Text
С. И. Баскаков
Радиотехнические цепи и сигналы.
Руководство к решению задач
Москва
Высшая школа
2002
Баскаков С. И. Радиотехнические цепи и сигналы. Руководство к
решению задач М.: Высшая школа, 2002, 214 с.
ISBN: 5-06-003994-3
Пособие содержит задачи по всем разделам одноименного курса. В
нем приведены условия задач, примеры решений, методические указания и
ответы. При работе с пособием рекомендуется пользоваться учебником
Баскакова С. И. "Радиотехнические цепи и сигналы" (М. : Высш, шк., 2000).
Во второе издание добавлены задачи по вейвлет-анализу сигналов и
методам оценки информационных характеристик радиоканала.
Предложены задачи, связанные с компьютерным анализом цепей и
сигналов с помощью программных продуктов MathCAD и Electronics
Workbench. Для студентов вузов, обучающихся по радиотехническим
специальностям.
ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
«Пример иногда полезнее правила»
И. Ньютон
Из собственного опыта читатель, безусловно, знает, что не-
отъемлемой частью процесса изучения точных — прежде всего,
математики и физики, а также многих естественных наук являет-
ся решение задач. Впервые столкнувшись с задачами в школьные
годы, мы затем настолько привыкаем к ним, что не утруждаем
себя вопросами о том, что же представляет собой задача как
таковая, в чем состоит ее познавательная роль. Более того, иные
учащиеся относятся к задачам как к неизбежному злу, которое
нужно просто терпеливо пережить. В связи с этим полезно от-
метить, что европейские наука и педагогика, история которых
насчитывает не одно тысячелетие, лишь к концу XVII века при-
шли к выводу о том, что обучение, основанное на механическом
заучивании теоретических положений, чрезвычайно неэффектив-
но. Слова Ньютона из его учебника «Алгебра», взятые в качестве
эпиграфа, удачно подчеркивают принцип, который вряд ли уста-
реет — залогом успешного учения служит активное познаватель-
ное творчество учащегося, который получает возможность на
собственном опыте увидеть теорию в действии.
Учебные задачи по своей природе близки к шахматным этю-
дам или, скорее к тем гаммам и арпеджио, без которых не
обошелся ни один начинающий музыкант. Хорошо составленная
задача несет в себе все черты небольшого научно-педагогического
сочинения — ее научная тематика строго очерчена и, что самое
главное, для успешного решения задачи нужно самостоятельно
сконструировать тот мыслительный алгоритм, который заранее
известен педагогу и который учащийся должен продемонстриро-
вать.
Как и все на свете, метод обучения с помощью решения задач
имеет собственное внутреннее ограничение: постановка задачи
неизбежно беднее той реальности, к которой эта задача относит-
ся. С этим обстоятельством непременно нужно считаться, соот-
нося выводы теории с практикой.
Как научиться решать задачи? По этому поводу написано
много серьезных книг. Ни в коей мере не претендуя на обобще-
ние, подчеркнем следующее.
Во-первых, следует выработать в себе отношение к этой де-
ятельности как к увлекательному труду, позволяющему широко
3
раскрыть интеллектуальные способности человека. Приемы раз-
нообразны — успешно решив задачу, подумайте, какие другие
схожие задачи можно решить найдет
1И
ям методом. Не забудьте
похвалить себя, если работа ладится. И главное, не впадайте
в уныние, если задача упорно «не желает решаться». Отдохнув,
принимайтесь за работу снова,— настойчивость в достижении
цели является непременной личностной чертой настоящего про-
фессионала. Если не удалось справиться с трудностью самосто-
ятельно и приходится обращаться к преподавателю, не ставьте
во главу угла «рецептурную» сторону дела — ведь цель не про-
сто получить верный ответ, а как можно глубже понять, почему
надо действовать именно так, а не иначе.
Во-вторых, открыв учебник, не следует сводить дело к по-
дыскиванию формулы, которая немедленно даст нужный ответ.
Формальное звание теории является необходимым, но отнюдь не
достаточным условием успе
III
юго решения задачи. Самой глав-
ной мыслительной процедурой всегда была некоторая догадка,
а это и есть, по сути дела, начало любого творчества. Если сразу
ясно, как решать ту или иную задачу, ею все равно не следует
пренебрегать. Аккуратное доведение до конца всех выкладок
н расчетов очень важно для формирования навыка самостоятель-
ной работы.
Пользуюсь возможностью высказать признательность рецен-
зенту книги — проф. М. П. Демину за полезные советы и благо-
желательную критику.
Автор
ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
Настоящая книга содержит материал к упражнениям по курсу
«Радиотехнические цепи и сигналы».
Раздел I включает шестнадцать отдельных тем, которые охва-
тывают всю программу курса. Тематические заголовки повторя-
ют названия глав учебника [1].
Подбор задач и их расстановка выполнена таким образом,
что учащимся предлагается внутренне организованная система
упражнений, отвечающая общим и частным принципам постро-
ения курса «Радиотехнические цепи и сигналы». Так, читатель
найдет здесь задачи, преследующие цель закрепить теоретичес-
кий материал. Имеются задачи следующей ступени сложности,
когда приемы и методы познавательной деятельности должны
быть обобщены учащимся для анализа более сложных ситуаций.
Наконец, в пособие включены задачи, предусматривающие пере-
нос знаний на новые объекты, выработку навыков творческого
мышления.
Раздел II пособия содержит указания к решению ряда задач.
В разделе Ш приведены образцы решений. Последний раздел IV
включает в себя ответы к задачам.
Автор стремился написать пособие, которое активно помога-
ло бы студенту в наиболее сложной фазе работы — в поиске
плана решения задач. Для этого была проведена классификация
всех помещенных в книге задач. Классификационные символы
располагаются в скобках вслед за номером задачи и имеют
следующий смысл:
УР — к задаче приведены указания (для хорошо подготовлен-
ных студентов, намеренных решить задачу «без подсказки») и ре-
шение;
Р — приведено только решение;
УО — данную задачу сопровождают указания и ответ;
У — приводится только указание;
О — приводится только ответ.
Изучение каждой темы следует начинать с проработки уста-
новочных задач типов УР и Р. При выполнении упражнений
студенту целесообразно иметь под рукой учебник по теории
цепей, например, [2] и математические справочники, такие, как [3]
и [4].
5
РАЗДЕЛ I
Задачи и упражнения
Тема 1
ОБЩАЯ ТЕОРИЯ РАДИОТЕХНИЧЕСКИХ СИГНАЛОВ
Ф Математические модели сигналов
1.1(Р). Импульсный сигнал «(О, имеющий размерность напря-
жения (В), описывается формулой
«(0=25 [ехр (— 1030-ехр(-2 Ю5/)] a(t).
Постройте график данного импульса. Определите максималь-
ное значение сигнала «ш, а также момент времени достижения
максимума tm„. Вычислите длительность импульса т„, определив
ее как длину отрезка времени от нуля до той точки, в которой
мгновенное значение сигнала уменьшается в 10 раз по сравнению
с максимальным значением.
12(0). Математическая модель импульсного сигнала задана
выражением
«(0=Ло/е'"<т(0.
Вычислите и постройте график данного сигнала в зависимо-
сти от безразмерного аргумента at. Определите длительность
импульса ти, приняв в качестве критерия окончания импульса
спад мгновенных значений до уровня 0.1 от максимального зна-
чения.
13(УО). Осциллограмма сигнала s(t) приведена на рис. 1.1.1.
Запишите математическую модель данного сигнала, применив
функции Хевисайда.
1.4(Р). Сигнал s(t) имеет математическую модель вида (рис.
1.1.2):
ГО , КО,
s(t)=<s0(t/t0), O^t^t0,
\.so ’ t>t0-
Представьте данную зависимость в виде суммы кусочно-ли-
нейных функций.
6
Рис. 1.1.1
1.5(0). На рис. 1.1.3, а, б, в изображены осциллограммы
импульсных сигналов 5i (t), s2(t) и s3(t). Найдите математические
модели данных сигналов, выраженные посредством сумм, кото-
рые составлены из произведений линейных функций и функций
Хевисайда.
1.6(0). Найдите формулы, описывающие математические
модели следующих импульсных сигналов (рис. 1.1.4): а) одно-
полярного импульса 51 (/), представляющего собой отрезок сину-
соиды с амплитудой А и частотой to0’> длительность импульса
равна половине периода (а); б) двухполярного импульса s2(t),
отвечающего целому периоду синусоиды с такими же парамет-
рами (6)
Рис 1.1.4
7
1.7(0). Математическая модель сигнала задана некоторой
функцией f(t), существующей в бесконечном промежутке времени
— со<г<сс. Представьте функцию f(t) в виде суммы четной
и нечетной частей:
/(г)=А(О+А(О
и найдите явные выражения для функций (f) и fm (t).
• Динамическое представление сигналов
1.8 (0). Используя функции Хевисайда, найдите динамическое
представление колебания 5 (г), описывающего переход некоторой
физической системы от нулевого уровня к постоянному уровню
В. Данный переход происходит за интервал времени Т по линей-
ному закону:
{О
вт,
В
t<0,
0<кТ,
t>T.
1.9 (0). Экспоненциальный видеоимпульс напряжения (В)
s(0=25exp(— 10б/)сг(/) действует на входе цепи, достаточно инер-
ционной для того, чтобы можно было приближенно представить
данный сигнал в виде л(0=Л<5(0- Определите числовое значение
коэффициента А.
1.10 (Р). Убедитесь, что при л-»со пределом последователь-
ности функций
/я(0=(л/2)е-м
служит функция Дирака <5 (О-
1.11 (Р). Докажите, что пределом по-
следовательности функций fn (0, одна
из которых изображена на рис. 1.1.5,
при л-» со является функция <5 (0-
1.12 (У). Докажите, что функция Дира-
ка <5(0 может рассматриваться как
предел последовательности класси-
ческих функций
- ехр( — nt2/2) при л-юс.
2л
8
• Геометрические методы в теории сигналов
1.13 (Р). Вычислите энергию Еи и норму ||и|| экспоненциального
видеоимпульса напряжения (В)
и=(0=30 exp (— Ю5/) a(t).
1.14 (0). Вычислите энергию Е, и норму |л| сигнала s(t),
представляющего собой прямоугольный видеоимпульс напряже-
ния (В) с амплитудой Uo и длительностью тв.
1.15 (0). Выведите формулу для нахождения энергии радиоим-
пульса длительностью тв с огибающей прямоугольной формы,
описываемого выражением
и(0=
О , /<0,
Um sin (cot+ф), Осгст,
О , />тв.
1.16 (F). Даны два сигнала: прямоугольный видеоимпульс
м(/)= 14[о’(0—o(t—Тц)] и экспоненциальный видеоимпульс v(t)=
= Uoe‘tr(t) (параметры Uo, а и тв — положительные веществен-
ные числа). Считая длительность тв фиксированной, найдите
величину параметра а, при которой расстояние р(и, v) ми-
нимально.
1.17 (F). Сигнал f(t)=t2 существует на отрезке времени
1. Найдите приближение к этому сигналу с помощью линейной
функции u(t)=At+B, наилучшее в смысле минимума расстояния
(метрики).
1.18 (0). На отрезке времени
— Г/2Г/2 задан импульсный си-
гнал и(0=С4со8(яГ/7), тождествен-
но обращающийся в нуль вне ука-
занного отрезка (рис. 1.1.6). Сигнал
v(0 представляет собой прямоуголь-
ный импульс длительностью 2/0,
вписанный в импульс и (г). Опреде-
лите параметр t0 таким образом,
чтобы расстояние р (u, v) было мини-
мальным.
• Теория ортогональных сигналов
1.19 (Р). Пусть {ц,(0}, л=1, 2, 3, ...— система ортогональных
сигналов, существующих на общем отрезке a^t^b и являющих-
ся векторами некоторого гильбертова пространства. Докажите,
что эта система сигналов линейно независима.
9
1.20 (Р). Докажите, что конечная система сигналов щ (г), и2 (/),...
uN(t), заданная на отрезке времени является линейно
зависимой в том случае, когда обращается в нуль определитель
Грамма:
(«1, «1) («1. «2)
(u2, ut) (u2, u2)
(«1, ww)
(“2. “w)
(“w. «1) («№ w2)
(«№ «W)
1.21 (0). Сигналы u(t) и v(r) представляют собой прямоуголь-
ные видеоимпульсы с амплитудами At и А2 и длительностями
тВ1 и Тя2 соответственно (рис. 1.1.7). Оба сигнала одновременно
отличны от нуля на отрезке времени длительностью т. Докажите,
что угол между этими сигналами, рассматриваемыми как
векторы в гильбертовом пространстве, не зависит от величин
Ai и А2. Получите формулу, определяющую угол ф.
1.22 (0). Два одинаковых по форме экспоненциальных видео-
импульса, разнесенных во времени на величину Го, описываются
выражениями
«1 (O=(7oe-"ff(O,
M2(O=C4e"e('-',,)ff(r-ro).
Определите зависимость угла между этими векторами от
параметра 10. Найдите величину t0, при которой <Д = 89° (прак-
тически ортогональные импульсы).
1.23 (У). В гильбертовом пространстве сигналов заданы два
вектора и и v с одинаковыми энергиями: ||u||2= ||v||2. Докажите,
что при этом сигналы s1 = u+v и s2=u-v ортогональны, т. е. (si,
52) = 0.
1.24 (У). Для произвольных сигналов u(t) и «(/), являющихся
элементами гильбертова пространства, докажите равенство па-
раллелограмма
||u+«||2+||u—v||2=2 ||u||2 + 2 Н2.
1.25 (Р). Сигналы u(t) и v (г) являются элементами некоторого
вещественного гильбертова пространства. Рассматриваемые сиг-
налы линейно независимы, т. е. равенство и=)л не имеет место
ни при каком значении вещественного параметра Л. Докажите
справедливость неравенства Коши — Буняковского
ю
|(u, ®)|<||u|| ‘M.
1.26 (У). Докажите, что в вещественном гильбертовом про-
странстве сигналов имеет место неравенство Минковского
11«+®11<И«11 + 1М.
1.27 (У). В гильбертовом пространстве сигналов заданы про-
извольный вектор и и вектор v, такой, что ||ю|| = 1. По аналогии
с геометрией обычных векторов на плоскости вектор w=(u,
v)v называют ортогональной проекцией вектора'» на напра-
вление v (рис. 1.1.8). Докажите, что вектор y=u—w ортогонален
вектору v.
1.28 (У). Обобщая результат задачи 1.27, докажите, что если
{vb v2,.... яд} — система взаимно ортогональных векторов с еди-
ничными нормами, то вектор
у=и-(и, Vi)vi-(u, v2)v2-...-(u, vN)vN
при любом и ортогонален по отношению к каждому из векторов
рассматриваемой системы.
1.29 (Р). Пусть в гильбертовом пространстве сигналов задана
система взаимно неортогональных векторов {go, g(, ..., g„, ...}.
Постройте на ее основе ортонормированную систему {»о, иь ...
..., ц,,...} таким образом, чтобы каждый вектор и* являлся линей-
ной комбинацией вида
«k=C*ogo + Cwg| + ...+Cfalg„+...
с постоянными коэффициентами.
1.30 (УО). Используя прием, найденный при решении задачи
1.29, вычислите три первых базисных вектора Ц), »| и и2, получа-
емых путем ортогонализации и нормировки системы степенных
функций {1, t, t2, ...} на отрезке —1<Г<1.
11
1.31 (УО). Найдите первые три коэффициента с0, ci и с2 обо-
бщенного ряда Фурье, получаемого при разложении сигнала
/(г)=е‘ на отрезке — по системе базисных функций {«*},
исследованных в задаче 1.30.
Вычислите норму
f- Y скик
к-о
абсолютной ошибки аппроксимации данного сигнала тремя
членами ряда. Получите числовую оценку для относительной
ошибки
f- Е
к-0
11/11
данной аппроксимации.
1.32 (УО). Решите предыдущую задачу в другой постановке:
найдите коэффициенты многочлена второй степени z(t)=
=A+Bt + Ct2 таким образом, чтобы данный многочлен с на-
именьшей среднеквадратичной ошибкой аппроксимировал сиг-
нал f(t)=d на отрезке — 1<г<1.
133(У). Докажите, что комплексные экспоненциальные фу-
нкции
. . 1 ( .2ялА „ . ,
«n(0=-7=exp(j— ), и=0, ±1, ±2, ...
Vr \ т /
на отрезке — Т/2<Г<Т/2 образуют ортонормированный базис.
134(У). На отрезке задана бесконечная полная си-
стема ортонормированных сигналов {«„(/)}, n=0, 1, 2, ... До-
кажите, что дельта-функция, сосредоточенная в некоторой внут-
ренней точке t0(a< t0<b), может быть представлена как бесконеч-
ный ряд
и—О
135(0). Сигнал s( о ), зависящий от безразмерного аргумента
о, на отрезке —1/2< о < 1/2 представляется формулой s(o)= 16 о 2.
Вычислите коэффициент с2 разложения данного сигнала в обо-
бщенный ряд Фурье по функциям Уолша:
*(«)= X c*wal(fc, ° )
*-0
12
1.36(0). Вычислите коэффициенты с0 и с2 в разложении сиг-
нала s( о)=45 ехр(—0,71 а |), заданного на отрезке —1/2< е < 1/2,
в обобщенный ряд Фурье по функциям Уолша.
1.37(УО). Найдите коэффициент обобщенного ряда Фурье
по функциям Уолша для сигнала /(/), рассмотренного в задаче
1.31.
Тема 2
СПЕКТРАЛЬНЫЕ ПРЕДСТАВЛЕНИЯ СИГНАЛОВ
• Периодические сигналы и ряды Фурье
2.1 (Р). Периодический сигнал s (t) с периодом Т на отрезке
— Т/2^/<Т/2 задан выражением s(t)=UoCOs(nt/T) (рис. 1.2.1).
Найдите выражения для коэффициентов Сл ряда Фурье этого
сигнала.
2.2 (УО). Периодическое колебание u(f) имеет период Т. На
отрезке — T/2^t^T/2 данное колебание представлено в виде
u(0=t7oexp(—/?|*|), причем параметр 0 велик настолько, что
рТ/2^>]. и поэтому отдельные импульсы, образующие периоди-
ческий сигнал, практически не «перекрываются» (рис. 1.2.2). Най-
дите коэффициенты ао/2 и а„ входящие в ряд Фурье данного
сигнала
. . 'V' 2яЛ|
ы(О=во/2+ X a„cos—.
2.3 (0). Периодический комплексный сигнал s (г) с периодом
Т представлен следующими выражениями:
{О
Лехр(/аг),
О
— Т/2<1<—т/2,
—т/2<Кт/2,
т/2<г<Т/2,
где А, а, т — заданные вещественные числа.
Рис. 1.2.2
13
Вычислите коэффициенты Ся(п=0, +1, +2, ...) рада Фурье
в комплексной форме для данного сигнала.
2.4 (0). График мгновенных значении вещественного периоди-
ческого сигнала s(t), относящихся к отрезку — Т/2< Г/2, изоб-
ражен на рис. 1.2.3. Получите формулу, определяющую общий
член последовательности {С„} коэффициентов комплексного рада
Фурье данного сигнала.
23(0). Прямоугольные видеоимпульсы положительной по-
лярности, образующие бесконечную последовательность с пе-
риодом Т, имеют амплитуду <70. Длительность каждого импуль-
са равна Т/3, точка Г=0 совпадает с серединой импульса. Вычис-
лите коэффициент С| комплексного рада Фурье указанного сиг-
нала.
2.6 (0). Периодический сигнал s(t) на отрезке — Т/2<г<Т/2
задан выражением s(r)=<7о(1 —2 \t\/T) (рис. 1.2.4). Получите выра-
жения, определяющие коэффициенты С„ рада Фурье для этого
колебания. Постройте график частичной суммы рада Фурье,
содержащей постоянную составляющую и две гармоники низших
номеров.
2.7 (УО). Осциллограмма периодического пилообразного сиг-
нала s (0 приведена на рис. 1.2.5. Получите выражения для коэф-
фициентов С„ комплексного рада Фурье. Запишите явное выраже-
ние этого сигнала в ваде суммы гармонических колебаний с крат-
ными частотами. Постройте график частичной суммы, состоящей
из трех первых членов. Сравните данное приближенное представ-
ление с исходным сигналом.
2Л(УО). Найдите связь между коэффициентами С„ (и—О, ± 1,
±2, ...) комплексного ряда Фурье периодического сигнала f(t)
и коэффициентами С„ ряда Фурье сигнала получен-
ного из исходного сигнала /(/) путем сдвига во времени на
t0 секунд.
2.9 (У). Комплексный периодический сигнал s(f) на отрезке
— T/2<z<T/2 имеет вид
Рис. 1.2.4
Рис. 1.2.3
14
s(t) = Sl (O+jSlO).
Покажите, что если функция Si (г) четна, a s2(t) — нечетна, то
коэффициенты Сл ряда Фурье при любом п являются веществен-
ными числами.
2.10 (0). Периодический вещественный сигнал s(t) на отрезке
задан выражением s(t)= Uoexp(—at) (рис. 1.2.6). Найдите
выражения для коэффициентов С„ комплексного ряда Фурье,
отвечающего данному сигналу. Вычислите амплитуду пятой гар-
моники As при следующих параметрах:
Uo=15 В, аТ=3.
2.11 (0). Найдите амплитуду А2 второй гармоники сигнала,
рассмотренного в задаче 2.1, если С7О=25 В.
2.12 (0). Применительно к условиям задачи 2.2 при Uo=300 В,
Т=2’10“5 с и /?=6‘10б с1 определите постоянную составля-
ющую ао/2, а также амплитуды первой, второй и третьей гармо-
ник сигнала.
2.13 (F). Периодический сигнал s (/), в общем случае комплекс-
ный, имеет заданный период Т. Получите выражение, связыва-
ющее среднюю за период мощность этого сигнала Р^ с коэф-
фициентами С„ его ряда Фурье.
Рис. 1.2.6
2.14 (УО). Найдите среднюю за период мощность сигнала,
рассмотренного в задаче 2.6, а также среднюю мощность Р^з),
отвечающую сумме постоянной составляющей, первой и второй
гармоник. Вычислите относительную погрешность 3 представле-
ния средней мощности указанным способом.
15
• Спектральные представления
непериодических сигналов. Преобразование Фурье
2.15 (F). Осциллограмма видеоимпульса напряжения s (t) пред-
ставлена на рис. 1.2.7. На отрезке времени 0</<тв=5 мкс функ-
ция s(t) имеет вид $(/)=Лехр(—at), где А и а — параметры,
определяемые видом осциллограммы. Найдите спектральную
плотность S(aj) данного импульса.
2.16 .(Р). Покажите, что спектральная плотность S(io) импуль-
са, рассмотренного в задаче 2.15, не обращается в нуль ни при
каких конечных значениях частоты со.
2.17 (F). Периодический сигнал 5^(0 образован бесконечной
последовательностью одинаковых импульсов 5о(О, повторяю-
щихся через одинаковые интервалы времени Т. Найдите фор-
мулу, связывающую коэффициенты С„(п=0, ±1, ...) ряда Фурье
периодического сигнала со спектральной плотностью So(&>) оди-
ночного импульса s0(t).
2.18 (F). Импульсная последовательность s(t) образована мно-
жеством 2^+l непересекающихся во времени одинаковых им-
пульсов (N — целое положительное число или нуль). Интервал
повторения последовательности равен Т (рис. 1.2.8).
Считая известной спектральную плотность So (со) одиночного
импульса, вычислите спектральную плотность S(co) последовате-
льности.
2.19 (Р). Вычислите спектральную плотность S(co) сигнала
s(t)=A(e~a—t~f,)a{t). Постройте график зависимости модуля
спектральной плотности от частоты для следующих значений
параметров: Л=6 В, а=106 с-1, /?=3‘ 106 с-1.
2.20 (F). Для сигнала s(t), рассмотренного в предыдущей зада-
че, выведите формулу, позволяющую рассчитать граничную ча-
стоту спектра сл^,, на которой модуль спектральной плотности
уменьшается в 10 раз по сравнению с тем значением, которое
имеет место на нулевой частоте. Получите числовое значение
Рис. 1.2.7 Рис. 1.2.8
16
(Огр применительно к тем параметрам а и fl, которые заданы
в условиях задачи 2.19.
2.21 (0). Экспоненциальный видеоимпульс тока (А) задается
выражением z(f)=0.75exp(—4‘ 107t)<r(t). Найдите модуль и ар-
гумент спектральной плотности данного колебания на частоте
/=10МГц.
2.22 (УО). Определите спектральную плотность S(co), отвеча-
ющую сигналу s(f)=Atexp(—at)<r(t).
2.23 (УР). На экране телевизионного приемника с длиной стро-
ки 500 мм требуется создать изображение вертикальной черной
линии шириной 3 мм (рис. 1.2.9). Электронный луч пробегает
строку телевизионного растра за отрезок времени длительностью
64 мкс. Оцените ширину спектра видеосигнала, управляющего
яркостью свечения экрана кинескопа в рассматриваемом случае.
2.24 (0). Найдите связь между спектральной плотностью S(co)
вещественного сигнала s (г) и спектральной плотностью Q(co)
сигнала q(t)=s(—t).
2.25 (УО). Четный сигнал qt (/) и нечетный сигнал q2(t) связаны
с исходным колебанием s(t) соотношениями:
?i(O=s(O+j(-O.
92<0=j(0-j(-0-
Найдите связь спектральных плотностей Ci(a>) и £Ь(<у) дан-
ных сигналов со спектральной плотностью S(co) сигнала s(f).
2.26 (0). Пусть s(t)++S(co). Найдите сигнал f(t), которому от-
вечает спектральная плотность: a) F(<a)=S2(co), б) F(co)=
= S(co) S* (а>)=IS(co)l2, в) F(to)=S* (co).
2.27 (0). Найдите спектральную плотность S(co) сигнала s(t),
математическая модель которого описывается л-й производной
функции £(/).
2.28 (Р). Определите спектральную плотность S(co) симмет-
ричного треугольного импульса s(t) (рис. 1.2.10).
Рис. 1.2.9
17
2.29 (F). Сигнал u(f) представляет собой последовательно-
сть из трех разнополярных видеоимпульсов с длительностью
Т и амплитудой <70 каждый (рис. 1.2.11). Вычислите спектраль-
ную плотность U (со) данного сигнала. Постройте график зависи-
мости спектральной плотности от безразмерного аргумента
соТ/2.
2.30 (УО). Найдите спектральную плотность S(co) несиммет-
ричного треугольного видеоимпульса s(f), осциллограмма кото-
рого изображена на рис. 1.2.12.
2.31 (У). На примере треугольного видеоимпульса, рассмот-
ренного в задаче 230, покажите, что значение спектральной
плотности на нулевой частоте равно площади импульса, т. е.
5(0)=Лт./2.
2.23 (УР). Импульсный сигнал s(t) отличен от нуля на отрезке
времени [0, tJ. Получите приближенное выражение спектральной
плотности S'(со) на достаточно низких частотах со, удовлетворя-
ющих условиях) сотн<к 1.
2.33 (УО). Осциллограмма импульса напряжения изображена
на рис. 1.2.13. Найдите приближенное числовое значение спект-
ральной плотности этого импульса на частоте со= 103 с-1.
234( УО). Осциллограмма импульса тока приведена на рис.
1.2.14. Вычислите приближенное значение спектральной плотно-
сти этого импульса на частоте со=5 • 103 с-1.
235(УР). Найдите сигнал s(t), спектральная плотность кото-
рого задана выражением
. . Sq
S(°,)=7—
1 Ч-агт^
где So,i — некоторые постоянные.
2.36(УО). Найдите сигнал s(t), исходя из его спектральной
плотности
So
5(щ)= - -.
1 +OJ т
237(УО). Определите функцию s(f), описывающую сигнал со
спектральной плотностью
S(co)=—Л
(я+ytD)3
где А — постоянная, а > 0 — вещественное число.
18
Рве. 1.2.11
2.38 (0). Найдите сигнал s(t), заданный своей спектральной
плотностью
S(a>) =--------------,
(a+ja>)O?+ja>)
где a>0, р>0, а^р.
2.39 (0). Найдите сигнал s(t), которому отвечает спектральная
плотность
S(co)=---------------------,
(со—Шо —/а) (со+со0 —ja)
где А, too, а — положительные вещественные числа.
2.40 (УР). Вычислите спектральную плотность U (со) сигнала
u(t), представляющего собой синусоиду, начинающуюся в мо-
мент времени 1=0: u(t)= Uosin &V a(t).
2.41 (УО). Найдите спектральную плотность S(co) импульса
включения комплексного экспоненциального сигнала, представ-
ляемого формулой s(f)=exp(jco0t) <r(t).
2.42 (УО). Вычислите спектральную плотность S(co) сигнала
/ч I1 . '<°>
$(!)=<
|ехр(/ г»), i>0,
где о — постоянное число.
19
2.43 (УО). Найдите спектральную плотность S(io) комплекс-
ного экспоненциального сигнала
5(0 =
'ехр(/соо0, *<0,
exp[/(o)0z+ й)], г>0,
имеющего скачок фазы на о радиан при г=0.
2.44 (0). Определите спектральную плотность S'(со) сигнала
s(0=cos2to0r, — co<t< + оо. Задачу решите двумя способами: а)
путем сведения заданного сигнала к сумме двух сигналов с из-
вестными спектрами, б) с помощью теоремы о спектре произ-
ведения двух функции.
2.45 (F). Непосредственным вычислением докажите, что
свертка
I u(r)v{t—T)dr
двух сигналов и (0 и v(0 с известными спектральными плот-
ностями U (со) и И (со) соответственно имеет спектральную плот-
ность F(co)= U (to) И (со).
2.46 (F). Вычислите свертку /(/) двух экспоненциальных видео-
импульсов ехр(—ait)<r(t) и л2(/)=Л2ехр(—a.2t)a (/) двумя
способами: а) прямым нахождением интеграла свертки, б) с по-
мощью теоремы о преобразовании Фурье свертки.
2.47 (УО). Вычислите сигнал q(t), являющийся сверткой двух
функций Хевисайда о (t).
• Преобразование Лапласа
2.48 (УР). Найдите оригинал u(t), которому отвечает изоб-
ражение 17(р)=1/р2.
2.49 (F). Найдите функцию f(t), которая является оригиналом
по отношению к изображению
(р+а)(р+Ь)(р+с)’
где а,Ь, с — постоянные числа.
2.50 (УР). Докажите следующий) формулу соответствия между
изображением по Лапласу и оригиналом:
(р+в)(р+6) Ь—а
2.51 (У). Докажите следующие соответствия между изображе-
ниями по Лапласу и оригиналами:
Ч Р • I /L ~bt ~аХ
а)---------=----(ое —се ),
(р+а)(р+Ъ) Ь-а
б)---------=ё (t) Н—1~(a2e‘zl—b2e~b').
(р+а)(р+Ь) Ь-а
2.5 Ky). Докажите, что изображению F(p) = l/(p+a)n+1 соот-
ветствует оригинал/(Z) = z"e-e//n! Здесь и^О — натуральное чис-
ло, a — произвольная величина.
2.53 (У). Докажите, что оригиналу cos(an+<p) отвечает изоб-
ражение по Лапласу (pcostp — tosia <р)/(р2 + а>2).
2.54 (УО). Найдите изображение по Лапласу U (р) для прямо-
угольного видеоимпульса u(t) с амплитудой С70 и длительностью
тя, который начинается в момент времени z=0.
2.55 (0). Сигнал s (t), начавшийся в момент времени /=0,
представляет собой бесконечную последовательность импульсов,
следующих во времени с периодом Т. Полагая известной функ-
цию 50(р) — изображение отрезка данного сигнала, отличного от
нуля на отрезке найдите преобразование Лапласа S(p)
для периодического сигнала.
2.56 (УО). Вычислите преобразования Лапласа Si(p), S2(p)
и S3(p) сигналов (Z), s2(z) и s3(f), описанных в условиях за-
дачи 1.5.
• Вейвлет-анализ
2.57(0). Напишите явные выражения функций, представля-
ющие вейвлеты Хаара 4*10(о ), 4*п( о ) и 4/<м( о ). Здесь о — безраз-
мерная переменная, связанная с текущим временем t и длитель-
ностью Т рассматриваемых сигналов соотношением о = ЦТ.
2.58(Р). На отрезке времени [0, 7] задан импульсный сигнал
треугольной формы s(z)=40(f/7), равный нулю в остальных точ-
ках оси г. Найдите коэффициент с1Ь входящий в расположение
этого сигнала по элементам вейвлет-базиса Хаара.
2.59(Р). В состав математической системы MathCAD входит
библиотечная функция wave(X), которая возвращает множество
коэффициентов разложения входного вектора X по элементам
вейвлет-базиса Добеши. Число компонентов вектора X должно
составлять 2”, где m — целое число. Имеется также функция
обратного вейвлет-преобразования iwave(F), которая восстанав-
ливает вектор отсчетов сигнала по известным коэффициентам
разложения.
21
Проведите численные эксперименты по вейвлет-анализу один-
очного прямоугольного видеоимпульса и его обратному вос-
становлению. Сделайте выводы о влиянии числа вейвлет-коэф-
фициентов, используемых при восстановлении сигнала.
Тема 3
ЭНЕРГЕТИЧЕСКИЕ СПЕКТРЫ СИГНАЛОВ.
ПРИНЦИПЫ КОРРЕЛЯЦИОННОГО АНАЛИЗА
• Обобщенная формула Рэлея.
Энергетические спектры
3.1 (УР). Используя обобщенную формулу Рэлея, найдите ска-
лярное произведение (u, v) экспоненциальных видеоимпульсов
u(/)=A1exp(—и v(/)=A2exp(—а2/)<т(Г).
3.2 (УО). В области физических частот о» 0 спектральные
плотности Su(a>) и S,(oj), которые отвечают сигналам u(t) и v(r),
представлены графически на рис. 1.3.1. Вычислите скалярное про-
изведение (и, v) данных сигналов.
33(УО). Вычислите скалярное произведение (u, v) экспоненци-
ального видеоимпульса u(Z)=Aexp(—at)a(f) и такого же им-
пульса v(/)=Aexp[—a(t— t0)]<r(t—t0), сдвинутого относительно
сигнала u(f) на г0(с) в сторону запаздывания.
3.4 (0). Найдите взаимный энергетический спектр (со) двух
гауссовых видеоимпульсов u(/)=A1exp( — Pit2) и ®(/)=Л2ехр *
х (—Pit2), заданных при — оо</< 4-оо.
33(0). Определите взаимный энергетический спектр ^(со)
гауссова видеоимпульса u(/)=Aiexp(—pt2) и экспоненциального
видеоимпульса v(/)=A2exp(—at)a(t).
3.6 (УО). Найдите взаимный энергетический спектр И^Ссо) пря-
моугольных видеоимпульсов u(t) и v(t) с амплитудами Uj и U2
соответственно, имеющих одинаковую длительность Т.
3.7 (0). Вычислите энергию Еи сигнала u(t), энергетический
спектр которого в области положительных частот задан графи-
чески на рис. 1.3.2.
3.8 (УР). Прямоугольный видеоимпульс u(t) имеет амплитуду
Uo и длительность т„. Выведите формулу для расчета энергии Х>»>
заключенной в пределах интервала положительных частот от
нуля до некоторой верхней граничной частоты (оъ.
3.9 (Р). Импульсное колебание задано формулой
s(/) = 15exp(— 107r)ff(0.
22
W, U>2 u
Рис. 1.3.1
Определите граничную частоту (Гц) таким образом, чтобы
в интервале частот (О, /т) было сосредоточено 90% всей энергии
импульса.
З.Ю(УО). Определите, какая доля полной энергии прямоу-
гольного видеоимпульса, имеющего длительность 5 мкс, содер-
жится в пределах частотного интервала от нуля до 575 кГц.
3.11(УО) Сигнал s (г) представляет собой прямоугольный ви-
деоимпульс. Найдите относительную долю полной энергии этого
сигнала, содержащуюся в пределах первых десяти лепестков спек
тра этого сигнала
• Автокорреляционная функция
3.12 (УР). Получите аналитическое выражение для автокор-
реляционной функции В,(т) двустороннего экспоненциального
видеоимпульса 5 (г) = А ехр (—/? |ф, где А — постоянная величина,
/?>0 — вещественное число.
ЗЛЗ(Р). Вычислите автокорреляционную функцию В, (г) сиг-
нала л(г)=Лехр(—a/)sin<DOt <r(t), имеющего экспоненциально
убывающую огибающую и гармоническое высокочастотное запо-
лнение.
3.14 (УО) Найдите функцию автокорреляции В,(т) экспонен-
циального видеоимпульса s(t)=А exp (—at) a (t)
3.15 (0). Сигнал s (t) представляет собой треугольный видео-
импульс (рис. 1.3 3), заданный выражениями:
Г<0,
0^/<ти,
Получите формулу, описывающую автокорреляционную функ-
цию Bs(r) данного сигнала.
23
3.16 (Р). Найдите аналитическое вы-
ражение для автокорреляционной фун-
кции Д,(т) радиоимпульса
{О , КО,
Acos(co0t+<p0), 0</<t„
О , />тя
Рве. 1.3.3 с огибающей прямоугольной формы.
3.17 (УО). Основываясь на условиях
задачи 3.12, определите интервал корреляции :,г_ рассматрива-
емого сигнала, понимаемый как сдвиг во времени т, при котором
величина В, становится равной 0.1 В, (0).
3.18 (УО). Вычислите автокорреляционные функции А (л) сле-
дующих пят>
II
озиционных дискретных сигналов: а) £]—(1,
1, 1,
-1, 1), б) 52 = (1, 1, -1,-1, 1).
• Функция взаимной корреляции
3.19 (0). Сигналы и (/) и v (/) являются прямоугольными радио-
импульсами с амплитудами и U2 соответственно; оба сигнала
имеют одинаковую длительность Т. Найдите функцию взаимной
корреляции Ви, (г) этих колебаний.
3.20 (УО). Получите аналитическое выражение функции взаим-
ной корреляции Д»(т) двух прямоугольных видеоимпульсов u(t)
и «(/), имеющих одинаковую амплитуду L/o и длительности
зую вещественную спект-
3.21 (У О). Сигнал u(f) имеет посто:
ральную плотность So в пределах полосы частот [ — а>„ <z»J. На
остальных частотах спектральная плотность этого сигнала равна
нулю. Сигнал v(/) получен из сигнала и(/) путем сдвига послед-
него во времени на /0 (с) в сторону запаздывания. Найдите
взаимную функцию корреляции Вм(т) этих сигналов.
3.22 (УО). Вычислите значения функции взаимной корреляции
для трехпозиционных дискретных сигналов u=(l, 1
-1)
Тема 4
МОДУЛИРОВАННЫЕ СИГНАЛЫ
• Сигналы с амплитудной модуляцией
4.1 (0). Однотона гтьный AM-сигнал описывается выражением
u(z) = 500(l +0.8cos(104f+45°))cos(107f+90°). Постройте в мас-
штабе векторную диаграмму данного сигнала, отвечающую мо-
менту времени Z=0.
4.2 (Р). Амплитудно-модулированный сигнал (В) описывается
следующим выражением:
и (Г) = 12 (1 + 0.6cos Qt+0.2cos 2Ш) cos a>Dt.
Найдите наибольшее и наименьшее значения огибающей U(t)
данного сигнала.
4.3 (У). Покажите, что для однотонального AM-сигнала и (/) =
= С70(1 +Afcos£h)cost(V коэффициенты модуляции «вверх» Ма и
«вниз» Мя совпадают: Ма=Мя=М.
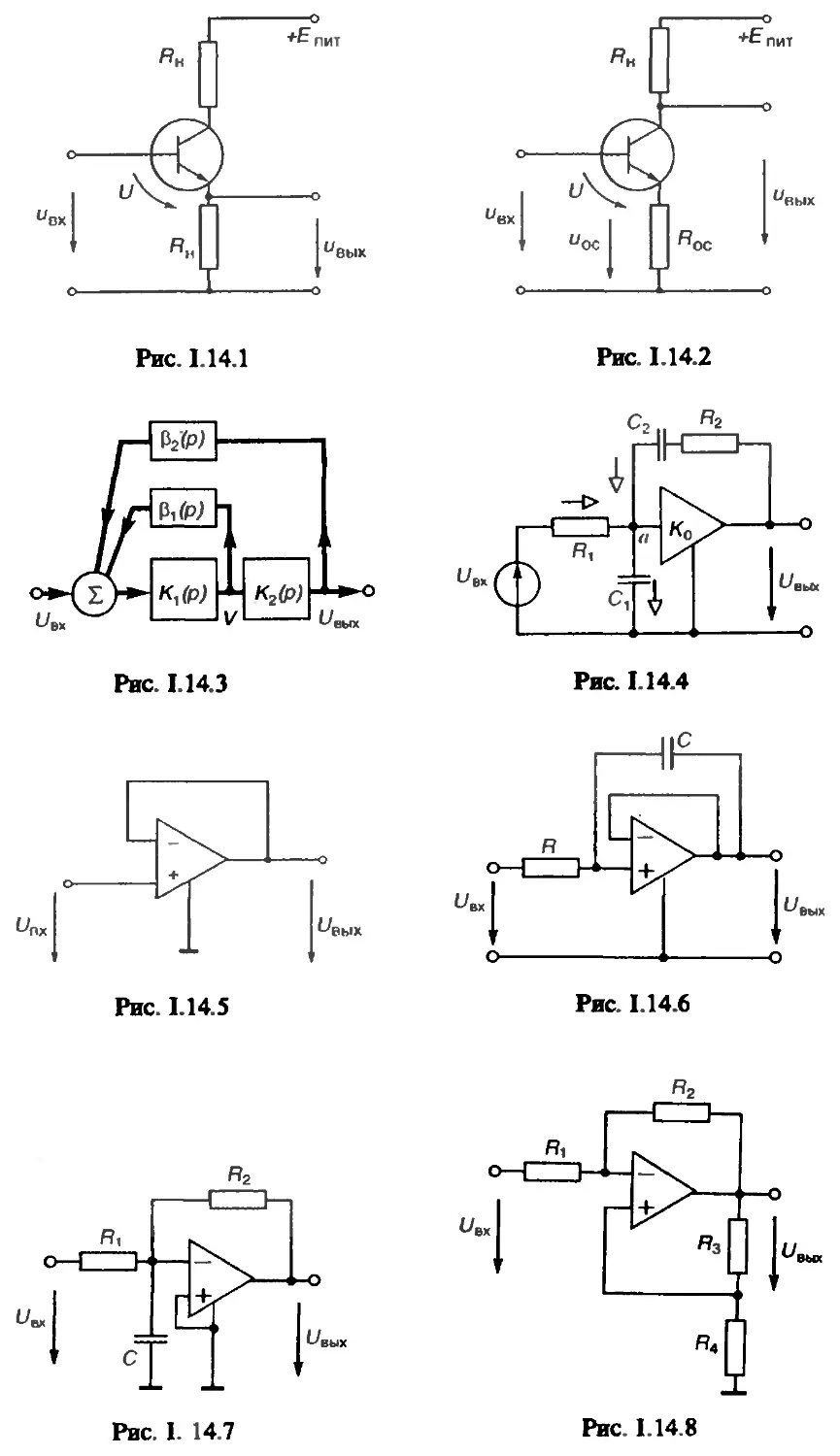
4.4 (УО). Осциллограмма однотонального AM-сигнала при
М<\ изображена на рис. 1.4.1. Получите формулу для расчета
коэффициента модуляции М на основании измерения экстремаль-
ных значений амплитуд Um„ и U^.
4.5 (УО). На рис. 1.4.2 изображена осциллограмма одното-
нального AM-сигнала и (<) при М > 1, когда имеет место явление
перемодуляции. Определите коэффициент модуляции М на ос-
новании известных значений амплитуд и Цш,.
4.6 (0). Однотональный AM-сигнал характеризуется тем, что
С7юах=13О В, (7^=20 В (см. рис. 1.4.1). Найдите коэффициент
модуляции М, а также амплитуду С70 несущего колебания.
4.7 (УО). Оцените ширину полосы частот П, занимаемую
в эфире телеграфным радиоканалом, работающим по принципу
AM со скоростью передачи 300 знаков/мин. Для упрощения
Рис. 1.4.2
Рис. 1.4.1
25
/о"^г to fo+^\ fo+^z f
Рис. 1.4.3
Рис. 1.4.4
расчета положите, что передаваемый сигнал является периоди-
ческой последовательностью точек кода Морзе. Длительность
паузы равна длительности передаваемого радиоимпульса (рис.
1.4.3).
4.8 (0). Спектральная диаграмма AM-сигнала, имеющего две
низкие частоты модуляции F] и F2, изображена на рис. 1.4.4.
Определите парциальные коэффициенты модуляции Mi и М2.
4.9 (Р). Источник ЭДС с амплитудной модуляцией u(t)=
= С70(1+Afcos£lz)cos<iV замкнут на резистивную нагрузку с со-
противлением R. Получите выражения для составляющих мгно-
венной мощности в нагрузке pa(f) и рго(0> которые изменяются
во времени с частотами Q и 2£1 соответственно.
4.10 (УО). Источник AM-сигнала создает на резистивной на-
грузке /?я=2кОм напряжение (В)
и (0=75 (1+0.4 cos lO’Ocos 10б/.
Вычислите минимальное Р^ и максимальное значения ак-
тивной мощности источника, усредненной за период несущего
колебания.
4.11 (0). Радиопередающее устройство с амплитудной модуля-
цией в режиме «молчания», т. е. при отсутствии модулирующего
сигнала, излучает мощность Р0=4 кВт. Найдите пиковое значе-
ние излучаемой мощности Рт., однотонального AM-сигнала, ес-
ли Л/=0.8.
• Сигналы с угловой модуляцией
4.12 (Р). Колебание с угловой модуляцией описывается выра-
жением
и (/) = 15 cos (108/ + 3 sin 1 Об/+1.4 sin 105«+л/4).
Найдите величину мгновенной частоты u)(t) данного сшнала
в момент времени t = 1 мкс.
26
4.13 (0). Найдите максимальное сот„ и минимальное зна-
чения мгновенной частоты co(t) ЧМ-сигнала, представляемого
выражением
u(t)= <70 (3 • 10’f+2sin 107Г+я/6).
4.14 (0). Однотональный ЧМ-сигнал имеет несущую частоту
_/о=50 МГц и частоту модуляции Г=7 кГц. Вычислите, в каких
пределах [/^п, /т.,1 должна изменяться мгновенная частота этого
колебания для того, чтобы индекс модуляции т был равен 40.
4.15 (УО). Получите спектральное представление сигнала с уг-
ловой модуляцией
u(0=8cos(106f+0.06sin 104/).
4.16 (0). Однотональный ЧМ-сигнал имеет частоту модуляции
F= 12 кГц и индекс модуляции т=25. Вычислите практическую
ширину спектра данного колебания.
4.17 (УО). Радиосигнал с фазовой модуляцией имеет индекс
т= 16. Оцените величину N — число боковых колебаний, присут-
ствующих в пределах полосы частот, центр которой совпадает
с несущей частотой, а ширина соответствует практической шири-
не спектра сигнала Ппр.^.
4.18 (УР). Однотональный ЧМ-сигнал имеет девиацию часто-
ты Дй)=6* 104 с"1. Найдите наибольшее из возможных значений
частот модуляции Пт.,, при котором в спектре сигнала будет
отсутствовать составляющая с несущей частотой.
4.19 (УО). Вычислите, при каком наибольшем значении моду-
лирующей частоты Гт., в спектре однотонального ЧМ-сигнала,
имеющего девиацию частоты Л/=40 кГц, будут отсутствовать
компоненты на частотах /п+Гт.» где f0 — частота несущего коле-
бания.
4.20 (УР). Для сигнала, рассмотренного в задаче 4.15, найдите
приближенные значения амплитуд Um2 и спектральных со-
ставляющих с частотами (Oq+TSL и соь+ЗП соответственно.
4.21 (УО). В радиопередающем устройстве, излучающем одно-
тональные ЧМ-сигналы, мгновенная частота колебаний изменя-
ется за счет того, что емкость конденсатора LC- контура в зада-
ющем генераторе переменна во времени
C(/)=C0+Cmcos£lZ.
Частота немодулированной несущей/о=28 МГц, емкость кон-
денсатора при отсутствии модуляции Со=30 пФ. Частота моду-
ляции Г=£1/(2я)=2 кГц; индекс модуляции /я=0.4. Вычислите
амплитуду изменения емкости Ст, обеспечивающую заданные
параметры сигнала.
27
• Сигналы с линейной частотной модуляцией
4.22(0). Прямоугольный ЛЧМ-импульс длительностью тв=
=40 мкс имеет значение базы В=500. Определите девиацию
частоты А/ в данном импульсе.
4.23(0). ЛЧМ-импульс с огибающей прямоугольной формы
имеет длительность тв=15 мкс. Девиация частоты за время им-
пульса А/=25 МГц. Определите базу В данного сигнала и ско-
рость нарастания частоты ц.
4.24(0). Вычислите величину энергетического спектра FTU пря-
моугольного ЛЧМ-импульса, имеющего девиацию частоты Асо =
= 10’ с-1, базу В=5~ 103 и амплитуду С7о=5О мкВ.
4.25(Р). Вычислите приближенное значение энергии Еи прямо-
угольного ЛЧМ-импульса u(f) длительностью ти с заданной амп-
литудой Uo и известной скоростью нарастания частоты д. Задачу
решите двумя способами: а) непосредственным интегрированием
во временной области, б) используя понятие энергетического
спектра сигнала Wu. Положите, что база сигнала В» 1.
4.26(0). Выведите формулу, определяющую связь величины
квадратичного слагаемого Oj фазового спектра прямоугольного
ЛЧМ-импульса на границе полосы частот сигнала со значением
базы В.
4.27(0). Найдите формулу, определяющую ширину основного
лепестка Ти» автокорреляционной
J функции ЛЧМ-импульса с заданны-
ми параметрами тв и В. Вычислите
L величину Тосж для импульса, име-
ющего базу В=2'103 и длитель-
Л \ ность тв=8 мкс.
-A I I - —------»- 4.28(УР). Найдите спектральную
х 1 ° \/'" * плотность S(oj) ЛЧМ-импульса
s(t) = Uoe~fil cos^co0f+^-^,
заданного в бесконечном интервале
Рис. 1.4.5 — со < / < + со и имеющего гауссову
форму огибающей (рис. 1.4.5).
• Сигналы для стереофонии
4.29(0). В системе стереофонического радиовещания сигналы
левого /(/) и правого r(z) каналов занимают область частот,
ограниченную сверху значением 10 кГц. Вычислите минимально
возможное значение поднесущей частоты fm, позволяющее избе-
28
жать наложения каналов друг на друга. Считайте, что наивысшее
значение частоты колебаний, воспринимаемых человеческим слу-
хом, составляет 18 кГц.
4.30(0). В левом канале стереофонической системы передается
низкочастотный гармонический сигнал с частотой 3 кГц, а в пра-
вом канале — такой же сигнал с частотой 5 кГц. Известно, что
частота поднесущего колебания равна 38 кГц. Найдите значения
частот всех спектральных составляющих, входящих в состав
сигнала с полярной модуляцией.
Тема 5
СИГНАЛЫ С ОГРАНИЧЕННЫМ СПЕКТРОМ
• Сигналы с ограниченным спектром
низкочастотного типа.
Ряд Котельникова
5.1 (Р). Сигнал s(t) с ограниченными спектром имеет спект-
ральную плотность
(О< —азя,
—со» < со < со,,
со>со,.
Получите представление данного сигнала в виде суммы двух
идеальных низкочастотных сигналов, спектральные плотно-
сти которых постоянны в пределах частотного интервала [—со,,
coj.
5.2 (0). Сигнал звукового сопровождения в телевизионном
канале ограничен верхней частотой ^=12 кГц. Определите ин-
тервал t0 между отсчетами этого сигнала, необходимый для
неискаженного воспроизведения сигнала при передаче его диск-
ретным способом.
5.3 (Р). Сигнал и (г), дискретизованный в соответствии с усло-
виями теоремы Котельникова, имеет два ненулевых отсчета,
изображенных на рис. 1.5.1. Вычислите мгновенные значения
исходного аналогового сигнала в момент времени t= 1 мкс.
5.4 (УО). Ряд Котельникова сигнала s (t) содержит три ненуле-
вых слагаемых (рис. 1.5.2). Все отсчеты измерены в вольтах.
Вычислите энергию Е, данного сигнала.
29
20В
15В
2-1 О 1 2 t, мкс
Рис. 1.5.1
20В
5.5 (УР). Гауссов видеоимпульс s(t)= (70ехр(—pt2), заданный
при — со «о < + оо, приближенно заменяется сигналом с ограни-
ченным спектром спектральная плотность которого в ин-
тервале частот Оссоссо, совпадает со спектральной плотностью
сигнала s(t), а при а» обращается в нуль. Найдите норму ||5ош11
сигнала ошибки подобной аппроксимации.
• Сигналы полосового типа. Комплексная огибающая
5.6 (У). Пусть $,(/), з2 (/)> ——сигналы, которым при выборе
в качестве опорной частоты некоторого конкретного значения
cdq соответствуют комплексные огибающие Oi(t), t72(f), До
кажите, что сумма произвольного числа таких сигналов имеет
комплексную огибающую, равную сумме комплексных огиба-
ющих отдельных слагаемых.
5.7 (0). Получите выражения для комплексных огибающих
следующих сигналов:
(C70coscd0z , /<0,
а S \U0cos((o0t+<p0), />0,
6)5(0=
U0cos<i30t , t<0,
C70cos(<o0+£l0)z, t^O.
В обоих случаях положите, что значение опорной частоты
равно (о0.
5.8 (0). Узкополосный сигнал /(г) имеет вид
f(t)= 10costlzcosav+[30sin£lf +
+ 5 sin (20/+л/4)] sin toot.
зо
Найдите выражение для комплексной огибающей С^(0 данного
колебания.
5.9 (УО). Найдите комплексную огибающую 0,(t), а также
синфазную амплитуду Л, (0 и квадратурную амплитуду B,(t) для
однотонального АМ-сигнала
s (t) = Um (1 + М cos Or) cos (cot+я/4).
5.10 (УО). Сигнал з(0 с однотональной угловой модуляцией
описывается зависимостью
з(0= Um cos (cot+т sin Qt).
Положив, что опорная частота сигнала равна несущей частоте со,
получите выражение для комплексной огибающей 0,(t), синфаз-
ной A,(t) и квадратурной B,(i) амплитуд сигнала. Докажите, что
частота сигнала ш,(/)=с£)+лпйсо5Пг
5.11 (Р). Найдите комплексную огибающую гармонического
сигнала з(/) = Uo sin co0t, — оо < t < + со, выбрав в качестве опорной
частоты величину <и0. Получите выражения для спектральной
плотности С,(со) комплексной огибающей, а также для спект-
ральной плотности S(co) колебания з(г).
5.12 (УО). Вычислите спектральную плотность S(co) узкопо-
лосного сигнала
(C70cosa)0r, t<0,
5 f А = <
(C70cos(ca0r+9>0), r>0.
Отдельно рассмотрите частный случай <ро= 180°.
5.13(УО). Найдите физическую огибающую U,(t}, полную фа-
зу и мгновенную частоту са,(0 однотонального ОБП-сиг-
нала с подавленной нижней боковой полосой:
з (г)=Uo cos coot+(MU0/2) cos (co0+Q)t,
где M< 1 — коэффициент амплитудной модуляции.
5.14(0). Вычислите минимальное сот\„ и максимальное
сотят значения мгновенной частоты простейшего сигнала с одной
боковой полосой (см. задачу 5.13) при следующих числовых
параметрах: со0= 10б с'1, £1= 104 с-1, М=1.
5.15(УО). Найдите физическую огибающую 17,(0, соответст-
вующую идеальному низкочастотному сигналу з (0, спектральная
плотность которого постоянна и равна 50 в интервале частот
— сов<со<сов, а на других частотах обращается в нуль.
31
5.16(0). Найдите комплексную огибающую Us(t) экспоненци-
ального радиоимпульса s(f)=Uoexp(—a/)sincjorcr(r). Получите
выражения спектральной плотности G,(a)) комплексной огиба-
ющей и спектральной плотности S(co) сигнала s(t).
5.17(0). Идеальный прямоугольный радиоимпульс длитель-
ностью тв описывается выражением
с°,
s(t)=< ^ocosev,
to,
t<zJ2,
t>tB/2.
Получите выражение комплексной огибающей (7,(f) данного
сигнала, полагая, что опорная частота равна а>0. Найдите спект-
ральную плотность S(ca) сигнала 5(0-
• Аналитический сигнал. Преобразования Гильберта
5.18 (Р). Спектральная плотность сигнала s(f) задана выраже-
ниями
ГО,
5(й))=<5оехр(-а|а)|),
to,
со< —й)п
а)>а)„
где So, а, — положительные числа. Найдите соответствующий
аналитический сигнал z,{t).
5.19 (УО). Сигнал s (0 имеет вещественную спектральную пло-
тность S((o), график которой при ш>0 изображен на рис. 1.5.3.
Вычислите аналитический сигнал z,(t) и определите закон измене-
ния во времени мгновенной частоты са,(г) рассматриваемого
сигнала.
5.20 (0). Сигнал s(t) при са>0 имеет спектральную плотность
5(a))=S0e~bo>. Найдите соответствующий аналитический сигнал
z,(0-
5.21 (У). Докажите, что если s (г)— сигнал с ограниченной
энергией, то он ортогонален по отношению к сигналу, сопряжен-
ному по Гильберту, т. е.
оо
J s(f).s(f)df=O.
— оо
32
5.22 (У). Докажите, что двукратное применение преобразова-
ния Гильберта к сигналу s(t) равносильно перемене знака сиг-
нала, т. е.
5.23 (0). Вычислите преобразование Гильберта s(t) сигнала
s (О=5(0, используя фильтрующее свойство 5-функции.
5.24 (УР). Прямоугольный видеоимпульс 5(0, симметричный
относительно начала отсчета времени (рис. 1.5.4, а), поступает на
вход системы, состоящей из идеального дифференциатора и квад-
ратурного фильтра КФ, выполняющего операцию преобразова-
ния Гильберта (рис. 1.5.4, б). Определите сигнал /(0 на выходе
системы.
5.25 (УО). Мгновенные значения сигнала 5(0 изменяются во
времени в соответствии с формулой 5(0=а/(“2 + 12). Вычислите
пребразование Гильберта s(t) данного колебания.
5.26 (У). Докажите, что мгновенная частота a)s(t) узкополос-
ного сигнала 5(0, которому соответствует преобразование Гиль-
берта 5(0, вычисляется по формуле
5.27 (УО). Вычислите преобразование Гильберта 5(0, отвеча-
ющее прямоугольному видеоимпульсу
2-415
33
Тема 6
ОСНОВЫ ТЕОРИИ СЛУЧАЙНЫХ СИГНАЛОВ
• Случайные события и их вероятности
6.1 (УР). Два лица, А и В, по очереди бросают игральную
кость. Игру начинает А. Выигрывает тот, кто первым выбро-
сит шесть очков. Найдите вероятность РА того, что выиграет
лицо А.
6.2 (УО). Некоторый цифровой сигнал представлен кодовы-
ми комбинациями — шестиразрядными двоичными числами, ко-
торые образованы случайными комбинациями нулей и единиц.
Вероятность появления символа «1» в каждом разряде состав-
ляет величину Pi=0.6, а вероятность символа «О» составляет
величину Р0=0.4. Найдите вероятность Р возникновения конкрет-
ной кодовой комбинации 101101, считая появления того или
иного символа в каждом разряде независимыми случайными
событиями.
6.3 (УО). В четырехразрядном цифровом сигнале (см. условия
задачи 6.2) появление нуля или единицы в первом разряде равно-
вероятно; в следующих разрядах перемена символа по сравнению
с предыдущим значением имеет вероятность 0.8, а сохранение
символа имеет вероятность 0.2. Найдите вероятность Р того, что
будет реализована кодовая комбинация 0110.
6.4 (УО). Изучение большой партии радиоэлектронных из-
делий показало, что из 10000 изделий в течение 4 лет исп-
равно работают 8200 экземпляров, а по прошествии 7 лет чис-
ло исправно работающих изделий составляет 3800. Определи-
те вероятность того, что случайно взятое изделие из числа
проработавших 4 года окажется также работоспособным через
7 лет.
6.5 (УО). Некоторая система, предназначенная для передачи
сигналов из точки а в точку Ь, изображена на рис. 1.6.1. Система
содержит элементы 1 и 2, резервирующие друг друга. Нормаль-
ное функционирование обеспечивается, если исправен хотя бы
один из этих элементов.
Известно, что в течение некоторого промежутка времени эле-
мент 1 исправен с вероятностью = 0.8, а элемент 2 — с вероят-
ностью Р2=0.7. Найдите вероятность Р исправной работы резер-
вированной системы за тот же промежуток времени.
6.6 (УО). На входы сумматора (рис. 1.6.2) поступают четыре
независимых постоянных во времени случайных напряжения иь
U2, из и Каждое из этих напряжений с равной вероятностью
принимает либо значение 0.5 В («низкий» уровень потенциала),
34
либо 4.5 В («высокий» уровень потенциала). Определите всю
совокупность напряжений иш на выходе сумматора вместе с ве-
роятностями их появления.
ф функция распределения и плотность вероятности.
Моменты
6.7 (0). Постройте график функции распределения Г(и№) для
случайной величины и^,, рассмотренной в задаче 6.6. Выведите
аналитическое выражение плотности вероятности p(un„).
6.8 (Р). Случайная величина X имеет плотность вероятности
Р(Х)~ {г/(1 +х)3,
х<0,
х>0.
Найдите функцию распределения F(x) данной случайной вели-
чины, а таже вероятность P(O<Af< 1) попадания случайной точки
внутрь отрезка [О, 1].
6.9 (УО). Случайная величина X может принимать лишь два
значения: х= 1 с вероятностью 0.25 и х= 1.5 с вероятностью 0.75.
Аналогично, случайная величина Y, независимая от X, может
принимать лишь два значения: у=3иу=5с одинаковыми веро-
ятностями 0.5. Найдите плотность вероятности случайной вели-
чины Z—X+ Y.
6.10 (0). Непрерывная случайная величина X имеет график
плотности вероятности р(х) треугольного вида (рис. 1.6.3). Пара-
метр а — заданное число, величина А заранее неизвестна. Полу-
чите формулу, описывающую функцию р(х).
6.11 (Р). Случайная величина X распределена по нормальному
закону с параметрами т=0, о—2. Найдите вероятность попада-
ния этой случайной величины в полуотрезок 0<х^2.
6.12 (0). Вычислите вероятность того, что случайная величина
X, рассмотренная в задаче 6.10, попадает в полуотрезок
0<х<а/2.
35
6.13 (Р). Найдите плотность вероят-
ности случайной величины Л — сопро-
тивления параллельного соединения
двух резисторов, один из которых име-
ет фиксированное сопротивление Ro,
в то время как сопротивление другого
резистора г — случайная величина, рав-
номерно распределенная на отрезке
[Но—а, Яо+а], где a<Ro — постоянное
число.
6.14 (Р). Независимые случайные ве-
личины X и Y имеют заданные плот-
ности вероятности />1(х) и р2(у) соответственно. Найдите плот-
ность вероятности Рз(г) случайной величины Z=X+ Y.
6.15(УО). Пусть X и Y — две независимые случайные вели-
чины, равномерно распределенные на отрезке [0, 1]. Найдите
аналитическое выражение функции p(z) — плотности вероятно-
сти суммы Z=X+ Y этих двух величин.
6.16(0). Вычислите плотность вероятности pz(z) случайной
величины Z, каждая реализация которой представляет собой
сумму реализаций независимых случайных величин X и Y с оди-
наковыми плотностями вероятности экспоненциального вида.
рх(х)=Ле“ьст(х), ру(у)=Ле~1уа(у).
6.17 (У). Докажите, что случайная величина X, имеющая рас-
пределение Коши с плотностью вероятности
р(х)=-------, — оо<х< + со,
л(1+х2)
характеризуется бесконечно большой дисперсией.
6.18 (0). Вычислите математическое ожидание и диспер-
сию случайного напряжения на выходе сумматора, рассмот-
ренного в задаче 6.6.
6.19 (Р). Вычислите среднее значение х и средний квадрат х2
случайной величины X, рассмотренной в задаче 6.8.
6.20 (0). Случайная величина U принимает значения 0.5, 0.8
и 1.3 с вероятностью 0.35, 0.45 и 0.2 соответственно. Вычислите
величины ти и а2.
6.21 (Р). Непрерывная случайная величина X равномерно рас-
пределена на полуотрезке а<х^Ь. Вычислите среднее значение
тх=х, средний квадрат т2=х2 и дисперсию а2=т2—т2 данной
случайной величины.
6.22 (УО). Случайная величина X имеет одностороннюю экс-
поненциальную плотность вероятности
36
(2ехр(—Лх) при х>0,
РХ (0 при х<0.
Найдите среднее значение х и дисперсию ст, этой случайной
величины.
6.23 (У). Докажите, что если X и Y — независимые гауссовы
случайные величины с математическими ожиданиями тх и ту
и дисперсиями <г2 и а2 соответственно, то случайная величина
Z=aX+bY, где а и b — константы, также обладает свойством
нормальности, имея математическое ожидание mz=amx+bmy
и дисперсию ax=a2ffx+b2fff.
6.24 (Р). Случайная величина X равномерно распределена на
отрезке [0, 1]. Найдите математическое ожидание и дисперсию
случайной величины Z, каждая реализация которой равна произ-
ведению длин отрезков, разделенных случайной точкой х.
ф Функциональные преобразования случайных величин.
Многомерные случайные величины
6.25 (Р). Найдите плотность вероятности случайной величины
Z, рассмотренной в задаче 6.24.
6.26 (0). Исходная случайная величина X имеет плотность
вероятности экспоненциального вида
, . (2ехр(—Лх), х>0,
х<0
с фиксированным значением параметра Л>0. Случайная вели-
чина Y получается из X путем функционального преобразования,
график которого изображен на рис. 1.6.4. Определите плотность
вероятности Рщ,(у) преобразованной случайной величины.
6.27(УО). Случайная величина X равномерно распределена на
отрезке [0, я/2]. Найдите среднее значение и дисперсию случайной
величины У, реализации которой связаны с реализациями случай-
ной величины Xследующим образом: y=5cosx+12cos2x.
6.28 (0). Случайная величина X рав-
номерно распределена на отрезке [а, 6].
Получите выражение, описывающее
плотность вероятности р(у) случайной
величины Y—X2. Найдите математи-
ческое ожидание ту и дисперсию а2.
6.29 (Р). Три независимые случайные
величины X, Y и Z имеют одинаковые
Рис. 1.6.4
нормальные плотности вероятности
37
р (О=exp ( - 2/(2<т2)/(л/2тгст), где — символ, соответствующий
х, у и z. Пусть (х, у, z) — три декартовы координаты точки
в трехмерном пространстве, связан
ме со сферическими коор-
динатами (г, о , ф) известными соотношениями:
X=rsin i) COS<p,
y=rsino sin<p,
z=rcoso .
Найдите одномерную плотность вероятности р(г) случайной
величины R, представляющей собой длину радиуса-вектора
в сферической системе координат.
• Характеристическая функция случайной величины
6.30 (0). Найдите характеристическую функцию случайной ве-
личины X, имеющей плотность вероятности рх (х) = А ехр х
х(-2х)п(х).
631(0). Вычислиie характеристическую функцию 0(и) слу-
чайной величины X, равномерно распределенной на отрезке
а^х^Ь.
6.32 (Р). Используя результат, полученный в задаче 6.31, най-
дите среднее значение х рассмотренной здесь случайной вели-
1Ы.
633(Р). Случайная величина X равномерно распределена на
отрезке — 1/2<х^ 1/2. Вычислите плотность вероятности случай-
ной величины У, каждая реализация которой равна сумме трех
независимых реализаций случайной величины X.
6.34 (0). Определите вероятность того, что модуль случайной
величины Y, рассмотренной в задаче 6.33, принимает значения,
превышающие единицу.
6.35 (УР). Случайная величина X имеет гауссову плотность
вероятности с известным математическим ожиданием тх и задан-
ной дисперсией Вычислите среднее значение случайной вели-
чины У, отдельные реализации которой связаны с реализациями
случайной величины X соотношением у=ехр (х).
Тема 7
КОРРЕЛЯЦИОННАЯ ТЕОРИЯ
СЛУЧАЙНЫХ ПРОЦЕССОВ
ф Функция корреляции и спектр мощности
7.1 (УР). Случайный процесс X (г) задан ансамблем своих ре-
ализаций вида х (t)=acosa>0t, где — фиксированная величина,
а — случайная величина с нулевым математическим ожиданием
а и конечной дисперсией п2=а2. Докажите, что процесс X(t) не
является стационарным в широком смысле.
7.2 (0). Случайный процесс X(t) имеет ансамбль постоян-
ных во времени реализаций, который описывается нормаль-
ным законом распределения с нулевым математическим ожида-
нием и некоторой известной дисперсией <т2. Найдите среднее
значение х и функцию автокорреляции Кх (г) данного случайного
процесса.
7.3 (У). Докажите, что случайный процесс, рассмотренный
в задаче 7.2, неэргодичен.
7.4 (У). Реализации случайного процесса X(t) представляют
собой гармонические колебания вида x(0=acosa>of+6sinav
с фиксированной частотой соь; амплитуды ан b являются случай-
ными величинами.
Докажите, что процесс X(t) стационарен в широком смысле
тогда и только тогда, если: 1) а=Ь=О; 2) Oa = ol', 3) ab=O.
7.5 (УО). Найдите функцию корреляции Лх(т) случайного про-
цесса X(t), рассмотренного в задаче 7.4, предполагая, что выпол-
нены все условия, обеспечивающие его стационарность в широ-
ком смысле.
7.6 (У). Докажите, что случайный процесс X (г), рассмотренный
в задаче 7.5, является эргодическим.
7.7 (Р). Пусть X(t) — стационарный дельта-коррелированный
случайный процесс (белый шум), имеющий нулевое математичес-
кое ожидание и функцию корреляции 1?х(т)= Ио5(г), где Ио —
постоянный на всех частотах спектр мощности данного процесса.
Случайный процесс У (г), реализации которого y(t) связаны с ре-
ализациями х (0 интегральным соотношением
I
y(t)=p(£)d£,
о
принято называть случайным процессом Винера.
Выведите формулу для функции корреляции этого случай-
ного процесса. Докажите, что процесс Винера нестациона-
39
рен Получите закон изменения дисперсии этого процесса во
времени.
7.8 (УО). Найдите спектр мощности FFx(ca) случайного процес-
са X(t), рассмотренного в задаче 7.5.
7.9 (0). Стационарный случайный процесс X(t) с размерно-
стью напряжения (В) на некоторой фиксированной частоте од
имеет значение спектра мощности Wx(од), равное 17 10“15 В2 с
Вычислите величины односторонних спектров мощности /\(<^о)
и Fx (f0).
7.10 (0). Найдите спектр мощности Wx (со) стационарного слу-
чайного процесса X(t), имеющего нулевое математическое ожи-
дание и функцию корреляции Ях(т)=о-2ехр х (—а|г|) созодг.
7.11 (0) Получите выражение для функции корреляции Лх(г)
стационарного случайного процесса Х(г) со спектром мощности
!Fx(to) полосового вида (рис. 1.7.1):
иг,
Wx(a>)=\ иг,
ОД----<СО<ОД-|----,
О при других со.
7.12 (Р). Найдите функцию корреляции Rx(t) случайного про-
цесса X (0 вида «случайного телеграфного сигнала» Его реализа-
ции х(/) (рис. 1.7.2) являются разрывными функциями, принима-
ющими с равными вероятностями лишь два значения: + а и — а.
В случайные моменты времени знак реализации изменяется скач-
ком. Вероятность события, состоящего в том, что за время
Т произойдет п перемен знака, описывается формулой закона
Пуассона
Рт(и)=^-ехр(-Л7),
л!
где Л>0 — параметр с размерностью частоты, определяющий
среднюю скорость протекания процесса
Ws(w)t
О' Ш
Рис. 1.7.1
Рис. 1.7.2
7.13 (0). Определите значение одностороннего спектра мощ-
ности Гх(су) случайного телеграфного сигнала Х(0, рассмотрен-
ного в задаче 7.12, на частоте со0=103 с-1 при следующих параме-
трах: а= 15 В; 2=3 104 с"1.
7.14 (0). Найдите интервал корреляции тк стационарного слу-
чайного процесса X(t) с односторонним спектром мощности
Л(ш)=
То,
о,
О^су^су,,
СУ>СУ»,
где су, — значение верхней граничной частоты спектра.
7.15 (УО). Найдите интервал корреляции т, случайного телег-
рафного сигнала X(t) (см. задачу 7.12) для значения 2=5 • 10б с-1.
Оцените значение со„ ограничивающее область частот 0<су<су»,
в пределах которой данный случайный процесс может прибли-
женно рассматриваться как белый шум.
ф Дифференциальные свойства случайных процессов
7.16 (Р). Стационарный случайный процесс X(t) имеет спектр
мощности низкочастотного вида:
1¥х(аз)=
— СУ.^СУ^СУ,,
СО< — СУ„ СУ>СУ».
Найдите спектр мощности про-
изводной Y(t)=dX/dt. Вычислите
функцию корреляции производной
ЗД.
7.17(УО). Определите эффектив-
ную ширину спектра Асу^ случай-
ного процесса У(/), рассмотренного
в задаче 7.16.
7.18 (УР). Гауссов стационарный Рис. 1.7.3
случайный процесс X(t) имеет одно-
сторонний спектр мощности, описанный в условиях задачи 7.14.
Получите формулу для расчета квазичастоты п(0) данного слу-
чайного процесса.
7.19 (УО). График частотной зависимости спектра мощности
стационарного гауссова процесса X(t) изображен на рис. 1.7.3.
Вычислите квазичастоту данного процесса.
41
• Узкополосные случайные процессы
7.20 (Р). Узкополосный нормальный случайный процесс X(t)
характеризуется дисперсией сг^= 10 В2. Найдите вероятность то-
го, что в некоторый фиксированный момент времени огибающая
этого процесса превосходит уровень 4 В.
7.21 (0). Узкополосный нормальный случайный процесс, име-
ющий дисперсию г2=2.5 В2, приложен ко входу идеального
детектора огибающей. Вычислите дисперсию и среднее значение
напряжения на выходе детектора.
7.22 (Р). Отдельные реализации огибающей U (г) нормального
узкополосного случайного процесса X(t) наблюдаются в течение
отрезка времени длительностью 1 с. Определите средние дли-
тельности суммарных промежутков времени, когда 4.9 В <С7<
<5.1 В при дисперсиях узкополосного процесса, равных 1 В2,
12 В2 и 96 В2 соответственно.
7.23 (0). Узкополосный случайный процесс X(t), нормальный
и стационарный в широком смысле, имеет функцию корреляции
(В2)
Rx (г) = 3.5ехр ( —10* |т|) cos 107 г.
Найдите функцию корреляции Rv(t) огибающей U{t) данного
процесса.
7.24 (0). Применительно к условиям задачи 7.24 найдите
спектр мощности fVv((o) (В2-с) огибающей U(t) рассматрива-
емого случайного процесса.
7.25 (Р). На основании результата, полученного в задаче 7.24,
определите эффективную ширину спектра огибающей с учетом
одного и двух членов в разложении функции корреляции.
7.26 (У). Докажите, что средний квадрат огибающей U (l) узко-
полосного нормального случайного процесса X(t) вычисляется
по формуле (72=2<т2, где <т2 — дисперсия процесса Х(1).
7.27 (У). Рассматривается сумма гармонического сигнала
u(f)= Umcos(DOt и узкополосного нормального шума X(t), спект-
ральная плотность мощности которого симметрична относи-
тельно центральной частоты <а0. Дисперсия ст2 случайного про-
цесса .Y(z) задана. Докажите, что средний квадрат огибающей
суммы этих двух колебаний вычисляется по формуле (72 =
= (72 + 2о-2.
7.28 (Р). Используя средства математической системы
MathCAD, составьте программу, позволяющую строить графики
распределения Райса в соответствии с формулой (7.78) из [1] при
произвольных отношениях Um/ox.
42
Тема 8
ВОЗДЕЙСТВИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
НА ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ СИСТЕМЫ
ф Дифференциальные уравнения линейных цепей.
Собственные колебания
8.1 (УР). Исследуйте собственные колебания цепи, схема кото-
рой приведена на рис. 1.8.1 вместе со стрелками, указывающими
положительные направления токов в ветвях, и знаками положи-
тельных напряжений на конденсаторах. Начальные напряжения
U|(0) и и2(0) на конденсаторах Q и С2 в момент времени 1=0
считаются заданными.
8.2 (УО). В соответствии с постановкой задачи 8.1, полагая
С] = С2=0.1 мкФ, 2?! = 1.6 кОм, /?2=2.4 кОм, /?3 = 6.8 кОм, вычис-
лите корни характеристического уравнения цепи. Найдите функ-
ции U|(/) и и2(/) при начальных условиях м((0) = 8 В, и2(0)=0.
Определите момент времени 10, начиная с которого прекращается
зарядка конденсатора С2.
8.3 (Р). Выведите характеристическое уравнение, описывающее
частоты собственных колебаний цепи, схема которой представ-
лена на рис. 1.8.2. Найдите частоты собственных колебаний в сле-
дующих частных случаях: а) Л/=0; б) R=co; в) /?=0.
8.4 (УО). Для ЯЬ-цепи, схема которой приведена на рис. 1.8.3,
запишите систему дифференциальных уравнений, описывающих
собственные колебания. Составьте характеристическое уравне-
ние данной системы и найдите его корни, положив Ri = R2=
= 3.9 кОм, R3= 1.6 кОм, Li= 15 мкГн, £г=35 мкГн.
8.5 (Р). Найдите ‘частоты собственных колебаний в системе
двух связанных колебательных контуров без потерь (рис. 1.8.4)
для частного случая 1^=1^=!,, Ct = C2 = C.
8.6 (0). Колебательный контур имеет добротность Q. Найдите
число полных периодов N собственных колебаний, которые со-
Рис. 1.8.1
Рис. 1.8.2
43
Рис. 1.8.3
Рис. 1.8.4
вершаются за отрезок времени от 1=0 до того момента времени,
когда амплитуда колебаний уменьшается в 10 раз по сравнению
с начальным уровнем.
• Передаточная функция н частотный коэффициент
передачи цепи
8.7 (0). В сложной ЛС-цепи (рис. 1.8.5) входным сигналом
служит напряжение u(t), а выходным сигналом — ток ic(f). Най-
дите передаточную функцию К(р) данной системы.
8.8 (0). Вычислите передаточную функцию К(р) цепи, схема
которой приведена на рис. 1.8.6. Входным сигналом служит ток
i(/), а выходным — напряжение u(t).
8.9 (0). Найдите передаточную функцию К(р) цепи (рис. 1.8.7),
равную отношению изображений токов i„„(0 и i„(l).
8.10 (F). Линейная цепь, схема которой изображена на рис.
1.8.8, возбуждается со стороны входа идеальным источником
тока 4х(0- Выходным сигналом служит напряжение Полу-
чите выражения передаточной функции К(р) = Um(p)/I„(p) и ча-
стотного коэффициента передачи K(jto). Выведите формулы, опи-
сывающие амплитудно-частотную характеристику (АЧХ) и фазо-
частотную характеристику (ФЧХ) данной цепи.
8.11 (0). Схема двухзвенного ЛС-фильтра приведена на рис.
1.8.9. Входным сигналом служит напряжение источника ЭДС e(t),
выходным сигналом является напряжение (1). Полагая извест-
ными значения R и С, выведите формулы для расчета передаточ-
ной функции К(р) и частотного коэффициента передачи K(jaf)
данной цепи. Получите выражения, описывающие АЧХ и ФЧХ.
Определите частоту cum„, на которой АЧХ достигает максимума,
если R=2 кОм, С=0.1 мкФ.
8.12 (УР). Схема трехзвенного ЛС-фильтра нижних частот
приведена на рис. 1.8.10. Получите выражение передаточной фун-
кции K(p)=Utta(p)/U„(p) данного фильтра. Положив Л=6.8 кОм,
С =0.2 мкФ, вычислите частоты J\ и f2 (Гц), на которых фазовый
сдвиг, вносимый фильтром, составляет —90° и —180° соответст-
венно.
44
8.13 (УО). Вычислите координаты полюсов передаточной фун-
кции трехзвенного ЛС-фильтра, рассмотренного в задаче 8.12,
при следующих параметрах цепи: J?=l МОм, С=1 мкФ.
8Л4(УР). На рис. 1.8.11 изображена схема линейного четырех
полюсника мостовой («скрещенной») структуры, который обра-
зован операторными сопротивлениями Zu Z2, Z3 и Z4. Выведите
формулу для расчета функции K(p)=Um(p)/U„(p).
8.15 (0). Найдите передаточную функцию K^—U^ipy/U^ip)
«перекрытого» четырехполюсника (рис. 1.8.12), образованного
линейными двухполюсниками с известными операторными со-
противлениями Zi(p), Z2(p), Z3(p), Z4(p).
8.16 (F). Основываясь на критерии Пэли-Винера, рассмотрите
вопрос о физической реализуемости фильтра нижних частот
с АЧХ гауссова вида
|^(/са)| = Х^ехр(—Ьй)2), 0<ш<оо.
ф Импульсная н переходная характеристики
8.17 (УО). Вычислите импульсную характеристику h(t) усили-
теля напряжения с апериодической нагрузкой (рис. 1.8.13). Диф-
ференциальную крутизну характеристики 5 электронного прибо-
ра в выбранной рабочей точке, а также внутреннее сопротивление
Ri положите известными.
8.18 (Р). Для учета инерционности процессов в биполярном
транзисторе часто используют упрощенную модель, согласно
которой статическая дифференциальная крутизна S является ком-
плексной и зависит от частоты
S (ш)=50/(1 +joi/(arp).
Здесь «Огр — граничная частота усиления транзистора.
Получите аналитическое выражение импульсной характери-
стики h (t) усилителя (см. рис. 1.8.13), в котором применен подоб-
ный транзистор.
8.19 (УР). Получите формулу, описывающую импульсную ха-
рактеристику h (/) для N ступенчатого усилителя малых сигналов
с одинаковыми апериодическими нагрузками, предполагая, что
частотный коэффициент передачи одной ступени
^(/Ш)=-Х0/(1+>тэ).
Здесь Ко — коэффициент усиления ступени на нулевой частоте,
тэ — эквивалентная постоянная времени ступени. Постройте гра-
фики импульсных характеристик для N=2, 3 и 4 в зависимости от
безразмерного аргумента //тэ.
46
Рис. 1.8.13
С
Рис. 1.8.14
8.20 (УО). Источником входного сигнала в ЛС-цепи (рис.
1.8.14) служит идеальный источник ЭДС. Выходное напряжение
снимается с резистора. Найдите импульсную характеристику дан-
ной цепи.
8.21 (0). Найдите импульсную характеристику Л(/) идеально-
го полосового фильтра, АЧХ которого изображена на рис.
1.8.15.
8.22 (0). Получите импульсную характеристику h(t) идеаль-
ного линейного фильтра нижних частот, коэффициент передачи
^(/ta) = |^(/ta)|e*’<(“) которого задается равенствами:
/О, (О< —со,,
|АГ(/си)| = < Ко, -со^со^со,
гфо, со<0,
Фх(ш)=5
(—фо. <о>0,
где фо — постоянная величина.
8.23 (Р). Найдите импульсную характеристику h (t) и переход-
ную характеристику g(t) цепи, принципиальная схема которой
изображена на рис. 1.8.16.
8.24 (0). Рассчитайте и постройте график переходной хара-
ктеристики g(t) двухконтурной цепи, рассмотренной в задаче
8.23. Параметры цепи: Л,—100 Ом, R2 = 2 кОм, £, = £г=15 мГн,
Л/=7 мГн.
8.25 (Р). Исследуйте способы, которые дают возможность
в индуктивно связанной цепи (см. задачу 8.23) улучшить качество
передачи на выход ступенчатого перепада входного напряжения,
т. е. сократить длительность фронта и уменьшить относительный
спад плоской части выходного сигнала.
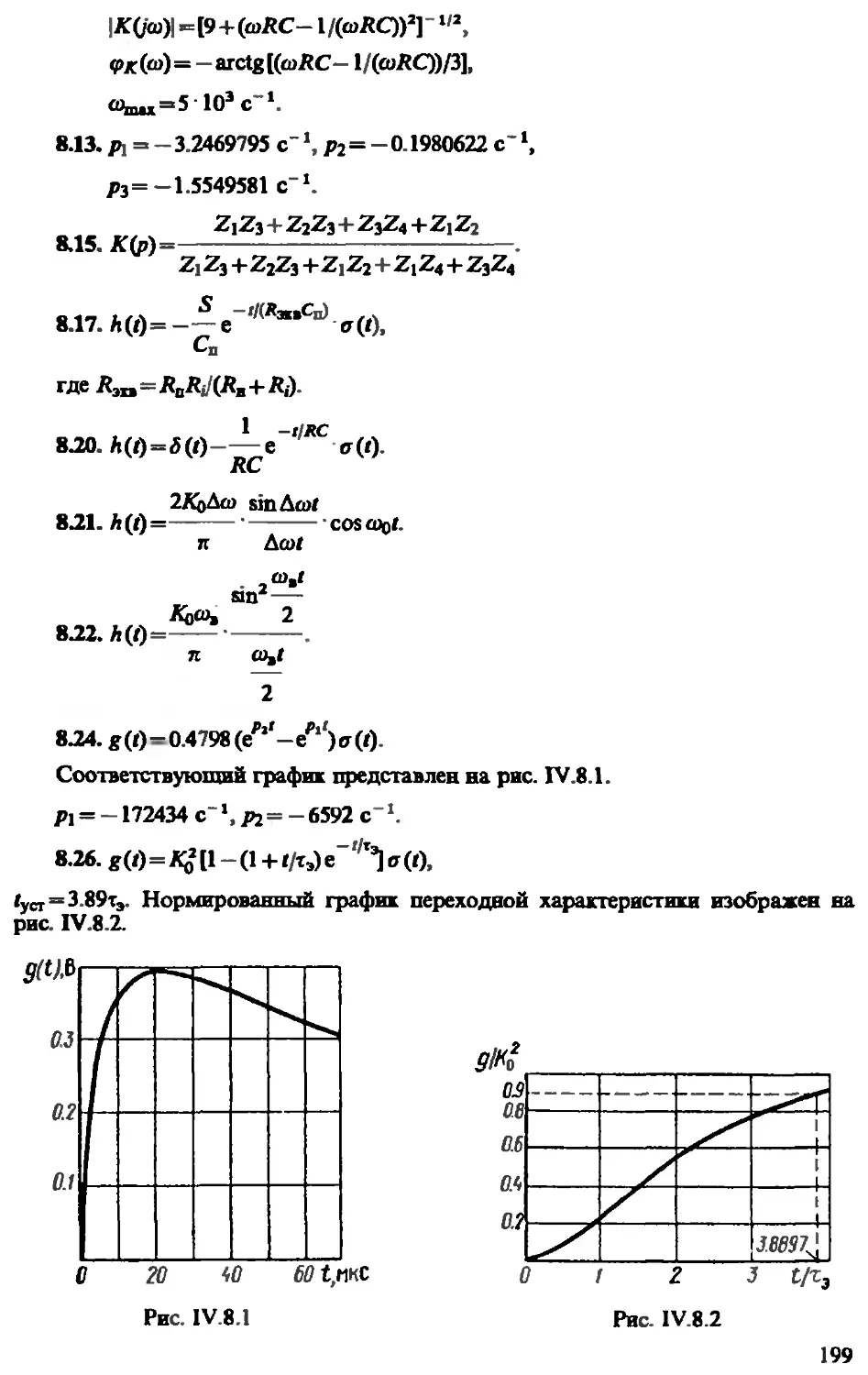
8.26 (УО). Определите переходную характеристику g(f) двух-
ступенчатого усилителя малых сигналов с одинаковыми ступеня-
47
Рис. 1.8.15
Рис. 1.8.16
ми, которые содержат резистивно-емкостные нагрузки. Зада-
ны величины: — коэффициент усиления одной ступени на ну-
левой частоте, т0 — эквивалентная постоянная времени ступени.
Постройте график переходной характеристики в зависимости
от аргумента //тэ. Определите время установления ^ст систе-
мы, понимаемое как отрезок времени, в течение которого напря-
жение на выходе достигает уровня 90% от установившегося
значения.
8.27 (УР). Вычислите импульсную и переходную характеристи-
ки симметричного ЛС-четырехполюсника мостового типа, схема
которого изображена на рис. 1.8.17.
8.28 (0). В последовательном LCR-ковтуре входной сигнал
создает идеальный источник ЭДС, подключенный к внешним
зажимам цепи. Выходной сигнал представляет собой ток i(t)
в цепи. Вычислите импульсную характеристику h (/) данной систе-
мы, если £=0.35 мГн, R= 15 Ом, С=4 нФ.
8.29 (УО). На входе сложного колебательного контура без
потерь с двумя конденсаторами G и С2 (рис. 1.8.18) действует
идеальный источник тока i(t). Выходным сигналом служит на-
пряжение и (/) на конденсаторе С2. Определите импульсную хара-
ктеристику h(t) данной цепи.
830(Р). Найдите переходную характеристику g(t) идеаль-
ного ФНЧ с заданными параметрами Ко и ta,. Определите вре-
мя установления колебаний в данной системе (см. задачу
8.26).
831(Р). Вычислите импульсную характеристику h(t) линейной
системы, частотный коэффициент передачи которой имеет вид
ГС
V |tf0exp(tf2ca2), ш<0
(Ко, ft — постоянные величины).
8.32 (УО). Импульсная характеристика h (i) стационарной
линейной системы представляет собой прямоугольный видео-
импульс длительностью Т с амплитудой А, начинающийся в
момент времени /=0. Найдите частотный коэффициент пере-
48
Рис. 1.8.17
дачи K(jto) и амплитудно-частотную характеристику данной си-
стемы.
8.33 (Р). Импульсная характеристика h(t) некоторой стацио-
нарной линейной системы представляет собой затухающую по-
следовательность разнополярных импульсов одинаковой длите-
льности Т (рис. 1.8.19). Амплитуды импульсов убывают по зако-
ну геометрической прогрессии, знаменатель которой а (0<а<
< 1) — вещественное число. Найдите частотный коэффициент пе-
редачи K(jto) данной системы.
8.34 (УО). Постройте график переходной характеристики g(t)
системы, рассмотренной в задаче 8.33 при а=0.8.
8.35 (0). Найдите частотный коэффициент передачи K(jto) ли-
нейной системы, импульсная характеристика h(t) которой изоб-
ражена на рис. 1.8.20.
8.36 (0). Импульсная характеристика некоторой линейной ста-
ционарной системы имеет вид
(°’
Л(о=
(*-0
t<0,
t>0,
где {а*} — последовательность вещественных коэффициентов,
Т— параметр с размерностью времени. Найдите частотный ко-
эффициент передачи KQ'to) данной системы. Изобразите струк-
турную схему ее реализации.
49
837(УР). Линейный стационарный фильтр, для которого
связь между входным сигналом uK(l) и выходным сигналом
(0 устанавливается с помощью соотношения
«вых (0 — “
«„юае,
принято называть фильтром «скользящего среднего». Здесь Т —
постоянный параметр с размерностью времени. Выведите выра-
жения для импульсной характеристики h(t) и частотного коэф-
фициента передачи K(jto) данной системы.
А Спектральный и операторный методы анализа
линейных систем
838(Р). Идеальный фильтр нижних частот с частотным коэф-
фициентом передачи
О, о < — to.
K(jto)=< Ко, -to,<to<to„
(j), СО>СОВ
возбуждается входным сигналом uKt(t)=UOl,(t). Найдите выход-
ной сигнал иш (/).
839(Р). Вход идеального ФНЧ с известными параметрами Ко,
ю, возбуждается прямоугольным видеоимпульсом, имеющим ам-
плитуду Uo и длительность тя. Передний фронт входного сигнала
возникает в момент времени /=0. Вычислите сигнал на выходе
фильтра.
8.40 (0). Найдите сигнал Uuu(/) на выходе, идеального полосо-
вого фильтра, частотный коэффициент передачи которого отоб-
ражается графиком на рис. 1.8.15, если ко входу фильтра прило-
жено колебание un(t)=Uoa(t). Фазовый сдвиг, вносимый
фильтром, равен нулю на всех частотах.
8.4Ц Р). На входе последовательной RL-цепи в момент време-
ни /=0 начинает действовать источник линейно нарастающей
ЭДС u„(t) = At(A>0). Определите закон изменения во времени
выходного напряжения uK(t), предполагая, что при t<0 запас
энергии в индуктивном элементе равен нулю.
50
• Интеграл Дюамеля
8.42(УР). На входе ЛС-цепи (рис. 1.8.21) действует источник
ЭДС, создающий прямоугольный видеоимпульс с амплитудой
Uo и длительностью тв:
(t) = Uo [<7 (Г) - О (t - Т.)].
Вычислите ВЫХОДНОЙ сигнал Una(t).
8.43 (Р). На входе АС-цепи (рис. 1.8.21) включен источник ЭДС
un(t)=ata(t), где а>0 — постоянное число. Найдите закон изме-
нения во времени выходного напряжения Постройте соот-
ветствующий график, выбрав в качестве аргумента отношение
r/т, где т=АС.
8.44 (УО). Ко входу АС-цепи (рис. 1.8.21) приложен источник
ЭДС, создающий одиночный импульс треугольной формы:
(О, г<0,
u„(Z)=< 1/ог/тв,
(О, />тв.
Полагая, что длительность импульса тя=АС, найдите выходной
сигнал Una (t) и постройте его график.
8.45 (УР). На входе мостовой RC-
цепи (см. рис. 1.8.17) с параметрами
Л = 5.6 кОм, С=0.02 мкФ действует
идеальный источник ЭДС, созда-
ющий прямоугольный видеоимпульс
с амплитудой £4=50 В и длитель-
ностью тв= 150 мкс. Вычислите и по-
стройте график импульса напряже- Рис. 1.8.21
ния на выходе »„(/).
Тема 9
ВОЗДЕЙСТВИЕ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ
НА ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ СИСТЕМЫ
• Частотные характеристики узкополосных цепей
9.1(УО). Одноконтурный резонансный усилитель малых сиг-
налов содержит колебательный контур с резонансной частотой
fpa=f>0 МГц и эквивалентной добротностью {?эи=40. Модуль
коэффициента усиления на резонансной частоте Аре, = 35. Вычис-
51
лите частотный коэффициент передачи усилителя K(j2.nf) на ча-
стотах f = 52 МГц и/2=68 МГц.
9.2(0). Амплитудно-частотная характеристика (АЧХ) одноко-
нтурного резонансного усилителя описывается выражением
---..... ....г
Vl+T’fa-COpc)2
где тх — постоянная времени колебательной системы. Определи-
те частоты ю1<2, на которых крутизна скатов АЧХ усилителя
максимальна.
93(Р). Резонансный усилитель образован каскадным включе-
нием N одинаковых одноконтурных ступеней с известным значе-
нием постоянной времени контура тх. Выведите выражение для
расчета полосы пропускания П0.707 данного усилителя.
9.4(0). Применительно к постановке задачи 9.3 определите
величину П0.707 при числе ступеней N= 1 и #= 5.
9.5(УО). Рассчитайте и постройте графики нормированных
АЧХ одно-, двух- и трехступенчатого резонансных усилителей.
Постоянные времени контуров тх и их резонансные частоты
(Орс одинаковы.
9.6(0). Резонансный усилитель, собранный из трех одинако-
вых ступеней, имеет частотный коэффициент передачи
K(j2nfpa)= —90. Найдите величину — модуль коэффициента
передачи одной ступени при f=fpn.
9.7(0). Одноконтурный резонансный усилитель имеет извест-
ные параметры Шро и тх. Найдите групповое время запаздывания
в таком усилителе для узкополосного радиоимпульса с часто-
той заполнения (о0=(Ора.
9.8(0). Обобщите результат, полученный в задаче 9.7, на
случай, когда (о^оЗра.
• Прохождение сигналов через узкополосные цепи
9.9 (Р). Усилитель образован каскадным включением двух ре-
зонансных ступеней с одинаковыми резонансными частотами
сора. Коэффициенты усиления Хр^ и и постоянные времени
тх1 и тх2 в общем случае различны. Найдите импульсную харак-
теристику h{t) данной узкополосной системы.
9.10 (УО). Вычислите импульсную характеристику h(t) двух-
ступенчатого усилителя, у которого коллекторной нагрузкой ка-
ждой ступени служит одиночный колебательный контур. Обе
ступени имеют одинаковые резонансные коэффициенты усиления
Кора и одинаковые постоянные времени тх. Резонансная частота
52
первого контура Wpd меньше резонансной частоты второго кон-.
тура 0^7 на величину Асо, такую, что Aco/Wpci 1. Постройте
ориентировочный график функции h (/).
9.11 (УО). Трехступенчатый резонансный усилитель содержит
колебательные контуры, настроенные на частоты copai=a)0—^a),
сорсЛ=а)о, сОреэз—<°о+Аш. Параметры и тж одинаковы для всех
трех ступеней. Система в целом является узкополосной, т. е.
2»1и Аш/сц0<^1- Вычислите импульсную характеристику Л (г)
усилителя. Изобразите примерный график этой функции. Резуль-
тат сравните с тем, который получен в задаче 9.10.
9.12 (УО). Узкополосный гауссов радиофильтр имеет часто-
тный коэффициент передачи, представляемый формулой
K(j(o)=Ко е-‘«“+“^+Ко е“Ь(ш*“”)2,
где Ко — масштабный коэффициент, со0 — центральная частота
полосы пропускания, b — размерная постоянная, такая, что
1. Найдите частотный коэффициент передачи K„(j£l) низ-
кочастотного эквивалента данного фильтра и соответствующую
импульсную характеристику
9.13 (0). Вычислите импульсную характеристику h(t) узкопо-
лосного гауссова радиофильтра, рассмотренного в задаче 9.12.
Проанализируйте возможность физической реализации данной
модели узкополосной системы.
9.14 (У). Докажите, что время установления колебаний в одно-
контурном резонансном усилителе малых сигналов при подаче на
его вход импульса включения гармонического сигнала с частотой
заполнения од=а>резые зависит от величины резонансной частоты
и вычисляется по формуле Густ=О.73/По 7о7, где П0.707 (Гц) — поло-
са пропускания колебательной системы по уровню 0.707 от резо-
нансного значения сигнала.
9.15 (УО). Одноконтурный резонансный усилитель напряже-
ния имеет параметры: ^«,=50, fpa= 1 МГц, (?эт,=80. На вход
усилителя подан AM-сигнал (мВ)
и„ (0=15 (1 + 0.8 cos 2я 104г) cos 2л • 106/.
Найдите напряжение ивых (t) на выходе усилителя.
9.16 (0). Применительно к условиям задачи 9.15 найдите вре-
мя запаздывания огибающей выходного сигнала по отноше-
нию к огибающей сигнала на входе.
9.17 (УР). Одноконтурный резонансный усилитель напряжения
имеет заданные параметры сорет, К^ и т,. Ко входу усилителя
приложен источник напряжения, имеющий скачок частоты при
/=0:
53
f Um COS tO^f, Z<0,
f (C7m COS (сОрез + йш)/, />0,
где Sa> — частотная расстройка.
Вычислите функцию Onnft) — комплексную огибающую вы-
ходного сигнала. Постройте графики зависимости от времени
физической огибающей (Z) при tko • тж= 1 и при баз • тж = 3.
9.18 (УР). Вычислите сигнал um(f), возникающий на выходе
узкополосного гауссова радиофильтра (см. задачу 9.12) при
подаче на его вход колебания u,K(t)= UDcosa)0to (t), частота за-
полнения которого совпадает с центральной частотой АЧХ
фильтра.
9.19 (0). Двухступенчатый резонансный усилитель малых сиг-
налов имеет одинаковые резонансные коэффициенты усиления
Лоре, и постоянные времени т, каждой ступени; резонансные часто-
ты контуров cDpai и (0^2=(Урез] + Асо различны. Ко входу усили-
теля приложен источник ЭДС
( о, '<0,
1^(°"114,С08(а^1Г+9>), *>о.
Найдите закон изменения во времени физической огибающей
Um(t) на выходе усилителя.
9.20 (F). Одноконтурный усилитель малых высокочастотных
колебаний имеет частотно-избирательную систему в виде просто-
го колебательного контура. Параметры усилителя К^, (о^ и
тж считаются заданными. На вход устройства подано колебание
«„(r)=a/cos[(cUp<3+5(n)l]‘ a(t), имеющее линейно нарастающую
во времени физическую огибающую и частоту заполнения, кото-
рая на величину 8<о превышает частоту Найдите выражение
комплексной огибающей Vm(t) выходного сигнала.
9.21 (УО). Одноконтурный резонансный усилитель имеет за-
данные параметры К^, а)^ и тк. На вход усилителя подан сигнал
ы»х(0= C/oe-e,cos[(a)pej + &o)f]o'(f), который имеет экспоненциаль-
но уменьшающуюся во времени амплитуду и частоту заполнения
со=сорез + 6со. Найдите комплексную огибающую U,M(t) сигна-
ла на выходе и соответствующую ей физическую огибающую
U,m(t).
9.22 (Р). Используя средства системы MathCAD, составьте
программу для анализа физической огибающей С7,ых сигнала,
изученного в задаче 9.21.
54
Тема 10
ВОЗДЕЙСТВИЕ СЛУЧАЙНЫХ СИГНАЛОВ
НА ЛИНЕЙНЫЕ СТАЦИОНАРНЫЕ ЦЕПИ
• Спектр мощности и функция корреляции
случайного сигнала на выходе линейной системы
10.1 (УР). Некоторая линейная стационарная система имеет
импульсную характеристику h(t). На входе системы действует
стационарный случайный сигнал X (0 с нулевым средним значе-
нием. Получите аналитическое выражение функции корреляции
/г) выходного случайного процесса У(0.
10.2(0). Основываясь на результате, полученном в задаче
10.1, получите формулы, описывающие функции корреляции
7^(0 на выходе линейных систем с импульсными характеристи-
ками вида:
а) й (0=J_exp (- ЦТ) а (0,
б)й(0=Л[а(0-а(/-7)]
(Л>0, Т>0 — постоянные величины).
В обоих случаях входным сигналом является белый шум с посто-
янным спектром мощности Wo.
10.3(Р). Линейная цепь (рис. 1.10.1) состоит из устройст-
ва задержки сигнала на Т (с) и сумматора. На входе цепи
действует стационарный случайный процесс X (0 с математичес-
ким ожиданием тх=0 и известной функцией корреляции 7?х(0.
Найдите функцию корреляции 7^(0 случайного процесса У(0 на
выходе.
10.4(УО). Применительно к условиям задачи 10.3 найдите
дисперсию случайного выхода сигнала, если известно выражение
функции корреляции случайного колебания на входе 7?х(0=
= <Т*Гх(0.
10.5(0). Найдите взаимную корреляционную функцию 7?Х),(0
случайных процессов X{t) и У(0 для линейной системы, которая
описана в условиях задачи 10.3.
Ю.6(УО). Некоторая линейная система осуществляет преоб-
разование входного сигнала х(0 таким образом, что выходной
сигнал
t
y(f)='T |x(Od£,
о
55
Рис. 1.10.1
Рис. 1.10.2
где Т— постоянный параметр с размерностью времени.
На вход системы подается напряжение, имеющее вид белого
шума с двусторонним спектром мощности Ио=Ю~12 В2-с.
Найдите значение времени t', за которое среднеквадратичный
уровень напряжения на выходе системы достигнет 0.2 В, если
Т— 1 мкс.
10.7(0). Электрическая цепь содержит два .RC-звена, разделен-
ных идеальным усилителем напряжения, коэффициент передачи
Ко постоянный на всех частотах (рис. 1.10.2). Входное сопротив-
ление усилителя неограниченно велико, а выходное равно нулю.
На входе цепи действует источник шумовой ЭДС (белый шум) со
спектром мощности Wo. Найдите спектр мощности вы-
ходного сигнала.
10.8(0). Колебательный LC-контур (рис. 1.10.3) подключен
к источнику шумового тока, имеющего функцию корреляции
/?,(т)=о'?ехр(—а|т|). Найдите спектр мощности Wu(a)) выход-
ного напряжения «(О-
10.9(0). Рассчитайте шумовую полосу Пш для AL-цепи (рис.
1.10.4).
Ю.10(УО). Получите формулу для расчета шумовой полосы
узкополосного гауссова радиофильтра с частотным коэффициен-
том передачи
K(j2nJ)=Ко f> 0.
Ю.11(УО). Получите выражения для дисперсии и функции
корреляции 7^ (т) выходного сигнала цепи, рассмотренной в зада-
че 10.7.
Рис. 1.10.3
Рис. 1.10.4
56
Рис. 1.10.5
10.12(0). На входе 7?С-цепи (рис.
1.10.5) действует источник шумовой
ЭД С, создающий случайный сигнал ви-
да белого шума, имеющий на всех ча-
стотах постоянную спектральную пло-
тность мощности Ио- Выходной слу-
чайный сигнал u(t) снимается с рези-
стора R. Найдите функцию корреляции
Л(г).
10.13(УО). Цепь представляет собой каскадное соединение
N одинаковых ЛС-цепей, между которыми включены идеальные
элементы развязки с единичными коэффициентами передачи (рис.
1.10.6). На входе цепи включен источник ЭДС вида белого шума
с односторонним спектром мощности Fo (В2*с). Получите вы-
ражение для расчета дисперсии о£ц выходного напряжения
«ых(0-
10.14(0). Цепь, схема которой изображена на рис. 1.10.7,
называют пропорционально-интегрирующим фильтром. На вхо-
де фильтра действует источник напряжения u„(z) с функцией
корреляции А„(т)=сг^ехр(—а |т|). Найдите дисперсию вы-
ходного сигнала 1^(1).
10.15(0). На входе RC-пепя (рис. 1.10.8) включен источник
напряжения вида белого шума с двусторонним спектром мощ-
ности Ио, постоянным на всех частотах. Получите выражение
функции корреляции Ru(r) выходного сигнала.
10.16(Р). Линейная система имеет частотный коэффициент
передачи
К (/со)=-(1-е /иГ),
Joi
где Л>0, Г>0 — постоянные величины. На входе системы дей-
ствует белый шум со спектральной плотностью мощности Ио-
Найдите функцию корреляции Rm(i:) выходного сигнала.
10.17(Р). Идеальный фильтр нижних частот, имеющий еди-
ничный коэффициент передачи в полосе частот 0 < со < со, и нуле-
вой коэффициент передачи на остальных частотах, возбуждается
57
со стороны входа источником стационарного шума X (/) с функ-
цией корреляции Rx (т)=ах ехр (—а |т|). Найдите дисперсию 07 вы-
ходного случайного процесса.
10.18(0). Линейный стационарный фильтр нижних частот
имеет коэффициент передачи по напряжению ЛЬ=250 в полосе
частот 0 </<140 кГц и нулевой коэффициент передачи на оста-
льных частотах. Ко входу фильтра подключен источник белого
шума с постоянным двусторонним спектром мощности Wo=
= 3'10“14 В2*с. Найдите эффективное напряжение шума ат на
выходе фильтра.
Ю.19(УО). На входе идеального полосового фильтра действу-
ет источник белого шума с односторонним спектром мощности
Fo (В2-с). Фильтр имеет постоянный коэффициент передачи Ко
в пределах полосы частот а>0—Лсо^со<<у0+Л(у. На остальных
частотах коэффициент передачи фильтра равен нулю. Определите
дисперсию Оу и функцию корреляции ЛДт) случайного процесса
Y(t) на выходе фильтра.
10.20(0). Источник ЭДС вида белого шума с односторонним
спектром мощности Fo подключен на вход последовательного
колебательного контура, образованного элементами L, С и R.
Найдите односторонний спектр мощности Ги(со) и функцию кор-
реляции Д,(т) напряжения u(f) на конденсаторе цепи. Положите,
что R<2y/L/C, т. е. свободный процесс в цепи имеет колебатель-
ный характер.
Ю.21(УО). Параллельный колебательный контур с потерями
(рис. 1.10.9) возбужден идеальным источником шумового тока,
шум с постоянным на всех частотах
двусторонним спектром мощности Ио-
Предполагая, что добротность контура
<2>>1, получите выражение функции
корреляции Rutt) выходного напряже-
ния u(r) в данной цепи.
10.22(0). На вход одноконтурного
резонансного усилителя малых колеба-
ний с параметрами /^,„=120, =
который создает
Рис. 1.10.9
58
=6.5 МГц, СЭ1>=55 подан случайный сигнал вида белого шума
с односторонним спектром мощности Fo=2' 10"18 В2/Гц. Опре-
делите величину — эффективное значение шумового напря-
жения на выходе усилителя.
• Источники шума в радиотехнических цепях
10.23(0). Идеальный фильтр нижних частот имеет полосу
пропускания 0 — 200 кГц. Коэффициент передачи напряжения
в полосе пропускания А^=300. На входе фильтра включен рези-
стор с сопротивлением 160 кОм, находящийся при температуре
400 К. Найдите эффективное напряжение шумового сигнала на
выходе устройства.
10.24(0). Найдите дисперсию о-2 шумового напряжения, воз-
никающего на конденсаторе простой ЛС-цепи под действием
теплового шума резистора. Вычислите эффективное напряжение
шума при следующих параметрах: С— 1 нФ, Г=300 К.
10.25(0). В электронном приборе протекает постоянный ток
10=4 мА. Вычислите дисперсию тока а}, относящуюся к ин-
тервалу частот 0.5 — 30 МГц.
10.26(0). Найдите вероятность Ро события, заключающегося
в том, что на анод электронного прибора со средним током 4=
=0.2 мкА за отрезок времени длительностью 10"12 с не поступит
ни одного электрона.
Ю.27(УО). Резистор R с сопротивлением 105 Ом, находящийся
при абсолютной температуре Т, включен в цепь, содержащую
диод, работающий в режиме насыщения, и источник постоянной
ЭДС (рис. 1.10.10). В цепи протекает ток со средним значением
4 = 1 мкА. Найдите величину Т, при которой удельные дисперсии
напряжений, создавамых на резисторе за счет дробового и тепло-
вого эффектов, оказываются равными.
10.28(0). Вход приемника соединен с антенной кабельной
линией передачи длиной 3 м. Погонное затухание волн в кабеле
составляет 1.4 дБ/м. Кабель находится при температуре окружа-
ющей среды 290 К. Найдите шумовую температуру Тш кабельной
линии, а также ее коэффициент шума F.
10.29(0). Усилитель образован каскад- \I
ным соединением трех ступеней. Коэффи- _ ( Л I
циенты усиления мощности ступеней рав- 'о П
ны КРХ, Кр2, Кп, а их коэффициенты шума т '
Fi, F2, F3 соответственно. Выведите фор- |
мулу, определяющую коэффициент шума
Г данного усилителя. рис поло
59
Тема 11
ПРЕОБРАЗОВАНИЯ СИГНАЛОВ
В НЕЛИНЕЙНЫХ РАДИОТЕХНИЧЕСКИХ ЦЕПЯХ
• Аппроксимация характеристик нелинейных
элементов
11.1(F). Полевой транзистор имеет три вывода — исток, сток
и затвор. На рис. 1.11.1 изображена экспериментально снятая про-
ходная характеристика 4(“э>) полевого транзистора КПЗОЗЕ —
зависимость тока стока 4 от управляющего напряжения на про-
межутке затвор — исток. Характеристика получена при постоян-
ном напряжении иа= 10 В. Получите аппроксимацию этой харак-
теристики многочленом 2-й степени на интервале —1.5
< —0.5 В, т. е. определите числовое значение коэффициентов ао,
aif а2, входящих в выражение 4=аь+П1 (ц>я+ 1)+а2(ии+1)2.
11.2 (УО). Вольт-амперная характеристика нелинейного двух-
полюсника приведена на рис. 1.11.2. Найдите коэффициенты ап-
проксимации этой характеристики в виде многочлена 3-й степени
в окрестности рабочей точки Uo= 10 В:
1=00+0] (и—10)+а2(ы—10)2 + а3(ы—10)3.
Аппроксимация должна быть пригодной в интервале напряжений
5 В<«<12.5 В.
113(0). Проходная характеристика биполярного транзистора
КТ306, т. е. зависимость 4=/(^бэ) (А), задана в виде
4 = 1.33 10"7 exp[«fe/(2.6 IO" 2)],
где «& — напряжение на промежутке база — эмиттер, В. Най-
дите многочлен 2-й степени, аппроксимирующий данную харак-
теристику в окрестности рабочей точки (70=0.25 В.
11.4 (0). Ток i (мА) в нелинейном резисторе зависит от прило-
женного напряжения и (В) следующим образом:
. [15м2 —30, «>1.41 В,
1 ( 0, «<1.41 В.
Найдите коэффициенты разложения этой вольт-амперной харак-
теристики в степенной ряд
i (м) = Оо+в] (м—2.5) + а2 (« — 2.5)2
при смещении Go = 2.5 В.
60
Рис.1.11.1
113(0). Вольт-амперная характеристика полупроводникового
диода при ы>0 задана выражением
i=io[e*p(u/uj-1],
где io—1-5 ’ 10“® А — обратный ток насыщения, «г=2.6 • 10“2 В —
температурный потенциал перехода. Определите напряжение и,
при котором дифференциальная крутизна характеристики 5ОТф со-
ставит 8 мА/В.
• Спектральный состав тока в нелинейном
двухполюснике
11.6 (Р). Ток в нелинейном резисторе i связан с приложенным
напряжением и кусочно-линейной зависимостью
О,
S(u-UJ,
u<Ua,
u>Ua,
где 5=15 мА/B, С7и=0.8 В. Найдите постоянную составляющую
тока 10 и амплитуду первой гармоники тока 1ь если напряжение
(В) «=0.5+0.5 cos cot.
11.7 (0). К нелинейному резистору с ВАХ вида
i (и) = 15+0.8 (и - 2.5) + 0,16) (« - 2.5)2 +
+ 0.07 (и-2.5)3
(ток измеряется в миллиамперах, а напряжение — в вольтах)
приложено напряжение и=2.5+0.6 cos cot. Найдите амплитуды
гармонических составляющих тока /0,1Х, /2 и 13.
61
11.8 (0). Проходная характеристика (мА) биполярного тран-
зистора в окрестности рабочей точки U0=l.2 В задана
многочленом
4= 154-40 (U&— l.2)+6.5(u6,-1.2)2 +
+ 2.5(«—1.2)3.
Найдите выражение колебательной характеристики /t=F(C7m),
полагая, что к базе транзистора приложено напряжение (В) Ufy=
= 1.2+44, cos со/.
11.9 (Р). Ко входу усилителя, транзистор которого имеет ВАХ,
заданную в условиях задачи 11.8, приложено напряжение (В) 14,=
=0.9+0.75 cos cot.
Определите постоянную составляющую коллекторного
тока 10.
11.10 (0). В одноступенчатом усилителе напряжения (рис.
1.11.3) использован полевой транзистор КПЗОЗЕ. К промежутку
затвор — исток приложено напряжение (В) u„= — 1 +0.5 cos со/.
Используя коэффициенты аппроксимации, полученные в задаче
11.1, определите постоянную составляющую 4о тока в стоковой
цепи. Влияние переменного напряжения на стоке считайте пренеб-
режимо малым.
11.11 (УО). Входная характеристика биполярного транзистора
КТ805, т. е. зависимость 4 =/(«&), аппроксимирована зависимо-
стью (мА),
4=
О,
Ю^-О.б),
14, < 0.6В,
14, >0.6 В.
К промежутку база — эмиттер приложено напряжение (В)
Ufy=0.4 + 0.75 cos cot. Определите мощность Р6, выделяемую в це-
пи базы.
Рис. 1.11.3
11.12(УО). К промежутку база —
эмиттер транзистора КТ803А подклю-
чен источник напряжения (В) Ufo=0.6+
+0.5 cos со^- Входная характеристика
/б=/(«вэ) допускает кусочно-линейную
аппроксимацию с параметрами: S=
= 0.66 A/В, 44=0.7 В. Определите вход-
ное сопротивление цепи Rmi по первой
гармонике.
11.13(Р)- Нелинейный резистор име-
ет ВАХ вида
62
г о,
/(«)=(и~
«<С4.,
и>ил.
К зажимам резистора приложено напряжение u=t70+ Umcoscot.
Получите формулы для расчета спектрального состава тока.
11.14 (0). Найдите постоянную составляющую /0 и амплитуду
первой гармоники тока 1Х в нелинейном элементе, рассмотренном
в задаче 11.13, при следующих данных: U„=l.5 В, С70—0.1 В,
(7В1=0.7 В, ил = 1.2 В, 5=6 мА/B.
11.15 (УР). В ряде случаев, например для описания свойств
мощных трансформаторов, оказывается удобной так называемая
кусочно-параболическая аппроксимация ВАХ:
i(u) =
О, u<Ut
B(u-Utf, u>U,
где В — численный параметр (A/В2), находимый эксперимента-
льно. Выведите формулы для расчета амплитуд гармонических
составляющих тока, возникающего под действием напряжения
u=Uo+Umcos ал.
11.16 (0). Полевой транзистор КПЗОЗЕ (см. задачу 11.1) при-
менен в одноступенчатом усилителе напряжения с резистивной
нагрузкой (рис. 1.11.3). На вход усилителя подана сумма гар-
монического сигнала uu(/)=l7mBX cos си/ и постоянного напряже-
ния смещения Uo- Найдите амплитуду второй гармоники напря-
жения ит2па на выходе усилителя, если Лв=5.1 кОм, UmK=0.25
В, С70= -1 В.
11.17 (УО). Применительно к условиям задачи 11.16 пост-
ройте график зависимости коэффициента нелинейных искаже-
ний kgn от амплитуд С/твх входного сигнала, изменяющейся
в пределах от 0 до 250 мВ. Положите, что напряжение смещения
С7о=-1 В.
• Нелинейные усилители гармонических колебаний.
Умножители частоты
11.18(Р). Резонансный усилитель собран по схеме, изображен-
ной на рис. 1.11.4. В усилителе применен транзистор КТ803А,
входная характеристика которого приведена в условиях задачи
63
Рис. 1.11.4-
11.12. Ток коллектора 4 связан с током
базы 4 линейной зависимостью 4=12ie.
Напряжение источника питания £„„-=70
В. Нагрузкой транзистора является коле-
бательный контур со следующими пара-
метрами: Ара = 30 кОм (относительно то-
чек а—Ь), коэффициент включения конту-
ра в цепь коллектора £„^=0.04. Ко входу
усилителя приложено напряжение (В)
«бэ=0.3+0.8 cos (Opat.
Пренебрегая инерционностью процес-
сов в транзисторе и обратным влиянием
коллекторного напряжения на ток базы,
рассчитайте следующие величины:
составляющие /об и Ли, а также амплитуды
/16 и /1х токов базы и коллектора соответ-
а) постоянные
первых гармоник
ственно;
б) полезную мощность Лш, выделяемую током первой гар-
моники в колебательном контуре;
в) мощность Ро, поступающую от источника питания, мощ-
ность Рвот, выделяемую в виде теплоты на коллекторе тран-
зистора, а также КПД г] усилителя;
г) амплитуды колебательных напряжений 17„к на коллекторе
и С^тжов на колебательном контуре;
д) коэффициент усиления мощности АР.
11.19(0). Одноконтурный резонансный усилитель питается от
источника с напряжением £шгг= 12 В. Резонансное сопротивление
контура (с учетом неполного включения) Ара=20 кОм. Постоян-
ное напряжение смещения на базе С70=0.5 В. Проходная харак-
теристика транзистора 4 =/(«&>) аппроксимирована кусочно-ли-
нейной функцией с параметрами S= 15 мА/B, £/„=0.8 В. Опреде-
лите амплитуду 17„„ входного сигнала, при которой усилитель
работает в критическом режиме. Частота входного сигнала со-
впадает с резонансной частотой контура.
11.20(0). На вход резонансного усилителя, рассмотренного
в задаче 11.19, подан гармонический сигнал с амплитудой
£/„„== 0.75 В. Определите напряжение смещения С70, при котором
в усилителе устанавливается критический режим.
11.21(0). Применительно к данным задачи 11.19 определи-
те мощность Ро, потребляемую усилителем от источника пита-
ния, полезную мощность Pt ,ых, выделяемую током первой гармо-
ники в колебательном контуре, мощность Рпстт, рассеиваемую
в виде теплоты на коллекторе транзистора, а также КПД т) усили-
теля.
64
11.22(0). Коллекторная цепь усилителя, рассмотренного в за-
даче 11.19, содержит колебательный контур, настроенный на
частоту второй гармоники входного сигнала. Резонансное со-
противление контура Rp„=8.6 кОм. Найдите амплитуду колеба-
тельного напряжения Umma на коллекторе транзистора.
11.23(Р). Резонансный удвоитель частоты работает в крити-
ческом режиме, т. е. амплитуда выходного напряжения Umm рав-
на напряжению источника питания Е^. Найдите зависимость
КПД удвоителя г] от величины угла отсечки тока при постоянной
амлитуде входного сигнала U„u-
• Амплитудная модуляция. Детектирование
АМ-сигналов
11.24 (F). Если в амплитудном модуляторе используют нели-
нейный элемент с кусочно-линейной характеристикой, то обычно
стремятся к тому, чтобы в режиме «молчания», т. е. при отсутст-
вии модулирующего сигнала, напряжение смещения Uo совпада-
ло с напряжением начала характеристики С7Ж. Постройте модуля-
ционную характеристику — зависимость первой гармоники тока
через элемент от величины {U0—Un)jU„ — нормированного от-
клонения рабочей точки.
11.25 (0). Используя 1рафик модуляционной характеристики,
полученный в задаче 11.24, оцените наибольшее значение коэф-
фициента модуляции Маи, при котором еще обеспечивается при-
ближенно линейность закона модуляции.
11.26 (УО). Детектор AM-колебаний содержит нелинейный ре-
зистивный элемент с квадратичной ВАХ вида
i—оь+а( (и — U0)+a2(u— U0)2.
Вычислите низкочастотную составляющую тока 4ч (0» протека-
ющего через нелинейный резистор для случаев:
а) детектирование однотонального АМ-сигнала
и = Uo + Um (1 + Af cos £lt) cos coDt,
б) детектирование ОБП-сигнала с подавленной нижней боко-
вой частотой
и— Uo+ U„ cos (0Dtcos (со0+П)л
2
11.27 (УО). Проходная характеристика транзистора, работа-
ющего в схеме коллекторного детектора (рис. 1.11.5), аппрок-
симирована многочленом второй степени:
3-415 65
i,=ад+(«fo- L70)+a2 (u& - U0)2.
На вход детектора подан сигнал
«бэ= С70+ Ц»(1+Mi cosQtt+M2cosQ2f)cosa)0t.
Найдите переменную низкочастотную составляющую ит„ (О на-
пряжения на выходе детектора.
11.28 (УР). Входное сопротивление диодного детектора (рис.
1.11.6) определяют как отношение амплитуды входного гармо-
нического напряжения UmKL к амплитуде первой гармоники то-
ка через диод: Л„= Докажите, что если SR*» 1, то Л„«
«ад.
11.29 (УР). На языке Pascal составьте программу для решения
трансцендентного уравнения, определяющего угол отсечки тока
в диодном детекторе. Исходные данные: сопротивление резисто-
ра нагрузки, крутизна ВАХ диода и абсолютная погрешность
вычислений е«10-3. Предусмотрите вывод на экран монитора
коэффициента детектирования kBCT=cos о.
11.30 (У). Используя средства программного продукта
Electronics Workbench, проведите моделирование процесса детек-
тирования AM-сигнала в схеме диодного детектора.
• Преобразование случайных сигналов
в нелинейных цепях
11.31 (F). На входе безынерционного нелинейного элемента
действует стационарный гауссов случайный процесс X(t), име-
ющий одномерную плотность вероятности
—-ехр
66
Характеристика, связывающая входной сигнал x(f) с выходным
сигналом у (/), задана системой равенств:
' 0, х<0,
ах2, х>0.
Найдите одномерную плотность вероятности рт (у) выходного
случайного сигнала.
1132(0). Решите задачу 11.31 для случая, когда нелинейный
элемент имеет двустороннюю квадратичную характеристику
у—ах2 (а>0).
1133(Р). Нелинейный элемент имеет характеристику следу-
ющего вида:
(Ь, х<0,
у=<
(а, х>0,
где а, b — постоянные числа. На вход элемента подан гауссов
случайный процесс X(t) с математическим ожиданием тх=0.
Найдите математическое ожидание ту и дисперсию а2 сигнала
Y(i) на выходе устройства.
1134(0). Безынерционный нелинейный элемент с характери-
стикой _у=а|х| возбуждается со стороны входа стационарным
нормальным шумом X(t) с нулевым средним значением и извест-
ной дисперсией а2. Найдите среднее значение ту и дисперсию
о2 выходного случайного процесса У(/).
11.35 (УО). Найдите функцию корреляции Ry(y) случайного
процесса Y(f), возникающего на выходе нелинейного звена с ха-
рактеристикой у=х2. На входе звена действует стационарный
нормальный случайный процесс X (/) с нулевым математическим
ожиданием и функцией корреляции Лх(у)=а2гх(т).
Тема 12
ПРЕОБРАЗОВАНИЕ СИГНАЛОВ
В ЛИНЕЙНЫХ ПАРАМЕТРИЧЕСКИХ ЦЕПЯХ
• Прохождение сигналов через резистивные
параметрические цепи. Преобразование частоты
12.1 (0). Идеальный источник ЭДС создает напряжение (В) и—
= 1.5 cos 2л-107/. К зажимам источника подключен резистивный
элемент с переменной во времени проводимостью (См) G(t)=
= 10-3 + 2-10-4sin 2л 106f. Найдите амплитуду тока 1т имеюще-
го частоту 9.9 МГц.
67
12.2 (0). Вещательный приемник длинноволнового диапазона
предназначен для приема сигналов в диапазоне частот от
Лтш=150 кГц до_4т„=375 кГц. Промежуточная частота прием-
ника /пр=465 кГц. Определите, в каких пределах следует пере-
страивать частоту гетеродина fT данного приемника.
12.3 (УО). В супергетеродинном приемнике гетеродин создает
гармонические колебания с частотой /J.=7.5 МГц. Промежуточ-
ная частота приемника /пр=465 кГц; из двух возможных частот
принимаемого сигнала основному каналу приема отвечает боль-
шая, а зеркальному каналу — меньшая частота. Для подавления
зеркального канала на входе пребразователя частоты включен
одиночный колебательный контур, настроенный на частоту ос-
новного канала. Найдите значение добротности Q этого контура,
при которой ослабление зеркального канала составит —25 дБ по
отношению к основному каналу приема.
12.4 (0). Дифференциальная крутизна резистивного парамет-
рического элемента, входящего в преобразователь частоты, изме-
няется по закону 5даф(/)='%+Si coscM> где Si —постоянные
числа, (Or — угловая частота гетеродина. Считая, что промежу-
точная частота сощ, известна, найдите частоты сигнала (о„ при ко-
торых возникает эффект на выходе преобразователя.
123(Р). Проходная характеристика полевого транзистора,
т. е. зависимость тока стока 4 (мА) от управляющего напряжения
затвор — исток (В) при —2 В, аппроксимирована квад-
ратичной параболой: ic=7.5(usa+2)2. Ко входу транзистора при-
ложено напряжение гетеродина un=C7mrcosct)rf. Найдите закон
изменения во времени дифференциальной крутизны харак-
теристики 4=/(«1я)-
12.6 (УО). Применительно к условиям задачи 12.5 выберите
амплитуду напряжения гетеродина U№ таким образом, чтобы
обеспечить крутизну преобразования 5^=6 мА/В.
12.7 (0). В преобразователе частоты использован полупрово-
дниковый диод, ВАХ которого описана зависимостью (мА)
Рис. 1.12.1
25 (и—0.2), и>0.2 В,
О, и<0.2 В.
К диоду приложено напряжение гете-
родина (В) «г= 1.2cosшг/. Вычислите
крутизну преобразования <5^ данного
устройства.
12.8 (УО). В диодном преобразова-
теле частоты, который описан в задаче
12.7, к диоду приложено напряжение
(В) и(0= Uo 4-1.2 cos (Ort. Определите,
68
при каком напряжении смещения Uo<0 крутизна преобразования
составит величину 1.5 мА/В.
12.9 (УО). Схема преобразователя частоты на полевом тран-
зисторе изображена на рис. 1.12.1. Колебательный контур настро-
ен на промежуточную частоту сОщ,=|сос—сог|. Резонансное сопро-
тивление контура Rpa= 18 кОм. Ко входу преобразователя при-
ложена сумма напряжения полезного сигнала (мкВ) Uc(0=
=50coswcz и напряжения гетеродина (В) ц. (0=0.8 cos а>?1. Ха-
рактеристика транзистора описана в условиях задачи 12.5. Най-
дите амплитуду итщ> выходного сигнала на промежуточной ча-
стоте.
• Прохождение сигналов через параметрические
реактивные цепи.
Параметрические усилители
12.10 (Р). Дифференциальная емкость параметрического дио-
да (варактора) в окрестности рабочей точки Uo зависит от при-
ложенного напряжения и следующим образом: Сля^(и)=Ь0+
+bt (и— Uo), где Ьо (пФ) и bi (пФ/B) — известные числовые коэф-
фициенты. К варактору приложено напряжение u=U0+ U„cos од.
Получите формулу, описывающую ток i(t) через варактор.
12.11 (УО). Дифференциальная емкость варактора описана вы-
ражением Ca^(u)=bD+bi(fi—Uo)+b2(u—Uo)2. К зажимам варак-
тора приложено напряжение и= Uo+ U„cosa>0t. Вычислите амп-
литуду 13 третьей гармоники тока через варактор, если fa—
= 10 ГГц, L7m= 1.5 В, ft2=0.16 пФ/В2.
12.12 (0). Варактор имеет параметры: *0=4 пФ, *2=0.25 пФ/В2.
К варактору приложено высокочастотное напряжение с амп-
литудой t/„=0.4 В. Определите, во сколько раз возрастет ам-
плитуда первой гармоники тока 1ь если величина Um станет рав-
ной 3 В.
12.13 (УО). Емкость параметрического конденсатора изменя-
ется во времени по закону С (/) = Соехр (—t/i) c(t), где Со, т — по-
стоянные величины. К конденсатору подключен источник линей-
но нарастающего напряжения u(t)=ata(t). Вычислите закон из-
менения во времени тока i(t) в конденсаторе.
12.14 (УО). Применительно к условиям задачи 12.13 найдите
момент времени в который мгновенная мощность, потребля-
емая конденсатором из источника сигнала, максимальна, а также
момент времени t2, в который максимальной оказывается мощ-
ность, отдаваемая конденсатором во внешние цепи.
12.15 (Р). Одноконтурный параметрический усилитель под-
ключен со стороны входа к источнику ЭДС (генератору) с внут-
69
ренним сопротивлением Аг=560 Ом. Усилитель работает на
резистивную нагрузку с сопротивлением Л,=400 Ом. Найдите
величину вносимой проводимости Gm, которая обеспечивает ко-
эффициент усиления мощности КР=25 дБ.
12.16 (0). Для параметрического усилителя, описанного в за-
даче 12.15, найдите критическую величину вносимой проводимо-
сти Gnup, при которой система оказывается на пороге самовоз-
буждения.
12.17 (УО). К зажимам управляемого параметрического кон-
денсатора приложено напряжение сигнала «(/)=C7mcos(et)c/+n/3).
Емкость конденсатора изменяется во времени по закону С(/) =
= Со[1 +/? cos (2&V+<?„)], где <ря— начальный фазовый угол ко-
лебания накачки. Выберите наименьшее по модулю значение
фв, которое обеспечивает нулевое значение вносимой проводи-
мости.
12.18 (0). Применительно к условиям задачи 12.17 для значе-
ний параметров Со=О.З пФ, /7=0.25 и сос=2л’ 109 с-1 вычислите
наибольшее по модулю значение отрицательной проводимости
G„m„, а также наименьший по модулю фазовый угол <ря, обес-
печивающий такой режим.
12.19 (Р). Двухконтурный параметрический усилитель пред-
назначен для работы на частоте fQ=2 ГГц. Холостая частота
усилителя /„л=0.5 ГГц. Использованный в усилителе варактор
изменяет свою емкость (пФ) с частотой накачки по закону
С(/)=2(1 + 0.15costoj). Источник сигнала и устройство нагрузки
имеют одинаковые активные проводимости Gr=GB=2‘ 10 3 См.
Вычислите величину резонансного сопротивления холостого ко-
нтура Лрехжол. при котором в усилителе возникает самовозбу-
ждение.
Тема 13
ОСНОВЫ ТЕОРИИ СИНТЕЗА
ЛИНЕЙНЫХ РАДИОТЕХНИЧЕСКИХ ЦЕПЕЙ
ф Синтез пассивных двухполюсников
13.1(УО). Среди функций, описывающих входную проводи-
мость двухполюсника:
Ч V / ч Р(Р2+025)
а) Г1(р)=———,
р +16
б) У2(р)=
(р2 + 1)(р2 + 25)
70
ч TZ , ч р(р* + 1.44)
в) У1(р)=------------------,
(р2+0.81) (р2+2.56)
ч v / \ р(р3+2р+0.5)
r) y<(?)=^i^'
найдите ту, которая отвечает физически реализуемой LC-цепи.
13.2(УР). Синтезируйте двухполюсник, имеющий входное со-
противление (Ом)
1бр3+4р
Z(p)=-------------.
(2р2 + 1)(бр2 + 1)
133(УО). Осуществите синтез двухполюсника с входным со-
противлением (Ом)
13.4(0). Получите аналитическое выражение входного сопро-
тивления последовательного LC-контура. На его основе синтези-
руйте цепь с входным сопротивлением (Ом)
8 lO'V+lO*
Z (р)=----—«-----•
4 10-вр
133(УО). Проведите синтез двухполюсника по заданному
входному сопротивлению (Ом)
„ б ю-^+ьг io-sp+i
Z(p)=
3 10“7р
13.6(0). Выведите формулу, описывающую входное сопротив-
ление параллельного LC-контура. Используя ее, синтезируйте
цепь, имеющую входное сопротивление (Ом)
Z(p)=
2 IO-2р
1.5 10-ир2 + 103’
13.7 (УО). Найдите схему двухполюсника, имеющего входное
сопротивление (Ом)
ч 1.5-10-V+2.5 10-*р+300
Z(p) = —
5 1О-,ор2 + 1
71
13.8 (УО). Осуществите синтез двухполюсника по заданному
входному сопротивлению (Ом)
ч 1.225’10-9ра + 1.05-10~ар
Z (п) =----------------------.
3.51O"sp+1.51Oa
13.9 (Р). Используя метод Кауэра, проведите синтез двухпо-
люсника с входным сопротивлением (Ом)
8рэ+4р
Зра+1'
13.10 (0). Синтезируйте схему двухполюсника, входное сопро-
тивление которого указано в задаче 13.9, таким образом, чтобы
первым элементом служила последовательно включенная индук-
тивная катушка с индуктивностью 2 Гн.
13.11 (УО). Осуществите синтез цепи со входной проводимо-
стью (См)
y(p)=-P^t2> ..
w (ра+1)^+3)
13.12 (УО). Синтезируйте двухполюсник, обладающий вход-
ным сопротивлением (Ом)
Z(p)=
10"‘р+2
ю-’р+ю-’*
13.13 (0). Найдите схему цепи, входное сопротивление (Ом)
которой описывается формулой
Z(p)=--------+-------.----------.
2 10"вр 3 10"6р+1/(0.125р)
13.14 (0). Найдите схему цепи, имеющей входную проводи-
мость (См)
У(р)=610"1Ор+--------------------------.
6 10"7р+--------------
1.3 10"’р +----
8.5 10" 7р
72
• Синтез фильтров нижних частот
13.15 (Р). Линейный стационарный четырехполюсник имеет
частотный коэффициент передачи мощности
Кр(ш»)=------;-----;
1+соя+0.5со*
Вычислите передаточную функцию К(р^ данного четырехпо-
люсника, зависящую от нормированной частотной переменной
Р-=>я.
13.16 (УО). Вычислите передаточную функцию четырехполюс-
ника, имеющего следующую зависимость частотного коэффици-
ента передачи мощности от нормированной частоты соя:
са?
1 +си*
13.17 (Р). Фильтр с частотной характеристикой максимально
плоского типа второго порядка имеет частоту среза/^=15 кГц
и коэффициент передачи на нулевой частоте Ко=0.92. Ко входу
фильтра подключен источник гармонического сигнала с амп-
литудой Um„=7.5 В и частотой 41 кГц. Определите величину
Unmx — амплитуду сигнала на выходе фильтра.
13.18 (Р). Покажите, что КС-цепь, нагруженная на резистор
Кя (рис. 1.13.1), имеет передаточную функцию по напряжению,
соответствующую ФНЧ с максимально плоской характеристикой
первого порядка. Подберите параметры К и С фильтра таким
образом, чтобы при К„=2 кОм получить значение частоты среза
ос=3-105 с-1.
13.19 (0). Покажите, что KL-цепь (рис. 1.13.2) имеет пере-
даточную функцию К(р) по напряжению, соответствующую
ФНЧ первого порядка с максимально плоской характеристикой
при заданной частоте среза. Найдите величину L, если Кя=450
Ом. о>с=2.8 Ю3 с-1.
13.20 (УО). Найдите передаточную функцию К(ря) фильтра
нижних частот четвертого порядка с характеристикой Баттервор-
Рис. 1.13.1
Рис. 1.13.2
73
та. Коэффициент передачи фильтра на нулевой частоте должен
быть равен 25.
13.21 (УО). Вычислите координаты полюсов передаточной фу-
нкции ФНЧ с максимально плоской характеристикой пятого
порядка, имеющего частоту среза 30 кГц.
13.22 (0). Фильтр нижних частот с максимально плоской ча-
стотной характеристикой передачи мощности вносит ослабление
Ai=—8.426 дБ на частоте со1 = 104 с1 и ослабление А2=
= —45.923 дБ на частоте ct)j=3 104 с-1. Вычислите частоту среза
фильтра сос и его порядок п.
13.23 (УО). Найдите наименьший порядок фильтра нижних
частот с максимально плоской характеристикой, исходя из того,
чтобы при изменении частоты от шс до 2шс усиление фильтра
изменялось бы не менее чем на 15 дБ.
13.24 (F). Схема ФНЧ, работающего от источника ЭДС на
резистивную нагрузку Rm представлена на рис. 1.13.3. Определите
номиналы элементов L и С таким образом, чтобы данная цепь
обладала частотным коэффициентом передачи по напряжению,
отвечающим характеристике Баттерворта второго порядка. Зада-
ны частота среза фильтра шс=7.5'104 с1 и сопротивление на-
грузки Ли= 1.2 кОм.
13.25 (Р). Выведите формулу для расчета ФЧХ фильтра ниж-
них частот с характеристикой типа Баттерворта второго порядка.
В качестве независимой переменной используйте нормированную
частоту щв.
13.26 (0). Найдите выражение, определяющее ФЧХ фильтра
нижних частот с максимально плоской характеристикой третьего
порядка. Каково предельно возможное значение фазового угла,
вносимого данным фильтром при соя-»оо?
13.27 (УО). ФНЧ с характеристикой Баттерворта первого по-
рядка имеет частоту среза 85 кГц. Для данного фильтра опреде-
лите групповое время запаздывания 7^ узкополосного сигнала
с центральной частотой спектра 40 кГц. Решите эту же задачу
применительно к фильтру третьего порядка с аналогичными
параметрами.
13.28 (Р). Выберите коэффициент е, входящий в выражение
частотной характеристики передачи мощности чебышевским
ФНЧ л-го порядка таким образом, что-
бы в пределах полосы пропускания не-
равномерность частотной характери-
L стики не превосходила 2 дБ.
Рис. 1.13.3
13.29 (УО). На плоскости нормиро-
ванной комплексной частоты рн опре-
делите координаты полюсов переда-
74
точной функции K(pJ для ФНЧ третьего порядка с харак-
теристикой чебышевского типа, имеющей неравномерность коэф-
фициента передачи мощности в полосе пропускания, равную
2 дБ.
1330(0). Применительно к условиям задачи 13.29 вычислите
передаточную функцию К(р^ рассматриваемого фильтра.
1331(У). На языке Pascal составьте программу расчета часто-
тного коэффициента передачи мощности Кр(со^) чебышевского
ФНЧ третьего порядка с некоторым заданным шагом д по
переменной соя. Положите, что заданным является безразмерный
параметр е — коэффициент неравномерности частотной харак-
теристики фильтра в пределах полосы пропускания.
Тема 14
АКТИВНЫЕ ЦЕПИ С ОБРАТНОЙ СВЯЗЬЮ
И АВТОКОЛЕБАТЕЛЬНЫЕ СИСТЕМЫ
• Цепи и системы с обратной связью
14.1 (Р). Получите формулу для расчета коэффициента усиле-
ния по напряжению Ктг=и^/и^г в схеме эмиттерного повторителя
(рис. 1.14.1) (в задачах 14.1 — 14.3 имеются в виду малые прира-
щения напряжений на входе и выходе).
14.2 (УО). В эмиттерном повторителе (рис. 1.14.1) применен
транзистор с дифференциальной крутизной проходной характе-
ристики S=8iI/du6i=7 мА/B. Сопротивление резистора нагрузки
Д=3 кОм. Вычислите коэффициент усиления данного устрой-
ства по напряжению. Определите, при каком направлении на
входе цепи величина напряжения «в,=0.15 В.
143(УР). Одноступенчатый транзисторный усилитель (рис.
1.14.2) содержит резистор нагрузки Яя и резистор обратной связи
Д». Полагая известной крутизну 5 проходной характеристики
транзистора ^=/(«6,) в окрестности выбранной рабочей точки,
выведите формулу для расчета коэффициента усиления Kv=
=um/un. Найдите параметр /?, определяющий коэффициент пе-
редачи цепи обратной связи.
14.4 (УО). Структурная схема системы с двухпетлевой обрат-
ной связью изображена на рис. 1.14.3. Найдите передаточную
функцию К(р) = (p)/Un (р).
14.5 (УР). Активный jRC-фильтр (рис. 1.14.1) содержит усили-
тель с вещественным и положительным коэффициентом усиления
по напряжению Д. Входное сопротивление усилителя бесконечно
велико, а выходное сопротивление равно нулю.
75
Рис. 1.14.1
Рис. 1.14.3
Рис. 1.14.5
Рис. 1.14.6
Выведите формулы, определяющие передаточную функцию
К(р)= Una.(p)/U„(p), а также АЧХ данного устройства. Найдите
критическое значение коэффициента усиления К^, при котором
система теряет устойчивость. Положив jR1=jR2=jR, Ci = C2=C,
Ко=2.95, постройте график нормированной АЧХ вы-
брав в качестве независимой переменной безразмерную величину
£=uRC.
14.6 (Р). Найдите передаточную функцию К(р) активной цепи,
схема которой изображена на рис. 1.14.5. Входящий в цепь иде-
альный усилитель имеет постоянный на всех частотах коэффици-
ент усиления Ко.
14.7 (УО). Решите задачу 14.6, предполагая, что передаточ-
ная функция операционного усиления (ОУ) описывается выра-
жением
*оу(р)=
Кр
где Тщ — постоянная времени ОУ, определяющая ширину по-
лосы пропускания усилителя, не охваченного цепями обратной
связи. Вычислите граничную частоту со^ рассматриваемого
устройства, определив ее как ту частоту, на которой модуль
коэффициента передачи по напряжению уменьшается до значения
0.707 от максимальной величины, достигаемой на нулевой ча-
стоте.
14.8 (УО). Активная цепь (рис. 1.14.6) содержит ОУ с вещест-
венным, не зависящим от частоты коэффициентом усиления Ко.
Получите выражение для передаточной функции K(p) = Una(p)l
IUn(p) данной системы.
14.9 (0). Цепь (рис. 1.14.7) содержит ОУ с бесконечно большим
входным и нулевым выходным сопротивлением. Коэффициент
усиления Ко постоянен на всех частотах. Найдите передаточную
функцию системы К(р) = С7вых(р)/17„(р).
14.10 (УО). Вычислите передаточную функцию K(p) = Una(p)l
/UM системы, принципиальная схема которой изображена на
рис. 1.14.8. Входящий в цепь идеальный ОУ на всех частотах
имеет бесконечно большой вещественный коэффициент усиления.
Определите, при каком наименьшем сопротивлении резистора
R* система становится неустойчивой, если /?, = 1 кОм, 1?2=5 кОм,
/?з = 15 кОм.
• Устойчивость цепей с обратной связью
14.11(Р). С помощью критерия Найквиста исследуйте устой-
чивость замкнутого контура из трех идентичных усилителей,
каждый из которых имеет передаточную функцию
77
К(р)=-Л
l+jn
где Ko,t — заданные числа.
14.12 (0). Решите предыдущую задачу для случая, когда име-
ется каскадное соединение нечетного числа п>3 идентичных уси-
лительных звеньев. Получите формулу для расчета — крити-
ческого значения коэффициента усиления по напряжению одного
звена на нулевой частоте, при которой происходит самовозбуж-
дение замкнутой системы.
14.13 (0). Напишите уравнение амплитудно-фазовой характе-
ристики для одноступенчатого усилителя с резистивно-емкостной
нагрузкой, у которого вход соединен с выходом посредством
идеальной линии задержки на То секунд. Выведите формулу для
расчета — критического значения коэффициента усиления на
нулевой частоте.
14.14 (0). Одноступенчатый усилитель (см. задачу 14.13) име-
ет параметры: 5=15 мА/B, /?ж=1.3 кОм, С„=60 пФ. Вход уси-
лителя соединен с выходом посредством идеальной линии за-
держки с параметром То. Пренебрегая влиянием выходного
сопротивления электронного прибора, определите критическое
значение Т^р, при котором система оказывается на границе
устойчивости.
14.15 (УО). Двухступенчатый усилитель с одинаковыми зве-
ньями имеет передаточную функцию по напряжению
Вход усилителя соединен с его выходом через дифференциру-
ющую цепь с передаточной функцией
Найдите критическое значение параметра Ко.
1+рт\
1+рТ2
L
-Кр
1+pt
-Ко
1+рп
Рис. 1.14.9
Рис. 1.14.10
14.16 (0). Решите предыдущую задачу при условии, что
где Т=0.1 т.
14.17 (УО). Исследуйте устойчивость замкнутой системы (рис.
1.14.9), в которой каскадное соединение двух идентичных усили-
тельных звеньев с апериодическими нагрузками замкнуто через
идеальный интегратор, имеющий передаточную функцию
Р(р) = 11(Тр), где Т— постоянный параметр.
14.18 (0). Исследуйте зависимость устойчивости замкнутой
системы (рис. 1.14.10) от величины коэффициента усиления Ко.
• Автогенераторы гармонических колебаний
14.19 (F). Схема ЯС-генератора гармонических колебаний при-
ведена на рис. 1.14.11. Найдите коэффициент усиления Ко актив-
ного звена, при котором происходит самовозбуждение системы,
если Д=/?2=3.6 кОм, С,=0.15 мкФ, С2=0.05 мкФ. Определите
значение генерируемой частоты а)т.
14.20 (УО). Автогенератор собран по схеме с трансформатор-
ной связью (рис. 1.14.12). Параметры системы: £=16 мкГн,
£^=3 мкГн, С=90 пФ, /?=25 Ом. Дифференциальная крутизна
проходной характеристики транзистора в выбранной рабочей
точке 1.4 мА/B. Найдите коэффициент связи к„ между
катушками автогенератора, при котором возникает самовозбуж-
дение данного устройства.
14.21 (0). Туннельный диод вместе с источником смещения
подключен к колебательному контуру (рис. 1.14.13). Дифференци-
альная крутизна ВАХ диода в рабочей точке 5Д1ф=—5 мА/В.
Резонансное сопротивление контура при полном включении
7{рс = 32 кОм. Определите, при каком минимальном значении
Рис. 1.14.11
79
ц
Рис. 1.14.13
коэффициента включения km активно-
го элемента в контур возникает само-
возбуждение системы.
14.22 (УО). Нелинейный двухполюс-
ник имеет ВАХ кусочно-линейного ви-
да со следующими параметрами: С7И=
=0.8 В, 5=45 мА/B. Вычислите сред-
нюю крутизну характеристики данного
элемента для случая, когда к зажимам
двухполюсника приложено напряжение
(В) и(t)=0.55+1.2cos cot.
14.23 (Р). В автогенераторе с трансформаторной связью при-
менен электронный прибор, у которого зависимость средней
крутизны 5[ (мА/B) от управляющего напряжения U (В) аппрок-
симирована многочленом 2-й степени:
5iW=ai + 3/4a3t72,
где ai=l мА/B, а3=— 2.5 мА/B3. Колебательный контур генера-
тора имеет параметры: to0=6’108 с-1, 0=25. Определите, при
каком минимальном значении коэффициента взаимоиндукции
ЛГщц, в системе возникнут автоколебания. Вычислите амплитуду
U„ в стационарном режиме, если A/=3A/min.
14.24 (0). Автогенератор содержит электронный прибор с ха-
рактеристикой средней крутизны (мА/B) следующего вида:
5, (С7)=4+0.3С72 —0.12I74,
где U — амплитуда управляющего напряжения (В). Известно,
что некоторый стационарный режим характеризуется амплиту-
дой U„= 1.5 В. Определите, устойчив ли этот режим.
Тема 15
ДИСКРЕТНЫЕ СИГНАЛЫ.
ПРИНЦИПЫ ЦИФРОВОЙ ФИЛЬТРАЦИИ
• Спектры дискретных сигналов.
Дискретное преобразование Фурье
15.1 (0). Аналоговый сигнал х(/) имеет спектр, ограничен-
ный верхней граничной частотой /в = 7.5 МГц. В некотором
устройстве обработки (например, в осциллографе с памятью)
проводится запись отрезка такого сигнала длительностью Т=
=60 мкс. Устройство осуществляет дискретизацию колебания
80
таким образом, что длительность интервала между выборка-
ми в 4 раза короче того значения, которое устанавливает тео-
рема Котельникова. Каждое выборочное значение отобража-
ется 8-битовым двоичным числом. Определите величину N —
объем памяти (бит), требуемой для записи данного отрезка сиг-
нала.
15.2 (УР). Сигнал £(г) представляет собой бесконечную пери-
одическую последовательность прямоугольных видеоимпульсов
единичной амплитуды. Период последовательности равен А, дли-
тельность одного импульса составляет т. Вычислите спектраль-
ную плотность St(co) данной последовательности.
15.3 (УО). Вычислите спектральную плотность 5Хд (со) дискрет-
ного сигнала хд(/), который возникает при дискретизации непре-
рывного колебания x(t) с помощью последовательности £(t),
рассмотренной в задаче 15.2. Спектральная плотность Sx(co) сиг-
нала x(f) предполагается известной. Постройте примерный гра-
фик модуля функции $Хд(со).
15.4 (0). Экспоненциальный видеоимпульс u(r)=(70expx
* (—at)o (t) дискретизируется во времени с шагом А. Выберите
величину А таким образом, чтобы на граничной частоте со^=п/&.
модуль спектральной плотности S^co^) уменьшался до уровня
0.015и(0).
153(УО). Применительно к условиям задачи 15.4 вычислите
величину 5] (0) — вклад в спектральную плотность дискретизи-
рованного сигнала на нулевой частоте, который вносится бли-
жайшими «копиями» спектра исходного колебания, имеющими
центральные частоты +2л/А.
15.6 (Р). Оцените величину 5доП(0)—дополнительный вклад
в спектральную плотность на нулевой частоте для дискретизиро-
ванного сигнала, описанного в задачах 15.4 и 15.5, который
вносится всей бесконечной совокупностью «копий» спектра ис-
ходного аналогового сигнала.
15.7 (0). Периодический дискретный сигнал хд(0 на интервале
своей периодичности задан пятью равноотстоящими отсчетами
(0.25, 0.8, 1, —1.5, —0.2). Вычислите постоянную составляющую
Со дискретного преобразования Фурье данного сигнала.
15.8 (У). Докажите, что если все N отсчетов дискретного сиг-
нала, заданные на интервале периодичности, равны между собой,
то все коэффициенты ДПФ такого сигнала, за исключением Со,
равны нулю.
15.9 (Р). Периодическая последовательность прямоугольных
видеоимпульсов с амплитудой Со, периодом Т и длительностью
отдельного импульса Т/3 дискретизована таким образом, что на
один период последовательности приходится N отсчетов. Вычис-
81
лите величины коэффициента Сх в ДПФ данного сигнала при N=
= 8 и при А=32.
15.10 (Р). Вычислите коэффициенты ДПФ Св (n=0, 1, 2)
дискретного периодического сигнала xa(t), заданного тремя от-
счетами (0, 10, 20).
15.11 .(У). Покажите, что коэффициент С3 ДПФ сигнала, рас-
смотренного в задаче 15.10. в точности равен коэффициенту Со.
15.12 (0). Дискретный периодический сигнал хд(/) задан че-
тырьмя отсчетами (1, 0, —1, 0). Вычислите коэффициенты ДПФ
С„ (и=0, 1, 2, 3).
15.13 {УО). Получите выражение периодического аналогового
сигнала x(t), каждому периоду которого отвечает дискретный
сигнал, состоящий из четырех равноотстоящих выборов (1, О,
-0.5, 0).
15.14 (УО). Восстановите аналоговый сигнал x(f) по коэффи-
циентам ДПФ, вычисленным в задаче 15.12. Убедитесь, что зна-
чения сигнала х(г) в отсчетных точках совпадают со значениями
дискретного сигнала. Предполагайте, что период Т сигнала задан.
15.15 (Р). На алгоритмическом языке Pascal напишите текст
программы для расчета коэффициентов ДПФ. Исходные данные
заключены в массиве вещественных отсчетов сигнала {х,} (i=0,...
..., N— 1) длиной N. Предусмотрите вывод на экран вещественной
и мнимой частей коэффициентов ДПФ.
15.1б (Р). Имеется дискретный периодический сигнал, отсчеты
которого на интервале периодичности образуют шестикомпо-
нентный вектор
Х= (1.5, 4, 5, 3.5, 7, -4).
Используя средства математической системы MathCAD, най-
дите вектор Y, являющийся быстрым преобразованием Фурье
(БПФ) исходного вектора X. Осуществите проверку полученного
результата, выполнив обратное преобразование вектора Y.
• Теория г-преобразования. Дискретная свертка
15.17 (УО). Получите формулу z-преобразования X (z) дискрет-
ной ступенчатой функции {jc*}, общий член которой задан выра-
жением
(О, и<0,
(1, п>0.
15.18 (0). Найдите z-преобразование X(z) дискретного сигнала
{х*}, имеющего общий член х„ = а, и=0, 1, 2...
82
15.19 (0). Получите формулу, описывающую z-преобразова-
ние AT(z) дискретного сигнала {х*.} с общим членом хя=а”/и!
при и>0.
15.20 (Р). Найдите дискретный сигнал {х„}, которому отвечает
z-преобразование
15.21 (0). Вычислите седьмой член х6 дискретной последова-
тельности {х„}, z-преобразование которой
У(г)=25/(1 —0.9z-1).
15.22 (УО). Задано z-преобразование
Л 14J —-------- — .
(i-a4z-,)(i-0A-1)
Найдите общий член х„ последовательности {х„}.
15.23 (Р). Найдите дискретный сигнал {х„}, z-преобразование
которого Af(z)=z-2.
15.24 (0). Вычислите z-преобразование F(z) свертки {/„} диск-
ретных сигналов {х„}=(1, 1, 1, О, 0,...) и {уя}=(0, О, 1, 1, О, 0,...).
15.25 (УО). Получите выражение свертки {/„} двух сигналов,
рассмотренных в задаче 15.24.
15.26 (Р). Путем непосредственного вычисления найдите сверт-
ку {/"„} дискретных сигналов {х„} = (15, 15, 7, 5, 3, 1, 0, ...)
и{уя}=(10, 5,2, 1,0, ...).
• Линейные стационарные цифровые фильтры
15.27 (Р). Трансверсальный (нерекурсивный) цифровой фильтр
(ЦФ) работает в соответствии с алгоритмом у,=4х,—2.5x,_i +
+0.8х,_2. Найдите импульсную характеристику {h„}, системную
функцию H(z) и частотный коэффициент передачи К (/со) этого
фильтра.
15.28 (0). Найдите частотный коэффициент передачи К (/со)
трансверсального цифрового фильтра второго порядка, имеюще-
го алгоритм у,=х,—2x,_i + x,_2. Исследуйте вид функции K(ja>)
при Дсо -»0.
15.29 (У). Покажите, что трансверсальный ЦФ, алгоритм кото-
рого описывается разностным соотношением у.— х,—Зх,_,+
+ 3х,_2—х,_3, осуществляет приближенно трехкратное дифферен-
83
пирование относительно медленных входных сигналов, спектр
которых содержит лишь частоты со, удовлетворяющие неравенст-
ву а)Д<£1.
1530(Р). Цф имеет системную функцию
Вычислите импульсную характеристику {й*} данного фильтра.
1531(УО). Некоторый ЦФ имеет следующий алгорим:
Л=*<-2+0.4у<_1 + 0.32у,_2.
Найдите системную функцию H(z), частотный коэффициент пе-
редачи К (jo) и импульсную характеристику {й*} фильтра.
1532(Р). Найдите аналитическое выражение m-го члена в им-
пульсной характеристике {й*} рекурсивного ЦФ, работающего
в соответствии с алгоритмом
У/=^+У/-1-0.5у/_2.
1533(0). Цифровой фильтр имеет следующий алгоритм:
yt= 1.5х,+4х,_!—0.85y_i.
Фильтр работает с шагом дискретизации по времени А=0.1 мс.
Найдите модуль |К(/со)| и фазовый угол <Рк(о) частотного коэф-
фициента передачи фильтра на частоте о=2•104 с-1.
1534(0). Собственные колебания в рекурсивном ЦФ второго
порядка описываются разностным уравнением
У*=У<-1—0.5у,_2.
Исследуйте устойчивость данного фильтра.
1535(УО). Аналоговый сигнал, поступающий на вход ана-
лого-цифрового преобразователя (АЦП), изменяется в пределах
от 0 до 15 В. Для представления отсчетов этого сигнала в АЦП
выделено восемь двоичных разрядов. Найдите величину шага
квантования qm а также дисперсию шума квантования.
1536(УО). Шум квантования, рассмотренный в задаче 15.35,
поступает на вход рекурсивного ЦФ первого порядка. Фильтр
преобразует последовательность входных отсчетов {х*} в после-
довательность {у*} отсчетов на выходе в соответствии с алгорит-
мом у,=0.9у,_ 1 +х,. Найдите дисперсию о^х шума квантования на
выходе фильтра.
84
1537(Р). На алгоритмическом языке Pascal составьте про-
грамму, позволяющую рассчитывать импульсную характеристи-
ку рекурсивного ЦФ второго порядка. Фильтр работает в соот-
ветствии с алгоритмом
У.=OoXi+biyt-i+Ьгу^2-
Тема 16
ОПТИМАЛЬНАЯ ЛИНЕЙНАЯ ФИЛЬТРАЦИЯ
СИГНАЛОВ
• Оптимальная фильтрация сигнала известной формы
16.1 (Р). На входе .RC-цепи (рис. 1.16.1) действуют два последо-
вательно включенных источника ЭДС. Один из них создает бе-
лый шум с постоянным на всех частотах значением спектра
мощности Ио- Второй источник создает гармонический сигнал
U„Mcos(Dot, амплитуда и частота которого известны. Определите
постоянную времени RC, при которой отношение сигнал/шум на
выходе Q= U„m/om окажется максимальным.
16.2 (0). Применительно к условиям задачи 16.1 найдите мак-
симально возможное отношение сигнал/шум на выходе ЛС-цепи
Объясните, почему эффективность работы данного фильтра ухуд-
шается с ростом частоты coq. Найдите амплитуду входного сиг-
нала (7ЯИ, при которой gm„=10, если соь=5- 10s с-1, Ио=3’ 10-14
В2 с.
163(0). Найдите максимальное значение отношения сиг-
нал/шум Qmu, которое достигается в оптимальном фильтре, со-
гласованном с прямоугольным радиоимпульсом. Заданными яв-
ляются плотность спектра мощности белого шума Wo, а также
амплитуда UmM и длительность тв радиоимпульса.
16.4 (Р). Одноконтурный резонансный усилитель имеет частот-
ный коэффициент передачи
K(jaj)=
-Аре,
1+Дв»-«>рез)Тж
На вход усилителя поступает сумма
белого шума с плотностью спектра
мощности Wo и прямоугольного ра-
диоимпульса, имеющего частоту за-
полнения соре,, длительность ти и ам-
плитуду 17„„. Определите предельно
достижимое значение Спред отноше-
ния сигнал/шум в данном усилителе.
85
Получите формулу для расчета оптимальной добротности
бот колебательного контура усилителя.
163(УО). Получите выражения частотного коэффициента пе-
редачи Krnttiai) и импульсной характеристики h (/) оптимального
линейного фильтра, согласованного с треугольным видеоим-
пульсом
[ 0 ,
sn(t)=<AtltOi
I 0 ,
г<0,
t>t0.
16.6 (0). Линейный фильтр согласован с треугольным видео-
импульсом (см. задачу 16.5). Параметры входного сигнала: г0=
= 15 мкс, Л=25 мкВ. Найдите максимальное значение сиг-
нала на выходе системы при условии, что фильтр имеет параметр
Л=1013 В"1 с"1.
16.7 (0). Сигнал 5Ш(О, выделяемый согласованным фильтром
из аддитивной смеси с белым гауссовым шумом, представля-
ет собой пачку радиоимпульсов с амплитудой Uo=3 мкВ и дли-
тельностью тв=2 мкс каждый. Плотность спектра мощности
белого шума ^0=1.5'10“17 В2,с. Определите, при каком числе
импульсов в пачке N отношение сигнал/шум на выходе достигнет
десяти.
16.8 (УО). Полезный сигнал представляет собой ЛЧМ-им-
пульс с огибающей прямоугольной формы. Импульс имеет дли-
тельность тв=8 мкс и девиацию частоты Д/=3.5 МГц. Для
выделения данного сигнала из смеси с нормальным белым шу-
мом применен согласованный фильтр. Найдите длительность
основного лепестка твш сигнала на выходе согласованного
фильтра.
16.9 (Р). Найдите частотный коэффициент передачи
оптимального линейного фильтра, обеспечивающего на своем
выходе максимально возможное отношение сигнал/шум при об-
работке сигнала известной формы с заданной спектральной плот-
ностью на фоне небелого шума, у которого известен спектр
мощности W(a>).
ф Оптимальная фильтрация случайных сигналов
16.10 (УО). Случайный процесс U (/) (полезный сигнал) имеет
нулевое математическое ожидание и функцию корреляции
7t('c)=ff2exp(—а|т|). Помеха V(t) представляет собой нормаль-
ный стационарный случайный процесс с нулевым математичес- 86
86
ким ожиданием и функцией корреляции Д,(т)=ст2 ехр (—/? |т|). По-
лучите выражение АЧХ оптимального фильтра, выделяющего
сигнал U (г) из смеси [7(0 + И(/) с минимальной среднеквадратич-
ной ошибкой.
16.11 (0). Выделяемый случайный процесс [7(0 имеет двусто-
ронний спектр мощности JFu(<u), плотность которого равна по-
стоянной величине А в пределах интервала частот (—со», со»). На
остальных частотах величина Wu(cd) равна нулю. Помеха И(0
имеет вид белого шума с постоянным параметром ИЪ- Получите
формулу для расчета минимально возможной дисперсии
ошибки выделения сигнала [7(f) из аддитивной смеси [7(0+
+ Г(Г).
16.12 (0). Применительно к постановке задачи 16.11 покажите,
что при А» Йо минимальная дисперсия ошибки, реализуемая
оптимальным фильтром, не зависит от уровня спектра мощности
полезного сигнала. Найдите для этих условий величину если
<а» = 610*с-1, 17о=510-14 В2 с.
16.13 (УО). Найдите минимально возможную дисперсию
ошибки выделения стационарного случайного процесса [7 (О с
функцией корреляции 7^(т)=ст2ехр (—а |т|) из аддитивной смеси
с гауссовым стационарным белым шумом К(0, который имеет
плотность спектра мощности JV0.
16.14 (0). Получите числовое значение дисперсии ст2^ для
случая оптимальной фильтрации сигналов, рассмотренных в за-
даче 16.13, при следующих числовых данных: Ио=Ю-12 В2 с,
ст2=0.02 В2, а=10бс“1.
16.15 (Р). Ко входу линейного стационарного фильтра прило-
жена сумма напряжений полезного сигнала u(t) и помехи и (О,
которые являются реализациями стационарных нормальных слу-
чайных процессов [7(0 и V(t) соответственно. Известно, что
полезный случайный процесс U(t) имеет функцию корреляции
7?„(т)=ст2ехр(—a|r|)coscu0r с заданными значениями дисперсии
ст2, а также параметров а и а)0. Случайный процесс помехи И(0
является дельта-коррелированным процессом вида белого шума,
характеризующимся постоянным на всех частотах значением спе-
ктральной плотности мощности Wo. Получите формулу, описы-
вающую частотную зависимость величины 1/Сигг О’со)| — модуля
частотного коэффициента передачи фильтра, который обеспечи-
вает минимум среднеквадратичной ошибки выделения полезного
сигнала из аддитивной смеси с помехой при условии, что выпол-
няется неравенство си0^>а. Исследуйте вопрос о физической ре-
ализуемости данного фильтра.
87
>ю кода ASCII (American Standart Code for Information
III
• Оценка информационных параметров радиоканала
16.16 (УО). По некоторому каналу связи передается сообще-
ние, представляющее собой слово «ИНФОРМАЦИЯ» на русском
языке. Найдите количество информации, заключенной в этом
сообщении.
16.17 (УО). Оцените энтропию Н источника сообщений, со-
здающего осмысленный текст на русском языке.
16.18 (0). Текстовая информация в компьютере записывается
С ПОМО1
Interchange), в котором каждая буква естественного языка коди-
руется восьмиразрядным двоичным словом. Найдите объем ин-
формации, содержащейся в книге на русском языке из 100 стра-
ниц, закодированной подобным образом. Считайте, что страница
состоит из 30 строк по 60 букв в каждой. Определите избыточ-
ность кодовой системы ASCII как отношение информационных
объемов сообщения после и до кодирования,
16.19 (0). Диктор читает одну страницу книжного текста (см.
предыдущую задачу) за две минуты. Электрический сигнал на
выходе микрофона лежит в интервале частот с верхней границей
6 кГц. Этот сигнал дискретизируется по времени в соответствие
с минимальным требованием теоремы Котельникова, а затем
каждый отсчет кодируется восьмибитовым двоичным словом.
Вычислите объем информации, которая содержится в записи
этого отрезка сигнала. Найдите избыточность описанного инфор-
мационного преобразования.
16.20 (Р). Проводной телефонный канал связи способен равно-
мерно пропускать колебания в интервале частот [0, 30 кГц]; на
более высоких частотах коэффициент передачи канала полагается
равным нулю. В канале присутствует белый шум, такой, что
отно
ности шума составляет 35 дБ. Вычислите пропускную способ-
ность С рассматриваемого канала.
ение средней мощности полезного сигнала к средней мощ-
РАЗДЕЛ П
Указания
Тема 1
1.3. Обратите внимание на то, что вид аргументов функций
Хевисайда должен отвечать наличию скачков сигнала при
t=—20, 20 и 30 мкс.
1.12. Воспользуйтесь значением табличного интеграла
СО _
Г -Л1 . Vя л
I е dx=— при а>0.
J 2^
о
1.23. Примите во внимание известные свойства скалярного
произведения двух сигналов.
1.24. Представьте квадраты норм в виде скалярных произве-
дений.
1.26. Вычислите квадрат нормы суммы двух сигналов и вос-
пользуйтесь неравенством Коши — Буняковского (см. задачу
1.25).
1.27. Вычислите скалярное произведение (u, ®).
1.28. См. указание к предыдущей задаче.
1.30. Обратите внимание на то, что полученные здесь функции
«о(О» «1(0 И и2(0 с точностью до постоянных коэффициентов
совпадают с известными из математики многочленами Ле-
жандра:
а(0=-[(г2-1)1 и=0, 1, 2, ...
At
1.31. Воспользуйтесь формулой для коэффициентов ряда
Фурье.
1.32. Найдите выражение для квадрата нормы ошибки ||/— 2||2.
Приравняв нулю частные производные по Л, £ и С, получите
систему линейных уравнений, определяющую искомые коэффи-
циенты. Убедитесь, что полученное решение в точности совпада-
ет с тем, которое получено в задаче 1.31 другим методом.
1.33. Воспользуйтесь формулой скалярного произведения ко-
мплексных сигналов.
89
1.34. Представьте дельта-функцию в виде формального ряда
6(t-t0)=Yla„u„(t)
и—О
с неизвестными пока коэффициентами а„. Умножьте скалярно
обе части этого равенства на функцию u„(t) с производным но-
мером т. Примите во внимание фильтрующее свойство дель-
та-функции.
137. Учтите, что амплитуды функции Уолша, заданных на
отрезке — должны равняться 1/у/2.
Тема 2
2.2. Исходя из условий задачи, перейдите к интегрированию
в бесконечных пределах.
2.7. Воспользуйтесь приемами, изложенными в решении зада-
чи 2.1.
2.8. В общей формуле для коэффициентов С„ введите новую
переменную £ = t—10.
2.9. В подынтегральном выражении формулы, определяющей
коэффициент Ст разложите функцию ехр(—jnoiit) по формуле
Эйлера.
2.14. Воспользуйтесь результатом, полученным в задаче 2.13.
2.22. Примените интегрирование по частям.
2.23. Положите, что верхняя частота в спектре сигнала при-
ближенно совпадает с границей основного лепестка графика зави-
симости модуля спектральной плотности сигнала от частоты,
т. е. /ш5>х=1/ти, где тв — длительность прямоугольного видеоим-
пульса.
2.25. Используйте результат, полученный в задаче 2.24.
2.30. Вычислите преобразование Фурье путем интегрирования
по частям. Полезно также решить эту задачу с помощью дву-
кратного дифференцирования импульса (см. задачу 2.28).
231. Воспользуйтесь приближенным разложением в ряд
Тейлора
->скв , <^2~я
е Вяв 1 -jart„—
и вычислите предел выражения 5(ш) при со-»0.
232. Сформированное в условиях задачи неравенство означа-
ет, что импульс является «коротким» в том смысле, что тв<с 1/со,
где со — характерное значение частоты в интересующей нас об-
ласти.
90
2.33. Воспользуйтесь результатом, полученным в задаче 2.32,
ограничившись учетом лишь момента Мо.
2.34. Убедитесь, что дополнительное слагаемое, вносимое мо-
ментом М2, пренебрежимо мало по сравнению с тем, которое
определяется моментом М\.
2.35. Воспользуйтесь методами теории вычетов, считая пере-
менную со комплексным числом. Обратите внимание на выбор
контура интегрирования в плоскости со.
2.36. Примените метод, изложенный в решении задачи 2.35.
2.37. Обратите внимание на то, что в точке co=ja подынтег-
ральная функция обратного преобразования Фурье имеет полюс
третьего порядка.
2.40. Воспользуйтесь теоремой о преобразовании Фурье про-
изведения двух сигналов.
2.41. См. указания к задаче 2.40.
2.42. Выделите в сигнале s(t) постоянную составляющую.
2.43. Воспользуйтесь результатом, полученным в задаче 2.41.
2.47. Обратите внимание на то, что при /<0 одна из функций,
входящих под знак интеграла свертки, не будет обладать поло-
жительным значением аргумента ни при каком значении пере-
менной интегрирования.
2.48. Для двух возможных случаев z>0 и /<0 замкните контур
интегрирования либо в левой, либо в правой части полуплоско-
сти переменной р. Воспользуйтесь теорией вычетов.
2.50. Разложите изображение на простые дроби. Восполь-
зуйтесь тем, что изображению 1/(р+а) отвечает оригинал
ехр(—at).
2.51. Разлагая изображение на простые дроби, выделите его
целую часть, дополнив числитель до величины знаменателя, а за-
тем вычтя прибавленное количество.
2.52. Предположите, что справедливо соответствие 1/(р+а)”=
=/" 'е^Дп—1)! и воспользуйтесь методом математической ин-
дукции, применяя теорему об оригинале, который отвечает про-
изведению двух изображений.
2.53. Воспользуйтесь свойством линейности преобразования
Лапласа.
2.54. Решите задачу двумя способами: а) прямым вычислени-
ем преобразования Лапласа, б) путем представления данного
колебания в виде разности двух сдвинутых во времени функций
включения.
2.56. Воспользуйтесь теорией об изображении сигнала, сме-
щенного во времени (см. формулу (2.62) из [1]).
91
Тема 3
3.1. Проверьте ответ, вычислив величину (и, v) во временной
области.
3.2. Примените обобщенную формулу Рэлея.
33. Воспользуйтесь табличным интегралом
со
Г cosax л
——-dx=—е , о>0, у>0).
J /Ч-x2 2у
о
3.6. Воспользуйтесь результатом, полученным в задаче 2.28.
3.8. Проведите интегрирование по частям.
3.10. Используйте результат, полученный в задаче 3.8. Вос-
пользуйтесь тем, что при значениях аргумента z» 1 имеет место
приближенное равенство
Si (z)»n/2—cosz/z.
3.11. См. указания к задаче 3.10.
3.12. Воспользуйтесь связью между энергетическим спектром
сигнала и его автокорреляционной функцией.
3.14. Обратите внимание на четность автокорреляционной
функции.
3.17. Для нахождения ткор составьте трансцендентное уравне-
ние. Решите это уравнение методом последовательных приближе-
ний, используя микрокалькулятор (см. решение задачи 1.1).
3.18. Обратите внимание на то, что сигнал з2 по сравнению
с сигналом Si имеет существенно больший уровень боковых
лепестков автокорреляционной функции.
3.20. Постройте совместно графики функций u(t) и v(t—т).
Определите интервалы значений аргумента, в которых импульсы
и и v «перекрываются».
3.21. Найдите взаимный энергетический спектр 1К»(со), вос-
пользовавшись формулой преобразования Фурье.
3.22. При выполнении операции сдвига дополните сигналы
и и v нулями на «пустых» позициях слева и справа.
Тема 4
43. Примите во внимание, что <70)/14>, Мя=
=(и0-и^)/и0.
4.4. Коэффициент модуляции М определяется из системы двух
равенств <7m„= С/о(1 +М); U^= <70(1 — М).
92
4.5. Воспользуйтесь двумя соотношениями, которые вытека-
ют из графика:
C/o(l+AO=t4i«; U0(l-M)=-Umn.
4Л. Приближенно положите, что ширина спектра огибающей
радиоимпульсов ограничена шириной основного лепестка ее спе-
ктральной диаграммы.
4.10. Исходите из того, что если U„ — амплитуда напряжения
на резистивной нагрузке, то активная мощность
Р=Ц*/(2Я).
4.15. Обратите внимание на то, что т=0.06 с 1 и поэтому
данный сигнал является узкополосным, содержащим лишь три
спектральные составляющие.
4.17. Примите во внимание, что в данном случае т'»-1. Вос-
пользуйтесь приближенным выражением для расчета Пщшт.
4.18. Воспользуйтесь тем, что наименьший корень уравнения
Л ("0=0 равен 2.405.
4.19. Основывайтесь на том, что уравнение Л(гп)=0 имеет
наименьший корень 3.832.
4.20. Разложите функции cos (т sin Q/) и sin (zn sin Q/) при т<1
в ряды Тейлора. Ограничьтесь двумя членами каждого ряда.
4.21. Убедитесь, что здесь девиация частоты мала по сравне-
нию со значением несущей частоты и поэтому приращение А/ре,
резонансной частоты контура связано с приращением емкости
АС соотношением A/pa=(d/'pra/dC) 'АС (производная вычисляется
при/=/0).
4.28. В данной задаче анализируется единственный, по-вцди-
мому, случай, когда спектральная плотность ЛЧМ-колебания
явно выражается через элементарные функции.
При решении используйте значение табличного интеграла
_-р sin
е (px2+2qx)dx=
cos
Г ад2 sin Г1 р ра2
——ехр —larctg —
*/а2+р2 L а +P*J«*L2 а <?+Р .
93
Тема 5
5.4. Воспользуйтесь принципом ортогональности системы ба-
зисных функций, входящих в ряд Котельникова.
5.5. Примите во внимание, что спектральные плотности сиг-
налов SaXf) и «ош (0 не «перекрываются» и поэтому данные сиг-
налы взаимно ортогональны.
5.6. Отдельные слагаемые суммы s=si+s2+--- представь-
те в виде ^(z^Re^^e*”0'). Воспользуйтесь тем, что операции
суммирования и вычисления вещественной части перестано-
вочны.
5.9. В качестве опорной частоты выберите частоту несущего
колебания.
5.10. Воспользуйтесь формулой (5.35) из [1].
5.12. Примените формулу (5.36) из [1].
5.13. При вычислении преобразования Гильберта учтите, что
здесь со>0 и поэтому sgnco=l.
5.15. Примите функцию U,(t) равной модулю аналитического
сигнала
5.19. Обратите внимание на то, что несимметрия графика
5 (со) относительно точки соо ведет к непостоянству во времени
мгновенной частоты. Рассмотрите отдельные частные случаи:
a) iSi=0, б) Sj=0, в) Si = S2-
5.21. Примените обобщенную формулу Рэлея.
5.22. Используйте связь между спектральными плотностями
сигналов, сопряженных по Гильберту. Примените обобщенную
формулу Рэлея.
5.24. Примените результат, полученный в задаче 5.23.
5.25. Разложите подынтегральное выражение в преобразова-
нии Гильберта на простые дроби.
5.26. Определите мгновенную частоту как производную
по времени от полной фазы 1Д, (z)=arctg(s/s). Воспользуйтесь
правилом дифференцирования сложной функции.
5.27. Отдельно рассмотрите случаи: а) точка t находится вне
интервала (—г0, f0), 6) — t0<t<t0.
Тема 6
6.1. Воспользуйтесь правилом вычисления вероятности суммы
несовместных событий.
6.2. Используйте правило умножения вероятностей.
6.3. См. указания к задаче 6.2.
6.4. Воспользуйтесь принципом определения эмпирической
вероятности.
94
6.5. Составьте полную группу событии, отвечающих исправ-
ной работе системы. Примените правило вычисления вероят-
ности группы несовместных событий.
6.6. Воспользуйтесь статистической независимостью входных
напряжений. Составьте полную группу событий.
6.9. См. указания к задаче 6.6.
6.15. Отдельно рассмотрите случаи и 1 <z<2.
6.17. Непосредственно рассмотрите интеграл, описывающий
средний квадрат данной случайной величины.
6.22. Воспользуйтесь табличным интегралом
СО
I л —ах , • —л—1
I х е ах=л!а
о
6.23. Примените свойство характеристической функции суммы
независимых случайных величин.
6.27. Используйте принцип усреднения функции от случайной
величины.
6.35. Воспользуйтесь выражением характеристической функ-
ции гауссовой случайной величины.
Тема 7
7.1. Убедитесь, что дисперсия a2 (t) явно зависит от времени.
7.3. Примените условие Слуцкого (см. формулу (6.47) из [1]).
7.4. Убедитесь, что х и х2 не зависят от времени, если справед-
ливы приведенные в задаче условия.
7.5. Обозначьте посредством а2 средние квадраты величин
а и Ь.
7.6. См. указания к задаче 7.3.
7.8. Воспользуйтесь выражением спектральной плотности гар-
монического колебания.
7.15. Положите, что на частоте со» спектр мощности уменьша-
ется до уровня 0.9 от того значения, которое наблюдается на
нулевой частоте.
7.17. Перейдите к одностороннему спектру мощности Fx((o).
7.18. Используйте формулу (7.34) из [1], приняв во внимание,
что здесь гх(т)=5Шй>»т/(си»т).
7.19. Выразите дисперсию производной случайного процесса
X(/) через его односторонний спектр мощности.
7.26. Воспользуйтесь выражениями для моментов рэлеевской
случайной величины.
95
7.27. Представьте огибающую в виде U (t)=y/(Um+А)г+В* у
где A (t) и В (t) — синфазная и квадратурная составляющие амп-
литуды случайного процесса.
Тема 8
8.1. Для составления системы дифференциальных уравнений,
описывающих динамику процессов в цепи, используйте метод
узловых потенциалов.
8.2. При нахождении момента времени t0 учтите, что режимы
заряда и разряда отличаются направлением тока в конденсаторе.
8.4. В качестве искомых функций используйте потенциалы
»1 и и2 узлов 7 и 2.
8.12. Введите вспомогательные величины — напряжения
Ua и Ub в узлах а и b соответственно. Примените метод узловых
потенциалов.
8.13. Для нахождения корней кубического уравнения исполь-
зуйте формулы Кардано. Обратите внимание на характер рас-
положения полюсов передаточной функции на комплексной плос-
кости.
8.14. Введите в рассмотрение переменные Ua и Ub — изоб-
ражения электрических потенциалов точек а и b соответственно.
При этом ит=иа— Ub.
8.17. Используйте выражение импульсной характеристики
ЛС-цепи.
8.19. Учтите, что при каскадном соединении звеньев их часто-
тные коэффициенты передачи перемножаются. Найдите импульс-
ную характеристику, применив методы теории вычетов.
8.20. Воспользуйтесь импульсной характеристикой 7?С-цепи,
у которой выходной сигнал снимается с конденсатора. Примите
во внимание спектральное представление «5-функции.
8.26. Время установления найдите, численно решив трансцен-
дентное уравнение методом последовательных приближений.
8.27. Обратите внимание на то, что при arc 1 значения g(r)a
«1, поскольку в начальной стадии процесса оба конденсатора
практически обеспечивают непосредственное соединение входа
с выходом. Напротив, если ar» 1, то g(t)~ — 1, так как резисторы
соединяют вход с выходом скрещенным образом.
8.29. Воспользуйтесь операторным методом. Введите в рас-
смотрение вспомогательное напряжение v(r) на конденсаторе С(.
Получив изображение импульсной характеристики, разложите
его на сумму простых дробей.
832. Обратите внимание на размерность величины А.
8.34. Воспользуйтесь тем, что A(r)=dg|/dr.
96
8.37. Положите u„ (£)=£(£). Воспользуйтесь фильтрующим
свойством ^-функции.
8.42. Примите во внимание, что при />гв входной сигнал
тождественно обращается в нуль.
8.44. Представьте входной сигнал в виде суммы трех колеба-
ний, заданных на полубесконечных интервалах времени,— двух
линейной нарастающих функций с разными знаками, сдвинутых
во времени на отрезок тн, и импульса включения с отрицательной
полярностью:
и«(0=— О-тя)аО-тя)-С7оа(/-тя).
ти ти
8.45. Воспользуйтесь выражением импульсной характеристи-
ки цепи, полученным в задаче 8.27.
Тема 9
9.1. Примените формулу (9.19) из [1].
9.5. Воспользуйтесь в качестве аргумента безразмерной пере-
менной £ = Гж (tO — СОри).
9.10. Получите выражение для частотного коэффициента пе-
редачи двухступенчатой системы. Перейдите к частотному коэф-
фициенту передачи низкочастотного эквивалента, взяв в качестве
опорной частоты величину соре,]. Воспользуйтесь операторным
методом, положив p=j£l.
9.11. Выберите в качестве опорной частоту соо. Импульсную
характеристику hm(t) низкочастотного эквивалента усилителя
найдите операторным методом.
9.12. Примените табличный интеграл
-л*1 j 1 h I ь3
е cosbxdx=- /-expi
2\] Р \ *Р,
о
9.14. Воспользуйтесь формулой связи между добротностью,
резонансной частотой и полосой пропускания колебательного
контура.
9.15. Представьте входной сигнал в виде суммы несущего
колебания и двух боковых составляющих. Примените принцип
суперпозиции.
9.17. Используйте метод интеграла Дюамеля применительно
к комплексным огибающим. В качестве опорной частоты выбери-
те величину й)р„. Введите безразмерный аргумент х=/тж.
9.18. Воспользуйтесь результатом, полученным в задаче 9.12.
4-415 97
9.21. Исходите из того, что комплексная огибающая сигна-
ла на входе O„(t)=Uoe a‘^Sa'a(f). Примените формулу (9.54)
из[1].
Тема 10
10.1. Рассмотрите конкретную реализацию x(t) и найдите
функцию у (г) методом интеграла Дюамеля. Проведите соответ-
ствующие усреднения.
10.4. Воспользуйтесь свойством четности функции корре-
ляции.
10.6. Используйте результат, полученный в задаче 7.7. Учтите,
что дисперсия случайной величины пропорциональна квадрату
постоянного коэффициента пропорциональности.
10.10. Для приближенного вычисления интеграла используйте
условие узкополосности bfo 1. Примите во внимание, что
Je *dx=yfnj2.
10.11. Примените спектральный метод и теорию вычетов.
10.13. Воспользуйтесь тем, что
dx (2Л'-3)!!
(1+х< <2jV-2)'!’
где N — целое число.
10.19. Обратите внимание, что дисперсия выходного сигнала
равна произведению квадрата коэффициента передачи, односто-
роннего спектра мощности Fo и полосы пропускания 2Дш.
10.21. Воспользуйтесь приближенным выражением импульс-
ной характеристики (см. формулу (8.84) из [!])
справедливым при 0» 1.
10.27. Примите во внимание, что и^д.проъ = 1уд.ДрОъ Я2.
98
Тема 11
11.2. В качестве узлов аппроксимации используйте точки и^=
=5, 7.5, 10 и 12.5 В.
11.11. Найдите по отдельности, а затем сложите мощности,
поступающие в цепь базы от обоих источников.
11.12. Входное сопротивление нелинейного элемента по пер-
вой гармонике определите в соответствии с формулой Л«1 =
= где UmK — амплитуда входного напряжения.
11.15. Введите угол отсечки тока
б =arccos[(U,-U0)/U„]
и найдите амплитуды гармоник тока в виде
L=BUi, уя(2, б ), л=0, 1, 2,...,
где уя(2, б ) — коэффициенты разложения при кусочно-параболи-
ческой аппроксимации
11.17. По определению, коэффициент нелинейных искажений
^=^^100%.
11.26. В случае детектирования AM-сигнала обратите внима-
ние на появление в низкочастотном компоненте тока состав-
ляющей с удвоенной частотой модуляции за счет нелинейного
взаимодействия двух боковых колебаний.
11.27. Положите, что на эквивалентной схеме транзистор мо-
жет быть заменен идеальным управляемым источником тока.
Считайте, что нагрузочная ВС-цепь полностью отфильтровывает
все высокочастотные компоненты спектра.
11.28. Воспользуйтесь тем, что при 5АЛ» 1 угол отсечки тока
б мал и поэтому можно воспользоваться приближенными выра-
жениями для тригонометрических функций, определяющих коэф-
фициенты Берга у, ( д).
ИЗО. Схема моделируемой цепи изображена на рис. II.11.1.
Отметим, что здесь использован стандарт графического изоб-
ражения схемных элементов, принятый в США.
Проводя моделирование, варьируйте частоты несущего коле-
бания и моделирующего си- ______ _______________
гнала, а также параметры Г и Т ~ ~ |
нагрузочной цепи детектора
таким образом, чтобы мож- ______________1 _______
но было оценить роль уело- |
вий неискаженного детекти- —
рования (11.51) из [1]. Рис. 11.11.1
99
11.35. Воспользуйтесь выражением двумерной плотности ве-
роятности гауссова случайного процесса
р(х, хт)=-----== ехр
2ка2у/\-Л2
х2 —2Rxxxt+x'i
2^(1-Я’)
Тема 12
123. Используйте точную формулу ^=Q(flfva—fva]J) для обо-
бщенной расстройки контура. Полученный результат округлите
до целого числа десятков.
12.6. Воспользуйтесь формулой (12.14) из [1].
12.8. Обратите внимание на то, что данная задача допускает
еще одно решение при С70 > 0.
12.9. Вычислите амплитуду выходного тока на промежуточ-
ной частоте, воспользовавшись понятием крутизны преобразо-
вания.
12.11. Примените тригонометрическую формулу
sinxcos2x= 1/4 (sin х+sin Зх).
12.13. Учтите, что заряд q=Си, в го время как ток i=dq/dt.
12.14. Обратите внимание на то, что знак напряжения неиз-
менен, в то время как ток меняет свой знак при t=r.
12.17. Имейте в виду, что уравнение sin4>=0 имеет корни
Ф=0, ±я, ±2я,...
Тема 13
13.1. Обратите внимание на расположение нулей и полюсов
проводимости на комплексной плоскости. Воспользуйтесь теоре-
мой о числе нулей и полюсов реализуемого двухполюсника.
13.2. Примените метод Фостера.
133. Перейдите от сопротивления к проводимости цепи.
133. Используйте результат, полученный в задаче 13.4.
13.7. Выделите целую часть функции Z (р) и примените резуль-
тат, полученный в задаче 13.6.
13.8. Выделите целую часть дроби и в остатке перейдите от
сопротивления к проводимости.
13.11. Перейдите от проводимости к сопротивлению. Приме-
ните метод Кауэра.
13.12. Воспользуйтесь методом Кауэра.
13.16. Выполните замену переменной pK=jojK и воспользуйтесь
принципом квадрантной симметрии.
100
13.20. Найдите корни уравнения 1+Ри=0, имеющие отрица-
тельные вещественные части.
13.21. Проведите денормирование частотной переменной
с учетом приведенного значения частоты среза фильтра.
13.23. Усиление (дБ), вносимое фильтром с максимально
плоской характеристикой, вычисляют по формуле
A(toB)= — 101g(l+ w„").
13.27. Фазовая характеристика фильтра третьего порядка по-
лучена в задаче 13.26.
13.29. Исходя из заданной неравномерности, определите пара-
метр е.
1331. Воспользуйтесь тем, что многочлен Чебышева третьего
порядка Т3(а)я)=4сОя —3(УЯ.
Тема 14
14.2. Воспользуйтесь тем, что ик=и63+иша.
143. Введите в рассмотрение напряжение v=Ue, и примите во
внимание, что переменная составляющая коллекторного тока
4=Sv. Пренебрегите влиянием внутреннего сопротивления тран-
зистора.
14.4. Введите в рассмотрение величину У(р) — изображение
сигнала в промежуточной точке (см. рис. 1.14.3).
143. Введите вспомогательную величину UB(p) — изображе-
ние напряжения в узле а. Примите во внимание, что входная цепь
усилителя не потребляет тока. Составьте уравнение состояния
цепи из условия обращения в нуль алгебраической суммы токов
в узле а.
14.7. Обратите внимание на эффект расширения полосы про-
пускания системы под действием обратной связи.
14.8. Введите в рассмотрение величину У(р) — изображение
напряжения на неинвертирующем входе усилителя. Учтите, что
ток между входными и выходными зажимами течет только по
ЛС-цепи, не ответвляясь ко входу усилителя из-за бесконечно
большого входного сопротивления.
14.10. Введите в рассмотрение вспомогательные напряжения
на инвертирующем и неинвертирующем входах усилителя с изоб-
ражениями У] и V2 соответственно. Положите вначале, что Ко —
конечная величина, перейдя затем к пределу при Кг* со. Границу
устойчивости системы определите из условия обращения в бес-
конечность модуля передаточной функции.
14.15. Составьте характеристическое уравнение системы. Вос-
пользуйтесь упрощенной формой критерия Рауса — Гурвица,
101
согласно которой характеристическое уравнение устойчивой си-
стемы третьего порядка должно содержать члены всех степеней
и иметь коэффициенты лишь одного знака.
14.17. Примените критерий Рауса — Гурвица.
1430. Как известно из теории цепей, Ла=ЛГ/^/£1£2.
1432. Вычислите угол отсечки о и воспользуйтесь функцией
Берга У1( д ).
Тема 15
153. Разложите функцию (/) в комплексный ряд Фурье и вос-
пользуйтесь формулой (2.35) из [1].
153. Примените теорему о спектре произведения двух сиг-
налов.
153. Обратите внимание на то, что величина S, (0) состоит из
двух комплексно-сопряженных слагаемых, которые отвечают по-
ложительным и отрицательным частотам.
153. Воспользуйтесь формулой суммы геометрической про-
грессии со знаменателем ехр(—у2лл/Л).
15.11. Проведите расчет коэффициента С3 по общей фор-
муле ДПФ.
15.13. Воспользуйтесь тем, что выборочные значения сигнала
вещественны.
15.14. Примените формулу (15.11) из [1].
15.17. Примените формулу суммирования бесконечной геоме-
трической прогрессии. Заметьте, что функция У (z) определена во
внешней области единичного круга, т. е. при |z|> 1.
1532. Разложите z-преобразование на простые дроби. Вос-
пользуйтесь приемом, использованным в задаче 15.20.
1535. Решите задачу двумя способами — путем обращения
z-преобразования и непосредственным вычислением.
1539. Рассмотрите характер функции K(jaj) при соД-»0.
Для проверки результата убедитесь, что данный алгоритм да-
ет нулевую последовательность {у*}> если {•**} представляет со-
бой равноотстоящие во времени отсчеты квадратичной пара-
болы.
1531. Разложите функцию H(z) на простые дроби. Восполь-
зуйтесь результатом, полученным в задаче 15.30.
1535. Положите, что случайные отсчеты шума квантования
имеют равномерный закон распределения.
1536. Импульсная характеристика рассматриваемого фильт-
ра имеет вид (1, 0.9, (0.9)2, (0.9)3, ...).
102
Темя 16
163. Для нахождения спектральной плотности входного сиг-
нала используйте прием, основанный на дифференцировании сиг-
нала и на свойстве спектра производной.
16.8. Воспользуйтесь формулой (16.40) из [1].
16.10. Стационарный случайный процесс с функцией корреля-
ции вида Я (т)=а2 ехр (- а |т|) имеет спектр мощности 1Г(со)=
=2аа2/(а*+а,2).
16.13. См. указания к задаче 16.10.
16.16. Положите, что алфавит русского языка состоит из 32
букв. Предположите для простоты, что появление любой буквы
в сообщении равновероятно.
16.17. Считайте, что весь текст записывается без учета того,
является ли буква строчной или прописной.
РАЗДЕЛ Ш
Решения
Тема 1
1.1. График изменения во времени мгновенных значении сиг-
нала приведен на рис. Ш.1.1. Из условия и'(*тм)=0 получаем
уравнение для определения t„„:
—ехр(-105/тжх)+2ехр(—2- 105zBUX)=0,
откуда
105^= — 1п(1/2),
т. е. /щи=6.931 • 10-6 с=6.931 мкс. При этом ыт.т=6.25 В.
Длительность импульса по условию задачи является корнем
уравнения
ехр(—Ю’тя)—ехр (—2 • 105т,)=0.025.
Введя безразмерную величину х= 105тн, имеем
ехр(—х)—ехр(—2х)=0.025,
откуда, переходя к уравнению, разрешенному относительно х,
получаем
х= - In (0.025+е-2х). (*)
Корни таких трансцендентных уравнении удобно находить
методом последовательных приближении [5], используя микрока-
лькулятор. Ориентируясь на график сигнала, выбираем нулевое
приближение Хо, достаточно близкое к предполагаемому корню.
Положим, что х0=3. Подставляя это значение в (*), находим
первое приближение
х, = — In (0.025 + е~б)=3.5943422.
Указанный процесс продолжаем по итерационному принципу:
х„= -In(0.025+е-2лп —1), п=2, 3,...
до тех пор, пока два последовательных приближенных значения
не станут отличаться на заданное заранее малое число, определя-
104
ющее точность расчета. Выполнив данные действия, находим
корень х= 3.6628862 (все цифры точные).
Сохранять значащие цифры во всех десятичных разрядах на
практике нет необходимости. Дело в том, что исходные данные
обычно известны с гораздо меньшей точностью. Поэтому пред-
ставление результата с большим количеством разрядов создает
лишь иллюзию достоверности. Принимая, что х=3.66, находим
ти=3.66 х 10 5 с=36 6 мкс.
1.4. Рассматриваемый сигнал s(t) можно представить как
сумму двух линейно нарастающих функций Sj(O и 52(0 (рис.
Ш.1.2) с одинаковыми по величине и различными по знаку
угловыми коэффициентами наклона. Отсюда
•s (0=(W'o) to (/) - (so/to) 0 - to) о (t-10).
1.10. Функция fn(t) является четной; площадь, ограниченная
правой половиной кривой,
je-"'dr=^je-<d^=l/2.
о о
Отсюда видно, что площадь, ограниченная всей кривой, равна
единице независимо от п.
При любом t^O предельное значение/„(/) равно нулю. Дейст-
вительно, по правилу Лопиталя
lim ne~"/= lim (Je"*)-1 =0.
л-»оо Л-»СО
Таким образом, пределом последовательности f„ (t) является
обобщенная функция d(t).
105
1.11. При п-»оо длина отрезка, на котором сосредоточена
функция /и (0, равная 2/и, стремится к нулю. При этом площадь,
ограниченная функцией/,, равна единице независимо от п.
1.13. По определению, энергия сигнала
«2dz=900 е 210/dz=4,5‘10 3В2-с.
о о
Норма данного сигнала
Hull =(£J1/2=6.708 Ю-2 В с1'2.
1.16. Квадрат расстояния между сигналами
рг(и, 1>)=
(и—v)2dz=
= U% j (1 -e"e')2dz+ U$ j e-2e/dz=
о г»
= С/оГ7--(1-е-<Пв)+ти .
I 2a a
По условию задачи требуется найти минимум функции
F(a)=-P-2(1 - е-ати)
al 2
2е “-1.5
Примерный график, приведенный на рис. III. 1.3, указывает на то,
что минимум функции F(a) существует и является единственным.
Из условия F'(a)=0 находим, что
параметр а должен являться корнем
трансцендентного уравнения
—<пя 0.75
а =--------.
l+atH
Решая это уравнение методом по-
следовательных приближений (см.
задачу 1.1), получаем а=0.961/ти.
106
1.17.
Р2(А «)= J (i2—At—B)2dt=
о
1 A (A1-ZB)
-------+------------+АВ+В2.
5 2 3
Приравнивая нулю производные dp2ldA и dpzjdB, получаем си-
стему линейных уравнений
2Л + ЗД=3/2,
Л + 2В=2/3,
имеющую единственное решение: В= —1/6, А=1.
1.19. Рассмотрим равенство
<2|U| + ejUj-F... + apuk=Q.
Умножим скалярно обе части на сигнал По причине ор-
тогональности системы функций в левой части отличным от нуля
окажется лишь скалярное произведение (to, щ). Равенство at (to,
«0=0 возможно лишь при at =0. Проведя аналогичные рассужде-
ния применительно к сигналам и2, и3, кк при любом к, убежда-
емся, что из ортогональности системы сигналов вытекает свойст-
во линейной независимости.
1.20. Допустим, что рассматриваемые сигналы линейно зави-
симы и поэтому равенство
<010 + O2U2+... + О/Д0^=0 (*)
возможно при некотором выборе коэффициентов at, а2, ---, ац, не
равных нулю одновременно. Умножив скалярно обе части (*) на
функции ub и2, ..., uN, получаем однородную систему уравнений
относительно коэффициентов а2,..., aN:
ах{иъ ut)+a20<b «2)+ - +On(«i, un)=0,
al(u2, И1)+в2(И2> «2)+ — + Оц(и2, UW)=0,
ul) + fl2(Ww> «2) + — + un)~ 0.
Для того чтобы данная система имела ненулевое решение,
необходимо и достаточно обращение в нуль ее определителя,
представляющего собой определитель Грамма.
107
1.25. Так как сигналы и и v линейно независимы, то (u+Av,
u+Av)>0, откуда
Л2(», «)+2А(и, »)+(«, и)>0.
Квадратичный трехчлен относительно А не имеет вещественных
корней и поэтому (и, u)(v, »)—(и, »)2>0, т. е. |(u, v)|< ||и|| • ||»||, что
и требовалось доказать.
1.29. Нормируем элемент g0 и положим «o=go/||goll • Вектор
A1=g1—(gt, и^и0 ортогонален к ио (см. задачу 1.27). Нормируя йь
получаем новый элемент ортонормированной системы: Ui =
=Л1/||й1||. Действуя по аналогии, получаем элемент A2=g2—
—(g2, uo)«o—(g2, Uj)«i, ортогональный как к щ, так и к и,. Нор-
мируем его и получаем и2 = й2/||й2||. Продолжая этот процесс,
имеем на к-м шаге (fc = 3, 4, ...):
ht=gk-(gk, «o>o-(gk, «i)ui-.-.-(g*«4-i)u*-i-
Данный способ построения ортонормированной системы ба-
зисных векторов известен в математике под названием процеду-
ры Грамма — Шмидта.
Тема 2
a>it
2.1. Так как s(t)= U0cos—, то
Г/2
2U0 A a>it
С„=— I cos—cosnco//dr.
Т J 2
О
Воспользуемся тем, что
cos х • cos у=[cos (х+у)+cos (х—у)].
Тогда
108
Т/2
217O(-1)"+1
л(4л2 —1)
о
2.13. Средняя за период мощность комплекснозначного си-
гнала
Т/2
ЛрЦ | 5(0^*(Od/.
-тр.
Так как
,(/)= £ с./”'1,
П— —00
ТО
Т/2
р<,=-т i f с-с~ Г
•* m—— con—— со J
— Т/2
Непосредственным вычислением убеждаемся, что
Т/2
| e*“*'dt=O
— Т/2
для всех 1. Итак,
Лр= z СвСп* = С0С0* + 2£ СЯС*
Л™—СО Л—1
2.15. Из рисунка, полагая 1=0, непосредственно находим А =
= 80 В. Так как 80ехр(—or 5 • 10-6)=20, to а=2.773,106 с-1.
Спектральная плотность
$(«)=—-[1-е-(в+>ш)1и],
a+jco
2.16. Значение частоты со, при котором спектральная плот-
ность обращается в нуль, должна удовлетворять уравнению
е-«и.е->«и=зЬ
109
или
е <n”coscnB= I,
е~”ж8П1йпи=0.
Очевидно, что эта система уравнений несовместна.
2.17. Коэффициент С„ комплексного ряда Фурье выражается
следующим интегралом:
Т/2
Ся=| J *(r)e_*"“d/.
—тр
Пределы интегрирования в последней формуле могут быть рас-
ширены от —оо до +оо, поскольку функция So (0 определена
только на отрезке — T/2<z<T/2. Таким образом,
C„=-S0(ncoi).
т
2.18. Используя теорему о спектре смещенного во времени
сигнала и группируя отдельные импульсы в пары, равноотсто-
ящие от начала отсчета, имеем
ад=So (®) ‘ (1+е*"г+е->иГ+ <faT+ c~fia,T+...
..^NaT+e~JNaT)=S0 (w) (1 + 2 cos a>T+
+2 cos 2шТ+...+2 cos NojT).
Для того чтобы проанализировать зависимость модуля спект-
ральной плотности от числа импульсов, введем функцию
Fn((dT) = |1 + 2 cos соТ+... + 2 cos МаТ].
На рис. Ш.2.1, а, б изображены графики функций Fi(caT) (после-
довательность из трех импульсов) и F2(to7) (последовательность
из пяти импульсов). Можно заметить следующую закономер-
ность: с ростом N функция Fn приобретает вид локализованных
«всплесков», расположенных в точках а>Т=2пп (n=0, 1, 2, ...).
В пределе при 2V-»oo происходит переход от непрерывного к ди-
скретному спектру; частоты отдельных спектральных составля-
ющих соответствуют гармоникам частоты повторения импульс-
ной последовательности.
2.19. Используя выражение для спектральной плотности экс-
поненциального видеоимпульса, имеем
по
S(ai)=A I---------
ya+jw P+fa,
(ap-<o2)+j(a+fi)to
При заданных числовых параметрах
|5(<u)|=
1.2 107
V(3 • Ю12 - о2)2 +1-6 ’ Ю13й?
Для построения графика удобно нормировать частоту, введя
новую переменную £ = со/10б. Тогда
15(01 =
1.2- 10-s
V(3-{2)2 + 16{2'
График данной зависимости приведен на рис. III.2.2.
2.20. Граничная частота удовлетворяет биквадратному урав-
нению
(сф - ш£>)2 + (а+0)2со2 = 100а2/?2,
положительный корень которого
Подставляя числовые значения а и Р, имеем
-720 -360 0 360 720 мТ.
111
й)ф=5.026 106 с"1.
2.23. Длительность видеоимпульса, создающего на экра-
не темную полосу, тн=3-64/500 = 0.384 мкс, откуда faesa= 1/тя=
=2.6 МГц.
2.28. Излагаемый ниже способ удобен для нахождения спект-
ральных плотностей импульсных колебании, представляемых от-
резками прямых. Дифференцируя исходный сигнал, получаем два
разнополярных прямоугольных импульса (рис. Ш.2.3); вторая
производная имеет вид трех ^-функций (рис. III.2.4). Математи-
ческая модель второй производной такова:
Спектральная плотность второй производной
G(co)=—le-----he-----2
\ 2 2 ?
4Af <utB \
=—I COS----1 ].
2 /
Используя связь между спектрами сигналов и их производных,
находим
_ **Л /
S(aj)=— G(aj)/aj2=——I 1—cos—
<ЛН\ 2 t
Следует заметить, что при со-»оо |5]~1/со2, т. е. модуль
спектральной плотности убывает здесь с ростом частоты гораз-
Рис. Ш.2.3
112
до быстрее, чем в случае прямоугольного видеоимпульса, для
которого |5]~1/со. Это связано с тем, что рассматриваемый
треугольный импульс описывается непрерывной функцией вре-
мени, в то время как прямоугольный импульс является раз-
рывным.
2.29. Пусть f(f)=du/dt и пусть имеет место соответствие
f(j)<->F(w). На основании математической модели исходного сиг-
нала функция /(г) выражается в виде суммы ^-функций:
(зг\ / т
t+- +2С70ф+-
2 7 \ 2,
(Т\ ( ЗТ
t— ) + С7о51 t-
2? V 2
Таким образом, ее спектральная плотность
ЗшТ а>Т
J~2~ J 2
F(aj)=ja)U(a))= — Uoe +2С70е —
а>Т ЗшТ
-J 2 2
—2UqS -4-t70e =
ЗсоТ соТ
= —j2[70sin-----|-j4C70sin—.
2 2
Отсюда
, ч 4Г0 . шТ 2U0 . 3(ОТ
U((o)=—sm-----------sm—.
со 2 со 2
Введя безразмерный аргумент х=а)Т/2, получаем
U (x)/(tZo7)=(2sinx—sin Зх)/х.
График нормированного модуля спектральной плотности,
рассчитанный по данной формуле, изображен на рис. Ш.2.5.
2.32. Рассмотрим импульсный сигнал s (Z), отличный от ну-
ля на отрезке времени [0, tJ. Спектральная плотность этого сиг-
нала
тн
S(w)=p(/)e’^'d/.
О
(*)
113
Будем интересоваться значениями функции S(co) на достаточно
низких частотах, удовлетворяющих неравенству со«:1/тв.
Малость безразмерной величины tot в показателе экспоненты,
входящей в (•), дает возможность воспользоваться рядом Мак-
лорена
-Jal , . сА2
е ------h...
2
Тогда, ограничиваясь учетом первых трех слагаемых, имеем
ти
5 (ш)« J5 (0 —fa* ““ =
о
со2
=MQ —j(oMt —— М2,
где символами Мо, и М2 обозначены определенные интегралы,
называемые моментами рассматриваемого импульса:
тя
A/B=j*s(Ofdf, л=0, 1,2, ...
О
Легко видеть, что точное разложение таково:
5(ш)= £ Мк{](о)к1К
к-0
Если длительность импульса тв-»0, то очевидно, что
lim S(co)=A/0,
rH-0
т. е. предельное значение спектральной плотности импульса,
длительность которого стремится к нулю, равна площади этого
импульса.
2.35. На основании обратного преобразования Фурье
Sb
J(0=-
2Л
Л»
е аш
1 +сЛ2
Здесь подынтегральная функция имеет два простых полюса,
определяемых из уравнения 1 +со2т2=0. Данные полюсы сосредо-
точены в точках с координатами со^= ±j/t.
Для вычисления сигнала s(t) при />0 следует провести интег-
рирование по контуру Ct (рис. Ш.2.6), включающему в себя
бесконечно протяженную вещественную ось и дугу бесконечно
большого радиуса, расположенную в верхней полуплоскости
1шсо>0. Интеграл по указанной дуге стремится к нулю с ростом
ее радиуса и поэтому
/ jot '
е аш _ / е
-----—=2nj res I--------—
l+co2t2 \1+ш2т2
Вычет подынтегральной функции в точке полюса
res=e
Итак,
jot -t/1
e da> ite
1 +ш2т2 T
Аналогичный результат, отличающийся знаком в показателе
экспоненты, будет получен для значений Г <0; при этом интег-
рирование следует провести по контуру, замыкающемуся дугой
бесконечно большого радиуса в нижней полуплоскости. В резуль-
тате получаем окончательно
5(r)=S0e-w/7(2t).
2.40. Воспользуемся тем, что
sin —jit [<5 (со—со0)—(ш + «о)],
a (со) +1 /(/со).
Тогда, вычисляя свертку этих спектральных плотностей,
имеем
115
co
— co
co
хГяй(й)-О+—ld£=-J; f 5(C-0)o)X
L j(e»-oj 2 j
x^rc-Ode-; f <5(£~cod-~ +
2 J co—f
— co
co
+j-2 j $(C4-e^(<»-e)de4-
— co
CO
1 Ioz>- 4 e S
+ ; £(C + COo)--=-J~S(co-cod-
2 J co—f 2
— co
1 Л c z x 1
---------1-j - 6 (co+tOo) 4 =
2(co-coo) 2 2(co+coo)
Л CUq
= ——COfl) —Й(со4-С0о)]-----------------;
2 ar—to;
2.45. В соответствии с определением понятия спектральной
плотности
со со
F(co)= J dteT*0' J u(t)v(t—r)dt.
— co — co
В данном выражении функцию v(t—t) можно выразить через
соответствующую спектральную плотность
СО
f PCri^dri.
2п J
— со
(**)
Подставив (**) в (*), а затем, изменив порядок следования опера-
ций интегрирования по переменным т и if, получим
116
F(w)=
d»?=
и(т)е ^dr.
Заметим, что внутренний интеграл здесь представляет собой
функцию U (»?). Тогда
со со
F(ai)= [ d^GOC/OoFl f .
J [2Я J
— co ~co
Так как
CO
- f
2л J
co
TO
co
F(co)= j дт]У(т])иМ^(г]-а})=У((о)и(а)),
— co
что и требовалось доказать.
2.46. а) По определению свертки
СО
Л0= j
— со
со
=AtA2 j e-e*('-°<T(z-Oe_e2{<T(Od£.
- со
Положим, что г>0. Графики сигналов s((r—{) и 52(О» образу-
ющих подынтегральное выражение, приведены на рис. III .2.7. Так
как произведение этих сигналов отлично от нуля лишь в проме-
жутке 0<£<t, то
117
f(t)=AiA2e
Если t<0, то графики сигналов st(t—%) и з2(%) оказываются
разнесенными во времени, произведение этих сигналов равно
нулю при любых { и поэтому /(0=0 (рис. Ш.2.8).
б) Преобразуя сигналы Si(0 и s2(t) по Фурье, имеем следу-
ющие соответствия:
aj+jcD a2+ja>
откуда
,
(oti+/a>)(a2+ja>)
T. e.
Л1Л2
/(0=—
2Л
e acu
(«i+je>)(«2+»
Разложив дробно-рациональную функцию подынтегрального вы-
ражения на простые дроби, имеем
1 1 / 1_________________________1_
(ai+ja>)(a2+j<o) a2—ai\ai+jto a2+jw
Воспользовавшись известной формулой для спектральной
плотности экспоненциального видеоимпульса, получаем от-
сюда
Рис. III.2.7
Рис. 111.2.8
118
/(0=—(e“e,'-e~ej'),
«2-«1
что, естественно, совпадает с результатом, полученным выше
прямым методом.
2.48. В точке р=0 функция U(p) имеет полюс второго поряд-
ка. Для />0 контур интегрирования состоит из бесконечной
вертикальной прямой с некоторой абсциссой а>0 (рис. Ш.2.9)
и дуги Ct радиуса /?-юо, расположенной в левой полуплоскости.
Так как при Л-»оо величина 1/р2-»0 равномерна относительно
аргумента р, то по лемме Жордана
г р1
I е
lim I — dp=0.
«-.оо J Р
С,
Точка полюса оказывается внутри контура интегрирования.
Вычет подынтегральной функции в точке полюса
=lim—(e₽,)=L
p-о p-о
Отсюда для />0
я+>00
1 г рг
,. 1 I е
w(0=— 3d/>='-
2ig J р1
a-J<o
Для вычисления функции и (г) при Г<0 контур интегрирования
следует замкнуть дугой С2, расположенной в правой полуплоско-
сти, где подынтегральная функция
не имеет особых точек. Поэтому при
t<0 имеем u(r)=0.
2.49. Заданное изображение пред-
ставим в виде
1 АВС
(р+а)(р+Ь)(р+с) р+а р+Ь р+с
Коэффициенты А, В и С можно
1айти обычным способом, который
используется при разложении на про- Рис. Ш.2.9
119
стые дроби. Однако это сопряжено с громоздкими выкладками.
Более короткий путь состоит в следующем. Из последней фор-
мулы видно, например, что величина А есть вычет функции,
стоящей в левой части, вычисленный при р= — а:
X=res| =------------.
₽“-« (А — а)(с—а)
Аналогично находим коэффициенты В и С:
Z?=res| =---------;
р—* (a—b)(c—b)
C=res| =----1----.
Р“-« (я—с)(Ь—с)
Отсюда
— al —bt —ct
е е е
(Л—я)(с—я) (я—А)(с—Л) (я—с)(Ъ—с)
250. Разлагая изображение на простые дроби, имеем
1 _ А В
(p+d)(p+b) р+а р+Ь
Неизвестные величины А и В удовлетворяют уравнению
рА+ЬА+рВ+аВ=Л.
Приравняв коэффициенты при одинаковых степенях р, получаем
систему двух алгебраических уравнений
л+в=о,
ЬА+аВ= 1,
решение которой очевидно:
Л=—; В= —-.
Ь—а Ь—а
Таким образом,
1 1 / 1_______________________________
(р+я)(р+Л) Ь—а\р+а р+Ь
откуда вытекает формула из условий задачи.
120
2.58. Принимая во внимание ре-
зультат, полученный в предыдущей
задаче, на основании формулы (2.69)
из [1] имеем:
2
Л-------1------1------
О 20 40 60
I
Рис. Ш.2.10
Си =40
л/2
2.59. Возможный текст рабочего листа программы представ-
лен ниже (рис Ш.2.10):
г=0.63,
X:=i/(f<32, 1, 0),
У: = wave (X),
Yit 0)
Z:=iwave(W/).
Здесь исследуемый сигнал представлен 64 отсчетами, первая
половина из которых положена равными единице, а остальные
нулю. Из этих отсчетов сформирован входной вектор X. Его
вейвлет-преобразованием является вектор Y. Затем из его пер-
вых двадцати компонентов формируется вектор W. Его обрат-
ным вейвлет-преобразованием служит вектор Z.
Следует заметить, что уменьшение числа компонентов, ис-
пользуемых при обратном преобразовании, ведет к появлению
характерных осцилляций сигнала в окрестностях точек разрыва.
Это явление хорошо изучено в математике и носит название
эффекта Гиббса.
Тема 3
3.1. Зная спектральные плотности данных сигналов, имеем
(u,t>)=——
2я J
d<u
(a1->)(a2+_/to)’
Разложим подынтегральную функцию на простые дроби:
121
1
(«1-»(а2+»
а1+а2 \«i-J(o «2+/ш
Интеграл от каждой из простых дробей вычисляем одним и тем
же приемом. Так,
dt0 p(a2-jw)dw р dfl)
---~= ---Г~ = а2 1----2
а2+усо J а^+о) J aj+ar
В результате имеем
(u, v)=AlA2/(ai +а2).
3.8. Возводя в квадрат вещественную спектральную плот-
ность прямоугольного видеоимпульса, получаем энергетический
спектр
Wu (со)
. 2в«>
sin^~
(сЯж/З)2'
По теореме Рэлея в узком смысле
Е
f sini(cna/2)
-------------dco.
J (on,/!)2
о
Выполнив замену переменной £=соТа/2, имеем
я
ШвТв/2
О
Интегрируя по частям, получаем
|^Si(co,TH)-
^ти «вХи
sin2
(ш.Гя/2)2
122
где
Si(z)=j^d£-
о
неэлементарная функция, называемая интегральным синусом [4].
3.9. Энергетический спектр рассматриваемого сигнала задает-
ся формулой
JF,(o)=
225
1024+а>2'
Граничная частота удовлетворяет уравнению
или
arctg (сОгр/107)=0.45л.
Решая его, находим <0^= 107 * tg0.45n, т. е. /j>= 10.049 МГц.
3.12. Спектральная плотность
со
S(co)=2B Гe~filcos cut
J /P+cu2
0
откуда энергетический спектр
Wt((o) =4B2p2l(P2+(o2)2.
Автокорреляционная функция Кя(т) представляется следу-
ющим интегралом Фурье:
71
I е do;
J (Д2+ш2)2’
Здесь подынтегральная функция имеет два полюса второго по-
рядка в точках с координатами аз= ±jfi. Для вычисления функции
Х,(т) при т>0 находим
123
_ d
»-JP d0)
(Д2+ш2)2 _
f»-JP
= -je-/”(l+j?T)/(4j?2).
Таким образом, при т>0
№. , л
е dcu _ , я -Btl+pt
-------=2nj'res=-e ------,
(Д’+ш2)2 2 р3
откуда, приняв во внимание четность автокорреляционной функ-
ции, имеем
ад=^е"™(1+/?М).
р
3.13. Здесь
00
К, (т)=А 2 Je aI sin toot' e-e(/+t) sin соь (t+r) df=
о
co
=A2e~”Je-2e/sinc)of sincoo(f+t)d*-
о
Известно, что
sin x • sin У=~ [cos (x—y)—cos (x+y)J.
Поэтому
aO co
.j г А2 C
—coscobt I e~^dt-------— e-2ercos(2a)oZ+(u0T)dL
о о
Используя табличный интеграл
co
I e-j“cos(ox+2)dx=—- — (pcosZ—<?sin2),
J P +4
о
124
получаем
3.16. Положим, что т>0. Тогда для 0<т<та имеем
К,(т)= J j(l)j(t+T)dt=
о
—Л2 J cos(w0f+9o)cos[w0(f+T)+<PQ]df.
о
Так как
cosx • cosy =Ц [cos (х—y)+cos (х+у)],
то
А2 Г А2 Г
КЛт)=— I costard Л— cos(2aV+<aoT+
2 J 2 J
о о
+2e>0 df=— (та— т) cos cOoT+
2
^2
4---sin [<D0 (2тж—T)+2pJ.
4«o
В практических случаях, как пра-
вило, й)о"га» 1, т. е. длительность ра-
Рис. Ш.3.1
125
диоимпульса значительно превосходит длительность одного пе-
риода высокочастотного заполнения. Тогда приближенно
т>та.
Соответствующий график изображен на рис. III.3.1.
Темя 4
4.2. Огибающая сигнала (В) задается выражением U(f)=
= 12 (1+0.6 cos О/+0.2 cos 2£2/). Введя безразмерный аргумент
x=£lt, видим, что значения х, при которых огибающая дости-
гает экстремальных значений, должны являться корнями урав-
нения
0.6 sinx+0.4 sin 2х=0.
(*)
Очевидный корень х=0 соответствует максимуму огибающей
t7m„=21.6 В. Другой корень уравнения (*) найдем, разделив
обе части на sinx^O, откуда cosx= —0.75, т. е. х=2.419 и 17^,=
=6.9 В.
4.9. Вычисляя мгновенную мощность, имеем
и2
(1+М cosQ/)2 cos2 ioot=
V2L л .,2 l+COS2Q/\
=— 11+2M cosOz+Л/2----------I x
R \ 2 J
(1+cos2o>oA
--------I.
2 /
Отсюда
pn(t)=^^-cosQt; P2a(t)=U^-—- cos2£2/.
R 4Л
4.12. Полная фаза данного сигнала
^(/)=108/+3sin 10б/+ 1.4sin 105/+7г/4.
Мгновенная частота есть производная от полной фазы:
126
(О (0 = 10е+3 • 106 cos 106/ +1.4 -10s cos 105f.
Подставляя значение t= 10“б с, получаем со =1.0176' 10е с-1.
4.18. Спектральная составляющая на несущей частоте будет
отсутствовать при всех значениях индекса модуляции т, которые
являются корнями трансцендентного уравнения Jo(m)=O. Мно-
жество таких корней бесконечно; наименьший корень т=2.405.
Этому значению соответствует наибольшая частота модуляции
0^=6104/2.405 = 24948 с’1.
4.20. Оставляя по два члена в разложении гармонических
функций малого аргумента, имеем
и (0 = Uo cos (т sin Qt) cos cogt—
— UD sin (m sin П0 sin coDt~ Uocos co0t (1 — (m2 sin2 Qt){2)—
— Uo sin co0t (m sin Sit—(m3 sin3 Slf)/6).
Раскрывая по известным правилам степени тригонометрических
функций, находим, что
17и2=17(>т2/8=3.610-3,
141э=17от3/48 = 3.6 10“5.
4.25. а). Полагая, что начало отсчета времени совпадает с се-
рединой импульса, имеем
Второе слагаемое в числителе подынтегрального выражения
представляет собой знакопеременную функцию; вклад от него
стремится к нулю с ростом базы сигнала. Таким образом,
E^Ufa/2.
б). Энергетический спектр сигнала практически постоянен
в пределах полосы частот Лсо=дтв и равен Wu—itUol{2p}. Тогда
энергия сигнала Еи— Wu-Еы/л= UoTn/2, что было получено выше
другим способом.
127
4.28. Представим спектральную плотность сигнала s(t) следу-
ющим образом: где
h = U0
e^
( 9"\
COS I CO0N--JCOS(Dfdf =
\ 2 /
и0
2
I pr21
cos (tt)o+co)f+— +
I 2 I
I II
+cosl (too—шкч— >df,
I 2 I)
I2=UO
e
cos I tzVH— Jsm<urdr=
\ 2 j
2
-ft1 J .
e <sin
—sin
Воспользовавшись табличным интегралом, приведенным в ука-
заниях к данной задаче (см. раздел II), получаем
с/ \ U° -««Oo+oOW’+P*/*)
Л(со)=----е х
хехр(-уЛ1)+-°-^=е-«--",,'ад‘"'Л’
2
хехр(/Л2),
где
. I р р р(ш0+ш)2
1 “ 2 аГС 6 2/? 20 8(Р2 +р2/4)’
1 р р(ш0-ш)2
2 *20 8(/Г2+р2/4)
128
Первое слагаемое в последней формуле описывает спектраль-
ные компоненты, имеющие максимум в области отрицательных
частот при <д~ —од; второе слагаемое соответствует той части
спектра, которая имеет максимум при со~од. Во всех случаях,
которые интересны для практики, обе указанные части спектра
взаимно не «перекрываются».
Темя 5
Отсюда видно, что рассматриваемый сигнал есть полусумма
двух идеальных низкочастотных сигналов с одинаковыми пара-
метрами So, од. Сигналы сдвинуты во времени на отрезки
+л/(2од) относительно начала отсчета времени.
5.3. В соответствии с рисунком определяем интервал диск-
ретизации г0=2* 10-6 с, откуда находим верхнюю частоту в спек-
тре сигнала од=яДо=1.57,1Об с-1. Ряд Котельникова рассмат-
риваемого сигнала имеет вид
швг to»r—я
из которого при Г=10 6 с получаем $(10 б)=22.28 В.
5.5. Так как энергетический спектр сигнала s(t)
и;(£у)=^е7ш1/(2Л)
5-415
129
то
Воспользовавшись известной неэлементарной функцией — инте-
гралом вероятностей [4]
Ф(х)=-1= f e"'1/2d/,
у/2л J
— со
для которой Ф(оо)= 1, получаем
"^=^Л('-фй)Ув
Если со,=0, то естественно, что ]|^<жпИ = П-УП- Действительно,
Ф(0)=0.5 и поэтому И^И = U0^/nl(2P)= |И|.
Функция Ф(х) быстро стремится к единице с ростом х. Это
ведет к тому, что при достаточно больших значениях со, норма
сигнала ошибки становится достаточно малой. Например, если
соя/у/р=3, то Ф(со,\//?)=0.9986 и ||sOT|| =0.052 ||s||.
5.11. Поскольку sinx=cos(x—90°), имеем
(u<fi e^Y
5 (0=Uo cos (a)ot—90°)—Re
откуда комплексная огибающая представляется постоянным во
времени числом
е7,= 17ое-Л/2=-;С7о.
Спектральная плотность комплексной огибающей
Gs(aj)= -j2nU06(aj).
Искомая спектральная плотность
S (со) = —jnU0[6 (со—(D0)—д (со+СОо)].
130
5.18. Здесь
«о 7
z,(O=— I e( o+'/1)“dw=
я J
Sff(<X+j’O —«ш, . -aa^ . •.
— [1—e coswBf—je smwB/J.
я(вг+»2)
5.24. Производная от входного колебания
s' (0= иоб (t+to)-U06(t—t0).
Сигнал на выходе квадратурного фильтра
00 00
_/Л f г<т+'о). и0 f S(*-»o) .
f(t)=— I ----------ат------I ---------ат=
я J 1-т Я J r-т
— co —co
Uo
2t/o Iq
я \»+<b t-to,
Тема 6
6.1. Обозначим выпадение шестерки символом X, выпадение
любого другого числа от единицы до пяти — символом У. К вы-
игрышу лица А приводят следующие ситуации: X — с вероят-
ностью 1/6, YYX — с вероятностью (5/6)2 • 1/6, YYYYX — с веро-
ятностью (5/6)4 • 1/6 и т. д. Отсюда легко видеть, что вероятность
выигрыша А
=0.545,
т. е. лицо, начавшее игру, имеет некоторое, хотя и небольшое,
преимущество.
6.8. По определению
FW_p(0d{=2J_^.
о о
131
Выполнив замену переменной f]= 1 + £, имеем
1+х
Р(х)=2 j d^3=l-(l+x)-2.
i
Далее,
Р(0<х<1)=Р(1)-Р(0)=0.75.
6.11. Основываемся на том, что
(Ь—т\ /а—т\
---I—Ф1-----|.
® / \ а /
В данном случае
Р(0<х<2)=Ф(1)-Ф(0)=0.341.
6.13. Так как Р=гРо/(г+Ло), то обратная функция г=
=RRo/(Ro—R); ее производная ir/dR=Ro/(Ro—Л)2. Плотность
вероятности сопротивления г имеет вид р(г)= 1/(2л), поэтому
p(P)=p(r)|dr/dP|=P02/(2^№-P)2).
Сопротивление R изменяется в пределах от
Ло(/?о—a) Хо(Ро+а)
«оап— ~~ ДО -Л'щжх— ~ •
2Ло—о 2Jtg+a
Окончательно
ЛО , R< Pm'm.
p(R)= S Л2/(2а(Л-Р)2), Лшш<R<Ram
to , R>Rmu.
6.14. Рассмотрим двумерную случайную величину W=(X, Y).
Так как Хи У независимы, тоpw(x, y)=Pi(x)p2(y). Перейдем от
аргументов (х, у) к новым аргументам (х, z), где z=x+y. Так как
якобиан преобразования D= 1, то в новых переменных двумерная
плотность вероятности pw(x, z)=p1(x)p2(z—х). Отсюда плот-
ность вероятности суммы есть свертка плотностей вероятности
слагаемых:
Рз(г)=
со
J Pi(x)p2(z-x)dx.
— со
132
Говорят, что данное выражение описывает композицию двух
законов распределения.
6.19. В соответствии с принципом усреднения
00 оо «х>
[jdL fa fa
J(i+o3 К К .
Нахождение среднего квадрата сводится к вычислению ин-
теграла
?=2 Г 0+_!--------------------1 1
Ja+o1 L 1+« 2(1+о\1
О
Таким образом, рассмотренная здесь случайная величина
имеет неограниченно большую дисперсию.
6.21. В данном случае
xp(x)dx=^~ Jxdx=^,
т. е. среднее значение совпадает с серединой отрезка.
Далее,
со b
хт= J x2p(x)dx=^— Jx2dx=fc +t^+a\
Наконец,
2 "2 \2 Ф
(7, =Х—(ХГ =---
12
6.24. Очевидно, что z=x(l — х). Плотность вероятностир(х)=
= 1. Тогда
z= I х(1 — x)dx= 1/6.
о
Далее,
133
Отсюда
z2=J х2 (1 —x)2 dx= 1/30.
о
<r2=1/30-1/36= 1/180.
6.25. Если z=x(l —x) (рис. Ш.6.1, а), то обратная функция x=
= l/2+-y/l/4—z двузначна (рис. Ш.6.1, б). Ее производная
dx_
& 2у/Щ-2
откуда
{0 , z<0,
l/Vl/4-z, 0<z<l/4,
0 , z>l/4.
6.29. Якобиан преобразования от переменных х, у, z к пере-
менным г, а, <р
sin о cos<p
sin о sin<p
cos fl
r COS fl cos<p
r cos й sin<p
— rsin fl
—r sin fl sin<p
rsin fl cos<p
0
= r2sinfl .
Таким образом, преобразованная плотность вероятности
Р(г, а , ф)=^^1ехр(-г2/(2«т2)).
(2я)3,2<г
Для нахождения одномерной плотности вычисляем:
Рис. Ш.6.1
134
fd« p(r, о, ф)=-^-^ехр(-г2/(2<т2)).
J (2л)1'2 аг3
2я
pW=|d<p
о о
6.32. Воспользуемся известной связью между моментами и ха-
рактеристической функцией:
«П=Г"0(Л)(О).
Производная характеристической функции
„ ibu Jau Ли Jau
1-----------ju(be -ае)-е +е
® («)=------'---------:-------• ( )
J(b-a) I?
При и-» О в правой части возникает неопределенность. Чтобы
раскрыть ее, следует воспользоваться разложениями
. 0*4* Au , b2U*
е =l+jau--------...; е = l+jbu-------...
2 2
Подставив эти выражения в правую часть (*), имеем
0(0)=-------; mi=x=-----.
2 2
6.33. На основании решения задачи 6.31
-Л/2
®х (и)= --------= sin (u/2)/(u/2),
Ju
откуда
®/u)=sin3(u/2)/(u/2)3.
Чтобы от характеристической функции перейти к плотности
вероятности р(у), необходимо вычислить интеграл Фурье
со
^0’)=^ j ®y(u)e~Jy“du,
— со
который в силу четности функции ®у(и) можно записать так:
135
co
pM=-
nJ «3
0
Соответствующий табличный интеграл
ОО
_ fsin3(u/2)cosj>u ,
Z= I--------,------au=
J «
о
приводит к следующему выражению плотности вероятности р (у)
приу>0:
/•3 , 1
, 0<у<-,
Очевидно, что функция р(у) является четной и должна быть
дополнена соответствующей ветвью при у<0. Скачанное здесь
отображается графиком на рис. Ш.6.2. Следует обратить внима-
Рис. Ш.6.2
ние на то, что плотность вероятности
суммы трех независимых случайных вели-
чин отображается вполне «гладкой» кри-
вой, несмотря на то, что плотность веро-
ятности отдельных слагаемых носит раз-
рывный характер. В этом проявляется за-
кон, согласно которому при неограничен-
ном увеличении числа слагаемых закон
распределения суммы асимптотически
стремится к нормальному (центральная
предельная теорема в теории вероятно-
стей).
136
6.35. По определению, характеристическая функция Qx(u)=
=ехр (/их), поэтому exp(x)=0x(—j). Для гауссовой случайной
величины 0x(u)=exp(jmxu—<т2и2/2), откуда ехр(х)=ехр(«х+
+<тх2/2).
Тема 7
_7.1. Среднее значение x(t) не зависит от времени: х(0=
=acosGV=0, однако дисперсия- o2(t)=a2cos2a)0t=a2(l +
+cos2cttf)/2 является функцией времени. Отсюда следует, что
случайный процесс X (0 нестационарен в широком смысле.
7.7. Так как х=0 при всех £, то
У= x(Od£=0.
Тогда
(/., я=у&)у&)= р?х(£ь «аел»
= w0
jd6p>(£|-£)d£2.
о о
Как видно из данного равенства, на плоскости & подынтег-
ральная функция равна нулю во всех точках, кроме точек прямой
с уравнением £2=£ь гДе эта функция имеет 6-образную способ-
ность. Эта прямая соответствует отрезку О А на рис. Ш.7.1, а, б,
где изображены прямоугольные области, в пределах которых
проводится интегрирование.
Возможны два случая. Если ti>t2 (рис. Ш.7.1, а), то интег-
рирование по & дает не равный нулю результат только вдоль
отрезка вида ВС, начальная точка которого В принадлежит об-
ласти Поэтому By(tlt t2)= FFo<2. если rt >t2.
В случае, когда t\<t2, интеграл по & вдоль любого отрезка
вида ВС равен единице всегда (рис. Ш.7.1, б). Отсюда Z2)=
= Woh, если G<t2. Так как в обоих случаях функция корреляции
явно зависит от или t2, а не от разности tx —12, то винеровский
случайный процесс нестационарен в широком смысле.
137
Рис. Ш.7.1
Полагая, что t1 = t2=t, находим, что дисперсия <J2=Ry(t, t)=
= Wot линейно растет во времени.
7.12. Очевидно, что х(0=0. Что касается величины
х(с)х(с+т), то она равна либо а2, либо —а2 в зависимости от
того, будет ли реализация процесса за отрезок времени т иметь
четное число скачков (включая нуль), либо нечетное. Используя
принцип усреднения, получаем при т>0
Лх(г)=х(/)х(/+т)=а2(Рт(0)+Рт(2)+...)-
—a(Pt(l)+Pt(3)+...)=
=a2e~it( 1 —Лт+— (Лт)2—— (Лт)3+..А=а2е-2Л.
\ 2! 3! J
Так как функция корреляции четна, то
Лх(т)=о2е-Лм.
7.16. Находим спектр мощности производной:
' 0 ,
. о ,
со< —аь,
—со»<со<со»,
и» (О,.
Далее,
Wo ? Wo Т
Л,(т)=— со2 cos сотdco=— I <!;2cos£d£.
п J ят3 J
О О
138
Используем табличный интеграл
z?cosfcxdx=-
к
2bzt
sinfcxd—-cosfcx,
где Zi=a+bx, a=Q, 6=1, fc=l, так что zi=£. В результате
получаем
Я
sinwaT 2со$ш1т
ш»т (а>,т)2
7.18. В данном случае коэффициент корреляции случайного
процесса г1(т)=8ш©1т/(ю1т). Поэтому
(о>вт)3 sin а>)Т+2o>sT' cos ауг—2 sin о>ат
rx (т)=-------------------------------.
В последнем выражении следует раскрыть неопределенность, воз-
никающую при т-»0. Для этого следует воспользоваться прави-
лом Лопиталя. Тогда r£(0)= —и£1Ъ, откуда л(0)=ш^(2л-у/3).
7.20. Известно, что плотность вероятности огибающей
p(U)="ezp(-t72/(2ff*)).
°х
Отсюда
00
P(U^U0)= f-^e“°’Z2*«dl7=
J ах
= J e~td^=e~u»Pe*=Q.449.
7.22. Так как длина отрезка [4.9 В, 5.1 В] достаточно мала по
сравнению с центральным значением 17=5 В, то вероятность
Р(4.9 В<С7<5.1 В)»р(5) 0.2.
Используя формулу распределения Рэлея, получаем таблицу
139
?,В!
3.72 10~6
0.0294
9.2-КГ1
Данные вероятности характеризуют собой относительное время
пребывания огибающей в пределах рассматриваемого полуин-
тервала. Переходя от относительных величин к абсолютным
длительностям, получаем таблицу средних длительностей пребы-
вания:
3.72 мкс
29.4 мс
9.2 мс
7.25. При учете одного члена разложения функции корреляции
огибающей соответствующий спектр мощности
Максимальное значение этой функции
Иг1Лп«= ИЪ(0)= 1.3745 10"4 В2 с.
Отсюда
Дшэф=—1— I ИЪ(со)с1со=
=4-10е
При учете двух членов разложения
5.498 10* 6.968'10s
Эта функция также имеет максимальное значение при ш=0:
ИЪ(0) = 1.418 10"4 В2 с.
Поэтому эффективная ширина спектра огибающей
140
00
A©*=3.877 • 10е ---—- +
J+lO’+a?
о
+4.914 107
Г d<0
J 1.6 lO’+w1
о
Рис. П1.7.2
= 3.238-104 с"1.
Таким образом, относительная ошибка, возникающая при
упрощенном представлении функции автокорреляции огибающей
лишь одним членом ряда, составляет около 3%.
7.28. Один из возможных вариантов решения задачи представ-
лен следующей программой (рис. Ш.7.2):
а:=3,
z:=0.01..8,
p(z):=z-exp
10 (az).
2
Интересно провести ряд экспериментов с этой программой,
наблюдая, в частности, как проявляется нормализация райсовс-
кого распределения при увеличении значения безразмерного от-
ношения а=ит(ах.
Тема 8
8.1. На основании первого закона Кирхгофа, считая положи-
тельным ток, входящий в узел, и отрицательным ток, выходящий
из узла, запишем уравнения баланса токов в узлах 7 и 2:
dt Ri R3
. U)
dw2 U2 «2-«1
— C/2------------—U.
dt R2 Лэ
Введем обозначения
1/Л13 = 1/Л1 + 1/Лз; l//?23=l//?2 + l//?3-
Тогда (1) приобретает вид системы линейных дифференциальных
уравнений первого порядка:
141
dU] Uj Uj
df AjjCi AjQ
Ui U2 d«2
Л3С2 Л23С2 d/
(2)
Решение системы (2) будем искать в виде: и^Ае’, и2=Ве‘
с неизвестными заранее постоянными А и В. Подставляя эти
выражения в (2) и сокращая на общий экспоненциальный множи-
тель, приходим к системе алгебраических уравнений относитель-
но А и В:
А—— =0,
ЛэС,
Ягз^
Для разрешимости этой системы необходимо потребовать, что-
бы ее определитель был равен нулю. Отсюда получаем харак-
теристическое уравнение системы
1 \( 1 \ 1
уч----) уч----I— ----=0,
' RuCtJy R23C2J R}C,C2
или
.2
Л13С1 Л23С2>
1 I
^1зЛ2з
о,
(4)
имеющее корни У( и у2.
Если величина у совпадает с yi или у2, то система (3) имеет
бесконечное множество решений, отличающихся друг от друга
общим коэффициентом пропорциональности. При этом на ос-
новании, например, первого уравнения из (3) получаем соот-
ношение
А I // 1 \
-=—/I уч-------)•
В /?ЗС1/ у Лое*!/
Таким образом, общее решение системы (2) приобретает вид
142
«2 (0 = Л3С1 (71 +——- )^1 е”‘ +
\ лиЧ/
(5)
+Я3С1 (уг+ )Л2еъ,
\ лич/
причем коэффициенты А\ и А2 должны быть найдены из началь-
ных условий при /=0:
А\+А2—Ui(0),
ЯзС,
Л2 =и2(0).
Решая эту систему, находим:
. (П+ 1/(Я1эС1))«1 (0)-«2 (0)/(ЛзС.)
"1—------------------------------->
72-71
. -(7! + 1/(Л1зС!))И1 (ORi^OJ/toC,)
А2----------------------------------.
72-71
(б)
Подставив коэффициенты (б) в (5), приходим к окончательным
выражениям, описывающим собственные колебания в рассмат-
риваемой цепи:
«2(0)
ЛС1
\ RaCiJ J
72-71
«г(0—------(vi
72—71 \ Я1зС1/|_ \ Я13С1/
-«2(0)
+——(ft+—тг) Г«2 (0)-
72-71 \ Л13С,/[_
— Л3С1 ( у! + ) U1 (0)
143
83. Выбрав в качестве динамических переменных токи i, и i2,
имеем следующую систему уравнении:
_ if. di?
Ц —+- Ifidr+M-=0,
dt cj dt
d/2 dii
Lj—+Л12+Л/—=0.
dr dt
Находя решения в виде ii(0=Je’‘, получаем систему
алгебраических уравнений
уД Ч— 1А+уМВ=0,
. ?с/
yMA+(yL2+R)B=0.
Для разрешимости этой системы необходимо, чтобы определи-
тель был равен нулю, откуда вытекает характеристическое урав-
нение
(y2LiC+l)(yL2+R)-y3M2C=0 (1)
Если М=0, то контуры оказываются несвязанными. Уравне-
ние (1) имеет три корня, один из которых yj = — R/Lq веществен,
а два других у2,з = — чисто мнимые. Корню yt отвечает
экспоненциально затухающий процесс в AL-цепи; корням у2.э со-
ответствуют гармонические колебания с частотой сособ=1/^/Е^С
в £С-контуре без потерь.
При R=оо ЛЛ-контур разомкнут; в LC-контуре могут су-
ществовать незатухающие гармонические колебания с частотой
Особ-
Если Л=0, то уравнение (1) приобретает вид
y2(LlL2-M2)C=-L2, (2)
откуда
где кс=М)у/LiLj. < 1 — коэффициент индуктивной связи конту-
ров. При этом в системе будут наблюдаться гармонические соб-
ственные колебания с частотой
144
C0co6= 1/7(1-к2}ЦС> \!у/цс.
(4)
Итак, наличие индуктивной связи с короткозамкнутым контуром
приводит к повышению собственной частоты колебательной си-
стемы.
8.5. Система дифференциальных уравнений рассматриваемой
цепи имеет вид:
d1/] i| dJi2
L -'++ЛЛ-, = 0,
dt2 C dt2
d2ij i? d2ii
L-'++M-' = G.
dr2 C dt2
(1)
Перейдем от переменных i'i и i2 к новым переменным £ и т] та-
ким, что относительно последних система (1) превратится в два
не связанных между собой дифференциальных уравнения. Если
такое преобразование возможно, то переменные £, т] называют
нормальными координатами системы. Переход к нормальным
координатам — важный прием в теории колебаний.
Для данного случая нормальные координаты находятся
просто:
Действительно, складывая и вычитая уравнения, входящие в (1),
получаем:
(L+Af)d2£/df2 + £/C=0, (3)
(L-M)d2f]/dt2 + T}/C=Q. (4)
Решениям уравнения (3) отвечают гармонические колебания
с частотой сомб! = 1/V(L+M)C. Аналогично для уравнения (4)
имеем частоту собственных колебаний cdco62= Гово-
рят, что в рассматриваемой системе возможны два нормальных
колебания, называемых также модами. Моды сложной колеба-
тельной системы полностью независимы друг от друга. Так, при
соответствующих начальных условиях в системе может быть
селективно возбуждена первая (низкочастотная или медленная
мода). При другом способе возбуждения можно добиться сущест-
вования лишь второй (высокочастотной или быстрой моды).
В общем случае в системе одновременно наблюдаются обе моды,
которые, интерферируя, образуют биения.
6-415 145
8.10. Между узлами а и b цепи включены ветви с оператор-
ными проводимостями
У!=рС+|; Y2=pC/(\+pRQ.
Изображения токов связаны уравнениями, вытекающими из за-
конов Кирхгофа:
4+4=/»*; lilh— У1/Уг-
Отсюда
l2=IMYl + Y2)
и поэтому передаточная функция
RY2 pr2c
У1 + У2 (ЛС)У+ЗЛСр+1
Обозначая т=RC и выполняя замену переменной p=ja>, находим
частотный коэффициент передачи
Отсюда нормированная АЧХ:
\K(jco)\IR=-
<(1 —со2т2)2+9со2т2
Фазочастотная характеристика фл(со) представляет собой раз-
ность аргументов двух комплексных чисел, стоящих в числителе
и знаменателе формулы (1). Если шт<1, то знаменатель отоб-
ражается точкой в первом квадранте комплексной плоскости
и поэтому
<pK(w)=|- arctg(3wr/(l - w2t2)).
Если же сот > 1, то точка, отображающая знаменатель, перемеща-
ется во второй квадрант, так что
фк (и) = - arctg [(со 2т2 -1 )/(Зшг)].
8.12. Пусть ко входу фильтра подключен идеальный источник
ЭДС с изображением (р). Выберем в качестве положительных
146
направления токов в ветвях, указанные стрелками на рис. Ш.8.1.
Равенство нулю алгебраических сумм токов в узлах а, b и с при-
водит к системе уравнений
да-рС^-(^в- ^)/Л=0,
(С4- Ub)/R-pCUb-(Ub-
(Ub-U^/R-pCUM=0.
Для нахождения передаточной функции цепи следует исклю-
чить вспомогательные переменные Ua и Ub. Выполнив эту опера-
цию, получаем
Un = (p3R3C2 + 5p2R 2С2 + 6pRC+1),
откуда
ад=(Р3Л3С3 + 5р2Л2С2+6рЛС+1)"1,
K(joj)=[(1 - 5со2Л 2 С2) +jaj (6RC- со2Л 3С3)]"1.
Отсюда фазочастотная характеристика
, ч <иЛС(б—<и2Я2С2)
Частота /, найдется из условия 1 —5со2Л2С2=0, соответственно
для частоты /2 имеем уравнение 6 — со2Л2С2=0. Используя число-
вые данные, приведенные в условии задачи, получаем f\ =
= 52.34 Гц, f2=286.65 Гц.
8.14. Здесь изображения потенциалов
г2иы ztun
------; иь=----.
Z[ +2J2 Z3+Z4
Тогда
г2____z4
Z[ +Z2 z3+z^
X(p)=-^^-.
(Zl+Z2)(Z3+Z4)
8.16. Рассмотрим интеграл
Г 1п|К(/ю)|<1<и
J 1 +<u2
— 00
00
Г inKo—bo)2
I----------dto.
J 1 +<u2
— 00
Рис. 111.8.1
147
Так как
lim [со2/(1 + со2)] = 1,
то данный интеграл расходится и поэтому рассматриваемый
фильтр физически нереализуем.
8.18. Частотный коэффициент передачи данной системы
^о^эШтр
(Orp+jaiiil+janS
откуда
2л
Л* .
е аш
(ш^+7ш)(1+/ал3)
На плоскости комплексной переменной со подынтегральная функ-
ция имеет два простых полюса в точках с координатами co^Jco^,
и со2=у/т3. Находя вычеты
“““ 7(1 -ШгрТ,)
и
“-ш> Я1-соп>Ъ)’
получаем
1-<"грЬ
8.19. Для jV-ступенчатой системы, собранной из идентичных
звеньев,
^Ow)=(-X0)n/(1+jcot3)n
Тогда
(—ЛЬ) Г e^'da)
2П „ О +Jan3')N
148
Подынтегральная функция имеет TV-кратный полюс в точке
со=У/тэ с вычетом
res |
ш-у/т,
. Л»"1 Г-*0'/ ; Лт
1 d е (й)-у/тэ)
(N-l)! . N-l N
* ’ dco L (1 т-усотэ) -*
•е"'/17тэ.
Отсюда
(N-l)> t3
е-"ъ <?(/).
На рис. III.8.2 представлены графики функции
ЛО/ьХ/ЛэЛ* ехр(—tM/(N-1)!,
пропорциональных импульсным характеристикам. Графики по-
строены для TV=2, 3 и 4. Видно, что рост числа ступеней усили-
теля ведет к увеличению задержки импульсного отклика.
8.23. Используя изображения напряжения и токов, имеем
систему уравнений
+pLtIi +рМ12,
О—R2I2 + pLah + pMIi.
Исключив с помощью второго уравнения данной системы изоб-
ражение It (р), получаем связь между и 12:
149
i2 в том направлении, которое принято за положительное, ведет
к повышению потенциала нижнего зажима резистора R2t т. е.
к уменьшению выходного напряжения. Используя обозначение
ЦЬа—M2 = LiL2(l —к2), где — коэффициент связи,
представим передаточную функцию в виде
Л//?2 р
К(р)=--------— •---------,
^£2(1-^) (P-PI)(P-P2)
где р1Л — корни характеристического уравнения
2 , LiR2 + LiRt Я|Л2
р +Р-------------------;—0.
Используя таблицы преобразований Лапласа, получаем
А = I ~Р2а
Ltlbd-kf) Pl-Pi
g(t)= .г.’ —— (e”*' -ей')С(0-
LiLad-ki) pi-Pi
8.25. Сокращения длительности фронта и уменьшения спада
плоской вершины можно добиться, если модуль одного из кор-
ней характеристического уравнения сокращать, а модуль другого
увеличивать. Так как
Рм=[ ~ (“1 + «г) ± ((«1 + «г)2 - 4 (1 - к2) х
ха.а2)1/2]/(2(1-Лс2)),
где а1 =Rl/Ll, a2=Ri/Li, то ясно, что имеются два пути: а) устре-
мить величину кс к единице, получив в пределе идеальный транс-
форматор без рассеяния; б) устремить «1 и (или) а2 к нулю, т. е.
увеличить постоянные времени первого и (или) второго контура.
8.27. Здесь
ад=^='—°,
рЛС+1 р+«
где а= 1/(ЛС). Импульсная характеристика является оригиналом
по отношению к передаточной функции. Используя таблицы
преобразований Лапласа, получаем
h (t) = д (?) — 2ае <r(z).
150
Аналогочно,
g(t)=K(p)!p- g(t)=(2e~a‘—l)a(/).
8.30. Воспользуемся тем, что переходная характеристика есть
интеграл от импульсной характеристики. Тогда
р sin со,
g(0=— —— d«.
л J сов<;
— co
Выполнив замену переменной х=<в,£, находим
Ко
g(‘) = ~
л
sinx
— dx.
Данный интеграл выражается через специальную функцию — ин-
тегральный синус
Так как
и, кроме того, Si(—оо)= — л/2, то
g(0=—Г;+Я(аМ)
л 2
График полученной зависимости приведен на рис. Ш.8.3.
Так как Si(oo)=n/2, то величина tycT должна удовлетворять
уравнению
л/2 + Si (совгуст/2) = 0.9л
или
Si (со,густ/2)= 1.2566.
151
По таблицам интегрального синуса [4] находим w,zyCT=2.8, т. е.
/уст=0.44//.-
8.31. Здесь
О оо
Л(0=— f e^^don-- fe^’^dc^Z.+Z^
2л J 2л J
— со О
Возьмем первое слагаемое в правой части и дополним выра-
жение P2(o2+(ot до полного квадрата:
B2U)2+(Ot = \ B(O-i--I------•
\ 2fiJ 4/F
Тогда
0
-е"Л4Д1 f e^'^dai
2л J
Вводя новую переменную rj — раз + t/(2P), получим
co
Ко , , Г ,
Zi = - e I e dn.
2nP J
o
Входящий сюда интеграл вычисляется так:
со оо
е4’ dtj = j* cos г] dr] +j J sin r]2 dr] = * (1 +j).
152
Таким образом,
Л Pe-^d+A
Аналогично вычисляем второе слагаемое:
Л /VW(1-A
2
Объединив оба результата, находим окончательно
A(z)=—=cos
VW
&
График импульсной характеристики представлен на рис. Ш.8.4.
8.33. Функцию А?(/со), являющуюся преобразованием Фурье от
импульсной характеристики Л (г), удобно вычислить следующим
образом. Находим производную
Л'($=Л5(0-Л(а+1)5(г-7)+Л(а+
+ а2)5(/-2Т)-Л(а3+а2)5(1-37)+Л(а4+
+ о3)5(Г-47)-...=Л5(0-Л(а+1)[5(/-
-7)-аЗ(1-2Т)+а250-37)-А25(1-47) + ...].
Ее преобразование Фурье
G (со)=А - А (а +1) е-/аГ[1 - а е-/шГ+ а3 е->2“г-...].
Суммируя бесконечную геометрическую прогрессию, получаем
7-415
153
(7(ш)=Л| 1-
(a+V)e°T
откуда
Несложные тригонометрические выкладки приводят к следу-
ющей формуле для нормированной АХЧ данной системы:
шТ
\K(ja>T)\_2 ап 2
ЛТ +2acos<oT+a2
На рис. Ш.8.5 представлены кривые, построенные по этой фор-
муле при а=0.4 и а=0.8.
8.37. Так как
Л(0=| J 5(0^,
t-T
то при точка £=0, в которой сосредоточена ^-функция,
принадлежит области интегрирования и поэтому h(f)= 1/Т. Если
же t<0 или t>T, то очевидно, что Л (0 = 0. Отсюда видно, что
данный фильтр является физически реализуемым. Выполнив пре-
образование Фурье, получаем
K(ja)=— (1—e-Jtor).
8.38. В соответствии с принципом спектрального метода
Utaa(t)=
С/оЛо UqKo fsina>t Г1 1
=-------1----I------dco=L70Ko| - + - Sl(w,0 I.
2 л J cd [_2 л J
о
Отметим, что аналогичное решение другим методом было полу-
чено в задаче 8.30.
154
839. Используя метод интеграла
Дюамеля, основываемся на том, что
импульсная характеристика идеаль-
ного ФНЧ
Л(0=-------.
Поскольку входной сигнал отличен
от нуля лишь на отрезке времени [О,
tJ, получим
,. UoKarn, Г апш,(/-т)
«жых(0 =----- -----r CdT-
О
Выполнив замену переменной x=co,(t—t), имеем
I (sinx/x)dx.
“W
Данный интеграл преобразуем следующим образом:
о>а(‘-Ч>
откуда
[ГпКл
На рис. Ш.8.6, а, б изображены графики зависимостей, построен-
ные по последней формуле применительно к достаточно корот-
ким импульсам (<овтв=1 и 2), а также применительно к более
длинному импульсу с параметром ш,тв=20 Следует обратить
внимание на различный характер искажений коротких и длинных
импульсов.
8.41. Передаточная функция системы
ад=_Л_-=_^_>
R+pL р+1/t
где t=LjR — постоянная времени цепи.
155
UR(P)=
Я(1/г)
^(p+l/z)
Используя соответствие
———=at—(1— е “),
p’O+e)
получаем выходной сигнал
ия(1)=А (1—т)+Ате~',\
t>0.
График полученной зависимости представлен на рис. Ш.8.7. Вид-
но, что напряжение ия при г-» со стремится к прямой, которая
повторяет закон изменения во времени входного напряжения,
будучи, однако, смещенной на постоянную времени t в сторону
запаздывания.
8.42. Воспользуемся выражением импульсной характеристики
ЛС-цепи:
При 1<тя имеем
, . I , ч ч . -t/RC I t/RC .
««х(0= и» (*)*('-*) dr=—е е dt=
= U0(l-e~,IRC).
Соответственно при />т„
156
t
о
Введем переменную интегрирования jc=£/t.
Тогда
»/»
Uua (f)=ate~‘lx Jxexdx
о
Интегрируя по частям, получаем
иив(0=от
График данной зависимости представлен на рис. Ш.8.8 (кривая
7). Здесь же изображена прямая 2, соответствующая входному
сигналу.
157
8.45. При Т<тж
m«(0= tfoj [5(/-t)-2ae““('-r)]dt=
О
t
= Go-laGoe-" je‘ndt= C70(2e“"-1).
о
При t> t,
Uex(z)= Uo J[5 (t-t)-2ae““(r-^dt=
о
= -2aG0e“'|e"dt= -2Goe“a'(e",,-l).
о
Рассчитанная осциллограмма выходного напряжения показана
на рис. Ш.8.9.
Тема 9
9.3. Частотный коэффициент передачи JV-ступенчатого уси-
лителя
К{}(О)=--------------.
[1 +Лж(<О-<Орсэ)1
Выражение АЧХ данной системы имеет вид
На граничной частоте полосы пропускания имеет место ра-
венство
[1+ti (Шгр-шРс)2]АГ/2=\/2’
откуда
По.707 = — 1.
158
9.9. В выражении для частотного коэффициента передачи
усилителя
K(j(o)=
[1 +j(fi>-copo)T1i][l +j(co-ajpa)Tl2]
делаем замену переменной со=сора+£1 и переходим к частотному
коэффициенту передачи низкочастотного эквивалента
Kn(JQ)=-----.
(1+Л>Тж1)(1+;ПТж2)
Соответствующая передаточная функция
(Р+В1)(р+В2)
где Кл=Ктп\К!„->, ai = l/tIb Используя таблицы преоб-
разований Лапласа, получаем
Л- (0о (О,
«2~“1
откуда
Л(0=--------(е — е ^cosojpatoit).
«2-«1
9.17. Комплексная огибающая сигнала на входе
U„, КО,
U„e'lau, t^O.
Так как
то при t<0
0^(0= |
— CD
«/’ж
^-K^U^-"4 | exdx=-^pe3C7m.
- 00
159
При
о
-со
I
fe«e-«-№de=
О
ЧЧ
V ТТ I -V-
ЛфезС/лС I в QX,
О
где b=6(o tK — безразмерный параметр, характеризующий от-
ношение частотной расстройки к полосе пропускания контура.
Проводя интегрирование, получаем
1+jb
Для построения графиков удобно ввести переменную х= t/tr При
этом физическая огибающая для i>0
C4»(x)=|tU(x)l=
=KpaUJ(x),
где
/(x)=-J= [cos2 bx+
y/l+b2
+(sin bx+b е-х)2]1/2.
Графики функции /(x) для случаев
b=l и b=3 представлены на рис.
Ш.9.1.
9.18. Здесь
0,(0=0о<Ф); е ,1/(46).
г^тЛ
Тогда
со
^(0= f t7«(r-4)A„,(4)d«=
J WW
со
где Ф (х) — интеграл вероятностей.
9.20. Используя метод интеграла Дюамеля, получаем
где Ь=6(О'тт — параметр, характеризующий расстройку колеба-
тельной системы относительно частоты заполнения входного
сигнала.
9.22. Возможный текст программы представлен ниже (рис.
Ш.9.2):
х:=О,О..1О
b:=5d:=0.0
Ко: = 25 U0:=2
U(x): = 1 ^U° <exP(~d X+J ь)~
1-d+jb
-ехр(-х))
Рис. Ш.9.2
161
В соответствии с обозначениями, принятыми в задаче 9.21,
здесь введено безразмерное время х, а также безразмерный пара-
метр b и d. Заданы также численные значения величин <70 и Ко-
Полезно провести серию численных экспериментов, подбирая
различные значения b и d и наблюдая за тем, как этот выбор
влияет на протекание процесса.
Тема 10
10.1. Реализация сигнала на выходе системы
откуда
СО
f 3^)Л(/-о^=о.
Далее,
со
j J^^b^Ao.-eoA^-^d^d^.
— со
Если входной процесс — белый шум со спектром мощности
Wo, то Д,(&, £2)= WoSПоэтому
ядп, /2)=^о J *(ri-e)A(r2-e)d{.
Обозначим *2=^4-т; 6 —£=>/; /2—{=ч+т.
Тогда
Ry(r)=W0 J h(ri)h(ri + T)dTi.
— 00
162
103. Рассмотрим два подхода к решению данной задачи,
а) Прямой метод
Ясно, что y(0=x(/)+x(Z—7). Тогда
=[х(0+х0-7)][х(/+т)+х(/+г-7)]=
=х(/)х(/+т)+х(0х(/+т-7)+
+х (t—Т) х (t + т)+х(/—7)х(/+т—7)=
=2Ях(т)+2?х(т- 7)+Лх(т + Т).
6) Спектральный метод.
Частотный коэффициент передачи цепи +е .
Квадрат модуля коэффициента передачи
K(jto) К* (jai)=2 (1 +cos со 7).
Если JPx(co)—спектр мощности входного случайного сигнала,
то по теореме Винера — Хинчина
1 f / >иГ4- ~J“a\
Я,(т)=- И'ЛшИ 1 +—у—je*vtdw=
“вс
=2Ях(т)+Ях(т-7)+2?х(т + П
что совпадает с результатом, который получен прямым методом.
10.16. Здесь
|Х0<о)|2=A 2Т2 ma(<0^2).
(шТ/2)2
Для нахождения функции корреляции необходимо вычислить
„ t ч И'оЛ’Т’ Гяп2(шТ/2)
ЛЖ1И('г)=---I-------^coscordco.
я J (а>Т[2)
о
Имеется табличный интеграл
Гп
fsin2ax'cos26x 1~(с—Ь), Ь<а,
—?—dx=r
i (о,
163
Таким образом,
;рм2(г-М),
'о,
kl<r,
|7|>Г.
10.17. Находим спектр мощности
РКх(ш)=2дх ie ” cos art di
J а2+аг
о
Односторонний спектр мощности
2ejja
я(а2+в»2)
Дисперсия сигнала на выходе
Тема 11
11.1. На основании графика ВАХ составляем таблицу значе-
ний аппроксимируемой функции в выбранных узлах:
Un, В -1.5 -1 -0.5
ic мА 0.5 1 2.5
Отсюда получаем систему уравнений
Оо—0-5в14- 0.25а2=0-5,
Оо=1.
До 4" 0.5в14" 0.25о2 —2.5.
Решив ее, находим, что а0=1 мА, ^=2 мА/B, а2=2 мА/В2.
11.6. Угол отсечки тока о находим из соотношения
164
0.8—0.5 Л ,
cos fl =------=0.6,
0.5
откуда в =0.927 рад=53°. Соответствующие коэффициенты Берга
Уо=- (sin fl — fl cos fl )=0.077,
Vi =- ( fl —sin fl • cos a )=0.142.
Спектральные составляющие тока
/о=5С7туо=О.581 мА,
Ii = SU„ yi = 1.067 мА.
Так как точность кусочно-линейной аппроксимации не слишком
велика, то полученные цифры целесообразно округлить: 10=
=0.6 мА, Ii = 1.1 мА.
11.9. Записываем ВАХ транзистора относительно рабочей
точки L70=0.9 В в виде
4=Oo+ai (wfo-0.9) + e2(wfe—0.9)2+
+сз(«бэ—0.9)3 мА.
При этом
в0=1ж| =15-40 0.34-6.5 0.09-
М61-09
-2.5 0.027=3.52 мА,
=40-13 0.34-7.5 0.09=
Мбэ-0-9
= 36.78 мА/В,
= 13 0.54-2.5-6 (-0.3)/2=
Мбэ-09
=4.25 мА/В2,
Л *
а3=-
6 «бэ-0.9
=2.5 мА/B3.
Отсюда
U1
Jo=во 4- в2—=4.7 мА.
2
165
11.13. Воспользуемся тем, что ВАХ данного нелинейного ре-
зистора есть разность двух кусочно-линейных функций. Вводим
два угла отсечки тока в, и в2в соответствии с формулами:
«Ли-Ц» С42-Ц)
cos 0i=-------; cos 62=------.
и„ ' Vn
Тогда
Z.=SDM(yR(o1)-yR(o2)).
11.15. На основании общих принципов вычисления коэффици-
ентов ряда Фурье имеем:
Уо(2, й)=- I (cosf—cos o)2df,
Я J
о
у„(2, о)=-J (cos cos o)2cosnfdf, n=l, 2,...
о
Явные выражения двух первых коэффициентов разложения име-
ют вид
у0(2, «)=-
Я
[0 |-+COS2 о
V
3 . „
— sin2 о
У1(2, о )=-
я
яп’о
sin о — о cos о------
3
Соответствующие графики представлены на рис. III.11.1.
11.18. Косинус угла отсечки
coso =(0.7—0.3)/0.8=0.5,
откуда д=л/3 = 1.047 рад.
Соответствующие коэффициенты Берга у0=0.109, yi=0.196.
Составляющие токов 7^=0.058 А, 1^=0.696 А, /16=0.103 А,
7,ж= 1.236 А.
Входное сопротивление колебательной системы
Л„ = /с2„Лрез=48 Ом.
Полезная мощность на выходе
166
Pi»»=^^=36.7 Вт.
Амплитуда колебательного напря-
жения на коллекторе
Um=1^= 59.3 В.
Амплитуда напряжения на контуре
£4™=^*.™=1480 В.
Мощность, потребляемая от источника питания,
Ро=/охДпгт=48.7 Вт.
Мощность потерь
7>пот=Ро—Pi.«=12 Вт.
КПД усилителя
>/ = —100% = 75.4%.
48.7
Мощность первой гармоники на входе
Pi«=Z4,«Zi<5/2=0.041 Вт.
Коэффициент усиления мощности
К/>=Р1»ЫХ/Р1„=89О или 29.5 дБ.
11.23. Мощность, потребляемая от источника питания,
Р3 = Ршгг^0=Рщгт‘5^41жх}’0 ( d).
Полезная мощность
Рг — UnmtJiP. ~ EvsnSUmn У? ( Й )•
Отсюда КПД
72(d) 1 sin2d-cosd — 2cos2dsind
tj =-----=- -----------------------
2y0(d) 6 sind — -Ocosd
График, построенный на основании этой формулы, изображен на
рис. III. 11.2. Из графика видно, что для обеспечения приемлемого
КПД угол отсечки тока в удвоителе следует выбирать существен-
но меньше 90°.
167
11.24. Так как Ii=SUmnyi( о), то для решения поставленной
задачи достаточно проанализировать зависимость безразмерной
величины Ii/(SUm)=yi от параметра £=(и0-ия)/ит= -cos о.
Известно, что
?! ( а)=- ( & —sin a cos fl ),
п
откуда
(0)=- [arccos (- 0+5 \Л~£2]-
Л
График, построенный по этой формуле, приведен на рис. III. 11.3.
11.28. Входное сопротивление детектора не зависит от амп-
литуды входного сигнала:
Так как е«:1, то
У1(в)=-( d — -sin 2 fl )»2fl3/(3n)
я \ 2 /
и из уравнения tgfl — о =л/(/?в5) следует, что
б3/з=л/(ад.
Итак,
yi(fl)»2/№S),
откуда
^аЛя/2.
11.29. Один из возможных вариантов текста программы при-
веден ниже:
MSUm)
11 Нх! 0.75 \ 0.5 Д- 0.25 0 30 60 90 120 9, грап Рис. III.11.2 168 Л" Z LLj P.g > 0,6 f ^^0,4 / °'2\ -1.0-Q&0&Q4-Q2 0 020,40.60.81.0 Uq-Uh ~Um Рис. III. 11.3
uses WinCrt;
var
E, R, S, T, B, Tl, KDET:real;
begin WriteLn(’PAC4ET ДИОДНОГО ДЕТЕКТОРА’);
WriteLn;
WriteLnfBBOAHM сопротивление нагрузки R’);
ReadLn(R);
WriteLnfBBO/iHM крутизну BAX диода S’);
ReadLn(S);
WriteLn(’BBOflHM погрешность вычисления угла отсеч-
ки’);
ReadLn(E);
B:=Pi/(R*S);
Т:=0;Т1: = 0;
repeat
T:=T1;
T1: =АгсТап(В+Т);
until Abs(Tl—Т)<Е;
WriteLn(’Yron отсечки=’, Т:5:3,‘радиан’);
WriteLn;
KDET: —cos(T);
WriteLn(’Ko304>HnHeHT детектирования = ’,KDET:5:3)
end.
Данная программа, а также другие Pascal — программы, при-
веденные в книге, написаны с использованием среды програм-
мирования Turbo Packal for Windows фирмы Borland. С неболь-
шими изменениями программа может быть воспринята любыми
другими компиляторами языка Pascal.
Имена переменных в программе выбраны следующим об-
разом: R — сопротивление резистора нагрузки, S — крутизна
ВАХ диода, Т — угол отсечки тока, Е — абсолютная погреш-
ность вычисления угла отсечки, KDET — коэффициент детекти-
рования, Т1 — вспомогательная переменная, необходимая для
организации итерационного процесса.
1131. В данном случае обратная функция х=у/у[а однознач-
на. Ее производная
dx_ 1 1_ 1
4У 2у/у/а ° 2у/ау
Так как всем отрицательным значениям входного сигнала, име-
ющим общую вероятность 1/2, отвечает единственное значение
выходного сигнала _у=0, то
169
О, у<0,
Аш(У)-<1г(>,)+_ е—у>0.
I2 2у/2паувх
1133. Так как математическое ожидание входного сигнала
равно нулю, то очевидно, что Ра—Рь—1/2. Используя принцип
усреднения, получаем
а+Ь
2 '
о —ч _ _ в2 h2 (o+h)2 (о—b):
*22 4 4
Тема 12
123. По определению, дифференциальная крутизна
S'„*=dic/d«M.
Подставляя сюда выражение для напряжения, создаваемого гете-
родином, получаем (мА/В)
8^=30+ 15 cos со,/.
12.10. Варактор является нелинейным конденсатором, ток
в котором
i= =(d9/d«) (du/dz)=Сгоф («) • (dw/dz).
В рассматриваемом случае
Ь\<й$и*
i (l) = — b0a)0Um sin a)ot--— sm 2о)0Л
Таким образом, данный варактор можно использовать для со-
здания удвоителя частоты гармонического сигнала.
12.15. По условию задачи усиление системы
A=101g/C,=201g—=25.
Gr + GH+GBH
Отсюда
Gm= -4.045Ю-3 См.
170
12.19. Для самовозбуждения усилителя необходимо обеспе-
чить вносимую отрицательную проводимость G„= —4 10 3 См.
Применим формулу для расчета активной проводимости, вноси-
мой в сигнальный контур данного усилителя [1]:
Gm— Р ДОсОДюлСо -Лрез.ход/4.
Подставив числовые значения, получаем 7?рг,тПп=4.5 кОм.
Тема 13
13.2. В соответствии с методом Фостера разложим входное
сопротивление на элементарные дроби:
Z(p)= 16р*+4р _ар+ь + cp+tf
W ~ (2P2+1) (бр3 +1) “ +1 бр2+1 ’
где a, b, с и d — подлежащие определению коэффициенты. При-
равнивая коэффициенты при одинаковых степенях р, получаем
систему уравнений
6а+2с=16,
66+2d=0,
а+с=4,
b+d=O,
из которой следует, что а=2, 6=0, с=2, J=0.
Таким образом,
гу, \
Z (р)=— ---I-—-—•
2^ + 1 6/Р + 1
Легко показать, что входное сопротивление параллельного LC-
контура
Z£c(p)=-r^--
Учитывая это, получаем схему синтезированной цепи, приведен-
ную на рис. Ш.13.1.
13.9. Проводя деление числителя на знаменатель, начиная со
старших степеней, на первом этапе получаем
_8р3+4р |Зр2+1
8р3 + 8р/3 8
4р/3 зр
171
Таким образом,
4р
Z<A=-3P+^-
Инвертируя остаток, имеем
„ 8 1
Z(p)=-pd—-—.
з 3j? + l
4р/3
Проводим следующий этап деления:
_3р2 + 1|4р/3
Зр2 9р/4’
1
Окончательно получаем представление функции Z (р) в виде цеп-
ной дроби:
8» 1
—ч—
4 4р
3
Легко видеть, что этой дроби отвечает цепь, схема которой
изображена на рис. III. 13.2.
Если делить числитель на знаменатель, начиная с младших
степеней, то на первом же этапе остаток получается отрица-
тельным:
_ 4р+8р3|1+Зр2
4р+12р3 4р
—4р3
что ведет к физически нереализуемой цепи.
13.15. Коэффициент передачи мощности как функция перемен-
ной ря выражается формулой
8/3 Гн
2Гн 2Гн 1Ф ЗФ Рис. Ш.13.1 172 9/4 Ф =к 4/3 Гн - — — Рис. III.13.2
Полюсами данной функции являются корни биквадратного урав-
нения
ря4-2р2+2=0,
равные
А1дм= ±У1±Л
Так как
то
Vi+J=v'2ew; у/1Ч=Х/гем'.
Имея в виду, что Kf(p^—K{p^ • К(—р^, получаем выражение для
/С(р„), учитывая лишь те полюсы, которые лежат в левой полу-
плоскости:
13.17. Нормированная частота источника сигнала
/„=41/15=2.733.
Коэффициент передачи мощности
^=Ло2/(1+/;*)=0.015.
Модуль коэффициента передачи напряжения
/^=^/2=0.122.
Отсюда амплитуда выходного сигнала
С4п»в=7.5 0.122«0.92 В.
13.18. Обозначив посредством Z' (р) операторное сопротивле-
ние параллельного соединения С и Rx:
2'(р)=ад+рад,
получаем следующее выражение передаточной функции фильтра
по напряжению:
173
R+Z’(p) l+pA'C’
где R'=RRJ(R+R^.
Отсюда следует, что функция К(р) имеет единственный полюс
в точке с вещественной отрицательной координатой pi= — 1/
!<R'C}. Если положить, что 1/(Л'С)=<вс, то рассматриваемая си-
стема имеет свойства ФНЧ с характеристикой Баттерворта пер-
вого порядка при заданной частоте среза.
Обращаясь к конкретному расчету, выберем R=RX=2 • 10э Ом.
При этом Л'=103 Ом, откуда С=1/(3‘ 108)=3.33 нФ.
13.24. Коэффициент передачи напряжения
л (р)=------------=
рЛ+Лж/(1 4-рЯ.С)
р1+2(ц>+в>Г
где а= 1/(2ЛжС), п>о= 1/(ЬС).
Данная функция имеет полюсы в точках с координатами
Ри= ±-«Ua/oJo-»2-
Для того чтобы фильтр обладал требуемой частотной харак-
теристикой, необходимо, чтобы
a=(ojy/i\ соо^Щс,
откуда
С= 1/^/21Цвс)=7.86 нФ; L=1/(<bc2Q=22.6 мГн.
13.25. Фильтр нижних частот с максимальной плоской харак-
теристикой второго порядка на плоскости нормированной комп-
лексной частоты имеет два полюса частотного коэффициента
передачи в точках с координатами р«и= —
Передаточная функция фильтра
ад=--------1----=|К| е>г.
(р-лМр-л)
Выбирая на вертикальной оси произвольную точку с ординатой
со. (рис. Ш.13.3), видим, что ФЧХ фильтра определяется двумя
углами ф( и <р2'
<Рк(“>я)=
174
Отсюда
Фк(<Ож)= -arctg(^/2 со,- l)-arctg(v/2cox+1).
График, рассчитанный по данной формуле, представлен на рис.
Ш.13.4.
13.28. Многочлены Чебышева Т„(сэ^) принимают значения,
лежащие в интервале (— 1, 1). На границе полосы пропускания
Тя(1)=1 при любом п. Таким образом, коэффициент недодачи
мощности колеблется в пределах от 1 до 1/(14-е2). Неравномер-
ность частотного коэффициента передачи, выраженная в децибе-
лах, составит величину А= 101g(l+e2). Из условия задачи нахо-
дим, что
£=V1O02-1=0.7648.
Тема 14
14.1. Выходное напряжение эмиттерного повторителя
u^a=RBiT=SR^ =SRa(un—uMay
Деля обе части этого равенства на величину и„, получаем
Kv=SRn(l-Kv),
откуда
Kv=
SRK
1+5Л,’
Следует отметить, что здесь параметр обратной связи /?= — 1.
Так как в данном случае все выходное напряжение приложено ко
175
входу цепи, имея полярность, противоположную полярности
входного сигнала, то говорят, что эмиттерный повторитель охва-
чен 100%-ной отрицательной обратной связью.
14.3. Так как входное напряжение uu=v + Uo« то напряжение
на резисторе обратной связи
Woc = SJ?Oc(u»x-Uoc),
откуда
““ 1 +
Возрастание тока коллектора ведет к понижению потенциала
коллектора относительно общей точки усилителя и поэтому
п . _ СП (1 |
\ l+SR^J
Отсюда коэффициент усиления
Kv=-SRJli + SR^R^R^.
Так как Kq= —SR„ то параметр 0= —RoJRK.
14.5. Условно примем в качестве положительных такие напра-
вления токов в ветвях, которые указаны стрелками на рис. 1.14.4.
На основании первого закона Кирхгофа имеем следующее урав-
нение состояния цепи, записанное относительно изображений Um,
Um и Ua:
U.m-Ug |
Лг+1/(Р^2)
(1)
Так как Um=KoU0, то из (1) следует, что
14ых(1-1/Ло) u^-u^IKq
R2+l/(pC2) Ri
UyaPCl
Ко
откуда
I-KWKq K(p) _
------------1----------------pCi=O.
Лг+1/(рС2) Ri Ko
(2)
Разрешив данное уравнение относительно К (р), получаем
176
(3)
К(р)=—----------------------------.
p^C.^Q+p^.q+AzCz-CXb-lJ^iCJ + l
Частотный коэффициент передачи K(j<o) находим, выполнив за-
мену переменной ]<о—р:
YJ™ J =-Z----------------------------
1 —e>JAiC|^2Cz+/to[^Ci + А2С2— (Ао— 1) AjCJ
Для того чтобы полюсы функции К(р) располагались в левой
полуплоскости переменной р (условие устойчивости), необходи-
мо, чтобы все коэффициенты при различных степенях р в знаме-
нателе формулы (3) были положительны. Отсюда получаем нера-
венство
Л1С1+Л2С2-(Ло-1)Л1С2>О.
Таким образом, критическое значение коэффициента усиления
активного звена
-г । _ А|С1+Й2С2
а.с2
При заданных в условиях задачи параметрах системы нор-
мированная АЧХ фильтра
|К(Ю1 1
*ь Vo-iV+ootose1’
где ^—(oRC. Соответствующий график приведен на рис. III. 14.1.
Можно сделать вывод о том, что рассмотренный 7?С-фильтр
пригоден для выделения полосового сигнала, спектральные со-
ставляющие которого концентрируются вблизи «резонансной»
частоты сорС1= 1/(ЯС).
14.6. Так как потенциалы на выходе и на инвертирующем
входе ОУ совпадают, то изображение выходного сигнала
С7.ых=А0(С7и-С7ип),
откуда
При AJj-»oo/C(p)-»l. Таким образом, данная цепь может быть
использована как повторитель уровня напряжения, имеющий
высокое входное и низкое выходное сопротивления.
177
14.11. Уравнение АФХ разомкнутой системы имеет вид
w О) = - К$/(\ +/<ат)3=- ~ ехр [/ (я -
(1 +вгт2г'а
—3arctgtor)].
Легко проверить, что argw(/0)=n, в то время как argwG'co)=
= —я/2. Это указывает на то, что годограф Найквиста, отвеча-
ющий интервалу частот 0<со< + со, имеет вид витка спирали.
Соответствующий чертеж представлен на рис. III. 14.2; виток,
отвечающий полубесконечному интервалу отрицательных ча-
стот, показан пунктиром. На частоте tob при которой я—
—3arctgto,T=0, аргумент АФХ равен нулю. Для того чтобы
замкнутая система была устойчивой, необходимо, чтобы
^/(1+шЬ2)3/2<1.
Так как согг= 1.732, то Ко<2.
14.19. Воспользуемся условием самовозбуждения [1]
Ко> 1 + (7?,^+/?2С2)/(/?2С1).
Подставляя сюда номиналы элементов, приведенные в условии
задачи, получаем, что Ко>2.33. Генерируемая частота
(0^=1/ч/ЛЛ2С1С2=3.208 • 103 с"1.
14.23. На пороге самовозбуждения, при 17=0, должно выпол-
няться
а,=RCjM^=IKtOoQM,^.
Отсюда Afmm=l/(aiCOoO=6.66 • 10 8
178
\l(a0QM)—'i.3A' 10 * См. Амплитуда колебании в стационарном
режиме должна удовлетворять уравнению
10~3-1.875 10-3С7*=3.34-10_*
решив которое получаем Va=0.596 В.
Тема 15
15.2. Коэффициенты комплексного ряда Фурье С„ при л=0,
+ 1» ±2,... равны
«л
„ 1 f -рял/д . тйп(ляг/Д)
Ся=- I е а/=----------------.
Д J Д mtt/Д
-t/2
Суммируя вклады всех гармонических составляющих, имеем
5{(<в)=— £ [sin(>wrr/A)(>wrr/A)]5(to—2ял/Д).
. Д „—в
15.6. Будем полагать, что интервал дискретизации Д мал
настолько, что А« 1/ot. Тогда приближенно
5дап(0)«2аС7о
1 1
(2я/Д)2 (4я/Д)2
+(бя/Д)2
2аЦ»Д2
1 1 1
-т-Ь-т-Ь-!
22 42 б2
Полученный здесь ряд суммируем, основываясь на том, что,
согласно [4]
Е(2^-1)-3=1+А+1+...4
k-l 3 3 8
£*-х=1+-+-+...= С(х),
*-| 2х 3х
где С(х) — так называемая дзета-функция Римана, имеющая ча-
стное значение С(2)=л2/6. Итак,
179
Отсюда ^допСО)» at/оД2/12- Следует отметить, что 5u(0)=L70/a
и поэтому 5доп(0)/5и(0)=(аД)2/12. Если, например, аД=я/100, то
S'nOII(0)/iS'u(0)=8.22 -10"’, т. е. дополнительный вклад в спектраль-
ную плотность, возникающий за счет дискретизации, достаточно
мал.
15.9. При #=8 в пределах импульса оказывается три отсчета.
Тогда, положив п=1, имеем
Суммируя геометрическую прогрессию, получаем
тг 1
С,=—— ---------=0.301 Uoe~J”°. (1)
8 1-е'*
Если #=32, то в пределах импульса оказываются 11 отсчетов.
Поэтому
ТТ Ю V 1 .-»*’**«
С,=-“ У «-** ‘=-"1^---------0.2814«,е-'*”’. (2)
32*е0 32
Легко найти, что коэффициент Q ряда Фурье аналогового
сигнала
С1=О.276С7ое-'“'. (3)
Сравнивая выражения (1), (2) и (3), убеждаемся, что с ростом
N коэффициент G ДПФ стремится к соответствующему коэф-
фициенту ряда Фурье того аналогового сигнала, который был
подвергнут дискретизации.
15.10. По общей формуле находим:
С0=Л (10+20)= 10,
С, = ‘ (1Ое-'120"+2Ое-'240”),
С2=^(10е‘:/240’+20е_'480’).
Так как
-/120° -/480° 1 .-УЗ
е =е =-------------]—.
2 2
180
-j2«f 1 , V3
e = —Fj—,
2 2
TO
15.15. Возможный текст программы приведен ниже:
uses WinCRt;
const
N=10;
var i,M:integer;
var X: arrayfl.. 16] of real;
var A,B,T:real;
begin
WriteLn(’PacHeT коэффициентов ДПФ*);
WritelnfMaccHBa действительных отсчетов4);
WriteLnf из ’,N,* Элементов*);
WriteLn;
\УгкеЬп(’Введите значения элементов массива*);
for i:=1 to N do Readln(X[i]));
WriteLn(’BenjecTBeHHa« и мнимая части ДПФ*);
WriteLn;
for i:=0 to N-l do
begin
Writein (’Гармоника номер*,!);
A:=0;B:=0;
for M:=0 to N-l do
begin
T:=2*pi*M*i/N;
A:=A+X[M]*cos(T);
B:=B+X[M]*sin(r);
end;
A:=A/N; B:=B/N;
WriteLn(A:7:3,B:7:3);
end;
end.
Для определенности длина входного массива N выбрана равной
десяти и описана в разделе констант. Перед компиляцией это
значение можно произвольно изменять.
15.16. Так как число компонент вектора X не совпадает с це-
лой степенью двойки, то по правилам системы MathCAD для
вычисления БПФ следует использовать библиотечную функцию
cfft(X). Результаты представлены ниже:
181
Вычисление прямого и обратного быстрого преобразования
Фурье средствами пакета MathCAD
1.5 6.94
4 - 3.266+2.12Н
Х: = 5 Y:=efT(X) Y: = - 0.408+3.536i
3.5 4.082
7 -0.408—3.5361
. -4. -3.266 -2.121i
Z:=icff(Y)
1.5
4
5
3.5
7
-4
15.20. Воспользумся разложением
(i-o-1=i+£+e+...
Тогда
X(z)=1 + 0.3z"1 +0.09z" 2+0.027z~ 3 +....
откуда
{хя}=(1, 0.3, 0.09, 0.027, ...).
Общий член последовательности хя=(0.3)".
15.23. Функция X(z) аналитична во всей z-плоскости, за ис-
ключением точки z=0. Поэтому в формуле обратного z-преоб-
разования интегрирование можно вести по любой замкнутой
кривой L, которая охватывает начало координат. Согласно те-
ореме Коши о вычетах
л=-1,
л#-1.
Отличным от нуля оказывается лишь отсчет
182
Итак, {х„} = (0, О, 1, О, О,...).
15.26. Используем алгоритм дискретной свертки [1]. На одной
полоске бумаги через равные интервалы записываем сигнал {х„},
а затем на другой полоске — сигнал {у„}, в котором позиции
расположены справа налево (рис. Ш.15.1, а). Совместив первые
позиции записей (рис. Ш.15.1, б) и перемножив отсчеты, находя-
щиеся на одной вертикали, находим 15• 10= 150. Чтобы полу-
чить величину /ь следует передвинуть полоски на одну позицию
(рис. Ш.15.1, в). Тогда/1 = 15’ 10 + 15’5=225. Выполняя эти опе-
рации до тех пор, пока ненулевые отсчеты не перестанут накла-
дываться, находим
{4}=(150, 225, 175, 130, 84, 42, 16, 5, 1, 0, 0, 0,...).
15.27. Импульсная характеристика
{й„}=(4, -2.5, 0.8).
Системная функция есть z-преобразование от {h„}:
#(z)=4-2.5/z+0.8/z2.
Выполнив замену переменной z=exp(/coA), получаем
К (joj)=4—2.5 ехр ( —jcoА)+0.8 ехр ( —j2xoА)=
=4—2.5 cos соА+0.8 cos 2шА —j (2.5 sin соА+
+ 0.8 sin 2шА).
1530. В соответствии с формулой обратного z-преобразо-
вания
При т#0 подынтегральная функция имеет один простой полюс
в точке z=0.6 с вычетом res=(0.6)”1. Отсюда по теореме Коши
йт=2.5(0.6)т~1. Если же/п=0, то
Рис. Ш.15.1
183
<i—dz- =о,
•J z(z—0.6)
поскольку вычеты в точках полюсов z=0 и z=0.6 равны по
модулю и противоположны по знаку: resi=l/(—0.6), res2=1/0.6.
Окончательно
, ( 0, ш=0,
Ат )
12.5(0.6)"“*, т= 1,2,3,...
1532. Выполнив ^-преобразование разностного уравнения
фильтра, имеем
Y (z) (1 —z~1 + 0.5z“ 2)=X(z).
Отсюда системная функция ЦФ
— - - — —
1—z-1+0.5z-2 z2—z+0.5
Общий член импульсной характеристики находим из обратного
z-преобразования:
” 2я/ J z2—z+0.5
Представим подынтегральную функцию в виде
т+1 т+1
Z Z
z2—z+0.5 (z—zi)(z—z2)
Очевидно, что точки полюсов имеют координаты
’«л 1 ±/*/4
zu=-(l+/)=-= е" .
2 ^2
Вычеты подынтегральной функции в точках полюсов
^4-' 2*1+1
гев] =----, res2=---.
Zj —Z2 ?2_г1
Сумма вычетов
У res,——— (z7+1 -zy+,)=2° ~mJ/2 sin Г- (m+1)
i *i-*2 L4
184
Отсюда
йи=2(1_т)/2г’
sin -(m+l) , zn=O, 1, 2, ...
1537. Возможный текст программы представлен ниже:
uses WinCrt;
const
аО=2.5;Ы = 1.5;Ь2= —1.33;
var
y,yl,y2:real;
X:array[l ..100] of real;
N:integer;
begin
{Подготавливаем массив входных данных}
for N: = l to 100 do
if N= 1 then X[N]:=1 else X[N]: =0;
yl:=0;y2:=0;
{рассчитываем импульсную характеристику фильтра}
for N: = l to 20 do
begin
y:=a0*X[N]+bl*yl +b2*y2;
y2:=yl:yl: = y;
WriteLn(N,y:12:3);
end;
end
Для простоты коэффициенты, входящие в алгоритм цифровой
фильтрации, конкретно определены в разделе констант. Массив
входных чисел выбран длиной в 100 отсчетов, что в данном
случае вполне достаточно. Следует провести ряд численных экс-
периментов с данной программой, подбирая значения коэффици-
ентов фильтра таким образом, чтобы реализовать как устой-
чивые, так и неустойчивые режимы работы ([1], с. 412).
Тема 16
16.1. Рассматриваемая цепь линейна. Для нее справедлив при-
нцип суперпозиции. Поэтому напряжения шума и гармоничес-
кого сигнала на выходе могут быть найдены по отдельности.
В данном случае
_ tZ’"“
®вых t'rawx ,---------------
V 2RC ^1 +{х,2А2С2
Отношение сигнал/шум удобно представить в виде
8-415 185
nn\l<o0W0 l+vfrRC)2'
Обозначим x=(OqRC. Функция
F(x)=v/x/(l+x2)
имеет единственный максимум при х= 1. Отсюда (RC)om= 1/со0.
16.4. Амплитуда выходного колебания в конце импульса
и»ых(т»)=-expt-TjTj).
Дисперсия шума на выходе усилителя
<йх=
Таким образом, при /=тв
Q_Umu(y -ехр (-Тд/Тж))
Jwoib
Преобразуем эту формулу, учтя, что оптимальный фильтр обес-
печивает отношение сигнал/шум
Сп»х =итпУ/т„/(2Wo) (см. задачу 16.3):
6 = 6m»xf(T«/Tx),
где
г-/ / ч l-exp(-W4)
Функция F(th/tk) принимает максимальное значение, равное 0.9
при т„/тж= 1.25. Итак, 2Оред=0-96т»х- Так как Tx=22/a)pi3, то 2ОПТ=
=0.4й)резти.
16.9. Пусть K^Qto) — частотный коэффициент передачи оп-
тимального фильтра, который нужно найти. Мысленно допол-
ним структурную схему устройства фильтрации так называ-
емым «отбеливающим» фильтром, который преобразует задан-
ный случайный процесс в белый шум с параметром Wo. Легко
видеть, что функция Кот6 (со) должна быть такова, чтобы
|AoT6(M2 W(co)=W0.
186
Для того чтобы не изменить общий частотный коэффициент
передачи, предположим, что отбеливающий фильтр каскадно
соединен с еще одним фильтром, имеющим частотную харак-
теристику 1/А^в(/а)) (рис. Ш.16.1).
В точке 1 полезный сигнал имеет спектральную плотность
Sn{<o)=Km6(j<o)Sn{<o). Поэтому звено, отмеченное на рисунке
пунктиром, должно работать как оптимальный фильтр при бе-
лом шуме и иметь частотный коэффициент передачи
/Г'(/Ш)=Я5Т1(Ш)АХ6(/Ш)е’>ш'0. (1)
Но, с другой стороны,
Х'(/Ш)=Хопт0Ш)/Хот6(/Ш). (2)
Приравнивая правые части (1) и (2), находим, что
или
Kom(i(o)=BW0S^)^°/W(W).
Видно, что числовые значения АЧХ такого фильтра должны
уменьшаться в той области частот, где велика спектральная
плотность мощности шума.
Концепция отбеливающего фильтра часто используется в те-
оретических исследованиях задач обработки сигналов при нали-
чии шумов.
16.15. Спектр мощности случайного процесса вида U(t) ис-
следовался в задаче 7.10. Условие too»a означает, что процесс
U (t) является узкополосным. Поэтому можно ограничиться лишь
первым слагаемым в формуле, определяющей спектр мощности
этого процесса, которое отвечает полубесконечному интервалу
положительных частот:
Wa (ш)=аа2/[а2+(w—ш0)2].
На основании формулы (16.50) из [1] при ш>0 имеем
Рис. Ш.16.1
187
,,, t. м »г(Ш) i
М^Чигг (/O))| — , , , •
FF„(cu) + IF0 1 + И70[<гЧ(ш-о>0)г]/(«гг)
дй фильтр физически нереализуем, так как его ФЧХ
Видно наличие резкого подъема АЧХ фильтра в окрестности
частоты а?о, что свойственно резонансной цепи. Однако, строго
говоря, даь
должна принимать нулевые значения на всех частотах (см. [1], с.
16.20. Воспользовавшись формулой (16.72) из [1], имеем:
С= 3 104 • 3.321g (1 +103 Ъ« 348.6 Кбит/с.
Полученная цифра достаточно оптимистична, однако не еле*
дует забывать, что она относится к случаю, когда мощность
сигнала в 3162 раза превышает мощность шума. Если эти j
ности окажутся равными (вполне вероятная ситуация для л
связи низкого качества), то пропускная способность снизится до
99.6 Кбит/с.
в
РАЗДЕЛ IV
Ответы
Тема 1
1.2. График сигнала приведен на рис. IV.1.1, ти=4.889/а.
(г-г0)<г(г-г0).
1Л».51(г)=^г<т(г)-^
(< - «о) О (г - Го) - -so О (t - Го).
*2(0 =
*з(0
(г—Го)а(г—г0)+
|(Г-Го)<т(Г-Го)-
1.6. Ji (r)=Asina>or
j2(r)=Asma>ot
-Г1)<7(Г-Г1) +------
1.7.Ar(0=lf(0+/(-01/2.
/m(0=[f(0-/(-01/2.
1.8. j
a(t—т)<1т.
1.9. A = 2.5 IO-5 B e.
1.14. £>1/^ WetZo7^.
1.15. Eu= 17^[2(<оти+ф)—ап2(шти+ф)]/(4ш).
1.18. Г0 =0.2277887’.
Рис. IV.1.1
189
1.21., ^=агсаи(т/у/ти1тя2).
1.22. ^=arccos(exp(-a/0)), *о=4.О48/а.
1.30. Ц)=1/у/2, «1=у/з/2/, u2=v/45/8 (Z2-1/3).
131 . Со“1.6620, Ci =0.9011, Сг**0.2263, абсолютная ошибка равна 0.037815,
относительная ошибка равна 0.0189.
1.3 1 Л =0.9963, В= 1.1036, С=0.5367.
135. С2=-1.
136. СЬ=37.9687, С2=3.3188.
137. Q =(е—е-1 — 2)/ч/2=0.768.
Тема 2
2.2. ao/2-=2U(J(PT),
_21/0 РТЦ2п)
а"~ п (РТ/(2п))2+п2'
Лтяп[(а—лш])т/2]
23. С„=---------------.
Т (а—жВ|)т/2
2.5. C1=O.276<7oexp(-J6O°).
2.6. Со= Uq/2; при |л| > 1
jV
2.7. Со=О, С„=—(—1) , л=±1, ±2, ...
пп
2U U 2V
s(t)=— sin<U|t--sin2<0|/4--sin3o>|t—...
я я Зя
График суммы трех первых членов ряда Фурье изображен на рис. 1V.2.1.
2.8. ^я=С„ехр(—J2nntolT),
где Т — пфиод сигнала.
2.10. Л0=2|С$| =0.903 В.
2.11. Л2 =2.122 В.
2.12. во/2=5 В, а, =9.967 В, в2=9-888 В, в3-9.754 В.
2.14. Рср=1/2/3=0.3331/э,
РсрО)=1/2(~+;4+яМ=0.3331/2.
\4 п 81 п J
^=(^cp-^cp(3))/^cp=5.749 10-‘.
190
221. 10-e A c, — 57°31'6".
А
2.22 . <S(co) =--.
(a+jto)1 2
224. e(a>)=S*(a>).
225. Ci (co)=2ReS(co),
C2 (a>)=2jlm S(co).
226. a)/(()= j
6)/(0= j
Рис. IV.2.1
в)/(О=л*(-О-
227. S(co)=(/co)".
233. S(103)=1.5 -IO-4 B e.
234. S(5‘103)=J10-13 A’C.
гл гл ' 't
236. s (I) =---e I cos-----------+sin —— 1.
* \
Л12 -at
237. s(r) =—e o(t).
2
Л _a/
238. s (г) =---(e —e ) a (r).
fl-a
239. s(t)---e a/sincuo to (t).
<o0
1
2.41. S(a>)=ni (to— cun) 4----.
j(oo-CDo)
1
2.42. 5(<и)=я(е*+1)<5(со)+—
jeo
e>tr_ j
2.43. 5(со)=я(ё,* + 1)й(а>—шв)Ч--------.
J(co-co0)
2.44. S (co)=nd (co)+[<5 (co — 2co0)+S (co+2coq)].
2.47. q(t) = ta(t).
191
2.54. U(p)=— (1-е /"и).
P
2.55. S(p)=So(p)/(l-e-pr).
~P‘o
•$0 pt~ ^0 ®
2.56. Sj (p)=—- (1 -e' °)-------,
ZoP2 p
50Г1 /1 /1 1 \ -pt. 1
Si(p}=- — — Г+------------ e +-------e
pUo Vo Vo ti-toJ h-to
e z_4 5° Г1 1 ~P‘o 1 ~P‘l . 1
<$з(р)=~;| “—~e---------e H--------
P Mo to h~ 0 h~h
(Jl, 0<0<l/4,
X57. *Р10(0)=Г -
1-V2, l/4< 0 <1/2,
(V2> 1/2 <0 <3/4,
'*'11(0)4 -
1-V2, 3/4<0<l,
(4, l/4<0<9/32,
'*'44(0) = ^
[-4, 9/32 < 0<5/16.
Тема 3
3.X (u, v)=A\A2<O\!n.
3.3. (w, г)=Л 2exp(—a/o)/(2a).
, . . яЛ*Л2 -^i/Px+i/p,).
3.4. **^((0)=——
y/PlPi
n -o/ms a
3.5. Wnfa^A^ /-e P----------
V P a2+a>2
sn2(a>T/2)
3.6. Ww(p>)^UxU2T2———
(wT/2)2
3.7. EM=0.191 B2 c.
3.10.0.974. 3.11.0.990.
3.14. ^(т)=Л2ехр(-а|т|)/(2а).
3.15. Bs(r}=U2
-ftn-kl)3
- 3т2 ’
+(tH-M)2
к1<ти-
192
3.17. rTOp=3.89//J.
3.18. а) Д>1(л)=(...,0,0,1,0,1,0,5,0,1,0,1,0,0,...),
6) itj (л)={...,0,0,1,0, - 3,0,5,0,- 3,0,1,0,0,...).
3.1». В„(?)-
о
|т|<Т,
Ц>Т.
(1/0(71-г),
3.20. При т>0 Дл,(т)=< Q
т<Т1,
г>Тх.
{V20T\,
О,
0>т>-(Г2-Г1),
-(Г2-Г1)>т>-Г2,
t<-T2.
3.21. Вм(&=
£*а>>Гяпв>1(/ло+*)
2я L ш.(»о+т)
ыпшв(»о—т)"
ы.('о-т) .
32L Значения функции Дд,(л) образуют множество (..., О, 1, 2, —1, —2, 1,
О, ...).
Тема 4
4.1. Векторная диаграмма сигнала изображена на рис. IV.4.1. Здесь ОК — ось
отсчета углов, О А — вектор несущего колебания, АВ — вектор верхнего боково-
го колебания, АС — вектор вившего бокового колебания, OD — вектор резуль-
тирующей амплитуды. Справа приведен масштаб чертежа.
1/fQgx lAnin
4.4. М=-----------.
6rnin
t/max-!" lAnm
45. M=------------.
t^max lAnin
4.6. A/=0.73, UO=75 B.
4.7. П=20 Гц.
4Л. A/1=0.8,A/2=0.6. d
4.10. Pmi»-0.506 Вт, Pmax=2.756 Вт. g
4.11. Z’miK=12.96 кВт. /
4.13. <^=3.02 10’ с'1, wmi0=2.98-10’ с *. ‘ '2K WO
4.14. /^=49.86 МГц,/„„=50.14 МГц.
____________________________
4.15. w(f)»8cosl06f+0.24cosl.01 10et- О К
—0 24 cos 0 99 106f. pgC iv 4 1
193
4.16. Ппржхт=624 кГц. 4.17. W=34.
4.19. Fm„=10 438 Гц.
4.21. Cm=8.57- 10"* пФ.
4.22. ДГ= 1-989 МГц.
4.23. В=2356, я=1047 • 10,а с-2.
4.24. Wu= 1.963 КГ23 В2 с2.
4.26. Ф] = — В/8. 4.27. тоа,=5.03'10-в с.
4.29. 28 кГц.
4.30. 3 кГц, 5 кГц, 38 кГц, 35 кГц, 33 кГц, 41 кГц, 43 кГц.
Тема 5
5.2.1 0=41.67 мкс. 5.4. £,=0.9 В2 • с.
5.7. а) 0,(0=
кО,
1>0.
б) 0«(О-| jo,.
t<0,
t>0.
5.8. fy(t) = 10cosfir+J 30 sin fir+5 ып
5.9. UJ(t)=Um(l+Mcostli)exp(jnl4'),
^Ю-Л,(0-(14.л£)(1 +Л/cos fir).
5.10. O,(f) — Um exp (Jm sin fit),
Л,(г)= l/m cos (m sin fir),
B, (t) = Um tin (m sin fir).
l/o(e>0-l)
-----------h
2j(o)-a)0)
(l+e^nU0
5.12. S(co)=------6(a)—n>o)+
(e М+1)яЦ) U0(e *41)
--------------3(n>+ci>o)+-----------.
2 2j(to+<uo)
Если фо =180°, то
О)
S(a))=j2U0—-----.
“-“о
Важно отметить, что при <ро= 180° в спектре сигнала отсутствуют ^-особенности
на частотах ±соо-
/ М2
5.13. и,(г) = Uo 11+Мcosfir+ —,
194
м
sin aigt+— sin (aio+Q)t
^,(O=aretg---------—-----------,
COS OiQt+—COS (й>0 +fi)z
M
ajoH----4—(wo+ft)cosftr
a>, (0=---------------;------•
7+Mcosftr+Af2/4
5.14. comin=0.99 106 с'1, 1.003 106 c"1.
SocoB|sin(a),//2)|
5.15. U,(f)=---------------
я I I
5.16.0,G)=-jt70e ff(0>
-JU0
Ga(fo)—----
a+jto
UtflOo
5(<o)=--------------------------.
[a+7(w-wo)] [a+/(a>—a>o)]
{0, t<-zJ2,
Uq,
0,
ибГ®п((<а~®»о)тж/2) sin((a+a>o)'rI/2)'
S(co)=— ---------------+---------------
2^L (аз-сооУгвР. (ю+юоИи/З .
W
5.19. z, (r) [5, (1 -e ")+52(e -1)],
уя/
(S2-S?)Aa>
0 - <uo +---—------------------
2 (S*++ 25,52 cos Дшг)
So
5.20.2,0= (Z>+j7).
я(Л2+12)
5.23. s (0 = 1/(я0-
5.25. s (O = t/(a2 + r2).
195
Ug t + tg
5.27. Если te[—tg, JqJ, to s (l)——In-;
я tg-t
в противном случае
l/0 * + *0
s(0=—In----.
Я t-tg
Теми 6
6.2. P=0.0207.
6.3. P=0.064.
6.4. P=3800/8200 =0.463.
6Л.
6.6. «,„= {2 B, 6 B, 10 B, 14 B, 18 B}.
Соответствующие вероятности: P(2)= 1/16, P (6) =4/16, P(10)=6/16, P(14)=4/16,
P(18)= 1/16. Обратить внимание на малые вероятности как предельно малых, так
и предельно больших значений выходного сигнала. Объясните данный результат.
6.7. График функции распределения F(utia) изображен на рис. IV.6.1,
Р(м«ых)— ^(м»ых —2)+ 3(Una ®) +
16 4
3 1 1
+" S (Una- Ю)+-<5 (Una-14)+— г("жых-18).
6.9. р (z)=0.1255 (z—4)+0.3755 (z-4.5)+0.1255 (z-6)+0.3755 (z- 6.5).
{0,
(fl+x)/fl2,
f \l 2
0,
x< —a,
—e<x<0,
0<x<a,
x>e.
6.12. P(0<x«e/^=0.375.
{0, z<0,
z, 0<z<l,
2-z, l<z<2,
0, z>2.
CO, z<0,
6A6.p(z)=< ,
(A2zexp(—Az), z>0.
6.18. mna= 10 B, aLx=16 B2.
6.20. mB=0.795, ^=0.081.
196
6.22.х=Щ,о1=Щ2.
!0, у<0,
(1-е )5(у) + Ле е х
x(xi-xft)/>>o+e ***5(у-_уо), Osjysjyo,
0. У>Уй-
637.у=3.183, 0^=99.833.
{0, У<а3,
---------------а2^у^Ь2,
2(Ь-а)у/у
0,--------у>ь2,
my^fa2 +ab+b2)/3,
4b6 +4tfi + 10Л1-9ab5-9asb
<=---------------—-----------
y 45 (b— a)2
630. 0(u)=2/(2-ju).
jbu jau
631. e(«)=e .
j(b—a)u
634. P(|y|> 1) =0.042.
Темя?
7.2. л=0, Xx(T)=i2=02.
73. Rx{c)=o2co&(Oqz.
73. Их(а>)=а2я[й(а>—а>о) + £(а>+ао)]-
73. Fx(coo)=5.41 • IO-16 B2 c, Fx(fo=3.4'10'15 В2/Гц.
7.10. 1Тх(а>)=<и72Г-------+-------?-----1
La2+(a>—cuq)2 a2+(co+cuo)2J
Да>
sin— т
Wifio) 2
7.11. Rx (t)----•-----• cos to0T.
n Дю
— т
2
7.13. Fx(iOo)=2.yS7-10-3 B2 c.
197
7.14. тк=л/(2<о1).
7.15. тк = 10-7 с, сов=3.332'10е с"1.
7.17. Лсиэф=<ив/3.
1 Га>’+а>2а>,+а>1а>2+а>’71/2
7.19. л (0)=----= I—---—-------.
2ял/6*- °>1+°>2 J
7.21. oj; =1.07 В2, (7=1.98 В.
7.23. Лг(т)=1.374ехр(-2 10*|т|)+0.087ехр(-4 10*|т|).
5.498 10* 6.968 Ю3
7.24. Wv(<o)=----------+------------.
4 1О"+со2 1.6 109+<о2
Тема 8
8.2. п = -4.86 103 с-1, у2= -8-5• 103 с“»,
«1 (/)= 1.714 exp(yif)+6.286ехр(угО>
М2(/)=0.490[ехр(71/)—ехрОъО], *ов 153.4 мкс.
duj Ki3<lu2
8.4. —Ч----ut----------=0,
dr Ц R3 dt
R23 duj dt<2 R23
-------+-----+-----U2 =0,
R3 dt dt La
где
Лв=R\R3{{R\ + 7?з); Л23—/?2^?з/№+^з)-
Харакгеристическое уравнение
(l-A3/?23//?32)72+(/?23/A2 + /?13/bi)y+/?13ll23/(L1L2)=0.
При выбранных значениях параметров
У! = -1.915 10" с‘ \ у2= -2.57 • 107 с“».
8.6. 7V — целое число, ближайшее к 0.733g.
1
8.7. К(р)=-------------.
Ri+il+RdRU/ipQ
Р2^2
8.8. К(р)=
pLifl+La/Lij+LaR/Li
R
8.9. К(р)=——.
pL+R
1
8.11. Х(р)=—---—-----.
3+pRC+l/(pRC)
1
-----------------,
3+j(a)RC-\/(c}RQ)
198
|K(/<u)| =(9+(<oAC- l/(oAQ)2]“ l'2,
Фл(л>)=-arctg[(toAC- l/(aiRCj)f3],
<om„=5 10a c~*.
8.13. pi = -3.2469795 c”\ p2= -0.1980622 c~*,
p3= -1.5549581 c-1.
Z1Z3+Z2Z3+Z3Z4 +Z1Z2
8.15. K(p)=---------------------------.
Z1Z3 +Z2Z3 4-Z1Z24-Z1Z44-Z3Z4
8.17. Л(»)= -— е~‘КЯзиС*> a(J),
где A3„=AIIAi/(AB4-Ai).
8.20. Л(0=5(0-^е"'/ЛС <7(f).
2К<>Дй) sin Д<о»
8.21. Л (0 =---•-----• cos wqI.
п Ла>1
. 2“.'
ЯП*----
2
8Л4. г(0 = 0.4798(еЛ'-еЛ')<7(0-
Соответствующий график представлен на рис. IV.8.1.
Р1 = -172434 с"*, р2= -6592 с-1.
8.26. г(0=Л?(1 -(1 +»/гэ)е-'/'э](7(0,
<уст=3.89тэ. Нормированный график переходной характеристики изображен на
рис. IV.8.2.
199
8.28. Л(»)=2.857 - 103 е'2143 10’'(cos8.449 10sr—
- 0.025 sin 8.449 10sr) a (t).
1
8.29. Л(г)=------(1— cos cunt) o(l).
Ci+C2
A -iaT
832. К(До)=—(1—e ),
|К(М1=ЛТ
(cuT/2).
8.34. Нормированный трафик функции g(t) изображен на рис. IV.8.3.
8.35. K(/a>)=—(1-2е >Г/2+е >“7)-
8.36. А?(/со) = аке ^акТ.
к-0
Структурная схема цени, реализующей
данную импульсную характеристику,
представлена на рис. IV.8.4. Она образова-
на сумматором, а также совокупностью
масштабных усилителей с коэффициента-
ми {а*} и устройств задержки с парамет-
рами Т, 2Т, ...
8.40. uam(t)=------[Si(co0+Aco)t)-
я
Si((co0—Да>)г)].
8.44. и,ых
200
о,
t<0,
I (t — r/A
Uol —1+e I OsStsSt,
I —r/r
'‘I7oe , i>t.
Соотвегствуклции график изображен на рис. IV.8.5.
Тема 9
•1.477 ->1.477
9.1. K(/2n/i)=-3-267;Х(/2л/2)=-3.267е
9.2. С01.2=С1>р<3±1/(^/2тж).
Г 12.73 кГц, А=1,
9.4. По 707 е 7
1.4.91 кГц, А =5.
9 Л. Нормированные АЧХ усилителей приведены на рис. IV.9.1 (кривая
I — одна ступень, кривая 2 — две ступени, кривая 3 — три ступени).
9.6. /^-4.48.
9.7. Ггр=тж.
‘Р l+CtBo-Wpo)2^ ТЖ \tj ^Dt/2 / Дсо\ xcosl Шрс! +— It. Ориентировочный график данной функции изображен на рис. 1V.9.2. 9.11. Л(/)= 4А^ез/'\2 -Г/ХЖЯП2Д<ОГ = - — ) е coscuof. тж \tj (Дол)2 Примерный вид графика данной функции изображен на рис. IV.9.3. 9.12 Ан,(Д1)=Л0е"“11, *о / f2\ Лт(0=—,= expl - J. 2yjnb \ 4*/ IKQ^I/Kmax /II Оо\ 'У г °А\ х 2 / / °-2\\ -4-3-2-1 0 1 2 31^-41^) Рис. IV.9.1 201
Ко 44
9.13. h (г) =—= e cos coot,
y/nb
Гауссов радиофильтр физически нереализуем.
9.15. »W<(') = -750[1 +0.424cos(2л 10*f- 1.012)]х
xcos2nl06f.
9.16. ^=16.1 мкс.
KqU„ /Г _х/ sini/xX!1
(co,,,-—)] +
[_x/l cosjjx
f)—e |-+»7------------sini/x
\»7 *1
где x = t/tx, tj=Дсо тж.
~ KpaUo —dx+jb —x
9.21. ^(f)-----(e -e ),
l-d+jb
где x=t[Tt, b=8axtK, d=axK.
Тема 10
10.2. а) ЯЛ(т)=(ИЪ/(27Э)ехр(-|т|/П
б) A/t)=
A2W0(T-\t\),
0,
10.4. ^=2^(1 +rx(7D).
10.5. Лх/г) = Кх(г) + Кх(т-П
202
10Л. t'=0.04 с.
10.7. H„»=-----------f-------Ц--.
(1+со2Г2)(И-си2Г2)
где Т1=Я1С1, 72=/?2^-2-
2aofco2
ЮЛ. WC(cu) =
1 С2(а2 + ш2)(а£-а>2):
где со2 = 1/(LQ.
10.9. Пш=Л/(4£).
10.10. Пт~у/п/(2Ь).
10.11. аг2
AgWb Т2
2 У\ + Т2)ТХ'
„ ^Wofe
ги (т)=---1 -
2(Г22Г2)\
ЮЛ 2. ги (т) = Wo а (г)--е
L 2RC
_nF0 (2A'-3)!’
na~2RC (2N-2Y.I
р (Л1+Л2)С+А2С2а
““= “ (Я1 + Я2)С[1 + а(Я1 + Я2)С]
Wo / Л1+Л2, \
и(т)=------------- ехрI-------т ).
2R1C(1+Ri/R2) \ RtR2C /
10.18. <7вых=0.023 В.
10.19. <г2=2Л^ГоД<о,
sin Дай
гу (т)=2Лд £оДа>---cos а>от.
Дап
10.20. Ги(а>)=
(со2 — coq)2 + 4a2 со2 ’
FoCOq -а|г|/ а
ги(т)=——е 1со$шстЧ— sincoc|T|
4» \ сос
203
где u)Q—\lyjLC, a=R/(2L), <ис=\/<0о—°2-
W*b -aft|/ a \
10.21. rv(t)=---e I coscoot------sincuoM L
4aC2 \ coo J
где co0= 1/x/bC, a=l/(2PC).
10.22. ffBiU=73.1 мкВ. 10.23. авых=7.97 мВ.
10.24. о^=ЛТ/С; «эф=2.03 мкВ.
10.25. of=3.776-10'14 А2.
10.26. Р0=0.2865. 10.27. Т=580 К.
10.28. Тш=473 К; F=2.63.
F2-l F3-l
10.29. F=F+---+-------.
Kpi КпКп
Тема 11
11.2. ао=1.25 мА, oi=0.68 мА/В,
02=0.14 мА/B2, oj=0.01 мА/В3.
11.3. 4 = 1-99’10-3+0.077(мбэ—0.25) +1.475(мбэ—0.25)2 А
11.4. оо=63.75 мА, oi=75 мА/B, о2=15 мА/В2,
оз=о4 = ...=0.
113. и=0.128 В.
11.7. Zo= 15.03 мА, Zi=0.49 мА, /2=029 мкА,
/з = 3.78 мкА.
11.8. ZI=40I4, + 1.875I/3.
11.10. 4,0=1.25 мА, 11.11. Рб= 1-52 мВт.
11.12. ЯМ1=4.05 Ом.
11.14. Z0=0.92 мА, Zi = 1.56 мА.
11.16. /4йвых=0-32 В.
11.17. График зависимости приведен на рис. IV. 11.1.
11.19. £7явх=0.42 В.
11.20. Г/о=0.19 В.
11.21. Ро=3.69 мВт,
Р1ВЫХ=3.35 мВт,
РПОТ=0.34 мВт,
»7=91%.
204
11.22. GmlMX=10.28 В.
11.25. Л/шжх=0.9.
1126. а) 4ч(0— a2MU^cosQt+
cos 201,
4
а2Л/ГД
6) 4ч(0=-------cosQt.
2
fl2G2/la
11J27. ивыхли(»)= ----— (4Mi cos£lir+
4
Рис. IV.11.1
+4M2cosQ2t+
+M|2cos2OIt+M2COs2Q2t+2M|M2cos(Q|+Q2)t+
4_2A/[A/2cos(Oj •—Од) ij*
{0, _y<0,
1 expf-—
I
y>0.
1134. my
1135. Ky(t)~2a%R’(t).
Тема 12
121. 4,-150 мкА.
122. Jknia=615 кГц. /^„=840 кГц.
123. Q=70.12.4. сос1=сог+шар, a>c2=tor—<Опр-
12.6. t/rar=0.8 В. 12.7. 5цр=7.846 мА/B.
123. Uo= -0.978 В. 12.9. Umnp=5A В.
1211. 73=8.48 мА. 1212 В 8.53 раза.
1213. i(r)=flCoe“'/T^l-~у
1214. h=0.382т, г2=2.618т.
1216. G„= -4.286 10"s См. 1217. фи=2я/3.
12.18. GBHm„= —2.356 10"* См, <ря= — 5п/6.
205
Тема 13
13.1. Физически реализумой £С-цепи отвечает лишь проводимость Yy (р).
133. Паралельяая КС-цепь с параметрами. К—3 кОм, С=3 нФ
13.4. Последовательные £С контур с параметрами элементов. L**2 мкГн,
С—0.4 нФ.
133. Последовательный £СК-контур с параметрами элементов: С=03 мкФ,
£-2 мГн, К-40 Ом.
13.6. Параллельный £С контур с параметрами элементов- £—20 мкГн,
С-750 пФ
13.7. Схема цепи изображена на рис. IV.13.1.
133. Схема цепи изображена на рис. IV. 13.2.
13.10. Схема цепи, отвечающая условию задачи, приведена на рис. IV.13.3.
Сравнивая данный результат с тем, который получен в задаче 13.9, убеждаемся
в неоднозначном характере процедуры синтеза.
13.11. Схема цепи приведена на рис. IV.13.4.
13.12. Схема цепи т введена на рис. IV.13.5.
13.13. Схема цепи приведена на рис. IV. 13.6.
13.14. Схема цепи приведена на рис. IV.13 7
13.16. K(pJ
К»
(Р«-е )(р«-е )
13.19. £-0 161 Гн.
13.20. —25/(р£+2.6132р.1+3.4143pJ+2.6132р,+1).
С25мГн
2мкФ
35нкГн
СО Си
Рис. IV.13.1
2 Гн ТФ
Рис. IV.13 4
Рис. IV.13.3
1 кОм
Рис. IV.13.5
206
1321. Ад--58.24831 ±
±/179.26992 с"*,
/>3.4=-152.49609 ±
±/’110.79489 с’*,
Pi=- 188.49555 с’*.
1322. coc=8‘10s с’*, л=4.
13.23 . »m;r=3. Усиление фильтра
составляет при этом —15.12 дБ.
13.26 . ч>к(<о^= -arctgco,-arctg(2coa-%/3)-
-arctg(2zoj+v/3); <рх(со)=Зя/2.
13.27 . 7^= 1.533 мкс для фильтра первого порядка,
4.295 мкс для фильтра третьего порядка.
1329. Л1.2= -0.18441 ±7’0.92303, рж3- -0.36883.
1
1330. Я(рл)=-------------------------------
р*+0.73766р* + 1.02203рж+0.32678.
Рис. IV.13.7
Тема 14
142. Ки=0.955, овх=3.3 В.
KiK2
14.4. К(р)=---------------
1-(Х1Д1+К2ВД.
КоККо+1)
14.7. К(р)=-----------,
1+7ноу/(К0+1)
o>rp=(Ko+l')/t0y.
Ко
142. Л(р)=---------.
1 + Kg+pRC
-Ко
14.9. К(р) =-----------------.
1+Я1(1+Яо)/Я2+рЯ,С
—Я2(Я3+Л4)
14.10. К[р) =----------.
Я1Я3 — Я2Л,
Система становится неустойчивой, если Я4 > 3 кОм.
14.12. Хожр(л)=1/со8(я/л).
Ко
14.13. w (/со) = ехр7 (я—со Го);
207
= ^/1 +я2 (то)2.
14.14. 7^=1.258 КГ* с. 14.15. К^у/з.
14.16. Л^-438.
14.17. Система неустойчива при любом Кое(О, со).
14.18. Для устойчивости системы необходимо одновременное выполнение
двух неравенств:
а)ЛЬ<1,б)ХЬ<(т+Т2)/Т1.
1430. кс,=0.23.14.21. Jt,„=0.08.
1432. S, = 16.57 мА/В.
1434. Рассмотренный в задаче стационарный режим устойчив.
Тема 15
15.1. N=28800 бит.
т “ sin (лят/Д) / 2ял\
153. 5.(<о)=- У —-—-----------------I.
Дя--оо \ Л/
Примерный вид зависимости |5Хд(со)| изображен на рис. IV. 15.1.
15.4. Дяел/(100а).
153. Si(0)=2«Uo/(«2+4a2/A2). 15.7. Со=О.О7.
15.12 . Со=О, q-1/2, С2-0, С3=1/2
15.13 . x(0 =0.125 +0.75cos(2jtf/7)+0.125cos(4nt/7).
15.14 . x(0=cos(2itl/7). 15.17. JT(z)=z/(z-l).
15.18 . 2f(z)=l/(l—az-1). 15.19. A'(z)=exp(az'1).
1531. x*= 13.286.15.22. x„= -2(0.4)"+3(0.6)".
z3+2z2+2z+l
1534. F(z)=-----------.
ЗГ
1535. {f„} =(0, 0, 1, 2, 2,1,0,0,...).
1538. ЛСш)= 1 -ге'^+е'72^.
Разлагая экспоненты в ряды Маклорена и ограничиваясь учетом первых трех
членов при соД-+0, находим, что /Г(/ш)яг(/соД)2, т. е. фильтр приближенно осуще-
ствляет операцию вычисления второй производной входного сигнала.
1
1531. Я(х)=-------------,
z2—0.4z—0.32
Л((<о) =------------,
е^-0.4е^-0.32
208
Рис. IV.15.1
JO, m=0, 1,
10.8333 (О-в)""1 -0.8333т=2, 3, ...
1533. |К(/ш)|=3.470, —0.862 рад.
1534. Рассматриваемый фильтр устойчив.
1535. =0.059 В, <^,=2.86-10'* В2.
1536. о2 =1.505 10“’В2.
Тема 16
16.2. бтм= Um вх/чА^О^О» Um вхв 1-22 мВ.
С ростом частоты coq должна расширяться полоса пропускания. Это ведет к тому,
что возрастает мощность шума, поступающего на выход цепи.
163.
163. ^„(/<0)=— (1-е ^°)+—
arto ja>
{0, КО,
BA(l~t/tQ), 0<t<to,
0, t>io-
16.6. m„=3.125 В. 16.7. ^=84.
163. твых=45.5 нс.
1
16.10. |Л(/со)|=------------------,
1 +fc(a2+co2)/(^2+co2)
где
к=Р<^/(аи^).
209
16.13.
16.11.
16.12.
<min
16.14.
со» AJV0
я A+Wo
=9.549 10"10 В2.
(а+2^/Ио)1/2’
= 10“* В2.
16.16. 50 бит.
16.17. 5 бит/символ
16.18. 900 кбит; 1.6 раза
16.19. 11.52 Мбит; 1280 раз.
Приложения
1. Некоторые трагомметрмескве формулы
. , 1
йп2х =-(l—cos2x).
COS2 Л 1 :=-(l+cos2x).
sin3x 1 =-(3 tin x—sin 3x).
COS3 л 1 :=- (3 cos x +cos 3x).
sin3x 1 =— (10 sinx—5 sin Зх+sin 5x).
COS3 л 1 (10 cosx+ 5 cos Зх+cos 5x).
X Связь между взображеавямв оркпымаие
f(p) /(»)
1 l/P l/P1 l/O+o) pl(p+a) o/bO+o)] 1 a(0 ff(r) < exp(—at) S(i)—oexp(—at) 1—exp(—at) 1 — at -bt (e —e )
(p+a)(p+b) p (p+a)(p+b) l/(P+o)2 pKp+a)1 b—a 1 , -bl -at (be —ae ) b—a —at te —at (1—et)e
ш/(р2+<о2) р/(р2+ш2) <оД(р+о)2+й>2] sin <or cos <or —at . e sin tot
211
Продолжение прилож.
Ж
F(p)
(p+fl) Л(р “Ьfl)2+60 2]
в’/[р2(р+яЯ
1
p(p + a)(p + d)
1
р[(р+о)2+й)2]
1
(p+a)(pa+ciD2)
P
(p+e)(p3+a>2)
P2
(p+a) (p2 + co2)
—at
е cosatf
— at
at—(\ — e )
1 г / а YI
—------ 1—е X |СО5ОИ+ ЯПОИ I
а2+Ф2|_ \ ш /-
1 / -«/ fl . \
—------| е — cos cot+-sin cot 1
a1 + co2 \ co /
—-----;(—ae cos a)f+ct) sin ail)
a2+ar
1 • -~al *
-------(ere — a co sin cot 4- ctreos cot)
cP+co2
РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА
II
1. Баскаков С. И. Радиотехнические цепи и сигналы.— М.: Высшая школа,
2000.
2. Попов В. П. Основы теории цепей.— М.: Высшая школа, 2000,
3. Прудшвсов А. П., Брычков Ю. А., Марячев О. И. Интегралы и ряды.— М.:
Наука, Главная редакция физико-математической литературы, 1981.
4. Янке £, Эйде Ф., Л
таблицы: Пер. с нем./ Под ред Л. И. Седова — М/ Наука, Главная редакция
физико-математической литературы, 1977.
5. Твхоаов А. Н., Костомаров Д. TL Вводные лекции по прикладной математи-
ке.— М.: Наука, Главная редакция физико-математической литературы, 1984.
6, Дьяконов В. П., Абраменкова И. В. MathCAD 7.0 в математике, физике
и в Internet.— М.: Изд-во Нолидж, 1999.
7. Грызлов В. И*, Грызлова Т. П. Туг
1998.
8. Карлащук В. И. Электронная лаборатория на IBM PC. Программа
Electronics Workbench и ее применение.— М/. Изд-во Солон-Р, 2000.
М.: Изд-во ДМК,
ОГЛАВЛЕНИЕ
Предисловие ................................................3
РАЗДЕЛ I. ЗАДАЧИ И УПРАЖНЕНИЯ ..............................6
Тема 1. Общи теория радиотехнических сигналов ..............6
Тема 2. Спектральные представления сигналов................13
Тема 3. Энергетические спектры сигналов. Принципы корреляционного
анализа ...................................................22
Тема 4. Модулированные сигналы ............................25
Тема 5. Сигналы с ограниченным спектром....................29
Тема 6. Основы теории случайных сигналов ..................34
Тема 7. Корреляционная теория случайных процессов..........39
Тема 8. Воздействие детерминированных сигналов на линейные
стационарные системы ......................................43
Тема 9. Воздействие детерминированных сигналов на частотно-
избирательные системы......................................51
Тема 10. Воздействие случайных сигналов на линейные стационарные цепи 55
Тема 11. Преобразования сигналов в нелинейных радиотехнических цепях 60
Тема 12. Преобразование сигналов в линейных параметрических цепях ...67
Тема 13. Основы теории синтеза линейных радиотехнических цепей .70
Тема 14. Активные цепи с обратной связью и автоколебательные системы 75
Тема 15. Дискретные сигналы. Принципы цифровой фильтрации.......80
Тема 16. Оптимальная линейная фильтрация сигналов ..............85
РАЗДЕЛ II. Указания ............................................89
РАЗДЕЛ III. Решения ...........................................104
РАЗДЕЛ IV. Ответы .............................................189
Приложения.....................................................211
Рекомендуемая литература.......................................213