Text
Алгебра һәм анализ башлангычлары 10-Г
Алгебра
Һәм анализ
башлангычлары
III- I 1
Татар урта гомуми
белем бирү мәктәбенең
10-11 нче сыйныфлары
өчен дәреслек
A. Н. Колмогоров редакциясендә
Россия Федерациясе Мәгариф һәм фән
министрлыгы тарафыннан тәкъдим ителгән
:‘р *
ОСТЬ · *: ’ ’ V*
Ж-ГТЛЛ·' < -7Я
Or liK! Xs
crgto
Н*«М1111ПАЛ*ХО ^.HUriA
’ t *
'ЛГИФ b*:.’
нлстрлыгы
мОГОРС*
ЛТ-миЦИГЛЛЬ
i<Z*!7il»1 6СЛЕЫ
eilp'i МУНИ^С-АЛЬ
yv.'bEXiHN-'.nrL
Казан ·
Москва
2007
«Мәгариф» нәш
• «Просвещение
;УГ> ШЖ'ЛКАЙ СРЕДНЯЯ 0wi£?i PAJCBVinfcl-i'i <’
0 y’.U'tJiHKHtH liiy-iEEHi-V ОТДЕЛЬНЫХ V.
•ияты .
J* « » 2C0-’ J
ОГРН 1021801975768
ИНН 1Ь1ДО$670 КПП 1^301001
»
УДК 373.167.1:51*10/11
ББК 22.14 я721
А47
Авторлары: А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудницын,
Б. М. Ивлев, С. И. Шварцбурд
Алгебра и начала анализа: Учеб, для 10—11 кл. общеобразо-
ват. учреждений / А. Н. Колмогоров, А. М. Абрамов, Ю. П. Дудни¬
цын и др.; Под ред. А. Н. Колмогорова.— 15-е изд.— М.: Просвеще¬
ние, 2006.
Охраняется Законом РФ *06 авторском праве и смежных правах».
Воспроизведение всей книги или ее части на любых видах носителей
запрещается без письменного разрешения издательства.
Переводное издание учебника выпущено в свет по Лицензионному
договору 3/67 от 14.06.07 г. Экземпляры переводного издания подлежат
распространению исключительно в Республике Татарстан, а также среди
татарской диаспоры на территориях других субъектов Российской
Федерации.
А47 Алгебра һәм анализ башлангычлары: Татар урта гомуми
белем бирү мәкт. 10—11 нче с-флары өчен д-лек/А. Н. Кол¬
могоров, А. М. Абрамов, Ю. П. Дудницин һ. б.; Русчадан
3. X. Билалова, В. 3. Закиров, Л. Ш. Галиева, Ф. М. Хафизова,
Л. X. Мөхәммәтҗанова тәрҗ.— Казан : Мәгариф, 2007.—
383 б.: рэс б-н.
ISBN 978-5-7761-1704-6
ISBN 978-5-7761-1704-6 © Издательство «Просвещение», 1990
© Художественное оформление.
Издательство «Просвещение», 2000
Все права защищены
© Татарчага тәрҗемә, «Мәгариф»
нәшрияты, 2001, үзгәрешләр белән
Суз башы
Сез яңа фән өйрәнә башлыйсыз. Китап исемендәге
«алгебра» сүзе сезгә инде таныш.
Курсның, асылда, яңа булган өлеше анализ башлангычларын
өйрәнүгә багышлана. Математик анализ (яки анализ) — мате¬
матиканың бер тармагы. Ул фән буларак XVIII йөздә форма¬
лашкан һәм ике төп өлкәне — дифференциаль һәм интеграль
исәпләү өлкәләрен — үз эченә ала. Анализ табигать фәннәренең
үсешендә гаять зур роль уйный. Төрле практик мәсьәләләр чиш¬
кәндә килеп чыккан функцияләрне тикшерүнең көчле, шактый
универсаль методы барлыкка килә. Анализның башлангыч тө¬
шенчәләре һәм методлары (чыгарылма, дифференциаллау, баш¬
лангыч функция, интеграл, функциянең максимум һәм минимум¬
нарын эзләү методы) белән танышу — курсның иң мөһим мак¬
сатларыннан берсе.
Дәреслектән ничек файдаланырга кирәклеге турында берничә
күрсәтмә биреп китәбез. Китап ахырында урнаштырылган эчтәлек
һәм атамалар күрсәткече сезгә кирәкле бүлекне, билгеләмә яки
теореманы тиз табарга ярдәм итәр. Күнегүләргә җаваплар һәм
күрсәтмәләр тиңдәшле бүлекләрдә бирелде. Тәкъдим ителгән
мәсьәләләрне чишүнең төп идеясе белән танышу өчен, В һәм
тамгалары белән аерып күрсәтелгән бик күп мисалларны чишү
үрнәкләре китерелде. Тагын шуны да искәртәбез: уртача билге
алу өчен, сез чишә белергә тиешле бу мәсьәләләр мәҗбүри
исәпләнгән әзерлек дәрәҗәсен күрсәтәләр. Калган мәсьәләләр
бераз катлаулырак.
Контроль эшкә әзерләнүне җиңеләйтү максатында, һәр бүлек
ахырында төп материалны кабатлау өчен сораулар һәм мәсьәләләр
китерелде. Бу сорауларга җавапларны һәм андый мәсьәләләрне
чишү үрнәкләрен тиңдәшле пунктларның текстында табарга була.
♦Тарихтан мәгълүматлар» дигән материалны укып, математик
анализны иҗат иткән кешеләр һәм өйрәнелә торган төшенчәләр¬
нең, термин һәм символларның ничек килеп чыгуы турында белә
аласыз.
Дәреслекнең кайбер пунктларында теоретик характердагы өстә¬
мә материал бар, ул !► һәм тамгалары белән аерып күрсәтелде.
Мәктәпне тәмамлаганда сезгә чыгарылыш имтиханнары бирер¬
гә туры киләчәк. Билгеле булганча, урта мәктәп курсының теоре¬
тик материалы кыскача «Математика. Белешмә материаллар» ки¬
табында бирелгән. Курсны кабатлау өчен, практик күнегүләр «Ка¬
батлау өчен сораулар һәм мәсьәләләр» дигән бүлектә урнашты¬
рылды. Ахырда йомгаклау бүлеге катлаулырак мәсьәләләрдән
тора.
3 Сүз башы
Уку ярдәмлегендә
кулланылган
тамгалаулар
N
— барлык натураль сан¬
нар күплеге
£(Л
— f функциясенең кыйм¬
мәтләре өлкәсе
Z
— барлык бөтен саннар
күплеге
Δχ
— х аргументының үсем-
тәсе
г0
— барлык тискәре бул¬
маган бөтен саннар
күплеге
Δ/(Χ.),Δ/
— f функциясенең х0
ноктасындагы үсем-
тәсе
Q
— барлык рациональ
саннар күплеге
Г<ж»>
— f функциясенең х0
ноктасындагы чыга¬
я
— барлык реаль саннар
рылмасы
күплеге, санлы туры
sin
— синус функциясе
[«; *>]
— очлары а һәм Ь булган
cos
— косинус функциясе
йомык аралык (ки¬
tg
— тангенс функциясе
семтә), монда a < Ь
ctg
— котангенс функциясе
(а; ь)
— очлары а һәм Ь булган
ачык аралык (интер¬
вал), монда а < Ъ
e
— е саны, (е1У=е1 бул¬
ган күрсәткечле функ¬
циянең нигезе
(«; Ь), |а; Ь)
— очлары о һәм Ь булган
ярымячык аралык
log.
— нигезе а булган лога¬
рифм
лар, монда a < Ь
Ig
— унарлы логарифм
(а; “).
[а; “).
(— ®; 6),
In
— натураль логарифм
(нигезе е булган лога
рифм)
(— °»; 6]
— чиксез аралыклар
max/
— / функциясенең [α; Λ]
( 0D- ао)
— чиксез аралык, санлы
туры
(“;*)
кисемтәсендәге ин зур
кыйммәте
ά
— векторның тамгала¬
min/
— / функциясенең [а; δ]
нышы
I·*»
кисемтәсендәге ин кеч¬
(α-<$; α+δ)
— α ноктасының <£ти
кенә кыйммәте
рәлеге
J fMdx
— / функциясенең а дан
[x]
— т санының бөтен ки¬
сәге
& га кадәр чикләрдәге
интегралы
{*}
— х санының вакланма
кисәге
aresin a
— а санының арксину¬
сы
|χ|
— х санының модуле
(абсолют зурлыгы)
arccoa a
— а санының арккоси
нусы
Их)
— f функциясенең х
ноктасындагы кыйм¬
arctg a
— а санының арктан¬
генсы
мәте
arcctg a
— а санының арнкотан-
D(f)
— f функциясенең бил-
тангенсы
геләнү өлкәсе
бүлек
Тригонометрик
функцияләр
§ 1.
Санча аргументның тригонометрик
функцияләре
1. Синус, косинус, тангенс һәм котангенс
(кабатлау)
1. Радианлы үлчәм. Сез почмакларны радианнарда
үлчәү белән таныш инде. 1 радианлы почмак — дугасының
озынлыгы әйләнә радиусына тигез булган үзәк почмак ул (1 нче
рәсем). Радианлы һәм градуслы үлчәм 180° = π радиан тигезлеге
белән бәйләнгән; па лы почмак Λ& радианга тигез.
Почмакларны радианнар белән үлчәгәндә, кайбер формулалар¬
ның күренеше гадиләшә төшә. Мәсәлән г радиуслы әйләнәдә α
радианлы дуганың озынлыгы
I = ar; (1)
формуласы буенча табыла; г радиуслы түгәрәкнең α радианлы
дуганы эченә алган сектор мәйданы S ны табу формуласы түбән¬
дәгечә булыр:
tr2
2
(2)
(1) Һәм (2) формулалар дугалары (п зурлыгындагы) градуслы
үлчәмдә бирелгән әйләнә дугасы озынлыгын һәм сектор мәйданын
исәпләп чыгару өчен кулланыла торган I - һәм S =
рәвешендәге аналогик формулалардан гадирәк. Радианлы үлчәм¬
нең байтак өстенлекләре булу (17 нче пунктны
да карагыз) тригонометриядә почмакларның
градуслы үлчәмен түгел, бәлки күбрәк радиан¬
лы үлчәмен куллануга китерде.
Алгебра курсыннан сез α радианлы (монда
α — теләсә нинди реаль сан) почмакка бору¬
ның ничек билгеләнүен беләсез. Шулай ук
сезгә α ның (α — почмак яки сан) синусы,
косинусы, тангенсы һәм котангенсы билгелә¬
мәләре дә таныш.
Тригонометрик функцияләр
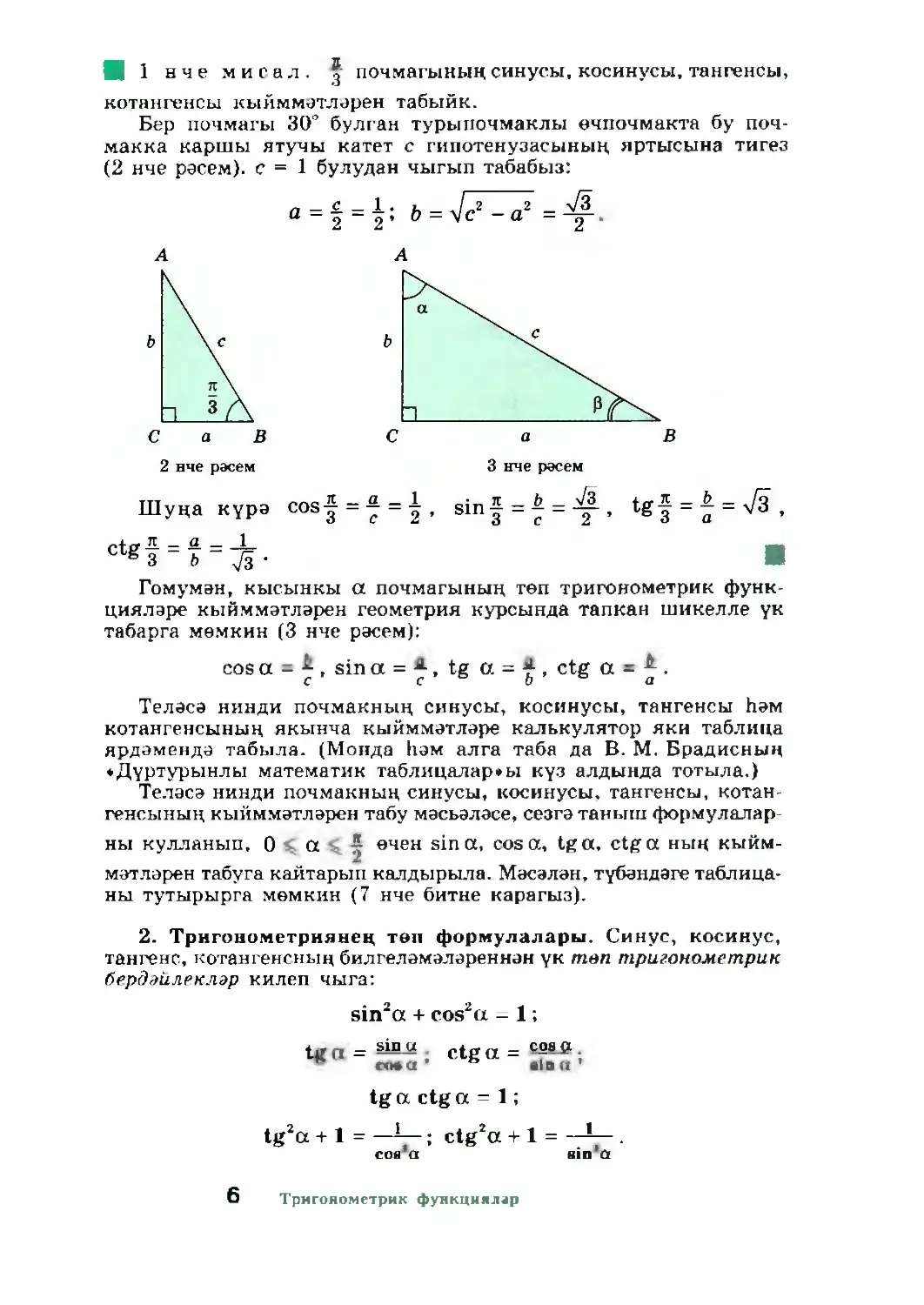
■ 1 нче мисал. ®- почмагының синусы, косинусы, тангенсы,
котангенсы кыйммәтләрен табыйк.
Бер почмагы 30° булган турыпочмаклы өчпочмакта бу поч¬
макка каршы ятучы катет с гипотенузасының яртысына тигез
(2 нче рәсем), с = 1 булудан чыгып табабыз:
С а В
c
a
В
2 нче рәсем
3 нче рәсем
Шуңа күрә
cosW = l·
sin π = ь _ V3
Sln3 c 2 ’
e+σ· ~ —
ctg 3 ь 7з ·
Гомумән, кысынкы α почмагының төп тригонометрик функ¬
цияләре кыйммәтләрен геометрия курсында тапкан шикелле ук
табарга мөмкин (3 нче рәсем):
cos α - , sin α = A, tg α = f·, ctg α - - .
с с о а
Теләсә нинди почмакның синусы, косинусы, тангенсы һәм
котангенсының якынча кыйммәтләре калькулятор яки таблица
ярдәмендә табыла. (Монда һәм алга таба да В. М. Брадисның
♦ Дүртурынлы математик таблицалар»ы күз алдында тотыла.)
Теләсә нинди почмакның синусы, косинусы, тангенсы, котан¬
генсының кыйммәтләрен табу мәсьәләсе, сезгә таныш формулалар¬
ны кулланып, 0ξ өчен since, cosa, tga, ctga ның кыйм¬
мәтләрен табуга кайтарып калдырыла. Мәсәлән, түбәндәге таблица¬
ны тутырырга мөмкин (7 нче битне карагыз).
2. Тригонометриянең төп формулалары. Синус, косинус,
тангенс, котангенсның билгеләмәләреннән үк men. тригонометрик
бердәйлекләр килеп чыга:
sin2a + cos2a = 1;
^а= sina ctga= essa;
co*a * eln a '
tg a ctg a = 1;
tg2a + 1 = ——; ctg2a + 1 = .
cos'a ein’a
6
Тригонометрик функцияләр
α
0
5.
6
*
4
X
3
к
2
2д
3
3S
4
5г
б
π
sin α
0
1
2
£
2
~2
1
Уз
2
1
2
0
cos α
1
Уз
2
4
2
1
2
0
2
2
_Уз
2
-1
tg a
0
Уз
1
—
-1
Jz
0
ctg a
—
-Уз
1
0
-I
-Л
—
a
75
6
3
ад
2
§2
3
Is
4
lit
6
2π
sin a
_1
2
ί^ί<Ν
1
1
-1
A
2
_^2
2
_1
2
0
cos a
_ ^3.
2
1
_1
2
0
1
2
2
2
1
tga
^3
1
—
-7з
-1
"i
0
ctg a
Л
1
1
Уз
0
__L
7з
-1
—
Кушу формулалары калган формулаларны чыгару өчен нигез
булып торалар:
cos (ot - β) = cos a cos β + sin a sin β;
cos (α + β) = cos α cos β - sin α sin β;
sin (α - β) = sin a cos β - cos a sin β;
sin (α 4- β) = sin α cos β + cos α sin β;
7
Тригонометрик функцияләр
sin(™±a), cos^±aj, tg^±a), ctg(^±a), n e Z,
күренешендәге аңлятмаларнын рәвешен үзгәртү очей, β - Μ0Η^
да η ε Ζ дип алып, кушу формулаларыннан китерү формулала
рын табабыз.
Бу формулаларны истә калдыру өчен, түбәндәге мнемоник ка¬
гыйдәдән файдалану уңайлы:
а) 0 < a < J булса, китерелгән функция алдына
башта бирелгән функция алдындагы тамга куела
(4 нче рәсем).
б) п так булса, функция *кофункциягә» үзгәрә;
п җөп булса, функция үзгәрми. (Косинус, синус,
котангенс, тангенс тиңдәшле рәвештә синус, косинус,
тангенс һәм котангенсның «кофункцияләре» дип
атала.)
4 нче рәсем
sin ' -Г; - a) - cos a; cos I * - aj = sin a;
tg^ + a) = -ctga; cos - a) = - sin a Һ.6.
Сезгә шулай ук синусларның (косинусларның) суммасы һәм
аермасы формулалары да таныш:
sin a + sin β = 2 sin cos-;
r 2 z
sin a - sin β - 2 sin 2^ cos :
cos a + cos β = 2 cos cos - ;
cos a - cos β = - 2 sin 1 cos .
r 2 z
8
Тригонометрик функцияләр
а = β дип алып, кушу формулаларыннан икелэтелган аргумент
формулалары чыгарыла:
sin2a = 2 sin a cos α;
cos 2α = cos2a - sin2a;
cos2a - 1 -2sin2a; cos 2a = 2 cos2a - 1;
tg2a-^L;
i-tgV
cos 2t « 1 - 2 sin21 һәм cos 2t = 2 cos21 - 1 формулаларына
t = 4 кыйммәтен куеп, ярты аргумент формулаларын табабыз:
a 1-cos a
sm ' =
Λ
(3)
(4)
2
1+сма
2
cos2 я =
*
2 нче мисал. Таблицалардан файдаланмыйча, (3) форму¬
ланы кулланып, sin кыйммәтен табыйк:
sin2 £ =
1-cos®
о
2
0 < , sin А > 0 булганга табабыз: sin A = ч- .
Җавапны гадиләштерергә мемкин:
72-Уз _ J4-2Уз _ 7<Уз -1)2 _ Уз-ι _ Уё-Уг
2 2У2 " 2У2 “ 2У2 " 4 ’
(3) тигезлекне (4) гә буынга-буын бүлсәк,
2« 1-cosa
** 2 1 + coea (5)
формуласы килеп чыгар.
2 . Sin5
tg - = —' тигезлегенең уң кисәгендә санаучысын да,
c.os“ ' π ’
ваклаучысын да 2cos® гә тапкырлап табабыз:
sin§ 2sin2cos§
a — 2 _ 2 2
2 cos® 2cosifl
5 3
sma
1 + cosa’
ягъни
_ sin a
6 2 l + cosa
(6)
9
Тригонометрик фу акция ләр
_ α sin 2 „
Аналогик рәвештә tg ^ = —- тигезлегенең уң кисәгендә са-
2 cos3
научысын да, ваклаучысын да 2sin-2· гә тапкырлап,
п 1 - сое α
:
6 2 sio α
формуласын чыгарабыз.
3 нче мисал. Таблица кулланмыйча tg^ кыйммәтен табыйк:
Ч !^ = - Л· = —г = тг4 = = ('β +1)*·
8 1+cos- ι_γ2 V2-1 2-1
4 2
A < < π икәнен искә алабыз. Шуңа күрә tg < 0 һәм, димәк,
i о ь
tg¥ = -(>/2 + 1).
В
(7)
2-1
4 нче мисал, coset = 0,8 һәм 0<α<^ булганда, sin*,
cos^ һәм tgy не табыйк.
у почмагы беренче чирекнеке, димәк, sin у > 0, cos * > 0,
tg > 0. Шуңа күрә
sin Л = = 70Д = 0,3162;
cos* = u·^· = V<K9 = 0,9487;
М=ЖЧ·0·3333·
Күнегүләр
Күнегүләр һәр пунктта ике өлешкә бүлеп бирелгән. Беренче
өлештә бирелгән мәсьәләләр шушы тема буенча мәҗбүри исәп¬
ләнгән хәзерлек дәрәҗәсен билгелиләр: уртача билгесе алу өчен,
шундый мәсьәләләрне чишә белергә кирәк. Күп очракта бу
мәсьәләләрне чишү ысуллары белән тиңдәшле пункт текстында
тикшерелгән мисалларны карап танышырга мөмкин.
1.-5« Почмакларның зурлыкларын радианлы үлчәмдә күрсә-
|тегез:
а) 45°, 36°, 180°; б) 120°, 310°, 360°;
I в) 60°, 72°, 270°; г) 150°, 216°, 90°.
1 0 Тригонометрик функцияләр
2.— Почмакларның зурлыкларын градуслы үлчәмдә күрсәтегез:
я' я
I
5π .
6)
2π
SS
_δ-
' з’
2 ’
36 ’
5 ’
4 ’
9’
3π
5 ’
π;
г)
is
4 ’
Зя
2 ’
-Is.
12 ·
3. — Аңлатманың санча кыйммәтен табыгыз:
a) sin 0 + cos £ + sin2 б) 3 sin * + 2 cos π + ctg2 *;
к в) 6 sin f - 2 cos 0 + tg2 £; r) 3tg ~ sin2 * + cos2 *.
4. -$ Түбәндәге тигезлекләр үтәлерлек α, β, γ саннары бармы?
!a) sin α = -0,5, cos β = <3, tg γ = -2,5;
б) since = cosp = -2,2, tg γ = 0,31;
в) sina = 1,3, cosP = , tg γ = 5,2;
г) sina = -^, cosp = 72,5, tg γ =-7,5.
5.- Бер үк санның синусы белән косинусы тиңцәшле рәвештә
тигез булулары мемкинме?
а) һәм б) 0,4 һәм 0,7;
В) -!■· Һәм Г) --!■ һәм 4-,
β.- Бер үк санның тангенсы белән котангенсы тиңцәшле рә¬
вештә тигез булулары мемкинме?
а) ~т һәм -|; б) (ч/з — 2) Һәм (V3 + 2);
О 0
в) 2,4 һәм - ; г) һәм .
7. - а) sina = -0,8, π < a < ;
б) cos a = - —, ί < a < π;
B)sina=^, 0<α<£; r)cosa = |i, < a < 2π
О Λ 1 ί
булганда, калган өч төп тригонометрик функциянең кыйм¬
мәтләрен табыгыз.
8. - Аңлатманы гадиләштерегез:
а) cos2 a - cos4 a + sin4 a; 6) -—*COif-P-;
’ cosp + sin p ’
в) (sin2 a - tg2a sin2 a) ctg a; r) —>f + tg21.
cos* t
1 1 Тригонометрик функцияләр
9.— Исәпләп чыгарыгыз:
cos Λ· coa 5c ~ a'n 3*n Λ
15 la _ 15 la
а)
gs)
cos0,3k sin0,2n + эшО.Зя cos0,2k ’
sin—® cos® - sin® cos^®
Г" I IB a V LB
81n|® 81Пү® - COS I® COS-j-®
tg^ - tg|®
- д 1^ ·
1 + ’
10.
11.-
12.
13.
14.
list
ti -®- ΙΛ ~
110 412t
sina = f, cos₽ = --^, |<α<π, f < β < π;
cosa = 0,6, sinp = -7r, Яг < « < 2π, π < β < Яг
' 1 ϊ Z ' ζ
булганда, sin 2a, cos 2β, sin (a - β) һәм cos (a + β) ны исәпләп
чыгарыгыз.
а)
б)
Аңлатманы гадиләштерегез:
. 2sinacosfl-sm(a-p) .
fl' cos(a-P)-2sinasinP ’
g\ l-cosa+cos2ot .
1 sin2a-sina ’
в)
2 sin.
sin a
г) ctg2a (1 - cos 2a) + cos2 a.
Тиңдәшле тригонометрик функциянең аргументы ^0; ' |
аралыгында булырлык итеп, бирелгән аңлатманың рәве¬
шен үзгәртегез:
а) sin^r, cos (- -5-7ή, tg0,6n,
б) tg^. sinJ-i®), cosl,8rt,
Аңлатманың санча кыйммәтен
а) 8 sin " cos Яг tg 4" ctg —;
б) lOctg sin cos ;
в) —9Ш - - соз(2л - t).
1 + sinl~® + 11
Тигезлек дөресме?
a) sin - sin ~
i z 1 z 2
в) sin + sin = cos Яг;
io Jo у
ctg (-1,2л);
ctg0,9ir.
табыгыз:
6) cos^ -cos" =
о 24
г)
cos + cos - - 72 cos .
<3 0 о
Тригонометрик функцияләр
15- a) cosa = -||, π < α < б) sina = |» | < a < π;
в) cosa = Л, 4* < a < 2π; г) sin a = π < α <
булса, sin &, cos·^, tgj не табыгыз.
16. а) a = 0,19; б) a = 1,37; в) a = 0,9; г) a =1,2 булганда,
калькулятор яки таблица ярдәмендә sin a, cos a, tg a, ctg a
ның кыйммәтләрен табыгыз.
17. - Калькулятор яки таблица ярдәмендә
а) 17°; 43°24'; 83°36'; 72°12' почмакларының радианлы
үлчәмен;
б) 0,384; 0,48; 1,11; 1,48 почмакларының градуслы үлчә¬
мен табыгыз.
18. — Дуганың радианлы үлчәме α га, әйләнәсенең радиусы R га
тигез булган дуганың озынлыгын исәпләп чыгарыгыз:
а) a=2, R = 1 см; б)а = ^, Я = 6см;
в) a = 0,1, R = 1 м; г) а = Я= 10 м.
19. — Түгәрәкнең радиусы R һәм секторның үзәк почмагының
радианлы үлчәме α билгеле булганда, секторның мәйданын
исәпләп чыгарыгыз:
а} a = 0,1, R= 1 м; 6)a = y, й = 3м.
20. — а) Тиңдәшле дугасының озынлыгы түгәрәк диаметрына
тигез булган секторның үзәк почмагының радианлы үлчә¬
мен табыгыз.
б) Сектор дугасының озынлыгы аның периметрыннан өч
тапкыр кыскарак. Аның үзәк почмагының радианлы үл¬
чәмен табыгыз.
Аңлатмаларның кыйммәтләрен табыгыз (21—22).
21. — а) a = 5 булганда, 3sin(2a - ‘ j + 2cos(3a- π);
б) a = -ү булганда, sin2 (a - ~ j + 3tg i ■'* j;
в) a = * булганда, 4 cos (3a - * 1 + ctg (a + ;
r) a = -·| булганда, cos (a + + tg2 (2a + ·*).
22. — a) i + булганда, cosa = ||, < a < 2π;
б) Д1Д u тав булганда, tg a = -;
iinawno J ’ s 4’
cosa + ctga . ■
— булганда, cos a = -1, π < a < “;
r) sin2 a - cos2 β булганда, cos2 a - sin2 β = 0,5.
13
23.— О < α < ’ булганда, тигезлекнең дөрес икәнен исбатлагыз:
а)
б)
sin α^Ι + tg2 * * *a = ,1 ;
cosajl + tg 2α
11 + cos а /1 -cosa
. I ■: , - 2 ctg a;
\ 1 - cosa \ 1 + cosa &
вj 71 — sin2 a _ cosa .
sina y/l-cos2a’
!r) 7sin2 a + tg2 a sin2 a = . 1 .
ycos2a + ctg2 a cos2 a
Бердәйлекне исбатлагыз (24—26).
24. a) sin(» + a) - eosfj - a); B) = 2.
25.
a)
6)
в)
r)
(sin2t + 2 sin t cos t - cos21)2 - 1 - sin 4i;
cosa - 2sin3a - cos5a
—T—5-—— = tg 3a;
sin 5a - 2 cos 3a - sin a
1 - 4 sin2 t - cos2t „„„о..
cos21 — sin21
sina + 2sin2a + sin3a
ό—s T- = tg 2a.
cosa + 2cos2a + соэЗа
26.- a)
1 - tg2 £ 2 tg ?
COS ί - 7-; 6) βϊηβ -
i + i + tg2|
27-- Таблица һәм калькулятор кулланмыйча исәпләп чыгарыгыз:
a) sin £ cos
б) (sin - sin -j^): cos ~;
sin2 ' - cos2 ~;
cosАң? - cos Д
r) 12 12
Sin!2
2. Тригонометрик функцияләр
һәм аларның графиклары
1. Синус Һәм косинус функцияләре. Үзәге коорди-
наталар башлангычында, ә радиусы 1 гә тигез булган әйләнәне
берәмлек әйләнә дип атыйлар. Берәмлек әйләнәнең Ра ноктасы
Ро (1; 0) ноктасын a радиан почмакка борып табылсын, ди. Ул
вакытта Ра ноктасының ординатасы — a почмагының синусы,
ә бу ноктаның абсциссасы a почмагының косинусы икәнлеген
аңлау кыен түгел (5 нче рәсем).
1 4 Тригонометрик функцияләр
5 нче рәсем
6 нчы рәсем
1 нче мисал, -ү радианлы почмакның синусын, косину¬
сын, тангенсын һәм котангенсын табыйк.
Тигезьянлы турыпочмаклы өчпочмакның үзлекләреннән фай¬
даланып, ноктасының координаталарын (6 нчы рәсем)
җиңел табып була: х = - —, у = . Шуңа күрә sin 11 = ,
cos^ = _^, tg^ = -l, ctg^ = -l.
Алга таба без барлык почмаклар да радианнарда үлчәнгән дип
исәпләрбез һәм шуңа күрә pad тамгасы, кагыйдә буларак, төшереп
калдырылыр. Почмакларны үлчәү берәмлеген (1 радиан) бил¬
геләнгән дип исәпләргә сүз куешып, мәсәлән, х санының синусын
х радианлы почмакның синусы буларак, х санының косинусын х
радианлы почмакның косинусы буларак табабыз һ. б.
Билгеләмә. у = sin х һәм у - cosх формулалары
белән бирелгән санлы функцияләрне тиңдәшле
рәвештә синус Һәм косинус дип атыйлар (һәм sin
һәм cos дип тамгалыйлар).
Бу функцияләрнең билгеләнү өлкәсе — барлык реаль саннар
күплеге. Берәмлек әйләнә нокталарының ординаталары да, абс¬
циссалары да барлык кыйммәтләрен -1 дән алып 1 гә кадәр ал¬
ганга күрә, [-1; 1] кисемтәсе синус һәм косинус функцияләре¬
нең кыйммәтләре өлкәсе була, f функциясенең билгеләнү өлкә¬
сен — D(f) аша, кыйммәтләре өлкәсен E(f) аша тамгалыйк. Ул
вакытта болай язарга мөмкин:
D(sin) = D (cos) — R; Е (sin) “ Е (cos) = [-1; 1].
Синус һәм косинус функцияләренең сезгә таныш түбәндәге
үзлекләрен исегезгә төшереп китәбез.
Теләсә нинди х өчен:
1) sin (-х) = -sin х, cos (-х) = cos х;
2) sin (х + 2πη) = sin х, cos (х + 2πη) = cos х
I (η — теләсә нинди бөтен сан) тигезлекләре дөрес.
15
Тригонометрик функцияләр
2. Синусоида. [0; 2π] кисемтәсендә синус функциясенең гра¬
фигын тезик. Моның өчен ординаталар күчәрендә — (0; -1)
һәм (0; 1) нокталарын, ә абсциссалар күчәрендә 2π абсциссалы
ноктаны билгелибез (игътибар итегез: [0; 2π] кисемтәсенең
озынлыгы якынча 6,28 гә тигез). [0; 2π] кисемтәсен һәм берәм¬
лек әйләнәне 16 тигез өлешкә бүләбез (7 нче рәсем). Графикның
α абсциссалы ноктасын төзү өчен, синусның билгеләмәсеннән
файдаланабыз: берәмлек әйләнәдә Ра ноктасын билгеләп, Р„ аша
абсциссалар күчәренә параллель туры үткәрәбез (7 нче рәсем).
Бу туры белән х = а турысының кисешү ноктасы эзләнелгән нокта
булыр, чөнки аның ординатасы Р„ ноктасының ординатасы белән
тәңгәл килә, a sin α билгеләмә буенча Р„ ның ординатасына тигез.
7 нче рәсемдә графикның 16 ноктасын төзү күрсәтелгән. Шул
нокталарны салмак кәкре сызык белән тоташтырып, синус графи¬
гының [0; 2π] кисемтәсендәге эскизын табабыз. Синус графигын
бу кисемтәдән тыш дәвам итү өчен, sin (х + 2πη) = sin х (η — теләсә
нинди бөтен сан) булуын искәрәбез. Шуңа күрә х0 + 2πη (монда
0 χθξ 2π) күренешендәге барлык нокталарда синусның кыйм¬
мәтләре тәңгәл киләләр һәм, димәк, синусның барлык турыдагы
графигы аның төзелгән графигын Ох күчәре буйлап (уңга һәм
сулга) 2π, 4π, 6π һ.б. га параллель күчәре ярдәмендә табыла (8 нче
рәсем). Синусның графигы синусоида дин атала. Безгә синусның
кыйммәтләрен табарга ярдәм иткән ординаталар күчәрендәге
[-1; 1] кисемтәсен кайвакыт синуслар сызыгы дип тә атыйлар.
Косинусның графигын төзү өчен, cosx = sm(x + ~ ι булуын
искә төшерәбез. Шулай булгач, косинусның теләсә нинди xQ нок¬
тасындагы кыйммәте синусның х0 + 5 ноктасындагы кыйммәтенә
тигез. Бу исә косинус графигы синус графигын Ох күчәре буйлап
тискәре юнәлештә ' ераклыкка параллель күчереп табыла дигән
8 нче рәсем
Тригонометрик функцияләр
У.
У = COS X
-2п 3π
-π π 0
π π 3π 2π 5π х
2
" ' 2 -1
2 2 2 -
9 нчы рәсем
сүз. Шуңа күрә у = cos х функциясенең графигы да синусоида
була (9 нчы рәсем).
3. Тангенс, котангенс функцияләре һәм аларның графиклары.
Билгеләмә. » = tgx һәм y = ctgx формулалары
белән бирелгән санлы функцияләрне тиңдәшле
рәвештә тангенс һәм котангенс дип атыйлар
(һәм tg һәм ctg дип тамгалыйлар).
Тангенс функциясенең билгеләнү елкәсе — косинусы нульгә
тигез булмаган (cos х * 0) барлык х саннары күплеге, ягъни ■£ + яп
га тигез булмаган барлык х саннары күплеге (п барлык бетен
саннар күплеге Z ны «йөгереп үтә» дип исәпләнә. Котангенсның
билгеләнү өлкәсе синусы нульгә тигез булмаган (sin х * 0) барлык
х саннары күплегеннән, ягъни п га тигез булмаган (монда п е Z)
барлык саннардан тора.
Берәмлек әйләнәгә Рф ноктасында I орынмасын үткәрәбез
(10 нчы рәсем), α — косинусы нульгә тигез булмаган (cosa^O)
теләсә нинди сан булсын, ди. Ул вакытта Pa (cos a; sin а) ноктасы
ординаталар күчәрендә ятмый һәм, димәк, ОРа турысы I ны
1 абсциссалы ниндидер Тв ноктасында кисеп үтә. Бу ноктаның
ординатасын табыйк.
Моның өчен ОРо турысының 0(0; 0) һәм Ра (cos a; sin a) нокта¬
лары аша үтүен искәрәбез. Шуңа күрә әлеге турының тигезләмәсе
у = х tg a була. Бу туры өстендә яткан Та ноктасының абсциссасы
1 гә тигез. ОРа турысы тигезләмәсеннән Та ноктасының ординатасы
10 нчы рәсем 11 нче рәсем
Тригонометрик функцияләр
12 нче рәсем
кисешү ноктасының ординатасы α ның тангенсына тигез. Шуңа
күрә I турысын тангенслар сызыгы дип атыйлар.
Шулай ук ОРа турысы белән Л ноктасы аша берәмлек әйлә-
2
нәгә үткәрелгән т орынмасының кисешү ноктасы Со ның абс¬
циссасы (11 нче рәсем) ctga тигез икәнен исбатлап була (sin a*0
дип алына). Шуңа күрә т турысын котангенслар сызыгы дип
атыйлар.
Тангенсның (котангенсның) кыйммәтләре өлкәсе — барлык сан¬
лы туры. Моны tg функциясе өчен исбатлыйк. у0 — теләсә нинди
реаль сан булсын. Т(1; (/„) ноктасын карыйк. Хәзер генә күрсәтел¬
гәнчә, ТОх почмагының тангенсы yQ гә тигез. Димәк, tg функциясе
теләсә нинди реаль у0 кыйммәтен кабул итә. Шуны исбатларга
кирәк иде дә-
tg һәм ctg функцияләренең сезгә таныш булган түбәндәге
үзлекләрен исегезгә төшереп китәбез:
1) tg (-x) = -tgx; ctg (-Х) - -ctg x;
2) tg (x + πη) - tg x; ctg (x + πη) = ctg x, n e Z.
i Д- _ „
\ 2’2/ интервалында тангенсның графигын төзү (12 нче рә¬
сем) синусның графигын төзүгә карата сөйләгәннәргә охшаш,
(tg функциясенең ноктадагы кыйммәте тангенслар сызыгы ярдә¬
мендә табыла.) tg (х + πη) = tg х (п е Z) бердәйлеге булу сәбәпле,
1 8 .
• ** Тригонометрик функцияләр
тангенс функциясенең барлык билгеләнү өлкәсендәге графигы
(13 нче рәсем) 2) интеРвалындагы графиктан Ох күчәре
буйлап (уңга һәм сулга), π, 2п һ. б. га күчерү юлы белән табыла
(13 нче рәсем), tg функциясенең графигын тангенсоида дип
атыйлар.
Котангенсның графигы 14 нче рәсемдә бирелгән.
Синус, косинус, тангенс һәм котангенсны еш кына төп три¬
гонометрик функцияләр дип атыйлар. Кайвакыт тагын төп ике
тригонометрик функция — секанс һәм косеканс кулланыла (тиң¬
дәшле рәвештә sec һәм cosec дип тамгалана).
Төп тригонометрик функцияләрнең ни өчен 6 булуын аңлау
өчен, кысынкы α почмагының тригонометрик функцияләрен
кысынкы почмагы α булган турыпочмаклы өчпочмакның яклар
чагыштырмасы буларак та билгеләргә мөмкин (3 нче рәсем).
Андый чагыштырмалар 6:
sinoc-■'*·; cosa = -; tga = r; ctga = A;
с ’ с ’ b ® а
sec а - £; cosec а = —. · Ж
Ь а
14 нче рәсем
1 9 Тригонометрик функцияләр
Күнегүләр
28. —а)а = |, a = f. а = б)<х = |, а = π, а = -|;
в)а = £, а = Д?, « = -■&; г)« = -£, а · 2π, « =
Ο Ζ 4 О 4
булса, берәмлек әйләнәдә Ра ноктасын билгеләгез.
29. — a тигез
ί я( I 8 _jr- б) 1 — — ·
ίа) 2 ’ 4 ’ ’ 1 6’3’2’
βϊ _π К Яп·· Γ) ЗА in
2 ’ 3 ’ ύπ’ ' 4 ’ 3’2
булса, берәмлек әйләнәдә Ра ноктасының координаталарын
табыгыз.
30. - a тигез
а) За, -2,7; б) 51, 1,8л, -3,2;
в) '7 . 1,9; г) -2,3π, 3,7
4 D У
булса, Ра ноктасы координаталар яссылыгының кайсы чи¬
регендә урнашкан?
31. - Санның тамгасын табыгыз:
а) sin-„-cos^tg2,3n; б) sin 1 cos 3 ctg5;
в) sin 1, Зл cos у tg2,9; г) sin 8 cos 0,7 tg6,4.
32. a тигез
а) 4π, -π; б) -5,5π;
в) π, -2π; г)
булса, α ның синусы һәм косинусы кыйммәтләрен табыгыз.
33.- Функциянең графигын төзегез:
а) у = cos^ + x);
в) У = cos(|-xj;
б) у = - sin(x + π);
г) г/ - tg(x + π).
34.— Берәмлек әйләнәдә координаталары түбәндәге шартны ка¬
нәгатьләндерүче Ро(х; у) ноктасын билгеләгез:
а) у = 0,5; х > 0; б) х = - , у > 0;
в)х = ^·, у > 0; г)у = -^, х < 0.
35.— а) sina= -0,5;
в) coso: = -0,4;
б) cos a = 0,3;
г) tga = 2
булганда, миллиметрлы кәгазьдә берәмлек әйләнә, ә ан¬
нары a үзәк почмагын төзегез.
20 Тригонометрик функцияләр
Бирелгән функциянең билгеләнү өлкәсен һәм кыйммәт¬
ләре өлкәсен табыгыз. Аның графигын төзегез (36—37).
36. — а) у = 2 + sin х;
в) у — cosx - 1;
37. — а) у = 2 sinx;
в) у = 0,5 tgx;
б) у = 1 + tg х;
г) у = 3 + sin х.
б) у = -1 cos г;
г) у = -1,5 sinx.
Функция графигының координата күчәрләре белән кисешү
нокталарының координаталарын табыгыз (38—39).
38.— а) у = sin х;
в) у — cos х;
б) у = 1 + cos х;
г) у = sinx- 1.
39.— а) у = х2 - Зх;
в) у = 2,5 + cosx;
б) у = sinx — 1,5;
г) У =7 + 1·
§2.
Функцияләрнең төп үзлекләре
3. Функцияләр һәм аларның графиклары
1. Санлы функция. Функция төшенчәсе белән сез ал¬
гебра курсында таныштыгыз. Анализ башлангычларын өйрән¬
гәндә, функциянең түбәндәге билгеләмәсен кабул итү уңайрак.
Билгеләмә D күплегендәге һәр х санына бил¬
геле бер кагыйдә буенча х ка бәйле у санын тиңдәш
итүче тиңдәшлек билгеләнү өлкәсе D булган саклы
функция дип атала.
Функцияләрне, гадәттә, латин (ә кайвакыт грек) хәрефләре
белән тамгалыйлар. Ирекле рәвештә алынган f функциясен
карыйк. Бәйсез үзгәрешле х ны функциянең аргументы дип
атыйлар, х санына тиңдәшле у санын f функциясенең х нок¬
тасындагы кыйммәте дип атыйлар һәм /(х) дип тамгалыйлар.
f функциясенең билгеләнү өлкәсен D (f) дип тамгалыйлар, х саны
f функциясенең билгеләнү өлкәсенә кергәндәге барлык f (х) санна¬
рыннан торган күплекне f функциясенең кыйммәтләре елкэсе
дип атыйлар һәм Е (/) дип тамгалыйлар.
Еш кына функция нинди дә булса формула ярдәмендә бирелә.
Бу вакытта, әгәр нинди дә булса өстәмә чикләүләр бирелмәсә,
үзгәрешленең формуланы мәгънәле иткән барлык кыйммәтлә¬
ре күплеге шул формула белән бирелгән функциянең билгеләнү
өлкәсе дип исәпләнә. Мәсәлән, /(х) = формуласының барлык
х * 0 өчен мәгънәсе бар, шуңа күрә нульгә тигез булмаган бар¬
лык реаль саннар күплеге /(х) = ς функциясенең билгеләнү өлкәсе
21 Тригонометрик функцияләр
дип исәпләнә. Аның кыйммәтләре өлкәсе билгеләнү өлкәсе белән
тәңгәл килә, һәм ул (-°о; 0), (0; ®) интервалларының берләшмә¬
сеннән гыйбарәт.
Гомумән, А һәм В күплегенең берсенә генә булса да кергән
барлык элементлардан торган күплек А һәм В күплекләренең
берләшмәсе дип атала. А һәм В күплекләренең берләшмәсе A u В
рәвешендә тамгалана. Мәсәлән, [0; 2] һәм [1; 3] кисемтәләренең
берләшмәсе [0; 3] кисемтәсе була.
vj символы санлы аралыкларның берләшмәсе рәвешендә күрсә¬
тергә мөмкин булган саннар күплекләрен тамгалау өчен уңай.
Мәсәлән, /(х) = ~ функциясе өчен
D(f) = E(/) = (-oo;0)u(0; оо). ◄
у = tgx функциясенең билгеләнү өлкәсе
+ ππ; f+ πη].
монда ne Z рәвешендәге барлык интервалларның берләшмәсен¬
нән тора, ә аның кыйммәтләре өлкәсе — барлык санлы туры:
Е (tg) = (-х; α>).
f(x) = p (х) (монда р (х) — күпбуын) рәвешендәге функцияләрне
бөтен рациональ функцияләр дип, ә /(х) = (монда р (х) һәм
q (х)— күпбуыннар) күренешендәге функцияләрне вакланма
. ...... _
рациональ функцияләр дип атыйлар. ( | өлешенең q(x) нульгә
әйләнмәгәндә мәгънәсе бар. Шуңа күрә /(х) = вакланма-
рациональ функциясенең билгеләнү өлкәсен q(x) күпбуынының
тамырларыннан башка барлык реаль саннар күплеге тәшкил итә.
1 нче мисал, /(х) = вакланма-рациональ
х’ - Зх2 + 2х
функциясенең билгеләнү өлкәсен табыйк.
х3 - Зх2 + 2х күпбуынының тамырлары — 0,1 һәм 2 саннары.
Шуңа күрә D(f) = (-»; 0) (0; 1) u (1; 2) и (2; «). gg
2. Функциянең графигы, у = f (х) булганда, координаталар
яссылыгының барлык (х; у) нокталары күплеген f функциясенең
графигы дип атыйлар, ә х исә f функциясенең барлык билгеләнү
өлкәсен «йөгереп үтә».
Координаталар яссылыгы асткүплегенең Оу күчәренә парал¬
лель теләсә нинди туры белән бердән дә артык уртак ноктасы
булмаса, бу күплек нинди дә булса функциянең графигы була.
Мәсәлән, 15 нче рәсемдә сурәтләнгән күплек функция графигы
булмый, чөнки аның ординаталары төрле: б, һәм Ь,_ булган,
ә абсциссасы бер үк, ягъни а га тигез булган ике ноктасы бар.
Әгәр без әлеге күплекне функция графигы дип уйласак, бу
функциянең х = а булганда һәм Ь2 гә тигез ике кыйммәте бар
дип исәпләргә туры килер иде, ә бу функция билгеләмәсенә каршы
килә.
2 Тригонометрик функцияләр
Функцияне еш кына график юл белән бирәләр. Ул вакытта
билгеләнү өлкәсендәге теләсә нинди х0 өчен функциянең аңа тиң¬
дәшле у = f (*(>) кыйммәтен табу кыен түгел (16 нчы рәсем).
3. Графикларны үзгәртеп төзиләр. Хәзергә сез графикларын
төзи ала торган функцияләр артык күп түгел. Болар — у = kx + Ь,
у = ах2 + Ьх + с, y = sinx, y = cosx, у = tg х, y = ctgx
функцияләре. Геометрия курсыннан фигураларны үзгәртеп төзү¬
ләр турындагы таныш мәгълүматларны кулланып, бу исемлекне
шактый арттыра алабыз.
1) Башта ординаталар күчәре буйлап (0; Ь) векторына па¬
раллель күчерүне карыйк. Монда һәм алга таба да әлеге үзгәртүдә
яссылыкның ирекле рәвештә алынган (х; у) ноктасы күчкән нок¬
таның координаталарын (х'; у') аша тамгалап, сезгә таныш бул¬
ган формулаларны табабыз;
|х' = х,
I
1/ = у + Ь.
(1)
f — билгеләнү өлкәсе D(f) булган ирекле рәвештә алынган
функция булсын. Әлеге күчерүдә бу функциянең графигы нинди
фигурага күчкәнен ачыклыйк. (1) формулалардан турыдан-туры
графикның теләсә нинди (х; f (х)) ноктасы (х; / (х) + Ъ) ноктасына
күчкәнлеген табабыз. Бу исә f графигы барлык (х; / (х) + Ь) (монда
хе D(f)) нокталарыннан торган фигурага күчкәнлекне белдерә.
Функция графигының билгеләмәсе буенча бу фигура у = f (х) +
+ Ъ функциясенең графигы була. Югарыда сөйләгәннәрдән чыгып,
шундый кагыйдә әйтә алабыз:
/(х) + Ъ (монда Ь — даими сан) функциясенең графи¬
гын төзү өчен, f графигын ординаталар күчәре буйлап
(0; Ь) векторына күчерергә кирәк.
■ 2 нче мисал, а) у = sin х + 2,б)у = х2-5 функцияләренең
графикларын төзик.
а) Кагыйдәгә туры китереп, у = sin х функциясенең графигын
(0; 2) векторга, ягъни Оу күчәре буйлап 2 берәмлеккә югарыга
таба күчерәбез (17 нче рәсем).
Тригонометрик функцияләр
17 нче рәсем
б) Төзү у = х2 параболасын (0; -5)
векторга, ягъни Оу күчәре буйлап
түбәнгә таба күчерү юлы белән баш¬
карыла (18 нче рәсем).
2) Оу күчәре буйлап k коэффици¬
енты белән сузу сезнең өчен яңа үз¬
гәртеп төзү булып тора. Бу үзгәртү
X - х,
У' = ky.
(2)
формулалары белән бирелә.
Сузганда бирелгән М' ноктасы
күчә торган М ноктасын төзү өчен
ΑΛί турысында (монда А—М ның.
Ох күчәренә проекциясе, 19 нчы
а рәсем) А үзәгенә карата М га го¬
мотетии нокта төзергә кирәк (го¬
мотетия коэффициенты сузу коэф¬
фициенты k га тигез). 19 нчы б рә¬
семдә һәм -2 коэффициенты белән
сузганда бирелгән нокталар күчә торган нокталарны төзү күрсә¬
телгән.
Сузганда f функциясенең графигы нинди фигурага күчкәнен
ачыклыйк. (2) формулаларыннан турыдан-туры f графигының
ирекле рәвештә алынган (х; f(x) ноктасы (х; ноктасына
күчкәнлеген табабыз. Моннан f графигының барлык (х; kf (х))
нокталарыннан торган фигурага күчкәнлеге килеп чыга (монда
xeD(f). Бу фигура (у = kf(x)) функциясенең графигы була.
Түбәндәге кагыйдә исбатланды:
у = kf(x) функциясенең графигын төзү өчен, у = / (х)
функциясенең графигын ординаталар күчәре буйлап
k тапкырга сузарга кирәк.
3 нче мисал, у = —2хг һәм у = -1 cosх функцияләренең
графикларын төзик.
Тригонометрик функцияләр
Беренче очракта төзү у = х2 функциясенең графигын фай¬
даланып башкарыла (20 нче рәсем), ә икенче очракта башта
j/ = cosx функциясенең графигын төзибез, аннары ордината¬
лар күчәре буйлап ή коэффициенты белән сузудан файдаланабыз
(21 нче рәсем).
Искәрмә. Әгәр 0< |л| < 1 булса, k коэффициенты белән
сузуны еш кына кысу дип атыйлар.
Мәсәлән, коэффициенты белән сузу 2 тапкырга кысу дип
атала. Әгәр k < 0 булса, y = kf(x) функциясенең графигын төзү
өчен, башта f функциясенең графигын k тапкырга сузарга, ә ан¬
нары аны абсциссалар күчәренә симметрияле итеп чагылдырырга
кирәк була (20 нче рәсемне карагыз).
21 нче рәсем
25
Тригонометрик функцияләр
3) Абсциссалар күчәре буйлап
(а; 0) векторга параллель күчерү
х' - х + а,
У" - У
(3)
формулалары белән бирелә.
(3) формулалары буенча / функ¬
циясе графигының һәр ноктасы
(х +а; f(x)) ноктасына күчә. Шуңа
күрә f графигы (х' f(x' - α)) ноктала¬
рыннан торган Ф фигурасына күчүен
х’, у’ үзгәрешлеләре ярдәмендә
язарга мөмкин, монда х’ үзгәрешлесе х + а күренешендәге барлык
кыйммәтләрне ала, х исә D(f) ны ♦йөгереп үтә».
х’ ның нәкъ шул кыйммәтләре өчен х' - а саны D(f) ныкы
була һәм f(x' - а} дип билгеләнә. Димәк, Ф фигурасы y = f(x- а)
функциясенең графигы була. Шулай итеп, нәтиҗә ясарга мөмкин:
y = f(x-a) функциясенең графигы f графигыннан
аны абсциссалар күчәре буйлап (а; 0) векторга кү¬
череп табыла.
Игътибар итегез: әгәр а > 0 булса, (а; 0) векторы абсциссалар
күчәренең уңай юнәлеше белән бердәй юнәлгән, ә а < 0 булса,
каршы юнәлгән.
4 нче мисал, у = >/х +1 һәм y = cos(x-·^) функция¬
ләренең графикларын төзү 22 нче һәм 23 нче рәсемнәрдә күрсә¬
телгән.
4) Ох күчәре буйлап k коэффициенты белән сузу
х’ = kx,
у'- У
(4)
формулалары белән бирелә.
Мондый сузу вакытында f функциясе графигының теләсә кай¬
сы ноктасы (Ах; /(х)) ноктасына күчә. Ә х', у’ үзгәрешлеләренә
килсәк, у = f(x) графигы (х'; f нокталарыннан торган фигура¬
га күчә дип әйтергә мөмкин, монда х’ үзгәрешлесе х' = Ах күрене¬
шендәге барлык кыйммәтләрне ала, ә хе £>(/).
23 нче рәсем
26
Трнгонометрнк функцияләр
24 нче рәсем
Бу фигура у = функциясенең графигы була. Шулай бул¬
гач:
У - f (функциясенең графигын төзү өчен, f функ¬
циясенең графигын абсциссалар күчәре буйлап k ко¬
эффициенты белән сузарга кирәк.
Q 5 нче мисал. у = cos2х һәм у = sinх функцияләренең
графикларын төзү 24 нче һәм 25 нче рәсемнәрдә күрсәтелгән.
4. Чагылдыру. Билгеләнү өлкәсе D һәм кыйммәтләре өлкә¬
се Е булган функцияне шулай ук D күплегенең Е күплегенә
чагылдыруы дип тә атыйлар. Мәсәлән, у = sinx формуласын
реаль саннар күплеге R ның [-1; 1] кисемтәсенә чагылдыруы
дип әйтергә мөмкин. «Функция» Һәм «чагылдыру* сүзләре —
синонимнар.
Еш кына билгеләнү өлкәсе яки кыйммәтләре өлкәсе (бәлки,
бу ике күплек тә) санлы күплекләр булмаган функцияләр (чагыл¬
дырулар) тикшерелә. Андый мисаллар белән сез, асылда,
геометрия курсында очраштыгыз инде. Мәсәлән, мәйданнарны
үлчәүнең билгеләнгән берәмлекләрендә «Күппочмак мәйданы»
функциясенең билгеләнү өлкәсе — яссылыкта күппочмаклар
күплеге. Ә бу функциянең кыйммәтләре күплеге — тискәре
булмаган саннар күплеге, («мәйданы юкка чыккан» күппочмаклар,
мәсәлән кисемтә, 0 мәйданга ия).
F фигурасын F' фигурасына күчерә торган хәрәкәт (охшаш
үзгәртү кебек үк) чагылдыру була, аның билгеләнү өлкәсе F һәм
кыйммәтләре өлкәсе F' нокталардан торалар.
Чагылдыру төшенчәсен еш кына гомуми математиканың төп
төшенчәләре исәбенә кертәләр. Аның ярдәмендә функциягә мон¬
дый билгеләмә бирергә мөмкин: D күплегенең һәр элементына
у - sin х
25 нче рәсем
27 Тригонометрик функцияләр
Е күплегенең тулысынча билгеләнгән бер элементы туры килгәндә
һәм Е күплегенең һәр элементы D күплегенең бер генә булса да
ниндидер элементына тиңдәш ителгәндә, D күплегенең Е күпле¬
генә чагылдыруы билгеләнү өлкәсе D һәм кыйммәтләре өлкәсе
Е булган функция дип атала.
Күнегүләр
40. — а) -1, 2 » Ю нокталарында /(х) = х + ·£·,
б) - * , 0, π нокталарында f(x) = 3 cos (х - γ |;
в) 0, 1, 2 нокталарында /(х) = 7бх - х2 ;
г) - }, 0, нокталарында /(х) = 2 - sin 2х
функцияләренең кыйммәтләрен табыгыз.
41. - a) х0, t + 1 нокталарында /(х) = х2 + 2х;
б) a, b - 1 нокталарында /(х) = tg 2х;
в) х0, а + 2 нокталарында /(х)= ‘ +1;
г) 2, Λ + π нокталарында f(x) = 2 cos функцияләренең
кыйммәтләрен языгыз.
42. - 26 нчы а—г рәсемнәрдә сурәтләнгән фигура функциянең
графигы буламы?
26 нчы рәсем
28 Тригонометрик функцияләр
һәр функциянең билгеләнү өлкәсен табыгыз (43—44).
43. -ia) fix) - г *. 1 „ ; б) f(x) = 4х2 - 9;
X - 4х + 3
в) f(x) - Л о*’ п; 0 fix) - 7зв №.
44. - a) f(x) = 4-: б) fix) - 2 tg х;
X
в) f(x) = 1 + ctgX; Γ)/(Χ) = Λ·
х
45. Һәр функциянең билгеләнү өлкәсен һәм кыйммәтләре өл¬
кәсен табыгыз:
а) у = 2cos(x-|); 6)^ = 2 + ^;
в) у = -1; г)у = 3 + 0,5 sin (*+*)-
46.
47.-
Графиклары 27 нче a—г рәсемнәрдә сурәтләнгән функ¬
цияләрнең билгеләнү өлкәсен һәм кыйммәтләре өлкәсен
табыгыз.
а) />(Л) - [ 2; 4], £(/) = [-3; 3];
б) D(f) = (-5; 3), Е (/) - (2; 6] булган нинди дә булса f функ¬
циясенең графигын сызыгыз.
27 нче рәсем
29
Тригонометрик функцияләр
48,— функцияләрнең графикларын бер үк координаталар систе¬
масында төзегез:
И У = Ь у = | + 2, у = ^-2;
I б) y = cosx, y = cosx-3, y = cos(x + -*j;
в) у = -х2, у = 4 - х2, у = -(х - 2)2;
r)y = sinx, y = sinx + 2, у = sin(x +’).
Функцияләрнең графикларын төзегез (49—50).
49. - а) у = r ; б) у = (х - 2)2 - 4;
в) у = 1-(х + 2)г; г) у = 2 + |.
50. - a) y = l + 2sinx; б) у = Vx + 1 -1;
в) у = 0,5 cos х - 1; г) у = 2 + Vx - 1.
_ , ] х, х ? 0 булса, Λ 1 Λ „
51.— a) fix) = -2;-£;0;5 нокталарында;
I -х, х < 0 булса; 3
б) /(х) =
х2-1, х>-1 булса,
-2; -1; 0; 4 нокталарында;
1 - х, х < -1 булса;
в) /(х) =
-|;0;
ΐ
6
sin х, х > 0 булса, π
cos х -1, х С 0 булса; 2
нокталарында функциянең кыйммәтләрен табыгыз.
52.— a) ABC өчпочмагының АС нигезе Ь га, BD биеклеге һ ка
тигез. BD биеклегенең К ноктасы аша АС га параллель
туры үткәрелгән. Бирелгән өчпочмакны бу туры белән бү¬
лүдән килеп чыккан фигураларның мәйданнарын ВК = х
ераклыгының функциясе буларак күрсәтегез.
- б) Үзәк почмакның радианлы үлчәме х ка, түгәрәкнең
радиусы R га тигез. Тиндәшле сегментның мәйданын
х ның функциясе буларак күрсәтегез.
в) Секторның үзәк почмагының радианлы үлчәме α га,
радиусы г га тигез. Секторның периметрын ос почмагының
функциясе буларак күрсәтегез.
, г) Квадратның диагоналенә параллель туры аны ике
фигурага бүлә. Квадратның ягы а га тигез булса, һәр
фигураның мәйданы һәм диагональдән әлеге туры белән
кисеп алынган кечерәк кисемтәнең озынлыгы х арасын¬
дагы бәйлелекне формула белән бирегез.
Тригонометрик функцияләр
53.— Функциянең билгеләнү өлкәсен табыгыз:
. х/Зх-2
. Jx + 2 .
У ~ 3 - 2х ·
б) У = ' Ifi гг ί
Ю X
. - χ2
Г> У- 1-2х ·
54.— Функцияләрнең билгеләнү өлкәсен һәм кыйммәтләре өл¬
кәсен табыгыз:
а) у = 1 + sin2x ;
в) у = Jx2 + 4 ;
«ϊ . х -1 .
б) у = х ;
г) у - 1,5 - 0,5 cos2 х .
Функцияләрнең графикларын төзегез (55—56).
55.-а) у = |х-1|;
б) V =
х2 -4, х 2 булса,
2-x, х <2 булса;
в) у = -~/2х - 2 ;
г)
3 - х2, х > 1 булса,
х - 2, х $ 1 булса.
56. а) у = sin3x - 1;
в) у = 1 + cos2x ;
б) у = |х3 + 2;
г) у = 1 + |х/х.
4. Җөп һәм так функцияләр.
Тригонометрик функцияләрнең периодиклыгы
1. Җөп һәм так функцияләр. Билгеләнү өлкәсе коор-
динаталар башлангычына карата симметрияле булган, ягъни бил¬
геләнү өлкәсендәге теләсә нинди х өчен (-х) саны шулай ук бил¬
геләнү өлкәсенә кергән функцияләрне тикшерик. Андый функция¬
ләр арасында җөп һәм так функцияләрне билгелиләр.
Билгеләмә. Әгәр билгеләнү өлкәсендәге теләсә
нинди х өчен f(-x) = f(x) тигезлеге үтәлсә, f функ¬
циясе xf&n функция дип атала (28 нче рәсем).
28 нче рәсем
31 Тригонометрик функцияләр
Билгеләмә. Әгәр билгеләнү өлкәсендәге теләсә
нинди х өчен f(-x) — ~f(x) тигезлеге үтәлсә, / функ¬
циясе так функция дип атала (29 нчы рәсем).
I 1 нче мисал. f(x) — x*— җөп функция, ә g (х) = х3 — так
функция. Чыннан да, бу функцияләрнең һәркайсының билгеләнү
өлкәсе (ул барлык санлы туры) 0 ноктасына карата симметрияле
Һәм теләсә нинди х өчен f (-х) = (-х)4 = х4 = f(x), g(~x) = (_х)8 =
= -х3 = -g (х) тигезлекләре үтәлгән. Бу функцияләрнең график¬
лары 30 һәм 31 нче рәсемнәрдә сурәтләнгән.
Җөп һәм так функцияләрнең графикларын төзегәндә, сезгә
алгебра курсыннан таныш булган түбәндәге әзлекләрдән файдала¬
нырбыз:
Iе. Җөп функциянең графигы ординаталар күчәренә
карата симметрияле.
2*. Так функциянең графигы координаталар башлан¬
гычына карата симметрияле.
Әлеге ике кагыйдәдән шундый нәтиҗә килеп чыга: җөп яки
так функциянең графигын төзегәндә, аның бер кисәген тискәре
булмаган х лар өчен төзеп, аннары килеп чыккан графикны
ординаталар күчәренә карата (функция җөп булган очракта) яки
координаталар башлангычына карата (так булган очракта)
чагылдыру җитә.
2 нче мисал, /(х) “ х + γ —так функция (моны мөстә¬
кыйль рәвештә исбатлагыз). Аның графигы координаталар баш¬
лангычына карата симметрияле (32 нче рәсем).
Төп тригонометрик функцияләрдән синус, тангенс һәм котан¬
генс — так, ә косинус — җөп функция. Шуңа күрә синус, тангенс
Тригонометрик функцияләр
һәм котангенсның графиклары координаталар башлангычына
карата симметрияле (8, 13, 14 нче рәсемнәрне карагыз), ә коси¬
нусның графигы (9 нчы рәсемне карагыз) ординаталар күчәренә
карата симметрияле,
3 нче мисал, fix) = ж,+ х — җөп функция, чөнки аның бил-
х ~х
геләнү өлкәсе х = 0 ноктасына карата симметрияле (ул -1,0 һәм
1 дән башка барлык саннардан тора) һәм барлык xeD(f) өчен
f(-x) = '■*' = f(x)
1 ' (-x)’-(-x) х - х3 x’-x v 7
тигезлеге үтәлгән.
Бу функциянең графигы Оу күчәренә карата симметрияле
(33 нче рәсем).
4 нче мисал, /(х) = х2 + х җөп функция дә, так функция
дә түгел. Аның билгеләнү өлкәсе 0 ноктасына карата симметрияле,
ләкин, мәсәлән, х = 1 булганда /(1) = /(-1) тигезлеге дә, f (1) =
= -/(-1) тигезлеге дә үтәлми, чөнки /(1) =■ 2, ә /(-1) = 0.
2. Периодик функцияләр. Тормышта безгә очрый торган про¬
цесс һәм күренешләрнең күбесе кабатлану үзенчәлегенә ия. Мәсә¬
лән, Кояш белән Җирнең үзара бертөрле торышы ел аша кабат¬
лана. Маятникның торышлары аның тирбәнү периодына тигез
период белән бер-берсеннән аерылып торган вакыт моментларында
бертөрле була.
Мондый төрдәге процессларны периодик процесслар дип,
ә аларны тасвирлап биргән функцияләрне периодик функцияләр
дип атыйлар.
Сезгә таныш булган төп тригонометрик функцияләр — перио¬
дик функцияләр. Әйтик, теләсә нинди х һәм теләсә нинди бөтен
33 Тригонометрик функцияләр
k саны өчен sin (х + 2rcfe) = sin х тигезлеге үтәлә. Моннан 2nfe- синус
функциясенең периоды (k # 0 — теләсә нинди бөтен сан) икәнлеге
килеп чыга.
Гомумән, f функциясенең периодиклыгы турында сөйләгәндә
билгеләнү өлкәсе D (/), һәр х ноктасы белән бергә, х ны Ох күчәре
буйлап (уңга һәм сулга) Т ераклыкка параллель күчергәндә килеп
чыккан нокталарны да үз эченә алырлык Т * 0 саны бар дип уйла-
ныла. Әгәр билгеләнү өлкәсендәге теләсә нинди х өчен функция¬
нең х, х - Т һәм х + Т нокталарындагы кыйммәтләре тигез, ягъни
f (х + Т) = f (х) = f (х - Т) булса, f функциясен периоды Т » 0 булган
периодик функция дип атыйлар.
Барлык санлы турыда билгеләнгән һәм теләсә нинди х өчен
sin (х + 2π) = sin х, cos (х + 2π) = cos х булганга күрә, синус һәм
косинус — периодлары 2π гә тигез булган периодик функцияләр.
Тангенс һәм котангенс — периодлары π гә тигез булган перио¬
дик функцияләр. Чыннан да, бу функцияләрнең билгеләнү өлкә¬
ләре, һәр х белән бергә, х + π һәм х - π саннарын да үз эчләренә
алалар һәм tg(x + π) = tgx, ctg(x + π) = ctgx тигезлекләре дөрес.
Үзеннән-үзе аңлашыла, әгәр / функциясенең периоды Т булса,
ул вакытта теләсә нинди бөтен п £ 0 өчен пТ саны шулай ук бу
функциянең периоды була. Мәсәлән, п = 3 булганда, берничә тап¬
кыр периодик функция билгеләмәсен кулланып табабыз:
/(х + ЗТ) = /((х + 2Т) + Т) - f (х + 2Т) = f ((х + Т) + Т) =
= /(х + Т) = /(х).
а) у = sin х һәм у = cos х функцияләренең иң кечкенә
уңай периодлары 2π гә тигез икәнен;
б) У ~ tg х һәм у = ctgx функцияләре өчен иң кечкенә
уңай период π саны икәнен исбатлыйк.
► а) Билгеләп үтелгәнчә, 2π саны sin һәм cos функцияләренең
периоды була. Шуңа күрә 2π дән кечкенәрәк уңай сан аларның
периоды була алмавын исбатлыйсы кала. Моны исбат итик.
Әгәр Т — косинусның, ирекле рәвештә алынган периоды бул¬
са, ул вакытта теләсә нинди α өчен cos (а + Т) = cos а. а = 0 дип
алып, cos Т = cos 0=1 икәнен табабыз, cos х = 1 булган иң кечкенә
уңай Т саны 2π.
Т — синусның ирекле рәвештә алынган уңай периоды булсын.
Ул вакытта теләсә нинди α өчен sin (α + Т) = sin α, α = * дип алып,
sin IT + j) = sin^ = 1 икәнен табабыз. Ләкин х - | + 2πη (neZ)
булганда гына sin х = 1. Шуңа күрә 2πη рәвешендәге иң кечкенә
уңай сан 2π.
б) Әгәр Т — тангенсның уңай периоды булса, ул вакытта tg Т =
— tg(O + Т) = tgO = 0. (0; π) интервалында тангенсның нульләре
булмаганга күрә, Т ·ι π. Алдарак tg функциясенең периоды π икән-
34 Тригонометрик функцияләр
у
34 нче рәсем
леге исбатланган иде, димәк, π тангенсның иң кечкенә уңай перио¬
ды була, ctg өчен исбатлау аналогик рәвештә башкарыла.
Кагыйдә буларак, «иң кечкенә уңай период» сүзе төшереп
калдырыла. Мәсәлән, тангенсның периоды π гә тигез, синусның
периоды 2π гә тигез дип сөйләү кабул ителгән.
Төп тригонометрик функцияләрнең периодиклыгыннан без ал-
дарак аларның графикларын төзегәндә файдаланган идек инде.
Түбәндәге раслау дөрес булыр.
Периоды Т булган периодик функциянең графигын
төзү өчен, аны Т озынлыгындагы кисемтәдә төзеп,
аннары килеп чыккан графикны Ох күчәре буйлап
уңга һәм сулга пТ ераклыкка күчерү җитә (34 нче
рәсем, монда п — теләсә нинди натураль сан).
Чыннан да, (х0; у0) — периодик f функциясе графигы ноктасы
булсын. Ул вакытта теләсә нинди бөтен п өчен х0 + пТ ноктасы
f ның билгеләнү өлкәсенә керә (пункт башындагы искәрмәне кара¬
гыз) һәм f ның периодик булуы сәбәпле, f(x0 + пТ) = /(х0) = у0
тигезлеге дөрес. Димәк, (х0; у0) ноктасын Ох күчәре буйлап
(пТ; 0) векторына параллель күчергәндә табылган (х0 + пТ; у0)
ноктасы да f графигыныкы була.
5 нче мисал. f(x) = 2cosx + l функциясенең графигын
төзик. Төзү өчен аның периоды 2π гә тигез периодик функция
булуыннан файдаланабыз. Чыннан да, f функциясе барлык турыда
билгеләнгән һәм, димәк, аның билге¬
ләнү өлкәсе, теләсә нинди х0 ноктасы
белән бергә, х0 не Ох күчәре буйлап
уңга һәм сулга 2π ераклыкка парал¬
лель күчерүдән килеп чыккан нокта¬
ларны да эченә ала. Моннан тыш, ко¬
синус периодик функция булганлык¬
тан, /(х + 2л) = 2 cos (х Η-2π) + 1 =
= 2 cos х-н 1 = /(х). Периодик функ¬
цияләрнең графиклары үзлегеннән
35 нче рәсем
файдаланып, f ның графигын башта
Тригонометрик функцияләр
36 нчы рәсем
[0; 2π] кисемтәсендә төзибез. Графикларны үзгәртеп төзүнең та¬
ныш кагыйдәләренә туры китереп косинусның графигын Оу кү¬
чәре буйлап 2 тапкырга сузабыз һәм аны 1 гә югарыга таба күче¬
рәбез (35 нче рәсем), ә аннары параллель күчерүләр ярдәмендә
аны барлык санлы турыда дәвам итәбез (36 нчы рәсем).
, 6 нчы мисал. f(x) = tg^2x — функциясенең периодик
һәм иң кечкенә уңай периоды | икәнен исбатлыйк. Тан¬
генс аргументның ! + πη (neZ) гә тигез булмаган барлык
кыйммәтләре өчен билгеләнгән. Шуңа күрә бирелгән функциянең
билгеләнү өлкәсе 2х — j Ф -ή + πη , ягъни х ϊ , ηεΖ шарты
үтәлгән х лардан тора. Моннан D[f), ирекле рәвештә алынган х
лар белән рәттән, х0+^, х0 - neZ рәвешендәге барлык
нокталарны да эченә алганлыгы килеп чыга.
f(x+ 5) = tg(2(x + |J- = tg((2x-i) + n) = tg(2x -|) = f(x)
булгач, * саны f функциясенең периоды икәнлеге күренеп тора.
* саны f функциясенең иң кечкенә уңай периоды икәнлеген
исбатлыйсы кала. ξ дән кечерәк булган То саны f ның периоды,
дип уйлыйк. Ул вакытта теләсә нинди χεί)(/) өчен f(x + T0) -
tg(2 (х + То) - |) = tg((2x - I) + 2Т0) = f(x) = tg (2х - , чөнки
То саны — f ның периоды. Ләкин бу 2Т0 саны f функциясенең
периоды икәнлеген белдерә. Безнең фараз итү буенча То < * һәм,
димәк, 2Т0 < π. Бу элек исбатлаганга каршы килә: тангенсның
иң кечкенә уңай периоды π гә тигез.
Гомуми раслау аналогик рәвештә исбатлана:
Әгәр f функциясе периодик һәм Т аның периоды
булса, ул вакытта Af(kx + b) функциясе, монда А,
k һәм b — даими зурлыклар, ә fe * 0, шулай ук
периодик була, шуның белән бергә, аның периоды
-J- га тигез.
*
Тригонометрик функцияләр
Бу раслаудан чыгып турыдан-туры, мәсәлән, sin |3х - 11 функ¬
циясенең периоды — санына, ә cos (- * + π) функциясенең
периоды 4π гә тигез икәнлеген табабыз.
Күнегүләр
Җөп функцияләр икәнлеген исбатлагыз (57—58).
57.- а) flx) = Зх2 + х4; б) f(x) = х5 sin f;
&
58.-
в) fix) - хг cosx; г) f(x) = 4х® - х2;
а) Лх)-008^—; б) fix) = 2^·,
B)f(Jt)- 32; г)/(х)-СО8Х.
jc 4 - г
Так функцияләр икәнлеген исбатлагыз (59—60).
59. a) f(x) = х3 sin х2; б) fix) = х2(2х - хэ);
в) ftx) = x5cos3x; г) f(x) = x(5 - x2) .
60, - a) f(x) = ; 6) f(x) = cosx\ ;
' 2xJ ’ 7 ' ' i(25-x2)
X ' “ J ’j
a) 6)
в) r)
37 нче рәсем
Тригонометрик функцияләр
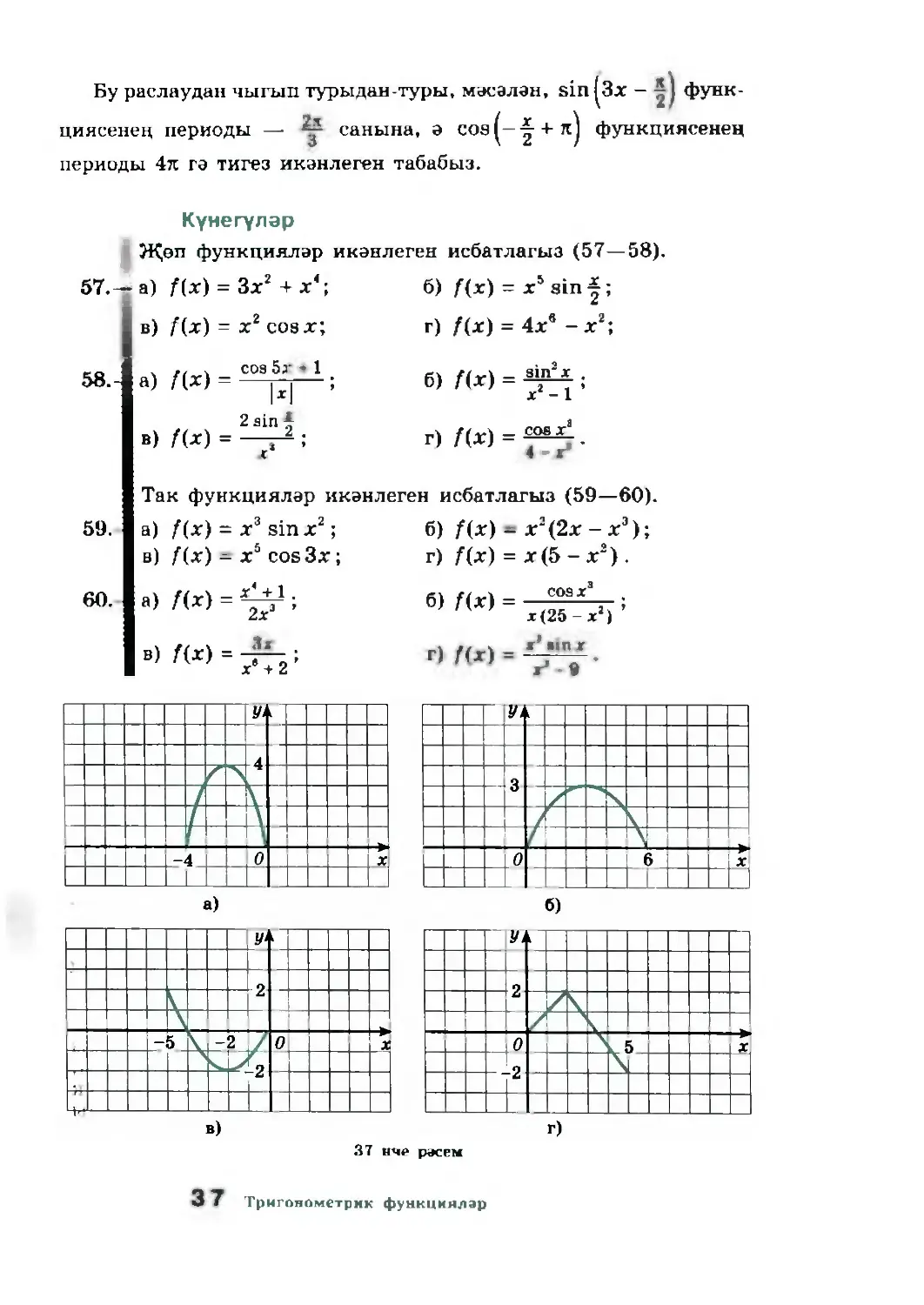
61.— 37 нче а—г рәсемдә х 0 (х 0) шартын канәгатьләндергән
барлык х лар өчен f функциясенең графигы төзелгән.
1) f — җөп функция; 2) f — так функция икәнлеге билгеле
булса, f функциясенең графигын төзегез.
62. ^а) r(x) = sinf, Т = 4π; б) f(x) = 2tg3x, T = <;
я в) f(x) = 3cos4x, T = j; г) f(x) = ctg|, T = 3π
булса, T саны f функциясенең периоды икәнен исбатлагыз.
63.
64.
65. -
f функциясенең периодик икәнен исбатлагыз:
а) /(х) = 2 - cos х ; б) f(x) = tg2x;
в) /(х) = sinх + cosx; г) f(x) = 3 + sin3x .
Һәр функциянең иң кечкенә уңай периодын табыгыз
(64—65).
а) У = I sin & ; б) у = 3 tg 1,5х ;
B)y = 4cos2x; r)y = 5tg|.
а) у - sin х cos х ;
в) у = sin2x - cos2x ;
б) у = sin х sin 4х - cos х cos 4х ;
г) у “ sin 3x cos х + cos 3x sin x .
Тригонометрик функциялор
66. — 38 нче а—г рәсемнәрендә периоды Т булган функция
, графигының бер өлеше сурәтләнгән. Бу функциянең
[-1,57; 2,57] аралыгындагы графигын төзегез.
67. Д Функциянең иң кечкенә уңай периодын табыгыз һәм
графигын төзегез:
а) у = sin 2х ; б) У = cos * ;
в) У - tg ; г) у = sin 1,5х .
68.
Укучы, f функциясе өчен ике тигезлекнең дөреслеген тик¬
шереп, 7 саны f ның периоды була дигән нәтиҗә ясады.
а) f(x) = sinx, sin| = |, sin(* + ^) = |, Т = ^;
б) /(х) = cosх, cos= 0, cos(·| + π) = 0, Т = π;
fU) = -j
в)
X + 1, x < 1 булса,
3 - х, х > 1 булса.
/•(-|) = 0,5, r(-| + 3) = 0,5, 7 = 3;
г)/(х) = х + |х|, f(-4) = 0, /(-4 + 3)-О,
ры өчен укучының бу раславы дөресме?
Т = 3 шартла-
Түбәндә күрсәтелгән функцияләрнең кайсылары — җөп,
кайсылары — так, кайсылары җөп тә, так та түгел (69—70)?
69.—а) у = sin х + ctgx - х; б) у - ————;
' 91П X COS X
70.¬
71.4
72.
в) у = х4 + tg’x + х sin х;
ч tgr-CtRX
г) " Ы
Бирелгән функциянең җөп яки так икәнен исбатлагыз
һәм аның графигын төзегез:
а) У = ; б) у = .
f һәм g функцияләре барлык реаль саннар күплегендә
билгеләнгән.
а) һ(х) = /(x)g2(x), f — җөп функция, g — так функция;
б) А(х) = /(х) - g(x), f һәм g — җөп функцияләр;
в) й(х) - f(x) + g(x), f һәм g — так функцияләр;
г) Λ(χ) - f(x) g(x), f һәм g — так функцияләр булса,
h җеп функция буламы?
39
Тригонометрик функцияләр
73. — Функциянең иң кечкенә уңай периодын табыгыз:
a)y = sin2x; 6)y = tgxctgx;
в) у = ат4х - cos4х; г) у = (sin^ + cos-| j .
74. —Функциянең графигын тезегез:
а) у = 1 - cosl, 5х; β) У = sin(2x - ’);
B)y = 2 + Sinf; r) y = tg(2x-j).
75. — Әгәр у = f (х) функциясе периодик булса, у = kf(x) + Ь функ¬
циясенең дә периодик икәнен исбатлагыз.
76. -2 саны функциянең периоды түгеллеген исбатлагыз:
а) у = х2-3; б) y*cosx; в) у = Зх-5; г) у = |х|.
5. Функцияләрнең үсүе һәм кимүе.
Экстремумнар
1. Функцияләрнең үсүе һәм кимүе. Үсүче һәм кимү¬
че функцияләрнең төшенчәләре белән сез инде таныш. Мәсәлән,
39 нчы рәсемдә [-1; 10] кисемтәсендә билгеләнгән функциянең
графигы сурәтләнгән. Бу функция [-1; 3] һәм [4; 5] кисемтәләрендә
үсә, [3; 4] һәм [5; 10] кисемтәләрендә кими, у = х2 функциясенең
(-со; 0] гә кадәр аралыкта кимегәнлеге, [0; “) кә кадәр аралыкта
үскәнлеге билгеле, х үзгәрешлесе -« тән ® кә кадәр үзгәргәндә,
бу функциянең графигы башта нульгә кадәр «төшә» (0 ноктасында
функциянең кыйммәте нульгә тигез), ә аннары чиксезлеккә кадәр
«күтәрелә» (20 нче рәсемне карагыз).
Билгеләмә. Әгәр Р күплегендәге теләсә нинди
х, һәм х2 өчен х2 > х, булганда f(xj > f (х,) тигез¬
сезлеге үтәлсә, Р күплегендә f функциясе үсә.
Билгеләмә. Әгәр Р күплегендәге теләсә нинди
Xj һәм х2 өчен х2 > X! булганда f (х2) < f(xt) тигез¬
сезлеге үтәлсә, Р күплегендә f функциясе кими.
Башка сүзләр белән әйткәндә, әгәр Р күплегендәге аргумент¬
ның зуррак кыйммәтенә функциянең зуррак кыйммәте туры
килсә, f функциясе бу күплектә үсүче функция дип атала. Әгәр
Р күплегендәге аргументның зуррак кыйммәтенә функциянең
кечерәк кыйммәте туры килсә, f функциясе бу күплектә кимүче
функция дип атала.
40 Тригонометрик функцияләр
И 1 нче мисал, f (г) = хп (ne N)
функциясе п так булганда барлык
санлы турыда үскәнен, ә п җөп бул¬
ганда f (х) = х" функциясе [0; «°) кә
кадәр аралыкта үскәнен, ә (-»; 0]
гә кадәр аралыкта кимегәнен исбат¬
лыйк.
Башта f(x) = х" функциясенең
теләсә нинди натураль п өчен [0;“)
кә кадәр аралыкта үскәнен исбат¬
ларбыз. х2 > х1 0 булсын. Ул ва¬
кытта дәрәҗәнең үзлеге буенча
х2 > х" , Хәзер п җөп булган оч¬
ракны карыйк. Xj < х2 ί 0 булсын. Ул вакытта -х > -х 0 һәм
(-Xj)" > (-Xj)" £ 0, ягъни х” > х2 . Нәкъ шушының белән п җөп
булганда, f (х) = х" функциясе (-»; 0] кадәр аралыкта кимегәнлеге
исбатлана. п так булган очракны карыйсы калды. Әгәр х < 0 < х.
булса, ул вакытта х" < 0 < х2. Әгәр хг < х2 ■ 0 булса, ул вакытта
-х1 > -х., > 0 һәм шуңа күрә (—X,)" > (-х2)" > 0, ягъни —х{* > -х" ,
моннан х2 > х“ . Шулай итеп, так п өчен х, > xL тигезсезлегеннән
х2 > х“ тигезсезлеге килеп чыкканлыгы исбатланды. Билгелә¬
мә буенча f(x) = х" функциясе п так булганда барлык санлы турыда
үсә.
2 нче мисал. Әгәр у = /(х) функциясе Р күплегендә үссә,
у = -/(х) функциясе Р күплегендә кимегәнлеген исбатлыйк,
х, һәм х, Р күплегендәге теләсә нинди ике сан һәм х2 > х, булсын.
-Hxz)<-f(x1), ягъни /(х,) < f (х2) икәнен исбатларга кирәк. Әмма
бу — f функциясенең Р күплегендә үсү шартының ачыктан-ачык
нәтиҗәсе.
3 нче мисал. /(х)= ү функциясе (-“; 0) һәм (0; <χ) ара-
лыкларының һәркайсында кими (мөстәкыйль рәвештә исбатла¬
гыз). Ләкин бу функция әлеге аралыкларның берләшмәсендә ки¬
мүче функция булмый. Мәсәлән, 1 > -1, ләкин /(1) >
Функцияләрне үсүгә һәм кимүгә тикшергәндә, үсү һәм кимү
аралыкларының максималь озынлыгын, чик нокталарны да кер¬
теп (әгәр чик нокталар бу аралыкларга керсәләр, билгеле), күрсәтү
кабул ителгән. Мәсәлән, f(x) = ү функциясе [2; 100] кисемтәсендә
кими дип әйтергә мөмкин. Бу дөрес, ләкин мондый җавап тулы
түгел.
Искәрмә. Җөп һәм так функцияләр өчен үсү һәм кимү
аралыкларын табу мәсьәләсе берникадәр гадиләшә: бу аралыклар¬
ны х J 0 булганда табу җитә (40 нчы рәсем).
Мәсәлән, f функциясе җөп һәм [а; &] аралыгында, монда
Ь > а $ 0 үссен, ди. Бу функциянең [-Ь; -а] аралыгында кимегәнен
исбатларбыз.
41 Тригонометрик функцияләр
Чыннан да, -а * хг>хг^ -Ь булсын. Ул вакытта / (—х2) - f (х2),
/(-х ) = /(х2), шул ук вакытта а ζ -х2 < -х, Ь, һәм f функциясе
[a; bj да үскәнлектән, f(-xt) > f(~x2), ягъни /(Xj) > f(x2).
2. Тригонометрик функцияләрнең үсүе һәм кимүе. Иң элек
синусның [-·| + 2πη; -| + 2nnj, neZ аралыкларында үсүен ис¬
батларбыз. Синус периодик булу сәбәпле, синусның < j ки¬
семтәсендә үскәнлеген исбатлау җитә. х2 > х{ булсын. Синуслар¬
ның аермасы формуласын кулланып табабыз:
sin х2 - sin х( = 2 cos **ζ** sin х" „ -*1.
(I)
- у £ X! < х2 тигезсезлегеннән 0 < һәм
й X.+Х, »
- 2 < ~2~ < 2 икәнлеге килеп чыга·
Шуңа күрә cos *■ *** > 0, sin Χ%Χ| > 0. (1) дән sinXj-sinx,
аермасының уңай, ягъни sinx2 > sinXj икәнлеге килеп чыга.
Шуның белән синусның күрсәтелгән аралыкларда үскәнлеге ис-
батлана. Аналогия буенча [ Ί + 2πη; + 2дп ] , neZ аралыклары
синусның кимү аралыклары булуы исбатлана.
Табылган нәтиҗәне берәмлек әйләнә ярдәмендә җиңел аңла¬
тырга мөмкин икәнлеген әйтеп китәбез: әгәр - ‘ % < t2 < 5 бул¬
са, билгеле Р,2 ноктасының ординатасы Р, ноктасының ордината¬
сыннан зуррак булыр (41 нче а рәсем). Әгәр < t2 ζ булса,
ул вакытта Р. ноктасынның ординатасы Р, ноктасы ордината¬
сыннан кечерәк (41 нче б рәсем).
Тригонометрик функцияләр
Косинусның үсү аралыклары — [-π + 2πη; 2πη] (монда neZ)
кисемтәләре, ә кимү аралыклары [2πη; π + 2ππ] (монда neZ)
кисемтәләре була. Синус эчен исбатлаган кебек үк диярлек исбат¬
ларга мөмкин. Китерү формуласы cosx - sin(x + |) дән файдала¬
ну гадирәк. Аннан турыдан-туры, мәсәлән, синусның үсү аралык¬
ларын j гә сулгарак күчерүдән табылган аралыклар косинусы¬
ның үсү аралыклары булганлыгы килеп чыга.
Тангенс функциясенең (-^ + πη; + монда neZ ара-
лыкларында үскәнен исбатлыйк. Тангенс периодик булу сәбәпле,
( 2? j) интервалы өчен исбатлау җитә.
х, һәм хг — шушы интервалдагы теләсә нинди саннар һәм
х2 > х, булсын. tgx2 > tgXj икәнен исбатларга кирәк. Табабыз:
tg*,
sin sin
cosx2 cosx,
sinr2cosxt - sinx*coax? _ sin(x2-xj
COSXjCOSXj COSXj cosx2 ‘
Фараз итү буенча -■^<X1 < x2 <4. Шуңа күрә cosx^O,
cosx2 > 0. Ә 0 < x2-Xj < π булганлыктан, sin(x2-x1) > 0 була.
Димәк, tg х2 - tg х, > 0, ягъни tg х2 > tg Xj, шуны исбатларга кирәк
иде дә.
ctg функциясе (πη; π + πη), монда neZ аралыкларында киме¬
гәнлеге аналогия буенча исбат ителә.
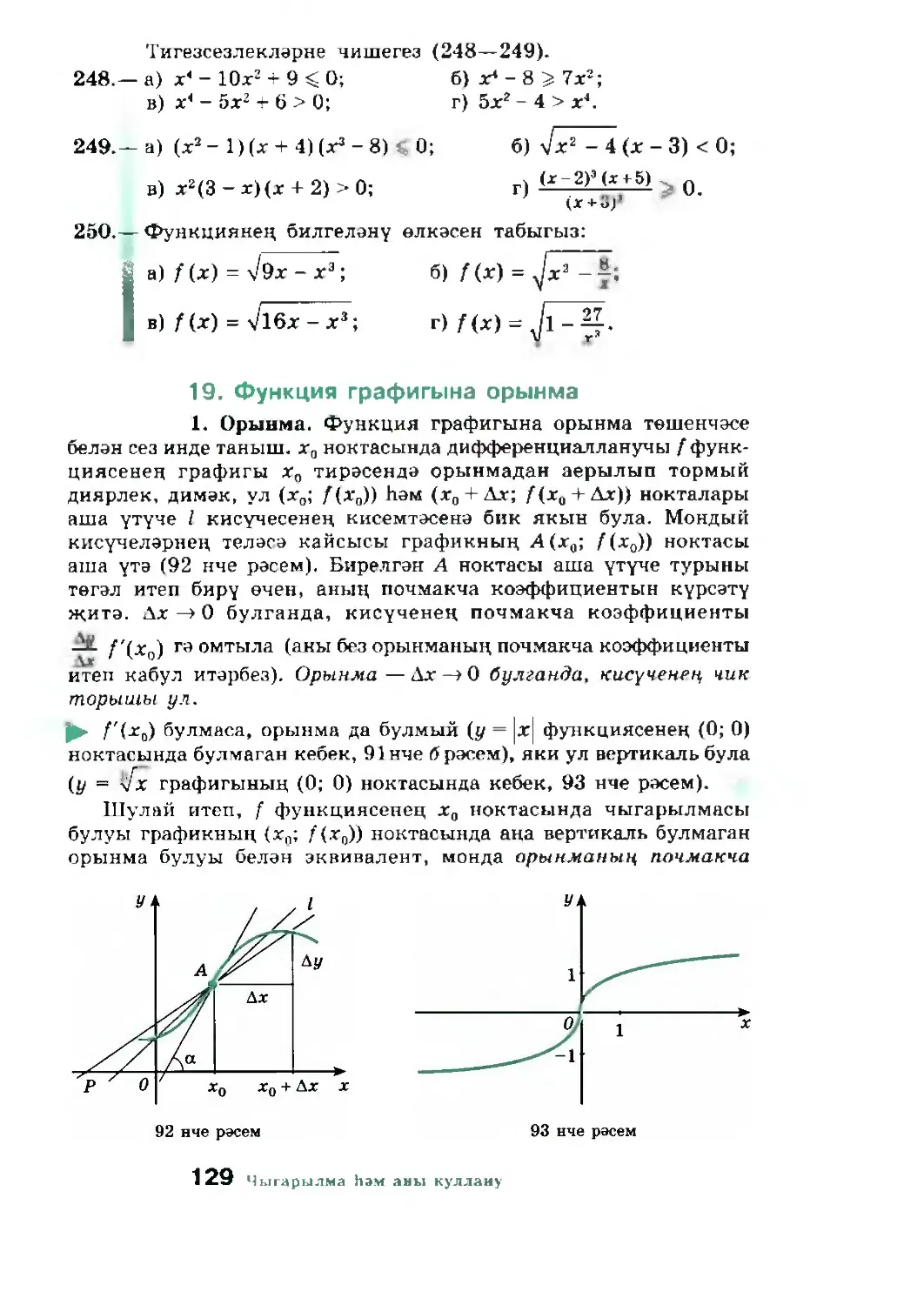
3. Экстремумнар. Функциянең кайбер нокта тирәсендә үз-үзен
тотышын тикшергәндә тирәлек төшенчәсеннән файдалану уңай.
а ноктасын эченә алган теләсә нинди интервал шул а ноктасы¬
ның тирәлеге дип атала. Мәсәлән, (2; 6) интервалы — 3 ноктасы
тирәлекләренең берсе, (—3,3; -2,7) интервалы — -3 ноктасының
тирәлеге.
39 нчы рәсемдәге графикны өйрәнеп, шундый нәтиҗәгә килергә
мөмкин: функциянең үсүе кимүгә алмашына торган х нокталары
43 Тригонометрик функишпюр
(3 һәм 5 нокталары) яки, киресенчә, кимүе үсүгә алмашына торган
нокталары (4 ноктасы) билгеләнү өлкәсенең иң «күренеп тора
торган» нокталары була. Бу нокталарны тиңдәшле рәвештә мак¬
симум нокталары (хга4Х = 3 һәм х^ = 5 ) һәм минимум нокталары
(хт = 4) дип атыйлар.
Нинди дә булса конкрет функциянең графигын төзегәндә башта
аның шундый нокталарын табу файдалы. Мәсәлән, sin функциясе
өчен бу — ±-| + 2пп, neZ рәвешендәге нокталар. Аныклык өчен
х0 = ’ дип алыйк. Бу нокта синусның үсү аралыгының уң чиге
була, һәм шуңа күрә, әгәр - % х < г, булса, 1 = sin х0 > sin х.
Моннан тыш, х0 = 7 — кимү аралыгының сул чиге һәм, шулай
булгач, < х < булганда sin х < sin х0. Шулай итеп, х0 =
ноктасының ί- тирәлегендә яткан теләсә нинди х өчен
sin j > sinx һәм шуңа күрә х0 = - синус функциясенең макси¬
мум ноктасы була.
-’2 ноктасында, киресенчә, функциянең кимүе үсүгә алма¬
шына дән сулда функция кими, ә уңда үсә). Аналогик рә¬
вештә фикер йөртеп, - ноктасының берникадәр тирәлегендә,
sin х > sin (“ *) = икәнен табабыз, һәм шуңа күрә — синус
функциясенең минимум ноктасы. Экстремум нокталарының тө¬
гәл билгеләмәләрен бирик.
билгеләмә Әгәр х0 ноктасының ниндидер тирә¬
легендәге барлык х өчен f (х) > / (х0) тигезсезлеге
үтәлсә, х0 ноктасы f функциясенең минимум нок¬
тасы дип атала (42 нче рәсем).
42 иче рәсем
44 Тригоиометрик функцияләр
нче рәсем
Билгеләмә Әгәр х0 ноктасының ниндидер тирә¬
легендәге барлык х өчен f(x) ζ f(x0) тигезсезлеге
үтәлсә, х0 ноктасы f функциясенең максимум нок¬
тасы дип атала (43 нче рәсем).
Билгеләмә буенча f функциясенең максимум ноктасы х0 дәге
кыйммәте әлеге функция өчен шул ноктаның ниндидер тирәлеген¬
дәге кыйммәтләреннән иң әурысы була. Шуңа күрә функциянең
х0 тирәлегендәге графигы, кагыйдә буларак, шома «калкулык»
(43 нче а рәсем һәм 44 нче рәсем — х2, х3 нокталары) яки
очлы «тау түбәсе» (43 нче б рәсем) рәвешен ала. Минимум нок¬
тасы тирәлегендә графиклар, кагыйдә буларак, шулай ук сал¬
мак (42 нче б рәсем — х0 ноктасы,
44 нче рәсем — х4, х5 нокталары) яки
текә төшкән «чокыр» (42 нче а рә¬
сем — х0 ноктасы һәм 44 нче рә¬
сем — хв ноктасы) рәвешендә сурәт¬
ләнә.
Функция графикларының мак¬
симум яки минимум нокталарында
үз-үзләрен тотышларына башка ми¬
саллар 45 нче (а — максимум нокта¬
сы), 46 нчы (а — минимум ноктасы)
һәм 47 нче (монда (-1; 0) аралыгын¬
да һәр нокта минимум ноктасы да,
максимум ноктасы да була) рәсем¬
нәрдә китерелгән.
45 нче рәсем 46 нчы рәсем 47 нче рәсем
45 Тригонометрик функцияләр
Функциянең максимум һәм минимум нокталары өчен гомуми
атама кабул ителгән — аларны экстремум нокталары дип атый¬
лар. Функциянең бу нокталардагы кыйммәтләрен тиңдәшле рә¬
вештә функциянең максимумнары һәм минимумнары дип атый¬
лар (гомуми атамасы — функциянең, экстремумы). Максимум
ноктасы хМ1 дип, ә минимум ноктасы хт1„ дип тамгалана. Функ¬
циянең бу нокталардагы кыйммәтләрен тиңдәшле рәвештә
һәм у,™ дип тамгалыйлар.
Күнегүләр
77.— Графиклары 48 нче а—г рәсемнәрдә сурәтләнгән функция¬
ләр өчен табыгыз:
£ а) функциянең үсү һәм кимү аралыкларын;
б) функциянең максимум һәм минимум нокталарын;
в) функциянең экстремумнарын.
78.
Функция графигының эскизын сызыгыз (78—80).
а) f функциясе (-«; 2] аралыгында үсә һәм [2; <») аралы¬
гында кими;
б) f функциясе (-co; -2] һәм [0; 3] аралыкларында үсә,
[-2; 0] һәм [3; «) аралыкларында кими;
в) f функциясе (-0°; 1] һәм [4; ») аралыкларында кими,
[1; 4] аралыгында үсә.
46 Тригонометрик функцияләр
79. - a) xm„ = -3, xmln = 4, /(-3) = 5. /(4) = -5;
б) Xmin = —2, Xmii> — 2, Хт*х “ θ>
Л-2) = Л2) = -3, Г(0) = 2;
в) х^-Ч», xM„=2, f(-5) = l, Л2) = 6;
* г) Хщы ~ —4, Хщ«х — 3, Χφϊο — 1’
I п-4) = 5, Г(3) = 2, Л-1) = -2.
I
80. - a) f — җөп функция, хт„ = -3, x„,in = О,
I Л-3) = 4. ЛО) = 0;
К б) f — так функция, х,.,,, = 2, хгат = 5,
I Л2) = 3, Л5) = -4;
! в) f — җөп функция, хт1п = 4, х^, = О,
I /(4) = -2, /(0) = 2;
I г) f — так функция, xmln = -4, xmax = -1,
I Л-4) = -3, Λ-D = I-
81. I y = kx + b функциясе a) k > 0 булганда R күплегендә үскәнен;
■ б) k < 0 булганда R күплегендә кимегәнен исбатлагыз.
I Функциянең үсү һәм кимү аралыкларын, максимум нок-
I таларын, минимум нокталарын, аның максимумнарын
I һәм минимумнарын табыгыз (82—85).
а) у = -х2 + 6х - 8;
в) у - х2 - 4х;
б) у = (х + 2)4 + 1;
Г) у = (х — З)4.
83.
а) у = А
в) у = -
б) у = -(х+3)5;
Г) у = (х -4)3.
84.
а) у - 3sinx - 1;
в) у - 2cosx + 1;
б) у = -2cosx + 1;
г) у = 0,5 sin х - 1,5.
а) у = 1 + 2tgx
в) у = -tgx;
б) у = sinx + 1;
г) у ж cos х - 1.
Саннарны чагыштырыгыз:
I а) соз^· һәм соз^5·; б) sin^ һәм sin^·;
I в) tg·^· һәм tg^·; г) sin^ һәм sin^.
87. 1 Саннарны үсә бару тәртибендә урнаштырыгыз:
Ia)sin3,2, sin3,8, sinl,3;
I б) cos0,9, cos 1,9, cos 1,3;
I в) tg0,5, tgl,4, tg(-0,3);
|r) sin 1,2, sin(-l,2), sin0,8.
47
Тригонометрик функцияләр
Үсү һәм кимү аралыкларын, экстремум нокталарын һәм
функциянең экстремум нарын табыгыз (88—89).
88-a)s = i^ + 1; β) (ί = 4|х| - х*;
в) у = — 2; г) у = х2 - 2 |х|.
у (г + 1)3 ν 6 * * * * 11
89.— а) У = cos(x + ^); б) У = 1 - sin(x - !*);
в) у = sin (х + ; г) у = 2 + cos (х - .
90.— Саннарны үсә бару тәртибендә урнаштырыгыз:
а) cos^|^, sin^, cos 4г > cos i-4г);
б) tg(-^j, tg^, ctg1^,
B) Ctg ** , Ctg 1 ’Л , tg Π , Ctg ;
ir) sin^-y^j, cos 4^, sin|y, sin^|^.
a) f(x) = х4 + Зх функциясе [0; ®) аралыгында үскәнен;
б) /(χ) = -χ3 - 2х функциясе R да кимегәнен;
в) /(χ) = χβ - 0,5 функциясе ( °°; 0] аралыгында кимегәнен;
г) /(х) = х5 + 1,5х функциясе R да үскәнен исбатлагыз.
92.
Түбәндәге фаразларның дөреслеген исбатлагыз:
а) / — җөп функция, х0 максимум ноктасы булса, ул
вакытта -х0 максимум ноктасы була;
б) f так функция булса һәм [a; ft] аралыгында кимесә,
f функциясе (-6; -а] аралыгында да кими;
в) / — так функция, х0 минимум ноктасы булса, ул ва¬
кытта -х0 ноктасы максимум ноктасы була;
г) f җөп функция булса һәм [a; ft] аралыгында үссә, ул
[-ft; -α] аралыгында кими.
6. Функцияләрне тикшерү
1. Функцияләрнең графикларын төзү. Элек сез функ¬
цияләрнең графикларын «нокталар буенча» төзедегез. Нокталар
санын җитәрлек күп билгеләгәндә, билгеле, бу метод күп очракта
яхшы нәтиҗәләр бирә. Ләкин бу вакытта функция кыйммәтләре¬
нең зур таблицаларын төзергә туры килә, ә иң мөһиме, функция¬
нең әһәмиятле үзенчәлекләрен күрми калып, графикны төзүдә
ялгыш җибәрергә мөмкин.
Тригонометрик функцияләр
49 нчы рәсем
Мәсәлән, функциянең 15 ноктада кыйммәтләрен исәпләп һәм
графикның тиңдәшле нокталарын координаталар яссылыгында
билгеләп, без 49 нчы рәсемне таптык, ди. Графикның эскизы
барлык бу нокталар аша үтүче өзлексез кәкрегә якын дип уйлау
табигый (50 нче рәсем). Шулай да «чын» график (билгеле, шушы
ук нокталар аша үтүче) бу эскизга бөтенләй охшамавы да мөмкин
(51—53 нче рәсемнәр).
Ялгышулардан котылу өчен, функциянең үзенә генә хас үзен¬
чәлекләрен ачыкларга, ягъни функцияне башта тикшерергә, өйрә¬
нергә кирәк. Мәсәлән, / функциясе турында түбәндәгеләр билгеле
булсын, ди:
— функция (-со; -10), (-10; 10), (10; <») аралыкларының бер¬
ләшмәсендә билгеләнгән;
— функциянең кыйммәте -11 һәм 0 нокталарында нульгә әй¬
ләнә, (-·»; -11), (-10; 0) интервалларында тискәре һәм (-11; -10),
(0; 10) һәм (10; “>) интервалларында уңай;
— функция (-оо; -Ю) һәм (-10; 10), [12; 15] аралыкларында
үсә һәм (10; 12], [15; «.) аралыкларында кими;
— функция 12 ноктасында минимумга ия, шул ук вакытта
f(12) = 16 һәм 15 ноктасында максимумга ия, шул ук вакытта
Г(15) = 19;
— ниһаять, аргументның кыйммәтләре -10 га һәм 10 га якын¬
лашканда, f ның кыйммәте абсолют зурлыгы буенча чиксез үсә.
Бу мәгълүматлар функция графигының эскизы 53 нче рәсемдә
сурәтләнгәнчә диярлек булуын аңларга мөмкинлек бирә.
49
Тригонометрик функцияләр
Тагын бер мисал карыйк: /(х) - ( функциясен тикшерик.
1) Функциянең билгеләнү өлкәсен табабыз. Әлеге очракта
D (/) — барлык санлы туры, чөнки ваклаучы х2 + 1 нульгә әйләнми.
2) f функциясенең җөп икәнен искәрәбез: теләсә нинди х өчен
«-*>*
Шуңа күрә функцияне тикшереп, аның х 0 өчен графигын
төзү җитә, аннары төзелгән графикны ординаталар күчәренә ка¬
рата чагылдырасы гына кала.
3) f графигының координата күчәрләре белән кисешү ноктала¬
рын табабыз, f графигы ординаталар күчәрен (0; /(0)) ноктасында
кисеп үтә. /(0) нең кыйммәте 1 гә тигез. Шуңа күрә f графигы
(0; 1) ноктасы аша үтә.
f функциясе графигының, абсциссалар күчәре белән кисешү
нокталарын табу өчен, /(х) = 0 тигезләмәсен чишәргә кирәк. (Аның
тамырларын функцияне», нульлэре дип атыйлар). = 0 тигез¬
ләмәсенең тамырлары юк. Димәк, f графигы абсциссалар күчәрен
кисел үтми.
4) / функциясе нинди аралыкларда — уңай кыйммәтләр, нинди
аралыкларда тискәре кыйммәтләр алганын ачыклыйк; аларны
функциянең даими тамга аралыклары дип атыйлар. Бу аралык¬
ларда функциянең графигы абсциссалар күчәреннән югарырак
(тиңдәшле рәвештә түбәнрәк) ята. Әлеге очракта теләсә нинди х
өчен х2 + 1 нең кыйммәте уңай булганлыктан, барлык санлы туры¬
да /(х) > 0.
5) Функциянең нинди аралыкларда үсүе яки кимүе турындагы
мәгълүматлар графикны төзүне шактый җиңеләйтә (бу аралык¬
ларны функциянең усу яки кимү аралыклары дип атыйлар).
Тикшерелә торган функция өчен (-<*>; 0] — үсү аралыгы, ә [0; оо)
кимү аралыгы икәнлеген исбатлыйк.
Xj һәм х2 саннары [0; оо) аралыгындагы ике кыйммәт, шул ук
вакытта х2 > xt булсын, х, һәм х2 уңай саннар булганлыктан, х2 > хл
шартыннан х2 > х2; х2 + 1 > х2 + 1 Һәм, ниһаять,
икәнлеге килеп чыга. Шулай итеп, /(х2) < /(х(), ягъни / функциясе
[0; оо) аралыгында кими.
/ функциясе (-оо; 0] аралыгында үсә. Исбатлау аналогик
рәвештә башкарыла (шулай ук / ның җөплегеннән дә файдала¬
нырга мөмкин).
6) Үсү кимүгә яки, киресенчә, кимү үсүгә алмашынган нок¬
таларда функциянең кыйммәтләрен табабыз. Безнең очракта
үсү арасына да, кимү арасына да керүче бары тик бер генә нокта
50
Тригонометрик функцияләр
54 нче рәсем 55 нче рәсем
бар — ул 0 ноктасы. О ноктасы /(х) = ( 1 f функциясенең макси¬
мум ноктасы; f(0) = 1.
7) Ниһаять, х чикләнмәгән рәвештә үскәндә х2 + 1 нең кыйм¬
мәте чикләнмәгән рәвештә үсүен һәм шуңа күрә f(x) = —нең
кыйммәтләре (уңай кала барып) нульгә якынлашканын искәрәбез.
f(x) = 1 функциясенең тикшерү барышында алынган үз¬
лекләре аның графигын төзү өчен җитә.
Графикның (0; 1) ноктасын төзибез. Без [0; «*>) — f функ¬
циясенең кимү аралыгы икәнен ачыкладык. Шуңа күрә 0 абсцис¬
салы ноктадан уңдарак графикны «түбән таба юнәлгән» кәкре
сызык рәвешендә сурәтлибез (54 нче рәсем). Теләсә нинди х өчен
Z(x) > 0 булганлыктан, бу кәкре абсциссалар күчәреннән түбән төшә
алмый, шул ук вакытта (7 нче пункттагы тикшерүне карагыз)
графикны уңга дәвам иткәндә, ул абсциссалар күчәренә чиксез якы¬
ная . f функциясенең җөп булуыннан файдаланасы калды; х 0 өчен
төзелгән кәкрене ординаталар күчәренә карата симметрияле чагыл¬
дырып, f функциясенең графигын табабыз (55 нче рәсем).
2. Функцияләрне тикшерү схемасы. Функцияләрне тикшергән¬
дә без тасвирланган схема буенча эш итәрбез. Гомуми очракта
тикшерү түбәндәге мәсьәләләрне карауны күз алдында тота:
1) Бирелгән f функциясенең билгеләнү һәм кыйм¬
мәтләре өлкәләрен табарга.
2) Функция тикшерүне җиңеләйтә торган үзенчәлек¬
ләргә ияме икәнен, ягъни f функциясе: а) жөп яки
так; б) периодикмы икәнен ачыкларга.
3) Графикның координата күчәрләре белән кисешү
нокталарының координатларын исәпләп чыгарырга.
4) f функциясенең тамгасы даими булган аралыклар¬
ны табарга.
5) f функциясенең нинди аралыкларда үскәнен, нин¬
ди аралыкларда кимегәнен ачыкларга.
5 1 Григокометрик функцияләр
6) Экстремум нокталарын табарга, экстремумның
төрен (максимум яки минимум) билгеләргә һәм бу
нокталарда f ның кыйммәтен исәпләп чыгарырга.
7) Билгеләнү өлкәсенә кермәгән үзенчәлекле нокта¬
лар тирәлегендә (мәсәлән, f(x) — у функциясе өчен
х = 0 ноктасы) һәм аргумент модуле буенча зур кыйм¬
мәткә ия булганда f функциясенең үз-үзен тотышын
тикшерергә.
Бу планның якынча характерда булуын истә тотарга кирәк.
Әйтик, абсциссалар күчәре белән кисешү нокталарын табу өчен,
f(x) = 0 тигезләмәсен чишәргә кирәк, ә без аны хәтта, мәсәлән,
f(x) бишенче дәрәҗәдәге күпбуын булса да чишә белмибез. (Дөрес,
күп очракларда андый тигезләмәнең тамырлары санын һәм та¬
мырларның үзен теләсә нинди төгәллек белән табу методлары
бар.) Шуңа күрә еш кына тикшерүнең теге яки бу этабын төшереп
калдырырга туры килә. Шулай да функцияне тикшерү барышын¬
да мөмкин кадәр әлеге схеманы сакларга киңәш ителә.
Функциянең үсү (кимү) аралыкларын һәм экстремум ноктала¬
рын эзләү, кагыйдә буларак, функцияне тикшерүнең иң авыр
этаплары булып тора. Киләсе бүлектә сез мондый мәсьәләләрне
чишүнең математик анализ методларын куллануга нигезләнгән
гомуми методлары белән танышырсыз.
(► f функциясенең графигы чикләнмәгән рәвештә якынлаша тор¬
ган вертикаль турыларны (мәсәлән, f(x) = у функциясе өчен х = 0
турысын яки 53 нче рәсемдә сурәтләнгән функциянең графи¬
гы өчен х = ±10 турысын) вертикаль асимптоталар дип атый¬
лар.
Әгәр функция вакланма рәвешендә булып, ваклаучысы
а ноктасында нульгә әйләнсә, ә санаучысы нуль булмаса, мондый
очракта график еш кына х = а вертикаль асимптотасына ия була.
Мәсәлән, f(x) ~ функциясенең графигы х = 0 вертикаль асимп¬
тотасына ия. /(х) = tgx функциясенең графигы өчен х = * + πη,
монда neZ турылары вертикаль асимптоталар булалар.
Әгәр х модуле буенча чикләнмәгән рәвештә үскәндә функ¬
циянең графигы чикләнмәгән рәвештә ниндидер горизонталь
(f(x) = ! функциясе очрагында бу у = 0 турысы, 55 нче рәсемне
карагыз) яки авыш (/(х) = х + функциясе графигы өчен у = х
турысы, 32 нче рәсемне карагыз) турыга якынлашса, андый ту¬
рыны горизонталь (тиңдәшле рәвештә авыш) асимптота дип
атыйлар.
5 2 Тригонометрик функцияләр
3. Графикларны «уку». Функцияләрнең графикларын төзүгә
югарыда тикшерелгән мисал һәм мәсьәләләрнең күбесендә сез
мондыйрак хәлләр белән очраштыгыз: функция формула белән
бирелгән, аның үзлекләрен тикшереп, f ның графигын төзергә.
Икенче мәсьәлә дә практик яктан шактый кызыклы: бирелгән
графигы ярдәмендә f функциясенең төп үзлекләрен санап чыгу
таләп ителә.
Моңа охшаш мәсьәләләр эксперименталь тикшерүләр бары¬
шында еш чишелә. Бу вакытта графикларны төзү төрле методлар
белән тормышка ашырыла. Мәсәлән, эксперименталь юл белән
табылган нокталар буенча. Шулай ук күп санлы үзьязгыч прибор¬
лар да бар. Мәсәлән, осциллографлар аларның экраннарында
электр тирбәнешләре күрсәтмәле график сурәткә әверелә. Күрсәт¬
мәле график язылышны алырга мөмкинлек бирә торган икенче
бер прибор — кардиограф; аның ярдәмендә алынган кардиограм¬
маны укып, врачлар йөрәк эшчәнлегенең торышы турында нәтиҗә
ясыйлар.
Язу өчен төгәл теориясе булдырылмаган реаль процессларны
тикшергәндә килеп чыга торган авырлыкларның шактый типик
мисалы белән сез 56 нчы рәсемне карап таныша аласыз. Монда
1974 елның февралендә Мәскәү өлкәсе өчен тәүлек дәвамында
уртача температура үзгәрешләренең графигы китерелгән. Калын
сызык белән һава торышының озак срокка исәпләнгән прогноз
нәтиҗәләрен күрсәтүче А һәм Б «теоретик кәкреләре» сурәтләнгән
(прогноз 5° ка кадәр төгәллек белән бирелгәнгә күрә, кәкреләр
ике). Бу графикны «укып», без, мәсәлән, өч «салкынаю дулкыны»
көтелүен күрәбез (4 еннән 10 ына кадәр, 17 сеннән 19 ына кадәр
һәм 23 еннән 26 сына кадәр). Шулай ук җепшек көннәр көтелми,
тулаем һава торышы салкынча (-17°...-22°) булачак дип уйланыл-
ган. Чынлыкта исә (фактик температура үзгәрешенең графигы
В нәзек сызыгы белән сурәтләнгән) температура нормадан 5—10°
ка югарырак була (күпьеллык күзәтүләр нәтиҗәсендә барлыкка
56 нчы рәсем
53 Тригонометрик функцияләр
килгән климатик норма Г сызыгы белән бирелгән), 4 еннән 8 нче
февральгә кадәр салкынаю түгел, ә җылыну күзәтелә һ. б. Прогноз
турында бу һәм башка мәгълүматларны һәм реаль картинаны
сез 56 нчы рәсемдә китерелгән графикларны «укып* белә аласыз.
Күнегүләр
93. — График белән бирелгән функцияне (57 нче рәсем) гомуми
схема буенча тикшерегез.
94. -* f функциясенең үзлекләре билгеле булганда (55 нче биттәге
таблицаны карагыз), функциянең графигын тезегез:
Һәр функцияне гомуми схема буенча тикшерегез һәм
аның графигын төзегез (95—99).
95. - а) /(х) = 5 - 2х ; б) f(x) = 3 - 2х - х2;
в) f(x) = Зх-2; г) f(x) - х2 - Зх + 2 .
96. - а)/(х) = |-2; б) f(x) = -(х - 3)«;
β)Λχ) = ^: г)/(х) = хэ-1.
97. - a) f(x) = Vx-3; б) /(х) = 4х-хг;
в) /(х) - Vx +1; г) f(x) = 4 - х2.
5 4 Гри1-омометрик функцияләр
Функциянең
үзлекләре
а)
б)
■>
г)
1
Билгеләнү
өлкәсе
Кыйммәтләре
өлкәсе
[-6; 6]
1-2; 5]
[-5; 4)
[0; 6]
1-4; 4J
1-3; 6]
(-5; 3]
[0: 5]
2
Графикның
кисешү
нокталары:
а) Ох күчәре
белән
б) Оу күчәре
белән
А(-4;0),
В (-2; 0)
С(0; 2,5)
0(0; 0)
А(-4; 0).
В(-1; 0),
С(2,5; 0)
0(0; -2)
А(3; 0)
В(0; 4,5)
3
Даими тамга
аралыклары:
а) fix) > 0
б) fix) < 0
(-6; -4),
(-2; 6]
(-4; -2)
(-5; 0),
(0; 4]
(-4; -1),
(2,5; 4]
(1; 2,5)
[-5; 3)
4
Аралыклар:
а) үсү
б) кимү
[-3; 1],
[4; -6]
(-6; -3].
fl; 4]
[-5; -2],
[0; 4]
(-2; 0]
ί-4; -2],
fi;4]
[-2; 1]
[-3; 1]
[-5; -З),
[1;3]
5
Максимум
нокталары,
функциянең
максимумы.
Минимум
нокталары,
функциянең
минимумы
ι./Ш-з
-з,
Г<-3>- -2
4, /(4) = 1
-2.
Г(-2)-2
0,Л0)-0
-2,
/(-2) = 2
1.
/(1) = -з
-3,
/(-3)=2
6
Графикның
өстәмә
нокталары
Н-в) = 3
Г(6)-5
Я-5) = 0,5
Г<4> -б
/(4) = 6
Г(-5) = 3
Ьәр функцияне гомуми схема буенча тикшерегез һәм
аның графигын төзегез (98—99).
а) /(х) - х4 + 4х2; б) f(x) = 1 - Vx + 4;
в) /(х) = х3 + х;
а) Дх) = х2 -2|х| + 1;
в) f(x) = |х| - х2;
г) /(х) = х/х-2 - 2.
б) Г(х) = 7тЬ
г) Лх) = ЦМ.
55 Тригонометрик функция лар
7. Тригонометрик функцияләрнең үзлекләре.
Гармоник тирбәнешләр
1. Тригонометрик функцияләрне тикшерү. Тикшере¬
лә торган функцияләрнең үзлекләрен үткән пунктта китерелгән
схема буенча язу уңай. Синус, косинус, тангенс, котангенс функ¬
цияләренең сезгә инде таныш булган үзлекләрен таблицада туплап
бирик. (Һәркайда neZ дип уйланыла.)
Функция
fix) = sin х
f(х) = cos х
f(x) = tgx
f(x) = ctgx
1.1
R
R
(_| + яя.« + жв'
(πη; π + πη)
1.2
[-1; П
l-i; П
R
R
2.1
Так
Җөп
Так
Так
2.2
2π
2π
π
π
3.1
(πη; 0)
(f+ πη;0)
(πη; 0)
(4 + «λ; θ)
3.2
(0; 0)
(0; 1)
(0; 0)
Юк
4.1
(2πη; π + 2πη)
(-^+2πη; τ£+2πη)
(πл; “ + πη)
^πη; J + πη)
4.2
(-π + 2πη; 2πη)
θ|+2πη; Д£ + 2ял)
γ + ЯП» πη)
(- 1 + πη; πη)
5.1
^-•g-+2rea; ^+2πη)
[-π + 2πη; 2πη]
2 + 2 + πη)
Юк
5.2
Γ^+2πη; 3^+2xnJ
[2πη; π + 2πη]
Юк
(πη; π + πη)
6.1
- I + 2πη
π + 2πη
Юк
Юк
6.2
-1
-1
Юк
Юк
6.3
Г; + 2πη
2πη
Юк
Юк
6.4
1
1
Юк
Юк
Таблицада f функциясенең үзлекләрен түбәндәгечә номерлап
бирү кабул ителгән:
1.1 — билгеләнү өлкәсе;
1.2 — кыйммәтләре өлкәсе;
Тригонометрик функцияләр
2.1 — җөплек (таклык);
2.2 — иң кечкенә уңай период;
3.1 — / графигының Ох күчәре белән кисешү нокталарының
координата лары;
3.2 — f графигының Оу күчәре белән кисешү нокталарының
координаталары;
4.1 — f уңай кыйммәтләр алган аралыклар;
4.2 — f тискәре кыйммәтләр алган аралыклар;
5.1 — үсү аралыклары;
5.2 — кимү аралыклары;
6.1 — минимум нокталары;
6.2 — функциянең минимумнары;
6.3 — максимум нокталары;
6.4 — функциянең максимумнары.
Тригонометрик функцияләрнең үзлекләре мәсьәләләр чишкән¬
дә еш кулланыла.
И 1 нче мисал, sin(-l), sinl, sin2, sin3, sin4 саннарын үсә
бару тәртибендә урнаштырыйк.
Китерү формулаларын файдаланып, бу саннарның аргумент
кыйммәтләре синусның бер үсү аралыгыныкы — | - " : ?, кисем¬
тәсенеке булырлык күренештә язабыз:
sin 2 = sin (π - 2), sin 3 = (π - 3), sin 4 = (π - 4).
-·*<-1<π-4<π-3<1<π-2<·|
£ £
икәнлеге ачык, шуңа күрә
sin(-l) < sin (π - 4) < sin (π - 3) < sin 1 < sin (π - 2).
Димәк, sin (-1) < sin 4 < sin 3 < sin 1 < sin 2.
57 Триговометрик функцияләр
59 нчы рәсем
fix) = 2sin^3x — ~'i функциясенең графигын карыйк (58 нче
рәсем). Ул түбәндәге эзлеклелектә үзгәртүләр ярдәмендә табыла:
а) у = sin х функциясенең, графигын абсциссалар күчәре буйлап
3 тапкырга кысып, у = sin Зх функциясенең графигын табабыз
(59 нчы рәсем).
б) у = sin Зх функциясенең графигын | о) векторга күчереп,
у = sin 3 (х - ’), ягъни у = sin (Зх - ' ι функциясенең графигын
табабыз (60 нчы рәсем),
в) у = sin (Зх - ') функциясенең графигын ординаталар күчә¬
ре буйлап 2 тапкырга сузып, у - 2 sin (Зх - -у J функциясенең
графигын табабыз (61 нче рәсем).
3 нче пунктта өйрәнелгән үзгәртүләрдә кәкренең «форма»сы
саклана (хәрәкәттәге һәм охшаш үзгәртүләрдәге кебек). Шуңа
күрә синусның графигын гына түгел, бәлки аңардан ординаталар
күчәре буйлап кысу (сузу), ә аннан соң хәрәкәт яки охшаш үзгәртү
ярдәмендә табылган теләсә нинди кәкрене дә синусоида дип атый¬
лар. Шушы ук искәрмә башка кәкре, мәсәлән, парабола яки гипер¬
бола өчен дә дөрес.
/(х) = A sin (kx + b) һәм f (х) = A cos (kx + i>) рәвешендәге функ¬
цияләрнең үзлекләре синусның (яки косинусның) үзлекләренә
аналогик булу андый функцияләрне чагыштырмача тиз тикшерер¬
гә: иң мөһиме, аларның периодларын һәм кыйммәтләре 0 гә
һәм ± А га тигез булган нокталарны табарга мөмкинлек бирә.
60 нчы рәсем
Тригонометрик функцияләр
61 нче рәсем
Η 2 нче мисал. f(x) = 2sin^3x - yj функциясен тикше¬
реп, аның графигын төзик.
/ функциясенең периоды ‘ кә тигез (4 нче пунктны карагыз).
Синус ππ, neZ күренешендәге нокталарда нульгә әйләнә, шуңа
күрә Зх - у = πη , ягъни х =-j +-у , ηεΖ булганда /(x) = 0.
Аннары /(x) = -2 һәм /(x) = 2 тигезләмәләрен чишеп таба¬
быз: Зх - у « - + 2πη булганда 81п(3х - '’'J = -1, моннан
x = , πεΖ Зх - &* = £ + 2πη булганда sin[3x - = 1,
12 3 4 2 · “ \ 4 J ’
моннан x = y^ + ^yneZ. Табылган нокталарны абсциссалар
күчәрендә билгелибез. Озынлыгы периодка тигез булган кисемтәне
карау җитә. Әлеге очракта сул очы функциянең минимум ноктасы
булган I у2 ’ 4 I кисемтәсен алу уңайлы
(62 нче рәсем). Аннары / функциясе¬
нең кисемтәсендә —2 дән 2 гә
кадәр үсүче, | jj· ~J кисемтәсендә
2 дән -2 гә кадәр кимүче графигын
төзибез. Бу вакытта график абсциссалар
күчәрен (г°) һәм Й:0'
рында кисеп үтәргә тиеш.
сенең барлык санлы турыдагы графигы¬
ның эскизы 62 нче рәсемдәге графигын
абсциссалар күчәре буйлап yy,neZ
кисемтәгә күчереп табыла (58 нче
рәсем). 62 нче рәсем
59 Тригонометрик функцияләр
2. Гармоник тирбәнешләр.
f(t) = A cos (ωί + φ) (1)
яки
f (0 = A sin (ωί + φ) (2)
законы буенча үзгәрә торган зурлыклар физикада мөһим роль
уйный. Мәсәлән, пружинага эленгән шарчыкның координатасы
шундый закон буенча үзгәрә (149 нчы рәсем). Шарчык гармоник
тирбәнешләр ясый, диләр.
(2) функциясен дә (1) функциясе рәвешендә язарга мөмкин:
A sin (ωί + φ) = A cos (ωί + φ - " j.
(1) тирбәнешен тулысынча билгели торган А, ω һәм φ па¬
раметрлары махсус атамаларга ия: А — тирбәнүнең амплиту¬
дасы, ω — тирбәнүнең циклик (яки әйләнү) ешлыгы, φ — тир¬
бәнүнең башлангыч фазасы (гадәттә, <ре [0; 2π] аралыгында алына).
Asin(oi + q>) һәм .4 cos (ωί + φ) функцияләренең — га тигез
периодын гармоник тирбәнү периоды дип атыйлар.
(1) һәм (2) функцияләренең үзлекләрен — механикадан
алынган түбәндәге мисал өстендә аңлатып бирү уңай. М ноктасы
R = А радиуслы әйләнә буенча ω почмакча тизлеге белән (ω > 0
булганда сәгать йөрешенә каршы, ә ω < 0 булганда сәгать йөреше
уңаена) тигез хәрәкәт итсен, ди. Шул ук вакытта башлангыч вакыт
моменты t = 0 дә ОМ векторы абсциссалар күчәренең уңай юнә¬
леше белән φ почмагы төзи (63 нче рәсем), t ның түбәндәге ике
функциясен — ноктаның абсциссалар һәм ординаталар күчәрлә¬
ренә проекцияләренең координаталарын — x(i) һәм y(t) функ¬
цияләрен карыйк.
t вакыт моментында ОМ векторы Ох күчәренең уңай юнәлеше
белән φ(ί) почмагын төзи, шул ук вакытта әйләнә буенча тигез
хәрәкәт законына таянып язабыз: <p(t) = φ + ωί. Синус һәм косинус
функцияләренең билгеләмәләре буенча
x(i) = Acos(i), ягъни x(i) = Acos(roi + φ),
у (t) = A sin (t), ягъни у (ί) = A sin (ωί + φ).
У
63 нче рәсем
Бу функцияләрнең үзлекләрен кине¬
матикага нигезләнеп өйрәнербез. Алар-
ның периоды нокта бер әйләнеш ясаган
вакыт Т га тигез икәнлеге ачык. Әйләнә¬
нең озынлыгы 2кА га тигез, ә ноктаның
сызыкча тизлеге υ = ωΑ, шуңа күрә
т _ 2πΑ _ 2π
1 f (1) ’
М ноктасы уң чик торышны, алган
вакыт моментларының берсе ί0 не ка¬
рыйк. Ул вакытта x(i0) - A, y(i0) = 0.
60 Тригонометрик функцияләр
Вакытның шушы моментыннан башлап xft) функциясе бер-бер
артлы периодның беренче яртысында А дан -А га кадәр кимер
һәм периодның икенче яртысында -А дан А га кадәр үсәр. Бу
вакытта х (t) функциясенең максимум нокталары ул ноктаның
уң чик торышны алган вакыт моментлары булыр, минимум
нокталары — сул чик торышка, ә нульләр югарыгы һәм түбәнге
торышларга туры килерләр.
у (/) функциясе дә аналогик үзлекләргә ия; аның максимум
һәм минимум нокталары — әйләнәдә нокталарның югарыгы һәм
түбәнге торышларына, ә нульләр уң һәм сул торышларына туры
килер.
A = 1, ω = 1 һәм φ = 0 булганда, x(t) һәм у (t) функцияләренең
тиңдәшле рәвештә cos t һәм sin t га тигез икәнен билгеләп үтәбез.
Ноктаның берәмлек әйләнә буйлап тиңдәшле хәрәкәтен карап,
бу функцияләрнең үзегезгә таныш үзлекләрен җиңел чыгарып
булуына мөстәкыйль рәвештә тикшереп ышаныгыз.
Күнегүләр
100. — Тригонометрик функцияләрнең үзлекләреннән файдала¬
нып, аңлатманы шул ук тригонометрик функциянең иң
кечкенә уңай аргументының аңа тигез кыйммәте белән
алмаштырыгыз:
j a) tg^, sin^; б) cos^-ijS-j, ctg(- у);
в) sintgp|*); г) cosctg
101. - Функциянең билгеләнү өлкәсен һәм кыйммәтләре өлкәсен
табыгыз:
a) f(x) = 3cos2x - 1; б) f(x) = 2- ctg3x ;
B)/(x) = 2tg|; r) /(*) = l + 0,5sin|.
102. - Функциянең даими тамга аралыкларын һәм нульләрен
табыгыз:
a) fix) = - sin Зх; б) f(x) = tg ;
в) f(x) = cos j ; г) f(x) = ctg2x .
103. - Функциянең үсү, кимү аралыкларын, максимум һәм ми¬
нимум нокталарын табыгыз:
a) /(х) = 4cos3x ; б) /(х) - 0,5 ctgj;
в) f(х) = 2 tg * ■ г) f(x) = 0,2 sin 4x.
1 Тригонометрик функцияләр
Функцияне тикшерегез һәм аның графигын төзегез (104—
105).
104. — а) /(х) = I cos I; б) /(х) = -2 sin 2х;
| в) f (χ) = -1,5 cos Зх; Г) f(x) = 3 sin |.
105. -1 a) 7(x) = |tg2x; б) /(х)--Зсоз^;
5 В) /(х) = -2ctg f; Г) f(x) = 2,5 sin .
106.4 Хәрәкәт итүче җисемнен координатасы (сантиметрларда
үлчәнгән) күрсәтелгән закон буенча үзгәрә. Тирбәнүнең
J амплитудасын, периодын» ешлыгын табыгыз. Түбәндәге
» бирелмәләр өчен җисемнең ί, вакыт моментындагы коор-
1 динатасын исәпләп чыгаРЬ1Гыз:
I а) х(0 = 3,5cos4jii, X, = с;
б) χ(ί) =5 cos
(3πί + β)
ti =4,5 с;
в) х (ί) = 1,5 cos 6πΖ, *ι = 1 з с;
г) х(х) -0,5cos|Zj = 8 с;
107.
Ток зурлыгы түбәндәге закон буенча үзгәреп торганда (ток
зурлыгы — амперларда» вакыт секундларда үлчәнгән),
аның амплитудасын, пеРи°Дын, ешлыгын табыгыз:
а) I (ί) = 0,25 sin 50πί;
в) I (t) = 0,5sinl0Ttt;
б) I (t) = 5 sin 20πί;
г) I(t) = 3 sin 30πΖ.
108.
Көчәнеш түбәндәге закон буенча үзгәреп торганда (көчә¬
неш — вольтларда, вакыт секундларда үлчәнгән), аның
амплитудасын, периодын һәм ешлыгын табыгыз:
a) U (X) = 220 cos 60nt; б) U (ί) =110 cos 30πΧ;
в) U(ί) = 360 cos 20πί; г) U (f) = 180 cos 45πί.
109.— Саннарны үсә бару тәртибендә урнаштырыгыз:
а) cos 4, cos 7, cos 9, cos (-12,5);
б) tg (-8), tg 1,3, tg 4, tg ιθ:
в) sin 6,7, sin 10,5, sin (-7), sin 20,5;
r) ctg 3,5, ctg (-9), ctg 5, ctg 15.
110.— Функциянең билгеләнү елкәсен табыгыз:
а) У -
в) У =
б) У = ^sin2| - cos21 ;
г) у = yjtgx + ctgx .
62 Тригонометрик фуякцияләр
111.— Функциянең кыйммәтләре әлкәсен табыгыз:
а) у = sin х - 7з cos х ; б) у = . * .;
в) у = V1-COS4X ; г) у = 1 + jg2x·
Функцияне тикшерегез һәм аның графигын төзегез (112—
113).
112. -a) f(x) = 2cos(x + |);
в) 7(х) =
113. —a) f(x) = sin(2x-
в) flx) = 4cos(f + *);
\ <5 <3 /
б) f(x) = |sin(f-x);
г) /*(х) = 1,5 cos ί | - х).
б) f(x) = ctg(| + ^j;
г) /(x) = tg(^-3x).
114.
64 нче рәсемдә сурәтләнгән графигы буенча ток зурлыгы¬
ның (яки көчәнешнең) амплитудасын, тирбәнү периодын
билгеләгез. Ток зурлыгының (яки көчәнешнең) вакытка
бәйлелек законын языгыз.
/,А1 U.BL
а) б)
63 Тригонометрик функциядер
115.— Хәрәкәт башланганнан алып исәпләгәндә, иң якын нинди
вакыт моменты t да (t > 0) х (ί) = 5 cos | 11 законы бу¬
енча гармоник тирбәнә торган ноктаның күчеше:
»а) максималь; б) 2,5 кә тигез;
в) 0 гә тигез; г) -5 кә тигез була?
§ 3.
Тригонометрик тигезләмәләрне
һәм тигезсезлекләрне чишү
8. Арксинус, арккосинус һәм арктангенс
1. Тамыр турында теорема. Тигезләмәләр чишкәндә
куллану өчен уңай булган мөһим раслауны бирик.
Теорема (тамыр турында). f функциясе I ара¬
лыгында үссен (яки кимесен), а саны f ның шушы
аралыкта кабул иткән теләсә кайсы бер кыйммәте
булсын. Ул вакытта /(х) = а тигезләмәсенең I ара¬
лыгында бердәнбер тамыры була.
Исбатлау. Үсүче f функциясен карыйк (кимүче функция
очрагында аналогик рәвештә фикер йөртәбез). Теореманың шарты
буенча I аралыгында f(b) = а булырлык бер Ь саны бар. Ь саны
f(x) = a тигезләмәсенең бердәнбер тамыры икәнен күрсәтербез.
I аралыгында f(c) = a булган тагын с*Ь саны бар, дип уйлыйк.
Ул вакытта я с < Ь, я с > Ь. Ләкин f функциясе I аралыгында үсә,
шуңа күрә тиңдәшле рәвештә я /(с) < /(Ь), я f (с) > /(Ь). Бу исә
/(с) = /(Ь) = а тигезлегенә каршы килә. Димәк, безнең фаразыбыз
дөрес түгел һәм /(х) = а тигезләмәсенең I аралыгында Ь саныннан
башка тамырлары юк.
I 1 нче мисал. Xs + х = 2 тигезләмәсен чишик.
/(х) = х3 + х функциясе R да үсә (бу — ике үсүче функциянең
суммасы). Шуңа күрә f (х) = 2 тигезләмәсенең тамырлары бердән
артык түгел, х = 1 аның тамыры икәнен күрү кыен түгел.
2. Арксинус. Белгәнебезчә, синус функциясе j 2'2] кисем‘
төсендә үсә һәм -1 дән 1 гә кадәрге барлык кыйммәтләрне ала.
Димәк, тамыр турындагы теорема буенча |а| 1 булган теләсә нин¬
ди а саны өчен sinx = а тигезләмәсенең ί аралыгындагы
бердәнбер тамыры Ь бар. Бу Ь санын а санының арксинусы дип
атыйлар һәм arcsin а аша тамгалыйлар (65 нче рәсем).
6 4 Тригонометрик функцияләр
65 нче рәсем
66 нчы рәсем
_ „ _ Г_8- 8 1
Билгеләмә. Синусы а га тигез булган I 2’ a I
кисемтәсендәге сан а санының арксинусы дип
атала.
I 2 нче мисал, arcsin -у не табыйк.
arcsin-y··*, чөнки sinA = jS һәм
3 нче мисал, arcsin ( | не табыйк.
Синусы (“2) гэ тигеэ булган сан ([“f· 2] аРалыгыннан j
- £ га тигез. Шуңа күрә arcsin (—|) = ~ $ · ff
3. Арккосинус. Косинус функциясе [0; π] кисемтәсендә кими
һәм 1 гә кадәрге барлык кыйммәтләрне ала. Шуңа күрә |α| <- 1
булган теләсә нинди а саны өчен cos .г = а тигезләмәсенең [0; π]
кисемтәсендә бердәнбер тамыры b бар. Бу b санын а санының
арккосинусы дип атыйлар һәм arccosa аша тамгалыйлар (66 нчы
рәсем).
Билгеләмә. Косинусы а га тигез булган, [0; я]
кисемтәсендәге сан а санының арккосинусы дип
атала.
I 1 4 нче мисал
|*[0; πΐ.
5 нче мисал
һәм е [0; π].
arccos4 = |. чөнки cose=4 һәм
arccos I - I 3л , чөнки cos (r --
Тригонометрик функцияләр
4. Арктангенс. (£· г/ интервалында тангенс функциясе үсә
һәм R дагы барлык кыйммәтләрне ала. Шуңа күрә " | интер¬
валындагы теләсә нинди а саны эчен tgx = а тигезләмәсенең бер¬
дәнбер тамыры b бар. Бу b санын а санының арктангенсы дип
атыйлар һәм arctga аша тамгалыйлар (67 нче рәсем).
Билгеләмә. Тангенсы а га тигез булган & * |
интервалындагы сан а санының арктангенсы дип
атала.
■ 6 нчы мисал, arctgl = чөнки tg^· = 1 һәм 1-4; f .
7 нче мисал. arctg^-Vs) = чөнки tg(-^| = -V3
һәм -4е(-4;4). ■
3 \ 2 2/ β
5. Арккотангенс. Котангенс функциясе (0, π) интервалында
кими һәм R дагы барлык кыйммәтләрне ала. Шуңа күрә (0, π)
интервалындагы теләсә нинди а саны өчен ctg х = а тигезләмәсенең
бердәнбер тамыры b бар. Бу Ъ санын а санының котангенсы дип
атыйлар һәм arcctga рәвешендә тамгалыйлар (68 нче рәсем).
Билгеләмә. Котангенсы а га тигез булган (Ο;π)
интервалындагы сан а санының арккотангенсы
дип атала.
67 нче рәсем 68 нче рәсем
66 Тригонометрик функцияләр
8 нче мисал. arcctg-^ = ^, чөнки ctg^ = -^ һәм
«1=1
e (0; π).
9 нчы мисал
һәм & е (0; π).
arcctg(->/3)
= , чөнки ctg = -7з
о и
Күнегүләр
Тигезләмәләрнең һәркайсының бирелгән аралыкка кергән
ничә тамыры бар (116—117)?
116.—а) х7 = 3, х е (-»; »); б) = -5, х е (-«; 1);
в) х6 = 4, х е (-оо; 0]; г) = 2, х е (-2; «).
117.— а) (х - З)3 = -4, х е (-со; <ю);
б) 2sinx = l,5, х е [-•J; *]:
в) (χ + 2)4 =5, х е [-2; ое); г) 0,5cosx = —J
х е [0; π].
Берәмлек әйләнәдә t ның тиңдәшле кыйммәтләре бирелгән
тигезлекне канәгатьләндерә торган Р, нокталарын бил¬
геләгез. t ның бирелгән аралыктагы кыйммәтен табыгыз
(118—120).
118- a) sine = 4» [-Μ]ί б) sini = -i, [44];
B)sint = -4· [4; 2j: r)sint = l, [44].
119. a) cost = 4, [0; π]; 6) cost = 4 . [0; π];
в) cost = - “, [0; π]; г) cost = 0, [0; π].
120. a) tgt = -1, (44); 6) ctgt = V3, (0; π);
в) tgt =7з, f): г) ctgt = -1, (0; π).
121.
Исәпләп чыгарыгыз (121—123).
a) arcsinO; 6) arcsin (--y-
b) arcsin 1; r) arcsin I - 4
67 Тригонометрик функцияләр
122—
123.
124.
125.-
a) arccosi ~4)ί
в) arccos ί-^Ι;
v 2 /
a) arctg 4=;
v·
в) arctg 0;
Аңлатмаларның мәгънәсе
a) arcsin
в) arcsinl,5;
a) arccos π;
в) arccosI-V3I;
6) arccos
r) arccos 1.
6) arctg (-1);
r) arctg V3.
бармы (124—125)?
б) arccos-/δ;
г) arccos .
б) arcsin (з - χ/2θ);
г) arcsin*.
Аңлатмаларның кыйммәтләрен табыгыз (126—128).
126.
a) arcsin 0 + arccos 0; б) arcsin 1- Др) + arccos |;
в) arcsin 4- + arccos --3 ; r) arcsin (-1) + arccos .
127.-
а) arccos (-0,5) + arcsin (-0,5);
б) arccos (-^1 - arcsin (-1);
в) arccos(-4) + arcsini- i|·
r) arccos - arcsin -J .
128.-
a) arctg 1 - arctg х/з; 6) arctg 1 - arctg (-1);
в) arctg 1 -χ/з J + arctg 0; r) arctg -4- + arctg х/з.
129.-
Саннарны чагыштырыгыз:
а) arcsin һәм arccos·^-;
б) arccos 1 ‘, 1 һәм arctg (-1);
a) arctg χ/з һәм arcsin 1;
г) arccos һәм arcsin i.
ι 2 I 2
68
Тригонометрик функцияләр
130.— Калькулятор яки таблицалар ярдәмендә аңлатманың
кыйммәтен табыгыз:
а) arcsin 0,3010; arctg 2,3;
б) arccos 0,6081; arctg0,3541;
в) arcsin 0,7801; arccos 0,8771;
г) arctg 10; arcsin 0,4303.
131.— Исәпләп чыгарыгыз:
а) 2 arcsin + arctg (-1) +arccos-ү·;
б) 3arcsin77 + 4arccos 1 |-arcctg| Vs);
в) arctg (-7з) + arccos I -yj + arcsin 1;
1 r) arcsin(-1) -1arccos | + 3 arctgI- -Ul.
132. — [-1; 1] аралыгындагы теләсә нинди Xj һәм x2 саннары өчен
х, < х2 тигезсезлегеннән
a) arcsin х, < arcsin х2; б) arccos xt > arccos х2
тигезсезлеге килеп чыкканын исбатлагыз.
133. — Теләсә нинди х, һәм х2 саннары өчен х, < х2 тигезсезлегеннән
1а) arctg х, < arctg х2; б) arcctgx, > arcctgx2
тигезсезлеге килеп чыкканын исбатлагыз.
Саннарны үсә бару тәртибендә урнаштырыгыз (134—135).
a) arcsin |, arcsin (-0,3), arcsin 0,9;
б) arcsin (-0,5), arcsin (-0,7), arcsin g ;
в) arccos 0,4, arccos (-0,2), arccos (-0,8);
r) arccos 0,9, arccos (-0,6), arccos ·|.
135.
а) arctg 100, arctg(-5), arctg0,7;
б) arcctgl,2, arcctgn, arcctg(-5).
9. Иң гади тригонометрик тигезләмәләрне чишү
1. cos t = а тигезләмәсе. Әгәр |α| > 1 булса,
cost = a (1)
тигезләмәсенең чишелешләре булмавы үзеннән-үзе аңлашыла,
чөнки теләсә нинди t өчен jcos t| 1.
|α| 1 булсын, cos t = а булган барлык t саннарын табарга ки¬
рәк. (1) тигезләмәнең [0; π] кисемтәсендә төгәл бер чишелеше
бар — ул arccos а саны.
69 Тригонометрик функцияләр
Косинус — җөп функция, димәк, [-π; 0] кисемтәсендә (1) тигез¬
ләмәнең шулай ук төгәл бер чишелеше бар — ул -arccosa саны.
Шулай итеп, cosf = а тигезләмәсенең 2тг озынлыгындагы [-π; π]
кисемтәсендә ике чишелеше бар: t = ±arccosa (a = 1 булганда тәң¬
гәл килүче).
cos периодик функция булганга күрә, калган чишелешләр мо¬
нысыннан 2πη (neZ) га аерылалар, ягъни (1) тигезләмәнең тамыр¬
лары формуласы түбәндәгечә була:
t = ± arccos а + 2пге, п е Z. (2)
(Игътибар итегез: бу формуланы бары тик |a| С 1 булганда гына
кулланырга ярый.)
(1) тигезләмәнең чишелешен берәмлек әйләнәдә күрсәтергә
мөмкин. Билгеләмә буенча cos t — берәмлек әйләнәнең Р, ноктасы
абсциссасы. Әгәр |a| < 1 булса, андый нокталар ике (69 нчы а рә¬
сем); ә a = 1 яки a = -1 булганда бер (69 нчы б рәсем).
a = 1 булганда, arccosa һәм -arccosa саннары тәңгәл киләләр
(алар нульгә тигез), шуңа күрә cos t = 1 тигезләмәсенең чишелеш¬
ләрен t = 2πη, neZ рәвешендә язалар.
a = -1 һәм а = 0 өчен (1) тигезләмәнең чишелешләрен «аерым»
формада язу кабул ителгән:
t - π + 2πη, η € Ζ булганда, cos t = -1;
t = £ + nn, n e Z булганда, cos t » 0.
Q 1 нче мисал, cosх = тигезләмәсен чишик.
(2) формула буенча
х = + arccos + 2πη, п e Ζ.
arccos I = § булганга күрә,
х = ± £ + 2πη, n e Ζ.
о
Тригонометрик функцияләр
2 нче мисал, cosx = -0,2756 тигезләмәсен чишик.
(2) формула буенча
х = ± arccos(-0,2756) + 2πη, neZ.
arccos(—0,2756) ның кыйммәтен калькулятор ярдәмендә таба¬
быз: ул якынча 1,8500 гә тигез. Шулай итеп,
х = ± χ0 + 2пп, neZ, монда х0 = 1,8500.
3 нче мисал. cos ^2х - j = --у тигезләмәсен чишик.
(2) формула буенча
2х - J = ± arccos (- + 2πη, п e Ζ,
ягъни 2x - 4 = ± + 2πη, моннан
4 О
X = Τ ± Η + ««, η € “
2. sin t = а тигезләмәсе.
sin t = a (3)
тигезләмәсенең ]α| > 1 булганда чишелешләре юк, чөнки теләсә
нинди t өчен |sint|^l. |α| О булганда (3) тигезләмәнең -·£; -J
кисемтәсендә төгәл бер чишелеше бар: tx = arcsin a. 7; -- j ара¬
лыгында sin функциясе кими һәм -1 дән алып 1 гә кадәр бар¬
лык кыйммәтләрне ала, шуңа күрә тамырлар турындагы теоре¬
ма буенча (3) тигезләмәнең бу кисемтәдә дә бер тамыры бар:
70 нче а рәсемнән бу тамырның π - arcsin α га тигез булган t2 саны
икәне күренә. Чыннан да, sin t2 = sin (π - t,) = sini, = а. Моннан
тыш, - *· ti ζ j булганга күрә яза алабыз: ~-g < < 7 һәм
π - C π - t, rt + ·|, ягъни t2 саны. кисемтәсенә керә.
71
Тригонометрик функцияләр
Шулай итеп, (3) тигезләмәнең [“o'· кисемтәсендә ике чи¬
шелеше бар: t, = arcsin а һәм ί2 — к — arcsin a (a = 1 булганда тәңгәл
килүче). Синусның периоды 2π икәнен искә алып, тигезләмәнең
барлык чишелешләрен язу эчен түбәндәге формулаларны табабыз:
t = arcsin a 4- 2πη, (4)
t = π-arcsin α + 2πη, η&Ζ. (5)
(3) тигезләмәнең чишелешләрен ике формула белән түгел,
ә бер формула белән язу уңайлы:
t = (-1)* arcsina + nk, keZ. (6)
(6) формуладан k = 2n (җеп) булганда — (4) формула белән
язылган барлык чишелешләр, ә k = 2п + 1 (так) булганда (5) фор¬
мула белән язылган барлык чишелешләр табылуына ышану кыен
түгел.
(3) тигезләмәнең чишелешен берәмлек әйләнәдә җиңел күрсә¬
теп була. Билгеләмә буенча sin t — берәмлек әйләнәдә Р, нокта¬
сының ординатасы. Әгәр Ια| < 1 булса, ул вакытта андый нокталар
ике (70 нче а рәсем); а = ±1 булганда бер (70 нче б рәсем).
Әгәр a = 1 булса, arcsin а һәм π - arcsin а саннары тәңгәл килә¬
ләр, шуңа күрә
sin f«1
тигезләмәсенең чишелешен
t = 5 + 2πη, п е Ζ
рәвешендә язу кабул ителгән.
а = -1 һәм а - 0 булганда түбәндәгечә язалар:
t = - ·| + 2πη, η & Ζ булса, sin t = -1,
t = πη, η € Z булса, sin t - 0.
4 нче мисал. sinx = ^ тигезләмәсен чишик.
(б) формула буенча
х = (-1)* arcsin-1^· + nk, k е Z, ягъни
х = (-1)* -j + πΛ, k € Ζ.
5 нче мисал, sinx = 0,3714 тигезләмәсен чишик.
(6) формула буенча
х = (-1)" arcsin 0,3714 + πη, п е Ζ.
Калькулятор ярдәмендә табабыз: arcsin 0,3714 = 0,3805.
6 нчы мисал, sin [ Д ) = тигезләмәсен чишик.
Синус — так функция. Шуңа күрә
7 2 Тригонометрик функцияләр
(6) формула буенча
£ - -Л- = (-1)* arcsin (-·*■/1 + π&, A е Z.
2 ιθ ' ' \ 2 /
arcsin булганга күрә яза алабыз:
2-ω'·’1»* (-*)■”'*·
X = ί + (-1)*+Ч + 2лЛ, ft е Z.
Д. tgt = β тигезләмәсе. Теләсә нинди а өчен (“2’2) интеРва
лында tg t = а булырлык төгәл бер t саны бар, бу — arctg α. Шуңа
күрә
tgi = a (7)
тигезләмәсенең π озынлыгындагы I - □ · 2) интеРвалында бердән¬
бер тамыры була. Тангенс функциясенең периоды π гә тигез.
Шулай булгач, (7) тигезләмәнең калган тамырлары әле табылган
тамырдан πη (neZ) га аерылалар, ягъни
t = arctg a + πη, ηεΖ. (8)
tg t = α тигезләмәсенең чишелешен тангенслар сызыгы ярдәмендә
күрсәтү уңайлы (71 нче рәсем), tg t — ул OPt турысының тангенслар
сызыгы белән кисешү ноктасы Tt ның ординатасы икәнен исегезгә
төшерәбез (1 нче пунктны карагыз). Теләсә нинди а саны өчен
тангенслар сызыгында ординатасы а га тигез булган бары тик бер
генә нокта бар, бу — Т(1; а) ноктасы. ОТ турысы берәмлек әйләнә
белән ике ноктада кисешә; бу вакытта
ярымәйләнәнең t, = arctg а булырлык
OPt) ноктасы туры килә.
■ 7 нче мисал. tgx = V§ тигез¬
ләмәсен чишик. (8) формула буенча
х - arctgVs + πη, п е Ζ
чишелешен табабыз. arctgV3 “ , шу¬
ңа күрә иң соңгы җавапны болай яза¬
быз:
х = -5- + πη, п е Ζ.
Λ
8 нче мисал, tgx = 5,177 тигез¬
ләмәсен чишик. (8) формуладан
х = arctg 5,177 + πη, neZ
икәнлеге килеп чыга. Калькулятор яр¬
дәмендә табабыз:
71 нче рәсем
arctg 5,177 « 1,3800.
73
Тригонометрик функцияләр
9 нчы мисал, ctgх = -у/З тигезләмәсен чишәбез.
Бу тигезләмә (8) формула ярдәмендә чишелә торган tg X = —1=
тигезләмәсенә тамырдаш:
х - arctg ί- -Μ + πη - - £ + πη, η e Ζ.
\ 431 6
Күнегүләр
I Тигезләмәләрне чишегез (136—143).
136.-
. „ 42
a) cosx = у-;
ία
в) cosx =
137.-
a) 2cosx + -Тз = 0;
в) 2cosx + V2 = 0;
138.
a) sinx =
в) sin x = - 2;
139.-
a) V2sinx + l = 0;
в) 2sinx -1 = 0;
140.
»> =
в) tg x = 1;
141.
a) tg x + л/З = 0;
в) V3tgx-1 = 0;
142.
a) sin2x = ^y·;
в) sin I = |;
143.-
a) sin x = -0,6;
в) cosx = 0,3;
б) cos х = - ;
г) cos x = -1.
6) ^2 cosx -1 = 0;
r) 2 cos x - 1 = 0.
6) sinx =
r) sinx = -1.
6) 2 sin х + л/з = 0;
г) 2sinx + >/2 =0.
6) ctgx = >/3;
г) tg х = 0.
6) ctgx + 1 = 0;
r) ^3 ctgx-1 = 0.
6) cos| = -|;
r) cos 4x - 0.
6) ctgx = 2,5;
r) tgx - -3,5.
Тигезләмәләрне чишегез (144—147).
144.—a) sin(-|) = -ώ;
б) tg(-4x) = X;
48
r) ctg(-f) = l.
74 Тригонометрик функцияләр
145. — а) 2cos [ή ^' = 73;
Β> J3tg(f + f) = 3;
146. —a) cos^- 2x) = -1;
в) *(МН:
6) 2sin(3x-|) = -χ/2;
r) sin(f-|) + l = O.
6) 2 sin (|- f) = 73;
г) 2cos(-| -Зх) = V2.
147. —a) sin3xcosx - cos3xsinx = ;
б) sin2 f - cos2 f = 1;
4 4
в) sin2xcos2x = -4;
r) sin 4 cos 7 - cos f sin f = ^.
148. — у = 2cos^2x - '; һәм j/ = sin(f + *j
функцияләре өчен аларның графиклары белән күрсәтелгән
турының уртак нокталары координаталарын табыгыз.
а) х = 4,5π; б) у = -1; в) у = 1; г) у = 0.
149. - cos(·^ ~ 2х) = 2» sin^2x + '( = -1 тигезләмәләрен чишегез
һәм һәркайсының:
а) иң кечкенә уңай тамырын;
б) ] аралыгындагы тамырларын;
* в) иң зур тискәре тамырын;
г) (-π; 5) аралыгындагы тамырларын табыгыз.
150. t “ arcctg a + πη, neZ формуласы буенча ctg t = а тигезлә¬
мәсенең барлык чишелешләре дә табылганын исбатлагыз.
10. Иң гади тригонометрик тигезсезлекләрне
чишү
Тригонометрик функцияләрне эченә алган тигезсезлек¬
ләрне чишү, кагыйдә буларак, sint ζ a, cost > a, tgt > а һ.б. иң
гади тигезсезлекләрне чишүгә кайтып кала.
Мисаллар өстендә аларны чишү ысулларын карыйк.
Я 1 нче мисал. sint>-* тигезсезлеген чишик.
Бирелгән тигезсезлекне канәгатьләндерүче t кыйммәтләре өчен
берәмлек әйләнәнең барлык Р, нокталарының ординаталары
75 Тригонометрик функцияләр
72 нче рәсем
73 нче рәсем
дэн зуррак яки аңа тигез була. 72 нче рәсемдә аерып күрсә¬
телгән I дугасы — барлык шундый нокталар күплеге. Pt нокта¬
сының шул дуганыкы булу шартын табыйк.
Р., ноктасы уң ярымәйләнәдә ята, Pf] нең ординатасы гә
тигез, димәк, ^сыйфатында t, = arcsin(“2) ~ “ б кыйммәтен алу
уңай. Без I дугасын ίξ ноктасыннан Р1л ноктасына кадәр сәгать
йөрешенә каршы йөреп чыгабыз дип күз алдына китерик.Ул ва¬
кытта t2 > Г, һәм t2 = π - arcsin I -A) = -~Λ икәнен аңлау җиңел.
Шул рәвешле, - ң ζ t ζ -γ булса, Р, ноктасы I дугасыныкы икәнен
табабыз. Димәк, тигезсезлекнең 2π озынлыгындагы [- 4; Яг] ара¬
лыгына кергән чишелеше ~ θ t рәвешендә була. Синус
периодик функция булганга күрә, калган чишелешләре табылганга
2πη, монда neZ рәвешендәге саннарны өстәп табыла. Җавап тү¬
бәндәгечә языла:
- i + 2πη ζ t < + 2πη, п e Ζ.
о О
2 нче мисал. sint<·^- тигезсезлеген чишик.
Бу тигезсезлек әлеге тигезсезлекне канәгатьләндерүче кыйм¬
мәтләре өчен берәмлек әйләнәнең барлык Р, нокталарының орди¬
наталары дән кечерәк булуын белдерә. 73 нче рәсемдә аерып
күрсәтелгән I дугасы — шундый барлык нокталар күплеге. Дуга¬
ның очлары Р(] һәм Р,г әлеге күплеккә керми, чөнки аларның
ординаталары дән кечерәк түгел, ә гә тигез. Р, ноктасының
к„ен керу не
табабыз, t = arcsin-^· = 4 не алабыз.
£, 4
76 Тригонометрик функцияләр
I дугасын Ptl ноктасыннан Pt2 гә сәгать йөреше уңаена йөреп
чыгуны карыйк; t2 < t, һәм ί2 = -π - arcsin 2 = ~ . Тигезсез¬
лекнең 2π озынлыгындагы ~ * аралыгында урнашкан бар¬
лык чишелешләре болай языла: - to < ί <’. Синусның периодик
булуын исәпкә алып, тигезсезлекнең барлык чишелешләрен та¬
бабыз:
- + 2πη < ί < * + 2πη, η eZ.
4 4
3 нче мисал, cos t < i тигезсезлеген чишик.
■ t
Берәмлек әйләнәнең абсциссалары дән кечерәк булган нокта¬
лары күплеге х = i турысыннан сулдарак яталар. Шулай булгач,
74 нче рәсемдә аерып күрсәтелгән I дугасы барлык шундый
нокталар күплеге булыр (аның очлары Рһ Һәм Р1г нокталары бу
күплеккә кермиләр), f, һәм t2 не табабыз. Р(| ноктасы югарыдагы
ярымәйләнәгә урнашкан, Р(1 нең абсциссасы гә тигез, димәк,
ti = arccos = ^. Р(] ноктасыннан Р(, ноктасына күчү I дугасы
буйлап сәгать йөрешенә каршы башкарыла, ул вакытта t2 > t,
һәм t2 = 2π - arccos-1 = to. < t < to шарты үтәлгәндә, нокта
Δ ο α
аерып күрсәтелгән l дугасыныкы була (аның очларыннан башка).
Тигезсезлекнең 2π озынлыктагы [0; 2π] аралыгына кергән чише¬
лешләре болай языла: I <t < to. Косинус периодик функция
булу сәбәпле, калган чишелешләре әлеге чишелешкә 2пп, монда
neZ рәвешендәге саннарны өстәп табыла. Тулы җавап түбәндәгечә
булыр:
·§■ + 2πη < t <. to + 2πη, η e Ζ.
ti a
4 нче мисал, tgt ζ 1 тигезсез¬
леген чишик.
Тангенсның периоды π гә тигез.
Шуңа күрә башта әлеге тигезсезлек¬
нең I - I; аралыгына кергән барлык
чишелешләрен табабыз, ә аннары тан¬
генсның периодиклыгыннан файдала¬
набыз. ί ның кыйммәтләре әлеге тигез¬
сезлекне канәгатьләндерә торган бар¬
лык Р, нокталарын уң ярымәйләнәдә
аерып күрсәтү өчен, тангенслар сызы-
77 Тригонометрик функцияләр
гына мөрәҗәгать итәбез. Әгәр t тигезсезлекнең чишелеше бул¬
са, Т ноктасының tgt га тигез булган ординатасы 1 дән кечерәк
яки тигез булырга тиеш. АТ нуры — шундый Т нокталары күплеге
(75 нче рәсем). Рәсемдә аерып күрсәтелгән I дугасы исә шул нур
нокталарына тиңдәшле Pt нокталары күплеге була (игътибар ите¬
гез: тикшерелә торган күплеккә Ptl ноктасы керә, ә Р, нокта-
ΐ
сы керми). Р( ноктасының I дугасына керү шартын табыйк,
е (- j; ^) һәм tg t,=l, шулай булгач, I, = arctg 1 = . Димәк,
t аргументы - шартын канәгатьләндерергә тиеш.
Бирелгән тигезсезлекнең oj аралыгына кергән барлык чи¬
шелешләре мондый була: (~υ» 4]· Тангенсның периодиклыгын
исәпкә алып, җавапны табабыз:
-·£ + ππ<ί^-5· + πη, п е Ζ.
Δ 4
5 нче мисал. cos2x^-J*-~ тигезсезлеген чишик. 2х ны
£
t аша тамгаласак, cosi Э —ү килеп чыга. 76 нчы рәсемдә тиң¬
/ \
дәшле I дугасы аерып күрсәтелгән. Табабыз: — arccos I - -у-1 =
= , f, = — « моннан
4 4 4
- + 2πη ζ t < ψ + 2πη, η e Ζ.
4 4
х үзгәрешлесенә күчәбез:
- "т + 2πη < 2х С + 2πη,
4 4
+ m ζ х + ил, η e Ζ.
Ο ο
7 8 Тригонометрик функцияләр
6 нчы мисал.
’ΜΐΉ тигезсезлеген
чишик.
Бирелгән тигезсезлекнең рәве¬
шен үзгәртәбез:
77 нче рәсем
2 — ΐ не ί аша тамгалыйк, ул вакытта tg t > — 2·. 77 нче рәсемдә
тиңдәшле / дугасы аерып күрсәтелгән. t] = arctg^--j-l = - ^
булганга күрә, -^ + Jtn<t<^+rtrt икәнлеге килеп чыга, х үз-
гәрешлесенә күчәбез:
' + πη < % - < £ + πη,
П Ζ о 2
+ 2πη < х < + 2πη, п е Ζ.
J о
Күнегүләр
Тиңдәшле ί кыйммәтләре бирелгән тигезсезлекне канә¬
гатьләндергән Pt нокталарын берәмлек әйләнәдә билгелә¬
гез. t ның тигезсезлекне канәгатьләндергән һәм күрсә¬
телгән аралыкка кергән кыйммәтләре күплеген табыгыз
(151 — 153).
151.
152.-
153.
a) sin t > 1, t е [0, π];
в) sin t > '.2 . t е [0; π];
a) cost>^,te[-j;f];
В) cost >|, t e j
a) tg/ > ^3.
в)
6) sin t - y, t ε [-π; 0];
г) sin t < - |, t € [-π; 0].
6)
r) cost<—^,te[|;^].
6) tgt<-^,te(-f;|);
r) tgt<-l,
79
Тригонометрик функцияләр
Тигезсезлекләрне чишегез (154—157).
154. — a) sinx £
. в) sinx >
155. -&а) cosx 4»
• I
в) cos х -у;
156. a) tgx < л/З;
в) tgx -%;
<3
157. а) 2 cos х -1 > 0;
в)2соэх-7з 0;
б) sm х < - -у;
г) sin х < - .
б) cos х < ;
И
1 J2
г) COSX < --у.
б) tg х > —L;
ч‘3
г) tgx < -1.
б) 2sinx + v'2 £ 0;
г) 3 tg х + 7з 0.
Тигезсезлекләрне чишегез (158—163).
158.— a)
sin 2x <
6) cosf
Ο Δ
в)
V
c
•гИ
s..
2 ’
r) tg5x > 1.
159.— а) 2 cos (2х + 1;
в) >/2sin(* + |)> 1;
б) V3tg(3x + |)<l;
г) 2cos^4x-^j> Vs.
160.— a) sin х cos % - cos x sin 4 £ 4»
Ο Ο Δ
161.
162.
5) sin 4 cos х + cos 4 sin x < - ;
'4 4 2
в) 4sin2xcos2x > V2;
r) cos 4 cos x - sin x sin 4 < ~ v ·
б ο Δ
a)ctgx^V3; б) >/3ctg|®-2x) > 1;
в) ctg3x £-JL··; r) 3ctg(| +*)>--Уз.
a) 3sin4 > 2; 6) 4 cos4 < -3;
e)5tg2x^3; r) 0,5sin4x <-0,2.
Тригонометрик функцмялвр
163.— Тигезсезлекнең күрсәтелгән аралыкка кергән чишелеш¬
ләрен табыгыз:
а) sinx>-|,xe(-f;^);
б) cos-J > х е Г-£; о"|;
в) tgx -1, х е *];
г) sin 2х < х е [0; π].
11. Тригонометрик тигезләмәләрне һәм
тигезләмәләр системаларын чишүгә мисаллар
9 нчы пунктта иң гади тригонометрик тигезләмәләрне
ничек чишәргә икәнлеге күрсәтелгән иде. Катлаулырак тигезләмә¬
ләрне чишү тригонометрик формулаларны белүне таләп итә. Бер¬
ничә мисал карап үтик.
Ц 1 нче мисал. 2sin2x + sinх- 1 = 0 тигезләмәсен чишик.
Яңа у = sin х үзгәрешлеген кертәбез. Ул вакытта бирелгән тигез¬
ләмәне 2у2 + у - 1 = 0 рәвешендә язарга мөмкин. Без квадрат тигез¬
ләмә таптык. У\ — !. һәм уг = -1 аның тамырлары булып хезмәт
итә. Шулай булгач, sinx = * яки sinx = -l. Беренче очракта
х = (-1>‘ arcsin^ + дА, ягъни х - (-1)* ~ + πΑ,keZ
чишелешен табабыз. Икенче очракта
х = - ± + 2пп, ns Z
булыр.
2 нче мисал. 6sin2x + 5 cosx - 2 = О тигезләмәсен чишик.
sin2x ны l-cos2x ка алмаштырып, cosx ка карата квад¬
рат тигезләмә табабыз: 6(1 — cos2x) 4-5cosx - 2 — 0, моннан
-6cos2x + 5cosx + 4 = 0, ягъни 6cos2x - 5cosx - 4 = 0. 1 нче мисал¬
дагы кебек үк, cos х = у яңа үзгәрешлесен кертәбез. Ул вакытта
бу2 - 5у - 4 = 0, моннан у = * яки у - 1 ‘ .
14 > 1 булганлыктан, cosx = 11 тигезләмәсенең чишелеше юк.
3 " о
cosx = - ^ тигезләмәсен чишеп табабыз:
х = ±3? + 2πΑ, k ε Ζ.
л
3 нче мисал, tgx + 2ctgx = 3 тигезләмәсен чишик.
tgx ны у аша тамгалыйбыз.
ctgx =
tgx
булганга күрә,
81 Тригонометрик функцияләр
тигезләмәсен табабыз. Ул у2 - Зу + 2 = 0 (у * 0 шарты
үтәлгәндә) квадрат тигезләмәсенә китерелә. Аның тамырлары
у = 2, у = 1.
1) tgx =2, х = arctg 2 +nk, ягъни х = xQ +πΑ, AeZ, монда
x0 = arctg 2 = 1,1072.
2) tgx =1, x = + nk, k e Z.
4 нче мисал. 3sin2x - 4sinxcosx + cos2x = 0 тигезләмәсен
чишик.
х ның cos х = 0 булгандагы кыйммәтләре бу тигезләмәнең
чишелешләре була алмый, чөнки cosx = 0 булса, 3sin2x = 0 ти¬
гезлеге дә үтәлергә тиеш, ә косинус һәм синус бер үк вакытта
нульгә тигез була алмыйлар. Шуңа күрә тигезләмәнең ике кисәген
дә cos2x ка (яки sin2x ка) бүлеп, бирелгән тигезләмә белән та¬
мырдаш 3 tg2x -4tgx + l= 0 тигезләмәсен табарга мөмкин, мон¬
нан tgх = 1 яки tgx = i · Димәк,
х = 7 + πη, η € Ζ яки х = arctg ' + πη, ne Ζ.
4 о
5 нче мисал. 6sin2x + 4 sin х cos х = 1 тигезләмәсен чишик.
Тигезләмәнең уң кисәгендәге 1 не sin2x + cos2x ка алмашты¬
рабыз. Тиешле рәвеш үзгәртүләрне башкарганнан соң 5 sin2 х +
+ 4 sin х cosx - cos2x = 0 килеп чыга. 4 нче мисалда тасвирланган
моңа охшаш тигезләмәне чишү алымыннан файдаланабыз. Нәти¬
җәдә табабыз: tg х - 1, tgx = -1. Димәк,
э
х = arctg А + πη, п е Ζ, яки х = -% + π/г, k е Z.
6 нчы мисал. sin2x - sin2x = 0 тигезләмәсе sin2x ны
2sinхcosx ка алмаштырганнан соң sin2x - 2sinxcosx = 0 рәве¬
шендәге тигезләмәгә китерелә.
Сул кисәген тапкырлаучыларга таркатабыз: sin х (sin х-
-2cosx = 0, моннан sinx = 0, ягъни х = πη, neZ, яки sinx-
~2cosx = 0, моннан tgx = 2 һәм х = arctg2 + πη, n<=Z, ягъни
x = x0 + πη, neZ, монда x0 = arctg2 « 1,1072.
4 нче мисалдагы кебек тигезләмәнең ике кисәген дә cos2x ка
бүлеп, tg2x-2tgx = 0 тигезләмәсен табарга да була. Әгәр дә
sin2x ка бүлсәк, х ның sin х = 0 булгандагы кыйммәтләре дә әлеге
тигезләмәнең чишелешләре икәнлеген исәпкә алырга кирәк. Шуңа
күрә sin2x ка бүлгәннән соң килеп чыккан ctg х - А =- 0 тигезләмә-
мәсенә sinx = 0 тигезләмәсенең тамырларын өстәргә кирәк була.
Башка бик күп тигезләмәләр, мәсәлән, sin2x - sinxcosx +
+ eos2x = 0 яки sin2x + 2 sin х cos х - 5 sin х cos2x + 2 cos3x = 0 һ.б.
шулай ук тигезләмәнең сул һәм уң кисәген тигезләмә белән бер
үк дәрәҗәдәге косинус (яки синус) дәрәҗәсенә бүлү юлы белән
чишеләләр. Алдан cos х = 0 ( sin"x нә бүлгәндә sin х = 0) булгандагы
82
Тригонометрик функцияләр
х ның кыйммәтләре бирелгән тигезләмәнең чишелешләреме икә¬
нен тикшерергә кирәк. Әйтик, икенче дәрәҗә тигезләмәне — cos2x
ка {яки sin2* ка), ә өченче дәрәҗәне cos3* ка (яки sin3* ка) бүләләр
дә tg* (яки ctg*) ны у ка алмаштырып, алгебраик тигезләмә
табалар.
I 7 нче мисал, cos 6х + cos 2* = 0 тигезләмәсен чишик. Коси¬
нуслар суммасын тапкырчыгышка үзгәртеп, 2 cos 4* cos 2* = О
тигезләмәсен табабыз, cos 4* = 0 яки cos 2х = 0, ягъни
x = j + яки x = ^ + ^,neZ
8 4 4 2
8 нче мисал.
булса, бу тигезләмә дөрес тигезлеккә әйләнә.
х~У = т-
t>
sin х = 2 sin у.
тигезләмәләр системасын чишик. Беренче тигезләмәдән табабыз:
(х - I = 2(sin*cos ' ,1 -
у = х-^·. Ул вакытта 2siny = 2sin
о
- cosх sin - 2 [sin х ·^ +—cos х I sinx + V3 cosx. Система-
a / \ z z
ның икенче тигезләмәсе sin x = sin x + <3 cos х рәвешен ала, мон¬
нан cosx = О, X = ' + πη, биредә neZ. Аннары табабыз:
y = x-^- = ^ + nn-^ = nn-^,neZ.
ό £ <3 Ο
Җавап: (■£ + πη; πη - η € Ζ.
Күнегүләр
Тигезләмәләрне чишегез (164—168).
164. —
165. ¬
166.¬
167.¬
168.
a) 2 sin2 x + sin x - 1 = 0;
в) 2 sin2 x - sin x - 1 = 0;
a) 6 cos2 x + cos x - 1 = 0;
в) 4 cos2 x - 8 cos x + 3 = 0;
a) 2 cos2 x + sin x + 1 = 0;
в) 4 cos x = 4 - sin2 x;
a) 3 tg2 x + 2 tg x - 1 = 0;
в) 2 tg2 x + 3 tg x - 2 = 0;
a) 2 cos2 x + 7з cos x = 0;
в) 7з tg2 x - 3 tg x = 0;
6) 3 sin2 * - 5 sin x - 2 = 0;
r) 4 sin2 x + 11 sin x - 3 — 0.
6) 2 sin2 x + 3 cos x = 0;
r) 5 sin2 х -I- 6 cos x — 6 = 0.
6) cos2 x + 3 sin x = 3;
r) 8 sin2 x + cos x + 1 = 0.
6) tg x - 2 ctg x + 1 = 0;
r) 2 ctgx-3tgx + 5 = 0.
6) 4 cos2 x - 3 - 0;
r) 4 sin2 x - 1 “ 0.
83 Тригонометрик функцияләр
Тигезләмәләрне чишегез (169—174).
169.— а) 3 sin2 х + sin х cos х = 2 cos2 х;
б) 2 cos2 х - 3 sin х cos х + sin2 х = 0;
в) 9 sin x cos x - 7 cos2 x = 2 sin2 x;
r) 2 sin2 x - sin x cos x «■ cos2 x.
170.— a) 4 sin2 x - sin 2x = 3;
в) sin 2x - cos x - 0;
6) cos 2x = 2 cos x - 1;
r) sin 2x + 4cos2 x = 1.
171.— a) 2 sin2 x = -73 sin 2x;
в) sinx + V3 cosx = 0;
6) м3 tg x - Vi ctg x = 2;
r) tgx = 3ctgx.
172.— a) sin 2x + 2 cos 2x = 1;
в) 3 sin 2x + cos 2x -2 cos2 x;
6) sin4 , - cos4 4 = 4;
4 Δ
г) 1 - cos x = 2 sin ■*.
173. — a) sin4x + sin2 2x = 0;
в) a,in5_ ·4 = 2;
J sin X + 4
174. — a) cos 5x - cos 3x = 0.
в) sin 5x - sin x - 0;
5tgx + 8
r) 1 - 8in2x = (cos-£ sin *)*.
6) sin 7x - sin x = cos 4x;
r) cos 3x + cos x = 4 cos 2x.
Тигезләмәләр системаларын чишегез (175—176).
175. - a)
в)
176. - а)
I в)
х + у = π,
cos х - cos у = 1;
6)
I х + у = π,
I sin х + sin у = 1;
sinx-cosy = 0,
sin2 x + cos2 у = 2;
sin x + cos у = 1,
sin2 x - cos2 у = 1;
г)
б)
г)
x-y = f,
cos2 х + sin2 у = 2;
x + y = f,
sin2 x - sin2 у = 1.
* + !/ = £,
tgxtgy =
x-y-R.
sin x cos у = I.
8 4 Тригонометрик функцияләр
Тарихтан мәгълүматлар
1. Почмакларны үлчәү берәмлекләренең килеп чыгуы турын¬
да. Почмакларны градусларда үлчәү безнең эрага кадәр күп еллар
элек борынгы Вавилонда барлыкка килгән. Жрецлар Кояш үзенең
көндезге юлын 180 «адымда» башкара, һәм, димәк, бер «адым*
җәелгән почмакның өлешенә тигез дип исәпләгәннәр. Вавилонда
алтмышарлы исәпләү системасы кабул ителгән була, ягъни,
асылда, саннар, безнең унарлы системада кабул ителгәнчә, 10 са¬
нының түгел, бәлки 60 санының дәрәҗәләре суммасы рәвешендә
язылганнар. Шуңа күрә табигый ки, почмакларны үлчәүнең
тагын да ваграк берәмлекләрен кертү өчен, бер «адым» эзлекле
рәвештә 60 өлешкә бүленгән.
Почмакларны үлчәүнең Вавилон системасы җитәрлек дәрәҗәдә
җайлы булып чыга һәм Греция, Рим математикларында сакланып
кала. Почмак зурлыкларының атамалары өчен без куллана торган
терминнар, нигездә, латинчадан алынган. «Градус» сүзе латинча
gradus (адым, дәрәҗә) дигәннән килеп чыккан. Minutus сүзенең
латинчадан тәрҗемәсе «кечерәйтелгән» дигәнне белдерә. Ниһаять,
secunda «икенче» мәгънәсендә тәрҗемә ителә. Монда түбәндәгеләр
күздә тотыла: градусның 60 өлешкә, ягъни минутларга бүленүе —
бу беренче бүленеш; минутның 60 секундка бүленүе — градусның
икенче тапкыр бүленеше. Сирәк кулланыла торган секундның
γ е атамасы — терцина, латинча tercina сүзе градусның «өченче»
тапкыр бүленүен белдерә.
Почмак зурлыкларын хәзер кабул ителгәнчә тамгалау систе¬
масы XVI һәм XVII гасырлар тирәсендә киң тарала; алардан
Н. Коперник һәм Т. Браге кебек атаклы астрономнар файда¬
ланган. Ләкин әле К. Птолемей ук (безнең эраның II гасырында)
градуслар санын — түгәрәк белән, минутлар санын — штрих,
секундлар санын ике штрих белән тамгалаган.
Почмакларны үлчәүнең икенче берәмлеге — радиан — күптән
түгел генә кертелә. Радиан терминын эченә алган беренче басма
(бу имтихан билетлары була) 1873 елда Англиядә дөнья күрә.
Башта нәкъ менә радианлы үлчәме күздә тотылуы тамга белән
күрсәтелгән (мәсәлән, s~ — бу ’ радианлы почмак), ләкин күп
тә үтми R (яки г) индексын төшереп калдыра башлыйлар. «Ради¬
ан» термины үзе латинча radius (энә, нур) сүзеннән алынган. Бер
радианлы почмакның билгеләмәсен искә төшерсәк (дугасының
озынлыгы әйләнә радиусына тигез булган үзәк почмак), мондый
почмакны атау өчен «рад» тамырын сайлап алу үзеннән-үзе аң¬
лашыла.
2. Тригонометрия тарихы турында. «Тригонометрия» сүзе бе¬
ренче мәртәбә 1505 елда немец теологы һәм математигы Пи-
тискусның китап исемендә очрый. Ул грек сүзеннән килеп чык¬
кан: τρίγωνον — өчпочмак, μετρεω — үлчәү. Икенче сүзләр белән
85 Тригонометрик функцияләр
78 нче рәсем
әйткәндә, тригонометрия — өчпочмакларны үл¬
чәү турындагы фән. Исеме чагыштырмача күп¬
тән түгел генә барлыкка килсә дә, хәзер триго¬
нометриягә кертелә торган күп кенә төшенчә
һәм мисаллар моннан инде ике мең еллар элек
билгеле була.
Синус төшенчәсенең бик озын тарихы бар.
Чынында өчпочмак һәм әйләнә кисемтәләре¬
нең төрле чагыштырмалары (асылда, тригоно¬
метрик функцияләр дә) безнең эрага кадәр
III гасырда ук инде Борынгы Грециянең бөек
математиклары — Евклид, Архимед,
Аполлоний Пергский хезмәтләрендә
очрыйлар. Рим периодында бу чагыштырмалар махсус исемнәргә
ия булмасалар да, Менелай (безнең эраның I гасырында) тара¬
фыннан җитәрлек дәрәҗәдә системалы рәвештә өйрәнелгән була.
Мәсәлән, хәзерге α почмагының синусы α зурлыгындагы үзәк
почмак таянган ярымхорда, яки икеләтелгән дуга хордасы буларак
өйрәнелгән (78 нче рәсем).
Аннан соңгы периодта математика озак вакытлар буена һинд
Һәм гарәп галимнәре тарафыннан шактый актив үстерелә. Атап
әйткәндә, IV—V гасырларда бөек һинд галиме Ариабхатаның
(476—550 еллар тирәсендә) астрономиядән хезмәтләрендә инде
махсус терминнар күренә башлый, (һиндстанның Җир тирәли
беренче иярчененә шушы галимнең исеме бирелгән.) AM кисем¬
тәсен (78 нче рәсем) ул ардхаджива (ардха — яртысы, джива —
җәя тәтесе — хорда шуны хәтерләтә) дип атый. Соңрак аның кыс¬
ка джива атамасын куллану гадәткә кереп киткән. IX гасырда
джива (яки джиба) сүзе гарәп математиклары тарафыннан гарәп¬
чәдән джайб (кабарынкылык) сүзенә алмаштырыла. XII гасырда
математиклардан гарәпчә текстларны тәрҗемә иткәндә бу сүз ла¬
тинча синус (sinus — бөгелеш, кәкрелек) сүзенә алмаштырыла.
Косинус сүзе исә күпкә яшьрәк. Косинус — ул латинча
complementy sinus, ягъни «өстәмә синус» (яки, башкача әйтсәк,
«өстәмә дуганың синусы»; cos α = sin(90° - α) икәнен исегезгә
төшерәбез) сүзләренең кыскартылып язылышы.
Тригонометрик функцияләр килеп керү белән, «өчпочмакларны
үлчәү» мәсьәләсенең чикләве шактый киңәя. Шуңа күрә танылган
математикФ. Клейн (1849—1925) «тригонометрик» функцияләр
турындагы белемнәрне башкача — гониометрия (латинча gonio
сүзе «почмак* дигәнне белдерә) дип атарга тәкъдим итә. Ләкин
бу атама кулланылышка кереп китми.
Тангенслар күләгәнең озынлыгын билгеләүгә мәсьәлә чишүгә
бәйле рәвештә барлыкка килә. Тангенс (шулай ук котангенс,
секанс һәм косеканс) X гасырда гарәп математигы Әбү-л-Вафа
тарафыннан кертелә. Ул шулай ук тангенс һәм котангенсларны
табу өчен беренче таблицаларны да төзи. Ләкин бу ачышлар озак
вакытлар Европа галимнәренә билгеле булмый. Ьәм тангенслар
86 Тригонометрик функцияләр
XIV гасырда башта инглиз галиме Т. Б р а в е р д и н, ә соңрак немец
математигы, астроном Региомонтан (1467 ел) тарафыннан
кабат ачыла. Латинча tanger (орыну) сүзеннән килеп чыгучы
♦тангенс» атамасы 1583 елда күренә башлый. Tangens — «оры¬
нучы» мәгънәсендә тәрҗемә ителә (исегезгә төшерегез: тангенслар
сызыгы — берәмлек әйләнәгә орынма ул).
Хәзерге arcsin һәм arctg тамгаланышы 1772 елда Вена мате¬
матигы Ш е р ф е р һәм атаклы француз галиме Ж. Л.Лагранж
хезмәтләрендә кулланыла. Дөрес, берникадәр элегрәк аларны
Я. Бернулли тикшергән була, ләкин ул башка символика
куллана. Бу символлар исә XVIII йөз ахырында гына гомуми
кулланылышка керә, «арк» кушымчасы латинча arcus (җәя, дуга)
сүзеннән килеп чыккан, бу arcsin х ның мәгънә төшенчәсе белән
тулысынча туры килә; мәсәлән, arcsin х ул синусы х ка тигез
булган почмак (дуга дияргә дә була).
Озак еллар буена тригонометрия геометриянең бер кисәге була¬
рак үсә, ягъни без хәзер тригонометрик функциянең терминнары
аша әйтеп бирә торган фактлар геометрик төшенчәләр, фаразлар
аша әйтеп бирелгән һәм исбатланган. Ихтимал, астрономиядән
практик кызыксыну тудырган мәсьәләләрне чишү (мәсәлән, судно¬
ның торган урынын билгеләү, Кояш, Ай тотылуларны алдан әйтү
һ.б.) тригонометриянең үсешенә иң зур этәргеч биргәндер. Астро¬
номнарны сферада яткан зур түгәрәкләрдән төзелгән сферик өч¬
почмакларның почмаклары белән яклары арасындагы бәйләнеш¬
ләр кызыксындырган. Борынгы заман математикларының без
IX класста шөгыльләнгән яссы өчпочмакларны чишү мәсьәлә¬
ләренә караганда шактый авыр мәсьәләләрне дә (сферик геометрия
турындагы китапларны укыгыз) чишә алуларын әйтеп китәргә
кирәк.
һәрхәлдә, сезгә тригонометриядән таныш формулаларның кү¬
бесе борынгы грек, һинд, гарәп математиклары тарафыннан гео¬
метрик формада ачылган һәм кабат ачылганнар. (Дөрес, тригоно¬
метрик функцияләрнең аермалары формулалары XVII гасырда
гына билгеле була — аларны тригонометрик функцияләр белән
исәпләүләрне җиңеләйтү өчен инглиз математигы Непер чыгара.
Ә синусоиданың беренче рәсеме 1634 елда барлыкка килә.)
К. Птолемей тарафыннан синусларның беренче таблицасы тө¬
зелү (ул озак вакытлар хордалар таблицасы дип аталып йөртелгән)
принципиаль әһәмияткә ия: гамәли мәсьәләләрнең күбесен, берен¬
че чиратта астрономия мәсьәләләрен, практик чишү чарасы бар¬
лыкка килә.
Әзер таблицалар белән эш иткәндә яки калькулятордан фай¬
даланганда без кайчандыр әле таблицаларның уйлап табылма¬
ган булуы турында уйламыйбыз. Аларны төзү өчен, зур күләмдә
исәпләү эшләре башкару таләп ителү белән бергә, таблицаларны
төзү ысулын да уйлап табарга кирәк була. Птолемей таблицалары
бишенче унарлы тамгага кадәр төгәллек белән төзелгәннәр.
87 Тригонометрик функцияләр
Эйлер Леонард
(1707-1783)
XVIII йөзнең күренекле математигы. Швейцариядә
туган. Озак еллар Россиядә яшәгән һәм эшләгән.
Петербург Фәннәр академиясе члены. Эйлерның
гаять зур фәнни мирасы математик анализ, гео¬
метрия, саннар теориясе, вариацион исәпләүләр,
механика һәм математиканың башка куллану өлкә¬
ләренә караган искиткеч нәтиҗәләрне эченә ала.
XVIII йөзнең бөек математигы Л. Эйлер (1707 —1783)
чыгышы белән швейцарияле, озак еллар Россиядә эшләгән, Петер¬
бург Фәннәр академиясе члены, тригонометриягә хәзерге күре¬
нешне биргән. Нәкъ Эйлер беренче булып тригонометрик функ¬
цияләрнең безгә таныш билгеләмәләрен кертә, ирекле рәвештә
алынган почмак функциясен тикшерә башлый, китерү формула¬
ларын таба. Бу — Эйлер үзенең тормышы дәверендә математикада
эшләргә өлгергән эшләренең бик кечкенә бер өлеше генә: ул 800
дан артык хезмәт калдыра, математиканың төрле өлкәләренә
кергән һәм соңыннан классик теорема булып киткән күп кенә
теоремаларны исбат итә. (1776 елда сукыраюга да карамастан,
Эйлер гомеренең соңгы көннәренә кадәр яңадан-яңа хезмәтләрен
әйтеп торып яздыруын дәвам итә.) Ләкин әгәр дә сез тригоно¬
метрик функцияләр белән геометрик формада, ягъни Эйлерга
кадәрге күпбуын математиклар кебек үк, эш итәргә омтылып
карасагыз, Эйлерның тригонометрияне системага салудагы хезмә¬
тен бәяли алырсыз. Эйлердан соң тригонометрия исәпләүләр
формасын ала: аерым мисаллар тригонометрик формулаларны
формаль куллану юлы белән исбатлана башлый, ә исбатлаулар
күпкә гадиләшә һәм җыйнаклана.
3. Функция төшенчәсе тарихыннан. Сез VII класста танышкан
функция төшенчәсе чагыштырмача әле күптән түгел барлыкка
килгән. Функция төшенчәсен кертү кирәклеген аңлау һәм аның
җитәрлек дәрәҗәдә төгәл билгеләмәсен булдыру өчен берничә буын
беренче класслы математикларның тырышлыгы кирәк булган.
XVII йөздә математикадагы революцион үзгәрешләр төрле илләр
һәм халыкларның вәкиле булган күп санлы галимнәрнең хез¬
мәтләре нәтиҗәсендә килеп чыккан. Шулай да беренче чиратта
П. Ферма (1601—1665), Р. Д е к а р т (1596—1650), И. Ньютон
(1643—1727), Г. В. Лейбницның (1646—1716) исемнәрен телгә
алырга кирәк.
Функция төшенчәсенең килеп чыгуы өчен кирәкле алшартлар
XVII гасырның 30 нчы елларында, аналитик геометрия барлыкка
килгәннән соң туа. Чөнки аналитик геометрия, Борынгы Греция
Тригонометрик функцияләр
Декарт Рене
(1596-1650)
Беек француз философы, математик. Аналитик
геометрияне иҗат итүчеләрнең берсе. Үзгәрешле
зурлык төшенчәсен керткән. Аның идеяләре күп
санлы «картезианчылар» (Декартның латинчалаш-
тырылган исеме — Картезий) тарафыннан дәвам
иттерелә. Төп хезмәтләре «Геометрия», «Метод
турында фикерләүләр»
геометрларының классик методларыннан аермалы буларак, гео¬
метрик мәсьәләләрне чишүдә алгебраны актив куллануы белән
үзенчәлекле. (Геометриядән координаталар методы белән мәсь¬
әләләр чишкәндә сез, асылда, аналитик геометрия методларыннан
файдаланасыз.) Француз математигы П. Ферма һәм Р. Декарт,
бер-берсенә бәйсез рәвештә, бер үк вакытта диярлек яссылыкта
координаталар системасын кертү һәм фигураларны аларның
тигезләмәләре аша бирү нәтиҗәсендә геометриянең күп мәсь¬
әләләрен геометрик фигураларның тигезләмәләрен тикшерүгә
кайтарып калдыру мөмкинлеген күрсәтәләр. Үзенең «Геометрия»
һәм «Метод турында фикерләүләр» дигән китапларында яңа ме¬
тодның җентекле аңлатмасын биргән Декарт хөрмәтенә туры¬
почмаклы координаталар системасы соңрак Декарт координата¬
лар системасы дип атала башлый. Шул ук вакытта алгебра да
формалаша, нәкъ менә сез хәзер алгебраик аңлатмаларның рәве¬
шен үзгәрткәндә, тигезләмәләр һәм текстлы мәсьәләләр чишкәндә
һ.б. куллана торган «хәвефле исәпләүләр» барлыкка килә.
Бөек инглиз галиме, математик һәм физик И. Ньютон хәрәкәт
итүче нокта координаталарының вакытка бәйлелеген тикшереп,
асылда инде функцияләрне тикшерү белән шөгыльләнгән була.
Бу төшенчәне Ньютон үзе кертмәсә дә, аның мөһимлеген яхшы
аңлый. Мәсәлән, 1676 елда ул болай дип билгеләп үтә: «Әгәр мин
фигураларны тикшерүдән читкә китеп, барысын да ординаталарны
гына тикшерүгә (ягъни чынлыкта вакытның функциясенә) кай¬
тарып калдырмаган булсам, билгеле, бу гомуми нәтиҗәләрне таба
алмаган булыр идем».
«Функция» термины үзе беренче мәртәбә бөек немец математи¬
гы һәм философы Г. Лейбницның кулъязмасында (1673 елда)
очрый, ә аннары басылып та чыга (1692 ел). Латин сүзе function
«эшләү», «үтәү» мәгънәсендә тәрҗемә ителә (fungor фигыле шу¬
лай ук «күрсәтү, аңлату» дип тәрҗемә ителә). Лейбниц бу төшен¬
чәне ноктаның яссылыктагы торышына бәйле параметрларны
исемләү өчен кертә. Лейбниц үзенең шәкерте — Швейцария мате¬
матигы И. Бернулли (1667—1748) белән үзара язышу бары-
89 Тригонометрик функцияләр
Ньютон Исаак
(1643-1727)
Бөек инглиз галиме, Г. Лейбниц белән бер үк ва¬
кытта математик анализ нигезләрен эшли. Клас¬
сик механиканы иҗат итүче. Ньютон оптикада, фи¬
зика һәм математиканың башка бүлекләрендә гү¬
зәл ачышлар ясый. Аның төп хезмәте — "Табигать
белеме философиясенең математик башлангыч¬
лары» — табигать фәннәре үсешенә гаять зур этәр¬
геч бирә.
шында әкренләп функциянең аналитик аңлатма булуына ышана¬
лар һәм 1718 елда ул мондый билгеләмә бирә: «Үзгәрешле
зурлыкның функциясе дип нинди дә булса ысул белән шул үзгә-
решледән һәм даимиләрдән төзелгән зурлык атала».
Л. Эйлер үзенең «Анализга кереш» (1748 ел) китабында функ¬
циягә мондый билгеләмә бирә: «Үзгәрешле зурлык функциясе —
шул үзгәрешле зурлыктан һәм саннардан яки даими зурлыклар¬
дан нинди дә булса ысул белән төзелгән аналитик аңлатма ул*.
Эйлер шулай функция өчен хәзер кабул ителгән тамгаланыш¬
ларны да кертә. Санлы функциянең бирелү ысулына бәйле бул¬
маган хәзерге төшенчәсе рус математигы Н. И. Лобачевский
(1834 ел) һәм немец математигы Л. Дирихле (1837 ел)тарафын-
нан бер-берсенә бәйсез рәвештә бирелә. Бу билгеләмәләрдәге төп
фикер шуннан гыйбарәт: һәр х ка у ның билгеле бер кыйммәте
ничек тиңдәш итеп куелуы әһәмиятле түгел (атап әйткәндә, ана¬
литик аңлатмасын бирү мәҗбүри түгел), бары тик бу тиңдәшлек¬
нең аныкланган булуы гына мөһим.
Ирекле рәвештә алынган билгеләнү өлкәсе һәм кыйммәтлә¬
ре өлкәсе белән бирелгән (санча кыйммәтләр булуы мәҗбүри тү¬
гел — 29 нчы битне карагыз) функциянең хәзерге заман төшенчә¬
се, асылда, бөтенләй күптән түгел, күплек теориясен иҗат итүче
Г. Канторның (1845—1918) хезмәтләреннән соң, агымдагы
гасырның беренче яртысында гына барлыкка килә.
Функция төшенчәсе катлаулы һәм, күреп үткәнебезчә, бик озын
гадәти үсеш юлы үтә. Яңа абстракт төшенчәне кертү кирәклегенә
төшенү өчен исә аны күп кенә конкрет мәсьәләләрне чишү бары¬
шында аерып күрсәтү, аның мәгънәсен мөмкин кадәр төгәл чагыл¬
дыра торган билгеләмә бирү таләп ителә.
Математиканың конкрет, катлаулы мәсьәләләре белән эш ит¬
кәндә һәм аны практикада кулланганда, математиклар функция
төшенчәсенең кирәклеге белән очрашалар. Бу көчле яңа тикшерү
аппаратын — интеграль һәм дифференциаль исәпләүләрне иҗат
итү барышында килеп чыга. Аның элементлары белән сез киләсе
Тригонометрик функцияләр
бүлектә танышырсыз. Эйлер үзәк төшенчәсе функция дип игълан
иткән («Чиксезләр анализы тулысынча үзгәрешле зурлык һәм
аларның функцияләре белән эш итә») интеграль һәм дифферен¬
циал ь исәпләүләрнең ачылуы математиканың мөмкинлекләрен
кискен арттыра.
Кабатлау өчен сораулар һәм мәсьәләләр
1. 1) 1 радианлы почмак нинди почмак ул? Почмакның радиан¬
лы һәм градуслы үлчәмнәрен бәйли торган формулаларны
языгыз.
2) Почмак зурлыгын радианлы үлчәмдә күрсәтегез:
а) 18°; б) -250°; в) - 360°; г) 225’.
3) Почмак зурлыгын градуслы үлчәмдә күрсәтегез;
а) π ; б) -2,5: в) ; г) 3.
□
2. 1) а санының синусы һәм косинусына билгеләмә бирегез.
2) Берәмлек әйләнәдә Ра ноктасын билгеләгез, а тигез
a) б) ~ү; в) -Д?; г) -| булса, sinot һәм cosa ның
кыйммәтләрен табыгыз (калькулятор яки таблица куллан¬
мыйча).
3) a тигез а) 23’24'; б) -1,7; в) -108’6'; г) 0,8 булса, sin a һәм
cosa ның кыйммәтләрен табыгыз.
3. 1) a санының тангенсы һәм котангенсына билгеләмә бирегез,
tga һәм ctg a ның нинди кыйммәтләре өчен билгеләнгән?
2) a тигез а) б) -·в) г) *- булса, tga һәм
ctg a ны табыгыз (калькулятор яки таблица кулланмыйча).
3) a тигез а) 1,7; б) -0,4; в) 2,3; г) -0,5 булса, tga һәм ctga
ның кыйммәтләрен табыгыз.
4. 1) Бер аргументның тригонометрик функцияләре кыйммәт¬
ләрен бәйли торган формулаларны языгыз.
2) Аңлатманы гадиләштерегез:
а) (tga + ctga)(1 + cosa)(1 -cosa);
6)
cos3 a + sin3 a
sin a
, cos3 a - sin3 a
+ cosa '
в Ϊ ■ + 1 z
1 + tg2a 1 + ctg2 a
r) sin’a(1 + ctga) + cos3a(l + tga).
3) Бердәйлекне исбатлагыз:
cosa _ 1 + sina .
' 1 - sin a cos a
- sina 1 + cosa,
B) Ί : ·
' 1 - cosa sina
1 - (sina + cosa)3 = 2t 2
sinacosa - ctga ®
r) tg2 a - sin2 a = tg2 a sin2 a.
Тригонометрнк функцияләр
5. 1) sina, cos a, tga, ctga ның тамгалары Pa ноктасы коорди-
наталарның кайсы чирегендә ятуга ничек бәйле? Бу тамга¬
ларны әйтеп чыгыгыз.
2) Тамгасын билгеләгез:
а) sin(-212°) һәм ctg^p б) cos 3059 һәм tg^-^5);
в) cos (-105°) һәм ctgijr; г) sin(-324°) һәм tg^5·.
3) Бер тригонометрик функциянең кыйммәте һәм α ның
кайсы аралыкныкы икәне бирелгәндә, калган өч төп триго¬
нометрик функциянең кыйммәтләрен табыгыз:
а) sin a = < a < π;
J ·—
в) a - t π < (К ;
б) ctg a = -3, < a < 2π;
г) cosa = l,0<a<4.
6.
1) Китерү формулаларын истә калдыру өчен, мнемоник ка¬
гыйдәне әйтеп бирегез. Берничә китерү формуласын языгыз.
2) Иң кечкенә уңай аргументның тригонометрик функциясе
кыйммәтенә китерегез:
а) sin(-i|£); б) ctg^; в) tg(-^); г) cos^.
3) Аңлатманы гадиләштерегез:
а) sin ' "· + cos + tg ;
о О 4
б)
sin (π - a) cos (π + a) tg (-a)
Sin(a-^)ctg(^ + a)cos(a + f)’
в) ctg Y + sin - cos
r)
sin (a - π) tg IJ + a)
COS p* + a) ctg (a - π)
7. 1) Сумманың (аерманың) синусы, косинусы, тангенсы форму¬
лаларын языгыз.
2) Аңлатманың кыйммәтен табыгыз:
а) sina-^ һәм 0 < a < ■§■ булса, sini^ + a);
б) cos-^ һәм tg~;
B)cosa = --7 һәм £<α<π булса, cos(4-a).
3 3 \ а >
3) Бердәйлекне исбатлагыз:
а) sin (a + -) + sin (a - j) = а/з sin a;
б) tg + x) - tg - x) = 2 tg 2x;
в)
tga + tg(* - a)
1 - tgatg{| - a)
• v3;
r)
sin (a г β)
cos a cosβ
- iga + tgp,
92 Тригонометрик функцияләр
8. 1) Икеләтелгән аргумент формулаларын языгыз.
2) Исәпләгез:
а) cos α = ~4»π<α<^ булса, sin 2α;
б) sin <х = fi · cos α < 0 булса, tg 2α;
в) sin α = булса, cos 2α;
r) cos α = ^,^<α<2π булса, tg 2α ны исәпләп чыгарыгыз.
3) Бердәйлекне исбатлагыз:
a) —g --(2cos2 α-1) = sin2α; 6) * - CQ8*° + _ tg a;
l-tg2a 1 + cos2a + sin2a ’
в) 1 - (cos a - sin a)2 = sin 2a; r) tg a (1 + cos 2a) = sin 2a.
9.
1) Синусларның (косинусларның) суммасы һәм аермасы фор¬
мулаларын языгыз.
2) Калькулятор яки таблицадан файдаланмыйча исәпләп чы¬
гарыгыз:
a) cos 117“ + cos 63°;
в) cos^£-cos^;
3) Бердәйлекне исбатлагыз:
sin a + sin 3a . _ o
s— = tg 2a;
cosa + cos3a 0 ’
(sin 2a + sin 4a)2 + (cos 2a + cos 4a)2 - 4 cos2 a;
sin2a + sin2B . , , a\
cos2a + cos2B =tg(a + |i);
sin 2a + sin 4a + sin 6a = 4 sin 3a cos 2a cos a.
sin 70" - sin 10’
6) :
r) sin 112° + sin 248°.
a)
6)
в)
r)
10. 1) Ярты аргумент формулаларын языгыз.
2) Табыгыз:
а) cos α = ·^,^<α<2π булса, cos ® ;
б) sin α = -|,π<α<^ булса, tg^;
в) sin a = π < a < булса, sin®;
<2 Lt
r) cos α = ~,“<α<2π булса, ctg £ .
' ә z “ - - 2
3) Аңлатманы гадиләштерегез:
а) , 81ttC( ctg - sin2 a;
’ 1 + cosa ” 2 ’
6) sin 2 a cosa
7 1 + cos 2a 1 + cos a
. 1 - cos a
• sin a
‘ 1 + cosa
93
Тригонометрик функцияләр
11. 1) Санлы функция, аның билгеләнү өлкәсе, кыйммәтләре
өлкәсе дип нәрсәгә әйтәләр?
2) Функциянең билгеләнү өлкәсен табыгыз:
а) У = ,3* + 1,д; б) У = ; в) и = ^4-х2; г) у = ——.
’ у χΛ - 7х +12 ’ ' х sinx’ ’ я ’ ' “ cosx
3) Функциянең кыйммәтләре өлкәсен табыгыз:
а) у = Зсозх -1;6)j/ = -j + 1;b)j/ = 2-sinx; г) у - 3 - χ4.
12. 1) Функциянең графигы нәрсә ул?
2) Функциянең графигын төзегез:
а) у - * |; б) у = 2 ~ cosx; в) у - Ίχ + 2; г) у = sinx - 1.
3) f функциясе графигының координата күчәрләре белән
кисешү нокталарын табыгыз:
a) f(x) = х3 - 4х; б) /(х) = ү + 1;
в) /(х) = 1 - х4; г) /(х) =
13. 1) Р күплегендә үсә (кими) торган функциянең билгеләмәсен
әйтеп бирегез.
2) Графигы 79 нчы рәсемдә сурәтләнгән функциянең үсү
һәм кимү аралыкларын табыгыз.
3) Функциянең үсү һәм кимү аралыкларын табыгыз:
а) у - 1 + 0,5cosх; б) у = - j»
в) у - 2х2 + 4х; г) у = 1,5sinx - 1.
14. 1) Максимум ноктасына, минимум ноктасына билгеләмә
бирегез. Функциянең экстремумы дип нәрсәгә әйтәләр?
2) Графиклары 79 нчы рәсемдә сурәтләнгән функцияләрнең
максимум нокталарын, минимум нокталарын күрсәтегез.
3) Функциянең максимум нокталарын һәм минимум нокта¬
ларын табыгыз:
Тригонометрик функцияләр
15. 1) Функцияне тикшергәндә нинди мәсьәләләр чишелә?
2) Функцияне тикшерегез:
a)y = sinx-2; б)</ = -у^;
в) у = х2 - 4х + 3; г) у - 2 cos х + 1.
3) Бу функцияләрнең графикларын төзегез.
16. 1) Җөп һәм так функциягә билгеләмә бирегез. Аларның
графиклары нинди үзлеккә ия?
2) Түбәндә күрсәтелгән функцияләрнең кайсылары — җөп,
кайсылары так икәнен ачыклагыз:
а) у = б) у = х + х5;
в) у = xcosx; г) у = Зх2 + х*.
3) Түбәндәге шартлар билгеле булганда f функциясенең гра¬
фигын төзегез:
а) f — так, f(x) = cosx - 1, хе (-«>; 0];
б) f — җөп, /(х) = (х - I)3, хе [0; °°);
в) f — җөп, f(x) - sin х, х е (-оо; 0];
г) f — җөп, /(х) = 4х - х2, х е [0; »).
17. 1) Периодик функция, функциянең периоды дип нәрсәгә әй¬
тәләр?
2) Функция нинди иң кечкенә уңай периодка ия?
а) у = cos х; б) у = tg х; в) у - sin х; г) у = ctg х.
3) Функциянең иң кечкенә уңай периодын табыгыз:
а) у = sin^; б) у = cos(4x + l); в) у = tg2x; г) у = cos 4.
18. 1) Синус функциясенең төп үзлекләрен санап чыгыгыз.
2) Синус функциясенең үзлекләреннән файдаланып, саннар¬
ны үсә бару тәртибендә урнаштырыгыз:
a) sin 0,3, sin 1,1, sin (-1,2); б) sin 4, sin 3,6, sin 2;
в) sin 0,4, sin (-0,9), sin 1,4; r) sin 4,3, sin 2,9, sin 1,9.
3) Функцияне тикшерегез һәм аның графигын төзегез:
а) у = sin (х - б) у = sin ;
в) у = 1 +1,5 sin х; г) у = sin 2х.
19. 1) Косинус функциясенең төп үзлекләрен санап чыгыгыз.
2) Косинус функциясенең үзлекләреннән файдаланып, сан¬
нарны үсә бару тәртибендә урнаштырыгыз:
a) cos 0,3, cos (-2,9), cos 1,8; б) cos 5,3, cos4,4, cos6,2;
в) cos 0,5, cos (-1,3), cos3; r) cos 6,1, cos 3,5, cos 4,9.
3) Функцияне тикшерегез һәм аның графигын төзегез:
а) у = cos(х + --θ; 6)y = -cosx;
в) у = 2cosx - 1; r)y = cos-|.
9 5 Тригонометрик функцияләр
20. 1) Тангенс функциясенең төп үзлекләрен санап чыгыгыз.
2) Тангенс функциясенең үзлекләреннән файдаланып, саннар¬
ны үсә бару тәртибендә урнаштырыгыз:
a)tg(-0,4), tgl,2, tg0,8; б) tg 2,8, tg3,9, tg 1,6;
в) tg0,6, tg(-l,3), tg(-0.7); r) tg4,3, tg 1,7, tg 2,5.
3) Функцияне тикшерегез һәм аның графигын төзегез:
a) y = -tgx·, б) = в) у-2 tgx; г) у = tg(x -.
21. 1) Тамыр турында теореманы әйтеп бирегез.
2) Санның арксинусы билгеләмәсен әйтеп бирегез. Арксинус
нинди саннар өчен билгеләнгән?
3) Аңлатманың кыйммәтен табыгыз:
a) arcsin (-1) + arcsin ?· ; б) arcsin - + arcsin | - ή^Ι;
в) arcsin- arcsin 1; r) arcsin 0 + arcsin
22. 1) Санның арккосинусы һәм арктангенсы билгеләмәләрен
әйтеп бирегез. Санның арккосинусы һәм арктангенсы нинди
саннар өчен билгеләнгән?
2) Аңлатманың кыйммәтен табыгыз:
a) arccos (-1) + arctg V3; б) arccos- + arcsin^;
Ja Л
в) arctg (-1) - arccos -т-; г) arccos 0 + arctg V-.
Z a
23. 1) Иң гади тригонометрик тигезләмәләр: sinx = а, cosx = a,
tg х = а ны чишү формулаларын языгыз.
2) Тигезләмәне чишегез:
а) 2cosx + у/з = 0; б) \/з tgx + 1 = 0;
в) 2 sin х - л/2 = 0; г) 2 cos х - 1 = 0.
24. Тигезләмәне чишегез:
1) а) 2sin2x + 3sinx = 2;
в) 2cos2x - 5cosx = 3;
2) а) 6 sin2 x - 2 sin 2x = 1;
в) 4 sin x cos х - у 3;
6) tg2 *x - 4tgx + 3 = 0;
r) 2sinzx + sinx = 0.
G
6) sin2x - cos2x =
r) cos4x - sin4x — 1.
25. Тигезсезлекне чишегез (башта берәмлек әйләнәдә х бирелгән
тигезсезлекне канәгатьләндерә торган нокталары күплеген
күрсәтегез):
1) а) sinx >^; б) 2созх + 1 <0; в) tgxc >/з.
2) а) Sin|cos|>-|; б) (sin cos
в) 2sin2^ ζ 1; г) cos2 I-sin* I
Тригонометрик функцияләр
Чыгарылма
һәм аны куллану
т
§4.
Чыгарылма
12. Функциянең үсемтәсе
Еш кына безне нинди да булса зурлыкның кыйммәте
түгел, бәлки аның ничек үзгәрүе кызыксындыра. Мәсәлән,
пружинаның сыгылу кече пружинаның озынаюына пропор¬
циональ; эш ул энергия үзгәрүе була; уртача тизлек — ул күчүнең
бу күчү башкарылган вакыт аралыгына чагыштырмасы һ.б.
f функциясенең ниндидер бер билгеләнгән ноктадагы кыйммә¬
тен аның х0 тирәлегендә ятучы төрле нокталардагы кыйммәтләре
белән чагыштыру өчен, f(x) - f(x0) аермасын, «аргумент үсемтәсе»
һәм «функция үсемтәсе» төшенчәләрен кулланып, х - х0 аермасы
аша күрсәтү җайлы була. Аларның мәгънәсен аңлатыйк.
х — билгеләнгән ниндидер х0 ноктасы тирәлегенең ятучы ирек¬
ле нокта булсын, х - х0 аермасы бәйсез үзгәрешленең (яки аргу¬
ментның) х0 ноктасындагы үсемтәсе дип атала һәм Δχ аша
тамгалана. Шулай итеп,
Δχ = х - х0,
моннан х = х0 + х икәнлеге килеп чыга.
х0 башлангыч кыйммәте х үсемтәсен алды, дип тә әйтәләр.
Моның нәтиҗәсендә f функциясенең кыйммәте
f(x) - = f(*o + Δχ) - f(x0)
зурлыгына үзгәрә.
Бу аерма f функциясенең х0 ноктасындагы Δχ үсемтәсенә тиң¬
дәш үсемтәсе дип атала һәм Δ/символы белән тамгалана («дельта
эф» дип укыла), ягъни билгеләмә буенча
ΔΖ =/(Хо + Δχ) -/(х0), (1)
моннан
f(x) = f(x0 + Δχ) = f(x0) + Δ/.
x0 билгеләнгәндә Δ/ үсемтәсенең Δχ тан функция булуына игъ¬
тибар итегез.
Δ/ ны бәйле үзгәрешленең үсемтәсе дип тә атыйлар һәм у — f(x)
функциясе өчен Δρ аша тамгалыйлар.
97 Чыгарылма һәм аны куллану
■ 1 нче мисал. Әгәр дә /(х) = х2, х0 = 2 һәм: а) х = 1,9;
б)х = 2,1 булса, Δχ һәм Δ/ ның х0 ноктасындагы үсемтәсен табыйк.
а) х = х-х0 = 1,9-2 = -0,1;
Δ/ - /(1,9) - /(2) = 1,92 - 22 = -0,39.
б) Δχ - х х0 = 2,1 - 2 0,1;
Δ/ = /(2,1) - /(2) = 2,12 - 22 = 0,41.
2 нче мисал. Аргументның үсемтәсе Δχ ка тигез булса,
/(х) = ү функциясенең х0 ноктасындагы үсемтәсе Δ/ ны табыйк.
(1) формула буенча табабыз:
— f (х0 + Δχ) /(х0) — . —
О ' ■ ■" ”0
_ χα - (χ0 + Δχ) _ Δχ
χβ(χ, + Δχ) ~ χ0(χ0+Δχ)*
3 нче мисал. Кабыргасы а булган куб бирелгән. Әгәр дә
кабырганың озынлыгын үлчәгәндә җибәрелгән хата Δχ булса, бу
кубның күләмен исәпләүдәге хата ΔΚ ны табыйк.
Үсемтәнең билгеләмәсе буенча х = α + Δχ, ул вакытта
ΔΚ = 1'(х) - F(a) = (α + Δχ)3 - α3 = 3α2Δχ + За(Дх)2 + (Δχ)3.
у = /(х) функциясенең графигын тикшерик. 80 нче рәсемгә
карап, Δχ һәм Δ/ (Δ/ үсемтәсен Δρ аша да тамгалыйлар) үсемтә-
ләренең геометрик мәгънәләрен аңларга мөмкин.
/ функциясе графигының теләсә нинди ике ноктасы аша үтүче
I турысын / графигына карата кисүче дип атыйлар. (х0; у0) һәм
(х; у) нокталары аша үтүче кисүченең почмакча коэффициен¬
ты -—— гә тигез. Аны Δχ һәм Δρ үсемтәләре аша күрсәтү уңай
х-х0
(80 нче рәсем):
k — tg α — .
98 Чыгарылма һәм аны куллану
(у = kx + b турысының почмакча коэффициенты абсциссалар
күчәре белән бу туры арасындагы α почмагының тангенсына тигез
икәнлеген искә төшерик.)
Үсемтәләрнең без кулланган тамгалары ярдәмендә (i0; t0 + Δί)
вакыт аралыгында хәрәкәтнең уртача тизлеген аңлату да җайлы
була. Әгәр дә нокта туры буйлап хәрәкәт итеп, аның координатасы
χ(ί) билгеле булса,
ί , * 1 _ *(<0 + Δί) — x(ip)
Бу формула Δί < 0 өчен дә ([ί0 + Δί; ί0] аралыгы өчен дә) дөрес.
Чыннан да, бу очракта ноктаның күчеше χ(ί0)- χ(ί0 + Δχ) ка ти¬
гез; вакыт аралыгы озынлыгы — Δί, һәм, димәк,
V ίKt\ - xPol-xUo + At) _ xUo + At)-xU») й
vvp\aif —Al Al иула.
.. _ f(x + Ax) - f(xo) _ _ .
Моңа охшатып, , - = —— аңлатмасын очлары х0 һәм
х0 + Δχ булган аралыкта функция үзгәрүенең уртача тизлеге дип
атыйлар.
Күнегүләр
177. — а) Турыпочмаклыкның яклары 15 м һәм 20 м га тигез.
Әгәр дә: 1) аның кечерәк ягын 0,11 м га озынайтсак;
2) зуррак ягын 0,2 м га озынайтсак, турыпочмаклык пери¬
метрының Һәм аның мәйданының үсемтәсен табыгыз,
б) Түгәрәкнең радиусы 2 см. Әгәр дә радиусның озынлы¬
гын үлчәгәндә хата: 1) 0,2 см; 2) АЛ; 3) 0,1 см; 4) һ ка
тигез булса, түгәрәк мәйданын исәпләгәндә җибәрелгән
хатаны табыгыз.
178. - a) f(x) = - J, х0 = -2, Δχ = 0,1;
б) /(х) = 2х2 - 3, х0 = 3, Δχ = -0,2;
в) Дх) = Зх + 1, х0 - 5, Δχ = 0,01;
г) Дх) = ^,х0 =2, Δχ = 0,1
булса, / функциясенең х0 ноктасындагы үсемтәсен та¬
быгыз.
179. а) Дх) = cos2 х, х0 = у, х = ^;
б) /(х) = 4х — х2, Хо = 2,5, х = 2,6;
В) Дх) = tgx,Хо =|,х = f
булса, Δχ һәм А/ функцияләренең х0 ноктасындагы үсем-
тәләрен табыгыз.
09 Чыгарылма һәм аны куллану
182.
81 нче рәсем
183.-
180. — Әгәр: a) f(x) = 1 - Зх2; б) /(х) -ах + Ъ; в) /(х) = 2х2;
г) f(x) = - булса, f функциясенең х ноктасындагы үсем-
I тәсен х0 һәм Δχ аша күрсәтегез.
181. -^ 81 нче рәсемдә автобус хәрәкәтенең графигы күрсәтелгән.
& Вакытның түбәндәге аралыкларында хәрәкәтнең уртача
~ тизлеген табыгыз.
а) [0; 3]; б) [3; 5]; в) [3,25; 5,25]; г) [0; 8].
Нокта кординаталар турысы буенча вакытның теләсә
кайсы моментында координатасы 3 + 12i - t2 булырлык
итеп хәрәкәт итә. Вакытның түбәндәге I аралыгы ечен
нокта нинди юнәлештә һәм күпмегә күчәр: а) [2; 2,5]; б)
[7; 8]; в) [4; 5]; г) [6; 8]? Аның уртача тизлеге күпме булыр?
(1; 3) ноктасы аша үтүче һәм почмакча коэффициентлары
түбәндәгечә булган турылар тезегез:
a) -1 һәм 2; б) £ һәм -3; в) 3 һәм -2; г) һәм -2.
һәр очрак ечен бу турыларның абсциссалар күчәре белән
нинди почмак (җәенкеме яки кысынкымы) төзегәнлеген
ачыклагыз.
f(x) ~^хг функциясе графигын кисүче һәм абсциссалары
х, һәм х2 булган нокталар аша үтүче турының почмакча
коэффициентларын табыгыз. Әгәр:
а)х, = 0, х2 — 1; б) х, =-1, х2 =-2;
в) х, = 1, х, = 2; г) х, = -1, х2 = 0
булса, кисүче Ох күчәре белән нинди (кысынкымы яки
җәенкеме) почмак төзер?
184.
185.— Кубның х кабыргасы х үсемтәсе алган. Кубның тулы өсле¬
. ге мәйданының үсемтәсен табыгыз.
100 Чыгарылма һәм авы куллану
186. — Δ/ һәм ны χ0 һәм Δχ аша күрсәтегез һәм табылган
аңлатмаларны үзгәртегез:
a) f(x) = -х3 + Зх; б) /(х) = ;
в) /(х) = х3 - 2х; г) f(x) = pl-j.
187. — Хәрәкәт законы түбәндәгечә булса, туры буйлап хәрәкәт
итүче ноктаның [ίϋ; +Δ0 аралыгында уртача тизлеген
табыгыз:
а) х (0 = vot - ; б) х (0 = -αί + b;
в) х (0 « ; г) х (0 = at - b.
13. Чыгарылма төшенчәсе
1. Функция графигына орынма турында төшенчә.
Сезгә практикадан билгеле булган барлык функцияләрнең график¬
лары шома кәкре сызык рәвешендә сурәтләнде. Андый кәкре¬
ләрнең геометрик яктан нинди булуын без у = х2 функциясенең
1 гә якын булган аргументның кыйммәтләре өчен төзелгән графи¬
гына конкрет мисал ярдәмендә карарбыз. Моның өчен масштаб
берәмлеген (82 нче рәсем масштабы белән чагыштырганда)
10 тапкыр зурайтыйк; у = х2 графигын бу масштаб белән [0,5; 1,5]
кисемтәсендә төзик (83 нче рәсем). Шуннан соң, масштабны тагын
10 тапкырга зурайтып, функциянең графигын [0,95; 1,05] кисем¬
тәсендә төзик (84 нче рәсем). Бу рәсемнән күренгәнчә, 1 гә якын
кыйммәтләр алганда у = х2 функциясенең графигы у = 2х - 1
турысының кечкенә кисемтәсеннән артык аерылып тормаган-
лыгын, ягъни бирелгән функция графигының нокталары бу туры
буйлап төзелгән кебек булуын күрербез.
Теләсә нинди шома кәкре мондый үзлеккә ия була: аның
теләсә нинди ирекле кечкенә кисәге ниндидер I турысының кисем¬
тәсеннән артык аерылып тормый. (ЭХМ нарда кулланыла торган
график төзүчеләрнең шома функция графикларын һәр ноктада
кечкенә кисемтәләр төзеп ясаулары кызыклы.) Шома кәкренең
һәр ноктасы өчен бу ноктага тиңдәш турының (ягъни кәкренең
кечкенә кисәген аның кисемтәсе ярдәмендә без күз алдына китерә
торган турының) билгеләнгән булуын әйтеп китик. Моны аңлау
өчен, түбәндәге күргәзмә иллюстрациягә игътибар итик.
Безгә синусоида, парабола яки гипербола һ.б. тиз генә төзү
өчен трафарет ясарга кирәк булсын, ди. Моның өчен башта милли¬
метрлы кәгазьдә, мөмкин кадәр төгәлрәк итеп, бу кәкренең графи¬
гын төзиләр. Кайчы ярдәмендә трафаретны төгәл итеп кисеп алгач,
аның чиге безгә кирәкле кәкре була. Кайчының һәр ноктадагы
торышы (ә ул бу ноктада эзләнелгән турыны бирә дә инде) төгәл
101 Чыгарылма һәм аны куллану
Η
- II
c
c
1
u
CM
σ
II
c
-л
cc
α
qC
Cfi
О|
О
d
о
ci
>
T
Ό
•
►
2
c
о
-
f
c
f
u
c
£_
r~
г
ιΗ
■ е
О
II
• :
31 -
сч
К Ί
CM
wH
_
00
d
co
о
1
и
cX
)
cO
я
о
Q>
c
>
q
a
c
Η
II
а»
н
" II '
□4-
—
—
—
’’j
OS
И
Ci
>
a
I*
—
—
I
—
—
—
00
2
φ
8
Е
СО
X
102 чыгарылма һәм аны куллану
билгеләнгән: кайчы кискәндә бу торыштан читкә тайпылса, чы¬
гынты хасил була яки трафарет киселә.
Практик яктан х х0 гә якын кыйммәтләр алганда, f функция¬
сенең графигы аның кисемтәсе белән туры килгәч һәм (х0; /(х0))
ноктасы аша үтүче турыны f функциясе графигының (х0; f(x0))
ноктасындагы орынмасы дип атыйлар. Алга табигый бер мәсьәлә
килеп баса: бирелгән функциянең графигына бирелгән ноктадагы
орынмасының торышын төгәл билгеләргә кирәк була.
f турысының бер ноктасының координаталары билгеле — бу
(х0; f(x0)) ноктасы. Орынманың почмакча коэффициенты k ны
табасы кала.
Мисал өчен, у = х2 функциясен карап китик. Аның графигы
х0 ноктасының кечкенә тирәлегендә I орынмасының кисемтәсенә
якын була. Шуңа күрә (х0; х0) һәм (xQ + Δχ; (х0 + Δχ)2) нокталары
аша үтүче кисүчеләрнең почмакча коэффициентлары, Δχ нульгә
чиксез якынлашса (ягъни х ноктасы х0 гә бик якын килсә),
k почмакча коэффициентына якын булалар.
(х0; у(х0)) һәм (х0 + Δχ; у(х0 + Δχ)) нокталары аша үтүче
кисүченең почмакча коэффициенты Α(Δχ) ка тигез (12 нче
пункт), монда Sy — у функциясенең х0 ноктасындагы Δχ үсемтә-
сенә тиңдәш үсемтәсе. у = х2 функциясе өчен
^( Д у) = — (■*<! + Ах)2 X? _
' ' Δχ Дх
2χ0Δχ + (ДхУ
Δχ
= 2х0 + Δχ
(1)
тигезлеге дөрес була.
Орынманың почмакча коэффициентын табу өчен, Δχ нульгә
якынайганда, fe(Ax) ның нинди кыйммәткә якын булуын ачык¬
лыйсы кала, k (Δχ) ның 2х0 гә якын булуы үзеннән-үзе аңлашыла.
Димәк, Δχ ның бик кечкенә кыйммәтләре өчен кисүченең поч¬
макча коэффициенты 2х0 гә якын. х„ = 1 булса, k = 2. Эзләнелә
торган орынманың (1; 1) ноктасы аша үтүен исәпкә алсак, орынма¬
ның тигезләмәсе у=2х- 1 була дигән нәтиҗәгә киләбез. Пунктның
башында ук без, фикер йөртеп, шушы ук нәтиҗәгә килгән идек.
2. Хәрәкәтнең моменталь тизлеге. Хәзер сезгә физикадан
билгеле булган мәсьәләгә кайтыйк. Ноктаның туры буенча
хәрәкәтен карап китик. Вакытның t моментында ноктаның х
координатасы x(t) га тигез булсын. Физика курсындагы кебек
үк, хәрәкәт тигез һәм салмак башкарыла, дип уйлыйк. Башкача
әйтсәк, сүз реаль тормышта күзәтелә торган хәрәкәтләр турында
бара. Ачыклык өчен сүз автомобильнең шоссе юлда туры сызыклы
кисәге буенча хәрәкәте турында бара, дип уйлыйк.
Мәсьәләне болай куйыйк: билгеле х (ί) бәйлелеге буенча вакыт¬
ның t моментында автомобиль хәрәкәт иткән тизлекне табыйк
(бу тизлекнең моменталь тизлек дип аталганлыгын сез инде
беләсез). x(t) бәйлелеге сызыкча бәйлелек булса, җавап бик гади:
1 03 Чыгарылма һәм авы куллаву
вакытның теләсә кайсы моменты өчен тизлек үтелгән юлның
вакытка чагыштырмасына тигез була. Хәрәкәт тигез хәрәкәт бул-
маса, мәсьәлә катлаулана.
Вакытның теләсә кайсы моментында автомобильнең ниндидер
(бу момент эчен) билгеле бер тизлек белән хәрәкәт итү факты
ачык. Вакытның ί0 моментында спидометрның фоторәсемен эш¬
ләсәк, бу тизлекне җиңел таба алырбыз (спидометр t моменты
өчен моменталь тизлекнең кыйммәтен күрсәтә), х (ί) билгеле булса,
ны табу өчен, физика дәресләрендә сез болай эшли
идегез.
Δί зурлыгындагы ί0 дән ί0 + Δί га кадәр булган вакыт аралы¬
гындагы уртача тизлек билгеле (12 нче пункт):
(2)
Без фараз иткәнчә, җисем салмак хәрәкәт итә. Шуңа күрә
болай уйлау табигый булыр: Δί бик кечкенә булса, вакытның бу
аралыгында тизлек үзгәрмәс. Ул вакытта (бу аралыкта) уртача
тизлек без эзләгән vM01feBTiJ,b(io) кыйммәтеннән аерылып тормас.
Ә бу моменталь тизлекне билгеләүнең түбәндәге ысулына китерә;
НуртДАГ) ны табарга һәм аның, Δί нульдән аерылып тормый дип
санап, нинди кыйммәткә якын булуын билгеләргә кирәк була.
Конкрет мисал карап китик. υ0 тизлеге белән югарыга ыргытыл¬
ган җисемнең моменталь тизлеген табыйк. Аның t моментындагы
биеклеге безгә билгеле һ (ί) = vot — *■- формуласы буенча табыла.
1) Башта ΔΛ ны табыйк:
ΔΛ (ί) = πο(ί0 + Δί) - - voto + = ι>0Δί - <ί0Δί -
(v0-gt0)&t - g&f-
2) <>„,,(Δί) « — 2_ = vo _ g/0 - JL·-. (3)
3) Δί ны нульгә якынайтып кечерәйтик (моны кыскача Δί
нульгә омтыла дип әйтәләр. Ул болай языла: Δί —> 0).
Бу очракта - нең шулай ук нульгә омтылганлыгы, ягъни
Δί —> 0 өчен — -> 0 икәнлеге җиңел аңлашыла.
г0 һәм -gt^, димәк, р0 - gi0 зурлыклары да даими булганлыктан,
(3) формуладан табабыз:
Δί —»0 өчен υ^ίΔί) -» υ0 - gt0.
Шулай итеп, ноктаның бу вакытның t0 моментындагы момен¬
таль тизлеге
-va-gta
формуласы буенча табыла.
104 Чыгарылма һам аны куллану
3. Чыгарылма. Абсциссасы х0 = 1 булган ноктада параболага
орынманың почмакча коэффициентын исәпләү һәм υ0 тизлеге
белән югарыга ыргытылган җисемнең моменталь тизлеген табу
турындагы без карап киткән ике мәсьәләнең әйтелешләре төрле
иде. Ләкин беэ һәр ике очракта да бер схемага таянып эш иттек.
Ирекле f функциясенә һәм аның билгеләнү өлкәсендәге теләсә
нинди х0 ноктасына карата кулланган бу схеманы болай тасвирлап
була.
1) f функциясен бирүче формула ярдәмендә функциянең х0
ноктасындагы үсемтәсен табабыз:
Δ/ “ f(x0 + Ax) - f(xQ).
2) ~ аермалы чагыштырмасы өчен аңлатма табабыз:
Δ/· _ /(х, әЛх) - f(x0) '
Αχ Αχ
аннары аны үзгәртәбез — гадиләштерәбез, Δχ ка кыскартабыз һ.б.
3) Δχ нульгә омтыла дип санап, ның нинди санга омтылуын
ачыклыйбыз.
Шулай итеп, табылган сан кайвакытта (физикадагы кебек)
функциянең х0 ноктасында үзгәрү тизлеге яки (ешрак) f функ¬
циясенең х0 ноктасындагы чыгарылмасы дип атала.
Билгеләмә f функциясенең х0 ноктасындагы
чыгарылмасы дип Δχ нульгә омтылганда
Δ( _ f (х0 + Δχ) - /(Хр)
Δχ Δχ
аермалы чагыштырмасы омтылган сан атала.
f функциясенең х0 ноктасындагы чыгарылмасы Л(х0) дип там¬
галана («х0 ноктасында эф штрих» дип укыла).
П 1 нче мисал. /(х) = х3 функциясенең х0 ноктасындагы
чыгарылмасын табыйк.
Югарыда күрсәтелгән схема буенча эш итик.
1) Δ/ = (х0 + Δχ)3 - xu* = 3χ2Δχ 4- 3χ0(Δχ)2 + (Δχ)3.
2) = 3xj + 3χ0Δχ + (Δχ)2 (Δχ * О).
3) 3X5 кушылучысы — даими, ә Δχ-»Ο өчен Зх,Дх ->0 һәм
(Δχ)2—>0 икәнлеге ачык, димәк, 3χθΔχ + (Δχ)2—>0. Шулай итеп,
табабыз:
Δχ —> 0 өчен ~ -ә Зха .
Δχ u
Димәк,
Г(ХО) = Зх2.
Чыгарылма һәм аны куллану
2 нче мисал. f(x} = kx + b функциясенең (k һәм b— даи¬
ми) x0 ноктасындагы чыгарылмасын табыйк.
1) Af=(k (x0 + Δχ) + b) - (kx0 + 6) = kAx.
2> й= k- '
3) k — даими, — теләсә нинди Δχ өчен даими сан, димәк,
Ах —> 0 өчен —> k. Моннан (kx + by — k.
х0 ноктасындагы чыгарылмасы булган функция бу ноктада
дифференциалланучы функция дип атала, f функциясе диффе-
ренциаллана торган нокталар күплеге Л, булсын. Нәр xcDj санына
Г(х) санын тиңдәш куеп D, күплегендә билгеләнгән яңа функция
табарбыз. Бу функция у = /(х) функциясенең чыгарылмасы дип
атала һәм /' яки у' дип тамгалана.
Бирелгән f функциясенең чыгарылмасын табу дифференциал-
лау дип атала.
Бу пунктта без дифференциаллауның түбәндәге формулаларын
таптык:
(х2)' = 2х, (х8)' = Зх2, (kx + ЬУ = k.
(kx + ЪҮ = k формуласында k = 0, b = C дип уйлап, биредә С —
ирекле даими сан, С — 0, ягъни даими санның чыгарылмасы нульгә
тигез икәнлеге табыла.
Күнегүләр
188. — f функциясенең графигын төзегез һәм аңа абсциссасы х0
булган нокта аша үтүче орынма үткәрегез. Рәсемнән файда¬
ланып, бу орынманың почмакча коэффициентының тамга-
й сын билгеләгез:
а) /(х) = х2 - 2х - 3, х0 = 0, х0 = 3, х0 = 2, х0 = -1;
б) f(x) = -у + 1, х0 = -2, х0= 1, х0 = -1, х0 = 2.
189. Функция графигына (85 нче рәсем) абсциссалары xt, х2,
х3, х4 булган нокталар аша үтүче орынманың (әгәр ул
булса) почмакча коэффициентының тамгасын билгеләгез.
Бу орынма абсциссалар күчәре белән нинди почмак (кы¬
сынкымы яки җәенкеме) төзер? Нинди нокталар тирәлеген¬
дә функциянең графигы шома кәкре була.
190. - Функциянең үсү һәм кимү аралыкларын языгыз (86 нчы
рәсем). Графикта күрсәтелгән һәр ноктада орынманың поч¬
макча коэффициентының тамгасын билгеләгез.
Чыгарылма һәм аны куллану
85 нче рәсем
191.-а)/(х) = 2х\ х0=1, Δχ = 0,5; ОД; 0,01;
б) /(х) = хг, хи = 1, Δχ = 0,5; 0,1: 0,01 булса, х0 ноктасында
! V
, ны исәпләгез.
Δχ
192.
а) = 8х0 + 4Δχ, х0 = 2; - 1;
б) дг ” + 3*οΔχ + (Δ*)2» хо = 1; ~21;
в) = -2х0 + Δχ, х0 = 1; 2
’ Δχ °
булса, Δχ —> 0 өчен — чагыштырмасы нинди санга омтылыр?
86 нчы рәсем
107 Чыгарылма һәм аны куллану
193.—a) f(x) = x3, х0 = 2; -1,5;
I] б) /(х) = 4 - 2х , х0 - 0,5; -3;
I в)/(х)-Зх-2, х0- 5; -2;
г) /(х)“Х2, х0 = 2,5; -1 булса, дифференциаллауның,
13 нче пунктта табылган формулаларын кулланып, /функ-
I циясенең х0 ноктасындагы чыгарылмасын табыгыз.
194.— Чыгарылма билгеләмәсеннән файдаланып,
а) /(х) = х2-3х ның -1; 2;
б) /(х) “ 2х3 ның 0; 1;
в) f(x) = -j нең - 2; 1;
г) f (х) = 4 - х2 ның 3; 0 нокталарындагы чыгарылмаларын
табыгыз.
195.— а) х0 = - 1; б) х0 = 3; в) х0 - 0; г) х0 -= 2 булса, f (х) = х2
функциясе графигының абсциссасы х0 булган нокта аша
үтүче орынмасының тигезләмәсен табыгыз.
196.— Билгеләмәдән файдаланып, х (0 законы буенча турысызын-
|лы хәрәкәт итүче ноктаның ί моментындагы моменталь
тизлеген табыгыз:
а) х (i) = -I2 + 8t, ί0 =6; б) х (ί) = 3ί2 + 2, t0 = 2;
I B)x(0= t0= 4; r) x(t) = 5i - 3, i0 = 10.
14. Функциянең өзлексезлеге һәм чикләмә
аша күчү төшенчәсе
t ноктасында моменталь тизлекне табу турындагы мәсьәләгә
кабат кайтыйк (13 нче пунктта (3) формуласын кара). υ^Λί) =
Уо - gt0 - g. Ύ функциясе Δί = 0 булганда билгеләнә алмый. Ләкин
L = v0 = gt0 саны өчен |Δί| кечерәйгәндә оурт, (Δί) — L аермасы
нульгә якынлаша. Шуңа күрә дә без Δί—>0 өчен υ^ίΔί)-» у0-
git, дип яздык.
Гомумән, /(х) - L аермасы теләсә никадәр кечкенә булса, ягъни
|f(x) - L\ |Δχ| кечерәйгәндә теләсә нинди һ > 0 дән кечерәк була
алса, х х0 гә омтылганда f функциясе L санына омтыла, дип
әйтәләр, биредә Δχ - х - х0. (Моменталь тизлекне табу турындагы
мәсьәләдәге кебек үк, х — х0 кыйммәте каралмый.)
Билгеле, х -> х0 урынына Δχ -> 0 дип тә язарга мөмкин, f функ¬
циясе буенча L санын табу чикләмә аша күчү дип атала. Сез чик¬
ләмә аша күчү белән башлыча түбәндәге төп ике очракта эш
итәрсез.
1 08 Чыгарылма һәм авы куллану
Беренче очрак — аермалы чагыштырмасында чикләмә аша
күчү, ягъни чыгарылма табу. Бу очрак белән сез алдагы пунктта
таныштыгыз.
Икенче очрак функциянең өзлексезлеге төшенчәсе белән бәй¬
ләнгән. Әгәр х —> х0 өчен f(x) —> f(xQ) булса, функция х0 ноктасын¬
да өзлексез, диләр. Биредә f(x)-L - f(x) - /(х0) = Δ/, |Δ/| бик
кечкенә |Δχ| өчен кечкенә була, ягъни аргументның х0 ноктасын¬
дагы кечкенә үзгәрешлеләренә функциянең кечкенә үзгәрешле-
ләре тиңдәш була. Сезгә билгеле булган барлык элементар функ¬
цияләр үзләренең билгеләнү өлкәләренең һәр ноктасында өзлексез
булалар. Мондый функцияләрнең графиклары билгеләнү өлкәсенә
кергән һәр аралыкта өзлексез кәкреләр белән сурәтләнәләр. Гра¬
фикларны сез һәрвакытта кулланылган «нокталар буенча» төзү
юлы шуңа нигезләнгән дә инде. Төгәлрәк әйткәндә, биредә без
тикшергән функциянең, чыннан да, өзлексез булуын алдан ачык¬
ларга кирәк була. Бик гади очракларда мондый тикшерүне өзлек¬
сезлек билгеләмәсенә нигезләнеп алып баралар.
В 1 нче мисал. Сызыкча f(x) = kx + b функциясенең санлы
турының һәр ноктасында өзлексез булуын исбат итик.
Безгә кечкенә |Δχ| лар өчен |Δ/| ның теләсә нинди һ > 0 дән
кечерәк була алуын күрсәтергә кирәк. Ләкин |Δ/| = |/(х0 + Δχ) -
-/■(х0)| = |*(χο + Δ*) + Ь) - (kx0 + ί>)| - |λ||Δχ| һәм |Δ/| һ>0 дән А # О
өчен Δχ < j|| итеп алсак кына кечерәк булыр (k - 0 өчен теләсә
нинди Δχ ны алырга була).
2 нче мисал. f(x) = 4х функциясенең х0 ноктасында
х0 > 0 өчен өзлексез булуын исбат итик.
Башта без Δχ ны |Δχ| ζ х0 булырлык итеп сайларга мөмкин
икәнлеген күрсәтеп китик, ул вакытта >/х = ^ха + Δχ билгеләнә.
Аермасын табыйк:
Әгәр |Δχ| ны ^хоһ нан кечерәк (без әйтеп киткәнчә, ходән ке¬
черәк) итеп алсак, |Δ/| ның һ > 0 дән кечерәк булуы күренә.
► Моменталь тизлекне табу мәсьәләсендә имоменталь(£0) саны гу1ИП(ЛГ)
функциясе нульдә имоменталь саны белән «тутырылганнан» соң бу
ноктада өзлексез функциягә әверелерлек итеп билгеләнгән иде.
Орынманың почмакча коэффициентын табу мәсьәләсендә дә шул
ук хәл g(0) = 2х0 дип санасак, £(Δχ) = 2χ0 + Δχ функциясе бу
ноктада өзлексез функциягә әверелә.
Чыгарылма һәм аны куллану
Алдагы пункттагы мисаллардан яңа операция — чикләмә аша
күчүнең — билгесез зурлыкларны табуның яңа чарасы булып тор¬
ганлыгы күренә. Бу бүлектә без аннан киң файдаланырбыз. Чик¬
ләмә аша күчү кагыйдәләрен әйтеп китик (аларны математик
анализ курсларында исбат итәләр).
I 1 нче кагыйдә, f функциясе х0 ноктасында өз-
I лексез булса, Δχ —> 0 өчен Δ/ —> 0.
2 нче кагыйдә, f функциясенең х0 ноктасында
чыгарылмасы булса, Δχ—>0 өчен 4? —» f'(x»)·
1 нче һәм 2 нче кагыйдәләр f функциясенең һәм чыгарыл¬
маның х0 ноктасында өзлексез булу турындагы билгеләмәләрдән
турыдан-туры килеп чыгалар.
3 нче кагыйдә, х —> х0 өчен f (х) —> A, g (х) —> В
булсын. Ул вакытта х —> х. (ягъни Δχ —> 0) өчен;
а) f(x) + g(x)—>А + В;
б) f(x)g(x)->AB;
в) -> д (В*0 өчен).
Өзлексез f һәм g функцияләре өчен
А = Дх0), В = g(x0),
һәм бу кагыйдәләр х0 ноктасында өзлексез функцияләрнең сумма¬
сы, тапкырчыгышы һәм өлеше (өлеш очрагында g(x)^O) х0 нок¬
тасында өзлексез булуларын аңлаталар.
Чикләмә аша күчү кагыйдәләре функцияләренең өзлексезле¬
ген исбатлаганда һәм дифференциаллау формулаларын чыгарган¬
да киң кулланылалар.
3 нче мисал. Һ(х) = 10х + >fx функциясенең (0; °°) ара¬
лыгының теләсә нинди х0 ноктасында өзлексез булуын исбатлыйк.
f(x) = 10х һәм g(x)= </х функцияләренең өзлексез булуы 1 нче
һәм 2 нче мисалларда исбат ителгән иде. Шулай булгач, һ функ¬
циясе өзлексез ике функциянең суммасы буларак өзлексез була
(3 нче а кагыйдәсе).
4 нче мисал.
f(x) = Vx.
1) Ирекле х0 ноктасы өчен
Δ/ - —=
V*. · у'х,>
(2 нче мисалны кара).
2>£ = -- ί ■
3) 1 нче кагыйдә буенча Δχ -» 0 өчен %/х0 + Δχ —> у'Х0 , чөнки
а/г функциясе х0 ноктасында өзлексез (2 нче мисалны кара), шуңа
/'(х) = - - икәнлеген исбатлыйк, биредә
2ух
110 Чыгарылма һәм аны куллану
күрә Δχ —> 0 өчен -Jx0 + у]х0 + Δχ —» 2^/χθ (3 нче а кагыйдәсе,
буенча) һәм Δχ —> О өчен —— * —> —(3 нче в кагыйдәсе,
^Χη+^Χο + Δχ 2^/Хд
буенча). Шулай итеп, теләсә нинди уңай х өчен (ух)' =
Күнегүләр
197. — Графигы 87 нче рәсемдә күрсәтелгән функция X,, х2, х3
нокталарының һәркайсында өзлексез булырмы?
198. -er f функциясенең графигын төзегез. Әлеге функциянең бил-
g геләнү өлкәсендә функция өзлексез булмаган нокта бармы?
х - 1, х ζ -1 өчен,
1 - х2, х > -1 өчен;
a) f(x) =
1 2 - х, х С 1 өчен,
б) f(x) = < _ . f
2х - 1, х > 1 өчен;
х + 2, х < 1 өчен.
в) ftx) -
1 өчен.
х2
в)
87 нче
рәсем
ыгарылма һәм аны куллану
199. — f функциясе бирелгән аралыкның һәр ноктасында өзлексез
булырмы?
' a) f(x) - х3 - 4х, (-<»; <»); б) /(х) - [2; «);
р в) f(x) - хг + 2х -1, [-10; 20];
Ί г) /(х) - 5х - Jx, (0; «).
I
200. | а) /(х) = х2 - Зх + 4, х -> 0, х -> 2;
I б) /(Х) = pyj. х -> 1, х -> 4;
I в) f(x) = 4-|,хч -2, х -ә 0;
г) /(х) - 4х - ·γ, х -ә -1, х - > 4
булса, f функциясе нинди санга омтыла?
201.
х —> 3 өчен /(х) -»1, g(х) —> -2 икәнлеге билгеле, х -> 3 бул¬
ганда функция нинди санга омтыла?
a) 3/(x)g(x);
. /(χ) - g(x).
' /(x) + g(x)’
в) 4 f (х) - g(x); г) (3 - g (х)) f (х).
202.
х —» -1 өчен /(х) —> 3, g(x) —> -0,5 икәнлеге билгеле.
х -> -1 булганда, функция омтылган санны табыгыз:
б) (/(x)-g(x))2;
. _ _ (g ίχ№
в) (/(х))2+2£(х); г)
203. — Функция нинди санга омтыла?
а) х —> 4 булганда, /(х) = х +3* + ~ .
х-о
б) х-ә-1 булганда, /(х) = f ;
X ^Х Г I
в) х —> 2 булганда, /(х) = ;
г) X -ә -1 булганда, f(x) = .
X + о
204. — Квадратның ягы 0,01 дм төгәллек белән үлчәнсә, аның
периметры нинди төгәллек белән табылган булыр?
205. -» Төзек өчпочмакның периметрын 0,03 дм төгәллек белән
г табу өчен, аның ягын нинди төгәллек белән үлчәү җитә?
206. -а Әйләнә озынлыгын 0,06 дм төгәллек белән исәпләү өчен,
£ аның радиусын нинди төгәллек белән үлчәргә кирәк?
112
Чыгарылма һәм апы куллану
207.— х -> а булганда, fix) -»A, g(x) -» В икәнлеге билгеле. Чик¬
ләмә аша күчү кагыйдәсен кулланып исбатлагыз:
а) Cf(x) -> С - А, биредә С — даими сан;
б) /(х) - g(x) -+А-В',
в) (/(x))2-(g(x))2 ^А2-В2;
9 г) (/(х))п -» Ая, биредә πεΖ.
15. Чыгарылмаларны исәпләү кагыйдәләре
1. Дифференциаллауныц тел кагыйдәләре. Чыга¬
рылмаларны исәпләүнең берничә кагыйдәсен чыгарыйк. Бу пункт¬
та и һәм V функцияләренең һәм аларның чыгарылмаларының
кыйммәтләре х0 ноктасында кыскача болай тамгалана: u(x0) = u,
р(х0) = υ, u'(x0) = u', υ'(χ0) = ν’.
1 нче кагыйдә, и һәм и функцияләре х0 нок¬
тасында дифференциаллансалар, аларның суммасы
да бу ноктада дифференциаллана һәм
(и + V)' = и' + ν'.
Кыскача болай әйтәләр: сумманың чыгарылмасы
чыгарылмаларның суммасына тигез.
1) Исбатлау өчен башта функцияләр суммасының без карап
киткән х0 ноктасындагы үсемтәсен исәплик:
Д(н + о) = и(х0 + Δχ) + и (х0 Ί- Δχ) - (u (х0) + и (х0)) =
= (и (х0 + Δχ) - и (х0)) + (и (х0 + Δχ) - V (х0)) = Ди + Δυ.
A(U + t>) _ Дц Д£
’ Δχ ~ Δχ Δχ*
3) и һәм и функцияләре хй ноктасында, ягъни Δχ —> 0 булганда
дифференциалдан алар,
Ди
Δχ
Δυ
Δχ
Ул вакытта Δχ —> 0 булганда —- > и + и (3 нче а кагыйдә,
ЛЛ*
чикләмәләрне исәпләү кагыйдәләрен кара — 14 нче п.) ягъни
(и + v)’ = и' + ν'.
Лемма. Әгәр f функциясе х0 ноктасында дифферен-
циалланса, ул чагында бу ноктада функция өзлексез
була: Δχ -> 0 булганда Д/ -» 0, ягъни Δχ —► 0 булганда
ί(χ0 + Δχ) -> f(x0).
Чыннан да, Δχ -» 0 булганда Δ/ = · Δχ —> f'(x0) 0, чөнки
Г(*о)> ә Δχ —» 0.
Шулай итеп, Дх —> 0 булганда Δ/ —* 0, ягъни дифференциалла¬
пмы функцияләр өчен Δχ -» 0 булганда f(x0 + Δχ) -» f(x0).
113
Чыгарылма һәм авы куллану
2 нче кагыйдә. Әгәр и һәм υ функцияләре ха
ноктасында дифференциалланса, аларның тапкыр¬
чыгышы да бу ноктада дифференциаллана һәм
(ut>)' = u'v + Uv'.
1) Башта тапкырчыгышның үсемтәсен табыйк:
Δ(ιζο) = и (х0 4- Δχ) υ (х0 + Δχ) - и (х0) υ (х0) =
= (u(x0) + Au)(o(x0) + Δυ) - u(x0)u(x0) =
= и (χ0) υ (χ0) + Δυυ (χ0) + и (χ0) Δυ + ΔιιΔυ - и (χ0) υ (χ0) =
= Δυυ (χ0) + υ (χ0) Δυ + ΔυΔν.
2) = ) + ц(х )Αϋ + Δι/^ϋ.
' Δχ Δχ ' “' ' υ' Δχ Δχ
3) и һәм υ функцияләре Δχ —> 0 булганда χ0 ноктасында диф-
ференциалланганга күрә —> и', —> ν', Δυ —» 0. Шуңа күрә
-> u'u(xo) + u(xo)u' + O-i/ - u'u(x0) + u(x0)i/, ягъни
(ui>)' = u'v + uv'. Моны исбатларга кирәк иде дә.
Нәтиҗә. Әгәр и функциясе х0 ноктасында диффе¬
ренциалланса, ә С — даими булса, Си функциясе дә
бу ноктада дифференциаллана һәм
(Си)' - Си'.
Кыскача болай әйтәләр: даими тапкырлаучыны
чыгарылма тамгасы алдына чыгарырга мөмкин.
Исбатлау өчен икенче кагыйдәдән һәм 13 нче пункттан билгеле
булган факттан файдаланабыз: С' = 0.
(Си)' = С'и + Си' = 0 и + Си = Си'.
3 нче кагыйдә, и һәм v функцияләре х нокта¬
сында дифференциалланса һәм υ функциясе бу нок¬
тада нульгә тигез булмаса, “ өлеше дә ул ноктада
дифференциаллана һәм
(и\ _ u'v - uv'
U/ ~ υ2
► Башта | 1 j формуласын чыгарыйк.
1) функциясенең үсемтәсен табыйк:
дЛ\ _ 1 I _ V (Хо) - V (ха + Дх) _ -Ду
" р(х0 + Дх) t?(x„) и(хи)у(х0 + Дх) у(х0)(р(х0) + Др) ‘
114
Чыгарылма һам аны куллану
2) Моннан
Δ(ν) Δχ
Δχ υ(χ0)(υ(χ0) + Δυ)'
3) Δχ —> 0 өчен —> ν' (чөнки υ χ() ноктасында дифференциал¬
лана), Δχ -> 0 (без исбатлаган лемма буенча). Шуңа күрә
' -» — - - 12, ягъни (I) - - у2.
Δχ l>u и2 1 1 Р2
Хәзер, функцияләр тапкырчыгышының чыгарылмаларын табу
кагыйдәсен кулланып, өлешнең чыгарылмасын табабыз:
1 1 нче мисал. Түбәндәге функцияләрнең чыгарылмаларын
табыйк: a) f(x) - х2 ‘: б) f(x) = t" , .
a) (1)' = - i- = - X. шуңа күрә (χ» -1)‘ = (х2)' - (|) = 2х -
-(-Л)‘2г + 4;
\ хг) х2
б, I х2 V (хг)'(х3 + 1) - х2 (xs + 1)' _ 2х (х3 + 1) - х2 ((х3)'+ 1)' _
Цх» + 1] “ (х’+1)2 (х*+1)2
_ 2х(хэ + 1)-х2(3х2 + 0) _ 2х4 + 2х - Зх4 _ 2х - х4
‘ (х3 + 1)2 " (х’+1)2 (х3+1)2* *
2. Дәрәҗәле функция чыгарылмасы, х" дәрәҗәле функциясе¬
нең чыгарылмасын исәпләү формуласы болай була (монда п саны
1 дән зуррак булган ирекле натураль сан):
(хя)' = ηχ·’. (1)
х2 функциясенең чыгарылмасы формуласы безгә инде билгеле:
(х2)' - 2х.
Тапкырчыгышны дифференциаллау формуласын кулланып
табабыз:
(х3)' = (х2 · х)' = (х2)'х 4- х2(х)' = 2х · х + х2 · 1 = Зх2;
(х3)' = (х3 · х)' = (х9)х 4- х3(х)’ = Зх2 · х 4- х3 · 1 = 4х3.
Хәзер (х2)' = 2Х2'1, (х3)' = Зх3"1, (х4)' = 4х4-1 икәнен искәртеп ки¬
тик, ягъни п = 2, 3 һәм 4 өчен (1) формула исбатланды. Шуңа
охшаш итеп исәпләүләрне дәвам итсәк, (1) формуланың п = 5, 6
һ.б. өчен дә дөрес икәнлегенә ышанырбыз.
' (1) формуланың теләсә нинди натураль η > 4 өчен дөрес икән¬
леген исбатлыйк.
115 Чыгарылма һәм аны куллану
(1) формула η = k өчен дөрес, ягъни
(Х*У = kx*1
булсын, ди.
Ул вакытта (1) формуланың п = k + 1 өчен дә дөрес булганлы¬
гын күрсәтик. Чыннан да,
(х**1)' = (х* · х)' - (х*)'х + х* · (х)' =
= ftx* 1 · X + X* “ fex* + X* = (k + 1) X*.
Шуңа күрә, (1) формула п = 4 өчен дөрес булганлыктан, аның
п = 5 өчен дә дөрес булуы килеп чыга, ә ул вакытта формула η = 6
өчен дә, димәк, п = 7 өчен дә һ.б. теләсә нинди натураль neN өчен
дә дөрес була (исбатлауны төгәл башкару математик индукция
методына нигезләнгән).
Әгәр п = 1 яки п = 0 булса, х * 0 өчен бу формула шулай ук
дөрес була. Чыннан да, х * 0 өчен (1) формула буенча
(х1)'= 1 · х1 1-lx0»!.
(х°У = 0 · х° 1 = 0,
ә бу безгә алдагы пункттан билгеле булган х һәм 1 функцияләре
чыгарылмаларының кыйммәтләре белән тәңгәл килә.
Ниһаять, п — тискәре бөтен сан булсын, ди. Ул вакытта п = -т,
монда т — натураль сан. Өлешне дифференциаллау кагыйдәсен
кулланып, һәм натураль т өчен инде исбатланган (1) формуланы
файдаланып, х * 0 булганда табабыз:
(хл)' = (х -г = (-^У = = -т =
= -тх’·' = ох"-1.
Шулай итеп, мондый нәтиҗә ясал була:
Теләсә нинди бөтен п һәм теләсә нинди х өчен (nil
булганда, х * 0)
(хпҮ = пхП
В 2 нче мисал, a) f (х) = х 5; б) f(x) = 3xT-A функциялә¬
ренең чыгарылмаларын табабыз.
а) (х 5) = -5х"5 1 = ~5х °;
б) (зх7-р-) = 3(х7)'-5(х э)'=3 7х«-5(-3)х ‘ = 21х6 + ^.
Дәрәҗәле функциянең дифференциаллануыннан һәм чыга¬
рылмаларны исәпләүнең төп кагыйдәләреннән
бөтен рациональ функцияләрнең (күпбуыннарның)
һәм вакланма-рациональ функцияләрнең билгеләнү
өлкәләренең һәр ноктасында дифференциаллану-
лары килеп чыга.
Чыгарылма һәм аны куллану
Күнегүләр
Функцияләрнең чыгарылмаларын табыгыз (208—211).
208. - a) f(x) = х2 + х3; б) f(x) = } + 5х - 2;
$ в) /(х) = х2 + Зх - 1; г) /(х) - х3 + Jx.
209. , a) f(x) = х3 (4 + 2х - х2); б) f(x) = 4х (2х2 - х);
в) Дх) = хг(3х + х3); г) Лх) = (2х-3)(1-х3).
210- а) у = б) у = : в) У ~ Βΐ1; г> У л
211- а) у = х® -Зх4 -х + 5; б) У = f-р-+>/*;
х* 3 ,
в) у = х1 - 4х5 + 2х -1; г) у = -ү + + 1.
212.
213-
214-
f функциясенең бирелгән нокталардагы чыгарылмасының
кыйммәтен исәпләгез:
а) f(x) - х2 - Зх, х = - 4, х = 2;
б) /(х) = х - 4>/х, х = 0,01, х = 4;
в) f(x) = х - |, х = V2, х = —V;
г) = fcf* = -з, х = 0.
al /(х) = 2х2-х; б) Лх) = -|х3+х2+12;
в) f (х) = 4г- - 1,5х2 - 4х; г) /(х) = 2х - 5х2 булса,
О
f(x) = 0 тигезләмәсен чишегез.
а) /(х) = 4х - Зх2; б) /(х) = х3 + 1,5х2;
в) /(х) = х2 - 5х; г) /(х) = 4х - 4 х3 булса,
f'(x)<0 тигезсезлеген чишегез.
215.— Функциянең чыгарылмасын табыгыз:
a)/(x) = f^p-; б) Πχ) = (| + χ2)(2-ν£):
В) /(X) = У~г ’, г) f(x> = (3χ5 - χ)·
216.-+
х ның f функциясе чыгарылмасының нульгә тигез булган¬
дагы кыйммәтләрен табыгыз:
а) /(х) = х5 - 3 4 ха + 5х; б) f(x) = 2х4 - х8;
о
в) /(х) = х4 + 4х; г) /(х) = X4 - 12х2.
117
Чыгарылма һәм аны куллану
217. — a) f(x) - х3 - 6х2 - 63х; б) /(ж) = Зх - 5х2 + х3;
в) f(x) = I х3 - 8х; г) /(х) = Зх2 - 9х - | х3
булса, f'(x) < 0 тигезсезлеген чишегез.
218. — Чыгарылмасы
а) 2х 4- 3; б) 16г3 - 0,4; в) 8х - 2; г) 9х2 - |
гә тигез булган кимендә бер функцияне формула аша бирегез.
219. — Әгәр:
а) Д(х) һәм f2(x) функцияләренең һәркайсыың х0 нокта-
I сында чыгарылмасы булмаганлыгы;
б) Л(х) ның х0 ноктасында чыгарылмасы булуы, ә f2(x) ның
чыгарылмасының булмавы билгеле булса, <р(х) = Д(х) -I- /г(х)
функциясенең х0 ноктасында чыгарылмасы юк дип әйтү
дөрес булырмы?
16. Катлаулы функциянең чыгарылмасы
1. Катлаулы функция. Мисалдан башлыйк.
1 нче мисал. z = Л (х) = 71 -х2 формуласы белән билге¬
ләнгән һ функциясе өчен х ның бирелгән кыйммәте буенча
г ның тиңдәш кыйммәтен исәпләргә кирәк булсын. Моның өчен
башта бирелгән х өчен
У = f (х) = 1 - х2
кыйммәтен, аннары у ның шул кыйммәте аша
2= е(у) = Jy
кыйммәтен исәпләргә кирәк.
Шулай итеп, f функциясе х санына у санын тиңдәш, ә g функ¬
циясе у ны z ка куя, һ функциясен у һәм f функцияләреннән
төзелгән катлаулы функция дип әйтәләр һәм
Л(х) = g(/(x))
рәвешендә язалар.
Ирекле х ноктасында катлаулы һ(х) = g(f(x)) функциясенең
кыйммәтен исәпләү өчен, башта «эчке» f функциясенең бу нок¬
тадагы кыйммәте у ны, аннан соң g(y) ны исәплиләр.
Катлаулы g(f(x)) функциясенең билгеләнү өлкәсе нинди була
соң? Ул — /(х) ның билгеләнү өлкәсенә кергән һәм аны g функция¬
сенең билгеләнү өлкәсенә керерлек иткән барлык х лар күплеге.
Без карап киткән мисалда f функциясенең билгеләнү өлкәсе
булып барлык санлы туры тора. Әгәр дә /(х) ның кыйммәте
g(y)=->Jy функциясенең билгеләнү өлкәсенә керсә, й/х)ның
кыйммәте билгеләнгән була. Шуңа күрә у 0 тигезсезлегенең
үтәлүе, ягъни 1 - х2 > 0 булу таләп ителә, димәк, g(f(x)) функция¬
сенең билгеләнү өлкәсе [-1; 1] кисемтәсе була.
118 Чыгарылма һач аны куллану
2. Катлаулы функциянең чыгарылмасы формуласы. Алдагы
пунктларда сез рациональ функцияләрнең, аерым алганда, күп¬
буыннарның чыгарылмаларын табарга өйрәндегез. Ләкин f(x) =
= (2х + 3)1СО функциясенең чыгарылмасын исәпләү күпбуынның
чыгарылмасын табуга кайтып калса да, зур күләмле эш башкаруны
таләп итә: (2х + 3),0° не күпбуын рәвешендә күрсәтергә һәм килеп
чыккан суммадагы 101 кушылучыны дифференциалларга кирәк
була. Катлаулы функциянең чыгарылмасын исәпләү кагыйдәсен
исбатласак, бу һәм башка мондый мәсьәләләрнең чишелешен
күзгә күренерлек дәрәҗәдә гадиләштереп була.
Әгәр f функциясенең х0 ноктасында, ә g функция¬
сенең уп = / (х0) ноктасында чыгарылмасы булса, ул
вакытта һ (х) = g (f (х)) катлаулы функциясенең
х ноктасында шулай ук чыгарылмасы була, өстәвенә
һ'(х„)-g (f(x(>)) f '(xn). (1)
(1) формуланы исбатлау өчен (алдагы кебек үк), Δχ^Ο
булганда -.j вакланмасын тикшерергә һәм Δχ -> 0 булганда
> g'(yo) икәнлеген күрсәтергә кирәк.
&У = f(xo + Δχ) - f(x„) = Δ/
тамгаланышларын кертик. Ул вакытта ΔΛ - һ (х0 + Δχ) — һ (х0) =
= g(f (*0 + Δχ)) - £(/(*«)) = 8 (Уо+ &У) - 8(Уо) = №■
Ау —> 0 булганда Δρ —> 0 була, чөнки / х0 ноктасында дифферен-
циаллана.
Без исбатлауны бары тик х0 ноктасының ниндидер тирәлегендә
Δ/ * 0 булырлык f функцияләре өчен генә башкарырбыз. Ул вакыт¬
та Δχ >0 булганда * Я'(Уо) · чөнки
ΑΛ Ay АХ .iy Aj
Δχ —> 0 булганда —> /'(х0), ә Δρ -»0 булганда -» g'(p0), ә бу
югарыда күрсәтелгәнчә) Δχ —> 0 булганда үтәлде.
■ 2 нче мисал. Алда куелган мәсьәләгә кайтыйк һәм Λ (х) =
= (2х + 3)10и функциясенең чыгарылмасын табыйк:
һ функциясен катлаулы Л(х) = g(f(x)) функциясе рәвешендә
күрсәтеп була, монда g(p) = р100, р = f (х) = 2х + 3. Ләкин f'(x) — 2,
g'(y) = 100 р", шуңа күрә Л'(х) = 2 · 100 р" = 200 (2х + 3)".
3 нче мисал, һ (х) = ^Зх2 +1 функциясенең чыгарылма¬
сын табыйк.
һ (х) = g(f{x)), монда у - f(x) = Зх2 + 1, g(y) = д/р , шуңа күрә
g'(y) - һәм р' = f'(x) = 6х, моннан
A'(x) = -L р' = ■6х = . Зх ■
2 VW 2^3хг + 1 ,/Зх2 + 1 "
икәнлеген табабыз.
Чыгарылма һәм аны куллану
Күнегүләр
220. —
221. —
Катлаулы Л(х) = функциясен төзүче элементар
f һәм g функцияләрен формулалар аша бирегез (220—221).
а) һ (х) = cos Зх; б) һ (х) = sin ^2х - у);
B)A(x) = tg-|; г) й (х) = cos (Зх + jk
а) Л (х) = (3 - 5x)s;
в) й(х) = (2х + 1)т;
б) й(х) = Vcosx;
г) Л(х) = tg
222.
223.
224.-
һәр функциянең билгеләнү өлкәсен табыгыз (222—223).
а) у = v'9 -х2; б) у - , ;
v'x‘-7x + lil
в) у - \0,25 - х2; г) у = , * .
»Л -ж’
а) у - v'cosx; б) (/ —Л—т.
Sin(x-f)
в) у = tg 2х; г) у = Vsinx.
Функцияләрнең чыгарылмаларын табыгыз (224—225).
а) Г(х) = (2х-7)8; б) (х) = ;
в) /(х) = (9х + 5)4; г) =
225.-
a) f (х) = (з - -j ) *;
в) /(х) = (4-1,5х)10;
б) f(x) = (jx-7)’-(l-2x)4;
г) f (х) = (5х - 2)13 - (4х + 7)’.
226. — Функциянең билгеләнү өлкәсен табыгыз:
а) у * V1 - 2 cos х; б) у = - 1;
в) У = Vsinx-0,5; г) у = +1.
227. — i(x) = 3-2x, g(x) = x2 һәм p(x) = sinx. Әгәр:
а) Л (х) = /(g(x)); б) А (х) = g(p(x));
в) һ (х) = g (f (х)); г) һ (х) = р (f (х)) булса,
катлаулы Л функциясен формула аша күрсәтегез.
Чыгарылма һ»м аны куллану
228.- = g(x) = cosx һәм p(x) = y/x функцияләре
бирелгән. Әгәр:
a) һ (х) - f (g (х)); б) h (x) = f (p (x));
в) A(x) = p(g(x)); г) Л(х) = p«(x)) булса,
катлаулы һ функциясен формула аша күрсәтегез, һ функ¬
циясенең билгеләнү өлкәсен табыгыз.
229. —· f(g(x)) = x булырдай f функциясен табыгыз:
a)g(x) = 2x; б)д(х)-ч/х;
I в) £(х) = Зх + 2; г) £(х) = х24-1, х^ 0.
230. — f функциясенең чыгарылмасын табыгыз:
I а) / (х) = (х3 - 2х2 + ЗГ; б) f (х) = + -Ц;
%* +3
в) /(х) = \/4х2 4-5; г) /(х) = (3 - х3)* 4- >/2х - 7.
17. Тригонометрик функцияләрнең
чыгарылмалары
1. Синус чыгарылмасы формуласы.
Синус функциясенең теләсә нинди ноктада чыгарыл¬
масы булуын һәм
(sin х)'= cos х. (1)
икәнлеген исбатлыйк.
sin a - sin β - 2 cos sin — %— формуласы кулланып табабыз:
Asinx _ sin(xa+Ax)-sinx0 _ 2cos^x0 + _
Δχ Δχ Δχ
2
(1) формуланы чыгару өчен:
sin^r
а) Δχ -> 0 булганда ———> 1;
2
б) Δχ -> О булганда cos ίχ0 4- j -» cos x0 икәнлеген күрсәтү
җитә.
By раслауларга таянып, (1) формуланы китереп чыгарабыз.
Чыннан да, Ах —> 0 өчен
■ ■ cos(x0 4- I -» 1 · cosх0
Δχ Δχ \ ° 2 J u
2
= COS x0
121 Чыгарылма һәм аны куллану
88 нче рәсем
► Без алда нигезләнеп эш иткән
а) һәм б) раслауларының күрсәт¬
мәле геометрик мәгънәләре бар.
а) Берәмлек әйләнәдә Ро ноктасы¬
ның ике ягына да ΙΔ*Ι озынлыкта
Р0А һәм Р0В дугаларын салыйк
(88 нче рәсем). Ул вакытта АВ
дугасының озынлыгы |Дх| ка, ә АВ
хордасының озынлыгы 2|sin
булыр. |Δχ| кечкенә булганда АВ
хордасының озынлыгы ул тартып
торган АВ дугасы озынлыгыннан
практик яктан караганда аерылып
тормый диярлек. (Сез геометрия курсында әйләнә озынлыгы
формуласын чыгарганда бу факттан файдаланган идегез инде.
Чыннан да, билгеле булганча, зур п нар өчен Р„ · С якынча
тигезлеге дөрес була, биредә Рл — камалган төзек п почмаклыкның
периметры, ә С — әйләнә озынлыгы. Димәк, мондый күппочмак
ягының озынлыгы ул тартып торган дуга озынлыгына якынча
тигез була.). Шулай булгач,
Ах —> 0 булганда
=
АВ
«ίη^
Δχ
2
б) Без АВ хордасы озынлыгының АВ дугасы озынлыгыннан
с. ... — Q ; Μ, η ΙΔχΙ
кечерәк булуын, ягъни 2 sin ~ < 2 · — икәнлеген искәртеп китик.
Косинуслар аермасы формуласы һәм бу тигезсезлектән файда¬
ланып табабыз:
cos (хо + ^) _ cos
|д J
Ләкин Δχ —> 0 өчен 0. Шуңа күрә Δχ —> 0 өчен
cos (х0 + ή*) -» cos х0 була.
I Мисал. Катлаулы функцияне дифференциаллау формуласы
буенча
(sin (ах + Ь)У = a cos (ах + Ь).
122 Чыгарылма һам аны куллану
2. Косинус, тангенс һәм котангенсны дифференциаллау фор¬
мулалары.
у = cos х, у = tg х, у = ctg х функцияләренең чыгарыл¬
малары аларыың билгеләнү өлкәләренең һәр нокта¬
сында булуын һәм түбәндәге формулаларның дөрес
икәнлеген исбатлыйк:
(cosx)' = -sinx, (2)
<**>' = Jrp (3)
= (4)
(2) формуланы чыгару cos х = sin - х), cos - х) = sin x
тигезлекләренә һәм катлаулы функцияне дифференциаллау ка¬
гыйдәсе:
(cosx)' = (sin| * - xjj = COSI ί; - xj· (-5 - xj = -sinx
ка нигезләнгән.
(3) һәм (4) формулаларны исбатлау өчен, өлеш чыгарылмасын
табу формуласын һәм синус, косинус чыгарылмаларының алдан
чыгарылган формулаларын кулланыйк:
.. .. (sinx) _ (sinx)'cosx - (cosx)'sinx _ cos2 x + sin2x _ 1 _
Г \CO8X) COS2 X cos2x cos2x’
' ·Lir rV- Icos-'l - (cos*)'slnx ~ (sinx)'cosx _ -sin2 x - cos2 x _ 1
' 1' \sinx/
sin2x
sin2x sin2x
Күнегүләр
Һәр функциянең чыгарылмасын табыгыз (231—233).
231.-£а) у = 2sinx;
,ΰί
5 в) у = -0,5 sin х;
б) у - 1 - sin х;
г) у = 0,5 + 1,5sinx
ж
232.- а) у “ 3cosx;
в) у = 1 - cosx;
б) у — х + 2cosx;
г) у = 2sinx + 1,5cosx.
233.- а) у = л/з ·- 3tgx;
б) у — cosx - tgx;
в) у = 1 tgx;
г) у - 2 tg х - sin х.
234,- a) f(x) - ± cos (2х - л); б) f (х) = х - tg (-2х);
в) /(х) = 3 sin (f - f); г) /(х) = 2 cos
булса, /'(0) һәм f'(n) ны табыгыз.
123
Чыгарылма һәм авы куллаву
235.-йa) fix) = Ix + cosx; 6) f(x) = x-tgx;
I в) fix) = 2 sin x - 1; r) fix) - x- cos x
I булса, fix) = 0 тигезләмәсен чишегез.
Функциянең һәркайсының чыгарылмасын табыгыз (236—
238).
236.— а)
/(х) - х3 sin2x;
6)
f(x) = x4 + tg2x;
в)
fix) =
r)
237.— а)
/(х) = sin2x;
6)
f (x) = tgx + ctgx;
в)
f (х) = cos2x;
r)
fix) = sin2x + cos2x.
238.— а)
f (x) = cos 2x sin x + sin 2x cosx;
| б)
fix) = cos2 f - sin2
в)
f (x) = sin 5x sin 3x + cos 5x cos 3x;
!г>
f (x) = sin 3x cos 3x.
239.-й· a) f(x) 2 sin2 х - л/2 х; б) f(x) = 2х + cos (4х - π);
!в) f(x) = cos2x; г) fix) = sin2x -а/Зх
булса, аларда fix) - 0, fix) > 0 булырлык нокталарны та¬
быгыз.
a) f (х) = 1 -sinx; б) fix) = 2cos2x;
в) fix) —cosx; г) fix) = 3sinx
булса, f функцияләренең кимендә берсен формула аша
күрсәтегез.
§5.
Өзлексезлекне һәм чыгарылманы
куллану
18. Өзлексезлекне куллану
1. Функциянең өзлексезлеге. 14 нче пунктта сез нок¬
тада функциянең өзлексезлеге төшенчәсе белән таныштыгыз. Әгәр
функция ниндидер бер I аралыгының һәр ноктасында өзлексез
булса, аны I аралыгында өзлексез дип атыйлар (I аралыгы f функ
циясенең өзлексезлек аралыгы дип атала). Бу аралыкның бер нок¬
тасыннан аңа якын икенче ноктасына күчкәндә функция кыйммә¬
те аз үзгәрә; бу аралыкта f графигы өзлексез сызык тәшкил итә,
бу сызык турында аны «карандашны кәгазьдән аермыйча ясап
була» диләр. (Мәктәп курсында өйрәнелә торган өзлексез функция¬
ләр белән эш иткәндә бу һәрвакыт дөрес була.)
124 Чыгарылма һәм авы куллану
15 нче пунктта күрсәтелгәнчә, х0 нокта¬
сында дифференциалланучы функция бу
ноктада өзлексез була. Барлык вакланмалы-
рациональ һәм төп тригонометрик функ¬
цияләр үзләренең билгеләнү өлкәләренең
барлык нокталарында дифференциаллана-
лар. Димәк, бу функцияләр алда әйтелгән
нокталарның һәркайсында өзлексезләр.
Мәсәлән, f(x) = x2 функциясенең ту¬
рының барлык нокталарында, ә f(x) = у
функциясенең (-ео; 0) һәм (0; <ю) арала¬
рында дифференциаллануыннан бу функ¬
цияләрнең тиңдәш араларда өзлексез булулары килеп чыга.
Өзлексез функцияләрнең түбәндәге үзлеген күрсәтеп китик:
Әгәр дә f функциясе (а; Ъ) интервалында өзлексез
булып нульгә әйләнмәсә, бу интервалда ул даими
тамгасын саклый.
89 нчы рәсем
Бу раслауның күргәзмәле интерпретациясе бар. (а; Ь) интер¬
валында f(Xi) < 0, ә /(х2) >0 булырлык х, һәм х2 нокталары табы¬
лыр, дип уйлыйк.
Ул вакытта у = 0 турысы аерып торган Αίχ,;/(х,)) һәм
В(х2;/(х2)) нокталарын тоташтыручы өзлексез кәкре (/ функ¬
циясенең графигы) бу турыны (у = 0 турысын) бирелгән интер¬
валны ниндидер х3 ноктасында кисеп үтәр (89 нчы рәсем), ягъни
/(х3) = 0 булыр.
А һәм В нокталары (а; Ь) интервалы белән сурәтләнгән елганың
төрле ярларында урнашкан дип күз алдына китерик. Туристка,
А дан В га эләгү өчен, ниндидер бер урында елганы кичү кирәклеге
ачык. Ә бу шартка каршы килә: f функциясе (а; Ь) интервалында
нульгә әйләнми (тигез кыйммәт алмый).
2. Интерваллар методы. Бер үзгәрешле тигезсезлекләрне чишү
методы (интерваллар методы) өзлексез функцияләрнең бу пункт¬
та тикшерелгән үзлегенә нигезләнгән (бу үзлекне тулысынча исбат¬
лау математик анализ курсларында китерелә). Аны аңлатып китик.
f функциясе I интервалында өзлексез булып, бу интервалның
чикле сандагы нокталарында нульгә әйләнсен. Өзлексез функция¬
ләрнең югарыда күрсәтелгән үзлеге буенча бу нокталар I не һәр¬
кайсында өзлексез функция f даими тамгасын саклап калган ин¬
тервалларга бүләләр. Бу тамганы билгеләү өчен, функциянең һәр
интервалының нинди дә булса бер ноктасындагы кыйммәтен исәп¬
ләү җитә. 2 (
1 нче мисал. — > 0 тигезсезлеген чишик.
, хг-5х+6
f (χ) = —ί— функциясе (ул — вакланмалы-рациональ
функция) үзенең билгеләнү өлкәсендәге һәр ноктада өзлексез була
125 Чыгарылма һәм аны куллану
+ - + - +
о ооо ►
-1 12 3
90 нчы рәсем
Һәм -1, 1 нокталарында нульгә әйләнә. Бу функциянең билгеләнү
өлкәсе булып ваклаучының нульләреннән, ягъни 2 һәм 3 нок¬
таларыннан тыш, санлы туры тора. Бу нокталар -1 һәм 1 нок¬
талары белән бергә f ның билгеләнү өлкәсен 5 аралыкка бүләләр
(90 нчы рәсем), аларның һәркайсында f функциясе өзлексез һәм
нульгә әйләнми. Рәсемдә тиңдәш һәр интервалда f ның тамгасы
күрсәтелгән, аны f интервалның эчке нокталарындагы кыйм¬
мәтләре тамгаларын табу юлы белән билгелибез.
Тигезсезлеге төгәл тигезсезлек түгел, шуңа күрә -1 һәм 1
нокталары (функциясенең нульләре) тиңдәшле аралыкларга кер¬
теләләр. Рәсемгә карап, җавапны табарга мөмкин: тигезсез¬
лекнең чишелеше булып (-°°; -1]; [1; 2) һәм (3; «) аралыкларның
берләшмәсе тора.
2 нче мисал, х3 + 2х - 2 = 0 тигезләмәсе тамырларының
берсен 0,1 гә кадәр төгәллек белән табыйк.
/(х) = х3 + 2х - 2 = 0 функциясе өзлексез, шуңа күрә аның
очларында f төрле тамгалы кыйммәтләр алырлык 0,2 озынлы¬
гындагы кисемтә табу җитә, f (1) = 1 > 0, f (0) = -2 < 0, шуңа күрә
тигезләмәнең тамыры бар һәм ул [0; 1] кисемтәсендә урнашкан,
f (0, 6) = 0,63 + 2 · 0,6 — 2 — -0,584 < 0 һәм /(1) > 0, димәк, тамыр
[0,6; 1] кисемтәсендә ята. Ниһаять, /(0, 8) = 0,112 > 0, ә f (0, 6) < 0,
шулай итеп, тамырның [0,6; 0,8] кисемтәсендә ятуы ачыклан¬
ды. Хәзер без аны таба алабыз: 0,1 төгәллек белән х0 = 0,7.
3. Өзлексез булмаган функциягә мисал. Без моңа кадәр эш
иткән барлык функцияләр үзләренең билгеләнү өлкәләренең телә¬
сә кайсы ноктасында өзлексез иделәр. Ләкин, шулай булса да, бу
хәл теләсә кайсы функция өчен дөрес дип уйларга ярамый.
Мисал китерик, f (х) = (х} функциясен карап китик, биредә
{х} — х санының вакланмалы кисәге (/(х) = {х} ның графигы
91 нче а рәсемдә сурәтләнгән); абсциссалар күчәренең теләсә нинди
бөтен санлы ноктасын, мәсәлән, х = 2 не алыйк.
х0 ноктасында өзлексез функциянең төп үзлеге (Δχ -»0 өчен
Чыгарылма һәм аны куллану
f (x0 + Δχ) -» -> /(x0)) бу очракта үтәлми. Чыннан да, Δχ -> 0 булсын.
Әгәр Δχ > 0 булса {х0 + Δχ} нульгә якын. Әгәр дә Δχ < 0 булса,
(х0 + Δχ} кыйммәте 1 гә якын. Шул ук вакытта f (х) = {х} функциясе
х = п нокталарыннан үзгә булган барлык нокталарда өзлексез,
биредә п — бөтен сан.
f(x) = {x) функциясенең бу үзлеген аңлау 91 нче а рәсемен
караганнан соң читен түгел.
4. Өзлексез булып та, бирелгән ноктада дифференциалланмау-
чы функциягә мисал. Мондый функциягә /(х) = |х| (91 нче б рә¬
сем) мисал була ала, ул өзлексез, ләкин нульдә дифференциалланмый;
ί х, х^ 0 өчен,
η
I -х, х < 0 өчен
икәнлеген искә төшереп китик.
f(x) = |х| функциясенең теләсә нинди ноктада (шул исәптән
нульдә дә) өзлексез булуы ачык.
Бу функциянең графигын карап китик. х0 > 0 ноктасының
ниндидер тирәлегендә теләсә нинди х > 0 өчен функция х ка тигез,
шуңа күрә мондый нокталарда аның чыгарылмасы х' гә тигез,
ягъни х 0 булганда |х| = 1; х < 0 булганда |х| = -х булганлыктан,
х ның тискәре кыйммәтләре өчен |х| =-1; 0 ноктасында
/(х) = |х| функциясенең чыгарылмасы булмый.
Моны киресеннән чыгып исбат итик, /(х) = |х| ның нульдә
чыгарылмасы бар, ягъни Δχ -> 0 булганда ниндидер А саны¬
на омтыла, дип уйлыйк. Ул вакытта җитәрлек кадәр кечкенә |Δχ|
өчен ~ кыйммәтләре А га якын булырлар, шул исәптән Δχ ның
кечкенә кыйммәтләре өчен
Δχ > 0 булганда |1 - А| < 1 тигезсезлеге дөрес, моннан
—I I А · 1, ягъни
Д/(0) л !
—: А < 1 тигезсезлеге үтәлергә тиеш.
(1)
Δχ < 0 булганда |-1 — А| < 1 тигезсезлеге дөрес, моннан
-1 < -1 - А < 1, ягъни
-2<А<0. (2)
(1) һәм (2) тигезсезлекләре үзара капма-каршылар. Шулай
булгач, ну льда /(х) = |х| функциясенең чыгарылмасы була дигән
фараз итү дөрес булмаган.
Димәк,
1, х > 0 өчен,
х - 0 өчен булмый,
-1, х < 0 өчен.
127 Чыгарылма һәм аны куллану
Күнегүләр
241.— а) /(х) = х4 - х + 1;
б) /(Χ) = ·
х +1, х -1 өчен,
х2 - х, х > -1 өчен;
в) f(x) = ■
1 - х2, х < О
5 - 2x, х О
өчен,
өчен;
г) f (х) = 2х - х2 + х3
• булса, Xj = 0 һәм х2 = —1 нокталарында f функциясе өзлек¬
сез булырмы?
242. - Функцияләр өзлексез булган аралыкларны табыгыз:
а) / (х) = х8 - 2х2; б^<х> = £^
в) f (х) = 2х4 - Зх2 + 4; г) /'(х) = X*~S*+6
X ~ н
243. - Бирелгән тигезләмәнең [0; 1] аралыгында ятучы тамыры
барлыгын исбат итегез һәм аны (тамырны) 0,1 гә кадәр
төгәллек белән табыгыз:
а) 1,4 - 10х2 - х3 = 0; б) 1 4- 2х2 - 100х4 = 0;
в) х3 - 5х + 3 = 0; г) х4 + 2х - 0,5 = 0.
Тигезсезлекләрне чишегез (244—245).
244.- а)х2-5х + 4>0;
б)
<♦3
хг+4х-5
?0;
в) х2 - Зх - 4 С 0;
Γ)^Ζ£±6<0.
' х-2
245. а)
(х-2)(х-4) . 0
х2+2х-3 '
2хг +5* J
2 + 5х+ 4
. хг-2х-3
Г) <
' (х+3)(х-4)
246.
Функциянең билгеләнү
өлкәсен табыгыз:
а) Г(х) =
. ,, ч /х*+7х + 12
в) / (х) = ;
247.—a) f(x) =
4 - х, х < 4 өчен,
(х - т)2, х 4 өчен;
б)/(х) =
х2 -Зх .
х2-т ’
. .. . Зх2 + т, х< 0 өчен, 5-*
B)/(x) = i я л r)f(x) = ——
х + 2, х>0 өчен; х +т
булса, f функциясе т нинди кыйммәтләр алганда санлы
турыда өзлексез булыр?
128 Чыгарылма һәм аны куллану
Тигезсезлекләрне чишегез (248—249).
248. —а) х4 - 10х2 + 9 0; б)х4-8^7х2;
в) х4 - 5х2 + 6 > 0; г) 5х2 - 4 > х4.
249. - а) (х2- 1)(х + 4) (х3 - 8) ζ 0; б) Vx2 -4(х-3) < 0;
в) х!(3-х)(х + 2)>0; г) (х~^*(у5) > 0¬
250.— Функциянең билгеләнү өлкәсен табыгыз:
I a) f (х) = V9x - х3; б) f (х) = >/х2”-К;
в) / (х) = V16x - х3; г) /(х) = J1 - ^·.
19. Функция графигына орынма
1. Орынма. Функция графигына орынма төшенчәсе
белән сез инде таныш. х0 ноктасында дифференциалланучы /'функ¬
циясенең графигы х0 тирәсендә орынмадан аерылып тормый
диярлек, димәк, ул (х0; /(х0)) һәм (χ0 + Δχ; /(χ0 + Δχ)) нокталары
аша үтүче I кисүчесенең кисемтәсенә бик якын була. Мондый
кисүчеләрнең теләсә кайсысы графикның А(х0; /(х0)) ноктасы
аша үтә (92 нче рәсем). Бирелгән А ноктасы аша үтүче турыны
төгәл итеп бирү өчен, аның почмакча коэффициентын күрсәтү
җитә. Δχ —> 0 булганда, кисүченең почмакча коэффициенты
— f'(xo) гә омтыла (аны без орынманың почмакча коэффициенты
итеп кабул итәрбез). Орынма — Δχ —»0 булганда, кисүченең чик
торышы ул.
f'(x0) булмаса, орынма да булмый (у = |х| функциясенең (0; 0)
ноктасында булмаган кебек, 91нче б рәсем), яки ул вертикаль була
(у = 4х графигының (0; 0) ноктасында кебек, 93 нче рәсем).
Шулай итеп, / функциясенең х0 ноктасында чыгарылмасы
булуы графикның (х0; /(х0)) ноктасында аңа вертикаль булмаган
орынма булуы белән эквивалент, монда орынманың почмакча
92 нче рәсем 93 нче рәсем
Чыгарылма һәм аны куллану
коэффициенты f’(x0) гә тигез. Чыгарылманың геометрик мәгънәсе
шуннан гыйбарәт.
х0 ноктасында дифференциалланучы f функциясенең
графигына орынма — (х0; /(х0)) ноктасы аша үтүче
һәм почмакча коэффициенты f'(x0) булган туры ул.
f функциясенең графигына х,, х2, х3 нокталарында орынмалар
үткәрик (94 нче а рәсем) һәм алар абсциссалар күчәре белән төзе¬
гән почмакларны билгелик (ул почмаклар күчәрнең уңай юнәле¬
шеннән уңай юнәлештә турыга кадәр булган почмаклар). Без
ος почмагының кысынкы, а3 почмагының җәенке икәнлеген,
ә а2 почмагының нульгә тигез булуын күрәбез, чөнки I турысы
Ох күчәренә параллель. Кысынкы почмакның тангенсы уңай,
җәенкенеке — тискәре, tg 0 = 0, шуңа күрә
f (х,) > 0, f'(x2) = 0, f(xs) < 0.
Аерым нокталарда орынма үткәрү графикларның эскизларын
төгәлрәк төзү мөмкинлеген бирә. Мәсәлән, синус функциясенең
графигы эскизын төзү өчен, алдан 0; к һәм π нокталарында синус¬
ның чыгарылмасы тиңдәшле рәвештә 1; 0 һәм -1 гә тигез икән¬
леген табабыз. Аннары (0; 0), |* ; 1) һәм (π; 0) нокталары аша үтүче
һәм почмакча коэффициентлары тиңдәшле рәвештә 1,0 һәм-1
булган турылар төзибез (94 нче б рәсем). Бу турылар һәм Ох
турысы белән төзелгән трапециягә синусның графигын, ул х = 0 гә,
* гә һәм π гә тигез булганда, тиңдәшле турыларга орынырлык
итеп камыйсы гына кала.
Синусның графигы нуль тирәлегендә у = х турысыннан аеры¬
лып тормаганлыгын күрсәтеп китик. Мисал өчен, күчәрләрдә масш¬
таблар бер берәмлектә 1 см кисемтә туры килерлек итеп сайланган
булсын, sin0,5 = 0,479425, ягъни |sin0,5 -0,5| =0,02, сайлап
алынган масштабта бу 0,2 мм озынлыгындагы кисемтәгә туры
килә. Шуңа күрә у — sinx функциясенең графигы (-0,5; 0,5)
интервалында у = х турысыннан (вертикаль юнәлештә) 0,2 мм
дан артмаган зурлыкка тайпыла ала, ә бу якынча үткәрелгән сы¬
зыкның калынлыгына туры килә.
а) б)
94 нче рәсем
130 Чыгарылма һәм аны куллану
2. Орынма тигезләмәсе. Хәзер f функциясе графигының
А(х0; /(*(,)) ноктасындагы орынмасының тигезләмәсен чыгарыйк.
Почмакча коэффициенты /'(х0) булган туры тигезләмәсе мон¬
дый рәвештә була:
У = f'(xa)-x + b.
Ь ны исәпләү өчен, орынманың А ноктасы аша үтүеннән файда¬
ланыйк:
/(х0) = /'(х0) ·χ0 + Ь, моннан b = f(x0) — f'(x0) ‘X9, димәк, орынма¬
ның тигезләмәсе мондый:
У = f'(x0)-x - f'(x0)-x0 +
яки
У = f(*o) + Г (*(>)(* - X<:)· (1)
I 1 нче мисал, f (х) = x3 - 2x2 + 1 функциясе графигының
абсциссасы 2 булган ноктадагы орынма тигезләмәсен табыйк.
Бу мисалда х0 = 2, f(xQ) = f(x0) “ f (2) = 23 - 2 ·22 + 1 = 1, /'(·*)=
= Зх2 - 4х, f'(x0) — f '(2)= 3 ·22-4 - 2 = 4. Бу саннарны (1) тигезләмәгә
куеп, у = 1 + 4(х-2), ягъни у = 4х-7 тигезләмәсен табарбыз.
2 нче мисал, у ~ х2 параболасының абсциссасы х0 булган
ноктадагы орынма тигезләмәсен чыгарыйк.
у(х0) = Хо, ә у‘(*о) = 2х0 икәнлеге билгеле. Бу кыйммәтләрне
орынманың (1) тигезләмәсенә куеп табабыз: у = х% + 2х0(х - х0),
ягъни у - 2хох - х£. Мәсәлән, х0 = 1 өчен тигезләмәсе у = 2х - 1
булган орынма килеп чыга.
Параболага А (х0; х;) ноктасындагы орынманың Ох лар кү¬
чәре белән кисешү ноктасы Т ның координаталарын табыйк
(95 нче рәсем). Әгәр дә Т ноктасының координаталары булса
(х,; 0), Т ноктасы орынма өстендә ята (шуңа күрә аның коорди¬
наталары орынманың тигезләмәсен канәгатьләндерәләр), моннан
0 = 2х0Х] - χθ. х0 * 0 булса, Xj =
Табылган нәтиҗә параболага аның (түбәдән башка) теләсә нин¬
ди ноктасында орынма төзүнең гади ысулына китерә: моның өчен
А ноктасын очлары 0 һәм х0 булган Ох күчәре кисемтәсен урталай
бүлүче Т ноктасы белән тоташтыру җитә;
АТ турысы — эзләнелгән орынма. х0 = 0
булса, орынма Ох турысы була.
3. Лагранж формуласы, f графигының
(а; Ь) интервалыннан абсциссасы с булган
ноктасында орынмасы барлыгын, аның
А(а·, B(b; f(b)) нокталары аша үтүче
кисүчегә параллель булуының дөреслеген
күргәзмәле аңлату өчен чыгарылманың
геометрик мәгънәсеннән файдаланыйк.
АВ га параллель һәм графикның [а; б]
аралыгына тиңдәш булган өлеше белән ур¬
так нокталары булмаган I турысын карап
95 нче рәсем
131
Чыгарылма һәм аны куллану
китик. Бу I турысын, ул АВ га параллель калырлык итеп, f гра¬
фигына таба күчерик. Турының графикның бу кисәге белән уртак
нокталары килеп чыккан Zoторышын билгелик. 96 нчы а рәсемнән
мондый «беренче» уртак нокталарның теләсә кайсы 1а турысының
f графигына орыну ноктасы икәнлеге күренә. Бу ноктаның
абсциссасын с аша тамгалыйк. Ул вакытта /'(c) = tga, монда
a — /0 турысы белән абсциссалар күчәре арасындагы почмак.
Ләкин III АВ, шуңа күрә a почмагы АВ кисүчесенең авышу
почмагына тигез була, ягъни
Г(с)~ tga =
Шулай итеп, функция дифференциалланса, (a; Ь) интервалында
но =
булырлык се(а; Ь) ноктасын табып була (96 нчы б рәсем).
Бу формуланы Лагранж формуласы дип атыйлар.
Күнегүләр
251.— f функциясенең нинди нокталарында орынма:
а) горизонталь була;
: б) абсциссалар күчәре белән кысынкы почмак този;
! в) абсциссалар күчәре белән җәенке почмак төзи (97 нче
рәсем)?
252.- Аргумент нинди (абсциссалар күчәрендә билгеләнгән)
кыйммәтләр алганда, график аша бирелгән функциянең
чыгарылмасы (98 нче рәсем): а) нульгә тигез; б) нульдән
зуррак; в) нульдән кечерәк?
f функциясе графигының бирелгән М ноктасы аша үтүче
орынманың абсциссалар күчәренә авышу почмагы танген¬
сын табыгыз (253—254).
253. а) f (х) = х2, Λί (-3; 9);
в) f(x) = xs, М (-1; -1);
б)/(х) = |х8 - х, М(2;£);
г) f(x) = х2 +2х, М(1; 3).
132 Чыгарылма һәм аны куллану
У‘>
254.—a) /(x) = 2cosx,
16) f (х) - -tg x, Μ (π; 0);
в) f (х) = 1 + sin x, Λί(π;1);
г) /(x) = -cosx, Μ (-π; 1).
133 Чыгарылма һәм аны куллану
256.
f функциясе графигының абсциссасы х0 булган ноктадагы
орынмасының тигезләмәсен языгыз (255—256).
255.a) f(x) = I, х0 - -1, х0 = 1;
б) f(x) = 2х - х2, х0 = 0, х0 = 2;
в) /(х) = х2 + 1, х0 = 0, х0 = 1;
г) /(х) = х3- 1, х0 = -1, х0= 2.
а) f (х) - 3 sin х, х0 = J . х0 =■ π;
б) /(х) = tgх, х0 = *·, х0 =|;
в) f (х) = 1 + cos х, х0 - 0, х0 = ;
г) /(х) = -2sinx, х0 = -у, х0 = π.
f функциясе графигының алардагы орынмаларның абс¬
циссалар күчәренә параллель булган нокталарны табыгыз
(257—258).
257. -а) /(х) = х3 - Зх2 + Зх; б) f(x) = |х4 + 16х;
в) f(x) = Зх" - 6х2 + 2; г) /(х) = х3 - Зх + 1.
258. — a) f (χ) = 2cosx + х; б) /(х) - sin2x + 73х;
> в) /(х) - cos(x - г) /(х) « V2x-2sinx.
259. —; Функциянең графигы Ох күчәре белән нинди почмак ясап
кисешер?
Й а)/(х) - Зх - х3; б) f(x) ~ sin(x + ®|;
К в) f (х) - х2 - Зх + 2; г) f (х) = - cos х.
260.4· Функциянең графигы Оу күчәре белән нинди почмак төзеп
L кисешер?
|а)/(х)=^; б) /(x) = ltg(x-|);
|в)/(х) = |(х-1)2; г)Г(х) = 8т(2х + |).
20. Якынча исәпләүләр
/(х) = х7-2х« + 3х2-х + 3
функциясенең х0 = 2,02 ноктасындагы якынча кыйммәтен исәп¬
ләргә кирәк булсын, ди. f ның 2,02 гә якын булган х0 = 2 ноктасын¬
дагы кыйммәте җиңел табыла: f(2) = 13. f ның графигы 2 нокта¬
сындагы тирәлектә у = f(xa) + f'(x0)(x - х0) турысына — аңа абс¬
циссасы 2 булган ноктада үткәрелгән орынмага якын. Шуңа күрә
/(2,02) -- у (2,02). Шулай булгач, /'(х) = 7х6 - 12х5 + 6х - 1,
Г(х0) = /'(2) = 75 һәм /(х) = у(х) = 13 + 75 0,02 = 14,5.
Чыгарылма һам аны куллану
Калькуляторда исәпләүләр /(2,02) = 14,57995 нәтиҗәсен би¬
рәләр.
Гомумән, х0 ноктасында дифференциалланучы f функциясе
графигы, Δχ нульдән аз аерылып торса (графикның абсциссасы
х0 булган ноктасына үткәрелгән), орынмага якын була, ягъни кеч¬
кенә Δχ лар өчен
/<х) = /(хо) + Г(*о)А*· (1)
х0 ноктасы /(х0) һәм /'(хи) кыйммәтләре чагыштырмача җиңел
табыла алырлык булса, (1) формула /(х) ның х булганда, х„ гә
җитәрлек кадәр якын булганнары өчен якынча кыйммәтләрен
табарга мөмкинлек бирә. >/4,08 нең кыйммәтен исәпләгәндә,
х0 сыйфатында 4 санын алу бик табигый, чөнки 4,08 саны 4 кә
якын һәм х0 = 4 булганда f (х0) - 7хо һәм f' (χ0) = *— кыйм-
1
мәтен табу авыр түгел: f (4) = V4 = 2, /'(4) =
(1) формула буенча Δχ = 0,08 булганда табабыз:
74,08 «2 + | 0,08 = 2,02.
. 1 нче мисал. (1) формуладан
71 + Δχ « 1 + | Δχ (2)
якынча формуласын чыгарыйк.
f (х) = \[х, Хо =1 һәм χ = χ0 + Δχ=1 + Δχ дип алыйк. Ул ча¬
гында /(х0) = 71 = 1 һәм /'(х) = —г-, моннан /'(х0) = /'(1) = г, ·
... . . 2-jx J
(1) формула буенча
f (х) = 71 + Δχ * 1 +1 Δχ.
Аерым алганда, 71,θθ = 71 + θ,θθ = 1 + ^ ■ 0,06 = 1,03.
74,08 кыйммәтен шулай ук (2) формула буенча табып була:
74,08 = 2Τΐ?02 = 2(1 + j 0,02) = 2,02.
2 нче мисал. (1) формуладан
(1 + Δχ)η *= 1 + ηΔχ (3)
якынча формуласын чыгарыйк.
/(х) = х", х0 = 1 һәм χ = χ0 + Δχ=1 + Δχ дип алыйк, f (х0) = 1,
/'(х) = пхя 1 не табыйк, моннан /'(х0) = η. (1) формула буенча
/(х) = (1 + Δχ)η = 1 + ηΔχ.
Мәсәлән, Ι,ΟΟΙ100 = (1 + 0,001 )100 = 1 + 100 0,001 = 1,1.
1,001100 нең калькулятор ярдәмендә исәпләп табылган кыйм¬
мәте 1,10512 гә тигез.
135 Чыгарылма һәм аны куллану
3
нче
мисал.
I ..
θ og7aB кыйммәтен исәпләү өчен, п =
= -30, Δχ = - 0,003 булганда, (3) формуладан файдалану уңай:
—^■ = (1-0,003) 30 = (1+(-30) (-0,003)) =1+0,09 =1,09.
(1) формуланы еш кына башка элементар, мәсәлән, тригоно¬
метрик функцияләрнең якынча кыйммәтләрен исәпләү өчен дә
кулланалар. Мәсәлән, sin 1° ны исәпләү өчен f(x) = sinx, хо = О
дип алу уңай, монда Δχ = л (чөнки 1° =
1 oil \ 1 olJ /
Шулай булгач, /(х0) = sin 0 = 0, f'(x0) - cos 0=1 һәм
sinx = /(х0) + f'(x())Ax = 0 + 1 Δχ = Δχ,
ягъни sin 1° « * 0,017453 . sin 1° ның кыйммәтен калькулятор
ярдәмендә исәпләп, sinl° » 0,0174525 икәнлеген табабыз.
Күнегүләр
261.— (1) формула ярдәмендә f функциясенең х, һәм х2 ноктала¬
, рындагы якынча кыйммәтләрен исәпләгез:
а) / (х) = х* + 2х, Xj = 2,016, х2 = 0,97;
б) 7(х) = х5 - х1 2, х, = 1,995, х2 = 0,96;
в) / (х) = х3 - х, Xj = 3,02, х2 = 0,92;
г) f(x) = х2 + Зх, xf = 5,04, х2 = 1,98.
(1) һәм (3) формулалар ярдәмендә якынча кыйммәтләрне
табыгыз (262—263).
262. а) 1,002'°°; 6)0,995°; в) 1,03м0; г) 0,998м.
263. а) 71,004; б) 725,012; в) 7θ,997; г) 74.0016.
(1) формула ярдәмендә якынча кыйммәтләрне исәпләгез
(264—266).
264.— a) tg44Q; б) cos61°; в) sin 31е; г) ctg47°.
265.-a) cos(| + 0,04);
в) sin(£ + 0,03);
6) sin(|-0,02);
r) tg(| + 0,05).
r*l — ·
’ 2,0016s ’
r) '
' 0,994s
Чыгарылма һ»м аны куллану
21. Физикада һәм техникада чыгарылма
1. Чыгарылмавың механик мәгънәсе. Физика курсында хәрә¬
кәт тизлегенең ничек билгеләнгәнлеген искә төшерик. Иң гади
очракны карап китик: материаль нокта координаталар турысы
буенча хәрәкәт итә, хәрәкәт законы бирелгән, ягъни бу х нокта¬
сының координатасы t вакытыннан билгеле бер x(t) функциясе
булсын, t0 дән t0 + Δί га кадәр вакыт арасы өчен ноктаның күчүе
х (t0 + Δί) - х (ί0) = Δχ ка, ә аның уртача тизлеге
= £ (1)
га тигез.
Δί < 0 өчен дә (1) формула дөрес: күчү χ(ί0) - χ(ί0 + Δ0 “ _Δχ
ка, ә вакыт арасы зурлыгы -Δί га тигез.
Хәрәкәтнең характеры, гадәттә, мондый була: кечкенә At лар
өчен тизлек практик яктан караганда үзгәрми, ягъни зур төгәллек
белән хәрәкәтне тигез хәрәкәт дип санарга була (13 нче пунктта¬
гы мисалны карагыз). Икенче төрле әйткәндә, уртача тизлекнең
кыйммәте At —»0 булганда, ниндидер бер билгеле булган кыйммәт¬
кә омтыла, аны t0 вакыты моментында бу ноктадагы моменталь
тизлек υ (t0) дип атыйлар да инде. Шулай итеп,
At -> 0 булганда, ^(Δί) = ~ -♦ υ(ί0).
Ләкин чыгарылма билгеләмәсе буенча At —> 0 булганда,
дГ х
Шуңа күрә моменталь тизлек υ(ί) (бары тик) теләсә нинди
дифференциалланучы χ(ί) функциясе өчен генә билгеләнә дип
саныйлар, өстәвенә
v(t) = x'(i). (2)
Кыскача болай әйтәләр: координатаның вакыт
буенча чыгарылмасы тизлек була. Чыгарылманың
механик мәгънәсе шуннан гыйбарәт.
Моменталь тизлек уңай кыйммәтләр дә, тискәре кыйммәтләр
дә һәм, билгеле, 0 кыйммәте дә алырга мөмкин. Вакытның нинди
дә булса (it, t2) аралыгында тизлек уңай булса, нокта уңай юнәлеш¬
тә хәрәкәт итәр, ягъни x(t) координатасы вакыт үтү белән үсә,
әгәр дә o(t) тискәре булса, x(t) координатасы кими.
Хәрәкәтнең тизләнеше белән дә шундый ук хәл. Ноктаның
хәрәкәт тизлеге и вакыт t га карата функция. Бу функциянең
чыгарылмасы хәрәкәтнең тизләнеше дип атала:
a = v'(t).
Кыскача болай әйтәләр: тизлекнең вакыт буенча
чыгарылмасы тизләнеш була.
137 Чыгарылма һәм аны куллану
η I нче мисал. Материаль ноктаның түбән төшүен карап
китик. Координаталар турысы аска таба вертикаль юнәлтелеп,
материаль ноктаның башлангыч торышы 0 гә туры килсә, физика¬
дан билгеле булганча, x(t) = у булыр. Ул чакта вакытның t мо¬
ментында ноктаның төшү тизлеге
υ = (f)' = St,
ә a = (gt)' = g тизләнеше даими зурлык булыр.
Гомумирәк очракны карап китик.
2 нче мисал. Туры буйлап хәрәкәт итүче нокта координата-
сының вакытка бәйләнеше түбәндәге формула аша күрсәтелсен:
х(0 = f + vot + х0,
монда а * 0, и0 һәм х0 — даими зурлыклар. Хәрәкәтнең тизлеген
һәм тизләнешен табабыз.
Бу хәрәкәтнең тизлеге мондый була:
v = x'(t) = t2 +vot + xo) = 2-|i + y0 = at + v0.
Хәрәкәт тизлеге вакытка карата функция икәнлеге билгеле,
шуңа күрә без бу хәрәкәтнең тизләнешен таба алабыз: о'(О“
= (at + υ0)' = а. Без квадратик законга буйсынган хәрәкәтнең тиз¬
ләнеше даими һәм а га тигез икәнлеген күрәбез, α > 0 булса, хә¬
рәкәт тигез тизләнешле, әгәр дә α < 0 булса, тигез әкренәюче була.
ов = о(0), ә х0 = х(0) икәнлеген дә күрсәтеп китик.
III бүлектә без туры буенча хәрәкәт иткәндә, тизләнеш даими
булса, хәрәкәтнең
х (t) = f ί2 + + Xq
квадратик законына буйсынганын исбатларбыз, биредә —нокта¬
ның башлангыч тизлеге, х0 — башлангыч координата.
► У = f(x) — ирекле, дифференциалланучы функция булсын. Ул
вакытта без материаль ноктаның координаталар турысы буенча
х - f(t) законына буйсынган хәлдә хәрәкәт итүен карап китә ала¬
быз. Чыгарылманың механик мәгънәсе дифференциаль исәп¬
ләүнең теоремаларын күргәзмәле интерпретацияләргә мөмкинлек
бирә.
М 3 нче мисал, f һәм һ ике дифференциалланучы функция¬
ләр булсын. Туры буенча түбәндәге (чагыштырма) хәрәкәтне карап
китик. Координаталарның поезд белән бәйләнгән хәрәкәтчел
системасы бирелсен, аның башы (машинист кабинасы) коорди¬
наталарның хәрәкәтсез системасы башына (станциягә) карата
х, = f(t) законы буенча хәрәкәт итсен. Координаталарның хәрәкәт¬
чел системасында материаль нокта х2 = һ (ί) законы буенча хәрәкәт
итә. Ул вакытта бу ноктаның координаталарның хәрәкәтсез сис¬
темасына карата х координатасы х = х, + х2 гә тигез, ә аның тиз-
138
Чыгарылма һәм аны куллану
леге υ(ί) = x'(t) була. Икенче яктан, тизлекләрне кушу законы
буенча и (t) — υ,(Ο + v/t) = *i(t) + xi(t). Шулай итеп, без чыгарыл¬
маның механик мәгънәсе ярдәмендә билгеле булган
(/ + АГ-Г + Л'
формуласын таптык.
4 нче мисал. Материаль нокта координаталар турысы
буенча х = f(t) законы буенча хәрәкәт итсен. Ул вакытта аның
[а; д] аралыгындагы урта тизлеге
vp ' b-a
га тигез.
y(t) моменталь тизлеге [α; ί>] арасы нокталарында һәрвакыт¬
та да уртачасыннан кечерәк (зуррак) була алмый. Димәк, ниндидер
ί0€ [α; 6] моментында моменталь тизлек уртача тизлеккә тигез була,
ягъни [а; б] аралыгында
v(t0)=Ht0)=^:a/(a) (з)й
булырлык t0 табыла.
Без Лагранж формуласының механик интерпретациясен
таптык.
2. Чыгарылма куллануга мисаллар. Функцияләрнең физик
күренешләрне характерлаучы чыгарылмалары ярдәмендә башка
физик зурлыклар да бирелә ала. Мәсәлән (билгеләмә буенча), егәр¬
лек ул эшнең вакыт буенча табылган чыгарылмасы була. Мисал
карап китик.
S 5 нче мисал. Бериш булмаган таякчык бирелгән, естәвенә
аның озынлыгының теләсә нинди I кисәгенең массасы т (/)
билгеле булсын (I таякчыкның билгеләнгән башыннан саналсын).
Таякчык бериш булмаса да, аның зур булмаган (I дан I + Δ/ га
кадәр) кисәгенең тыгызлыгы якынча бер үк дип уйлау
табигый, естәвенә, Δ/ никадәр кечкенә булса, тыгызлык бу арада
шулкадәр кечкенә чикләрдә үзгәрер. Шуңа күрә таякчык тыгыз¬
лыгының I га бәйле буларак таралышы характеристикасы итеп
d(l) = т’(1) сызыкча тыгызлыгын кабул итәләр.
6 нчы мисал. Механика мәсьәләләренең күбесендә нокта¬
ның яссылыктагы яки пространстводагы хәрәкәте карала. Ул ва¬
кытта тизлек вектор зурлык була. Әгәр дә ноктаның t моментын¬
дагы координаталары x(t) һәм y(t) га тигез булсалар, тизлек
векторы p(f) ның координаталары х'(0 һәм y'(t) га тигез була
икән. Моннан файдаланып, кинематика нигезендә тригонометрик
функцияләрнең чыгарылмалары формулаларын чыгарып була.
Радиусы 1 булган әйләнә буенча сәгать угына каршы юнәлеш¬
тә 1 гә тигез почмакча тизлек белән тигез хәрәкәт карап китик
(99 нчы рәсем). Ул чагында вакытның ί моментында М ноктасы¬
ның координаталары мондый була: х (0 = cos t, у (ί) = sin t. Физика
139 Чыгарылма һам аны куллану
У
99 нчы рәсем
курсыннан сезгә билгеле булганча, тизлек векторы υ (f) әйләнәгә
орынма юнәлешендә булып, аның озынлыгы 1 гә тигез (|о| = wR =
— 1 ·1 = 1). Димәк, бу вектор координаталары cos (t + " | — - sin t
һәм sin (t + ' | — cost булган OP, + s векторы белән тәңгәл килә.
Икенче яктан, u(t) векторының координаталары тиңдәшле рә¬
вештә x'(t) (ягъни cos't) һәм y'(t) (ягъни sin't) га тигез. Безгә
таныш булган формулалар табылды:
cos't = -sin t, sin'i = cost.
7 нче мисал. Параболаның оптикада һәм техникада кул¬
ланыла торган үзлеген чыгарыйк.
у — ах2 параболасын Оу күчәре тирәсендә әйләндерүдән барлык¬
ка килә торган өслек әйләнү параболоиды дип атала. Параболоид¬
ның эчке өслеге — көзгеле өслек, һәм бу параболик көзге Оу кү¬
чәренә параллель булган яктылык нурларының бәйләме белән
яктыртыла дип күз алдына китерик.
Бу көзгенең Оу күчәре аша үтүче а яссылыгы белән төзелгән
кисемен карап китик. Бу кисем у = х2 параболасы кебек үк пара¬
бола була (Ох күчәрен кисем яссылыгында сайлыйбыз, a = 1). Оп
тика законнары буенча яктылыкның кайтарылган нуры <х яссы¬
лыгында ятачак, өстәвенә бу нур параболага орынма белән төшүче
МА нуры ясаган почмак белән тигез почмак төзер (100 нче рәсем).
Без Оу күчәренә параллель барлык нурларның чагылганнан
соң Оу күчәренең бер үк ноктасында кисешүләрен исбат итәрбез.
Чагылган ирекле нурның Оу күчәре белән кисешү ноктасын
F аша тамгалыйк. АТ турысы параболага А ноктасында орынма
булыр. Яктылыкның чагылдыру законнарыннан (100 нче рәсем)
/ТАМ - /FAP икәнлеге шунда ук килеп чыга. Ләкин МА нуры
Оу күчәренә параллель, шуңа күрә /FPA = /ТАМ. Димәк, /FPA =
1^0 ‘ Г 1.11 .ф1Л ,·* 1ам< I·»’ WV. i.iail V
= Z.FAP, ягъни FPA өчпочмагы — тигезьянлы һәм FA = FP. А (х0; у0)
ноктасы парабола өстендә ята, шуңа күрә у0 = xj. АТ орынмасының
тигезләмәсе у = 2хох - х£ рәвешле була. Аннан Р ноктасының ур
ординатасын табабыз. Ул ур = 2х0 0 - х£, ягъни ур = -</а. F нокта¬
сының ординатасын у дип тамгаласак, FP = у + yQ булыр. Озынлык
FA = у''хо + (Уо - у)2, шуңа күрә (FA — FP икәнлеген искә төше¬
рик) (у + р0)2 - xl + (у0 - у)2 тигезлеге дөрес, ягъни у2 + 2уу0 + у2 =
= (/ο + ^ό-2(/ί/» + ί/2> моннан ±ууй-у0 һәм (уа*Ъ булганлыктан)
Шулай итеп, параболик көзгенең күчәренә параллель булган
барлык нурлар чагылганнан соң бер ноктага җыела, ул ноктаны
параболик көзгенең фокусы дип атыйлар (F ноктасын шулай ук
у = х2 параболасының фокусы дип атыйлар).
Параболик телескопларның төзелеше бу үзлеккә нигезләнгән.
Ерак йолдызларның нурлары безгә параллель бәйләм рәвешендә
килеп җитә. Параболик телескопны ясап, аның фокусына фото¬
пластинка куйсак, без йолдыздан килгән яктылык сигналын кө¬
чәйтү мөмкинлегенә ирешәбез. Радиосигналларны көчәйтү мөм¬
кинлеген биргән параболик антенналар эшләү дә шушы ук прин¬
ципка нигезләнгән.
Параболик көзге фокусында яктылык чыганагы урнаштырсак,
бу чыганактан килүче нурлар, көзгенең өслегеннән чагылганнан
соң таралмыйча, көзгенең күчәренә параллель булган тар бәйләмгә
җыелалар. Бу факт прожекторлар һәм фонарьлар, төрле проектор¬
лар ясаганда кулланыла, аларның көзгеләрен параболалар форма¬
сында эшлиләр.
Күнегүләр
267. — Материаль нокта х (ί) = - -t3 + 2t2 + 5t законы буенча туры¬
сызыклы хәрәкәт итә.
а) Хәрәкәтнең тизлеген t вакытының теләсә нинди момен-
I тында исәпләү өчен, формула чыгарыгыз, б) t = 2с ка тигез
S моменты өчен тизлекне табыгыз. (Күчү метрларда үлчәнә.)
в) Хәрәкәт башланып ничә секунд үткәч, нокта туктап ка¬
лыр?
268. - Материаль нокта x(t) = t3 - 4t2 законы буенча турысызык¬
лы хәрәкәт итә. t = 5с моменты өчен тизлекне һәм тизлә¬
нешне табыгыз. (Күчеш метрларда үлчәнә.)
269. - Җисем үз күчәре тирәли <p(t) = 3t2 - 4t + 2 законы буенча
әйләнә. Ирекле t моментында һәм i = 4 булганда, почмакча
тизлек ω(0 ны табыгыз (φ (t) — радианнарда үлчәнгән
борылу почмагы, ω (f) — секундына радиан белән үлчәнгән
тизлек, t — секундларда үлчәнгән вакыт).
141 Чыгарылма һәм аны куллану
276. -
I
■
|
277. -#
S
I
278. у
270. — Маховик тоткарлау нәтиҗәсендә t вакыт эчендә φ (t) = 4t -
g - 0,3t2 почмакка борыла. 1) Вакытның t = 2с моментында
в маховикның почмакча әйләнү тизлеге ω(ί) ны; 2) вакыт-
I ның кайсы моментында аның әйләнүдән туктаганын табы-
I гыз. (ω(0 — радианнар белән үлчәнгән почмак, t — секунд-
I лар белән үлчәнгән вакыт.)
271. — Нокта x(t) = 2ί3 + t - 1 законы буенча туры сызык буйлап
хәрәкәт итсен. Вакытның t моментында тизләнешне табы¬
гыз. Вакытның кайсы моментында тизләнеш a) 1 см/с2;
б) 2 см/с2ка тигез булыр? (x(t) — сантиметрларда үлчәнгән
күчү, t — секундларда үлчәнгән вакыт.)
272. — Нокта, х (0 = - -g- + 3t2 - 5 законына буйсынып, туры сызык
буйлап хәрәкәт итсен (вакыт — секундлар, координата метр¬
лар белән үлчәнә), а) Ноктаның тизләнеше нульгә тигез
булган вакытның t моментын; б) бу моментта нокта нинди
тизлек белән хәрәкәт иткәнен табыгыз.
273. — Нокта, х (t) = -Jt законына буйсынып, туры сызык буйлап
хәрәкәт итә. Аның тизләнеше тизлекнең кубына пропор¬
циональ икәнлеген күрсәтегез.
274. — х(0 = 2i3 - t2 законы буенча турысызыклы хәрәкәт итүче
т массалы материаль ноктага, t = 2 булганда, тәэсир итүче
F көчен табыгыз.
275. — Массасы 2 кг булган җисем х(/) = t1 + t + 1 законы буенча
туры сызык буйлап хәрәкәт итә. х координатасы — санти¬
метрлар белән, вакыт секундлар белән үлчәнә, а) Тәэсир
итүче көчне; б) хәрәкәт башланып 2 секундтан соң җисем¬
нең кинетик энергиясе Е ны табыгыз.
Озынлыгы 20 см булган АВ таякчыгының А ноктасыннан
I (см) ераклыкта урнашкан теләсә нинди С ноктасы өчен
таякчыкның АС кисәге массасы граммнарда т(1) = 31г -I- 5(
формуласы аша табылуы билгеле булсын, а) АВ кисемтәсе¬
нең уртасында; б) таякчыкның В очында сызыкча тыгыз¬
лыкны табыгыз.
Ике материаль нокта туры сызык буйлап xjt) = 4t2 - 3
һәм x2(i) = t3 законнары буенча хәрәкәт итә. Кайсы вакыт
аралыгында беренче ноктаның тизлеге икенчесенең тизле¬
геннән зуррак булыр?
0 пунктыннан араларындагы почмак 60° ка тигез булган
ике нур буенча ике җисем: берсе 5 км/сәг тизлек белән —
тигез, икенчесе s(t) = 2t2 + t законы буенча хәрәкәт итә.
Алар бер-берсеннән нинди тизлек белән ераклашалар? (а —
километрлар, t — секундлар белән үлчәнә.)
142 Чыгарылма һәм аны куллану
§6.
Функцияне тикшергәндә чыгарылма
куллану
22. Функциянең үсүе (кимүе) билгесе
6 нчы пунктта без функцияләрне тикшерүнең төп
мәсьәләләреннән берсе бу функциянең үсә яки кими торган
аралыкларын табу икәнлеген күреп киттек. Мондый тикшерүне
чыгарылма ярдәмендә җиңел башкарып була. Тиешле раслаулар¬
ны әйтеп китик.
.1* >. . ί» ■ ■
Әгәр da I интервалының һәр ноктасында
Г (х) > 0 булса, f функциясе I дә үсә.
Ф V ■! К IJ. ϋ *·. М *
I интервалының һәр ноктасында f'(x) < 0 булса,
f функциясе I да кими.
Бу билгеләрне исбатлау Лагранж формулаларына нигезләнеп
алып барыла (19 нчы пунктны карагыз). Интервалда теләсә нинди
х, һәм х2 саннарын алыйк, х, < х2 булсын. Лагранж формуласы
буенча
H/J-ZUD (1)
д3 * Х1
булырлык се(Хр х2) саны бар. с саны I интервалына керә, чөнки
хт һәм хг нокталары I гә керәләр, хе1 өчен f’(x) > 0 булса, f'(c) > 0,
һәм шуңа күрә f ix^ < /(х2) бу (1) формуладан килеп чыга, чөнки
х2 - х, > 0. Шулай итеп, I дә f функциясенең үсүе исбатланды.
Әгәр хе/ өчен f'(x) < 0 булса, /'(с) < 0, һәм шуңа күрә f(xx) > f(x2)
бу (1) формуладан килеп чыга, чөнки x2-Xj>0. Шулай итеп,
/ дә f функциясенең кимүе исбатланды.
Бу билгеләрнең күргәзмәле мәгънәләре түбәндәге физик фикер
йөртүләрдән ачыкланыр (ачыклык өчен үсү билгесен карап китик).
Ординаталар күчәре буенча хәрәкәт итүче нокта ординатасы
вакытның ί моментында у - f(t) булсын. Ул чакта вакытның
t моментында бу ноктаның тизлеге f'(t) га тигез булыр (21 нче
пунктны кара). I аралыгында вакытның теләсә нинди моменты
өчен f'(t) > 0 булса, нокта ординаталар күчәренең уңай юнәлешен¬
дә хәрәкәт итәр, ягъни ί] < ί2 булса, /(М < Ә бу α функция¬
сенең I аралыгында үсүен аңлата.
143
aapM.iHn һәм алы куллану
1 нче мисал. / (х) = х - хэ функциясенең үсү (кимү) ара¬
лыкларын табыйк һәм аның графигын төзик.
Бу функция барлык реаль саннар күплегендә билгеләнгән.
f'(x) = 1 - Зх1 2 тигезлегеннән 1 - Зх2 > 0 булса, f'(x) > 0. Бу тигез¬
сезлекне интерваллар методы белән чишеп (101 нче а рәсем),
( ’77з)
интервалында f'(x) > 0 һәм, димәк, бу интервалда f ның
үскәнен белербез.
Шуңа охшаш рәвештә
-ое; -U һәм
х I аралыкларында
f'(x) < 0, шуңа күрә бу аралыкларда f кими. Хәзер f ның
һәм 4- нокталарындагы кыйммәтен исәплик:
■у о
73
z(__14 = __L _/_ 1 V β 2 .
' \ 7з/ ,з \ 7з/ зтз ’
(1 9 ί , 1 2
- һәм NI —; ——
λ/3 3ν3 / \ ч*3 Зу'З
X)
73 /
Һәм 1Ч=;оо] аралыкларында кимүче функциянең графигын төзик
V I
(101 нче б рәсем).
Рәсемнән күренгәнчә
1 . 1
Зз ’ 7з
нокталарын билгелик,
f функциясе
7з ’ Taj аРалыгында үсү46, (-«;
Һәм 4^- нокталарында өзлексез
кисемтәсендә үсә, ә
-4; 001 аралыкларында кими.
/
һәм
101 нче рәсем
1 нче искәрмә. Әгәр f функ¬
циясе үсү (кимү) аралыгының кай¬
сы да булса бер очында өзлексез бул¬
са, ул вакытта бу ноктаны әлеге ара¬
лыкка кертәләр (1 нче мисалдагы
- η һәм нокталары кебек).
Без бу фактны исбатламыйча гы¬
на кабул итәрбез.
2 нче искәрмә. /'(•г)>0һәм
f'(x)<0 тигезсезлекләрен чишү
өчен, интерваллар методын (Дарбу
теоремасын) куллану уңай була:
аларда чыгарылма 0 гә тигез яки ул
144 Чыгарылма һәм аны куллану
булмаган нокталар f функциясенең билгеләнү өлкәсен аларның
һәркайсында f даими тамга саклый торган аралыкларга бүләләр.
(Бу факт математик анализ курсында исбат ителә.) /' ның кыйм¬
мәтен аралыкның нинди дә булса ноктасында исәпләп, тамганы
билгеләп була.
В 2 нче мисал, f (х) - 2х + функциясенең үсү (кимү) ара¬
лыкларын табыйк һәм аның графигын төзик.
Бирелгән функциянең билгеләнү өлкәсе булып (-°о;О) һәм
(0;«) аралыклары берләшмәсе тора; /*(х) = 2-р·; шуңа күрә
х - 1 булганда, f'{x) = 0. 0 һәм 1 нокталары f функциясенең
билгеләнү өлкәсен өч аралыкка: (-°°; 0), (0; 1) һәм (1; «) аралыкла¬
рына бүләләр. 2 нче искәрмә буенча, аларның һәркайсында
f үзенең даими тамгасын саклый. Бу аралыкларның һәрберсендә
чыгарылманың тамгасы 102 нче а рәсемдә күрсәтелгән.
Шулай булгач, бирелгән функция 0) һәм (1; ») аралыкла¬
рында үсә. f функциясе 1 ноктасында өзлексез, шуңа күрә бу
ноктаны (1 нче искәрмә нигезендә) f функциясе үскән аралыкка
кертергә мөмкин.
Нәтиҗәдә f ның (-»; 0) һәм [1; °0) аралыкларында үскәнле¬
ген табабыз. Аннары (0; 1) интервалында f'(x) < 0 һәм шуңа күрә
f (1 нче искәрмәне искә алганда) (0; 1 ] аралыкта кими.
0 ноктасы D (/) ка керми, ләкин, х 0 гә омтылганда, кушы¬
лучысы чиксез үсә. Шуңа күрә / ның кыйммәтләре дә чиксез
үсә. 1 ноктасында функция 3 кә тигез кыйммәт ала.
Хәзер координаталар яссылыгында Λί(1; 3) ноктасын билге¬
лик һәм (—оо; 0), [1; ■») аралык¬
ларында үсүче, ә (0; 1] аралыкта
кимүче функциянең графигын сы¬
зыйк (102 нче б рәсем).
3 нче мисал, /(х)= -2х +
+ sin х функциясенең үсү (кимү)
аралыкларын табыйк.
Функция барлык санлы турыда
билгеләнгән. Аның чыгарылмасы
мондый була:
f'(x) = -2 + cosx.
IcosxI С 1 булганлыктан, бар¬
лык реаль х лар өчен f'(x) < 0 булуы
җиңел табыла. Ә бу f (х) = -2х + sin х
функциясенең барлык санлы туры¬
да кимегәнлеген аңлата.
145 Чыгарылма һәм аны куллану
279. -
280. -
281. -
282. -
283. -
284. -
285. -
286. -
Күнегүләр
Функцияләрнең үсү һәм кимү аралыкларын табыгыз
(279—281).
а)/(х) = 3-|х; б) f(x) = -х2 + 2х-3;
в) f (х) - 4х - 5; г) f (х) - 5х2 - Зх + 1.
а)Г(х) = -| + 1; б) /(х) = х2(х - 3);
в)Нх) = ^; г) /(х) = х3-27х.
а) /(х) = 12х + Зх2 - 2х3; б) /(х) = 4-х4;
в) /(х) = х(х2-12); г)Г(х) = ^.
Түбәндәге шартларны канәгатьләндерүче f функциясе
графигының эскизын төзегез:
а) D(f) = [-2; 5], f'(x) > 0, хе (-2; 5) өчен;
б) D(f) = [1; 6], Λ(χ) < 0, хе(1; 3)U(3; 6), Г(3) = 0 өчен;
в) D(f) = [-2; 5], f'(x)> 0, хе(-2; 1)U(1; 5), /'(1) = 0 өчен;
г) D(f) = [1; 6], f'(x) < 0, хе(1; 6) өчен.
Функцияләрнең үсү һәм кимү аралыкларын табыгыз
аларның графикларын төзегез (283—284).
а) /(х) = х3 + Зх3 - 9х + 1; б) f(x) = 4х3 - 1,5х4;
в) /(х) = 2 + 9х + Зх2 - х3; г) /(х) = х4 - 2х2.
а> /’<χ) = 2-ό^Η: б) Г(х) = |х-3|-2;
в)/(х) = 8х2-х4; г) fix) = II 1|.
f функциясенең R да үсүен, ә g функциясенең R да кимүен
исбат итегез:
a) f (х) = Зх + cos 2х; б) g (х) = - -у - х;
в) f (х) = х7 + 2х5 +3; г) g (х) = -4х + sin х.
Бирелгән Pj һәм Р2 аралыкларының һәркайсында тигезлә¬
мәнең бары тик бер генә тамыры булуын исбат итегез:
а) х3 - 27х + 2 = 0; Р, - [-1; 1], Р2 = [4; 6];
б) х4 - 4х - 9 = 0; Pj = [-2; 0], Р2 - [2; 3];
в) х4 + 6х2 - 8 = 0; Р, = [-2; -1], Р2 = [1; 2];
г) -1 + Зх2 - х3 = 0; Pj = [-2; 0]; Р2 = [2; 3].
146 .
1игарылма һәм аны куллану
23. Функцияләрнең критик нокталары, аның
максимумнары һәм минимумнары
Без f'(x)> 0 һәм булган аралыкларда функ¬
циянең үзен тотышын карап киттек. Чыгарылма булмаган яки
ул нульгә тигез булган функциянең билгеләнү өлкәсендәге эчке
нокталары бу функциянең критик нокталары дип атала. Ул
нокталар, функциянең графигын төзегәндә, зур роль уйныйлар,
чөнки бары тик алар гына функциянең экстремум нокталары
була ала (103 һәм 104 нче рәсемнәр). Тиешле раслауны әйтеп
китик, аны Ферма теоремасы (француз математигы Пьер
Ферма хөрмәтенә) дип атыйлар.
Э к с т р е м у м н ы ң кирәклек билгесе.
Әгәр х0 ноктасы f функциясенең экстремум нок¬
тасы булып бу ноктада аның чыгарылмасы бул¬
са, ул нульгә тигез: = 0-
f'(x) > 0 очрагын карап китик. Чыгарылманың билгеләмәсе
буенча х —> х0 булганда, чаГыштырмасы f'(x0) уңай са¬
нына омтыла, димәк, ул үзе дә хи гә җитәрлек кадәр якын булган
барлык х лар өчен уңай була. Мондый х лар өчен
f(x) - f(x0) > θ
X-Xq '
Һәм, димәк, х0 нең ниндидер тирәлегендәге барлык х > х0 өчен
fix) > /(х0). Шуңа күрә х0 максимум ноктасы була алмый.
Әгәр х<хп булса, /(х) < /(х0) һәм, димәк, χΌ ноктасы f ның
минимум ноктасы да булмый.
f'(x)<f) очрагы да шулай ук тикшерелә.
Ферма теоремасының экстремум булу өчен кирәкле шарт кына
булуын кисәтеп үтү зур әһәмияткә ия: хп ноктасында чыгарыл¬
маның нульгә әйләнүеннән функция бу ноктада экстремумга ия
дип әйтү дөрес булмас иде. Мәсәлән, f(x) = x3 функциясенең чы¬
гарылмасы 0 ноктасында нульгә тигез, ләкин функциянең бу
ноктада экстремумы юк (105 нче рәсем).
103 нче рәсем 104 нче рәсем
147 Чыгарылма һәм аны куллану
Хәзергә кадәр без чыгарылмалары нульгә тигез булган критик
нокталарны тикшердек. Чыгарылмалары булмаган критик нокта¬
лар да бар, аларны да карап үтәргә кирәк. (Мәсәлән, 0 ноктасының
у - функциясе өчен критик нокта булмаганлыгын күрсәтеп
китик: бу ноктада чыгарылма юк, ләкин ул билгеләнү өлкәсенең
эчке ноктасы булмый.) Бу нокталарда функциянең экстремум-
нары булырга да, булмаска да мөмкин.
I 1 нче мисал, /(х) = |х| функциясен тикшерик (106 нчы
рәсем). 0 ноктасында бу функциянең чыгарылмасы юк. Димәк,
бу нокта — критик нокта. 0 ноктасында функциянең минимумы
булуы ачык.
2 нче мисал. f(x) = 2х + |х| функциясен карыйк (107 нче
рәсем). Графиктан 0 ноктасында бу функциянең экстремумы бул¬
мавы күренә. Бу ноктада функциянең чыгарылмасы да юк.
Чыннан да, f функциясенең 0 ноктасында чыгарылмасы бар
дип уйласак, /(х) - 2х ның да 0 дә чыгарылмасы булыр иде. Ләкин
f (х) - 2х = I х I, ә I х I функциясе 0 ноктасында дифференциаллан-
мый (18 нче пунктны карагыз), каршылык килеп чыкты.
Димәк, f функциясенең 0 ноктасында чыгарылмасы юк.
Ферма теоремасыннан функциянең экстремум нокталарын та¬
бу өчен, беренче чиратта аның критик нокталарын табарга кирәк
икәнлеге килеп чыга. Тикшерелгән мисаллардан күренгәнчә, би¬
релгән критик ноктаның экстремум ноктасымы, юкмы икәнлеген
белү өчен, өстәмә тикшерү үткәрергә кирәк була. Шуның белән
бергә, еш кына ноктада экстремумның булуы өчен түбәндәге җи¬
тәрлек шартлардан файдалану ярдәм итә.
Функциянең максимумы билгесе Әгәр
f функциясе х0 ноктасында өзлексез, э (а; х0) ин¬
тервалында f'(x0) > 0 һәм (х0; 6) интервалында
f'(x0) < 0 булса, х0 ноктасы f функциясенең макси¬
мум ноктасы була.
Теореманы гадирәк итеп әйтсәк, куллану өчен уңайрак булыр.
Чыгарылма х0 ноктасында тамгасын плюстан минус¬
ка үзгәртсә, х0 максимум ноктасы була.
148
Чыгарылма һәм аны куллану
Исбатлау. f'(x)>0 чыгарылмасы (α; х0) интервалында,
ә / функциясе х0 ноктасында өзлексез, димәк (22 нче пунктны
кара), f функциясе (а; х0] аралыкта үсә һәм шуңа күрә (а; х0)
интервалындагы барлык х лар өчен f(x)<f(x0).
[хс; Ь) аралыгында функция кими (исбатлау алдагыга охшаш
итеп алып барыла) һәм шуңа күрә (х0; Ь) интервалындагы барлык
х лар өчен f(x) < f(x0).
Шулай итеп, (а; Ь) интервалындагы барлык х*х0 өчен /(х)<
< f (х0), ягъни х0 ноктасы f функциясенең максимум ноктасы була.
Максимум билгесенең бик гади механик мәгънәсе бар. Без
f(x) ул — Оу күчәре буйлап хәрәкәт итүче ноктаның вакытның
х ноктасындагы координатасы, ә /'(х) — ноктаның бу моменттагы
тизлеге дип саный алабыз. Шарт буенча вакытның х0 дән алдан
килүче аралыгында нокта тизлеге уңай. Шуңа күрә бу вакыт эчен¬
дә нокта, уңай юнәлештә хәрәкәт итеп, Оу күчәре буенча f(xa) нок¬
тасына кадәр күтәрелә, ягъни х <х0 булганда, f(x) </(х0). Нокта х0
моментында бер мизгелгә туктап тора (вакытның бу моментында
аның тизлеге нульгә тигез була яки анык түгел), аннан соң ул
күчәр буйлап төшә башлый (шарт буенча f'(x) тизлеге, х > х0 бул¬
ганда, нульдән кечерәк), ягъни / (х) < /(х0). Шулай итеп, х0 тирәле¬
гендә f(x)<f(x0) һәм х0 ноктасы — максимум ноктасы.
Функциянең минимумы билгесе, fФунк¬
циясе х0 ноктасында өзлексез, э (а; х0) интерва¬
лында f(x0) < 0 һәм (х0; 6) интервалында f’(x0) > 0
булса, х0 ноктасы f функциясенең минимум нок¬
тасы була.
Гадәттә, бу теореманың гадиләштерелгән әйтелешеннән файда¬
ланалар.
I Чыгарылма х0 ноктасында тамгасын минустан плюска
үзгәртсә, х0 минимум ноктасы була.
Бу билгене исбатлау максимум
билгесен исбатлауга охшаш (аны
мөстәкыйль башкару файдалы бу¬
лыр).
□ 3 нче мисал. f(x) = 3x-x3
функциясенең экстремум ноктала¬
рын табыйк.
Бу функциянең 3 - Зх2 ка тигез
чыгарылмасы барлык нокталарда
билгеләнгән һәм -1 һәм +1 нокта¬
ларында нульгә әйләнә. -1 нокта¬
сында чыгарылма тамгасын минус¬
тан плюска үзгәртә (х < -1 булганда,
149
Чыгарылма һәм аны куллану
f'(x) < 0, һәм, -1 < х < 1 булганда, /'(х) > 0). 1 ноктасында чыгарыл¬
ма тамгасын плюстан минуска үзгәртә. Максимум һәм минимум
билгеләреннән файдаланып, f функциясе өчен —1 ноктасының —
минимум, ә 1 ноктасының максимум ноктасы икәнен табабыз.
Функциянең графигы 108 нче рәсемдә сурәтләнгән.
Күнегүләр
287. — Графигы 109 нчы рәсемдә сурәтләнгән функциянең критик
нокталарын табыгыз.
288. — Функциянең критик нокталарын табыгыз:
a) = 4 - 2х + 7хг; б) /(х) = 1 + cos 2х;
'1 в) f (х) = х - 2 sin х; г) f (х) = 4х - дг.
м
289. Графигы 110 нчы рәсемдә сурәтләнгән f функциясенең
J максимум һәм минимум нокталарын табыгыз. Тиңдәш
ноктада чыгарылма булырмы? Ул булса, аның кыйммәте
нинди булыр?
290. - Функциянең критик нокталарын табыгыз. Аларның кай¬
сылары — максимум нокталары, ә кайсылары минимум
нокталары булыр?
a) f (х) = 5 + 12х - х3; б) /(х)= 9 + 8х2 - х4;
в) f(x) = 2х3 + Зх2-4; г) f (х) = | х4 - х2.
291. f функциясенең критик нокталары булмаганлыгын исбат¬
лагыз:
a)f(x)=Jx; 6)/(x) = tgx;
в) /(х) = Зх - 7; г) / (х) = Зх5 + 2х.
f функциясенең критик нокталарын табыгыз (292—293).
292.-»- a) f (х) = sin2 х — cosx; б)/(х) = 2х +-Д-;
в) /(х) = 10cosx + sin2x- 6х; г) f(x) = х3 - 4х + 8.
150 Чыгарылма һәм аны куллану
293.— a) f (х) = (х - 2)3; б) f (х) =
< х < 1 булганда,
х < -2 булганда,
в) f(x) = f + |; г) /(х) = ·
295.->
-х - 2, х С -1 булганда
х, 1
2 - х, х > 1 булганда;
х + 6,
х2, -2 ί χζ 2 булганда,
6 - х, х > 2 булганда.
294.— Түбәндәге үзлекләргә ия булган функция графигының эс¬
кизын тезегез:
| a) D(f) - [-3; 5], /'(х) > 0 хе(-3; 1) өчен, /'(х) < 0 хе(1; 5)
һәм /'(1) = 0 өчен;
б) D(f) = [-3; 5], Г(х)<0*€(-3; 1)өчен, f(x)>Oxe(l; 5)
өчен һәм 1 ноктасында f функциясенең чыгарылмасы бул¬
мый;
в) D(/) = [a; ft], xt — функциянең минимум ноктасы, х2 —
аның максимум ноктасы,
г) D(f) = [α; δ], х, — максимум ноктасы, х2 — минимум
ноктасы, f(a) f(b).
Функциянең үсүен, кимүен тикшерегез һәм экстремумы
булу-булмавын ачыклагыз. Функциянең графигын төзегез:
a) f(x) = |x4-8х2; б)/(х) =
в) /,(х) = 2х-|х3; г) /(х)= χ2;272
24. Функцияне тикшергәндә чыгарылма
куллануга мисаллар
Сез (4 нче пункттан) функциянең графигын төзүне аны тикше¬
рүдән башлауның яхшырак икәнлеген беләсез, ә ул түбәндәгедән
гыйбарәт: бирелгән функция өчен: 1) аның билгеләнү өлкәсен
табалар; 2) f функциясенең так яки җөп, периодик булу-булмавын
ачыклыйлар. Моннан соң 3) f функциясе графигының коорди¬
наталар күчәрләре белән кисешү нокталарын; 4) аның тамгасы
даими булган аралыкларны; 5) үсү һәм кимү аралыкларын;
6) экстремум нокталарын һәм бу нокталарда f ның кыйммәтләрен
151 Чыгарылма 1юм аны куллану
табалар һәм 7) «аерым» нокталар һәм модуле буенча зуррак
х лар тирәлегендә функциянең үзен тотышын тикшерәләр.
Шул рәвешле тикшерү нәтиҗәсендә функциянең графигы төзелә.
Функциянең үсүен (кимүен) һәм экстремумы булу-булмавын
тикшерү чыгарылма ярдәмендә башкару уңай. Моның өчен башта
f функциясенең чыгарылмасын һәм аның критик нокталарын
табып, аннары аларның кайсылары экстремум нокталары булуын
ачыклыйлар.
|1 нче мисал. /(х) = 3xs - 5х3 + 2 функциясен тикшерик
һәм аның графигын төзик.
Тикшерүне югарыда күрсәтелгән схема буенча башкарыйк.
1> £>(/) = Я, чөнки f — күпбуын.
2) f функциясе так та, җөп тә булмый (моны үзлегегездән ис¬
батлагыз).
3) , 4) f графигы ординаталар күчәре белән (0; /(0)) ноктасында
кисешә; f графигының абсциссалар күчәре белән кисешү нокта¬
ларын табу өчен, Зх5 - 5х3 +2 = 0 тигезләмәсен чишәргә кирәк,
аның тамырларының берсе (х=1) җиңел табыла. Тамырларның
башкалары (әгәр алар булса) якынча гына табыла алалар. Шуңа
күрә бирелгән бу функция өчен без графикның абсциссалар күчәре
белән башка кисешү нокталарын һәм тамганың даими аралыкла¬
рын табып тормыйбыз (4 нче пунктта күрсәтелеп киткәнчә, ките¬
релгән схема якынча характерда гына була).
5), 6) f функциясенең чыгарылмасын табабыз:
/'(х) = 15х< - 15х2 = 15х2(х2 - 1).
= R,шуңа күрә f’(x) булмаган критик нокталар юк.
х2(х2- 1) = 0 булса, ягъни аргументның 0, -1 һәм 1 гә тигез
кыйммәтләре өчен /'(х) = 0 икәнлеген искәртеп китик. Без тик¬
шергән функциянең өч критик ноктасы бар.
Таблица төзибез:
X
(“«; -1)
-1
0
(0;1)
1
(1; °°)
Γ(χ)
+
0
-
0
-
0
+
/(X)
4
2
0
max
min
Бу таблицаның беренче юлында үсү тәртибендә функциянең
критик нокталары һәм алар белән чикләнгән интерваллар бирел¬
гән. Икенче юлда бу интервалларда чыгарылманың тамгалары
күрсәтелгән. (Мондый һәр интервалда чыгарылманың тамгасы
үзгәрешсез кала, аны табу өчен чыгарылманың тикшерелә торган
интервалдагы нинди дә булса ноктада тамгасын билгеләү җитә.)
Өченче юлда бирелгән функциянең ничек үзгәрә баруы: « у » —
үсә, « \ » — кими, дүртенчесендә критик нокталарның рәвешләре
турындагы нәтиҗәләр язылган (югарыда бирелгән схеманың 5 нче
Чыгарылма һәм ямы куллану
һәм 6 нчы пунктлары), f функциясе¬
нең критик ноктасы булган 0 ноктасы
экстремум ноктасы булмый, шуңа күрә
ул таблицаның дүртенче юлында күр¬
сәтелмәгән. Функциянең критик нокта¬
лар арасындагы аралыкта ничек үзгәрә
баруы турындагы нәтиҗәне еш кына
(чыгарылманың тамгасын билгеләү
урынына) функциянең бу аралыклар
очындагы кыйммәтләрен чагыштырып
ясап була. Мәсәлән, f(0) < /(-1) булган¬
да, (-1; 0) аралыгында функция кими
(һәм, димәк, бу аралыкта f < 0 була).
Функциянең графигын төзибез
111 нче рәсем
(111 нче рәсем). Төзүне таблицада күрсәтелгән аралыкларда баш¬
кару уңай. Мәсәлән, таблицада f ның (0; 1) интервалында кимүе
күрсәтелгән. fO һәм 1 нокталарында өзлексез (чөнки ул һәр җирдә
өзлексез), шуңа күрә ул [0; 1] кисемтәсендә кими. Шуның өчен
графикны [0; 1] кисемтәсендә /(0) = 2 кыйммәтеннән /(1) = 0 кыйм¬
мәтенә кадәр кими торган итеп ясыйбыз. Бу вакытта 0, ±1 нок¬
таларында графикка орынмалар горизонталь булырга тиешләр,
таблицаның икенче юлында бу нокталарда чыгарылма нульгә
тигез диелгән. Башка аралыкларда да график шулай ук төзелә.
2 нче мисал. 2х3 - Зх2 - 12х - 11 = 0 тигезләмәсенең та¬
мырлары санын табыйк.
/(х) = 2ха - Зх2 - 12х - 11 функциясен карап китик. Аның бил¬
геләнү өлкәсе D(f) — (-°°; °°). Бу f функциясенең критик ноктала¬
рын эзләп табу өчен, аның чыгарылмасын табабыз: /'(х) = 6х2 —
- 6х - 12. Бу чыгарылма х=1 һәм х = 2 нокталарында нульгә
әйләнә.
Таблицаны тутырыйк:
JC
(-«;-!)
-1
(-1;2)
2
(2; «I
Г(х)
+
0
-
0
+
ί(χ>
-4
-31
max
min
(-<»; -1] аралыкта функция тән -4 кә кадәр үсә. Шуңа күрә
бу аралыкта /(х) = 0 тигезләмәсенең тамырлары булмый; [-1; 2]
аралыкта тигезләмәнең тамырлары шулай ук булмый, чөнки бу
аралыкта / функциясе -4 тән -31 гә кадәр кими; ниһаять, [2; <»)
аралыкта функция -31 дән чиксезлеккә кадәр үсә, шуңа күрә бу
аралыкта f (х) - 0 тигезләмәсенең төгәл бер тамыры була (тамырлар
турындагы теорема буенча). Шулай итеп, 2ха-Зх2- 12х-11 =0
тигезләмәсенең бер тамыры бар (бу тамыр да (2; «>) интервалында
була).
153 Чыгарылма һәм алы куллану
Күнегүләр
296.—
298.¬
299.
Функцияне тикшерегез һәм аның графигын төзегез (296—
297).
a) f(x) = х2 -2х + 8; б) f (х) = - + х + |;
в) /(х) =-х2+5х + 4; г> ^(χ) = Τ + Ίβ +4*
a) f (х) - -х3 + Зх - 2; б) f (х) - х4 - 2х2 - 3;
в) f (х) » х3 + Зх + 2; г) f(x) = 3x2-x3.
Функциянең үсү һәм кимү аралыкларын табыгыз:
а) f (х) - 1 + 1,5х - Зх2 - 2,5х3;
б) /(х) = ^-^-6х + 1;
в) / (х) = ^ + 8х - 5; г) / (х) = Xs - 6х2 - 15х - 2.
f функциясенең R күплегендә үсүен исбатлагыз:
a) /(х) - 2х - cosx; б) f(x) = х5 + 4х;
в) /(х) - sinx + ^; г)/(х) =2х*+Х-5.
Функцияне тикшерегез һәм аның графигын төзегез (300—
302).
300. -а) /-(χ) = 1χ2-|х5; б) /(х) = 4х2 - х4;
в) /(х) = |х® - 1|х3; г) /(х) = 5х3 - Зх5.
□ о
301. -а) /(х)-хЧ'1 + χ; 6)Ηχ) = ^ν-?:
В) /(х) - хл/2-x; г)/(х) = _2^_.
302. -» а) / (х) = sin2 х + sin х; б) / (х) = г ;
I в) f (х) - cos2 х - cos х; г) f (х) = .
303. й f функциясенең бирелгән аралыкта уңай кыйммәтләр ал-
I ганлыгын исбат итегез:
I a) /(x) = tgx-x; / =
I б) f (х) - Jx - 1; I = [1; <»);
в) / (х) = х - sin х; I = (0; оо);
г) /(х) = х + —-cosx; I = ί-|; |].
154 Чыгарылма һәм аны куллану
304,— Тигезләмәнең ничә тамыры бар?
а) 4х3 - Зх2 - Збх -10 = 0; б) ^--х3-^ + 3х = 0;
J в) х4 - 4х3 -9 = 0; г) х2 - - 1 - 0.
25. Функциянең иң зур һәм иң кечкенә
кыйммәтләре
Бик күп практик мәсьәләләрне чишү еш кына кисем¬
тәдә әзлексез булган функциянең иң зур һәм иң кечкенә кыйм¬
мәтләрен табуга кайтып кала. Анализ курсларында [а; &] кисемтә¬
сендә өзлексез f функциясенең, бу кисемтәдә иң зур һәм иң кеч¬
кенә кыйммәтләр алуын, ягъни [а; t>] кисемтәсендә / функциясе
иң зур һәм иң кечкенә кыйммәтләр алырлык нокталар булуын
раслаучы Вейерштрасс теоремасы исбатлана.
[а; &] кисемтәсендә f функциясе өзлексез булып кына калмыйча,
бу кисемтәдә аның чикле санда гына критик нокталары да булган
очрак өчен f ның иң зур һәм иң кечкенә кыйммәтләрен табу ка¬
гыйдәсен күрсәтик.
Башта f ның [а; һ] кисемтәсендә критик нокталары юк, дип
уйлыйк. Ул вакытта (23 нче пункт) f бу кисемтәдә үсәр (112 нче
рәсем) я кимер (113 нче рәсем), һәм, димәк, f функциясенең [а; Ь]
кисемтәсендәге иң зур һәм иң кечкенә кыйммәтләре булып f
ның а һәм Ь очларындагы кыйммәтләре торыр.
Хәзер [а; һ] кисемтәсендә f функциясенең критик нокталары
чикле санда булсын. Бу нокталар [a; Ь] кисемтәсен эчке өлешлә¬
рендә критик нокталар булмаган чикле сандагы кисемтәләргә бүлә¬
ләр. Шуңа күрә (алдагы абзацны кара) f иң зур һәм иң кечкенә
кыйммәтләрен мондый кисемтәләрнең очларында, ягъни функ¬
циянең критик нокталарында яки а һәм Ь нокталарында алыр.
Шулай итеп, кисемтәдә критик нокталары чикле сан¬
да булган функциянең иң зур һәм иң кечкенә кыйм¬
мәтләрен табу өчен, аның барлык критик ноктала
рындагы һәм кисемтә очларындагы кыйммәтләрен
исәпләргә һәм табылган саннарның иң зурысын һәм
иң кечкенәсен сайлап алырга кирәк.
155 Чыгарылма һәм аны куллану
■ 1 нче мисал, у (х) = х3 - l,5x2 - 6х + 1 функциясенең
[-2; 0] кисемтәсендәге иң зур һәм иң кечкенә кыйммәтләрен
табыйк.
Башта критик нокталарны табабыз, у'(х) = Зх2 - Зх - 6 чыга¬
рылмасы теләсә кайсы х өчен билгеләнгән, шуңа күрә у'(х) = 0
тигезләмәсен чишәргә кала. Аны чишеп табабыз: х = -1 һәм х = 2.
Хәзер у(-2) = -1, t/(-l) = 4,5 һәм у(0)- 1 саннарының иң зу-
рысын һәм иң кечкенәсен сайлап алырга кирәк (х = 2 критик
ноктасы тикшерелә торган кисемтәгә керми). Кыйммәтләрнең
иң кечкенәсе -2 ноктасында һәм ул -1 гә тигез, ә иң зурысы -1
ноктасында һәм аның 4,5 кә тигез булуы ачык. Аны кыскача
болай язалар:
таху(х) = у(-1) = 4,5; miny(x) = у (-2) = -1.
1-2; 0| 1-2; 0|
Функциянең иң зур һәм иң кечкенә кыйммәтләрен табуның
югарыда бирелгән методын күп төрле практик мәсьәләләрне чиш¬
кәндә дә кулланырга була. Бу очракта түбәндәге схема буенча эш
итәләр:
1) мәсьәлә функцияләр теленә ♦күчерелә». Моның өчен җайлы
булган х параметрын сайлап алалар һәм аның аша безне кызык¬
сындырган зурлыкны /(х) функциясе итеп күрсәтәләр;
2) анализ чаралары ярдәмендә бу функциянең ниндидер ара¬
лыктагы иң зур һәм иң кечкенә кыйммәтләре эзләнә;
3) функцияләр телендә табылган нәтиҗәнең (баштагы мәсь¬
әләнең терминнарында) нинди практик мәгънәсе булуы ачык¬
лана.
Гомумән алганда, практик мәсьәләләрне математика чаралары
белән чишү, кагыйдә буларак, төп өч этапны эченә ала: 1) форма¬
лизация (баштагы мәсьәләне математика теленә күчерү); 2) килеп
чыккан математик мәсьәләне чишү һәм 3) табылган нәтиҗәгә
интерпретация (аны математика теленнән баштагы мәсьәлә тер¬
миннарына »кучеру»).
Бу гомуми метод белән (аны математик модельләштерү методы
дип атыйлар) сез инде танышкан идегез, бу схема буенча алгебра
курсында текстлы мәсьәләләр чишелде. Аны куллануга мисал
китерик.
80 2 нче мисал. Ягы а булган квадрат формасындагы калай¬
дан аның почмакларыннан кечкенә квадратлар кисеп алырга да
(114 нче рәсем), кырыйларын бөгеп, өсте ачык тартма ясарга кирәк.
Тартманың күләме максималь булсын өчен, аның нигез ягы нинди
булырга тиеш?
Чишү. 1) Тартманың нигез ягы озынлыгын х дип алыйк. Ул
чакта кисеп алынган квадратларның яклары озынлыгы ;(а-х),
ә тартманың күләме ^(а -х)х2 ка тигез булыр. Мәсьәләнең мәгъ¬
нәсе буенча х саны 0 < х < а тигезсезлеген канәгатьләндерергә,
156 Чыгарылма һәм аны куллану
114 нче рәсем
ягъни (0; α) интервалына керергә тиеш. Шулай итеп, безгә
V(x) = (а - х) х2 функциясенең (0; а) интервалындагы иң зур
кыйммәтен табарга кирәк.
2) Функциянең иң зур һәм иң кечкенә кыйммәтләрен табу
кагыйдәсе кисемтә өчен әйтелгән иде. V(x) функциясе барлык
саннар турысында өзлексез, шуңа күрә аның иң зур кыйммәтен
[0; а] кисемтәсендә эзләп, аннан соң гына без чишә торган мәсь¬
әлә өчен нәтиҗә ясарбыз. Функциянең критик нокталарын та¬
быйк:
V'(x) = ах -%хг, ах-|х2»0,
п 2
ягъни х — 0 яки х = g а.
V(0) = 0 һәм V(a) = 0, шуңа күрә V функциясе үзенең иң зур
о
кыйммәтен х = - α булганда ала, ягъни
о
maxV(x)-
[0; □) '
2_а3
27 а
Функция [0; а] кисемтәсенең, димәк, (0; а) интервалының
эчендә дә иң зур кыйммәт ала.
3) х ның бирелгән шартларда мөмкин булган күләмнең макси¬
мумына ия булган тартманың нигез ягы озынлыгы булганлыгын
искә төшерәсе кала.
2
Табылган нәтиҗә нигез ягы g а булган тартманың иң зур
күләмле булуын аңлата.
157 Чыгарылма һәм аны куллану
Күнегүләр
305. — f функциясенең иң зур һәм иң кечкенә кыйммәтләрен
табыгыз:
а) f(x) = х4 - 8х2 - 9; [-1; 1] һәм [0; 3] аралыкларында;
б) f(x)= ——; [_4; -1] һәм [1; 3] аралыкларында;
в) /(х) = Зх5 - 5х3; [0; 2] һәм [2; 3] аралыкларында;
г) /(х) = ; [-3; -2] һәм [1;5] аралыкларында.
306. — Функциянең Р} аралыгындагы иң зур кыйммәтен Р2 ара¬
лыгындагы иң кечкенә кыйммәте белән чагыштырыгыз.
I a) f(x) = х3 + Зх2 - 9х; Рх = [-4; 0], Р2 = [3; 4];
3 б) /(х) - х4 - 2х2 + 4; /> = [-|; , Р2 = [2; 3].
307. Материаль нокта β (t) = 12t2 -1t3 законы буенча туры сызык
■ ·
буйлап хәрәкәт итә, монда s(t) — метрларда юл һәм t —
секундларда вакыт. Вакытның [4; 10] аралыгындагы кай¬
сы моментында ноктаның хәрәкәт итү тизлеге иң зур бу¬
лыр һәм ул күпмегә тигез?
308. - Аргумент [-2; 5] аралыгында нинди кыйммәтләр алганда,
fix) = 21х + 2х2 —— функциясенең үзгәрү тизлеге иң зур
О
яки иң кечкенә булыр?
309. - Турысызыклы хәрәкәт итүче материаль ноктаның тизлеге
v(t) = gt3- 12t законы буенча үзгәрә (тизлек секундына
метрларда үлчәнә). Хәрәкәт Г( = 10 с тан t, = 50 с ка кадәр
аралыкта тикшерелсә, вакытның кайсы моментында хәрә¬
кәтнең тизләнеше иң кечкенә булыр?
310.— f функциясенең бирелгән аралыктагы иң зур һәм иң кеч¬
кенә кыйммәтләрен табыгыз:
а) /(х)= 2sinx+ cos2x; [0; 2π];
б) /(х)= 1,5х2 + ~; [1; 4];
в) Лх)= 2sinx + sin2x; [О; у·];
г) /•(х) = х+тГ2 ; I-5!’2,5].
311.—■ Квадратлары суммасы иң кечкенә булырлык итеп, 24 са¬
нын тискәре булмаган ике кушылучының суммасы рәве¬
шендә күрсәтегез.
Чыгарылма һәм аны куллану
312. — Тапкырчыгышы иң зур булырлык итеп, 4 санын тискә¬
ре булмаган ике кушылучының суммасы рәвешендә күр¬
сәтегез.
313. — Озынлыгы 48 м булган тимерчыбык кисәген турыпочмак¬
лык килеп чыгарлык итеп бөккәннәр. Турыпочмаклык¬
ның мәйданы иң зур булсын өчен, аның яклары нинди
озынлыкта булырга тиеш?
314. — Тапкырчыгышлары иң зур булырлык итеп, 54 санын уңай
өч кушылучының суммасы рәвешендә күрсәтегез, кушылу¬
чыларның икесе 1 һәм 2 саннарына пропорциональ булсын.
315. — Квадратлары суммасы иң кечкенә булырлык итеп, 16 санын
ике уңай санның тапкырчыгышы рәвешендә күрсәтегез.
316. — Турыпочмаклыкның мәйданы 64 см2. Периметры иң кеч¬
кенә булсын өчен, турыпочмаклыкның яклары нинди
озынлыкта булырга тиеш?
317. — Нигезе квадрат булган турыпочмаклы параллелепипед фор¬
масындагы өсте ачык мичкә 13,5 л сыеклык сыйдырырга
тиеш. Үлчәмнәре нинди булганда, мичкәне ясау өчен, иң
аз материал кирәк булыр?
318. — Нигезе 60 см һәм ян ягы 50 см булган тигезьянлы өчпоч¬
макка иң зур мәйданлы турыпочмаклык камалган. Туры¬
почмаклыкның ике түбәсе өчпочмакның нигезендә, ә кал¬
ган икесе аның ян якларында яталар. Турыпочмаклык¬
ның яклары озынлыгын табыгыз.
319. —Түгәрәк бүрәнәдән, турыпочмаклы кисемнең мәйданы иң
зур булырлык итеп, балка кисеп алганнар. Әгәр бүрәнәнең
кисем радиусы 20 см булса, балка кисеменең үлчәмнәрен
табыгыз.
320. — Бораулау вышкасы таш юлның иң якын ноктасыннан
9 км ераклыкта урнашкан. Бу ноктадан юл буйлап 15 км
Р ераклыкта урнашкан (юлны туры сызык дип алабыз) торак
I пунктка бораулау вышкасыннан курьер җибәрергә кирәк.
Й Курьер, велосипедка утырып, басудан 8 км/сәг, таш юлдан
И 10 км/сәг тизлек белән барса, югарыда әйтелгән пунктка
№ иң кыска вакыт эчендә барып җитү өчен, аңа таш юлның
S нинди ноктасына таба хәрәкәт итәргә кирәк?
321. $ Көймә ярның иң якын А ноктасыннан 3 км ераклыкта.
» Көймәдәге пассажир А ноктасыннан 5 км ераклыкта яр
гё буенда урнашкан В авылына барып җитәргә уйлый. Көймә
р 4 км/сәг тизлек белән хәрәкәт итә, ә пассажир, көймәдән
и төшсә, сәгатенә 5 км юл үтә ала. В авылына иң кыска
L вакытта барып җитү өчен, ул көймә белән ярның нинди
0 пунктына килеп туктарга тиеш?
159 Чыгарылма һәм аны куллану
322. — Үзенең квадраты белән суммасы иң кечкенә кыйммәт алыр¬
лык санны табыгыз.
323. — Бирелгән гипотенузалы барлык турыпочмаклы өчпочмак¬
лардан тигезьянлысының мәйданы иң зур булганлыгын
исбат итегез.
324. — Әйләнәгә камалган барлык турыпочмаклыклар арасыннан
иң зур мәйданлысын табыгыз.
325. — Бирелгән түгәрәккә камалган барлык тигезьянлы өчпоч-
I маклар арасыннан тигезьяклысының мәйданы иң зур бул-
I ганлыгын күрсәтегез.
Тарихтан мәгълүматлар
1. Терминнар һәм тамгаланышларның килеп чыгышы. Мате¬
матиканың чыгарылмаларны һәм аларның функцияләрне тик¬
шергәндә куллануны өйрәнүче кисәген дифференциалъ исәпләү
дип атыйлар. Аермаларны күрсәтүче Δ/ рәвешендәге үсемтәләр
чыгарылмалар белән эш иткәндә сизелерлек дәрәҗәдә зур роль
уйныйлар. Шуңа күрә calculis differenlialis (ул аермалар исәпләү
дип тәрҗемә ителә) дигән яңа исәпләүнең исеменә латин тамыры
differentia (аерма) килеп керү бик табигый; бу исем инде XVII га¬
сыр ахырында ук барлыкка килә.
«Чыгарылма» термины (аны 1797 елда Ж. Лагранж (1736—
1813) керткән) француз сүзе derivee нең турыдан-туры татарчага
тәрҗемәсе булып тора; хәзерге у', f тамгаланышларын да Ж. Ла¬
гранж керткән. Мондый исем төшенчәнең мәгънәсен чагылды¬
ра (туры килә): f'(x) f(x) тан китереп чыгарыла, f(x) тан чыга¬
рылма булып тора. И. Ньютон чыгарылма функцияне — флюкция
дип, ә функциянең үзен флюента дип атаган. Г. Лейбниц диффе¬
ренциалъ чагыштырма турында сүз алып барган һәм чыгарылманы
дип тамгалаган. Болай тамгалау хәзерге әдәбиятта еш очрый.
df символын Лейбниц f функция¬
сенең дифференциалын тамгалау
өчен сайлап алган, / функциясенең
df дифференциалы ул — Л(х0) чы¬
гарылмасының Δχ үсемтәсенә тап¬
кырчыгышы, ягъни df = f'(x0)Ax·
Әгәр дә Δχ ны dx белән алыштыр¬
сак, болай язып була: df = f'(xa) dx,
моннан f'(x0) = ~. Дифференциал¬
ның геометрик мәгънәсе 115 нче рә¬
семнән ачык күренә: монда df =АВ,
ә I турысы — графикка орынма.
y = f(x)
I
AB = df
χο
115 нче рәсем
х0 + Δχ
160 Чыгарылма һәм
аны куллану
Лейбниц Готфрид Фридрих
(1646-1716)
Бөек немец галиме. Философ, математик, физик,
юрист, тел белгече. Ньютон белән беррэттэн мате¬
матик анализга нигез салучы. Зур әһәмияткә ия
булган математик мәктәл оештыручы. Лейбниц
идеяләренең математик логика үсешенә тәэсире
шактый зур булды.
Дифференциаль исәпләүдә кабул ителгән терминология турын¬
да сөйләү чикләмә һәм чиксез кечкенә зурлык төшенчәләреннән
башка тулы булмас иде. Чикләмә турында түбәндә җентекләбрәк
сөйләнер, ә хәзергә барлык кулланмаларда чыгарылманың чик¬
ләмә буларак билгеләнүен кисәтеп китик. Югарыда кабул ител¬
гән Ах -> 0 булганда, -> f'(x) тамгаланышы урынына f'(*o) “
= lim - дип язалар.
Δ±-»0
lim тамгаланышы — латин сүзе limes нең (межа, чик) кыскарт¬
масы; Ах ны кечерәйтеп, без ~ ның кыйммәтен f'(x0) «чигенә»
омтылдырабыз. «Чикләмә» терминын Ньютон керткән.
Чиксез кечкенә зурлык мисалы булып Ах тан (Δχ)2 функциясе
хезмәт итә ала, чөнки Ах —► 0 булганда, (Δχ)2 —» 0. Гомумән,
lim α (х) = 0 булса, α (х) — чиксез кечкенә дип әйтәләр.
Чиксез кечкенәләр математик анализда зур роль уйныйлар,
шуңа күрә аны еш кына чиксез кечкенәләр анализы дип тә
атыйлар.
Ниһаять, «экстремум» сүзенең латин extremum (кырый) сү¬
зеннән килеп чыкканлыгын искәртеп китик. Maximum — иң зур,
ә minimum — иң кечкенә буларак тәрҗемә ителә.
2. Дифференциаль исәпләү тарихыннан.
1) Дифференциаль исәпләү Ньютон һәм Лейбниц тарафыннан
чагыштырмача күптән түгел, XVII гасырның ахырында барлыкка
килгән. Моннан бик күп еллар элек Архимедның спираль кебек
катлаулы кәкрегә (чикләмә аша күчү кулланып) орынма төзү генә
түгел, бәлки f (х) = х2(а - х) функциясенең максимумын да таба
алуы гаҗәпкә калдыра.
Орынма төшенчәсе (ул, сез белгәнчә, чыгарылма төшенчәсенә
бәйләнгән) эпизодик рәвештә Италия математигы Н. Тарталья
(1500—1557) хезмәтләрендә очрый. Биредә орынма туптан атылган
161 Чыгарылма һәм авы куллану
Ферма Пьер
(1601-1665)
ί Франция математигы һем юристы. Үз вакытының
’ иң танылган математикларыннан берсе. Ферма¬
ның саннар теориясе өлкәсендә зур әһәмияткә
ия булган хезмәтләре бар. Ул аналитик геометрия¬
не төзүче, аналитик геометриядә зур нәтиҗәләргә
ирешә.
ядрәнең иң зур ераклыкка очуын тәэмин итүче авышу почмагын
өйрәнгәндә карала. И. Кеплер орынманы бирелгән радиуслы
шарга камалган параллелепипедның иң зур күләмлесен табуга
багышланган мәсьәләне чишкәндә тикшерә.
XVII гасырда Г. Галилейның хәрәкәт тәгълиматы ниге¬
зендә чыгарылманың кинематик концепциясе актив үсеш алды.
Болай аңлатуның терле мәсьәләләргә карата кулланылган ва¬
риантлары Р. Декартта, француз математигы Роберваль-
дә (1602—1675), инглиз галиме Д. Грегорида (1638—1675),
И. Барроу (1630—1677) һәм, ниһаять, И. Ньютон хезмәтлә¬
рендә очрыйлар.
Декарт, линзаларның оптик үзлекләрен өйрәнгәндә, орынма
һәм нормальне (орыну ноктасына орынмага перпендикуляр итеп
үткәрелгән турыны шулай атыйлар) карау кирәклеге турындагы
фикергә килгән. Аналитик геометрия методлары һәм үзе уйлап
тапкан аныксыз коэффициентлар методы ярдәмендә ул төрле
кәкреләргә, шул исәптән эллипска да, нормальләр төзү мәсьәлә¬
ләрен чишә алган.
1629 елда П. Ферма күпбуынның экстремумнарын табу кагый¬
дәләрен тәкъдим иткән. Бу кагыйдәләрне чыгарганда. Ферманың,
максимум һәм минимум булуның иң гади дифференциала шарт¬
ларын белә торып, чикләмә аша күчүне актив куллануын әйтеп
үтәргә кирәк.
Математиканы үстерүдә Ферманың роле зур булды. Лаеклы
рәвештә аның исемен йөртүче теоремалар сезгә анализдан бил¬
геле булган теорема белән чикләнми, Ферманың бөек теоремасы
(«хп ■+■ уп = ζ” тигезләмәсенең икедән зуррак булган натураль п
өчен натураль саннарда чишелеше юк»), хәзергә кадәр исбатлан-
маса да, саннар теориясе проблемалары өстендә аның уйланула¬
рының берсенең генә нәтиҗәсе булып тора. Ферма — аналитик
геометрияне төзүчеләрнең берсе. Ул оптика белән дә шөгыльлән¬
гән. Ферма принцибы («Яктылык нуры аны үтү вакыты иң
162 Чыгарылма һәм аны куллану
кечкенә булырлык итеп тарала») күп¬
ләргә билгеле, ул хәзерге физикада да
кулланыла.
Бу принципның зур әһәмияткә ия
булган нәтиҗәләрен сез үзлегегездән
чыгара аласыз. Яктылык кайтарылу
законы («Кайтарылу почмагы төшү
почмагына тигез») Ферма принцибы
буенча билгеле бер геометрик мәсьәлә¬
гә кайтып кала. Яктылыкның сыну
законын чыгару ечен, сезгә билгеле
булган экстремум табу кагыйдәләрен
кулланырга кирәк була. (Мондый
мәсьәлә чишәргә кирәк (116 нчы рә¬
сем): «Яктылык нуры астагы ярымъ-
яссылыкның М ноктасыннан өстәге ярымъяссылыкның N нокта¬
сына үтә. Яктылыкның астагы ярымъяссылыктагы (бериш ти¬
рәлектә) тизлеге даими һәм р, гә тигез, ә өстәге ярымъяссылык¬
тагы тизлеге о2. Нокта юлны иң аз вакытта үтә алсын өчен, ул
нинди юл буенча хәрәкәт итәргә тиеш?»)
Чыгарылмалар турындагы систематик тәгълимат Лейбниц һәм
Ньютон хезмәтләрендә үсеш алган. Ньютон — анализның ике
төп проблемасын әйтеп бирүче кеше:
«1. Үтелә торган юлның озынлыгы даими рәвештә (ягъни ва¬
кытның теләсә нинди моменты өчен) биреп барыла; хәрәкәтнең
әйтелгән вакыттагы тизлеген табарга кирәк.
2. Хәрәкәтнең тизлеге даими рәвештә бирелә: әйтелгән вакыт
эчендә үтелгән юлның озынлыгын табарга».
Беренче проблема элементлары белән сез инде бу бүлектә та¬
нышкан дифференциаль исәпләүнең үсеш программасын бирә.
Икенчесе интеграль исәпләүгә карый (III бүлекне кара).
Әгәр Ньютон, нигездә, механика мәсьәләләреннән чыгып эш
итсә (Ньютон анализы Ньютон классик механикасы белән бер үк
вакытта барлыкка килә), Лейбниц исә күбесенчә геометрик мәсь¬
әләләрдән чыгып эш иткән.
Анализ идеяләренең моннан соңгы үсеше турында сөйләгән¬
дә (ә алар бик тиз таралдылар һәм үзләрен яклаучылар тапты¬
лар), беренче чиратта Лейбниц укучылары — бертуган Я. һәм
И. Бернуллиларны атап китәргә кирәк.
И. Бернулли укучысы А. Лопиталь (1661—1704) 1696 ел¬
да дифференциаль исәпләү буенча беренче басма курсын бас¬
тырып чыгарган, бу курс яңа методларның киң таралуына ки¬
тергән.
Лагранж да яхшы нәтиҗәләргә ирешкән, аның хезмәтләре
анализ нигезләрен ачыклауда зур роль уйнаган.
163 Чыгарылма һәм аны куллаяу
Математиканың күп кенә башка бүлекләрендәге кебек мате¬
матик анализны үстерү буенча Л. Эйлер һәм К. Ф. Гаусс
(1777—1855) керткән өлеш аерата зур.
Кыскача очеркта XVIII гасырда һәм соңрак башкарылган
ачышларның асылы турында сөйләп бетерергә мөмкин түгел.
Ләкин юнәлешләрнең берсе турында искә алмау мөмкин түгел.
Сүз функцияләрне дәрәҗәле рәтләргә таркату, ягъни функция¬
ләрне кушылучылар саны чиксез булган күпбуыннар рәвешендә
күрсәтү турында бара. Чиксез сумманың (санлы рәтнең) бер ми¬
салы сезгә таныш: чиксез периодик вакланмалар чиксез сандагы
кушылучылар суммасы рәвешендә күрсәтелделәр. Санлы һәм
функциональ рәтләр белән Ньютон гына түгел, аннан алда яшәгән
галимнәр дә эш иткәннәр, шуңа күрә Тэйлор формуласы исеме
бик үк гадел түгел (Б. Тэйлор (1685—1731) — инглиз матема¬
тигы, ул аны 1715 елда бастырып чыгарган). Түбәндәге бик билгеле
бәйләнеш:
f(x0 +Δχ) = /(χ0) + ^Γ1δλ: + 4?Α(Δχ)2 + +···
бу исемне йөртә (биредә fw(x0) — f функциясен х0 нокта¬
сында п тапкыр дифференциаллаганнан соң табылган кыйммәт,
ә п! = 1 2 · ... - п). Чыгарылмалар формулаларын, мәсәлән, sinx
һәм cosx өчен белеп, сез аларны үзегез Тэйлор рәтенә тарката
аласыз.
Күп очракта чиксез санлы кушылучыларны алып ташлап,
функцияләргә күпбуыннар аша шактый якынлашуга мөмкинлек
бирә торган формулалар табып була.
2) Бик күп мәсьәләләрне чишәргә мөмкинлек биргән яңа, көчле
метод барлыкка килү сәбәпле туган энтузиазм XVIII гасырда
анализның көчле үсүенә китерде. Ләкин бу гасыр ахырында диф-
ференциаль һәм интеграль исәпләүләрне төзүчеләр алдына баскан
проблемалар кискен алга куелды.
Кыенлыкларның иң зурысы чикләмә, өзлексезлек, реаль сан
кебек төп төшенчәләрнең төгәл билгеләмәсе булмауда иде (моңа
бәйле рәвештә фикерләүләрдә логик җитешсезлекләр һәм хәтта
хаталар да бар иде). Өзлексезлек билгеләмәсе характерлы мисал
булып тора. Эйлер, Лагранж һәм хәтта Фурье (ә ул XIX гасыр
башында эшли башлаган иде) өзлексез функция дип үзенең бил¬
геләнү өлкәсендә бары тик бер аналитик аңлатма аша бирелгән
функцияне атыйлар иде.
Шулай итеп, «яңа* математика грек математикларының клас¬
сик үрнәкләрендә тәрбияләнгән галимнәр өчен гадәти булган төгәл¬
лек стандартларына җавап бирмәде. Математикларга бик кирәк
булган интуиция математика фәненнән аерылгысыз булган логика¬
дан алга чыкты. Ньютон, Лейбниц, Эйлер кебек гигантларның
интуицияләре аларга хата ясамаска мөмкинлек бирде. Ләкин нык
логик нигезләр кирәк иде.
Чыгарылма һәм авы куллану
Коши Огюстен Луи
(1789-1857)
Франция математигы. Анализ, комплекслы үзгә-
решлеле функцияләр теориясе, дифференциаль
тигезләмәләр теориясе һ.б. өлкәләрдәге зур
әһәмияткә ия булган шактый күп теоремаларны
исбат иткән. Кошиның зур хезмәте анализ курсын
эшкәртүгә багышланган, анда ул, аерым алганда,
классик билгеләмәгә әверелгән билгеләмәләр —
чикләмә, функциянең өзлексезлеге билгеләмәлә¬
рен биргән.
.ИКвВЯММНММКкЯЯКГfl·ымк
XVIII гасыр өчен түбәндәге әйтелмәләр характерлы. Танылган
математик М. Ролль: «Яңа исәпләү ул — гениаль хаталар кол¬
лекциясе»,— дип язды. Ә Франциянең бөек фикер иясе Вольтер
исә: «Исәпләүләр — барлыгын төгәл исбатларга мөмкин булмаган
нәрсәләрне исәпләү һәм төгәл үлчәү осталыгы»,— дип әйткән.
XIX гасырның 20 нче елларында Франция математигы
О. Кош и (1789—1857) анализга нык фундамент салуга зур өлеш
керткән, ул функция һәм эзлеклелек чикләмәләренең төгәл бил¬
геләмәләрен тәкъдим иткән һәм алар нигезендә анализның күп
кенә фундаменталь теоремаларын исбатлаган. Алардан бераз
элегрәк (1821 елда) чикләмә һәм өзлексезлек билгеләмәләрен бир¬
гән, шактый гына башка, зур әһәмияткә ия булган нәтиҗәләргә
(шул исәптән аралыкта өзлексез булып та, аның бер ноктасында
да чыгарылмасы булмаган данлыклы функциягә мисал китергән)
ирешкән чех математигы Б. Больцано (1781—1848) турында
әйтеп китәргә кирәк. Ләкин аның хезмәтләре соңрак билгеле
булды.
Коши функция чикләмәсенә мондый билгеләмә биргән: «Теләсә
нинди е>0 саны өчен 0< |χ-α|<δ тигезсезлеген канәгать¬
ләндерүче барлык х лар өчен | f(x) - А| < ε булырлык δ > 0 санын
табып булса, А саны х а га омтылганда, /(х) функциясенең чик¬
ләмәсе дип атала (ягъни lim f(x) = А).
X —· 4
Бу билгеләмәгә нигезләнеп, ноктада өзлексезлек билгеләмәсен
бирү кыен түгел: lim /(х) = f (х0) булса, f функциясе х0 ноктасында
өзлексез була. х-,а
Эзлеклелек чикләмәсенең (интеграл билгеләмәсе бу төшенчәгә
бәйле; 30 нчы пунктны кара) билгеләмәсе болай әйтелә: «Теләсә
нинди ε > 0 саны өчен | ап - А | < ε тигезсезлеген канәгатьләндерүче
барлык η > N өчен шундый N номеры булса, А саны а„ эзлекле-
легенең чикләмәсе дип атала.
Коши чикләмәләр турындагы без чыгарылмаларны исәпләгәндә
кулланган (14 нче пунктта аларны чикләмә аша күчү кагыйдәлә¬
ре дип атаган идек) түбәндәге теоремаларны исбат итте:
Чыгарылма һәм аны куллану
Әгәр lim/'(x)=A һәм lim g (х) = В булса, сумма¬
х -■* а х -> а
ның һәм аерманың, тапкырчыгышның, өлешнең
(limg(x)*O булганда) чикләмәләре бар һәм
lim(/(x) ±g(x)) = А±В,
lim(/(x)g(x)) = А В,
х -» а
!и"йй=вбула-
«Коши»ча исбатлауга мисал китерик (еш кына: «эпсилон-
дельта телендә» дип әйтәләр). Сумманың чикләмәсе турындагы
теореманы исбатлыйк.
Теләсә нинди уңай е > 0 санын алыйк. Ул вакытта ' > 0 һәм
шуңа күрә (Коши билгеләмәсе буенча):
1) lini/(x) = A шартыннан 0< Ix-oHSl тигезсезлеген канә-
х ■> α
гатьләндерүче барлык х лар өчен
lf(x)-A|<| (1)
булырлык, δ санын табып була;
2) limg(x) = B шартыннан түбәндәге килеп чыга:
г d
0 < I х — a I < δ2 тигезсезлеген канәгатьләндерүче барлык х лар
өчен
|g(x) В|<| (2)
булырлык δ2 > 0 бар.
δ( һәм δ, саннарының иң кечкенәсен δ аша тамгалыйк. Ул
вакытта 0 < |х - а | < δ тигезсезлеген канәгатьләндерүче теләсә нин¬
ди х өчен (1) һәм (2) тигезсезлекләр үтәлә; бу х лар өчен табабыз:
|/(х) + g(x)- (А + В)| -
- |(f(x)-A) + U(x)-B)| ζ |/(χ)-Α| 4- Ιί(χ)-Β| < f + f = ε.
Моның белән lim(f(x) + g(x)) = A + В икәнлеге исбатлана.
τ —» и
Кагыйдәләрнең башкалары (тапкырчыгыш һәм өлеш өчен)
шуңа охшаш рәвештә исбатлана.
XVII гасырда күп кенә математикларның лозунглары мондый
иде: «Алга барыгыз, ирешкән нәтиҗәләрегезнең дөреслегенә ыша¬
ныч сезгә соңрак килер».
3. Реаль сан төшенчәсе турында. Математик анализ XVIII га¬
сырда барлыкка килә. Ләкин аңа бары тик XIX гасырның ахы¬
рында О. Коши (160 нчы битне карагыз) тарафыннан барлыкка
китерелгән чикләмәләр теориясеннән соң ук немец математикла¬
ры Р. Дедекинд (1831—1916), К. Вейер шт расе (1815 —1897)
166 Чыгарылма һәм аны куллану
Кантор Георг
(1845-1918)
Немец математигы, математиканың үсешенә, ма¬
тематика нигезләрен аңлауга аның идеяләренең
һәм хезмәтләренең тәэсире зур булды. Күплекләр
теориясен төзүче. Чиксез күплекләр теориясенә,
реаль саннар теориясенә кагылышлы булган шак¬
тый күп нәтиҗәләргә иреште.
һәм Г. Кантор (1845—1918) берьюлы берничә төрле формада
реаль саннар теориясен төзегәннән соң гына тулысынча нигез
салына.
Саннар турындагы беренче күзаллаулар тормыш-көнкүреш
таләпләре тәэсирендә әкренләп барлыкка килгән. Бик күптәннән
үк санау һәм зурлыкларны үлчәү өчен саннар кулланылган.
«Бирелгән чикле күплек ничә элементны эченә ала?* дигән
сорауга һәрвакыт я натураль сан, я нуль саны белән күрсәтелә
дип җавап бирелә. Димәк, тискәре булмаган барлык бөтен саннар
күплеге
{0; 1; 2; 3; ...}
санауның барлык ихтыяҗларын канәгатьләндерә.
Зурлыкларны үлчәгәндә, эш башкачарак. Мәсәлән, ике пункт
арасы 3,5 километрга, бүлмәнең мәйданы 16,45 квадрат метрга
тигез булуы мөмкин һ.б.
Зурлыклар төрле төрдә була. Ике мисал китерик.
1. Нокталар арасындагы ераклыклар, кисемтәләрнең, сынык
һәм кәкре сызыкларның озынлыклары — болар бер үк төрдәге
зурлыклар. Ал арны сантиметрларда, метрларда, километрларда
һ.б. күрсәтәләр.
2. Вакыт аралыкларының дәвамлылыгы — шулай ук бер үк
төрдәге зурлыклар. Аларны секундларда, минутларда, сәгатьләрдә
һ.б. күрсәтәләр.
Бер үк төрдәге зурлыкларны үзара чагыштырырга һәм кушар
га мөмкин:
1 м > 90 см
300 с < 1 сәг
350 м + 650 м - 1 км
2 сәг + 3 сәг -= 5 сәг
Ләкин 1 метрмы, әллә 1 сәгать зурракмы дип сорауның
мәгънәсе юк, шулай ук 1 метр белән 30 секундны да кушарга
ярамый. Вакыт аралыкларының дәвамлылыгы белән ераклыклар
да — төрле төрдәге зурлыклар. Төрле төрдәге зурлыкларны
чагыштырырга һәм кушарга ярамый.
167 Чыгарылма һам аны куллану
Вейерштрасс Карл Теодор Вильгельм
(1815-1897)
Немец математигы, ул математиканың төрле өлкә¬
ләрендәге классик теоремаларны исбатлаучы
Вейерштрассның математик анализны нигезләүгә
багышланган хезмәтләре асылда төгәл һәм төзек
теория булдыруны тәмамладылар.
Зурлыкларны уңай саннарга һәм нульгә тапкырларга мөмкин.
а зурлыгын тискәре булмаган х санына тапкырлау нәтиҗәсендә
шул ук төрдәге Ь = ха зурлыгы килеп чыга. Берничә мисал ки¬
терик:
5 20 см = 100 см - 1 м
0,01 20 см = 0,2 см = 2 мм
0 20 см = 0 см
Нинди дә булса е зурлыгын үлчәү берәмлеге буларак кабул
итеп, аның ярдәмендә шул ук төрдәге теләсә нинди икенче а зур¬
лыгын үлчәргә мөмкин. Үлчәү нәтиҗәсендә табабыз: а = хе, монда
х — сан.
Бу х саны, е ны үлчәү берәмлеге итеп алганда, а зурлыгының
санча кыйммәте дип атала. Мәсәлән, үлчәү берәмлеге 1 м булганда,
(е = 1 м), бүлмә озынлыгының санча кыйммәте 5,6 була, ә үлчәү
берәмлеге бер сантиметр (е = 1 см) булганда, шул ук озынлыкның
санча кыйммәте 560 була.
Үлчәү берәмлеге бер үк е булганда, а һәм Ь зурлыкларының
санча кыйммәтләре х һәм у ка тигез, ягъни а = хе, Ь = уе булсын.
Әгәр Ь * 0 булса, — чагыштырмасын а ның Ь зурлыгына чагыш¬
тырмасы дип атыйлар.
Зурлыклар турындагы иң гади мәгълүматлар шуннан гыйба¬
рәт. Монда китерелгән зурлыклар турындагы төшенчә саннар тө¬
шенчәсенә таяна. Ләкин тарихи юл башкача була: уңай реаль
саннар зурлыклар чагыштырмасы (дөресрәге, кисемтәләрнең озын¬
лыклары чагыштырмасы) буларак килеп чыга.
Берәмлек квадратның диагонале аның ягы белән үлчәмсез
булуы ачылганнан соң, кисемтәләрнең озынлыклары чагыштыр¬
масы натураль саннар белән генә түгел, хәтта рациональ саннар
белән дә һәрвакыт күрсәтелә алмавы мөмкин икәнлеге ачыклана,
һәр кисемтәнең санча кыйммәтен билгеле бер үлчәү берәмлеген¬
дә билгеләү өчен, яңа саннар — иррациональ саннар кертү таләп
ителгән.
168 Чыгарылма һәм аны куллану
Практикада барлык зурлыкларны да үлчәү якынча характерда.
Аларның нәтиҗәләрен таләп ителгән төгәллек белән рациональ
вакланмалар ярдәмендә яки махсус рәвештә чикле унарлы ваклан¬
малар ярдәмендә аңлатырга мөмкин. Мәсәлән, ягы 1 м лы квадрат¬
ның диагонален бер сантиметрга кадәр төгәллек белән үлчәгәндә,
без аның озынлыгы якынча 1,41 м га тигез икәнен беләбез. Бер
миллиметрга кадәр төгәллек белән үлчәгәндә, бу озынлыкның
якынча 1,414 м га тигез икәнен табабыз.
Ләкин математикада еш кына практик исәпләүләрнең якынча
характерда булуын читләтеп үтәләр. Кисемтәләрнең озынлыкла¬
рын үлчәүгә эзлекле рәвештә теоретик якын килү чиксез унарлы
вакланмаларны тикшерү кирәклегенә китерә. |J = 0,666...; ^2 =
= 1,41421356... ; π = 3,14159265... саннары нәкъ шундый ваклан¬
малар белән күрсәтеләләр.)
Теләсә нинди кисемтәнең үлчәү берәмлеге итеп кабул ителгән
кисемтә озынлыгына чагыштырмасы чиксез унарлы вакланма рә¬
вешендә күрсәтергә мөмкин булган сан белән аңлатыла.
Реаль саннарның тулы теориясе шактый катлаулы һәм урта
мәктәп программасына керми. Ләкин аларны төзүнең бер ысулы
белән без гомуми күренештә танышып китәрбез.
1. Кабул итәләр:
а) һәр реаль санга (аның язылышы сыйфатында) чиксез унарлы
вакланма туры килә:
х-а0, at, аг,
б) һәр чиксез унарлы вакланма реаль санның язылышы була.
Ләкин монда чиксез тугызлыклар эзлеклелегенә тәмамланган
унарлы вакланмаларны чиксез нульләр эзлеклелегенә тәмамлан¬
ган унарлы вакланманы аңлаткан санның икенче төрле язылышы
дип исәпләү табигый:
0,9999... = 1,0000...; 12,765999... = 12,766000... .
Мондый килешүне мисал ярдәмендә аңлатыйк:
0,(9) = 3 0,(3) - 3 I = 1·
Бары тик периодта тугыз булган унарлы вакланмаларны карау¬
дан төшереп калдырып кына, без реаль саннар күплеге белән
чиксез унарлы вакланмалар күплеге арасында үзара беркыйммәтле
тиңдәшлек табабыз:
а0 саны — ул уңай х санының бетен кисәге, ә х - а0 = 0,
α1α2α3...α„... — х санының вакланма кисәге.
х„ = а0,а1ага3...ап санын—х ның 10" кадәр төгәллектә
киме белән алынган унарлы якынлашуы, ә х'„ = хп + 10 " санын
х - а0,а1а2а3...а„... санының 10 " кадәр төгәллектә артыгы белән
алынган унарлы якынлашуы дип атыйлар.
169 Чыгарылма һам аны куллану
Әгәр х саны тискәре, ягъни
булса, ул вакытта
х' = -ай,а1а2а3...ап һәм х„ = х' - Ю”
дип уйланыла.
2. Ике реаль санны чагыштыру кагыйдәсен кертәләр. Кимендә
бер п өчен х„ < у„ тигезсезлеге үтәлгәндә, билгеләмә буенча х саны
у саныннан кечерәк була. х„ һәм уп — монда х һәм у өчен 10 ’
кадәр төгәллектә киме белән алынган унарлы якынлашулар. (Без
чикле унарлы вакланмаларны чагыштыру кагыйдәсе таныш булу¬
дан файдаландык.)
3. Реаль саннар өстендә арифметик гамәлләрне билгелиләр
(монда шулай ук чикле унарлы вакланмалар өчен бу гамәлләрнең
билгеләнгән булуыннан чыгып эш итәбез).
Теләсә нинди п өчен
+ Уп < * + У < < + у'.
тигезсезлеге үтәлгәндә, г реаль санын х һәм у реаль саннарының
суммасы (х + у дип тамгалана) дип атыйлар.
Математик анализ курсында андый санның барлыгы һәм
бертөрле генә билгеләнүе исбатлана.
Аналогик рәвештә, тискәре булмаган х һәм у саннарының
тапкырчыгышы дип теләсә нинди п өчен
х„Уп < *У < <Уп
тигезсезлеге үтәлгән г саны (ху дип тамгалана) атала.
Андый сан бар һәм бертөрле генә билгеләнә. Монда төрле
тамгадагы реаль саннар өчен тискәре булмаган |х| һәм |у| сан¬
нарының тапкырчыгышы инде билгеләнгән дип эш итәләр,
ху = -1 х I I у I дип уйланыла; калган очракларда ху = | х 11 у |, (Гадәт¬
тә, αθ,α^...^... санын α0,α1α2...αη... һәм -а0,а1а2...аЛ... саннарының
һәркайсының модуле дип атыйлар.)
Алу гамәле кушуга кире гамәл буларак билгеләнә: х һәм у
саннарының аермасы х - у дип у + г = х тигезлеге үтәлгән ζ саны
атала. Ә бүлү гамәле тапкырлау гамәленең киресе буларак билге¬
ләнә: х: у өлеше дип уг = х тигезлеге үтәлгән ζ саны атала.
4. 3 нче пунктта күрсәтелгәнчә билгеләнгән тигезсезлекләр
һәм арифметик гамәлләр аларга рациональ саннар күплегендә
хас булган төп үзлекләрнең сакланганлыгын күрсәтәләр.
Кабатлау өчен сораулар һәм мәсьәләләр
1. 1) Аргумент үсемтәсе һәм функция үсемтәсе нәрсә ул?
2) Δχ һәм Δ/ үсем тә л әренең геометрик мәгънәсе нидән гый¬
барәт? чагыштырмасыныкы?
3>s не х0 һәм Δχ аша күрсәтегез:
a) f (х) = х2 - х; б) /(х) = х3 + 2; в) /(х) = Зх - 1; г) /(х) = j .
Чыгарылма һәм аны куллану
117 нче рәсем
2. 1) Функциянең ноктадагы чыгарылмасының билгеләмәсен
әйтегез.
2) Билгеләмәдән файдаланып, f функциясенең х0 ноктасын¬
дагы чыгарылмасын табыгыз:
a) f(x) = x2 + 1, х0 = -2; б) f (х) = у, х0 = 3;
в) f (х) = 2х - 1, х0 = -4; г) f(x) = х3, х0 - 2.
3. 1) Чыгарылмаларны исәпләү кагыйдәләрен әйтегез, f (х) = х"
функциясенең чыгарылмасы күпмегә тигез булыр (п — бетен
сан)?
2) Дифференциалланучы f функциясе график аша бирелгән
(117 нче рәсем), f графигында күрсәтелгән нокталарда орын¬
ма төзегез һәм чыгарылманың a,b,c,d нокталарындагы якын¬
ча кыйммәтләрен табыгыз.
3) Функцияне дифференциаллагыз:
а) /(х) = (х + 2) sinx; б) f(x) =
в) /(х) = х3 - У + cos Зх; г) f(x) - ууд.
4. 1) Нинди функцияне аралыкта өзлексез функция дип атый¬
лар?
2) Функциянең өзлексезлек аралыкларын табыгыз:
a) Λ*) = ; б) f(x) = 1 - 2tgх;
в) “ x»-V-10: г) /(х) = х^ - Зх2 + 7.
3) Тигезсезлекне интерваллар методы белән чишегез:
a>774+lti>1; б) х< - 15х2 - 16 < 0;
в) *2~3ζ"4 С 0; г) (х-1)(х-2)(х + 4) > 0.
171 Чыгарылма һәм аны куллану
5. 1) Нинди турыны / функциясенең графигына (х0; f (х0)) нокта¬
сындагы орынмасы дип атыйлар?
2) Чыгарылманың геометрик мәгънәсе нидән гыйбарәт?
3) / функциясе графигының (х0; /(х0)) ноктасындагы орынма¬
сының тигезләмәсен языгыз:
а) /(х) = cos х, х0 = У; б) /(х) - |, х0 - 2;
в) /(х) = sinх, х0 = π; г) /(х) = х2, х0 =
β. 1) х0 ноктасында дифференциалланучы функциянең якынча
кыйммәтен исәпләү эчен кулланылган гомуми формуланы
языгыз.
2) Функциянең кыйммәтен якынча исәпләү өчен, форму¬
лалар языгыз:
а) /(х) = хя; б) /(х) —cosx;
в)/(х)=л/х; г)/(х)=|.
3) Якынча кыйммәтләрне исәпләгез:
а) ΪΟΟΪ^; 6)sin59°: в) 79.009; г) 0,999ls.
7. 1) Чыгарылманың механик мәгънәсе нидән гыйбарәт?
2) Җисем туры буйлап х(0 законы буенча хәрәкәт итә. Ва¬
кытның t моментында җисемнең тизлеген һәм тизләнешен
табу формулаларын языгыз.
3) a) х(0 — i8 9 - 2t2 + 5, t0 - 4; б) x(t) = 3cos2f, t0 =
в) x (0 = 5t - i2, t0 — 2; r) x(i) = 2t2 + t - 4, t0 = 4
булса, ноктаның t моментындагы тизлеген һәм тизләнешен
табыгыз.
8. 1) Лагранж формуласын языгыз.
2) Функциянең үсү билгесен (кимү билгесен) әйтегез.
3) Функцияне үсүгә һәм кимүгә тикшерегез:
а) у = х2Х+9 > б) у = Зх - sin Зх;
в) у - х4 - 4х; г) у = х2 + »
9. 1) Функциянең критик ноктасы дип нинди ноктаны атый¬
лар?
2) Функциянең максимумы (минимумы) билгесен әйтегез.
3) Функцияне максимумга һәм минимумга тикшерегез:
а) у = - х4; б) у = 2 sin х + cos 2х;
в) у — х8 - Зх; г) у = х - tg х.
172 Чыгарылма һәм аны куллану
10. 1) Функцияне тикшерү схемасын сөйләгез.
2) Функцияне чыгарылма ярдәмендә тикшерегез:
a)f(x) = ^ + 4-x2: 6)/(x) = J + f;
Ίο ·* A
в)/(х) = х®-3х2-9х; г) /(х) ~ 4 .
3) f функциясен гомуми схема буенча тикшерегез һәм аның
графигын төзегез:
а)/(х) = х2 - у; б) f(x) = х2(х-2)2;
в) f{x) = 2х2 + 3х- 1; г)/(х) = +х2-3х+1.
11. 1) Функциянең кисемтәдәге иң зур һәм иң кечкенә кыйм¬
мәтләрен табу кагыйдәсен әйтегез.
2) Функциянең бирелгән кисемтәдәге иң зур һәм иң кечкенә
кыйммәтләрен табыгыз:
а) Нх) = 0,8х5 - 4ха, [-1; -2]; б) /(х) = х - sin2x, [о; |];
в) / (х) = Зх2 - 2х®, [-1; 4]; г) f(x) = х2(6 - х), [-1; 5].
3) а) Ике санның аермасы 8 гә тигез. Беренче сан кубының
икенчесенә тапкырчыгышы иң кечкенә булсын өчен, бу сан¬
нар нинди булырга тиеш?
б) Машиналар куеп тору өчен, бер ягы бина стенасы белән
туры килә торган турыпочмаклык формасындагы мәйданчык
бүлеп бирделәр. Мәйданчыкның өч ягын 200 м озынлыкта¬
гы металл челтәр белән тоткач, мәйдан иң зур булып чыккан.
Мәйданчыкның үлчәмнәре нинди?
Башлангыч функция
һәм интеграл
1 ■ ■ ■
I
§ 7.
Башлангыч функция
26. Башлангыч функциянең билгеләмәсе
Механикада кулланылган мисалны искә төшерик. Әгәр
вакытның башлангыч t = 0 моментында җисемнең тизлеге 0,
ягъни о(0) = 0 булса, җисем ирекле төшкәндә, t вакыты момен¬
тына
8(0 = ^- (I)
юл үтәр иде.
(1) формуланы Галилей эксперименталь юл белән тапкан була.
Дифференциаллап тизлекне табабыз:
s'(O = f(O = ^· (2)
Икенче дифференциаллау тизләнешне бирә:
ι>'(ί) = α(0 = £. (3)
ягъни тизләнеш даими зурлык була.
Механика өчен башкача бер фикер урынлы: ноктаның a(t)
тизләнеше билгеле (бу очракта ул даими), υ(ί) тизлегенең үзгәрү
законын һәм шулай ук s (t) координатасын табарга кирәк. Башка¬
ча әйтсәк, a (t) га тигез булган бирелгән υ'(0 чыгарылмасы буенча
o(t) ны табарга, ә аннан соң o(t) га тигез булган s'(t) чыгарылмасы
буенча s(0 ны табу сорала.
Мондый мәсьәләләрне чишү өчен, дифференциаллауга кире
операция интеграллау операциясе кулланыла. Без аның белән
шушы бүлектә танышырбыз.
Билгеләмә Бирелгән аралыкта барлык х лар өчен
булса, F функциясе бу аралыкта f функциясенең
башлангыч функцилее дип атала.
г t-3
1 нче мисал. F(x) = ^- функциясе (-®; +оо) интервалда
f (х) = х2 функциясе өчен башлангыч функция була, чөнки барлык
хе(-“>; оо) өчен
ILtuijiauruq функции һәм интеграл
F'(x) = 1^-1 = |(x3)' = | Зх2 = х2 = f(x).
\ t ό ό
— + 7 нең дә чыгарылмасы х2 икәне җиңел аңлашыла һәм
О
шуңа күрә х2 өчен ул R да шулай ук башлангыч функция була.
Билгеле 7 урынына биредә теләсә нинди даими санны куярга
мөмкин. Шулай итеп, без башлангыч функцияне табу мәсьәләсе¬
нең чиксез күп чишелешләре булуын белдек. Киләсе пунктта сез
бу чишелешләрнең барысын да ничек табарга икәнен күрерсез.
2 нче м и с а л . (0; оо) интервалда f (х) = —г- функциясе өчен
УХ
F(x) = 2y/x функциясе башлангыч функция булыр, чөнки бу ин¬
тервалдагы барлык х лар өчен
Г(ж).(2Л)' = 2^--^ = /(х)
1 нче мисалдагы кебек үк, С теләсә нинди даими зурлык булганда
да, F(x) = 2 \[х + С функциясе шул ук (0; оо) интервалда / (х) — -U
Ух
функциясе өчен башлангыч функция була.
3 нче мисал. (-»;<») аралыкта/(х)=—— функциясе өчен
F(x) = у функциясе башлангыч функция түгел, чөнки F'(x) = /(х)
тигезлеге 0 ноктасында үтәлми. Шулай да (-оо; 0) һәм (0; оо) ара-
лыкларының һәркайсында F функциясе f өчен башлангыч функ¬
ция була. О
Күнегүләр
326.— Күрсәтелгән аралыкта f функциясе өчен F функциясенең
башлангыч функция икәнен исбатлагыз:
й a) F(x) = X6, /(х) = 5Х*, Х€(-оо, co);
й б) F(x) х 3, f(x) — -Зх 4, хе(0; оо);
В) F(x)= |хт, /(Х) = Х®, Хё(-оо; оо);
г) F(x) = -1χ«, /(χ) = χ-γ, Х€(О; оо).
о
327,-
Күрсәтелгән аралыкта f функциясе өчен F функциясе баш¬
лангыч функция була аламы?
а) F(x) = 3 - sin х, f(x) = cos х, х<=(-оо, оо);
б) F(x) = 5 - X4, /(X) = -4Х3 > Х€(-оо, оо);
в) F(x) = cosx - 4, f(x) = -sinx, хе(-оо, оо);
г) F(x) = х-2 + 2, /<лг>-X€(0, oo).
башлангыч функция һәм интеграл
f функциясе өчен R да башлангыч функцияләрнең берсен
j табыгыз (328—329).
a) f(x) = 3,5; б)/(x) = cosx;
в) У(х) = 2х; г) / (х) “ sin х.
a) /(х) = —sinx; б) f(х) = -х;
в) f(x) = -4; г) /(х) = -cosx.
330. — Күрсәтелгән аралыкта f функциясе өчен F функциясе баш¬
лангыч функция икәнен исбатлагыз:
а) F(x) = sin2x, f(x) - sin2x, хеЯ;
б) F(x)= icos2x, /(x) =-sin 2x, хеЯ;
в) F (x) = sin 3x, f (x) = 3 cos Зх, хеЯ;
г) F(x)-3 + tgy, /(x) = 1 , Χ€(-π;π).
Δ 2cos2v
331. — Күрсәтелгән аралыкта F функциясе f функциясе өчен баш¬
лангыч функция була аламы?
а) F (х) - 2х + cos j, f (х) = 2 -1 sin |, х е Я;
б) F(x) = V4-x\ f(x) = --₽=£=, х e (-2; 2);
■J4-X2
в) F(x) = ^·,/(x) = 14--^, хе (0;w);
r) F(x) ~ 4xVx, f (x) - 6>/x, x € (0; «).
332.— f функциясе өчен Я да башлангыч функцияләрнең берсен
табыгыз: 2
a)f(x) = x + 2; б) f (х) = (sin | - cos |;
в) f (х) = sin2x + cos2x; г) /(х) = Зх2 + 1.
333.— f функциясе өчен ике башлангыч функция табыгыз:
a) /(х) - 2х; б) /(х) - 1 - sin х;
в) /'(х) = х2; г) /(х) = cosx + 2.
334.— Бирелгән өч функция арасыннан башка ике функция тиң¬
дәшле рәвештә аның чыгарылмасы һәм башлангычы бул¬
ган функцияне күрсәтегез:
а) f(x) = 4-, £(х) = -у, й(х) = -р-;
б) f (х) = 4- - cos х, g (х) = 1 + cos х, һ (х) = х + sin х;
в) f (х) “ 1, g (х) = X + 2, Л(х) = -£■ + 2х;
г) f (х) = 3 - 2 sin х, g (х) = Зх + 2 cos х, һ (х) « -2 cos х.
176
Башлангыч функция һәм интеграл
27. Башлангыч функциянең төп үзлеге
1. Башлангыч функцияләрнең гомуми рәвеше. Инте¬
граллау операциясе бирелгән функция өчен аның барлык башлан¬
гыч функцияләрен табудан гыйбарәт. Бу мәсьәләне чишкәндә,
функциянең даимилек билгесе төп рольне уйный.
Функциянең даимилек билгесе. Әгәр
ниндидер I аралыгында F'(x) = 0 икән, F функциясе
бу аралыкта даими була.
Исбатлау. I аралыгында ниндидер х0 ноктасы билгеләп
куйыйк. Ул вакытта, Лагранж теоремасы буенча, шушы ара¬
лыктагы теләсә кайсы х саны өчен
F (х) - F (х0) = F'(c) (х - х0)
булырлык итеп, х һәм х0 аралыгында урнашкан с санын күрсәтергә
мөмкин, cel булганга күрә, шарт буенча F'(c) = 0, димәк,
F(x) - F(x0) = 0.
Шулай итеп, I аралыгындагы барлык х лар өчен
F(x) = F(x0),
ягъни F функциясе даими кыйммәтен саклый.
f функциясенең барлык башлангыч функцияләрен /функциясе
өчен башлангыч функцияләрнең гомуми рәвеше дип аталган бер
формула ярдәмендә язарга мөмкин. Түбәндәге теорема дөрес була
(башлангыч функцияләрнең төп. үзлекләре).
Теорема I аралыгында f функциясе өчен телә¬
сә нинди башлангыч функция
F(x) + C (1)
рәвешендә языла ала, биредә F(x) функциясе —
I аралыгында fix) функциясе өчен башлангыч
функцияләрнең берсе, әС — ирекле даими зурлык.
Башлангыч функциянең кыскача әйтелгән ике үзлеге турын¬
дагы әлеге фикерне ачыклыйк:
1) (1) аңлатмадагы С урынына нинди генә сан куйсак та,
I аралыгында f функциясе өчен башлангыч функция табылыр;
2) I аралыгында / өчен нинди генә Ф башлангыч функциясен
алсак та, I аралыгындагы барлык х өчен
Ф(х) = F(x) + C
тигезлеге үтәлерлек С санын сайлап алырга мөмкин.
177
Башлангыч функция һәм интеграл
У
Исбатлау. 1) Шарт буенча F функциясе — 1 аралыгында
f функциясе өчен башлангыч функция. Димәк, теләсә нинди хе/
өчен F'(x) ~ fix), шуңа күрә
(F(x) + C)’ = F'(x)+C' =■ f(x) + О = /(х),
ягъни f функциясе өчен F (х) + С — башлангыч функция.
2) Ф(х) — шул ук I аралыгында f функциясе өчен башлангыч
функцияләрдән берсе булсын, ягъни барлык хе/ өчен Ф'(х) = f(x)·
Ул вакытта
(Ф(х) - F(x))' = Ф'(х) - F'(x) = f(x) - f(x) = О.
Моннан күренгәнчә, функциянең даимилек билгесе буенча Ф(х) -
-F(x) аермасы I аралыгында берникадәр даими С кыйммәтен ка¬
бул итүче функция була.
Шулай итеп, 1 аралыгындагы барлык х лар өчен Ф(х) ~ F(x) =
= С тигезлеге дөрес була, шуны исбатларга кирәк иде дә.
Башлангыч функцияләрнең төп үзлегенә геометрик мәгънә
бирергә мөмкин:
Функция өчен теләсә кайсы ике башлангыч функция
нең графиклары берсе икенчесеннән Оу күчәре буйлап
параллель күчереп табыла (118 нче а рәсем).
2. Башлангыч функцияләрне табуга мисаллар.
■ 1 нче мисал. / (х) = -х3 функциясе өчен R да башлангыч
функцияләрнең гомуми рәвешен табыйк.
f функциясенең башлангыч функцияләреннән берсе - икә-
нен искәрик, чонкм
= -х3. Исбатланган теорема нигезендә
178
Ьашлангыч функция һәм интеграл
(2)
Димәк,
f функциясе өчен башлангыч функцияләрнең гомуми рәвеше тү¬
бәндәгечә:
Г(х) = -^- + С.
2 нче мисал. (0; <*>) аралыгында f(x) = А функциясе өчен
х = 1 булганда, 1 кыйммәтен кабул итүче башлангыч функция
F(x0) не табыйк.
f функциясенең теләсә кайсы башлангыч функциясе F(x) =
= - — + С рәвешен алуын җиңел тикшерергә була. Чөнки шарт
буенча F (1) = 1 булганга күрә, -1 + С = 1 рәвешендәге тигезләмәне
(С га карата) табабыз, моннан С = 2, һәм, димәк, F0(x) = -у + 2.
3 нче мисал. Нокта даими а тизләнеше белән туры буйлап
хәрәкәт итә. t0 = 0 башлангыч моментында ноктаның башлангыч
координатасы хоһәм башлангыч тизлеге v0. Ноктаның χ(ί) коор-
динатасын вакытка карата функция буларак табыйк.
x'(t) = V (ί) һәм и'(0 = a (t) булганга, а (0 = а шартыннан υ'(0 = α
икәнлеге килеп чыга. Моннан
v(t) = at + С,.
(2) формулага t0 = 0 не куеп табабыз: С, - и0 һәм
х'(0 = υ(ί) = at + v0.
г
х(0= +itf + C2. (3)
С2 не табу өчен, (3) тигезлеккә ί0 = 0 кыйммәтен куябыз; моннан
С2 — х0. Шулай итеп,
*0) = ^ + νοί + χβ. Җ
Искәрмә. F ның башлангыч функциясен тапканда, кыска¬
лык өчен f бирелгән аралык, гадәттә, күрсәтелми. Бу вакытта
мөмкин кадәр озын булган аралыклар күздә тотыла. Мәсәлән,
түбәндәге мисалда / (х) = -7- функциясе (0; аралыгында би-
Ух
релгән дип исәпләү табигый.
4 нче мисал. f(x) = — функциясе өчен графигы М (9; -2)
. . '<у . . »
ноктасы аша үтә торган башлангыч функцияне табыйк.
f (х) = -А функциясенең теләсә нинди башлангыч функциясе
Ух
2у'х + С
рәвешендә языла. Әлеге башлангыч функцияләрнең графиклары
118 нче б рәсемдә сурәтләнгән. Эзләнелә торган башлангыч
функция графигының М (9; -2) координатасы ноктасы 2-^9 +
+ С = -2 тигезләмәсен канәгатьләндерергә тиеш. Моннан С = -8
икәнен табабыз. Димәк, F(x) = 2-Ух - 8.
Түбәндә кайбер функцияләрнең башлангыч функцияләре таб¬
лицасы китерелгән:
179 Башлангыч функция һәм интеграл
Функция f
k
(даими
зурлык)
х"
(neZ,
п*-1)
1
sinx
COS X
1
COS2X
1
sin2x
f башлангыч
функция¬
ләрнең
гомуми
рәвеше
һх + С
үл ♦ !
+ с
/1 + 1
2yfx +С
-cos х + С
sinx + С
tgx + С
-ctg х + C
Таблица дөрес тутырылганмы? Үзегез тикшерегез.
Күнегүләр
f функциясе өчен башлангыч функцияләрнең гомуми рәве¬
шен табыгыз (335—336).
335. ~а) /(х) = 2-х4; б) f(x} x + cosx;
в)/(х) = 4х; г)/!(х) = -3.
336. - а) f (х) = х6; б) f (х) = ± - 2;
в)/(х)=1-^г; г)/(х) = х5.
337. - f функциясе өчен бирелгән кыйммәтне күрсәтелгән ноктада
кабул итүче башлангыч функция F ны табыгыз:
а) /(х) = г(|) = -12; б) f (х) = ^, Г(|) = 0;
в) /(х) = х3, F(-l) = 2; г) f (х) = sinx, F (-π) = -1.
338.— F функциясенең f функциясе өчен башлангыч функция
икәнен тикшерегез. Әгәр дә:
а) F (х) = sin х - х cos х, f(x) = х sin х;
б) F(x) = Vx2 + 1, f (х) = -=£=;
7χ2 +ι
в) F (х) - cos х + х sin x, f (х) = x cos x;
r) F(x) = x-1 f(x) = Hil
Λ X*
булса, f өчен башлангыч функцияләренең гомуми рәвешен
табыгыз.
339.— f функциясе өчен графигы бирелгән М ноктасы аша үтүче
башлангыч функцияне табыгыз:
а) f (х) - 2 cos х, ΜI * ; 1);
б) / (х) = 1-х2, М(-3; 9);
в) r(x) = sin(x +|),Λί(γ; -1);
г) /(χ) = ^·,Μ(|;3).
180 Башлангыч функция һәм интеграл
340. — f функциясе өчен графикларының тиңдәш нокталары (ягъ¬
ни абсциссалары тигез булган нокталары) арасындагы ерак¬
лык а га тигез булган ике башлангыч функцияне табыгыз:
a) f (х) - 2 - sin х, α = 4; б) f (х) = 1 + tg2 х, α = 1;
в) /(х) = sin2 - cos2 a = 0,5; r) f(x) = -L, a = 2.
- *■ ύ
341. — Туры буенча a(t) тизләнеше белән нокта хәрәкәт итә.
t0 башлангыч моментында аның координатасы х0 гә тигез,
э тизлеге и0. Ноктаның х (t) координатасын вакытка карата
функция буларак табыгыз:
ί· a) a(t)“-2t, f0 = 1, х0 = 4, = 2;
L б) a(f) = sini, t0 = x0 = 2, ua-l;
в) a(t) = 6t, t0 - 0, x0 · 3, v0 = 1;
r) a (t) — cos t, t0 - π, x0 “ 1, v0 = 0.
28. Башлангыч функцияләрне табуның өч
кагыйдәсе
Әлеге кагыйдәләр дифференциаллауның тиңдәшле кагыйдәлә¬
ренә охшаш.
1 нче кагыйдә. Әгәр дә f өчен башлангыч функ¬
ция F, ә g өчен башлангыч функция G икән, ул ва¬
кытта f+g өчен башлангыч функция F + G була.
Чыннан да, F’ = а һәм G' - g булганга күрә, сумманың чыга¬
рылмасын табу кагыйдәсе буенча:
(F + G)' = F' + G' = / + g.
2 нче кагыйдә. Әгәр дә/өчен башлангыч функ¬
ция F, ә k даими зурлык икән, ул вакытта kf өчен
башлангыч функция kF була.
Чыннан да, даими тапкырлаучыны чыгарылма тамгасы тышы¬
на чыгарырга мөмкин, шуңа күрә
(kF)' - kF' - kf.
3 нче кагыйдә. Әгәр дә /(х) өчен башлангыч
функция F (х), ә k һәм Ь — даими зурлыклар, өстәве¬
нә k * 0 икән, f(kx + ί>) функциясе өчен башлангыч
функция ^F(kx + b) була.
Чыннан да, катлаулы функциянең чыгарылмасын табу кагый¬
дәсе буенча:
(IF(kx + b)}' = IF'(kx + b) k = f(kx + b).
Бу кагыйдәләрне куллануга мисаллар китерик.
181 Башлангыч функция һәм интеграл
Q 1 нче мисал, f(x) = x3 + функциясе өчен башлангыч
функцияләрнең гомуми рәвешен табыйк.
х3 функциясе өчен башлангыч функцияләрнең берсе , ә —
функциясе өчен башлангыч функцияләрнең берсе ’ булганга,
1 нче кагыйдә буенча f(x) = х3 + Л· функциясе өчен башлангыч
функцияләрнең берсе — - — булыр.
4 х
Җавап. F(x) = ^-| + С.
2 нче мисал./(х) «5 cos х функциясе өчен башлангыч функ¬
цияләрдән берсен табыйк.
cos х функциясе өчен башлангыч функцияләрнең берсе sin х,
шуңа күрә 2 нче кагыйдәне кулланып җавапны табабыз: F(x) **
= 5 sin х була.
3 нче мисал, р = sin(3x-2) функциясе өчен башлангыч
функцияләрнең берсен табыйк.
sin х функциясе өчен башлангыч функцияләрнең берсе — cos х
булганга күрә, 3 нче кагыйдә буенча эзләнелә торган башлангыч
функция F (х) “ _ з cos (Зх - 2) гә тигез.
4 нче мисал, /(х) = функциясе өчен башлангыч
(7 - Зх)5
функцияләрнең берсен табыйк.
функциясе өчен башлангыч функция - ( гә тигез, шуңа
күрә 3 нче кагыйдә буенча эзләнелә торган башлангыч функция:
- I
F (х) = — _ .
-3 4(7-3x)* 12(7-Зх)*
5 нче мисал. Массасы 2 кг булган материаль нокта Ох
күчәре буенча бу күчәр буйлап юнәлгән көч тәэсирендә хәрәкәт
итә. t вакыты моментында әлеге көч F(t) = 3t-2 гә тигез. Әгәр
дә, t “ 2 с булганда, ноктаның тизлеге 3 м/с ка, ә координата 1 гә
тигез (F — ньютоннарда алынган көч, t ~ секундларда алынган
вакыт, х — метрларда үлчәнгән юл) икәне билгеле булса, ноктаның
хәрәкәт законы х(() ны табыгыз.
Ньютонның икенче законы буенча F = та, биредә а — тизлә¬
неш. Шуңа күрә
α(0 = £ = |ί-1.
Ноктаның тизлеге и (t) аның тизләнеше a (t) өчен башлангыч
функция була, шуңа күрә
υ(Ο = |ί2 -t + С2.
182 Ба шлангым функция һәм интеграл
С\ константасын о (2) = 3 шартыннан табабыз:
~ 4 - 2 + С, = 3, ягъни Cj = 2 Һәм v (t) = т t2 _ t + 2.
x(t) координатасы v (i) тизлеге өчен башлангыч функция була,
шуңа күрә
x(O = |i3 ~^t2+2t + C2.
С2 константасын х (2) = 1 шартыннан табабыз:
1 8 - j 4 + 4 + С2 = 1, С2 = -3.
Шулай итеп, ноктаның хәрәкәт законы:
x(i) = |i3-~t2 + 2t-3. ■
Күнегүләр
/ функциясе өчен башлангыч функцияләрнең гомуми
рәвешен табыгыз (342—344).
342,—
343.
а) f (х) - 2 - х* + -р-;
») f (х) - ~г ~ sinx;
a) f(x) = (2x-3)s;
в) / (х) = (4-5х)’;
б) f (χ) = х - -ь cos х;
г) f(x) ~ 5х2 -1.
б) f (х) = 3sin2x;
г) f(x) = -|cos(f-f)·
344. а)/Чх) = —;
(4—15х)4
б) f(x) =
2 г.
cos2^ -xj
В) f (X) = i—
' ' ’ (Зх-1)2
f(X) = -^ +
1
cos2 (Зх -1)
345.
/ функциясе өчен графигы М ноктасы аша үтүче башлан¬
гыч функцияне табыгыз:
а) /(х) = 4х + -Ь, М (-1;4);
б) Дх) = х3 +2, ЛГ(2;15);
в) /(х) = 1 - 2х, М (3; 2);
г) f(x) = i-10x*+3,M(l; 5).
Башлангыч функция һәм интеграл
346.— Түбәндәге функцияләр өчен башлангыч функцияләрнең
гомуми рәвешен табыгыз:
а) /(х) - 1 - cos3x + 2sin(“ -х);
б) Г(х) = ^4т-
sin- 4х
в) f (х) = —77?—гг - 3 sin (4 - х) + 2х;
cos- (Зх +1)
г) f (х) = —ί + 3 - 2 cosi-y - х]
(3-2x)s j5x-2 U )
-Зх2;
347. — Әгәр F графигындагы М ноктасының координаталары бил¬
геле булса, f функциясе өчен башлангыч F функциясен
формула белән бирегез:
а) /(х) = 2х + 1, М(0; 0);
б) /(х) = 3х2-2х, М(1; 4);
в) f(x) = x + 2, М(1; 3);
г) /(х) =-х2 + Зх, Af(2; -1).
348. — Туры сызык буенча хәрәкәт итүче ноктаның тизлеге i>(t) =
= t2 + 2t - 1 тигезләмәсе белән бирелгән. Әгәр вакытның
башлангыч моментында (е = 0) ноктаның координаталар
башында урнашуы билгеле булса, нокта координаталары
х ның t вакытына бәйлелек формуласын языгыз.
349. — Туры сызык буенча хәрәкәт итүче ноктаның тизлеге υ (е) =
- 2 cos формуласы белән бирелгән. Әгәр t = с момент¬
ында ноктаның координаталар башыннан 4 м ераклыкта
урнашуы билгеле булса, нокта координаталарының вакыт¬
ка бәйлелеген аңлаткан формуланы табыгыз.
350. — Нокта туры сызык буенча a(t) = 12t2 + 4 тизләнеше белән
хәрәкәт итә. Әгәр t = 1 с моментында аның тизлеге 10 м/с
ка тигез булып, координатасы 12 гә тигез булса (а ның
үлчәү берәмлеге 1 м/с2 ка тигез), ноктаның хәрәкәт итү
законын табыгыз.
351. — т массалы материаль нокта Ох күчәре буенча әлеге күчәргә
параллель юнәлгән кеч тәэсирендә хәрәкәт итә. t вакыты
моментында бу көч F(t) га тигез. Әгәр дә t = t0 булганда,
; ноктаның тизлеге и0 гә тигез, ә аның координатасы х0 гә
J тигез икәне билгеле булса (F(t) — Ньютоннарда, t — се-
jg кундларда, с — секундка туры килгән метрларда, т —
(килограммнарда үлчәнә), х(() ның t вакытына бәйлелек
формуласын табыгыз:
g a) F(e) = 6-9t, t0= 1, υ0 = 4, х0--5, m = 3;
' б) F (0 = 14 sin i, t0 = π, ι>0 = 2, χ0 = 3, m = 7;
ί в) F(t) = 25cost, t0 = f , υ0 = 2, χα = 4, /η-5;
tl г) F(t) = 8t + 8, e0 = 2, ue - 9, x0 = 7, m = 4.
184
Башлангыч функция һәм интеграл
352.— f функциясе өчен булган Fx башлангыч функциясенең гра¬
фигы М ноктасы аша, ә F2 башлангыч функциясенеке N
ноктасы аша үтә. Әлеге башлангыч функцияләрнең аерма¬
сы ничек? Әгәр дә:
а) f (х) - Зх2 - 2х + 4, Af (-1; 1), N(0; 3);
б) / (х) = 4х - 6х2 + 1, Af(O; 2), N(1; 3);
I в) / (х) = 4х - х3, М(2; 1), JV (-2; 3);
I г) /(х) = (2х + I)2, М(-3; -1), Аг(1; б|) булса, F, һәм F, гра-
I фикларының кайсысы югарырак урнашыр?
§8.
Интеграл
29. Кәкресызыклы трапециянең мәйданы
Ох күчәренең [а; Ь] кисемтәсендә тамгасын үзгәртми
торган өзлексез f функциясе бирелсен, ди. Әлеге функциянең
графигы, [а; 6] кисемтәсе һәм х - а һәм х = Ь турылары белән
чикләнгән фигураны (119 нчы рәсем) кәкресызыклы трапеция
дип атыйлар. 119 нчы а—д рәсемнәрендә кәкресызыклы трапе¬
циягә төрле мисаллар китерелгән.
119 нчы рәсем
185 Башлангыч функции һәм интеграл
Кәкресызыклы трапецияләрнең мәйданнарын исәпләп чыгару
ечен, түбәндәге теоремадан файдаланалар.
Теорема Әгәр /функциясе — [а; &] кисемтәсендә
езлексез һәм тискәре булмаган функция, ә F шу¬
шы кисемтәдә аның башлангыч функциясе бул¬
са, ул вакытта кәкресызыклы трапециягә тиц-
дәш мәйдан (120 нче рәсем) башлангыч функция¬
нең [а; б] кисемтәсендәге усемтәсенә, ягъни
S = F(b)~F(a) (1)
га тигез.
Исбатлау, [а; б] кисемтәсендә билгеләнгән S (х) функциясен
тикшерик. Әгәр а<х$Ь икән, S(x) мәйданы М(х;0) ноктасы
аша үтүче вертикаль турыдан сулдарак урнашкан кәкресызыклы
трапециянең бер өлешенә тигез була (120 нче а рәсем). Әгәр х = а
булса, S (о) - 0 була. Шул ук вакытта S (i>) = S икәнен искәрәбез
(S — кәкресызыклы трапеция мәйданы).
s'(x) - f(x) (2)
икәнен исбатлыйк.
Чыннан да, чыгарылма билгеләмәсе буенча
Δχ —> 0 булганда, * -> /(х) (3)
икәнен исбатларга кирәк.
Δ5 (х) санаучысының геометрик мәгънәсен ачыклыйк. Гадилек
өчен Δχ > 0 очрагын тикшерик. Δ5 (х) = S (х + Δχ) - S (х), шуңа
күрә AS(x) 120 нче б рәсемендә штрихланган фигураның мәйда¬
ны булыр. Хәзер шундый ук AS(x) мәйданлы турыпочмаклык
алыйк, ул [х; х + Δχ] кисемтәсенә таянган булсын (120 нче в рә¬
сем). Турыпочмаклыкның өске ягы, f функциясенең өзлексез
булуы нәтиҗәсендә, аның графигын абсциссасы с е [х; х + Δχ]
булган ниндидер ноктада кисеп үтә (киресенчә булганда, әлеге
турыпочмаклык я кәкресызыклы трапециянең бер өлешендә
[х; х + Δχ] кисемтәсе өстендә була, яисә үзе трапецияне эченә ала;
аның мәйданы тиңдәшле рәвештә Δ£(χ) мәйданыннан кечерәк
120 нче рәсем
186 Башлангыч функция һәм интеграл
яки зуррак була). Турыпочмаклыкның биеклеге f(c) ка тигез.
Турыпочмаклыкның мәйдан формуласы буенча табабыз: Δ5 (х) -
= /(с)Дх, моннан '7,'1 = f(c)· (БУ формула Δχ < 0 булганда да
дөрес.) с ноктасы х һәм х + Δχ арасында ятканга күрә, Δχ —>0
булганда, с ноктасы х ка омтыла, f функциясе өзлексез бул¬
ганлыктан, Δχ —> 0 гә омтылганда, f (с) -> /(х). Шулай итеп,
Δχ -> 0 гә омтылганда, —: > j (х).
(2) формула исбатланды.
Без S (х) функциясенең f (х) функциясе өчен башлангыч функ¬
ция булуын таптык. Шуңа күрә башлангыч функцияләрнең төп
үзлеге буенча барлык хе[а;б] өчен
S(x) = F(x) + C
икәне табыла, биредә С — ниндидер даими зурлык, ә F(x) исә
f функциясе өчен башлангыч функцияләрнең берсе. С ны табу
өчен х = а ны куябыз:
F(a) + С = S(a) = 0,
моннан C = -F(a). Димәк,
S(x) = F(x)-F(a). (4)
Кәкресызыклы трапециянең мәйданы S (Ь) га тигез булганлык¬
тан, (4) формулага х = Ь ны куеп табабыз:
S = S(fe) = F(b) - F(a).
-- Мисал. /(х) = х2 функциясенең графигы һәм у = 0, х-1,
х = 2 турылары белән чикләнгән кәкресызыклы трапециянең мәй¬
даны S ны исәпләп чыгарыйк (121 нче рәсем).
f (х) = х2 функциясе өчен башлан¬
гыч функцияләрнең берсе булып
F(x) = -j- хезмәт итә. Димәк,
S = F(2)-F(1) = ^-H =1 yg
4 4 Λ
' ■ ' Сез функциянең чыгарылмасын
табу күпчелек очракта исәпләү ха¬
рактерындагы кыенлыкларга гына
бәйле икәнен күрдегез. Башлангыч
функцияләрне тапканда исә, эш кы¬
енрак тора.
Мәсәлән, бирелгән функциянең
башлангыч функциясе бармы-юкмы
икәне башта ук ачык билгеле дә тү¬
гел. Шуңа күрә аралыкта өзлексез
булган теләсә нинди функциянең бу
аралыкта башлангыч функциясе бар
икәнен әйтеп китәбез. Югарыда ките¬
релгән (2) формуланың исбатланышы
121 нче рәсем
187 Башлангыч функция һәм интеграл
бу мәсьәләгә ачыклык кертә. Шулай да кайбер шактый гади
функцияләрнең дә башлангычын мәктәптә өйрәнелә торган функ¬
цияләр ярдәмендә язып булмаска мөмкин. Мәсәлән, у = Vx3 +1
функциясе моңа мисал була ала.
Күнегүләр
Түбәндәге сызыклар белән чикләнгән фигураның мәйданын
исәпләп чыгарыгыз (353—354).
353.-48 а) у = х2, у = 0, х - 3; б) у = cos х, у = 0, х — 0, х *· J;
в) у = sin х, у = 0, х = 0, х = π;
г) у - ±, у - 0, х = 1, х = 2.
354.-
а) у = х3 + 1, у = 0, х = 0, х = 2;
б) у = 1 -I- 2 sin х, у = 0, х = 0, х = ;
в) у — 4 - х2, у — 0;
г) у = 2 cosx, у = 0, х - - 2 > х = 2’
355. — Түбәндәге сызыклар белән чикләнгән фигураның мәйда¬
нын исәпләп чыгарыгыз (355—356).
а) у = (х + 2)2, у = 0, х = 0;
б) У = j—рГ +1. ί/ = 0, х = 0, х = 2;
в) у = 2х - х2, у = 0; г) у = -(х -1)3, у - 0, х = 0.
356. - а) у = 3sin(x + &). у = 0, х = х =
б) у = 2 cos 2х, у = 0, х = - |. х = I;
|в) у = sinx у = 0, х = J, х =
г) р = 1-со8Х,у = 0,х = -^ х = |.
30. Интеграл. Ньютон — Лейбниц формуласы
1. Интеграл турында төшенчә. Кәкресызыклы трапе¬
циянең мәйданын икенче төрле юл белән дә исәпләргә мөмкин.
Гадилек өчен f функциясен тискәре түгел һәм [а; 6] кисемтәсендә
өзлексез дип алырбыз; ул вакытта тиңдәшле кәкресызыклы трапе¬
циянең S мәйданын якынча түбәндәгечә исәпләргә мөмкин булыр:
[а; 5] кисемтәсен х0 = a < х, < х2 < ... < хл_, < х„ = Ь нокталары
белән бердәй озынлыктагы п кисемтәгә бүлик, һәм Δχ = =
- xk ~ х*., булсын, монда Λ- 1,2 .... п-1, п. Ьәр [х*.,; х*] кисемтәсен
Башлавгыч функция һәм интеграл
нигез итеп алып, /(rt l) биеклегендәге турыпочмаклык төзибез.
Бу турыпочмаклыкның мәйданы:
f(xlt_l)Ax = ~-f(xk_1)
ә барлык мондый турыпочмаклыкларның мәйданнары суммасы
(122 нче рәсем):
S„ = ^(/(x0) + /(xt) + ... + f(xB.1))
f функциясенең өзлексезлеге нигезендә, п зур булганда, ягъни
Ах кечкенә булганда төзелгән турыпочмаклыкларның берләшмәсе
безне кызыксындырган трапеция белән «тәңгәл килә диярлек*.
Шуңа күрә п зур булганда, S„^S дигән фараз барлыкка килә,
һәм бу якынча тигезлек теләсә нинди төгәллек белән дә үтәлә.
(Кыскача «п чиксезлеккә омтылганда, S, зурлыгы S ка омтыла*
диләр һәм п —> *> омтылганда, S„ —> S дип язалар.)
Бу фараз дөрес. Моннан да бигрәк [а; &] кисемтәсендә өзлексез
булган теләсә нинди f функциясе өчен (тискәре булмау мәҗбүри
түгел) (п —> оо булганда) ниндидер санга омтыла. Бу санны (бил¬
геләмә буенча) f функциясенең а дан Ь га кадәр интегралы дип
*
атыйлар һәм J f (х) dx дип билгелиләр, ягъни
о Ь
п —* оо кә омтылганда, S„ —> J f (x)dx (1)
a
(«эф икс дэ иксның а дан Ь га кадәр интегралы» дип укыла).
а һәм Ь саннары интеграллау чикләре дип атала: а — түбәнге
чик, Ь — югарыгы чик. / тамгасы — интеграл тамгасы дип атала.
f функциясе — интеграл асты функциясе дип, ә х үзгәрешлесе
интеграллау үзгәрешлесе дип атала.
Шулай итеп, әгәр [a; fe] кисемтәсендә /(х) 0 булса, кәкресы¬
зыклы трапециянең мәйданына тиңдәш S мәйданы
ь
S = jf(x)dx (2)
а
Башлангыч функция һәм интеграл
► Интегралны якынча исәпләү өчен, S„ суммасын карарга мөм¬
кин. Шулай да f функциясе уңай булган очракта, 123 нче рәсемдә
күрсәтелгәнчә, кушылучылары кәкресызыклы трапециягә «камал¬
ган» һәм сынык сызыклар белән чикләнгән трапеция мәйданнары¬
на тигез булган
ft \ it Ct f
суммасыннан файдалану яхшырак.
Чыннан да, трапеция мәйданы формуласын кулланып табабыз:
ς + b-a + b-a
2 ' п 2 п *
2. Ньютон — Лейбниц формуласы. Кәкресызыклы трапеция
мәйданы өчен булган формулалар
»
S = F(b)-F(a) һәм S = jf(r)dx
ны чагыштырып нәтиҗә ясыйбыз.
Әгәр F [a; ft] кисемтәсендә f өчен башлангыч функция
булса, ул вакытта
ь
f (х) dx - F {b) F (а).
u
(3)
(3) формула Ньютон — Лейбниц формуласы дип атала. Ул [a; ft]
кисемтәсендә өзлексез булган теләсә нинди f функциясе өчен дөрес.
Ньютон — Лейбниц формуласын куллануга мисаллар карыйк.
2
И 1 нче мисал, j x2dx ны исәпләп чыгарыйк, х2 функциясе
-1
өчен башлангыч функция булу сәбәпле,
2
ί x3dx = £ - » 3.
-1
F(b) - F(α) аермасын ([a; ft] кисемтәсендә F функциясенең үсем¬
тәсен) язу җайлы булсын өчен, аны кыскача F (г) | , ягъни
F(b)-F(a) = F(x)\b'
рәвешендә тамгалау кабул ителгән.
190 Башлангыч функция һәм интеграл
Шушы тамгалаулардан файдала
нып, Ньютон — Лейбниц формуласын,
гадәттә,
p(x)dx = r(x)i; (4)
α
рәвешендә язалар.
π
2 нче мисал, j sin х dx ны исәп-
о
ләп чыгарыйк.
Кабул ителгән тамгалардан файда¬
ланып табабыз:
УА
124 нче рәсем
J sin х dx = - cosx I* = - cos π - (- cos 0) - 2.
0
1 нче искәрмә. Интегралга без биргән билгеләмә ‘ функ¬
циясенең -1 дән 2 гә кадәр интегралы турында сөйләргә мөмкин¬
лек бирми әле, чөнки бу функция [—1; 2] кисемтәсендә өзлексез
түгел. Шушы ук кисемтәдә функциясе — функциясе өчен
„ х I
башлангыч була алмый, чөнки бу кисемтәдәге 0 ноктасы — функ¬
циясенең билгеләнү өлкәсенә керми.
~ 3 нче мисал, у = 1 - х һәм у = 3 - 2х - х2 сызыклары белән
чикләнгән фигураның мәйданын исәплик.
Әлеге функцияләрнең графикларын сызабыз (124 нче рәсем)
һәм графикларның кисешү нокталарының абсциссаларын 1 - х =
= 3 - 2х - х2 тигезләмәсеннән табабыз. Бу тигезләмәне чишеп, х = 1
һәм х = -2 икәнен беләбез. Эзләнелә торган мәйданны кәкресызык¬
лы BADC трапециясе һәм ВАС өчпочмагы мәйданнарының аерма¬
сы буларак табарга мөмкин. (2) формула буенча
Sbadc = J (3-2x-x=)dx = /зх-х2
= [з-1-|]-(з(-2)-(-2)2 = 9.
Sabac =jAB BC = j ·3·3 = |.
Димәк, штрихланган фигураның мәйданы:
S — &BADC ~ &А.ВАС — 9 “ 9 = ~ 4,5.
191 Башлангыч функция һәм интеграл
2 нче искәрмә, а b булганда, билгеләмә буенча
b a
jf(x)dx = -$f(x)dx
a b
дип алып, интеграл тешенчәсен киңәйтергә җайлы.
Шушындый килешү булганда, Ньютон — Лейбниц формула¬
сы теләсә нинди а һәм Ъ өчен дөрес була (аерым алганда,
4
j/(x)dx = 0).
а
Күнегүләр
Интегралны исәпләгез (357—358).
357. —
358. -|
359.
2
a) J x4dx;
1
1
«)
J (2x+l)2
2
б) Jcosx dx;
β
б) J 3 cos у dx;
о
дөреслеген
в) ί x3dx;
10
в) ί
г)
J COS2 X
0
я
2
г) I sin 2x dx.
4
Тигезлекнең
a) ί = ί dx;
J cos2x J
о 0
rc J-
2 Й
в) jcosxdx = J x2dx;
ΰ о
исбатлагыз:
з .
6) ί sinxdx = ί
о iVx
16
1 2
r) J (2x +1) dx = j (x3 -1) dx.
О 0
4
360.
361.
Сызыклар белән чикләнгән фигураның рәсемен ясагыз
һәм исәпләп чыгарыгыз (360—361).
а) у — х4, у — 0, х - -1; х = 1;
б) у = х4, у = 1;
в) у = х2 - 4х + 5, у = 0, х = 0, х = 4;
г) у = х2 - 4х + 5, у = 5.
а) у = 1 - х3, у = 0, х = 0;
б) у = 2 - хэ, у = 1, х = -1, х = 1;
в) у = -х2 - 4х, у = 0, х = -3, х = -1;
г) у = -х2 - 4х, у - 1, х = -3, х = -1.
192 Вашлангыч функция һам интеграл
Интегралларны исәпләп чыгарыгыз (362—363).
2я 2
362.-a) isin^dx; б) ( , dr ;
9 θ < j Xr * 5
ж 2 v
2ж
B’iA; 4 a
363.— a) j isin-+cos-| dx;
1
6) J(l + 2x)’dx;
0
ж
0
12
в) j (1 + cos2x)dx;
0
r> j(x+i‘dJf·
Сызыклар белән чикләнгән фигураның рәсемен ясагыз
һәм мәйданын исәпләп чыгарыгыз (364—366).
364. — а) у = х3, у = 8, х = 1;
б) у = 2 cos х, у = 1, х = - I , х = з ;
в) у = х2 - 2х + 4, у = 3, х = -1;
г) у = sinx, у = 2> х = 6» х = -g-·
365. — а) у = 4х - х2, у = 4 - х; б) у = р. у = 2х, х = 4;
в) у = х2; у = 2х; г) у = 6 - 2х, у = 6 + х - х2.
366. — а) у = х2 - 4х + 4, у = 4 - х2;
б) у = х2 - 2х + 2, у = 2 + 6х - х2;
в) у = х2, у = 2х - х2;
г) у = X2, у = X3.
367. — у = 8х - 2х2 функциясенең графигы белән һәм шул парабо¬
ланың түбәсеннән үткәрелгән орынма һәм х = 0 турысы
белән чикләнгән фигураның мәйданын исәпләп чыгарыгыз.
Й
368. — /(х) = 8 - О,5х2 функциясенең графигы, аңа х = -2 абсцис¬
салы ноктадан үткәрелгән орынма һәм х =1 турысы белән
? чикләнгән фигураның мәйданын исәпләп чыгарыгыз.
369. -М Тигезлекне исбатлагыз:
a) J (/ (х) + g (х)) dx - J f (х) dx + J g (x) dx;
д a a
b b
t 6) J kf (x) dx — k j f (x) dx (биредә k — даими).
193 Башлангыч функция һәм интеграл
31. Интегралны куллану
1. Җисемнәрнең күләмнәрен исәпләү. V күләмле җи¬
сем бирелсен, ди, өстәвенә шундый бер туры бар (125 нче рәсем),
бу турыга перпендикуляр итеп нинди генә яссылык алсак та, ул
яссылык белән җисемнең кисешү мәйданы S безгә билгеле була.
Ләкин Ох күчәренә перпендикуляр яссылык күчәрне ниндидер х
ноктасында кисеп үтә. Димәк, һәрбер х санына ([а; &] кисемтәсен¬
нән, 125 нче рәсемне карагыз) бердәнбер S(x) саны — җисемнең
әлеге яссылык белән кисешү мәйданы тиңдәш була. Шуның белән
[а; £>] кисемтәсендә S(x) функциясе бирелә. Әгәр S(x) функциясе
[а; Ь] кисемтәсендә өзлексез булса,
*
(I)
формуласы дөрес була. Бу формуланың тулысынча исбатланышы
математик анализ курсларында бирелә, ә биредә бу формулага
китерә торган күргәзмәле фикерләүләргә тукталыйк.
[а; б] кисемтәсен х0 = a < < х2 < ... < хп _, < Ь = хп нокталары
белән тигез озынлыктагы п кисемтәгә бүлеп чыгыйк,
Δχ = = х* - k = 1,2,п
булсын (30 нчы пунктны карагыз). Һәрбер хк ноктасы аша Ох
күчәренә перпендикуляр яссылык үткәрәбез. Бу яссылыклар би
релгән җисемне катлауларга бүлә¬
ләр (126 нчы а, б рәсемнәр), и, ,
һәм ак яссылыклары арасындагы
катлауның күләме п җитәрлек ка¬
дәр зур булганда, S(xkl) кисеменең
мәйданын «катлау калынлыгы*
Δχ ка тапкырлаганга якынча тигез
була һәм шуңа күрә
V *■ S (х0) Δχ + S (Xj) Δχ + ... +
+ 5(χ„.,)Δχ = Vn.
а)
126 нчы рәсем
194 Башлангыч функция һәм интеграл
Җисем никадәр юкарак катлау¬
ларга киселсә, ягъни п никадәр зур
булса, әлеге якынча тигезлекнең тө¬
гәллеге шулкадәр югары була. Шуңа
күрә п —> » омтылганда, Vn —»V. Инте¬
гралның билгеләмәсе буенча
127 иче рәсем
п « кә омтылганда, —>
а
11 нче мисал. Биеклеге Н һәм нигезләренең мәйданнары
S һәм s булган кисек пирамиданың күләме (S + s + VSs) ка
тигез икәнен исбатлыйк.
О ноктасы »тулы» пирамиданың түбәсе булсын (127 нче рәсем).
О ноктасы аша, пирамиданың нигезенә перпендикуляр итеп.
Ох күчәрен үткәрәбез. Кисек пирамиданың нигезләре Ох күчәрен
а һәм Ь нокталарында кисеп үтә. Ох күчәренә перпендикуляр
һәм әлеге күчәрдәге [a; Ь] кисемтәсен х ноктасында кисеп үтүче
һәр яссылык кисемдә пирамиданың нигезенә охшаш күппочмак
бирә. Шуңа күрә кисем мәйданы S(x) kx- ка тигез, э аерым алганда.
ь
s — S(a) = ka2 һәм S — S(b) — kb2.
Кисек пирамиданың күләмен (1) формула буенча исәпләп чыга¬
рабыз:
Ь ъ
V= ikx2dx = *f =4(63 -a*) = ^(kb2 +kab + ka2) =
J d О d
a
d
2 нче мисал. Кәкресызыклы трапеция Ох күчәренең [a; b]
кисемтәсенә таяна һәм өске яктан [а; Ь] кисемтәсендә тискәре бул¬
маган, өзлексез f функциясенең графигы белән чикләнә. Бу кәкре¬
сызыклы трапецияне Ох күчәре тирәсендә әйләндергәндә, күләме
а)
б)
128 нче рәсем
Башлангыч функция һәм интеграл
b
V = J nf 2(x) dx (2)
0
формуласы буенча табыла торган җисем табабыз (128 нче а рәсем).
Чыннан да, Ох күчәренә перпендикуляр һәм бу күчәрнең [а; 6]
кисемтәсен х ноктасында кисеп үтә торган һәрбер яссылык, җисем
белән кисешкәндә, f (х) радиуслы һәм S (х) = nf2(x) мәйданлы түгә¬
рәк бирә (128 нче б рәсем). Моннан (1) формуласы буенча (2)
формула табыла.
2. Үзгәрешле (алмаш) көчнең эше. Р көче тәэсирендә туры
сызык буенча хәрәкәт итүче материаль ноктаны тикшерәбез. Әгәр
тәэсир итүче көч даими булып туры буенча юнәлсә, ә күчеш s ка
тигез булса, физикадан билгеле булганча, әлеге көчнең эше Рз
тапкырчыгышына тигез булыр. Хәзер үзгәрешле көч башкарган
эшне исәпләү өчен формула чыгарабыз.
Нокта Ох күчәре буенча проекциясе Ох күчәренә х тан f функ¬
циясе булган көч тәэсирендә хәрәкәт итсен, ди. Бу вакытта без
f ны өзлексез функция дип фараз итәрбез. Әлеге көч тәэсирендә
материаль нокта Μ (а) ноктасыннан М (Ь) ноктасына күчә (129
нчы а рәсем). Бу очракта А эшенең
ь
A = ^f(x)dx (3)
а
формуласы буенча исәпләнүен күрсәтербез.
[а; &] кисемтәсен бердәй Δχ = - - озынлыгындагы п кисемтәгә
л
бүләбез. Әлеге кисемтәләр [a; xj, [х,; х2]..., [х„ һ] була (129 нчы б
рәсем). Барлык [a; Ь] кисемтәсендә көчнең эше әлеге көчнең та¬
былган кисемтәләрдәге эшләр суммасына тигез, / функциясе х тан
өзлексез функция булганлыктан, җитәрлек кадәр кечкенә [а; х,]
кисемтәсендә көчнең эше якынча f(a)(xl-a) га тигез (без / ның
кисемтәдә үзгәрүен исәпкә алмыйбыз). Шушыңа охшаш рәвеш¬
тә икенче [x^xj кисемтәсендә көчнең эше /(х()(х,-х,) гә ти¬
гез һ.б.; п нчы кисемтәдә көчнең эше якынча f(x„_d(b ~ χ„-ι)гә тигез.
Димәк, барлык [а; һ] кисемтәсендә көчнең эше якынча
А = Αη = /(α) Δχ +/(х,) Δχ +... +/(χΓ_,)Δχ =
= ^£(Г(а) + Г(х1) + ... + Г(х, ,))
гә тигез һәм [a; fe] кисемтәсе никадәр кыскарак кисемтәләргә бүл¬
гәләнсә, якынча тигезлекнең төгәллеге шулкадәр югары була.
м (а) М(Ъ) М (a) Af (ft)
—1 1 » ■ ο I - I—β ►
О о Ь х 0 а = х0 х, х2 ...х„ L x„=ft χ
а) б)
129 нчы рәсем
196 Ва
шлангыч функция һәм интеграл
О х О х х
а) б)
130 нчы рәсем
Әгәр дә η —> ο» дип исәпләсәк, әлеге якынча тигезлекнең төгәл
тигезлеккә күчүе табигый:
А. =4£(/(о) + ИХ|) + ...4/(х.-|П-» А.
п —> co кә омтылганда, А„ тикшерелә торган функциянең а дан
Ь га кадәрге интегралына омтылганга күрә (30 нчы пунктны
карагыз), (3) формула чыгарылды.
3 нче мисал, 5 см га сузылган пружинаның эластиклык
көче 3 Н га тигез. Пружинаны 5 см га сузар өчен, күпме эш баш¬
карырга кирәк?
Гук законы буенча пружинаны х зурлыгына суза торган
F көче F = kx формуласы буенча исәпләп чыгарыла, биредә k —
даими пропорциональлек коэффициенты (130 нчы рәсем), О нок¬
тасы пружинаның ирекле торышына туры килә. Мәсьәлә шар¬
тыннан 3 = fe-0,05 икәне чыга. Димәк, k = 60 һәм көч F = 60x,
ә (3) формула буенча
А = j 60х dx = 30х2|“'°5; А = 0,075 Дж.
0
3. Массалар үзәге. Массалар үзәген тапканда, түбәндәге кагый¬
дәләрдән файдаланалар.
1) Туры өстендә хп х2, ... , х„ координаталы нокталарда урнаш¬
кан гп2, ... , тп массалы А,, А2, ... , Ап материаль нокталары
системасының массалар үзәге координатасы х'
х' - +'П2хг + ... + т„х„ .
т, + т2 + ... + т„ ' ’
формуласы буенча табыла.
2) Массалар үзәге координатасын исәпләгәндә, фигураның телә¬
сә кайсы өлешен материаль нокта белән алыштырырга мөмкин,
бу ноктаны әлеге өлешнең массалар үзәгенә урнаштырып, ә масса¬
сын фигураның тикшерелә торган өлешендәге массасына тигез
дип алалар.
_ 4 нче мисал. Таяк буенча, ягъни Ох күчәренең [а; Ь] кисем¬
тәсе буенча, р (х) тыгызлыгындагы масса бүленеп урнашсын, биредә
р(х) — өзлексез функция. ь
а) Таякның суммар массасы М ның J р (х) dx ка тигез икәнен;
Л һ
б) массалар үзәге координатасы х' ның п j хр (х) dx
икәнен күрсәтик. ‘ а
ка тигез
Ьашлангыч функция һәм интеграл
[a; ft] кисемтәсен a — х0 < χΊ < х2 < ... хп = Ь нокталары белән
тигез η өлешкә бүләбез (129 нчы б рәсем), η зур булганда, әлеге
η кисемтәнең һәркайсында тыгызлыкны даими һәм k нчы ки¬
семтәдә якынча р(л*-1) гә тигез дип әйтергә (р(х) ның өзлексез
булуы сәбәпле) була. Ул вакытта k нчы кисемтәнең массасы
тк =-—p(x*-i) гә якынча тигез, ә таякның барлык массасы
■~~(Р(Хо) + р(Х]) + ,.. + p(xn.j)) гә тигез, η кечкенә кисемтәләр¬
нең һәркайсын х*_, ноктасында урнашкан т* массалы материаль
нокта дип санап һәм (4) формула буенча массалар үзәгенең коорди-
натасын якынча табабыз:
, ~(Χ<ιΡ(Χο) + ΧιΡ(Χι) + ... + Χ„-ιΡ(Χη-ι))
X = —а
(P(xj + P(xl) + -+P(*,,-1))
Ь
Хәзер инде η -♦ ® кә омтылганда, санаучының J хр (х) dx инте¬
гралына, ә ваклаучы таякның (барлык массасын аңлатучы зурлык)
Ъ
jp(x)dx интегралына омтылуын игътибарга алыйк.
л
Яссылыктагы яки пространстводагы материаль нокталар систе¬
масының массалар үзәге координаталарын табу өчен дә, (4) форму¬
ладан файдаланалар.
Күнегүләр
370. — а) у = х2_+ 1, х = 0, х = 1, р = 0;
б) у = ч/х, х —1,х = 4, у = Q;
I в) у = у[х, х = 1, у = 0;
г) у = 1 - х2, у - 0
сызыклары белән чикләнгән кәкресызыклы трапецияне
абсциссалар күчәре тирәсендә әйләндергәндә табылган җи¬
семнең күләмен табыгыз.
371. - а) у = х2; у = х; б)у = 2х, у = х + 3, х = 0, х = 1;
в) у = х 4- 2, у = 1, х - 0, х = 2; г) у = Jx, У = х
сызыклары белән чикләнгән фигураны абсциссалар күчәре
тирәсендә әйләндергәндә барлыкка килгән җисемнең күлә¬
мен табыгыз.
372. а) Радиусы R һәм биеклеге Н булган шар сегментының
күләмен табыгыз.
б) Биеклеге Н, нигез радиуслары R һәм г булган кисек
конусның күләме өчен формула чыгарыгыз.
198
Башлангыч функция һәм интеграл
373. — Әгәр 2 Н кеч пружинаны 1 см га кысса, пружина 4 см га
i кысылсын өчен, күпме эш башкарырга кирәк?
374. -14 Н көч пружинаны 8 см га суза. Пружинаны 8 см га сузу
I өчен, күпме эш башкарырга кирәк?
375. — g зурлыгындагы электр корылмасы тәэсирендә электрон
туры буенча а ераклыгыннан Ь ераклыгына кадәр күчә.
Корылмаларның үзара тәэсир итешү көче башкарган эшен
табыгыз. (Ике очракны тикшерегез: 1) a < b, q < 0; 2) Ь < а,
q > 0. Кулон законын аңлаткан формуладагы пропорцио¬
нальлек коэффициентын γ га тигез дип алыгыз.)
376. — Каналның киселеше тигезьянлы трапеция формасында:
аның биеклеге һ, нигезләре а һәм Ь. Каналны тутыручы
суның плотинага ясаган басым көчен табыгыз (a > b, а —
трапециянең өске нигезе).
377. — Нигез яссылыгыннан төбендәге тишем аша цилиндрсыман
мичкәгә бирелә торган су мичкәне тутыра. Бу вакытта са¬
рыф ителгән эшне табыгыз. Мичкәнең биеклеге Λ ка, ниге¬
зенең радиусы г га тигез.
378. — Шарны суга батырганда этеп чыгару көченә каршы башка¬
рылган эшне табыгыз.
379. -1 I = 20 см озынлыгындагы бериш металл таяк горизонталь
яссылыкта әлеге таяк очыннан үткән вертикаль күчәр ти¬
рәсендә әйләнә. Әйләнүнең почмакча тизлеге са - Юлс *.
Таякның аркылы кисем мәйданы 8 = 4 см2, таякның ясал¬
ган материалының тыгызлыгы р = 7,8 г/см3. Таякның
кинетик энергиясен табыгыз.
380. Бериш туры түгәрәк конусның массалар үзәген табыгыз.
Тарихтан мәгълүматлар
1. Терминнар һәм тамгаланышларның килеп чыгуы турында.
Интеграл төшенчәсенең тарихы квадратуралар табу мәсьәләләре
белән тыгыз бәйләнгән. Хәзерге вакытта без мәйданнарны исәпләү
мәсьәләләре дип караган мәсьәләләрне Борынгы Греция һәм Рим
математиклары теге яки бу яссы фигураның квадратурасы ту¬
рындагы мәсьәләләр дип атаганнар. Латин сүзе quadratura «квад¬
рат формасы бирү» дип тәрҗемә ителә. Махсус термин кирәклеге
безнең өчен гадәти саналган реаль саннар турындагы күзаллаулар¬
ның борынгы греклар һәм римлылар яшәгән заманда (һәм соңрак,
XVIII йөзгә кадәр) җитәрлек дәрәҗәдә үсеш алмаган булуы белән
аңлатыла. Математиклар аларның геометрик аналоглары белән
199 Кашдангыч функция һәм нитеграл
яки үзара тапкырлап булмый торган скаляр зурлыклар белән эш
иткәннәр. Шуңа күрә мәйданнарны табу мәсьәләләрен түбәндәгечә
әйткәннәр: «Бирелгән түгәрәккә тигез зурлыкта итеп квадрат тө¬
зергә». («Түгәрәкнең квадратурасы турында» гы әлеге классик
мәсьәлә, билгеле булганча, циркуль һәм линейка ярдәмендә чише¬
лә алмый.)
J символы Лейбниц тарафыннан 1675 елда кертелә. Әлеге тамга
латин хәрефе S ны үзгәртеп алынган (suinma сүзенең беренче хә¬
рефе). Интеграл сүзен Я. Бернулли (1690 елда) уйлап тапкан.
Ихтимал, ул баштагы халәтенә китерергә, кире кайтарырга дип
тәрҗемә ителә торган латин сүзе integro дан алынгандыр. (Чыннан
да, интеграллау гамәле дифференциаллау юлы белән табылган
интеграл асты функциясен яңадан «баштагы халәтенә кайтара».)
Бәлки, интеграл термины башкача килеп чыккандыр: integer
сүзе бөтен дигәнне аңлата.
Үзара хат язышулар барышында И. Бернулли һәм Г. Лейбниц
Я. Бернулли тәкъдиме белән килешәләр. Шул ук 1696 елда матема¬
тиканың яңа тармагының исеме — интеграль исәпләү (calculus
integralis) барлыкка килә, аны И. Бернулли кертә.
Сезгә билгеле интеграль исәпләүләргә караган башка термин¬
нар шактый соң барлыкка килә. Хәзерге көндә кулланыла торган
башлангыч функция моннан шактый элегрәк Лагранж (1797 ел)
тарафыннан кертелгән «примитив функция»не алыштырды.
Латин сүзе primitivus «башлангыч» днп тәрҗемә ителә: Г(х) =
= | f (х) dx fix) өчен башлангыч функция, ул F (х) ны дифференци¬
аллау юлы белән табыла.
Хәзерге әдәбиятта /(х) функциясе өчен барлык башлангыч
функцияләр күплеге шулай ук анык булмаган интеграл дип ата¬
ла. Бу төшенчәне Лейбниц кертә, ул барлык башлангыч функция¬
ләрнең бер-берсеннән ирекле константалары белән аерылып тору-
ь
ларын күреп ала. Ә j f (x)dx ны анык интеграл дип атыйлар (там-
•
таланышын К. Фурье (1768—1830) керткән, ә инде интеграллау
чикләрен Эйлер күрсәткән).
2. Интегралны исәпләү тарихыннан. Борынгы Греция матема¬
тикларының яссы фигураларның квадратураларын (ягъни мәй¬
даннарын исәпләү) һәм шулай ук җисемнәрнең кубатураларын
(күләмнәрен исәпләү) табуга бирелгән мәсьәләләрне чишүдә шак¬
тый зур уңышлары Евдокс Книдский (б. э. кадәр якынча 408—
355 еллар) тарафыннан кертелгән тәмамлау методы куллануга
бәйле. Әлеге метод ярдәмендә Евдокс, мәсәлән, ике түгәрәкнең
мәйданнары чагыштырмасы аларның диаметрларының квадрат¬
лары чагыштырмасы кебек, ә конусның күләме нигезе һәм биек¬
леге шундый ук булган цилиндр күләменең 1 енә тигез икәнен
исбатлаган.
200 Кашлангыч функция һәм интеграл
Архимед
(6. э. кадәр якынча 287—212 еллар)
Боек галим. Математика һәм механикада күп кенә
фактларны һәм методларны беренче булып ачучы,
күренекле инженер. Архимедның мәйдан һәм кү¬
ләмнәрне исәпләп чыгаруга, механика мәсьәләлә¬
рен чишүгә бәйле тирән һәм үткен идеяләре, асыл¬
да, 2000 елдан соң диярлек эшләнгән математик
анализ ачышларына караганда алдан уйлап та¬
была.
Евдоксның методы Архимед тарафыннан камилләштерелә. Бу
үзгәрешләр сезгә билгеле: геометрия курсында тәкъдим ителгән
түгәрәк мәйданының формуласын чыгару Архимед идеяләренә
нигезләнгән. Архимед методын чагылдырган төп этапларны исе¬
гезгә төшерик: 1) түгәрәк мәйданы аны камаган теләсә нинди
төзек күппочмак мәйданыннан кечерәк, ә теләсә нинди камалган
күппочмак мәйданыннан зуррак булуы исбатлана; 2) яклары са¬
нын чиксез икеләткәндә, әлеге күппочмакларның мәйданнары
аермасы нульгә омтылуы исбатланды; 3) түгәрәкнең мәйданын
исәпләп чыгару өчен, төзек күппочмакның яклары санын чиксез
икеләткәндә, мәйданы чагыштырмасы омтылган кыйммәтне
табасы кала.
Архимед тәмамлау методы һәм барлык башка тапкыр фикер¬
ләр (шул исәптән механика модельләрен дә кертеп) ярдәмендә
күп кенә мәсьәләләрне чиште. Ул π санының кыйммәтен бәяләде
(3 < π < 3 γ), шар һәм эллипсоид күләмен, парабола сегменты¬
ның мәйданын Һ. б. тапты. Бу нәтиҗәләрне Архимед үзе үк югары
бәяли; аның теләге буенча кабер ташына цилиндрга камалган
шар чокып ясала (Архимед мондый шарның күләме цилиндр
күләменең - сенә тигез икәнен күрсәткән).
Архимед интеграль исәпләүнең күп кенә төшенчәләрен алдан
уйлап таба. (Өстәвенә чикләмәләр турындагы беренче теоремалар
да гомумән аның тарафыннан исбатланган.) Ләкин әлеге төшенчә¬
ләр ачык аңлаешлы аңлатма булып исәпләү дәрәҗәсенә кадәр җит¬
керелсен өчен мең ярым елдан да артыграк вакыт кирәк була.
Күп кенә яңа нәтиҗәләр тапкан XVII гасыр математиклары
Архимед хезмәтләреннән өйрәнәләр. Борынгы Грециядә туган баш¬
ка метод — бүленми торган зурлыклар методы да — шулай ук
киң кулланыла (бу метод беренче чиратта Демокритның ато¬
мистик карашларына бәйләнгән). Мәсәлән, кәкресызыклы трапе¬
цияне (131 нче а рәсем) алар /(х) озынлыгындагы вертикаль
кисемтәләрдән төзелгән дип күз алдына китергәннәр һәм чиксез
кечкенә f(x)dx зурлыгына тигез мәйдан биргәннәр. Шуннан чыгып,
201 Вашлангыч функция hjM интеграл
Риман Георг Фридрих Бернхард
(1826-1666)
Немец галиме, XIX гасырның иң күренекле матема¬
тикларыннан берсе. Саннар теориясендә һәм ком¬
плекслы үзгәрешле функцияләр теориясендә ис¬
киткеч ачышлар ясый. Ееклидча булмаган яңа гео¬
метриягә нигез салган, соңыннан ул Риман исемен
алган. Коши нәтиҗәләрен гомумиләштерүче инте¬
грал теориясен барлыкка китергән
ь ΊΪΜΊιιΠ ιι WBWHi iBilWHhiiMl ΙΙιιΜΜίΡ
эзләнелә торган мәйдан чиксез күп сандагы чиксез кечкенә мәйдан¬
нарның суммасына
S= Σ fMdx
a < ж < b
ка тигез дип исәпләнгән. Кайчак хәтта бу суммадагы һәр кушы¬
лучының аерым төрдәге нульләр булуы һәм чиксез күп кушы¬
лучыларның суммасы тулысынча билгеле булган уңай сумманы
бирүе турында басым ясап әйтелгән.
И. Кеплер (1571 —1630), хәзерге көндә шикле булып күрен¬
гән алымга нигезләнеп, үзенең «Яңа астрономия* (1609) һәм
«Сыра мичкәләре стереометриясе» (1615) исемле әсәрләрендә күп
кенә мәйданнарны (мәсәлән, эллипс белән чикләнгән фигураның
131 нче рәсем
202
Башлангыч функция һәм интеграл
Чебышев Пафнутий Львович
(1821-1894)
Рус математигы һәм механигы. Аның дөнья күлә¬
мендә танылган тикшеренүләре күпбуынлы функ¬
циянең якынлашу теориясенә (“Чебышее күпбуын¬
нарының» иң яхшы якынлашуы), интеграль исәп¬
ләүгә, ихтималлылык теориясенә, механизмнар
теориясенә карый.
мәйданын) һәм күләмнәрне (җисемнәрне чиксез юка пластинка¬
ларга кискәләп) дөрес исәпләп чыгарган. Бу тикшеренүләрне Ита¬
лия математиклары Б. Кавальери (1598—1647) һәм Э. Тор¬
ричелли (1608—1647) дәвам иткән. Б. Кавальери тарафыннан
әйтелгән принцип үзенең әһәмиятен безнең көннәргә кадәр югалт¬
маган. Аның бу принцибы берникадәр өстәмә фаразлар ярдәмендә
бирелгән.
131 нче б рәсемдә сурәтләнгән фигураның мәйданын табарга
кирәк булсын, ди. Бу фигураны югарыдан Һәм түбәннән чикләүче
кәкреләр у ~ f(x) һәм у = f (х) + с тигезләмәләре белән бирелгән.
Әлеге фигураны Кавальери терминологиясе буенча «бүлеими
торган» чиксез нәзек баганачыклардан тора дип күз алдына китер¬
сәң, аларның барысы өчен дә уртак озынлык с булыр. Аларны
вертикаль юнәлештә күчерә барып, нигезе b-а һәм биеклеге с
булган турыпочмаклык төзи алабыз. Шуңа күрә эзләнелә торган
мәйдан табылган турыпочмаклыкның мәйданына, ягъни S~Sl~
= с(Ь - а) га тигез.
Яссы фигураларның мәйданнары өчен Кавальериның гомуми
принцибы түбәндәгечә әйтелә.
Параллельләрнең кайбер бәйләмендәге турылары
Ф, һәм Ф2 фигураларын тигез озынлыктагы кисемтә¬
ләр буйлап кисеп үтсен, ди (131 нче в рәсем). Ул ва¬
кытта Ф) һәм Ф.> фигураларының мәйданнары тигез.
Моңа охшаш принцип стереометриядә дә бар, ул күләмнәрне
тапканда уңайлы. Кавальери принцибының гади нәтиҗәләрен
сез үзегез чыгара аласыз. Мәсәлән, нигезләре һәм биеклекләре
уртак булган туры һәм авыш цилиндрларның күләмнәре тигез
икәнен исбатлагыз.
XVII гасырда интеграль исәпләүгә каралган күп кенә ачышлар
ясала. Мәсәлән, П. Ферма 1629 елда ук теләсә нинди у = хп (биредә
п — бөтен сан) кәкресенең квадратурасы мәсьәләсен чишә (ягъни,
асылда, (xndx = —Ц-хп+| формуласын чыгара), шуның нәтиҗәсендә
J п +1
203 Ьшилангыч функция һәм интеграл
Лебег Анри
(1875-1941)
Француз математигы. Үлчәү (мәйдан һәм күләм
төшенчәсен гомумиләштерү) теориясен барлыкка
китерә һәм шуның нигезендә интегралның яңа
теориясен эшкәртә.
дә авырлык үзәкләрен табуга күп кенә мәсьәләләрне чишә. И. Кеп¬
лер үзенең атаклы планеталар хәрәкәте законнарын чыгарганда,
асылда, якынча интеграллау идеясенә таяна. Ньютонның укыту¬
чысы И.Барроу (1630—1677) интеграллау һәм дифференциал-
лау арасындагы бәйләнешне аңлауга якынрак килә. Функцияләрне
дәрәҗәле рәтләр рәвешендә күрсәтү буенча башкарылган эшләр
зур әһәмияткә ия була.
Шулай да XVII гасырның күп кенә көчле уйлап табучы ма¬
тематиклары тапкан нәтиҗәләр шактый зур булса да, исәпләү
эшләре әле башкарылмаган була. Күп кенә аерым мәсьәләләрне
чишүнең нигезендә яткан уртак идеяләрне аера белергә һәм шу¬
лай ук җитәрлек дәрәҗәдә уртак алгоритм бирүче дифференциал-
лау операцияләре арасында бәйләнеш булдыру кирәк була. Болар
бер-берсенә бәйсез рәвештә Ньютон һәм Лейбниц тарафыннан эш¬
ләнә, һәм ул сезгә таныш Ньютон — Лейбниц формуласы исемен
йөртә. Шушының белән гомуми метод тәмам формалаша. Ләкин
күп кенә функцияләрнең башлангыч функцияләрен табарга өйрә¬
нәсе, яңа исәпләүне логик яктан нигезлисе һ.б. эшлисе кала әле.
Ләкин иң әһәмиятлесе эшләнә: дифференциаль һәм интеграль
исәпләүләр барлыкка килә.
Киләсе йөз елда математик анализ методлары актив үсә (бе¬
ренче чиратта элементар функцияләрне интеграллауны системалы
рәвештә тикшерүне төгәлләгән Л. Эйлер һәм И. Бернулли
исемнәрен әйтергә кирәк). Интеграль исәпләүне үстерүдә рус мате¬
матиклары М. В. Остроградский (1801—1862), В. Я. Буня-
ковский (1804—1889), П. Л. Чебышев (1821 — 1894) катна¬
шалар. Аерым алганда, Чебышев нәтиҗәләре принципиаль әһәми¬
яткә ия була. Ул элементар функция аша аңлатып булмый торган
интегралларның барлыгын исбат итә.
Интеграл теориясенең төгәл язылышы узган гасырда гына бар¬
лыкка килә. Бу мәсьәләнең чишелеше 0. Коши, зур математиклар¬
ның берсеннән саналган немец галиме Б. Риман (1826—1866),
204 Ьашлангыч функция һам интеграл
француз математигы Г. Дар бу (1842—1917) исемнәре белән
бәйле.
Фигураларның мәйданнары һәм күләмнәре барлыгына бәйле
күп кенә сорауларга җаваплар К. Жордан (1838—1922) тара¬
фыннан үлчәү берәмлекләре теориясе эшләнгәч табыла.
Безнең гасыр башында интеграл төшенчәсенең төрлечә гому-
миләштерелүе француз математиклары А. Лебег (1875—1941)
һәм А. Даижуа (1884—1974), совет математигы А. Я. X инч и н
(1894—1959) тарафыннан башкарыла.
Кабатлау өчен сораулар һәм мәсьәләләр
1. 1) Башлангыч функциянең билгеләмәсен әйтегез.
2) F функциясенең R да f функциясе өчен башлангыч функ¬
ция икәнен исбатлагыз:
а) f (х) = 2х + 3, F (х) - х2 + Зх + 1;
б) (х) = sin2х + 3, /-’(х)- + 3х;
в) f(x) = -х3 +5, F(x) = -~ + 5х + 2;
г) f (х) = - cos 4 + 1, F (x) = -2 sin 4 + x.
3) Бирелгән аралыкта F функциясе f функциясе өчен башлан¬
гыч функция була аламы?
а) F (х) - х2 - х, f (х) - 2х -1 R да;
б) F (х) = р· - sin х, f (х) = - - cos х R да;
в) F (х) = х1 + 1, f (х) - -ү + х R да;
г) F (х) = х + cos х, f (х) = 1 - sin х R да.
2. 1) Бирелгән аралыкта функциянең даимилек билгесен әйте¬
гез. Башлангыч функциянең төп үзлекләрен әйтегез.
2) Түбәндәге функцияләр өчен башлангыч функцияләрнең
гомуми рәвешен языгыз:
a) i(x) = kx + b (k һәм b — даими); б) /(х) =
в) /(х) ~ х" (п — бөтен сан, п*-1); г) /"(х) = cos х.
3) f функциясе өчен бирелгән ноктада бирелгән кыйммәтне
кабул итүче башлангыч F функциясен табыгыз:
a) f (х) - sin х - cos х, F (π) = 1; б) f (х) = ~ - -Д, F (3) = 5;
в) /(x) = 2x-5,F(l) = -2; r) /(x) =-J—, F(6) = 10.
Jx-2
205 Башлангыч функция һәм интеграл
3. 1) Башлангыч функцияләрне табуның өч кагыйдәсен әйтегез.
2) Түбәндәге функцияләр өчен башлангыч функцияләрнең
гомуми рәвешен табыгыз:
a)/(x) = sin3x--^-; б)/(х) = 4-тг^
cos’ = x 2Vx
в) f (x) = (4 - 5x)3 - г) f (х) = x -10cos2x.
3) f(x) функциясе өчен графигы М ноктасы аша үтүче баш¬
лангыч функцияне табыгыз:
a) Г(х) = (2-Зх)2,М(1;2); б) /(х) = sin2х, М (|; -2);
в) f{x)= V2cosx, М(^;2); г) f (х) = —^—,М(0;3).
4. 1) Нинди фигураны кәкресызыклы трапеция дип атыйлар?
Кәкресызыклы трапециянең мәйданын исәпләү өчен, форму¬
ла языгыз.
2) Кәкресызыклы трапециягә мисаллар китерегез.
3) Бирелгән сызыклар белән чикләнгән кәкресызыклы трапе¬
цияне сурәтләгез һәм аның мәйданын табыгыз:
а) у = sinx, у = 0, х = ^. х = б) у = -х3, у = 0, х = -2;
в) у = (х - I)2, у = 0, х = 3;
г) у = 3 - 2х - х2, у = 0, х = 0, х = —2.
5. 1) Интегралның нәрсә икәнен аңлатыгыз.
2) Ньютон — Лейбниц формуласын языгыз. Интегралны
исәпләгез:
3 2 я 3
а) ί 6) ί 77= в) Jsin*dx; г> ί*Μχ.
-3 * « о
3
3) Түбәндәге сызыклар белән чикләнгән фигураның мәйда¬
нын исәпләп чыгарыгыз:
а) у = х2, у “ Зх; б) у = х2 - 4х + 6, у = 1, х = 1, х = 3;
в) у = 4 - х2, у = 3; г) у = cosx, у = 1, х = х =
IV
бүлек
Күрсәткечле һәм
логарифмик
функцияләр
§9.
Дәрәҗә төшенчәсен гомумиләштерү
32. п нчы дәрәҗә тамыр һәм аның үзлекләре
1. Тамырны билгеләү, а саныннан квадрат тамыр тө¬
шенчәсе сезгә таныш инде: бу — квадраты а га тигез сан, а санын¬
нан п нчы дәрәҗә тамыр да моңа охшаш рәвештә билгеләнә, биредә
п саны — ирекле натураль сан.
Билгеләмә » нчы дәрәҗәсе а га тнгез булган
сан α саныннан п нчы дәрәҗә тамыр дип атала.
Ί 1 нче м ис ал . 27 саныннан өченче дәрәҗә тамыр 3 кә тигез,
чөнки 3® = 27. 2 һәм -2 саннары 64 саныннан алтынчы дәрәҗә
тамыр була, чөнки 2е = 64 һәм (-2) 6 = 64.
Әлеге билгеләмә буенча а саныннан п нчы дәрәҗә тамыр —
х“ = а тигезләмәсенең ирекле чишелеше. Бу тигезләмәнең тамыр¬
лары саны п һәм а га бәйле, /(х) = х" функциясен тикшерик.
Билгеле булганча, [0; <») аралыкта бу функция теләсә нинди
п өчен усә һәм [0; 00) аралыктагы барлык кыйммәтләрне ала.
Тамыр турындагы теорема буенча (8 нче пункт), теләсә нинди
ае[0; о°) өчен хп = а тигезләмәсенең тискәре булмаган, өстәвенә
бердәнбер тамыры була. Аны а саныннан п нчы дәрәҗә арифметик
тамыр дип атыйлар һәм tfa дип тамгалыйлар; п санын тамыр
күрсәткече дип, а санын тамырасты аңлатмасы дип атыйлар.
Тамыр тамгасы ·/ радикал дип атала.
Билгеләмә, л нчы дәрәҗәсе а га тигез тискәре
булмаган сан а саныннан η нчы дәрәҗә арифме¬
тик тамыр дип атала.
□ 2 нче мисал. а)^8;б) кыйммәтен табабыз.
а) χ/δ = 2, чөнки 2® = 8 һәм 2 > 0;
207 Күрсәткечле һәм логарифмик функцияләр
б> \'ltt = I* ЧӨНКИ (I) = 16 Һәм 2 > °·
п җөп булганда, f(x) = х" функциясе җөп була. Моннан, әгәр
а > 0 булса, ул вакытта х” = а тигезләмәсенең xt= tfa тамырыннан
тыш, х2 = —Уа тамыры була. Әгәр а = 0 булса, бер тамыр: х = 0;
әгәр а < 0 булса, бу тигезләмәнең тамырлары булмый, чөнки теләсә
нинди санның җөп дәрәҗәсе — тискәре булмаган сан.
Шулай итеп, п җөп булмаганда, теләсә нинди уңай а саныннан
п нчы дәрәҗә ике тамыр бар; 0 саныннан п нчы дәрәҗә тамыр
нульгә тигез; тискәре саннан җөп дәрәҗә тамыр булмый.
^3 нче мисал, х4 =81 тигезләмәсенең ике тамыры бар: бу
3 һәм -3 саннары. Шулай итеп, 81 дән дүртенче дәрәҗә ике та¬
мыр бар. Бу вакытта </81 — тискәре булмаган сан, ягъни У81 = 3,
ә -3 = -</81.
4 нче мисал, х4 - 3 тигезләмәсенең уңай тамыры Уз саны.
Бу — иррациональ сан (-Уз саны кебек). Аның унарлы тамгала¬
рын бер-бер артлы исәпләп чыгарырга мөмкин:
1 < Уз < 2, чөнки I4 < 3 < 24;
1,3 < Уз < 1,4, чөнки 1,34 < 3 < 1,44 һ.б.
(УЗ - 1,31607... икәненә ышаныгыз).
п ның так кыйммәтләре өчен /(х) = хл функциясе барлык сан¬
лы турыда үсә; барлык реаль саннар күплеге — аның кыйммәтләре
өлкәсе. Тамыр турындагы теореманы кулланып, хл = а тигезләмәсе
а теләсә нинди һәм, аерым алганда, а < 0 булганда да, төгәл бер
тамырга ия була. Бу тамырны а ның теләсә нинди кыйммәте өчен
(шул исәптән һәм тискәре а өчен) Уа дип тамгалыйлар.
I Шулай итеп, п так булганда, теләсә нинди а саныннан
I п нчы дәрәҗә тамыр бар, һәм ул бердәнбер.
Так дәрәҗәдәге тамырлар өчен
У^а =-Уа
тигезлеге дөрес.
Чынлыкта исә
(-Уа)" = (-D* . (Уа)я = -1 а = -а,
ягъни -Уа саны -а саныннан п нчы дәрәҗә тамыр ул. п так бул¬
ганда. мондый тамыр бердәнбер. Димәк, У-α = -Уа.
У-а = а (п так булганда) тигезлеге тискәре саннан так дәрә¬
җәдәге тамырны шул ук дәрәҗәдәге арифметик тамыр аша аңлатыр¬
га мөмкинлек бирә. Мәсәлән, У-71 = -^71, У-27 = -У27 = -3.
208
Күрсәткечле һәм логарифмик функцияләр
1 нче искәрмә. Теләсә нинди х өчен
п җөп булса, х|;
п так булса, х була.
(Бу үзлекне үзегез исбатлагыз.)
2 нче искәрмә, а саныннан беренче дәрәҗә тамыр а га
тигез дип әйтү җайлы. Белгәнегезчә, саннан икенче дәрәҗә тамыр¬
ны квадрат тамыр дип атыйлар, ә язган вакытта тамыр күрсәт¬
кече 2 не төшереп калдыралар (мәсәлән, 7 дән квадрат тамырны
гади генә \П дип тамгалыйлар). Өченче дәрәҗә тамырны куб та¬
мыр дип атыйлар.
5 нче мисал, а) х5 - -11; б) Xs = 7 тигезләмәләрен чишәбез.
а) п нчы дәрәҗә тамырның билгеләмәсе буенча х саны -11
дән бишенче дәрәҗә тамыр. Тамыр күрсәткече — так 5 саны,
шуңа күрә мондый тамыр бар, һәм ул бердәнбер: >(/-11.
Җавапны болай язалар: х = -V11.
б) п нчы дәрәҗә тамыр билгеләмәсе буенча х8 = 7 тигезләмәсе¬
нең чишелеше у/1 саны була. 8 саны җөп булганга күрә, —v7
шулай ук бирелгән тигезләмәнең чишелеше була. Шулай итеп,
X; = </1. х2 = -(/7. Җавапны болай язарга мөмкин: х = ±^7.
2. Тамырларның төп үзлекләре, п нчы дәрәҗә арифметик
тамырларның сезгә билгеле үзлекләрен исегезгә төшерик.
Теләсә нинди натураль сан п, бөтен k өчен һәм теләсә
нинди тискәре булмаган а һәм Ь саннары өчен түбән¬
дәге тигезлекләр үтәлә:
1°. -Jab = · Ф>.
3°. = 'tfa (k > 0).
4°. <α = να6 (Λ > 0).
5°. tfak = (л/β)* (әгәр k С 0 булса, ул вакытта а * 0).
1° үзлеген исбатлыйк. Билгеләмә буенча i/ab — п нчы дәрәҗәсе
ab га тигез булган тискәре булмаган сан.
yfa ■ </b саны — тискәре булмаган сан. Шуңа күрә натураль күр¬
сәткечле дәрәҗә үзлегеннән һәм п нчы дәрәҗә тамыр билгеләмә¬
Күрсәткечле һәм логарифмик функцияләр
сеннән (να vft)’ = at) тигезлегенең дөреслеген тикшерү дә җитә:
(t/а &Уу = (у/аУ (^Ь)" = ab.
Түбәндәге өч үзлек моңа охшаш рәвештә исбатлана:
4^0 һәм = А = ί·
№ 0 һәм (^Г= ((^)")Л = «£)* = а;
Ча ? 0 һәм (у/аУ* = ((у/а)пУ‘ = а*.
Хәзер 5° үзлеген исбатлыйк. (\/а)* санының η нчы дәрәҗәсе
а* га тигез икәнен искәртик:
(вКуУ = (Уаук = ((^аУУ = α*.
Арифметик тамырның билгеләмәсе буенча (</а)* = \/а* (чөнки
vfoy^o).
Тамырлар кергән санлы аңлатмаларның рәвешләрен үзгәртүгә
мәсьәләләр чишкәндә, 1°—5° үзлекләрен куллануга мисаллар ки¬
терик.
Ц 6 нчы мисал. Аңлатмаларның рәвешләрен үзгәртик:
a) V8 · V4; б) ^5^; в) #7; г) ^128; д) V128».
a) V8 · V4 = = ^32 = 2 (1° үзлек);
бМ5 ά = $ = |= -1 <2° Үзле«);
в) VV7 = *^7 (3° үзлек);
г) χ/128 = = V2 (4° үзлек);
д) 5° үзлекне кулланып табабыз: V1283 = (·ί/128)3 = 23 = 8.
Арифметик тамырның түбәндәге үзлеген исбатлыйк.
6°. 0 < а < Ь булган теләсә нинди а һәм Ь саннары
. өчен
Va < v'h
I тигезсезлеге үтәлә.
Исбатлауны киресеннән чыгып башкарабыз. > Vh булсын.
Ул вакытта натураль күрсәткечле дәрәҗәләрнең үзлеге буенча
(?/аУ (у/b)", ягъни a Ь була. Бу a < Ь шартына каршы килә.
210
Күрсәткечле һәм логарифмик функцияләр
7 нче мисал, ү2 һәм үЗ саннарын чагыштырыйк.
^2 һәм Уз не бердәй күрсәткечле тамырлар рәвешенә ките¬
рик: </2 = ‘У21 - *У32, ә Уз = ү/з3 = Ч/27 (бу вакытта без 4° үз¬
лектән файдаландык). 32 > 27 тигезсезлегеннән һәм 6° үзлектән
*У32 > 'У27 икәне күренә, һәм, димәк, У2 > Уз була.
8 нче мисал. х15 > 20 тигезсезлеген чишик.
Бу тигезсезлек хв - 20 > 0 тигезсезлегенә тамырдаш. f(x) =
= хв — 20 функциясе өзлексез булганлыктан, интерваллар методын¬
нан файдаланырга мөмкин. х® - 20 = 0 тигезләмәсенең ике тамыры
бар: У20 һәм -У20. Бу саннар турыны өч аралыкка бүләләр. Би¬
релгән тигезсезлекнең чишелеше — аларның икесенең берләшмә¬
се: -У20) һәм (У20; <х).
Күнегүләр
Тигезлекнең дөреслеген тикшерегез (381—382).
381. - а) У16 =2; б) У-ϊ = -1;
1в) 'У1024 = 2; г) У-243 - -3.
а) *У1 = 1; б) Уб4 = 2; в) У-343 = -7; г) *Уо = 0.
Исәпләп чыгарыгыз (383—384).
383. а) У—27; б) </81; в) 4-32; г) Уб4.
384. a) (/gj·. б) у^’· в> 8 ’ r) 4256
385.
386. ¬
387.
388.
Тигезләмәләрне чишегез (385—388).
a) Xs + 4 = 0; б) х6 = 5; в) х3 = 4; г) х4 = 10.
а) х10 -15 = 0; б) х7 + 128 = 0; в) хв - 64 = 0; г) х5 = 3.
а) 16х4 -1=0; б) 0,01х3 + 10 = 0;
в) 0,02х®-1,28 = 0; г)12|-|х2 = 0.
а) </ί = -0,6; б) Ух = 3; в) ^х = 5; г) Цх ~ -1.
211 Күрсәткечле һәм логарифмик функцияләр
Санлы аңлатманың кыйммәтен табыгыз (389—394).
389—а) (-УЙ)4; б) (2</=2)5; в) «/?)’; г) (-</2)6.
390.- а) </16 625; б) </32 243; в) </8 343; г) </0,»001 16.
391— a) </160 625; б) </24 ■ 9; в) </48 · 27; г) </75.45.
392.^а)</9 </9; б) </16 </=8; в) </27 · </9; г) ?/=25 ■ </25.
395.
г) «/з| 1| + Д.
V в 2 <80
Түбәндәге саннарның беренче ике унынчы тамгасын (өтер¬
дән соң) табыгыз:
а) </2; б) </б; в) ^7; г) </3.
Таблицалардан яки калькулятордан файдаланып, 0,01 гә
кадәр төгәллек белән тамырның якынча кыйммәтен табы¬
гыз (396—397).
396. а) </10.17; б) 7П: ») л/13.21; г) </п.
397. - в) ζ'13.7; б) </10; в) УО; г) </Гз.
Саннарны чагыштырыгыз (398—401).
398. в) ^0»2 һәм 0;
в) ν'1,8 һәм 1;
399. а)|</2 һәм ;/’f;
в) </2 һәм </3;
400. в) <0.3 һәм <|0.05.
в) </7 һәм </40;
б) 'У0.4 һәм
г) <ιΌ.2 һәм уо.з.
б) '* ■? һәм 'Vo, 43;
г) 'VO,8 һәм 1.
б) ч4 һәм </й;
г) <5 һәм <‘500.
212 Күрсәткечле һәм логарифмик функцияләр
401. -
402. -I
403. ¬
404.
405.
406.
407.
408. ¬
409.¬
410.¬
411.
412.
a) V-0.4 һәм <-0,3; б) V-5 һәм V-3;
в) V-2 һәм V-4; г) V-5 һәм V-3.
Тапкырлаучыны тамыр тамгасы тышына чыгарыгыз (а > 0,
ь>оу.
а)^64а8д11; б) V-128a7; в) ^6а12Ь6; г) faa'0.
Тапкырлаучыны тамыр тамгасы эченә кертегез (а > 0, Ь > 0):
а) б) ab^fa; в) afa; г)-abV-4.
а ның кыйммәтләре нинди булганда тигезлек дөрес (404—
405)?
а) fa = -а; б) ία7 = а; в) = |а|; г) fa = а.
a) fa » -а; б) 'fa = -а; в) -fa = |а|; г) fa = а.
Аңлатманы ваклаучысында тамыр тамгасы булмаган рә¬
вешкә китерегез (406—407).
\ 3 . α — V2 я . 1 . ч/б +1
a)V7-^’
а)-уг; в) —г) fa.
V2 2>/х xiii 3V5
Санлы аңлатманы afa рәвешенә китерегез, биредә а —
рациональ сан, ә Ь — натураль сан (408—409).
■>й‘ в,®= г,№·
а) '■&; 61 в) г) fl'· Й.
Тигезләмәне алмаштырып кую юлы белән чишегез t = fa
яки t ·» %/х:
a) Vx-5Vx+6 = 0; б) fa + Vx = 2;
в) fa - 3fa + 2 = 0; r)fa-5fa=6.
Тигезсезлекне чишегез (411—412).
ia)x4<3; б) х11 ^7; в) х10 > 2; г) х3 £ 5.
ia)\/x<-7; б) Vx > 2; в) fa > 2; г) fa 3.
213 Күрсәткечле һәм логарифмик функцияләр
Аңлатманы гадиләштерегез (413—414).
413. — а) \[а6, биредә а 0; б) Уа4, биредә а > 0; в) Уа5.
414. — а) Уа3 - Уа2, биредә а < 0; б) Уа4 + 2Уа7, биредә а 0;
в) Уа5 -Уа6, биредә а 0; б) Уа3 + 3 Уа8, биредә а ζ 0;
415. — Аңлатманың кыйммәтен табыгыз:
а) У10 + У73 · У10 - УтЗ; б) Г + У17;
ү4-ү17
в) У9-У65 · У9 + Уб5; г) Уз - Уб ■ Уз + Уб,
416. — Аңлатманы ваклаучысында радикал булмаган вакланма
, рәвешендә күрсәтегез:
а) 1 . б) 2 . в) 2 . г) За
V2-V3’ α-Vft’ V5+V7’ V^-V^ + У^
33. Иррациональ тигезләмәләр
Үзгәрешлесе тамыр тамгасы астында булган тигезләмә¬
ләрне иррациональ тигезләмәләр дип атыйлар. Мәсәлән, Ух -2 = 0.
Иррациональ тигезләмәләрне чишүгә мисаллар китерик.
Ί 1 нче мисал. Ух2-5=2 тигезләмәсен чишик.
Бу тигезләмәнең ике кисәген дә квадратка күтәреп, х2 - 5 = 4
не табабыз.
Моннан х2 = 9, ягъни х = 3 яки х = —3 табылыр.
Табылган саннар (1) тигезләмәнең чишелешләре буламы икә¬
нен тикшерик. Чыннан да, ул саннарны тигезләмәгә куйганда,
дөрес тигезлекләр килеп чыга:
Уз2 -5 = 2 һәм У<-3)2 -5 = 2.
Димәк, х = 3 һәм х = -3 тигезләмәнең чишелеше икән.
2 нче мисал. Ух=х-2 тигезләмәсен чишик.
Тигезләмәнең ике кисәген дә квадратка күтәреп табабыз: х =
= х2 - 4х + 4. Гадиләштерүдән соң х2 - 5х + 4 = 0 квадрат тигез¬
ләмәсе килеп чыга, аның тамырлары х = 1 һәм х - 4. Табылган
саннар бирелгән тигезләмәнең чишелешеме икәнен тикшерик.
4 санын тигезләмәгә куйганда, У4 =4-2 дөрес тигезлеген табабыз,
ягъни 4 — бирелгән тигезләмәнең чишелеше була. 1 санын куй¬
ганда исә, уң кисәктә -1, ә сул кисәктә 1 саны килеп чыга. Димәк,
1 саны тигезләмәнең чишелеше була алмый, аны бирелгән тигез¬
ләмәне әлеге ысул белән чишү нәтиҗәсендә табылган чит тамыр
дип әйтү кабул ителгән. Җавап: х — 4.
214 Күрсәткечле һәм логарифмик функцияләр
Күргәнебезчә, иррациональ тигезләмәләрне чишкәндә табылган
чишелешләрне тикшерү таләп ителә, мәсәлән, дөрес булмаган
тигезлекне квадратка күтәрү дөрес тигезлек бирергә мөмкин.
Чыннан да, дөрес булмаган 1 = -1 тигезлеген квадратка күтәрү
дөрес тигезлек бирә: I2 =» (-1)2.
■ 3 нче мисал. ух2 - 2 = 4х тигезләмәсен чишик. Бу тигез¬
ләмәнең ике кисәген дә квадратка күтәрик: х2 - 2 = х. Гадиләште¬
рүләрдән соң х2 — х ~ 2 = 0 тигезләмәсен табабыз, аның тамырлары
х — -1 һәм х = 2. Ί саны тигезләмәнең тамыры түгеллеге үзеннән-
үзе аңлашыла, чөнки х “ -1 булганда, бу тигезләмәнең ике кисәге
дә билгеләнми. Тигезләмәгә 2 санын куйганда, л/22 - 2 = ^2 дөрес
тигезлеген табабыз. Шулай булгач, бары тик 2 саны гына бирелгән
тигезләмәнең чишелеше була.
4 нче мисал. -Jx -6 = -У4 - х тигезләмәсен чишик.
Бу тигезләмәнең ике кисәген дә квадратка күтәреп, х - 6 =
= 4 - х, 2х = 10 һәм х = 5 не табабыз. Куеп карау юлы белән
5 санының бирелгән тигезләмәнең тамыры түгеллегенә ышана¬
быз. Шуңа күрә аның чишелешләре юк.
Кайвакыт иррациональ тигезләмәләрне тигезкөчле күчешләр¬
дән файдаланып чишү уңайрак була.
П 5 нче мисал. -Ух - 2 = х - 8 тигезләмәсен чишәбез.
Билгеләмә буенча Vx - 2 — квадраты тамырасты аңлатмасына
тигез булган тискәре булмаган сан. Башка сүзләр белән әйткәндә,
Ух - 2 = х - 8 тигезләмәсе
|х - 2 = (х - 8)2,
]х-8>0
системасына тигезкөчле. Системаның х2 - 17х + 66 = 0 тигезләмә¬
сенә тигезкөчле беренче тигезләмәсен чишеп, 11 һәм 6 тамырларын
табабыз, әмма х - 8 > 0 шарты бары тик х = 11 өчен генә үтәлә.
Шуңа күрә бирелгән тигезләмәнең бер тамыры бар: х = 11.
6 нчы мисал, х — 1 = Vx2 - х — 1 тигезләмәсен чишәбез.
Моннан алда тикшерелгән мисаллардан аермалы буларак, әлеге
иррациональ тигезләмәдә квадрат тамыр түгел, ә өченче дәрәҗә
тамыр. Шуңа күрә, «радикалдан котылу өчен», тигезләмәнең ике
кисәген дә квадратка түгел, ә кубка күтәрергә кирәк: (х-1)3“
= ха — х-1. Рәвешүзгәртүләрдән соң табабыз:
х3 - Зх2 + Зх-1 = х2-х-1,
х3 — 4Х2 Ί- 4х = 0,
х(х-2)2 = 0.
Шулай итеп, х, = 0, х2 = 2.
215 Күрсәткечле һәм логарифмик фуакцияләр
7 нче мисал.
чишәбез.
Vx + Vi/ = 4.
х + у = 28
тигезләмәләр системасын
и — у/х һәм и = у/у дип алып,
и + V = 4,
и3 + υ3 = 28
системасын табабыз.
Икенче тигезләмәнең сул кисәген тапкырлаучыларга тарката¬
быз: и3 + υ3 = (и + υ) (и2 - uv + υ2) һәм аңа беренче тигезләмәдән
и + и = 4 не куябыз. Ул вакытта икенче тигезләмәгә тигезкөчле
и + V = 4,
и2 -uv + v2 =7
системасын табабыз.
Беренче тигезләмәдән табылган и ның (υ — 4 - и) кыйммәтен
икенче тигезләмәгә куеп,
и2 — и(4 - и) + (4 - и)2 = 7, ягъни и1 - 4и + 3 = 0
тигезләмәсен табабыз.
Табылган квадрат тигезләмәнең ике тамыры бар: и, = 1 һәм
иг = 3. V ның тиңдәш кыйммәтләре: υ, = 3 һәм υ2 = 1. х һәм у
үзгәрешлеләренә күчеп табабыз:
■Ух = Ui, ягъни Xj = u3 = 1; = v3 = 27; х2 = ίι» = 27; р2 = у? - 1.
Җавап: (1; 27); (27; 1).
Күнегүләр
417, —
I
418, ¬
419.
420.
Тигезләмәне чишегез
а) у/х4 +19 =10;
в) л/б1 - х2 = 5;
а) у/х +1 = х - 5;
в) \/2х -1 = х - 2;
а) у/2х +1 = у/х2 - 2х + 4;
в) у/х + 2 = у/2х - 3;
а) х = Ух3 +х2 -6х + 8;
в) х = у/х3 - х2 - 8х + 20;
—420).
б) Ух2 - 28 = 2;
г) Vx-9 = -3.
б) х + у/2х + 3 = 6;
г) 3 + л/Зх + 1 = х.
б) у/х = у/х2 - х - 3;
г) у/9- х2 = у/х + 9.
б) х - 2 = Ух2 -8;
г) х +1 = Ух3 +2х2 +х.
Күрсәткечле һәм логарифмик функцияләр
421.— Тигезләмәләр системасын чишегез:
tfx + 2$/y=l, \it/x-tfy =2>/2,
л) · _ _ б) · _ _
3</x-Vy = 10; |2</х + 3^/у =8V2;
> 2ΐ/χ+^ = 7, г /х+З^у =5ү/б,
4^/у-3#х=6; 57у-2/х=75.
Тигезләмәләрне чишегез (422—425).
422,— a) Vx + 1 Vx + 6 = 6;
в) — = ·<'3χ + 2;
^χ-2
423— а) 75 + ^773 = 3;
в) J18 - Vx + 10 = 4;
424— а) у/х - 3 = 1 + <'х-4;
б) * + 1 = -Jx - 1;
V2*-l
г) Vx V2 - х = 2х.
б) 7Vx2 -16 + х = 2;
г) Vx-\/x2 -5 = 1.
б) \1х + 2 - у/х-б - 2;
в) 2 + л/10 - х = \/22 - х;
г) V1 - 2х - 3 = л/16 + х.
425— а) л/х-З - 6 = Vx - 3; б) Vx + 1 + 2Vx +1 = 3;
в) </х-5 =30-Vx-5; г) 3lVx2 -3 + Vx2 - 3 = 4.
Тигезләмәләр системасын чишегез (426—427).
426— а)
2\/х - у[у =5,
б)
л/б + х -3yj3y + 4 =-10,
4 V3y + 4 -5^6 + х = 6;
»)
[2 Vx -2 + у]5у + 1 = 8,
)з<х-2-2ч/5у+ 1 =-2.
427. - а)
■)
х- у - 16
ylx + tfy = 5,
XI/ = 216;
|х - у - 32;
l/x -tfy = 2,
ху = 27.
217 Күрсәткечле һәм логарифмик функцияләр
34. Рациональ күрсәткечле дәрәҗә
Сезгә бөтен күрсәткечле дәрәҗә төшенчәсе таныш
инде. ап аңлатмасы, η £0 булганда, а = 0 очрагыннан тыш, барлык
а һәм η өчен билгеләнгән. Мондый дәрәҗәләрнең үзлекләрен
исегезгә төшерәбез.
Теләсә нинди a, Ь саннары һәм теләсә нинди бөтен т
һәм η саннары өчен түбәндәге тигезлекләр дөрес:
ап · а” = а"+"; ат : а" = ат'п (а # 0);
(атУ = атп;
(аЬУ = ап · Ь"; (Ь * 0);
а1 = а; а° = 1 (а # 0).
Шулай ук түбәндәге үзлекне дә билгеләп үтик.
I Әгәр т> η булса, а > 1 булганда, ат > а" була, һәм,
I 0 < а < 1 булганда, ат < ап була.
5 _1
Әлеге пунктта без, 20,3, 87, 4 2 һ.б. төрдәге аңлатмаларга
мәгънә биреп, санның дәрәҗәсе төшенчәсен гомумиләштерербез.
Бу вакытта рациональ күрсәткечле дәрәҗәләр бөтен күрсәткечле
дәрәҗә үзлекләренә (я булмаса аларның кайберләренә) ия булыр-
ϋ
лык билгеләмә бирү табигый. Ул вакытта, аерым алганда, а"
санының η нчы дәрәҗәсе а~ нчы дәрәҗәсенә тигез булырга тиеш.
Чыннан да, әгәр (α₽)ϊ = аи үзлеге үтәлсә,
щ ®
(а")л =а’ = ат
үзлеге дә үтәлә.
Соңгы тигезлек (п нчы дәрәҗә тамырның билгеләмәсе буенча)
а
а" санының ат саныннан η нчы дәрәҗә тамыр икәнен аңлата.
Шулай итеп, түбәндәге билгеләмәгә киләбез.
Билгеләмә, χ/α™ саны г = ~ рациональ күрсәт¬
кечле а > 0 санының дәрәҗәсе дип атала, биредә
т — бөтен сан, әп — натураль сан (л > 1).
Шулай итеп, билгеләмә буенча
0 санының дәрәҗәсе бары тик уңай күрсәткечләр өчен генә
билгеләнә: теләсә нинди г > 0 өчен билгеләмә буенча 0г = 0.
218 Күрсәткечле һәм логарифмик функцияләр
Ί 1 нче мисал. Рациональ күрсәткечле дәрәҗәнең билгелә¬
мәсе буенча
7 4 = V7; 2® = \/2а = ^32; a ,s =
1 3 2
2 нче мисал. 73, 814 һәм 128 7 санлы аңлатмаларының
кыйммәтләрен табабыз.
Күрсәткечле дәрәҗә билгеләмәсеннән һәм тамыр үзлекләрен-
1 ■ 3 ; ί—
нән файдаланып табабыз: 83 = ү8 - 2, 814 = у813 = (у81)3 =
- З3 = 27, 128 7 = V128-2 = (V128) 2 = 2"г = |.
1 нче искәрмә. Күрсәткечле дәрәҗә билгеләмәсеннән те¬
ләсә нинди уңай а өчен һәм теләсә нинди рациональ г өчен аг
саны уңай икәне шунда ук килеп чыга.
2 нче искәрмә. Теләсә нинди рациональ санны вакланма
рәвешендә төрлечә язарга мөмкин, чөнки теләсә нинди натураль
k өчен — = т' ■ а' нең кыйммәте шулай ук рациональ г санын
я яд
язу формасына бәйле түгел. Чынлыкта исә тамырлар үзлегеннән
а '* = гхУа'”* = х/с'" — α " икәне килеп чыга.
3 нче искәрмә. а<0 булганда, а санының рациональ
дәрәҗәсе билгеләнми, бу очраклы түгел. Әгәр дә без (1) формуланы
1
α < 0 өчен дә дөрес дип уйласак, ул вакытта, мәсәлән, (-8)’ нең
кыйммәте V-8 гә, ягъни -2 гә тигез булыр иде. Ә икенче яктан,
1 = I, һәм шуңа күрә -2 = (-8)3 = (-8)® = fy'(-8)2 = v8z - 2 ти-
ti о
гезлеге үтәлергә тиеш. Хәзер югарыда рациональ күрсәткечле
дәрәҗә өчен әйтелгән билгеләмәдә бөтен күрсәткечләр өчен дөрес
булган дәрәҗәнең төп үзлекләре саклана (аерма бары тик шунда:
моннан соң китерелә торган үзлекләр уңай нигезләр өчен генә
дөрес).
Теләсә нинди рациональ сан г һәм s өчен һәм теләсә
нинди уңай а һәм Ь өчен түбәндәге тигезлекләр
дөрес:
1°. <Га’ = аг*’.
2°. аг: а‘ = аГ‘.
3°. (а’У^аГ1.
4°. (аЬУ = аг ■ Ъг.
»··(!)■-г·
219 Күрсәткечле һәм логарифмик функцияләр
Бу үзлекләрне исбатлау өчен, рациональ күрсәткечле дәрәҗә
билгеләмәсеннән һәм 32 нче пунктта исбатланган тамыр үзлек¬
ләреннән файдаланырга кирәк. Әйтик, 1°, 3° һәм 4° үзлекләрен
исбатлыйк, г - һәм S = у булсын, биредә п һәм q — натураль
саннар, ә т һәм р — бөтен саннар. Ул вакытта:
аг-а‘ = yjam tia' = ■’Уа"' = а^ат<1+П1’ =а л" = а"‘·,
(а'У = <1(агУ = \>(4ат У = να4* = α ” = a'·;
(aby - \](аЬу = >jambn‘ = \lam ■ \ibm = ar br.
2* һәм 5° үзлекләр моңа охшаш рәвештә исбатлана (мөстәкыйль
рәвештә фикер йөртегез).
.— I .3
I 3 нче мисал. V40 24:5 4 аңлатмасының кыйммәтен
табабыз. Ул вакытта:
.— 1 .а / 1 3 4.1 1.4
</’40 24:5 4 = </23 5 24 54 = 24 4 54 4 = 21 51 = 10.
4 нче мисал
а)
а1.2_62.1
б) аңлатма-
ларының рәвешен үзгәртәбез.
Табабыз:
. а2-Ьг _ (а‘)’-(*4)2 _ (а}-г>4)(в4+Ь’) _ i 3
а) — ; ;— а -б ,
а*+Ь* а*+Ь* а* + Ь*
= = 0.4 _ Ь0,7 Ж
' ай* +aa,b°‘l +b'·* +aBib°·'’ + «>0·7)2
Рациональ күрсәткечле дәрәҗәнең түбәндәге ике үзлеген
билгеләп үтик.
6°. г — рациональ сан һәм 0 < а < Ь булсын. Ул вакытта
г > 0 булганда, ar < Ьг,
г < 0 булганда, аг > Ъ' була.
7°. Теләсә нинди г һәм з рациональ саннары өчен
г > з тигезсезлегеннән
α > 1 булганда, аг > а’,
0 < α < 1 булганда, а' < а’ икәне чыга.
б° үзлекне исбатлыйк. Әгәр г > 0 булса, ул вакытта г ны
г = рәвешендә язарга мөмкин, биредә т һәм п — натураль сан¬
нар. 0 < a < Ь тигезсезлегеннән һәм бөтен күрсәткечле дәрәҗә
220 Күрсәткечле һәм логарифмик фувкцияләр
үзлегеннән ат < If икәне чыга. Тамырлар үзлеге буенча (32 нче пункт,
6° үзлек) бу тигезсезлектән табабыз: ^ат < \[b'T, ягъни аг < If
г < 0 очрагында шушыңа охшаш фикер йөртәбез.
7° үзлекне исбатлау өчен, башта г һәм з рациональ саннарын
уртак ваклаучыга китерәбез: г = һәм s - —, биредә п — нату-
• *· л
ж , ж “ л · > s тигезсезлегеннән т> р
раль сан, ә т һәм р — бөтен саннар, г >
1
икәне килеп чыга. Әгәр а > 1 булса, a" = \ia > 1 була һәм бөтен
I
1
күрсәткечле дәрәҗә үзлеге буенча (а")" > (а"у.
1 m 1 Р
(а")" - ап — аг һәм (ап)р - а" = а’ икәне аңлашыла.
0 < α < 1 очрагы моңа охшаш рәвештә тикшерелә.
2
I 5 нче мисал, у 8 һәм 23 саннарын чагыштырыйк.
</δ ны рациональ күрсәткечле дәрәҗә рәвешендә язабыз;
г- 1 3 3 , .
у8 = 25. 7° үзлек буенча 23 > 25 була, чөнки > т-
6 нчы мисал. 2a<w һәм З200саннарын чагыштырыйк.
Бу саннарны бердәй күрсәткечле дәрәҗәләр рәвешендә языйк:
2*» = (23)100 = 8100; З200 = (З2)100 - 9100.
8 < 9 булганлыктан, 6° үалек буенча табабыз:
8,0° < д.оо, ягъни 2зоо < 32<ю j
Күнегүләр
428. —■ Аңлатманы саннан тамыр алу рәвешендә күрсәтегез:
? 1
а) З1·2; б) 5 э; в) 41·25; г) 6 2.
429. —■ Аңлатманы рациональ күрсәткечле дәрәҗә рәвешендә күр¬
сәтегез:
a) Va-2; б) </зБ; в) г) VF.
430.
431.
Санлы аңлатманың кыйммәтен табыгыз (430—431).
a) 24304; б) fe'P; в) 165; г) ·.
I О J l 1 6J f "
a) 82:(8® 9*);
21
B) 8 3:810·75;
8 —
6)3/100 (>/2)* (I)3;
Күрсәткечле һәм логарифмик функцияләр
Тапкырлаучыларга таркатыгыз (432—433).
432.¬
433.¬
434.
435.¬
436.
437.-
а) (ах)3 + (ау)3; б)а-а2; в)3 + 32; г) (Зх)2 - (5х)2.
1 1 1 I
- a) X3yi - X3 - у3
в) 4-4^;
I 1
б) С2 + с ,
г) а + Ь2 + а2 + а2Ь\
Аңлатманы
. а-b .
а) 1 ·
аг-Ь2
а) х~у
’ 2 11
х4 + х2у4
гадиләштерегез (434—435).
г~8
б> “ Ϊ
г3 +2г3 + 4
г) —
2 11
а3 -а3Ъ3 +Ь
5 . 2
X +
В)^1
V^ + 2a2;
<?-1
1
\ а3-Ь3 .
a + a'2b'2 а-а№/ a2+ab + b2>
Саннарны чагыштырыгыз:
·· ..
а) уЗ3 һәм Зе; б) 0,4 ' һәм ί
в) Уб5 һәм 61·7; г) һәм
Аңлатманың кыйммәтен табыгыз:
. 1 . 3
·> »■ *·* Чгһ)' (ώ) ’=
-1 2 ,1
б) 0,001 3 -(-2)-2643 -8 3 +(9в)2;
в) 273 +(^) -2504;
г) (-0,5)4 -6250·24 -(2|)’1 +19(-3)-s.
Күрсәткечле һәм логарифмик функцияләр
438.—Аңлатманы гадиләштерегез:
439. — Аңлатманы рациональ күрсәткечле дәрәҗә рәвешендә күр¬
сәтегез:
а) ах3; б) у/a2 у/а;
в) ξ'Γ* Vh; г) |-^27^х.
440. — Аңлатманы тамыр рәвешендә күрсәтегез:
а) 3 2 6; б)а4:д5; в) 2Ъ 3; г) ьМ.
441. — Саннарны чагыштырыгыз:
а) (73) β һәм ^З’1 «/J б) З600 һәм 54М1;
ί а
в) (1) 7 һәм V2 214; г) 730 һәм 440.
442. — Аңлатманың мәгънәсе бармы?
1 _. . -4
а) (-3) , б) (-2) ; в) 53; г) 0 7.
443. — Аңлатманың билгеләнү өлкәсен табыгыз:
а)(х + 1)Һ б)х^; в)хЛ г)(х-5)3.
444. — Үзгәрешленең кыйммәтләре нинди булганда тигезлек дө-
|рес?
a)(fli)e = a; б) (αψ =-α;
I в) (αβ) = г) (а0·7) 7 = -а.
223 Күрсәткечле һәм логарифмик функцияләр
§ 10.
Күрсәткечле һәм логарифмик
функция
35. Күрсәткечле функция
1. Иррациональ күрсәткечле дәрәҗә. Уңай а санын
а
билгелибез дә һәр санына а " санын тиңдәшле рәвештә куябыз.
Шуның белән рациональ саннар күплеге Q да билгеләнгән һәм
34 нче пунктта санап үткән үзлекләргә ия булган f(x) = ах санлы
функциясен табабыз, a = 1 булганда, а* функциясе даими, чөнки
теләсә нинди рациональ х өчен Iх = 1.
Башта калькулятор ярдәмендә 2Х кыйммәтен [-2; 3] кисем¬
тәсендә I адымы белән (132 нче а рәсем), ә аннан соң | адымы
белән (132 нче б рәсем) исәпләп, 2Х функциясе графигының берни¬
чә ноктасын билгелик. Шундый ук төзүләрне 1 , 1 һәм башка
шундый адымнар белән күңелдә дәвам итеп табылган нокталарны
салмак кәкре белән тоташтырсак, бу кәкрене барлык санлы турыда
m
билгеләнгән һәм үсә баручы рациональ х — нокталарында 2'
кыйммәтен кабул итүче кайбер функциянең графигы итеп кабул
итү табигый булыр (132 нче в рәсем), у = ( *| функциясе графи¬
гында җитәрлек санда нокталар төзегәннән соң, без әлеге функция¬
нең дә аналогик үзлекләргә ия булуын күрәбез (аерымлык шунда;
^=(1) ФУнкциясе да кими)·
Әлеге күзәтүләрдән күренгәнчә, һәр иррациональ α өчен 2“ һәм
саннарын у = 2Х һәм у = формулалары белән бирелгән
функцияләр өзлексез булырлык итеп билгеләргә мөмкин, өстәвенә
у = 2Х функциясе барлык саннар турысында үсә, ә у = функ¬
циясе кими.
a > 1 булганда, иррациональ α өчен д“ санының ничек билгелә¬
нүен гомуми рәвештә әйтеп китик.
Без у = а* функциясенең үсә баручы функция булуын телибез.
Ул вакытта г < а < г2 булырлык теләсә нинди рациональ η һәм г2
өчен а“ ның кыйммәте а'1 < аа < а'2 тигезсезлекләрен канәгать¬
ләндерергә тиеш.
х ка якынлашучы г, һәм г, кыйммәтләрен сайлаганда, а'1 һәм
аг- гә тиңдәш кыйммәтләрнең дә бер-берсеннән бик аз аерылганын
искәрербез. Барлык рациональ rt саннарына туры килгән барлык
224 Күрсәткечле һәм логарифмик функцияләр
225 Күрсәткечле һәм логарифмик функцияләр
аг' дән зур, ә барлык г2 рациональ саннарына туры килгән барлык
й<г дән кечкенә булган бер генә һәм бары тик бер генә у саны
барлыгын исбатларга мөмкин. Әлеге у саны — билгеләмә буенча
аа ул.
Мәсәлән, 2Т функциясенең хп һәм х' нокталарындагы кыйм¬
мәтен, биредә хп Һәм х' х = -Уз санының унарлы якынлашуы, каль¬
кулятор ярдәмендә исәпләгәннән соң, хп һәм х' у/з кә никадәр
якын булсалар, 2*" ның 2Л" тан шулкадәр азрак аерылганын кү¬
рәбез.
1 < уЗ <2 булганга күрә,
21 = 2 < 2^ < 22 - 4.
1,7 <л/3 < 1,8 һәм, димәк,
2’7 = 3,2490096 < 2^ < 21·8 · 3,4822022.
л/з ның киме һәм артыгы белән алынган түбәндәге унарлы
якынлашуларын моңа охшаш рәвештә тикшереп, тигезсезлекләр
язабыз:
21·73 = 3,3172782 < 2 4/3 < 21·74 ~ 3,3403517;
21 732 = 3,3218801 < 2^ < 21·™ « 3,3241834;
21.732° я 3,321801 < 2^< 21·7321 « 3,3221104;
21,73205 я 3,3219952 < 2^ < 2 1 73206 · 3,3220182;
21,732О5о β 3,3219952 < 2^ < 21·732051 · 3,3219975.
2^ нең калькуляторда исәпләнгән кыйммәте түбәндәгечә;
----- 3,321997.
0 < α < 1 өчен аа саны шушыңа охшаш рәвештә билгеләнә. Мон¬
нан тыш, теләсә нинди α өчен Iе = 1 һәм α > 0 өчен 0“ = 0 дип
алалар.
2. Күрсәткечле функциянең үзлекләре
Билгеләмә, у = ах формуласы белән бирелгән
функция (биредә а > 0, a * 1) а нигезле күрсәткеч¬
ле функция дип атала.
Күрсәткечле функциянең төп үзлекләрен санап чыгыйк (алар
мәктәп курсында исбатланылмый).
1. а* функциясенең билгеләнү өлкәсе реаль саннар
күплеге R була.
2. аг функциясенең кыйммәтләре өлкәсе барлык уңай
реаль саннар күплеге Я+ була.
3. α > 1 булганда, а’ функциясе барлык санлы турыда
үсә, 0 < α < 1 булганда, ах функциясе Я күплегендә
кими.
226 Күрсәткечле һәм логарифмик функцияләр
а > 1 һәм О < а < 1 очраклары өчен күрсәткечле функцияләр¬
нең графиклары 133—134 нче рәсемнәрдә сурәтләнгән.
4. х һәм у ның теләсә нинди реаль кыйммәтләре
өчен
аха» = а“'; £ = а‘>;
(αθ)-=α·θ·; («)'-£;
(αχ)ν = α4'
тигезлекләре дөрес.
Бу формулаларны дәрәҗәләрнең төп үзлекләре дип атыйлар.
3 нче һәм 4 нче үзлекләр башта бары тик рациональ х лар
өчен генә билгеләнгән а1 функциясенең үзлекләре барлык саннар
турысында билгеләнгән ах функциясе өчен дә дөрес булуын аңла¬
талар (34 нче пункттагы 1°—7° үзлекләрен карагыз).
Күнегүләр
445. — Функциянең үзлекләрен санап чыгыгыз һәм аның графи¬
гын төзегез:
а) у = 4’; б) у = 0,2*; в) у - 0,7х; г) у = 2,5*.
446. - Функциянең кыйммәтләре өлкәсен табыгыз:
а)у = -2*; б)у = (|) +1; в) у - -г)р = 5*-2.
447. - Саннарны чагыштырыгыз:
а) (I) 2 һәм 1; б) 3-^ һәм
г Λ ί
в) 2,5"v* һәм 1; г) 0,3 β һәм 0,33.
227 Күрсәткечле һәм логарифмик функцияләр
448.— Исәпләп чыгарыгыз:
a)((V2)^)^; б) 3*-гЛ-91^3; в)8'й:2а'5; г) (3^)^.
Аңлатманы гадиләштерегез (449—450).
449. а)а>‘ б) х· Vr’:x4";
в) (аЛ)А; г) у*
450. - a) +1; б) (^-ΐΗ+Λ.»*)
(а^-Ь^Р в<А-а'«
. I „ . *
в) “Та—ТТл—ТГ: г) + У")’ - (4 *уУ ·
_ ' лЛ л_ :
а 3 +а 3 b 3 +Ъ 3
451. — Түбәндәге кыйммәтләрне (таблицалар яки калькулятордан
файдаланып) 0,1 гә кадәр төгәллек белән исәпләп чыгары¬
гыз:
a) Ю1·41 һәм Ю1·43; б) 10мн һәм Ю'·415;
в) Ю3·33 һәм Ю2,24; г) Ю2·236 һәм 102,ззт.
452. — 451 нче мәсьәләдә табылган нәтиҗәләрдән файдаланып,
10“ һәм 10^5 кыйммәтләрен 0,2 гә кадәр төгәллек белән
табыгыз.
453. — Бирелгән функцияләрнең кайсылары R күплегендә үсә
баручы, кайсылары кими баручы икәнен күрсәтегез:
а) У = (72)·, у = б)!/ = (^-2)-,!/ = ;^7;
·> » = (»)’■ У * (?)*! П » " (» - /Т)'. У -
454. -* Функциянең кыйммәтләре өлкәсен табыгыз:
a)i/ = 3,+’-3; б) iZ = |2’r-2|;
в) у = (A)* 1 + 2; г) у - 4|х|.
455. - ί Функциянең R да иң зур һәм кечкенә кыйммәтен табыгыз:
а)у = (|)’“х; б)у = 5 + 3'“·*';
в)у = 4С1МХ; Г>У = (1) -2.
456. -· Тигезләмәнең тамыр тамгасын табыгыз:
а) р-Г = 10; б) 0,3х = 0,1; в) 10х = 4; г) 0,7х = 5.
228 Күрсәткечле һәм логарифмик функцияләр
Тигезләмәләрне график юл белән чишегез (457—458).
457. — а) 3' = 4 - х; б) = х + 3;
в) (Ц = х + 1; г) 4* = 5 - х.
458. — а) З1 = 2х - 1; б) 4’ + 1 = 6 - х;
в)2'-2 = 1-х; г)3'=-|.
459. - /(х) = а’ күрсәткечле функциясенең:
а) экстремумнары булуы;
■ б) ниндидер х0 ноктасында иң зур кыйммәт кабул итүе;
в) ниндидер ноктада нульгә тигез кыйммәт алуы;
г) җөп (так) булуы дөресме?
36. Күрсәткечле тигезләмәләрне һәм
тигезсезлекләрне чишү
1. Тигезләмәләр. Иң гади күрсәткечле тигезләмәне
тикшерик
a‘ = b, (1)
биредә а > 0 һәм а * 1.
у = а1 функциясенең кыйммәтләре өлкәсе — уңай саннар
күплеге. Шул сәбәпле Ь < 0 яки 6 = 0 очрагында (1) тигезләмәнең
чишелешләре булмый.
Ь > 0 булсын, a > 1 булганда, у = функциясе (-°0; °°) аралы¬
гында үсә (0 < a < 1 булганда кими) һәм барлык уңай кыйммәт¬
ләрне ала. Тамыр турындагы теореманы кулланып (8 нче пункт),
1 дән башка теләсә нинди уңай а һәм Ь > 0 өчен (1) тигезләмәнең
бердәнбер тамыры булганын табабыз. Бу тамырны табу өчен, Ь ны
Ь = ас рәвешенә китерергә кирәк, с ның а1 = тигезләмәсе чише¬
леше икәне үзеннән-үзе аңлашыла (134 нче рәсем).
■ 1 нче мисал. 7'2 = ^49 тигезләмәсен чишик.
2
49 = 72, ә v49 - 73 икәнен искәрик. Шуңа күрә бирелгән тигез-
2
ләмәне 7*”2 = 7* рәвешендә язарга мөмкин. Димәк, бирелгән ти¬
гезләмәнең тамыры х — 2 = j тигезлеге үтәлерлек х саны, ягъни
X = 2 j була. Җавап: х = 2 |.
2 нче мисал, δ*2-2* 1 =25 тигезләмәсен чишик. Аны
gx*-fa-i _ 52 рәвешендә языйк. Бу тигезләмәнең тамырлары
булып х2 - 2х - 1 = 2 тигезлеге үтәлә торган х саннары тора. Мон¬
нан тамырлары 3 һәм -1 саннары булган квадрат тигезләмәне
чишәбез. Җавап: 3; -1.
229 Күрсәткечле һәм логарифмик функцияләр
3 нче мисал. 6х*1 + 35 · 6' 1 = 71 тигезләмәсен чишик.
61*' - Зб ’ 61 1 икәнен искәрик. Шуңа күрә бирелгән тигезләмәне
36 · 6Х * + Зб · б'-1 = 71, ягъни 71■6Х1 = 71 рәвешендә язарга мөм¬
кин, моннан 6Х 1 = 6°, х - 1 = 0 һәм х = 1. Җавап: 1.
4 нче мисал. 4Х - 5 · 2Х + 4 - 0 тигезләмәсен чишик, t = 2х
үзгәрешлесе белән алмаштырабыз. Биредә 4х = (2Х)2 = t2 була. Шуңа
күрә бирелгән тигезләмә t2 - 5t + 4 = 0 рәвешен ала. Әлеге квад¬
рат тигезләмәнең чишелешен табабыз: = 1 һәм ί2 = 4. 2х = 1
һәм 2х = 4 тигезләмәләрен чишеп табабыз: х = 0 һәм х = 2.
Җа ва п : 0; 2.
2. Тигезсезлекләр һәм тигезләмәләр системасы. Иң гади күр¬
сәткечле тигезсезлекләрне чишү у - ах функциясенең билгеле үз¬
легенә нигезләнгән: бу функция α > 1 булганда үсә һәм 0 < α < 1
булганда кими.
| 5 нче мисал. 0,57 Зх < 4 тигезсезлеген чишик.
0,5 2 = 4 икәненнән файдаланып, бирелгән тигезсезлекне
0,57 Зх < 0,5 2 рәвешендә күчереп языйк.
у = 0,5ж күрсәткечле функция кими (чөнки 0,5 нигезе 1 дән
ким). Шуңа күрә бирелгән тигезсезлек 7 - Зх > -2 тигезсезлегенә
тамырдаш, моннан х < 3. Җавап: 3).
6 нчы мисал. 6χ2χ2χ>63 тигезсезлеген чишик.
у = 6Х күрсәткечле функция үсә. Шуңа күрә бирелгән тигезсез¬
лек х2 + 2Х > 3 тигезсезлегенә тамырдаш. Әлеге тигезсезлекне чи¬
шеп, җавапны табабыз: (-<»;-3) һәм (1; оо).
7 нче мисал. - з^й, +3<0 тигезсезлеген чишик.
t = ) алыштыруны кулланабыз, ул вакытта = t2 һәм ти¬
гезсезлек ί2-^ί+3<0 рәвешендә языла, моннан < t < 9.
lJ ίί
Димәк, бИР®лгән тигезсезлекнең чишелеше булып | ' | <9
тигезсезлеген канәгатьләндерүче х саннары һәм бары тик шундый
саннар гына хезмәт итә. Әмма | = (|), 9 = (|) , ә у = функ¬
циясе кими, чөнки 1 < 1. Шуңа күрә | < 9 тигезсезлегенең
чишелеше булып -2 < х < 1 тигезсезлеген канәгатьләндерүче х
саннары була. Җавап: (-2; 1).
8 нче мисал. Тигезләмәләр системасын чишик:
2Х +2* = 12,
З2’-·' = 3.
Системаның икенче тигезләмәсеннән 2х - у ~ 1 не табабыз, мон¬
нан у 2х - 1· Беренче тигезләмәгә у урынына 2х - 1 аңлатмасын
куеп, 2Х + Я2"1 = 12 не табабыз, моннан 2Х + · 22х = 12. 2х не t аша
230 Күрсәткечле һәм логарифмик функцияләр
билгеләп, t2 + 2t — 24 = 0 квадрат тигезләмәсен табабыз, моннан
tj = -6, f2 = 4. 2х = -6 тигезләмәсенең чишелешләре юк. 2Х = 4
тигезләмәсенең тамыры х ~~ 2 саны, у ның моңа тиңдәш кыйммәте
3 кә тигез. Җавап: (2; 3).
Күнегүләр
Тигезләмәләрне чишегез (460—464).
460— а) 4Х = 64; б) = 27; в) 3' = 81; г)
462. - а) З6'х = 38*’2;
в) 7зх = 9;
463. - а) 7Х+2 + 4 · Т'+1 = 539;
| в) 4Х+1 + 4Х = 320;
464. - а) 9Х-8 Зх-9 = 0;
в) 36* - 4 6* - 12 = 0;
465. Тигезләмәләр системасын
б) м'в'-1 = Vi27*;
г) = 4^2.
б) 2·3Χ+1 -3х =15;
г) 3-5Х+3 + 2 6х*1 =77.
б) 100х -11 10х +10 = 0;
г) 49х - 8 · 7х +7 =0.
4”» « 16,
4*·1*= I;
чишегез:
I б3*"" = \6,
|2*'3х =
3Χ’*+2 = 27;
Тигезсезлекләрне чишегез (466—467):
466.
467.
а)(|Г>27;
в) 0,2* <
a) 4s-2х <0,25;
в) 0,42хИ >0,16;
6) (7б)х<^;
г) 1,5х < 2,25.
б) 0,37+4х > 0,027;
г) З2 х < 27.
Тигезләмәләрне чишегез
468.
i а) 3х'1 - 2 · 3х 2 = 75;
(468—470).
6>(i) -(I) =4-8;
г) 5 9х + 9х-2 = 406.
231 Күрсәткечле һәм логарифмик функцияләр
469. —a) 5X+1 = 8X+1; б) (1)‘'*· (’)*в) 7х’г = 42 x.
470. -a) 3х + 33 x =12; 6)4^+16 = 10 2^;
в) 4,96; r) 4x-0,25xZ = 15.
471. — Тигезләмәләр системасын чишегез:
5Х+» = 125,
4<»-»ι*-ι — j.
б)
х + у = 5,
4х + 4« = 80;
в)
3* + 3* = 12,
6X+* =216;
г)
]4Х+* = 128,
|5Sl-2i,-3 _ j.
Тигезсезлекләрне чишегез (472—474).
472.- а) 2χ2 > (I)" 3; б) < (7б)х’*8·™;
г)ЙГ>64^<
473.¬
474.-1
475.-
a) (j)" + (|У * > 2,5; б) 221’1 + 22xi + 2’xa < 448;
•’(j)'''-(s)'’ra: r)3-+3-<28.
a) πχ - π2χ 0; 6) (j)21'1 -10 3 x + 3 < 0;
в) 4X - 2t+1 - 8 > 0; r) (ij" -5 6 1 - 6 ζ 0.
Тигезсезлекләрне график юл белән чишегез:
а)2х^3-х; б) ^2х + 5;
в) (-j)’> 2х +1; г)Зх>4-х.
37. Логарифмнар һәм аларның үзлекләре
1. Логарифм. ах = Ь тигезләмәсенә кайтыйк, биредә
α > 0 һәм а * 1. Моннан алдагы пунктта әйтелгәнчә, Ь 0 булганда,
әлеге тигезләмәнең чишелешләре юк һәм Ь > 0 очрагында бердән¬
бер тамыры була. Бу тамырны а нигезе буенча Ь ның логарифмы
дип атыйлар һәм logo& дип тамгалыйлар, ягъни
Ing ό .
a - = Ь.
Билгеләмә Ъ санын табу өчен, α нигезен күтә¬
рергә тиешле дәрәҗә күрсәткече α буенча Ъ саны¬
ның логарифмы дип атала.
232 Күрсәткечле һәм логарифмик функцияләр
α'ο*“(>= Ь формуласын (биредә Ь > 0, α > 0 һәм а * 1) төп лога
рифмик бердәйлек дип атыйлар.
1 нче мисал, a) log2 32; б) log5 0,04 нең кыйммәтен табабыз:
а) 32 = 2s икәнен күрәбез, ягъни, 32 санын табу өчен, 2 не би¬
шенче дәрәҗәгә күтәрергә кирәк. Димәк, log232 = 5.
б) 0,04 = g = 5 2 икәнен искәрик, шуңа күрә log50,04 = -2
була. .
2 нче мисал. Нигезе үЗ буенча θ санының логарифмын
табыйк.
(х/З)-4 = икәнен искәрик. Шуңа күрә логарифм билгеләмәсе
буенча log^ | = -4.
„ .. 1 „ 3 _
3 нче мисал, a) loge х = 3 ; б) log, 8 = - ^ булырлык х санын
табыйк.
Төп логарифмик бердәйлектән файдаланабыз:
1
а) х = 8|ог»х - 83 = 2;
з _« .
б) х'°«*8 - 8, ягъни х 4 = 8, моннан х = 8 3 = А.
10
2. Логарифмнарның төп үзлекләре. Логарифмнар белән эш¬
ләгәндә, күрсәткечле функция үзлекләреннән чыга торган алар-
ның түбәндәге үзлекләре кулланыла.
Теләсә нинди α > 0 булганда (a * 1) һәм теләсә нинди
уңай х һәм у өчен түбәндәге тигезлекләр үтәлә:
1°. logel = 0.
2°. log.a = 1.
3°. logaxy = logux + logajf.
4°. log„y = log.x - logay.
5°. Теләсә нинди реаль р өчен loga Xя = р loge х.
3° нче кагыйдәне исбатлау өчен, төп логарифмик бердәйлектән
фай д ал анабыз:
x = a'0<“\ у=а^у. (1)
Бу тигезләмәләрне буынлап тапкырлап табабыз:
X teg V Ing X + Ing у
xy = aa · а в' = а а а ,
ягъни ху = αοβ·Ι + Ιο<"ί'. Димәк, логарифмның билгеләмәсе буенча
loga(xj/) = log„x + log., у.
Тапкырчыгышның логарифмы логарифмнар сумма¬
сына тигез.
233
Күрсәткечле һәм логарифмик функцияләр
4° нче кагыйдәне яңадан (1) тигезлек ярдәмендә исбатлыйк:
X _ д'*' * _ lo« a * - toia V
V ~ а"*”" ’
димәк, билгеләмә буенча logd = logB х - loga у.
Өлешнең логарифмы логарифмнар аермасына тигез.
5° нче кагыйдәне исбатлау эчен, х = а1ое“* бердәйлегеннән фай¬
даланабыз, моннан хр = . Димәк, билгеләмә буенча logax₽ =
- plogax.
Дәрәҗәнең логарифмы әлеге дәрәҗәнең күрсәткече
белән шул ук дәрәҗәнең нигезе логарифмы тапкыр¬
чыгышына тигез.
Логарифмнарның төп үзлекләре логарифмнарны эченә алган
аңлатмаларның рәвешен үзгәртү барышында киң кулланылалар.
Мәсәлән, логарифмның бер нигезеннән икенче нигезенә күчү фор¬
муласын исбатлыйк:
(Әгәр бу формуланың ике кисәгенең дә мәгънәсе булса, ягъни
х > 0, a > 0 һәм a * 1, Ь > 0 һәм 6*1 булса, бу формула дөрес
була.)
Дәрәҗәне логарифмлау кагыйдәсе буенча һәм төп логарифмик
бердәйлек буенча язабыз:
logt х = log, (a11*·'),
моннан
log(,x = logBx · log, a.
Әлеге тигезлекнең ике кисәген дә log,a га бүлеп кирәкле
формуланы табабыз.
Ниндидер бер Ь нигезгә төзелгән логарифмнар таблицасы
булганда, күчү формуласы ярдәмендә ирекле а нигезле логарифм¬
ның кыйммәтен табарга мөмкин. Унарлы һәм натураль логарифм¬
нар таблицалары аеруча киң кулланыла (нигезе 10 булган лога¬
рифмнарны унарлы логарифмнар дип атыйлар һәм 1g дип там¬
галыйлар, ә натураль логарифмнар белән сез 41 нче пунктта
танышырсыз).
I 4 нче мисал. log0 3 7 не табабыз.
Калькулятордан (яки таблицалардан) файдаланып табабыз:
lg 7 ~ 0,8451 һәм 1g 0,3 - 0,4771 - 1 = -0,5229. Димәк, күчү
. „ . „ 0,8451 _
формуласы буенча log03 7 0 = -1,6162.
Күрсәткечле һәм логарифмик функцияләр
5 нче мисал. log25 = a һәм log23 = b икәне билгеле.
log2300 не α һәм Ь аша күрсәтик.
Логарифмнарның төп үзлекләреннән файдаланып табабыз:
log2 300 = log, (3 · 52 · 22) = log, 3 + 2 log2 5 + 2 log, 2 = b + 2a + 2.
6 нчы мисал. 8α3 \[b* аңлатмасының логарифмын log2 a
һәм log,Ь аша аңлатыйк. (Кыскача болай әйтәләр: бирелгән аңлат¬
маны 2 нигезе буенча логарифмлыйбыз.)
Логарифмнарның төп үзлекләреннән файдаланып табабыз:
log2(8a3tfb*) = log2(23 α3 Ь7)= 3log2 2 + 3log, a +| log2 b =
= 3 + 3 log2 a + I log2 b.
7 нче мисал. Әгәр log5 х = log5 7 + 2 log5 3-3 log5 2 булса,
х ны табыйк. Башта логарифмнарның төп үзлекләреннән файдала¬
нып, бирелгән тигезлекнең уң кисәгенең рәвешен үзгәртәбез:
logs* = log5 7 + bgs32 - logs 23 = log5^r =
о О
ягъни log5x = log5^ һәм шуңа күрә х = ^=7,875.
, Ig72-lg9
в нче мисал. |g 28-lg7 аңлатмасының кыйммәтен табыйк.
Логарифмнарның төп үзлекләреннән файдаланып, әлеге ваклан¬
маның санаучысының һәм ваклаучысының рәвешен үзгәртәбез:
lg72 - lg9 - ]g^ = lg8 = 31g 2; lg28 - Ig7 = lg^ = lg4 = 21g2.
Димәк,
Ig72-lg9 _ 3lg2 _ 3
Ig28-lg7 ~ 2lg2 ” 2’
Күнегүләр
a нигезле дәрәҗә рәвешендәге санның а нигезе буенча лога-
| рифмын табыгыз (476—478).
476. -1 а) З2 = 9; б)23=|; в) 42 = 16; г)52=^.
й Z&
1 1 1
477. - а) 95 = 3; б) 7° = 1; в) 325 = 2; г) 3 1 = |.
[ о
2 ? ? ?
478. - а) 273 = 9; б) 325 = 8; в) 814 = 27; г) 125’ = 25.
Күрсәткечле һәм логарифмик функцияләр
Тигезлекләрнең дөреслеген тикшерегез (479—482).
479.- a) log3 А. = -4; б) log](j χ _ θ.
в) log,16 = 2; г) log5125 « 3.
480. —
I
481. *
482. -
a) log5 0.04 = -2;
б) log7 343 = 3;
в) lg0,01 = -2;
г) Iog3 2I3 = -5.
a) 8 = 6;
б) logjj 27 = -6;
в) log! 9 = -2;
3
г) log0 5 4 = -2.
a) log2jrl28 = M;
6) logo г 0,008 = 3;
в) logj^ 0,2 = -2;
г) logo 2125 = -3.
483.-
Бирелгән саннарның логарифмнарын а нигезе буенча та¬
быгыз:
а) α = 5 булганда 25, -, <ә; б) α = 8 булганда 64, 2;
в) α = 2 булганда 16, 1. V2; г) α = 3 булганда 27, ч/з.
Ч XT
х санын табыгыз (484—486).
484.
a) log3 х = -1; б) logi х = -3;
В
в) logs X = 2; г) log7 х = -2.
485.
a) log, х = -3; б) log^ х = 0;
в) logi х = 1; г) log! х = -3.
Т 2
486.
a) log, 81 = 4; б) log,^ = 2; в) log,! = -2; г) log,27 = 3.
487.
Санны а нигезле логарифм рәвешендә языгыз:
а) а - 4 булганда 2; 1; 0;
б) α = 3 булганда 3; —1; —3; 1;
в) а = 2 булганда 3; -*·; 0; -1;
г) α = 5 булганда 1; —2; 0; 3.
Төп логарифмик бердәйлектән файдаланып, аңлатманы га¬
диләштерегез (488—490).
488.
а) 1,7ΙοβΙ·7ί; 6)πΙο<*5·2; в) 21О<25; г) 3,8loese
489.-
а) 5ltl0isS
б) Ю1'1"2;
Β)(1),“*·Ι,; r)321oga18.
236 Күрсәткечле һәм логарифмик функцияләр
490. —
491. -й
a)421-3; 6)5S1’4 в) (|р*; г) б21*‘\
3 нигезе буенча логарифмлагыз (α > О, b > 0):
a)(V^b)'; 6)(^) ‘ B)9a<^: r)27?'
492.
493. -
10 нигезе буенча логарифмлагыз, биредә α > 0, b>0, с > О
(492-493). г_
a)100V^; б)-^-т=; в) </1бА4с’; r)5^.
0,1 Cvc? „2.3
a о
I J 2 Ϊ
a) 103a4b2c 3; 6) ; в) 10'4a2b5c3; r)——
10 ° c IQ’aV
494.— log6 2 = а һәм log. 3 = b икәне билгеле: а һәм b аша аңла¬
тыгыз:
a) log572; 6)log515; B)log512; r)log530.
Исәпләп чыгарыгыз (495—496).
495.— a) Ig8 + lgl25;
I в) log12 4 + logi2 36;
496 J a) 2£8±kl8.
4W.-№ aj 2Ig2 + lg3 ’
в) logs 11 - lo&2 44;
497.-r- a) log6 x = 3 log6 2 + 0,
6) Igx = |lg5a -31g 5
6) log27-log2^;
r) lgl3-lgl30.
, logs 16 .
’ log, 4 ’
r) logo 3 9 - 2 logo 3 Ιθ-
ί logs 25 - 2 log6 3;
+ 41gc;
в) 1g x = 51g m +11g η -11g p;
r) log4 х ~ 1 log4 216 - 2 log410 + 4 log4 3 булса, х иы та¬
быгыз.
498.+ Исбатлагыз:
a) log, 3 + log31 < -2;
2 z
B) 10g3 7 + log; 3 > 2;
6) 4l<,is7 = 7,o*s 4-
r)
237
Күрсәткечле һәм логарифмик функцияләр
38. Логарифмик функция
а саны 1 гә тигез булмаган уңай сан булсын.
Билгеләмә.
y = log„x (1)
формуласы беләв бирелгән функцияне а нигезле
логарифмик функция дип атыйлар.
Логарифмик функциянең төп үзлекләрен санап китик.
I 1. Логарифмик функциянең билгеләнү өлкәсе — бар¬
лык уңай саннар күплеге Я+, ягъни P(loga) = R+.
Чыннан да, моннан алдагы пунктта әйтелгәнчә, һәрбер уңай х
санының а нигезе буенча логарифмы бар.
I 2. Логарифмик функциянең кыйммәтләре өлкәсе —
I барлык реаль саннар күплеге.
Чынлыкта логарифм билгеләмәсе буенча теләсә нинди реаль
у өчен
loga(at') = y (2)
тигезлеге дөрес, ягъни у = logax функциясе х0 = α5/0 ноктасында у0
кыйммәтен кабул итә.
3. Логарифмик функция барлык билгеләнү өлкәсендә
үсә (а > 1 булганда) яки кими (0 < а < 1 булганда).
Мәсәлән, а > 1 булганда, функциянең үсүен исбатлыйк
(0 < а < 1 очрагында да шушыңа охшаш фикер йөртелә).
х, һәм х2 — ирекле уңай сан, һәм х2 > х, булсын. logax2 > logax1
икәнен исбатларга кирәк. Киресеннән чыгып исбатлыйбыз, ягъни
logex2 logax1. (3)
a > 1 булганда, күрсәткечле функция у = а1 үсә, шуңа күрә (3)
тигезсезлектән
(4)
чыга. Ләкин ο10*11*2 — х2, a’°s“X1 = хг (логарифмның билгеләмәсе
буенча), ягъни (4) тигезсезлек х2 х, икәнен аңлата. Бу исә х2 > х,
дип фараз итүгә каршы килә.
График төзү өчен, логарифмик функциянең 0 кыйммәтен
1 ноктасында кабул итүен искәрик: теләсә нинди a > 0 булганда,
log01=0, чөнки а° = 1.
238 Күрсаткечле һом логарифмик функцияләр
а > 1 булганда, функциянең үсүе нәтиҗәсендә х > 1 булганда,
логарифмик функция — уңай кыйммәтләр, ә 0 < х < 1 булганда,
тискәре кыйммәтләр ала.
Әгәр 0 < а < 1 булса, ул вакытта у = logax да кими, шуңа
күрә 0 < х < 1 булганда logax > 0 һәм х > 1 булганда logdx < 0
була.
Исбатланган үзлекләргә таянып, a > 1 (135 нче а рәсем) һәм
0 < a < 1 булганда (135 нче б рәсем) у = logex функциясенең гра¬
фигын төзү кыен түгел.
Түбәндәге раслау дөрес (исбатлануны 40 нчы пункттан кара¬
гыз).
Нигезләре бердәй булган күрсәткечле һәм логариф¬
мик функцияләрнең графиклары у = х турысына ка¬
рата симметрик була (136 нчы рәсем).
Логарифмик функциянең үзлекләрен куллануга мисаллар тик¬
шерик.
136 нчы рәсем
239
К .рсәткечле һәм логарифмик функцияләр
У 1 нче мисал.
f (х) = log,(4 - 5х) функциясенең бил¬
геләнү өлкәсен табыйк.
3
5
2
7
Логарифмик функциянең билге-
137 нче
рәсем
ләнү өлкәсе — Я. күплеге. Шуңа күрә
бирелгән функция х ның бары тик
4 - 5х > 0 була торган, ягъни х < 0,8
булгандагы кыйммәтләре өчен генә
билгеләнә. Димәк, бирелгән функциянең билгеләнү өлкәсе булып
(-во; 0.8) интервалы хезмәт итә.
2 нче мисал. / (х) = log2(х2 - Зх - 4) функциясенең билге¬
ләнү өлкәсен табыйк.
Моннан алдагы мисалдагы кебек f функциясе х ның х2 - Зх -
- 4 > 0 булырлык кыйммәтләре өчен билгеләнә. Әлеге квадрат
тигезсезлекне чишеп, D(f) ның (-оо; -1) һәм (4; <») интерваллары
берләшмәсе икәнен табабыз.
3 нче мисал, f (х) = log.— функциясенең билгеләнү
өлкәсен табабыз.
2х + 3
. > 0 тигезсезлеген интерваллар методы белән чишеп,
γ) икәнен табабыз (137 нче рәсем).
4 нче мисал. Саннарны чагыштырыйк: a) log35 һәм
log97; б) log 15 һәм logi7; в) log310 һәм log412.
з з
а) Нигезе 1 дән зур булган логарифмик функция барлык санлы
турыда үсә. 7 > 5 булганлыктан, log37 > log35 була.
б) Әлеге очракта логарифмның нигезе 1 дән кечкенә, шуңа
күрә у = logi х функциясе кими һәм, димәк, log ι 7 < log ι 5.
э зз
в) 10 > 9 — З2 икәнен искәрик, шул сәбәпле log310 > 2, икенче
яктан 12 < 16 = 42 һәм, димәк, log412 < 2. Шулай итеп, log310 >
>log412.
5 нче мисал. Кайсысы зуррак: log,3 +log,7 ме, әллә
log2(3 + 7) ме?
Логарифмнарның төп үзлекләре буенча log.3 +log,7=log,21.
log,(3 + 7) = log210 һәм 10 < 21 булганлыктан, ә логарифмның
нигезе 2 саны 1 дән зур булу сәбәпле, log, 10 < log221, димәк,
log,3 + log27 > log2(3 + 7).
240
Күрсәткечле һәм логарифмик функцияләр
Күнегүләр
* Аңлатманың билгеләнү өлкәсен табыгыз (499—500).
499.— a) logJlO -5х);
в) log3(x - 4);
б) log3(9-x2);
г) log03(x2 - 16).
500.-5» a) log^(6 + х х2);
в) logo,9 5-2χ ’
б) lg^;
г) log^(x2 2x 3).
Саннарны чагыштырыгыз (501—503).
501. - a) log23,8 һәм log24,7; б) log ι 0,15 һәм logι 0,2;
а з
в) log3 5,1 һәм log3 4,9; г) log021,8 һәм log0.22,l.
502. - allog^S һәм 1; б) log ι 1,9 һәм log ι 2,5;
Λ
B)log„2,9 һәм 1; r)log07>/2 һәм logojO^.
503. a) log2 10 һәм logs 30; 6) log032 һәм log33;
в) log3 5 һәм log7 4; r) log310 һәм loge57.
504.
Функциянең төп үзлекләрен санап чыгыгыз һәм аның
графигын төзегез;
а) у = logs х; 6)i/ = logix;
2
B)y = log4x; г) у = log j х.
з
505. — Аңлатманың билгеләнү өлкәсен табыгыз:
a) log2sinx; б) log3(2* -1); в) logi cosx; г) lg(l-3*).
2
506. — Аңлатманың кыйммәтен табыгыз:
а) log2 2 sin ~ + log2 cos -Д;
б) log4(ξ/7 - χ/з) + log,(V49 + </21 + </9);
в) lgtg4 + lgctg4;
г) logJ5 + 2x/6) + log„(5-2V6).
507. — Функциянең графигын төзегез:
а) У = 10g3(x-2); 6).v = -log1X;
2
в) у = log,(x + 1); Г) у = logiX + 2.
241
Күрсәткечле һем логарифмик ФУ“кциплар
508. — Тигезләмәне чишегез:
а) log3 х = 2 log9 6 - log, 12;
б) log j х = log02 35 - 2 log0.2 25 x/7;
I
в) logs x = j logs144 + logs 0,75;
r) log, x = 3 log0 j 4 + 21og0>l1|·
509. — Тигезләмәне график юл белән чишегез:
a) lg х = 1 - х; б) log ι х = х - 4;
3
в) log ι х = х - 6; г) log2 х = 3 - х.
Б
510. — Логарифмик функциянең
а) экстремумнары булуы; б) так булуы;
в) периодик булуы; г) җөп булуы дөресме?
511. — / аралыгында f функциясенең иң зур һәм иң кечкенә
кыйммәтләрен табыгыз:
а) /(х) = log|X, I = [1; 4J; б) /(х) = log9 х, I = [|;9];
в) /(х) = logj х, I = Ң; 1]; г) /(х) = iog± х, I = [|; 4].
39. Логарифмик тигезләмәләр һәм
тигезсезлекләрне чишү
Иң гади
loga х = Ь
логарифмик тигезләмәсен тикшерик. (0; «) аралыкта логарифмик
функция үсә (яки кими) һәм шул ук аралыкта барлык реаль
кыйммәтләрне ала (135 нче рәсем). Тамыр турындагы теоремадан
күренгәнчә (8 нче пункт), теләсә нинди Ь өчен бирелгән тигезлә¬
мәнең чишелеше бар һәм бары тик бердәнбер. Санның логарифмы
билгеләмәсеннән шунда ук аь нең шундый чишелеш икәнлеге
күренә.
1 нче мисал. 1 oga(х2 + 4х 4- 3) = 3 тигезләмәсен чишик.
х ның х2 4- 4х 4- 3 = 23 тигезлеге үтәлерлек кыйммәтләре генә
бирелгән тигезләмәне канәгатьләндерә. Без х2 4- 4х — 5 = 0 квадрат
тигезләмәсен таптык. Аның тамырлары 1 һәм -5 саннары. Димәк,
бирелгән тигезләмәнең тамыры ике сан: 1 һәм -5.
2 нче мисал. log5(2x + 3) = log5(x+ 1) тигезләмәсен чишәбез.
Бу тигезләмә х ның бары тик 2х + 3 > 0 һәм х 4- 1 > 0 тигез¬
сезлекләре үтәлердәй кыйммәтләре өчен генә билгеләнә, х ның
мондый кыйммәтләре өчен бирелгән тигезләмә 2х + 3 = х + 1
242 Күрсәткечле һәм логарифмик функцияләр
тигезләмәсенә тамырдаш була. Моннан х — -2 не табабыз, х ның
мондый кыйммәтләре өчен бирелгән тигезләмә 2х + 3 = х + 1
тигезләмәсенә тамырдаш була. Моннан х = -2 не табабыз, х - -2
саны х + 1 > 0 тигезсезлеген канәгатьләндерми. Димәк, бирелгән
тигезләмәнең тамырлары юк.
Шушы ук тигезләмәне башкача да чишәргә була. Бирелгән
тигезләмәнең нәтиҗәсе 2х + 3 = х + 1 тигезләмәсен тикшергәндә,
х = -2 икәнен табабыз, һәрвакытта тигезләмәләрне тамырдаш
булмаган үзгәртүләр вакытында табылган кыйммәтне баштагы
тигезләмәгә куеп карап тикшерү таләп ителә. Әлеге очракта
= logs (-1) тигезлеге дөрес түгел (аның мәгънәсе юк).
3 нче мисал, log, (х2 - 2х + 2) = 1 тигезләмәсен чишәбез.
Бу тигезләмәне х ның х > 0 һәм х ψ 1 тигезсезлекләре (х —
логарифмик функциянең нигезе) һәм х2 - 2х + 2 = х, ягъни
х2 - Зх + 2 = 0 тигезлеге үтәлерлек кыйммәтләре генә канәгать¬
ләндерә. Табылган квадрат тигезләмәнең тамырлары 1 һәм 2.
Ләкин х = 1 бирелгән тигезләмәнең чишелеше була алмый. Ди¬
мәк, бары тик 2 саны гына бирелгән тигезләмәнең чишелеше
була ала.
4 нче мисал. logi(5 - 2х) > -2 тигезсезлеген чишәбез.
з
-2 саны log ί 9 га тигез. Шуңа күрә бирелгән тигезсезлекне
з
iogi(6-2x) > log ί 9 рәвешендә күчереп язарга мөмкин. Нигезе
3 3
1 булган логарифмик функция билгеләнгән һәм, , < 1 булганга
О
күрә, R. да кими. Димәк, икенче тигезсезлекне бары тик 0 < 5 -
- 2х < 9 шарты үтәлә торган х саннары гына канәгатьләндерә,
моннан -2 < х < 2,5.
Шулай итеп, (-2; 2,5) интервалы бирелгән тигезсезлекнең
чишелеше була.
5 нче мисал, log2 х - log^ х — 3 — 0 тигезләмәсен чишегез.
Икенче кушылучыда 5 нигезенә күчәбез һәм, t = log5 х дип алып,
алыштыру ясыйбыз, ул вакытта
log с х = "’-ь г = — = 21.
logsV5 1
Хәзер бирелгән тигезләмәне t2 - 2t - 3 = 0 рәвешендә язабыз.
Әлеге квадрат тигезләмәнең тамырлары 3 һәм -1. Алыштырыл-
ган log5 х = 3 һәм log5x = -l тигезләмәләрен чишеп табабыз:
х — 5* = 125 һәм х = 5 1 = 0,2.
6 нчы мисал. Тигезләмәләр системасын чишәбез:
Ilg(y-X)= lg2,
I log2 х - 4 = log2 3 - log, у.
243 Күрсәткечле һәм логарифмик функцияләр
Системаның беренче тигезләмәсе у - х = 2 тигезләмәсен»,
ә икенчесе А = — тигезләмәсенә тигезкөчле, өстәвенә х > 0 һәм
10 у
у > 0. £/ = х + 2неү^- = — тигезләмәсенә куеп, х (х + 2) = 48 не та¬
бабыз, моннан х2 + 2х - 48 = 0, ягъни х = -8, яки х = 6.
х > 0 булганлыктан, х = 6 һәм ул вакытта у = 8 була. Шулай
итеп, бирелгән тигезләмәләр системасының бер чишелеше бар:
х — 6, у — 8.
Тагы шуны искәрик: логарифмнар ярдәмендә теләсә нинди
а‘ = Ь рәвешендәге күрсәткечле тигезләмәнең тамырын язарга мөм¬
кин (36 нчы пункттагы мисалларны чишкәндә, без моны эшли
алмый идек әле), х = loga Ь саны әлеге тамыр була.
7 нче мисал. 5‘'3х = 7 тигезләмәсен чишәбез.
Логарифмның билгеләмәсе буенча 1 - Зх = logs 7 һәм х = 3 —
-Ilog 7. St
О ■*
Күнегүләр
Тигезләмәләрне чишегез (512—515).
512. - а) 9Х= 0,7; б)(0,3)'=7; в)2'-10; г) 10' = π.
513.—a) log5х = 2; 6)log04x = -l; в) log9x = -г) Igx = 2.
514.-r
.J
516.
517.
a) logi (2x - 4) = -2; 6) log, (x2 + 2x + 3)
B)log03(5 + 2x) = 1; r) log, (3 - x) = 0.
a) (0,2)4 ' = 3; 6) 5'2 = 7; в) 32 3x - 8; r) 72x = 4.
Тигезсезлекне чишегез (516—517).
a) log3x > 2; 6) log0Sx > -2;
в) log0.7x <1; r) log2 5 x < 2.
a) log4(x - 2) < 2; 6) logi (3 - 2x) > -1;
3
в) log5(3x + 1) > 2; r) logi (4x + 1) < -2,
7
” log, 6;
Тигезләмәне чишегез (518—520).
518. - a) logax = 2 loga3 + loga 5; 6) 1g (x - 9) + 1g (2x - 1) = 2;
в) logax = loga10 - loga2; r) log3(x + 1) + log3(x + 3) = 1.
519. a) I log2 (x - 4) + I log2 (2x - 1) -= log, 3;
б) 1g (3x2 + 12x + 19) - 1g (3x + 4) = 1;
в) 1g (x2 + 2x - 7) - Ig (x - 1) = 0;
r) log5 (*2 + 8) - log5 (x + 1) = 3 log5 2.
244 Күрсәткечле һәм логарифмик функцияләр
520.— a) log? х + log4 Vx -1,5 = 0;
в) logg x - logs x = 2;
6) lg2 x - Igx2 + 1 = 0;
r) log| x - 2 log3 x - 8 = 0.
521.
Тигезләмәләр системасын чишегез:
в) + У =7’
[lg х + lg у = 1;
ίχ + у = 34,
в)J
[log2 х + log2 у = 6;
Тигезләмәләрне чишегез
522.- a) —? + τ-Ц = 1;
lgx + 1 lgx+5
рЧ 21g-*—= 1:
’ lg(5x-4) *’
r)
)og4(x + y) = 2,
log3 x + log3 у = 2 + log3 7;
log4 x - log4 у = 0,
x2 ~5y2 + 4 = 0.
(522—524).
6) log21 =
4 log2j-l
r\ 1— + —5— -
lgx-6 lgx + 2
523.— a) loga x = log£ 2 + log, 3;
a
в) log3 x-21ogi X = 6;
3
6) log, 2 - log4 x + ~ = 0;
r) log2S x + log5 x = log, 7β.
8
524.— a) log2 (9 - 2X) = 3 - x;
6) log2(25x*3 - 1) = 2 + log2(5x,;l + 1);
Vb) log4 (2 ■ 4х"2-1) = 2x - 4;
' r) log2 (4X + 4) - log2 2X + log2 (2X+1 - 3).
Тигезсезлекләрне чишегез (525—528).
525. — a) lg (2x - 3) > lg (x + 1);
* 6) log0 3(2x-4) > log03(x + l);
I в) lg (3x - 7) c lg (X + 1);
I* r) logO 5 (4x - 7) < log0 5 (x + 2)·
526. +* a) log0,s x > 1°&г (3 “ 2x)l
6) log„(x+ 1) + log,x < log,2;
' в) lg x + lg (x - 1) < lg 6;
r) log2 (x2 - x - 12) < 3.
527. a) logi X “ 1°&2 X 6;
в) lg2 x + 2Igx > 3;
6) log3 x - 4 > 0;
r) log2 x - 9 < 0.
528.
a) log2sin| < -1;
в) log] cos2x > 1;
2
6) |3-log2x| < 2;
r) |31gx - 1| < 2.
245 Күрсәткечле һәм логарифмик функцияләр
Тигезләмәләр системасын чишегез (529—530).
529.— а)
log^x + у) = 2,
3
log3(x-y) = 2;
б)
lg(x2 + у2) = 2,
log48 х + log48 у = 1;
в)
530.- /0
6)
и)
log! х + log! у = 2,
3 3
1 log! х - log! у = 4;
3 3
lg(x2 + у2) = 1 + lgl3;
lg(* + y) = lg(x-y) + lg8.
3y 9' = 81,
lg(x + y)2 - Igx = 21g 3;
lQi*i*'**0 _ 50,
1g (x + y) + lg (x - y) = 2 - 1g 5;
3X 2^=576, [igx-lgy = lgl5-l,
logj-(y - x) = 4; Г) 110le(3r+2<z’ = 39.
40. Кире функция турында тешенчә
1. Функцияләрнең кайтмалылыгы. Төрле функция¬
ләрне тикшерү барышында сез берничә тапкыр шундый мәсьәлә
чиштегез: бирелгән х0 аргументының кыйммәте буенча / функция¬
сенең кыйммәтен исәпләп чыгарырга. Еш кына моңа кире мәсь¬
әләне дә тикшерергә туры килә: аргументның f функциясе бирел¬
гән у0 кыйммәтен кабул иткәндәге кыйммәтен табарга.
■ 1 нче мисал, f (х) = fex + b (k * 0) булсын, х аргументының
/■(х) “ у0 булгандагы кыйммәтен табу ечен, /(х) = у0 тигезләмәсен,
ягъни kx + Ь = уй тигезләмәсен чишәргә кирәк. Аны чишеп, теләсә
нинди у0 өчен бу тигезләмәнең чишелеше х = барлыгын һәм
бары тик бер генә икәнен беләбез.
2 нче мисал. /(х) = х2 функциясе өчен у0 > 0 булганда,
f (х) = у0 тигезләмәсенең ике чишелеше бар: х, =Jy0, х2 =
(әгәр у0 = 0 булса, чишелеше бер: х0 = 0).
Үзенең һәрбер кыйммәтен билгеләнү өлкәсенең бердәнбер
ноктасында кабул иткән функцияне кайтма функция дип атый¬
лар. Шулай итеп, k * 0 булганда, f(x) = kx + Ь функциясе кайтма,
ә /(х) = х2 функциясе (барлык санлы турыда билгеләнгән) кайтма
була алмый.
Искәрмә. Кайтма функция билгеләмәсеннән мондый нәти¬
җә чыга: әгәр / функциясе кайтма булып, а саны Е (f ) кыйммәтләре
өлкәсенеке булса, ул вакытта /(х) = а тигезләмәсенең чишелеше
була һәм өстәвенә бары тик бер генә.
246 Күрсәткечле һәм логарифмик функцияләр
2. Кире функция, f — ирекле кайтма функция булсын. Теләсә
нинди уп өчен бу функциянең Е (f) кыйммәтләре өлкәсендә D (/)
билгеләнү өлкәсенеке булган /(х0) = у0 итәрлек төгәл бер χϋ кыйм¬
мәте бар. Һәр уп кыйммәтенә х0 нең әлеге кыйммәтен тиңдәш
итеп, билгеләнү өлкәсе Е (/) һәм кыйммәтләр өлкәсе D (/) булган
яңа g функциясен табабыз. Мәсәлән, кайтма функция f(x) = kx + b
(k £ 0) өчен ирекле у0 ноктасындагы яңа g функциясенең кыйм¬
мәте
формуласы белән бирелә.
g функциясенең аргументы өчен үзебез күнеккән х тамгаланы¬
шын сайлап,
.. \ х-ь
#(*)= -д
икәнен табабыз.
Әгәр g функциясе кайтма f функциясенең кыйммәтләр өлкә¬
сендәге һәрбер х ноктасында f(y) = х булырлык у кыйммәтен кабул
итсә, g функциясе f функциясенә кире функция, диләр.
Югарыда күрсәтелгәнчә, f (х) = kx + b (k Ψ 0) функциясенә кире
функция £(х) = ' функциясе була. Икенче бер мисал тик¬
шерик.
■ 3 нче мисал. f(x) = х3 функциясенең кайтма булуын исбат¬
лыйк һәм f ка кире у = g (х) функциясен бирүче формула чыга¬
рыйк.
Кире функция билгеләмәсе буенча башта f (у) - х тигезләмәсенең
х ның кыйммәте теләсә нинди булганда да бердәнбер у чишелеше
булуын исбатларга кирәк. Әлеге очракта бу тигезләмә у3 = х, һәм
аның теләсә нинди х өчен бердәнбер чишелеше у = -Ух була (8 нче
пунктны карагыз). Шуңа күрә /(х) = х3 функциясе кайтма функция
138 нче рәсем
247 Күрсәткечле һәм логарифмик функцияләр
һәм g(x) = үх функциясе ада кире функция була. Әлеге функция¬
ләрнең графиклары 138 нче рәсемдә сурәтләнгән.
Әгәр кайтма / функциясенең графигы бирелсә, f ка кире булган
g функциясенең графигын түбәндәгечә фикер йөртеп төзү кыен
булмас.
! ( функциясенең һәм аңа кире булган g функциясе¬
' нең графиклары у ~ х турысына карата симметрик
! булалар.
Бу үзлекне исбатлыйк, f функциясенең графигы буенча / функ¬
циясенә кире g функциясенең ирекле а ноктасындагы кыйммәтен
график юл белән табарга мөмкин. Моның өчен а координаталы
ноктаны гадәттәгечә горизонталь күчәрдә түгел, ә вертикаль күчәр¬
дә алырга кирәк. Кире функция билгеләмәсеннән күренгәнчә, g(a)
ның кыйммәте Ь га тигез (139 нчы а рәсем).
Шулай итеп, әгәр дә берникадәр гадәти булмаган координата¬
лар системасы сайлап алынган дисәк (аргумент вертикаль күчәргә
салына, ә функциянең кыйммәте горизонталь күчәргә), ул вакытта
f ка кире булган g функциясенең графигы — f функциясенең
(гадәттәге координаталар системасында төзелгән) графигы ул дип
әйтергә мөмкин, g графигын үзебез гадәтләнгән координаталар
системасында сурәтләү өчен, ( ның графигын у = х турысына ка¬
рата чагылдырырга кирәк (139 нчы б рәсем).
Әгәр g функциясе f функциясенә кире функция булса, ул ва¬
кытта f функциясе кайтма була һәм аңа f функциясе кире функ¬
ция була. Шуңа күрә f һәм g функцияләрен үзара кайтма функ¬
цияләр дип әйтәләр.
(кире функция турында ). Әгәр / функ
циясе I аралыгында үссә (яки кимесә), ул кайт
ма функция була, f ка кире һәм f кыйммәтләре
влкәсендә билгеләнгән g функциясе шулай ук үсә
баруны (тиңдәшле рәвештә кими баручы) була.
248
логарифмик φ>Ήκπι«;υΐίΐρ
У
f(x) = x2
а) б) в)
140 нчы рәсем
Исбатлау. Ачыклык өчен f функциясен үсә баручы функ¬
ция дип алыйк, f функциясенең кайтмалылыгы — тамыр ту¬
рындагы теореманың ап-ачык нәтиҗәсе ул (8 нче пункт). Шуңа
күрә f ка кире g функциясенен Е (/) күплегендә үсүен исбатлыйсы
кала.
Xj һәм х2 — Е (/) ның ирекле кыйммәтләре, х2 > χγ һәм
= g^i), Уг = g(^i)
булсын. Кире функциянең билгеләмәсе буенча
х, = һәм х2 = f(y2).
Шарттан (f — үсә баручы функция) файдаланып табабыз, у{ j? уг
дип алу /(j/j) > f (у2) нәтиҗәсенә, ягъни х, > х2 гә китерә. Бу х2 > Xj
фаразына каршы килә. Шуңа күрә у2 > ylt ягъни х2 > Х] шартыннан
#(х2) > £(Xj) булуы күренә.
Нәкъ менә шуны исбатларга кирәк иде дә.
® 4 нче мисал. Югарыда әйтеп үтелгәнчә, f(x) = х2 функциясе
кайтма функция түгел. Ләкин [0; «>) аралыкта /*(х) = х2 форму¬
ласы белән билгеләнгән f* функциясе әлеге аралыкта үсә һәм,
димәк, кире функция була. g(x) = Vх функциясе /* функциясенә
кире була. Бу функцияләрнең графиклары 140 нчы а рәсемдә
сурәтләнгән.
Гомумән, /(х) функциясе теләсә нинди натураль п өчен [0; <»)
аралыкта үсә һәм шуңа күрә кире функциягә ия. g (х) = Vi функ¬
циясе f (х) = х" функциясенә кире функция була, п ның кайбер
кыйммәтләре өчен әлеге функцияләрнең графиклары 140 нчы б,
в рәсемнәрдә сурәтләнгән.
249 Күрсәткечле һәм логарифмик функцияләр
Күнегүләр
Бирелгән f функциясенә кире булган g функциясен бирүче
формуланы чыгарыгыз, g функциясенең билгеләнү елкә-
сен һәм кыйммәтләре елкәсен күрсәтегез (531—532).
531. — a) f (х) = 2х + 1;
в) / (х) = -2х 4-1;
532. -а) Г(х)= 1;
в)^х> = 772;
б) f(x) = |x-l;
г) /(х) = -|х~ 1.
б) f(x) = 2хг (х > 0);
г) f (х) = '/x + l.
533.-·
f ка кире функциянең графигын тезегез:
a) f (х) = 2х3 4-1;
в) f (х) = -2х3 4-1;
б) /(х) = (х 4-1)2, х е (-co; -1];
г) /(х) = (х -1)2, х е [1; co).
егчо рәсем
250 Күрсәткечле һәм логарифмик функцияләр
534.— f функциясенең графигы буенча (141 нче рәсем) f ка кире
булганда, g функциясенең -2, 1 һәм 3 нокталарындагы
кыйммәтләрен табыгыз, g функциясенең графигын төзе¬
гез, аның билгеләнү өлкәсен һәм кыйммәтләре өлкәсен
күрсәтегез:
a) f (х) = Л (х); б) f (х) = f2 (х);
в) f (х) = f3 (х); г) f (х) = Л (х).
Күрсәтелгән аралыкта f функциясенең кире функциягә
ия булуын исбатлагыз, f функциясенә кире функциянең
графигын төзегез (535—536).
а) / (х) = хг + 1, х 0;
в) / (х) = i/x, х > 0;
а)/(х) = sinx, хе
в) / (х) = cosx, хе[0; π];
б) f(x) = 2х, (-ое; оо);
г) /(х) = X3 + 1, (-00; оо).
6)/(x) = tg х, хе(-|;-|);
г) / (х) = ctg х, хе(0; π).
§ 11.
Күрсәткечле һәм логарифмик
функциянең чыгарылмасы
41. Күрсәткечле функциянең чыгарылмасы
1. е саны. Алдагы пунктларда күрсәткечле функция¬
нең графиклары һәр ноктасында орынма үткәрергә мөмкин булган
шома сызыклар (сыныксыз) рәвешендә бирелде. Ә функция графи¬
гының х0 ноктасы аша орынма үткәрергә мөмкин булуы — әлеге
функцияне х0 ноктасында дифференциаллап була дигән сүз. Шуңа
күрә күрсәткечле функция барлык нокталарда да дифференциал-
лана дип фараз итү табигый.
α = 2; 2,3; 3; 3,4 ечен у = а1 функциясенең берничә графигын
сызыйк (142 нче рәсем) һәм аңа абсциссасы 0 булган ноктада
орынмалар үткәрик. Бу орынмаларның абсциссалар күчәренә авы¬
шу почмаклары тиңдәшле рәвештә якынча 35°, 40°, 48° һәм
51° ка тигез, ягъни а ның үсүе белән у = а1 функциясенең графи¬
гына М (0; 1) ноктасында үткәрелгән орынманың почмакча коэф¬
фициенты әкренләп tg 35° тан tg 51° ка кадәр арта, а ны 2 дән 3 кә
кадәр арттыра барганда, а ның аңа тиңдәш орынманың почмакча
коэффициенты 1 гә тигез (ягъни авышу почмагы 45° ка тигез)
булырлык кыйммәте табылуы үзеннән-үзе аңлашыла. Бу фараз¬
ның төгәл әйтелеше (без аны исбатламый гына кабул итәбез)
түбәндәгечә:
251 Күрсәткечле һәм логарифмик функцияләр
у = е1 күрсәткечле функциясенең 0 ноктасында 1 гә
тигез чыгарылмасы, ягъни
I
Δχ 0 гә омтылганда, —т > 1 (1)
булырлык 2 дән зуррак һәм 3 тән кечерәк е саны бар.
Искәрмә, е санының иррациональ икәнлеге һәм шуңа күрә
периодик булмаган чиксез унарлы вакланма рәвешендә язылуы
исбат ителгән. Электроник хисаплау машиналары ярдәмендә
е санының ике меңнән дә артыграк унарлы тамгалары та¬
былган. Бу вакланманың беренче тамгалары түбәндәгечә: е =
= 2,718281828459045... .
е1 функциясен еш кына экспонента дип атыйлар.
2. Күрсәткечле функциянең чыгарылма формуласы.
1 нче теорема, е* күрсәткечле функциясе билге¬
ләнү өлкәсендәге һәр ноктада дифференциаллана
Һәм
(е*)' е*.
Исбатлау. Башта у «■ е* функциясенең х0 ноктасында үсем¬
тәсен табыйк:
Ду = ~ 1).
252 Күрсәткечле һәм логарифмик функцияләр
(1) шарттан файдаланып, Δχ 0 гә омтылганда язабыз:
Δ» _ ег',(сЛг-1)
■
-1
> 0*0
&х ■
Чыгарылма билгеләмәсе буенча моннан теләсә нинди х өчен
у' — е*, ягъни (ех)' “ & икәнлеге килеп чыга.
ЕЗ 1 нче мисал, у = е 5х функциясенең чыгарылмасын таба¬
быз: ,
(е5*)' = е®х · (5х)‘ = 5е5х.
е саны — уңай һәм 1 гә тигез булмаган сан, шуңа күрә
логарифмнар е нигезе буенча билгеләнә.
Билгеләмә.е нигезе буенча логарифм натураль
логарифм (In дип тамгалана) дип атала:
1п х = log, х. (2)
Төп логарифмик бердәйлек буенча теләсә нинди уңай а саны
өчен е>па “ а. Шуңа күрә ах күрсәткечле функция
ах = (е,пу = ех,"“ (3)
рәвешендә языла ала.
Хәзер а ның ирекле рәвештә алынган кыйммәте өчен күрсәт¬
кечле функциянең чыгарылмасы формуласын чыгарыйк.
2 нче теорема, ах күрсәткечле функциясе
билгеләнү олкәсенец һәр х ноктасында дифферен¬
циаллана һәм
(α*)' = οχ1ηα (4)
була.
Исбатлау. (3) формуладан катлаулы функциянең чыгарыл¬
масы турындагы теорема буенча күрсәткечле функциянең һәр
ноктада дифференциаллануын күрәбез:
(а*)' = (е*1п“У = ех1па1п a = a11п а. (5)
Нәтиҗә. Күрсәткечле функция үзенең билгеләнү
өлкәсенең һәр ноктасында өзлексез, ягъни х —> х0 гә
омтылганда, а* —> а‘°.
Бу күрсәткечле функциянең дифференциаллануыннан һәм
дифференциаллана торган функциянең өзлексезлеге турындагы
леммадан чыга (120 нче битне карагыз).
1 2 нче мисал, у =2‘ һәм у = 5‘3х функцияләренең чыгарыл¬
маларын табыйк.
(4) формула буенча:
(2ХГ = 2Х 1п 2; (5’37 = (-3) ■ 5’3х 1п 5.
Күрсәткечле һәм логарифмик фуикциялар
г/А
3 нче мисал. f(x} = хе* функ¬
циясен үсүгә (кимүгә) һәм экстре-
мумга тикшерик.
Бу функциянең чыгарылмасын
табабыз:
143 нче рәсем
f'(x) = (хех)' = х'е* + х(ехУ =
= е* + хе* = е*(1 + х).
Теләсә нинди х өчен ех > 0 бул¬
ганлыктан, f тамгасы (1 + х) ның
тамгасы белән туры килә. Димәк,
(-1; <») аралыкта f'(x) > 0 була, шуңа
күрә [-1; оо) аралыкта f үсә. -1)
аралыкта f'(x)<0, шуның өчен
(-οβ; -1) аралыкта f кими.
хе = -1 ноктасында чыгарылма үзенең тамгасын минустан
плюска үзгәртә, димәк, х0 = -1 минимум ноктасы була.
Функциянең графигы 143 нче рәсемдә күрсәтелгән.
3. Күрсәткечле функциянең башлангыч функциясе.
л 1
3 нче теорема. R да ах функциясе өчен т——
функциясе башлангыч функция була.
Чыннан да. In а — даими һәм шуңа күрә теләсә нинди х өчен
144 нче рәсем
- -р— · (ахУ = ах Ιηα = ах.
\1па/ Ιηα ' ' Ιηα
α *
Моның белән ‘‘ ! ның а* функциясе
өчен R да башлангыч функция икән¬
леге исбатланды. Ә (е1)' тигезлеген¬
нән исә барлык х өчен е* ның R да
е* функциясе өчен башлангыч функ¬
ция икәнлеге чыга.
Д 4 нче мисал, а) /(х) = 5ж;
б) g (х) - 4 ■ 2Х; в) һ (х) = 4efa - 10 · 0,6х
функцияләре өчен башлангыч функ¬
цияләрне табыйк.
3 нче теоремадан һәм башлангыч
функцияләрне табу кагыйдәләреннән
файдаланып, җавапларны язабыз:
а) F(x) = ^ + C;
б) G(x) = T^ + C;
в) Н(х) = |е--10.^ + С.
Күрсәткечле һәм логарифмик функцияләр
5 нче мисал, у = 3х, у = 0, х = -1, х = 2 сызыклары белән
чикләнгән фигураның мәйданын табыйк.
Әлеге фигура — кәкресызыклы трапеция (144 нче рәсем). Шуңа
күрә аның мәйданы S ны кәкресызыклы трапециянең мәйданы
формуласы буенча табабыз:
’ 9 3 1 26
, - йз" һГз - 31п3
Күнегүләр
537—
Натураль логарифмнар таблицасы буенча (яки калькулятор
ярдәмендә) табыгыз:
a) In 3, In 5,6, In 1,7; б) In 8, In 17, In 1,3;
в) In 2, In 35, In 1,4; r) In 7, In 23, In 1,5.
I
538. -1
539. -
Һәр функциянең чыгарылмасын табыгыз (538—539).
а) у = 4с1 + 5; б) у = 2х + Зе х;
в) у - 3 - | ех; г) у = 5ех - х2.
а) у = е1 cos х;
в) у = 3х- Зх2;
б) у = Зе* + 2х;
г) у = х2е*.
540.
Абсциссасы х булган ноктада f функциясенең графигына
орынма тигезләмәсен языгыз:
a) f (х) = е х, х0 =0; б) f (х) = 3*, х0 = 1;
в) f (х) - Хо - 0; г) f (х) - 2“х, х0 - 1.
541.
Түбәндәге функция өчен башлангыч функцияләрнең гому¬
ми рәвешен табыгыз:
а)/(х) = 5ех; 6)/(χ) = 2·3χ;
в)/(х) = 4*;
г) №) = |е* + 1.
s · / »,Лг · та
542.-
Интегралны исәпләп чыгарыгыз:
a)j0,5*dx;
П
б) f е2* dx;
η
1
в) j 2хdx;
-2
г) J 3х dx.
2
Һәр функциянең чыгарылмасын табыгыз (543—544).
543—а) у = ех* sinf;
Ci
I j в) у - е^1 cos2x;
6)j/ = 72tg3x;
г) у = 2-xctgi.
255 Күрсәткечле һәм логарифмик функцияләр
»>» = «Τ7τ; '>»=■&·
2+5 V.r+0,5
545.— Түбәндәге функцияне үсүгә (кимүгә) һәм экстремумга тик¬
шерегез:
a)f(x) = xe5x; б) f (х) = х2 2 J;
в) f (х) = хе1; г) f (х) = х10,5*.
546.— Түбәндәге функция өчен башлангыч функцияләрнең гому¬
ми рәвешен табыгыз:
a) f (х) = е3’21; б) f (х) = 2 · 0,9х - 5.6 х;
в)/(х) = 2’10х; г) /(х) = е" 4- 2,31+х.
Түбәндәге сызыклар белән чикләнгән фигураның мәйда¬
нын табыгыз (547—548).
547. — а) у = ех, у = 0, х = 0, х = 1; б) у — 3х, у = 9Х, х — 1;
в) у = 2х, у = 0, х = -1, х - 2; г) у - у = х - 1.
548. - а) у = (I)', у = 3, х = 1; б) у = е\ у = е*, у = е;
в) у = у = 1, х = -2; г) у = у = 4х, у = 4.
42. Логарифмик функциянең чыгарылмасы
Башта логарифмик функциянең һәр ноктада диффе-
ренциаллануын күрсәтик, у = iogo х һәм у = а1 функцияләренең
графиклары у = х турысына карата симметрик. Күрсәткечле
функция теләсә нинди ноктада дифференциаллана, ә аның чыга¬
рылмасы нульгә әйләнми, шуңа күрә күрсәткечле функциянең
графигы һәр ноктада горизонталь булмаган орынмага ия. Шуңа
күрә логарифмик функциянең графигы да теләсә нинди ноктада
вертикаль булмаган орынмага ия. Ә бу исә логарифмик функ¬
циянең үзенең билгеләнү өлкәсендә дифференциаллануына тигез
көчле.
Хәзер билгеләнү өлкәсендәге теләсә нинди х өчен логарифмик
функциянең чыгарылмасы
1пх = | (1)
формуласы буенча табылуын исбатлыйбыз.
Төп логарифмик бердәйлек буенча барлык уңай х өчен х = е|Т|Х,
ягъни әлеге тигезлекнең уңында һәм сулында R+ да билгеләнгән
бер үк функция тора. Шуңа күрә х һәм е|пх функцияләренең
чыгарылмалары тигез, ягъни
х' = (е'“х)'. (2)
256 Күрсәткечле һәм логарифмик функцияләр
х' = 1 икәне билгеле. Уң кисәкнең чыгарылмасын катлаулы
функциянең чыгарылмасын табу кагыйдәсе буенча һәм 1 нче
теорема буенча (41 нче пункт) исәпләп чыгарабыз: (е |п *)' =
— х = xln' х. Табылган чыгарылмаларны (2) тигезлеккә куябыз:
I — х In х, моннан In х — х .
В 1 нче мисал. Функцияләрнең чыгарылмаларын табыйк:
а) у - In (5 + 2 х); б) у = log3x; в) у = logr2x.
а) (In (5 + 2х))'= 5^(5 + 2х)‘ = ^;
б) (iog3xy = | - yb;
X /1 /о ҮХЛ Zln2xV _ 2 _ 1
в) (log7(2x)) ln7 f 2xln7 - xln7 .
2 н ч е м и сал. /(х) = хЧп х функциясен үсүгә, кимүгә, экстре-
мумга тикшерик һәм аның графигын төзик.
х > 0 булганда, функция билгеләнә. Бу функциянең чыгарыл¬
масын табабыз:
f(x) = 2х In х + х2 · т = 2 х In х + х =
х > 0
булганга күрә, чыгарылманың тамгасы
2 J ««Ч
тамгасына туры килә. Моннан күренгәнчә
аралыкта
Г(х) > 0 һәм шуңа күрә
аралыкта функция үсә;
аралыкта чыгарылма тискәре, шуңа күрә f
аралыкта
кими.
ноктасында чыгарылма үзенең тамгасын плюска үз-
1
2е '
гортә, димәк, бу — минимум ноктасы: f
Функция графигының эскизы 145 нче рәсемдә бирелгән. Ж
(1) формула (0; оо) аралыкта — функциясе өчен теләсә
нинди башлангыч функциянең In х + С рәвешендә
языла алуын күрсәтә.
Т функциясенең (-°0; 0) аралыкта да башлангыч функциясе
була, бу — In (-х) функциясе. Чыннан да,
(in (- x»'=b <- x)'=Z7·<-!> - 7·
х > 0 өчен |х| — х һәм х < 0 өчен |х| = -х булганлыктан.
257 Күрсәткечле һәм логарифмик функцияләр
без 0 ноктасын эченә алмаган теләсә нинди аралыкта
1 функциясенең башлангыч функциясе In |х| икә¬
нен исбатладык.
3 нче м и с а л. -3 не эченә алмаган теләсә нинди аралыкта
функциясе өчен башлангыч функцияләр In |х + 3| + С га тигез.
5^7 функциясе өчен башлангыч функциянең гомуми күре¬
неше (- 5 ноктасын эченә алмаган теләсә нинди аралыкта)
In | |5χ + 7| + С була.
4 нче мисал, у = 7, у - 0, х - 1, х = 2 сызыклары белән
чикләнгән фигураның мәйданын табыйк (146 нчы рәсем).
х > 0 булганда, In х функциясе — ү өчен башлангыч функция,
шуңа күрә безне кызыксындырган кәкресызыклы трапециянең
мәйданы
S = In 2 - In 1 = In 2
гә тигез.
Күнегүләр
Һәр функциянең чыгарылмасын табыгыз (549—550).
549. -Г а) у - In (2 + Зх); б) у = log0 s х + sin х;
Ι в) у = In (1 + 5х); г) у = lg х - cos х.
550. - а) у = х2 log, х; б) у = ; в) у = х In х; г)р~^~.
551. - Түбәндәге функция өчен башлангыч функцияләрнең гому¬
ми рәвешен табыгыз:
э 12
а)Г(х) = 7^Т; ®>/(х)- 7-775;
в)/(х)-7^2 5 г)/(х)-|.
258 Күрсәткечле һәм логарифмик функцияләр
552.- Әгәр _ _
а) /(х) = In (х + 1), х0 = 0; б) Г(х) = 1g х + 2, х0 = 1;
)в)/(х) = 2 In х, х0 = е; г)/(х) = log, (х - 1), х0 = 2
булса, f функциясенең графигына абсциссасы х0 булган
ноктада үткәрелгән орынманың тигезләмәсен языгыз.
Интегралны исәпләгез:
7 ι е . з
. Г dx . [41 . f dx
a) J x , 6) J 3_2x , в) J x , r) J 3л+1 .
1 -ι 1 о
554.— Функциянең чыгарылмасын табыгыз:
1п(5+3х)
а) У - , , ··
х1 +1
х2
в) у - . , ;
* 1п5х
б)Р 1»(1-2х) ’
Функцияне үсүгә (кимүгә) һәм экстремумга тикшерегез
(555—556).
555.— a) f (х) = ух In х;
в) / (х) = 2х - In х;
,. ч Ιηχ
б) Ζ(χ)= —;
г) /(х) — х In х.
556.— а) /(х) = х In2 х;
в) f
б)/(х)=>;
г) f(x) = у + In х.
557.-» Түбәндәге сызыклар белән чикләнгән фигураның мәйда-
9 нын исәпләп чыгарыгыз:
1а)у = * + 2, у = 0, х = 2, х = 6;
4>, _1;
В) У = 2х . У = 0. X = 4 . х = 2;
г) у = 3 - 4 , у = 0, х = -6, х = - 3.
43. Дәрәҗәле функция
1. Дәрәҗәле функция һәм аның чыгарылмасы. Теләсә
нинди α реаль саны һәм һәр уңай х өчен х« саны билгеләнгән
булуын сез беләсез ниде. α санын (0; <») аралыкта билгелибез.
Билгеләмә, /(х) = ха формуласы белән бирелгән
функция дәрәҗәле (дәрәҗә күрсәткече а) функция
дип атала.
259 Күрсәткечле һәм логарифмик функцияләр
Әгәр а > 0 икән, дәрәҗәле функция х = 0 булганда да
билгеләнә, чөнки Οα = 0. α бөтен сан булганда, дәрәҗәле функция
f(x) = Xя х < 0 өчен дә билгеләнә, α җөп булганда, әлеге функция
җөп, ә α так булганда, функция так була. Шуңа күрә дәрәҗәле
функцияне бары тик (0; *>) аралыкта гына тикшерү дә җитә.
Курсның алдагы бүлекләрендә сез у = х“ функциясенең чыга¬
рылмасы формуласын бары бөтен дәрәҗә күрсәткечләре һәм
шулай ук α =-| өчен генә таптыгыз. Хәзер безгә формуланы
α ирекле булганда чыгарасы кала. Билгеләнү өлкәсендәге теләсә
нинди х өчен дәрәҗәле функциянең чыгарылмасы түбәндәгечә
булуын исбатлыйк:
(χ“)'·= αχ0*1. (1)
Чыннан да, х = е|ох булганлыктан, х® = е°1пж була. Моннан кат¬
лаулы функциянең чыгарылмасын исәпләү кагыйдәсе буенча
табабыз:
(х«)' = (е °1,1= е °,n * (a In х)' = х° · α · j = αχ ° * ’.
(1) формула исбатланды.
α < 0 булганда, дәрәҗәле функция (0; аралыкта кими, чөнки,
х > 0 булганда, (х°)' = ах ° “1 < 0. α > 0 булганда, (х°)' = αχ “ “1 > 0,
шуңа күрә дәрәҗәле функция х > 0 булганда үсә. Моннан тыш,
х = 0 булганда, дәрәҗәле функциянең нульгә тигезлеген һәм
х —> 0 һәм х > 0 булганда, х ° —»0 икәнен истә тотарга кирәк.
Шуңа күрә 0 ноктасы үсә бару аралыгына тоташа, ягъни, α > 0
булганда, дәрәҗәле функция [0; аралыкта үсә. α теләсә нинди
кыйммәткә ия булганда, дәрәҗәле функция графикларының
мисаллары 147 нче рәсемдә китерелгән.
(1) формуласыннан /(х) = х" дәрәҗәле функциясенең чыгарыл¬
масы дәрәҗәле функция булуы (/(х) = αχ ®-1) күренә. Дәрәҗәле
функциянең башлангыч функциясе белән эш башкача тора.
α* -1 булганда, fix) - х® дәрәҗәле функциясенең башлангыч
„а+1
функцияләренең гомуми рәвеше F(x) - + С икәнен җиңел
тикшерергә була.
α — -1 булганда, билгеле булганча, f ның башлангыч функциясе
F (х) = In |х| + С була.
Күрсәткечле һәм логарифмик функцияләр
2. Дәрәҗәле функциянең кыйммәтен исәпләп чыгару.
(1 + Δχ)“»1 + αΔχ (2)
якынча формуласын чыгарабыз.
/ (х) = х ° функциясен тикшерәбез һәм х<>= 1 һәм х = 1 + Δχ
өчен 20 нче пункттан билгеле булган f (х) - f (х0) + f (хо) Δχ (3) фор¬
муласыннан файдаланып табабыз: f(xo) = /(1) » 1, /'(х) - αχ“ *,
моннан Л(х0) = f(l) = α · 1“ 1 = α. (3) формула буенча
f (х) = (1 + Δχ)α · 1 + α Δχ.
Барыннан да ешрак бу формуланы тамырларны исәпләү өчен
кулланалар, α = — дип алып табабыз:
^1+Δχ = (1+Δχ)£ -1+ v- <4>
I Мисал. Якынча кыйммәтләрне исәплибез:
а) <1?08 ; б) 3/27,03 ; в) ^ЮОО .
(4) формуладан файдаланабыз:
а) {/1,08 = (1 + 0,08)4 = 1 + | ■ 0,08 = 1,02;
б) </27?03 - ^27(1 + = з . >/ι 4.^ = з (1 + | s
s 3,0011. ^/27,03 нең өтердән соң сигез тамгалы кыйммәте түбән¬
дәгечә: 3/27,03-3.0011107;
Β)2,β= 1024 икәнен беләбез. Ул вакытта: ^/1000 “
[1-·^)- 1.995.
Күнегүләр
® f функциясенең графигын төзегез һәм аның чыгарыл-
fl масын табыгыз (558—559).
В э -
558. -1 a) f(x) =Х 2; б) f(x) = ХЛ ;
I ?
|в)/(х)-Х3; г) f (х) = Х-7* .
559. -I а) f(x) = х'; б) /(х) = ;
I в) f (х) = Xя; г) f (х) = (2х) 1Я 3.
281 „ . _ J .
V ι Күрсәткечле һәм логарифмик функцияләр
(4) формула ярдәмендә якынча кыйммәтләрне исәпләп
чыгарыгыз (560—561).
‘ . -г- .
560. - а) 24’; б) ^625 3 ; в) V81; г) V48 ■
561. ^ а) ^30 ; б) ^90 ; в) >/9,02 ; г) ^33 ·
562. -I I аралыгында f функциясенең иң зур һәм иң кечкенә кыйм-
X мәтен табыгыз:
* 2 - Г1 1
а)/(х)= х5, / = [1; 32]; б)/(х)=х 3,/=Ls;27J;
1 4 « Г 1 ♦ Я11
В) Лх) = х\/ = [2;1]; r)f(x)- х4,/ = Lie ’ 81J'
563. - Түбәндәге функция өчен башлангыч функцияләрнең гому¬
ми рәвешен табыгыз:
а)/-(х) = -|х-^; б)/(х) = х2^;
в)/(х)=3х1; г)/(х) = хЕ.
564. - Интегралны исәпләп чыгарыгыз:
a)jx2dx; 6)j-~: в) f2x’dx; г) JSx'dx.
1 1 X3 <■ 1β
565. — Түбәндәге сызыклар белән чикләнгән фигураның мәйданын
исәпләп чыгарыгыз:
а)у = х^, у = 0, х=1; б) у = , у ■ - , у = ·| ;
в) у = х°·8, у = О, х=1, х = 32;
г) У “7 . У = 0, х = 3, х= 5.
566. — Миллиметрлы кәгазьдә у = vх , у = >/х , у = у х (х ^0) функ¬
цияләренең графикларын төзегез.
1) График ярдәмендә
a) V2.V3; б) >/3,^5; в)^2?5, </3;
г) >/2,5, >/2 нең якынча кыйммәтләрен табыгыз.
2) Әлеге тамырларның кыйммәтләрен калькулятор ярдә¬
мендә табыгыз.
3) Аларның якынча кыйммәтләрен (4) формуланы файда-
ll ланып исәпләп чыгарыгыз. Күрсәтмә: 2,5 = 1,62 - 0,06;
I 2,5 = 1,33+ 0,303; 2,5 = 1,254 + ; 2 = 1,42 + 0,04;
Н 3-1,4Я + 0,256; 3 = 1,3*= 0,1439.
I 4) Табылган нәтиҗәләрне чагыштырыгыз.
262 Күрсәткечле һам логарифмик фуикциялар
567.— f (х) — х'1^ функциясенең түбәндәге үзлекләргә ия булуы
дөресме?
а) Билгеләнү өлкәсендә очларында функция төрле
тамгалы кыйммәтләр кабул итә алган кисемтәне табарга
|була.
б) Җөп функция була, в) Экстремумнары бар.
г) Функциянең иң кечкенә кыйммәт ала торган х0 нок¬
тасы бар.
44. Дифференциаль тигезләмәләр турында
төшенчә
1. Турыдан-туры интеграллау. Табигать белеме мәсь¬
әләләрен чишү барышында еш кына кайбер функциянең чыгарыл¬
маларын (беренче, икенче һ. б.) бу функциянең үзе һәм бәйсез
үзгәрешле белән ялгаучы бәйләнешләр килеп чыга. Мәсәлән,
Ньютонның икенче законы буенча даими т массалы материаль
нокта туры буенча хәрәкәт иткәндә, F = та формуласы дөрес була,
биредә F — хәрәкәтне барлыкка китерүче көч, а — ноктаның
тизләнеше. F көче бары тик вакыт t га гына бәйле булсын, ягъни
F = F(t). Тизләнешнең вакыт буенча алынган координатаның
икенче чыгарылмасы икәнен искә алып, (а (0 = х" (ί)). х (0 функ¬
циясенә карата дифференциаль тигезләмә табабыз:
„ F(t)
F (ί) = тх (О, ягъни х (t) = , моны чишү өчен башта х (0
м
ны функциясенең башлангыч функциясе буларак, ә аннан
соң х (0 ны да υ(ί) = х' (ί) функциясенең башлангыч функциясе
буларак табабыз. Гомуми чишелеш ирекле ике константага бәйле.
Аларны табу өчен, гадәттә, координатаны һәм тизлекне нинди дә
булса t вакыты моментында бирәләр.
1 нче мисал. Авырлык көче тәэсирендә вертикаль рәвештә
хәрәкәт иткәндә берәмлек массалы ноктаның координатасы һ (t)
дифференциаль тигезләмәне канәгатьләндерә (Oz күчәре вертикаль
рәвештә аска юнәлгән):
H'(t)=g.
Бу тигезләмәнең гомуми чишелеше түбәндәге рәвештә була:
ft (t) = ft0+ vot + — , биредә ft0= һ (0), = и (0).
й0 һәм о0 не биреп, без бердәнбер чишелеш табабыз.
Гомумән, f функциясе өчен F башлангыч функциясен иц гади
дифференциаль тигезлзмэ
F'(x) = fix) (1)
ның чишелеше итеп карап була, биредә /(х) — бирелгән функция,
Г(х) — әлеге тигезләмәнең чишелеше.
Күрсәткечле һәм логарифмик функцияләр
2. Күрсәткечле үсүнең һәм күрсәткечле кимүнең дифферен¬
циал ь тигезләмәсе. Физика, техника, биология һәм социаль фән¬
нәрнең күп кенә мәсьәләләрен чишү
f(x) = kf(x) (2)
дифференциаль тигезләмәсен канәгатьләндерүче функцияне табу
мәсьәләсенә кайтып кала, биредә k — нинди дә булса константа.
Күрсәткечле функциянең чыгарылмасы формуласын белгәндә,
Г(х) = Се** (3)
рәвешендәге теләсә нинди функция (2) тигезләмәнең чишелеше
булуына төшенү читен түгел, биредә С — константа. С ирекле
булганга күрә, (2) дифференциаль тигезләмәнең чишелешләре
чиксез күп.
(2) тигезләмәнең (3) рәвешендәге функциядән башка чише¬
лешләре юклыгын исбат итик. Моның өчен (2) тигезләмәне
канәгатьләндерүче ирекле / функциясен һәм ярдәмче функциясен
тикшерербез:
£(х) = /(х)е **. (4)
g функциясенең чыгарылмасын табыйк:
g' (х) = f (х) е »' + f (х) (е-‘х)' = f (х) ег* - kf (х) е
f (х) урынына аның (2) тигезләмәдәге kf(x) кыйммәтен куйсак
табабыз:
g'(x) = kftxye *1 - kf(x)e ** “ 0.
g функциясенең чыгарылмасы нульгә тигез, шуңа күрә барлык
х лар өчен g(x) = С. (4) тигезләмәдән
/(х) е'*·1 = С, моннан /(х) = Се*ж
ны табабыз, шуны исбатларга кирәк иде дә.
Искәрмә. Югарыда китерелгән фикер йөртүләрдә без
f функциясе билгеләнгән һәм барлык санлы турыда (2) тигезлә¬
мәне канәгатьләндерә дип исәпләдек. Конкрет мәсьәләләрдә еш
кына (2) тигезләмәне бары тик берникадәр аралыкта гына канә¬
гатьләндерә торган функцияләрне карарга туры килә. Мондый
очракта (2) тигезләмәне кулланырга мөмкин булган аралыкта
гына (3) формула мәсьәләнең гомуми чишелешен бирүе табигый.
(2) дифференциаль тигезләмәнең мәгънәсе түбәндәгедән гый¬
барәт: функциянең х ноктасында үзгәрү тизлеге функциянең бу
ноктадагы кыйммәтенә пропорциональ. Бу тигезләмә практик
мәсьәләләрне чишкәндә еш очрый.
2 нче мисал. (Радиоактив таркалу.) Вакытның башлангыч
моментында радиоактив матдәнең массасы
m(O) = /no (5)
булсын. Матдә массасы т (t) ның кимү тизлеге t вакыты үтү белән
матдә микъдарына пропорциональ булуы, ягъни m'(t) =
264 Күрсәткечле Һәм логарифмик функцияләр
тигезләмәсе үтәлүе, биредә k > 0, эксперименталь рәвештә ис-
батланган. Югарыда әйтелгәннәрдән чыгып, т (t) = Се *' ны язабыз.
С константасы (5) шарттан табыла. Атап әйтсәк, ί = 0 булганда
т0 = т (0) = Се * 0 = С, ягъни С = т0.
Нәтиҗәдә:
m0(t) = тае~*'. (6) ф
Бу мисал типик: дифференциаль тигезләмәнең чиксез күп
сандагы чишелешләре арасыннан бер чишелешен аерып алу өчен,
гадәттә, тагы «башлангыч шарт»ны (безнең очракта (5) шартны)
кабул итү сорала.
Радиоактив матдә массасының ике тапкыр кимүе өчен киткән
вакыт аралыгы Т ны бу матдәнең ярымтаркалу периоды дип
атыйлар. Т ны белгәндә, k ны табарга мөмкин.
т(Т) = т0, ягъни тое " = | т0
булганга, е‘‘т - .
Димәк, е*Т “2, kT = In 2, моннан k = .
Мәсәлән, радий өчен Т =1 550 ел. Шуңа күрә (әгәр вакыт еллар
„ 1п2
белән исәпләнсә) k = 1&5θ = 0,000447. Миллион елдан соң радий¬
ның башлангыч массасы т0 дән бары тик т (Ю6) = тое 447 =
= 0,6 · 10 ,м т0 генә кала.
3. Гармоник тирбәнешләр, f функциясе чыгарылмасы f тан
чыгарылманы f функциясенең икенче чыгарылмасы дип атыйлар
һәм /" дип тамгалыйлар (<*эф ике штрих» дип укыла). Мәсәлән:
sin' х = cos х, sin" х = cos' х = -sin х,
cos' х = -sin x, cos" x = -sin' x = -cos x. (7)
Икенче чыгарылма функциянең торышын җентекләбрәк тик¬
шерергә ярдәм итә. Беренче чыгарылма — функциянең үзгәрү
тизлеге, ә икенче чыгарылма әлеге тизлекнең үзгәрү тизлеге ул.
(7) формуланы анализлаганнан соң, синус һәм косинусның
икенче чыгарылмалары функцияләрнең үзләреннән бары тик
тамга белән генә аерылып торуларын күрергә мөмкин. Икенче
төрле әйтсәк, бу функцияләрнең икесе дә t аргументының барлык
кыйммәтләре өчен
f(t) = -f(t)
тигезләмәсен канәгатьләндерәләр.
Физикада, аерым алганда механикада,
(8)
тигезләмәсен канәгатьләндерүче f функцияләре зур роль уйный,
биредә ω — уңай константа.
Күрсәткечле һәм логарифмик функцияләр
148 нче рәсем
149 нчы рәсем
Механикадан шундый рәвештәге тигезләмәгә китерә торган
мәсьәләне тикшерәбез, т массалы шарчыкка горизонталь урнаш¬
тырылган пружина беркетелсен, ә аның икенче очы стенага
беркетелсен (148 нче рәсем), һәм тигезләнеш торышында шарчык
үзәгенең координатасы х нульгә тигез булсын. Үзәкне х # 0 коор-
динаталы ноктага күчергәндә, шарчыкны тигезләнеш торышына
кайтарырга омтылучы көч барлыкка килә. Гук законы буенча бу
көч х ның күчешенә пропорциональ, ягъни F = -kx, биредә k —
уңай константа (149 нчы рәсемне карагыз). Ньютонның икенче
законы буенча F = та, шуңа күрә туры буенча хәрәкәт иткәндә
тизләнеш координатаның икенче чыгарылмасы булуын исәпкә
алсак:
та (i) -= тх" (f) = F, ягъни х" (ί) = - х (ί) була.
Икенче төрле әйткәндә, шарчык үзәгенең хәрәкәте эластиклык
көчләре тәэсирендә, ω = ~ булганда, (8) тигезләмәгә бәйләнгән.
(8) тигезләмәгә тиңдәшле рәвештә вакытка карап үзгәрүчән
физик зурлыкның гармоник тирбәнеш (7 нче пунктны карагыз)
башкаруын күрсәтик. (8) тигезләмәнең үзен гармоник тирбәнеш¬
ләрнең дифференциалы тигезләмәсе дип атыйлар.
f(f) = A cos (ωί + φ) (9)
функциясенең, А һәм φ теләсә нинди даими зурлык булганда, (8)
тигезләмәнең чишелеше икәнен тикшерик. Чыннан да, катлаулы
функция чыгарылмасы өчен булган формуладан файдаланып
табабыз:
f (ί) = *А ω sin (ωί + φ),
f" (ί) = -A co2 cos (ωί + φ) = -ω2 f (ί).
Киресе дә дөрес: (8) тигезләмәнең теләсә нинди чишелеше (9)
рәвешендәге функция була, өстәвенә, гадәттә, А 0, φβ [0; 2π) не
сайлыйлар. Моны исбатлау мәктәп курсына керми.
Әгәр башлангыч шартлар /(О) = уо, Г(0) = ι>0 бирелгән булса,
ирекле константалар А һәм φ не билгеләргә мөмкин.
4. Атмосферада җисемнәрнең төшүләре. Тагы да катлаулы¬
рак мисал тикшерик. Җисем атмосферада төшкән вакытта һава
каршылыгын исәпкә алырга кирәк. Эксперименталь юл белән
һаваның каршылык көче хәрәкәт тизлегенә пропорциональ, ягъни
җисемгә тәэсир итә торган F көче F(t) = mg - kh'(t) га тигез икәне
расланган, биредә т — җисемнең массасы, g — ирекле төшү
Күрсәткечле һәм логарифмик функцияләр
тизләнеше, һ (t) — туры өстендәге координата (Oh күчәре верти¬
каль рәвештә аска юнәлгән), k — пропорциональлек коэффи¬
циенты. Ньютонның икенче законы буенча F = та. шуңа күрә
тг" (t}= mg - kz' (t), ягъни г" (t)=g ~~2' 0}
тигезләмәсен табабыз. Бу тигезләмәне хәрәкәт тизлеге u(t) = z' (t)
га карата дифференциаль тигезләмә буларак тикшерү җайлы:
</(0 = g~bv (Г), биредә Ь - — > 0.
(Ю)
Бу тигезләмәне таныш рәвешкә китерү өчен, яңа билгесез
y(t) = у - υ(ί) функциясен кертәбез, ул вакытта y'(t} =
= = - v'(t) һәм (10) тигезләмә ~у' (t) = by (t), ягъни
y'(t) — -Ьу(/)рәвешендә языла, аның чишелеше безгә билгеле:
у (ί) — Сегы. Димәк,
f(0= f-y(t)= f-Ce “
у = е'1" функциясе R да кими, бу вакытта аның кыйммәте
t үскәндә чикләнмәгән рәвештә кими (ягъни теләсә нинди С өчен,
ί -> оо омтылганда, Се~ы —> оо кә). Бу исә тизлекнең пропорциональ-
g
лек коэффициенты зурлыгы k га һәм масса т га бәйле булган "ζ
даими кыйммәтенә якынлашуын аңлата. Мәсәлән, озакка сузылган
сикерүләрдә, парашют ачылмаган очракта, бу тизлек якынча
50 м/с ка тигез, ә парашютчының җиргә тигәндәге тизлеге
(k шактый зур була) якынча 4—5 м/сәг.
Бу мисаллар дифференциаль тигезләмәләрнең ни дәрәҗәдә
көчле тикшерү аппараты булуларын аңларга мөмкинлек бирә.
Еш кына нинди дә булса процесс белән идарә итүче элементар
законнар дифференциаль тигезләмәләр рәвешендә языла, ә бу
процессның вакыт үтү белән ничек барышын ачыклау өчен, әлеге
дифференциаль тигезләмәләрне чишәргә туры килә.
Күнегүләр
568.— y(t) функциясенең бирелгән дифференциаль тигезләмәнең
чишелеше булуын тикшерегез:
Й а) у (t) = 3 cos (2t + π), у" = - 4у;
Ι б) y(t)=4 sin (lf-Σ), y" = -1 y-
I в) у (t) = 2 cos 4/, y" + 16y = 0;
I r) y(t) = I sin (0,1t + 1), y" + 0,01y = 0.
267 Күрсәткечле һәм логарифмик функцияләр
569. — y = 5eJl функциясенең у' - Зу тигезләмәсен канәгатьлән¬
дерүен исбатлагыз.
570. — у- 7е 21 функциясенең у'=-2у тигезләмәсен канәгать¬
ләндерүен исбатлагыз.
571. у - Зе 11 функциясенең у’ = -Ту тигезләмәсен канәгатьлән¬
дерүен исбатлагыз.
572. - Дифференциаль тигезләмәнең нинди дә булса нульдән үзгә
чишелешен табыгыз:
а) у" - -25у; б) |у"+ 4у = 0;
в) 4у" + 16</ = 0; г)/'=-|у.
573. - Гармоник тирбәнешнең дифференциаль тигезләмәсен
языгыз:
а) х = 2cos (2t - 1); б) х = 6,4 cos (о, It +;
в) х - 4sin(3t - г) х = 0,71 sin (0,3t - 0,7).
574. — Ике гармоник тирбәнеш xjt) = Atcos («V + <pt) һәм x2(t) -
= A2 cos (ω2ί + φ2) нең суммасы ешлыкларның чагыш¬
тырмасы г рациональ сан булганда һәм бары шул вакытта
<Ц.
гына (ягъни — = г) периодик функция булганын исбат-
ωζ
лагыз.
575. — т, мг С радиеннан t мин радиоактив таркалудан соң η мг
калган. С радиеның ярымтаркалу периодын табыгыз.
576. — Радиоактив таркалу башланганда 1 г А радие була. Әгәр
аның ярымтаркалу периоды 3 мин ка тигез булса, ничә
минуттан соң ул 0,125 г калыр?
577. — Радиоактив матдәнең ярымтаркалу периоды бер сәгатькә
тигез. Ничә сәгатьтән соң аның микъдары 10 тапкыр
кимер? Әгәр радийның ярымтаркалу периоды 1550 елга
тигез булса, 1000 елдан соң радийның күпме өлеше ка¬
луын исәпләп чыгарыгыз.
578. — Бер җисемнең температурасы 200’, ә икенчесенең — 100°.
Бу җисемнәр 0° температуралы һавада 10 мин торганнан
соң, беренче җисем — 100° температурага кадәр, ә икенчесе
80° температурага кадәр суынган. Күпме вакыттан соң
җисемнәрнең температуралары тигезләшер? (Җисемнең
T(t) температурасы F(t)-fe (Т-Т,) тигезләмәсен канә¬
гатьләндерә, биредә Т, —әйләнә-тирәдәге температура.)
268 Күрсәткечле һәм логарифмик функцияләр
579. — Ике җисемнең дә температуралары 100 әр градус. 0° тем¬
пературалы һавада 10 мин торганнан соң бер җисемнең
температурасы 80°, ә икенчесенең 64° була. Суына башла¬
ганнан соң ничә минут үткәч, аларның температуралары
аермасы 25° булыр?
580. — Моторлы көймә 30 км/сәг тизлек белән хәрәкәт итә. Мо-
I торны сүндергәннән соң 3 мин үткәч, көймәнең тизлеге
күпме булыр? (Көймәнең тизлеге ο(ί) (м/мин белән)
v'(t) = -ka (/), дифференциаль тигезләмәсен канәгатьлән-
5 u
дерә, биредә k = . Шуннан файдаланыгыз.)
Тарихтан мәгълүматлар
1. Терминнар һәм тамгаланышларның килеп чыгуы
турында. Күп кенә мәсьәләләрнең чишелеше тигез тапкырлашу¬
чыларны тапкырлауга китерә. Натураль күрсәткечле дәрәҗә ту¬
рындагы төшенчә Борынгы Грециядә үк барлыкка килә (санның
квадраты аңлатмасы — квадратның мәйданын исәпләгәндә,
ә санның кубы кубның күләмен тапканда барлыкка килә). Ләкин
а*, а3 тибындагы хәзерге тамгаланышларны XVII гасырда Декарт
керткән.
Вакланма күрсәткечле дәрәҗә һәм вакланма күрсәткечле
дәрәҗәләр өстендә гамәлләрнең иң гади кагыйдәләре XIV гасырда
француз математигы Η. О р е м (1323—1382) хезмәтләрендә очрый.
Билгеле булганча, Шюке (1445—1550 еллар чамасы) тискәре
һәм нуль күрсәткечле дәрәҗәләрне тикшергән. С. Стевин не
Ja тамыры итеп тәкъдим иткән. Ләкин системалы рәвештә
рациональ күрсәткечләрне беренче булып Ньютон куллана.
Немец математигы М. Штифель (1487—1567), а*1 булган¬
да, а° = 1 гә билгеләмә биргән һәм күрсәткеч (немецча Exponent
сүзенең хәрефләрдән торган тәрҗемәсе) атамасын керткән.
Немецча potenzieren дәрәҗәгә күтәрүне аңлата.
(logG f (х) = loga g (х) => α|θί“ *(*)= α10*- ?(χ)) тибындагы күчеш¬
ләрдә еш кулланыла торган потенцирлау сүзе шуннан чыккан.)
Exponenten термины үз чиратында грек сүзенең бик үк төгәл
булмаган тәрҗемәсеннән алынган. Диофант аның аша билгесез
зурлыкның квадратын билгеләгән.
XII гасырда кертелгән радикал һәм тамыр терминнары ике
кыйммәткә ия булган як һәм тамыр мәгънәсендәге латин сүзе
radix тан алынган. Грек математиклары «тамыр алырга» диясе
урынга «квадратның ягын аның бирелгән зурлыгы (мәйданы)
буенча табарга» дип әйткәннәр. Тамыр тамгасы V/ символы рә¬
вешендә беренче тапкыр 1525 елда барлыкка килә. Хәзерге заман
269 Күрсәткечле һам логарифмик функцияләр
символы Декарт тарафыннан кертелә, ул горизонталь сызык ести.
Ньютон исә тамыр күрсәткечләрен ести: у/~ , \ .
Логарифм сүзе грек сүзләре λόγοφ (сан) һәм αρΐνμοφ (чагыш¬
тырма) сүзләреннән алынган һәм, димәк, саннарның чагыштырмасы
дип тәрҗемә ителә. Логарифмнарны уйлап табучы (1594 ел)
Дж. Непер тарафыннан мондый исемнең сайлап алынуы лога¬
рифмнарның берсе арифметик прогрессия буыны, ә икенчесе
геометрик прогрессия буыны булган (түбәндәгене карагыз) ике
санны чагыштырганда барлыкка килүе белән аңлатыла. Нигезе е
булган логарифмнарны Спейдел (1619 ел) кертә. Ул 1пх функ¬
циясе өчен беренче таблицаларны төзи. Шактый соңрак барлыкка
килгән натураль (табигый) атамасы әлеге логарифмның «таби-
гыйлеге белән» аңлатыла. Н. Меркатор (1620—1687) әлеге
исемне бирүче 1пх ның у у гиперболасы астындагы мәйдан икә¬
нен әйтә. Ул шулай ук гиперболик исемен тәкъдим итә.
2. Логарифмнар тарихыннан. XVI гасыр дәвамында төрле
мәсьәләләрне һәм беренче чиратта турыдан-туры практикада
кулланыла торган астрономия мәсьәләләрен (аерым алганда,
судноларның торышын йолдызлар һәм Кояш буенча билгеләгәндә)
чишү барышында якынча исәпләүләр үткәрү белән бәйле эшләр¬
нең күләме бик тиз арта. Тапкырлау һәм бүлү операцияләрен
(гамәлләрен) башкарганда иң зур кыенлыклар тууын аңлау кыен
түгел. Әлеге операцияләрне, кушу гамәленә китереп, өлешчә гади¬
ләштереп караулар (мәсәлән, 1 дән алып 100 000 гә кадәр бөтен
саннарның квадратлары таблицалары төзелә, алар ярдәмендә ab -
= I (а + Ь)2 — (а + Ь)2 формуласы буенча тапкырчыгышларны
исәпләргә мөмкинлек туа) зур уңыш китерми. Шуңа күрә
саннарны тапкырлау һәм бүлү урынына аларның логарифмнарын
кушуга һәм алуга китергән логарифмнарны ачу, Лапласның әйтүе
буенча, хисаплаучыларның гомерләрен озынайта.
Логарифмнар практикада гаҗәеп киң кулланылыш табалар.
Логарифмны уйлап табучылар яңа теорияне тирәнтен өйрәнү белән
генә чикләнмиләр. Хисаплаучыларның хезмәт җитештерүчән-
лекләрен бик тиз күтәрүче практик кулланма — логарифмнар
таблицалары төзиләр. Шуны өстәп әйтергә кирәк: инде 1623 елда
ук, ягъни беренче таблицалар басылганнан соң нибары 9 ел үтүгә,
инглиз математигы Д. Гантер тарафыннан күп буын хезмәт¬
кәрләре өчен эш инструменты саналган беренче логарифмик ли¬
нейка уйлап чыгарыла. (Соңгы вакытта безнең күз алдыбызда
электроник хисаплау һәр җирдә киң таралган вакытта логарифм¬
нарның роле, исәпләүләр җайланмасы буларак, бик нык кими.)
Шотландия математигы Дж. Непер (1550—1617) һәм Швей¬
цария математигы II. Бюрги (1552—1632) бер-берсенә бәйсез
рәвештә логарифмнарның беренче таблицаларын төзегәннәр.
* Логарифмнарның гаҗәеп таблицаларын тасвирлау» (1614 ел)
270 Күрсәткечле һәм логарифмик функцияләр
Непер Джон
(1550-1617)
Инглиз математигы. Логарифмнарны уйлап табуны,
логарифмнарның беренче таблицаларын төзеп,
хисаплаучыларның эшен җиңеләйтүче һәм мате¬
матиканың кулланылышы үсешенә зур өлеш
керткән кеше.
Һәм «Гаҗәеп логарифмнар таблицаларының төзелеше» (1619 ел)
исемендә китап булып чыккан Непер таблицаларына 1 минутлы
адым белән 0 дән 90° ка кадәр почмакларның синуслары,
косинуслары һәм тангенсларының кыйммәтләре кергән. Бюрги
үзенең саннар логарифмнары таблицаларын 1610 елда хәзерләп
бетергән, күрәсең, ләкин алар Непер таблицалары басылып
чыкканнан соң 1620 елда гына дөнья күрә, шуңа күрә аның таб¬
лицалары күзгә ташланмый.
Логарифмнарны уйлап табуның нигезендә яткан мөһим
идеяләрнең берсе билгеле була инде. Штифель (1487—1567)
һәм башка математиклар
а 3, а 2, α 1,1, а, аг, а3,...
геометрик прогрессия буыннарын тапкырлау һәм бүлү
...,-3, -2,-1,0,1, 2, 3, ...
арифметик прогрессия төзүче күрсәткечләрне кушуга һәм алуга
тиңдәш булуга игътибар итәләр.
Ләкин бер идея генә җитми. Мәсәлән, 2 санының бөтен дәрә¬
җәләр «челтәре» артык сирәк; күп кенә саннар «логарифмнарсыз
кала», шул сәбәпле тагын бер идея кирәк була: берәмлеккә бик
< 1Г, Λ ί V+1
1н ' һәм 1ч дәрәҗә-
10’/ \ 10"/
ләре, п ның кыйммәтләре бик зур булганда, үзара якын икәнен
күреп, Непер һәм Бюрги охшаш чишелеш кабул итәләр: Непер —
нигез итеп |1—I санын, ә Бюрги 11+ — | санын ала.
1 10/ \ 10</
Аларның моннан соң фикер йөртүләре һәм хисаплауларының
схемаларын тасвирлауларын сөйләп бирү шактый кыен, чөнки
шактый катлаулы аерым моментлар күп һәм, гомумән, XVI гасыр
текстлары шактый буталчык. Шуны искәрик: моннан соң Непер —
I V0’ / 1 V°*
нигезен, ә Бюрги + нигезен ала. Бу — эшнең
якын санны дәрәҗәгә күтәрү.
Күрсәткечле һәм логарифмик функцияләр
асылын үзгәртми (сезгә билгеле булганча, log w. х = —logo*
шуңа күрә әлеге үзгәртүләр логарифмда өтернең урынын күчерүгә
генә китерә), шулай да хисаплауны һәм таблицаларның үзләрен
берникадәр гадиләштерергә мөмкинлек бирә.
Шулай итеп, логарифмнарны уйлап табучыларның икесе дә,
нигездә, (1 + Л,) рәвешендә дәрәҗәләрне тикшерү максатка
ярашлы булыр дигән нәтиҗә ясыйлар, биредә М — бик зур сан.
Мондый рәвешле саннарны тикшерү Цщ (1 + —j буларак бил¬
геләнгән сезгә билгеле е санын белдерер (эзлеклелек чикләмәсенең
билгеләмәсе «Тарихтан мәгълүматлар»да бирелгән, III бүлектә).
Логарифмнарның нигезе сыйфатында е санын кабул итү идеясенә
күп калмый (Бюргиның логарифмнар таблицалары нигезе өченче
тамгага кадәр төгәллек белән е га туры килә. Неперның лога¬
рифмнары таблицаларының нигезе - санына якын).
Унарлы логарифмнарның беренче таблицалары (1617 ел)
Непер киңәше буенча инглиз математигы Г. Бриггс (1561—1630)
тарафыннан төзелә. Аларның күбесе Бриггс тарафыннан чыгарыл¬
ган якынча формула
ярдәмендә табыла, т һәм п кыйммәтләре зур булганда, әлеге фор¬
мула җитәрлек дәрәҗәдә төгәл. Бриггс т һәм п ның кыйммәт¬
ләрен икенең дәрәҗәләре рәвешендә алган: бу аңа tfa һәм V10
исәпләүләрен эзлекле рәвештә квадрат тамыр алуга кайтарып
калдырырга мөмкинлек бирә.
Бриггсның икенче идеясе кайбер саннарның унарлы лога¬
рифмнарының кыйммәтләрен таблицалар ярдәменнән башка мөс¬
тәкыйль рәвештә табарга мөмкинлек бирә. Бөтен сан логариф-
масының бөтен өлеше санның үзендәге цифрлар саныннан бергә
ким. Шуңа күрә, мәсәлән, өч урынга кадәр төгәллек белән lg2 не
табу өчен, 2‘°3 дәге цифрлар санын табу җитә. Бу бик үк кыен түгел.
Логарифмнар таблицаларын төзегәндә, Непер һәм Бюргиның
у = log„ х функциясе өчен булган ирекле х0 ноктасындагы Δχ һәм
Δι/ үсемтәләре арасындагы бәйләнешне табу зур роль уйнаган.
Аларның аңлату системасының детальләренә артык игътибар
итмичә, төп нәтиҗәне болай белдерергә мөмкин: — = —, биредә
k — нинди дә булса константа. Әгәр логарифмнарның нигезе
(1+·“) дәрәҗәсе булса, биредә л — шактый зур сан, ул вакытта
Ди 1 ~
. - — була.
Δχ х
Күрсәткечле һәм логарифмик функцияләр
Δχ ны нульгә омтылдырып, у' = ү дифференциал* тигезләмәсен
табабыз, ә аның чишелеше,— белгәнегезчә, 1пх + С функциясе.
*0 .
. ί dx , , „ ,
In χ0 нең J — буларак табылуы баштан ук билгеле, ягъни
In х0 гипербоЛа, абсциссалар күчәре
һәм х = 1, х = х0 турылары белән чикләнгән кәкресызыклы тра¬
пециянең мәйданы. Әлеге билгеләмәдән чыгып, сезгә билгеле
булган логарифмнарның үзлекләрен чыгару бик үк җиңел
булмаган, ләкин сезгә аңлашылырлык мәсьәлә.
Кабатлау өчен сораулар һәм мәсьәләләр
1. 1) Саннан п нчы дәрәҗә тамырга билгеләмә бирегез, п нчы
дәрәҗә арифметик тамыр нәрсә ул?
2) Кыйммәтен табыгыз:
а) </«27 ; 6)^625; в) </-128; г) д) | ·
3) Тигезләмәне чишегез:
a) х«-125; б)х4 = 64; г)х4»-16.
2. 1) Арифметик тамырларның теп үзлекләрен әйтегез.
2) Аңлатманың рәвешен үзгәртегез:
3) Саннарның кайсысы зуррак?
а) </128 яки ч4 ; б) 2100 яки 10020;
в) </26 яки </б ; г) </б яки </з .
3. 1) Рациональ күрсәткечле дәрәҗәгә билгеләмә бирегез һәм
мондый дәрәҗәләрнең төп үзлекләрен әйтегез.
2) Кыйммәтен табыгыз:
б) </б4 : 2 5 ■ j 210 I ;
в) 16 4;
3) Саннарның кайсысы
a) VI6 яки 24 ;
*
в) 0,37 яки 0,3 7;
зуррак?
„ з
б) з э яки 9 4 ;
г
г) 5*з яки 5"°'*.
273
Күрсәткечле һәм логарифмик функцияләр
4. 1) Күрсәткечле функциянең төп үзлекләрен әйтегез.
2) Функциянең графигын төзегез:
а) У = 4'; б) у = ||| ; в) у = 6Л; г) у = ||) .
3) Саннарның кайсысы зуррак?
Л с г
а) 2°·4 яки 2 1; б) 1,2 1 яки 1,2 ** ;
в) Ц) яки |i) ; г) 0,3 "яки 0,3 я.
5. 1) а1 = ае (а > 0, a * 1) тигезләмәсенең тамырларын табыгыз,
б) а* > а' тигезсезлеген чишегез (ике очракны тикшерегез:
0 < α < 1 һәм а > 1).
2) Тигезләмәне чишегез:
1
a) 271 = 95; б) 9'41 + 3*42 = 18;
в) 0,5,”ж 2i=/2; г) З*42 - 3х = 72.
3) Тигезсезлекне чишегез:
а)5*2,>|; б) 0,2χ2-2 > 5;
в)3х<|; г) (I)Х,>4·
6. 1) Санның логарифмына билгеләмә бирегез.
2) Табыгыз:
a) Iog2 16^2; 6)log0225; в) lg 0,01; r)logiV3.
3
3) Төп логарифмик бердәйлекне языгыз һәм исәпләгез:
.... _ /nlt-log23 ... ...
а)324|ов»5; б) И) ; в)51 + |адз2; г) 0,2' + |"«о.г&.
7. 1) Логарифмнарның төп үзлекләрен санап чыгыгыз.
2) а нигезе буенча аңлатманы логарифмлагыз (е > 0, Ь > 0):
а) а = 2 булганда 16б7 Vc;
б) α = 10 булганда ;
^/ЮОЬ"
в) а = 3 булганда ;
с’
г) а = 0,7 булганда .
^•Jc
274
Күрсәткечле һәм логарифмик функцияләр
3) a) log3 х = 2 log, 7 + j log3 27 - | log,16;
б) log, x = 2 log2 5 - I log2 8 + log2 0,2;
в) log, x «log, 1,5+I log, 8;
r) lgx = l + 2 1g 3-jig 125
булса, х ны табыгыз.
8. 1) Логарифмик функциягә билгеләмә бирегез һәм аның төп
үзлекләрен санап чыгыгыз.
2) Функциянең графигын төзегез:
а) у = log4 х; б) у = log , (х - 1);
5
В) у = log5x; г) у = log, (х + 1).
4
3) Кайсы сан зуррак?
а) lg 7 яки 3 lg 2; б) log ι 5 яки logι 6;
3 3
в) log35 яки log36; г) log2 3 яки log3 2.
9. 1) a) loga х = b (a > 0, о * 1) тигезләмәсенең барлык тамыр¬
ларын күрсәтегез.
б) logd х > log„c тигезсезлеген чишегез (ике очракны карагыз:
0 < a < 1, a > 1).
2) Тигезләмәне чишегез:
а) log2(x - 15) = 4; б) lg2x + 2 lg х = 8;
в) In2 (х - 2) = 4; г) lg (х2 - 2х - 4) = lg 11.
3) Тигезсезлекне чишегез:
а) log0e х > 2; б) lg х < -2;
в)1пх>-3; r)log7x<l.
10. 1) у - ех, у ” ах функцияләре өчен чыгарылма формуласын
языгыз.
2) Функциянең чыгарылмасын табыгыз:
а)ц(х)=5-2е4 б) u(x) = 3 · 57х ';
B)g(x) = e ’x; г)/(х)-(f)te.
3) Түбәндәге функция өчен башлангыч функцияләрнең
гомуми рәвешен табыгыз:
а) и (х) = е5х - 7е4х; б) и (х) = 5е°,Тх;
в) g (х) = е Зх; г) / (х) - е2*.
275 Күрсәткечле һәм логарифмик функцияләр
11.
12.
13.
14.
1) у = logo х функциясенең чыгарылмасы нинди? f(x)= —
функциясе өчен башлангыч функцияләрнең гомуми рәвешен
табыгыз.
2) Функциянең чыгарылмасын табыгыз:
а) у = х In Зх; б) у = log2 (7 - 2х);
B)j/ = 2 1ogjX; г)у = 1пу.
3) Түбәндәге функция өчен башлангыч функцияләрнең го¬
муми рәвешен табыгыз:
а)/(х)=^: 6)ί(χ)- гЦ; в)и(х)=ү; г)Л(х)=-^т.
1) у = ха дәрәҗәле функциясенең чыгарылмасы нинди?
2) Түбәндәге функциянең графигын төзегез һәм аның чыга¬
рылмасын табыгыз: <¬
а) у = х7; б) у = х 4; в) у = х'0·3; г) у « х'г.
3) Якынча кыйммәтне табыгыз:
а) ^32,02 ; б) 7127,9 ; в) 7θ4,3 ; г) ^80,6 .
1) Нинди тигезләмәләрне иррациональ тигезләмәләр дип
атыйлар?
2) Тигезләмәне чишегез:
а) Ух -3 = 2х -7; б) У2х + 3 =2;
в)х-Ух = 12; Г) х + 3 = Узз + х2 .
3) Тигезләмәләр системасын чишегез:
а)
Ь
1
II
W
* «
б)
х + у - у/ху = 6,
X - у = 9;
ху = 16;
■) .
•Jx + yfy =4,
г) .
х2 + у - 7
н
1
II
00
х2у = 12.
1) Ике үзгерешлеле ике тигезләмә системасының чишелеше
дип нәрсәне атыйлар?
2) Тигезләмәләр системасын чишегез:
а) .
N> Н
* 1
и co
II
й|н- "
·♦ сл
•
б)
52*-» =0,2
5*-х = 125;
в)
2ху = 9,
^Χ-2μ _
г)
з3х+* = Уз,
5х - 4у = 15.
3) Тигезләмәләр системасын чишегез:
а)
х-р-4.
log2 х - log2 у = 1;
З'2’ = 1,
lgx + lg(y + 5) = 2;
в)
log3 (5х - у)
ху = 2;
= 2,
г)
х2 + у2 = 26,
log5 х = 1 + log5 У-
276 Күрсәткечле һәм логарифмик функцияләр
Кабатлауга
мәсьәләләр
’ I
§ 1.
Реаль саннар
1. Рациональ һәм иррациональ саннар
1. Түбәндәге раслаулар дөресме?
а) Әгәр натураль сан 6 га бүленсә, ул 3 кә бүленә.
б) Әгәр ике санның суммасы җөп сан булса, кушылучы¬
ларның һәркайсы җөп сан була.
в) Әгәр ике санның тапкырчыгышы нульгә тигез булса, тап¬
кырлаучыларның һәркайсы нульгә тигез.
г) Әгәр ниндидер санның кубы 8 гә бүленсә, бу җөп сан
була.
2. Эзлекле килүче өч натураль сан суммасының 3 кә бүленүен,
ә аларның тапкырчыгышының 6 га бүленүен исбатлагыз.
3. 523 санының уң ягына ике сан өстәп языгыз, килеп чыккан
бишурынлы сан а) 3 һәм 5 кә; б) 8 һәм 9 га бүленсен.
4. ΙΟ56 -1 санының 3 кә һәм 11 гә бүленүен исбатлагыз.
5. Икеурынлы санның берәмлекләр цифры дистәләр цифрын¬
нан 2 берәмлеккә зуррак. Сан үзе 30 дан зуррак һәм 40 тан
кечкенәрәк. Бу санны табыгыз.
6. Әгәр вакланмасы кыскартылмас вакланма булса,
вакланмасының да кыскартылмас икәнен исбатлагыз.
7. а) |а| = ]-о|; б) х < |х|; в) |х|2 - х2
икәнен исбатлагыз.
8. Аңлатмаларның кыйммәтләрен табыгыз (8—9).
2,75:1,1 + з|
в) Ңг;
2,5-0л(-з|)
3|: 10 +0,175
в) (1,4-3,5 : 1|): 2,4 +3,4 : 2|;
2 0.25
А
- 1 + 2.2 10
277 Кабатлауга масьәлалар
v‘ 0,52-0,5 1,22-1,82
a’ 0,4!+0,l!+2 0,4 0,1 ’ и О.2-1.2 0,8 5
в) 0,62+0,l2-2 0,6 0,1 . r) Λ |V _ (4 5 2,.
1,5-1,52 15/ V 8 / »
10. Санның якынча кыйммәте язылышындагы дөрес цифрларны
күрсәтегез:
а) 3,82 ± 0,1; б) 1,980 · Ю4 ± 0,001 ■ Ю4;
в) 7,891 ±0,1; г) 2,8 · Ю4 ± 0,3 · Ю4.
11. (1 + х)"~ 1 + пх формуласыннан файдаланып, якынча исәп¬
лән чыгарыгыз:
a) 1,002s; б) 0,9974; в) 2,0043; г) 3,015.
12. а = 11,5, 6 = 3,8 икәне билгеле, а) α + 6; б) За - 6; в) аб; г)-^
аңлатмасының якынча кыйммәтен табыгыз.
13. Гади вакланма рәвешендә языгыз:
а) 2,(3); б) 0,(66); в) 1,0(8); г) 1,(33).
14. а)7б; 6)277; в)7б+1, г)ү саннарының
һәркайсының рациональ сан булмавын исбатлагыз.
15. а) а һәм 6 — рациональ саннар;
б) α һәм б — иррациональ саннар;
в) α — рациональ, а 6 иррациональ сан булса, а һәм Ь санна¬
рының суммасы (тапкырчыгышы) рациональ (иррациональ)
сан була дип әйтү дөресме?
16. 0,01 төгәллеккә кадәр табыгыз:
а) 72+|; б)7б-|; в) 73г) 7б
17. Саннарны үсә бару тәртибендә тезегез. Аларның кайсысы —
рациональ, ә кайсысы иррациональ сан икәнен күрсәтегез.
а) 72 ;-2; -1,7; f; б) log23; -1; |; -7б;
в) 0,(2); I; г) е; -1,(6); 710 ; lg 100.
Саннарны чагыштырыгыз (18—19).
18. а) һәм ή; б) (75+2) Һәм 717 .
в) log37 һәм logT3; г) (77 + з) һәм 731 .
278 Кабатлауга масьаләлар
19. а) 15|0*э>» һәм б) (72 + 7з) һәм (73О -7з);
в) sin 2,1 һәм sin 7,98; г) (Ти + 7б) һәм (7з + 71θ).
20 Санның рациональлеген исбатлагыз:
б) (V2 + 1)2 +(1 - Τϊ)2 - (77 4- 1)(7? - 1);
в) 211Х!. _ 7з5 ; г) (з718 + 278 + 4VsO): 72.
v7 -v5 ■ ·
2. Процентлар. Пропорцияләр
21. Әгәр: а) х саны 320 нең 2,5% ы булса; б) х санының 2,5% ы
75 кә тигез булса; в) 2,8 саны 84 санының ничә процентын
тәшкил итсә, х шул процентлар санына тигез була; г) х саны
35 нең 140% ын төзесә, х санын табыгыз.
22. 1987 елда предприятиенең продукция эшләп чыгаруы —
4% ка, ә икенче елда 8% ка артты. Ике ел вакыт эчендә
уртача еллык продукция үсешен табыгыз.
23. Бирелгән дүрт санның беренче өчесе 5, 3, 20 саннарына
пропорциональ, ә дүртенче сан өченчесенең 15% ын тәшкил
итә. Әгәр икенче сан калганнарының суммасыннан 375 кә
кимрәк булса, ул саннарны табыгыз.
24. Көзге-кышкы чорда яшелчәләргә бәя 25% ка артты. Яшел¬
чәләрнең бәясе элеккечә булсын өчен, яз көне аларның
бәясен ничә процентка төшерергә кирәк?
25. Пропорциянең билгесез буынын табыгыз:
а)12:| = х:·^; б) х : (-0,3) = 0,15 : 1,5;
О оО
0,13 . 26 .
х 3Г
26. Тигезләмәне чишегез:
я! 2 _ б .
2,5 х ’
в) 1 3 — 6,5
х-2 1,5
б) -Ξ— = I’8
х + 5 1,2
γΊ
’ 1,2 х + 3
27. ABC өчпочмагында АВ ягының Е ноктасы аша АС ягына
параллель итеп туры үткәрелгән.
а) АВ = 22,5 см, АЕ = 18 см, ВС = 15 см булса, ВС ягының
туры бүлгән кисемтәләрен;
б) АВ = 7,5 см, АЕ = 5 см, ә ABC өчпочмагының мәйданы
72 см2 булса, ABC өчпочмагының бүлгәләнгән фигура мәйдан¬
нарын табыгыз.
Кабатлауга мәсьәләләр
28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
3. Прогрессияләр
Беренче буыны 2 гә, ә җиденче буыны 20 гә тигез булса,
арифметик прогрессиянең 20 буынының суммасын табыгыз.
4 һәм 40 саннары арасыннан, бу саннарны да кертеп, ариф¬
метик прогрессия төзерлек дүрт сан табыгыз,
9 , log 2 ’ log1 2 саннаРы арифметик прогрессиянең
эзлекле килүче өч буыны булуын исбатлагыз.
Арифметик прогрессиянең беренче һәм бишенче буын¬
нарының суммасы 26 га, ә икенче һәм дүртенче буынна¬
рының тапкырчыгышы 160 ка тигез. Прогрессиянең беренче
алты буынының суммасын табыгыз.
а, Ь, с, d саннарының шушы тәртиптә алганда геометрик
прогрессия төзүләре билгеле булса, (а - с)2+(Ь - c)2+(b - d)2-
- (a - d)2 аңлатмасын гадиләштерегез.
V2+1 1 , 1 _ _
, „ /ζ Һәм л- саннарының геометрик прогрессия тө-
V2-1 ··*< z
зүен исбат итегез.
Геометрик прогрессиянең дүртенче буыны икенчесеннән
24 кә зуррак, ә икенче һәм өченче буыннарының суммасы
6 га тигез. Беренче буынны һәм прогрессиянең тапкырлыгын
табыгыз.
Беренче, икенче һәм соңгы буыннары тиңдәшле рәвештә
3 кә, 12 гә һәм 3072 гә тигез булган чикле геометрик
прогрессиянең буыннары санын табыгыз.
Чикле геометрик прогрессиянең тапкырлыгы 4 гә тигез,
О
аның дүртенче буыны — гә, ә барлык буыннары суммасы
ЭЧ
гә тигез. Бу прогрессиядә барлыгы ничә буын?
Кырыйдагы лары суммасы 14 кә, ә уртадагылары суммасы
12 гә тигез һәм беренче өчесе — геометрик прогрессияне,
а соңгы өчесе арифметик прогрессияне төзегән дүрт санны
табыгыз.
Чиксез кими баручы геометрик прогрессиянең тапкырлыгын
һәм суммасын табыгыз. Монда Ь *= \/3 , Ь= ———.
»' 3 ♦ 1
Чиксез кими баручы геометрик прогрессиянең беренче өч
буыны суммасы 10,5 кә, ә прогрессия суммасы 12 гә тигез.
Аның беренче буынын һәм тапкырлыгын табыгыз.
Һәркайсы а нигезле (а > 0, а * 1 ) дәрәҗә булган өч сан гео¬
метрик прогрессия төзиләр. Әлеге саннарның логарифмнары
арифметик прогрессия төзүен исбатлагыз.
Кабатлауга мәсьәләләр
§2.
Бердәй рәвешүзгәртүләр
4. Алгебраик аңлатмаларның рәвешен
үзгәртү
41. Тапкырлаучыларга таркатыгыз.
а) а2 + Ь2 + 2а - 2Ь - 2 ab; б) х3 + (у - 1) х + у;
в) а6- 8; г) х* - х2 (у2 + 1) + у2.
42. а) п е N булса, п4 + 2п3 - п2 - 2п ның 24 кә бүленүен;
б) п е N булса, (пг + 4п + 3) (п2 + 6л + 8) нең 24 кә бүленүен;
в) п е N булса, п3 - п ның 6 га бүленүен;
г) п е N, п — җөп сан булса, п3 - 4л ның 48 гә бүленүен
исбатлагыз.
43. Вакланманы кыскартыгыз:
а3 + а2 - а -1 х2+л -12
а> α2+2α+1 ’ 6> х2 + 8х + 16’
2аг-5а + 2 х3-27
αί>-2ί>-3α+6 ’ г) х2у + 3ху +9у '
Аңлатмаларны гадиләштерегез (44, 45).
лл 4mn). т п 2тп 1.
\ m+nf I т+п п-т т2+п2)
6) +
a+b V ) а + Ъ аг_
V ( х _ 8 х2-2х х + 8 .
В' VXa-4 x2+2xj 4-х х+2*
Г) f 1 + 2c , 1 Y (e-3)412c
^c2+3c + 2 c2+4c + 3 c2 + 5c+6y 2
45. a) /_3 2 1 V : ·
\2x-y 2x + y 2x-5y) ’ 4x2-4y2 ’
~ ( 3 , 4 , 2α V 3 Г1 a-12 .
* ^α-З + a2 -5a + 6 a-2 ) ’ (2a+ 1/ 3(3-a) ’
. (x’-8 o i. ,V« *-l
} I x-2 +2X l'\4 X ) 2-x :
/
r) k2 9-Λ2 . 27 + Ла/3, & ϊ
1 з+k k2_Ak g-л ·( з-fe I*
281 Кабатлауга мэсьалэләр
5. Радикаллар һәм вакланма күрсәткечле
дәрәҗәләр кергән аңлатмаларның рәвешен
үзгәртү
46. Ваклаучыда иррациональлектән котылыгыз:
47. Исәпләгез:
Аңлатмаларны гадиләштерегез (48—51).
г)
282 Кабатлауга мәсьәләләр
Illi
к_ . а3 -2аяЪ3 +abs -*
51. a) a »;
5 4 1 ? 2
a* -a3b3 -ab3 + a3b
6)
в)
Г)
' ! 1
2(г«-У4 )
1 _1 -1 _1
<x2 у 4 -X 4 у 2
с4 + с2 с2 + 1
3{αί>)? -ЗЬ
а-һ
6. Тригонометрик аңлатмаларның рәвешен
үзгәртү
Аңлатмаларны гадиләштерегез (52, 53).
52. a) tg2 a - sin2 a - tg2 a sin2 a;
б) Jsin'! β (1 + ctg β) + cos2 β (1 + tg p);
в) (3 sin a + 2 cos a)2 + (2 sin a - 3 cos a)2;
cos ptgP
r> sin2 β “ ct^ β cos β.
283 Кабатлауга млсьэлэлар
53. a) 2tg α-tg (α - π) + ctg^-α);
*■(-«) ΜΙ—), «»« .
ώη(π-α) ctga Sin(f+a)’
tg (π- β) cos (π- β) tg - β)
Β) 9ίη(|-β)οίβ(*+a)tg(^+a) ’
tgi^+alsin^sinHicos^
р) \ 4 / Z Io
ctg (я-а)сов— sin-^cosZn
7 Ιο V
Бердәйлекне исбатлагыз (54, 55).
* tgatg β(α+β) 2P* 1 + cos 2α + sin 2α ® *
«>8ία+β)+οο8(α-β) sinα-sin3α _ λ1.„9„
В) ein(a+0)+ein(a-p) tg^ Γ) cosα-cos3α “ Ctg2a*
55. а) π < α < 2π булганда, Jl + ^cosa = cos^ ;
u £ Z V 4 Z 4
б) π < a< 3’ булганда, Jl - J-g-- 4-cos 2a = VScosi^-·^) ;
в) у < a < 2π булганда, у |+1 2 +1cos = -cos ’
г) < a < 2π булганда, ^1 + ^7 -1 cos a = V2 cos (J - .
56. Тигезлекнең дөреслеген исбатлагыз:
а) cosy cos у cosy w ;
б) tg 20* - 4 sin 20* sin 50° - -2 sin 20°;
в) —> 4 sin 70* = 2;
sin 10’
r) cos 20°+ 2 sin2 55° - ^2 sin 65° - 1.
57. Тигезлекнең дөреслеген исбатлагыз:
а) 0 < х < у булганда, tg х + ctg х > 2;
284 Кабатлауга мәсьәләләр
«ini-J+α) Γ
б) 77—n 7 /г,—TT + “ a*n ' 2v3 .
’ Λ(,νίΗ!Η)
в) (1 + sin φ + cos φ) (l-sin<p + cos φ) (1 + sin φ - cos φ)χ
x (sin φ + cos φ -1)^1;
г) 2 sin 4 a sin 2 α + cos б α > - 1.
Исәпләгез (58, 59).
58. a) sin 2 α = 2 булса, cos4 α + sin4 α;
б) tg*=zn булса,
в) sin a tg α = у булса, cos α;
г) tg·^· - -λ/2 , π < α < булса, sin α, cos 2α, cosy.
59. a) 1g tg 1° + 1g tg 2° + ... + 1g tg 89°;
6) 1g tg 1’ · 1g tg 2° · ... · 1g tg 89°.
60. Санны нуль белән чагыштырыгыз:
а) 1g sin 32° ■ 1g cos 7’ · 1g tg 40’ · 1g ctg 20’;
б) 1g tg 2’ + lg tg 4°+lg ctg 2’+lg ctg 4°.
61. cosx=r®y, cosi/=y^y, cosz=yyy, a + b + c *0 булса,
tg2 7 + tg2 4+ tg2у суммасын табыгыз.
7. Дәрәҗә һәм логарифмнар кергән
аңлатмаларның рәвешен үзгәртү
Саннарны чагыштырыгыз (62, 63).
62. а) З400 һәм 4’00; б) -log5·^ һәм 7logjl;
э
в) 5200 һәм 2500; г) log, -72 һәм log3 .
63. a) log, 2 + log, 7 һәм log, (2 + 7);
б) log, 5 - log, 3 һәм log, (5 - 3);
в) 3 log7 2 һәм log7 (3 - 2);
г) log31,5 + log3 2 һәм log3 1,52.
64. Аңлатманы гадиләштерегез:
a) 814’2logs4 + 251081*68; б) 241о*«я - 5ζΙΟ*Λ“ - a°.
285 Кабатлауга мәсьәләләр
65. Санны унарлы вакланма рәвешендә языгыз:
. . . _ I - 5 . . -
а) 491-|о*’2 + 5; 6) 362 +2-|’«г,°.
66. Аңлатманың кыйммәтен табыгыз:
а) УЛ*? ; 6) 2 log0 З3 - 2 logo,ДО;
iigz + igo
в) ’ г) (2 1о£122 + logl23 ) (2 log126 - log123).
Jg 1 о — lg 1OU
67. Аңлатманы а нигезе буенча логарифмлагыз:
а) α = 5 булганда, 25ft3 vrT ;
л о t n л « 0,0016b*
б) α = 0,2, b > 0, с > 0 булганда, —— .
с\1сг
68. a) log4x = 21ogJ0 + |log681 - | log4125;
4 о
б) log! х = I log 1 16-log 1 8 + logt 28 булса, х ны табыгыз.
3*3 3 3
69. Таблица ярдәмендә исәпләгез:
.) 7.832 Уйй м . 102.3'
5,2562 V92.14 6,341
70. Аңлатманы гадиләштерегез һәм якынча кыйммәтен табыгыз:
loga2 · log43 ■ log54 ■ loge5 · ... ■ logl09.
71. log2( Vs +1) + log2( Ve - 2)=Д икәне билгеле.
log2( V3 - 1)+ log2( V6 + 2) суммасын табыгыз.
§3.
Функцияләр
8. Рациональ функцияләр
72. Тигезьянлы трапециянең бер нигезе ян ягына тигез, нигез
янындагы почмагы 30°.
а) Трапециянең мәйданын ян ягының функциясе буларак;
б) трапециянең периметрын аның биеклеге функциясе
буларак формула белән күрсәтегез.
73. Өчпочмаклы төзек призманың ян кабыргасы нигез янына
тигез.
а) Нигез ягының функциясе буларак призманың күләмен;
б) күләмнең функциясе буларак призманың ян өслеге мәйда¬
нын формула белән бирегез.
286 Кабатлауга мәсьалаләр
74. Материаль нокта, турысызыклы хәрәкәт итеп, гармоник
тирбәнешләр ясый.
а) Вакытның функциясе буларак ноктаның координатасын;
б) вакытның функциясе буларак ноктаның тизлеген фор¬
мула белән бирегез.
75. 150 нче рәсемдә А һәм В пунктларыннан бер үк вакытта
кара-каршы чыгучы ике туристның хәрәкәт графиклары
сурәтләнгән.
а) Туристлар А һәм В пунктларына кайсы вакытта килеп
җиткәннәр?
б) Аларның һәркайсы юлда күпме вакыт булган?
в) Туристның һәркайсы тукталыш урынына кайсы вакытта
килеп җиткән?
г) Аларның һәркайсы күпме вакыт ял иткән?
д) Тукталышка кадәр һәм аннан соң һәр турист нинди тизлек
белән хәрәкәт иткән?
е) Ьәр туристның уртача хәрәкәт итү тизлеге нинди?
76. Функциянең графигы буенча (151 нче рәсем) сорауларга
җавап бирегез:
1. Функциянең үсү аралыклары нинди?
2. Функциянең кимү аралыклары нинди?
3. Функциянең максимум һәм минимум нокталарын әйте¬
гез. Бу нокталарда функция нинди кыйммәтләр ала?
4. [-2; 2] кисемтәсендә функциянең иң зур һәм иң кечкенә
кыйммәтләре күпмегә тигез?
5. Функция нинди нокталарда өзлексез түгел һәм функция¬
нең бу нокталарда кыйммәтләре нинди?
6. Функция нинди аралыкларда өзлексез?
7. Функцияләрнең кайсылары җөп һәм кайсылары так?
287 Кабатлауга масьалалэр
а)
б)
в)
151 нче расем
288 Кабатлауга масьалалар
77.
78.
Функциянең билгеләнү өлкәсен табыгыз:
X1
б)у- -J—;
х'-1
_ . X
в)^ х*-9х2 + 20’ г)-й‘зх’-5хн·
Функция өчен өзлексез аралыкларын табыгыз:
V2 1
а) у =
б) у =
хг +
1
г) У =
7».
_ __ _ - -
Зха-2х2+б
исбатлагыз:
Функциянең җөп (так) икәнен
а) у = х3 - Зх;
6x3
б)У-
|х| + 2
г> У~ ,1 ·
в) у = х4 (х2+2);
80.
Функциянең даими
тамга аралыкларын табыгыз:
. Х-1
а^= “зГ;
. х2-4х-5
б)у- 9-’
2-Г-3
в) у - 1 5 , ;
г) у = 2х2 - 5х + 2.
81.
Функциянең үсү (кимү) аралыкларын һәм минимум нок¬
таларын табыгыз:
а) у = 4х2 + Зх - 1;
б)у - Ι-f;
в)у = (х-I)4-2;
ч Х+*
г) у = —г.
' 3 х-1
Функцияне тикшерегез һәм аның графигын төзегез (82, 83).
82.
а) у = Зх - 5;
б) у = 2х2 - 7х + 3;
в) у = 2“х;
г) у = 12 - 4х - х2.
83.
. о 3
а) у = 2 -у;
' X Ч 1
б)у = (х-2)я-1;
. *4·».
в) у - :
г)у “ 4 (х + 2)4.
Функцияләрнең һәркайсының графигын төзегез (84—86).
;84.
а)у = Зх-2; б)у =
х2 - 4х - 5; в)у=-^-1; г)у = х3 + 2.
*85.
а)у=3х + |х|;
6) у = |-х2 - * + 2|;
в) у = 2х - |х-3|;
г) у = х2 - 4]х| + 3.
86.
1 х4· сч
β)ί/=Ίψ; б)У =
Х+2; .,„.(±1;
X2 х **
289 Кабатлауга масьәлэлар
87. Функция графикларының уртак нокталары бармы?
а) у = х2 һәм у = х + 6; б) у = — һәм у = 4 (х + 1);
в) у = х4 Һәм у = 2хг + 1; г) у = һәм у = х2 - 2.
88. Тигезләмәнең бирелгән I аралыгында тамыры барлыгын ис¬
бат итегез:
а) х3 - 6х + 2 = О, I = [О; 1]; б) х4 - Зх2 + j = 0, 1= [1; 2];
в) Xs + Зх = 5, I = [1; 21; г) 4 + 2х* - Xs = О, I = (-1; 2].
Тигезләмәләрне (тигезсезлекләрне) график юл белән чишегез
(89, 90).
89.
а) 4 - Зх х + 2;
в) , = 4х;
б) х2 - 2х = - х;
г) х2 + 2х + 2 ? х + 1.
90.
б) |1-х| = 2-|х|;
г) |х-1| = 3-|х|.
91. у = ах + Ь функциясенең графигы А (2; 1), В (5; 10) нокталары
аша үтә. а һәм Ь ны табыгыз.
92. Квадрат функция графигы буенча (152 нче рәсем) а, Ь, с һәм
D дискриминантының тамгаларын билгеләгез.
93. Сызыкча яки квадратик функция а) җөп; б) так; в) периодик
була аламы?
94. Функцияне җөп һәм так функцияләрнең суммасы рәвешендә
күрсәтегез:
а)у=ТхГ’ б)у= х3-х|х| + 3;
в) У Х +.Х · г) у ~ 2xs + х4 Зх + 8.
95. Функция җөпме яки такмы?
а) у = 5х5 - 2х2 - 3; б) у = 4х5 - 2х* + х;
9. Тригонометрик функцияләр
Функцияләрнең билгеләнү өлкәсен табыгыз (96, 97).
96.
а) у - —;
сон’ X
б^ = Ϊ Г.Ь ’
в) у =
У = X
sin g cos 2
290 Кабатлауга мәсьәләләр
291 Кабатлауга иәсьәлэлар
а) У = 1+ З‘п2х : б> у = л/1-cos 4х ;
в) У “ ; г) у = tg х + ctg х.
100. Функциянең даими тамга аралыкларын табыгыз:
а) у = Зсоз (х +1) ; б) у = 1 - tg Зх;
в) у - 1 - 72 sin j; г) у = 1 + 2cos 2х.
101. Бирелгән функцияләрнең кайсылары җөп, кайсылары так
була?
а) у = tg Зх - ctg |; б)у= ;
в)у = з1п-^—г)у-—- cosx.
102. Бирелгән функцияләр арасыннан периодик функцияләрне
күрсәтегез һәм ул функцияләрнең иң кечкенә уңай период¬
ларын табыгыз:
а) у - 1 - sin 5х; б) у = х sin2 х - х cos2 х;
в) у = 3tg (у ~ ; г) у = (sin х + cos х)2.
103. Функциянең үсү (кимү) аралыкларын, максимум һәм ми¬
нимум нокталарын табыгыз:
a)p = l + sin(x-|); б) у =
в) у = 0,5 cos( | - 2х); г) у = 71 - sin2 х .
104. Функциянең иң зур һәм иң кечкенә кыйммәтләрен табыгыз
(әгәр алар булса):
а) у = cos 2х + sin2 х; б) у = 1 - 4 sin Зх;
в) у - sin х - cos х; г) у = 1 +1 tg х|.
Функцияләрнең графикларын төзегез (105, 106).
105. а) у = 2 sin2·^ ;
в) у = 1+ 2cos 2х;
106. Я) У = l*l8in* ;
X
в) у = cos х + [cos х|;
107. Функцияне тикшерегез
в) у - 1 +1 COS (r4 - x);
б) у - 71 - cos2 x ;
r) y = sin(x -- 2.
б) у = (sin x - cos x)2;
г) у = sin x ctg x.
һәм аның графигын төзегез:
г) у = 1 - tg 2х.
292 Кабатлауга мәсьәләләр
108. х0 нең ft = х3 тигезләмәсенең тамыры икәнлеге билгеле.
Моннан (—х0) саны әлеге тигезләмәнең тамыры була дип
әйтеп буламы?
109. Саннарны чагыштырыгыз:
a) sin (π + £ 1 һәм cos (π + ~
в) tg 2 һәм ctg 2;
1; б) tg π3 һәм ctg π2;
г) sin 1 һәм cos 1.
110. а) 0 < α < к булса, sin α + cos α > 1;
б) cos (sin α) > 0, α € Я икәнен исбатлагыз.
111. Тигезләмәне график юл белән чишегез:
a) sin x = -x;
в) tg x = x, -f < x < 1;
6) tg x ■» \/2 cos x, - < x < ;
r) cos x = 1 - X2.
10. Дәрәҗәле, күрсәткечле
һәм логарифмик функцияләр
Функцияләрнең билгеләнү өлкәсен табыгыз (112—114).
112. a) у = V16x - x3 ;
1
_ 1
г) У" 7x’+x-2O ·
113. a)p= Vx2 3* -3*+1 ;
б) у - ^2einx -1 ;
в) у - iog3 (4 - Зх + X3 j;
г)у = log2sinx.
... Jx3-5x+e
114. a)y- y y ;
lg(x + 10)3
б) у « 71ogs cosx ;
ln(3x-2)
г) у = ^lg (Зх2 - 2х).
Функцияләрнең һәркайсының билгеләнү өлкәсен табыгыз
(115, 116).
115. а) у = 2Vx +1 ;
в) у - 2 1g х + 1;
б) у = 51 * - 1;
г) у = 3 х 2;
116. а) р = 2с"1;
в)р= 1 + |log2 х|;
б)у = 2-Ух;
r)y=l + |Vi|.
293 Кабатлауга мәсьәләләр
Функцияләрнең даими тамга аралыкларын табыгыз (117,
118).
117.
118.
а>У-НГ-4;
в) у = 2 - 3*;
а) у = 4х + 2-4\
в) у = ·Τχ + 3 ;
б) у = log4(x + 3);
г) у = ух - 4.
б) у = ]g (х - 2) - 1;
Г) у - 2 Vx.
Бирелгән функцияләр арасыннан җөп һәм так функцияләрне
табыгыз (119, 120).
119. а)у = 5г+5х;
в)у = (|) ;
б) у = 1g (1 - х2);
г) у - χξ'χ.
120. a)j/= J;
б) у = 3* - 3 «;
в) μ = З"**; г) jr ■ Vx4 + 1.
121. Функцияне тикшерегез һәм аның графигын төзегез:
а) у = 2-Ух -1;
б)у = 4*-*-2;
в)у= j log2(x+l); г)у=ух-2 + 1.
Функцияләрнең графикларын төзегез (122, 123).
122. в) у -
г7х-2 + 1: б)У=(|)'*;
и) у - 2 - tix + Ι; г) у = 1 + log2 (х + 2).
123. а) у = 5 |οβ5 (х υ; б)у = logix-l;
2
в) у = 21*1; г) у = log2 х2.
124.
Функциянең иң зур
(әгәр алар булса):
а) у = V36-X2 ;
һәм иң кечкенә кыйммәтләрең табыгыз
б) у = ·
0x7 булганда,~ .
-2 ζ х < 0 булганда, х3 + 1;
в) у = 3 а1П
(х -1)’, -1 х <1 булганда,
log 2 х х 8 булганда.
125. Тигезләмәне график юл белән чишегез:
a) logi х = х - 3 ;
в) log2x = 25x;
б) Vx-2 = I ;
г) 2W = 11-1*1·
294 Кабатлауга мәсьәлалар
126. Тигезсезлекне график юл белән чишегез:
а) log ι х > х - 3; б) -2 £ ;
2 1
в) 2 *^х2+1; г) logi х > 2х- 7.
3
127. у = (log2 3)*п * һәм у = (log3 2)°°·* функцияләренең иң зур
кыйммәтләре тигез булуын исбатлагыз.
128. a) f (х) = -г— - V1 - х2 , f (х0) = 0;
б) f (х) - 1g (х + 15) + Igx, f (х0) = 2 булса, х0 аргументының
кыйммәтен табыгыз.
129. a) f(x) = ι ' I функциясенең R күплегендә кимүен;
б) f(x) = log, Зх функциясенең (0; ®) аралыгында үсүен
исбатлагыз.
§4.
Тигезләмәләр, тигезсезлекләр,
тигезләмәләр һәм тигезсезлекләр
системалары
11. Рациональ тигезләмәләр һәм
тигезсезлекләр
Тигезләмәләрне чишегез (130, 131).
130. а) 3 (х - 2) - 5 = 4 - (5х - 1); б)
в) 7 - 2 (3 - х) = 4(х - 1) + 5; г)
2х - 3 = 5;
4 - Зх = 2 .
131.
15 ’
х-3 3(5-2х)
в) 1 —у- = х - ;
б)
г)
^ + 5=4;
132. а ның нинди кыйммәтләре өчен тигезләмәнең бердәнбер
чишелеше бар; чишелешләре юк; чишелешләре чиксез күп?
а) ах - 2х = 3(х-1); б) a (1 - х) + 2 = Зх - ах;
в) х (2 - а) - х = 5 + х; г) 5 + 3(х + За) = 9а 4- 5.
Тигезсезлекләрне чишегез (133—135).
х-1 . _ . _ _ „ 5х-2 3-х .
133. а) 4- х < 1,5х 4- 3,5; б) —д — > 1;
в) х - 4(3 - х) > 2х + 7; г) 3 + -—< 2х.
295 Кабатлауга мәсьәләләр
134. а) 4х — 3| < 5; б) |2х + 5] ? 1;
в) ^<2; г)4|2-х|^12.
■« ас \ 2х-3 к х + 2 < q
135. а) у > 5; б) |^-ь 4| *
в) (х-4)|5-Зх|<0; г) |2х+ 7|(3-х) < 0.
136. Тигезләмәне чишегез:
a) xz + 2х - 15 = 0; б)7х2+5х = 0;
в)(х-3)(х-2)-6(х-3); г) х2-^+| =0.
137. а нинди кыйммәт алганда тигезләмәләрнең уртак тамырлары
була?
а) х2- ах = 0 һәм х2- х - За = 0;
б) х2 - (а - 1)х = 3 һәм 4х2 - (4а + 3)х + 9 = 0;
в) х2 + ах + 8 = 0 һәм х2 + х + а = 0;
г) 2х2 + (За - 1) х = 3 һәм 6х2 - (2а - 3)х = 1.
138. Тигезләмәнең бер генә тамыры булсын өчен, k ның кыйм¬
мәтләрен табыгыз:
a) (A - 1)х2 + (A + 4)х + k + 7 = 0; б) 9х2 - 2х + k = 6 - Ах;
в) (2А - 5)х2 - (2А - 1)х + 3 = 0; г) ЗАх2 - 6х + А -2 - 0.
139. Зх2 - 5х - 2 = 0 тигезләмәсен чишми генә а) тамырлары сум¬
масын; б) тамырлары тапкырчыгышын; в) тамырларының
квадратлары суммасын; г) тамырларының кублары сумма¬
сын табыгыз.
Тигезләмәләрне чишегез (140, 141).
140. a) =i; б)2х±1+^.=5;
х-1 х-1 * ах + 1
, 2 3 _ 15 . r 14 4 3 з
В* х*+5х 2х-10 х2-25 ’ х2-4 (2-х)2 (х + 2)2
141. а) -Г- + -Г 2> б)2х4-5х2 + 2 = 0;
х2 + 4 х2 + 5
в) ί—V-з(—) + 2 =0; г) I —= 2,5.
\ х ) \ х I х х-+1
Тигезсезлекләрне чишегез (142—144),
142. а) 2х2 + 6х + 17 > 0; б)х2-3,2х<0;
в) (Зх - 2)2 - 4х (2х - 3) > 0;
г) (6х - 1) (1 + 6х) + 14 < 7х (2 + 5х).
143. а) > 0;
х-3
\ х~2 п.
В) (х-3)(х-5) °’
б)
г)
х2 + 2х-3 Л
ί 0;
х2-2х+8
х2+5х+4 θ
х2-5х-6
296 Кабатлауга мәсьәләләр
144. а) (г -1) (г + 2) (х - 3) (х - 4) < 0;
в)^£> 1_.
х-5 1-х
б) х4 - Зх2 + 2 < 0;
г) 1 + — < — .
х2 X
145. Тигезсезлекнең дөреслеген исбатлагыз:
а) т + — 5 4, т > 0 булганда; б) — т - ί 1;
т 1-» т2
в) г ♦ ~ > 2, а > 0, Ь > 0 булганда;
О 41
г) £ < , α > 0, fe > 0, с > 0, а < Ь булганда.
0 р + с
12. Иррациональ тигезләмәләр һәм
тигезсезлекләр
Тигезләмәләрне чишегез (146—149).
146. а) х2 + 2х + 10 = 2х-1;
в) ,/17 + 2х-3х2 = х + 1;
147. а) 7х+ 17 - 7^7 = 4;
в) 7Х + 7 + 7Х _2 = 9 ;
б) yjx2 -16 = х2-22;
г) 7*2+9 = х2—11.
б) 27x^1 + 7*-ϊ = 3;
г) 2^/х +Ϊ + |/х +1 = 6 .
146. а) Vx - --== + 72+ х = θ;
' y/ifX
149. а) 7225+ х2 = X2 -47;
в) 7х2 +36 = х2 - 54;
б) Vx + ух -2 = 0;
г) ?/Зх + 1 - 73х +1 = 0 -
б) 7χ-2 = х-2;
г) 7х3 -5х2 +16х-5 = х - 2.
Тигезсезлекләрне чишегез (150, 151).
150. а) 7х2-5 ^2; б) 7(* ” 2)(1 - 2х) > -1 ;
в) у/х2-16^1; г) (Vx - з)(х2 + 1) > 0.
... . I ■> Л 7*2-2х + 3 _ Л
151. a) Jx2 - 6х + 9 > 3 ; б) -— ■ 0 ;
Жг* +х>1
в) 725-20х + 4х2 ζ 1; г) ^2χ-χ2 + 15 (Зх-х2 - 4) С 0.
Кабатлауга мәсьәләләр
13. Тригонометрик тигезләмәләр һәм
тигезсезлекләр
Тигезләмәләрне чишегез (152—158).
152. a) cos х + 2 cos 2х - 1;
в) 2 cos2 х + 4 cos х = 3 sin2 х;
б) 4 sin 2х - 3 sin (2х )= 5;
г) cos2x + 4 sin2 х = 2 sin2 2х.
153. a) sin’x - cos3x = 1 + "Μ ;
в) cos4x - sin4 x - ii-;
2
154. a) cos 4x + 2 cos2 x = 1;
в) cos 3x + sin x sin 2x = 0;
6) cos (f + x) + cos (j - x) = 1;
r) sin (I + x) - sin (f - x) = 1.
6) 4 (1 + cos x) - 3sin24 cos ;
r) 4 (1 - cos x) = 3sin — cos2 <·, .
155. a) cos 2x - cos 6x = 0; 6) sin x + sin 2x + sin 3x = 0;
в) sin x + sin Зх = 0; r) cos (+ 5x) + sin x = 2 cos 3x.
156. a) . 6 , о = 3 - ctg x; 6) 1 + 2 cos 3x cos x - cos 2x = 0;
' Ctg X + ά ° '
®) Ήηχ+Τ = 11 - 2 sin r) ctg x + j^-2.
157. a) tg 3x - tg x - 0; 6) tg x - sin x =2 sin2^;
в) sin x tg x - cos x + tg x; r) sin x + sin 2x = tg x .
158. a) arccos 1+2x = тг! 6) arctg (2x - 1) = - T 5
Ο ό
в) arcsin -^4^ = _ ^ ί r) arctg (2 “ θχ) “ “ *
4 o
Тигезсезлекләрне чишегез (159—162).
159. a) sin( \
б) V3tg(f-x)> -1;
в) sin 2 x sin у - cos 2x cos > у;
r) sin 3x cos x + sin x cos 3x $ Л— .
160. a) 2sin2x ζ 1; 6) 3 tg22x 1;
B)4cos2xi3; r)tga|-l>0.
298 Кабатлауга мәсь»лал»р
161. a) |cos х - 1| ζθ,5;
В) |sin2x + || <i j;
162. a) sin х - -Уз cos x;
в) sin x + cos x < 1;
6) sin x < cos x;
r) tgx + ctg x > 0.
6) log o,5 sin x > 1;
r) logjj cos x > -1.
14. Күрсәткечле тигезләмәләр һәм
тигезсезлекләр
Тигезләмәләрне чишегез (163—167).
163. a)(O,2)'2-lto iTS= 5^5; б) 2х’-3· 5х’ 3 = 0,01 · (10х ψ;
Β)2χΙ-6χ+0·ί г) — = -32L·,
7 16ч/2 2-1Ь б12’12'
164. а) 5Эх-2 · б3*"’- 3 · 53х 2 = 60; б) 4х-3х 0·5 = 3χ+0·δ - 22х~1;
в) 2Sxl +25х'2 + 23х"3 = 896; г) 52х'1 + 22х - 52х-22х + 2.
165. а) 9х’ *-36 · 3χ2'3+ 3-0: б) 5Эх+1 + 34 · 52х- 7 ■ 5х;
в) 16х - 50 · 22х = 896; г) 7“х-8 · 7^*+ 7 = 0.
166. а) 3 · 4Х+ 2 · 9х = 5 · 6х; б) 8Х + 18х = 2 ■ 27х;
в) 2 · 25х - 5 · 10"+ 2 · 4х = 0; г) 3 · 16х+ 2х · 81х = 5 ■ 36х.
167. а) З2^ + З2^-1- З2^"2 = 11; б) 5 ’*»2χ-25 ?°·χ=0; ,
в) 2,1П’Х + 2С“’Х = 3; г) 3 ■ 91 + 61 = 2 ■ 4 * .
Тигезсезлекләрне чишегез (168—170).
168. a) > (|)а + Х ; б) 3χί*χ < 10“β;
в) 3 ’ (т£·) <9: г)4х2+х-11>5’<*!4.
169. а) 0,04х - 26 · 0,2х + 25 < 0; б) 9х - 84 · 3 2х + | > 0;
и
в)4х-10-2х + 16<0; г)22х+1 + (|)”
170. а) х2 · Зх - Зх+* < 0; 6)3,7 х*4 >1;
в) х2 · 5х-52+х < 0; г) 2Х + 2 - 2Х + 3 - 2Х*4 > 5Х + 1- 5х + 2<
299 Кабатлауга масьәлаләр
15, Логарифмик тигезләмәләр һәм
тигезсезлекләр
Тигезләмәләрне чишегез (171—175).
171. a) logj х = 4-31og3x; б) |lg(2x -1) = 1 - lg s/x-9;
в) log3 λ/χ-5 + log3 >/2x -3 = 1;
г) 3 lg2 (x - 1) - 10 lg (x - 1) + 3 - 0.
172. a) 2 log, (lg x) = log, (10 - 9 lg x);
б) lg (3' + x - 17) = x lg 30 - x;
в) 2 lg (lg x) - lg (3-2 lg x);
г) x - x lg5 = lg (2* + x - 3).
173. a) log,x + j^-2 = 5; 6) log3x + log^ x - log l x = 6;
Кж 3
B) log^ x + log* 1=3; r) log^ x + 4 logr2 + log8x = 16.
174. a) x V’2 - 8; 6) x· - 125x2;
в) x'<x= 10 000; г)х,в«*'-4
175. a) 3 log2 sinx + log2 (1 - cos 2x) = 2;
б) log0, sin 2x + lg cos x = lg 7;
в) log, 5^*2 - (x - 4) log, 5;
r) lg (3 · 5* + 24 · 20х) = x + lg 18.
Тигезсезлекләрне чишегез (176—179).
176. a) log2 (x2 — x — 4) < 3; 6) log^.j (5 - 2x) > 2;
в) lg(x2-x + 8) > 1; r) log^_j(3-2x) < 2.
177. a) 2 log2 x < log2 (x + 3);
б) logi (10 - x) + logi (x - 3) > -1;
β β
в) logi(x-2)+ log±(12-x) >-2;
a 3
r) log0r5 (4 - x) log0 s 2 - l°£o.$ (*“!)·
178. a) lg(x2 + x - 6) - lg(x + 3) < lg3; 6) log3 yy < 1;
в) ln(x2 + 3x - 10) - ln(x - 2) > In 4; r) log3 yy ζ 1.
179. a) log2 (4x - 5 · 2X + 8) > 2; 6) log2»., x + 6 > 5 log0iS x;
в) lg2 x lg x + 2; r) log i (6X+1 - 36*) > -2.
300 Кабатлауги масыъталәр
16. Рациональ тигезләмәләр һәм
тигезсезлекләр системалары
Тигезләмәләр системасын чишегез (180—183).
180. а) |2х + Зу = - 1
|бх + 4у = 1;
х + 2у =7,
2х Зу = 5;
£ + £ =12
х х 6 ’
х + у = 5;
Ϊ =2,
181.
182.
183.
в)
а)
в)
а)
в)
а)
в)
(х - у)2 + у2 = 1;
(х - у)(х2 - у2} = 45,
х + У = 5;
х2у3 = 16,
х3у2 = 2;
х3 + у3 = 7,
х3у3 = -8;
х3 + у3 = 9,
ху = 2;
б)
г)
б)
г)
Зх - 9у =12,
4х - 12у =16;
|5х - 8у = 0,
[х - 1,6у = 1.
х - у = 1,
х3 - у3 = 7;
I х3 + у3 =35,
[х + у = 5.
б) |х2у3 + х3уг = 12,
|х2у3 -х3у2 = 4;
г) х2 - ху = 28,
у2 - ху = -12.
б) I х2 + у4 = 5,
ху2 = 12;
— + — = 5,
х у
г)
.2 у.
184. а нинди кыйммәткә ия булганда тигезләмәләр системасының
бердәнбер чишелеше бар; чишелешләре юк; чишелешләре
чиксез күп?
a) ix-5y = 7,
[αχ - у = -3;
в) [χ + ay = α,
Зх - 2y = -6;
б)
г)
х + 2у = а,
2х + 4у - 5;
х - У = 2,
2х - 2у = 2а.
185. Тигезсезлекләр системасын чишегез:
х+1 х+4 х-
Х 2 3 4
1,5х-2,5 < х;
а) 2х > 3
| + |(χ_7)<3ψ0;
б)
301 Кабатлауга мәсьәләләр
в)
x + l X ъ Х-1 „ л
——-х-2,
0,5х < 2 - х;
г) [2(3х - 1) < 3(4х + 1) +16,
4(2 + х) < Зх + 8.
17. Иррациональ тигезләмәләр системалары
Тигезләмәләр системасын чишегез (186—188).
186. a)
Ух - Уу -4,
б)
ΗΊ
+
II
00
•
2Ух + 3^y = 18;
4χ ■ 4у -15;
в)
зУх - 4у ~ 8,
г)
/ху = 12,
•
Jx + 2^/y = 19;
Ух + Уу =7.
187. a)
х-Уу ~ y4x = 30,
б)
х + у - Уху= 7,
Ух + Уу = 5;
ху = 9;
в)
и!
+
*Ti
II
o>
·*
г)
ху = 64,
X - У = 12;
х - у + 4ху= 20.
188. a)
4x + Уу - 26,
б)
4х-4у = з|.
Ух + Уу = 6;
ху = 1;
в)
4χ - У у = 5,
г)
«
1
11
+
t£-^ = i;
txy = 8.
18. Тригонометрик тигезләмәләр
системалары
Тигезләмәләр системасын чишегез (189, 190).
189. a) isin х cos у = 0,25, б) ίχ-ys-l*
[siny cosx = 0,75; |созг _ cog2 = θ.
в) i4sinxsiny = 3, г) sin2 χ = COSXCO9y>
|tgxtgy-3, j cos2 x = sin x sin y.
190. a) itgx + tgy = 3,
cosx cosy =
6) χ + у = ,
. “ z
sinx + cos2y = -1;
302 Кабатлауга мэсьалаләр
в)
sin х sin у =4,
w 4 ’
ctg x ctg у = 3;
г)
cos 2y + cos x = 1,
x + y = l·
19. Күрсәткечле һәм логарифмик
тигезләмәләр системалары
Тигезләмәләр системасын чишегез (191 —196).
191. a)
9I+tz ~729,
З**'’1 = 1;
в)
(>/5)"'' = 25,
2βμ-χ-1 _ J.
192. a)
4log<21 — у = —1,
52Х-» +5- =5,2;
в)
3ΐο«3(χ + μ) _ 2,
22ж + » ·~ 16;
193.
a) З1-7» = 63,
6)
2Ж - 2* = 16,
x + у = 9;
Зж + Зу = 28,
x-y = 3.
2Ж +3" = 17,
2*42 -З**’ = 5;
г) ilog^ (y-x) = 4,
13* +2-3*'-2 =171.
в)
|3Ж + 7*' = 16;
4Ж · 4“ = 64,
4Ж + 4» = 63;
6)
r)
194.
а)
Igx - \gy = 1,
lg2 x + lg2 у = 5;
в)
I lg х - lg у = 7,
I Igx + Igy = 5;
log2 (*2 + У2) = 5>
21og4 x + log2 у = 4;
log2(x +1) = log2 (y + ‘J,
log2x-21og2 (y-|) = 0·
195. a)
в)
У - log3 x = 1,
х» = 312;
log5x + 3,e«’» = 7,
х» = 512;
6) = 15,
log3 (x2 -y2)-log3(x -y) =0;
О 9(.
5 v ' = 2Ә,
log5(x2 -y2) = logs(x + y)·
303
Кабатлауга масьаләләр
196. a) log< х - log2 у = О,
х2 - 2y2 = 8;
в) log9 x - log3 у = 0,
x2 - by2 + 4 = 0;
б) 32Л-Л _ 81,
lg Jxy = 1 + lg3;
r) 2log2x-3*'= 15,
З* log2 x = 21og2 x + 3*+1.
20. Тигезләмәләр һәм тигезләмәләр
системалары төзүгә мәсьәләләр
197. Автобус яңа расписание буенча 325 км араны элеккегә
караганда 40 мин ка тизрәк үтә. Автобус элекке расписаниедә
каралган уртача тизлеген 10 км/сәг кә арттыра. Автобусның
яңа расписание буенча уртача тизлеген табыгыз.
198. Акмый торган суда тизлеге 15 км/сәг булган моторлы көймә,
агым уңаена 139^ км араны үтеп, кире кайткан. Әгәр ул
барлык юлны 20 сәг тә үткән булса, елганың агым тизлеген
табыгыз.
199. Поезд 220 км араны билгеле бер вакытта үтәргә тиеш иде.
2 сәг баргач, ул 10 мин туктап торырга мәҗбүр була
һәм, калган юлны билгеләнгән вакытта үтү өчен, тизлеген
5 км/сәг кә арттыра. Поездның баштагы тизлеген табыгыз.
200. Ике теплоход очрашканнан соң, аларның берсе — көньякка,
ә икенчесе көнбатышка таба китә. Очрашудан соң 2 сәг
үткәч, алар арасындагы ераклык 60 км була. Әгәр берсенең
тизлеге икенчесенекеннән 6 км/сәг кә артыграк икәне
билгеле булса, һәр теплоходның тизлеген табыгыз.
201. Аралары 390 м булган ике ноктадан бер-берсенә каршы ике
җисем хәрәкәт итә. Җисемнең берсе беренче секундта 6 м
юл үтә, ә аннан соңгы һәр секундта алдагысына караганда
6 м га күбрәк үтә. Икенче җисем 12 м/с тизлек белән тигез
хәрәкәт итә һәм беренче җисемгә караганда 5 с ка соңрак
хәрәкәт итә башлый. Алар беренче җисем хәрәкәт итә
башлаганнан соң ничә секунд үткәч очрашырлар?
202. Тимер юл магистрале төзелешендә төзүчеләр бригадасы план
буенча берничә көндә 2160 м3 балчык күчерергә тиеш иде.
Беренче өч көндә бригада план буенча билгеләнгән көнлек
норманы үти, ә аннан соң һәр көн норманы 80 м3 га арттырып
үти һәм шуңа күрә срогыннан бер көн элек 2320 м3 балчык
күчерә. Бригаданың план буенча көнлек нормасы күпме
булган?
203. Эшчеләрнең ике бригадасы, бергә эшләп, тәҗрибә учас¬
тогында агач утыртуны 4 көндә төгәлләгән. Бер бригада үзе
генә бу эшне икенчесенә караганда 6 көн тизрәк төгәлли
304 Кабатлауга мәсьәләләр
алса, ал арның һәркайсына бу эшне башкару өчен ничә көн
кирәк булыр иде?
204. 60 т йөкне ташу өчен берничә машина кирәк була, һәр
машинага планда каралганнан 0,5 т га кимрәк төяү сәбәпле,
өстәмә рәвештә тагын 4 машина сорала. Башта ничә машина
планлаштырылган була?
205. Ике кисек җизнең массасы 30 кг. Беренче кисәктә — 5 кг,
ә икенчесендә 4 кг саф бакыр бар. Әгәр икенче кисәктә
бакырның концентрациясе беренчесенә караганда 15% ка
артык булса, җизнең беренче кисәгендә бакыр ничә процент?
206. 40 г тозы булган эремәгә 200 г су өстәделәр, шуннан соң
аның концентрациясе 10% ка кимеде. Эремәдә күпме су
бар һәм аның концентрациясе нинди булган?
207. Ике автомашина бер пункттан бер үк вакытта һәм бер үк
юнәлештә юлга чыгалар. Машиналарның берсе — 50 км/сәг,
икенчесе 40 км/сәг тизлек белән хәрәкәт итә. Ярты сәгатьтән
соң шул ук пункттан шул ук юнәлештә өченче машина юлга
чыга. Ул беренче машинаны икенчесенә караганда 1 сәг
30 мин ка соңрак узып китә. Өченче машинаның тизлеген
табыгыз.
208. Хәрәкәтсез күзәтүче яныннан даими тизлек белән 7 с та үткән
һәм шул ук тизлек белән озынлыгы 378 м булган платформа
буйлап үтү өчен, 25 с сарыф иткән поездның тизлеген һәм
озынлыгын табыгыз.
209. Аралары 50 км булган А һәм В пунктларыннан бер үк
вакытта бер-берсенә каршы ике җәяүле чыга, 5 сәг тән соң
алар очрашалар. Очрашканнан соң, А дан В га баручы җәяүле
тизлеген 1 км/сәг кә киметә, ә икенчесе 1 км/сәг кә арттыра.
Беренче җәяүле В га, икенче җәяүле А га барып җиткәнгә
караганда, 2 сәг кә иртәрәк килеп җитә. Һәр җәяүленең
баштагы тизлеген табыгыз.
210. Заводта А тибындагы бер электр двигателен җитештерү
өчен — 2 кг бакыр һәм 1 кг кургаш. В тибындагы бер электр
двигателен җитештерү өчен 3 кг бакыр һәм 2 кг кургаш
тотыла. Әгәр 130 кг бакыр һәм 80 кг кургаш тотылган
булса, электр двигателенең һәр тибы ничәшәр данә җитеш¬
терелгән?
211. Ике эшче бергә бер эшне 12 көндә үти алалар. Әгәр эшнең
яртысын — бер эшче, ә аннан соң икенче яртысын икенче
эшче үтәсә, бу эш 25 көндә тәмамланыр иде. Һәр эшче бу
эшне үзе генә ничә көндә башкара ала?
212. Тыгызлыклары 1,2 г/см3 һәм 1,6 г/см3 булган ике сыек¬
лыктан 60 г катнашма ясалган. Әгәр 8 см3 катнашманың
массасы катнашмадагы җиңелрәк сыеклыкның барлык
массасы кадәр булса, һәр сыеклык ничәшәр грамм алынган
һәм катнашманың тыгызлыгы күпме?
305
Кабатлауга мәсьәләләр
213. Эретмәне 3 кг чиста көмеш белән эреткәндә, 90% комеше
булган эретмә табалар, ә аны 90% көмеше булган 2 кг эретмә
белән эретеп, 84% масса өлеш көмеше булган эретмә табалар.
Көмешнең баштагы бакыр белән эретмәсендәге массасын һәм
масса өлешен (процентларда) исәпләгез.
214. Озынлыгы 60 м булган әйләнә буйлап ике нокта бер үк
юнәлештә тигез хәрәкәт итә. Нокталарның берсе икенчесенә
караганда тулы әйләнешне 5 с ка тизрәк ясый һәм минут
саен аны куып җитә. Нокталарның тизлекләрен табыгыз.
215. Икеурынлы уңай санның цифрлары квадратлары суммасы
13 кә тигез. Әгәр ул саннан 9 ны алсаң, шул ук цифрлар
белән язылган кире тәртиптәге сан килеп чыгар. Ул санны
табыгыз.
216. Квадратлары аермасы 55 кә тигез булган натураль саннарның
барлык парларын табыгыз.
§ 5.
Чыгарылма, башлангыч функция,
интеграл һәм аларның кулланылышлары
21. Чыгарылма
217. a) f(x)- |х2 , х0 = 1 , Δχ = 0,1;
б) f(x) = Vx - 1 , х0 - 2 , Δχ - 0,21;
в) /(х) = 3-2х, x0 = 2, Δχ = 0,2
булса, f функциясе өчен чагыштырмасын табыгыз.
218. a) f (х) = 1 - 4х, х0 = 3; б) f(x) = 1,5 х2, х0 = 2;
в)/(х) = Зх + 2, х0= 5; г) f(x) = х3 + 1, х0=-1
булса, билгеләмәдән файдаланып, х0 ноктасында f функция¬
сенең чыгарылмасын табыгыз.
Функцияләрнең чыгарылмаларын табыгыз (219—222).
219. а) /(х)= |х4-|х3+|х2-х + 5;
б) f (х) = (4 - х2) sin х;
в) f (х) = (х2 + 5) (х3 - 2х + 2);
г) =
Соа г
2-х4 ’
306
Кабатлауга мәсьәләләр
220. a)f(x)=-L-Vx +J=; б)/(x) = (2 - Vi) tg x;
x1 tlx ' '
β)Πχ)“Τ27: γ^<χ>=Γ^7·
221. a) f (x) = 2* + 1g x; 6) f (x) - e * + 2 log, 2x;
в) f(x) = x3 · 5*; r)/(x)= lnx .
ex+e *
222. a) f (x) = sin 3x + cos 5x; 6) f (x) = Vl + x2 + — ί
(2x-l)3
в) f (x) = (3 - 2x«)»; r) f (x) = 1g (3x) - 3tg (2x -.
223. a) fix) = x4 - 2x2 + 1; 6) f(x) = 1,5 sin 2x - 5 sin x - x;
в) f (х) “ - у- + Цр- - 9x; г) / (х) = x + cos 2 x
булса, f (x) = 0 тигезләмәсен чишегез.
224. Функция график белән бирелгән (153 нче рәсем).
1) Билгеләнгән нокталарның кайсыларында
a) f (х) >0; б) f (х) <0; в) f (х) = 0 икәнен күрсәтегез;
2) a) f (х) > 0; б) f (х) < 0; в) f (х) = 0 булган аралыкларны
күрсәтегез.
3) (a; Ь) интервалының кайсы нокталарында f функциясенең
чыгарылмасы юк?
153 нче рәсем
307 Кабатлауга мәсьәләләр
154 нче рәсем
Чыгарылмаларның кыйммәтләрен бирелгән нокталарда
чагыштырыгыз (225, 226).
225. а) һәм х2; б) xt һәм х3; в) х2 һәм х4; г) х3 һәм х5 (154 нче
рәсем).
226. a) X) һәм х2; б) хэ һәм х8; в) х4 һәм xs; г) х2 һәм х4 (155 нче
рәсем).
227. и, V, w функцияләре х ноктасында дифференцирланалар.
(и, и, w)' = и' V w + и υ' и> + и υ w' икәнен исбатлагыз.
22. Чыгарылманы функция тикшерүдә
куллану
228. Функциянең х( һәм х2 нокталарындагы якынча кыйммәтен
исәпләгез:
а) f(x) = jx’-x, х,- 2,0057, х2 = 1,979;
б) f(x) = 2 + 4х-х2 + |х«, х1 = 3,005, х2-1,98.
229. Аңлатманың якынча кыйммәтен исәпләгез:
а) 79,009 ; б) 1,000115; в) 0.999 s; г) 78,008 .
Функцияләрнең үсү һәм кимү аралыкларын, максимум һәм
минимум нокталарын табыгыз (230, 231).
230. a) f (х) = |х3 + 4х2 - 7х + 18;
3
В)/(Х) =
231. a) f (х) = cos 2 х - 2 cos х;
в) f (х) = 2 sin х + cos 2 х;
6)/(r)=f^;
г)/(х)=5^.
6)/(x) = 2-sinf;
г) f (х) = Зх - cos 3 х.
Функцияне тикшерегез һәм
234).
232. a) f (х) = х2 (х - 2)2;
аның графигын төзегез (232—
6)Г(Х)= Ι + f;
в) f (х) - х3 - Зх2 - 9х;
308 Кабатлауга мәсьәләләр
233. а)/(х) = 1 - 2 sin 2х;
б) f (х) = cos2 х - cos х;
в) /(x) = 3-cos|;
234. a) f (х) = Vx In х;
в)/(х) = 2«*
235. f функциясенең бирелгән
кыйммәтләрен (әгәр алар
а) / (х) = 18х2 + вх3 - Зх\
б) f (х) = 2 cos х - cos 2х,
г) f (х) = sin2 х - sin х.
б)/(х)=
г) f (х) = х - In х.
аралыкта иң зур һәм иң кечкенә
булса) табыгыз:
(I; 3J;
|0; π];
г) f(x) = sin χ-χ, [-π; π].
236. 10 санын саннарның кублары суммасы а) иң зур; б) иң
кечкенә булырлык итеп, тискәре булмаган ике кушылу¬
чының суммасы рәвешендә күрсәтегез.
237. Турыпочмаклы өчпочмакның катетлары озынлыгы суммасы
20 см га тигез. Өчпочмакның мәйданы иң зур булсын өчен,
катетлар нинди озынлыкта булырга тиеш?
238. Параллелограммның диагональләре озынлыгы суммасы
12 см га тигез. Аның барлык якларының квадратлары
суммасының иң кечкенә кыйммәтен табыгыз.
239. Ике урам буйлап 40 км/сәг һәм 50 км/сәг даими тизлек
белән юл чатына таба ике машина килә. Урамнарның туры
почмак ясап кисешүен искә алып һәм ниндидер вакыт
моментында автомашиналарның юл чатыннан 2 км һәм
3 км ераклыкта (тиңдәшле рәвештә) булуларын белеп, алар
арасындагы ераклык күпме вакыттан соң иң кечкенә булуын
белегез.
240. 1,4 м лы картинаның түбәнге кырые күзәтүче күзеннән
1,8 м биеклектә итеп эленгән. Картинаны карау уңай булсын
өчен (ягъни вертикаль буенча күрү почмагы иң зур булсын
өчен), күзәтүче стенадан нинди ераклыкта торырга тиеш?
241. 4 м лы статуяны биеклеге 5,6 м булган колоннага куйганнар.
Буе (күзгә кадәр алганда) 1,6 м булган кеше, статуяны иң
зур почмак белән күрү өчен, нинди ераклыкта басарга
тиеш?
242. Күләмнәре 16 км3 булган барлык цилиндрлар арасыннан
тулы өслеге иң кечкенә мәйданлы цилиндрны табыгыз.
243. R радиуслы шарга камарга мөмкин булган иң зур күләмле
цилиндрның биеклеген табыгыз.
244. Нигез радиусы R, биеклеге Н булган конус эченә тулы өслеге
иң зур булган цилиндр камарга кирәк. Цилиндрның ра¬
диусын таыгыз.
309 Кабатлауга мәсьәләләр
245. Бирелгән цилиндрны камаучы иң кечкенә күләмле конус
төзергә (цилиндр һәм конусның нигез яссылыклары тәңгәл
киләләр).
246. R радиуслы шарны камаучы иң кечкенә күләмле конусның
биеклеген табыгыз.
247. Конус нигезенең үзәге шар үзәгендә ятарлык итеп, В радиуслы
ярымшарны камаучы иң кечкенә күләмле конус төзелгән.
Конусның биеклеген табыгыз.
248. 40 см диаметрлы түгәрәк бүрәнәдән, кисемендә нигезе Ь,
биеклеге һ булырдай турыпочмаклык килеп чыгарлык итеп,
балка кисеп алырга кирәк. Балканың ныклыгы Ъһ2 ка
пропорциональ. Ь һәм һ ка нинди кыйммәтләр биргәндә,
балканың ныклыгы иң зур булыр?
249. Тәрәзә ярымтүгәрәк белән тәмамланган турыпочмаклык
формасында. Бирелгән периметр өчен мәйданы иң зур булган
тәрәзәнең үлчәнешләрен табыгыз.
250. Әйләнә өстендә А ноктасы бирелгән. А ноктасындагы орын¬
мага параллель булган ВС хордасын ABC өчпочмагының
мәйданы иң зур булырлык итеп үткәрегез.
251. Бирелгән тигезьянлы өчпочмакка камаулы түгәрәкнең ра¬
диусы иң зур булсын өчен, бу өчпочмакның мәйданы бил¬
геле булганда, аның түбә янындагы почмагы нинди булырга
тиеш?
252. у = х2 параболасында А (2; 0,5) ноктасына кадәрге ераклыгы
иң кечкенә булган ноктаны табыгыз.
253. Өчпочмаклы төзек призманың күләме V га тигез. Призманың
тулы өслеге иң кечкенә булсын өчен, нигезенең ягы нинди
булырга тиеш?
23. Чыгарылманы физикада һәм
геометриядә куллану
254. Туры буенча ике нокта хәрәкәт итә. Әгәр:
а) xt(i) = 2ft3. x2(t) = 2t-3;
б) х,(О = 9г2+1, x2(t) = t3
булса, беренче ноктаның тизлеге икенчесеннән кимрәк
булгандагы вакыт аралыгын табыгыз.
255 Җисемнең күчәр тирәсендә борылу почмагы вакытка бәйле
рәвештә <p(t) = 0,lt2-0,5t + 0,2 законы буенча үзгәрә. Җи¬
семнең t = 20 с вакыт моментындагы почмакча тизлеген та¬
быгыз. (Почмак радианнарда үлчәнә.)
256. Түгәрәк металл диск җылытканда киңәеп, радиусы 0,01 см/с
ка бертөрле арта. Дискның радиусы 2 см га тигез булган
моментта дискның мәйданы нинди тизлек белән арта?
310 Кабатлсуга мэсьалалэр
257. А пунктыннан арадагы почмаклары 60° булган ике туры буй¬
лап бер үк вакытта ике җисем хәрәкәт итә башлый. Берен¬
чесе — 5 км/сәг тизлек белән тигез, икенчесе s(t) = 2t2 - t
законы буенча хәрәкәт итә. t = 3 сәг моментында алар бер-
берсеннән нинди тизлек белән ераклашалар? (s — кило¬
метрларда, t сәгатьләрдә үлчәнә.)
258. 5 м озынлыктагы АВ кисемтәсенең очлары координаталар
күчәре буйлап шуышалар. А очының күчү тизлеге 2 м/с ка
тигез. А очы координаталар башлангычыннан 3 см ерак¬
лыкта булганда, В очының күчү тизлеге нинди булыр?
259. Вертикаль торучы баскычның озынлыгы 5 м га тигез.
Баскычның түбәнге очы 2 м/с даими тизлек белән шуыша
башлый, t вакыты моментында баскычның югарыгы очы
нинди тизлек һәм нинди тизләнеш белән түбән төшә?
260. Бериш булмаган АВ таякчыгының озынлыгы 12 см. Аның
AM өлешенең массасы М ноктасының А очыннан ераклыгы
квадратына пропорциональ рәвештә үсә һәм, AM = 2 см
булганда, 10 г га тигез. 1) АВ таякчыгының барлык
массасын һәм аның теләсә кайсы ноктасындагы сызыкча
тыгызлыгын; 2) таякчыкның А һәм В нокталарындагы
сызыкча тыгызлыгын табыгыз.
261. Тәгәрмәч борылу почмагы вакытның квадратына пропорцио¬
наль булырлык итеп әйләнә. Беренче әйләнешне тәгәрмәч
8 с та башкара. Тәгәрмәчнең әйләнә башлауга 48 с вакыт
үткәннән соңгы почмакча тизлеген табыгыз.
262. Җисем 10 м биеклектән 40 м/с башлангыч тизлек белән
вертикаль юнәлештә югарыга ыргытылган. Түбәндәге со¬
рауларга җавап бирегез: а) 5с тан соң ул җир өслегеннән
нинди биеклектә булыр? б) Ничә секундтан соң җисем иң
югары ноктага җитәр һәм ул җирдән нинди ераклыкта булыр
(g = 10 м/с2 дип исәпләргә)?
263. у = “ V _1 параболасының кайсы ноктасында орынма абс¬
циссалар күчәренә а) 45°, б) 135° почмак белен авышкан?
264. Орынмалары абсциссалар күчәренә 135° лы почмак белән
авышса, f(x) - х® + ' хг- х - 3 функциясе графигы ноктала¬
рының абсциссаларын табыгыз.
265. f (х) - х3 +1 х2 + х - 3 функциясе графигына теләсә нинди
орынманың абсциссалар күчәрен кисеп үтүен исбатлагыз.
266. f (х) = х5 + 2х - 7 функциясе графигына теләсә нинди орын¬
маның абсциссалар күчәре белән кысынкы почмак төзүен
исбатлагыз.
267. f(x) = (х + 2)2 һәм g(x) = 2 - х2 функцияләре графикларының
уртак ноктасы һәм шул ук нокта аша үтүче уртак орынмасы
булуын исбатлагыз.
311
Кабатлауга мәсьәләләр
24. Башлангыч функция
268. Түбәндәге функцияләр өчен башлангыч функцияләрнең го¬
муми күренешен табыгыз:
a) f (х) = 4sin х + cos Зх; б) f (х) = х2 + х5 + x2 + j3;
вП(х)=2 + -Ц; г)/(х) — Ϊ—.
х ~ 1 соз2 2х sin2 Зх
269. f функциясе өчен графигы М ноктасы аша үтүче башлангыч
функцияне табыгыз:
а) / (х) = I. Л/ (1;2); б) f (х) = х 2 + cosх, М
в) f (х) - х ♦, М (2; -3); г) f (х) = sin 2 х, М (0; 1).
270. Теләсә нинди х ноктасында чыгарылмасы 2х - 3 кә һәм
2 ноктасындагы кыйммәте 2 гә тигез булган функцияне
табыгыз.
271. Абсциссасы х булган ноктадагы орынманың почмакча коэф¬
фициенты Зх2 ка тигез булганда, А(2; 3) ноктасы аша үтүче
кәкренең тигезләмәсен табыгыз.
272. Материаль нокта координаталар турысы буйлап o(t) = sin t х
х cos t тизлеге белән хәрәкәт итә. t = j өчен аның коорди-
натасы 3 кә тигез булса, нокта хәрәкәтенең тигезләмәсен
табыгыз.
25. Интеграл
273. Исәпләгез:
Зя
2
a) j cos (1,5π + 0,5х) dx;
я
Я
6
в) J (cos 3 х - sin 2 X) dx;
η
12
2
б) f (х 2 + х2) dx;
ι
-2
г) J (5 - 6х - X2) dx.
-s
274. Интегралның иң зур һәм иң кечкенә кыйммәтләрен та¬
быгыз:
α 4 Л
Л 2
a) jcos|dx, aeR; б) J cos2xdx,aeK.
о »
275. Түбәндәге сызыклар белән чикләнгән фигураның мәйданын
исәпләп чыгарыгыз:
а) у = 0,5х2 - 2х + 3, у = 7 - х;
б) у = (х - 2)2, у = 4 - х2;
в) у = х2-Зх + 4, у = х+1;
г) у = х2 - 2х + 2, у = 2 + 4х - х2.
Кабатлауга мәсьәләләр
276. у = х + 4 турысы фигураны у= τ,χ2 һәм у = 8 сызыклары
белән чикләнгән фигураларга бүлгәли, һәр фигураның мәй¬
данын табыгыз.
277. у = 2,5 + 2х - 0,5х2, х = -1 сызыклары һәм бирелгән парабола
абсциссасы х = 3 булган нокта аша үткәрелгән орынма белән
чикләнгән фигураның мәйданын табыгыз.
278. у = х2 - 4х + 5 параболасы һәм аның абсциссалары х = 1 һәм
х = 3 булган нокталары аша үткәрелгән орынмалар белән
чикләнгән фигураның мәйданын табыгыз.
279. Квадратның мәйданы аның ике чиктәш түбәсе аша үтүче
һәм бер ягына аның уртасында орынучы парабола белән
нинди чагыштырмада бүленә?
280. а нинди кыйммәткә ия булганда у — х2 4- 4х 4- d (а 0), х — 0,
х = 2 һәм у = 2 сызыклары белән чикләнгән фигураның
мәйданы 12 гә тигез? (Фигураның өске ярымъяссылыкта
ятуы билгеле.) 2
281. /(х) - a sin πχ 4- Ь функциясе/'(2) = 2, J f (x) dx = 4 шарт-
o
ларын канәгатьләндергән а һәм Ь саннары парларын табыгыз.
11
VI
бүлек
Катлаулырак
мәсьәләләр
— “ f
Г
I
§ 1
Саннар. Аңлатмаларның рәвешен үзгәртү
1. Бөтен саннар
1. Исбатлагыз: а) әгәр р — гади сан һәм р > 3 булса, р2 - 1
саны 24 кә бүленә; б) әгәр a + Ь + с саны 6 га бүленсә, а3 + Ь3 + с3
саны 6 га бүленә (а, Ь, с — бетен саннар); в) әгәр а2 + Ь2 саны
7 гә бүленсә, а2 + Ь2 саны 49 га да бүленә (а һәм Ь — бетен
саннар); г) л2 + 5л + 16 саны п теләсә нинди бөтен сан
булганда да 169 га бүленми.
2. а ның нинди бөтен кыйммәтендә х2 + ах + б = 0 тигезләмә¬
сенең ике тамыры да бөтен сан була?
3. Исбатлагыз: а) төзелмә N санының иң кечкенә бүлүчесе
(1 гә тигез булмаган) ν'Λ' нан артмый; б) N — төгәл квадрат
булганда һәм шул вакытта гына N санының так сандагы
бүлүчеләре була.
4. п санының бүлүчеләре санын табыгыз: а) п = 1024 булса;
б) η = 210 булса; в) п = р^р^ ... р“* (α,, α2, ... ак — натураль,
рг, р2, ... , р„ — төрле гади саннар) булса; г) п = 10! (fe! —1 · 2 х
х 3 ·... · k тапкырчыгышның тамгаланышы) булса.
5. а) Төгәл квадратларны 3 кә, 4 кә бүлгәндә нинди калдыклар
булуы мөмкин?
б) Бөтен коэффициентлы квадрат тигезләмәнең дискри¬
минанты 23 кә тигез булуы мөмкинме?
в) Турыпочмаклы өчпочмакның барлык якларының озын¬
лыклары — бөтен саннар. Катетларының озынлыклары так
саннар булуы мөмкинме?
г) 12 урынлы N санының унарлы язылышында 2 һәм 9 цифр¬
лары 2 шәр тапкыр очрый, ә калганнары — берәр тапкыр.
N төгәл квадрат буламы?
6. а) Санның унарлы язылышында 300 берлек һәм берничә
нуль бар (башка цифрлар юк). Бу сан төгәл квадрат буламы?
б) 1987 урынлы а саны 9 га бүленә, а ның цифрлары сум¬
масы — Ь саны, Ь ның цифрлары суммасы — с саны, с ның
цифрлары суммасы — d саны, d ны табыгыз.
7. а) 5 кә; б) 3 кә; в) 9 га бүленүчәнлек билгеләрен исбатлагыз.
314 Катлаулырак мәсьәләләр
Тигезләмәләрне бөтен саннарда чишегез (8—9).
8. а) 3' = 1 +
в) х2 - у2 = 91;
б) 2‘ - 1 = у2;
г) 2* + 1 = у2.
9- а)13х-7у = 6; б) х! + у! = (х + у)1;
в) 27х - 9(/= 15; г) 1! + 2! 4-... + х! - у2.
Ю· γ вакланмасын (биредә I — бөтен сан) нинди бөтен k сан¬
нарына кыскартып була?
11· Бирелгән: lg 16 = 1,20412... . 125100 санының цифрлары са¬
нын һәм беренче цифрын табыгыз.
2. Математик индукция методы
12—15 нче мәсьәләләрнең чишелеше математик
индукция принцибына нигезләнә, бу принципны еш кына ариф¬
метиканың бер аксиомасы буларак кабул итәләр. Әлеге принцип
түбәндәгечә тәгъбирләнә:
Натураль п санына бәйле раслау:
а) ниндидер п = п0 башлангыч кыйммәт өчен дөрес
булса һәм
б) ул п = k (биредә k £ па — ирекле натураль сан)
өчен дөрес дип кабул иткәннән соң, п = k + 1 өчен дә
дөрес раслау чыкса, бу раслау теләсә нинди натураль
п > п0 өчен дә дөрес була.
Тигезләмәләрне математик индукция методы белән исбат¬
лагыз (п е N) (12—13).
12. а)Г + У + У+... + л^"(л+ув + 1);
б) I2 + З2 + 52 + ... + (2n - I)2 = и<2п *2^2!;
в) 1® + 3® + 5® + ... + (2л - I)3 - п2 (2п2 ~ 1);
г) 1 · 11 + 2 ■ 2! + 3 · 3! + ... + п ■ л! = (п + 1)! - 1.
13. я) JL + L + L + + 1 _ "
’ 4 5 * 5 6 т 6 7 *'"* (л+3)(а + 4) “ 4(я + 4) ’
б) 22 + 62 + ... + (4л - 2)2 = .
3
в) _Z_ а. + 7 + + 7 - 1 — 1 ·
’ 1 8 8 15 Г 15-22**··* (Τη-βχΤη + Ι) “ 7л + 1 ’
г) 78 + Г12 + ΪΓ16 * ··· * 7п-(4’п +4) =16“Ti(bl)·
315 Катлаулырак мәсьәлалар
14. Тигезсезлекләрне математик индукция методы белән исбат¬
лагыз (п е N):
a) |sinnx| <n|sinx|; б) +... + > 1;
в) (1 + Л)" > 1 + пһ, теләсә нинди натураль п 2, һ > -1 һәм
һ * 0 өчен (Бернулли тигезсезлеге);
г) (1 + һ)л > 1 + пһ + 1' һ2, теләсә нинди натураль п 3
һәм һ > 0 өчен.
15. Математик индукция методы белән исбатлагыз. Теләсә нинди
натураль п өчен:
а) б2"+1 + 1 саны 7 гә кабатлы;
б) 33п + 2 + 24л +1 саны 11 гә кабатлы;
в) 4" + 15η - 1 саны 9 га кабатлы;
г) 72п 1 саны 48 гә кабатлы.
3. Реаль саннар
16- Теләсә нинди рациональ санны чиксез периодик унарлы
вакланма рәвешендә күрсәтергә мөмкин икәнен исбатлагыз.
17. Теләсә нинди чиксез периодик унарлы вакланманың нин¬
дидер рациональ санның язылышы булуын исбатлагыз.
18. Натураль а саны тулы квадрат булмаса, -Уа ның иррациональ
сан булуын исбатлагыз.
19. Түбәндәгеләрнең рациональ сан булуы мөмкинме:
а) ике иррациональ санның суммасы;
б) иррациональ санның иррациональ дәрәҗәсе?
Саннарның иррациональ булуын исбатлагыз (20—22).
20. a) 73 ; б) </з ; в) lg 5; г) log2 9.
21- а) 7з + 7δ ; б) 72 + 7з ; в) ς1 г-; г) 72 + 7з .
22. a) k^2 + *73 , биредә k һәм р — нульгә тигез булмаган бөтен
саннар;
б) 3,272772777277772... (беренче икелектән соң бер җиде,
икенчесеннән соң — ике, өченчесеннән соң — өч һ. б.,
п нчы икелектән соң — п җиделек һ. б.).
Аңлатмаларны гадиләштерегез (23—24).
23. а) 72 - 73 ; б) >/129 - 5б7б ;
в) 77 + 2710 ; г) ^57 +12715 .
24. а) 7б7-4272 + 719 - б72 ;
б) ү51 - 4777 - ^47 -4733 .
316 Катлаулырак мәсьәләләр
25. Ваклаучыдагы иррациональлектән котылыгыз:
26. Түбәндәге саннар бер үк геометрик прогрессиянең буыннары
булырга мөмкинме?
а) 10, 11,12; 6)81,-36,24.
27. + +? θ - 1(| санының рациональ булуын исбат¬
лагыз.
28. Теләсә нинди М саны өчен
1
суммасы М нан зуррак булырлык натураль п саны табылуын
исбатлагыз.
4. Аңлатмаларның рәвешен үзгәртү
29. Тапкырлаучыларга таркатыгыз:
а)х4 + 4; б)х4 + х2+1; в)х* + х + 1;
г) (х2 + у2)3 + (z2 - х2)3 - (у2 + z2)3;
д) (х + у + г)3- х3-у3- г3;
е) х3 + у3 + z3 - 3 xyz.
30. Бердәйлекне исбатлагыз:
(а2 + Ь2} (х2 + у2) = (ах + by)2 + (ау- Ьх)2.
31. Формулаларны исбатлагыз:
32. α + β + γ = π булуы билгеле, биредә α, β, γ — уңай.
Бердәйлекне исбатлагыз:
а) sin α + sin β + sin γ = 4 cos ” cos cos ;;
б) cos2 α + cos2 β + cos2 γ = 1 - 2 cos α cos β cos γ;
в) cos 2 α + cos 2β + cos 2γ= -1 - 4 cos a cos β cos γ,
г) sin2 α + sin2 β + sin2 γ= 2 + 2 cos α cos β cos γ.
317 Катлаулырак мәсьәләләр
33. Тигезлекне исбатлагыз:
а) arcsin х + arccos х - j , теләсә нинди х € (-1; 1] өчен;
б) arctg х + arcctg х = ; в) cos (arctg x) = , 1 ;
y/1 + x2
r) tg (arccos x) = '*1 ~ T , теләсә нинди х € [-1; 1] һәм х * 0
X
өчен.
Исәпләгез (34—35).
34. а) —-— + ;
cos 290° V3 sin 250е
б) sin8 α + cos6 α, әгәр sin a + cos a = т булса;
в) cos 84* cos 24*cos 48° cos 12°;
r) cos8 a - sin8 a, әгәр cos 2a = т булса.
35. a) arcsin (sin 10);
в) arctg (tg 2);
6) arccos (cos 12);
r) arcctg (ctg 3).
36.
x0 саны arctg =
тигезләмәсенең тамыры булуын тик-
шерегез, xQ =
7 a-ι
7a-ri
37.
α + β + γ— π, = sinY икәне билгеле.
‘ a Ь с
a2 = b2 + с2 - 2bc cos α икәнен исбатлагыз, өстәвенә α, β, γ ның
уңай саннар булмавы да мөмкин.
38. sin 47° + sin 61°-sin 11° - sin 25° - cos 7° икәнен исбатлагыз.
39. a)IogIu = a, log!,u = t>, log2u = c булса, logllw и ны табыгыз,
б) log, 12 = a, log12 24 = b булса, log54 168 не табыгыз.
40. a) х > 1 булса, 2^og2* = x^log*2 икәнен исбатлагыз.
б) Таблица кулланмыйча гына исәпләгез: 2^1овг^ - 3^1оКз2 .
5. Прогрессияләр
41. Тигезләмәне бөтен саннарда чишегез:
£zl+£z?+£z? + ...+ 1=з.
XXX X
42.
Теләсә нинди φ е (0; -j) өчен тигезлекнең дөреслеген ис¬
батлагыз:
1 - tg φ + tg2 φ - tg3 φ + ... -
■J2 cost?
2sin(* + <p) *
Катлаулырак масьәлаләр
43. Геометрик прогрессияне тәшкил итүче дүрт санның сум¬
масы -40 ка, ә аларның квадратлары суммасы 3280 гә тигез.
Бу саннарны табыгыз.
44. Өчурынлы санның цифрлары — геометрик прогрессия,
ә аңардан 400 гә кечерәк санның цифрлары арифметик
прогрессия тәшкил итсә, әлеге өчурынлы санны табыгыз.
45. а ның нинди кыйммәтендә б14 х+ 5,_\ -g, 25х + 25 * саннары
(бирелгән тәртиптә) арифметик прогрессия тәшкил итәрлек
х лар табылыр?
46. х, у, ζ саннары (бирелгән тәртиптә) геометрик прогрессия
тәшкил итәләр, х + у, у + ζ, ζ + х саннары — арифметик
прогрессия. Геометрик прогрессиянең тапкырлыгын
табыгыз.
47. Арифметик прогрессиянең беренче т һәм п буыннарының
суммалары тигез икәне билгеле, ягъни Sm = S„. Sm + n ны
табыгыз.
48. Геометрик прогрессиянең беренче п буынының суммасы А
һәм аларга кире булган зурлыкларның суммасы В (В * 0)
икәнлеге билгеле булса, беренче п буынның тапкырчыгышын
табыгыз.
49. Арифметик (а„) һәм геометрик (б„) прогрессияләрнең
буыннары = t»40 >0, aw = bw > 0 шартларын канәгатьлән¬
дерә. Кайсы зуррак: а50 яки bw?
50. Сумманы табыгыз:
a) 1 + 11 + ...+ 111...1; б) х + 2х2 + Зх3 + ... + пх";
п. берлек
В’ fe(A + l) + (fe + l)(A + l) ’ (fe + п -l)(fc + n) ’
г) sin х + sin 2x + ... + sin nx.
§2.
Элементар функцияләр һәм аларның
үзлекләре
6. Функцияләрне тикшерү
51. Функциянең билгеләнү өлкәсен табыгыз:
... ~ ^8-2ж-х«
а^-^2Г‘ 6>У= σώχ-ί
. arcsin0,5x , I T~. Г
в) у = —I : г) у = ^cos (sin х)
v*‘-l
д) У “ 1о& .in r cos х; е) у = , 1/——, ..
lg (ι-7χ2-ι)
319 Катлаулырак мәсьәләләр
52, у = f (х) функциясенең билгеләнү өлкәсе — [-1; 2] кисемтәсе.
Функциянең билгеләнү өлкәсен табыгыз:
а) у = / (х) + 1;
г) у = f (2х);
ж)у= |/(х)|;
к)у-/(1 -|х|);
б) у = f (х+ 1);
д) у = f (-х);
з)у = /(|х|);
л) у = f(Vx);
В) У = 2/ (х);
е) У - ~f (х);
и) у = /(1 - х):
м)у = /(х2).
Һәр функциянең кыйммәтләре
өлкәсен табыгыз (53—54),
53.
а) у = cos2 х - cos х;
б) у = >/1 - sin х ctgx ;
в) у = 3 cos х — 4 sin х - 1;
г) У- , .
tg2|+2
54.
а) у = cos2 х - cos4 х;
б)у = [х]2;
в) у = 3 sin2 х - 4 sin х - 2; г) у = · ——у .
55. Функция җөпме (яки такмы)?
а) /(х)=^у; ·Μ(Χ)-Ιβίψ + φτ* + 1);
(/(|г*5Г - {/(*-5)' , /х>1\
ΒΗ(χ)=·ϊ --?у Γ)Ηχ)-Ιοβ.(ττϊ).
56. а) Билгеләнү өлкәсе 0 ноктасына карата симметрик булган
теләсә нинди f функциясе өчен у = ——функциясе җөп,
Г(х) f( ж)
Э У = 2 функциясе так булуын исбатлагыз.
б) Билгеләнү өлкәсе 0 ноктасына карата симметрик булган
теләсә нинди функцияне җөп һәм так функцияләрнең
суммасы рәвешендә (өстәвенә бер генә рәвештә) күрсәтергә
мөмкин булуын исбатлагыз.
в) Бер үк вакытта җөп һәм так булган барлык функцияләрне
табыгыз.
57. f Һәм g функцияләре — уртак Т периоды белән периодик
функцияләр, у = f (х) + g(x) һәм у - f (x)g(x) функциялә¬
ренең Т периодлы периодик функцияләр булуын исбатлагыз.
58. Барлык саннар турысында билгеләнгән һәм уртак периоды.,
булмаган ике өзлексез периодик функция суммасының
периодик булмавын исбатлагыз.
59. а) Барлык рациональ саннар — бу функциянең периоды,
ә барлык иррациональ саннар периоды булмаган; б) барлык
иррациональ саннар — бу функциянең периоды, ә барлык
рациональ саннар периоды булмаган периодик функцияләр
бармы?
320 Катлаулырак мәсьәләләр
60. Функциянең периодик булмавын исбатлагыз:
a) f (х) = cos х cos(x\/2 j; б) f (х) = cos х + cos (х\
в) f (х) = sin xz; г) f (х) - sin Vx .
61. Функциянең иң кечкенә уңай периодын табыгыз:
а) у = cos3 х; б) у = ^|sin2x| ;
в) y = cos(xx/2) + cos г)у = {-1-2х}.
62. Функциянең периодик булмавын исбатлагыз:
a)y=Vx; 6)y = sin|x|;
в) у = х2 + х + 1; г) у = sin х + sin (х ^2 ).
63.
64.
65.
66.
67.
68.
69.
70.
Саннарны чагыштырыгыз:
a) log23 һәм logb8; б) logB 10 һәм 1g 11;
в) 23'00 һәм З2'50; г) cosec һәм 4 (1 - sin .
Саннарны үсү тәртибендә урнаштырыгыз:
а) sin 4°, cos 2, tg 3, ctg 6;
б) sin 10°, cos 275°, tg 190°, ctg 100°.
у = f (х) функциясенең I аралыгында 1) үсүе; 2) кимүе бил¬
геле. Әгәр: a) k > 0; б) k < 0 булса, у — kf (х) функциясе
I аралыгында үсүче (яки кимүче) функция буламы?
f — барлык саннар турысында үсүче һәм уңай функция
булсын.
Түбәндәге расламаны исбатлагыз:
а) у = Г (х) функциясе R да үсә;
б) у = уууу функциясе R да кими;
в) у = ү/(х) функциясе R да үсә;
г) у = 1g /(х) функциясе R да үсә.
Әгәр f: а) җөп; б) так; в) периодик функция икәнлеге билгеле
булса, п ның нинди кыйммәтләрендә f функциясенең тогәл
п экстремумы була?
f (х) = ах + Ь рәвешендәге функцияләр арасыннан теләсә нин¬
ди х өчен: a) f (f(x)) = f (х); б) f (f(x}) = x булганнарын
табыгыз.
Әгәр: а) / (х) = 3 - х; б) f (х) = у-; в) f (х) = -ру булса, (х) =
= f (/(X)). f3 (Х) = f (Н/(х))) һ. б., fn (х) = f ... (f (х)...))
функцияләрен һәм / (х) ның билгеләнү өлкәсен табыгыз.
1 вх+6 ,
У = У7ТТ’ °' У = ~^d РәвешенДәге Функцияләр арасыннан
үзләренең кире функцияләре белән тәңгәл килүче барлык
функцияләрне дә табыгыз.
321 Катлаулырак мәсьәләләр
71. [0; 1] кисемтәсендә билгеләнгән һәм ике экстремум ноктасы
булган кайтма функциягә мисал китерегез.
Бирелгәнгә кире функцияне табыгыз. Табылган функция¬
ләрнең графикларын төзегез (72—73).
72. а)у = Vx + 1 ; 6)y = lg(l-x); в) у = ; г) у = yftgx .
73. а) у = sin х, х е [-б) у = cos х, х е (0; π);
B)y = tgx, г) у = ctg х, х € (0; π).
7. Функцияләрнең графиклары
74. а) Җөп функциянең графигы ординаталар күчәренә карата
симметрик; б) так функциянең графигы координаталар
башлангычына карата симметрик булуын исбатлагыз.
75. 156 нчы рәсемдә сурәтләнгән функцияләрнең графикларын
иң кечкенә уңай Т периодлы периодик функция график¬
ларына кадәр өстәп төзегез (әгәр бу мөмкин булса), шуның
өстенә алар: а) җөп; б) так булсын.
76. 157 нче рәсемдә барлык саннар турысында билгеләнгән пе¬
риодик функция графигының бер өлеше сурәтләнгән, / функ¬
циясенең иң кечкенә уңай периоды нинди булыр?
156 нчы рәсем
157 нче рәсем
322 Катлаулырак мәсьәләләр
158 нче рәсем
у = f (х) функциясенең графигы сурәтләнгән (158 нче рәсем).
Функция графигының эскизын төзегез (77—78).
77. а) у = f (~2х); б) у = f (|х|); в)!/ = Г(1-х); г) у = |f(x)|.
78. а)у--2/(х); б)Г?^!
в) у — f(2x + 4); г) у - -/ (- |х|).
79. f функциясе графигы ярдәмендә <р функциясе графигы
табылырга мөмкин булган рәвешүзгәртүләр эзлеклелеген
табыгыз:
а) f (х) = sin х, φ (х) = sin х + cos х;
б) f (х) = sin2 х, φ (х) = sin4 х + cos4 х.
80. Теләсә нинди вакланмалы сызыкча у = (с * 0 һәм
'' ad - be Φ 0) функциясенең графигы у = — функциясе графи¬
гыннан параллель күчерү ысулы ярдәмендә табылырга мөм¬
кин булуын исбатлагыз, k коэффициентын табыгыз.
81. R да функциянең иң зур һәм иң кечкенә кыйммәтләрен
табыгыз:
a) f (х) = 2 cos 2 х + sin2 х; б) f (х) - , 1 - ;
V2x2-4x+3
в) f (х) = 2 sin2 х - cos 2 х; г) f (х) = cos2 х + cos х + 3.
82. Функциянең үсү (кимү) аралыкларын, максимумнарын һәм
минимумнарын табыгыз:
. « . , « хг+х-2
а) у = 2 sin х + 3 cos х; б) у = —;—■— ;
в) у = cos 2 х - 2 cos х; г) у = lg sin х.
83. Функция графигының асимптоталарын табыгыз:
. х х2 + 1 . х2 . *’+<
а)1/ = —2; б)у-—; в){/=^п; г)у=—.
323 Катлаулырак мәсьәләләр
Функциянең графигын төзегез (84—85).
84. а) у = {1,5 х - 1}; б) у = 1 ’
. Jl - cos2 х .. Jl + 2x + x2
в^= cosz ; l)j/ X + 1 ·
85. а) у = sin x7cos2 х + cos x7sin2 х;
б) у = 71 - cos2 х + sinx;
в) у — sin2(7tg *) + cos2x(7tgx); г) у = 71 — sin2 х + cos х .
Функциянең графигын төзегез (86—89).
86. а) у = |{х} - ||; б)у = 2‘*··; в)у= 2ΐΙοβ2ΐΙ + ι; г) у = log,
87. a)i/=7[x]; б)у=7{х}; в) у = {х}2; г) у = {х2}; д) у = t·
88. а) у — 4х + 7—х ;
в) у = ctg I sin х ;
89. а) у = sin (arcsin х);
в) у = cos (2 arccos х);
б) у = 71о£2«ю cos2000 х ;
г) у = {cos х}.
б) у = arcsin (sin х);
г) у = arctg (tg х).
90. Графикларның эскизлары ярдәмендә тигезләмәнең чише¬
лешләре санын табыгыз:
a) sin х = 100 х; б) arcsin х = х;
в) lg х = cos х; г) х2 + tg2 х = 100.
91. 159 нчы рәсемдә
у - ах3 + bx2 + cx + d
функциясенең графигы сурәтләнгән, a, b, с, d коэффициент¬
ларының тамгаларын билгеләгез.
Координаталар яссылыгында координаталары түбәндәге
шартларны канәгатьләндерүче нокталар күплеген сурәтләгез
(92—96).
92. а) х (у - 2) = 0; б)
У
3 1
х2 - 2х|;
в) (х - 2) (у + 4) = 0; г)
У
= sin х.
93. а)
х| < 1. 1 у < 1; б)
х
-3
1. |у-4| < 1;
в)
у 1 > 1X +11; г)
х + у
+
v
1
Ч:
1
V
to
94.
_ г#2
а)-? У
х2 + у8-1
ζθ;
в) 7* + у > |х|;
б) I XI +1 у I = 4;
ху+£ £+1
} ху-1 у-1‘
324 Катлаулырак мәсьәләләр
159 нчы рәсем
95. а) у2 + соз2 х = 1; б) х2 + у2 - х2 у2 + 1;
в) |у| = logi ||х + 2| - 1| ·
96. a) Jx + y^ У|х|; б) | х | - | у | < а; в) [xj < (у]; г) {х} > {у};
д) — > -; е) sin х > sin у, ж) min (х; у) = 1; э) ху + 1 > 0.
■ X у ■ ~ ' ·" - -
§3.
Тигезләмәләр, тигезсезлекләр һәм
системалар
8. Рациональ алгебраик тигезләмәләр
97. а ның кыйммәтләре нинди булганда бирелгән тигезләмәнең
чишелеше була?
а) х2 - 2 (а - 1) х + 2а + 1 = 0;
б) (а - 3) х2 - 2 (За -4) х + 7а - 6 = 0.
98. а) а ның нинди кыйммәтләре эчен
(а - 2) х2 - 2 (а + 3) х + 4а = 0
тигезләмәсе тамырларының берсе 3 тән зурак, ә икенчесе
2 дән кечерәк була?
325 Катлаулырак мәсьәләләр
6) α ның нинди кыйммәтләре өчен
(2а + 3) х2 + (α + 1) х + 4 = 0
тигезләмәсенең ике тамыры да [-2; 0] кисемтәсендә ятар?
99. Xi һәм хг саннары — х2 + рх + q = G тигезләмәсенең тамырлары,
а) х2+ х2; б) х? + х2;
в) Т7 + г) xf+xi не р һәм q аша белдерегез.
100. х2-4х +р = 0 тигезләмәсе тамырларының квадратлары
суммасы 16 га тигез, р ны табыгыз.
б) а ның нинди кыйммәтләрендә х2+ 2e (х - 1) + 1 = 0 тигез¬
ләмәсенең тамырлары суммасы бу тамырларның квадрат¬
лары суммасына тигез була?
101. ах2 + Ъх + с = 0 тигезләмәсенең тамырлары юк, өстәвенә
α + б + с < 0. С ның тамгасын билгеләгез.
102. Әгәр ах2 + ί>χ + с = 0 һәм Ьх2 + сх + а = 0 (а # 0) тигезләмә¬
ләренең уртак тамыры булса, сх2 + ах + Ь = 0 тигезләмәсенең
дә тамыры шул ук булуын исбатлагыз.
103. Исбатлагыз: а) әгәр бөтен коэффициентлы а^х" + α,χ""1 + ...+
+ а„ — 0 тигезләмәсенең х0 = — тамыры кыскармаслык вак¬
ланма булса, р — ап ның бүлүчесе, ә q саны а„ нең бүлүчесе
була; б) Р (х) күпбуынын (х - а) бербуынына бүлгәндәге
калдык бу күпбуынның а ноктасындагы кыйммәтенә тигез
(аерым алганда, а саны — Р (х) күпбуынының тамыры булса,
бу күпбуын (х - а) га калдыксыз бүленә).
104. 103 нче мәсьәлә нәтиҗәсеннән файдаланып, тигезләмәне
чишегез:
а) 2х® - х2 + х + 1 = 0;
б) Юх3 - Зх2 - 2х + 1 = 0;
в) х4 + хэ + х2 - х - 2 = 0;
г) 2х4 + 7х® + бх2 + 7х - 6 = 0.
Тигезләмәне чишегез (105—114).
105. а) (х + 1) (х + 2) (х + 4) (х + 5) = 40;
б) (х - I)6 + (х + З)5 = 242 (х + 1);
в) (х + 1) (х + 2) (х + 3) (х + 4) = 100;
г) х4 + (х + 2)4 = 17.
106. а) —3—г — = А; 6)6 — = 4х - х2;
' х(х+2) (х+1)1 12 х2-4х+10
х 1 I 2 « .
(х+2)(х-7) (х-2)(х-3) *’
г) (х2 - Зх + 1) (х2 + Зх + 2) (х2 - 9х + 20) = -30.
107. a) х2 + ± + 2(х + I) = 6;
б) ——— + —— 2
х2 + 2х+3 х2+7х+3
108. а) х4 - 2х8 + 4х2~ 2х + 1 = 0; б) 2х4 + х3 - Зх2 + х + 2 = 0;
4
в) х4 - 2Х3 - Зх2+ 4х + 4 - 0; г) х4 - 4Х3 - Ιβχ2- 12х + 9 = 0.
326 Катлаулырак мәсьәләләр
109. а) 8х4 + δχ3 - х- 190 = 0; 6) 4х4 - 4Х3 + f = 66.
110. а) х1 + 4х ~ 1 = 0; б) х4 - 4х3 -1=0.
111. а) 2 (х2 + х + I)2- 7 (х - I)2 - 13 (ха - 1);
б) (х2 — х + 1)2+2 (х2 + 1) = (х+ I)2.
Or2 -и 2
6,χ!+ϊ±?-1·
113. а)х2+[х| -2 = 0; б) х2 - 2х - 3 = | Зх - 3 |.
114. а) I |||х -1| + 2| -1| + 1| = 2;
б) 2|х + б|-1х|-|х-б| = 18;
в) 2х - 3 I = j х2 - 2х - 6 I;
г) х + 1|-|х| + 3|х-1|-2|х-2| = х + 2.
9. Рациональ алгебраик тигезсезлекләр
Тигезсезлекләрне чишегез (115—118).
. . 3(х-1)(х + 2)2 Л
115. а) (х2 + Зх + 1) (х2 + Зх - 3) 5; б) . \-Л ' . > 0.
(х2+1](х + 1) (х-2)
116. а) х4 + Зх3 + 2х2 + Зх + 1 > 0;
б) (х - 1) (х - 3) (х - 4) (х - 6) 17.
117. а) х18 - х13 + х10-х7 + х2 -х + 1 > 0;
б) х12 - х9 + х4 - х + 1 < 0.
118. a) j х2 - 2х |< х; б) Зх2-| х - 3 I > 9х- 2.
119. Тигезсезлекне исбатлагыз:
а) Tab (а > 0, Ь > 0); б) а + 1 > 2 (а > 0);
Л л
в) a+t>*—- > yjabed (а. b,c,d — уңай саннар);
г) > tfabc (α > 0, Ь > 0, с > 0).
3
Тигезсезлекләрне исбатлагыз (120—124).
120. а) а3 + Ъ2 + с2 > ab + ас + Ьс;
б) (а + Ь) (Ь + с) (с + а) 8 abc (а 0, Ь 0, с ? 0);
в) әгәр a + Ь + с = 1 булса, а2 + Ь2 + с2 ? ;
г) а4 + Ь4 + с4 £ abc (а + Ь + с).
121.
— + — + —— .
2г З2 η2 п
327 Катлаулырак мэсьэлалар
122. (а + b) (а3 + b3) <2 (α4 + fe4).
123. 5α2 - Gab + 5b2 > 0 (a2 + b2 * О).
124. ^(а + с)(& + й) > Jab + Jed (а О, b О, с О, d О).
10. Рациональ алгебраик тигезләмәләр
системалары
Тигезләмәләр системаларын чишегез (125—134).
125.
а)
(х - у)(х2 - у2) = За3,
(х + у) [х2 + у2^ = 15а3;
б)
х2 - ху + у2 - 21,
у2 - 2ху + 15 = 0.
126.
а)
и + и = 2,
1 Зи - и 1 = 1;
б)
1х-1| + |у-2| = 1,
у + |х-1| = 3.
127.
а)
■
х + у - 2 = 2,
2х - у + 4z « 1,
-х + бу - ζ - 5;
б)
■
х + у + ζ - -2,
х - у + 2г = -7,
2х + Зу - ζ - 1.
128.
а)
х + у = 3,
х4 + у4 -17;
б)
х + у + ху - 0,
х3 + у3 +х3у3 = 12.
129.
а)
х - у + ху = 17,
х2 + у2 = 34;
б)
(х2 + 1)(у2 +1) = 10,
(х - у)(ху + 1) = -3.
130.
а)
х2 - 2ху - Зу2 = 0,
х2 - 2ху + у2 =6;
б)
•
ЬО и И
co
* + £
+ * II
II N
' " μ-
11 ω
N
Μ
ь
131.
а)
х2 - у2 = 3,
х2 + ху + у2 = 7;
б)
(x2+y2)J = 6,
(х2-у2)у = х.
132.
а)
х3 - у3 =19(х-у),
х3 + у3 = 7(х + у);
б)
х3 = 5х + у,
у3 = х + бу;
в)
X2 + У + 2 = 2,
X + у2 + 2 = 2,
х + у + г2 = 2;
г)
J N н
II II II
N N »
» Η Η
<Ν CM <Μ
+ + +
η см
Η Sh N
328 Катлаулырак мәсьәләләр
133. a) 2x(—+ —) = 15.
\г yf
б)
134. а)
В)
-13;
х3 + у3 - z“ - xyz = -4,
х3 - у3 + ζ3 - xyz = 8,
I -x3 + у3 + ζ3 - xyz - -2;
x + у + ζ = 4,
х2 + у2 + ζ2 = 14,
I ху + xz + yz = 9;
б)
г)
xy _ 6
x + y 5 ’
xz _ 3
— — — *
Χ + Ζ ■
zy
z + y
4x2 + 4y +1 = 0,
4y2 + 4z +1 = 0,
4z2 + 4x +1 = 0.
х2 + ху + у2 - 37,
х2 + xz + ζ2 = 28,
у2 + yz + ζ2 - 19.
4 *
2
3 '
11. Тигезләмәләр һәм тигезләмәләр
системаларын төзүгә мәсьәләләр
133. 1,2 м озынлыктагы әйләнә буенча даими тизлекләр белән
ике нокта хәрәкәт итә. Алар, төрле юнәлештә хәрәкәт итсәләр,
һәр 15 с саен очрашалар. Бер юнәлештә хәрәкәт иткәндә, бер
нокта икенчесен һәр 60 с саен куып җитә. Кәр ноктаның
тизлеген табыгыз.
136. Өчурынлы санның цифрлары суммасы 17 гә тигез, аларның
квадратлары суммасы 109. Бирелгән саннан 495 не алгач,
шул ук цифрлар белән, ләкин кире тәртиптәге язылган сан
килеп чыга. Санны табыгыз.
137. Метродагы пассажир хәрәкәт итүче эскалатор буйлап 24 с та
төшә. Әгәр хәрәкәтсез торган эскалатор буйлап шул ук тизлек
белән барса, 42 с та аска төшеп җитә. Пассажир хәрәкәт
итүче эскалатор баскычында басып торса, күпме вакыт эчендә
аска төшеп җитәр?
138. А, В һәм С пунктлары турысызыклы юллар белән тоташкан.
АВ юлының кисемтәсенә ягы | АВ га тигез булган квадрат
формадагы кыр тоташа, ВС кисемтәсенә ягы ВС га тигез
булган квадрат кыр тоташа, АС кисемтәсенә буе АС га тигез,
ә киңлеге 4 км булган турыпочмаклык рәвешендәге урман
участогы тоташа. Урманның мәйданы квадрат кырларның
мәйданнары суммасыннан 20 км2 га зуррак. Урманның мәй¬
данын табыгыз.
139. Мәктәп олимпиадасында җиңүчеләрне тәбрикләү өчен, бер¬
төрле китаплар һәм бер үк төрле значоклар сатып алганнар.
Китаплар өчен — 1056 сум, значоклар өчен 56 сум түләгән¬
нәр. Китапларны значокларга караганда 6 данәгә артыграк
сатып алганнар. Ничә китап сатып алганнар?
329 Катлаулырак масьәлалар
140. Портфель, авторучка һәм китаплар сатып алу өчен, укучы
берникадәр акча сарыф иткән. Үз бәясенә караганда
портфель 5 тапкыр арзаирак, авторучка 2 тапкыр арзанрак,
китап 2,5 тапкыр арзанрак торса, сатып алынган әйберләр
80 сум торыр иде. Әгәр портфель 2 тапкыр арзанрак, китап
3 тапкыр арзанрак, ә авторучка 4 тапкыр арзанрак торса,
шул ук сатып алынган әйберләргә укучы 120 сум түләгән
булыр иде. Барлык сатып алынган товар күпме тора һәм
кайсы әйбергә күбрәк түләнгән: портфельгәме яки авторуч¬
кагамы?
141. Алтын белән көмешнең өч төрле эретмә кисәкләре бар.
Өченче кисәкнең 2 г эретмәсендәге алтын беренче һәм
икенче эретмәдән 1 әр грамм алынган кисәкнеке кадәр.
Өченче кисәкнең массасы 10 г алтын кергән беренче кисәк
белән 80 г алтын кергән икенче кисәкнең суммар массасына
тигез. Беренче кисәккә караганда 4 тапкыр зуррак булган
өченче кисәктә 75 г алтын бар. Беренче кисәктә күпме алтын
бар?
142. А пунктыннан В пунктына иртән сәгать 8 дә тизйөрешле
поезд чыга. Шул ук вакытта В дан А га таба пассажир һәм
курьер поездлары чыга, пассажир поездының тизлеге курьер
поездына караганда 2 тапкыр кечерәк. Тизйөрешле поезд
В пунктына шул ук көнне 17 сәг 50 мин та килеп җитә,
ә курьер поезды белән ул иртәнге 10 сәг 30 мин тан да иртә¬
рәк очрашмый. Әгәр тизйөрешле поезд һәм курьер поезды
очрашкан вакыт белән тизйөрешле поезд һәм пассажир поез¬
ды очрашкан вакыт арасы бер сәгатьтән дә ким булмаса, пас¬
сажир поездының А пунктына килеп җитү вакытын табыгыз.
143. Самолет очып килеп җиргә төшкәннән соң берникадәр вакыт
дәвамында о тизлеге белән тигез хәрәкәт итә. Моннан соң
очучы тормозлый, самолетның хәрәкәте тигез акрыная
башлый һәм һәр секунд саен тизлеге 2 м/с ка кечерәя. Җиргә
төшү урыныннан тәмам туктаганга кадәрге юл 4 км га тигез.
Самолетның беренче 400 м юлны үткән вакытының җир
буйлап үткән барлык юл вакытына чагыштырмасы 4 : 65 кә
тигез, и тизлеген табыгыз.
12. Иррациональ тигезләмәләр һәм
тигезсезлекләр
Тигезләмәләрне чишегез (144—152).
144. а) Jl-Vx< -хг = х - 1;
б) χ/x2 -Зх + З + χ/x2 -Зх + 6 = 3;
I 1 " ■ ■ Jx+Ϊ . Jx-1 _ л 1
в) χ/1 + хух2 - 24 = х - 1; г) γχ-1 γ r + 1 1 4 ’
330 Катлаулырак мәсьәләләр
145. а) 7х + 7х-1 = 1; б)
в) х + 7х = 2; г)
146. a) 71 + cosx = sinx;
в) 74 -3cosx = -2cosx;
710-х-73-х =1;
7o~7x + l + V? + 7x +1 = 4 .
6) 71 -2cosx = sinx;
r) 72 sin2x = -2 sin x.
147. a) \/x - 1 - 27x - 2 + 7x + 7 - 67x - 2 = 2;
6) x/x + 3 - 47x - 1 + >/x + 8 - б7х - 1 - 1.
148. a) 7x - 2 + 71 -x = 17;
6) -\x(2 - x) + χ/χ4(2 - x)7(x + 3)5 + ^(x - 2)(x + l)x2 +
+ 7(x + 2)(x + 6) = 2.
149. a) tf(x + I)2 + 27х2 -1 = β7(Χ -1)2;
6) ^(2 - x)2 + 7(7 + x)2 = 7(7 + x)(2-x).
iso. a) 7χ + ι + 7зх +1 = 7χ-ΐ; 6) 7i + 7χ-ΐ6 - 7χ-8.
151.
a)
ζ/12 + x _ 64 7
12 3 V
6) x2 — 5x — 4Tx +13 = 0.
152.
- 27
153. Ьәр реаль а саны өчен тигезләмәнең барлык чишелешләрен
табыгыз:
а) х + 71 - х2 = α ; б) 7х2 - 1 + X = а .
Тигезсезлекләрне чишегез (154—158).
154. а) 7х2 - Зх + 2 > 2х - 5; б) 7зх - х2 < 4 - х;
в) зТх - 7х + 3 >1; г) х - ^1 -1 х I < 0.
155. a) < з; б) + 1 1;
X X
в) 4х2 + 12x71+ Х $ 27(1 + х);
г) 7х + 7х + 7 + г7х2 +7х < 35 - 2х.
156. а) х2 - 2х + 3 < 74 - Г2; б) 73-х - 7х + 1 > | ·
331 Кнтлаулырак масьэлалар
157.
>15.
12’
а) х + —=
158. а) Тэ + З1 -2 >9-3*;
в) log2(>/x + 3 - х -1) О;
г) V4rxl +17 - 5 > 2х.
Тигезләмәләр системасын чишегез (159—162).
159. а)
\ixjy + y/xtfy = 12,
ху = 64;
Vx + tfy = 4,
X + у = 28;
!6°. а) [зух + 2у + з^х - у + 2 = 3,
2х + у - 7;
Л> (х2 + 2у + ^х2 + 2у + 1 = 1,
(2х + у = 2;
в)
х - у + Jx2 - 4у2
xiyjx2 - 4у2 = 0;
= 2,
161. а)
х2 - Ух/ху = 36,
у2 - Х\[ху = 72;
162. а)
xVx + 3yjx = 36,
у/у + Sxyjy = 28;
б> ί2</χ -2^У = З^у,
х — у = 63;
■)
Зх - у[ху + 2у = 29,
2х - </ху - у = 20;
+^х2-у2 _ 5 + J7
7*2 +у2 - Jx2 -у* S--J?
Xs + 2уа = 118.
332 Катлаулырак мэсьалалар
13. Тригонометрик тигезләмәләр,
тигезсезлекләр һәм системалар
Тигезләмәләрне чишегез (163—165).
163. а) 3 + 2 sin 2х = tg х + ctg х;
б) tg х - sin х = 1 - tg х sin х;
в) sin2x + sin2 2x = sin2 3x;
r) V6sin x - 2 cos x = 0.
164. a) |x[ sinx + x = 0; 6) Vsinx - 1 + 2x - 0;
в) |x| cosx - x = 0; г) r I = sjn I.
165. a) cos\ χ - tg4 x = 17; 6) tg 3x - tg x = 2 (sin 4x - sin 2x);
в) 3 (log2 sin x)2 + log2(l - cos2x) = 2; r) 22t<2 0081 - 4.
166. Формуланы исбатлагыз:
2tg§
l-tg2f
a) sin a ~ ; 6) cos a
i + tg2f '
2tg|
B)tga r>cl*a
167. Тигезләмәне чишегез:
1 + t«22
1-f’f
a) sin 2x + tg x = 2; 6) sin x + ctg·^ = 2.
168. Бердәйлекне исбатлагыз:
a sinx + Ь cos x = A sin (x + φ),
биредә φ түбәндәге шартларны канәгатьләндерә:
cos φ = ! а , sin φ = , ° , Α = , α .
Тигезләмәләрне чишегез (169—175).
169. a) sinx - у/з cos х = 1; б) 2 sinx + 3 cos х = 4.
170. л/2 (sinx + cos х) = tg х + ctg х.
πχ 2πχ „ 4πχ _ 8πχ Ιβπχ 1
• С03^С08-зГС05-зГС08-зГС08^Г = й·
172. a) sin8x + cos8x = χχ ; б) sinl<M)x + cos,oax = 1.
173. 2 cos -j£=2r + 2 ·«.
333 Катлаулырак мәсьәләләр
174. х2 + 2x sin (ху) +1 = 0.
175. 8 sin х= +
176. (sin х + Уз cos х) sin 4х - 2 тигезләмәсенең чишелешләре
булмавын исбатлагыз.
Тигезсезлекләрне чишегез (177—178).
177. а) х/з tg2 х - 4tg х + χ/з > 0; б) ** . <11-2 sinx;
olll Λ * 1
в) < 2 - tg х; г) tgx + ctgx > х/З + -jU.
178. a) cos 2x < cos 3x - cos 4x;
б) cos2 x + cos2 2x + cos2 3x + cos2 4x > 2;
в) sin 2x + 2 sin x > 0;
г) (1 + cos 2x) (tg x - х/з ) > 0.
179. Тигезсезлекнең дөреслеген исбатлагыз:
а) Jcostp < у/2 cos |, әгәр -* < φ < * булса;
б) sin4 α + cos4 α ~ , теләсә нинди а өчен.
ί
Тигезсезлекләрне чишегез (180—181).
180. sin I cos πχ j > .
181. χ/б - 2sinx 6 sin х - 1.
182. 0 < х < булса, cos sin х > sin cos х булуын исбатлагыз.
183. А, В һәм С — өчпочмакның почмаклары булса, cos А +
+ cos В + cos С С ~ булуын исбатлагыз.
Тигезләмәләр системаларын чишегез (184—186).
184. а)
sin х — = sin у,
sinx σ
cos х — = cos у;
cosx v
sin (y - 3x) = 2 sin3 x,
cos(y - 3x) = 2 cos3 x.
185.
tg — ·+· tg ,
g2 g2 7a’
tgx + tgy = 2x/3.
186.
tgxtgy =
tgytgz -
mu—+ 3,
cosx cos у
-
cos у cosx
-5,
tg X tg 2 =
sin у
“
COSX COS 2
334 Катлаулырак мәсьәләләр
14. Күрсәткечле һәм логарифмик
тигезләмәләр һәм тигезсезлекләр
Тигезләмәләрне чишегез (187—189).
187. а) * р5-ч24)’ = 10; б) 3Х + 4Х- 26;
■) (2 ♦ >/з)* + (2 - 7з)‘ = 4; г) (2 - 7з)’ + (2 - 7з)' = 4’.
188. а> |x-3|fai-w»+3-l; б) хГ2ства1 = -tfx ;
в) |х - 2| **·-** 1 = 1; г) 2^1 - sin х2·
189. a)2"nSx+4 · 2«·!χ = 6;
1
В) 43 + 2 co.ix_ 7.41+00. 2χ_ 42 .
6) 3'“«x-2 · 3
r) (2 sin x)0" * = 1.
190. a) а ның нинди кыйммәтләрендә a (2* + 2'x) = 5 тигезләмәсе¬
нең бердәнбер чишелеше була?
Тигезсезлекләрне чишегез (191—192).
191. а) 2Х + 2Н > 2<2 ;
б) 25 · 2х - 10х-!-5х > 25;
в) аж < 52*1;
г)
2”*+1
2.
192. a)(x-2)*i’ta+s> 1;
б) 9^-8 + з < з^’-э .за.
&
193. а) 4х - а · 2х - а + 3 < О тигезсезлегенең кимендә бер чишелеше
булырлык итеп, а ның барлык кыйммәтләрен табыгыз.
194. Тигезләмәләр системасын чишегез:
а) (з2х +42v = 82,
3х - 4» = 8;
б) ί(2χ+1 -3) 2V 1 = L
[73х+"у2 = х + у;
в)
2«»z .j. — 5.
г)
021<х+соау _ 3
θοοβρ = 2
Тигезләмәләрне чишегез (195—197).
195. a) V1 + 1о₽2 х + \/41og“ х - 2 = 4;
б) log6 2Х + 3- loge|3x - 3 ·= х;
в) logi(3 + |smx|) = 2H - 2;
Я
г) + lg tg х + Vl - 1g tg х = 2.
Катлаулырак мәсьәләләр
196. а) 9х'** + 91 x'lf 1 = 60; б) |х - 1)'°*’”Ι<*2'* = |х - 1|3 ;
2 Iff ΙθΦ — Ί х
в) х" » «0,1; г) log,M (х2 + х~ 6) = 4.
197. a) lg (arctg x) + lg (arcctg x) — a;
б) log, + i (x2 - 9x + 8) · log,., (x + 1) = 3;
в) arcsin (lg x2) + arcsin (lg x) = ^ ;
Г) log., -4x2 (9 - 16x<) = 2 + 4 -ү .
log2(3-4x2)
198. а ның нинди кыйммәтләрендә 2 logjx - |log3 x| + a = 0 ти¬
гезләмәсенең дүрт чишелеше була?
199. а ның нинди кыйммәтләрендә Зх lg х = 1 + a lg х тигезлә¬
мәсенең: а) бер чишелеше; б) ике чишелеше була?
200. а ның нинди кыйммәтләрендә х In |х| = а тигезләмәсенең бер
тамыры була?
Тигезсезлекләрне чишегез (201—203).
201. а) log2 (1 + log! х~ loge χ) < 1;
б) logi (* “ I)2 iog0.5 (х - 1) > 5;
в) log ί (log2 log,. j9) > 0; r) log2 (log j log5 x) > 0.
2 3
202. a) log2 (21-Dlog! (2I + 1-2) > 2; 6) 3l0^1 + xlot** <6;
2 , ,
в) 31®1*2 < 3 lf2x + 5-2; г) 5Ьг5Л +x,0«5r< 10.
203. a) log,_3 (x - 4) < 2;
6) 2 1<*2-χ<ιγ2 + ®·γ + 16»< 1;
. ί 4x-5 1
? =
г) log, (log» (3'- 9)) < 1.
204. log0 (x2 - x - 2) > loga (3 + 2x - х2) тигезсезлегенең х = « бул¬
ганда дөрес булуы билгеле. Бу тигезсезлекнең барлык чише¬
лешләрен табыгыз.
Тигезләмәләр системасын чишегез (205—206).
205. а)
log, у = 2,
log,., (у + 23) = 3;
б) (х + уУ =(х-уҮ ,
log, х = 1 + log2 у',
в)
(х-у)2*’1 =125,
lg2(x - у) = 1;
г) 2 log2 х — 3ν = 15,
3* ■ log2 х = 2|О*2Г +3**‘.
336 Катлаулырак мәсьәләләр
206. а)
сой у
3”βχ = ш ■
log2 (sin х - cos x) - log2 (sin x + cos x) = -1;
6) ί log2 sin x + log2 sin у = -2,
[log., cosx + log, cosy = 1 - log, 4.
§4.
Анализ башлангычлары
15. Чыгарылма
207. а) Функциянең үсү билгесен исбатлагыз: әгәр I аралыгын¬
дагы аргументның теләсә нинди ике кыйммәте х һәм х + Δχ
өчен (биредә Δχ * 0) > 0 шарты үтәлсә һәм бары тик шул
вакытта f функциясе I аралыгында үсә;
б) I аралыгында функциянең кимүе турында охшаш билгене
әйтегез һәм исбатлагыз.
208. Исбатланган билгеләрдән файдаланып (207 нче күнегүне
кара), функциянең үсү һәм кимү аралыкларын табыгыз:
а)/(х) = 2х2; б) f (х) - 3 - 4х;
в) f (х) = 3 - х2; г) f (х) = 1 - | .
209. Чыгарылманың билгеләмәсеннән файдаланып, f функция¬
сенең х0 ноктасында дифференциаллануын исбатлагыз, әгәр:
а) f (х) = х|х|, х0 = 0; б) |х2 - 1|(х+1), х0 = -1;
х2 - 1,х £ 1 булса,
в)/(х)= _ _
хл - х, х > 1, х0 =1 булса;
х2, х > 0 булса,
ОМ" 3 А ОЛ
х3, х < 0, х0 = Обулса.
210. Әгәр f функциясе саннар турысының һәр ноктасында диф¬
ференциал ла нса һәм теләсә нинди х. Һәм х2 кыйммәтләре
өчен /(х, + х,) = f (х,) + f (х2) тигезсезлеге үтәлсә, f (х) ның
даими булуын исбатлагыз.
211. a) fix) = Vx2 функциясенең 0 ноктасында чыгарылмасы бул¬
мавын исбатлагыз.
212. a) ft (х) функциясе х0 ноктасында дифференциалланса,
ә f2 (х) функциясе дифференциалланмаса;
б) ике функциянең дә х0 ноктасында чыгарылмасы булмаса,
х0 ноктасында φ (х) = (х) · f2 (х) функциясенең чыгарыл¬
масы булмый дип әйтү дөресме?
337 Катлаулырак мәсьәләләр
213. f функциясе саннар турысының һәр ноктасында диффе-
ренциалланса һәм теләсә нинди х, һәм х2 кыйммәтләре өчен
/(xj + х2) = /(х,) · f(x2) тигезлеге үтәлсә, / (х) - е01 яки f(x) = 0
булуын исбатлагыз.
214. Кире тригонометрик функцияләрнең чыгарылмалары фор¬
мулаларын табыгыз:
a) arcsin' х = , * ; б) arccos' х = ——>·;
Vl-χ» у/1-хг
в) arctg' х = ; г) arcctg' χ - ·
215. Функциянең чыгарылмасын табыгыз:
а) у = х*’, б) у = (sin х)*.
216. Функциянең п нчы чыгарылмасын табыгыз: у= -——.
хг -Зх + 2
217. х > х0булганда, f (х0) = g(xQ) һәм, f (х) > / (х) булса, х > х0
булганда, f (х) > g (х) була.
218. Сумманы исәпләгез:
а) 1 + н—“ 4 Һ ·». + —-—:
’ 2 22 2а 2’-‘
б) 2 + 3·| + 4·-τ + 5—+ ... + (η + 1)’“·
2 22 23 ν ’ 2"-'
16. Функцияләрне тикшерүдә чыгарылмалар
куллану
Функциянең үсүен (кимүен) һәм экстремумнарын тик¬
шерегез (219—220).
219. a)/(x) = x2(Vx-1); б)/(х) = х2<’1 - 2х ;
в) /(*)=“ 6 sin х - cos 2х; г) f (х) = 2 sin х + 3 соа х.
220. a) f (х) = -0,2х5 + 0,5х4- х3 - х2 - х;
б) f (х) = 0,8х5 - х4 + 4х3 + 2х2 + 4х.
221. f функциясе R да үсүче булырлык итеп, а ның барлык кыйм¬
мәтләрен табыгыз:
а) f М = 3"1 х3+ (α - 1) х2 + 2х + 5;
б) f (х) = 2х8 - 3 (а + 2) х2 + 48ах + 6х - 5.
222. Бирелгән тигезләмәнең бердәнбер тамыры булуын исбат¬
лагыз:
a) cos х = - х; б) sin х = -х - п.
223. Тигезсезлекне чишегез:
а) 2 + sin х > ——-; б) 2 - cos х > , * , .
’ 1 + х2 1 + х
338
Катлаулырак мәсьәләләр
224. Теләсә нинди х3 + ах2 + Ъх + с = 0 куб тигезләмәсенең кимендә
бер реаль тамыры булуын исбатлагыз.
225. и дәрәҗәсендәге күпбуынның п нан да артык булмаган
тамыры һәм (п -J) дән дә күп булмаган экстремум ноктасы
'< булуын исбатлагыз.
226.
227.
п нчы дәрәҗәдәге күпбуын үзенең һәр кыйммәтен п тап¬
кырдан артыграк алмавын исбатлагыз.
Я (х) = -у—т вакланмалы рациональ функция (п — Р (х) ның
дәрәҗәсе, т — Q (х) ның дәрәҗәсе) булсын.
a) R (х) үзенең һәр кыйммәтен х ның k = max (т, п) кыйм¬
мәтләреннән артыграк алмавын;
б) Я(х) ның, әгәр 1Я*п булса, (zn + n-l) дән артыграк
булмаган экстремум нокталары һәм, әгәр т = п булса,
(т + п -2) дән артыграк булмаган экстремум нокталары
булуын исбатлагыз.
228. Функциянең иң зур һәм иң кечкенә кыйммәтләрен табыгыз:
a) f (х) = 4х3 - х |х - 2| [О; 3] да;
б) f (х) = max — + cos х
' r U2 + 4nx + 41
229. Д, В, С пунктлары бер турыда ятмыйлар, өстәвенә Z ABC = 60°.
Бер үк вакытта А ноктасыннан — автомобиль, ә В нокта¬
сыннан поезд чыга. Автомобиль В юнәлешендә —80 км/сәг
тизлек белән, поезд С юнәлешендә 50 км/сәг тизлек белән
хәрәкәт итә. АВ = 200 км булса, нинди вакыт моментында
(хәрәкәт башлангычыннан алып) поезд белән автомобиль
арасы иң кечкенә була?
230. Кәгазь битендә текст 384 см2 биләп торырга тиеш. Өске һәм
аскы буш кырлар — 3 әр см, уң һәм сул кырлар 2 шәр см
булырга тиеш. Кәгазьне экономияләү ягыннан караганда,
кәгазь битенең иң отышлы үлчәүләре нинди булырга тиеш?
231. Пароход өчен ягулык чыгымнары ике өлешкә бүленә.
Беренчесе тизлеккә бәйле түгел һәм сәгатькә 480 сум тәшкил
итә. Чыгымнарның икенче өлеше тизлекнең кубына
пропорциональ, һәм, тизлек 10 км/сәг булганда, чыгымның
бу өлеше сәгатенә 30 сумга тигез. Тизлек нинди булганда
1 км юлга төшкән чыгымнарның гомуми суммасы иң кеч¬
кенә була?
232. Λ/(0; 1) ноктасыннан f (х) = ——-- функциясе графигына ка-
4л/3х*
дәрге иң кыска араны табыгыз.
233. Кайсы зуррак?
а) З^2 яки 2^ ; б) Ь-)1эет яки .
339 Катлаулырак мәсьәләләр
234. х € (О; ; булса, түбәндәгеләрне исбатлагыз:
a) cos х > 1 - 4-; б) sin х > х - -77-;
* Ό
B)cosx< 1 -γ + g; r)sinx<x-£ + ^.
235. Тигезсезлекне исбатлагыз:
а) х > 0 булганда, е* > 1 + х;
б) х > 0 булганда, In (1 + х) < х.
236. Тигезләмәне чишегез:
a) In х = 1 - х; б) 21 = 3 - х.
237. Бирелгән тигезләмәнең тамырлары санын а параметрына
бәйләп табыгыз:
а)х3-3х = а; б) |х2-4х + 3| —ах.
238. а киңлегендәге елгага туры почмак белән Ь киңлегендәге
канал үткәрелгән. Каналга керә алу өчен, пароходлар нинди
максималь озынлыкта булырга мөмкин (а һәм Ь метрларда
үлчәнә)?
239. (0; 10) интервалында функциянең минималь кыйммәтләрен
табыгыз:
f(x) = 2x+ + COS X.
17. Чыгарылманы физика һәм геометриядә
куллану
240. R радиуслы тәгәрмәч туры буйлап тәгәри, t секунд эчендә
тәгәрмәчнең борылу почмагы φ = t + у тигезләмәсе белән
билгеләнә. Тәгәрмәч үзәге хәрәкәтенең тизлеген һәм тиз¬
ләнешен табыгыз.
241. Туры горизонталь юл өстеннән 12 м биеклеккә лампа бер¬
кетелгән. Бу юл буйлап баручы кеше лампадан 50 м/мин
тизлек белән ераклашса, аның күләгәсе нинди тизлек белән
озыная барыр (кешенең озынлыгы 1,8 м)?
242. у = 8 - х Һәм у - 4 -Ух + 4 функцияләренең графиклары үзара
нинди почмак ясап кисешәләр?
243. М ноктасы аша узучы f функциясе графигына орынманың
тигезләмәсен языгыз:
а)/(х)=|, М(0; 3); б) f (х)° х2 - 4х +1, М(-1; -3);
в) f(x) = ч/2х-1 , М(-1; 0); г) /(х) - yfa-x2 , Af(0; 6).
244. Аргументның f (х) = 3 cos 5х Һәм g (х) “ 5 cos 3x4-2 функ¬
цияләре графикларына бу нокталардан үткәрелгән орын¬
малар параллель булырлык кыйммәтләрен табыгыз.
340 Катлаулырак мәсьәләләр
245. у — — гиперболасына орынманың координаталар күчәрләре
арасында яткан кисемтәсе орыну ноктасы белән урталай
бүленә дигән расламаны исбатлагыз.
246. ху = а2 гиперболасына орынма белән координаталар күчәр¬
ләре арасында хасил булган өчпочмакның мәйданы даими
2а2 ка тигез булуын, ә орыну ноктасының бу өчпочмакны
камаучы әйләнәнең үзәге булуын исбатлагыз.
247. а ның нинди кыйммәтендә f(x) = функциясенең гра¬
фигы абсциссалар күчәрен 45° лы почмак белән кисә (кимендә
бер кисешү ноктасында)?
248. а һәм Ь ның нинди кыйммәтләрендә у = 1х - 2 турысы
y = ax2 + bx + 1 функциясе графигына A (1; 5) ноктасында
орына?
249. а ның теләсә нинди кыйммәтләре өчен f (х) = х2 - ах функ¬
циясе графигының у = -х турысына перпендикуляр булган
орынмасы барлыгын исбатлагыз.
250. Координаталар яссылыгында Mk нокталары күплеген сурәт¬
ләгез, биредә Mk (А=1, 2...) — М (х, у) ноктасыннан у = х2
параболасына k орынма үткәрергә мөмкин булган нокталар
күплеге.
18. Башлангыч функция
R да f функцияләре өчен барлык башлангыч функцияләрне
табыгыз (251, 252).
251. а)/(х)= |х|; б)/(х) = |х - 11; в)/(х) = |хг - 11.
252. a) f (х) = хх/1 + х2 ; б) f (х) = хе**;
в) / (х) = ctg х, х е (0; π); г) f (х) - tg х, х е (“ ® · ч) ·
253. а) Г (х) = һәм / (3) - -1;
б) Г (х) =3-х, /(0)=1, Г (1) = 0;
в) f' (х) = cos х һәм f (е) = π;
г) f" (х) “ -1 Һәм f (0) = f (2) = 0 булса,
барлык f функцияләрен табыгыз.
254. f функциясе өчен графигы М ноктасы аша узучы башлангыч
функцияне табыгыз. Башлангычның графигын төзегез.
COSX, хеОбулса,
a) f(x) =
1,
1,
х^Обулса, Af(O;O).
х < 1 булса,
б) 7 (х) _L х^1булса, М(4;0).
чЖ
341 Катлаулырак мәсьәләләр
255. |-α; α| интервалда билгеләнгән өзлексез так функциянең
теләсә нинди башлангычы җөп функция булуын исбатлагыз.
256. |-α; а| интервалда билгеләнгән өзлексез җөп функциянең
кимендә бер так башлангычы булуын исбатлагыз.
257. Ике җисем бер ноктадан бер үк вакытта туры буйлап хәрәкәт
итә башлый. Беренчесенең тизлеге и (0 = 3ί2 - 60 икенче-
сенеке и (0 = 10/ + 20. Алар кайсы моментта һәм башлангыч
ноктадан нинди ераклыкта очрашырлар? (Тизлек м/с та
үлчәнә.)
258.
Туры буйлап хәрәкәт итүче т массалы җисемнең х коор-
динаталы ноктада потенциаль энергиясе и (х) ка тигез.
Исбатлагыз:
а) туры буйлап хәрәкәт иткәндә җисемнең х (0 координатасы
дифференциаль = -и'(х) тигезләмәсен канәгатьләндерә;
б) х" = огх гармоник тирбәнеш башкаручы т массалы матди
, ч kx2 ,
ноктаның потенциаль и (х) энергиясе —гә тигез, биредә
k = τηω2 (и (0) = 0) дип алыгыз.
259. Ньютонның икенче законы буенча туры буйлап хәрәкәт итүче
.л
ти
т массалы матди ноктаның тулы энергиясе Е =~^~ + и(х)
ның саклануын исбатлагыз (и (х) — потенциаль энергия).
260. х, (0 һәм х2 (0 х" (0 = - <о2х (0 тигезләмәсенең ике чишелеше
булсын. Xj(0 - х2(0 һәм /гХ[ (0 функцияләре (k — ирекле сан)
шулай ук бу тигезләмәнең чишелешләре булуын исбатлагыз.
261. х" (0 = - <о2 х (0 тигезләмәсенең х = A cos (ωί + φ) рәвешендәге
һәм башлангыч х (0) = х0, х' (0) = и0 шартларын канәгать¬
ләндергән чишелеше барлыгын исбатлагыз.
262. 260—261 нче күнегүләрдәге мәсьәләләренең нәтиҗәләреннән
файдаланып, дифференциаль тигезләмә х" (0 = -ω2χ (0 ның
теләсә нинди чишелешен х = A cos (ωί + φ) рәвешендә язарга
мөмкин икәнлеген исбатлагыз.
263. Бердәйлекне функциянең даимилек билгесеннән файдаланып
исбатлагыз:
a) arcsin х + arccos х = ; б) arctg х + arcctg х = .
264. у'у2 = 2 һәм у (2) = 2 икәнлеге билгеле булса, у функциясен
табыгыз.
265. Функцияләрнең башлангычларын табыгыз:
е1 sin х һәм е1 cos х.
342 Катлаулырак мәсьәләләр
19. Интеграл
266. Матди нокта туры буйлап хәрәкәт итә. Исбатлагыз:
I
а) х (t) = х0 + J V (t) dt (теләсә нинди t моментында ноктаның
ί0
тизлеге υ (t) һәм координатасы башлангыч 10 моментында
х0 гә тигез булуы билгеле булса);
t
б) у (t) = и0+ J a (i) dt (теләсә нинди t моментында ноктаның
*0
тизләнеше a (t) һәм башлангыч t0 моментында тизлеге и0 гә
тигез булуы билгеле булса).
267. f (х) — дәрәҗәсе 3 тән зуррак булмаган күпбуын булсын.
Исбатлагыз:
ь
J f (х) dx = (j/l + 4рг + р3),
п
а
биредә р, = /(а), у2= f |^)» Va~f(b).
268. Исбатлагыз:
а
а) j f (х) dx = 0, f (х) так функция булса;
U о
б) j / (х) dx = 2 j (х) dx, f (х) җөп функция булса.
-а ΰ
269. 268 нче күнегүдәге мәсьәләнең нәтиҗәләреннән файдаланып
исәпләгез:
3 я
а) ί (tg х + sin х) dx; б) J х cos х dx.
_ι ’
8
270. Исәпләгез:
к
28
β .
в) Jx^l-|dx ;
2
I
б) j хе χ3 dx;
о
2
г) J (cos2 х + cos4 x) dx.
343 Катлаулырак масьәлаләр
271. Интеграл ярдәмендә чикләмәне табыгыз:
(η - Ιΐ·^
η
a) Ит -
х^ п
, п
sin - + sin — + ... + sm
η η
6)
lim ί—Ц- + —
гн>а,\и + 1 л +
η + η) '
. ,. lf + 2' + ... + л" η
в) Ит , ρ > 0;
X —»» П'"
Inf-' nf-1
-I
(η + 1)'’ (η+2)’’
272. Исәпләгез:
2π 2я
a) J cos2 nxdx (n e N); 6) j sin kx cos mx dx (me N, he N);
о 0
Jl я
в) J sin2 x dx; r) j sin 3x cos 5x dx.
π 0
273. Интегралның геометрик интерпретациясеннән файдаланып
исәпләгез:
2 ι
a) J Jх| -1| dx; б) J V1 - х2 dx ;
-2 -1
3 5
в) j |х2 - 1| dx; г) J|{x}-|| dx.
о о
274. Эллипс эчендә яткан нокталардан төзелгән фигураның мәй¬
данын исәпләгез. (Эллипс дип нокталарының координа¬
та лар ы:
х2 У2
1 1 тигезлеген канәгатьләндерүче фигура атала.)
е* 1г
275. а, Ь, с параметрларының нинди кыйммәтләрендә интеграл
билгеләнә?
a 0 α
276. Сызыклар белән чикләнгән фигураның мәйданын табыгыз:
а) у = I х2 - 11 һәм у = 5 +1 х |; б) у = 2х - х2.
277. у = ~, у = 2x^1 » х = 2, х = а, у = 0 сызыклары белән чик¬
ләнгән фигураның мәйданы In-i- кә тигез, а ны табыгыз.
344 Катлаулырак мәсьәләләр
278. у = х2 параболасы белән абсциссалар күчәренә параллель
булган ирекле туры арасында яткан параболик сегментның
мәйданы турыпочмаклык мәйданының 3 сенә тигез булуын
исбатлагыз. Бу турыпочмаклыкның түбәләре — туры белән
параболаның кисешү нокталары һәм кисешү нокталарыннан
абсциссалар күчәренә төшерелгән перпендикулярларның
нигезләре.
279. Пружина 180 Н лы көч тәэсирендә 2 см га сузыла. Пру¬
жинаның баштагы озынлыгы 20 см га тигез. Пружинаны
25 см га кадәр сузу өчен, нинди эш башкарырга кирәк?
280. а ның нинди кыйммәтендә Ох күчәре, у = х3 + Зх2 + х + а
функциясе графигы һәм бу функциянең экстремум нокта¬
ларындагы х = const вертикальләре белән чикләнгән фигу¬
раның мәйданы иң кечкенә кыйммәткә ия була?
281. Башлангыч массасы М булган су тамчысы авырлык көче
тәэсирендә аска төшә һәм, секунд саен т массасын югалта
барып, парга әйләнә. Тамчы төшә башлаганнан алып тулы-
сынча парга әйләнеп беткәнгә кадәр вакыт эчендә авырлык
көченең эше нинди?
282. Биеклеге Н һәм нигез радиусы R булган конус формасындагы
ком өеме ясау өчен, авырлык көченә каршы нинди минималь
эш башкарырга кирәк? Комның тыгызлыгы р га тигез һәм
комны конусның нигез яссылыгыннан күтәрәләр.
283. Нигезе α = 40 см һәм биеклеге һ = 30 см булган бериш өч¬
почмаклы пластина үз нигезе тирәсендә даими почмакча
тизлек ω = 5π с 1 белән әйләнә. Әгәр пластинаның калын¬
лыгы d = 0,2 см, ә материалының тыгызлыгы р = 2,2 г/см3
булса, пластинаның кинетик энергиясен табыгыз. (Пластина
калынлыгын исәпкә алмаска.)
284. R радиуслы бериш ярымтүгәрәкнең массалар үзәген табыгыз.
285. R радиуслы бериш ярымшарның массалар үзәген табыгыз.
286. Бериш җисемне суга батырганда, суның этеп чыгару көченә
каршы башкарылган эшнең pgVh ка тигез икәнлеген ис¬
батлагыз, биредә р — суның тыгызлыгы, g — ирекле төшү
тизлеге, һ — суга батырылган өлешнең массалар үзәгенең
батырылу тирәнлеге, V — батырылган өлешнең күләме.
Күнегүләргә җаваплар һәм
күрсәтмәләр
1 1 I I I I I '
I бүлек
1· г) Ь* t β" : ’ · 2. г) 225’ ; 270’; -105’. 3. в) 4; г) 3. 4. в) Юк; әйе; әйе.
6 5 2
_ Я . Я . 15
5. в) Юк; т) әйе. 6. в) Юк; г) әйе. 7. г) эт α - - ; tg α - - —; ctg α - - — .
17 id 6
8.г)-1.9.в)1. 10.6)-j|;|||;g:-g. 11. B)tga. 12. tgf; -cos£;
д 4 1
cos ; -ctg 0,1 rt. 13. r) 1. 14. в) Юк; г) әйе. 15. г) г— ; * /тт ; -4.
□ V17 w I ί
16. в) 0,7833; 0,6216; 1,2602; 0,7936. 17. б) 22’6"; 27’30"7"; 63’35'54";
84’47'52". 18. в) 0.1 м; с) 9 им. 19. в) 0,05 мг. 20. б) 1. 21. в) 3; г) .
- ’ ■ ' о
22. ■ 27. г) -2. 30. в) IV; IV; И. 31. г) Плюс. Зв. в) D (у) - R,
3
Е (у) - [- 2; 0]. 37. г) D (у) = R, Е (у) = [- 1,5; 1,5]. 38. г} (0; -1); + 2яп; о) .
в g Z. 39. в) (0; 3.5). 41. в) ~ + 1; ТТ5 + 1. 42. в) Юк. 43. в) (-®; -4) 11
■*0 «6 · Л
(J (-4; 2) IJ (2; »). 44. πη саннарыннан башка санлы туры, монда п е Ζ.
1 нче рәсем
45. в) D (у) - Е (у) - (-·; -1) (J (“Ъ «)·
46. г) D (р) - [-4; 3]. Е (у) = [-1; 4 ].
49. г) 1 вче рәс. 50. в) у - cos х функциясенең
графигын ординаталар күчәре буйлап сузабыз
(к = 0,5), ә аннары (0; -1) векторына күчерәбез,
I е ЛА
2 нче рәс. 52. г) S, (х) - хг, D (SJ = [0; |;
(_ αν2 I
0;—j-i .
53. в) [-2; 1,5) U (1,5; ®). 54. г) D (у) - R.
Е(у) - [1; 1,5]. 64. г) 3 π. 65. в) π. 67. г) .
~ ’
68. в), г) Юк. 69. Так. 70. Җеп тә түгел, так та
346 Күнегүләргә җаваплар һәм күрсәтмәләр
У
у = 0,5 cosx - 1
2 нче рәсем
түгел. 72. г) Җеп. 73. г) 2 к. 77. г) [-4; -2 ], [0; 2], [4; 6] да үсә: [-6; -4].
[-2; О], [2; 4] да кими; х„,.Л - -2, х " 2, х„,„ = -4, х„, = О. х„и - 4. у (-2) =
= у (2) - 3, у(О) — 0, у (-4) - р(4) - -2. 82. г) [3; “) да үсә, (-®; 3] да кими;
= 3· и» “ о. 83. в) (-®; -3), (-3; ®) да үсә; экстремум нокталары юк.
84. [ - I + 2ял; 5 + 2ял] да үсә, [ ? + 2πη: 4г + 2ял) да кими. х = 5 + 2ял.
л* ί ύ Л
+ 2ял) = -1, х^ =( - ■ + 2ял), у (- % + 2ял) = -2, ле Ζ. 85. г)[ - я + 2ял; 2πη]
да үсә, [2яп; я + 2ял J да кими; х,^ - 2дл, р(2яп) - 0, х^„- к + 2πη, у (к + 2πη) - -2;
η € Ζ. 88. в) Беренчесе зуррак. 87. г) sin (-1,2). sin 0,8, sin 1,2. 88. г) ( ®; -1],
[0,1] да кими, [-1;0], [1; ®) да үсә. х т - 0, у (0) -0, xni, - ±1, р(-1)“«(1)-
= -1. 89. в) Г- + 2ял; 4 + 2ял , да үсә, . 4 + 2ял; + 2πη , да кими>
L о о J 1_о о J
х|ж>. - I + 2πη. у (J + 2ял) =1, х„” + 2дя. у(у + 2ял) = -1, в <= Z.
90. в) ctg j’* , ctg jf , ctg Цр , tg у . 91. в), г) Күрсәтмә, у - xe һәм
у = х* функцияләренең үзлекләреннән файдаланыгыз. 92. Күрсәтмә.
-Ь < X) < хг < -а булсын, ул вакытта а ς -х2 < -xt < Ь һәм f(~xt) > f(~x}), ченки
f [β; t>] да кими, димәк, f(xt) < /(х,). 93. в) 1) !>(/} = (-8; 6], E(f) - [-2; 2];
2) функция так; 3) (-4; 0), (0; О), (4; 0) — Ох күчәре белән кисешү нокталары,
(0; 0) — Оу күчәре белән кисешү ноктасы; 4) (-4; 0), (4: 6] да f (х) > 0, [-6; -4),
(0; 4) да Дх) < 0; 5) [-6; -2], [2; 6] да үсә, [-2; 2] да f кими. 6) xmln - 2,
/(2) - -2, Жт.х= -2, А-2) - 2. 96. г) 1) D(f) - £(/) - Я; 2) (1; О), (0; -1) -
координата күчәрләре белән кисешү нокталары; 3) (-“; 1) да /(х) < 0, (1; ®) да
f (х) > 0; 4) f функциясе Я да үсә. 97. в) 1) D(f) - [-1; ®), E(f) - [0; »); 2) (-1; 0),
(0; 1) — күчәрләр белән кисешү нокталары; 3) (-1; ®) да / (х) > 0; 4) (-1; =>) да
f үсә. 98. в) 1) D (Л = Е (D - Я; 2) функция так; 3) (0; 0) — күчәрләр белән кисешү
ноктасы; 4) (-®; 0) да /(х) < 0, (0; «) да ,<<х) > 0; 5) f функциясе Я да үсә;
347 Күнегүләргә җаваплар һәм күрсәтмәләр
г) 1) D (у} — [2; *>), Е (f) = [-2; ±>); 2) (6; 0) — Ох күчәре белән кисепгү ноктасы;
3) [2; 6) да Дх) < 0, (6; ®) да fix) > 0; 4) f функциясе [2; «>) да үсә. 99. в) 1) D (/) — Я,
Е (f) — (-<»; J ] ί 2) функция җөп; 3) (0; 0), (-1; 0), (1; 0) — күчәрләр белән кисешү
нокталары; 4) (-»; 1), (1; «>) да f(x) < 0, (-1; 0), (0; 1) да f (х) > 0; 5) (-«; -*J ,
[0; 0,5] да f үсә, [-0,5; 0], [0,5; ®) да f кими; хт,,^ ±0,5, у(-0,5)“
-у(0,5) - 0,25, x„to - 0, р(0) - 0. 100. r) -cos", 101. e) Z>(/) =
he Z, E(f) = R. 102. г) -y <■ * < ~4+~2^ булганда, f(x) > 0,
π itn л(п + 1] п ли
— + — < x < = булганда, f(x) <0, x - ~t + -5-; n e Z булганда, fix) - 0.
4 Ζ Z 4 z
Г 2W»1 Г 5 π« . 3,1 ™Ί л ал
ЮЗ. |_- g + -у, 8 + -yj да үсә, [ у + -у; -у + -yj да кими, х^= g +
хш1л = ч + "2 ’ п € Ζ" Ιθ4' <*>УНКЦИЯН€Ч графигы 3 нче рәсемдә сурәтләнгән.
105. в) Функциянең графигы 4 нче рәсемдә сурәтләнгән. 100. г) А ■= 0,5, Т - 4,
ω =· ί , x(f() = 1.110. в) Я, 2кл, η ε Z саннарыннан тыш. 111. в) [0; ^2 Һ г)(0; 2].
113. в) Функциянең графигы 5 нче рәсемдә сурәтләнгән. 114. в) Л = 12, Т = 1,2,
1(f) = 12 ein . 115. г) 2 j . 118. - " ; г) 120. г) . 121. г) - .
*> о о 2 4 4
3 нче рәсем
348 Күнегүләргә җаваплар һәм күрсәтмәләр
4 нче рәсем
122. в) ; г) О. 124. в) Юк; г) әйе. 125. б) Юк. 126. г) - ί .127. в) £ ; г) - Д .
О d 2 1 £
128. в) ; г) ΐ - 129. в) Беренчесе кечерәк. 130. в}0,8948; 0,5010. 131. г) - .
132. б) α = arccos x,. β - arccos ζ, тамгаланышларын кертәбез, α β дип уйлыйк,
α Һәм β [0; π] аралыгында ятканлыктан, косинус монда кими, cos a. cos β, ягъни
х,)хг не табабыз, ә бу шартка каршы килә. 133. Күрсәтмә. 132 нче б күнегүнең
чишелешендә язылган алымны файдаланыгыз. 136. в) ± + 2πη, п е Ζ.
138. г) - ~ + 2πη, η e Ζ. 139. г) (-1)” *1 · ?
2 4
•·χ _
142. (-1)” · -=· + 4πη, η e Ζ. 143. в) ± arccos 0,3
Ο
η e Ζ. 146. Γ)
d
+ πη, η € Ζ. 141. в) 5 + πη.
ο
- Ρχ
+ 2пл, η e Ζ, 145. г) - + 4πη.
6^>^Ζ *47·
г) (-1)" + ДД + 3πη, η e Ζ.
4 Ο
349 Күнегүләргә җаваплар һәм күрсәтмәләр
148. .) (|±| + W4l),(.«+4ftn;l).n<Z. 14». г) - * . О, * , - * .
151- ») Й=т)· 152 в) (-|;з)·188· г) Η;“ΐ)· 154 Г> (-¥ + 2w«
- ц + 2ял), neZ. 155. в) - ^ + 2πη; g + 2πη j, ηε Z. 156. г) I - " + πη, - -j + яп),
η € Z. 159. в) (4κλ; π + 4itn), n € Z. 160. r) (4^· + 2πη; - + 2πη), η € Z.
16L r) (- 5 + 2πη; π + 2яп), ηε Ζ 162. rt(- ? + 4 arcsin 4 + ; -- 4 arcsin 4 + ,
η ε Ζ. 163. в) [ J
4 . 164. (-1)" · arcsin 4 + ял, η ε Ζ. 165. г) 2 πη, ± arccos 4 +
4 J 4 5
+ 2πη, η ε Ζ. 166. г) π + 2πη, ηε Ζ. 167. в) χ2+ πη, χ2 + πη, χ, - -arctg 2 = -1,1071.
χ2 = arctg 4 “ 0,4636, η e Ζ. 168. г) ± g + πη, η e Ζ. 169. в) + πη, arctg 3,5 +
+ πη, η e Ζ. 171. г) ± * + πη, η е Ζ. 172. в) (-1)" · 4 arcsin 4 + ” , η e Ζ.
173. в) (-iy‘ · | + πη, neZ. 174. в) , g + ; ft, η ε Ζ. 175. г) (j - ял; яп) ,
η ε Ζ. 176. в) I * +· 2nfe; + πη I, η e Ζ, к e Ζ.
II бүлек
177. б) 3) 1,2881; 4) пһ (2R + ft). 178. г) 0,205. 179. г) Δχ = 0,125, Δ/ = 0,1,
180. г) χ8.ΫΪ ’ 65 км/саг· I®2· г) Тискәре юнәлеште 4 кә. ν* = -2.
Δ/ -2χ0-Δχ
184. 1,5, кысынкы. 185. в) 6(2χ + Δχ)Δχ. 186. г) д; = т ~ ν~, ..
((«ο+Δπ) +1j(jr» + 1)
187. в) (2t0 + Δ0. 188. б) Минус, плюс, минус, плюс. 191. б) 2,5; 2,1; 2,01.
192. г) -2, -4. 193. г) 5, -2. 194. в) -1, -1. 195. г) у = 4х - 4. 196. в) 2; г) 5.
197. в) Х[, х2 нокталарында өзлексез. х5 ноктасында өзлексез түгел. 200. в) 5; 4.
201. в) 6. 202. г) 0,25. 204. һ = 0,04 дм.
206. һ 0,01 дм. 208. г) Зх2 +
2Л·
209. г) + 9х3+ 2. 210. в) —. 211. в) 7Х6 - 20х* + 2; г) х - 9х 4.
(5х+8)2
Зхг(2х’-4х3+5)
212. в) 1,5; 4. 213. в) 4; -1. 214. г) (-«; -2), (2; ~). 215. в) —— .
('-’·)
350
Күнегүләргә җаваплар һәм күрсәтмәләр
216. в) -1. 217. г) (-«; 3), (3; β» ). 218. г) Мәсәлән, Зх3 - |х. 219. а) Юк.
220. г) /(х) - Зх + ' , g(x) = сое х. 221. в) f(x) - 2х + 1, g(x) - х3.
222. в) (-0,5; 0,5]. 223. г) (2ял; я + 2πβ], п е Ζ. 224. г) - .
225. г> 65(5х - 2)” + 24(4х + 7)’’. 220. в) + 2ял; + 2лл] , η 6 Ζ.
227. а) 3 - 2х!; в) (3 - 2х)3. 228. б) -ξ~- , [О; 1) U (1; в) Vcosx ,
[-| + 2ял; I + 2ял] , л е Ζ. 229. б) f(x) [0; «); г) fix) - -7х - 1 .
230. г) -15х3 (3 - х3)4 + . 232. 2 сое х - 1,5 sin х. 233. в) .
V2x-7 2соегх
jg * ял|. л € Z. 240. в) Мәсәлән. f(x) = -sin х. 241. г) Әйе, әйе.
234. г) 0; -1. 235. г) -5+ 2ял. η € Z. 237. 6} -4соа2х . 239. г) ± А+ я»,
л sin22x
(’ П +
242. в) Я; г) (-«; 2), (2; <»). 243. в) 0,7. Күрсәтмә, f (О, 8) < О, f (0, 6) > О икәнен
тикшерегез. 244. г) (-«>; 1), (2; б). 245. в) (-«; -4), [-2; -1), [2; «).
240. г) (-«■; -3] U (-1; 1) U [3; ®). 247. г) т > 0. 248. г) (-2; -1), (1; 2).
249. в) (-2; 0), (0; 3); г) (-»; -5), [2; «). 250. в) (-<»; -4] (J [О; 4). 253. в) 3.
254. г) 0. 255. г) у - Зх + 1, у - 12х - 17. 256. в) у = 2, у - 1 + | - х.
257. в) (-1; -1), (0; 2), (1; -1). 258. г) ( J + 2яд; Л ( J + 2πη - l)j . (- £ + 2ял;
72 ^2ял + 1 - j 11 , п е Z. 259. а) (0; 0) ноктасында arctg 3, (-Уз ; 0) һәм ( 7з ; 0)
нокталарында я - arctg О; г) I | + 2яв; 0j нокталарында -j, (- + 2ял; 0 j нокта¬
ларында , пе Z. 260. а> ; г) . 261. в) 24,52; -0,16; г) 40,52, 9,86.
283. г) 2,0004. 284. г) 0,9302. 265. в) 0,526. 266. в) 0,1247. 267. а) (-Г2 + 4Г + 5) м/с;
в) 5 с. 268.35 м/с; 22 м/с1. 269. (6t - 4) рад/с, 20 рад/с. 270. а) 2,8 рад/с. 271.12t см/с;
а) у^с; б) |с. 272. а) 6 с; б) 18 м/с. 274. 22т. 275. а) 0,04 Н; б) 0,0025 Дяс.
, 8гг-91+21
276. а) 65 г/см; б) 125 г/см. 277. 0 < t < 24. 278. t < 0булганда, I. , . .
* V<f — w-tXl
280. г) (-«; -3], (3; «■) да үсә; [-3; 3] да кими. 281. в) (-»; -2], [2; да үсә,
(-2; 2] де кимн. 283. г) Функциянең графигы 6 нчы рәсемдә сурәтләнгән.
284. Функция графигы 7 нче рәсемдә сурәтләнгән. 286. г) /(х) - -Зх3 + 6х -
= Зх (2 - х), (-«; 0) һәм (2; аралыкларыннан барлык х очен / (х) < 0, шулай
351 Күнегүләргә жаваплар һәм күрсәтмәләр
6 нчы рәсем
7 ичг рәсем
булгач, f функциясе [-2; 0] һәм [2; 3] да кими, ( (-2) > 0, ДО) < 0, /(2) > 0, f (3} <
< 0, тамыр турындагы теорема буенча тигезләмәнең [-2; 0], [2; 3] аралыкларының
һәркайсында бердәнбер чишелеше бар. 287. 6) х2, х4, х6, х„ х,. 288. в) ± ' + 2кп,
neZ; г) ±2. 290. в)х„„ = -1, хм„ = 0; г)х„ь„-±1, - 0. 291. a) f'(x) - 5
бернинди х өчен дә f' (х) * 0; х = 0 булганда, f' (х) була алмый, ләкин бу нокта
т 2
[0; «) аралыгы өчен эчке нокта булмый. 292. в) (—1)"+1 ■ g + яп, п е Z; г) ± TJ .
293. в) ± 3; г) 0; ± 2. 295. г) Функциянең графигы 8 нче рәсемдә сурәтләнгән.
297. г) Функциянең графигы 9 нчы рәсемдә сурәтләнгән. 298. г) (-®; -1], [5; «)
/20
да үсә, [- 1; 5J да кими. 300. з) D (f) — D (f) - R; f — так; х = 0, х — ± ''“з" булганда,
352 Күнегүләргә җаваплар һәм күрсәтмәләр
10 жчы росгм
х е
4
[2; ®) да үсә; / функциясе [- 2; 2] да кими; хм, - -2, f (-2) 4 үг
икән, f(x)>0 була; әгәр
икән, Дх) < 0 була; f функциясе (-»; -2],
Д2) = - 4 ; г) Dif) - £(f) - R; f — так функция; х = 0, х - ±
fix} - 0; х е
булса, fix) > 0; әгәр х е
— 2,
булса, fix} < 0: f [- 1; 1] да үсә, (-»; -1], [1; ®) да кими; x„,„ - -1.
Д-1) - -2; = 1, f(l) - 2. 301. в), г) Функцияләрнең графиклары 10, 11 нче
рәсемнәрдә сурәтләнгән. 302. в), г) Функцияләрнең графиклары 12, 13 нче
рәсемнәрдә сурәтләнгән. 304. в) 2; г) 3. 305. в! max f (х) = f (2) = 56, min f (x} -
- f(l) - -2; max f (х) - f (3) - 594, rain f (x) = f(2) = 56; r) max f (x) = f (-2) - 2,
353 Күнегүләргә җаваплар һәм күрсәтмәләр
min /(x> f (-3) - 1,5: min /(x)-/(l>-
l· *1 2
max f (x) = f (5) = | . 307. 6 c. 72 м/с.
[·=»]
308. min f (x) - f (-2) = 9, max f(x) “ f (2) -
I t ‘I I «··!
3/3
Я
= 25. 30». 10 c. 310. в) max Дх) - f
r) max flx^*
/ ( 3> - 4. min / (x) - /( 5) - - 5 ‘.
311. 24 - 12 + 12. 312. 4-2 + 2. 313. 12 м.
12 м. 314. 54 - 12 I 24 t 18. 315. 16-4-4.
310. 8 cm, 8 cm. 317. Биеклеге — 1,5 дм, нигезенең ягы — 3 дм. Чиш ү. х — бак
нигезенең ягы булсын (х > 0). Авың биеклеген күләм һәм нигезенең ягы аша
» . « . · ■ . 13,5 _ , , п , . . 13,5
күрсәтәбез. 13,5 - х2 · Λ, п — . Бакның еслеген табабыз: — хг + 4х ■ =
■' ' ,s · г»
— х* + — . S(x) - х2 + — функциясенең (0; аралыгында иң кечкенә кыйм-
54 _ - —
мәтен табабыз. (х) — 2х - —, х - 3 — критик нокта. Функция (0; 3) да кими,
х2
[3; да үсә. Димәк, min S (х) - S(3) = 27. 318. 30 см. 20 см. 31». 20/2 см.
Г (°·")
20 v 2 см. 320. Авылдан 3 км һәм таш юлның бораулау вышкасына иң якын
ноктасыннан 12 км ераклыктагы ноктага. 321. В дан 1 км ераклыктагы АВ
кисемтәсе ноктасына. 322. -0,5. 324. Квадрат.
III бүлек
327. г) Юк. 32». в} Мәсәлән, -4х. 331. в) Юк. 332. в> Мәсәлән, х. 334. г) /(х) -
= 3-2 sinx. 336. в) х + ^ + С. 337. г) -cosx - 2. 33». в) -cos^x + ^j - 2.
341. г) x(t) = -coat. 343. г} -sin (ϊ-ϊ)+°· 344 в) “з(ЗхИу +С- 34в¬
- -i- - 2 Xs + Зх + 4,5. 340. в) х- tg (Зх + 1) - Зсов (4 - х) + х’ + С.
2х2 d
347. г) -£ + |x’-4i. 348. χ(ί) = |<а + t! - t. 349. х(0 - 4sin| +2.
350. x(t) - е + 2t2 +21 + 7. 351. г) x(t) -±t’+f2 + t- lg. 352. в) -2; икенче.
353. в) 2; г) j . 354. в) 101 ; г) я + 1. 355. в) 1’ ; г) | . 356. в) Уз - j.
354 Күнегүләргә җаваплар һәм күрсәтмәләр
357. г) 1. 358. в) 0.9. 360. г) 10 | . 301. г) б|. 302. г) 4. 363. в) yj + | .
364. г) 73 - * . 365. г) 4.5. 306. г) Д . 367. 51.368. 4.5. 369. a) F(x)функциясе -
f(x) өчен башлангыч, G(x) функциясе g(x) өчен башлангыч функция булсын. Ул
вакытта F(x) + G(x) функциясе — /(х) 4- g(x) өчен башлангыч функция. Шуңа
күрә f (/(х) + g(x»dx - (F(x) + G(x)) I - Fib) + G(b} - F(a) - G<a)- F(b> - F(a) +
+ G (6) - G(a) - J ftx)dx + j g(x)dx. 370. r) yy . 371. r) |. 372. a) (ЗЛ - H);
- ·
б) у + Яг + F). 373. 0,16 Дж. 374. 0.16 Дж. 375. W · j . Күрсәтмә.
_ . . Л. „ ... . t i ya \ ,
F (x) = - , , монда γ > 0 — ниндидер даими сан. Шуңа күрә А - ί ( - — I dx “
Г Λ χ2 3 4Ι
УЧ
х
пял (о 4" 25}ft /пгчп лгчо
370. - —-— ,\g (376 — 378 нче күнегүләрдә р — суның тыгызлыгы,
6
g —ирекле төшү тизләнеше). Күрсәтмә. Сыеклыкка батырылган (вертикаль)
*г
пластинкага ул сыеклыкның басым көче Р - pg j S(x)dx формуласы буенча
*ι
исәпләнә, монда S(x) — пластинканың мәйданы, батыру тирәнлеге (ft) ft) дән ft.ra
кадәр үзгәрә. 377, ЖГ>*>Р< . 378. 4 W· 379. pS^' ' " 4 160 000 я2 эрг.
2 3 6
Чишү. Стерженьның 14 нче рәсемдә билгеләнгән өлешенең массасы ρίΔχ ка
тигез; стерженьның диаметрын исәпкә алмыйбыз (билгеләнгән өлешнең
озынлыгын Δχ озынлыгындагы кисемтә дип исәплибез), ул чагында бу өлешнең
һәр ноктасының сызыкча тизлеге Dx тәртибендәге төгәллек белән ω х ка тигез
була. Стерженьның (0; х] өлешенең кинетик энергиясен £(х) аша билгелибез.
Кинетик энергиянең [х; х + Δχ] кисемтәсе исәбенә үсемтәсе якынча
та2
2 гә, ягъни
ρ8ω2χ2Δχ
2
ρ8ω2χ2
гә тигез, шуңа күрә £' (х) - <j · “ 0 һэм> Димәк, эзләнелә
торган энергия Е(1) - J Е' (х) dx -
ι pSa>2x2dx „ . х1 , ρ8ω2ί2
- J -—2 = Ρ S ω ~2 dx “ — ·
380. Түбәсеннән исәпләгәндә конус биеклеге-
14 нче рәсем
3
нең -у ераклыгында ятучы нокта.
4
355 Күнегүләргә җаваплар һәм күрсәтмәләр
IV бүлек
384. в) - I . 388. в) ± 2. 387. ± J17 . 388. г) -1. 391. в) β. 392. -5. 393. г) 2.
394. в) . 395. г) 1,44. 396. г) 2,22. 397. в) 1,29. 399. в), г) Беренчесе кечкенәрәк.
400. в), г) Беренчесе зуррак. 401. в) Беренчесе зуррак. 402. в) a3b
403. г) ^4а358 . 404. в) а д 0; г) a f 0. 405. а - 0; б) α ζ 0; г) барлык а өчен.
406. г) 7?2^ . 407. г) . 408. г) 5 ^4 . 409. г) | ^320 , 410. г) б9.
5 3 з
411. г) (-■»; ^5 ]. 412. г) [0; 81]. 414. в) 0. 415. г) 2. 416. в) ^25 fo5 + ^49 .
6
417. в) ± в. 418. г) 8. 419. г) 0, -1. 420. в) -10; 2. 421. в) (16; 81). 422 г) 0; 0,4.
424. г) -12. 425. г) ±2. 426. в) (16; 4), (зб; 1|). 427. г) (27; 1), (-1; -27).
428.
г)
6“3 . 429. в) b 'з . 430. в) 32.
431. в) 432. г) х1
3* - 52 .
433.
г)
а2
434. г) а
+ Ь3 . 435. г) х - 1. 435. Беренчесе
1
а
кечкенәрәк. 437. г) 10. 438. г) - . 440. г) W . 441. в) Тигезләр.
vZ/n
442. г) Юк. 443. в) (0; 444. в) а = ± 1; г) а = 0. 446. г) (-2; со). 447. г) Беренчесе
кимрәк. 448. г) 9. 450. г) |х" - у’|, 451. в) 169,8; 173,8. 452. 10'^ = 172,4.
453. г) у = (3 - 41У — кими, у — \т) — 7С9, г’
-1 , 457. в) 0; г) 1, Күрсәтмә. Графикларның эскизлары ярдәмендә кисешү
з
ноктасының абсциссасы х - 1 не табабыз, башка кисешү нокталарының булмавын
исбатлыйсы кала. Моның өчен күрсәткечле һәм сызыкча функцияләрнең тиңдәш¬
ле үзлекләреннән файдаланабыз, х > 1 булганда, у = 41 функциясе — 4 тәи зуррак
кыйммәтләр, ә у - 5 - х функциясе 4 тән кечерәк кыйммәтләр ала. (х < 1 булганда,
функцияләр тиңдәшле рәвештә 4 тән кечерәк һәм зуррак кыйммәтләр алалар.)
Димәк, графикларның башка кисешү нокталары юк. 458. г) -1. 461. в) 4; г) 4.
482. в) 4; г) -3; 1. 463. в) 3; г) -1. 464. в) 1; г) 1; 0. 485. в) (-2; -3); г) 4^.
466. в) [2; »); г) (-«; 2). 467. в) (-»; 0,5); г) (-1; *). 468. в) -2; г) 2. 469. в) -1;
г) 2. 470. в) 2; г) 2. 471. в) (1; 2), (2; 1); г) (2; 1,5). 472. в) [-3; -1}; г) ,
(4; ®). 473. в) (-2; ®); г) (-»); 1). 474. в) (2; ®); г) [-1; «). 475. в) (-«; 0];
356 Күнегүләргә җаваплар һәм күрсәтмәләр
г) (1; ®). 484. г) i . 486. г) 8. 48в. г) 3. 487. г) logs 5, log, X , log, 1,
log, 125.
488. г) 1.490. г)
491. г) 2 log, b - 3 -7 log, а. 493. г) lg с - 7 -
I
„ т‘и’
- flga - 81g b. 494. г) 1+β + ί>. 496. в) -2. 497. в»—j-. 498. в) Чишү.
Р"
Тигезлекнең уң һәм сул кисәкләрендәге аңлатмалар арасында булган аерманы
карыйбыз, аны нуль белән чагыштырабыз: log, 7 +-
1 2. logJ7-2log,7 +1
log,3 ‘
(l-log37)Z
log, 3
> 0; г) Чишү. Тигезлекнең сул кисәген үзгәртәбез: 3 |о*’4 —
ь»,а 5
> 5 1м,1 «Ч,» - б1”**4 1 = 5'«*г». 499. г) (-«; -4)U(4; ®).
500. в) ( jj ; 2 1) . 502. в), г) Беренчесе кимрәк. 503. в), г) Беренчесе зуррак.
505. в) + 2πη; + 2яп ) , η € Ζ. 508. в), г) 0. 507. г) Функциянең графигы
15 нче рәсемдә сурәтләнгән. 508. г) π !. 509. в) 5. 510. г) Юк. 511. в) 0; -1.
512. в) log, 10. 513. г} 100. 514. в) -2,35. 515. в) | - log, 2. 518. в) (0,7; ®).
517. в) (8; ®); г) (12; ®>. 518. в) 5; г) 0. 519. в) 2; г) 0; 8. 520. в) 25. | ; г) 27, 1.
□ 3
521. в) (32; 2), (2; 32); г) (1; 1). 522. в) 4; г) 100. 10". 523. в) 9; г) |. 524. в) 2;
г) 2. 526. в) (1; 3); г) (-4; -3)11(4; 5). 527. в) (0; 0,001)U(Ю; ®); г) [д ! 2?1.
528. в)
-■5 + яп; - I + ял) U Ц + «η; | + «I
η€Ζ; г) ( <*0.1 ; 10).
529. в) (Х; з), г)<9; 7). 530. в) (2; 8); г) (9; 8). 531. в) g(x) - ,
15 нче рәсем
357 Күнегүләргә җаваплар һәм күрсәтмәләр
D(g) -- E(g) = It. 532. r)g(x) = x2 - 1, D(g)= |0; »>, £(g) - |- 1; ®). 533. г) График
16 нчы рәсемдә сурәтләнгән. 535. в) g(x) - х‘.
х < 0; г) g(x) - ^х-1 .
538. в) -1 «*. 53». 2хе' + х2е. 540. в) у - 1 + х; г) у = 1 -1 (х - 1} In 2.
л δ Δ
541. г) 1 е* + х + С. 542. в) щ, - 2,5247. 543. г) -2 ' In 2 ctg | + - - .
\ 3 /
3*{2* In 1,5+5* In 0,6
544. в) . 545. (-®; 1] аралыгында үсә, [1; ») аралыгында
(2· + 6.)
хини; ж.„ - 1. ! <1> -1. 54». г) + С. МТ. г| -' «■-· ■» 1.
г о III ώ,ο Ζ Ζ
548.
в) Д- - 2 <= 2,3. 549.
In 2
"» 1^7 ■ 550. г) . 551. в) In |х + 2| + С.
,_2 ! х(21п5х-1) / ,1
552. г) у - - · . 553. г| ’ In 10 » 0,7675. 554. в) . 555. 10; J I да
1п2 3 ' In2 5х t 2J
кими, [β; I) да үсә; х„,„ = |
/■(•|·) = 1 + In 2. 556. в) (0; е2] да үсә, (е2; да кими,
х„„ = е2. rte2) = 2 . 557. в) A In 8 == 1.0397.
<? 2
558. г) -7δχ . Графигы 17 нче рәсемдә
сурәтләнгән. 559. г) 2 In 3 · (2х)м ·, графигы
18 нче рәсемдә сурәтләнгән. 560. г) 2,63.
561. г) 2,0125. 562. г) 27, А . 563. г) ' + с.
И f т I
564. г) 844. 565. г) In 11 = 0,5108.
567. в) Юк;г) х0 = 0. 572. г) Мәсәлән, у =
= 2 cos 1.573. в) х" = -9х. 575. в) (|> '^п д .
358 Күнегүләргә җаваплар һәм күрсәтмәләр
576. 9 мин. 577. сәг ~ 3,322 саг; 0,6394. 578.
580. 500е 4 м/мия = 3.37 м/мин.
101g 2
1(1.6
14,75 мив.
МИЯ “
V бүлек
1. а) Әйе; б), в) юк; г) әйе. 3. а) 52 305; 52 335; 52 365; 52 395; 52 320; 52 350; 52 380;
б) 52 344. 5. 35. 6. К у рсәтмә. вакланмасы d санына кыскарсыи, ди, d —
ab ның бүлүчесе, шуңа күрә яисә a. d саннарының, яисә b, d саннарының уртак
d' бүлүчесе бар; аныклык өчен d' саны а һәм d ның бүлүчесе булсын, ул вакытта
d' ка бүленә, шулай булгач, Ь саны d' ка бүленә, димәк, вакланмасы
_ „ _ Р
p€Z,q€N. — — кыскартылмас вакланма.
сГ ка бүленә. 13. в) 1
Р
у > 0 булсын, шуңа күрә р һәм q ны натураль саннар дип исәпләргә була. Ул
. Р2 . . . , - .
вакытта 5 - — , ягъни р2 = 5дг, моннан р2 ның, димәк, р ның да 5 кә бүлевүе
9*
килеп чыга, ягъни р = 5к. p = 5k вы рг = 5<?3 тигезлегенә куеп, 25Λ2 - 5дг, q* - 5А2
ны табабыз. Соңгы тигезлектән q ның 5 кә бүленүе күренә. Алда ясалган фараз
- Р ,
белән каршылыкка очрадык: — кыскартыла торган вакланма булып чыкты;
- г (монда г рациональ) икән, ул вакытта уЬ · г - I рациональ
була, ә бу у5 нең иррациональлегенә каршы килә. 19. а) Тигезләр; в) беренчесе
кечерәк; г) беренчесе зуррак. 31. 87 яки 69. 32. 0. 34. 6, = 0,2; q = 5. 36. 5.
37. 12,5; 7,5; 4,5; 1.5 яки 2; 4; 8; 12. 38. q = 1 - ; S = 3. 39. bt ” 6; q - 0,5.
43. г) у-. 44. г) 2. 45. г) 3. 47. в) 1; г) 1. 48. в) хЛ - Л . 49. г) -Λ - .
‘ ( I һ . е*4 , . „ „
50. б) ab4 la +б ; г) —-—-. 51. в) с! ; г) 3. 52. б) |βιηβ + сое β ; г) am β.
\ ) с +2
53. в) 1. 58. б) 4^; г) sin а - - ; cos # = - 4-; сое 2а - - X ; 59. а) 0.
60. а) 0 дән кечерәк. 81. 1. 62. г) Беренчесе зуррак. 63. в) Беренчесе зуррак.
64. а) 4 1. 65. б) 0,34. 66. в) -3; г) 1. 67. б) 4 + 4 log^h - | log^c. 68. б) 14.
69. г) 365.06446. 70. lg 2 - 0,3010. 71. 2 - А. 73. б) S - 3?Р^- ■
V О
77. в) (-»; -Л)11(-Т5 ; -2)U(2; >/&)U(-A; «). 80. в) һәм (5; «) да
f(x) > 0, (j . 5 ) Да /W < 0. 81. г) (-»; 1) һәм (1; «) да кими. 85. г) 19 вчы
359 Күнегүләргә жаваплар һәм күрсәтмәләр
РА Ум
-1
19 нчы рәсем 20 нче рәсем
рәсемне кара. 86. а) 20 нче рәсемне кара. 87. в), г) Әйе. 88. в) f(x) = х* + Зх -5
булсын, /(х) әзлексез, бу вакытта /(1) 1< О, f(2) = 33 > 0. 91. а - 3, Ь = - 5.
92. в) а > О, Ь < 0, с > О, D < О; г) а < О, t> < О, с ~ О, D > О; д) а < О, b < 0, с < О,
D < 0. 93. а) Була алалар (у = ахг + Ь рәвешендәге квадратик һәм у = Ь рәвешендәге
Хг Х3-Х π
сызыкча). 94. в) у “ β* -1 х4 -1 ' ®·· в> ± g + 2ял рәвешендәге саннардан
, , Гя Зж Ί
тыш, барлык саннар, Д € Ζ. 97. в) + ял;+ яд1, η € Ζ. 98. г) (-1; 1).
99. г){-co;-2] J[2; оо). 100. в) (-^ + 4ял; | + 4лл) да р > 0, + 4ял; + 4ял)
да у < Ο, η ΕΖ. 101. в)Так; г)җен. 102. г) я. 103. в) |> ♦ ял; & + ял] да кими,
Г- " + яд: £ + ЯЛ I да үсә, х^,“ ‘j + ял, хш = £ 4- ял, л eZ. 104. г) min у = 1,
L "
max у юк. 105. 6) Күрсәтмә, у = |sin х|. 108. Әйе. 109. в) tg2 < -1 < ctg 2.
Д|,)
111. в) 0; г) 0. 112. в) <-«>; O)U[1; 4]. 113. в) (-«>; «); г) (2ял; я + 2яд), neZ.
114. в) (j; 2) U(2; о=). 115. г) (0; «□). 116. в) [1; ·), 117. в) (-00; log3 2) да
У > 0, (logj 2; со) да у < 0. 118. в) [0; ») да у > 0. 119. Җеп тә түгел, так та түгел.
120. в) Җеп. 123. а) Күрсәтмә, х > 1 булганда, у = х - 1. D(y) = (1; co).
124. г) min у = y(l) - 0, min у = ι/(-1) = 4. 125. г) ± 3. 126. г) (О; 3). 128. а) О;
[-и] 1>=»1
ф1.133.Г> ft ;-). 134. в) |1; 13]; г) |-1;-5]. 135. г)-3.5 Нам ]3; ->.
137. г) -6; г) 2; Ц . 138- а) 1; 2; 71; в) | ; 4; г) О; -1; 3. 139. а) | ; в) ;
г) . 140. в) : г) -4; I . 141. η) -1; г) 1. 142. в) (-»; со); г) (1; 13).
360 Күнегүләргә җаваплар һәм күрсәтмәләр
143. г) (-<»; -4)U(6; «). 144. в) (1; 3)U(3: 5); г) (3; 4). 146. в) 2; г) -4; 4.
147. в) 2; г) 63. 148. в) 4; г) - | ; 0. 14». в) -8; 8; г) -1; -3. 150. в) (-«>; -J17JU
U[V17; -J; г)(9;«=). 151. в) [2; 3]; г) [-3; 5]. 152. а) -π + 2 πη; ± arccos | + 2πη,
π 1 4 л й- η г
η ζΖ; 6) -д - 2 arccos 5 + πη (яки arctg 0.5 + πη. η ε Ζ — җавапның башка
формасы); г) arctg 0,5 + πη, η GZ, 153. в) + + πη, η εΖ; г) (-1 ("arccos + πη,
ηεΖ. 154. в) £ + an, ν + тг · η€Ζ; г) 2πη, 2 · (-1)" · arcsin | + 2πη, neZ.
155. в) ψ. n€Z; г) « * у . "|+ πη, η€Ζ. 156. в) (iy| + πη, ηεΖ;
r) l-iyy + an, ηεΖ. 157. в) (-1>" + ,| + ал, ηεΖ; г) an; » 5 ♦ 2 πη,
ηεΖ. 158. а) - т ; б) 0; в ) -2 Л -2; г) 0. 159. в) I 4* ♦ 4"л ; I ,
ηεζ; г) Г-# + ^; A + η€Ζ. 160. в) Г ? + πη; + ал! , nGZ;
I о Z I £ £ J L *·> J
+ 2πη
2πη),ηεΖ. 161.a)[-| + 2πη;
0 ^-π + 2πη; - j
I + 2πη; π +
neZ;·) Г- ’ + πη, anj.neZ; г) [πη; | + πη],ηεΖ. 162. a) + 2πη; π + 2πη) ,
η εΖ; в) ( ’ + 2πη; 2π + 2πη|, л εΖ; г) | + 2πη; | + 2nnj , л εΖ. 163. в) 1; 5;
г) 3; 9. 164. в) 2; г) 1. 165. в) 3; г) 0; | . 166. в) + log5 2 : г) 0; | .
2
167. 6) ± arccos - 1) + 2πη. η εΖ; г) -1. 168. в) (-«; - ; г) (-«>; -4)U
(J(3; »). 169. в) (1; 3); г) (-»; -1ЦД0: ”>- 170. 6) (-5; 3)(J (4; ®). 171. в) 6;
г) 1001; 1 + V10 · 172. в) 10; г) 3. 173. г) 64. 174. в) 100; ; г) 3; 9.
175. а) (-1)" J + πη. η εΖ; б) arcsin + 2πη, η εΖ. 176. а) {-3; U
U (^ΊΓ^ ;4); г) -1:1)· IT7· a) (0; 6): r) (1: 2JU13: 4) *78· B) (2;
r) (|;*)· 17»· в)(0; 0.1) U [100; «); r) (-«·; 0]|J[log.5; 1). 180. в) ( 31 ; ’) ; r) 0.
181. в) (0,4; 0,8); r)(2; 3); (3; 2). 182. в) (0,5; 4); г) (7; 3); (-7;-3). 183. в) (1;2);
(2; 1); г) (| ; |) ; (|; . 185. в) [-3; ; г) (-3,5: 0). 186. а)(25; 49); г) (9; 16);
(16; 9). 187. в) (16; 4); г) (16; 4); (-4; -16). 188. в) (81; 16); г) (-1; -8);
(-8; -1). 189. а) - (-1)* £ + πη - ”* ; « + (-1)‘ " + πη + ). Λ. ηεΖ;
у Ч 1Ζ Ζ 4 LZ 1л /
361
Кунегүларгә җаваплар һәм күрсәтмәләр
б) - (l. ; j + |),лСЖ. в) + πη + nk; + πη - oft), (-| + πη + πΛ; -2+xn-«fej,
ft,neZ;r)U + - л + 2πη), ft. nSZ. 190.6) (πη; - πη) ^(-ΐ)’*1 | + πη;
^ + (-1)"|-πη), neZ; в) (j + πη + πΑ; £ + πη - π*) , ί-^ + πη + π*;
~^+πη-πλ
ftSZ. neZ; г) θ£ + πη;-πη), (.* + 2πη; £ - 2πη) , ί-|+2πη;
^-2πη) , η eZ. 191. a) (2; 1); б) (5; 4); в) (5; 1); г) (3; 0). 192. а) (1; 3); б) (3; 2);
в) (2; 0); г) (2; 6). 193. а) (2; 1); (log, 7; log, 9); б) (4;1). 194. а) (100; 10); (0,1; 0,01);
(4; 4); в) (1000 000; 0,1); г) (|; 1) 195. а) (27; 4); ; - з) ; б) (2; -1); в) (125; 4);
(625; 3); г) (3; 2). 196. а) (4; 2); б) (25; 36); в) (1; 1); (4; 2); г) (512; 1).
197. 75 км/сэг. 198. 4 км/саг. 199. 55 км/сэг. 200. 18 км/сэг, 24 км/сэг.
201. 10 с. 202. 240 м3. 203. 6 һам 12 көн. 204. 20. 205. 25%. 206. 160 г, 20%.
207. 60 км/саг. 208. 21 м/с, 147 м. 209. 6 км/сэг, 4 км/сэг. 210. 20; 30.
211. 20 һам 30 кев. 212. 12 г, 48 г. 1,5 г/см3. 213. 3 кг, 80%. 214. 4 м/с, 3 м/с.
215. 32. 216. 8 һәм 3; 28 һәм 27.
220. г) -508Χ-~2- . 221.
(1-2совх)*
(х3-2) sinx + 3x2cosx
218. в) 3; г) 3. 219. г) 1
(*-«·)’
ez+«’’ - xie'-e'-'jlnx .
г) J . 222. г) !— -
и , v 'xlnlO
■ —Ή ■ 223· г> (-1)’ А + ■ η е 2 г25· в) r) < 0 <
cos!l2x - —I ' ' 12 2 J *
<f(xs). 228.6) 25,375; 9,84. 229. в) 1,005; г) 2 + » 2,00067. 230. в) (1; -)
да үсә, (-», 1] да кими, xmln - 1; г) (-» ; 4) да һәм (4; «) да үсә.
231. в)Г- ~ + 2πη; £ + 2πη1, Г 5 + 2πη; + 2πηΊ да үсә, + 2πη; £ + 2πηΊ,
L л o j L * J Lo J
+ 2,w; т 4 *"] да кими’ x«“«= 6 + 2ял’ “ т + 2жл‘ f + πη>
neZ; r) (-=■>; ®) да үсә. 232. a). 6) 21 нче рәсемне кара. 234. а), б) 22 нче рәсемне
кара. 235. в) max f - 1) - 4 4 ; mln/ - f (1) - 3; г) max f - /(-π) - π;
[:■] [:■·] ι*·ι
min / - - {(π) - -π. 236. a) 10 + 0; 6) 5 + 5. 237. 10 см, 10 см. 238. 72 см2. 239.
/А сэг. 240. 2,4 м. 241. 4>/2 м. 242. Һ = 2г. 243. .245. Я - 1,5 сэг. 246. 4R
V3
247. Н - Я>/3.248. Ъ = см, h = 4oJ2 см. 249. Я ; Н - .
^/3 ¥3 Л + 4 π+4
362
Күнегүләргә җаваплар һәм күрсәтмәләр
21 нче рәсем
250. Орыну ноктасыннан 1,5 Я ераклыкта. 251. 60°. 252. М (1; 1). 253. -У4V .
254. а) (о; |1; б) (6; ®). 255. 3,5 рад/с. 256. 0,04 л см2/с. 257. 8 км/сәг.
4·· 100
258. I ι> I -1,5 м/с- 259. ;— м/с, п гг м/с2. 260. 1) 360 г; 5хг/см;
'/25-4f2 J[25-4t2)
22 нче рәсем
363 Күнегүләргә җаваплар һәм күрсәтмәләр
2) О; 60 г/см. 261. 3 я рад/с. 262. а) 85 м; б) 4 с, 90 м. 263. а) М (-1; -1,5);
б) Μ (1; -1,5). 264. ; О. 266. Теләсә нинди х өчев f - 5х* + 2 > 0.
268. в) 2х + 3 In |х - 1|+ С; г) tg 2х - ct« Зх + С. 269. в) ---L-- 2 ;
Зх’ 24
г) - сов2х ι-1 . 270. х1 - Зх + 4. 271. у - х» - 5. 272. -1 сов 21 + 3.
273. в) 7~2 |.~3^ ; г) 39. 274. а) 2; -2; б) 0.5; -0,5. 275. в) я ; г) 9.
276. 18 һәм тг . 277. 101.278. |. 279. 2; 1. 280. |. Чишү. Күрсәтелгән
·» V V о
фигура рәсемдә штрихланган (23 нче а рәсем а < 2 гә тиңдәш, ә 23 нче б рәсем
a J 2 га тиңдәш), а < 2 булганда, әлеге фигураның мәйданы 4 кә тигез булган
г
ОАВС квадратының мәйданыннан кечерәк, ә α > 2 булганда, S = ( (х1 + 4х + a) dx
о
364 Күнегүләргә жаваплар һәм күрсәтмәләр
VI бүлек
1. г) Күрсәтм ә. пг + 5п + 16 = (п - 4)2 + 13п саны 13 кә η — 13* + 4 булганда
гына бүленә, ул вакытта (п - 4)2 саны 169 га бүленә, ә 13п бүленми. 2. ± 5; * 7.
3. б) К ү р с ә т м ә. Әгәр d саны N ның бүлүчесе булса, ул вакытта ү шулай ук N
ның бүлүчесе була, эстәвенә d - } N - d1 булганда гына мөмкин. 4. в) (а( + 1) х
х(а2 + 1) ... (а, + 1). 5. б) Юк; в) юк: г) юк. Күрсәтмә. N ны 3 кә бүлгәндә,
калдыкта 2 була, (а) ны кара. 6. а) Юк; сан 3 кә бүлеаә, ә 9 га бүленми; б) 9.
Күрсәтмә. 5 $ 1987 ■ 9 =17 883, с < 9 · 4 + 1 = 37, d < 11 һәм d саны 9 га бүленә.
8. а)(х; у)- (0; 0). К үрсәтмә. № 5, а ны кара; б)(0; 0); (1; 1); (1; -1). Күрсәтмә,
х ' 2 булганда, у2 санын 4 ка бүлгәндә, калдыкта 3 калырга тиеш (№ 5, а ны
кара); в) (46; 45); (46; -45); (-46; -45); (-46; 45); (10; 3); (10; -3); (-10; -3);
(-10; 3). Күрсәтмә, (х + у) Һәм (х - у) — 91 нең бүлүчеләре; г) (3; 3); (3; -3).
Күрсәтмә, (у - 1) һәм (у + 1) саннары — х > 0 булганда, 2 санының дәрәҗәләре.
9. а)(7*+1; 13* + 1), k е Z; б)(1;1); г) (1:1); (1;-1); (3; 3); (3;-3). К ү рсәтмә.
х > 4 булганда, 1! + 21 + ... + х! саны 3 кә тәмамлана. 10. ± 13. 11. 210; 4.
Күрсәтмә, lg 2 - 0,30103, lg 5 - 1 - lg 2 = 0,69897 (0,00001 кадәрге төгәллек
белән) һәм lg 125lw] - 300 lg 5 - 209,691. Әгәр N санының k цифры булса,
k - 1 й IgN < k була. Моннан тыш, lg4 < 0,691 < lg5. 14. б) Күрсәтмә.
3^+2 + Зп'-ГЗ + ЗйТ4 > п +Т ■ 17· Күрсәтмә. Чиксез периодик унарлы
вакланма чикле унарлы вакланма беләв ваклаучы 10* (* — периодтагы цифрлар
саны) булган чиксез геометрик прогрессия суммасын кушып табыла. 19. а) Әйе;
б) әйе (мисал: (Уг)21’12* = 3). 20.6) Уз = дип фараз итик, биредә p€Z, qeN.
о Р3
— — кыскартылмаучы вакланма. Ул вакытта 3 - — , ягъни р3 - Зд3, моннан
р ның 3 кә бүленүе килеп чыга, р — 3* ны р3 — Здэ тигезләмәсенә куеп, 27k3 - 3q3
ны табабыз, ягъни 9*2 = q3. Соңгы тигезлектән q ның 3 кә бүленүе килеп чыга.
Каршылыкка килеп чыктык; — вакланмасы 3 кә кыскартыла; в) lg5 = булсын,
Ч Ч
бу вакытта lg 5 > 0 икәнен истә тотсак, р һәм q — натураль саннар дип исәпләргә
>
була, lg 5 = — тигезлегеннән 10’ = 5 не табабыз, моннан (О’ = 5’, ә бу тигезлек
дөрес түгел: аның сул ягы җөп сан була, ә уң ягы юк. 21. а) 7з + 7б = г булсын,
биредә г — рациональ сан. Ул вакытта 3 + 27з ■ 7б +· 5 = г1, моннан 715 = —у— ,
ә бу 715 нең иррациональ булуына каршы килә. 22. Күрсәтмә. * — бу
вакланманың периоды озынлыгы булсын, * нчы икеледән соң килүче цифрдан
башлап, * цифр карыйк. Бу барлык цифрлар — җиделеләр, шуңа күрә
365 Күнегүләргә җаваплар һәм күрсәтмәләр
бу вакланманың периоды (77.„77)гә тигез булырга тиеш, бу лерес түгел, бу
/3-1
очракта моннан соңгы барлык цифрлар җиделе булырга тиеш. 23. а) ——-
>/2
б) 4^5 - 7; в) <5 + -?2; г) 2<3 + З^б . 24. а) 6; б) <» - Л . 25. а) Башта /З
тән котылыгыз: (7Й + Й) · ( (ty' - /2 - + ) = (Vi)’ + (й)’ = 2^2 е 3;
б) башта санаучыны һәм ваклаучыны >/2 е /З - /5 кә тапкырлагыз; в) № 29.
е ның нәтиҗәсеннән файдаланыгыз. 26. а), б) Юк. 27. Күрсәтмә. Кубка күтә¬
реп, х = + нең х1 - 5х - 12 - 0 тигезләмәсенең тамыры
булуын исбатлагыз, ә бу тигезләмәнең бер генә реаль тамыры бар: х = 3. Димәк,
бирелгән сан 3 кә тигез. 28. Теләсә нинди натураль k очей
2^1+ 2^2 +·■■■*■ 2^ >^+2^+"+^"i· 29· β) (x’ ~2x + 2)X
x(x2 + 2x + 2); б) (хг + x + 1) (x2 - x + 1); в) (х2 + x + 1) (x3 - хг + 1);
г) 3(x2 ι у2) (у2 1 г2) (х - г) (х + г); д) 3(у + г) (г + х) (х + у); е) (х + у + ζ) х
х (х2 + у2 ι г2 - ху - yz - гх). 33. а) а = arccos х булсын, ул вакытта <C0S ° *’ һәм,
[б α ξ π.
беренчедән.
π < π _ π
2'2 2 · θ икенчедән.
sin I" - «j = cos α - х. димәк.
х санының арксинусы билгеләмәсе буенча
34. a) J*g ;
- - a — arcsin х.
2
б) 1 - 3 (т2 - I)2; в) 16 ; 0 -W ■ 35. а) Зд - 10; б) 4д - 12; в) 2 - π;
г) 3. 36. Күрсәтмә, tg у = формуласыннан файдаланыгыз.
39. а)
аЬс _ . ай +1
аб + ас + бс ’ а;8 - 56
40. а) Күрсәтмә. 2 нигезе буенча ике кисәкнең
дә логарифмнары тигез; б) 0. 41. 7. 43. 2; -6; 18; -54. 44. 931. 45. а 12.
.» , „ л .„ Mb .п ν ρα .99 10· 1
46. 1 яки -2. 47. 0. 48. g j . 49. aso 6И. 50. я)Күрсәтмә. iri.J = —g— ;
Һ цифр
б) күрсәтм ә. S — Sx = х + х2 + ... + х" - пх"* *; в) | _ * + п . 51- а) х * ,
neZ; b)(-2;-1)U(1;21; г) Я; е) (-^2 ; -1)0(1; >?2). 52. б) [-2; 1); г)[*2;1];
366 Күнегүләргә җаваплар һәм күрсәтмәләр
з) [-2; 2]; к) [-2; 2]; л) [О; 4]. 53. а} [-<5*]» в) [-в; 4]; г) («И £
. / 10 . si ЧГЛ Ч КЛ Ч Ч > Л п/Л
54. в) V "У ‘ S J ’ г) Ч· 5®· а) f W = 0 теләсә ниңди х € D (/) ечев, естэвенэ D (f)
О ноктасына карата симметрик. 59. а) Әйе (мәсәлән, Дирихле функциясе,
х рациональ булса, бу функциянең кыйммәте 1 гә тигез, һәм х иррациональ булса,
0 г» тигез); б) юк (әгәр авдый функция булса, Һәм 1 -7г саннары аның
периодлары булырга тиеш, ә аларның суммасы 1 юк). 60. Күрсәтмә,
а) 1 кыйммәтен функция бер ноктада, 0 ноктасында гына ала. 61. б) ‘ ; в) 2x^2 ;
г) 1. 63. Күрсәтмә, а) log,3 > 1,5 > loga8. 64. a) ctg 6; сое2; tg3; sin 4’.
67. а) Теләсә нинди n да; б) җеп п да; в) андый η нар юк. 68. a) f (х) = Ь яки
f(x) = х; б) f(x) · х яки fix) - Ь - х. 69. а) Җеп п да х, так л да 3 - х, билгеләнү
елкәсе R; в) η саны 3fc рәвешендә булганда, п саны Зк + I рәвешендә булганда,
, п саны 3k + 2 булганда, Σζΐ; п - 1 булганда, D (f) - (-®; 1) (J (1; “") һәм,
1-х х
п > 2булганда, D(fn)- (-·; 0)(J(0; 1)U(1; “·>· 70. а)у - — , a#О; б)р-хякн
αχ+b ~
р - ^х_а (he * -а2). 71. 24 нче рос. кара. 75. Өстәп булмый; б) җепкә кадәр;
а) һәм б) так функциягә кадәр. 76. а) Т > 2; б) Т - 3, Т > Т#, биредә Т„ = 6,5;
в) Т > Тл, биредә Го = 5. 77. 25 нче рәс. кара. 81. a) min/ - -1; max f *■ 2;
б) max f - 1, иң кечкевә кыйммәте булмый. 83. х ® кә омтылганда, у = х - 1,
я
х -» кә омтылганда, у х - 1; г) у - 1, х — 3, х - -3. 84. в) Күрсәтме.
24 нче рәсем
367
Күнегүләргә җаваплар һәм күрсәтмәләр
25 нче рәсем
sin х > О булганда, у = tgx һәм, sin х £ О булганда, у = - tg х. 90. a) 1; б) 1;
в) 3; г) 14. 91. а) а > О, b > 0, с < 0. d > 0; б) а > О, Ъ < 0, с < 0, d > 0. 92. а) х - О
һәм у = 2 турылар пары; б) у - хг - 2х һәм у = 2х -х2 (ике парабола). 94. 26 нчы
, ху+1 J/+1 И1-*) .
рэс. кара; г) күрсәтмә. ~~ j > jpj » (др-lU.-fl >°· 95. б) (х2 - 1)κ
х (у2 - 1) = О — 4 туры. 96. в), г) 27 нче рэс. кара. 97. a) a <S. О һәм а 4, а < - !,
булганда — терле тамгалы, а 5 4 булганда — уңай; -4 < а < 0 булганда —
тискәре. 98. а) 2 < а < 5. 99. а) р2 - 2q; р' - 4pZq + 2q2. Күрсәтмә. Виет теоремасын
кулланыгыз. 100. а) р = 0; б) андый а лар юк. 101. a + Ь + с - /(1) < 0, шуңа күрә
с = /(0) < 0. 102. Күрсәтмә. Бу тамырның 1 булуын исбатлагыз, ул вакытта
а + Нс-О һәм х = 1 — сх2 + Ьх + а ·· 0 тигезләмәсенең тамыры. 103. Күрсәтмә.
р
а) х0 - ~~ ны тигезләмәгә куегыз һәм р һәм q саннары үзара гади булуыннан
файдаланыгыз; б) Р(х) ны Р(х) = Q(x) (х - а) + т рәвешендә күрсәтегез, биредә г —
Р (х) яы (х ~ а) санына бүлгәндәге калдык; х = а ны куеп, Р (а) - г ны табабыз.
104. .) * 1; И-»; 0.5. 105. .>
106. г) Күрсәтмә. (х2 + Зх + 2) (х2- 9х + 20) = (х + 1) (х + 2) (х - 4) (х - 5) =
- (х2 - Зх - 4) (х2 - Зх - 10). у = х2 - Зх + 1 булсын, ул вакытта у (у - 5)х
Күнегүләргә жаваплар һәм күрешмәдер
х(у - 11) - -30, моннан (№ 103 ве кара) у, - 6, у2 3= 5 ± ч'ЗО - 107. а) 1, -2 * уЗ .
-9 ± 733 1 1
б) 1; 3; . 108. а) 2; |; 6) күрсәтмә, у = х + булсын, ул вакытта
2/ + у-7 = 0; в)-1; 2; г) 1 + 7т ± 7зТ7 + 5 . 109- а)2; -|; б) 1 *
110. Күрсәтмә, а) (х2 + I)2 - 2(х -I)2, моннан х2 + 1 - ± 7з (х - 1); б) чишүнең
бер ысулы — у алыштыруы белән а) га китерү. 111. a) 2; 4; -1; --j ;
“ x I it 3
б) күрсәтмә, у = —— булсын, ул вакытта у2 + 2у - 1 = 0.112. а) —j— .
113. а) ±1; б) 5; -3. 114. а) 1; б) [6; ®). 115. а) (-·; -4]|J{-2; -1]U(1; “>)·
11β. а) (-<»; U ( Ц7. а) (-«; «); б) 0. 118. а) (1; 3);
. , . a + b c + d
а· I ~ 4--Л91 / 4 + V19 I a+b+c+d 2 + 2
б) —з—I UI —з—119. в)Күрсәтмә. - > 2 >
la-t-b c+d п=—т= , a + fe+c
V 2 " 2 * ■ чсв = Globed ;г)күрсәтмә. d — 3 дип исәнләгез.
125. б) (з7з;Тз); (з7з; - 7з); (4; 5); (-4; -5). 128. а) (|; |); (|ί|)ί
б) (1 ± (3 - V· 2 С Vo * 3. 127. a) (1; 1; 0); б) (-3; 2; -1). 128. a) (1; 2); (2; 1);
б) (1 + 7з ; 1 -7з ); (1 -7з ; 1 + 7з ). 129. а) (5; 3); (-3: -5); (717; 717);
(-717; -717); б) (2; -1); (1; -2); (-2; -1); (1; 2); (0; 3); (-3; 0).
юа ./1+713 1+71з\ /1-713 -1+71з\ I з(з+7в9) з+;й I
130. .) (—j—; 2~); Ң—; —I ц) t —io~j!
(3(а^”).цД |. w 10.^ (.»,»,!») 131. .>(2,1»
(.V а): ( д‘ л)·
(Ч,247·*'^)· 132.а)(0;0); (7?; 7т); (-7?;-ТЙ; (3; 2); (2; 3); (-3;-2); (-2;-3);
(719; -719); (-719; 719); б) (0; 0); (2; -2); (-2; 2); (7б; 7в); (~7в; -7б);
(+ у/з β ~у/1 + \/3 A ί —у/7 + 9 у/ί + у/з (>/7 “ ^3 ф —у/7^у/3 ф
1 2 * 2 J; 2 ; 2 Г 2 * 2
рТ7-7з;77-7з\ в) ( х + _х + ч^. . j + ;jk е1 _;'3. _! _;3>
I Л л ϊ
-1 -7з); (0; 1; 1); (1; О; 1); (1; 1; 0); (2; -1; -1); (-1; 2; -1); (-1; -1; 2); г) (1; 0; 1);
(-1; 0; -1); (|; ||) ; (-1; - |; - |) . 133. а) (3; 2; 1); (3; -2; -1); (-3; 2; -1);
370
Күнегүләргә җаваплар һәм күрсәтмәләр
(-3; -2; 1);б) (3; 2; 1). 134.β)(2; х/з: 6): 6) (- 1; -1; -
в) 0; г) ( I : - Н-! (- ^;-X; (4; 3; 2); (-4; -3; -2).
W3 73 7з/ \ 73 75 73/
135. 3 м/мин; 1,8 м/мин. 136. 863. 138. 40 км*. 139. 8. 140. 280 сум, портфель
авторучкадан кыйммәтрәк. 141. 12,5 г. 142. 16 сәг. 45 мин. 143. 100 м/с.
144. а) I; б) 1; 2: а) 7; г) ± Щ · 145. а) 1; 5) 2; 11; в} 1; г) 0. 146. а) π + 2ял;
+ 2πη, ηεΖ; б) + 2г. п, neZ; в) 0; г) πη; + 2кл, neZ. 147. a) [3: 11];
_ _ ~ „ 63 9 .. „
6) [5; 10]. 148. a) 0; 6) 2. 149. a) gg ; γ ; б) күрсәтмә. Ике кисәген дә
^(7+х)2 ка бүлегез. 150. a)-1; б) 8; 8 ± j1*’2 . 151. а) ; 6)0.
_ _ а-Л—а^ . . _ а+72—а*
152. 0.153. а) 0, a < -1 булса; х = , -1 < a < 1 булса; х - ,
1 si a < 4z булса; х - , α - 72 булса; 0, α > 72 булса; б) 0, α < -1 булса;
аг+1 а2+1
х = —х— , -1 · ο < 0 булса; 0, 0 ζ а < 1 булса; 0, 0 $ а < 1 булса; х = ——- ,
ха о
о 1 булса. 154. а) (-“; 1](J
17 + 713
6
б) [0; 3]; в) (1; »);
г)
155. „>[-Ь«) и Н; 5>[1;®1:в)
81-9797 „ Г„ ч.ц\
—s—: °; г> L0: πΐ) · 15β·а) 0:
157. а) (1; |) (J (|б) (-«; - U(3; «). 158. аЩ; «»
б) (о; {J и(4; «);
в)
-з+7б
2 :
11; г) (2; »).
159. a) (1; 64); (64; 1); б) (4; 1);
(1; 4); в) (1; 27); (27; 1); г) (1; 8); (8; 1). 160. а) (2; 3); (’’ ; - | | ; б) (2; -2);
в)(4;2); Q-.-j); г) (8; 27); (-27; -8). 161. а) (-2; -8); 6) (*}; 24 ); (j; | ) .
162. а) (9; 1); б)(64; 1); (-1; -64); а)(9; 4); ):
г|М>1(<^).
163. а) (-1)" + -^. η εΖ; б) + ял, пе Ζ; в) g · V . ял, п е Ζ; г) g + 2πη,
neZ. 164. a) 0; -ту + 2яп, |-2πη. neW; 6)0; в) 0; 2 πη. π - 2πη, η ε ΛΓ; г) 0.
165. a) ± arccos + ли, л еИ; б) πη; , ηε2; в) (-1)" ,. + πη, л εΖ;
371 Күнегүләргә җаваплар һәм күрсәтмәләр
2
ж а . af . г nil, /с uj
I ft X/. * Vf£F« a) X) x- I
+ πη, n eZ;
6)0. 170. + 2πη, neZ. 171. 2k, k e Z, биредә A ^31/, I e Z;
Ц(2п+1), neZ, n*33m + 16. meZ. 172. a) £ + ™
ηεΖ; б) -ү, neZ.
173.0. 174. (-1; - £ + 2πη ); (1; - % + 2πη j.aeZ. 175. - yg + ; g + an,neZ.
177. a) ( - -^ + πη; | + ivi j; (g + ππ; * + πη j, η εΖ; 6) (g + 2πη; + 2πη ), η εΖ;
в) (- ^ + πη; - ^ + πη J ; (πη; + πη
πη; $+πτι
< ο .
πη; + πη
Δ
η €
ηεΖ. 178. а) Γ-^ + 2πη;-| + 2πηΙ [-|+2πη;-| + 2πη], [|+ 2πη; &® + 2πη1,
neZ; 6) -ί + πη, ^ + πη;-® + πη, Λ +πη; Λ + πη , Η ♦ «л; ♦ Wi L
Δ I 1ϋ 4 10 10 II 10
η е Ζ; в) (2πη; π + 2πη), ηεΖ; г) § + πη; * + πη L 180. Күрсәтмә. cos πχ = -1
13 ζ _
яки | \ cos πχ ч g - 181. + 2πη; ^*2ltn | , η e Ζ. 182. Күрсәтмә,
cos sin x > cos x > sin cos x, 184. a) I 5(" » к(2ж + *|; k, п e Z;
β) (ί · ; π + 2πΑ ), *, η € Ζ 185. f gaiTtg1^^10 +2πΑ; Заг^е1 -^-10 + 2πη ,;
14 4 / V3 <3 /
2arctg-—Ц^- + 2дА; 2arctg * 'θ + 2πη I;
у'З 73 I
(«♦2π*;5>2πη)
‘.О о ί
k ε Ζ, η е Ζ.
186.+ πτη; * +πη; - ^ + π (2ρ - т - η); (- |■ +· πηι;- + πη;^ + π (2p-m-n+l |).
т, η, ρεΖ. 187. а) ± 2; 6) 2; в) ±1; Γ) 1. 188. а) |; 2; 4; 6) 1; ; ± | .
η e Ν; в) - д ; ; 1; 3; г) 0. 189. а) о + πη, η e Ζ; б) arcfg 10 + πη, ηεΖ; в) ± g +πη,
η е Ζ; г) 2 + 2πη, (-If θ + πη, η ε Ζ. 190. a = | . 191. (-«; log,, (^2 -1)] U (0,5; «];
6) (0; 2); г) (-«; ®). 192. а) (2; 3) (J (4; «); б) (-^7;-Л) L) (ч/З; J?) . 193. а > 2.
372 Күнегүләргә җаваплар һәм күрсәтмәләр
194. а) (2; 0); б) (1; 1); в) ® + лА; ®- + 2itnj , + πΛ; 2ют—11, Л, л е Z;
г) (πη;2πΛ±5). Л, п е Z. 195. а) 8; б) log., J ' j4* ; в) 0; г) | + πη, neZ.
J? =£“ 1 1
196. a) 10 1 * ; 10 * 3 ; 6) 2; g ; в) 10: ; г) 0. 197. Күрсәтмә. arctgx +
JL
+ arcctg x = J ; arctg x arcctg x — 10°; 6) 0; в) 10; r) ± 0,5. 198. 0 < a < g .
199. a) a < 0; 6) a > 0. 200. |e| > |. 201. a) 11: з); 6) (3; *)U<1; + 2 1“):
в) (4; 10); г) (1; tfa). 202. a) 0; 6) I * з); B) Jog8—J—; «/; r) Q: δ).
203. a) (4; «■); 6) (-4 - J2 ; -5) (J (-3; -4 + 72 )(J(1; 2); в) [ 7б-1; 2)U(2; 5);
г) (loga10; »). 204. (2; 2,5). 205. (2; 4); 6) Ij. : в) (13; 8); г) (512; 1).
206. а) (| + 2ял; +^ + 2π*
ι]; ■*?+2πη; ι *+2я*1, η, keZ;6)(*
I \ ο a I \6
® + 2πη;|+2Η*),
,. Г(х)-Г(О)
η, keZ. 209. а) Г (0) =
- lim
- 0. 210. Чагыштырма
, . Δ/
табыйк: ■
/(χ+Δχ)-/(χ)
нинди х өчен (чөнки /(0) - /(0 +0)
/(х)+/(δχ)-/(χ) _ Ζ(Δχ)-Λθ) ,(Λ. .
= » τ (0) теләсә
Λχ Δχ
- /(0) + /(0) - 2/(0), ягъни /(0) - 0).
211. Күрсәтмә. —χΠ-0— ” ~χ
, бу функциянең х нульгә омтылганда
чикләмәсе булмый. 212. Гомумән алганда, юк. Мисаллар: a) f^x) - х, f^x) — |х|,
χ0 - 0; 6) /,(χ) - /2 (χ) - Vx2, χ„ = 0. 214. a) / (χ) - arcsin χ функциясенең диффе-
_. _ .. .. I « . « λ
реишиллялучы i<r) - ·ιηχ (бмлгелакү олмәсә I “ 2 > 2 J I- функциясенә кире
функция буларак чыгарылмасы була, sin (arcsin х) » х тигезлеген диффе¬
ренциаллап табабыз: cos (arcsin х) · (arcsin х)' _ 1, моннан (arcsin х)' —
- —~ ; arcsinх -αбулганлыктан,cosα = Ji-sin! α = 71-χ1
cos(arcsinxj Jl-χ1 ' ’
_ _ λ- - , ,™ , cos' χ - sin* χ In em χ
була, чөнки cos α > 0. 215. a) x” (In χ + 1); б) (sin х)"· * ; .
sinx
216. Күрсәтмә. —— 1 , . 217. Күрсәтмә, һ (х) - / (х) - g(x)
х2-Зх + 2 х~^· 1-1
373 Күнегүләргә җаваплар һәм күрсәтмәләр
п + 2 п + 2 л(л+1)
функциясе (х0; ») да үсә. 218. а) 4 - ; б) 16 - — - - ■ t— = 16 -
л2 + 5п+8
у Г · 221 “) Λ “З. а 1; б) 0 а 28. 222. а) Күрсәтм ә. f (х) -
-cos х + х функциясе (-»; ®) да үсә. 223. а) (-»; as); б) (-со; 0) IJ (0; <=).
224. Күрсәтмә. Җитәрлек дәрәҗәдә зур уңай х ларда бу тигезләмәнең сул
кисәге уңай, ә җитәрлек дәрәҗәдә модуле буенча зур тискәре х ларда тискәре
икәнлеген исбатлагыз. 225. Күрсәтмә. Математик индукция методыннан һәм
Лагранж теоремасыннан файдаланыгыз (Лагранж теоремасы буенча, күпбуынның
ике тамыры арасында бу күпбуын чыгарылмасының тамыры бар). 226. Р(х)
р тапкыр А кыйммәтен алсын, р> п. Ул вакытта Р (х) — А күпбуынының дәрәҗәсе
п һәм аның п нан күбрәк тамыры була, ә бу моңа кадәрге мәсьәлә нәтиҗәсенә
каршы киле. 227. Күрсәтмә, a) R (х) - С булса, ул вакытта С — p(x)-Cq (х)
күпбуынының тамыры k дәрәҗәсеннән югарырак түгел; б) q(x)p'(x)~
t ,'Г Ί'ί) i»|rly I I 'I
- p (x) д' (x) = 0 булганда, R\x) - — һәм K(x) - 0,
m · п булса,
бу тигезләмәнең сул ягы — дәрәҗәсе т + п - 1 дән югарырак булган күпбуын,
һәм, т = п булса, дәрәҗәсе т + п - 2 дән югарырак булмаган күпбуын.
228. min /(χ) = λ | !=·=·; maxf(x) = / (з) - 105. 229. 1Ц сәг. 230. Кәгазь
[о;з] 27 М 43
'Т
битенең буе 30 см, киңлеге 20 см. 231. 20 км/сәг. 232. (/> . 233. а) Беренчесе
зуррак; б) икенчесе зуррак. 236. a) 1; б) 1. 237. |а| > 2 булганда, 1 тамыр;
|а| —2 булганда, 2 тамыр; |а| < 2 булганда, 3 тамыр; б) -4 -ү12 < а < 0
булганда, тамыры юк; а — ~4 - у'12 булганда, 1 тамыр; а < -4 - vl2 , а - 0 һәм
α > 4 булганда, 2 тамыр; <1 = 4- 712 булганда, 3 тамыр; 0 < α < 4 - 712 булганда.
4 тамыр. 238.
/ г 2
а3 + Ь’
239. /(3π) - 12π - 1. 240. Я + Rt, R.
160 о
241. у7 м/мин. 242. 90°. 243. а) у - - j х + 3; у - -3, у - -12х - 15;
в) у - -Ь(х + 1); г) у - ±7зх + 6. 244. πη, ί · , neZ. 247. α - 4.
v3 “ ’
α + 1
248. α = 3, 6—1. 249. Күрсәтмә, х = —g— булганда, f (х) - 2x - а һәм
f (x) = 1. 250. Afe— у — х2 параболасының «эчлеге», Λί( — парабола үзе. М2 — бу
374 Күнегүләргә җаваплар һәм күрсәтмәләр
x jx|
параболаның «тышкы өлеше», Mk — k J 3 булганда буш. 251. a) ., + С;
б) F(x) =
х2 -χ + С, χ 1 булганда,
~^х2+х+С-1, х < 1 булганда;
х ■ -1 булса.
£ . 4 ι C
3 3 ·
в) F(x) =
- 1 < x < 1 булса,
ra
3
x · θ » C, x > 1 булса.
О
252. a) 4 (1 +
О
χ2)γ'1 + x2 + C; 6) -|e'xa
+ С; в) In sin x + C; r) —in ccs x + C.
253. a) In |x - 11 - In 2 - 1; 6)
x* ♦ 3x- - 5x + 1: в) sin x - ein e + π; г) - *1 + х.
п -г г 2
254. a)F(x) =
sin х,
х»
х < 0 булса,
х > 0булса;
6) ₽(х) -
2-Jx - 4,
x - 3,
x > 1 булса,
х < 1 булса.
255. Күрсәтмә. (F(x) - F(-x)’ = F'(x) + У(-х) = f (x) - /(x) = 0, ягъни G(x) -
= F(x)-F{-x) —даими. Моннан тыш, G (0) = F (0) — F(0) = 0, моннан F(x) =
= F(-x). 256. Күр сәтм ә. G(x) = F(x) + F(-x) булсын, ул вакытта G' (х) = f(x)~
- f (x) = 0, ягъни G(x) — С, биредә C — даими, F(0) — 0 булса, C = 0. 257. 10 c,
700 м (чөнки t > □). 264. у = ^/бх-4 · Күрсәтмә, (у3)' = Зу'у2 = 6.
t
sinх-cosx , sinx + cosx . , ™ . . ί . . . ~
265. е* һәм е*. 266. а) Табабыз: х (1) = (х0 + I υ(ζ) dzf =
Zu И *
<0 ■"
= x'Q + (о(0 - o(t0))' = 0 + ν' (1) = ν’ (ί) һәм Χο = Χο + j ν(ζ) dz = χ0 + 0 = χ0.
'ο
267. Күрсәтмә. Формуланы у = 1, у = х, у = х2 һәм у = х2 өчен тикшерегез.
268. а) Күрсәтмә. № 255 не кара; б) күрсәтмә. № 256 ны кара; jF(x)+ F(-x) =
= С, бу вакытта х = 0 не куеп, С = 2F(0) не табабыз, моннан теләсә нинди х өчен
X
j f(z]dz = F(x) - F (-х) = 2(F(x) - F (0)), шулар арасында х = а өчен дә.
-х
2 г
269. а) 0; б) 0. 270. а) ■ 135,6; в) -1 у . Күрсәтмә, у = 1 - -х формуласы
π 1
буенча үзгәрешлене алыштырыгыз. 271. a) -g ! б) 1п2. Күрсәтмә. — ны җәя
тышына чыгарыгыз; в) -;
г) (21 1).
272. а) д. Күрсәтмә.
375 Күнегүләргә җаваплар һәм күрсәтмәләр
„ l + 2cosnx
cos2 nt 2 —
6) 0; в) π; г) 0. Чиш ү.
Jsin Зх cos 5х dx = i |(sin 8x -
о о
, .«
-sin 2x)dx = -I|-lcos8x + lcos2x|l . 273. a) 2;
Δ \ 6 2 t 1
и
б) I ; в) 7 j ;
MI9,
274. nab.
275.
α > 2.
булганда;
b ■ 2
б) С < 0 һәм
г)
С > 3;
в)
!«<-С
|6<-€i
(а>-С
[а>-С
. 1 _ „ 2
булганда. 276. а) 24 j ; о) 2 д . 277. 8;
1_2-2<21
5 ’
279. 25 Дж. 280. о = -1. 281.
«рй’/Гг
“ ~ \g—ирекле төшү тизләнеше). 282. ———
6m 12
285. R радиуслы бериш ярымшарның массалар үзәге шар үзәгеннән g ерак¬
лыгында, аның симметрия күчәрендә ята.
Атамалар күрсәткече
Аралыкта эзлексез функция 134
аргументның үсемтәсе 105
арккосинус 69
арккотангенс 70
арксинус 68
арктангенс 69
асимптота
— авыш 55
— вертикаль 55
— горизонталь 55
Башлангыч 185
башлангычларның гомуми рәвеше
188
башлангычларның төп үзлеге 185
башлангычны табу кагыйдәләре 192
берәмлек әйләнә 15
бетен рациональ функция 23
бетен сан 178
бүленмәүчелек методы 214
Вакланмалы рациональ функция 23
Вейерштрасс теоремасы 165
Гармоник тирбәнешләр 63, 278
гармоник тирбәнешләрнең амплиту¬
дасы 63
гармоник тирбәнешләрнең башлан¬
гыч фазасы 63
гармоник тирбәнешләрнең ешлыгы 63
гармоник тирбәнешләрвең периоды 63
гармоник тирбәнешнең тигезләмәсе
279
Даиминең чыгарылмасы 113
дифференциалланучы функция 114
дифференциаллау 114
диффереициаллау кагыйдәләре 121
дифференциаль исәпләү 170
дәрәҗәле функция 273
дәрәҗәле функциянең башлангычы
273
дәрәҗәле функциянең чыгарылмасы
124
дәрәҗәләрнең төп үзлекләре 232
е саны 263
Зурлык 178
Интеграл 200, 212
— анык 212
— анык булмаган 212
интеграл исәпләү 212
интеграллау 201
интеграллау чикләре 201
интерваллар методы 135
иррациональ күрсәткечле санның дә¬
рәҗәсе 236
иррациональ сан 179
иррациональ тигезләмә 227
Кавальери принцибы 215
кайтма функция 259
катлаулы функция 127
катлаулы функциянең чыгарылмасы
127
квадрат тамыр 222
377 Атамалар күрсәткече
кимүче функция 43
кире функция 259
кире функция турында теорема 261
китерү формулалары 7
косеканс 20
косинус 15
котангенс 18
котангенслар сызыгы 18
куб тамыр 222
кәкресызыклы трапеция 196
кәкресызыклы трапециянең мәйдан
формуласы 198
күплекләрнең берләшмәсе 23
күрсәткечле тигезләмә 242
күрсәткечле тигезләмәләр система¬
лары 243
күрсәткечле тигезсезлек 243
күрсәткечле функция 239
күрсәткечле функциянең башлан¬
гычы 267
күрсәткечле үсүнең (кимүнең) диф¬
ференциала тигезләмәсе 277
Лагранж формуласы 142
логарифм 246
логарифмик тигезләмәләр система¬
лары 256
логарифмик тигезсезлек 256
логарифмик функция 251
логарифмик функциянең чыгарыл¬
масы 269
логарифмнарның теп үзлекләре 246
Максимум ноктасы 47
массалар үзәге 209
минимум ноктасы 47
моменталь тизлек 111, 147
Натураль логарифм 266
натураль сан 178
л нчы дәрәҗә арифметик тамыр 220
л нчы дәрәҗә тамыр 220
ноктада функциянең өзлексезлеге 117
Ньютон Лейбниц формуласы 202
Парабола фокусы 151
периодик функция 36
Радиан 5
радикал 220
рациональ күрсәткечле санның
дәрәҗәсе 231
рациональ сан 177
реаль сан 177
Санлы функция 22
саннарның аермасы 181
саннарның суммасы 181
саннарны чагыштыру кагыйдәләре 181
саннарның унарлы якынлашуы 181
санның бетен өлеше 180
санвың вакланма өлеше 180
санның рациональ күрсәткечле
дәрәҗәсе 231
секанс 20
синус 15
синуслар сызыгы 16
синусоида 17
сызыкча тыгызлык 150
Так функция 34
тамыр күрсәткече 220
тамырларның төп үзлекләре 222
тамыр турында теорема 67
тангенс 18
тангенслар сызыгы 18
тангенсоида 20
тизләнеш 148
тригонометрик тигезләмәләр система¬
лары 86
тригонометрик тигезсезлек 79
тригонометрик функцияләрнең баш¬
лангычы 191
тригонометрик функцияләрнең кыйм¬
мәтләре тамгасы 7
тригонометриянең төп формулалары 7
378 Атамалар күрсәткече
Тэйлор формуласы 174
теп логарифмик бердәйлек 246
Ферма теоремасы 157
функция аргументы 22
функция графигына орынма 110
функция графигына орынма тигезлә¬
мәсе 140
функция графигының рәвешен үз¬
гәртү 24
функциянең билгеләнү елкәсе 22
функциянең графигы 24
функция дифференциалы 171
функциянең даимилек билгесе 188
функциянең даими тамга аралыгы 53
функциянең иң зур кыйммәте 165
функциянең иң кечкенә кыйммәте
165
функциянең кимү аралыгы 53
функцияне тикшерү схемасы 54
функциянең кимү билгесе 153
функциянең критик ноктасы 157
функциянең кыйммәте 23
функциянең кыйммәтләре елкәсе 23
функциянең максимумы 48
функциянең максимумы билгесе 159
функциянең ноктадагы чыгарылмасы
113
функциянең нуле 53
функциянең периоды 36
функциянең чикләмәсе 175
функциянең чыгарылмасы 114
функциянең экстремумы 48
функциянең үсемтәсе 105
функциянең үсү аралыгы 53
функциянең үсү билгесе 153
Унарлы логарифм 248
Чагылдыру 28
чикләмә 171
чикләмәле күчү 117
чикләмәле күчү кагыйдәләре 118
чиксез кечкенә зурлык 171
чит тамыр 228
чыгарылманың геометрик мәгънәсе
139
чыгарылманың механик мәгънәсе 147
Эзлеклелекнең чикләмәсе 176
Экстремум ноктасы 48
Үзара кире функцияләр 261
үзгәрешле көчнең эше 207
үсүче функция 43
Җисем күләме формуласы 206
җөп функция 33
Эчтәлек
. I
Сүз башы 3
I
бүлек
ТРИГОНОМЕТРИК ФУНКЦИЯЛӘР
§1-
Санча аргументның тригонометрик функцияләре
1. Синус, косинус, тангенс һәм котангенс (кабатлау)
5
2. Тригонометрик функцияләр һәм аларның графиклары 14
§2.
Функцияләрнең төп үзлекләре
3. Функцияләр һәм аларның графиклары 21
4. Җөп һәм так функцияләр. Тригонометрик функцияләрнең периодик¬
лыгы 31
5. Функцияләрнең үсүе һәм кимүе. Экстремумнар 40
6. Функцияләрне тикшерү 48
7. Тригонометрик функцияләрнең үзлекләре. Гармоник тирбәнешләр 56
§3.
Тригонометрик тигезләмәләрне һәм тигезсезлекләрне
чишү
8. Арксинус, арккосинус һәм арктангенс 64
9. Иң гади тригонометрик тигезләмәләрне чишү 69
10. Иң гади тригонометрик тигезсезлекләрне чишү 75
11. Тригонометрик тигезләмәләрне һәм тигезләмәләр системаларын
чишүгә мисаллар 81
Тарихтан мәгълүматлар 85
Кабатлау ечен сораулар һәм мәсьәләләр 91
и
бүгек
ЧЫГАРЫЛМА ЬӘМ АНЫ КУЛЛАНУ
§4.
Чыгарылма
12. Функциянең үсемтәсе 97
13. Чыгарылма төшенчәсе 101
14. Функциянең өзлексезлеге һәм чикләмә аша күчү төшенчәсе 108
15. Чыгарылмаларны исәпләү кагыйдәләре 113
16. Катлаулы функциянең чыгарылмасы 118
17. Тригонометрик функцияләрнең чыгарылмалары 121
380
§5.
Өзлексезлекне һәм чыгарылманы куллану
18. Өзлексезлекне куллану 124
19. Функция графигына орынма 129
20. Якынча исәпләүләр 134
21. Физикада һәм техникада чыгарылма 137
§6.
Функцияне тикшергәндә чыгарылма куллану
22. Функциянең үсүе (кимүе) билгесе 143
23. Функциянең критик нокталары, аның максимумнары һәм минимум¬
нары 147
24. Функцияне тикшергәндә чыгарылма куллануга мисаллар 151
25. Функциянең иң зур һәм иң кечкенә кыйммәтләре 155
Тарихтан мәгълүматлар 160
Кабатлау ечев сораулар һәм мәсьәләләр 1 γθ
III
бу лек
БАШЛАНГЫЧ ФУНКЦИЯ ҺӘМ ИНТЕГРАЛ
§7.
Башлангыч функция
26. Башлангыч функциянең билгеләмәсе
27. Башлангыч функциянең төп үзлеге
28. Башлангыч функцияләрне табуның өч кагыйдәсе
174
177
181
§8.
Интеграл
29. Кәкресызыклы трапециянең мәйданы 185
30. Ньютон — Лейбниц формуласы 188
31. Интегралның куллану 194
Тарихтан мәгълүматлар 199
Кабатлау очсн сораулар һәм мәсьәләләр 205
IV
бүлек
КҮРСӘТКЕЧЛЕ ҺӘМ ЛОГАРИФМИК
ФУНКЦИЯЛӘР
§9-
Дәрәҗә төшенчәсен гомумиләштерү
32. п нчы дәрәҗә тамыр һәм аның үзлекләре
207
33. Иррациональ тигезләмәләр 214
34. Рациональ күрсәткечле дәрәҗә 218
§ 10.
Күрсәткечле һәм логарифмик функция
35. Күрсәткечле функция 224
36. Күрсәткечле тигезләмәләрне һәм тигезсезлекләрне чишү 229
37. Логарифмнар һәм аларның үзлекләре . 232
381
ЗВ. Логарифмик функция 238
39. Логарифмик тигезләмәләр һәм тигезсезлекләрне чишү 242
40. Кире функция турында төшенчә 246
§11
Күрсәткечле һәм логарифмик функциянең
чыгарылмасы
41. Күрсәткечле функциянең чыгарылмасы 251
42. Логарифмик функциянең чыгарылмасы 256
43. Дәрәҗәле функция 259
44. Дифференциаль тигезләмәләр турында төшенчә 263
Тарихтан мәгълүматлар 269
Кабатлау ечея сораулар Ьэм мәсьәләләр 273
бүлек
КАБАТЛАУГА МӘСЬӘЛӘЛӘР
§ 1.
Реаль саннар
1. Рациональ һәм иррациональ саннар
2. Процентлар. Пропорцияләр
277
279
3. Прогрессияләр 280
§2.
Бердәй рәвешүзгәртүләр
4. Алгебраик аңлатмаларның рәвешен үзгәртү 281
5. Радикаллар һәм вакланма күрсәткечле дәрәҗәләр кергән аңлатма¬
ларның рәвешен үзгәртү 282
6 Тригонометрик аңлатмаларның рәвешен үзгәртү 283
7. Дәрәҗә һәм логарифмнар кергән аңлатмаларның рәвешен үзгәртү 285
§3
Функцияләр
8. Рациональ функцияләр 286
9. Тригонометрик функцияләр 290
10. Дәрәҗәле, күрсәткечле һәм логарифмик функцияләр 293
§4.
Тигезләмәләр, тигезсезлекләр, тигезләмәләр һәм
тигезсезлекләр системалары
11 Рациональ тигезләмәләр һәм тигезсезлекләр 295
12. Иррациональ тигезләмәләр һәм тигезсезлекләр 297
13. Тригонометрик тигезләмәләр һәм тигезсезлекләр 298
14. Күрсәткечле тигезләмәләр һәм тигезсезлекләр 299
15. Логарифмик тигезләмәләр һәм тигезсезлекләр 300
16. Рациональ тигезләмәләр һәм тигезсезлекләр системалары 301
17. Иррациональ тигезләмәләр системалары 302
18. Тригонометрик тигезләмәләр системалары 302
382
19. Күрсәткечле һәм логарифмик тигезләмәләр системалары 303
20. Тигезләмәләр һәм тигезләмәләр системалары төзүгә мәсьәләләр 304
§5.
Чыгарылма, башлангыч функция, интеграл һәм
аларның кулланылышлары
21. Чыгарылма 306
22. Чыгарылманы функция тикшерүдә куллану 308
23. Чыгарылманы физикада һәм геометриядә куллану 310
24. Башлангыч функция 312
25. Интеграл 312
VI
буГМиг
§1.
Саннар. Аңлатмаларның рәвешен үзгәртү
1. Бөтен саннар 314
2. Математик индукция методы 315
3. Реаль саннар 316
4. Аңлатмаларның рәвешен үзгәртү 317
5. Прогрессияләр 318
§2.
Элементар функцияләр һәм аларның үзлекләре
6. Функцияләрне тикшерү 319
7. Функцияләрнең графиклары 322
§3.
Тигезләмәләр, тигезсезлекләр һәм системалар
8. Рациональ алгебраик тигезләмәләр 325
9. Рациональ алгебраик тигезсезлекләр 327
10. Рациональ алгебраик тигезләмәләр системалары 328
11. Тигезләмәләр һәм тигезләмәләр системаларын тезүгә мәсьәләләр 329
12. Иррациональ тигезләмәләр һәм тигезсезлекләр 330
13. Тригонометрик тигезләмәләр, тигезсезлекләр һәм системалар .... 333
14. Күрсәткечле һәм логарифмик тигезләмәләр һәм тигезсезлекләр . . 335
§4.
Анализ башлангычлары
15. Чыгарылма 337
16. Функцияләрне тикшерүдә чыгарылмалар куллану 338
17. Чыгарылманы физикада һәм геометриядә куллану 340
18. Башлангыч функция 341
19. Интеграл 343
Күнегүләргә җаваплар һәм күрсәтмәләр 346
Атамалар күрсәткече 377
Учебное издание
Колмогоров Андрей Николаевич
Абрамов Александр Михайлович
Дудницнн Юрий Павлович и др.
Алгебра
и начала анализа
Учебник для 10—11 классов
общеобразовательных учреждений
Казань. Издательство «Магариф». 2007
Перевод с русского на татарский язык
Уку-укыту басмасы
Колмогоров Андрей Николаевич
Абрамов Александр Михайлович
Дудницин Юрий Павлович Һ. б.
Алгебра Нам
анализ башлангычлары
Татар урта гомуми белем бирү мәктәбенең
10—11 нче сыйныфлары өчен дәреслек
Редакция мөдире Л. X. Мөхэммэтҗанова
Редакторлары Л. Р. Хафизова, Ф. М. Хафизова,
Л. X. Мвхзммгтҗанова
Бизәлеш редакторы Р.А. Сайфуллина
Техник редакторы Л. И, Матвеева
Компьютерда биткә салучысы В. С. Тимошкин, Л. И. Матвеева
Корректорлары С. 3. Гыймалетдинова, Г. Р. Ногманова, Г. Г. Мвхэммэтҗанова
Оригинал-макеттан басарга кул куелды 27.12.07. Форматы 60x90'/,,. Офсет кәгазе.
«Школьная· гарнитурасы. Офсет басма. Басма табагы 24,0 + форз. 0,25.
Нәшер-хисап табагы 21,07 -һ форз. 0,39. Тиражы 9500 д. Заказ C-I615.
• Мәгариф» нәшрияты. 420059. Казан, Оренбург тракты, 20а.
Тел./факс (843) 277-52-88; 277-52-62.
E-mail:inagarif(g)niail.ru
•Идел-Пресс» полиграфия-нәшрият комплексы» ААҖ.
420066. Казан, Декабристлар урамы, 2.