Author: Ласица А.М. Кондратьева Т.Н. Павловская О.Ю.
Tags: физика термодинамика молекулярная физика методические указания
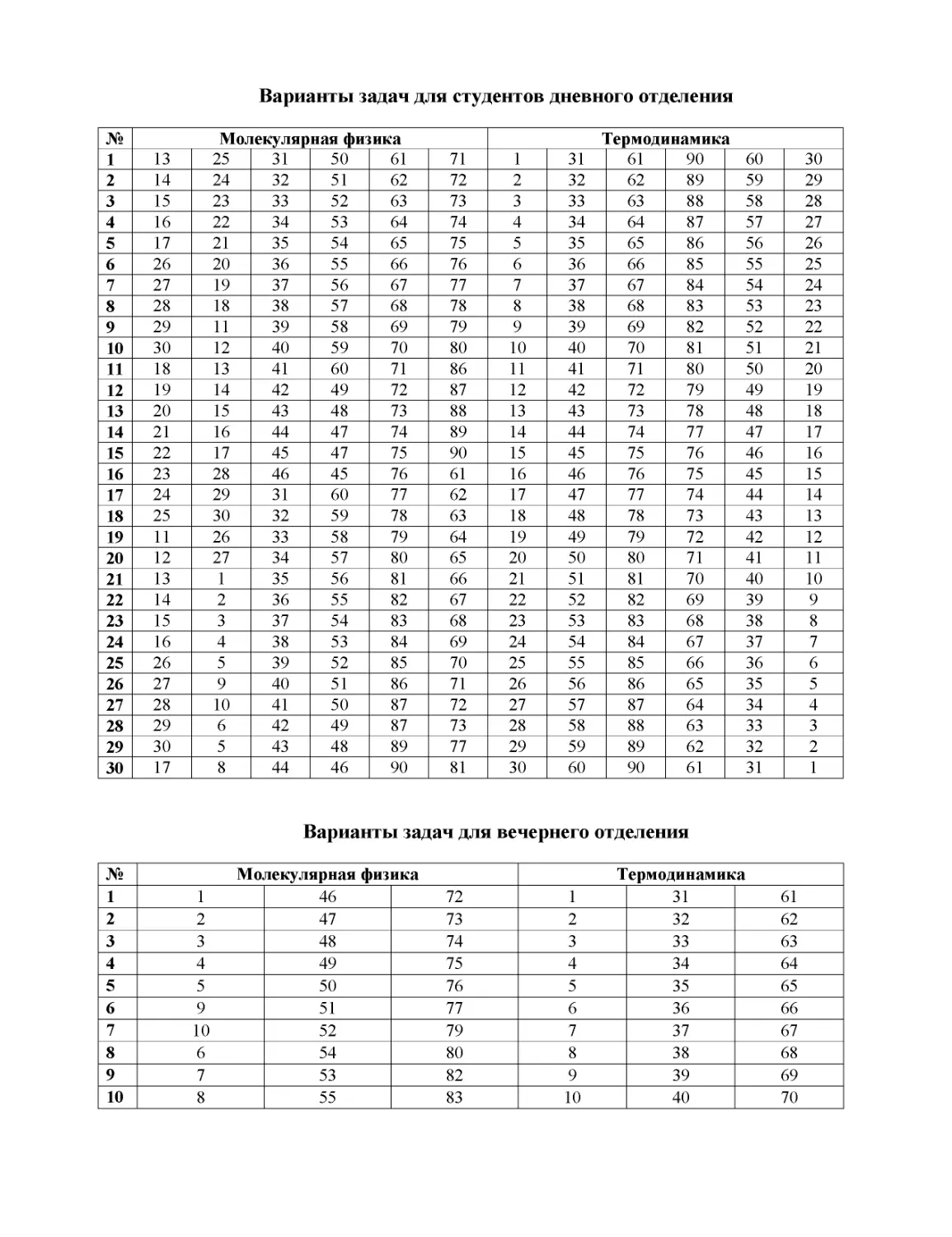
Year: 2004
Text
МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
Методические указания по решению задач
Омск 2004
Составители:
Ласица
Александр Михайлович
;
Кондратьева
Тамара Николаевна
;
Павловская
Ольга Юрьевна.
Печатается по решени
ю редакционно
-
издательского совета Омского госуда
р-
ственного технического университета.
Молекулярная физика и термодинамика
–
разделы физики, в которых изуч
а-
ются макроскопические процессы, связанные с огромным числом содерж
а
щихся в
телах атомов и молекул. Для исследования этих процессов применяются два кач
е-
ственно различных метода: статистический и термодинамический. Первый лежит в
основе молекулярной физики, второй
–
термодинамики.
Основные положения
молекулярной физики
Мо
лекулярная физика
–
раздел физики, изучающий строение и свойства в
е-
щества, исходя из молекулярно
–
кинетических представлений, основывающих
ся на
том, что
все тела состоят из молекул, находящихся в непрерывном движении.
Наиболее полное описание любой системы
состояло бы в определении ура
в-
нений движения всех тел
,
входящих в нее, однако из
-
за большого числа частиц вх
о-
дящих в макроскопическую систему
,
данная задача является принципиально нера
з-
решимой.
С
остояние системы в молекулярной физике определяется небольшим
н
а-
бором величин, называемых параметрами состояния (термодинамическими пар
а-
метрами) характеризующих свойства системы в целом.
В
качестве
основных
пар
а-
метров состояния выб
ирают температуру Т, давление р
и объем
V
.
Если система
находится во внешнем поле
, то
к параметрам состояния добавляются характерист
и-
ки поля.
Параметры состояния
в большинстве случаев не являются независимыми, они
связаны между собой некоторым уравнением, называемым уравнением состояния
.
Одной из основных задач молекулярной физики являет
ся установление явного вида
уравнения состояния и установление связи между параметрами состояния и усре
д-
ненными характеристиками движения
частиц
,
входящих в систему. Для решения
такой задачи приходится прибегать к рассмотрению различных физических мод
е-
лей
вещества. Одной из самых простых моделей является модель идеального газа.
Идеальным называют газ, удовлетворяющий следующим условиям:
1)
собственный объем молекул газа пренебрежимо мал по сравнению с объемом
сосуда;
2)
потенциальной энергией взаимодействия мол
екул можно пренебречь;
3)
столкновения молекул между собой и со стенками сосуда абсолютно упругие.
Модель идеального газа можно использовать при изучении реальных газов,
так как в условиях, близких к нормальным, а также при низких давлениях и выс
о-
ких темпера
турах
они
близки к идеальному газу. Кроме того, внеся поправки на
собственный размер молекул и действующие молекулярные силы, можно перейти к
теории реальных газов.
Уравнение состояния идеального газа носит название уравнение Менделеева
-
Клапейрона и имеет
вид
,
V
RT
RT
m
p
n
m
=
=
где
=
m
/
число молей газа,
R
=
8,31
Дж/(моль
К)
универсальная газовая постоя
н-
ная. Данное уравнение является обобщением установленных экспериментально з
а-
конов повед
е
ния идеального газа к которым относятся
законы
:
1)
Бойля
-
Мариотта
:
p
V
=
const
при
Т
,
m
=
const
;
2)
Шарля
:
const
T
P
=
при
V
,
m
=
const
;
3)
Гей
-
Люссака
:
const
T
V
=
при
P
,
m
=
const
;
4)
Дальтона
давление смеси идеальных газов равно сумме парциальных давл
е-
ний входящих в нее газов
:
p
=
p
1
+
p
2
+
p
3
+
,
(р
1
, р
2
,
…
-
парциальные давления
–
давления, которые оказывали бы газы смеси, е
с-
ли бы они одни занимали объем, равный объему смеси при той же те
м
пературе)
;
5)
Авогадро
-
моли любых газов при одинаковых температуре и давлении зан
и-
мают одинаковые объемы
(п
ри нормальных у
словиях
p
= 1,013
10
5
Па
,
Т
=
273,15 К
,
для одного моля
этот объем
V
=
22,41
10
-
3
м
3
)
.
По определению, в одном моле различных веществ содержится одно и то же
число молекул, называемое постоянной Авогадро:
N
A
=
6,022
10
23
моль
-
1
.
Уравнение Менделеева
-
Клап
ейрона может быть переписано в другом виде
:
nkT
p
=
,
где
n
–
концентрация молекул газа,
6
10
38
.
1
/
23
-
ᅲ
=
=
A
N
R
k
–
постоянная Больцм
а-
на.
Основным уравнением молекулярно кинетической теории идеального газа н
а-
зывается уравнение связывающее давл
ение
,
оказываемое идеальным газом на сте
н-
ки сосуда с характеристиками его молекул
:
£
=
ᅲ
ᅲ
=
0
2
0
3
2
3
1
e
u
n
m
n
p
:
(
m
0
–
масса молекулы газа
;
£
=
2
u
u
:
-
средняя квадратичная скорость молекул,
£
0
e
-
средняя кинетическая энергия пост
упательного движения одной молекулы
).
Принимая во внимание уравнение Менделеева
–
Клапейрона
,
получаем
kT
m
2
3
2
2
0
0
=
=
u
e
.
Средняя кинетическая энергия поступательного движения одной молекулы
идеального газа пропорциональна термодинамической температуре
и зависит тол
ь-
ко от нее.
Более детальное описание системы заключается в определении не только
средней скорости, но и закона распределения молекул по скоростям. Этот закон
теоретически выведен Максвеллом.
Закон Максвелла описывается некоторой фун
к-
цией
f
(
)
, называемой функ
ци
ей распределения молекул по скоростям. Если ра
з-
бить диапазон скоростей молекул на малые интервалы, то на каждый интервал
скорости будет приходиться некоторое число молекул
dN
(
)
, имеющих скорости в
интервале от
до
+
d
, пропорци
ональное ширине интервала
d
.
u
u
u
d
f
N
dN
ᅲ
=
)
(
)
(
и
u
u
u
d
N
dN
f
ᅲ
=
)
(
)
(
,
где
N
–
число молекул газа.
Таким образом, функция
f
(
)
определяет относительное число молекул
N
dN
/
)
(
u
, скорости которых лежат в интервале от
до
+
d
. Можно также с
к
а-
зать, что функция
f
(
)
определяет вероятность
попадания скорости молекулы в и
н-
тервал
от
до
+
d
.
│
₩
ᅲ
-
ᅲ
ᅲ
ᅲ
│
₩
ᅲ
=
kT
m
kT
m
f
2
exp
2
4
)
(
2
0
2
2
/
3
0
u
u
p
p
u
.
График функции представляет с
о-
бой немонотонную кривую обр
а-
щающуюся в ноль при
=
0 и
=
.
При увеличении температ
уры ма
к-
симум функции распределения ст
а-
новится более пологим и смещается
в область больших скоростей. Ск
о-
рость при которой достигается ма
к-
симум функции распределения н
а-
зывается наиболее вер
о
ятной скор
о-
стью
В
.
Этой скоростью и близкой
к ней обладает наиболь
шее число
молекул. Кривая несимметрична относительно
В
.
Расчеты показ
ы
вают
, что
m
u
u
RT
m
kT
2
2
0
=
=
=
.
С помощью функции распределения можно установить среднее значение л
ю-
бой величины
X
зависящей от скорости
u
u
u
d
f
X
X
)
(
)
(
0
ᆬ
=
£
Например,
среднее значе
ние скорости
0
0
2
0
3
2
/
3
0
0
8
2
1
exp
2
4
)
(
m
kT
d
kT
m
kT
m
d
f
ᅲ
=
│
₩
ᅲ
ᅲ
-
ᅲ
ᅲ
│
₩
=
ᅲ
ᅲ
=
ᆬ
ᆬ
p
u
u
u
p
p
u
u
u
u
,
среднее значение квадрата скорости
m
u
u
u
p
p
u
u
u
u
RT
m
kT
d
kT
m
kT
m
d
f
3
3
2
1
exp
2
4
)
(
0
0
2
0
4
2
/
3
0
0
2
2
=
=
│
₩
ᅲ
ᅲ
-
ᅲ
ᅲ
│
₩
ᅲ
=
ᅲ
ᅲ
=
ᆬ
ᆬ
.
Если газ находится в поле внешних сил,
то
кроме распределения по скоростям
устанавливается распределение по координатам. В случае поля тяготения Земли это
приводит
к тому, что концентрация молекул и давление газа
из
меняются с высотой.
Закон изменения установлен Больцманом для изотермической атмосферы
:
│
₩
ᅲ
ᅲ
-
=
│
₩
ᅲ
ᅲ
ᅲ
-
ᅲ
=
│
₩
ᅲ
ᅲ
-
ᅲ
=
│
₩
ᅲ
ᅲ
ᅲ
-
ᅲ
=
kT
h
g
m
p
T
R
h
g
p
p
kT
h
g
m
n
T
R
h
g
n
n
0
0
0
0
0
0
exp
exp
,
exp
exp
m
m
где
p
0
и
n
0
-
давление и концентрация молекул на высоте
h
=
0.
Первая из формул н
а-
зывается рас
пределением Больцмана, вторая
-
барометрической формулой.
Молекулы газа, находясь в состоянии хаотического движения, непрерывно
сталкиваются друг с другом. Между двумя последовательными столкновениями
молекулы проходят некоторый путь
, который называется
длиной свободного пр
о-
бега. В общем случае длина пути между последовательными столкновениями ра
з-
лична,
поэтому
можно говорить о средней длине свободного пробега молекул <
>.
За
единицу времени
молекула проходит путь, равный <
> и
,
если <
z
>
-
среднее
число
столкновений за единицу времени, то
£
£
=
£
z
/
u
l
.
Расчеты показывают
, что
2
2
2
1
,
2
d
n
d
n
z
p
l
u
p
=
>
<
=
(
d
эффективный диаметр молекулы).
В термодинамически неравновесных системах возникают особые необра
ти
-
мые процессы, называемые явлениями переноса,
в результате которых происходит
про
странственный перенос энергии (теплопроводность), массы (диффузия),
и
м-
пульса
(внутреннее трение).
Уравнения
,
описывающие явления переноса называю
т-
ся
:
1.
закон
ом
теплопроводности
Фурье
:
dt
dS
dx
dT
dQ
ᅲ
ᅲ
-
=
k
(
£
=
l
u
r
k
V
c
3
1
коэффициент теплопроводности, с
V
удельная теплоемкость
при постоянном объеме),
2.
закон
ом
диффузии
Фика
:
dt
dS
dx
d
D
dM
ᅲ
ᅲ
-
=
r
(
l
u
3
1
=
D
коэффициент диффузии
),
3.
закон
ом
внутреннего трения
Ньютона
:
dt
dS
dx
d
dp
ᅲ
ᅲ
-
=
u
h
(
l
u
r
h
3
1
=
коэффициент внутреннего трения (вязкость)).
Знак минус в
уравнениях показывает, что перенос энергии, массы и импульса идет
в направлении противоположном направлению возрастания температуры, плотн
о-
сти и скорости соответственно
. Коэффициенты
,
D
и
связаны простыми соо
т-
ношениями:
.
,
V
c
D
ᅲ
=
=
h
k
r
h
Примеры решения задач
Задача №
1
В сосуде объёмом
V
= 1
л
находится углекислый газ массой
m
= 0,2 г. При
температуре
T
=2600
K
н
екоторая часть молекул диссоциировала на молекулы к
и-
слорода и ок
и
с
и углерода. При этом давление газа в сосуде оказалось равным 108
кПа.
Опр
е
делить какая часть молекул диссоциировала.
Решение:
Рассмотрим уравнение диссоциации углекислого газа
2
2
2
2
O
CO
CO
+
Таким образом
,
каждый моль углекислого газа
,
распадаясь вызывает
появление одного моля окисла углерода и половину моля кислорода.
В результате распада части молекул в сосуде будут находит
ь
ся
три
г
а-
за:
CO
2
,
CO
,
O
2
. По закону Дальтона
на
йдём выражение для давления
,
создаваемого данной смесью газов
2
2
O
CO
CO
p
p
p
p
+
+
=
.
Введём степень диссоциации
a
-
отношение числа молей распавшихся
мол
е-
кул к начальному числу молей вещества
0
ᄑ
@0
ᄑ
ᄆ
=
.
Тогда число мо
лей
CO
2
ᄆ
(1
0
@0
0
CO
2
-
=
=
n
n
n
n
-
,
ч
исло молей
CO
ᄆ
0
@0
CO
ᅲ
=
=
n
n
n
,
ч
исло молей
O
2
(с учётом уравнения реакции)
2
ᄆ
2
0
@0
O
2
ᅲ
=
=
n
n
n
.
Из уравнения Менделеева
–
Клапейрона
V
V
ᄆ)
(1
RT
p
0
C0
CO
2
2
-
=
=
n
n
,
V
V
RT
ᄆ
RT
p
0
C0
CO
n
n
=
=
,
V
V
2
RT
ᄆ
RT
p
0
0
O
2
2
n
n
=
=
.
Общее давление будет связано со степенью диссоциации
a
уравнением
Дано:
V
= 1
л
m
= 0,2 г
Т=2600 К
Р=108
кПа
α
-
?
│
₩
+
=
│
₩
+
+
-
=
2
1
RT
2
1
RT
p
0
0
a
n
a
a
a
n
V
V
.
Так как
m
n
m
=
0
(
= 44·10
-
3
кг/моль
–
молярная масса
CO
2
)
, то
│
₩
+
=
2
1
a
m
V
mRT
p
.
Выражая
a
и производя расчет
,
получим
2
,
0
1
2
=
│
₩
-
=
mRT
V
p
m
a
.
Ответ
:
степень диссоциации газа
=
0,2.
Задача № 2
Используя функцию распределения Максвелла по скоростям
,
найдите наиб
о-
лее в
е
роятное значение кинетической энергии атомов гелия
,
который
при давлении
P
= 10
5
Па имеет плотность
=160
г/м
3
.
Решение:
Запишем функцию распределения Максвелла по скоростям.
│
₩
-
│
₩
ᅲ
ᅲ
=
kT
m
kT
m
f
2
exp
2
4
)
(
0
2
3
0
2
p
u
p
u
.
Поскольку
нужно найти
наиболее вероят
ное значение энергии
,
имеет смысл перейти от
распределения по скоростям к распредел
е
нию по энергиям
f(
e
).
П
о смыслу функции распределения относ
и
тельное число молекул скорости
которых лежат в интервале
ск
о
ростей
u
d
,
которому
соответствует интервал эне
р-
гий
e
d
, р
авно
e
e
u
u
d
f
d
f
N
dN
)
(
)
(
=
=
.
Из данного выражения можно
получить соотношение связывающе
е две фун
к-
ции распределения
:
e
u
u
e
d
d
f
f
)
(
)
(
=
.
И
з
формулы видно
:
для перехода от распред
е-
л
ения по скоростям к распределению по энергиям недостаточно просто выразить
скорость через энергию.
Поскольку
2
2
0
u
e
m
=
,
0
2
m
e
u
=
,
то
производная
e
e
u
0
2
1
m
d
d
=
, и выражения для распределения по энергиям будет иметь ви
д.
(
)
│
₩
-
ᅲ
=
-
KT
KT
f
e
e
p
e
exp
2
)
(
2
1
2
3
.
Дано:
p
= 10
5
Па
160
=
r
г
/м
3
2
e
-
?
Наиболее вероятное значение энергии
2
e
соответствует максимуму функции
распределения. Соответственно производн
ая
e
e
d
df
)
(
должна
быть равна нулю
:
0
exp
)
(
2
)
(
2
1
2
3
=
│
₩
│
₩
-
=
-
kT
kT
d
d
d
df
e
e
p
e
e
e
,
(
)
0
2
1
exp
2
2
1
2
1
2
3
=
│
₩
-
│
₩
-
-
-
kT
kT
kT
e
e
e
p
,
0
2
1
2
/
1
2
/
1
=
-
kT
2
2
e
e
,
2
kT
2
=
e
.
Обращаем внимание, что выражение для наиболее вероятной энергии нельзя
получить подставив в формулу
2
2
0
u
e
m
=
выражения для наиболее вероятной скор
о-
сти
0
2
m
kT
B
=
u
(в этом с
лучае получилось бы
kT
=
e
).
Из уравнения Менделеева
Клапейрона следует, что
R
P
T
r
m
=
, значит
A
B
N
P
R
P
k
ᅲ
ᅲ
=
ᅲ
=
r
m
r
m
e
2
2
(в последней формуле учтено, что
R
=
N
A
·
k
)
.
Подставляя данные из условия и
м
о-
лярную массу гелия
m
= 4·10
-
3
кг/моль
,
получим
21
10
2
-
ᅲ
=
B
e
Дж
.
Ответ
:
наиболее вероятное
значение кинетической энергии
атома гелия
21
10
2
-
ᅲ
=
B
e
Дж
.
Задача № 3
Ротор
центрифуги,
заполненный радоном
,
вращается с частотой
n
= 50
Гц
.
Радиус ротора
a
= 0,5 м. Определить давление газа на стенку ротора, если в его
центре давление
p
0
= 10
5
Па. Температуру по всему об
ъ
ёму считать постоянной
,
равной
Т=300
К
.
Решение:
Рассмотрим
находящийся в це
н-
трифуге
цилиндрический слой
воздуха бесконечно малой то
л-
щины
dr
,
такой,
что можно
сч
и-
тать,
что все молекулы данного
слоя нах
о
дятся на
одинаковом
расстоянии
r
от оси вращения.
Запишем для данного слоя вто
рой закон Нь
ю-
тона :
F
=
ma
Под силой
F
в данном случае нужно понимать
разность
сил давления дейс
т
вующих
с внешней и внутренне
й
стороны слоя
F
= ((
p
+
d
p
)
-
p
)
2
p
r
h
=
d
p
2
p
r
h
,
где произведение 2
p
r
h
даёт площадь боковой
поверхности слоя воздуха. Массу
данного слоя можно
получить,
умножив плотность воздуха
на объём слоя
dV
= 2
p
r
dr
h
;
m
=
r
dV
=
r
2
p
r
dr
h
.
Все молекулы данного слоя вовлечены во
вращательные движения с угловой скоростью
w
и находятся на одинаковом ра
с-
стоянии
r
от оси вращения
,
с
ледовательно
,
обладают одинаковым нормальным у
с-
кор
е
нием
r
a
2
w
=
.
Объединяя выражения
,
получим
dp
=
r
dr
·
r
ᅲ
2
w
(в правой и левой части сокращён одинаковый множитель 2
p
r
h
). Из уравнения
Менделеева
–
Клапейрона следует
RT
p
m
r
=
.
П
одставляя в пред
ыдущее выражение и
разделяя перем
енные
,
получим
RT
dr
r
p
dp
ᅲ
ᅲ
=
2
m
.
Проинтегрируем полученное
уравнение
:
A
RT
r
p
+
ᅲ
=
2
ln
2
2
m
где А
-
некоторая постоянная
интегрирования
. Представим её в виде нат
у
рального
логарифма о
т некоторой другой постоянной С
:
A
=
ln
C
. Т
огда
C
RT
r
p
ln
2
ln
2
2
+
ᅲ
=
m
Дано:
n
= 50
Гц
a
= 0,5 м.
p
0
= 10
5
Па.
Т=
300 К.
p
-
?
или
│
₩
ᅲ
=
RT
r
C
p
2
exp
2
2
m
.
По условию задачи
на оси
центрифуги давление должно быть
p
0
, это возмо
ж
но
только в
случае,
когда
C
=
p
0
.
Заменяя
C
на
p
0
,
определим
давление
как фун
кцию
расстояния до оси вращения
:
│
₩
=
RT
r
p
p
2
exp
2
2
0
m
.
Вспоминая, что
p
w
2
=
,
получим
расчетную формулу
для давления
│
₩
=
RT
r
p
p
2
2
exp
2
2
2
0
n
p
m
.
Подставляя в последнюю формулу
r
=
a
= 0,5 м
и
молярную
массу радона
m
= 0,222 кг/моль
,
вычислим дав
лени
е газа на стенку центрифуги
p
= 3
10
5
Па
.
Ответ
:
давление на стенку ротора p
0
=
3
10
5
Па
.
Задача № 4
Стальной стержень длиной
ℓ = 20
см
с площадью поперечного сечения
S
= 3
см
2
нагревается с одного конца до температуры
t
1
= 300
0
С, а другим концом упир
а-
е
тся
в
лёд. Предполагая, что передача тепла происходит исключительно вдоль
стержня (без потерь через стенки), по
д
считать массу льда
,
растаявшего за время
t
=
10
мин. Теплопроводность стали
= 60
Вт/
(
м
∙
К
)
.
Решение:
Найдём количество теплоты полученное льдом. Для этого запишем
уравнение теплопроводности.
dSdt
dx
dT
Q
k
d
-
=
.
Считая, что поток тепла не изменяе
тся
со временем и постоянен в
пределах сечени
я стержня, данную формулу можно записать в виде
t
k
S
dx
dT
Q
-
=
.
Производная
dx
dT
представляет собой градиент температуры в стержне. Так как
длина стержня равна
ℓ,
а разность температур на его концах
t
1
-
t
2
, можно прои
з
вести
Дано:
t
1
= 300
0
С
S
= 3см
2
t
2
= 0
0
С
ℓ = 20
см.
t
= 10мин.
=
6
0
Вт/м
∙
К
m
-
?
замен
у
(
)
l
2
1
t
t
dx
dT
-
=
.
Знак минус в выражении
Q
можно не учит
ы
вать, так
как он
показывает,
что направле
ние переноса теплоты противоположно направлению во
з-
растания температуры. С учётом этого количеств
о
теплоты получё
н
но
е льдом
:
(
)
l
t
k
S
t
t
Q
2
1
-
=
.
Так как всё это количество теплоты идёт на плавление льда,
Q
=
m
(
=
3,3
10
5
Дж/кг
–
удельная теплота плавления льда
)
. Объединяя выражения
и
производя ра
с
четы
получим
(
)
.
49
049
,
0
1
2
3
:
=
=
-
=
b
t
k
l
S
t
t
m
Ответ
:
масса растаявшего льда
m
=
0
,049
кг
=
49
г.
Задача №
5
В результате некоторого процесса вязкость некоторого идеального газа ув
е-
личилась в
2
=
a
раза, а коэффициент диффузии
–
в
4
=
b
раза. Во сколько раз ув
е-
личилось давление газа.
Решение:
Согласно молекулярно кинетической теории
,
£
=
l
u
3
1
D
,
r
l
u
h
£
=
3
1
,
где
n
d
2
2
1
ᅲ
ᅲ
=
£
p
l
средняя длина свободного пробег
а,
0
8
m
kT
ᅲ
=
£
p
u
-
средняя скорость движения молекул,
=
m
0
n
-
плотность газа.
По основному уравнению МКТ
nkT
p
=
, поэтому
0
0
0
T
n
nT
p
p
=
.
Подставим в
выражение для
значения
£
l
,
u
и
,
тогда
2
2
/
3
0
2
0
2
0
3
2
2
3
8
2
3
1
d
m
kT
d
m
kT
d
m
ᅲ
ᅲ
ᅲ
ᅲ
=
ᅲ
ᅲ
ᅲ
ᅲ
ᅲ
ᅲ
=
ᅲ
ᅲ
£
ᅲ
=
p
p
p
p
u
h
;
Из формул видно, что
h
~
T
, значит
,
2
2
0
2
0
a
h
h
=
=
T
T
.
Для того чтобы найти отн
о-
шение
0
n
n
,
свяжем между собой
h
и
D
.
И
з формул видно
, что
n
Dm
D
0
=
=
r
h
.
О
т-
Дано
:
h
=
0
a
0
D
D
b
=
0
p
p
-
?
сюда
0
Dm
n
h
=
, а отношение
b
a
h
h
=
ᅲ
=
D
D
n
n
0
0
0
. В итоге
получаем
отношени
е
давл
е-
ний
2
3
2
0
=
=
=
b
a
b
a
a
P
P
.
Ответ
:
давление возрастет в два раза.
Зад
ачи,
рекомендуемые для аудиторных занятий
1.
12 г газа занимают объем 4 дм
3
при температуре 7
0
С. После нагревания газа
при постоянном давлении его плотность стала равна 0,6 мг/см
3
. До какой темпер
а-
туры нагрели газ?
Ответ:
до
1400 К
.
2.
В сосуде находит
ся 14 г азота и 9 г водорода при температуре 10
0
С и давл
е-
нии 1 МПа. Найти молярную массу смеси и объем сосуда.
Ответ: 4,6 г/моль; 12 дм
3
.
3.
В двух сосудах емкостями 3 и 4 л находится газ под давлениями 0,2 и 0,1 МПа
соответственно. Температура в обоих
сосудах одинакова. Под каким давлением б
у-
дет находиться газ, если соединить сосуды трубкой?
Ответ: 140 кПа
.
4.
В баллоне емкостью 150 см
3
содержится газ при температуре 30
0
С. Вследс
т-
вие утечки из колбы вышло 4
∙10
18
молекул. Определить, на сколько пониз
илось при
этом давление газа?
Ответ: 112 Па
.
5. Плотность некоторого газа равна 6
∙10
-
2
кг/м
3
, средняя квадратичная скорость
молекул этого газа равна 500 м/с. Найти давление, которое газ оказывает на стенки
с
о
суда.
Ответ: 5 кПа
.
6.
В баллоне емкостью 5 л
находится 25
∙10
21
молекул азота. Найти среднюю
квадр
а
тичную скорость его молекул, если давление в баллоне
P
= 720 мм рт.ст.
Ответ: 1100
м/с
.
7. Найти число молекул азота в 1 см
3
при нормальных условиях и обладающих
скоростью: а) между 99 м/с и 101 м/с; б)
между 499 м/с и 501 м/с.
Ответ: 8,6
∙10
18
; 4,9
∙10
19
.
8. Найти для газообразного азота температуру, при которой скоростям молекул
υ
1
= 300
и
υ
2
= 600
м/с соответствуют одинаковые значения функции распредел
е
ния
Максвелла.
Ответ: 330
К
.
9. Полагая
температуру воздуха и ускорение свободного падения не зависящими
от высоты, определить, на какой высоте
h
над уровнем моря плотность воздуха
мен
ь
ше своего значения на уровне моря в 2 раза. Температура воздуха
t
= 0
0
С.
Ответ: 5,5 км
.
10.
Вычислить среднюю
длину свободного пробега молекул воздуха при темп
е-
ратуре 17
0
С и нормальном давлении. Эффективный диаметр молекул воздуха пр
и-
нять равным 3
∙10
-
8
см.
Ответ: 10
-
7
м
.
11. Определить среднее число всех столкновений между молекулами, которые
происходят в течен
и
е
1
с в 1 см
3
кислорода при температуре 17
0
С и давлении 5 мм
рт. ст. Эффективный диаметр молекулы кислорода 2,9
∙10
-
8
см.
Ответ: 2,27
∙10
24
.
12. Найти среднюю длину свободного пробега азота, если его динамическая вя
з-
кость 17 мк
Па
с,
d
= 0,3 нм.
Ответ:
0,09
нм
.
13. Найти коэффициент теплопроводности воздуха при температуре 10
0
С и да
в-
лении 100 кПа, если диаметр молекулы воздуха принять равным 0,3 нм.
Ответ: 13 мВт/
(
м
ʘ
К
).
14. Вычислить коэффициент диффузии и динамическую вязкость азота при да
в-
лении 0,1
МПа и температуре 7
0
С.
Ответ:14
ʘ
10
-
6
м
2
/с и 17
ʘ
10
-
6
Па
ʘ
с
.
Зада
чи для самостоятельного решения
1.
Сколько молекул содержится в 2 л кислорода, находившегося при температ
у-
ре 17
0
С и давлении 0,2 МПа?
2.
Сосуд емкостью 1 л содержит 1,5 г некоторого газа под да
влением 0,25 МПа.
Определить среднюю квадратичную скорость молекул газа.
3.
Среднеквадратичная скорость молекул газа при давлении 0,1 МПа составл
я
ет
500 м/с. Определить плотность газа при этих условиях.
4.
При какой температуре средняя квадратичная скорость атом
ов гелия станет
равной второй космической скорости (11,2 км/с)?
5.
Определить массу одной молекулы углекислого газа.
6.
В сосуде
емкостью 5 л находится 0,2 моля
некоторого газа. Определить, к
а-
кой это газ, если его плотность 1,12 кг/м
3
.
7.
Газ при температуре 309 К
и давлении 0,7 МПа имеет плотность 12 кг/м
3
. О
п-
ределить молярную массу этого газа.
8.
Сколько молекул газа содержится в баллоне вместимостью 30
л при темпер
а-
туре 300 К и давлении 5 МПа?
9.
Плотность некоторого газа 0,06
кг/м
3
, средняя квадратичная скорость мол
е
кул
этого газа 500 м/с. Найти давление, которое газ оказывает на стенки сосуда.
10.
Давление газа 1
МПа; концентрация молекул 10
10
см
-
1
. Найти температуру г
а-
за и среднюю кинетическую энергию поступательного движения одной молекулы.
11.
Плотность воздуха при те
мпературе 0
0
С и давлении 760 мм рт. ст. равна
0,001293 г/см
3
. Сколько весит литр воздуха при температуре 27,3
0
С и давлении
750 мм рт. ст.?
12.
Баллон содержит газ при
t
1
= 50
0
С и давлении 30 атм. Каково давление, к
о
гда
из баллона будет выпущена половина
массы газа, а температура понизится до
t
2
= 10
0
С?
13.
Сосуд ёмкостью
V
= 0,01 м
3
содержит азот массой
m
1
= 7 г и водород ма
с
сой
m
2
= 1 г при температуре
Т
= 280 К. Определить давление
P
смеси газов.
14.
Найти плотность
ρ
газовой смеси, состоящей по ма
ссе из одной части вод
о-
рода и восьми частей кислорода
,
при давлении
P
= 0,1 МПа и температуре
Т
= 290 К.
15.
Баллон емкостью
V
= 15 л содержит смесь водорода и азота при темпер
а
туре
Т
= 300 К и давлении
P
= 1,23 МПа. Масса смеси
m
=
145 г.
Определить массу
m
1
водорода и массу
m
2
азота.
16.
Газовая смесь, состоящая из кислорода и азота, находится в баллоне под да
в-
лением
P
= 1 МПа. Считая, что масса кислорода составляет 20% от массы смеси,
определить парциальные давления
P
1
и
P
2
от дельных газо
в.
17.
Два сосуда с объемами
V
1
= 1 л и
V
2
= 3 л соединены трубкой с краном. До
открытия крана в первом сосуде содержался азот под давлением
P
1
= 0,5 атм и при
температуре
t
1
= 0
0
С, а во втором
-
аргон под давлением
P
2
= 1,5 атм и при темп
е-
ратуре
t
2
= 100
0
С. Определить, какое давление установится в смеси газов, если о
т-
крыть кран. Температура смеси 79
0
С.
18.
Плотность газа
ρ
при давлении
P
= 720 мм рт. ст. и температуре
t
2
= 0
0
С
равна 1,3 г/л. Найти массу моля
μ
газа.
19.
Сколько молекул водорода находится в
объеме 1,55 л при температуре 27
0
С
и давлении 750 мм рт. ст.?
20.
Найти число молекул
N
в 1 см
3
и плотность
ρ
азота при давлении
1,00
10
-
11
мм рт. ст. и температуре 15
0
С.
21.
Два баллона соединены трубкой с краном. В первом находится газ по
д да
в-
лением 10
5
Н/м
2
, во втором
–
при 6
ʘ
10
4
Н/м
2
. Емкость первого баллона 1 л, вт
о
рого
–
3 л. Какое давление установится в баллонах (в мм рт. ст.), если открыть кран? Те
м-
пературе постоянна. Объемом трубки можно пренебречь.
22.
Найти число
ν
молей и число
N
мо
лекул, содержащихся в объеме
V
= 1см
3
водяного пара при температуре
t
= 4
0
С.
23.
В баллоне емкостью
V
= 20 л находится аргон под давлением
P
1
= 800 кПа и
температуре
Т
1
= 325 К. когда из баллона было взято некоторое количество арг
о
на,
давление в баллон
е снизилось до
P
2
= 600 кПа, а температура установ
и
лась
Т
2
= 300 К. Определить массу
m
аргона, взятого из баллона.
24.
Баллон емкостью
V
= 40 л заполнен азотом. Температура азота
Т
= 300 К.
К
огда часть азота израсходовали, давление в баллоне пон
изилось на
∆
P
= 400 кПа.
Определить массу израсходованного азота. Процесс считать изотермическим.
25.
В баллоне находился идеальный газ при давлении 4
ʘ
10
7
Па и температуре
300 К. Затем 3/5 содержащегося в баллоне газа выпустили, а температура пониз
и-
лась до
240 К. Под каким давлением находится оставшийся в баллоне газ?
26.
Какой объем
V
занимает смесь азота массой
m
1
= 1 кг и гелия
m
2
= 1 кг при
нормальных условиях
–
давлении 760 мм рт. ст. и температуре 273 К?
27.
Один баллон емкостью
V
1
= 20 л содержит азот п
од давлением
P
1
= 24 атм,
другой
–
емкостью
V
2
= 44 л содержит кислород под давлением
P
2
= 16 атм. Оба
баллона были соединены между собой и оба газа смешались, образовав однородную
смесь (без изменения температуры). Найти парциальные давления
P
1
и
P
2
обо
их г
а-
зов в смеси и полное давление
Р
.
28.
В сосуде при температуре
t
= 100
0
С и давлении
P
= 4
ʘ
10
5
Па находится 2
м
3
смеси кислорода и сернистого газа
SO
2
. Определить парциальные давления комп
о-
нентов, если масса сернистого газа
т
2
= 9 кг.
29.
Три баллона емкость
ю 3 л, 7 л и 5 л наполнены соответственно кислородом
(2 ат
м
), азотом (3 ат
м
) и углекислым газом (0,6 ат
м
) при одной и той же температ
у-
ре. Баллоны соединяют между собой, причем образуется смесь той же температуры.
Как
о
во давление смеси?
30.
Газовая смесь, сос
тоящая из кислорода и азота, находится в баллоне под да
в-
лением
P
= 720 мм рт. ст. Считая, что масса кислорода составляет 40
% от массы
смеси, определить концентрацию молекул отдельных газов при температуре 290 К.
31.
Зная функцию распределения молекул по скор
ости, вывести формулу наиб
о-
лее вероятной скорости.
32.
Используя функцию распределения молекул по скорости, получить фун
к
цию,
выражающую распределени
е
молекул по относительным скоростям
u
(
u
=
υ/υ
в
).
33.
Определить относительное число молекул идеального газа, ск
орости кот
о
рых
заключены в пределах от нуля до одной сотой наиболее вероятной скорости.
34.
Какая часть молекул азота при 150
0
С обладает скоростями от
300
до 325
м/с?
35.
Какая часть молекул кислорода при 0
0
С обладает скоростью от 100
до
110 м/с?
36.
Кака
я часть молекул азота, находящегося при температуре
Т
, имеет скор
о
сти,
лежащие в интервале от
υ
в
до
υ
в
+
∆
υ
, где
∆
υ
= 20
м/с,
Т
= 400
К.
37.
Определить температуру кислорода для которой функция распределения по
скоростям будет иметь максимум при скорости
υ
= 4
20 м/с.
38.
Определить температуру водорода, при которой средняя квадратичная ск
о-
рость молекул больше их наиболее вероятной скорости на
∆
υ
= 400 м/с
.
39.
Во сколько раз средняя квадратичная скорость молекул водорода больше
средней квадратичной скорости молекул в
одяных паров при той же температуре?
40.
Азот находится под давлением
p
= 10
5
Па при температуре
Т
=300
К. Найти
относительное число молекул азота, скорости которых лежат в интервале от
υ
в
до
υ
в
+
∆
υ
, где
∆
υ
= 1 м/с.
41.
Зная функцию распределения молекул по с
коростям, определить среднюю
арифметическую скорость
<
υ
>
молекул.
42.
По функции распределения молекул по скоростям определить среднюю ква
д-
ратичную скорость
<
υ
кв.
>
.
43.
Найти среднюю арифметическую, среднюю квадратичную и наиболее вер
о-
ятную скорости молекул газа
, плотность которого при давлении 300 мм рт. ст. равна
0,3 г/л.
44.
При какой температуре средняя квадратичная скорость молекул азота бол
ь
ше
их наиболее вероятной скорости на 50 м/с?
45.
Какая часть общего числа
N
молекул имеет скорости: 1) больше наиболее в
е-
роя
тной скорости и 2) меньше наиболее вероятной скорости?
46.
Пылинки, взвешенные в воздухе, имеют массу
m
= 10
-
18
г. Во сколько раз
уменьшится их концентрация
n
при увеличении высоты на
∆
h
=10
м? Температура
воздуха
Т
= 300 К.
47.
Масса
т
каждой из пылинок, взвеш
енных в воздухе, равна 1 аг. Отношение
концентрации
n
1
пылинок на высоте
h
1
= 1 м к концентрации
п
0
их на высоте
h
0
= 0
равно 0
,
787. Температура воздуха
Т
= 300 К. Найти по этим данным значение п
о-
стоянной Авогадро
N
A
.
48.
На
сколько уменьшится атмосферное да
вление
p
= 100 кПа при подъеме н
а-
блюдателя над поверхностью Земли на высоту
h
= 100 м? Считать, что темпер
а
тура
Т воздуха равна 290 К и не изменяется с высотой.
49.
На какой высоте
h
над поверхностью Земли атмосферное давление вдвое
меньше, чем на её поверхно
сти? Считать, что температура
Т
воздуха равна 290 К и
не изменяется с высотой.
50.
Барометр в кабине летящего вертолета показывает давление
p
= 90 кПа. На
какой высоте
h
летит вертолет, если на взлетной площадке барометр показывал да
в-
ление
p
0
= 100 кПа? Счита
ть, что температура
Т
воздуха равна 290 К и не
изменяе
т-
ся с высотой.
51.
Найти изменение высоты
∆
h
, соответствующее изменению давления на
∆
p
= 100 Па, в двух случаях:
1) вблизи поверхности Земли, где температура
T
1
= 290
К, давление
p
1
= 10
0 кПа; 2) на некоторой высоте, где температура
Т
2
= 220 К, давл
е
ние
p
2
= 25 кПа.
52.
Барометр в кабине летящего самолета все время показывает одинаковое да
в-
ление
p
= 80 кПа, благодаря чему летчик считает высоту
h
полета неизменной. О
д-
нако темпера
тура воздуха изменилась на
∆
Т
= 1
К.
К
акую ошибку
∆
h
в определ
е
нии
высоты допустил летчик? Считать, что температура не зависит от высоты и что у
п
о
верхности Земли давление
p
0
= 100 кПа.
53.
Высотная космическая станция расположена на горе Алагез в Армении
на
высоте 3250 м над уровнем моря. Найти давление воздуха на этой высоте. Темпер
а-
туру воздуха считать постоянной и равной 5
0
С. Массу одного киломоля воздуха
принять равной 29 кг/моль. Давление воздуха на уровне моря равно 760 мм рт. ст.
54.
На какой высоте да
вление воздуха составляет 75
% от давления на уровне
моря? Температуру считать постоянной и равной 0
0
С.
55.
Пассажирский самолет совершает полеты на высоте 8300
м.
чтобы не сна
б-
жать пассажиров кислородными масками, в кабинах при помощи компрессора
поддержи
вается постоянное давление, соответствующее высоте 2700
м.
Найти ра
з-
ность давлений внутри и снаружи кабины. Среднюю температуру наружного возд
у-
ха сч
и
тать равной 0
0
С.
56.
Найти в предыдущей задаче, во сколько раз плотность воздуха в кабине
больше плотности в
оздуха вне её, если температура наружного пространства равна
минус
20
0
С и температура внутри кабины 20
0
С.
57.
Какова масса
1 м
3
воздуха: 1) у поверхности Земли, 2) на высоте 4
км от п
о-
верхности Земли? Температуру воздуха считать постоянной и равной 0
0
С. Д
авл
е-
ние воздуха у п
о
верхности Земли равно 10
5
Па
.
58.
На какой высоте плотность газа составляет 50
% от
его плотности
на уровне
моря? Температуру считать постоянной и равной 0
0
С. Задачу решить для: 1) во
з-
духа и 2) водорода.
59.
На поверхности Земли барометр
показывает 101 кПа. Каково будет давл
е
ние
при подъеме барометра на высоту 540 м. Температуру считать одинаковой и равной
7
0
С.
60.
Определить высоту горы, если давление на её вершине равно половине да
в-
ления на уровне моря. Температура всюду одинакова и равна
0
0
С.
61.
Найти количество азота, прошедшего вследствие диффузии через площадку
10 см
2
за 5 с, если градиент плотности азота в направлении, перпендикулярном пл
о-
щадке, 1,26 мг/см
4
. Коэффициент диффузии 1,42 см
2
/с.
62.
За какое время 720 мг углекислого газа проди
ффундируют из почвы в атм
о-
сферу через 1 м
2
её поверхности при градиенте плотности 500 мг/см
4
? Коэфф
и
циент
диффузии принять равным 1,42 см
2
/с.
63.
Определить динамическую вязкость кислорода при нормальных условиях.
Принять среднюю длину свободного пробега моле
кул 100 нм.
64.
При некоторых условиях длина свободного пробега молекул водорода ра
в
на
0,5 мкм. Определить диаметр молекулы, если эти условия таковы: давление
0,2 МПа, температура 17
0
С.
65.
Найти количество азота, прошедшего вследствие диффузии чере
з площадку
100 см
2
за 10 с, если градиент плотности в направлении, перпендикулярном к пл
о-
щадке, равен 1,26 кг/м
4
.
66.
Коэффициенты диффузии и внутреннего трения кислорода при некоторых
условиях соответствуют 0,12 Мм
2
/с и 19,5 мкПа
ʘ
с. Найти при этих условиях п
ло
т-
ность кислорода.
67.
В сосуде объемом 2 л находится 4,0
ʘ
10
22
молекул двухатомного газа. Коэ
ф-
фициент диффузии равен 2,0
ʘ
10
-
5
м
2
/с. Определить коэффициент теплопроводности
г
а
за при этих условиях.
68.
Какой толщины следовало бы сделать деревянную стену здания, ч
тобы она
давала такую же потерю теплоты, как кирпичная стена толщиной 40 см при один
а-
ковых температурах внутри и снаружи здания? Коэффициенты теплопроводности
кирпича и дерева равны соответственно 0,70
и
0,175 Вт/
(
м
ʘ
К
)
.
69.
Между двумя пластинками, находящим
ися на расстоянии
1
мм друг от друга,
находится воздух. Между пластинками поддерживается разность температур 1
0
С.
Площадь каждой пластины равна 100
см
2
. Какое количество тепла передается за
счет теплопроводности от одной пластины к другой за 10 мин? Считат
ь, что воздух
н
а
ходится при нормальных условиях. Диаметр молекулы равен 0,3 нм.
70.
Найти коэффициент теплопроводности водорода, если известно, что коэфф
и-
циент внутреннего трения для него при этих условиях 8,6 мкПа
ʘ
с.
71.
Средняя длина свободного пробега молекул
ы углекислого газа при нормал
ь-
ных условиях равна 50 нм. Определить среднюю арифметическую скорость мол
е-
кулы и число соударений, которое испытывает молекула.
d
=
0,7
нм.
72.
В колбе объемом 100
см
3
находится 0,5 г азота. Найти среднюю длину св
о-
бодного пробега
молекул азота при этих условиях
,
d
= 0,3 нм.
73.
В сосуде объемом 0,5 л находится кислород при нормальных условиях. На
й-
ти общее число столкновений между молекулами кислорода за одну минуту.
d
= 0,3 нм.
74.
Найти среднее время между двумя послед
овательными столкновениями м
о-
лекул азота при температуре 10
0
С и давлении 1 мм рт. ст.
d
= 0,3 нм.
75.
Какое предельное число молекул газа должно находиться в 1 см
3
сферическ
о-
го сосуда диаметром 15 см, чтобы молекулы не сталкивались друг с другом? Ди
а-
метр мол
екулы газа принять равным 0,3 нм.
76.
Как изменится число ударов молекул одноатомного газа о стенку баллона
площадью 1м
2
за 1 с, если давление газа увеличится в 4 раза в 1) изотермическо
м
и
2) изохорно
м
процесс
ах
?
77.
При каком давлении средняя длина свободного
пробега молекул азота ра
в
на
1 мм, если при нормальном давлении она равна 8
ʘ
10
-
6
см?
d
= 0,3 нм.
78.
Плотность фотосферы, оцениваемая оптическими методами, составляет
2
ʘ
10
-
4
кг/м
3
. Определить длину свободного пробе
га атомов водорода в фотосфере,
d
=
0,23 нм.
79.
В сосуде вместимостью 1 дм
3
находится азот при температуре 7
0
С и давл
е-
нии 0,2 МПа. Определить число столкновений мо
лекул азота в этом сосуде за 1с,
d
= 0,3 нм.
80.
Какое давление нужно создать в колбе диаметром 0,1 м, содержащей азот
при температуре 20
0
С, чтобы получить вакуум?
d
= 0,3 нм.
81.
Средняя длина свободного пробега молекул водорода при некотором давл
е-
нии и температуре 21
0
С равна 90 нм. В результате изотермического процесса да
в-
ление газа увеличилось в 3 раза. Найти среднее ч
исло столкновений молекул вод
о-
рода за 1
с в конце процесса.
d
= 0,23 нм.
82.
При каком давлении средняя длина свободного пробега молекул водорода
равна <
λ> = 2,5
см? Температура
t
=68
0
С,
d
= 0,23 нм.
83.
В баллоне вместимостью 10 дм
3
находится гелий массой 2 г.
Определить
среднюю длину с
вободного пробега молекул гелия,
d
= 0,2 нм.
84.
Средняя длина свободного пробега молекул гелия при нормальных усл
о
виях
230 нм. Найти среднюю продолжительность свободного пробега молекул г
е
лия при
давлении 1,0 МПа и температуре 17
0
С
,
d
= 0,2 нм.
85.
В сферическом сосуде вместимостью 2 дм
3
находится водород. При какой
плотности водорода молекулы его практически не будут сталкиваться друг с др
у-
гом?
d
= 0,23 нм.
86.
Определить коэффициент диффузии двухатомного газа, находящегося в с
о-
суде об
ъемом 2,0 л с числом молекул 4,0
ʘ
10
22
, если коэффициент теплопроводности
эт
о
го газа 144 мВт/
(
м
ʘ
К
)
.
87.
Определить среднюю длину свободного пробега молекул кислорода, если
при температуре 0
0
С коэффициент диффузии кислорода 0,20 см
2
/с,
d
= 0,3 нм.
88.
Найти коэфф
ициент теплопроводности водорода, если коэффициент вязк
о
сти
для него при этих условиях 8,6 мкПа
ʘ
с.
89.
Определить коэффициент диффузии гелия, если средняя длина свободного
пробега атомов гелия при нормальных условиях 180
нм.
90.
Углекислый газ и азот находя
тся п
ри одинаковых температурах и давлениях.
Найти для этих газов отношение коэффициентов диффузии, внутреннего трения,
теплопроводности. Диаметры молекул этих газов:
d
1
= 0,4 нм,
d
2
= 0,3 нм.
Основные положения
термодинамики
Терм
одинамика
–
раздел физики, изучающий общие свойства макроско
пи
чес
-
ких систем и процессы перехода между различными состояниями. В основе терм
о-
динамики лежат установленные из опыта и подтверждающиеся всей совокупностью
вытекающих из них следствий законы, н
азываемые началами термодинамики.
Первое начало термодинамики
по существу представляет собой закон сохр
а-
нения энергии
,
примененный к термодинамическим процессам
: количество тепл
о-
ты, сообщенное термодинамической системе
,
идет на увеличение ее внутренней
эне
ргии
U
и совершение системой работы против внешних сил.
A
U
Q
+
D
=
.
Для процессов, в которых термодинамические параметры системы меняются
бесконечно мало можно записать первое начало в дифференциальной форме.
A
dU
Q
d
d
+
=
.
Под вну
тренней энергией системы подразумевают
энергию этой системы за
вычетом кинетической энергии системы как целого и потенциальной энергии си
с-
темы в поле внешних си
л. Внутренняя энергия, в отличие
от работы и количества
теплоты, является функцией состояния.
Выражение для внутренней энергии пр
е-
дельно упрощается
при
рассмотрения простейшей термодинамической системы
–
идеального газа. В этом случае
RT
m
i
U
m
2
=
.
где
i
-
число степеней свободы молекул газа (
i
=
3 для одноатомного
,
i
=
5 для дву
х-
атомн
ого,
i
=
6 для многоатомного газа
с жесткой связью ме
ж
ду атомами в молек
у-
ле).
Элементарная работа
,
совершаемая газом против внешних сил при изменении
его объема
:
pdV
A
=
d
. При изменении объема газа от
V
1
до
V
2
газ совершит работу
=
2
1
)
(
V
V
dV
V
p
A
.
где
p
(
V
)
зависимость давления от объема в процессе расширения газа. Для изоб
а-
рического процесса эта формула принимает вид
)
(
1
2
V
V
p
A
-
=
,
а для изотермического
1
2
ln
V
V
RT
m
A
m
=
.
Для расчета количества теплоты
,
переданного
системе
,
вводится понятие те
п-
лоемкости
–
величины, равной количеству теплоты, не
об
хо
димому для нагревания
вещества на 1
К:
dT
Q
C
d
=
.
У
доб
но
вв
ести
также удельн
ую
теплоемкость
–
велич
и-
н
у
, равн
ую
количеству теплоты, не
об
хо
димому для наг
ревания 1
кг вещества на
1
К:
mdT
Q
c
d
=
и молярн
ую
теплоемк
ость
–
величину, равную
количеству теплоты,
необходимому для нагревания
одного
моля вещества на 1 К:
dT
Q
C
n
d
n
=
. Удельная
теплоемкость связана с молярной
соотношением
m
n
c
C
=
.
Различают теплоемкости при постоянном давлении и постоянном объеме, е
с-
ли в процессе нагревания вещества поддержива
е
тся постоянным соответственно
давление и
ли
объем.
В случае нагревания при постоянном объеме не совершается
работа проти
в внешних сил, поэтому теплоемкость при постоянном объеме меньше
теплоемкости при постоянном давлении. Применяя первое начало термодинамики
,
можно получить выражения для молярных теплоемкостей при постоянном объеме и
давлении, а т
акже уравнение связи межд
у ними
:
.
,
2
2
,
2
R
C
C
R
i
C
R
i
C
V
P
P
V
+
=
+
=
=
Последнее выражение называется уравнением Майера.
Адиабатическим называется процесс, происходящий без теплообмена с окр
у-
жающей средой, при адиабатическом процессе
давление, объем и температура газа
связаны уравнениями Пуассона
:
const
TP
const
TV
const
PV
=
=
=
-
-
g
g
g
g
1
1
,
,
,
где
i
i
C
C
V
P
2
+
=
=
g
отношение теплоемкостей при постоянном давлении и объеме
,
которое называют показателем адиабаты или коэффициентом Пуассона. Работа в
адиабатическом процессе совершается за счет
убыли внутренней энергии
U
-
A
D
=
и выражается следующими формулами
:
│
₩
│
₩
-
-
=
│
₩
-
-
=
-
=
-
1
2
1
1
1
2
1
2
1
1
1
,
1
1
),
(
2
g
g
n
g
n
n
V
V
RT
A
T
T
RT
A
T
T
R
i
A
.
Круговым процессом или циклом называется процесс, при котором система,
пройдя через ряд состояний, возвращается в исходное. Коэффициентом полезног
о
действия тепловой машины
называется выражение, определяемое формулами
:
%
%
Q
Q
Q
Q
Q
Q
A
-
=
-
=
=
1
h
,
где А
работа
,
совершенная рабочим веществом тепловой машины за цикл,
Q
Н
количество теплоты
,
полученное рабочим веществом от нагревателя,
Q
Х
колич
е-
ство т
еплоты
,
отданное рабочим веществом холодильнику за то же время.
Второе начало термодинамики определяет направление протекания термод
и-
намических процессов и может быть сформулировано несколькими эквивалентн
ы-
ми способами. Наиболе
е часто встречаются формулир
овки
Клаузиуса и Томсона
:
1)
невозможен процесс, единственным результатом которого является передача т
е-
плоты от холодного тела к горячему
;
2)
невозможен процесс, единственным резул
ь-
татом которого является совершение работы за счет охлаждения одного тела.
Осн
о-
вываясь на втором начале термодинамики, Карно вывел теорему, нос
я
щую его имя:
из всех периодически действующих тепловых машин, имеющих одинаковые темп
е-
ратуры нагревателя и холодильника, наибольшим КПД обладают обратимые маш
и-
ны; при этом КПД обратимых
машин, работающих при одинак
о
вых температурах
нагревателей и холодильников, равны друг другу и не зависят от конструкции м
а-
шин.
Введя в рассмотрение абстрактный обратимый цикл
,
состоящий из двух из
о-
терм и двух адиабат
,
Карно установил формулу максимально в
озможного КПД те
п-
ловой машины
%
T
T
T
-
=
max
h
(Т
Н
,
Т
Х
температуры нагревателя и хол
о
дильника).
Введя специа
льную функцию состояния системы
энтропию
S
, можно дать
еще одну формулировку второго начала термодинамики
:
энтропия
адиабатически
изоли
рованной
системы при любых процессах
,
происходящих в ней
,
не уменьшае
т-
ся
она возрастает при необратимых процессах и остается постоянной при обрат
и-
мых
0
ᄈ
D
S
. Е
сли система совершает переход из
состояния 1 в состояние 2, то и
з-
менение энтро
пии
+
=
ᄈ
-
ᄈ
D
-
2
1
2
1
1
2
2
1
T
A
dU
T
Q
S
S
S
d
d
,
(знак равенства относится к обратимым процессам). Физический смысл энтропии
раскрывает формула Больцмана
W
ln
k
S
=
, где
k
-
постоянная Больцмана,
W
те
р-
модинамическая вероятность состояния системы
-
число способов, кот
орыми может
быть реализовано данное состояние макросистемы.
Примеры решения задач
Задача № 1
Газ, занимавший объем 2
л
при давлении 0,
1 МПа, расширился из
о
термически
до
4
л. После этого, охлаждая газ изохорически, уменьшили давление в 2 раза. Д
а-
лее г
аз изобарически расширился до 8
л. Начертите график зависимости давления
от объема, найдите работу
,
совершенную г
а
зом.
Решение:
П
острои
м
график зависимости давления от объе
ма.
Первый процесс
,
происходящий с газом
,
является изотермическим. Выразим давление
через объём и температуру при помощи ур
авнения Менделеева
–
Клапейрона
V
RT
p
n
=
.
Так как
T
=
const
,
давление
в данном процессе
обратно пропорционально объёму
, и линия
,
изображающая да
н
ный
процесс на
p
-
V
диаграмме
,
будет участком гиперболы начинающ
е
й-
ся в точке
V
1
,
p
1
и заканчива
ю
щ
ей
ся в точке
V
2
,
p
2
.
Второй
процесс,
происходящий с газом
,
является изохорическим. В этом пр
о-
цессе объём не изменяется
и
,
следователь
но
,
на
P
-
V
диаграмме он изображается в
виде вертикальной прямой
,
идущей из точки
V
2
,
p
2
в точку
V
2
,
p
3
.
Третий процесс происходящий с газом
,
по усл
о
вию задачи
,
изобарический. На
P
-
V
диаграмме он будет выглядеть как горизонтальная линия
,
идущая из точки
V
2
,
p
3
в точку
V
3
,
p
3.
Дано:
V
1
= 2
л
P
1
=
0
,1
МПа
V
2
= 4
л
P
3
=
2
2
P
V
3
= 8
л
A
-
?
Последовательно изображая все процессы
,
получим следу
ю-
щую
P
-
V
ди
а
грамму.
Рассчитаем работу
,
совершенную газом. Так как раб
о-
та
,
совершаемая газом
,
аддитивная
величина
А = А
1
+А
2
+А
3
,
где А
1
–
работа
,
совершенная в изотермическом п
роцессе,
А
2
–
работа
,
совершенная в изохорическом процессе, А
3
–
р
а-
бота
,
совершенная в изобарическом процессе. Каждую из р
а
бот можно вычислить
по формуле
dV
V
p
A
V
V
=
2
1
)
(
(
V
1
и
V
2
–
начальные и конечные объёмы занимаемые г
а-
зом
)
. Прим
е
ним эту фор
мулу для определения работы А
1
. Согласно уравнению
Менделеева
–
Клапейрона
,
зависимость
p
(
V
) им
е
ет вид
V
RT
V
p
n
=
)
(
.
Следовательно
,
работа
│
₩
ᅲ
=
=
=
1
2
1
ln
2
1
2
1
V
V
RT
V
dV
RT
dV
V
RT
A
V
V
V
V
n
n
n
.
Множитель
n
RT
вынесем из
-
под знака инт
еграла как посто
янную величину
,
з
аменяя её на
p
1
V
1
,
получим
63
,
138
ln
1
2
1
1
1
=
=
V
V
V
p
A
.
В изохорическом процессе изменение объёма газа не происходит, следов
а-
тельно
,
А
2
= 0.
При вычислении работы А
3
учтём, что давление, как постоянная величина
,
может быть вы
н
есена из под знака интеграла
)
(
2
3
3
3
3
3
3
2
3
2
V
V
p
dV
p
dV
p
A
V
V
V
V
-
=
=
=
.
Для расчёта необходимо знать давление
P
3
. Так как первый процесс изотермич
е-
ский,
2
1
1
2
V
V
p
p
=
.
По условию задачи
2
1
1
2
3
2
2
V
V
P
p
p
=
=
,
следовательно
,
100
)
(
2
2
3
2
1
1
3
=
-
=
V
V
V
V
P
A
.
Общая раб
ота
А = А
1
+А
2
+А
3
= 238,63 Дж
.
Ответ
:
работа
,
совершенная газом А
=
238,63 Дж.
В качестве дополнения заметим, что существует еще один способ определ
е-
ния работы
,
совершаемой газом
,
–
графический. Как известно
,
площадь на ди
а-
грамме
p
V
между линией
,
изображаю
щей процессы
,
происходящие с газом
,
и
осью объема по модулю равна работе. Если объём газа увеличится, то работа пол
о-
жительна, в противном случае
отрицательна. В ряде случаев этот метод позволяет
найти работу
,
не прибегая к вычисл
е
нию интегралов.
Задача
№ 2
Азот
находящийся
при температуре 400 К, подвергли адиабатическому ра
с-
шир
е
нию, в результате которого его объём увеличился в
n
= 5 раз, а внутренняя
энергия уменьшилась на 4 кДж. Определите массу азота
,
считая его идеальным г
а-
зом.
Решение:
Составим выражение изменения внутренней энергии азота,
сч
и
тая его идеальным газом.
Δ
U
=
n
V
!
Δ
T
=
(
)
│
₩
-
=
-
1
2
2
1
2
1
1
2
T
T
T
m
R
i
T
T
m
R
i
m
m
Учитывая, чт
о процесс расширения происходил адиабатич
е
ски
,
воспользуемся уравнением Пуассона
,
связывающим
температ
у
ры
и
объёмы
1
2
2
1
1
1
-
-
=
g
g
V
T
V
T
(
i
i
C
C
V
P
2
+
=
=
g
-
показатель адиаб
а
ты). С
помощью данного уравнения сведём неизвестное отношение те
м-
ператур к и
звестному отношению объ
ё
мов
:
1
1
2
1
1
2
1
-
-
│
₩
=
│
₩
=
g
g
n
V
V
T
T
.
Для изменения внутренней энергии в итоге получаем формулу
│
₩
-
│
₩
=
D
-
1
1
2
1
1
g
m
n
T
m
R
i
U
.
Выра
зив
массу
и произведя расчеты
,
получим
кг.
Ответ
:
масса азота
m
=
0.028
кг.
Задача № 3
Определите показатель
адиабаты
для смеси газов
,
содержащей гелий массой
1
m
= 8
г
и водород массой
2
m
=
2
г. Газы считать идеальными.
Решение:
По определению
V
P
c
A
=
g
. Рассчитаем удельные теплоёмкости
для смеси газов. Перв
о
й вычислим теплоёмкость при постоя
н-
ном объёме. Колич
е
ство тепл
оты
,
необходимое для нагревания
смеси газов на
Δ
T
,
с одной стороны
,
по определению теплоё
м-
кости
,
равно
T
m
m
c
Q
V
D
+
=
)
(
2
1
.
Дано:
m
=
28
г/моль
i
= 5
T
1
= 400
K
V
2
= nV
1
n
= 5
Δ
U
=
-
4 кДж
m
-
?
Дано:
1
m
= 8г.
m
1
= 4·10
-
3
кг/моль
2
m
= 2г.
m
2
= 2·10
-
3
кг/моль
g
-
?
028
,
0
1
1
2
1
1
=
│
₩
-
│
₩
ᅲ
D
=
-
g
m
n
RT
i
U
m
С другой стороны
,
данное количество
теплоты может быть представлено
как
сумма теплот
,
идущих на нагре
вание двух газов по отдел
ь
ности
:
T
m
c
T
m
c
Q
Q
Q
V
V
D
+
D
=
+
=
2
1
2
1
2
1
.
Приравнивая выражения
,
получим
2
1
2
1
2
1
m
m
m
c
m
c
C
V
V
V
+
+
=
.
Удельные теплоёмкости газов можно выразить через число степеней свободы
молекул и молярные массы газов
:
1
1
1
2
m
R
i
c
V
=
;
2
2
2
2
m
R
i
c
V
=
,
где
1
i
= 3,
2
i
= 5.
После подстановки получаем
2
1
2
2
2
1
1
1
2
2
m
m
m
R
i
m
R
i
c
V
+
+
=
m
m
.
Аналогичные рассуждения дадут для удельной теплоёмкости при постоянном
давлении
2
1
2
2
2
1
1
1
2
)
2
(
2
)
2
(
m
m
m
R
i
m
R
i
c
P
+
+
+
+
=
m
m
.
Соответственно
,
показатель
адиабаты п
осле подстановки полученных выр
а-
жений
545
,
1
)
2
(
)
2
(
2
2
2
1
1
1
2
2
2
1
1
1
=
+
+
+
+
=
=
m
m
m
m
g
m
i
m
i
m
i
m
i
c
c
V
P
.
Ответ
:
показатель адиабаты
545
,
1
=
g
.
Задача № 4
Некоторая тепловая машина работает по циклу
,
состоящему из адиабаты, изобары и изохоры
,
изобр
а-
женному на
рисунке
. Определить
теоретический
к. п. д.
такого двигателя если степень сжатия (отношение ма
к-
симального объёма к мин
и
мальному)
n
= 10, а в качестве
рабочего тела используется идеальный двухато
м
ный газ.
Решение:
Теоретически
й КПД тепловой машины можно определить по формуле
│
₩
-
=
-
=
H
X
H
X
H
Q
Q
Q
Q
Q
1
h
.
Рассмотрим
p
-
V
диаграмму цикла
,
совершаемого тепловой машиной. На уч
а-
стке 1
-
2 машина не получает и не отдаёт теплоту
,
так как этот процесс адиабатич
е-
ский
.
На участ
ке 2
-
3 при постоянном давлении прои
с
ходит уменьшение объёма, это
возможно только в том случае
,
если уменьша
ю
тся температура газа, а следовател
ь-
но
,
и его внутренняя энергия. Кроме того
,
работа
,
совершённая газом на этом учас
т-
ке
,
тоже отриц
а
тель
на.
З
начит
,
с
огласно первому началу термодинамики (
Q
=
A
+
Δ
U
)
,
отрицател
ь
ным будет и количество теплоты
,
получаем
ой
системой в данном
процессе. Последнее означает, что процесс 2
-
3
это процесс
,
в котором система о
т-
дает теплоту холоди
л
ь
нику
:
Q
X
=
-
Q
23
(в
формуле поста
влен знак минус потому, что в выражении КПД стоят модули к
о-
личеств теплоты
,
полученных и отданных тепловой машиной
)
.
Рассмотрим участок 3
-
1: на данном участке при постоянном объёме увелич
и-
вается давление газа. Из уравнения Менделеева
Клапейрона следует,
что увел
и-
чива
ю
тся температура газа и его внутренняя энергия. Так как работа в данном пр
о-
цессе не совершается (
V
=
const
), количество теплоты
,
полученное системой
,
равно
изменению внутренней энергии и является положительной величиной
-
на участке
3
-
1 тело
находится в контакте с нагревателем и
Q
H
=
Q
31
.
С учётом всего вышесказанного можно преобразовать выражение КПД
(
)
(
)
(
)
3
1
2
3
3
1
2
3
31
23
1
1
1
1
T
T
T
T
T
T
C
T
T
C
Q
Q
Q
Q
V
P
H
X
-
-
+
=
-
-
+
=
+
=
-
=
g
h
,
где
i
i
2
+
=
g
показатель адиаб
а-
ты.
Используя уравнение изобары
,
можно получить связь между температура
ми
T
2
и
T
3
=
T
2
/
n
.
Температуры в первом и во втором состояниях
можно связать с помощью
уравнения
Пуассона
:
const
TV
=
-
1
g
.
Примен
яя его к перво
му
и второ
му
состоян
и-
ям
,
получим
.
,
)
(
,
1
2
1
1
1
2
1
1
1
1
2
2
1
1
1
-
-
-
-
-
=
=
=
g
g
g
g
g
n
T
T
nV
T
V
T
V
T
V
T
Подставляя выражения
для
T
1
и
T
3
в формулу КПД
,
получим
Дано:
n
= 10
i
= 5
h
-
?
(
)
(
)
1
1
1
1
1
1
1
1
1
1
1
1
2
1
2
2
2
-
-
-
=
-
-
+
=
-
│
₩
-
+
=
-
│
₩
-
+
=
-
-
g
g
g
g
g
g
g
g
h
n
n
n
n
n
n
n
n
T
n
T
T
n
T
.
Учитывая, что для двухатомного газа
i
= 5 и
4
,
1
=
g
, проводя расчёты
,
получим
48
,
0
=
h
.
Ответ
:
48
,
0
=
h
.
Задача № 5
Определить КПД тепловой машины
,
работающей по
циклу
,
изо
браженному на рисунке
,
если известно, что
V
2
= 2
V
1
, Т
2
= 2Т
1
,
а рабочим телом является идеальный
трехатомный газ.
Решение:
Прежде всего проанализируем процессы
,
происходящие с газом. Проце
ссы 2
–
3 и 4
–
1,
как
видно из рисунка
,
являются изохорическ
и
ми.
В процессах 1
–
2 и 3
–
4 температура прямо про
-
порциональна объёму.
Значит
,
данные процессы
являются изобарическими.
Перерисуем цикл машины в координатах
p
–
V
. По усл
о-
вию задачи температур
ы
в начале и конце изохорического
процесса отличаются в 2 раза. Значит
,
во столько же раз дол
ж-
ны отличаться давлени
я
газа и мож
но
записать
, что
p
2
= 2
p
1
.
КПД цикла
,
по определению
,
равен отношению работы
,
совершенной газом к количеству те
плоты
,
полученн
ой от нагревателя
:
=
Q
A
=
h
.
Работа
,
соверш
аема
я газом за цикл
,
численно равна площади
,
ограничи
ваемой
циклом на диаграмме
p
-
V
. В
данном
случае эта площадь представляет
собой
прям
о-
угольник, с
ледователь
но
:
A
= (
p
2
-
p
1
)(
V
2
-
V
1
) =
p
1
V
1
.
Испол
ьзуя рас
суждения
,
аналогичные приведенным в предыдущей задаче
,
можно прийти к выводу, что тело получает теплоту от нагревателя на участках 1
-
2 и
2
-
3 (на участках 3
-
4 и 4
-
1 рабочее тело тепловой машин
ы отдаёт теплоту холодил
ь-
нику)
:
Q
н
=
Q
12
+
Q
34
.
Рассчита
ем количество теплоты
Q
12
=
n
С
V
(
T
2
-
T
1
)
.
С
V
= 3
R
молярная
тепл
о-
емкость трёхатомного газа при постоянном объёме
.
У
чте
м
, что для трёхатомного
газа число степеней свободы
i
=
6
. Т
1
и Т
2
температур
ы
в соответствующих точ
ках
цикла. Раск
рывая скобки и учитывая, что
Дано:
Т
2
= 2Т
1
V
2
= 2
V
1
h
-
?
n
RT
1
=
p
1
V
1
;
n
RT
2
=
p
2
V
1
= 2
p
1
V
1
,
получим
Q
12
= 3R
n
(T
2
-
T
1
) = 3 (
n
RT
2
-
n
RT
1
) = 3(2
p
1
V
1
-
p
1
V
1
)
=3
p
1
V
1
.
Аналогич
но, можно записать
Q
23
=
n
С
p
(
T
3
-
T
2
)
.
С
р
= 4
R
–
мол
ярная
теплоёмкость
трёхатомного идеального газа при постоянном объёме. Учитывая, что
n
RT
3
=
p
2
V
2
= 4
p
1
V
1
,
запишем
Q
23
= 4
R
n
(
T
3
-
T
2
) = 4(4
p
1
V
1
–
2
p
1
V
1
) = 8
p
1
V
1
,
Q
Н
=
Q
12
+
Q
23
= 11
p
1
V
1
.
Рассчитаем коэффициент полезного действия
09
,
0
11
1
11
1
1
1
1
=
=
=
=
V
P
V
P
Q
A
=
h
.
Ответ
:
09
,
0
=
h
.
Задача №
6
В двух сосудах одного и того же объёма находится гелий массой 10
г
(
m
1
= 4·10
-
3
кг/моль) и азот массой 56
г (
m
2
= 28·10
-
3
кг/моль). Давление и температ
у-
ра газов одинаковы. Сосуды соединяют и начинается процесс диффузии. Опред
е-
лить изм
е
нение энтропии системы в данном процессе.
Решение:
Процесс диффузии в данной задаче можно рассматривать как
процесс изотермического расширения. В этом случае изменени
T
э
н
тропии гелия
1
1
1
1
1
Q
T
Q
T
T
Q
S
=
=
=
D
d
d
.
Так как процесс изотермический
,
Q
1
=
A
1
.
Вычисляя
работу в из
о-
термическом процессе
,
получим
2
ln
V
V
ln
RT
1
2
1
1
2
1
2
1
2
1
ᅲ
=
ᅲ
=
=
=
=
RT
V
dV
RT
dV
V
RT
pdV
A
V
V
V
V
V
V
1
1
1
n
n
n
n
.
В последней формуле учтено, что
V
2
= 2
V
1
, так как
по условию объёмы обоих
сосудов равны. Следовательно
,
2
ln
2
ln
1
1
1
1
ᅲ
=
ᅲ
=
=
D
R
m
R
T
Q
S
m
n
1
.
Аналогичные вычисления для второго газа
дают
2
ln
2
2
2
ᅲ
=
D
R
m
S
m
.
Полное изменение энтропии всей системы
Дано:
m
1
= 10
г
m
1
= 4
г/моль
m
2
= 56
г
m
2
=28
г/моль
Δ
S
-
?
6
92
,
25
2
ln
2
2
1
1
2
1
=
│
₩
+
ᅲ
=
D
+
D
=
D
m
m
m
m
R
S
S
S
.
Ответ
:
изменение энтропии системы в данном процессе
6
92
,
25
=
D
S
.
Задачи,
рекомендуемые для аудиторных заняти
й
1. Азот массой 5 кг, нагретый на 150 К, сохранил неизменный объем. Найти к
о-
личество теплоты, сообщенное газу, изменение его внутренней энергии и сове
р-
шенную газом работу.
2.Водород массой
m
= 4 г был нагрет на
∆
T
= 10 К при постоянном давлении.
Опр
е
дел
ить работу расширения газа.
3. При изотермическом сжатии двух киломолей азота, находившегося при те
м-
пер
а
туре 20
°С, до давления 2
атм.
терм
остату отдано
20 кДж
теплоты
. Определить
давление, под которым находился азот до сжат
и
я, и работу, соверше
н
ную над г
азом
при сжатии.
4. Водород при нормальных условиях имел объем
V
1
=
100 м
3
. Найти изменение
внутренней энергии газа при его адиабат
ическом
расширении до объема
V
2
= 150
м
3
.
5. В цилиндре под поршнем находится водород мас
c
ой
m
= 0,02 кг при темпер
а-
туре Т
1
= 300 К. Водород сначала
рас
ширился адиабат
ически
, увеличив свой об
ъ
ем
в пять раз, а затем
был
сжат изотермически, причем объем газа уменьшился в пять
раз. Найти температуру Т
2
в конце адиабатного расширения и полную работу
,
с
о-
вершенную газом. Изобразить
процесс графически.
6. Кислород массой 2 кг занимает объем 1 м
3
и находится под давлением 0,2
МПа. При нагревании газ расширился при постоянном давлении до объема 3 м
3
, а
затем давление его возросло до 0,5 МПа при неизменном объеме. Найти изменение
внут
ренней энергии газа, совершенную им работу и переданное газу количество т
е-
пл
о
ты.
7.
Каков
а
удельн
ая
теплоемкост
ь
с
v
смеси газов, содержащей кислород
m
1
=
10
г
и азот
m
2
=
20
г?
8. Идеальный двухатомный газ, содержащий количество
вещества
=
1 кмоль,
совершает замкнутый цикл, график к
о-
торого изображён
на рис
унке
. Определить 1) количество те
п-
лоты полученное
,
от
нагревателя; 2) количество теплоты
,
п
е-
реданное охл
а
дителю;
3) работу
,
совершаемую газом за цикл;
4) к.п.д цикла
.
P
МПа
1,6 2 3
1,5
1,4
1,3 1 4
1,2
0 1 2 3
V,
м
3
9. Идеальный двухатомн
ый газ совершает цикл Кар
н
о,
график которого изображен на рис
унке
. Объемы газа в с
о-
стояниях В и
C
соответс
т
венно
V
1
=
12 л и
V
2
= 16 л.
Найти
к.п.д цикла
.
10. Вычислить приращение энтропии
∆S
при нагревании
1 кмол
ь
трехатомного
газа от 0
°С до 500
°
С, если процесс нагревания происходит:
а) при постоянном об
ъ-
еме; б) при постоянном давлении.
11.
2 кг льда, находящегося при
t
=
18°С, нагрели и превратили в пар. Опред
е-
лить изменение энтропии в этом процессе. Температура плавления 273 К, темпер
а-
тура пар
ообразования 373 К
(удельная теплоемкость льда с
л
=
2,1
·
10
3
Дж/(кг
К)
,
удельная теплоемкость воды с
в
=
4,2
·
10
3
Дж/(кг
К)
, удельная теплота пла
в
ления льда
=
3,3
·
10
5
Дж/(кг
К)
, удельная теплота парообразования
r
=
23
·
10
5
Дж/кг
).
Задачи для самостоятельн
ого решения
1.
При адиабатном расширении кислорода с начальной температурой
T
1
=
320
K
внутренняя энергия уменьшилась на
∆
U
=
8,4 кДж, а его объем увеличился в
n
= 10
раз. Определить массу
m
кислорода.
2. Баллон вместимостью V = 20 л содержит водород при
температуре
T
=
300 К
под давлением р = 0,4 МПа. Каковы будут температура
T
1
и давление р
1
,
если газу
с
о
общить количество теплоты
Q
= 6 кДж?
3. Водород занимает объем 10 м
3
при давлении 10
5
Па. Газ нагрели при постоя
н-
ном объеме до давления 3
·
10
5
Па. Опред
елить изменение внутренней энергии газа,
раб
о
ту, совершенную газом, и количество теплоты, сообщенное газу.
4. Азот нагревался при постоянном давлении, причем ему соoбщено количество
теплоты
Q
= 21 кДж.
Определить работу
A
, которую совершил при этом газ, и
и
з-
менение его внутренней энергии
∆
U
.
5. Кислород при неизменном давлении р = 80 кПа нагревается. Его объем увел
и-
чивается от
V
1
= 1 м
3
до
V
2
= 3 м
3
. Определить: 1) изменение внутренней энергии
кислорода; 2) работу
,
совершенную им при расширении; 3) количест
во теплоты
,
с
о-
общенное газу.
6. Д
л
я нагревания углекислого газа на 50
°С при постоянном давлении требуе
т
ся
3,3
·
10
5
Дж тепла. Определить массу углекислого газа, работу расширения и измен
е-
ние внутренней энергии.
7. Азот массой
m
= 200 г расширяется изотерм
ически при температуре
Т = 280 К, причем объем газа увеличивается в два раза. Найти: 1) изменение вну
т-
ренней энергии газа; 2) совершенную при расширении газа работу; 3) количество
теплоты
,
п
о
лученное газом.
8. Азот, занимавший объем
V
1
= 10
л под давлением р
1
=
0,2 МПа, изотермиче
-
ски расширился до объема
V
2
=
28 л. Определить работу расширения газа и количе
-
ство теплоты
,
полученное газом.
p A
p
2
B
D
p
1
C
V
1
V
2
V
9. При изотермическом расширении кислорода, содержавшего количество вещ
е-
ства
= 1
моль и имевшего те
мпературу Т = 300 К, газу было передано количество
теплоты
Q
= 2 кДж. Во сколько раз увеличился объем газа?
10. При адиабатном сжатии кислорода массой
m
= 20 г его внутренняя энергия
увеличилась на
∆
U
= 8 кДж и температура повысилась до Т
2
= 900 К. Найти:
1) п
о-
вышение температуры
∆
Т; 2) конечное давление газа Р
2
, если начальное давл
е
ние
Р
1
= 200 кПа
.
11. Кислород массой 10
г, находящийся при температуре
370 К, подвергли ади
а-
батическому расширению, в результате которого его давление уменьшилось в
4 раза. В результате последующего изотермического процесса газ сжимается до
первоначального давления. Определить: 1)
температуру газа в конце процесса;
2) количество теплоты, отданное газом; 3) приращение внутренней энергии газа;
4) работу, соверш
енную газом.
12. Некоторая масса газа, занимающего объем
V
1
=
0,01 м
3
, находится при давл
е-
нии
Р
1
=
0,1 МПа и температуре Т
1
=
300 К. Газ нагревается вначале при постоя
н-
ном объеме до температуры Т
2
=
320 К, а затем при постоянном давлении до темп
е-
ратуры Т
3
=350 К. Найти работу, совершаемую газом при переходе из
начального
состояния в
конечное
.
13. Кислород массой 5 кг занимает объем 1,5 м
3
и находится под давлением
3 атм. Газ нагрет сначала при постоянном давлении до объема 4 м
3
, а затем при п
о-
сто
янном объеме до давления 5 атм. Найти изменение внутренней энергии газа и
сове
р
шенную им работу.
14.
Водород массой 40 г, имевший температуру 300 К, адиабатно расширился,
ув
е
личив объем в 3 раза. Затем при изотермическом сжатии объем газа уменьшился
в
2 раза. Определить полную работу, совершенную газом, и конечную температуру
г
а
за.
15. Кислород массой 200 г занимает объем 100 л и находится под давлением
200 кПа. При нагревании газ расширился при постоянном давлении до объема 300
л, а затем его давле
ние возросло до 500 кПа при неизменном объеме. Найти измен
е-
ние внутренней энергии газа, совершенную им работу и теплоту, переданную г
а
зу.
16. Моль идеального газа имеет первоначально температуру 290 К. Газ расшир
я-
ется изобарически до тех пор, пока его об
ъем не возрастет в два раза. Затем газ о
х-
лаждается изохорически до первоначальной температуры. Определить приращение
внутренней энергии газа, работу, совершенную газом, и количество теплоты, пол
у-
че
н
ное газом.
17. В цилиндре под поршнем находится водород ма
ссой 0,02 кг при температуре
300 К. Водород сначала расширился адиабатически, увеличив свой объем в 5 раз, а
затем был сжат изотермически, причем объем газа уменьшился в 5 раз. Найти те
м-
пературу в конце адиабатического расширения и полную работу, совершен
ную г
а-
зом. Изобразить процесс графически на диа
грамме "давление
-
температура".
18. Некоторая масса кислорода занимает объем V
1
=3 л
при температуре
t
1
=
27°С и давлении
p
1
=
8,2
·
10
5
Па.
Во втором с
о
стоянии газ имеет параметры
V
2
=4,5 л и
p
2
=6
·
10
5
Па. Найти: количество тепла, полученного газом;
работу, с
о
вершенную газом при расширении; изменение
внутренней энергии газа.
Задачу решить при условии, что перевод газа из первого
состояния во второе осуществл
я
ется: 1) путем АСВ и 2) путем А
D
В.
19.
Азот массой
m
=
50 г находится при температуре
T
1
=
280
K
.
В результате
изохорного охлаждения его давление уменьшилось в 2 раза, а з
а
тем в результате
изобарного расширения температура газа в конечном состоянии стала равной пер
-
воначальной. Определите:
1)
работу, совершенную газом; 2) изм
е
нение внутренней
энергии газа.
20.
Двухатомный идеальный газ занимает объем
V
1
=
1 л и находится под давл
е-
нием
p
1
=
0,1 МПа. После адиабатического сжатия газ характеризуется объемом
V
2
и да
в
лением
p
2
. В результате послед
ующего изохорного процесса газ охлаждается
до первоначальной температуры, а его давление
p
3
=
0,2 МПа. Определить: 1) объем
V
2
; 2) давление
p
2
.
21. Считая азот идеальным газом, определить его удельную теплоемкость: 1) для
изохорного процесса; 2) для изобар
ного процесса.
22. Определить удельные теплоемкости
c
v
и
c
p
смеси углекислого газа массой
m
1
= 3 г и азота массой
m
2
= 4
г.
23. Определить удельную теплоемкость
с
p
смеси кислорода и азота, если
кол
и-
чество вещества первого компонента равно 2 мол
ь
, а колич
ество
вещества втор
о
го
4 мол
ь
.
24. Смесь газов состоит из хлора и криптона, взятых при одинаковых условиях и
в равных объемах. Определить удельную теплоемкость с
p
смеси.
25. Вычислить удельные теплоемкости
c
v
и с
p
газов: 1) гелия; 2) водорода; 3) у
г-
лекис
лого газа.
26. Разность удельных теплоемкостей (
c
р
-
с
v
) некоторого двухатомного газа
ра
в-
на 260
Дж/(моль
К)
. Найти молярную массу
газа и его удельные теплоемкости
с
v
и с
р
.
27. Дана смесь газов, состоящая из неона, масса которого
m
1
= 4 кг и водород
а,
масса которого
m
2
= 1 кг. Газы считать идеальными. Определить удельные теплое
м-
кости смеси газов в процессах: р
=
со
nst
,
V
=
со
nst
.
28. Принимая отношение теплоемкостей для двухатомных газов
n
=
1,4, вычи
с-
лить удельные теплоемкости кислорода.
29.
Найти о
тношение с
p
/с
v
для смеси газов, состоящей из 10 г гелия и 4 г водор
о-
да.
30.
Вычислить отношение
c
р
/с
v
для смеси 3 мол
ь
аргона и 5 мол
ь
кислорода.
31. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и
двух изобар, причем наибольшее давле
ние газа в два раза больше наименьшего, а
наибольший объем в четыре раза больше наименьшего. Определить к.
п.
д.
ци
к
ла
.
32. Идеальный газ, совершающий цикл Карно, 2/3 количества теплоты
Q
1
, пол
у-
че
н
ного от нагревателя, отдает охладителю. Температура Т
2
ох
ладителя равна 280
К. Определить температуру Т
1
нагревателя.
33. Идеальный газ совершает цикл Карно. Температура Т
2
охладителя равна
290 К. Во сколько раз увеличится к.
п.
д. цикла, если температура нагревателя по
-
высится от 400 К до 600 К?
34. Идеальн
ый газ совершает цикл Карно. Температура Т
1
нагревателя в три раза
выше температуры
T
2
охладителя. Нагреватель передал газу количество теплоты
Q
1
= 42 кДж. Какую работу А совершил газ?
35. Газ совершил цикл Карно. Абсолютная температура нагревателя в три
раза
выше, чем температура холодильника. Нагреватель передал газу количество тепл
о-
ты 5 кДж. Какую работу совершил газ?
36. Газ совершает цикл Карно. За счет теплоты 4200 Дж, полученной от нагрев
а-
теля, он совершает работу 598 Дж. Каков
к.
п.
д.
цикла? Во ск
олько раз абсолютная
температура нагревателя больше абсолютной температуры холодильника?
37. Газ совершает цикл Карно. Работа изотермического расширения газа 5 Дж.
Определить работу изотермического сжатия, если КПД цикла равен 0,2.
38. Идеальный газ соверш
ает цикл Карно, Температура нагревателя
220
°С, те
м-
пература холодильника 7
°С. При изотермическом расширении газ совершает раб
о-
ту 120 Дж. Определить количество теплоты, которое газ отдает холодильнику при
изоте
р
мическом сжатии.
39. В результате кругового
процесса газ совершил работу 5 Дж и отдал хол
о-
дильнику 16,8 Дж теплоты. Определить
к.
п.
д.
цикла.
40. Совершая замкнутый процесс, газ получил от нагревателя количество тепл
о-
ты
Q
1
= 4 кДж. Определить работу А газа при протекании цикла, если его к.
п.
д.
=
0,1.
41.В результат кругового процесса газ совершил работу А
=
1 Дж и передал о
х-
ладителю количество теплоты
Q
2
=
4,2 Дж. Определить
к.
п.
д.
цикла.
42.Идеальный газ, совершающий цикл Карно, произвел работу 600 Дж. Темп
е
-
ратура нагревателя 500 К, х
олодильника 300 К. Определить: 1) к.
п.
д. цикла;
2) колич
е
ство теплоты, отданное холодильнику за один цикл.
43.Идеальный газ, совершающий цикл Карно, 70
% количества теплоты, пол
у-
ченной от нагревателя, отдает холодильнику. Количество теплоты, пол
учаемое от
нагревателя, равно 5 кДж. Определить: 1) к.
п.
д. цикла; 2) работу, совершенную
при полном цикле.
44. Наименьший объем газа, совершающего цикл Карно, равен 153 л. Опред
е-
лить наибольший объем, если объем газа в конце изотермического расширения с
о-
ставл
я
ет 189 л, а в конце изотермического сжатия
160 л.
45. Определить
к.
п.
д.
цикла, состоящего из двух адиабат и двух изохор, с
о
вер
-
шаемого идеальным газом, если известно, что в
процессе адиабатного расширения
а
б
солютная температура газа Т
2
=
0,75
·
Т
1
,
а в процессе адиабатного сжатия
Т
4
=
0,75
·
Т
3
.
46. Идеальная тепловая машина, работающая по циклу Карно, имеет температ
у-
ру нагревателя 227
°С, температуру холодильника 127
°С. Во сколько раз нужно
увеличить температуру нагревателя, чтобы
к.
п.
д.
машины увеличился в 3 раза?
47. Идеальная тепловая машина, работающая по циклу Карно, получает за ка
ж-
дый цикл от нагревателя 2514 Дж. Температура нагревателя 400 К, холодильника
-
300 К. Найти работу, совершаемую машиной за один цикл, и количество тепла
, о
т-
даваемое холодильнику за один цикл.
48.
Идеальная тепловая машина работает по циклу Карно. При этом 80
% тепла,
получаемого от нагревателя, передается холодильнику. Количество тепла, получа
е
-
мого от нагревателя, равно 6,3 кДж. Найти: 1)
к.
п.
д.
цикла;
2) работу, соверше
н
-
ную при полном цикле.
49. Один киломоль кислорода совершает цикл Карно в интервале температур от
27
°С до З27
°С. Известно, что отношение максимального за цикл давления к мин
и
-
мальному
равно 20. Вычислить: 1)
к.
п.
д.
цикла; 2) колич
ество теплоты, получе
н
-
ное от нагревателя за цикл ; 3) количество теплоты, отданное холодильнику за цикл;
4) работу, совершаемую газом за цикл.
50. Идеальный газ совершает цикл Карно. Температура Т
1
нагревателя равна
470 К, температура Т
2
охладителя рав
на 280 К. При изотермическом расшир
е
нии
газ совершает работу А = 100 Дж. Определить к.
п.
д. цикла
, а также колич
е
ство
тепл
о
ты
Q
2
, которое газ отдает охладителю при изотермическом сжатии.
51. Идеальный газ совершает цикл Карно. Температура
T
1
нагревателя
в четыре
раза выше температуры
T
2
охладителя. Какую долю количества теплоты, получа
е-
мого за один цикл от нагревателя, газ отдает охладителю?
52. Идеальная тепловая машина. работающая по циклу Карно, совершает за одни
цикл работу 7,35
·
10
4
Дж. Температура н
агревателя 100
°С, температура холодил
ь-
ника 0° С, Найти: I)
к.
п.
д.
машины; 2) количество тепла, получаемого маш
и
ной за
один цикл от нагревателя; 3) количество тепла, отдаваемого за один цикл холодил
ь-
нику.
53. Многоатомный идеальный газ совершает цикл
Карно, при этом в процессе
адиабатического расширения объем газа увеличивается в 4 раза. Определить к.
п.
д.
ци
к
ла.
54.Идеальный двухатомный газ, содержащий количество вещества
= 1 моль,
совершает цикл, состоявший из двух изохор и двух изобар Наимен
ьший объем
V
min
= 10 л, наибольший
V
max
=
20 л, наименьшее давление
p
min
= 246 кПа, наибол
ь-
шее
p
max
=410 кПа. Построить график цикла. Определить
к.
п.
д.
55. Идеальный газ совершает цикл Карно, к.
п.
д. которого 0,4. Определить раб
о-
ту изотермического сжатия
газа, если работа изотермического расширения 400 Дж.
56. Газ совершает цикл Карно. Температура холодильника 280 К, нагревателя
380 К. Во сколько раз увеличится коэффициент полезного де
й
ствия цикла, если
темпер
а
туру нагревателя повысить на 200 К?
57.Опере
делить
к.
п.
д.
цикла
изображенного на рисунке.
Р
абочим телом является идеальный
одноатомный
газ,
p
2
=
2
p
1
,
V
2
=
4
V
1
.
58. Тепловая машина, рабочим телом которой является
идеальный
двухатомный
газ, совершает цикл, изображенный
на рис
унке
. Найт
и
к.
п.
д.
этой машины, если
p
2
=
2
p
1
,
V
2
=
4
V
1
.
59.
Идеальная тепловая машина работает по циклу Карно.
Определить КПД цикла, если известно, что за один цикл б
ы
ла произведена работа,
равная 3000 Дж, и холодильнику б
ы
ло передано 13,4
к
Дж тепла.
60
. В результата циклического процесса газ совершил работу А = 100 Дж и пер
е-
дал холодильнику 400 Дж теплоты. Определить коэфф
и
циент полезного действия
ци
к
ла.
61. Смешали воду массой m
1
= 5 кг при температуре T
1
= 280 K с водой массой
m
2
= 8 кг при температур
е T
2
= 350 K. Найти: 1) температуру смеси; 2) изменение
э
н
тропии
∆S
, происходящее при смешивании.
62. В результате изохорного нагревания водорода массой m = 1 г давление p газа
увеличилось в два раза. Определить изменение
∆S
энтропии газа.
63. Найти измене
ние
∆S
энтропии при изобарном расширении азота массой m =
4 г от объема V
1
= 5 л до объема V
2
= 9 л.
64. Кусок льда массой m = 200 г, взятый при температуре
t
1
=
-
10 °С, был нагрет
до температуры
t
2
= 0
°С и расплавлен, после чего образовавшаяся вода была
нагр
е-
та до температуры
t
1
= 10 °С. Определить изменение
энтропии
∆S
в ходе указанных
процессов.
65.
Лед массой m
1
= 2 кг при температуре
t
1
= 0 °С был превращен в воду той же
температуры с помощью пара, имеющего температуру
T
2
= 100 °С. Определить ма
с-
су m
2
израсходованного пара. Каково изменение энтропии
∆S
системы лед
-
пар?
66.
Кислород массой m = 2 кг увеличил свой объем в 5 раз один раз изотермич
е-
ски, другой
-
адиаб
атно. Найти изменение
энтропии в каждом из указанных проце
с-
сов.
67.
Вычислить изменение эн
тропии двух молей идеального двухатомного газа,
если его температура изохорически повышается от 200 К до 300 К. Убывает энтр
о-
пия г
а
за или возрастает?
68.
Вычислить изменение энтропии при изотермическом сжатии трех молей ид
е-
ального газа от 20 до 15 л. Убыва
ет энтропия газа или возрастает ? Газ двухато
м-
ный.
69. Вычислить изменение энтропии при изотермическом изменении давления
шести молей идеального одноатомного газа от 9 до 6 МПа при комнатной темпер
а-
туре. Уменьшается или увеличивается при этом энтропия газа
?
70. Вычислить изменение энтропии при изотермическом изменении давления
трех молей идеального двухатомного газа от 5 до 7 МПа при комнатной температ
у-
ре.
71.
Вычислить изменение энтропии при изобарическом нагревании пяти молей
идеального одноатомного газа
от 200 до 300 К. Увеличивается или умен
ь
шается при
этом энтропия газа?
72. Вычислить изменение энтропии двух молей идеального двухатомного газа,
если его давление изохорически увеличивается от 2 до 3 МПа. Увеличивается или
уменьшается энтропия газа в это
м случае?
73. Вычислить изменение энтропии восьми молей идеального одноатомного газа,
если его температура изохорически убывает от 325 до 285 К. Убывает или возраст
а-
ет энтропия газа ?
74. Вычислить изменение энтропии трех молей идеального одноатомного газа
,
если ему изобарически сообщается 5 кДж тепла. Первоначальная температура газа
равна 300 К. Увеличивается или уменьшается энтропия газа в этом случае ?
75. Вычислить изменение энтропии семи молей идеального одноатомного газа,
если его давление изохорическ
и уменьшается от 7 до 5 МПа. Увеличивается или
уменьшается энтропия газа?
76. Вычислить изменение энтропии пяти молей идеального одноатомного газа,
если у него изохорически отнимается 3 кДж тепла. Начальная температура газа ра
в-
на 350 К. Увеличивается или
уменьшается энтропия газа?
77. 1 кмо
ль двухатомного идеального газа
наход
и
тся при некоторой температ
у
ре,
охлаждается изохорически, вследствие чего его давление уменьшается в два раза.
Затем газ изобарически расширяется так, что в конечном состоянии его тем
п
е
ратура
равна первоначальной. Найти приращение энтропии.
78. Водород массой
m
= 100 г был изобарно нагрет так, что его объем, увеличи
л-
ся в 3 раза, затем водород был изохорно охлажден так, что давление его уменьш
и-
лось в 3 раза. Найти изменение
∆
S
энтропии
в ходе указанных процессов.
79. Вычислить изменение энтропии двух молей идеального двухатомного газ
а,
если ему изохорически сообщаю
тся 5 Дж тепла. Начальная температура газа равна
250 К.
80. Вычислить изменение энтропии четырех молей идеального одноатом
ного г
а-
за, если он изотермически отдает количество тепла 7 кДж. Температур газа равна
350 К. Увеличивается или уменьшается энтропия газа?
81. Вычислить изменение энтропии трех молей идеального двухатомного газа,
если ему изотермически сообщается количеств
о тепла 4 кДж. Температура газа ра
в-
на 300 К.
82. Вычислить изменение энтропии пяти молей идеального двухатомного газа,
если от него изобарически забирают 3 кДж тепла. Начальная температура газа равна
330 К.
83. Найти приращение энтропии при превращении 200
г льда,
находившегося
при температуре минус
10,7
°С, в воду. Теплоемкость льда считать не зависящей от
температуры. Температуру плавления принять равной 273 К.
84. Вычислить изменение энтропии трех молей идеального двухатомного газа,
если газ изобарическ
и сжимают от 2 до 1 л при комнатных температурах. Увелич
и-
вается или уменьшается при этом энтропия газа?
85. Найти изменение энтропии при переходе 8 г кислорода от объема в 10 л
при
температуре 80
°С к объему в 40 л при температуре 300
°С.
86. 6,6 г вод
орода расширяется изобарически изобарически до увеличения объ
е-
ма в два раза. Найти изменение энтропии при этом расширении.
87. Найти изменение энтропии
∆
S
5 г водорода
,
изотермически расширившегося
от объема 10 л до объема 25 л.
88. Найти приращение энтроп
ии
∆
S
при расширении 2 г водорода от объема 1,5 л
до объема 4,5 л, если процесс расширения происходит при постоянном давлении.
89. 10 г кислорода нагревают от
t
1
=
50 °С до
t
2
=
150 °С. Найти изменение энтр
о-
пии, если нагревание происходит: 1) изохорически;
2) изобарически.
90. При нагревании 1 кмоль
двухатомного газа его абсолютная температура ув
е-
личивается в 1,
5 раза. Найти изменение энтропии
, если нагревание происходит
1) изохорически; 2) изобарически.
Варианты задач для студентов дневного отде
ления
№
Молекулярная физика
Термодинамика
1
13
25
31
50
61
71
1
31
61
90
60
30
2
14
24
32
51
62
72
2
32
62
89
59
29
3
15
23
33
52
63
73
3
33
63
88
58
28
4
16
22
34
53
64
74
4
34
64
87
57
27
5
17
21
35
54
65
75
5
35
65
86
56
26
6
26
20
36
55
66
76
6
36
66
85
55
25
7
27
19
37
56
67
77
7
37
67
84
54
24
8
28
18
38
57
68
78
8
38
68
83
53
23
9
29
11
39
58
69
79
9
39
69
82
52
22
10
30
12
40
59
70
80
10
40
70
81
51
21
11
18
13
41
60
71
86
11
41
71
80
50
20
12
19
14
42
49
72
87
12
42
72
79
49
19
13
20
15
43
48
73
88
13
43
73
78
48
18
14
21
16
44
47
74
89
14
44
74
77
47
17
15
22
17
45
47
75
90
15
45
75
76
46
16
16
23
28
46
45
76
61
16
46
76
75
45
15
17
24
29
31
60
77
62
17
47
77
74
44
14
18
25
30
32
59
78
63
18
48
78
73
43
13
19
11
26
33
58
79
64
1
9
49
79
72
42
12
20
12
27
34
57
80
65
20
50
80
71
41
11
21
13
1
35
56
81
66
21
51
81
70
40
10
22
14
2
36
55
82
67
22
52
82
69
39
9
23
15
3
37
54
83
68
23
53
83
68
38
8
24
16
4
38
53
84
69
24
54
84
67
37
7
25
26
5
39
52
85
70
25
55
85
66
36
6
26
27
9
40
51
86
71
26
56
86
65
35
5
27
28
10
41
50
87
72
27
57
87
64
34
4
28
29
6
42
49
87
73
28
58
88
63
33
3
29
30
5
43
48
89
77
29
59
89
62
32
2
30
17
8
44
46
90
81
30
60
90
61
31
1
Варианты
задач для вечернего отделения
№
Молекулярная физика
Термодин
амика
1
1
46
72
1
31
61
2
2
47
73
2
32
62
3
3
48
74
3
33
63
4
4
49
75
4
34
64
5
5
50
76
5
35
65
6
9
51
77
6
36
66
7
10
52
79
7
37
67
8
6
54
80
8
38
68
9
7
53
82
9
39
69
10
8
55
83
10
40
70
Библиографический список
1.
Савельев И. В. Курс общей фи
зики. В 5 Кн. Кн. 3. Молекулярная физика и те
р-
модинамика: Учеб. Пособ. для втузов.
М.
:
ООО
”
ИздательствоАстрель
”
,
2003
.
-
208
с.
2.
Трофимова Т. И. Курс физики: Учеб. пособ. для инж.
–
техн. специальностей в
у-
зов. 4
-
е изд.., испр. М.: Высш. школа., 1997. 542 с.
3.
Детлаф А. А., Яворский Б. М. Курс физики: Учеб. пособ. для втузов. М.., 1989.
608 с.
4.
Савельев И. В.
Сборник вопросов и задач по общей физике
:
Для втузов.
-
2
-
е изд.,
перераб.
–
М.
:
Наука,1988.
-
288с.
5.
Чертов А. Г., Воробьёв А. А. Задачник по физике.
–
5
-
е изд.
, перераб. и доп.
–
М.,
1988. 526 с.
6.
Иродов И. Е. Задачи по общей физике
:
Учеб. пособ.
-
СПб.
:
Издательс
т-
во
”
Лань
”
,2001.
-
416с.
7.
Трофимова Т. И., Павлова З. Г. Сборник задач по курсу физики с решениями
:
Учеб. пособ. для вузов. М.
:
Высш. шк., 1999.
-
591с.
8.
Белону
чкин
В. Е.
, Заикин
Д. А.
,
Кингсеп А. С
.
и др.
Задачи по общей физике
:
Для студентов техн. вузов.
М.
:
Физматлит
.
, 2001
.
-
333с.
9.
Мурзов В. И.
Общая физика в задачах и решениях
:
Учебн. пособие для инж.
-
техн.
спец. вузов.
-
Минск.
:
Вышейш. шк.
-
1986.
-
164с.
10.
Механи
ка, молекулярная физика и термодинамика: Учеб. пособие /Сост.: А. И.
Блесман, В. П. Шабалин, О. В. Кропотин и др.
-
Омск: Изд
-
во ОмГТУ
.
-
1
999.
-
76 с.