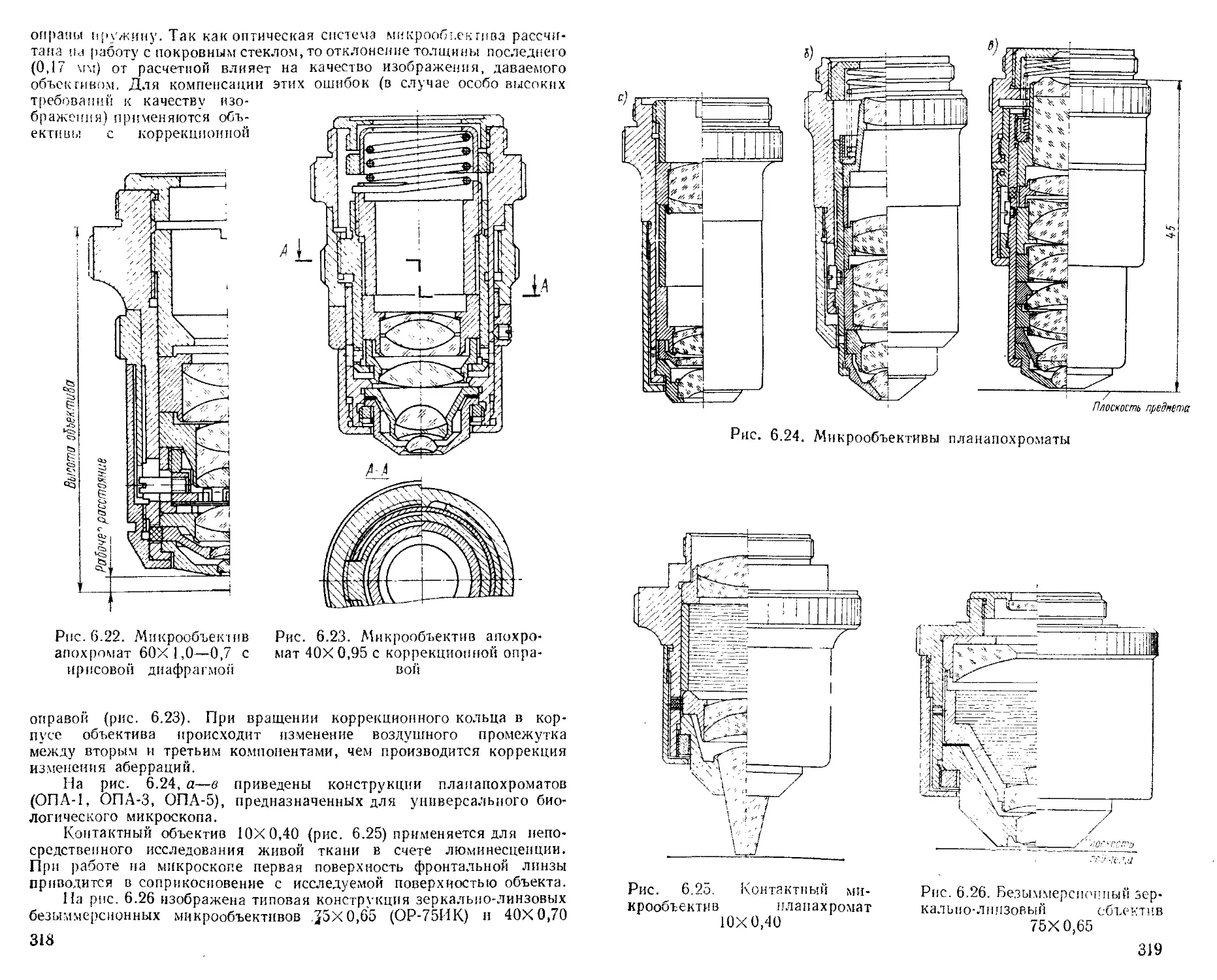
Author: Панов В.А. Кругер М.Я. Кулагин В.В.
Tags: применение оптики в целом приборостроение механика оптика
Year: 1980
Text
СПРАВОЧНИК КОНСТРУКТОРА оптико-МЕХАНИЧЕСКИХ ПРИБОРОВ
Третье издание, переработанное и дополненное
Под общей редакцией д-ра техн, наук В. А. ПАНОВА
ЛЕНИНГРАД сМАШИНОСТРОЕНИЕ» ЛЕНИНГРАДСКОЕ ОТДЕЛЕНИЕ 19 8 0
ББК 34.9я2
С74
УДК 535.8 (031)
Авторы: В. А. ПАНОВ, | М. Я. КРУГЕР |, В. В. КУЛАГИН, Г. В. ПОГАРЕВ, А. М. ЛЕВИНЗОН, И. М. ДОЛИНСКИЙ, Н. А. МИХАЙЛОВ, Б. Г. РЕЗНИЦКИЙ, М. И. КАЛИНИН, Р. М. РАГУЗИН
Рецензент канд. техн, наук В. В. Хваловский
Справочник конструктора оптико-механических С74 приборов./В. А. Панов, М. Я. Кругер, В. В. Кулагин и др.; Под общ. ред. В. А. Панова. — 3-е изд., перераб. и доп. — Л.: Машиностроение, Ленингр. отд-ние, 1980.—742 с., ил.
В пер.: 2 р. 70 к.
В справочнике приведены краткие сведения о физической и геометрической оптике, основные формулы расчета оптических систем, методика расчета аберраций, допуски на изготовление и сборку оптических деталей н узлов.
Третье издание (2-е нзд. 1967 г.) дополнено новым материалом по расчету важнейших элементов н узлов приборов, основам конструирования механической части оптических приборов, структурному анализу подвижных систем, защите от коррозии и покрытиям деталей. В справочник включены новые данные по оптическим бесцветным, цветным и светорассеивающим стеклам, пластмассам, волоконно-оптическим жгутам, светораесеивающим экранам.
Справочник предназначен для инженерно-технических работников оптико-механических предприятий.
СХ5О-58» г51'8”'
ББК 34.9я2
6П5.8
© Издательство «Машиностроение», 1980 г.
ПРЕДИСЛОВИЕ
Современные оптико-механические приборы представляют собой сложные технические устройства/построенные на основе использования разнообразных свойств световой энергии, электронно-оптических систем и точных механизмов.
Для дальнейшего научного и технического прогресса, повышения производительности труда и качества выпускаемых изделий требуется интенсивная разработка и расширение производства новых совершенных приборов. В связи с этим растет потребность в технической литературе и справочниках.
Со времени опубликования второго издания «Справочника конструктора оптико-механических приборов» прошло более десяти лет. За этот период времени появились новые технические материалы, ГОСТы, нормали, введена Единая система конструкторской документации (ЕСКД) и т. д. В связи с этим возникла необходимость в третьем издании данного справочника.
В настоящем справочнике материал по сравнению со вторым изданием переработан и приведен в соответствие с появившейся новой технической документацией по проектированию и расчету оптико-мехаиических приборов.
Добавлены сведения по фотометрическим расчетам приборов, источникам и приемникам световой энергии, светофильтрам, дифракционным решеткам, объективам, окулярам, гибким волоконно-оптическим жгутам, светорассеивающим стеклам и экранам, оптическому цветному стеклу, полимерам для оптических деталей, оптическому конструкционному стеклу, пластмассам и другим техническим материалам. Приведены новые типовые конструкции оптико-механических узлов и дополнены примеры крепления оптических деталей. Расчеты допусков при изготовлении и сборке оптических деталей и узлов выделены в отдельную главу. В гл, 9 изложена новая методика анализа структуры кинематической схемы механизма.
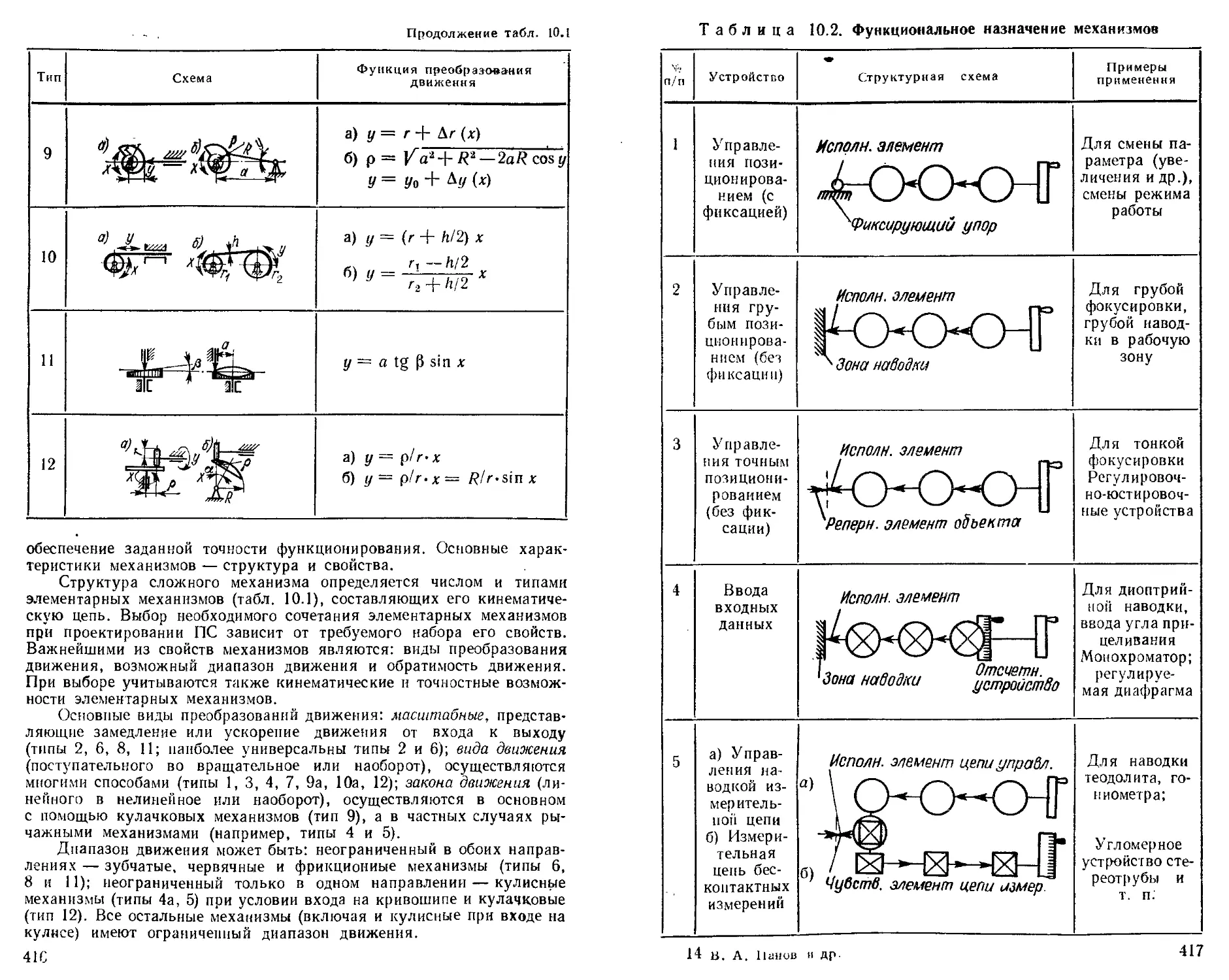
Включены сведения о функциональных назначениях механизмов и подвижных систем оптических приборов, рассмотрены особенности проектирования таких механизмов, внесены уточнения в их расчет.
ОГЛАВЛЕНИЕ
Предисловие .............................................. 3
Глава 1. Физическая оптика (Ф. А. Панов).................... 5
Электромагнитная природа света.......................... —
Электромагнитные волны. Спектр электромагнитных колебаний................................... —
Уравнения волнового движения................ 6
Интерференция света. Основы теории интерферометров 7
Оптическая длина пути ................................. 8
Область и поле интерференции............... —
Входные и выходные зрачки и поле интерферометров —
Ширина щели при нелокализованных полосах..... 9
* Допустимый размер входного зрачка при локализованных полосах ............................................. —
Интерференция в пластинках ....................... 10
Кольца Ньютона ............................. 11
Принцип создании интерференционной картины в интерферометре .......................................... 12
Дисперсия света. Основы теории спектральных приборов 14
Принципиальная оптическая схема спектральных при-
о
Светосила спектрального прибора ...................... 15
Линейная дисперсия призменных спектральных приборов —
Теоретическая разрешающая способность спектральных приборов.............................................. 17
Фраунгоферова дифракция от круглого отверстия .... 18
Увеличение прибора, имеющего спектральные призмы 19
Кривизна спектральных линий .......................... 20
Реальная разрешающая способность спектрального прибора ................................................. 21
Дифракционные решетки ................................. —
Угловая и линейная дисперсии решетки ................. 22
Разрешающая способность прибора с дифракционной решеткой............................................ 23
Излучение и поглощение света............................ —
Монохроматическое и сложное излучение.................. —
Законы теплового излучения АЧТ........................ 25
Излучение тел, не являющихся абсолютно черными 30
Соотношение между энергетическими и светотехническими
величинами ........................................... 31
Расчет световых свойств потока на основе кривой распределения энергии по спектру.......................... 33
Светотехнические величины ............................. 34
Излучение равнояркостных поверхностей................. 38
Реакция приемников лучистой энергии на падающий поток излучения ...................................... 39
Отражение света ...................................... 41
Поляризация света при отражении ...................... 42
Виды поляризации света ............................... 43
Потери света в оптических приборах.................... 44
Просветление стекол ................................... —
Расчет светопропускания и светопоглощен и я бесцветного стекла ............................................... 45
Потери света при отражении и поглощении в светофильтрах ................................................. 46
Расчет интегрального коэффициента пропускания свето-
фильтра для видимой области спектра при сложном .
излучении ............................................. —
Светофильтры переменной плотности (фотометрические клииья) .............................................. 47
Расчет коэффициента светопропускания оптических приборов ................................................ 48
Формулы для вычисления оптической плотности некоторых отдельных элементов оптической системы.......... 51
Распространение света в анизотропной среде (кристаллы) 54
Двойное лучепреломление в одноосных кристаллах . . —
Положительные и отрицательные кристаллы. Волновые поверхности Френеля .................................. 55
Поляризаторы....................................... —
Поляризационные призмы............................ 56
Примеры расчета симметричного поля поляризации призм ................................................ 59
Оптические компенсаторы .............................. 60
Расчет интерференционной окраски кварцевой пластинки при параллельных николях ............................. 61
Глава 2. Геометрическая оптика (В. А. Панов) .............. 63
Основные понятия геометрической оптики.................. —
Строение пучка лучей .................................. —
Основные законы геометрической оптики ................. —
Параксиальная оптика .................................. 65
Правила знаков ........................................ —
Главные точки, главные плоскости, фокусы и фокусные расстояния ........................................... 66
Формулы, определяющие положение сопряженных точек.
Линейное увеличение в сопряженных плоскостях ... 67
Угловое н продольное увеличения ...................... 68
Узловые точки ..................................... 69
Построение изображения ............................ —
Построение изображения с помощью узловых точек 70
Преломление луча через сферическую поверхность . . . —
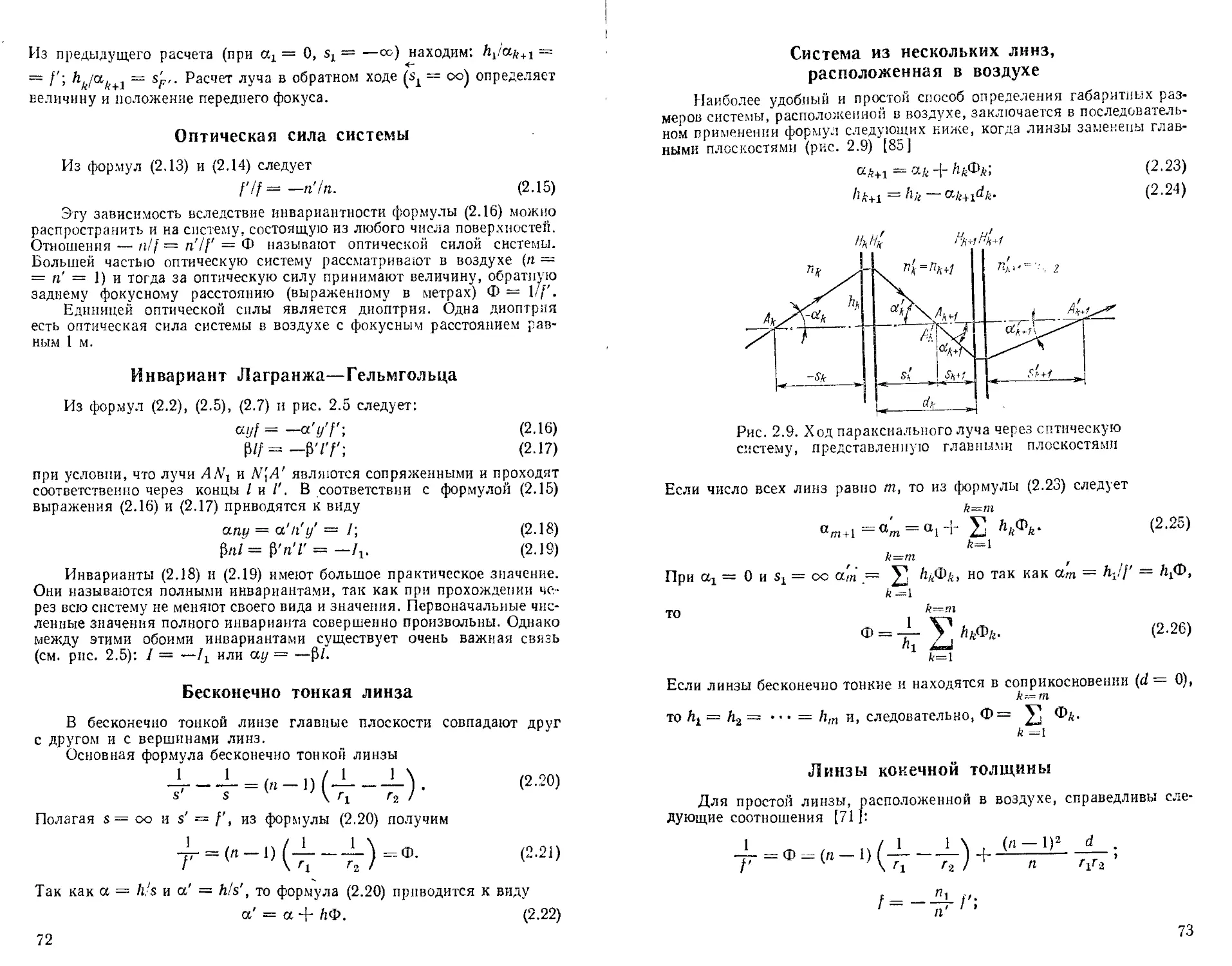
Преломление через несколько сферических поверхностей 71
Оптическая сила системы ........................... 72
Бесконечно тонкая линза .............................. —
Система из нескольких линз, расположенная в воздухе 73
Линзы конечной толщины................................ —
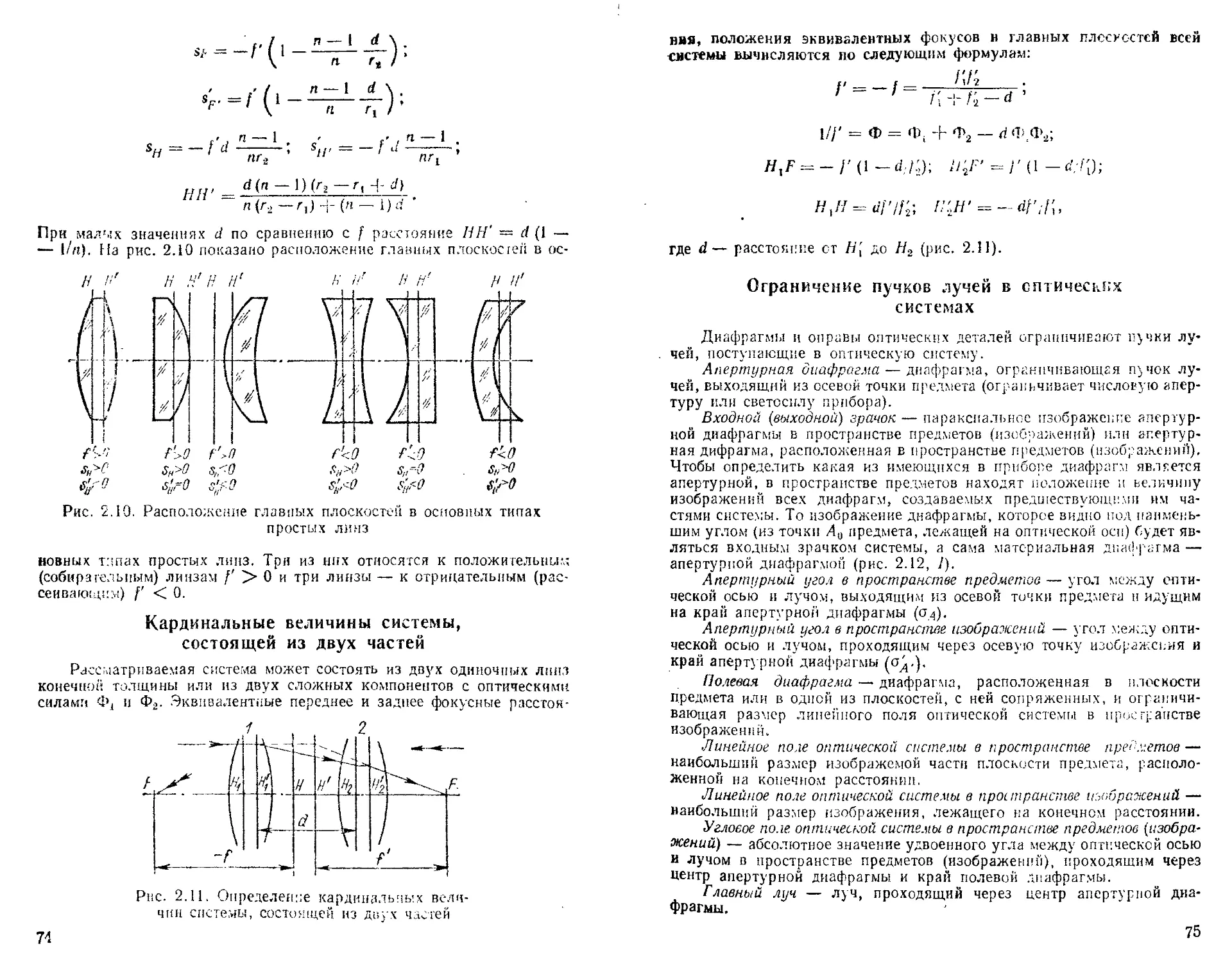
Кардинальные величины системы, состоящей из двух частей .............................................. 74
ч/ Ограничение пучков лучей в оптических системах .... 75
Геометрическое виньетирование ...................... 76
Положение зрачков и окон в основных типах оптических систем ............................................. 77
Соотношения между линейным полем и светосилой системы (инварианты Лагранжа—Гельмгольца) .... 78
Видимое увеличение оптических приборов........ 79
Видимое увеличение лупы ............................ 80
Видимое увеличение лупы, работающей с аккомодирующим или аметропическим глазом................. —
Телескопические или афокальные системы........ 81
Сложный микроскоп .................................. 82
Передача перспективы оптическими приборами .... 85
Естественное впечатление .............. 86
Общие формулы для светосилы оптического прибора —
Светосила оптического прибора при малой передней апертуре (объективы зрительной трубы, фотографические объективы для ландшафтных съемок и т. д.)........... 87
Светосила оптического прибора при малой задней апертуре (проекционные приборы, осветительные системы, прожекторы и др.) ................................... —
Разрешающая способность оптических приборов........ 88
Согласование разрешающей способности прибора с разрешающей способностью глаза ......................... —
Дифракционная разрешающая способность прибора . . —
Глубина изображаемого пространства .............. . 90
Глубина резкости телескопической системы...... 92
Глубина резкости лумы и микроскопа .................. —
Глубина резкости при аккомодации глаза......... —
Аберрации центрированных систем ...................... 93
Аберрации третьего порядка. Коэффициенты Зейделя —
Коэффициенты аберраций третьего порядка бесконечно тонких компонентов ................................. 94
Сферическая аберрация......................... 96
Кома....................................... 97
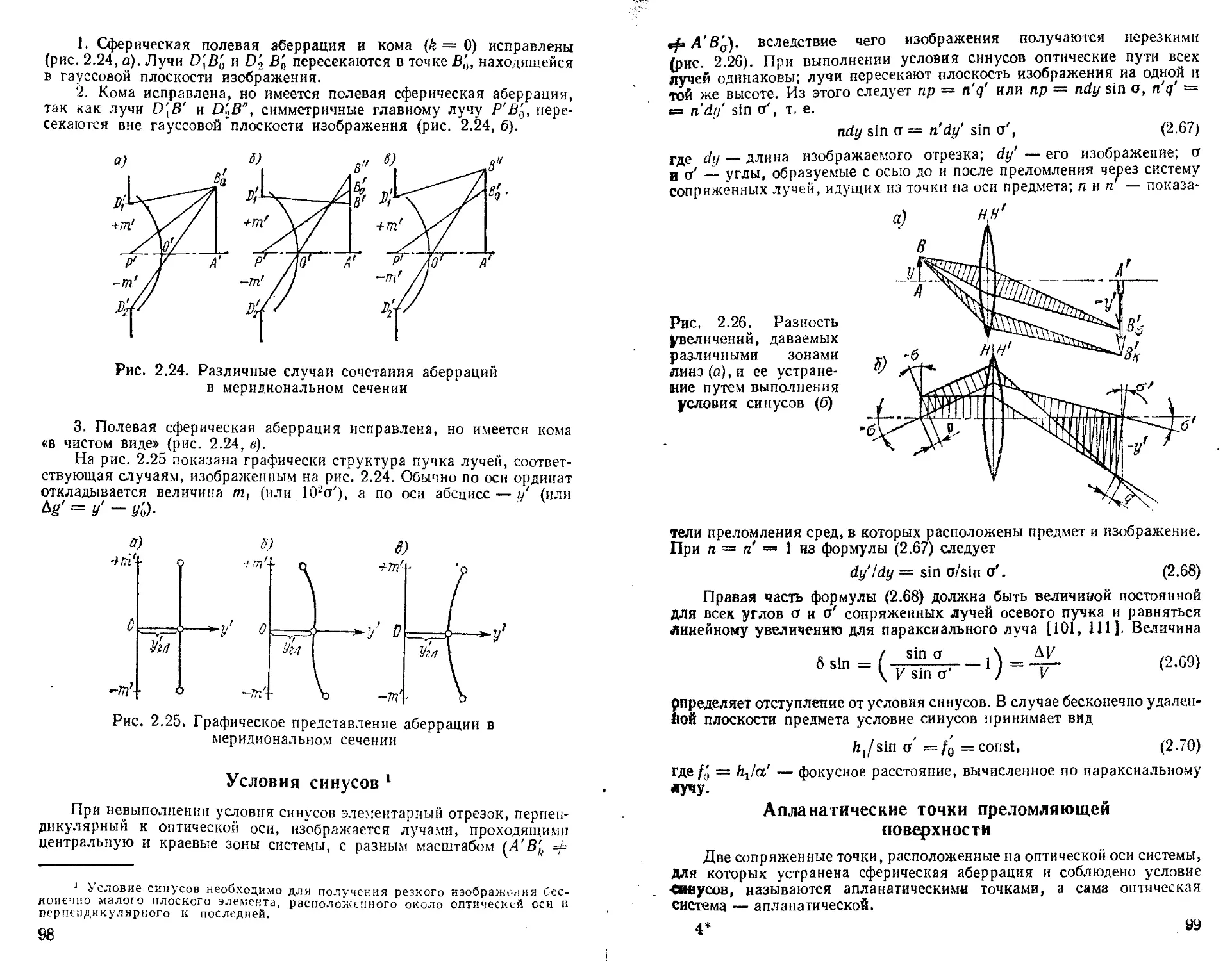
Условие синусов ................................... 98
Апланатические точки преломляющей поверхности ... 99
Формы апланатических менисков ....................... 100
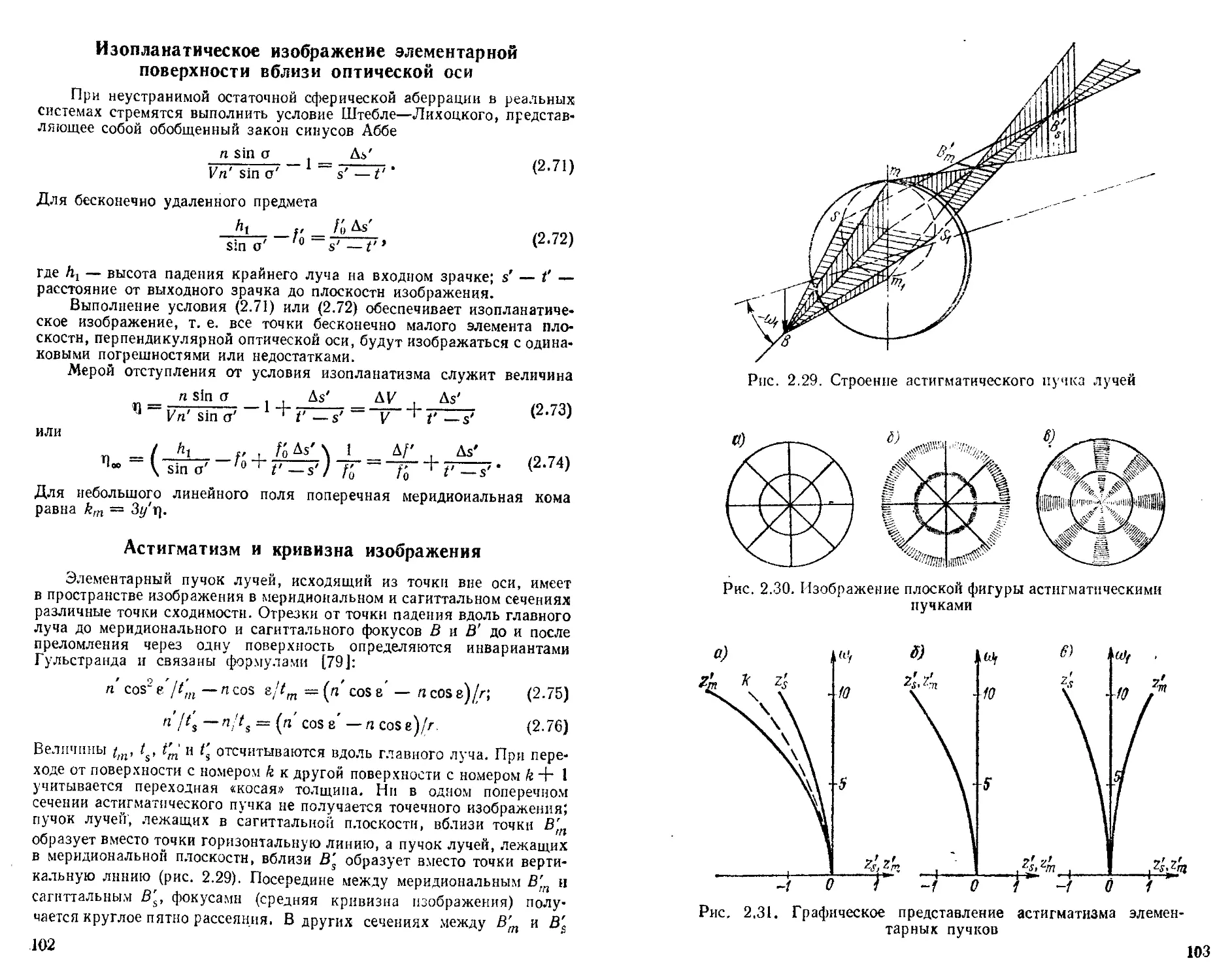
Изопланатнческое изображение элементарной поверхности вблизи оптической оси 102
Астигматизм и кривизна изображения............. —
Дисторсия ........................................... 101
Хроматические аберрации ........................... 105
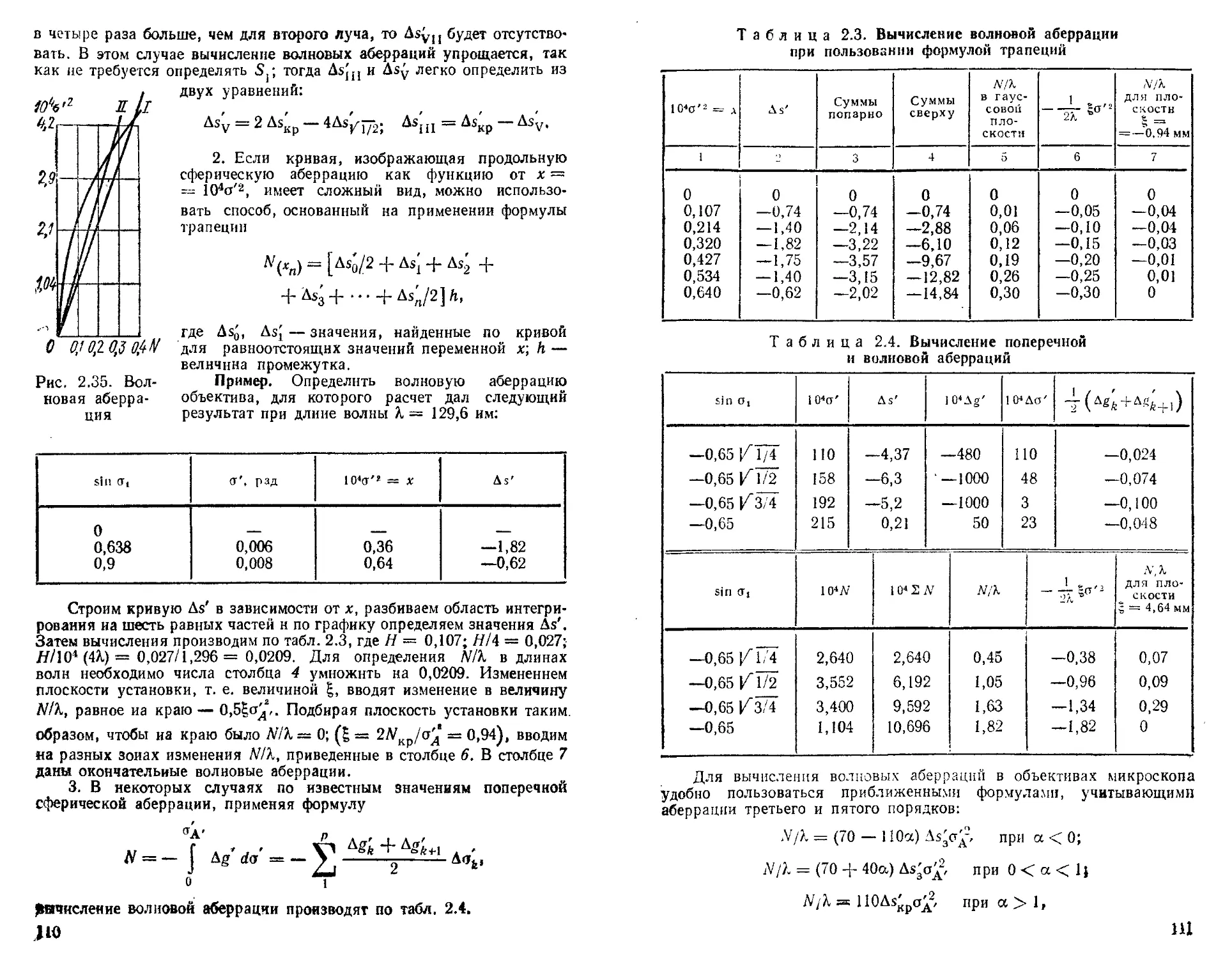
Зависимость между волновой и продольной аберрациями 108
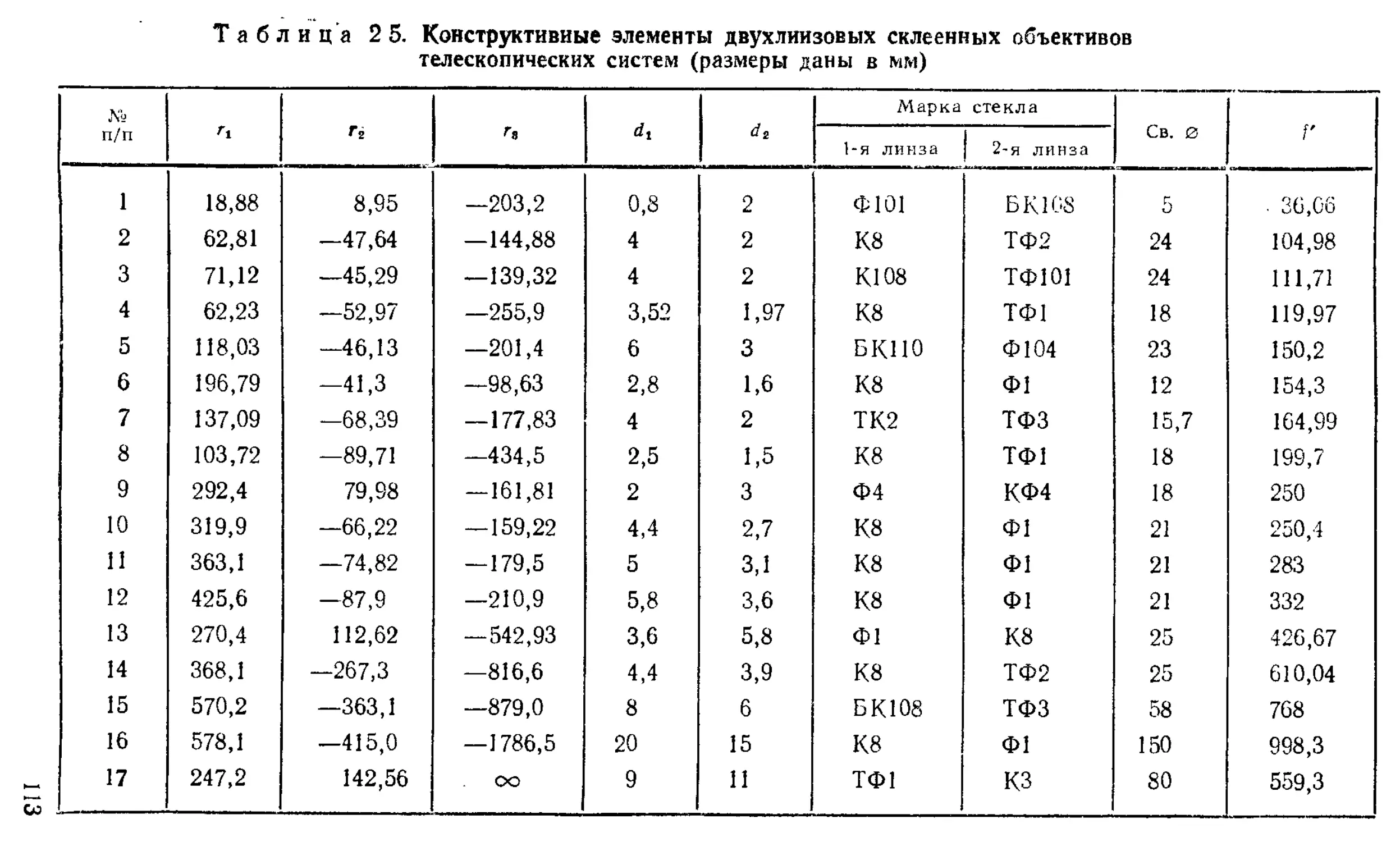
Объективы из двух склеенных лннз .................... 112
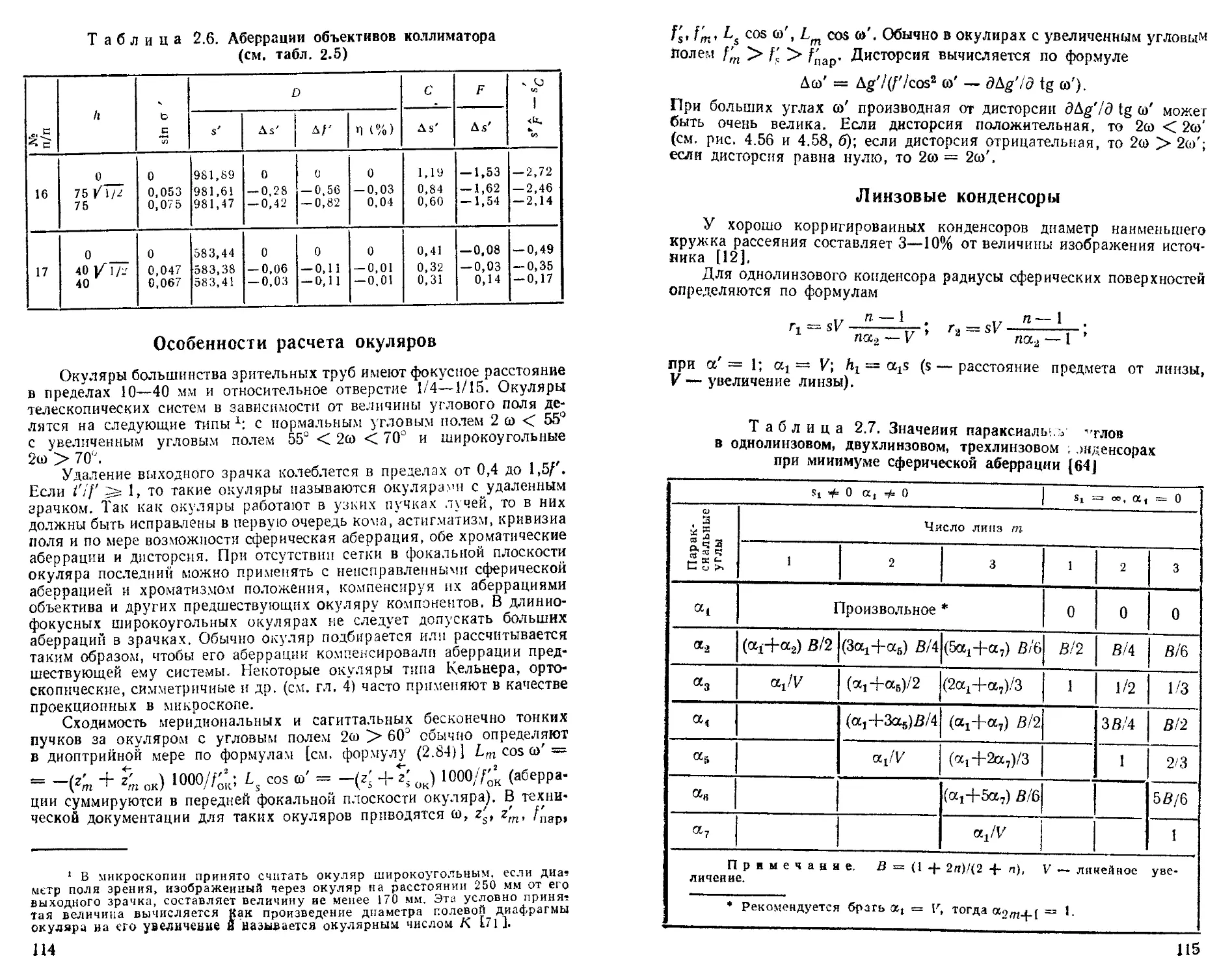
Особенности расчета окуляров ........................ 114
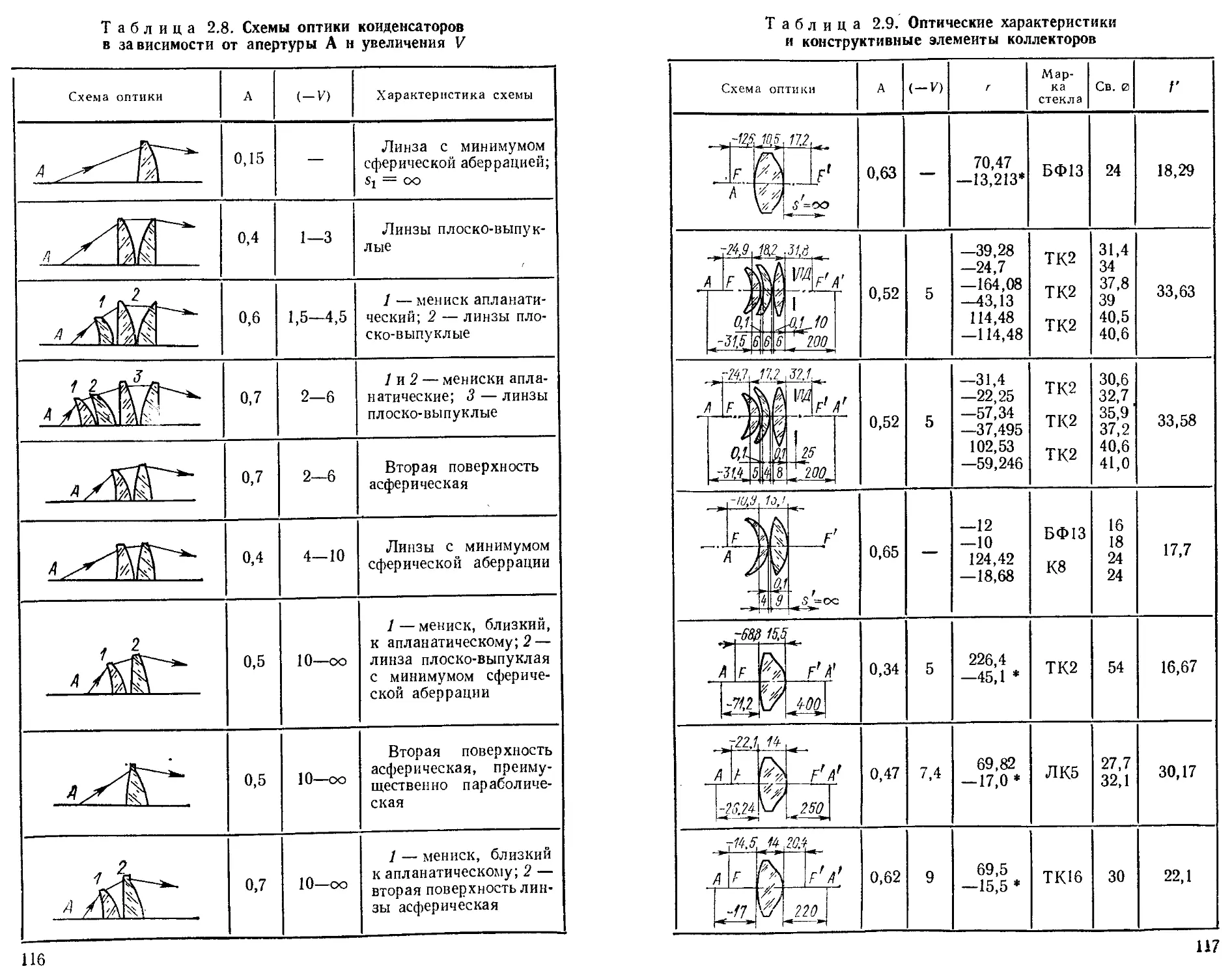
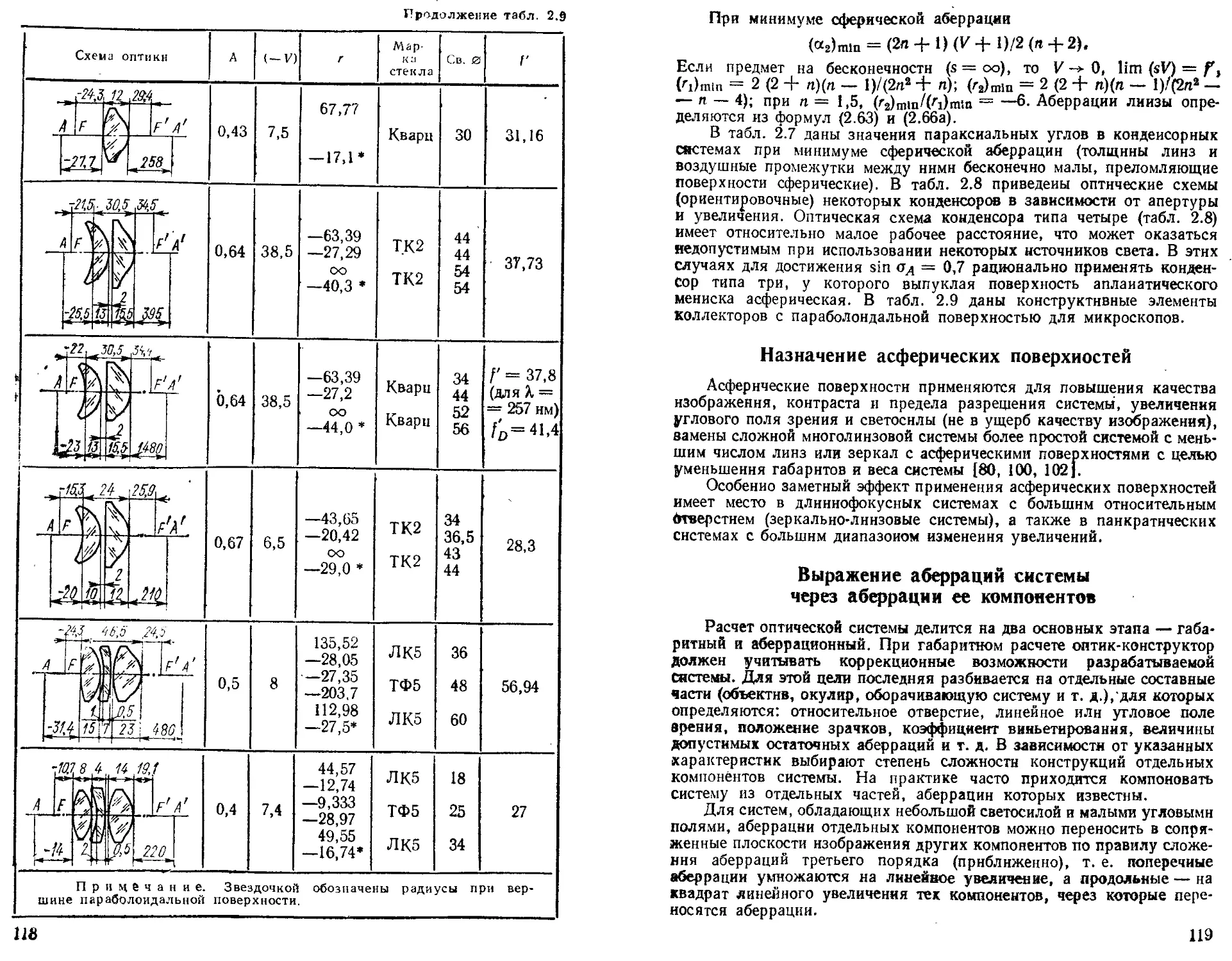
Линзовые конденсоры........................... 115
Назначение асферических поверхностей........... . 119
Выражение аберраций системы через аберрации ее компонентов ............................................ —
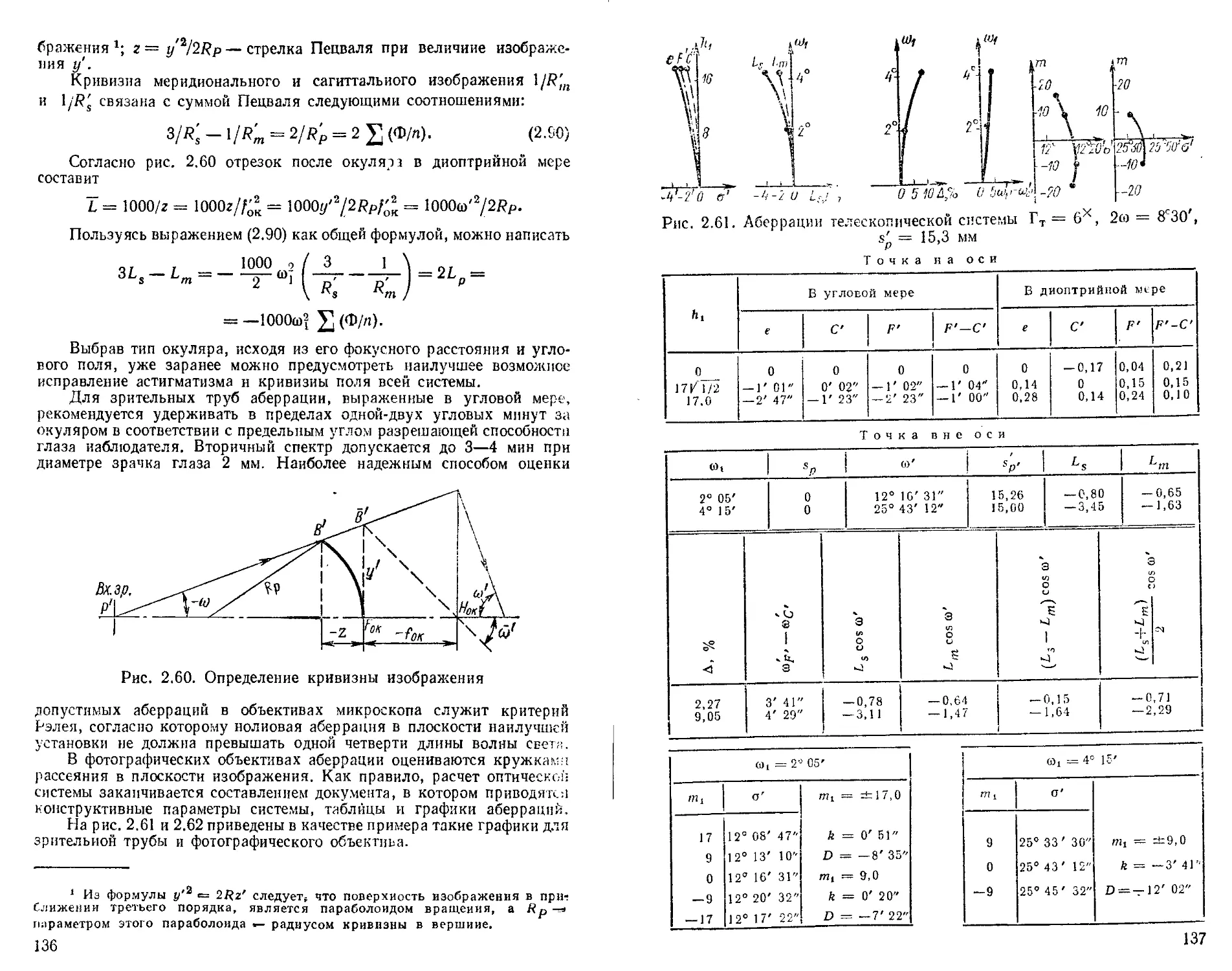
Формулы для вычислений аберраций системы после окуляра .......................................... 120
Анализ кривой широкого наклонного пучка в меридиональном сечении ................................... 123
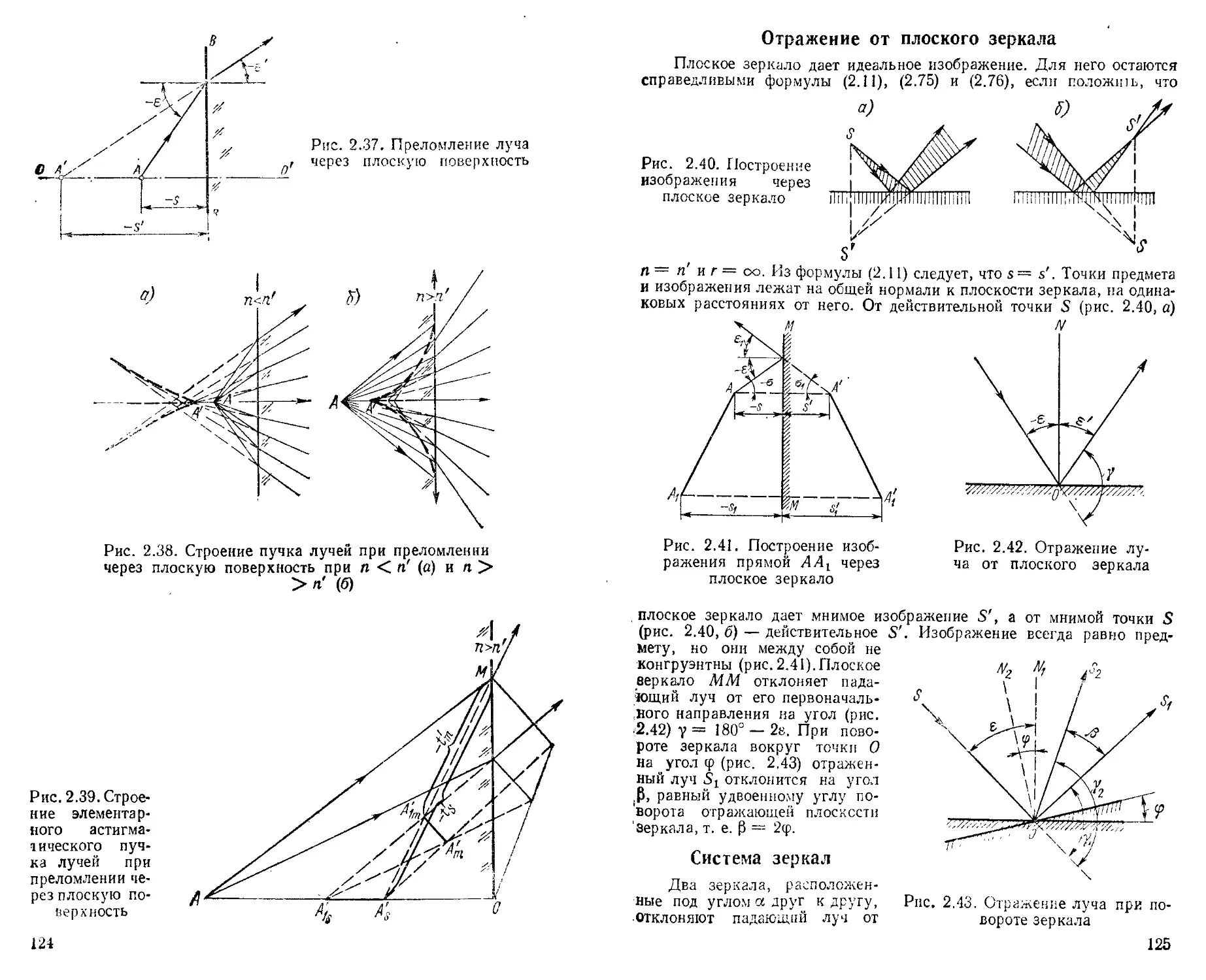
Отражение и преломление на плоских поверхностях оптических деталей ..... ............................... —
Преломление луча через плоскость .................... 123
Отражение от плоского зеркала ....................’ 125
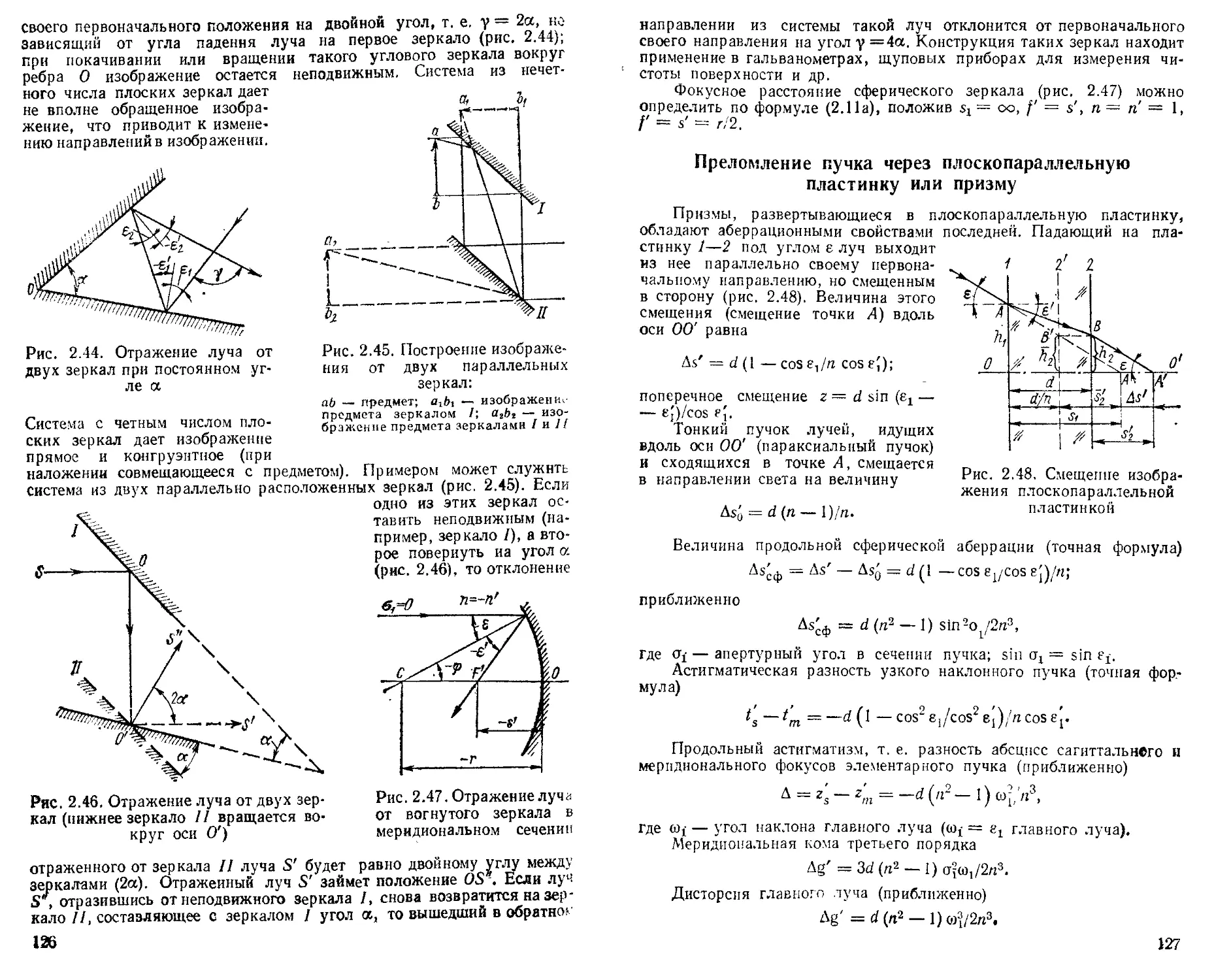
Система зеркал....................................i —
Преломление пучка через плоскопараллельную пластинку или призму.................................... 127
Графическое построение хода луча через плоскопараллельную пластинку (или любую ей эквивалентную призму) методом редуцирования ....................... 128
Преломление лучей через призму в ее главном сечении — Преломление луча, проходящего через призму вне плоскости главного сечения (внемериднональный луч) . , . 129
Дисперсия призм ................................ . 130
Ахроматические клинья ............................... 133
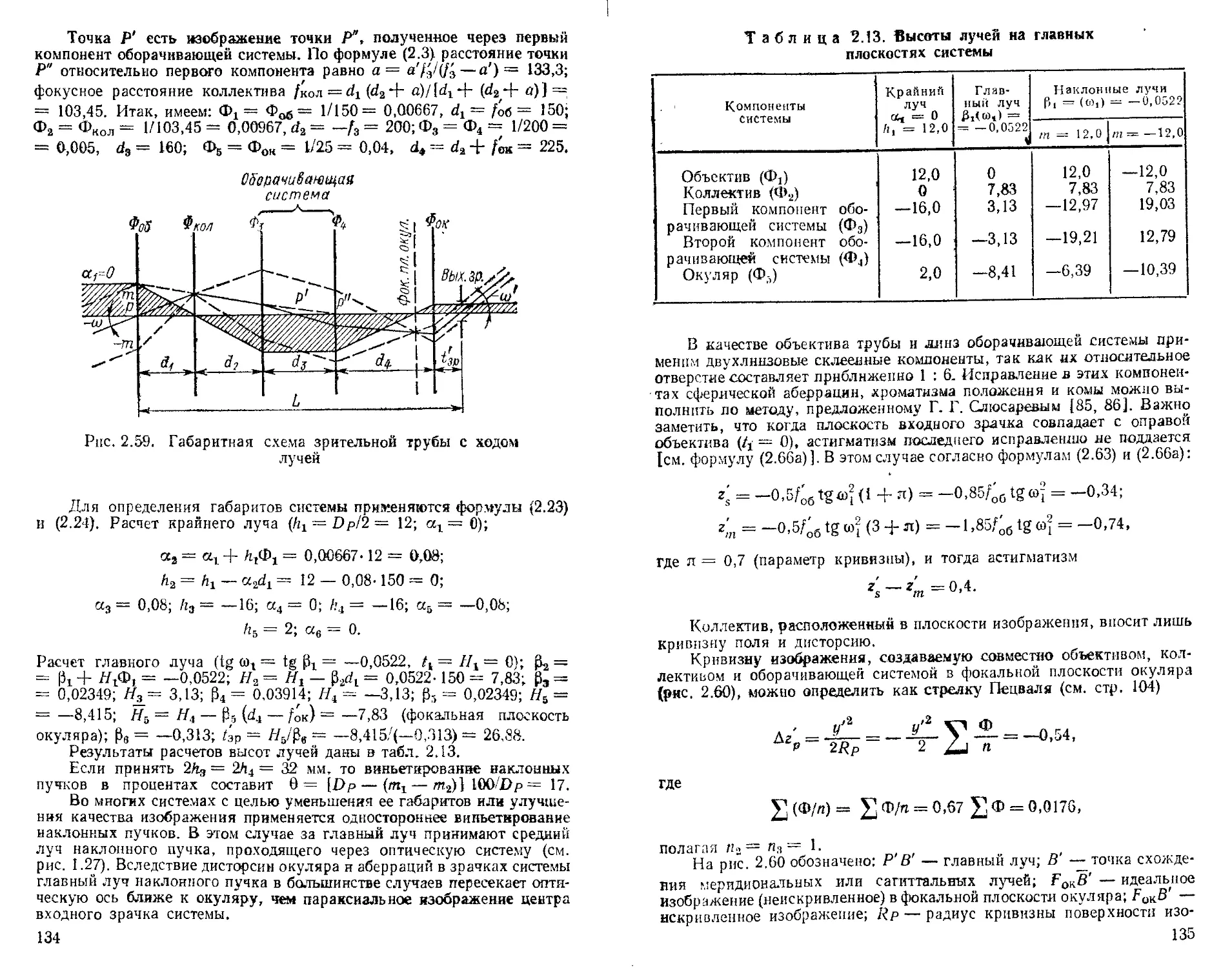
Габаритный расчет зрительной трубы . * , .............. —
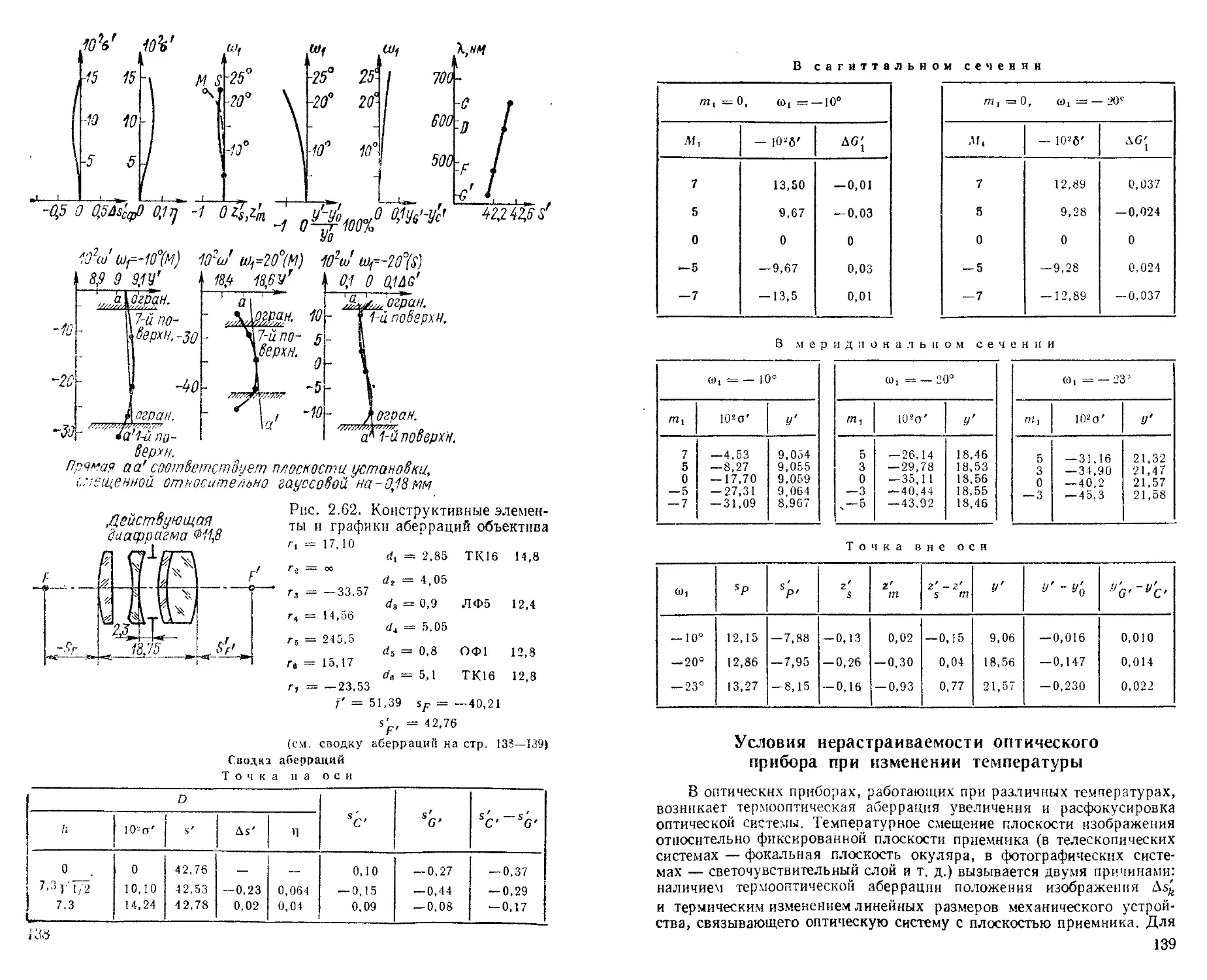
Условия нерастраиваемости оптического прибора при изменении температуры ............................... 139
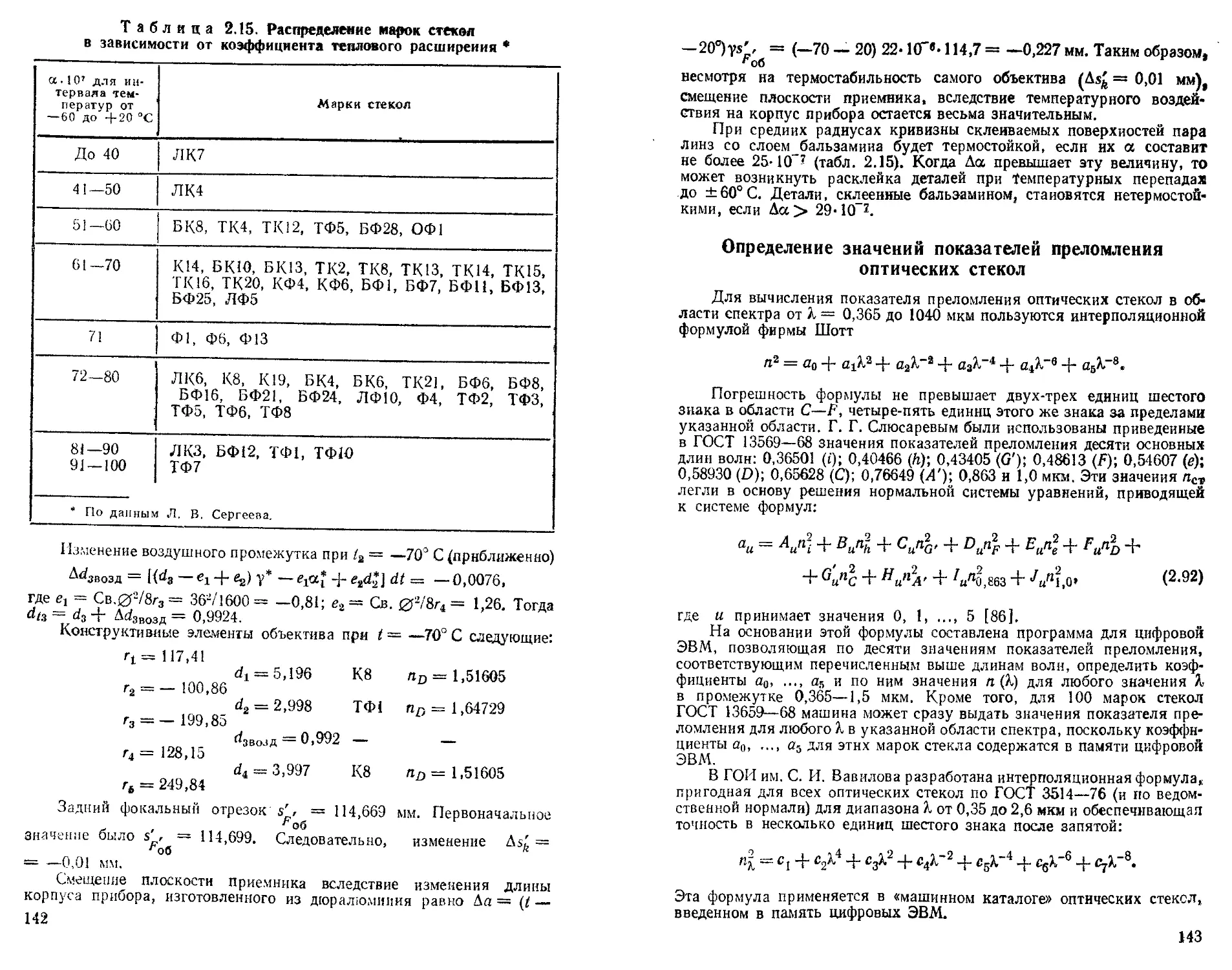
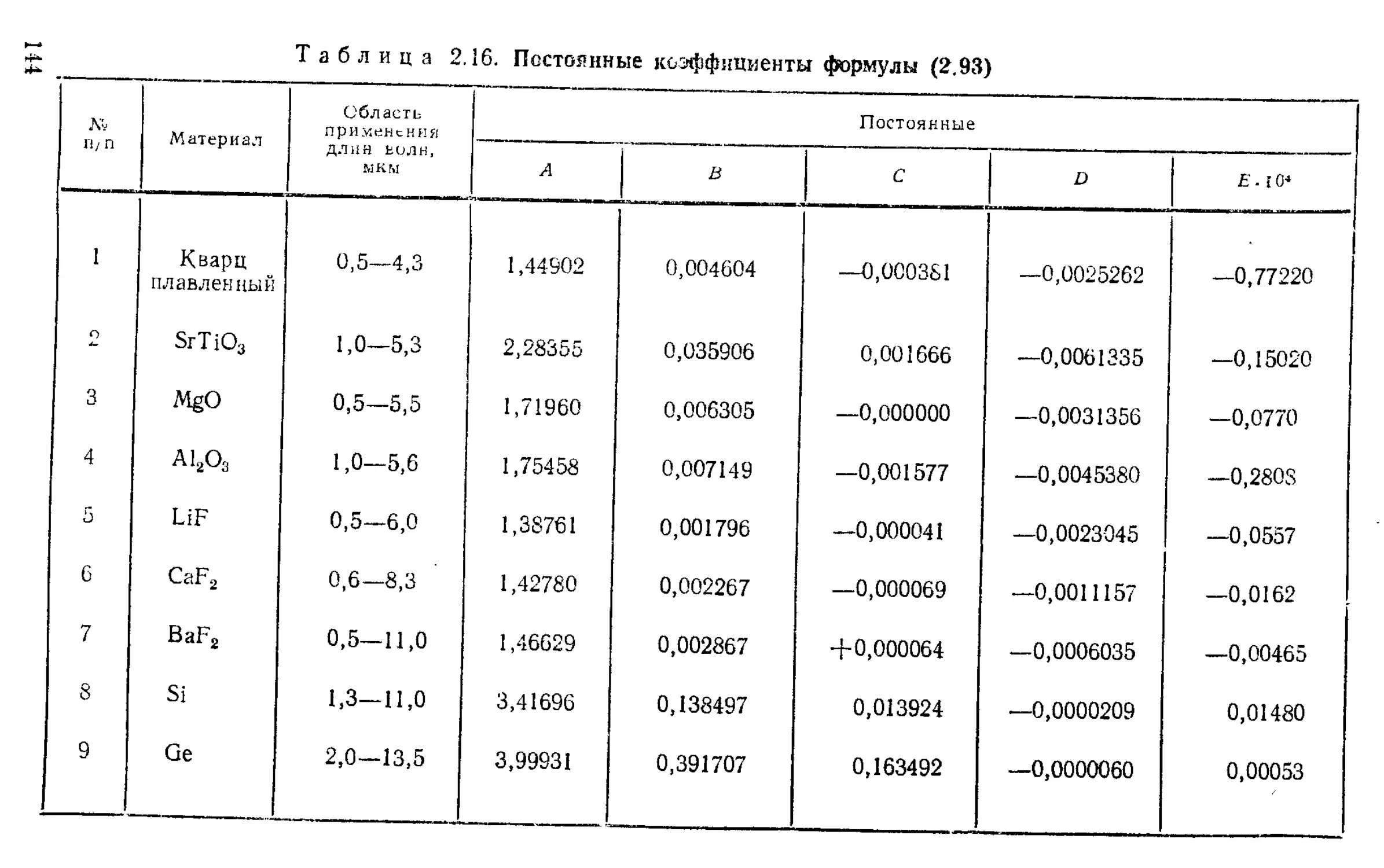
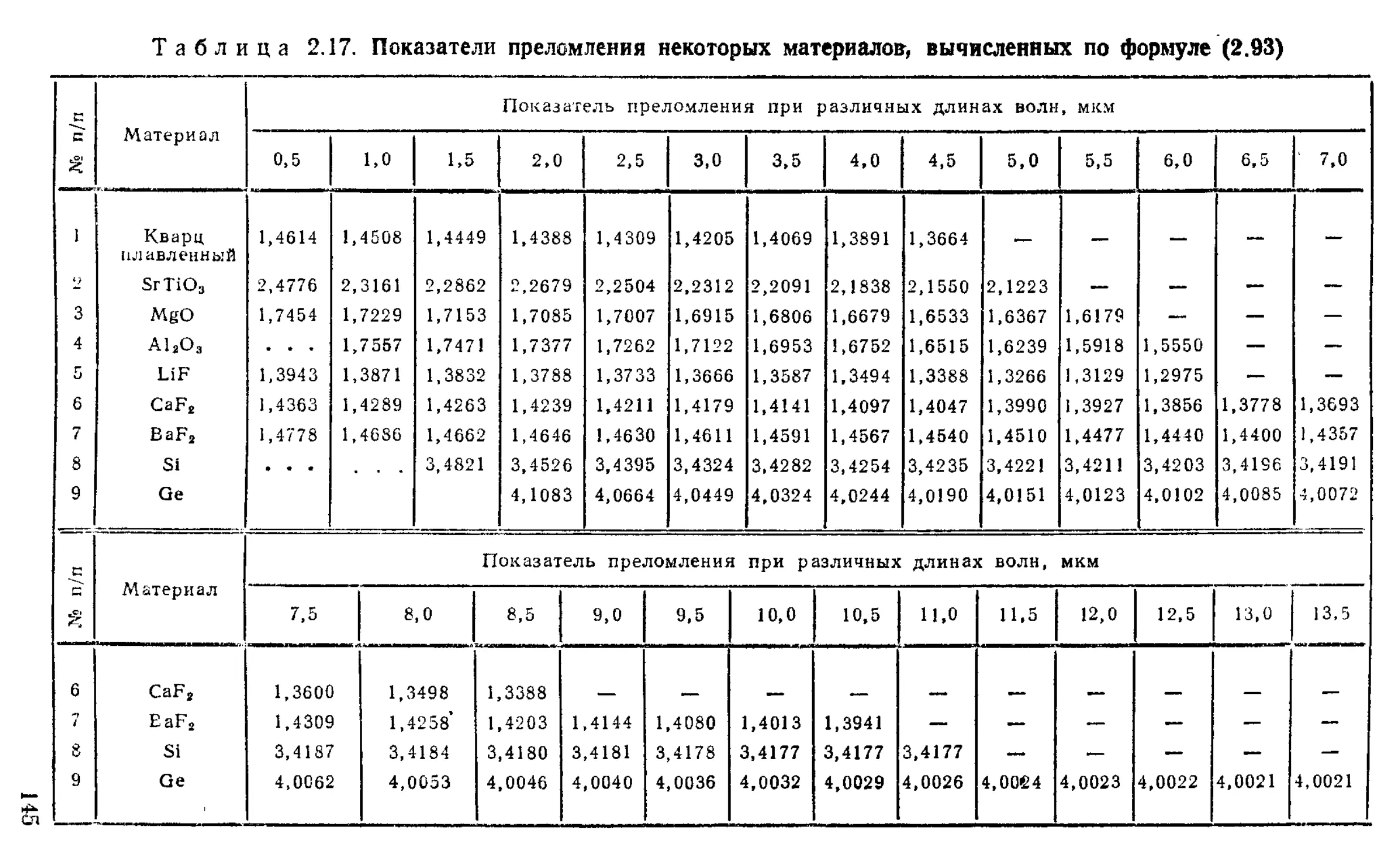
Определение значений показателей преломления оптических стекол ................................... . 143
Интерполяционные формулы М. Герцбергера для вычисления показателя преломления в инфракрасной области спектра .................................. 146
Глава 3. Глаз как оптический инструмент (Л4. Я- Кругер) 147
Строение и свойства глаза ............................. —
Аккомодация глаза .............................L , 148
Недостатки зрения .............................У'» —
Влияние на остроту зрения условий освещенности .149 Световые пороги ....................................... —
Контрастная чувствительность.................. 150
Разрешающая способность ............................... —
Бинокулярное зрение........................... 151
Цветоощущение................................. 152
Воздействие невидимых излучений................. —
Глава 4. Оптические детали и узлы (Л4. >7. Кругер, В. А. Панов) .......................................♦ . 154
Общие сведения ......................................... —
Условные обозначения, применяемые на чертежах и схемах — Требования к оформлению чертежей оптических деталей, узлов и схем.......................................... 155
Общие требования ...................................... —
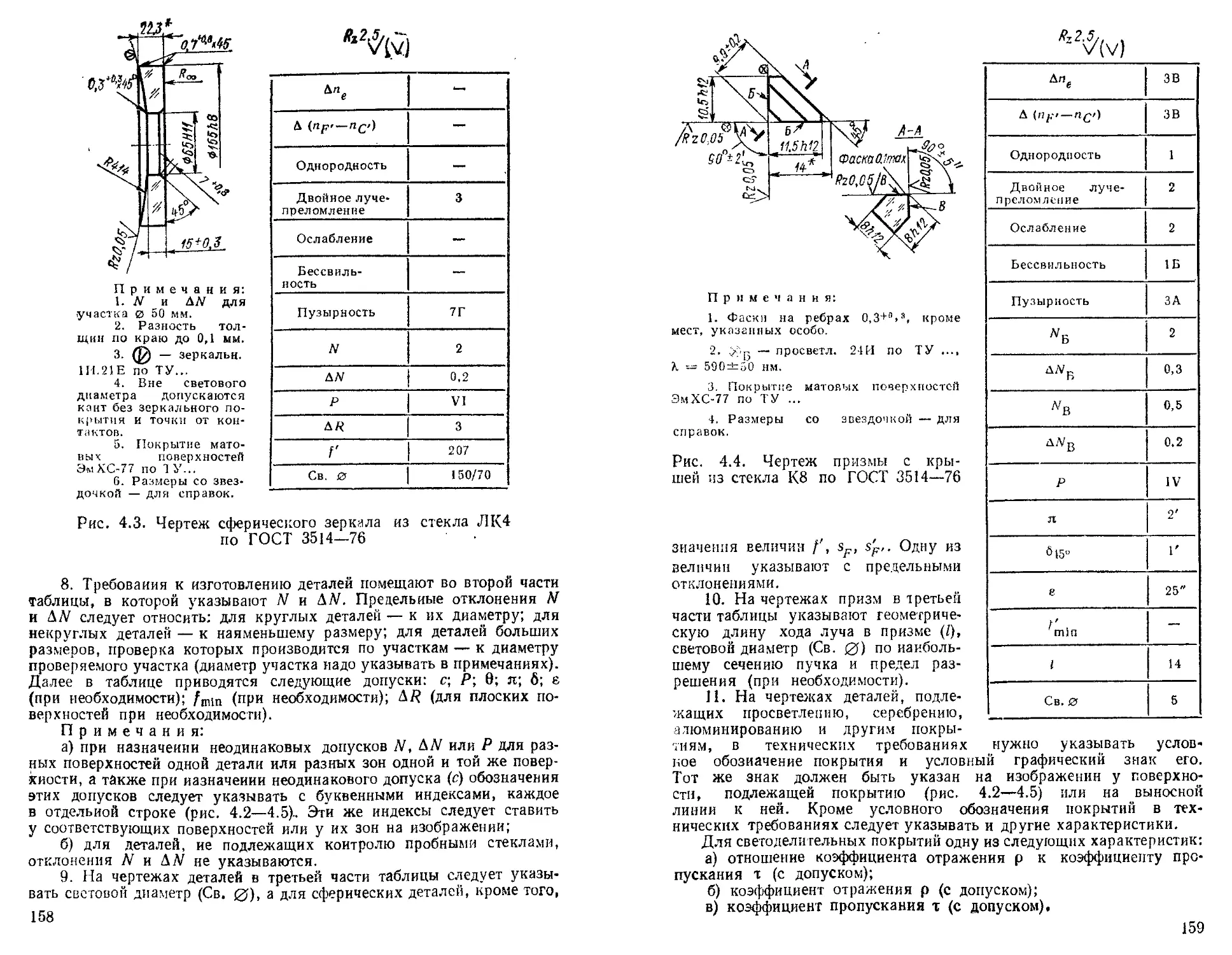
Оформление рабочих чертежей деталей................. 156
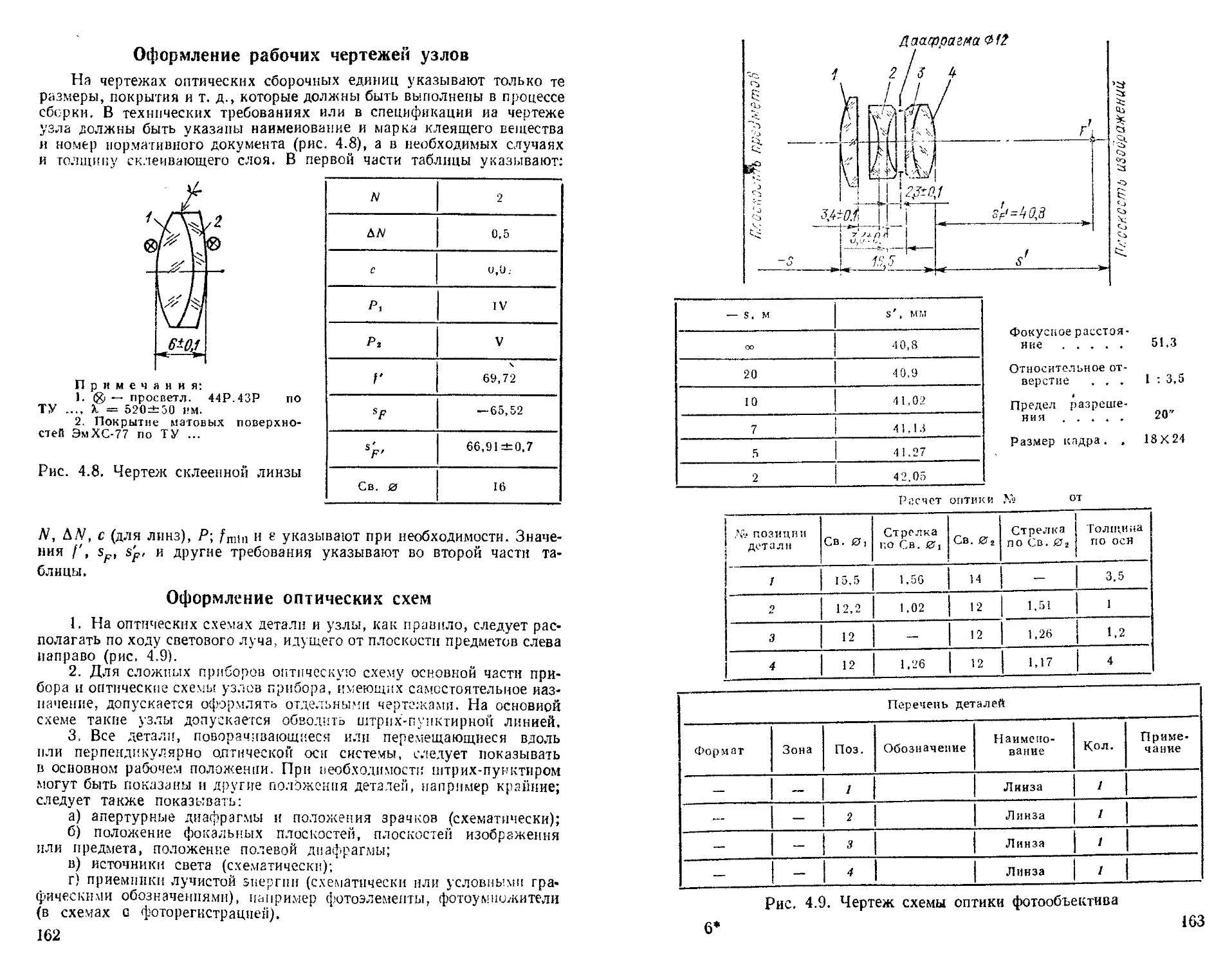
Оформление рабочих чертежей узлов................... 162
Оформление оптических схем......................... —
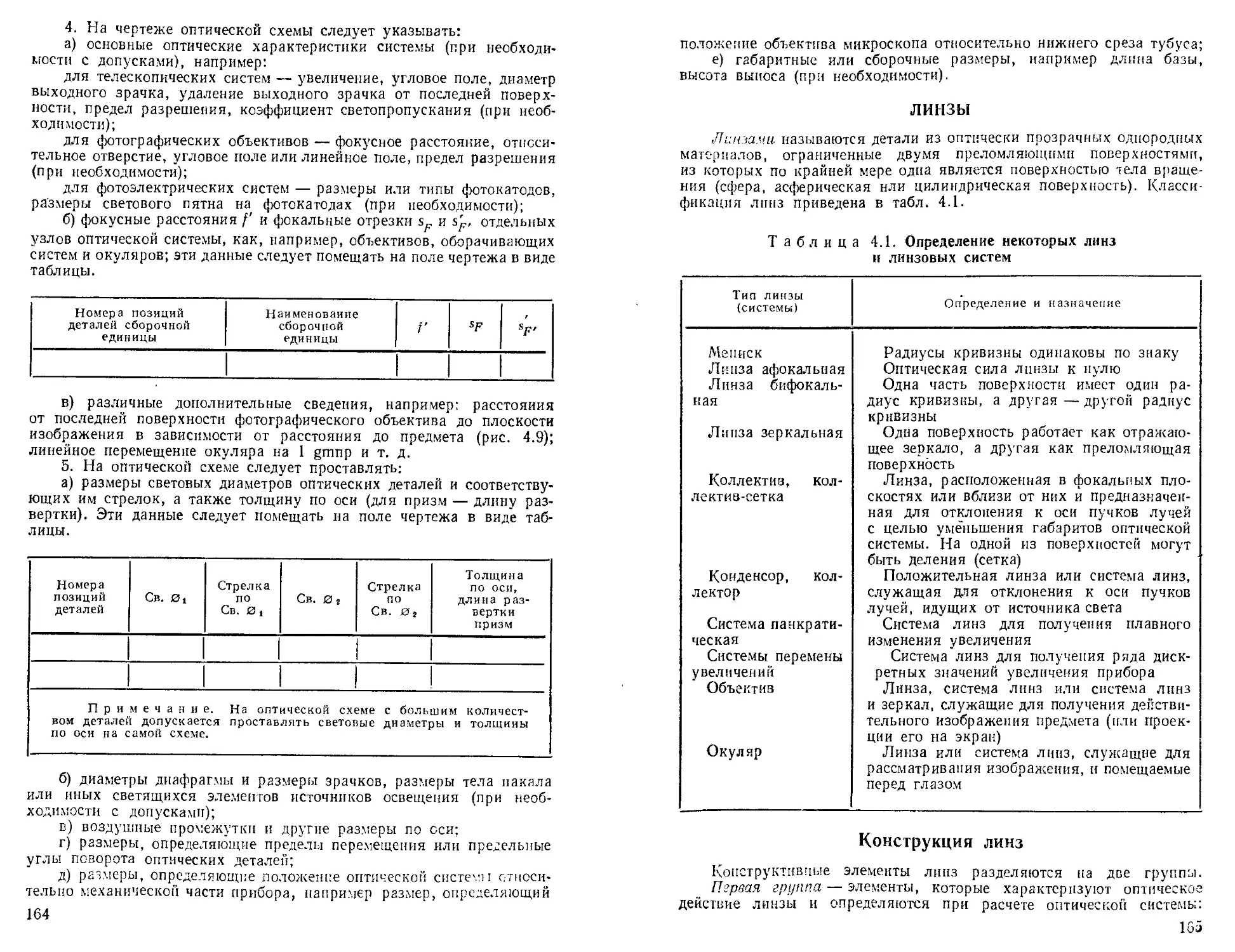
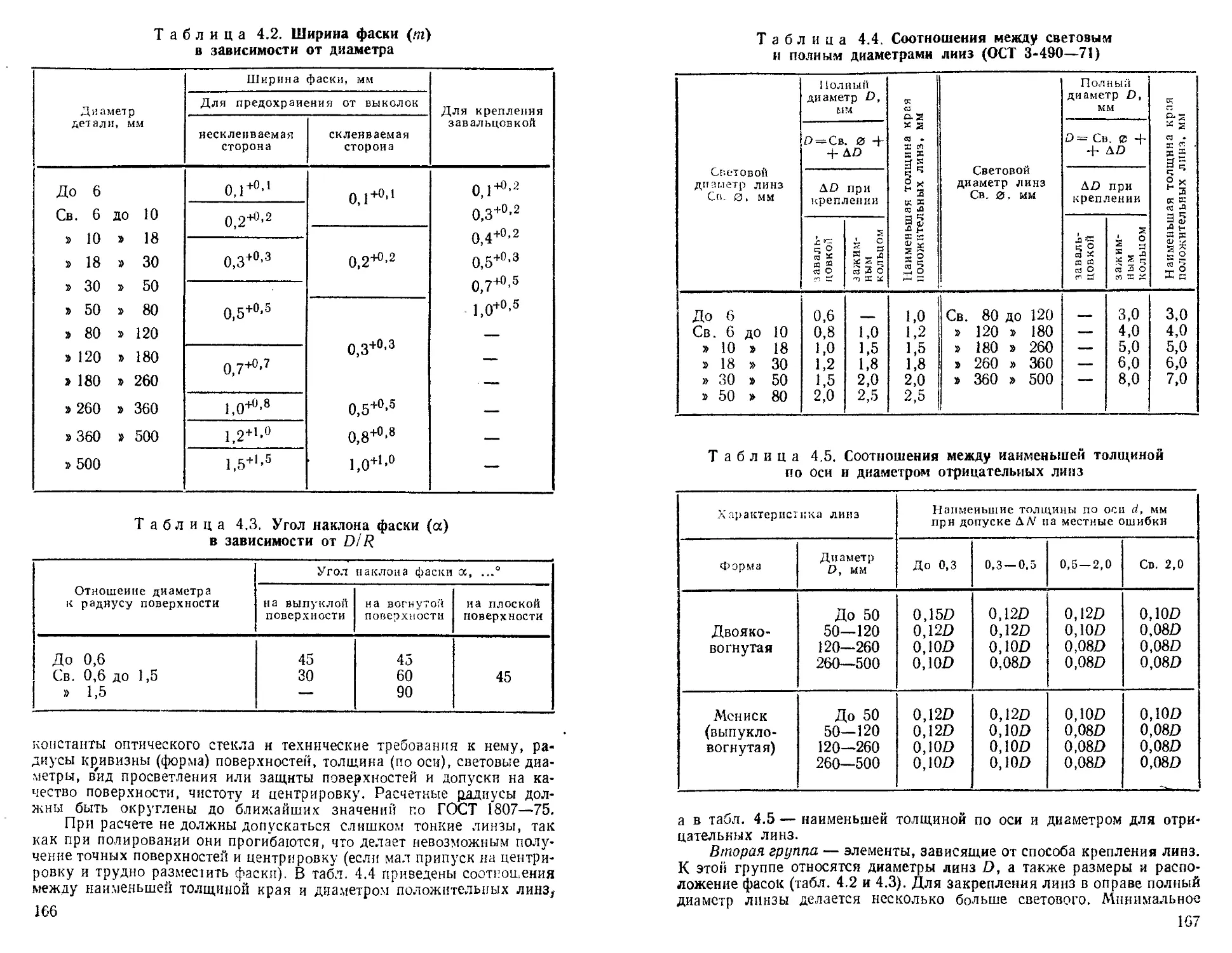
Линзы ................................................ 165
Конструкция линз ...................................... —
Фаски на оптических деталях круглой формы (линзы, сетки, светофильтры и Др.) .......................... 168
Зеркала ................................................ —
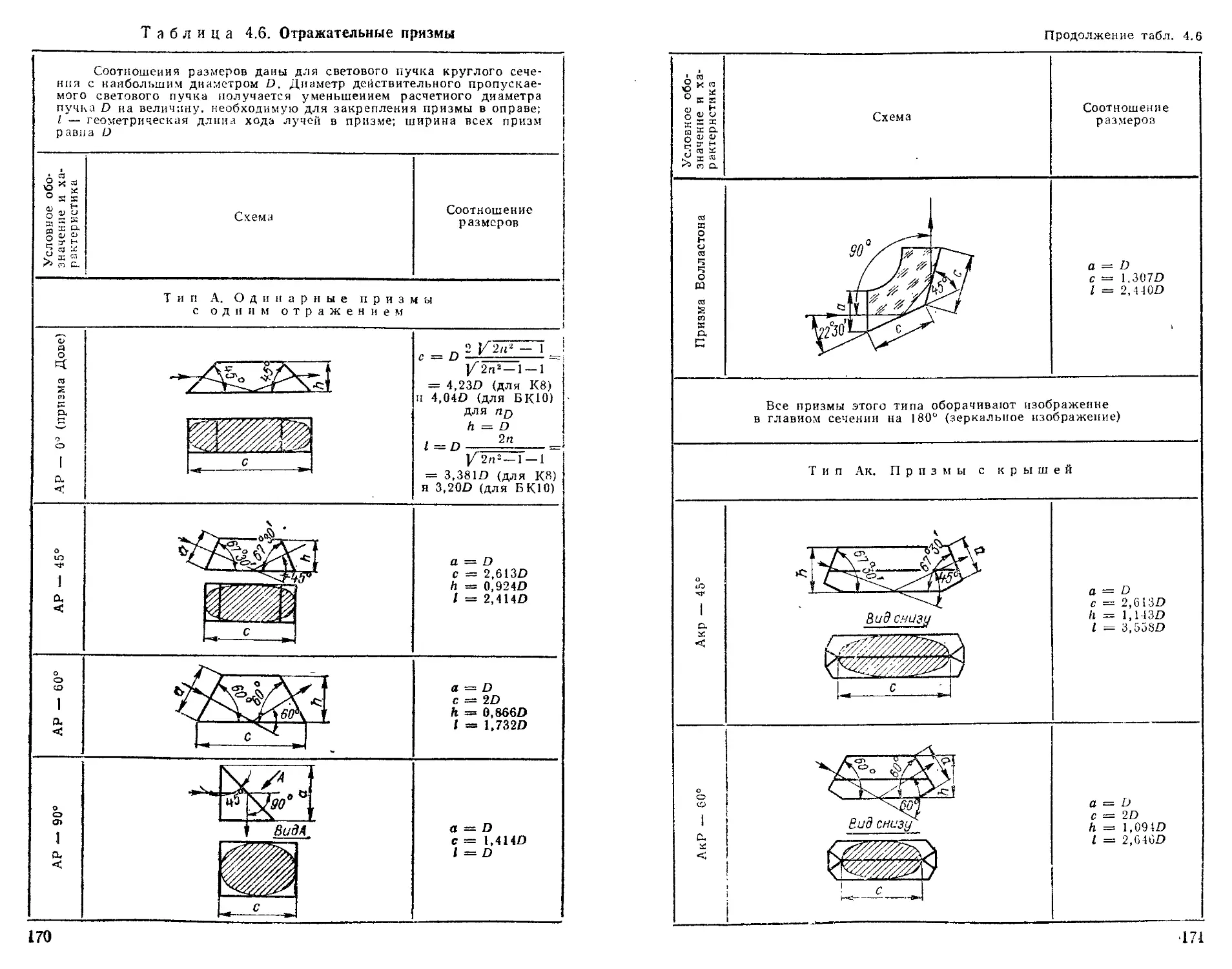
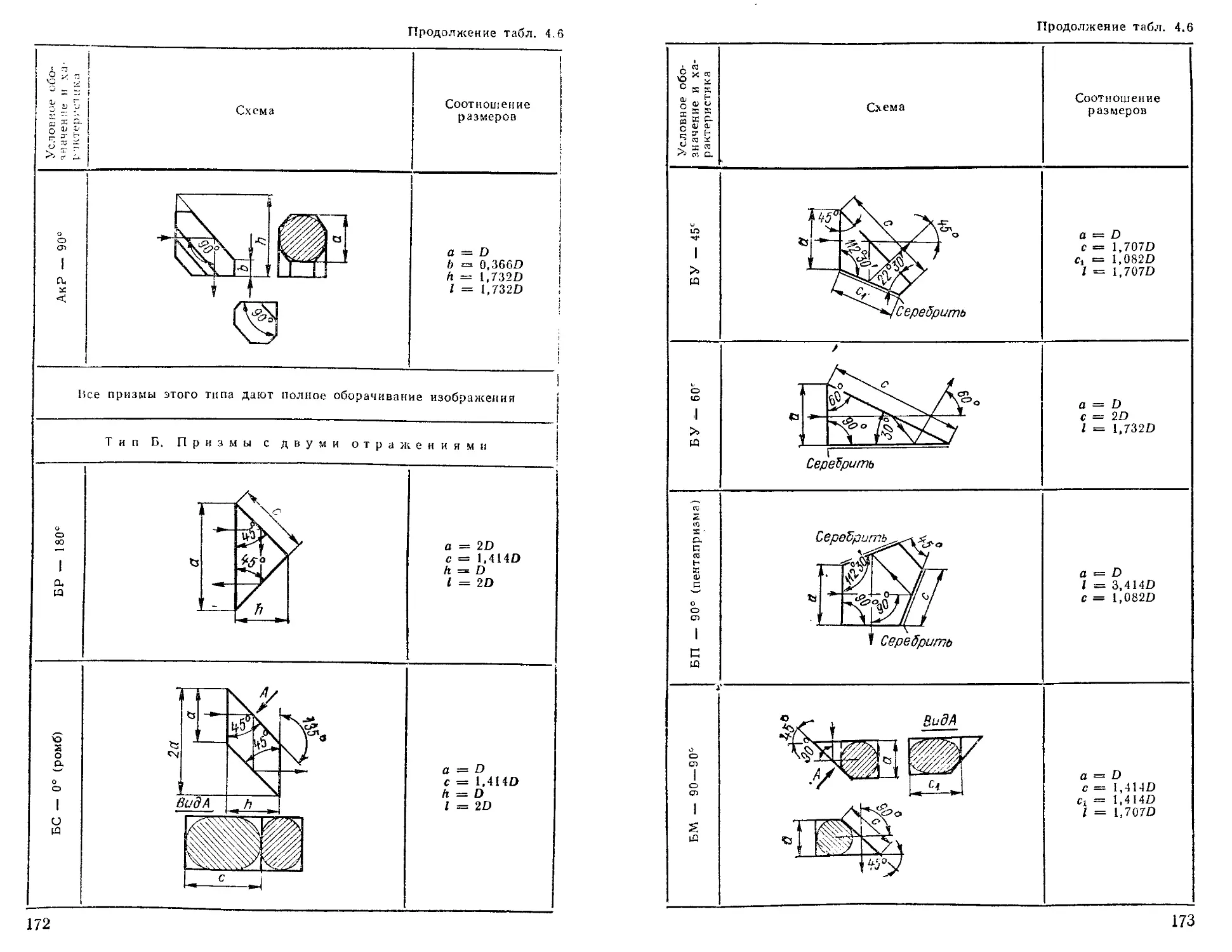
Призмы................................................ 169
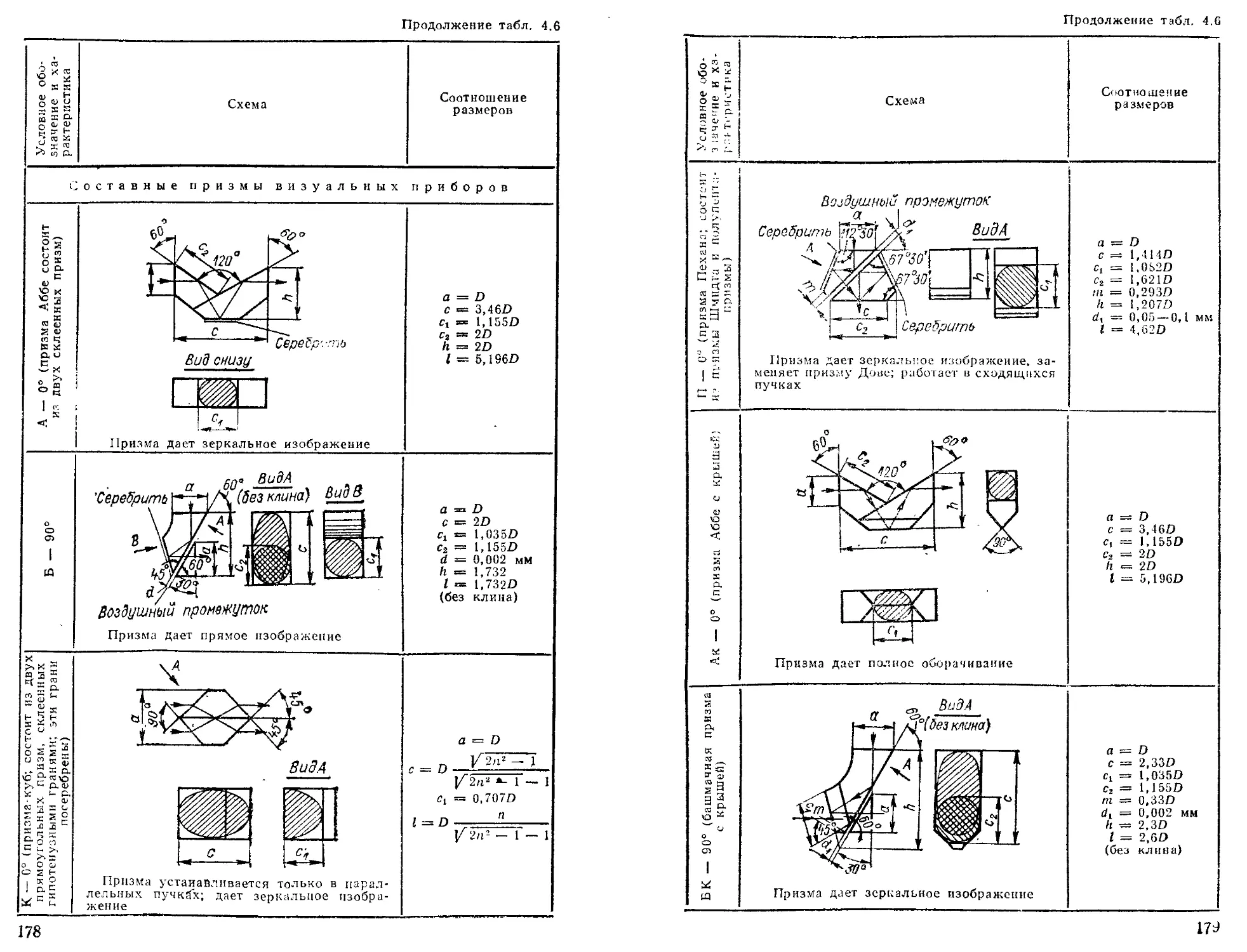
Составные призмы .................................... 181
Расчет размеров призм ................................. —
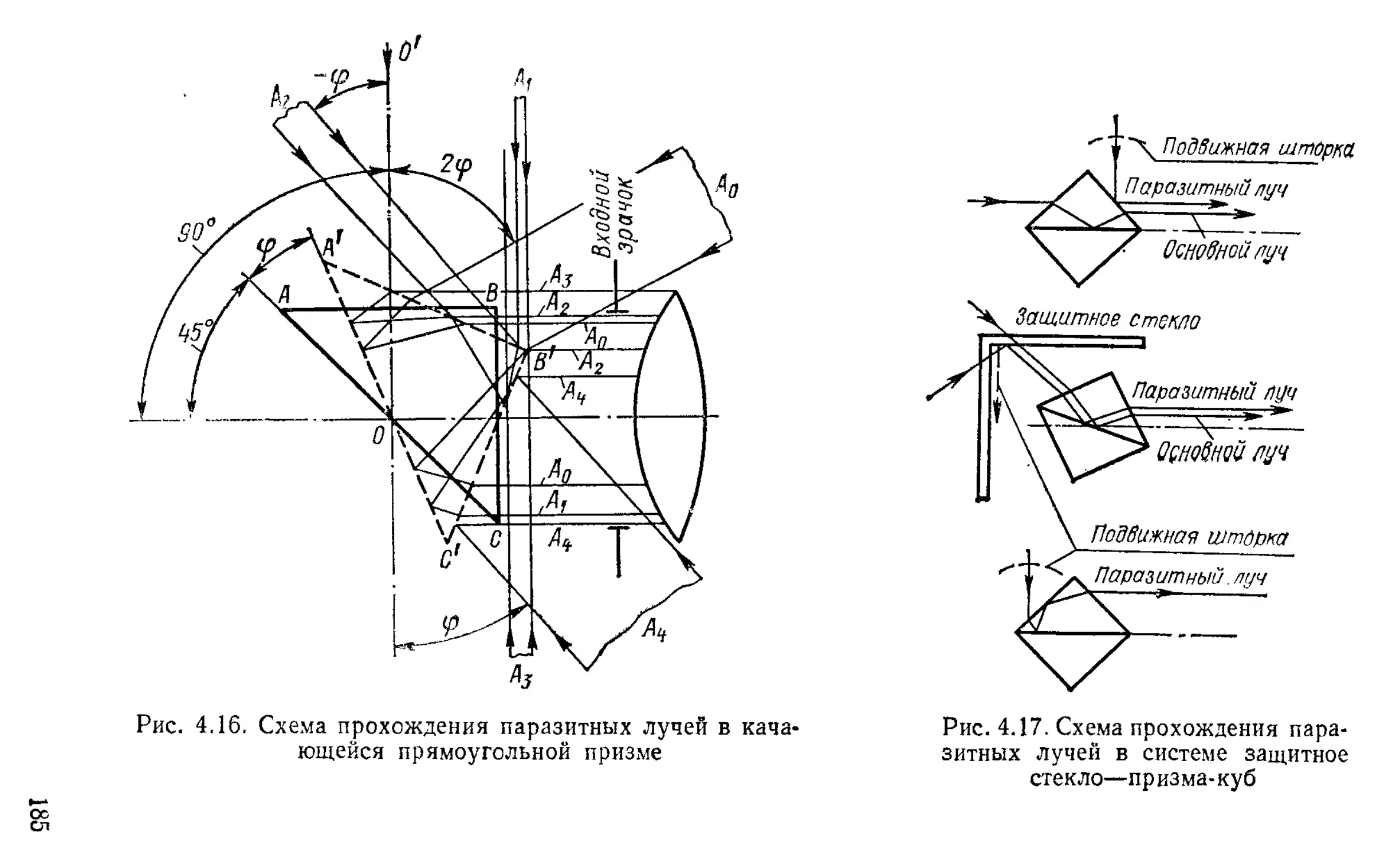
Призмы с одной отражающей гранью (тип А)............. 183
Паразитные отражения в призмах....................... 184
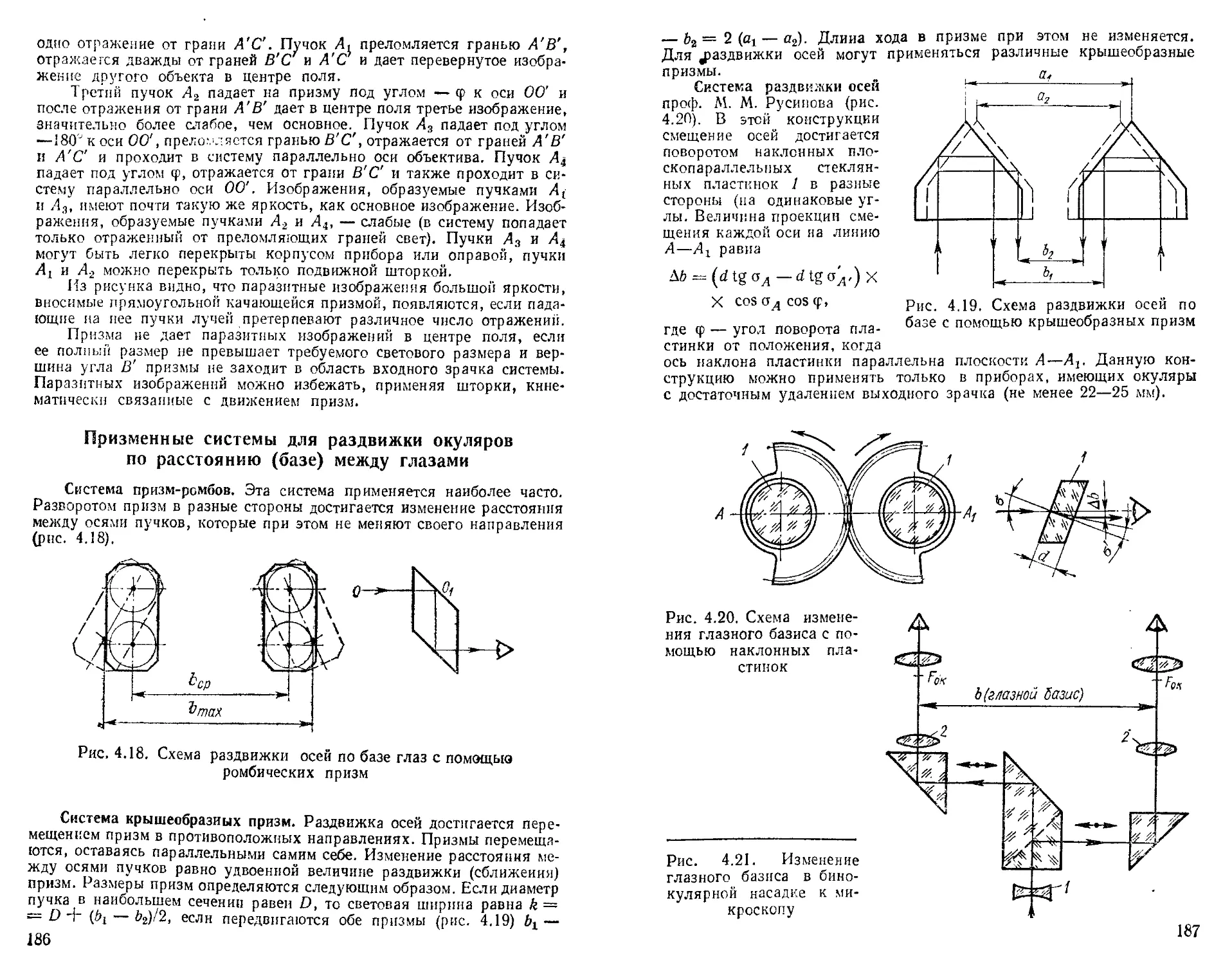
Призменные системы для раздвижки окуляров по расстоянию (базе) между глазами......................... 186
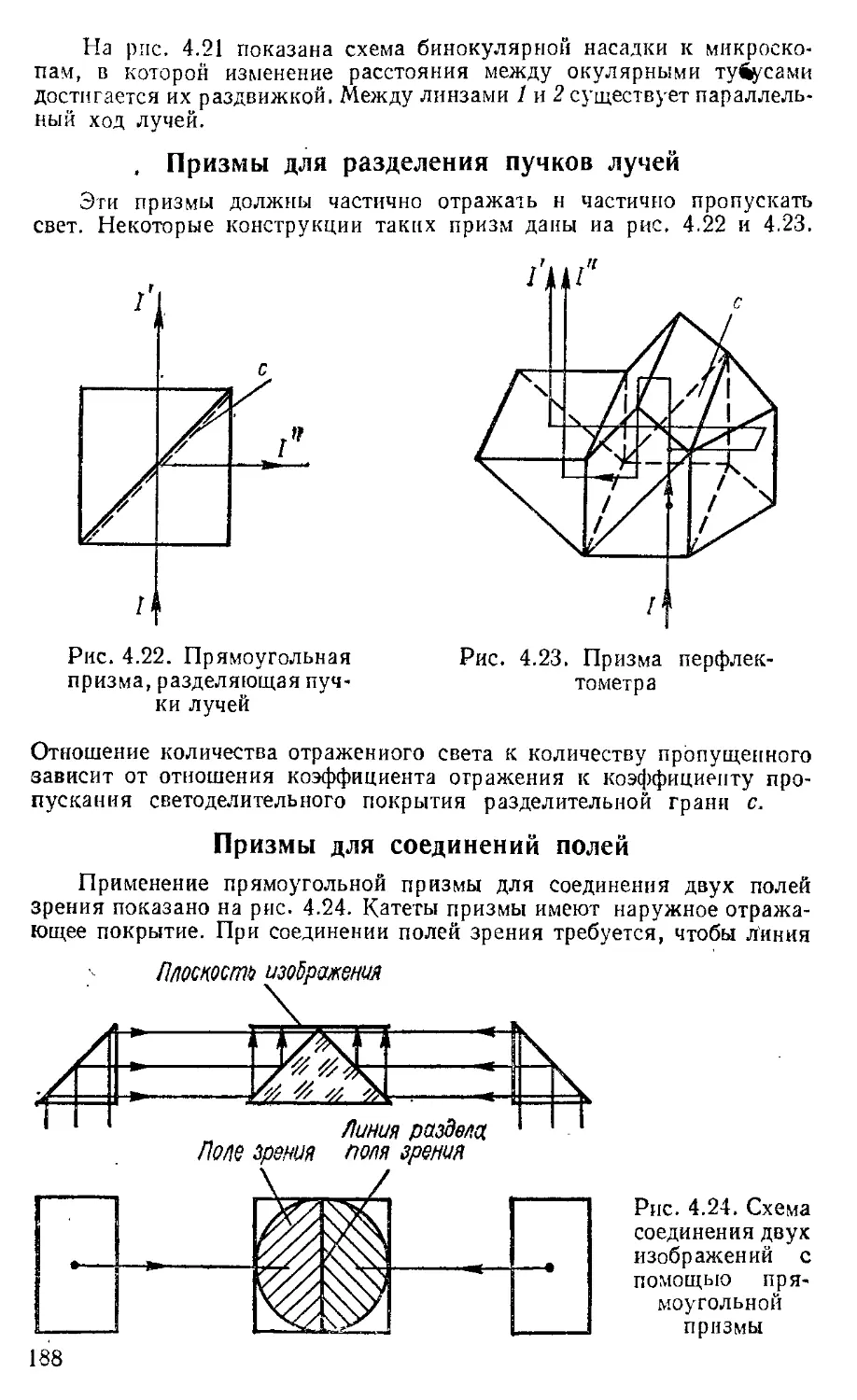
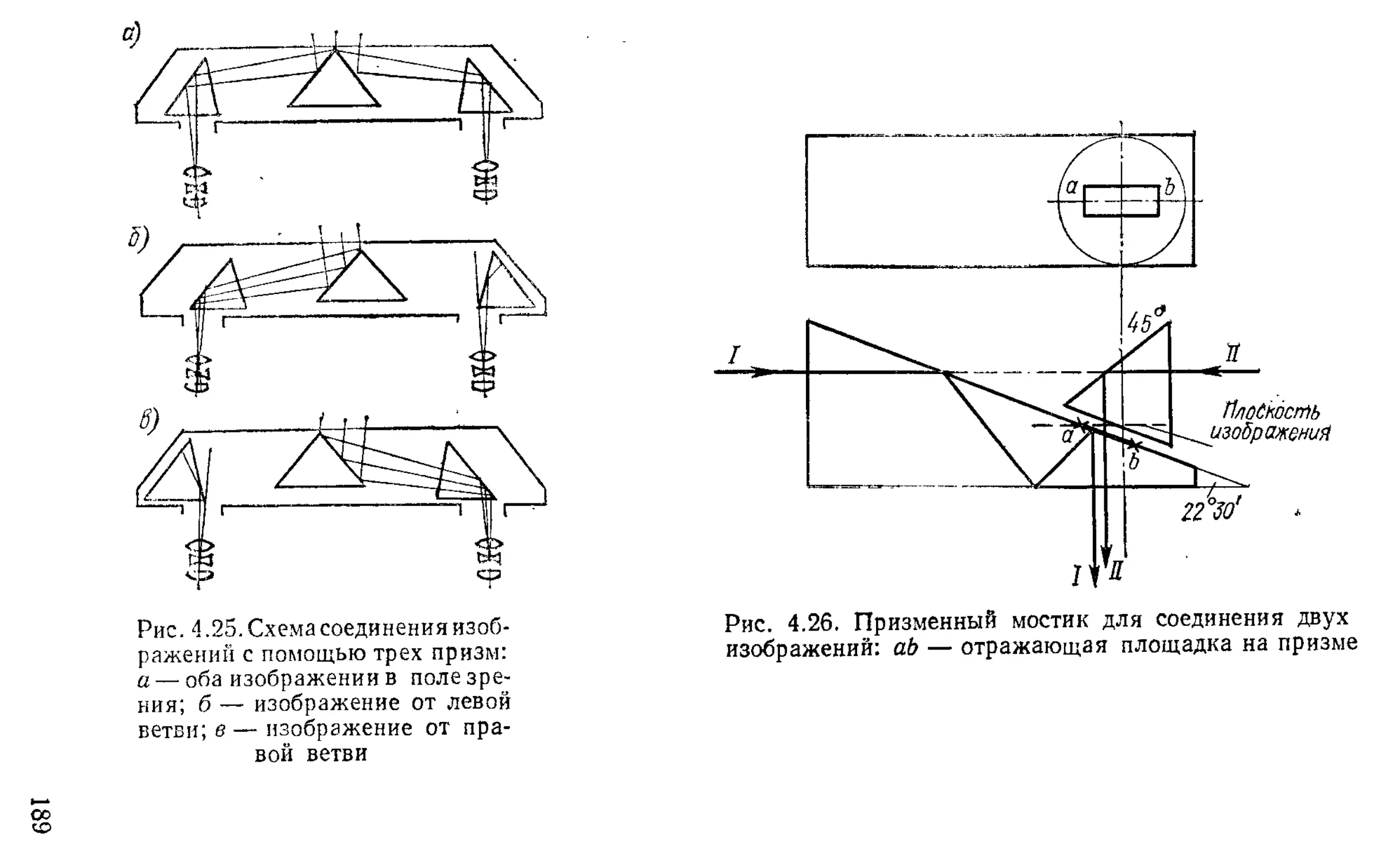
Призмы для разделения пучков лучей.............. 188
Призмы для соединения полей .............. . . . <
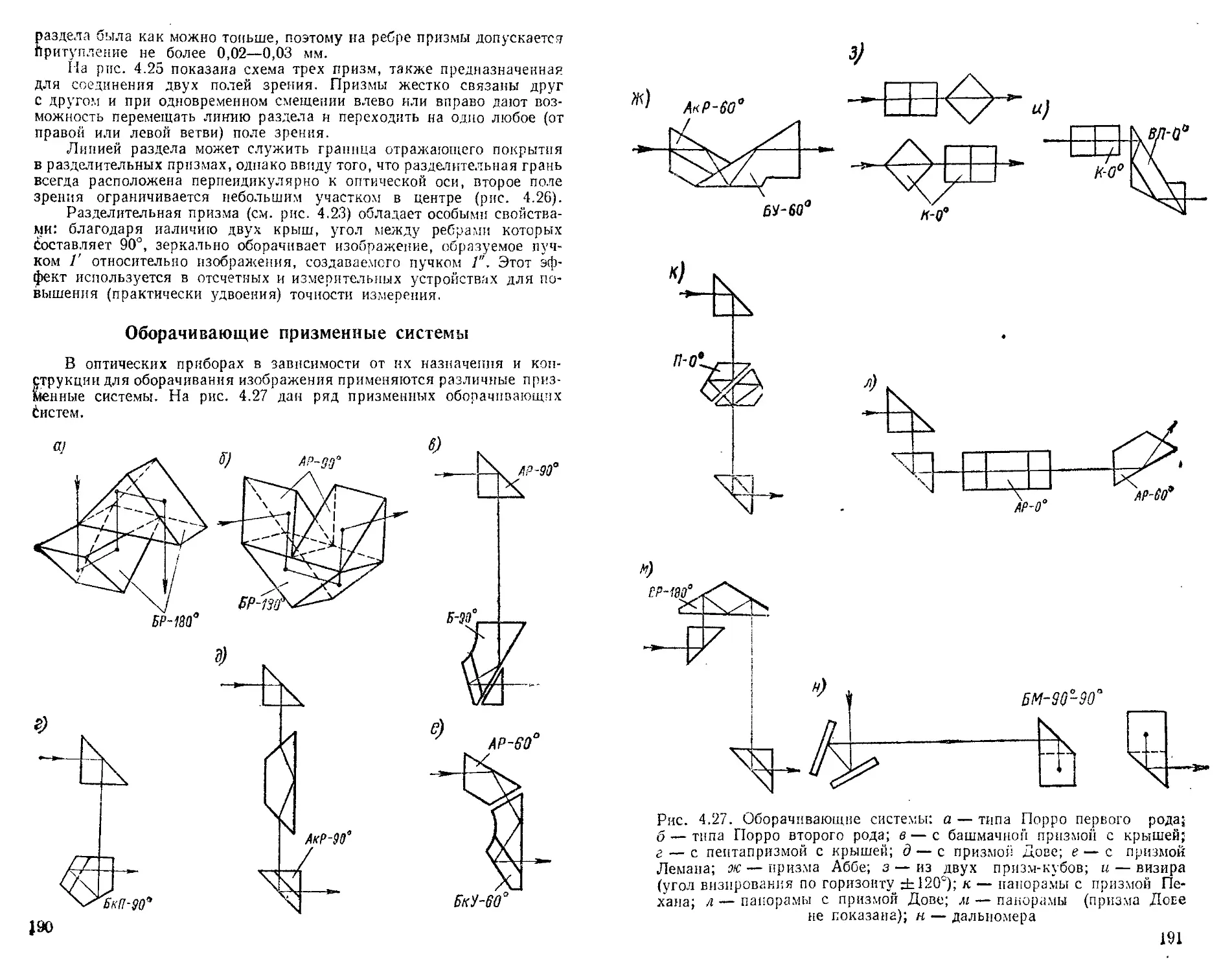
Оборачивающие призменные системы ................ .
Оптические шарниры ................................
Клинья ............................ .................
Фаски иа призмах и иекруглых пластинках..............
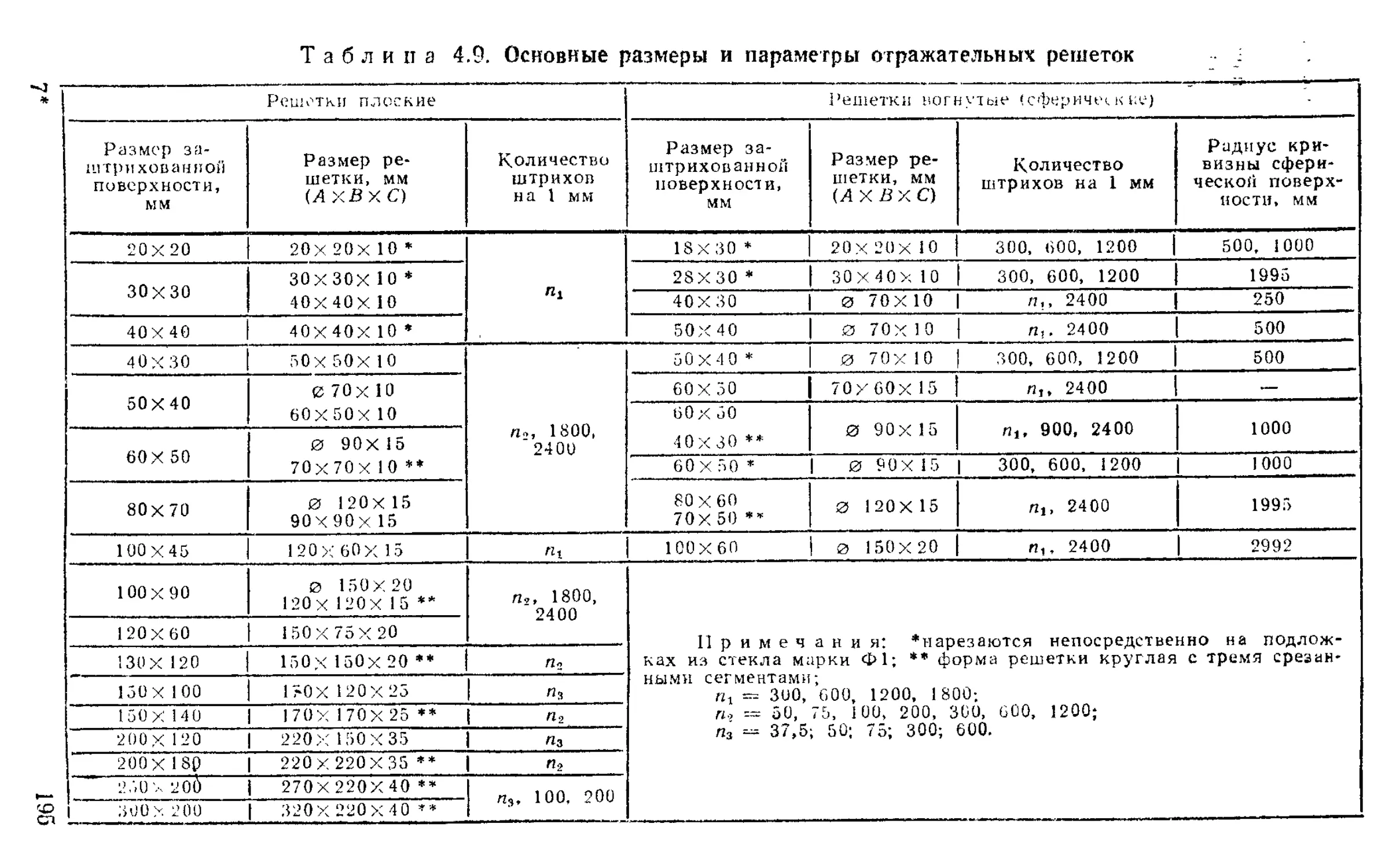
Дифракционные решетки ...............................
Сетки ...............................................
Растровые (трансверсальные) сетки . ...............
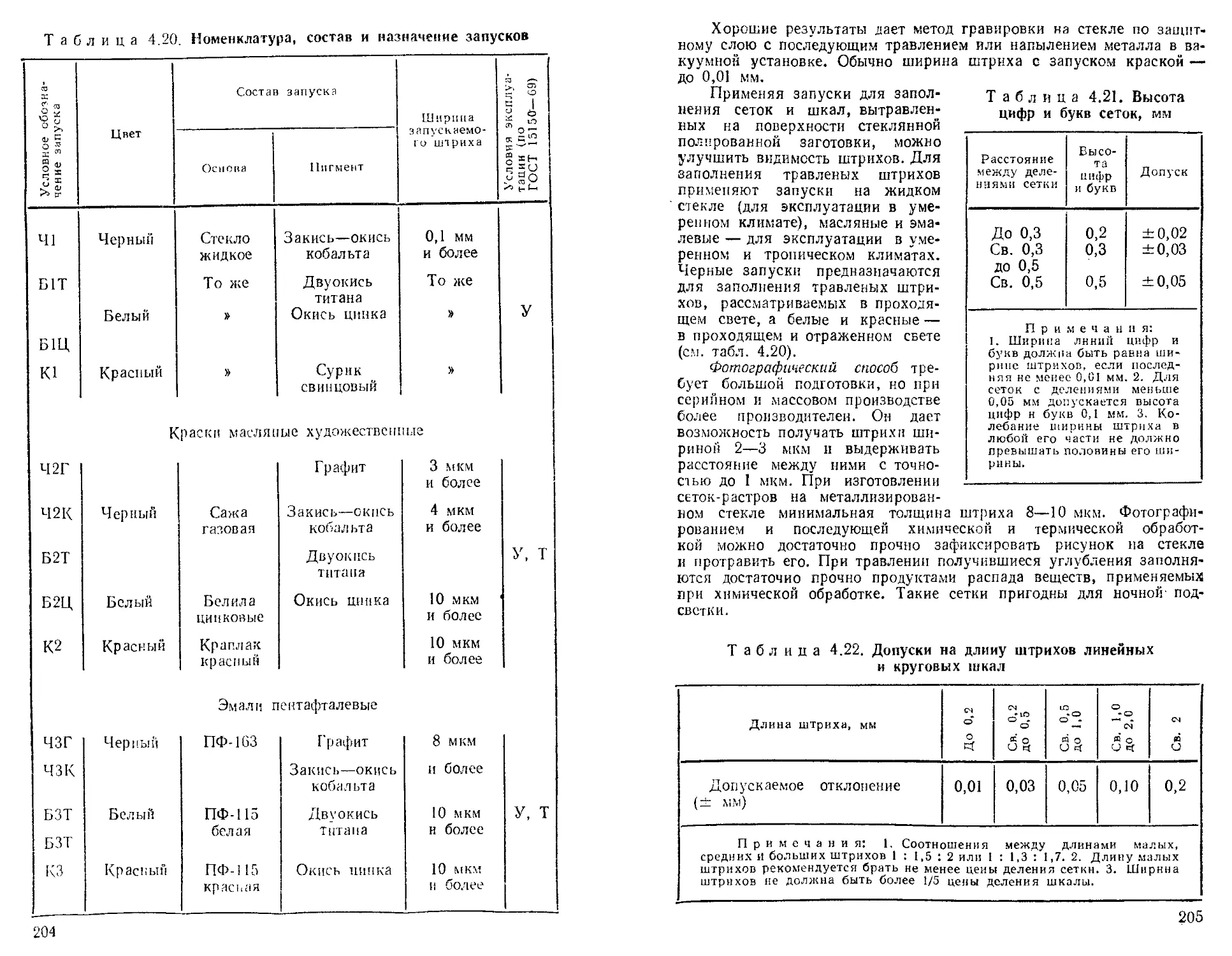
Допуски на изготовление заготовок сеток и лимбов. Выбор марки стекла ..............
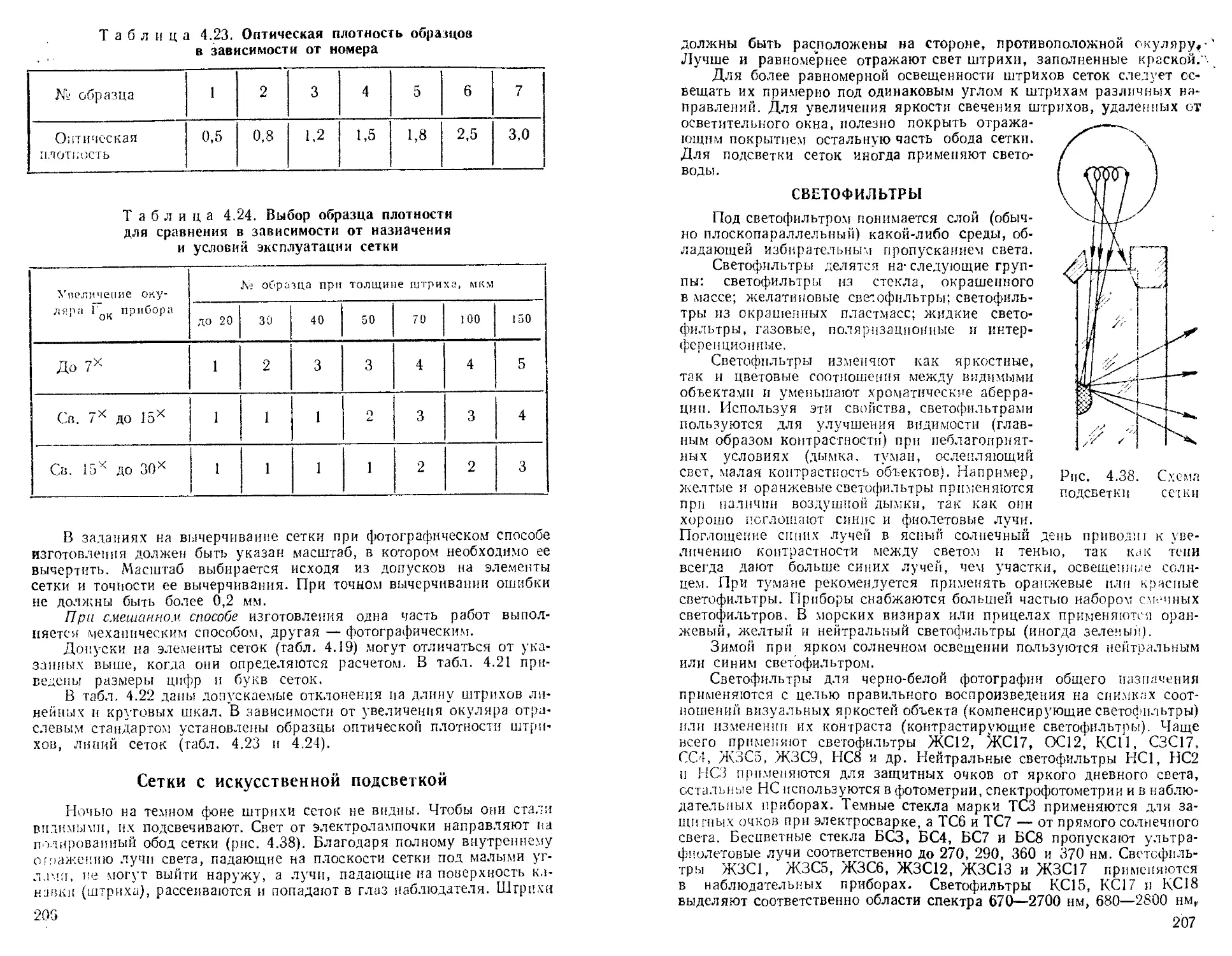
Методы и точность нанесения делений на сетках . * ♦ Сетки с искусственной подсветкой ..................
Светофильтры.........................................
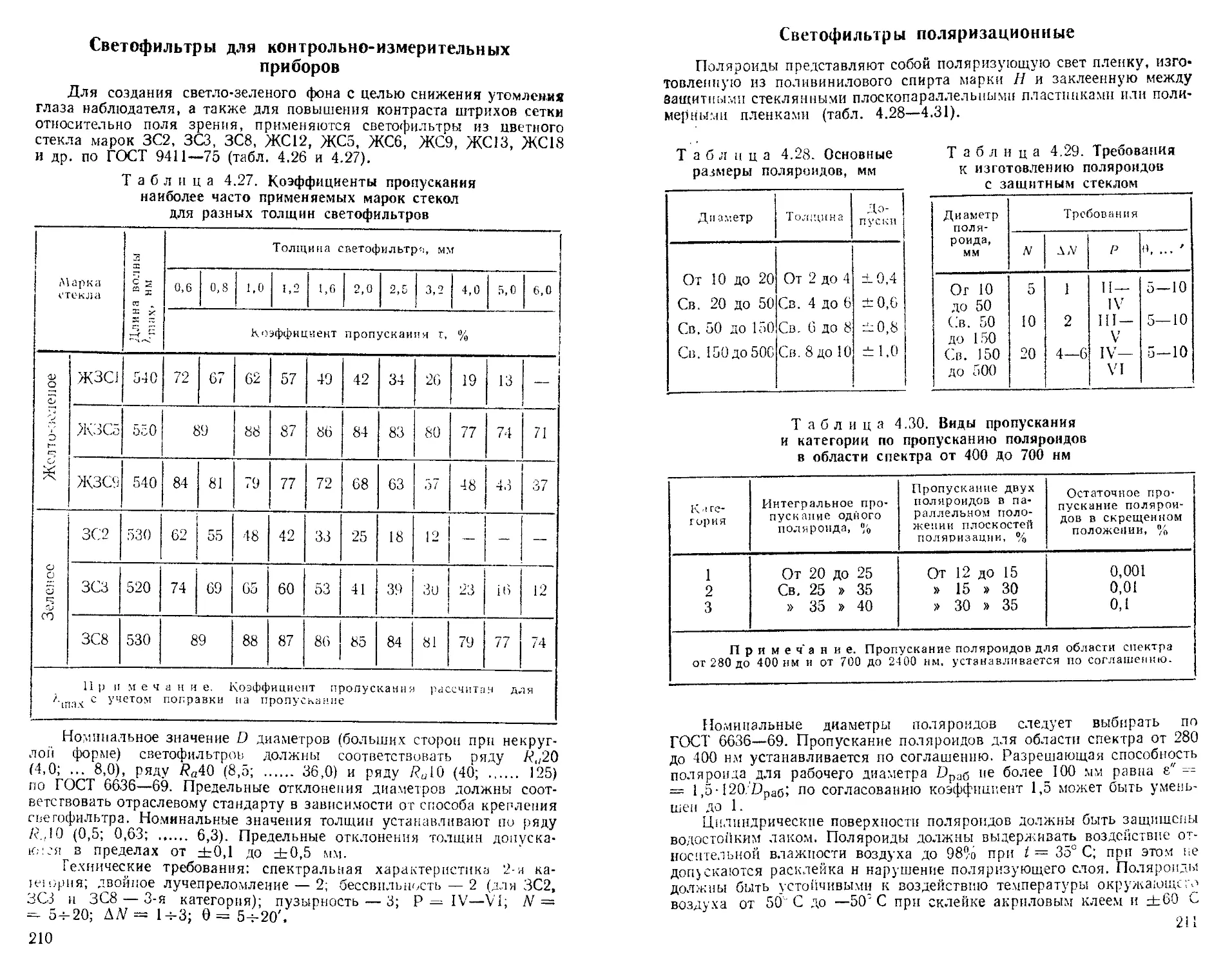
Стеклянные светофильтры для микроскопии . . . . . Светофильтры для контрольно-измерительных приборов Светофильтры поляризационные ......................
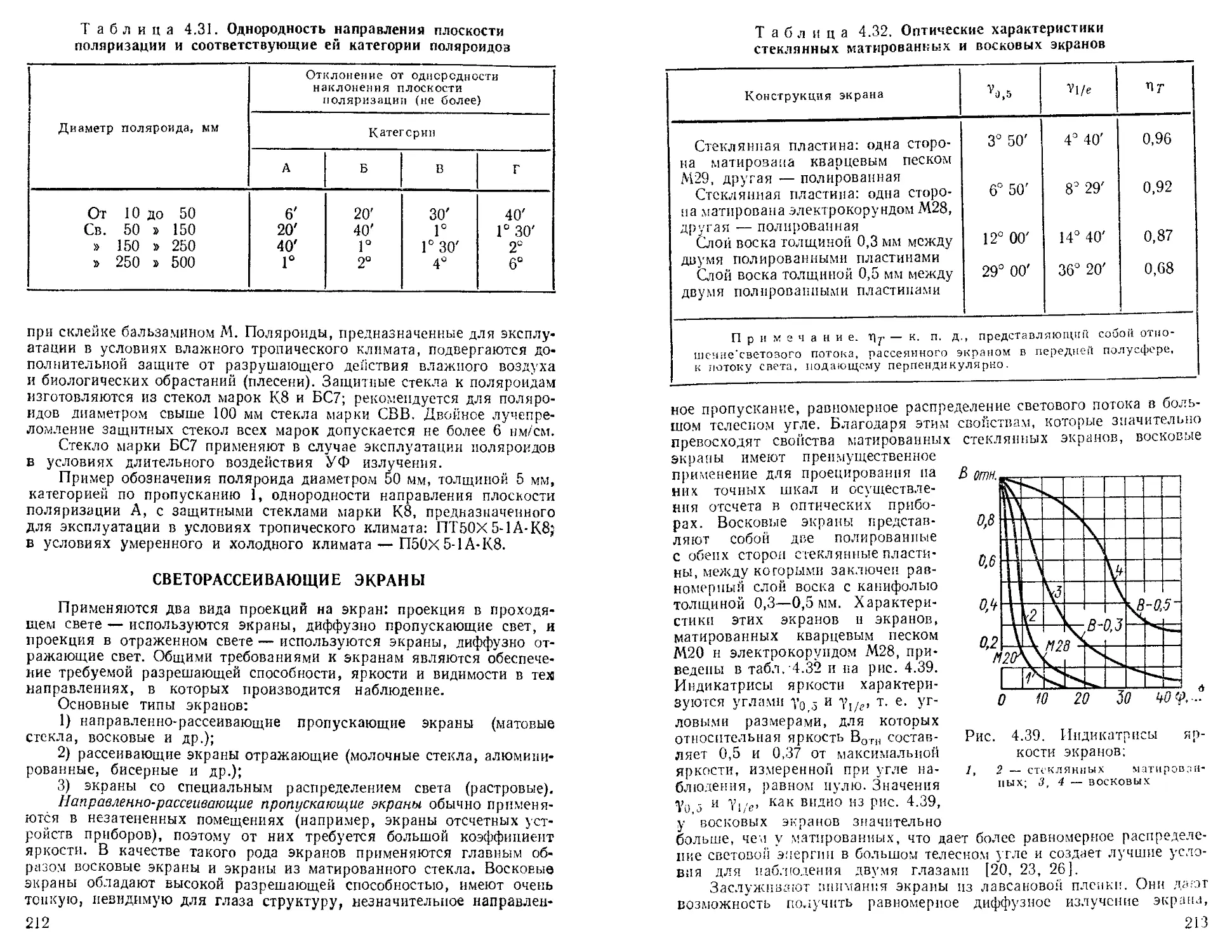
Светорассеивающне экраны ............................
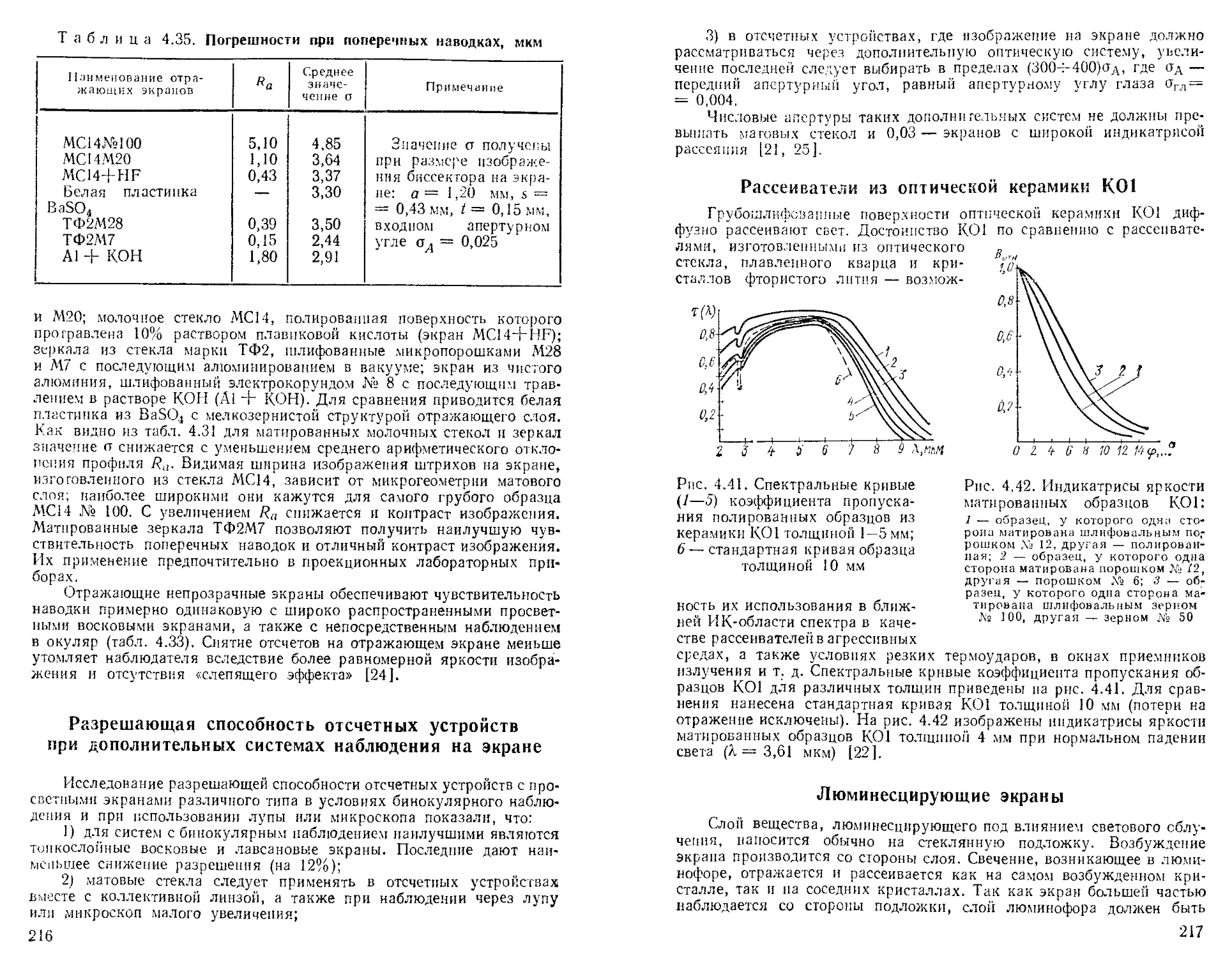
Чувствительность визирования штрихов на просветных экранах ...........................................
Чувствительность визирования штрихов на непрозрачных отражающих экранах ............................
Разрешающая способность отсчетных устройств при дополнительных системах наблюдения на экране . . . Рассеиватели из оптической керамики КО1............
Люминесцирующие экраны ............................
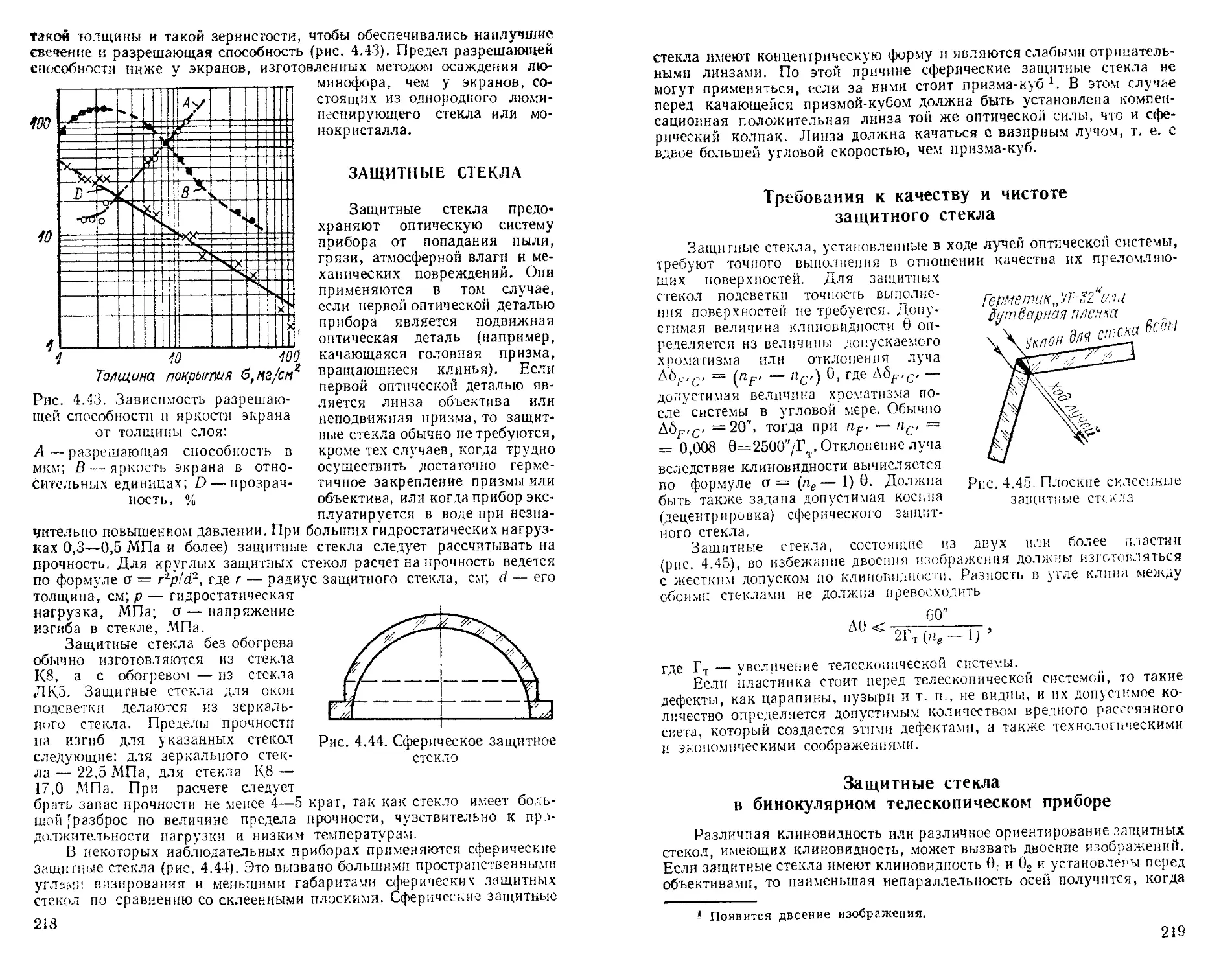
Защитные стекла .....................................
Требования к качеству и чистоте защитного стекла . . . Защитные стекла в бинокулярном телескопическом приборе ...........................................
Защитные стекла с обогревом .......................
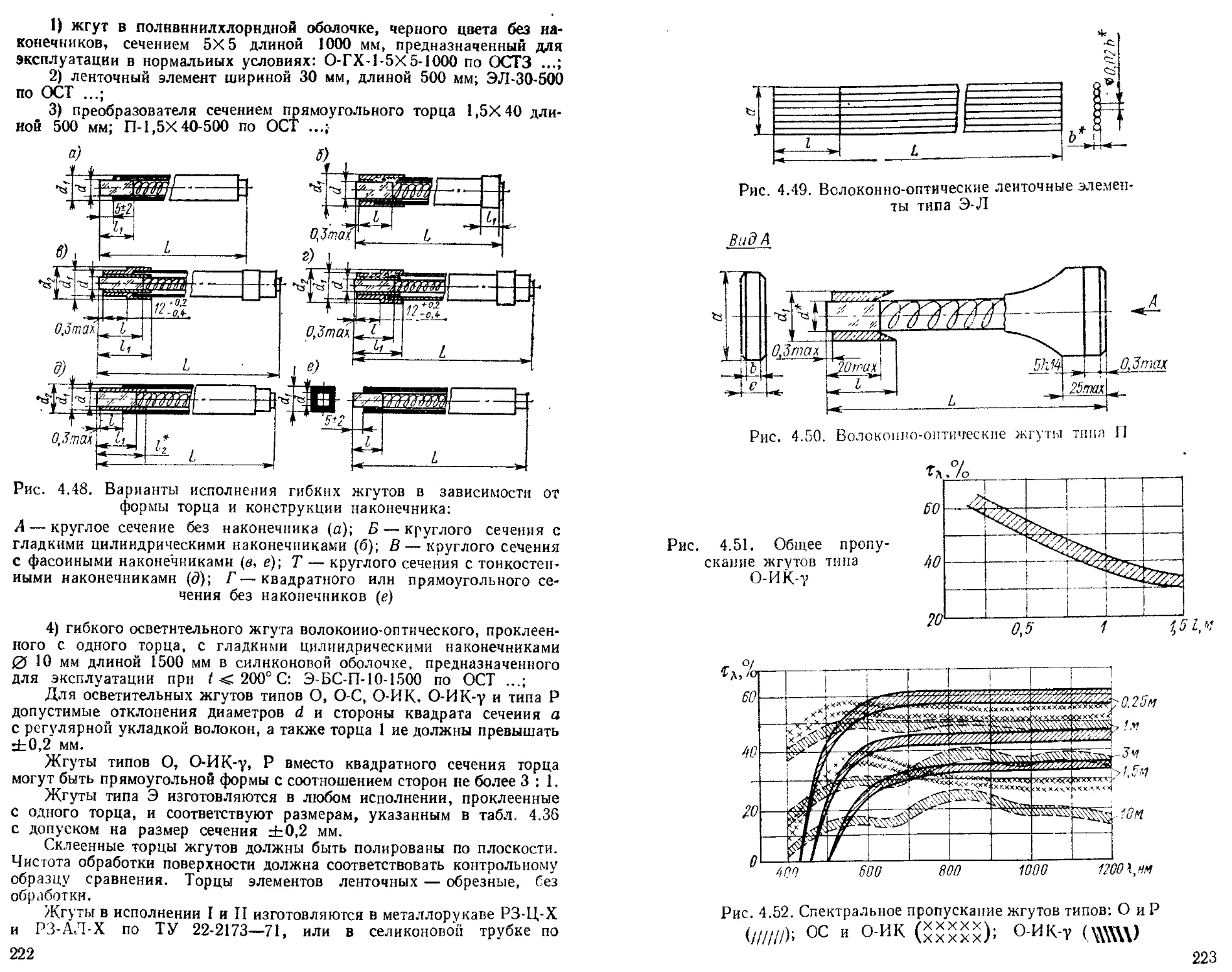
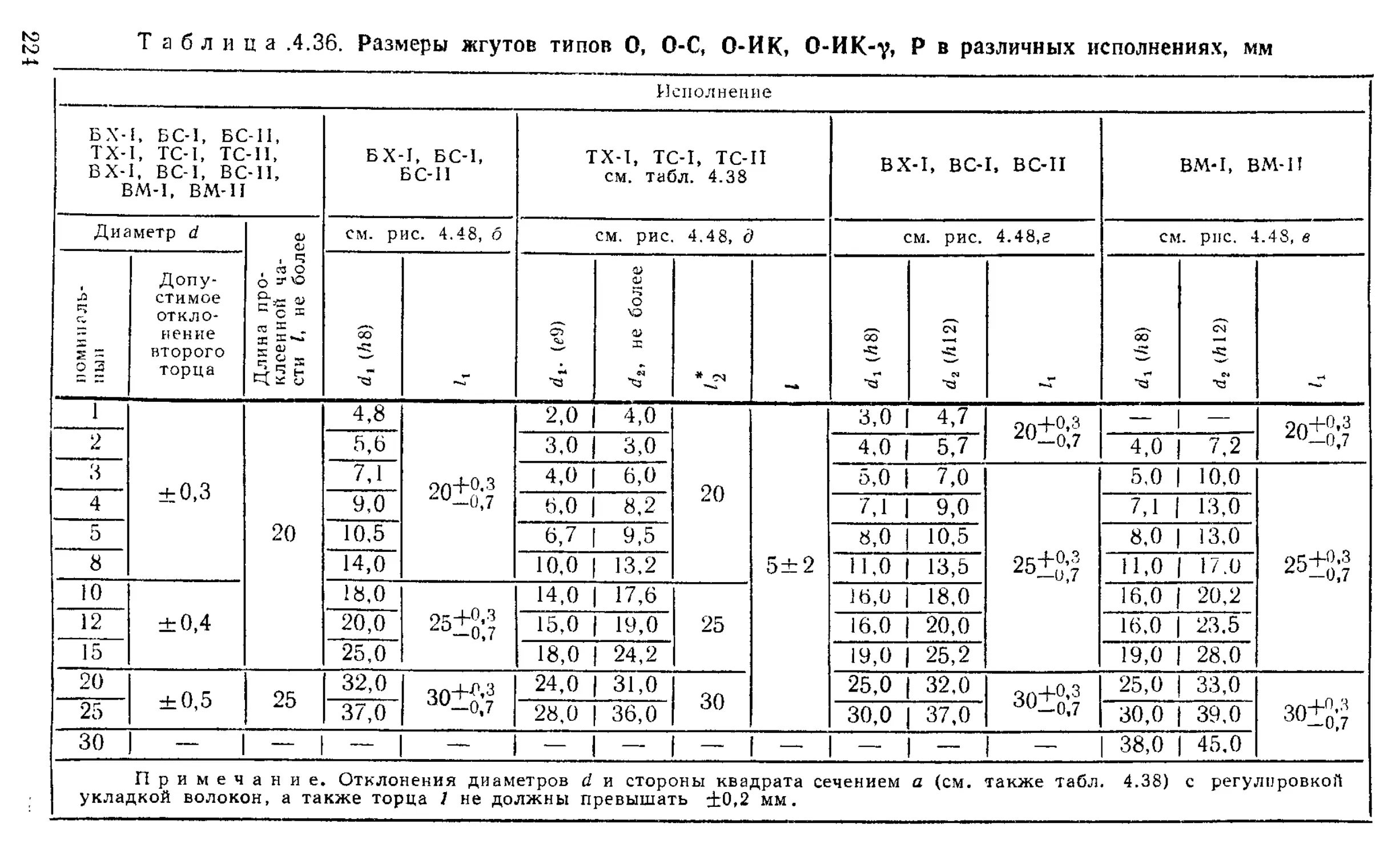
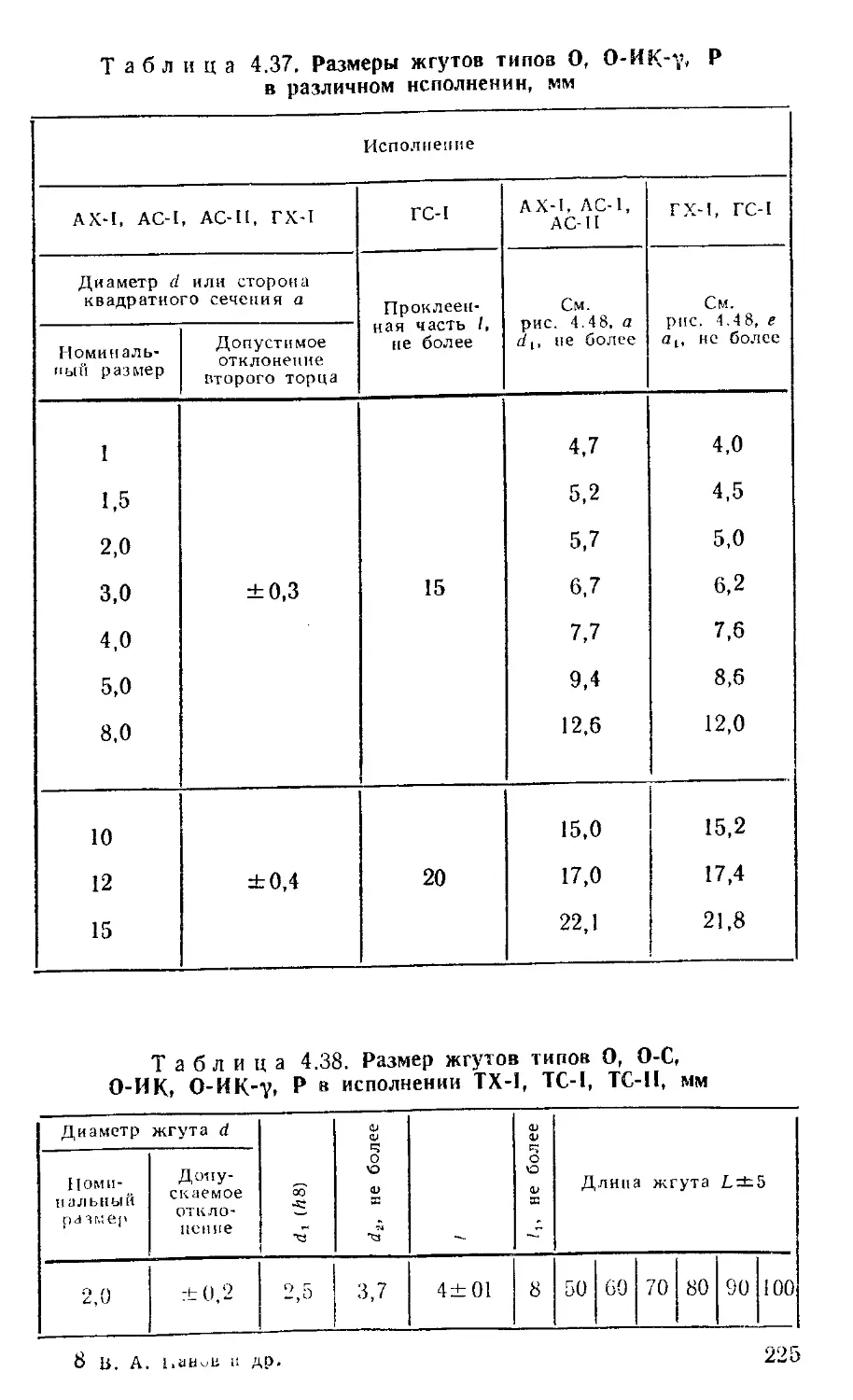
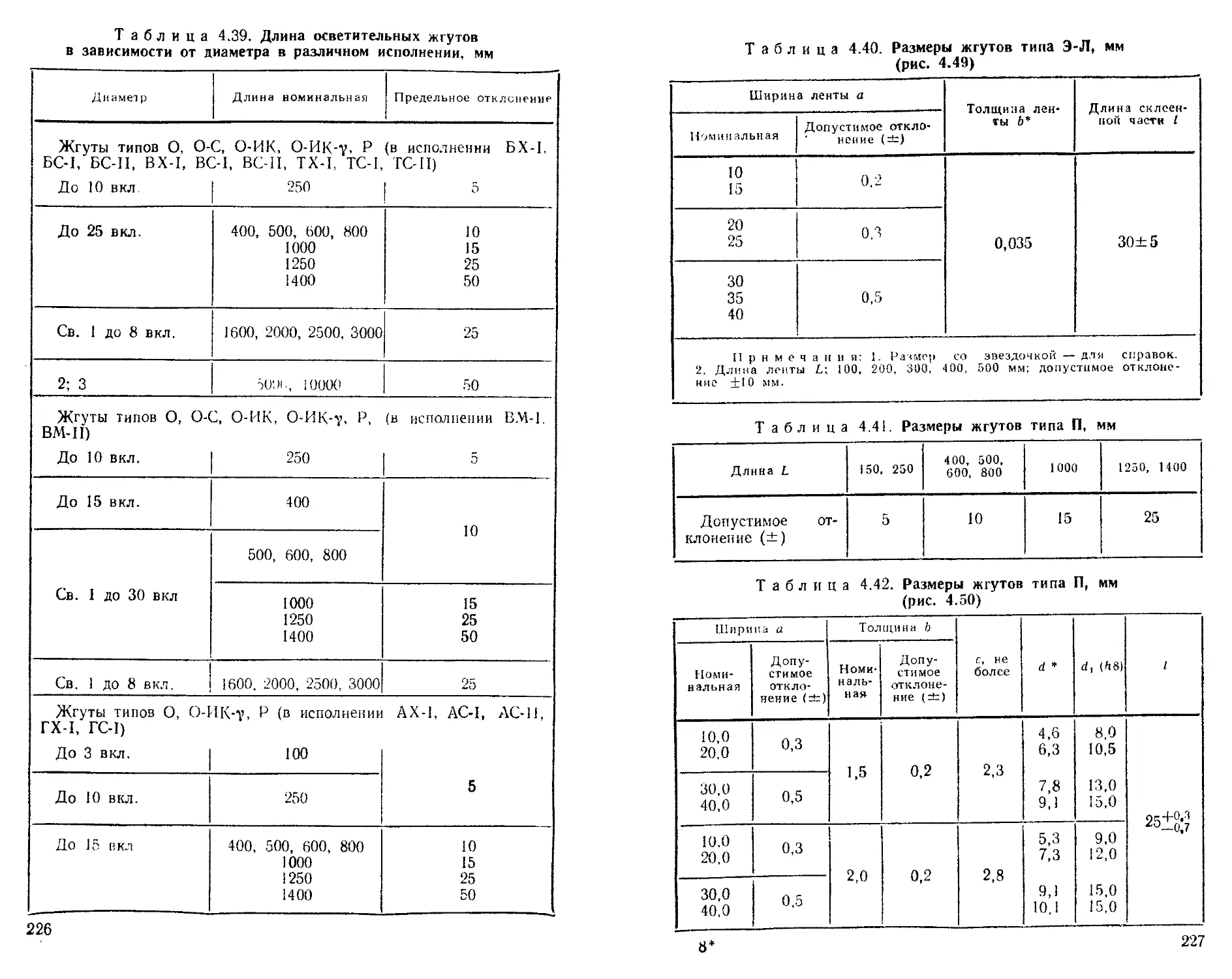
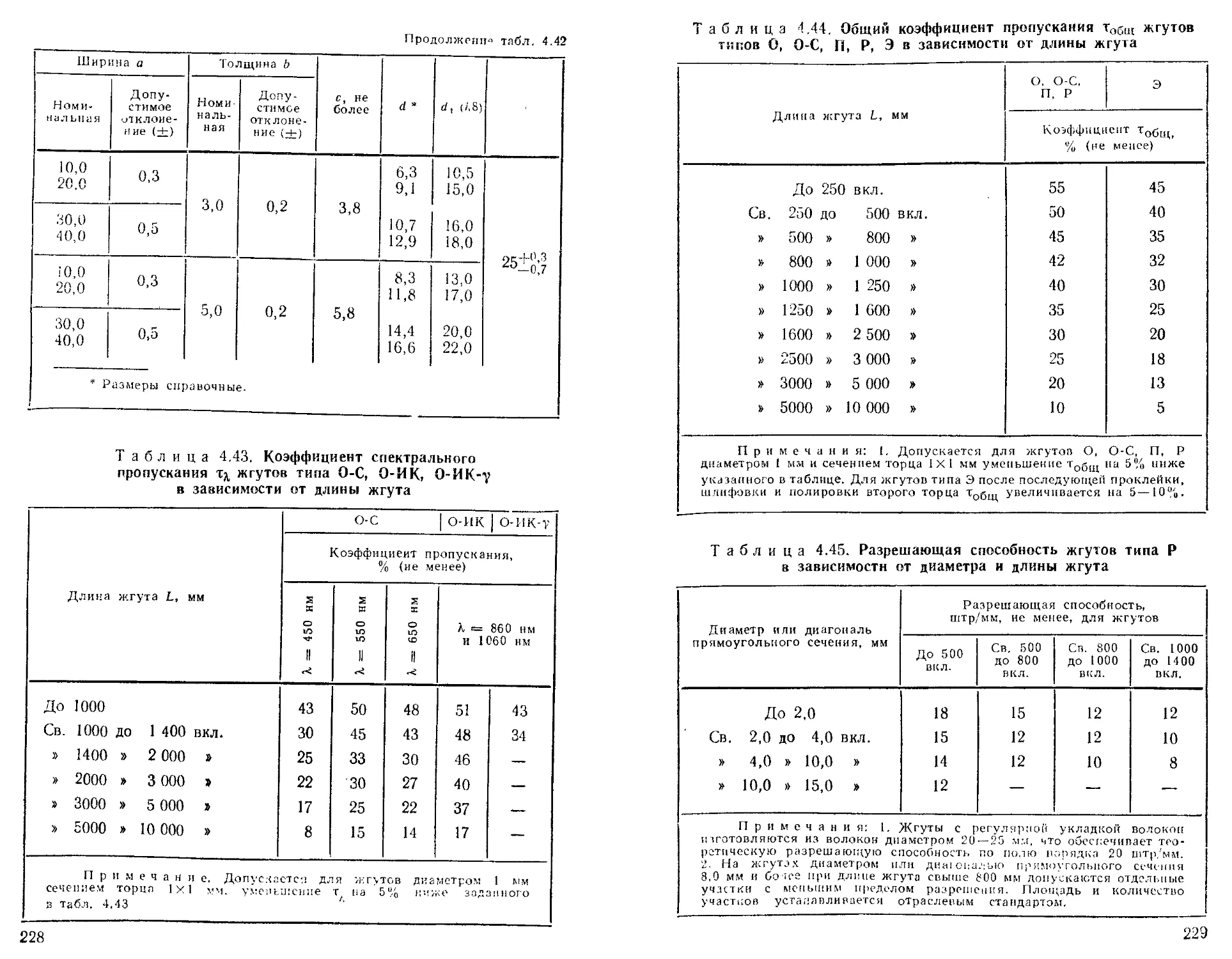
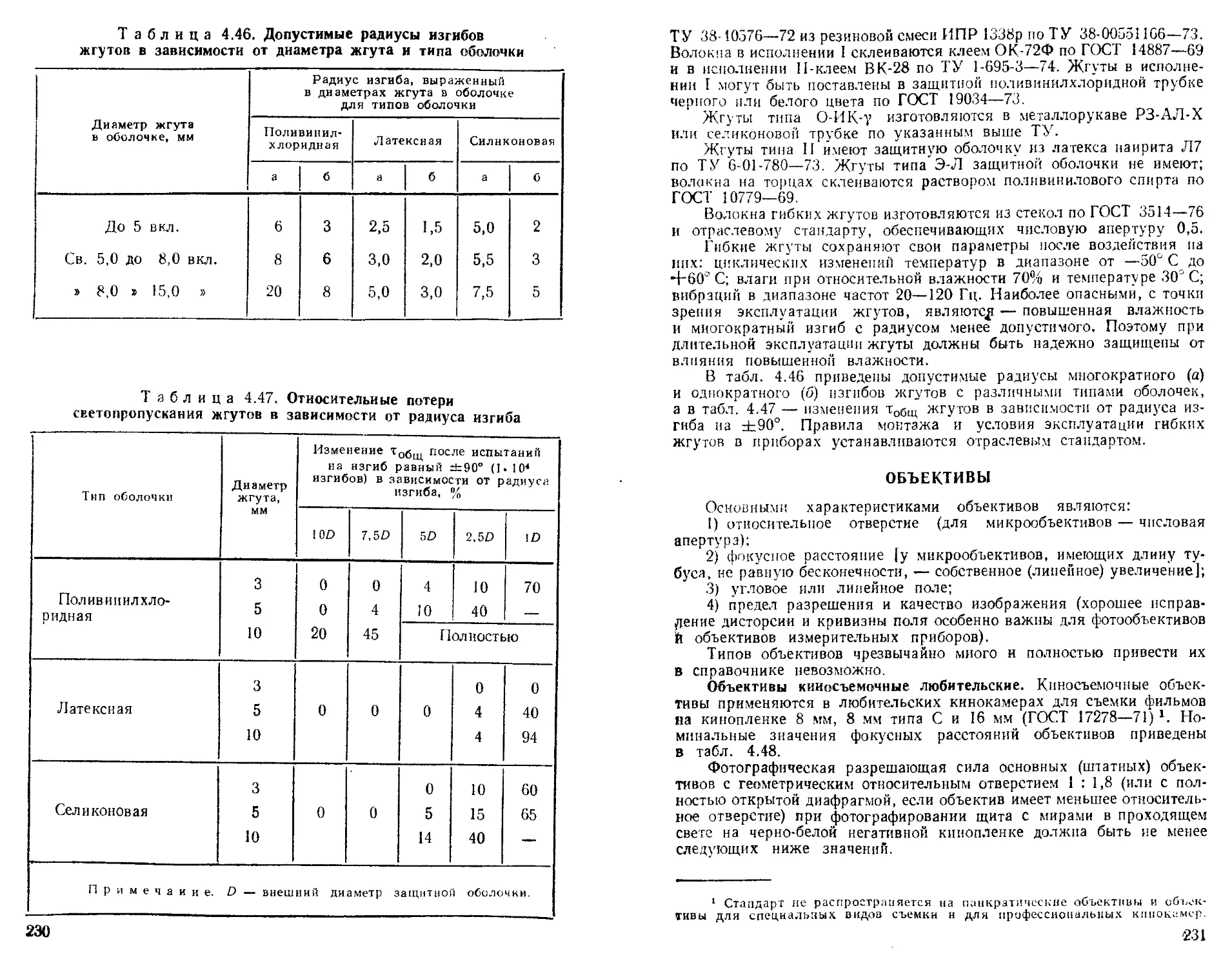
Жгуты волоконно-оптические гибкие....................
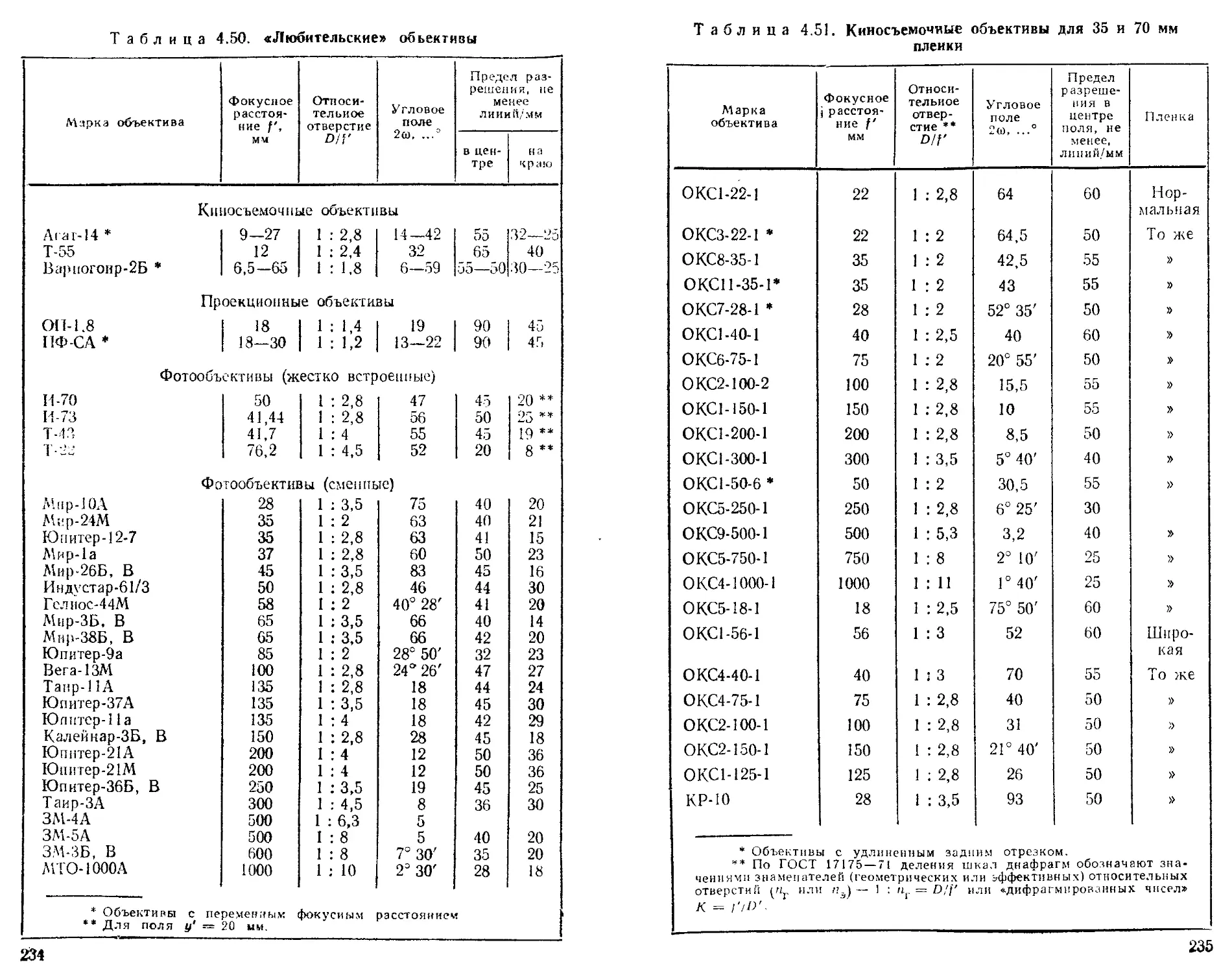
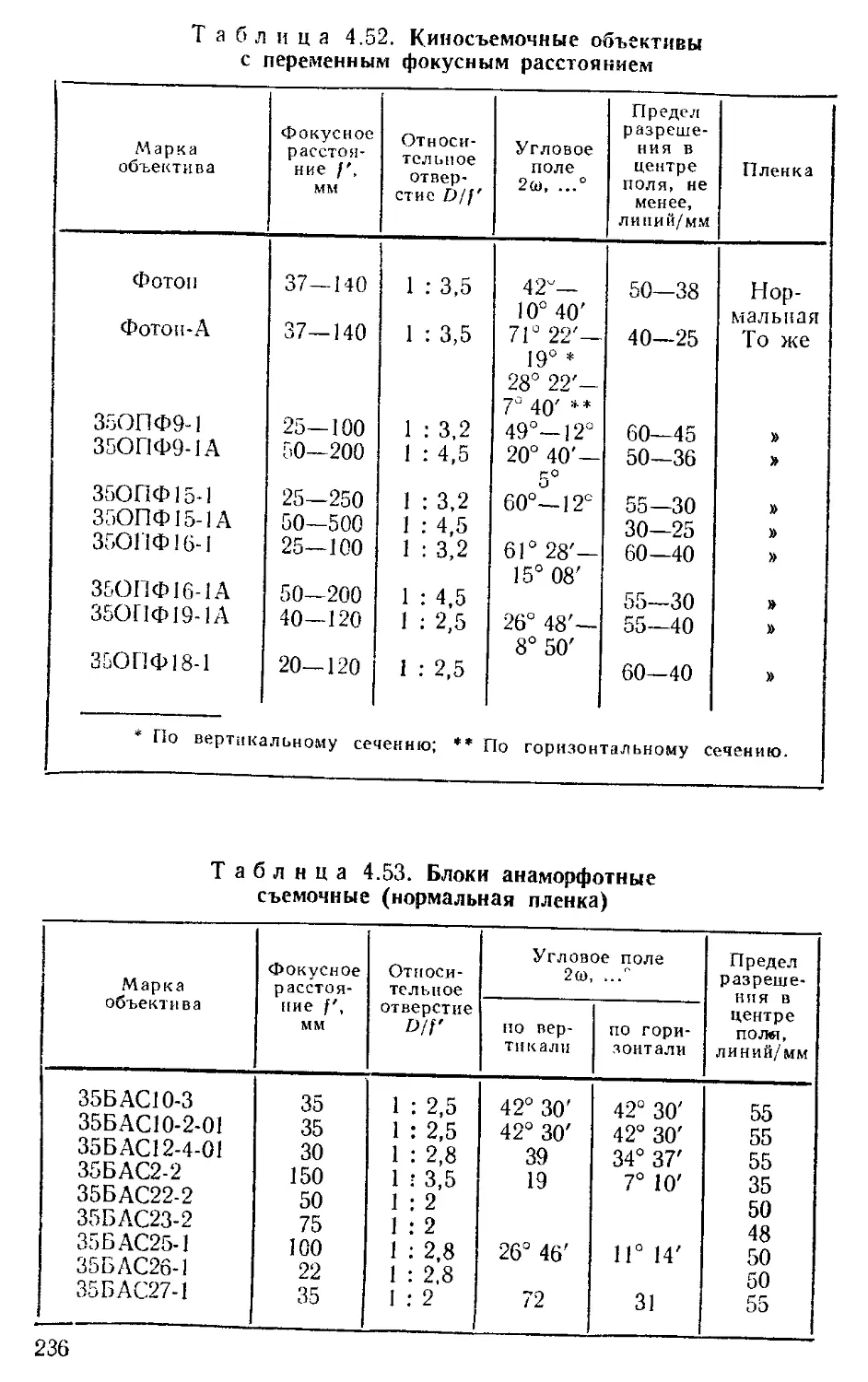
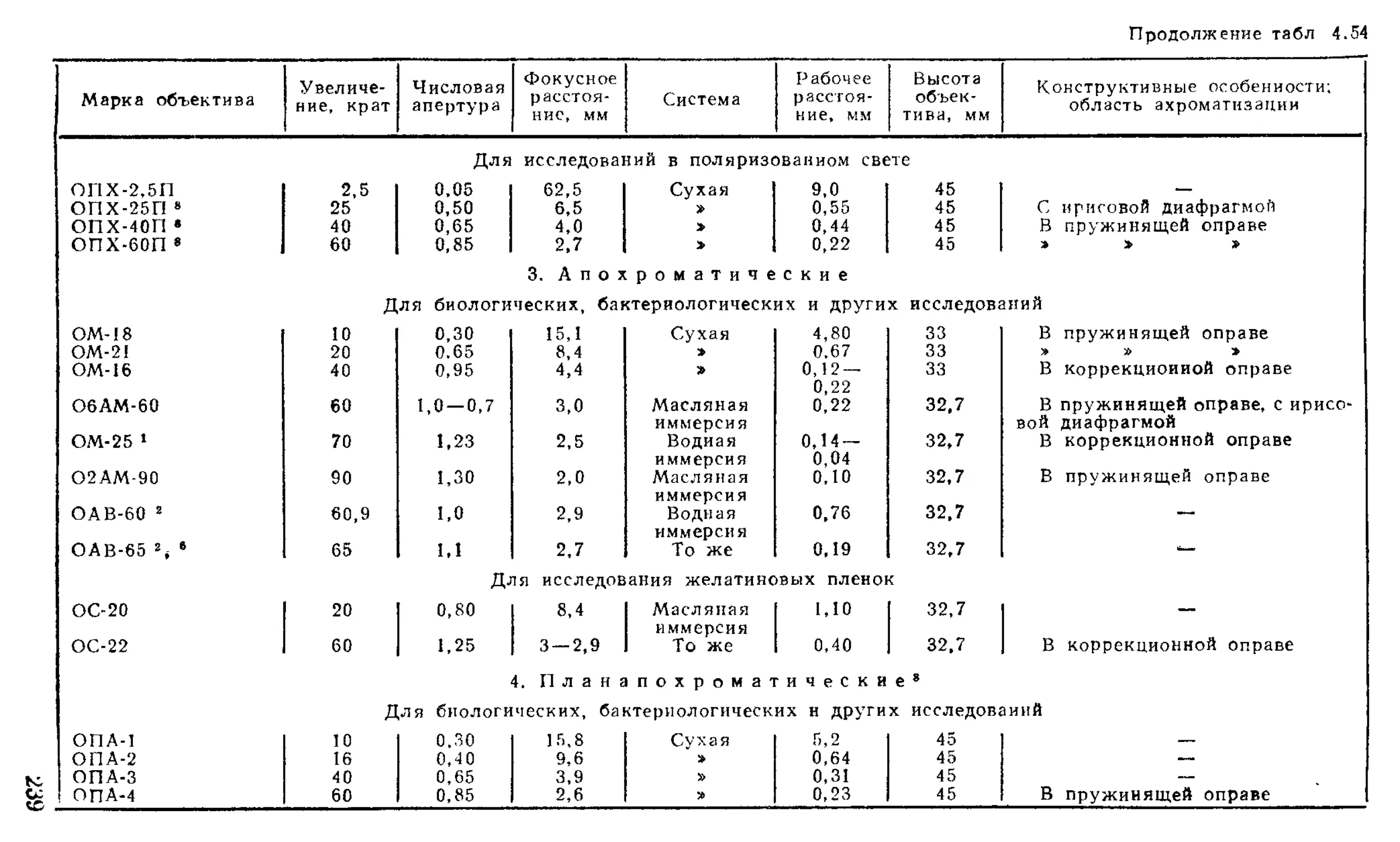
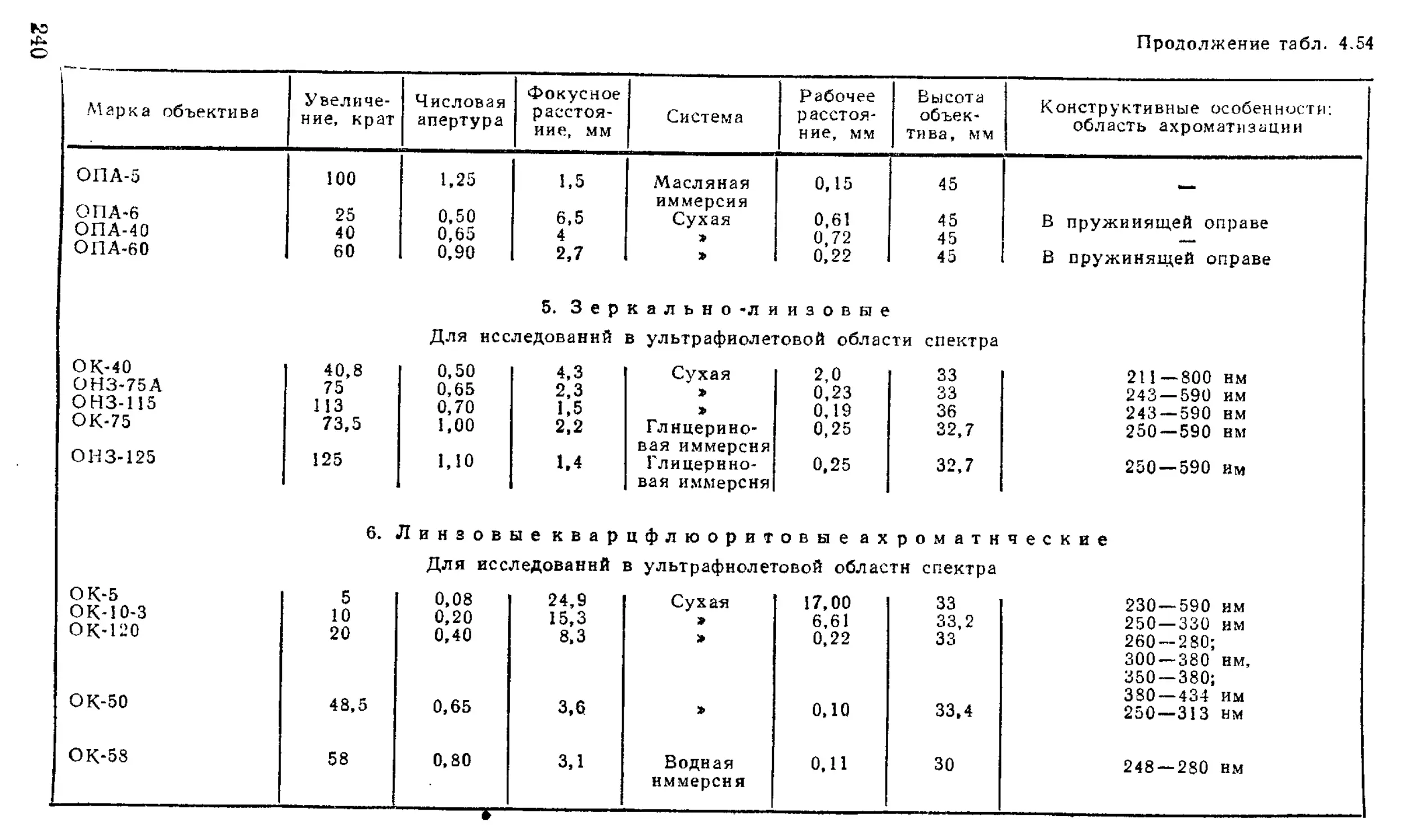
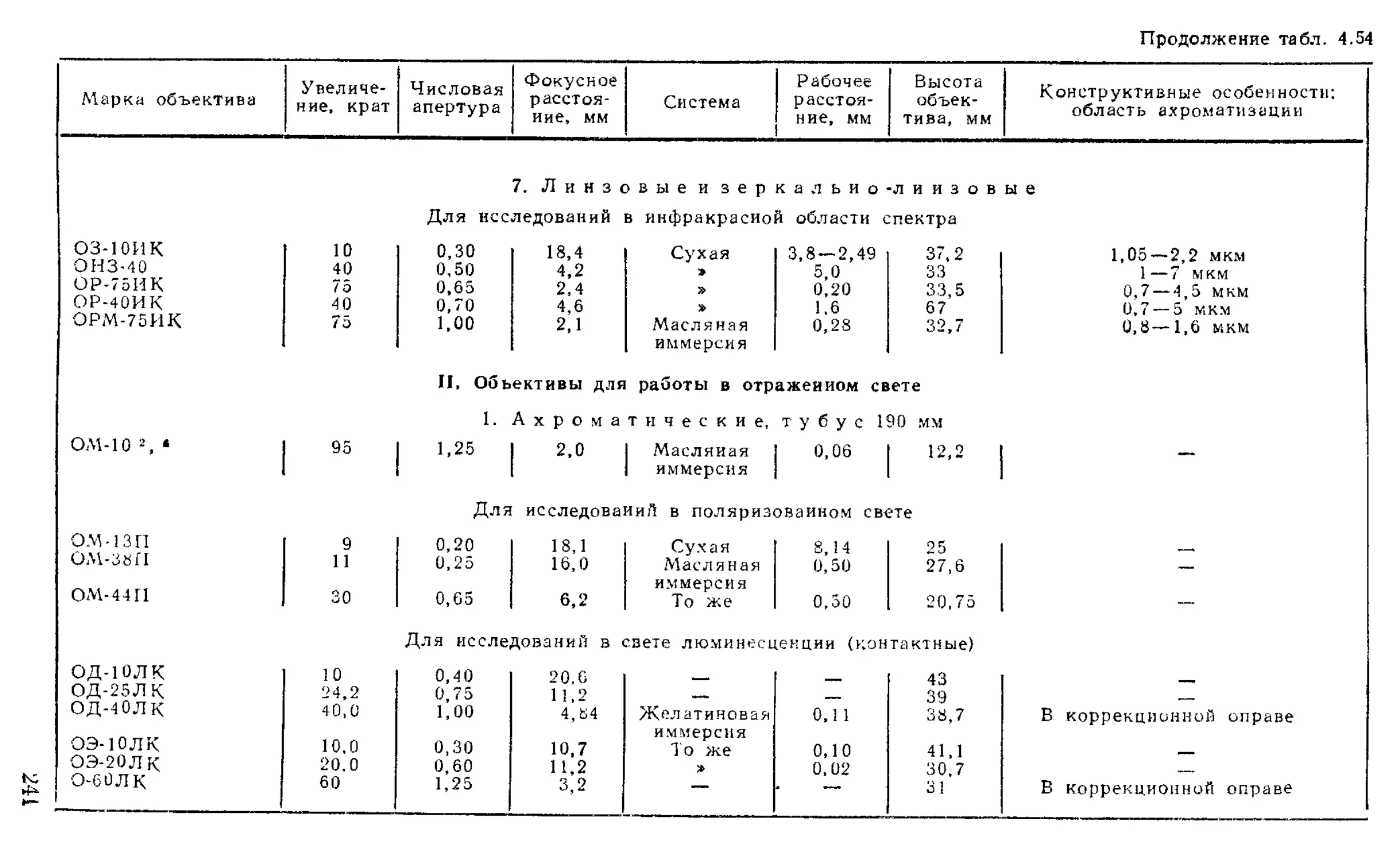
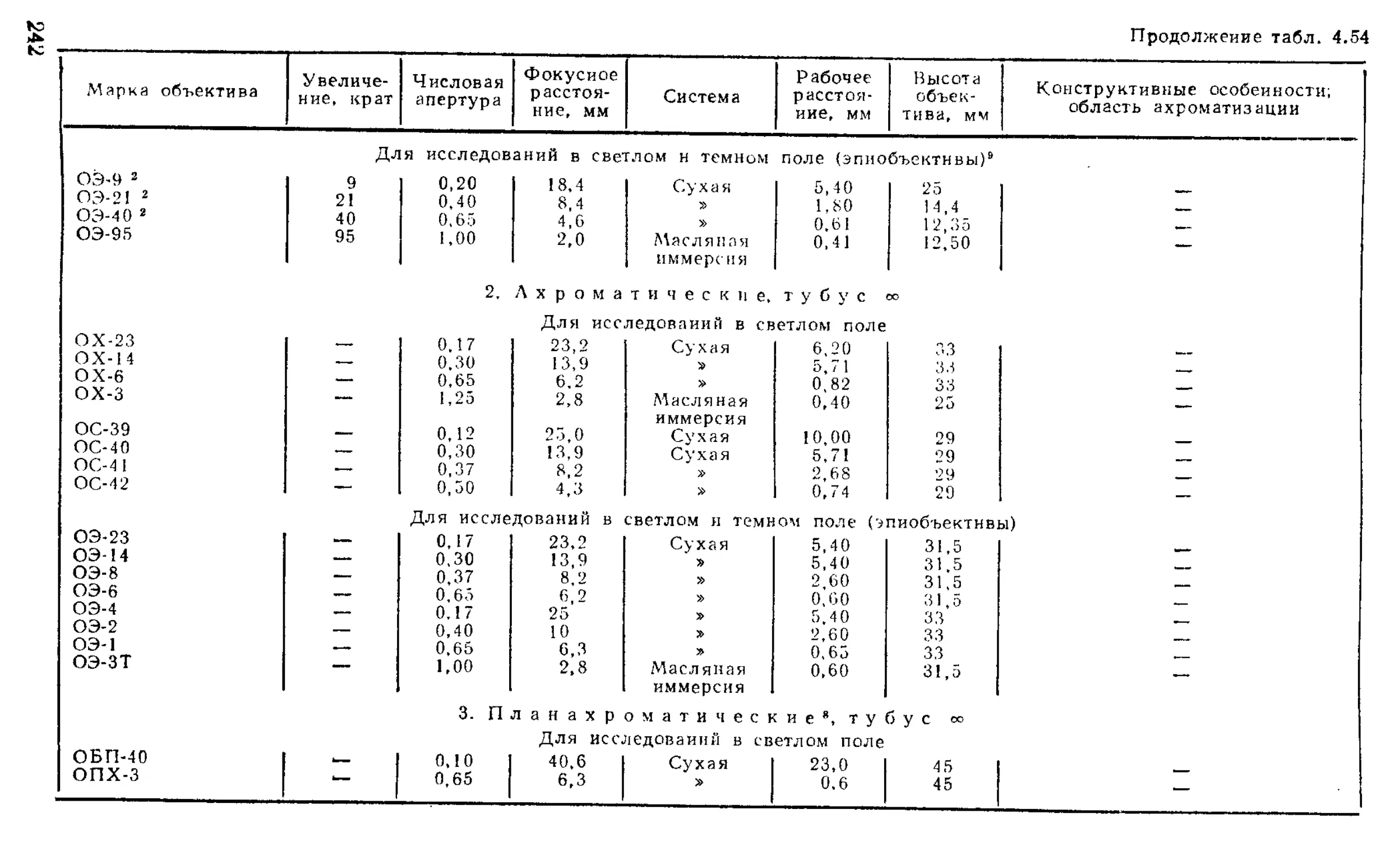
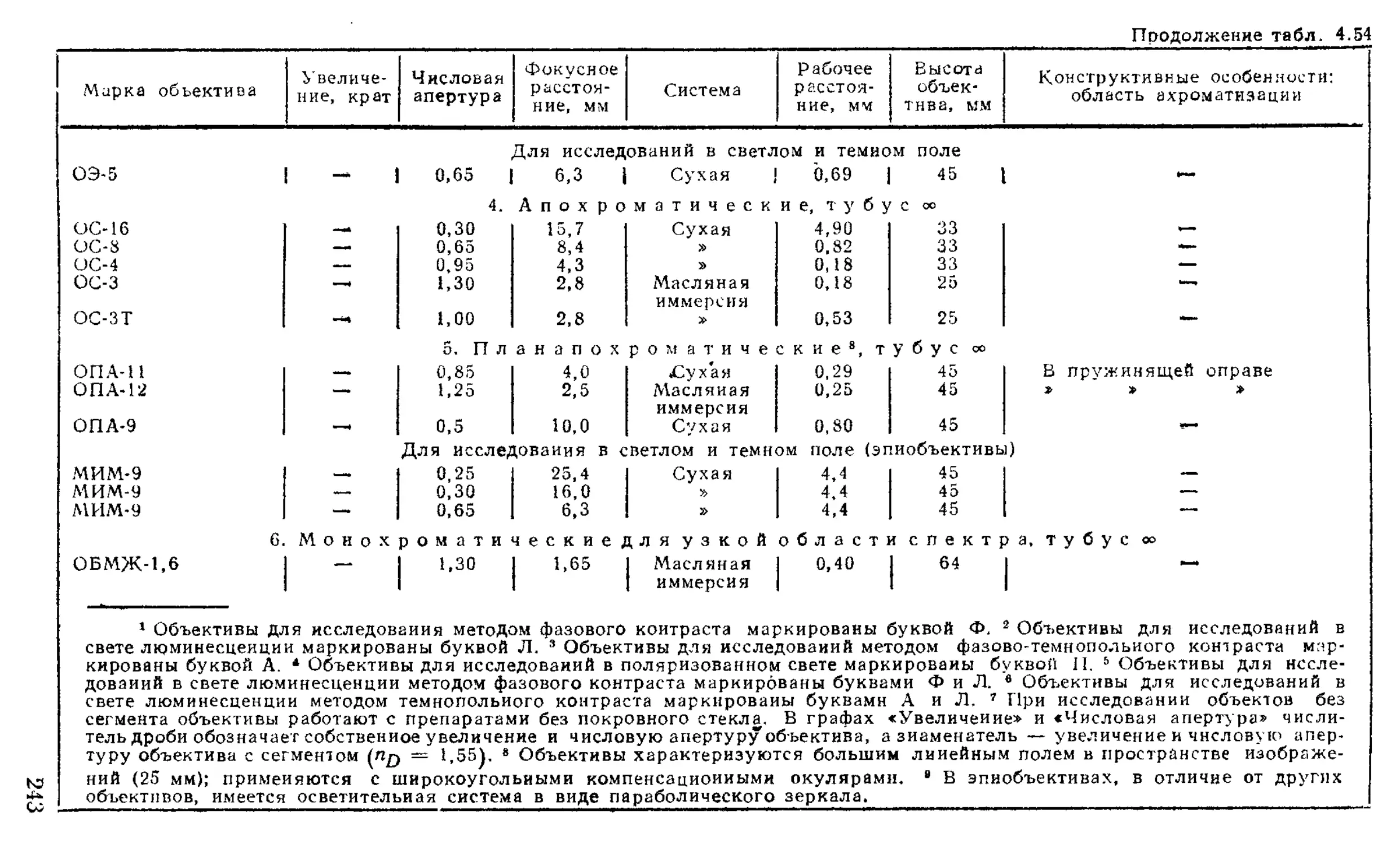
Объективы ...........................................
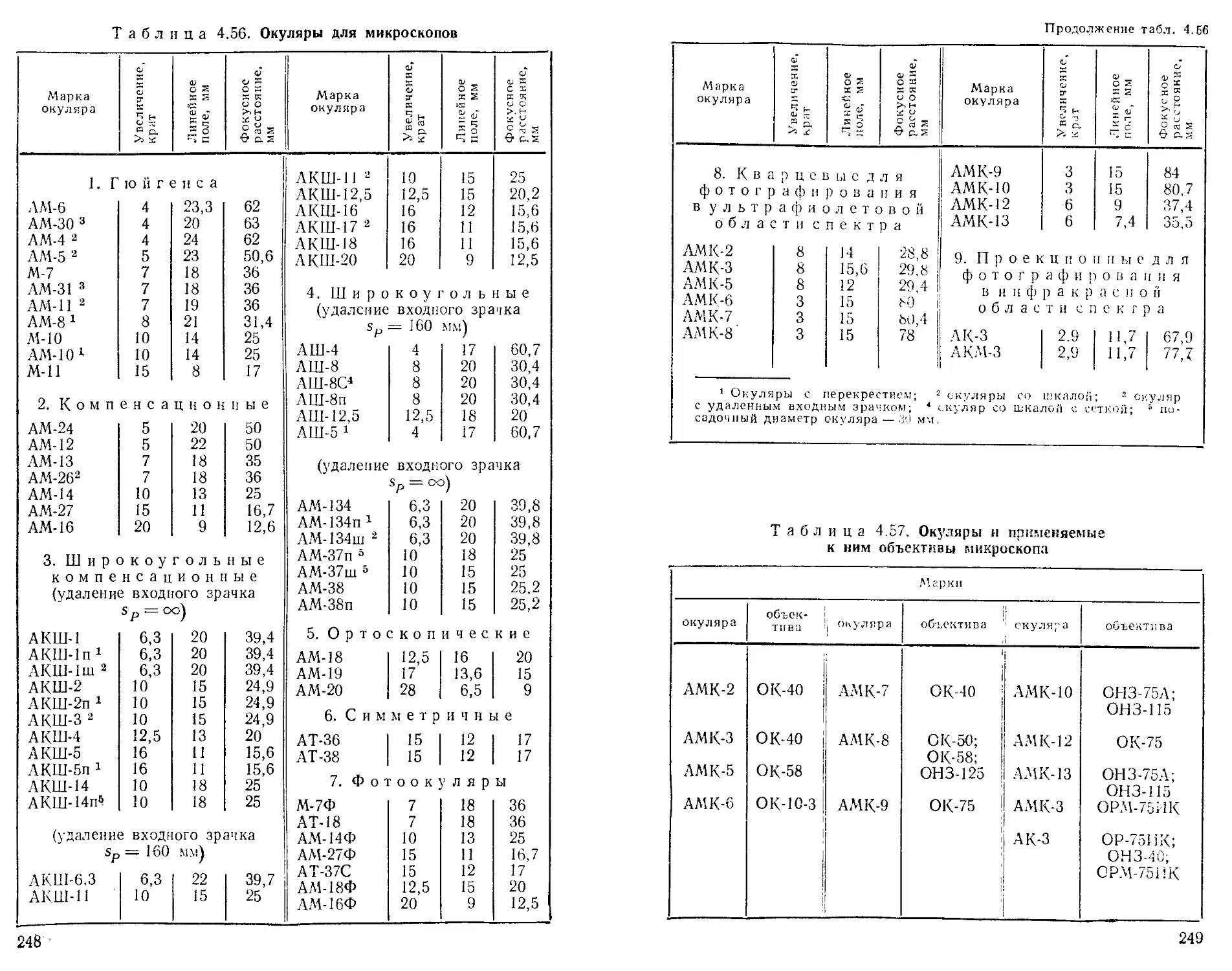
Окуляры..............................................
Типы окуляров и их характеристики..................
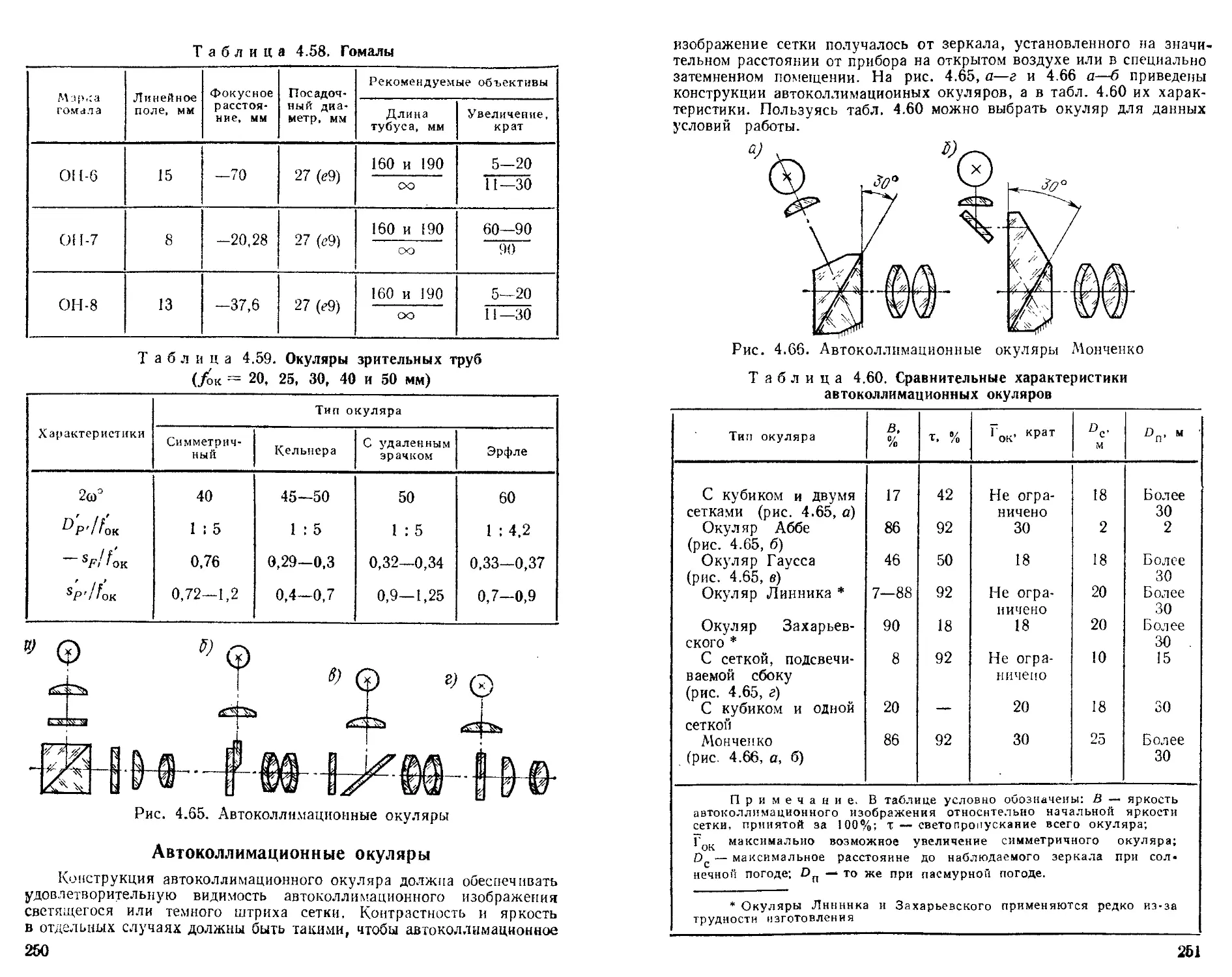
Автоколлимационные окуляры ........................
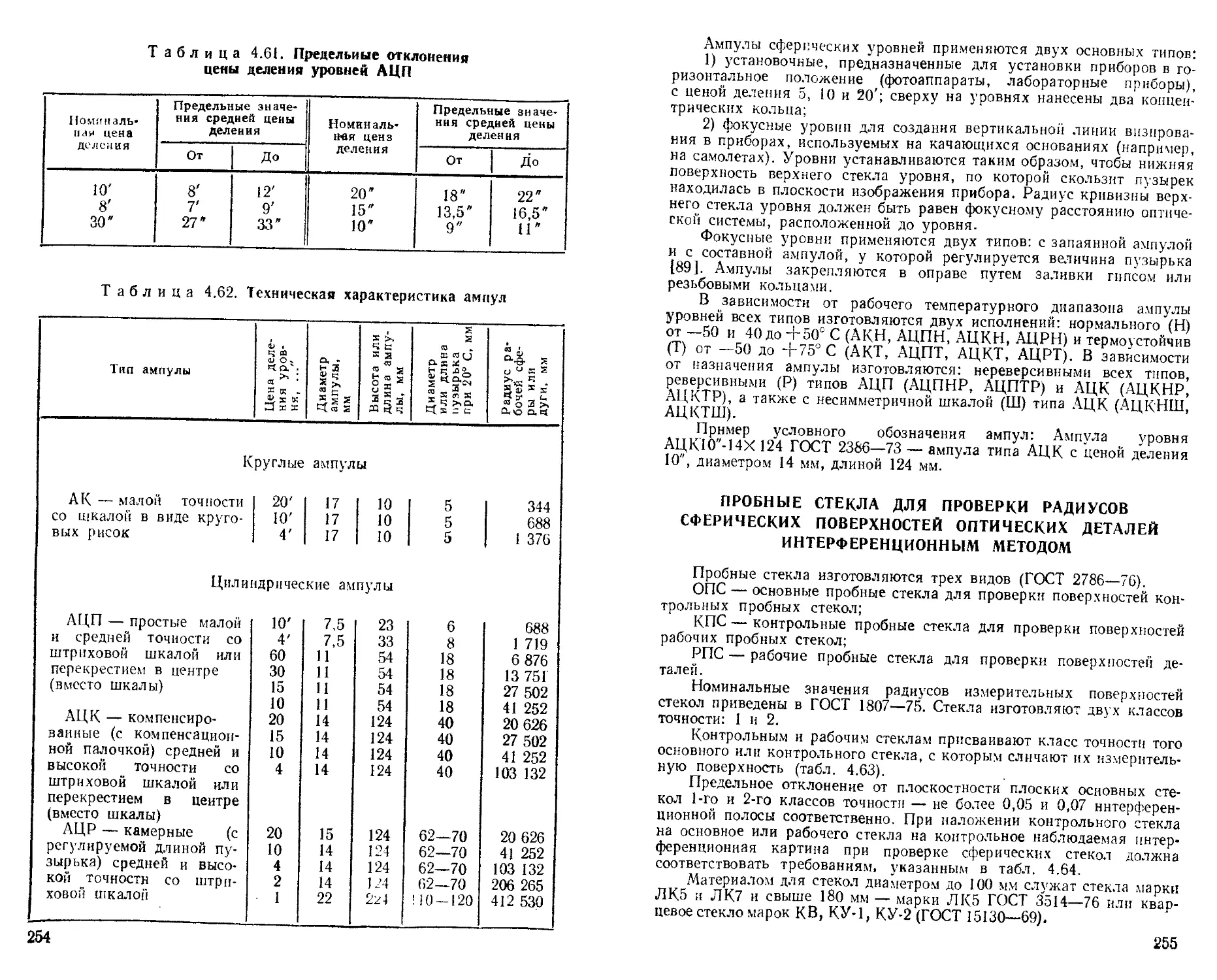
Уровни ..............................................
Пробные стекла для проверки радиусов сферических поверхностей оптических деталей интерференционным методом ...............................................
Допуски на чистоту поверхностей оптических деталей Глава 5. Крепление оптических деталей (Я. А. Михайлов)
Общие положения .....................................
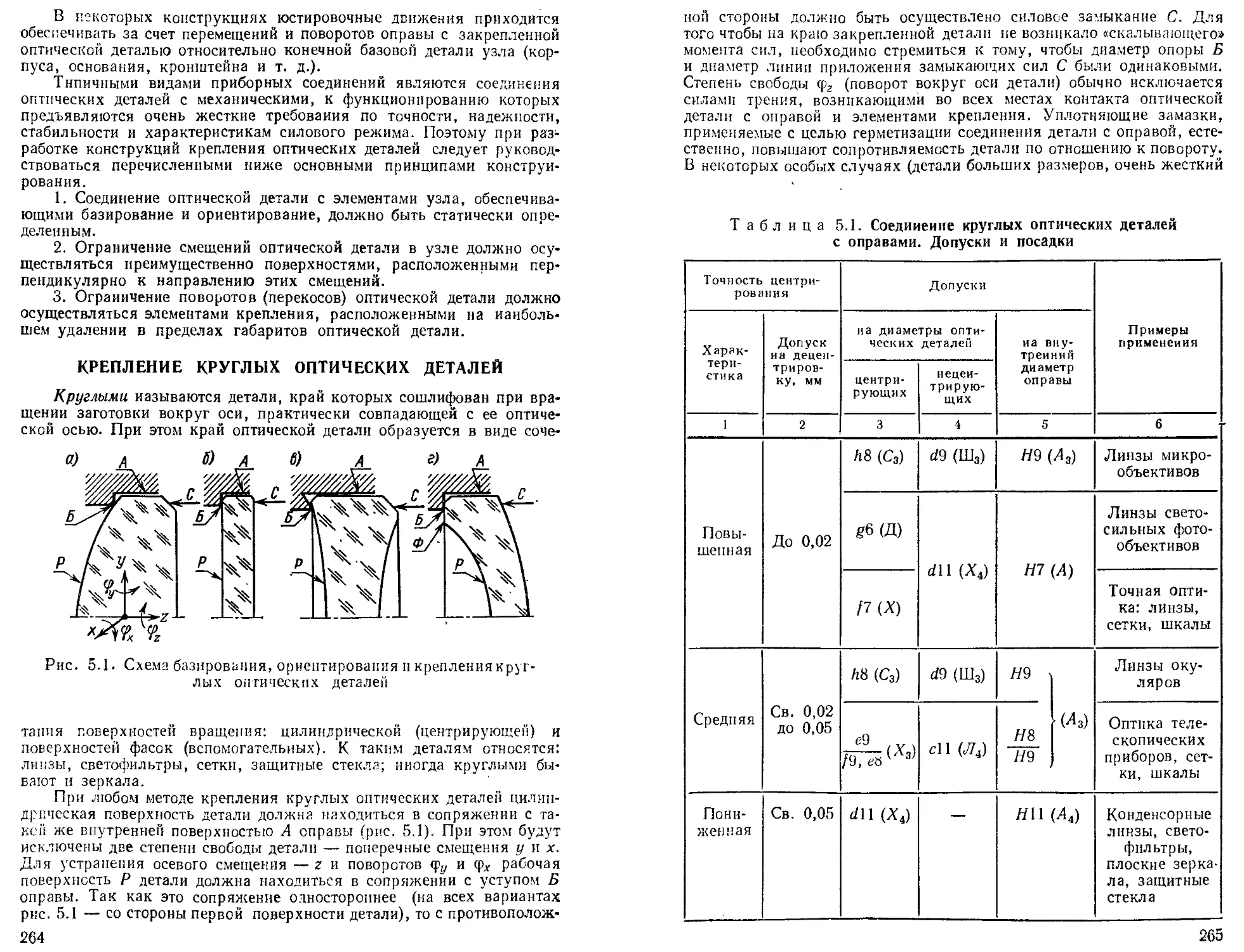
Крепление круглых оптических деталей.................
Крепление завальцовкой.............................
Крепление резьбовым кольцом........................
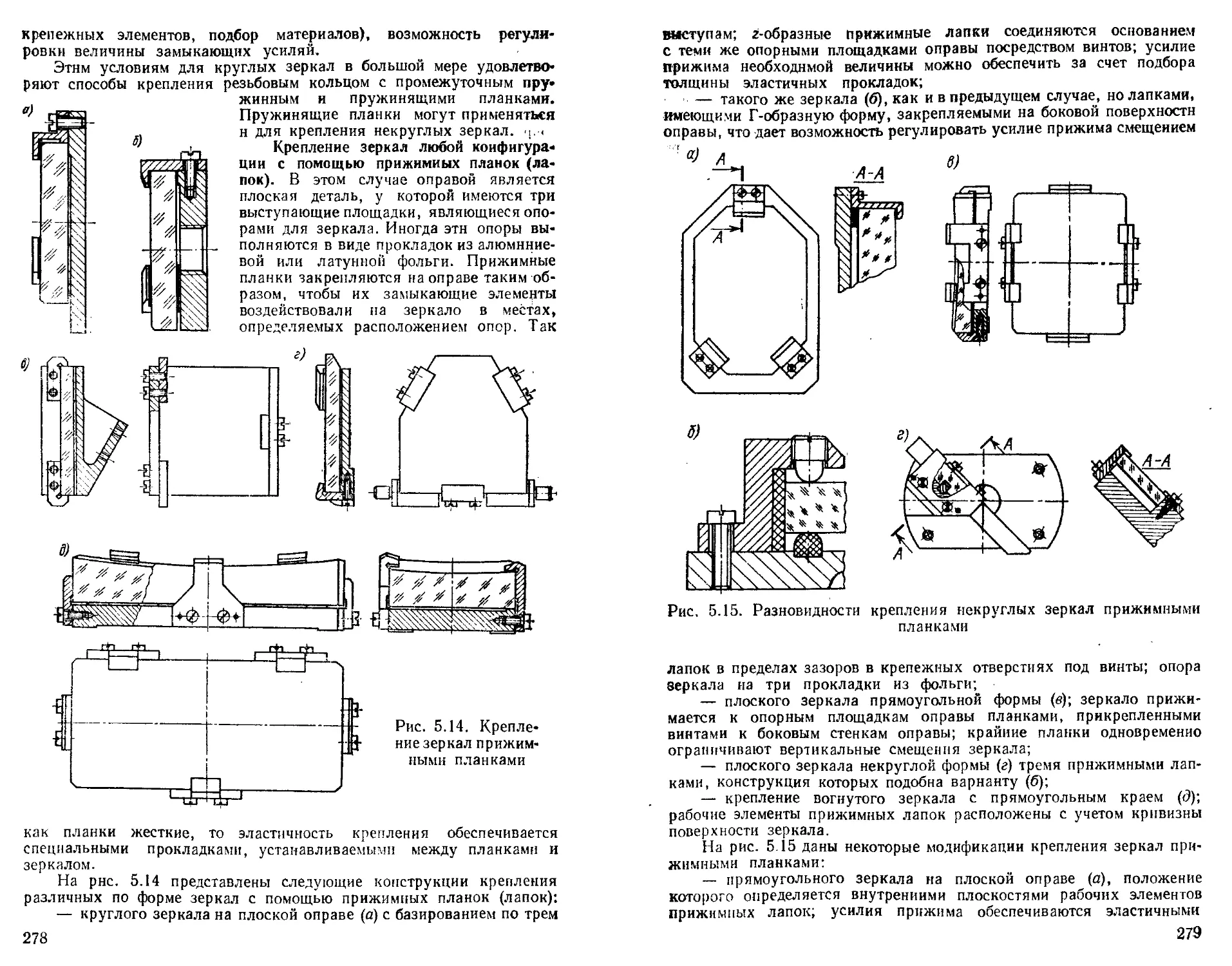
Крепление пружинящими планками ....................
Крепление проволочным кольцом .....................
Крепление приклеиванием ...................... . .
Крепление зеркал ....................................
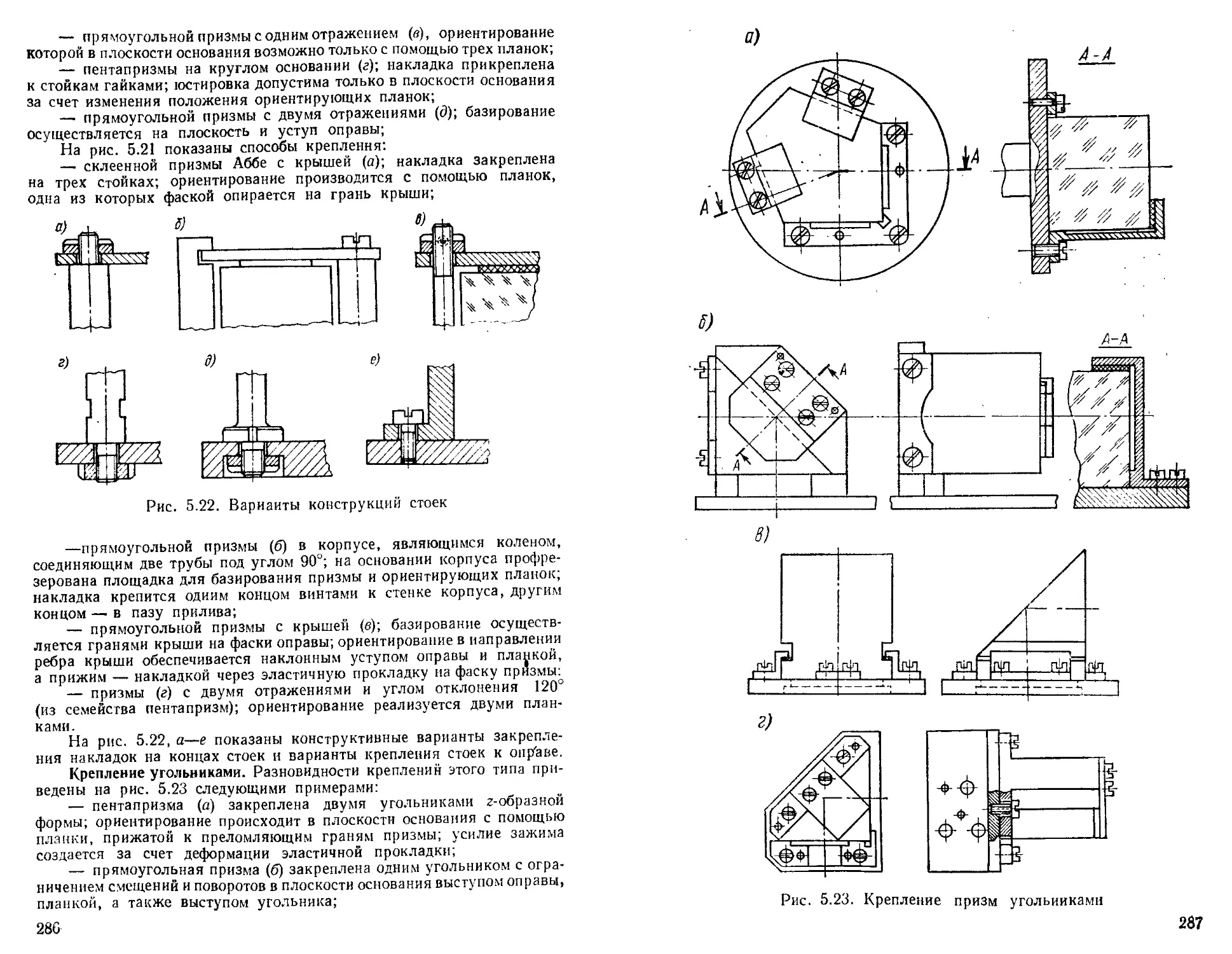
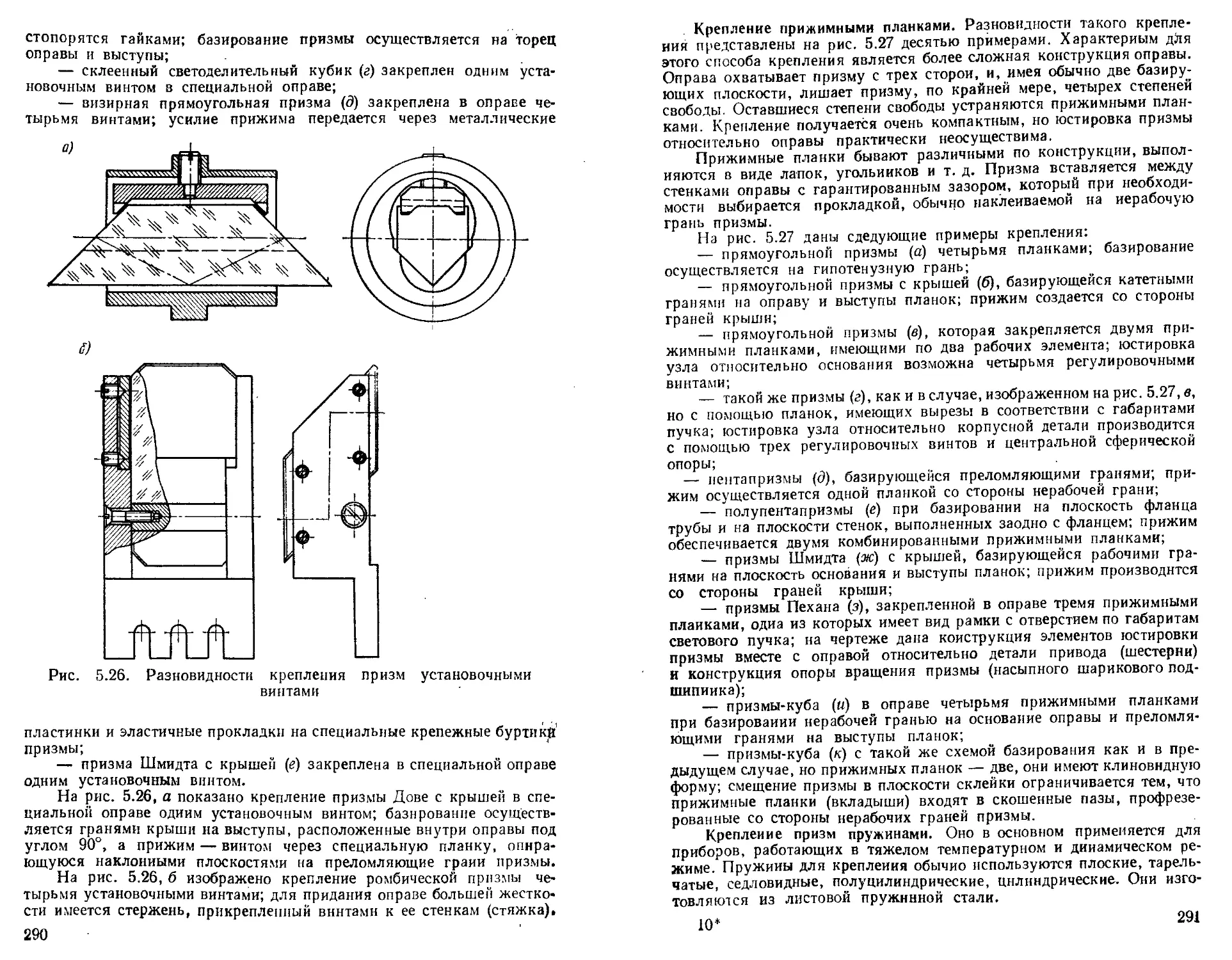
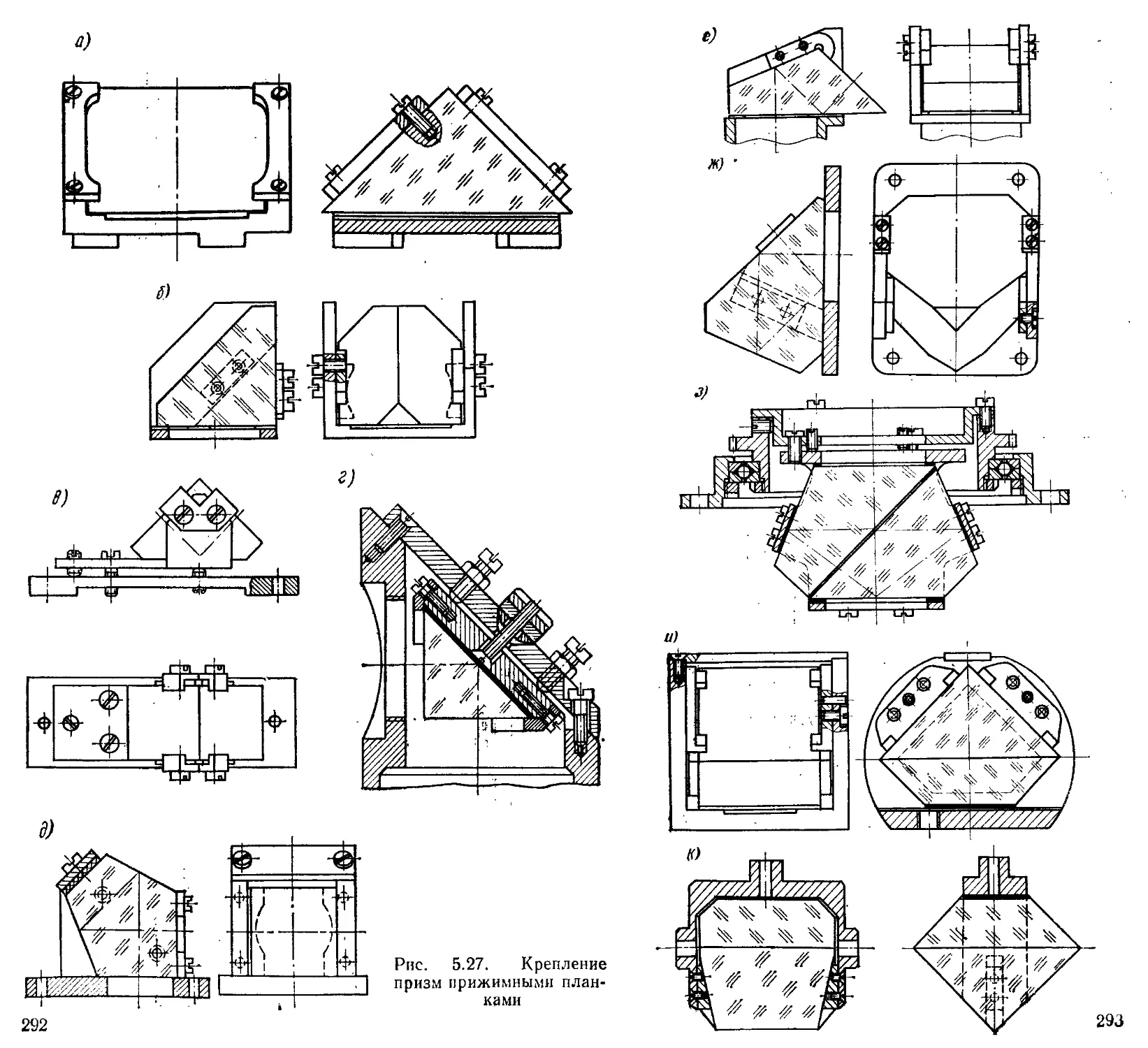
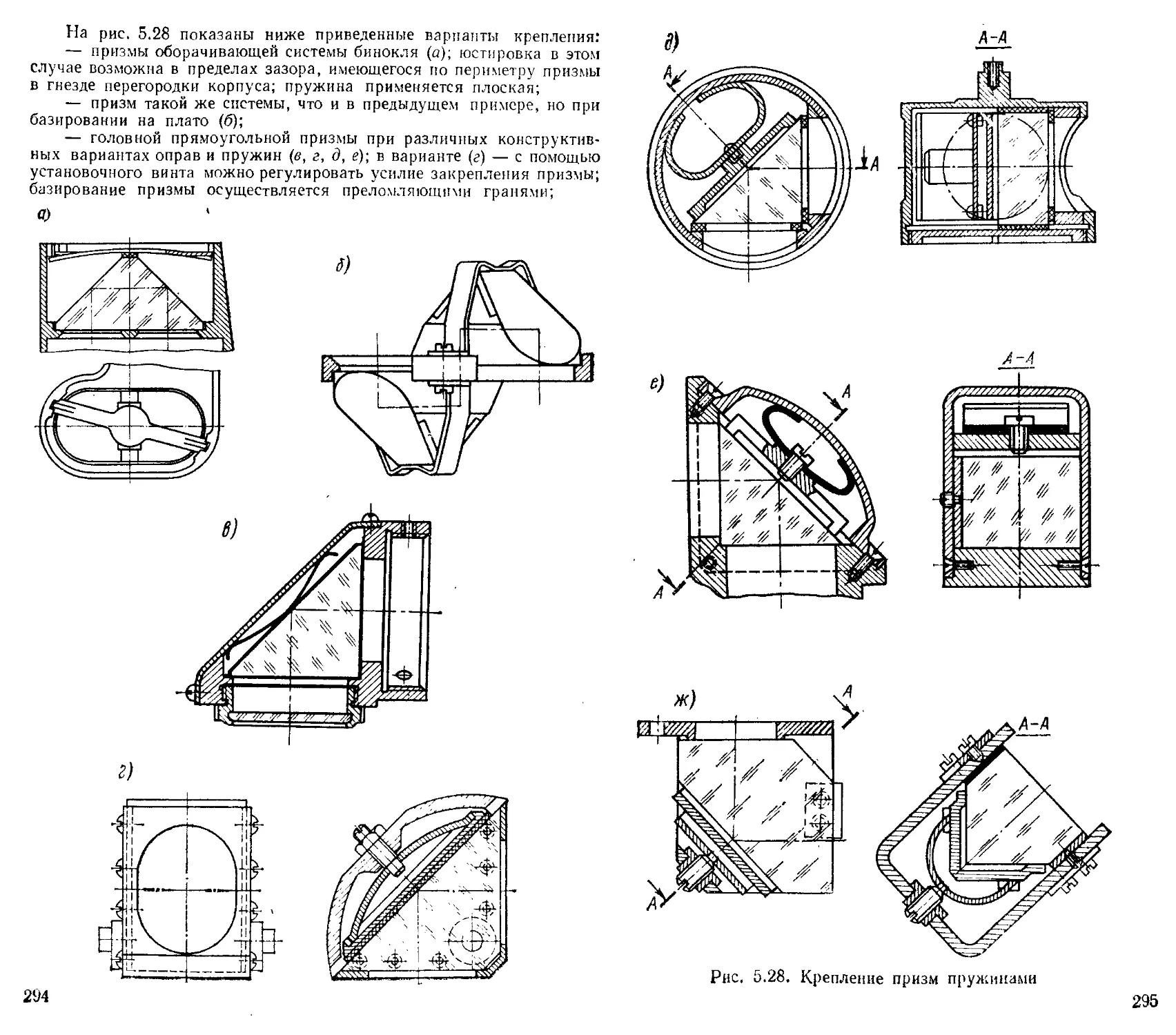
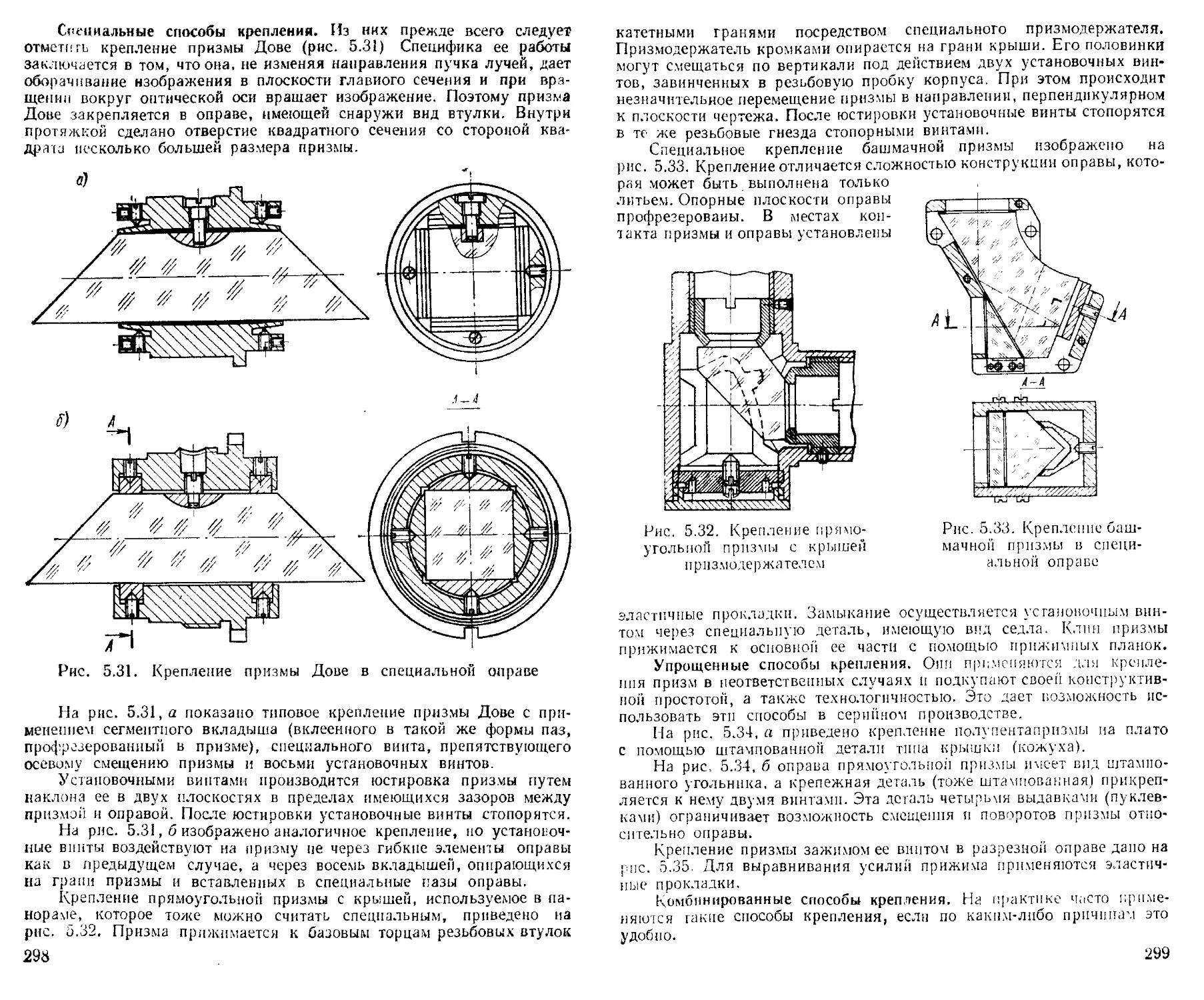
Крепление призм .....................................
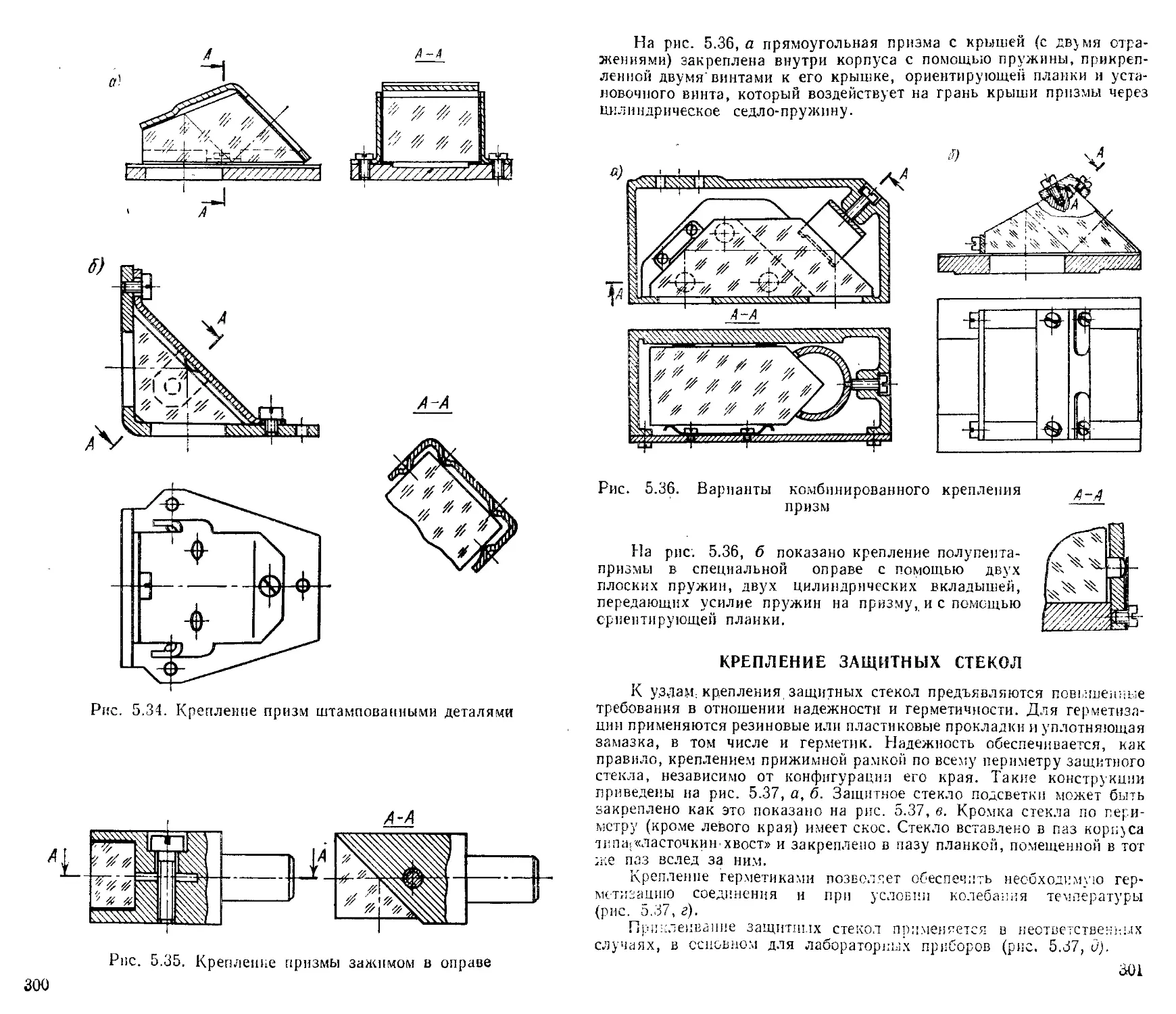
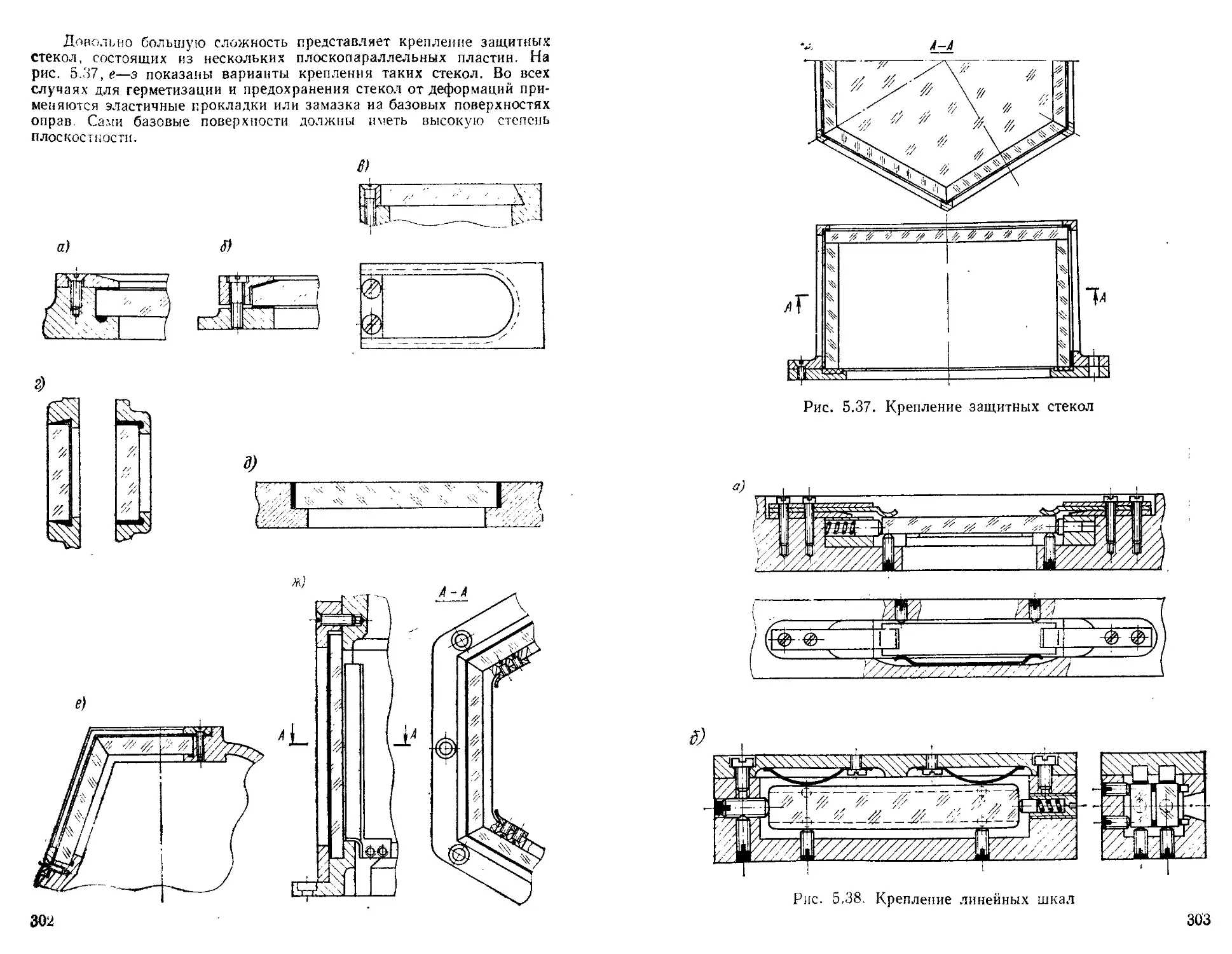
Крепление защитных стекол ...........................
Крепление линейных шкал .............................
Глава 6. Типовые конструкции оптико-мехаиических узлов (74. >7. Кругер, В. А. Панов, Р. М. Рагузин и И. М. Долинский) .......................................
188
190
192
193
194
198
201
202
206
207
209
210
211
212
214
215
216
217
218
219
220
• 221
231
244
250
252
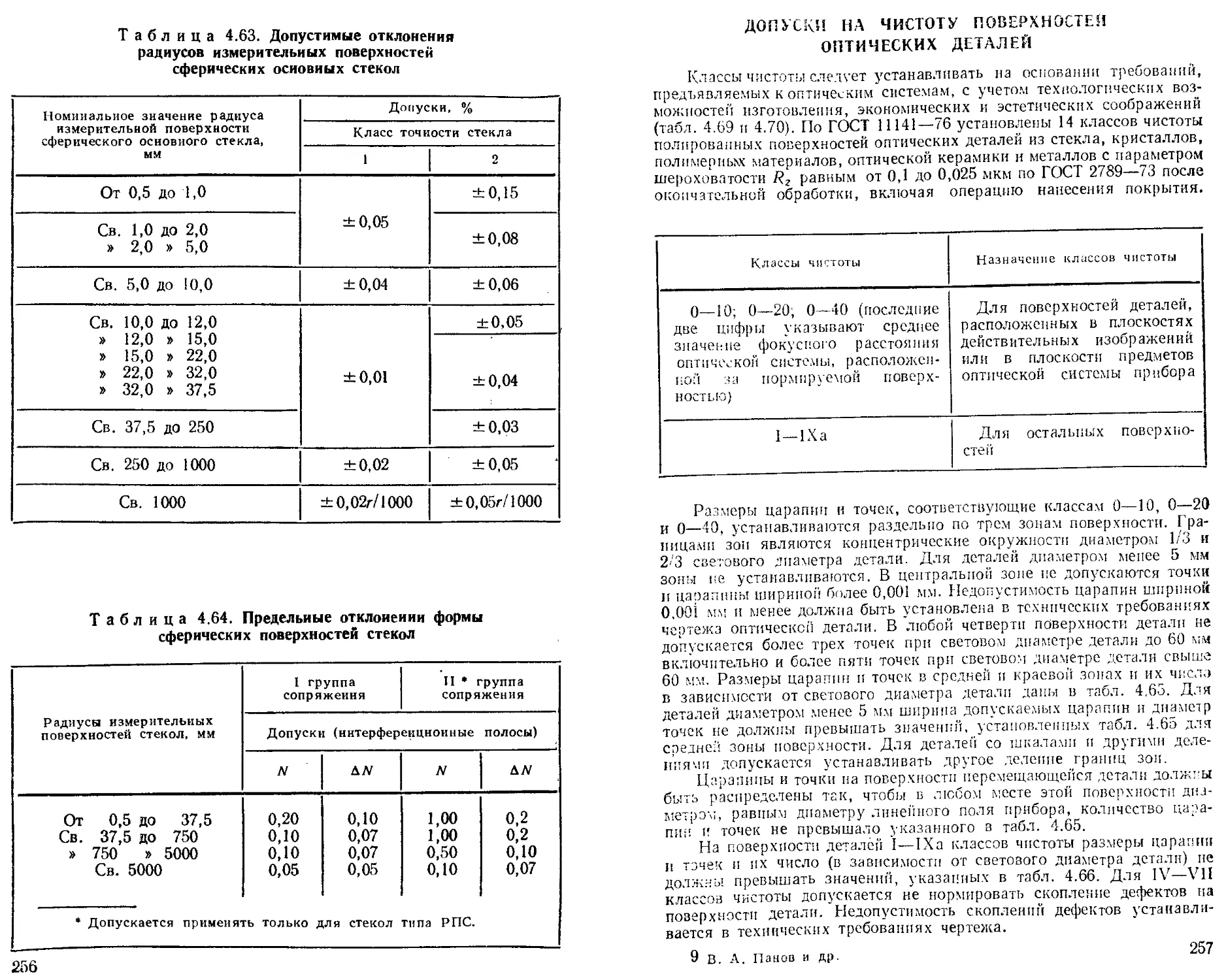
255
257
263
264
267
269
273
275
277
283
301
304
305
737
Узлы крепления защитных стекол ..................... 305
Системы визирования ................................ —
Объективы телескопических приборов ................. 311
Зеркально-линзовые объективы ....................... 312
-> Фото- и кинообъективы .............................. 313
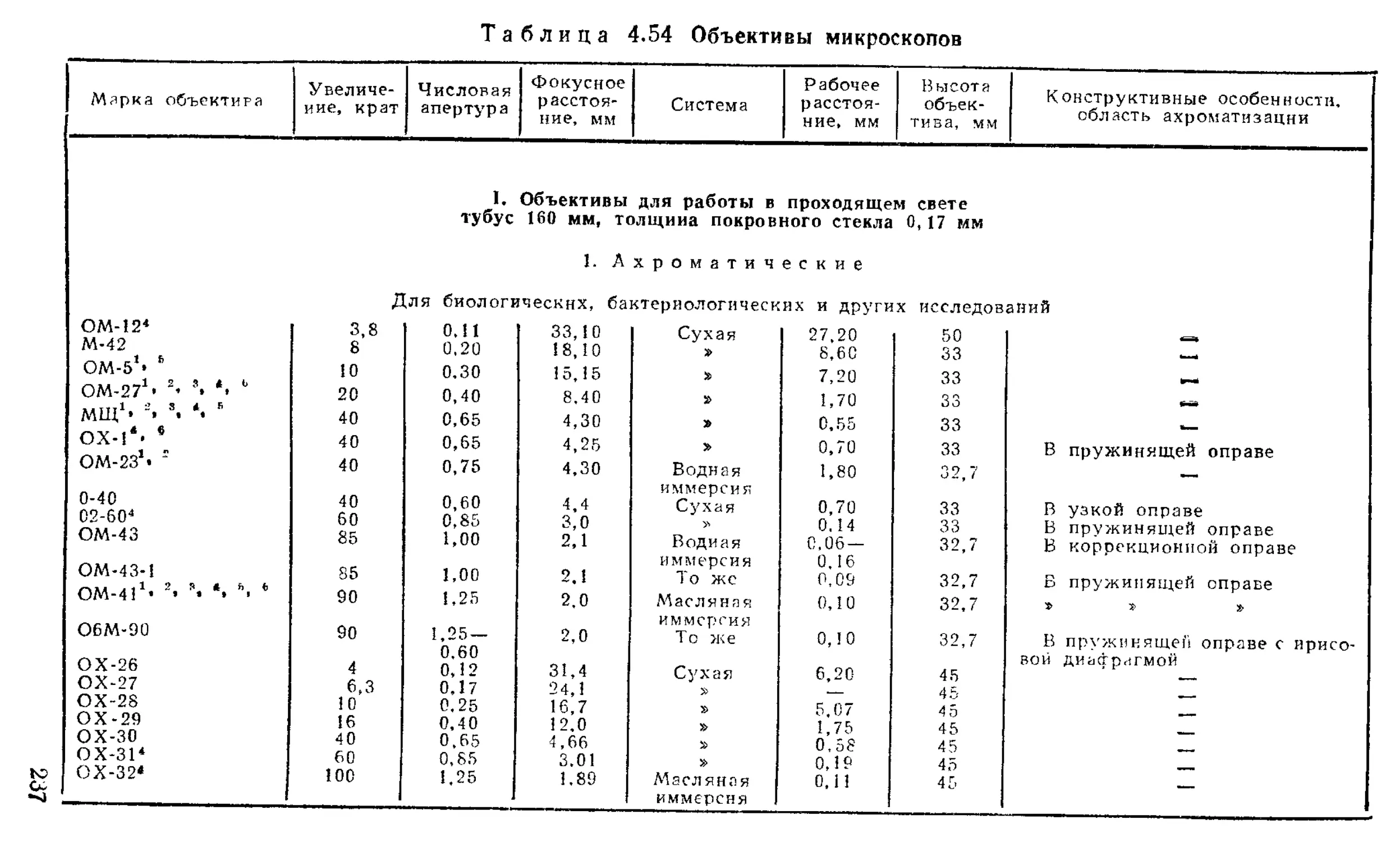
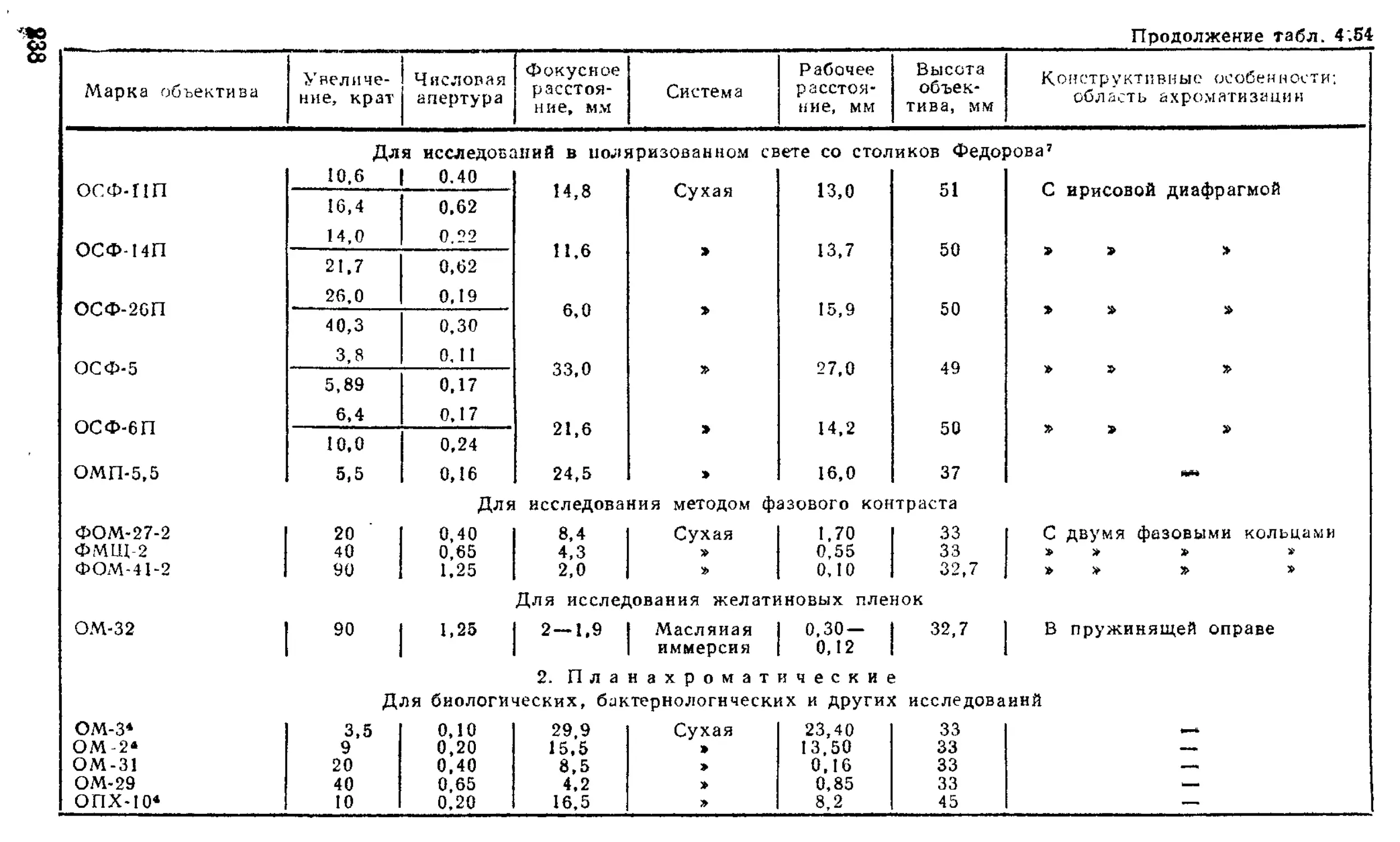
Микрообъективы ..................................... 316
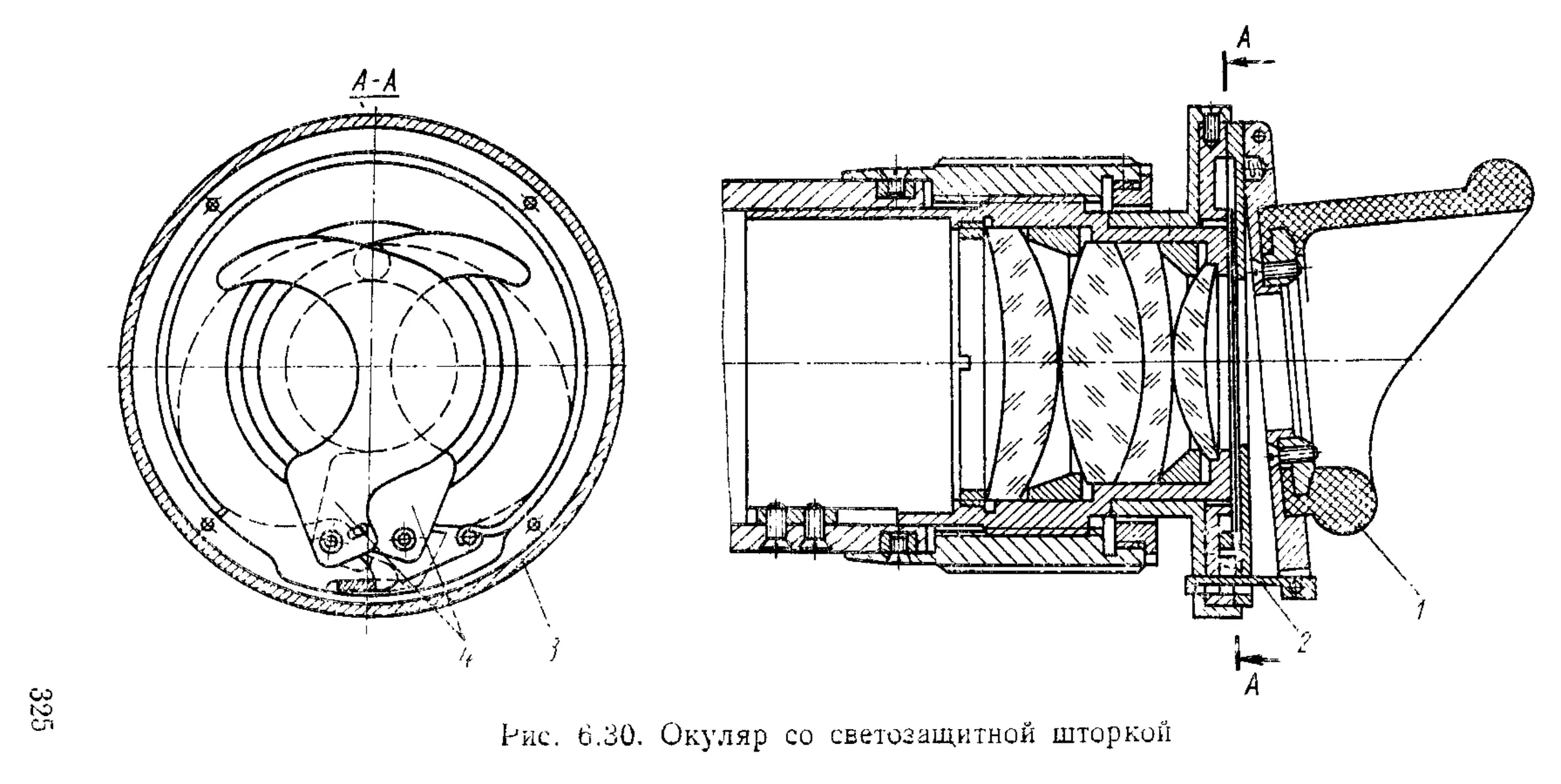
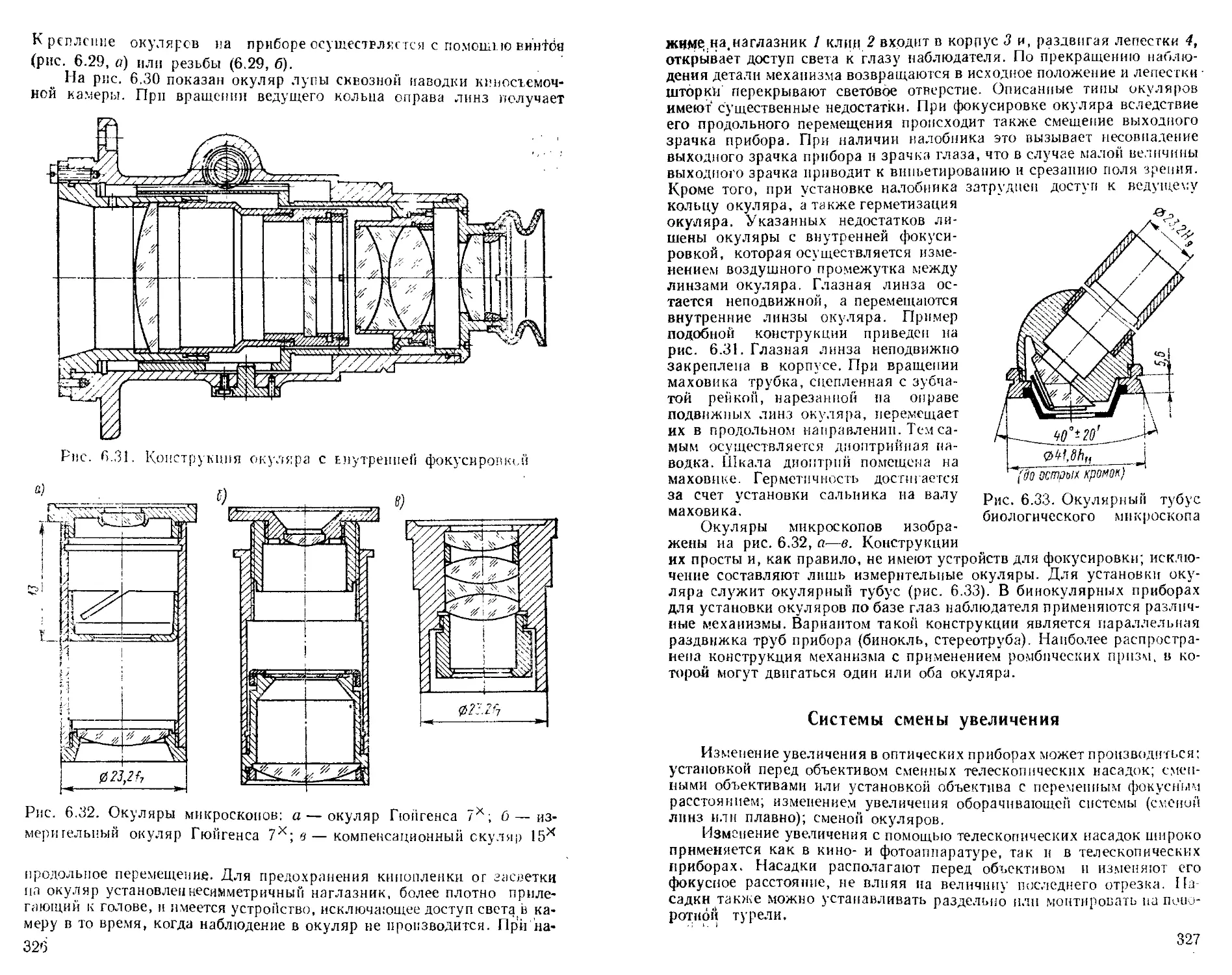
Окуляры............................................. 320
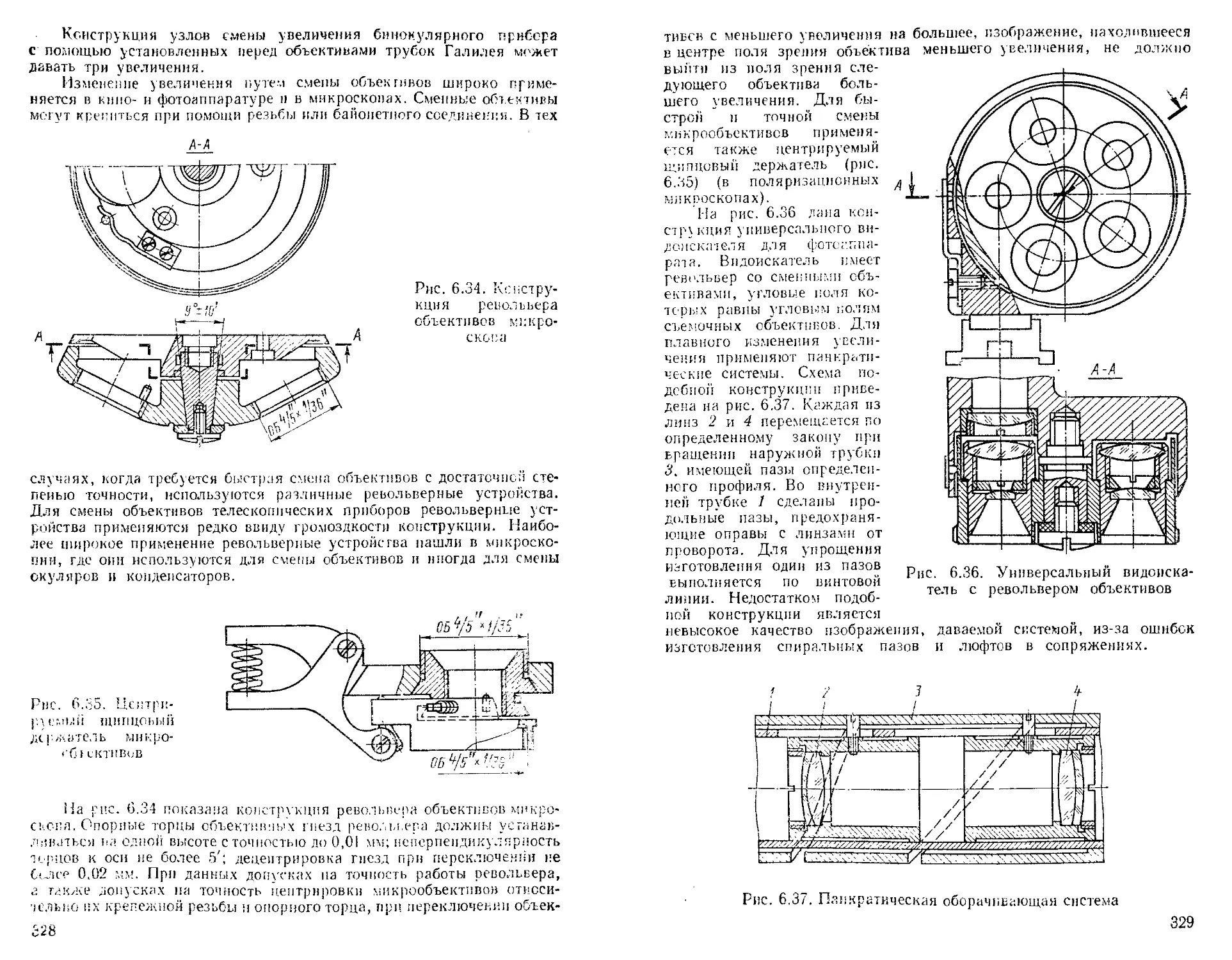
Системы смены увеличении ........................... 327
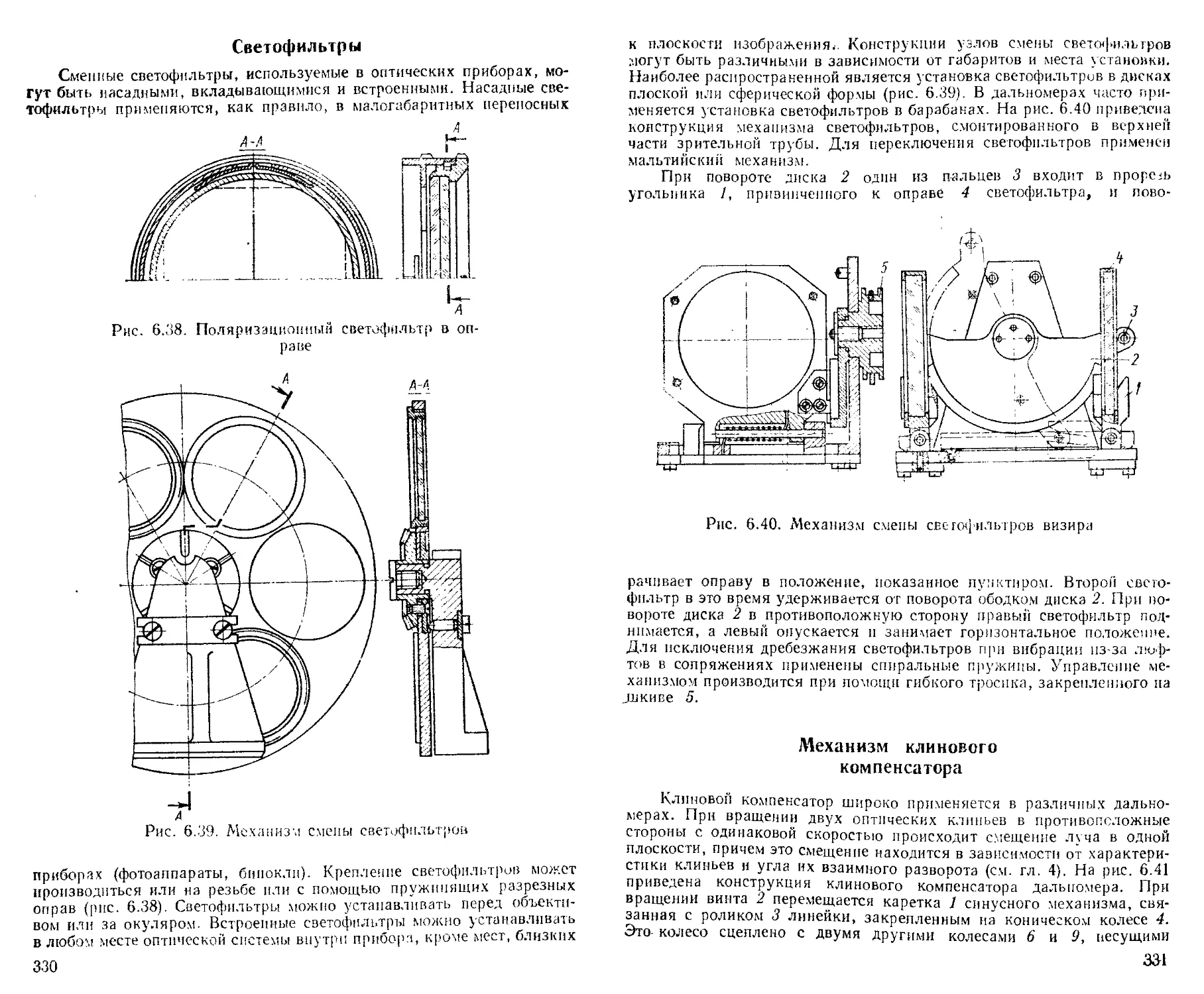
Светофильтры........................................ 330
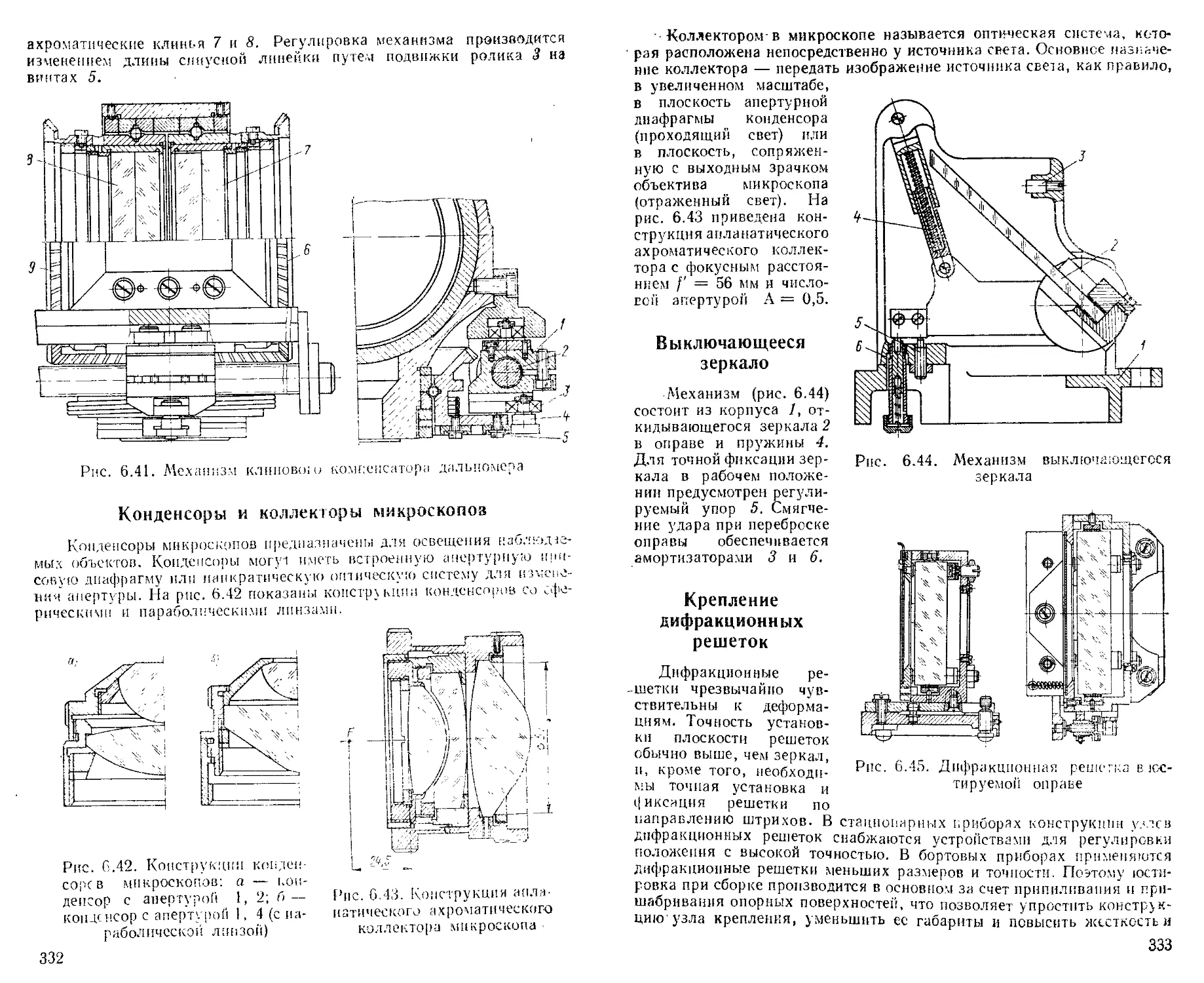
Механизм клинового компенсатора.................... 331
Коиденторы и коллекторы микроскопов................. 332
Выключающееся зеркало............................... 333
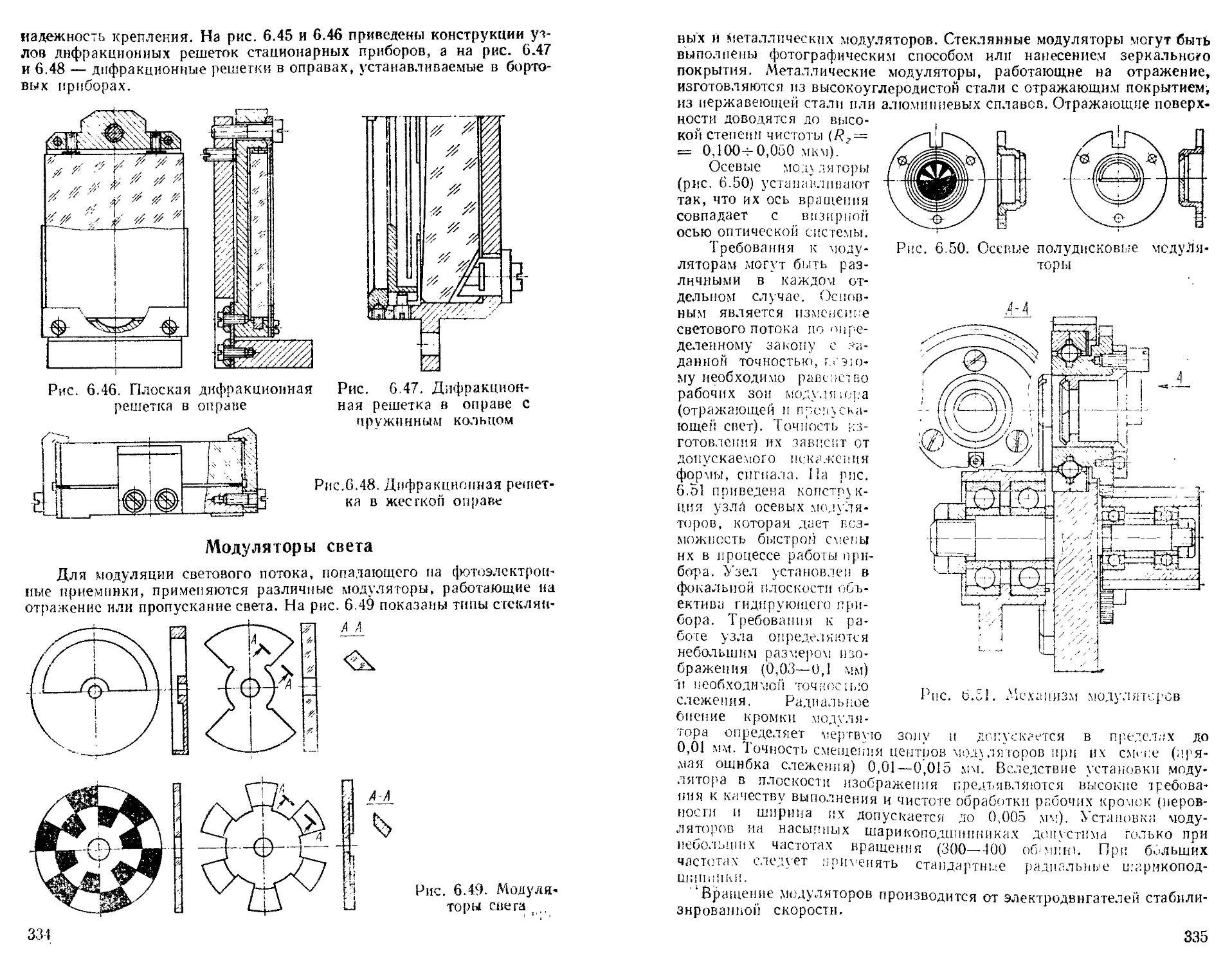
Крепление дифракционных решеток .................. '' —
Модуляторы света.................................... 334
Фокусировочиые механизмы ........................... 336
Глава 7. Диафрагмы, щели, бленды, наглазники и налобники (М. Д. Кругер, Б. Г, Резницкий, В. А. Панов) 338
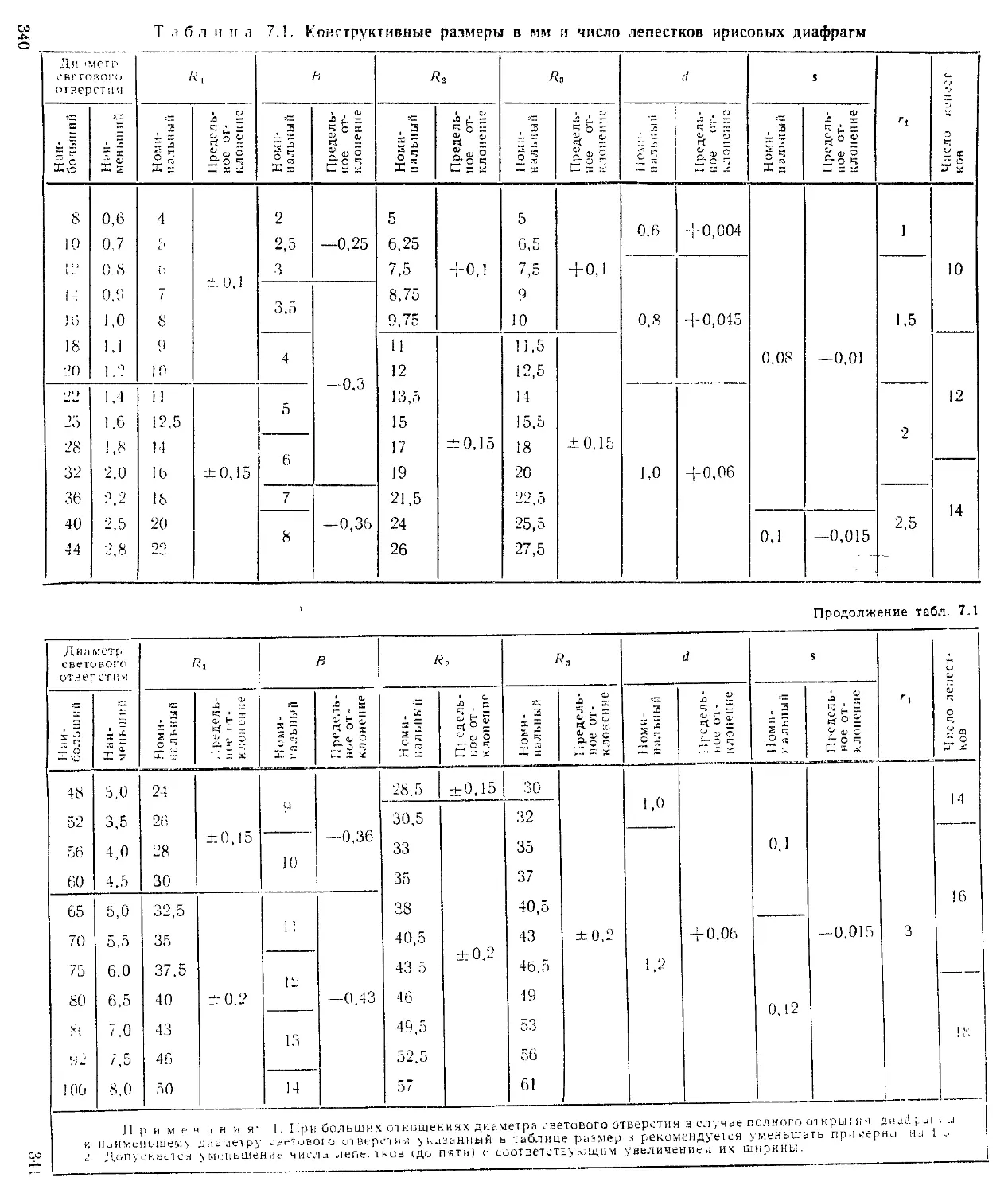
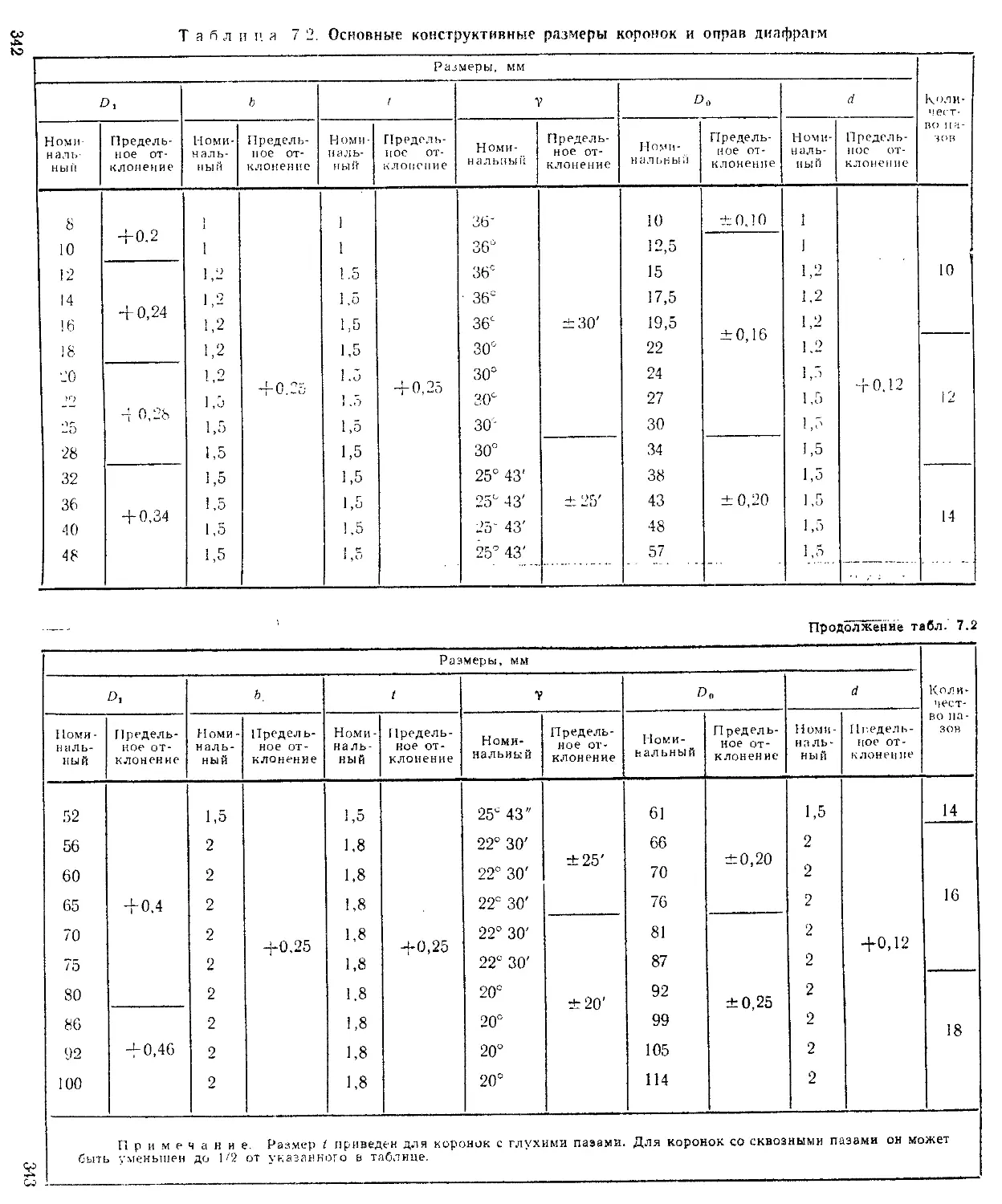
Диафрагмы............................................... —
Расчет ирисовых диафрагм ...................... . 345
Щелевые диафрагмы................................... 346
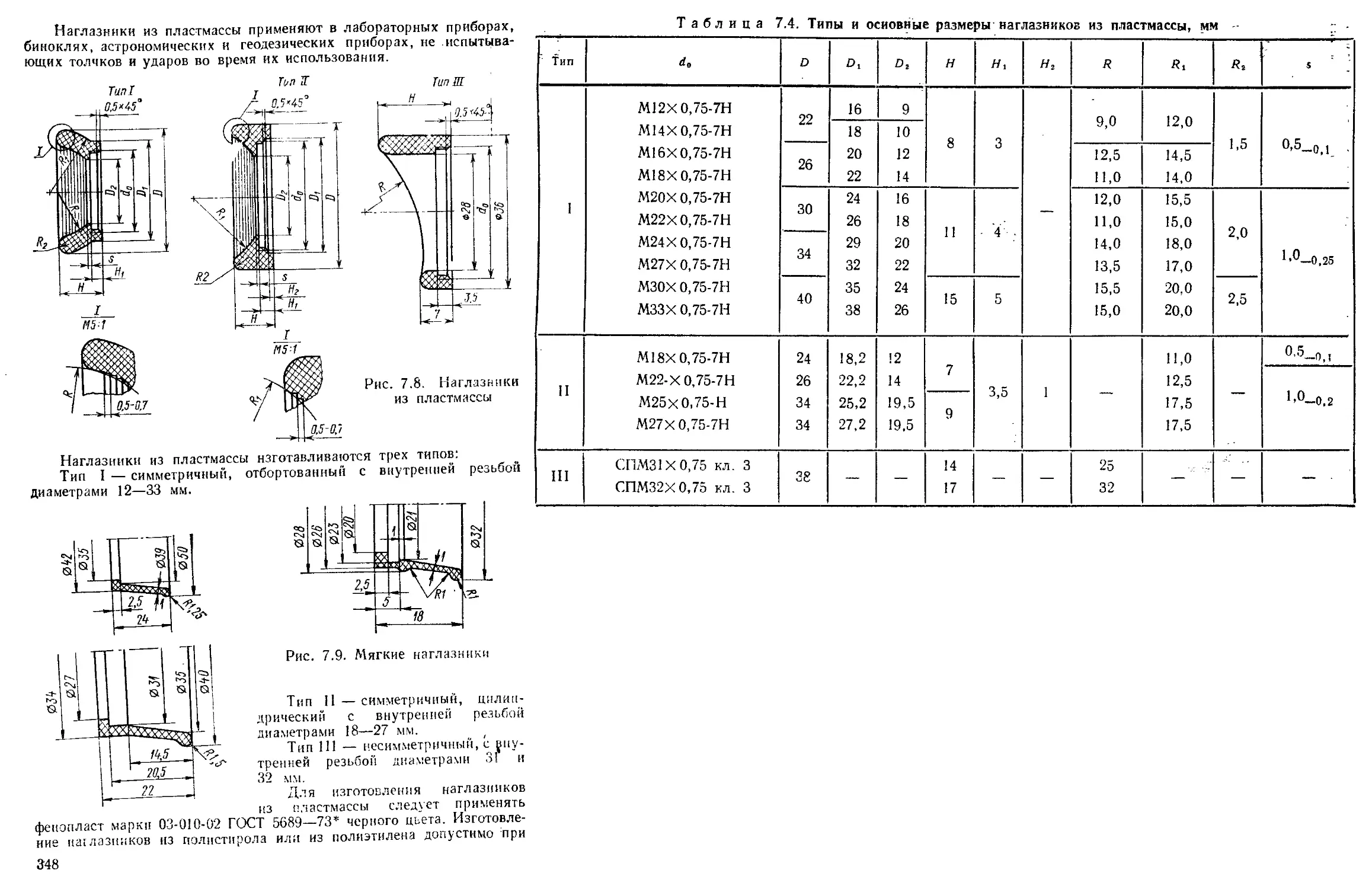
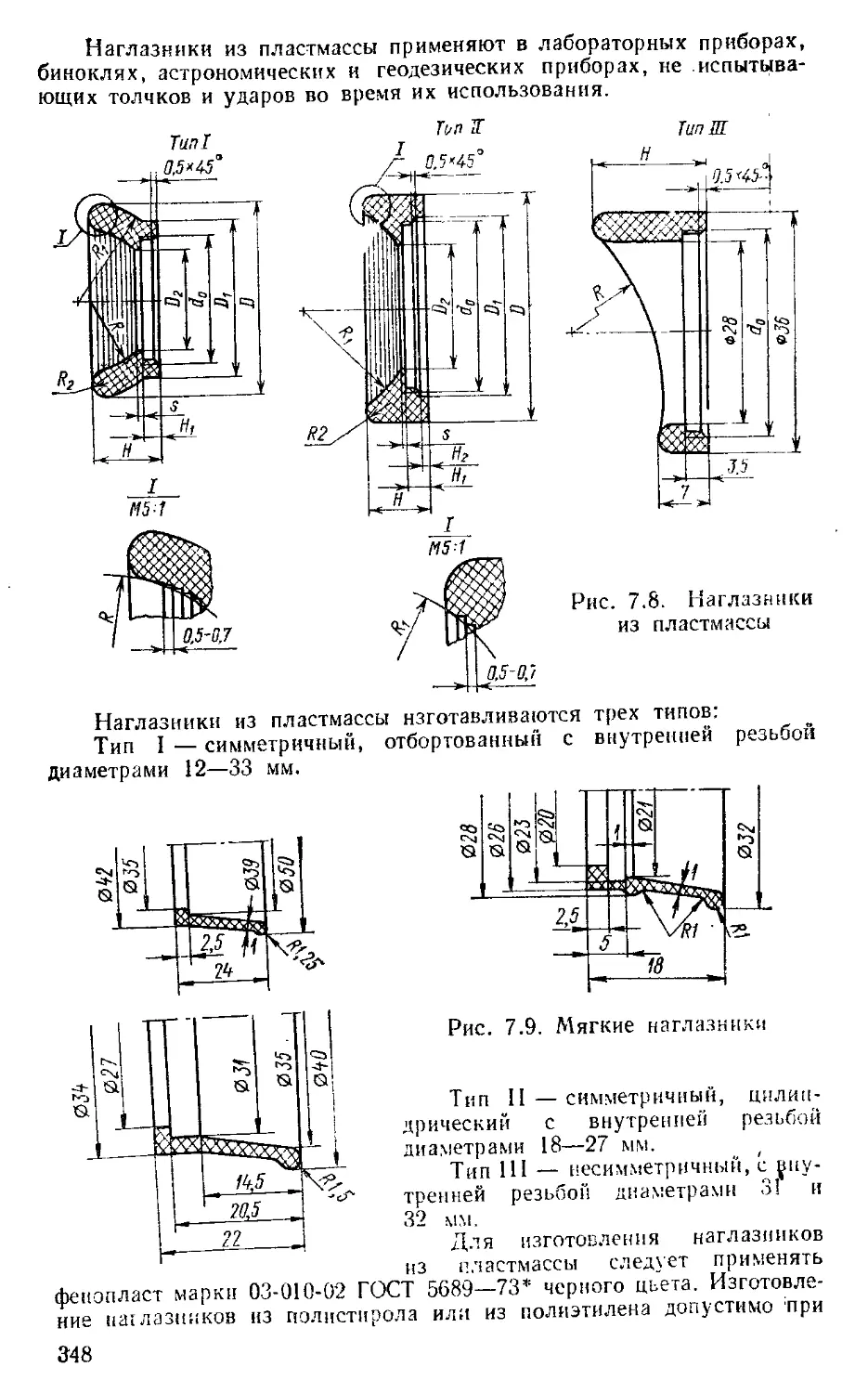
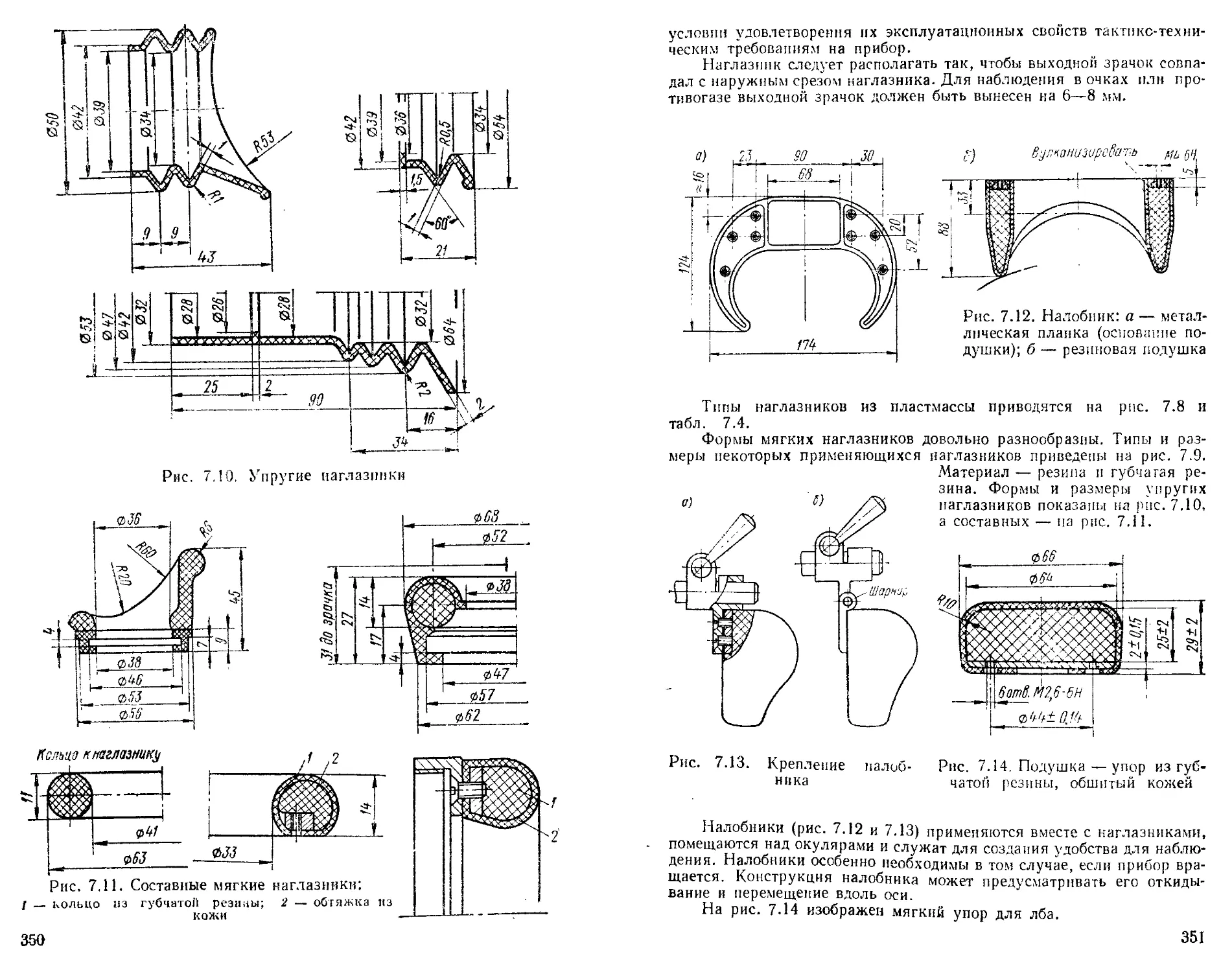
Наглазники и налобники ............................... 347
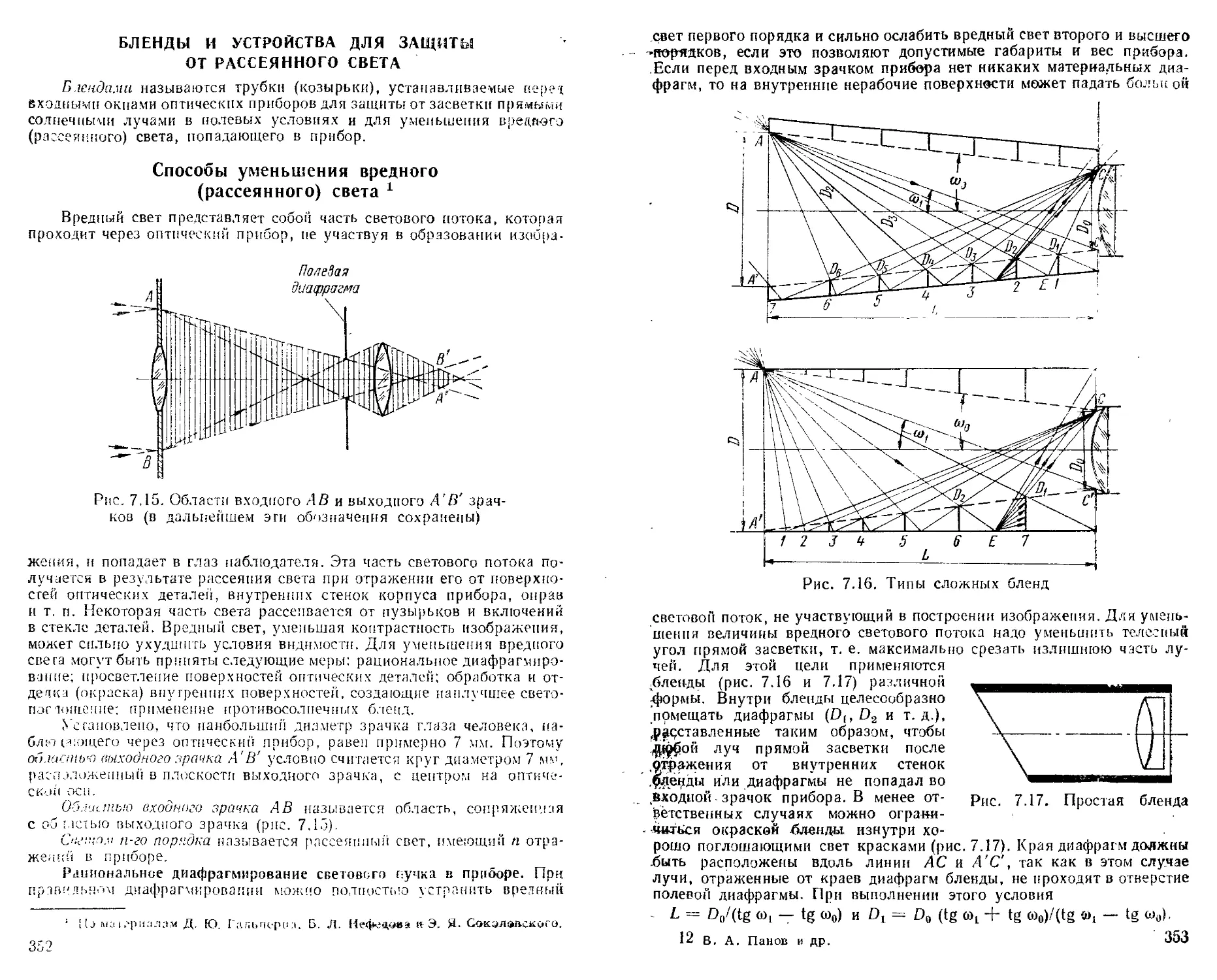
v Бленды и устройства для защиты от рассеянного света . . 352
Способы уменьшения вредного (рассеянного) света ... —
Глава 8. Расчет допусков на изготовление и сборку оптических деталей, узлов и приборов (Г. В. Погарев) 357
Критерии оценки качества изображения и допуски на дефекты оптической, системы.......................... 358
Расчет допусков на оптические поверхности и детали, перпендикулярные оси системы......................* 362
Расчет допусков на наклонные оптические поверхности н пластинки ........................................ 365
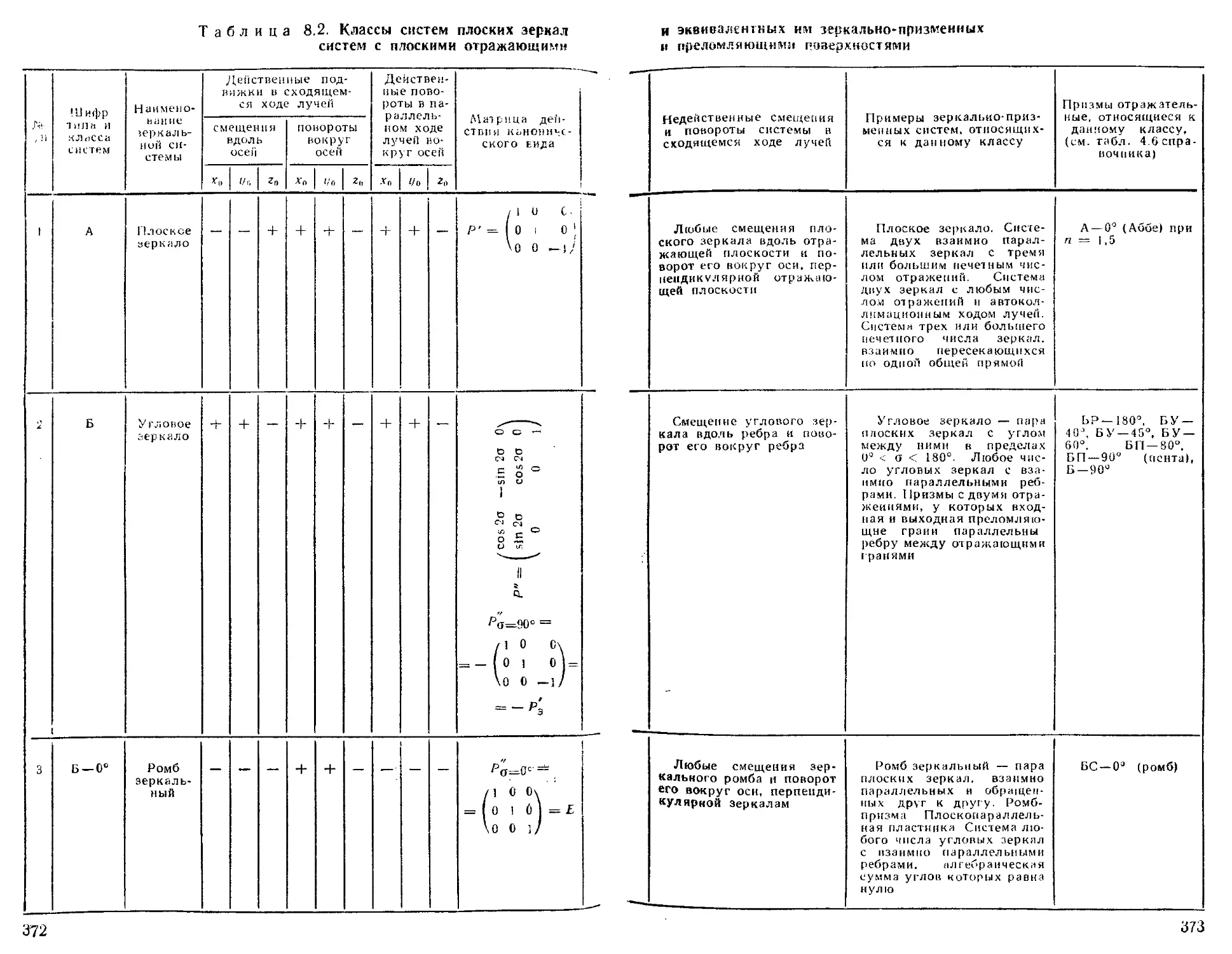
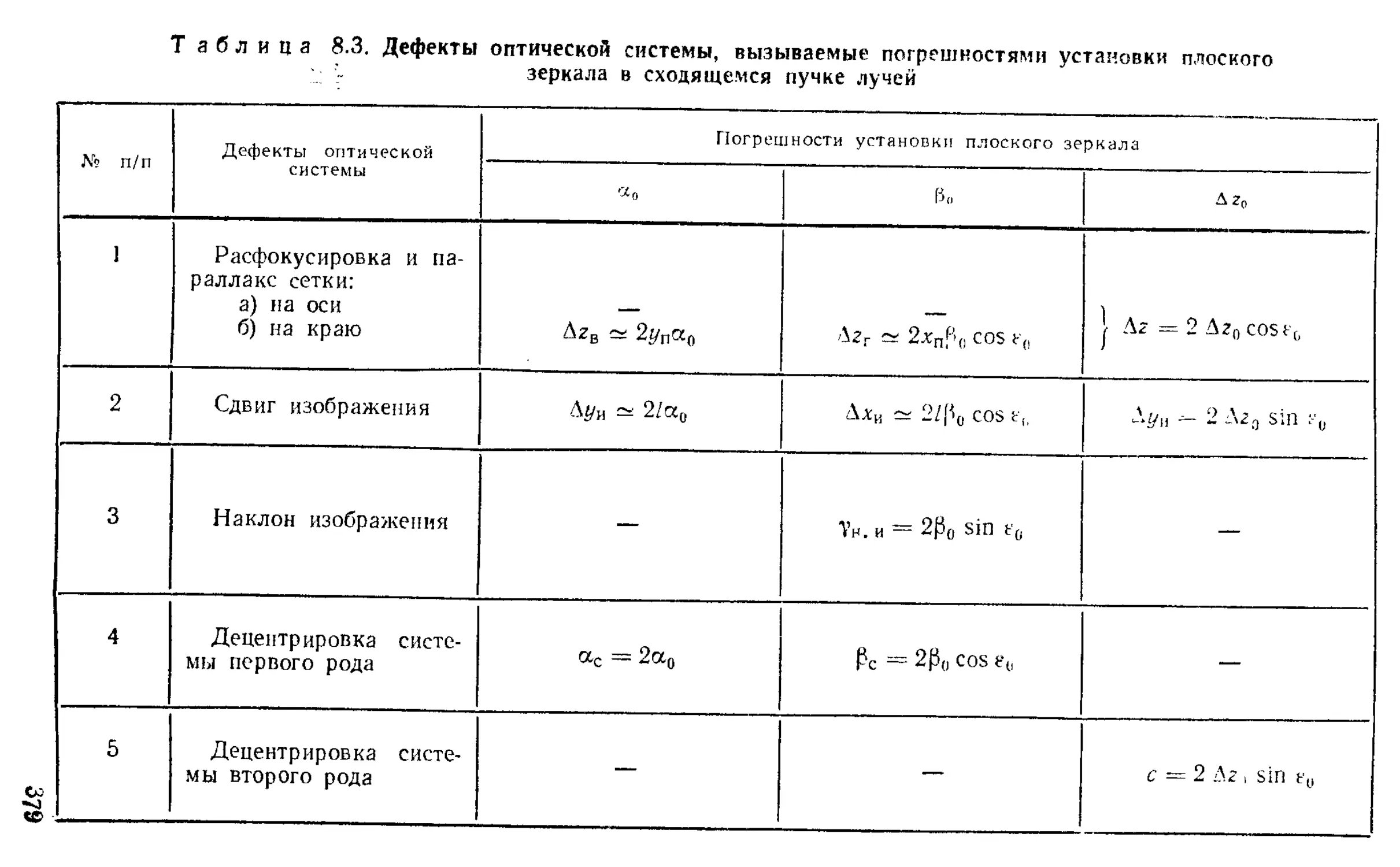
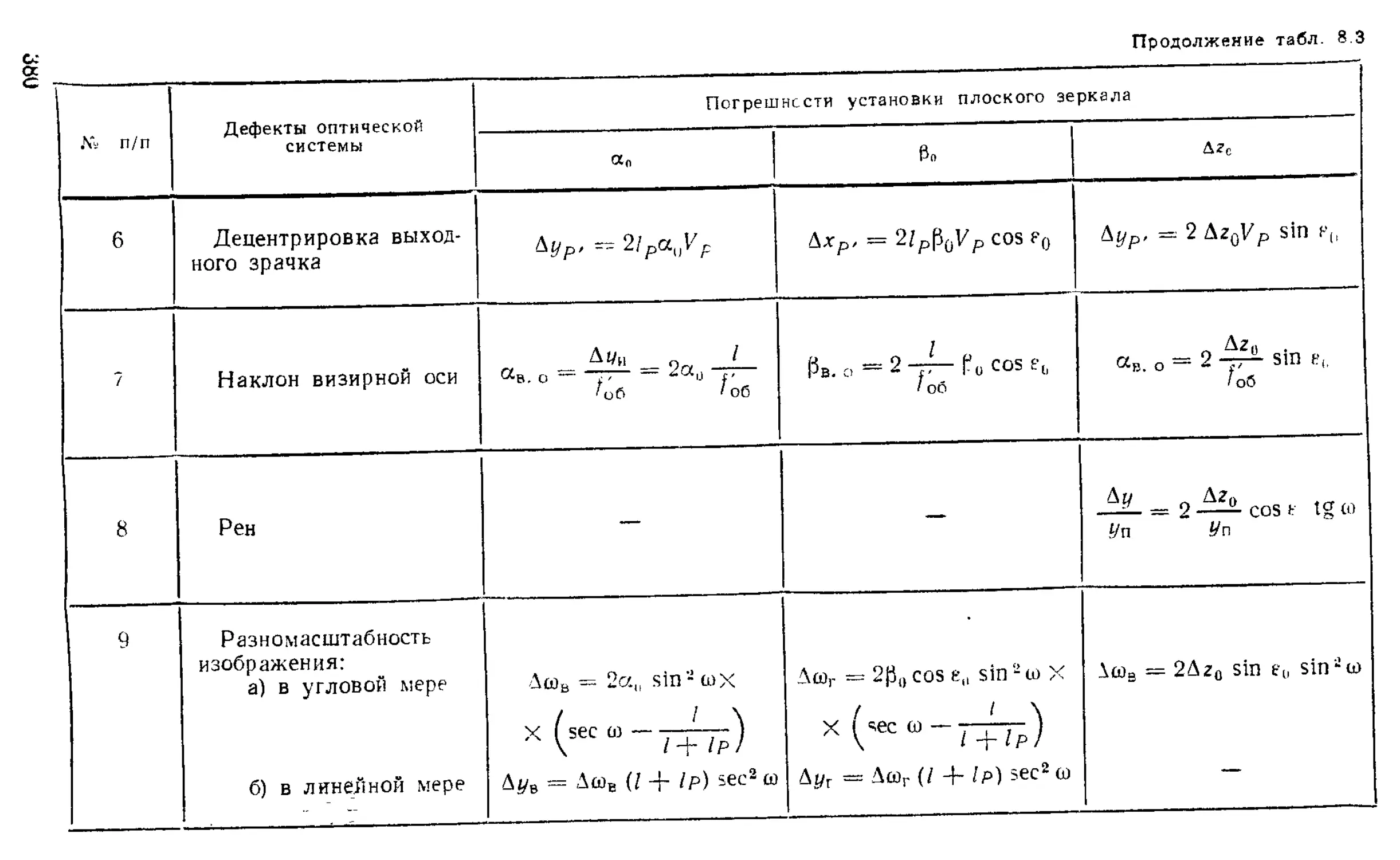
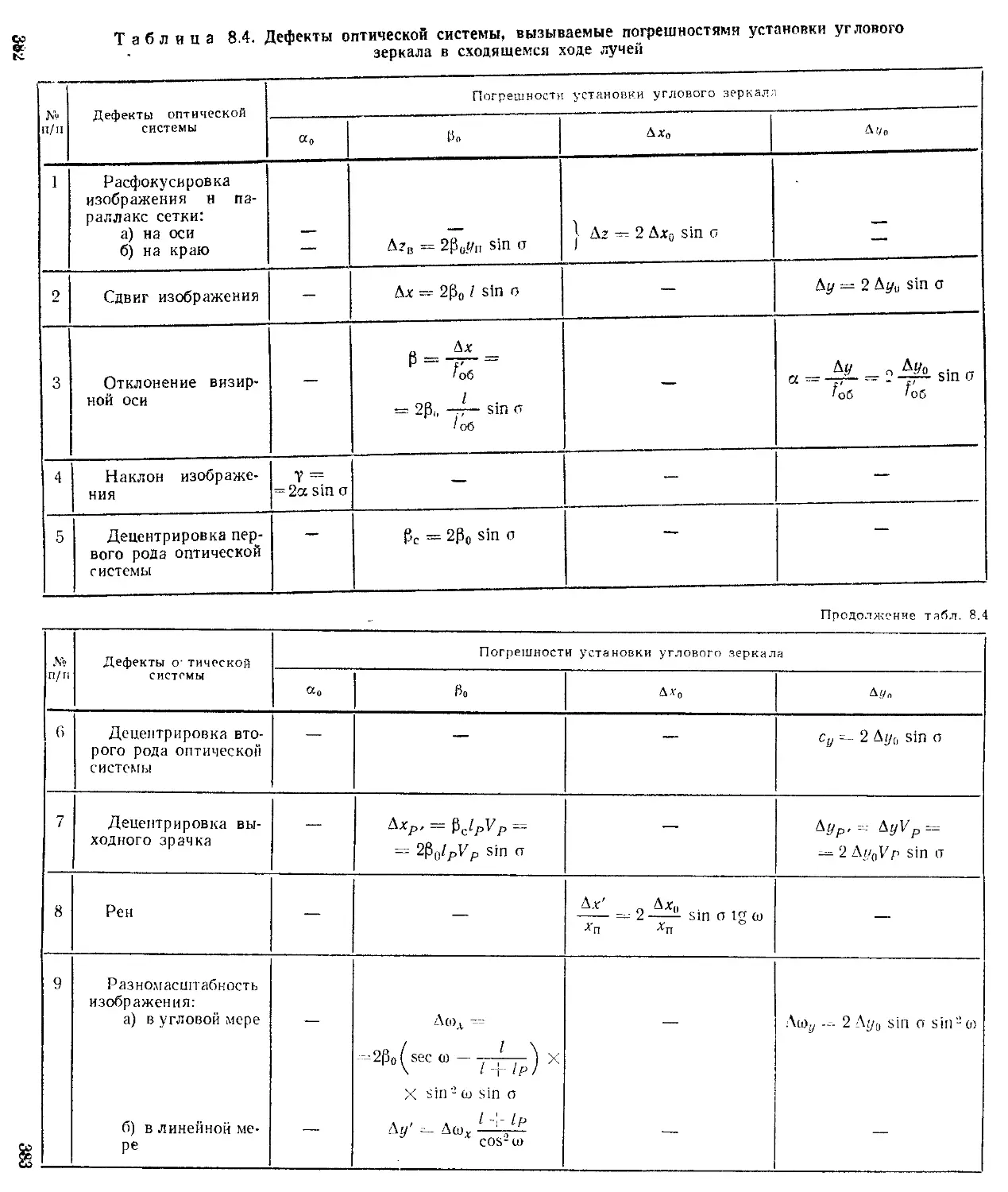
Влияние смещений и поворотов зеркально-призменных систем на положение н ориентировку изображения . . . 367
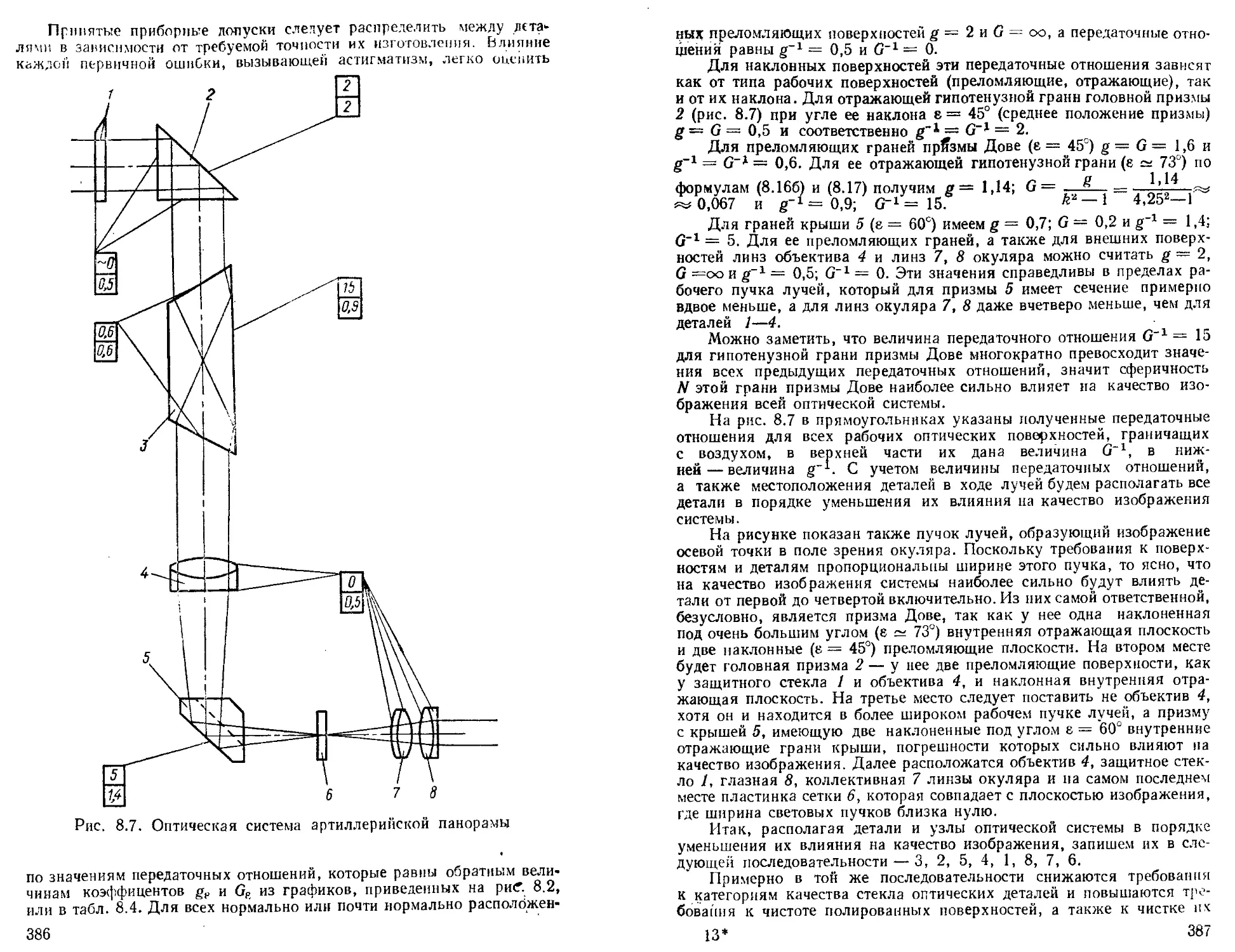
Расчет допусков на оптические детали с учетом требований к точности функционирования и к сборке приборов 376 Пример расчета допусков на оптические детали артиллерийской панорамы ................................. 385
Глава 9. Методика структурного анализа механизмов приборов (И. М. Долинский)............................ 396
Общие сведения ......................................... —
Основные определения ................................. —
Избыточные связи и местные подвижности в механизме 398
Методика структурного анализа ......................... 399
Определение общего числа подвижностей в кинематических парах анализируемого механизма и числа контуров в нем .............................................. 401
Таблица для структурного анализа механизмов ... —
Структурный анализ механизмов с упругими звеньями 406
Структурный анализ неподвижных соединений .... 407
Рекомендации по нзложенной методике................. 413
Глава 10. Расчет и конструирование подвижных систем оп-
тических приборов (В. В. Кулагин)............ 414
Механические системы оптических приборов.......... —
Механизмы подвижных систем оптических приборов ' (ПСОП) ..............................................
Замечания к проектированию механизмов ПСОП . . . . 420
Характеристики точности механизмов ПСОП ...... 423
Причины и виды ошибок механизмов .................... 424
Определение ошибок механизмов ....................... 428
Расчетные формулы ошибок механизмов ................. 431
Расчеты на точность при проектировании (виды расчетов, исходные данные н условия) ..................... 435
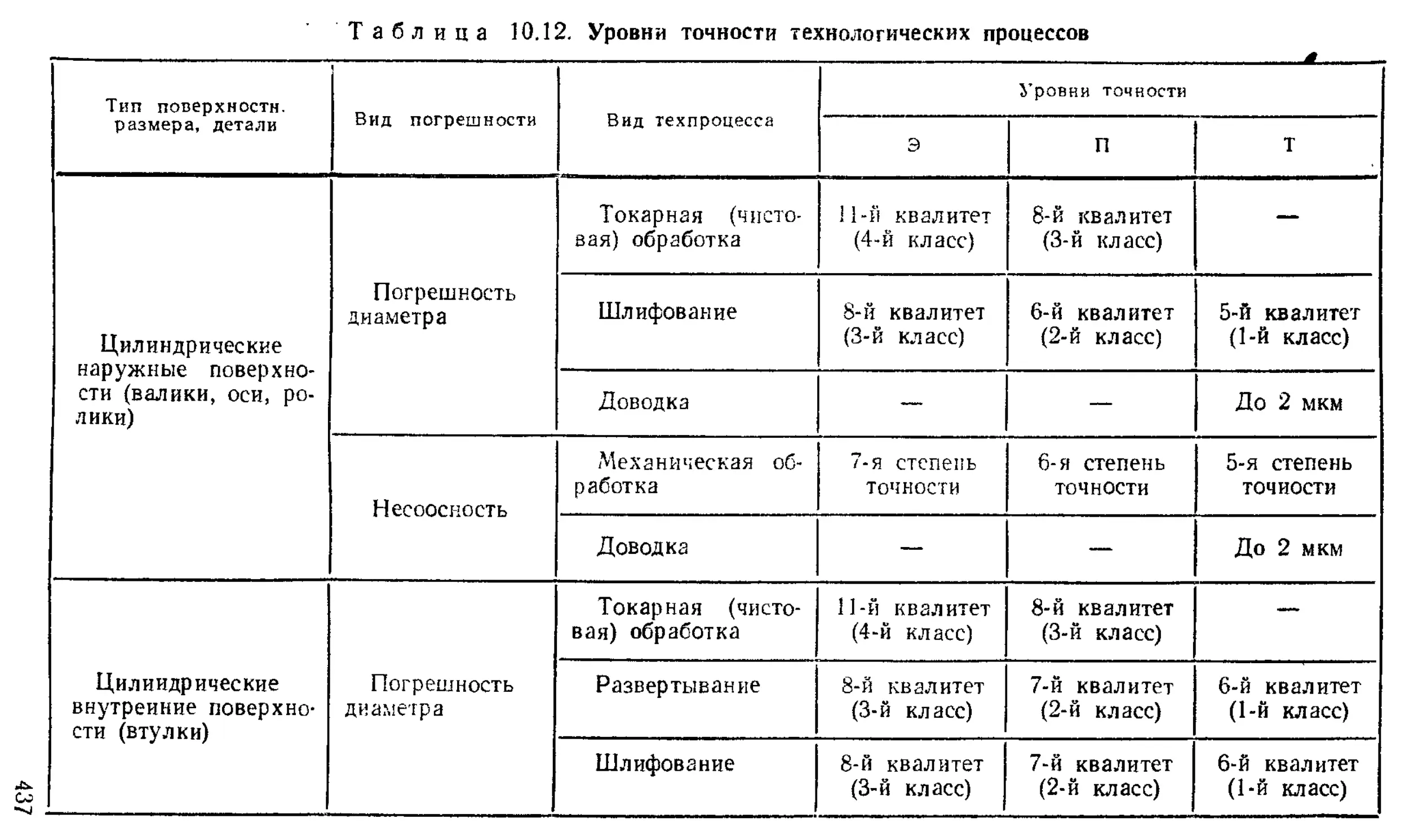
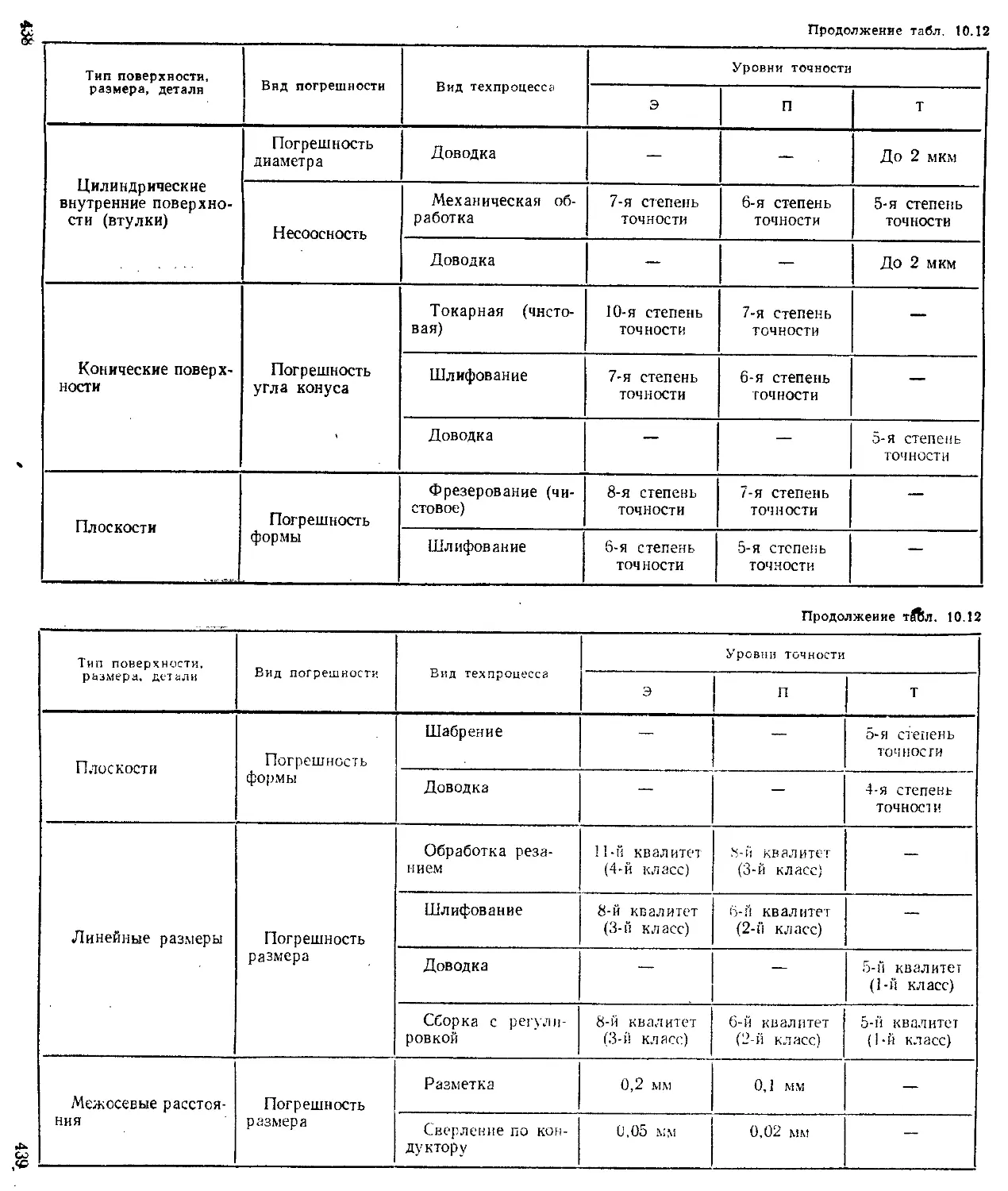
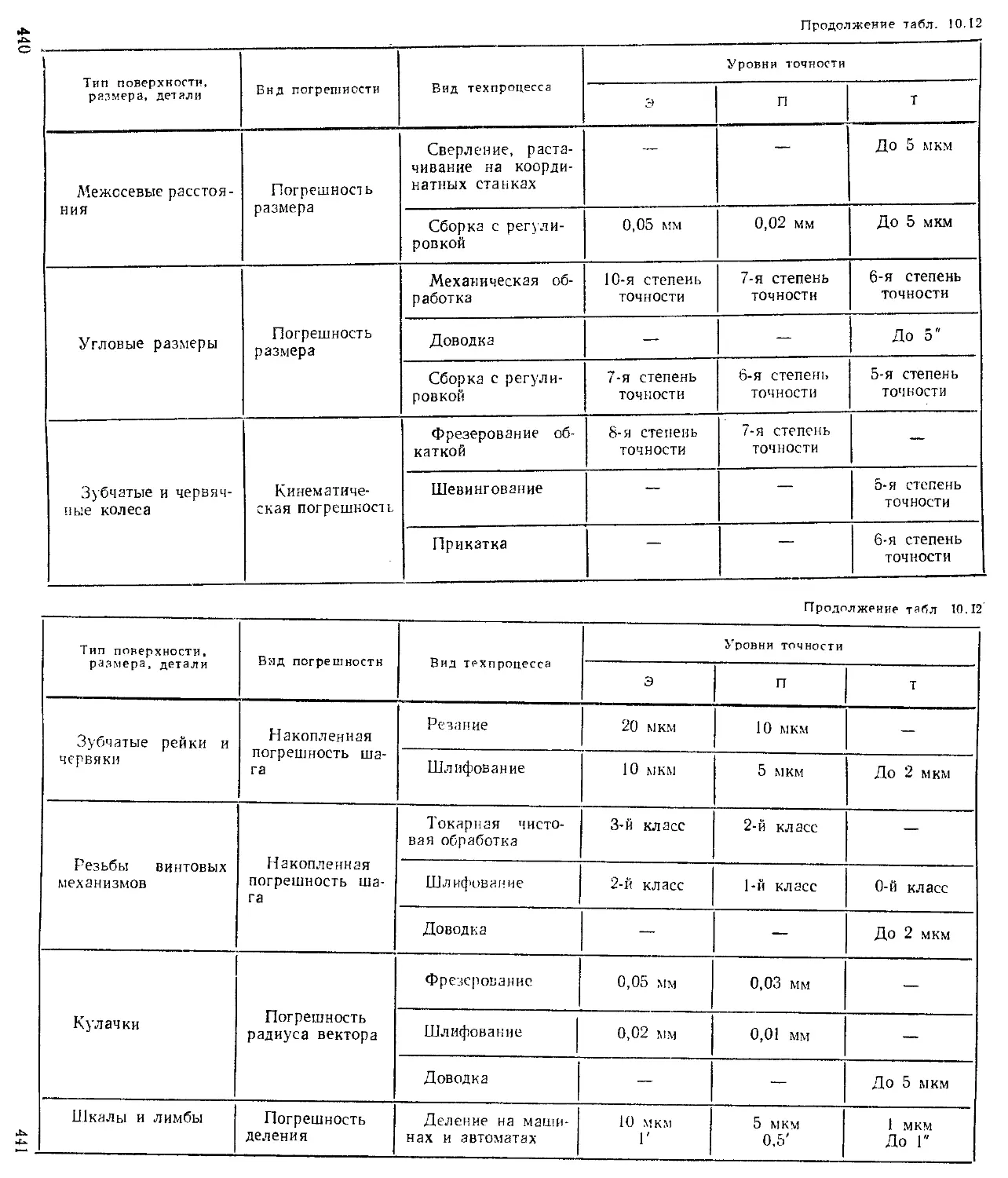
Критерии технологичности конструкций ................ 436
Критерии степени влияния ошибок...................... 442
Методы компенсации ошибок механизмов................. 444
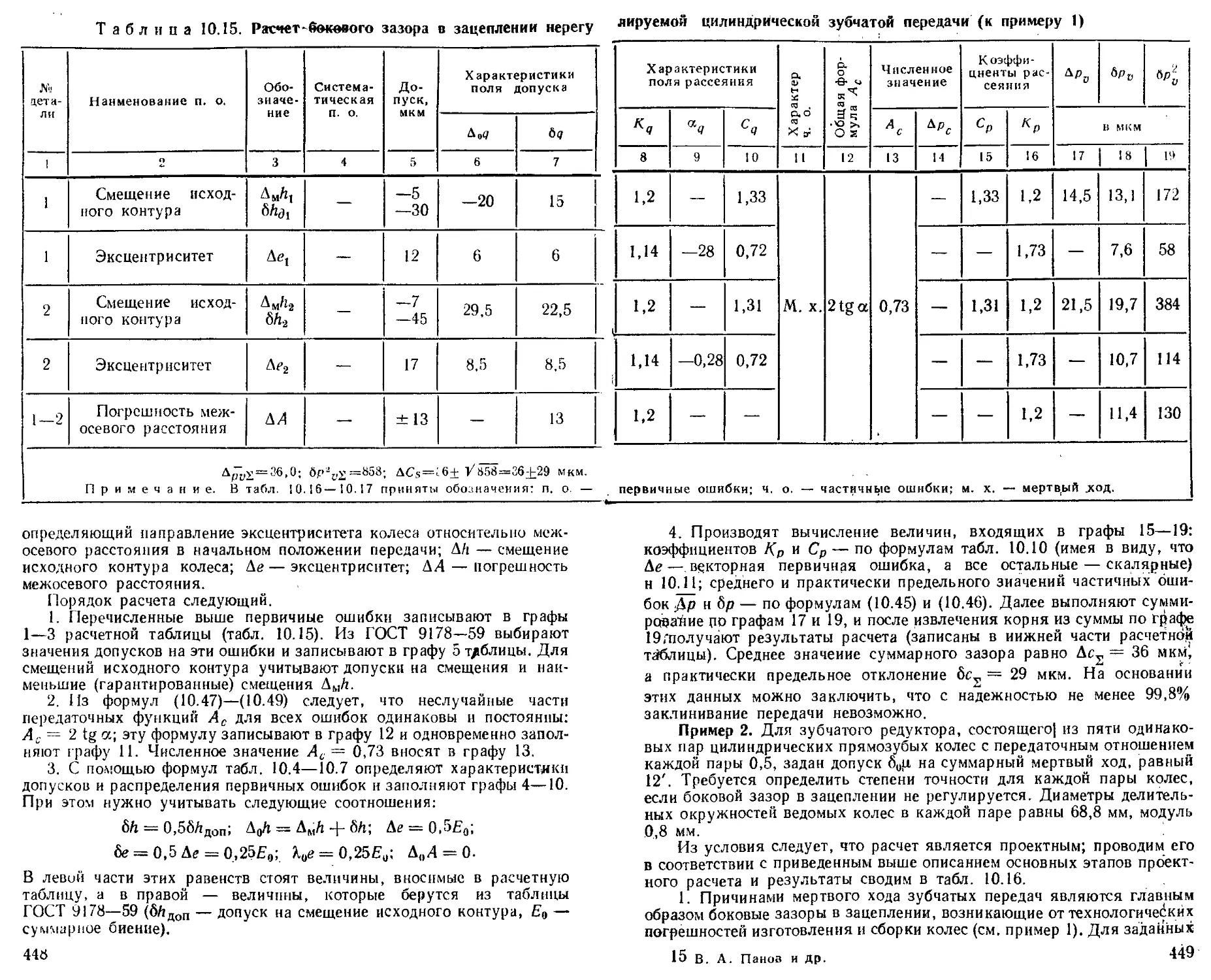
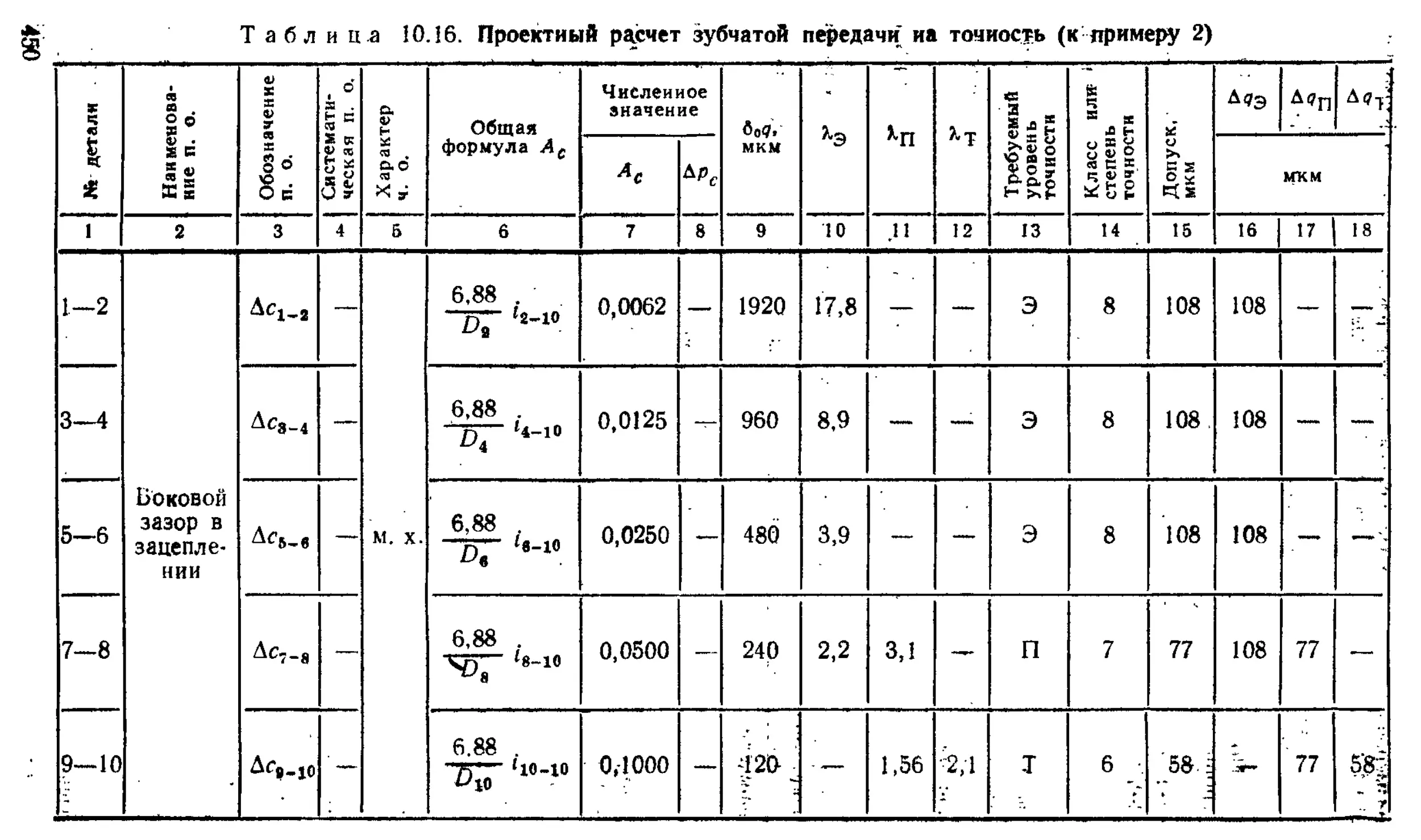
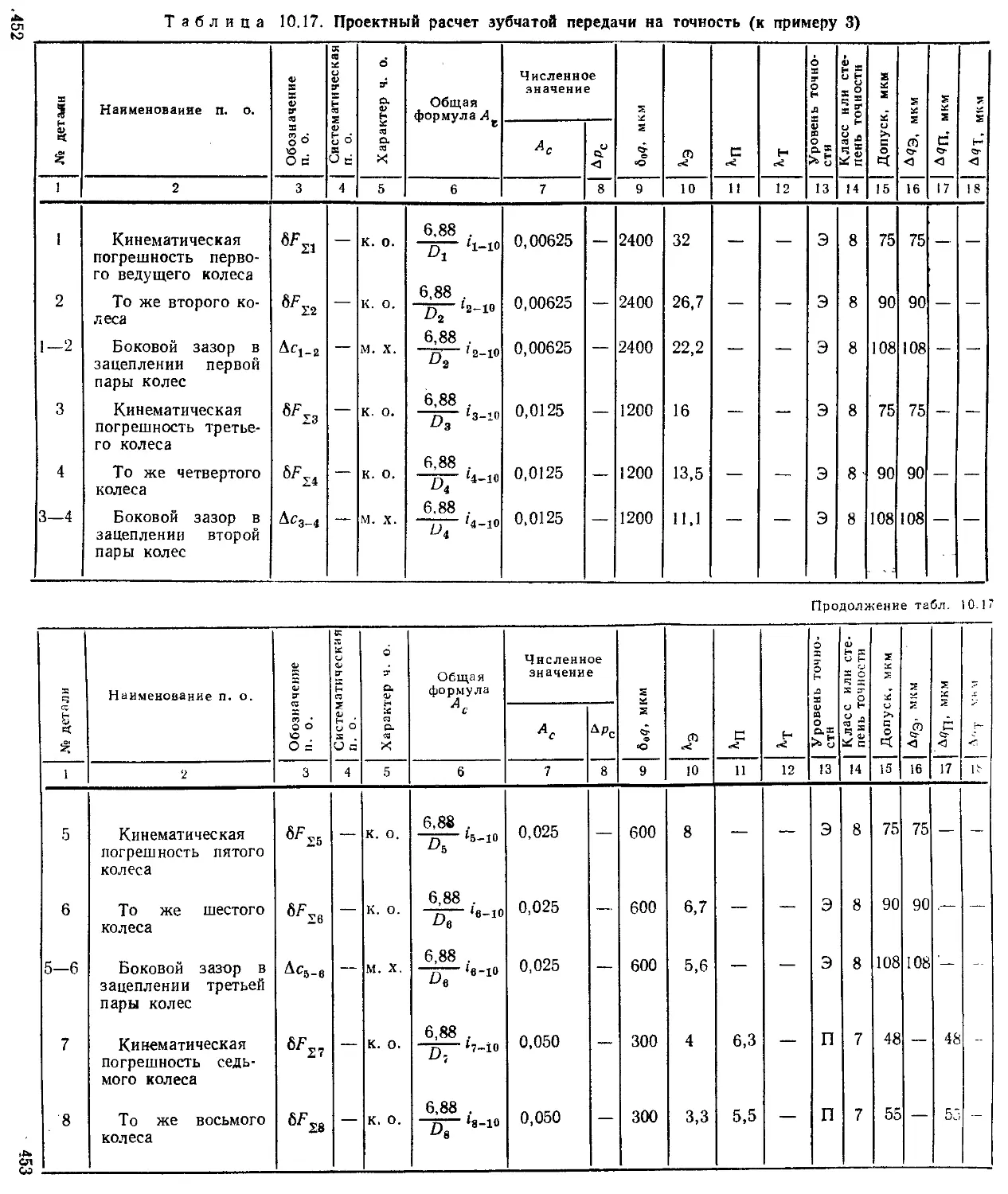
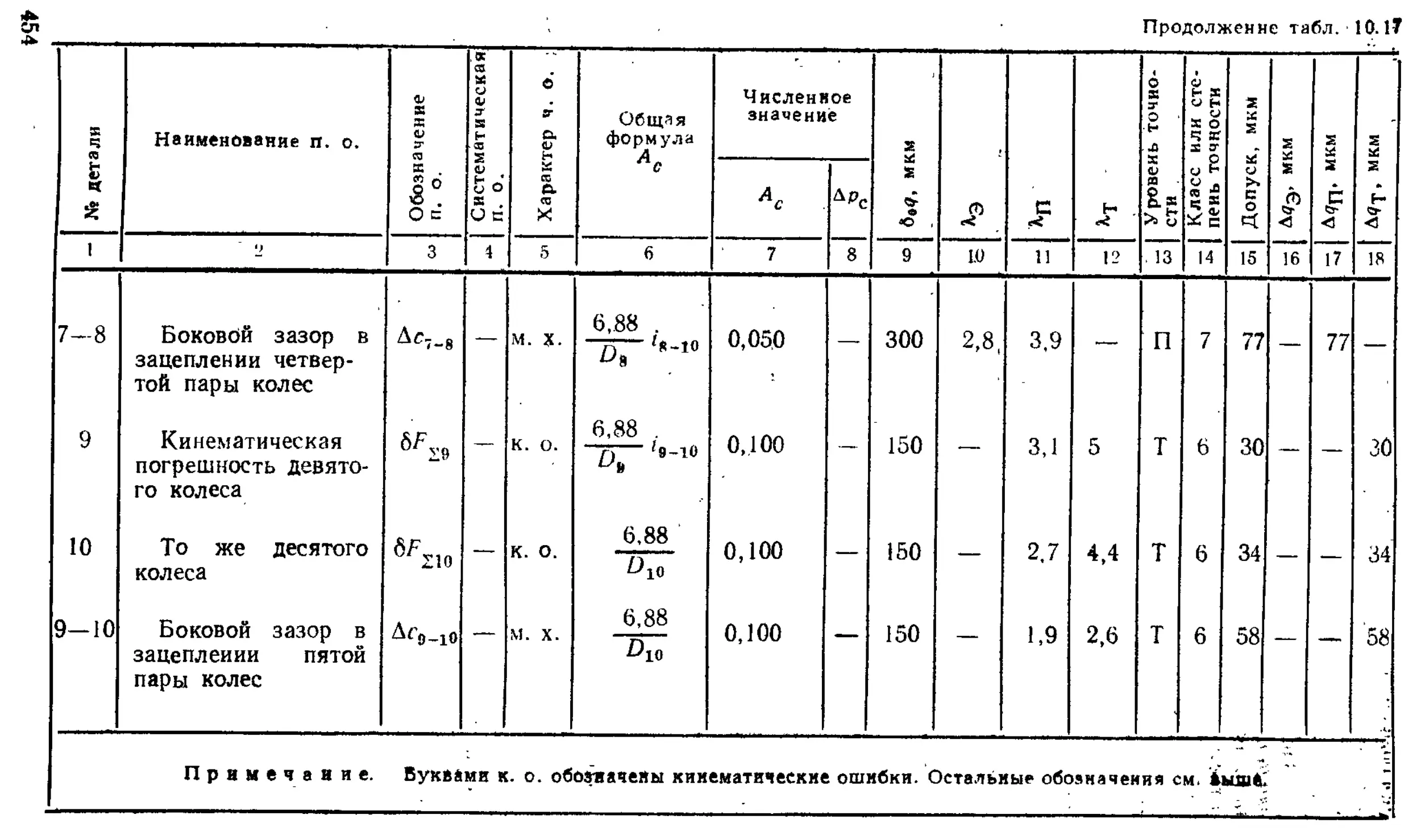
Проектный расчет механизмов на точность ...... 445
Проверочный расчет механизмов на точность ..... 446
Примеры расчета механизмов на точность............... 447
Глава 11. Направляющие для прямолинейного и вращательного движения (Л4. Д. Кругер, Л4. И, Калинин) ................................................... 456
Общие сведения ........................................ —
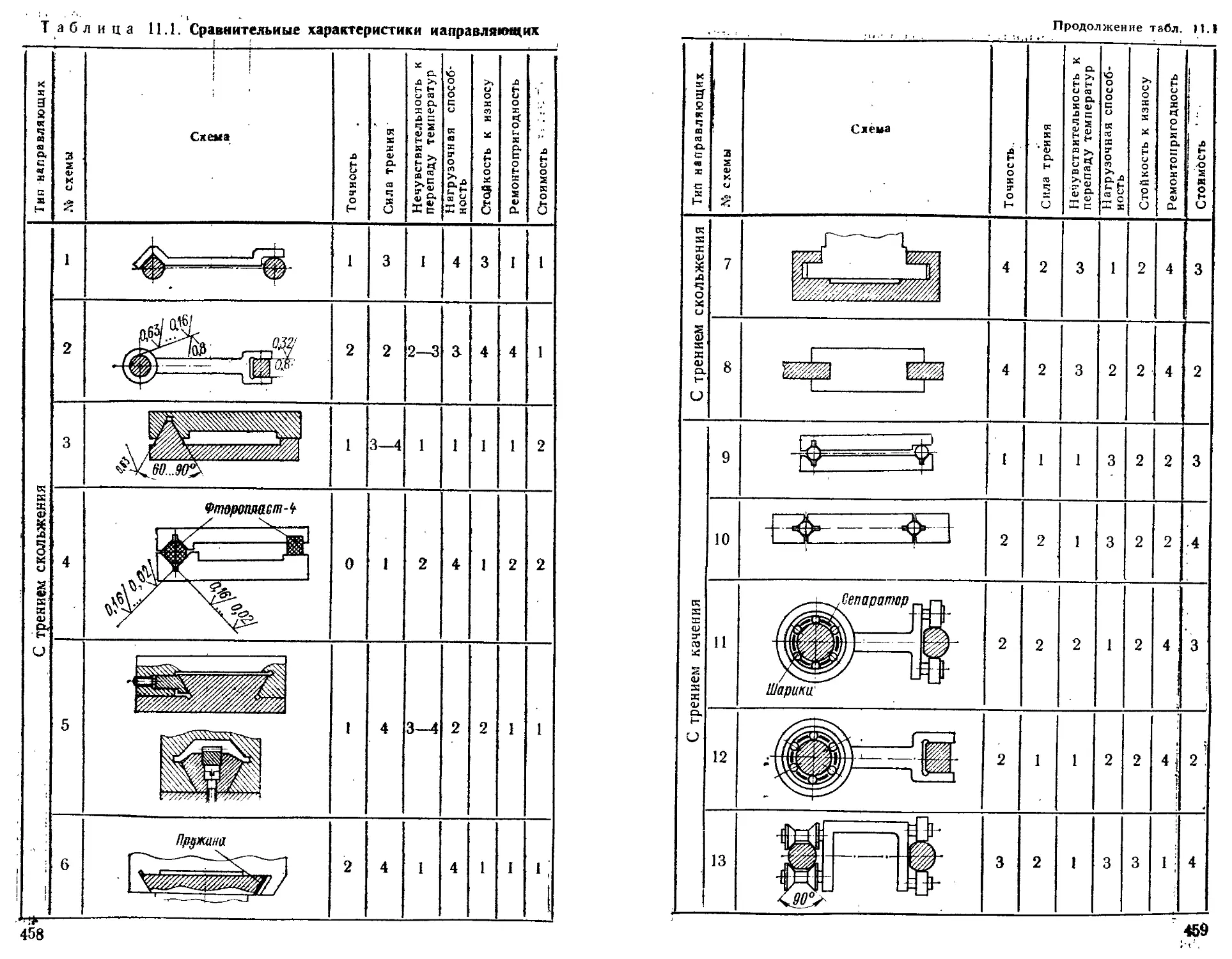
Принципы коиструнровання направляющих......... 457
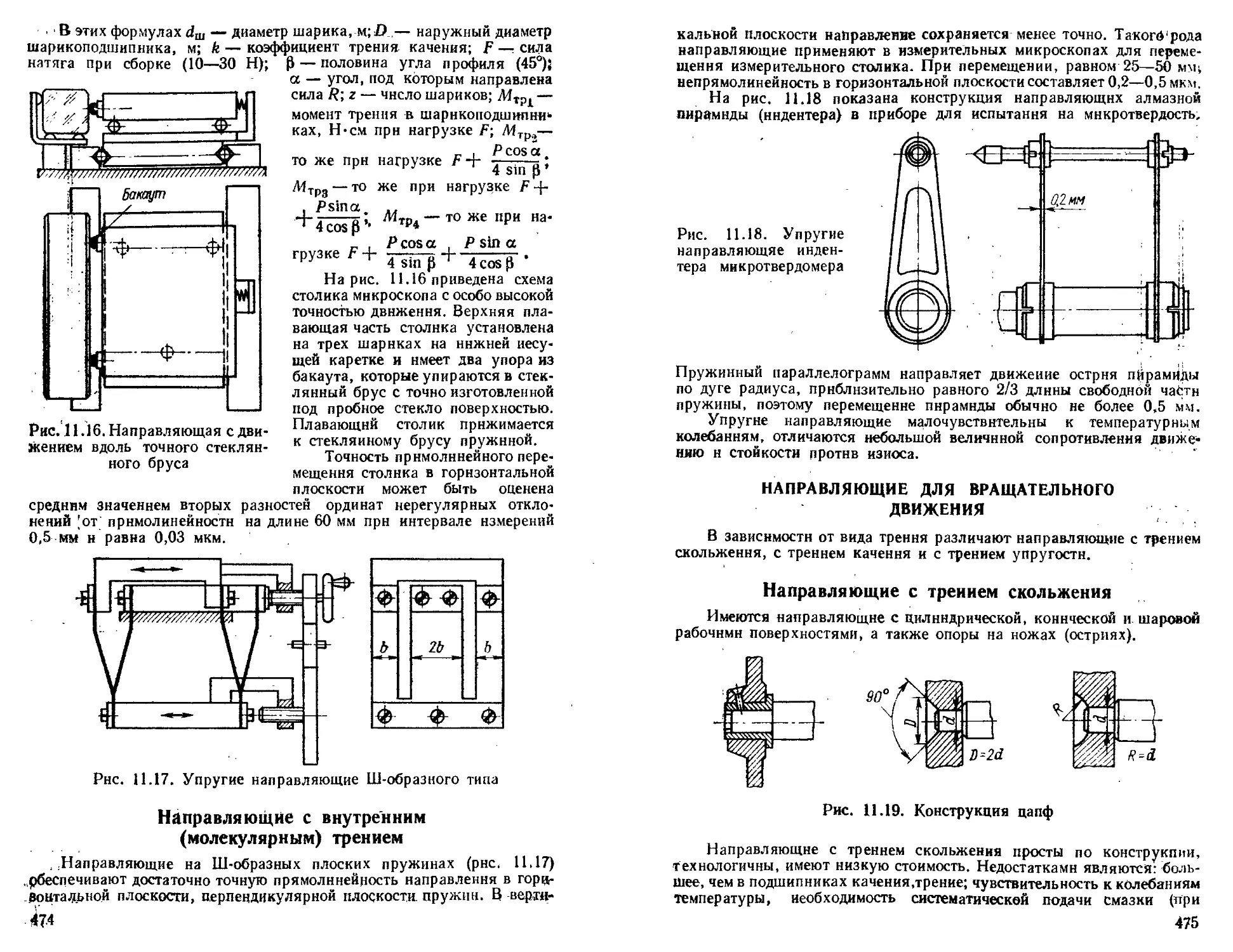
Направляющие для прямолинейного движения ..... —
Направляющие с треннем скольжения............. —
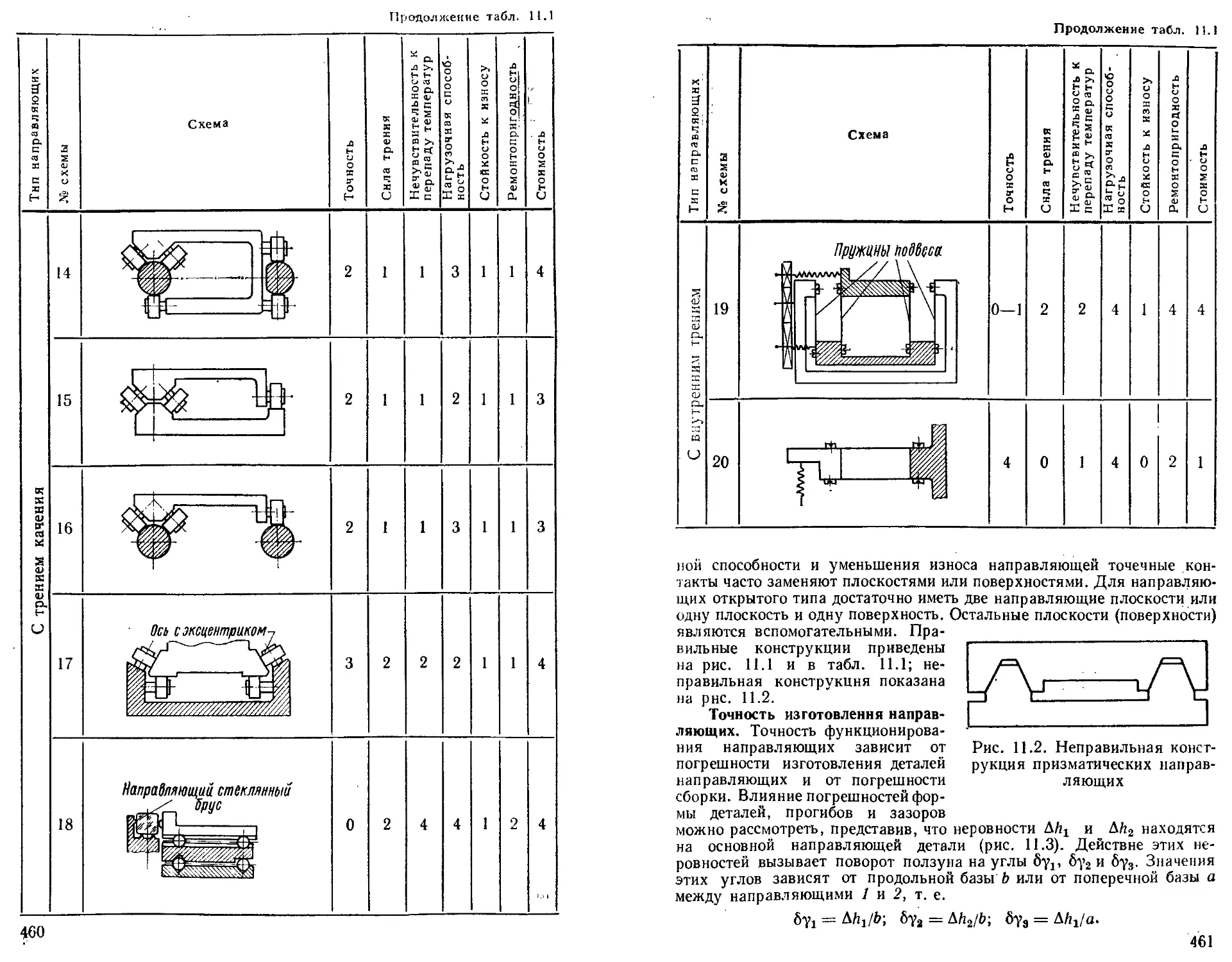
Направляющее с трением качения ...................... 468
Направляющие с внутренним (молекулярным) треннем 474
Направляющие для вращательного движения....... 475
Направляющие с трением скольжения............. —
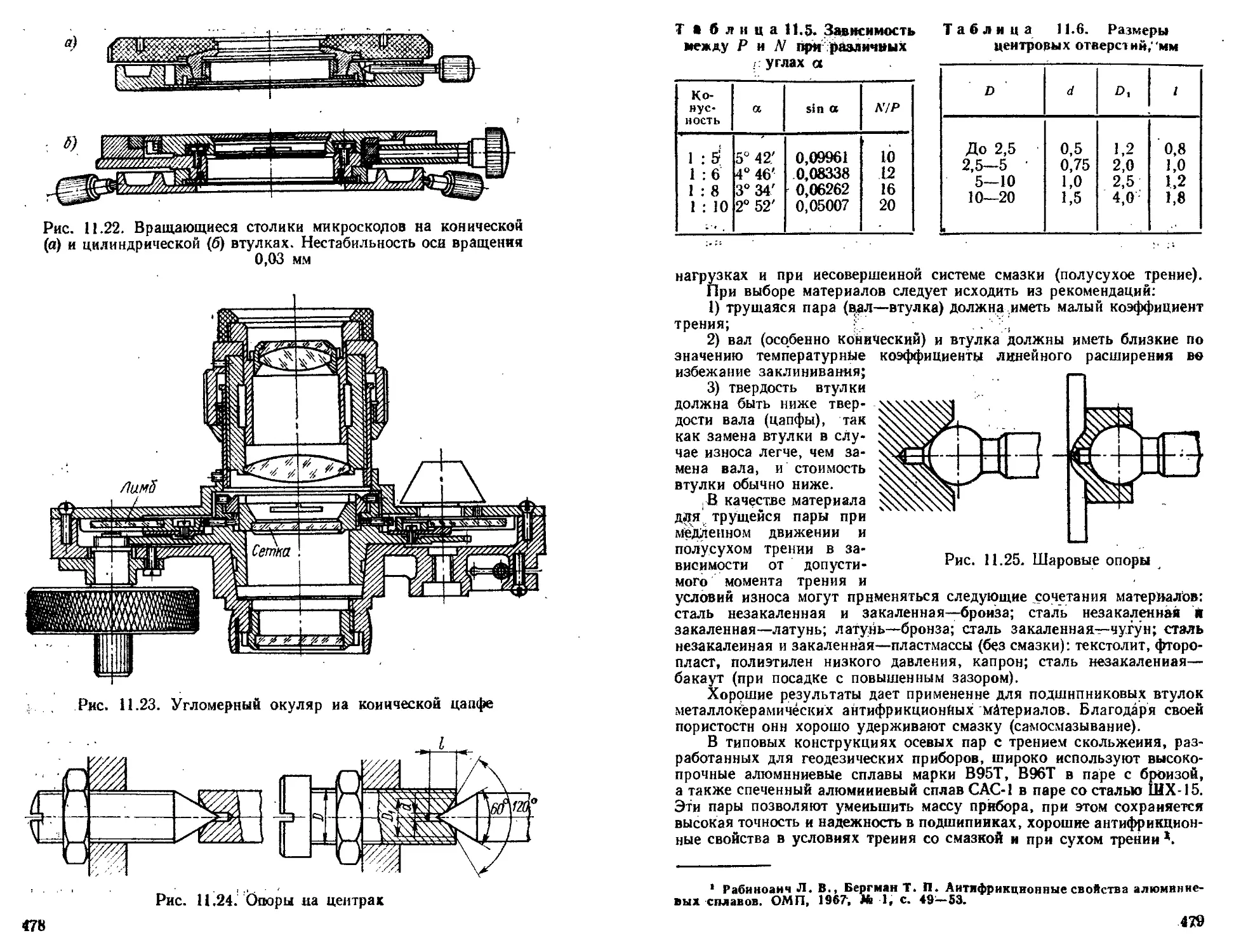
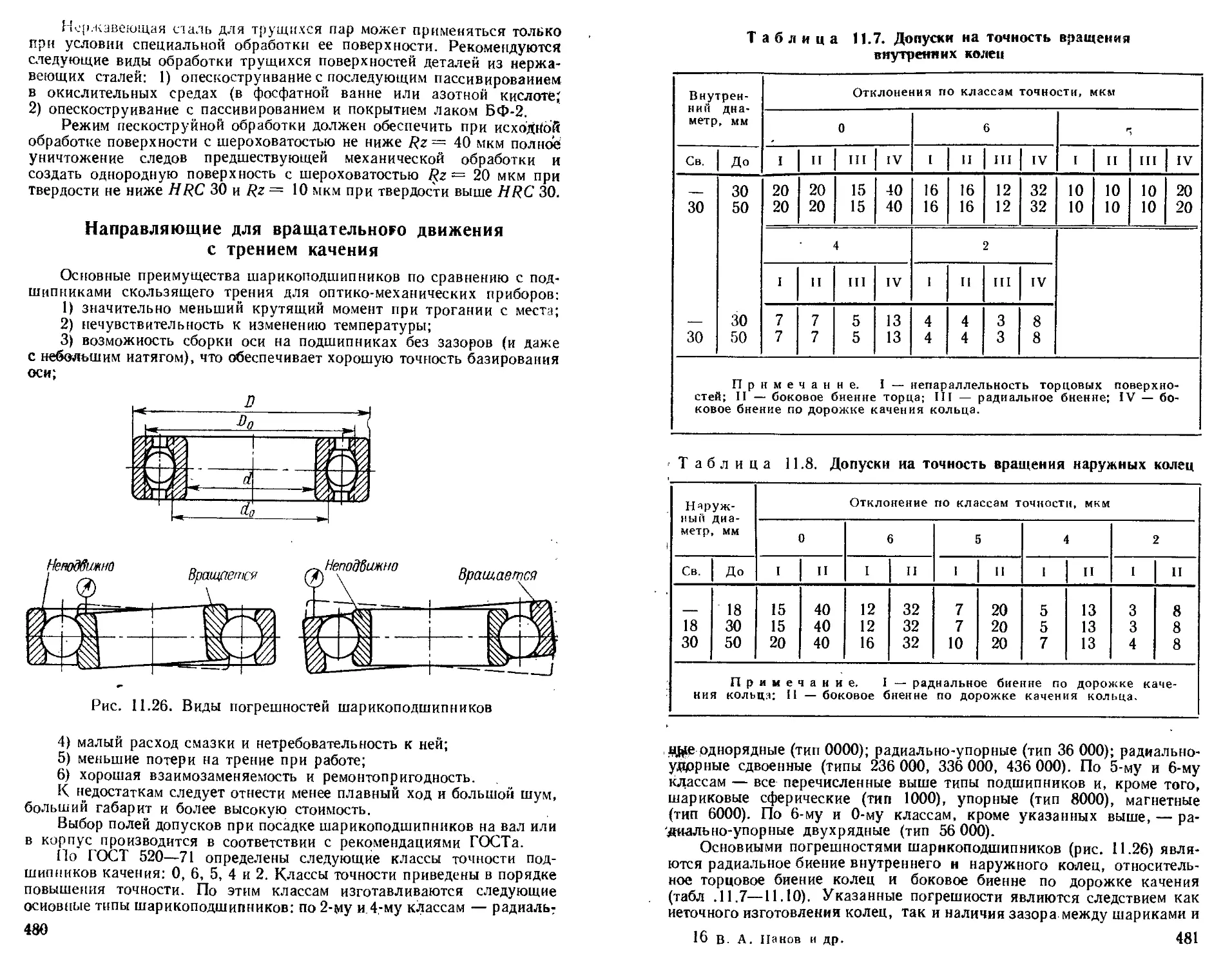
Направляющие дли вращательного движения с трением качения ............................................. 480
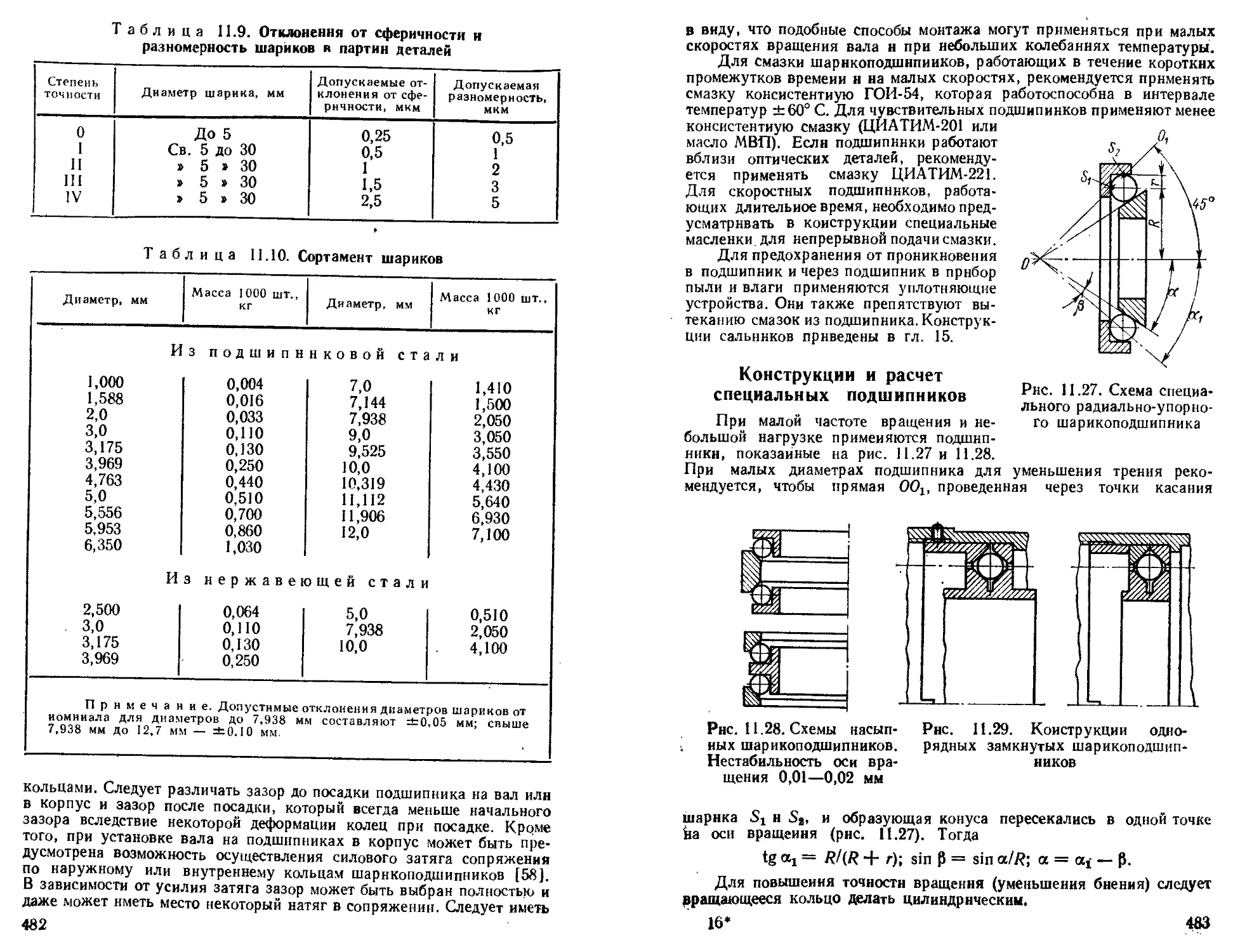
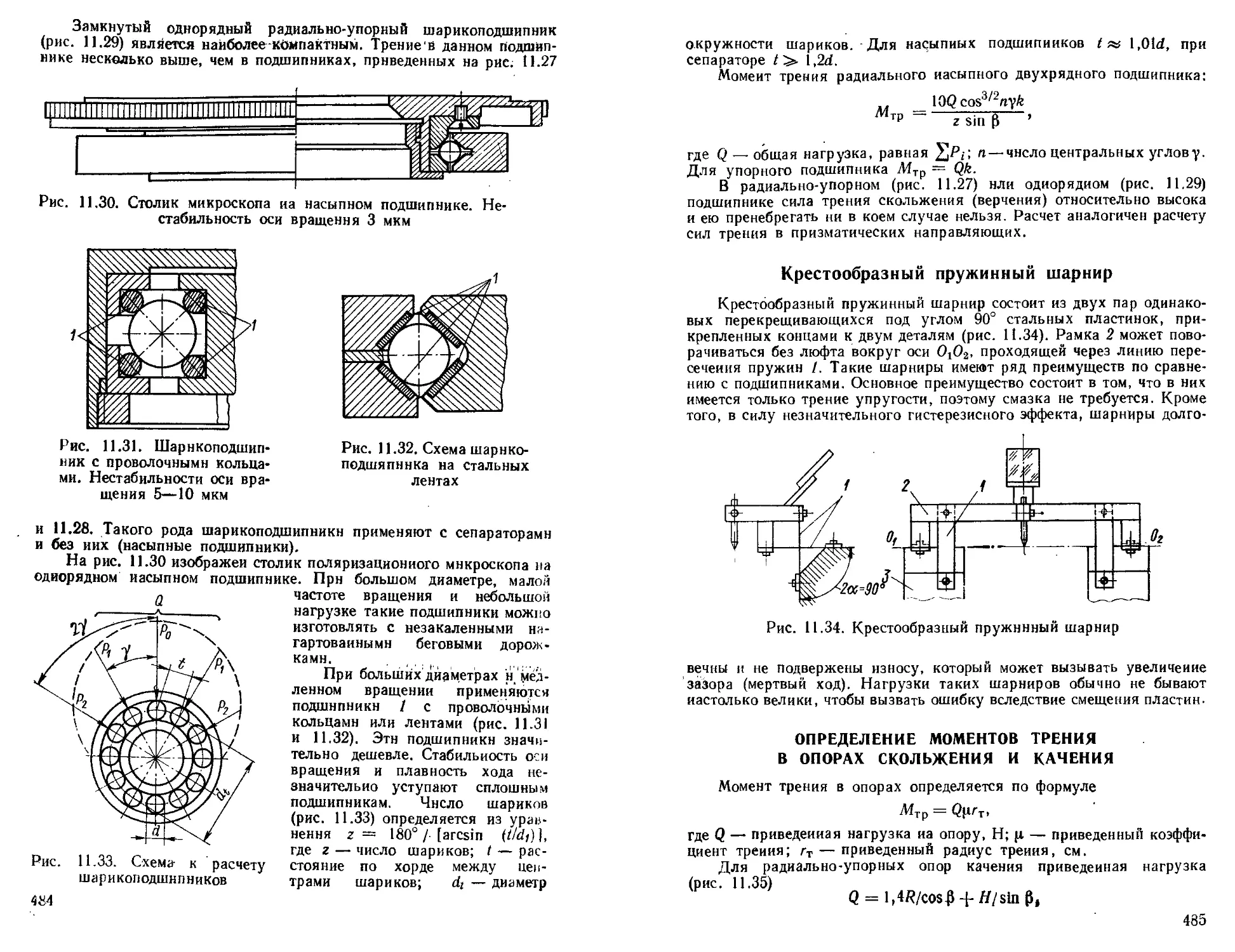
Конструкции н расчет специальных подшипников . . . 483
Крестообразный пружинный шарнир .................... 485*
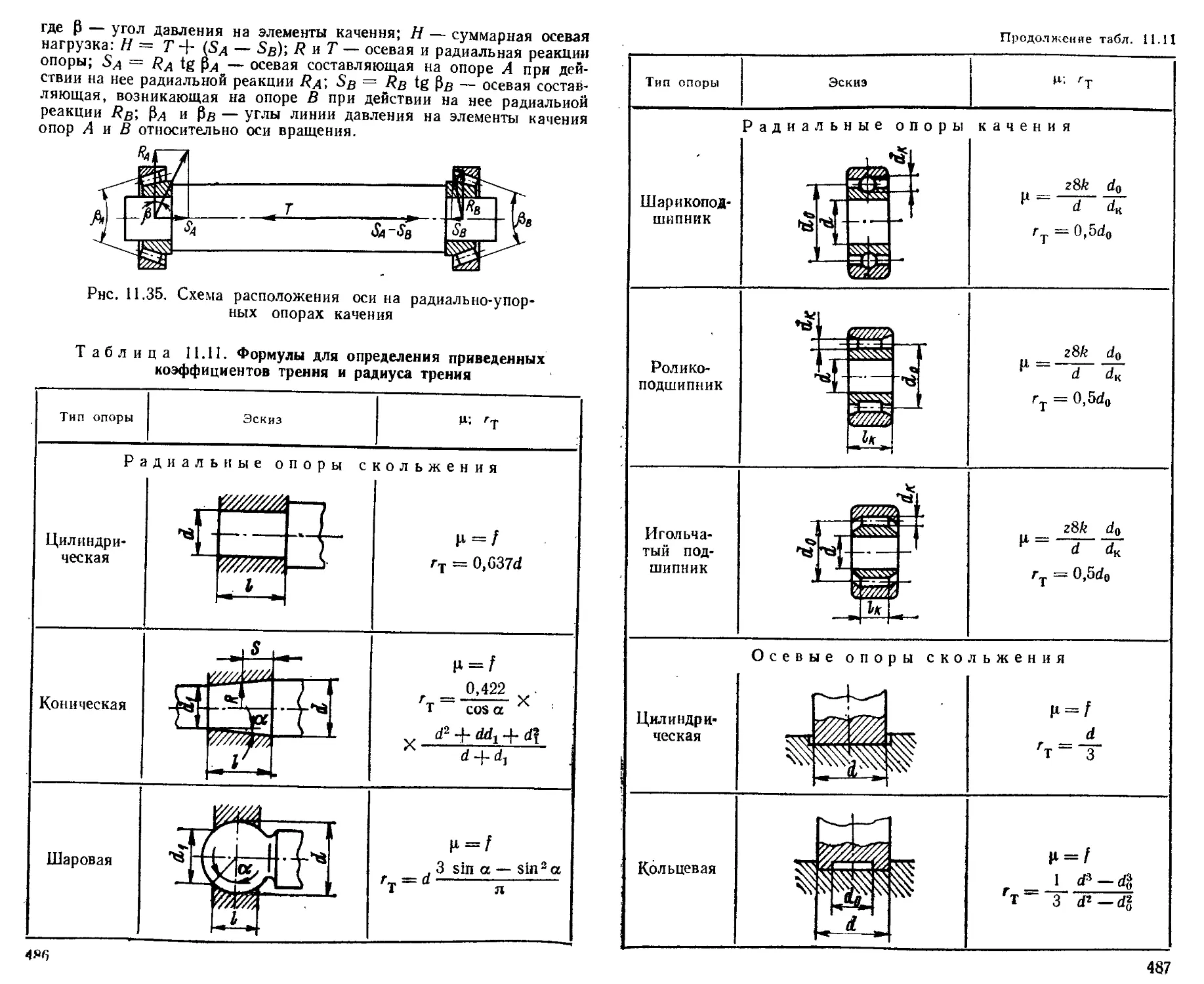
Определение моментов трення в опорах скольжения и качения ................................................ —
Глава 12. Винтовые механизмы (AL Д. Кругер, В. А. Панов) 491 Винтовые механизмы точного движения ........ —
Расчет винтовых механизмов .......................... 492
Точность винтовых механизмов ............ 494
Конструкции отсчетных иинтовых механизмов............. 495
Точность изготовления ................................. —
Материалы для винтовых пар........................... 499
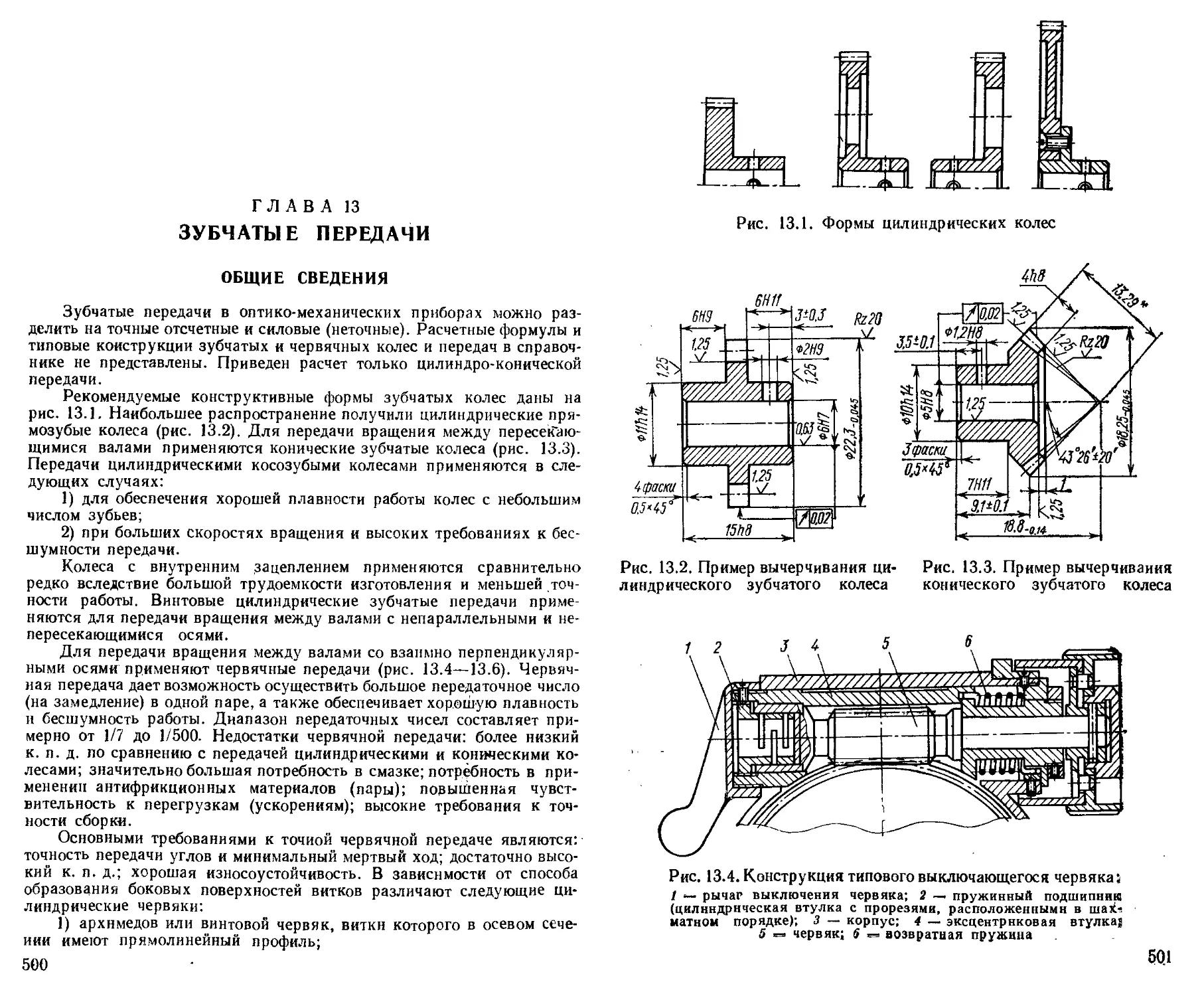
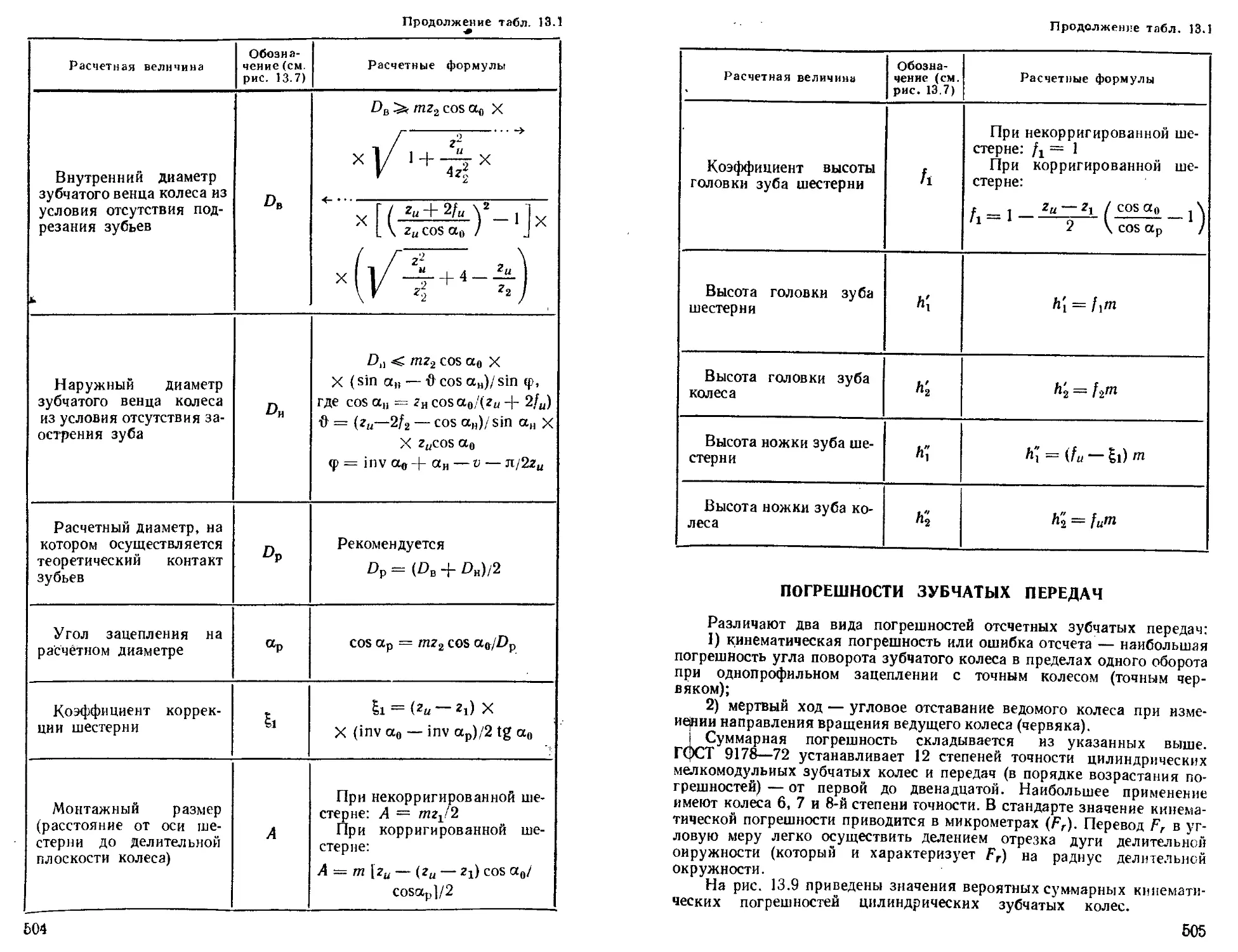
Глава 13. Зубчатые передачи (Л4. Я. Кругер, Л4. И. Калинин) 500 Общие сведения.............................................. —
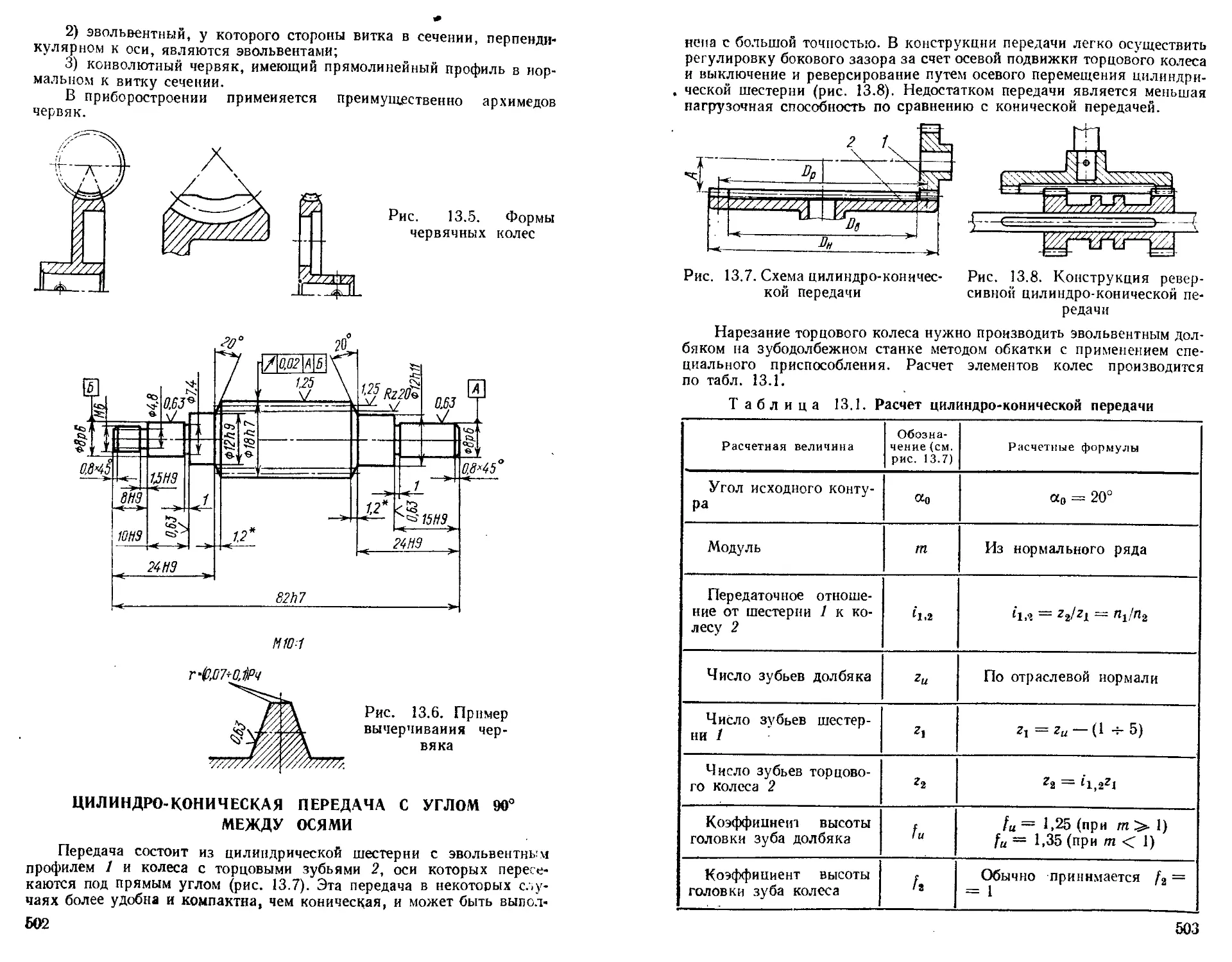
Цилиндро-коническая передача с углом 90° между осями 502
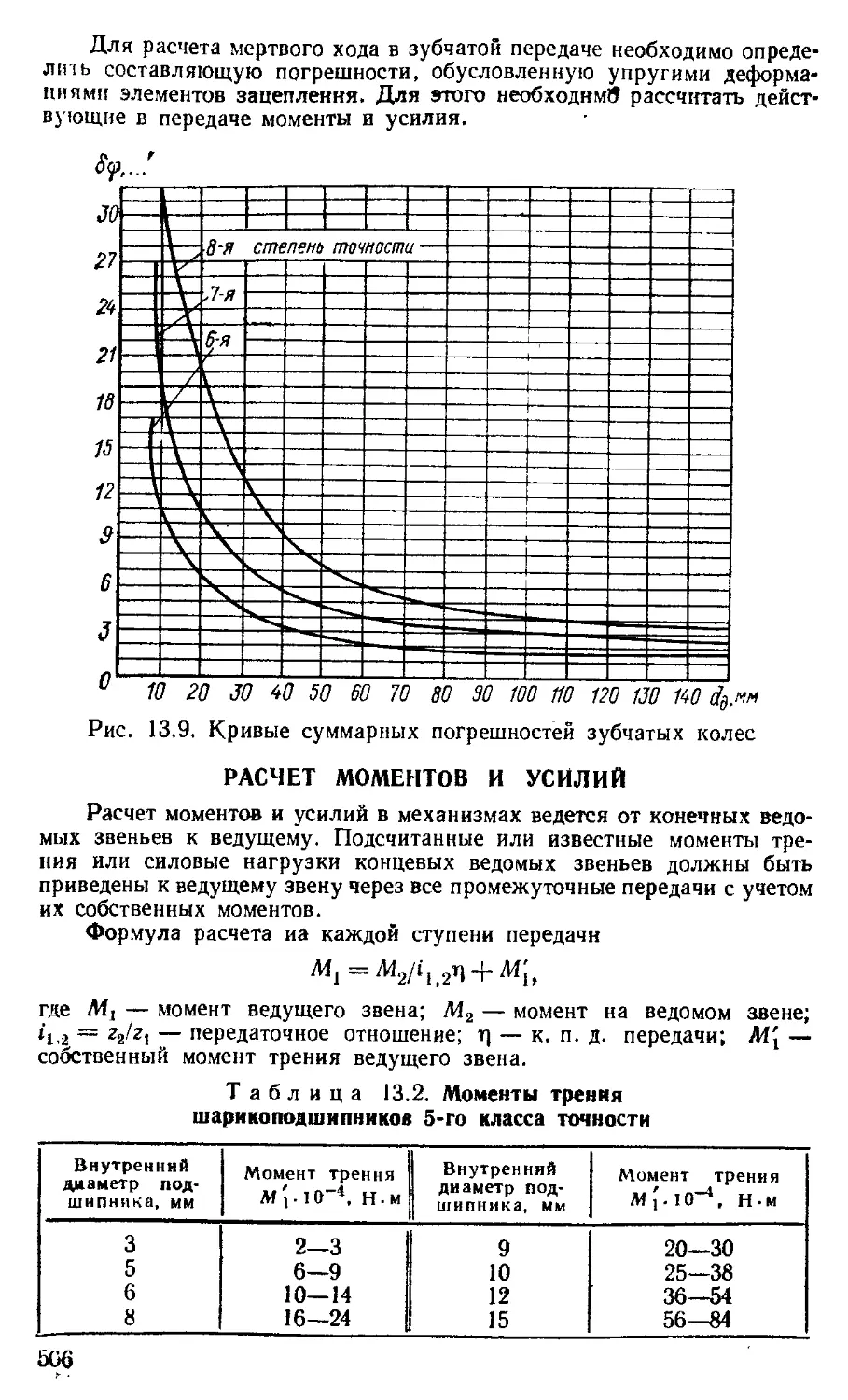
Погрешности зубчатых-передач.......................... 505
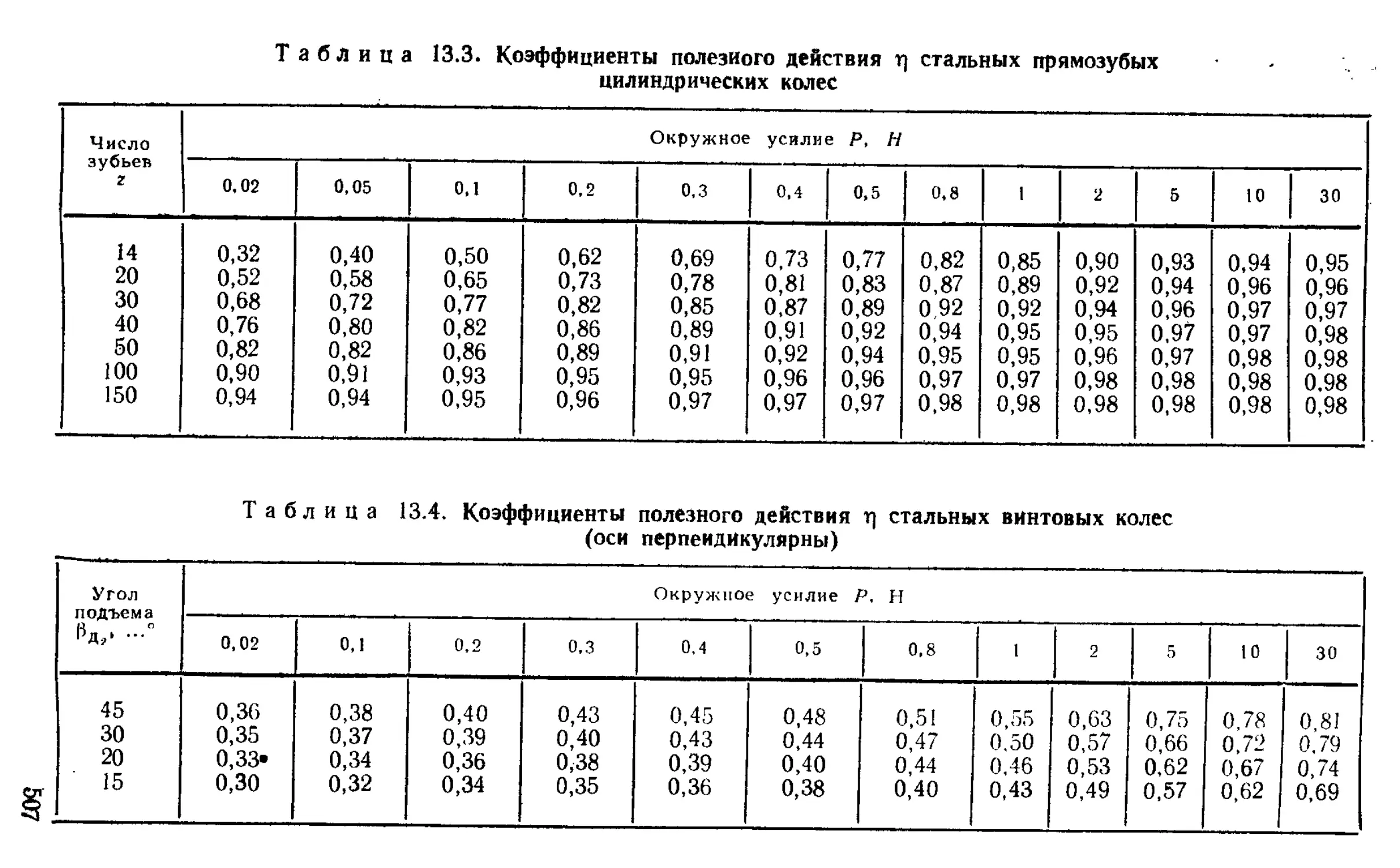
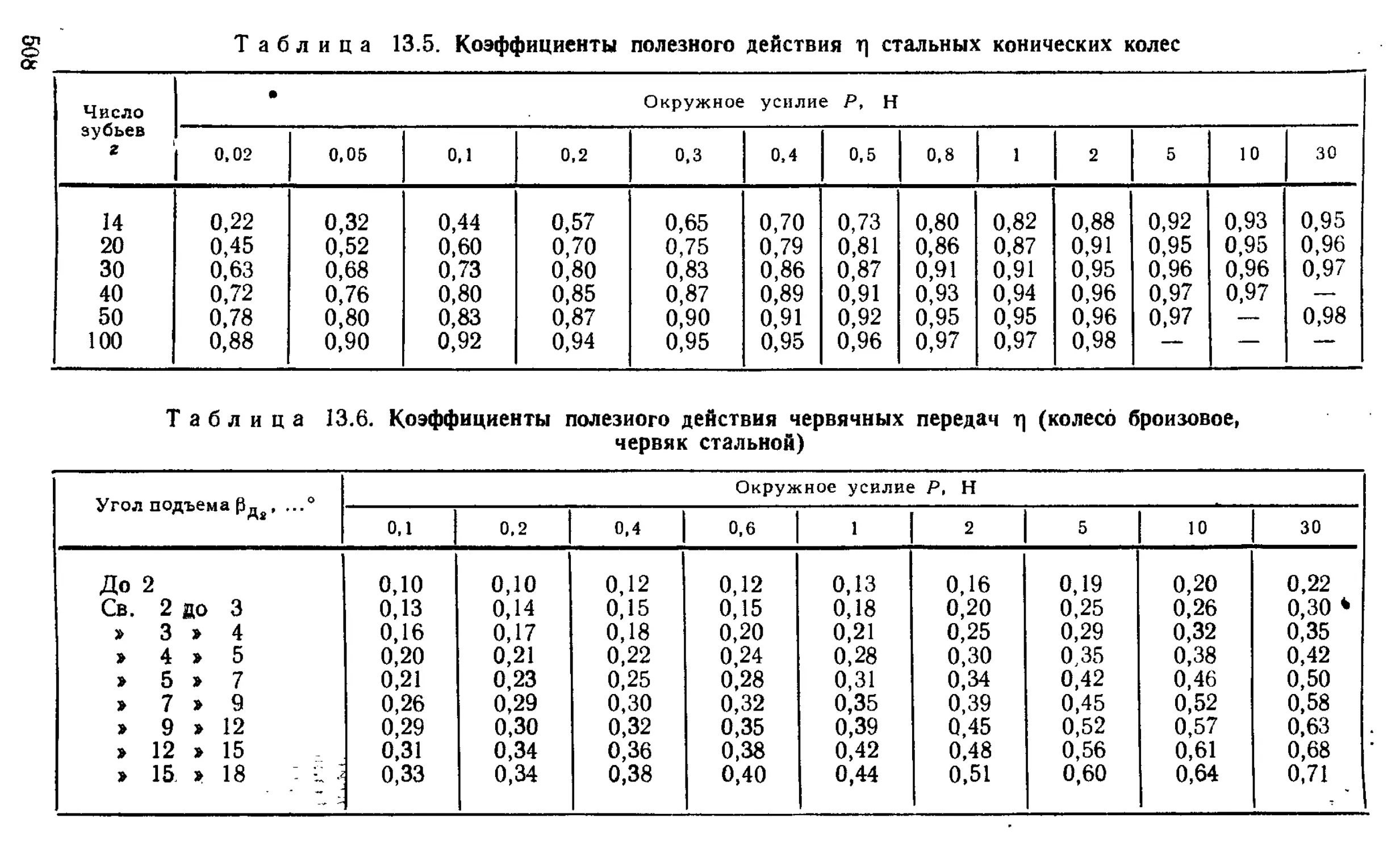
Расчет моментов и усилий .............................. 506
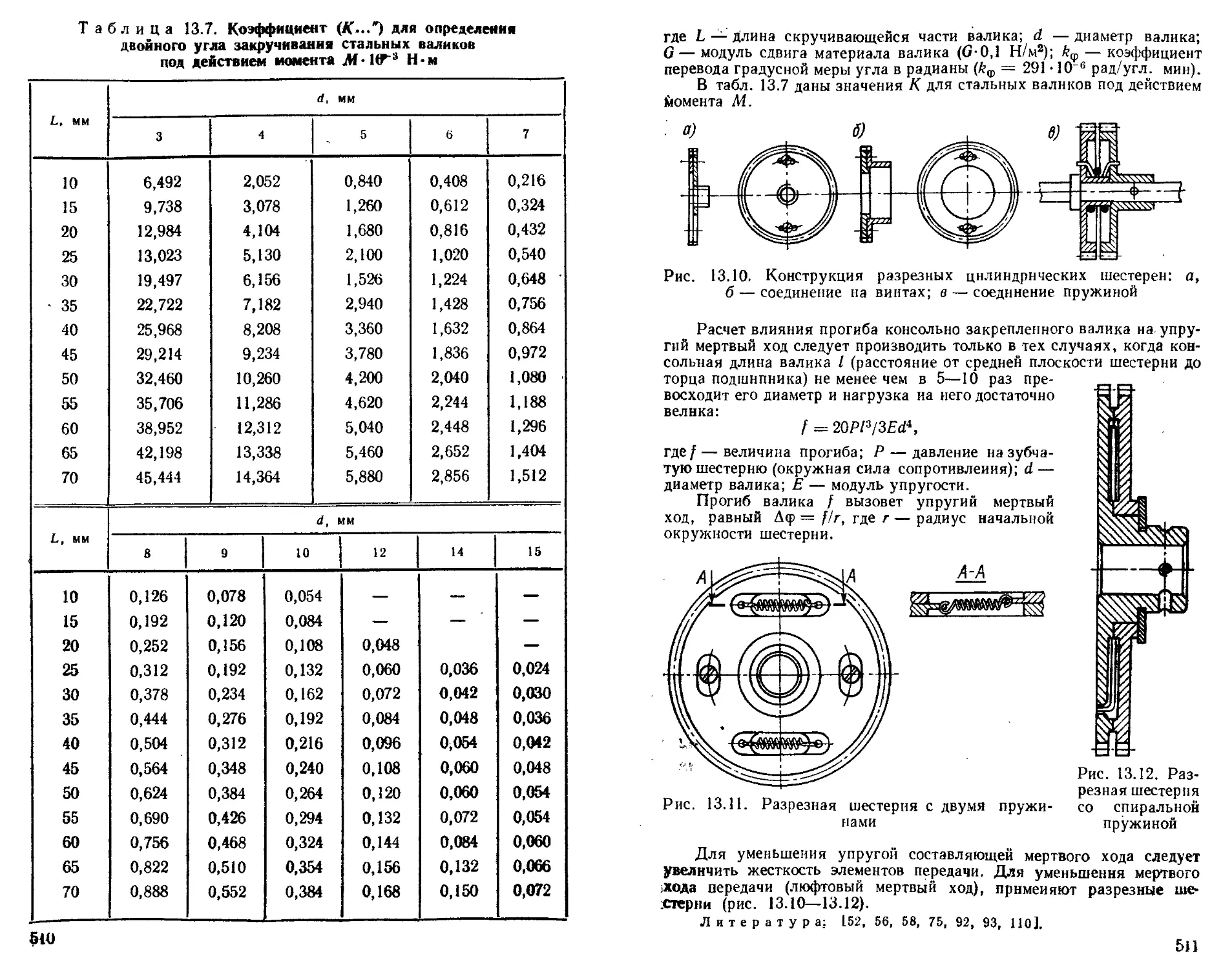
Расчет мертвых ходов ................................. 509
Глава 14. Отсчетные устройства (Л!. Д. Кругер, В, А. Панов) 512 Оптические отсчетные устройства............................. —
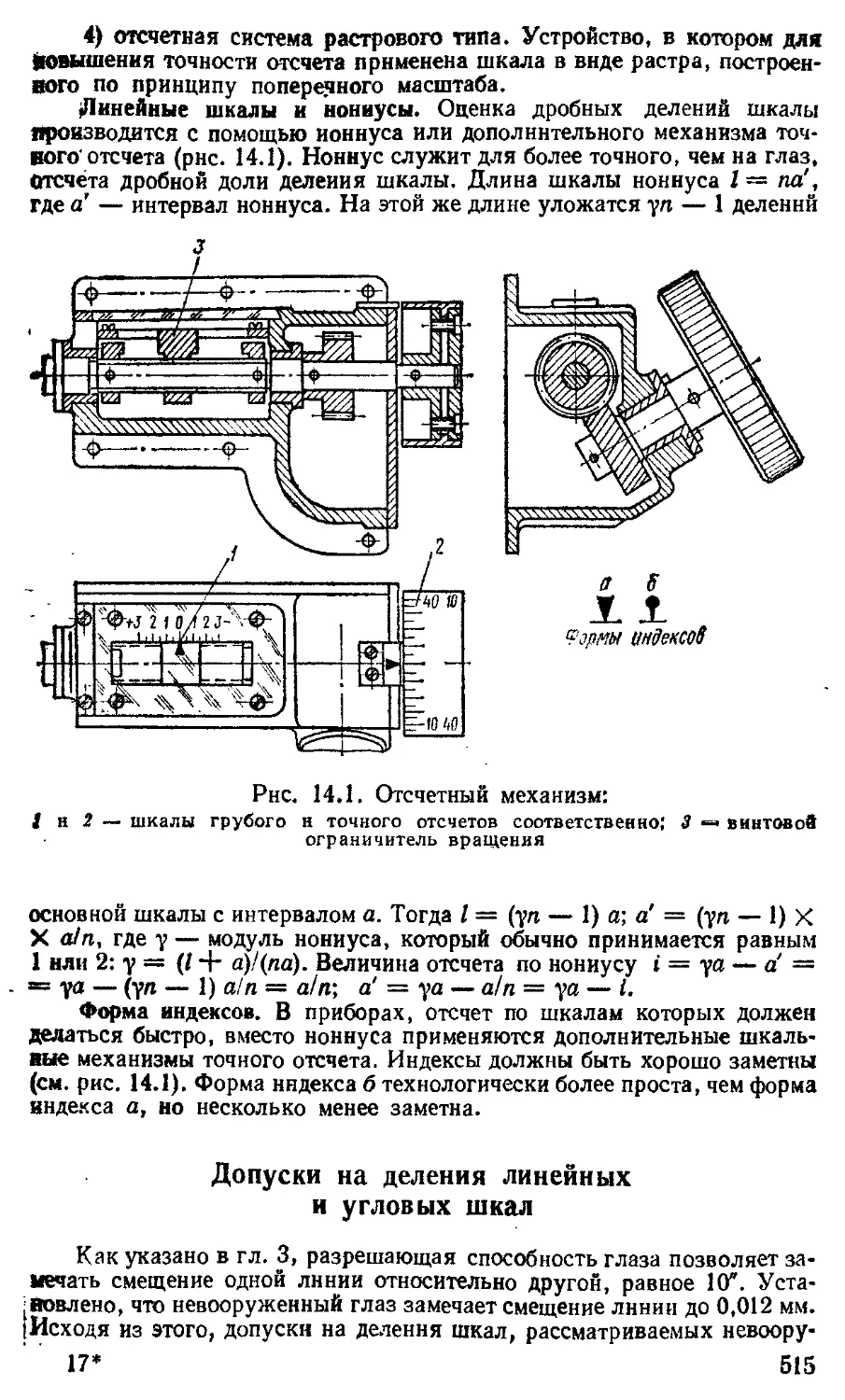
Оптические отсчетные устройства непосредственного отсчета ................................................. —
Оптические отсчетные устройства с микрометрами ... 513
Шкаловые отсчетные устройства ............. —
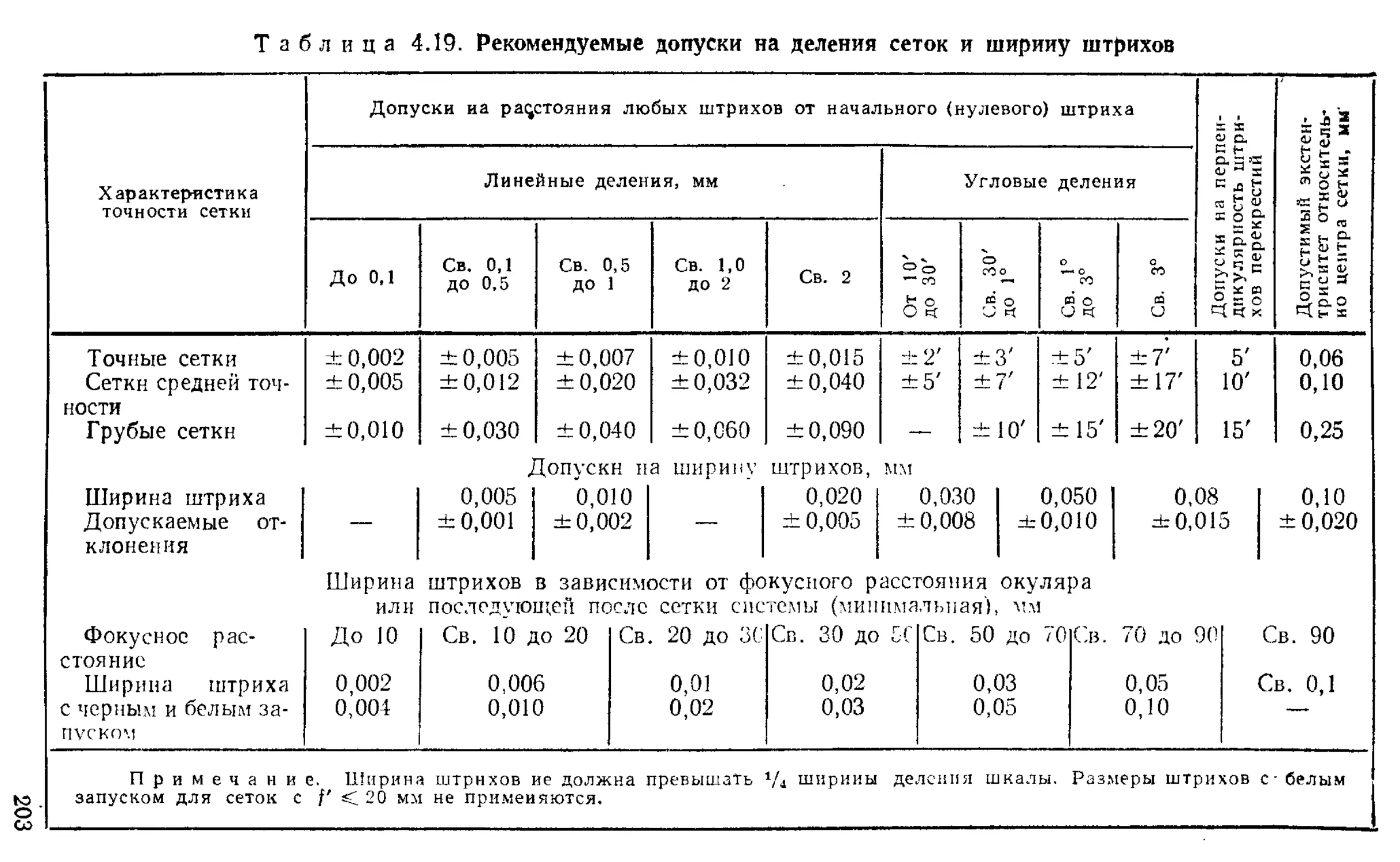
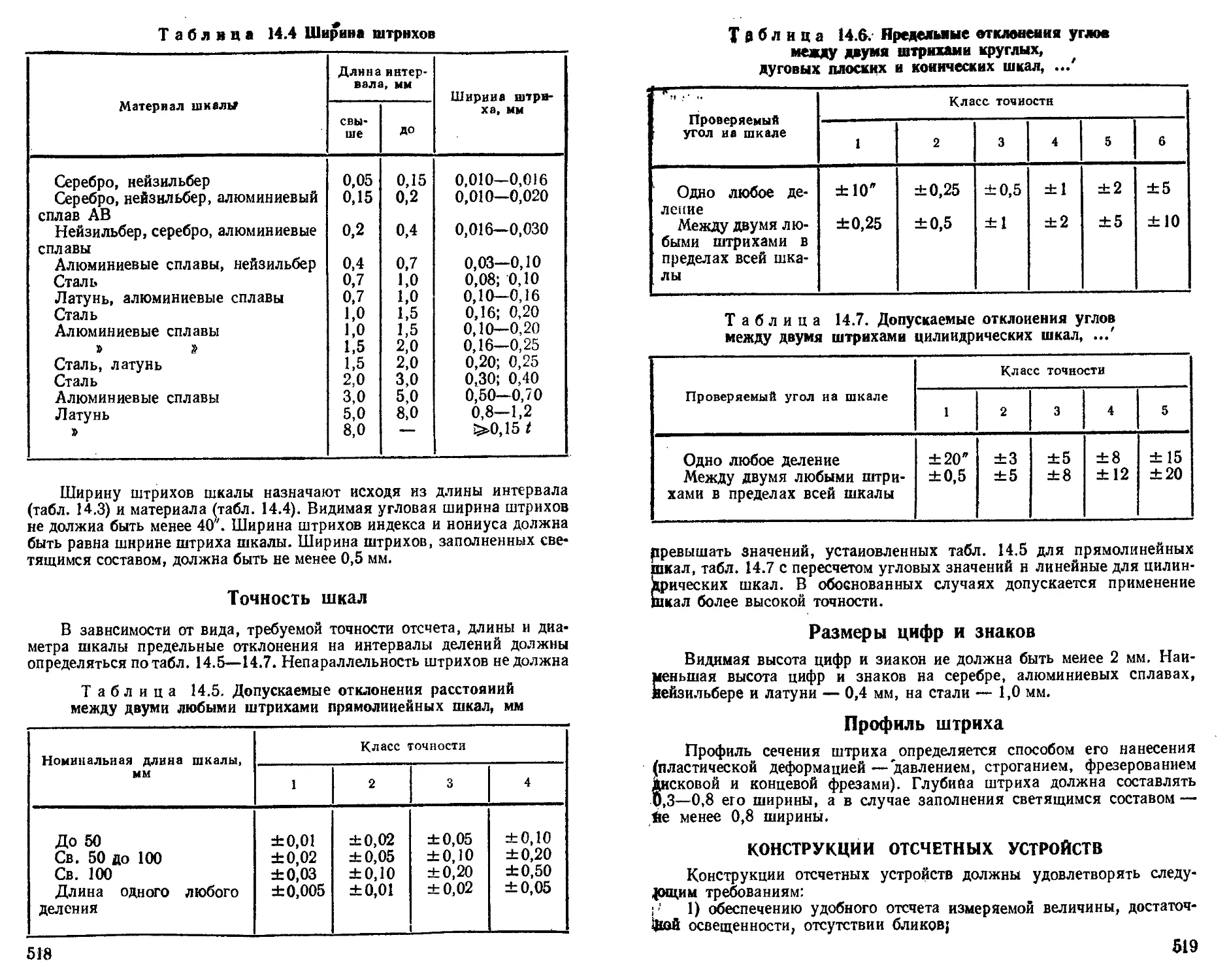
Допуски на деления линейных и угловых шкал .... 515
Шкалы на металле .................................... 517
V Размеры штрихов ...............................
Точность шкал ..................................... 518
Размеры цифр и знаков ............................... 519
Профиль штриха ..................................... —
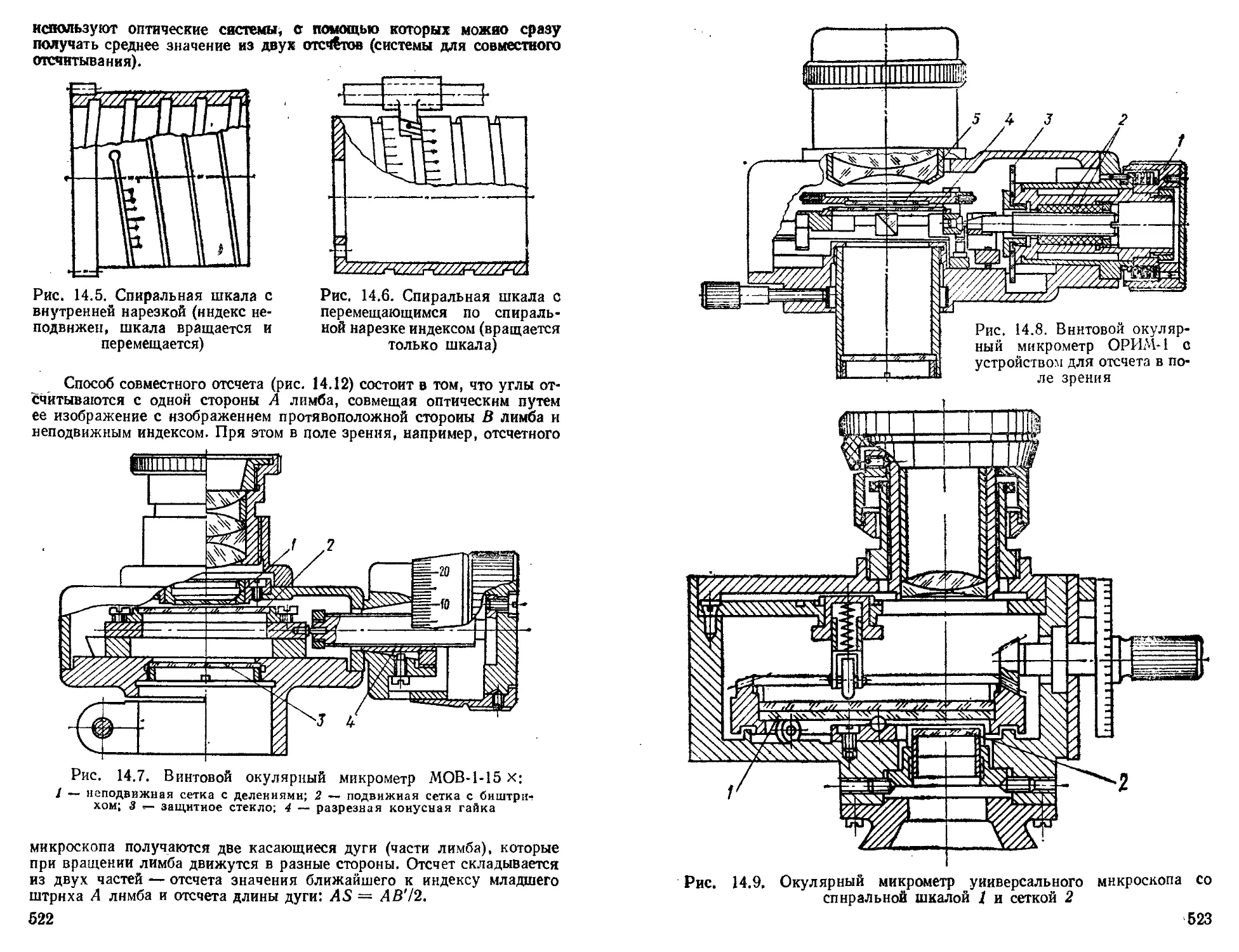
Конструкции отсчетных устройств...................... 519
Применяемые материалы .............................. 525
Точные фиксаторы ................................... 526
Глава 15. Герметизация и осушка приборов (Л4. Я. Кру-гер, Б, Г. Резницкий) .................................... 529
Общие сведения ......................................... —
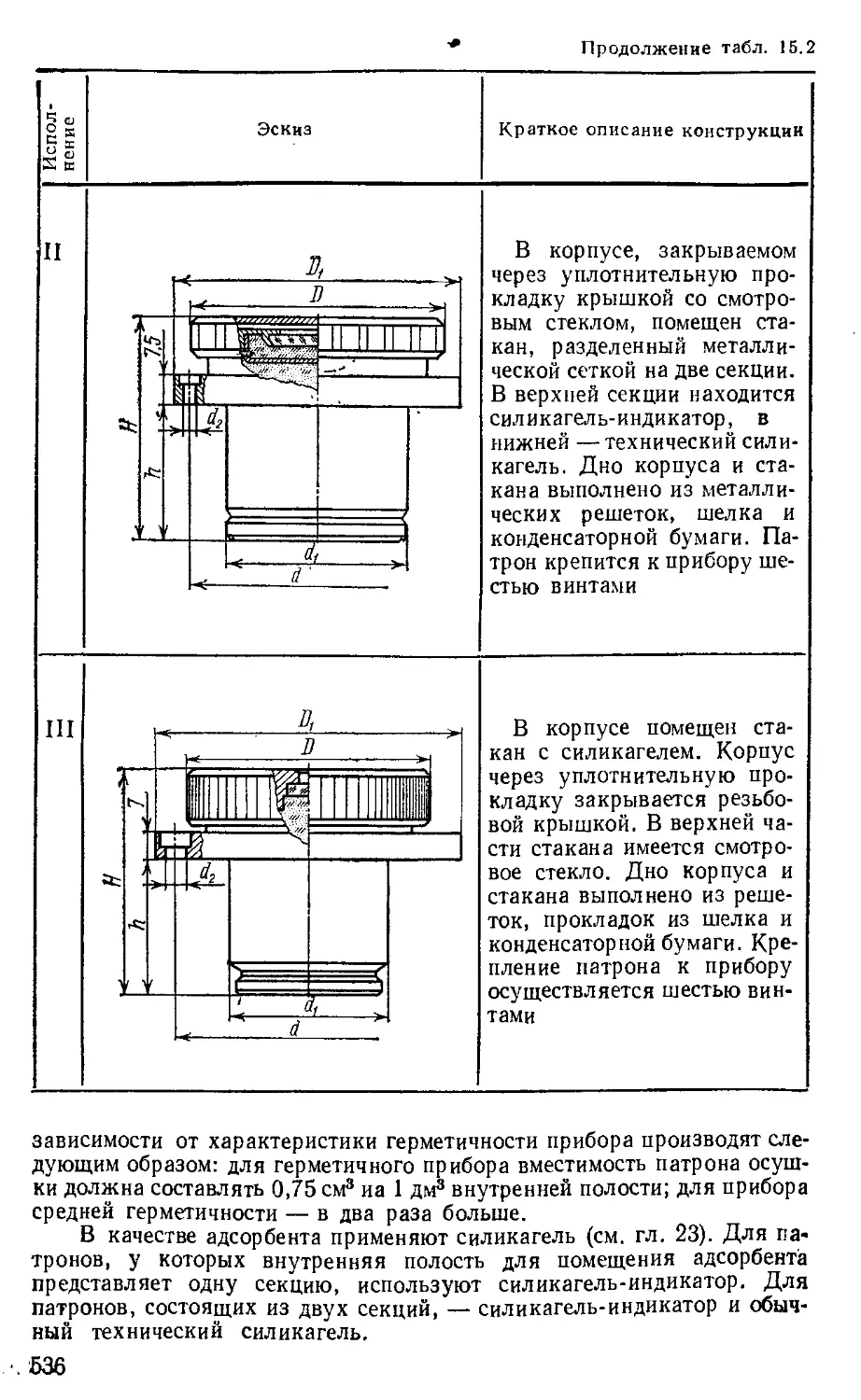
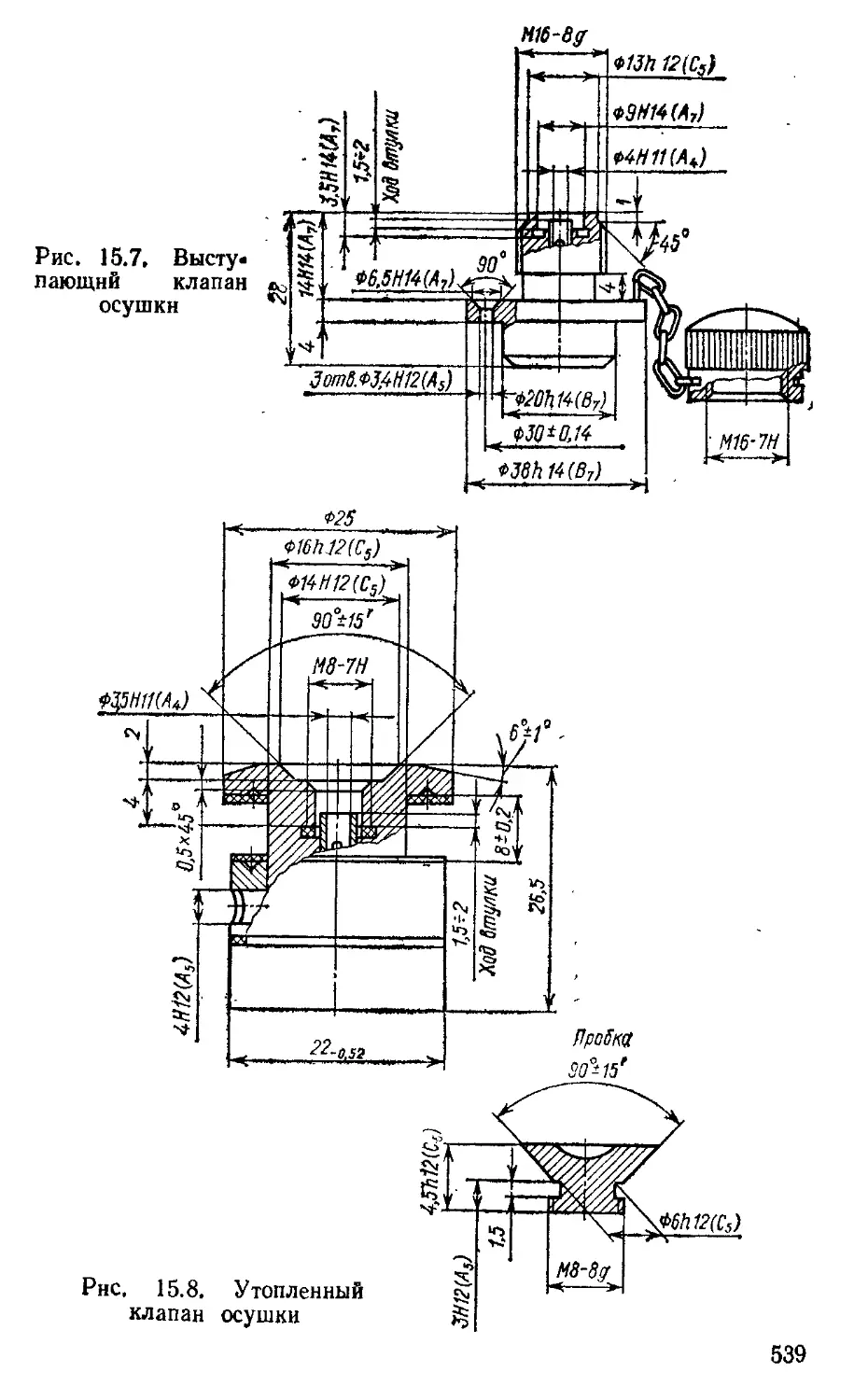
Конструкции корпусов приборов, сальников, патронов и клапанов осушки ...................................... 530
Расчет элементов уплотнения .......................... 531
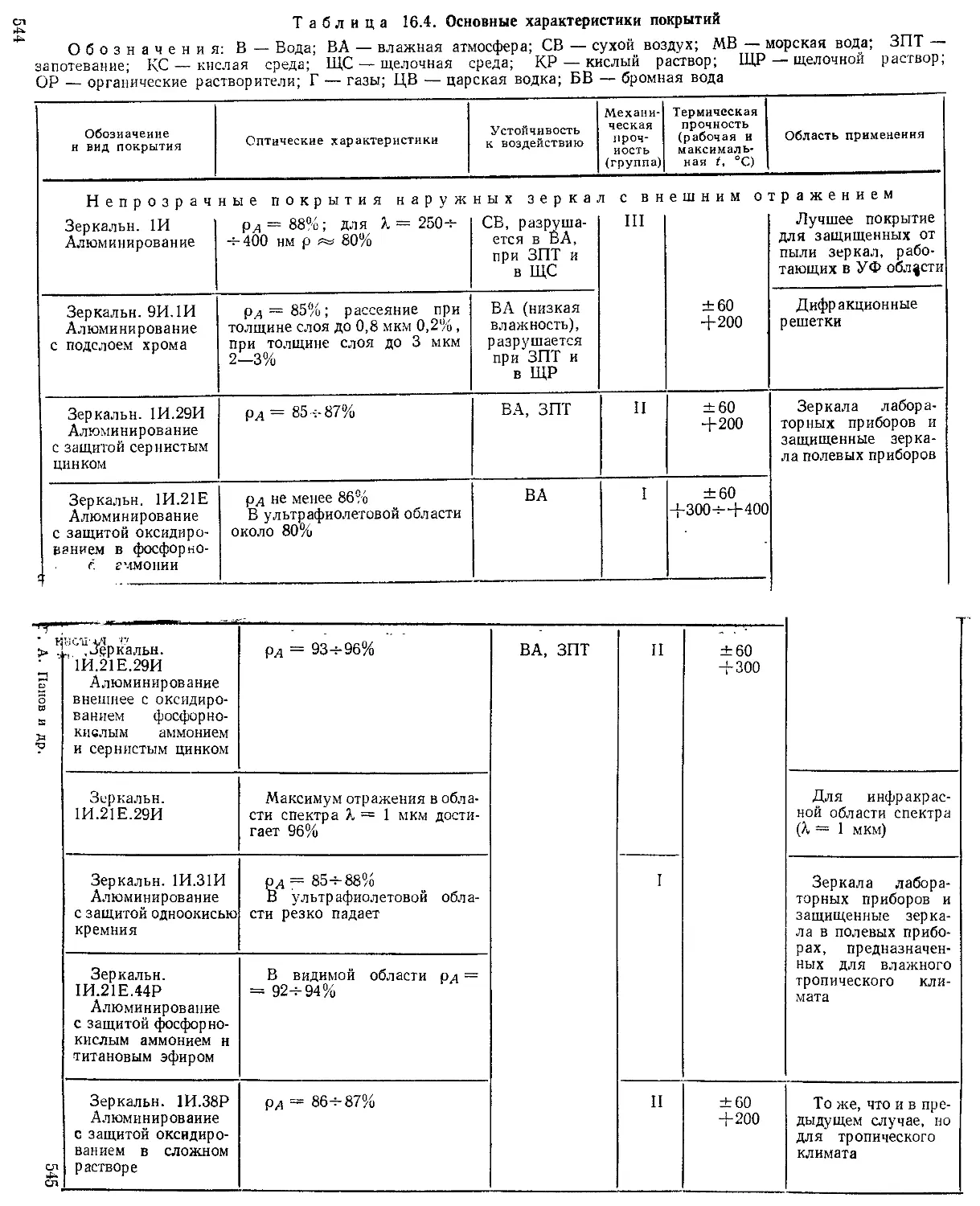
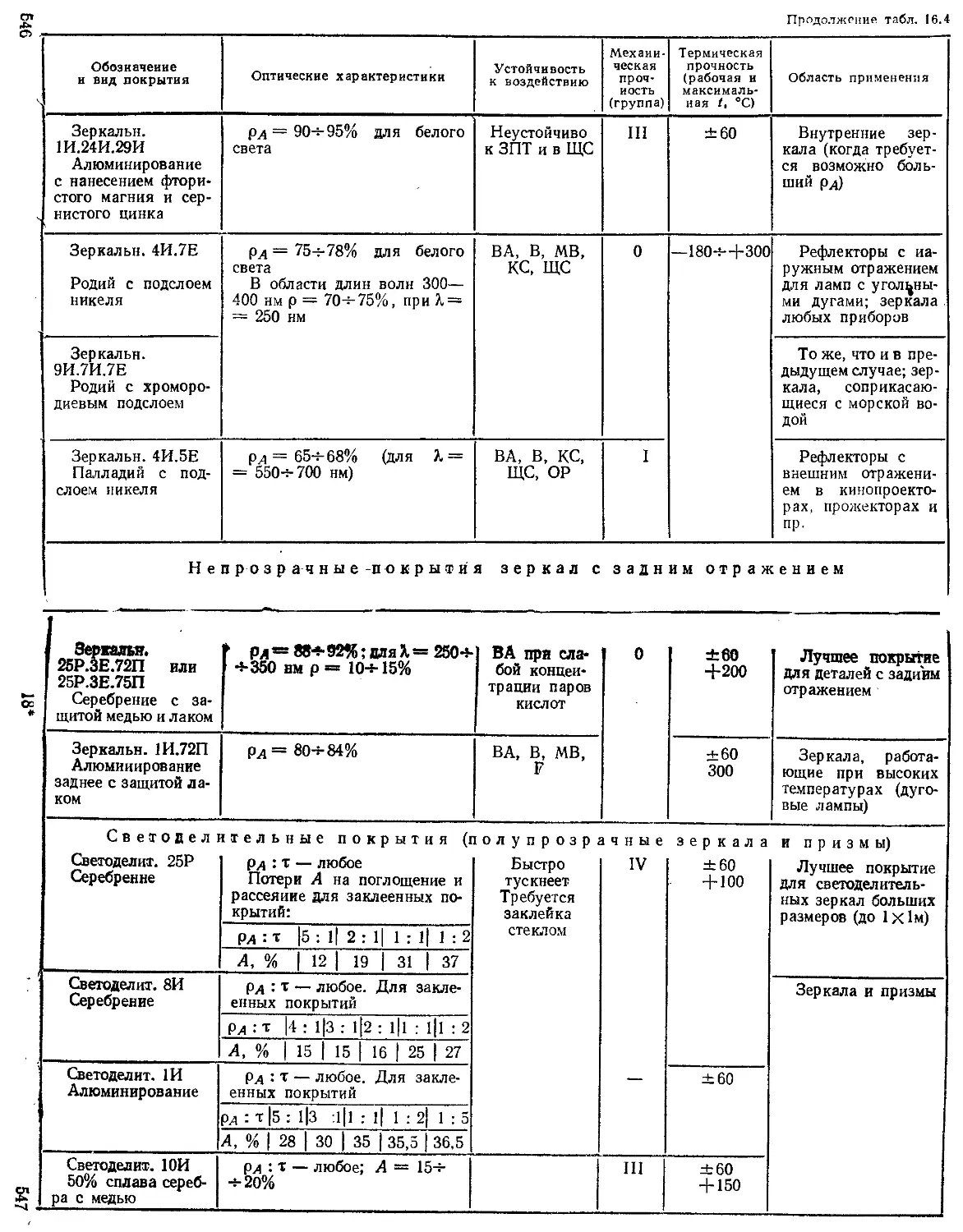
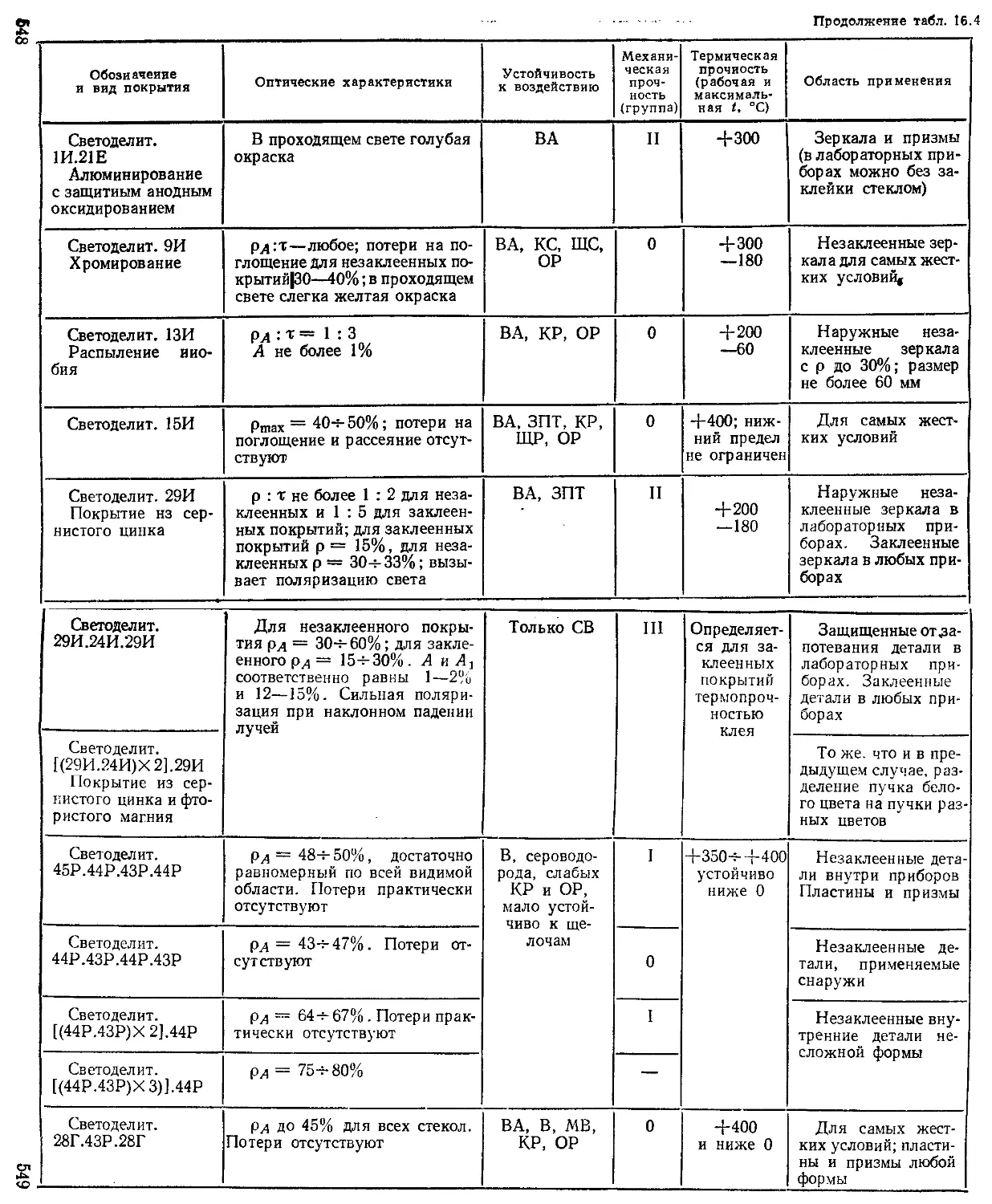
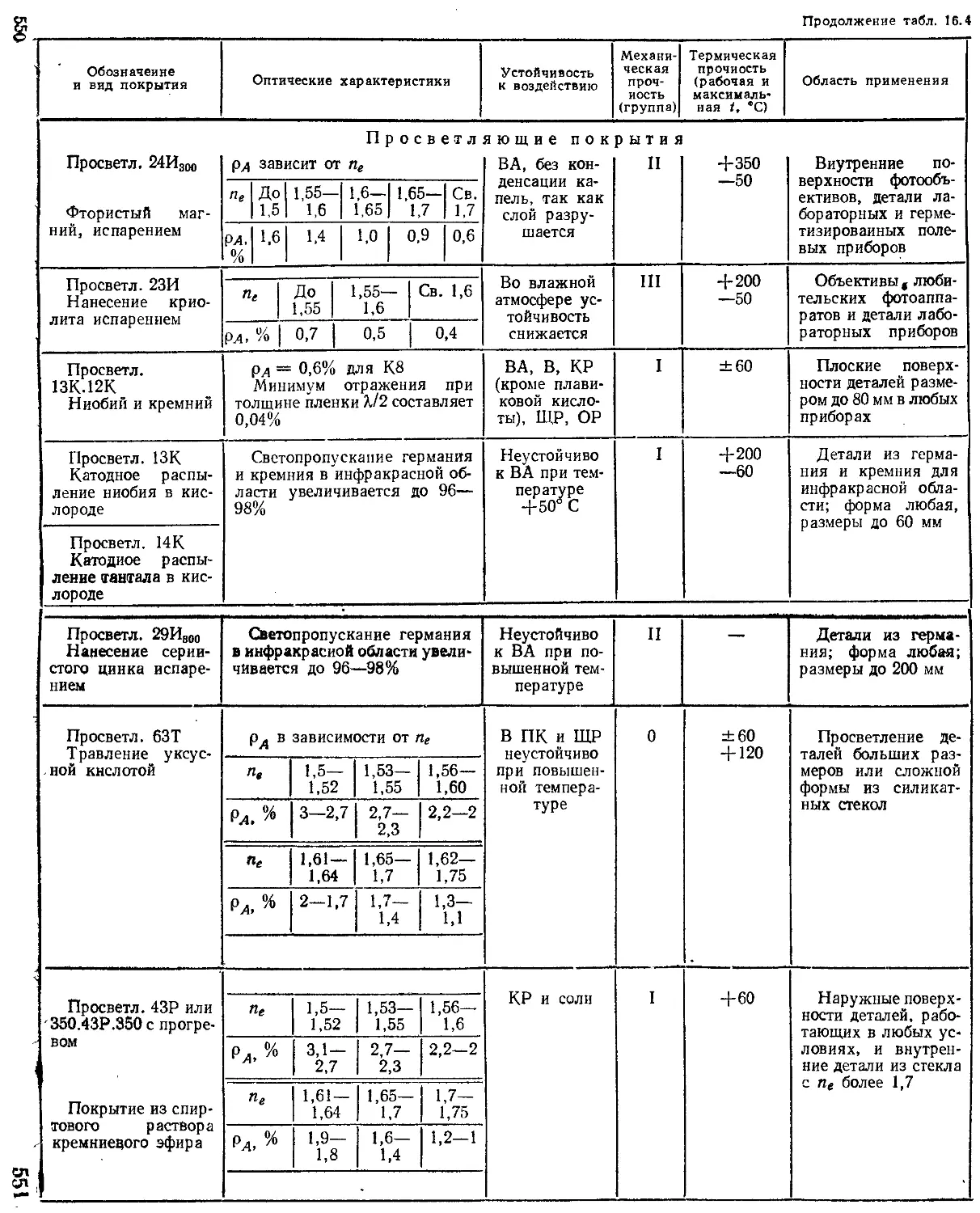
Глава 16. Покрытия оптических деталей (М. Я. Кругер, В. Л. Панов) ....................................... 541
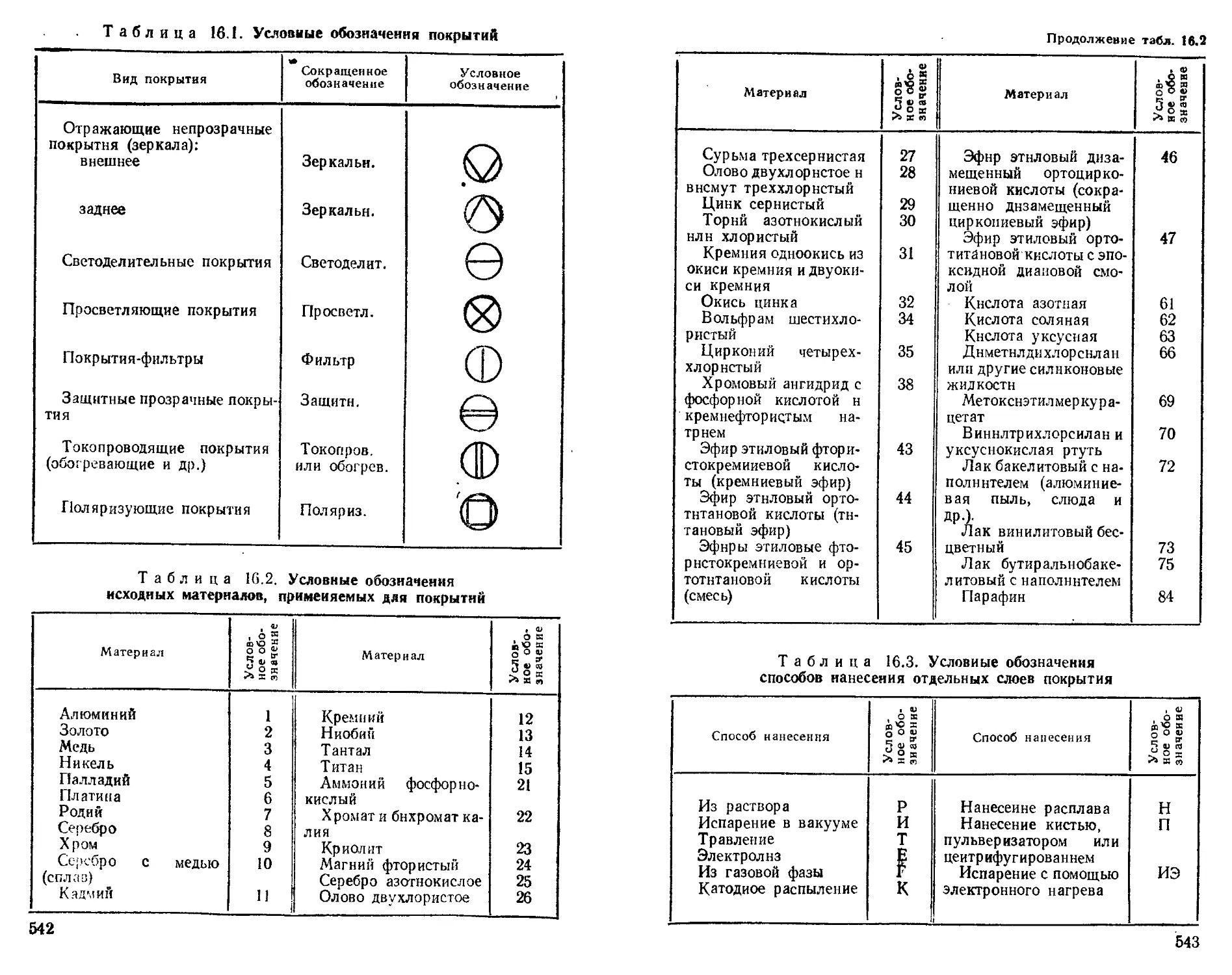
Виды покрытий........................................... —
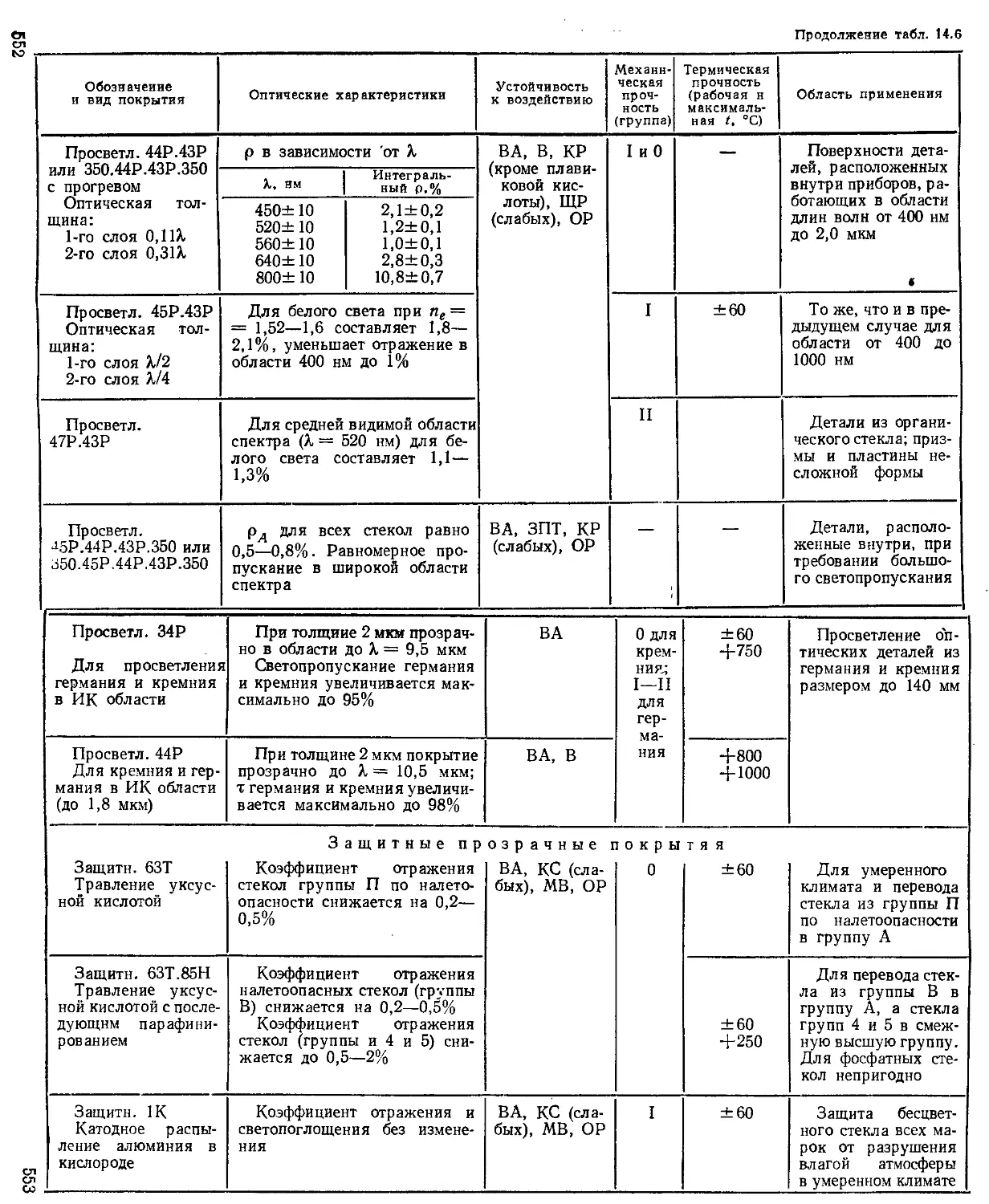
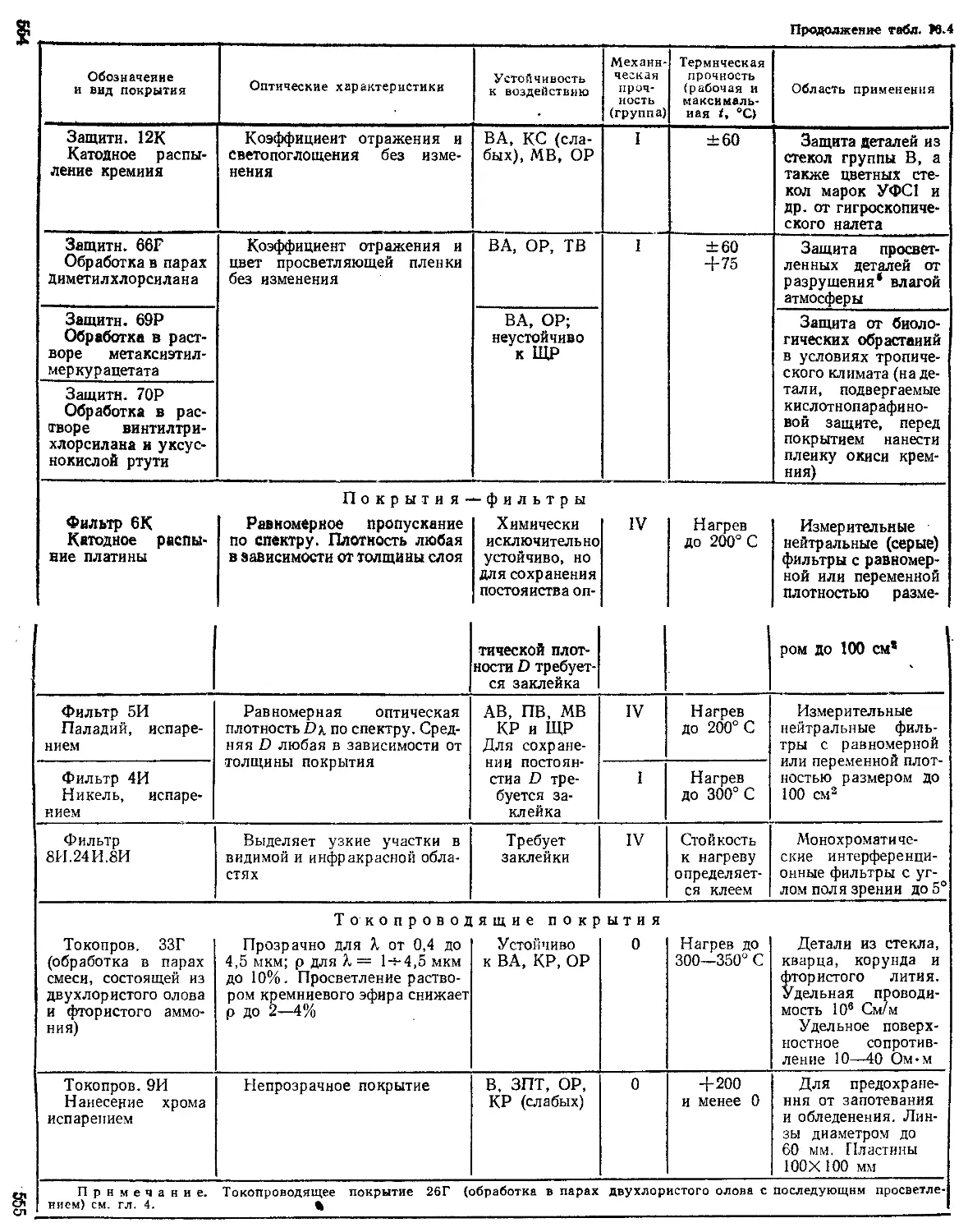
Основные характеристики и выбор покрытий ....... 556
Глава 17. Защита от коррозии. Покрытия деталей оптико-механических приборов (Л. 7И. Левинзон) . . . 558
Общие сведения о коррозии .............................. —
Металлы и сплавы, применяемые без покрытий........... —
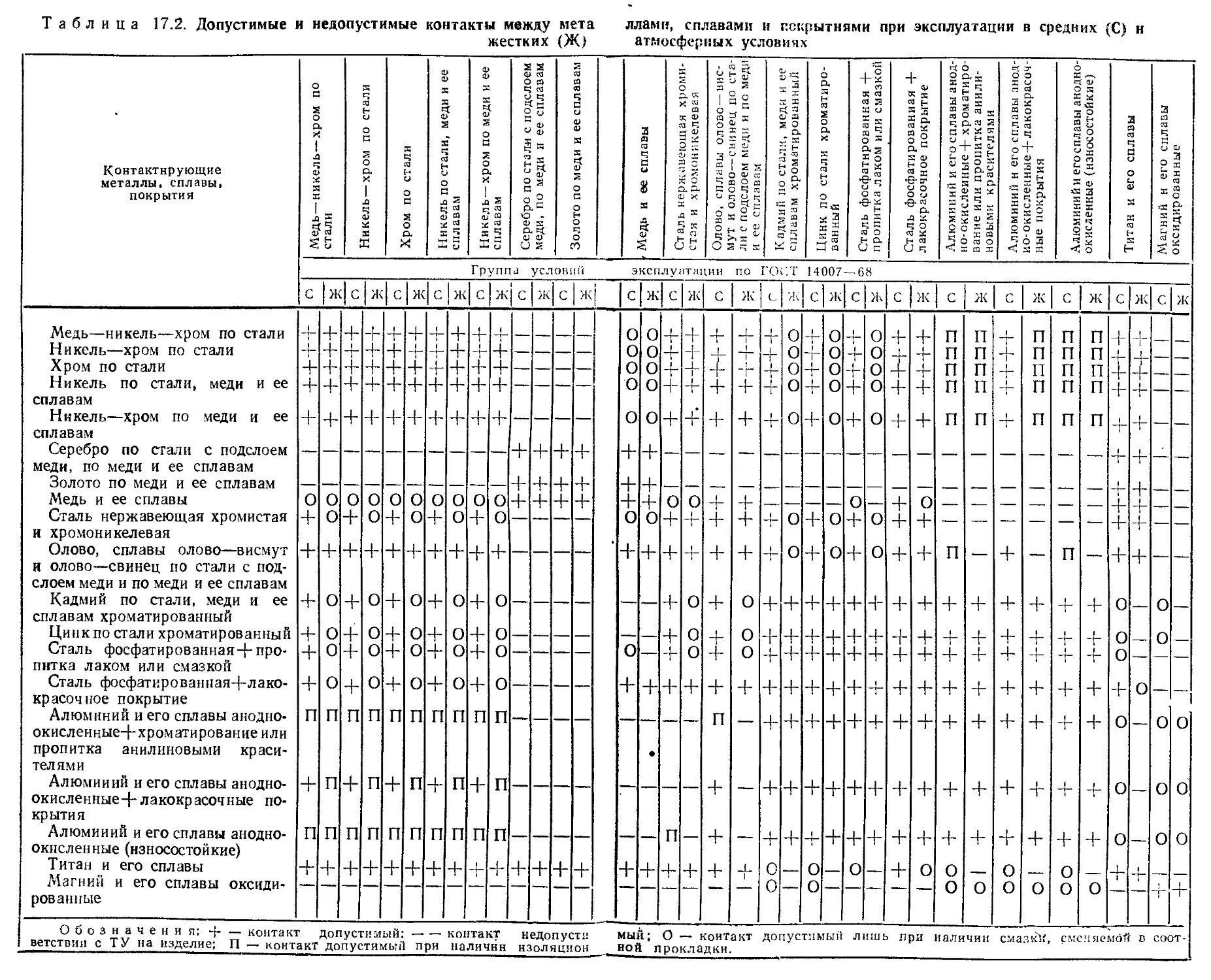
Контактная коррозия .................................. 559
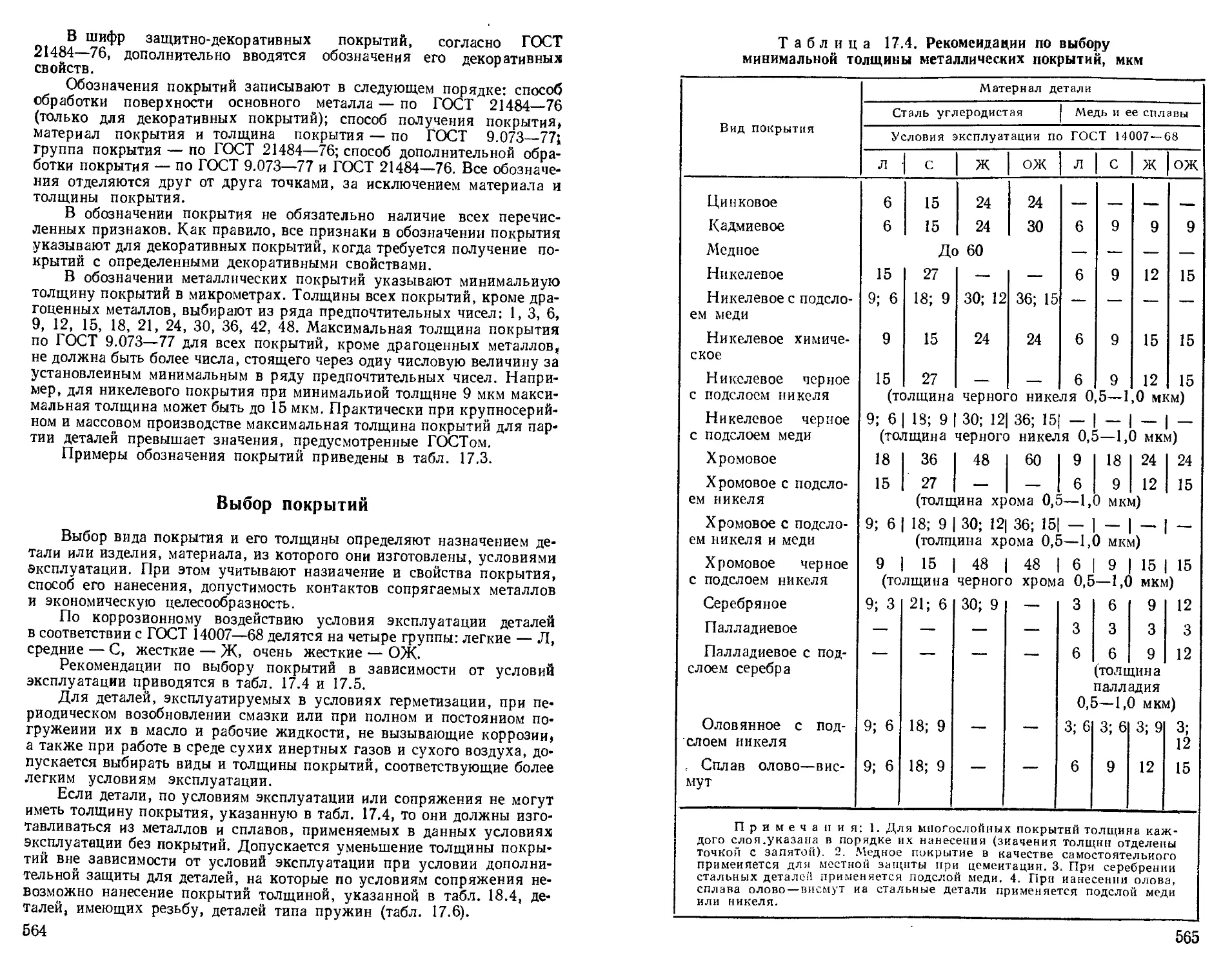
Нанесение на чертежах обозначений покрытий........... 562
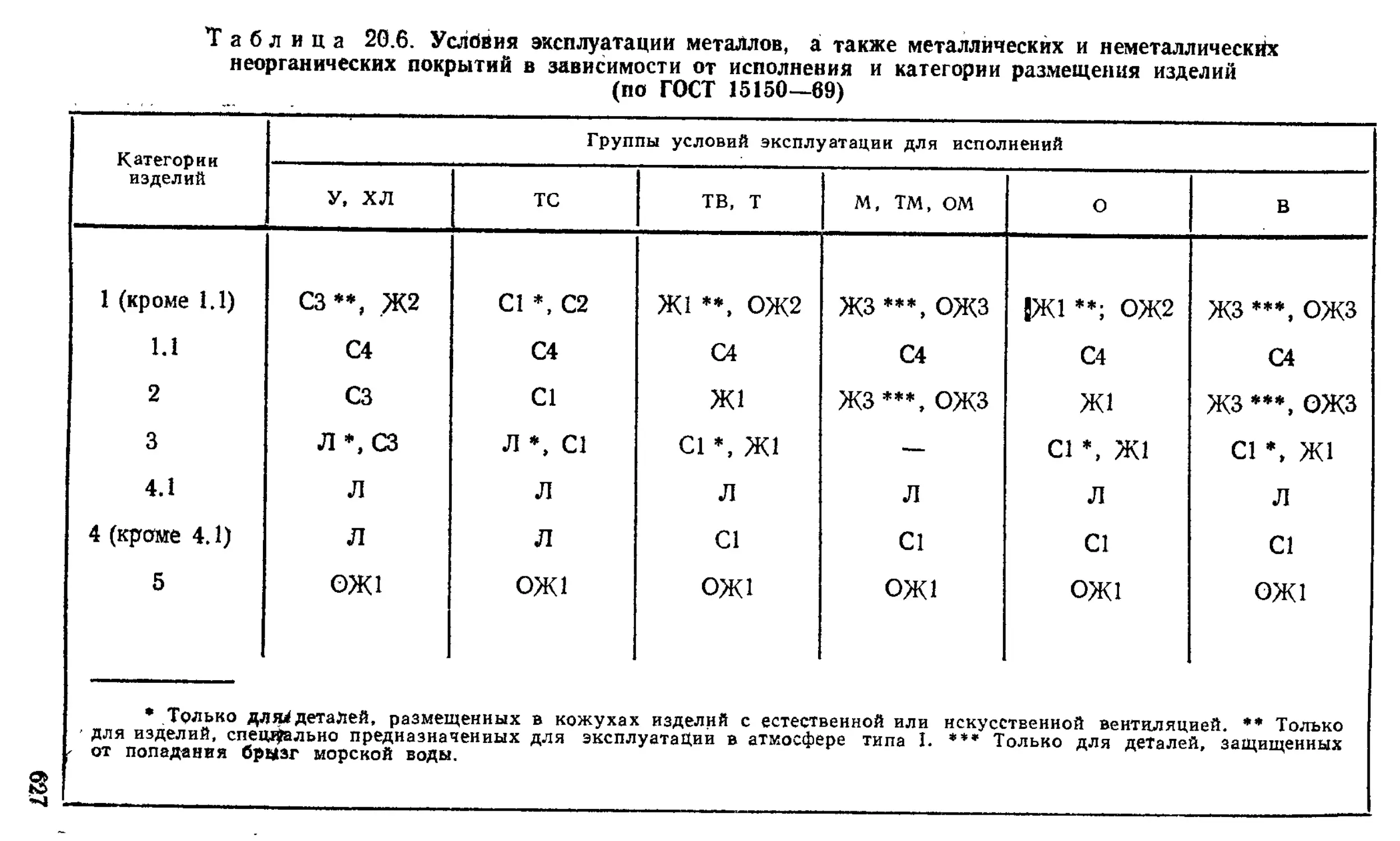
Покрытия металлические и неметаллические неорганические ................................................. —
Краткая характеристика покрытий ...................... —
Обозначения покрытий ............................... 563
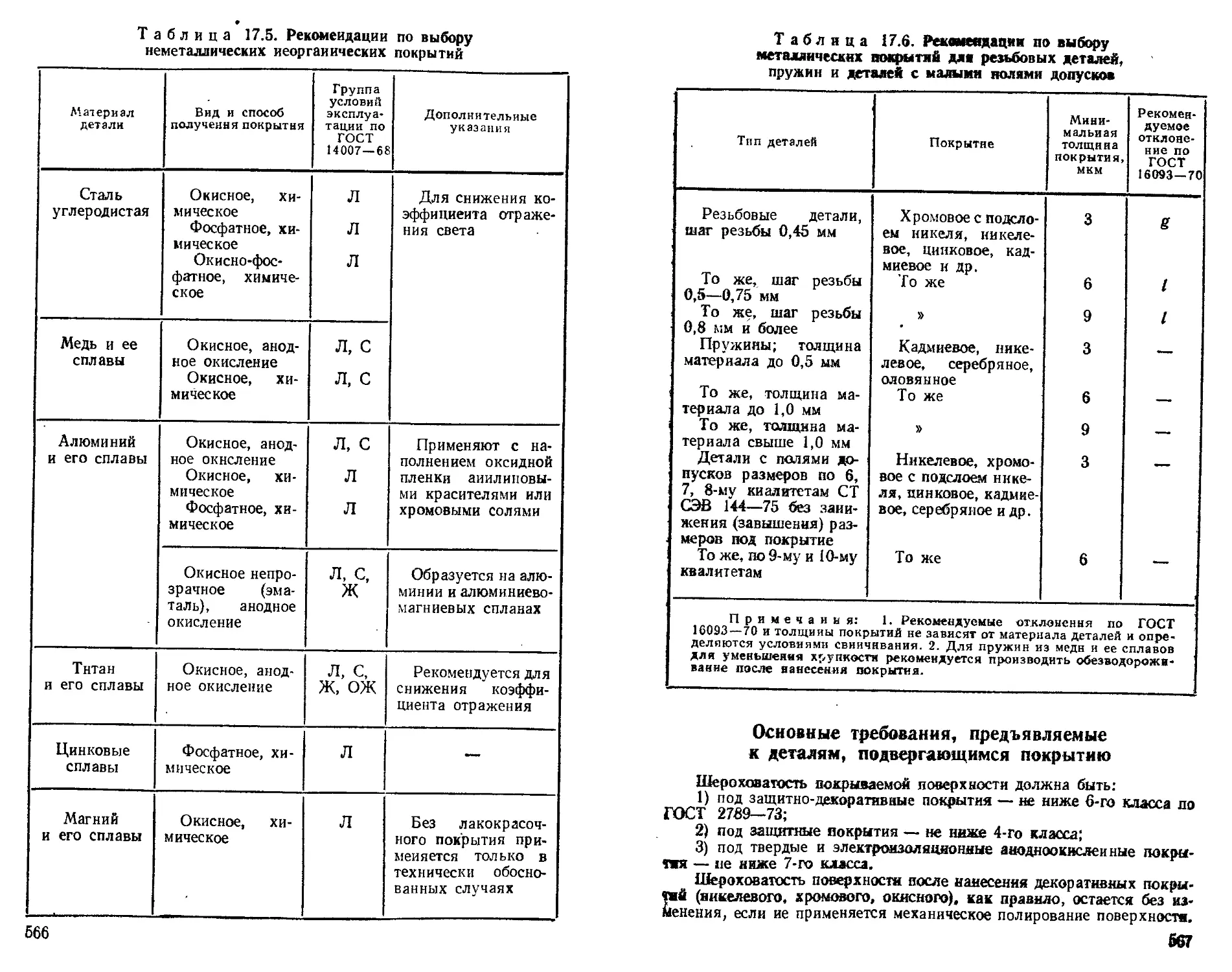
Выбор покрытий ....................................... 564
Основные требования, предъявляемые к деталям, подвергающимся покрытию................................ 567
Основные характеристики металлических покрытий . . ч 569
Основные характеристики неметаллических неорганических покрытий ..................................... 572
Покрытия лакокрасочные ................................. 574
Краткая характеристика покрытий....................... —
Обозначения лакокрасочных покрытий.................... 575
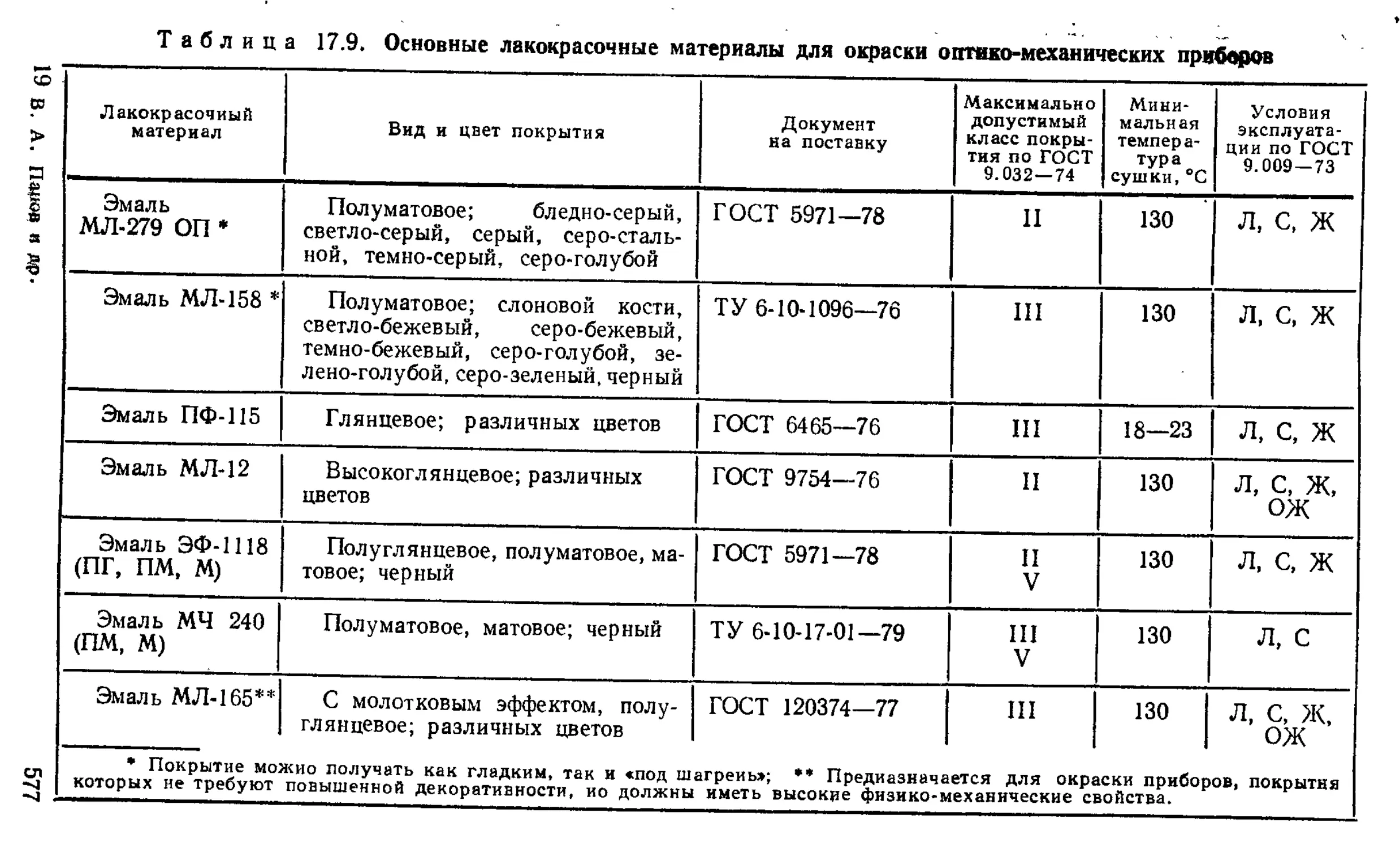
Выбор лакокрасочных материалов для окраски деталей 576
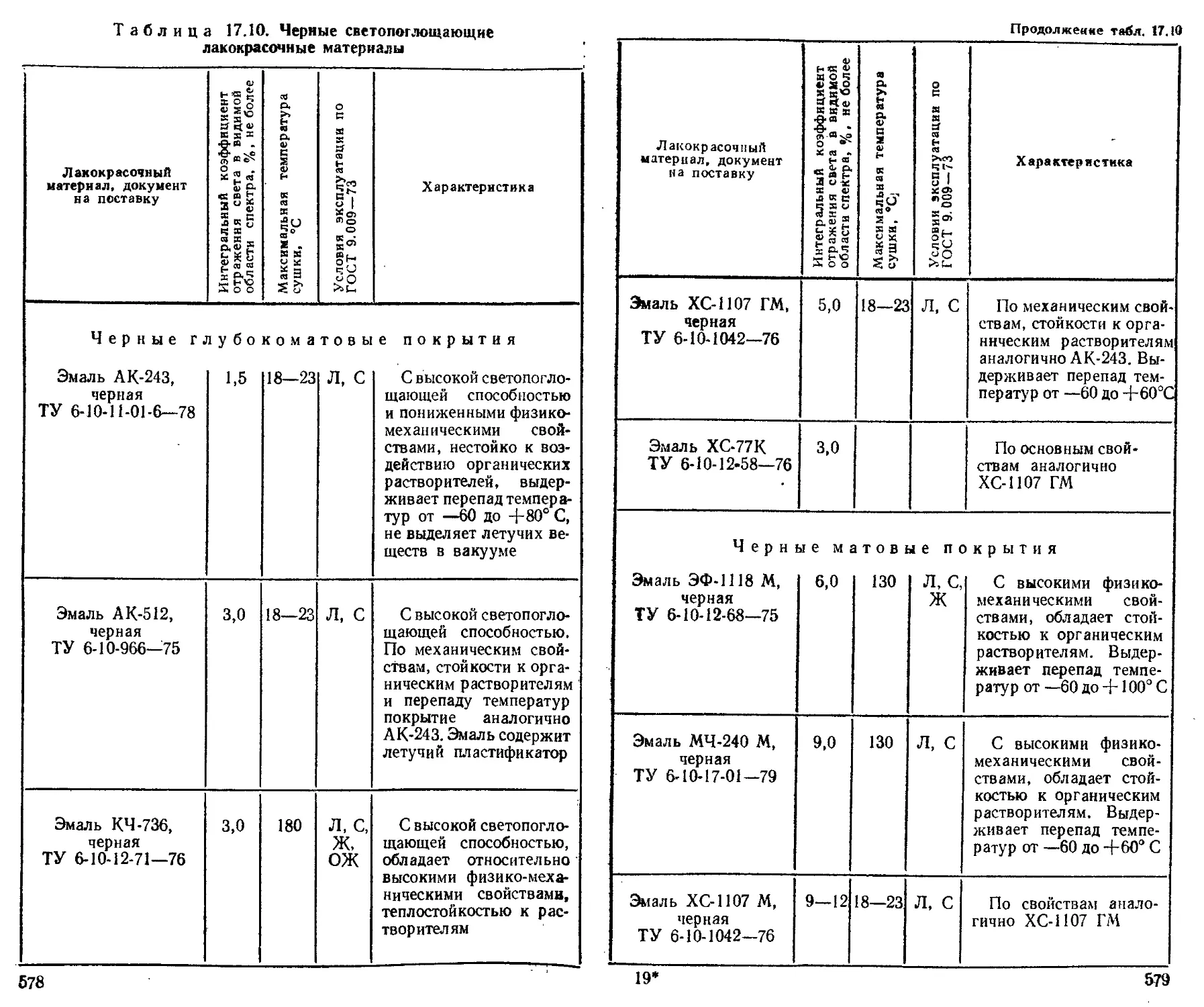
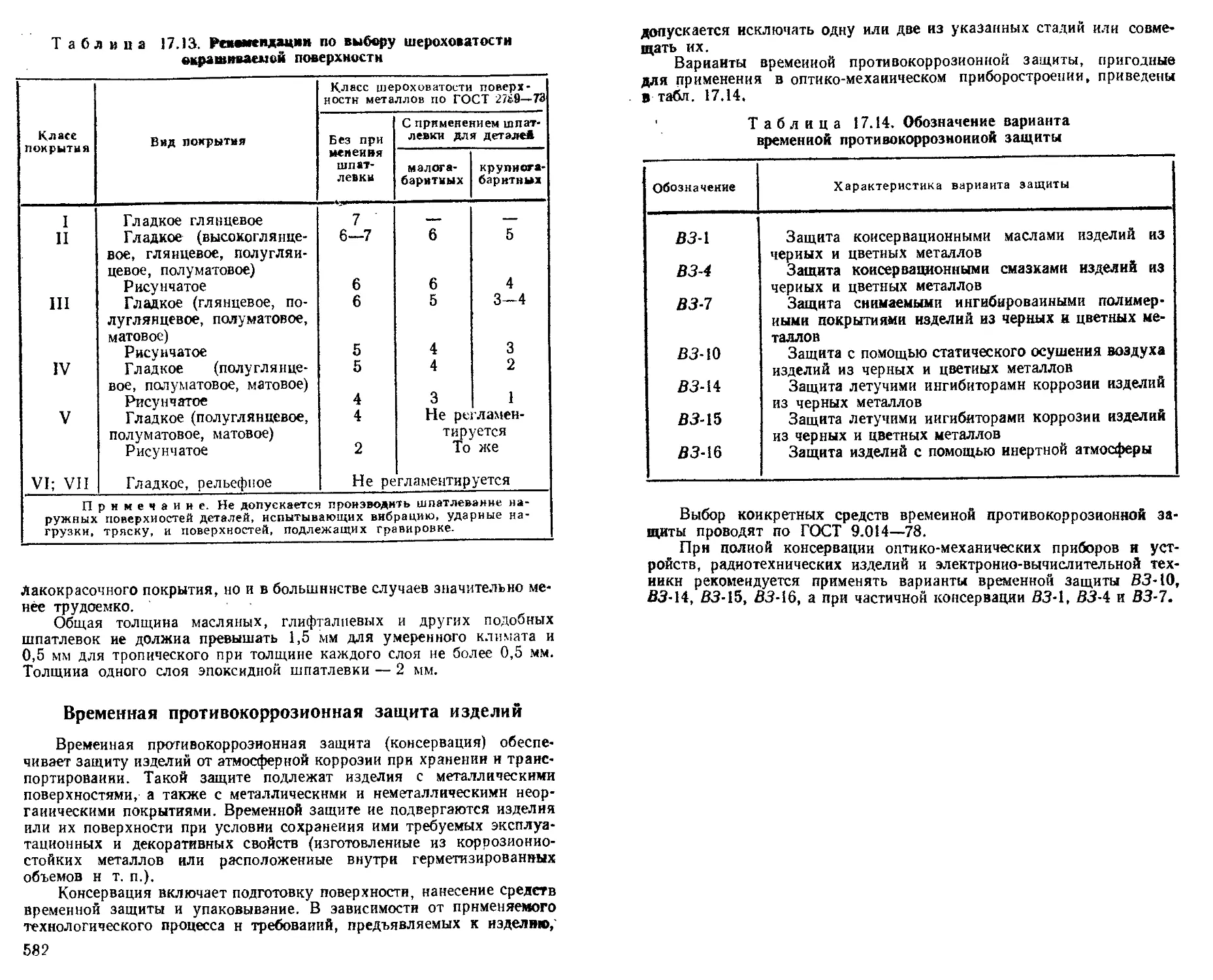
Специфические лакокрасочные материалы, применяемые в оптико-механическом приборостроении ........ 581
Требования к окрашиваемым деталям ................• —
Временная противокоррозионная защита изделий . . . 582
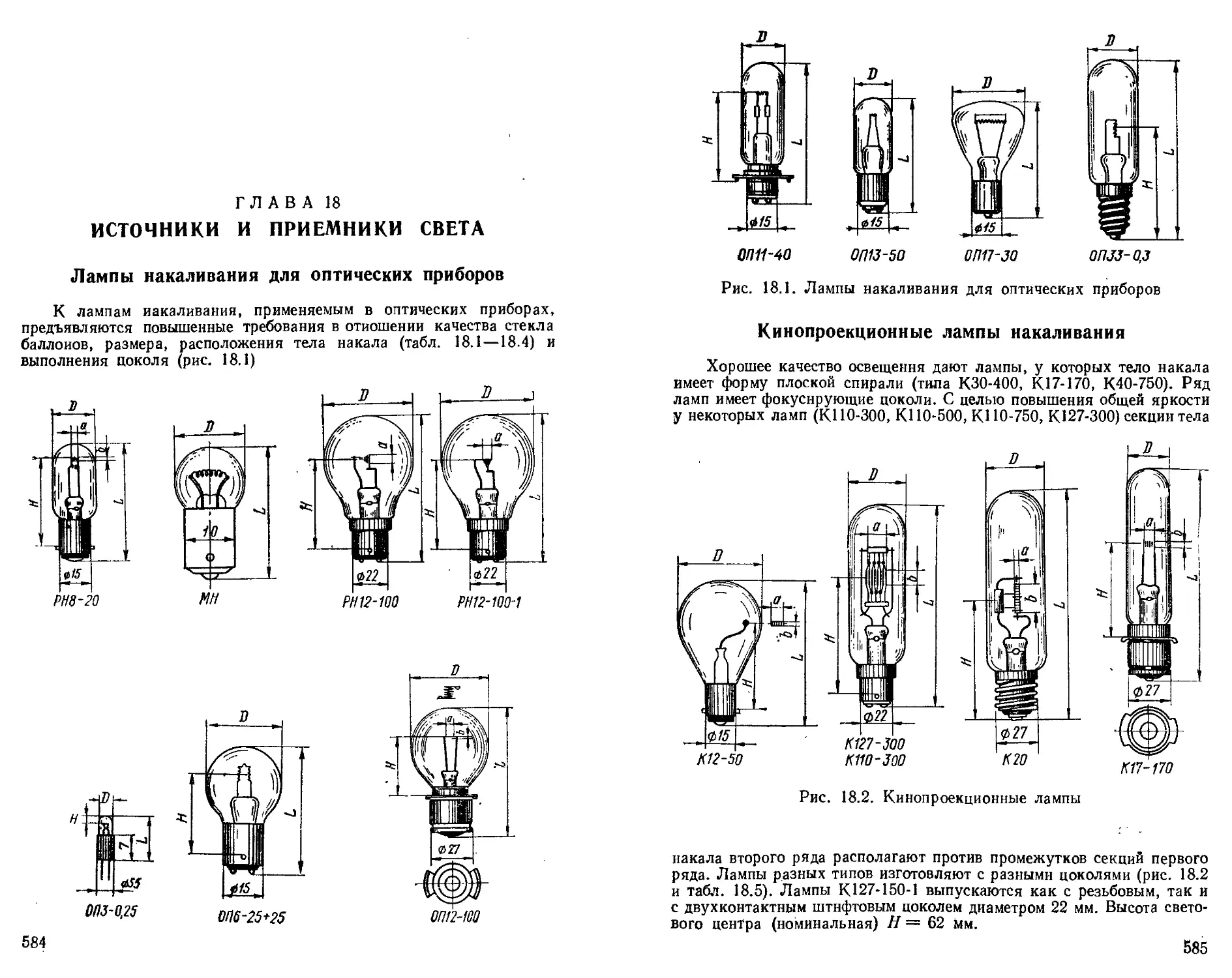
Глава 18. Источники и приемники света (В. Л. Панов, М. Я* Кругер)....................................... 584
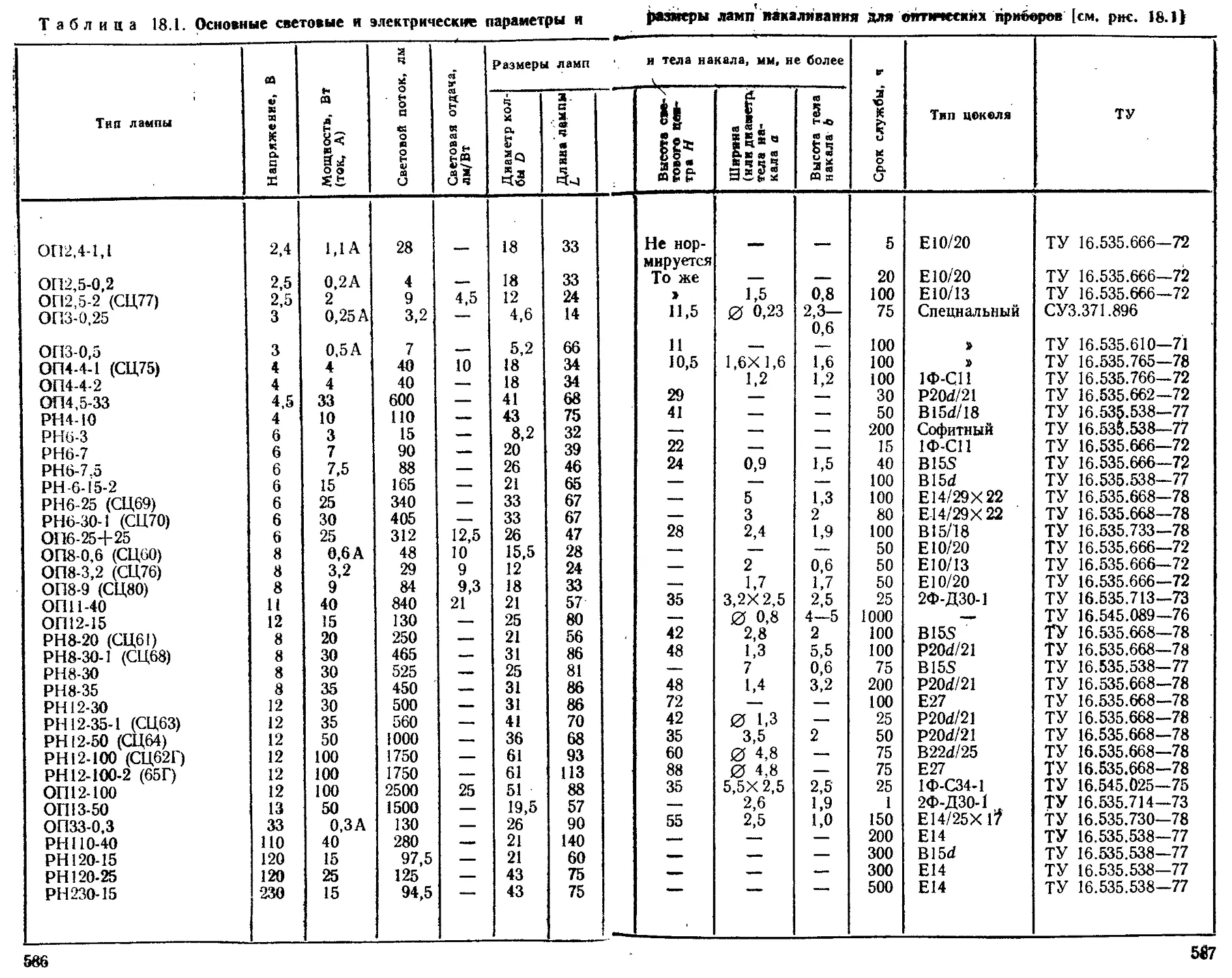
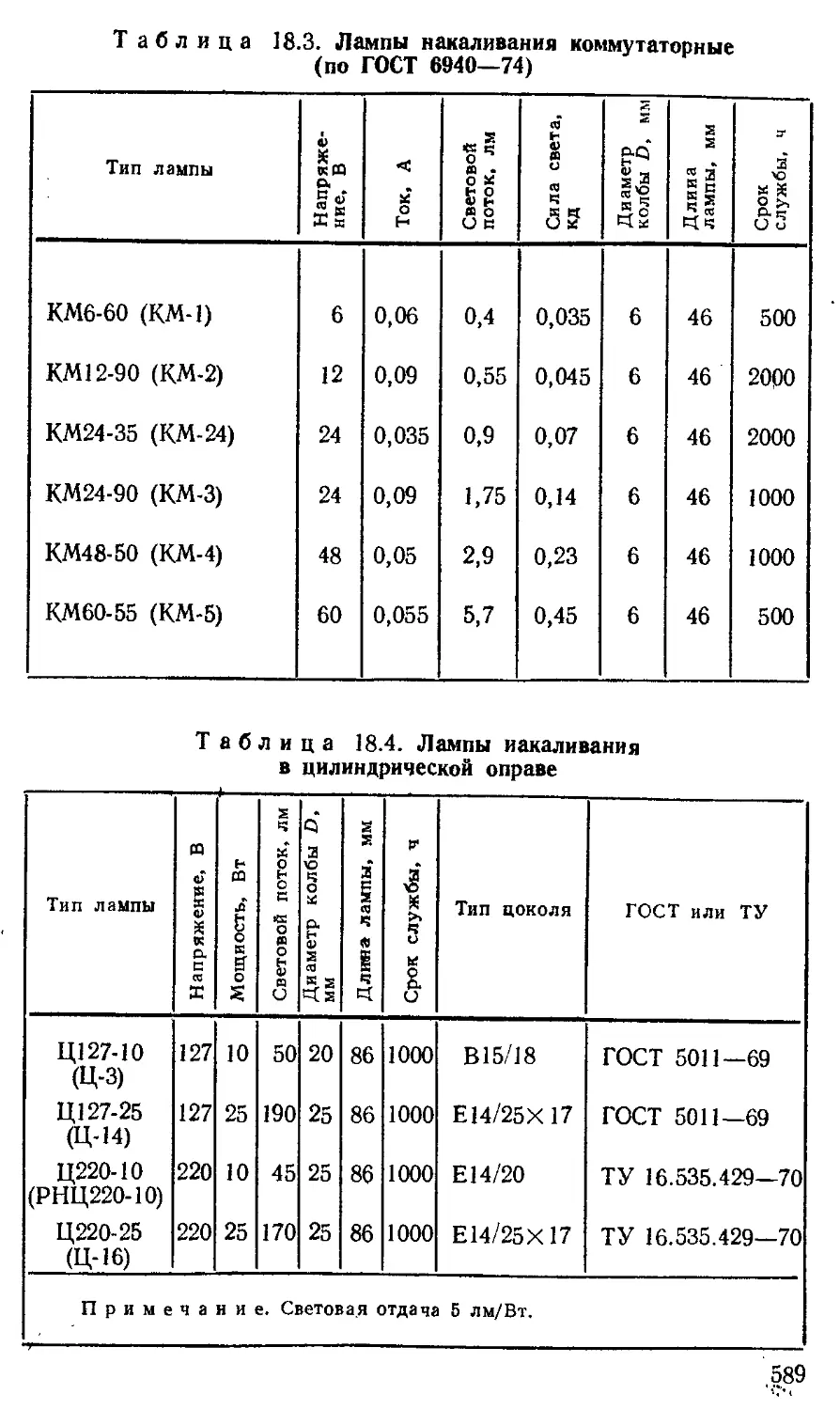
Лампы накаливания для оптических приборов.......... —
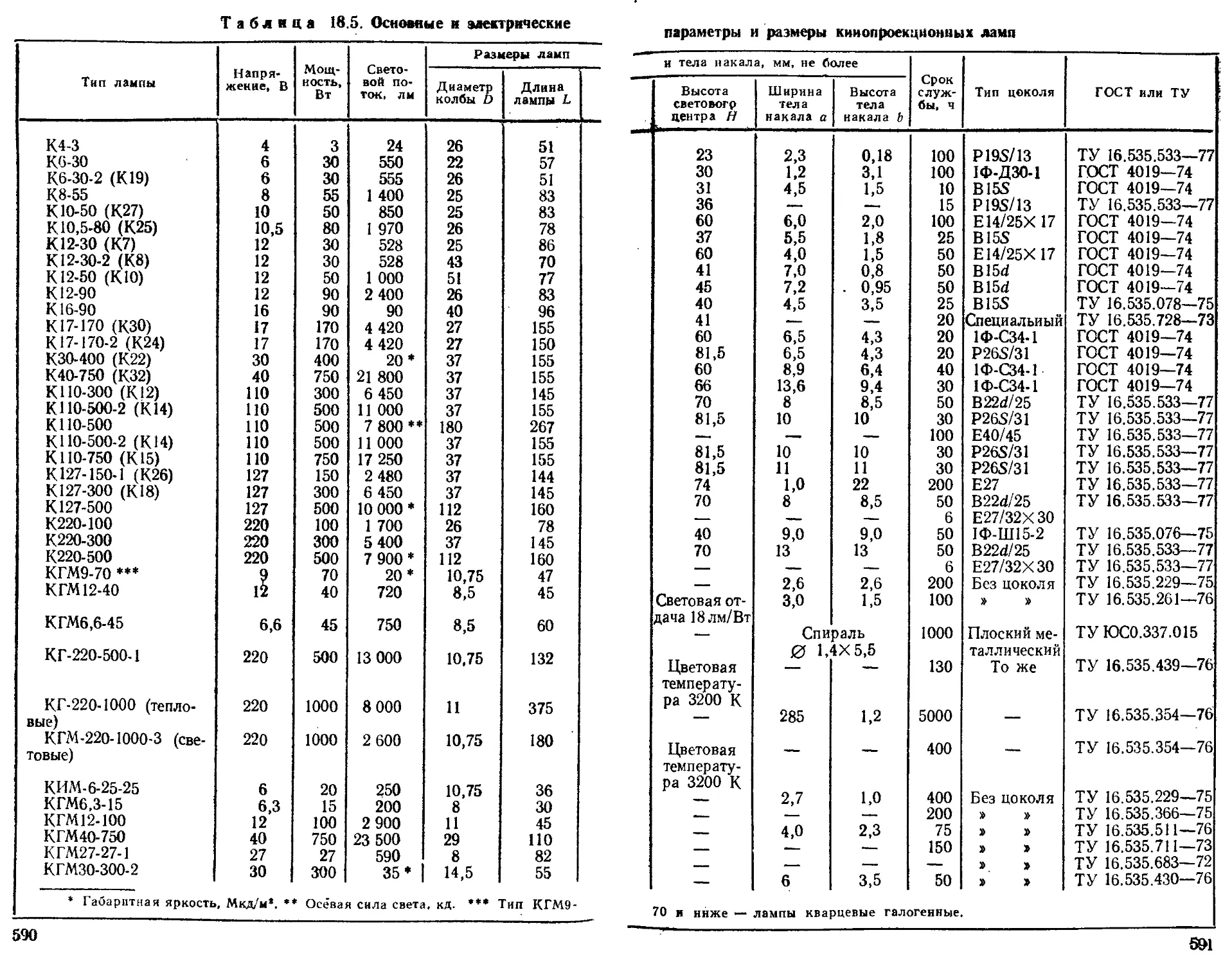
Кинопроекционные лампы накаливания........ 585
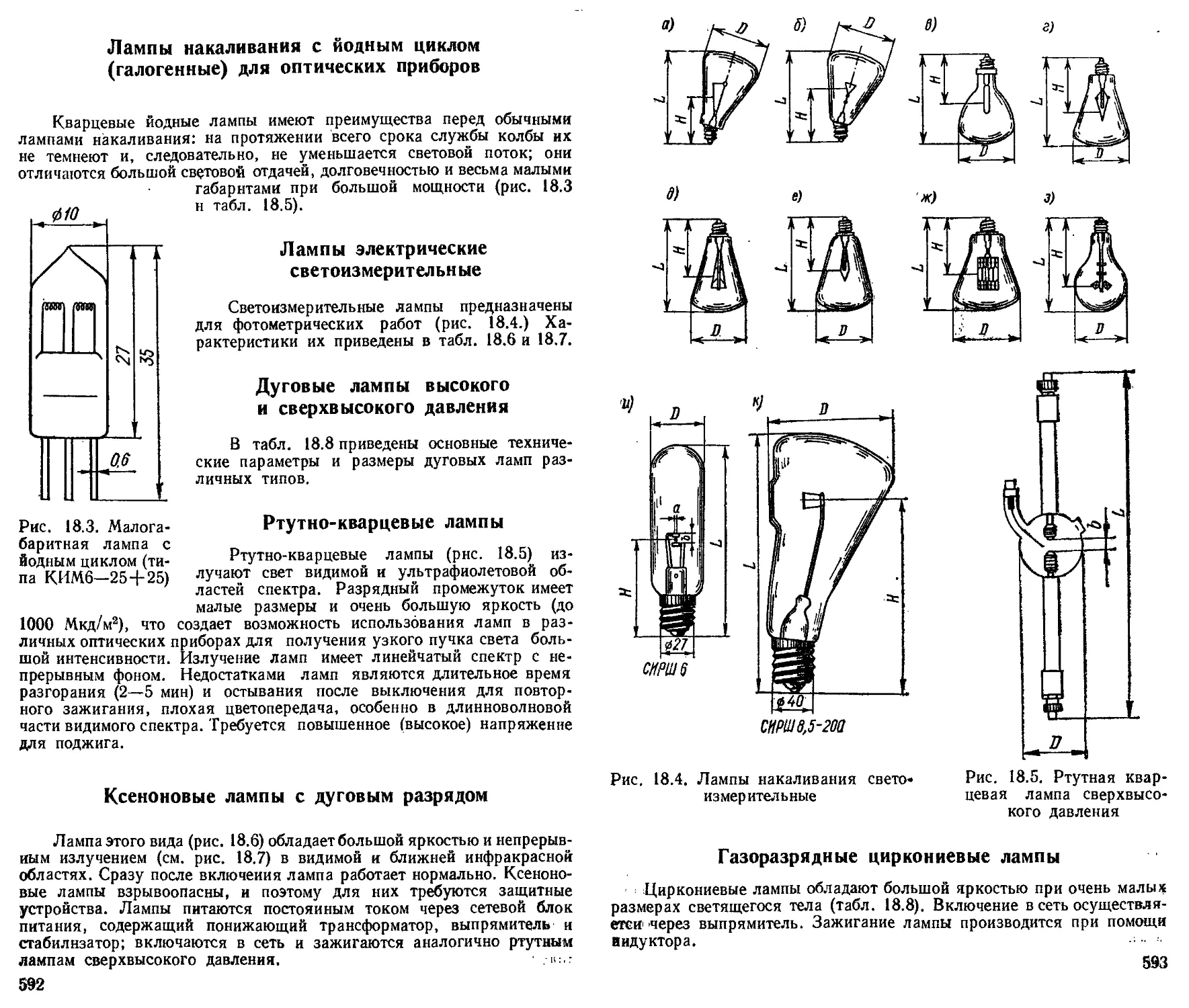
Лампы накаливания с йодным циклом (галогенные) для оптических приборов ................................ 592
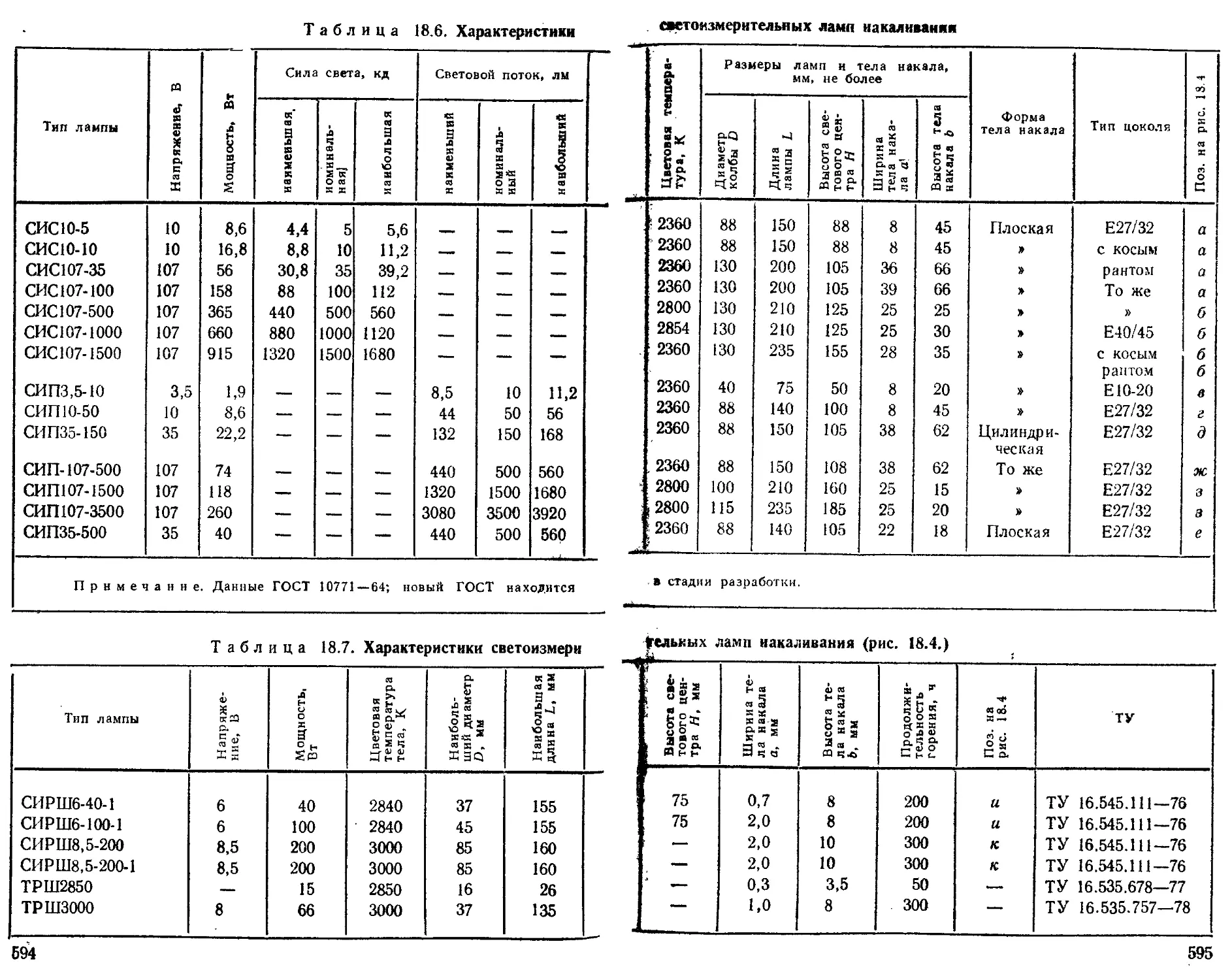
Лампы электрические светоизмерительные..............
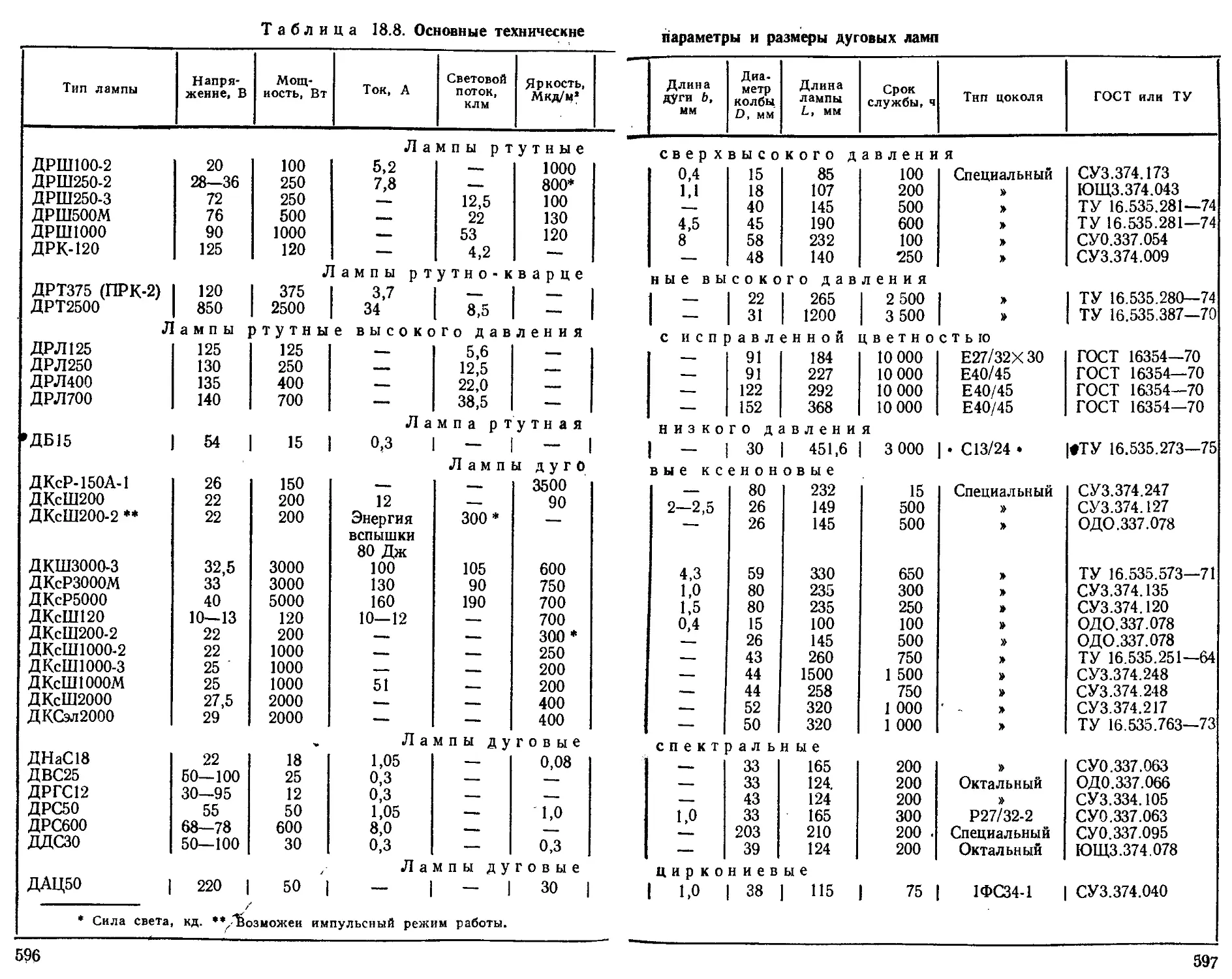
Дуговые лампы высокого и сверхвысокого давления . . .
Ртутно-кварцевые лампы .............................
Ксеноновые лампы с дуговым разрядом ................
Газоразрядные циркониевые лампы .................... 593
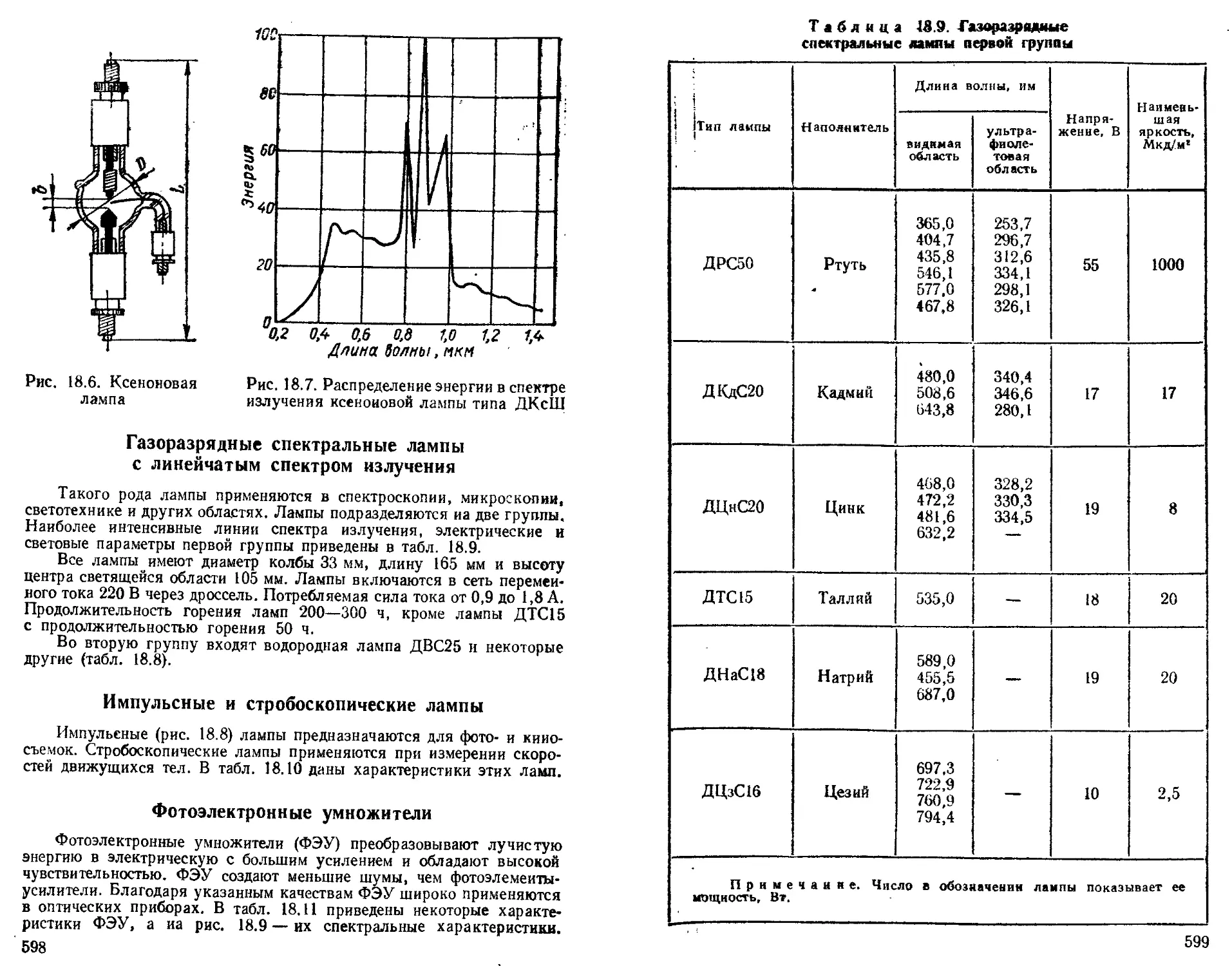
Газоразрядные спектральные лампы с линейчатым спектром излучения................................. 598
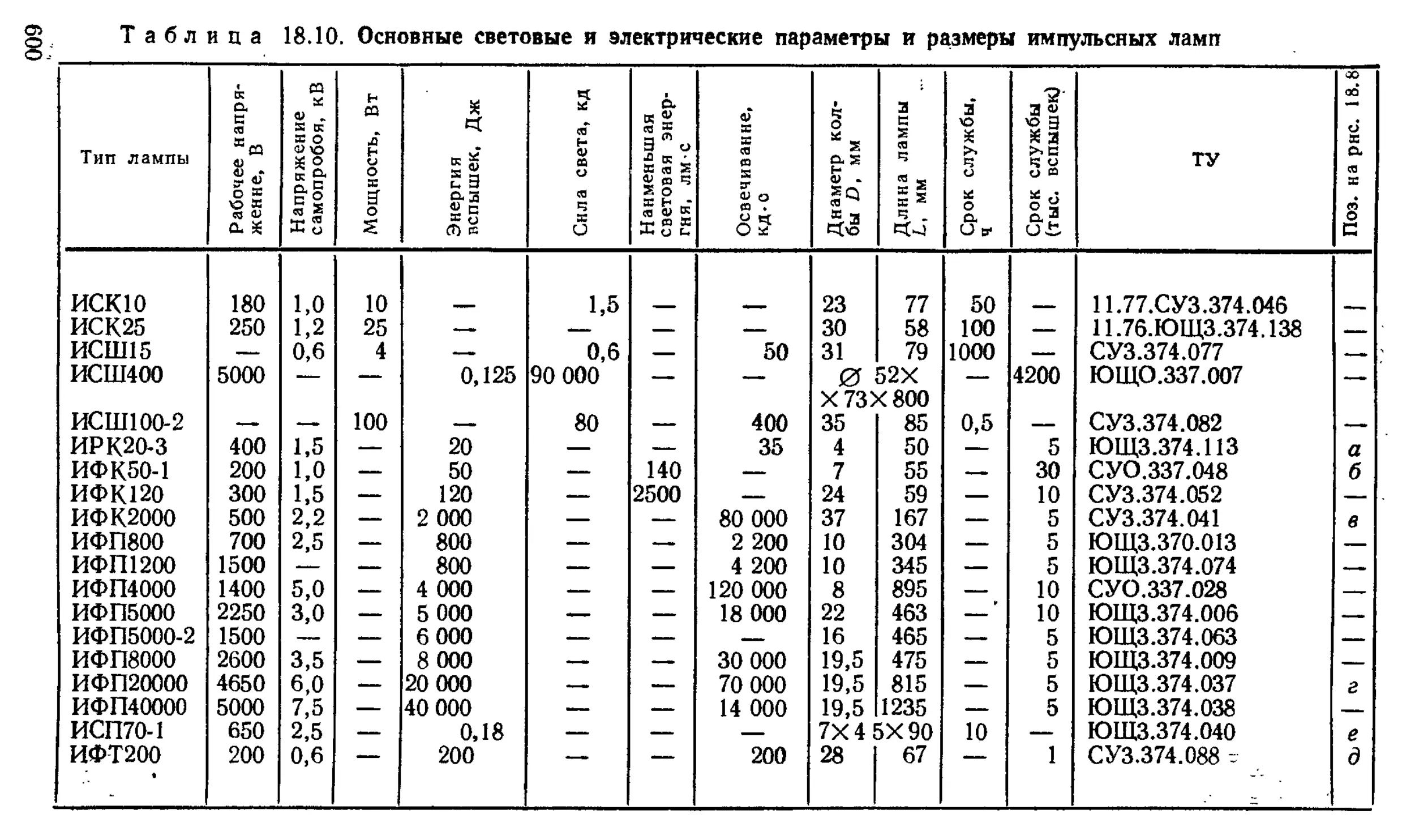
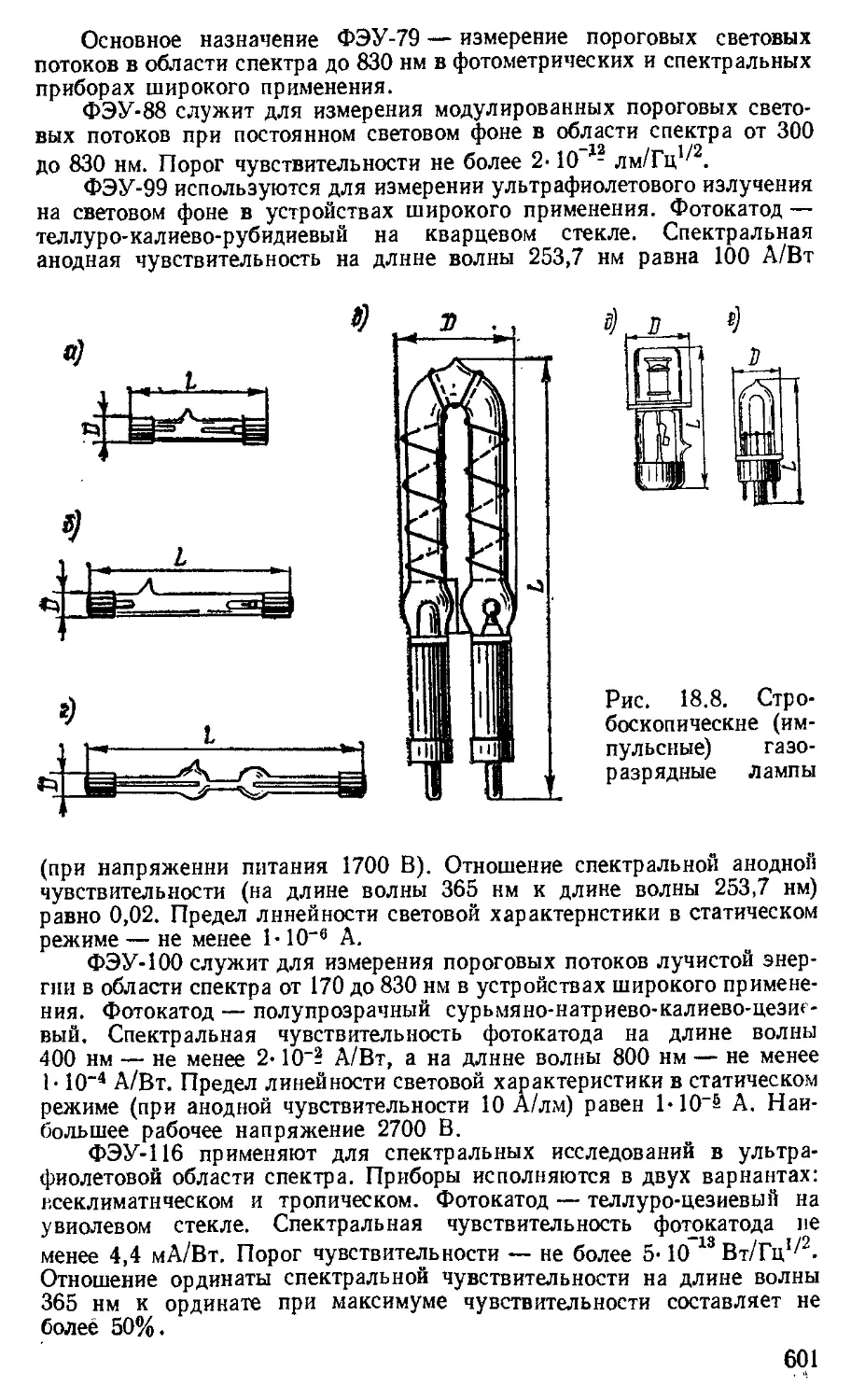
Импульсные и стробоскопические лампы.................. —
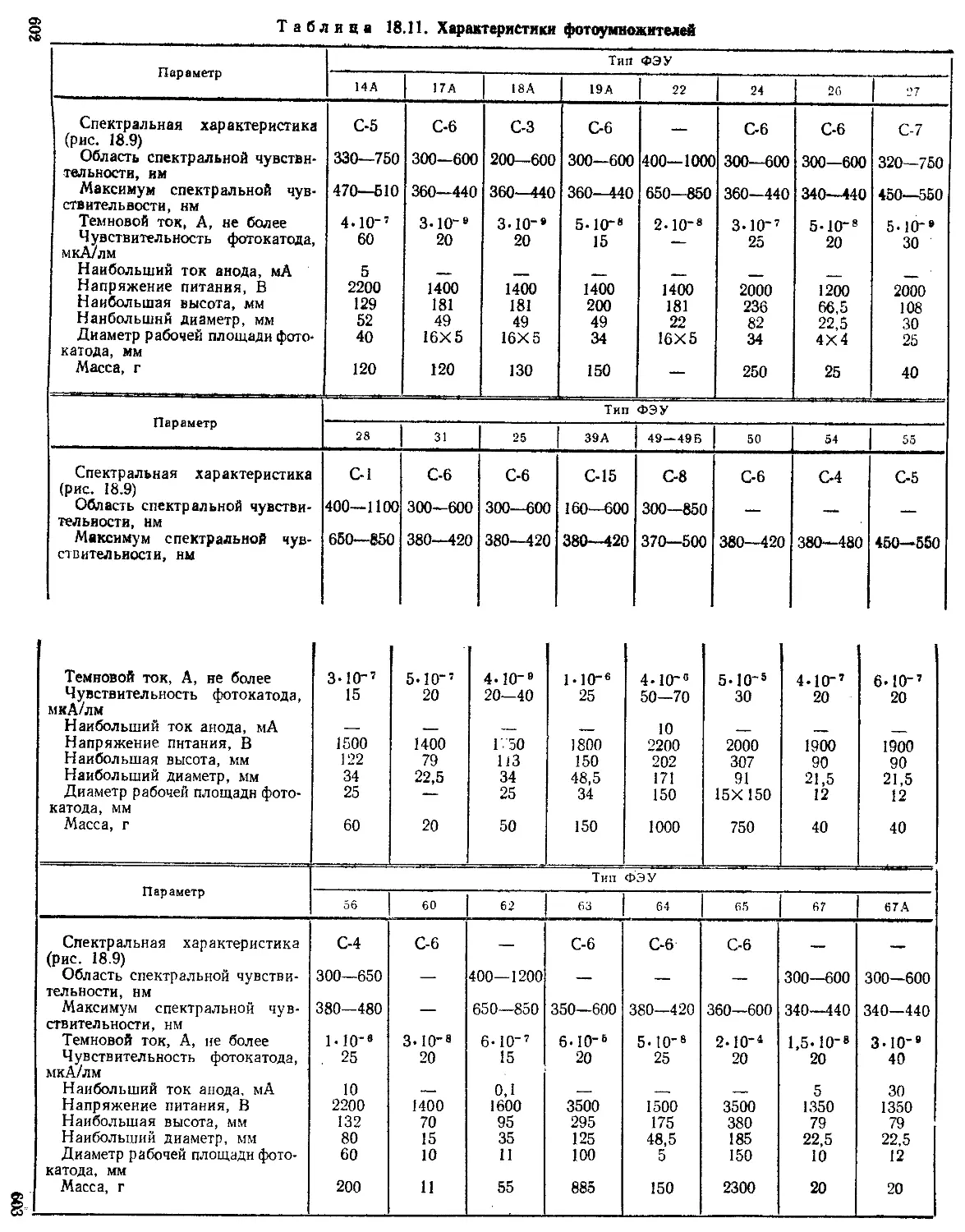
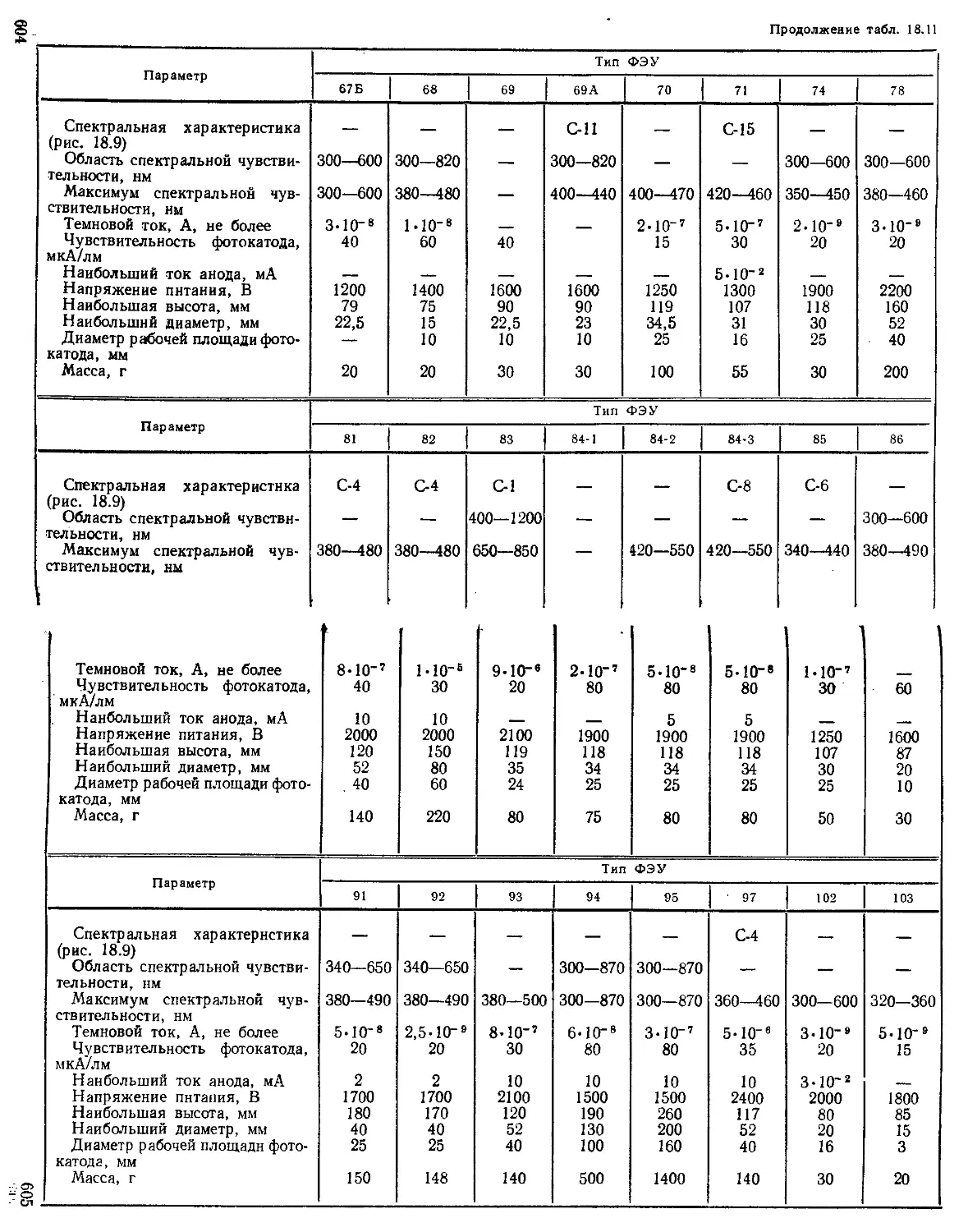
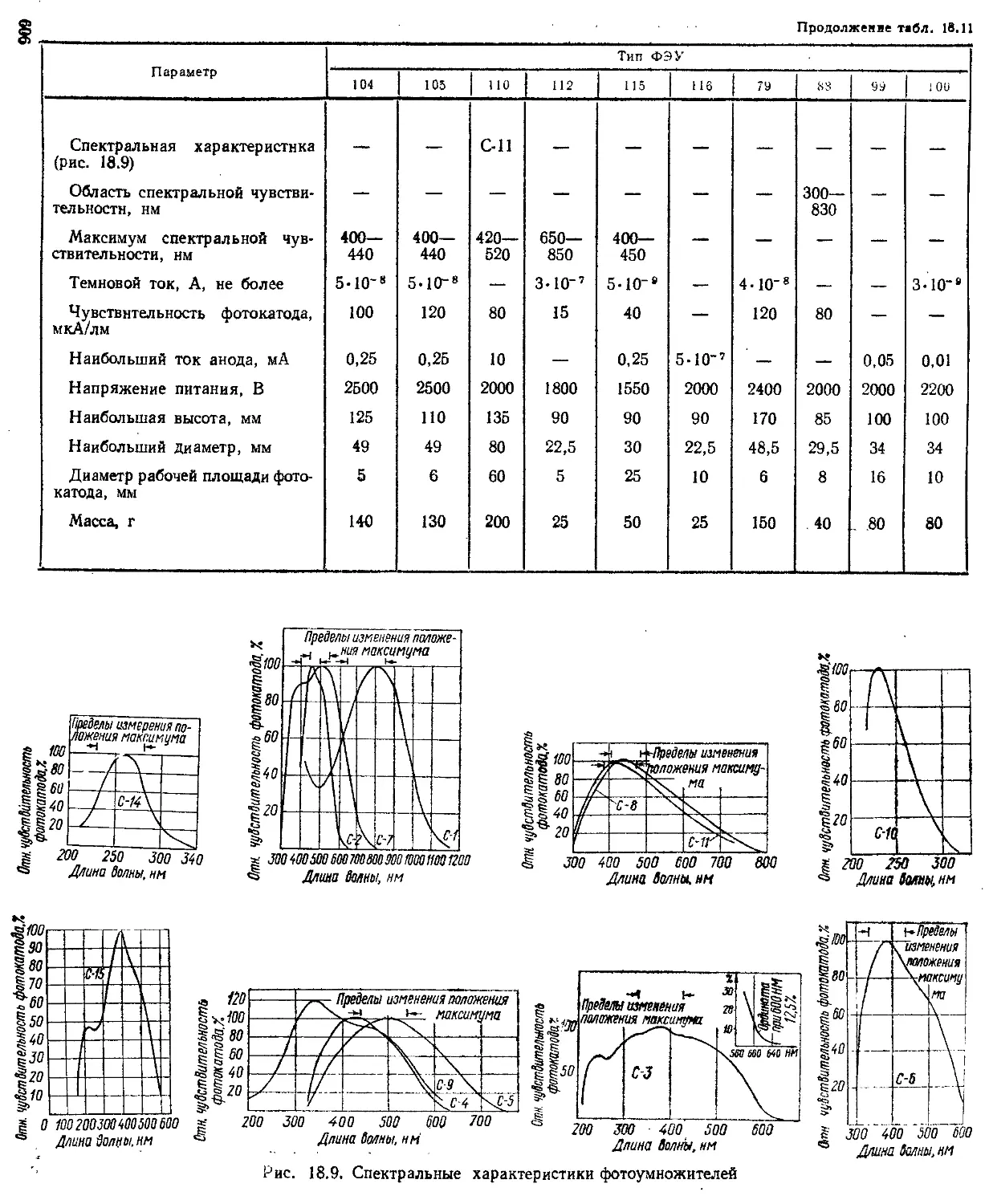
Фотоэлектронные умножители ........................... —
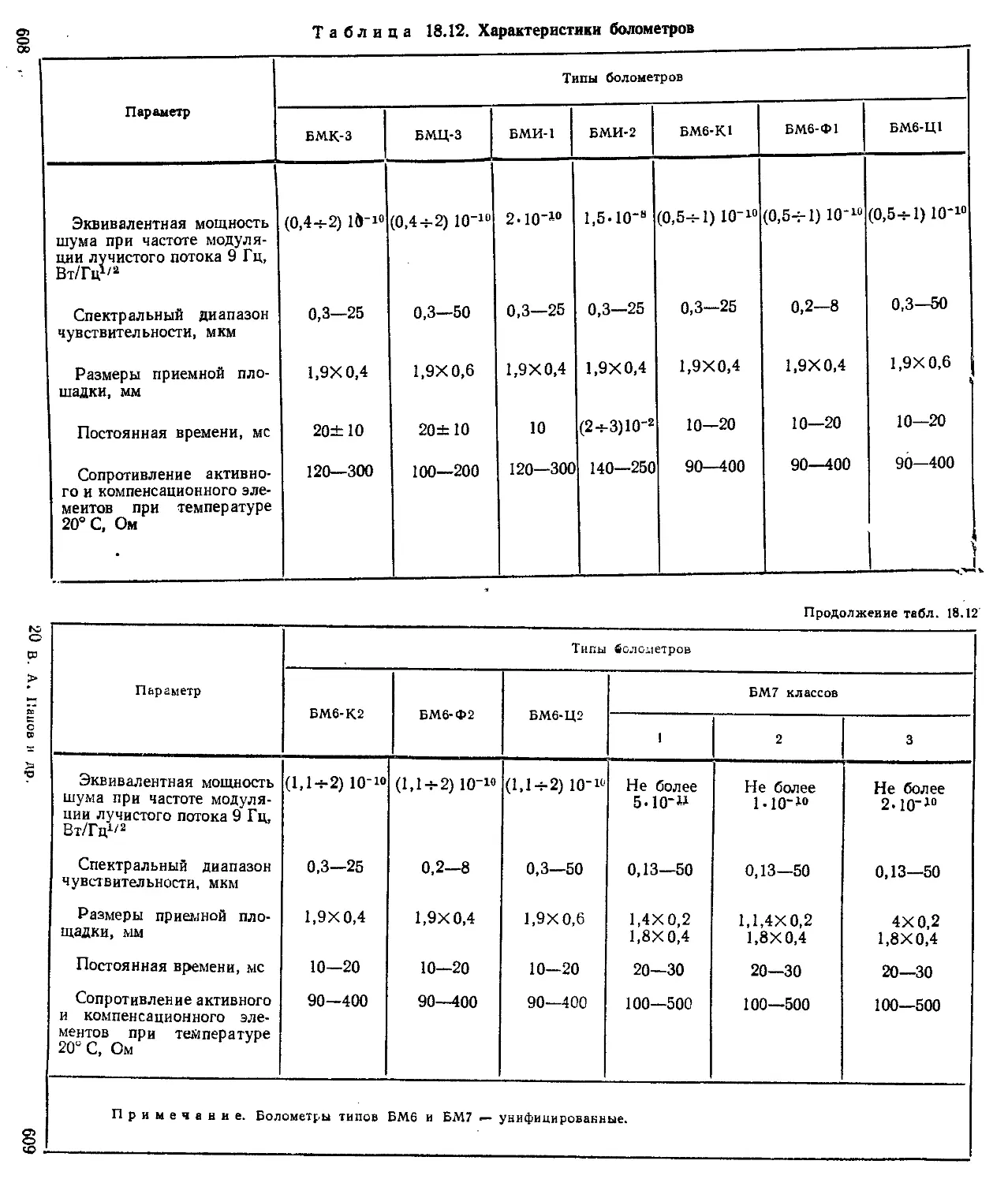
Болометры .......................................... 512
Электронно-оптические преобразователи (ЭОП) • • • • 612
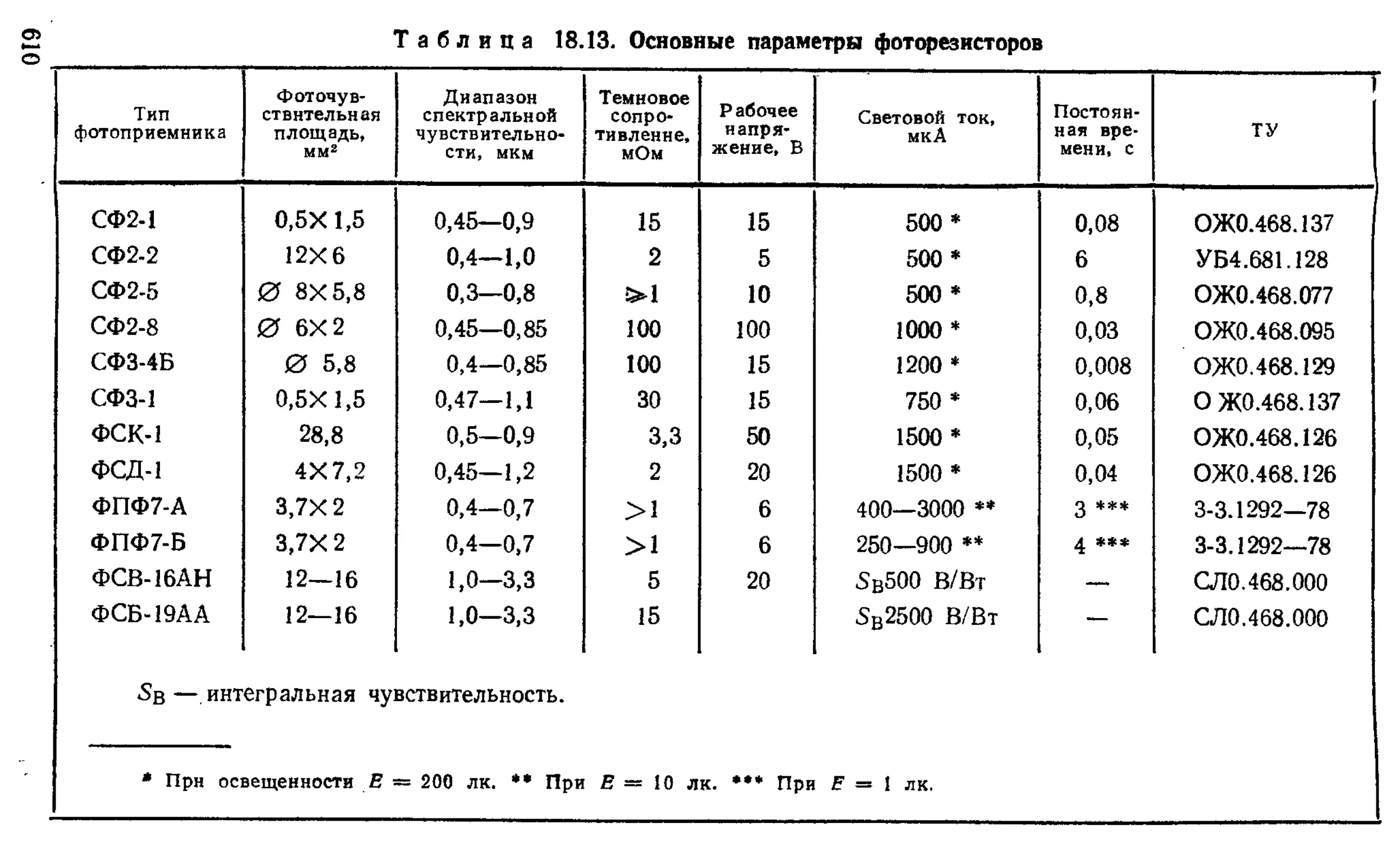
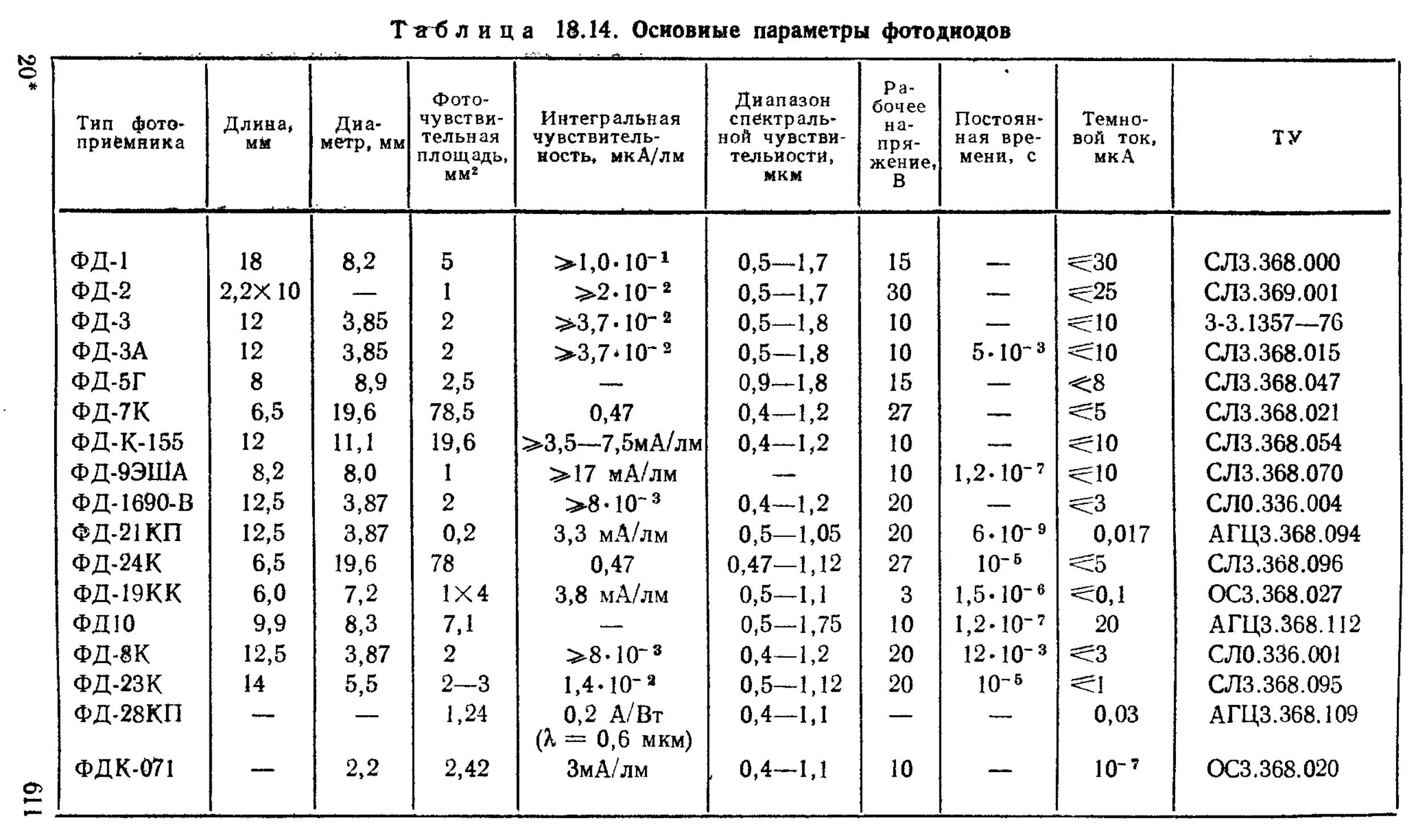
Фоторезисторы и фотодиоды............................ —
Глава 19. Организация рабочего места и органы управления приборами (AL Я* Кругер, Р. 7И. Рагузин) 613
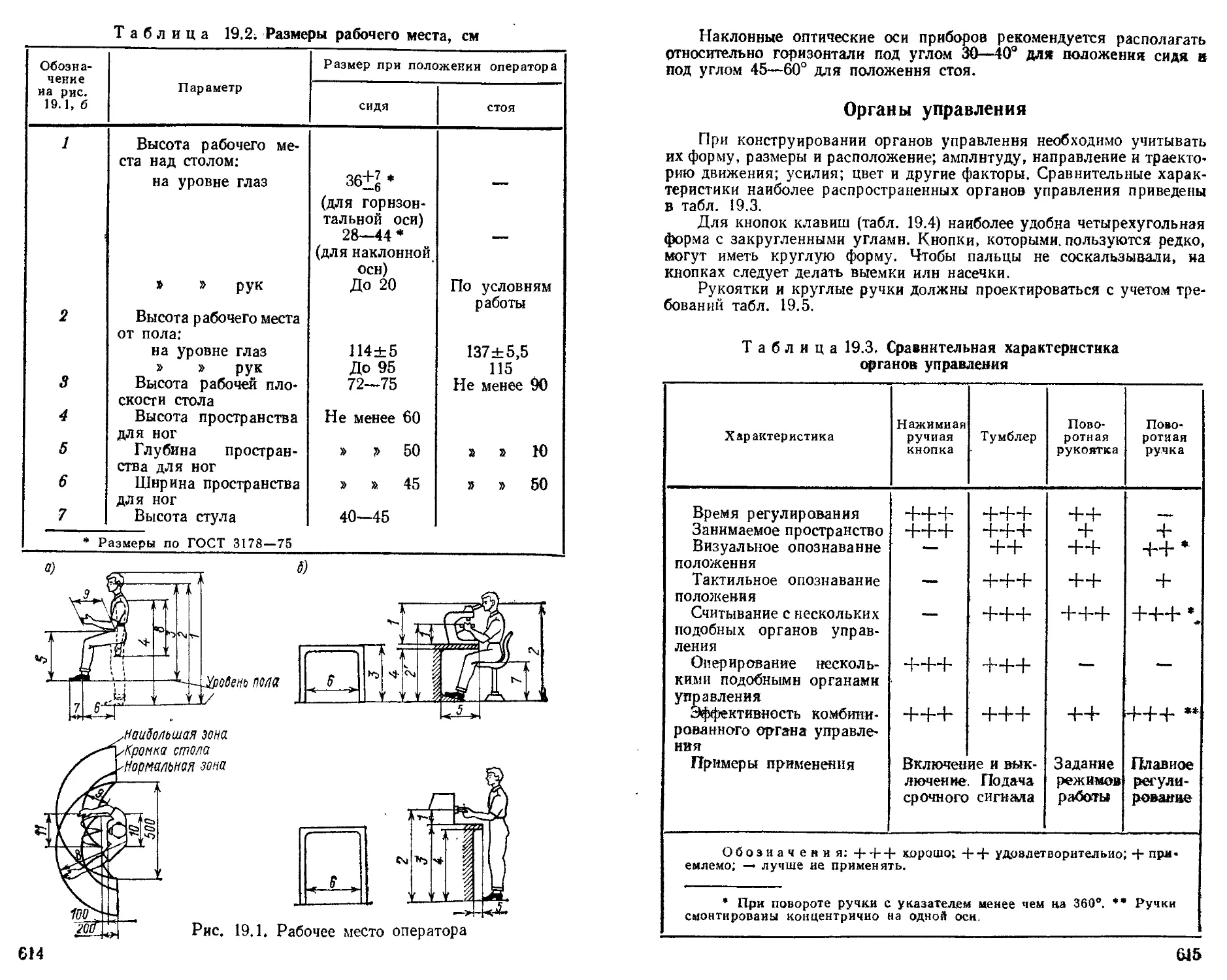
Рабочее место оператора .............. —
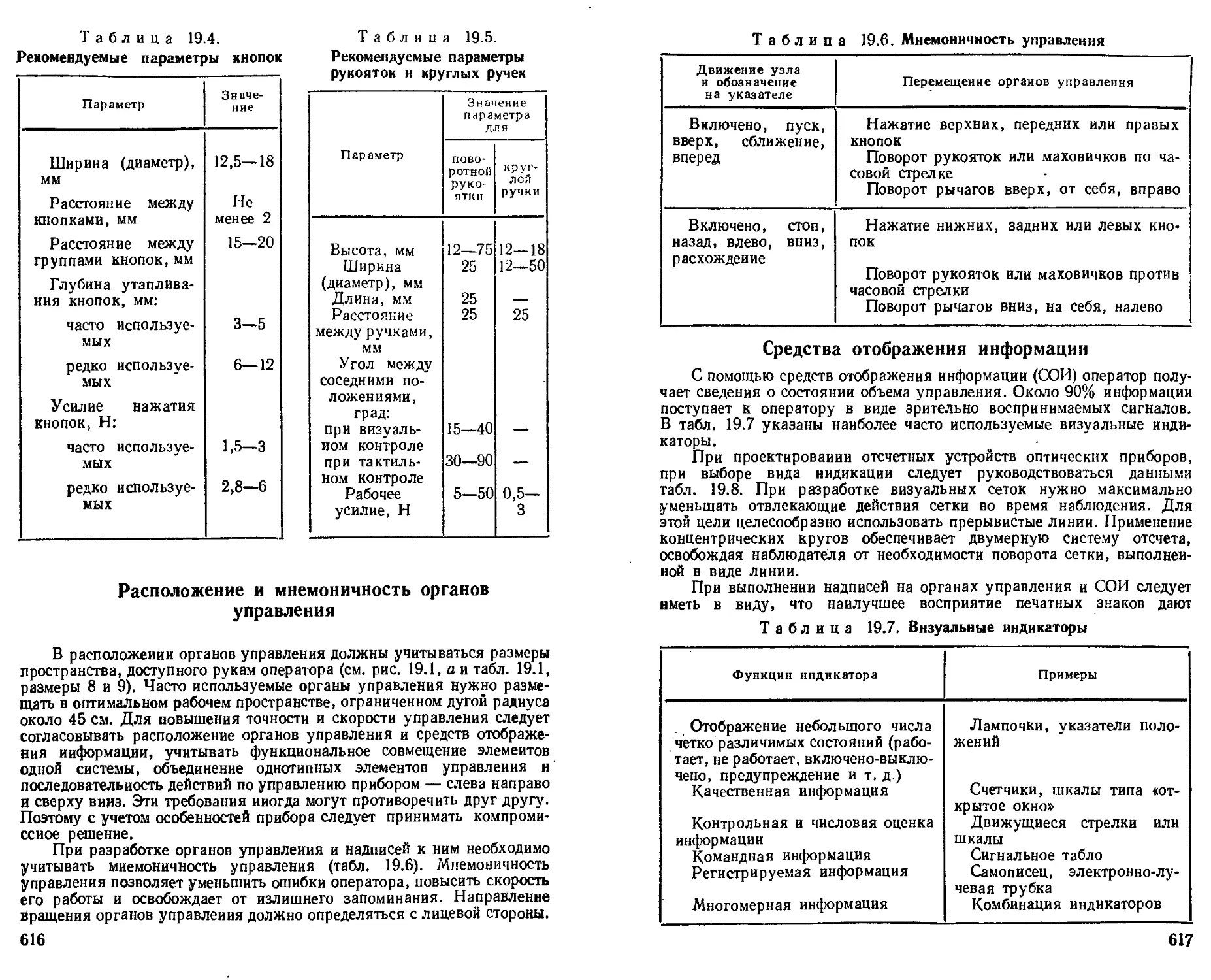
Органы управления............................ 615
Расположение и мнемоничность органов управления 616
Средства отображения информации ................... 617
Пульты управления ................................. 618
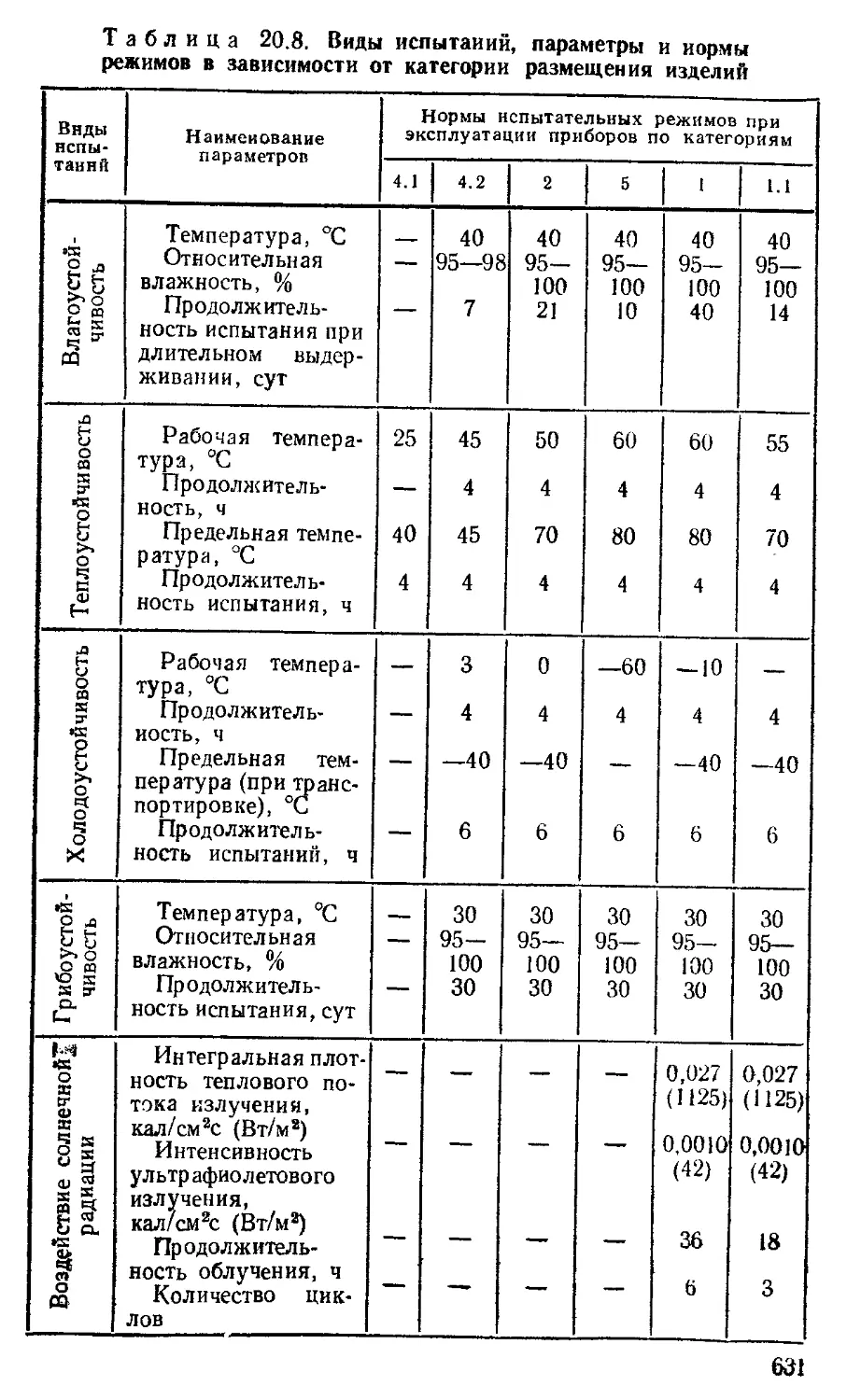
Глава 20. Технические требовании к оптико-механическим приборам (Б, Г. Резницкий) .............................. 619
Общие требования ............................ • • • —
Требования по стандартизации и унификации .... —
Требования к консервации и упаковке ................. —
Эргономические требования и требования технической эстетики ........................................... 620
Требования по безопасности труда.............. —
Требования к составным частям приборов ........... —
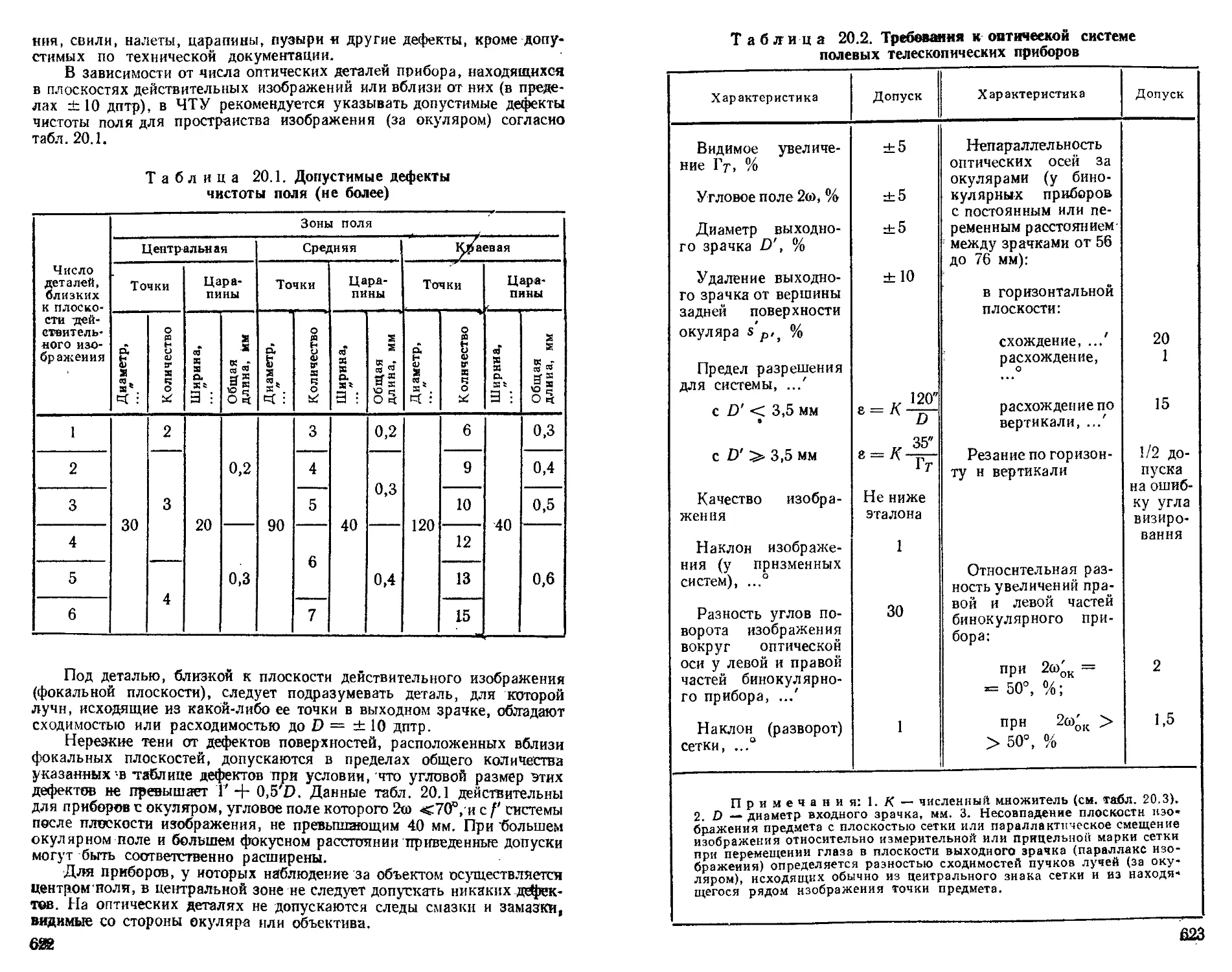
Требования к оптическим деталям.............. 621
Требования к оптическим деталям, находящимся в оптических системах ...................................... —
Требования к телескопическим приборам ............... 624
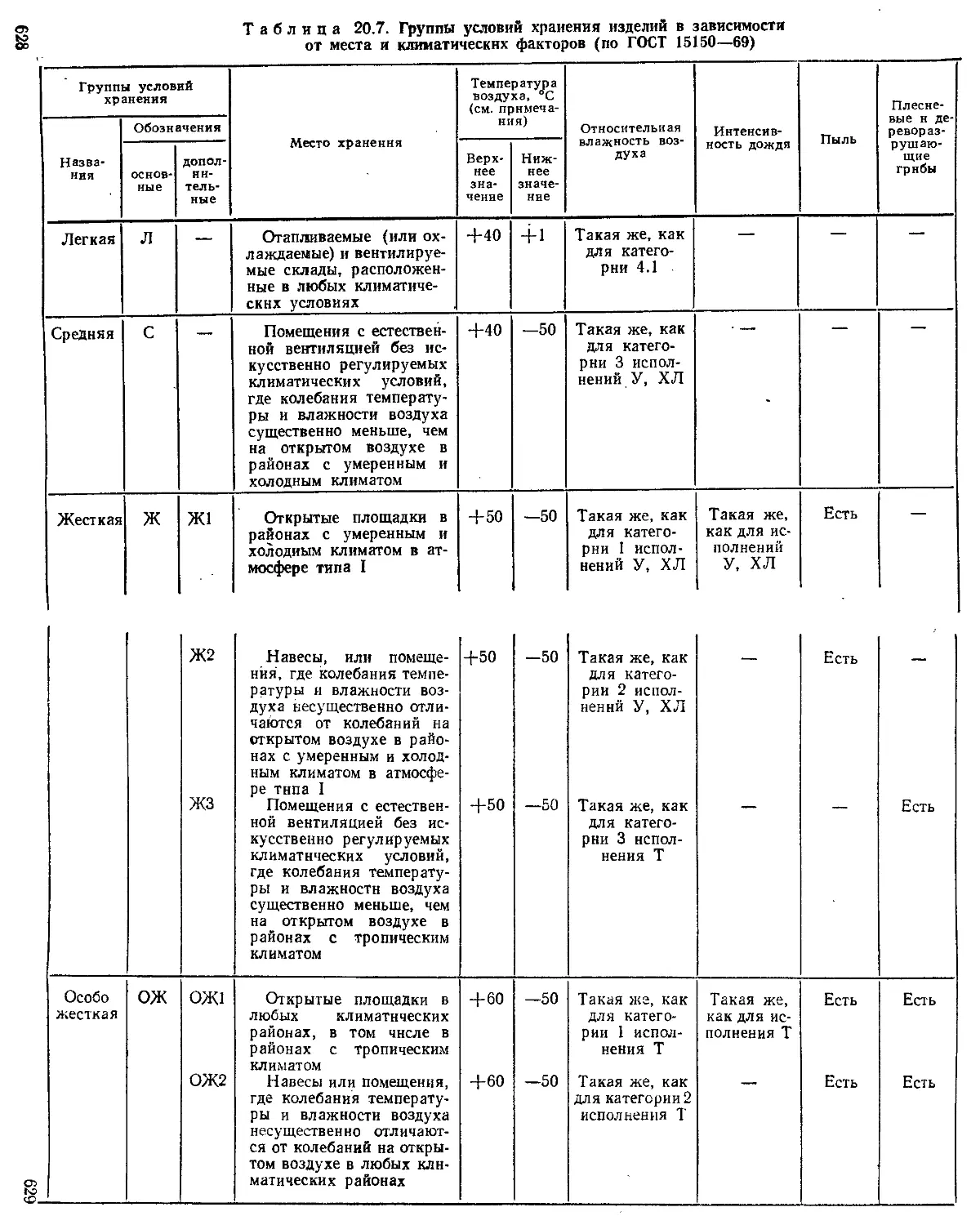
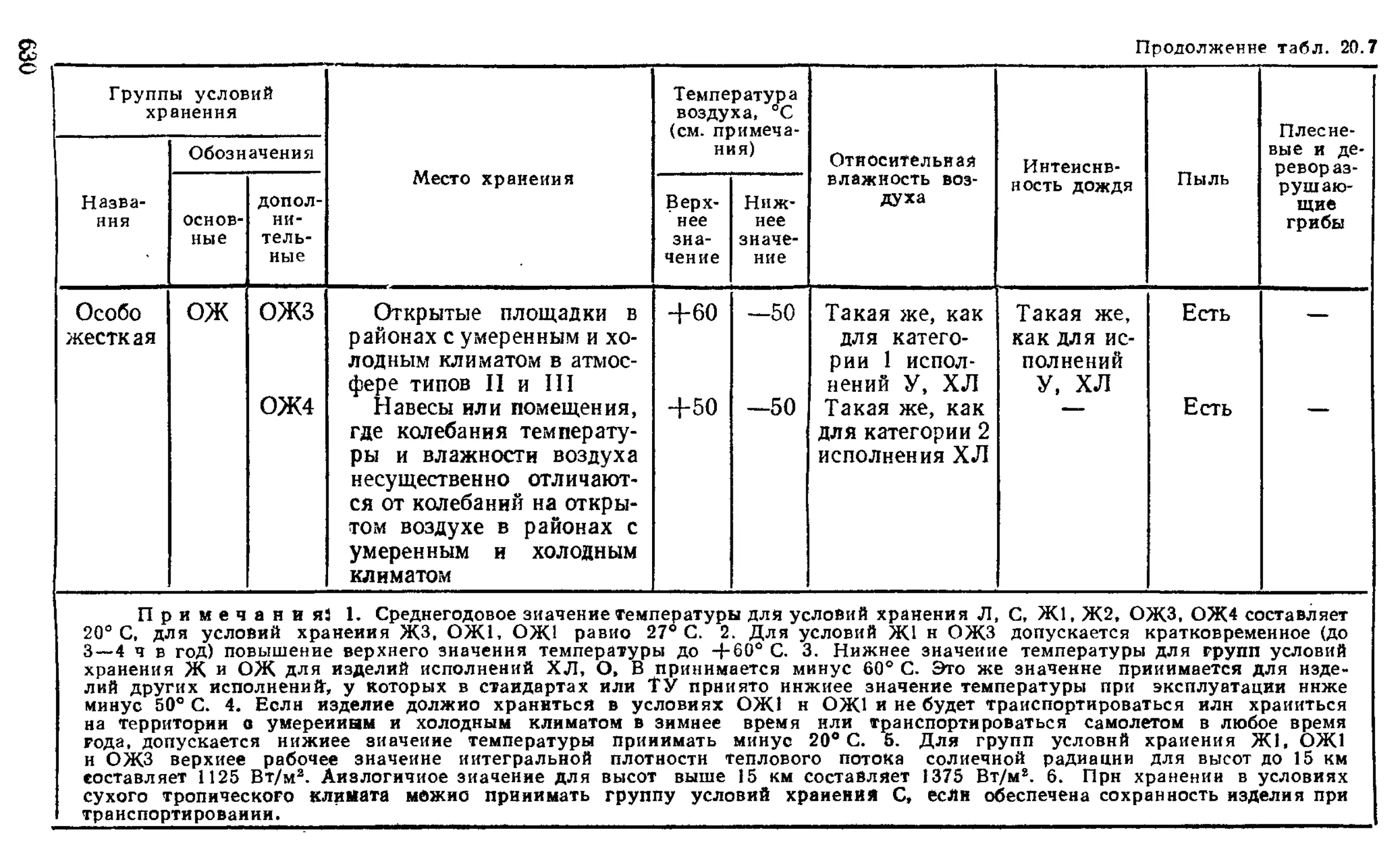
Требования к устойчивости приборов к внешним воздействиям при эксплуатации ........................... —
Требования к приборам, предназначенным для работы в районах с тропическим климатом ............. 633
Глава 21. Основные правила разработки конструкторской
документации (Б, Г. Резницкий) ....... 636
Стандарты, используемые в начальной стадии разработки конструкторской документации.................... —
Стандарты, используемые при разработке чертежей —
Стандарты, используемые при разработке технических условий ............................................ 644
Стандарты, используемые при разработке эксплуатационной документации ............................... —
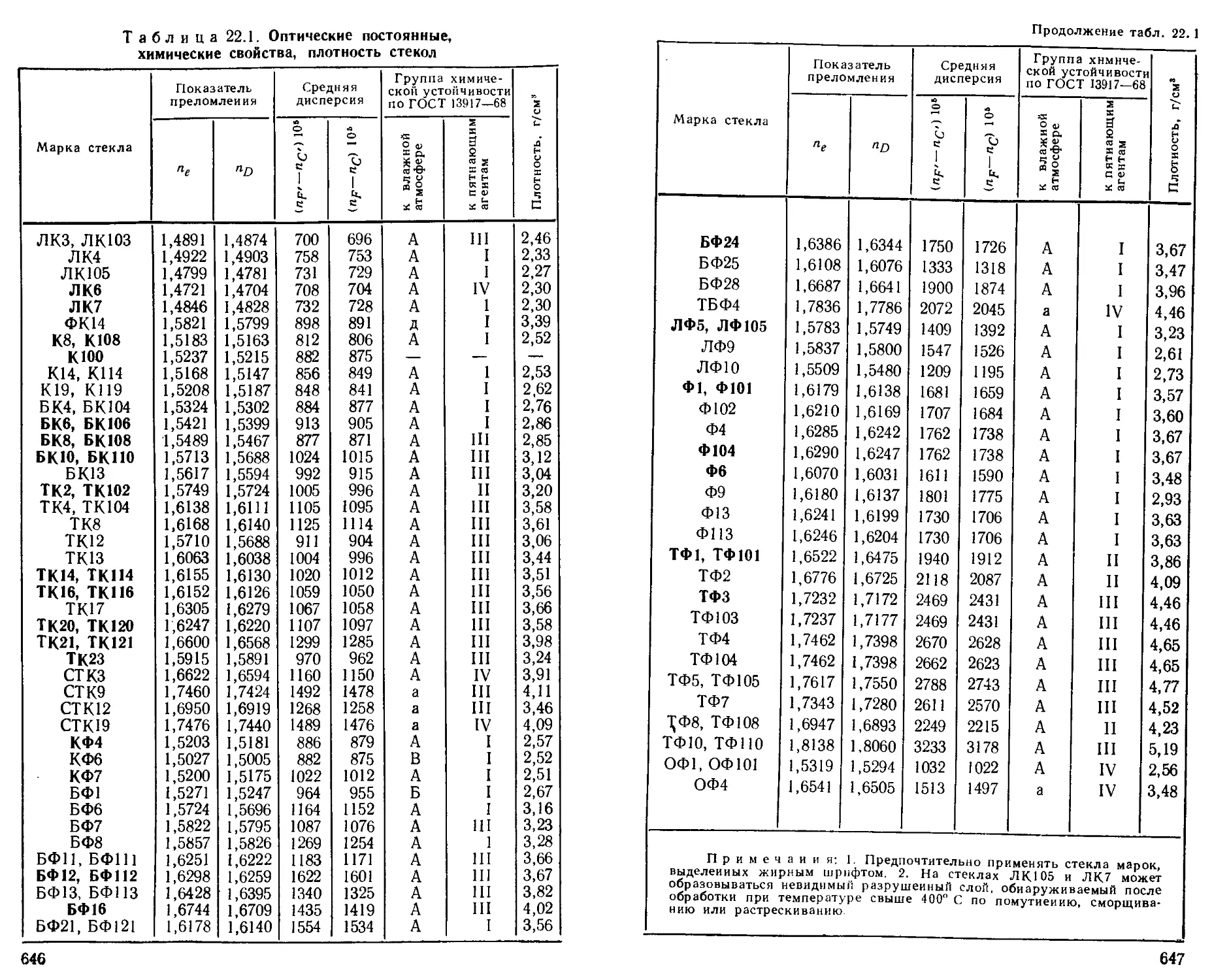
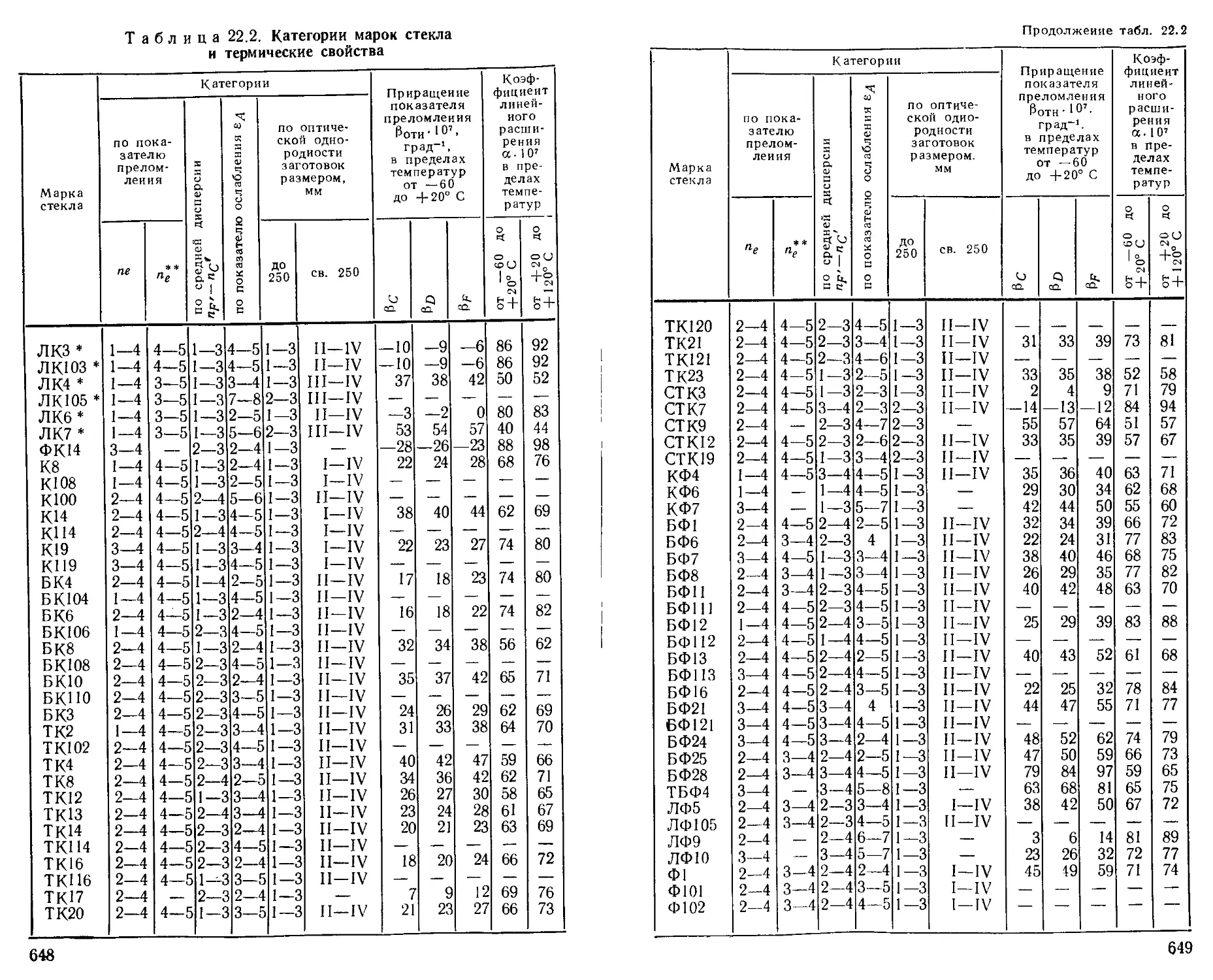
Глава 22. Оптические материалы (В. А. Панов) . . . . 645
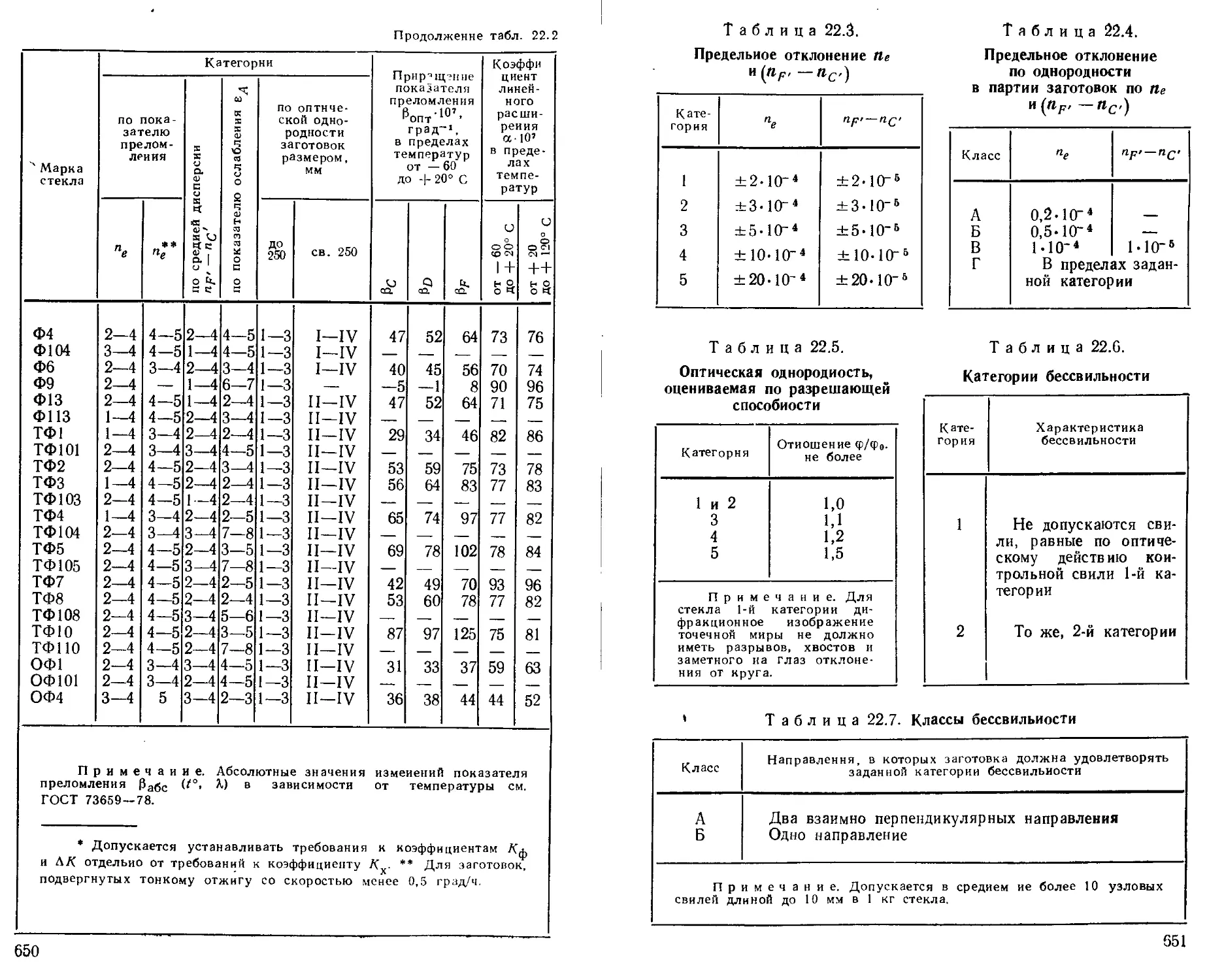
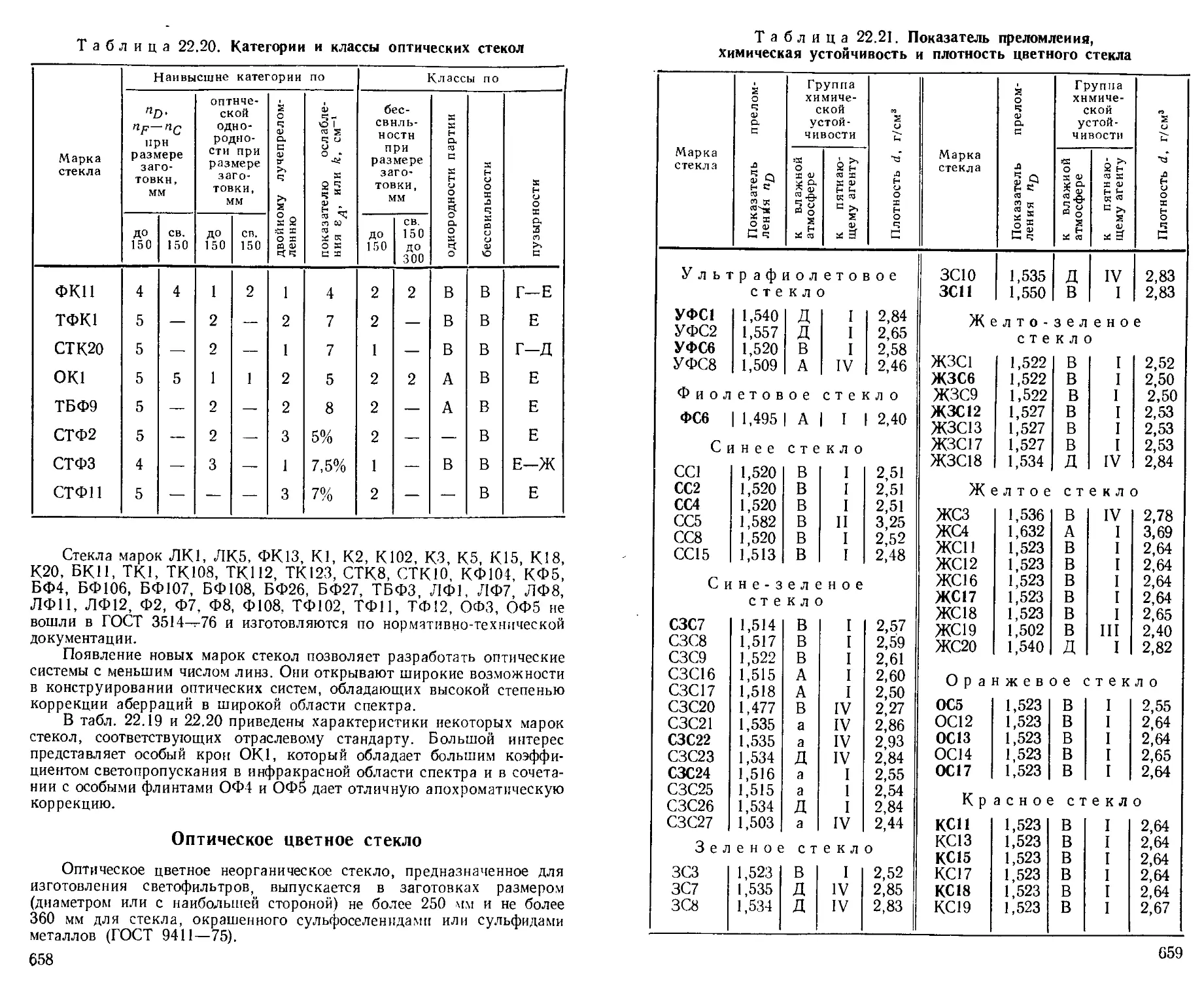
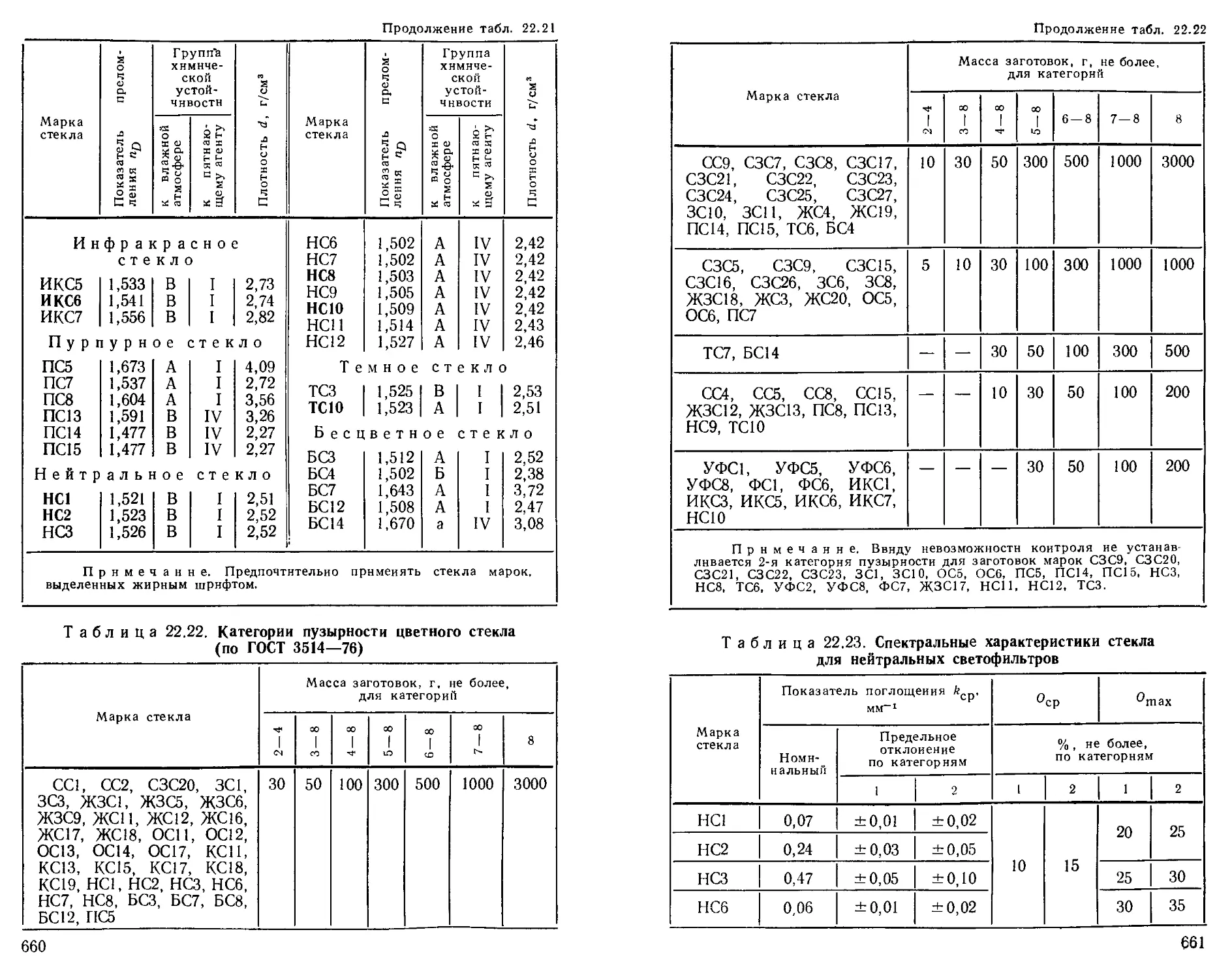
Оптическое бесцветное стекло ............... —
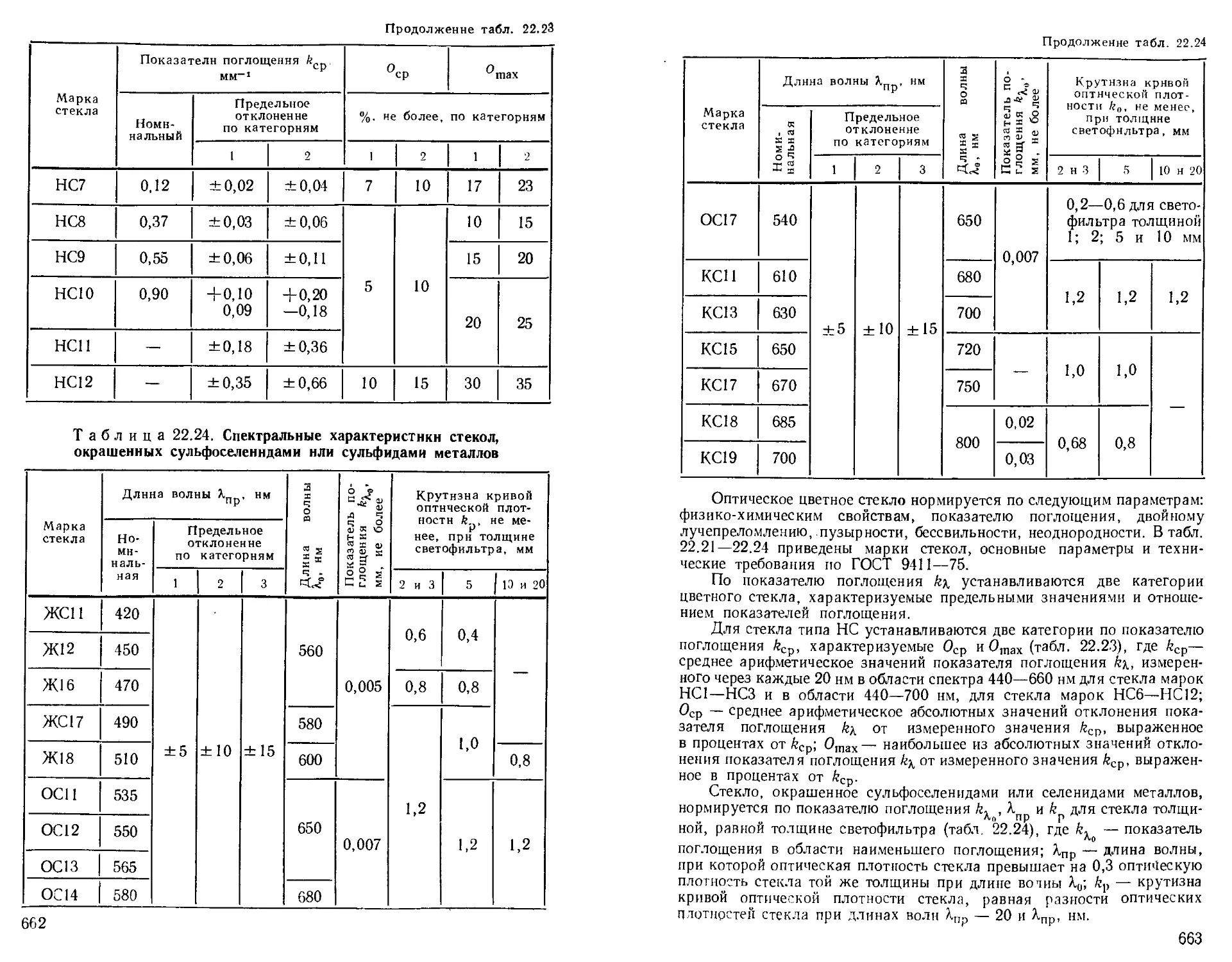
Оптическое цветное стекло ............. 658
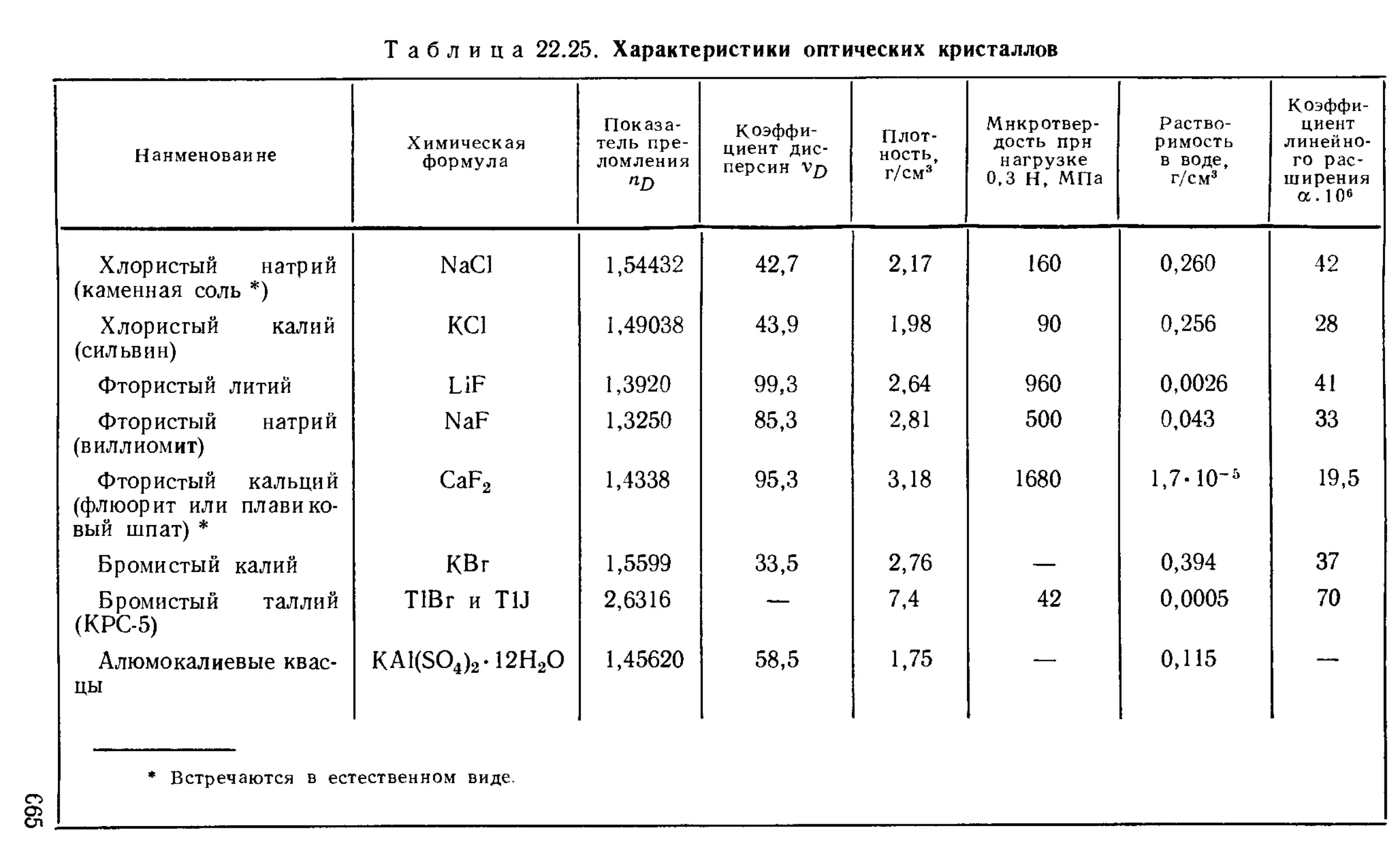
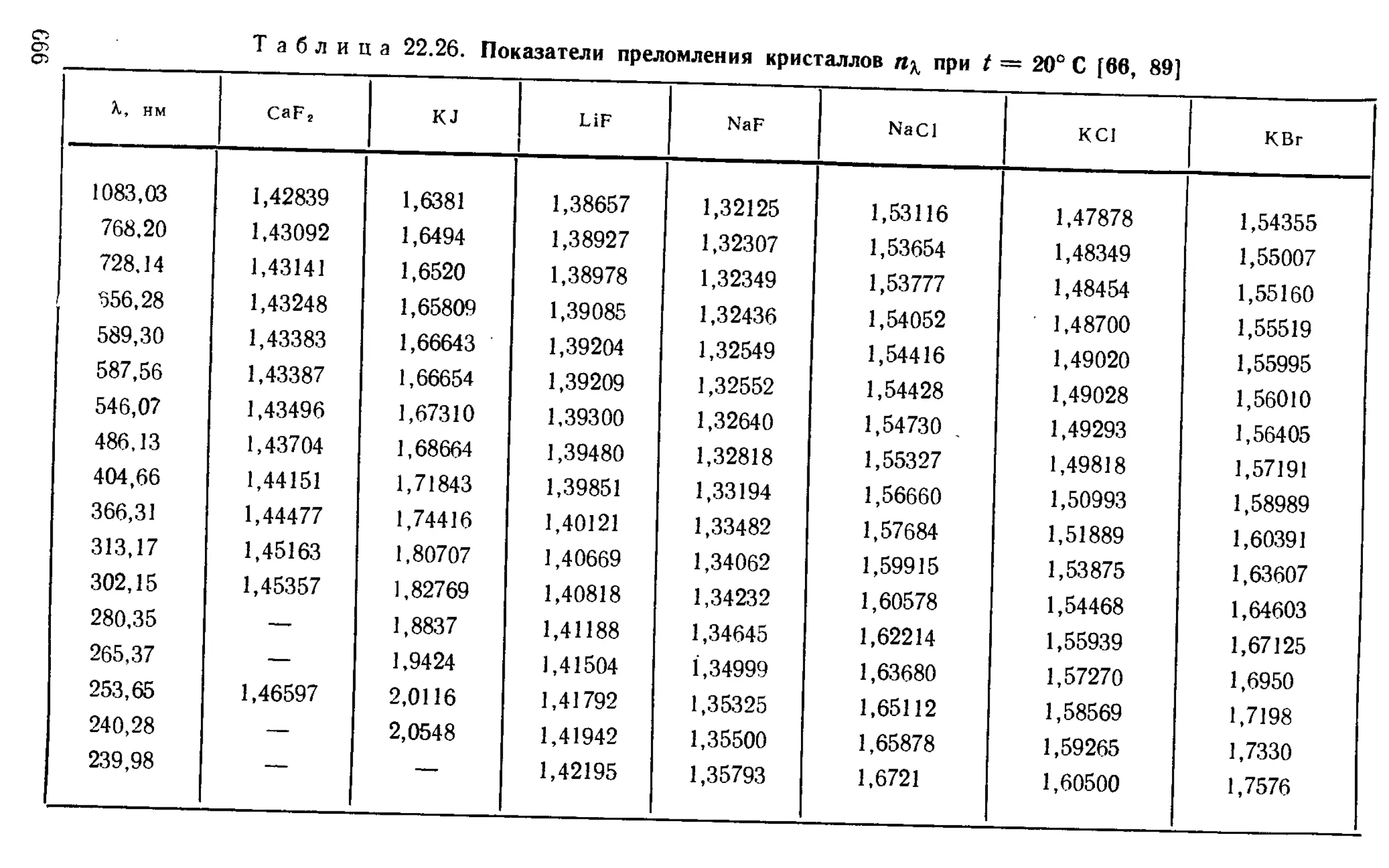
Оптические кристаллы .......................... , 664
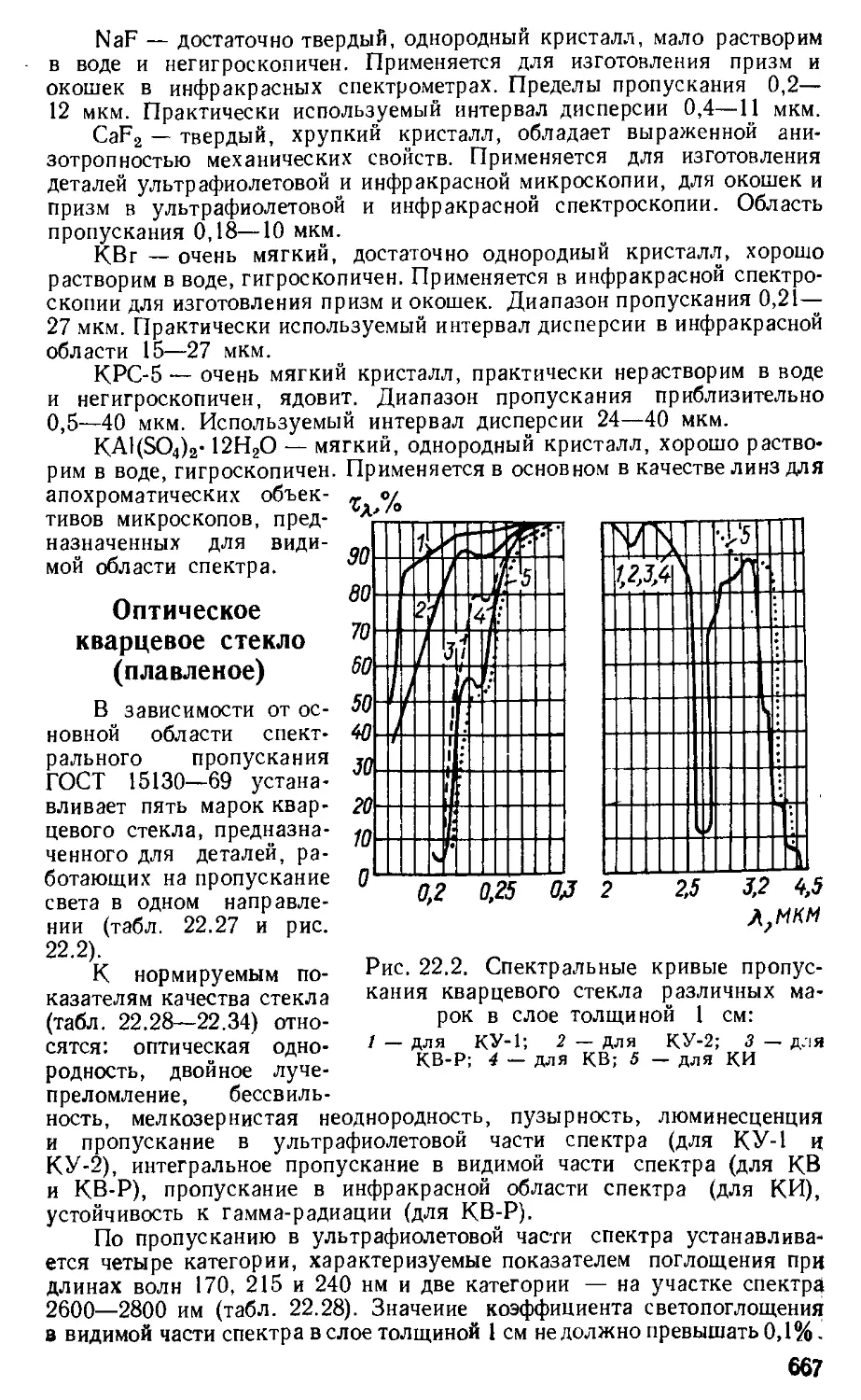
Оптическое кварцевое стекло (плавленое)....... 667
Оптические ситаллы ................................ 671
Оптическая керамика ............................... 673
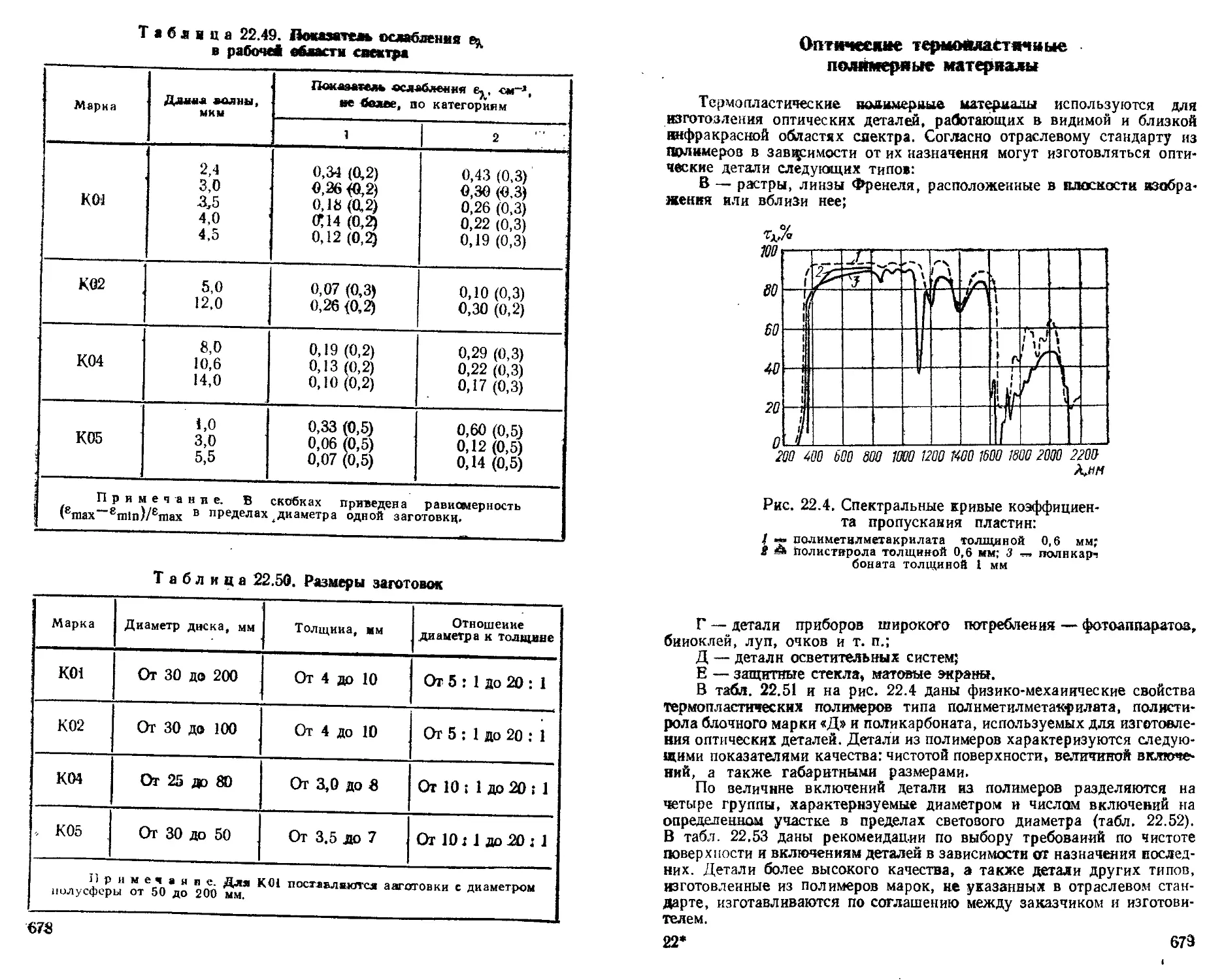
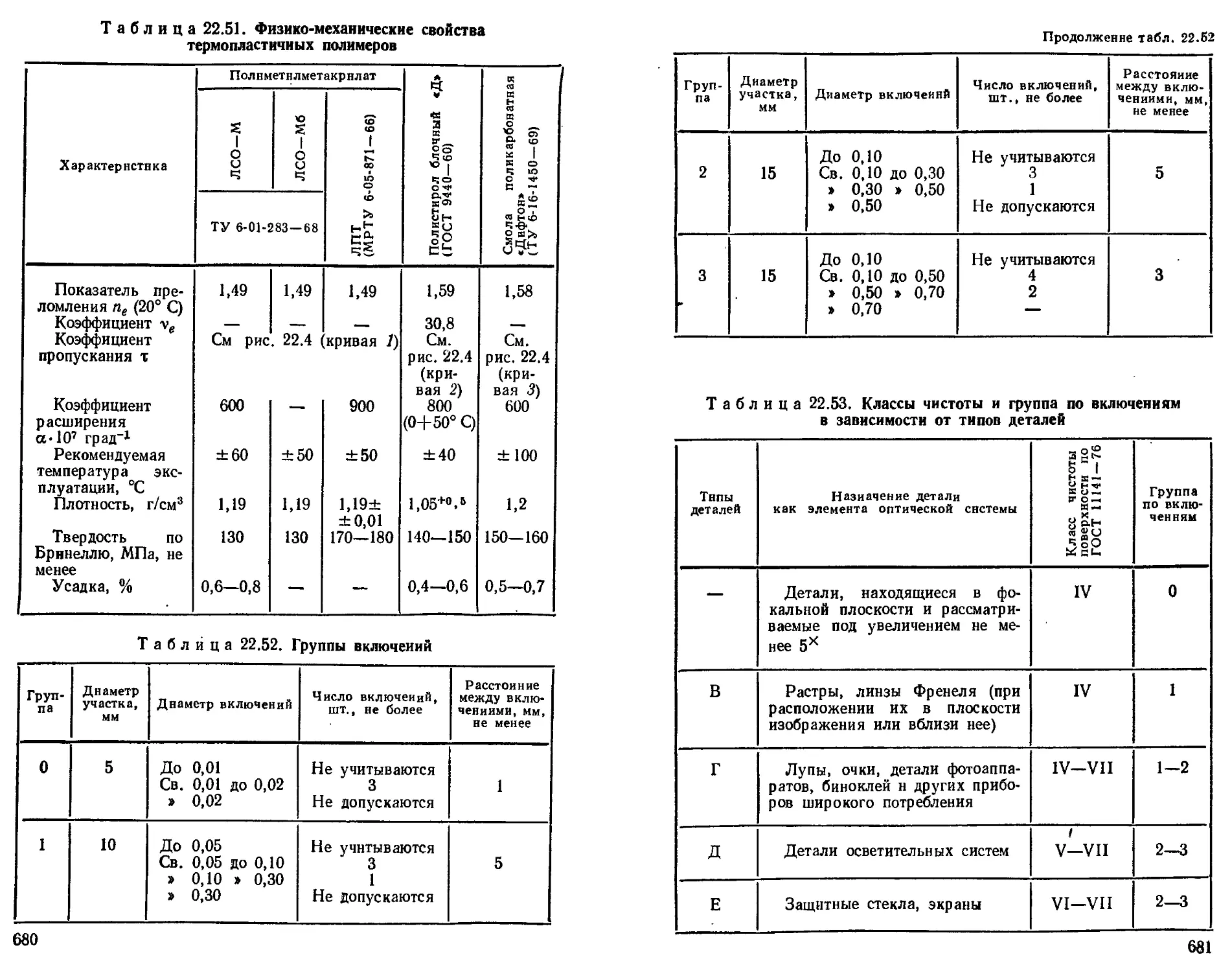
Оптические термопластичные полимерные материалы. . 679
Стекло органическое конструкционное ............... 683
Светорассеивающие стекла .......................... —
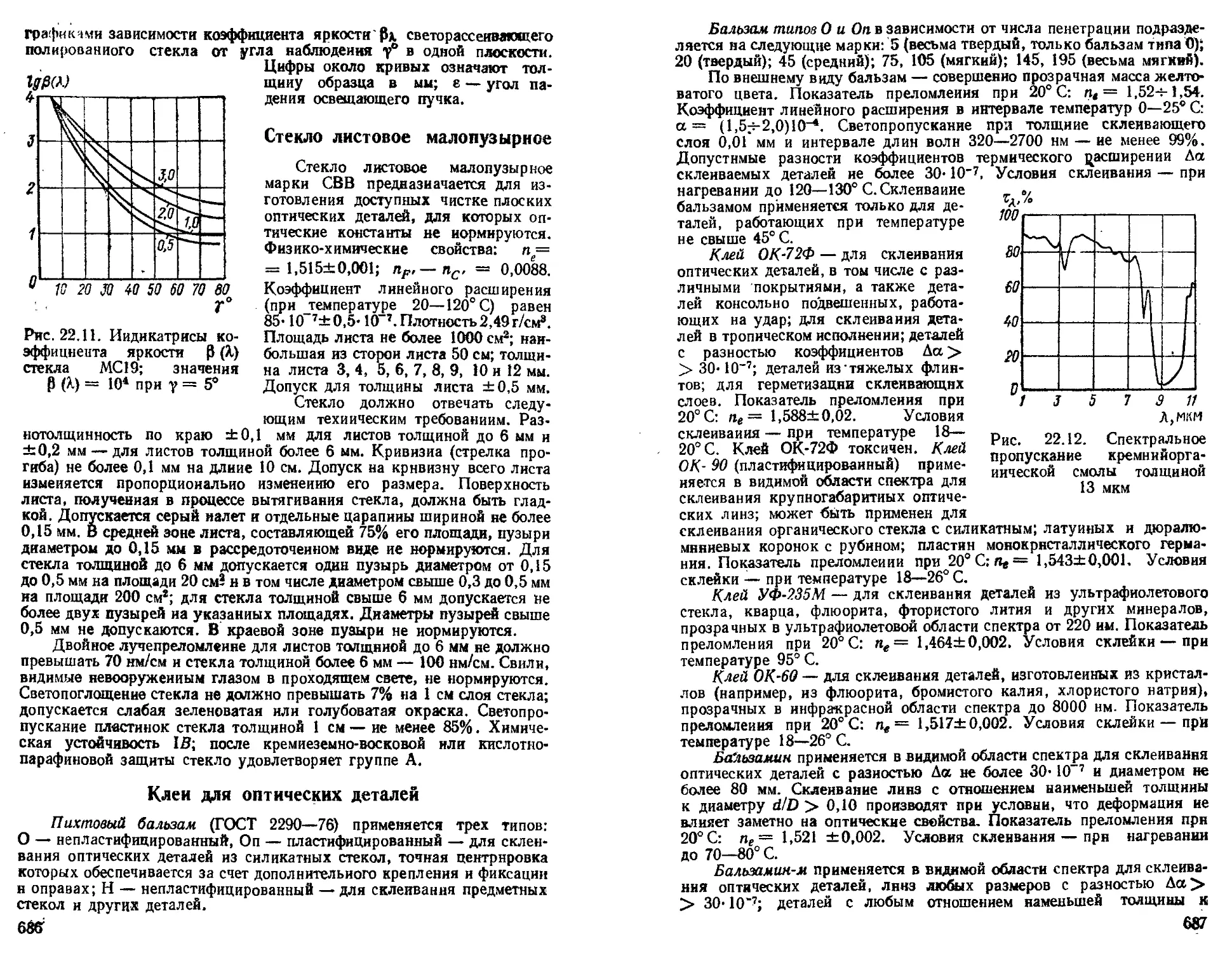
Стекло листовое малопузырное ...................... 686
L Клеи для оптических деталей ........................... —
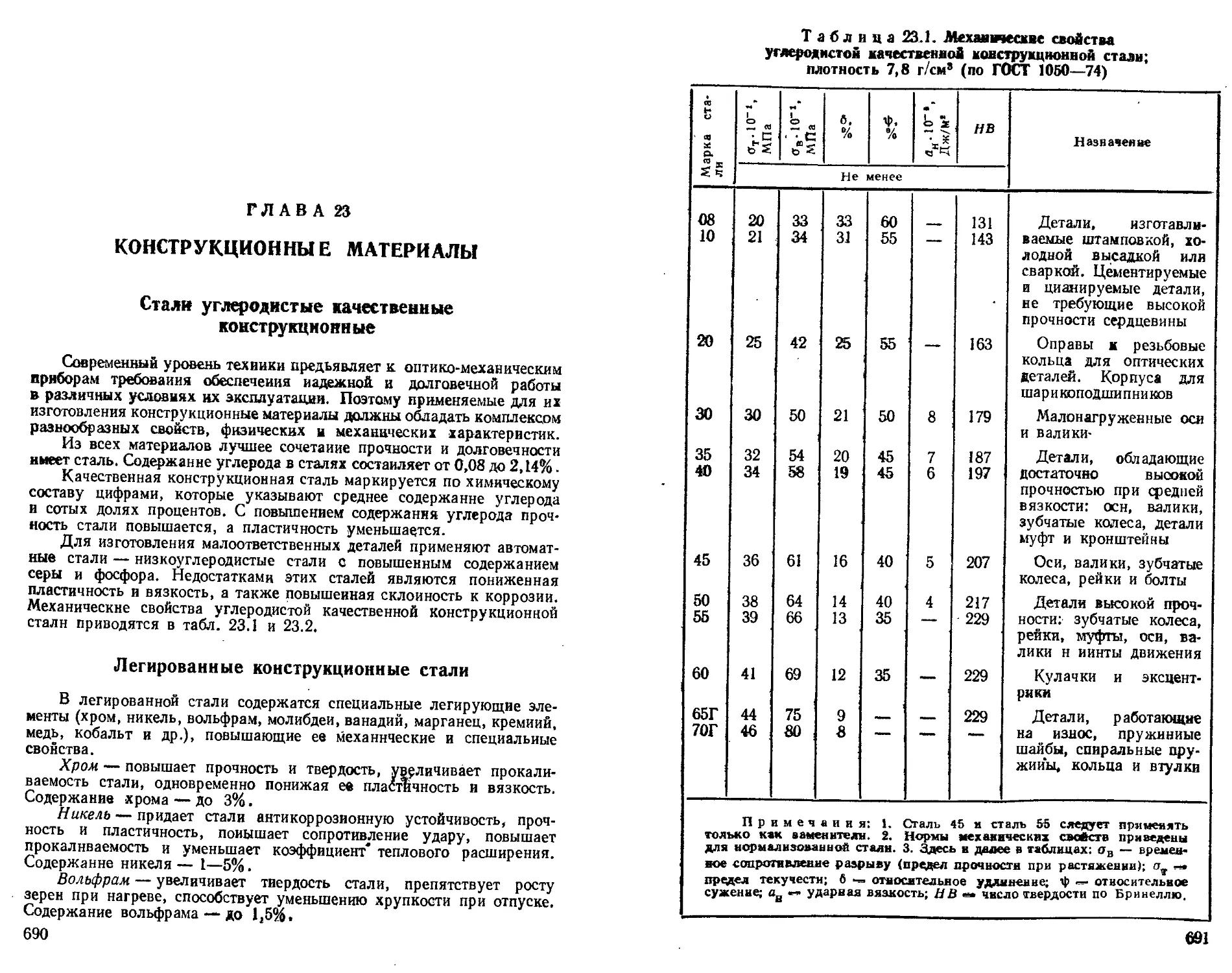
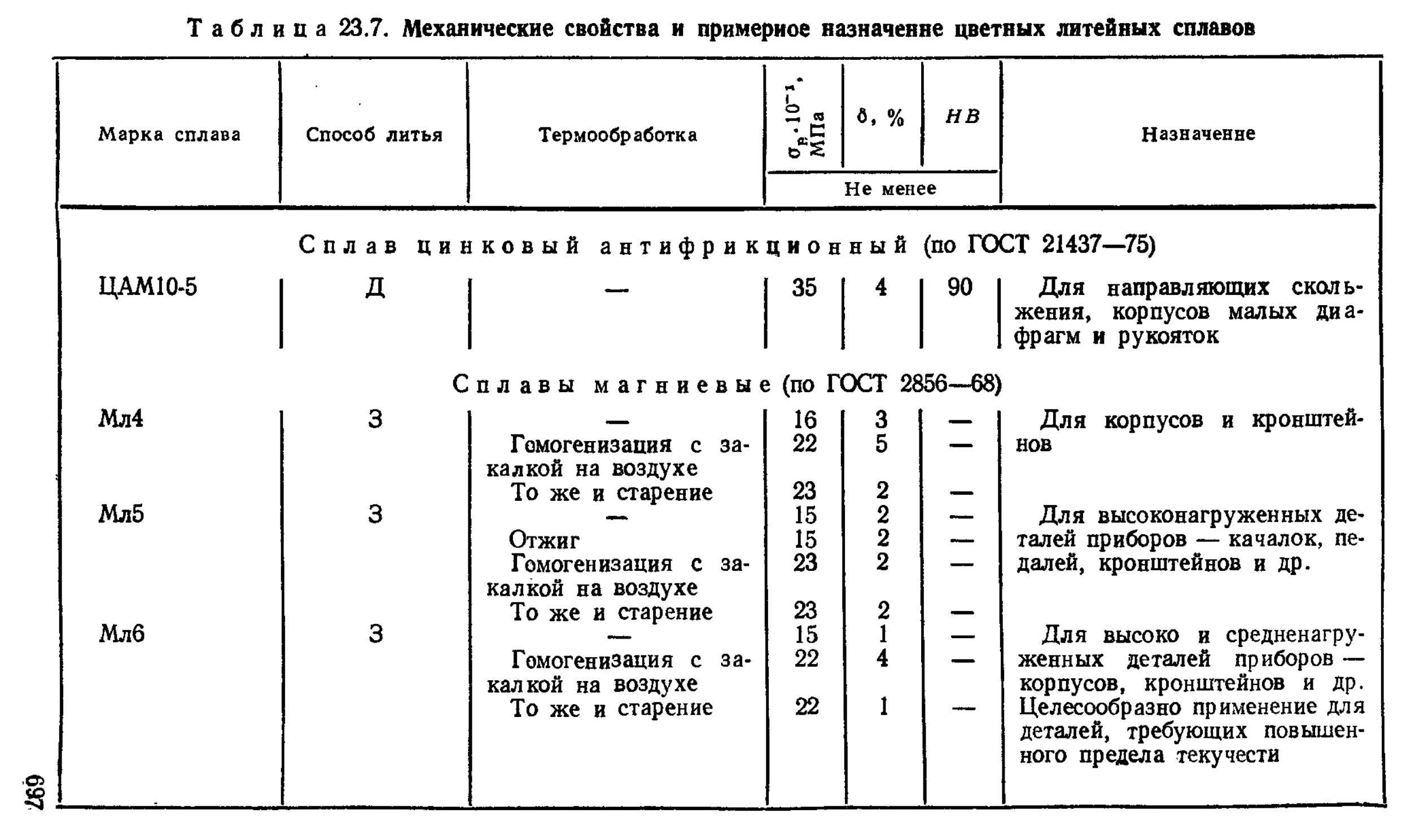
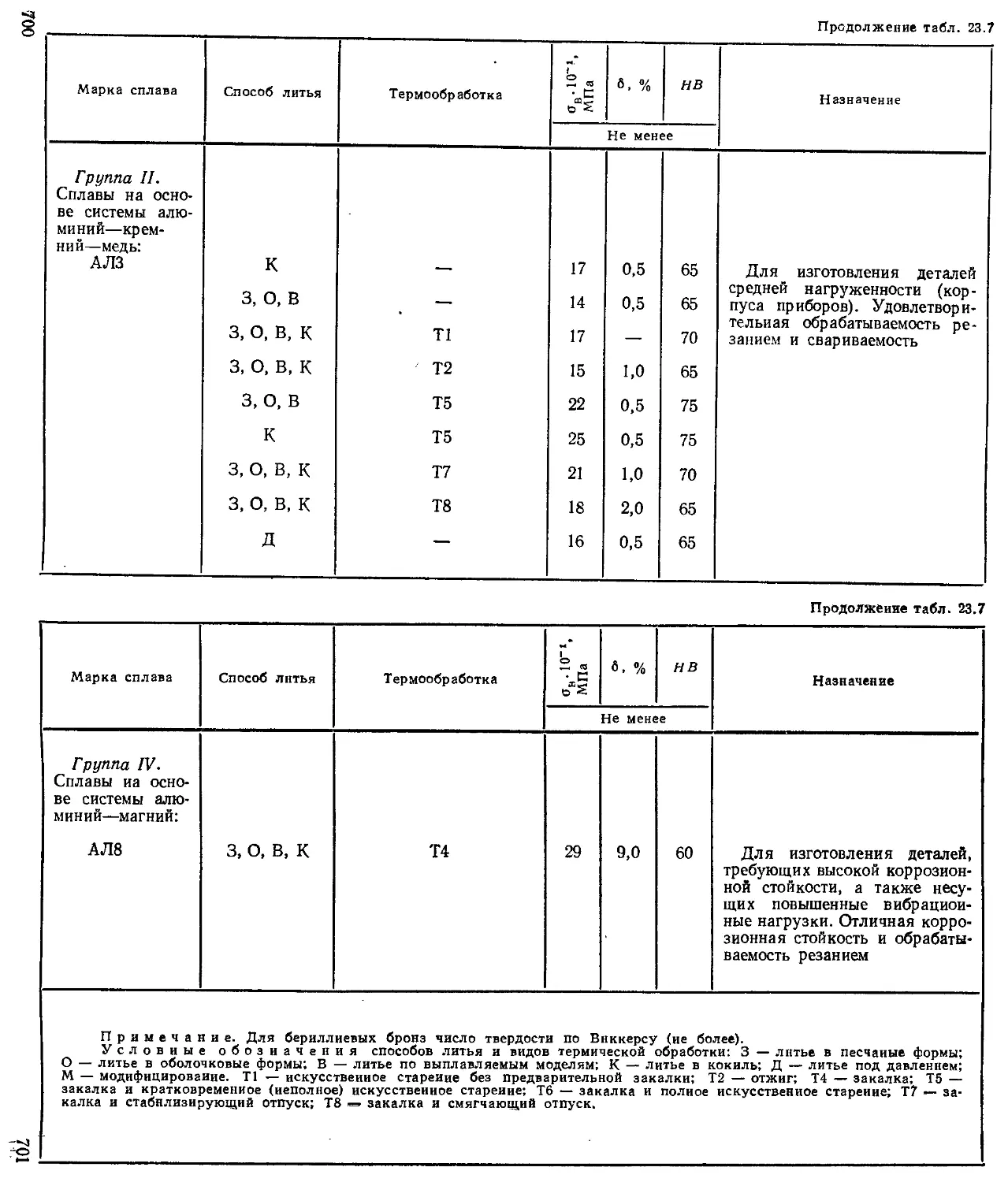
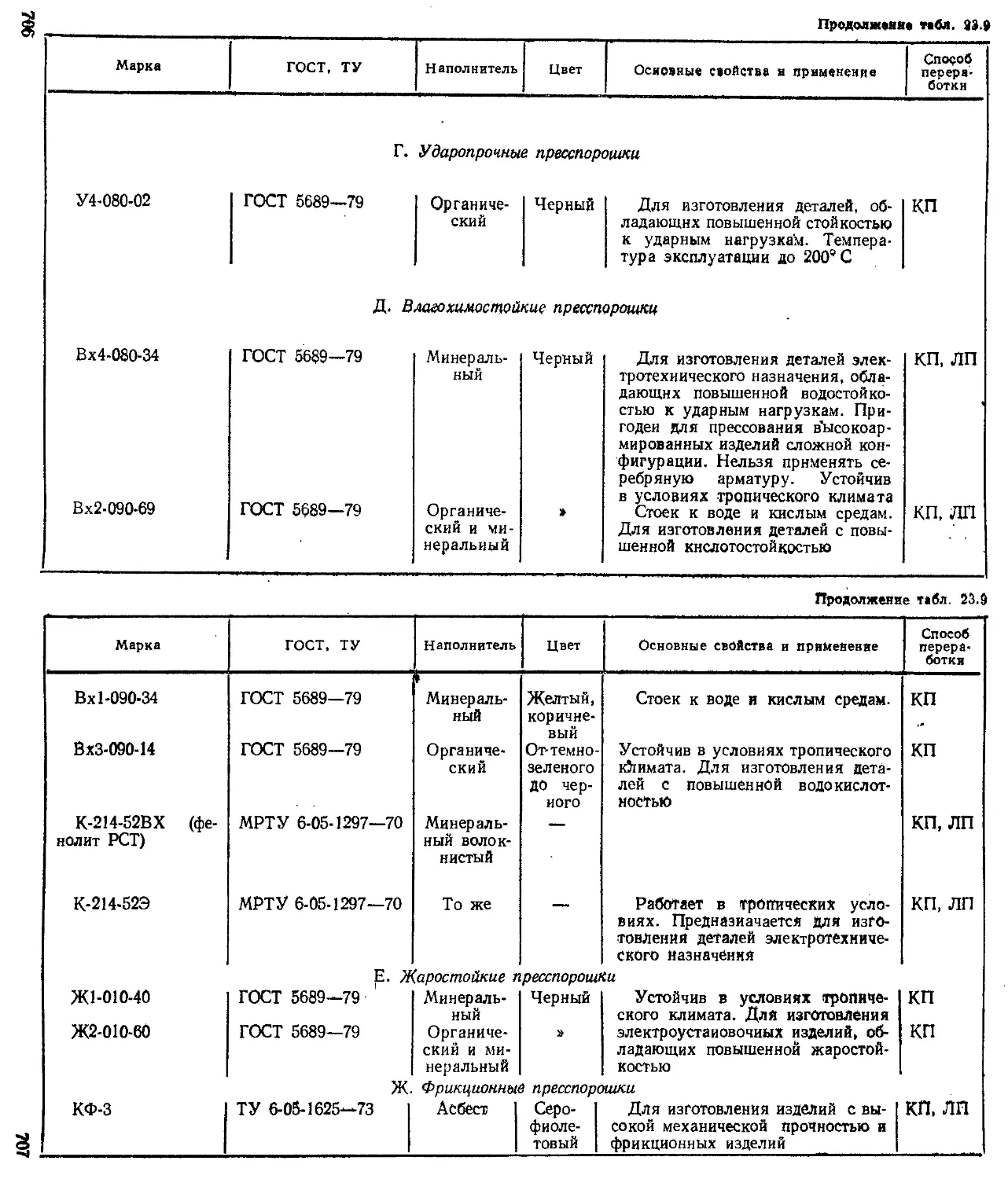
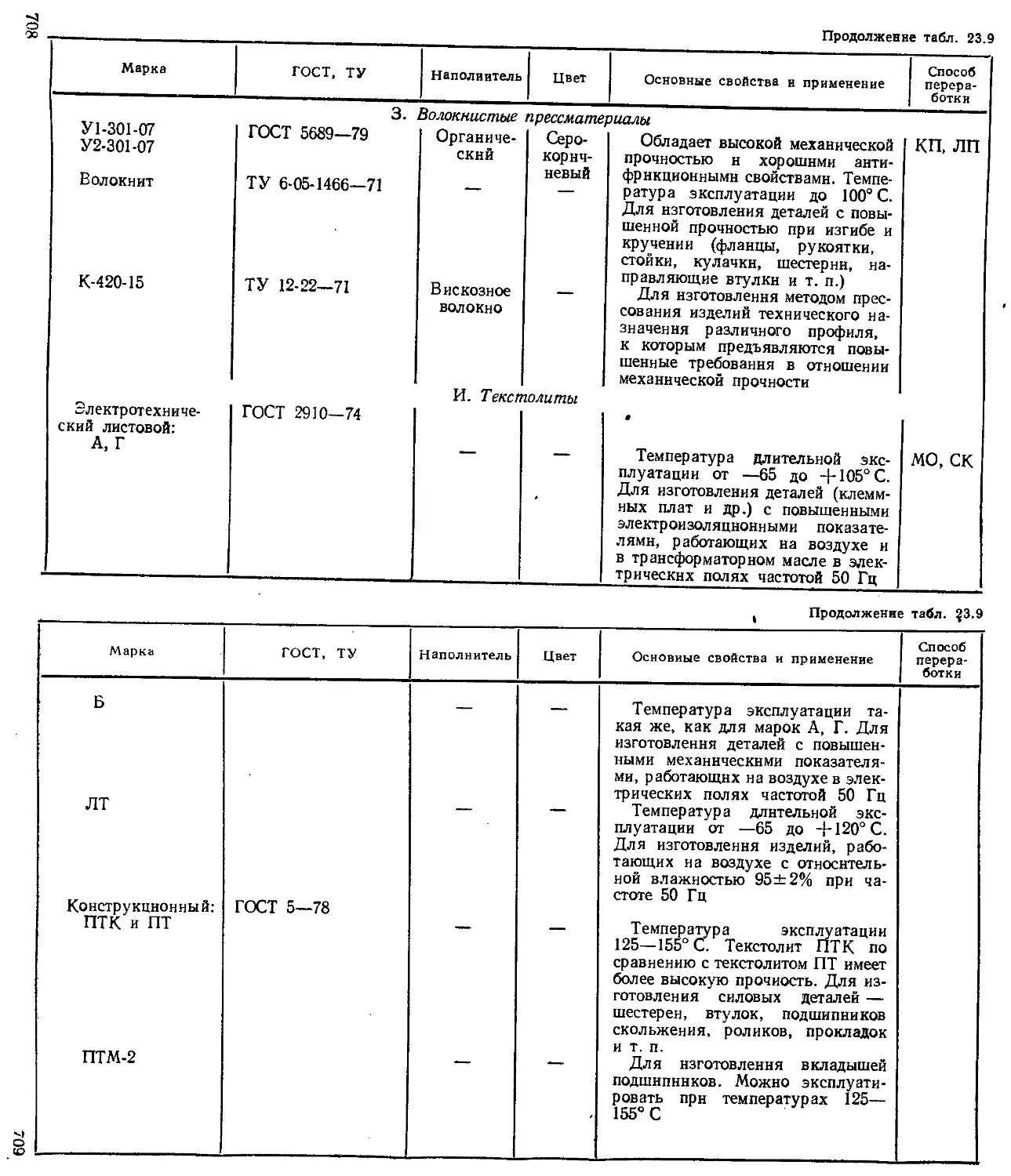
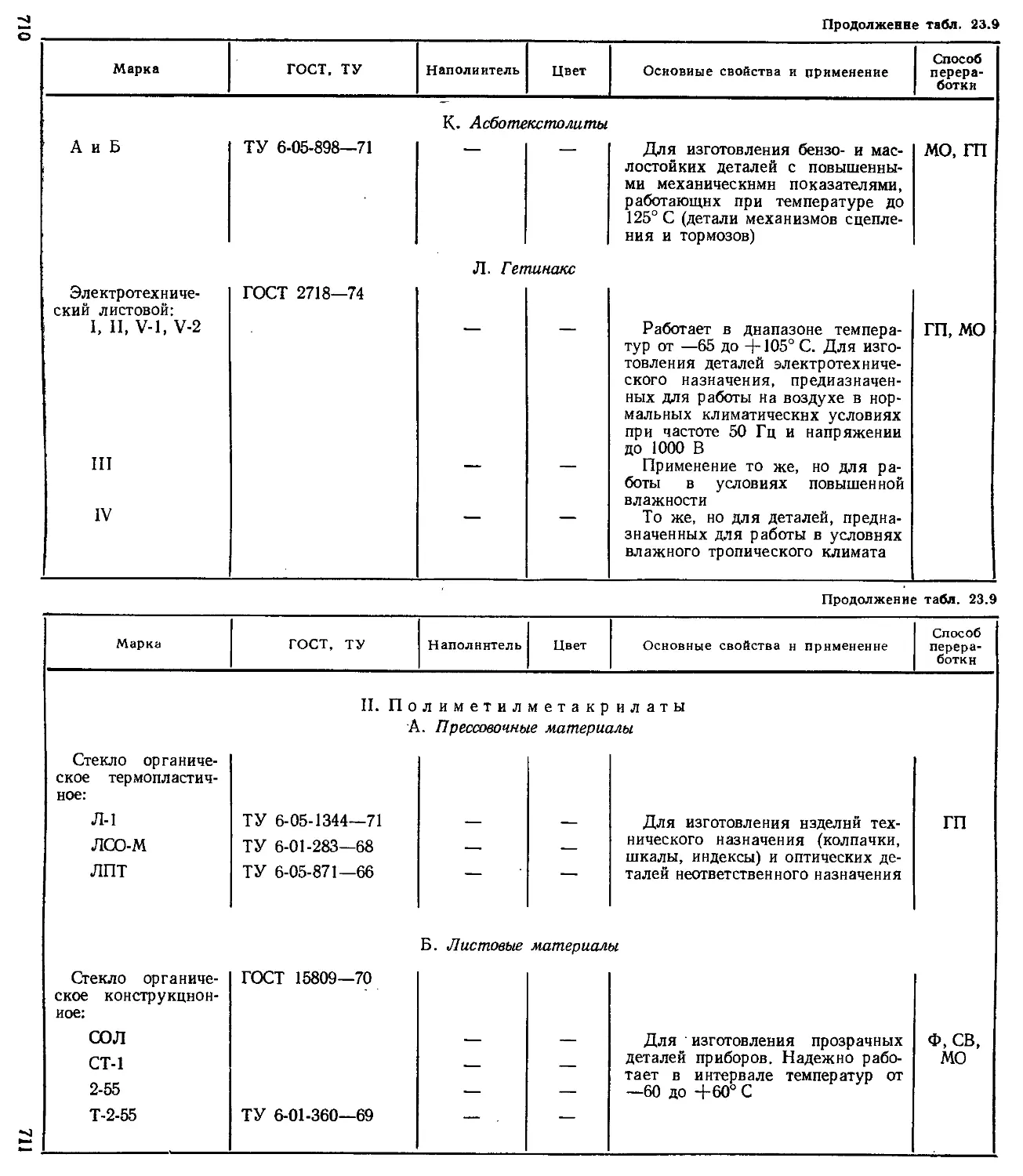
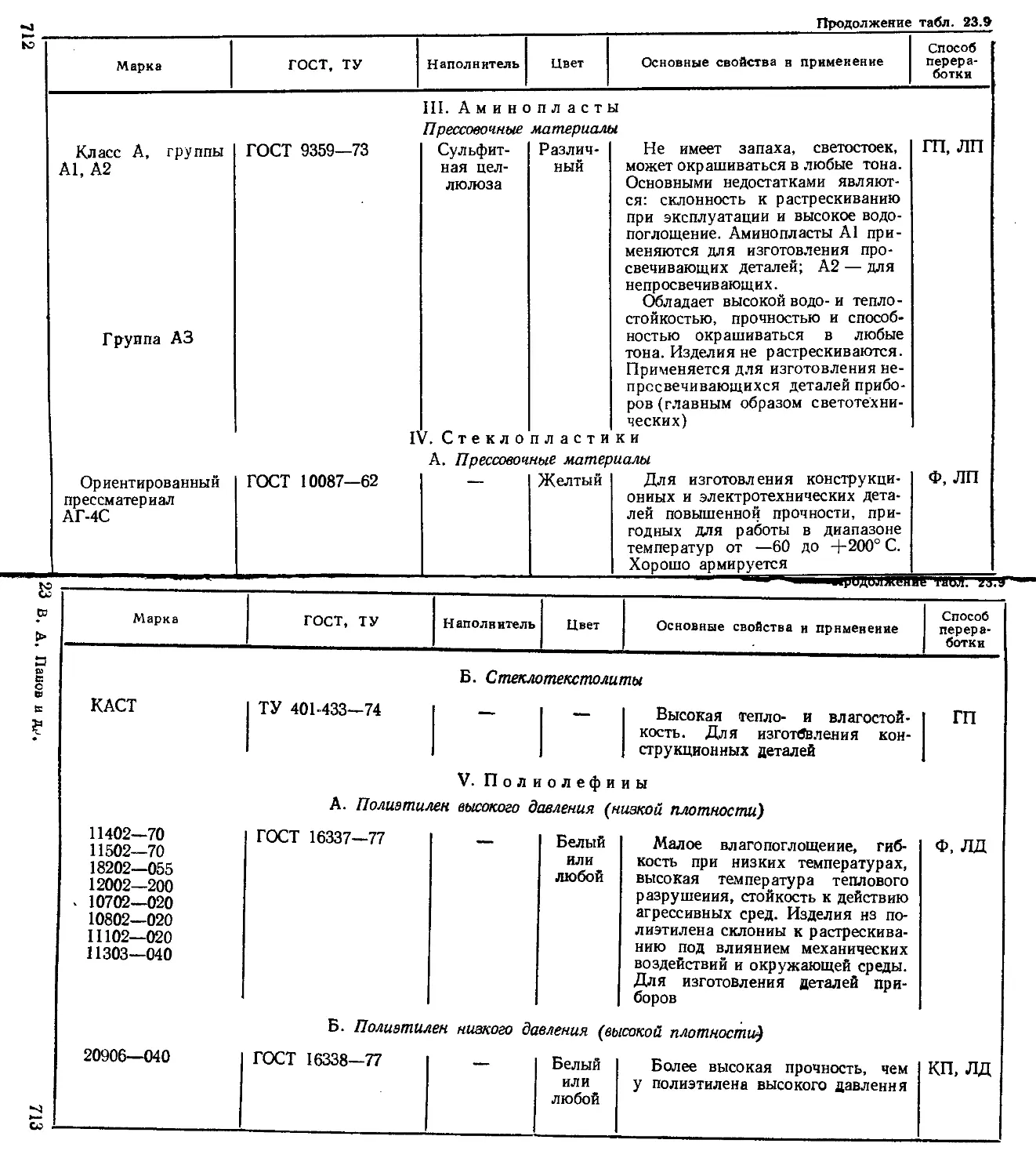
Глава 23. Конструкционные материалы {Б. Г. Резницкий) 690
Стали углеродистые качественные конструкционные . . —
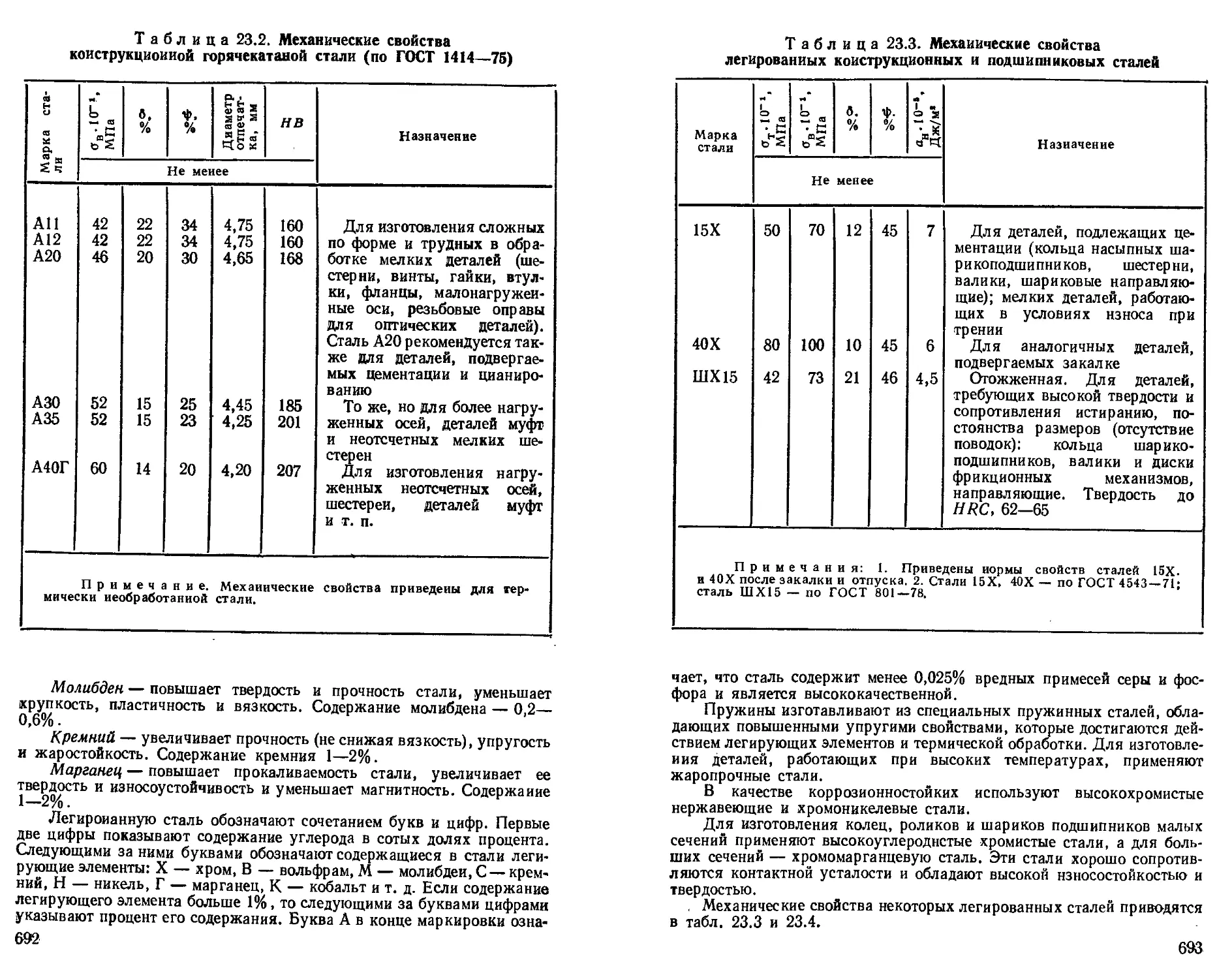
Легированные конструкционные стали........... —
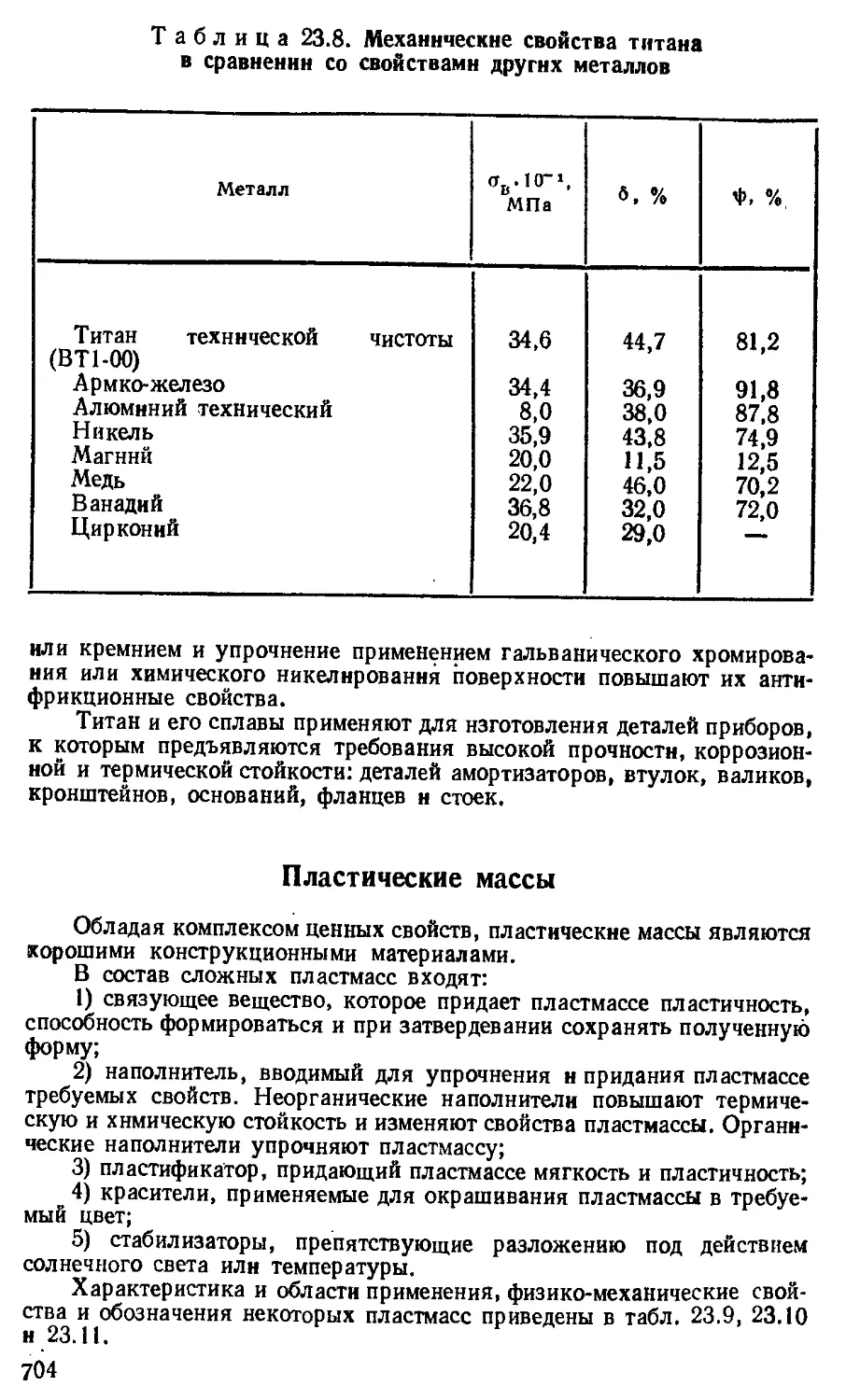
v<n vw vwiv/iyium,nmn i^annuamn допп тм1п» А), ультрафиолетовую (от 50 А до 380 им),
километров), оптический диапазон (X меняется от 50 А1 до 1 мм), и диапазон у-лучей (длина волны X < 50 А). Оптический диапазон излучений делят на четыре области со следующими границами длин воли: рентгеновскую (от 0,1 до 50 " ‘ ’ --- •
видимую (от 380 им до 770 нм) (табл. 1.1) и инфракрасную (от 770 нм до 1 мм). Инфракрасную область в свою очередь
T а б л и ц а 1.1. Видимые цвета
Таблица 1.2. Длины волн излучений, испускаемых различными элементами
Область спектра Длина волны, нм Обозначение линий спектра Элемент
Ультрафиолетовая 365,0 1 Hg
404,7 и Hg
434,1 в' н
435,8 g F Hg
480,0 Cd
Види- 486,1 F Н
мая 546,1 е Hg
587,6 d Не
589,3 D Na
643,8 С Cd
656,3 С H
766,5 А' К
Видимые цвета Диапазон длин волн, нм
Фиолетовый Синий Голубой Зеленый Желто-зеленый Желтый Оранжевый Красный 380-450 450—480 480-510 510-550 550-575 575—585 585-620 620—780
подразделяют на коротковолновый участок (от 0,77 до 1,5 мкм), средневолновый (от 1,5 до 20 мкм), длинноволновый (от 20 мкм до 1,0 мм). Указанные границы диапазонов и областей длин волн условны, а сами длины волн даны для вакуума. В табл. 1.2 приведены длины волн излучений, испускаемых некоторыми элементами.
Уравнения волнового движения
Колебание монохроматической волны может быть описано одним из уравнений:
у = a sin 2л (1IT — х/Х);
у — a sin (2 л/Т) (/ — х/с);
у = a sin (<»/ — хх);
у = а sin 2л (yt — kx),
где v — фазовая скорость; » = 2л/Т — угловая скоросж; х — угловое волновое число; v = 1/7" — частота; к = 1/Х — восжжое число; а — амплитуда колебания (наибольшее отклонение точки волны от положения равновесия); X — длина волны — расстояние, на которое 2
2 С I января 1980 г. в соответствен с СТ СЭВ 1€52—78 смеете един иды длины ангстрем обязательному применению подлежит единица длины метр (1 А = 10~« м).
распространяется фронт монохроматической волны за один период колебания.
Для практики представляют интерес три вида волн:
., 1) плоские волны (параллельный пучок лучей), распространяющийся в идеально прозрачной среде, имеющие постоянную амплитуду а паи любых значениях х;
2) сферические волны, в которых а убывает пропорционально х, т> е. а — ajx — начальная амплитуда); энергия волн пропорциональна а? и убывает пропорционально х2;
3) плоские волны, распространяющиеся в поглощающей среде, ах *
т. е. аое 2 (а — коэффициент поглощения).
ИНТЕРФЕРЕНЦИЯ СВЕТА.
ОСНОВЫ ТЕОРИИ ИНТЕРФЕРОМЕТРОВ
Под интерференцией света понимается явление, возникающее при взаимодействии когерентных1 волн и состоящее в том, что интенсивность результирующей световой волны в зависимости от разности фаз взаимодействующих волн может быть больше или меньше суммы их иитеясивностей. При своем взаимодействии когерентные волны способны образовывать новую волну, амплитуда колебания которой в каждой
ее точке получается как векторная сумма амплитуд отдельных колебаний (рис. 1.1). В случае интерференция двух волн 0 и 1 с амплитудами Sj и результирующая волна 2 характеризуется формулой
У = Уо + У1 = «о sin ф + «1 sin (<р + б);
_ У = sin (ф + Ф),
Где А0-1 — результирующая амплитуда;
= (atf + a, cos б)2 + (а, sin о)25
A$-i — а% а? 2а0а1 cos б.
1 Когерентные волны — волны одинаковой частоты, колебания в которых отличаются постоянной разностью фаз, не изменяющейся во времени, достаточном для наблюдения.
Если а0= а] = а, то
Л2_, =2а2(1 +cos6) = 2а2 [1 + cos (2лД/Л)].
В случае интерференции п волн с амплитудами а0, сц, а2.ап,
и одинаковой взаимной разностью фаз равнодействующая амплитуда равна
лл=(аи+ S°ncos"6 +(S°nSin"6 ;
\ / \ I /
п
У ап sin иб
tg®=—Ц---------------•
До + ап cos иб
I
Возможность наблюдения интерференции практически ограничивается углом 2а около оси светового пучка, выходящего из источника, диаметр которого 2г, т. е. 2r sin о < Л/4.
Оптическая длина пути
Если после разделения пучка света иа два пучка последние будут распространяться в различных средах, то при подсчете приобретаемой волнами разности фаз необходимо учитывать изменение длины волны при переходе из вакуума в среду (Лср = Л/пСр)-
Оптической длиной пути называется произведение показателя преломления п на геометрическую длину пути d, I.
Область и поле интерференции
Полем интерференции называется поверхность или плоскость, в которых исследуется интерференционная картина. Полем интерфе" реиции может быть фокальная плоскость лупы или микроскопа, через которые рассматривается интерференционная картина, плоскость фотопластинки и т. п. Интерферометры, в которых осуществляется интерференция в результате взаимодействия двух пучков лучей, называются двухлучевымн, трех пучков лучей — трехлучевыми, многих пучков лучей — многолучевыми [44].
Входные и выходные зрачки и поле ин терфероМЪтров
Теорию интерферометров проще всего строят на основе вычисления производных функций от разности хода, применяя при этом законы геометрической оптики.
Большинство технических интерферометров имеет две ветви, каждая из них представляет собой отдельную оптическую систему.
На рис. 1.2 дана принципиальная оптическая схема двухлучевого интерферометра. Источник света L совмещен с входным зрачком интер-8
ферометра*, плоскость В, в которой наблюдается интерференционная картина, служит полем интерференции. Две ветви интерферометра имеют общий входной зрачок н общее поле. Каждая из ветвей интерферометра дает изображение
входного зрачка, и, следова- ,Lt
тельио, в общем случае имеют
два выходных зрачка Lt и Д2. В
Интерферометр также имеет два /, Р
входных поля Bj и В2, явля- ’ ----- "
ющнхся изображением выход- о
вого поля интерференции. В не- °2
которых конструкциях интер- рис । 2. Зрачки и окна интерферо-ферометра и Lg нлн Bt и Вг г метра
совпадают друг с другом. Со- F
вскупиость входного зрачка
L и двух входных полей н В2 можно отнести к пространству предметов, а совокупность выходных зрачков Lt и L2 и выходного поля В — к пространству изображений.
Ширина щели при нелокализованных полосах
Для получения хорошего контраста смещение интерференционных полос от крайних точек входного зрачка (щели) не должно превышать Д с Х/4. На рис. 1.3 показано, что Д = Ощр, поэтому допустимая ширина щели равна Цщ. доп= Угол Р зависит от расположения входного зрачка и входных полей. Например, если Л = 0,55 мкм и р = 20", то ширина щели а™. доп — = 1,5 мм. При р = 1°
значение ащ. доП = 0,01 мм. Критический размер щели Ощ. кр Л./р.
Допустимый размер входного зрачка при локализованных полосах
Рнс. 1.4. Схема определения ширины щели при локализованных полосах
Локализованные полосы появляются в результате интерференции лучей, полученных из одного первичного луча. Поэтому точка L входного зрачка и точки Bt и В2 входных полей расположены на одной пря
мой. Разность хода, возникающую- на краях входного зрачка (рис. 1.4) относительно точки L, можно вычислить по формуле Д ~-~ сощ/8!/ (7+ с). Если q с, то Д = ссщ/З?2 = сс~/2. Для получения хорошего контраста при Д = Х/4 необходимо, чтобы оД0П = К
при 1 = 0,55 мкм величина с= 0,02 мм, сДоП = Т°- Если с— 1! ?.:•», то 1°. Критический угловой размер круглой даафрагмы определяется из условия А = X, т. е. аКр = V
Интерференция в пластинках
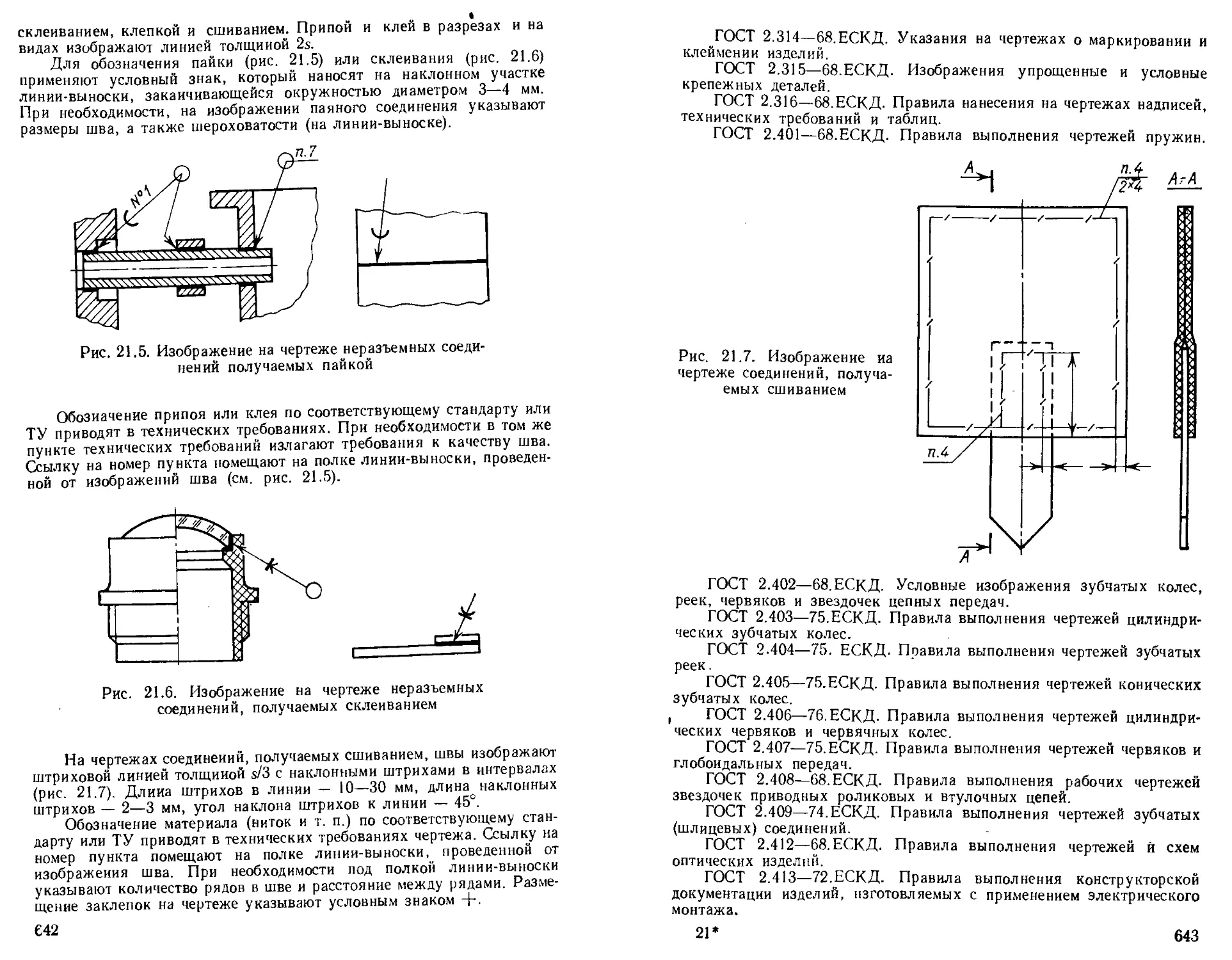
Явления интерференции в пластинках используются в различных схемах интерферометра. Примеры интерференционных схем даны иа рис. 1.5:
1) источник света L (рис. 1.5, а) и поле интерференции В находятся на произвольных конечных расстояниях от испытуемой пластинки ' ' типа);
2) источник излучения расположен на произвольном расстоянии (рис. 1.5,6), а поле отнесено на бесконечность (наблюдаются полосы равного наклона);
3) источник света расположен в бесконечности (рис. 1.5, в), а поле находится па произвольно конечном расстоянии (наблюдаются полосы равной толщины);
4) поле Р и источник света L удалены в бесконечность (рис. 1.5, г). Плоскости L и В сопряжены, поэтому через каждую точку поля можно провести множество лучей.
В первых трех случаях источник света L не сопряжен с полем В, поэтому через каждую точку поли проходят только два вполне определенных луча, показанных на рисунке.
Углы пересечения <о учитывают ширину интерференционных полос е = Угол р определяет критическую ширину источника света (щели), при которой контрастность полос падает до нуля.
Полоал равного наклона — интерференционные полосы, локализованные в бесконечности и образующиеся в -результате прохождения света через плоскопараллельный слой, причем одинаковому наклону лучен в слое соответствует определенное положение интерференционной полосы (рис. 1.5,6).
Оптическая разность хода с учетом потери полуволны при отражении от первой поверхности (n> tij)
А = 2/гКл2 — sin2s-i-,
или
А = 2/iftcose'—(1.1)
изменение разности хода в зависимости от изменения угла в
dA = 2nh sin e'de'.
Полосы равной толщины — интерференционные полосы, образующиеся вдоль линий равных оптических толщин слоя (при угле падения е= const), в котором происходит интерференция (рис. 1.5, в). Из формулы (1.1) при постоянных в' и п следует, что dA = 2n cos в' dh.
Интерференционные полосы могут служить для очень точных измерений толщин пластинки или для обнаружения небольших неровностей на понерхиостя. Если принять, что чувствительность соответствует 0,1 шяряны полосы (изменение разности хода на 0,1 А или 0,06 мкм), то погрешность определения толщины (в мкм) прн нормальном падении луча (8 = 0) составляет
dA 0,06
0,03
Для воздушных пластинок dh — 0,03 мкм. С увеличением угла падения е чувствительность метода понижается.
Кольца Ньютона
Кольца Ньютона представляют частный Рнс. 1.6. Схема об-
случай полос равной толщины. Они образу- разования колец
Ньютона
ются в тонком воздушном слое между двумя
поверхностями стеклянных деталей, из которых одна обычно служит эталоном. При нормальном падении лучей (е= 0) на испытуемую деталь разность хода Д = 2d + А/2. В точке контакта деталей Д = А/2. Система интерференционных колец, наблюдаемых в отраженном свете, образует темный центр. При монохроматическом свете темные кольца находятся от точки контакта на расстояниях, при которых 2d равно целому числу волн 2d = (N — 0, 1, 2, 3, ...). Если радиус г сферической поверхности испытуемой детали нелик (рис. 1.6), то стрелка d = — R2/2r. При наложении на такую поверхность плоской эталонной пластинки радиус N-ro кольца, наблюдаемого в отраженном свете, равен /?т~V_rKN = с K/V, радиус светлого кольца = — V гА K/V + 1/2 = с V V+ 1/2. По измеренному диаметру кольца 2R и его порядковому номеру при дайной длине волны А можно вычислить радиус сферической поверхности исследуемой детали. В табл. 1.3. приведены формулы для вычисления разности радиусов испытуемой поверхности и пробного стекла.
Каждое кольцо (полоса) соответствует приращению толщины воздушного промежутка на А/2. Если А = 0,5-10 3 мм, то число интерференционных полос
Зависимость между фокусным расстоянием и числом интерференционных колец в плоскопараллельной пластинке, установленной перед системой в качестве защитного стекла или светофильтра,
—_____и
4АА/(д—1)
N =Nt±Ne,
где JVj и — числа колец на каждой стороне пластинки.
Таблица 1.3. Формулы для вычислении разности радиусов испытуемой поверхности и пробного стекла о отраженном свете
Разность радиусов Предел измерения
Дг= 4Хг2/П2 (D/r) < 1
Дг = kN cos ос/2 (1 — cos а) (D/r) > 1 при касании пробного стекла краями
Дг = X/V/2 (1 — cos а) (D/r) г> 1 при касании пробного стекла серединой
Примечания: 1.0 ференциониой картины; 2. bin ос = 2R — диаметр наблюдаемой интер-= О/2л
Если обе поверхности пластинки являются одновременно выпуклыми или вогнутыми, то Л\ и Na складывают. Если одна из сторон
выпуклая, а другая — вогнутая, то N равно разности чисел колец.
Пример. Определить допустимую разность N защитного стекла (светофильтра), если его фокусное расстояние не должно быть меньше 1000 м. Диаметр светофильтра 50 мм, п=1,5,
Рис. 1.7. К расчету контрастности ин-
X = 0,6 мкм.
О2 502
N ~ 4Х (п — 1) Г “ 4 0,5 6 10-* • 10«
терференционных полос
Принцип создания интерференционной картины в интерферометре
Создание интерференционной картины основано на принципе разделения пучка лучей на два самостоятельных пучка, которые после прохождения внутри оптической системы снова сводятся в один пучок.
Элементарная освещенность в некоторой точке Р', создаваемая от источника света площадью dS в случае а9 = ах = а,
ЛЕ = 2а2
H-cos2n^dS.
(12)
В интерферометрах источник света (например, апертурная диафрагма) имеет конечные размеры. Поэтому разность хода можно представить суммой двух величин Д = До + 6Д (До — разность хода лучен, исходящих из центра апертурной диафрагмы; 6Д — приращение разности хода между осевым лучом и лучом, выходящим нз некоторой произвольной точки апертурной диафрагмы). По ней выбирается источник света для освещения интерферометра. Небольшое отклонение Д9 от нуля не вызывает заметного изменения контрастности. Однако при 12
значительном Д вследствие недостаточной монохроматичности приме* няемого света контрастность интерференционных полос понижается. Величина ДА зависит от размеров апертурной диафрагмы. Суммарная освещенность в данной точке Р найдется интегрированием формулы (1.2)
Е = 2a2S+2aJ cos (А0-|-ЙД)] dS. (1.3)
s
При вычислении освещенности в некоторой точке поля интерферометра задача сводится к нахождению 6Д и вычислению интеграла too площади действующей апертурной диафрагмы (прямоугольной, круглой, щелевой н т. д.). Контрастность интерференционных полос в данной точке
Ь — ^niax 7? mln
Ещах 4- Е mm ’
где Ещах и Ещщ — соответственно наибольшая и наименьшая освещенность н рассматриваемой точке поля.
Для вычисления Етах и Етщ формула (1.3) приводится к виду
Е =2«> [s+ Рcos (2”5»j -е ,» (Ц&)] , где
(3) (S)
На рис. 1.7 по осям координат отложены отрезки Р и Q. Конец вектора р (точка Af) имеет координаты (Р и Q), <р — полярный угол вектора р с осью х. Из рис. 1.7 следует
Р — р cos ф, Q sin ф, р = Kes Q2. то! да
Е = 2а* |$+ рcos (bt -42-4- ф)] .
Наибольшая освещенность получается, когда
[ 2л До , \ , 2л До , _
cos (—-----1- ф) 1 вли —^-2> 4- ф = 2nv,
где V — 0, 1, 2, 3, .... и будет равна Етах = 2a2 (S-J- р).
Наименьшая освещенность соответствует cos (2лД0/А,4* ф) — —1> т. е. при 2лД0/Х4- ф = (2v4~ 1) л, тогда Emln = 2d2 (S — р).
Формула для контрастности интерференционных полос примет вид
. р _ КгЧ-<?2
S — S
В интерференционных фазовых микроскопах особое значенве имеет предел разрешения по глубине (фазовый предел разрешения), так как здесь структура объекта наблюдается при сдвиге фазы. Для отраженного света фазовый предел разрешения составляет около 1/20, для проходящего света — 1/10 (п — 1) и не зависит от числовой апертуры, если принять во внимание, что оценка производится до одной десятой полосы. Точность измерения сдвига фазы (толщины или нзме-
ненки мкмапеля преломления} момию налучия» посредством досох-пиши ими фшншетрвроваашя гораздо большей. S>эгам случае ариден раамвемия мажет быть на аврндтс пмпг, z. е. мЮО a X/W0 <м — 1).
Эта лрмищм разрешаем ари оиродененяык услеашх могут быть достигнуты при помощи многолучевой интерференции без фотометри-рования и даже превзойдены в некоторых конструкциях интерференционных микроскопов. Так, например, точность измерения сдвигов фаз в ширииг-микроскопе и микроскопе акад. А. А. Лебедева с кри-смяжичесаими элементами при благоприятных условиях достигает W3M.
Методы фазового и интерференционного контраста в микроскопе и сяемы шащрфарепшюиных микроскопов для биологических микроскопов [105].
ДИСПЕРСИЯ СПЕТА.
ОСНОВЫ ТЕОРИИ СПЕКТРАЛЬНЫХ ПРИБОРОВ
Явления, обусловленные зависимостью показатели преломления неиевсвва от длины волны света п = / (1), называют дисперсией. Для всех прозрачных веществ п монотонно возрастает с уменьшением Л, т. е. фиолетовые лучи преломляются сильнее красных, что соответствует нормальной дисперсии. Для оптических стекол зависимость п от Л для видимой области спектра определяется по эмпирической формуле Гартмана
п = п® -ф с/(К —А®}«.
При а = 1 показатель преломления п определяется с точностью до двух-трех единиц пятого знака в области длин волн от 440 до 660 им. Постоянные л®, с и Л® можно вычислить по трем известным значениям длины волны К и соответствуюигнм им показателям преломления п для данной марки стекла. Зависимость « f (&) оптического стекла См. гл. 22.
Принципиальная оптическая схема спектральных приборов
В зависимости от способа разложения свеча спектральные приборы делятся на призменные, дифракционные и интерференционные [63, 97].
Рнс. 1.8. Принципиальная оптическая схема прибора с линзовой оптикой
Принципиальная схема спектрального прибора дана на рас. 1.8. Осветительная система L изображает источник света I на входную щель S, расположенную в передней фокальной плоскости объектива входного коллиматора. Входная щель S изображается с помощью объективов Ох и Ot в задней фокальной плоскости Р объектива О®. Между 14
объективами О, и Ог в параллельных пучках расположена диспергирующая иризма D. В плоскости Р может быть установлена фотопластинка для регистрации спектров. Прибор, построенный по этой схеме, вазы-вжэся еквят^к^юфак. Если вместо фотопластинки применяется щель, то адобор называемся аииохдажадеарлм. Вместо првзмы Е> может быть усишжлеяа плоская дифракционная решетка с жекоторым кзменеаием осей входного и выходного коллиматоров.
Светосила спектрального прибора
Светосила характеризует освещенность Е\ в спектре, даваемую прибором, или лучистый поток Фэх, проходящий через выходную щель прибора [63]. Лучистый поток вычисляется по формуле
Фа — для спектрально!} линии Ф3Х —
для участка ДХ непрерывного спектра, где В^ — яркость входной щели, представляющая среднюю величину яркости по длинам волн данного участка непрерывного спектра или интегральную яркость в случае отдельной спектральной линии; S — площадь входной щели;
— коэффициент светопропускапия системы; ДХ — определяется геометрическим изображением входной щели.
Если лучистый поток полностью проходит через выходную щель прибора и попадает на приемник (иапрнмер, фотоэлемент), то светосила по лучистому потоку определяется выражением
= Фэх/^Л = SShx = SQ4 дХ. (1.4)
В случае фотографирования спектра имеет значение освещенность, создаваемая на фотопластинке. Освещенность Е^ соответственно для спектральной линии и непрерывного спектра равна
Et=BK^-Q4 или Е^=В^-^-ОтьДХ, <L5)
где S' — площадь фотопластинки, на которую падает лучистый поток ФзК.
Светосила в этом случае
S S
или Ях=-уГйт4.Д1.
Из сопоставления формул (1.4) и (1.5)сл*дучт, что светосила спектрального прибора определяется различно ври фотоэлектрической и фотографической регистрации спектра. При визуальном рассмотрении спектра светосила определяется освещенностью на сетчатке глаза.
Лишенная дисиереия
призменных спектральных приборов
Линейный отрезок dl, соответствующий угловой дисперсии dy, создаваемой призменной системой между двумя лучами с соответствующими длинами волн X и X + dX (рнс. 1.9) в фокальной плоскости f.2 объектива камеры, равен
di =-^--1^1 нли dl____________dL
sine “sine нли dX “ dX sine’
где е — угол наклона плоскости спектра к оптической оси объектива камеры. Величина dlldk называется линейной дисперсией прибора и измеряется числом миллиметров, приходящихся на единицу интервала спектра (мм/А, мм/нм, мм/мкм). На практике обычно пользуются величиной, обратной линейной дисперсии dkldl и выражают ее А/мм, нм/мм, мкм/мм. В табл. 1.4 даиы линейная дисперсия и разрешающая
Рис. 1.9. Схема определения линейной дисперсии
способность трех типов спектральных приборов. Линейная дисперсия для любой длины волны, проходящей призму в минимуме отклонения, равна
0
,, 2fe sin —- ,, ,
dl _______________2 /2 dn
dk ~ -i / if sin e dk~ ’
J/ 1—n3sjn2-^—
где k — число призм; 6 — преломляющий угол призмы.
Таблица 1.4. Линейная дисперсия и разрешающая способность спектральных приборов [63]
Тип прибора Линейная дисперсия на 1 мм Разреш ающая способность
Призменные с малой и средней дисперсией Большие призменные приборы и дифракционные решетки И птерференцион и ые loo-ю А ю—1 А о,1—о,о1 А 103—ю5 10»—5-10» До нескольких миллионов
Теоретическая разрешающая способность спектральных приборов
Разрешающая способность ограничивается явлением дифракции света от действующего отверстия призмы или от отверстия коллиматорных объективов. При дифракции иа одной щели (см. рис. 1.13) положение минимумов при нормальном падении света определяется формулой a sin <р — тК, (1.6)
•где <р — угол дифракции; т — порядок минимума; а — ширина щели.
В основу оценки разрешения двух спектральных линий равной интенсивности положен критерий Рэлея, в соответствии с которым
указанные спектральные линии считаются разрешенными, если центральный дифракционный максимум второй линии совпадает с первым минимумом первой линии (см. рис. 2.20). Критерий Рэлея является условным и в некоторых случаях заниженным, например, современные фотоэлектрические установки и контрастная фотопла-
Рис. 1.10. Определение величины основания призмы
стинка регистрируют различие в освещенностях или в световых потоках до 5% и менее.
Принимая во внимание ди-
фракцию в действующем отверстии СЕ = D (рис. 1.9) по формуле (1.6) прн m= 1, угол ф = Х/О (при малом угле <р) дает угловое расстояние между центральным дифракционным максимумом и первым минимумом. По условию Рэлея этому угловому расстоянию
<р должно соответствовать угловое расстояние Ду между двумя разрешенными спектральными линиями, отличающимися на ДХ по длине волны. Угловое расстояние Ду можно выразить через угловую дисперсию dyidL призмы: Ду = dyAZ/dZ. По условию Рэлея <р = Ду, тогда A./D = dyAVdA. и
X „ dy г —-----— D ——
dA, dX ’
(1.7)
т. е. разрешающая способность определяется двумя величинами: D — действующим отверстием прибора (в данном случае отверстием призмы) я угловой дисперсией призмы. Эта формула справедлива для всех спектральных приборов.
Принимая во внимание тот случай, когда призма находится в минимуме отклонения, формуле (1.7) можно дать иное выражение
Из рис.
_ X _ 20 sin -А-
Д 1 Л. 2 . 3 6
у 1— reasm3—g-
1.10 при
20 sin /- = --
у 1 — п2 sin2-^-
dn
dT”
имеем
_ ?, _ dn r~M~L dk ’
(1.8)
т. e. разрешающая способность спектрографа пропорциональна основанию призмы (если она полностью заполнена пучком света) и дисперсии ее материала. Если прибор содержит А одинаковых призм, то
r==kLST
(1.9)
В случае неполного заполнения призмы пучком света вместо L в формулу (1.8) следует подставить разность геометрических путей
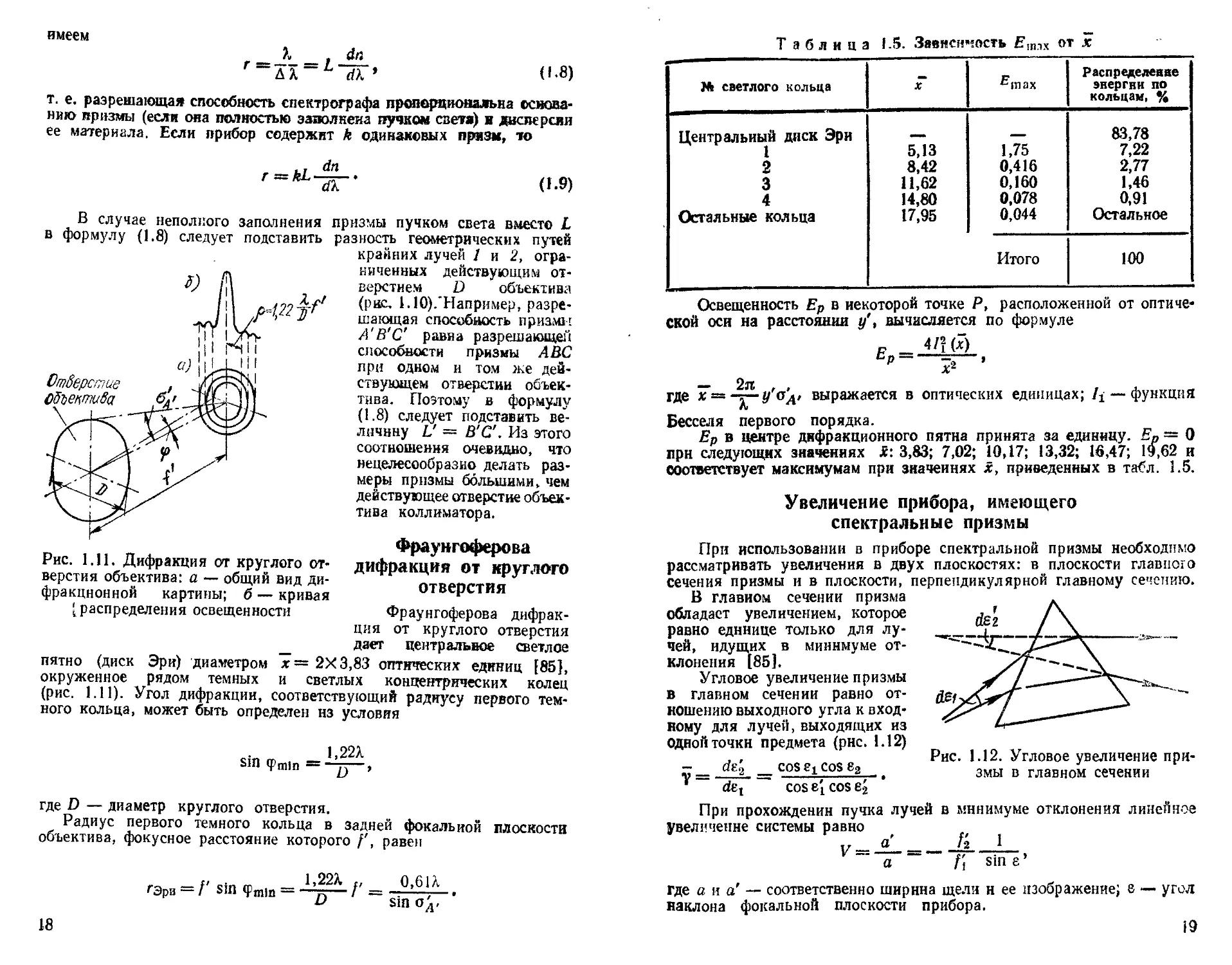
Рис. 1.11. Дифракция от круглого отверстия объектива: а — общий вид дифракционной картины; б — кривая (распределения освещенности
крайних лучей 1 и 2, ограниченных действующим отверстием D объектива (рис. 1.10).'Например, разрешающая способность призмы А'В'С равна разрешающей способности призмы АВС при одном и том же действующем отверстии объектива. Поэтому в формулу (1.8) следует подставить величину L' = В'С'. Из этого соотношения очевидно, что нецелесообразно делать размеры призмы большими, чем действующее отверстие объектива коллиматора.
Фраунгоферова дифракция от круглого отверстия
Фраунгоферова дифрак
ция от круглого отверстия
дает центральное светлое пятно (диск Эри) диаметром х= 2X3,83 оптических единиц [85],
окруженное рядом темных и светлых концентрических колец (рис. 1.11). Угол дифракции, соответствующий радиусу первого темного кольца, может быть определен нз условия
1.22Х sm фппп ———
где D — диаметр круглого отверстия.
Радиус первого темного кольца в задней фокальной плоскости объектива, фокусное расстояние которого равен
. 1,22Х 0,6 IX
гэрв-/ Sin q>mlB -=
Таблица 1.5. Зависимость Е!ППХ от х
№ светлого кольца X £|пах Распределение энергии по кольцам, %
Центральный диск Эри __ 83,78
1 5,13 1,75 7,22
2 8,42 0,416 2,77
3 11,62 0,160 1,46
4 14,80 0,078 0,91
Остальные кольца 17,95 0,044 Остальное
Итого 100
Освещенность Ер в некоторой точке Р, расположенной от оптической оси на расстоянии у', вычисляется по формуле
Е __ 4/' ₽ хг ’ — 2л , , , ,
где х = -^—у аА, выражается в оптических единицах; /у — функция Бесселя первого порядка.
Ер в центре дифракционного пятна принята за единицу. Ер = О при следующих значениях Я: 3,83; 7,02; 10,17; 13,32; 16,47; 19,62 и соответствует максимумам при значениях Я, приведенных в табл. 1.5.
Рис. 1.12. Угловое увеличение призмы в главном сечении
Увеличение прибора, имеющего спектральные призмы
При использовании в приборе спектральной призмы необходимо рассматривать увеличения в двух плоскостях: в плоскости главного сечения призмы и в плоскости, перпендикулярной главному сечению.
В главном сечении призма обладает увеличением, которое равно единице только для лучей, идущих в минимуме отклонения [85].
Угловое увеличение призмы в главном сечении равно отношению выходного угла к входному для лучей, выходящих из одной точки предмета (рис. 1.12) de а _______cos gj cos e3
’ det cos e[ cos e3
При прохождении пучка лучей в минимуме отклонения линейное увеличение системы равно
д Л 1
a /; sine’
где она' — соответственно ширина щели н ее изображение; в — угол наклона фокальной плоскости прибора.
Так как входная щель располагается параллельно преломляющему ребру призмы, то ее линейное увеличение в плоскости, перпендикулярной главному сечевик», равно отношению V — h'/h— —f2lf'u где h и h' — соответственно высота щелн н высота ее изображения.
Кривизна спектральных линий
Бесконечно удаленная прямая линия, параллельная ребру призмы (например, изображение щели или спектральной линии S, расположенной в переднем фокусе объектива (Д коллиматора; см. рис. 1.8) и рассматриваемая через призму, кажется искривленной по дуге окружности с вогнутостью, обращенной в коротковолновую область спектра. Когда призма не находится в положении наименьшего отклонения лучей, кривизна н стрелка прогиба линий, рассматриваемых в задней фокальной плоскости объектива О2, соответственно равны [97, 99 J
_ 1_____и2 — 1 sin б
Р ~ R ~ nf2 cos е'( cos в2 *
где у — угол, под которым из центра объектива О2 видна данная точка линии (щели), расположенная в плоскости изображения.
Если призма находится в положении минимума отклонения, то
1 2 (п2 - 1) Sitl 2 2(n"--l)tgf,.
R nf'! 1/1 2 c- 2 0 ~
у \ — II2 Sin2 —
Если н приборе имеется несколько призм, то кривизна, вызываемая отдельными призмами, не просто складывается, а каждая кривизна р должна быть умножена на увеличение в главном сечении следующих за ней призм.
Спектр, даваемый призмой, менее удобен, чем нормальный спектр дифракционной решетки, так как его фиолетовая часть растянута значительно сильнее красной (см. табл. 2.12). Дисперсия в призматическом спектре меняется обратно пропорционально л3. Поэтому при исследовании распределения интенсивности в непрерывных спектрах следует всегда вносить поправку на зависимость дисперсии от длины волны; чтобы получить спектр приближающимся к нормальному, необходимо все ординаты интенсивностей призменного спектра разде--яить на X3.
Реальная разрешающая способность спектрального прибора
Реальная разрешающая способность прибора зависит от следующих факторов:
1) ширины щели спектрального прибора и условия ее освещения (когерентное или некогерентное освещение);
2) разрешающей способности приемника излучения (фотоэлемент, фотопластинка, глаз и т. д.);
3) погрешности оптической системы.
Реальная разрешающая способность спектрографа (фотографическая регистрация спектра) определяется по формуле
______X h ft dy р_____р sin е dh ’
где р — предельное разрешимое пластникой расстояние в мм.
Разрешающая способность прямо пропорциональна f'2. Однако светосила прибора резко уменьшается, если увеличить f,.
Эффективное действующее отверстие прибора определяется по
формуле х 1
Для определения разрешающей способности пользуются нормальной шириной входной щели (44, 63]: аа = Kf\lD = лй, где — фокусное расстояние объектива переднего коллиматора. Прн этой ширине щели геометрическое изображение ширины спектральной линии (а' — = af2lfi) равно дифракционной ширине (пДИф = X/^/D), т. е. той наименьшей ширине, которую может обеспечить прибор при бесконечно
тонкой щели.
Вследствие конечных размеров ширины щели практический предел разрешения меньше теоретического и может быть вычислен по формуле
гпр = гтеор X [sd/f X2/ /{2sd X/ )] 1, где s — ширина щели; /' — фокусное расстояние объектива коллиматора; d — действующая ширина светового пучка.
Для оптимальной ширины щели $опг = = XfId следует гпр = 0,75гтеор.
В инфракрасных лучах, когда работают с широкой щелью, которая по энергетическим причинам превышает оптимальный размер, частота спектра определяется условием
7? = rTCOpX (srf// + X] Ч
Рис. 1.13. Схема прозрачной дифракционной решетки: а — ширина щели; b — величина непрозрачного промежутка; d = а -|-ф-6— постоянная, или период решетки
Дифракционные решетки
По форме рабочей поверхности дифракционные решетки делятся на плоские и вогнутые, а по свойству материала — па прозрачные и отражательные.
Прозрачная дифракционная решетка (рис. 1.13) представляет собой совокупность строго параллельных щелей, разделенных непрозрачными промежутками.
Современные решетки, как правило, работают иа отражение. Отражательные решетки представляют собой совокупность штрихов —
канавок, расположенных на определенном расстоянии друг от друга (рис. 1.14). Отражающим свет элементом служит отражающая грань. Наклон грани к общей плоскости РР' решетки определяет угол «блеска» решетки; прн дифракции света в направлении этого угла решетка дает максимальную интенсивность света.
Д', Nz
Рис. 1.14. Теоретический профиль штриха ступенчатой решетки: N1 — нормаль к поверхности решетки; — нормаль к грани решетки; е — угол падения лучей; ф— угол дифракции
Р----
Угловая и линейная дисперсии решетки
Положение главных максимумов решетки определяется нз основного уравнения [63, 97]
d (sin е + sin ф) — k\,
(1.10)
где k — положительные илн отрицательные целые числа, так как угол <р может быть расположен по обе стороны от регулярно отраженного луча ф = е. Каждому значению k = 1, 2, 3 н т. д. соответствуют спектры 1, 2, ..., fe-ro порядка.
Практически решетки применяются при углах в и ф до 65°, что позволяет наблюдать предельную длину волны доХпр = 1,8d; поэтому решетка с 3600 штр/мм пригодна только до Z = 500 нм.
Изменение утла ф, соответствующее изменению длины волны на единицу, носит название угловой дисперсии решетки. Дифференцируя (1.10) по длине волны X прн постоянном угле падения е для всех длин волн, получим формулу для вычисления угловой дисперсии
dq> _ k
d7. dcos ф
Дисперсия минимальна при ф = 0°. При малых значениях ф косинус изменяется медленно, поэтому угловая дисперсия практически остается постоянной. Такие спектры с постоянной дисперсией, расположенные вблизи нормали к решетке, называют нормальными.
Разрешающая способность прибора с дифракционной решеткой
С вопросом о разрешающей способности спектрографа связано понятие о ширине спектральной линии. Для бесконечно узкой нли «иор-ральной» щели прибора принято считать, что ширина спектральной линии определяется угловым размером Д<р центрального дифракционного максимума по формуле
Д ф = Х/М4 cos ф = X//cos ф. (1.11)
Его линейная ширина з = Дф/2/sin е; Nd — I — ширина заштрихованной части решетки; — фокусное расстояние объектива камеры.
Пример. X = 6000 А, /=100 мм, ф = 0°, тогда Дф=6-10"* ми 1,2". Формула (1.11) определяет угловой размер дифракционного максимума при дифракции в действующем отверстии решетки, равном 1 cos ф для угла дифракции ф. Предел разрешения дифракционной решетки пропорционален порядку спектра k н числу штрихов N'.
r — — (1.12)
А Л
где ДХ — разность волн двух спектральных линий, дифракционные максимумы которых видны раздельно; [X — средняя длина волны разрешаемых линий.
Предел разрешения можно вычислить по формуле
Nd , . ... I , , , . .
т — (sin е+ sin ф) =у (sin е + sin ф), (1.13)
Для автоколлнмационной установки при е = <р имеем г — = 2/ sin ф/Х.
В предельном случае ф = 90°, поэтому г = 21/к.
С точки зрения повышения дисперсии прибора выгодно работать в высшем порядке спектра. Так как интенсивность спектральных линий быстро падает с увеличением порядка спектра, то обычно не пользуются порядком выше четвертого.
В настоящее время широко используются копии с дифракционных решеток (реплики), получаемые методом копирования на основе применения полимеризирующихся пластмасс (см. гл. 4).
ИЗЛУЧЕНИЕ И ПОГЛОЩЕНИЕ СВЕТА
Монохроматическое и сложное излучение
Процесс испускания электромагнитных волн материальным телом называется излучением. Излучения различаются по мощности (количественная характеристика) н по спектральному составу (качественная характеристика).
Монохроматическое излучение — излучение вполне определенной длины волны X; характеризуется мощностью или потоком излучения.
Различают два вида сложного излучения:
1) излучение, состоящее нз конечного числа монохроматических излучений (прерывный линейчатый спектр). Полная характеристика такого излучения определяется мощностью входящих в его состав Монохроматических излучений;
Рис. 1.15. Зависимость спектральной плотности потока Дх излучения от длины волны Л
2) излучение, состоящее из непрерывного ряда монохроматических излучений; оно характеризуется общей мощностью и ее непрерывным распределением по длинам волн внутри всего спектрального диапазона.
Если в спектральном промежутке от Л до 1 + ДА, энергетический поток излучения равен г/Фэл, то отношение | dfyoJd'k 1^_>о — Рк~ = / (Л) характеризует монохроматический поток излучении с длиной волны Л и называется спектральной плотностью потока излучения.
Спектральной кривой лучистого потока илн кривой распределения энергии по спектру называется такая кривая, у которой абсциссами являются длины волн, а ординаты р\ таковы, что pdk выражает мощность, передаваемую лучистым потоком в виде излучений, длины волн которых заключены между А и А+ДЛ (рис. 1.15). Величина р^ выражается в единицах мощности на единицу длины волны, например Вт/мкм.
Поток излучения в пределах длин волн от до Xj равен
Фэсх.-г,) = J = [ №.
Величина ФЭ(Х,-Х) определяется заштрихованной площадью (рис. 1.15).
Поток лучистой энергии можно рассматривать: 1) с энергетической точки зрения и характеризовать мощность Фэ в ваттах; 2) с точки
зрения производимых нм световых ощущений и характеризовать световым потоком Ф в люменах.
В каждом случае поток энергии характеризуется плотностью излучения, яркостью, спектральным составом (плотностью распределения энергии по длинам волн) и т. д. Для описания распределения лучистою потока в пространстве служит система лучистых величин.
Между лучистыми величинами существуют те же соотношения, что и между световыми величинами. Однако, чтобы отличить световые величины от лучистых для последних приняты особые краткие термины (табл. 1.6) [83].
На практике характеристика источников излучения какого-нибудь тела определяется путем сравнения с характеристикой излучения абсолютно черного тела (АЧТ).
Таблица 1.6. Сопоставление некоторых лучистых величин
Термины, содержащие названия аналогичных световых величин Специальные термины
Энергетическая освещенность Облученность
светимость Излучательность
» сила света Сяла излучения
» яркость Лучистость
Законы теплового излучения АЧТ
Согласно закону Кирхгофа для одной и той же точки тела отношение излучательной способности, оцениваемой спектральной интенсивностью плотности излучения к его поглощательной способности, оцениваемой спектральной поглощательной способностью (коэффициентом поглощения) ах, для одной длины волны н температуры есть величина постоянная г\1/ах1 — гК2/а>.2 = = гКп/акп = f (КТ).
Тело, которое поглощает все падающее на него излучение (а^т = = 1), называется абсолютно черным телом.
При данной температуре АЧТ обладает наибольшей излучательной способностью по сравнению с другими телами. Излучаемая телом энергия пропорциональна коэффициенту поглощения. Величина этого коэффициента зависит от физических свойств тела, состояния его поверхности, температуры, а также от спектра излучения, падающего на тело. АЧТ является идеальным ламбертовым (косинусным) излучателем [1, 32, 83, 104, 115].
В природе существует ряд веществ, которые по поглощательной способности весьма близки к черному телу (сажа, платиновая чернь и др.). АЧТ служит эталонным прибором, по которому калибруются источники и приемники излучения.
Спектральная плотность энергетической светимости (излучатель-ность) вычисляется (Вт-м"2-мкм-1) по формуле Планка [102, 104, 115]
г; = 3,71 108А"5 (енз80АГ _ I )~т, (1.14)
где А выражается в мкм; Т — в К, е = 2,718 основание натурального логарифма.
На основании закона Вина максимальное излучение имеет место на длине волны кт (мкм) при данной абсолютной температуре Т
и его плотность (Вт-м 2 мкм"1) определяется соотношением
. / Т \5
'" = 130,0(т«ю) • (1J6>
Для интервала спектра от до А2:
Кз
/?э*а1.хг) = (l-П)
Интегральная энергетическая светимость по закону Стефана— Больцмана
оо
о
где 0 — 5,67-10"8 Вт-м"2-К"4.
Энергетическая яркость (лучистость) излучения определяется формулами:
для интервала спектра от до к*
К, интегральная энергетическая яркость
Яэ*.инт 1 Г ... аР 5,67 / Т
э. ИНТ ~ п — я J к п л \ 100 / ’
о
где t>£ — спектральная плотность энергетической яркости.
Лучистый поток, излучаемый во входной зрачок 'оптической системы, можно вычислить по формулам:
d<b'3K = nSA2dB3\ = SA2r’dX;
Ха
Фэ (Ki-K,) =nS^B3(kt-kt) = SAX(lrl,) = SA2 j (L19)
Kt 00
< инт = SA2/?;. иит = SA2 J r*Kdk = oTW, (1.20)
о
где S — площадь поверхности АЧТ; A — входная числовая апертура системы.
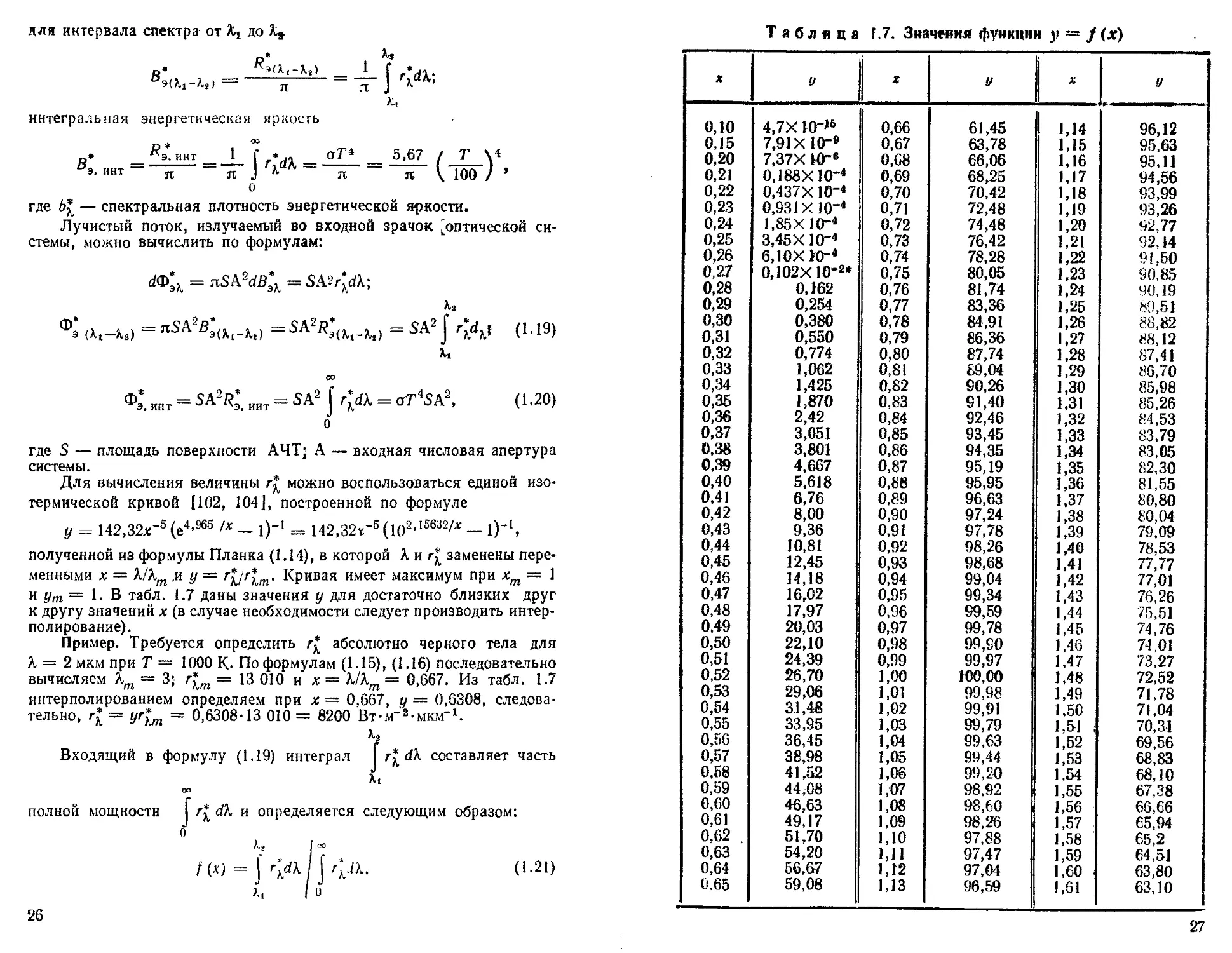
Для вычисления величины можно воспользоваться единой изотермической кривой [102, 104], построенной по формуле
у = 142,32х'5 (е4,965 /х — 1)-1 = 142,32т-5 (ю2-15632/* — 1)-1, полученной из формулы Планка (1.14), в которой X и заменены переменными х = к/кт ,и у = Кривая имеет максимум при xm — 1 и ут = 1. В табл. 1.7 даны значения у для достаточно близких друг к другу значений х (в случае необходимости следует производить интерполирование).
Пример. Требуется определить г?* абсолютно черного тела для к = 2 мкм при Т = 1000 К- По формулам (1.15), (1.16) последовательно вычисляем кт — 3; г*_т = 13 010 и х = к/кт = 0,667. Из табл. 1.7 интерполированием определяем при х — 0,667, у = 0,6308, следовательно, = У*кт ~ 0,6308-13 010 = 8200 Вт-м-2-мкм-1.
Xj
Входящий в формулу (1.19) интеграл J dk составляет часть К,
оо
полной мощности J dk и определяется следующим образом:
о
X. I се
f(x) = j r*Kdk рх (1.21)
М I о
Таблица 1.7. Значения функции у = / (х)
X У X У X У
0,10 4,7Х 10~>6 0,66 61,45 1,14 96,12
0,15 7,91X10-» 0,67 63,78 1,15 95,63
0,20 7,37Х 10-» 0,68 66,06 1,16 95,11
0,21 0,188X10-» 0,69 68,25 1,17 94,56
0,22 0,437 X 10”» 0,70 70,42 1,18 93,99
0,23 0,931X10-» 0,71 72,48 1,19 93,26
0,24 1,85X10-» 0,72 74,48 1,20 92,77
0,25 3,45X10-» 0,73 76,42 1,21 92,14
0,26 6,10X10-» 0,74 78,28 1,22 91,50
0,27 0,102X10-2* 0,75 80,05 1,23 90,85
0,28 0,162 0,76 81,74 1,24 90,19
0,29 0,254 0,77 83,36 1,25 89,51
0,30 0,380 0,78 84,91 1,26 88,82
0,31 0,550 0,79 86,36 1,27 88,12
0,32 0,774 0,80 87,74 1,28 87,41
0,33 1,062 0,81 89,04 1,29 86,70
0,34 1,425 0,82 90,26 1,30 85,98
0,35 1,870 0,83 91,40 1,31 85,26
0,36 2,42 0,84 92,46 1,32 84,53
0,37 3,051 0,85 93,45 1,33 83,79
0,38 3,801 0,86 94,35 1,34 83,05
0,39 4,667 0,87 95,19 1,35 82,30
0,40 5,618 0,88 95,95 1,36 81,55
0,41 6,76 0,89 96,63 1,37 80,80
0,42 8,00 0,90 97,24 1,38 80,04
0,43 9,36 0,91 97,78 1,39 79,09
0,44 10,81 0,92 98,26 1,40 78,53
0,45 12,45 0,93 98,68 1,41 77,77
0,46 14,18 0,94 99,04 1,42 77,01
0,47 16,02 0,95 99,34 1,43 76,26
0,48 17,97 0,96 99,59 1,44 75,51
0,49 20,03 0,97 99,78 1,45 74,76
0,50 22,10 0,98 99,90 1,46 74,01
0,51 24,39 0,99 99,97 1,47 73,27
0,52 26,70 1,00 100,00 1,48 72,52
0,53 29,06 1,01 99,98 1,49 71,78
0,54 31,48 1,02 99,91 1,50 71,04
0,55 33,95 1,03 99,79 1,51 ; 70,31
0,56 36,45 1,04 99,63 1,52 69,56
0,57 38,98 1,05 99,44 1,53 68,83
0,58 41,52 1,06 99,20 1.54 68,10
0,59 44,08 1,07 98.92 1,55 67,38
0,60 46,63 1,08 98,60 1,56 66,66
0,61 49,17 1,09 98,26 1,57 65,94
0,62 51,70 1,10 97,88 1,58 65,2
0,63 54,20 1,11 97,47 1,59 64,51
0,64 56,67 1,12 97,04 1,60 63,80
0.65 59,08 1,13 96,59 1,61 63,10
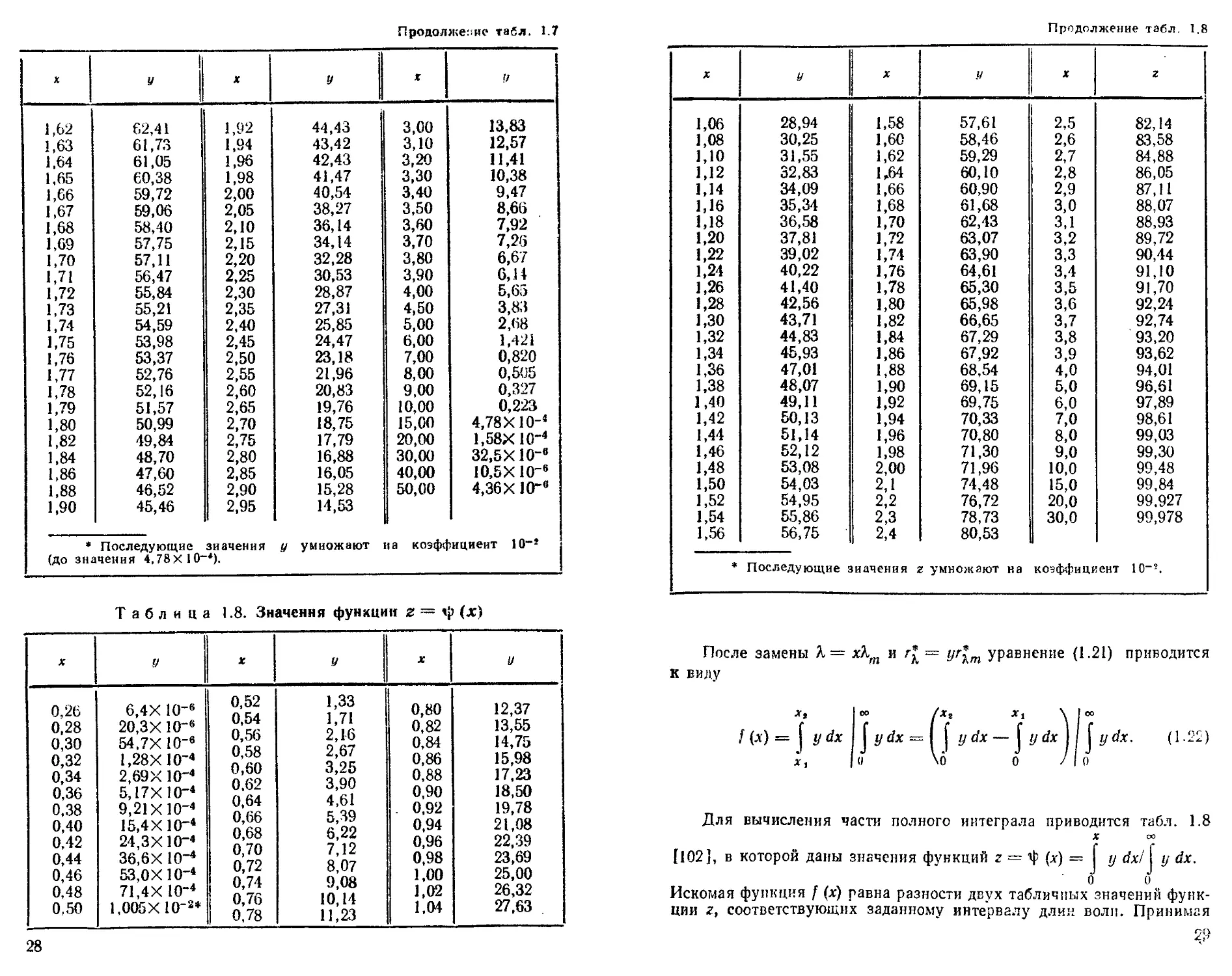
Продолжение таел. 1.7
X • X У X У
1,62 62,41 1,92 44,43 3,00 13,83
1,63 61,73 1,94 43,42 3,10 12,57
1,64 61,05 1,96 42,43 3,20 11,41
1,65 60,38 1,98 41,47 3,30 10,38
1,66 59,72 2,00 40,54 3,40 9,47
1,67 59,06 2,05 38,27 3,50 8,66
1,68 58,40 2,10 36,14 3,60 7,92
1,69 57,75 2,15 34,14 3,70 7,26
1,70 57,11 2,20 32,28 3,80 6,67
1,71 56,47 2,25 30,53 3,90 6,14
1,72 55,84 2,30 28,87 4,00 5,65
1,73 55,21 2,35 27,31 4,50 3,83
1,74 54,59 2,40 25,85 5,00 2,68
1,75 53,98 2,45 24,47 6,00 1,421
1,76 53,37 2,50 23,18 7,00 0,820
1,77 52,76 2,55 21,96 8,00 0,505
1,78 52,16 2,60 20,83 9,00 0,327
1,79 51,57 2,65 19,76 10,00 0,223
1,80 50,99 2,70 18,75 15,00 4,78 XI О-4
1,82 49,84 2,75 17,79 20,00 1,58X10"4
1,84 48,70 2,80 16,88 30,00 32,5Х10-«
1,86 47,60 2,85 16,05 40,00 10,5Х IO"6
1,88 1,90 46,52 45,46 2,90 2,95 15,28 14,53 50,00 4,36Х 10-«
* Последующие значения (До значения 4,78X10“*). у умножают ta коэффициент 10“*
Таблица 1.8. Значения функции г ~ ф (х)
X У X У X У
0,26 6,4Х Ю-6 0,52 0,54 0,56 0,58 0,60 0,62 0,64 0,66 0,68 0,70 0,72 0,74 0,76 0,78 1,33 1,71 2,16 2,67 3,25 3,90 4,61 5,39 6,22 7,12 8,07 9,08 10,14 11,23 0,80 12,37
0,28 20,ЗХ 10~6 0,82 13,55
0,30 54,7X10-® 0,84 14,75
0,32 1,28X10'4 0,86 15,98
0,34 2,69Х 10-4 0,88 17,23
0,36 5,17X10"4 0,90 18,50
0,38 9,21 ХЮ"4 . 0,92 19,78
0,40 15,4Х IO"4 0,94 21,08
0,42 0,44 24,ЗХ10-4 36,6Х ю-4 0,96 0,98 22,39 23,69
0,46 0,48 0,50 53,0X10"4 71,4Х IO’4 1.005Х Ю"2* 1,00 1,02 1,04 25,00 26,32 27,63
Продолжение табл. 1.8
X у X у X Z
1,06 28,94 1,58 57,61 2,5 82,14
1,08 30,25 1,60 58,46 2,6 83,58
1,10 31,55 1,62 59,29 2,7 84,88
1,12 32,83 1,64 60,10 2,8 86,05
1,14 34,09 1,66 60,90 2,9 87,11
1,16 35,34 1,68 61,68 3,0 88,07
1,18 36,58 1,70 62,43 3,1 88,93
1,20 37,81 1,72 63,07 3,2 89,72
1,22 39,02 1,74 63,90 3,3 90,44
1,24 40,22 1,76 64,61 3,4 91,10
1,26 41,40 1,78 65,30 3,5 91,70
1,28 42,56 1,80 65,98 3,6 92,24
1,30 43,71 1,82 66,65 3,7 92,74
1,32 44,83 1,84 67,29 3,8 93,20
1,34 45,93 1,86 67,92 3,9 93,62
1,36 47,01 1,88 68,54 4,0 94,01
1,38 48,07 1,90 69,15 5,0 96,61
1,40 49,11 1,92 69,75 6,0 97,89
1,42 50,13 1,94 70,33 7,0 98,61
1,44 51,14 1,96 70,80 8,0 99,03
1,46 52,12 1,98 71,30 9,0 99,30
1,48 53,08 2,00 71,96 10,0 99,48
1,50 54,03 2,1 74,48 15,0 99,84
1,52 54,95 2,2 76,72 20,0 99.927
1,54 1,56 55,86 56,75 2,3 2,4 78,73 80,53 30,0 99,978
* Последующие значения умножают на коэффициент 10~?.
После замены Х= xkm и г£ = уг%т уравнение (1.21) приводится К виду
*>
/ (Л ) = J у dx X <
j ydx = (I
(1-22)
Для вычисления части полного интеграла приводится табл. 1.8 X а>
1102], в которой даны значения функций г = ф (л) = J у dx/j у dx.
Искомая функция f (х) равна разности двух табличных значений функции г, соответствующих заданному интервалу длин волн. Принимая
во внимание (1.17), (1.18) и (1.21), интеграл, входящий в (1.19), будет равен
Kg оо
^□(Х^Х,) = j rX ^ = / (*) j ~ ' W ^э.лнт =
X, О
Излучение тел, не являющихся абсолютно черными
Все тела, отличающиеся по характеру излучения от АЧТ, условно делятся на селективные и серые.
Тела, для которых еуу — спектра.*ная излучательная способность или спектральный коэффициент излучения — меняется с изменением температуры и длины волны (т. е. излучение имеет селективный характер) называются селективными телами. Они не подчиняются законам излучения АЧТ, за исключением закона Кирхгофа. Примером таких тел является вольфрамовая нить лампы накаливания. Для таких тел можно записать:
ГК — ехтгх;
dBA = b^-£d^eKT~dk-,
Kg Ле Kg Ле
Вэ(Х,-Ха) = J dB9X = J bkd^ = — j rkd’K — f ekTrkd^>
X, X, X, X,
00 00 00
4 Л - 4-M -
0 0 0
00
= 44 eKTrKdk-0
Излучательная способность серого тела — f (T) = не зависит от длины волны. Величина е-у сильно зависит от характера обработки поверхности материала излучателя [1, 102]. Строго говоря, в природе серых тел не существует, однако в пределах сравнительно узких диапазонов многие тела практически могут рассматриваться как серые и к ним можно применить следующие зависимости:
х = еДх;
87.x. Д dB* = -Д-i— Л л
ь в.., X ) = — ( 5(Л1~Л2) л J л Xi
В Ш1Т = SL 7 г* <Д = — аТ4 = 5,67 ( -ХтУ 5
э.ипт я J х л л \ 100 /
о
^э.инт ~ 8Г^э.инт = е70^ = ет 100 ) ‘
Кривая распределения энергии серого тела отличается от кривой АЧТ при той же температуре только постоянным множителем.
Пример. Определить величину лучистого потока в интервале длин волн от А = 2 до 6 мкм, испускаемого серым телом с поверхности S = = 2 см2 и поступающего в оптическую систему с числовой апертурой А — 0,1, если температура тела Т = 1500 К, а излучательная способность еу = 0,97. Воспользуемся формулой (1.19); найдем сначала Я*(Х X )> затем по формуле (1.15) определяем = 2 мкм; вычисляем x1 = k1/km = 1; х2 = КАп = 3. Из табл. 1.8 находим гл = = ’l’ (*1) — Ф (О — 0,25; z2 = ф (х2) = ф (3) = 0,88. Согласно формуле (1.18) определяем R*3— 5,67 (15)4 = 28,7-104. Следовательно, х2
^э(х1-л2) = j г1^^=(г2 — г1) Кэ = 18,08-104 Е-т-м-2. Принимая л,
во внимание (1.19), получим
Фэ(Х!-М) =8ГФЭ(М-Л») = eTSA" (г2 ~г1) ^э.шгг =
= 0,97-2-0,1М8,08 — 0,351 Вт.
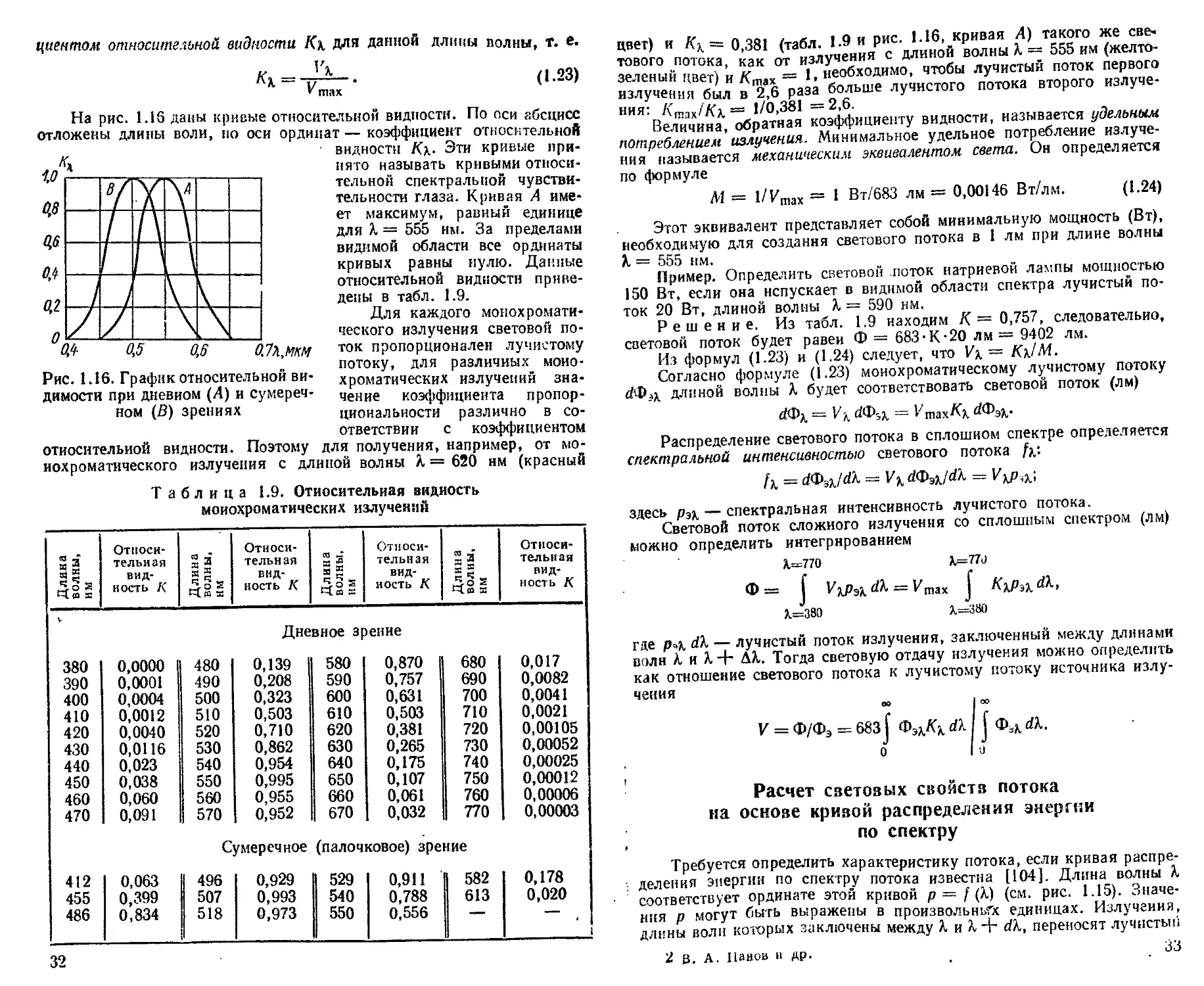
Соотношения между энергетическими и светотехническими величинами
Отношение светового потока к лучистому потоку этого излучения V — Ф/Ф, (лм/Вт) называется световой отдачей сложного излучения.
Отношение Их = Ф^/ФэЛ называется коэффициентом видности или коэффициентом отдачи монохроматического излучения.
Коэффициент видности есть функция длины волны Л рассматриваемого монохроматического излучения.
На границах видимого спектра ординаты кривой приближаются к нулю. Ее максимум Ешах приходится на длину волны 555 нм, т. е. на такое излучение, для которого чувствительность глаза при равных энергетических потоках максимальна.
Величина Етах служит соотношением между энергетическим и световым потоками и называется световым эквивалентом лучистого потока.
Практически установлено, что Етах= 683 лм/Вт, т. е. при длине волны X = 555 нм монохроматический лучистый поток в 1 Вт эквивалентен монохроматическому световому потоку (желто-зеленого цвета) 683 лм. Отношение коэффициента видности при длине волны X к максимальному значению этого коэффициента Ешах называется коэффи-31
циентом относительной видности Кк для данной
длины полны, г. е.
max
(1.23)
Рис. 1.16. График относительной видимости при дневном (А) и сумеречном (В) зрениях
На рис. 1.16 даны кривые относительной видности. По оси абсцисс отложены длины воли, но оси ординат — коэффициент относительной видности Кх- Эти кривые принято называть кривыми относительной спектральной чувствительности глаза. Кривая А имеет максимум, равный единице для к = 555 нм. За пределами видимой области все ординаты кривых равны нулю. Данные относительной видности приведены в табл. 1.9.
Для каждого монохроматического излучения световой поток пропорционален лучистому
потоку, для различных монохроматических излучений значение коэффициента пропорциональности различно в со-
ответствии с коэффициентом относительной видности. Поэтому для получения, например, от монохроматического излучения с длиной волны к = 620 нм (красный
Таблица 1.9. Относительная видиость монохроматических излучений
2 з 44» S Относительная вид-ность Л 2 з* я ~ я S Е Ч в- W ® 4Й Д Относительная вид-ность К 2 а »« 44 оа к Относительная ВИДИОСТЬ К 2 з 35 ж s 5 е Ч w So s 44» к Относительная вид-ность К
V Дневное зрение
380 0,0000 480 0,139 580 0,870 680 0,017
390 0,0001 490 0,208 590 0,757 690 0,0082
400 0,0004 500 0,323 600 0,631 700 0,0041
410 0,0012 510 0,503 610 0,503 710 0,0021
420 0,0040 520 0,710 620 0,381 720 0,00105
430 0,0116 530 0,862 630 0,265 730 0,00052
440 0,023 540 0,954 640 0,175 740 0,00025
450 0,038 550 0,995 650 0,107 750 0,00012
460 0,060 560 0,955 660 0,061 760 0,00006
470 0,091 570 0,952 1 670 0,032 770 0,00003
Сумеречное (палочковое) зрение
412 0,063 496 0,929 529 0,911 582 0,178
455 0,399 507 0,993 540 0,788 613 0,020
486 0,834 518 0,973 550 0,556 ~ 1
цвет) и А'х = 0,381 (табл. 1.9 и рис. 1.16, кривая А) такого же светового потока, как от излучения с длиной волны к — 555 им (желто-зеленый цвет) и Ктах = 1, необходимо, чтобы лучистый поток первого излучения был в 2,6 раза больше лучистого потока второго излучения: Кт3х/Кк= >/0,381 =2’6- _
Величина, обратная коэффициенту видности, называется удельным потреблением излучения. Минимальное удельное потребление излучения называется механическим эквивалентом света. Он определяется по формуле
М = 1/Vmax = 1 Вт/683 лм = 0,00146 Вт/лм. (1.24)
Этот эквивалент представляет собой минимальную мощность (Вт), необходимую для создания светового потока в 1 лм при длине волны к = 555 нм.
Пример. Определить световой .поток натриевой лампы мощностью 150 Вт, если она испускает в видимой области спектра лучистый поток 20 Вт, длиной волны к = 590 нм.
Решение. Из табл. 1.9 находим К — 0,757, следовательно, световой поток будет равен Ф = 683-К-20 лм = 9402 лм.
Из формул (1.23) и (1.24) следует, что Vx = Кк!М.
Согласно формуле (1.23) монохроматическому лучистому потоку йФ?Х длиной волны к будет соответствовать световой поток (лм)
<M>X =V’k = Г max^X ^®3X-
Распределение светового потока в сплошном спектре определяется спектральной интенсивностью светового потока /х’-
/х = йФ3х/dk = Их di&pjdk = РхР-х!
здесь рэх — спектральная интенсивность лучистого потока.
Световой поток сложного излучения со сплошным спектром (лм) можно определить интегрированием
X—770 Х=77о
Ф= J РхРэХ = Уmax J ^ХРэХ^>
Х=380 X—380
где р,х dk — лучистый поток излучения, заключенный между длинами волн к и А.+ &к. Тогда световую отдачу излучения можно определить как отношение светового потока к лучистому потоку источника излучения
ОО | 00
V = Ф/Фэ = 683j Фэх^х dk J Ф3х dk. о I о
Расчет световых свойств потока на основе кривой распределения энергии ' по спектру
Требуется определить характеристику потока, если кривая распре-; деления энергии по спектру потока известна [104]. Длина волны к соответствует ординате этой кривой р = f (к) (см. рис. 1.15). Значения р могут быть выражены в произвольных единицах. Излучения, длины волн которых заключены между к и к + dk, переносят лучистый
2 В. А. Панов и др. 33
поток, пропорциональный pd't.. Соответствующий световой поток равен dd> = aV^p dl или <М> = аК\р diJM (а — постоянная, зависящая от масштаба ординат р). Световой поток, соответствующий всей со
рассматриваемой совокупности излучений, равен ф = /Сд,/? с/Л,/Л1;
о
ос
лучистый поток для того же излучения Фа = a J р dX; к. п. д. т] = о
= Л1Ф/ФЭ = J Kip rfX/J р d/.', световая отдача V = Ф/Фэ = т]/Л4; о о
удельное потребление С = Фэ/Ф = /И/г).
Практически надо построить на миллиметровой бумаге спектральные кривые лучистого и светового потоков. Абсциссами обеих кривых будут служить длины волн, ординатами первой кривой — значения р, ординатами второй — значение г = Кр. Отношение двух площадей
дает величину т], затем по приведенным выше формулам легко опре-
деляются световая отдача и удельное потребление.
Пример. Даны кривая А — спектральная кривая лучистого потока для излучения, испускаемого кратером обычной вольтовой дуги
Ряс. 1.17. Спектральные кривые лучистого н светового потоков излучения кратера обычной вольтовой дуги
(подобная спектральной кривой черного тела при 3750 К), и кривая S’-спектральная кривая светового потока для твго же излучения (рис. 1.17). Отношение двух площадей непосредственно дает г) = 0,068. Следовательно, световая отдача излучения V — 0,068 X 683 = = 46,4 лм/Вт; удельное потребление С=\/У — — 0,022 Вт/лм.
Фотометрические характеристики какого-либо излучатели определя-
ются спектрофотометрическим сравнением их с излучением абсолютно черного тела, характеризуемого законами Планка, Стефана—Больцмана, Вина и др. 132, 115].
Светотехнические величины
Светотехнические величины применяются для оценки визуального действия лучистого потока. За основную светотехническую единицу принята единица силы света — кандела (кд).
Сила света. Понятие сила света относится лишь к точечным источникам. Часто встречаются случаи, когда размеры источника света очень малы по сравнению с расстоянием от источника до освещаемой поверхности, поэтому' такой источник называют точечным, хотя размеры его конечны. Если, например, используя понятие силы света, вычислить 34
освещенность поверхности в случае, когда расстояние до источника в 10 раз больше его размеров, то получающаяся ошибка составляет около 0,5%.
Сила света точечного источника в некотором направлении есть приходящийся на единицу телесного угла световой поток, излучаемый этим источником в данном направлении: I = df^ldd или I = Ф/й.
Единица силы света кандела соответствует силе света точечного источника, который испускает световой поток в 1 лм, распределенный равномерно внутри телесного угла в 1 ср.
Применительно к излучателю, представляющему собой абсолютно черное тело, за единицу силы света принята кандела (кд), равная силе света, испускаемой с площади 1/600 000 м2 сечения полного излучателя
в перпендикулярном этому сечению направлении при температуре излучателя, равной температуре Затвердевания платины при давлении 101 325 Па.
Средняя сферическая сила света /0 представляет собой отношение всего излучаемого источником светового потока к максимальному телесному углу й, /9 = ЯК Фд/Йд = Фд/4Л = яхФо/12,56.
Световой поток. Это
понятие определяется как мощность лучистой энер-
Рис. 1.18. Освещенность площадки точечным источником света, расположенным на бесконечности
гни, оцениваемая по производимому ею световому ощущению. Единицей для измерения светового потока является люмен (лм). Люмен
равен световому потоку, испускаемому точечным источником в телесном угле 1 ср при силе света 1 кд.
Мощность светового потока излучения пропорциональна силе света I источника и телесному углу й, который это излучение заполняет: йф = Ida, или Ф = /Ф. Световой поток можно определить как поток излучения, оцененный светоадаптированным глазом согласно выра-
00
жению Ф = 683 J dl. о
Освещенность. Это понятие характеризуется плотностью светового потока, падающего на поверхность. Она определяется отношением светового потока к освещаемой площади: Е = d®/dS, или Е = Ф/S. За единицу освещенности принят люкс, т, е. освещенность поверхности площадью 1 м2 при падающем на нее световом потоке 1 лм. Освещенность можно выразить следующим соотношением: Е — 1 лм/1 м2 = 1 лк.
Рассмотрим три случая освещенности от точечного источника света.
1. Телесный угол Й = 0. Когда точечный источник света расположен на большом расстоянии от освещаемой площадки или последняя очень мала, можно считать, что падающие лучи будут параллельны между собой (рис. 1.18). Если световой поток освещает площадку Se, перпендикулярную к падающим лучам, и площадку Se, наклонную под утлом е к этим лучам, то Es = Еа cos е, т. е. освещенность
поверхности наклонным пучком лучей прямо пропорциональна косинусу угла падения лучей на поверхность.
2. Точечный источник света L излучает расходящийся световой поток Ф внутри телесного угла й (рис. 1.19). Этот световой поток создает освещенность на площадках Sj и S2, перпендикулярных коси пучка лучей, £, = Ф/S,, Е2 = Ф/52, но S2/Si = r'ijr'j, тогда £,/£2 = £?/r?, т. е. освещенность изменяется обратно пропорционально квадрату расстояния от освещаемой поверхности до источника света.
3. Общий случай. Предположим, что в вершине телесного угла расположен источник света £, сила света которого I (рис. 1.19). Световой поток Ф, излучаемый источником внутри телесного угла Q, создает на наклонной площадке SR освещенность £f= £0 cos е, где £0 =Ф/£0 — освещенность, полученная тем же световым потоком на площадке Sn, перпендикулярной к оси световой трубки, т. е. Ф = 1Q и О = Sjr2, тогда
„ Ф
£е = -г- COS 8 = Xl
= —cosе — —cose. (1.25) Oj г
Из формулы (1.25) следует, что освещенность поверхности? создаваемая точечным источником света, прямо пропорциональна силе света истюч-на поверхность и обратно прост источника света до освеща
емой поверхности.
Пример. Определить освещенность, создаваемую электролампой силой света I = 400 кд, на горизонтальной поверхности стола в центре и на расстояниях 1,0 и 2,0 м от центра, если лампа подвешена над центром стола на высоте Л = 2 м от его поверхности.
Решение. Воспользуемся формулой (1.25). Для освещенности в центре стола е = 0, cos е = 1, г = Л, £ = 400/22 = 100 лк.
Для освещенности в радиусе R — 1 м от центра стола rf = R2 + + Л2 = 5, /j = Кб, cos е, = h/r = 2/К5, £, — 1 cos = 400 X X 2/5 Кб = 71 лк.
Для освещенности в радиусе /?= 2 м от центра стола г| = /?2 + + Л2 = 8, г2 = 2 К2, cos е2 — h!rt = К2/2, £2 = / cos е2/г| — 400 X X К2/16= 35 лк.
Светимость. Светимость какой-либо светяше1”ся поверхности есть световой поток, испускаемый единицей поверхности, или плотность излучаемого потока
Рис. 1.19. Освещенность площадок расходящимся пучком лучей
ника, косинусу угла падения лучей порциональна квадрату расстояния
О
1.26)
где R — светимость поверхности; Фр — световой поток, испускаемый поверхностью (лм); S — площадь поверхности (м2).
Пример. Определить светимость листа Селей бумаги площадью S = 240 см2, отражающей 90% падающего на него светового потока Фо = 80 лм.
Таблица 1.10. Основные энергетические и световые величины
Энергетические величины Световые величины
Наименование Определяющее уравнение Единица измерения Наименование Определяющее уравнение Единица измерения
Поток излучения (лучистый поток) Энергия излучения Энергетическая сила света (сила излучения) Энергетическая светимость (излучательность) Энергетическая освещенность (облученность) Энергетическая яркость (лучистость) Энергетическое количество освещения ос 0 t F, =--= [ Фэ (0 dt б ' d<2 Лэ~ dS, р <1фэ р ~ d'^ t Н> = j Е3 (!) dt 0 Вт Дж Вт • ср'1 Вт • м'2 Вт-м'2 Вт-м" 2-ср'1 Дж-м'2 Световой поток Световая энергия Сила света Светимость Освещенность Яркость Количество освещения 00 Ф=68.3 [ KkpKdX 0 t W = ( Ф (/) d' б ' ~"ЗГ п * dSj _ d® Е “ dS2 в d!s' E1 dijCOSfj t H =•- j E (t) dt 0 ЛМ лм • с кд (св) лм/м2 лк кд/м- (нт) лк-с
Примечание, ft — телесный угол; t — время; е — угол между нормалью к плоскости и лучом; — излучающая поверхность; S2 — облучаемая поверхность.
Решение. Величина светового потока, отраженного листом бумаги, равна Ф„=0,9 Ф0=72 лм; тогда согласно формуле (1.26), R = Фр/S = 300 лм/м2.
Яркость. Яркостью светящейся поверхиостн называется отношение силы света, излучаемой в данном направлении, к проекции светящейся поверхности на плоскость, перпендикулярную к направлению излучения.
На рис. 1.20 S — светящаяся поверхность, в — угол между направлением ОМ излучения и нормалью ON к светящейся поверхности, So — проекция светящейся поверхности на плоскость, перпендикулярную к направлению излучения.
Пусть 1е — сила света в направлении излучения М, В—яркость светящейся поверхности, тогда
Рис. 1.20. К вычислению яркости светящейся поверхности
Для направления, перпендикулярного к светящейся площадке S (угол в = 0, cos в = 1), из формулы (1.27) имеем
В = /0/5. (1.27а)
За единицу яркости принята 1 кд/ма. Яркостью в 1 кд/м2 обладает равномерно светящаяся плоская поверхность, излучающая в перпендикулярном к ' ней
направлении свет силой в 1 кд с 1 м2; В = 1№IS = 1 кд/1 м2. До 1965 г. была принята другая единица яркости — стильб (сб). Стильб — яркость равномерно светящейся плоской поверхности, излучающей в перпендикулярном направлении силу света 1 кд с 1 см2 поверхности.
Пример. Определить яркость вольфрамовой нити лампы накаливания в осевом направлении, если сила света лампы в том же направлении /0 = 300 кд, а площадь светящейся поверхности нити равна 0,20 см2.
Применяя формулу (1.27а), получим В =/0/S = 300/0,00002 = = 1,5-107 кд/м2.
В табл. 1.10 приведены основные энергетические н световые величины.
Излучение равнояркостных поверхностей
Светящиеся поверхности излучают или отражают свет с различной яркостью в разных направлениях. Однако часто пользуются поверхностями, которые диффузно излучают или отражают свет по закону Ламберта с яркостью практически одинаковой во всех направлениях (см. рис. 1.22, в) или в пределах некоторых телесных углов (белая матовая бумага, молочные стекла ламп накаливания, абсолютно черное тело н т. д.). Поскольку яркость во всех направлениях одинакова, то из (1.27) и (1.27а) следует, что 1е — /0 cos в; по этой формуле построена фотометрическая кривая (окружность, касательная к поверхности), характеризующая распределение силы света от равнояркостного источника S (см. рис. 1.22, в). Световой поток, излучаемый в полусферу плоской поверхностью конечных размеров, равен Ф = 38
Таблица 1.11. Соотношения световых величин для равнояркостных излучающих или отражающих поверхностей *
Характеристики световых величин Формулы
Сила света в направлении, составляющем угол е с нормалью к испускающей энергию площадке (/0 — сила света вдоль нормали к поверхности) Яркость излучающей поверхности Световой поток отражающей поверхности (Ф и Ф' — падающий и отраженный потоки, р — коэффициент отражения) Светимость отражающей поверхности Световой поток, излучаемый элементом dS поверхности внутри конуса, ограниченного углами 8 и е + de Световой поток в интервале от 0 до 8 Световой поток внутри полусферы * Матовые поверхности, имеющие по в ковую яркость, называются поверхностями поверхностям, имеющим направленное отраз менимы. /s — l0 COS 8 л ф' = рф D ф' ф „ = р—= р£ d<I> = 2лВ sin е cos в X X de dS Ф = лВЗ sin2 в ф = лВ8 сем направлениям одина-Ламберта. К глянцевым кение, формулы не при-
Соотношения между светимостью и яркостью. Так как l&t/S = = R — светимость поверхности, а /0/5 — В — яркость этой поверхности, то R — лВ. Если яркость выразить в кд/м3, то светимость получится в лм/м3 (лк).
Соотношения между освещеииостью н яркостью. Так как R = = рЕ и R = лВ, то Е = лВ/p или В = рЕ/л, где освещенность выражена в лк, а яркость — в кд/м3, р — коэффициент отражения.
В табл. 1.11 даны соотношения световых величин для равнояркостных излучающих или отражающих поверхностей.
Реакция приемников лучистой энергии на падающий поток излучения
Приемники лучистой энергии делятся на неселективные и селективные [12, 102, 115].
Реакция неселективных приемников (болометр, термоэлемент и др.) зависит только от потока энергии и не зависит от длины волны. Чувствительность приемника (г/Вт) равна
о dW ~ dW3 ’
где d\v — реакция приемника; йФэ — падающий поток излучения.
тока излучения и>эх вычисляется
Л
Рис. 1.21. Схема определения интегрального коэффициента пропускания
Размерность реакции приемника зависит от свойств самого приемника. Например, г выражается в вольтах или амперах при электрическом токе, вызываемом в приемнике потоком излучения.
Пороговая чувствительность приемника — способность реагировать на минимальный поток излучения.
Селективные приемники (фотоэлементы, ФЭУ, глаз, фотопластинки и др.) характеризуются спектральной и интегральной чувствительностью.
Реакция приемника от действия на него монохроматического по-по формуле cW — 5хФэх, где Sx коэффициент, характеризующий
спектральную чувствительность
приемника.
Относительная спектральная чувствительность приемника s>, = ~ 5х/5х.тах (^Лшах — максимальная чувствительность приемника при длине волны Лп1;,х).
В фотоэлектронных приборах (фотоэлемент, ФЭУ и др.) преобразующих лучистую энергию в электрическую, чувствительность S определяется отношением изменения фототока к изменению падающего на приемник лучистогд потока S = d/4/Ф, (мкА/Вт) или светового потока S = 4///ФФ (мкА/лм).
Спектральная чувствительность определяется отношением изменения фототока к изменению монохроматического излучения с длиной волны X : Sx, = d/лА/Фэх (мкА/Вт) или Sx = й/д/йФл (мкА/лм).
Интегральная чувствительность приемника — чувствительность к иеразложенному свету определенного источника излучения. Стандартным источником света может служить лампа накаливания с вольфрамовой спиралью, работающей в определенном режиме при температуре тела накала 2850 К. Интегральная чувствительность приемника, выраженная в энергетических единицах, равна
СО со
S = j 5ХФЛ dl j ФэХ dl [A/Вт], ь о
Если интегральная чувствительность определяется как отношение полного фототока к падающему световому потоку, то
« Ла
s = J Sx®x dA/683 J dX> о x,
где Xf и Х2 — границы видимой области спектра.
Пределы интегрирования при определении величины фототока могут быть сужены со стороны ультрафиолетовой области спектра границей пропускания окна, через которое освещают фс-тоэлемент; со стороны инфракрасного излучения — порогом фотоэффекта (фотоэлемент становится нечувствительным).
Если селективный приемник лучистой энергии, например фотоэлемент, глаз, фотографический слой и т. д. применяется совместно со светофильтром, то необходимо знать интегральный коэффициент т2 пропускания этого светофильтра и чувствительность приемника лучистой энергии по спектру. Интегральный коэффициент пропускания светофильтра равен т2 = j где ®о —
поток, падающий на светофильтр; Ф' — поток, прошедший через светофильтр; Фх — спектральная интенсивность падающего излучения; Ух — спектральная чувствительность приемника; тх — спектральный коэффициент пропускания светофильтра. Интегралы формулы можно вычислить графо-аналитическим способом (рис. 1.21). Для этой цели в прямоугольной системе координат строят кривые Фх, Ул и тх. Перемножив соответствующие ординаты кривых Фх и Ух, строят кривую ФхУь а затем, перемножив ординаты кривых ФхКх и ?х, наносят кривую ФаУхТл- Площадь Ф' соответствует интегралу, стоящему в числителе, а площадь Фо — интегралу в знаменателе приведенной выше формулы.
Отражение света
Характер отражения света от поверхности зависит от качества ее обработки и материала.
Отражение света можно подразделить на три вида: зеркальное (угол падения равен углу отражения), которое дают хорошо полированные поверхности (рис. 1.22, а); направленно-рассеянное, при котором максимум силы света совпадает с направлением зеркального отражения (рис. 1.22, б); диффузное (рассеянное) отражение, которое дают идеально рассеивающие поверхности молочного стекла (рис. 1.22, в).
Рис. 1.22. Три вида отражения
Силу света или яркость отраженного от тела света можно характеризовать с помощью фотометрической поверхности, образуемой концами радиусов векторов, определяющих указанные величины.
В случае рассеянного или полурассеянного отражения пользуются понятием коэффициента яркости га = Ва/В0, где Ва—яркость поверхности в данном направлении; Во — яркость идеально матовой белой поверхности при равных освещенностях.
Общий коэффициент отражения р складывается из коэффициентов направленного и диффузного отражений. Величина р всегда меньше единицы. Коэффициент га может быть больше единицы (рис. 1.23). Окружность / изображает распределение удельной силы света, отраженного идеально рассеивающей поверхностью, а кривая 2 —
полурассеянное отражение от некоторой поверхности при той же освещенности. Коэффициенты яркости для направлений OD и ОС равны отношению векторов roD=ODIOC"> 1; гос= О ЛЮС < 1. Коэффициенты яркости зависят от угла падения, поэтому они даются для случая нормального падения света. Для естественного света коэффициент отражения преломляющей поверхности можно вычислить по формуле Френели (1.28).
Рис. 1.24. Схема ромбов Френеля (а) и Муни (б)
Рис. 1.23. Распределение удельной силы света
Поляризация света при отражении
Для расчетов отраженного света от поверхности прозрачных сред с показателем преломления п при угле падения света в пользуются формулами Френеля [113]. Если электрический вектор Е перпендикулярен к плоскости падения свеча, тор± = /,//±=sin2(e—e')/sina (в-|-Ч- s'); sin в' = sine/я. Если вектор Е параллелен плоскости падения света, то ри = 1 ц r/Z(( = tg2 (s — e')/tg2 (в + в'), где lf и I — интенсивности отраженного и падающего света. Степень поляризации при отражении Р = | (р±—Р ц )/(Рх + Р ц) | становится равной 1, если р У =0, т. е. если в + в' = 90°. Отсюда следует, что отраженный свет становится линейно поляризованным. Этот случай соответствует условию tg Вр = п (закон Брюстера) х.
Отношение интенсивностей поляризованных компонент дает q=* = D.JD и = [2n/(l + я2)]4"1. Например, при я — 1,5163 (К8) имеем q = 0,714m.
В табл. 1.12 даны ер для некоторых сред.
Ромб Френеля — стеклянная ромбическая призма, в которой пучок лучей, дважды испытывая полное внутреннее отражение, приобретает сдвиг фазы л/2 (рис. 1.24, а). Если показатель преломления стекла я = 1,51 и свет падает по нормали, то каждый преломляющий угол ромба должен быть равен 0 = 54,6°.
В тех случаях, когда учитывается сдвиг фазы на входной и выходной поверхностях, оптимальное значение угла 0 подбирается методом проб. Если пучок света падает на ромб не по нормали, то сдвиг фазы будет иным.
1 Для случая преломления линейно поляризованного света под углом Брюстера потери света равны нулю. Это явление широко используется в лат верной технике.
Таблица 1.12. Угол поляризации ер
Вещество nD при t ~ 20° С Ер
Вода 1,333 53° Т
Стекло марки К8 1,516 56° 36'
» » ТФ10 1,806 61° 1'
Периклаз Кристаллический кварц: 1,737 60° 4'
«0 1,544 57° 4'
пе 1,553 57° 13'
Ромб Муни [113], имеющий п = 1,65 и преломляющие углы 0 = = 60°, позволяют использовать пучки со значительным угловым расхождением (рис. 1.24,6).
Виды поляризации света
Состояние светового вектора можно представить двумя взаимно перпендикулярными слагающими х и у этого вектора в плоскости волны [89]
СО
х = J a sin (<о< 4- 6j) d<o;
о
у = J b sin (<в< 62) d<B. о
Здесь а и Ь — амплитуды; и 6а — фазы, зависящие от угловой скорости <в.
Исключая время t нз уравнений, получим уравнение эллипса +-fr —5-cos <s* -6з) =-sin2 (Si -6s)-
Рассмотрим частные случаи поляризации света:
1) 6j — 6а = 0 и fa — эллипс вырождается в прямую (линейная поляризация) х/а ±: y!b — 0;
2) 6j — о2 = (2n + 1) л/2 и а = Ь — эллипс принимает вид круга.
Следовательно, различают три вида предельной поляризации света; линейную, круговую и эллиптическую (с вращением вектора вправо или влево; см. рис. 1.28).
Для полной характеристики состояния поляризации светового пучка требуется знание четырех величин [113]: интенсивности естественного света; интенсивности подмешанного поляризованного света; азимутов осей эллипса; эксцентриситета эллипса.
Линейно поляризованный свет вполне определяется только указанием-плоскости поляризации, т. е. плоскости, перпендикулярной к световому (электрическому) вектору.
Для характеристики света, поляризованного по кругу, достаточно указать направление вращения. Для эллиптически поляризованного необходимо определить азимут осей, эксцентриситет и направление вращения. Все четыре признака полностью требуются для определения состояния поляризованного света.
Потери света в оптических приборах
В оптических приборах различают три вида потерь света: потери на отражение на преломляющих поверхностях; потери на поглощение н рассеивание внутри массы стекла; поглощение света в отражающих металлических поверхностях.
Коэффициенты отражения р, пропускания т я поглощения а светового потока выражают долю отражаемой Фр, пропускаемой Фс и поглощаемой Фа частей светового потока по отношению ко всему падающему потоку Фо, т. е. р = Фр/Ф0, т = Фг/Ф0, а = Фа/Ф0- Поскольку Фр + Фг + Фа = Фо, то р + т + а — 1. Коэффициент отражения света на преломляющей поверхности, разделяющей две среды, вычисляется по формуле Френеля
Фр _ 1 Г tg2(e'-r) , sinks'-г) 1
Р-Ф„ 2 L tg2(K' + e) sinks' 4-е) J ’ 1 ’
Для малых углов падения применение закона преломления п sin е = п' sin s' дает
Р = !(«'—«)/(»'4-«)1а> ’ (1.28а)
где пип' — показатели преломления до и после преломления; для углов 30—40° последнее выражение дает достаточно точное значение р. Для значений Пстекло^воздух 2,5 это выражение дает завышенный результат, поэтому необходимо учитывать вторичные отражения [12].
Просветление стекол
Просветление стекол применяется с целью увеличения светопро-пускаиия и повышения контрастности изображения вследствие устранения рефлексов при отражении. Просветление оптики достигается нанесением пленок на поверхности стекла. Показатель преломления п и толщина пленки h подбираются так, чтобы суммарная интенсивность светового потока, отраженного от поверхности пленки и стекла вследствие интерференции света, была равна нулю.
Согласно формуле (1.28), пнтенсис-ности отраженных лучей будут равны при выполнении условия [(п3 — п2)/(л3 + п2) ]а = [(n2 — nj/ln^r + n4 ]2, откуда п2 = Й” i^n,, при /г( = 1.
Разность хода лучей при нормальном падении А = 2d = 2Л/г2.
Для гашения отраженного света необходимо, чтобы А = М2 = = 21шг, т. е. ftn2 = d = М4. В общем случае d = (2ft 4* 1) М4 (ft = 0, 1, 2, 3, ...). Общая толщина пленки для X = 550 им должна быть равна d = 137,5 нм и для более общего случая d = 137,5 + 275 ft. Пленка отражает свет избирательно, н просветленная поверхность стекла приобретает интерференционную окраску, характерную для тонких пленок. Покрытия оптических деталей описаны ц гл, 17, 44
Расчет светопропускания и светопоглощен ня бесцветного стекла
Под светопропусканнем т' среды понимается отношение светового потока Ф, прошедшего через среду, к Фо падающему. Если световой поток проходит через ряд сред с коэффициентами пропускания т2, in, то вся система будет иметь коэффициент пропускания т = == TjTgTg, ...» Tfl.
Логарифм величины, обратной пропусканию, называется оптической плотностью D' = 1g (1/т') = —1g т'. Суммарная оптическая плотность системы, состоящей из п числа сред, равна D==D1 + D2-\-•+•••• + Dn, т. е. имеет место закон аддитивности. Формулы, определяющие т или D, применимы в тех случаях, когда падающий поток является монохроматическим, а среды селективны, нли когда падает поток любого спектрального состава, но среды не селективны.
Светопропускание пластинки из бесцветного стекла вычисляется по формуле
^ = -^ = (i-p)2^ad = ^ (1.29)
где р — коэффициент отражения от одной полированной поверхности; (1 — р2) = R — поправка на отражение, выраженная в единицах пропускания.
Коэффициент поглощения а вычисляется при его экспериментальном определении по формуле
где 1g е = 0,4343; d выражается в см.
Светопропускание в любой заданной толщине для монохроматического света находится по формуле
IgTw ='^rL или
прн х~ 1
1g т(1) = -g*(rf)- ИЛИ £>(1) =-^р-.
Пример I. Определить а стекла К8 (п = 1,5163), если т'= 0,84 и R ~ 0,918, толщина стекла d = 10 см.
Решение. —1g т' = —1g 0,84 = —(0,924 — 1) = 0,076; lg R = 1g 0,918 = 0,963 — 1 = —0,037; a = (0,076 — 0,037)/10 X X 0.4343 = 0,009 или a = 0,9%.
Пример 2. Определить светопропускание стекла ТФ1 толщиной 10 мм для X = 365 нм, есля при d = 40 мм D' = 0,860.
Решение. Поправка на отражение Do = —2 lg (1 — р) = = 0,060.
Оптическая плотность слоя стекла толщиной d = 40 мм равна D = D' — Dp= 0,860 — 0,060 = 0,8. Плотность прн толщине d — = 10 мм равна D (10) = 10-0,8/40 = 0,200; следовательно, = 0,200 + 0,060 = 0,260.
Для перехода от D' к т' и обратно пользуемся табл. 1.16. В первом ее столбце даны значения D' через 0,1, а в верхней строке — сотые доли. На пересечении строк со столбцами приведены значения т', отвечающие любым значениям плотности от 0,01 до 1,99. Из этой таблицы по плотности 0,260 находим т/ = 0,55 или 55%.
Потери света при отражении и поглощении в светофильтрах
Спектральная характеристика светофильтра выражается численными значениями показателя поглощения fex для различных длин волн и спектральными кривыми оптической плотности D и коэффициента пропускания т'. За светопоглощение оптического цветного стекла принимается отрицательный десятичный логарифм светопропу-скания в толщине слоя 1 мм. Оптическая плотность стекла толщиной d = 1 мм называется показателем поглощения и определяется из формулы /г? = —1g (t,d./d, где светопропускание стекла толщиной d (мм).
Оптическая плотность Од. массы стекла для монохроматического света с длиной волны X связана с k\ и тд выражением D\ — —1g тл = — d.
При расчете плотности необходимо учитывать потери на отражение на двух поверхностях стекла. Светопропускание светофильтра толщиной d (мм) монохроматического света дайной длины волны вычисляется по формуле
< = (1-Р)2Ч=(1-Р)2Ю-м. * . (1.30)
где 10- М = тх — светопропускание светофильтра в толщине d.
Оптическая плотность £)£ светофильтра дли дайной длины волны D'x = ~ «8 Ч = - 2 1g О ~ Р) = DK + = V +
Пример 1. Требуется определить показатель поглощения стекла, если при d == 3 мм для дайной длины волны = 0,355 и Dp — 0,04.
Решение. Из табл. 1.16 находим = 0,45. Следовательно, DK = D'K — Dp = 0,45 - 0,04 = 0,41; kK = DyJd = 0,41/3 = 0,137.
Пример 2. Определить D'K и т/ светофильтра толщиной d = 2,5 мм для длины волны Л, если kt, — 0,30 и Dp — 0,04.
Решение. Из табл. 1.16 находим = 0,162.
Для характеристики вещества с сильным поглощением (металлы и т. д.) показатель поглощения относится не к 1 см или 1 мм, а к длине полны, деленной иа 4л, т. е. х = /А/4л или х* = аЛ/4л. Тогда т из формул (1.29) и (1.30) принимает вид [32]
т =e"1IW’rf/x или т = 10~4я*4/х.
Расчет интегрального коэффициента пропускания светофильтра для видимой области спектра при сложном излучении
Коэффициент пропускания светофильтра для видимой области спектра может быть вычислен, если даны [104]: 1) кривая спектра, определяющая ординату р для падающего излучения в зависимости от 46
длины волны 1 (Ф^ = рсГк — спектральная интенсивность); 2) спектральная кривая пропускания поглощающей пластинки, выражающая вависимость т от Л,; 3) кривая относительной видности, дающая коэффи-
Рис. 1.25. Спектральная кривая пропускания аммиачного раствора медного купороса (а) н схема определения интегрального коэффициента светофильтра для сложного излучения (б)
пропущенного излучения, ординаты которой г' = t',,pKk- Отношение площади, ограничиваемой второй кривой, к площади, ограничиваемой первой кривой, дает коэффициент пропускания Т для рассматриваемого падающего излучения
. 770 ч I ,770 ,
Т =| j TxpKKdk\ I j рК^сГ/. |.
\380 /I \380 /
Пример. На рис. 1.25, а дана спектральная кривая пропускания кюветы, содержащей аммиачный раствор медного купороса. Падающим излучением является излучение лампы накаливания, для которой распределение энергии по спектру в видимой области представлено кривой 1 на рнс, 1.25, б; масштаб ординат выбран произвольно. Кривая 2 получена умножением каждой ординаты кривой 1 на соответствующее значение т. е. на значение кривой рис. 1.16. Кривая 3 получена умножением ординат кривой 2 на значение коэффициента т;, снятых с кривой рис. 1.25, а. Коэффи-
циент пропускания т равен отношению площадей, ограниченных кривыми 3 и 2.
Светофильтры переменной плотности (фотометрические клинья)
Светофильтры переменной плотности представляют собой равномерно нарастающую толщину
Рис. 1-26. Схема линейною фотометрического клина: 1 — поглощающий слой клина; 2 подклин
однородного поглощающего слоя. Плотность любого места клина вычисляется по формуле
D—kl-\-Da,
где Do — начальная плотность клина; k — константа клина, т. е. приращение оптической плотности на 10 мм длины клина.
Для получения равномерной плотности по фотометрическому полю применяется подклин с той же константой (рис. 1.26).
Расчет коэффициента светопропускаяия оптических приборов
Коэффициент светопропускания оптической системы можно вычислить по формуле [3, 12]
т’ = (1 — Р1). ..(1 —pfl) (1 — a,) \ ..(1 ..Rt.. ,R3Tt...Tp,
(1-31)
где р — коэффициент отражения от поверхности деталей на границе воздух—стекло для непросветленных деталей из стекла с показателем преломления п; р = (п— 1)г/(п+ I)1 2; а — коэффициент поглощения стекла (ГОСТ 3514—67) оптических деталей системы I — длина хода осевого луча в деталях (см); R — коэффициент отражения зеркальных непрозрачных покрытий и светоделительных покрытий (определяется из нормали иа покрытие, см. гл. 17); Т — коэффициент пропускания свето-делительных покрытий; m — число деталей системы, кроме зеркал с внешним отражающим покрытием; q — число поверхностей, граничащих с воздухом, кроме поверхностей с зеркальным и светоделительным покрытиями; s — число поверхностей с зеркальным непрозрачным покрытием и светоделительным покрытием в условиях работы иа отражение; р — число поверхностей со светоделительным покрытием в условиях работы на пропускание света.
Формулой (1.31) не учитываются потери пря отражении на поверхностях склейки деталей, если на них нет светоделительиых покрытий, и на поверхностях призм при полном внутреннем отражении, так как потери на этих поверхностях незначительны. При расчете коэффициента пропускания оптических систем удобнее пользоваться формулой (1.32), по которой сначала вычисляют оптическую плотность системы D’ = = —1g т', а затем по вычисленному значению D' находят коэффициент пропускания т'.
D' = (18/11 + • • • + lirfcAm + ^l^pl + • • + AqDpq -f- BiDfa -f-
+ • • • + BpDp/t 4- CiDn + . •» + CpDfp, (1.32)
где Dp = —1g (1 — p); DR = —1g R; DT = —lg T; lt, .... lm — суммарная длина хода луча (см) в деталях из стекла с одинаковым показателем ослабления + • • • + 8дт, т. е. из стекла одной категории по показателю ослабления (по ГОСТ 3514—76); Л(, ..., Aq — число непросветленных н просветленных поверхностей с одинаковым числом отражения; Bj, .... Bh — число поверхностей с зеркальным и светоделительным покрытием одинакового коэффициента отрагхепия. В это число вхо-
1 Вчесто а аз ГОСТ 3514 — 76 берется натуральный показатель ослабле-
ния ед — а.
дят поверхности со светоделительным покрытием, работающие в проходящем ходе лучей оптической системы; Cit Ср — число поверхностей светоделительных покрытий.
Для оптического бесцветного стекла (ГОСТ 3514—76) установлен десятичный показатель ослабления (величина, обратная расстоянию на котором поток излучения источника А по ГОСТ 7721—76 ослабляется в результате поглощения и рассеяния в стекле в 10 раз; см. табл. 22.10). В табл. 1.13 даны значения натурального показателя ослабления е'А = e^/lg е — ел/0,4343. Числениое значение е'А — а = = k‘ + а', где k' на’ — соответственно натуральные показатели поглощения и рассеяния. Для прозрачных оптических сред (стекло и многие кристаллы) практически о' 0 [32].
Оптическая плотность D и т слоя стекла толщиной 1 см в зависимости от еА н категории (ГОСТ 3514—76) приведены в табл. 1.13.
Таблица 1.13. Значения еА, еА и а в зависимости от категории стекла н й; t в зависимости от еА
ПО 4-76 ь ослаб-10*, см'1 ный по-эслабле-)4, СМ'1 Коэффициент светопропускания т Плот-н ость D. 10* По ПОСТ 3514 — 67
X щ е л — е л . 14
Категор ГОСТ 3 Показа? ления е Натура, казател: НИЯ 8Д При толщине (/ = 1 см • К ч.' 4, £ х О Ц л £• ~ 5 , > О ‘° * ь- «ю
1 2—4 5—10 0,9995—0,9990 2—4
2 5—9 11—22 0,9989—0,9978 5—10 000 20
3 10—17 23-40 0,9977—0,9960 10—17 00 40
4 18—25 41-59 0,9959—0,9941 17—26 0 60
5 26—35 60—80 0,9940—0,9920 26—35 1 80
6 36-45 81—104 0,9919—0,9896 35-45 2 100
7 46—65 105—149 0,9895—0,9851 46—65 3 150
8 66—130 150—300 0,9850—0,9700 66—132 4 300
0,040 0,96 177
0,050 0,95 223
0,060 0,94 269
В табл. 1.14 н 1.15 даны поправки иа отражение от непросветленной поверхности в зависимости от показателя преломления.
При расчете коэффициента пропускания оптической системы с небольшим ходом луча в стекле деталей величину D достаточно брать с точностью до 0,001. По табл. 1.13 можно находить величины D0 для просветленных поверхностей с коэффициентом отражения р. Например, для р = 0,6% в табл. 1.13 имеется значение еА = 0,006, которому соответствует D = 0,0026. Эта величина одновременно является и величиной Do.
Коэффициенты отражения от просветленных поверхностей, непрозрачных зеркальных покрытий и коэффициенты отражения и пропу-49
Т а б л и ца 1.14. Поправки на отражение Dp от непросветленной поверхности в зависимости от показателя преломления
п 00 .01 02 03 .04
1,4 0,0122 0,0127 0,0133 0,0138 0,0144
1,5 0,0177 0,0183 0,0189 0,0195 * 0,0201
1,6 0,0238 0,0244 0,0250 0,0257 0,0263
1,7 0,0302 0,0309 0,0316 0,0322 0,0329
1,8 0,0370 0,0377 0,0384 0,0391 0,0398
1,9 0,0440 0,0447 0,0454 0,0462 0,0469
2,0 0,0512 0,0519 0,0526 0,0534 0,0541
2,1 0,0585 0,0592 0,0599 0,0607 0,0614
2,2 0,0658 0,0666 0,0673 0,0681 0,0688
п .05 .06 .07 .08 .09
1,4 0,0149 0,0155 . 0,0160 0,0166 0,0171
1,5 0,0207 0,0213 0,0219 0,0226 0,0232
1,6 0,0269 0,0276 0,0282 0,0288 0,0295
1,7 0,0336 0,0343 0,0350 0,0356 0,0363
1,8 0,0405 0,0412 0,0419 0,0426 0,0433
1,9 0,0476 0,0483 0,0490 0,0498 0,0505
2,0 0,0548 0,0555 0,0563 0,0570 <0,0578
2,1 0,0621 0,0628 0,0636 0,0643 0,0651
2,2 0,0696 0,0703 0,0711 0,0718 0,0726
Таблица 1.15. Поправки на отражение Dp от непросветленной поверхности в зависимости от п > 2,3
п .0 .1 .2 .3 .4
2 0,073 0,081
3 0,125 0,132 0,139 0,147 0,154
4 0,194 0,200 0,206 0,213 0,219
п .5 .6 .7 .8 9
2 0,088 0,095 0,103 0,110 0,118
3 0,161 0,168 0,175 0,181 0,188
4 0,225 0,231 0,237 0,243 0,249
Таблица 1.16. Коэффициент пропускания т' в % в зависимости от плотности D'
D' .00 .01 .02 .03 .04 .05 .06 .07 .08 .09
0,0 100,0 97,7 95,5 93,8 91,2 89,1 87,1 85,1 83,2 81,3
0,1 79,4 77,6 75,9 74,1 72,4 70,8 69,2 67,6 66,1 64,6
0,2 63,1 61,7 60,3 58,9 57,5 56,2 54,9 53,7 52,5 51,3
0,3 50,1 49,0 47,9 46,8 45,7 44,7 43,7 42,7 41,7 40,7
0,4 39,8 38,9 38,0 37,1 36,3 35,5 34,7 33,9 33,1 32,4
0,5 31,6 30,9 30,2 29,5 28,8 28,2 27,5 26,9 26,3 25,7
0,6 25,1 24,5 24,0 23,4 22,9 22,4 21,9 21,4 20,9 20,4
0,7 19,9 19,5 19,1 18,6 18,2 17,8 17,4 17,0 16,6 16,2
0,8 15,8 15,5 15,1 14,8 14,5 14,1 13,8 13,5 13,2 12,9
0,9 12,6 12,3 12,0 11,7 11,5 11,2 11,0 10.7 10,5 10,2
1,0 10,0 9,8 9,5 9,3 9,1 8,9 8,7 8,5 8,3 8,1
1,1 7,9 7,8 7,6 7,4 7,2 7,1 6,9 6,8 6,6 6,5
1,2 6,3 6,2 6,0 5,9 5,8 5,6 5,5 5,4 5,2 5,1
1,3 5,0 4,9 4,8 4,7 4,6 4,5 4,4 4,3 4.2 4,1
1,4 4,0 3,9 3,8 3,7 3,6 3,5 3,5 3,4 3,3 3,2
1,5 3,2 3,1 3,0 3,0 2,9 2,8 2,8 2,7 2,6 2,6
1,6 2,5 2,5 2,4 2,3 2,3 2,2 2,2 2,1 2,1 2,1
1,7 2,0 2,0 1,9 1,9 1,8 1,8 1,8 1,7 1,7 1,6
1,8 1,6 1,6 1,5 1,5 1,5 1,4 1,4 1,4 1,3 1,3
1,9 1,3 1,2 1,2 1,2 1,2 1,1 1,1 1,1 1,1 1,0
Скания светоделительных покрытий берутся из технических условий на соответствующий вид покрытия, а затем вычисляют или находят по табл. 1.13 нли 1.16 соответствующие поправки Dp, Dr и Dr. По формуле (1.32) с помощью табл. 1.16 находят коэффициенты пропускания т' оптической системы. Величину D' прЬдварительно округляют до второго знака после запятой. С помощью этой таблицы можно также находить величины Dr и Dr по известным значениям R и Т. Например, оптические детали лабораторных и полевых приборов, служащие в качестве зеркал с внешним отражением, обычно имеют покрытие зеркальное 1И.21Е; коэффициент отражения покрытия R не менее 86%. Следовательно, по табл. 1.16 интерполированием находят Dr= 0,065.
Коэффициент пропускания светоделительного покрытия Т =20%. По табл. 1.16 ближайшей величиной является т' = 19,9, которому соответствует величина Dr = 0,70.
Формулы для вычисления оптической плотности некоторых отдельных элементов оптической системы
1. Для лииз, пластин, призм полного внутреннего отражения
О' = ID + 2D0,
где I — толщина линз и пластин по оптической оси и длина хода осевого луча в призмах (см).
2. Для склеенной системы из двух линз
D' — /jD, 4- Z2£>2 4- О()1 4- Doi.
3. Для зеркала с задним отражением
D' = 21D 4- 2Dp + Dr. • (1.33)
4. Для светоделителя незаклеенного
D’ = ID 4- Du 4- DT. (1.34)
Оптическая плотность в отраженном холе лучей вычисляется по формуле (1.33). По формуле (1.34) вычисляется оптическая плотность в прямом ходе лучей системы.
5. Для светоделителя, заклеенного покровным пеклом
D' = 4- l2D2 4- Dp, + Do2 4- Dr. (1.35)
По формуле (1.35) вычисляется оптическая плотность в прямом ходе лучей оптической системы. При вычислении D' в отраженном ходе лучей в формулу (1.35) вместо Dr подставляется Dr.
Приращение оптический плотности ДО' системы после облучения прибора заданной дозой гамма-излучения вычисляется по формуле
ДО = ZjADj 4- 12&D2 -J- • • • 4-
где ДО — приращение оптической плотности стекла иа 1 см.
/ ладный луч
Рис. 1.27. Схема огыики визира
Оптическая плотность D'p() системы после облучения О^б = О' 4* 4- ДО'. По вычисленному значению Орб в табл. 1.16 находят коэффициент пропускания т'б оптической системы после облучения.
На рис. 1.27 дана схема оптики визира, для которой приводится [ асчет светопропускания (табл. 1.17 и 1.18).
Окончательно получаем для системы с непросветленной оптикой О' = = 0,042 + 0,333 = 0,375, т' = 42%. После просветления D'— = 0,042 + 0,121 = 0,163, т' = 69%.
Таблица 1.17. Расчет потерь в оптической системе, состоящей из защитного стекла, объектива, призмы Шмидта с крышей, сетки и окуляра
№ поз. по рис. 1.27 Наименование детали Марка стекла nD Длина хода, см SA Категория № поверхности детали Вид просветления р при просветлен и и
/ Защитное стекло К8 1,5163 0,6 0,0025 4 1 2 63Т 63Т 0,03 0,03
1 ТК16 1,6126 0,7 0,0045 6 3 44Р.43Р 0,011
и Объектив 2 ТФ5 1,7550 0,5 0,0045 6 5 44Р.43Р 0,011
3 ТК21 1,6568 0,7 0,0045 6 6 44Р.43Р 0,011
7 44Р.43Р 0,011
11/ Призма Шмидта БКЮ 1,5688 10 0,0017 3 8 9 24И 24И 0,014 0.014
/V Сетка К8 1,5163 0.4 0,0025 4 10 11 — 0,04 0,04
1 ТК21 1,6568 0,7 0,0045 6 12 44Р.43Р 0,011
13 —— —
V Окуляр 2 ТФ5 1,7550 0.5 0,0045 6 14 — —
3 ТК16 1,6126 0,6 0,0045 6 15 44Р.43Р 0,011
4 ТК16 1,6126 1,3 0,0045 6 16 44Р.43Р 0,011
17 63Т 0,03
Примечание. Общая длина хода осевого луча в деталях системы 16 civ , число поверхностей, гранича-
щих с воздухом, 14.
Таблица 1.18. Результаты расчета светопропускания
№ поз. по рис. 1.27 ‘d Марка стекла без просветления Вид просветления Л Ор при просветлении
/, IV II, V Ill LiPt — = 1-0,0025 = = 0,0025 ' 1^2 ~ = 5 0,0045 = = 0,0225 I3D3 = = 10-0,0017 = = 0,0170 К8 ТК16 ТФ5 ТК21 БКЮ 4-0,0187 = = 0,075 4-0,0246 = = 0,098 1-0,0340 = = 0,034 3-0,0274 = = 0,082 2-0,0218 = = 0,044 63Т 44Р-43Р 24И 3-0,0132 = = 0,040 7-0,0048 = = 0,034 2-0,0061 = = 0,012 2-0,0177 = = 0,035
£ 16 0,042 14 0,333 14 0,121
РАСПРОСТРАНЕНИЕ СВЕТА
В АНИЗОТРОПНОЙ СРЕДЕ (КРИСТАЛЛЫ)
В зависимости от оптических свойств кристаллы делятся на три группы-.
а) правильной системы; эти кристаллы оптически изотропны;
б) одноосные кристаллы (тригональные, тетрагональные и гексагональные системы); имеют лишь одно направление, вдоль которого не происходит двойного лучепреломления (кварц, исландский шпат);
в) двуосные кристаллы (ромбическая, одноклинная и триклинная системы); имеют два направления, вдоль которых не происходит двойного лучепреломления [116].
Двойное лучепреломление в одноосных кристаллах
При преломлении на границе с анизотропной средой луч естественного света расщепляется на два луча: обыкновенный (о-луч) и необыкновенный (е-луч).
Обычному закону преломления подчиняется о-луч, и он имеет постоянное значение показателя преломления во всех направлениях в кристаллах. Показатель преломления е-луча непостоянен и зависит от его направления. В плоскости главного сечения поляризован о-луч, а е-луч поляризован перпендикулярно к указанному сечению. Показатели преломления лучей вдоль оптической оси в направлении, перпендикулярном к оси, называются главными показателями преломления (н , и п£).
Разность фаз о- и е-лучей зависит от угла падения, положения оптической оси и толщины кристалла.
На рнс. 1.28 показаны вектор ОС, характеризующий направление и амплитуду колебаний плоскополяризованного света, падающего на кристаллическую пластинку, ОА и ОВ — соответствующие векторы, дающие определенную разность фаз. Характер поляризации в кристалле зависит от длины пути прохождения света.
Рис- 1.28. Поляризация света при прохождении через кристаллическую пластинку
Положительные и отрицательные кристаллы. Волновые поверхности Френеля
Для характеристики распространения света в кристаллах пользуются волновыми поверхностями Френеля. Волновая поверхность обыкновенной волны изображается шаровой поверхностью, а необыкновенной— эллипсоидом вращения (рис. 1.29). Одноосные кристаллы, у которых пе < п., называются отрицательными (исландский шпат); кристаллы, у которых пе > п0 называются положительными (кварц).
Рис. 1.29, Двойная поверхность показателя преломления кварца (а) и исландского шпата (б):
0—0-ч оптическая ось; п0 и ng — главные показатели преломления
Эллипсоид френелевой волновой поверхности у отрицательных кристаллов удлинен в направлении, перпендикулярном к оптической оси, а у положительных — в направлении, параллельном этой оси.
Поляризаторы
Поляризатором называется оптическое устройство, преобразующее нроходищий через него естественный свет в поляризованный. Поляризатор, предназначенный для обнаружения поляризации, называется анализатором. Действие поляризационных приборов основано на одном из физических явлений [113]:
а) на отражении и преломлении на границе двух диэлектриков (например, воздух — стекло);
С) двойном лучепреломлении;
в) на дихроизме (явлении различного поглощения о- и е-лучей).
Двупреломляющие поляризаторы обычно изготовляются из исландского шпата (СаСО8) с прозрачностью от 240 нм до 1,8 мкм. За пределами этой области вещество обладает, сильным поглощением и некоторым дихроизмом. Другим подходящим материалом является натровая селитра (NaNO3). Кварц для поляризаторов применяется редко, так кик разность пе — п0 = 0,009 очень мала, но часто используется для фа-з ;гых пластинок.
I
Поляризационные призмы
Для поляризации при двойном лучепреломлении применяются призмы из кварца или исландского шпата. В двойных призмах Николя, Глава—Томсона, Франка—Риттера н др. обыкновенный луч пре-
Рис. 1.30. Призма Николя: а — вид сбоку; б — вид по направлению луча (штриховкой показано направление оптической оси в плоскости чертежа, стрелками и точками — направление колебания электрического вектора на лучах)
терпевает на поверхности раздела между призмами полное внутреннее отражение. Необыкновенный луч проходит сквозь призму и становится линейно поляризованным.
Оптическая ось v кристалла
Рис. 1.31. Призма Франка—Риттера
Призма Николя изготовляется из ромбоэдра исландского шпата. Последний рассекается плоскостью, перпендикулярной к главному сечению кристалла, проходящему через оптическую ось кристалла и его длинное ребро. Обе призмы скленваютсн канадским бальзамом, акриловым клеем или льняным маслом (рис. 1.30). Призма Николя пробе
пускает полностью поляризованный свет в пучках с углом до 29°. Поле поляризации несимметричное. Существует несколько типов призм,
входные грани которых перпендикулярны к длинным ребрам и оси кристалла отличаются ориентацией, что обеспечивает более симметричное поле поляризации (призмы Глава—Томсона, Глазебру-ка, Франка—Риттера,
Осипова и др.).
На рис. 1.31 приведена призма Франка— Риттера; материал призмы — исландский шпат; симметричное поле поляризации около 28°. Двойная призма Франка— Риттера показана на рис. 1.32, а. Склеивающим веществом служит обычное льняное масло или акриловый клей. Симметричное поле поляризации около 28° 30'. На рис. 1.32, б дана схема выреза поляризатора из кристалла исландского шпата. Объем призмы 2870 мм3, минимальный объем кристалла 1900 мм3.
Призма Плана с воздушным промежутком показана на рис. 1.33, а (симметричное поле зрения 8°), а на рис. 1.33, б— схема выреза призмы из кристалла исландского шпата. Объем призмы
Рис. 1.32. Двойная призма Франка — Риттера
Таблица 1.19. Показатели преломления склеивающих составов для поляризационных призм (для 1 = 589,3 нм)
Матери ад Г1
Акриловый клей Льняное масло Маковое масло Канадский бальзам Гедамин-раствор мбчевиноформальдегидных смол в бутиловом спирте; прозрачен для X = 250 нм и менее 1,485 1,485 1,463 1,526 1,52
Ос
Поле поляризации
Рис. 1.33. Призма Глава с воздушным промежутком
2030 мм8, минимальный объем кристалла 6650 мм8. Светопропускание призмы Глана составляет около 50%. В табл. 1.19 даны показатели преломления склеивающих составов для призм.
Примеры расчета симметричного поля поляризации призм
1. Произведем расчет призмы Глана с воздушным промежутком (см. рис. 1.33, а). Материал призмы — исландский шпатр^, = 1,6584, пс = 1,4864), и ъет — углы полного внутреннего отражения обыкновенного и необыкновенного лучей; а0 и ае — углы соответствующих лучей с осью, ограничивающих поля поляризации в призме; 0 — угол призмы. Применяя закон отражения, получим: sin еот = 1/п0, еот = = 37° 05'; sin ееп — 1/пе = 0,6728, еет = 42° 17'. Из условия симметрия поля поляризации а' = о' = а' = (егт — «,,т)/2 = 2° 36'; 0 = — («от + «етУЗ — 39° 4Г. Поле поляризации в воздухе равно 2а = 8°.
2. Произведем расчет призмы Франка—Риттера (см. рис. 1.32, а). Материал призмы — исландский шпат, склеивающее вещество — акриловый клей. Так как пе = нклея, то о-луч испытывает на склеиваемой поверхности полное внутреннее отражение (угол падения на этой поверхности становится больше предельного). Согласно рис. 1.32, а имеем sin е0— пКЛея/»о — пе/п0 = 1,4864/1,6584 = 0,897; 0 = 90° — “ (е„ + °о)‘
Зависимость поля поляризации от угла среднего клина и склеивающего вещества приведена в табл. 1.20.
Таблица 1.20. Зависимость поля поляризации от угла среднего клина и склеивающего вещества
Угол среднего клина 20, ...° Симметричное поле поляризации, ...°
Канадский бальзам Акриловый клей Маковое масло
35 18,5 29,9 35,5
40 10,2 21,5 27,0
43 5,2 16,5 22,0
44 3,5 14,8 20,3
45 1,9 13,1 18,7
Двоякопреломляющие призмы преобразуют падающий иа них луч естественного света в два линейно поляризованных луча, расходящихся под некоторым углом. Один из лучей может быть выделен с помощью диафрагм, тогда призмами можно пользоваться в качестве поляризаторов. Различные конструкции трехгранных призм нз Аристал-лов даны на рис. 1.34. Поток лучей, ие изменяющий при прохождении через призму своего направления, ахроматичен; у отклоняющихся лучей угол отклонения зависит от длины волны. Угол расхождения лучей у призм Рошона и Сенармона у = (п0 — пе) tg 0, где 0 — преломляющий угол призмы.
Призма Волластона дает удвоенный угол расхождения; для Л. = = 589,3 км и 0 = 30° угол расхождения 2у = 5° 45'.
Поляризаторы (поляризационные светофильтры), основанные па дихроизме, см. гл. 4.
Рис. 1.34. Двоякопреломляющие призмы: а — призма Рошона; б — призма Сенармона; в — призма Волластона (точки означают, что оптическая ось перпендикулярна чертежу)
Оптические компенсаторы 1
Компенсатор Бабине. Состоит из двух кварцевых клиньев, вырезанных так, что оптические оси в них взаимно перпендикулярны (рис. 1.35). Один из клиньев В неподвижен и снабжен посредине крестом и штрихом. Другой клин А можно перемещать с помощью микрометрического винта с делительным барабаном. Луч обыкновенный
Рис. 1.35. Компенсатор Бабине Рнс. 1.36. Компенсатор Солейля
в верхнем клине становится необыкновенным в нижнем клине, и наоборот. В том месте, где d, = d2 между лучами ие возникает разности фаз. Меняя разность толщин (dt — j2), можно получить любую разность фаз.
Компенсатор Солейля. Компенсатор (рис. 1.36) представляет собой видоизмененный компенсатор Бабине, в котором клинья заменены пластинками с той же ориентацией осей кварца. Нижняя пластинка разрезана на две клиновидные части А и В; перемещение части А плавно изменяет общую толщину пластинок. Компенсаторами могут служить плоскопараллельные пластинки из одноосных и двухосных кристаллов, вырезанные в определенном направлении относительно кристаллографической оси (рнс. 1.37 и 1.38).
1 Поляризационные приспособления, применяемые для анализ* подари кованного света.
Широкое применение имеют пластинки с разностью хода А/4 и А/2 (пластинка «четверть волны» и «полуволны») из одноосных кристаллов с поверхностями, вырезанными параллельно оси. Пластинки (ком-
пенсаторы) изготовляются из слюды, селенита, гипса и кварца. Так, толщина пластинки в «.четверть
Оптическая ось кристалла
Рис. 1.38. Слюдяная пластинка, заклеиваемая между защитными стеклами К8, с оптической разностью хода 375 нм
Рис. ).37. Кварцевая пластинка с разностью хода 530—570 нм
волг.!-» первого порядка
(мм) из слюды для А == 0,589 мкм равна
А 0,589-10'3
4(пг — п0) ~ 4-0,008
= 0,0184.
Для измерения небольших величин эллиптичности поляризованного света и очень малых разностей хода двупреломления в объектах применяется поворотная пластинка (эллиптический компенсатор) из слюды толщиной 11—4 мкм, что составляет разность хода А/10— —А/30.
Расчет интерференционной окраски кварцевой пластинки при параллельных николях
Разность хода между обыкновенными и необыкновенными волнами в кварцевой пластинке (падающий луч нормален к поверхности пластинки) равна
Д = d (па — п0) (1.36)
или числу волн
N = Д/А = d (па — пп)/Х, (1.37j
где па — пг, — разность показателей преломления в направлении, перпендикулярном к пластинке; А — длина волны в воздухе.
Наибольшая разность хода возникает, когда пластинка вырезана параллельно оптической оси, т. е. когда па = пе.
Если разность хода равна нечетному числу полуволн (2п + 1) А/2, то обыкновенный и необыкновенный лучи после выхода из николя гасят ДРУГ друга. При М = nA лучн усиливают друг друга, и суммарная яркость света равна удвоенной яркости каждого из слагаемых лучей. Во всех других случаях лучи либо частично усиливают, либо ослабляют друг друга. По формулам (1.36) и (1.37) можно произвести приближенный расчет спектрального состава интерференционной окраски кристаллической пластинки при параллельных николях, если известен спектральный состав света, проходящего через нижний николь. Для лучей разного цвета па— п0 и пе — п0 у кварца приблизительно одинаковы
Таблица 1.21. Характер цвета в зависимости от разности хода, выраженного в числах волн в кварцевой пластинке d — 0,1 мм
Число волн N == Д/Х Характер цвета Число волн N = ДД Характер цвета
2*/4 2 Р/, Фиолетовый Синий Зеленый Р/2 р/2 1V4 Желтый Оранжевый Красный
Поэтому расчет можно вести для среднего значения величины двупреломления (Л = 589,3 нм). Для кварцевой пластинки, вырезанной параллельно оптической осн, Л = 0,0091d.
В табл. 1.21 даны разности хода, выраженные числом волн для каждого цвета в кварцевой пластинке d = 0,1 мм. Как видно из таблицы, фиолетовые лучи, имеющие разность хода 2*/4 (или смещение X/4), после интерференции дадут яркость, равную яркости каждого нз них. Тот же эффект дадут зеленые н красные лучи. Яркость синих лучей (М = 2) равна арифметической сумме яркостей интерферирующих слагаемых; желтый и оранжевый лучи (М = Р/2) гаснут. Скрещивание никелей увеличивает разность хода на Х/4.
Литература: (1, 3, 12, 42, 44, 63, 67, 82, 83, 87, 99, 102, 104, 113, 115, 116].
ГЛАВА 2
ГЕОМЕТРИЧЕСКАЯ ОПТИКА
ОСНОВНЫЕ ПОНЯТИЯ ГЕОМЕТРИЧЕСКОЙ ОПТИКИ
Строение пучка лучей
Световым лучам геометрической оптики соответствуют нормали к поверхности волны в физической оптике.
Строение пучка лучей определяется совокупностью лучей. Если лучи выходят из одной точки или сходятся в одной какой-либо точке, то такой пучок лучей называется гомоцентрическим. Пучки лучей бывают расходящиеся, сходящиеся и параллельные. Гомоцентрический пучок лучей образует одну точку изображения S', называемого точечным изображение образовано пересечением
или стигматическим. Если самих лучей, то оно называется действительным (рис.2.1, а), а если изображение образовано их геометрическими продолжениями, то оно называется мнимым (рис. 2.1, б). В геометрической оптике под светящейся точкой подразумевается источник света, не имеющий размера и объема.
Рис. 2.1. Изображение точки
Основные законы геометрической оптики
Закон прямолинейного распространения света. Принято считать, что в прозрачной н однородной (изотропной) среде свет распространяется вдоль прямой линии, называемой лучом. Геометрическая оптика не рассматривает явления дифракции от края отверстия диафрагмы, при котором свет заходит в область геометрической тенн. Однако в реальных оптических приборах нужно учитывать явление дифракции, так как оно сильно портит изображение, если свет проходит сквозь узкое отверстие, размеры которого соизмеримы с длиной волны света.
Закон независимого распространения света. Предполагается, что отдельные лучи и пучки после пересечения продолжают распространяться по прежним направлениям. При определенных условиях в месте пересечения могут возникнуть интерференционные йвлепия, но в геометрической оптике они не рассматриваются.
Таблица 2.1. Значения предельных углов гт полного внутреннего отражения и углов (—81) падения на входную грань прямоугольной призмы
Марка стекла «о е771 е>
К8 1,5163 41° 16' 5°4Г
БК10 1,5688 39° 36' 8° 29'
ТК2 1,5724 39° 30' 8° 4 Г
ТК16 1,6126 38° 19' 10° 47’
ТФ1 1,6475 37° 22' 12° 38'
ТФ5 1,7550 34° 44' 18° 13'
Закон отражения н преломления. Если лучи, распространяясь в определенной среде, встречают среду, отличную по показателю преломления от первоначальной, то они иа поверхности раздела этих сред
частично отражаются и преломляются или полностью отражаются в определенном направлении [100]. При этом соблюдаются следующие
закономерности:
1) падающий, преломленный и отраженные лучи лежат в одной
плоскости с нормалью к поверхности в точке падения луча;
2) при отражении действует закон отражения — е= еь т. е. угол падения равен углу отражения;
3) отношение синуса угла падения к синусу угла преломления для двух данных сред — величина постоянная н равная относительному показателю преломления этих двух сред
sin е/sin s' = п'!п. (2.1)
Падающий н преломленный лучи взаимно обратимы. Если принять, что п = —п', то уравнение (2.1) дает закон отражения. Показатель преломлении данной среды по отно-
Рис. 2.2. Определение полного
внутреннего отражения в,прямо- шениюк воздуху называется абсо-
угольной призме лютпым показателем преломления.
Показатель преломления воздуха принимается равным единице, хотя его точное значение п = 1,000274 (при нормальном давления 1013 ГПа и температуре 20° С).
Полное внутреннее отражение. При переходе луча нз более плотной среды в менее плотную преломленный луч отклоняется от нормали т. е., е' > в. При увеличении угла падения наступит момент, когда sin в' = 1, т. е. преломленный луч будет скользить по поверхности границы раздела (в = 90°). В этом случае предельное значение угла падения определяется по формуле sin = n'ln или в случае преломления луча нз среды в воздух (я = 1) sin ет — \/п.
При всяком угле падения, большем е.я, луч полностью отражается внутрь той среды’, из которой он распространяется (табл. 2.1, рис. 2.2) На явлении полного внутреннего отражения основано устройство некоторых оптических деталей (призм полного внутреннего отражения, освещение сеток в приборах и т. д.).
Если лучи падают на отражающую грань призмы под углом, меньшим, чем р7П1 то на такую грань наносится зеркальное покрытие (см. гл. 16).
ПАРАКСИАЛЬНАЯ ОПТИКА
Законы параксиальной (гауссовой) оптики относятся к бесконечно малой области, окружающей оптическую ось системы. Эта область исследуется с помощью нулевых лучей. Изображение предметов с помощью нулевых лучей строится на положениях солинейного сродства 178, 79].
Правила знаков
Положительным направлением вдоль оптической оси считается направление света слева направо. Оптическую систему принято изображать так, чтобы ее первая (входная) поверхность располагалась на рисунке слева (рис. 2.3). При расчете оптической системы следует придерживаться следующих правил [89]:
Рис. 2.3. Правило обозначения размеров и угловых величин
1) угол луча с оптической осью считается положительным, если луч, пересекая ось, идет сверху вниз, и отрицательным — снизу вверх;
2) линейные величины предмета и изображения, а также отрезки высот лучей считаются положительными, если они расположены над осью, и отрицательными — под осью;
3) радиус кривизны поверхности считается положительным, если ее центр кривизны находится справа от поверхности, а отрицательным — слева от поверхности, т. е. отсчет производится от поверхности К центру;
4) величины толщин н воздушных промежутков между преломляющими поверхностями при движении света слева направо всегда считаются положительными;
3 В. А. Панов и др, 6о
5) углы между лучом и нормалью к поверхности в точках падения луча е и е' (углы падения и преломления) считаются положительными, если нормаль должна быть повернута по ходу часовой стрелки, чтобы совпасть с направлением луча;
6) угол <р между нормалью в оптической осью считается положительным, если оптическая ось должна быть повернута по направлению движения часовой стрелки, чтобы совпасть с нормалью;
7) при отражении на поверхности изменяется знак у показателя преломления п', угла отражения е' и величины расстояния между отражающей поверхностью и следующей (при движении света справа налево);
8) фокусные расстояния считаются положительными по направлению света от главных плоскостей;
9) при преломлении или отражении лучей на сферической поверхности за начало отсчета отрезка принимается вершина поверхности (точка О). Отрезки считаются положительными, если _оин откладываются вдоль оси справа от точки О по направлению распространения света, и отрицательным, когда откладываются слева от точки О. В случае отрицательных значений указанных выше величии перед ними ставится знак минус.
Соответственные (одноименные) и сопряженные точки, отрезки и углы в пространстве предметов и в пространстве изображений указываются одинаковыми буквами, но обозначения, относящиеся к пространству изображений, отличаются знаком «штрих» вверху каждой буквы.
Главные точки, главные плоскости, фокусы и фокусные расстояния
Две сопряженные плоскости, расположенные перпендикулярно к оптической оси, для которых линейное увеличение равно плюс единице, называются главными плоскостями. Различают переднюю и заднюю главные плоскости (рис. 2.3).
Задняя главная плоскость П' определяется пересечением идущих параллельно осн в пространстве предметов лучей с их продолжением после преломления через систему (это вытекает нз постоянства величин Н'F' — h:a').
Передняя главная плоскость Н определяется аналогично задней, если провести параллельно оси луч в обратном направлении (со стороны пространства изображения).
Точки пересечения главных плоскостей с оптической осью есть главные точки системы.
Задний фокус системы есть точка F', сопряженная с бесконечно удаленной точкой, расположенной на оси системы в пространстве предметов.
Передний фокус системы есть точка F, сопряженная с бесконечно удаленной точкой, расположенной на оси системы в пространстве изображений.
Заднее фокусное расстояние — расстояние от задней главной плоскости до заднего фокуса F' (Н'F' = /').
Переднее фокусное расстояние — расстояние от передней главной плоскости до переднего фокуса (HF — —f).
Задний вершинный фокальный отрезок — расстояние от вершины последней поверхности системы до заднего фокуса (О'F' — s'F,y
Передний вершинный фокальный отрезок — расстояние от вершины первой поверхности системы до переднего фокуса (OF = —s/.).
Передняя и задняя фокальные плоскости — перпендикулярные к оптической оси плоскости, проходящие соответственно через фокусы F и F'.
Расстояние передней главной плоскости от вершины первой поверхности системы sh — sp — f.
Расстояние задней главной плоскости от вершины последней поверхности системы з'И, — з'р, —
Согласно рис. 2.4 следует f ~ hia и f == h а.
Формулы, определяющие положение сопряженных точек. Линейное увеличение в сопряженных плоскостях
Положение сопряженных точек А и Д' на осп системы относительно фокусов системы определяются отрезками г и г' (рис. 2.4).
Линейное (поперечное) увеличение
V = у'/у = -z'lf = -//г, (2.2)
откуда получается формула Ньютона гг' = ff.
Если система находится в однородной среде, то/' = —f и гг' — —
Расстояния гиг' считаются положительными, если точки А и Д' расположены правее фокусов F и F' (на рис. 2.4 г < 0 и г' > 0). Положение сопряженных точек А и Д' на оси системы связаны зависимостью относительно главных точек И и Н'
j'ia' + //а = 1
или для системы, находящейся в однородной среде
1/а'— 1'а= 1//'. (2.3)
Согласно формуле (2.2) и рис. 2.5
V = an'a'a' = а'п'ап'. (2.4)
Расстояния от передней главной плоскости до предмета и от задней главной плоскости до изображения равны а = (1 — V)flV и а = = (» - V) Г-
3* 67
Угловое и продольное увеличения
Под угловым увеличением W7 понимают величину (рис. 2.5)
W = а' /а = а/а' (2.5)
или
Г = а'/а = f/z' = zlf. (2.5a)
Это угловое увеличение относится к лучам, проходящим через осевые точки А н Д' предмета у и изображения у'. Можно говорить об угловом увеличении для любой пары сопряженных точек. Так, например, для лучёй ВН и Н'В', проходящих через главные точки Н и Н' и образующих с осью соответственно углы (3^ и (см. рис. 2.4), имеем W и~ = = У'а'Уа' или на основании формул (2.4) и (2.5а) =
= -///'•
Рис. 2.5. Соотношения между линейным, угловым и продольным увеличениями
Угловое увеличение для произвольных точек Р н Р’ (рис. 2.5) равно W — Прн этом сопряженные лучн ВР н В'Р' проходят через плоскости предмета и изображения соответственно на высоте у и у'.
Из формул (2.2) и (2.5а) следует, что W = //г' = —flVf или WV = = —f/f. Произведение углового увеличения на линейное есть величина постоянная для любой пары сопряженных точек на оси и равно угловому увеличению в главных точках Н и Н', т. е.
W V = WPVP = Wh = - ///'. (2.6)
Из рнс. 2.5 следует
Рр = Г/1 = а'е'/ае. (2.7)
Отношение е'/е = Q есть увеличение отрезка между точками АР и А'Р', т. е. продольное увеличение отрезка вдоль осн. Согласно формулам (2.5) и (2.7) Q = Vp/W — V/W,,, или по формуле (2.6)
Q = е'/е = —VVp/f = п' VVpln\ (2.8)
при п' — п = 1 (система в воздухе) Q = Wo> где V и Vo — линейное увеличение в точках А и А', Р и Р'.
Если точку Р бесконечно близко приближать к точке А, то отрезок е становится бесконечно малым. В этом случае Vp -> V, a -> W 68
и увеличение Q переходит в элементарное продольное увеличение q в точке А. Из формулы (2.8) следует
о = lim Q = —-4—V lim Ур = —-г- V2 = — V2, е->0 t <?->() / п
при п = п = 1, <7 = V2. Согласно формуле (2.6) qWiV = 1. Продоль-
ное увеличение в точке Р равно qp = Ир или qpWp/Vp = 1.
Для практических расчетов удобно пользоваться следующими формулами:
e' = f'(Vp-V). (2.10)
Узловые точки
Узловыми точками называются такие точки, в которых угловое увеличение Wp = 1. Из формулы (2.5а) следует: при Wp = 1, z = f и z' — f, т. e. передняя узловая точка находится от переднего фокуса на расстоянии, равном заднему фокусному расстоянию, а задняя узловая точка от заднего фокуса па расстоянии, равном переднему фокусному расстоянию.
Луч, пересекающий оптическую ось в передней узловой точке в пространстве предметов под некоторым углом, пересекает в пространстве изображения ось в задней узловой точке под тем же углом.
Из формулы (2.6) вследствие Wp = 1 следует, что Vp — Wh, т. е. линейное увеличение в узловых точках равно угловому увеличению в главных точках. Если первая и последняя среды одинаковы, то главные и узловые точки системы совпадают.
Построение изображения
Если в системе известны положения главных точек и обоих фокусов, то можно определить графически положение и величину изображения по положению и величине предмета, и наоборот. Ддя этого надо построить ход двух лучей, исходящих из точки предмета (см. рис. 2.4). Один из этих лучей направить параллельно оптической оси (у = h = = /Т), а другой через F — передний фокус. Высоты лучей на передней главной плоскости переносятся без изменения в знаке и абсолютной величине на заднюю главную плоскость. Первый луч выйдет из системы через точку jV[ — изображение точки Nt — и пройдет через F — задний фокус системы. Второй луч, проходящий через F — передний фокус системы, пересечет переднюю главную плоскость в точке Л^-и выйдет через точку N\ (изображение точки А,) параллельно осп по направлению ЛГ.,В'. Точка В'—пересечение лучей N{F' и N[B'—есть изображение точки В. Опуская из точки В' перпендикуляр на оптическую ось, получим точку Д', которая и явится изображением точки А предмета у = АВ, а отрезок А’В1 = у' его изображением. Все поперечные величины при построении условны, так как на самом деле они бесконечно малы.
Построение изображения с помощью узловых точек
Пользуясь построением, основанным на свойстве узловых (или главных, если п = п') точек, легко определить: величину изображения бесконечно удаленных предметов в задней фокальной плоскости -оптической системы; направление в пространстве изображений любсго луча, если известно его направление в пространстве предметов; найти положения любых сопряженных точек на сопряженных лучах.
Пространство между главными плоскостями отдельных линз или Сложных компонентов ни для расчета, ни для построения изображения роли ие играет. Поэтому обе главные плоскости обычно ссемсщают
Рис. 2.6. Построение изображения точки Л( с помощью узловых точек системы:
1 — пространство предметов; // — пространство изображений
в одну общую плоскость. Однако для действительного положения изображения в реальной оптической системе следует учесть алгебраическую сумму расстояний между главными плоскостями.
По данному направлению одного из лучей, принадлежащего параллельному пучку, падающему под углом <о к оптической оси (рис. 2.6), требуется определить величину изображения у' в фокальной плоскости F' и направление заданного луча в пространстве изображения. Проведя без преломления через главную точку Н луч /ЛИ'параллельио лучу SN, получим в плоскости £' точку М'. Последняя является нзображениембесконечно удаленной точки, образуемым параллельным пучком, из которого выделены два луча SJV и НМ'. Величина изображения у' — —f tg го. Отсюда следует, что в пространстве изображения искомый луч пройдет через точку М1 и его направление будет NM'.
Если светящаяся точка Л, лежит на луче SN вне оптической оси, то ее изображение должно находиться па луче NM'. Поэтому соединяя Л( с Н и продолжая этот луч до пересечения с НМ' в точке А', можно заключить, что Л? есть изображение точки ЛР Точка Л' на оси есть изображение точки Л.
Преломление луча через сферическую поверхность
В параксиальной области высота Л параксиального луча бесконечно мала и углы а, в и <р стремятся к нулю (рис. 2.7),. поэтому <р = Л/г; а — h/s\ а' = h/s'; в = а — <р; в' = а' — <р; п (а — <р) = п' (а' — <р).
Из этих соотношений легко получить нулевой инвариант или инвариант Аббе
п (1/s — 1/г) = п' (Х/s' — 1/г), (2.11)
n'/s' — nfs = (n' — n)lr (2. t la)
и1я a'n' — an = h (n' — n)!r = ЛФ. (2.12)
•;г Каждая преломляющая поверхность имеет свой инвариант Аббе.
Рис. 2.7. Преломление луча через сферическую поверхность
Такие инварианты называются неполными, или частичными [111]. Положив в уравнении (2.11а) величину s ----- оо, найдем расстояние
заднего фокуса от преломляющей поверхности (рис. 2.8, а, б)
s' = f — n'/Ф =
<=n'rl(n—п). (2.13)
Аналогично из формулы (2.11а) определяется переднее фокусное расстояние, если принять s' = оо:
S = f = —пг/(п' — п).
(2.14)
Преломление через несколько сферических поверхностей
Расчет хода паракси-
Л,-' п'=п
Рис. 2.8. Определение фокусного расстояния преломляющей поверхности
ального луча через си-
стему, состоящую из k поверхностей заключается в последовательном Применении формулы (2.12) и формулы h<; = h:^1 — а-к d;f.i [85], т. е.
«1^1 , М-'-;—»t) .
п2 ‘ n.j\
h-л =k1—a2dl;
= j. HjMZZoi, nk+l it
Из предыдущего расчета (при at = 0, st= —оо) находим: hv'a/i+1 = = ЛА/а/е+1 = s'F,. Расчет луча в обратном ходе = оо) определяет величину и положение переднего фокуса.
Оптическая сила системы
Из формул (2.13) и (2.14) следует
/7/ =—п'/п. (2.15)
Эту зависимость вследствие инвариантности формулы (2.16) можно распространить и на систему, состоящую из любого числа поверхностей. Отношения — n/f = п'//' = Ф называют оптической силой системы. Большей частью оптическую систему рассматривают в воздухе (п = = п' — 1) и тогда за оптическую силу принимают величину, обратную заднему фокусному расстоянию (выраженному в метрах) Ф = 1//'.
Единицей оптической силы является диоптрия. Одна диоптрия есть оптическая сила системы в воздухе с фокусным расстоянием равным 1 м.
Инвариант Лагранжа—Гельмгольца
Из формул (2.2), (2.5), (2.7) и рис. 2.5 следует:
ayf =—а'у'Г; (2.16)
р//=-р77'; (2.17)
при условии, что лучи ANr и N\A' являются сопряженными и проходят соответственно через концы I и Г. В соответствии с формулой (2.15) выражения (2.16) и (2.17) приводятся к виду
any = а' п' у' = I; (2.18)
Рп/= Р'п'Г = —/v (2.19)
Инварианты (2.18) и (2.19) имеют большое практическое значение. Они называются полными инвариантами, так как при прохождении через всю систему не меняют своего вида и значения. Первоначальные численные значения полного инварианта совершенно произвольны. Однако между этими обоими инвариантами существует очень важная связь (см. рис. 2.5): I = —или ау = —(3Z.
Бесконечно тонкая линза
В бесконечно тонкой линзе главные плоскости совпадают друг с другом и с вершинами линз.
Основная формула бесконечно тонкой линзы
4---Г = ('г-1)(т--7-)- (2'20)
Э i> \'1 ' 2 '
Полагая s = оо и s' = f, из формулы (2.20) получим
<221>
Так как а = Л/s и а' = Л/s', то формула (2.20) приводится к виду
а' = а + ЛФ. (2.22)
Система из нескольких линз, расположенная в воздухе
Наиболее удобный и простой способ определения габаритных размеров системы, расположенной в воздухе, заключается в последовательном применении формул следующих ниже, когда линзы заменены главными плоскостями (рис. 2.9) [85]
ал+1 = «& + Л&Ф*; (2.23)
/А+1 = К/г+i^ft- (2.24)
Рис. 2.9. Ход параксиального луча через оптическую систему, представленную главными плоскостями
Если число всех линз равно т, то из формулы (2.23) следует
k~m
%+l=°m = Ol + S (2.25)
/?=м
k~m
При = 0 и sx = ос ат — но так как ат = hjf' — Л/D,
А-=1
то k~m
ф = J- У h^k. (2.26)
к=1
Если линзы бесконечно тонкие и находятся в соприкосновении (d = 0),
то ht = Л2 = . •. = hm и, следовательно, Ф = У Фд.
k =1
Линзы конечной толщины
Для простой линзы, расположенной в воздухе, справедливы следующие соотношения [71]:
/ \ Л1 гг / л riri
d(n — l)(r2 — r, 4- d}
n(r2— r,) + (n — 1)« ’
При малых значениях d по сравнению с f расстояние НН’ — d (1 — — l/л). На рис. 2.10 показано расположение главных плоскостей в ос-
Рис. 2.10. Расположение главных плоскостей в основных типах
простых линз
новных типах простых линз. Три из них относятся к положительны.'.; (собирательным) линзам f > 0 и три линзы — к отрицательным (рассеивающим) f < 0.
Кардинальные величины системы, состоящей из двух частей
Рассматриваемая система может состоять из двух одиночных линз конечной толщины или из двух сложных компонентов с оптическими силами Ф, и Ф2. Эквивалентные переднее и заднее фокусные расстоя-
Рис. 2.11. Определение кардинальных величин системы, состоящей из двух частей
нвя, положения эквивалентных фокусов н главных плоскостей всей системы вычисляются по следующим формулам:
1//' = ф = ф. + Ф2 — rf ф ф2;
— — (1 = /' (1
til’ll nw = -dt’;i\,
где d— расстояние ст //[ до Н2 (рис. 2.11).
Ограничение пучков лучей в оптических системах
Диафрагмы и оправы оптических деталей ограничивают пучки лучей, поступающие в оптическую систему.
Апертурная диафрагма — диафрагма, ограничивающая пучок лучей, выходящий из осевой точки предмета (ограничивает числовую апертуру или светосилу’ прибора).
Входной (выходной) зрачок. — параксиальное изображение апертурной диафрагмы в пространстве предметов (изображений) или апертурная дифрагма, расположенная в пространстве предметов (изображений). Чтобы определить какая из имеющихся в приборе диафрагм является апертурной, в пространстве предметов находят положение и величину изображений всех диафрагм, создаваемых предшествующими им частями системы. То изображение диафрагмы, которое видно под наименьшим углом (из точки До предмета, лежащей на оптической оси) будет являться входным зрачком системы, а сама материальная диафрагма — апертурной диафрагмой (рис. 2.12, /).
Апертурный угол в пространстве предметов — угол между оптической осью и лучом, выходящим из осевой точки предмета п идущим на край апертурной диафрагмы (од).
Апертурный угол в пространстве изображений — угол между оптической осью и лучом, проходящим через осевую точку изображения и край апертурной диафрагмы (<^-).
Полевая диафрагма — диафрагма, расположенная в плоскости предмета или в одной из плоскостей, с ней сопряженных, и ограничивающая размер линейного поля оптической системы в пространстве изображений.
Линейное поле оптической системы в пространстве предметов — наибольший размер изображемой части плоскости предмета, расположенной на конечном расстоянии.
Линейное поле оптической системы в пространстве изображений — наибольший размер изображения, лежащего на конечном расстоянии.
Угловое поле, оптической системы в пространстве предметов (изображений) — абсолютное значение удвоенного угла между оптической осью и лучом в пространстве предметов (изображений), проходящим через Центр апертурной диафрагмы и край полевой диафрагмы.
Главный луч — луч, проходящий через центр апертурной диафрагмы.
Виньетирующая диафрагма — любая материальная диафрагма, кроме апертурной и полевой, которая ограничивает пучки лучей, выходящих из точек предмета, лежащих вне оптической оси и вызывает геометрическое виньетирование (ГОСТ 7427—76).
Входное (выходное) окно — параксиальное изображение виньетирующей диафрагмы в пространстве предметов (изображений) Ч
Рис. 2.12. Ограничение пучков лучей в пространстве предметов (7) н влияние виньетирующей диафрагмы (выходного окна) на ограничение внеосевых лучей в пространстве изображений (//—V): (II—точка изображения В\ без виньетирования — граничный случай; /// — точка изображения В'г, главный луч проходит вне зоны виньетирования; IV — точка изображения В’3, главный луч находится в зоне виньетирования; V — точка изображения B’t при полном виньетировании — граничный случай)
Геометрическое виньетирование
Под геометрическим виньетированием понимается явление срезания диафрагмой наклонных пучков лучей, исходящих из точек предмета, расположенных вне осп системы. Виньетирование вызывает в изображении постепенное падение освещенности о.г некоторой точки предмета к краю поля. На рис. 2.12, / даны: диафрагма Д.. — входной зрачок, диафрагма Д, — виньетирующая (входное окно), диафрагма Д2, край которой лежит выше луча А^В^ не вызывает виньетирования и поэтому из дальнейшего рассмотрения исключается. В пределах от AL
1 Ранее применявшиеся термины «люки» ГОСТ 7427 — 76 отменены.
до Л2 будет происходить виньетирование, вызываемое входным окном. Влияние виньетирующей диафрагмы (выходного окна) на ограничение внеосевых пучков лучей в пространстве изображений представлено на рис. 2.12 (77—V)- Виньетирование оценивают коэффициентом линейного виньетирования /гы = 2m/2h, где 2т — отрезок в меридиональной плоскости зрачка для наклонного пучка лучен, a 2h — отрезок в той же плоскости для осевого пучка лучей.
Глаз человека малочувствителен к падению освещенности на краю поля зрения прибора, и виньетирование для 50% глаз практически не ощущает. В некоторых приборах (перископы, широкоугольные объективы) в целях уменьшения поперечных размеров оптических деталей виньетирование допускается до 70% н более.
Положение зрачков и окон в основных типах оптических систем
В симметричных фотографических объективах апертурная (обычно ирисовая) диафрагма находится в середине воздушного промежутка, разделяющего обе части объектива (рис. 2.13). Ее изображение a\b't через переднюю половину объектива является входным зрачком, а изображение а'2Ь'2 через заднюю — выходным зрачком. Оба зрачка находятся в главных плоскостях объектива, поэтому линейное увеличение в зрачках объектива равно единице. Луч Ва\, направленный в край входного зрачка, т. е. в точку а\, пройдя компонент 1, коснется края диафрагмы (в точке а) и выйдет по направлению СВ'. На продолжении этого
Рис. 2.13. Апертурная диафрагма, расположенная внутри оптической системы
луча находится точка а', — край выходного зрачка. По мере увеличения угла (0 главного луча последний займет такое положение МР, при котором вся верхняя половина пучка будет экранирована, т. е. виньетирование достигнет 50%. Оправа компонента I — входное окно объектива, а ее изображение через всю систему — выходное окно. Если и оправа компонента 7/ также экранирует наклонные пучки лучей, то она будет вторым выходным окном, а ее изображение через объектив в обратном ходе — вторым входным окном.
В несимметричных объективах (триплеты, тессары, типа Пепваля и т. д.) входной и выходной зрачки находятся внутри объектива, вблизи апертурной диафрагмы.
В призменных биноклях входным зрачком является оправа объектива (она же и апертурная диафрагма), выходным — ее изображение через окуляр. Если выходной зрачок прибора больше зрачка глаза, то последний становится выходным зрачком для прибора, а его изображение через всю систему в обратном ходе — входным зрачком.
В биноклях Галилея выходным зрачком всегда является зрачок глаза, входным окном служит оправа объектива.
В большинстве зрительных труб входным зрачком (одновременно и апертурной диафрагмой) служит оправа объектива. В некоторых системах входным зрачком является призма или плоское зеркало, стоящее порет объективом.
Соотношение между линейным полем и светосилой системы (инварианты «Лагранжа—Гельмгольца)
Рис. 2.14. К выводу инварианта Лангран-жа—Гельмгольца
На рис. 2.14 дано: ОО'—оптическая ось системы, состоящая нт р числа линз: Л'Л', и N'N\—соответственно входной и выходной зрачки, ограничивающие падающий в систему пучок лучей, выходящих из точки А, изображением которой является точка Д'. Произвольные, ио сопряженные точки Р и Р' (см. рис. 2.5) перенесены в центры Р п Р' зрачков (см. рис. 2.13), радиусы которых обозначены чепез р и р'. На основании формул (2.7) и (2.19), полагая р и р' вместо I и /', линейное увеличение в зрачках Г’,, = р'/р = == Р/ц-Р'Лр. Глаз наблюдателя, помещенный в точку Р, будет наблюдать предмет у под углом Р, а его изображение у' из точки Р' под углом (У (система в воздухе п, = = п' = 1). Отношение этих углов равно угловому увеличению в зрачках системы Р'.’р =
== \JV(,= Wp. Аналогично этому линейное увеличение для предмета V=al,a^= MW. На основании формул (2.13i и (2.19) получакнся два полных инварианта Лагранжа—Гельмгольца:
«!!/!«! = rhy'a’ = п,у..а, = ... = пР+1ур+^Р+1; (2.18а)
"iPtoi = = п2p2f}2 = ... = «p^p.n+t'iy+t, (2.19а)
причем yh а.и = —р*^. Здесь рп р2, ..., р^, и т. д. радиусы зрачков отдельных линз, а поэтому р. и рр — суть радиусы малых площадок входного и выходного зрачков для всей системы. Инварианты (2.18а) и (2.19а) шавливают определенные соотношения между линейным полем и светосилой системы.
Видимое увеличение оптических приборов
Под видимым увеличением понимается отношение
Г = tg y'/tg у, (2.27)
Где y — угол, под которым наблюдатель видит предмет левое раженным глазом; у' — угол, под которым глаз наблюдателя видит изображение предмета через оптический прибор.
Рис. 2.15. Геометрическое соотношение к определению видимого увеличения оптических систем
На рис. 2.15 центр глаза наблюдателя помещен в точку О, из которой предмет у, находящийся от псе па расстоянии k, рассматривается под углом
у = arctg . . (2.28)
Глаз наблюдателя, расположенный в точке О', рассматривает изображение у' с расстояния k' под углом
y' = arctg(-^-). (2.29)
Из формул (2.28) и (2.29) следует;
Г = tg т'/tg у = y'k'yk' = Vk.'k'. (2.30)
Отрезки k и k' отрицательны, так как они отсчитываются от центра зрачка по направлению прохождения света, который всегда идет от предмета пли его изображения к глазу. Вместо формулы (2.30) на основании
рис. 2.15 получим
tg<o' е' k tgw е k'
Согласно формуле (2.19а)
п e'k 1
п'
(2.31)
(2.32)
Выражение (2.32) представляет окончательный вид общей формулы для видимого увеличения любой оптической системы.
Видимое увеличение лупы
Выходным зрачком лупы (и апертурной диафрагмой) обычно служит зрачок глаза (е = k’). Из формулы (2.32) при п = п = 1 следует Гл = kleVp. Согласно выражению (2.9)
= (jr-1)- <2'33)
Рассматриваемый предмет находится в переднем фокусе, т. е. г = 0: согласно формуле (2.2) увеличение И = сю. Поэтому из выражения (2.33) следует, что eVp = —Принимая расстояние наилучшего зрения для невооруженного глаза k = —250, получим Гл = = kleVv = 250//'.
Видимое увеличение лупы, работающей с аккомодирующим или аметропическим глазом
В этом случае предмет находится на расстоянии г от переднего фокуса F лупы, а его изображение через лупу — на расстоянии г' от заднего фокуса F' (рис. 2.16). Зрачок глаза, служащий выходным зрачком лупы, находится на расстоянии г' от F' лупы: с — расстояние от зрачка глаза до изображения у’ — есть расстояние, на которое аккомодирует
Рис. 2.16. Определение видимого увеличения лупы, работающей совместно с аметропическим глазом
глаз, а в случае аметропического глаза — расстояние до его дальней точки. Если расстояние с выражено в мм, то с = 1000/Д, где Л — напряжение аккомодации (или аметропия глаза во втором случае) в диоптриях. Из рис. 2.16 следует
г'= гр-ф 1000/Л (2.34)
Подстановка в формулу (2.30) значений k = —250 мм и k' = с = = 1000/4, г' нз формулы (2.34) и V из формулы (2.2) дает
р 250 Л , (2.35)
1 /' \ ' 1000 J •
При А = 0 формула (2.35) переходит в выражение для Го неаккомодирующего глаза (эмметропа): Го = 250//' формула (2.35) принимает вид - ( Аг r^=r«V+-iw
Если зрачок глаза наблюдателя находится в задней фокальной плоскости лупы, т. е. г’р = 0, тогда Гл = Го, т. е. видимое увеличение лупы не зависит от аккомодации и аметропии глаза наблюдателя.
Телескопические или афокальные системы
Параллельный пучок, попадающий в телескопическую систему, выходит из нее параллельным. К телескопическим системам относятся астрономические и геодезические трубы, бинокли, перископы, различные зрительные трубы.
Простейшая телескопическая система состоит из двух основных компонентов — объектива и окуляра, причем задний фокус объектива совмещен с передним фокусом окуляра. Оптическая сила такой системы равна нулю. Главные плоскости системы находятся в бесконечности. Так как система находится в воздухе, то из формул (2.6) и (2.8) Q = = V/W = V2; q = V2. Все три увеличения V, W н Q постоянны.
В телескопических системах зрачок глаза совмещен с выходным зрачком прибора, т. е. г' = k' и е = k. Из формулы (2.32) следует, что
Рис. 2.17. Простая телескопическая система
Гт= 1/Кр = 1/V = W = tg w'/tg Wj, т. е. видимое увеличение есть величина постоянная и равная угловому увеличению системы. Продольное увеличение q= 1/Г^. Из рис. 2.17 следует, что tg со = у' и tg со' = y'/f'oK.
Увеличение телескопической системы, состоящей из объектива и окуляра, может быть определено по формуле
Гт = foc/foK = Dp/Dp,. (2.36)
Если в систему входит еще и оборачивающая система с линейным увеличением V, то Гт = Vf'a6if’3K.
Сложный микроскоп
Кардинальные точки, фокусы, главные плоскости упрощенной оптической системы. На рис. 2.18 приведена схема оптической системы микроскопа, состоящего из объектива 1 н окуляра 2, с указанием расположения главных плоскостей и фокусов, фокусных расстояний, а также и расстояния между ее компонентами. С целью упрощения рисунка объектив и окуляр заменены простыми линзами. Как показано на рис. 2.18, в случае положительного окуляра задний фокус микроскопа F' лежит впереди второй главной эквивалентной плоскости Н' и поэтому заднее фокусное расстояние микроскопа является отрицательным; тем не менее его система не эквивалентна простой отрицао льной линзе.
Рнс. 2.18. Схема оптической системы микроскопа
При наблюдении нормальным пеаккомодированным глазом предмет совмещен с передним фокусом всего микроскопа. Задний фокус объектива и передний фокус окуляра находятся друг от друга па расстоянии оптического интервала Ао = —/об Роб- Заднее фокусное расстояние микроскопа вычисляется по формуле
__ /об/ок _____ /об/ок
Расстояние заднего фокуса микроскопа F' от заднего фокуса окуляра fox
^'=-/ок4к/Лэ = /;х/Ао-
Соответственно расстояние переднего фокуса микроскопа от переднего фокуса объектива
ZF = /об/об/А0 — —Гм/^О-
Расстояние передней главной плоскости микроскопа от переднего фокуса объектива равно
гн = гг-Л
Расстояние задней главной плоскости системы микроскопа от заднего фокуса окуляра
г' =?',—/'= ^ок (/ок + /об)
Апертурная диафрагма АД микроскопа расположена в задней фокальной плоскости объектива, а полевая диафрагма ПД — в передней фокальной плоскости окуляра.
Оптическая система микроскопа с осветительным устройством дл» проходящего света. На рис. 2.19 приведена принштпальнаяоити-ческая схема микроскопа с упрощенной осветительной системой, выполненной по принципу Кёлера. Отдельные ее узлы заменены главными плоскостями и расположены на одной прямой. Коллектор 2 изображает источник света 1 в апертурную ирисовую диафрагму 4 конденсора 5, который проецирует полевую диафрагму 3 коллектора в плоскость предмета 6. Выходящие из конденсора параллельные пучки лучей равномерно освещают прозрачный предмет в пределах изображения диа-
Рис. 2.19. Принципиальная оптическая схема микроскопа с упрощен ной осветительной системой
метра полевой диафрагмы коллектора. После взаимного пересечения на освещаемом участке предмета пучки лучей расходятся, направляясь в обьектив 7 микроскопа. Угол, образуемый с оптической осью лучом, выходящим из центра предмета и направляющимся в край зрачка, являеа-я апертурным углом. Предмет расположен перед передним фокусом объектива микроскопа, который дает действительное, перевернутое и увеличенное изображение предмета в передней фокальной плоскости окуляра 10 (т. е. в плоскости полевой диафрагмы 9 микроскопа) Выходящие из окуляра параллельные пучкн лучей попадают в эмметропическпй глаз и собираются на его сетчатке, где образуется окончи (ельное изображение рассматриваемого предмета. Изображение же источника света получается в задней фокальной плоскости объектива микроскопа, в которой происходит пересечение параллельных лучей. В этой же плоскости располагается и апертурная диафрагма 8 микроскопа. Еще раз изображение источника света создается в выходном зрачке микроскопа 11, являющемся изображением апертурной диафрагмы 8. Зрачок глаза наблюдателя совмещен с выходным зрачком 11 микроскопа, а следовательно, изображение источника света располагается па зрачке глаза, а изображение рассматриваемого предмета — на его сетчатке. Наличие в осветительной системе ирисовых апертурной и полевой диафрагм позволяет раздельно регулировать величину числовой апертуры п диаметр освещаемого поля зрения.
Видимое увеличение микроскопа. Масштаб изображения. Принято считать, что увеличением микроскопа называется отношение изображения, получаемого на сетчатой оболочке глаза при помощи микроскопа, к изображению того же объекта на сетчатке невооруженного глаза. При этом предмет рассматривается невооруженным глазом на расстоянии
наилучшего зрения D = —250 мм; тогда в соответствии с рис. 2.18 увеличение микроскопа будет равно
Г м = =------42- = УобГок- (2.37)
/м /об /ок
В современных конструкциях микроскопов между объективом и окуляром, как правило, находятся оптические компоненты, которые, обладая оптической силой, влияют на увеличение микроскопа.
Приведем формулы расчета увеличения микроскопа для случаев, когда в нем применяются следующие компоненты:
а) линза, смещающая изображение, даваемое объективом, и увеличивающая его в масштабе Кл. с:
Г м = УобГокУл. с; (2.38)
б) проекционная система (фотообъективы, проективы и т. д.), передающая изображение, даваемое микроскопом, на экран, фотопленку и другие приемники световой энергии с увеличением Упр:
м=Тмупр; (2.39)
в) окуляр в качестве проекционной системы, передающий изображение, даваемое объективом, на конечное расстояние (микрофотонасадки типа МФН) с увеличением Кою
М = УозУок- (2.40)
«ь
Часто при фотографировании с окуляром, увеличение последнего определяется величиной К — коэффициентом увеличения камеры, тогда
М=ТмК, (2.41)
где К = s'/250 (s' — расстояние от задней главной плоскости проекционного окуляра до изображения; например, если s' == 150 мм, то К = 150/250= 0,6).
При применении в микроскопе микрообъектива, рассчитанного для бесконечно удаленного изображения, и тубусной линзы с фокусным расстоянием л увеличение микроскопа равно
Гм = Аг. л^ок//об (2.42)
или
г — 250 /т. л р у, - ,п
*м— "250 I °к — 1об^ГОк) ( •
• об
где Го6 = 250,7об — увеличение объектива, соответствующее увеличению лупы; qx — коэффициент увеличения тубусной линзы.
При применении тубусной линзы с дополнительными компонентами, соответствующими условиям а—в [формулы (2,38)—(2.40)], увеличения микроскопа можно представить следующими формулами:
Гм = 4^-Гл.сГок; (2.41)
/об
М = rMV1Ip = VnpF’OK; (2.45)
/об
д; = л- /<, или М = л Кок. (2.46)
/об /об
Зависимость между диаметром выходного зрачка и увеличением микроскопа. Поскольку в системе микроскопа выполнено условие синусов, то с достаточной степенью приближения диаметр выходного зрачка микроскопа можно вычислить по формуле [100]
Dp, = 2п sin aAfM = 2Af'K. (2.17)
Подставив = 250/Гм из формулы (2.37), получим Dp' = = 500А/Гм. Так, например, если Гм = 500А, то Dp' = 1 мм; при Гм = 1000А имеем Dp’ = 0,5 мм.
Линейное поле микроскопа. При визуальном наблюдении линейное поле микроскопа определяется диаметром того круга в плоскости предмета, изображение которого заполняет полевую диафрагму окуляра. Чтобы определить величину линейного поля всего микроскопа в пространстве предметов, необходимо линейное поле окуляра разделить на увеличение объектива, а в случае применения дополнительных линзовых компонентов, размещенных в тубусе микроскопа между объективом и окуляром, — на их общее увеличение. Линейное поле микроскопа D = 2у = 500 tg <о7Гы.
Передача перспективы оптическими приборами
Центром перспективы в пространстве предметов служит центр входного зрачка, а в пространстве изображений — центр выходного зрачка. Характер перспективы меняется в зависимости от того, где расположен входной зрачок системы относительно предмета и самого прибора [100, 111].
Наблюдение предметов через лупу. 1) Нормальная перспектива — зрачок глаза расположен между лупой и её задним фокусом; предмет, более близкий к лупе, виден под большим углом, чем предмет более далекий. 2) Гиперцентрическая перспектива — зрачок глаза расположен за задним”фокусом лупы; предмет, более близкий к лупе, виден под меньшим углом, чем предмет более далекий. 3) Телецентрическая перс--Пектина — зрачок глаза совпадает с задним фокусом лупы; в пространстве предметов главные лучи идут параллельно оптической оси, т. е. входной зрачок расположен в бесконечности. Такой ход лучей называется телецентрическим и имеет большое практическое значение 85
в измерительных приборах, так как устраняются ошибки измерения при установке на резкость [100).
Линейное поле зрения лупы 2у = где D — световой диа-
метр лупы, t' — расстояние зрачка глаза от лупы.
)
\ I Естественное впечатление
Из рис. 2. ЕУтледует, что tg со = —p/e; tg у' = —tj'ik'. По условию естественного впечатления требуется, чтобы со = у'. Следовательно, yie— y'/k', откуда 1'е = y'/yk' = V'ik'. Принимая во внимание формулу (2.30), Г = k'e. При фотографировании далеких предметов (ландшафтная съемка) можно положить е — k. Тогда для получения естественного впечатления от такого снимка требуется Г = 1. С другой стороны, из формулы (2.36) следует: для того чтобы Г = 1, необходимо f = 250 мм. Если f < 250 мм, то для получения естественного впечатления от снимка прибегают к увеличительному стеклу.
Положив видимое увеличение Г = 1, из формулы (2.36) найдем условие естественного впечатления от изображения на экране k' = = Л1/', где k' — расстояние от экрана до глаза наблюдателя, рассматривающего изображение; f — фокусное расстояние киносъемочной камеры; М — масштаб изображения, даваемый проекционным аппаратом. _
Пример. Дано: b — ширина кадра (ширина изображения на пленке) равна 22 мм; /)' = 100 мм; В — ширина экрана. Тогда k' = М','к == = Bf'klb = В100/224,5В.
Общие формулы для светосилы оптического прибора
Светосилой оптического прибора принято называть величину, характеризующую освещенность изображения.
Входящий в оптическую систему световой поток, заполняющий входной зрачок (см. рис. 2.12), вычисляется по формуле 1106]
Ф — лВ dS sin2 оА.
Выходящий из системы световой поток равен
ф' = тФ = лтй dS sin2 оА,
(2.48)
где т — коэффициент пропускания системы; В — яркость элементарней площадки dS, расположенной на оптической оси перпендикулярно к последней; Од — апертурный угол в пространстве предметов. Величину выходящего светового потока можно вычислить по формуле
ф’ = лВ dS' sin 'о.,,
где оА, — апертурный угол в пространстве изображения; В' — яркость изображения элементарной площадки </5'.Так как В' — n\Bltii, то
Ф = л хВ dS sin2 оА,. (2.49)
Световой поток, излучаемый площадкой dS, распределяется в пространстве изображений по площади dS'. Величина светового потока, 86
приходящего на единицу площади, определяет освещенность в пространстве изображения. Вследствие этого величина светосилы [ 111 ]/7 = s=®7SrfS'. Из формулы (2.48) Н— пт d S sin2 <3A/dS', но так как dS’/dS — V, sin Од, = sin oA/V, следовательно,
И = пт (sin Од/И)2 = пт 51П2Од,. (2.50)
Светосила оптического прибора при малой передней апертуре (объективы зрительной трубы, фотографические объективы для ландшафтных съемок и т. д.)
Подстановка в формулу (2.50) значенийзт од = Dp!'2e и g = лт/4 дает Н = g (Dp!eV)2; приняв во внимание (2.9) и п — п' — 1, получим / V V / D„ \2
,м,)
Для бесконечно удаленных предметов V = 0 из формулы (2.51) получим выражение для физической светосилы объектива Н = g (D
Если положить g— 1, тогда //() = (Dp//'fi)2 представляет собой квадрат относительного отверстия и характеризует геометрическую светосилу объектива. При съемке предметов с конечного расстояния светосила уменьшается. Например, при репродукции снимка в масштабе V= —1 симметричным объективом (Vp = 1) из формулы (2.51) получим Н = 0,25g (Dp;fт. е. светосила уменьшается в четыре раза по сравнению с той, когда s, = оо. Квадрат диаметра выходного зрачка D'p, зрительной трубы принято называть относительной светосилой трубы.
Пример. Определить величину светового потока, поступающего на фотокатод ФЭУ, от имитатора неба (яркость 20 000 кд/м2) через объектив с фокусным расстоянием /' = 100 мм и 2Л,= 5О мм, если диаметр фотокатода dKaT=8 мм и светопропускание оптической системы т=0,8.
Решение. Применим формулу (2.49). Так как оптическая система, передающая световую энергию на фотокатод, расположена в воздухе, то n — n' — 1. Найдем площадь фотокатода: dS' = =л d2aT /4= 0,5-10" 4 м2; выходная числовая апертура объектива (увеличение в зрачках V = 1) равна sin а'А' = D'p^f'^ — 0,25; по формуле (2.49) найдем Ф' = 0,16 лм.
Светосила оптического прибора при малой задней апертуре (проекционные приборы, осветительные системы, прожекторы и др.)
Подстановка в формулу (2.5,0) величины sin _ Dp.fte' дает И = лтРр, '4е'2 = tS'/c'2, (2.52)
где D'.,. и S' — соответственно диаметр и площадь выходного зрачка, е* — расстояние от выходного зрачка до плоскости изображения.
Освещенность, создаваемая действием прожектора, вычисляете t по формуле Маижена
£ = xSS'/e'2. (2.53)
РАЗРЕШАЮЩАЯ СПОСОБНОСТЬ ОПТИЧЕСКИХ ПРИБОРОВ
Согласование разрешающей способности прибора с разрешающей способностью глаза
Предположим, что изображение у получается такой величины, что оно из точки О', являющейся центром зрачка глаза, рассматривается под углом у', равным в — предельному углу разрешающей способности глаза. Угол cflj, под которым находящийся на пределе разрешения предмет у виден из центра входного зрачка прибора, является также предельным углом со. Главный луч в пространстве изображения при згом образует угол со' — со' (см. рис. 2.15). Пользуясь рис. 2.15, можно определить в линейной мере величину предмета, находящегося на границе разрешения: у = —йе/Г. В случае лупы или микроскопа k = = —250 мм (е в рад), тогда у = 250 е/Г = /'в.
Для прибора дальнего действия (зрительные трубы, бинокли и т. д.) удобнее выражать разрешающую способность через угол со, являющимся предельным углом разрешающей способности всей системы, состоящей из прибора и глаза наблюдателя: со = Ае/Г1е. Так как для прибора дальнего действия k = е, то со = в/Гт.
Пример. Призменный бинокль имеет Гт -- 15х. Если принять е = Г, то со = 60"/15 = 4 с.
На разрешающую способность прибора влияет кроме разрешающей способности глаза еще и степень коррекции аберраций оптической системы. В фотографических объективах разрешающую способность принято определять числом линий N на 1 мм. Теоретически ?/т = = 1/1.22КХ, где К= (f /Dp)—диафрагменное число; если % = = 0,5 мкм, тогда N 1600/К. Практически разрешающая способность зависит от аберраций фотообъективов и свойств фотографических слоев. Так, например, у высокочувствительных крупнозернистых эмульсий разрешающая способность равна 40—50 линиям на 1 мм, у мелкозернистых 100—150, у фотоматериала специального назначения 200— 800. Как правило, разрешающая способность системы, состоящей из фотографического объектива и светочувствительного слоя, значительно меньше, чем теоретическая разрешающая способность объектива (с\г. табл. 4.50—4.53).
Дифракционная разрешающая способность прибора
Явление дифракции от краев диафрагм, ограничивающих пучок лучей, вызывает понижение разрешающей способности. Наименьшее расстояние между двумя светящимися точками (или линиями), которые еще /могут быть различимы, является мерой разрешающей силы. Для определения предела разрешения микроскопа применяются тест-сбъекты (диатомеи), для зрительных труб и фотообъективов — штриховые миры. При визуальном испытании контраст светлых и темных полос — решающий фактор. На рис. 2.20 даны изображения двух точек, частично налагающихся одно на другое. Картина распределения освещенности представлена штриховой линией с некоторым .минимумом. Разность между этим минимумом и соседним максимумом составляет 5% и является для глаза предельно допустимой. Эга разность в освещеп-88
ности соответствует наименьшему расстоянию между двумя точками определяемому в оптических единицах значением [85]
= 2лг'од,/Л = 3,3, (2.54)
где г' — расстояние между центрами изображения двух точек (или двух прямых линий), соответствующее угловой величине «ДИф- На рис. 2.20 показано, что адиф = г'/f'oC; о'А, = Рр/2/;б, где Рр — диаметр входного зрачка объектива телескопической системы; f'o6 — фокусное расстояние объектива. При xt = 3,3 из выражения (2.54) получим аДИф = l,05A./Dp. Если X = 0,000560 мм, то аДИф в секундах дуги составит
ади*= 120W- (2.55)
где Dp — выражается в миллиметрах.
Рис. 2.20. Определение дифракционного предела разрешения оптической системы
По формуле (2.55) можно определить разрешающую способность глаза. Так для диаметра входного зрачка глаза £)сд = 0,5 мм, «ДИф = = 4\ Если Ргл = 2 мм, то «дись = Г. При 2 мм разрешающая 'способность глаза вследствие физиологических свойств не увеличь" •ваетяя-.'" ~ ------------ '
Предел разрешения микроскопа определяется дифракционными явлениями, возникающими в плоскости предмета,, микроструктура которого действует на световые волны подобно дифракционной решетке. Максимальная разрешающая способность микроскопа при косом освещении определяется по формуле [100]
X X
Аоб + А,“-2А^’ <2’56)
где Аод и А/г — соответственно числовая апертура объектива и конденсора микроскопа.
Чтобы полностью использовать разрешающую способность микроскопа, определяемую формулой (2.56), необходимо иметь соответствующее полезное увеличение микроскопа. Это увеличение должно быть настолько большим, чтобы наименьшее разрешаемое микроскопом расстояние г/диф составляло в пространстве изображений микроскопа углов} ю величину, не меньшую, чем предельный угол разрешающей способности глаза наблюдателя е = d£vjk. Подставив в эту формулу
Значение,/ из (2.56) nk— —250мм, найдем Гм = 250'0,00029е А/0.ГА= = —е Л/6.9Л. (где е выражается в минутах, А — в миллиметрах). Полагая величину е в пределах от 2 до 4', получим
А/3.45А < | Гм | < А/1.72А; (2.57)
для видимой области спектра (А. — 0,000589 мм)
500А < | Гм | < 1000А. (2.58)
Значения Гм, удовлетворяющие неравенству (2.58), называются значениями полезного увеличения микроскопа.
Полезное увеличение телескопической системы определяется из условия, что разрешающая способность телескопической системы может быть использована глазом наблюдателя в полной мере, т. е. что угловое расстояние, между изображениями двух точек за окуляром должно быть не меньше определенной величины, например Г. При таком условии разрешающая способность системы определяется разрешающей способностью объектива. Из формул (2.27) и (2.55)
адиф = адифГт = 120 Гт/£)р,
Если адиф = е= Г, то Гт = 0,50р называется полезным увеличением зрительной трубы. Чтобы увеличить угловое поле, яркость и диаметр выходного зрачка системы в большинстве случаев принимают Гт < < Dp (Dp в мм).
Полезное действие зрительной трубы определяется коэффициентом L — £>'/£>, где Ъ — острота зрения невооруженного глаза, Ь' — острота зрения глаза, вооруженного зрительной трубой при тех же условиях наблюдения. Как принято в физиологической оптике Ь — 1/е и Ь' = 1т (в и е — угловые размеры в минутах наименьших деталей объекта, разрешаемых соответственно невооруженным и вооруженным глазом).
Для реальных приборов отношение полезного действия к увеличению Гг, т. е. Л7 = ЛГТ, называемое коэффициентом использования увеличения, всегда меньше единицы. Коэффициент Л' определяет рациональность выбора основных оптических характеристик зрительной трубы применительно к заданным условиям наблюдения.
ГЛУБИНА ИЗОБРАЖАЕМОГО ПРОСТРАНСТВА
Глубина изображаемого пространства определяется допус гш.и.й величиной кружка рассеяния ?' в плоскости изображения. Допустимая ветчина г' зависит от назначения оптической системы и условия наблюдения. Плоскости, названные на рис, 2.21 передней и задней плоскостями, ограничивают то пространство, которое изобра?кается еще редко при фокусировке объектива на плоскость наведения. Кружки pac.ei--ния в изображении должны быть видны наблюдатетю под предельны : углом г. величина которого колеблется в зависимости от условий ш-блюденкч от 1 до 4'. Действительный диаметр кружка рассеяния пр < наблюдении с условного расстояния г' — 250 tg е = 250 sin е = 250ь sin 1'. Кружок рассеяния г', спроектированный обратно па плоек'-ггь наведения, равен г = г'/У (У—масштаб изображения иль линейн'.е увеличение). Расстояние между передним и задним, планами 90
Д, + Д2 определяет геометрическую глубину резкого изобрел сиия и вычисляется по формуле
Тт = А, + А2 ® 2е»е/Р,
rJle Aj = егя^[) 4- ее); Д2 = е2е/(£> — ее); е выражается в радианах; g д_ расстояние от входного зрачка до плоскости наведения.
Если снимок будет получен контактным печатанием с негатива, то необходимо, чтобы на негативе все кружки рассеяния не превышали допустимой угловой величины. Поэтому г <: ek (k — расстояние, с которого будет рассматриваться снимок). Чтобы при этом восстановить
правильную перспективу предметов, расстояние k должно бить равно фокусному расстоянию примененного объектива. При этом условии г' = f'e и г = г'/Е = )'е/Е — ее; е, = De:{D + ее); е2 = De, (D — ее). Рассмотрим следующие случаи фокусировки.
1. Если фокусировать на бесконечность (плоскость наведения е = = оо), то «j = От.
2. Если фокусировать так, чтобы задний план был в бесконечности (е2 = сс), то ej = D/2e, т. е. в последнем случае расстоянье до переднего плана вдвое меньше, а глубина, следовательно, больше. Поэтому выгодно фокусировать не на бесконечность, а на плоскость Л2. Эту плоскость называют началом бесконечности, так как дальше нее все точки пространства изображаются в фокальной плоскости резко. Диафрагмированием объектива можно увеличить глубину и приблизить начало бесконечности.
Если фотографирование производится короткофокусным объективом и снимки получаются увеличением негатива в М раз, то допуск на диаметр кружка рассеяния на негативе должен быть уменьшен соответственно в М раз. В этом случае г' < f'e/M, г = ее/Л1;
с _____De De
1 D-i-eejM1 ^-D — eejM"
Глубина резкости телескопической системы
Глубина резкости, выраженная в диоптрийной мере, телескопической системы, у которой зрачок глаза действует как апертурная диафрагма, равна глубине изображения глаза Тгл — 1/3,5£Хл, уменьшенной в Г, раз
7Т = Тгл/Гт = 1 /3,5ОглГт. (2.59)
Это равенство справедливо и в том случае, когда увеличение телескопической системы больше нормального, т. е. когда диаметр выходного зрачка прибора меньше зрачка глаза. В этом случае в формулу (2.59) вместо Дгл глаза подставляется диаметр выходного зрачка прибора Dp1 По сравнению с глубиной аккомодации глубина изображения в телескопической системе очень мала, так же как и в лупе.
Глубина резкости лупы и микроскопа
Глубина резкости лупы вычисляется по формуле
= (2.ед
" 1Т°ГЛ
где Drn — диаметр зрачка глаза; f — фокусное расстояние лупы. Если для лупы принять в среднем Огл = 3 мм и е = Г (0,00029 рад), то Тл = 12,5/Гл мм.
Исключив из формулы (2.60) £>гл и f с помощью формул (2.37) и (2.47), глубину резкости микроскопа (мм) можно вычислить по формуле
rM = J^L. (2.61)
АГМ
Так как в пределах полезного увеличения микроскопа диаметр выходного зрачка 1 мм, то при определении глубины резкости в микроскопе следует исходить из волновой теории света (дифракции)
т —
м ~ 2А2 '
Глубина резкости при аккомодации глаза
В приведенных выше случаях предполагалось, что глаз наблюдателя аккомодирован на определенную плоскость. Однако глаз может аккомодировать от своей ближней точки до дальней (А = 1/а — 1/u^). Поэтому глубина резкости изображаемого пространства должна быть увеличена с учетом и глубины аккомодации.
Для лупы и микроскопа глубина аккомодации в пространстве предметов (мм), сопряженная с границами области аккомодации невооруженного глаза, может быть вычислена по формуле
т = f 250 Y А = -
а к 1\, 7 1000 1000 л’
где ?! — объем аккомодации глаза, (дптр). 92
Объем аккомодации для нормального глаза (эмметропа) при ар = = 250 мм составляет 4 дптр, тогда Та = 250/Г2 — 0,004/'2, где /' — заднее фокусное расстояние системы (мм). У лупы и микроскопа область аккомодации распространяется от передней фокальной плоскости всего прибора, оптически сопряженной с дальней точкой нормального глаза, в направлении к прибору.
Если изображение проецируется на экран или матовое стекло, то Та = 0. У зрительной трубы, установленной на бесконечность, дальная точка лежит на расстоянии (м) а'д = а^Г2 от входного зрачка.
У всех приборов глубина аккомодации обратно пропорциональна квадрату увеличения. Она играет существенную роль у приборов с малым увеличением в основном у слабых луп. Следует помнить, что изменением аккомодации нельзя получить резкое изображение всех предметов, расположенных в пределах глубины Та одновременно.
АБЕРРАЦИИ ЦЕНТРИРОВАННЫХ СИСТЕМ
Вследствие аберраций оптической системы точка объекта изображается в виде фигур рассеяния, а прямые линии — нерезкими и искривленными. Существует семь основных аберраций. Две из них — хроматические (продольная хроматическая аберрация, или короче — хроматизм положения и хроматизм увеличения), остальные пять относятся к монохроматическим аберрациям. Монохроматические аберрации можно разбить на аберрации широкого пучка (сферическая и кома) и полевые аберрации (астигматизм, кривизна поля и дисторсия).
Аберрации третьего порядка.
Коэффициенты Зейделя
При расчете оптических систем широко применяется теория аберрации третьего порядка [85, 86, 100, 102].
Поперечные аберрации третьего порядка для плоскости предмета, расположенной на конечном расстоянии, можно представить по степеням заднего апертурного угла при условии нормировки ар = 1; hx = а^; Pi = 1; <! = (высота пересечения второго параксиального луча с поверхностью):
—2n' Ag' = а' (а'2 ф- ф'2) St -ф (ЗсГ2 + ф'2) ©jSn ф-+ а'ш'2 (351п -ф- Z"S1V) ф- W;SV;
—2п' AG' = ф' (а'2 ф- ф'2) Si ф- га’ф'ш^ц ф-+ 4’ ®2 (SH1 + Z2S1V),
(2.62)
где / — е, = t, — s,; Agp и AGp — аберрации в меридиональном И сагиттальном сечениях соответственно.
Поперечные аберрации по степеням координат т, и на входном зрачке, когда плоскость предмета расположена на бесконечности (at= О, «г = —оо) при условии ар = 1; hj = 1; ij = ffr> / = —п ~ —1:
О„.Л„, + , 3/и?+.A«f (л
' bg-------------~pi *1® ' f’ +
+ wiwi (^iiioo 4-Sjv) + svx’
+ 'wi<0I(siii» + s1V)-
Здесь S|, Sn, Sin, Siv, Sy—соответственно поверхностные коэффициенты сферической аберрации, комы, астигматизма, кривизны поля и днсгорсия третьего порядка.
Л;. — высота пересечения с k-ii поверхностью первого параксиального луча; а и ч.'.. — углы с осью первого параксиального луча до и после преломления с k-ii поверхностью [проходящего через точку предмета, расположенную на оси (рис. 2.5) ]; и — углы с осью второго параксиального луча (проходящего через центр входного зрачка).
Коэффициенты аберраций третьего порядка бесконечно тонких компонентов *
В бесконечно тонких компонентах й и 11 постоянны. Принято обозначать через Р* и 1F* значение сумм Р% и W* по всем поверхностям «-го кэм.чж.л.-гз. Положив S (<р/л) = л(-, где ф — приведенные оптические 94
силы линз «-го компонента, из (2.64) можно получить для т тонких компонентов формулы
Из формул (2.65) вытекают два важных следствия.
1. Плоскость предметов находится на конечном расстоянии (<4 0)
S\ = slVP*‘, Su =t1P*— V
$ш = -^ P* - 2 (/, -S1) A. W* + (i _ v);
о J ’ '’I Ct J
S|V =ту(I-V); 51 (2.66)
+ ('1-s1)2 (-|~У (3 + я)(1 -V),
при условии a, = И; — sxV; tt = /7t; = 1; 1 = nx (tt — s,) V.
2. Плоскость предмета бесконечно удалена (а, = 0, s, = —сю)
S^ = P-> Sllx=tlP + W-, + U
Siv = jt; SVo. = /> + 3^ + ^(3 + n) (2.66a) при условии 04 = 1; ht = 1; f)1 = 1; tx = I — —nt — —1 . Если плоскость входного зрачка совпадает с тонким компонентом tx = 0, то 5|„ = Р, S,,. = W-, $и|я> = 1; S1Vw = л; 5Voo=:0; т. е. астигматизм, определяемый коэффициентом Siu, не поддается исправлению и имеет постоянное значение; дисторсия равна нулю.
Параметры Р и W (характеризуют аберрации тонких компонентов в случае а, = 0 и s, = оо) и Р* и W* (в случае а, ~!= 0) имеют линейную Зависимость; Р = [Р* — 4аW* + а (а' —а) ] [(4 Ц- 2л) а + а' ]/(а' — >-а)3; W= [W* — а (а' — а)(2 + л)]/(а' — а)2; величины Р, W 95
и л называются основными параметрами [85, 86]. Они зависят только от внутренних элементов компонента (радиусов поверхностей и от показателей преломления стекол) и полностью определяют все пять аберраций третьего порядка монохроматического луча. Практически я = 0,64-0,7.
Сферическая аберрация
Продольной сферической аберрацией называется разность по оптической оси отрезков sz' для лучей, выходящих из точки на оси и падающих на входной зрачок системы на высоте /1* (например, лучи 1, 2,4
Рис. 2.22. Сферическая аберрация линзы. Образование каустики
на рис. 2.22, а), и Sq— для параксиального луча, т. е. As' = s'k — s't. Продольная сферическая аберрация может быть выражена четной функцией переменной а иля h [85, 86, 100, 102]
Д^ф = ао'2 + &о'4 -[- со'6 + • • •,
где а, Ь, с и т. д. — соответственно коэффициенты аберраций третьего, пятого и седьмого порядков. При наличии сферической аберрации строение преломленного пучка остается симметричным относительно оптической оси. Поперечная сферическая аберрация равна Ag' = Аз'ф tg o'. Согласно формуле (2.62) поперечная сферическая аберрация третьего порядка Д81Игф=_o'3SlZ2n', а формуле (2.63) Лй;11сф = —
Поверхность, огибающая лучи, называется каустикой (рис. 2.22, а). В рассматриваемом пучке существует наиболее узкое место каустики, соответствующее наименьшему пятну рассеяния, где верхний луч пересекается с нижней ветвью каустики. Расчет распределения энергии в изображении показывает, что наилучшая плоскость установки, в которой получается наиболее резкое изображение, ие совпадает с плоскостью наименьшего поперечного сечения каустической поверхности. Построив (рафик поперечной сферической аберрации, можно с его помощью определить такую плоскость установки, в которой кружки рассеяния
наименьшие (рис. 2.22, б). Для этой цели из начала координат проводится прямая аа таким образом, чтобы кривая поперечной сферической аберрации вправо и влево от нее имела одинаковые отступления.
На рис. 2.22, б смещение плоскости установки определяется углом ф — наклона прямой аа' относительно оси ординат. Величина смещения (дефокусировка) плоскости установки параксиального изображения
До-',о'. Кружки рассеяния будут определяться расстоянием точек кривой до прямой аа’. Практически удобный способ нахождения наклона прямой, определяющей величину смещения плоскости установки, в которой кружки рассеяния наименьшие, заключается в следующем: проводят две касательные к кривой поперечной сферической аберрации, построенной симметрично относительно оптической оси. При этом касательные должны проходить через конечные точки В и В' кривой ВОВ'. Прямая, проведенная параллельно касательным и проходящая через начало координат О, будет искомой прямой аа'. (Для определения наклона прямой аа' можно ограничиться одной касательной.)
Кома
Под комой понимают асимметрию широкого наклонного пучка, вышедшего из точки предмета вне оси, по отношению к главному лучу пучка [12, 100J. На рис. 2.23 показан один из случаев меридиональной комы. Главный луч ВР пучка пересекает плоскость изображения на высоте у'гп. Верхний и нижний лучи, проходящие входной зрачок на
Вх.зр. Вых.зр.
Рис. 2.23. Строение широкого меридионального пучка лучей; возникновение комы
высоте ±т, пересекают плоскость изображения на расстоянии у'11П Я У-т от оси. Величина меридиональной комы k = (У+т+ yim)/2 —у'л. При наличии комы внеосевая точка предмета изобразится в виде пятна рассеяния, по форме напоминающего комету с ярко освещенной вершиной и довольно широким хвостом, плотность энергии в котором быстро убывает. Например, яркое пятно будет расположено в точке В'и, а хвост направлен в сторону от оси (внешняя кома). Из формулы (2.62) меридиональная кома третьего порядка (ф' = 0) равна = —3o'2a>1S[I/2/f'
Встречаются различные случаи сочетания комы со сферической полевой аберрацией. На рис. 2.24 схематически даны три случая строе-Иия пучка лучен в пространстве изображений [12].
4 В. А. Папон и др. 97
1. Сферическая полевая аберрация и кома (k = 0) исправлены (рис. 2.24, а). Лучи D\B’O и D2 В'„ пересекаются в точке B’t, находящейся в гауссовой плоскости изображения.
2. Кома исправлена, но имеется полевая сферическая аберрация, так как лучи D\B' и D'2B", симметричные главному лучу Р'В^, пересекаются вне гауссовой плоскости изображения (рис. 2.24, 6).
Рис. 2.24. Различные случаи сочетания аберраций в меридиональном сечении
3. Полевая сферическая аберрация исправлена, но имеется кома «в чистом виде» (рис. 2.24, в).
На рис. 2.25 показана графически структура пучка лучей, соответствующая случаям, изображенным на рис. 2.24. Обычно по оси ординат откладывается величина т, (или 102а'), а по оси абсцисс — у' (или = У' — Уд-
Рис. 2.25. Графическое представление аберрации в меридиональном сечении
Условия синусов 1
При невыполнении условия синусов элементарный отрезок, перпендикулярный к оптической оси, изображается лучами, проходящими центральную и краевые зоны системы, с разным масштабом (Д'В'к
1 Условие синусов необходимо для получения резкого изображения бес-конечно малого плоского элемента, расположенного около оптической оси и перпендикулярного к последней.
A'Bq), вследствие чего изображения получаются нерезкими (рис. 2.26). При выполнении условия синусов оптические пути всех лучей одинаковы; лучи пересекают плоскость изображения иа одной и той же высоте. Из этого следует пр — п' q' или пр = ndy sin о, п q — = ndy sin o', т. e.
ndy sin a = n'dy' sin a', (2.67)
где dy — длина изображаемого отрезка; dy' — его изображение; a И a' — углы, образуемые с осью до и после преломления через систему сопряженных лучей, идущих из точки на оси предмета; я и п — показа-
Рис. 2.26. Разность увеличений, даваемых различными зонами линз (а), и ее устранение путем выполнения условия синусов (б)
тели преломления сред, в которых расположены предмет и изображение. При я = я' — 1 из формулы (2.67) следует
dy'ldy = sin a/sin o'. (2.68)
Правая часть формулы (2.68) должна быть величиной постоянной для всех углов а и а' сопряженных лучей осевого пучка и равняться линейному увеличению для параксиального луча [101, 111]. Величина
к . / sin a , \ ДУ сл.
6 sin = ( -----;---1 ) = —- (2.69)
\ V sin a J V
определяет отступление от условия синусов. В случае бесконечно удаленной плоскости предмета условие синусов принимает вид
fcj/sin o'=/0 = const, (2.70)
где /у = hja,' — фокусное расстояние, вычисленное по параксиальному лучу.
Апланатические точки преломляющей поверхности
Две сопряженные точки, расположенные на оптической оси системы, Для которых устранена сферическая аберрация и соблюдено условие •Синусов, называются апланатическими точками, а сама оптическая система — апланатической.
4* 99
Сферическая преломляющая поверхность может иметь три пары сопряженных анланатических точек.
Первая пара: обе точки совпадают с вершиной поверхности s = = s' = 0, линейное увеличение V ~ 1.
Вторая пара: обе точки совпадают с центром кривизны, т. е, $ = = s' = r, V=n/n'.
Третья пара: сопряженные точки расположены на расстояниях s и s'.
В первой и третьей парах астигматизм отсутствует, во второй паре астигматизм не равен нулю.
Формы апланатических менисков
Существуют четыре формы апланатическнх менисков, которые дают апланатнческое изображение точки на оси при больших апертурах
вплоть до предельных.
Первая форма. Передняя поверхность а пл апатична к положению предмета, центр второй поверхности совпадает с центром изображения от первой поверхности (рис, 2.27, а). Мениск действует рассеивающе (выходная апертура больше входной). Его
Рис, 2.27, Формы апланатическнх менисков
радиусы = s1/(n + 1); г2 = Sj/n — d; линейное увеличение V = 1/п; фокусное расстояние
р __ 1_______si —„
п — 1 s( — d (п + 1) р
Вторая форма. Концентрические мениски — центры обеих поверхностей сов ца дают с центром предмета (рис. 2.27, б).
Третья ферма. Обе поверхности действуют апланатическп. Выходящий пучок смещается параллельно входящему (рис. 2.27, в)
t\ = sL/(n + 1); г2 = (Sj — nd)!(n + 1); V = 1,
Четвертая форма. Центр передней поверхности совпадает с центром предмета, вторая поверхность апланатична к предмету (рис. 2.27, г).
Для первой поверхности — sj = rj; Vi = 1/п;
для второй поверхности s2 = rr — d; r2 ~ nsJ(n-\~ 1); s'2 = ns2;
V2 = n2.
Линейное увеличение мениска в сопряженных точках А и А' равно V — п, фокусное расстояние
р п2 s — d ~~ п — 1 d + /zsx 01 ’
выходная апертура sin а3 = sin aj/V = = sin af/n. Мениск действует соби-рающе. Так,например, мениск из марки стекла ТК16 (nD = 1,6126), снижает апертуру выходного пучка в 1,6126 раза. Три апланатических мениска,
Рис. 2.28. Построение апланатических точек
установленных последовательно один за другим будут иметь выходную апертуру sin а7 = sin at/n3. Однако число примененных апланатических
менисков ограничено тем, что эти мениски становятся толстыми, а радиусы их поверхностей малыми. Поэтому практически невыгодно последовательно применять более трех менисков.
Апланатические мениски не дают действительного изображения. Чтобы получить действительное изображение необходимо иметь по крайней мере одну неапланатическую поверхность. Апланатические
поверхности играют большую роль в конструкциях сильных микрообъективов, у которых входная апертура доходит до 0,95 в сухих системах и до 1,5—1,6 в иммерсионных.
На рис. 2.28 показано построение апланатических точек А и А' Для преломляющей сферической поверхности с радиусом г < 0 и отделяющей две среды с показателями преломления п~ 1,5 и п'= 1 (воздух). Радиусы окружностей, концентричных преломляющей поверхности M0N (г = СО), равны СА = пг!п и СА' = пг!п'. Незави-
симо от величии углов о все лучи, вышедшие из точки А, находящейся на расстоянии s = 5т/3, преломляясь на сферической поверхности M0N, проходят через сопряженное с точкой А мнимое изображение А', находящееся на расстоянии s' = 5г/2. Линейное увеличение в апланатических точках А и А' равно V ~ п2 = 1,52 = 2,25. Конструкция таких менисков применяется в иммерсионных микрообъективах
Изопланатнческое изображение элементарной поверхности вблизи оптической оси
При неустранимой остаточной сферической аберрации в реальных системах стремятся выполнить условие Штебле—Лихоцкого, представляющее собой обобщенный закон синусов Аббе
Vn - 1 = -7^77 • (2.71)
Vn sin о s — t
Для бесконечно удаленного предмета
—^-7 —=4-^7, (2.72)
sin о и s — t * '
где hx — высота падения крайнего луча на входном зрачке; s' — t' — расстояние от выходного зрачка до плоскости изображения.
Выполнение условия (2.71) или (2.72) обеспечивает изопланатиче-ское изображение, т. е. все точки бесконечно малого элемента плоскости, перпендикулярной оптической оси, будут изображаться с одинаковыми погрешностями или недостатками.
Мерой отступления от условия изопланатизма служит величина п sin о As' AV . As'
4 ~ Vn' sin a' l + V *" V —s' ^2‘73^
ИЛИ
n — / -___4. _L ™ As* /2.74)
r°° \ sin o' 0 —s'/ /J /q ' ¥—s'* '* ’
Для небольшого линейного поля поперечная меридиональная кома равна km == 3z/'q.
Астигматизм и кривизна изображения
Элементарный пучок лучей, исходящий из точки вне оси, имеет в пространстве изображения в меридиональном и сагиттальном сечениях различные точки сходимости. Отрезки от точки падения вдоль главного луча до меридионального и сагиттального фокусов В и В’ до и после преломления через одну поверхность определяются инвариантами Гульстранда и связаны формулами [79]:
п cos2 в /tfn—и cos = (//cos 8 —n cos в) /г; (2.75)
n/ts — = (n cos s —/zcose)/r (2.76)
Величины /$, t'm и /' отсчитываются вдоль главного луча. При переходе от поверхности с номером k к другой поверхности с номером k + I учитывается переходная «косая» толщина. Ни в одном поперечном сечении астигматического пучка не получается точечного изображения; пучок лучей, лежащих в сагиттальной плоскости, вблизи точки В'п образует вместо точки горизонтальную линию, а пучок лучей, лежащих в меридиональной плоскости, вблизи В' образует вместо точки вертикальную линию (рис. 2.29). Посередине между меридиональным В'гп и сагиттальным В', фокусами (средняя кривизна изображения) получается круглое пятно рассеяния. В других сечениях между В'гп и B's 102
Рис. 2.29. Строение астигматического пучка лучей
Рис. 2.30. Изображение плоской фигуры астигматическими пучками
тарных пучков
фигура рассеяния имеет форму эллипса с различной ориентацией осей. Координаты фокусов элементарного астигматического пучка в области аберраций третьего порядка определяются по формулам (2.62):
4 = - -§r (3S.H + /2SiV); < = - -g. (Sni + /2«iv).
Проекция астигматической разности на ось системы г' — z’m = •— со 511 j/zi >
На рис. 2.30, а дано изображение плоской фигуры, состоящей из рада концентрических окружностей с центром на оси и их радиусов. Радиальные линии изображаются резко сагиттальными пучками, а концентрические окружности получаются размытыми (рис. 2.30, б); меридиональные же пучки дают обратные явления (рис. 2.30, в).
Средняя кривизна изображения равна 1/R' ~ (1,'Я'г + 1/.А?');2. Кривизна меридиональной и сагиттальной поверхностей равна
1/< = 2гт/у’2-, 1 / R's = 2z's/у'1. (2.77)
Если система не имеет аберраций высших порядков и астигматизм уничтожен (Sju == 0), то обе фокальные астигматические поверхности сливаются и изображение располагаетси на поверхности Пецваля, кривизна которой, согласно выражениям (2.64) и (2.77), вычисляется по формуле
УКр = = l/Rs = ~пlSIV = Л1 S fyl/r.
Стрелка поверхности Пецваля Д^ = у'2/2R'p — fyi/r. Из
теории аберрации третьего порядка z'm — &г'р = 3 — Дг'), 0ТКУДа
Д?р — (Згу — z^j/2. Можно соответствующим расчетом уничтожить астигматизм (z's — z'm = 0), но кривизна изображения будет оставаться (рис. 2.31, б) и, наоборот, уничтожить среднюю кривизну k (рис. 2.31, а) изображения, но тогда остается астигматизм (рис. 2.31, в).
Дисторсия
Нарушение подобия в геометрической форме между предметом и его изображением называется дисторсией (рис. 2.32). Изображение квадратной сетки (рис. 2.32, а) принимает подушкообразный (положительная дисторсия Д > 0, рис. 2.32, б) или бочкообразный вид (отрицательная дисторсия Д < 0, рис. 2.32, в). Дисторсия не вызывает нерезкости в изображении. Линейная величина дисторсии может быть определена как разность Дг/' = у’ — y'Qt где у' — действительная величина изображения предмета в гауссовой плоскости, образуемого главным лучом, проходящим через центр входного зрачка системы; ?/(' — идеальное изображение предмета г/, полученное с помощью формул гауссовой оптики, не учитывающей дисторсии у'о = Vy. Дисторсия в относительной (2 62) А = Дисторсия третьего порядка из формулы
Ag'=-^J-SV. • (2.78)
Если Ag — 0, у' = у'о при всех значениях у' = Vy, т. е. истинное значение V для всех отрезков остается постоянным:
у „ _ V' -s')tg<y
У tgtoi
= const - V.
В этом случае система дает неискаженное, т. е. ортоскопическое, изображение. Если Ag' 0, то у’ = у$ + Ag'; V = V + &g!y\
Ду V — V = &g'/y.
(2.79)
Ограничиваясь областью аберраций третьего порядка, из формул (2.78) и (2.79) получим
д v = - ТТ7 Sv‘ <2>8°)
Оптическая система дает ортоскопическое изображение, если AV/V = 0. Необходимым и достаточным условием ортоскопии в области
Рис. 2.32. Искажение изображений дисторсией
аберраций третьего порядка является Sv— 0. Когда предмет находитси на бесконечности, выражение (2.80) теряет смысл. Из формулы (2,63) при tg иц — (ох следует
г
~~ У Уо = 2ц' *
или Agr'/£/6 — tg2co1SVoo/2n'. Если SVoo = 0, то Ar/Z = 0, и, следовательно, у' ~ уQ, т. е. для всех углов поля зрения <ог при выполнении условия ортоскопии должно соблюдаться условие —у*Itg (Ох = % — = const, т. е. фокусные расстояния, вычисленные по действительным главным лучам, должны оставаться постоянными и равными фокусному расстоянию, вычисленному по параксиальным лучам [12, 79].
В системе, у которой отношение у’7tg (Dt остается с достаточной степенью точности постоянным для углов сог, но не равным параксиальному фокусному расстоянию считается исправленной так называемая фотограмметрическая дисторсия.
В зрительных трубах допускается дисторсия от 3,5 до 10%. В аэросъемочных объективах «Руссар», рассчитанных пр оф, М. М. Русиновым для целей картографии, дисторсия не превышает 0,04%.
Хроматические аберрации
Хроматические аберрации возникают при преломлении белого света на оптических поверхностях; при этом происходит разложение света на спектральные составляющие, Это свойство преломляющей среды носит название дисперсии.
При расчете оптических систем различают два вида хроматических аберраций: хроматизм положения и хроматизм увеличения.
Хроматизм положения определяет окрашенность изображения осевой точки предмета, а хроматизм увеличения — внеосевой точки.
Область ахроматизацнн оптической системы зависит от ее назначения. Для визуальных приборов хроматическая коррекция производйтся для цветов лучей С н F, поскольку глаз обладает наибольшей чувствительностью к средней части указанного интервала спектра (Л = 550 нм) [12, 85], В случае передачи изображения с помощью микроскопа с большим увеличением на фотографическую пленку применяют коррекцию, при которой соединяют изображения трех длин волн: D, С и G'.
Хроматическая аберрация положения. Эта аберрация определяется расстоянием между гауссовыми плоскостями изображения для двух цветов и вычисляется по формуле [85]
1 Р
^Sxp ip
„ 6а* с Дл* А
где С* — о —— ; Дл* = — разность показателей пре-
ломления для длин волн Х2 и Xi (условно соответствующих, например-, цветам F и С); ц* ~ 1/л*; а* — углы с осью первого параксиального луча, принятого для средней длины волны — (Лх + Х2)/21 соответствующей основному показателю преломления л0.
Для простой тонкой линзы в воздухе
о
VI 6а* Дп* _ а' — а & __ ЛФ
Zj 6ц* л* ~ 1 — п “ v
1
где V — (nD — 1)/(Лг — псУ ® — оптическая сила линзы.
Для системы, состоящей из т бесконечно тонких линз, хроматизм положения для случая ах =£= 0 вычисляется по формуле
д4р = - (^i/vi + %Ф2/у2 + • • • + ^Om/vm) a'2.
Для одной бесконечно тонкой линзы в воздухе
Asxp= -s'2/fv; AsKp„ = -f'/v.
Условия ахроматизации двух линзового склеенного объектива
<Pi Д- <рз = 1;
21 _L 21 - A. m - V1 .
vt v2 Vt — v2
Хроматическая аберрация увеличения в относительной мере [85]
Для компонента, состоящего из т бесконечно тонких линз в соприкосновении, хроматизм увеличения вычисляется по формуле
Пример. Определить хроматизм увеличения для простой линзы из стекла БФ21 (v = 40), если предмет расположен на бесконечности, а входной зрачок — в переднем фокусе линзы Oj = —1).
Решение. А^р/У = ®x/v = — 1/v — —0,025 (2,5%).
Вторичный спектр. Расчетом оптических сил и ср2 марок стекол отдельных линз системы можно совместить в плоскости изображения
в одну точку два луча различных длин волн (например, С и F), но при этом лучи других волн (например, D) не пересекут ось в той же точке. Такой остаточный хроматизм As'dp “ sf — sd ПРИ условии — — = 0 называется вторичным
спектром. На рис. 2.33 приведена кривая для системы, у которой одновременно с исправлением хроматизма для линии С и F устранен вторичный спектр для линии D (апохроматическая коррекция). Изображения для этих цветов расположены в одной плоскости. Оптические системы, в которых устранен хроматизм положения для двух цветов (напримерн,- С и F), называются ахроматическими.
Апохроматическую коррекцию
Рис. 2.33. Графики коррекции хроматизма положения:
имеют астрономические приборы, некоторые микрообъективы и репродукционные объективы для цветной фотографии, геодезические зрительные трубы н другие системы, где требуется большое увеличение.
Вторичный спектр двухлинзовых
I — неисправленная система; II — визуальная коррекция; III — апси хроматическая коррекция; / V — актиническая коррекция (фотограф фическая)
положения =£ 0, то
объективов. Если хроматизм
As
“ Vq — 1(^£)г)з V1 (Pdf)\ ~
s'2 (Ppp)?
f' 4 — vt
Когда As'(F_C)o = 0,
ь'2 (Pdf)* (Pdf)i +•/
Если предмет на бесконечности, то s' ~ fr, тогда s'-'/' “ /'. Величина вторичного спектра пропорциональна отношению разности частных относительных дисперсии PDF — (nF— (nF — к разности коэффициентов средней дисперсии. Эти величины для каждой марки стекла берутся из ГОСТ 13659—78.
Величина вторичного спектра зависит от того, для каких двух лучен устранен хроматизм положения данного объектива. В оптических приборах визуального назначения (лучи С и F соединены) вторичный спектр равен s''/2000/'. В системах, служащих для фотографирования
с визуальной наводкой на фокус (фотообъективы и некоторые астрономические объективы), вторичный спектр для цвета F (когда соединены
D и О'), равен s'2/1300/'.
Величины относительных частных дисперсии, например для линий
спектра С, F и G', для
Рис. 2.34. Гр афическое представление сферохроматической аберрации
большинства силикатных стекол могут быть выражены следующей эмпирической фор-мулон Р0.с = f (yCFy.
РО’С = (.пО' =
= 1,674 — 0,0018vcr — а + bvCF.
Зависимость, представленная формулой, выражает собой некоторую прямую линию. Применение особых марок стекол и кристаллов (ОФ4, ОФ5, OKI, ОК2, CaF2, LiF и др.), не лежащих на указанной прямой, значительно уменьшает величину вторичного спектра [85].
Хроматическая разность сферических аберраций (сферохроматическая аберрация). Сферическая аберрация для различных длин волн имеет различные значения (рис. 2.34); для лучей двух длин волн сферическая аберрация вычисляется по формуле
AsXF ~ (SF sc)h (SF Sc)d*
где h и 0 указывают, что ход соответствующих лучей определен на высоте h входного зрачка и в параксиальной области.
При наличии сферохроматической аберрации хроматизм исправляется для средней зоны (обычно для К 3/4).
Зависимость между волновой и продольной аберрациями
Волновая аберрация вычисляется по формуле [85 J
N == — J (As' — £) sin a* rfa'.
Для малых углов а'
W = -V ( (As'-g)rf(a'2),
где As' = па'2 -J- -ф со'6 -J- • • -.
После интегрирования в единицах длин волн
Ж = —а'2 (па'2/2 + Ьо'Чз + са'6/4 — g)/2X =
= —а'? Asm/2 + ASy/3 + Asvii/4)/2a + gaz3/2X,
где Asj((, А$у, AsyH— аберрации третьего, пятого и седьмого порядков; £а'2/2Х — дефокусировка, определяющая плоскость наилучшей установки от гауссовой плоскости.
Таблица 2.2. Вычисление волновой аберрации
bin щ Д s' Ю2а' д$ш Asv AsVII
—0,4 КТ/4 -0,4 К172 —0,4 К 3/4 -0,4 —0,8 -2,5 1,02 1,45 1,70 2,05 —0,71 — 1,42 —2,13 —2,84 0,29 1,15 2,58 4,60 —0,07 —0,52 —1,77 -4,20
sin од AsIJI Vsv 2 1 f 3 + А SVII + 4 __ q'2 2Х N X с к Л7Х в плоскости установки
СЧ 1 "Ф 1 ’—1 Х-<~ 1 со TF т* о о о о 1111 —0,28 —0,46 —0,65 —0,94 —0,089 —0,178 —0,267 —0,356 0,02 0,08 0,17 0,34 —0,08 —0,17 —0,25 —0,34 —0,06 —0,09 —0,08 0
Способы вычисления волновых аберраций.
I. Если As' достаточно плавная, то вычисление Az очень удобно производить по методу Е. Г. Яхонтова: определяют по кривой или непосредственно вычисляют As' для края апертуры о^р и о'0|1а = = <?кр' V 2>
Вычисляют продольную сферическую аберрацию третьего порядка = —Ц/25{/2/?/ [см. формулу (2.62)] и затем из двух уравнений AsKp = AsiII + AsV + Asvn и As30Ha ~ ~ ^SIIl/2 + ^sv/4 +
+ Д$уП/8 определяют Asyn = 2As^p— 8As^— + 2AsJI{ и A$y = = As^p — ASyH— As[H. Дальнейшие вычисления производят по табл. 2.2.
Пример. Определить волновую аберрацию микрообъектива 20X0,40, для которого вычислены следующие величины: As^0 = —2,5 мм, As' =-0,8 мм; 102<т'р = 2,03; 1С2а^_= 1,45; = —2,84;
As; = 4,60; AsyH = —4,20. Промежуточные значения As[H, Asy, Asyn пропорциональны соответственно второй, четвертой и шестой степеням sin Плоскость установки для края N — 0 (см. табл. 2.2)
смещена на В = ;VKp2Z <з'~ = —0,34,0,356 = —0,96 мм. Эта плоскость (рис. 2.35) определяется прямой /, проходящей через начало координат и последнюю точку кривой волновой аберрации, пос1роенной по данным Лг (табл. 2.2). Прямая // построена так, что расстояние точек кривой (волновые аберрации), измеряемые в направлении оси абсцисс, от точек прямой наименьшие. Если разность As^p — AsJn для краевого луча
Рис. 2.35. Волновая аберрация
в четыре раза больше, чем для второго луча, то Asyn будет отсутствовать. В этом случае вычисление волновых аберраций упрощается, так как fie требуется определять S ; тогда Asfn и Asy легко определить из двух уравнений;
Asy = 2 AsKp — 4Asj< 1/2; ^siп = A$Kp Asv*
2. Если кривая, изображающая продольную сферическую аберрацию как функцию от х = -- 104а'2, имеет сложный вид, можно использовать способ, основанный на применении формулы трапеции
“ [д$о/2 + +
+ А$3ф ••• ф Asn/2]
где Asq, As{ — значения, найденные по кривой для равноотстоящих значений переменной х; h —
величина промежутка.
Пример. Определить волновую аберрацию объектива, для которого расчет дал следующий результат при длине волны X = 129,6 им:
sin <Tt <У', рзд Ю*ог'2 = X As'
0 0,638 0,9 0,006 0,008 0,36 0,64 —1,82 —0,62
Строим кривую As' в зависимости от х, разбиваем область интегрирования иа шесть равных частей н по графику определяем значения As'. Затем вычисления производим по табл. 2.3, где Н = 0,107; ///4 — 0,027; Z//104(4X) = 0,027/1,296 = 0,0209. Для определения Nik в длинах волн необходимо числа столбца 4 умножить на 0,0209. Изменением плоскости установки, т. е. величиной £, вводят изменение в величину Nik, равное иа краю — 0,5£а^. Подбирая плоскость установки таким, образом, чтобы иа краю было Nik — 0; (В = 2/VKp/o^8 = 0,94), вводим на разных зонах изменения Nik, приведенные в столбце б. В столбце 7 rmba окончательные волновые аберрации.
3. В некоторых случаях по известным значениям поперечной сферической аберрации, применяя формулу
Зачисление волновой аберрации производят по табл. 2.4,
Таблица 2.3. Вычисление волновой аберрации при пользовании формулой трапеций
10*0'2 = Л As' Суммы попарно Суммы сверху N/K в гауссовой плоскости 1_ Sit'2 2/. ‘° Лг/л для плоскости 6 = = — 0,94 мм
1 3 4 5 6 7
0 0 0 0 0 0 0
0,107 —0,74 —0,74 —0,74 0,01 -0,05 —0,04
0,214 — 1,40 —2,14 —2,88 0,06 —0,10 —0,04
0,320 — 1,82 —3,22 —6,10 0,12 -0,15 -0,03
0,427 —1,75 —3,57 -9,67 0,19 —0,20 —0,01
0,534 — 1,40 —3,15 — 12,82 0,26 —0,25 0,01
0,640 —0,62 —2,02 — 14,84 0,30 —0,30 0
Т а б л и ц а 2.4. Вычисление поперечной и волновой аберраций
sin 0i 1О40' As' 1 04Ag' 104До' 4(д^ :+Л^ + |)
—0,65 Ц1/4 ПО "4,37 -480 НО -0,024
—0,65 158 -6,3 к -1000 4 18 -0,074
—0,65 С3/4 —0,65 192 215 -5,2 0,21 -1000 50 г Г J >3 -0,100 -0,048
sin <rt 104Л/ 104 2 N ж — Л’д для плоскости 3 — 4,64 мм
—0,65 Ц1/4 2,640 2,640 0,45 —0,38 0,07
—0,65 К1/2 3,552 6,192 1,05 —0,96 0,09
—0,65 СЗ/4 —0,65 3,400 1,104 9,592 10,696 1,63 1,82 -1,34 -1,82 0,29 0
Для вычисления волновых аберраций в объективах микроскопа удобно пользоваться приближенными формулами, учитывающими аберрации третьего и пятого порядков:
N/к = (70 — 110а) As'Од, при а < 0;
jV/Z — (70 + 40а) As'o^, при 0 < а < 1 j
N/Z = ИОДЗкрСГд, при а > 1,
ш
где а — As'p/As'; As' — сферическая аберрация для апертурного угла К Ь2од'.
Допустимое значение вторичного спектра и кривизны изображения при /, — 0,000589 мм составляет N/k — 850<;Од,, где £ — величина дефокусировки. Подставив вместо § значение величин вторичного спектра, меридиональной или сагиттальной кривизны и задаваясь левой части равенства, определяют допустимые значения этих величин [711.
Объективы из двух склеенных линз
Разработанный Г. Г. Слюсаревым метод расчета двух линзовых склеенных объективов дает возможность определить пару стекол, удовлетворяющую требуемым параметрам Р, W и С, с помощью которых исправляются сферическая аберрация, кома и хроматизм положения [85, 86].
При заданном значении С приближенно вычисляют Р$ — Р — — 0,84 X (W— 0,15)2. Затем по cp&, Qo и PQ из таблиц [85, 86] подбирают подходящую пару стекол. Предел относительного отверстия двухлинзовых склеенных объективов зависит от остаточных аберраций высших порядков и ие должен превышать следующие значения:
Dlf 1 : 4 1 : 5 1 : 6 1 : (8-5-10)
ff, мм 150 До 300 До 500 До 1000
В табл. 2.5 даны конструктивные элементы двухлинзовых склеенных объективов, а в табл. 2.6 — остаточные аберрации для точки на оси объективов коллиматора, приведенных в табл. 2.5 строки 16 и 17.
Линзы объективов, у которых световой диаметр превышает 60— 70 мм, рекомендуется применять несклеенными или соединять оптическим контактом, воздушный промежуток между линзами должен быть порядка 0,05 мм. Поле зрения не должно превышать в среднем 10—15° при малых и 7—10° при больших
Двухлинзовые объективы применяются в качестве компонентов оборачивающих систем, половинок симметричных фотографических объективов, микрообъективов с числовой апертурой до 0,1. Прибавляя к двухлинзовому объективу простой мениск, можно повысить (D//')oej до 1 : 3,5.
Система двух одинаковых склеенных объективов, поставленных вплотную друг к другу с одинаковым расположением радиусов кривизны, увеличивает почти вдвое относительное отверстие по сравнению с одним компонентом [86, 100].
Два компонента из двух склеенных линз, разделенных большим воздушным промежутком, применяются в качестве проекционных объективов (Diff ~ 1 : 2 и 2со— 20— 22°) и микрообъективов с числовой апертурой до 0,4.
Таблица 2 5. Конструктивные элементы двухлиизовых склеенных объективов телескопических систем (размеры даны в мм)
№ п/п п Г* г8 б?! ^2 М ар к а стекла Св. 0 Г
1-я линза 2-я линза
1 18,88 8,95 —203,2 0,8 2 Ф101 БК108 5 36,06
2 62,81 —47,64 —144,88 4 2 К8 ТФ2 24 104,98
3 71,12 —45,29 —139,32 4 2 КЮ8 ТФ101 24 111,71
4 62,23 —52,97 —255,9 3,52 1,97 К8 ТФ1 18 119,97
5 118,03 —46,13 —201,4 6 3 БК110 Ф104 23 150,2
6 196,79 —41,3 —98,63 2,8 1,6 К8 Ф1 12 154,3
7 137,09 —68,39 —177,83 4 2 ТК2 ТФЗ 15,7 164,99
8 103,72 —89,71 —434,5 2,5 1,5 К8 ТФ1 18 199,7
9 292,4 79,98 —161,81 2 3 Ф4 КФ4 18 250
10 319,9 —66,22 — 159,22 4,4 2,7 К8 Ф1 21 250,4
11 363,1 —74,82 —179,5 5 3,1 К8 Ф1 21 283
12 425,6 —87,9 -210,9 5,8 3,6 К8 Ф1 21 332
13 270,4 112,62 —542,93 3,6 5,8 Ф1 К8 25 426,67
14 368,1 —267,3 —816,6 4,4 3,9 К8 ТФ2 25 610,04
15 570,2 —363,1 —879,0 8 6 БКЮ8 ТФЗ 58 768
16 578,1 —415,0 —1786,5 20 15 К8 Ф1 150 998,3
17 247,2 142,56 оо 9 11 ТФ1 КЗ 80 559,3
Таблица 2.6. Аберрации объективов коллиматора (см. табл. 2.5)
№ п/п А sin о ' D с * F 1 «k co
s' As' А/' n (%) As' As'
0 0 981,89 0 0 0 1,19 — 1,53 — 2,72
16 75 V 0,053 981,61 — 0,28 — 0,56 — 0,03 0,84 — 1,62 — 2,46
75 0,07 5 981,47 — 0,42 — 0,82 0,04 0,60 — 1,54 — 2,14
0 0 583,44 0 0 0 0,41 -0,08 — 0,49
17 40 /1Д' 0,047 583,38 — 0,06 — 0,11 — 0,01 0,32 — 0,03 — 0,35
40 0,067 583,41 — 0,03 — 0,11 — 0,01 0,31 0,14 — 0,17
Особенности расчета окуляров
Окуляры большинства зрительных труб имеют фокусное расстояние в пределах 10—40 мм и относительное отверстие 1/4—1/15. Окуляры телескопических систем в зависимости от величины углового поля делятся на следующие тины 7 с нормальным угловым полем 2 со < 55° с увеличенным угловым полем 55° < 2со < 70° и широкоугольные > 70°.
Удаление выходного зрачка колеблется в пределах от 0,4 до 1,5/'. Если /'//' 1, то такие окуляры называются окулярами с удаленным
зрачком. Так как окуляры работают в узких пучках лучей, то в них должны быть исправлены в первую очередь кома, астигматизм, кривизна поля и по мере возможности сферическая аберрация, обе хроматические аберрации и дисторсия. При отсутствии сетки в фокальной плоскости окуляра последний можно применять с неисправленными сферической аберрацией и хроматизмом положения, компенсируя их аберрациями объектива и других предшествующих окуляру компонентов, В длиннофокусных широкоугольных окулярах не следует допускать больших аберраций в зрачках. Обычно окуляр подбирается или рассчитывается таким образом, чтобы его аберрации компенсировали аберрации предшествующей ему системы. Некоторые окуляры типа Кельнера, орто-скопические, симметричные и др. (см. гл, 4) часто применяют в качестве проекционных в микроскопе.
Сходимость меридиональных и сагиттальных бесконечно тонких пучков за окуляром с угловым полем 2<о > 60° обычно определяют в диоптрийной мере по формулам [см. формулу (2.84)1 Lm cos со' = = -(4 + ок) Ю00Хк; £s cos со' = -(г; + ок) 1000/^к (аберра-ции суммируются в передней фокальной плоскости окуляра), В технической документации для таких окуляров приводятся со, z'st z'm, f^ap.
1 В микроскопии принято считать окуляр широкоугольным, если диа^ метр поля зрения, изображенный через окуляр на расстоянии 250 мм от его выходного зрачка, составляет величину не менее 170 мм. Эта условно приняв тая величина вычисляется Как произведение диаметра нолевой диафрагмы окуляра на его увеличение в называется окулярным числом К [71].
f', L3 cos co\ Lm cos й>\ Обычно в окулярах с увеличенным угловым Молем f'm > /' > . Дисторсия вычисляется по формуле
Дсо' == Ag7(/7cos2 cd' — dkg'ld tg co')-
При больших углах со' производная от дисторсии dkg id tg со' может быть очень велика. Если дисторсия положительная, то 2со < 2со' (см. рис. 4.56 и 4.58, б); если дисторсия отрицательная, то 2<о > 2со'; если дисторсия равна нулю, то 2ю = 2со'.
Линзовые конденсоры
У хорошо корригированных конденсоров диаметр наименьшего кружка рассеяния составляет 3—10% от величины изображения источника [12],
Для однолинзового конденсора радиусы сферических поверхностей определяются по формулам
д — 1 , Т7 п— 1 ------—; га = sV па, — V па2 —
при а' = 1; == V; hL = 04s (s — расстояние предмета от линзы,
V — увеличение линзы).
Т а б л и ц а 2.7, Значения параксиалыь ’тлов в однолинзовом, двухлинзовом, трехлинзовом ; шденсорах при минимуме сферической аберрации [64J
$1 0 =/= 0 Sj = оо, а, = 0
Параксиальные углы 1 Число линз m
1 2 3 1 2 3
oq Произвольное * 0 0 0
«2 (04+04) (З04+04) В/4 (504+04) В1'^ В/2 В/4 S/6
аз (а,+а6)/2 (2а1+а7)/3 1 1/2 1/3
а4 («,+305)3/4 (04+04) В/2 ЗВ/4 В/2
at/V (at+2a7)/3 1 2/3
а6 (ai+5a,) В/6 5#/6
а7 04/V 1
Примечание. В = (1 -f- 2я)/(2 -f- л), V — линейное увеличение. ♦ Рекомендуется брать — F, тогда ао/П^.[ ~ 1-
Т а б л и ц а 2.8. Схемы оптики конденсаторов в зависимости от апертуры А н увеличения V
Схема оптики А (-V) Характеристика схемы
А 0,15 — Линза с минимумом сферической аберрацией; 5г = ОО
.^1 ¥ 0,4 1—3 Линзы плоско-выпуклые /
.лЛ 0,6 1,5-4,5 1 — мениск апланати-ческий; 2 — линзы плоско-выпуклые
А fc 0,7 2—6 1 и 2 — мениски апла-нэтические; 3 — линзы плоско-выпуклые
0,7 2—6 Вторая поверхность асферическая
0,4 4—10 Линзы с минимумом сферической аберрации
0,5 10—оо 1—мениск, близкий, к апланатическому; 2 — линза плоско-выпуклая с минимумом сферической аберрации
* 0,5 10—оо Втор ая повер хность асферическая, преимущественно параболическая
U 0,7 10—оо 1 — мениск, близкий к апланатическому; 2 — вторая поверхность линзы асферическая
т а б л и ц а 2.9, Оптические характеристики и конструктивные элементы коллекторов
( Зхема оптики А (-Ю г Марка стекла Св. 0 Г
.,-^7 Ж, 17,2 0,63 -— 70,47 —13,213* БФ13 24 18,29
F Г И F1
Л VZ г /= оо
&,9 8,2 М 0,52 5 —39,28 —24,7 —164,08 —43,13 114,48 —114,48 ТК2 ТК2 ТК2 31,4 34 37,8 39 40,5 40,6 33,63
А f и Л /<д ЧК1 \пд F' а'
— ОЛ 1х>1 I 4^ 10 юо —*
51,5 6 —* >4 6^6 „ 1
к J 'Ц 52,1. 4Г 0,52 5 —31,4 —22,25 —57,34 —37,495 102,53 —59,246 ТК2 ТК2 ТК2 30,6 32,7 35,9' 37,2 40,6 41,0 33,58
А г к //?\ 1/И
Ay/i OJ^. л 4 8 _ 25
0,65 -— —12 —10 124,42 —18,68 БФ13 К8 16 18 24 17,7
F /\Х f С\д F'
/ 1 J < 1\\ 1 F 1 4>J 0.1 S =с<
> 9
f?
_ -98$ 152 F'm 0,34 5 226,4 —45,1 * - TK2 54 16,67
у I г г
*4-00
-22J /4 FrAf 0,47 7,4 69,82 — 17,0* ЛК5 27,7 32,1 30,17
А
292^ J50^
А ~14,5 0,62 9 69,5 —15,5 * TK16 30 22,1
г А f'a'
J20^
Продолжение табл. 2.9
!•
Схема оптики А (-V) Г Марка стекла Св. 0 Г
г2‘ А |Г U 12_ 29,4 irU F' А' 0,43 7,5 67,77 — 17,1* Кварц 30 31,16
-25,6 -«——l К/ -ЛлГ цк f 2 г f' а' 0,64 38,5 —63,39 —27,29 оо —40,3 * ТК2 ТК2 44 44 54 54 37,73
ш 5g,^.5y? 1- * 7 Ц 155 J.4 F1 А1 80 -*Ч 0,64 38,5 —63,39 —27,2 • оо —44,0 * Кварц Кварц 34 44 56 Г = 37,8 (для X — — 257 нм) />41,4
тг/д 4|А / I’"' ^24^252 ' \ ч/ эдл U .АА d 0,67 6,5 —43,65 —20,42 оо —29,0 * ТК2 ТК2 36,5 43 44 28,3
-24J 4 ft г*— 4Ь\5 ,1 < »г w 'ij 25\л ^4 У f' а' ,4Sg 0,5 8 135,52 —28,05 —27,35 —203,7 112,98 —27,5* ЛК5 ТФ5 ЛК5 36 48 60 56,94
л к 1 А I-/4O f-<—-—> > ,4 /4 16 »U»l!« >|<> кУи£и., Г $5 г Т ГТ 7 _г'/ 7/?г 0,4 7,4 44,57 —12,74 —9,333 —28,97 49,55 —16,74* ЛК5 ТФ5 ЛК5 18 34 27
Примечание. Звездочкой обозначены радиусы при вершине параболоидальной поверхности.
пе
При минимуме сферической аберрации
(аг)тш = (2п + 1) (V + 1 )/2 (п + 2),
Если предмет на бесконечности (s — оо), то V -> 0, lim (sV) = f 9 Wmin = 2 (2 + п)(п — l)/(2n2 + л); (г^щ = 2 (2 + п)(п — 1)/(2п2 — — л ~ 4); при п = 1,5, (r^min/Wmtn ~ “б- Аберрации лиизы определяются из формул (2.63) и (2.66а).
В табл. 2.7 даны значения параксиальных углов в конденсор ных системах при минимуме сферической аберрация (толщины линз и воздушные промежутки между ннмн бесконечно малы, преломляющие поверхности сферические). В табл. 2.8 приведены оптические схемы (ориентировочные) некоторых конденсоров в зависимости от апертуры и увеличения. Оптическая схема конденсора типа четыре (табл. 2.8) имеет относительно малое рабочее расстояние, что может оказаться недопустимым при использовании некоторых источников света. В этих случаях для достижения sin — 0,7 рационально применять конденсор типа три, у которого выпуклая поверхность аплаиатического мениска асферическая. В табл. 2.9 даны конструктивные элементы коллекторов с параболоидальной поверхностью для микроскопов.
Назначение асферических поверхностей
Асферические поверхности применяются для повышения качества изображения, контраста и предела разрешения системы, увеличения углового поля зрения и светосилы (не в ущерб качеству изображения), замены сложной многолинзовой системы более простой системой с меньшим числом линз или зеркал с асферическими поверхностями с целью уменьшения габаритов и веса системы (80, 100, 102].
Особенно заметный эффект применения асферических поверхностей имеет место в длиннофокусных системах с большим относительным бтверстнем (зеркально-линзовые системы), а также в панкратнческих системах с большим диапазоном изменеиня увеличений.
Выражение аберраций системы через аберрации ее компонентов
Расчет оптической системы делится на два основных этапа — габаритный и аберрационный. При габаритном расчете оптик-конструктор должен учитывать коррекционные возможности разрабатываемой системы. Для этой цели последняя разбивается на отдельные составные части (объектив, окулир, оборачивающую систему и т. д.),*для которых определяются: относительное отверстие, линейное илн угловое поле зрения, положение зрачков, коэффициент виньетирования, величины допустимых остаточных аберраций и т. д. В зависимости от указанных характеристик выбирают степень сложности конструкций отдельных компонентов системы. На практике часто приходится компоновать систему из отдельных частей, аберрации которых известны.
Для систем, обладающих небольшой светосилой и малыми угловыми полями, аберрации отдельных компонентов можно переносить в сопряженные плоскости изображения других компонентов по правилу сложения аберраций третьего порядка (приближенно), т. е. поперечные аберрации умножаются на линейное увеличение, а продольные — на квадрат линейного увеличения тек компонентов, через которые переносятся аберрация.
Если AgJ, Л^2* •••> &g'k и ^2» ...» Vk соответственно поперечные аберрации и линейные увеличения первого, второго и Анго компонентов, то поперечные аберрации всей системы в пространстве изображения k-то компонента будут
Ag' = ^g\V.y3- Vk + Ag.'V3V4- • -Vk + • • • + Agfe.jVft + Ag; (2.81) и продольные аберрации
As' = As^- + As>j^ >V2 + • > + + As^. (2.82)
Формулы для вычислений аберраций системы после окуляра
1. Аберрации в угловой мере (мин) можно вычислить, определив суммарные поперечные аберрации в передней фокальной плоскости окуляра
Дсо' = +.1 ~ Ag°K 3438, (2.83)
f ок
где Ag{ — поперечная аберрация системы до окуляра, вычисленная в прямом ходе лучей; Ag0K — поперечная аберрация окуляра, вычисленная в обратном ходе.
2. Продольные аберрации, не зависящие от апертуры (кривизна поля, астигматизм, хроматизм положения и т. д.), принято определять в диоптрийной мере L по следующей формуле:
Аз' + АзД ^к/юоо ’
(2.84)
где /'к (мм); Az= f^/1000 — величина продольной аберрации в пе-редней фокальной плоскости окуляра, соответствующая продольной аберрации в пространстве изображений в одну диоптрию.
Пример. Определить аберрации всей системы в передней фокальной плоскости окуляра и после окуляра телескопической системы, содержащей двухкомпонентную оборачивающую систему с параллельным ходом и V — —2х (см. рис. 2.59). Фокусные расстояния и относительные отверстия компонентов трубы даны в табл. 2.10, аберрации — в табл. 2.11.
Сложение аберраций системы (без окуляра). Продольная сферическая аберрация для основной длины волны = 589,3 нм [см. формулу (2.82)] Д5сф = AsodV2 + Asi V2 + As2 — (Aso6 + Asi) V2 + As2 = = (—0,15+ 0,25) 4 — 0,05 — 0,35.
По этой формуле были вычислены следующие продольные аберрации:
1) хроматизм положения на «оси» = —1,3 (для параксиаль-
ных лучей);
2) хроматизм положения на «краю» (йкр = 10), AsIf-C) = 0,38;
3) сагиттальная и меридиональная кривизна г' — 1 и г^= —4. Поперечные аберрации (см. формулу (2,81)]
Таблица 2.10. Характеристика компонентов телескопической системы
Характеристика Компоненты системы
Объектив + коллектив Оборачивающая система (компонент) Окуляр
первый второй
Фокусное расстояние, мм 100 200 400 25
Относительное отверстие 1 : 5 1 : 5 1 : 10 1 : 10
1) хроматизм увеличения &у{г-с) = (&y'(F-C)—&y'(F-О.) J v| + + Щр-С)г = (°-02 - 0,02) 2+ 0,01 = 0,01;
2) дисторсия Дг/' = (0,05+ 0,15) 2 — 0,20— 0,20;
3) условие изопланатизма ц (%) — т)об—Ц1+Ц2~—0>20 + + 0,10 + 0,15 = 0,05.
Вычисление аберраций системы после окуляра. Аберрации в диоптрийной мере [см. формулу (2.84)]
(As'+ As'к) 1000 (0,35 —0,10)1000
Деф =--------—j-------=-------2^---------= -0,4 дптр;
/ок
<F-C)q~2’2> ^(F-C)vta ” кр
1 >0»
Аберрации в угловой мере
Дс4> сф =
(As'4-As'K) tgg'
/ок
3438 =
(0,35 —0,10) (-0,05) 3438 = __1ЧЗ, 25
или
ДаЬ сф = hK?L3438/1000 = 1,25 (—0,4) 3,44 = —1 '43";
4<f_C|, , (0,38 -0,03) (-0,03) 3438 _ _г,г4..
к. р 20
4<,;м, - ж8 „ №»! + »да Ж8 _
foK
Дадист
3438 = 1С22'.
Остаточные суммарные аберрации сведены в табл. 2.11. Кривизна поля в случае исправления астигматизма
Ч (32S ” 4)/2 - (3 + 4)/2 = 3,5.
Таблица 2.11. Аберрации компонентов зрительной трубы, мм
Компоненты системы Хроматизм ds(F-C)„ Точка на оси Точка вне оси
\р “ 1 ° W —2° 3 '
As'z)c4> щ % As(r— С) у' гз Г гт ДУ(/?„С) Дудист
Объектив —0,15 —0,15 —0,20 —0,08 10 —3,5 —6,5 0,02 0,05
Первый компонент оборачивающей системы —0,20 0,25 —0,10 0,10 10 4,0 5 0,02 —0,15
Второй компонент оборачивающей системы . 0,10 —0,05 0,15 0,30 20 —1,0 2 0,01 —0,20
Окуляр —0,08 —0,10 —0,30 —0,03 20 —3,0 5 —0,02 0,40
Суммарная аберрация всей системы L ~ 2,2 | L = —0,4 —1'43’ | 0,05 В диоптрийной мере | L - -0,6 | - | L3 - 3,2 | Lm = -1,6 В угловой мере —2' 24" | — | — | — - 4'8' | 1°22"
Примечание. Стрелка показывает, что аберрации первого компонента оборачивающей системы и окуляра вычислены в обратном ходе лучей.
Анализ кривой широкого наклонного пучка в меридиональном сечении
Поперечная кома k (рис. 2.36) определяется расстоянием, измеренным вдоль оси у’ от точки О, соответствующей координате главного луча до прямой, соединяющей концы кривой поперечной аберрации. £ = = (^ерх + ^нжн)/2 ~ У'гл = (8.75+ 9,05)/2 - 9 = -0,1. Тангенс
угла наклона tg ср касательной в точке О определяет величину меридионального искривления изображения равную величине поперечной ме
ридиональной кривизны At/, деленной на соответствующий апертурный угол, т. е. tg <р = Д//Д102а'=5.
Поперечная «полевая» сферическая
аберрация
^сф “ (а1 “
= [(—0,4) — (4-0,2)]/2 = —0,3.
Продольная сферическая аберра-ция Дз'ф = Лй'ф/tg о' = —0,3/0,03= = —10 мм.
Если вычислен коэффициент Пец-валя Siv -- —11 6р/г), то можно
определить по стрелке Пецваля Д?р = f/'2SIV/2 величину сагиттального искривления изображения zs = = (2Агр + <,)/3.
Рис. 2.36. График поперечной аберрации широкого наклонного пучка в меридиональной плоскости
ОТРАЖЕНИЕ И ПРЕЛОМЛЕНИЕ НА ПЛОСКИХ ПОВЕРХНОСТЯХ ОПТИЧЕСКИХ ДЕТАЛЕЙ
Преломление луча через плоскость
Изображение светящейся точки А находится на пересечении с осью OOL продолжения преломленного луча на расстоянии s' от преломляющей плоскости ВВ (рис. 2.37) и вычисляется по фор .му ле (2,75) при г = оо
s' = sn cos e'/n cos e. (2.85)
В случае перпендикулярного падения луча на плоскость из формулы (2.85) следует «о = n's/n.
Продольная сферическая аберрация (рис. 2.38) а ' — n's / cos \
5сФ “ л \ cos в / ’
Расстояние от точки меридионального и сагиттального пучков после преломления (рис. 2.39)
= *т п’ cos2 e7n c°s2 е; /п-
Полагая, что чп ~ астигматическая разность вдоль оси
будет равна г'$ — z/n = t (1 — cos“ е /cos2 е).
Рис. 2.37. Преломление луча через плоскую поверхность
Рис. 2.38. Строение пучка лучей при преломлении через плоскую поверхность при п < п' (а) и п >
>п' (6)
Рис. 2.39. Строение элементарного астигматического пучка лучей при преломлении через плоскую поверхность
Рис. 2.40. Построение изображения через плоское зеркало
Отражение от плоского зеркала
Плоское зеркало дает идеальное изображение. Для него остаются справедливыми формулы (2.11), (2.75) и (2.76), если положшь, что
п = п' и г — оо. Из формулы (2.11) следует, что s = s'. Точки предмета и изображения лежат на общей нормали к плоскости зеркала, на одинаковых расстояниях от него. От действительной точки S (рис. 2.40, а)
Рис. 2.42. Отражение луча от плоского зеркала
Рис. 2.41. Построение изображения прямой AAt через плоское зеркало
плоское зеркало дает мнимое изображение S', а от мнимой точки S (рис. 2.40, б) — действительное S'. Изображение всегда равно предмету, но они между собой не конгруэнтны (рис.2.41).Плоское зеркало ММ отклоняет падающий луч от его первоначального направления на угол (рис.
>2.42) у == 180 — 2в. При повороте зеркала вокруг точки О на угол ср (рис. 2,43) отраженный луч Sj отклонится на угол {Р, равный удвоенному углу поворота отражающей плоскости ‘зеркала, т. е. £ = 2ф.
Система зеркал
Два зеркала, расположенные под углом а друг к другу, Отклоняют падающий луч от
Рис. 2.43. Отражение луча при повороте зеркала
своего первоначального положения на двойной угол, т. е. у = 2а, но зависящий от угла падения луча на первое зеркало (рис, 2.44); при покачивании или вращении такого углового зеркала вокруг ребра О изображение остается неподвижным. Система из нечет-
ного числа плоских зеркал дает не вполне обращенное изображение, что приводит к изменению направлений в изображении.
Рис. 2.44. Отражение луча от
Рис. 2.45. Построение изображе-
двух зеркал при постоянном угле а
ния от двух параллельных зеркал:
Система с четным числом плоских зеркал дает изображение прямое и конгруэнтное (при
ab — предмет; агЬ^ — изображена предмета зеркалом /; — азо-
бражение предмета зеркалами lull
наложении совмещающееся с предметом). Примером может служить Система из двух параллельно расположенных зеркал (рис. 2.45). Если
Ряс. 2.46, Отражение луча от двух зеркал (нижнее зеркало 77 вращается вокруг оси О')
одно из этих зеркал оставить неподвижным (например, зеркало 7), а второе повернуть иа угол а (рис. 2.46), то отклонен не
Рис. 2.47. Отражение луча от вогнутого зеркала в меридиональном сеченин
отраженного от зеркала П луча S' будет равно двойному углу между зеркалами (2а). Отраженный луч S' займет положение OS'. Если луч S , отразившись от неподвижного зеркала 7, снова возвратится на зеркало 7/, составляющее с зеркалом 7 угол а, то вышедший в обратно* 126
направлении из системы такой луч отклонится от первоначального своего направления на угол у=4а. Конструкция таких зеркал находит применение в гальванометрах, щуповых приборах для измерения чистоты поверхности и др.
Фокусное расстояние сферического зеркала (рис. 2.47) можно определить по формуле (2.11а), положив sx = оо, f' = s', n ~ п = 1, /' = s' = /72.
Преломление пучка через плоскопараллельную пластинку или призму
Призмы, развертывающиеся в плоскопараллельную пластинку, обладают аберрационными свойствами последней. Падающий на пластинку 1—2 под углом е луч выходит из нее параллельно своему первоначальному направлению, но смещенным в сторону (рис. 2.48). Величина этого смещения (смещение точки Л) вдоль оси ОО' равна
As' — d (1 — cos гу/п cos ej);
поперечное смещение z~ d sin (ex — — e[)/cos fj.
Тонкий пучок лучей, идущих вдоль осн 00' (параксиальный пучок) и сходящихся в точке Л, смещается в направлении света на величину
As' = d (п — 1 )//2.
Рис. 2.48. Смещение изображения плоскопараллельной пластинкой
Величина продольной сферической аберрации (точная формула)
Аз'ф = As' — Asq = d (1 —cos ej/cos ej)/«;
приближенно
As'$ = d (n2 — 1) sin^o^n3,
где Of — апертурный угол в сечении пучка; sin оу — sin Астигматическая разность узкого наклонного пучка (точная фор-
мула)
—tm — —d (1 — cos2 gj/cos2 cos ej.
Продольный астигматизм, т. e. разность абсцисс сагиттальнего и меридионального фокусов элементарного пучка (приближенно)
Д = — г'т = —d О*2 — 1) ДД’3>
где (Oi — угол наклона главного луча (<14 = главного луча). Меридиональная кома третьего порядка
Ag' = 3d (п2 — 1) о^(о1/2п3.
Дисторсия главного луча (приближенно)
Ag' = d(n2 — l)w3/2n3.
Продольная хроматическая аберрация
^S(F-C) ~ (Vrtc d*
Хроматизм увеличения в одной общей плоскости установки
^Р-С — Ур Ус — О!^С 1/ftp)
Плоскопараллельная пластинка или эквивалентная искажают изображения, когда
ей призма не параллельных
Рис. 2.49. Определение положения F'oG относительно призмы
опи находятся на пути лучей (защитное стекло перед объективом и т. д.). В сходящемся пучке лучей (например, после объектива) они вносят аберрации.
Пример. Определить положение заднего фокуса объектива F'o$ относительно выходной грани прямоугольной призмы, расположенной за объективом (рис. 2.49).
Для параксиальных лучей (а—е) /i2 ~ — a'd = h± — ad/n = й2,
поэтому s2 = $2 ~ si—d!n. Для рассматриваемого случая = so — а — —d/n. Если в системе имеется несколько призм, то
sp = «О — L “возд - S
Графическое построение хода луча через плоскопараллельную пластинку (или любую ей эквивалентную призму) методом редуцирования
Толщину стеклянной пластинки с показателем преломления п приводят к воздушной толщине d/n (см. рис. 2.48). Падающий луч проводят без преломления до встречи с выходной гранью 2' воздушной пластинки. Затем высоту /г2 откладывают на выходной грани2 стеклянной пластинки. Ход лучей определяется в стекле прямой АВ. С помощью редуцирования упрощается графическое построение лучей при габаритном расчете системы в параксиальной области или при малых углах падения е.
Преломление лучей через призму в ее главном сечении
На рис. 2.50 изображен ход луча в главном сечении призмы MAN (в плоскости, перпендикулярной преломляющему ребру) с преломляющим углом 0, расположенной в воздухе. Из рис. 2,50 следует, чти е2 — & + а“ —£i + е'| + е2— ° — угол отклонения луча ст
первоначального направления SElt На основании закона преломления для точек В и D имеем sin et = п sin еsin = п sin е2
соз-^С^' + ег)
sin (0 а) ==.-----------j-----------п sin — 0. (2.86)
cos (S1 + 60
Для постоянного значения угла 0 и при данном показателе преломления п вещества призмы угол о будет изменяться, если менять вели-
чину угла падающего луча SB с нормалью. Значение минимального угла отклонения amm в зависимости от п и 0 призмы определяется по формуле
sin — (9 -f- onlln)~
= п sin-i- 0. (2.87)
В этом случае 8, — - (0 + amin)/2; ej = 0/2; в1 = — е' и ej = е2.
Ход луча в призме бу-
Рис. 2.50. Отклонение луча призмой в главном ее сечении
дет симметричен относитель-
но гранен, т. е. перпендикулярен
биссектрисе угла 0. Формула
используется для определения показателя преломления п вещества призмы; углы 0 и omin измеряются на гониометре или спектрометре. Формула для вычисления отклонения луча через призму с малым углом 0 при больших углах падения е
а = arcsin [9 Vл2 — sin2гх sin ед] — 4- 0)
или приближенно
а = 0 []/"4- (л2 — 1) tg2 — 1 ].
При малых углах 9 и имеем о = 0 (п— 1).
Если призма находится не в воздухе, т. е. =^= 1 и п3 ф 1, минимум (или максимум) отклонения вычисляется по формуле to е' = (/г — — cos 0)/sin 9, где k = К (л2 — —п'1)> — показатель прелом-
ления призмы.
Преломление луча, проходящего через призму вне плоскости главного сечения (внемеридиональный луч)
Косой (внемеридиональный) луч РВ может быть определен углом у, образуемым лучом со своей проекцией Р’В на плоскость главного сечения (рнс. 2.51) и углом ехо между упомянутой выше проекцией и
5 В. А. Панов и др, 129
Рис. 2.51. К вычислению хода внемеридионального ‘луча через призму
нормалью к грани призмы. Последовательное применение к двум граням призмы закона преломления дает следующие результаты [85]:
1) угол луча со своей проекцией после преломления у'2 равен (до преломления), т. е. иаклон луча к плоскости главного сечения не меняется;
2) проекция луча и а главное сечей ие ведет себя как световой луч, т. е. удовлетворяет законам преломления, если за величину показателя преломления стекла принять А/ = = Ип2 Н- (П* — 1) tg2 у,.
Зависимость этого условного показателя преломления У от наклона у вызывает искривление спектральных линий.
Дисперсия призм
Простая призма в воздухе дает при постоянном угле падения лучей — 0 угловое отклонение do между двумя лучами с разностью показателей преломления dn для длин волн X и 1+ dk
Угловой дисперсией призмы называется отношение doldn\ значение для него можно получить, если продифференцировать формулу (2.87)
do min__________2 Sin (0/2)________dn
dA. ~ /1 — n2 sin2 (0/2) ’
(2.88)
Для k одинаковых призм, расположенных в минимуме отклонения, dt/min _ 2fe sin (0/2) dn
dX [Л [ —n2 sin (0/2)
Угловую дисперсию можно увеличить, если отказаться от симметричного хода лучей в призме (или от принципа наименьшего угла отклонения о). В случае произвольного хода луча света в призме угловая дисперсия призмы определяется по формуле
do __ sin 9 da
dk ” cos ej cos ^2 dk
При малых углах 0 и do = 0dn, при минимуме отклонения do = —2 tg a^dn/n.
Угловая ширина спектра определяется угловым расстоянием До между лучами данного спектра и с достаточной степенью точности вычисляется по формуле (2.88). Участку ДХ длин волн между AL и соответствует изменение показателя преломления Ап. Поэтому
Да? sin (0/2) Д/ь
V 1 — п2 sin* (0/2)
Для 60-градусной призмы До = гДп/!^ 4 — й2, где п —среднее значение показателя преломления для длины волны с симметричным 130
кодом луча в призме в данном интервале длин волн. Например, для кварца в интервале длин волн от X — 1852 A (n = 1,6759) до к = 7685 А (л — 1,5391) средней длиной волны будет Хср = 2500 А (Лер — 1,607); Дл = 0,1368, До = 0,2325 в радианной мере (или 13,3°). Для стекла ТФ1 в интервале длин волн от X — 3650 (п = 1,7002) до Х = 8630 А 1,6326) Аср= 4600 А (лср = 1Л66); Дп== 0,0676, До== 0,1222
В радианной мере (или 7°).
Дисперсия вещества призмы dnldk для видимой области спектра обычно вычисляется по интерполяционной формуле Гартмана [89].
Увеличения дисперсии можно достигнуть увеличением преломляющего угла призмы. Однако предел этому ставит полное ви угрей нее
Рис. 2.52. Призма Амичи
Рис. 2,53. Призма Цинкера
отражение иа второй поверхности призмы. Можно построить призму с большим преломляющим углом, если ее поместить в среду с показателем преломления nf > 1. В этом случае формула (2.87) примет вид
6 t 6 Опии
п Sin -гт- = п Sin -----Чг™ -
da _ / 1 dn 1 dn'
dk ~~ \ п dk п' dk
п sin (9/2) /п'а—п3 sin3(9/2)*
Область значений 0, как это следует из подкоренного выражения предыдущей формулы, увеличена до sin (9/2) < пЧп. Если принять п— 1,66 и п' = 1,5 [флиитовая призма находится в среде из кронового стекла (рис. 2.52), то .угол 0 может достигать значений до 120°. Угловая дисперсия такой сложной призмы определяется по формуле
da__________2
dk ~~ cos ех cos е2
Л dfla Л
sm 02 cos — sin 9
* 1 dk
dnt "dk
9
Где — преломляющий угол внешних кроновых призм, которые предполагаются одинаковыми; 02 — преломляющий угол средней флин-товой призмы; Si и. е2 — углы падения луча соответственно иа первую и вторую поверхности.
Угол полного отклонения луча призмы o~2(Si+0i — 9г)« Призмы прямого зрения. К ним относится призма Амичи (Броу-виига, рис. 2.52). Оиа состоит из одной флинтовой призмы, обладающей (большой дисперсией, и двух крайних кроновых призм с малой дисперсией. Угол средней флинтовой призмы определяется по формуле
tg (02/2) = v К-!)/«!,-4).
Где и Пф — показатели преломления крона и флинта для того луча, который системой не отклоняется (обычно принимают Х = 486,1 нм).
5* 131
Таблица 2.12. Дисперсия трсйнсй призмы Амичи БКЗ (По = 1,5183 v 10,3); ТФ5 (по 1,7550 v - 27,5) 01 = 03 ==99с 53'; СЪ = —109 46'
Спектралъпая линия, нм Дисперсия Спектральная линия, нм Дисперсия
766,5 (А') 750 700 656,3 (С) 600 7° 11,Т 6° 59,5' 6° 21,8' 5° 41' 4° 27,6' । 587,6 (ф 500 486,1 (8) 435,8 fe) 434,1 (О') 400 1 Ч. *. *. о ст. ю ~ сч Г- О LO N’T о те lq о оо о о о о о о СО СО-J ОО
Часто призмы конструируют из двух (трех) флинтовых и трех (четырех) кроновых призм. Пяти пр и змеиные системы могут быть рассчитаны так, чтобы кривизна некоторых спектральных линий была уничтожена. В табл. 2.12 приведены значения дисперсии тройной призмы Амичи.
Рис. 2.54. Призма Вернике
Рис. 2.55. Призма Резерфорда
Призма Цпнкера (рис. 2.53) состоит из двух одинаковых по величине призм различной дисперсии, но имеющих одинаковый показатель преломления для одной определенной длины волны. Свет на первую
Рис. 2.57. Призма с постоянным отклонением 60°
поверхность призмы падает перпендикулярно, поэтому потери ьш отражение в ней меньше, чем в призме Амичи.
14а рис. 2.54 дана призма Вернике, обладающая большой дисперсией; по конструкции она представляет собой двойную призму Цинкера. На рис. 2.55 показана призма Резерфорда, состоящая из флинтовой 132
призмы с большим преломляющим углом (90—120°) и двух одинаково симметричных, наклеенных на нее призм из крона. Конструкции некото-
рых призм с постоянным углом отклонения приведены на рис. 2.56 и
Алроматическпе клинья
Призму, ограниченную двумя преломляющими поверх костями с малым углом (0 с 6°) между ними принято называть клипом. Предполагая, что углы 0 клиньев, а также углы е луча с нормалью к грани
клиньев малы, получаем условие ахроматизма клина, составленного из двух простых клиньев (рис. 2.58). При этом их отклонение равно о — («1 — 1) 0Х + («3 — 1) х X 02, откуда
9, = a/(v, — v2) A/i,;
9» = —&/(У1 — v2) An2,
Рис. 2.58. Ахроматический клин
где vr и v2 — коэффициенты дисперсии; 0Х и 02 — углы клиньев, 'имеющие разные знаки, т. е. клинья обращены преломляющими ребрами в противоположные стороны. Приведенные выше формулы являются приближенными. Если угол отклонения луча велик (более 2—3°), то следует пользоваться более строгой теорией ахроматизации призменных систем [85, 86].
При прохождении лучей через клип происходит трансформирование пучка. Коэффициент анаморфозы или трансформирования [3, 85, 89] ka = тЧт (рис. 2.58).
Габаритный расчет зрительной трубы
Требуется рассчитать систему со следующими характеристиками: Гт ~ 6х, 2(1)! = 6°, длина системы L — 750-^780 мм, диаметр выходного зрачка D'p, ~ 4 мм и /' не менее 15 мм, входной зрачок всей системы совпадает с оправой объектива (рис. 2.59). Применяем двухликзо-Вую симметричную оборачивающую систему V — —1 и /з == /X- С целью иаилучшего исправления астигматизма в ней, примем Д-0,8Д. Главные лучи делят в точке Р' расстояние (7? пополам, и тогда вследствие симметричности хода между компонентами автоматически исправляются кома, дисторсия и хроматизм увеличения. Для сопряжения точек Р и Р' применяется коллектив, установленный в плоскости изображения, создаваемого объективом. Чтобы выполнить условие >s 15 мм. примем/qK = 25 мм (окуляр типа Кельнера). По формуле (2.36) диаметр входного зрачка (объектива) Dp — D'p,r = 4 X 6 — 24. Фокусное -расстояние объектива /'б = /°КГТ = х ^0. Полагая L = ,зж 750 мм, определим /'половины оборачивающей системы: Д ~ =
(Z- — dY — — /зр)/2 = 200 мм.
Точка Р* есть изображение точки Р\ полученное через первый компонент оборачивающей системы. По формуле (2.3) расстояние точки Р" относительно первого компонента равно а= —а1) = 133,3; фокусное расстояние коллектива /кол = d± (d2 + a)/Mi + №+ #)) = = 103,45. Итак, имеем: Фх = 1/150 = 0,00667, = /об = 150;
Ф2 = Фкол = 1/103,45 = 0,00967, d2 = ~/3 = 200; Ф3 = ф4 == 1/200 = = 0,005, d3 = 160; Ф5 = Фок - 1/25 - 0,04, d4 - d2 + /от = 225,
Оборачивающая
система
Рнс. 2.59. Габаритная схема зрительной трубы с ходом лучей
Для определения габаритов системы применяются формулы (2.23) и (2.24). Расчет крайнего луча (hi — Dp/2 — 12; аг = 0);
а2 = = 0,00667* 12 = 0,08;
h2 = — a2di = 12 — 0,08-150 = 0;
«з — 0,08; /tj — —16; a4 = 0; /z4 = —16; a5 = —0,08;
= 2; cc6 — 0.
Расчет главного луча (tg шг — tg — —0,0522, = //х — 0); = = + ЯхФг - —0,0522; H2 - Z/j - = 0,0522-150 - 7,83; £3 =
== 0,02349; //3 == 3,13; ₽4 = 0,03914; Я4 == —3,13; p5 = 0,02349; ZZ5 = = —8,415; ZZ5 = Z/4 — P5 (d4 — /OK) — —7,83 (фокальная плоскость окуляра); рб = —0,313; dp = ZZ5/₽6 = —8,415/(—0,313) = 26,88.
Результаты расчетов высот лучей даны в табл. 2.13.
Если принять 2Лз = 2Л4 = 32 мм, то виньетирование наклонных пучков в процентах составит 0— [Dp — (/гц. — m2)) 100/Dp = 17.
Во многих системах с целью уменьшения ее габаритов или улучшения качества изображения применяется одностороннее виньетирование наклонных пучков. В атом случае за главный луч принимают средний луч наклонного пучка, проходящего через оптическую систему (см. рис. 1.27). Вследствие дисторсии окуляра н аберраций в зрачках системы главный луч наклонного пучка в большинстве случаев пересекает оптическую ось ближе к окуляру, чем параксиальное изображение центра входного зрачка системы.
Таблица 2.13. Высоты лучей на главных плоскостях системы
. 1 Компоненты системы Крайний луч «1 — 0 /г, = 12,0 Главный луч = —0,0522 Наклонные лучи р, = (01) == — 0,0522
т — 12,0 т ~ —12,0
Объектив (Ф5) Коллектив (Ф2) Первый компонент обо- 12,0 0 —16,0 0 7,83 3,13 12,0 7,83 —12,97 —12,0 7,83 19,03
рачивающей системы (Ф3) Второй компонент обо- —16,0 —3,13 —19,21 12,79
рачивающей системы (Ф4) Окуляр (Ф-,) 2,0 -8,41 —6,39 —10,39
В качестве объектива трубы и линз оборачивающей системы применим двухлннзовые склеенные компоненты, так как их относительное отверстие составляет приближенно 1 : 6. Исправление в этих компонентах сферической аберрации, хроматизма положения и комы можно выполнить по методу, предложенному Г. Г. Слюсаревым [85, 86]. Важно заметить, что когда плоскость входного зрачка совпадает с оправой объектива (4 — 0), астигматизм последнего исправлению не поддается [см. формулу (2.66а)]. В этом случае согласно формулам (2.63) и (2.66а):
< = -0,5/;6tg^ (1 + л) = -0,85/;б tg wj’ = -0,34;
гт = -0,5/'б tg wf (3 4- л) = -1,85,^б tg = -0,74,
где л = 0,7 (параметр кривизны), и тогда астигматизм
< - 4 = о-4-
Коллектив, расположенный в плоскости изображения, вносит лишь кривизну поля и дисторсию.
Кривизну изображения, создаваемую совместно объективом, коллективом и оборачивающей системой в фокальной плоскости окуляра (рнс. 2.60), можно определить как стрелку Пецваля (см. стр. 104)
где
У, (Ф/л) = £ Ф/л = 0,67 2 Ф = 0,0176,
полагая /м — л3 = 1-
На рис. 2.60 обозначено: Р’ В' — главный луч; В’ — точка схождения меридиональных или сагиттальных лучей; F0K8' — идеальное изображение (пейскривленное) в фокальной плоскости окуляра; F0KS' — искривленное изображение; Rp — радиус кривизны поверхности изо-
135
бражения1; г~ y^/ZRp—стрелка Пецваля при величине изображения у’.
Кривизна меридионального и сагиттального изображения
и 1/Z?' связана с суммой Пецваля следующими соотношениями:
3/7?;-1/^ = 2//?; = 2^(Ф/п). (2.50)
Согласно рис. 2.60 отрезок после окуляр з в диоптрийной мере составит
L = 1000/г = 1000г//;® = 1000//'2/2#Р/;2 = 1000(о'2 !2Rp.
Пользуясь выражением (2.90) как общей формулой, можно написать
= —1000(1)? 2 (Ф/п).
Выбрав тип окуляра, исходя из его фокусного расстояния и углового поля, уже заранее можно предусмотреть наилучшее возможнее исправление астигматизма н кривизны поля всей системы.
Для зрительных труб аберрации, выраженные в угловой мере, рекомендуется удерживать в пределах одной-двух угловых минут за окуляром в соответствии с предельным углом разрешающей способности глаза наблюдателя. Вторичный спектр допускается до 3—4 мин при диаметре зрачка глаза 2 мм. Наиболее надежным способом оценки
Рис. 2.60. Определение кривизны изображения допустимых аберраций в объективах микроскопа служит критерий Рэлея, согласно которому нолновая аберрация в плоскости наилучтен установки не должна превышать одной четверти длины волны свети. В фотографических объективах аберрации оцениваются кружками рассеяния в плоскости изображения. Как правило, расчет оптическсн системы закапчивается составлением документа, в котором приводятся конструктивные параметры системы, таблицы и графики аберраций.
На рис. 2.61 и 2.62 приведены в качестве примера такие графики для зрительной трубы и фотографического объектива.
1 Из формулы у’% = 2Z?z' следует₽ что поверхность изображения в прит
Слижении третьего порядка, является параболоидом вращения, a Rp ~^> параметром этого параболоида <- радиусом кривизны в вершине.
Рис. 2.61. Аберрации телескопической системы Гт = 6х, 2со = 8с30', Sp — 15,3 мм
Точка на оси
hi В угловой мере В диоптрийной мере
€ С' F' Л' —С' I е С' F' F'-C'
0 0 0 0 0 0 -0,17 0,04 0,21
17^1/2 — Г 01" 0' 02" — 1' 02" — 1' 04" 0,14 0 0,15 0,15
17.0 — 2' 47" — 1' 23" — 2' 23" — Г 00" 0,28 0,14 0,24 0,10
Точка вне оси
(0t SP V 4
4^ КЗ о е — О СП сл » ч. 0 0 12° 1G' 31" 25° 43' 12" 15,26 15,00 — 0,80 — 3,45 — 0,65 — 1,63
% ‘V /3® — L - cos to' £* cos co' tri (L3- £m)cosw' 7, .co sec —— — (ш7+57)
2,27 9,05 Л. GO » ч КЗ 4^ — 0,78 — 3,11 — 0,64 — 1,47 — 0,15 — 1,64 — 0,71 —2,29
Git — 2° 05'
a' ~ 1 7,0
17 12° 08' 47" k = 0' 51"
9 12° 13' 10" D — — 8' 35"
0 12° 16' 31" /?2t — 9,0
— 9 12° 20' 32" k == 0' 20"
— 17 12° 17' 22" D ~ —7' 22"
©i = 4е 15' I
o'
9 25° 33' 30" пц — zt9,0
0 25° 43' 12" k = —3' 41"
—9 25° 45' 32" D——12' 02"
102ш lpf-1lf(M) > у 9 9,19'
-
\ 7-й по-
верху -зо
107ш' ш^20л(М)
>< /8,4 18,6Vr
' Д| ‘ * -
1 - \7-йпо-
\Sepxn.
IQ
102ш Wf-20°(S)
h 0,1 0 0,1 ag'
I и I--1 *—
огран.
11-й поверху
\а'
д огра у
ст 1-иповерхн.
ограи.
77?
аЧ~й поверху Прямая аа' соответствует плоскости установки, смещенной относительно ,
гауссовой на-0,18 мм
О
Действующая диафрагма $11,8
Рис. 2.62. Конструктивные элементы и графики аберраций объектива П — 17, ю
rfi == 2,85 ТК16 14,8
Г.> ™ ОС
d2 ~ 4,05
гл — —33,57
Щ = 0,9 ЛФ5 12,4 г4 — 14,56
di — 5,05 г з — 245,5
rf5 = 0,8 ОФ1 12,8
га = 15,17
dR — 5,1 ТК16 12,8
г, —23,53
f = 51,39 sF —40,21
s' = 42,76 F'
(см. сводку аберраций на стр. 133—139)
Сзодкт аберраций
Точка на оси
D SC' SG' SC' S6'
h 103o' s' As' n
0 0 42,76 —— 0,10 — 0,27 — 0,37
7'31'172 10,10 42,53 — 0,23 0,064 — 0,15 — 0,44 — 0,29
7,3 14,24 42,78 0,02 0,04 0,09 — 0.08 — 0,17
i Л*5
В сагиттальном с е ч е н и н
т 1 — 0, (ох — - -10°
ЛТ - Ю*б' AG'
7 13,50 — 0,01
5 9,67 -0,03
0 0 0
—5 — 9,67 0,03
— 7 — 13,5 0,01
тх — 0, Ct»! — — 20е
— 102б'
7 12,89 0,037
5 9,28 — 0,024
0 0 0
— 5 — 9,28 0,024
— 7 — 12,89 — 0,037
меридиональном сечении
(!)i = — 10°
mi 10s<T' У'
7 — 4,53 9,054
5 — 8,27 9,055
0 — 17,70 9,059
— 5 — 27,31 9,064
— 7 — 31,09 8,967
(о1 — _ 20°
10*сг' у'
5 — 26,14 18,46
3 — 29,78 18,53
0 — 35,1 1 18,56
— 3 — 40,44 18,55
— 5 — 43,92 18,46
(0t
102а' У'
5 — 31,16 21,32
3 — 34,90 21,47
0 — 40,2 21,57
— 3 — 45,3 21,58
Точка вне оси
(01 Sp SP' z' s z' m . £ N 1 м У' /7G' УС'
— 10Q 12,15 — 7,88 — 0,13 0,02 — 0,15 9,06 — 0,016 0,010
— 20° 12,86 — 7,95 — 0,26 — 0,30 0,04 18,56 — 0,147 0,014
— 23° 13,27 -8,15 — 0,16 — 0,93 0,77 21,57 — 0,230 0,022
Условия нерастраиваемости оптического прибора при изменении температуры
В оптических приборах, работающих при различных температурах, возникает термооптическая аберрация увеличения и расфокусировка оптической системы. Температурное смещение плоскости изображения относительно фиксированной плоскости приемника (в телескопических системах — фокальная плоскость окуляра, в фотографических системах — светочувствительный слой и т, д.) вызывается двумя причинами: наличием термооптической аберрации положения изображения и термическим изменением линейных размеров механического устройства, связывающего оптическую систему с плоскостью приемника. Для
Рис. 2.63. Эффект температурного смещения плоскостей изображения:
Д — положение плоскости приемника при начальной температуре прибора 20э С, находящейся на расстоянии ОД =s я' от п ос л еди ий поверкиост и о пт и ч с с к о й“ системы; О А ~ Sj — положения изображения при температуре t
1.27) при изменении температуры от
устранения эффекта температурного смешения плоскости изображения относительно плоскости приемника должно быть выполнено условие (рис. 2.G3) [89]
Д£ = Дз^—Да = 0, (2.91)
где — температурное смешение плоскости изображения относительно фиксированной плоскости приемника, вызванное термооптической аберрацией (As,' = sj — положения оптической системы и термическим изменением Да размеров механического устройства, связывающего оптическую систему с фиксированной плоскостью приемника. Из формулы (2.91) следует, что Д$£=Ла. Если термическое изменение линейных размеров механического устройства, связывающего оптическую систему с приемником, компенсирует изменение расстояния от последней поверхности оптической системы до плоскости приемника, то Д£ — 0. Это и есть условие иерасстраивае-мости оптического прибора в отношении температурной дефокусировки изображения относительно плоскости при-емника.
Пример. Определить Дб£ — величину смещения задней фокальной плоскости объектива визира (см. рис. G = 20 до G = —70° С.
Предварительные замечания. С изменением температуры происходят изменения: показателей преломления стекол, радиусов кривизны поверхностей линз, толщин линз и также воздушного промежутка между линзами из-за теплового расширения материала промежуточного кольца. Показатель преломления стекла при температуре f вычисляется по формуле
П/=П2О+ ₽*('-20),
где п-га — показатель преломления стекла при 1—20° С (приводится в ГОСТ 3514—76 или ведомственной нормали); р* — коэффициент, характеризующий приращение показателя преломления для той длины волны, для которой исправлены монохроматические аберрации объектива (приводится в ГОСТ 13659—78).
Радиус кривизны поверхности при температуре вычисляется по формуле/7 = r0 (1 + а*/) илн г/ == r20 (1 -ф Д/а*), где а* — температурный коэффициент линейного расширения определенных марок стекол; г0 и г2о — радиусы кривизны соответственно при t0 = 0° и 20° С; Д£ = t — Go-
Для поверхности склейки двух стекол а* принимается равным среднему арифметическому величин коэффициентов расширения этих 140
Таблица 2.14. Конструктивные элементы объектива ш rje
и значения а и Вр
Радиусы поверхностей Толщины по оптической оси Марка стекла rlD Св. С а*. 1С7 е-о юв
> > > > > сл Ы ts w II II II II II КО — I | — СП ВО 1 | _ О ОО Ю —‘ "-Т § о со со со со di = 5,2 d2=3 ,<1БОЗД:= 1 dA ~ 4 К8 ТФ1 К8 1,5163 1,6475 1,5163 36 72 83 72 • 2,8 3,4 2,8
стекол. Изменение величины воздушного промежутка можно вычислить по приближенной формуле
&dt = [(d — ег -|- е2) у* — е/х* + е/**]
где сх и е2 — величины «стрелок», отсчитываемых от вершин преломляющих поверхностей с учетом их знака (см. правила знаков стр. 65); у* — коэффициент линейного расширения материала, из которого изготовлено промежуточное кольцо длиной L = d — 4~ е2.
Конструктивные элементы г, d, п объектива из трех линз даны в табл. 2.14. В этой таблице а* и ££ даны для марок стекол К8 и ТФ1, применяемых в объективе.
Кольцо из дюралюминия (у* = 22- 10~е) длиной L --- d3 — ех + е2.
Решение. Вычисляем Ц/, г/, df при t2 = —70'С, если /х ~ 20~ С. А/ = 12 — Гх = —90° С.
Для марки стекла К 8
nz = n2O-[-₽2> (С—20) = 1>5103 + 2.8 10"6(—90) = 1,51005;
для марки стекла ТФ1:
nt = +о + (Н — 20) = 1,6475 +3,4.10'6 (—90) = 1,64729;
rti = ri (1 +«; At) = 117,49 [1 + 72-10"7 (—90)] = 117,41;
rt2 = г2 [ 1 + (а1 + аз) Д^/2] ~
= —100,93 [1 + 78 10-7 (-90)] = - 100,86;
г,3=г3(1 +а2*Д/) = _200 [1 + 83.10~7 (—90) J = —199,85;
г/4 = /-4(1 +а} А/) = 128,23 [1 +72.10"7 (—90)] = 128,15;
rts = гБ(1 +а] А/) = 250 [1 + 72.10'7 (—90)] = 249,84;
dzl = dj (1 + а] At) =5,196;
dt2=d-(l + А/) = 2,998; dti = d4 ( 1 + а] А/) = 3,997.
Таблица 2.15. Распределение марок стекол в зависимости от коэффициента теплового расширения *
а. 107 для интервала температур от — 60 до +20 °C Марки стекол
До 40 ЛК7
41—50 ЛК4
51—60 БК8, ТК4, ТК12, ТФ5, БФ28, ОФ1
61-70 К14, БКЮ, БК13, ТК2, ТК8, ТК13, ТКИ, ТК15, ТК16, ТК20, КФ4, КФ6, БФ1, БФ7, БФН, БФ13, БФ25, ЛФ5
71 Ф1, Ф6, Ф13 ,
72—80 ЛК6, К8, К19, БК4, БК6, ТК2], БФ6, БФ8, БФ16, БФ21, БФ24, ЛФ10, Ф4, ТФ2, ТФЗ, ТФ5, ТФ6, ТФ8
81—90 91 — 100 ЛКЗ, БФ12, ТФ1, ТФ1О ТФ7
* По данным Л. В. Сергеева.
Изменение воздушного промежутка при = —70° С (приближенно) А^звозд “ —е14“ %) Y* "— Д' dt = —0,0076,
где ег - Св.02/8г3== 36V1600 = —0,81; Св. 02/8г4 = 1,26. Тогда rf/з d3 4“ Д^звозд ” 0,9924.
Конструктивные элементы объектива при t ~ —l(f С следующие:
rt= 117,41
^ = 5,196 К8
г2 = — 100,86
d2 = 2,998 ТФ1
г3 — — 199,85
^звозд “ 0,992 — г4 = 128,15
d4 -3,997 К8
г6 = 249,84
Пр = 1,51605 по = 1,64729
Пв = 1,51605
Задний фокальный отрезок s', = 114,669 мм. Первоначальное ^об
значение было = 114,699. Следовательно, изменение SsL ~ Лоб
= —0,01 мм.
Смещение плоскости приемника вследствие изменения длины корпуса прибора, изготовленного из дюралюхмипия равно Да = (/ —
—20°)ysS = (—70 — 20) 22-10"’-114,7 = —0,227 мм. Таким образом.
*об
несмотря на термостабильность самого объектива = 0,01 мм)* смещение плоскости приемника, вследствие температурного воздействия на корпус прибора остается весьма значительным.
При средних радиусах кривизны склеиваемых поверхностей пара линз со слоем бальзамина будет термостойкой, еслн их а составит не более 25-10 7 (табл. 2.15). Когда Да превышает эту величину, то может возникнуть расклейка деталей при Температурных перепадая до ±60°С. Детали, склеенные бальзамином^ становятся нетермостойкими, если Да> 29*10 г.
Определение значений показателей преломления оптических стекол
Для вычисления показателя преломления оптических стекол в области спектра от 1 = 0,365 до 1040 мкм пользуются интерполяционной формулой фирмы Шотт
л2 = До 4~ 4“ 4“ 4'
Погрешность формулы не превышает двух-трех единиц шестого знака в области С—F, четыре-пять единиц этого же знака за пределами указанной области. Г. Г. Слюсаревым были использованы приведенные в ГОСТ 13569—68 значения показателей преломления десяти основных длин волн: 0,36501 (t); 0,40466 (А); 0,43405 (О'); 0,48613 (F); 0,54607 (е); 0,58930 (£>); 0,65628 (С); 0,76649 (Л'); 0,863 н 1,0 мкм. Эти значения лст легли в основу решения нормальной системы уравнений, приводящей к системе формул:
аи = + &unh + CunG' + DunF + ^ипе + +
+ GunC + + ^/*0,863 + A/11,0» (2.92)
где и принимает значения 0, 1, ..., 5 [86].
На основании этой формулы составлена программа для цифровой ЭВМ, позволяющая по десяти значениям показателей преломления, соответствующим перечисленным выше длинам волн, определить коэффициенты а0, ..., и по ним значения п (X) для любого значения X в промежутке 0,365—1,5 мкм. Кроме того, для 100 марок стекол ГОСТ 13659—68 машина может сразу выдать значения показателя преломления для любого X в указанной области спектра, поскольку коэффициенты д0, tz5 для этих марок стекла содержатся в памяти цифровой ЭВМ.
В ГОИ им. С. И. Вавилова разработана интерполяционная формула* пригодная для всех оптических стекол по ГОСТ 3514—76 (и по ведомственной нормали) для диапазона X от 0,35 до 2,6 мкм и обеспечивающая точность в несколько единиц шестого знака после запятой:
= Cj 4“ с2^4 + С3^2 + СА’2 + 4“ сб^”6 + ^Л”8»
Эта формула применяется в «машинном каталоге» оптических стекол,, введенном в память цифровых ЭВМ.
Таблица 2.16. Постоянные коэффициенты формулы (2.93)
Л'у П/ п Материал Область применения длин волн, мкы Постоянные
А В С D Е - {О4
1 Кварц плавленный 0,5—4,3 1,44902 0,004604 —0,000381 —0,0025262 —0,77220
о SrTiO3 1,0—5,3 2,28355 0,035906 0,001666 —0,0061335 —0,15020
3 MgO 0,5—5,5 1,71960 0,006305 —0,000000 —0,0031356 —0,0770
4 А12О3 1,0—5,6 1,75458 0,007149 —0,001577 —0,0045380 —0,2803
5 LiF 0,5—6,0 1,38761 0,001796 —0,000041 —0,0023045 —0,0557
6 CaF2 0,6— 8,3 1,42780 0,002267 —0,000069 —0,0011157 —0,0162
7 BaF2 0,5—11,0 1,46629 0,002867 4-0,000064 —0,0006035 —0,00465
8 Si 1,3—11,0 3,41696 0,138497 0,013924 —0,0000209 0,01480
9 Ge 2,0—13,5 3,99931 0,391707 0,163492 —0,0000060 0,00053 /
Таблица 2.17. Показатели преломления некоторых материалов, вычисленных по формуле (2.93)
сл
№ п/п Материал Показатель преломления при различных длинах волн, мкм
0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 4,5 5,0 5,5 6,0 6,5 ' 7,0
1 ч 3 4 5 6 7 8 9 Кварц плавленный SrTiO3 MgO А1аО3 LiF CaF2 BaF2 Si Ge 1,4614 2,4776 1,7454 • • • 1,3943 1,4363 1,4778 • • • 1,4508 2,3161 1,7229 1,7557 1,3871 1,4289 1,4686 1,4449 2,2862 1,7153 1,7471 1,3832 1,4263 1,4662 3,4821 1,4388 2,2679 1,7085 1,7377 1,3788 1,4239 1,4646 3,4526 4,1083 1,4309 2,2504 1,7007 1,7262 1,3733 1,4211 1,4630 3,4395 4,0664 1,4205 2,2312 1,6915 1,7122 1,3666 1,4179 1,4611 3,4324 4,0449 1,4069 2,2091 1,6806 1,6953 1,3587 1,4141 1,4591 3,4282 4,0324 1,3891 2,1838 1,6679 1,6752 1,3494 1,4097 1,4567 3,4254 4,0244 1,3664 2,1550 1,6533 1,6515 1,3388 1,4047 1,4540 3,4235 4,0190 2,1223 1,6367 1,6239 1,3266 1,3990 1,4510 3,4221 4,0151 1,6179 1,5918 1,3129 1,3927 1,4477 3,4211 4,0123 1,5550 1,2975 1,3856 1,4440 3,4203 4,0102 1,3778 1,4400 3,4196 4,0085 1,3693 1,4357 3,4191 4,0072
п/п I 1 Материал Показатель преломления при различных длинах волн, мкм
7,5 8,0 8,5 9,0 9,5 10,0 10,5 11,0 11,5 12,0 12,5 13,0 13,5
6 7 8 9 CaF2 EaF2 Si Ge 1,3600 1,4309 3,4187 4,0062 1,3498 1,4258 3,4184 4,0053 1,3388 1,4203 3,4180 4,0046 1,4144 3,4181 4,0040 1,4080 3,4178 4,0036 1,4013 3,4177 4,0032 1,3941 3,4177 4,0029 3,4177 4,0026 4,0064 4,0023 4,0022 4,0021 4,0021
Интерполяционные формулы JVL Герцбергера для вычисления показателя преломления в инфракрасной области спектра
За последние годы появился широкий ассортимент оптических материалов для инфракрасной области спектра. Для реализации этих материалов необходимо знать их оптические константы. Для этой цели можно применить интерполяционную формулу М. Герцбергера
4 — BL+ CU + DW+ Е№ + (2.93)
где L = (X5?— 0,02В)”1, постоянные А, В, ..., Е вычисляются при известных показателях преломления для пяти длин волн. Зная эти постоянные для данного материала (табл. 2.16), можно определить и для любой заданной длины волны для 14 материалов в ИК-области (плавленный кварц, LiF\ MgO, CaF2, Si, Ge, BaF2, Ai2O3, JR-20, As2S3 н др.) (табл. 2.17) [117].
Если известны ..., zz5, то показатель преломления для призволь-ной длины волны можно вычислить по универсальной интерполяционной формуле М. Герцбергера
п (X) = ai (X) nJ. + а2 (X) п2 — а3 (X) th + (X) п4 + а5 (X) п5. (2.94)
В табл. 2.18 приведены величины коэффициентов (X), вычисленные через интервал 0,5 мкм для области от 1,5 до 5 мкм.
Таблица 2.18. Коэффициенты сц (X) универсальной формулы (2.94), вычисленные для восьми длин волн X от 1,5 до 5,0 мкм в интервале 0,5 мкм
А (А) а2 (А) (А) (Л) а, (X)
1,5 1 0 0 0 0
2,0 0,116994 2,034777 —3,274872 2,437882 —0,314781
2,5 0 1 0 0 0
3,0 —0,004907 0,269321 1,344831 —0,676081 0,066836
3,5 0 0 1 0 0
4,0 0 0 0 1 0
4,5 —0,002182 0,062725 —0,647779 1,320303 0,266933
5,0 0 0 0 0 1
В качестве примера использования табл. 2.17 и 2.18 вычислим показатель преломления SrTiO3 для X = 2 мкм:
п (2,0) = 0,11699 X 2,2862+ 2,03478 X 2,2504 — 3,27487 X
X 2,2091 + 2,43788 X 2,1838 — 0,31478 X 2,1223 = 2,2679.
Литература: [1, 3, 12, 18, 19, 57, 61, 64, 66, 67, 69, 71, 78 — 82, 85, 86, 89, 100, 102, 103, 111, 112, 117].
ГЛАВА 3
ГЛАЗ КАК ОПТИЧЕСКИЙ ИНСТРУМЕНТ
Строение и свойства глаза
Схематический горизонтальный разрез глаза дан на рис. 3.1 Р — роговица; Л — хрусталик; ЦУ — центральное углубление; СП — слепое пятно; КВ — камерная влага; СТ — стекловидное тело; О — центр вращения глаза; У—ЦУ — линия наилучшего видения — зрительная ось; У ОК — оптическая ось.
Сетчатая оболочка (или сетчатка), выстилающая дно глаза, состоит из нервных волокон, заканчивающихся так называемыми палочками и
Кольцевая мышца
Склера
Рис, 3.1, Схематический горизонтальный разрез глаза
колбочками, являющимися светочувствительными элементами глаза. Палочки более светочувствительны, но не различают цветов; колбочки чувствительны к цветам, но менее светочувствительны. В месте сетчатки, находящемся против зрачка, имеется так называемое центральное углубление, размер которого соответствует пространственному углу обзора около Iе, в котором расположены одни колбочки. Вокруг него находится овальный участок с угловым размером примерно 6—7°, называемый желтым пятном, в котором имеются также палочки, но в значительно меньшем количестве, чем колбочки.
Желтое пятно, и в особенности центральное углубление, являются областями наибольшей остроты зрения.
Поле зрения одного глаза: вниз 70°, вверх 55°, к носу 60° и к виску 90° (125° по вертикали и 150° по горизонту). Поле зрения обоих глаз около 180°. Поворот глаз в сторону ±45—50°.
Поле зрения одного глаза условно можно разделить на три зоны:
1) зона наиболее четкого видения — центральная с полем зренья около 2°;
2) зона ясного видения, в пределах которой (при неподвижном глазе) возможно опознавание предметов без различия мелких деталей с полем зрения около 30° по горизонту и около 22° по вертикали;
3) зона периферического зрения, в пределах которой предметы нс опознаются, но опа имеет важное значение для ориентации.
Аккомодация глаза
Аккомодация — способность глаза изменять кривизну поверхностей хрусталика, что дает возможность видеть отчетливо различно удаленные предметы. Точка предмета, изображение которой получается на сетчатке при покое аккомодации, называется дальней точкой глаза R\ точка, изображение которой получается при максимальном напряжении аккомодации, называется ближней точкой Р (рис. 3.2).
Расстояние между дальней и ближней точками называется объемом аккомодации. Видеть резко предметы, расположенные ближе, чем ближняя точка, без очков нельзя. С возрастом ближняя точка отодвигается от глаза, так как способность аккомодации, а отсюда и объем аккомоцянии постепенно уменьшаются. В возрасте около ЗОлет ближнее
расстояние ар около 125 мм. Если это расстояние становится более 250 мм, то для работы на близком расстоянии необходимы очки. Объем л 1000 1000
аккомодации в диоптриях: А&~-------------
°*
Недостатки зрения
Нормальным (эмме тропическим) называется зрение, если при полностью ослабленном мускуле хрусталика отрезок ар равен оо. Такой глаз видит резко без напряжения аккомодации далекие предметы.
При близорукости (миопии) дальнаяя точка расположена на конечном расстоянии, которое тем меньше, чем больше близорукость.
Дальнозоркость характеризуется Тем, что дальная точка находится за глазом (отрезок ар положительный). Величина аметропии Л^ == 148
= 1000 1/а^, выраженная в диоптриях, характеризует степень близорукости или дальнозоркости. Прн близорукости отрицательна.
В приборах для коррекции близорукости и дальнозоркости применяется подвижка окуляров. В приборах, не имеющих диоптрийной подвижки окуляров, следует их установку делать в пределах —0,5— 1 дптр.
Наличие аберраций в глазе вызывает явления иррадиации, при котором размеры светлых фигур, отверстий или источников света на темном фоне кажутся больше, чем такие же размеры темных фигур. Например, белые штрихи на черных шкалах кажутся большими, чем черные штрихи на белом фоне.
Влияние на остроту зрения условий освещенности
Адаптация — способность глаза приспосабливаться к очень сильным различиям в освещенности [например, отношение яркостей предметов, видимых днем при солнечном освещении, и предметов, видимых ночью (слабые звезды), достигает 1012 : 1].
Адаптация осуществляется путем изменения размера зрачка глаза, диаметр которого изменяется от 2 до —8 мм (площадь зрачка меняется в 16 раз), и за счет восстановления или разложения зрительного пурпура и перемещения зерен черного пигмента. При слабых яркостях работают только палочки, поэтому значительно падают острота зрения и цвето-чувствительность.
Интенсивное освещение тормозит деятельность палочек, и зрение осуществляется главным образом при помощи колбочек. Максимальная чувствительность палочек приходится на длину световых волн порядка 510 нм. а колбочек — на длину 550 нм. Это сказывается в том, что синеватые цвета начинают казаться при слабой освещенности более светлыми по сравнению с желтыми и красными, в то время как при сильном освещении они были одинаковыми по яркости (явление Пур-ки нье).
При различных освещенностях чувствительность сетчатки изменяется примерно в IО3 раз. Процесс темновой адаптации требует большого времени (при резком уменьшении освещенности до 1 ч).
При точных измерениях необходимо обеспечить наиболее благоприятную освещенность и не допускать ее колебаний. Наиболее благоприятной освещенностью признан интервал между 100—400 лк.
Когда наблюдение ведется одним глазом, на остроту зрения влияют световые раздражения второго глаза. Так, например, при наблюдении темных объектов на светлом поле острота зрения выше, если второй глаз также освещен. Обратное действие получается при наблюдении светлых объектов на темном поле.
Световые пороги
Световым порогом Л' глаза называется наименьшее количество луч иглой энергии, вызывающее ощущение света. Световая чувствительность глаза 1//V, Световые пороги выражаются в эр г/с или освещенностью на зрачке в лк/Величина абсолютного светового порога глаза очень мала и колеблется у разных людей от 1-10 10 до 5-КГ1* эрг/с (в среднем соответствует освещенности на зрачке,порядка 1-10 9 лк). Спектральные границы зрительного ощущения существенно зависят от плотности энергии воспринимаемого ощущения.
Контрастная чувствительность
Видимость предметов основана на контрасте — яркостном или цветовом. Яркостный контраст определяется величиной k = — B&)/B$ (BQ — яркость объекта; Вф — яркость фона). Отношение ДВ/Вф (АВ — минимальная различимая глазом разность яркостей объекта и фона) называется порогом контрастности. Зависимость порога контрастности от яркости фона показана па рис. 3.3. С увеличением яркости фона контрастная чувствительность растет, достигая максимального значения при 130—640 кд/м2, а при еще более высоких яркостях снижается (слепящее действие).
Рис. 3,3. Зависимость порога контрастной чувствительности А В/В от яркости фона
Рис. 3.4. Зависимость остроты зрения от яркости фона
Разрешающая способность
Разрешающей способностью глаза называется способность различать раздельно близко расположенные друг к другу точки, линии или другие фигуры. Принято считать разрешающую способность глаза в среднем равной одной угловой минуте, при этом острота зрения принимается за 1. Если глаз разрешает 30", то острота зрения равна 2 и т. д. При наблюдении сдвига одной части линии относительно другой разрешающая способность значительно выше (в среднем 10"). Средняя ошибка опытных наблюдателей при этом иногда не превышает 3". Острота зрения при оценке смещения линий — нониальная острота зрения — играет большую роль при измерениях и отсчете по шкалам и нониусам. При передвижении к боковым частям сетчатки острота зрения сильно падает. Если остроту зрения в центре принять за 1, то при смещении на 5° от центра острота зрения падает до 0,3, на расстоянии 10° она падает до 0,2 и т. д.
Разрешающая способность зависит от контраста наблюдаемой картины и яркости фона.
Так как с увеличением яркости фона Вф зрачок глаза уменьшается, то, следовательно, при малых диаметрах зрачка (2—3 мм) разрешающая способность глаза оптимальна. С уменьшением контраста разрешающая способность сильно снижается. Например, при яркости фона около 1 кд/м2 при контрасте 0,929 разрешающая способность 8 = 1,2', при контрасте 0,284 е — 2,2', а при контрасте 0,096 8 равна всего лишь 6,3't т. е. разрешающая способность ухудшается почти в 5 раз. Контраст 150
цветных изображений можно повысить применением светофильтра. Большое влияние иа остроту зрения оказывает правильная и стабильная освещенность (рис. 3.4),
.41 Очень велика чувствительность глаза к малым перемещениям объектов, движущихся достаточно медленно. Установлено, что глаз замечает перемещение, равное в угловой мере 10". При непрерывном движении наименьшая угловая скорость, которую замечает глаз, приблизительно равна 1—2 град/с.
Рис. 3.5. Различение разно-удаленности точек А и С при наблюдении двумя глазами: Лд и — изображения точек А и С в левом глазу; А'п н — то же в правом глазу
Бинокулярное зрение
Расстояние между центрами глаз b называется глазной базой. У подавляющего большинства людей это расстояние находится в пределах 56—72 мм. Эти пределы приняты при конструировании бинокулярных приборов. Однако, если диаметры выходных зрачков прибора более 4—5 мм, можно допустить наименьшее расстояние между центрами окуляров 58 мм, а при больших диаметрах окулярных линз наименьшее расстояние приходится делать не менее 60 мм (т. е. равным диаметру оправы окуляров в ее наиболее толстой части).
Зрительной осью глаза называется линия, проходящая через центр хрусталика н середину центрального углубления на сетчатке.
Угол схождения между зрительными осями глаз называется углом конвергенции. Угол расхождения осей называется углом дивергенции.
Изменение угла конвергенции тесно связано с изменением аккомодации. Изменение угла конвергенции и связанное с этим ощущение напряжения глазных мышц позволяет судить о дальности объектов. Максимальный угол конвергенции ~ 32°.
Стереоэффект. При наблюдении одним глазом наблюдатель оценивает разноудаленность предметов по их относительной величине, если они ему знакомы, или по изменению видимости (иначе по воздушной перспективе). Оценка равноудаленности предметов значительно точнее производится при наблюдении двумя глазами. Чем больше угол конвергенции, тем больше аккомодация глаз. Поэтому, если рассматриваемый предмет находится в бесконечности, оси глаз параллельны и аккомодация равна нулю. В связи с этим к бинокулярным приборам предъявляются следующие требования:
1) если осн окуляров непараллельны, то из окуляров должны выходить пучки расходящихся лучей, соответствующие аккомодации ?лаз при данном угле конвергенции;
2) если оси окуляров параллельны, то из окуляров должны выходить пучки параллельных лучей.
На рис. 3.5 дана схема наблюдения двумя глазами. Ра естся ине между изображениями точек А и С в левом глазу (5Л) и в правом (S t) различны. Если наблюдатель ощущает эту разницу, то он воспринимает и разноудаленное™ точек А и С н ощущает пространство стереоскопически. Углы ад и ас называются углами параллакса. Чем дальше наблюдаемые предметы (4 и С), тем меньше угол параллакса. Разность — 5’п пропорциональна разности углов параллакса.
Тренированный наблюдатель ощущает изменения параллактического угла между осями глаз при наблюдении достаточно контрастных объектов порядка 10" (порог стереоскопического зрения).
При больших расстояниях R имеем а' ~ b/R. Если b — 65 мм и а' — 10"— 0,00005 рад, то невооруженными глазами стереоэффект будет ощущаться иа расстоянии /?тах — Ь/а' — 1300 м.
Предельное расстояние, на котором еще ощущается стереоэффект, называется радиусом стереоскопического зрения. Если увеличение бинокулярного оптического прибора Гт и расстояние между оптическими осями объективов в /V раз больше, чем расстояние между осями глаз, то радиус стереоскопического зрения возрастает пропорционально произведению этих величин.
Непараллельное™ оптических осей бинокулярных приборов сверх допустимого предела (см. гл. 20) вызывает двоение изображения.
Разность увеличений или разворот изображений свыше допустимых пределов в обоих половинках прибора также вызывает двоение изображения в приборе.
Цветоощущение
Глаз ощущает излучения с длиной волны примерно 780—380 нм. Согласно некоторым данным, при значительной мощности излучения глаз видит излучения с длиной волны до 950 н 320 нм. Глаз способен различать свыше 100 цветовых тонов и оттенков.
Дополнительными цветами называются такие цвета, которые при смешении дают белый (или серый) цвет: красный (656 нм) и синеватозеленый (492 нм); оранжево-красный (608 нм) и голубовато-зеленый (490 нм); желтый (585 нм) и синий (485 нм); желто-зеленый (574 нм) и сипнн (482 нм); зелено-желтый (564 нм) и фиолетовый (433 нм).
Если некоторое время пристально смотреть иа фигуру, окрашенную в какой-либо насыщенный цвет, а затем перевести взгляд на поверхность белого цвета, то на этой поверхности глаз будет видеть в течение некоторого времени этот же объект, окрашенный в дополнительный цвет.
Небольшой объект белого цвета, помещенный на цветном поле, кажется окрашенным в цвет, дополнительный к цвету поля. Окраска двух смежных объектов, окрашенных в дополнительные цвета, кажется более интенсивной, чем если рассматривать каждый объект отдельно.
Воздействие невидимых излучений
Ультрафиолетовые лучи с X менее 313 нм при значительных дозах вызывают воспаление роговицы и соединительных оболочек глаза, а также сильные боли, которые начинаются ие сразу, а по прошествии 152
нескольких часов после облучения. Ультрафиолетовые лучи с X более 313 нм в значительной степени задерживаются хрусталиком, kgto- v рый при этом начинает сильно флуоресцировать. Ближние инфракрасные лучи с X от 809 до 1350 им, достигая сетчатки, вызывают ее нагрев, который при недлительном воздействии обычно безвреден. Однако при длительном интенсивном воздействии таких инфракрасных лучей (например, наблюдение за солнце'н незащищенными глазами) может вызвать выгорание сетчатки в том ее месте, где находилось изображение ’• солнца.
Инфракрасное излучение с X свыше 1350 им сильно поглоща-ется камерной влагой, что может привести к помутнению хрусталика глаза (образуется катаракта).
Литература: [3, 12, 32, 54, 100, 103, 105].
ГЛАВА 4
ОПТИЧЕСКИЕ ДЕТАЛИ И УЗЛЫ
ОБЩИЕ СВЕДЕНИЯ
Совокупность оптических деталей, установленных в положении, заданном расчетом и конструкцией, составляет оптическую систему прибора,
Оптические детали разделяются на следующие виды: линзы, зеркала, призмы и клинья, дифракционные решетки, сетки, экраны, светофильтры, защитные стекла, поляризационные призмы, поляфилытры компенсаторы, световоды.
В качестве узлов рассматриваются части, состоящие из деталей, соединяемых склеиванием или устанавливаемых на оптическом контакте, а также объективы, окуляры, сложные (составные) призмы и типовые призменные системы.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ, ПРИМЕНЯЕМЫЕ НА ЧЕРТЕЖАХ И СХЕМАХ
1. Обозначения физических величин
Показатели преломления для линий C't F', е1 прр, пр', п
С
Средняя дисперсия ............................. пр' — tipp
Коэффициент дисперсии , ................ . V
V
Длина волны, отвечающая границе пропускания по спектру............................
Длина волны, отвечающая максимуму пропускания по спектру.................................
Hid X
Предел разрешения в угловых секундах ... «
Количество полос (линий) на 1 мм
«.V
2. Обозначения элементов оптических деталей
Световая зона...................................... Св.
Световой диаметр................................... Св. 0
Длина хода луча в призме (геометрическая) /
1 В ГОСТ 3514 — 76 в качестве основной длины волны приняты длина волны зеленой линии «с» спектра ртути (К ~ 546,1 нм), а средняя дисперсия (tip' — пС') определяется по голубой (F') и красной (О') линиям спектра кад? мня (Кр' — 480,0 нм и ^Qr — 643,8 нм), вместо линий D, С н F в ГОСТ 3514 — 67.
3. Обозначения предельных отклонений Предельные отклонения показателя преломления пл........................................... Дл
Предельные отклонения средней дисперсии пр» — ПС'..........................................д
Предельное отклонение стрелки кривизн» по-верхност» детали от стрелки кривизны поверхности пробного стекла, выраженное числом интерференционных колец или полос, или допускаемая сферичность плоской поверхности в том же измерении...................... . , N
Предельное отклонение формы поверхности от сферы нли плоскости, выраженное числом интерференционных колец или полос (местные ошибки)......................................... ДА/
Наименьшее допускаемое фокусное расстояние пластинок или призм, как результат сферичности их поверхностей, в миллиметрах пли метРах......................................... fmln
Допускаемая децентрировха каждой поверхности (для линз) в миллиметрах................................ £
(При необходимости вместо с указывается разность толщин по краю)
Предельная клиновидность пластинки в минутах или секундах или разпотолщинность в миллиметрах . . 6
Предельная пирамидальность 1 призмы в минутах нли секундах .......................................... Л
Предельная разность равных по номиналу углов призмы (с цифровым индексом угла прнзмы, например, для прямоугольной призмы б45о) в минутах или секундах 6
Классы чистоты полированных поверхностей............. Р
Класс точности пробного стекла, назначаемой по
ГОСТ 2786 — 76, или предельные отклонения от значения расчетного радиуса поверхности в процентах А/?
1 Наличие угла между
ребрами призмы и противолежащими гранями.
ТРЕБОВАНИЯ К ОФОРМЛЕНИЮ ЧЕРТЕЖЕЙ ОПТИЧЕСКИХ ДЕТАЛЕЙ, УЗЛОВ И СХЕМ
Общие требования
Правила выполнения чертежей и схем оптических изделий установлены ГОСТ 2.412—68,
1. Оптические схемы» детали и узлы следует изображать на черту’-е по ходу луча, идущего слева направо.
2, При выполнении чертежей и схем оптических изделий применяют обозначения основных величии физической оптики — по ГОСТ 7601—78, основных величин геометрической оптики — по ГОСТ 7427—76, элементов оптических детален, предельных отклонений
физических величин и допускаемой неточности изготовления оптических деталей (см. выше условные обозначения, применяемые на чертежах и схемах), шероховатости поверхностей — по ГОСТ 2.369—73, специальных оптических покрытий (см. гл. 16), классов чистоты полированных поверхностей — по ГОСТ 11141—76.
3. На чертежах поверхности оптических детален обозначают прописными буквами русского алфавита, которые наносят на полках линий-выносок. Поверхности, к которым предъявляют одинаковые требования по точности и качеству изготовления, допускается обозначать одной и той же буквой.
4. В правой верхней части чертежа помещают таблицу, состоящую из трех частей: требования к материалу, требования к изготовлению,
Рис. 4.1. Изображение фасок на чертежах оптических детален
расчетные данные. Па чертежах оптических сборочных единиц указанная таблица должна состоять из двух частей: требования к изготовлению, расчетные данные.
5. На чертежах оптических деталей фаски изображают, как показано на рис. 4.1, а. Защитные (предохранительные) фаски допускается графически ^не изображать. Размеры фаски указывают на полках линии-выноски (рис. 4.1, б) или в технических требованиях надписью т X а, где т — ширина фаски, а — угол ее наклона. Если угол наклона фаски для предохранения от выкалывания не нормируется, то на чертежах или в технических требованиях указывают только ширину фаски (рис. 4.1, в).
Оформление рабочих чертежей деталей
1. Радиусы сферических поверхностей деталей должны выбираться по ГОСТ 1807—75.
Асферические поверхности линз и зеркал должны определяться координатами точек поверхности или уравнением кривой, использованной для ее построения (рис. 4.2).
2. Толщину по краю линз и неплоских зеркал и габаритную толщину менисков рекомендуется указывать в качестве справочных размеров (рис. 4.2 и 4.3).
3. На чертежах призм, пекруглых защитных стекол и зеркал следует кроме линейных и угловых размеров, определяющих их геометрическую форму, указывать номинальные размеры световых зон поверхностей, если для световых зон предъявляются более высокие требования в отношении класса (группы) дефектов, чем для краевой зоны (рис. 4.4 и 4.5).
Примечания:
1. Д2р ±=0.5%.
2. Диаметр кружка рассеяния — не более 0,2 мм.
3. ® др — лросветл. 44Р.43Р по ТУ ..., Х — 560+50 мм.
4. Покрытие матовых поверхностей ЭмХС-77 по Т\ ...
5. Размеры со звездочкой — для справок.
Рис. 4.2. Чертеж параболической линзы из стекла БКДО по ГОСТ 3514—76
4. Световые зоны ограничивают тонкой штрих-пунктирной линией (рис. 4.5) с указанием на полке линии-выноски обозначения «Св.».
5. Для деталей из бесцветного оптического стекла по ГОСТ 3514— 76 в первой части таблицы помешают следующие требования к ма-
(V)
Дг,г ЗВ
A (пр' — пс') ЗВ
Однородность 3
Двойное лучепреломление 3
Ослабление 2
Бессвильность ЗВ
Пузырность 2Б
^АБ В 5
ллДб 0,5
с 0,05
РА IV
РБ V
Д«АБ 3
Г 47,87
SP — 42,65
SF' 48,71 ±= 0,81
Св. Св. 0 5 26,1 28.1
териалу: категорию и класс по показателю преломления и средней дисперсии; категорию по оптической однородности; категорию по двойному лучепреломлению; категорию по радиационно-оптической устойчивости (стекла серии 100); категорию по показателю ослабления; категорию и класс бессвильности; категорию и класс пузырности.
6. Для деталей из цветного оптического стекла по ГОСТ 9411—75 в таблице следует указывать категории по спектральной характеристике, двойному лучепреломлению, бессвильности и пузырности (рис. 4.G).
7. Для деталей из других оптических материалов (кварцевое стекло, естественные и искусственные кристаллы и др.) первую часть таблицы заполняют в соответствии с действующими техническими условиями на эти материалы.
Примечания: N и AW для участка 0 50 мм.
2. Разность толщин но краю до 0,1 мм.
3. (^ — зеркальн. 1И.21Е по ТУ...
4. Вне светового диаметра допускаются кант без зеркального покрытия и точки от контактов.
5. Покрытие матовых поверхностей
ЭмХС-77 по 4 У...
6. Размеры со звездочкой — для справок.
Лле ^пИ
A (пр' — П(у)
Однородность РИ
Двойное лучепреломление 3
Ослабление
Бессвиль-ность
Пузырность 7Г
W 2
AW 0,2
Р VI
лр 3
г 207
Св. 0 150/70
Рис. 4.3. Чертеж сферического зеркала из стекла ЛК4 по ГОСТ 3514-76
8. Требования к изготовлению деталей помещают во второй части таблицы, в которой указывают V и ДА/. Предельные отклонения У и AN следует относить: для круглых деталей — к их диаметру; для некруглых деталей — к наименьшему размеру; для деталей больших размеров, проверка которых производится по участкам — к диаметру проверяемого участка (диаметр участка надо указывать в примечаниях). Далее в таблице приводятся следующие допуски: с\ Р; 0; л; 6; е (при необходимости); ^min (при необходимости); Д/? (для плоских поверхностей при необходимости).
Примечания:
а) при назначении неодинаковых допусков /V, &N или Р для разных поверхностей одной детали иля разных зон одной и той же поверхности, а также при назначении неодинакового допуска (с) обозначения этих допусков следует указывать с буквенными индексами, каждое в отдельной строке (рис. 4.2—4.5). Эти же индексы следует ставить у соответствующих поверхностей или у их зон на изображении;
б) для деталей, ие подлежащих контролю пробными стеклами, отклонения N и ДА/ не указываются.
9. На чертежах деталей в третьей части таблицы следует указывать световой диаметр (Св. 0), а для сферических деталей, кроме того, 158
Примечания:
1. Фаски на ребрах 0,3+3>3, кроме мест, указанных особо.
2. — просветл. 24И по ТУ ...»
X ~~ 590±5’о нм.
3. Покрытие матовых поверхностей ЭмХС-77 по ТУ ...
4. Размеры со звездочкой — для справок.
Рис. 4.4. Чертеж призмы с крышей из стекла К8 по ГОСТ 3514—76
значения величин sF, s'F,r Одну из величин указывают с предельными отклонениями.
10. На чертежах призм в третьей части таблицы указывают геометрическую длину хода луча в призме (Z), световой диаметр (Св. 0) по наибольшему сечению пучка и предел разрешения (при необходимости).
11. На чертежах деталей, подлежащих просветлению, серебрению,
Алг с ЗВ
А — «£>) ЗВ
Однородность 1
Двойное лучепреломление 2
Ослабление 2
Бессвилыюсть 1Б
Пуз ыр кость ЗА
2
0,3
;VB 0,5
a.VB 0,2
р IV
л 2'
615“ 1*
е 25"
Н min —
1 14
Св. 0 5
алюминированию и другим покры-
тиям, в технических требованиях нужно указывать условное обозначение покрытия и условный графический знак его. Тот же знак должен быть указан на изображении у поверхности, подлежащей покрытию (рис, 4.2—4.5) или на выносной линии к ней. Кроме условного обозначения покрытий в технических требованиях следует указывать и другие характеристики.
Для свело делительных покрытий одну из следующих характеристик: а) отношение коэффициента отражения р к коэффициенту пропускания т (с допуском);
б) коэффициент отражения р (с допуском);
в) коэффициент пропускания т (с допуском)*
^(v)
Примечания:
I. Фаски на ребрак 0,3+0>8 Х45°. Фаски на углах 1°»4Х45°.
2. — просветл. 44Р. 43Р по
ТУ .... X = 520^50 им,
3. Покрытие матовых поверхностей ЭмХС-77 по ТУ ...
4. Размеры со звездочкой *-» для справок.
Рис. 4,5. Чертеж призмы со световыми зонами из стекла К8 по ГОСТ 3514—76
Для просветляющих, светоделительных и отражающих покрытий: среднюю рабочую длину волны света (с допуском), для которой рассчитано покрытие, если она отличается от средней длины волны для белого света (550 нм), или участка спектра, для которого покрытие предназначено.
Для покрытий-фильтров:
а) для нейтральных (серых) — оп-
Дм 2В
Д (пр,—пС') 2В
Однородность 2
Двойное луче-преломленне 2 i
Ослабление 1 1
Бессвильность 1Б
Пузырность ЗА
"а 3
д"а 0,3
1
АЛБ 0,2
РА V
IV
Л 3'
3'
8 5"
Г гшп —
1 48
тическую плотность (с допуском); .
б) для интерференционных (узкополосных) — длину волны А-юзх» отвечающую середине полосы пропускания, коэффициент пропускания ттах для этой длины волны, полуширину полосы пропускания определяемую как разность длин волн, соответствующих ттах/2, и минимальное пропускание тт1п по обе сто-
роны от полосы пропускания.
12. При окраске нерабочих матовых поверхностей детали в технических требованиях помещают указания в соответствии с требованиями ГОСТ 2.310—68 (рис. 4.2—4.6)
Пример оформления чертежа сетки показан на рис. 4.7.
0,5 t0‘^55a /^2сраски
Рис, 4.6. Чертеж светофильтра из стекла ОС1 по ГОСТ 9411—75
Спектральная характеристика 2
Двойное лучепреломле-н ие 3
Бессвильность 2
Пуз ыр кость 5
А 4
ДА 0.5
Р V
0 5'
Г . in in 5 м
Св. 0
Примечания:
1. Ширина штрихов — —0,015^= =1=0,003 мм.
2. Разность штрихов по ширине у одной детали не более 0.003 мм.
3. Разность штрихов по длине у одной детали не более 0,015 мм.
4. Отклонение расстояний от начального штриха до любого другого не более 0,005 мм.
5. Остальные требования к штри-
хам по ТУ ...
6. Штрихи и цифры травить и заполнить запуском ... по I * ...
7. Шрифт 0,5 по ТУ ...
R. 2.5 (V)
д% 4 В
4В
Однородность 4
Двойное лучепреломление 3
Ослабление 3
Бессвильность 2В
Пузырность 1
А ——
ДА —
Р 1—20
0 15'
Св. 0 14
Рис. 4,7. Чер теж сетки из стекла БК10 по ГОСТ 3514—76
6 В. А. Панов и др.
Оформление рабочих чертежей узлов
На чертежах оптических сборочных единиц указывают только те размеры, покрытия и т. д., которые должны быть выполнены в процессе сборки. В технических требованиях или в спецификации иа чертеже узла должны быть указаны наименование и марка клеящего вещества и номер нормативного документа (рис. 4.8), а в необходимых случаях и толщину склеивающего слоя. В первой части таблицы указывают:
Примечания:
1.0“ просветл. 44Р.43Р по ТУ .... 1 “ 520±30 нм.
2. Покрытие матовых поверхностей ЭмХС-77 по ТУ ...
Рис. 4.8. Чертеж склеенной линзы
Л/ 2
ДЛ/ 0,5
с
Р, IV
Pi V
Г 69,72
SF “65,52
SF’ 66,91 =±=0.7
Св. 0 16
(V, АЛ/, с (для линз), Р; fmJ11 и е указывают при необходимости. Значения /', s^, s'p, и другие требования указывают во второй части таблицы.
Оформление оптических схем
1. На оптических схемах детали и узлы, как правило, следует располагать по ходу светового луча, идущего от плоскости предметов слева направо (рис. 4.9).
2. Для сложных приборов оптическую схему основной части прибора и оптические схемы узлов прибора, имеющих самостоятельное назначение, допускается оформлять отдельными чертежами. На основной схеме такие узлы допускается обводить штрих-пунктирной линией.
3, Все детали, поворачивающиеся или перемещающиеся вдоль пли перпендикулярно оптической осн системы, следует показывать в основном рабочем положении. При необходимости штрих-пунктиром могут быть показаны и другие положения деталей, например крайние; следует также показывать:
а) апертурные диафрагмы и положения зрачков (схематически);
б) положение фокальных плоскостей, плоскостей изображения или предмета, положение полевой диафрагмы;
в) источники света (схематически);
г) приемники лучистой энергии (схематически или условными графическими обозначениями), например фотоэлементы, фотоумножители (в схемах с фото регистрацией).
— S. м s', мм
оо 4 0,8
20 4 0,9
10 4 1,02
7 41,13
5 41.27
2 4 2,05
Расчет оптики
Фокусное расстоя-и не 51,3
Относительное отверстие . , . 1 : 3,5
Предел разрешения 20"
Размер кадра. . 18X24
от
1 позиции ! детали Св. 01 Стрелка по Св. 01 Св. 02 Стрелка ПО Св. 0г Толщина по осн
1 15,5 1,56 14 — 3.5
2 12,2 1,02 12 1,51 1
3 12 — 12 1,26 1,2
4 12 1.26 12 1,17 4
Перечень деталей
Формат Зона Поз. Обозначение Наименование Кол. Примечание
— 1 Линза 1
— ’— 2 Линза 1
— — 3 Линза 1
— 4 Линза 1
4. На чертеже оптической схемы следует указывать:
а) основные оптические характеристики системы (при необходимости с допусками), например:
для телескопических систем — увеличение, угловое поле, диаметр выходного зрачка, удаление выходного зрачка от последней поверхности, предел разрешения, коэффициент светопропускания (при необходимости);
для фотографических объективов — фокусное расстояние, относительное отверстие, угловое поле или линейное поле, предел разрешения (при необходимости);
для фотоэлектрических систем — размеры или типы фотокатодов, размеры светового пятна на фотокатодах (при необходимости);
б) фокусные расстояния f' и фокальные отрезки и отдельных узлов оптической системы, как, например, объективов, оборачивающих систем и окуляров; эти данные следует помещать на поле чертежа в виде таблицы.
Номера позиций деталей сборочной единицы Наименование сборочной единицы Г SF Г
в) различные дополнительные сведения, например: расстояния от последней поверхности фотографического объектива до плоскости изображения в зависимости от расстояния до предмета (рис. 4.9); линейное перемещение окуляра на 1 gmnp и т. д.
5. На оптической схеме следует проставлять:
а) размеры световых диаметров оптических деталей и соответствующих им стрелок, а также толщину по оси (для призм — длину развертки). Эти данные следует помещать на поле чертежа в виде таблицы.
Номера позиций деталей Св. 01 Стрелка по Св. 01 Св. 05 Стрелка по Св. 02 Толщина по оси, длина развертки призм
Примечание. На оптической схеме с большим количеством деталей допускается проставлять световые диаметры и толщины по оси на самой схеме.
б) диаметры диафрагмы и размеры зрачков, размеры тела накала или иных светящихся элементов источников освещения (при необходимости с допусками);
в) воздушные промежутки и другие размеры по оси;
г) размеры, определяющие пределы перемещения или предельные углы поворота оптических деталей;
д) размеры, определяющие положение оптической системы относительно механической части прибора, па пример размер, определяющий
положение объектива микроскопа относительно нижнего среза тубуса;
е) габаритные или сборочные размеры, например длина базы, высота выноса (при необходимости).
ЛИНЗЫ
Линзами называются детали из оптически прозрачных однородных материалов, ограниченные двумя преломляющими поверхностями, из которых по крайней мере одна является поверхностью тела вращения (сфера, асферическая нли цилиндрическая поверхность). Классификация линз приведена в табл. 4.1.
Таблица 4.1. Определение некоторых линз и линзовых систем
Тип линзы (системы) Определение и назначение
Мениск Линза афокальная Линза бифокальная Линза зеркальная Коллектив, коллектив-сетка Конденсор, коллектор Система панкрати-ческая Системы перемены увеличений Объектив Окуляр Радиусы кривизны одинаковы по знаку Оптическая сила линзы к нулю Одна часть поверхности имеет один радиус кривизны, а другая—другой радиус кривизны Одна поверхность работает как отражающее зеркало, а другая как преломляющая поверхность Линза, расположенная в фокальных плоскостях или вблизи от них и предназначенная для отклонения к оси пучков лучей с целью уменьшения габаритов оптической системы. На одной из поверхностей могут быть деления (сетка) Положительная линза или система линз, служащая для отклонения к оси пучков лучей, идущих от источника света Система линз для получения плавного изменения увеличения Система линз для получения ряда дискретных значений увеличения прибора Линза, система линз или система линз и зеркал, служащие для получения действительного изображения предмета (или проекции его на экран) Линза или система линз, служащие для рассматривания изображения, и помещаемые перед глазом
Конструкция линз
Конструктивные элементы линз разделяются на две группы.
Первая группа — элементы, которые характеризуют оптическое действие линзы и определяются при расчете оптической системы:
Таблица 4,2. Ширина фаски (т) в зависимости от диаметра
Диаметр детали, мм Ширина фаски, мм Для крепления завальцовкой
Для предохранения от выколок
несклеиваемая сторона склеиваемая сторона
До 6 Св. 6 до 10 » 10 » 18 » 18 » 30 » 30 » 50 » 50 » 80 » 80 » 120 » 120 » 180 > 180 » 260 » 260 » 360 »360 » 500 » 500 О,!*0’1 0.1+0'1 CM CM СО Ю ю о о о © Q а Д « to 1 ъ I । । । I । о о о о о —
О,2+0’2
о.г+о-2
О,3+0’3
О,5+0-5
О,3+0’3 О.8+0-8 1,0+1-°
О.7+0-7
1,0+О'8
1>2+1.о
1,5+1’5
Таблица 4.3. Угол наклона фаски (а) в зависимости от D/R
Отношение диаметра к радиусу поверхности Угол наклона фаски а, ...°
на выпуклой поверхности на вогнутой поверхности иа плоской поверхности
До 0,6 45 45
Св. 0,6 до 1,5 30 60 45
» 1,5 — 90
константы оптического стекла н технические требования к нему, радиусы кривизны (форма) поверхностен, толщина (по оси), световые диаметры, вид просветления или защиты поверхностей и допуски на качество поверхности, чистоту и центрировку. Расчетные радиусы должны быть округлены до ближайших значений по ГОСТ 1807—75.
При расчете не должны допускаться слишком тонкие линзы, так как при полировании они прогибаются, что делает невозможным получение точных поверхностей и центрировку (если мал припуск на центрировку и трудно разместить фаски). В табл. 4.4 приведены соотношения между наименьшей толщиной края и диаметром положительных линз^ 166
Таблица 4.4, Соотношения между световым и полным диаметрами л низ (ОСТ 3-490—71)
Световой диаметр линз Св. 0, мм Полный диаметр D, мм Наименьшая толщина края положительных линз, мм Световой диаметр линз Св. 0 , мм Полный диаметр £>, мм Наименьшая толщина края положительных линз, мм
/О = Св. 0 4 4-Д£> D ~ Св. 0 4~ + &D
&D при креплении &D при креплении
заваль-ЦОВКОЙ зажимным КОЛЬЦОМ заваль-ЦОВКОЙ зажимным кольцом
До 6 Св. 6 до 10 » 10 » 18 » 18 » 30 » 30 » 50 » 50 » 80 0,6 0,8 1,0 1,2 1,5 2,0 1,0 1,5 1,8 2,0 2,5 1,0 1,2 1,5 1,8 2,0 2,5 Св. 80 до 120 » 120 » 180 » 180 » 260 » 260 » 360 » 360 » 500 3,0 4,0 5,0 6,0 8,0 3,0 4,0 5,0 6,0 7,0
Т а б л и ц а 4,5. Соотношения между наименьшей толщиной по оси н диаметром отрицательных линз
Характеристика линз Наименьшие толщины по оси d, мм при допуске A7V па местные ошибки
Форма Диаметр D, мм До 0,3 0,3 —0.5 0,5 —2,0 Cd. 2,0
До 50 0,152? 0,120 0,120 0,100
Двояко- 50—120 0,120 0,120 0,100 0,082?
вогнутая 120—260 0,102? 0,102? 0,082? 0,082?
260—500 0,102? 0,080 0,082? 0,082?
Мениск До 50 0,122? 0,120 0,100 0,100
(выпукло- 50—120 0,120 0,100 0,080 0,080
вогнутая) 120—260 0,100 0.10D 0,082? 0,082?
260—500 0,100 0,100 0,082? 0,080
а в табл. 4.5 — наименьшей толщиной по оси и диаметром для отрицательных линз.
Вторая группа — элементы, зависящие от способа крепления линз. К этой группе относятся диаметры линз D, а также размеры и расположение фасок (табл. 4.2 и 4.3). Для закрепления линз в оправе полный диаметр линзы делается несколько больше светового. Минимальное
значение полного диаметра в зависимости от светового даны в табл. 4.4. Окончательный его размер округляется до ближайшего (большего) нормального диаметра по ГОСТ 6636—69.
Фаски на оптических деталях круглой формы (линзы, сетки, светофильтры и др.)
Фаски снимаются: а) для предохранения детали от выколок (защитные фаски); б) для крепления линз завальцовкой или обеспечения центрировки; в) для удаления излишков стекла (конструктивные). Первые два вида фасок нормализованы и выбираются из табл. 4.2 и 4.3 в зависимости от диаметра линз; конструктивные фаски не нормализованы и определяются из конструктивных соображений.
При малой толщине оптической детали на краю размер фаски может быть уменьшен. Фаски на оптических деталях, которые крепятся закаткой должны быть концентричны по отношению к наружному диаметру.
На выпуклых поверхностях при отношении диаметра D к радиусу поверхности больше 1,5 фаску ие снимают; при отношении D/R от 1,3 до 1,5 фаска допускается, ио не является обязательной. Ширина и допустимость фасок, попадающих в световой пучок, которые должны быть минимальными или отсутствовать совсем, устанавливаются конструктором. Угол наклона фаски (а) в зависимости от отношения D/R выбирать по табл. 4.3 Если конструктивная фаска образует с сопрягаемой поверхностью линзы угол меньше 110°, то следует снимать дополнительно фаску от выколок согласно табл. 4.2, 4.3 и 4.8.
ЗЕРКАЛА
Применяются плоские, сферические и асферические зеркала с наружным и задним отражающим покрытием (сплошным или частично отражающим и частично пропускающим свет). Плоские зеркала применяются в тех случаях, когда они дают выигрыш в весе и простоте конструкции по сравнению с отражательными призмами.
Плоские зеркала, участвующие в построении изображения в визуальных системах приборов или используемые в точных измерительных приборах (например, интерферометрах), требуют высокой точности изготовления. Как правило, отражающий слой на этих зеркалах наносится на наружной стороне. Это делается для того, чтобы избежать влияния ошибок изготовления зеркала, например клиновидности, на качество оптической системы. Зеркала с задней отражающей поверхностью нельзя устанавливать в сходящихся пучках, так как они вызывают двоение изображения, а при наклонном положении также астигматизм и асимметрию в строении пучка. Плоские зеркала невысокой точности имеют широкое применение в неответственных узлах (осветительные устройства, видоискатели фотокамер, рисовальные устройства микроскопов и т. н.).
Формы зеркал весьма разнообразны. Толщина зеркал зависит от размера, способа крепления и главным образом от требуемой точности поверхностей. Чем точнее зеркало, тем больше должна быть его толщина. Толстые зеркала меньше деформируются при креплении. Зеркала концевых отражателей дальномеров при допуске иа подгонку под пробное стекло 0,1—0,3 полосы и при размерах сторон 60—80 мм имеют толщину 10—12 мм. Рекомендуется применять следующие соотношения между толщиной d и наибольшим размером I (или диаметром) зеркала:
а) особо точные зеркала (зеркала интерферометров, концевые отражатели дальномеров) d (1/5—1/7) /, б) точные зеркала (визуальных систем наблюдательных и прицельных приборов) d>.(l/8—1/10) I, в) грубые зеркала (осветительные системы) d (1/15—1/25) I. Размер зеркала с задней отражающей поверхностью (рис. 4.10) определяется по формуле
двоение изображения и хро-
cos е ]/' п- — sin2 е’ где D — ширина зеркала.
Клиновидпость зеркала вы: матизм.
Для изготовления точных зеркал, входящих в оптическую систему прибора, применяется стекло марки К8, для концевых отражателей дальномеров — кварцевое стекло, малочувствительное к изменениям температуры. Для таких же целей в менее ответственных случаях применяется стекло марки ЛК5, в неответственных случаях — зеркальное стекло.
Сферические и асферические зеркала (параболические, гиперболические, эллиптические), внеосевые с внешней и с задней отражающими поверхностями применяются для объективов астрономических приборов, объективов микроскопов, телеобъективов фотоаппаратов, для прожекторов и различных осветительных устройств.
ПРИЗМЫ
Призмы применяются для следующих целей: для изменения хода лучей в приборах; изменения направления оптической оси системы; изменения направления линии визирования; оборачивания изображения; уменьшения габаритного хода лучей; разделения пучков лучей; вращения изображения или компенсации поворота изображения (например, в панорамических приборах); разложения света (в спектральных приборах); поляризации света (табл. 4.6 и 4.7).
Преимущества призм:
1) углы между гранями призмы неизменны, в то время как углы между зеркалами должны регулироваться с большой точностью при сборке и система зеркал может разъюстироваться в процессе эксплуатации;
2) потери света у призм от граней с полным внутренним отражением равны нулю,в то время как при отражении от поверхностей зеркал потери довольно велики. Кроме того, покрытия зеркал могут с течением времени портиться;
3) некоторые призмы нельзя заменить зеркалами (например, призму Дове или спектральную призму).
Призмы отражательные подразделяются на одинарные (из одного куска) и составные.
Таблица 4.6. Отражательные призмы
Соотношения размеров даны дня светового пучка круглого сечения с наибольшим диаметром О. Диаметр действительного пропускаемого светового пучка получается уменьшением расчетного диаметра пучка D на величину, необходимую для закрепления призмы в оправе: I — геометрическая длина хода лучей в призме; ширина всех призм равна D
О О
О
<и о
м о
ч и
я X
S
и
X
гг я X СП
Схема
Соотношение размеров
о н
Тип А. Одинарные призмы с одним отражением
а о
<3J
со
с
о-
О
о
о о ст>
60
о « 00
ВидА
„2 1/ 2/г2 — 1 с ~ D —------------------
— 4,230 (для К8) и 4,040 (для БК10)
Для nD h = D
У 2и2—1—1
= 3,3810 (для КЗ) и 3.20D (для БКЮ)
а — D с h
I = 2,4140
2.613D 0,9240
а =
С ~
2D
0,8660
I 1,7320
а — О с = 1,4140
Все призмы этого типа оборачивают изображение в главном сечении на 180° (зеркальное изображение)
Тип Ак. Призмы с крышей
а = D с = 2,6130 h = 1,1430 I = 3,5380
।
Соотношение размеров
*
f I
а « D b = 0,3660 й = 1,7320 I = 1,7320
Все призмы этого типа дают полное оборачивание изображения I
Тип Б. Призмы с д в у м и отражениями
СС * S Р о
S CL Ф Р
* го
Схема
Соотношение размеров
Серебрить
а — D
I = 3.4I4D
с = 1.082D
а = D
с = 1,414D d = 1,4140
I = 1.707D
-и
<v о ж а о ч
GJ
Я
О
(У н
СП
у
Схема
Соотношение размеров
а — О с = 1,4140 ?! = 1,3050 I = 1,9540
Призма БР — 180е дает зеркальное изображение предмета, призма БС — 0° и призмы типа БУ и БН — прямое изображение, призмы типа БМ — полное оборачивание
крышей и одним отражением
Призмы
1 и л
с
а = 2,2250 с = 1,4140 I == 2,9570
а « 1,2370 о => 1,0820 I = 2,1110
о АО О
СУ о
и о
и
Г'Ъ
Схема
Соотношение размерив
Вид А
а = D с — сг = h =
I =
1.155D 2,6180 1,61 80 2,8020
Схема
Соотношен не размеров
а — D с = 2,50
Ci ~ 2D
I = 4,330
Схем а
Соотношение размеров
Т и п Вк. Призмы с крышей и двумя отражающими поверхностями
о in
а — D г — ,уП ct = 2,6180 т = 0,3570
I = 4,5350
с = 1,7810
= 1,3630
/ = 3,040
с = 2,6180 h = 0,9340 I = 2,8020
Призмы ВкЛ — 0° и ВкР — 45° дают полное оборачивание, а призма ВкР — 180° — зеркальное изображение
Схема
Соотношение размеров
Составные призмы визуальных приборов
а = D
с 3,46D
Ci = 1,155D
Cj 2D
h = 2D
I = 5J96D
Призма дает зеркальное изображение
'Серебрит
В ид А (Ззз клина)
о о о
45
Вид В
%
I,
Воздушный промежуток
Призма дает прямое изображение
а = D
с = 2D
сх з= l,035D
с-2 = 1,155D d — 0,002 мм h « 1,732
I 1.732D (без клина)
к га Р.
а — D
D
— 1
|/*2н2 >- 1 — 1 = 0.707D
Призма устанавливается только в параллельных пучкйх; дает зеркальное изображение
<ь о X
Схема
Соотношение размеров
Призма дает зеркальное изображение, заменяет призму Дове; работает в сходящихся пучках
а
м К а с
a — D с = 1,4140 ct = 1,0520 с2 == 1,6210 т = 0,2930
h =* 1,2070
dx — 0,05 — 0,1 мм I = 4,620
а — О с ® 3,460 ct — 1,1550 с2 = 20
h с= 20
I = 5.19GD
а = О с = 2,330
Cj — 1,0350 с 2 -”* 1,15 5 О т — 0,330
— 0,002 мм h — 2,30
I = 2,60 (без клина)
щ
Призма дает зеркальное изображение
А сп _ X W хэ « й
о <ъ
I s S д К U о v И » Ь £ се & . х га
Схема
Соотношение размеров
а = D с = 1,780 = 1,080 с2 = 1,4140 т — 0,390 h = 1,2310 di = 0,1 мм I = 4,750
Призма дает полное оборачивание
m m 2 S m
X В CU X с о
а = О b — D с = 1,55 (Л + О) h ~ 0,333 (Л + О) I = 1,115 (Л + О) (без клииа)
Каждая призма обозначается двумя буквами и числом, разделяемых между собой знаком тире. Первая буква указывает число отражающих граней, вторая буква — характер конструкции призмы. Число указывает угол отклонения осевого луча в градусах,
Примечания: 1. Крыша условно считается за одну грань. Обозначается индексом «к» у первой буквы,
2. Если осевой луч отклоняется внутри призмы в двух плоскостях, то цифры условного обозначения указывают углы отклонения в этих плоскостях.
Призмы с одной отражающей гранью обозначаются буквой А; с двумя отражающими гранями — буквой Б; с тремя отражающими гранями буквой В; призмы с крышей—Ак, Бк, Вк.
В зависимости от характера конструкции призмы второй буквой обозначается: Р — равнобедренная призма; П — пентапризма, У — полупентапризма, С— ромбическая призма, М — призма дальномерного типа и Л — призма Лемана.
В табл, 4.6 приведены данные отража- *
тельных призм.
Составные призмы
Каждая призма обозначается одной буквой и числом, разделяемых знаком тире. Пример обозначения: призма-куб — К—0°, башмачная призма — Бк—90°. Условные обозначения проставляются на рабочих чертежах вместе с названием призм.
Отражательные призмы развертыва-
ются в плоскопараллельную пластинку. Развертка призмы выполняется путем пере-
Рис. 4.11. Развертка
прямоугольной приз-
мы
вертывания контура сечения призмы вокруг каждой стороны этого контура, соответствующей отражающей грани, в той последовательности, в которой происходят отражения луча от этих граней. На рис. 4.11—4.13 даны примеры развертки призм и определения геометрической длины хода осевого луча в призме I.
Рис. 4.12. Развертка пентапризмы
Расчет размеров призм
Чаще всего огибающая поверхность пучков лучей, проходящих через призму, является конической поверхностью с круглым основанием. Поэтому для определения размеров призм следует задаться размерами конуса пучка лучей и положением одной из граней призмы.
Рассмотрим случай, когда задана грань, на которой сечение пучка будет меньшим (рис. 4.14). Для решения задачи вводится эквивалентная развертке призмы воздушная пластинка толщиной l/п (п — показатель преломления призмы, I — геометрическая длина луча в призме берется по типу призмы из табл. 4.6), Для определения толщины воздушной призмы надо найти величину D на ее выходной грани. Зная
угол конуса лучей 2а и обозначая l/D ~ kt можно определить величи-ну D из выражения
D — 2 (г + a tg а) + 2Dk tg а/л, откуда
D _ 2 (г + q tg а)
1 — 2k tg а/л *
Решение аналогичной задачи, когда задается положение грани
с большим сечением пучка, просто, так как D в этом случае известно и размеры призмы берутся из табл. 4.6.
Если призма с двумя или тремя отражениями имеет крышу,
выходящую только иа одну
Рис. 4.14. Схема расчета призмы
преломляющую грань (входную или выходную), то вместо полученного размера надо брать размер
sin у
где у — угол между ребром крыши и рассматриваемой гранью. Если в призмах с одним отражением (типа АР) крыша выходит на две грани (например, у прямоугольной прнзмы), то
К1 -ф sin2у sin у
Если призма не развертывается в плоскопараллельную пластинку, то она действует как клин с большим преломляющим углом и вызывает хроматизм и искажение изображения. Такие призмы применяются с дополнительным (компенсирующим) клином (например, башмачная призма Б—90е). Угловое поле любой призмы ограничено н зависит
Таблица 4.7. Предельные углы 2о для различных призм из стекла К 8 и БК10
Тип призмы Зрачок на входной (выходной) грани Зрачок в середине раззертки призмы
2<т, о • • г
К 8 Б К1 О КЗ БК 10
АР—90э 85э 24' 89° 06' 2а -> 90° 2а -> 90°
БР—180° 43° 10' 44° 44' 85° 24' 89° 06'
БП—90° 25° 59' 26° 54' 50° 27' 52° 20'
АР—45° 36° 37° 06' 70J 58' 73° 48А
АР—0° 25° 36' 26° 30' 50° 56' 55° 48'
П—0 18° 43' 19° 26' 37° 26' 38° 45'
Формула
Формула sin о — —— I р sin а — п
V1 -р 4&2 1 /с2
от ее конфигурации и показателя преломления стекла (табл. 4.7). Предельный угол о определяется по формуле sin or с n-(V Т 4й2).
Если входной зрачок поместить в середине развертки призмы, то угол а определяется по формуле sin а л/(К* 1 + /г2)-
Призмы с четным числом отражающих граней и ходом луча в одной плоскости дают прямое изображение. При качании такой призмы в этой плоскости выходящий пучок лучей не отклоняется.
Призмы с нечетным числом отражающих граней и ходом луча в одной плоскости дают зеркальное изображение предмета. При качань'и их в этой плоскости лучи отклоняются на двойной угол. Если у призмы с нечетным числом отражающих граней одну из них заменить двумя гранями, расположенными под прямым углом (крышей), то такая призма будет давать полное оборачивание (на 180е). При этом общий угол отклонения пучка не изменится.
Все размеры призм вычисляются в зависимости от наибольшего диаметра светового пучка D, проходящего через призму, с учетом припуска на фаску и крепление.
По характеру отклонения луча призмы делятся на призмы с ходом осевого луча в одной плоскости н призмы с пространственным ходом осевого луча.
Призмы с одной отражающей гранью (тип А)
Призмы этого типа дают зеркальное изображение и при нормаль’ ном падении луча на входную грань угол его отклонения равен углу при вершине. При наличии крыши на отражающей грани изображение получается развернутое вокруг оптической оси на 180°.
Призма Дове АР—0°. Эта призма носит также название призмы прямого зрения — ее оптическая ось параллельна отражающей грани и угол отклонения равен 0°. Употребляется как компенсационная призма для поворота изображения вокруг оси прибора. Угол поворота изображения в два раза больше угла поворота призмы. Отражающая грань с не требует нанесения зеркального покрытия (см. табл. 4.6). Призма развертывается в плоскопараллельную пластинку, наклоненную к оси под углом 45°, поэтому она устанавливается только в параллельном ходе лучей.
В визирной (качающейся) прямоугольной призме, как правило, отражающую грань следует серебрить. Размеры призмы зависят от диаметра пучка лучен и угла качания. Для получения наименьших размеров призму следует помещать так, чтобы входной зрачок системы находился в середине призмы или как можно ближе к ней.
При больших углах качания, чтобы избежать больших габаритов призмы, которые при этом получаются, применяют призму-куб, состоящую из двух прямоугольных призм, склеенных гипотенузными гранями. Гипотенузные грани должны иметь отражающее покрытие.
Если возможно применение качающейся призмы из стекла с большим пе, то отражающее покрытие может не понадобиться.
При положении призмы-куба, изображенной на рис. 4.15, а, работает только одна половина призмы; по мере поворачивания ее для визирования в зенит (рис. 4.15, 6) начинает включаться вторая половина призмы н при визировании в зенит работают обе половины. Призма-куб дает возможность визировать в пределах угла 210—220°. Недостатки этой призмы заключаются в следующем:
1) призма может работать только в параллельных пучках лучей; в сходящихся пучках лучей происходит двоение изображения;
2) трудность изготовления, так как ошибки углов половинок призмы и склейки даже порядка нескольких секунд вызывают двоение изображения. Допустимая угловая величина двоения изображения 30"/Гт (Гт — увеличение системы, расположенной после призмы);
3) если входной зрачок расположен перед призмой, вместо круглого получается зрачок, показанный на рис. 4.15, в\ это ухудшает условия работы с прибором и ведет к снижению разрешающей способности.
В прямоугольной призме с двумя отражающими поверхностями типа БР—180° ошибка в угле 90е, равная 6, вызовет отклонение выходящего пучка 26/г в главном сечении призмы.
Ошибка пирамидальности, равная л, дает отклонение выходящего пучка лучей на 2л/г в плоскости, перпендикулярной главному сечению. Ошибка в острых углах не вызывает отклонения выходящего пучка,
Призма-куб (К—0°)
но вызывает его смещение иа величину Z6/n, где I — геометрическая длина хода лучей в призме, 6 — ошибка в острых углах, отличающаяся только знаком.
В зависимости от конфигурации отражательные призмы могут удлинять нли сокращать габаритную длину хода лучей. Сокращение габаритного хода лучей вызывают призмы с многократным отражением, например, пентапризма БП—90°, призма Шмидта ВР—45°, призма БУ—45°, призма Пехана и некоторые другие. Призма Аббе А—0° при размерах, указанных в табл. 4.6, и при п = 1,5 не дает смещения изображения при ее включении в ход лучей.
Паразитные отражения в призмах
Призмы или призменные системы должны проверяться на возможность появления вредных (паразитных) отражений, которые могут вызвать появление дополнительных изображений или бликов. Паразитный ход лучей может появляться, например, в прямоугольной визирной призме (рис. 4.16) при указанном на рисунке положении или в призме-кубе в положении, изображенном на рис. 4.17.
При повороте прямоугольной равнобедренной призмы АВС, расположенной перед объективом телескопической системы, на угол (р от начального положения (при начальном положении отражающая грань АС расположена под углом 45° к оси объектива) могут возникать паразитные изображения. На рис. 4.16 показан ход пучков лучей, образующих эти добавочные изображения. Основной пучок Ао, падающий на призму под углом 2(р к нулевой оси визирования ОО', испытывает 184
ОС
Сл
Рис. 4.16. Схема прохождения паразитных лучей в качающейся прямоугольной призме
Подвижная шторка
Рис. 4.17. Схема прохождения паразитных лучей в системе защитное стекло—призма-куб
одно отражение от грани А'С'. Пучок А, преломляется гранью А'В', отражается дважды от граней В'С? и А'С и дает перевернутое изображение другого объекта в центре поля.
Третий пучок Д2 падает на призму под углом —ф к оси ОО' и после отражения от грани А'В' дает в центре поля третье изображение» значительно более слабое, чем основное. Пучок А3 падает под углом —180J к оси ОО', преломляется гранью В'С', отражается от граней А'В' и А'С' и проходит в систему параллельно оси объектива. Пучок А^ падает под углом (р, отражается от грани В'С' и также проходит в систему параллельно оси 00', Изображения, образуемые пучками и Л3, имеют почти такую же яркость, как основное изображение. Изображения, образуемые пучками А2 и Д4, — слабые (в систему попадает только отраженный от преломляющих граней свет). Пучки А3 и А^ могут быть легко перекрыты корпусом прибора или оправой, пучки и А.2 можно перекрыть только подвижной шторкой.
Из рисунка видно, что паразитные изображения большой яркости, вносимые прямоугольной качающейся призмой, появляются, если падающие на нее пучки лучей претерпевают различное число отражений.
Призма ие дает паразитных изображений в центре поля, если ее полный размер не превышает требуемого светового размера и вершина угла В' призмы не заходит в область входного зрачка системы. Паразитных изображений можно избежать, применяя шторки, кинематически связанные с движением призм.
Призменные системы для раздвижки окуляров по расстоянию (базе) между глазами
Система призм-ромбов. Эта система применяется наиболее часто. Разворотом призм в разные стороны достигается изменение расстояния между осями пучков, которые при этом не меняют своего направления (рис. 4.18).
Рис. 4.18, Схема раздвижки осей по базе глаз с помощью ромбических призм
Система крышеобразиых призм. Раздвижка осей достигается перемещением призм в противоположных направлениях. Призмы перемещаются, оставаясь параллельными самим себе. Изменение расстояния между осями пучков равно удвоенной величине раздвижки (сближения) призм. Размеры призм определяются следующим образом. Если диаметр пучка в наибольшем сечении равен Dt то световая ширина равна k == = D + — b^, если передвигаются обе призмы (рис. 4.19) Ь± —
— 2 (ах — а2). Длина хода в призме при этом не изменяется.
Для раздвижки осей могут применяться различные крышеобразные
призмы.
Система раздвижки осей проф. М. М. Русинова (рис. 4.20). В этой конструкции смещение осей достигается поворотом наклонных плоскопараллельных стеклянных пластинок 1 в разные стороны (на одинаковые углы. Величина проекции смещения каждой оси на линию Д—А± равна
A6 = (dtg ал—dtg ал.)х
Рис. 4.19. Схема раздвижки осей по базе с помощью крышеобразных призм
X cos Ол COS ф,
где ф — угол поворота пла
стинки от положения, когда
ось наклона пластинки параллельна плоскости А—Д3. Данную конструкцию можно применять только в приборах, имеющих окуляры с достаточным удалением выходного зрачка (не менее 22—25 мм).
Рис. 4.20, Схема изменения глазного базиса с помощью наклонных пластинок
Рис. 4.21. Изменение глазного базиса в бинокулярной насадке к микроскопу
На рис. 4.21 показана схема бинокулярной насадки к микроскопам, в которой изменение расстояния между окулярными тубусами Достигается их раздвижкой. Между линзами 1 и 2 существует параллельный ход лучей.
, Призмы для разделения пучков лучей
Эти призмы должны частично отражать н частично пропускать свет. Некоторые конструкции таких призм даны иа рис. 4.22 и 4.23.
Рис. 4.22. Прямоугольная призма, разделяющая пучки лучей
Рис. 4.23. Призма перфлек-тометра
Отношение количества отраженного света к количеству пропущенного зависит от отношения коэффициента отражения к коэффициенту пропускания с вето дел и тельного покрытия разделительной грани с.
Призмы для соединений полей
Применение прямоугольной призмы для соединения двух полей зрения показано на рис. 4.24. Катеты призмы имеют наружное отражающее покрытие. При соединении полей зрения требуется, чтобы линия
Плоскость изображения
Лоле зрения поля зрения
Рис. 4.24. Схема соединения двух изображений с помощью прямоугольной призмы
Со
to
Рис. 4.25. Схема соединения изображений с помощью трех призм: а — оба изображении в поле зрения; б — изображение от левой ветви; в — изображение от правой ветви
Рис. 4.26. Призменный мостик для соединения двух изображений: ab — отражающая площадка на призме
раздела была как можно тоньше, поэтому на ребре призмы допускается притупление не более 0,02—0,03 мм.
На рис. 4.25 показана схема трех призм, также предназначенная для соединения двух полей зрения. Призмы жестко связаны друг с другом и при одновременном смещении влево или вправо дают возможность перемещать линию раздела и переходить на одно любое (от правой или левой ветви) поле зрения.
Линией раздела может служить граница отражающего покрытия в разделительных призмах, однако ввиду того, что разделительная грань всегда расположена перпендикулярно к оптической оси, второе поле зрения ограничивается небольшим участком в центре (рис. 4.26).
Разделительная призма (см. рис. 4.23) обладает особыми свойствами: благодаря наличию двух крыш, угол между ребрами которых Составляет 90°, зеркально оборачивает изображение, образуемое пучком /' относительно изображения, создаваемого пучком Г. Этот эффект используется в отсчетных и измерительных устройствах для повышения (практически удвоения) точности измерения.
Оборачивающие призменные системы
В оптических приборах в зависимости от их назначения и конструкции для оборачивания изображения применяются различные призменные системы. На рис. 4.27 дан ряд призменных оборачивающих бистем.
J90
Рис. 4.27. Оборачивающие системы: а —• типа Порро первого рода; б — типа Порро второго рода; в — с башмачной призмой с крышей; г — с пептапризмой с крышей; д — с призмой Дове; е — с призмой Лемана; ж — призма Аббе; з — из двух призм-кубов; и — визира (угол визирования по горизонту ±120°); к — панорамы с призмой Пе-хана; л — панорамы с призмой Дове; м — панорамы (призма Досе не показана); н — дальномера
Оптические шарниры
Оптические призменные шарниры дают возможность изменять углы между оптическими осями двух и более ветвей в приборе без враще-. ния изображения. Оптические шар-
Рис. 4.28. Визирная система (оптический шарнир) с «горизонтальным столом»
пиры могут быть плоскими или пространственными, К плоским шарнирам можно отнести системы с качающимися в одной плоскости
Рис. 4.29. Визирная система (оптический шарнир) с «наклонным столом»
визирными призмами, а к пространственным — систему панорамы.
Если к этой системе в качестве куб, то может быть осуществлен
головной призмы поставить призму-непрерывный обзор больше чем полусферы. По геометрическим свойствам различаются системы визирования с «горизонтальным столом» и «наклонным столом».
В системе с «горизонтальным столом» (рис. 4.28) углы с помощью построительного механизма проще строить в горизонтальной и вертикальной плоскостях. В системе с «наклонным столом» (рис. 4.29) углы с помощью построительного механизма проще строятся в вертикальной и наклонной плоскостях.
Рис. 4.30. Пространственный оптический шарнир; компенсация наклона изображения путем вращения призмы 1 вокруг оси Zj— Zj на величину половины угла поворота призмы 2 вокруг оси
Z—Z
Еще один вид оптического шарнира показан на рис. 4.30.
клинья
Клинья применяются для получения и измерения малых углов отклонения луча. Измерительные клинья (компенсаторы) бывают двух типов: клин, перемещающийся вдоль оси в сходящемся пучке (рис. 4.31, а) и пара вращающихся клиньев (рис. 4.31, б). Оба типа применяются в дальномерах. Для устранения хроматизма клинья склеиваются из двух простых
клиньев (из крона и флинта), ориентированных в разные стороны. Точность угла отклонения достигается разворотом клиньев при склейке. В первой системе с клином, перемещающимся вдоль оп-
Рис. 4.31, Тины измерительных клиновых компенсаторов: а) перемещающийся вдоль оси клин; б) система вращающихся клиньев
тической оси и установленном в сходящихся пучках, изображение смещается с оси па величину
Д/ = </[ —'/а = г (п — 1) 6, где 0 — угол клина; z — перемещение клина.
Во второй системе два одинаковых клипа, поворачивающиеся в разные стороны на одинаковые углы, образуют клин с переменным углом. Угол отклонения луча о в зависимости от угла р поворота каждого клина от начального положения а = ат cos р, где от ™ = О( + О>, а1 и а2 — углы отклонения луча каждым клином.
ФАСКИ НА ПРИЗМАХ И НЕКРУГЛЫХ ПЛАСТИНКАХ
Ширина фасок (т) на ребрах двугранных углов и па трехгранных углах в зависимости от длины короткого ребра детали выбирается по табл. 4.8. Допустимость фасок на ребрах двугранных углов призм с крышей и призм-кубов, попадающих в световой пучок, устанавливается конструктором. Фаски для предохранения от выкалывания снимаются перпендикулярно биссектрисе угла между гранями на двугранных углах до 110и включительно. Если угол наклона фасок для предохранения от выкалывания особо не оговаривается, то в чертежах следует указывать только ширину фасок, например: «фаска на ребрах О,4+0,5». На трехгранных углах, у которых угол между двумя гранями (из трех) более 110°, необходимость фаски для предо-
7 В. А. Панов и др.
Т а б л и ц а 4.8. Фаски на ребрах для предохранения деталей от выколок
Дли на ребра, мм Ширина фаски (ш|, мм
на ребрах на трех-грапных углах
До 6 0,1+0'2 0,з+«.з
Св. 6 до 10 О2+0-3 0,5+0,3
Св. 10 До 18 О,3+0’4 1,0+0’4
Св. 18 до 30 0,4+0’5 1,5+<J’5
Св. 30 до 50 О,5+0-6 2,О+0’6
Св. 50 до 80 О/Г^-8 2,5+0,8
Св. 80 до 120 О,8+0-9 3,0+|-2
Св. 120 до 150 1,0+1’° 3,5+1,5
Св. 150 1,2+|-2 4,0+"’°
хранения от выкалывания устанавливается конструктором. В чертежах необходимо указывать ширину фаски на трехгранных углах и угол, определяющий ее положение.
Конструктивные фаски снимаются на ребрах и углах призм для обеспечения условий удобного крепления их* в оправе или для уменьшения их веса, Расположение конструктивных фасок определяется типом призмы и конструкцией крепления. Наибольшие размеры фасок ограничиваются размерами призмы, необходимыми для пропускания расчетного светового пучка лучей. Размеры фасок, указанные в табл. 4.8, на конструктивные фаски не распространяются.
ДИФРАКЦИОННЫЕ РЕШЕТКИ
В зависимости от назначения и формы поверхности дифракционные решетки, применяемые в спектральных приборах, подразделяются на плоские отражательные, вогнутые (сферические и тороидальные) отражательные, эшелетты, плоские прозрачные, поляризаторы, измерительные н другие.
Плоские и вогнутые отражательные решетки применяются в спектральных приборах для рентгеновской, вакуумной ультрафиолетовой, ультрафиолетовой, видимой и инфракрасной областей спектра. Решетки изготовляются на слоях металла, нанесенного испарением в вакууме па подложку из стекла марки ЛК7, или кварцевого стекла марки КВ, непосредственно на подложках из стекла марки Ф1 пли путем копирования на подложках из стекла марки ЛК7. В табл. 4.9—4.10 приведены основные размеры и параметры плоских и сферических отражательных решеток. Разрешающая способность по отношению к теоретическому значению составляет не менее 0,9 и 0,8 соответственно для групп А и Б. Спектральные липни — резкие симметричные. Вблизи линий в пределах трех-четырех нормальных щелей могут наблюдаться сильные спутники и фон. Коэффициент отражения в максимуме концентрации для области спектра более 200 нм составляет: для группы А не менее 70% в перво м порядке и не менее 60% — во втором порядке; для группы Б — не менее 50% в первом и втором порядках. Коэффициент отражения в максимуме концентрации для области спектра короче 200 нм составляет в первом порядке не менее 50 и 40% соответственно для групп А и Б. Угол «блеска» имеет значения в пределах от 1 до 70°, кроме решеток, изготовленных на стекле Ф1, для которых угол блеска колеблется от Р до 5°. Относительная интенсивность «духов» Роуланда в первом и втором порядках должна составлять не более 0,1% и в третьих и в более высоких порядках — не более 0,2%. Относительная интенсивность «духов» Лаймана — не более 0,01%.
Тороидальные решетки имеют количество штрихов на 1 мм 300, 600, 1200, 1800, 2400; изготовляются с заштрихованной поверхностью 50X40 мм (размер решетки 60Х 50Х 10 мм). Радиус кривизны в меридиональном сечении гт — 500 мм и в сагиттальном сечении г$ — 313,4; 325,8; 333,4; 344,4 и 404,6 мм. Решетки изготовляются с заштрихованной поверхностью 60X50 мм (размер решетки 70Х60Х 15 мм) с радиусами кривизны гт = 1000 мм и rs ~ 668,3 мм.
Эшеллеты применяются в спектральных приборах для ИК области спектра; изготовляются на металлических подложках из алюминиевого сплава марки ЛМЦ по ГОСТ 4784—74 или путем копирования на подложках из стекла марки ЛК7. Основные размеры эшеллетов приведены в табл, 4.11. Эшеллеты имеют количество штрихов на 1 мм, 2, 4, 6, J94
Таблица 4.9. Основные размеры и параметры отражательных решеток
Решетки плсекие Решетки вогнутые (сферические)
Размер за-111 трихованяон поверхности, мм Размер решетки, мм (ЛхВхС) Количество штрихов на 1 мм Размер заштрихованной поверхности, мм Размер решетки, мм (Л X В 'Л С) Количество штрихов на 1 мм Радиус кривизны сферической поверхности, мм
20 X 20 20Х 20Х Ю * 18X30 * 20 X 20 X 10 300, 600, 1200 500, 1000
30X30 зохзох ю * 40Х 40Х 10 28Х 30 * ЗОХ 40 X 10 300, 600, 1200 1995
40X30 0 70Х 10 /7,, 2400 250
40Х 40 40Х40Х 10 * 50X 40 0 70Х 10 л,. 2400 500
40 X 30 5 0 X 5 0 X 10 п», 1800, 2400 50 X 40 * 0 70X10 300, 600, 1200 500
50X40 60Х 50 0 70x10 60 X 50 X 10 0 90X15 70х 70Х 10 ** 60X 50 | 70/ 60х 15 П], 2400 —
60X 50 40X 30 ** 0 90X15 nlt 900, 2400 1000
60x 50 * 0 90X 15 300, 600, 1200 1000
80X70 0 120x15 90х 90х 15 80 X 60 70X 50 •* 0 120X15 щ, 2400 1995
100X45 120Х бОх 15 ЮОХ 60 0 150X20 п,, 2400 2992
юох 90 120х 60 0 150x20 120х 120Х 15 ** 150Х 75 X 20 п„ 1800, 2400 Примечания: *нарезаются непосредственно на подложках из стекла марки Ф1; ** форма решетки круглая с тремя срезанными сегментами; пг = 300, 600, 1200, 1800; я, == 50, 75, 100, 200, 300, 600, 1200; п3 37,5; 50; 75; 300; 600.
130Х 120 150Х 150х 20 ** П2
150Х 100 1S0X 120Х 23 «3
150X140 I70X 170Х 25 ♦* i п2
200Х 120 220 X 150X 35 Пз
200X 1 SQ 220X 220X 35 **
250 X 20б 300 К. 200 270Х 220Х 40 ** 320X 220X 40 ** п3, 100, 200
Таблица 4.10. Рабочие порядки спектра при различном количестве штрихов на 1 мм в отражательных решетках
Количество штрихов и а 1 мм Порядки спектра Количество штрихов на 1 мм Порядки спектра
Группа А Группа Б Группа А Группа Б
37,5 50 75 100 200 300 i; 2 1; 2 1; 2 1; 2 1; 2 От 1 до 100 ! » 1 » 75 » 1 » 50 » 1 » 36 » 1 » 18 » 1 » 12 600 900 1200 1800 2400 1; 2 1; 2 1 От 1 ДО 6 1; 2 1; 2 1 1
12, 24, 50, 75 и 100 с рабочими порядками первым и вторым. Спектральные линии резкие, симметричные, без заметных дефектов.
Плоские прозрачные решетки подразделяются на амплитудные, у которых штрихи имеют прозрачные и непрозрачные (из слоя алюминия) участки, и фазовые, которые являются прозрачными копиями плоских отражательных решеток. Ре-
Основные размеры э шел лето в
Размер заштрихованной поверхности, мм Размер эшеллета, мм (А X ВХ С)
50 X 50 70Х70Х 10
70X70 S0X 90 X 15
100Х 100 120Х 120Х 15
1Б0Х 150 170Х 170X25
200X200 220X220X35
250X 250 270X270X40
300X 300 320X320X40
тетки изготовляются на подложках из стекла марки К8. Амплитудные решетки имеют число штрихов па 1 мм от 0,5 до 1200. Фазовые решетки имеют число штрихов на 1 мм 50, 100, 150, 200, 300, 600 и обеспечивают в первом порядке в видимой и ближней И К областях спектра качество спектральных линий, а также интенсивность «духов» Роуланда и Лаймана такие же как и у отражательных решеток. Угол «блеска» от 1 до 35°.
Решетки- поля риза торы примени-ются для поляризации проходящего инфракрасного излучения. Решетки изготовляются на прозрачных в инфракрасной области спектра подложках (табл. 4.12). Поляризаторы на подложках из стекла марки ИКС25 имеют ко-» эффпциент пропускания для неполяри-зованного излучения не менее 25%?
а поляризаторы всех остальных типов — не менее 30% прн степени поляризации не менее 9526 и размере решетки не более 45X45 мм2.
И эмеритальные решетки предназначены для измерения линейных перемещений по методу интерференционных муаровых полос. Решетки изготовляются на металлических слоях, нанесенных на подложки из стекла марки К 8 или путем копирования на подложках из стекла той же марки. Измерительные решетки применяются в комплектах, состоящих из двух прозрачных, а также из прозрачной и отражательной решеток, одна из которых является шкалой, а другая — индексом (табл. 4.13 и 4.14).
Таблица 4.12. Параметры решеток-поляризаторов
Материал подложки Количество штрихов на 1 мм Рабочая область длин волн, мкм
Фторопласт Ф-32Л марки «В» или «Н» (ОСТ 05-432—78) 1200 От 2 до 7
2400 От 1,5 до 7
Полиэтилен (пленка полиэтиленовая, стабилизированная типа А нли Б (ГОСТ 10354—73) 1200 Св. 4
По л и мет и л мета к рил ат марки ЯСОМ 1200 От 2 до 3,2 » 3,6 » 5,5
2400 От 1,5 до 3,2 » 3,6 » 5,5
Кальций фтористый ФК-И 1200 Ог 3 до 9
2400 Ог 2 до 9
Барий фтористый 1200 От 3 до 12
Слоило ИКС25 1200 От 6 до 16
Т а б л и ц а 4.13. Основные размеры прозрачных и отражательных решеток-шкал и прозрачных решеток-индексов
Тип решетки Размер заштрихованной поверхности, мм Форма и размер решетки, мм (А X В X С)
Решетка-индекс 35X35 40X40X5
Решетка-индекс 0 20 0 20Х 5.5 *
Решетка-шкала 23Х 13 25Х 15Х 13
То же 35 X 35 40X40X5
» 100X35 110Х40Х 10
» 150X35 160Х 40Х 10
>> 200X35 210Х40Х 15
» 250Х 35 260Х40Х 15
» ЗООХ 35 310Х40Х 15
* Фокусное расстэян не решетки » 50 мм.
Таблица 4.14. Основные параметры комплектов измерительных решеток
Цепа полосы, мкм Решетки комплекта Количество штрихов на 1 мм Длина волны, при которой контраст достигает максимального значения
Решетка-индекс Решетка-шкала
10,0 Две прозрачных 100 100 Св. 0,6
8,0 Прозрачная и от- 62,5 31,25 0,9
ражательпая
4,0 То же 125 62,5 0,9
2,0 » 250 125 0,9
1,0 500 250 0,9
0,8 » 625 312,5 0,9
0,5 1000 500 0,5
0,4 » 1250 625 0,5
Примечали е. Допускается отклонение цены полосы е от поминального значения только в меньшую сторону на величину, не более 2•10~4t\
СЕТКИ
Сетками обычно называются стеклянные плоскопараллельные пластинки с нанесенными на них перекрестиями, шкалами или иными знаками (марками), устанавливаемые в плоскостях изображения оптических систем. Иногда в качестве сеток применяются плосковыпуклые линзы (коллектив-сетка) или другие сферические детали.
По назначению и виду гравировки сетки можно разделить на следующие основные группы:
1) прицельные (визирные) сетки, предназначенные только для наведения прибора на объект (цель);
2) измерительные сетки (шкалы, растры);
3) сетки смешанного вида и с различными специальными марками (сетки стереодальномеров и др.).
Визирные сетки (рис. 4.32, а, б) обычно имеют перекрестие с разрывом в центре, с угловой величиной разрыва 3—4 тысячных дистан-
Таблица 4.15. Диаметр D н толщина d сеток, мм
d De9 d De$ <1
До 6 Св. 6 до 18 1±0,2 1,5± 0,2 Св. 18 до 30 » 30 » 50 2.5+0.5 4,0± 0,5 Св. 50 до 80 » 80 > 120 Св. 120 до 150 6,0± 0,5 8,0±0,Б 10,0± 0,5
Г! римечаиие. Размеры фасок берутся по таблицам для линз.
ции. Наличие разрыва увеличивает точность наведения, так как штрихи не закрывают цель. Линейная величина разрыва рассчитывается по формуле I — и/71000, где п — угловая цена разрыва в тысячных дистан-ции; — фокусное расстояние объектива или всей системы до сетки. Толщину сетки берут в зависимости от диаметра (табл. 4.15).
Рис, 4,32. Типы сеток
Измерительные сетки разных типов даны па рис. 4.32, в—4,35. Наведение с помощью биссектора точнее, чем наведение с помощью перекрестия. Ошибка наведения по одинарному штриху равна примерло
Рис. 4.33. Б иссек-
Рис. 4,34. Сетка со спиральным би-штрих ом
тор
половине толщины штриха; ошибка наведения но биссектору (двойному штриху) равна примерно 1/3 толщины штриха. В случае примете ния Госсектора наибольшая точность обеспечивается при толщщ / штриха t s,3 и ширине промежутка а = (2-ьЗ) s (рис. 4.33). Толщи: а штриха зависит от увеличения окуляра и равна f Так к
предельный угол разрешения глаза е = Г, то например, при f'K == — 25 мм толщина штриха t— 0,007 мм. Для таких окуляров большей частью принимают t — 0,0084-0,02 мм. Обычно угловой размер штриха 2—4'. Следует иметь в виду, что изготовление штрихов тоньше 0,01 мм затруднительно.
Рис. 4.35. Сетка-калибр
Таблица 4.16. Допустимая величина зазора при
^30 °’ ММ
f OK Dp,
2 4 6
20 0,06 0,03 0,02
25 0,09 0,047 0,03 —
30 0,13 0,06 0,045 0,033
40 0,24 0,12 0,08 0,06
50 0,37 0,19 0,12 0,09
В измерительных приборах используются также сетки со спиральным двойным штрихом. С г! о мощью такой сетки можно осуществлять измерения с точностью до 2 мкм. Шаг спирали обычно 0,5 мм (рис. 4.34), толщина штриха 0,01—0,015 мм, расстояние между штрихами 0,06 мм. Применяются также сетки, на которые наносят два измерительных контура для измеряемой ве-
личины, т. е. верхний и нижний пределы отклонений. Если необходимо иметь большее число различных измерительных марок, пользуются так называемыми револьверными сетками, На рис. 4.35 изображена сетка инструментального микроскопа, на которой нанесены профили резьб. Эта сетка закреплена в револьверном устройстве; поворачивая его, поле зрения различные участки сетки. В измеритель-
Рис. 4.36. Схема жду
к расчету зазора ме-сетками
можно вводить в поле зрения различные участки сетки. В измерительных приборах иногда применяют двойные сетки, одна из которых — неподвижная со шкалой, вторая — подвижная с индексом (например, у винтового окулярного микрометра, (см. рнс. 14.7). В этом случае между сетками должен быть зазор. Конструктивно зазор следует выбирать не менее 0,05 мм, а иногда н 0,01 мм (табл. 4.16). Наличие зазора вызывает паралаке между шкалой и индексом, который может давагь ошибку отсчета (рис. 4.36). При зазоре^ угловая величина паралакса
в минутах равна
2 (р + 4к/<Ь) 0.00029’
Растровые (трансверсальные) сетки
Для точных отсчетов, особенно если они производятся на экране, применяются растровые (трансверсальные) сетки, построенные по принципу поперечного масштаба. Такие сетки имеют наклонные к вертикали липни, состоящие из биссекторов (рис. 4.37), квадратов или точек.
О, Щ
^0 9 8 \7 6 5 3 2 1 О
Н П II ||| П Н I! И п II 110 п и h п и и н и и и /
Н II II II II II II II II II I
II II II II II II II II II II
II II l| II II 11 II II II II *
II II 1| II II II II II II II
II II 11 II II II II II II II «
|| || |||П II II II II II II 7
II II II II II II II II II II 8
II II II jll II II 11 II II II 9
II II II II II II II II II И HW
0 2 Ч- 6 В 10
; jSSSi ЕЕ-:::::;:;
8 SHuiiSi!!
" 7 J 5 7 9
Рис. 4.37. Растровые (трансверсальные) сетки
Сдвиг в горизонтальном направлении бнссекторов, лежащих на наклонных линиях, равен расстоянию между наклонными линиями, деленному на число биссекторов на наклонной линии. С биссекторами совмещают индекс, имеющий вид вертикального штриха.
Растровая сетка устанавливается в пл ос кос*! и изображения и вместе с индексом проецируется на экран.
Лучшим экраном является восковой экран (см. стр. 213), имеющий наиболее тонкую структуру рассеивающей поверхности.
Точность отсчета с помощью растровых шкал может достигать 0,001 мм. Хорошие результаты показало сочетание светло-зеленого
фона экрана и прозрачных бесцветных марок растра.
Допуски на изготовление заготовок сеток и лимбов. Выбор марки стекла
Отклонение плоскостей (поверхностей) сеток, а также и лимбов не оказывает заметного влияния на качество изображения, поэтому допуски на качество поверхности задаются достаточно широкие —
Таблица 4,17. Марки стекол для лимбов в зависимости от способа наиесёиня иа них делений
и знаков
Способ нанесения делений и знаков Марка стекла
Фотографирование Гравировка алмазом Травление для ширины штрихов не менее 0,03 мм не более 0,05 мм Вакуумное напыление К8, К Ю8 К8, К Ю8 К8 К Ю8, БКЮ БКЮ, СВВ Ф8, Ф108, Ф18 БКЮ, БКИ0
Таблица 4.18. Марки стекол для сеток в зависимости от способа нанесений делений и знаков
Способ нанесения делений и знаков Марка) стекла'
Фотоспособ Хромирование в вакууме делений, нанесение по лаку Гравирование алмазом t =* = 1,54-3,0 мкм Травление t — З-гб мкм t — 5-5-40 мкм t— 504-500 мкм К8, КЮ8 К8, КЮ8 К8, ТФ2, КЮ8 Ф8 БКЮ, БК! Ю, Ф108 К8, К108, БФ24
до Л7 = 104-15 и AN — 2. Клиновидность может допускаться от 5' до 10\ Чистота поверхностей сеток Р = 0 — 20 н Р = 0 — 40. Обычно в телескопических приборах в центральной трети поля зрения не допускается никаких дефектов. Количество дефектов в остальной части поля зрения указывается в частных технических условиях на прибор. Чистота поверхности лимбов Р= 0—20 (для рабочей зоны) и PV (для нерабочей зоны).
Рекомендуется диаметр сетки изготовлять с отклонением с9. Допускаются отклонения: dll — для сеток, имеющих специальное юстировочное устройство, и Я8 — для сеток, требующих повышенной точности центрировки. У сеток е подсветкой обработка заготовок по цилиндрической части должна выполняться точность, равная Rz = 0,L
Материал выбирается в зависимости от способа нанесения делений (табл. 4.17 и 4.18). Требования к стеклу: = Д — 4В,
однородность 3—4, показатель ослабления е == 6, двойное лучепреломление — 3, бессвильность — 2В, пузырность — 1 (для рабочей зоны).
Методы и точность нанесения делений на сетках
Сетки и шкалы на стекле условно можно разделить по точности на три класса (см. табл. 4.19). В зависимости от назначения, конфигурации рисунка, толщины штриха и класса точности выбирается способ изготовления шкалы или сетки. Существуют три способа нанесения рисунка иа сетках и шкалах: механический, фотографический, смешанный.
Механический способ оправдывает себя при изготовлении простых сеток и шкал на пантографе или делительной машине. Точность линейных размеров 0,01—0,02 мм, 202
Таблица 4.19. Рекомендуемые допуски на деления сеток и ширину штрихов
Характеристика точности сетки Допуски иа расстояния любых штрихов от начального (нулевого) штриха Допуски на перпендикулярность штрихов перекрестий Допустимый экстен-триситет относительно центра сетки, мм'
Линейные деления, мм Угловые деления
До 0,1 Св. 0,1 до 0,5 Св. 0,5 ДО 1 Св. 1,0 до 2 Св. 2 1 1 От 10' до 30' Св. 30' о! or о . о со Ю о о п Св. 3°
Точные сетки Сеткн средней точности Грубые сеткн Ширина штриха ±0,002 ± 0,005 ±0,010 ±0,005 ±0,012 ±0,030 0,005 ±0,007 ±0,020 ±0,040 Цопускн II 0,010 ±0,010 ±0,032 ±0,060 а ширину ±0,015 ±0,040 ±0,090 штрихов, 0,020 ±2' ± 5' мм 0,03 ± ± 0 3' -т / / 10' ±5' ±12' ±15' 0,050 -4- у' ±17' ±20' 0, 5' 10' 15' 08 0,06 0,10 0,25 0,10
Допускаемые отклонения Ширина или ±0,001 штрихов последую] ±0,002 в зависим! дей после эст и от фо сетки сис ±0,005 кусного р темы (мип ±0,008 асстояния пмальная), ±0,010 окуляра мм ±0,015 ± 0,020
Фокусное расстояние Ширина штриха с черным и белым запуском До 10 0,002 0,004 Св. 10 до 20 Св. 0,006 0,010 20 до 30 0,01 0,02 Св. 30 до 0,02 0,03 5С Св. 50 до 0,03 0,05 70 Св. 70 до 0,05 0,10 90 Св. 90 Св. 0,1
Примечание. Ширина штрихов ие должна превышать */4 ширины деления шкалы. Размеры штрихов с - белым запуском для сеток с f' С 20 мм не применяются.
ю о со
Т а б л и ц а 4.20. Номенклатура, состав и назначение запусков
Условное обозначение запуска Цвет Состав запуска Ширина запускаемого штриха Условия эксплуатации (по ГОСТ 15150—69)
Основа Пигмент
41 Б1Т Б1Ц К1 Ч2Г Ч2К Б2Т Б2Ц К2 чзг чзк БЗТ БЗТ КЗ Черный Белый Красный К Черный 1^4 О Белый Красный Черный Белый Красный Стекло жидкое То же » 'раски масляi Сажа газовая Белила цинковые Краплак красный Эмали п ПФ-163 ПФ-115 белая ПФ-115 красная Закись—окись кобальта Двуокись титана Окись цинка Сурик свин цовый [ые художествен! Графит Закись—окись кобальта Двуокись титана Окись цинка ентафталевые Графит Закись—окись кобальта Двуокись титана Окись пинка 0,1 мм и более То же » » иле 3 мкм и более 4 мкм и более 10 м км и более 10 мкм и более 8 мкм и более 10 мкм и более 10 мкм и более У У, т У, т
Хорошие результаты дает метод гравировки на стекле по защит-
ному слою с последующим травлением или напылением металла в вакуумной установке. Обычно ширина штриха с запуском краской — до 0,01 мм.
Применяя запуски для заполнения сеток и шкал, вытравленных на поверхности стеклянной полированной заготовки, можно улучшить видимость штрихов. Для заполнения травленых штрихов применяют запуски на жидком стекле (для эксплуатации в умеренном климате), масляные и эмалевые — для эксплуатации в умеренном и тропическом климатах. Черные запуски предназначаются для заполнения травленых штрихов, рассматриваемых в проходящем свете, а белые и красные — в проходящем и отраженном свете (см. табл. 4.20).
Фотографический способ требует большой подготовки, но при серийном и массовом производстве более производителен. Он дает возможность получать штрихи шириной 2—3 мкм и выдерживать расстояние между ними с точностью до 1 мкм. При изготовлении
Т а б л и ц а 4.21. Высота цифр и букв сеток, мм
Расстояние между делениями сетки Высота цифр и букв Допуск
До 0,3 0,2 ±0,02
Св. 0,3 0,3 ±0,03
до 0,5
Св. 0,5 0,5 ±0,05
мен ьше
Примечания:
I. Ширина линий цифр и букв должна быть равна ширине штрихов, если последняя не менее 0,61 мм. 2. Для сеток с делениями
0,05 мм допускается высота цифр н букв 0,1 мм. 3. Колебание ширины штриха в любой его части не должно превышать половины его ширины.
сеток-растров на металлизирован-
ном стекле минимальная толщина штриха 8—10 мкм. Фотографированием и последующей химической и термической обработкой можно достаточно прочно зафиксировать рисунок на стекле и протравить его. При травлении получившиеся углубления заполня
ются достаточно прочно продуктами распада веществ, применяемых при химической обработке. Такие сетки пригодны для ночнотг под
светки.
Таблица 4.22. Допуски на длину штрихов линейных и круговых шкал
Длина штриха, мм До 0,2 Св. 0,2 до 0,5 Св. 0,5 до 1,0 Св. 1,0 до 2,0 Св. 2
Допускаемое отклонение (± мм) 0,01 0,03 0,05 0,10 0,2
Примечания: 1. Соотношения между длинами малых, средних и больших штрихов 1 : 1,5:2 или 1 : 1,3 : 1,7. 2. Длину малых штрихов рекомендуется брать не менее цеиы деления сетки. 3. Ширина штрихов не должна быть более 1/5 цены деления шкалы.
Таблица 4.23. Оптическая плотность образцов в зависимости от номера
М1 образца 1 2 3 4 5 6 7
Оптическая плотность 0,5 0,8 1,2 1,5 1,8 2,5 3,0
Таблица 4.24. Выбор образца плотности для сравнения в зависимости от назначения и условий эксплуатации сетки
Увеличение окуляра Г прибора № образца при толщине штриха, мкм
до 20 30 40 50 70 100 150
До 7 х 1 2 3 3 4 4 5
Св. 7х до 15х 1 1 1 2 3 3 4
Св. 15х до 30х 1 1 1 1 2 2 3
В заданиях на вычерчивание сетки при фотографическом способе изготовления должен быть указан масштаб, в котором необходимо ее вычертить. Масштаб выбирается исходя из допусков на элементы сетки и точности ее вычерчивания. При точном вычерчивании ошибки не должны быть более 0,2 мм.
При смешанном способе изготовления одна часть работ выполняется механическим способом, другая — фотографическим.
Допуски на элементы сеток (табл. 4.19) могут отличаться от указанных выше, когда они определяются расчетом. В табл. 4.21 приведены размеры цифр и букв сеток.
В табл. 4.22 даны допускаемые отклонения иа длину штрихов линейных и круговых шкал. В зависимости от увеличения окуляра отраслевым стандартом установлены образцы оптической плотности штрихов, линий сеток (табл. 4.23 и 4,24).
Сетки с искусственной подсветкой
Ночью на темном фоне штрихи сеток не видны. Чтобы они стали видимыми, нх подсвечивают. Свет от электролампочки направляют на полированный обод сетки (рис. 4.38). Благодаря полному внутреннему огпаженню лучи света, падающие на плоскости сетки под малыми углами, не могут выйти наружу, а лучи, падающие и а поверхность канавки (штриха), рассеиваются и попадают в глаз наблюдателя. Штрихи 206
Рис. 4.38. Схема подсветки сетки
день приводиг к уве-
должны быть расположены на стороне, противоположной окуляру^-Лучше и равномернее отражают свет штрихи, заполненные краской. '
Для более равномерной освещенности штрихов сеток следует освещать их примерно под одинаковым углом к штрихам различных направлений. Для увеличения яркости свечения штрихов, удаленных от осветительного окна, полезно покрыть отражающим покрытием остальную часть обода сетки. Для подсветки сеток иногда применяют световоды.
СВЕТОФИЛЬТРЫ
Под светофильтром понимается слой (обычно плоскопараллельный) какой-либо среды, обладающей избирательным пропусканием света.
Светофильтры делятся на- следующие группы: светофильтры из стекла, окрашенного в массе; желатиновые светофильтры; светофильтры из окрашенных пластмасс; жидкие светофильтры, газовые, поляризационные и интерференционные.
Светофильтры изменяют как яркостные, так и цветовые соотношения между видимыми объектами и уменьшают хроматические аберрации. Используя эти свойства, светофильтрами пользуются для улучшения видимости (главным образом контрастности’) при неблагоприятных условиях (дымка, туман, ослепляющий свет, малая контрастность объектов). Например, желтые и оранжевые светофильтры применяются при наличии воздушной дымки, так как они хорошо поглотают синие и фиолетовые лучи. Поглощение синих лучей в ясный солнечный
личению контрастности между светом и тенью, так как тени всегда дают больше синих лучей, чем участки, освещенные солнцем. При тумане рекомендуется применять оранжевые или красные светофильтры. Приборы снабжаются большей частью набором сменных светофильтров. В морских визирах или прицелах применяются оранжевый, желтый и нейтральный светофильтры (иногда зеленый).
Зимой при ярком солнечном освещении пользуются нейтральным или синим светофильтром.
Светофильтры для черно-белой фотографии общего назначения
применяются с целью правильного воспроизведения на снимках соотношений визуальных яркостей объекта (компенсирующие светофильтры) или изменении их контраста (контрастирующие светофильтры). Чаще всего применяют светофильтры ЖС12, ЖС17, ОС12, КС11, СЗС17, СС4, ЖЗС5, ЖЗС9, НС8 и др. Нейтральные светофильтры НС1, НС2 и НСЗ применяются для защитных очков от яркого дневного света, остальные НС используются в фотометрии, спектрофотометрии и в наблюдательных приборах. Темные стекла марки ТСЗ применяются для защитных очков при электросварке, а ТС6 и ТС7 — от прямого солнечного света. Бесцветные стекла БСЗ, БС4, БС7 и БС8 пропускают ультрафиолетовые лучи соответственно до 270, 290, 360 и 370 нм. Светофильтры ЖЗС1, ЖЗС5, ЖЗС6, ЖЗС12, ЖЗС13 и ЖЗС17 применяются в наблюдательных приборах. Светофильтры КС15, КС17 и КС18 выделяют соответственно области спектра 670-—2700 нм, 680—2800 нмг
Т а б л и ц а 4,25, Области применения светофильтров
Марка стоил а Назначение светофильтра
СС4 СС5 СС8 СС9 СЗС24, СЗС25 ЗС1 зсз 3C7 жсз осн КС 13 КС15 ПС7 ПС8 пен Выделение области 340—470 нм Трехцветная проекция; выделение области 370—500 нм Синий сигнальный; цветное освещение Светофильтр дневного света Тсплофпльтр поглощает ИК-область от X > 750-ь800 им Трехцветная проекция; выделение области 480—570 нм; фотография Зеленый сигнальный светлый; цветное освещение Выделение узких участков спектра; в комбинации с ОС13 — линии ртутного спектра 578 нм Выделение линии ртутного спектра 313 им (в комбина- ция с УФС2) Фотография: наблюдательные приборы Трехцветная проекция, красный сигнальный Светофильтр для оптических пирометров; фотография Выделение линии ртутного спектра в комбинации с ОС11 и ОС 12; градуировочный светофильтр Колориметрия; поглощение области 500—550 нм Выделение области 250—460 нм; поглощение области 460—660 нм
Таблица 4,26, Коэффициент пропускания марок стекол для разных толщин светофильтров
То лщина светофильтров, мм
Марка стекла Длина волны, им 0,6 1,0 1,6 2,5 4,0
Коэффициент пропускания т, %
ОС17 555 87 84 77 -
жзс1 540 72 62 49 34 19
ЖЗС5 550 89 88 86 83 77
НС8 555 65 54 37 21 8
Примечание, Рассчитан с учетом поправки на отражение.
800—2800 нм. В табл. 4,25 приведены области применения некоторых светофильтров.
Точность выполнения плоскостей светофильтров, а также допуск на клиновпдность назначаются в соответствии с требованиями к системе. Например, для фотографии плоскости светофильтров должны быть, выполнены с точностью до 1—2 полос. Технические требования на светофильтры, устанавливаемые внутри оптической системы, опреде-208
ляются при .расчете последней. Технические требования на светофильтры, устанавливаемые за окуляром (ориентировочно): N = 10, AN = 3, 0 = 10', PIV. В табл. 4.26 приведены марки стекол светофильтров, применяемых в геодезических приборах для ослабления и излишней яркости фона, или наблюдаемого объекта и усиления контрастности последнего.
Номинальное значение диаметра D (мм) светофильтров должно соответствовать ряду /?а10 и /?а20, толщина d — ряду Ra5 (ГОСТ 6G36—69). Предельное отклонение толщины от номинального значения не более 10%. Толщину светофильтра из стекла ОС17 не рекомендуется делать более 2 мм, так как иначе резко ухудшается контрастность изображения. Требования к стеклу: спектральная характеристика — 2; двойное лучепреломление — 3; бессвильность — 2В; пузырность — 4; требования к обработке поверхностей для D < 20 мм не более — N — 10, AN — 2, 0—10'; для £) > 20 мм, не более — /V = 20, A;V = 3 и 0 < 15'.
Светофильтры для выделения инфракрасной области спектра применяются двух видов: а) абсорбционные (из цветных стекол, германия, кремния и др.); б) интерференционные, изготовляемые путем нанесения тонких оптически однородных слоев из диэлектриков или полупроводников на подложку, прозрачную в требуемой спектральной области. Существенным недостатком абсорбционных фильтров является невозможность выделения с их помощью узких участков спектра с высоким т. Этого недостатка лишены интерференционные светофильтры.
Стеклянные светофильтры для микроскопии
Синие светофильтры применяются при микрофотографировании с апохроматическими объективами для усиления контраста бесцветных препаратов. Светофильтр СС1 при освещении от лампы накаливания придает препарату окраску, сходную с окраской от дневного света.
Зеленые светофильтры увеличивают контраст препаратов, имеющих красную окраску, и полезны при работе с апохроматами, у которых недостаточно хорошо исправлен хроматизм для синих лучей. Они применяются также с фазово-контрастными устройствами и при фотографировании, так как они задерживают синие лучи, повышая контрастность изображения.
Желто-зеленые и желтые светофильтры дают большую контрастность, чем зеленые. Наибольшая контрастность достигается при фотографировании с оранжевыми светофильтрами.
Теплозащитные светофильтры СЗС16 и СЗС24 (термически устойчивые) не пропускают инфракрасных лучей; коэффициент линейного расширения при (20—120)° С равен 67-10~7 и 55* 10“7 соответственно.
Светофильтры УФС, ФС и СС служат для выделения возбуждающего света из спектра источника в люминесцентной микроскопии, а также для выделения узкой области спектра в ультрафиолетовой микроскопии (УФС1 выделяет X == 240—400 нм; УФС2 — А = 270-^360 нм; ФС1 — А = 330 4-460 нм; ФС6 — область 290—460 и 720—1200 нмС Светофильтры ЖС и ЖЗС, пропускающие свет люминесценции и задерживающие возбуждающий свет помещают между препаратом н окуляром.
Светофильтры для контрольно-измерительных приборов
Для создания светло-зеленого фона с целью снижения утомления глаза наблюдателя, а также для повышения контраста штрихов сетки относительно поля зрения, применяются светофильтры из цветного стекла марок ЗС2, ЗСЗ, ЗС8, ЖС12, ЖС5, ЖС6, ЖС9, ЖС13, ЖС18 и др. по ГОСТ 9411—75 (табл. 4.26 и 4.27).
Таблица 4.27. Коэффициенты пропускания наиболее часто применяемых марок стекол для разных толщин светофильтров
Марка стек л г) Длина водны Толщина светофильтра, мм
0,6 0,8 1.0 1,2 1,6 2,0 2,5 3,2 4,0 5,0 6,0
Коэффициент пропускания г, % 1
Желто-зеленое жза 540 72 67 62 57 49 42 34 2G 19 13 i ।
ЖЗС5 Сп О 89 88 87 86 84 83 80 77 74 71
ЖЗС9 540 84 81 79 77 72 68 63 37 48 43 37
i Зеленое 1 ЗС2 530 62 55 48 42 33 25 18 12 — — —
ЗСЗ ! 520 74 69 1 65 60 53 41 39 30 23 16 12
ЗС8 530 89 88 87 86 85 84 81 79 77 74
11 р и меча н и е. Коэффициент пропускания рассчитан для с учетом поправки на пропускание
Номинальное значение D диаметров (больших сторон при некруг-лоп форме) светофильтров должны соответствовать ряду А,20 (4,0; ... 8,0), ряду Яа40 (8,5; .. 36,0) и ряду /?J0 (40; ... 125)
по ГОСТ 6636—69. Предельные отклонения диаметров должны соответствовать отраслевому стандарту в зависимости от способа крепления светофильтра. Номинальные значения толщин устанавливают по ряду /<,,10 (0,5; 0,63; . 6,3). Предельные отклонения толщин допуска-
клея в пределах от ±0,1 до ±0,5 мм.
Технические требования: спектральная характеристика 2-и каин при я; двойное лучепреломление — 2; бессвильность — 2 (для ЗС2, ЗСЗ и ЗС8 — 3-я категория); пузырность — 3; Р = IV—VI; N =* =- 5-20; AV = 1д-3; 0 = 5-20'.
Светофильтры поляризационные
Поляроиды представляют собой поляризующую свет пленку, изготовленную из поливинилового спирта марки Н и заклеенную между защитными стеклянными плоскопараллельными пластинками или полимерными пленками (табл. 4.28—4.31).
Таблица 4.28. Основные размеры поляроидов, мм
Диаметр Толщина Допуски
От 10 до 20 От 2 до 4 ± 0,4
Св. 20 до 50 Св. 4 до 6 ± 0,6
Св.50 до 150 Св. 6 до 8 ±0,8
Св. 150до50С Св. 8 до 10 ±1,0
Таблица 4.29. Требования к изготовлению поляроидов с защитным стеклом
Диаметр поляроида, мм Требовавия
N A>V Р н, ... '
Ог 10 до 50 Св. 50 до 150 Св. 150 до 500 5 10 20 I 2 4—6 И— IV III-V IV— VI С1 СП СИ »—• . 1—- ООО
Т а б л и ц а 4.30. Виды пропускания и категории по пропусканию поляроидов в области спектра от 400 до 700 нм
К-l ге-гирия Интегральное пропускание одного поляроида, °/о Пропускание двух поляроидов в параллельном положении плоскостей поляризации, % Остаточное пропускание поляроидов в скрещенном положении, %
1 От 20 до 25 От 12 до 15 0,001
2 Св. 25 » 35 » 15 » 30 0,01
3 » 35 » 40 » 30 » 35 0,1
Примечая ие. Пропускание поляроидов для области спектра
от 280 до 400 нм и от 700 до 2400 нм, устанавливается по соглашению.
Номинальные диаметры поляроидов следует выбирать по ГОСТ 6636—69. Пропускание поляроидов для области спектра от 280 до 400 нм устанавливается по соглашению. Разрешающая способность поляроида для рабочего диаметра Лраб не более 100 мм равна е"— == 1,5 ‘120/Рраб; по согласованию коэффициент 1,5 может быть уменьшен до 1.
Цилиндрические поверхности поляроидов должны быть защищены водостойким лаком. Поляроиды должны выдерживать воздействие относительной влажности воздуха до 98% при I — 35° С; при этом не допускаются расклейка н нарушение поляризующего слоя. Поляроиды должны быть устойчивыми к воздействию температуры окружающего воздуха от 50 С до —50J С при склейке акриловым клеем и ±60 С
Т а б л и ц а 4.31. Однородность направления плоскости поляризации и соответствующие ей категории поляроидов
Диаметр поляроида, мм Отклонение от однородности наклонения плоскости поляризации (не более)
Категории
А Б Б Г
От 10 до 50 6' 20' 30' 40'
Св. 50 » 150 20' 40' 1° 1° 30'
150 » 250 40' 1о 1°30' 2°
250 » 500 1° 2° 4° 6°
при склейке бальзамином М. Поляроиды, предназначенные для эксплуатации в условиях влажного тропического климата, подвергаются дополнительной защите от разрушающего действия влажного воздуха и биологических обрастаний (плесени). Защитные стекла к поляроидам изготовляются из стекол марок К8 и БС7; рекомендуется для поляроидов диаметром свыше 100 мм стекла марки СВВ. Двойное лучепреломление защитных стекол всех марок допускается не более 6 нм/см.
Стекло марки БС7 применяют в случае эксплуатации поляроидов в условиях длительного воздействия УФ излучения.
Пример обозначения поляроида диаметром 50 мм, толщиной 5 мм, категорией по пропусканию 1, однородности направления плоскости поляризации А, с защитными стеклами марки К8, предназначенного для эксплуатации в условиях тропического климата: ПТ50Х 5-1А-К8; в условиях умеренного и холодного климата — П50Х5-1А-К8.
СВЕТОРАССЕИВАЮЩИЕ ЭКРАНЫ
Применяются два вида проекций на экран: проекция в проходящем свете — используются экраны, диффузно пропускающие свет, и проекция в отраженном свете — используются экраны, диффузно отражающие свет. Общими требованиями к экранам являются обеспечение требуемой разрешающей способности, яркости и видимости в тех направлениях, в которых производится наблюдение.
Основные типы экранов:
1) направленно-рассеивающие пропускающие экраны (матовые стекла, восковые и др.);
2) рассеивающие экраны отражающие (молочные стекла, алюминированные, бисерные и др.);
3) экраны со специальным распределением света (растровые).
Направленно-рассеивающие пропускающие экраны обычно применяются в незатененных помещениях (например, экраны отсчетных устройств приборов), поэтому от них требуется большой коэффициент яркости. В качестве такого рода экранов применяются главным образом восковые экраны и экраны из матированного стекла. Восковые экраны обладают высокой разрешающей способностью, имеют очень топкую, невидимую для глаза структуру, незначительное направлен-212
Табл и ц а 4.32. Оптические характеристики стеклянных матированных и восковых экранов
Конструкция экрана Vs У\/е
Стеклянная пластина: одна сторона матирована кварцевым песком М29, другая — полированная 3° 50' 4° 40' 0,96
Стеклянная пластина: одна сторона матирована электрокорундом М28, другая — полированная 6° 50' 8Э 29' 0,92
Слой воска толщиной 0,3 мм между двумя полированными пластинами 12° 00' 14° 40' 0,87
Слой воска толщиной 0,5 мм между двумя полированными пластинами 29° 00' 36° 20' 0,68
Примечание. — к. п. д., представляющий собой отио-шение'светозого потока, рассеянного экраном в передней полусфере, к потоку света, подающему перпендикулярно.
, равномерное распределение светового потока в боль-свойствам, которые значительно стеклянных экранов, восковые
ное пропускание шом телесном угле. Благодаря этим превосходят свойства матированных экраны имеют преимущественное применение для проецирования па них точных шкал и осуществления отсчета в оптических приборах. Восковые экраны представляют собой две полированные с обеих сторон стеклянные пластины, между которыми заключен равномерный слой воска с канифолью толщиной 0,3—0,5 мм. Характеристики этих экранов и экранов, матированных кварцевым песком М20 н электрокорупдом М28, приведены в табл. 4.32 и иа рис. 4.39. Индикатрисы яркости характеризуются углами т0 5 и yi/e, т. е. угловыми размерами, для которых относительная яркость Вотн составляет 0,5 и 0,37 от максимальной
Рис. 4.39. Индикатрисы яркости экранов;
яркости, измеренной при угле наблюдения, равном нулю. Значения То о и Yi/е» как видно нз рис. 4.39,
1, 2 — стеклянных матировок
пых; 0, 4 — восковых
у восковых экранов значительно
больше, чел у матированных, что дает более равномерное распределение световой энергии в большом телесном угле и создает лучшие условия для наблюдения двумя глазами [20, 23, 26].
Заслуживают внимания экраны из лавсановой пленки. Они дают
возможность получить равномерное диффузное излучение экраега,
применить источники света с меньшими габаритными яркостями, не утомляют зрения.
Чтобы получить более равномерную освещенность поля -рения применяют коллективную линзу, которая переносит изображение выходного зрачка системы в плоскость зрачка глаза [21, 25]. В этом случае экраном может служить матированная плоская поверхность коллектива. Однако при этом появляется необходимость фиксированного положения глаза и наблюдение становится возможным только одному наблюдателю. Растровые светопропускающие экраны представляют собой рифленое стекло или пластмассу типа линз Френеля или набор мелких положительных линз. По опубликованной в соответствующей литературе данным [12] они имеют максимальный коэффициент яркости fjmax = 3,2, т = 49% (стекло) и т—• 43% (пластмасса).
Растровые отражающие экраны представляют собой совокупность малых оптических элементов в виде сферических лунок [12, 89]. Растровые экраны имеют лучшее распределение света, чем алюминированные или бисерные.
Чувствительность визирования штрихов на просветных экранах
Чувствительность поперечных и продольных наводок зависит главным образом от разрешающей способности оптической системы, формы совмещаемых объектов и характера рассеяния света структурой экрана. Точность отсчета тем выше, чем меньше ширина штрихов и расстояние между ними (если это расстояние не выходит за пределы разрешения оптической системы и глаза) [21]. При использовании бнссектора и штриха в окуляре в том случае, когда зазоры, образующиеся между штрихами после совмещения, равны толщине среднего более широкого штриха, чувствительность наводки в самом благоприятном случае составляет примерно 0,1 теоретического предела разрешения (см. стр. 89), т. е. 8 — 0,061 л/sin ад. Если X = 0,55 мкм и sin Од — 0,025, то 8= 1,36 мкм. Значение sin Од должно равняться расчетному при диаметре зрачка глаза £%л “ 2 мм [21].
Таблица 4.33. Средние квадратичные значения погрешностей, мкм
Наименование экрана Поперечная наводка Продольная паводка
Биссектор
№ 1 № 2 № 3 № 3
Без экрана (наблюдение в окуляр) 3.51 4,38 5.05 0,45
К8М28 3,21 3,40 5,54 0,60
К8М28 + HF 3,69 3,91 4,58 0,49
Ь-0.3 3,37 4,29 4,39 0,54
В-0.5 5,26 0,68
Свс товсд 2,65 4,34 5,83 0,44
Таблица 4,34, Размеры штрихов биссекторов, мм
Номер биссектор з a $ t a/s
1 | 1,20 0,43 0,10 2,80
9 | 2.31 0.67 0,34 3,50
3 j 2,88 i 1,50 0,72 1,92
размеров на следующих экранах:
Рис. 4,40. Индикатрисы яркости экранов:
1.3 — стеклянных матированиих;
2 — световода; 4, 5 — восковых
Теоретическую чувствительность продольных наводок (мкм) можно вычислить по формуле
Лг' — 2л.’6 sin2 од = 0,2/sin2 Од.
В табл, 4.33 приведены средине квадратичные значения погрешностей наведения при поперечных и продольных наводках, проводи-пнях с помощью биссектора разных матовые экраны из стекла марки К8, шлифованные с одной стороны электрокорундом М28, один из экранов протравлен 20% раствором плавиковой кислоты: восковые экраны В-03 и В-0,5 толщиной 0,3 и 0,5 мм соответственно; световод с разрешением 40 штр/мм. Другая сторона экранов — полированная. На рис. 4.40 даны сравнительные кривые яркости этих экранов. Индикатрисы яркости характеризуются углом половинной яркости То,ь (углом между нормалью к поверхности и направлением, в котором яркость равна половине ее значения по нормали).
Как видно из таблицы 4,33 данные измерения грубее теоретического значения (3.51 мкм вместо 1,36). Очевидно объясняется это тем, что размеры даже самого мелкого биссектора (табл. 4.34) в семь раз превышают пределы разрешения оптической системы, чувствительность поперечных и продольных наводок в проекционных отсчетных устройствах (при проецировании изображения объекта на восковые экраны, матовые стекла, световод и др,) остается примерно той же, что и при непосредственном отсчете в окуляре [21. 25]. Однако при использовании экрана наблюдатель меньше утомляется, поэтому чувствительность наводки сохраняется при длительной работе.
Чувствительность визирования штрихов на непрозрачных отражающих экранах
В табл. 4,35 приведены средине квадратичные значения погрешностей при поперечных наводках па экраны, представляющие собой: молочное стекло 5VC14, матированное абразивными порошками Лд 100
Таблица 4.35. Погрешности при поперечных наводках, мкм
Наименование отражающих экранов Среднее значе-ченне о Примечавне
МС14№100 МС14М20 MC14+HF Белая пластинка BaSO4 ТФ2М28 ТФ2М7 Al + КОН 5,10 1,10 0,43 0,39 0,15 1,80 4,85 3,64 3,37 3,30 3,50 2,44 2,91 Значение ст получены при размере изображения биссектора на экране: а — 1,20 мм, s = = 0,43 мм, t — 0,15 мм, входном апертурном угле ~ 0,025
и М20; молочное стекло MCI4, полированная поверхность которого протравлена 10% раствором плавиковой кислоты (экран MC14+HF); зеркала из стекла марки ТФ2, шлифованные микропорошками М28 и Л17 с последующим алюминированием в вакууме; экран из чистого алюминия, шлифованный электрокорундом № 8 с последующим травлением в растворе КОН (А1 + КОН). Для сравнения приводится белая пластинка из BaSO4 с мелкозернистой структурой отражающего слоя. Как видно из табл. 4.31 для матированных молочных стекол и зеркал значение о снижается с уменьшением среднего арифметического отклонения профиля /%. Видимая ширина изображения штрихов на экране, изготовленного из стекла МС14, зависит от микрогеометрни матового слоя; наиболее широкими они кажутся для самого грубого образца MCI4 № 100. С увеличением снижается и контраст изображения. Матированные зеркала ТФ2М7 позволяют получить наилучшую чувствительность поперечных наводок и отличный контраст изображения. Их применение предпочтительно в проекционных лабораторных приборах.
Отражающие непрозрачные экраны обеспечивают чувствительность наводки примерно одинаковую с широко распространенными просветными восковыми экранами, а также с непосредственным наблюдением в окуляр (табл. 4.33). Снятие отсчетов на отражающем экране меньше утомляет наблюдателя вследствие более равномерной яркости изображения и отсутствия «слепящего эффекта» [24].
Разрешающая способность отсчетных устройств при дополнительных системах наблюдения на экране
Исследование разрешающей способности отсчетных устройств с просветными экранами различного типа в условиях бинокулярного наблюдения и при использовании лупы или микроскопа показали, что:
1) для систем с бинокулярным наблюдением наилучшими являются тонкослойные восковые и лавсановые экраны. Последние дают наименьшее снижение разрешения (на 12%);
2) матовые стекла следует применять в отсчетных устройствах вместе с коллективной линзой, а также при наблюдении через лупу или микроскоп малого увеличения;
3) в отсчетных устройствах, где изображение на экране должно рассматриваться через дополнительную оптическую систему, увеличение последней следует выбирать в пределах (300-У400)Од, где Од — передний апертурный угол, равный апертурному углу глаза агл = = 0,004,
Числовые апертуры таких дополни тельных систем не должны превышать матовых стекол и 0,03 — экранов с широкой индикатрисой рассеяния 121, 25].
Рассеиватели из оптической керамики КО1
Грубошлифсваипые поверхности оптической керамики КО1 диффузно рассеивают свет. Достоинство КО1 по сравнению с рассеивате
лями, изготовленными из оптического стекла, плавленного кварца и кристаллов фтористого лития — возмож-
Рис. 4.42. Индикатрисы яркости матированных образцов КО1: 1 — образец, У которого одна сторона матирована шлифовальным по,-рошком .\'j 12, другая — полированная; 2 — образец, у которого одна сторона матирована порошком № /2, другая — порошком Ха 6; 3 — образец, у которого одна сторона матирована шлифовальным зерном
<№ 100, другая — зерном № 50
Рпс. 4.41. Спектральные кривые (/—5) коэффициента пропускания полированных образцов из керамики 1<О1 толщиной 1—5 мм; 6 — стандартная кривая образца толщиной 10 мм
ность их использования в ближней ИК-области спектра в качестве рассеивателей в агрессивных
средах, а также условиях резких термоударов, в окнах приемников излучения и т. д. Спектральные кривые коэффициента пропускания образцов КО1 для различных толщин приведены па рис. 4.41. Для сравнения нанесена стандартная кривая КО1 толщиной 10 мм (потери на отражение исключены). На рис. 4.42 изображены индикатрисы яркости матированных образцов КО1 толщиной 4 мм при нормальном падении света (/.--3,61 мкм) [22].
Люминесцирующие экраны
Слои вещества, люминесцирующего под влиянием светового облучения, наносится обычно на стеклянную подложку. Возбуждение экрана производится со стороны слоя. Свечение, возникающее в люминофоре, отражается и рассеивается как на самом возбужденном кристалле, так и на соседних кристаллах. Так как экран большей частью наблюдается со стороны подложки, слой люминофора должен быть
таком толщины и такой зернистости, чтобы обеспечивались на и лучшие свечение и разрешающая способность (рис. 4.43). Предел разрешающей способности ниже у экранов, изготовленных методом осаждения люминофора, чем у экранов, состоящих из однородного люми-несцирующего стекла или монокристалла.
Рис. 4.43. Зависимость разрешающей способности п яркости экрана от толщины слоя:
А —разрешающая способность в мкм; В — яркость экрана в относительных единицах; D — прозрачность, %
ЗАЩИТНЫЕ СТЕКЛА
Защитные стекла предохраняют оптическую систему прибора от попадания пыли, грязи, атмосферной влаги н механических повреждений. Они применяются в том случае, если первой оптической деталью прибора является подвижная оптическая деталь (например, качающаяся головная призма, вращающиеся клинья). Если первой оптической деталью является линза объектива или неподвижная призма, то защитные стекла обычно пе требуются, кроме тех случаев, когда трудно осуществить достаточно герметичное закрепление призмы или объектива, или когда прибор экс-
плуатируется в воде при незначительно повышенном давлении. При больших гидростатических нагрузках 0,3—0,5 МПа и более) защитные стекла следует рассчитывать на прочность. Для круглых защитных стекол расчет на прочность ведется по формуле о = r~p!d-, где г — радиус защитного стекла, см; d — его
толщина, см; р — гидростатическая нагрузка, МПа; о — напряжение изгиба в стекле, МПа.
Защитные стекла без обогрева обычно изготовляются из стекла К8, а с обогревом — из стекла ЛК5. Защитные стекла для окон подсветки делаются из зеркального стекла. Пределы прочности на изгиб для указанных стекол следующие: для зеркального стекла — 22,5 МПа, для стекла 1\8 —
Рис. 4.44. Сферическое защитное стекло
имеет боль-к пр>
17,0 МПа. При расчете следует
брать запас прочности не менее 4—5 крат, так как стекло
шой ,'разброс по величине предела прочности,
чувствительно
должительности нагрузки и низким температурам.
В некоторых наблюдательных приборах применяются сферические защитные стекла (рис. 4.44). Это вызвано большими пространственными углами визирования и меньшими габаритами сферических защитных стекол по сравнению со склеенными плоскими. Сферические защитные
стекла имеют концентрическую форму и являются слабыми отрицательными линзами. По этой причине сферические защитные стекла не могут применяться, если за ними стоит призма-куб1. В этом случае перед качающейся призмой-кубом должна быть установлена компенсационная положительная линза той же оптической силы, что и сферический колпак. Линза должна качаться с визирным лучом, т. е. с вдвое большей угловой скоростью, чем призма-куб.
Требования к качеству и чистоте защитного стекла
Защитные стекла, установленные в ходе лучей оптической системы, требуют точного выполнения в отношении качества их преломляющих поверхностей. Для защитных
стекол подсветки точность выполнения поверхностен пе требуется. Допустимая величина клпиовидпости 0 определяется из величины допускаемого хроматизма или отклонения луча Ддг.,с, = Где Д6Г,С, —
допустимая величина хроматизма после системы в угловой мере. Обычно Дб^,^ — 20", тогда при пр, — пс, = = 0,008 0—2500"/Гт, Отклонение луча вследствие клипов идности вычисляется по форм}'ле о = (пе — 1) 0. Должна быть также задана допустимая косина (децентрировка) сферического защит-
Герметик,, У Г-32 цила ёитбаоная пленка
Рис. 4.45. Плоские склеенные защитные стекла
кого стекла.
Защитные стекла, состоящие из двух пли более пластин (рис. 4.45), во избежание двоения изображения должны изготовляться с жестким допуском по клипивидпости. Разность в угле клина между обоими стеклами не должна превосходить
ДО <
G0"
2Гт(»г-1) ’
где Гт — увеличение телескопической системы.
Если пластинка стоит перед телескопической системой, то такие дефекты, как царапины, пузыри и т. п., не видны, и их допустимое количество определяется допустимым количеством вредного рассеянного света, который создается этими дефектами, а также технологическими и экономическими соображениями.
Защитные стекла в бинокулярном телескопическом приборе
Различная клиновидность или различное ориентирование защитных стекол, имеющих клиновидность, может вызвать двоение изображений. Если защитные стекла имеют клиновидность 0- и 02 и установлены перед объективами, то наименьшая непараллельность осей получится, когда
4 Появится двоение изображения.
клинья ориентированы в одном направлении. В этом случае вызванная ими непараллельность осей 6' — (п— 1)-(^j — 02)Гт. Если — — 02 ~ ДО, то ДО — 67(п — 1)ГТ. Допуск д' имеет различные предельные значения для непараллельности в вертикальной и горизонтальной плоскостях.
В бинокулярных приборах иногда специально применяют клипо-видные защитные стекла для юстировки параллельности осей. Отступление пластинки от плоскостности делает се слабей линзой. Если расстояние £>0 — начало бесконечности для данного прибора, то допустимо, чтобы защитное стекло имело фокусное расстояние [' не менее По.
Если пластинка с обеих сторон имеет примерно одинаковую сферичность разных знаков, то допустимый радиус сферы г = £>() = = Dp.V^ /tg Г. Число допустимых колец N — где R — радиус стекла; к — длина волны. При Л = 0,0005 мм получим
1,7Ор/Г"
При диаметре пластинки 2R — 36 мм. Dp' = 3 мм и 1\ = 8^ получим М = 1.
Защитные стекла с обогревом
Для предохранения от запотевания и образования льда на защитных стеклах применяется обогрев. В качестве токопроводящих покрытий используется пленка двуокиси олова (SnO2), так как она об
Рис. 4.46. Зависимость температуры нагрева токонесущей поверхности от мощности при t = 15—20 е С
Рис. 4.47. Пример расположения токоироводов на защитном стекле
ладает высокой проводимостью и прозрачностью, обеспечивает достаточно равномерный нагрев стекол любых размеров. Расход энергии небольшой (рис. 4,46). Условное обозначение покрытия 26Г (гл. 16).
В зависимости от условий эксплуатации прибора необходимая удельная мощность может колебаться в пределах 0,1 — I В т/см2. Для морских приборов обычно удельная потребляемая мощность 0,5 Вт/см3, для авиационных приборов — 0,6—0,9 Вт/см2,
Пленка имеет прочную адгезию со стеклом —20,0 МПа и с клеящими веществами —15,0 МПа. Твердость покрытия сравнима с твердостью стекла. Показатель преломления пленки 1,98. Светоиоглоще-нке в видимой области до 4% при толщине пленки до 0,5 мкм. Коэф-220
фициент отражения в видимой области до 18% в зависимости от марки стекла.
Просветлением пленки можно снизить коэффициент отражения до 4%. Пленка прозрачная для Л от 400 до 2000 нм, устойчива к воде и влажной атмосфере, действию кислот, щелочей и органических растворителей. Она защищает химически неустойчивые стекла от налетов и пятнания; выдерживает нагрев до 400е С и охлаждение не менее чем до 60е С. Удельная проводимость пленки у от 105 до 5* 105 См/м, удельное поверхностное сопротивление р$ при толщине пленки до 0,5 мкм — 500—100 Ом*см. Для подвода тока на пленку наносят катодным распылением полоски топкого слоя инвара, затем их лудят и припаивают к ним токопроводы. Таким образом получается достаточно прочное и стойкое соединение.Токопроводящие полоски должны быть расположены так, чтобы обеспечивался равномерный подвод тока к токопроводящей пленке (рис. 4.47).
Для регулирования обогрева применяются термоэлементы (термисторы), которые вклеиваются в специальные пазы в защитных стеклах и включаются в цепь автоматического регулятора обогрева. Применяются также термореле с биметаллическим контактом, устанавливаемые в непосредственной близости от защитного стекла.
ЖГУТЫ ВОЛОКОННО-ОПТИЧЕСКИЕ ГИБКИЕ
Гибкие жгуты из оптического стекловолокна разделяются на 8 типов следующего назначения:
<Ф » — жгуты с регулярной укладкой волокон для подсветки и считывания информации;
«П » — жгуты для преобразования формы светового сечения;
«Э » — гибкие волоконно-оптические элементы, склеенные с одного торца;
«Э -Л» — волоконно-оптические ленточные элементы, состоящие из одного слоя волокна, склеенного на определенную длину;
остальные четыре типа жгутов — осветительные и предназначены для передачи света: «О» — в видимой области спектра; «О-С» — без искажения цветности; «О-ИК» — в ближней ИК-области спектра и «О-ИК-у» — У устойчивые.
Гибкие волоконно-оптические жгуты поставляются в следующих вариантах:
1) в зависимости от формы торца и конструкции наконечника варианты А, Б, В, Г и Т (рис. 4.48—4.50);
2) в зависимости от вида защитной оболочки:
X — в поливинхлоридной защитной оболочке; С — в силиконовой оболочке; М — в металлорукаве;
3) в зависимости от температурных условий эксплуатации: первые — предназначены для эксплуатации в диапазоне температур от —50е С до +60° С; вторые — предназначены для эксплуатации в диапазоне температур —50° С до +200° С.
В табл. 4.36—4.47 даны размеры жгутов и их характеристики. Общее и спектральное пропускания жгутов приведены на рис. 4.51 и 4.52.
Обозначение жгута состоит из обозначения типа и вариантов исполнения с указанием диаметра или сторон прямоугольного торца и длины с ссылкой на номер отраслевого стандарта; для жгутов в поливинилхлоридной оболочке должен быть указан цвет оболочки»
Примеры условных обозначений:
1) жгут в поливинилхлоридной оболочке, черного цвета без наконечников, сечением 5X5 длиной 1000 мм, предназначенный для эксплуатации в нормальных условиях: ОТХ-1-5X5-1000 по ОСТЗ
2) ленточный элемент шириной 30 мм, длиной 500 мм; ЭЛ-30-500 ПО ОСТ
3) преобразователя сечением прямоугольного торца 1,5X40 длиной 500 мм; П-1,5X40-500 по ОСТ ...;
Рис. 4.48. Варианты исполнения гибких жгутов в зависимости от формы торца и конструкции наконечника:
А — круглое сечение без наконечника (а); Б — круглого сечения с гладкими цилиндрическими наконечниками (б); В— круглого сечения с фасонными наконечниками (в, е)\ Т — круглого сечения с тонкостенными наконечниками (б); Г—квадратного илн прямоугольного сечения без наконечников (е)
4) гибкого осветительного жгута волоконно-оптического, проклеенного с одного торца, с гладкими цилиндрическими наконечниками 0 10 мм длиной 1500 мм в силиконовой оболочке, предназначенного для эксплуатации при t < 200° С: Э-БС-П-10-1500 по ОСТ ...;
Для осветительных жгутов типов О, О-С, О-ИК, О-И К-у и типа Р допустимые отклонения диаметров d и стороны квадрата сечеиия а с регулярной укладкой волокон, а также торца 1 ие должны превышать ±0.2 мм.
Жгуты типов О, О-ИК-у, Р вместо квадратного сечения торца могут быть прямоугольной формы с соотношением сторон не более 3:1.
Жгуты типа Э изготовляются в любом исполнении, проклеенные с одного торца, и соответствуют размерам, указанным в табл, 4.36 с допуском на размер сечения ±0,2 мм.
Склеенные торцы жгутов должны быть полированы по плоскости. Чистота обработки поверхности должна соответствовать контрольному образцу сравнения. Торцы элементов ленточных — обрезные, без обработки.
Жгуты в исполнении I и II изготовляются в металлорукаве РЗ-Ц-Х и РЗ-АЛ-Х по ТУ 22-2173—71, или в селиконовой трубке по 222
Рис. 4.49. Волоконно-оптические ленточные элементы типа Э-Л
Вид А
Рис. 4.51. Общее пропускание жгутов типа
О-И К-у
Рис. 4.50. Волоконно-онтя'геские жгуты типа П
Рис. 4.52. Спектральное пропускание жгутов типов: О и Р 0/////); ос и оик (ххххх); О-ИК-у (\\\\\\)
to to -4-*
T аблица .4.36. Размеры жгутов типов О, 0-С, О-ИК» О-ИК-у, Р в различных исполнениях, мм
Исполнение
БХ-1, БС-1, БС TX-I, TC-I, ТС BX-I, ВС-1, ВС BM-I, BM-II >11, -П, -II, БХ-I, БС-1, БС-П ТХ-1, TC-I, тс-п см. табл. 4.38 ВХ :-I, BC-I, вс-п BM-I, вм-п
Диаметр d ф ф см. рис. 4.48, б см. рис. 4.48, д см. рис. 4.48,г см . рис. 4 .48, в
номинальный Допустимое отклонение второго торца Длина проклеенной части 1, не бол ОО wi ^3 d2, не более * rs] So г* сч ч—с ^3 оо T-f ^3 d2 (Л 12) w-4
1 4,8 2,0 4,0 3,0 4,7 0,7 — — 2о±2;73
2 5,6 3,0 3,0 4,0 5,7 4,0 7,2
3 ±0,3 7,1 2о±0-3 0,7 4,0 6,0 20 5,0 7,0 5,0 10,0
4 9,0 6,0 8,2 7,1 9,0 7,1 13,0
5 20 10,5 6,7 9,5 8,0 10,5 25±°:? 8,0 13,0
8 14,0 10,0 13,2 СП 1+ го 11,0 13,5 11,0 17.0 70 О ± 1 1Л см
10 18,0 25+°.з °—0,7 14,0 17,6 16,0 18,0 16,0 20,2
12 ± 0,4 20,0 15,0 1 19,0 25 16,0 20,0 16,0 23,5
15 25,0 18,0 24,2 19,0 25,2 19,0 28,0
20 ±0,5 25 32,0 qq+ДЗ 24,0 31,0 30 25,0 32,0 3O±o’J 25,0 33,0
25 37,0 ^—0,7 28,0 36,0 30,0 37,0 30,0 39,0 ЗО+по;3
30 __ — — — — ( — — 1 — — ‘ 38,0 45,0
Примечание. Отклонения диаметров d и стороны квадрата сечением укладкой волокон, а также торца 1 не должны превышать ±0,2 мм. а (см. также табл . 4.38) с регулировкой
Таблица 4.37. Размеры жгутов типов О, О-ИК-у, Р в различном исполнении, мм
Исполнение
AX-I, АС-1, АС-И, ГХ-1 ГС-1 AX-I, АС-1, AC-II ГХ-1, ГС-1
Диаметр d или сторона квадратного сечения а Проклеенная часть /, не более См. рис. 4.48, а dt, не более См. рис. 4.48, е alt нс более
Номинальный размер Допустимое отклонение второго торца
1 4.7 4,0
1.5 СМ СО 4.5
2,0 5,7 5,0
3,0 ±0,3 15 6,7 6,2
4,0 7,7 7,6
5,0 9.4 8,6
8,0 12,6 12,0
10 15,0 15,2
12 ±0,4 20 17,0 17,4
15 22,1 21,8
Таблица 4.38. Размер жгутов типов О, О-С, О-ИК, О-ИК-у, Р в исполнении TX-I, ТС-1, TC-II, мм
Диаметр жгута d ОО 33 d2, не более не более Длина жгута L±5
Номинальный ра змер Допускаемое отклонение
2,0 ± 0,2 2,5 3,7 4± 01 8 50 60 70 80 90 100
8 В. А. ьан^в и др.
225
Т а б л и ц а 4.39. Длина осветительных жгутов в зависимости от диаметра в различном исполнении, мм
Диамет р Длина номинальная Предельное отклонение
Жгуты типов О, О-С, О-ИК, O-ИК-у, Р БС-I, БС-11, BX-I, ВС-1, BC-II, ТХ-I, TC-I, (в исполнении ТС-11) БХ-1,
До 10 вкл. 250 о
До 25 вкл. 400, 500, 600, 800 1000 1250 1400 10 15 25 50
Св. 1 до 8 вкл. 1600, 2000, 2500, 3000 25
2; 3 50’Х, ЮООО 50
Жгуты типов О, О-С, О-ИК, О-ИК-?, Р, ВМ-П) (в исполнении ВМ-1,
До 10 вкл. 250
До 15 вкл. 400 10
500, 600, 800
Св. 1 до 30 вкл 1000 1250 1400 15 25 50
Св. 1 до 8 вкл. 1600. 2000, 2500, 3000 25
Жгуты типов О, О-ИК-V, Р (в исполнении ГХ-1, ГС-1) АХ-1, АС-1, АС-11,
До 3 вкл. 100
До 10 вкл. 250 5
До 15 вкл 400, 500, 600, 800 1000 1250 1400 10 15 25 50
Т а б л и ц а 4.40. Размеры жгутов типа Э-Л, мм (рис. 4.49)
Ширина ленты а Толщина ленты 6* Длина склеенной части 1
Номинальная Допустимое откло-' некие
10 15 0,2
20 0,3
25 0,035 30±5
30
35 0,5
40
Прнмечани я: 1. Размер со звездочкой — для справок. 2. Длина ленты L: 100, 200, 300, 400, 500 мм; допустимое отклонение ±10 мм.
Таблица 4.41, Размеры жгутов типа П, мм
Длина L 150, 250 400, 500, 600, 800 1000 1250, 1400
Допустимое отклонение (±) 5 10 15 25
Т а б л и ц а 4.42. Размеры жгутов типа П, мм (рис. 4.50)
Ши pm; а а Толщина b с, не более d * dj i
Номинальная Допустимое отклонение Номинальная Допустимое отклонение
10,0 20,0 О.з 1,5 0,2 2,3 4,6 6,3 7,8 9,1 8.0 10,5 13,0 15,0 0,7
30,0 40,0 0,5
10.0 20.0 0,3 2,0 0,2 2,8 L3 9,1 10,1 9,0 12,0 15,0 15,0
30,0 40.0 0.5
Продолжение табл, 4.42
Ширина а Толщина b с, не более d * (л 8) -
Номинал ьная Допустимое отклонение (±) Номинальная Допустимее отклонение (ЧН)
10,0 20,0 0,3 3,0 0,2 3,8 6,3 9,1 10,5 15,0
30,0 40,0 0,5 10,7 12,9 16,0 18,0 окД-0,3 0,7
0,0 20,0 0,3 5,0 0,2 5,8 8,3 11,8 13.0 17,0
30,0 40,0 0,5 14,4 16,6 20,0 22,0
* Размеры справочные.
Таблица 4,43. Коэффициент спектрального пропускания тд, жгутов типа О-С, О-И К, О-ИК-V в зависимости от длины жгута
о-с о-ик O-I4K-V
1 (оэффициеит пропускания, % (ие менее)
Длина жгута L, мм X — 450 нм ин OSS = ин 0S9 = Л — 860 нм и 1060 нм
До 1000 Св. 1000 до 1 400 вкл. » 1400 » 2 000 » » 2000 » 3 000 » » 3000 » 5 000 » » 5000 » 10 000 » 43 30 25 22 17 8 50 45 33 •зо 25 15 48 43 30 27 22 14 51 48 46 40 37 17 43 34
Примечание. Допускается для жгутов диаметром сечением торца 1x1 мм. уменьшение т, на 5% ниже зад в табл. 4.43 1 мм знкого
Таблица 4,44, Общий коэффициент пропускания тобщ жгутов типов О, О С, П( Р, Э в зависимости от длины жгута
Длина жгута L, i ЙМ о, О-С, п, Р э
Козффици % (не еит тобщ, менее)
До 250 в кд. 55 45
Св 250 до 500 вкл. 50 40
» 500 » 800 » 45 35
800 » 1 000 » 42 32
» 1000 » 1 250 » 40 30
» 1250 » 1 000 » 35 25
1600 » 2 500 )> 30 20
» 2500 » 3 000 25 18
» 3000 » 5 000 » 20 13
» 5000 » 10 000 » 10 5
Примечания: I, Допускается для жгутов О, О-С, П, Р диаметром 1 мм и сечением торца 1X1 мм уменьшение т0^щ на 5% ниже указанного в таблице. Для жгутов типа Э после последующей проклейки, шлифовки и полировки второго торца тобщ увеличивается на 5—10%,
Таблица 4.45. Разрешающая способность жгутов типа Р в зависимости от диаметра и длины жгута
Диаметр или диагональ прямоугольного сечения, мм Разрешающая способность, штр/мм, не менее, для жгутов
До 500 вкл. Св, 500 до 800 вкл. Св. 800 до 1000 вкл. Св. 1000 до 1400 вкл.
До 2,0 18 15 12 12
Св. 2,0 до 4,0 вкл. 15 12 12 10
» 4,0 » 10,0 » 14 12 10 8
» 10,0 » 15,0 » 12 — — —*
Примечания: 1, Жгуты с регулярной укладкой волокон изготовляются из волокон диаметром 20 — 25 мм, что обеспечивает теоретическую разрешающую способность по полю порядка 20 штр/мм. 2. На жгутах диаметром или диагональю прямоугольного сечения 8,0 мм и бо гее при длине жгута свыше 800 мм допускаются отдельные участки с меньшим пределом разрешения. Площадь и количество участков устаиавли вается отраслевым стандартом.
Таблица 4.46. Допустимые радиусы изгибов жгутов в зависимости от диаметра жгута и типа оболочки
Диаметр жгута в оболочке, мм 1 Радиус изгиба, выраженный в диаметрах жгута в оболочке для типов оболочки
Поливинилхлоридная Латексная Силиконовая
а б а б а б
До 5 вкл. 6 3 2,5 1,5 5,0 2
Св. 5,0 до 8,0 вкл. 8 6 3,0 2,0 5,5 3
» 8,0 » 15,0 » 20 8 5,0 3,0 7,5 5
Т а б л и ц а 4.47. Относительные потери светопропускания жгутов в зависимости от радиуса изгиба
Тип оболочки Диаметр жгута, мм Изменение т0^щ после испытаний на изгиб равный ^z90° (Ь 104 изгибов) в зависимости от радиуса изгиба, %
10D 7,50 50 2,50 Ю
Поливинилхлоридная 3 5 10 0 0 20 0 4 45 4 10 10 40 70
Полностью
Латексная 3 5 10 0 0 0 0 4 4 0 40 94
Сел иконовая 3 5 10 0 0 0 5 14 10 15 40 60 65
Примечание. D — внешний диаметр защитной оболочки.
ТУ 38-10576—72 из резиновой смеси ИПР 1338р по ТУ 38-00551166—73. Волокна в исполнении I склеиваются клеем ОК-72Ф по ГОСТ 14887—69 и в исполнении 11-клеем В К-28 по ТУ 1-695-3—74. Жгуты в исполнении I могут быть поставлены в защитной поливинилхлоридной трубке черного или белого цвета по ГОСТ 19034—73.
Жгуты типа О-ИК'У изготовляются в металлорукаве РЗ-АЛ-Х или селиконовой трубке по указанным выше ТУ.
Жгуты тина II имеют защитную оболочку из латекса иаирита Л7 по ТУ 6-01-780—73. Жгуты типа Э-Л защитной оболочки не имеют; волокна на торцах склеиваются раствором поливинилового спирта по ГОСТ 10779—69.
Волокна гибких жгутов изготовляются из стекол по ГОСТ 3514—76 и отраслевому стандарту, обеспечивающих числовую апертуру 0,5.
Гибкие жгуты сохраняют свои параметры после воздействия иа них: циклических изменений температур в диапазоне от —50°С до +60° С; влаги при относительной влажности 70% и температуре 30й С; вибраций в диапазоне частот 20—120 Гц. Наиболее опасными, с точки зрения эксплуатации жгутов, являются — повышенная влажность и многократный изгиб с радиусом менее допустимого. Поэтому при длительной эксплуатации жгуты должны быть надежно защищены от влияния повышенной влажности.
В табл. 4.46 приведены допустимые радиусы многократного (а) и однократного (б) изгибов жгутов с различными типами оболочек, а в табл. 4.47 — изменения тобЩ жгутов в зависимости от радиуса изгиба иа ±90°. Правила монтажа и условия эксплуатации гибких жгутов в приборах устанавливаются отраслевым стандартом.
ОБЪЕКТИВЫ
Основными характеристиками объективов являются:
I) относительное отверстие (для микрообъективов — числовая апертура);
2) фокусное расстояние [у микрообъективов, имеющих длину тубуса, не равную бесконечности, — собственное (линейное) увеличение];
3) угловое или линейное поле;
4) предел разрешения и качество изображения (хорошее исправление дисторсии и кривизны поля особенно важны для фотообъективов Й объективов измерительных приборов).
Типов объективов чрезвычайно много и полностью привести их в справочнике невозможно.
Объективы киносъемочные любительские. Киносъемочные объективы применяются в любительских кинокамерах для съемки фильмов на кинопленке 8 мм, 8 мм типа С и 16 мм (ГОСТ 17278—71)г. Номинальные значения фокусных расстояний объективов приведены в табл. 4.48.
Фотографическая разрешающая сила основных (штатных) объективов с геометрическим относительным отверстием 1 : 1,8 (или с полностью открытой диафрагмой, если объектив имеет меньшее относительное отверстие) при фотографировании щита с мирами в проходящем свете на черно-белой негативной кинопленке должна быть ие менее следующих ниже значений.
1 Стандарт не распространяется на панкратические объективы и объективы для специальных видов съемки и для профессиональных кинокамер.
Т а б л и ц а 4.48. Номинальные значения фокусных расстояний объективов
Формат кинопленки, мм Значения фокусных расстояний, мм
8 10 12 15 — 25 50 100 — 200 —
8 (тип С) 10 12 15 — 25 50 — 100 200 — —
16 10 12 15 20 25* 50 75* 100 150* 200 300
Примечания: 1) Значения фокусных расстояний, расположенные слева и справа от ломаной липни, относятся соответственно к широкоугольным и длиннофокусным объективам для данного формата пленки. 2. Значения фокусных расстояний, расположенные внутри ломаной линии относятся к основным (штатным) объективам для данного формата кинопленки. 3. Значения фокусных расстояний, отмеченные знаком звездочка применять не рекомендуется.
1. При съемке на 8 мм н 8 мм типа С кинопленке:
65 линип/мм — в центре поля изображения;
40 лшшй/мм — на краях поля изображения у' = 2,7 мм для 8 мм кинопленки, у' = 3,2 мм для 8 мм типа С кинопленки.
2. При съемке на 16 мм кинопленке:
55 линий/мм — в центре поля изображения;
35 линий/мм — на краях поля изображения (у* = 5,6 мм, где у — расстояние от центра поля изображения до края поля изображения по диагонали).
Кинопленка КН-1 по ГОСТ 5554—70, применяемая при испытании, должна иметь разрешающую способность не ниже 135 линий/мм по ГОСТ 2819—68 и общую светочувствительность 11 единиц по ГОСТ 10691—63. В случае применения других типов кинопленок необходимо определять поправочный коэффициент. Коэффициент света-пропускания основных (штатных) объективов в центре поля изображения должен быть не менее 0,8. Коэффициент светорассеяния основных (штатных) объективов с геометрическим относительным отверстием 1 : 1,8 (пли при полном открытии диафрагмы, если объектив имеет меньшее геометрическое относительное отверстие) должен быть не более 0,025.
, Освещенность изображения на краях поля {у' = 2,7 мм, у' = 3,2 мм и у = 5,6 мм для 8 мм, для 8 мм типа С н 16 мм кинопленки соответственно) по отношению к центру поля, освещенность которого принимается за 100%, должна быть не менее 30%.
Просветление оптических поверхностей объективов должно обеспечивать цветопередачу без искажений на цветной кинопленке,
Объективы нормального фокусного расстояния для фотоаппаратов. ГОСТ 19322—73 устанавливает ряды нормальных фокусных расстояний объективов для фотоаппаратов общего назначения с форматами кадров 18X24, 28X28, 24X36, и 60X60 мм (табл. 4.49). Стандарт не распространяется на специальные объективы (например, широко-232
Т а б л и ц а 4.49. Номинальные значения нормальных фокусных расстояний объективов
Вид аппарата Формат кадра, мм Номер ряда Номинальное фокусное расстояние, мм
Ш кал ь 1 ю-дал ь номерные с жестковстроепным объективом 18X24 1 25, 28, 30, 32, 35
24X36 28X28 2 32, 35, 38, 40, 42, 45, 48, 50, 53, 55
Зеркальные 24X36 3 48, 50, 53, 55, (58)
Зеркальные и шкаль-но-делыюмериые 60X60 4 75, 80, 85, (90)
Примечания. 1. Предпочтительным является меньшее значение в ряде по отношению к соседнему. 2. Значения ряда 2 — 32 и 35, ряда 3 — 55. ряда 4 — 85 следует применять для светосильных или упрощенных объективов. 3. Значения в скобках предпочтительное*
угольные, длиннофокусные, панкратические, а также на объективы для макроподводной съемки).
В табл. 4.50—4.53 приведены характеристики объективов.
Объективы для микроскопов. В СССР выпускаются объективы, рассчитанные для длины тубуса 160 мм и толщины покровного стекла препарата d = 0,17 мм, а также для длины тубуса «бесконечность» и 190 мм (применяются без покровного стекла) (табл. 4.54 и 4.55).
По степени исправления аберраций и области спектра, в которой они работают, объективы разделяются на следующие группы:
1) ахроматические, в которых исправлены сферическая аберрация, кома и хроматическая аберрация положения для двух цветов; кривизна изображения не исправлена;
2) апохроматические, в которых лучше, чем в ахроматических объективах, исправлены сферическая аберрация н кома и почти полностью устранен вторичный спектр; не исправлена кривизна изображения; хроматическая аберрация увеличения составляет 1—2% и для ее исправления применяются компенсационные окуляры;
3) зеркальные и зеркально-линзовые для УФ, И К и видимой областей спектра (апохроматы);
4) линзовые кварцфлюоритовые для ультрафиолетовой области спектра в пределах длин волн 250—330 нм;
5) монохроматические для узкой области спектра;
6) планобъективы, в которых дополнительно исправлена кривизна изображения.
По назначению объективы разделяются на следующие категории:
1) нормальные;
2) для исследований фазово-контрастным и фазово-темнополь-ным методами;
3) для исследований в поляризованном свете;
4) для люминесцентных и фазово-люминесцентных исследований;
Т а б л и ц а 4.50. «Любительские» обьективы
Марка объектива Фокусное расстояние мм Отвоси-тельиое отверстие D/f' Угловое поле 2со, ...° Предел разрешения, не менее лииий/мм
в центре на краю
Киносъемочные объективы
Агаг-14 * 9—27 1 : 2,8 14—42 55 32—25
Т-55 12 1 : 2,4 32 65 40
Варногонр-2Б * 6,5—65 1 : 1,8 6—59 55—50 30-25
Проекционные объективы
ОП-1.8 18 1 : 1,4 19 90 45
НФ-СА * 18—30 1 : 1,2 13—22 90 45
Фотообъективы (жестко встроенные)
И-70 50 1 : 2,8 47 45 20 **
И-73 41,44 1 : 2,8 56 50 25 **
Т-43 41,7 1 : 4 55 45 19 **
Т-32 76,2 1 : 4,5 52 20 g **
Фотообъективы (сменные)
Мнр-10А 28 1 : 3,5 75 40 20
Мир-24М 35 1 : 2 63 40 21
Юпитер-12-7 35 1 : 2,8 63 41 15
М ир-1а 37 1 : 2,8 60 50 23
Мир-26Б, В 45 1 : 3,5 83 45 16
Индустар-61/3 50 1 : 2,8 46 44 30
Гслнос-44М 58 1 : 2 40° 28' 41 20
Мир-ЗБ, В 65 1 : 3,5 66 40 14
Мир-38Б, В 65 1 : 3,5 66 42 20
Юпитер-9а 85 1 : 2 28° 50' 32 23
Вега-13М 100 1 : 2,8 24° 26' 47 27
Тапр-11А 135 1 : 2,8 18 44 24
Юпитер-37А 135 1 : 3,5 18 45 30
Юпитер-11а 135 1 : 4 18 42 29
Калейнар-ЗБ, В 150 1 : 2,8 28 45 18
Юпнтер-21А 200 1 : 4 12 50 36
Юпитер-21М 200 1 : 4 12 50 36
Юпитер-ЗбБ, В 250 1 : 3,5 19 45 25
Таир-ЗА 300 1 : 4,5 8 36 30
ЗМ-4А 500 1 : 6,3 5
3AV5A 500 I : 8 5 40 20
ЗМ-ЗБ, В 600 1 : 8 7° 30' 35 20
МТО-1ОООА 1000 1 : 10 2° 30' 28 18
* Объективы с переменным фокусным расстоянием
*• Для поля у1 — 20 мм.
Т аблица 4.51. Киносъемочные объективы для 35 и 70 мм пленки
Марка объектива Фокусное j расстояние f' мм Относительное отверстие ** D/f' Угловое поле 2(0, ...° Предел разрешения в центре поля, не менее, линий/мм Плен к а
ОКС1-22-1 22 1 : 2,8 64 60 Нормальная
ОКСЗ-22-1 * 22 1 : 2 64,5 50 То же
ОКС8-35-1 35 1 : 2 42,5 55 »
ОКСИ-35-1* 35 1 : 2 43 55 »
ОКС7-28-1 * 28 1 : 2 52° 35х 50 »
ОКС1-40-1 40 1 : 2,5 40 60 »
ОКС6-75-1 75 1 : 2 20° 55х 50 »
ОКС2-100-2 100 1 : 2,8 15,5 55 »
ОКС1-150-1 150 1 : 2,8 10 55
ОКС1-200-1 200 1 : 2,8 8,5 50 »
ОКС1-300-1 300 1 : 3,5 5° 40' 40
ОКС1-50-6 * 50 1 : 2 30,5 55 »
ОКС5-250-1 250 1 : 2,8 6° 25х 30
ОКС9-500-1 500 1 : 5,3 3,2 40
ОКС5-750-1 750 1 : 8 2° 10х 25 »
ОКС4-1000-1 1000 1 : 11 1° 40х 25 »
ОКС5-18-1 18 1 : 2,5 75° 50х 60 »
ОКС1-56-1 56 1 : 3 52 60 Широкая
ОКС4-40-1 40 1 1 3 70 55 То же
ОКС4-75-1 75 1 : 2,8 40 50 »
ОКС2-100-1 100 1 : 2,8 31 50 »
ОКС2-150-1 150 1 : 2,8 21° 40х 50 »
ОКС1-125-1 125 1 ; 2,8 26 50 »
КР-Ю 28 1 : 3,5 93 50 »
* Объективы с удлиненным задним отрезком. * * По ГОСТ 17175 — 71 деления шкал диафрагм обозначают значениями знаменателей (геометрических или эффективных) относительных отверстий или — 1 : п — D/Г или «.дифрагмнрованных чисел» К = Г/D',
Таблица 4.52. Киносъемочные объективы с переменным фокусным расстоянием
Марка объектива Фокусное расстояние мм Относительное отверстие D/f' Угловое поле 2си, ...° Предел разрешения в центре поля, не менее, ли НИЙ/мм Пленка
Фотон 37—140 1 : 3,5 42"— 10° 40' 50—38 Нормальная
Фотон-А 37—140 1 : 3,5 71° 22'— 19° * 28° 22'- 7° 40' ** 40—25 То же
35ОПФ9-1 25—100 1 : 3,2 49°—12° 60—45 »
35ОПФ9-1А 50—200 1 : 4,5 20° 40'— 5° 50—36
35ОПФ1 а-1 25—250 1 : 3,2 60°— 12е 55—30 »
35ОПФ15-1А 50—500 1 : 4,5 30—25 »
35ОГ1Ф16-1 25—100 1 : 3,2 61° 28'— 15° 08' 60—40
35ОГ1Ф16-1А 50—200 1 : 4,5 55—30 »
35ОПФ19-1А 40—120 1 : 2,5 26° 48'— 8° 50' 55—40
35ОПФ18-1 20—120 1 : 2,5 60—40 »
* Но вертикальному сеченню; ** Ло горизонтальному сечению.
Таблица 4.53. Блоки анаморфотные съемочные (нормальная пленка)
Марка объектива Фокусное расстояние f', мм Относительное отверстие D/f' Угловое поле 2(0, Предел разрешения в центре полет, линий/мм
по вертикали по горизонтали
35БАС10-3 35 1 : 2,5 42° 30' 42° 30' 55
35БАС10-2-01 35 1 : 2,5 42° 30' 42° 30' 55
35БАС12-4-01 30 1 : 2,8 39 34° 37' 55
35БАС2-2 150 1 : 3,5 19 7° 10' 35
35БАС22-2 50 1 : 2 50
35БЛС23-2 75 1 : 2 48
35БАС25-1 100 1 : 2,8 26° 46' 11° 14' 50
35БАС26-1 22 1 : 2,8 50
35БАС27-1 35 1 : 2 72 31 55
Таблица 4.54 Объективы микроскопов
Марка объектива Увеличение, крат Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности, область ахроматизацни
I. Объективы для работы в проходящем свете тубус 160 мм, толщина покровного стекла 0,17 мм 1. Ахроматические Для биологических, бактериологических и других исследований
ОМ-124 3,8 0,11 33,10 Сухая 27,20 50
М-42 8 0,20 18,10 8,60 33 ^4
ОМ-51» ' 10 0,30 15,15 7,20 33
__1 2 3 А Ь ОМ-27 • ♦ » » 20 0,40 8,40 » 1,70 33
1 1 Tt т ** 3 Л мщ» » • • 40 0,65 4,30 0,55 33
ОХ-1*» в 40 0,65 4,25 0,70 33 В пружинящей оправе
ОМ-231» “ 40 0,75 4,30 Водная иммерсия 1,80 32,7
0-40 40 0,60 4,4 Сухая 0,70 33 В узкой оправе
02-604 60 0,85 3,0 0.14 33 В пружинящей оправе
ОМ-43 85 1,00 2,1 Водная иммерсия 0.06— 0,16 32,7 В коррекционной оправе
ОМ-43-1 85 1,00 2.1 То же 0,09 32,7 В пружинящей оправе
ОМ-41 • » • * 90 1,25 2.0 Масляная иммерсия 0,10 32,7
О6М-90 90 1,25 — 0,60 2,0 Те же 0,10 32,7 В пружинящей оправе с ирисовой диасграгмой
ОХ-26 4 0,12 31,4 Сухая 6,20 45 1 ii<
ОХ-27 6,3 0,17 24,1 » — 45 1»
ОХ-28 10 0,25 16,7 » 5,07 4 5
ОХ-29 16 0,40 12,0 » 1,75 45 -
ОХ-ЗО 40 0,65 4,66 0,58 45
ОХ-314 60 0,85 3.01 » 0,19 45 нчв
ОХ-32* 100 1,25 1.89 Масляная иммерсия 0,11 45
Марка объектива Увеличение, крат 1 Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности; область ахроматизацин
ОСФ-ПП ОСФ-14П ОСФ-26П ОСФ-5 ОСФ-6П ОМП-5,5 ФОМ-27-2 ФМЩ-2 ФОМ-41-2 ОМ-32 ОМ-34 ОМ-2* ОМ-31 ОМ-29 ОПХ-Ю4 Для исследов: 10,6 | 0.40 1НИЙ В ПОЛ] 14,8 11,6 6,0 33,0 21,6 24,5 исследова 8,4 4,3 2,0 Для иссле; 2 — 1,9 2. П л а {еских, бак 29,9 15,5 8,5 4,2 16,5 яризованном св Сухая » » » » ния методом ф< Сухая » » ^ования желать Масляная иммерсия нахромат тернологнческь Сухая » » » » ете со стол 13,0 13,7 15,9 27,0 14,2 16,0 азового кон 1,70 0,55 0,10 1НОВЫХ пле1 0,30 — 0,12 и ч е с к и е IX и други? 23,40 13,50 0,16 0,85 8,2 и ков Фе до] 51 50 50 49 50 37 траста 33 33 32,7 чок 32,7 : исследова 33 33 33 33 45 зова7 С ирисовой диафрагмой » » > > > > » х> > » » » С двумя фазовыми кольцами » » » * » » > » В пружинящей оправе инй
16,4 14,0 0,62 0.22
21,7 26,0 0,62 0,19
40,3 3,8 0,30 0, 11
5,89 6,4 0,17 0,17
10,0 5,5 20 40 90 90 д. 3,5 9 20 40 10 0,24 0,16 Для 0,40 0,65 1,25 1,25 ля биологи1 0,10 0,20 0,40 0,65 0,20
Марка объектива Увеличение, крат Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности; область ахроматизацни
Для исследований в поляризованном свете
ОПХ-2,5П 2,5 0,05 62,5 Сухая 9,0 45
ОПХ-25Г! 8 25 0,50 6,5 0,55 45 С ирисовой диафрагмой
ОПХ-40П • 40 0,65 4,0 0,44 45 В пружинящей оправе
ОПХ-60П 8 60 0,85 2,7 0,22 45 > > »
3. А п о х роматиче с к и е
Для биологических, бактериологических и других исследований
ОМ-18 10 0,30 15,1 Сухая 4,80 33 В пружинящей оправе
ОМ-2! 20 0.65 8,4 0.67 33
ОМ-16 40 0,95 4,4 » 0,12 — 33 В коррекционной оправе
0,22
О6АМ-60 60 1,0 —0,7 3,0 Масляная 0,22 32,7 В пружинящей оправе, с ирисо-
иммерсия вой диафрагмой
ОМ-25 1 70 1,23 2,5 Водная 0,14 — 32,7 В коррекционной оправе
иммерсия 0,04
О2АМ-90 90 1,30 2,0 Масляная 0,10 32,7 В пружинящей оправе
иммерсия
ОАВ-60 2 60,9 1,0 2,9 Водная 0,76 32,7 ——
иммерсия
ОАВ-65 2, 6 65 1,1 2,7 То же 0,19 32,7
Для исследования желатиновых пленок
ОС-20 20 0,80 8,4 Масляная 1,10 32,7 —
иммерсия
ОС-22 60 1,25 3 — 2,9 То же 0,40 32,7 В коррекционной оправе
4. Плана 1похроматически е 8
Для биологических, бактериологических и других исследований
ОПА-1 10 0.30 15,8 Сухая 5,2 45
ОПА-2 16 0,40 9,6 > 0,64 45 ——
ОПА-3 40 0,65 3,9 » 0,31 45 —
ОПА-4 60 0,85 2,6 0,23 45 В пружинящей оправе
240
Продолжение табл. 4.54
Марка объектива Увеличение, крат Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности: область ахроматизации
ОПА-5 100 1,25 1,5 Масляная иммерсия 0,15 45
О ПА-6 ОПА-40 25 40 0,50 0,65 6,5 4 Сухая » 0,61 0,72 45 45 В пружинящей оправе
ОПА-60 60 0,90 Для нсс 2,7 5. 3 е р ледованнй > к а л ь н о -л и в ультрафиоле! 0,22 и з о в ы е "свой облас 45 ти спектра В пружинящей оправе
ОК-40 40,8 0,50 4,3 Сухая 2,0 33 211 — 800 нм
ОНЗ-75А 75 0,65 2,3 » 0,23 33 243 — 590 им
ОНЗ-115 ИЗ 0,70 1,5 » 0,19 36 243—590 нм
ОК-75 73,5 1,00 2,2 Глицериновая иммерсия 0,25 32,7 250—590 нм
ОНЗ-125 125 6. 1,10 Л и н з о в Для исс 1,4 ы е к в а р ледованнй Глицериновая иммерсия цфлюорит в ультрафноле! 0,25 о в ы е ах говой облас 32,7 р о м а т и тн спектра 250 — 590 им ч е с к и е
О К-5 5 0,08 24,9 Сухая 17,00 33 230 — 590 им
ок-ю-з О К-120 10 20 0,20 0,40 15,3 8,3 » 6,61 0,22 33,2 33 250 — 330 им 260 — 280; 300 — 380 нм, 350 — 380; 380 — 434 им
ОК-50 48,5 0,65 3,6 » 0,10 33,4 250—313 нм
ОК-58 58 0,80 3,1 Водная иммерсия 0,11 30 248 — 280 нм
Марка объектива Увеличение, крат Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности: область ахроматизации
оз-юик ОНЗ-40 ОР-75ИК ОР-40ИК ОРМ-75ИК ОМ-10 2, • ОМ. 13 п ОМ-38 И ОМ-44 [1 од-юлк ОД-25Л К ОД-40ЛК 10 40 75 40 75 95 9 И 30 10 24,2 40,0 Для нсс 0,30 0,50 0,65 0,70 1,00 II, Обь 1. 1,25 Для 0,20 0,25 0,65 Для иселе 0,40 0,75 1,00 7. Линзе ледований 18,4 4,2 2,4 4,6 2,1 ективы для А х р о м а 2,0 исследова 18,1 16,0 6,2 дований в 20,6 11,2 4,84 ) в ы е и з е р в инфракрасно! Сухая > » Масляная иммерсия работы в отр т и ч е с к и е, I Масляная I иммерсия Ний в поляриз Сухая Масляная иммерсия То же гвете люминесь Желатиновая к а л ь и о й области с 3,8 — 2,49 5,0 0,20 1.6 0,28 ажеииом св тубус 1’ 0,06 □ванном св< 8,14 0,50 0,50 1енции (кон 0,11 л и и з о в пектра 37,2 33 33,5 67 32,7 ете 30 мм 12 2 1 ?те 25 27,6 20,75 тактные) 43 39 38,7 ы е 1,05 — 2,2 мкм 1—7 мкм 0,7 — 4,5 мкм 0,7 — 5 мкм 0,8—1,6 мкм В коррекционной оправе
4^ ОЭ-10ЛК ОЭ-20Д к о-солк 10,0 20,0 60 0,30 0,60 1,25 10,7 11,2 3,2 иммерсия То же 0,10 0,02 41,1 30,7 31 В коррекционной оправе
Марка объектива Увеличение, крат Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности; область ахроматизации
Для исследований в светлом н темном поле (эпиобъектнвы)9
ОЭ-9 2 9 0,20 18,4 Сухая 5,40 25
03-21 2 21 0,40 8,4 1,80 14,4 **
03-4 0 2 40 0,65 4,6 » 0,61 12,35 1 1
03-95 95 1,00 2,0 Масляная 0,41 12,50 —
иммерсия
2, Л х р о м а т и ч е с к п е, тубус X
Для исследований в светлом поле
ОХ-23 0.17 23,2 Сухая 6,20 33
ОХ-14 0,30 13,9 » 5,71 33
ОХ-6 < 1 * 0,65 6,2 » 0,82 33
ОХ-3 1,25 2,8 Масляная 0,40 25 —-
иммерсия
ОС-39 — 0,12 25,0 Сухая 10,00 29 —
ОС-40 0,30 13,9 Сухая 5,71 29
ОС-4 1 I* 0,37 8,2 » 2,68 29
ОС-4 2 0,50 4,3 » 0,74 29 —
Для исследований в светлом и темном поле (эпиобъектнвы)
03-23 0,17 23,2 Сухая 5,40 31,5
03-14 — 0,30 13,9 5,40 31,5
03-8 —* 0,37 8,2 » 2 60 31,5
03-6 1 Ш' 0,65 6,2 » 0,60 31,5
03-4 0,17 25 5,4 0 33
03-2 0,40 10 » 2,60 33
03-1 — 0,65 6,3 » 0,65 33 1
ОЭ-ЗТ 1,00 2,8 Масляная 0,60 31,5 —
иммерсия
3. П л а н а х р ом этические8, ту бус оо
Для исследований в светлом поле
ОБП-40 0,10 40,6 Сухая 23,0 4 5 -
ОПХ-3 0,65 6,3 » 0.6 45 —
Марка объектива Увеличение, крат Числовая апертура Фокусное расстояние, мм Система Рабочее расстояние, мм Высота объектива, мм Конструктивные особенности: область ахроматизацин
Для исследований в светлом и темном поле
ОЭ'5 1 -* ! 0,65 6,3 | Сухая 1 0,69 45
4. А п о х р о матическ и е, тубу С со
ОС-16 -*** 0,30 15,7 Сухая 4,90 33
ОС-8 0,65 8,4 » 0,82 33
ОС-4 ма 0,95 4,3 » 0,18 33
ОС-3 1,30 2,8 Масляная 0,18 25
иммерсия
ос-зт **** 1,00 2,8 » 0,53 25
5, П л а н а п о х роматиче с к и е *, т у б у с СО
ОПА-11 **»* 0,85 4,0 .Сухая 0,29 45 В пружинящей оправе
ОПА-12 1,25 2,5 Масляная 0,25 45 » » »
иммерсия
ОПА-9 0,5 10,0 Сухая 0,80 45
Для исследования в светлом и темном поле (эпиобъективы)
МИМ-9 0,25 25,4 Сухая 4,4 45 —
МИМ-9 0,30 16,0 4,4 45 —
МИМ-9 0,65 6,3 » 4,4 45 ——
6. М о и о х р о м а т и ческиедляузкой области спектра, тубус оо
ОБМЖ-1,6 1,30 1,65 Масляная 0,40 64
иммерсия
243
1 Объективы для исследования методом фазового контраста маркированы буквой Ф. 2 Объективы для исследований в свете люминесценции маркированы буквой Л. 3 Объективы для исследований методом фазово-темнопольиого контраста маркированы буквой А. 4 Объективы для исследований в поляризованном свете маркированы буквой II. 5 Объективы для исследований в свете люминесценции методом фазового контраста маркированы буквами Ф и Л. 6 Объективы для исследований в свете люминесценции методом темнопольиого контраста маркированы буквами А и Л. 7 При исследовании объектов без сегмента объективы работают с препаратами без покровного стекла. В графах «Увеличение» и «Числовая апертура» числитель дроби обозначает собственное увеличение и числовую апертуру объектива, а знаменатель — увеличение и числовую апертуру объектива с сегментом — 1,55), 8 Объективы характеризуются большим линейным полем в пространстве изображений (25 мм); применяются с широкоугольными компенсационными окулярами. 8 В эпиобъективах, в отличие от других объективов, имеется осветительная система в виде параболического ;зеркал а.
Таблица 4.55. Микропланары для микросъемки
/Л арка Увеличение, крат Относительное отверстие Фокусное расстояние, мм Конструктивная особенность
ОГ1-15 15 1 : 4,5 40 С ирисовой диафрагмой
ОП-16 10 1 : 4,5 65 » » )/
ОП-17 5 1 : 4,5 100 » » »
ОФ-1Н 0,5—1,0 1 : 6,3 150 » ъ »
5) для исследований толстослойных желатиновых пленок;
6) контактные;
7) для исследований при высоких температурах (с большим рабочим расстоянием).
Кроме того, объективы микроскопов характеризуются следующими конструктивными параметрами: длиной тубуса, рабочим расстоянием и высотой объектива.
Длиной тубуса называется расстояние на тубусе микроскопа от нижнего опорного торца для объектива до верхнего опорного торца для окуляра. Объективы для длины тубуса оо работают с дополнительной ахроматической линзой, устанавливаемой за объективом (см. гл.2).
Рабочим расстоянием называется расстояние от верхней поверхности покровного стекла до оправы первой линзы объектива.
Высотой объектива называется расстояние от плоскости предметов до опорной плоскости объектива.
ОКУЛЯРЫ
Окуляр — оптическая система, расположенная непосредственно перед глазом и предназначенная для рассматривания изображения, образованного предыдущей оптической системой.
Требования, предъявляемые к окулярам, изложены в гл. 2.
Рис. 4.53. Схема окуляра Рамс- Рис. 4.54. Схема окуляра Гюй-дена генса
По левая Виа азо а ем а
Типы окуляров и их характеристики
Окуляр Рамсдена (рис. 4,53). Хроматизм неисправлен, полевые аберрации исправлены для 2со 40е; Sp,^(0,25— 0,3)/'. Окуляр Рамсдена применяется в простых геодезических приборах.
Окуляр Гюйгенса. Такой окуляр (рис. 4.54) применяется в микроскопах. По сравнению с окуляром Рамсдена в нем несколько лучше исправлен хроматизм. Передний фокус мнимый и лежит между линзами; Spf = /'/3.
Окуляр Кельнера. Этот тип окуляра (рис. 4.55) самый распространенный. В нем хорошо исправлены аберрации в пределах 2(0 — 45—50°; —s^/73; Sp^f/2.
Симметричный окуляр. Такие окуляры (рис. 4.56) применяются в телескопических приборах. Они хорошо исправлены в пределах 2(о = 40° —sF - sp,^ 0,75/7
Ортоскопический окуляр. Подобные окуляры (рис, 4.57) применяются преимущественно в измерительных приборах и микроскопах. Они хорошо исправлены на все аберрации, особенно на дисторсию в пределах 2(о - 40°; — s„ /72;
s;, - 0,75/'.
Широкоугольные окуляры Эрфле. Существуют два типа таких окуляров: первый (рис. 4.58, а) исправлен в пределах 2(0 = = 65°; — sf^/75; sp,= = /72; второй тип (рис. 4.58,6) исправлен в пределах 2(о = 60 -г 65°; s = -/75; s^,= (0,5-r 4-0,75) f.
Окуляр с удаленным зрачком. Для таких окуляров (рис. 4.59) 2(о = = 45°; s'pf = /'. Окуляры с угловым полем 2(о — 80° обычно имеют параболическую глазную линзу, как, например, окуляр, изображенный на рис. 4.57. Окуляры с угловым полем 61 и 53° приведены на рис. 4.60 и 4.61, а окуляры с внутренней фокусировкой, применяемые при высоких требованиях к герметичное ги прибора, — на рис, 4.62, а и
Рис. 4.55. Схема окуляра Кельнера
Рис. 4.56, Схема симметричного окуляра
Рис. 4.57. Схема ортоскопического окуляра
Рис. 4.58. Схема окуляра Эрфле; а — первого типа; б — второго типа
4.62, б. Окуляр, показанный на рис. 4.62, а, имеет пределы диоптрий-» ной установки от —5 до 4-6 и изменяется от 0,30 до 11,3 мм; окуляр, изображенный на рис. 4.62, б имеет пределы диоптрийной установки ±5 и d8 — изме-
няется в пределах от 1,42 до 11,47 мм.
На рис. 4.63 даны графики аберраций окуляров, изображенных на рис. 4.62, а и 4.62, б. В табл. 4.56—4.59 приведены данные некоторых распространенных окуляров.
На' рис. 4.64 приведены оптические схемы некоторых новых ком-
Рис. 4.59. Схема окуляра с удаленным зрачком
пенсационных окуляров
с постоянным по полю зрения приблизительно 2%. Окуляры
хроматизмом увеличения, равным предназначены для высококаче-
Рис. 4.60. Схема окуляра с угловым полем 61°
, (IvdSuXHM чситЪ
Г-35
Рис. 4.61. Схема окуляра с угловым полем 53°
Рис. 4.62. Схемы окуляров с внутренней фокусировкой: а — первого типа; б — второго типа
9 fo=25,0
Подвижная часто
ственных планапохроматических объективов микроскопа, у которых хроматическая разность увеличения составляет 1,5—2%. Они имеют хорошую коррекцию монохроматических аберраций и их
применение с апохроматическими объективами обеспечивает^практически бесцветное изображение в микроскопе (71J. Окуляр Г = 6,3х является развитием окуляра Гюйгенса, а окуляры 10 и 16 < —схемы
Рис. 4.63. Графики аберраций окуляров: а — по рис. 4.62, а; б — по рнс. 62, б
Рис. 4.64. Оптические схемы новых компенсационных окуляров микроскопа: а — Г = 6,3х; б — Г — 10х; в — Г = 12,5х; г — Г — 16х
Кельнера. По оптической схеме рис. 4.60, в разработай комплект симметричных окуляров с увеличением 10, 12,5 и 20х; с угловым полем 2со ~ 40J и = 0,6/4
Т а б л и ц а 4.56. Окуляры для микроскопов
Марка окуляра Увеличение, кр ат Линейное поле, мм Фокусное расстояние, мм Марка окуляра Увеличение, крат Линейное поле, мм Фокусное расстояние, мм
1. Г IO й Г < 211 с а АКШ-11 2 10 15 25
23,3 АКШ-12,5 12,5 15 20,2
АМ-6 4 62 АКШ-16 16 12 15,6
АМ-30 3 4 20 63 АКШ-17 2 16 11 15,6
АМ-4 2 4 24 62 АКШ-18 16 11 15,6
АМ-5 2 5 23 50,6 АКШ-20 20 9 12,5
М-7 7 18 36
АМ-31 3 7 18 36 4. Ш и р о к о у Г 0 Л Ь 1 ч ы е
AM-11 2 АМ-8 1 7 8 19 21 36 31,4 (удаление sn входного зрачка = 160 м\Л
М-10 10 14 25 60,7
AM-10 4 10 14 25 А Ш-4 4 17
М-11 15 8 17 АШ-8 8 20 30,4
АШ-8С4 8 20 30,4
2. Комп е н с а цнон н ы е АШ-8п 8 20 30,4
АШ-12,5 12,5 18 20
АМ-24 5 20 50 АШ-5 1 4 17 60,7
AM-12 5 22 50
AM-13 7 18 35 (удаление входного зрачка
АМ-262 7 18 36 s_ — СХ ))
АМ-14 10 13 25 р 20 39,8
АМ-27 15 11 16,7 AM-134 6,3
AM-16 20 9 12,6 АМ-134п 1 6,3 20 39,8
АМ-134ш 2 6,3 20 39,8
3. Ш и р < компе ) к оу голь н ы е АМ-37п 5 10 18 25
н с а п ионные АМ-37ш 5 10 15 25
(удаление входного зрачка S р •— оо) АМ-38 АМ-38п 10 10 15 15 25,2 25,2
АКШ-1 6,3 20 39,4 5. О р т о 2 К 0 П и ч е с кие
АКШ-ln 1 6,3 20 39,4 AM-18 12,5 16 20
АКШ-1 ш 2 6,3 20 39,4 АМ-19 17 13,6 15
АКШ-2 10 15 24,9 АМ-20 28 6,5 9
АКШ-2п 1 10 15 24,9 6. Сим
АКШ-3 2 10 15 24,9 метр и ч н ы е
АКШ-4 12,5 13 20 АТ-36 15 12 17
АКШ-5 16 11 15,6 АТ-38 15 12 17
АКШ-5п 1 16 11 15,6
АКШ-14 10 18 25 /. Фотоокуляр ы
АКШ-14п5 10 18 25 М-7Ф 7 18 36
АТ-18 7 18 36
(удаление входного зрачка АМ-14Ф 10 13 25
SP ,= 160 мм) АМ-27Ф 15 11 16,7
ЛКШ-6.3 АКШ-11 6,3 10 22 15 39,7 25 АТ-37С АМ-18Ф AM-16Ф 15 12,5 20 12 15 9 17 20 12,5
Марка окуляра Увеличение, крат Линейное ноле, мм Фокусное расстояние, мм Марка окуляра У в ел и ч е н и е, крат Линейное поле, мм Фокус ное расстояние, м м
8. К в а о ц е в ы е л л я AM К-9 3 15 84
фотограф» р о в а и и я АМК-Ю 3 15 80,7
В V л ь т р афиолетовой АМК-12 6 9 37,4
области с п е к т р а АМК-13 6 7,4 35,5
AM К-2 8 14 28,8 9. П р о е к ц и о г н ы е л л я
AM К-3 8 15,6 29.8 ф о т о г р а ф и р о в а н и я
AM К-5 8 12 29,4 । В И II Ф пак о а с и о и
AM К-6 AM К-7 3 3 15 15 80 80,4 облас т и спектра
AM К-8 3 15 78 А К-3 А КМ-3 2.9 2,9 ИД Н,7 67,9 77,7
1 Окуляры с перекрестием; 2 окуляры со шкалой ; ” окуляр
с удаленным входным зра1 садочный диаметр окуляра КОМ; 4 — 30 мм <,куляр со шкалой с сеткой; 6 по-
Таблица 4,57. Окуляры и применяемые к ним объективы микроскопа
Марки
окуляра объектива i окуляра объектива 1 ! ' окуляр а объектива
АМК-2 О к-40 AM К-7 1 S 1 ок-4о 1 i АМК-Ю ОНЗ-75А; ОНЗ-115
ДМ К-3 AM К-5 OK-40 ОК-58 AM К-8 ОК-50; ОК-58; ОНЗ-125 АМК-12 АМК-13 ОК-75 ОН 3-75 А; ОНЗ-115
AM К-6 ок-io-з 1 АМК-9 OK-75 I 1 АМК-3 А К-3 ОРМ-75ИК ОР-75ИК; OH3-40; ОРМ-751 !К
Таблица 4.58. Гомалы
М ар<:а гомала Линейное поле, мм Фокусное расстояние, мм Пос адоч-ный диаметр, мм Рекомендуемые объективы
Длина тубуса, мм Увеличение, крат
011-6 15 —70 27 (<?9) 160 и 190 со и-»* Н-* СП 1 1 оэ to о о
Of 1-7 8 —20,28 27 (е9) 160 и 190 60—90 90
ОН-8 13 —37,6 27 (е9) 160 и 190 со 5—20 11—30
Таблица 4.59. Окуляры зрительных труб (/ок = 20, 25, 30, 40 и 50 мм)
Характеристики Тип окуляра
Симметричный Кельнера С удаленным зрачком Эрфле
гй) 40 45—50 50 60
&P'/fок 1 : 5 1 : 5 1 : 5 1 : 4,2
sf! ?ок 0,76 0,29—0,3 0,32—0,34 0,33—0,37
sP'/foK 0,72—1,2 0,4—0,7 0,9—1,25 0,7—0,9
Рис. 4.65. Автоколлимационные окуляры
Автоколлимационные окуляры
Конструкция автоколлимационного окуляра должна обеспечивать удовлетворительную видимость автоколлимационного изображения светящегося или темного штриха сетки, Контрастность и яркость в отдельных случаях должны быть такими, чтобы автоколлимационное 250
изображение сетки получалось от зеркала, установленного на значительном расстоянии от прибора на открытом воздухе или в специально затемненном помещении. На рис. 4.65, а—г и 4.66 а—б приведены конструкции автоколлимациоиных окуляров, а в табл. 4.60 их характеристики. Пользуясь табл. 4.60 можно выбрать окуляр для данных условий работы.
Рис. 4.66. Автоколлимационные окуляры Монченко
Т а б л и ц а 4.60. Сравнительные характеристики автоколлимациоиных окуляров
Тип окуляра В, % т. % гок. крат ПС’ м ^л’ м
С кубиком и двумя сетками (рис. 4.65, а) 17 42 Не ограничено 18 Более 30
Окуляр Аббе 86 92 30 2 2
(рис. 4.65, б)
Окуляр Гаусса (рис. 4.65, в) 46 50 18 18 Более 30
Окуляр Линника * 7—88 92 Не ограничено 20 Более 30
Окуляр Захарьевского * 90 18 18 20 Более 30 .
С сеткой, подсвечиваемой сбоку 8 92 Не ограничено 10 15
(рис. 4.65, г)
С кубиком и одной 20 —— 20 18 30
сеткой
Монченко (рис. 4.66, а, б) 86 92 30 25 Более 30
Примечание. В таблице условно обозначены: В — яркость автоколлимационного изображения относительно начальной яркости сетки, принятой за 100%; т — светопропускание всего окуляра;
Г максимально возможное увеличение симметричного окуляра; Ос — максимальное расстояние до наблюдаемого зеркала при солнечной погоде; Оп — то же при пасмурной погоде.
* Окуляры Лннннка и Захарьевского применяются редко из-за трудности изготовления
УРОВНИ
Уровнями называют устройство для установки визирных линий или плоскостей в горизонтальное (или вертикальное) положение, а также для определения малых углов отклонения плоскостей от горизонта. Уровни характеризуются чувствительностью к отклонениям и точностью измерения угла отклонения. Широкое применение в различных лабораторных и полевых измерительных приборах (например, в геодез и че-
Рис. 4.67» Принцип действия уровня (HHi— линия горизонта)
Рис. 4.68. Цилиндрический уровень
ских), а также в прицельных устройствах находят пузырьковые уровни [67]. Уровни состоят из стеклянной ампулы и металлической оправы различной конструкции.
Ампула уровня представляет собой закрытый стеклянный сосуд в виде трубки, внутренней поверхности которой придана бочкообразная форма, или в виде низкого цилиндрического стаканчика, верхней торцевой поверхности которого придана сферическая форма. При горизонтальном положении ампулы середина пузырька уровня находится посередине ампулы (рис. 4.67, а). Если ампулу наклонить на угол а, то пузырек, стремясь занять наивысшее положение, переместится из точки Л1 в точку (рис. 67, б). Его перемещение можно определить по формуле Л1Л43 = л/?а/180.
Для установки уровня в горизонтальное положение и определения угла наклона на ампулах наносятся штрихи со стандартным расстоянием между ними 2 ± 0,5 мм. Угол, на который требуется наклонить уровень для перемещения пузырька на одно деление, называется угловой ценой деления данного уровня. Разность между ценой деления и фактическим углом наклона уровня для перемещения пузырька иа одно деление характеризует его точность и ие должна превышать 20% цены деления.
Чувствительность уровня зависит от радиуса кривизны и качества шлифования внутренней поверхности ампулы, свойств наполнителя, длины пузырька и температуры. При низких температурах вязкость жидкости возрастает и чувствительность понижается.
По форме различают уровни цилиндрические (рис. 4.68) и круглые (рис. 4.69). Иногда круглые уровни называют сферическими. Характеристики отдельных ампул (ГОСТ 2386—73) приведены в табл. 4.61 и 4.62. Ампулы заполняют маловязкой и не замерзающей при температуре до —60е С жидкостью и запаивают с обоих концов, оставляя пузырек паров данной жидкости. Цилиндрические ампулы изготовляют
Рис. 4. 69. Сферический уровень (а), ампула (б) и корпус (в)
из молибденового стекла. Наполнитель низкоточных (5—10') ампул — спирт этиловый, иногда смесь эфира со спиртом; высокоточных — эфир этйловый. Размер пузырька уровня составляет, примерно, 1/3 длины ампулы. При изменении температуры изменяется также и длина пузырька. Чтобы исключить это явление применяют компенсированные и камерные уровни [89].
Для повышения точности установки пузырька на середину уровни снабжены призменными системами и лупами, позволяющими совместить изображения противоположных концов пузырька (контактные уровни).
Установлено, что пузырек обычного уровня устанавливается на середине с ошибкой ±0,14т", контактного — с ошибкой ±0,04т", а контактного уровня с лупой — с ошибкой ± 0,04 т"/Гл, где Гл — увеличение лупы (обычно 2—3х) [67].
Т а б л и ц а 4.61. Предельные отклонения цены деления уровней АЦП
Номинальная цена деления Предельные значения средней цены деления Номин аль-№ая ценз деления Предельные значения средней цены деления
От До От До
10' 8' 12' 20" 18" 22"
8' 7' 9’ 15" 13,5" 16,5"
30" 27" 33" 10" 9" 11'
Т абл и ц а 4.62. Техническая характеристика ампул
Тиа ампулы Цена деле-ния уровня, ..." Диаметр ампулы, мм Высота или длина ампулы, мм Диаметр или длина пузырька при 20° С, мм Радиус рабочей сферы или дуги, мм
Круглые ампулы W
А К — малой точности 20' 17 10 5 344
со шкалой в виде круго- 10' 17 10 5 688
вых рисок 4' 17 10 5 1 376
Цилиндрические ампулы
АЦП — простые малой 10' 7,5 23 6 688
и средней точности со 4' 7,5 33 8 1 719
штриховой шкалой или 60 11 54 18 6 876
перекрестием в центре 30 11 54 18 13 751
(вместо шкалы) 15 11 54 18 27 502
10 и 54 18 41 252
АЦК — компенсиро- 20 14 124 40 20 626
ванные (с компенсациои- 15 14 124 40 27 502
ной палочкой) средней и 10 14 124 40 41 252
высокой точности со штриховой шкалой или перекрестием в центре (вместо шкалы) 4 14 124 40 103 132
АЦР — камерные (с 20 15 124 62—70 20 626
регулируемой длиной пу- 10 14 124 62—70 41 252
зырька) средней и высо- 4 14 124 62—70 103 132
кой точности со штри- 2 14 1 24 62—70 206 265
ховой шкалой 1 22 224 ! 10-120 412 530
Ампулы сферических уровней применяются двух основных типов:
1) установочные, предназначенные для установки приборов в горизонтальное положение (фотоаппараты, лабораторные приборы), с ценой деления 5, 10 и 20'; сверху на уровнях нанесены два концентрических кольца;
2) фокусные уровни для создания вертикальной линии визирования в приборах, используемых на качающихся основаниях (например, на самолетах). Уровни устанавливаются таким образом, чтобы нижняя поверхность верхнего стекла уровня, по которой скользит пузырек находилась в плоскости изображения прибора. Радиус кривизны верхнего стекла уровня должен быть равен фокусному расстоянию оптической системы, расположенной до уровня.
Фокусные уровни применяются двух типов: с запаянной ампулой и с составной ампулой, у которой регулируется величина пузырька [89]. Ампулы закрепляются в оправе путем заливки гипсом или резьбовыми кольцами.
В зависимости от рабочего температурного диапазона ампулы уровней всех типов изготовляются двух исполнений: нормального (Н) от —50 и 40 до+50° С (АКН, АЦПН, АЦКН, АЦРН) и термоустойчив (Т) от —50 до Ч~75° С (АКТ, АЦПТ, АЦКТ, АЦРТ). В зависимости от назначения ампулы изготовляются: нереверсивными всех типов, реверсивными (Р) типов АЦП (АЦПНР, АЦПТР) и АЦК (АЦКНР, АЦКТР), а также с несимметричной шкалой (Ш) типа АЦК (АЦК'НШ, АЦКТШ).
Пример условного обозначения ампул: Ампула уровня АЦК10"-14Х 124 ГОСТ 2386—73 — ампула типа АЦК с ценой деления 10", диаметром 14 мм, длиной 124 мм.
ПРОБНЫЕ СТЕКЛА ДЛЯ ПРОВЕРКИ РАДИУСОВ СФЕРИЧЕСКИХ ПОВЕРХНОСТЕЙ ОПТИЧЕСКИХ ДЕТАЛЕЙ ИНТЕРФЕРЕНЦИОННЫМ МЕТОДОМ
Пробные стекла изготовляются трех видов (ГОСТ 2786—76).
ОПС — основные пробные стекла для проверки поверхностей контрольных пробных стекол;
КПС — контрольные пробные стекла для проверки поверхностей рабочих пробных стекол;
РПС — рабочие пробные стекла для проверки поверхностей деталей.
Номинальные значения радиусов измерительных поверхностей стекол приведены в ГОСТ 1807—75. Стекла изготовляют двух классов точности: 1 и 2.
Контрольным и рабочим стеклам присваивают класс точности того основного или контрольного стекла, с которым сличают их измерительную поверхность (табл. 4.63).
Предельное отклонение от плоскостности плоских основных стекол 1-го и 2-го классов точности — не более 0,05 и 0,07 интерференционной полосы соответственно. При наложении контрольного стекла на основное или рабочего стекла на контрольное наблюдаемая интерференционная картина при проверке сферических стекол должна соответствовать требованиям, указанным в табл. 4.64.
Материалом для стекол диаметром до 100 мм служат стекла марки ЛК5 и ЛК7 и свыше 180 мм — марки ЛК5 ГОСТ 3514—76 или кварцевое стекло марок КВ, КУ-1, КУ-2 (ГОСТ 15130—69),
Таблица 4.63. Допустимые отклонения радиусов измерительных поверхностей сферических основных стекол
Номинальное значение радиуса измерительной поверхности сферического основного стекла, мм Допуски, %
Класс точности стекла
1 2
От 0,5 до 1,0 ±0,05 ±0,15
Св. 1,0 до 2,0 » 2,0 » 5,0 ±0,08
Св. 5,0 до 10,0 ± 0,04 ± 0,06
Св. 10,0 до 12,0 » 12,0 » 15,0 » 15,0 » 22,0 » 22,0 » 32,0 » 32,0 » 37,5 ±0,01 ±0,05 ±0,04
Св. 37,5 до 250 ±0,03
Св. 250 до 1000 ±0,02 ±0,05
Св. 1000 ± 0,02г/1000 ± 0,05г/1000
Таблица 4,64. Предельные отклонении формы сферических поверхностей стекол
Радиусы измерительных поверхностей стекол, мм I группа сопряжения И * группа сопряжения
Допуски (ннтерфер еицноиные полосы)
N ал/ N A7V 1
От 0,5 до 37,5 Св. 37,5 до 750 » 750 » 5000 Св. 5000 0,20 0,10 0,10 0,05 0,10 0,07 0,07 0,05 1,00 1,00 0,50 0,10 0,2 0,2 0,10 0,07
* Допускается применять только для стекол типа РПС.
ДОПУСКИ НА ЧИСТОТУ ПОВЕРХНОСТЕН ОПТИЧЕСКИХ ДЕТАЛЕЙ
Классы чистоты следует устанавливать на основании требований, предъявляемых к оптическим системам, с учетом технологических возможностей изготовления, экономических и эстетических соображений (табл. 4.69 и 4.70). По ГОСТ 11141—76 установлены 14 классов чистоты полированных поверхностей оптических деталей из стекла, кристаллов, пол и мерный материалов, оптической керамики и металлов с параметром шероховатости R2 равным от 0,1 до 0,025 мкм по ГОСТ 2789—73 после окончательной обработки, включая операцию нанесения покрытия.
Классы чистоты Назначение классов чистоты
0—10; 0—20; 0—40 (последние две цифры указывают среднее значение фокусного расстояния оптической системы, расположенной за нормируемой поверхностью) Для поверхностей деталей, расположенных в плоскостях действительных изображений или в плоскости предметов оптической системы прибора
1 —1Ха Для остальных поверхностей
Размеры царапин и точек, соответствующие классам 0—10, 0—20 и 0—40, устанавливаются раздельно по трем зонам поверхности. Границами зон являются концентрические окружности диаметром 1/3 и 2''3 светового диаметра детали. Для деталей диаметром менее 5 мм зоны не устанавливаются. В центральной зоне не допускаются точки н царапины шириной более 0,001 мм. Недопустимость царапин шириной 0.001 мм и менее должна быть установлена в технических требованиях чертежа оптической детали. В любой четверти поверхности детали не допускается более трех точек при световом диаметре детали до 60 мм включительно и более пяти точек при световом диаметре детали свыше 60 мм. Размеры царапин и точек в средней и краевой зонах и их число в зависимости от светового диаметра детали даны в табл. 4,65. Для деталей диаметром менее 5 мм ширина допускаемых царапин и диаметр точек не должны превышать значений, установленных табл. 4.65 для средней зоны поверхности. Для детален со шкалами и другими делениями допускается устанавливать другое деление границ зон.
Царапины и точки на поверхности перемещающейся детали должны быть распределены так, чтобы в любом месте этой поверхности диаметром, равным диаметру линейного поля прибора, количество царапин и точек не превышало указанного в табл. 4.65.
На поверхности деталей I—1Ха классов чистоты размеры царапин л точек и их число (в зависимости от светового диаметра детали) не должны превышать значений, указанных в табл. 4.66. Для IV—VII классов чистоты допускается не нормировать скопление дефектов на поверхности детали. Недопустимость скоплений дефектов устанавливается в технических требованиях чертежа.
9 В. А. Панов и др. 257
Таблица 4.65. Размеры допускаемых дефектов, мм
Класс чистоты Зона Царапины Точки
Ширина, не более Суммарная длина, не более Диаметр, не более Число, не Солее, при светонем диаметре
От 5 до 20 Св. 20 до 60 Св. 60
0—10 Средняя 0,002 0,2 X Осв 0,004 1 3 5
Краевая 0,004 0,3 X £>св 0,006 3 6 10
0—20 Средняя 0,004 0,2 X Осв 0,010 1 3 5
Краевая 0,006 0,3 X ОСв 0,015 3 6 10
0—40 Средняя 0,006 0,2 X DCB 0,015 I 3 5
Краевая 0,008 0,3 X DCB 0,025 3 6 10
Таблица 4.66. Допускаемые дефекты на поверхностях, расположенных вне плоскостей изображения
Царапины Точки Скопление дефектов
Класс частот ы Ширина, мм, не более Суммарная длина, мм, не более Диаметр, мм, не более Число, не более Диаметр ограниченного участка, мм Площадь царапин и точек, мм2, не более
I 11 III IV V VI VII 0,004 0,006 0,010 0,020 0,040 0,060 0,100 2,0 X Осв 0,020 0,050 0,100 0,300 0,500 0,700 1,000 0,5 X DCB 1,0 1,2 2,0 5,0 10,5 25,0 50,0 0,004 0,006 0,020 0,100 0,400 3,000 10,000
VIII 0,200 2,000 0,4 X DCB
Villa 0,300 1.5 X £>ев
IX 2,0 X DCB 3,000 0,3 X DCI,
IXa 0,400 1,5 X Dca
Таблица 4.67. Допускаемые дефекты различных классов чистоты, мм
Класс чистоты Ширина царапни Диаметр точек Класс чистоты Ширина царапин Диаметр точек
I. II 0,001 0,002 VI 0,008 0,040
III 0,002 0,004 VII 0,010 0,100
IV 0,004 0,010 VIII, Villa 0,014 0,140
V 0,006 0,020 IX, IXa 0,020 0,200
Таблица 4.68. Рекомендуемые классы чистоты в зависимости от материала детали
Класс чистоты Материал детали Диаметр детали, мм. не более
0—10 и грубее Стекло оптическое групп А, Б, а, у по ГОСТ 13917—68 и по ГОСТ 9411—75
III и грубее Стекло оптическое групп В, д по ГОСТ 13917—68 и по ГОСТ 9411—75 -
V и грубее VI » » IV » » Кристаллы: фториды гигроскопические, пластинчатые, твердые (корунды), полупроводниковые 100
V и грубее Полимеры 250
V и грубее Металлы —
Царапины и точки размером, указанным в табл. 4.67 и менее, пе учитываются. Скопление этих дефектов не учитывают, если общая площадь участков, запятых под скоплением, не превышает 30% площади рабочей (световой) части поверхности деталей.
Для III—1Ха классов чистоты число точек и суммарная длина царапин размером от предельного для принятого класса по табл. 4.66 не должны быть более 50% от общего допускаемого числа точек и допускаемой суммарной длины царапин. Необходимость нормирования дефектов вне рабочей зоны устанавливают в технических требованиях
9* 259
Таблица 4.G9. Рекомендуемые классы чистоты в зависимости от назначения детали
Класс чистоты Виды оптических деталей
0—10 Сетки и коллективы в приборах с окуляром /01С— 10* -*15 мм; шкалы и лимбы, рассматриваемые под Гок> > 25Х; дифракционные решетки
0—20 Сетки и коллективы в приборах с фокусным расстоянием окуляра /ок= 15 4- 25 мм; шкалы и лимбы, рассматриваемые под увеличением в пределах от 25 до 10х
0—40 Сетки и коллективы в приборах с окуляром /ои > 25 мм; шкалы и лимбы, рассматриваемые под ГОк < 10х; подложки растров и детали, находящиеся в плоскости изображения фотоэлектронных систем, работающие в ПК области спектра
I Первая линза широкоугольных окуляров; первые линзы микрообъектов с увеличением более 10х
II Призмы, коллективы, первые линзы широкоугольных окуляров и другие детали, расположенные вблизи от плоскости действительного изображения оптической системы; подложки для диэлектрических зеркал в световой зоне, применяемые в твердотельных ОКГ и приборах, разработанных на основе ОКГ
III Линзы окуляров телескопических систем; окулярные призмы; линзы окуляров микроскопов и измерительных лабораторных приборов, выравнивающие стекла фотоаппаратов; линзы обтекателей и линзы объективов, работающих в инфракрасной области в условиях солнечной засветки
IV Линзы окуляров, объективов и оборачивающих систем, призмы и пластины телескопических приборов. Лупы, Линзы конденсоров и объективов, работающих в инфракрасной области в условиях отсутствия солнечной засветки. Выравнивающие стекла фотокамер. Подложки для интерференционных фильтров
2ёо
Продолжение та5л. 4,69
Класс чистоты Виды оптических детален
V Линзы объективов и оборачивающих систем, головные призмы, призмы в параллельных пучках и защитные стекла в телескопических приборах; линзы н зеркала фотографических и линзы проекционных объективов диаметром от 20 до 50 мм; линзы конденсоров и объективов, работающих в инфракрасной области в условиях отсутствия солнечной засветки; активные элементы (торцевая поверхность); цилиндрические двухканальные отражатели (внешняя и внутренняя поверхности), применяемые в ОКГ
VI Линзы объективов и оборачивающих систем телескопических приборов; линзы и зеркала фотографических и линзы проекционных объективов диаметром от 50 до 100 мм
VII Линзы и зеркала фотографических и астрономических объективов диаметром от 100 до 300 мм; смотровые стекла размером до 300 мм
VIII, IX Линзы и зеркала фотографических и астрономических объективов диаметром от 300 до 500 мм; смотровые стекла размером от 300 до 500 мм
Villa, IXa Линзы и зеркала фотографических и астрономических объективов диаметром более 500 мм; смотровые стекла размером более 500 мм
Т абл и ц а 4.70. Зависимость класса чистоты от диаметра рабочего отверстия
Диаметр рабочего отверстия, мм Класс чистоты
0 (плоскость изображения) 0—10, 0—20, 0—40
До 0,5 Св. 0,5 до 1,5 » 1,5 » 4,5 » 4,5 » 10 >10 » 25 » 25 » 50 » 50 I II III IV V VI VII—IXa
чертежа оптической детали. Краевые выколки размером более 0,8 мм должны быть заматованы. Для разных участков поверхности допускается применять различные классы чистоты. Для обозначения классов чистоты устанавливается буква Р с добавлением номера класса (например, PV).
Допускается устанавливать различные классы чистоты по царапинам и точкам (например, РIVI Pill соответственно).
При наличии в приборе нескольких плоскостей действительного изображения, в которых установлены детали, следует учитывать общее количество дефектов иа этих деталях. Для поверхностей, на которые будут наноситься просветляющие или отражающие покрытия, рекомендуется требования по чистоте ужесточать на один класс. В табл. 4.68— 4.70 даны рекомендуемые классы чистоты для оптических деталей.
Литература: [1, 3, 11, 12, 13, 14, 15, 20—27, 33, 44, 45, 61, 66, 67, 71, 72, 78, 79, 81, 82, 85—89, 101, 102, 103, 105, 1 1 1, 112 ].
ГЛАВА 5
КРЕПЛЕНИЕ ОПТИЧЕСКИХ ДЕТАЛЕЙ
ОБЩИЕ ПОЛОЖЕНИЯ
Конструирование узла крепления любой оптической детали предполагает обеспечение ее базирования, ориентирования и закрепления в соединении с базовой механической основой, обычно называемой оправой детали.
Конкретное конструктивное решение узла крепления зависит от многих факторов: вида оптической детали, ее назначения, материала, размеров и формы, от требований, регламентирующих функционирование этой детали в оптической системе прибора, от назначения прибора и условий его работы, а также от вида производства.
При выборе типа крепления и разработке конструкции узла необходимо обеспечить выполнение следующих общих требований:
1) крепление должно быть надежным, т. е. во время работы прибора положение оптической детали относительно оправы не должно изменяться;
2) замыкающие усилия, необходимые для осуществления сопряжения между оптической деталью и оправой, не должны вызывать опасных деформаций и напряжений;
3) базовая основа узла, ориентирующие и крепежные детали или их элементы должны быть расположены вне габаритов светового пучка. Поверхности этих элементов, находящиеся вблизи пучка, не должны быть причиной появления рассеянного света и бликов в системе;
4) крепления должны быть технологичны, как в отношении изготовления деталей, так и в отношении сборки.
Часто при конструировании узлов крепления оптических деталей приходится учитывать особые требования, связанные со специфическими условиями работы тех или иных приборов. Так, для приборов, работающих в нестабильном тепловом режиме, при больших перепадах температуры, необходимо иметь в виду температурные деформации, которые могут существенно повлиять на качество крепления. Для некоторых приборов отдельные узлы крепления должны быть герметичными, т. е. в местах соединения оптической детали и оправы следует предусмотреть специальное уплотнение.
Во многих случаях к узлам крепления предъявляются дополнительные требования, обусловленные особенностями производства оптических приборов, когда необходимая точность взаимного ориентирования оптических деталей достигается путем юстировки. В этих случаях крепление оптической детали должно допускать необходимые юстировочные движения детали относительно оправы.
В некоторых конструкциях юстировочные движения приходится обеспечивать за счет перемещений и поворотов оправы с закрепленной оптической деталью относительно конечной базовой детали узла (корпуса, основания, кронштейна и т. д.).
Типичными видами приборных соединений являются соединения оптических деталей с механическими, к функционированию которых предъявляются очень жесткие требования по точности, надежности, стабильности и характеристикам силового режима. Поэтому при разработке конструкций крепления оптических деталей следует руководствоваться перечисленными ниже основными принципами конструирования.
1. Соединение оптической детали с элементами узла, обеспечивающими базирование и ориентирование, должно быть статически определенным.
2. Ограничение смещений оптической детали в узле должно осуществляться преимущественно поверхностями, расположенными перпендикулярно к направлению этих смещений.
3. Ограничение поворотов (перекосов) оптической детали должно осуществляться элементами крепления, расположенными на наибольшем удалении в пределах габаритов оптической детали.
КРЕПЛЕНИЕ КРУГЛЫХ ОПТИЧЕСКИХ ДЕТАЛЕЙ
Круглыми называются детали, край которых сошлифован при вращении заготовки вокруг оси, практически совпадающей с ее оптической осью. При этом край оптической детали образуется в виде соче-
Рнс. 5Д. Схема базирования, ориентирования н крепления круглых оптических детален
та ни я поверхностей вращения: цилиндрической (центрирующей) и поверхностей фасок (вспомогательных). К таким деталям относятся: линзы, светофильтры, сетки, защитные стекла; иногда круглыми бывают и зеркала.
При любом методе крепления круглых оптических деталей цилиндрическая поверхность детали должна находиться в сопряжении с такси же внутренней поверхностью А оправы (рис. 5.1). При этом будут исключены две степени свободы детали — поперечные смещения у и х. Для устранения осевого смещения — z и поворотов ф/у и ф.г рабочая поверхность Р детали должна находиться в сопряжении с уступом Б оправы. Так как это сопряжение одностороннее (на всех вариантах рис. 5.1 — со стороны первой поверхности детали), то с противополож-264
ной стороны должно быть осуществлено силовое замыкание С. Для того чтобы на краю закрепленной дезали не возникало «скалывающего» момента сил, необходимо стремиться к тому, чтобы диаметр опоры Б и диаметр линии приложения замыкающих сил С были одинаковыми. Степень свободы ср2 (поворот вокруг оси детали) обычно исключается силами трения, возникающими во всех местах контакта оптической детали с оправой и элементами крепления. Уплотняющие замазки, применяемые с целью герметизации соединения детали с оправой, естественно, повышают сопротивляемость детали по отношению к повороту. В некоторых особых случаях (детали больших размеров, очень жесткий
Таблица 5.1. Соединение круглых оптических деталей с оправами. Допуски и посадки
Точность центрирования Допуски Примеры применения
Характеристика Допуск на децентрировку, мм на диаметры оптических деталей иа внутренний диаметр оправы
центрирующих нецеи-трирую-щих
1 2 3 4 5 6
Повышенная До 0,02 Л8 (С3) d9 (Ш3) W9 (Л3) Линзы микрообъективов
g6 (Д) dll (Х4) 7/7 (Л) Линзы светосильных фотообъективов
П (X) Точная оптика: лйнзы, сетки, шкалы
Средняя Св. 0,02 до 0,05 Л8 (С3) d9 (Ш3) Я9 ’ Из) Линзы окуляров
С1 1 (Л4) Н8 т Оптика телескопических приборов, сетки, шкалы
Пониженная Св. 0,05 dll (Х4) —— НИ (Л4) Конденсорные линзы, светофильтры, плоские зеркала, защитные стекла
Таблица 5.2. Допуски на посадочные диаметры деталей, покрываемых эмалью
1 Посадочный диаметр детали, мм Рекомендуемые поля допусков
до покрытия после покрытия „
Св. 3 до 6 » 6 » 180 ( {Л) 1 <Х) §6, Л8 (Д, С,)
Св. 3 до 6 » 6 > 180 (Ш) 1 (Л) Г (X)
Св.
» »
»
Толщина слоя эмали, мм
Таблица 5.3. Толщина слоя эмали в зависимости от диаметра детали
Посадочный диаметр детали, мм
3 до 10 0,008—0,012
10 » 30 0,010—0,016
30 » 80 0,012—0,020
80 » 180 0,016—0,025
динамический режим работы прибора) приходится прибегать к специальным устройствам, препятствующим вращению детали.
Необходимо учесть, что для более правильного ориентирования оптической детали в оправе опора ее иа уступ Б должна осуществляться рабочей (полированной) поверхностью (рис. 5.1, а—в), э не фаской, в расположении которой относительно оптической оси возможны большие погрешности. Поэтому, если опора реализуется вогнутой поверхностью детали, приходится усложнять форму уступа оправы (рис. 5.1, в). Исключение допускается только при наличии плоской конструктивной фаски Ф, перпендикулярной оси детали (рис. 5.1, г). В этом случае на перпендикулярность плоскости фаски по отношению к оптической оси • приходится назначать жесткие допуски.
Посадка круглой оптической детали в оправу по своему характеру должна быть посадкой с гарантированным зазором. Отраслевой стандарт ОСТ 3-2124—74 устанавливает выбор допусков на диаметры оправ и деталей (одиночных и склеенных) при различных требованиях к точности центрировки (табл. 5.1).
В блоке склеенных оптических деталей (например, линз) центрирующей считается деталь с наивысшими требованиями по децен-трмрованню; при одинаковых требованиях — с наибольшей толщиной по краю.
На одиночные (несклеенные) детали назначаются допуски по данным столбцов 3 или 4 (табл. 5.1) в зависимости от требований к децен-трированшо. Для защитных стекол, к которым предъявлены требования по герметизации, следует применять поле допуска е9 (ЛСЯ).
Оптические детали, требующие повышенной точности центрирования, посадочные поверхности которых должны быть покрыты эмалью, рекомендуется изготовлять с уменьшенным размером по диаметру, применяя допуски r соответствии с данными табл. 5.2. В этом случае на чертеже детали следует указывать размеры диаметров до и после покрытия.
Толщину слоя эмали рекомендуется выбирать в соответствии с величинами, указанными в табл. 5.3.
При особо жестких требованиях к точности центрирования наименьший посадочный зазор обеспечивается растачиванием оправы по конкретному значению диаметра линзы с указанием в чертеже: «поверхность ... обработать по линзе ... с зазором ... — ... мм». Такой метод, естественно, допустим только для единичного и мелкосерийного -производств.
Оправы для крепления круглой оптики обычно изготовляются нз стали, алюминиевых сплавов и латуни. Коэффициенты линейного расширения этих материалов и оптического стекла имеют существенное отличие (в 2—3 раза). Поэтому для больших перепадов температуры величина посадочного зазора должна быть проверена на отсутствие натяга в посадке оптической детали для нижнего предела температурного интервала и, в случае необходимости, зазор должен быть увеличен. Однако, при нагревании до верхнего предела температурного интервала зазор может достичь величины, недопустимой с точки зрения точности центрирования.
При очень жестких температурных условиях работы приборов, в особенности если оправы оптических деталей имеют большие размеры, применяют титановые сплавы, коэффициенты линейного расширения которых близки к коэффициентам линейного расширения стекла.
Поверхности оправ для антикоррозионной защиты и для уменьшения отражающего действия (рассеянный свет, блики) должны иметь черное покрытие в виде оксидных пленок или слоя матовой эмали. В особенности это важно для внутренних посадочных и свободных поверхностей. На протяженных гладких внутренних поверхностях (цилиндрических, конических) целесообразно применять противо-бликовое рифление (ОСТ 3-777—72).
Все, о чем было сказано выше, определяет то общее, что присуще различным способам крепления круглой оптики, независимо от их конкретной конструктивной реализации. Различия же способов крепления заключаются лишь в средствах закрепления деталей в оправах.
Существуют следующие способы крепления: крепление завальцов-кой (закаткой), крепление резьбовым (зажимным) кольцом, крепление пружинящими планками, проволочным («разрезным») кольцом и крепление приклеиванием. Первые два вида крепления используются наиболее широко, так как они являются универсальными для большого числа типоразмеров деталей.
Крепление завальцовкой
При этом способе оптическая деталь удерживается в оправе тонкой ее кромкой, которая приобретает свою конечную форму в результате пластического деформирования металла во время завальцовки. Такое крепление является неразъемным. Крепежная кромка оправы после завальщлзки находится в сопряжении с конусной поверхностью специальной фаски, сошлифованной на детали под углом 45°, при этом она не должна выступать за пределы фаски.
Профиль крепления завальцовкой показан на рис. 5.2, размеры в миллиметрах элементов крепления в зависимости от диаметра детали D даются в табл. 5.4.
Диаметр опорного уступа d2 определяется величиной светового диаметра рабочей поверхности детали, базирующейся на него. Глубина
расточки оправы h определяется геометрией края линзы с учетОхМ толщины края, ширины фаски, величины d2 и данных табл. 5.4.
Крепление завальцовкой применяется для оптических деталей диаметром до 80 мм и для склеенных блоков до 50 мм. Такое ограничение объясняется тем, что крепежная кромка предельной толщины в 0,5 мм не в состоянии обеспечить необходимую надежность крепления для тяжелых деталей, в особенности при наличии перегрузок (вибрации, тряска, удары). Увеличить же толщину кромки невозможно, так как в процессе завальцовки могут появиться выколки по краю детали. Кроме того, только тонкая завальцованная кромка обладает пружинящими свойствами, обеспечивая
Рис. 5.2. Размеры элементов оправы для крепления завальцовкой
необходимое силовое замыкание детали и оправы при отсутствии пережатий, а также хорошую компенсацию осевых температурных деформаций.
Материалы оправ при этом методе крепления должны обладать высокой пластичностью. Наилучшим является латунь ЛС59-1; применяются также: латунь Л62, дюралюминий марок Д1, Д6, Д16, низкоуглеро-
дистые конструкционные стали (сталь 20, сталь 30).
На рис. 5.3 показаны конструкции оправ, наиболее часто применяемых для крепления круглых деталей средних разме-
ров. Все оправы имеют резьбу для соединения их с базовой деталью узла и средства для завинчивания — накатку на буртике (а), отверстия под ключ (б) и шлицы под ключ (я).
Соотношения между размерами отдельных элементов оправ для наиболее типовых конструкций устанавливаются стандартом пред
приятия.
Таблица 5.4. Размеры элементов оправ под завальцовку
D S 1 /1
До 10 От 0,2 до 0,3 0,3-0,4 1,6 0,3
Св. 10 до 30 0,5-0,7 2,0 0,5
Св. 30 до 50 От 0,3 до 0,4 1,0-1,2 2,5 0,8
Св. 50 до 80 От 0,4 до 0,5 1,2—1,6 3,0 1,0
На рис. 5.4 даны следующие типовые примеры крепления заваль-цовкой:
— отрицательной линзы малого диаметра (а), закрепленной в оправе, имеющей базовые поверхности в виде цилиндрической наружной поверхности и двух параллельных плоских торцов, перпендикулярных оси линзы;
Рис. 5.3. Конструкции оправ для креплении завальцовкой
— линзового склеенного блока (например, объектива телескопической системы) (б) закрепленного в оправе, имеющей крепежную резьбу и опорный буртик;
— плосковыпуклой линзы (в), завальцованной в оправу аналогичной конструкции, причем завальцовка осуществлена со стороны буртика оправы;
— Системы трех несклеенных линз и двух промежуточных колец (а), закрепленных в общей оправе;
Рис. 5.4. Примеры крепления завальцовкой
— плоскопараллельной пластинки с приклеенной к ней линзой в оправе (д), базовыми поверхностями которой являются наружная цилиндрическая и две плоскости торцов.
Крепление резьбовым кольцом
При этом способе крепления оптическая деталь прижимается к опорному уступу оправы резьбовым кольцом, кромка которого нажимает на деталь с противоположной стороны. Это крепление разъемное, как и всякое соединение деталей с использованием резьбы.
На рис. 5.5 показаны следующие примеры конструкций узлов крепления оптических деталей резьбовым кольцом:
— двояковыпуклой линзы в оправе («), имеющей базовые элементы в виде резьбы и буртика;
— глубокого положительного мениска в оправе (б), базовыми элементами которой являются центрирующая наружная цилиндрическая поверхность и параллельные опорные торцы;
— склеенного блока двух линз (в), базирующегося иа уступ оправы вогнутой поверхностью; оправа, кроме крепежной резьбы и буртика, имеет центрирующий поясок; для более равномерного зажима между резьбовым кольцом и линзой установлено промежуточное кольцо;
— блока трех склеенных линз (г), причем резьбовое кольцо имеет внутреннюю резьбу н навинчивается снаружи на оправу, нажимая
Рис, 5.5. Примеры крепления резьбовым кольцом
на плоскую фаску линзы буртиком; для навинчивания кольца в буртике имеются отверстии под ключ;
— оптического клина (д), при этом к наклонной плоскости клина 1 примыкает промежуточное клинообразное кольцо 3 так, что они вместе составляют блок с параллельными внешними кромками; между зажимным кольцом 2 и промежуточным кольцом установлена эластичная прокладка для компенсации возможной непараллельности; клин предохраняется от проворота в оправе с помощью цилиндрического штифта 4, который опирается на полуцилиидрическую выемку в стенке оправы и призматическую выемку клина; кольцо 3 предохраняется от проворота стопорным винтом;
— круглого зеркала (г); оио используется в неответственных случаях, когда требования к плоскостности рабочей поверхности зеркала невысоки; для выравнивания зажимающих усилий по обе стороны от зеркала помещаются эластичные прокладки;
— системы четырех линз, из которых три — склеенные (ж); между одиночной линзой и склеенным блоком расположено промежуточное кольцо; зажимное рззьбовое кольцо — втулка, одновременно выполняет функции диафрагмы:
— сетки (з), причем для лучшей фиксации положения сетки между резьбовым кольцом и оптической деталью помещено промежуточное кольцо;
— тонкой плоскопараллельной пластинки (например, светофильтра) (и); кольцо с внутренней резьбой.
Крепление резьбовым кольцом, в отличие от крепления за вальцовкой, является жестким. Поэтому, при работе в сложном температурном режиме, возможно существенное ухудшение качества крепления (потеря стабильности при высоких температурах и пережатие — при низких). Кроме того, при этом методе трудно обеспечить равномерный прижим оптической детали по всей окружности опорного уступа из-за
погрешностей изготовления резьбы, погрешностей расположения торца зажимного кольца (неперпендикулярность), а также погрешностей формы уступа и торца.
Применение резьбового кольца с внутренней резьбой дает некоторое сокращение осевых габаритов узла (рис. 5.5, а, и), что бывает важно при малых расстояниях между оптическими элементами системы. Кроме того, достаточно тонкая прижимная кромка кольца, обладая меньшей жесткостью, способна в некоторой степени выравнять усилие зажатия при температурных деформациях.
Иногда для некоторого выравнивания усилия зажима применяют тщательно изготовленное промежуточное кольцо (рис. 5.5, в), с помощью которого может быть ослаблено действие погрешностей изготовления резьбового кольца. Температурные деформации при этом не компенсируются.
Крепление резьбовым кольцом применяется для линз диаметром от 10 мм. Для меньших размеров оно ие технологично вследствие трудностей изготовления внутренней резьбы. Для линз больших диаметров у этого способа крепления практически ограничений нет. Известны случаи его применения для линз диаметром 300 мм и более.
Для существенного повышения качества крепления применяются пружинные кольца, устанавливаемые между линзой и зажимным резьбовым кольцом (рис. 5и6). При наличии пружинного кольца крепление
становится эластичным, что позволяет избежать нежелательного действия осевых температурных деформаций.
При креплении толстых линз (илн склеенных линзовых блоков), работающих в условиях больших перепадов температуры, главной задачей является компенсация температурных деформаций. Она может быть решена применением пружинного кольца с гладкими торцами, имеющего два илн более рядов прорезей.
Рис. 5.7. Конструкции оправ для крепления резьбовым кольцом
Пружинные кольца с тремя выступами, расположенными под углом 120°, применяются для крепления тонких линз средних и больших диаметров, зеркал и других деталей с целью устранения возможных изгибающих усилий, по отношению к которым они очень чувствительны. В этом случае оптическая деталь должна опираться только на три выступающие участка оправы, расположенные также под углом 120° (на «три точки»). Такие площадки фрезеруются на опорном уступе оправы (рис. 5.6, а—в) или обеспечиваются прокладками (рис. 5.6, г, д). При этом пружинное кольцо должно быть ориентировано так, чтобы
его выступы находились против выступов оправы. Это достигается специальными фиксирующими устройствами, например с помощью установочного винта в оправе и продольного паза в кольце, как это показано на рис. 5.6, б, в. Три силы, приложенные к детали в точках контакта пружинного кольца компенсируются тремя силами реакции в точках контакта детали и оправы (опасных изгибающих моментов при этом не возникает).
На рис. 5.7, а—в изображены типовые оправы для крепления резьбовыми кольцами. Примерные соотношения размеров в мм: d, = = D; d2 ~ + 0,2, где D — полный и D± — световой диаметры
линзы; Dp + 0,2 + 2/73, где Н} — высота профиля резьбы
0,54Р); Sp = (64-10) Р\ Ь2 = dp + (24-10) (ip определяется особенностями конструкции всего узла); = (64-10) Р'\ Р и Рг —-шаги 272
резьб внутренней и наружной соответственно. Обычно применяется мелкая резьба с шагом 0,5; 0,75; 1 мм в зависимости от толщины стенки оправы и кольца. При креплении линз больших диаметров применяется резьба и с более крупным шагом.
Для завинчивания резьбовые кольца и оправы должны иметь шлицы или отверстия под ключ. Все резьбовые соединения, в том числе и резьбовые кольца должны предохраняться от самоотвинчивания стопорными винтами или краской.
-На рис. 5.8 представлены резьбовые кольца наиболее распространенных типов. Соотношения их размеров определяются геометрией посадочных мест оправы под кольцо и световым диаметром линзы иа ее рабочей поверхности со стороны кольца.
Рис. 5.10. Типы пружинных колец
На рис. 5.9 даны типы колец, которые могут применяться, как промежуточные, в узлах крепления нескольких оптических деталей, разделенных воздушным промежутком, а также, из конструктивных соображений, могут устанавливаться между резьбовым кольцом и оптической деталью или между резьбовым и пружинным кольцами.
На рис. 5.10 даны два варианта конструкций пружинных колец (с одним и двумя рядами прорезей). Тип и размеры пружинного кольца определяются массой закрепляемой детали (или деталей) с учетом инерционных перегрузок, которые зависят от условий работы прибора. Максимальный прогиб каждого пружинящего элемента кольца не должен быть больше половины ширины прорези.
Стандартами предприятий более подробно определяются соотношения между размерами элементов оправ и деталей крепления для наиболее употребимых вариантов конструкций.
Кроме материалов, используемых при креплении деталей завальцовкой, для изготовления оправ, резьбовых и промежуточных колец могут применяться автоматные стали А12, А20, закаленный дюралюминий ДГ1‘, Д6Т, Д16Т. Для оправ в серийном производстве могут применяться литейные алюминиевые сплавы АЛ2, АЛ9, АЛ 13. Для пру-жшшых колец применяются обычно стали: сталь 40, сталь 50.
Крепление пружинящими планками
По своим свойствам этот вид крепления аналогичен креплению оптических деталей с помощью пружинного и резьбового колец «на трех точках». Суть крепления заключается в том, что в трех небольших зонах («точках»), расположенных под углом 1203, на оптическую деталь нажимают три одинаковые плоские пружины или три выступа одной
пружины, обеспечивая силовое замыкание детали иа базирующий уступ оправы. Эти плоские пружины обычно н называются пружинящими планками. Прижимные пружинящие планки прикрепляются к оправе винтами, их конструкция и расположение относительно оправы могут быть самыми разнообразными. Конкретное конструктивное решение зависит от особенностей конструкции оправы и всего узла.
На рис. 5.11 показаны следующие варианты крепления круглых оптических деталей пружинящими планками:
— тремя радиально расположенными планками (а), каждая нз которых прикрепляется двумя винтами к широкому фланцу оправы; концы планок нажимают на выступающую поверхность детали; вариант невыгоден в отношении поперечных габаритов узла;
— тремя планками (б), для закрепления которых иа оправе требуется меньшая ширина торца; планки при этом имеют более сложную форму (в);
— пружинящими планками (г), прикрепленными к лыскам иа стенке оправы снаружи;
— светофильтра (д) накладным кольцом с тремя пружинящими выступами;
— круглого зеркала (е) накладным кольцом с шестью пружинящими элементами;
— линзы (ж) тремя специальными пружинящими планками, прикрепленными винтами к внутренней поверхности стенки оправы.
Крепление пружинящими планками целесообразно применять для оптических деталей большого диаметра (80 мм и более), так как при этом относительное увеличение габаритов узла будет невелико. Однако 274
некоторые варианты конструкций могут использоваться в неответственных случаях и для деталей малого диаметра (рис. 5.11, д, е). Прижимные планки изготовляют из сталей марок 65Г и У8А.
Крепление проволочным кольцом
Этот способ конструктивно прост и технологичен, но используется Только для крепления круглых оптических деталей в наименее ответственных случаях, когда ие предъявляется высоких требований к точности-, надежности и герметичности соединения. К таким деталям относятся: светофильтры, защитные стекла (не в оптической системе), рассеиватели, небольшие круглые экраны, конденсорные линзы, осветительные зеркала.
Рнс. 5.12. Крепление круглых деталей проволочным кольцом
На рнс. 5.12 приведены примеры конструкций такого крепления. Из рисунка ясно, что оптическая деталь находится между уступом оправы и выступающей частью проволочного кольца, помещенного в специальную канавку. Каиавка обычно выполняется прямоугольного сечения (рис. 5.12, а). Ее ширина равна диаметру проволоки, глубина — половине диаметра. Для облегчения сборки, развернутая длина кольца должна быть такой, чтобы между его концами после установки в канавку оставался промежуток в несколько миллиметров. Наружный диаметр свободного кольца (до сборки) должен быть больше внутреннего диаметра канавки. Кольца изготовляются из пружинной проволоки; ее диаметр (обычно 0,5—1,5 мм) зависит от размера оптической детали. Во избежание выколок, сопряжение оптической детали и кольца должно осуществляться по поверхности ее фаски. Ввиду наличия отклонений в размерах глубины расточки н ширины канавки в оправе, а также толщины детали по краю, это сопряжение возможно только с осевым зазором, в пределах которого оптическая деталь может смещаться и перекашиваться.
На рис. 5.12, б, г показаны варианты крепления светофильтра и зеркала в штампованных оправах. На рис. 5.12, в приведено крепление линзы конденсора. В этом случае проволочное кольцо упирается в поверхность конусной расточки. Осевая составляющая сил реакции на линии контакта будет действовать на линзу и прижимать ее к уступу. Для этого угол конуса и жесткость кольца должны быть рассчитаны с учетом массы линзы и возможных перегрузок.
Крепление приклеиванием
В конструктивном отношении этот способ является самым простым, так как он не требует других элементов крепления, кроме оправы и склеивающего вещества. Однако, этот вид крепления применяется
с некоторыми ограничениями. Крепление неразъемное и жесткое. При больших перепадах температуры, из-за разницы коэффициентов термического расширения материалов оптической детали и оправы, возможно расклеивание или возникновение недопустимых напряжений в стекле и деформаций детали. Поэтому при таких условиях работы, этот способ применяется в основном для неответственных деталей (осветительные зеркала и линзы, светофильтры, защитные стекла).
В лабораторных приборах, для которых тепловой режим более стабилен, приклеивание используется и для крепления деталей с высокими требованиями к качеству функционирования (например, таких,
Рис. 5.13. Крепление круглых деталей приклеиванием
как линзы объективов), в особенности в тех случаях, когда реализация других способов крепления затруднительна (детали очень малого диаметра). При этом следует учитывать, что некоторые склеивающие вещества при затвердевании (испарении растворителя или полимеризации) сильно уменьшаются в объеме (усаживаются), что может вызвать появление напряжений в оптической детали сразу же после завершения процесса склейки. Так, например, акриловый клей имеет усадку до 50%. Следовательно, для лабораторных приборов в ответственных случаях крепление приклеиванием допустимо применять только для деталей малого размера и жестких по своей конструкции (относительно бол ь ш о й тол щи вы).
Естественно, что качество крепления будет выше при следующих условиях: если рабочий температурный интервал уже, клей имеет наименьшую усадку и после завершения цикла склейки клеевой шов не превращается в твердое вещество, а приобретает податливость, причем не пластичную, а упругую, т. е. шов становится эластичным. При соблюдении этих условий способ приклеивания может быть распространен и на детали больших размеров. В наиболее ответственных случаях нежелательные воздействия приклеивания должны проверяться расчетом и в эксперименте.
Конструктор, использующий этот способ крепления, де л кен учитывать и особенности технологии. Например, что цикл затвердевания (сушки) — длительный (от нескольких часов до нескольких суток). Режим сушки часто требует применения термостатированных камер и характеризуется повышенными значениями температуры. Для точного базирования и ориентирования детали относительно оправы в процессе склейки и сушки необходимы специальные приспособления.
На рис. 5.13 показаны следующие семь вариантов конструкций крепления круглых деталей приклеиванием:
— плоскопараллельной пластинки (а), когда клеевой шов формируется за счет фасок детали и оправы, а базирование осуществляется по внутренней поверхности расточки и уступу;
— фронтальной линзы микрообъектива (б), базирующейся на фаску; клеевой шов располагается в пределах зазора между сопрягаемыми поверхностями;
— плоскопараллельной пластинки (а), если клеевой шов формируется специально увеличенным зазором в посадке; осевое базирование производится на уступ оправы;
— осветительного зеркала в оправе (г); клеевой шов усилен за счет периметра выступающего края детали и торца оправы;
— плосковыпуклой линзы малого диаметра (б); клеевой шов находится в зазоре между расточкой оправы и наружной поверхностью линзы в пределах глубины расточки (базирование на плоскость расточки);
— линзы с достаточно большой толщиной по краю (с); для создания клеевого шва используются специальная расточка оправы и фаска линзы;
— простейшего крепления посредством клеевого шва (ж), который формируется только за счет фаски оправы.
Для приклеивания оптических деталей к металлическим оправам могут применяться: оптические клеи по ГОСТ 14887—69 (акриловый, эпоксидные ОК-50П, ОК-72Ф и полиэфирный клей ОК-90 пластифицированный), технические клеи по РТМ 3-522—74 (полиуретановый ПУ-2, шеллачный), герметики по ОСТ 3-1927—73 (УТ-32, УТ-34), герметик УЗО м (ГОСТ 13489—68). Наибольшей эластичностью обладают полиуретановый клей и герметики.
КРЕПЛЕНИЕ ЗЕРКАЛ
Как известно, оптические зеркала, несмотря иа кажущуюся ксн-структивную простоту, требуют особого подхода при разработке конструкций узлов их крепления. Это объясняется тем, что искажение формы рабочей поверхности зеркала сильно влияет на качество изображения. Ввиду того что зеркало является относительно топкой деталью, оно очень чувствительно к деформациям, в особенности к изгибу.
Дзя неответственных зеркал круглой формы (например, осветительных) могут применяться обычные жесткие способы крепления или упрощенные, о которых говорилось выше.
Для крепления зеркал, которые участвуют в построении изображения и находятся в основном пучке оптической системы, обязательными являются: условие статической определенности соединения (опора «на три точки»), эластичность соединения (создание трех замыкающих усилий с помощью пружинных элементов), компенсация воздействия колебаний температуры (наличие посадочных зазоров, эластичных
крепежных элементов, подбор материалов), возможность регулировки величины замыкающих усилий.
Этим условиям для круглых зеркал в большой мере удовлетворяют способы крепления резьбовым кольцом с промежуточным пру»
жинным и пружинящими планками. Пружинящие планки могут применяться н для крепления некруглых зеркал, и. <
Крепление зеркал любой конфигурации с помощью прижимных планок (лапок). В этом случае оправой является плоская деталь, у которой имеются три выступающие площадки, являющиеся опорами для зеркала. Иногда этн опоры выполняются в виде прокладок из алюминиевой или латунной фольги. Прижимные планки закрепляются на оправе таким образом, чтобы их замыкающие элементы воздействовали на зеркало в местах, определяемых расположением опор. Так
Рис. 5.14. Крепление зеркал прижимными планками
как планки жесткие, то эластичность крепления обеспечивается специальными прокладками, устанавливаемыми между планками и зеркалом.
На рнс. 5.14 представлены следующие конструкции крепления различных по форме зеркал с помощью прижимных планок (лапок):
— круглого зеркала на плоской оправе (а) с базированием по трем
выступам; г-образные прижимные лапки соединяются основанием с теми же опорными площадками оправы посредством винтов; усилие прижима необходимой величины можно обеспечить за счет подбора толщины эластичных прокладок;
— такого же зеркала (б), как и в предыдущем случае, но лапками, имеющими Г-образную форму, закрепляемыми на боковой поверхности оправы, что дает возможность регулировать усилие прижима смещением
Рис. 5.15. Разновидности крепления некруглых зеркал прижимными планками
лапок в пределах зазоров в крепежных отверстиях под винты; опора зеркала на три прокладки из фольги;
— плоского зеркала прямоугольной формы (в); зеркало прижимается к опорным площадкам оправы планками, прикрепленными винтами к боковым стенкам оправы; крайние планки одновременно ограничивают вертикальные смещения зеркала;
— плоского зеркала некруглой формы (г) тремя прижимными лапками, конструкция которых подобна варианту (б);
— крепление вогнутого зеркала с прямоугольным краем (д); рабочие элементы прижимных лапок расположены с учетом кривизны поверхности зеркала.
На рис. 5.15 даны некоторые модификации крепления зеркал прижимными планками:
— - прямоугольного зеркала на плоской оправе (а), положение которого определяется внутренними плоскостями рабочих элементов прижимных лапок; усилия прижима обеспечиваются эластичными
прокладками, помещенными между зеркалом и оправой; за счет разности высот лапок возможен перекос зеркала относительно оправы;
— крепления плоского зеркала (б) с базированием на сферические концы установочных винтов; силовое замыкание осуществляется за счет деформации эластичной прокладки между зеркалом и оправой; с помощью винтов можно легко регулировать усилие, но при этом изменяется положение базирующих элементов и зеркало перекашивается;
Рис. 5.16. Консольное крепление зеркал
такое совмещение функций не всегда приемлемо. На рисунке хорошо видна другая эластичная прокладка, расположенная между краем зеркала и стойкой прижимной лапки; она нужна для ограничения продольных сдвигов зеркала при одновременной компенсации действия температурных деформаций;
— крепления вогнутого зеркала симметричной конструкции (б); зеркало опирается на две выступающие площадки, расположенные в средней части оправы вдоль ее длинных сторон; прижим создается двумя лапками, каждая из которых имеет по два рабочих элемента; опорные площадки в этом случае требуют доводки;
— крепления зеркала, в котором участвует только часть его длины (г); применяется при ограниченных габаритах; на разрезе видно, что зеркало прижимается к плоскости оправы планкой и Г-образнсй лапкой, продольные смещения зеркала ограничиваются с помощью вкладыша типа шпонки.
Консольное крепление. Оно применяется для крепления зеркал, работающих в качестве светоделителей, и должно выполняться на таком
удалении от рабочей зоны зеркала, чтобы деформации, вызываемые креплением не влияли на качество его поверхности. Закрепляемый
край зеркала обязательно базируется на оправу через прокладку (рис. 5.16, я, б); эластичные прокладки нужны и в местах контакта крепежных деталей. В особенности это важно для зеркал, испытывающих перегрузки [(например, в момент фиксации переключающегося зеркала (рис. 5.16,6)].
При особо жестких требованиях в отношении деформаций зеркала, для крепления используют специальные, предусмотренные иа нем выступы (рис. 5.16, б). На . рисунке показано крепление зеркала пентагональ-ного отражателя. Полированная плоскость выступов находится в сопряжении с притертыми площадками оправы; прижимные планки воздействуют на зеркало через эластичные прокладки.
На рис. 5.16, г приведена конструкция концевого отражателя дальномера. Кварцевые зеркала и кре
пежное основание соединены сваркой в единый блок, который базируется на трех сферических подпятниках. Прижим обеспечивается с помощью самоустанавливающегося диска и трех шариков. Усилие создается завинчиванием гайки, которая действует па диск через сферическую шайбу. Поперечные смещения ограничиваются тремя угольниками через эластичные прокладки. Юстировка отражателя производится изменением высоты подпятников н подвижкой угольников. Крепление довольно сложно по конструкции, но позволяет сохранить высокую точность формы и положения зеркал при колебаниях температуры и перегрузках.
Для крепления зеркал (чаще круглых) используют и пружины. На рис. 5.17 даны две такие конструкции; замыкающее усилие создается проволочной винтовой пружиной сжатия. На рис. 5.17, а показано, что усилие не регулируется, базирование зеркала осуществляется на плоскую кромку кольца. Во втором варианте усилие регулируется специальным винтом, положение которого стопорится гайкой (рис. 5.17, 6).
Зеркало базируется на уступ оправы. Между зеркалсм и пружиной обязательно наличие пластины с выступом по краю. С ее помощью усилие равномерно распределяется по кромке зеркала. Крепление пружиной обеспечивает стабильность формы зеркала при колебаниях температуры. Возможно улучшение этих вариантов за счет базирования на три площадки и прижима в трех точках. Вместо винтовых пружин иногда применяют пластинчатые. Посадка зеркала в оправу должна быть с гарантированным зазором при любой температуре в пределах рабочего диапазона.
Крепление зеркала в трубе. Такой вариант крепления показан на рис. 5.18. Чаще всего так закрепляются наклонные зеркала, расположенные под углом 45° к оси трубы. Боковая поверхность зеркала — Цилиндрическая; она сошлнфована в приспособлении при наклоне заготовки на 45° по отношению к осн вращения. Рабочая отражающая поверхность зеркала ограничена эллипсом, малая ось которого равна посадочному диаметру оправы. :
Зеркало базируется на наклонную плоскую кромку опорной втулки, предварительно вставленной в оправу. После регулировки по углу
Рис. 5.18. Крепление наклонного зеркала в трубе
Рнс. 5.19. Упрощенные конструкции крепления зеркал
поворота втулка стопорится. Крепление зеркала осуществляется с противоположной стороны посредством подобной же втулки, только с отверстием для прохода отраженного света. Эта втулка может фиксироваться резьбовым кольцом (рис. 5.18, а) или винтом (рис. 5.18, б). Возможны деформации зеркала от неравномерного зажатия и температурных влияний. Качество крепления может быть улучшено при использовании пружинного кольца, которое должно быть установлено между резьбовым кольцом и прижимной втулкой.
На рис. 5.19, а—в представлены некоторые упрошенные варианты крепления зеркал, которые могут применяться в неответственных случаях прн низких требованиях к точности зеркала. Такие крепления допустимы для зеркал небольших размеров.
Крепление крупногабаритных зеркал. При этом способе крепления (например, в астрономических приборах) приходится учитывать действие большой массы зеркала. Трех опор при этом уже недостаточно. Зеркало устанавливается на большее число опор, как осевых, так и радиальных. Опоры выполняются самоустанавливающнмися и регулируемыми. Применяются также дополнительные пружинные опоры для разгрузки основных базирующих. Весьма важной является проблема 282
автоматической компенсации разницы температурных деформации зеркала и оправы. Решение этой проблемы связано с расчетом и конструированием различных термокомпенсаторов. Подробно изложить всю специфику разработки конструкции крепления астрономических зеркал в ограниченном объеме главы справочника не представляется возможным. Это особая область конструирования н она требует использования специальной литературы.
КРЕПЛЕНИЕ ПРИЗМ
Конструкции узлов крепления призм в практике оптического приборостроения весьма разнообразны. Это определяется в первую очередь многообразием типов призм. Наиболее часто встречаются следующие способы крепления, которые можно считать типовыми: крепление накладкой, угольниками, установочными винтами, прижимными планками (лапками), пружинами, приклеиванием. В принципе выбор крепления мало зависит от типа призмы и определяется в основном конструктивными, технологическими и эксплуатационными требованиями. Иногда применяются комбинации элементов крепления различных типовых способов; в некоторых случаях нз-за особенностей функционирования призмы или особенностей ее формы применяются специальные способы крепления.
Все конструкции крепления прнзм должны удовлетворять тем общим требованиям, которые изложены в начале главы. Дополнительно можно отметить следующее.
1. Рабочие и нерабочие поверхности призмы — плоскости, поэтому только эти плоскости могут быть базовыми элементами призмы. Чаще основной базовой плоскостью бывает одна — нерабочая грань призмы. При сопряжении ее с опорной плоскостью оправы (основания, плато) призма лишается трех степеней свободы. Замыкание сопряжения осуществляется со стороны противоположной грани призмы элементом крепления, по названию которого н определяется название всего способа (накладка, угольник и т. д.). Остальные три степени свободы отнимаются ориентирующими планками, которые прижимаются к другим граням призмы вне светового пучка и закрепляются на оправе.
2. Опорная плоскость оправы, на которую базируется призма, должна иметь высокую степень плоскостности; только при этом будет обеспечена определенность положения на плоскости и исключена возможность изгибающих деформаций. При больших размерах призмы, для уменьшения влияния погрешностей формы основания, в середине его делают выборку, тогда призма базируется краевым участком по периметру базирующей грани или на два протяженных элемента опоры. В особо ответственных случаях применяют базирование и на три выступающие площадки основания, но при этом, для исключения изгибающих деформаций, прижим призмы нужно производить тоже в трех точках на противоположной грани.
3. Между призмой й крепежным элементом, как правило, следует ставить эластичную прокладку, которая компенсирует погрешности в расположении крепежного элемента относительно призмы и распределяет усилие по большей площади.
4. Ребра призмы, во избежание выколок, не должны контактировать с базирующими, ориентирующими н крепежными элементами конструкции.
5. В некоторых случаях удобно базировать призму на рабочую Грань (илн две грани). Если это преломляющая грань, то фактически
базирование будет происходить на четыре участка грани за пределами ее светового диаметра. Если это отражающая грань с зеркальным покрытием, то базирование не должно испортить покрытия. В случае
Рис. 5.20. Крепление призм накладкой
использования отражающей грани с полным внутренним отражением базирование может осуществляться только по краю грани тоже за пределами габаритов светового пучка.
6. Призмы являются довольно жесткими деталями и хорошо противостоят деформациям. Поэтому, очевидно, в большинстве способов не предусматривается специальных устройств для равномерного распределения зажимающих усилий или для компенсации температурных деформаций, кроме эластичных прокладок в местах крепления. К таким
способам крепления (мы называем их жесткими) относятся все, кроме крепления пружинами. Наиболее чувствительно к температурным деформациям крепление приклеиванием. Наилучшим образом компенсируются температурные деформации при креплении пружинами.
7. Часто требуется в узле крепления призмы обеспечить возможность ее юстировки относительно оправы. Не все способы допускают это в одинаковой мере. Приклеивание, как неразъемное соединение, после завершения цикла склейки юстировок не допускает. Очень затруднительно или совсем невозможно обеспечить такую юстировку при реализации способа крепления призмы прижимными планками (лапками). В этих случаях приходится разрабатывать конструкцию юстировоч-
Рис. 5.21. Разновидности крепления призм накладкой
него устройства оправы с закрепленной призмой относительно базовой детали всего узла (основания, кронштейна, корпуса и т. п.).
Остальные способы крепления легко обеспечивают юстировку призмы относительно оправы в виде поворотов и смещений в плоскости базовой грани. При креплении пружиной с одновременным базированием на две грани удается обеспечить различную юстировку в широких пределах.
Крепление накладкой. Такое крепление показано на рис. 5.20 и 5,21. Во всех конструкциях призма устанавливается на плоскость оправы п прижимается накладкой через эластичную прокладку. Концы накладки прикрепляются к стойкам, жестко соединенным с оправой.
На рис. 5.20 представлены следующие примеры креплении:
— прямоугольной призмы с одним отражением (ц), базирующейся на плоскость оправы и уступы; накладка расположена на двух стойках круглого сечения; юстировка затруднена и возможна только за счет дополнительной обработки уступов;
— пента приз мы (б) с базированием на плоскость оправы и кромки ориентирующих планок; оправа закреплена относительно монтажной основы узла (кронштейна) на сферическом подпятнике с возможной юстировкой в виде малых поворотов вокруг трех осей;
— прямоугольной призмы с одним отражением (в), ориентирование которой в плоскости основания возможно только с помощью трех планок;
— пентапризмы на круглом основании (г); накладка прикреплена к стойкам гайками; юстировка допустима только в плоскости основания за счет изменения положения ориентирующих планок;
— прямоугольной призмы с двумя отражениями (д); базирование осуществляется на плоскость и уступ оправы;
На рис. 5.21 показаны способы крепления:
— склеенной призмы Аббе с крышей (я); накладка закреплена на трех стойках; ориентирование производится с помощью планок, одна из которых фаской опирается на грань крыши;
Рис. 5.22. Варианты конструкций стоек
— прямоугольной призмы (б) в корпусе, являющимся коленом, соединяющим две трубы под углом 90°; на основании корпуса профре-зерована площадка для базирования призмы и ориентирующих планок; накладка крепится одним концом винтами к стенке корпуса, другим концом — в пазу прилива;
— прямоугольной призмы с крышей (в); базирование осуществляется гранями крыши на фаски оправы; ориентирование в направлении ребра крыши обеспечивается наклонным уступом оправы и планкой, а прижим — накладкой через эластичную прокладку на фаску призмы:
— призмы (г) с двумя отражениями и углом отклонения 120° (из семейства пентапризм); ориентирование реализуется двуми планками.
На рис. 5.22, а—е показаны конструктивные варианты закрепления накладок на концах стоек и варианты крепления стоек к онр'аве.
Крепление угольниками. Разновидности креплений этого типа приведены на рис. 5.23 следующими примерами:
— пентапризма (п) закреплена двумя угольниками г-образной формы; ориентирование происходит в плоскости основания с помощью планки, прижатой к преломляющим граням призмы; усилие зажима создается за счет деформации эластичной прокладки;
— прямоугольная призма (б) закреплена одним угольником с ограничением смещений и поворотов в плоскости основания выступом оправы, планкой, а также выступом угольника;
a)
Рис. 5.23. Крепление призм угольниками
Рис. 5.24. Крепление песклеснноп баш-мачной призмы угольником
— прямоугольная призма (в) базируется на рабочую преломляющую грань; прижим призмы к основанию обеспечивается низкими угольниками через прокладки за закраины призмы, образовавшиеся после фрезерования канавок на боковых нерабочих гранях;
— прямоугольная призма (г) крепится составным угольником аналогично варианту, приведенному на рис. 5.23, а.
На рис. 5.24 показано крепление башмачной призмы с крышей; угольник составной и имеет два рабочих элемента, так как призма состоит из двух несклеенных между собой частей. Основная часть устанавливается на плоскость основания и кромки ориентирующих планок; клин базируется на плоскость основания и рабочую плоскость основной части призмы через прокладку из фольги, выполненную в виде рамки.
Крепление установочными винтами. Подобный тип крепления представлен на рис. 5.25 следующими примерами:
— пентапризма (о) закреплена тремя установочными винтами; концы винтов упираются в углубления прижимной пластины; между пластиной и призмой имеется эластичная прокладка; оправа охватывает призму
с трех сторон, но базирующая плоскость у нее одна; смещения и повороты призмы в плоскости основания ограничиваются двумя ориентирующими планками;
— прямоугольная призма (б) закреплена двумя установочными винтами в жесткой оправе; смещения вдоль гппотенузпой грани ограничиваются за счет сил трения;
— прямоугольная призма (в) зафиксирована на конце трубы; два установочных винта завинчены в планку, прикрепленную концами к специальным выступам оправы; после поджима призмы винты
стопорятся гайками; базирование призмы осуществляется на торец оправы и выступы;
— склеенный светоделительный кубик (г) закреплен одним установочным винтом в специальной оправе;
— визирная прямоугольная призма (д) закреплена в оправе четырьмя винтами; усилие прижима передается через металлические
Рис. 5.26. Разновидности крепления призм установочными винтами
пластинки и эластичные прокладки на специальные крепежные буртикД1 призмы;
— призма Шмидта с крышей (е) закреплена в специальной оправе одним установочным винтом.
На рис. 5.26, а показано крепление призмы Дове с крышей в специальной оправе одним установочным винтом; базирование осуществляется гранями крыши на выступы, расположенные внутри оправы под углом 90°, а прижим — винтом через специальную планку, опирающуюся наклонными плоскостями на преломляющие граии призмы.
На рис. 5.26, б изображено крепление ромбической призмы четырьмя установочными винтами; для придания оправе большей жесткости имеется стержень, прикрепленный вннтамн к ее стенкам (стяжка).
Крепление прижимными планками. Разновидности такого крепления представлены на рис. 5.27 десятью примерами. Характерным для этого способа крепления является более сложная конструкция оправы. Оправа охватывает призму с трех сторон, и, имея обычно две базирующих плоскости, лишает призму, по крайней мере, четырех степеней свободы. Оставшиеся степени свободы устраняются прижимными планками. Крепление получается очень компактным, но юстировка призмы относительно оправы практически неосуществима.
Прижимные планки бывают различными по конструкции, выполняются в виде лапок, угольников и т. д. Призма вставляется между стенками оправы с гарантированным зазором, который при необходимости выбирается прокладкой, обычно наклеиваемой на нерабочую грань призмы.
На рис. 5.27 даны следующие примеры крепления:
— прямоугольной призмы (а) четырьмя планками; базирование осуществляется на гипотенузную грань;
— прямоугольной призмы с крышей (б), базирующейся катетными гранями на оправу и выступы планок; прижим создается со стороны граней крыши;
— прямоугольной призмы (в), которая закрепляется двумя прижимными планками, имеющими по два рабочих элемента; юстировка узла относительно основания возможна четырьмя регулировочными винтами;
— такой же призмы (г), как и в случае, изображенном на рис. 5.27, в, но с помощью планок, имеющих вырезы в соответствии с габаритами пучка; юстировка узла относительно корпусной детали производится с помощью трех регулировочных винтов и центральной сферической опоры;
— нентапризмы (д), базирующейся преломляющими гранями; прижим осуществляется одной планкой со стороны нерабочей грани;
— полупентапризмы (е) при базировании на плоскость фланца трубы и на плоскости стенок, выполненных заодно с фланцем; прижим обеспечивается двумя комбинированными прижимными планками;
— призмы Шмидта (ж) с крышей, базирующейся рабочими гранями на плоскость основания и выступы планок; прижим производится со стороны граней крыши;
— призмы Пехана (з), закрепленной в оправе тремя прижимными плаиками, одиа из которых имеет вид рамки с отверстием по габаритам светового пучка; на чертеже дана конструкция элементов юстировки призмы вместе с оправой относительно детали привода (шестерни) и конструкция опоры вращения призмы (насыпного шарикового подшипника);
— призмы-куба (н) в оправе четырьмя прижимными планками при базировании нерабочей гранью на основание оправы и преломляющими гранями на выступы планок;
— призмы-куба (к) с такой же схемой базирования как и в предыдущем случае, но прижимных планок — две, они имеют клиновидную форму; смещение призмы в плоскости склейки ограничивается тем, что прижимные планки (вкладыши) входят в скошенные пазы, профрезе-рованные со стороны нерабочих граней призмы.
Крепление призм пружинами. Оно в основном применяется для приборов, работающих в тяжелом температурном и динамическом режиме. Пружины для крепления обычио используются плоские, тарельчатые, седловидные, полуцилиндрические, цилиндрические. Они изготовляются из листовой пружинной стали.
Рис. 5.27. Крепление призм прижимными планками
На рис. 5.28 показаны ниже приведенные варианты крепления: — призмы оборачивающей системы бинокля (й); юстировка в этом случае возможна в пределах зазора, имеющегося по периметру призмы в гнезде перегородки корпуса; пружина применяется плоская;
— призм такой же системы, что и в предыдущем примере, но при базировании на плато (б);
— головной прямоугольной призмы при различных конструктивных вариантах оправ и пружин (в, г, д, г); в варианте (г) — с помощью установочного винта можно регулировать усилие закрепления призмы; базирование призмы осуществляется преломляющими гранями;
Ф
8)
Рис. 5.28. Крепление призм пружинами
— окулярной прямоугольной призмы с крышей (ж); базирование производится преломляющими гранями иа плоскость оправы и выступы угольников, прикрепленных винтами к стенкам оправы; усилие полу-цилиндрической пружины регулируется винтом.
крепления призм пружинами
Рис, 5.29. Варианты
На рис. 5.29 также представлены следующие варианты крепления пружинами:
— башмачной призмы (£7) цилиндрической пружиной, которая вставляется с натягом между выемкой корпуса и выемкой металл и че-296
ской планки, нажимающей на призму; базирование осуществляется по двум граням основной части призмы; клин призмы приклеен к основной части с помощью боковых стеклянных накладок;
— прямоугольной призмы с крышей (6), расположенной внутри колена, соединяющего две трубы; юстировка возможна смещением призмы в двух направлениях с помощью резьбовых втулок, торцы которых являются базовыми опорами для призмы;
— такой же призмы (в), как и в примере, приведенном на рис. 5.29, б, по с обеспечением юстировки поворотом вокруг осн, пер-
Рис. 5.30. Крепление призм приклеиванием
пенднкулярной плоскости главного сечения; крепление осуществляется с помощью полупилиндрической пружины и двух винтов; призма может юстироваться установочными винтами посредством наклона замыкающей пружины; поворот происходит вокруг оси цилиндрического вкладыша, приклеенного к призме, и опирающегося иа цилиндрическую выемку оправы;
— прямоугольной призмы в колене трубы (г) при базировании катетными гранями на кольцевой выступ оправы и торец резьбового кольца; крепление осуществляется с помощью тарельчатой пружины, усилие которой передается посредством специального вкладыша иа гипотенузную грань и может регулироваться по величине с помощью резьбовой втулки;
— крепление пружиной призмы-ромба (о) в окулярном блоке бинокулярного прибора; юстировка призмы в этой конструкции крепления не предусмотрена.
Крепление призм приклеиванием. Такое крепление применяется в неответственных случаях и имеет такие же ограничения, как и в случае крепления круглых оптических деталей (см. выше). На рис. 5.50 даны четыре варианта крепления. Конструктивные особенности каждого из них понятны из рисунка.
Специальные способы крепления. Из них прежде всего следует отметить крепление призмы Дове (рнс. 5.31) Специфика ее работы заключается в том, что она, не изменяя направления пучка лучей, дает оборачивание изображения в плоскости главного сечения и при вращении вокруг оптической оси вращает изображение. Поэтому призма Дове закрепляется в оправе, имеющей снаружи вид втулки. Внутри протяжкой сделано отверстие квадратного сечения со стороной квадрата несколько большей размера призмы.
Рис. 5.31. Крепление призмы Дове в специальной оправе
На рис. 5.31, а показано типовое крепление призмы Дове с применением сегментного вкладыша (вклеенного в такой же формы паз, профрезерованпый в призме), специального винта, препятствующего осевому смещению призмы и восьми установочных винтов.
Установочными винтами производится юстировка призмы путем наклона ее в двух плоскостях в пределах имеющихся зазоров между призмой и оправой. После юстировки установочные винты стопорятся.
На рис. 5.31, б изображено аналогичное крепление, но установочные винты воздействуют на призму не через гибкие элементы оправы как в предыдущем случае, а через восемь вкладышей, опирающихся на грани призмы и вставленных в специальные пазы оправы.
Крепление прямоугольной призмы с крышей, используемое в панораме, которое тоже можно считать специальным, приведено на рнс. 5.32. Призма прижимается к базовым торцам резьбовых втулок 298
катетными гранями посредством специального призмодержателя. Призмодержатель кромками опирается на грани крыши. Его половинки могут смещаться по вертикали под действием двух установочных винтов, завинченных в резьбовую пробку корпуса, При этом происходит
незначительное перемещение призмы в направлении, перпендикулярном к плоскости чертежа. После юстировки установочные винты стопорятся в те же резьбовые гнезда стопорными винтами.
Специальное крепление башмачной призмы изображено на рнс. 5.33. Крепление отличается сложностью конструкции оправы, кото-
рая может быть выполнена только литьем. Опорные плоскости оправы профрезероваиы. В местах контакта призмы и оправы установлены
Рис. 5.32. Крепление прямоугольной призмы с крышей прпзмодержа телем
Рнс. 5.33. Крепление башмачной призмы в специальной оправе
эластичные прокладки. Замыкание осуществляется установочным винтом через специальную деталь, имеющую вид седла. Клин призмы прижимается к основной ее части с помощью прижимных планок.
Упрощенные способы крепления. Они применяются для крепления призм в неответственных случаях п подкупают своей конструктивной простотой, а также технологичностью. Это дает возможность использовать эти способы в серийном производстве.
Н а рис. 5.34, а приведено крепление полу пента пр из мы на плато с помощью штампованной детали типа крышки (кожуха).
На рис. 5.34, б оправа прямоугольной призмы имеет вид штампованного угольника, а крепежная деталь (тоже штампованная) прикрепляется к нему двумя винтами. Эта деталь четырьмя выдавками (пуклев-ками) ограничивает возможность смещения и поворотов призмы относительно оправы.
Крепление призмы зажимом ее винтом в разрезной оправе дано на рнс. 5.35. Для выравнивания усилий прижима применяются эластичные прокладки.
Комбинированные способы крепления. На практике часто применяются такие способы крепления, если по каким-либо причинам это удобно.
А-4
А-А
Рис, 5.34. Крепление призм штампованными деталями
Рис. 5.35. Крепление призмы зажимом в оправе
На рис. 5.36, а прямоугольная призма с крышей (с двумя отражениями) закреплена внутри корпуса с помощью пружины, прикрепленной двумя’винтами к его крышке, ориентирующей планки и установочного винта, который воздействует на грань крыши призмы через цилиндрическое седло-пружину.
Рис. 5.36. Варианты
комбинированного крепления
призм
На рис. 5.36, б показано крепление полупентапризмы в специальной оправе с помощью двух плоских пружин, двух цилиндрических вкладышей, передающих усилие пружин на призму, и с помощью ориентирующей планки.
КРЕПЛЕНИЕ ЗАЩИТНЫХ СТЕКОЛ
К уздаМ; крепления защитных стекол предъявляются повышенные требования в отношении надежности и герметичности. Для герметизации применяются резиновые или пластиковые прокладки и уплотняющая замазка, в том числе и герметик. Надежность обеспечивается, как правило, креплением прижимной рамкой по всему периметру защитного стекла, независимо от конфигурации его края. Такие конструкции приведены на рис. 5.37, а, б. Защитное стекло подсветки может быть закреплено как это показано на рис. 5.37, в. Кромка стекла по периметру (кроме левого края) имеет скос. Стекло вставлено в паз корпуса т nnai «ласточки ш хвост» и закреплено в пазу планкой, помещенной в тот же паз вслед за ним.
Крепление герметиками позволяет обеспечить необходимую герметизацию соединения и при условии колебания температуры (рис. 5.37, г).
Приклеивание защитных стекол применяется в неответственных случаях, в основном для лабораторных приборов (рис. 5.37, и).
Довольно большую сложность представляет крепление защитных стекол, состоящих из нескольких плоскопараллельных пластин. На рис. 5.37, е—з показаны варианты крепления таких стекол. Во всех случаях для герметизации и предохранения стекол от деформаций применяются эластичные прокладки или замазка и а базовых поверхностях оправ. Сами базовые поверхности должны иметь высокую степень плоскостности.
S)
Рис. 5.37. Крепление защитных стекол
Рис. 5.38. Крепление линейных шкал
КРЕПЛЕНИЕ ЛИНЕЙНЫХ ШКАЛ
Важными требованиями при разработке конструкций узлов крест-ления шкал точных измерительных приборов являются: недопустимость деформаций шкал и возможность их юстировки посредством смещений и поворотов. Поэтому, как правило, шкалы закрепляются с точным соблюдением принципа статической определенности (шесть опорных точек) и с силовым замыканием под действием усилий пружин. Подвижные опоры для юстировки выполняются в виде юстировочных винтов.
На рис. 5.38, а, б приведены две конструкции крепления таких шкал. Концы опорных винтов и неподвижные опоры должны иметь высокую твердость, правильную форму и малую шероховатость. После юстировки винты стопорятся (обычно клеем или краской).
Литература: [2, 30, 31, 37, 38, 73).
ГЛАВА 6
ТИПОВЫЕ конструкции
ОПТИКО-МЕХАНИЧЕСКИХ УЗЛОВ
Узлы крепления защитных стекол
На рис. 6.1 изображена головка визира, снабженная стеклоочистителем и устройством для обогрева защитного стекла. Обогревательная токопроводящая пленка нанесена на внутренней поверхности стекла. Для подвода питания по краям стекла нанесен распылением слой инвара, к которому припаяны металлические шайбы. К этим шайбам винтами крепятся провода.
Головка визира (рис. 6.2) закрыта сферическим защитным стеклом, рассчитанным на работу в воде с большим давлением. Герметизация соединения достигается за счет установки прокладок.
Рис. 6.1. Защитное стекло со стеклоочистителем и обогревательным устройством Рис. 6.2. Головка визира
Системы визирования
В паиорамических приборах для визирования по вертикали и горизонтали применяются призмы и плоские зеркала. В качестве визирных призм используются прямоугольные призмы и призмы-кубы. Визирование по горизонтали в приборах обычно связано с вращением изображения. Для стабилизации изображения используют вращающиеся призмы Дове или Пехана.
На рис. 6.3 приведен узел вертикального обзора бинокулярного визира. Качающийся призменный мостик установлен своими цапфами
в подшипниках корпуса прибора. Две прямоугольные призмы в оправах крепятся к мостику на юстировочных винтах, служащих для согласования визирных осей. На мостике установлен зубчатый сектор для связи с механизмом наведения.
Рнс. 6.3. Качающийся призменный мостик
Узел визирной призмы (рис. 6.4) снабжен лимбом для отсчета углов визирования с точностью до г . Лимб установлен на трех центрирующих винтах. Для точной центрировки лимба на его поверхности одновременно с гравировкой делений наносят круговую риску, центр которой точно совпадает с центром делений. Для исключения эксцентриситета шкалы при сборке производится центрировка лимба по кольцевой риске относительно оси вращения оправы.
Рнс. 6.4. Визирная призма с лимбом
Механизм вертикального наведения визира (рис. 6.5) состоит из призмы-куба 1 в оправе 2, установленной на юстировочных винтах в качающейся оправе 3. Оправа 3 вращается в шарикоподшипниках, закрепленных в кронштейнах на основании 5. Для исключения отклонения плоскости движения визирного луча от вертикальной плоскости ось качания призмы должна быть параллельна опорной плоскости основания. Качание призмы производится системой шток—рейка— зубчатый венец, причем в качестве рейки используется червяк. Червяк 6 имеет лыску и фиксируется от поворота шпонкой 7} закрепленной во 306
втулке 5, которая может поворачиваться, благодаря чему достигается точная установка визирного луча без осевого смещения червяка. Мерт-
вый ход в кинематической цепи выбирается винтовой пружиной 4.
Панорамная головка (рис. 6.6) состоит из узла качающейся призмы и механизма наведения, который позволяет производить визирование в двух взаимно перпендикулярных плоскостях. Горизонтальное наведение осуществляется вращением червячного колеса 8, на котором установлен кронштейн 9, несущий призму 3. Вертикальное наведение происходит при вращении червячного колеса 7, установленного на шарикоподшипниках н имеющего втулку с внутренней резьбой. Ходовой
Рис. 6.6. Панорамная головка с качающейся визирной призмой: 307
Рнс. 6.5. Механизм вертикального наведения
винт 5 имеет выступ, на которым опирается зубчатая рейка 2, сцепленная с сектором 1 качающейся призмы. При вращении колеса 7 винт 5, вращение которого ограничено шпонкой 4, будет двигаться по направляющей колонке 6, перемещая при этом рейку 2, которая в свою очередь будет качать оправу с призмой. При вращение колеса 8 рейка 2 будет скользить опорным торцом по плоскости выступа винта 5 и не будет перемещаться в вертикальном направлении.
Рис. 6.7. Панорамная головка с качающимся зеркалом
На рис. 6.7 изображена головка прибора с качающимся зеркалом. Применение зеркала возможно только при малых углах визирования в плоскости, перпендикулярной плоскости зеркала. При больших углах качания габариты зеркала недопустимо увеличиваются. Горизонтальное наведение осуществляется поворотом несущего кронштейна /, установленного на червячном колесе 9. Вертикальное наведение производится качанием оправы 3 с зеркалом при помощи зубчатого сектора 4 и рейки 2. Перемещение рейки осуществляется сухарем 5, свободно сидящим вместе с оправой 6 па хвостовике винта 7. Винт имеет только осевое перемещение при вращении приводного колеса 8.
Компенсация поворота изображения, как указывалось выше, производится вращающимися призмами. На рис. 6.8 приведена конструкция >зла с призмой Дове.
Рис. 6.8. Окулярная
часть панорамного визира
Рис. 6,9. Визирная головка с дистанционным приводом
Схема устройства дистанционного наведения визира показана на рис. 6.9. Устройство состоит из головной призмы и системы следящего электропривода. Исполнительным элементом является маломощный управляемый электродвигатель; обратная связь осуществляется с помощью двух вращающихся трансформаторов (ВТ) — грубого и точного отсчета. Наличие двух элементов обратной связи объясняется
Рис. 6,10. Оптический шарнир
их невысокой точностью по сравнению с необходимой точностью визирования. Редуктор механизма состоит из цилиндрических прямозубых зубчатых колес. Для выборки мертвого хода в цени призма—ВТ точного отсчета применены разрезные зубчатые колеса z.> и г4. Соединительная муфта также выполнена безлюфтовой.
В качестве датчиков обратной связи можно применять потенциометры, сельсины и другие элементы, обеспечивающие необходимую точность.
Конструкция оптического шарнира приведена на рис. 6.10. На основании 4 закреплена пружиной прямоугольная призма 5. В отверстиях основания установлены две одинаковые призменные головки, состоящие из корпуса о в котором установлена прямоугольная призма 2, закрепленная пружиной 1. Усилие прижима регулируется эксцентри-310
ком 6. 11л корпусах головок установлены зубчатые секторы 7, сцепленные между собой В начальном положении все три призмы должны лежать в одной плоскости. Угловая ошибка зубчатой передачи вызовет такой же величины наклон изображения.
Объективы телескопических приборов
Телескопические приборы (визиры, зрительные трубы и т. п. имеют, как правило, двухлипзовые объективы. В бинокулярных при
борах (бинокль, стереотруба) одним из основных условий работы является параллельность визирных осей обеих труб. Крепление одного из объективов такой системы в эксцентриковой оправе дает возможность устранить непараллельность осей, т. е. компенсировать ошибки изготовления деталей и погрешности сборки.
В некоторых прицельных приборах эксцентриковые оправы объективов предназначены для совмещения визирной оси системы с геометрической осью трубы прицела.
На рис. 6.11 приведены
Рис. 6.11. Объективы в эксцентриковых оправах
два типа эксцентриковых креплений. Объектив укрепляется в эксцентриковой оправе заваль цов коп или резьбовым кольцом. Вращением оправы и втулки объектива самым изменять эксцентриковая кольцом.
относительно эксцентриковой втулки относительно корпуса можно смещать оптический центр в плоскости, перпендикулярной оси трубы, и тем положение визирной оси системы. После юстировки оправа жестко закрепляется в корпусе зажимным
Рис. 6.12. Устройства для фокусировки объективов
Для устранения отклонений от расчетных вершинных отрезков линз используют продольное перемещение объектива для совмещения плоское in изображения объектива с плоскостью сетки. Для этой цели применяются различные компенсаторы: установка оправы объектива из резьбе (рис. 6.12, я), подрезка оправы (рнс. 6.12,6) и установка проклздьых колец (рис. 6.12, в); подбором толщины и подрезкой про-
Рис. 6.13. Объектив с регулировкой фокусного расстояния
хладных колец производится фокусировка. Фокусные расстояния линз выдерживают при изготовлении с точностью ±2%, поэтому в тех случаях, когда фокусное расстояние объектива должно точно соответствовать расчету (или когда у двух объективов фокусные расстояния должны быть равны между собой, например, у дальномера), применяются несклеенные объективы с регулируемым воздушным промежутком, изменением которого достигают требуемой величины фокусного расстоя в и я. К он стр у кция,
показанная на рис. 6.13, состоит из корпуса,в котором на направляющих шпонках установлены оправы с линзами. Между оправами имеется распорное кольцо, на-распорного кольца изменяют
воздушный промежуток между линзами. Обе оправы закрепляются в корпусе резьбовыми кольцами. Вращение распорного и резьбовых колец производится через окна в корпусе; для этой же цели на кольцах имеются отверстия.
винченное на одну из них. Вращением
Зеркально-линзовые объективы
Зеркально-линзовые объективы применяются, когда нужно получить небольшую длину системы при большом фокусном расстоянии объектива, апохроматическую коррекцию при большом относительном
Рис. 6.14. Зеркально-линзовые объективы
отверстии и т. д. Эти объективы чрезвычайно чувствительны к точности центрировки и усилию зажима зеркал. Поэтому в конструкции должны быть предусмотрены центрировка зеркал в оправах методом автоколлимации и регулировка усилия зажима зеркал.
На рис. 6.14, а приведена конструкция зеркально-линзового объектива, состоящего из мениска с отражающей поверхностью малого диаметра на его первой поверхности и зеркала Манжена. Каждая оптическая деталь крепится и центрируется в своей справе, а затем вставляемся в тубус. На наружную поверхность оправ наклеивается слой пробки, служащей упругим элементом для выборки радиального 312
зазора между оправами и тубусом. От смещения в оправах зеркала удерживают пробками из фосфатцемента.
Зеркально-линзовый объектив, изображенный на рис. 6.14, б, имеет более сложную конструкцию. Крепление зеркал за ободок отверстия уменьшает их деформацию от усилия зажима. Малое зеркало объектива имеет температурный компенсатор, который дает возможность сохранить положение фокальной плоскости при колебаниях температуры; он состоит из алюминиевой шайбы, установленной между оправами зеркала и первой линзы.
Фото- и кинообъективы
Фото- и кинообъективы можно разделить на следующие группы: сменные объективы для фотокамер с дальномером; сменные объективы для зеркальных фотокамер и кинокамер; жестко встроенные объективы; объективы с переменным фокусным расстоянием. Основной особенностью этих объективов является высокое качество изображения Объективы первых двух групп должны обеспечивать возможность быстрой установки в камеру с необходимой точностью (0,01—0,02 мм в осевом направлении) без юстировки. Для присоединения объективов в камере используются резьбовое и байонетное соединения.
Объективы первой группы состоят из собственно объектива, включающего оптические узлы, корпуса, механизма диафрагмы, механизма фокусировки и механизма привода дальномера (объективы второй группы отличаются от объективов первой только отсутствием последнего механизма). Связь перемещения объектива с воспринимающим рычагом дальномера камеры осуществляется дальномерным кольцом, жестко связанным с оправой оптического блока. При использовании объективов с фокусным расстоянием, отличным от основного для данной! камеры, дальномерное кольцо связывается с оптическим блоком посредством специального механизма (дифференциальной резьбы).
На рис. 6.15 приведены объективы различных конструкций. Объектив (рис. 6.15, а) имеет телескопический убирающийся тубус 3 с байонетной фиксацией в рабочем положении. Оправы с линзами 1 и 6 установлены на резьбе в оправе 2, которая в свою очередь крепится резьбовым кольцом 5 во втулке 3. Подрезкой прокладного кольца 4 выдерживают рабочий отрезок (расстояние от базового торца оправы до задней фокальной плоскости) объектива при сборке. Фокусировка производится перемещением кольца 7 по резьбе кольца 8. Поводок кольца 7 имеет фиксацию в положении «бесконечность». Связь с дальномером камеры осуществляется торцом кольца 7.
Объектив, показанный на рис. 6.15, б, состоит из оптического блока 2 с механизмом диафрагмы, дистанционного кольца 7, дальномерного кольца 4 и корпуса 3. Все эти узлы связаны между собой механизмом дифференциальной резьбы. Принцип действия этого механизма состоит в следующем (рис. 6.16). При вращении кольца 7, имеющего внешнюю правую резьбу Ml с шагом Р^ происходит его перемещен к е в осевом направлении относительно неподвижного корил са 2. В случае, если резьба М2 имеет шаг Р.2, отличный от шага то кольцо 3 начнет перемещаться с шагом, равным разности шагов Рх и Р2.
Если же резьба М2 имеет другое направление (левая реьба), то перемещение кольца 3 будет равно сумме шагов и Р2, Если кольцо 3 связано с кольцом 7 резьбой М2 того же шага и направления, то его перемещения ге произойдет. Подбирая соотношение шагов резьб и их направление, можно получить различные линейные перемещения л пух
Рис. 6.15. Конструкции фотообъективов
Рис. 6.16. Схема дифференциальной резьбы
деталей (например, оптического блока и дальномерного кольца, (рис. 6.15, б) при вращении одной из них, связанной с дистанционной шкалой. В конструкциях фотообъективов без дальномерного кольца и в кинообъективах фокусировка может производиться или перемещением оптического блока относительно корпуса объекива, или фоку-сировочпым кольцом съемочной камеры (рис. 6.15, в). Объектив, изображенный на рис. 6.17, имеет насыпную конструкцию (все линзы завал ьцоваиы в оправах
одного диаметра). Фоку-сиройка производится перемещением оправы оптического блока по резьбе корпуса.
На рис. 6.18 приведена конструкция объектива, вмонтированного в центральный фотозатвор. Здесь центрировка переднего и заднего компонентов осуществляется через детали фотозатвора, поэтому качество изображения, даваемого таким объективом, ниже, чем у объективов, имеющих общий корпус.
Особую группу составляют объективы с переменным фокусным расстоянием. Оптическая система таких объективов обычно состоит
Рис. 6.17. Фотообъектив насыпной конструкции
Рис. 6.18. Центральный фотозатвор с объективом
из основного объектива и телескопической насадки с переменным увеличением. Изменение увеличения достигается осевым перемещением отдельных компонентов насадки. Перемещение различных компонентов происходит одновременно и по различным законам. Для перемещения применяются вращающиеся оправы со спиральными пазами. Основную трудное 1Ь их изготовления составляют выдерживание точности пазов и получение минимальных люфтов в сопряжениях.
Ми крообъекти в ы
Конструкции микрообъективов разнообразны и зависят от назначения объектива. Крепление к тубусу микроскопа производится при помощи специальной объективной резьбы, профиль и размеры которой приведены в табл. 6.1. Для крепления объективов, имеющих большой диаметр, применяется резьба М27Х0,75. Размеры сопряжения микрообъективов с тубусом приведены в табл. 6.2.
Таблица 6.1. Резьба для объективов микроскопов (по ГОСТ 3469—74). Все размеры даны в мм
Р
Наружный диаметр резьбы Средний диаметр резьбы Внутренний диаметр резьбы Шаг резьбы Гл у- ’ бина резьбы Рабочая высота витка Зазор по профилю
d D d 2 О, Р н2 Hi г
Болт 20.270 Гай-ка 20,320 Болт 19,818 Гайка 19,868 Болт 19,366 Гайка 19,416 <0,705 0,452 0,428 0,05
Обозначение резьбы: ОБ 4/5" X 1/36" ГОСТ 3469 — 74.
При сборке микрообъективов производятся их центрировка и подрезка базового торца, причем размер от базового торца до плоскости предмета должен быть одинаков для всех объективов, применяемых для определения типа микроскопа (за исключением иммерсионных объективов. у которых этот размер во избежание повреждения объекта делается на 0,2—0,3 мм меньше).
На рис. 6.19 изображен простейший объектив ахромат 8X0.20. Линзы в оправах установлены в общий корпус и закреплены резьбовым кольцом. В конструкции, приведенной на рис. 6.20, для компенсации погрешностей изготовления деталей и сборки оправа второй линзы 316
посажена в корпус с радиальным зазором. Перемешенном 3'1 Ci! линзы в плоско-
сти, перпендикулярной оси
объектива, добиваются требуемого качества изображения. Такая система юстировки применяется во многих объективах микроскопов.
Эпиобъективы (рис. 6.21) используются для работы в отраженном свете. Конструктивно такой объектив состоит из микрообъектива и параболического зеркала, служащего для освещения п редмета н а клон н ы м н пучками (наблюдение в темное поле).
Объектив на рис. 6.22 снабжен ирисовой диафрагмой, предназначенной для изменения апертуры объектива. Управление диафрагмой осуществляется наружным кольцом.
Иммерисионнын объек-
тив 90X 1,25 (см. рис. 6.20) имеет устройство, предохраняющее от порчи препарат и фронтальную линзу объектива. При упоре оправы
Рис,. 6.19. .Микрообъектив ахромат ЪХ 0,2'0
Таблица 6.2. Сопряжение микрообъектива с тубусом (по ГОСТ 11200—75).
Все размеры даны в мм
Обозначение резьбы 1 * не более не менее
ОБ 4,5"Х 19 4,8 3
XI /36"
М27Х0.75 26 5,5 4
М42Х0.75 41 5,5 4
* Размеры для справок.
фронтальной линзы в покровное стекло внутренний корпус останавливается,сжимая имеющуюся в верхнем части
Рис. 6.21. Эпиобъектив ахромат 40X0,65, тубус 190 м?л
Рис. 6.20. Микрсобъектив ахромат 90Х 1,25 масляной иммерсии
оправы пружину. Так как оптическая система микрообъекгква рассчитана на работу с покровным стеклом, то отклонение толщины последнего (0,17 мм) от расчетной влияет на качество изображения, даваемого объективом, Для компенсации этих ошибок (в случае особо высоких требований к качеству изображения) применяются объ- Лм. t „ j —-
Рис. 6.22. Микрообъектив апохромат 60X1,0—0,7 с ирисовой диафрагмой
Рис. 6.23. Микрообъектив апохромат 40X0,95 с коррекционной оправой
оправой (рис. 6.23). При вращении коррекционного кольца в корпусе объектива происходит изменение воздушного промежутка между вторым и третьим компонентами, чем производится коррекция изменения аберраций.
На рис. 6.24, а—в приведены конструкции планапохроматов (ОПА-1, ОПА-3, ОПА-5), предназначенных для универсального биологического микроскопа.
Контактный объектив 10X0,40 (рис. 6.25) применяется для непосредственного исследования живой ткани в счете люминесценции. При работе на микроскопе первая поверхность фронтальной линзы приводится в соприкосновение с исследуемой поверхностью объекта.
На рис. 6.26 изображена типовая конструкция зеркалыю-линзовых безыммерснонных микрообъективов ,J5X0,65 (ОР-75ИК) и 40X0,70 318
Рис. 6.24. Микрообъективы планапохроматы
Рис. 6.25. Контактный микрообъектив плапахромат 10X0,40
Рис. 6.26. Безыммерсиовпый зеркально-линзовый объектив 75X0,65
(ОР-40), рассчитанных для области спектра от 0,580,до 5,5 мкм и применяемых в инфракрасных микроскопах [711. .
/7 тттзсть предмета
На рис. 6.27 дана конструкция зеркально-линзового объектива ОР—II с большим рабочим расстоянием (st = 40,6 мм), предназначенного для высокотемпературного микроскопа, а также микроспектрального локального анализа с помощью лазерного излучения |71].
На рис. 6.28 приведены типовые конструкции проек-
Рис. 6.27. Зеркально-линзовый объектив с большим рабочим расстоянием (ff ~ = 9,9 мм, А — 0,4, тубус сю)
ционных объективов «Корректар» ОФ-1 II и микропланаров ОП-15, ОП-16, ОП-17, предназначенных для макро- и микрофотографии на пластинку размером 12Х 18 см.
Рис. 6.28. Проекционные объективы: а — «Корректар»; б — микропланар
Окуляры
Для рассматривания изображения, создаваемого объективом» в оптических приборах используются окуляры. По оптическим схема' и конструктивным особенностям окуляры могут быть подразделены l 320
окуляры телескопических приборов и окуляры микроскопов. Для телескопических приборов применяются окуляры с внешней и внутренней фокусировкой. Особую группу составлю? автоколлимационные окуляры.
Для наблюдателя, страдающего близорукостью или дальнозоркостью, с целью резкого видения фокальная плоскость окуляра должна быть смещена в ту или другую сторону относительно плоскости изображения. Величина этого смещения, соответствующая аметропии глаза А/ дптр, определяется по формуле г == (V/^/1000 мм. Окуляры
Рис. 6.29. Конструкции окуляров с внешней фокусировкой и .мягким наглазником
обычно рассчитываются на смещение, соответствующее 4—5 дптр, в каждую сторону.
Конструкции окуляров с внешней фокусировкой приведены на рис. 6.29. Такие окуляры ввиду простоты конструкций являются наиболее распространенными. Фокусировка производится перемещением оправы с линзами окуляра по резьбе корпуса. Для получения малого угла поворота ведущего кольца (менее 360~ при наличии на ведущем кольце диоптрийной шкалы) при большом осевом перемещении и тонкостенных оправах применяется многоходовая окулярная резьба (табл. 6.3).
Кроме резьб, указанных в табл. 6.3, допускается применение одноходовой резьбы с шагом 1 мм для всех диаметров.
Недостатком таких окуляров является то, что при фокусировке происходит вращение наглазника, укрепленного на оправе. Это осложняет работу с прибором и затрудняет установку несимметричных наглазников. Для исключения указанны,х недостатков конструкция окуляра выполняется так, чтобы при вращении ведущего кольца происходило только линейное перемещение оправы линз с установленным Наглазником. С целью предохранения оправы линз окуляра от про-*Ьрачивапия применяются направляющие шпонки из:: i л ифты.
П В. Л. Ы И’н ь др 321
Т а б л и ц а 6.3. Окулярная резьба (по ГОСТ 5359—77)
Нс мн и ал ь-Nbiii диаметр с/, мм Шаг Р, мм Число заходов
1 2 4 6 8 16 12 16 20 24
Ряд 1 Ряд 2 Ход резьбы Pfa, мм :
10 1,5 1,5 3
12 1,5 3 6
14 1,5 3 6
'6 1,5 3 6 9
1,5 3 6 9 —
20 1,5 3 6 9 12 15
21 1,5 3 G 9 12 15
22 1,5 3 6 Q 12 15
23 1,5 3 (5 9 12 15
24 1,5 3 6 9 12 15
25 1,5 3 6 9 12 15
26 1,5 3 6 9 12 15
27 1,5 з 5 9 12 15
2« 4 _ 1,5 3 6 9 12 15
29 1,5 3 6 9 12 15
зО 1.5 3 6 9 12 15 24
31 1.5 з 6 9 12 15 18 24
32 1.5 3 6 9 12 15 18 24
33 1,5 з 6 9 12 15 18 24
34 1,5 з 6 9 12 1; / 18 24
35 1,5 3 6 9 12 15 18 24 1
Номинальный диаметр d, мм Шаг Р, мм Число заходов
1 2 4 6 8 10 12 16 20 24
Ряд 1 ряд 2 Ход резьбы Р^, мм
36 1,5 1,5 3 6 9 12 15 18 24
37 1,5 3 6 9 12 15 18 24
38 1,5 3 6 9 12 15 18 24
39 1,5 3 6 9 12 15 18 24
40 1,5 3 6 9 12 15 18 24
41 1,5 3 6 9 12 15 18 24
42 1,5 3 6 9 12 15 18 24
43 1,5 3 6 9 12 15 18 24
44 1,5 3 6 9 12 15 18 24
45 1,5 3 6 9 12 15 18 24
46 1,5 3 6 9 12 15 18 24
47 1,5 3 6 9 12 15 18 24
48 1,5 3 6 9 12 15 18 24
49 1,5 3 6 9 12 15 18 24
50 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 24 32 40 48
52 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 24 32 40 48
55 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 ’?4 32 40 48
58 1 1,5 1,5 | 3 6 9 12 15 | 1 18 24 30 36
АН 0X3
II*
Нсминаль* П Ь) Й ДИВ' метр д’, мм Шаг Р, мм Числе заходов
1 2 4 6 г 10 12 16 20 24
Ряд 1 Ряд 2 Ход резьбы Р^,мм
53 2 8 16 24 32 40 48
СО 1,5 1 5 1 ,о 3 6 9 12 15 18 24 30 Зь
2 8 16 24 32 40 48
С* 2 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 2-1 32 40 48
С 5 1,5 1,5 3 9 12 15 18 24 30 36
2 8 16 24 32 40 48
(8 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 24 32 40 48
70 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 24 32
72 1,5 1,5 3 6 9 12 15 18 24 30 36
2 8 16 24 32 40 48
75 1,5 1,5 3 6 9 1 2 15 18 24 30 36
2 8 16 24 32 40 48
7,ч 1.3 1,5 3 6 9 ! 9 1 ** 15 18 24 30 36
2
30 1.5 1,5 3 ь 9 12 15 18 24 30 36
О 4-г 8 16 24 32 40 48
И р и м е ч а л и е, Одноходовая окулярная резьба всех диаметров ?coj‘.t,7 быть изготовлена с шагом I мм
А-А
со to CJ-i
Рис. (
Окуляр со светозащитной шторкой
Крепление окуляров па приборе осуществляется с помешт.ю вн'н^дя (рис. 6.29, а) или резьбы (6.29, б).
На рис. 6,30 показан окуляр лупы сквозной наводки киносъемочной камеры. При вращении ведущего кольца оправа линз получает
Рис. 6,31. Конструкция окуляра с внутренней фокусировкой
а)
023,2f7
Рис. 6.32. Окуляры микроскопов: а — окуляр Гюйгенса 7х; б—измерительный окуляр Гюйгенса 7х; в— компенсационный скуля;) 15х
продольное перемещение. Для предохранения кинопленки or засветки па окуляр установлен несимметричный наглазник, более плотно прилегающий к голове, н имеется устройство, исключающее доступ света в камеру в то время, когда наблюдение в окуляр не производится. При'на-326
жнмена4наглазник 1 клин 2 входит в корпус 3 и, раздвигая лепестки 4, открывает доступ света к глазу наблюдателя. По прекращению наблю-
затруднен доступ к веду
Рис. 6.33. Окулярный тубус биологического микроскопа
дения детали механизма возвращаются в исходное положение и лепестки • шторки перекрывают световое отверстие. Описанные тины окуляров имеют существенные недостатки. При фокусировке окуляра вследствие его продольного перемещения происходит также смещение выходного зрачка прибора. При наличии налобника это вызывает несовпадение выходного зрачка прибора и зрачка глаза, что в случае малой величины выходного зрачка приводит к виньетированию и срезанию поля зрения. Кроме того, при установке налобника кольцу окуляра, а также герметизация окуляра. Указанных недостатков лишены окуляры с внутренней фокусировкой, которая осуществляется изменением воздушного промежутка между линзами окуляра. Глазная линза остается неподвижной, а перемещаются внутренние линзы окуляра. Пример подобной конструкции приведен на рис. 6.31. Глазная линза неподвижно закреплена в корпусе. При вращении маховика трубка, сцепленная с зубчатой рейкой, нарезанной на оправе подвижных линз окуляра, перемещает их в продольном направлении. Тем самым осуществляется диоптрийная наводка. Шкала диоптрий помещена на маховике. Герметичность достигается за счет установки сальника иа валу маховика.
Окуляры микроскопов изображены иа рис. 6.32, а—в. Конструкции
их просты и, как правило, не имеют устройств для фокусировки; исключение составляют лишь измерительные окуляры. Для установки окуляра служит окулярный тубус (рис. 6.33). В бинокулярных приборах для установки окуляров по базе глаз наблюдателя применяются различные механизмы. Вариантом такой конструкции является параллельная раздвижка труб прибора (бинокль, стереотруба). Наиболее распространена конструкция механизма с применением ромбических призм, в которой могут двигаться один или оба окуляра.
Системы смены увеличения
Изменение увеличения в оптических приборах может производиться: установкой перед объективом сменных телескопических насадок; сменными объективами или установкой объектива с переменным фокусным расстоянием; изменением увеличения оборачивающей системы (сменой линз или плавно); сменой окуляров.
Изменение увеличения с помощью телескопических насадок широко применяется как в кино- и фотоаппаратуре, так н в телескопических приборах. Насадки располагают перед объективом и изменяют его фокусное расстояние, не влияя на величину последнего отрезка. На садки ^также можно устанавливать раздельно или монтировать на поно-ротнои турели.
Конструкция узлов смены увеличения бинокулярного прибера с помощью установленных перед объективами трубок Галилея может давать три увеличения.
Изменение увеличения путем смены объективов широко применяется в кино- и фотоаппаратуре и в микроскопах. Сменные объективы метут крепиться при помощи резьбы или байонетного соединения. В тех
Рис. 6.34. Конструкция револьвера объективов микроскопа
случаях, когда требуется быстрая смена объективов с достаточной степенью точности, используются различные револьверные устройства. Для смены объективов телескопических приборов револьверные устройства применяются редко ввиду громоздкости конструкции. Наиболее широкое применение револьверные устройства нашли в микроскопия, где они используются для смены объективов и иногда для смены окуляров и конденсаторов.
Ряс. 6.35. Цснтрк-рл е мы й щипцовый держатель мнкро-гбисктнвов
На рпс. 6.34 показана конструкция револьвера объективов мн кро-скс-ка. Спорные торцы объективных гнезд револьвера должны устанавливаться на одной высоте с точностью до 0,01 мм; непсрпеиднкулярность торцов к оси не более 5'; децептрировна гнезд при переключении не б<ысе 0.02 мм. При данных допусках на точность работы револьвера, а так/ке допусках па точность центрировки микрообъективов относительно их крепежной резьбы н опорного торца, при переключении объек-
тиесв с меньшего увеличения на большее, изображение, находившееся в центре поля зрения объектива меньшего увеличения, не должно
выйти из поля зрения следующего объектива большего увеличения. Дл я бы -строй и точной с мен ы микрообъективов применяется также центрируемый щипцовый держатель (рис. 6.35) (в поляризационных микроскопах).
*На рис. 6.36 дана конструкция универсального видоискателя для фотоаппарата. Видоискатель имеет револьвер со сменными объективами, угловые поля которых равны угловым полям съемочных объективов. Для плавного изменения увеличения применяют пан критические системы. Схема подобной конструкции приведена на рис. 6.37. Каждая из линз 2 и 4 перемещается по определенному закону при вращении наружной трубки 3. имеющей пазы определенного профиля. Во внутренней трубке 1 сделаны продольные пазы, предохраняющие оправы с линзами от п роворота. Дл я упрощения
Рис. 6.36. Универсальный видоискатель с револьвером объективов
изготовления один из пазов выполняется по винтовой линии. Н едоста тко м п о доб -пой конструкции является невысокое качество изображения, даваемой системой, из-за ошибок
пазов и люфтов в сопряжениях.
изготовления спиральных
Рис. 6.37. Панкратическая оборачивающая система
Светофильтры
Сменные светофильтры, используемые в оптических приборах, могут быть насадными, вкладывающимися и встроенными. Насадные светофильтры применяются, как правило, в малогабаритных переносных
.4
4-4 Н
А
Рис. 6.38. Поляризационный светофильтр в оправе
А
Рис. 6.39. Мехл низсмены светофильтров
приборах (фотоаппараты, бинокли). Крепление светофильтров может производиться или на резьбе или с помощью пружинящих разрезных оправ (рис. 6.38). Светофильтры можно устанавливать перед объективом или за окуляром. Встроенные светофильтры можно устанавливать в любом месте оптической системы внутри прибора, кроме мест, близких 330
к плоскости изображения.-, Конструкции узлов смены светофильтров могут быть различными в зависимости от габаритов и места установки. Наиболее распространенной является установка светофильтров в дисках плоской пли сферической формы (рис. 6.39). В дальномерах часто применяется установка светофильтров в барабанах. На рис. 6.40 приведена конструкция механизма светофильтров, смонтированного в верхней части зрительной трубы. Для переключения светофильтров применен мальтийский механизм.
При повороте диска 2 один из п-альцев 3 входит в прорежь угольника /, привинченного к оправе 4 светофильтра, и пово-
Рис. 6.40. Механизм
смены светофильтров визира
рачивает оправу в положение, показанное пунктиром. Второй светофильтр в это время удерживается от поворота ободком диска 2. При повороте диска 2 в противоположную сторону правый светофильтр поднимается, а левый опускается и занимает горизонтальное положение. Для исключения дребезжания светофильтров при вибрации из-за люфтов в сопряжениях применены спиральные пружины. Управление механизмом производится при помощи гибкого тросика, закрепленного па .шкиве 5.
Механизм клинового компенсатора
Клпновоп компенсатор широко применяется в различных дальномерах. При вращении двух оптических клиньев в противоположные стороны с одинаковой скоростью происходит смещение луча в одной плоскости, причем это смещение находится в зависимости от характеристики клиньев и угла их взаимного разворота (см. гл. 4). На рис. 6.41 приведена конструкция клинового компенсатора дальномера. При вращении винта 2 перемещается каретка 1 синусного механизма, связанная с роликом 3 линейки, закрепленным на коническом колесе 4. Это- колесо сцеплено с двумя другими колесами 6 и 9, несущими
ахроматические клинья 7 и 8. Регулировка механизма производится изменением длины синусной линейки путем подвижки ролика 3 на винтах 5.
Рис. 6.41. Механизм клиновою компенсатора дальномера
Конденсоры и коллекторы микроскопов
Конденсоры микроскопов предназначены для освещения наблюдаемых объектов. Конденсоры могут иметь встроенную апертурную ирисовую диафрагму или напкратическую оптическую систему для изменения апертуры. На рнс. 6.42 показаны конструкции конденсоров со сферическими и параболическими линзами.
Рис. 6.42. Конструкции конденсоре в микроскопов: а — конденсор с апертурой К 2; б — конденсор с апертурой 1, 4 (с параболической линзой}
Рис. 6.43. Конструкция апла-иатического ахроматического коллектора микроскопа
Коллектором в микроскопе называется оптическая система, которая расположена непосредственно у источника света. Основное назначение коллектора — передать изображение источника света, как правило,
в увеличенном масштабе, в плоскость апертурной диафрагмы конденсора (проходящий свет) или в плоскость, сопряженную с выходным зрачком объектива микроскопа (отраженный свет). На рис. 6.43 приведена конструкция апланатического ахроматического коллектора с фокусным расстоянием f = 56 мм и числосей апертурой А = 0,5.
Выключающееся зеркало
Механизм (рис. 6.44) состоит из корпуса /, откидывающегося зеркала 2 в оправе и пружины 4. Для точной фиксации зеркала в рабочем положе-
Рис. 6.44. Механизм выключающегося
нии предусмотрен регулируемый упор 5. Смягчение удара при переброске оправы обеспечивается амортизаторами 3 и 6.
Крепление дифракционных решеток
Дифракционные ре--шеткн чрезвычайно чувствительны к деформациям. Точность установки плоскости решеток обычно выше, чем зеркал, ц, кроме того, необходимы точная установка и фиксация решетки по
зеркала
Рис. 6.45. Дифракционная решетка в юстируемой оправе
направлению штрихов. В стационарных приборах конструкции узле в дифракционных решеток снабжаются устройствами для регулировки положения с высокой точностью. В бортовых приборах применяются дифракционные решетки меньших размеров и точности. Поэтому юстировка при сборке производится в основном за счет прнпнливапия и прн-шабрнвания опорных поверхностей, что позволяет упростить констр^к-циюузла крепления, уменьшить ее габариты и повысить жесткость и
надежность крепления. На рис. 6.45 и 6.46 приведены конструкции узлов дифракционных решеток стационарных приборов, а на рис. 6.47 и 6.48 — дифракционные решетки в оправах, устанавливаемые в бортовых приборах.
Рис. 6.46. Плоская дифракционная решетка в оправе
Рис. 6.47. Дифракционная решетка в оправе с пружинным кольцом
Рис.6.48. Дифракционная решет ка в жесткой оправе
Модуляторы света
Для модуляции светового потока, попадающего па фотоэлектронные приемники, применяются различные модуляторы, работающие на отражение или пропускание света. На рис. 6.49 показаны типы стекляи-
Рис. 6.49. Модуляторы света р(,
ных н металлических модуляторов. Стеклянные модуляторы могут быть выполнены фотографическим способом или нанесением зеркального покрытия. Металлические модуляторы, работающие на отражение, изготовляются из высокоуглеродистон стали с отражающим покрытием, из нержавеющей стали пли алюминиевых сплавов. Отражающие поверх
ности доводятся до высокой степени чистоты (/??== с= 0,100л-0,050 мкм).
Осевые моду ляторы (рис. 6.50) устанавливают так, что их ось вращения совпадает с визирной осью оптической системы.
Требования к модуляторам могут быть раз
Рис. 6.50. Осевые полудисковые модуляторы
личными в к а ж д о м от
дельном случае. Основным является изменение светового потока по определен ному закону с з а -данной точностью, г.сэю-му необходимо равенство рабочих зон модулятора (отражающей и пронхекающей свет). Точность изготовления их зависит от допускаемого искажения формы, сигнала. Па рис. 6.51 приведена конструкция узла осевых модуляторов, которая дает возможность быстрой смены нх в процессе работы прибора. Узел установлен в фокальной плоскости объектива гиднрующего прибора. Требования к работе узл а он редел я юте я небольшим разх^ерох: изображения (0,03—0,1 мм) "и необходихюп точяоендо слежения. Радиальное биение кромки модуля-
Рис. 6.61. Механизм модуляторов
тора определяет мертвую зону и допускается в пределах до 0,01 мм. Точность смещения центров модуляторов при их емгпе (прямая ошибка слежения) 0,01—0,015 мм. Вследствие установки модулятора в плоскости изображения предъявляются высокие требования к качеству выполнения и чистоте обработки рабочих кромок (неровности и ширина их допускается до 0,005 мм)- Установка модуляторов иа насыпных шарикоподшипниках допустима только при небольших частотах вращения (300—400 об/мин). При больших частотах следует применять стандартные радиальные шарикопод-
шипники.
Вращение модуляторов производится от электродвигателей стабилизированной скорости.
Фокусировочные механизмы
Фокусировочные механизмы предназначены для получения резкого изображения объекта в микроскопах и контрольно-юстировочных устройствах.
В настоящее время в микроскопостроенин известно большое число различных схем и конструкций фокусировочных механизмов, часть 'из которых опубликована в литературе по микроскопии [61], 176}, остальные в патентах.
Рис. 6ЛЗ. Кривошипно-шатунный механизм тонкого перемещения
Рис. 6 52. Рычажно-винтовой механизм тонкого перемещения
Рис, 6.54. Клиповой механизм тонкого перемещения
Обычно, фокусировочные механизмы состоят из раздельно функционирующих механизмов для грубого п тонкого перемещения.
В качестве механизма грубого перемещения чаще всего используют зубчато-реечную передачу, состоящую из косозубой шестерни и рейки. Применение такой передачи обусловлено необходимостью получить плавное перемещение ведомого элемента механизма.
Плавность движения ведомых элементов фокусировочных механизмов является основным требованием, которое предъявляется к этим механизмам.
В качестве механизмов топкого перемещения используют самые различные механизмы. Чаще других применяют механизмы, схемы которых изображены па рисунках, приведенных ниже.
Jia рис. 6.521 изображена схема рычажно-винтового механизма тонкого перемещения, где вращением рукоятки 1 поступательно перемешают винт, который своим фланцем А поворачивает рычаг 2. Поворот рычага 2 вызывает поступательное движение каретки 3. Контакт каретки 3 с рычагом 2 и рычага с фланцем винта, осуществляемый парами Ьго класса (см. гл. 9, табл. 1) обеспечивается силовым замыканием с помощью пружины 4. Кинематические параметры рассматриваемого механизма таковы: шаг винта — 0,5 мм, отношение длин плеч коленча
1 111 рис. 6.52--6.5Т римскими цифрами ouojuaucnu кл ко>1 кикслити-ческик нар (см. гл. 9>.
того рычага Ц : /2 = 1:2. Рабочий диапазон перемещения каретки 3— 2 мм. Зя одни оборот рукоятки 1 каретка 3 перемещается в своих папрае* ляющнх па 0,25 мм. Для уменьшения мертвого .хода в механизме коле! -чатый рычаг 2 следует подвесить па упругом крестообразном шар it и ре (см. гл. II, рис. 11.34).
( В механизме, и юираженном на рис. 6.53, перемещением винта / поворачивают рычаг 2, малое плечо которого является кривошипом в кривошипно-шатунном механизме, состоящим из шагу на 3 и ползуна 4. Таким образом, поворот рычага 2 через шатун 3 преобразовывается в поступательное перемещение каретки (ползуна) 4. Кинематические параметры рассматриваемого механизма: отношение длин плеч рычага 2— li : l> ~ 1 : 4. За один оборот впита 1 каретка 4 перемещается на 0,2 мм. Рабочий диапазон перемещения каретки 4 составляет 2 мм. Контакт звеньев между собой обеспечивается силовым замыканием с помощью пружины 5.
В механизме, который приведен на рис. 6,54, вращение винта 1 вызывает поступательное перемещение клина 2 вдоль осп впита. Перемещение клина вызывает перемещение каретки 4. Контакт каретки 4 с клином 2 осуществляется силовым замыканием с помощью пружины 5. Для уменьшения трения и увеличения плавности движения каретки 4 контакт ее с клином осуществляется через ролик 3,
В качестве направляющих для кареток рассмотренных механизмов чаще всего используют направляющие тина «ласточкин хвост» или обычные шариковые направляющие замкнутого типа (см, гл. 11, табл. 1, поз. 5 и 10).
Из трех рассмотренных механизмов тонкого перемещения наиболее предпочтительным является механизм, изображенный на рис. 6.54. Конструкция его проще и технологичнее двух других механизмов.
Литература: [36, 56. 61, 74, 76, 77, 89 1.
ГЛАВА 7
ДИАФРАГМЫ, ЩЕЛИ, БЛЕНДЫ, НАГЛАЗНИКИ И НАЛОБНИКИ
ДИАФРАГМЫ
Диафрагмами в оптических приборах называются детали и устройства, предназначенные для ограничения диаметра пучка лучей, проходящих через оптическую систему. Так как оптические системы центрированные, то диафрагмы, как правило, имеют круглые отверстия.
Рис. 7.1. Ирисовая диафрлма фиюобьектива:
1 — ведущее кольцо: 2 — ссевий штифт; 3 — коронка; 4 — ведущий штифт; з — оправа
По оптическому действию следует различать диафрагмы, ограничивающие входящие в прибор пучки — апертурные диафрагмы и диафрагмы, ограничивающие линейное (или угловое) поле (кадровая рамка в кино- и фотоаппаратах, отверстия в оправах сеток визуальных приборов, диафрагмы в окулярах микроскопов) — полевые диафрагмы. Полевые диафрагмы, как правило, имеют неизменяемое отверстие, однако в микроскопах и некоторых других приборах применяются поле-238'
вые диафрагмы с изменяющимся отверстием. Не изменяются отверстия апертурных диафрагм, являющихся входными зрачками в телескопиче-
ских системах.
В микроскопах, фотоаппаратах и осветительных приборах почти
всегда должна быть предусмотрена возможность изменения диаметра отверстия апертурной диафрагмы для регулирования освещенности.
Для этой цели в простейших
Рнс. 7.2. Ирисовая диафрагма микроскопа
приборах применяются либо сменные, либо револьверные диафрагмы в виде диска с рядом отверстий. Обе эти диафрагмы неудобны в эксплуатации, так как не позволяют плавно изменять освещенность, а последние к тому же имеют большие габариты. Поэтому широкое применение получили ирисовые диафрагмы, плавно изменяющие в заданных пределах световое отверстие объектива или осветительной системы.
Ирисовая диафрагма состоит из набора тонких дугообразных пластинок (лепестков), кольцевой оправы и поворотного кольца (коронки). Лепестки имеют па концах штифты. Один штифт (осевой) каждого лепестка входит в отверстие кольцевой оправы,
Рнс. 7.3. Лепесток диафрагмы
другой (ведомый) — в соответствующий радиальный паз поворотного кольца. При повороте коронки все лепестки поворачиваются в оправе, изменяя диаметр отверстия диафрагмы. Ирисовые диафрагмы (рис. 7.1 и .7.2) различаются размерами предельных отверстий, наружной формой, наличием рукоятки или ведущего кольца и шкалой. Рукоятка обычно применяется в микроскопах, ведущее кольцо — в фотообъективах.
В табл. 7.1 приведены конструктивные размеры лепестков ирисовой диафрагмы в зависимости от пределов измерения диаметра светового отверстия диафрагмы и числа лепестков. Данные настоящей таблицы, так же как и приводимой ниже табл. 7.2 не применимы при конструировании ирисовых диафрагм специальной конструкции и назначения, (с лепестками особой формы, с пропорциональной шкалой и т. д.).
.....размеры лепестков выбирают по рис. 7.3 и табл. 7.1.
Таблица 7.1. конструктивные размеры в мм и число лепестков ирисовых диафрагм
Ди отегр светового отверстия /< h Яэ d 3 fl Число лепесг-ков
На it-больший Нацмен ыиий Номинальный Предельное отклонен ие Номинальный 1 I Предельное отклонение | 1 Номинальный Предельное отклонение Номи-н а л ы i ы г) Предельное отклонение I i о м; ’ -ПИЛЬНЫЙ Предельное отклонение Ном Ti- ll альпый Предельное отклонение
8 10 1 i) 1 14 16 18 20 0,6 07 0.8 0.9 1,0 12? 4 5 t) 7 8 ft 10 ±0.1 2 2,5 3 —0,25 5 6,25 7,5 8,75 + 0,1 О ЬО -м О СП СЛ СЛ + 0,1 0.6 4-0,004 0,08 —0,01 1 10
0.8 + 0,045 1,5
3,5 -0.3
4 11 12 13,5 15 17 19 21,5 24 26 ±0,15 11,5 12,5 14 15,5 18 20 22,5 25,5 27,5 ±0,15 12
оо 23 28 32 36 40 44 1Л 1.6 1.8 2.0 2.2 2,5 2,8 11 12,5 14 16 18 20 2е ±0,15 5 1,0 +0,06 2
6
14
7 —0,3b 2,5
8 0,1 —0,015
Продолжение табл. 7Л
Диаметр светового отверстия Ki Я Я, АД d S Ь4 у
П ни-больший Н а и -МРНЫШ'Й Поминали ный .’.ре дельное отклонение Ц (ЧНЧГЬ’Л -ИИЮ Pi i Предельное отклонение Н ом и -мальмы it ан напои-и -ко ООН -qu-oVoilLl Номинальный Нредель-i ное от-i клонение | Номинальный Прсдель-| ное отклонение J 1оми - > 1 Й 71Ь11 bi Й j Предель-1 ное от~ S клонение Ч fl в I Число ле; 1 ков
48 3.0 24 28.5 ±0,15 30 1,0 14
52 3,5 26 ±0,15 9 --0,36 30,5 32
56 60 4,0 4.5 28 30 10 33 35 35 37 0 1
65 5,0 32,5 38 40,5 16
70 5,5 35 1 ? 1 1 40,5 ±0.2 43 ±0,2 + 0,06 —0,015 3
75 6.0 37,5 43 5 46.5 1,2
80 6,5 40 ±0.2 1± —0.43 46 49 0,12
pt 42 7.0 7,5 43 46 13 49,5 52.5 53 56 !3
106 8,0 50 14 1— р/ 61 ИЧ—М *** МММ . — ~—
Примечания- 1. При бол ьших от ношениях диаметра светового отверстия в случае полного откры; ня днсДрш к наименьшему диаметру сееТивою отверстия упаянный в таблице размер 5 рекомендуется уменьшать примерно на 1 --г Допускается уменьшение число лепе.тьов ^до пяти) с соответствующим увеличение»! их ширины.
Со
Co л. ю
Т а бл п и а 7 2. Основные конструктивные размеры коронок и оправ диафрагм
Размеры, мм Коли* честно пазов
D. Ь 1 V d
Номинал ь-н ы и Предельное отклонение Номи-н аль-ный Предельное отклонение Номи-наль-н ы й Предельное отклонение Номи-н альиый Предельное отклонение Номинальный Предельное отклонение Номинал fa- il ы й Предельное отклонение
8 10 12 14 16 18 20 25 28 32 36 40 j 48 + 0,2 сл сл сл СЛ СП Ст с го ьо ьо to tc . . . ю С J СП СП Сп СП СЛ О ’ С1 С * СТ СП СП СП + 0,25 36' 36° 36е ' 36е 36е 30" 30й 30е 30" 30° 25° 43' 25" 43' 25' 43' 25° 43' ±30' 10 12,5 15 17,5 19,5 22 24 27 30 34 38 43 48 57 ±0,10 1 1 1,2 1.2 1,2 1,2 1,5 1,5 1,6 1,5 1,5 1,5 1,5 1,5 + 0.12 10
±0,16
+ 0,24
12
4 0,28
± 25' ±0,20
+ 0,34 14
Продолжение табл. 7.2
Размеры, мм Количество пазов
Di Ъ. t Y d
Номи -наль-ный Предельное отклонение Коми -наль-ный Предельное отклонение Номи -на льны Ц Предельное отклонение Номинальный Предельное отклонение Номинальный Предельное отклонение Номи -на льны й Предельное отклонение
52 56 60 65 70 **» /о 80 86 92 100 + 0,4 1,5 2 2 2 2 2 2 2 2 2 +0,25 юооооосоооооооооооо <4 г- е, +0,25 25е 43" 22° 30' 22° 30' 22е 30' 22° 30' 22° 30' 20° 20е 20° 20° ±25' 61 66 70 76 81 87 92 99 105 114 ±0,20 1,5 2 2 2 2 2 2 2 2 2 +0,12 14
16
±20' ±0,25
18
+ 0,46
Примечание. Размер t приведен для коронок с глухими пазами. Для коронок со сквозными пазами он может быть уменьшен до 1/2 от указанного в таблице.
В табл. 7.2 приводятся конструктивные размеры оправ и коронок ирисовых диафрагм. Их основные размеры следует устанавливать но табл. 7.2 и рис. 7.4, а остальные размеры — по конструктивным соображениям. Размер D должен быть не менее 2 (R + В) (см. табл. 7.2 и рис. 7.3).
Размеры штифтов выбирают в соответствии с рис. 7.5 и табл. 7.3.
Лепестки изготовляют нз стальной ленты по ГОСТ 21996—+76,; ГОСТ 21997—76 или ГОСТ 503—71. Допускается изготовление из
ленты сплава АМг по ГОСТ 4784—74. Штифты делают из латунной проволоки марки Л62 по ГОСТ 1066—75. Оправы и коронки могут изготовляться из сплавов АЛ2, АМг2 или нз сплава Д16АТ.
Рис. 7.4. Типы коронок
Рнс. 7.5. Штифт диафрагмы
Установлены следующие допуски на диаметр отверстия диафрагм микроскопов: для полевых диафрагм до 5%; для апертурных— до 8%. Для диафрагм фотоаппаратуры допускается отклонение по седьмому классу точности.
Лепестки диафрагм должны окрашиваться в черный цвет.
При необходимости конструирования диафрагм, имеющих диаметр светового отверстия более 100 мм иля диафрагм специальной конструкции следует произвести расчет по приводимой ниже методике.
Г а б л и ц а 7.3. Размеры штифтов для лепестков диафраш
Размеры, мм
Дли диафрагм с наибольшим thlTOBMM диа- метром D d L
Номинальный Предельное отклонение Номинальный Предельное отклонение Н ом и -пальмы и Предельное отклонение
8—10 12—20 •'2 F2 50—100 1,0 1,2 1,5 2,0 —0,06 —0,12 0,6 0,8 1,0 1,2 —0,04 —0,045 1,2 1,5 1,5 1,8 —0,25
Расчет ирисовых диафрагм
Исходными данными для расчета являются диаметры наибольшего и наименьшего световых отверстий диафрагмы 2р, а также предельная наибольшая толщина ее по осн.
Прн расчете определяют (рис. 7.4 и 7.6): внутренний и наружный радиусы кривизны лепестка гвн и гн; толщину лепестка s; радиус окруж-
Рис. 7.6. Схема к расчету ирисовой диафрагмы
пости, по которой расположены отверстия под штифты г; угол между штифтами лепестка у; минимальное число лепестков п\ толщину диафрагмы по оси Т; шкалу углов поворота коронки (J в зависимости от диаметра отверстия диафрагмы.
Внутренний радиус лепестка равен радиусу наибольшего светового отверстия диафрагмы. Расстояние между штифтами лепестка должно быть ОУО2 т + гвн (рис. 7.6, а), в противном случае при некотором угле поворота коронки штифт выйдет из паза.
Радиус окружности расположения отверстий под штифты определяется по формуле
' = Т + V7гви - 3pmln (2,вн - Рт1п)].
Наружный радиус лепестка гн берется равным 2г — гвн. Угол между штифтами лепестка находится из треугольника ОО2О1 по формулам: sin Л- = Y = 2 arcsin --^ Гвн .
Радиус закругления края лепестка г1 = г — гвн.
Для компенсации допусков отверстие под ведомый штифт в лепестке смещают на 0,5—1 мм.
Минимальное число лепестков и определяют исходя из наименьшего необходимого перекрытия одного лепестка другим при наименьшем отверстии диафрагмы (рис. 7.6, б):
„360. ft
rt — —- , Е — pj — Ра. 8
Из треугольника А00' имеем
cos Рз — (гвн pmin)/(2г ви).
Из треугольника Д]О(У получаем
—р • V—г^
□ ~\вн ГПИП/ н
COS Pi —----5-------------г---.
2гвн (гвн pmin)
Полученное значение п округляют в сторону увеличения до ближайшего целого числа.
Наибольшая толщина Т диафрагмы (по лепесткам): Т = sny/360, где s == 0,05—0,1 мм.
На ведущем кольце наносится шкала диафрагмы.
Зависимость светового отверстия диафрагмы от угла поворота 0 ведущего кольца (коронки) находится из треугольника ОгОО' (рнс. 7.6, в)
Р = 'вн — У = гвп — 2г sin -2-,
л . a rBB p
Отсюда sin-jy- =—, где a — угол поворота лепестка.
Приближенно p — 2a, тогда sin ~ •
Более точные формулы для Р, получаемые из треугольника 00 VA,
cos a — &tgy\ .
г . / Y ,
------sin (4
a \ 2
a — + 2 arcsin-^-r—- ; а — г —гвн; k ~
Погрешности светового диаметра диафрагмы при ближенной формуле не превышают 4%.
Щелевые диафрагмы
Щелевые регулируемые диафрагмы применяются тельно в лабораторных приборах (спектроскопах, монохроматорах).
расчете по при-
почти ИСКЛЮЧИ-спектрографах,
Конструкция щелевой диафрагмы (рис. 7.7, а) позволяет изменять ширину щели с точностью до 0,01 мм.
Ножи диафрагмы /, имеющие форму клиньев, движутся в направляющих 2, расположенных под углом, благодаря чему можно изменять ширину щели. Ножи прижимаются к направляющим пружинами 3 и 4. Для передвижения ножей служит микрометрический винт 5 с от-чи -
диаф-
Рис. 7.7. Щелевая рагма:
1 — ножи; 2 — направляющие;
3, 4 — пружины; 5 — микрометрический винт; 6 — шкала
счетной шкалой 6. Цена деления шкалы 0,01 мм. Обратное движение ножам дает пружина 3.
На рис. 7.7, б показана схема диафрагмы типа «кошачий глаз». Перемещение ножей 1 в оправе 2 должно происходить симметрично. При изменении диагонали а площадь отверстия диафрагмы изменяется пропорционально а2. Кромки ножей должны лежать в одной плоскости.
НАГЛАЗНИКИ И НАЛОБНИКИ
Наглазником называется деталь окуляра, облегчающая совмещение и фиксацию зрачка глаза с выходным зрачком оптического прибора. Одновременно наглазники выполняют и другие функции: защищают глаз наблюдателя от попадания посторонних лучей, от ветра и дождя, от ушибов при толчках во время наблюдения.
Различают жесткие и мягкие наглазники. Жесткие наглазники изготовляют из пластмассы, мягкие — из резины.
Наглазники из пластмассы применяют в лабораторных приборах, биноклях, астрономических и геодезических приборах, не испытывающих толчков и ударов во время их использования.
<----
Наглазники из пластмассы изготавливаются трех типов:
Тип I — симметричный, отбортованный с внутренней резьбой диаметрами 12—33 мм.
Рис. 7.9. Мягкие наглазники
Таблица 7.4. Типы и основные размеры наглазников из пластмассы, мм
Тип rfo D Di Dz н н. н2 R . ..... (Л, .... Ri ' ; * $
М12Х0.75-7Н 22 16 9 9,0 12,0
М14ХО.75-7Н 18 10 8 3 1,5 °’5—0,1 •
М16Х0.75-7Н 26 20 12 12,5 14,5
М18Х0.75-7Н 22 14 11,0 14,0
1 М20Х0.75-7Н 30 24 16 12,0 15,5
М22Х 0.75-7Н 26 18 11 - 4' ? 11,0 15,0 2,0 *
М24ХО.75-7Н 29 20 14,0 18,0
М27Х0.75-7Н 34 32 22 13,5 17,0 1’°—0,25
МЗОХ 0,75-7Н 35 24 15,5 20,0
МЗЗХ 0.75-7Н 40 38 26 15 5 15,0 20,0 2,5 -
М18Х0.75-7Н 24 18,2 12 11,0 °’5—0,1
11 М22-Х0.75-7Н 26 22,2 14 7 3,5 1 12,5
М25хО,75-Н 34 25,2 19,5 9 1 17,5 " 1 0,2
М27Х0.75-7Н 34 27,2 19,5 - 17,5
III СПМ31Х0.75 кл. 3 СПМ32Х0.75 кл. 3 38 1 14 17 ——” — 25 32 — —
Тип Н — симметричный, цилиндрический с внутренней резьбой диаметрами 18—27 мм.
Тип 111 — несимметричный, с внутренней резьбой диаметрами 31 и 32 мм.
Для изготовления наглазников
।
из пластмассы следует применять
фенопласт марки 03-010-02 ГОСТ 5689—73* черного цвета. Изготовление наглазников нз полистирола или из полиэтилена допустимо при
Наглазники из пластмассы применяют в лабораторных приборах, биноклях, астрономических и геодезических приборах, не испытывающих толчков и ударов во время их использования.
Рис. 7.8. Наглазники
из пластмассы
Наглазники из пластмассы изготавливаются трех типов:
Тип I — симметричный, отбортованный с внутренней резьбой диаметрами 12—33 мм.
Тип II — симметричный, цилиндрический с внутренней резьбой диаметрами 18—27 мм.
Тип 111 — несимметричный, с внутренней резьбой диаметрами 31 и 32 мм.
Для изготовления наглазников из пластмассы следует применять
фенопласт марки 03-010-02 ГОСТ 5689—73* черного цвета. Изготовле-
ние наглазников из полистирола или из полиэтилена допустимо 'при
Таблица 7.4. Типы и основные размеры наглазников из пластмассы, мм
Тип rfo D Di н Hi R Ri $
М12Х0,75-7Н 22 16 9 9,0 12,0
М14ХО.75-7Н 18 10 8 3 1,5
М16Х0.75-7Н М18Х0.75-7Н 26 20 22 12 14 12,5 11,0 14,5 14,0
1 М20Х 0.75-7Н М22Х 0.75-7Н 30 24 26 16 18 11 - 4 ? — 12,0 11,0 15,5 15,0 2,0
М24Х0.75-7Н М27Х 0.75-7Н 34 29 32 20 22 14,0 13,5 18,0 17,0 1’°—0,25
МЗОХ 0,75-7Н л п 35 24 с 15,5 20,0 2,5
МЗЗХ 0.75-7Н 38 26 10 0 15,0 20,0
М18Х0.75-7Н 24 18,2 12 11,0 °’5—0,1
11 М22-Х0.75-7Н 26 22,2 14 7 3,5 1 12,5 0,2
М25ХО.75-Н М27Х0.75-7Н 34 34 25,2 27,2 19,5 19,5 9 1 17,5 17,5
III СПМ31Х0.75 кл. 3 СПМ32Х0.75 кл. 3 38 14 17 — 25 32 — —*
Рис. 7.10. Упругие наглазники
Рис. 7.11. Составные мягкие наглазники:
/ — кольцо аз губчатой резаны; 2 — обтяжка нз кожи
условии удовлетворения их эксплуатационных свойств тактике-техническим требованиям на прибор.
Наглазник следует располагать так, чтобы выходной зрачок совладал с наружным срезом наглазника. Для наблюдения в очках пли противогазе выходной зрачок должен быть вынесен на 6—8 aim.
Рис. 7.12. Налобник: а — металлическая планка (основание подушки); б — резиновая подушка
Типы наглазников из пластмассы приводятся на рнс. 7.8 и табл. 7.4.
Формы мягких наглазников довольно разнообразны. Типы и раз
меры некоторых применяющихся
Рис. 7.13. Крепление налобника
наглазников приведены на рис. 7.9. Материал — резина и губчатая резина. Формы и размеры упругих наглазников показаны на рис. 7.10, а составных — па рис. 7.11.
Рис. 7.14. Подушка — упор из губчатой резины, обшитый кожей
Налобники (рис. 7.12 и 7.13) применяются вместе с наглазниками, помещаются над окулярами и служат для создания удобства для наблюдения. Налобники особенно необходимы в том случае, если прибор вращается. Конструкция налобника может предусматривать его откидывание и перемещение вдоль оси.
На рис. 7.14 изображен мягкий упор для лба.
БЛЕНДЫ И УСТРОЙСТВА ДЛЯ ЗАЩИТЫ ОТ РАССЕЯННОГО СВЕТА
Блендами называются трубки (козырьки), устанавливаемые иере-х входными окнами оптических приборов для защиты от засветки прямыми солнечными лучами в нолевых условиях и для уменьшения вредного (рассеянного) света, попадающего в прибор.
Способы уменьшения вредного (рассеянного) света 1
Вредный свет представляет собой часть светового потока, которая проходит через оптический прибор, не участвуя в образовании изоира-
Поледая
Рис. 7.15. Области входного АВ и выходного А'В' зрачков (в дальнейшем эги обозначения сохранены)
жения, н попадает в глаз наблюдателя. Эта часть светового потока по-лучается в результате рассеяния света при отражении его от поверхностей оптических деталей, внутренних стенок корпуса прибора, оправ и т. п. Некоторая часть света рассеивается от пузырьков и включений в стекле деталей. Вредный свет, уменьшая контрастность изображения, может сильно ухудшить условия видимости. Для уменьшения вредного света могут быть приняты следующие меры: рациональное диафрагмирование; просветление поверхностей оптических деталей; обработка и отделка (окраска) внутренних поверхностей, создающие нанлучшее свето-пог лощение; применение противосолпечных бленд.
Установлено, что наибольший! диаметр зрачка глаза человека, на-блю тающего через оптический прибор, равен примерно 7 мм. Поэтому областью выходного зрачка А'В' условно считается круг диаметром 7 мм, раса сложенный в плоскости выходного зрачка, с центром на оптической осн.
Обнятые входного зрачка АВ называется область, сопряженная с об {тслью выходного зрачка (рис. 7.15).
С-чг:но.и n-го порндка называется рассеянный свет, имеющий п отражений в приборе.
Рациональное диафрагмирование светового пучка в приборе. При правильном диафрагмировании можно полностью устранить вредный
; l Ю лы i ?р и злам Д. Ю. Га пьпери :i. Б. Л. Нефедова и- Э. Я. Сокулэасксн о.
свет первого порядка и сильно ослабить вредный свет второго и высшего - -порядков, если это позволяют допустимые габариты и вес прибора.
Если перед входным зрачком прибора нет никаких материальных диафрагм, то на внутренние нерабочие поверхности мажет падать больной
Рис. 7.16. Типы сложных бленд
световой поток, не участвующий в построении изображения. Для уменьшения величины вредного светового потока надо уменьшить телесный
угол прямой засветки, т. е. максимально чей. Для этой цели применяются
.бленды (рис. 7.16 и 7.17) различной формы. Внутри бленды целесообразно помещать диафрагмы (Df, О2 и т. д.), доставленные таким образом, чтобы ^доой луч прямой засветки после ,ртфажения от внутренних стенок бленды или диафрагмы не попадал во входиойзрачок прибора. В менее ответственных случаях можно огра ни- читкея окраской бленды изнутри хо-
срезать излишнюю часть лу-
Рис. 7.17. Простая бленда
рошо поглошающими свет красками (рис. 7.17). Края диафрагм должны быть расположены вдоль линии АС и А'С'Г так как в этом случае
лучи, отраженные от краев диафрагм бленды, не проходят в отверстие полевой диафрагмы. При выполнении этого условия
L = O0/(tg со1 — tg со0) и = Do (tg + tg w0)/(tg “ tg
12 в. А. Панов и др.
353
Лучи прямой засветки после первого отражения ст нерабочих поверхностей (стенки, оправы, цилиндрические поверхности линз, матированные грани призм) не должны проходить через область выходного зрачка под углом к оптической осн, меньшими, чем угол со. В проекционных приборах и фотоприборах эти лучи не должны проходить через отверстие тюлевой диафрагмы. Число и расположение диафрагм находится графически.
На рис. 7.18 изображена простейшая телескопическая система, в которой выполнено указанное выше требование. Любой л\ч прямой засветки, упавший на поверхность корпуса тт, не проходит через область выходного зрачка. Свет, рассеянный участком корпуса т'т",
Рнс. 7.18. Устранение рассеянного света первого порядка
расположенный за полевой диафрагмой, также не будет вредным, так как лучи этого света выйдут из окуляра под углами большими, чем со'. Некоторые принципы построения и расчет бленд см. [82].
Внутренняя часть бленды должна как можно меньше отражать и рассеивать свет, т. е. необходимо, чтобы попавшие иа стенку лучи поглощались. В наиболее ответственных случаях, когда от прибора требуется предельная разрешающая способность н высокий контраст изображения, к конструкции и материалу бленды предъявляются особые требования. Заслуживают внимания перегородки бленды, изготовленные из соответствующего стекла с коэффициентом отражения р <0 0,016 при полном отсутствии светопропускаиия [82].
Особое внимание должно быть уделено вопросу устранения бликов при расчете оптической системы. Если последняя сконструирована таким образом, что каждый ее компонент изображает впереди стоящий оптический узел на последующий, то в такой системе не требуется установки защитных диафрагм от рассеянного света первого порядка, отражающегося от стенок прибора и оправ линз. Чем больше компонентов в системе, тем надежнее она защищена от постороннего света. Однако наличие в системе значительных остаточных аберраций может вызвать появление рассеянного света.
Следует не допускать проникновения каких-либо механических деталей в область световых лучей и завышения световых размеров оптических деталей. Лишние части оптических деталей становятся проводниками и источниками рассеянного света. При этом надо обратить особое внимание иа обработку поясков оправ, близлежащих к линзам.
Если конструкция прибора не позволяет устранить полностью
354
Рис. 7.19. Устранение рассеянного света от нерабочей
грани призмы
5)
а)
Рифленая
Коническая канавка в стекле
Рис. 7.20. Устранение рассеянного света от
Фаска вместо конической канавки
оправ и линз
Рис, 7.21, Устранение рассеянного света второго порядка
12*
йрсдный cect первого порядка, то в таких случаях необходимо обеспечить отсутствие его хотя бы в центральной части поля прибора.
На рис. 7.19 приведена простая телескопическая система, у которой вследствие малых размеров призмы и отсутствия бленды свет первого порядка, отраженный от матированных граней призмы, проходит крайние участки отверстия полевой диафрагмы и область выходного зрачка (заштрихованная часть пучка). Другие лучи (например, луч исходящие от матовой поверхности призмы и проходящие через нейтральную часть поля, не попадают в область выходного зрачка и, следовательно, не являются вредными.
Рифленые поверхности также выполняют функции системы лив-фра гм, но они менее эффективны, чем система, состоящая из небольшого количества диафрагм. Рифление следует применять только в тех случаях, когда оио конструктивно или технологически выгоднее системы диафрагм.
Вредный свет первого порядка возникает также в результате отражения лучей прямой засветки от цилиндрических матовых поверхностен линз и от внутренних цилиндрических поверхностей оправ линз (рис. 7.20, а). Свет (лучи 1 и 2), попадающий на эти поверхности, после отражения может частично проходить через отверстие полевой диафрагмы и область выходного зрачка.
На рис. 7.20, б показаны варианты правильной конструкции узла.
Ослабление вредного света второго и высших порядков. Полное устранение вредного света второго н высших порядков невозможно, его удается лишь ослабить в большей или меньшей степени.
Лучи рассеянного света любого порядка, отраженные от стенок корпуса, не должны проходить через область выходного зрачка под углами, меньшими, чем со' (рис. 7.21). Для того чтобы обеспечить указанное выше требование, достаточно трех диафрагм, которые размещаются так, что если смотреть через любую точку отверстия полевой диафрагмы на внутренние боковые стенки корпуса, то последние либо не видны (закрыты диафрагмами), либо видны, но линии визирования на них не пересекают области входного зрачка прибора (участок В этом
случае из прибора будет выходить рассеянный свет второго и высших порядков, отраженный от поверхностей оптических деталей.
Побочное вредное изображение. В оптических приборах в результате неправильного выбора параметров оптической системы иногда наблюдается наложение друг на друга основного и побочного изображений. Побочное изображение в телескопических системах возникает в тех случаях, когда вследствие неправильного выбора размеров призменной системы различные пучки лучей имеют неодинаковое число отражений. Для устранения побочного изображения, даваемого качающимися визирными призмами, иногда приходится вводить подвижные шторки (см. рис. 4.17).
Чернением и окраской внутренних поверхностей стенок корпуса прибора, диафрагм, оправ и матированных поверхностей оптических деталей может быть достигнуто значительное ослабление вредного света. О способах чернения и применяемых при этом материалах см. в гл. 18.
Литература: L17, 5G, 621
ГЛАВА 8
РАСЧЕТ ДОПУСКОВ НА ИЗГОТОВЛЕНИЕ И СБОРКУ ОПТИЧЕСКИХ ДЕТАЛЕЙ, УЗЛОВ И ПРИБОРОВ
Расчет и задание всесторонне обоснованных допусков на точность изготовления оптических деталей, на сборку узлов и приборов в целом — обязательный и важнейший этап проектирования оптических приборов. На точность функционирования приборов влияют ошибки как механических, так и оптических деталей и устройств, в частности, такие грешности как дефекты качества изображения, параллакс и разворот шкал и сеток, наклон н перекос изображении, отклонение, биение пли увод визирной оси и другие. Правильно заданные допуски па изготовление и установку оптических деталей и узлов позволяют обеспечить высокое качество выпускаемых приборов при наименьшей их себестоимости.
В данной главе основное внимание уделяется расчету допусков для оптических деталей, узлов и оптических систем в целом.
Оптические системы должны давать изображение высокого качества, обеспечивать требуемую точность работы прибора и иметь заданные характеристики.
На качество изображения оптической системы и на некоторые другие ее характеристики влияет множество погрешностей, которые можно объединить в три основные группы.
1. Погрешности оптических материалов — отклонения величины основного показателя преломления пе, средней дисперсии Пр. — пс, и других констант материалов, из которых изготовляются основные детали, от принятых при расчете табличных величин, а также такие дефекты как оптическая неоднородность, двойное лучепреломление, свили и т. д. (см. гл. 23).
2. Погрешности обработки оптических деталей — отклонение формы их рабочих поверхностей от заданной (А, АЛ', А/?), доцентри-"рОвка линз или их поверхностей (С), клиновидность пластинок (0) и разверток призм.
3. Погрешности сборки, вызывающие деформации оптических рабочих поверхностей, нарушение взапмоположения деталей и узлов в приборе, децентрирование частей системы, расфокусировку изображения, отклонения визирных осей.
Некоторые отклонения констант оптических материалов, например, показателен преломления, а также отдельные погрешности изготовления деталей их формы, толщины, вызывающие отклонения фокусного расстояния линз или дефекты качества изображения, могут быть
взаимно скомпенсированы при сборке продольным смещением оптических легален, изменением воздушных промежутков между ними и т. д. Благодаря агой возможности удается существенно расширить допуски на изготовление оптических деталей, снизить требования к материалам, из ко;орых они изготовляются.
Критерии оценки качества изображения и допуски на дефекты оптической системы
Из существующих критериев опенки качества изображения, даваемого оптическими системами, (по вычисленной величине кружка рассеяния, образуемого совокупностью лучей, по вычисленному распределению интенсивности света в дифракционной картине и других) на практике при испытании узлов и приборов в процессе сборки применяют критерий Рэлея и функцию контраста или частотно-контрастную характеристику (ЧКХ) [71, 85].
Вследствие дифракции даже идеальной оптической системой с круглым зрачком точки предметов изображаются в виде пятен конечных размеров, в пределах которых волновая разность хода достигает величины 0,61Л, где л — длина волны используемого света. Аберрации усложняют вид дифракционного изображения.
Согласно критерию Рэлея качество изображения точек считается еще первоклассным, если волновые аберрации не превосходят величины Дв — л/4 в пределах рабочего пучка лучей.
Рабочим пучком назовем пучок лучей наибольшего сечения, который в поле оптической системы образует изображение осевой точки предмета н по выходе из системы целиком попадает в зрачок глаза наблюдателя или иного приемника световой энергии.
При достаточной освещенности диаметр зрачка глаза наблюдателя £>3# г ~ 2 мм. Если выходной зрачок прибора больше 2 мм, то зрачок глаза наблюдателя, формируя выходящие пучки, становится выходным зрачком прибора.
Соответственно рабочей зоной, в отличие от световой зоны, назовем участок поверхности оптической детали, па который падает рабочий пучок лучей.
Полагая для видимой области спектра среднюю длину волны Аср — = 0,55 мк.м для допустимой величины волновой аберрации визуальных систем, согласно критерию Рэлея, получим До 0,14 мкм. Нз этого допуска иа все «технологические» аберрации, которые возникают вследствие дефектов изготовления и сборки оптических деталей, рекомендуется выделить только его часть, выраженную в мкм, не более
(Ав)доп = 0,1. (8.1)
Такова величина допустимой суммарной волновой аберрации на все оптические детали системы, влияющие на качество ее изображения., Расчет допусков на оптические детали и поверхности наиболее просто и быстро можно выполнить, пользуясь принципом таутохронизма. Согласно этому принципу (см. гл. I), волновые деформации в пределах рабочего пучка лучей не изменяют своей величины при ходе через любую последующую оптическую систему [40, 7о, 89]. Волновые же деформации, которые возникают при прохождении пучка лучей через оптические детали, имеющие дефекты материала в изготовления, алгебраически суммируются.
На рис. 8.1, « показано прохождение плоского волнового фронта UZ через плоскую границу между двумя средами с показателями пре-3S8
ломлен и я и п2, причем а на плоскости раздела сред имеется
местная неровность глубиной —Л* Участок волнового фронта, проходящий через неровность, отстанет от основной его части, и на выходящем в воздух волновом фронте W возникнет местная деформация Дв
Согласно принципу таутохронизма, т. е. из условия равенства времени прохождения пути между волновыми фронтон 1Г и U ' но крайнему и среднему лучам найдем
Лв. п = (^ 2)
Для волнового фронта, отраженного от тон же плоскости раздела в среде с показателем преломления и, аналогично можно получить
о. п
(8,3)
Из формул видно, что проходящий через преломляющую поверхность или отраженный от зеркальной поверхности плоский волновой фронт в некотором масштабе повторяет дефекты рабочей поверхности. Коэффициент пропорциональности в первом случае равен разности показателей! преломления nt — п2 на границе сред, а во втором — удвоенной величине показателя преломления среды, в которой отражается волновой фронт. Отсюда следует, что дефекты зеркальных поверхностей,
Рис. 8.1. Влияние дефектов плоской оптической преломляющей поверхности на выходящий волновой фронт: а — местной неровности на границе двух сред с различными показателями преломления > п%, » б — микрошероховатости; в — цплипд-ричности; г — клиновидности; д — сферичности
1 <: <
особенно с задним отражением, вызывают во много раз (в 4—6 н более) большее искажение волнового фронта, чем преломляющие поверхности. Наименьшие деформации вызывают дефекты поверхностей склейки, так как разность показателей преломления па них обычно мала.
В качестве передаточного отношения возьмем отношение величины возникшей деформации волнового фронта Ав к высоте дефекта поверхности А. Чем оно меньше, тем очевидно и ниже требования к точности обработки этой поверхности. Для рабочих поверхностей объектива театрального бинокля, изготовленного из стекол крон марки К8 (пе ~ —а 1,518), а также флинт марки Ф1 (пе = 1,615) и склеенного бальзамом
(п€ ~~ 1,53 ± 0,01), из формулы (8.2) получим передаточные стпошепия: д
для поверхности кроновой линзы, граничащей с воздухом, 0,52,
Ai
Ав
Дм Я флинтов ой линзы
0,61, для поверхности склейки— кроно-
линзы -0,01 ± 0,01, флинтовой линзы —— 0,08 — 0,1 мкм, то даже i;
В СИ
Лели на каждый дефект дать допуск Ав
условии получим следующие допуски на каждую поверхность Aj ~ ~ 0,2 мкм, А2 ~ 5,0 мкм, Д3 ~ 1,2 мкм и А4 ~ 0.17 мкм. Следовательно, обе внешние поверхности линзы, граничащие с воздухом, требуют обработки с помощью оптической полировки по самым высоким классам чистоты. Поверхность склейки, особенно кроновая, в которой разность показателей преломления между стеклом и бальзамом мала (не болте 0,02), может быть обработана шлифовкой мелким наждаком и ее неровности после склейки почти не испортят качество изображения, так как вызовут микродеформации волнового фронта в 50 раз меньшей
величины.
Как видно, допуски на дефекты изготовления и сборки оптических элементов даже с преломляющими рабочими поверхностями получаются весьма строгими. Для некоторого их расширения учитывают как конструктивную сложность оптических систем, так и специфику их работы. Например, вводят коэффициент сложности К > 1, па который умножают величину теоретического предела разрешения оптической системы при определении предельно допустимого его значения.
Допустимые аберрации большинства фотографических и проекционных систем могут значительно превышать критерий Рэлея, т.ж как структура фотоэмульсии обычно грубее дифракционной структуры оптического изображения [85|.
В некоторых оптических системах треб j'e гея высокое качество изображения только в одном направлении, например, в шкаловых отсчетных устройствах — поперек штрихов, в спектральных приборах — вдоль спектра. В указанных случаях разворотом деталей в процессе юстировки можно добиться улучшения качества изображения штрихов или спектральных линий, ориентируя соответствующим образом направление размытия штрихов и линий вследствие, например, технологического астигматизма.
Дефекты оптических поверхностей и деталей вызывают различные по характеру деформации проходящего или отраженного волнового фронта, а именно нерегулярные микроиеровности вследствие микрошероховатостей или волнистости рабочих поверхностей (рис. 8.1, б), искажение его формы вследствие несферичпости (цилиндричности) поверхностей (рнс. 8.1, в) пли их местных и зональных ошибок. При нс; пользовании белого света возникает также поперечный хроматизм'; например, за счет клиновидиости деталей (рпс. 8.1, г) и продольный хроматизм вследствие их фокусностн (рис. 8.1, б).
Допуск на поперечный и продольный хроматизм можно также задавать в волновой мере: допуск на поперечный хроматизм — величиной взаимного смещения волновых фронтов для линий F' и С' в пределах рабочего пучка лучей, а допуск на продольный хроматизм — величиной &hp,c. разности стрелок волновых фронтов для того же пучка лучей. Для самых ответственных случаев можно положить, чтобы оба эти волновых допуска А^,с, и &hF,c, не превосходили 0,1 мкм [40].
Поскольку клиновидность деталей по ГОСТ 2.412—68 задается в угловой мере, то и допуск на поперечный хроматизм удобнее выражать в той же мере. За окуляром допустимый угловой хроматизм яри диаметре рабочего выходного зрачка Dp будет равен
. х _ (AF'C')acn
(ЛС7’С')доп ~ Гр и р
(8.4).
Полагая волновой допуск (Др^сОдоп Равным 0,1 мкм, получим для допустимого хроматизма (в угловых секундах)
20"
При диаметре рабочего выходного зрачка D’p — 2 мм допуск (ДоF,с,)"оп составит всего 10". Поскольку хроматизм сказывается на работе прибора не так существенно как, например, двоение изображения, то обычно задают более широкие допуски на призматический хроматизм — до 20" для каждой детали, независимо от диаметра выходного зрачка и сложности оптической системы [101).
Общий допуск на «технологические» аберрации оптической системы необходимо разделить на допуски для отдельных деталей и их элементов (поверхностей и углов) исходя из предположения, что действия первичных ошибок будут суммироваться как случайные величины по квадратичному закону. Необходимо также учесть, что некоторые ошибки являются скалярными (например, хроматизм положения), а другие — векторными (например, хроматизм за счет клиновидиости деталей).
Величину волнового допуска (Ав)ск на каждый источник скалярных ошибок при общем их числе тск можно найти по формуле
(Дв)ск = .
Г ™ск
(£.6)
Величину волнового допуска (Ав)вк на каждый источник векторных ошибок можно найти из той же формулы (8,6), но умноженной на коэффициент К > 1, учитывающий благоприятное влияние на величину суммарной погрешности дисперсии первичных ошибок по фазе. Прн равновероятном распределении векторных ошибок по фазе и большом их числе можно положить 76 “ 1^2, тогда получим
(Дв)вк = / 2. (8.7)
V
При юстировке во многих случаях взаимным разворотом оптических деталей можно уменьшить до некоторого минимума суммарный хроматизм и астигматизм. Благодаря этому удается значительно расширить допуски как на клиновидность деталей, так и на астигматизм поверхностей [69].
Расчет допусков на оптические поверхности и детали, перпендикулярные оси системы
Для допуска на высоту микронеровностей оптических поверхностей из формулы (8.2) получим
А = - = йгЛ,. (8.8)
II । *—• /12
Здесь gn — коэффициент, обратный передаточному отношению; чем больше его величина, тем шире допуск можно задать на дефекты данной поверхности. Это относится к дефектам, которые непосредственно ухудшают качество изображения.
Единичные дефекты иодированных поверхностей в виде царапин, выколок, прошлифованных пузырей, а также пороки материала (пузыри, камни) регламентируют не по их глубине, а по величине отношения площади указанных дефектов к площади поперечного сечения рабочего пучка лучей в месте их нахождения; но ГОСТ 11141 — 76 допустима величина отношения указанных площадей не более 1%.
Расчетную формулу для допуска ДЛ'р на дефекты оптической поверхности в пределах ее рабочей зоны легко получить, воспользовавшись тем же коэффициентом g; действительно
~ = R A..VB. (8-0
/ v у /V у £
Здесь АЛ и Дйв — наибольшая допустимая разность стрелок оптической поверхности и соответственно выходящего волнового фронта в пределах рабочего сечения пучка лучей; A.-VB — волновой допуск на астигматизм и местные деформации выходящего волнового фронта в пределах рабочего пучка лучей, заданный величиной наибольшей допустимой разности числа интерференционных полос, которая наблюдается при контроле формы оптической поверхности под пробным стеклом; X — длина волны света, применяемого для освещения при контроле формы поверхности (для белого света при контроле по полосам красного цвета принимают к — 0,55 мкм).
Предельное значение допустимого волнового допуска ЛЛ7В для визуальных систем не должно превышать величины
_ (Айв)лоп < О-1 мкм
~~ л/2 0,28 мкм
(8.10)
Коэффициент g в формуле (8.9) определяется соответственно типу поверхности: для преломляющих — по формуле (8.2), для отражающих — по формуле (8.3).
Допуск на несферичиость (астигматичность) поверхностей в пределах светового диаметра (приводимые иа чертеже оптической детали) увеличивают на величину квадрата отношения светового диаметра к рабочему диаметру D пучка лучен, поэтому
(8.11)
Допуски на дефекты нерегулярного характера (местные вырывы, Зональные ошибки) в пределах светового диаметра задают той величины, какой они получились по формуле (8.9) для рабочей зоны поверхности.
Допуск N иа общее отклонение поверхности, перпендикулярной К оси системы, от расчетной формы можно определить исходя из допу-362
стимых аберраций, в частности, продольного хроматизма, или из условия удобства контроля заданного допуска ДА/ на местные ошибки, или из требований взаимозаменяемости деталей.
Для деталей неответственного назначения этот допуск задают исходя из возможностей технологии серийного оптического производства или из удобства контроля несферичности. В последнем случае принимают N не более чем в 3—5 раз больше допуска A/V.
‘ Допуск на клиновидность пластинок, разверток призм и на косину линз определяют по формуле
где —допустимый угловой хроматизм за окуляром прибора,
определяемый по формуле (8.4); D и Dp — диаметры сечения рабочего пучка лучей в месте расположения детали и диаметр рабочего выходного зрачка соответственно; W — угловое увеличение оптической системы, стоящей за дайной деталью, равное отношению тех же диаметров.
В сходящемся ходе лучей клип вызывает также кому, величину которой в угловой мере за системой, расположенной за клином, можно вычислить по формуле [18]
Да = -39 ^=4 а'2,г, (8.13)
к л
где о^, — апертурный угол пучка лучей в месте расположения клипа.
Клиновидность разверток отражательных призм может возникнуть вследствие двух причин: из-за отклонения углов между ее рабочими гранями от номинала, которое вызывает появление клнповидности 0С в плоскости главного сечения и из-за пирамидальности л, которая обусловливает клиновидность Од в плоскости, перпендикулярной главному сечению. В силу взаимоперпендикул яркости обеих составляющих клиновидность развертки призм равна 9= J, 0^ ~г 9^.
При расчете допусков и контроле призм, согласно ГОСТ 2412—63, каждая из ошибок рассматривается самостоятельно. Связь между ошибками отдельных углов призм и клиновидностыо 0С, между пирами-дальностью призм и клиновидностыо 0д находится из разверток призм.
Отклонение угла крыши Дкрш от прямого вызывает двоение изображения, когда пучок световых лучей падает одновременно на обе ее грани. Задаваясь двоением изображения за окуляром не более 20*, допуск на отклонение угла крыши вычисляют по с юрмуле
г Дкрш т «р/—;— । (8.14)
ь 1 4nU cose ' '
где п показатель преломления призмы; е — угол падения осевого луча на ребро крыши; W—угловое увеличение системы, стоящей за призмой для осевой точки ребра крыши.
Допуск на де центрировку линзы из поперечного хроматизма равен с < > (8.15)
где Д^,с, = 0,1 мкм волновой допуск на хроматизм в пределах рабочего диаметра D линзы.
Для близко расположенных друг к другу линз, составляющих ахроматическию пару, при расчете по формуле (8,15) получатся одинаковые допуски, так как по условию ахроматизации Vj/J = — vjy.
Дсцептриропка лиаз вызывает не только хроматизм, но и кому на оси н другие аберрации, что необходимо учитывать в ответственных системах.
Приближенную величину угловой комы, которую вызывает на оси системы одиночная линза, наклоненная па угол 0, можно вычислить по формуле
Д<гк = -зе^^ДоУ(1/2-1)1Г
где Од, — апертурный угол в пространстве изображений линзы, V — ее линейное увеличение.
Рис. 8.2. Влияние наклона отдельной линзы на кому на оси
Эта формула получает я, если представить, что наклоненная линза отличается от центрированной добавлением спереди и сзади одинаковых сферических клиньев с равными и противоположными по знаку углами О в —0 (рис. 8.2). Применяя к каждому из этих клиньев формулу (8.13;, найдем их суммарную кому, а после преобразований получим приведенную выше формулу.
Из формул (8.1 J)—(8.15) видно, что допуски на отдельные погрешности оптических поверхностей и деталей зависят от их местонахождения в ходе лучей; в первую очередь они зависят от диаметра D сечения рабочего пучка лучей: чем шире это сечение, тем строже все указанные допуски для детали. В такой же зависимости от размера сечения рабочего пучка находятся и требования к материалам для оптических деталей в отношении оптической однородности, двойного лучепреломления и др. Поэтому для деталей, расположенных в широком сечении рабочего пучка (т. е. дальше от плоскости изображения), следует назначать материалы более высоких категорий, чем для деталей, стоящих в узком пучке (т. е. ближе к плоскости изображения), для которых допустимо применять материалы пониженных категорий. Требования же к чистоте полировки поверхностей и к таким дефектам материала как пузыри, камни, царапины, выколки, наоборот, возрастают с уменьшением сечения рабочего пучка. Известно, что самые строгие требования предъявляются к деталям и поверхностям, расположенным близко к плоскости изображения, т. е. в узких световых пучках, к которым относятся коллективы ц особенно сетки.
Расчет допусков на наклонные оптические поверхности и пластинки
Коэффициент gE, который связывает высоту неровности Л с вызванной ею деформацией Дв проходящего волнового фронта для наклоненной под углом 8 плоскости, разделяющей среды с показателем преломления и п2 и имеющей неровность высоты А, вычисляется из более сложного выражения вида
д ____________
g& — “г~ = — Ohcos * — ~ sin 2 . (8.16)
^в
Из общей формулы (8.16) для поверхностей различного типа получим:
для преломляющей поверхности, граничащей с воздухом ~ 1;
л) _________
£пе = — (cos к — Кн- — sin2 е)"1;
для зеркал с внутренним отражением (;?, ~ — п.2 — п) _ 1
8о-«-----2л cos « :
для зеркал с наружным отражением (п ~ 1)
1 е‘к~- 2cose*
(8.16а)
(8.166)
(8.16в)
Абсолютные величины и графики коэффициентов gv для поверхностей трех типов при п — 1,5 приведены в табл. 8.1 и на рис. 8.3, которые позволяют ускорить и упростить расчет допусков.
Таблица 8,1. Величина коэффициентов для расчета допусков на оптические детали с преломляющими и отражающими рабочими поверхностями в зависимости от угла их наклона [при п = 1,5j
К оэффинневч ы Величина угла наклона е, ...с
с 30 45 60 90
2.0 1,8 1,6 1,4 0,9 .
«0 0,5 0,6 0,7 1,0 ос
«о.п о,з 0,4 0,5 0,7 ос:
6„ СО 5,4 1.6 0,5 0
ОС 1,7 0,7 0,3 о.:
Go. 11 со 1.2 0.5 0,2 0.
(?е 1.0 0,8 0,6 0,3 .— 1
Расчетные формулы (8.8) и (8.11) для допусков на микронеровности и на ! асферичность пригодны и для наклонных поверхностей, если в них вместо g подставить коэффициент соответствующий типу по
верхности и углу ее наклона.
В отличие от перпендикулярных к оси наклонные плоские поверхности имеют не один, а два источника астигматизма. Кроме пи-линдричности, атигматизм вызывает также и сферичность наклонной поверхности, так как при наклонном падении пучка лучей круговою сечения на строго сферическую поверхность выходящий волновой фронт деформируется неодинаково: больше в
плоскости падения (вдоль длинной оси рабочего участка эллиптической формы) и меньше в перпендикулярном направлении (вдоль его короткой оси). В результате возникает астигматизм волнового фронта, равный наибольшей разности его стрелок. Допуск па сферичность наклонной пл ос к ост и, о п р едел я е м ы й
числом полос Л;р вдоль малой! оси рабочего участка, равен tfp = jA-j-AA'^GeAA',,,
(8.17)
где k — отношение длин, большой и малой осей рабочего участка эллиптической формы.
Рис. 8.3. График коэффициентов g£f Ск и для расчета допусков на дефекты преломляющих и отражающих поверхностей и на клиновидность пластинок в зависимости от угла наклона (при показателе преломления п =
= 1 > 5) Согл асно ГОСТ 2.412—68,
допуск N для пекруглых деталей следует задавать вдоль наименьшего светового размера О/. /т{п, поэтому
Д' = Д'Р (£8Д™1»у. (8.18)
Для призм, развертка которых перпендикулярна оси пучка, и зеркал с внешних! отражением знаменатель в формуле (8.17) определяется из равенства k'1 — 1 = tg2 £, и тогда
0e = geCtg28. (8.19)
Величины коэффициентов G& даны в табл. 8.1 и на графиках’ рис. 8.3. При угле е == 45° имеем (?45о = g45O и в этой точке соответствующие графики взаимно пересекаются.
Допустимую клиновидность для наклонной пластины можно рассчитать по формуле (8.19), если умножить ее па коэффициент Q& (см. табл. 8.1 и рис. 8.3), меньший единицы, учитывающий возрастание углового хроматизма с увеличением угла наклона) пластинки е, причем
(8.20)
\ » /
Последняя формула получена из известного выражения для величины угла отклонения преломленного луча, падающего наклонно на входную грань клина, в плоскости его главного сечения
= е (п — 1) (i -j- 1 tg2 ф .
(8.21)
Требования к точности поверхностей и параллельности пластинок, как видно из табл. SJ и графиков рис. 8.3, следующим образом зависят от типа поверхностей и угла их наклона.
1. Требования к точности обработки отражающих поверхностей, нормальных к осп пучка (кривые gfe для допусков на местные ошибки и кшкронеровносги) в четыре (для наружных) и даже в шесть раз (для внутренних) выше, чем к обработке преломляющих поверхностен, граничащих с воздухом. Однако по мере возрастания угла наклона поверхностей в эти требования изменяются неодинаково — для преломляющих они ужесточаются более чем вдвое (при е — 90е), а для отражающих снижаются, так как допуски растут до бесконечности (при 90е). Это подтверждается известным фактом, что при скользящем ходе лучен даже шероховатые (шлифованные) поверхности дают изображение хорошего качества.
2. Требования к сферичности преломляющих и отражающих плоских поверхностей (кривые Ge) с ростом угла наклона 8 непрерывно и быстро ужесточаются.
3. Требования к параллельности пластинок и разверток призм с ростом угла наклона 8 также непрерывно ужесточаются (кривые Qe).
Влияние смещений и поворотов зеркально-призменных систем на положение и ориентировку изображения
Погрешности установки зеркал и призм нарушают положение и ориентировку изображения в поле оптической системы и вызывают децентрировку ее частей.
При расчете допусков на точность установки зеркально-призмен-ных систем нередко возникают пространственные задачи, для решения которых пользуются методами аналитической, начертательной геометрии, сферической тригонометрии, а также векторной алгеброй, матричным исчислением к кватернионами [29, 34, 35, 41, 53, 57, 60, 64, 69, 73, 74, 81, 84, 89, 94—96].
. . Направление орта луча, отраженного от плоского зеркала или преломленного поверхностью, разделяющей среды с показателями преломления пип', можно найти из следующих векторных выражений:
А{ ~ A—2N {AN)
и соответственно
А' ~ А -ф xV I cos 8 — cos 8х п \ п
(8.22)
(8.23)
Здесь; А — орт направления падающего луча; /V — орт нормали отражающей и преломляющей плоскости, направленной навстречу падающему лучу; е и 8х — углы падения и преломления луча. При k 367
чиск? отражений в зеркальной системе нием в матричной форме
удобнее «ользоваться вы-nw-
/ ^11 "НА _
д(*) = Л1(Ъд _ , 1 /I, (8-с4)
"'J
где — матрица действия зеркальной системы, записанная в тон /се
системе координат осей, в которой задан орт А направления падко него луча; /нп, ш12.. Мдз—элементы матрицы от первого до девятого.
Для плоского зеркала из формулы (8.22) найдем
-зл'Л 1-2Л2 -2а;л; .
-2.VaJV, -2Х^г 1-2Л'У
Здесь А'х, /Vy, Уг — проекции орта нормали зеркала в произвольной системе осей хцг
Матрица ЛГ общего вида преобразуется в матрицу Р' канонического вида, если ее записать в так называемой основной системе осей хоц:1го, неизменно связанной с плоским зеркалом, ось г,, которой направлена по нормали зеркала. При этом /V = /е0, вследствие чего из формулы (8.25) получим
Л о о\
/>'= | 0 ! 0 1. (ri.26)
\0 0 — 1/
Матрица действия углового зеркала имеет более сложный вид лг =
y sin a
г 22ir 2 1 г J I
Icos 2o4-2f) sin (J I — p sin 2ff+2p p sin a I | p sin 2<тЩ2г? p sitT u ]
I. A JLc Л I/ j I Lf A £ J
[pz sin 2o -f-2p
[— P
SHI J
Л sin a
sin 2<H-2p p sirTa if A *C
(8,27)
Здесь px, рц, p7 — проекции орта ребра углового зеркала, образованного пересечением его зеркал; о — двухграниый угол между зеркалами, отсчитываемый со стороны орта ребра р от первого по ходу луча ко второму зеркалу (положительным считается угол, отсчитываемый «ротив направления движения часовой стрелки).
У прямоугольного зеркала или крыши a = 90°. В этом случае матрица действия может быть представлена в виде
/ l~2Pi -2РхРу -2₽хРЛ
AIa=90 = - I — 2РХРУ 1 - 2ру —2РуРг I • (8.28)
\~2РХРг —2Pvpz 1 ~ 2^1/
Из совпадения полученной матрицы с формулой (8.25) (они отличаются друг от друга лишь противоположным знаком) следует, что пр я-368
мо у голь ное зеркало н крыша действуют на .направлщше^ШййШйИйс лучей так же, как плоское зеркало, перпендикулярное их ребру;-если у всех ортов пространства предметов поменять знаки на обратные.
У зеркального ромба (пара взаимопараллельных плоских зеркал) и у ромб-призм угол о=0, вследствие чего из формулы (8.27) найдем
Г ° °\
I о 1 О I = £, (8г29)
\0 О 1/
т. е. их матрица действия является единичной. Это означает, что-обе указанные зеркальные системы не влияют на направление отраженных лучей — выходящие из них лучи всегда остаются параллельными падающим.
Каноническая матрицаР" для углового зеркала с произвольным углом о между зеркалами получится из его матрицы общего вида ЛГ, если формулу (8.27) записать в основной системе координатных осейх0, //о* zb, неизменно связанной с угловым зеркалом, ось г0 которой совпадает с его ребром — ортом р. Тогда р == k0, в результате чего получим. -
(cos 2а —sin 2а 0\
sin 2а cos 2а 0 |. (8г30)
О 0 1/
Преломляющий клин в параллельном ходе лучей дейсгвуег<^шэ«о-гично угловому зеркалу с углом оил, который равен половине угла поворота ф преломленного луча вокруг ребра клина по отншдааню к падающему лучу. Для клина с малым преломляющим углом 9 угол поворота равен [73, 74]
if = 0 (1 - Уп-л 4- (Я3 — 1) tg2 е), (8.31)
где £ — угол падения луча на входную грань клина.
В первом приближении величина угла поворота ф вокруг ребра клина преломленного луча по формуле (8.31), зависит лишь от угла падения е луча на его входную грань, мо не зависит от ориентировки плоскости падения по отношению к плоскости главного сечения клина [74].
Положение изображения точки, отраженной k раз в системе плоских зеркал, в сходящемся ходе лучен можно определить радиусом-вектором причем согласно (рис. 8.4, а) имеем
7<fc) -k М(8.32)
/ ‘rsep(ft> — радиус-вектор изображения точки предмета Т, с которой Совмещено начало О неподвижных координатных осей х, р, г, после'^-го (: отражения; к—переменный скалярный множитель; A(k) — орт направления отраженного луча, определяемого по. формуле (8.24). -
Для наиболее распространенных зеркал найдем следующее-соотношения:
; л для плоского (рис. 8.4, а)
р =(1 __ Af')“4-2W (8.33)
для углового (рис. 8.4, б)
р" = (1 — Д|') (7+ ф (8.34)
для тройного (рис. 8.4, в)
р’" = (1 -ЛП(< + /~ц). (8.35)
З.^есь г — радиус-вектор точки С, вокруг которой вращается плоское, хгловое или тройное зеркало; Z—расстояние от точки С до отражающей плоскости зеркала; N — орт направления нормали зеркала; ЛГ, Л Г и
Рнс. 8.4. Отражение точки предмета и падающего луча от произвольной системы плоских зеркал (л), от плоского (6), углового и тройного зеркала (в)
ЛГ — матрица действия плоского зеркала, определяемая по формуле (8.25), углового зеркала — по формуле (8.27) и тройного зеркала соответственно; I и /ц — радиус-вектор точки пересечения ребра углового зеркала с перпендикуляром, опущенным из точки С, и радиус-вектор центра Ц системы зеркал относительно точки С.
Матрица ЛГ" трехзеркальной системы общего вида может быть найдена как произведение матриц 2 по формуле (8.27) первой по ходу 370
луча пары зеркал 1 и 2, образующих угловое зеркало с углом о1<2 и ортом pt>:! направления ребра, на матрицу ЛГ5 третьего зеркала по фор* муле (8.25).
Для зеркального ромба формула (8.34) вырождается в неопределенность вида 0* сю. Поскольку изображение Т" точки предмета Т после отражения в зеркальном ромбе смещается на расстояние 2d вдоль нормали Nt к первому по ходу луча зеркалу, восстановленной в точке Tt то для радиуса-вектора получим
рромб — 2dN 1, (8. Зб)
где d — толщина ромба, т. е. расстояние между отражающими плоскостями его зеркал.
Формула (8.36) применима и к плоскопараллельной пластинке, которая также смещает изображение Т" точки предмета Т вдоль нормали входной грани, по по ходу луча, на величину
А Л COS Г Ъ 1 Л , /О Ч-7Ч
А — I 1---. . —- ]d -------d sect:, (8.37)
V № — sin 2 г/ n
где n — показатель преломления пластинки; d — ее толщина; е — уюл падения луча на пластинку, косинус которого равен скалярному произведен и ю орта А направления падающего луча иа орт Л\ нормали входной грани.
Существует большое число разнообразных конструкций зеркально-призменных систем. В табл. 46 (см. гл. 4) включено 34 липа призм н призменных систем, а в книге [53] рассмотрено около 80 призм и систем, что далеко не исчерпывает всего их многообразия. Для понимания их свойств, действия и юстировки целесообразно пользоваться научной классификацией призменных и зеркальных систем, предложенной И. В. Лебедевым [57J. Согласно этой классификации все зеркальнопризменные системы с плоскими рабочими гранями, расположенные в сходящемся ходе лучей, можно разделить на семь классов, приведенных в табл. 8.2. Первые пять систем простые: плоское зеркало (класс Л), угловое зеркало (класс Б) и его частный случай — зеркальный ромб (класс Б — 0), тройное зеркало (класс В) и его частный случай — триэдр прямоугольный (класс В — 180е). В индексе ромба и триэдра указан угол отклонения выходящих лучей, соответственно 0е и 180.
Последние две системы сложные. Шестая система класса Л+£—0° представляет собой сочетание плоского зеркала с перпендикулярным ему зеркальным ромбом, а седьмая класса Б~]-Б—0и—сочетание углового зеркала с перпендикулярным его ребру зеркальным ромбом.
В графах 4 и 5 табл. 8.2 знаком + отмечены в основной системе координатных осей х0, г/0, гп действенные подвижки зеркальных систем соответственно в сходящемся и параллельном ходе лучей. Ось z0 основной системы координат совпадает с так называемым основным неизменным направлением зеркально-призменных систем: у плоского зеркала— с нормалью отражающей плоскости; у углового зеркала — с ребром; у тройного зеркала — с центром, в котором взаимно пересекаются зеркала, и направлена по лучу, который после отражения в системе трех зеркал выходит строго противоположно падающему лучу. У прямоугольного триэдра класса В — 180° направление оси не имеет значения, поскольку эта система любой луч отражает в строго противоположном направлении.
Таблица 8.2. Классы систем плоских зеркал систем с плоскими отражающими
, и * •! ифр 1Ш1И и класса систем Наи мено-ван не зеркальной системы Действенные подвижки в сходящемся ходе лучей Действенные повороты в параллельном ходе лучей вокруг осей Матрица действии канонического Еида -1^
смещения вдол ь осей повороты вокруг осей
г(( lit, (/о 2(т *0 Vo 2о
1 А Плоское зеркало — — -у + -р — -р -р — /10 С- Р' = 1 0 I 0 [ \0 0 ^1/
Б У гловое зеркало + II 1 || /cos2o — sin 2о 0\ 1 о — о g Р" — 1 sin 2о cos 2о 0 | A j J \ о oj — о о II _____
3 Б —0° Ромб зеркальный — — — -р -р — — — 11 о о — Cl * © - о [I — о- © ‘т? '— II - ь,
и эквивалентных им зеркально-призменных и преломляющими поверхностями
Недейственные смещения и повороты системы в сходящемся ходе лучей Примеры зеркально-призменных систем, относящихся к данному классу Призмы отражательные, относящиеся к данному классу, (см. табл. 4 6 справочника)
Любые смещения плоского зеркала вдоль отражающей плоскости и поворот его вокруг оси, перпендикулярной от р а ж а ю-щей плоскости Плоское зеркало. Система двух взаимно параллельных зеркал с тремя или большим нечетным числом отражений. Система двух зеркал с любым числом отражений и автокол-лнмационным ходом лучен. Система трех или большего нечетного числа зеркал, взаимно пересекающихся по одной общей прямой А —0° (Аббе) при п — 1,5
Смещение углового зеркала вдоль ребра и поворот его вокруг ребра Угловое зеркало — пара плоских зеркал с углом между ними в пределах 0° < о < 180°. Любое число угловых зеркал с взаимно параллельными ребрами. 11ризмы с двумя отражениями, у которых входная и выходная преломляющие грани параллельны ребру между отражающими гранями ЬР—180°. БУ — 40°, БУ —45°, БУ-600. БП —80°. БП—90° (пента), Б—90°
Любые смещения зеркального ромба и поворот его вокруг осн, перпендикулярной зеркалам Ромб зеркальный — пара плоских зеркал, взаимно параллельных и обращенных друг к другу. Ромб-призма Плоскопараллельная пластинка Система любого числа угловых зеркал с взаимно параллельными ребрами. алгебраическая сумма углов которых равна нулю БС — 0° (ромб)
.\и Л1 п Ш нфр типа и класса систем Наименование зеркальной системы Действенные и один /к к и в сходящемся ходе лучей Действенные повороты в параллельном ходе лучей вокруг осей Матрпп.-i действия канонического вида —
смещен ня идол ь осей поворотов вокруг осей
(/к г„ 'А. го Л' 1/л *0
4 В 7 ройное зеркало + + -U + 4- 4* 4" Q 5 % /cos2oCi —sin 2о, 0\ Щ 1 1 о Р = — I sin 2о_ cos 2о 0 ! - У* о 13 з I $ II \ 0 0 1/
5 В—180° Тр и эдр прямо-уголь НЫЙ + -J- — ~~ — ~— — — р'" — / 1 0 0\ — 0 1 0 | \о о I/
6 Ai^° Плоское зеркало с пер-пендику-лярным ем у зеркальным ромбом — — 4” 4" — Iff " f Р =Ра=(Г.Рэ = э = ер' = р'
7 Б4-Б-— оа Угловое зеркало с перпендикулярным его ребру зеркальным ромбом 4~ 4- 11 4'” к '«•" v “ Л '1 О II О -L > II 4? . еГ щ lL II |!
ГТродолжение табл. 8 2
Недействен пью смещен и я и повороты системы в сходящемся ходе лучей Примеры зеркалъно-приз-менных систем, относящихся к данному классу Призмы отражательные, относящиеся к данному классу, (см. табл. 4 6 справочника)
Только поворот тройного зеркала вокруг оси, проходящей через точку взаимного пересечения зеркал и параллельной лучу, который в тройном зеркале отражается в строго противоположном себе направлении Система трех произвольно расположенных зеркал, имеющих общую точку пересечения, Призмы с двумя отражающими гранями, вместо одной из которых нарезана крыша БкУ —45°, БкУ — 60°, БкП---90°, БкМ — 100° —90°. БК —90° (башмачная)
Любые повороты прямоугольного 1р>юдра вокруг точки взаимоиересечепия зеркал Система трех плоских зеркал, расположенных взаимно перпендикулярно. Световозвращатель, уголковый отражатель или три-пель- призма БкР—ISO"
Любые смещения зеркальной ей сто мы вдоль отражающей плоскости ее эквивалентного плоского зеркала Система трех плоских зеркал, перпендикулярных общей плоскости и не пересекающихся по одной общей прямой. Равнобедренные призмы с одним или тремя отражениями АР —0° (Дове), АР —45°. АР —60°, АР —90°, АР- 1050, ВЛ —0° (Лемана). ВР — 4 5° (Шмидта), ВР — 180°, А —0° (Аббе) при и 1,5, К —0°, П —0°, ВП — 0°
Смещение зеркальной системы вдоль ребра эквивалентного углового зеркала в поворот ее вокруг этого ребра Система четырех плоских «зеркал, расположенных произвольно. Все зеркальные и зеркально-пр и змеиные оборачивающие систе-м ы АкР — 45°, АкР — 60°, АкР —80°, АкР —90°, БМ— 60°—90°, БМ— 80°—90°, БМ — 90°—90°, БМ — 100°—90°, БМ — 120°— 90°, ВкЛ — 0°, ВкР —45°, ВкР—180°, Ак —0°, (Аббе), ПК-0°
В пг.раллелььох) ходе лучей все зеркальио-лризмеиные системы л р и р од д тс я лишь к in сети классам — к системам с единичной матрицей действия £ iio.io/кнтельного (ромб класса £—0) и отрицательного знака (триэдр класса — В — 180’); к системам с матрицей действия Р' иоложнтслиного знака (плоское зеркало класса /1) и отрицательного сиапи (прямоугольная крыша класса В с углом о — 90 ); к системам с матрицами'действия Р" положительного знака (угловое зеркало класса Б общего вида) и отрицательного знака (тройное зеркало класса £). В графе 6 приведены перечисленные матрицы действия канонического вида.
Далее указаны недейственные подвижки (графа 7), приведены гримеры зеркально-призменных систем каждого класса (графа 8) и наконец — шифр призм с распределением их по классам из табл. 4.6 настоящего справочника.
Расчет допусков на оптические детали с учетом требований к точности функционирования и к сборке приборов
Для оценки точности работы прибора первостепенное значение имеют дефекты оптической системы, наблюдаемые в ее поле. Рассмотрим основные из них в неподвижной системе координатных осей, с началом О в плоскости полевой диафрагмы, направив ось г по оптической оси, ось х — горизонтально, ось //— вверх. Погрешности изготовления и установки оптических детален, расположенных до полевой диафрагмы, могут вызвать следующие ошибки положения и ориентировки изображения.
1. Поперечные сдвиги изображения в плоскости полевой диафрагмы вдоль осей х и у соответственно на величины Ах и А//, что приводит к децеитрировке второго рода, т. е. к параллельному сдвигу частей оптической системы, а при наличии сетки еще и к отклонению визирной оси; в бинокулярных приборах указанные сдвиги вызывают, кроме того, взаимную непараллельность осей выходящих пучков лучей,
2. Продольное смещение изображения вдоль оси z иа величину Аг дает расфокусировку, а при наличии сетки — параллакс и рен.
3. Наклоны осевого луча и ортогональной ему плоскости изображения вокруг осей х и у соответственно на углы а и (3, что приводит к де-пентрировке первого рода, т. е, взаимному наклону частей оптической системы, который влечет за собой кому, нередкость на краях поля и перспективные искажения или разномасштабность изображения по полю.
4. Поворот изображения вокруг оси г на угол у в приборах с призменно-зеркальными системами или цилиндрическими линзами, что приводит к повороту, наклону или перекосу изображения.
Допуски и а указанные дефекты обычно задаются техническими' ' условиями на изготовление оптико-механических приборов.
В визирных системах, работающих совместно с глазом, требуется, f чтобы изображение было видно одновременно резко с сеткой или шкалой, причем допустимое смещение изображения от плоскости последних не должно превосходить величины
0,2 мкм й е
Дг=-----, (8.38)
°А'
где Од, — апертурный угол рабочего пучка в месте расположения сетки или шкалы.
Рис. 8.5. Плоское зеркало 3 в сходящемся ходе лучей между объективом Об и окуляром Ок коленчатого визира
Если при этом остаточный параллакс превосходит допустимую величину, то допуск Az следует соответственно ужесточить.
Для задания всесторонне обоснованных допусков на изготовление к установку оптических деталей и узлов следует вычислить их значения ьсходя из всех основных требований к прибору, а в качестве окончательных допусков принять наиболее строгие из полученных величин. При этом необходимо учесть как технологические возможности производства, так и экономические соображения.
Пересчитав по формуле Ньютона величину Az в пространстве предметов и изображений, получим выражение (м) для так называемой «практической бесконечности» в пространстве предметов
гс0= 1,25 (£)ру (8.38а)
в пространстве за окуляром г>1,25(^. (8.386)
Здесь Dp и Dp — диаметр рабочею входного и соответственно выходного зрачка, мм.
При разработке конструкций приборов, включающих зеркально-призменные системы, а также при их сборке и юстировке, кроме того, необходимо учитывать как свойства самих зеркал и призм, так и влияние их подвижек (смещений и наклонов) на свойства оптических систем
в целом и в первую очередь на каче-
ство изображения. Любая отражательная призма представляет собой совокупность системы плоских зеркал и преломляющей плоскопараллельной пластинки, толщина которой определяется методом развертки. Прежде всего следует отметить, что любая система плоских зеркал безаберрационпа в любом ходе лучей, т. е. она не вносит никаких расчетных аберраций. Такие системы, вообще говоря, не требуют юсти
ровки, т. е. плоские зеркала можно устанавливать произвольно, не допуская лишь срезания рабочих световых пучков, если приемник изображения — экран, окуляр, щель имеет все подвижки необходимые для совмещения его с плоскостью изображения. На практике таков случай встречается редко, так как почти всегда приемная часть прибора конструктивно базируется определенным образом по отношению к проекционной его части. Тем самым задаются (нередко однозначно) также и Садр! для установки зеркально-призменных систем. Погрешности установки зеркал и призм по отношению к этим базам вызывают ряд существенных дефектов прибора, в первую очередь взаимную децентрировку линзовых частей оптической системы, между которыми зеркально-призменные элементы устанавливаются.
Рассмотрим три типовых случая — установку плоского зеркала, углового зеркала и зеркальной крыши в сходящемся пучке лучей. ’
Плоское зеркало. Расточки корпуса коленчатой трубы (рис. 8.5) базируют с одной стороны объектив, с другой — окуляр. Базой для установки плоского зеркала и являются оси этих расточек. В точке взаимного пересечения этих осей поместим начало О системы координатных осей хс, z0( направив ось перпендикулярно осям обеих расточек,
а ось zu — no биссектрисе угла между ними. В поминальном положении зеркала эга система осей для него является основной, при этом нормаль зеркала должна совпадать с осью г0, а его отражающая плоскость — с началом О системы осей, т. е. с точкой пересечения осей расточек.
При указанном номинальном положении зеркала 3 луч, совпадающий с оптической осью объектива Об, после отражения от зеркала будет совпадать с оптической осью окуляра Ок, благодаря чему система линз будет центрированной, как показано на рис. 8.5 штриховыми линиями при выпрямленном ходе лучей.
В действительности плоское зеркало будет иметь три погрешности установки; сдвиг отражающей плоскости вдоль нормали на величину Дг0, поворот вокруг оси х‘о на угол а0 п наклон вокруг оси у0 на угол 0П.
Каждая погрешность приводит к децеитрпровке линзовой системы, т. е. к взаимному наклону оптических осей объектива и окуляра (децентрировка первого рода) или же к их взаимному сдвигу (децентрн-ровка второго рода). Остальные три возможные подвижки, т. е. сдвиги в плоскости отражения вдоль осей х0 и //п, а также поворот вокруг сси г0 очевидно не будут действенными.
В табл. 8.3 перечислены дефекты, вызываемые действенными погрешностями установки зеркала и приведены расчетные формулы. Из таблицы видно, что каждая первичная погрешность, кроме взаимной децентрировкп частей оптической системы, между которыми зеркало находится, вызывает п другие существенные дефекты, ухудшающие качество изображения пли точность работы прибора. Степень влияния этих дефектов зависит от ряда конструктивных величин, в том числе от угла е наклона зеркала к оптической оси, расстояний I и (1р + /) от плоскости изображения до зеркала и соответственно до входного зрачка, величины линейного г/п и углового со поля системы, фокусного расстояния объектива и линейного увеличения Vp в зрачках.
Приведенные в таблице расчетные формулы позволяют решать как прямую задачу — по техническим требованиям к прибору определять допустимые величины любых из подвижек плоского зеркала, так и обратную — по наблюдаемому за окуляром дефекту при юстировке прибора определять величину и знак подвижки, необходимой для устранения этого дефекта.
Каждая первичная ошибка установки зеркала вызывает специфические дефекты системы. Например, сдвиг Д?о зеркала вдоль его нормали влечет за собой расфокусировку па оси (табл. 8.3, № 1), децентрировку второго рода (№ 5) и реп (№ 8); наклон зеркала на угол (30 вызывает наклон изображения и децептрнровку первого рода системы по горизонту и т. д. Однако некоторые дефекты появляются вследствие влияния двух или даже трех ошибок (см. № 1, б; 2; 4; 6; 7; 9), Следует подчеркнуть, что указанные ошибки взаимно пе компенсируются, а а как бы заслоняют друг друга. Так, например, если децептрнровка выходного зрачка (№ 6) вследствие ошибок а0 и Аг0 равны друг Другу, но противоположны по знаку, то между ними имеет место соотношение се0/р = Аг0 sin е0. Однако если зеркало расположено вблизи входного зрачка, т. е. 1р мало, то в этом случае даже при малом сдвиге зеркала Дг0 вдоль нормали будет незаметно допущен значительный угол его поворота, так как а0 — Az0 При 1р = 20 мм, е0 _ 45е будет се0 ~ 1р
~ 0,03 Az0, т. е. при сдвиге зеркала всего на 1 мм зеркало следует повернуть от правильного положения на угол 2\ При этом на оси системы появится значительная кома.
Т а б л и ц а 8.3. Дефекты оптической системы, вызываемые погрешностями установки плоского зеркала в сходящемся пучке лучей
Со
№ п/п Дефекты оптической системы Погрешности установки плоского зеркала
[% A Zq
1 Расфокусировка и параллакс сетки: а) на оси б) на краю Дгв с± 2//п01о Агг 2хпро cos е(! | Az = 2 Az0 coseG
2 Сдвиг изображения Д//и 2/а0 Дхи ~ 2/р0 cos 'A-z/jj -— 2 A2q sin *i
3 Наклон изображения — Тн. и = 20о sin t0 —
4 Децентрировка системы первого рода ас = 2а0 0c = 200 cos t?o --
5 Децентрировка системы второго рода — " c = 2 Аг i sin
зъо
Продолжение табл. 8.3
,\у П/П Дефекты оптической системы Погрешности установки плоского зеркала
«0 Ьо A?e
6 Децентрировка выходного зрачка 2/ \хр, = 2ZpP0Vp cos f0 &yp, = 2 Az0Vp sin F(,
7 Наклон визирной оси А Q 1 О’В. о — / — 2ОС0 'об 'об 0В. о — 2 f. f*0 cos e(l f 00 ав. о = 2 sin e(, /об
8 Рен 1 Aw Л Az0 —— — 2 —- cos e tg co Уп Уп
9 Разно масштабность изображения: а) в угловой мере б) в линейной мере Дсов ~ 2ctl( sin - сох / / \ X ( sec оз \ 1 1р / Дув == ДсоЕ (Z + Ip) sec2 со Acor = 2p0 cos e0 sin2 co X f { \ X ( sec co — \ / + Ip/ &yT = Лсог (Z + Ip) sec2 co Xcos — 2Az0 sin eu sin2 co
и призм в процессе пх гости-исключить заслонение одних
Рис. 8.6. Угловое зеркало с углом о между зеркалами 1 и 2 в сходящемся ходе лучей между объективом Об и окуляром Ок коленчатого
внзира
Если же зеркало расположено вблизи полевой диафрагмы, т. е. I мало,то даже при малом сдвиге зеркала вдоль нормали от прагмзпнего положения потребуется повернуть его на значительный угол для цен грирования изображения в полевой диафрагме (№ 2). При этом czG/ = ==• Дги sin £f). Из последнего соотношения видно, что в данной случае также возможно незаметное введение большого поворота зеркала и это приведет к значительной коме на оси.
Следовательно, при контроле зеркал ровкн необходимо следить за тем. чтобы погрешностей другими; особенно важно выявлять повороты и наклоны зеркал, т. е. ошибки а0 и рн, вызывающие децентрировку первого рода.
Угловое зеркало. В о гл и ч не ст плоского зеркала угловое «еркало имеет в сходящемся пучке лучей четыре действенные подвижки, так как смещение углового зеркала вдоль ею ребра и поворот вокруг ребра недейственны (рис. 8.6). В табл. 8.4 рассмотрены дефекты, вызываемые действенными погрешностями установки углового зеркала и приведены расчетные формулы Подвижки углового зеркала рассмотрены также в основной для него системе осей x0z/0z0, которая ориентирована так, что при номинальном положении углового зеркала ось г0 совпадает с его ребром, а оси х(; и — с особыми его направлениями. Одно из них параллельно биссектрисе угла между падающим и выходящим лучами 2о (по нему направлена ось п,.), а другое — перпендикулярно первому' (с ним совпадает ось х0).
Известны свойства указанных особых направлений [57, 73 |. Смещение углового зеркала вдоль оси на Ах0 вызывает только расфокусировку Лг~2 Axu sin о, наклон вокруг том же осп на угол а0 — только поворот изображения у — 2cct) sin о Смещение зеркала вдоль оси у0 на Ду0 дает поперечный сдвиг изображения Az; ~ 2 Ар0 sin о, а наклон вокруг этой же оси на угол ptJ вызывает лишь отклонение выходящего луча на угол р — 2f30 sin о.
По иному, чем в случае плоского зеркала, влияют и остальные подвижки углового зеркала Наименьшее число дефектов вызывают две еголодвнжки: наклон на угол <х0 дает только наклон изображения, а децентрировка системы при этом не нарушается, сдвиг зеркала вдоль осн вызывает лишь расфокусировку изображения (табл. 8.4, № I) и соответствен но реп (№ 8).
Смещение углового зеркала вдоль оси i/0 вызывает децентрнровку второго рода по вертикали и дает пять дефектов, правда, не очень существенных. Наиболее существенные семь дефектов обусловливает последняя четвертая подвижка — наклон углового зеркала вокруг оси z/0 на угол р(). При этом возникает децентрировка первого рода системы, в связи с чем ухудшаются качество изображения (вследствие комы па оси) и точность измерений (вследствие параллакса и разномасштабности).
Таблица 8.4. Дефекты оптической системы, вызываемые погрешностями установки углового зеркала в сходящемся ходе лучей
Ku п/п Дефекты оптической системы — Погрешности установки углового зеркала
«о 0о Л I/O
1 Расфокусировка изображения н параллакс сетки: а) на оси б) на краю Д?в — 2₽ог/п sin а | А? — 2 Ах0 sin о —
2 Сдвиг изображения кх = 2р0 f sin ° — ку = 2 Аг/у sin а
3 Отклонение визирной оси 1 Дх р ~ г = ' об = 2р„ sin <т 1 об а=_^_ = о Д^О sino /об 'об
4 Наклон изображения Y = 2а sin о — —
5 Децентрировка первого рода оптической системы ' Рс = 2р0 sin о
Продолжение табл. 8.4
Ко п/п Дефекты о‘ тической системы Погрешности установки углового зеркала
а0 Д Л"о Д.(/п
6 Децентрировка второго рода оптической системы ' 1 1 — — су -- 2 А//о sin о
7 Децентрировка выходного зрачка — Ахр/ — Рс/рУр = = 2р0/р1/р sin о ^Ур* р 2 Aw0Pp sin о
8 Рен — — Ах' Ах0 — 2 sin 0 0) Л п хп —
9 Разномасштабность изображения: а) в угловой мере 6) в линейной мере АсоЛ -- ~-2p0(sec X \ 1 -у / Р / X sin2 (о sin о L\y’ ДСО, XX COS-U) —— Л(о^ --- 2 Ai/0 sin о sin2 w
Таким образом, в системах, содержащих угловое зеркало в сходящемся пучке лучей, наиболее вероятно ухудшение качества изображения в направлении, параллельном ребру углового зеркала. Для сравнения отметим, что погрешности установки плоского зеркала (его поворот на угол а0 и наклон на угол р0), как было показано (см. табл. 8.3), приводят к ухудшению качества изображения по всем направлениям поля системы.
Следует указать еще иа одно существенное обстоятельство, встречающееся при сборке коленчатых труб. При рассмотрении влияния подвижек плоского и углового зеркал предполагалось, что оси расточек под объектив и окуляр в корпусе взаимно пересекаются в общей точке. В действительности же всегда имеется некоторая величина непересечен и я этих осей. В этом случае для компенсации сдвига изображения вдоль оси к (см. рис. 8.5) необходимо было бы наклонить на некоторый угол как плоское, так и угловое зеркало вокруг оси г/0. В результате появится дополнительная децентрировка первого рода системы и как следствие — кома па оси.
Таким образом, в обоих случаях погрешности механической обработки корпуса коленчатого визира нельзя скомпенсировать наклонами зеркал, а эти погрешности должны быть ограничены заданием соответствующих допусков па непересечение осей расточек, или же скомпенсированы взаимным сдвигом объектива и окуляра.
В визире с угловым зеркалом (см. рис. 8.6) невозможно скомпенсировать никакими поворотами зеркала (если угол о между зеркалами неизменный) также и отклонение угла между осями расточек под объектив и окуляр (в номинале он равен 180° — 2о). В этом случае необходимо регламентировать допуском величину угла между осями расточек корпуса.
Прямоугольная крыша. Такая зеркальная система дает полное обращение изображения и для этого часто она применяется. ЛАагрица действия крыши в параллельном пучке лучей; равна (отличаясь лишь противоположным знаком)-матрице действия эквивалентного плоского зеркала, перпендикулярного ребру крыши, поэтому влияние обоих поворотов крыши и в сходящемся пучке лучей будет аналогичным влиянию поворотов указанного эквивалентного зеркала (см. влияние погрешностей сх0 и Ро в табл. 8.3). Сдвиг ребра крыши в плоскости (см. рис..8.5) влияет аналогично сдвигу плоского зеркала вдоль его нормали на ту же величину.
В отличие от плоского зеркала крыша имеет четвертую действенную подвижку — сдвиг ее ребра перпендикулярно плоскости, задаваемой осями расточек корпуса под объектив и окуляр. На рис. 8.5 показано, что сдвиг ребра вызывает удвоенной величины поступательный сдвиг выходящего луча в том же направлении, но без удлинения его хода, т. е. без возникновения расфокусировки 173]. Таким сд^рэ^ крыши легко можно скомпенсировать имеющееся непересечение осей расточек под объектив и окуляр в корпусе коленчатого визира.
Таким образом, имеющимися у крыши четырьмя действенными подвижками-можно скомпенсировать любую < погрешность механической обработки; коленчатогожорпуса.-и получить щ результате центрированную систему.
Призмы с одним отражением (типа АР), с двумя отражениями (типа БУ) или с одним отражением и крышей (типа АкР) имеют на одну действенную подвижку меньше, чем исходные для них зеркальный*системы, за счет наличия дополнительной плоскопараллельной пластийки, рабочие грани которой должны быть установлены перпендикулярно 384
оптичёской оси системы. Это ограничивает рассмотренные выше возможности-компенсации ошибок, механической обработки корпуса подвижками указанных призм.
Пример расчета допусков на оптические детали артиллерийской панорамы
Применим приведенные выше формулы к расчету допусков для деталей оптической системы панорамы, включающей детали различных типов: преломляющие, отражающие, неподвижные и вращаемые.
Оптическая система панорамы имеет следующие характеристики: видимое увеличение Гт = 4х» диаметр входного зрачка Dp ~ 16 мм; пределы изменения углов — горизонтальных ф = 360°, вертикальных i = ±18°; точность установки углов не ниже Аф = At = + 0,001 рад. Основными оптическими деталями и узлами панорамы являются (ряс. 8.7): защитное стекло /, головная призма 2, компенсационная призма Дове 3, объектив 4, призма с крышей 5, пластинка с сеткой б, линзы окуляра 7 и 8. Наименьший световой размер всех поверхностей и всех деталей примем равным 16 мм. Положение первых трех деталей 1—3 при работе панорамы может изменяться по отношению к последним подвижным деталям 4—7. При визировании по высоте головная призма/ поворачивается вокруг горизонтальной оси на угол tn = t/2 — ±9°, а при панорамировании по горизонту головка, заключающая в себе детали 1 и 2, вращается вокруг вертикальной оси на неограниченный угол ф и одновременно вокруг той же оси и в том же направлении, но на половинный угол ф/2 вращается также компенсационная призма Дове 3. Это необходимо учитывать, когда задаются допуски на оптические детали, так как при взаимном развороте деталей изменяется сумма ошибок векторного характера.
Панорама является серийным прибором. Ее оптическая система включает в себя три сложные в изготовлении призмы: Дове, прямоугольную с крышей и головную. Поэтому в данном случае можно задать допуски, несколько превосходящие критерий Рэлея, и принять за окуляром допустимый астигматизм до Адоп =0,45 дптр, допустимый хроматизм ДО — 0,3 .
В случае пересчета этих допусков в волновую меру в пределах зрачка глаза наблюдателя, являющегося рабочим входным зрачком панорамы, при условии, что £>з г — 2 мм, a D'p = 4 мм > D3 г, получим:
1) допуск на астигматизм, выраженный допустимой разностью стрелок выходящего волнового фронта с радиусом кривизны (в м) а
(A/it!)n =.= 0,5АДОП = 0,5-0,45 0,2 мкм;
2) допуск на хроматизм, выраженный линейным смещением волновых фронтов по краю рабочего пучка лучей для линий F'и С', = 0,2 мкм, что вдвое больше допустимого по формуле (8.5).
В волновой мере оба допуска оказались примерно равными по величине и превосходящими критерий Рэлея, поэтому качество изображения в панораме уже может заметно отличаться от идеального.
В пределах светового размера выходного зрачка D'p = 4 мм допустимый астигматизм выражается разностью стрелок выходящей волны A/ifi = 0,8 мкм или разностью числа полос AWB ~ 3.
13 в. А. Панэв и др, 385
Принятые приборные допуски следует распределить между деталями в зависимости от требуемой точности их изготовления. Влияние каждой первичной ошибки, вызывающей астигматизм, легко оцепить
Рис. 8.7. Оптическая система артиллерийской панорамы
по значениям передаточных отношений, которые равны обратным величинам коэффицентов g? и G? из графиков, приведенных на ри<Г. 8.2, или в табл. 8.4. Для всех нормально или почти нормально расположен-386
ных преломляющих поверхностей g=~2nG- oo, а передаточные отношения равны g”1 = 0,5 и G-1 — 0.
Для наклонных поверхностей эти передаточные отношения зависят как от типа рабочих поверхностей (преломляющие, отражающие), так и от их наклона. Для отражающей гипотенузной грани головной призмы 2 (рис. 8.7) при угле ее наклона е= 45° (среднее положение призмы) g = G = 0,5 и соответственно g~* = G"1 — 2.
Для преломляющих граней прйзмы Дове (е = 45е) g = G = 1,6 и g~* = G”x = 0,6. Для ее отражающей гипотенузной грани (е ~ 73°) по формулам (8.166) и (8.17) получим g — 1,14; G = —К— — —Ы?..
0,067 и g"1 = 0,9; G"1 = 15. — 1 4,252—1
Для граней крыши 5 (е = 60е) имеем g = 0,7; G = 0,2 и g-1 = 1,4; G'1 = 5. Для ее преломляющих граней, а также для внешних поверхностей линз объектива 4 и линз 7, 8 окуляра можно считать g — 2, G —оо и g-1 — 0,5; G"1 = 0. Эти значения справедливы в пределах рабочего пучка лучей, который для призмы 5 имеет сечение примерно вдвое меньше, а для линз окуляра 7, 8 даже вчетверо меньше, чем для деталей 1—4.
Можно заметить, что величина передаточного отношения G"1 = 15 для гипотенузной грани призмы Дове многократно превосходит значения всех предыдущих передаточных отношений, значит сферичность N этой грани призмы Дове наиболее сильно влияет на качество изображения всей оптической системы.
На рис. 8.7 в прямоугольниках указаны полученные передаточные отношения для всех рабочих оптических поверхностей, граничащих с воздухом, в верхней части их дана величина G"1, в нижней— величина g"\ С учетом величины передаточных отношений, а также местоположения деталей в ходе лучей будем располагать все детали в порядке уменьшения их влияния на качество изображения системы.
На рисунке показан также пучок лучей, образующий изображение осевой точки в поле зрения окуляра. Поскольку требования к поверхностям и деталям пропорциональны ширине этого пучка, то ясно, что на качество изображения системы наиболее сильно будут влиять детали от первой до четвертой включительно. Из них самой ответственной, безусловно, является призма Дове, так как у нее одна наклоненная под очень большим углом (е ~ 73°) внутренняя отражающая плоскость и две наклонные (в = 45°) преломляющие плоскости. На втором месте будет головная призма 2— у нее две преломляющие поверхности, как у защитного стекла / и объектива 4, и наклонная внутренняя отражающая плоскость. На третье место следует поставить не объектив 4, хотя он и находится в более широком рабочем пучке лучей, а призму с крышей 5, имеющую две наклоненные под углом & = 60° внутренние отражающие грани крыши, погрешности которых сильно влияют на качество изображения. Далее расположатся объектив 4, защитное стекло /, глазная 8, коллективная 7 линзы окуляра и на самом последнем месте пластинка сетки 6, которая совпадает с плоскостью изображения, где ширина световых пучков близка нулю.
Итак, располагая детали и узлы оптической системы в порядке уменьшения их влияния на качество изображения, запишем их в следующей последовательности — 3, 2, 5, 4, 1, 8, 7, 6.
Примерно в тон же последовательности снижаются требования к категориям качества стекла оптических деталей и повышаются требования к чистоте полированных поверхностей, а также к чистке нх 13* 387
при сборке. Указанные требования зависят и от длины- хода лучей в деталях.
Полученная запись расположения деталей в порядке уменьшения их влияния на качество изображения оптической системы может помочь конструктору при проектировании оправ и устройств для закрепления и юстировки оптических деталей, обращая его особое внимание на те из них, которые более всего портят качество изображения. Технологу такая запись последовательности деталей позволяет рациональнее построить процесс сборки оптического прибора, обеспечивающий, в первую очередь, получение высокого качества изображения; наметить эффективную методику контроля качества оптических узлов, поступающих на общую сборку прибора; предложить быстрый способ определения местоположения дефектной детали или узла в сложной системе, имеющей дефекты качества изображения; оперативно провести инспекцию правильности задания допусков на оптические детали.
При изготовлении панорамы особое внимание следует обратить на то, чтобы избежать деформаций призмы Дове, которая легко изгибается при закреплении в оправе и в процессе юстировки, т. е. при ее наклонах с помощью регулировочных винтов для установки отражающей грани призмы параллельно оси вращения. По формуле (8.9) легко найти величину предельно допустимой стрелки прогиба отражающей грани призмы Дове из условия, что приборный допуск ДУВ = 3 целиком отпущен на одну лишь эту грань. Даже при этом условии для нее получим всего лишь AN = gon = 1,14*3 ~ 3,5 нлн менее одного микрометра.
Переходя к расчету допусков на детали панорамы, примем передаточное отношение для нормально расположенной преломляющей поверхности, равное g"1 = 0,5, за единицу. Удваивая ранее полученные величины передаточных отношений, получим нормированные передаточные отношения, которые в дальнейшем будем обозначать буквой «£» с соответствующим индексом.
В панораме имеется следующее количество типовых поверхностей, вызывающих астигматизм:
1) двенадцать преломляющих, нормальных к оси пучка (не считая пластинки 6 сетки, для которой допуски свободные, так как сечение световых пучков в ее плоскости близко к нулю) с = 2/gu — 1;
2) одна внутренняя отражающая, наклоненная под углом & — 45° с двумя равными передаточными отношениями k2 = 2/gon = 2/Gon ~ 4;
3) две преломляющих, наклоненных под углом е— 45°с двумя равными передаточными отношениями k3 — 2/gu = 2/Gu — 1,2;
4) одна внутренняя отражающая, наклоненная под углом е= 73° с = 2/gon = 1,8 и k5 = 2/Gon = 30;
5) две внутренних отражающих, наклонных под углом в= 60° с h 2/gon = 2,8 и k-t - 2/Gon = 10.
В соответствии с формулой (8.7), подставляя полученные данные, найдем величину единичного допуска для нормальной к оси внешней преломляющей поверхности
ДуУед = /2A.Vd (+ 2fei + 4fe2 + kl + kl + 2k% + 2fe?)-"’5 = = /2 3 (12-1 —|- 2-42 —|- 4-1,2s + 1,8s + 30s + 2'2,82 2’102)*2'’5 ==
= /2-3 (1169)-°'6 = 0,1225 2=0,12.
Таким образом, для всех нормально стоящих внешних преломляющих поверхностей волновой допуск на астигматизм в пределах осевого пучка лучей составляет ДМед — 0,12, для гипотенузной грани призмы 2, он будет вчетверо больше, т. е. составит AV = 0,49, для входной и выходной грани призмы Дове ДМ — 0,15, а для ее отражающей грани АV-- 0,22 на цилнндричность и ДМ = 3,7 — на сферичность. После умнбжёиия этих волновых допусков на соответствующие коэффициентыполучим допуски на цилнндричность и сферичность поверхностей, одинаковые по величине для всех деталей в пределах сечения осевого пучка лучей. Например, для отражающих граней головной призмы 2, призмы Дове 3 и граней призмы с крышей 5 получится АА2о = 0,5-0,49 - 0,25 - Л'2О; АА30 - 1,14-0,22 - 0,25 и А30 =-= у^3,7 = 0,25. Примерно такой же величины допуски получатся и для всех преломляющих поверхностей. Например, для входной и выходной граней призмы Дове будет ААЗП — 1,6-0,15 — 0,25 = Азп.
Аналогично для допуска на угловой хроматизм каждой детали, вызывающей этот дефект (их в панораме имеется десять) по той же формуле (8.7) найдем (Аог,с,) ед ~ К 2-0,3' • 10"0,5 — 0,14'.
Переходя непосредственно к расчету и заданию допусков на отдельные детали панорамы, необходимо учесть все основные требования, предъявляемые к ним. Сюда относятся требования к качеству изображения, точности работы прибора, взаимозаменяемости сменных и запасных частей, а также к технологии изготовления, сборки и контроля деталей и экономические требования. Целесообразно было бы рассчитать допуски, исходя из каждого из указанных требований, и в качестве окончательного допуска принять наиболее строгий из них. Обычно учитывают лишь некоторые, наиболее важные в каждом случае, требования, что ускоряет и упрощает расчет. Рассчитаем допуски для всех деталей оптической системы.
1. Защитное стекло из стекла К8 (пе ~ 1,5; ve ~ 64; АА8 = 0,12;
= 0,14). Для плоскопараллельного защитного стекла необходимо указать W, ДМ, 0, /т1п н &" (предел разрешения в угловых секундах).
По формулам (8.17), (8.11) и (8.12) найдем М = оо; ДМ ~ 0,25; 9 = 4'.
Допуск на сферичность поверхностей определим также из допустимой фокусности /min защитного стекла, которое в этом случае действует как слабая одиночная линза с тем же фокусным расстоянием. Оиа вызывает хроматизм положения величины ДНр,с, = h/v, где h — стрелка выходящего сферического волнового фронта, а также расфокусировку изображения и параллакс. Ограничивая хроматизм в пределах рабочего пучка величиной Д/i^,^., С 0,1 мкм, для допустимой фокусности
Dp Dp 82-10“3
найдем /шш = = 8bhF,c,v = 8-0,1-10 3-64 = 1,25М’
Это очень большая фокусность, которая хотя и не вызывает заметного хроматизма изображения, но недопустима, если требуется, чтобы стекла были взаимозаменяемы, т. е., чтобы при замене одного стекла (разбитого, поцарапанного) другим из ЗИПа в приборе не возникло нн расфокусировки, ни параллакса, превосходящих установленные допуски. Глаз не замечает расфокусировки за окуляром панорамы в 0,2 дптр, что соответствует практической бесконечности 2^ ~ 5 м,
вычисленной по формуле (8.38, 6). Допуская для защитного стекла фокусность / не менее величины практической бесконечности
в пространстве предметов, по формуле (8.38, а) найдем допуск fmin :> = 1,25(0р)2 = 1,25-82= 80 м.
Если защитное стекло имеет форму двояковыпуклой или двояко-
162-103’п 8-80-103Х/2
вогнутой линзы с поверхностями равной кривизны, то получим допуск h Dp
на сферичность ее поверхностей N — —- = -------—
Л/2 о/ mln^/2
Фокусность защитного стекла вызовет угловой параллакс сетки , £>/>3440 16-3440
в пространстве предметов менее и — -г-..... -- = „ 0,7 .
/mln 10° оО- 10й
Ужесточая допуск, ограничим фокусность величиной fmin — 100 м.
Учтем, что при визировании по высоте под предельными углами е— ±18° защитное стекло работает как наклонная пластинка. Определим допуск на сферичность по формуле (8.17). Он будет равен N = = Ge AjVb = g(> ctg2 e AjVb = 2 ctg2 18°-0,12 2,4. Ввиду малого веса
влияния погрешностей защитного стекла в общей сумме погрешностей всех деталей, можно почти без всякого ущерба для качества изображения панорамы расширить полученные расчетом допуски и задать N = = 2 и AV= 0,5.
Проверим допустимость клиновидности защитного стекла 0=4' с точки зрения заданной точности измерения углов панорамой. Клино-видность защитного стекла в вертикальной плоскости при качаниях головной призмы вокруг горизонтальной оси вызовет ошибку измере-п2 — 1 ния угла At, которая равна по формуле (8.21) At ~ Аое ——------ X
— 0,040 или At — 0,16'. Клиновйд-плоскости вызовет увод визирной , оси
X 0 tg2 е = 7 1 0 tg2 18°
ность стекла в горизонтальной по вертикали тоже очень малой величины, которая определится с помощью формулы (8.31). Она равна Аае ~ 0,06х.
Таким образом, клиновидность 0=4' вполне допустима и из требований точности измерения углов,
В соответствии с ОТУ (см. табл. 21.2) предел разрешения для телескопических систем с размером выходного зрачка 3,5 мм и больше 35
определяется в угловых секундах по формуле е" = k где Гт — ви-1 т
димое увеличение телескопической системы, k — коэффициент, учитывающий ее конструктивную сложность и выбираемый в пределах от 1,05 до 2,2. Для защитного стекла, беря £= 1, получим 8" 120"
что ниже теоретического предела е" = ~[4~~
Таким образом, окончательно устанавливаем следующие
iV = 2; АД/ = 0,5; 0 = 4'; /т1п = 100 м; е" = 8,75".
2. Головная призма из стекла К8 (пе 1,5; ve — 64,1;
= 0,12; АД/ро = 0,49; AoF,c, = 0,14). Для прямоугольной
= 8,75",
допуски
A/VBI1 -призмы необходимо указать следующие допуски: Nn и A7Vn — для преломляющих граней, No и A7V0 — для отражающей гипотенузной грани, л — на пирамидальность, А,ив —для отклонения прямого угла, —для разности углов 45° и предел разрешения е".
Для преломляющих граней призмы можно задать те же допуски, что и для защитного стекла N = 2; AN = 0,5. Для отражающей грани по формулам (8.18) и (8.11) получим Лг = 0,5*0,49= 0,25 и АЛГ— = 0,25.
Клнновидность развертки призмы 0 имеет две взаимоперпендикулярные составляющие: 0Л — клнновидность за счет пирамидальное™ л и 0с клнновидность за Лет ошибок углов. Принимая допуск на клнновидность развертки призмы 0=4', и разделяя его поровну между составляющими получим 0Я =
Рис. 8.8. Клиновид-ность развертки прямоугольной призмы в плоскости главного сечения Ос вследствие неравенства острых углов Л и В и в перпендикулярной плоскости 0л за счет пнрамидаль-ности я
'45°
Из развертки прямоугольной призмы (рис. 8.8) видно, что ее клиновидность в плоскости главного сечения определяется разностью острых углов А + В ~ 0с = о45о, т. е. не зависит от величины угла С, а клиновидность 0Л в перпендикулярной плоскости связана с пирамидальиостыо соотношением 0Я = Р^2л;, где л — угол между гипо-теиузной гранью призмы и ребром противолежащего угла С. Для допусков получим соответственно л= 0Я 2'; 645О — 0с =
— 3'; Д90е—свободный, В последнем слу* чае зададим легко выдерживаемый при изготовлении призмы Д90о — 10'.
При визировании по высоте под углом i=±18° головная призма качается лишь на половинный угол, поэтому клиновидность ее.развертки вызовет ошибки, примерно вчетверо меньшие, чем давала клиновидность защитного стекла. Предел разрешения головной призмы можно задать тот же е"=8,75".
Окончательно зададим допуски: 7Vn = 2
A/Vo = 0,25; л = 2'; б = 3; А90О = 10' и s" = 8,75".
3. Компенсационная призма Дове из стекла К8 (he = 1,5; —
= 64,1; А^вп — 0,15; АА\)0 = 3,7; Ааг,с, = 0,14'). Призма Дове представляет собой усеченную прямоугольную призму, поэтому для иее следует указать те же допуски, что и для головной призмы. Для преломляющих и отражающих граней по формулам (8.18) и (8.11) най-дем Л'п = 1,6-0,15= 0,25= A<Vn; = -1 3,7 = 0,25 и AW =
1 о
= 1,14-0,22— 0,25. Ввиду малого влияния ошибок преломляющих граней по сравнению с ошибками отражающей грани можно без ущерба для качества изображения расширить допуски до Nn = AATn — = 0,5.
В соответствии с ГОСТ 2.412—68 допуск N на сферичность задается вдоль короткой стороны рабочих поверхностей, т. е. в нашем случае в пределах ширины пучка 16 мм. Длина отражающей грани призмы Дове в 4,23 раза больше ее ширины, поэтому допуск на ее сферичность вдоль длинной стороны будет в (4,23)2 раза больше полученного нами допуска и составит (4,23)2 0,25^4,4. Допустимый радиус кривизны
A;Vn = 0,5; NQ = 0,25;
поверхности при этом должен быть не менее
162ГО-«
8-0,67-10-3
км 0,5 км.
Допуски на ошибки углов и пирамидальность призмы Дове, исходя из требований качества изображения, т. е. из допустимого хроматизма Дб = 0,14', получатся несколько более строгими, чем для головной призмы, так как входная грань данной призмы наклонена под углом 45
Рис. 8.9. Влияние пира ми дальности призмы Дове на направление выходящих лучей
и коэффициент Q = 0,6 (см. рис. 8.3 и табл. 8.1). Поэтому найдем Ос = 0Л = 2'.
Разность углов 64Г)О в главном сечении призмы Дове не влияет на точность работы панорамы, так как в процессе юстировки призмы дополнительным наклоном ее отражающей грани к собственной оси вращения влияние этой ошибки автоматически компенсируется.
Отклонение же лучей в плоскости, перпендикулярной главному сечению призмы, за счет пирамидальности юстировкой не может быть скомпенсировано, так как ее отражающая грань параллельна плоскости отклонения лучей, вследствие чего при панорамировании возникнут ошибки переменной величины как при измерении горизонтальных, так и вертикальных углов. Это связано с тем, что призма Дове поворачивается на угол, вдвое меньший угла поворота головки. Рассчитав допуск на пирамидальность призмы, исходя из до-
пустимого хроматизма, в этом случае получим л = °л 2' , ы й
— ~~ — =1,4. Необходимо определить,
К 2 К2
какой величины погрешности измерения углов эта ошибка вызовет. Ход луча вне главного сечения клина с углом 0Л найдем с помощью матрицы
действия преломляющего клина по формуле (8.27) с учетом формулы (8.31).
Клиновидность развертки призмы Дове за счет пнрамидальности 0л на рис. 8.9 показана условно ортом ркл ребра клина, совпадающим с входной гранью и направленным так (вершина пирамиды расположена за плоскостью рисунка), что этот угол положителен. Падающий луч (орт А — —k) и отражающая грань призмы параллельны оси г. Направление выходящего луча найдется из выражения
А — М к л А = Л4кл
где /щ3, /»аз, т33 — третий, шестой и девятый элементы^ матрицы
Из рис.
8.9 для орта р*л имеем рКл =
Подставляя
элементы из ф°РмУЛы (8.27) и преобразуя, найдем
Видно, что лучи, выходящие из призмы Дове, вследствие пирами-дальности отклоняются в плоскости главного сечения на весьма малый ф3 ф
угол ct ~----—, а в перпендикулярном направлении на угол р •
г *
Для величины угла поворота ф луча вокруг ребра по формуле (8.31) при пе 1,52 получим ф = —О,890Я1 а из допуска на хроматизм 0Я = = 2' найдем ф = — 0,89-2' = —1,8'.
Такое отклонение луча — оно непосредственно входит в ошибку горизонтального и вертикального углов — следует считать недопустимым, поскольку суммарная погрешность панорамы не должна превышать 0,001 рад. Ужесточая допуск вдвое, получим для призмы Дове обычный допуск на пирамидальность я — 40".
Окончательно зададим следующие допуски для призмы Дове: Nn = 0,5; A;Vn - 0,5; No == 0,25; AjV0 = 0,25; я = 40"; = 2';
Д90о = 10'; e" - 9".
4. Первая линза объектива из стекла К8 (/' = 40 мм, пе = 1,5; \ = 64; = 0,12; = 0,14' или 0,08 мкм.
Для склеенной линзы необходимо указать допуски /Уп, ДУП (для внешней поверхности), УУСкл, АЛ^скл (для склеиваемой поверхности) и с на децентрировку. Для внешней поверхности зададим те же допуски, что и для защитного стекла 7Vn = 2; ДУУП = 0,5. Для склеиваемой поверхности их можно несколько расширить до ;VCKJI = 3 и АУСКЛ = ОД Допуск на децентрировку обеих линз объектива по формуле (8.15) с = Др,_, %- == 0,08-10-3^^ ~ 0,02 мм.
1 ь Up о
5. Призма с крышей из стекла К8 (пе ~ 1,5; ve=64; ДУВП — 0,12; A7VBO = 1,2; и А#во = 0,34, = 0,14', угловое увеличение для
призмы 2х). Для данной призмы следует задать допуски Л'п, ЛУП для преломляющих граней, 7V01 A7V0 — для отражающих граней крыши, л, S.f-.c, Ду0о, Дкрш и е .
На преломляющие поверхности аналогично предыдущему, ио учтя, что нх световой размер вдвое больше рабочего сечения пучка, зададим Nn = 3, AiVn — 1- Для отражающих граней крыши по формулам 48.18) и (8.11) найдем ~ 1, AjV0 = I-
Под пирамидальностью призмы с крышей следует понимать разворот ребра крыши, т. е. неперпендикулярность этого ребра по 393
отношению к ребру противолежащего прямого угла. Найдем связь между указанным разворотом ребра крыши и кли нови дн остью раз-
вертки призмы.
В призме AkP — 90° номинальной формы (рис. 8.10) ребро крыши направлено по орту р0, который совпадает с плоскостью рисунка. Осевой луч, идущий по орту А и перпендикулярный_входной грани, после
отражения от крыши, очевидно, выйдет по орту Aq, который тоже -перпендикулярен выходной грани.
Если ребро развернуто на угол пирамидальности я, то его орт запишется так: р = sin ш + —==: cos л/-— cosn/г. Для орта А" на-
/2 /2
правления луча, отраженного от крыши, пользуясь матрицей по форму-муле (8.28), получим
Таким образом, при развороте ребра крыши развертка призмы становится как бы клиновидной, причем угол клина 0 = ]f 2л, а ребро его
примерно параллельно оси у. По аналогии с прямоугольной- головной призмой, зададим
Рис. 8.10. Влияние пирамидальности (разворота ребра) призмы с крышей на направление выходящих лучей
на данную призму следующие допуски л == — 4' и 64-о = 6'.
По формуле (8.14) на угол крыши полу-читси весьма строгий допуск Акрит ~ 2". С учетом этого следует проверить допуски Nq и ДУ0 на неплоскостность граней крыши, так как
при наличии неплоскостности неопределенным становится само понятие «угол крыши». Полагая
радиус кривизны грани крыши равным /?Кры, н а идем, ч то у гол между к а сател ь н ы мн к ее крайним точкам составит величину 6 =•-где / — ширина грани крыши. В слу-16
чае панорамы I — —— ~ 11 мм. Допуская 6 с 2
С 0,5", для минимального радиуса кривизны
крыши
найдем
Якрш - tgg
~ 4 км. В поло-
сах эта величина составит всего N = 0,01 полосы, что практически невыполнимо. По*виднмому, следует задать N и ДА7 не более 0,05.
Таким образом, получим Nn — 3; AWn = 1; JV0 0,05; ДЛ?0 ~ = 0,05; л — 4'; = 6х; ДУ0О == 1 О'; Дкрш = 2"; в" = 35". Невысокая
разрешающая способность данной призмы связана с тем, что ее величина ограничивается шириной нормальной проекции каждой грани крыши на сечение пучка лучей.
6. Заготовка сетки. Допуски на преломляющие грани и на клинови дность свободные, обычно задают легко выполнимые на производстве N ~ 10; ЛУУ = 2; 0 = 10'. Требуется особая чистота полированных поверхностей Р = 1—20 (/'к = 20 мм),
' '7.-Линзы окуляра.Допуски для линз окуляра также получаются широкие, т. е. N н AW могут быть в 16 раз больше, чем для линз объектива, так как для окуляра отношение светового размера к диаметру рабочего пучка в четыре раза меньше. Зададим легко выполнимые и не затрудняющие склейку окулярных линз допуски N = 5; AW — 0,5. Допуск на децентрировку линз окуляра по формуле (8.15) получится с 0,05 мм.
Литература: [34, 35, 40, 41, 53, 57, 60, 64, 69, 71, 73, 74, 81, 84, 89, 94, 95, 96, 101].
ГЛАВА 9 методика структурного анализа МЕХАНИЗМОВ ПРИБОРОВ
ОБЩИЕ СВЕДЕНИЯ
Точность, надежность функционирования приборов и технологичность их конструкций существенно зависят от структурных параметров механизмов. Рациональные структурные параметры повышают точность н надежность функционирования механизмов при существенном снижении трудоемкости их изготовления. Выбирать такие параметры во время проектирования механизма можно только по результатам структурного анализа его функциональной схемы. Поэтому структурный анализ механизмов все шире внедряется в современную практику проектирования механизмов приборов, способствуя повышению качества и эффективности проектных работ.
Основные определения
Механизм — это замкнутая (контурная) кинематическая цепь, целесообразное движение которой относительно ее неподвижного звена (стойки механизма) однозначно определяется заданными законами движения ведущих звеньев.
Совокупность звеньев, соединенных шарнирами образует кинематическую цепь. Шарниры состоят из кинематических пар, число которых в шарнире определяют по формуле
Рш ~ т — 1,
(9.1)
где рш — число кинематических пар в шарнире; т — число звеньев, которое соединяет шарнир.
Таким образом, кинематическая пара — это простейшее соед и пение двух звеньев, допускающее их относительное движение. Способ соединения звеньев кинематической пары накладывает ограничения па относительное движение каждого звена пары; эти ограничения называют связями пары. Число связей — от единицы до пяти, поэтому все кинематические пары разделяют на пять классов по числу связей, налагаемых на относительное движение их звеньев. Конструктивные схемы кинематических пар в зависимости от их классов показаны в табл., 9.1,
Кинематическая цепь, звенья которой образуют замкнутый контур, является замкнутой (контурной) цепью. В общем случае^звенья замкиу-ЗЯ6
Таблица 9.1. Конструктивные схемы кинематических пар
Литейные стали .................................... 694
Сплавы алюминиевые для холодной обработки......... 695
Сплавы алюминиевые литейные ....................... 696
Сплавы алюминиевые спеченные ................. . 702
Сплавы цветные литейные.............................. —
Нейзильбер .............................. ........ —
Титан и его сплавы ................................ 703
Пластические массы ................................ 704
Смазки н масла .................................. 720
Замазки ............................................. “
v Адсорбенты для осушки приборов ...................... 726
Список литературы ....................................... 726
ИБ № 1893
Виктор Алексеевич ПАНОВ, Марк Яковлевич КРУГЕР, Василий Васильевич КУЛАГИН, Георгий Васильевич ПОГАРЕВ, Александр Матвеевич ЛЕВИНЗОН, Израиль Моисеевич ДОЛИНСКИЙ, Николай Александрович МИХАЙЛОВ, Бенедикт Григорьевич РЕЗНИЦКИЙ, Михаил Иванович КАЛИНИН, Рэм Михайлович РАГУЗИН
СПРАВОЧНИК КОНСТРУКТОРА ОП ТИ КО-МЕХА Н И Ч ЕС КИ X ПРИБОРОВ
Редакторы М. Г. Оболдуева и И. А, Денина Художественный редактор С. С. Венедиктов Технические редакторы; Л. В. Щетинина, Т. Н. Витошикская
Корректоры: Т. Н. Гринчук, И. Г. Жукова Переплет художника С. И. Знначева
Сдано в набор 03.03.80. Подписано в печать 24.10.80. М-40237.
Формат 84Х108*/а2. Бумага типографская № >.
Гарнитура литературная. Печать высокая. Усл. печ. л. 39,06. Уч.-нзд. л. 47,78. Тираж 25000 экз. Заказ 100. Цена 2 р. ВО к.
Ленинградское отделение издательства «Машиностроение» 191065, Ленинград, Д-65, ул. Дзержинского, 10
Ленинградская типография № 6 ордена Трудового Красного Знамени Ленинградского объединения «Техническая книга» нм. Евгении Соколовой Союзполнграфпрома при Государственном комитете СССР по делам издательств, полиграфии и книжной торговли.
193144, Ленинград, С-144 ул. Моисеенко, 10.
тон цепи могут образовать не один, а несколько замкнутых контуров, число k которых определяют по формуле
& = н, (9.2)
где k — число контуров в замкнутой кинематической цепи; п — число звеньев замкнутой цепи без учета ее стойки; р — число пар.
Кинематические цепи, равно как и механизмы разделяют на плоские и пространственные. К плоским цепям (механизмам) относят цепи (механизмы), все точки звеньев которых описывают траектории, лежащие в одной или параллельных плоскостях. К пространственным — цепи (механизмы), все точки звеньев которых описывают неплоские траектории или траектории, расположенные в пересекающихся плоскостях. Разделение механизмов на плоские и пространственные — относительно и имеет смысл лишь для теоретических исследований. В действительности из-за неизбежных технологических погрешностей изготовления звеньев, их упругости и других причин все реальные механизмы — пространственные.
Основное назначение механизма — это преобразование движения по наперед заданному закону, представляющему собою уравнение, связывающее текущие координаты перемещений ведомого и ведущего звеньев механизма между собою. Точное выполнение данного уравнения является главной задачей механизмов приборов. Успешное решение ее во многом зависит от того, насколько правильно при проектировании механизма выбраны его структурные параметры, т. е. число подвижных звеньев и число кинематических пар с указанием их класса.
Правильно выбрать структурные параметры механизма во время его проектирования можно лишь по результатам структурного анализа схемы проектируемого механизма.
Избыточные связи и местные подвижности в механизме
При анализе структуры механизмов могут встретиться степени свободы и условия связи, которые не влияют на характер движения механизма в целом. Такие степени свободы — создают в механизме избыточные — местные подвижности, а условия связи — избыточные связи в механизме.
Избыточные связи н местные подвижности влияют иа точность и надежность функционирования механизмов, но степень их влияния различна. Избыточные связи порождают статическую неопределимость механизма, вследствие чего его сборка без объемных деформаций невозможна. Последние увеличивают напряжение в звеньях н тренне во время работы механизма, и все это отрицательно сказывается на точности его функционирования. Повысить точность и надежность функционирования такого механизма можно только за счет доводок и специальных регулировок при его изготовлении, следовательно, избыточные связи всегда приводят к повышению трудоемкости изготовления.
Местные подвижности в механизме не влияют на его статическую неопределимость. Их влияние на точность функционирования механизма (следовательно, и на трудоемкость изготовления) — второго порядка малости по сравнению с влиянием избыточных связей. Местные 398
подвижности в механизме вызывают нейтральные звенья 1 и кинематические пары более высокого класса чем это необходимо для сборки и функционирования механизма.
Избыточные связи в механизме вызывают избыточные звенья и кинематические пары более низкого класса, чем это необходимо для работы и сборки реального механизма без объемных деформаций.
Конструирование механизмов без избыточных связей и местных подвижностей является сложной задачей, так как выявить наличие избыточных связей и местных подвижностей в проектируемом механизме можно только по результатам структурного анализа, выполняемого в процессе проектирования механизма.
МЕТОДИКА СТРУКТУРНОГО АНАЛИЗА
Проектирование механизма начинается с разработки его функциональной схемы, во время которой конструктор анализирует ряд вопросов. Чтобы правильно выбрать структурные параметры механизма, нужно сделать структурный анализ его функциональной схемы:
1) выявить наличие в схеме проектируемого механизма избыточных связей и местных подвижностей;
2) установить причину их возникновения;
3) определить число и место расположения избыточных связей в механизме;
4) устранить избыточные связи в проектируемом механизме, а если это не удалось, то изыскать возможность уменьшения их числа.
Для выполнения перечисленных работ нужна методика структурного анализа, которая должна удовлетворять следующим требованиям:
1) учитывать характер относительных движений сопрягаемых звеньев в каждой кинематической паре в зависимости от ее класса и вида;
2) давать правильный результат структурного анализа независимо от наличия избыточных, в частности нейтральных звеньев в механизме;
3) раздельно выявлять избыточные связи и местные подвижности в механизме;
4) выявлять место расположения избыточных связей и местных подвижностей в механизме;
5) установить число избыточных связей и местных подвижностей в механизме;
6) установить причину возникновения выявленных избыточных связей и определить возможность ее устранения.
Разработанная методика базируется на следующих основных положениях.
1. Все реальные механизмы — пространственные;
2, Любой механизм без избыточных связей собирается без объемных деформаций даже тогда, когда линейные и угловые размеры его звеньев имеют значительные отклонения от номиналов;
3. Сборка одного пространственного замкнутого контура без объемных деформаций требует в совокупности для всех кинематических пар контура шесть независимых движений; в числе этих движений должны быть три поступательных перемещения по трем взаимно перпендикуляр
1 Т. е. такие избыточные звенья, рабочее движение которых сопровождается дополнительной подвижностью, не искажающей основной характер рабочего движения. Нейтральные звенья не вызывают избыточных связей в механизме.
ным направлениям г, у, г, и три поворота <рх, фу, <рг вокруг тех же направлений.
При сборке механизма его звенья могут быть состыкованы не только за счет поступательных перемещений, но и за счет поворотов. Поэтому поступательное перемещение звена в момент сборки механизма может быть заменено поворотом его и сопрягаемого с ним звена вокруг осей, перпендикулярных направлению поступательного перемещения. Нужно только проверить, имеется ли в анализируемом механизме такое звено, поворот которого вокруг соответствующей оси компенсировал
Рис. 9.1. Схема сборки параллелограмма, у которого шатун меньше стойки
бы отсутствующее поступательное смещение сопрягаемых звеньев в нужном направлении и без нарушения этой подвижности в мертвых точках механизма.
Пример. В реальном параллелограмме длина шатуна 2 оказалась меньше длины стойки на величину хг (рис. 9.1, а). В результате шатун 2 и коромысло 3 не состыковались. Чтобы состыковать эти два звена и замкнуть контур, нужно мысленно жестко скрепить кривошип 1 и шатун 2 в шарнире В, затем сдвинуть их вправо на величину хг (рис. 9.1, б) или, не трогая их, сместить коромысло 3 (рис. 9.1, в) влево на величину хР
Отсутствие в рассматриваемом механизме поступательных движений в кинематических парах не позволяет замкнуть контур ни одним из указанных способов. Но здесь имеются звенья, повороты которых вокруг осей г, перпендикулярных оси г, дают возможность компенсировать отсутствующее необходимое поступательное перемещение вдоль оси хи состыковать шатун 2 с коромыслом 5, замкнув таким образом контур механизма. В данном примере состыковать шатун 2 с коромыслом 3 можно, во-первых, повернув шатун 2 против часовой стрелки вокруг шарнира В при неподвижном кривошипе /, а коромысло 3 — против часовой стрелки вокруг шарнира Д (рис. 9.1, г); во-вторых, мысленно закрепив шатун 2 в шарнире В и повернув кривошип 1 против часовой 400
стрелки вокруг шарнира А и коромысло 3 — против часовой стрелки вокруг шарнира D (рис. 9.1» д). В обоих вариантах замыкание контура механизма осуществляется без объемных деформаций.
4. Если имеется избыток поворотов, то наличие трех поступательных перемещений х, у, г не обязательно. Если же этого избытка нет, то отсутствие хотя бы одного поступательного перемещения означает наличие объемных деформаций и избыточную связь.
5. Две поступательные подвижности одного вида в одноконтурном механизме указывают на местную подвижность в механизме.
6. Два поворота вокруг одной оси в одноконтурном механизме, из которых ни один не используется на замыкание контура, также указывают на местную подвижность в механизме.
7. Для сборки многоконтурного механизма без объемных деформаций число поступательных перемещений и поворотов, необходимое для такой же сборки одноконтурного механизма, следует увеличить в k раз (k — число контуров в многоконтурном механизме).
Все эти основные положения позволили разработать новый метод структурного анализа, при котором число избыточных связей и местных подвижностей в механизме определяют по числу подвижностей в кинематических парах и числу контуров механизма, а ответы на остальные перечисленные вопросы получают, анализируя виды подвижностей каждой кинематической пары.
Определение общего числа подвижностей в кинематических парах анализируемого механизма и числа контуров в нем
Для определения общего числа подвижностей в кинематических парах нужно независимые подвижности каждой пары связать с осями координат. Затем общее число подвижностей всех кинематических пар в механизме представить как арифметическую сумму поступательных перемещений вдоль каждой координатной оси х, у, г и сумму поворотов вокруг каждой оси. При определении подвижностей в парах нужно рассматривать каждую пару как независимую свободную пару. При представлении подвижностей пар по осям координат для каждой из них может быть использована своя система координат с произвольной ориентацией осей.
Чисто замкнутых контуров в анализируемом механизме определяют по формуле (9.2). Чтобы выявить и определить число избыточных связей и местных подвижностей в механизме, нужно установить общее число подвижностей в его кинематических парах, что делается с помощью специально разработанной структурной таблицы, позволяющей также проанализировать структуру механизма.
Таблица для структурного анализа механизмов
Таблица (табл. 9.2) состоит из трех частей. В первой части приведены схемы и структурные параметры анализируемого механизма, т. е. исходные данные для анализа. Во второй — для каждой кинематической пары указаны имеющиеся в ней поступательные и угловые подвижности. В третьей части приведен структурный анализ рассматриваемого механизма и его результат.
Таблица 9.2. Структурный анализ механизмов
Решение примеров помогает понять и практически освоить структурный анализ механизмов с помощью таблицы.
В табл. 9.2 приняты следующие обозначения: k — число замкнутых контуров в механизме; х — смещение по оси х, у — по оси у и г — по оси г; ф* — поворот вокруг оси х, ф^ — вокруг оси у и ф2 — вокруг оси г; f — число местных подвижностей в механизме; q — число избыточных связей в механизме; w — число независимых рабочих движений (число ведущих звеньев в механизме).
Арабскими цифрами на схеме механизма обозначены его звенья, а римскими — классы кинематических пар; индекс при римских цифрах указывает порядковый номер кинематической пары в механизме.
Пример 1. В первой части табл. 9.2 приведена схема синусного механизма (№ 1) со всеми его структурными параметрами. Требуется по этим исходным данным выполнить структурный анализ механизма.
Решение. 1. По формуле (9.2) по исходным данным анализируемого механизма определить число замкнутых контуров в нем. Для рассматриваемого синусного механизма получаем k—p — п=^ 4—3 = = 1 — механизм одноконтурный.
2. Выбрать систему координат, относительно которой нужно рассмотреть подвижности каждой пары анализируемого механизма. Система координат для синусного механизма изображена в табл. 9.2»
3. Рассмотреть подвижности каждой пары анализируемого механизма независимо от других кинематических пар и результат занести во вторую часть таблицы.
В синусном механизме пара /,соединяющая кривошип со стойкой — вращательная пара V класса. Она имеет одну подвижность — поворот вокруг оси г, которая отмечена цифрой 1 в клетке,стоящей на пересечении строки фг со столбцом порядкового номера пары V класса. Пара 2, соединяющая кривошип с ползушкой—сферическая пара II класса (см. табл. 9.1 и 9.2). Оиа допускает четыре подвижности: 1) поступатель-вое смещение по оси г; 2) поворот вокруг оси х — фх; 3) поворот вокруг оси у — фу; 4) поворот вокруг оси z — фг. Поэтому в столбце порядкового номера пары 2 все четыре подвижности отмечены в соответствующих клетках. Пара 3, соединяющая ползушку с кулисой механизма — поступательная пара V класса. Она имеет только одну поступательную подвижность вдоль оси у, которая отмечена в клетке па пересечении третьего столбца со строкой у. Наконец, пара 4> соединяющая кулису 404
со стойкой механизма — также поступательная пара V класса. Она имеет одну подвижность вдоль осн х, что отмечено в клетке на пересечении строки х со столбцом порядкового номера этой пары.
4. После заполнения соответствующих клеток столбцов, обозначенных порядковыми номерами пар анализируемого механизма, нужно просуммировать число единиц, стоящих в каждой строке второй части таблицы. Результат суммирования записать в столбец, обозначенный
|5 . По результату суммирования подвижностей в парах нужно установить характер и степень их реализации в рассматриваемом механизме.
Для синусного механизма суммирование подвижностей в парах показало, что в механизме есть три поступательные подвижности — по одной вдоль каждой из координатных осей — и четыре угловых поворота; вокруг оси х, вокруг оси у и два поворота вокруг оси г. Итак, в синусном механизме общее число подвижностей равно семи.
Механизм одноконтурный, следовательно, имеющиеся в нем три поступательные смещения вдоль координатных осей и три поворота вокруг тех же осей реализуются на замыкание контура (на сборку механизма без объемных деформаций), а четвертый поворот срг вокруг оси г является рабочим движением кривошипа. В третьей части табл. 9.2 (№ 1) это показано стрелкой, направленной из клетки на пересечении строки срг со столбцом S к столбцу W.
Здесь и далее число стрелок, направленных к столбцу W, выражает число рабочих подвижностей в рассматриваемом механизме или число независимых ведущих звеньев в нем. Синусный механизм имеет одну рабочую подвижность (№ = 1) и соответственно одно ведущее звено — кривошип механизма.
Таким образом, проведенный с помощью табл. 9.2 структурный анализ синусного механизма показал, что в нем нет избыточных связей (q ~ 0), следовательно, он статически определен и собирается без объемных деформаций. В этом механизме нет также местных подвижностей (/ = 0).
Пример 2. Требуется провести анализ крпвошиппо-шатуиного механизма (табл. 9,2, №2), причем, если кривошип с шатуном соединены цилиндрической парой IV класса, а шатун с ползуном—сферической парой III класса (см. табл. 9.1).
Решение. В соответствии с изложенной в предыдущем примере последов а тел ь ность ю оп р едел яем:
1) число замкнутых контуров в механизме: k = р — п— 4 — 3 = 1;
2) систему координат (помещается в первой части табл. 9.2 рядом со схемой механизма № 1);
3) подвижности в каждой кинематической паре, которые записывают во второй части табл. 9.2;
4) построчные суммы подвижностей пар механизма (записывают в соответствующих клетках столбца S, табл. 9.2);
5) характер и степень реализации имеющихся в механизме подвижностей.
Из столбца S видно, что анализируемый механизм имеет трн поворота вокруг оси г, один из которых является рабочим движением (стрелка а), второй компенсирует недостающее смещение по осн у (стрелка б), а третий — замыкает контур механизма.
Анализ показал, что рассматриваемый кривошипно-шатунный механизм является также одноконтурным механизмом без избыточных связей (q == 0) и местных подвижностей (/ = 0). Механизм собирается без объемных деформаций.
Пример 3. Нужно проанализировать параллелограмм (табл. 9.2, № 3), если Щатун соединен с кривошипом сферической парой IV класса, а с коромыслом — сферической парой третьего класса (табл. 9.1).
Решение. Как и в предыдущих примерах, устанавливаем: 1) параллелограмм — одноконтурный механизм;
2) в механизме нет поступательных подвижностей вдоль осей координат;
3) четыре поворота (<рг = 4) вокруг оси г позволяют скомпенсировать недостающие поступательные подвижности (стрелки б, в и ^11в таблице);
4) при выбранных кинематических парах параллелограмм не имеет избыточных связей (q = 0) и местных подвижностей (/ = 0); он собирается без объемных деформаций.
Таким образом, анализируя каждый проектируемый механизм с помощью таблицы, конструктор получает все необходимые сведения о его структуре. Примеры, приводимые ниже, показывают, что эти сведения являются одновременно исчерпывающими.
В табл. 9.2 № 4 дан анализ параллелограмма с избыточным шатуном. Механизм — двухконтурный. Для сборки без объемных деформаций в нем должно быть по два смещения вдоль каждой оси координат н по два поворота вокруг каждой оси. В действительности, при указанных на схеме парах, в нем имеются три поворота вокруг оси х и три поворота вокруг оси yt одно поступательное смещение вдоль оси z (цилиндрическая пара IV класса, соединяющая кривошип 1 с шатуном 2) и шесть поворотов вокруг той же оси..Реализация имеющихся в механизме подвижностей показана стрелками.
Из таблицы видно, что в анализируемом механизме имеется одна местная подвижность (поворот шатуна 4 вокруг своей оси) и одна избыточная связь (избыточный шатун 4), не позволяющая собрать механизм без объемных деформаций. Собрать такой механизм можно только за счет деформации его звеньев вдоль оси х. При наличии избыточных связей в механизме деформация звеньев для его сборки зависит от точности их изготовления: с повышением точности изготовления деформация уменьшается. Поэтому кинематические пары и механизмы с избыточными связями чрезвычайно трудоемки в изготовлении и сборке, причем трудоемкость эта возрастает с числом избыточных связен. Следовательно, если во время проектирования не удается разработать механизм без избыточных связей, то нужно стремиться к уменьшению их числа в нем.
В табл. 9.2 (№ 5 и 6) выполнены анализы зубчатой передачи и механизма Мейера для фокусировки микроскопа.
Структурный анализ механизмов с упругими звеньями
В приборах широко применяют механизмы с упругими звеньями, отличающиеся от обычных отсутствием кинематических пар, роль которых выполняют звенья. Движение жестких звеньев осуществляется здесь за счет простых упругих деформаций упругих звеньев. Поворот жесткого звена (в зависимости от схемы механизма) осуществляется за счет кручения или изгиба, а поступательное перемещение — только за счет изгиба упругих звеньев. Если рассматривать упругие звенья как кинематические пары, налагающие определенное число условий связи на относительное движение жестких звеньев механизма, то для 406
структурного анализа таких механизмов полностью приложима изла*
гаемая методика.
Широкое распространение получили три типа упругих звеньев: круглая проволока, широкая плоская пружина (ширина во много раз больше толщины) и кольцевая плоская диафрагма. Проволока эквивалентна паре первого класса; она препятствует перемещению вдоль ее осн и оставляет пять возможных движений: два поступательных, перпендикулярных к ее оси, и три вращательных вокруг трех координатных осей, если одну из осей совместить с осью проволоки.
Плоская пружина налагает три условия связи: препятствует двум поступательным перемещениям вдоль координатных осей у и z, распо-
ложенных в плоскости пружины, и вращению вокруг оси х, перпендику'
лярной плоскости пружины (рис. 9.2, а). Она эквивалентна паре III класса, допускающей поступательное движение вдоль оси х и поворот вокруг осей у и z. Кольцевая плоская диафрагма эквивалентна паре V класса. Она допускает одно поступательное перемещение вдоль перпендикуляра к плоскости диафрагмы.
Примем упругие звенья па схемах механизмов изображать прямой линией с черными точками (рис. 9.2, б), что позволит безошибочно определять вид
Рис. 9.2. Упругое звено механизма
анализируемого механизма.
Пример 4. Требуется выяснить число избыточных связей в пружинном параллелограмме (табл. 9.2, № 7).
Решение. Поскольку упругие звенья рассматриваются как кинематические пары, анализируемый механизм представляет собой замкнутую цепь, состоящую из одного подвижного звена и двух пар. Подставив в формулу (9.2) р= 2 и п = I, пол уч им k = I. Механизм — одноконтурный. Для сборки без объемных деформаций в нем должны быть три перемещения вдоль осей у, х, г и три поворота вокруг тех же осей.
Структурный анализ неподвижных соединений
Для выявления с помощью разработанной методики наличия избыточных связей и местных подвижностей в неподвижных соединениях и определения причины их возникновения необходимо соблюдение следующих условий:
I) считать неподвижное соединение частным случаем замкнутой кинематической цепи, в которой закрепляемый элемент играет роль подвижного звена, а связи — кинематических пар;
2) рассматривать одну точечную связь как кинематическую пару I класса, две — пару II класса, а три — пару III класса.
Пример 5. Проверить неподвижное соединение кубика на наличие в ием избыточных связей, если задано число и расположение опорных точек (обозначены кружочками) на координатных плоскостях (табл. 9.2, № 8).
Решение. В этом соединении шесть точек, ориентирующих кубик в пространстве, размещены равномерно — по две точки на
Таблица 9.3. Результаты структурного анализа * ~ механизмов оптикомеханическнх приборов.
№
Схема н структурные параметры механизма
Итог анализа
Схема н структурные параметры механизма
Итог анализа
№
1
2
3
4
5
б
7
8
К?
10
У
х
Ш2 2_______ш3
11
VS:9 б_________tyg
7
В 2 Г
%
У
f
< X
2 /T--4-J
s' X . 2 К~-4~3^1
О
О
1
О
9
О
О
О
о
О
3
о
о
о
0
О
1
О
Z
о
о
Схема и структурные параметры механизма
Итог анализа
Схема и структурные параметры механизма
Итог анализа
Продолжение табл. 9.3
' ‘ • "ГДт.
Схема и структурные параметры механизма
Итог, зиа-! лиза
Итог ана-Схема и структурные лиза параметры механизма
О 1
каждой плоскости. Согласно перечисленным условиям кубик и опорные точки можно рассматривать как замкнутую цепь, в которой кубик — подвижное звено, а шесть опорных точек — три пары II класса (р — 3). Число контуров k в такой цепи равно k — р — п — 3 — 1 ~ 2.
Для устранения избыточных связей в соединении должно быть по две подвижности каждого вида. Если это требование выполнено, то опорные точки в координатных плоскостях расположены правильно.
Результат анализа (табл. 9.2) показал, что опорные точки в рассматриваемом соединении размещены правильно. Соединение не иу^ет избыточных связей, следовательно, оно статически определимо.
Пример 6. Выяснить, как повлияло изменение расположения опорных точек в координатных плоскостях на статическую определимость неподвижного соединения кубика (табл. 9.2 № 9).
Изменение опорных точек в рассматриваемом случае отразилось на распределении поворотов кубика вокруг каждой оси координат. Вместо необходимых двух поворотов — один поворот вокруг оси у и три поворота вокруг осн z. Такое распределение подвижностей в рассматриваемом соединении приводит к тому, что соединение подвижно и статически неопределимо. Оно имеет одну местную подвижность (/ = 1) и одну избыточную связь (q = I).
Рекомендации по изложенной методике
При выполнении структурного анализа механизмов нужно:
определять виды и число подвижностей в каждой паре без учета зазора в ней;
считать, что в кинематических парах нет избыточных связен и местных подвижностей;
считать, что в волновой передаче зацепление гибкой оболочки и сопряжение ролика с нею осуществляются парами I класса, а участок цилиндрической оболочки против каждого ролика является одновременно парой V класса и звеном.
В табл. 9.3 приведено 50 механизмов, для каждого из которых указаны целесообразные структурные параметры, полученные в результате анализа, выполненного согласно перечисленным рекомендациям х.
1 Волновые передачи № 47 н 48 заимствованы из книги: Решетов Л. Н. Конструирование рациональных механизмов. М.» Машиностроение, 1972.
ГЛАВА 10
РАСЧЕТ И КОНСТРУИРОВАНИЕ ПОДВИЖНЫХ СИСТЕМ ОПТИЧЕСКИХ ПРИБОРОВ
Механические системы оптических приборов
Характерной особенностью оптических приборов (ОП) является органичность сочетания и взаимодействия в них оптических и механических систем. Последние подразделяются на два основных вида: несущие и подвижные системы.
Несущие системы представляют собой комплексы неподвижных элементов (оснований, кронштейнов, стоек, плат и пр.) и предназначаются для базирования и внутреннего взаимного ориентирования оптических и других схемных элементов прибора. Они определяют общую компоновку конструкции, ее жесткость, технологичность сборки, надежность. Характерной особенностью является широкое применение в них регулировочно-юстировочных устройств, обусловленное высокими требованиями к точности ОП, а также сравнительно низкий уровень унификации конструктивных решений.
Подвижные системы (ПС) осуществляют механическое перемещение оптических систем и их элементов, обусловленное их функциональным назначением; образуют измерительные цепи приборов; являются основой устройств управления различными видами позиционирования, широко применяемого в ОП; выполняют разнообразные простейшие транспортирующие функции. Подвижные системы представляют конструктивную реализацию кинематических цепей, поэтому проектирование их базируется на выборе типов исходных механизмов и на определении их параметров.
Механизмы подвижных систем оптических приборов (ПСОП)
Назначение, типы и свойства механизмов. Механизмы служат для осуществления заданного вида и закона механического движения. По условиям применения в ПСОП механизмы подразделяются на силовые (обычно тихоходные приводы), выполняющие простые транспортирующие функции; ходовые (быстроходные приводы; применяются в основном при автоматизированном управлении движением) и точные механизмы. К первым предъявляются требования легкости и плавности хода, ко вторым — требование малости потерь на трение, к третьим — 414
Таблица 10.1. Типовые элементарные механизмы
Тип Схема Функция преобразования движения
1 4 rJk ьшь т~^з „ । - У=^ заходов бы kp 2л Х резьб! , где k — число >i; P шаг резь-
9 . о , 11у Ь 7 Ь Hi' ' v ||L У = а ~ь~х
3 J -<М <S ,•'.. О Z7^7 1 ГМ ЗГ/Л - 4’4^ кмк: А и а) у Q у- = arc sin (х/г) — arctg (х/г)
4 ж. "А &Z г=г Л а) У 6) у = г sin х = rtg X
5 0 „ У ef’-Tas- а) У + Kz2 -- г sin х -/- — (г cos х — е)2
М j '1 г*— >4 t-* а>1 б) У = arct' r sin х тг э 1 — Г COS X
а) 5)^^ ё)
6 Тта ЩОффй y= \zl!zi-x\
7 уй|4г rx = mzft> x
8 тш У = 1 2^22’ «1
Тип Схема Функция преобразования движения
9 а) у = г + Аг (х) б) р = У”о2+Я2—2aRcosy у = у» + Ду (х)
10 а) у = (г + h/2) х л r^—h/2 61 ’ - '2 *
11 ШЕ * зТс у == a tg р sin х
12 -‘т|< • ж? а) у = р!г-х б) у = p!r-x= R/r-sinx
обеспечение заданной точности функционирования. Основные характеристики механизмов — структура и свойства.
Структура сложного механизма определяется числом и типами элементарных механизмов (табл. 10.1), составляющих его кинематическую цепь. Выбор необходимого сочетания элементарных механизмов при проектировании ПС зависит от требуемого набора его свойств. Важнейшими из свойств механизмов являются: виды преобразования движения, возможный диапазон движения и обратимость движения. При выборе учитываются также кинематические и точностные возможности элементарных механизмов.
Основные виды преобразований движения: масштабные, представляющие замедление или ускорение движения от входа к выходу (типы 2, 6, 8, 11; наиболее универсальны типы 2 и 6); вида движения (поступательного во вращательное или наоборот), осуществляются многими способами (типы 1, 3, 4, 7, 9а, 10а, 12); закона движения (линейного в нелинейное или наоборот), осуществляются в основном с помощью кулачковых механизмов (тип 9), а в частных случаях рычажными механизмами (например, типы 4 и 5).
Диапазон движения может быть: неограниченный в обоих направлениях — зубчатые, червячные и фрикционные механизмы (типы 6, 8 и 11); неограниченный только в одном направлении — кулисные механизмы (типы 4а, 5) при условии входа на кривошипе и кулачковые (тип 12). Все остальные механизмы (включая и кулисные при входе на кулисе) имеют ограниченный диапазон движения.
Таблица 10.2. Функциональное назначение механизмов
п/п Устройство Структурная схема Примеры применения
1 Управления позиционированием (с фиксацией) Исполн. элемент Фиксирующий упор г Для смены параметра (увеличения и др.), смены режима работы
2 Управления грубым позиционированием (без фиксации) Исполн. элемент ' Зона наводки Для грубой фокусировки, грубой наводки в рабочую зону
3 Управления точным позиционированием (без фиксации) Исполн. элемент 1 / Д । \—' К-У неперн. элемент овьекта Для тонкой фокусировки Регулировочно-юстировочные устройства
4 Ввода входных данных Исполн. элемент 'дона наводки чсиетн. троист о во Для диоптрийной наводки, ввода угла прицеливания Монохроматор; регулируемая диафрагма
5 а) Управления наводкой измерительной цепи б) Измерительная цепь бесконтактных измерений Исполн. элемент цепь а) \ Z~\ z~x^ < Чувств, элемент цепь г управ г азмер Л. Для наводки теодолита, гониометра; Угломерное устройство стереотрубы и т. п.
14 ь. А. Ианов и ДР
417
№ п/п Устройство Структурная схема Примеры применения
6 То же, что в схеме 5, при совмещении цепей а и б Исполн. элемент цепи управл. Для глубинных измерений на микроскопе, наводки по углу Отсчетные микрометры
zj"4
Чувств, элемент цепи измер.
1 Измерительная цепь контактных измерений Чувств. элемент Объект Оптиметр; оп-тикатор; интерферометр контактный; индикаторные приборы
8 а) Неточный привод непрерывного перемещения б) Точный привод непрерывного перемещения Ислмн. элемент 'Исполн. элемент с о Для перемотки пленки Лентопротяжный механизм; привод следящей системы
Примечания: I, Кружками обозначены структурные элементы (СЭ) цепей управления, квадратиками — СЭ измерительных цепей (совмещение их в схеме 6 означает, что одни н те же СЭ выполняют обе функции). 2. Перекрещивание СЭ означает, что цепь точная (должна рассчитываться на точность) 3, Схема 5 применяется, когда в измерительной цепи имеются немеханическне СЭ, схема 6 — когда измерительная цепь состоит нз механизмов.
Необратимость движения — свойство, присущее в основном вин-товым механизмам (тин 1) и червячным передачам (тип 8а); оно используется, например, в механизмах управления позиционированием (табл. 10.2). ,tt1
Функциональное назначение механизмов в ОП. В оптических приборах в основном встречается три вида задач, решаемых с помощью механизмов: 1) позиционирование исполнительного элемента механизма в заданное положение; 2) передача измерительного сигнала от чувствительного элемента измерительной цепи на регистрирующее устройство; 3) осуществление процесса движения с целью перемещения (непрерывного или прерывистого) некоторого рабочего элемента (кино- или магнитной ленты и т. п.). Типовые структурные схемы механизмов для этих видов задач и конкретные примеры применения приведены 418
в табл, 10.2, где кружками обозначены структурные элементы механизмов управления позиционированием, квадратами — структурные элементы измерительных цепей. Перекрещивание кружка или квадрата означает, что конечный результат функционирования механизма зависит от точности функционирования данных структурных элементов.
Признаками, характеризующими механизмы управления позиционированием (схемы 1, 2, 3, 4, 5а, 6а), являются: замедление движения от входа к выходу; независимость результата то точности функционирования структурных элементов цепи, Процесс позиционирования заключается либо в приведении исполнительного элемента в заданное положение с последующей остановкой (при ручном управлении), либо в «удержании» исполнительного элемента в этом положении (при автоматическом сложении). Особым случаем позиционирования является придание цепи заданного положения с помощью «входных данных», устанавливаемых по отсчетным устройствам, расположенным на входе механизма (схема 4). Здесь точность результата зависит от точности структурных элементов цепи.
Признаками, характеризующими механизмы измерительных цепей (схемы 56, 66, 7), являются: точная фиксация входа цепи (чувствительного элемента) относительно объекта измерения (входного сигнала); ускорение движения от входа к выходу (рёгистрирующему элементу); зависимость точности результата измерения от точности функционирования структурных элементов цепи. При бесконтактных измерениях (схемы 5 и 6) фиксация чувствительного элемента выполняется путем совмещения реперных элементов чувствительного элемента и объекта измерения. Это совмещение является обычным позиционированием и выполняется с помощью механизмов управления.
Признаками, характеризующими механизмы третьей группы (схема 8), являются: непрерывное (более или менее длительное) движение в непрерывном или дискретном режиме; замедление движения; автоматизация процесса перемещения. Здесь имеет значение не точность результата, а точность процесса перемещения рабочего элемента.
Кинематические характеристики механизмов. Основной харгкте-ристикой является функция преобразования движения (ФПД)1 :
y = f(x,qs), (Ю.1)
где у и х — выходная и входная обобщенные координаты механизма; q$ — конструктивные параметры.
Для типовых элементарных механизмов ФПД приведены в табл. 10.1; для сложных механизмов эту функцию определяют на основе ФПД исходных элементарных механизмов: если yY ~ (хг),
У» = /а (уд...Уп = fn (Уп). то ФПД цепи
Уп — fn (Уп-1) — fn {/п-1, • • • , /а [/1 (-*1))} • (10-2)
* ‘ Кроме ФПД при проектировании используют прямую Аух и обратную Аху передаточные фнукции:
— dy/dxi (10.3)
Aty—dxjdy. (10.4)
Передаточные функции характеризуют кинематическую чувствительность механизмов*, прямая — для измерительных цепей, кратная — для механизмов управления позиционированием.
1 Ее называют также законом движения 1.9законом преобразования движения, функцией положения 128].
14* 419
Для линейных механизмов Аух и Аху — постоянные величины, их называют прямым и обратным передаточными коэффициентами и определяют численные значения по формулам:
Аух — у/х; (10.3а)
AxV — x/y. (10.4а)
Замечания к проектированию механизмов ПСОП
При проектировании механизмов основные трудности связаны с решением следующих трех задач: I) выбора оптимального сочетания элементарных механизмов (ЭМ) при составлении цепей сложных механизмов; 2) распределения общего значения передаточной функции цепи между передаточными функциями составляющих ЭМ; 3) определения численных значений параметров цепи (т. е. выполнения кинематического расчета). Эти трудности связаны с неоднозначностью возможных решений и ограниченностью исходных данных технических заданий (ТЗ).
При выборе исходных ЭМ (1-я задача) руководствуются качественными характеристиками типовых ЭМ, а именно: кинематическими и точностными возможностями, показателями силового режима, технологичностью и др. (см. табл. 10.1; подробнее см. в специальной справочной литературе).
Кинематические возможности ЭМ характеризуются видами возможных преобразований движения и ограничениями возможных значений передаточных функций (табл. 10.3).
Т а б л и ц а 10.3. Примеры ограничений значений передаточных функций
Наименование механизма Ограничения
Винтовой механизм Зубчатая реечная передача Рычажный двуплечий механизм Зубчатая передача Червячная передача Кулачковый механизм kP/360 [мм/град] 2лг/360 [мм/град] alb [мм/мм] Zj/za [град/град] гх!г2 [град/град] 0,003Р<Л^<0,01Р Аух — 0,02г 1/6 Аих 6 1/6 с АуХ < 6 aZ < 1/6' У А Угол давления ₽^зо°
Точностные возможности ЭМ определяются технологичностью изготовления кинематических пар и числом нх в цепи: чем короче кинематическая цепь (меньше число пар), тем точнее механизм (при прочих равных условиях)х.
1 Сведения о технологичности типовых кинематических вар см, в литературе по технологии приборостроения [39, 52, 68].
Показателям^ силового режима механизма являются: момент (сила) трогания с места, характеризующий «силовую чувствительность» механизма; среднее значение момента сопротивления, характеризующее силовую нагрузку при установившемся режиме движения; колебания момента сопротивления, характеризующие «силовую плавность» движения. Все эти показатели важны главным образом для механизмов первой и третьей групп (см. пояснение к табл. 10.2 на с. 418). Опыт показывает, что лучшие результаты по первому и второму показателям дают кинематические пары с трением качения, а по третьему — с тре
нием скольжения.
При распределении передаточной функции цепи между составляющими ЭМ можно руководствоваться следующими общими принципами:
для цепей, работающих на замедление, если доминирующим требованием является точность, следует делать наибольшее возможное замедление на выходе, постепенно снижая его к входу (рис. 10.1, кривая /); для цепей, работающих па ускорение, при том же условии выгодно иметь наибольшее ускорение на входе, постепенно уменьшающееся к выходу (кривая 2).
При выполнении кинематических расчетов обычно недостает исходных данных ТЗ для определения всех неизвестных параметров механизма, входящих в его ФПД. В этих случаях приходится путем
Рис. 10.1. Закономерности изменения передаточных функций, составляющих кинематическую цепь
анализа эксплуатационных, конструктивных и технологических ограничений искать дополнительные данные для расчета. Примеры подобных ограничений приведены в табл. 10.3, другим примером может служить широко применяемая регламентация чувствительности измерительных цепей и тонких перемещений.
Для измерительных цепей выражение чувствительности, как известно, имеет вид: Sy ~ da/dQ^ Aa/AQt где Ла — изменение выходного сигнала, AQ — входного. Если Ла и AQ физически выражаются через перемещения (например, указателя и чувствительного элемента), то Sy численно равна прямой передаточной функции измерительной цепи; Sf/ — Аух == dy/dx Лу/Лх. Приняв за Лу перемещение, соответствующее линейному или угловому интервалу шкалы (счетчика) отсчетного устройства, а за Лх — перемещение чувствительного элемента, соответствующее цене деления шкалы (счетчика), получим регламентированное значение чувствительности или, что то же, значение передаточной функции: Ла/ЛО. = Лу/Лх. Это соотношение и используется для кинематических расчетов измерительных цепей.
Пример 1. Формула ФПД измерительной цепи оптиметра (рис. 10.2) у (2/г) имеет четыре неизвестные величины: у — видимое
перемещение автоколлимационного блика (выходная координата цепи); г — длина плеча рычага; Гок — видимое увеличение окуляра; /об — фокусное расстояние объектива. Здесь х — перемещение измерительного стержня (чувствительный элемент) — представляет входную координату и регламентируется пределами измерения прибора. Передаточная функция цепи: Аух = у/х — (2/г) ГоК/об- У оптимегра видимая
величина интервала шкалы ДаНн == 0,9 мм, а цена деления шкалы Д(?ц д — 1 мкм. Отношение этих величин AaFH/AQu. д = = 0,9 мм/1 мкм = 900, следовательно, (2/г) Гок/об = 900. В получен-
Рис. 10.2. Схема оптиметра:
1 — рычаг с зеркалом; 2 — плоскость изображения: е — поворот рычага с зеркалом: 8 «== (1/г) х; у' — смещение автоколлимациопиого блика: у — fog2e;
видимое изображение у ® Г у'
отношению червячной передачи: шкала точного отсчета имеет
ной расчетной формуле с помощью других дополнительных даиных осталось определить только две неизвестные величины.
Пример 2. Угломерное червячное устройство (рис. 10.3), применяемое для измерительного углового перемещения оптической зрительной трубы, соединенной с червячиым колесом, имеет вход иа колесе (трубе) и выход на отсчетном устройстве, соединенном с червяком. Его ФПД выражается формулой z/=z2/z1*x, где у— перемещение шкалы точного отсчета (вме-
сте с червяком); г2 — число зубьев червячного колеса; zA — число заходов червяка; х—угол поворота колеса с трубой. Передаточная функция измерительной цепи равна передаточному А ух — z2/zx. В этих устройствах обычно п = 100 делений с угловым
интервалом 3,6°; цена деления может быть различной. Примем цену деления равной 3,6' (что соответствует одной тысячной дистанции).
Рис. 10.3. Червячное угломерное устройство
Тогда Дцин/Дфц. д= 3,6Q/3,6' ™ = 60. Приравниваем передаточную функцию цепи полученному значению: Ау* = zjzy = 60. Выбираем число заходои червяка (обычно zA — 1), после чего определяем число зубьев колеса z2 — 60.
Рис. 10.4. Бинговой механизм тонкой фокусировки микроскопа:
1 — объект наблюдения; 2 — предметный столик
Для механизмов управления позиционированием, работающих на замедление, чувствительность удобно характеризовать отношением пере-
Рис. 10.5. Рычажный винтовой механизм тонкого наведения:
1 — визирная ось зрительной трубы; 2 — угломерное отсчетное устройство
мещсния на входе (органе управления) к перемещению на выходе (исполнительном элементе), т. е. величиной, обратной передаточной функции. Чувствительность позиционирования тем выше, чем больше это отношение. При высоких требованиях к точности позиционирования данное отношение регламентируют, основываясь на опытных данных х: приняв за единицу перемещения на выходе перемещение исполнительного элемента, равное допуску на точность позиционирования, выбирают соответствующее перемещение на входе в пределах 0,5—Г для лабораторных приборов и в пределах 2—5° — для военных. Таким образом, с помощью указанной регламентации определяют необходимое значение обратной передачтоной функции: Аху — Дх/Ду = Дхрег/Дудоп, где Дхрег — регламентируемое, Д*/доп — допустимое значения.
Пример 3. Винтовой механизм, применяемый для тонкой фокусировки в микроскопе «Биолам» (рис. 10.4), имеет ФПД вида; у = Р/2л-х, где у — перемещение объекта (или объектива) при фокусировке (выходная координата механизма); Р — шаг резьбы; х — перемещение рукоятки управления (входная координата). Обратная передаточная функция равна Аху — — 2л/Р. В качестве допуска на точность фокусировки примем величину, равную 1 мкм, а регламентируемое перемещение на входе выберем Дхрег — 0,72°. Находим их отношение 0,72°/1 мкм = 12,58 рад/мм. Прирав-
няв передаточную функцию этому значению, получим 2л/Р — 12,58, откуда Р = 0,5 мм. Таким образом, здесь благодаря определению чувствительности оказался возможным полный расчет.
Пример 4. Рычажно-винтовой механизм тонкого наведения (рис. 10.5), применяемый в высокоточных углоизмерительных приборах (например, теодолитах) для точного позиционирования (наведения) зрительной трубы на объект, имеет ФПД вида: у~- kP/(2nR) х и обратную передаточную функцию Аху — 2лР !(kP), где у — угол поворота трубы (выходная координата механизма); k — число заходов; Р — шаг резьбы; R — длина рычага; х — угол поворота рукоятки управления (входная координата). За единицу перемещения на выходе примем Iя; регламентируемое перемещение иа входе Дхрег = 1°. Тогда по их отношению 171я = 3600 получим Аху— 2iiR/(kP) — 3600, откуда и иайдем неизвестные параметры механизма (обычно принимают k — 1; наименьшее технологически надежное значение шага резьбы Р = 0,35 мм, тогда определяется и необходимая длина рычага: /?^200 мм).
Характеристики точности механизмов ПСОП
Виды характеристик точности зависят от функционального назначения механизмов (см. табл. 10.2). Механизмы управления позиционированием на точность не рассчитываются (кроме схемы 4), так как для них имеет значение только точность результата, зависящая от пороговой чувствительности механизма к перемещениям. В случае
1 См,; Елисеев С. В. Геодезические инструменты н приборы, WL; Недр.!, 1973.
плзипчонпровзния чувствительного элемента измерительной цепи (схемы 5 и 6)по грешность позиционирования относится к методическим погрешностям процесса измерения, и ее нужно учитывать ири оценке точности результата измерения.
Механизмы измерительных цепей (схемы 56, 6 и 7), а также меха-низмы позиционирования по входным данным (схема 4) необходимо рассчитывать на точность. Характеристиками точности в общем случае являются: ошибки положения, перемещения и мертвого хода. Ошибка положения представляет собой разность действительного и идеального (поминального или расчетного) значений выходной координаты при фиксированном значении входной координаты механизма. Ошибкой перемещения называю! разность значений перемещений действительного и идеального (поминального, расчетного) на выходе механизма при заданном перемещении на входе. Ошибкой мертвого хода называют отставание ведомою звена механизма при реверсировании движения (в литературе встречается также наименование «ошибка обратного хода»). Основной характеристикой кинематической точности механизмов с непрерывным движением является ошибка перемещения; ошибка положения здесь служит для определения ошибок перемещения и мертвого хода. Для механизмов прерывистого движения основной характеристикой является ошибка положения.
Характеристики точности механизмов третьей группы (табл. 10.2, схема 8) зависят от вида движения: при непрерывном движении характеристикой является ошибка скорости, при прерывистом — ошибка положения.
В приборах, работающих в условиях вибраций, возникают также динамические ошибки, действие которых проявляется в виде дополнительною смещения исполнительного элемента механизма (оценивается экспериментально).
Перечисленные характеристики точности механизмов ПСОП — переменные величины; изменения их происходят в пределах диапазона движения, при повторении циклов движения, с течением времени. По характеру изменения в диапазоне движения различают ошибки накопленные, периодические и местные (последние носят нерегулярный характер). Рассеяние ошибок при повторении циклов движения происходит вследствие деформаций в слоях смазки, люфтов и трения в кинематических парах и характеризует случайную составляющую инструментальной ошибки прибора. Изменение ошибок с течением времени вырг^жается в постепенном снижении точности механизмов вследствие износа деталей, ослабления креплений и расстройства регулировок и характеризует точностную (параметрическую) надежность механизма.
Причины и виды ошибок механизмов
Различают два вида причин ошибок механизмов — допущения, принимаемые при проектировании, и первичные ошибки механизмов. Допущения принимаются с целью повышения точности или упрощения конструкции подвижной системы прибора. Наиболее часто встречаются допущения в функции преобразования движения (например, для нелинейного механизма при малом отклонении от линейности ФПД принимается линейной), называемые схемными; встречаются также допущения в определении параметров механизма, допущения в конструировании высших контактных пар. Ошибки механизмов, возникающие о г допущений, называют теоретическими (или структурными, схемными); они всегда имеют систематический характер.
Перечными ошибками механизмов являются погрешности размеров, формы и положения деталей, возникающие при изготовлении и работе механизма. Они характеризуются величиной и направлением: если направление определенное (погрешности размеров, деформации от сил тяжести деталей и т. п.), первичные ошибки называют скалярными, если же неопределенное (несоосности, эксцентриситеты, перекосы вращающихся деталей и т. п.) — векторными. При расчетах на точность для скалярных первичных ошибок учитывается только величина, для векторных — величина и направление. Наибольшее влияние на точность механизмов оказывают нижеследующие виды первичных ошибок.
Технологические первичные ошибки [4—7; 28; 43]. Они представляют собой производственные погрешности изготовления деталей
Таблица 10.4. Вероятностные характеристики рассеяния технологических первичных ошибок
Наименование Обозначение Расчетные формулы
Половина поля допуска Среднее значение Среднее квадратичное отклонение Ьд Л<7 а(Д<?) = 0,5 (Д?в — Д.?н) Д? — ~Ь &q$q — Cq$q О (Д?) = KqSq/3
Примечание. Л^в и Д^н — верхнее и нижнее предельные отклонения поля допуска (при расчетах подставляются со своими знаками); Д04 — 0,5 (Д*?в 4- Д<7Н) — координата середины поля допуска; <Хд — коэффициент относительной асимметрии поля рассеяния погрешности; — коэффициент асимметрии поля допуска; — коэффи- циент относительного рассе5шия погрешности в поле допуска.
Таблица 10.5. Расчетные формулы для коэффициента асимметрии поля допуска Cq
Расположение поля допуска Формула
Одностороннее с гарантированным отклонением То же, но без гарантированного отклонения Симметричное ~ Д(?7; б;/ J cLq | С^ ± 1 ~ | Cq^0
Примечание. Значения До^ и bq вычисляются по формулам табл. 10.4 и подставляются со своими знаками. Верхние знаки в формулах относятся к размерам элементов деталей типа «отверстие», а нижние — типа «вал».
Т а б л и ц а 10.6. Значения коэффициентов и Кд скалярных первичных ошибок
Расположение поля допуска Метод обработки Уровень точности К,
Симметричное Любой Э п т 0 0 0 1 1,1-1,3 1,3—1,5
Несимме- Автоматический э п т о © н-*О 1 1 => © о Ю — 1 1,1-1,2 1,2-1,3
тричное Пробными проходами э п т 0,1—0,2 0,2—0,3 0,3—0,4 1,1-1,2 1,2-1,3 1,3-1,4
Примечания: 1. Даны усредненные значения и при их выборе руководствуются конкретным состоянием оборудования. 2. Для указаны абсолютные значения; знак должен выбираться по правилу: минус — для размеров элементов деталей типа «отверстие», плюс — типа «вал». 3. Уровень точности Э, D и Т см. в табл. 10.12.
Таблица 10.7. Значения коэффициентов а7 и Kq векторных первичных ошибок
Распределение первичной ошибки
По закону Рэлея
По закону модуля разности
—0,28
—0,30
Примечание. Значения коэффициентов указаны для теоретических законов распределения 15, 6].
(погрешности размеров деталей, погрешности расположения и формы рабочих поверхностей) и погрешности сборки (смещения, переносы и пр.). Характер проявления этих ошибок случайный, поэтому рас4^ их производится по вероятностным характеристикам рассеяний» которые определяются по характеристикам поля допуска и предполагаемым законам распределения соответственных погрешностей (табл. 10.4— 10.7).
Погрешности размеров являются скалярными первичными ошибками и вызывают накопленные ошибки перемещения и отклонения скоростей ведомых звеньев. Погрешности расположения рабочих поверхностей, а также сборочные смещения и перекосы бывают скалярные и векторные; в первом случае они вызывают накопленные ошибки пере-426
мещения и отклонения скоростей, а во втором — периодические ошибки перемещения и колебания скоростей. Погрешности формы рабочих поверхностей выбывают всегда переменные нерегулярные ошибки перемещения и колебания скоростей.
Смещения в зазорах кинематических пар. Эти смещения определяются величинами зазоров, направления смещений— направлением действующих усилий. Зазоры являются технологическими ошибками, имеют случайный характер и определяются вероятностными характеристиками рассеяния — средним значением (Дс) и практически предельны м отклонением от среднего значения (бс): _____________________________ п _____ &С ~ У Д?1
(Ю.5)
(10.6)
Здесь Aq, Кд и — характеристики рассеяния погрешностей размеров, участвующих в образовании зазора (определяются по формулам табл. 10.4—10.6); КДс — коэффициент относительного рассеяния зазора; принимается равным 1—1,2 в зависимости от Кд и п (п — число погрешностей, образующих зазор).
Регулярные и плавные смещения в зазорах вызывают накопленные ошибки перемещения нли отклонения скорости ведомого звена; скачкообразные смещения, возникающие при реверсировании движения, являются основными причинами появления мертвых ходон механизмов.
Силовые деформации деталей. Причинами этих деформаций являются силы тяжести деталей, внешние (нагрузочные) силы, силы трения, усилия, возникающие в сборке при статически неопределенной конструкции. Наибольшее влияние иа точность механизмов оказывают обычно деформации от внешних сил, однако в приборах, имеющих массивные конструкции (например, астрономических), имеют большое значение и деформации от сил тяжести деталей.
Деформации могут быть следующих видов: объемные (растяжения, сжатия, изгиба, кручения), контактные и деформации в слоях смазки. При неблагоприятных условиях все оня могут оказывать заметное влияние на точность механизмов. Объемные деформации определяются достаточно точно обычными методами сопротивления материалов; наибольшее влияние оказывают деформации поперечного изгиба и кручения. Расчет контактных деформаций производится о помощью формул Герца и является тем более приближенным, чем грубее поверхности (так как эти формулы ие учитывают микропрофиль поверхностей). Достаточно надежным расчет можно считать при шероховатости поверхности не ниже 9-го класса. Расчет деформаций в слоях смазки обы^яо не производится ввиду отсутствия методов расчета и данных, а смещения принимаются равными зазорам.
Следствиями силовых деформаций могут быть все виды ошибок механизмов, при этом ошибки перемещения и скорости определяются изменением значений и знака деформаций; мертвые ходы (упругие) определяются изменением знака деформаций прн реверсировании движения. По характеру проявления эти ошибки считаются систематическими.
Температурные деформации деталей. Эти деформации возникают от колебаний теплового режима работы прибора (за начало отсчета колебаний температуры среды и деталей принимается +20с С). При
изменении теплового режима с малой скоростью, а также при установившемся режиме, отличном от начального, происходит пропорциональное изменение всех размеров деталей на величину
Д/ = lat (t — (10.7)
где / — размер детали; а/ — коэффициент линейного расширения материала; t и t$ — значения текущей и начальной температур детали. При неустановившемся тепловом режиме кроме изменений размеров происходят также изменения формы деталей, не поддающиеся строгому расчету. В этих случаях прибегают к различным методам защиты ответственных деталей от воздействия переменного теплового излучения (герметизация корпусов, обогрев, экранирование и др.). Следствием температурных деформаций явлиются ошибки перемещения и ошибки скорости ведомого звена; те и другие принимаются при расчетах как систематические.
Влияние сил трения в кинематических парах. Силы трения вызывают деформации, износ и смещения деталей в зазорах. Деформации деталей от сил трения являются главными причинами упругих мертвых ходов, играющих особенно большую роль при длинных кинематических цепях. Износ деталей — одна из характеристик параметрической надежности работы механизмов точных приборов. Нерегулярные смещения деталей в кинематических парах вследствие непостоянства сил трения — основные причины невоспроизводимости положений ведомых звеньев (например, измерений и отсчетов).
Колебания и вибрации прибора в процессе работы не только вызывают динамические ошибки (см. выше), но и оказывают влияние на не-воспроизводимость положений механизма. Причинами колебаний и вибраций в точных приборах, кроме внешних условий, являются неуравновешенность вращающихся с большой скоростью деталей, зазоры и трение в кинематических парах, недостаточная жесткость несущих конструкций, отсутствие или недостаточность амортизирующих устройств. Ошибки механизмов, возникающие в процессе работы, называют эксплуатационными.
Определение ошибок механизмов
В общих расчетных формулах приняты следующие условные обозначения: Др — первичная ошибка механизма; Др — ошибка положения механизма; Др — ошибка перемещения механизма; Др. — ошибка мертвого хода; As— полная суммарная ошибка механизма; Дю — ошибка скорости ведомого звена.
Чтобы различить ошибки по видам и свойствам, к основным обозначениям добавляются индексы: тр — для теоретических, тх — для технологических, э — для эксплуатационных, с — для систематических, v — для случайных, £ — для суммарных ошибок. Дополнительные индексы в случае необходимости будут оговариваться в тексте. к
Общие зависимости ме*ду ошибками механизмов. Все виды ошибок определяются при расчетах с помощью так называемых ошибок положения [9, 10]. Ошибки положения связаны с первичными ошибками следующими зависимостями:
= АЧ *<! <108>
п п
д-1/£==2_й"А?=2л’д?’ (10-9)
где &yA{J — частичная ошибка положения (вызванная отдельной первичной ошибкой); Д^ — суммарная ошибка положения механизма; dyldq — Aq — передаточная функция ошибки \ п — число ошибок.
Из формулы fl 0.9) вытекает принцип наложения ошибок (или принцип взаимонезависнмости действия первичных ошибок [9, 10], соответствующий алгебраическому суммированию всех видов ошибок механизмов. Передаточные функции (Aq) выражаются через номинальные значения конструктивных параметров и координаты звеньев механизма. Величины Ау и &q (а значит и Д^) могут быть постоянными, не зависящими от положения механизма, и переменными.
Рис. 10.6. Зависимости между ошибками: а — перемещения и положения; б — мертвого хода на выходе от мертвого хода на входе:
у0 — ФПД идеального механизма; у — то же реального; — значение перемещения ведомого звена идеального механизма; р — то же реального; А(/н — ошибка положения в начальном положении механизма; Дг/ — то же в текущем; Др — сшибка перемещения механизма; рпх — выходная координата прн прямом ходе механизма; рох — то же при обратном; Др — мертвый ход механизма; Дц — ошибка мерт-у вого хода механизма
Ошибки перемещения выражаются через ошибки положения формулой
Др = Д//т —Д//п, (10.10)
где by-f и Д*/н — значения ошибок положения для текущего и начального положений механизма (рис. 10.6, а).
Из формулы (10.10) видно, что ошибки перемещения представляют собой изменения ошибок положения в заданном диапазоне движения. Расчетные формулы для определения Др по вытекающие из формулы (10.10), приведены в табл. 10.8. При постоянных значениях ,Ад и"Ад (т. е. при отсутствии изменения ошибки положения) ошибка перемещения равна нулю. Расчет технологических ошибок перемещения, всегда регламентируемых допусками, производится по формуле типа (11) в табл. 10.8, а расчеты эксплуатационных ошибок (от деформаций) — по формулам типов (III) и (IV).
1 Ее называют также передаточным отношением и коэффициентом влияния ошибки.
Т а-б л и п а 10.6. Общие формулы ошибок перемещения
л ; Лервичшая ошибка * Передаточная функция Частичная ошибка перемещения
Постоянная ’ * Переменная 1 » Постоянна Переменна Постоянна Переменна Др = 0 (1) Др = (Л^ — Л^н) Ду (II) Др = Aq (Дут — Дун) (И I) Az? = Л^т Д^т Aqu Д^н (JV)
Ошибки мертвых ходов для заданных положений механизмов в общем случае выражаются разностью ошибок положения для прямого и обратного ходов ведомого звена
— Д^/пх ДУэх» (10-11)
где Дупх и ДроХ — значения ошибок положения для заданного по ложения механизма при прямом и обратном ходах ведомого звена (рис. 10.6, 6).
Ошибки скорости ведомого звена механизма определяются дифференцированием по времени формул соответственных ошибок положения
Ду — у — у0 = (d/dt) (Дг/). (10.12)
Здесь у и у0— действительное и идеальное (номинальное, расчетное) значения скорости ведомого звена; t — время.
В табл. 10.9 и на рис. 10.6 приведены все виды зависимостей между ошибками механизмов ПСОП.
Таблица 10.9. Общие зависимости между ошибками ПСОП
Ошибки Связи между ошибками Зависимости от первичных ошибок
Положения Исходная величина * А А * Ду = -g- Ду = Л Ду
Перемещения Др = Дут — Аун Ар = Ад? Дут — Л^п Дуц о ,
Мертвого хода Ар, = Дупх Дуох г Др = Aq пх Д(?пх Ауох Ау&х
Скорости Ду = -37 (Ду) Ду = 4г (А/ Ду) at
Определение ошибок положения механизмов. Практические методы определения ошибок положения основаны на принципе наложения ошибок, на основании Жоторого частичные ошибки можно находить раздельно [9, 10].
Общим методом определения ошибок положения, в соответствии с формулой (10.9), является метод дифференцирования функции преобразования движения по параметрам, погрешности которых являются первичными ошибками. Однако этот метод непригоден для первичных ошибок, представляющих погрешности «нулевых параметров» (погрешности формы деталей). В этих случаях применяют вспомогательные графо-аналитические методы: метод плана малых перемещений и геометрический [51, 109]. Практическая методика определения ошибок положения в этом случае распадается на два этапа: сначала находят указанное смещение как промежуточную ошибку положения, пользуясь длн этого одним из вспомогательных методов, а затем находят передаточную функцию кинематической цепи от детали, получившей смещение, до ведомого звена механизма; искомая ошибка положения равна их произведению
= Аух ДХд?, (10.13)
где А^х —передаточная функция участка цепи; ДхД(?— промежуточная ошибка положения.
В соответствии с формулой (10.8)
А^ = ^А? = ^А<?- (ЮЛ4)
где dxnp/dq — AQX — передаточная функция промежуточной ошибки положения; &q — первичная ошибка механизма.
Передаточная функция Аух определяется в общем случае дифференцированием ФГЩ участка кинематической цепи от детали, получившей упомянутое смещение, до ведомого звена
АуХ~ду/дхпр, (10.15)
где хпр — координата звена, включающего данную деталь.
Для механизмов с линейным законом движения передаточная функция определяется как простое отношение перемещений соответственных звеньев механизма
Аух ~ У/Хпр- (10.16)
Расчетные формулы ошибок механизмов
При. расчетах на точность необходимы расчетные формулы частичных й суммарных ошибок механизмов; первые используются главным образом при расчетах в процессе проектирования, вторые — при полном расчете. Суммирование ошибок производится для тех положений механизма, где суммарная ошибка имеет наибольшие значения (по абсолютной величине). Эти положения определяются по виду формул частичных ошибок или графо-аиалитическим анализом частичных ошибок [108].
Ниже приводятся расчетные формулы для ошибок перемещения и ошибок мертвых ходов механизмов, основанные на исходных общих зависимостях (10.8), (10.10), (10.11); расчетные формулы для ошибок скорости ведомого звена определяются с помощью выражения (10.12).
432
..-Таблица 10.10. Формулы частичных ошибок и значения коэффициентов Ср и Кр дли типичных векторных первичных ошибок механизмов
Вид ошибок Общая формула частичной ошибки w (».,) cp Численное значение Лр
. Ошибки мертвого хода нерегулируемой зубчатой передачи от эксцентриситетов колес Др = ACAV At? sin (<p -r 0K) 0 0 j/4-(K«+gc«) 1,73
Ошибки мертвого хода регулируемой зубчатой передачи от эксцентриситетов колес Др = AeAv &q 1 + cos (tp + 0H) 1 Ca ю| CO to •Cl К e u. 3,20
Ошибки перемещения механизмов от эксцентриситетов и перекосов шкал, биений валиков, ходовых винтов и т. п.» от несоосности муфт &р ~ ACAV At? sin (<p 4- 0H) — — sin 0И 0 0. Sin | |/ 2 + 9C;) при 180° sin == 1 3,45 (при <р^180с)
Ошибки перемещения зубчатой передачи от эксцентриситетов колёс . Др == ACAV At? sin (ср + « + 0h) — — sin (a + 0H) 0 0
Примечай н*е. А '— неслучайная часть передаточной функции ошибки; Av — случайная часть передаточной функции; ср — текущее значение угловой координаты детали; 0н — угловая координата векторной первичной ошибки в начальном положении механизма.
Ошибки перемещения теоретические (от допущений). Эти ошибки имеют систематический характер и суммируются алгебраически:
Ч ДДтр — Утч Упр! (10-17)
ПТр
«10-18>
Здесь г/тц и г/Пр — точное и приближенное значения выходной (расчетной) координаты механизма при отсутствии и принятии допущения соответственно; nTf> — число частичных теоретических ошибок.
Методы расчета частичных ошибок см. [49, 109]; в тех, случаях когда формулу (10.17) затруднительно привести к простому расчетному виду, пользуются табличным методом.
Ошибки перемещения технологические. Формулы частичных ошибок, вытекающие из формулы (II) табл. 10.8, для скалярных и векторных первичных ошибок имеют вид
= А Д^ск» (Ю. 19)
~ Д*7вк* (10.20)
где Ас — неслучайный передаточный коэффициент; Av — случайная часть передаточной функции векторной первичной ошибки (примеры см. в табл. 10.10). Определение Дртх при расчетах в процессе проектирования производится по предельным значениям Ае, Ао и Д?.
Суммирование технологических ошибок производится по вероятностным характеристикам рассеяния; расчетные формулы следующие:
Л^тх 2 = &Ртк 2 ± &Ртх £> (10.21)
___ птх
Лртх s = S (10.22)
1 1/ ТХ
4x2= К-К (10.23)
Здесь Дртх2 — среднее значение суммарной технологической ошибки перемещения; 6ртх2 — практически предельное отклонение от среднего значения; Ср и Кр — коэффициенты, зависящие от расположения поля допуска, вида и распределения первичной ошибки (определяются по табл. 10.10 и 10.11); — коэффициент относительного рассеяния сум-
марной ошибки (принимается равным 1 — 1,1 в зависимости от числа первичных ошибок и их распределений); птх — число технологических первичных ошибок.
Предельное значение технологической суммарной ошибки равно
тх | /----
ч,»,-<««>
По этим же формулам рассчитываются ошибки перемещения от смещений'в зазорах кинематических пар в тех случаях, когда эти смещения не связаны с реверсированием и имеют* регулярный характер; только значения 6</, Ср и Кр определяются с учетом формул (10.5) и (10.6).
433
Таблица 10.11. Исходные формулы для коэффициентов Ср и Кр
Первичная ошибка с₽ Кр
Скалярная Ср— Kq
Векторная Ср = CqM (Ав) кр =
Примечание. /М (А^) — математическое ожидание, о 0С) — среднее квадратическое отклонение случайной части передаточной функции первичной ошибки; остальные обозначения прежние (см. выше). 2л «г Al (А ) = -L 1 4„rf0„: \ J/ 2л j он 0 2л a2(^) = -ST i А^н. 0 где 0H—угол, определяющий направление векторной первичной ошибки в начальном положении механизма (случайная величина, распределенная в пределах от 0 до 2л по закону равной вероятности).
Ошибки перемещения эксплуатационные. Частичные ошибки перемещения от деформаций силовых и температурных рассчитываются непосредственно по формулам (III) н (VI) табл. 10.8. При определенном характере действия сил и установившемся тепловом режиме эти ошибки носят систематический характер н суммируются алгебраически
пэ-
S Ч»
(10.25)
где п3 — число частичных ошибок.
О расчетах самих деформаций см. с. 424 «Причины и виды ошибок механизмов».
Ошибки мертвых ходов механизмов от смещений в зазорах кинематических пар (люфтовые). Расчетные формулы подобны формулам технологических ошибок перемещения и приводятся без пояснений:
Ди = A A •
С V “вк’
(10.26)
(10.27)
(Ш.28)
(10.29)
(10.30)
(10.31)
где Д^ск — скалярная первичная ошибка; Д^вк — векторная первичная ошибка; пл — число люфтовых первичных ошибок.
Остальные обозначения подобны соответственным обозначениям технологических ошибок перемещения.
Ошибки мертвых ходов механизмов от деформаций детален (упругие), Расчет частичных ошибок упругих мертвых ходов производят по формуле (10.11) или непосредственно используя изменение деформаций Д/ под действием изменения момента ДЛ1 или силы Д/7 по формуле
Др^ — Ас (F)» (10.32)
где Ас — представляет собой передаточную функцию кинематической цепи от детали, испытывающей деформацию, до выходного звена [см. формулы (10.15) и (10.16)].
Ошибки упругих мертвых ходов являются систематическими ошибками н суммируются алгебраически
пу
дНс2 = S АМе, (Ю.ЗЗ)
где пу — число рассчитываемых упругих мертвых ходов.
Полная суммарная кинематическая ошибка механизма. Общий
вид расчетных формул следующий:
Д$ = Asc Д$у; (10.34)
= (10.35)
Д$о — ДртхЕ + Дри£ ± |/ fipTxS+fylflZ’ (10.36)
Здесь Д$с систематическая, Asy — случайная составляющие полной суммарной ошибки.
Конкретный состав слагаемых полной суммарной ошибки определяется требованиями к точности механизма. На практике встречаются расчеты только ошибок перемещения (при одностороннем рабочем движении), только мертвых ходов (с системами отработки с обратными связями) и полной суммарной ошибки (для большинства измерительных и счетно-решающ их приборов).
Расчеты на точность ври проектировании (виды расчетов, исходные данные и условия)
Основным видом расчета на точность при проектировании является проектный расчет. При разработке кинематической схемы производят анализ возможности получеиия технологичной конструкции и определяют требования к точности отдельных узлов; в процессе эскизной разработки конструкции производят оценку степени влияния на точность отдельных ошибок с целью выбора нанвыгоднейших параметров конструкции. После окончания эскизного проектирования выполняют полный анализ технологичности конструкции н расчет допусков на техноло-
гические первичные ошибки по заданному допуску на суммарную ошибку механизма.
Кроме проектного расчета находит применение проверочный расчет для сравнения ряда вариантов конструкции (см. с. 446, пример 1); он применяется также, когда допуски на технологические первичные ошибки уже назначены и необходимо проверить соответствие их заданным требованиям к точности механизма.
Все виды расчетов на точность осуществляются на основе приведенных выше расчетных формул с помощью специальных критериев технологичности конструкций и степени влияния ошибок (см. ниже) и с учетом применения компенсаторов ошибок.
Исходными данными для расчетов являются заданный техническими условиями допуск на точность механизма (60s), разработанные схема и конструкция механизма (или узлов) и сведения о производственной базе и объеме производства. Допуск 60$ определяет поле допустимых значений суммарной ошибки механизма; для ошибок перемещения это поле симметрично относительно нуля, для мертвых ходов оно одностороннее.
Исходным условием для расчета является обеспечение заданной точности
As (у) с | 6us |, (10.37)
(у — координата ведомого звена механизма) при минимуме стоимости изготовления механизма.
Критерии технологичности конструкций
Точностная технологичность конструкций точных приборов характеризуется уровнями точности требуемых технологических процессов обработки детален и сборки. В зависимости от достижимой точности, оборудования, оснащения и методов выполнения технологические процессы отделочных операций обработки деталей и сборки, применяемые в точном приборостроении, распределяются по трем уровням точности: экономическому, производственному и техническому, являющимся критериями точностной технологичности конструкции.
Экономический уровень точности (Э) для механической обработки соответствует точности, получаемой в серийном производстве с помощью типовых (нормализованных) инструментов и приспособлений на обычном универсальном и автоматическом оборудовании. Экономический уровень для сборки соответствует операциям, выполняемым без пригонок и специальных регулировок.
Производственный уровень точности (П) для механической обработки соответствует предельной точности, достижимой на обычном оборудовании с помощью специальных инструментов, приспособлений и методов. Производственный уровень для сборки соответствует сборке с регулировками, контроль которых выполняется производственными методами.
Технический уровень точности (Т) для механической обработки находится за пределами возможностей обычного оборудования н может быть достигнут с помощью специального оборудования или ручной доводки деталей. Технический уровень для сборки соответствует сборке с пригонками и регулировками, требующими лабораторных матодов контроля. В табл. 10.12 приведены ориентировочные значения уровней точности для наиболее распространенных типов технологических процессов и различных деталей, установленные на основе данных приборостроительных предприятий н литературных источников. Эти значения 436
Таблица 10.12. Уровни точности технологических процессов
Тип поверхности, размера, детали Вид погрешности Вид техпроцесса Уровни точности
э п т
Цилиндрические наружные поверхности (валики, оси, ролики) Погрешность диаметра Токарная (чистовая) обработка 11-й квалитет (4-й класс) 8-й квалитет (3-й класс) —
Шлифование 8-й квалитет (3-й класс) 6-й квалитет (2-й класс) 5-й квалитет (1-й класс)
Доводка — До 2 мкм
Несоосность Механическая обработка 7-я степень точности 6-я степень точности 5-я степень точности
Доводка — — До 2 мкм
Цилиндрические внутренние поверхности (втулки) Погрешность диаметра Токарная (чистовая) обработка 11-й квалитет (4-й класс) 8-й квалитет (3-й класс) —
Развертывание 8-й квалитет (3-й класс) 7-й квалитет (2-й класс) 6-й квалитет (1-й класс)
Шлифование 8-й квалитет (3-й класс) 7-й квалитет (2-й класс) 6-й квалитет (1-й класс)
Тип поверхности, размера, детали Вид погрешности Вид техпроцесса Уровни ТОЧНОСТИ
Э п т
Цилиндрические внутренние поверхности (втулки) Погрешность диаметра Доводка — —— До 2 мкм
Несоосность Механическая обработка 7-я степень точности 6-я степень точности 5-я степень точности
Доводка — — До 2 мкм
Конические поверхности Погрешность угла конуса Токарная (чистовая) 10-я степень точности 7-я степень точности —
Шлифование 7-я степень точности 6-я степень точности
Доводка — — 5-я степень точности
Плоскости Погрешность формы Фрезерование (чистовое) 8-я степень точности 7-я степень точности —
Шлифование 6-я степень точности 5-я степень точности —
Продолжение тЙЬл. 10.12
Тип поверхности, размера, детали Вид погрешности Вид техпроцесса Уровни точности
э П т
Плоскости Погрешность формы Шабрение " 1 — 5-я степень точности
Доводка —- — 4-я степень точности
Линейные размеры Погрешность размера Обработка резанием 11-й квалитет (4-й класс) S-й квалитет (3-й класс)
Шлифование 8-й квалитет (3-й класс) 6-й квалитет (2-й класс) —*
Доводка ’ — 5-й квалитет (1-й класс)
Сборка с регулировкой 8-й квалитет (3-й класс) 6-й квалитет (2-й класс) 5-й квалитет (1-й класс)
Межосевые расстояния Погрешность размера Разметка 0,2 мм 0,1 мм —
Сверление по кондуктору 0,05 мм 0,02 мм —
Тип поверхности, размера, детали Вид погрешности Вид техпроцесса Уровни точности
э п т
Межссевые расстояния Погрешность размера Сверление, растачивание на координатных станках — —- До 5 мкм
Сборка с регулировкой 0,05 мм 0,02 мм До 5 мкм
Угловые размеры Погрешность размера Механическая обработка 10-я степень точности 7-я степень точности 6-я степень точности
Доводка — " — До 5"
Сборка с регулировкой 7-я степень точности 6-я степень точности 5-я степень точности
Зубчатые и червячные колеса Кинематическая погрешность Фрезерование обкаткой 8-я степень точности 7-я степень точности
Шевингование — 5-я степень точности
Прикатка — — 6-я степень точности ,
Продолжение табл 10,12
Тип поверхности, размера, детали Вид погрешности Вид техпроцесса Уровни ТОЧНОСТИ
э п т
Зубчатые рейки и червяки Накопленная погрешность шага Резание 20 мкм 10 мкм —
Шлифование 10 мкм 5 мкм До 2 мкм
Резьбы винтовых механизмов Накопленная погрешность шага Токарная чистовая обработка 3-й класс 2-й класс
Шлифован не 2-й класс 1-й класс 0-й класс
Доводка — — До 2 мкм
Кулачки Погрешность радиуса вектора Фрезерование 0,05 мм 0,03 мм
Шлифование 0,02 мм 0,01 мм
Доводка — До 5 мкм
Шкалы и лимбы Погрешность деления Деление на машинах и автоматах 10 мкм Г 5 мкм 0,5' 1 мкм До 1"
определяют зоны, в пределах которых допуски соответствуют данному уровню точности. Для грубых ориентировочных оценок можно принимать, что экономическому уровню точности соответствует в среднем 3-й, производственному — 2-й и техническому — 1-й классы точности стандартных допусков на обработку деталей и сборку.
Анализ технологичности конструкций заключается в сопоставлении допусков на технологические первичные ошибки с уровнями точности. Конструкция технологична (в отношении допусков), если эти допуски соответствуют экономическому и производственному уровням точности отделочных и сборочных технологических процессов. Если значительное число первичных ошибок требует допусков на техническом уровне точности, то конструкцию следует признать нетехнологичнон для серийною производства (но она может быть приемлемой для мелкосерийного или штучного производства). В таких случаях необходимо исследовать возможность применения компенсаторов для расширения допусков, а если такой возможности нет, то изменить конструкцию.
Критерии степени влияния ошибок
Для упрощения расчетов целесообразно отбрасывать ошибки, влияние которых на точность механизма ничтожно. Общим критерием ничтожности влияния ошибок является условие, чтобы отбрасываемые ошибки не изменяли суммарную ошибку более чем на 5—10%. Исходя из этого, для предварительной грубой оценки влияния ошибок пользуются правилом: если из двух или более ошибок одна меньше остальных по крайней мере в 10 раз для систематических и в 5 раз для случайных ошибок, эту ошибку можно отбросить. Так, заранее отбрасывают ошибки от погрешностей микропрофиля рабочих поверхностей, погрешностей формы поверхностей для низких кинематических пар, от контактных деформаций в высших кинематических парах при малых нагрузках и т. и.
Для технологических ошибок более строгую и глубокую оценку степени их влияния производят с помощью предельных допусков и уровней точности (см. выше). Предельный допуск определяется из условия, что точность механизма зависит только от одной данной первичной ошибки
(10.38)
где — предельный допуск на первичную ошибку; Ас — неслучайная часть передаточной функции ошибки (см. выше); — допуск и а технологическую составляющую суммарной ошибки механизма, определяемой по формуле
60so=60s-Asc. (10.39)
Здесь 60s—полный допуск на точность механизма; Asc — систематическая составляющая суммарной ошибки (сумма теоретических и эксплуатационных систематических ошибок).
Степень влияния ошибок характеризуется требуемыми для допусков уровнями точности: чем сильнее влияние, тем выше уровень точности. Действительные значения требуемых допусков в процессе проектирования неизвестны (они рассчитываются на заключительном этапе проектирования), ио для сравнения с уровнями точности можно пользоваться предельными допусками, связанными с действительными допусками зависимостью 67 — где Азап 1 — коэффициент, зависящий
Таблица 10.13. Зависимость степени влияния ошибок от уровней точности
Соот н ош е н и я м еж ду коэффициентами влияния Степень влияния частичной ошибки Требуемый уровень точности допуска
с Лэ АП < ^0 < A-т < Слабое Сильное Очень сильное Допуск HI Экономический Производственный Технический ^выполним
от числа ошибок (чем больше число ошибок, тем меньше Кзап)- Наиболее полный и строгий анализ степени влияния ошибок производится с помощью коэффициентов влияния, устанавливающих непосредственное соотношение между величинами соответствующих ошибок и заданным допуском на точность механизма
(10.40)
где X— коэффициент влияния ошибки; As— частичная ошибка.
Для систематических ошибок Хс определяется по формуле (10.40) и степень влияния оценивается по общему критерию (см. выше): если окажется, что лс 20, ошибку можно отбросить как ничтожную; если 20>Хс^10, малые ошибки можно отбрасывать при условии, что число их ие более двух; в противном случае по этому неравенству нужно проверить %2с, найденный по сумме малых ошибок. Для случайных ошибок нельзя пользоваться непосредственно формулой (10.40), так как величины ошибок заранее неизвестны; оценка их влияния производится с помощью табл. 10.13, входными величинами для которой служат коэффициенты влияния, соответствующие предельным значениям уровня точности по табл. 10.12
(10.41)
и наименьшее допустимое значение коэффициента влияния Хо
1 - ±1/
Ло = “Т у -----г«2>
(10.42)
где rtf — число частичных ошибок, имеющих систематическую составляющую, Ti е. среднее значение (для них Ср =f= 0); п2 — число ошибок, н^ъимеющих систематической составляющей (Ср = 0).
Как видно из табл. 10.13, степень влияния ошибок связывается с уровнем точности, т. е. с технологичностью конструкции. Критерием ничтожного влияния случайных ошибок является условие (Лв — коэффициент влияния ничтожных ошибок).
Для ошибок, входящих в группу (Ср =/= 0), Хн 10, а для ошибок, входящих в группу п2 (Ср == 0),
>-н ~ ]АН (10-43)
где — число ничтожно влияющих ошибок из группы
Таблица 10.14. Наименьшие допустимые значения коэффициента влияния [к формуле (10.42)]
П> «1
0 1. 2 3 4 5 6 7 8 9 10
0 0,00 1,00 1,70 со № см 3,00 3,62 4,29 4,83 5,42 6,00 6.58
1 1,00 1,62 2,23 2,82 3,41 4,00 4,58 5,16 5,73 6,30 6,87
2 1,41 2,00 2,58 3,16 3,73 4,30 4,87 5,44 6,00 6,56 7,12
3 1,73 2,30 2,87 3,44 4,00 4,56 5,1 2 5,68 6,24 6,79 7,35
4 2,00 2,56 3,12 3,68 4,24 4,79 5,35 5,90 6,45 7,00 7,55
5 2,24 2,79 3,35 3,90 4,45 5,00 5,55 6,10 6,65 7,20 7,74
6 2,45 3,00 3,55 4,10 4,65 5.19 5,74 6,29 6,83 7,37 7,91
7 2,65 3,19 3,74 4,29 4,83 5,38 5,92 6,4 6 7,00 7,54 8,08
8 2,83 3,37 3,92 4,46 5,00 5,54 6,08 6,62 7,16 7,70 8,24
9 3,00 3,54 4,08 4,62 5.16 5,70 6,24 6,78 7,32 7,86 8,36
10 3,16 3,70 4,24 4,78 5,32 5,86 6,40 6,93 7,46 8,00 8,54
11 3,32 3,85 4,39 4,93 5,46 6,00 6,54 7,07 7,61 8,14 8,67
12 3,46 4,00 4,54 5,07 5,61 6,14 6,67 7,25 7,74 8,28 8,81
13 3,61 4,14 4,67 5,21 5,74 6,28 6,81 7,34 7,87 8,41 8.94
14 3,74 4,28 4,81 5,34 5,87 6,41 6,94 7,4 7 8,00 8,53 9,06
15 3.87 4,41 4,94 5,47 6.00 6,53 7,06 7,59 8,12 8,65 9,18
16 4,00 4,53 5,06 5,59 6,12 6,65 7,18 7,71 8,24 8,77 9,30
17 4,12 4 .65 5,18 5,71 6,24 6,77 7,30 7,83 8,36 8,89 9.42
18 4,24 4,77 5,30 5,83 6,36 6,89 7,42 7,94 8,47 9,00 9,53
19 4,36 4,89 5,4 2 5,94 6,47 7,00 7,53 8,06 8,58 9,11 9,64
20 4,47 5.00 5,53 6,06 6,58 7,11 7,64 8,16 8,69 9,22 9,74
21 4,58 5,11 5,64 6,16 6,69 7,22 7,74 8,27 8,80 9,32 9,85
22 4,69 5,22 5.74 6,27 6.80 7,32 7,85 8,37 8,90 9,42 9,95
23 4,80 5.32 5.85 6,37 6,90 7,42 7,95 8,47 9,00 9,52 10,05
24 4,90 5,42 5,95 6,47 7,00 7,52 8,05 8.57 9,10 9,62 10,15
25 5,00 5,52 6,02 6,57 7,10 7,62 8,15 8.67 9.20 9.72 10,24
Применение указанных критериев степени влияния ошибок см. с. 449, примеры 2 и 3. Численные значения л0 (в зависимости от числа первичных ошибок) приведены в табл. 10.14.
Методы компенсации ошибок механизмов
Компенсация применяется для ошибок, оказывающих наиболее сильное влияние на точность механизма и требующих допуски на техническом уровне точности. Компенсация заключается в уменьшении (иногда даже в полном устранении) действия отдельных сильно влияющих ошибок (или групп ошибок) с помощью специальных мероприятий или устройств, называемых компенсаторами. На практике применяются следующие методы компенсации [6, 8, 28, 39, 62]. L
1. Специальные организационно-технические мероприятия. Широкими возможностями уменьшения ошибок обладают так называемые обычные регулировки, применяемые при установках нулевых положений н согласовании движений на выходе и входе механизмов. С помощью таких регулировок производится, например, «половинение мертвых ходов»; возможно существенное уменьшение и ошибок перемещения |4, 5, 62]. Другим методом из этой группы является применение селекции при обработке и сборке [62] (сюда же относится и широко применяемый в мелкосерийном производстве метод комплектации при сборке).
2. Технологические пригонки и доводки деталей, выполняемые при сборке. К данным методам прибегают в основном для получения подвпж-444
ных замкнутых сопряжений с посадками выше 2-го класса точности и для уменьшения погрешностей формы рабочих поверхностей деталей в высшнх кинематических парах. Эти методы компенсации наименее желательны, так как весьма дороги.
3. Конструктивные методы, основанные на использовании регулировок при сборке, экономичны и эффективны, имн можно воздействовать одновременно на ряд ошибок. Конструктивные устройства, применяемые для регулировки, весьма разнообразны и основные их идеи хорошо известны (см. [4, 5, 49, 62, 109]). Недостатком этих устройств является нестабильность с течением времени, поэтому их избегают применять в конструкциях приборов высокой точности; другой недостаток заключается в некотором усложнении сборки, что ограничивает их применение в приборах крупносерийного и массового производства (здесь более целесообразно применение специального оборудования, дающего повышенную точность обработки по сравнению с обычным).
Проектный расчет механизмов на точность
Общие цели проектного расчета и решаемые им задачи: анализ технологичности конструкции; выбор рациональных параметров конструкции, определение требований к точности отдельных деталей, соединений и узлов; расчет допусков на технологические первичные ошибки. Характер и содержание расчета зависят от этапов проек-тмроваиия.
На первом этапе проектирования прн разработке кинематической схемы механизма определяют ианвыгоднейшие параметры схемы и делают предварительный анализ технологичности конструкции. Для этого выявляют основные ожидаемые источники ошибок, представляющие укрупненные (комплексные) первичные ошибки, и для них определяют предельные допуски [с помощью формулы (10.38) по максимальным значениям передаточных коэффициентов Ас], которые затем сравнивают с уровнями точности. На этом этапе производят также расчет н анализ теоретических ошибок. Если представляется возможным определить на этом этапе общее ожидаемое число первичных ошибок, следует произвести более полный анализ с помощью коэффициентов влияния [формулы (10.40)—(10.43) см. с. 447, пример 1].
На втором этапе проектирования прн разработке конструкции расчет сводится к оценке степени влияния отдельных ошибок с целью выбора наивыгоднейшего варианта конструкции. Расчет заключается, как н в предыдущем случае, в определении предельных допусков и установлении требуемых уровнен точности.
На завершающем этапе проектирования производят полный анализ степени влияния ошибок и технологичности конструкции и рассчитывают допуски на технологичные первичные ошибки. Последовательность расчета следующая.
' Выявление и исследование источников ошибок* Здесь выявляют действительные (поэлементные) первичные ошибки — технологические и эксплуатационные (см. «Причины и виды ошибок механизмов»). Исследование первичных ошибок заключается в определении их свойств и предварительной оценке степени влияния.
Определение частичных ошибок механизмов. Производят вывод формул частичных ошибок — сначала ошибок положения, а затем, пользуясь формулами (10.10)—(10.12), и основных ошибок, требуемых условиями расчета (т. е. ошибок перемещения, мертвого хода, скорое;и). Из полученных формул устанавливают выражения для Ас — неслучгй-
ной части передаточных функций ошибок, необходимые для дальнейших расчетов.
В процессе вывода формул производят оценку степени влияния ошибок с целью отбрасывания ошибок, оказывающих ничтожное влияние на точность механизма.
Расчет коэффициентов и ошибок. С помощью приведенных выше формул (см. «Расчетные формулы ошибок механизмов») рассчитывают все систематические ошибки механизма — теоретические и эксплуатационные (от деформаций) и определяют Дзс — систематическую составляющую суммарной ошибки [по формуле (10.35)]. Для каждой частичной ошибки нужно определить коэффициент влияния лс [по формуле (10.40)] н оценить степень ее влияния на точность механизма. При слишком малых значениях Хс необходимо заранее внести соответствующие изменения в конструкцию, чтобы ослабить влияние соответственных систематических ошибок (следует иметь в виду, что чем меньше Д$с, тем больше допуск на технологическую составляющую суммарной ошибки и тем дешевле будет прибор). Далее, с помощью формулы (10.39) определяют допуск иа технологическую составляющую ошибки и рассчитывают предельные допуски bQq [по формуле (10.38)] для всех учитываемых технологических ошибок, а по формулам (10.42) и (10.43) определяют значения коэффициентов влияния Хо и Хн. После этого производят анализ степени влияния технологических ошибок сначала по формуле Хэ а затем по табл. 10.13. В результате для многих ошибок устанавливают требуемые уровни точности. В тех случаях, когда необходимо получить конкретное численное значение допуска, пользуются формулой
&? = -Т—г4гг-’ (10.44)
где 67 — половина поля искомого допуска; остальные обозначения см. выше.
При несимметричном поле необходимо по найденному значению б^ определить верхнее и иижнее отклонения поля допуска. Для этого определяют с помощью формул табл. 10.5 значение коэффициента Cq (предварительно выбрав из табл. 10.6 или 10.7 значение «<?), затем по формулам табл. 10.4 рассчитывают Д^в и Д?н. Если среди найденных допусков некоторые окажутся на техническом уровне точности, целесообразно проверить возможность применения «условия компенсированного влияния» ошибок. Сущность этого условия заключается в возможности расширения допусков иа сильно влияющие ошибки за счет некоторого ужесточения допусков на слабо влияющие ошибки. Если, например, большинство первичных ошибок требует экономического уровня со значительным превышением Хэ над Ад, то для них целесообразно ужесточить допуски до предельных значений экономического уровня точности; это позволит расширить допуски для ошибок, требующих технического уровня, до производственного, илн производстве^ЙоГо до экономического.
Оформление всего расчета рекомендуется выполнять по форме табл. 10.16 и 10.17 (см. с. 449 и 455, примеры 2 и 3).
Проверочный расчет механизмов на точность
Расчет заключается в определении суммарной ошибки механизма по заданным допускам на первичные ошибки. Основные этапы расчета следующие.
Первый этап (выявление и исследование источников ошибок) и второй (определение частичных ошибок) — такие же, как и при проектном расчете (см. выше). Третий этап (расчеты коэффициентов и ошибок) состоит в следующем. Сначала находят систематические ошибки — теоретические и эксплуатационные (от деформаций) и определяют суммарную систематическую составляющую Л$с [см. формулу (10.35)]. Затем с помощью табл. 10.4—10.7 и 10.11 определяют характеристики полей допусков и распределения технологических первичных и частичных ошибок. Из формул частичных ошибок устанавливают и вычисляют Ас, по которым затем рассчитывают средине и практически предельные значения технологических частичных ошибок, пользуясь для этого формулами:
ЛРп-ЛСА; (10.45)
(ю.46)
где — среднее, а 8рп — практически предельное значение частичной ошибки; остальные обозначения см. выше. Формулы приведены для ошибок перемещения, но онн справедливы и для люфтовых мертвых ходов (вместо Лрп и &рп надо подставить и Далее производят суммирование технологических ошибок по формулам (10.22) и (10.23) или (10.29) и (10.30) и полное суммирование по формулам (10.35) и (10.36). Результат сравнивают с формулой (10.37).
Оформление проверочных расчетов рекомендуется выполнять по форме табл. 10.15.
Примеры расчета механизмов на точность
Пример 1. Требуется проверить возможность заклинивания цилиндрической прямозубой передачи при сопряжении вида С, если передаточное отношение i == 1/4, делительные диаметры колес dx — 16 мм, d2 ~ 64 мм и модуль т = 1; боковой зазор в зацеплении не регулируется степень точности 7-я.
Для данных условий достаточно определить вероятностные характеристики рассеяния бокового зазора в зацеплении и сравнить среднее значение и практически предельные отклонения от среднего значения зазора; если первое с достаточной надежностью превышает второе, то заклинивание невозможно.
Существенное влияние иа боковой зазор оказывают смещения исходного контура у обоих колес, эксцентриситеты колес и погрешности межосевого расстояния (влиянием остальных погрешностей можно пренебречь). Частичными ошибками являются здесь боковые зазоры в зацеплении от каждой из перечисленных ошибок. Зависимость бокового, зазора, измеренного по делительной окружности, от рассматриваемых первичных ошибок выражается формулами:
ДСдЛ = 2 tg а Дй; (10-47)
ДсДе = 2 tg а cos (<р + 0Н) Де; (10.48)
Дсдл = 21^аДД, (10.49)
где ДСдд. —боковые зазоры от смещения исходного кои-
тура, эксцентриситета и погрешности межосевого расстояния соответственно; ф — угол поворота колеса; a — угол зацепления; 0Н — угол,
Таблица 10.15. Расчет -бокового зазора в зацеплении нерегу лируемой цилиндрической зубчатой передачи (к примеру 1)
№ детали Наименование п. о. Обозначение Систематическая п. о. Допуск, мкм Характеристики поля допуска Характеристики поля рассеяния Характер ч. о. Общая формула Ас Численное значение Коэффициенты рассеяния 6pD
К, % сч Ас Ьрс Ср в мкм
1 п 4- 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
1 Смещение исходного контура dh^ — -5 —30 —20 15 1,2 1,33 М. х. 2tga 0,73 4 — 1,33 1,2 14,5 13,1 172
1 Эксцентриситет — 12 6 6 1,14 —28 0,72 " - — 1,73 — 7,6 58
2 Смещение исходного контура Дм^2 dh2 — —7 —45 29,5 22,5 1,2 — 1,31 1,31 1,2 21,5 19,7 384
2 Эксцентриситет Дг2 — 17 8.5 8,5 Е 1,14 —0,28 0,72 1,73 10,7 114
1—2 Погрешность межосевого расстояния ЬА -—- ±13 — 13 1.2 4 — — — 1,2 ' П.4 130
A~,,y^6,U; бр^^==858; ДСя=-Д6± Г858=36±29 мкм. . .
Примечание. В табл. 10.16—10.17 приняты обозначения: п. о. — первичные ошибки; ч. о. — частичные ошибки; м. х. — мертцый .ХОД.
определяющий направление эксцентриситета колеса относительно межосевого расстояния в начальном положении передачи; Д/i — смещение исходного контура колеса; Де — эксцентриситет; Д4 — погрешность межосевого расстояния.
Порядок расчета следующий.
1. Перечисленные выше первичные ошибки записывают в графы 1—3 расчетной таблицы (табл. 10.15). Из ГОСТ 9178—59 выбирают значения допусков на эти ошибки и записывают в графу 5 т/блицы. Для смещений исходного контура учитывают допуски на смещения и наименьшие (гарантированные) смещения ДМА.
2. Из формул (10.47)—(10.49) следует, что неслучайные части передаточных функций Ас для всех ошибок одинаковы и постоянны: Ас — 2 tg а; эту формулу записывают в графу 12 и одновременно заполняют графу 11. Численное значение А6. — 0,73 вносят в графу 13.
3. С помощью формул табл. 10.4—10.7 определяют характеристики допусков и распределения первичных ошибок и заполняют графы 4—10. При этом нужно учитывать следующие соотношения;
dh — 0,5б/гдоп; ДЛ = ДМЛ + б/i; Де = О,5£о;
бе = 0,5 Де = 0»25Е0; Хое — 0,25Е^ Д<(4 — 0.
В левой части этих равенств стоят величины, вносимые в расчетную таблицу, а в правой — величины, которые берутся из таблицы ГОСТ 9178—59 (6йдоП — допуск на смещение исходного контура, Е() — суммарное биение).
448
4. Производят вычисление величин, входящих в графы 15—19: коэффициентов Кр и Ср — по формулам табл. 10.10 (имея в виду, что Де—векторная первичная ошибка, а все остальные — скалярные) н 10.11; среднего и практически предельного значений частичных ошибок Др н dp — по формулам (10.45) и (10.46). Далее выполняют суммирование цо графам 17 и 19, и после извлечения корня из суммы по графе 19гполучают результаты расчета (записаны в иижней части расчетной таблицы). Среднее значение суммарного зазора равно Дс2 = 36 мкм, а практически предельное отклонение — 29 мкм. На основании этих данных можно заключить, что с надежностью не менее 99,8% заклинивание передачи невозможно.
Пример 2. Для зубчатого редуктора, состоящего] из пяти одинаковых пар цилиндрических прямозубых колес с передаточным отношением каждой пары 0,5, задан допуск боц на суммарный мертвый ход, равный 12х. Требуется определить степени точности для каждой пары колес, если боковой зазор в зацеплении не регулируется. Диаметры делительных окружностей ведомых колес в каждой паре равны 68,8 мм, модуль 0,8 мм. ‘
Из условия следует, что расчет является проектным; проводим его в соответствии с приведенным выше описанием основных этапов проектного расчета и результаты сводим в табл. 10.16.
1. Причинами мертвого хода зубчатых передач являются главным образом боковые зазоры в зацеплении, возникающие от технологических погрешностей изготовления и сборки колес (см, пример 1). Для заданных
15 В. А. Панов и др. 449
Г 1;; ;'СО 5—6 ОЭ 1 1—2 № деталя
1 1
о 00
Боковой зазор в зацеплении ю Наименование п. о.
> Г о > г» 1 00 > г» CR 1 <3» > г» 0» ( tfb > г» ь* ( W Обозначение п. 0.
j 1 1 1 1 Систематическая п. о.
м. х. СП Характер ч. о.
*г* о G 1 С 6.88 . - - I _ - <4 00 ' г-00 1 н* а о *• г-а> 1 , G 6J8 _ 6,88 . Dt ‘4-10 » 00 го*’ 1 ь* , с. О» Общая формула Лс
oooi-o 0,0500 1 0,0250 0,0125 О 8 О кэ Численное значение
j I 1 I 1 00 > тз гь
to <р - 240 480 960 1920 (О бо<7* мкм
2,2 3,9 00 гО 871 о >* « 0)
»—* ъ< СУ» — 3,1 1 1 1 *•* *•* ьп
* * < ГЭ 1 1 1 1 W >* м
4-] □ а» 0) 0) W Требуемый уровень точности
Oi 00 00 00 *-* Класс или i степень точности
’ СП 9° in 11; 1 L. .... *"SI^ / 108 108 108 *-* СИ Допуск, мкм
Г 108 108 108 108 *-* СП 5 £ > -Q 0)
1 1 1 *-* ! ' * щ v
' ’ '0? 1 >. t /- -, . 1 ' 1 00 > -Q
Таблица 10.16. Проектный расчет зубчатой передачи иа томность (к примеру 2)
размеров колес суммарные боковые зазоры, рассчитанные по формулам |10.47)—(10.49), имеют следующие величины:
-Степень точности........................ 8 7 в
Суммарный боковой зазор* мкм........... 108 77 68
По указанным данным заполняют графы 1—5 и 16—18 табл, 10.16 (уровни точности для зубчатых колес принимают по табл. 10.12), \
2. Зависимость углового мертвого хода зубчатой пары колес (в минутах) от бокового зазора в зацеплении, измеренного по делительной Окружности ведомого колеса пары, выражается формулой
6,88 д
ДНК = ~dT Асы <1о5о>
о
Где — делительный диаметр ведомого колеса пары; — суммарный зазор в зацеплении пары; 6.88 — размерный коэффициент. 1
Частичный мертвый ход передачи от мертвого хода каждой отдельной пары равен
Ди ==i. Ди = Дс„. (10.51)
г п k-n г к fe-ft Sfc» ' '
где 4-л — передаточное отношение от данной пары до выходного з?ена редуктора.
Таким образом, передаточные функции Ас для всех пар выразятся формулой
Ае = ik-n, (10.52)
«К
* конкретные выражения которой для соответственных нар редуктора вносят в графу 6. !
3. Систематические ошибки здесь отсутствуют, поэтому расчеты проводят сразу для Ас, предельных допусков и коэффициентов влияния. Заметим, что все первичные ошибки (суммарные боковые зазоры) относятся к группе (Ср 0, см. с, 443). Вычисляют прежде всего передаточные функции и записывают результаты в графу 7; по формуле1 (10.38) определяют значения предельных допусков, которые вносят в графу 9; по формуле (10.41) находят значения и записывают их в графу 10. Производят предварительный анализ степени влияния ошибок, имея в виду формулы Хэ и лн^ 10. Из полученных значений лн видно, что для первой пары лэ = 17,8 10, следовательно,
влиянием первой пары можно пренебречь; это означает, что без расчета допусков для этой пары можно назначить экономический уровень точности (8-ю степень точности по ГОСТ 9178—59х).
По оставшимся четырем первичным ошибкам 4, л2 6) определяют с помощью формулы (10.12) наименьшее допустимое значение Xq — 3 н производят полный анализ степени влияния всех ошибок и технологичности конструкции редуктора. Находим, что втор ур и третью пары колес можно выполнять на экономическом уровне точности (8-я степень), так как для них Хэ = 3; четвертая пара колес не
к - • ' )
1 Ввиду того что расчеты носят иллюстрационный характер, исходные Данные величин (допусков) взяты из ГОСТ 9178—59. »
15* 0J
Таблица 10.17. Проектный расчет зубчатой передачи на точность (к примеру 3)
№ детали Наименование п. о. Обозначение п. о. Систематическая п. о. Характер ч. о. Общая формула А Численное значение S г «О сп е«г с е«г е? Уровень точности Класс нли степень точности । Допуск, мкм S £ S сп о <1 S X S с о мкм
О О
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
1 Кинематическая погрешность первого ведущего колеса ^21 — К. О. 6,88 . Р, (1-10 0,00625 — 2400 32 — Э 8 75 75 —— —
2 То же второго колеса — К. О. 6,88 . Р2 12-10 0,00625 — 2400 26,7 — э 8 90 90 —
1—2 Боковой зазор в зацеплении первой пары колес — М. X. 6,88 . ”7)’ *2-1° 0,00625 — 2400 22,2 — — э 8 108 108 — —
3 Кинематическая погрешность третьего колеса — К. О. 6,88 . D3 ‘3-10 0,0125 — 1200 16 — — э 8 75 75 —
4 То же четвертого колеса ——- К. О. 6,88 . р, (4-1° 0,0125 — 1200 13,5 — ——™ э 8' 90 90 " '
3—4 Боковой зазор в зацеплении второй пары колес А^з-4 — М. X. 6,88 . Р, '4-10 0,0125 — 1200 11,1 — э 8 108 108 —*
Продолжение табл. 10.17
№ детали Наименование п. о. Обозначение и. о. | Систематическая ; п. о. Характер ч. о, i Общая формула Ас Численное значение WMW СП е«г Е е«г Уровень точности Класс или степень точности Допуск, мкм ими мкм X
Ас
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1b
5 Кинематическая погрешность пятого колеса —. К. О. 6,88 . р5 ,5-10 0,025 — 600 8 — — э 8 75 75 — —
6 То же шестого колеса ^26 — к. о. 6,88 . Рв ‘в-10 0,025 —-4 600 6,7 — э 8 90 90 d —н—
5—6 Боковой зазор в зацеплении третьей ^С5-6 — М. х. 6,88 . Р« 'в'10 0,025 — 600 5,6 — — э 8 108 108 — --
пары колес
7 Кинематическая — к. о. 6,88 . П h-io 0,050 —* 300 4 6,3 — п 7 48 — 48 —
погрешность седьмого колеса и<
8 То же восьмого колеса — К. О. 6,88 . р8 **-1° 0,050 — 300 3,3 5,5 п 7 55 — 55 —
СЛ
№ детали Наименование п. о. Обозначение п. о. Системат ическая П. О. Характер ч. о. ; Общая формула Ао Численное значение мкм 1 Уровень точности . Класс или степень точности Допуск, мкм S £ % СП сз-<3 мкм * 1 wmw
Ас дрс
1 2 3 4 5 6 7 8 9 1,0 11 12 . 13 14 15 16 17 18
7—8 Боковой зазор в зацеплении четвертой пары колес Дс7_8 " 1М. х. 6,88 . D 9 '*-10 0,05.0 — 300 2.8. 3,9 П 7 77 — 77 1
9 Кинематическая погрешность девятого колеса 6fV6 — к. о. 6,88 . Г) г9-10 0.100 — 150 -—— 3,1 5 т 6 30 — — — 30
10 То же десятого колеса ^Х10 - К. О. 6,88 D10 0,100 1 150 1 2,7 4.4 т 6 34 — 34
9—10 Боковой зазор в зацеплении пятой пары колес AC{j_iO .— М. X. 6,88 Dio 0,100 150 — 1,9 2,6 т 6 58 — 1 58 л»
Примечание. Буквами к. о. обьёиачейы кинематические ошибки. Остальные обозначения см. 1ъш1£ , -
__ Ц ,, --- | ' —. . . .Ь» - - „ *
укладывается в экономический уровень ~ 2,2 < Хо), но может быть выполнена на производственном уровне (Хп = 3,1 > Хо), а пятая — выходная, пара редуктора — не укладывается даже в технический уровень ТОЧНОСТИ (А-р — 2,1 < Xq).
Проверка возможности применения условия компенсированного влияния (см. с. 445—446) показывает, что если первые две пары выполнить i(a пределе экономического уровня точности (по 8-й степени), а третью и четвертую — по производственному уровню (по 7-й степени), то получится «запас точности», достаточный для того, чтобы и пятую пару выполнить на производственном уровне; суммарный мертвый ход» хотя и не уложится в номинал заданного допуска, но будет отличаться от него всего иа5%> что для практики обычно считается приемлемым.
Таким образом, выполнение данного редуктора по заданному допуску возможно, но при условии изготовления и сборки трех hap колес из пяти по производственному уровню точности.
Пример 3. Для зубчатого редуктора, рассмотренного в примеру 2, заДан допуск на полную суммарную ошибку (т. е. на ошибку перемещения и мертвый ход вместе), равный 15'. Требуется определить степени точности для всех пар колес, если боковой зазор в зацеплении не регулируется и все колеса изготовляются по допускам ГОСТ 9178Ц-59. Принимаем, что влияние погрешностей сборки и подшипников на ошибку (Перемещения учитывается допусками указанного ГОСТа.
. Полная кинематическая ошибка передачи определяется кинематическими погрешностями колес и суммарными боковыми, зазорами в зацеплении; те и другие являются комплексными первичными ошибками. Формулы частичных ошибок и численные значения величин, относящиеся к зазорам, используем из примера 2. Для кинематических погрешностей колес можно написать только приближенные формулы частичных ошибок перемещения, подобные формулам ошибок от эксцентриситетов колес (см. табл. 10.10), приняв эти погрешности в качестве векторных первичных ошибок (преобладающую роль в них играют эксцентриситеты — до 80% величины Общий вид этих формул, приведенных к выходу редуктора:
д₽=ал (4-SF х) • <10-53)
Здесь Ас — неслучайная часть передаточной функции ошибок [определяется по формуле (10.52)J; A#—случайная часть передаточной функции (см. табл. 10.10).
Из этого условия определяют и численные значения коэффициентов Ср и Ко (см. табл. 10.10 и 10.11), приняв, что углы поворота для всех колес больше 180°. Описание расчета здесь не приводится, так каю'оно аналогично изложенному в предыдущих примерах; результаты расчета сведены в табл. 10.17. Как и в примере 2, здесь использовано условие компенсированного влияния ошибок.
Литература: [4 — 10, 28, 39, 43, 48 —5Г, 62, 68, 89, 109L
ГЛАВА 11 НАПРАВЛЯЮЩИЕ ДЛЯ ПРЯМОЛИНЕЙНОГО И ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
ОБЩИЕ СВЕДЕНИЯ
Направляющими называют сборочные единицы, детали или отдельные их поверхности, которые обеспечивают перемещение других деталей или сборочных единиц в требуемом направлении. Различают направляющие для поступательного движения в плоскости и направляющие для вращательного движения вокруг некоторой оси или точки. В зависимости от вида трения, возникающего при взаимном перемещении деталей
Рис. 11.1. Типы направляющих для прямолинейного движения
направляющих, различают направляющие: с трением скольжения; с трением качения; с трением упругости (внутренним или молекулярным).
Взаимная ориентация деталей направляющих при функционировании может осуществляться за счет внешней силы (собственного веса каретки; усилия замыкающей пружины и т. п.) или за счет замыкания формой деталей направляющей. В первом случае направляющие называют открытыми с силовым замыканием; во втором случае — замкнутыми с замыканием формой. Открытые направляющие (рис. 11.Г, а) 456
применяют в основном в стационарных приборах,-замкнутые направляющие (рнс. 11.1,6, в) функционируют независимо от направления действующих сил.
ПРИНЦИПЫ КОНСТРУИРОВАНИЯ НАПРАВЛЯЮЩИХ
При конструировании направляющих для прямолинейного или вращательного движения следует учитывать принципы статической определенности конструкции, ограничения смещений н принцип баз. В соответствии с указанными принципами при конструировании необходимо обеспечить для подвижной детали направляющей одну степень свободы (поступательного нли вращательного движения). Остальные пять степеней свободы для подвижной детали нужно ограничить наложением необходимого числа точечных связей. При этом следует располагать ограничивающие плоскости (поверхности) по возможности нормально к направлению ограничиваемого перемещения и на максимально возможной базе.
Соблюдение указанных принципов позволит обеспечить требуемую точность функционирования направляющих, а именно:
1) сохранение параллельности движущейся детали заданной базе;
2) наличие минимальных смещений по нефункциональным направлениям,
В противоречие указанным выше принципам конструирования требования к плавности движения, стойкости против износа и возможности компенсации износа приводят к появлению большого числа конструкций направляющих.
НАПРАВЛЯЮЩИЕ ДЛЯ ПРЯМОЛИНЕЙНОГО ДВИЖЕНИЯ
Точность поступательного перемещения подвижной детали — ползуна, легкость и плавность движения, малый износ при требуемой грузоподъемности — важнейшие требования, которые необходимо обеспечить при конструировании, изготовлении деталей и сборке направляющих. Для приборов, работающих в условиях больших перепадов температур, эти требования должны соблюдаться во всем диапазоне колебания температуры.
В табл. 11.1 приведены конструктивные схемы различных типов направляющих и дана их сравнительная оценка по соответствующим классам. Высшим является нулевой или первый класс.
Типы направляющих классифицированы по виду трения:
1) направляющие с трением скольжения: по цилиндрическим, по плоским или комбинированным поверхностям;
2) направляющие с трением качения: на шариках, на роликах илн иголках;
3) направляющие с внутренним трением (упругие).
Направляющие с трением скольжения
Идеальной с точки зрения теории точности является конструкция направляющей, представляющая ползун формы параллелепипеда, опирающийся на три точечных контакта в горизонтальной плоскости (контакты образуют равносторонний треугольник) и на два контакта . По боковой поверхности, к которой ползун прижимается упругим ‘элементом (пружиной). Однако на практике для повышения нагрузоч-
00
' С трением скольжения Тип направляющих
о Cn 4ь co N? H* № схемы
Пружина 1 . 1 Фторопласт-^ ш'', ^jjp _ *n Xi x'Az v^, \Z \fe- i JU !P v yo~: - Jg » 1 и < 1 1 “J i i I » t h t 1 i Схема .
tO О r—* tO Точность
4ь 4b ft* co 1 4b to co Сила трения
►*** co 1 N? IO L >*4t Нечувствительность к перепаду температур
4b tO 4х >M« ^Л? 4b Нагрузочная способность
r—* to ft* 4b CO Стойкость к износу
h**# to r—* 4b *** Ремонтопригодность
Г-* tO to *— Стоимость ” • ' ~ 1
=5
E га
£
3
s
65*
С трением качения С трением скольжения Тип направляющих
со Г-* to о (© ос № схемы
1 1. ( Шарики: r I*-— b С ft- г Е
VI ri 1
- - ^enapamop _r- J Й»
СО ю to to >*4t 4X 4X Точность..
to to to to to Сила трения
Иац* to t— co CO Нечувствительность к перепаду температур
со to co • co to r—* Нагрузочная способность
со to to to to to to Стойкость к износу
4Х ’ ри J .ф Г. * г. - 4X to to 4X 4b Ремон то пр иго дно сть
4b to CO ' co to w Стоймдсть
p
ft
fjs
О Ja
я ft ж
Тнп направляющих № схемы Схема Точность Сила трения Нечувствительность к перепаду температур Нагрузочная способность Стойкость к износу Ремонтопригодность Стоимость
С трением качения 14 н tfTLr _j 2 1 1 3 1 1 4
15 2 1 1 2 1 1 3
16 г~ \j— -[ k 1 2 1 1 3 1 1 3
17 - 1 1сь с эксцентриком- 3 2 2 2 1 1 4
18 lanpafym [ r-F ющий стеклянный Spyc ММ 0 2 4 4 1 2 4 М 1
ной способности и уменьшения износа направляющей точечные контакты часто заменяют плоскостями или поверхностями. Для направляю
Рис. 11.2. Неправильная конструкция призматических направляющих
щих открытого типа достаточно иметь две направляющие плоскости или одну плоскость и одну поверхность. Остальные плоскости (поверхности) являются вспомогательными. Правильные конструкции приведены на рис. 11.1 и в табл. 11.1; неправильная конструкция показана на рнс. 11.2.
Точность изготовления направляющих. Точность функционирования направляющих зависит от погрешности изготовления деталей направляющих и от погрешности сборки. Влияние погрешностей формы деталей, прогибов и зазоров можно рассмотреть, представив, что неровности ДЛХ и Дй2 находятся на основной направляющей детали (рис. 11.3). Действие этих неровностей вызывает поворот ползуна на углы 6у2 и 6у3. Значения этих углов зависят от продольной базы b или от поперечной базы а между направляющими I и 2, т. е.
Shx/b; 6у2 =
Наклоны ползуна на углы и буз вызывают продольное Д/ и поперечное Д& смещения точки ползуна, зависящие от высоты // расположен ня этой точки иад уровнем направляющих:
Д/ = (H/L) Mil, А* == (я/д) д*ь Да = (£/*) > * *
Суммарное смещение точки О± от действии поперечного наклона подула и его поворота в горизонтальной плоскости
А*су« =-у ДЛ* + “Г АЛг
1 Из прнведевиых формул н рис. 11.3 видно, что для большей точности перемещения таиих точек ползуна (0^» 02) следует помещать эти точки
(По возможности ближе к линии, проходящей через точку опоры толкателя (03) и параллельной направляющим, и как можно ближе (по высоте) к плоскости направляющих. Для уменьшения смещения этих точек по ;высоте наиболее выгодно располагать их вблизи середины ползуна.
Достижимая точность изготовления (в мм) деталей направляющих ;на стандартном оборудовании приведена ниже.
Цилиндрические направляющие (валики)
На токарном станке:
диаметр (до 50 мм) , . . цнлиндрнчность . . . . конусность.............
На круглошлнфовальном стайке: диаметр (до 100 мм) . . цнлиндрнчность . . . . конусность . . . . . .. . прямолинейность . . .
Плоек На плоскошлнфональиом станке: прн грубом, шлифовании « точном шлифовании Шабрение ...................
Притирка «од пробное стекло
0,01—0,02
0,01 на длине 300 мм
0,02 < . « 300 мм
0,005
0,003 — 0,01 на длине 500 ми
0.005-*-0,01 « « 500 мм
0,005 — 0,01 « « 500 мы
о с т н
0.03 на длине 1000 мм
0,01 « « 1000 мы
0,01 — 0,02 на длине 1000 мм
0,05 мкм на длине 100 мм
Ддя .обеспечения высокой точности и плавности работы направляющих,., особенно с трением скольжения, требуется высокое качество обработки сопрягаемых поверхностей. Параметр шероховатости Ra обычно следует назначать в пределах от 1,0 до 0,1 мкм. Увеличение точности, плавности, износостойкости достигается применением поверх-нрстей с. .регулярным . рельефом, нанесенным, например, с помощью виброобкатывания по методу профессора Ю. Г. Шнейдера. Такие поверхности позволяют улучшить эксплуатационные характеристики направляющих за счет наиболее оптимальных условий работы смазки в зазоре сопрягаемых поверхностей и за счет упрочнения поверхностного слоя материала сопрягаемых поверхностей [114].
Высокую точность и плавность движения дают направляющие со стержнями из фторопласта 4 (табл. 11.1,. схема 4). Такие направляющие обеспечивают точность перемещения ползуна 0,03—0,05 мкм, характеризуемую средним значением вторых разностей ординат нерегулярных отклонений на длинах 60—200 мм при интервале измерительных перемещений от 0 до 0,5 мм. Характерно, что эти направлиющиё обеспечивают плавность работы и без наличия смазки.
В табл. 11.2 приведены данные по точности движения в направляющих различного типа.
Таблица 11.2. Точность прямолинейного движения в направляющих
к т Тип ^направляющих № схемы (см. табл. 11.1> Шероховатость рабочих поверхностей Ra, мкм Длина хода, мм Точность, МКМ
Цилиндрические с тре- 1 До 100 5
нием скольжения 1; 2 Ю,2—0,5 » 300 10
Призматические с 3; 5 0,1—0,2 » 10 0,5—1
трением скольжении 0,1—0,2 > 50 1—2
0,2—0,5 » 50 2—5
0,2—0,5 » 300 10 ,,
Призматические с 10 0.1 >1 1—2 .
трением качения (на ша- 10 0,1 г 100 О
риках или иголках) 9; 10; 11 0,5 » 100 3-£
Призматические и ци- 14—17 0,1—0,2 > 300 10—20
линдрические на шари- 14—17 0,2—0,5 > 1000 16—26
коподшипниках * 13—17 0,5—1 » 1000 18—30
С направляющим сте- 18 Rz 0,05 » 60 0,5
клянным брусом 18 Rz 0,05 » 0,5 0,03 ♦♦
Призматические со 4 0,05—0,15 » 60 0,5
стержнями из фторо- 4 0,05—0,15 > 0,5 0,03 ♦♦
пласта
На Ш-образных пло- 19 » 50 0,5
ских пружинах
♦ Точность указана в зависимости от класса шарнкоподшнп-
ников. Величина вторых разностей ординат нерегулярных отк л о-
нений.
Трение в направляющих. При конструировании направляющих производят расчет сил сопротивления движению ползуна с целью: а) расчета требуемого усилия пружины, осуществляющей силовое замыкание с приводом направляющей; б) расчета приведенного момента на валу ручного или электромеханического привода; в) обеспечения плав-( пости движения и отсутствия силового заклинивания.
При отсутствии действия внешних сил на ползун сопротивление движению ползуна в направляющей характеризуется силой трения Q, возникающей под действием массы ползуна Sx и располагаемого на нем объекта S2> т. е. Q = (Sx + S2) Ц, где р — коэффициент трения скольжения (качения). Для приведения в движение ползуна необходимо приложить внешнюю силу /?, которая должна быть больше силы трения Q, так как помимо трения скольжения (качения) сила R должна
Рис. 11.4. Схема воздействия сил на направляющую
преодолевать момент инерции неподвижного тела и силу молекулярного сцепления (трение покоя). Сила 7? может быть приложена различным образом: точка приложения силы расположена в средней плоскости направляющей под некоторым углом а к этой плоскости (рис. 11.4, п); точка приложения и сама сила находятся в параллельной плоскости, отстоящей от средней на длину I (рис. 11.4, б).
; При конструировании направляющих, в случае несоответствия размеров конструкции системе действующих на ползун сил, возможна ситуация, когда внешняя сила R не в состоянии привести ползун в движение, т. е. возникает силовое заклинивание. Следует различать также температурное заклинивание,которое получается при больших перепадах температур, при неправильно выбранных материалах деталей и вида посадки сопрягаемых поверхностей.
Силовое заклинивание. Внешнюю силу R, действующую под углом а (рис. 11.4, а), можно разложить на составляющие Р и Т. Сила Р осуществляет смещение ползуна, а сила Т прижимает ползун к направляющим, создавая препятствие движению за счет возникающих сил трения.
Из* уравнений равновесия ползуна:
F1 = ^2 + = Р2 + R sin а;
P2b — Th — Rh sin а
получим силы реакции F. = —£— R sin а и F2 = ~т~ R sin а, которые о и
вызывают силу трения.
Условие отсутствия заклинивания можно записать так:
Р = Я cos a > Q=(FX4- F2) р.
Используя выражения для сил Ft и Ft, можно записать п „2Л + & . . b
« cos а >/?-f-И sm « нли tga <
Отсюда следует условие отсутствия заклинивания
& 2ц tg а h 1 — р, tg а
Характерно» что наличие или отсутствие заклинивания не зависит от значения силы /?, а определяется только конструктивными параметрами — базой Ь, плечом h и углом действия силы а.
К ±0,08
27 М
Рис. 11.5. Направляющая типа ласточкина хвоста
Часто сила R действует параллельно направляющей, ноприложена на некотором расстоянии I от оси направляющей (рис. 11.4, б). В этом случае она создает момент М ~ /?/, уравновешивающийся моментом пары сил реакции в опорах, т. е. Rl = Fb. Реакция опор создает силу треиия в направляющих
2RI —
Условие отсутствия заклинивания R > Q можно выразить -через 2RI 21
конструктивные параметры R > р, или окончательно —- р, < 1.
Опыт эксплуатации направляющих показывает, что для обеспечения отсутствия заклинивания, хорошей плавности хода и небольшого износа рекомендуются следующие соотношения:
для плоских направляющих прямоугольного типа (см. табл. П.1, схемы 1 и 8) р < 0,25;
для призматических направляющих типа ласточкина хвоста (см. табл. 11.1, схемы 5, 6) а И < 0>25, где а — угол профиля ласточкина хвоста (рис. 11.5);
I
для цилиндрических направляющих (табл. 11.1, схемы 1, 2) < 0,25, где г == 1,27 — радиус трения.
Таблица 11.3. Коэффициенты трения скольжения материалов сопрягаемых деталей
Материал ПОДВИЖНОЙ детали Материал неподвижной детали
Конструкционная сталь 30—50 Сталь У8А Чугун Бронза Латунь ЛС59—1 Дюралюминий Медь Текстолит По-лн-эти-леи
незакаленная закаленная незака-леииая закаленная
СС БС СС БС СС БС СС БС СС БС СС БС СС БС СС БС СС БС СС БС
Конструкционная сталь, 30-50 0,18 0,12 0,18 0,05 0,10 0,15 0,08 0,10 0,15 0,05 0,10 0,15 0,05 0/15 0,15 0,09 0,13 0,10 0,15 0,13 0,15 0,19 0,19 — 0,15 0,22 0,08 0,04
Латунь ЛС59-1 0,10 0,19 0,10 0,14 0,10 0,19 0,10 0,14 —» 0,14 0,02 0,15 0,02 0,17 0,16 0,26 0,22 0,20 0,03 0,16 0,23 —
Броняй . оловяни-стая 0,09 0,13 0,16 0,09 0,13 0,16 0,09 0,13 0,16 — 0,15 — 0,21 0,07 0,10 0,20 — 0,22 — — —
Бронзы, не содержащие олово — 1 0,18 — 0,18 —> — — — — — "Г
Дюралюминий -—- 0,19 0,19 — 0,19' 0,19 —- 0,18 — 0,22 — 0,26 — 0,26 0,29 —
Силумин — — — — — — — V — — —- 0,34 ; — .
; • и S “ - ... ; . . г е -д , Примечание. СС — со смазкой; БС *- без Смазки. - * *; У
Ия приведенных соотношений видно, что эксплуатационные ,харак-Тернстжки направляющих зависят от коэффициента трения сколбжеЬия р, который в значительной степени определяется выбором материала Сопрягаемых деталей, качеством их обработки и наличием или отсутствием смазки в зазоре, средние данные коэффициентов трения.скольжения? для различных сочетаний материалов приведены в табл!. 11.3. ? Температурное заклинивание. Для приборов, работающих при Значительных колебаниях температуры окружающей среды, следует Производить расчеты на возможность температурного заклинивания при неправильном выборе посадки сопрягаемых поверхностей и их материала! При этом следует стремиться для достижения большей точности сопряжения, с одной стороны, к минимально возможному зазору, а с другой — к незначительному изменению этого зазора при значительных колебаниях температур. Реализовать эти условия можно, если конструировать направляющие из материалов, имеющих одинаковые или мало отличающиеся друг от друга температурные коэффициенты линейного расширения а (ТКЛР). Проверка зазора при назначенной посадке сопрягаемых деталей производится по формуле ДСв = — D2,
где — наименьший диаметр или линейный размер охватывающей детали; D2 — наибольший диаметр или линейный размер охватываемой дчалн.
' При значениях температуры в реальных условиях эксплуатации, отличных от нормальных (/0 — +20° С) величина зазора будет зависеть от ТКЛР ах и а2 соответствующих материалов сопрягаемых деталей:
ДС —D2 -j- (a^ -—OC2D2) (t — /q) = ДС# (^1^1 — Д^«
Приближенно можно записать, считая Dr = D2 == D:
ДС *= ДС0 + («! — «з) D At,
При симметричном диапазоне перепада температур (например ± 50° Q целесообразно выбирать для охватывающей детали материал с меньшим, чем у охватываемой а2, так как опасность защемлеиня при охлаждении больше ввиду большего перепада температуры (Д/ == —70° С при охлаждении, тогда как Д/~ +30° С при нагреве).
Мало чувствительны к изменениям температуры направляющие с трением скольжения открытого типа, с треиием упругости, с трением качения, и особенно на шарико- и роликоподшипниках. В табл. 11.4 приведены температурные коэффициенты линейного расширения различных конструкционных материалов.
Износ направляющих. Износ направляющих зависит от удельного давления контактирующих пар деталей, коэффициента трения материалов, их твердости и качества обработки, а также от свойств смазочных материалов, заполняющих зазор в направляющих.
- Проверка удельного давления производится по формуле q — = N/S < [<?], где N — нормальное давление; S — площадь контакта сопрягаемых пар деталей; (</] —допускаемое удельное давление. При малых скоростях перемещения (до 200 мм/мин) каретйи, допускаемые удельные давления выбирают в пределах 15-Ю5 Н/м2; при больших скоростях [(/1 « 4* 105 Н/м2. Следует иметь в виду, что площадь контакта S обычно меньше геометрической площади наименьшей из сопрягаемых поверхностей. Контакт, как правило, осуществляется по некоторым малым площадкам (пятнам), количество которых в сопряжении трудно определить до сборки направляющих. С целью увеличения определенности количества и расположения пятен контакта при йзго-товленин направляющих производят шабрение поверхностей, взаимную
Таблица 11.4. Коэффициенты линейного расширения (при t = ±70° С)
Материал а. 10» Материал а. 10е
Алюминий Алюминиевомаг-ниевый сплав Бронза Гипс Дюралюминий Инвар Иридий Кобальт Константан Латунь Т итан Медь 24—27 28,5 18 25 23 1,6 6,5 12,6 15 18,5 8 17 Нейзильбер Никель Платина Полиэтилен Платиноиридий Серебро Сталь Стекло техниче- ское Стекло кварцевое Фарфор Фторопл аст Цинк Чугун 18 13 9—13 100—800 8,8 19—20 И 16 0,4 3 55—110 29 10
притирку деталей направляющих или доводку поверхностей. Эти операции часто производят совместно с регулировкой (выборкой) зазора, для чего в конструкциях направляющих предусматривают возможность поджатия одной из деталей направляющих. Такие конструкции направляющих обычно весьма ремонтоспособны. Характеристики по ремонтоспособности и стойкости против износа различных типов направляющих приведены в табл. 11.1.
Направляющие с трением качения
Направляющие с трением качения обладают значительно меньшим трением, чем направляющие с трением скольжения; это обеспечивает возможность перемещения каретки при небольших величинах прилагаемых внешних сил. Кроме того, они практически нечувствительны к колебаниям температуры, и поэтому их можно собирать без зазора и даже с небольшим натягом. К недостаткам направляющих с трением качения следует отнести: более низкую точность, обусловленную погрешностями поверхностей и шариков (роликов); меньшую грузоподъемность вследствие наличия контакта по точке или по линии, что также ухудшает и плавность хода; несколько больший габарит и большая стоимость изготовления.
Однако отмеченные выше достоинства способствуют широкому использованию этих направляющих в точных приборах. Применение трения качения необходимо при изготовлении направляющих из нержавеющей стали, так как при трении скольжения они склонны к задиранию (заеданию). Направляющие с трением качения выполняются на роликах или иголках и на шариках.
Направляющие на роликах (рис. 11.6 и 11.7). При жесткой конструкции требуется оставлять зазор между роликами и направляющими для компенсации биения ролика, неточности формы направляющих и микронеровностей. Зазор должен быть не менее 0,04—0,08 мм. Жесткай 468
конструкция не обеспечивает хорошей точности перемещения каретки. Целесообразно конструировать направляющие на роликах с силовым замыканием с помощью пружины. В качестве роликов для получения легкого хода обычно используют шарикоподшипники. При замыкании
Рис. 11.6. Направляющие на роликах
пружиной перемещающаяся каретка испытывает линейные и угловые колебания, зависящие от величины биения роликов, точности (прямолинейности) н шероховатости поверхности направляющих, расстояния
между роликами.
Направляющие на шариках. Наибольшее распространение получили призматические направляющие на шариках (рис. 11.8), отличаю
щиеся компактностью, технологичностью и достаточно легким ходом. Недостатком их является износ, вследствие наличия, кроме трения качения, трения верчения. Обычно эти направляющие работают мало и на небольших скоростях, поэтому износ практически невелик.
Рис. 11.7. Каретка на шарикоподшипниках
Расстояние между крайними шариками L (рис. 11.9) выбирается меньше рабочей длины направля
ющих на половину максимального
перемещения s с некоторым запасом а. Для работы направляющей вполне достаточно иметь три шарика — два с одной стороны и один с противоположной. Обычно используют по два шарика с каждой стороны, а при значительной нагрузке и большой базе между шариками 469
может быть установлено и по три шарика с каждой стороны карами. Большее число шариков нежелательно, так как возможно базирование каретки ие на крайние, а иа средние шарики. В этом случае точность направления и условия работы ухудшаются.
Требуемое расстояние между шариками выдерживается заР'^ет сепараторов. Сепараторы бывают свободные н с принудительный движением. Свободные сепараторы применяются двух типов: у сепараторов первого типа имеется только ограничение движения (рис. И. 10);
Рис. 11.8. Призматические направляющие на шариках
второго типа — кроме ограничения движения и фиксация при крайних положениях движущейся детали.
Сепараторы первого типа следует применять только н горизонтально работающих направляющих. При использовании таких сепараторов в направляющих, работающих наклонно, в результате действия массы шариков и сепаратора может происходить постепенное проскальзывание
Рис. 1L9. Схема движения каретки на шариках
шариков вниз и в конечном счете заклинивание направляющих. Сепаратор второго типа несколько надежнее, так как оба его крайних положения контролируются штифтами (рис. 11.11).
Если направляющая работает в условиях значительной тряски, вибраций или ударов, необходимо применить сепаратор с принудительным движением (рис, 11.12). При движении каретки относительно детали 5 ось шестерни 2, закрепленной на сепараторе Л движется со скоростью в два раза меиьшей, чем каретка. Шестерня 3 находится в зацеплении с рейками 4, закрепленными иа каретке и направляющей.
Сепараторы изготавливают из листовой стали, латуни, дюралюминия или пластмасс.
Расчет силы треи и я в призматических направляющих. Касание шарика и поверхности направляющей вследствие их упругости происходит не в точке, а на некоторой площадке, называемой площадкой
соприкасания. Поэтому при качении шарика возникает не только тление качения, но и трение скольжения (верчения), которое весьма существенно. Задача нахождения закона распределения давления по
1 I I i F * *
Рис. 11.10. Сепаратор с одним ограничительным штифтом
Рис. 11.11. Сепаратор с двумя ограничительными штифтами
Рис. 11.12. Сепаратор с принудительным движением
общей поверхности касания двух упругих тел решена Г. Герцем. При сжатии шарика диаметром d я плоскости при одинаковых материалах давление распределится в круге, ограниченном радиусом г, который зависит от сжимающей силы Р и модуля упругости Е материала:
г = 0,88 УрЗ]Ё.
При качении шара по призматической направляющей происходит его относительное вращение вокруг перемещающегося центра площадки соприкасания, являющегося мгновенным центром вращения шарика. Момент трения верчения шарика равен
Af3 ~ О,5]Л
V 4P*d/E
cos 45°
Здесь Р ~ ; Q — нагрузка на направляющие, в которую
должна войти и сила натяга (если направляющие собраны с натягом); р — коэффициент трения скольжения. Тогда
м 0 5hQ j/ Qd . ' ж
“ cos2 45° V 4£cos45°* ’
Сопротивление движению каретки R равно:
d cos 45° "T" d cos 45°
(2Fz + Q),
где k — коэффициент трения качения. Второе слагаемое представляет собой сопротивление движению, создаваемое трением качения.
Рис. 11.13. Столик микроскопа на призматических шариковых направляющих
На рнс. 11.13 показан столик микроскопа, который можно передвигать по двум направлениям на призматических шариковых направляющих. На рис. 11.14 приведена конструкция цилиндрической направляющей на шариках с принудительным движением сепаратора при помощи шестерни, закрепленной на сепараторе, и двух реек: одна рейка нарезана на валу, другая закреплена на трубе винтами.
На рис. 11.15 изображены игольчатые направляющие для перемещения по вертикали массивного столика микроскопа (тонкая наводка на резкость).
Усилие R для перемещения каретки, нагруженной силой Р [56], рассчитывают по формулам:
а) на восьми шарикоподшипниках (рис. 11.7)
4 nJnri Pcosa , Р sin а X — 2k { 2F 4- . Q + —---
D L \ 4 sin p 4 cos p /
+ ^тр! + .4fTP2 + AfTP3 + AfTp4 ;
б) на шариках (рис. 11.8), причем влияние трения верчения не учитывается ввиду сложности расчета
sin р
cos а sin ₽
Рис. 11.14. Цилиндрические шариковые направляющие с принудительным движением сепаратора
Рис. 11.15. Игольчатые направляющие микрометрического движения столика микроскопа:
J сферическая пята; 2 — игла
В этих формулах— диаметр шарика, m;D_.— наружный диаметр шарикоподшипника, м; k — коэффициент трения качения; F — сила натяга при сборке (10—30 Н); р — половина угла профиля (45°);
Рис. 11.16. Направляющая с движением вдоль точного стеклянного бруса
то же прн
^трз то
. Psina.
4 cos р ’*
а — угол, под которым направлена сила R; z — число шариков; AfTpjl — момент трения в шарикоподшипник ках, Н*см прн нагрузке F; Мтр;>— _ , Р cos а
нагрузке F + ;
же при нагрузке F +
Мтр4 — то же ПРИ на-Pcosa Р sin а
4 sin р 4 cos (J
На рис. 11.16 приведена схема столика микроскопа с особо высокой точностью движения. Верхняя пла-
вающая часть столика установлена на трех шариках на ннжней несущей каретке и имеет два упора из бакаута, которые упираются в стеклянный брус с точно изготовленной под пробное стекло поверхностью. Плавающий столик прижимается к стеклянному брусу пружиной.
Точность прямолинейного перемещения столика в горизонтальной
плоскости может быть оценена
средним значением вторых разностей ординат нерегулярных отклонений ^от прямолинейности на длине 60 мм прн интервале измерений 0,5 мм н равна 0,03 мкм.
Рнс. 11.17. Упругие направляющие Ш-образного типа
Направляющие с внутренним (молекулярным) трением
, Направляющие на Ш-образных плоских пружинах (рнс. 11.17) рбеспечивают достаточно точную прямолинейность направления в горц-воыталыюй плоскости, перпендикулярной плоскости, пружин. В вертн-47-4
калькой плоскости направление сохраняется менее точно. Такого‘рода направляющие применяют в измерительных микроскопах для перемещения измерительного столика. При перемещении, равном 25—50 мм* непрямолинейность в горизонтальной плоскости составляет 0,2—0,5 мкм.
На рис. 11.18 показана конструкция направляющих алмазной пирамиды (нндентера) в приборе для испытания на мнкротвердость,
Рис. 11.18. Упругие направляющие инден-тера микротвердомера
Пружинный параллелограмм направляет движение острия пйрамйДы по дуге радиуса, приблизительно равного 2/3 длины свободной ча£тн пружины, поэтому перемещение пирамиды обычно не более 0,5 мм.
Упругие направляющие малочувствительны к температурным колебаниям, отличаются небольшой величиной сопротивления движению н стойкости против износа.
НАПРАВЛЯЮЩИЕ ДЛЯ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
В зависимости от вида трення различают направляющие с трением скольжения, с треннем качения и с трением упругости.
Направляющие с трением скольжения
Имеются направляющие с цилиндрической, конической и шаровой рабочими поверхностями, а также опоры на ножах (остриях).
Рис. 11.19. Конструкция цапф
Направляющие с треннем скольжения просты по конструкции, технологичны, имеют низкую стоимость. Недостатками являются: большее, чем в подшипниках качения,трение; чувствительность к колебаниям Температуры, необходимость систематической подачи смазки (при
быстром и длительном вращении). Формы цапф и Подшипников разнообразны (рис. 11.19—11.25). .
С целью уменьшения трения и износа материалы для т^ущ’йхся деталей следует подбирать с минимально возможным коэффициентом трения и обеспечивать требуемую шероховатость поверхности.
Материал вала обычно выбирают тверже материала втулки. Шероховатость обработки поверхности вала (Ra 0,14-0,5 мкм) должна быть на 1—2 класса выше чем у втулки. Негладкая поверхность втулки позволяет лучше удерживать смазку. Известно, что^трение двух полированных поверхностей без смазки значительно выше, чем трение полированной поверхности о негладкую, так как в первом случае сказываются силы молекулярного сцепления.
Рис. 11.20. Формы цапфн подшипников
Силовой расчет. При наличии смазки, момент трения в цилиндрических опорах (при малых скоростях) определяется по формуле [109]
Мтр = + Ррг,
где г — радиус цапфы; — начальный момент при нагрузке Р = 0 fl — коэффициент трения скольжения.
Мо зависит от вязкости смазки, зазора, площади трущейся поверхности, а также от качества сборки (например, от перекоса валика во втулке)'
Приближенно можно принять Л1о = krs, где k — коэффициент, зависящий от вязкости смазки и от зазора, Н/м2; S — площадь трущейся поверхности, м2. Так как S = 2лг/, где I — длина цапфы, то Л40 — — 2&лг2/.
Для ориентировочных расчетов можно принять при нормальной температуре k~ (4<-8) 102 Н/м2.
Недостатки цилиндрических опор*, наличие зазора в сопряжении, увеличение этого зазора при износе и невозможность его устранения без замены деталей. Поэтому вал при знакопеременной нагрузке может занимать практически любое положение в пределах этого зазора, что приводит к биению вала и к его перекосам.
Наиболее точное положение оси вращения вала даже после некоторого износа обеспечивают направляющие с конической рабочей поверхностью (рис. 11.21). Трение в конических цапфах выше, чем в цилиндрических. Момент трения при осевой нагрузке Р (рис. 11.21, а) равен
Л!тр = 1,27ргсрР/sin а = l,27|irCpW:
У —P/Sina; Гер = (''наиб+ ''наим)/2);
при радиальной нагрузке
/Йтр ~ l,27jircpP/cosa.
. . Если угол а мал, то давление /V— слишком большое. Для предотвращения возможного заклинивания в этом случае конические цапфы разгружают в осевом направлении с помощью торцовой опоры (рис. 11.21» 6) или винтового подпятника (рис. 11.21, в).
Если вал базируется на одну коническую цапфу, как в геодезически^ приборах, то цапфа должна иметь достаточную длину для обеспечения требуемой точности базирования и устойчивости. При этом конусность следует выбирать не менее 1 : 6. Минимальный зазор обеспечивается подгонкой деталей или притиркой в сборке. При большой
Рис. 11.21. Конические цапфы
протяженности конической поверхности сопряжение происходит на неопределенной базе и усложняется процесс прнгонки. Поэтому в средней части конуса вала (или втулки) делают выточки. Аналогично обрабатывают и протяженные цилиндрические опоры. Ширина выточки определяется из условий требуемой износоустойчивости направлиющей и может быть рассчитана при заданной силовой ситуации по допустимому удельному давлению для соприкасающихся поверхностей.
Конические цапфы применяются редко, преимущественно в геодезических и астрономических приборах, а также в микроскопах [предметный столик (рис. 11.22), угломерный окуляр (рис. 11.23)]. Применяемые углы конуса и соотношения сил даны в табл. 11.5.
Опоры с двумя коническими цапфами (опоры на центрах, рис. 11.24) применяются для легких деталей, требующих точного центрирования. Рабочие поверхности винта следует калить до твердости HRC 50—60. Геометрические соотношения для опоры на центрах даны в табл. 11.6. Шаровые цапфы (рис. 11.25) применяются тогда, когда требуется кроме вращения вала вокруг оси обеспечить возможность поворота вала вокруг центра шаровой цапфы.
Выбор материала втулки и вала. В оптико-механических приборах подшипники скольжения работают обычно при малых скоростях и
Рис. 11.22. Вращающиеся столики микроскодов на конической (а) и цилиндрической (б) втулках. Нестабильность оси вращения 0,03 мм
Рис. 11.23. Угломерный окуляр иа конической цапфе
I '
Рис. 11.24. Осюры на центрах
Таблица 11.$. Зависимость между Р и N ври различных углах Л
Конусность а sin а Л/Р
1 : S 1 : 6 1 : 8 1 : 10 • ♦ в 5° 42' 4° 46' 3° 34' 2° 52' 0,09961 0,08338 0,06262 0,05007 10 12 16 20
Таблица 11.6. Размеры центровых отверст ий; мм
D d 1
До 2,5 0,5 1,2 0,8
2,5—5 ' 0,75 2,0 1,0
5—10 1,0 2,5 1.2
10—20 • 1,5 4,0 1,8
нагрузках и при несовершенной системе смазки (полусухое трение).
При выборе материалов следует исходить из рекомендаций:
1) трущаяся пара (вал—втулка) должна иметь малый коэффициент трения; > .
2) вал (особенно конический) и втулка должны иметь близкие по
значению температурные коэффициенту линейного расширения во
избежание заклинивания;
3) твердость втулки должна быть ниже твердости вала (цапфы), так как замена втулки в случае износа легче, чем замена вала, и стоимость втулки обычно ниже.
В качестве материала для трущейся пары при медленном движении и полусухом трении в зависимости от допусти
Рис. 11.25. Шаровые опоры
мого момента трения и
условий износа могут применяться следующие сочетания материалов: сталь незакаленная и закаленная—бронза; сталь незакаленная я закаленная—латунь; латунь—бронза; сталь закаленная—чугун; сталь незакалеиная и закаленная—пластмассы (без смазки): текстолит, фторо
пласт, полиэтилен низкого давления, капрон; сталь незакалениая— бакаут (при посадке с повышенным зазором).
Хорошие результаты дает применение для подшипниковых втулок металлокерамических антифрикционйых материалов. Благодаря своей пористости они хорошо удерживают смазку (самосмазывание).
В типовых конструкциях осевых пар с трением скольжения, разработанных для геодезических приборов, широко используют высокопрочные алюминиевые сплавы марки В95Т, В96Т в паре с бронзой, а также спеченный алюминиевый сплав САС-1 в паре со сталью ШХ-15. Эти пары позволяют уменьшить массу прибора, при этом сохраняется высокая точность и надежность в подшипниках, хорошие антифрикционные свойства в условиях треиия со смазкой и при сухом трении
1 Рабиноаич Л. В., Бергман Т. П. Антифрикционные свойства алюминиевых сплавов. ОМП, 1967, М 1, с. 49—53.
Нержавеющая сталь для трущихся пар может применяться только при условии специальной обработки ее поверхности. Рекомендуются следующие виды обработки трущихся поверхностей деталей из нержавеющих сталей: 1) опескострунвание с последующим пассивированием в окислительных средах (в фосфатной ванне или азотной кислоте; 2) опескострунвание с пассивированием и покрытием лаком БФ-2,
Режим пескоструйной обработки должен обеспечить при исходной обработке поверхности с шероховатостью не ниже Rz ~ 40 мкм полное уничтожение следов предшествующей механической обработки и создать однородную поверхность с шероховатостью Rz = 20 мкм при твердости не ниже HRC 30 и Rz ~ 10 мкм при твердости выше HRC 30.
Направляющие для вращательного движения с трением качения
Основные преимущества шарикоподшипников по сравнению с подшипниками скользящего трения для оптико-механических приборов:
1) значительно меньший крутящий момент при трогании с места;
2) нечувствительность к изменению температуры;
3) возможность сборки оси на подшипниках без зазоров (и даже с небольшим иатягом), что обеспечивает хорошую точность базирования оси;
Рис. 11.26. Виды погрешностей шарикоподшипников
4) малый расход смазки и нетребовательность к ней;
5) меньшие потери на трение при работе;
6) хорошая взаимозаменяемость и ремонтопригодность.
К недостаткам следует отнести менее плавный ход и большой шум, больший габарит и более высокую стоимость.
Выбор полей допусков при посадке шарикоподшипников на вал или в корпус производится в соответствии с рекомендациями ГОСТа.
По ГОСТ 520—71 определены следующие классы точности подшипников качения: 0, 6, 5, 4 и 2. Классы точности приведены в порядке повышения точности. По этим классам изготавливаются следующие основные типы шарикоподшипников: по 2-му и 4,-му классам — радиаль:
Таблица 11.7. Допуски на точность вращения внутренних колец
Внутрен- Отклонения по классам точности, мкм
П И 11 метр дпа-, мм 0 6 1
Св. До I п in IV I Н III IV I п III IV
30 30 50 20 20 20 20 15 15 40 40 16 16 16 16 12 12 32 32 10 10 10 10 10 10 20 20
4 2
I н in IV 1 П III IV
30 30 50 7 7 7 7 СП СЛ 13 13 4 4 4 4 3 3 ОО ОО
Примечание. I — непараллельность торцовых поверхностей; П — боковое биение торца; III — радиальное биение; IV — боковое биение по дорожке качения кольца.
Таблица 11.8. Допуски иа точность вращения наружных колец
Наружный диаметр, мм Отклонение по классам точности, мкм
0 6 5 4 2
Св. До I II I II 1 11 1 II I П
___— 18 15 40 12 32 7 20 5 13 3 8
18 30 15 40 12 32 7 20 5 13 3 8
30 50 20 40 16 32 10 20 7 13 4 8
П р и м е 1 I а н и е. I — радиальное биение по дорожке каче-
ния кольца: 11 — боковое биение по дорожке качения кол ьца.
рднорядные (тип 0000); радиально-упорные (тип 36 000); радиально-упорные сдвоенные (типы 236 000, 336 000, 436 000). По 5-му и 6-му классам — все перечисленные выше типы подшипников и, кроме того, шариковые сферические (тип 1000), упорные (тип 8000), магнетные (тип 6000). По 6-му и 0-му классам, кроме указанных выше, — ра-даально-упорные двухрядные (тип 56 000).
Основными погрешностями шарикоподшипников (рис. 11.26) являются радиальное биение внутреннего н наружного колец, относительное торцовое биение колец и боковое биение по дорожке качения (табл ,11.7—11.10). Указанные погрешности явлиются следствием как неточного изготовления колец, так и наличия зазора между шариками и
Таблица 11.9. Отклонения от сферичности и равномерность шариков r партии деталей
Степень точности Диаметр шарика, мм Допускаемые отклонения от сферичности, мкм Допускаемая разномерность, мкм
0 До 5 0,25 0.5
I Св. 5 до 30 0,5 1
II » 5 » 30 1 2
III » 5 » 30 1.5 3
IV » 5 » 30 2.5 5
Таблица 11.10. Сортамент шариков
Диаметр, мм Масса 1000 шт., кг Диаметр, мм Масса 1000 шт., кг
И 1,000 1,588 2,0 3,0 3,175 3,969 4,763 5,0 5,556 5,953 6,350 И 2,500 . 3,0 3,175 3,969 3 подшипн 0,004 0,016 0,033 0,110 0,130 0,250 0,440 0,510 0,700 0,860 1,030 з н е р ж а в е i 0,064 0,110 0,130 0,250 нковой ста 7,0 7,144 7,938 9,0 9,525 10,0 10,319 11,112 11,906 12,0 ощей стали 5,0 7,938 10,0 Л И 1,410 1,500 2,050 3,050 3,550 4,100 4,430 5,640 6,930 7,100 0,510 2,050 4,100
Примечание. Допустимые отклонения диаметров шариков от номинала для диаметров до 7,938 мм составляют ±0,05 мм; свыше 7,938 мм до 12,7 мм — ±0.10 мм. «
кольцами. Следует различать зазор до посадки подшипника на вал или в корпус и зазор после посадки, который всегда меньше начального зазора вследствие некоторой деформации колец при посадке. Кроме того, при установке вала на подшипниках в корпус может быть предусмотрена возможность осуществления силового затяга сопряжения по наружному или внутреннему кольцам шарикоподшипников [581. В зависимости от усилия затяга зазор может быть выбран полностью и даже может иметь место некоторый натяг в сопряжении. Следует иметь
в виду, что подобные способы монтажа могут применяться при малых скоростях вращения вала н при небольших колебаниях температуры.
Для смазки шарикоподшипников, работающих в течение коротких промежутков времени н на малых скоростях, рекомендуется применять смазку консистентную ГОИ-54, которая работоспособна в интервале температур ±60° С. Для чувствительных подшипников применяют менее консистентную смазку (ЦИАТИМ-201 или масло МВП). Если подшипники работают вблизи оптических деталей, рекомендуется применять смазку ЦИАТИМ-221. Для скоростных подшипников, работающих длительное время, необходимо предусматривать в конструкции специальные масленки для непрерывной подачи смазки.
Для предохранения от проникновения в подшипник и через подшипник в прибор пыли и влаги применяются уплотняющие устройства. Они также препятствуют вытеканию смазок из подшипника. Конструкции сальников приведены в гл. 15.
Конструкции и расчет специальных подшипников
При малой частоте вращения и небольшой нагрузке применяются подшипники, показанные на рис. 11.27 и 11.28. При малых диаметрах подшипника для
мендуется, чтобы прямая OOlt проведенная через точки касания
Рнс. 11.27. Схема специального радиально-упорного шарикоподшипника
уменьшения трения реко-
Рнс. 11.28. Схемы насыпных шарикоподшипников. Нестабильность оси вращения 0,01—0,02 мм
Рнс. 11.29. Конструкции однорядных замкнутых шарикоподшипников
шарика Si и и образующая конуса пересекались в одной точке на оси вращения (рнс. И.27). Тогда
tg — /?/(/?+ г); sin Р = sin а//?; а = — р.
Для повышения точности вращения (уменьшения биения) следует Вращающееся кольцо делать цилиндрическим,
Замкнутый однорядный радиально-упорный шарикоподшипник (рис. 11.29) является наиболеекомпактным. Трениев данном подшипнике несколько выше, чем в подшипниках, приведенных на рис. 11.27
Рис. 11.30. Столик микроскопа иа насыпном подшипнике. Нестабильность оси вращения 3 мкм
Рис. 11.31. Шарикоподшипник с проволочными кольцами. Нестабильности оси вращения 5—10 мкм
Рис. 11.32. Схема шарикоподшипника на стальных лентах
и 11.28. Такого рода шарикоподшипники применяют с сепараторами и без иих (насыпные подшипники).
На рис. 11.30 изображен столик поляризационного микроскопа на однорядном насыпном подшипнике. Прн большом диаметре, малой частоте вращения и небольшой нагрузке такие подшипники можно изготовлять с незакаленными на-гартоваинымн беговыми дорожками.
Рис. 11.33. Схема к расчету шарикоподшипников
При больших диаметрах н медленном вращении применяются подшипники 1 с проволочными кольцами или лентами (рис. 11.31 и 11.32). Этн подшипники значительно дешевле. Стабильность оси вращения и плавность хода незначительно уступают сплошным подшипникам. Число шариков (рис. 11.33) определяется из уравнения z~ 180° / [arcsin (/Zrf/) L где г — число шариков; / — расстояние по хорде между центрами шариков; — диаметр
окружности шариков. Для насыпных подшипников t ж 1,01d, при сепараторе / 1,2г/.
Момент трения радиального насыпного двухрядного подшипника:
.. 10Qcos3/2nyA!
= zlinT - •
где Q — общая нагрузка, равная п—число центральных углову. Для упорного подшипника Л4тр ~ Qk.
В радиально-упорном (рис. 11.27) или одиорядиом (рис. 11,29) подшипнике сила трения скольжения (верчения) относительно высока и ею пренебрегать ни в коем случае нельзя. Расчет аналогичен расчету сил трения в призматических направляющих.
Крестообразный пружинный шарнир
Крестообразный пружинный шарнир состоит из двух пар одинаковых перекрещивающихся под углом 90° стальных пластинок, прикрепленных концами к двум деталям (рис. 11.34). Рамка 2 может поворачиваться без люфта вокруг оси проходящей через линию пересечения пружин /. Такие шарниры имеют ряд преимуществ по сравнению с подшипниками. Основное преимущество состоит в том, что в них имеется только трение упругости, поэтому смазка не требуется. Кроме того, в силу незначительного гистерезисного эффекта, шарниры долго-
Рис. 11.34. Крестообразный пружинный шарнир
вечны и не подвержены износу, который может вызывать увеличение зазора (мертвый ход). Нагрузки таких шарниров обычно не бывают настолько велики, чтобы вызвать ошибку вследствие смещения пластин.
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ТРЕНИЯ В ОПОРАХ СКОЛЬЖЕНИЯ И КАЧЕНИЯ
Момент трения в опорах определяется по формуле
^тр = Qpr т»
где Q — приведенная нагрузка иа опору, Н; р — приведенный коэффициент треиия; гт — приведенный радиус треиия, см.
Для радиально-упорных опор качения приведенная нагрузка (рис. 11.35)
Q — 4- Я/sin
где [J — угол давления на элементы качения; Н — суммарная осевая нагрузка: Н = Т + (5л — Sb); R и Т — осевая и радиальная реакции опоры; 5л = tg рл — осевая составляющая на опоре Л прн действии на нее радиальной реакции Ra\ $в = Rb tg Рв — осевая составляющая, возникающая на опоре В при действии на нее радиальной реакции Rg; рл и Рв — углы линии давления на элементы качения опор А и В относительно оси вращения.
Рнс. 11.35. Схема расположения оси на радиально-упорных опорах качения
Таблица 11.11. Формулы для определения приведенных коэффициентов трення и радиуса трения
Тип опоры
Эскиз
Радиальные опоры скольжения
Цилиндрическая
Коническая
Шаровая
|Х=/ гт = 0,6374
р = /
0,422 т ~ cos а
3 sin а — sin3а
Тип опоры Эскиз
Радиальные опоры качения
Роликоподшипник
Z$k da ==~d~ ~d^ Гт = 0,5do
Игольчатый подшипник
z8k da
Гт = O,5do
Осевые опоры скольжения
Цилиндрическая
Кольцевая
d
z =-----
т з
Тип опоры Эскиз И;
Осевые опоры качения
Упорный шарикоподшипник
Упорный роликоподшипник
Тил опоры
Эскиз
м; 'т
Радиально-упорные опоры качения
Радиальный шарикоподшипник при действии радиальной и осевой реакций опор
°к rT = 0,5do
Радиальноупорный шарикоподшипник
р =- 2k
rT = O,5do
Конический роликоподшипник
Примечания: 1. Угол в радиальном шарикоподшипнике при осевой нагрузке р = arcsln (ЮС/rfJ, С — осевая игра. 2. При коиических роликах d^ — средний диаметр ролика. 3. При расчетах все размеры следует принимать в см. 4. Цилиндрическая опора скольжения с буртиком и шаровая могут противостоять радиальной и осевой нагрузке одновременно. В этом случае следует определять отдельно моменты трения от радиальной и осевой реакций и складывать их. Момент треиня для осевой реакции определяется так же, как для кольцевой опоры.
Перед равнодействующей (Зд — Sb) осевых составляющих опор ставят знак плюс,если ее направление совпадает с направлением силы Т и минус, если ее направление противоположно.
В приведенных выше формулах Н всегда берется со знаком плюс (модуль). Дополнительная осевая нагрузка Н действует только иа одну из двух радиально-упорных опор. Формулы для опор скольжения справедливы при следующих условиях: охватываемое звено является жестким (отсутствует деформация изгиба); материал втулки изотропен, т. е. подчиняется закону Гука; в результате деформации опор не происходит перекоса оси вала; предварительный натяг отсутствует. Расчетные формулы приведены в табл. 11.11.
Выбор величины коэффициента трения при расчете производится иа основе следующих рекомендаций: большие значения коэффициентов трення скольжения берутся для тихоходных открытых механизмов, меньшие — для быстроходных закрытых механизмов при условии хорошей смазки (см. табл. 11.3).
Коэффициенты трения качения приведены ниже.
Тип опоры качения
k, см
Шариковый подшипник............. . . 0.005
Роликовый » ............... 0,07
Игольчатый » ...................0,01
Литература: [56, 58, 109, 114].
ГЛАВА 12
ВИНТОВЫЕ МЕХАНИЗМЫ
ВИНТОВЫЕ МЕХАНИЗМЫ ТОЧНОГО ДВИЖЕНИЯ
Винтовой механизм движения предназначен для преобразования вращательного движения (винта или гайки) в поступательное перемещение
7 = Р/>ф/2л, где / — перемещение винта (гайки); Ph —ход нарезки; ф— угол поворота винта (гайки).
Винтовые механизмы точного движения широко применяются в точных приборах благодаря большому отношению поворота винта (гайки) к поступательному перемещению и возможности получения достаточно высокой точности при сравнительно простой конструкции. Возможны четыре вида кинематических схем винтовых механизмов движения.
1. Гайка неподвижна — винт вращается и движется поступательно. Этот вид винтового механизма дает наибольшую точность. Однако габариты механизма при дайной схеме получаются наибольшими (равны сумме длины гайки и двойной длины хода винта), поэтому такая схема, как правило, применяется при малых длинах хода (до 25—50 мм).
Примерами таких механизмов служат измерительные микрометры, винтовой окулярный микрометр и т. п. (рис. 12.1).
2. Винт вращается — гайка имеет поступательное движение (рис. 12.2). Габарит этого механизма почти вдвое меньше (равен длине хода плюс длина гайки). Точность этого вида ниже, конструкция сложнее.
3. Гайка вращается — винт движется поступательно.
4. Гайка совершает оба движения — винт неподвижен.
Последние два вида применяются очень редко, так как конструкция их сложнее, а точность такого же порядка, как и у второй схемы.
Для точных винтовых пар применяются два вида стандартных резьб: метрическая остроугольная (угол профиля 60°) по СТ СЭВ 180—75 и 182—75, трапецеидальная (угол профиля 30°) по ГОСТ 9484—73. Выбор резьбы определяется требованиями точности, к. п. д. и технологическими соображениями. Для винтов, служащих для движения каких-либо частей со значительными нагрузками, рекомендуется применять трапецеидальную резьбу, так как трение в резьбе уменьшается с уменьшением угла профиля резьбы. Наименьшим треиием обладает прямоугольная резьба, однако оиа трудна в изготовлении и осевой люфт в паре трудно устранить.
Для винтов, работающих с небольшой нагрузкой, когда работа вннта незначительна и трение не играет роли, а также при требованиях малого шага применяется метрическая треугольная резьба с углом профиля 60°.
Рис. 12.1. Отсчетные винтовые механизмы с полиэтиленовыми гайками
Подвижная каретка-'
Рис. 12.2. Винтовой механизм с перемещающейся разрезной ганкой
Расчет винтовых механизмов
К. п. д. ходового винта определяется по формуле
n = tg ф/tg (ф + а),
где ф — угол подъема винтовой линии; а — угол профиля резьбы. Приведенный угол трения
Р = arctgf//cos-2-) ,
где f — коэффициент трения скольжения.
Самоторможение винта наступает, когда угол подъема равен углу трення, т» е. tg ф = tg р, где р — угол трения.
492
Расчет винта на растяжение и сжатие производится по формулам Q < -4- 0Р или Q < асж, где Q — сила, действующая вдоль оси винта, Н; ор — допускаемое напряжение на растяжение, Па; осж — допускаемое напряжение на сжатие, Па; — внутренний диаметр резьбы винта, мм:
dj5sl/^Z,lJW
3 г Я [о]р л [О]сж
где Qn — фиктивная нагрузка, приближенно равная 1,3Q—1,4Q. Допустимая длина винта (при работе на сжатие)
т л i/* ej min h “ 2 V 5Q ’
где Е—модуль упругости; Jmin == nd|/64—минимальный полярный момент.
Угол подъема винтовой линии ф определяется по формуле tg ф = Рп'/л^ср, где п — число заходов.
Длина гайки b — пР, где Р — шаг резьбы, мм; п — число витков гайки
п —- 4(?/л? (dg — d~), где q~ (75—125) 105 Па (для бронзы); d0—номинальный диаметр резьбы.
Для обеспечения нужной прочности и износоустойчивости резьбы гайки ее длину следует принимать не менее d0.
Усилия и моменты определяют следующим образом. Момент вращения винта при нагрузке на гайку Q более 30 Н вдоль оси винта (без учета силы трения в опорах) находят по формуле
М = Qr tg (ф -J- Р);
при нагрузке менее 30 Н
М — Qr tg (ф 4- Р)/е;
поправочный коэффициент е равен е — (N -ф- 150)/(A/-j- 240). В этих формулах N — сила, нормальная к винтовой поверхности, Н; г — средний радиус винта; р — приведенный угол трения.
Момент вращения винта, нагруженного силой Q, действующей перпендикулярно оси винта (без учета сил трения в опорах), для гайки4 двигающейся только по винту:
A'i = nfrQ/% sin .
. Момент вращения винта, нагруженного силой Q более 30 Н, действующей на плече а на ганку (без учета трения в опорах):
М ~ Qr tg (ф Р) + fada/fcsin при Q менее 30 Н
Л1 _ Qr tg (ф -ф- р)/е fZida/b sin
где b — длина гайки, мм.
Точность винтовых механизмов
Мтр
Рис. 12.3. Схема изгибающих сил в винтовой паре
только метрические резьбы, при
К точности винтовой пары можно предъявлять одно из следующих требований: высокая точность осевого перемещения или высокая точность осевого перемещения и точное направление винта (гайки).
Исходя из первого требования, выгоднее применять трапецеидальную резьбу, так как благодаря меньшему углу профиля такой резьбы местные ее погрешности, а также зазор в резьбе вызывают меньшие ошибки. Осевые ошибки выражаются формулой Ах = A^/cos а, где Д</ — погрешности профиля резьбы или зазора, измеренные по нормали к профилю.
Для метрической и трапецеидальной резьб разница в осевой ошибке, составляет 13% от Д?. Однако трапецеидальную резьбу можно применять только с шагом, превышающим 1 мм, так как при меньшем шаге ее технологически очень трудно изготовлять и нельзя шлифовать. Трудность изготовления точных метрических резьб, наоборот, растет с увеличением шага. Поэтому при малых шагах до 1 мм включительно применяют больших шагах — преимущественно
трапецеидальные. Лучшее направление винту (гайке) дает метрическая резьба. Поперечное смещение Az/ = Д^/sin а. Практически желательно, чтобы шаг резьбы был ие менее 1 мм, в крайнем случае 0,5 мм, так как изготовление более мелких резьб представляет затруднение.
Диаметр резьбы выбирают исходя из соображений достаточной жесткости винта при его нарезании и работе. Можно рекомендовать следующее соотношение длины винта к среднему диаметру: L < 15-i-*5-20dcp.
Винтовые механизмы имеют две группы первичных ошибок: погрешности резьбы и погрешности направления движения винта (гайки). Из погрешностей резьбы для винтовых механизмов движения важны: погрешности шага; погрешности угла профиля; погрешности среднего диаметра. Главнрй из них является погрешность шага. Погрешности шага резьбы бывают двух видов: периодические, повторяющиеся на каждом обороте винта, и накопленные (прогрессивные), появляющиеся на некоторой длине хода винта. Накопленная ошибка всегда больше, чем периодическая. Ошибки угла профиля резьбы винта и гайки обычно ие оказывают влияния на ошибку перемещения винта (гайки), так,^ак они постоянны по величине на длине резьбы и влияют только на износ резьбы и плавность хода. Погрешность среднего диаметра влияет на мертвый ход и износ резьбы.
Раньше считали, что на точность механизма влияют только по-
грешности резьбы винта. Как показали труды некоторых исследователей, ошибки гайки также оказывают влияние на точность механизма.
Кроме перечисленных погрешностей резьбы и направления движе-
ния периодическую ошибку может вызвать неперпеидикуляриость (биение) опорного торца винта и втулки подшипника в механизме второго вида (стр, 491). В механизме первого вида такая погрешность устраняется тем, что упорный конец винта делается сферическим, и
центр сферы располагается на оси вращения винта. Для этой цели технологически целесообразно сделать торцовую выточку, в которую завальцовывают нормальный шарик.
На точность винтового механизма неблагоприятно влияет трение между винтом и гайкой. Особенно невыгодно сказывается трение при длинных винтах небольших диаметров (происходит скручивание винта) и в конструкциях с плавающей гайкой, если направляющая деталь, служащая для удержания гайки от поворота (например, шпонка), расположена очень близко от оси винта (величина I мала). В этом случае сила давления А\, равная Мтр//, где /Итр — момент трения в винтовой паре, будет большой и вызовет увеличение трения в механизме и изгибающую винт силу реакции N2 (рис. 12.3), которая будет вызывать прогиб винта, упругий мертвый ход и неплавиость работы механизма.
КОНСТРУКЦИИ ОТСЧЕТНЫХ винтовых МЕХАНИЗМОВ
Область применения отсчетных винтовых механизмов — измерительные устройства приборов (микрометры, измерительные микроскопы, делительные машины и т. п.). К отсчетным винтам предъявляются высокие требования в отношении сопротивляемости износу, поэтому большое значение имеют правильный выбор материалов и их обработка. Винтовой механизм должен обеспечивать неизменное число витков, находящихся в контакте с гайкой, на всей длине рабочего хода.
Точность изготовления
На точных резьбошлифовальных станках можно изготовлять винты
с точностью (ошибка по шагу) 0,002 мм на длине 25 мм, на менее точных
станках—с точностью 0,01 мм на длине 300 мм.
Нельзя использовать винт в качестве основной направляющей для гайки, когда точка приложения силы к гайке значительно смещена от оси винта во избежание
заклинивания. Это особенно Рис. 12.4. График ошибок винта опасно при трапецеидальной резьбе.
Разрезные гайки несколько ухудшают точность работы винтовой Пары и, кроме того, повышают скорость износа. Поэтому для компенсаций мертвого хода более целесообразно применять пружины. Иногда применяют одновременно разрезные гайки н пружины.
В конструкциях точных винтовых механизмов должны быть предусмотрены возможности уменьшения осевого и радиального зазоров в паре с целью уменьшения мертвого хода и ошибок от биения опорных торцов винта (гайки) и, кроме того, возможность уменьшения зазора в резьбе в процессе эксплуатации.
Ошибки (прогрессивные и периодические) винта могут быть в каждом отдельном случае исправлены специальными коррекционными устройствами, если позволяют габариты и конструкция. Для этого пару винтов проверяют и составляют диаграмму ошибок винта (рис. Г2.4).
Рис. 12.5. Схема Рис. 12.6. Гайка,
коррекционного ус- стягиваемая вин-
тройства том
Для компенсации выявленных ошибок нужно, поворачивая виит на расчетные углы, дополнительно повернуть гайку на такой угол, чтобы ее перемещение вдоль винта исправляло ошибки винта. Для осуществления указанного поворота гайка 1 такого устройства (рис. 12.5) снабжается хвостовиком 2, который перемещается по криволинейному торцу планки 3, Коррекциоииая кривая строится в соответствии с диаграммой ошибок винта (пары). Расчет кривой производится следующим образом: в зависимости от требуемой (и возможной) точности и конструктивных соображений выбирается масштаб. Далее кривая рассчитывается по формуле у = R tg <рх, где <рх — угол поворота гайки для компенсации ошибки винта.
На рис. 12.4 по оси абсцисс отложены перемещения гайки, а по оси ординат — линейные перемещения хвостовика в плоскости коррекционной кривой. Указаное устройство может служить и для решения обратной задачи, сообщить гайке неравномерное перемещение по заданному закону при равномерном вращении винта. Прижим хвостовика к криволинейному торцу планки 3 производится с помощью пружины.
По этому же принципу строится коррекционное устройство для компенсации температурных влияний. Коррекционная кривая устанавливается под углом р, тангенс которого пропорционален разности коэффициента линейного расширения материала винта и детали^ относительно которой движется ходовая гайка.
Если необходимо компенсировать только температурное влияние, компенсационная кривая превращается с достаточным приближением в прямую, устанавливаемую под углом р к направлению движения ходовой гайки (см. рис. 12.3). Угол р в обоих случаях определяется но формуле
tg р = Ria (/ — /0) 2л/Р,
где /? — плечо гайки; / — ход винтового механизма; а — рази^сть коэффициентов линейного расширения ходового винта и детали, относительно которой движется гайка; t — фактическая температура; — нормальная температура, на работу при которой рассчитан прибор (обычно +20° С); Р— шаг винта.
Для того чтобы получить наименьший мертвый ход, используют различные конструктивные решения, которые сводятся либо к уменьшению зазора в резьбе, либо к применению пружин, обеспечивающих постоянный прижим гайки к одной стороне витков резьбы вданта. Наиболее широко применяют различные конструкции разрезной стягиваемой или пружинящей гайки.
такого рода механизмов
4 6
Рис. 12.7. Гайка из двух половин, соединенных резьбой
пол иэт иле новой гай кой должен быть полиэтилен
В отсчетном винтовом механизме винтового окулярного микрометра МОВ-1-15* (см. рис. 14.7) винт вращается и движется поступательно в разрезной конической гайке. На рис. 12.2 показана раздтяд-кость такой конструкции. Гайка, навинченная на коническую резьбу разрезной гайки, стягивает последнюю. Сжатие разрезной гайки с целью компенсации зазора в резьбе неизбежно искажает характер сопряжения, которое происходит не по всей резьбе, а на отдельных ее участках. Худшей в этом'отношении является конструкция, показанная на рис. 12.2.
Применение притирки после поджатия гайки улучшает сопряжение, но исключает взаимозаменяемость и повышает трудоемкость изготовления. Несмотря на эти недостатки, приведенные конструкции весьма распространены и обеспечивают точность отсчета передвижения винта около 0,001—0,005 мм. Чувствительность с течением времени несколько ухудшается вследствие загустения и загрязнения смазки. Износ резьбовой пары не всегда может быть скомпенсирован подтягиванием гайки без новой притирки, так как износ винта может быть неравномерным на рабочей длине.
Указанных недостатков лишены конструкции аналогичных механизмов с полиэтиленовыми неразрезными гайками, разработанные И. М. Долинским, Г. А. Матвеевой и Л. Ф. Ямшановым. Полиэтилен обладает хорошей упругостью, очень малым коэффициентом трения и легко обрабатывается резанием. Винтовая пара с не требует смазки. Материалом для гайки
низкого давления марки П, спресованный в виде блоков.
Гайки рекомендуется точить резцами, режущая кромка которых имеет закругление примерно 0,5 мм. Длина гайки должна быть такая же, как и у металлической гайки (не менее 1—1,5 диаметра винта); толщина стенки не менее 2 мм. Нарезание резьбы метчиком нужно обязательно делать «на проход», для этого диаметр хвостовика у метчика должен быть меньше внутреннего диаметра резьбы. Для создания легкости хода необходимо сделать несколько проходов резьбы метчиком. Гайка может быть выполнена и в виде конуса, но без разрезки; в этом случае обжатие гайки достигается за счет упругости полиэтилена.
Винтовой механизм окулярного микрометра МОВ-1-15 х (см. рис. 12.1, а) дает погрешность не более 2—4 мкм. Погрешность винтового механизма с шагом винта 0,5 мм, диаметром 6 мм и длиной перемещения 12 мм при грузоподъемности 7 Н (рис. 12.1, б) не превышает 1 мкм при почти полном отсутствии мертвого хода. Крутящий момент 0,1Н •м. Испытанный механизм после 10 000 полных ходов винта без смазки не подвергся износу.
На рис. 12.6—12.8 показаны другие конструкции с устройством для компенсации (уменьшения) зазора в резьбе. В конструкции, изображенной на рис. 12.6, сжатие гайки достигается с помощью стягивающего винта (винтов) 1, Эту конструкцию рекомендуется применять только для метрической резьбы. Гайка, показанная на рис. 12.7, состоит из двух половин А и Б, свинченных между собой, причем шаг резьбы половины А отличается от шага резьбы половины-Б. Вращением одной половины гайки относительно другой достигается уменьшение зазора между винтом и гайкой. В конструкции, приведенной на рис.-12.8, обе половины
гайки прижимаются к винту пружинами, что дает возможность быстро отключать гайку от вянта. Такая конструкция пригодна только для метрической резьбы.
Рис. 12.8. Гайка с пружинным замком
Рис. 12.9. Дифференциальный винт
Дифференциальный винт (рис. 12.9) имеет две нарезки с незначительно отличающимся шагом. Перемещение ганки А за один оборот винта равно разности шагов резьбы (Рг — Р2)- Предел перемещения гайки А (Рг — Р2) LlPb где L — перемещение винта В.
Дифференциальный винт применяется в тех случаях, когда гайке необходимо сообщить очеиь малые перемещения. Следует, однако, иметь в виду, что ошибка дифференциального виита вдвое больше, чем обычного винта. На рис. 12.10 дана конструкция отсчетного винтового механизма перемещения прицельного перекрестия оптического прицела для охотничьих ружей. Требуемая точность шага винта 0,01 мм. / Винтовой механизм, показан? ный иа рис. 12.11, является отсчетно-силовым. Нагрузка направлена вдоль оси и смещена на величину а. Обычно винтовые механизмы работают в таких условиях неудовлетворительно, вплоть до отказа из-за заклинивания резьбы. Для разгрузки винта предусмотрена установка вилки, двигающейся по направляющим на шарикоподшипниках и воспринимающей нагрузку плавающей ганки. Шарикоподшипники установлены на эксцентриковых осях, служащим для регулировки. Торцовые поверхности гайки выполнены сфернче-498
сними, что допускает некоторый перекос оси вннта относительно направляющих н предохраняет вннт от заклинивания. Механизм приводится в действие электродвигателем следящей системы и снабжен концевыми выключателями для ограничения хода. Приведенная конструкция обеспечивает легкий ход вннта при значительном смещении точки приложения нагрузки.
Материалы для винтовых пар
При малых нагрузках (5—10 Н), при которых обычно работают отсчетные винтовые пары, износ их незначителен. В таких случаях винт рекомендуется изготовлять из стали У8А без термообработки, а гайку — из латуни, оловяннстой бронзы или полиэтилена. При больших нагрузках и применении металлических гаек виит целесообразно изготовлять из стали У8А или У10А с последующей закалкой до тнердости HRC 50—55 и шлифованием.
Шероховатость обработанной поверхности незакаленного винта от Rz 3,2 до Rz 1,6, закаленного винта — от Rz 1,6 до Rz 0,8.
В измерительных устройствах часто применяются сопряжении звеньев, места контактов которых выполнены в виде сферы или плоскости, например сопряжение ведущего (толкающего) виита с кареткой. К такому сопряжению предъявляется требование неизменности расстояния между контактирующими деталями при работе.
В момент начала движении коэффициент трення (у металлов) значительно превышает коэффициент трения при движении. Это вызывает иеплавиость движения ведомого звена, что приводит к понижению точности механизма. В зоне контакта даже при закалке часто наблюдается эрозия поверхностей. Требуется, чтобы сопрягаемая пара имела характеристику трения, практически обеспечивающую равенство статического и кинематического коэффициентов трения и независимость усилий трогания от величины нагрузки. Материалами таких пар являются фторопласт-4, полиэтилен НД марки П и некоторые термопластичные полимеры в сочетании со сталью1. Однако следует учитывать хладотекучесть этих материалов, которая, если не примить специальных мер, может вызвать самопроизвольное смещение ведомого звена во времени даже прн постоинном силовом замыкании. Эти смещения существенно зависят от радиуса сферы и усилия замыкания.
Литература: [33, 48, 56, 89, 92, 93].
1 По материалам исследований И. М. Долинского к Г. А. Матвеевой.
ГЛАВА 13
ЗУБЧАТЫЕ ПЕРЕДАЧИ
ОБЩИЕ СВЕДЕНИЯ
Зубчатые передачи в оптико-механических приборах можно разделить на точные отсчетные и силовые (неточные). Расчетные формулы и типовые конструкции зубчатых и червячных колес и передач в справочнике не представлены. Приведен расчет только цилиндро-конической передачи.
Рекомендуемые конструктивные формы зубчатых колес даны на рис. 13.1. Наибольшее распространение получили цилиндрические прямозубые колеса (рис. 13.2). Для передачи вращения между пересевающимися валами применяются конические зубчатые колеса (рис. 13.3). Передачи цилиндрическими косозубыми колесами применяются в следующих случаях:
1) для обеспечения хорошей плавности работы колес с небольшим числом зубьев;
2) при больших скоростях вращения и высоких требованиях к бесшумности передачи.
Колеса с внутренним зацеплением применяются сравнительно редко вследствие большой трудоемкости изготовления и меньшей точности работы. Винтовые цилиндрические зубчатые передачи применяются для передачи вращения между валами с непараллельными и не-пересекающимися осями.
Для передачи вращения между валами со взаимно перпендикулярными осями применяют червячные передачи (рис. 13.4—13.6). Червячная передача дает возможность осуществить большое передаточное число (на замедление) в одной паре, а также обеспечивает хорошую плавность и бесшумность работы. Диапазон передаточных чисел составляет примерно от 1/7 до 1/500. Недостатки червячной передачи: более низкий к. п. д. по сравнению с передачей цилиндрическими и коническими колесами; значительно большая потребность в смазке; потребность в применении антифрикционных материалов (пары); повышенная чувствительность к перегрузкам (ускорениям); высокие требования к точности сборки.
Основными требованиями к точной червячной передаче являются: точность передачи углов и минимальный мертвый ход; достаточно высокий к. п. д.; хорошая износоустойчивость. В зависимости от способа образования боковых поверхностей витков различают следующие цилиндрические червяки:
1) архимедов или винтовой червяк, витки которого в осевом сече-иии имеют прямолинейный профиль;
Рис. 13.1. Формы цилиндрических колес
6H1f
Рис. 13.2. Пример вычерчивания цилиндрического зубчатого колеса
Рис. 13.3. Пример вычерчивания конического зубчатого колеса
Рис. 13.4. Конструкция типового выключающегося червяка! / «— рычаг выключения червяка; 2 —> пружинный подшипник (цилиндрическая втулка с прорезями, расположенными в шакч матном порядке); 3 — корпус; 4 — эксцентриковая втулка^ 5 » червяк; 6 « возвратная пружина
2) эвольвентный, у которого стороны витка в сечении, перпендикулярном к оси, являются эвольвентами;
3) конволютный червяк, имеющий прямолинейный профиль в нормальном к витку сечении.
В приборостроении применяется преимущественно архимедов червяк.
Рис. 13.5. Формы червячных колес
М10-1
т-(№7*0,ЦРч
Рис. 13.6. Пример вычерчивания червяка
ЦИЛИНДРО-КОНИЧЕСКАЯ ПЕРЕДАЧА С УГЛОМ 90° МЕЖДУ ОСЯМИ
Передача состоит из цилиндрической шестерни с эвольвентным профилем / и колеса с торцовыми зубьями 2, оси которых пересекаются под прямым углом (рис. 13.7). Эта передача в некоторых случаях более удобна и компактна, чем коническая, и может быть выпол-
йена с большой точностью. В конструкции передачи легко осуществить регулировку бокового зазора за счет осевой подвижки торцового колеса и выключение и реверсирование путем осевого перемещения цилиндри-, ческой шестерни (рис. 13.8). Недостатком передачи является меньшая нагрузочная способность по сравнению с конической передачей.
Рис. 13.7. Схема цилиндр о-кон и ческой передачи
Рис. 13.8. Конструкция реверсивной цилиндро-конической передачи
Нарезание торцового колеса нужно производить эвольвентным дол-бяком на зубодолбежном станке методом обкатки с применением специального приспособления. Расчет элементов колес производится по табл. 13.1.
Таблица 13.1. Расчет цилиндро-конической передачи
Расчетная величина Обозначение (см. рис. 13.7) Расчетные формулы
Угол исходного контура «0 сс0 = 20°
Модуль т Из нормального ряда
Передаточное отношение от шестерни 1 к колесу 2 4,2 t'1,2 == ^2^1 ~ ^1/^2
Число зубьев дол бяка По отраслевой нормали
Число зубьев шестерни 1 м [| м е
Число зубьев торцового колеса 2 г2 —
Коэффициент высоты головки зуба долбяка fu fu — 1,25 (при т 1) fu = 1,35 (при т. < 1)
Коэффициент высоты головки зуба колеса Обычно принимается /2 ~ = 1
Расчетная величина Обозначение (см. рис. 13.7) Расчетные формулы
Внутренний диаметр зубчатого венца колеса из условия отсутствия подрезания зубьев DB DB mz2 cos а0 X £
1 1 х 1 3I л* 1 сТ e -U -L О 3 3 N N bi N ( г к
Наружный диаметр зубчатого венца колеса из условия отсутствия заострения зуба Вн с mz2 cos а0 X X (sin ан — fl cos ан)/ sin tp, где cos ан ~ гн cosot0/(?w + 2/J fl = (г«—2f2 — cos aH)/sin ан x X zwcos а0 ср = inv ae + aH — v — n/2zu
Расчетный диаметр, на котором осуществляется теоретический контакт зубьев Ор Рекомендуется Dp = (DB + £>H)/2
Угол зацепления на расчётном диаметре ар cos ар = mz2 cos afr/Dp
Коэффициент коррекции шестерни ь h = (ги — ?i) X X (inv ae — inv ap)/2 tg ae
Монтажный размер (расстояние от оси шестерни до делительной плоскости колеса) А При некорригировэнной шестерне: А = mZj/2 При корригированной шестерне: А = т \zu — (ги — 2i) cos а0/ cosap]/2
Расчетная величина ч Обозначение (см. рис. 13.7) Расчетные формулы
Коэффициент высоты головки зуба шестерни /1 При некор риг ир ова иной шестерне: = 1 При корригированной шестерне: t I / cos ОСр . \ 1 ~~ 2 \ cos otp /
Высота головки зуба шестерни A'i = fjtn
Высота головки зуба колеса К h'2 =
Высота ножки зуба шестерни я; = (fu — 51) m
Высота ножки зуба колеса a; Лз = fum
ПОГРЕШНОСТИ ЗУБЧАТЫХ ПЕРЕДАЧ
Различают два вида погрешностей отсчетных зубчатых передач: 1) кинематическая погрешность или ошибка отсчета — наибольшая погрешность угла поворота зубчатого колеса в пределах одного оборота при однопрофильном зацеплении с точным колесом (точным червяком);
2) мертвый ход — угловое отставание ведомого колеса при изме-иерии направления вращения ведущего колеса (червяка).
| Суммарная погрешность складывается из указанных выше. Г0СТ 9178—72 устанавливает 12 степеней точности цилиндрических мелкомодульиых зубчатых колес и передач (в порядке возрастания погрешностей) — от первой до двенадцатой. Наибольшее применение имеют колеса 6, 7 и 8-й степени точности. В стандарте значение кинематической погрешности приводится в микрометрах (Fr). Перевод Fr в угловую меру легко осуществить делением отрезка дуги делительной окружности (который и характеризует Fr) на радиус делительной окружности.
На рис. 13.9 приведены значения вероятных суммарных кинематических погрешностей цилиндрических зубчатых колес.
Для расчета мертвого хода в зубчатой передаче необходимо определись составляющую погрешности, обусловленную упругими деформация ми элементов зацепления. Для этого необходима рассчитать действующие в передаче моменты и усилия.
Рис. 13.9, Кривые суммарных погрешностей зубчатых колес
РАСЧЕТ МОМЕНТОВ И УСИЛИЙ
Расчет моментов и усилий в механизмах ведется от конечных ведомых звеньев к ведущему. Подсчитанные или известные моменты трения или силовые нагрузки концевых ведомых звеньев должны быть приведены к ведущему звену через все промежуточные передачи с учетом их собственных моментов.
Формула расчета иа каждой ступени передачи
где Afi — момент ведущего звена; М2 — момент на ведомом звене; 4,2 ™ 2J2\ — передаточное отношение; т] — к. п. д. передачи; М[ — собственный момент трения ведущего звена.
Таблица 13.2. Моменты трения шарикоподшипников 5-го класса точности
Внутренний диаметр подшипника, мм Момент трення М Ю"4, Н-м Внутренний диаметр подшипника, мм Момент трения М J. I О'4, Н-м
3 2—3 9 20—30
5 6—9 10 25—38
6 10—14 12 36 ~“54
8 16—24 15 56—84
Т а б л и ц а 13.3. Коэффициенты полезного действия rj стальных прямозубых цилиндрических колес
Число зубьев г Окружное усилие Р, /7
0,02 0,05 0,1 0,2 0,3 0,4 0,5 0,8 1 2 5 10 30
14 0,32 0,40 0,50 0,62 0,69 0,73 0,77 0,82 0,85 0,90 0,93 0,94 0,95
20 0,52 0,58 0,65 0,73 0,78 0,81 0,83 0,87 0,89 0,92 0,94 0,96 0,96
30 0,68 0,72 0,77 0,82 0,85 0,87 0,89 0,92 0,92 0,94 0,96 0,97 0,97
40 0,76 0,80 0,82 0,86 0,89 0,91 0,92 0,94 0,95 0,95 0,97 0,97 0,98
50 0,82 0,82 0,86 0,89 0,91 0,92 0,94 0,95 0,95 0,96 0,97 0,98 0,98
100 0,90 0,91 0,93 0,95 0,95 0,96 0,96 0,97 0,97 0,98 0,98 0,98 0,98
150 0,94 0,94 0,95 0,96 0,97 0,97 0,97 0,98 0,98 0,98 0,98 0,98 0,98
Таблица 13.4. Коэффициенты полезного действия г) стальных винтовых колес (оси перпендикулярны)
Угол подъема Рд,. Окружное усилие Р, Н
0,02 0,1 0,2 0,3 0,4 0,5 0,8 1 2 5 10 30
45 0,36 0,38 0,40 0,43 0,45 0,48 0,5! 0,55 0,63 0,75 0,78 0,81
30 0,35 0,37 0,39 0,40 0,43 0,44 0,47 0,50 0,57 0,66 0,72 0,79
20 0,33* 0,34 0,36 0,38 0,39 0,40 0,44 0,46 0,53 0,62 0,67 0,74
15 0,30 0,32 0,34 0,35 0,36 0,38 0,40 0,43 0,49 0,57 0,62 0,69
S Таблица 13.5. Коэффициенты полезного действия г| стальных конических колес
Число • Окружное усилие Р, Н
зуоьев 2 1 0,02 0,05 0,1 0,2 0,3 0,4 0,5 0,8 1 2 5 10 30
14 0,22 0,32 0,44 0,57 0,65 0,70 0,73 0,80 0,82 0,88 0,92 0,93 0,95
20 0,45 0,52 0,60 0,70 0,75 0,79 0,81 0,86 0,87 0,91 0,95 0,95 0,96
30 0,63 0,68 0,73 0,80 0,83 0,86 0,87 0,91 0,91 0,95 0,96 0,96 0,97
40 0,72 0,76 0,80 0,85 0,87 0,89 0,91 0,93 0,94 0,96 0,97 0,97 — — *
50 0,78 0,80 0,83 0,87 0,90 0,91 0,92 0,95 0,95 0,96 0,97 МИН * 0,98
100 0,88 0,90 0,92 0,94 0,95 0,95 0,96 0,97 0,97 0,98 — — —
Таблица 13.6. Коэффициенты полезного действия червячных передач г) (колесо бронзовое, червяк стальной)
Угол подъема рд*, ...° Окружное усилие Р, Н
0,1 | 0,2 0,4 0,6 1 2 5 10 30
До 2 Св. 2 до 3 » 3 » 4 » 4 » 5 > 5 » 7 » 7 » 9 > 9 > 12 > 12 > 15 » 15. > 18 - : 0,10 0,13 0,16 0,20 0,21 0,26 0,29 0,31 0,33 0,10 0,14 0,17 0,21 0,23 0,29 0,30 0,34 0,34 0,12 0,15 0,18 0,22 0,25 0,30 0,32 0,36 0,38 0,12 0,15 0,20 0,24 0,28 0,32 0,35 0,38 0,40 0,13 0,18 0,21 0,28 0,31 0,35 0,39 0,42 0,44 0,16 0,20 0,25 0,30 0,34 0,39 0,45 0,48 0,51 0,19 0,25 0,29 0,35 0,42 0,45 0,52 0,56 0,60 0,20 0,26 0,32 0,38 0,46 0,52 0,57 0,61 0,64 0,22 0,30 * 0,35 0,42 0,50 0,58 0,63 0,68 0,71
Собственный момент трения ведущего звена чаще всего является моментом трения шарикоподшипников, в которых оно установлено. В табл. 13.2 приведены собственные моменты трения наиболее употребительных шарикоподшипников 5-го класса точности. В табл. 13.3— кЗ.6 приведены значения к. п. д. зубчатых и червячных передач. При i =/= 1 следует пользоваться соотношением т|i>2 = (jli + где Th,2 “ к. п. д. передачи с передаточным отношением t\,2 = И т]/—к. п. д. передачи с передаточным отношением £XlX = zjzx — 1; Лг — к* п. д. передачи с передаточным отношением 1'2,2 = ?2/г2 = 1; T)i и т]а берут из таблиц для соответствующих окружных усилий Р.
РАСЧЕТ МЕРТВЫХ ХОДОВ
Удобнее всего расчет ошибок н мертвых ходов производить в единицах той величины, которая вырабатывается механизмом и отсчитывается на его шкалах. Для этого необходимо определить цену оборотов всех звеньев кинематической цепи механизма илн прибора.
Ценой оборота А вала называется число отсчетных единиц, соответствующих полному обороту вала (детали):
А2 = АХ/Х(2,
где Ах и А2 — цены оборотов ведущего н ведомого звеньев пары в отсчетных единицах; Jx,2 — передаточное отношение пары.
Мертвый ход ДА рассчитывают по следующим формулам: для цилиндрической прямозубой реечной н конической передач
ДА = 2А (k -J- епш -J- /)/(^?);
для цилиндрической передачи с косозубымн колесами
ДА = 2А (k + епш + f)l(mz cos 0Д);
для червячной передачи
ДА = A (k 4- епш 4- cos со).
Здесь k — коэффициент, учитывающий боковой зазор между зубьямн и зависящий от класса точности колес, а также от наличия нли отсутствия регулировки межцентрового расстояния; епш — радиальный зазор в подшипнике; f — суммарное значение упругих линейных деформаций (изгиба валика, зуба, опоры); этот коэффициент должен учитываться при наличии достаточно больших нагрузок и невысокой жесткости передачи; т — модуль; z — число зубьев.
Методика н примеры расчета суммарных ошибок зубчатой передачи приведены в гл. 10.
Упругий мертвый ход, вызванный деформациями деталей передачи, зависит главным образом от закручивания валиков, а также от прогиба длинных консольных валиков. Упругнй мертвый ход может стать особенно заметным при большой цене оборота валика, а также при большой нагрузке, длине и малом диаметре валика. Расчет угла закручивания валика производится по формуле
Дер =Л7ИА/216000, где М —скручивающий момент на валике (/И-10~4, Н-м); А — цена оборота валика в отсчетных единицах; К — коэффициент для определения двойного угла закручивания участка валика.
Величину К вычисляют по формуле
А = 640L/nd4G^,
Т абл и ца 13.7. Коэффициент (К-..*) для определения двойного угла закручивания стальных валиков под действием момента ЛЬ КГ3 Н«м
d, мм
L, мм
3 4 5 6 7
10 6,492 2,052 0,840 0,408 0,216
15 9,738 3,078 1,260 0,612 0,324
20 12,984 4,104 1,680 0,816 0,432
25 13,023 5,130 2,100 1,020 0,540
30 19,497 6,156 1,526 1,224 0,648 '
' 35 22,722 7,182 2,940 1,428 0,756
40 25,968 8,208 3,360 1,632 0,864
45 29,214 9,234 3,780 1,836 0,972
50 32,460 10,260 4,200 2,040 1,080
55 35,706 11,286 4,620 2,244 1,188
60 38,952 12,312 5,040 2,448 1,296
65 42,198 13,338 5,460 2,652 1,404
70 45,444 14,364 5,880 2,856 1,512
d, * 4М
L, мм
8 9 10 12 | 14 15
10 0,126 0,078 0,054 1 —м
15 0,192 0,120 0,084 1
20 0,252 0,156 0,108 0,048 —
25 0,312 0,192 0,132 0,060 0,036 0,024
30 0,378 0,234 0,162 0,072 0,042 0,030
35 0,444 0,276 0,192 0,084 0,048 0,036
40 0,504 0,312 0,216 0,096 0,054 0,042
45 0,564 0,348 0,240 0,108 0,060 0,048
50 0,624 0,384 0,264 0,120 0,060 0,054
55 0,690 0,426 0,294 0,132 0,072 0,054
60 0,756 0,468 0,324 0,144 0,084 0,060
65 0,822 0,510 0,354 0,156 0,132 0,066
70 0,888 0,552 0,384 0,168 0,150 0,072
где L — длина скручивающейся части валика; d —диаметр валика; G — модуль сдвига материала валика (6-0,1 Н/м2); — коэффициент
перевода градусной меры угла в радианы (kw — 291 • 10~б рад/угл. мин).
В табл. 13.7 даны значения К для стальных валиков под действием Момента М.
Рис. 13.10. Конструкция разрезных цилиндрических шестерен: а, б — соединение на винтах; в — соединение пружиной
Расчет влияния прогиба консольно закрепленного валика на упругий мертвый ход следует производить только в тех случаях, когда кон
сольная длина валика I (расстояние от средней плоскости шестерни до
торца подшипника) не менее чем в 5—10 раз превосходит его диаметр и нагрузка иа него достаточно велнка:
f = 20PZ3/3Ed4,
где / — величина прогиба; Р — давление на зубчатую шестерню (окружная сила сопротивления); d — диаметр валика; Е — модуль упругости.
Прогиб валика f вызовет упругий мертвый ход, равный Аф = //г, где т — радиус начальной окружности шестерни.
Рис. 13.12. Разрезная шестерня со спиральной
Рис. 13.11. Разрезная шестерня с двумя пружи-
нами
пружиной
Для уменьшения упругой составляющей мертвого хода следует увеличить жесткость элементов передачи. Для уменьшения мертвого ‘Хода передачи (люфтовый мертвый ход), применяют разрезные шестерни (рис. 13.10—13.12).
Литература: 152, 56, 58, 75, 92, 93, 110],
ГЛАВА 14
ОТСЧЕТНЫЕ УСТРОЙСТВА
ОПТИЧЕСКИЕ ОТСЧЕТНЫЕ УСТРОЙСТВА
Оптические отсчетные системы можно разделить следующим образом:
1) по принципу действия оптических систем — телескопические и системы типа микроскопов;
2) системы для линейных и угловых измерений;
3) системы прямого отсчета и системы отсчета с микрометрами;
4) по типу отсчетных шкал—системы шкалового отсчета, системы с штрихом-оценщиком, нониусного типа н со шкалами, построенными по методу поперечного масштаба;
5) по способу воздействия на отсчетную систему — шкаловые механического устройства (если отсчет производится непосредственно в плоскостях расположения самих шкал или их изображений) и оптические микрометры или компенсаторы (если воздействие производится на лучи, передающие изображение шкал);
6) системы последовательного и параллельного действия (одинарного и двойного изображения);
7) по способу возможных математических действий—системы множительные одинарного изображения и суммирующие двойного изображения.
Точность отсчетных устройств определяется точностью оптических систем, точностью изготовления и сборки отсчетных элементов — шкал и нониусов, а также точностью совмещения штрихов при производстве отсчета. На точность совмещения влияет контраст изображения и его освещенность, параллакс изображения, утомление наблюдателя. Применением оптических микрометров или фотоэлектронного устройства для наведения на штрих можно значительно повысить точность совмещения.
Оптические отсчетные устройства непосредственного отсчета
К ним относятся устройства прямого отсчета, отсчета по- нониус-ной и растровой шкалам.
1 Устройства прямого отсчета. Отсчет производится по положению индекса, без совмещения со штрихом шкалы, с оценкой доли деления на глаз. Оптическая система служит только для увеличения видимых размеров шкалы.
2. Отсчет по ноннусной шкале (верньеру). Нониусной называется шкала, имеющая деления несколько меньшие (или большие), чем деления основной шкалы, что дает возможность отсчитывать доли делений основной шкалы по номеру совмещенного штриха шкалы ноннуса. Такой способ отсчета точнее, чем оценка доли делений основной шкалы на глаз.
3. Отсчет по растровой шкале (по шкале поперечного масштаба или Трансверсальной). Растровая шкала имеет наклонные к вертикали линии, состоящие из марок в виде точек, квадратиков или бнссекторов (см. рис. 4.37). Сдвиг штрнха-индекса с одной марки на соседнюю по вертикали соответствует горизонтальному смещению шкалы на величину а — s/Л/, где s — расстояние между наклонными линиями, a N — число марок в наклонной линии.
Оптические отсчетные устройства с микрометрами
1. Винтовые окулярные микрометры. Наиболее часто применяются оптические микрометры с измерительным винтом, у которых сетка с биссектором устанавливается в плоскости изображения окуляра. Отсчет дробных делений производится по шкале на барабане винта; в последних моделях шкала проектируется в поле зрения окуляра (см. рис. 14.7 и 14.8). Цена деления 0,01 мм.
2. Окулярные микрометры со спиральной шкалой (см. рис. 14.9). В этом микрометре шкала на сетке имеет внд двойной (биссекториаль-ной) спирали Архимеда. Расстояние между спиралями 0,012 мм, шаг спирали 0,1 мм. Внутри спирали находится круговая шкала, имеющая 100 равномерных делений (см. рис. 4.34). На расстоянии 0,1 мм расположена вторая неподвижная сетка; на ней по радиусу спирали Архимеда имеются два параллельных штриха, вдоль которых нанесена равномерная шкала с ценой деления 0,1 мм. Минимальная цена деления спирального микрометра равна 0,1/100 ~ 0,001 мм, где 0,1 — шаг спирали, мм; 100 — число делений круговой шкалы.
3. Оптические микрометры, смещающие изображение. С помощью оптических микрометров смещение индекса от ближайшего штриха шкалы измеряется путем перемещения изображения штриха до совмещения с индексом и измерения этого перемещения. Оптические микрометры делятся на две основные группы: с использованием изменения направления лучей — оптические компенсаторы; с использованием смещения лучей без изменения их направления. В качестве оптических элементов, служащих для смещения изображения, применяются вращаемые плоскопараллельные пластинки, оптические клинья, длиннофокусные линзы и для грубых измерений — зеркала. В табл. 14.1 даны характеристики оптических микрометров.
Шкаловые отсчетные устройства
К ним относятся:
1) отсчетная система со шкалой (шкалами) н индексом;
2) отсчетная система со штрихом-оценщиком в плоскости шкалы объекта или ее изображения помещен индекс в виде штриха или биссектора (двойного штриха);
3) отсчетная система нониусного типа. Снятие отсчета с основной шкалы производится совмещением ее с другой, выполненной в ином масштабе шкалой;
17 в, д. пййсМв и др. 513
Таблица 14.1. Характеристика оптических микрометров
Характер смещения детали относительно оптической оси системы
Влияние смещения или поворота оптических деталей
Плоскопараллельные пластинки (одна или две)
Один клии (ахроматический)
Два клина
Линзовый компенсатор
Смещение: вдаль осн поперек осн
Поворот: вокруг оптической осн
вокруг оси, перпендикулярной оптической оси
Не влияет » »
В сходящемся пучке! н акл онная пл асти н ка вызывает движение изображения по кругу, в параллельном ходе не влияет
В сходящемся пучке вызывает смещение на d sin ал
Лучи смещаются параллельно самим себе в главном сечении клина. В сходящемся пучке смещение изображения равно (при пе = 1,5) у' = 0,5as'. В параллельном ходе у' = 0,5а/ , где f — фокусное расстояние системы, образующей изображение после клина
В сходящемся пучке изображение двигается по кругу радиуса г —
Не применяется
Вращение пары клиньев во взаимно противоположных направлениях на равные углы отклоняет луч в одной плоскости на угол а = (oi+ а2) cos р, где at — а2 — угол отклонения луча каждым клином; р — угол поворота каждого клина от начального положения (главные сечення совмещены)
Не применяется
Смещение изображения в угловой мере о == а//л» где а — смещение линзы
Примечание. s'—> расстояние от клина до изображения; а — угол поворота пластинки; ст — угол отклонения луча клииом.
4) отсчетная система растрового типа. Устройство, в котором для повышения точности отсчета применена шкала в виде растра, построенного по принципу поперечного масштаба.
Линейные шкалы и нониусы. Оценка дробных делений шкалы производится с помощью ионнуса или дополнительного механизма точного'отсчета (рнс. 14.1). Ноннус служит для более точного, чем на глаз, Отсчёта дробной доли деления шкалы. Длина шкалы ноннуса I == па', где а* — интервал ноннуса. На этой же длине уложатся уп — 1 делений
Формы индексов
ff
Рнс. 14.1. Отсчетный механизм:
1 н 2 — шкалы грубого н точного отсчетов соответственно; 3 —• винтовой ограничитель вращения
основной шкалы с интервалом а. Тогда Z = (уп — 1) а; а' = (уп — 1) X X а/п, где у — модуль нониуса, который обычно принимается равным 1 нли 2: у — (I + а)!(па). Величина отсчета по нониусу i = уа — а' = - == уа — (уп — 1) а/п = а/n; а! = уа — а/л — уа — I.
Форма индексов. В приборах, отсчет по шкалам которых должен делаться быстро, вместо ноннуса применяются дополнительные шкальные механизмы точного отсчета. Индексы должны быть хорошо заметны (см. рис. 14.1). Форма индекса б технологически более проста, чем форма индекса а, но несколько менее заметна.
Допуски на деления линейных и угловых шкал
Как указано в гл. 3, разрешающая способность глаза позволяет замечать смещение одной линии относительно другой, равное 10". Уста-'йовлено, что невооруженный глаз замечает смещение линии до 0,012 мм. |Исходя из этого, допуски на деления шкал, рассматриваемых невоору-
17* 515
женным глазом, не следует назначать#меньше указанной величины. При рассматривании шкалы через лупу нлн микроскоп с увеличением Г этот допуск можно уменьшить в Г раз.
Допуски назначают исходя из технических требований к прибору, причем следует назначать наибольшие нз рекомендуемых допусков. В табл. 14.2 приведена ширина штрихов, рекомендуемая для некоторых линейных шкал.
Таблица 14.2. Ширина штрихов
Шкалы Ширина штрихов, мм
Шкалы, наблюдаемые невооруженным глазом: лабораторных приборов военных приборов рассматриваемые при удалении 0,8— 1 м с делениями, заполненными светосоставом временного действия * наблюдаемые в лупу илн микроскоп Особо точные шкалы лабораторных приборов или станков О,15+0"05 0,25—0,35+0,1 0,8—1+0,2 (и более) Не менее 0,8 0,15/Г, где Г — увеличение лупы илн микроскопа 0,002—0,05 **
* Ширина штрихов цифр не менее 1 мм, глубина делений не менее 0,5 мм. ** В зависимости от цены деления и увеличения.
Наибольший допуск на угловые деления не должен превышать 1/4 цены деления. Для грубых шкал диаметром до 80—100 мм, как правило, нет необходимости назначать допуск точнее 10'. Предельная величина допуска должна быть такой, чтобы на глаз не было заметно неравномерности делений шкалы. Например, шкала барабанчика угломерного прибора диаметром 40 мм имеет число делений 100, угловой размер деления 3,6° (216'), шнрниу штриха 0,25 мм (45' в угловой мере). Можно назначить допуск 10—15', так как при этом смещение штриха будет ие более 1/3 его ширины и не более 1/10 цены деления. Допуск на все деления назначается на отклонение угла между данным штрихом и нулевым.
Промежутки между ближайшими делениями всех шкал не должны быть меньше двух-трехкратной ширины штрихов. У шкал с отсчетом по нониусу часть, на которой нанесены деления, должна быть равна рабочей части шкалы плюс длина нониуса. Для повышения точности отсчета рекомендуется в начале и в конце шкалы, а также в конце нониуса наносить по два дополнительных штриха.
Шкалы на металле
Точность отсчета, условия освещения и средства отсчета определяют наименьшую линейную величину интервала шкалы. Установлено, что отсчет по индексу невооруженным глазом для наименьших линен-жых вёличнн интервалов 0,5; 0,8 и 1,0 мм достигается в долях интервала ^соответственно с точностью 1/1, 1/5, 1/10. При наблюдении в лупу с увеличением Тл наименьшие интервалы уменьшаются в Г раз. При отсчете по нониусу невооруженным глазом наименьший линейный интервал равен 0,8 мм, а с лупой — 0,8/Г мм. Точность отсчета в долях деления по нониусу зависит от числа его'основных делений (м). Расстояние между нулевым и последним штрихом основных делений нониуса равно длине (л— 1) илн (2л— 1) делений шкалы (примой нониус) и (п + 1) или (2л + 1) ее делений (обратный нониус).
Наименьший интервал шкалы, изготовленной нз алюминиевого сплава, равен 0,5 мм, стали — 0,5 мм, латуни — 0,2 мм, нейзильбера — 0,05 мм, серебра — 0,05 мм.
Размеры штрихов
Длина штрихов зависит от значения наименьшего интервала шкалы (/). Следует назначать: а) длину малого штриха в пределах: = (1,2 -~ ±2) t при t С 0,8 мм и lt = 1^-21 при t > 0,8 мм; б) соотношении длин малых, средних и больших штрихов Ц : Z2 : Z3 = 1 : 1,6 : 2,6 илн Zj : Z2 : : /3 ~ 1 : 1,5 : 2; в) если шкала имееттолько малые или большие штрихи, то ?! : Z3 = 1 : 1,5 или Zt : Z3 = 1 : 2.
Длина штриха индекса при расположении его рядом со шкалой должна быть равна для шкал: а) с одной длиной штрихов — длине штриха шкалы; б) с двумя длинами штрихов — полусумме длин большого и малого штрихов шкалы; в) с тремя длинами штрихов — длине Среднего штриха шкалы. При расположении индекса в плоскости изображении шкалы длина штриха индекса ие нормируется.
Длина штрихов нониуса должна быть равна длине соответствующих штрихов сопряженной с ней шкалы. При шкале с одной длиной штрихов длина нулевого и последнего штрихов нониуса принимается равной 1,5 от длины штриха шкалы. Предельные отклонения длин однозначных штрихов для разных деталей устанавливаются ±10% от соответствующих значений, дли одной детали — ±5%.
Таблица 14.3. Допуски на ширину штрихов, мм
Ширина штриха Предельное отклонение Допустимая разность ширины штрихов в одной шкале
От 0,010 до 0,012 ±0,003 0,002
» 0,016 » 0,030 ±0,006 0,004
0,05 ±0,01 0,006
Ог 0,08 до 0,10 ±0,02 0,012
» 0,12 » 0,20 ±0,03 0,020
» 0,25 » 0,40 . ±0,04 0,030
» 0,50 » 1,20 ±10% от ширины 10% от ширины
> - штриха штриха
Таблица 14.4 Ширина штрихов
Материал шкалы Длина интервала, мм Ширина штриха, мм
свыше ДО
Серебро, нейзильбер 0,05 0,15 0,010—0,016
Серебро, нейзильбер, алюминиевый 0,15 0,2 0,010—0,020
сплав АВ Нейзильбер, серебро, алюминиевые 0,2 0,4 0,016—0,030
сплавы Алюминиевые сплавы, нейзильбер 0,4 0,7 0,03—0,10
Сталь 0,7 1,0 0,08; 0,10
Латунь, алюминиевые сплавы 0,7 1,0 0,10—0,16
Сталь 1,0 1,5 0,16; 0,20
Алюминиевые сплавы 1,0 1,5 0,10—0,20
» £ 1,5 2,0 0,16—0,25
Сталь, латунь 1,5 2,0 0,20; 0,25
Сталь 2,0 3,0 0,30; 0,40
Алюминиевые сплавы 3,0 5,0 0,50-—0,70
Латунь 5,0 8,0 0,8—1,2
8,0 1 1 >>0,15 t
Ширину штрихов шкалы назначают исходя из длины интервала (табл. 14,3) и материала (табл. 14.4). Видимая угловая ширина штрихов не должна быть менее 40". Ширина штрихов индекса и нониуса должна быть равна ширине штриха шкалы. Ширина штрихов, заполненных светящимся составом, должна быть не менее 0,5 мм.
Точность шкал
В зависимости от вида, требуемой точности отсчета, длины и диаметра шкалы предельные отклонения на интервалы делений должны определяться по табл. 14.5—14.7. Неп а рал дельность штрихов не должна
Таблица 14.5. Допускаемые отклонения расстояний между двуми любыми штрихами прямолинейных шкал, мм
Номинальная длина шкалы, мм Класс точности
1 2 3 4
До 50 Св. 50 до 100 Св. 100 Длина одного любого деления ±0,01 ±0,02 ±0,03 ±0,005 ±0,02 ±0,05 ±0,10 ±0,01 ±0,05 ±0,10 ±0,20 ±0,02 ±0,10 ±0,20 ±0,50 ±0,05
Таблица 14.6. Предельные отклонения углов между двумя штрихами круглых, дуговых плоских и конических шкал, ...'
-г; Проверяемый угол иа шкале Класс точности
1 2 3 4 5 6
Одно любое деление Между двумя любыми штрихами в пределах всей шкалы ±10" ±0,25 ±0,25 ±0,5 ±0,5 ± 1 ±1 ±2 ±2 ±5 ±5 ± 10
Таблица 14.7. Допускаемые отклонения углов между двумя штрихами цилиндрических шкал,
Проверяемый угол на шкале Класс точности
1 2 3 4 5
Одно любое деление Между двумя любыми штрихами в пределах всей шкалы ±20" ±0,5 ±3 ±5 ±5 ±8 ±8 ± 12 ± 15 ±20
рревышать значений, установленных табл. 14,5 для прямолинейных шкал, табл. 14.7 с пересчетом угловых значений н линейные для цилиндрических шкал. В обоснованных случаях допускается применение шкал более высокой точности.
Размеры цифр и знаков
Видимая высота цифр и знаков ие должна быть меиее 2 мм. Наименьшая высота цифр и знаков на серебре, алюминиевых сплавах, нейзильбере и латуни — 0,4 мм, на стали — 1,0 мм.
Профиль штриха
Профиль сечения штриха определяется способом его нанесения (пластической деформацией — давлением, строганием, фрезерованием «исковой и концевой фрезами). Глубийа штриха должна составлять ,3—0,8 его ширины, а в случае заполнения светящимся составом — йе менее 0,8 ширины.
КОНСТРУКЦИИ ОТСЧЕТНЫХ УСТРОЙСТВ
Конструкции отсчетных устройств должны удовлетворять следу-ДОцим требованиям:
г' 1) обеспечению удобного отсчета измеряемой величины, достаточ-1Дой освещенности, отсутствии бликов^
2) собственная ошибка отсчетных устройств (шкала, индекс) должна быть значительно меньше, чем ошибка измерительного устройства прибора;
3) должно быть предусмотрено удобство юстировки нулевого положения шкал;
4) во избежание ошибки от параллакса края штрихов шкалы и ин-
7 / декса должны быть расположены
в одной плоскости и с малым разрывом;
5) толщина штрихов шкалы и нониуса (индекса) должна быть одинаковой;
6) необходимо предусматривать подсветку шкалы для пользования ею в ночное время.
Некоторые типовые конструкции отсчетных устройств даны на рис. 14.1—14.8. На рис. 14.9 показана конструкция отсчетного окуляра инструментального микроскопа.
Рис. 14,2. Типовой отсчетный барабан прицела: а — без фиксатора:
1 — шкала; 2 — гайка; 3 — плаика с индексом;
б — с фиксатором:
1 — подшипник; 2 — пружинное кольцо, закрепленное в двух точках иа подшипнике /ив двух точках на кольце 3;
3 — кольцо с торцовыми зубьями; 4 — фланец с торцовыми зубьями
В винтовом окулярном микрометре ОРИМ-1 (Г = 15Х), показанном на рис. 14.8, отсчетная шкала с ценой деления 0,01 мм представляет собой стеклянный лимб закрепленный на вращающейся вместе с барабаном 1 микрометра гайке 2. Изображение шкалы лимба оптической системой проецируется в плоскость сеток 4 и 5. На неподвижной сетке 4 нанесена шкала (в миллиметрах), на неподвижной сетке 5 имеется индекс. На рис. 14.10 показан винтовой окулярный микрометр МОВУ-1-15Х с угломерным устройством (цена деления 6').
В оптической отсчетной системе координатно-расточного стайка (рис. 14.11) на шкалу 2 растрового типа оптической системы проецируется отсчетный штрих 3 линейной или круговой шкалы, закрепленной на неподвижной части станка. Рамка со шкалой 2 подвешена на двух
плоских пружинах 1. С помощью дифференциального винта 6 и сухаря 5 шкалу 2 можно смещать, при этом механический индекс 7 перемещается с большей скоростью вдоль шкалы 5, цена деления которой составляет 1/10 цены деления растровой шкалы. Винт 4 служит для установки растровой шкалы на нуль.
Более часто применяются отсчетные устройства, в которых растровая шкала установлена в фокальной плоскости проекционного объектива. В эту же плоскость проецируется изображение отсчетной линейки или
/ /2
Рис. 14.3, Отсчетный барабан с шайбо-кулачковым ограничителем вращения:
1 — шкала; 2 — стопор; 3 — винт; 4 — фиксирующий кулачок; 5 — кулачковая шайба; 6 — упорный штнфт
шкалы, а затем изображение штриха линейки и растр совместно проецируются на экран, на котором наблюдают совмещение штриха с требуемым делением растра. Такая система позволяет исключить ошибки
проецирующей системы (они одинаковы для штриха линейки и для растра). По описанной схеме построен ряд отсчетных оптических устройств для точных металлорежущих станков.
Рис. 14.4. Микрометрический винт со шкалами грубого 1 и точного 2 отсчетов перемещения столика микроскопа
Одной из доминирующих ошибок в угломерных приборах является ошибка от эксцентриситета круговых шкал, которая равна Дф == = е sin <р/7?, где е — эксцентриситет; R — радиус окружности делений; Ф угол поворота шкалы от начального положения. Для исключения . . этой ошибки применяется отсчет в двух диаметрально расположенных точках шкалы, причем берется средняя величина отсчета. Часто
v .621
используют оптические системы* в помощью которых можно сразу получать среднее значение из двух отсчетов (системы для совместного отсчитывания).
Рис. 14.6. Спиральная шкала с перемещающимся по спиральной нарезке индексом (вращается только шкала)
Рис. 14.5, Спиральная шкала с внутренней нарезкой (индекс неподвижен, шкала вращается и перемещается)
Способ совместного отсчета (рис. 14.12) состоит в том, что углы отсчитываются с одной стороны А лимба, совмещая оптическим путем ее изображение с изображением противоположной стороны В лимба и неподвижным индексом. Пря этом в поле зрения, например, отсчетного
Рис. 14,7. Винтовой окулярный микрометр МОВ-1-15 X:
1 — неподвижная сетка с делениями; 2 — подвижная сетка с биштрихом; 3 защитное стекло; 4 — разрезная конусная гайка
микроскопа получаются две касающиеся дуги (части лимба), которые при вращении лимба движутся в разные стороны. Отсчет складывается из двух частей — отсчета значения ближайшего к индексу младшего штриха А лимба и отсчета длины дуги: 4S = А В'/2.
Mllllllllllllllllllllll
m
:“:5яя®к
Рис. 14.8. Винтовой окулярный микрометр ОРИМ-1 с устройством для отсчета в поле зрения
Рис. 14.9. Окулярный микрометр универсального микроскопа со спиральной шкалой 1 и сеткой 2
Угломерное устройство
винто-
Рис. 14.10.
вето окулярного микрометра МОВУ-1-15Х;
1 — угломерная шкала; 2 — нониусы
Рис. 14.11. Механизм растровой сетки оптического отсчетного устройства координатно-расточного станка
полос на чет-полос. Благо-при движении свет попадает на фотоэле-
На рис. 14.13 показан фотоэлектр веский датчик для измерения перемещения с растровой системой. На перемещающейся части установлена линейка 2 с нанесенными на ней чередующимися прозрачными и непрозрачными штрихами равной ширины. За нею неподвижно расположена такая же линейна 3. Число полос на линейке-мо-жет быть 100 и более на 1 мм. Свет от источника 1 через линейки (решетки) 2 и 3 направляется на разделительную призму 4, которая верхнюю часть пучка направляет на фотоэлемент 5, а нижнюю — на фотоэлемент 6. У неподвижной линейки 3 верхняя часть полос, через которую идет свет на фотоэлемент 6, сдвинута по отношению к нижней части ‘
верть шага даря этому линейки 2 поочередно менты , импульсы от которых идут попеременно. Таким способом можно производить счет полос и определять величину перемещения, его скорость по частоте импульсов и направление по последовательности сигналов. Еще большую точность измерения перемещения можно получить, используя растр в виде так называемых муаровых полос (рис. 14.14). Точность отсчета повышается примерно пропорционально ctg р. Широкое применение микрометры двойного изображения. Метод двойного изображения повышает точность измерения и дает возможность быстрого и точного наведения на центр симметрии контура фигуры, отверстия. Показателем наведения на центр симметрии контура фигуры является полное совпадение или точное симметричное расположение контуров зеркально раздвоенных изображений фигуры. При 524
получили окулярные
А
А'
Рис. 14
.12. Схема совмест кого отсчета
Рис. 14.13. Схема фотоэлектрической растровой отсчетной системы
этом одно изображение зеркально повернуто, как показано на рис. 14.15.
Окулярный микрометр двойного изображения ОГУ-22 и ход лучей в нем см. [27, 33].
Рис. 14.14. Схема растра с муаровыми полосами:
1 и 2 — подвижные решетки; 3 — вид муаровых полос
Рис. 14.15. Вид поля зрения в ОГУ-22 при измерении расстояния между центрами отверстия
Применяемые материалы
В качестве материала для гравируемых шкал применяются металлы и пластмассы.
Латунь ЛС59-1. Деления получаются чистыми, обработка не вызывает затруднений. Требуется отделка для защиты от коррозии (хромирование, никелирование или окраска).
Дюралюминий твердый и отожженный. Твердый обрабатывается хорошо, деления получаются чистые; отожженный дает менее чистые деления. Применяется с отделкой (окраска, оксидирование, хромирование) и без отделки.
Нейзильбер. Рекомендуется для высокоточных угломерных шкал с наиболее тонкими делениями, наблюдаемыми через лупу или микроскоп. Отделка не требуется.
Нержавеющая сталь. Обрабатывается значительно хуже, чем ранее перечисленные материалы.
Серебро. Иногда применяется для особо точных угловых шкал с самыми тонкими делениями, наблюдаемыми через лупу или микроскоп.
Сталь конструкционная. Применяется главным образом для больт ших шкал, наблюдаемых невооруженным глазом. Чистота делении невысокая; требует защитной отделки.
Поверхность металлических шкал делают матовой во избежание появления вредных бликов.
Пластмассы. Применяются все виды твердых пластмасс. Для прозрачных гравированных шкал применяется главным образом органи-
ческое стекло. Деления на шкалах из пластмасс гравируют, или получают при прессовании, за исключением шкал из органического стекла. При прессовании деления, как правило, делаются выпуклыми. Углубленные деления получать прессованием трудно и большей частью невыгодно вследствие высокой стоимости пресс-форм. Деления на шкалах и индексы заполняют красками. Заполнение делений светящимися составами постоянного действия запрещено ввиду наличия гамма-излучения. Светящиеся составы временного действия (требующие зарядки на свету) применяются мало.
Точные фиксаторы
Фиксаторы служат для остановки и удержания движущихся дета* лей в определенном положении относительно неподвижных частей. Усилие, развиваемое фиксатором при остановке деталей, должно превышать усилие, необходимое для движения детали вне зоны действия фиксатора. Точные фиксаторы применяют в различных отсчетных устройствах для фиксации положений шкал, визирных призм или других измерительных элементов (например, точных винтов), а также-для фик-
Рнс. 14.16. Конструкция жесткого фиксатора:
f — дужка с пазами фиксации защелки; 2 — защелка; 3 — винт^ удерживающий защелку от выпадания; 4 — корпус; 5 — упор для пальца; 6 — кнопка
сации сменных оптических узлов (револьвера с микрообъективами* переключающихся призм, линз, сеток и т. п.).
Для точной фиксации требуется, чтобы фиксатор имел минимальный люфт или обеспечивалось полное отсутствие люфта. Фиксатор входит в фиксирующую лунку и своим усилием заставляет движущуюся деталь дойтн до требуемого фиксируемого положения.
В приборах применяются жесткие и упругие фиксаторы. Жесткие фиксаторы (запоры) устроены так, что для смещения фиксированной детали требуется предварительно вывести запирающую деталь из зацепления с фиксируемой деталью. Жесткие фиксаторы более надежно 526
работают в условиях ударов и вибраций. Однако жесткие фиксатора ие обеспечивают безлюфтовой фиксации. При применении жестких фиксаторов следует использовать конструкции, в которых отпиравие
У 2
Рис. 14.17. Схема действия сил в упругом фиксаторе: 1 ♦— пружина; 2 движущаяся деталь
Рис. 14.18. Точный пружинный фиксатор:
1 зуб фиксатора; 2 — пружина; 3 фиксируемая деталь
(вывод фиксирующей детали) производится
нажатием пальца, а ие вы-
таскиванием фиксатора. Пример такой рис. 14.16.
Практически безлюфтовая фиксация достигается в некоторых конструкциях упругих фиксаторов или с помощью зажимов. Надо иметь в виду, что даже при безлюфтовой фиксации некоторый угловой люфт вращающейся детали может оставаться за счет зазора в подшипнике.
В конструкциях с упругими фиксаторами деталь выводится из фиксированного положения при приложении усилия, большего, чем усилие, необхо
коиструкции показан на
Рис. 14.19. Точный пружинный фиксатор
димое для ее движения вне зоны действия фиксатора. Принцип действия упругого фиксатора показан иа рис. 14.17. Усилие, развиваемое фиксатором в напра* £лении движения детали 2 должно быть больше силы трения движения (или вращения) этой детали. Тогда фиксатор при входе в фиксирующую
лунку своим усилием заставит движущуюся деталь дойти до требуемого точно фиксированного положения. Чтобы это произошло, сила пружины 1 фиксатора Р должна быть больше силы трения фиксируемой детали в соотношении lP/R ctg а >• 1,3-ь1,5.
Во избежание постоянного трения и износа фиксатора и поверхности, по которой мог бы скользить фиксатор на фиксируемой детали, целесообразно, чтобы действие фиксатора начиналось только вблизи от места фиксации. Конструкции фиксаторов такого рода, дающих без-люфтовую фиксацию, показаны на рис. 14.18 н 14.19. Торцовые зубчатые фиксаторы на мембранных пружинах (см. рис. 14.2, б) обеспечивают достаточно точную фиксацию и хорошую устойчивость при ударах. Не-
Рис. 14.20. Зажим с предохранением от деформации фиксируемой детали:
1 — плоская пружина; 2 — зажимной винт; 3 — тормозные колодки
правильно для фиксации одной детали применять два одновременно работающих фиксатора, например пружины, так как фиксация будет нечеткой из-за неодновременной их работы.
Широко распространенные упругие шариковые фиксаторы [93] работают достаточно надежно и дают меньший износ фиксируемых деталей, но не могут быть выполнены безлюфтовыми вследствие неизбежного зазора между шариком и несущей его втулкой. Практически без люфта работают зажимы (тормоза). Однако при жестких конструкциях тормозов часто возникают смещения или деформации фиксируемых деталей. Поэтому следует фиксацию осуществлять через гибкую деталь (рис. 14.20). Конструкцию тормозов см. также в [92, 93].
Литература: [27, 28, 30, 31, 33, 56, 58, 61, 89, 92, 93].
ГЛАВА 15
ГЕРМЕТИЗАЦИЯ И ОСУШКА ПРИБОРОВ
ОБЩИЕ СВЕДЕНИЯ
Приборы, работающие на открытом воздухе в различных атмосферных условиях, должны быть защищены от попадания во внутренние полости пыли и влаги, а также от запотевания при низких температурах или при резких колебаниях температуры окружающего воздуха.
Как правило, такого рода приборы не имеют полной герметичности, так как обеспечение ее усложняет и удорожает конструкцию. Важно, "чтобы обмен находящегося во внутренних полостях воздуха с наружным был, по возможности, затруднен. Этот обмен помимо естественной диффузии усиливается вследствие изменения давления воздуха внутри йрибора при изменениях температуры окружающей среды. Скорость обмена воздуха зависит от степени герметичности, которая должна замедлить этот обмен настолько, чтобы установленные в приборах патроны осушки успевали поглощать влагу из воздуха, проникающего в прибор.
Процесс запотевания оптических деталей происходит следующим образом. Прн охлаждении прибора влага из воздуха, находящегося внутри прибора, в первую очередь конденсируется на металлических деталях, имеющих большую теплопроводность по сравнению с оптическими деталями, особенно на внутренних стенках корпусов, крышек и т. п. Если оптические детали успевают охладиться до тех пор, пока еще не вся влага конденсировалась, то часть ее может осесть на них.
. При нагреве охлажденного прибора металлические детали нагреваются быстрее, и осевшая на них влага, испаряясь, оседает на оптические детали, которые вследствие меньшей теплопроводности нагреваются медленнее. Поэтому в этот период наблюдается особенно интенсивное запотевание оптики, которое по мере прогревания оптических деталей исчезает. Такое явление иногда наблюдается при испытании приборов охлаждением, когда только что вынутый из камеры прибор вносят в помещение с нормальной температурой.
Герметичными приборами считают такие, у которых избыточное давление в 19 600 Па понижается на 50% не быстрее чем за 6 ч. Приборами средней герметичности считают такие, у которых указанное выше понижение давления происходит не менее чем за 10 мин.
Герметичность обеспечивается следующими мероприятиями.
1. Места соединений наружных оптических и механических деталей должны быть уплотнены эластичными прокладками или уплотнительными замазками. В качестве уплотнительных прокладок применяются: резина по ТУ 38-105376—72 или ТУ 38-105537—73, фторопласт |гли полихлорвинил. Перечень и характеристики уплотнительных замазок приводятся в гл. 23.
Основными деталями, определяющими герметичность приборов, являются корпуса и крышки. Поэтому особенно важно тщательно уплотнять места разъемов и соединений наружных деталей с корпусом (крышкой). Число разъемся должно быть минимальным.
2. Корпуса и другие наружные детали не должны иметь сквозных раковин и пор.
3. Все выходящие наружу подвижные детали должны иметь салы-никовые уплотнения. Следует применять посадки с малыми зазорами при достаточно длинных сопряжениях валов и втулок. Необходимо стремиться к тому, чтобы воздушные полости внутри прибора были по возможности меньшими.
КОНСТРУКЦИИ КОРПУСОВ ПРИБОРОВ, САЛЬНИКОВ, ПАТРОНОВ И КЛАПАНОВ ОСУШКИ
Корпуса предохраняют оптические системы, электрические устройства и механизмы приборов от повреждений и внешних воздействий. Конструкция закрытых корпусов должна быть удобной для монтажа и регулировки механизмов и электрических устройств, юстировки оптических систем, а также для ремонта прибора. Форма и внешнее оформление корпусов должны соответствовать требованиям технической эстетики. Технологически наиболее удобна конструкция корпуса, состоящая из основания (цоколя), иа котором монтируются узлы прибора, и съемного кожуха, закрывающего внутренние части прибора. Способ закрепления кожуха на основании, наряду с обеспечением требуемой плотности соединения, не должен вызывать деформации основания.
Рис. 15.1. Схемы компенсации н уплотнения корпусов:
1 — корпус; 2 — крышка; 3 — замазка или эластичная прокладка
Рнс. 15.2. Уплотнения между деталями:
1 — прокладка; 2 — замазка
Схемы компоновки корпусов показаны на рнс. 15.1, примеры уплотнений между деталями — на рис. 15.2.
Литые корпуса и крышки приборов, к которым предъявляются требования высокой герметичности, необходимо проверять на отсутствие сквозных раковнн н пор. Не рекомендуется делать сквозные резьбовые отверстия. Разъем корпуса с крышкой (кожухом) должен удовлетворять следующим требованиям:
1) число и расположение точек прижима (соединительных винтов) должно обеспечивать достаточное и равномерное прижатие крышки (кожуха) по всему периметру разъема;
2) соединительные винты должны располагаться снаружи относительно герметизирующей прокладки на небольшом расстоянии от иеё, 530
( , .„Количество точек прижима зависит от жесткости прижимаемой «тали в данном сечениц,. жесткости прокладки, требующейся степени герметизации н диаметра винтов. Конструкция откидных кожухов ТКрышек) на петлях менее надежна по Яоддетизацир/ так как не обеспечивает возможности равномерного прижима по периметру.
РАСЧЕТ ЭЛЕМЕНТОВ УПЛОТНЕНИЯ
Усилие сжатия крышки и корпуса Яри достаточной их жесткости, в соответствии со схемой (рнс. 15.3), вычисляется Йо формуле
г — т гп,
Где Pk = ncfyp/4— сила отрыва, зависящая от внутреннего давления; Рп == ₽= ftdfibzpn — сила сжатия прокладки, обеспечивающая требуемую герметичность; Ь2 — ширина прокладки в сжатом достоянии; рп ~ ph2'!р — необходимое ^снлие сжатия прокладки, пропорциональное выталкивающему усилию ph2 на единицу длины прокладки; /?2 — толщина Сжатой прокладки; р, = ph2ipn — коэффициент пропорциональности, представляющий собой отношение максимального
Рк
р
р
Рис. чету
15.3. Схема к рас-элементов уплотнения
усилия, приходящегося на единицу длины прокладки, противодействующего ее выталкиванию, К давлению прижима прокладки, создающего это усилие.
Приближенно р. определяется нз равенства силы трения и выталкивающей силы, приходящихся на единицу длины прокладки, т. е. ph2
Таблица 15.1, Допускаемые напряжения сжатия для резиновых прокладок
Характеристика и группа резины по ТУ 38-105376—72 Предел прочности при разрыве, 10» Па, не менее Условия работы
ВМ 40 Небольшие нагрузки
ВС 45 Средние нагрузки
Морозостойкая мягкая ММ 35 Небольшие нагрузки
Морозостойкая средней твердости МС 40 Средние нагрузки
Примечание. Допускаемое напряжение О в 5—8 раз меньше указанного предела прочности. Верхний предел — для корпусов при* боров, работающих в сложных условиях длительное время.
= FTp *= pnb22f, где /— коэффициент трения прокладки о корпус; л
отсюда рп~ — dnh%p. Окончательно
4Л2 "
Wn.
р-
Наибольшая допускаемая толщина Л2 сжатой прокладки в зависимости от допускаемого напряжения сжатия ее материала о, определяю-
щего допускаемое давление сжатия Рп, может быть найдена после замены Рп~(Рп) ~ = (о). Допускаемые напряжения для резины приведены в табл. 15.1.
Число винтов определяется из выражения
Рвп^Р<
зтс1{)
(Ов) п,
где Рв — усилие, приходящееся на одни винт; (ов)—предел прочности на разрыв материала винта; dQ — внутренний диаметр вннта.
Число винтов необходимо выбирать возможно большим, а их диаметр — меньшим, чтобы уменьшить усилие Рв и получить допускаемый для данного фланца корпуса и крышки изгибающий момент и стрелу прогиба на участках между винтами. Жесткость фланца и крышки должна быть достаточной. В случае необхо-
димости ее увеличения следует пред-Рнс. 15.4. Типы фетровых усматривать вдоль фланца ребро же-с аль ников сткостн.
Конструкцию крепления и размеры деталей для прижима защитных стекол определяют исходя из допустимых деформаций стекла. Допускаемую деформацию для защитных стекол оптических систем рассчитывают с учетом обеспечения сохранения качества изображения и прочности стекла. Прочность силикатного стекла на изгиб составляет (84-16) 107 Па.
На рис. 15.4 приведены конструкции сальников обычного типа. Эти
конструкции просты и широко применяются для малоответственных случаев. Сальники обеспечивают герметизацию прн избыточном давлении 20- Ю3—40* 103 Па. Их конструкции имеют следующие недостатки:
1) для получения хорошей герметичности соединения необходимо сильно поджимать уплотнительное кольцо, что приводит к возрастанию момента трения на валике;
2) сальниковое кольцо, изготовляемое из фетра или из войлокаf быстро деформируется или изнашивается, ухудшая герметичность соединения.
Этот недостаток мало ощущается, если диаметры валиков не превышают 15 мм, но становится существенным при больших диаметрах. Поэтому в некоторых случаях целесообразно применять так называемые мембранные сальники (рис. 15.5), которые практически не изнашиваются
и сохраняют постоянным момент трення. Уплотнение с одной мембраной (рис. 15.5,а) обеспечивает герметичность в пределах (20 -ь 30) 103 Па.
Материал, применяемый для мембран: бронза
БрКМЦ-3-5, ГОСТ 4748—70, толщиной 0,1—0,3 мм; лента стальная пружинная, ГОСТ 21996—76, толщиной
Рис. 15.5. Мембранные сальники
0,1—0,3 мм. Рекомендуется мембраны притирать и ставить на смазку. Прогиб мембраны должен быть таким, чтобы обеспечивалось плотное прилегание по кольцевой поверхности. Мембранные сальники можно выполнять и с несколькими мембранами (рнс. 15.5, б). В этом
Рис, 15.6. Передача вращения в герметичный корпус:
1 — резиновый колпачок; 2 — коленчато-изогнутый валик; 3 — металлический колпачок; 4 — металлический колпачок; 5 — валнк с пазом на фланце
случае их изготавливают нз ленты толщиной 0,08—0,1 мм. На рнс. 15.6 показан полностью герметизированный ввод враща* ющегося валика в корпус.
Для постоянного поглощения водяных паров с целью избежания конденсации влаги или образования инея на поверхностях оптических деталей применяют патроны осушки. Типы, исполнения, габаритные ^размеры и краткое описание патронов осушки, применяемых в оптических приборах, приведены в табл. 15.2. Вместимость внутренней полости ^патрона, предназначенной для помещения адсорбента (силикагеля), Iследует выбирать нз табл. 15.3, Выбор вместимости патрона осушки в
Т а б л и ц а 15.2. Характеристика патронов осушки
Исполнение
Эскиз
Краткое описание конструкций;
Патроны осушки с резьбовым креплением (типа ПОР)
В кор пусе, закрыв аемом резьбовой крышкой со смотровым стеклом, помещается силикагель. Дном корпуса патрона служит пористое стекло. Крепление к прибору осуществляется с помощью наружной резьбы
II
В корпусе патрона помещается капсула с силикагелем. Капсула закрыта крышкой со смотровым стеклом и через уплотнительную резиновую прокладку при помощи резьбы на крышке соединяется с корпусом. Дном корпуса служит пористое стекло, Патрон крепится к прибору с помощью резьбы на нижней части кожуха
III
Помещенный в корпусе стакан с силикагелем закрыт резьбовой крышкой со смотровым стеклом. Между крышкой и стаканом помещается уплотнительная резиновая прокладка, а между стаканом и дном корпуса — пружина. Дном корпуса служит пористое стекло, Крепление патрона к прибору осуществляется при помощи резьбы на корпусе
8g « а о ф
Эскиз
Краткое описание конструкции
IV
В корпусе помещена капсула, в которой находится бумажный стакан с шелковым мешочком, наполненным силикагелем. Капсула через уплотнительную прокладку закрывается крышкой со смотровым стеклом. В корпусе имеется подпружиненная втулка. При смене капсулы в патроне втулка под действием пружины поднимается до упор а и перекрывает отверстия корпуса, соединяющие полость патрона с полостью прибора, исключая поступление наружного воздуха в прибор. На корпусе патрона имеется наружная резьба, с помощью которой он крепится к прибору
Патроны осушки с фланцевым креплением (типа ПОФ)
Конструкция патрона аналогична исполнению IV ПОР. Крепление патрона осуществляется четырьмя винтами
Краткое описание конструкции
В корпусе, закрываемом через уплотнительную прокладку крышкой со смотровым стеклом, помещен стакан, разделенный металлической сеткой на две секции. В верхней секции находится силикагель-индикатор, в нижней — технический силикагель. Дно корпуса и стакана выполнено из металлических решеток, шелка и конденсаторной бумаги. Патрон крепится к прибору шестью винтами
В кор пусе помещен стакан с силикагелем. Корпус через уплотнительную прокладку закрывается резьбовой крышкой. В верхней части стакана имеется смотровое стекло. Дно корпуса и стакана выполнено из решеток, прокладок из шелка и конденсаторной бумаги. Крепление патрона к прибору осуществляется шестью винтами
зависимости от характеристики герметичности прибора производят следующим образом: для герметичного прибора вместимость патрона осушки должна составлять 0,75 см3 иа 1 дм3 внутренней полости; для прибора средней герметичности — в два раза больше.
В качестве адсорбента применяют силикагель (см. гл. 23). Для патронов, у которых внутренняя полость для помещения адсорбента представляет одну секцию, используют силикагель-индикатор. Для патронов, состоящих из двух секций, — силикагель-индикатор и обычный технический силикагель,
Таблица 15.3. Основные данные патронов осушки
Тип и исполнение Вместимость патрона, см8 Габаритные и присоединительные размеры, мм
d D н h ^2
Предельные отклонения
6g ±0.16
ПОР-1 1,0 М18Х0.75 - - - 15,5 23,0 15,2 10,7 6,7 1 ' —
ПОР-1 1,5 М18Х0.75 15,5 23 19,7 15,2 10,7
ПОР-П 1,5 М20Х 0,75 — 27 26,0 12,0 '
ПОР-1 2,5 М18Х0,75 15,5 23 28,6 24,1 19,6 —
ПОР-П 2,5 М20Х 0,75 — 27 34,8 12,0
ПОР-Ш 2,5 М20Х 0,75 25 27,0 17,0 8,5
ПОР-1 4,0 М20Х0.75 17,5 25 32,1 27,6 23,1 1 1
ПОР-П 4,0 МЗОХ 0,75 —— 37 23,3 12,0 ' 1 — —
ПОР-Ш 4,0 М20Х0.75 — — 25 39,9 29,9 15,0 —
ПОР-1 6,0 М20Х 0,75 —— 17,5 25 44,9 40,4 35,9 — 1 1
ПОР-1 6,0 МЗОХ 0,75 27,5 35 17,5 13,0 8,5 — 1
ПОР-П 6,0 МЗОХ 0,75 1 1 37 28,6 12,0
ПОР-Ш 6,0 М20Х 0,75 1 1 25 52,4 42,4 21,0 —
ПОР-Ш 6,0 • МЗОХ 0,75 — — — 36 25,0 15,0 8,0 —
ПОР-1 10,0 МЗОХ 0,75 27,5 35 28,6 24,1 19,6 —“
ПОР-1 10,0 М36Х1 34,0 44 24,9 19,4 24,9 —
ПОР-П 10,0 МЗОХ 0,75 37 39,0 12,0 —
ПОР-П 10,0 М36Х1 — — ' 43 29,0 12,0 — 11
со Продолжение табй.
Тип и исполнение Вместимость патрона, сма Габаритные и присоединительные размеры, мм
d D н h di Z>1
Предельные отклонения
6g ±0.16
ПОР-Ш 10,0 МЗОХ 0,75 36 35,0 25,0 13,0
ПОР-Ш 10,0 М36Х1 — — 41 27,2 17,2 9,0
ПОР-1 20,0 М36Х 1 — — 34,0 44 35,0 29,5 25,0
ПОР-1 20,0 М42Х1 — — 40,0 50 30,7 25,2 20,7 —II
ПОР-П 20,0 М36Х1 — — 43 45,2 12,0 II 1 II 1
ПОР-П 20,0 М42Х1 1 49 34,8 12,0
ПОР-Ш 20,0 М36Х1 — — 41 40,2 30,2 15,0
ПОР-Ш 20,0 М42Х1 — — — — 47 32,6 22,6 12,0 VMM
ПОР-Ш 30,0 М42Х1 — 47 41,9 31,9 16,0 wns чии ф
ПОР-IV 30,0 М39Х1 — — 48 67,1 47,0 35,0
ПОФ-1 30,0 — 54 ±0,28 37,0 44 63,6 45,3 4,8 64
ПОФ-П 50,0 — — 66 47,0 66 58,0 35,0 3,5 74
ПОФ-П 80,0 — — 84 55,0 76 57,0 33,5 5,5 94
ПОФ-Ш 80,0 — 84 56,0 78 57,0 34,0 Vtw 5,5 94
ПОФ-П 200,0 — — 104 73,4 100 87,0 56,0 6,5 118
ПОФ-Ш 200,0 104 73,4 100 80,0 56,0 — — 6,5 118
Приме чание. Допуск ±0,16 относится к размерам 66; 84 и 104.
12(С9)
Рис. 15.7, Высту* лающий клапан осушки
H>38h14(B7)
Наличие патронов не полностью обеспечивает осушку приборов в условиях повышенной влажности. В таких случаях приборы периодически просушивают сухим воздухом с помощью осушительных май!ин. Для соединения оптико-механических приборов со штуцером шланга осушительных машин, отбирающих влагу из нагнетаемого в прибор воздуха служат клапаны осушки. В зависимости от расположения на приборе клапаны осушки бывают выступающими и утопленными. *
Присоединительные размеры выступающего клапана должны соответствовать указанным на рис. 15.7, а утопленного — на рис. 15.8.
Запирающее устройство клапана должно обеспечивать соблюдение герметичности при пневматическом давлении на клапан 0,2 МПа. При отжатии втулки клапана до предела воздух должен свободно проходить через клапан в прибор и из него. При этом площадь сечения открывающихся отверстий должна быть не менее 0,1 см2. С прекращением отжима втулки клапан должен под воздействием пружины или другого устройства возвращаться на свое место, надежно запирая проход воздуха.
Литература; [89, 92 ].
ГЛАВА 16
ПОКРЫТИЯ ОПТИЧЕСКИХ ДЕТАЛЕЙ
ВИДЫ ПОКРЫТИЙ
Оптические детали изготовляются в двух вариантах: Bx- — в обычном исполнении, В2 — в тропическом исполнении в соответствии с руководящими техническими условиями. Последние устанавливают рекомендации по защите оптических деталей от действия влаги, воздуха и биологического обрастания (плесени) в условиях влажного тропического климата, а также по нанесению интерференционных просветляющих, светоделительных и зеркальных покрытий и по склеиванию этих деталей.
Покрытия могут быть однослойными и многослойными. Условные обозначения видов покрытий строятся по следующей схеме:
1) сокращенное обозначение покрытия (табл. 16.1);
2) обозначение исходного материала для обозначения первого слоя покрытия (табл. 16.2).
3) обозначение способа нанесения первого слоя покрытия (табл. 16.3);
4) то же (пп. 2 и 3) для второго и последующих слоев покрытия.
Если на оптическую деталь требуется нанести последовательно несколько покрытий, то обозначение покрытия складывается из условных обозначений всех наносимых на деталь видов покрытий в последовательности их нанесения слева направо.
Многослойные покрытия, состоящие из чередующихся слоев, можно обозначить сокращенно по следующим формулам:
а) для четного числа слоев: (ab)*n/2 (а и b — чередующиеся слои; п — число слоев);
б) для нечетного числа слоев: (ab) (п—1)/2-а.
К условному обозначению покрытий добавляют еще цифру, показывающую температуру предварительного прогрева детали, на которую наносится покрытие, или последующей термообработки слоев покрытия, если температура прогрева 300—350° С.
Температуру прогрева деталей следует изображать следующим образом:
а) в виде индекса у буквы, если покрытие износится на нагретую деталь, например: Просветл. 24И300;
б) в виде цифры перед буквой (перед сокращенным наименованием покрытия) с точкой между ними, если покрытие наносится на предварительно прогретую деталь после ее охлаждения, например: Просветл. 300.44Р.43Р;
в) в виде цифры после буквы (после условного обозначения покрытия) с точкой между ними, при последующей термообработке слоев покрытия, например: Просветл. 45Р.44Р.43Р.300.
Вид покрытия Сокращенное обозначение Условное обозначение р
Отражающие непрозрачные покрытия (зеркала): внешнее заднее Светоделительные покрытия Просветляющие покрытия Покрытия-фильтры Защитные прозрачные покрытия Токопроводящие покрытия (обогревающие и др.) Поляризующие покрытия Зеркальн. Зеркальн. Светоделит. Просветл. Фильтр Защити. Токопров. или обогрев. Пол я риз.
Таблица 16.2, Условные обозначения исходных материалов, применяемых для покрытий
Материал Условное обозначение Материал Условное обозначение
Алюминий 1 Кремний 12
Золото 2 Ниобий 13
Медь 3 Тантал 14
Никель 4 Титан 15
Палладий 5 Аммон и й фосфор но- 21
Платина 6 кислый
Родий 7 Хромат и бнхромат ка- 22
Серебро 8 ЛИЯ
Хром 9 Кр иол ИТ 23
Серебро с медью 10 Магний фтористый 24
(сплав) Серебро азотнокислое 25
Кадмий 11 Олово двухлористое 26
Материал Условное обозначение Материал Условное обозначение
Сурьма трехсернистая 27 Эфир этиловый диза- 46
Олово двухлорнстое н 28 мещенный ортоцирко-
висмут треххлорнстый Цинк сернистый 29 ниевой кислоты (сокращенно днзамещенный
Торнй азотнокислый 30 циркониевый эфир)
нлн хлористый Эфир этиловый орто- 47
Кремния одноокись из 31 титановой кислоты с эпо-
окиси кремния и двуоки- си кремния Окись цинка 32 ксидной диаиовой смолой Кислота азотная 61
В ол ьфр ам шестихло- 34 Кислота соляная 62
ристый Кислота уксусная 63
Цирконий четырех- 35 Днметнлдихлорсилан 66
хлористый Хромовый ангидрид с 38 или другие силиконовые жидкости
фосфор ной кисл ото й н Метокснэтил мер ку р а- 69
кремнефтористым натрием цетат Виннлтрихлорсилан и 70
Эфир этиловый фтори- 43 уксуснокислая ртуть
стокремииевой кисло- Лак бакелитовый с на- 72
ты (кремниевый эфир) Эфир этиловый орто- 44 полннтелем (алюминиевая пыль, слюда и
титановой кислоты (титановый эфир) Эфиры этиловые фто- 45 др.). Лак винилитовый бесцветный 73
рнстокремниевой и ор- Лак бутиральнобаке- 75
тотнтановой кислоты (смесь) литовый с наполнителем Парафин 84
Таблица 16.3. Условные обозначения способов нанесения отдельных слоев покрытия
Способ нанесения Условное обозначение Способ нанесения Условное обозначение
Из раствора Испарение в вакууме Травление Электролиз Из газовой фазы Катодное распыление Р И т F К Нанесение расплава Нанесение кистью, пульверизатором или центрифугированием Испарение с помощью электронного нагрева 1 н п ИЭ
Обозначения: В — Вода; ВА — влажная атмосфера; СВ — сухой воздух; МВ — морская вода; ЗПТ запотевание; КС — кислая среда; ЩС — щелочная среда; КР — кислый раствор; ЩР — щелочной раствор; ОР — органические растворители; Г — газы; ЦВ — царская водка; БВ — бромная вода
Обозначение и вид покрытия Оптические характеристики Устойчивость к воздействию Механическая прочность (группа) Термическая прочность (рабочая и максимальная t, °C) Область применения
Непрозрач Зеркальн. 1И Алюминирование ные покрытия н а р у ж Рд ~ 88%; для Л = 250-ь -ь-400 нм р 80% ных з е р к а. СВ, разрушается в ВА, при ЗПТ и в ЩС ч с в н III е Ш Н И М О ± 60 +200 тражением Лучшее покрытие для защищенных от пыли зеркал, работающих в УФ области
Зеркальн. 9И.1И Алюминирование с подслоем хрома рл = 85%; рассеяние при толщине слоя до 0,8 мкм 0,2% , при толщине слоя до 3 мкм 2-3% ВА (низкая влажность), разрушается при ЗПТ и в ЩР Дифракционные решетки
Зеркальн. 1И.29И Алюминирование с защитой сернистым цинком РД= 85-5-87% ВА, ЗПТ II ±60 +200 Зеркала лабораторных приборов и защищенные зеркала полевых приборов
Зеркальн. 1И.21Е Алюминирование с защитой оксидированием в фосфорно-ё аммонии > рд не менее 86% В ультрафиолетовой области около 80% ВА I ± 60 +300-5-+400
Панов и др.
КНСТг+Л Г' Г .Зеркальн. 1И.21Е.29И Алюминирование внешнее с оксидированием фосфор но-кислым аммонием и сернистым цинком рд = 93-5-96% ВА, ЗПТ II ±60 +300
Зеркальн. 1И.21Е.29И Максимум отражения в области спектра л — 1 мкм достигает 96% Для инфракрасной области спектра (X = 1 мкм)
Зеркальн. 1И.31И Алюминирование с защитой одноокисью кремния РД= 85-ь 88% В ультрафиолетовой области резко падает I Зеркала лабораторных приборов и защищенные зеркала в полевых приборах, предназначенных для влажного тропического климата
Зеркальн. 1И.21Е.44Р Алюминирование с защитой фосфорнокислым аммонием н титановым эфиром В видимой области рд = = 92-5-94%
Зеркальн. 1И.38Р Алюминирование с защитой оксидированием в сложном растворе РД = 86-5- 87% II ±60 +200 То же, что и в предыдущем случае, но для тропического климата
Обозначение и вид покрытия Оптические характеристики Устойчивость к воздействию Механическая прочность (группа) Термическая прочность (рабочая и максимальная /, °C) Область применения
Зеркальн. 1И.24И.29И Алюминирование с нанесением фтористого магния и сернистого цинка рд = 90-5-95% для белого света Неустойчиво к ЗПТ и в ЩС III ± 60 Внутренние зеркала (когда требуется возможно больший рд)
Зеркальн. 4И.7Е Родий с подслоем никеля рл = 75-=-78% для белого света В области длин волн 300— 400 нм р = 70-н75%, при X — ™ 250 нм ВА, В, МВ, КС, ЩС 0 —180+4-300 Рефлекторы с наружным отражением для ламп с угольными дугами; зеркала любых приборов
Зеркальн. 9И.7И.7Е Родий с хроморо- диевым подслоем То же, что и в предыдущем случае; зеркала, соприкасающиеся с морской водой
Зеркальн. 4И.5Е Палладий с подслоем никеля рл = 65-*-68% (для X == — 550-5-700 нм) ВА, В, КС, ЩС, ОР I Рефлекторы с внешним отр ажени-ем в кинопроекторах, прожекторах и пр.
Непрозрачныеиокрытия зеркал с задним отражением
1 Зеркальн. 1 25Р.ЗЕ.72П или 25Р.ЗЕ.75П Серебрение с защитой медью и лаком " Рд== 88*92%; дляХ = 250+ +350 им р= 10+15% ВА при слабой концентрации паров кислот 0 ±60 4-200 Лучшее покрытие Для деталей с задним отражением
Зеркальн. 1И.72П Алюминирование заднее с защитой лаком Рл — во-*- 84% ВА, В, МВ, F + 60 300 Зеркала, работающие при высоких темпер ату р а х (дуговые лампы)
Светодел! Светоделит. 25Р Серебрение цельные покрытия (г Рл : т — любое Потери А на поглощение и рассеяние для заклеенных покрытий: ЮЛ у П Р озр £ Быстро тускнеет Требуется заклейка стеклом i ч н ы е IV зеркала ±60 Н~юо и призмы) Лучшее покрытие для светоделительных зеркал больших размеров (до 1x1м)
Рл : Т |б : 1 2 : I 1 : 1 1 : 2
А, % 12 19 31 37
Светоделит. 8И Серебрение рл : т — любое. Для заклеенных покрытий Зеркала и призмы
Рл 4 : 1 3 : 1 2 : 1 1 : 3 [1:2
А, % 15 15 16 25 27
Светоделит. 1И Алюминирование Рл : т — любое. Для заклеенных покрытий ±60
Рл : т 5 : 1 3 :1 1 : 1 1 : 2 _1 : 5
А, % 28 30 35 35,5 36,5
Светоделит. 10И 50% сплава серебра с медью Ра : т — любое; А — 15+ + 20% III ±60 4-150
Обозначение и вид покрытия Оптические характеристики Устойчивость к воздействию Механическая прочность (группа) Термическая прочность (рабочая и максимальная /, °C) Область применения
Светоделит. 1И.21Е Алюминирование с защитным анодным оксидированием В проходящем свете голубая окраска ВА II 4-300 Зеркала и призмы (в лабораторных приборах можно без заклейки стеклом)
Светоделит. 9И Хромирование рл:т—любое; потери на поглощение для незаклеенных по-крытий|30—40%; в проходящем свете слегка желтая окраска ВА, КС, ЩС, ОР 0 4-зоо —180 Незаклеенные зеркала для самых жестких условий*
Светоделит. 13И Распыление ниобия рл : т = 1 : 3 А не более 1% ВА, КР, ОР 0 4-200 —60 Наружные незаклеенные зеркала с р до 30%; размер не более 60 мм
Светоделит. 15И Ртах ~ 40-5-50%; потери на поглощение и рассеяние отсутствуют ВА, ЗПТ, КР, ЩР, ОР 0 4-400; нижний предел не ограничен Для самых жестки х условий
Светоделит. 29И Покрытие нз сернистого цинка р : т не более 1 : 2 для незаклеенных и 1 : 5 для заклеенных покрытий; для заклеенных покрытий р == 15%, для незаклеенных р == 30-^33%; вызывает поляризацию света ВА, ЗПТ II 4-200 —180 Наружные незаклеенные зеркала в лабораторных приборах. Заклеенные зеркала в любых приборах
Светоделит. 29И.24И.29И Для незаклеенного покрытия рд = ЗО-т-60%; для заклеенного р/ = 15-5-30%. А и А] соответственно равны 1—2% и 12—15%. Сильная поляризация при наклонном падении лучей Только СВ III Определяется для заклеенных покрытий термопрочностью клея Защищенные от .запотевания детали в лабораторных приборах. Заклеенные детали в любых приборах
Светоделит. [(29И.24И)Х2].29И Покрытие из сернистого цинка и фтористого магния
То же, что и в предыдущем случае, разделение пучка белого цвета на пучки разных цветов
Светоделит. 45Р.44Р.43Р.44Р Р/ = 48н-50%, достаточно равномерный по всей видимой области. Потери практически отсутствуют В, сероводорода, слабых КР и ОР, мало устойчиво к щелочам I 4-350-^-4-400 устойчиво ниже 0 Незаклеенные детали внутри приборов Пластины и призмы
Светоделит. 44Р.43Р.44Р.43Р РЛ — 43-5-47%. Потери от-сут ствуют 0 Незаклеенные детали, применяемые снаружи
Светоделит. [(44Р.43Р)Х 2J.44P р/ = 64-5-67%. Потери практически отсутствуют I Незаклеенные внутренние детали несложной формы
Светоделит. [(44Р.43Р)ХЗ)].44Р РЛ = 75-ь 80%
Светоделит. 28Г.43Р.28Г Рл до 45% для всех стекол. Потери отсутствуют ВА, В, МВ, КР, ОР 0 4"400 и ниже 0 Дл я с амых жестких условий; пластины и призмы любой формы
Обозначение и вид покрытия Оптические характеристики Устойчивость к воздействию Механическая прочность (группа) Термическая прочность (рабочая и максимальная t. ФС) Область применения
Просветляющие покрытия
Просветл. 24И300 Фтористый магний, испарением рл зависит от пе 1 ВА, без конденсации капель, так как слой разрушается п +350 —50 Внутренние поверхности фотообъективов, детали лабораторных и герметизированных полевых приборов
пе До 1,5 1,55- 1,6 1,6— 1,65— Св. 1,65 1,7 1,7
РЛ. 1.6 % 1.4 1,0 0.9 0,6
Просветл. 23И Нанесение криолита испарением Во влажной атмосфере устойчивость снижается III +200 —50 Объективы а любительских фотоаппаратов и детали лабораторных приборов
Пе До 1,55 1,55— 1,6 Св. 1,6
рл, % 0,7 0,5 0,4
Просветл. 13К.12К Ниобий и кремний рд — 0,6% для К8 Минимум отражения при толщине пленки Х/2 составляет 0,04% ВА, В, КР (кроме плавиковой кислоты), ЩР, ОР I ±60 Плоские поверхности деталей размером до 80 мм в любых приборах
Просветл. 13К Катодное распыление ниобия в кислороде Светопропускание германия и кремния в инфракрасной области увеличивается до 96— 98% Неустойчиво к В А при температуре 4-50*С I 4-200 —60 Детали из германия и кремния для инфракрасной области; форма любая, размеры до 60 мм
Просветл. 14 К Катодное распыление тантала в кислороде
• 1
Просветл. 29И800 Нанесение сернистого цинка испарением Светопропускание германия в инфракрасной области увеличивается до 96—98% Неустойчиво к ВА при повышенной температуре II Детали из германия; форма любая; размеры до 200 мм
Просветл. 63Т Травление уксусной кислотой рЛ в зависимости от пе В ПК и ЩР неустойчиво при повышенной температуре 0 ±60 4-120 • Просветление деталей больших размеров или сложной формы из силикатных стекол
пе 1,5- 1,52 1,53— 1,55 1,56— 1,60
Рд.% 3—2,7 2,7- 2,3 2,2—2
л* 1,61 — 1,64 1,65— 1,7 1,62— 1,75
Ра % 2—1,7 1,7- 1,4 1,3- 1,1
Просветл. 43Р или '350.43Р.350 с прогре-- вом Покрытие из спиртового раствора - кремниевого эфира 1 КР и соли I 4-60 Наружные поверхности деталей, работающих в любых условиях, и внутренние детали из стекла с Пе более 1,7
Пе 1,5- 1,52 1,53— 1,55 1,56— 1,6
Ра % 3,1-2,7 2,7- 2,3 2,2—2
пе 1,61 — 1,64 1,65— 1,7 1,7-1,75
рд, % 1,9- 1,8 1,6- 1,4 1,2-1
Обозначение и вид покрытия Оптические характеристики Устойчивость к воздействию Механическая прочность (группа) Термическая прочность (рабочая н максимальная tt °C) Область применения
Просветл. 44Р.43Р или 350.44Р.43Р.350 с прогревом Оптическая толщина: 1-го слоя 0,11Z 2-го слоя 0.31Z р в зависимости 'от X ВА, В, КР (кроме плавиковой кислоты), ЩР (слабых), ОР I и 0 Поверхности деталей, расположенных внутри приборов, работающих в области длин волн от 400 нм до 2,0 мкм с
X, нм Интегральный р,%
450± 10 520± 10 560± 10 640± 10 800± 10 2,1±0,2 1,2±0,1 1,0±0,1 2,8±0,3 10,8±0,7
Просветл. 45Р.43Р Оптическая толщина: 1-го слоя Z/2 2-го слоя Х/4 Для белого света при пе~ = 1,52—1,6 составляет 1,8— 2,1%, уменьшает отражение в области 400 нм до 1% I ±60 То же, что и в предыдущем случае для области от 400 до 1000 нм
Просветл. 47Р.43Р Для средней видимой области спектра (X = 520 нм) для белого света составляет 1,1— 1,3% II Детали из органического стекла; призмы и пластины несложной формы
Просветл. J5P.44P.43P.35O или 350.45Р.44Р.43Р.350 рл для всех стекол равно 0,5—0,8%. Равномерное пропускание в широкой области спектра ВА, ЗПТ, КР (слабых), ОР г i —— Детали, расположенные внутри, при требовании большого светопропускания
Просветл. 34Р Для просветления германия и кремния в ПК области При толщине 2 мкм прозрачно в области до X = 9,5 мкм Светопропускание германия и кремния увеличивается максимально до 95% ВА 0 для кремния; I—II ДЛЯ германия ±60 +750 Просветление оптических деталей из германия и кремния размером до 140 мм
Просветл. 44Р Для кремния и германия в ПК области (до 1,8 мкм) При толщине 2 мкм покрытие прозрачно до X = 10,5 мкм; т германия и кремния увеличивается максимально до 98% ВА, В +800 +1000
Защити. 63Т Травление уксусной кислотой Защитные пр Коэффициент отражения стекол группы П по налето-опасности снижается на 0,2— 0,5% озрачные г ВА, КС (слабых), МВ, ОР I о к р ы 0 т Я Я ±60 Для умеренного климата и перевода стекла из группы П по налетоопасности в группу А
Защити. 63Т.85Н Травление уксусной кислотой с последующим п ар афи н и-рованием Коэффициент отражения налетоопасных стекол (группы В) снижается на 0,2—0,5% Коэффициент отражения стекол (группы и 4 и 5) снижается до 0,5—2% ±60 +250 Для перевода стекла из группы В в группу А, а стекла групп 4 и 5 в смежную высшую группу. Для фосфатных стекол непригодно
Защити. 1К Катодное распыление алюминия в кислороде Коэффициент отражения и светопоглощения без изменения В А, КС (слабых), МВ, ОР I ±60 Защита бесцветного стекла всех марок от разрушения вл аго й атмосфер ы в умеренном климате
Обозначение и вид покрытия Оптические характеристики Устойчивость к воздействию • Механическая прочность (группа) Термическая прочность (рабочая и максимальная Л °C) Область применения
Защити. 12К Катодное распыление кремния Коэффициент отражения и с вето пог лощения без изменения ВА, КС (слабых), МВ, ОР I ±60 Защита деталей из стекол группы В, а также цветных стекол марок УФС1 и др. от гигроскопического налета
Защити. 66F Обработка в парах Диметилхлорсилана Коэффициент отражения и цвет просветляющей пленки без изменения ВА, ОР, ТВ I ±60 +75 Защита просветленных деталей от разрушения* влагой атмосферы
Защити. 69Р Обработка в растворе метаксиэтил-меркурацетата Защити. 70Р Обработка в растворе винти л трихлорсилана и уксуснокислой ртути ВА, ОР; неустойчиво к ЩР Защита от биологических обрастаний в условиях тропического климата (на детали, подвергаемые кислотнопарафи новой защите, перед покрытием нанести пленку окиси кремния)
Фильтр 6К Катодное распы-ние платины Покрытия- Равномериое пропускание по спектру. Плотность любая в зависимости от толщины слоя -фильтры Химически исключительно устойчиво, но для сохранения постоянства оп- тической плотности D требуется заклейка IV Нагрев до 200° С Измерительные нейтральные (серые) фильтры с равномерной или переменной плотностью разме- ром до 100 см’ ч
Фильтр 5И Паладий, испарением Равномерная оптическая плотность D& по спектру. Средняя D любая в зависимости от толщины покрытия АВ, ПВ, МВ КР и ЩР Для сохранении постоянен! а D требуется заклейка IV Нагрев до 200°С Измерительные нейтральные фильтры с равномерной или переменной плотностью размером до 100 см2
Фильтр 4И Никель, испарением I Нагрев до 300° С
Фильтр 8И.24И.8И Выделяет узкие участки в видимой и инфракрасной областях Требует заклейки IV Стойкость к нагреву определяется клеем Монохроматические интерференционные фильтры с углом поля зрении до 5°
Токопров. ЗЗГ (обработка в парах смеси, состоящей из двухлористого олова и фтористого аммония) Токопровод Прозрачно для к от 0,4 до 4,5 мкм; р для X — 1-^4,5 мкм до 10%. Просветление раствором кремниевого эфира снижает р до 2—4% я щ и е п о к р Устойчиво к ВА, КР, ОР ы т и я 0 Нагрев до 300—350° С Детали из стекла, кварца, корунда и фтористого лития. Удельная проводимость 10е См/м Удельное поверхностное сопротивление 10—40 Ом-м
Токопров. 9И Нанесение хрома испарением Непрозрачное покрытие В, ЗПТ, ОР, КР (слабых) 0 +200 и менее 0 Для предохранения от запотевания и обледенения. Линзы диаметром до 60 мм. Пластины 100Х 100 мм
Примечание, нием) см. гл. 4. Токопроводящее покрытие 26Г (обработка в парах двухлористого олова с последующим просветле-
ОСНОВНЫЕ ХАРАКТЕРИСТИКИ И ВЫБОР ПОКРЫТИЙ
При выборе покрытий необходимо исходить нз технических требований к данной детали, условий эксплуатации прибора, температурного режима, расположения детали в приборе, условий чистки деталей н их формы.
Рис. 16.1. Спектральное отражение от поверхности стекла после трехслойного просветления в области: а — видимой части спектра;
б — к — 5004-900 нм
Уменьшения интенсивности отраженного света в широком интервале длин волн можно достигнуть с помощью трехслойного просветления. Ахроматичность трехслойного просветления (45Р.44Р.43Р) иллюстрируется спектральной кривой коэффициента отражения, приведен-
Рис. 16.2. Спектральное светопропускание стекла после трехслойного просветления для
Х = 1,94-2,1 мкм
иой на рис. 16.1, а для пленки толщиной 400—450 нм, нанесенной на поверхность стекла К 8 и рассчитанной иа среднюю видимую часть спектра (X — 5404-550 нм). Вследствие равномерности отражения в различных участках видимой области спектра такое покрытие не вызывает появление окраски поля зрения прибора в проходящем свете при наличии большого числа поверхностей. Практически можно получить трехслойное просветление, дающее низкие значения коэффициента отражения в ши-556
роком интервале длин волн любой области спектра [46]. В качестве примера на рнс. 16.1, б дано спектральное отражение от поверхности стекла после трехслойного просветления в области длин волн 500—950 им. Как видно нз рис. 16.1, б, отражение на краях области ие превышает 2%, вблизи границ X = 350 нм и X — 800 нм отражение практически равно нулю. На рис. 16.2 приведены кривые коэффициента пропускания для шести поверхностей стекла К8 до н после просветления в области длин волн 0,9—2,1 мкм.
Основные характеристики покрытий: оптические свойства; химическая устойчивость; коррозионная устойчивость; механическая и термическая прочность. Оптические свойства покрытий характеризуются данными табл. 16.4.
Для всех видов зеркальных покрытий дается коэффициент отражения рл для источника света цвета А (цветовая температура 2854 К) при угле падения луча 15°; а для некоторых покрытий — коэффициент отражения по спектру.
Для светоделительных покрытий указываются предельно возможные отношения коэффициента отражения р к коэффициенту пропускания т (при источнике света А), потери на поглощение и рассеяние в Зависимости от отношения. Для св етодел и тельных интерференционных покрытий указывается предельно возможное значение коэффициента отражения рл при угле падения луча 15°. Потери на поглощение и рассеяние в этих покрытиях практически равны нулю.
В зависимости от толщины пленки максимум отражения может быть получен для различных участков спектра. Для просветляющих покрытий дается величина рд также прн падении лучей под углом 15°.
Примеры обозначения поляризующих покрытий:
1) покрытие девятислойное из растворов титанового и кремниевого эфиров: Полярнз. [(44Р.43Р)Х4].44Р;
2) покрытие однннадцатислойное нз растворов титанового и кремниевого эфиров: Поляриз. [(44Р.43Р)Х5J.44P;
3) покрытие одиннадцатислойное из растворов азотнокислого то-рня и кремниевого эфира: Поляриз. f(30P.43P)X5].30P;
4) покрытие тринадцатнслойное: Поляриз. [(30Р.43Р)Хб].30Р, Литература: [46, 55, 106].
ГЛАВА 17
ЗАЩИТА ОТ КОРРОЗИИ.
ПОКРЫТИЯ ДЕТАЛЕЙ
ОПТИКО-МЕХАНИЧЕСКИХ ПРИБОРОВ
ОБЩИЕ СВЕДЕНИЯ О КОРРОЗИИ
Разрушение металлов (сплавов) вследствие химического или электрохимического взаимодействия их с коррозионной средой получило название коррозии. Механизм протекания коррозионных процессов кожет иметь химический, электрохимический или смешанный характер.
Химическая коррозии — разрушение металлов происходит в результате непосредственного химического воздействия внешней среды. При электрохимической коррозии разрушение металлов происходит в присутствии электропроводной среды (вода, влажные газы, растворы солей, кислот, щелочей и т. д.) и сопровождается появлением электрического поля и переносом зарядов.
Электрохимическая коррозия протекает как два в значительной Мере самостоятельных (но сопряженных) процесса: окислительный (растворение металлов на одних участках) и восстановительный (выделение катиона из раствора или восстановление окислителей на дру-гйх участках). В некоторых случаях коррозия в электролитах может осуществляться по химическому механизму параллельно с электрохимическим, т, е. по смешанному механизму.
МЕТАЛЛЫ И СПЛАВЫ, ПРИМЕНЯЕМЫЕ БЕЗ ПОКРЫТИЙ
Как правило, для обеспечения защиты деталей от коррозии применяются покрытия, внд и толщина которых зависят от металла детали и условий эксплуатации.
Если по условиям сопряжения невозможно нанести покрытие толщиной, обеспе ивающей необходимую защиту от коррозии, то детали должны быть изготовлены из коррозионностойких металлов и сплавов, В табл. 17.1 указаны основные металлы и сплавы, применяемые без покрытий. Условия эксплуатации указаны согласно ГОСТ 14007—68, Улучшение качества поверхности повышает коррозионную стойкость металла. Класс шероховатости поверхности деталей, применяемых без покрытиц» не должен быть ниже 7а по ГОСТ 2789—73.
; В процессе эксплуатации на деталях из коррозионностойких ме-Йдлов допускается возможное потемнение поверхности, отдельные йки или пятна коррозии на ней.
Таблица 17.1. Коррозиоиностойкие металлы и сплавы, применяемые без покрытий
Металлы, сплавы Группа условий Эксплуатации по ГОСТ 14007 — 68
Золото, платина, палладий, родий, серебро Хромоникелевые стали с содержанием хрома не ниже 17% и никеля 2% типа 12Х18Н9Т, 14Х17Н2 Высокохромистые стали с содержанием хрома не ниже 18% типа 95X18 Стали с содержанием хрома 13% типа 20X13 Бронзы БрКМцЗ-1, БрАЖ9-4, БрБ2, БрАЖМцЮ-3-1,5 и др. Латуни: ЛС59-1, Л63, Л68, ЛК80-3 и др. Титановые сплавы Мельхиор, константан, нейзильбер Вольфрам Никель Пермаллой л, с, ж, ож л, с, ж, ож л, с, ж, ож л л, с, ж, ож л, с, ж л, с, ж, ож л, с, ж л, с, ж Л, С, Ж, ОЖ * л, с
КОНТАКТНАЯ КОРРОЗИЯ
При контакте двух разнородных в электрохимическом отношение металлов один из них, обладающий более отрицательным потенциалом^ Начинает функционировать в качестве анода элемента и усиленно корро* Днровать, а другой, более положительный, становится катодом. Me* таллы, обладающие наиболее отрицательным потенциалом, могут разрушаться со скоростями, значительно Йревышающими скорости з^ор? рознн ртих металлов в отсутствие контакта. Опасность возникновения контактной коррозии возрастает с ужесточением условий эксплуатации.
В изделиях, предназначенных для эксплуатации в легких условиях, допустимы контакты любых металлов, кроме магниевых сплавов. Для Магниевых сплавов в легких условиях допустимы следующие контакты при условии защиты их грунтами или смазками: с алюминйево-магние-Выми сплавами; со сплавами иа цинковой основе; С любым металлом, покрытым цинком, кадмием, оловом.
Защита конструкций и узлов от контактной коррозии может быть Осуществлена следующими методами: правильным выбором контакти-руемых металлов; электрической изоляцией контактируемых металлов; рациональными методами конструирования; изоляцией контактных Пай от воздействия внешней среды и др.
Наиболее эффективным методом борьбы с контактной коррозией является правильный выбор контактирующих металлов; можно ре$кО Снизить контактную коррозию и избежать ее совсем, если исключит^ явно недопустимые контакты. В табл. 17,2 приведены допустимые и недопустимые контакты между металлами, сплавами и покрытиями в средних и жестких условиях эксплуатации.
Таблица 17.2. Допустимые и недопустимые контакты между мета лламн, сплавами и покрытиями при эксплуатации в средних (С) н жестких (Ж) атмосферных условиях
ч Контактирующие металлы, сплавы, покрытия Медь —никель—хром по стали пикель—хром по стали Хром по стали Никель по стали, меди и ее сплавам Никель —хром по меди и ее сплавам Серебро по стали с подслоем меди, по меди и ее сплавам Золото по меди и ее сплавам < Медь и ее сплавы Сталь нержавеющая хромистая и хромоникелевая Олово, сплавы олово—висмут и олово—свинец по стали с подслоем меди и по меди и ее сплавам Кадмий по стали, меди и ее сплавам хроматированный Цинк по стали хроматированный Сталь фосфатированная + пропитка лаком или смазкой Сталь фосфатированная + лакокрасочное покрытие — 1 Алюминий и его сплавы анод-но-окислеиные + хроматирование или пропитка анилиновыми красителями Алюминий н его сплавы анод-ио-окисленные 4* лакокрасочные покрытия 1 Алюминий и егосплавы анодно-окисленные (износостойкие) Титан и его сплавы Магний н его сплавы оксидированные
Группа услов> [й эксплуатации по ГОСТ 14007—68
С ж с Ж С ж С ж С ж С ж С ж| 1 С ж (2 ж С ж С ж (2 ж С >11 С Ж С ж с ж С ж С ж (2 ж
Медь—никель—хром по стали Никель—хром по стали Хром по стали Никель по стали, меди и ее сплавам Никель—хром по меди и ее сплавам Серебро по стали с подслоем меди, по меди и ее сплавам Золото по меди и ее сплавам Медь и ее сплавы Сталь нержавеющая хромистая и хромоникелевая Олово, сплавы олово—висмут и олово—свинец по стали с подслоем меди и по меди и ее сплавам Кадмий по стали, меди и ее сплавам хроматированный Цинк по стали хроматированный Сталь фосфатированная+ пропитка лаком или смазкой Сталь фосфатированпая+лако-красочное покрытие Алюминий и его сплавы анодно-окисленные+хроматирование или пропитка анилиновыми красителями Алюминий и его сплавы анодно-окисленные-|-лакокрасочные покрытия Алюминий и его сплавы анодно-окисленные (износостойкие) Титан и его сплавы ?4агний и его сплавы оксидированные О + п + п + О О О О О О п п п О + п ч- п ( ( ( ( ( ( ] ] 1 ч з з 3 з з 3 л п л ( ч ч 1 1 ч 3 h h п н л h ( ( ( ( ( ( 1 1 1 ч 3 3 3 3 3 3 л л л ( ч ч ч 1 1 ч 3 Н н л h л ( ( ч ( ( ( ( 1 1 I 3 3 н 3 3 3 3 л л л ( ч 1 I 3 л h л ( ( ( ( ( ( ] 1 I j । 3 ) 3 3 3 3 л л л + ь + + — а О О О О О + О + О + + < ( ( ( ( ( ч 3 3 3 3 3 н 3 • h О п ( ( ( ( • 3 3 3 3 1 Л < ( ( 3 3 3 1 ~г О О ( ( ( ( ( ( ( 3 3 3 3 3 3 3 1 + О О ( ( ( ( ( ( ( 3 3 3 3 3 3 3 F Н О + + О О О О О О О О + —j ( 3 0 п п п п п п О О п п п п п О Г 3 □ П п п п п + О п п п п п п О О п п п п п О + О О О О О О -К i j ( 3 О О О О О J Т О О О
О б ° з н а ч е н и я; 4- — контакт допустимый: —— контакт недопусти мый; О — контакт допустимый лишь при наличии смазки, сменяемой в соот- ветствии с ТУ на изделие; П — контакт допустимый при наличии нзоляцион __ ной прокладки.
НАНЕСЕНИЕ НА ЧЕРТЕЖАХ ОБОЗНАЧЕНИЙ ПОКРЫТИЙ
Правила нанесения иа чертежи деталей обозначений покрытий (металлических, неметаллических неорганических, лакокрасочных) устанавливаются ГОСТ 2.310—68.
Обозначения покрытия указывают в технических требованиях чертежа после слова «Покрытие». При необходимости нанесения на все поверхности детали одного и того же покрытия запись делают nd типу: «Покрытие ...» (далее следует обозначение).
При наиесеиии покрытия на поверхности, которые можно обозначить буквами или однозначно определить словами (наружная или внутренняя поверхности и т. п.) запись производят по типу: «Покрытие поверхностей А...», «Покрытие наружных поверхностей,..».
При нанесении одинакового покрытия на несколько поверхностей их обозначают одной буквой и запись производят по типу: «Покрытие поверхностей А ...».
При нанесении различных покрытий на несколько поверхностей детали их обозначают различными буквами и запись производят по типу: «Покрытие поверхности А..., поверхности Б...».
Если необходимо нанести покрытие на поверхность сложной конфигурации или на часть ее, которую нельзя однозначно определить, то такие поверхности обводят штрих-пунктирной утолщенной линией на расстоянии 0,8—1,0 мм от контурной линии, обозначают одной буквой и проставляют размеры, определяющие положение этих поверхностей; запись производят по типу: «Покрытие поверхности А ...».
Размеры, определяющие положение поверхности, можно не вро-ставлять, если они ясны из чертежа.
ПОКРЫТИЯ МЕТАЛЛИЧЕСКИЕ И НЕМЕТАЛЛИЧЕСКИЕ НЕОРГАНИЧЕСКИЕ
Краткая характеристика покрытий
Металлические покрытия по полярности относительно Защищаемого металла подразделяются на катодные с более положительным и анодиыЗ С более отрицательным, чем защищаемый металл, потенциалом. Необходимо учитывать, что полярность покрытий зависит не только от приводы металлов, но и от внешних условий. Например, олово по отношению к железу в растворах солей является катодным покрытием^ а в среде, содержащей смесь органических веществ (консервы) — анодным.
Принято считать, что катодное покрытие может быть защитным при условии полного отсутствия пор и других несплошностей в нем, так кай оно Защищает основной металл только механически. Анодные покрытия рассматривают как покрытия, которые оказывают помимо кроющего эффекта и электрохимическое защитное действие путем катодной поляризации защищаемого металла в несплошностях покрытия. Примером анодного покрытия является цинк по стали. Однако в свете современных представлений об анодной пассивности металлов стало ясно, что в определенных условиях несплошные катодные покрытия могут защищать нижележащий металл электрохимически путем анодной поляризации оголенных участков металла, способствуя тем самым их пассивации.
Металлические покрытия характеризуются хорошим сцеплением с металлом, высокими защитными и физико-механическимн свойствами. Стойкостью к органическим растворителям, широкой гаммой специаль* 662
пых свойств (твердость, электропроводность, отражательная способность и мн. др.),
К основным недостаткам следует отнести появление хрупкости в покрываемом металле из-за наводороживания его в процессе осаждения покрытия и неизбежная неравномерность толщины покрытия как на различных участках одной и той же детали, так и на различных деталях в партии в результате неравномерности электрического поля при осаждении покрытия.
Химические (оксидные, фосфатные) покрытия характеризуются равномерностью и малой толщиной слоя, хорошим сцеплением с лакокрасочными покрытиями. К недостаткам следует отнести невысокие защитные и механические свойства этих покрытий.
Обозначения покрытий
Обозначение покрытий производится в соответствии с ГОСТ 9.073—77, в котором принята буквенно-цифровая ^система обозначений.
Таблица 17,3. Примеры обозначения металлических н неметаллических неорганических покрытий
Наименование покрытия Обозначение
Хромовое с подслоем полублестящего никеля толщиной 12 мкм, полученное на сатинированной поверхности Хромовое с подслоем никеля толщиной 12 мкм Хромовое с подслоем меди толщиной 18 мкм и двухслойного никеля толщиной 15 мкм Никелевое полублестящее толщиной 12 мкм, нанесенное по матированной поверхности Цинковое толщиной 15 мкм блестящее с радужным хроматированием Никелевое черное по никелю толщиной 6 мкм, защищенное прозрачным лаком Анодно-окисное покрытие алюминия, полученное на механически и электрохимически полированной поверхности, наполненное раствором черного красителя Анодно-окнсное покрытие алюминия, наполненное раствором черного красителя Анодно-окисное покрытие бесцветное, полученное иа поверхности после алмазной обработки Химическое окнсно^ покрытие, Хроматированное и промасленное Химическое фосфатное покрытие, матовое, хроматированное, защищенное лаком стн. Н12. пб. X. пб Н12.Х М18.Нд15.Х.б мт.М6.Н12,пб Ц15.б.хр.радужное Н6.Н,ч/лак мп.эп.Ан.Окс, черный, б Ан.Окс.черный алм.Ан.Окс.зк, Хим.Оке. хр. при. Хим.Фос.м.хр/лак
В шифр защитно-декоративных покрытий, согласно ГОСТ 21484—76, дополнительно вводятся обозначения его декоративных свойств.
Обозначения покрытий записывают в следующем порядке: способ обработки поверхности основного металла — по ГОСТ 21484—76 (только для декоративных покрытий); способ получения покрытия, материал покрытия и толщина покрытия — по ГОСТ 9.073—77; группа покрытия — по ГОСТ 21484—76; способ дополнительной обработки покрытия — по ГОСТ 9.073—77 и ГОСТ 21484—76. Все обозначения отделяются друг от друга точками, за исключением материала и толщины покрытия.
В обозначении покрытия не обязательно наличие всех перечисленных признаков. Как правило, все признаки в обозначении покрытия указывают для декоративных покрытий, когда требуется получение покрытий с определенными декоративными свойствами.
В обозначении металлических покрытий указывают минимальную толщину покрытий в микрометрах. Толщины всех покрытий, кроме драгоценных металлов, выбирают из ряда предпочтительных чисел: 1, 3, 6, 9, 12, 15, 18, 21, 24, 30, 36, 42, 48. Максимальная толщина покрытия по ГОСТ 9.073—77 для всех покрытий, кроме драгоценных металлов* не должна быть более числа, стоящего через одну числовую величину за установленным минимальным в ряду предпочтительных чисел. Например, для никелевого покрытия при минимальной толщине 9 мкм максимальная толщина может быть до 15 мкм. Практически при крупносерийном и массовом производстве максимальная толщина покрытий для партии деталей превышает значения, предусмотренные ГОСТом.
Примеры обозначения покрытий приведены в табл. 17.3.
Выбор покрытий
Выбор вида покрытия и его толщины определяют назначением детали или изделия, материала, из которого они изготовлены, условиями Эксплуатации. При этом учитывают назначение и свойства покрытия, способ его нанесения, допустимость контактов сопрягаемых металлов и экономическую целесообразность.
По коррозионному воздействию условия эксплуатации деталей в соответствии с ГОСТ 14007—68 делятся на четыре группы: легкие — Л, средние — С, жесткие — Ж, очень жесткие — ОЖ.
Рекомендации по выбору покрытий в зависимости от условий эксплуатации приводятся в табл. 17.4 и 17.5.
Для деталей, эксплуатируемых в условиях герметизации, при периодическом возобновлении смазки или при полном и постоянном погружении их в масло и рабочие жидкости, не вызывающие коррозии, а также при работе в среде сухих инертных газов и сухого воздуха, допускается выбирать виды и толщины покрытий, соответствующие более легким условиям эксплуатации.
Если детали, по условиям эксплуатации или сопряжения не могут иметь толщину покрытия, указанную в табл. 17.4, то они должны изготавливаться из металлов и сплавов, применяемых в данных условиях эксплуатации без покрытий. Допускается уменьшение толщины покрытий вне зависимости от условий эксплуатации при условии дополнительной защиты для деталей, на которые по условиям сопряжения невозможно нанесение покрытий толщиной, указанной в табл. 18.4, деталей, имеющих резьбу, деталей типа пружин (табл. 17.6).
Таблица 17.4. Рекомендации по выбору минимальной толщины металлических покрытий, мкм
Материал детали
Вид покрытия Сталь углеродистая Медь и ее сплавы
Условия эксплуатации по ГОСТ 14007—68
л • с Ж ож Л с Ж ож
Цинковое Кадмиевое Медное Никелевое Никелевое с подслоем меди Никелевое химическое Никелевое черное с подслоем никеля Никелевое черное с подслоем меди Хромовое Хромовое с подслоем никеля Хромовое с подслоем никеля и меди Хромовое черное с подслоем никеля Серебряное Палладиевое Палладиевое с подслоем серебра Оловянное с подслоем никеля , Сплав олово—висмут 6 6 15 9; 6 9 15 (тс 9; 6 (toj 18 15 9; 6 9 (то 9; 3 9; 6 9; 6 15 15 Дс 27 18; 9 15 27 элщина 18; 9 ицина 36 27 (толп 1 18; 9 1 (ТОЛП! 15 лщина 21; 6 18; 9 18; 9 24 24 > 60 30; 12 24 черног 30; 12] черногс 48 щна хр 30; 12| (ина хр 48 черног 30; 9 24 30 36; 15 24 'о нике 36; 15 ) нике;: 60 ома 0,f 36; 15 ома 0,1 48 о хром 6 6 6 6 ля 0 - [я 0J 9 6 >-1, 5—1, 6 а 0,5 3 3 6 0,1 3; 6 6 9 9 9 9 ,5-1 — 18 9 9 мкт ) мкт 9 6 3 6 (тол в палл 5-1,< 3; 6 9 9 12 15 12 ,0 мь — 9 мкт 24 12 л) — 1 л) 15 1 МКТ/ 9 3 9 тина ад и я 9 мкт 3; 9 12 9 15 15 15 :м) <1) 24 15 15 О 12 3 12 л) 3; 12 15
Примечания: 1. Для многослойных покрытий толщина каждого слоя.указана в порядке их нанесения (значения толщин отделены точкой с запятой). 2. Медное покрытие в качестве самостоятельного применяется для местной защиты при цементации. 3. При серебрении стальных деталей применяется подслой меди. 4. Прн нанесении олова, сплава олово—висмут иа стальные детали применяется подслой меди или никеля.
Таблица 17.5. Рекомендации по выбору неметаллических неорганических покрытий
Материал детали Вид и способ получения покрытия Группа условий эксплуатации по ГОСТ 14007 — 68 Дополнительные указания
Сталь углеродистая Окисное, химическое Фосфатное, химическое Ок иен о-фосфат ное, химическое Л Л л Для снижения коэффициента отражения света
Медь и ее сплавы Окисное, анодное окисление Окисное, химическое л, с л, с
Алюминий и его сплавы Окисное, анодное окисление Окисное, химическое Фосфатное, химическое л, с л л Применяют с наполнением оксидной пленки анилиновыми красителями или хромовыми солями
- Окисное непрозрачное (эма-таль), анодное окисление л, с, ж Образуется на алюминии и алюминиево-магниевых сплавах
Тнтан и его сплавы Окисное, анодное окисление Л, с, ж, ож Рекомендуется для снижения коэффициента отражения
Цинковые сплавы Фосфатное, химическое л ч ••
Магний и его сплавы Окисное, химическое л Без лакокрасочного покрытия применяется только в технически обоснованных случаях
Т а б л и ц а 17.6. Рекомендации по выбору металлических покрытий для резьбовых деталей, пружин и деталей с малыми нолями допусков
Тип деталей Покрытие Минимальная толщина покрытия, мкм Рекомендуемое отклонение по ГОСТ 16093— 70
Резьбовые детали, шаг резьбы 0,45 мм То же, шаг резьбы 0,5—0,75 мм То же, шаг резьбы 0,8 мм й более Пружины; толщина материала до 0,5 мм То же, толщина материала до 1,0 мм То же, толщина материала свыше 1,0 мм Детали с полями допусков размеров по 6, 7, 8-му киалитетам СТ СЭВ 144—75 без занижения (завышения) размеров под покрытие То же, по 9-му и 10-му квалитетам Хромовое с подслоем никеля, никелевое, цинковое, кадмиевое к др. То же » я Кадмиевое, никелевое, серебряное, оловянное То же » Никелевое, хромовое с подслоем никеля, цинковое, кадмиевое, серебряное и др. То же 3 6 9 3 6 9 3 6 *» - - 1 1 1 I I
Примечания: 1. Рекомендуемые отклонения по ГОСТ 16093-—70 и толщины покрытий не зависят от материала деталей и определяются условиями свинчивания. 2. Для пружин из медн и ее сплавов для уменьшения хрупкости рекомендуется производить обезводорожя-ваиие после нанесения покрытия.
Основные требования, предъявляемые к деталям, подвергающимся покрытию
Шероховатость покрываемой поверхности должна быть:
1) под защитно-декоративные покрытия — не ниже 6-го класса по ГОСТ 2789—73;
2) под защитные покрытия — не ниже 4-го класса;
3) под твердые и электроизоляционные аиодноокислеиные покрытия — не ниже 7-го класса.
Шероховатость поверхности после нанесения декоративных покры-21Й (никелевого, хромового, окисного), как правило, остается без из-енения, если ие применяется механическое полирование поверхности.
Класс шероховатости поверхности после нанесения защитных покрытий в зависимости от исходной поверхности и типа электролита либо остается без изменений, либо снижается иа одну-две единицы.
Поверхность деталей, изготовленных из горячекатаного металла, должна быть чистой (без травильного шлама, окалины, ржавчины и других загрязнений).
На поверхности литых и кованых деталей не должно быть пор, газовых и усадочных раковин, шлаковых включений, спаев, недоливов, трещин, помимо допускаемых технической документацией на отливки и кованые детали. На поверхности деталей не должно быть забоин, вмятин, раковин, расслоений, прижогов, трещин, заусенцев, пор и дефектов от рихтовочного инструмента.
Острые углы, кромки деталей должны быть скруглены радиусом не менее 0,5 мм или иметь фаски для обеспечения равномерного нанесения покрытий методом катодного восстановления. При конструировании следует избегать углублений, вогнутостей, острых углов и т. п.
Необходимо иметь в виду, что при нанесении металлических и неметаллических неорганических покрытий на узлы, имеющие клепаные, развальцованные, штифтовые, резьбовые соединения, а также на детали с точной сваркой или со сложной конфигурацией трудно, а иногда практически невозможно произвести полную отмывку электролита. Трудно удалить электролит из пор линейных деталей, металл о керам и-.ческих деталей и деталей, имеющих глухие отверстия и полости или глубокие отверстия малых диаметров. Остатки электролита часто являются причиной возникновения коррозии деталей и снижения качества покрытия.
В связи с этим предъявляется ряд требований при конструировании подобных узлов и деталей. Не допускается нанесение покрытий разъемных узлов в собранном виде. Не допускается нанесение покрытий на сборочные единицы, имеющие зазоры, из которых невозможно удалить остатки электролита. Сварные и паяные детали, на которые наносят покрытия, должны иметь по всему периметру непрерывные швы, исключающие возможность затекания электролита. Точечную сварку деталей под покрытия необходимо производить по герметизирующим материалам. Рекомендуется наносить покрытия до проведения точечной сварки. Для легких и средних условий эксплуатации допускается наносить покрытия без заполнения шва герметизирующим материалом.
При назначении покрытий на сварные и паяные детали, литые детали из металлокерамики, различные сборочные единицы, имеющие зазоры и глухие полости, рекомендуется выбирать покрытия, которые наносятся из разбавленных, относительно неагрессивных электролитов (фосфатные, оксидо-фосфатные, никелевые и т. д.).
На детали, соединяемые в сборочные единицы клепкой, запрессовкой, свинчиванием, покрытия должны наноситься, как правило, до проведения этих операций. Не рекомендуется нанесение покрытий на металлическую арматуру после частичной ее запрессовки в пластмассу. Недопустимо производить анодное окисление алюминиевых литейных сплавов с арматурой из стали, меди и ее сплавов.
Нанесение покрытий нескольких видов на одну и ту же деталь в массовом и серийном производствах представляет значительные трудности, а в ряде случаев и невыполнимо.
Если необходимо, чтобы на стальную или латунную деталь наносились два покрытия — черное и декоративное светлое, то можно рекомендовать окисное химическое в сочетании с однослойным хромовым покрытием.
Основные характеристики металлических покрытий
Цинковые покрытия. Цвет покрытия — светло-серый или серебристо-белый с синеватым оттенком. Цинк электрохимически защищает сталь от коррозии в атмосферных условиях при температуре до +70° С; при более высоких температурах он защищает сталь только механически.
Для повышения коррозионной стойкости цинковое покрытие подвергают хроматированию или фосфатированию. Без указанных обработок покрытие допускается применять только при необходимости снижения переходного электрического сопротивления для деталей, работающих в легких условиях. Для изделий, работающих в условиях затрудненного обмена воздухом между внутренним пространством и внешней средой и при наличии в замкнутом пространстве органических материалов, которые при старении выделяют агрессивные вещества, цинковые покрытия рекомендуется применять с дополнительной защитой лакокрасочными покрытиями.
При электролитическом цинковании наиболее сильное наводоро-живаиие и связанное с ним охрупчивание основного металла происходит в цианистых электролитах. Электролитическое цинкование не допускается для деталей, изготовленных из сталей с прочностью более 1400 МПа. Допустимая рабочая температура цинкового покрытия до 4-300° С. Микротвердость покрытия, наносимого электролитическим способом, составляет 500—600 МПа. Оно выдерживает развальцовку, гибку; неустойчиво при запрессовке. Декоративные свойства покрытия невысоки, покрытие применяется в основном, для защиты от коррозии стальных деталей изделий, эксплуатируемых в промышленных районах. Кадмиевые покрытия. Цвет покрытия — светло-серый или серебристо-белый. Кадмий защищает сталь от коррозии в морской атмосфере и в морской воде электрохимически, в пресной воде — преимущественно механически. Кадмиевые покрытия характеризуются высокой пластичностью и эластичностью, выдерживают развальцовку, штамповку и вытяжку. Покрытие легко притирается; микротвердость — 350— 500 МПа.
Кадмий значительно более стоек, чем цинк, в кислых и нейтральных средах. В условиях атмосферы промышленных центров кадмиевые покрытия менее стойки, чем цинковые. Покрытие нестойко в контакте с деталями, пропитанными или покрытыми олифой или маслами, особенно в закрытых объемах. При кадмировании происходит наводороживание стали и связанное с этим повышение ее хрупкости. Для устранения наво-дороживания проводят обезводороживание нагревом. Для повышения коррозионной стойкости покрытия рекомендуется производить его хроматирование или фосфатирование. Допускаемая рабочая температура 4-250° С.
Покрытие применяется:
для стальных деталей, подвергающихся действию морской воды или морских испарений;
для снижения контактной разности потенциалов при контакте с алюминиевыми и магниевыми сплавами деталей из стали и медных сплавов;
для защиты от коррозии деталей типа-пружин;
для деталей кинопроекционной аппаратуры, которые в процессе работы соприкасаются с кинопленкой;
для получения покрытий, обладающих высокой пластичностью, хорошей притираемостью и свинчиваемостью.
В связи с дефицитностью кадмия применять кадмиевые покрытия необходимо только в технически обоснованных случаях, когда приме* некие других покрытий не обеспечит получения требуемых свойств.
Никелевое покрытие. Цвет покрытия—серебристо-белый с желтоватым оттенком. Однослойное никелевое покрытие является катодным по отношению к стали, алюминию и алюмнииевым сплавам и обеспечивает их защиту от коррозии механически. Никелевые покрытия могут наноситься как методом катодного восстановления, так и методом химического восстановления.
Покрытие выдерживает запрессовку, изгибы; при расклепке и раз-ральцовке возможны случаи отслаивания. Покрытие хорошо полируется, мнкротвердость его составляет 2000—5000 МПа. Допустимая рабочая температура — до +650° С. Никель стоек к действию ряда органических кислот, минеральных солей и растворов щелочей; в атмосфере, йасыщенной агрессивными газами и влагой, покрытие окисляется и туск-реет. Для защиты от потускнения на никелевое покрытие наносится слой хрома толщиной 0,5--1,0 мкм.
При введении в состав электролита для нанесения никеля блеско-Образующих добавок покрытие получается блестящим непосредственно й ванне.
Для уменьшения пористости и повышения защитных свойств применяются подслой меди, двухслойные н трехслойные никелевые щжрытия.
Никелевые покрытия рекомендуются преимущественно для получения защитно-декоративных покрытий иа наружных деталях сложной конфигурации и внутренних деталях изделий; для защитно-декоративных покрытий деталей, подвергающихся расклепке, завальцовке.
Никелевое черное покрытие. Цвет покрытия от темно-серого до верного. Покрытие имеет невысокие физико-механические свойства и малую декоративность. Применяется в качестве светопоглощающего. Интегральный коэффициент отражения в видимой области спектра при нанесении на полированную поверхность составляет 8—10%. Коррозионная стойкость определяется подслоем нанесенным под черный иикель.
Хромовое покрытие. Цвет покрытия—серебристо-стальной с синеватым оттенком. По отношению к стали, алюминиевым и цинковым сплавам является катодным и обеспечивает защиту от коррозии механически. Покрытие отличается хорошим сцеплением с основным металлом, йовышенной твердостью и износоустойчивостью. Твердое блестящее громовое покрытие обладает низкой пластичностью, эффективно работает на трение при нанесении на твердую основу. Микротвердость 7500— II 000 МПа. Хромовые покрытяя длительное время не тускнеют в атмосфере, на них не действует сероводород. Поэтому хром наносится в качестве поверхностного слоя толщиной 0,5—1,0 мкм по никелевому декоративному покрытию.
К недостаткам хромовых покрытий относятся: снижение пластических свойств стали из-за наводороживаиия, значительная неравномерность распределения хрома на покрываемой поверхности.
Хромовые покрытия применяются для получения защити о-декоративных покрытий по никелевому подслою и без него; дли повышения износостойкости и твердости стальных деталей; для восстановления размеров изношенных деталей.
Хромовое черное покрытие. Цвет покрытия—черный; обладает более высокими, чем у черного инкеля, защитными и физико-механиче-ркнми свойствами. Коэффициент отражения этого покрытия по поверхности, обработанной электрокорундом, составляет 2—3%. Для повьине-670
ния коррозионной стойкости покрытия применяется подслой никеля. Рекомендуется в качестве светопоглощающего покрытия.
Медные покрытия. Цвет покрытия от светло-розового до красного. Медное покрытие является катодным по отношению к стали, алюминиевым и цинковым сплавам. Покрытие обладает высокой электропроводностью, пластичностью, выдерживает глубокую вытяжку, развальцовку, облегчает приработку и свинчивание. Микротвердость составляет 600— 1200 МПа. В качестве самостоятельных медные покрытия не применяются из-за малой устойчивости на воздухе. Допустимая рабочая температура — до +300° С.
Применяется в качестве подслоя под декоративные никелевые и хромовые серебряные и другие покрытия; для местной защиты от науглероживания при цементации; для повышения притирочных свойств поверхности и пластичности при глубокой вытяжке.
Оловянные покрытия. Цвет покрытия от светло-серебристого до серого. В атмосферных условиях по отношению к стали оловянное покрытие является катодным, во многих органических средах — анодным. Покрытие хорошо выдерживает развальцовку, штамповку, запрессовку, в свежеосажденном состоянии хорошо паяется. При хранении олово окисляется н теряет способность к пайке; оплавленное покрытие дольше сохраняет способность к пайке. Микротвердость — 120— 200 МПа.
При хранении на поверхности олова, нанесенного по подслою меди или латуни, образуются нитевидные токопроводящие кристаллы (так называемое иглообразование), что может привести к нарушению работы приборов. Для исключения иглообразования олово наносится по подслою никеля. Замена оловянных покрытий сплавом олово—висмут, содержащим 0,5—1,5% висмута, также уменьшает иглообразование и сохраняет способность к пайке на более длительное время.
Покрытия применяют для деталей, подвергающихся панке; для снижения контактной разности потенциалов, при сопряжении стальных деталей с деталями из алюминиевых сплавов.
Серебряные покрытия. Цвет покрытия—серебристо-белый. Серебряное покрытие является катодным по отношению к стали, алюминию, медным сплавам.
Под действием сернистых соединений, находящихся в воздухе, покрытие тускнеет, покрывается черным налетом сульфида серебра. Сульфидная пленка не снижает коррозионной стойкости, но повышает переходное сопротивление, что ограничивает применение серебра для покрытия контактов, работающих при малых контактных давлениях и малых токовых нагрузках. Для уменьшения переходного сопротивления на серебряные покрытия износят дополнительно палладий, золото или родий.
Допустимая рабочая температура покрытия — до +700° С. Серебряные покрытия характеризуются наиболее высокой по сравнению с остальными металлами электро- и теплопроводностью» а также высокой отражательной способностью. Серебряные покрытия мягки, хорошо выдерживают гибку, развальцовку, облегчают свинчивание, хорошо паяются. Микротвердость — 700—800 МПа. Не рекомендуется применять для деталей, работающих в контакте с органическими материалами, содержащими серу.
Серебряные покрытия применяются для снижения переходного сопротивления токопроводящих деталей; для повышения поверхностей проводимости; для получения зеркальных покрытий, в том числе, для оптических квантовых генераторов,
Палладиевые -покрытия. Цвет покрытия — светло-серый. Покрытие является катодным по отношению к покрываемым металлам» обладает высокой стойкостью в атмосферных условиях и при воздействии сероводорода. Покрытие характеризуется высокими теплостойкостью, электропроводностью, износостойкостью, отражательной способностью.
Палладиевые покрытия не рекомендуется применять в замкнутых объемах, при затрудненном обмене воздухом между внутренней и внешней средой, при наличии во внутреннем объеме органических веществ, которые взаимодействуют с палладием с образованием на поверхности покрытия темных пленок, увеличивающих переходное электрическое сопротивление контактирующих поверхностей.
Микротвердость — 2000—4000 МПа. Покрытия не тускнеют на воздухе при температуре до 400° С. Применяются преимущественно для деталей из меди и медных сплавов, требующих низкого переходного сопротивления и работающих на истирание; для защиты серебряных покрытий от окисления; для получения покрытий с высоким коэффициентом отражения.
Родиевые покрытия. Цвет — светло-серебристый с голубоватым оттенком. Покрытие является катодным по отношению к покрываемым металлам. Обладает большой коррозионной стойкостью как в атмосферных условиях, так и в коррозионно-активных средах, высоким коэффициентом отражения света, высокой электропроводностью и износостойкостью.
Родиевые покрытия отличаются способностью длительное время сохранять хорошую проводимость в контактах. Интегральный коэффициент отражения в видимой области спектра составляет 76—81%. Микротвердость достигает до 9000 МПа.
Применяются для получения зеркал, работающих в жестких условиях эксплуатации; для повышения износостойкости ответственных трущихся и контактных деталей при необходимости сохранения постоянства переходного сопротивления.
Золотые покрытия. Цвет покрытия—от золотисто-желтого до темножелтого. Золотое покрытие является катодным по отношению к покрываемым металлам. Обладает хорошей пластичностью, мягкостью, полиру емостью, способностью к пайке, высокой электропроводностью и теплопроводностью.
Покрытие характеризуется высокой химической стойкостью. Микротвердость — 400—600 МПа. Микротвердость сплава золото—никель, содержащего 1% никеля, увеличивается до 900—1000 МПа, при этом другие свойства сплава изменяются незначительно.
Применяется для покрытия деталей высокочастотной аппаратуры^ требующих низкого переходного сопротивления и длительного сохранения электрических параметров; для обеспечения стабильного коэффициента отражения света.
Основные характеристики неметаллических неорганических покрытий
Анодно-окисные прозрачные покрытия на алюминии и его сплавах. Покрытия характеризуются: высокими защитными свойствами, хорошим сцеплением с основным металлом и с лакокрасочным покрытием, наносимым по окисной пленке; высокой микропористостью и, как следствие, способностью окрашиваться неорганическими и органическими красителями; высокой твердостью, износостойкостью и электроизоля-цйонными свойствами. В зависимости от технологических параметров 572
процесса и состава сплава могут быть получены покрытия: защитные, защитно-декоративные, износостойкие, электроизоляционные.
Защитные, защитно-декоративные покрытия имеют толщину 10— 20 мкм. Для придания деталям декоративного вида покрытия наполняются растворами красителей или для повышения защитных свойств растворами хромовых солей или водой. Твердые износостойкие и электроизоляционные покрытия характеризуются повышенной толщиной (30—150 мкм и более), твердостью, хрупкостью. Удельное электрическое сопротивление пленки достигает 1014 Ом*см, пробивное напряжение — до 30 В/мкм. При анодном окислении размеры деталей увеличиваются, как правило, на 0,5 толщины покрытия (на сторону).
Покрытия применяется для получения защитно-декоративных пленок; для повышения твердости и износостойкости детали; для придания электроизоляционных свойств; в качестве грунта под лакокрасочное покрытие.
Анодно-окисные непрозрачные (эмата левые) покрытия и а алюминии и его сплавах. Является разновидностью анодно-окнсного покрытия. Эматалевое покрытие непрозрачно, по внешнему виду напоминает стеклянное эмалевое покрытие. Естественный цвет — от светлосерого до темно-серого в зависимости от марки металла. Покрытие характеризуется высокими декоративными свойствами; высоким удельным сопротивлением и пробивным напряжением, износостойкостью. Эматалевое покрытие стойко к резким перепадам температур, выдерживает гибку, неглубокую вытяжку.
Высоко-декоративные эматалевые покрытия образуются на чистом алюминии и алюминиево-магниевых сплавах типа АМГ-2. Эматалевые пленки хорошо окрашиваются в растворах органических красителей. Применяются для получения высокодекоративных покрытий, обладающих повышенной твердостью и износоустойчивостью.
Анодно-окисные покрытия иа титане и его сплавах. Цвет пленки может приобретать различные цвета спектра и зависит от режимов ее получения. Толщина покрытия от долей до нескольких десятков микрометров. Для декоративных целей и покрытий черного цвета применяются покрытия толщиной до 1 мкм. Применяются для получения черных светопоглощающих покрытий и для улучшения антифрикционных свойств.
Аиодно-окисные покрытия на меди и ее сплавах. Цвет покрытия — черный. По сравнению с химическим окисным покрытием обладает лучшими защитными и механическими свойствами. Применяется для получения светопоглощающих покрытий.
Окисные покрытия на стали. Цвет покрытия на углеродистой стали — черный с синеватым оттенком. Стали, содержащие легирующие добавки, оксидируются хуже. Толщина оксидной пленки до 1 мкм. Защитные свойства покрытий невелики, для их повышения покрытия пропитывают маслами или подвергают гидрофобной обработке.
Применяются для получения декоративных покрытий на деталях с точными размерами, кроме деталей, изготовленных методом литья, деталей из металлокерамики и Уборочных" единиц; для получения светопоглощающих покрытий; для повышения сцепления с последующим лакокрасочным покрытием.
Фосфатные покрытия на стали. Цвет покрытия — от серого до серо-черного в зависимости от марки стали и состава раствора. Покрытие характеризуется невысокими защитными свойствами в связи с пористым строением пленки. Для повышения защитных свойств фосфатные покрытия подвергают пропитке маслами, гидрофобизированию или 573
другой обработке. Толщина покрытия 10—15 мкм. Фосфатные покрытия обладают высокой адсорбционной способностью, высоким электрическим сопротивлением, хорошо прирабатываются. К недостаткам покрытия следует отнести низкую механическую прочность, которая увеличивается после пропитки лаками.
Покрытие применяется в качестве грунта под лакокрасочные покрытия; как ващитное для пористых деталей и сборочных единиц.
Окисно-фосфатиые покрытия на стали. Цвет покрытия от темносерого до черного в зависимости от марки стали. Механические свойства аналогичны окисным. Защитные свойства несколько выше, чем у окисных. Толщина покрытия 2—3 мкм. Так как покрытие наносятся из разбавленных растворов, его применение предпочтительно для деталей из металлокерамики, литейных деталей и сборочных единиц, имеющих поры, зазоры и глухие полости.
Окисные химические покрытия на алюминиевых сплавах. Цвет покрытия—темио-серый или радужно-желтый в зависимости от марки сплава и состава раствора. Толщина покрытия 3—5 мкм. Механические и защитные свойства ниже, чем у анодно-окисных покрытий. Окисные покрытия служат хорошим грунтом под последующее лакокрасочное покрытие.
Применяются для литейных алюминиевых сплавов для улучшения сцепления с лакокрасочным покрытием.
Фосфатные покрытия иа алюминии и его сплавах. Цвет покрытия— золотисто-желтый. Покрытие характеризуется токопроводностью, толщина слоя 3—5 мкм. Применяется для детален, где необходимо сочетание защитных свойств с сохранением токопроводимостн.
Окисные покрытия на магнии и его сплавах. Цвет покрытия от светло-желтого до черного в зависимости от марки сплава н состава раствора. Покрытие характеризуется невысокими защитными свойствами, хорошей адгезией с лакокрасочными материалами. Толщина покрытии 2—4 мкм. Применяется для межоперационной защиты от коррозии при изготовлении деталей; в качестве грунта под лакокрасочное покрытие.
ПОКРЫТИЯ ЛАКОКРАСОЧНЫЕ
Краткая характеристика покрытий
Лакокорасочиые покрытия характеризуются высокими защитными и декоративными свойствами, возможностью реставрации. Лакокрасочные материалы в зависимости от их марки и технологии нанесения могут образовывать гладкие и рельефные рисунчатые покрытия различной степени блеска: глянцевые, полуглянцевые, полуматовые, матовые, глубокоматовые. К специфическим материалам, используемым в оптикомеханическом приборостроении, относятся черные матовые и глубокоматовые эмали, белые матовые и глубокоматовые эмали, эмали для окраски нерабочих поверхностей деталей из стекла.
По температуре сушки лакокрасочные материалы подразделяются на высыхающие при комнатной или прн повышенной температуре. Как правило, лакокрасочные материалы горячей сушки образуют покрытия 0 повышенными защитными, фнзнко-механическими свойствами н более высокой стойкостью к органическим растворителям и маслам.
Обозначения лакокрасочных покрытий
Условное обозначение лакокрасочных покрытий должно соответствовать требованиям ГОСТ 9.032—74. В обозначение покрытия входит сочетание слов, букв и цифр, определяющих вид и свойства покрытия, в следующем порядке: покровный лакокрасочный материал, цвет, обозначение стандарта на данный материал, класс покрытия, условия эксплуатации.
В зависимости от климатических условий, от категории размещения приборов условия эксплуатации согласно ГОСТ 9.009—73 подразделяются на четыре группы: легкие — Л, средние — С, жесткие — Ж, особо жесткие — ОЖ.
По внешнему виду, качеству нанесения лакокрасочные покрытии согласно ГОСТ 9.032—74 делятся на семь классов.
В табл. 17.7 приводятся рекомендации по выбору класса покрытии для различных групп оптико-мехаиических приборов. Примеры обозначений лакокрасочных покрытий приведены в табл. 17.8.
Т а б л и ц а 17.7. Рекомендации по выбору класса лакокрасочных покрытий
Класс покрытия (ГОСТ 9.032—74) Область применения
II Наружные поверхности деталей любительской фото-н киноаппаратуры высокого класса, оправ объективов, теодолитов, дальномеров
III Наружные поверхности микроскопов, спектральных приборов, профессиональной киноаппаратуры, измерительных приборов и любительской проекционной аппаратуры
IV Наружные поверхности астрономических, фотометрических приборов, рефрактометров, профессиональной кинопроекционной и „усилительной аппаратуры, укладочных ящиков
V Наружные поверхности приборов, к которым не предъявляются повышенные декоративные требования, внутренние поверхности деталей приборов, окрашиваемых по II—IV классам
VI Наружные поверхности станков и другого оборудования
VII Внутренние поверхности станков
Таблица 17.8. Примеры обозначения покрытий
Вид покрытия
Эмалью МЛ-279 ОП по III классу, светло-серого цвета; эксплуатируется в легких условиях
Эмалью МЛ-158 по IV классу, светло-бежевого цвета «под шагрень»; эксплуатируется в легких условиях
Эмалью ХС-1107 по V классу, черного цвета глубокоматовое; эксплуатируется в средних условиях
Эмалью XВ-785 по V классу, серого цвета; подвергается воздействию растворов кислот и щелочей и эксплуатируется в жестких условиях
Лаком УР-231 по V классу, бесцветное, электроизоляционное, эксплуатируется в средних условиях
Обозначение
Эмаль МЛ-279 ОП светло-серая; - ГОСТ 5971—78. III. Л
Эмаль МЛ-158 шагрень светло-бежевая; ТУ 6-10-1096—76. IV.Л
Эмаль ХС-1107 ГМ черная;
ТУ 6-10-1042—77.V.C
Эмаль XВ-785 серая; ГОСТ 7313—75.V. 7/1-Ж
Лак УР-231 бесцветный;
ТУ 6-10-863—76.V.9-C
Примечание. Обозначение покрытий стойких в особых средах (химически стойкие, малостойкие, термостойкие и др.), приведены в ГОСТ 9.032 — 74.
Выбор лакокрасочных материалов для окраски деталей
Выбор лакокрасочного покрытия определяется требованиями, предъявляемыми к внешнему виду (цвет, степень блеска, фактура, класс покрытия), условиями эксплуатации, свойствами лакокрасочных материалов и допустимым режимом сушки. Для окраски деталей оптико-механических приборов можно применять лакокрасочные материалы, используемые в машиностроении, автомобилестроении и других отраслях промышленности. Многие из этих материалов имеют существенные недостатки и не обеспечивают высокого качества окраски: плохой розлив, недостаточно высокий перетир, ограниченную и мало пригодную цветовую гамму, темные, тусклые тона.
В последнее время для оптико-механического приборостроения разработаны специальные приборные эмали, которые характеризуются повышенными декоративными и физико-механическими свойствами. Эти эмали образуют пол у.матовые покрытия (как гладкие, так и рельефные) спокойных цветов, хорошо гармонирующие друг с другом.
Разработанные эмали (МЛ-158, МЛ-279 ОП, ЭФ-1118) позволяют наряду с гладкими полуматовыми покрытиями получать и рельефные декоративные, по внешнему виду напоминающие шагреневую кожу. Благодаря рельефной поверхности маскируются дефекты поверхности деталей, а значит, уменьшается трудоемкость процесса подготовки поверхности под окраску.
Изменяя технологические параметры нанесения и сушки эмали, можно регулировать характер рисунка покрытия. На практике приходится выбирать различный рисунок для различных изделий, учитывая габариты прибора.
В табл. 17.9 приведены основные материалы^ применяемые для окраски оптико-механических приборов.
Панов и др.
Таблица 17.9. Основные лакокрасочные материалы для окраски оптико-механических приборов
Лакокрасочный материал Вид и цвет покрытия Документ на поставку Максимально допустимый класс покрытия по ГОСТ 9.032—74 Минимальная температура сушки, °C Условия эксплуатации по ГОСТ 9.009—73
Эмаль МЛ-279 ОП * Полуматовое; бледно-серый, светло-серый, серый, серо-стальной, темно-серый, серо-голубой ГОСТ 5971—78 II 130 Л, С, ж
Эмаль МЛ-158 * Полуматовое; слоновой кости, светло-бежевый, серо-бежевый, темно-бежевый, серо-голубой, зелено-голубой, серо-зеленый, черный ТУ 6-10-1096—76 III 130 Л, С, ж
Эмаль ПФ-115 Глянцевое; различных цветов ГОСТ 6465—76 III 18—23 л, С, ж
Эмаль МЛ-12 Высокоглянцевое; различных цветов ГОСТ 9754—76 II 130 л, с, ж, ож
Эмаль ЭФ-1118 (ПГ, ПМ, М) Полуглянцевое, полуматовое, матовое; черный ГОСТ 5971—78 II V 130 л, с, ж
Эмаль МЧ 240 (ПМ, М) Полуматовое, матовое; черный ТУ 6-10-17-01—79 III V 130 л, с
Эмаль МЛ-165** С молотковым эффектом, полуглянцевое; различных цветов ГОСТ 120374—77 III 130 л, с, ж, ож
* Покрытие можно получать как гладким, так и «под шагрень»; •* Предназначается для окраски приборов, покрытия которых не требуют повышенной декоративности, ио должны иметь высокие физико-механические свойства.
Таблица 17.10. Черные светопоглощающие лакокрасочные материалы
Лакокрасочный материал, документ на поставку Интегральный коэффициент отражения света в видимой области спектра, %, не более i Максимальная температура ; СУШКИ, °C Условия эксплуатации по ! ГОСТ 9.009 — 73 । Характеристика
Черные глубокома т О В ы е покрытия
Эмаль АК-243, черная ТУ 6-10-11-01-6—78 1,5 18—23 Л, С С высокой светопоглощающей способностью и пониженными физико-механическими свойствами, нестойко к воздействию органических растворителей, выдерживает перепад температур от —60 до +80° С, не выделяет летучих веществ в вакууме
Эмаль А К-512, черная ТУ 6-10-966—75 3,0 18—23 Л, С С высокой светопоглощающей способностью. По механическим свойствам, стойкости к орга- ; ническим растворителям и перепаду температур покрытие аналогично АК-243. Эмаль содержит летучий пластификатор
Эмаль КЧ-736, черная ТУ 6-10-12-71—76 3,0 180 л, с, ж, ож С высокой светопоглощающей способностью, обладает относительно высокими физико-механическими свойствами, теплостойкостью к растворителям
Лакокрасочный материал, документ на поставку Интегральный коэффициент отражения света в видимой области спектра, %, не более Максимальная температура сушки, °Cj । ' । ।» и ** Условии эксплуатации по ГОСТ 9.009 — 73 Характеристика
Эмаль ХС-1107 ГМ, черная ТУ 6-10-1042—76 5,0 18—23 Л, С По механическим свойствам, стойкости к органическим растворителям аналогично АК-243. Выдерживает перепад температур от —60 до +6О°С
Эмаль ХС-77К ТУ 6-10-12-58—76 3,0 По основным свойствам аналогично ХС-1107 ГМ
Черные матовые покрытия
Эмаль ЭФ-1118 М, черная ТУ 6-10-12-68—75 6,0 130 л, с, ж С высокими физикомеханическими свойствами, обладает стойкостью к органическим растворителям. Выдерживает перепад температур от —60 до +100° С
Эмаль МЧ-240 М, черная ТУ 6*10-17-01— 79 9,0 130 л, с С высокими физикомеханическими свойствами, обладает стойкостью к органическим растворителям. Выдерживает перепад температур от —60 до +60° С
Эмаль ХС-1107 М, черная ТУ 6-10-1042—76 9—12 18—23 л, с По свойствам аналогично ХС-1107 ГМ
Таблица 17.11. Основные лакокрасочные материалы для получения диффузных белых светоотражающих покрытий
Лакокрасочный материал, документ на поставку Интегр альный диффузный коэффициент отражения в видимой области спектра, % Минимальная темпер атура сушки, °C Условия эксплуатации по ГОСТ 9.009—73 (. г- ч; Характеристика
Эмаль АК-512, белая ТУ 6-10-967—76 80—83 18—23 Л, С Выдерживает перепад температур от —60 до +200° С; нестойко к органическим растворителям
Эмаль ВЛ-548, белая ТУ 6-10-12-30—76 76—80 18—23 Л Выдерживает перепад температур от —60 до +80° С
Эмаль АК-1102, белая ТУ 6-10-1408—72 80 18—23 л, с Обладает высокой светостойкостью; выдерживает перепад температур от —60 до +1206 С
Эмаль АК-573, белая ТУ 6-10-1352—73 82—87 18—23 л, с Нестойко к органическим растворителям
Эмаль АК-194 ТУ 6-10-901—75 75—80 100 л, с Отличается повышенной белизной и теплостойкостью при 140—150° С; выдерживает перепад температур от —60 до +Wc —
Специфические лакокрасочные материалы, применяемые в оптико-механическом приборостроен и и
При изготовлении оптико-механических приборов применяют лакокрасочные материалы со специальными свойствами: светопоглощающие, светоотражающие, для окраски нерабочих поверхностей деталей из стекла. В табл. 17.10—17.12 приведены основные лакокрасочные материалы, используемые для указанных целей, и дана краткая их характеристика.
Таблица 17.12. Лакокрасочные материалы для окраски нерабочих поверхностей деталей из стекла
Лакокрасочный материал Документ на поставку Минимальная температура суш кн, °C Условия эксплуатации по ГОСТ 9.009—73
Эмаль ХС-543, черная ТУ 6-10-12-32—76 18—23 Л, с
Эмаль ХС-1107М, черная ТУ 6-1042—76 18—23 л, с
Эмаль ЭП-51, черная с введением 10% микроталька * ГОСТ 9640—75 18—23 л, с, ж
Эмаль КО-843, черная ** ТУ 6-10-11-01-61—76 100 л, с, ж
* Можно применять для подк-раски фасок и оправ после заваль-цовки линз.** Покрытие стойко к органическим растворителям; выдерживает воздействие температуры +300° С и развальцовку.
Требования к окрашиваемым деталям
Детали должны поступать на окраску после проведения сварочных* слесарных, механических работ. Поверхности деталей не должны иметь заусенцев, не удаленных сварочных брызг и флюсов, наплывов пайки, острых кромок радиусом менее 0,3 мм.
На поверхностях литых деталей не должно быть неметаллических макровключений, пригара формовочной земли, нарушений сплошности металла в виде раковин, трещин, спаев и других неровностей.
Шероховатость поверхности, обеспечивающая получение покрытий заданного класса отделки без шпатлевки и со шпатлевкой, должна ’ удовлетворять требованиям табл. 17.13.
Шпатлевка служит для сглаживания неровностей окрашиваемой Поверхности. Необходимо отметить, что шпатлевание снижает механические и защитные свойства покрытия, так как толстые слои шпатлевки Подвержены растрескиванию и скалыванию. В связи с этим необходимо Стремиться устранять дефекты поверхности не шпатлеванием, а предварительной механической обработкой, что не только повышает качество
Таблица 17.13. Рекомендации по выбору шероховатости окрашиваемой поверхности
Класе покрытия Б ид покрытия Класс шероховатости поверхности металлов по ГОСТ 27*9—73
Без при мемеивя шпатлевки С применением шпатлевки для деталей
малогабаритных крупногабаритных
I Гладкое глянцевое 7 ' ——
II Гладкое (высокоглянцевое, глянцевое, полу глянцевое, полу матовое) 6——7 6 5
Рисунчатое 6 6 4
III Гладкое (глянцевое, по-луглянцевое, полуматовое, матовое) 6 5 3-4
Рисунчатое 5 4 3
IV Г л адкое (полу гл я нце- вое, полуматовое, матовое) 5 4 2
Рисунчатое 4 3 1
V Гладкое (полуглянцевое, полуматовое, матовое) 4 Не регламентируется
Рисунчатое 2 То же
VI; VII Гладкое, рельефное Не ре гламентируется
Примечание. Не допускается производить шпатлевание на ружных поверхностей деталей, испытывающих вибрацию, ударные на грузки, тряску, и поверхностей, подлежащих гравировке.
Лакокрасочного покрытия, но и в большинстве случаев значительно менее трудоемко.
Общая толщина масляных, глифталпевых и других подобных шпатлевок ие должна превышать 1,5 мм для умеренного климата и 0,5 мм для тропического при толщине каждого слоя не более 0,5 мм. Толщина одного слоя эпоксидной шпатлевки — 2 мм.
Временная противокоррозионная защита изделий
Временная противокоррозионная защита (консервация) обеспечивает защиту изделий от атмосферной коррозии при хранении и транспортировании. Такой защите подлежат изделия с металлическими поверхностями, а также с металлическими и неметаллическими неорганическими покрытиями. Временной защите ие подвергаются изделия или их поверхности при условии сохранения ими требуемых эксплуатационных и декоративных свойств (изготовленные из коррозионно-стойких металлов или расположенные внутри герметизированных объемов н т, п.).
Консервация включает подготовку поверхности, нанесение средств временной защиты и упаковывание. В зависимости от применяемого технологического процесса н требований, предъявляемых к изделию/ 582
допускается исключать одну или две из указанных стадий или совмещать их.
Варианты временной противокоррозионной защиты, пригодные для применения в оптико-мехаиическом приборостроении, приведены В табл. 17*14.
Таблица 17.14. Обозначение варианта временной противокоррозионной защиты
Обозначение Характеристика варианта защиты
33-1 Защита коисервационными маслами изделий из черных и цветных металлов
33-4 Защита коисервационными смазками изделий из черных и цветных металлов
33-7 Защита снимаемыми ингибированными полимерными покрытиями изделий из черных и цветных металлов
33-10 Защита с помощью статического осушения воздуха изделий из черных и цветных металлов
33-14 Защита летучими ингибиторами коррозии изделий нз черных металлов
33-15 Защита летучими ингибиторами коррозии изделий из черных и цветных металлов
33-16 Защита изделий с помощью инертной атмосферы
Выбор конкретных средств временной противокоррозионной защиты проводят по ГОСТ 9.014—78.
Прн полной консервации оптико-механических приборов и устройств, радиотехнических изделий и электронно-вычислительной техники рекомендуется применять варианты временной защиты ВЗ-10, ЯЗ-14, ВЗ-15, 33-16, а при частичной консервации 33-1, 33-4 и 33-7.
ГЛАВА 18
ИСТОЧНИКИ И ПРИЕМНИКИ СВЕТА
Лампы накаливания для оптических приборов
К лампам накаливания, применяемым в оптических приборах, предъявляются повышенные требования в отношении качества стекла баллонов, размера, расположения тела накала (табл. 18.1—18.4) и выполнения цоколя (рис. 18.1)
0ПЗ~0,25 0П6-25+25
л
D
0П13-5О
0П17-30
Рис. 18.1. Лампы накаливания для оптических приборов
Я
ООН- OJ
Кинопроекционные лампы накаливания
Хорошее качество освещения дают лампы, у которых тело накала имеет форму плоской спирали (типа К30-400, К17-170, К40-750). Ряд ламп имеет фокусирующие цоколи. С целью повышения общей яркости у некоторых ламп (К 110-300, КН0-500, К110-750, К127-300) секции тела
Рис. 18.2. Кинопроекционные лампы
накала второго ряда располагают против промежутков секций первого ряда. Лампы разных типов изготовляют с разными цоколями (рис. 18.2 и табл. 18.5). Лампы К127-150-1 выпускаются как с резьбовым, так и с двух контактным штифтовым цоколем диаметром 22 мм. Высота светового центра (номинальная) Н = 62 мм.
Таблица 18.1. Основные световые и электрические параметры и размеры ламп накаливания для оптических приборов [см. рис. 18.1 J
а ч м и а Г М-* Размеры ламп и тела накала, мм, не более < — г
Тип лампы в I Напряжение, Мощность, Вт (ток, А) Световой поте Световая отда дм/Вт Диаметр колбы D Длина дампы L 1 Высота све*/| тового цев* тра Н Ширина (или диаметр тела накала а Высота тела накала Ь Срок службы Тип декеля ТУ
002,4-1,1 2.4 1,1 А 28 18 33 Не нор- 5 Е10/20 ТУ 16.535.666—72
мируется
0112,5-0,2 ОП2.5-2 (СЦ77) 2,5 2,5 0,2А 2 4 9 4,5 18 12 33 24 То же > 1,5 0 0,23 0,8 20 100 Е10/20 Е10/13 ТУ ТУ 16.535.666—72 16.535.666—72
ОПЗ-О.25 3 0,25 А 3,2 4,6 14 11,5 2,3-0,6 75 Специальный СУ3.371.896 >
ОПЗ-0,5 3 0,5 А 7 •mW 5,2 66 И 100 в ТУ 16.535.610—71
ОП4-44 (СЦ75) 4 4 40 10 18 34 10,5 1.6Х 1,6 1,6 100 в ТУ 16.535.765—78
ОП4-4-2 4 4 40 HIM 18 34 1.2 1,2 100 1Ф-С11 ТУ 16.535.766—72
ОП4.5-33 4,5 33 600 41 68 29 —- 30 P20J/21 ТУ 16.535.662—72
РН440 4 10 по 43 75 41 —- —- 50 B15d/18 ТУ 16.535.538—77
РН6-3 6 3 15 8,2 32 —- —- —- 200 Софитный ТУ 16.535.538—77
РН6-7 6 7 90 20 39 22 —- —- 15 1Ф-С11 ТУ 16.535.666—72
РН6-7.5 6 7,5 88 26 46 24 0,9 1,5 40 B15S ТУ 16.535.666—72
PH-645-2 6 15 165 -HIM 21 65 —- — 100 BI5d ТУ 16.535.538—77
РН6-25 (СЦ69) 6 25 340 33 67 —- 5 1,3 100 Е14/29X22 ТУ 16.535.668—78
РН6-30-1 (СЦ70) 6 30 405 — ..IR 33 67 3 2 80 Е14/29Х 22 ТУ 16.535.668—78
ОП6-25+25 6 25 312 12,5 26 47 28 2,4 1,9 100 В15/18 ТУ 16.535.733—78
ОП8-0.6 (СЦ60) 8 0,6 А 48 10 15,5 28 —- — 50 Е10/20 ТУ 16.535.666—72
ОП8-3.2 (СЦ76) 8 3,2 29 9 12 24 2 0,6 50 Е10/13 ТУ 16.535.666—72
ОП8-9 (СЦ80) 8 9 84 9,3 18 33 —- 1,7 3,2X2,5 1,7 2,5 50 Е10/20 ТУ 16.535.666—72
ОП11-40 U 40 840 21 21 57' 35 25 2Ф-Д30-1 ТУ 16.535.713—73
ОП1245 12 15 130 -HIM 25 80 —- 0 0,8 4—5 1000 ТУ 16.545.089—76
РН8-20 (СЦ61) 8 20 250 21 56 ₽ 42 2,8 2 100 B15S ТУ 16.535.668—78
РН8-30-1 (СЦ68) 8 30 465 31 86 48 1,3 5,5 100 P20J/21 ТУ 16.535.668—78
РН8-30 8 30 525 25 81 —- 7 0,6 75 BI5S ТУ 16.535.538—77
РН8-35 8 35 450 31 86 48 1,4 3,2 200 P20J/21 ТУ 16.535.668—78
PH 12-30 12 30 500 чм 31 86 72 —- —- 100 Е27 ТУ 16.535.668—78
PH 12-35-1 (СЦ63) 12 35 560 41 70 42 0 1,3 —* 25 Р204/21 ТУ 16.535.668—78
PH 12-50 (СЦ64) 12 50 1000 — ..IR 36 68 35 3,5 2 50 P20d/21 ТУ 16.535.668—78
РН12-100 (СЦ62Г) 12 100 1750 1 61 93 60 0 4,8 —- 75 B22d/25 ТУ 16.535.668—78
PH 12-100-2 (65Г) 12 100 1750 61 113 88 0 4,8 75 Е27 ТУ 16.535.668—78
ОП12-100 12 100 2500 25 51 88 35 5,5X2,5 СО СП сч — 25 1Ф-С34-1 ТУ 16.545.025—75
ОШ 3-50 13 50 1500 19,5 57 —- 2,6 1 2Ф-Д30-1 . ТУ 16.535.714—73
опзз-о,з 33 0,ЗА 130 26 90 55 2,5 1,0 150 Е14/25Х ТУ 16.535.730—78
PH 110-40 110 40 280 21 140 * —- 200 Е14 ТУ 16.535.538—77
PH 120-15 120 15 97,5 21 60 —- 300 B15J ТУ 16.535.538—77
PH 120-25 120 25 125 43 75 •W—' —— 300 Е14 ТУ 16.535.538—77
PH 230-15 230 15 94,5 43 75 1*— J 500 Е14 ТУ 16.535.538—77
Таблица 18.2. Лампы накаливании миниатюрные и сверхминиатюрные
Тип лампы Напряжение, В Ток, А Световой поток, лм Диаметр колбы D, мм Длина лампы, мм Срок службы, Ч Тип цоколя ГОСТ или ТУ
МН 1-0,068 (МН1) 1 Л £ 0,068 м п ы м И Н И ! 12 а т ю р 24 н ы е 300 Е10/13 ГОСТ 2204—74
МН2,5-0,068 (МН2) 2,5 0,068 —- 12 24 250 Е10/13 ГОСТ 2204—74
МН2,5-0,15 (МНЗ) 2,5 0,15 2,3 12 24 45 Е10/13 ГОСТ 2204—74
МН2,5-0,29 (МН4) 2,5 0,29 4,0 16 30 300 B9S/14 ГОСТ 2204—74
МН2,5-0,4 (МН5) 2,5 0,40 9,0 12 24 15 Е10/13 ГОСТ 2204—74
МН2,5-0,54 (МН7) 2,5 0,54 7,0 16 30 550 B9S/14 ГОСТ 2204—74
МН2,5-0,72 (МНЮ) 2,5 0,72 12 16 30 120 Е10/13 ГОСТ 2204—74
МНЗ-0,14 (МН 12) 3,0 0,14 3,7 12 24 6 Е10/13 ГОСТ 2204—74
МН2,5-0,068-1 2,5 0,068 12 24 1500 Е10/13 ТУ 16.535.514—75
МНЗ,5-0,26 (МН 13) 3,5 0,26 7,5 12 24 25 Е10/13 ГОСТ 2204—74
МН6,3-0,3 (МН 14) 6,3 0,30 8,5 12 24 1000 Е10/13 ГОСТ 2204—74
МН 13,5-0,16 (МН 16) 13,5 0,16 12 12 24 100 Е10/13 ГОСТ 2204—74
MH26-0J2 (МН 17) 25 0,12 12 11 28 200 Е10/13 ТУ 16.535.494—70
МН26-0,12-1 (МН 18) 26 0,12 11 11 31 200 Е10/13 ТУ 16.535.494—70
МН36-0,12 (МН24) 36 0,12 12 11 30 100 B9S/14 ТУ 16.535.309—69
МН 18-0,1 (МН23) 18 0,10 12 11 31 200 Е10/13 ГОСТ 2204—74
СМН6,3-20 6,3 Ламп 0,02 ы с в е р 0,26 я со со н и ат 9 юр нь 600 I е Специальный ТУ 16.535.446—76
СМН6,3-20-2 6,3 0,02 0,26 32 600 Без цоколя ТУ 16.535.446—76
СМН9-60 9 0,055 1,4 3,0 9 500 Специальный ТУ 16.535.453—76
СМН9-60-2 9 0,055 О rf* 3,0 27 500 Без цоколя ТУ 16.535.453—76
СМН10-55 10 0,05 3,0 9 1500 Специальный ТУ 16.535.453—76
СМН10-55-2 10 0,05 1.0 3,0 27 1500 Без цоколя ТУ 16.535.453—76
Т абл и ца 18.3. Лампы накаливания коммутаторные (по ГОСТ 6940—74)
Тип лампы Напряжение, В Ток, А Световой поток, лм Сила света, кд Диаметр колбы Ь, мм Длина лампы, мм Срок службы, ч
КМ6-60 (КМ-1) 6 0,06 0,4 0,035 6 46 500
КМ 12-90 (КМ-2) 12 0,09 0,55 0,045 6 46 2000
КМ24-35 (КМ-24) 24 0,035 0,9 0,07 6 46 2000
КМ24-90 (КМ-3) 24 0,09 1,75 0,14 6 46 1000
КМ48-50 (КМ-4) 48 0,05 2,9 0,23 6 46 1000
КМ60-55 (КМ-5) 60 0,055 5,7 0,45 6 46 500
Т а б л и ц а 18.4. Лампы накаливания в цилиндрической оправе
Тип лампы Напряжение, В Мощность, Вт Световой поток, лм Диаметр колбы £>, мм Длина лампы, мм Срок службы, и Тип цоколя ГОСТ или ТУ
Ц127-10 (Ц-3) 127 10 50 20 86 1000 В15/18 ГОСТ 5011—69
Ц127-25 (Ц-14) 127 25 190 25 86 1000 Е14/25X17 ГОСТ 5011—69
Ц220-10 (РНЦ220-10) 220 10 45 25 86 1000 Е14/20 ТУ 16.535.429—70
Ц220-25 (Ц-16) 220 25 170 25 86 1000 Е14/25Х17 ТУ 16.535.429—70
Приме '7 11 ч а И и е. Световая отдача Б лм/Вт.
Световой поток, лм Размеры ламп
Тип лампы Напряжение, В Мощность, Вт Диаметр колбы Ь Длина лампы
К4-3 Кб-30 Кб-30-2 (К19) К8-55 К10-50 (К27) К 10,5-80 (К25) К12-30 (К7) К12-30-2 (К8) К12-50 (КЮ) К12-90 К16-90 К17-170 (КЗО) К17-170-2 (К24) K30-400 (К22) К40-750 (К32) К110-300 (К12) К110-500-2 (К14) К110-500 К1Ю-500-2 (К14) К1Ю-750 (К 15) К127-150-1 (К26) К127-300 (К 18) К127-500 К22О-1ОО К220-300 К220-500 КГМ9-70 *** КГМ12-40 КГМ6.6-45 КГ-220-500-1 КГ-220-1000 (тепловые) КГМ-220-1000-3 (световые) КИМ-6-25-25 КГМ6.3-15 КГМ12-100 КГМ40-750 КГМ27-27-1 КГМЗО-ЗОО-2 * Габаритная яркость 4 6 6 8 10 10,5 12 12 12 12 16 17 17 30 40 110 по по по по 127 127 127 220 220 220 ,? 6,6 220 220 220 6 6,3 12 40 27 30 , Мкд/м*. * 3 30 30 55 50 80 30 30 50 90 90 170 170 400 750 300 500 500 500 750 150 300 500 100 300 500 70 40 45 500 1000 1000 20 15 100 750 27 300 * Осёва 24 550 555 1 400 850 1 970 528 528 1 000 2 400 90 4 420 4 420 20* 21 800 6 450 И ООО 7 800 ** 11 000 17 250 2 480 6 450 10 000 * 1 700 5 400 7 900* 20* 720 750 13 000 8 000 2 600 250 200 2 900 23 500 590 35* ) я сила светг 26 22 26 25 25 26 25 43 51 26 40 27 27 37 37 37 37 180 37 37 37 37 112 26 37 112 10,75 8,5 8,5 10,75 П 10,75 10,75 8 11 29 8 14,5 ь кд. **• ’ 51 57 51 83 83 78 86 70 77 83 96 155 150 155 155 145 155 267 155 155 144 145 160 78 145 160 47 45 60 132 375 180 36 30 45 ПО 82 55 Гип КГМ9-
параметры и размеры кинопроекционных ламп
и тела накала, мм, не более Срок службы, ч Тип цоколя ГОСТ или ТУ
• Высота световогр центра Н Ширина тела накала а Высота тела накала b
23 2,3 0,18 100 P19S/13 ТУ 16.535.533—77
30 1,2 3,1 100 1Ф-Д30-1 ГОСТ 4019—74
31 4,5 1,5 10 B15S ГОСТ 4019—74
36 15 P19S/13 ТУ 16.535.533—77
60 6,0 2,0 100 Е14/25Х 17 ГОСТ 4019—74
37 5,5 1,8 25 В15$ ГОСТ 4019—74
60 4,0 1,5 50 Е14/25X17 ГОСТ 4019—74
41 7,0 0,8 50 BI5rf ГОСТ 4019—74
45 7,2 . 0,95 50 В154 ГОСТ 4019—74
40 4,5 3,5 25 B15S ТУ 16.535.078—75
41 20 Специальный ТУ 16.535.728—73
60 6,5 4,3 20 1Ф-С34-1 ГОСТ 4019—74
81,5 6,5 4,3 20 P26S/31 ГОСТ 4019—74
60 8,9 6,4 40 1Ф-С34-1 ГОСТ 4019—74
66 13,6 9,4 30 1Ф-С34-1 ГОСТ 4019—74
70 8 8,5 50 В224/25 ТУ 16.535.533—77
81,5 10 10 30 P26S/31 ТУ 16.535.533—77
100 Е40/45 ТУ 16.535.533—77
81,5 10 10 30 P26S/31 ТУ 16.535.533—77
81,5 11 11 30 P26S/31 ТУ 16.535.533—77
74 1,0 22 200 Е27 ТУ 16.535.533—77
70 8 8,5 50 В224/25 ТУ 16.535.533—77
— 1 6 Е27/32Х 30
40 9,0 9,0 50 1Ф-Ш15-2 ТУ 16.535.076—75
70 13 13 50 В224/25 ТУ 16.535.533—77
1 6 Е27/32Х 30 ТУ 16.535.533—77
1 2,6 2,6 200 Без цоколя ТУ 16.535.229—75
Световая отдача 18 лм/Вт 3,о 1,5 100 » » ТУ 16.535.261—76
— Спираль 1000 Плоский ме- ТУ ЮС0.337.015
0 1,4X5,5 таллический
Цветовая температура 3200 К 1 130 То же ТУ 16.535.439—76 ТУ 16.535.354—76
। 285 1,2 5000 ।
Цветовая температура 3200 К —— 400 ТУ 16.535.354—76
2,7 1,0 400 Без цоколя ТУ 16.535.229—75
200 » » ТУ 16.535.366—75
4,0 2,3 75 » » ТУ 16.535.511—76
— 1 150 ТУ 16.535.711—73
» ТУ 16.535.683—72
6 3,5 50 ТУ 16.535.430—76
70 и ниже — лампы кварцевые галогенные.
Лампы накаливания с йодным циклом (галогенные) для оптических приборов
Кварцевые йодные лампы имеют преимущества перед обычными лампами накаливания: на протяжении всего срока службы колбы их не темнеют и, следовательно, не уменьшается световой поток; они отличаются большой световой отдачей, долговечностью и весьма малыми
Рис. 18.3, Малогабаритная лампа с йодным циклом (типа КИМ6-25+25)
1000 Мкд/м2), что
габаритами при большой мощности (рис. 18.3 н табл. 18.5).
Лампы электрические светоизмерител ьн ые
Светоизмерительные лампы предназначены для фотометрических работ (рис. 18.4.) Ха-рактеристики их приведены в табл. 18.6 и 18.7.
Дуговые лампы высокого и сверхвысокого давления
В табл. 18.8 приведены основные технические параметры и размеры дуговых ламп различных типов.
Ртутно-кварцевые лампы
Ртутно-кварцевые лампы (рнс. 18.5) излучают свет видимой и ультрафиолетовой областей спектра. Разрядный промежуток имеет малые размеры и очень большую яркость (до создает возможность использования ламп в раз-
личных оптических приборах для получения узкого пучка света большой интенсивности. Излучение ламп имеет линейчатый спектр с непрерывным фоном. Недостатками ламп являются длительное время разгорания (2—5 мин) и остывания после выключения для повторного зажигания, плохая цветопередача, особенно в длинноволновой части видимого спектра. Требуется повышенное (высокое) напряжение
для поджига.
Ксеноновые лампы с дуговым разрядом
Лампа этого вида (рис. 18.6) обладает большой яркостью и непрерывным излучением (см. рис. 18.7) в видимой и ближней инфракрасной областях. Сразу после включения лампа работает нормально. Ксеноновые лампы взрывоопасны, и поэтому для них требуются защитные устройства. Лампы питаются постоянным током через сетевой блок питания, содержащий понижающий трансформатор, выпрямитель и стабилизатор; включаются в сеть и зажигаются аналогично ртутным лампам сверхвысокого давления.
СНРШв,5-20в
Рис. 18.4. Лампы накаливания свето* измерительные
Рис. 18.5. Ртутная кварцевая лампа сверхвысокого давления
Газоразрядные циркониевые лампы
Циркониевые лампы обладают большой яркостью при очень малых размерах светящегося тела (табл. 18.8). Включение в сеть осуществляется через выпрямитель. Зажигание лампы производится при помощи индуктора.
H H n n n n •о n s x s x и и *o w Й E Ё E Ё 8 8 S ? 9 S о о yi СЛ crcgr Ф Ф . — О о •—* w Тип лампы
00 . 00 00 o> о ' СИ СИ Напряжение, В
ьоьэ»— С) •—* Q О О 05 сл о о о о Мощность, Вт
оз ко оо со то t© ф до Ф О ОО 00 ф СП ф ф 4^ цх о О О О О Ф Цветовая температура тела, К
оо *— оо до rf*. оо *ч ф си сл сл -ч Наибольший диаметр £>, мм
»—* Нн* Нн* Нн* Нм* оо ьэ о> со сп сл СЛ Ф О Ф си СП Наибольшая длина L, мм
1 1 1 I СЛ СП Высота светового центра Н, мм гслькых ламп пака; jL
о to to ю о о оо о о о -ч Ширина тела накала а, мм
ОО ОО о о 00 00 СП Высота тела накала Ь, мм Еивания (рис. 18.4.) *
со w w to to SSS8SS Продолжительность горения, ч
| Поз. на рис. 18.4
ТУ 16.545.111—76 ТУ 16.545.111—76 ТУ 16.545.111—76 ТУ 16.545.111—76 ТУ 16.535.678—77 ТУ 16.535.757—78 ТУ
Примем СИП35-500 СИП107-3500 СИП-107-500 СИП 107-1500 СИП35-150 СИПЗ.5-10 СИП 10-50 СИС107-1500 СИС 107-1000 СИС 107-500 СИС107-100 СИСЮ-5 СИСЮ-10 СИС 107-35 Тип лампы г
инне 00 СП 107 107 107 со ел ° . со In 107 107 107 107 107 Нм* О ф Напряжение, В
!. Данные ГОСТ rfs О 260 811 2? to to to 00 05 ' ф 915 099 365 158 СП 05 16,8 00 05 Мощность, Вт 1
1 1 1 1 1 1 1 1320 880 440 00 ОО 30,8 00 00 4». 4». наименьшая, Сила
о 1 1 1 1 1 1 1 1500 11000 500 1 100 00 сл ф СП номинальная) о ш 3 fts С\
1 — 64; новый ГО 1 1 1 1 1 1 1 (35 ОО Ф 1120 560 112 со ф “to о I! 5,6 наибольшая с» X я £ fS to
440 3080 1320 440 132 rfs ' rfs ОО СП 1 1 1 1 1 1 1 наименьший ’ о а го о и се ф X to
п ж оо X 500 3500 1500 500 150 СП Ф О 1 1 1 1 1 1 1 номинальный о 55= д о о *s Ж 4 X
о Зя X о V. сл ф о 3920 1680 560 Ф ОО СИ О> 11.2 1 1 1 1 1 1 1 наибольший я *• ь к q s ж X
1 — -
в стад’ to to to to СО 00 00 оо ^7^ О О О о 2360 2360 2360 ю оо 05 о to 00 СП ю 00 ф ф ю 8 ф й ф ф У ф ю со S Цветовая температура, к $
X тз в> W х; 00 00 сл 100 со 00 00 ОС 00 00 о 130 130 i 03 о со ф со ф 00 Оо 00 ОС Диаметр колбы Ь Разы 5s £ •s s
аботки. ОМ to со сл 210 150 150 140 1 । Си 235 ) 210 to о го <5 200 сл о 150 Длина лампы L еры ла мм s £ г
। 105 185 091 108 105 100 СП О 155 125 125 105 I 1 105 00 ОС ос 00 Высота светового центра Н мп и тела накала, ;, не более : ламп
ю ю to СЛ to Сп со со со 00 00 00 to 00 to СП to СП со ф 8? 00 00 Ширина тела накала а’ s to Ж s s
00 to ф СЛ Ф to 05 to СП to ф 00 СП СО ф to СП СП СП Высота тела накала Ъ i X X
Плоская *5 V То же Цилиндрическая & & V * * * * Плоская 1 Форма тела накала
m то го m to w to ГП to СО to го to со to Е27/32 го ю G0 to Е10-20 с косым раитом Е40/45 То же рантом с косым Е27/32 Тип цоколя J
j пь QJ со 8 ©j C\j сь ©5 ©5 ©\ ©\ £> р Е» Поз. на рис. 18.4
Таблица 18.8. Основные технические
Тип лампы Напряжение, В Мощность, Вт Ток, А Световой поток, клм Яркость, Мкд/м*
Лампы р т у т н ы е я
ДРШ100-2 20 100 5,2 1000
ДРШ250-2 28—36 250 7,8 800*
ДРШ250-3 72 250 » 12,5 100
ДРШ500М 76 500 •Пч 22 130
ДРШ1000 90 1000 53 120
ДРК-120 125 120 » 4,2 ——»
Лампы р т у т н о - к в а р ц е
ДРТ375 (ПРК-2) 120 375 3,7
ДРТ2500 850 2500 34 8,5 ——»
Л а м п ы ртутные высокого дав ления
ДРЛ125 125 125 5,6
ДРЛ250 130 250 -W 12,5
ДРЛ400 135 400 » 22,0
ДРЛ700 140 700 38,5 »
Л а м п а р т у т н а я
’ДБ15 54 15 0,3 - vwt* |
Ламп! ы д у Г 0
ДКсР-150А-1 26 150 3500
ДКсШ200 22 200 12 90
ДКсШ200-2 ** 22 200 Энергия 300* — -
вспышки
80 Дж
ДКШ3000-3 32,5 3000 100 105 600
ДКсРЗОООМ 33 3000 130 90 750
ДКсРбООО 40 5000 160 190 700
ДКсШ120 10—13 120 10—12 700
ДКсШ200-2 22 200 мч* 300*
ДКсШЮОО-2 22 1000 мч* 250
ДКсШЮОО-З 25 ' 1000 * 1 мч* 200
ДКсШЮООМ 25 1000 51 200
ДКсШ2000 27,5 2000 400
ДКСЭЛ2000 29 2000 » 1 400
"V Ла мпы дуговые
ДНаС18 22 18 1,05 0,08
ДВС25 50—100 25 0,3 ™ !
ДРГС12 30—95 12 0,3 ™ !
ДРС5О 55 50 1,05 1,0
ДРС600 68—78 600 8,0
ддсзо 50—100 30 0,3 1 — 0,3
Л а мпы ду г о в ы е
ДАЦ5О 220 | 50 — | — 1 30 I
/
♦ Сила света , кд. ♦♦/возможен импульсный режим работы.
параметры и размеры дуговых ламп
Длина дуги Ъ, мм Диаметр колбы D, мм Длина лампы L, мм Срок службы, ч Тнп цоколя ГОСТ или ТУ
свер хвысо кого д а в л е н и я
0,4 15 85 100 Специальный СУЗ.374.173
1.1 18 107 200 ЮЩ3.374.043
™ ! 40 145 500 ТУ 16.535.281—74
4,5 45 190 600 ТУ 16.535.281—74
8 58 232 100 » СУ0.337.054
—— 48 140 250 СУ3.374.009
н ы е вы С 0 к о го дав л е и и я
22 265 2 500 1 * 1 ТУ 16.535.280—74
31 1200 3 500 1 * 1 ТУ 16.535.387—70
с исправл е н н о й цв етн о с т ь ю
™ ! 91 184 10 000 Е27/32Х 30 ГОСТ 16354—70
" 91 227 10 000 Е40/45 ГОСТ 16354—70
—— 122 292 10 000 Е40/45 ГОСТ 16354—70
— 152 368 10 000 Е40/45 ГОСТ 16354—70
низко год; а в л е н и я
1 — 30 | 451,6 | 3 000 | • С13/24 • |»ТУ 16.535.273—75
в ы е кс е и о н о в ы е
—- 80 232 15 Специальный СУЗ.374.247
2—2,5 26 149 500 » СУЗ. 374.127
— 26 145 500 ОДО.337.078
4,3 59 330 650 ТУ 16.535.573—71
1,0 80 235 300 СУЗ.374.135
1,5 80 235 250 СУ3.374.120
0,4 15 100 100 » ОДО.337.078
" 26 145 500 » ОДО.337.078
—— 43 260 750 ТУ 16.535.251—64
—— 44 1500 1 500 СУ3.374.248
44 258 750 » СУЗ.374.248
52 320 1 000 * - » СУ3.374.217
— 50 320 1 000 ТУ 16.535.763—73
спектраль н ы е
33 165 200 » СУ0.337.063
" 33 121 200 Октальный ОДО.337.066
™ ! 43 124 200 » СУ3.334.105
1,0 33 165 300 Р27/32-2 СУ0.337.063
203 210 200 . Специальный СУ0.337.095
— 39 124 200 Октальный ЮЩ3.374.078
ц и р к о и и е в ы е
1 1,0 38 115 75 1ФС34-1 | СУЗ.374.040
Рис. 18.6. Ксеноновая лампа
Рис. 18.7. Распределение энергии в спектре излучения ксеноновой лампы типа ДКсШ
Газоразрядные спектральные лампы с линейчатым спектром излучения
Такого рода лампы применяются в спектроскопии, микроскопии, светотехнике и других областях. Лампы подразделяются иа две группы. Наиболее интенсивные линии спектра излучения, электрические и световые параметры первой группы приведены в табл. 18.9.
Все лампы имеют диаметр колбы 33 мм, длину 165 мм и высоту центра светящейся области 105 мм. Лампы включаются в сеть переменного тока 220 В через дроссель. Потребляемая сила тока от 0,9 до 1,8 А. Продолжительность горения ламп 200—300 ч, кроме лампы ДТС15 с продолжительностью горения 50 ч.
Во вторую группу входят водородная лампа ДВС25 и некоторые другие (табл. 18.8).
Импульсные и стробоскопические лампы
Импульсные (рис. 18.8) лампы предназначаются для фото- и киносъемок. Стробоскопические лампы применяются при измерении скоростей движущихся тел. В табл. 18.10 даны характеристики этих ламп.
Фотоэлектронные умножители
Фотоэлектронные умножители (ФЭУ) преобразовывают лучистую энергию в электрическую с большим усилением и обладают высокой чувствительностью. ФЭУ создают меньшие шумы, чем фотоэлемеиты-усилители. Благодаря указанным качествам ФЭУ широко применяются в оптических приборах. В табл. 18.11 приведены некоторые характеристики ФЭУ, а иа рис. 18.9 — их спектральные характеристики. 598
Таблица 43.9. Газоразрядные спектральные лапши первой группы
: ] ! Тип лампы 1 Наполнитель Длина волны, им Напряжение, В Наименьшая яркость, Мкд/.мЕ
видимая область ультрафиолетовая область
ДРС50 Ртуть 365,0 404,7 435,8 546,1 577,0 467,8 253,7 296,7 312,6 334,1 298,1 326,1 55 1000
ДКдС20 Кадмий 480,0 508,6 643,8 340,4 346,6 280,1 17 17
ДЦнС20 Цинк 468,0 472,2 481,6 632,2 328,2 330,3 334,5 19 8
ДТС15 Таллий 535,0 —— 18 20
ДНаС18 Натрий 589,0 455,5 687,0 19 20
ДЦзС16 Цезий 697,3 722,9 760,9 794,4 —— 10 2,5
Примечание. Число в обозначении лампы показывает ее мощность, Вт.
Тип лампы Рабочее напряжение, В Напряжение самопробоя, кВ Мощность, Вт Энергия вспышек, Дж Сила света, кд Наименьшая световая энергия, ЛМ' с Освечиванне, кд. с Диаметр колбы D, мм Длина лампы L, мм Срок службы, ч Срок службы (тыс. вспышек)
Поз. на рнс. 18.8
Таблица 18.10. Основные световые и электрические параметры и размеры импульсных ламп
ту
ИСК10 ИСК25 180 250 1,0 1,2 10 25 1,5 — 23 30 77 58 50 100 11.77.СУ3.374.046 11.76.ЮЩ3.374.138 -
ИСШ15 —- 0,6 4 —Ч 0,6 50 31 79 1000 — СУ3.374.077 1 »
ИСШ400 5000 — — 0,125 90 000 ——- ——- 0 52Х X 73Х 800 — — 4200 ЮЩО.337.007 ——-
ИСШ100-2 —Ч —Ч 100 —Ч 80 — 400 35 85 0,5 — СУ3.374.082 чч
ИРК20-3 400 1,5 — 20 — 35 4 50 — 5 ЮЩ3.374.113 а
ИФК50-1 200 1,0 50 140 7 55 30 СУО.337.048 б
ИФК120 300 1,5 120 Чч, 2500 Чч, 24 59 10 СУ3.374.052 —
ИФК2000 500 2,2 2 000 — 80 000 37 167 ч— 5 СУ3.374.041 в
ИФП800 700 2,5 — 800 —Ч 2 200 10 304 1 5 ЮЩ3.370.013
ИФП1200 1500 II Чч, 800 Чч, 4 200 10 345 5 ЮЩ3.374.074 чч
ИФП4000 1400 5,0 Чч, 4 000 — 120 000 8 895 ч * 10 СУО.337.028 —
ИФП5000 2250 3,0 Чч, 5 000 18 000 22 463 10 ЮЩ3.374.006 1 »
ИФП5000-2 1500 — Чч, 6 000 ^а* 16 465 —* 5 ЮЩ3.374.063 Ча*
ИФП8000 2600 3,5 8 000 —Ч —Ч 30 000 19,5 475 —* 5 ЮЩ3.374.009 чч
ИФП20000 4650 6,0 20 000 1 » ч_ 70 000 19,5 815 5 ЮЩ3.374.037 г
ИФП40000 5000 7,5 40 000 ч_ Чч, 14 000 19,5 1235 1 5 ЮЩ3.374.038 —
ИСП70-1 650 2,5 Чч, 0,18 7Х 4 5Х 90 10 — ЮЩ3.374.040 е
ИФТ200 • 200 0,6 ч— 200 ч— 200 28 67 Ча* 1 СУ3.374.088 - д
Основное назначение ФЭУ-79 — измерение пороговых световых потоков в области спектра до 830 нм в фотометрических и спектральных приборах широкого применения.
ФЭУ-88 служит для измерения модулированных пороговых световых потоков при постоянном световом фоне в области спектра от 300 до 830 нм. Порог чувствительности не более 2* 10 х- лм/Гц1^2.
ФЭУ-99 используются для измерении ультрафиолетового излучения на световом фоне в устройствах широкого применения. Фотокатод — теллуро-калиево-рубидиевый на кварцевом стекле. Спектральная анодная чувствительность на длине волны 253,7 нм равна 100 А/Вт
Рис. 18.8. Стробоскопические (импульсные) газоразрядные лампы
(при напряжении питания 1700 В). Отношение спектральной анодной чувствительности (на длине волны 365 нм к длине волны 253,7 нм) равно 0,02. Предел линейности световой характеристики в статическом режиме — не менее 1-10“6 А.
ФЭУ-100 служит для измерения пороговых потоков лучистой энергии в области спектра от 170 до 830 нм в устройствах широкого применения. Фотокатод — полупрозрачный сурьмяно-натриево-калиево-цезш-вый. Спектральная чувствительность фотокатода на длине волны 400 нм — не менее 2* 10"? А/Вт, а на длине волны 800 нм — не менее Ь 10“4 А/Вт. Предел линейности световой характеристики в статическом режиме (при анодной чувствительности 10 А/лм) равен 1*10"^ А. Наибольшее рабочее напряжение 2700 В.
ФЭУ-116 применяют для спектральных исследований в ультрафиолетовой области спектра. Приборы исполняются в двух вариантах: всеклиматнческом и тропическом. Фотокатод — теллуро-цезиевый на увиолевом стекле. Спектральная чувствительность фотокатода не менее 4,4 mA/Вт. Порог чувствительности — не более 5* 10 13 Вт/Гц1^2-Отношение ординаты спектральной чувствительности на длине волны 365 нм к ординате при максимуме чувствительности составляет не более 50%.
Параметр Тип ФЭУ
14А 17А 18А 1 19А 22 24 26 27
Спектральная характеристика (рис. 18.9) С-5 С-6 С-3 С-6 11— С-6 С-6 С-7
Область спектральной чувствительности, им Максимум спектральной чув- 330—750 300—600 200—600 300—600 400—1000 300—600 300—600 320—750
470—510 360—440 360—440 360—440 650—850 360—440 340—440 450—550
ствительвости, нм
Темновой ток, А, не более 4. 10’7 3.10“9 3.10’» 5-10*8 2.10"8 3.1O-7 5-10“8 5.IO*9
Чувствительность фотокатода, мкА/лм Наибольший ток анода, мА 60 20 20 15 — 25 20 30
5 лам- -
Напряжение питания, В 2200 1400 1400 1400 1400 2000 1200 2000
Наибольшая высота, мм 129 181 181 200 181 236 66,5 22,5 108
Наибольший диаметр, мм 52 49 49 49 22 82 30
Диаметр рабочей площади фото-катода, мм 40 16X5 16X5 34 16X5 34 4X4 25
Масса, г 120 120 130 150 — 250 25 40
Параметр Тип ФЭУ
28 31 25 39А 49—-49Б 50 54 55
Спектральная характеристика (рис. 18.9) С-1 С-6 С-6 С-15 С-8 С-6 С-4 С-5
Область спектральной чувстви- 400—1100 300—600 300—600 160—600 300—850 —- —-
тельиости, им Максимум спектральной чувствительности, нм 650—850 380—420 380—420 380—420 370—500 380—420 380—480 450—550
Темновой ток, А, не более 3-10-7 5-10’7 4.10-8 1-10-« 4.10-® 5-10-’ 4.10-’ 6.10-’
Чувствительность фотокатода, мкА/лм 15 20 20—40 25 50—70 30 20 20
Наибольший ток анода, мА .1 -» 10 1 1 1
Напряжение питания, В 1500 1400 1 50 1800 2200 2000 1900 1900
Наибольшая высота, мм 122 79 113 150 202 307 90 90
Наибольший диаметр, мм 34 22,5 34 48,5 171 91 21,5 21,5
Диаметр рабочей площади фото- 25 25 34 150 15X150 12 12
катода, мм
Масса, г 60 20 50 150 1000 750 40 40
--,41 »«, -1 -'. 1 1 Тип ФЭУ
Параметр 67А
56 60 62 63 64 65 67
Спектральная характеристика С-4 С-6 С-6 С-6 С-6 *•— ^*41*
(рис. 18.9)
Область спектральной чувстви- 300—650 — 400—1200 — —— —— 300—600 300—600
тельиости, нм
Максимум спектральной чув- 380—480 — 650—850 350—600 380—420 360—600 340—440 340—440
ствительности, нм
Темновой ток, А, не более Ь10*8 3.10-8 6- ю-’ 6.10-6 5.Ю-8 2-Ю'4 1,5-10-8 3.10-’
Чувствительность фотокатода, мкА/лм Наибольший ток анода, мА 25 20 15 20 25 20 20 40
10 1 0,1 — —J « *—- 5 30
Напряжение питания, В 2200 1400 1600 3500 1500 3500 1350 1350
Наибольшая высота, мм 132 70 95 295 175 380 79 79
Наибольший диаметр, мм 80 15 35 125 48,5 185 22,5 22,5
Диаметр рабочей площади фото- 60 10 11 100 5 150 10 12
катода, мм
| Масса, г 200 11 55 885 150 2300 20 20
Параметр Тип ФЭУ
67Б 68 69 69А 70 71 74 78
Спектральная характеристика (рис, 18,9) — — С-Н ' — С-15 —
Область спектральной чувстви- 300—600 300—820 — 300—820 — 300—600 300—600
тельности, нм Максимум спектр ал ьнон чувств и тельности, нм 300—600 380—480 — 400—440 400—470 420—460 350—450 380—460
Темновой ток, А, не более 3-10-8 МО"8 2-10-’ 5.10-’ 2.10-в 3.10-8
Чувствительность фотокатода, JLf К Д / П U 40 60 40 15 30 20 20
Наибольший ток анода, мА •_ 5-Ю"2 ——
Напряжение питания, В 1200 1400 1600 1600 1250 1300 1900 2200
Наибольшая высота, мм 79 75 90 90 119 107 118 160
Наибольший диаметр, мм 22,5 15 22,5 23 34,5 31 30 52
Диаметр рабочей площади фотокатода, мм 1' 10 10 10 25 16 25 40
Масса, г 20 20 30 30 100 55 30 200
Параметр Тип ФЭУ
84-1 84-2 | 84-3
81 82 83 85 86
Спектральная характеристика (рис. 18.9) С-4 С-4 С-1 —* С-8 С-6 —
Область спектральной чувствительности, нм — 400—1200 — 300—600
Максимум спектральной чувствительности, нм 380—480 380—480 650—850 420—550 420—550 340—440 380—490
1
* h
Темновой ток, А, не более 8-Ю-7 1-10-6 ЭНО-’ 2-10-’ 5.10-8 5-10-® ыо-’ — —
Чувствительность фотокатода, i/v А /пи 40 30 20 80 80 80 30 60
Мл Лт. Наибольший ток анода, мА 10 10 5 5
Напряжение питания, В 2000 2000 2100 1900 1900 1900 1250 1600
Наибольшая высота, мм 120 150 119 118 118 118 107 87
Наибольший диаметр, мм 52 80 35 34 34 34 30 20
Диаметр рабочей площади фото- , 40 60 24 25 25 25 25 10
катода, мм
Масса, г 140 220 80 75 80 80 50 30
Параметр Тип ФЭУ
91 92 93 94 95 97 102 103
Спектральная характеристика (рис. 18.9) —- — —* — С-4 —* —
Область спектральной чувстви- 340—650 340—650 — 300—870 300—870 —*
тельности, нм
Максимум спектральной чув- 380—490 380—490 380—500 300—870 300—870 360—460 300—600 320—360
ствительности, нм
Темновой ток, А, не более Чувствительность фотокатода, * г тл Д / TT'MJ 5.10-8 2.5-10-» 8-10-’ 6.10-8 3-10-’ 5.10-в ЗИ0-» 5-10-»
20 20 30 80 80 35 20 15
МаА/ J1M Наибольший ток анода, мА 2 2 10 10 10 10 3-10-2
Напряжение питания, В 1700 1700 2100 1500 1500 2400 2000 1800
Наибольшая высота, мм 180 170 120 190 260 117 80 85
Наибольший диаметр, мм 40 40 52 130 200 52 20 15
Диаметр рабочей площади фото- 25 25 40 100 160 40 16 3
катода, мм
Масса, г 150 148 140 500 1400 140 30 20
Параметр Тип ФЭУ
104 105 110 112 115 116 79 .S3 99 1 00
Спектральная характеристика - - - - - - - С-11 - 1 - -
(рис. 18.9)
Область спектральной чувстви- — — — — 300— ——
тельиости, нм 830
Максимум спектральной чув- 400— 400— 420— 650— 400— 1 — — —
ствительности, нм 440 440 520 850 450
Темновой ток, А, не более 5-10-’ 5.10"» —* 3-10-’ 5-10-’ — 4-IO"8 — З-Ю'®
Чувствительность фотокатода, мкА/лм 100 120 80 15 40 — 120 80 1 —-
Наибольший ток анода, мА 0,25 0,25 10 — 0,25 5-10-’ " — 0,05 0,01
Напряжение питания, В 2500 2500 2000 1800 1550 2000 2400 2000 2000 2200
Наибольшая высота, мм 125 ПО 135 90 90 90 170 85 100 100
Наибольший Диаметр, мм 49 49 80 22,5 30 22,5 48,5 29,5 34 34
Диаметр рабочей площади фото- 5 6 60 5 25 10 6 8 16 10
катода, мм
Масса, г 140 130 200 25 50 25 150 40 . 80 80
g ж жжшшшшт
<§ Длина волны, нм
Рис. 18.9. Спектральные характеристики фотоумножителей
Длина волны, нм
£ m~^oo lob воо е Длина fc/ш, нм
о Т а б л и ц а 18.12. Характеристики болометров
00 ________________________________________
Параметр Типы болометров
БМК-3 БМ.Ц-3 БМИ-1 БМ.И-2 БМ6-К1 БМ6-Ф1 БМ6-Ц1
Эквивалентная мощность шума при частоте модуляции лучистого потока 9 Гц, Вт/Гц1'2 (0,4+2) (0,4+2) 10’10 2.1O'10 1,5.10-® (0,5+1) 10-10 (0,5+1) Ю"10 (0,5+1) Ю'10
Спектральный диапазон чувствительности, мкм 0,3—25 0,3—50 0,3—25 0,3—25 0,3—25 0,2-8 0,3—50
Размеры приемной площадки, мм 1,9X0,4 1,9X0,6 1,9X0,4 1,9X0,4 1,9X0,4 1,9X0,4 1,9X0,6 । <
Постоянная времени, мс 20± 10 20 ± 10 10 (2+3)10-* 10—20 10—20 10—20
Сопротивление активного и компенсационного элементов при темпер атуре 20° С, Ом • 120—300 100—200 120—300 140—250 90—400 90—400 90—400 S
Продолжение табл. 18.12
Параметр Типы болометров
БМ6-К2 БМ6-Ф2 БМ6-Ц2 БМ7 классов
1 2 3
Эквивалентная мощность шума при частоте модуляции лучистого потока 9 Гц, Вт/Гц1/2 (1,1+2) 10-ю (1,1 + 2) 10-1° (1,1+2) 10-1° Не более 5.10-w Не более 1.10-1“ Не более 2.10"10
Спектральный диапазон чувствительности, мкм 0,3—25 0,2—8 0,3—50 0,13—50 0,13—50 0,13—50
Размеры приемной площадки, мм 1,9X0,4 1,9X0,4 1,9X0,6 1,4X0,2 1,8X0,4 1,1,4X0,2 1,8X0,4 4X0,2 1,8X0,4
Постоянная времени, мс 10—20 10—20 10—20 20—30 20—30 20—30
Сопротивление активного и компенсационного элементов при температуре 20° С, Ом 90—400 90—400 90—400 100—500 100—500 100—500
Примечание. Болометры типов БМ6 и БМ7 унифицированные.
о о
Таблица 18.13. Основные параметры фоторезисторов
Тип фотоприемника Фоточувств нтельная площадь, мм2 Диапазон спектральной чувствительности, мкм Темновое сопротивление, мОм Р абочее напряжение, В Световой ток, мкА Постоянная времени, с ТУ . . . ,
СФ2-1 0,5X1,5 0,45—0,9 15 15 500 * 0,08 ОЖО.468.137
СФ2-2 12X6 0,4—1,0 2 5 500 * 6 УБ4.681.128
СФ2-5 0 8X5,8 0,3—0,8 ^•1 10 500 * 0,8 ОЖ0.468.077
СФ2-8 0 6X2 0,45—0,85 100 100 1000 * 0,03 ОЖО.468.095
СФЗ-4Б 0 5,8 0,4—0,85 100 15 1200 * 0,008 ОЖО.468.129
СФЗ-1 0,5X1,5 0,47—1,1 30 15 750 * 0,06 ОЖО.468.137
ФСК-1 28,8 0,5—0,9 3,3 50 1500 * 0,05 ОЖО.468.126
ФСД-1 4X7,2 0,45—1,2 2 20 1500 * 0,04 ОЖО.468.126
ФПФ7-А 3,7X2 0,4—0,7 J 6 400—3000 ** 2 *** 3-3.1292—78
ФПФ7-Б 3,7X2 0,4—0,7 1 6 250—900 ** 4 *** 3-3.1292—78
ФСВ-16АН 12—16 1,0—3,3 5 20 SB500 В/Вт — СЛ0.468.000
ФСБ-19АА 12—16 1,0—3,3 15 Sg2500 В/Вт — СЛ0.468.000
Sb —, интегральная чувствительность.
* Прн освещенности В ~ 200 лк. ** При 8—10 лк. ••* При В = 1 лк.
NO
0>
T а б лица 18.14. Основные параметры фотодиодов
Тип фото-приёмника Длина, мм Диаметр, мм Фото-чувствительная площадь, мм2 Интегральная чувствительность, мкА/лм
ФД-1 18 8,2 5 >1,0-10-1
ФД-2 2,2Х 10 — 1 >2-10-2
ФД-3 12 3,85 2 >3,7-10-2
ФД-ЗА 12 3,85 2 >3,7* 10“ 3
ФД-5Г 8 8,9 2,5 —•
ФД-7К 6,5 19,6 78,5 0,47
ФД-К-155 12 11,1 19,6 >3,5—7,5мА/лм
ФД-9ЭША 8,2 8,0 1 >17 мА/лм
ФД-1690-В 12,5 3,87 2 >8-10~3
Ф Д-21 КП 12,5 3,87 0,2 3,3 мА/лм
ФД-24К 6,5 19,6 78 0,47
ФД-19КК 6,0 7,2 1X4 3,8 мА/лм
ФД10 9,9 8,3 7,1 —
ФД-8К 12,5 3,87 2 >8-10-®
ФД-23К 14 5,5 2—3 1,4-10-3
ФД-28КП — 1,24 0,2 А/Вт (X = 0,6 мкм)
ФДК-071 — 2,2 2,42 ЗмА/лм
Диапазон спектральной чувствительности, мкм Рабочее напряжение, В 4 Постоянная времени, с Темновой ток, мкА ТУ
0,5—1,7 15 ^30 СЛЗ.368.000
0,5—1,7 30 — ^25 СЛ3.369.001
0,5—1,8 10 — 3-3.1357—76
0,5—1,8 10 5-Ю"3 ^10 СЛ3.368.015
0,9—1,8 15 — <8 СЛ3.368.047
0,4-1,2 27 СЛ3.368.021
0,4—1,2 10 ^10 СЛ3.368.054
— 10 1,2-10-’ СЛЗ.368.070
0,4-1,2 20 ^3 СЛ0.336.004
0,5—1,05 20 6-10'9 0,017 АГЦ3.368.094
0,47—1,12 27 10~Б СЛ3.368.096
0,5—1,1 3 1,5- 10-е =^0,1 OC3.368.027
0,5—1,75 10 1,2-10“7 20 АГЦЗ.368.112
0,4-1,2 20 12-Ю-3 СЛ0.336.001
0,5—1,12 20 10“6 J СЛЗ.368.095
0,4-1,1 — " 0,03 АГЦ3.368.109
0,4-1,1 10 — 1-1 10-’ OC3.368.020
Болометры
В качестве приемников инфракрасного излучения применяются болометры. Основными элементами болометра (рис. 18.10) являются два термочувствительных сопротивления в виде тонких висмутовых слоев, нанесенных на подложку из нитроцеллюлозы и помещенных в стеклянный или металлический баллон. Одно сопротивление (приемный элемент) подвергается воздействию измеряемой радиации, другое ___________ (компенсационный элемент) — служит для п /- —7' компенсации влияния изменения темпер а-"и ТУРЫ внешней сРеДы- В табл. 18.12 приве-1 дены характеристики некоторых болометров.
Электронно-оптические преобразователи (ЭОП)
Эти преобразователи применяют для преобразования изображения, полученного в невидимых лучах, в видимое. Для преобразования изображения, полученного в инфракрасных лучах с длиной волны до 1,2 мкм, применяют ЭОП типа П-4 (ОДО.335.084ТУ). Эти же преобразователи, только с увиолевым или кварцевым окном, используют для преобразования изображения, полученного в ультрафиолетовом свете с длиной волны
Рис. 18.10. Болометр типа БМК-3
220 им.
Характеристики ЭОП типа П-4: экран сульфидио-селенидиый желто-зеленого свечения; фотокатод кислородно-цезиевый; рабочее напряжение — 18 кВ; диаметр фотокатода — 20 мм; разрешающая способность в центре — 30 линий/мм (в плоскости фотокатода 18 линий/мм); область спектральной чувствительности 0,8—1,2 мкм; увеличение 0,6*; дисторсия — 10—12%. Срок службы не менее 500 ч.
Фоторезисторы и фотодиоды
В основе работы фоторезисторов лежит изменение электропроводности чувствительного слоя приемника при его облучении. Величина чувствительности по напряжению фоторезисторов зависит от схемы, в которую включен приемник. В табл. 18.13 приведены основные параметры и характеристики некоторых фоторезисторов.
Фотодиодами принято называть фотоэлектрические полупроводниковые приборы, в которых при воздействии лучистой энергии возникает фототок.Фотодиоды могут включаться в схемы как с внешним источником питания, так и без него (включение в вентильном режиме). В табл. 18.14 приведены основные параметры и характеристики фотодиодов.
Литература; [3, 12, 45, 89, 105, 115].
ГЛАВА 19
ОРГАНИЗАЦИЯ РАБОЧЕГО МЕСТА И ОРГАНЫ УПРАВЛЕНИЯ ПРИБОРАМИ
Рабочее место оператора
При конструировании приборов следует обеспечивать наилучшие условия для восприятия информации, управления системой и наименьшую утомляемость оператора. Разработку рабочего места наблюдателя нужно производить с учетом требований инженерной психологии.
Габариты рабочего места оператора должны основываться на антропометрических данных.Размеры человеческого тела, которые необходимо учитывать при разработке рабочего места, приведены в табл. 19.1 и на рис. 19.1, а. Рациональные размеры рабочего места приведены в табл. 19.2 и на рис. 19.1, б.
Таблица 19.1. Размеры человеческого тела, см
Обозначение размера на рис. 19.1, а Наименование размера Мужчины Женщины
X а X а
1 Рост 168 5,8 156,7 5,7
2 Высота глаз (стоя) 156,9 5,8 145,8 5,5
3 Высота глаз (сидя) 118 4,3 по 4,2
4 Высота плеч 137 5,5 128,1 5,2 3,5
5 Высота до верхнего края согнутой ноги 56 3,6 51,3
6 Расстояние от туловища до края согнутой ноги 33 3,6 31 3,5
7 Расстояние от края колена до конца ноги 21 2,6 18 2
8 Длина руки 75 3,5 69,7 3,1
9 Рассто я в и е от локтя до конца кисти 46,5 2 42,7 1,8
10 Ширина плеч 41 2 37 1,8
11 Ширина бедер 34,4 2,1 38,8 3,1
Обозначения: X — среднее значение; о — среднее квадратическое отклонение.
Таблица 19.2; Размеры рабочего места, см
Обозначение иа рис. 19.1, б Параметр Размер при положении оператора
сидя СТОЯ
1 1 Высота рабочего места над столом: на уровне глаз 36^6 * (для горизонтальной оси) 28—44* (для наклонной осн)
2 » » рук Высота рабочего места от пола: на уровне глаз » » рук До 20 114+5 До 95 По условиям работы 137±5,5 115
3 4 Высота рабочей плоскости стола Высота пространства для ног 72—75 Не менее 60 Не менее 90
б Глубина пространства для ног » » 50 > > Ю
€ 7 * р Ширина пространства для ног Высота стула азмеры по ГОСТ 3178—75 » % 45 40—45 » » 50
Наклонные оптические оси приборов рекомендуется располагать относительно горизонтали под углом 30—40° для положения сидя и под углом 45—60° для положения стоя.
Органы управления
При конструировании органов управления необходимо учитывать их форму, размеры и расположение; амплитуду, направление и траекторию движения; усилия; цвет и другие факторы. Сравнительные характеристики наиболее распространенных органов управления приведены в табл. 19.3.
Для кнопок клавиш (табл. 19.4) наиболее удобна четырехугольная форма с закругленными углами. Кнопки, которыми, пользуются редко, могут иметь круглую форму. Чтобы пальцы не соскальзывали, на кнопках следует делать выемки илн насечки.
Рукоятки и круглые ручки должны проектироваться с учетом требований табл. 19.5.
Таблица 19.3. Сравнительная характеристика органов управления
Характеристика Нажимная ручная кнопка Тумблер Поворотная рукоятка Поворотная ручка
Время регулирования Занимаемое пространство Визуальное опознавание положения Тактильное опознавание положения Считывание с нескольких подобных органов управления Оп ер ир ован ие веско л ь-кими подобными органами управления Эффективность комбинированного органа управления Примеры применения ++• +++\ _L_J Плавное регулирование
-4-
-д
1 1 -
Задание режимов работы
+++ ие и вык-Подача сигнала
Включен люченне срочного
О б о з и а ч е в и я: 4-4-+ хорошо; 4- 4~ удовлетворительно; 4" прьи* емлемо; —» лучше ие применять. * При повороте ручки с указателем менее чем на 360°. Ручки смонтированы концентрично на одной оси.
Таблица 19.4.
Рекомендуемые параметры кнопок
Параметр Значение
Ширина (диаметр), мм 12,5—18
Расстояние между кнопками, мм Не менее 2
Расстояние между группами кнопок, мм 15—20
Глубина утапливания кнопок, мм:
часто используемых 3—5
редко используемых 6—12
Усилие нажатия кнопок, Н:
часто используемых 1,5—3
редко используемых 2,8—6
Таблица 19.5.
Рекомендуемые параметры рукояток и круглых ручек
Параметр Зн ачение параметра для
поворотной рукоятки круглой ручки
Высота, мм 12—75 12—18
Ширина (диаметр), мм 25 12—50
Длина, мм 25
Расстояние между ручками, мм Угол между соседними положениями, град: 25 25
при визуальном контроле 15—40
при тактильном контроле 30—90
Рабочее усилие, Н 5—50 0,5— 3
Расположение и мнемоничность органов управления
В расположении органов управления должны учитываться размеры пространства, доступного рукам оператора (см. рис. 19.1, а и табл. 19.1, размеры 8 и 9). Часто используемые органы управления нужно размещать в оптимальном рабочем пространстве, ограниченном дугой радиуса около 45 см. Для повышения точности и скорости управления следует согласовывать расположение органов управления и средств отображения информации, учитывать функциональное совмещение элементов одной системы, объединение однотипных элементов управления н последовательность действий по управлению прибором — слева направо и сверху вниз. Эти требования иногда могут противоречить друг другу. Поэтому с учетом особенностей прибора следует принимать компромиссное решение.
При разработке органов управления и надписей к ним необходимо учитывать мнемоничность управления (табл. 19.6). Мнемоничность управления позволяет уменьшить ошибки оператора, повысить скорость его работы и освобождает от излишнего запоминания. Направление вращения органов управления должно определяться с лицевой стороны. 616
Таблица 19.6. Мнемоничность управления
Движение узла и обозначение на указателе Перемещение органов управления
Включено, пуск, вверх, сближение, вперед Нажатие верхних, передних или правых кнопок Поворот рукояток или маховичков по часовой стрелке Поворот рычагов вверх, от себя, вправо
Включено, стоп, назад, влево, вниз, расхождение Нажатие нижних, задних или левых кнопок Поворот рукояток или маховичков против часовой стрелки Поворот рычагов вниз, на себя, налево
Средства отображения информации
С помощью средств отображения информации (СОИ) оператор получает сведения о состоянии объема управления. Около 90% информации поступает к оператору в виде зрительно воспринимаемых сигналов. В табл. 19.7 указаны наиболее часто используемые визуальные индикаторы.
При проектировании отсчетных устройств оптических приборов, при выборе вида индикации следует руководствоваться данными табл. 19.8. При разработке визуальных сеток нужно максимально уменьшать отвлекающие действия сетки во время наблюдения. Для этой цели целесообразно использовать прерывистые линии. Применение концентрических кругов обеспечивает двумерную систему отсчета, освобождая наблюдателя от необходимости поворота сетки, выполненной в виде линии.
При выполнении надписей на органах управления и СОИ следует иметь в виду, что наилучшее восприятие печатных знаков дают
Таблица 19.7. Визуальные индикаторы
Функции индикатора Примеры
Отображение небольшого числа четко различимых состояний (работает, не работает, включено-выклю-чено, предупреждение и т. д.) Качественная информация Контрольная и числовая оценка ин^юрмации Командная информация Регистрируемая информация Многомерная информация Лампочки, указатели положений Счетчики, шкалы типа «открытое окно» Движущиеся стрелки или шкалы Сигнальное табло Самописец, электронно-лучевая трубка Комбинация индикаторов
Таблица 19.8. Сравнительные данные индикаторов отсчетных устройств
Функции индикатора Тнп
Движущийся указатель Движущаяся шкала Счетчик
Количественное считывание Контрольное чтение Отправление информации Слежение +++ + +++ +++ —| ** —|-| -
Обозначения: + + хорошо, 4--f- удовлетворительно,
+ приемлемо, — лучше ие применять.
следующие сочетания цвета знака с цветом фона (в убывающем порядке): черный на белом, черный на желтом, синий на белом, зеленый на белом, красный на белом, красный на желтом.
Пульты управления
Пульты управления должны обеспечивать удобное и достаточное по размерам рабочее пространство для оператора, свободный проход к пульту, рациональное размещение на пульте органов управления
Рис. 19.2. Схемы пультов управления
и СОИ. На пультах должно быть место для ведения документации. Схемы некоторых пультов приведены на рис. 19.2.
Органы управления и СОИ, которые используются наиболее часто, следует располагать в доступных местах. Визуальные индикаторы должны быть установлены так, чтобы параллакс и блесткость были минимальны. Пульт управления необходимо снабдить сиденьем, обеспечивающим удобную, ненапряженную позу наблюдателя.
Литература: L16, 70, 107, 108].
ГЛАВА 20
ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ К ОПТИКО-МЕХАНИЧЕСКИМ ПРИБОРАМ
Общие требования
Конструкция приборов должна удовлетворять техническому заданию (ТЗ) на ее разработку, отвечать требованиям контролепригодности, метрологического обеспечения, эргономики, технической эстетики и безопасности труда. Конструкция приборов должна быть технологичной и отвечать требованиям ГОСТ 14.201—73, ГОСТ 14.202—73 и отраслевым стандартам.
Требования по стандартизации и унификации
В ТЗ должна быть предусмотрена взаимная унификация приборов, а также сокращение номенклатуры составных частей, комплектующих изделий, средств обслуживания и ремонта, материалов и сырья. С этой целью задаются коэффициенты применяемости, повторяемости и межпроектной унификации. Для обеспечения выполнения этих качественных показателей следует:
1) предусматривать использование оригинальных составных частей только тогда, когда невозможно обеспечить выполнение ТЗ применением стандартных, унифицированных и базовых конструкций;
2) по возможности унифицировать составные части разрабатываемых приборов и изделии, с которыми оин должны совместно работать в соответствии о ТЗ;
3) соблюдать тнпоразмерные ряды н параметрические требования, установленные на разрабатываемые приборы;
4) выбирать н применять комплектующие элементы в соответствии с требованиями соответствующих стандартов;
5) не допускать выполнения требований по стандартизации и унификации за счет снижения качества и технического уровня приборов.
Требования к консервации и упаковке
Консервация и упаковка должны обеспечивать сохраняемость приборов прн транспортировании всеми видами транспорта и в условиях «ранения, указанных в отраслевых стандартах, в течение сроков, указанных в ТЗ. Требования к средствам н методам консервации должны соответствовать указанным в отраслевых стандартах.
Эргономические требования и требования технической эстетики
Конструкция приборов должна соответствовать требованиям действующих стандартов на систему человек—машина (СЧМ). Конкретные характеристики и численные значения этих требований должны выбираться из стандартов СЧМ и действующих нормативно-технических документов исходя из возможностей конструктивного построения и функционирования приборов.
Требования технической эстетики, которые рекомендуется выполнять на этапах инженерного и художественного конструирования, должны включать следующие положения:
1) достижение нужного уровня эстетического совершенства приборов исходя из тенденции формообразования промышленных изделий;
2) соответствие композиционных средств и формы в целом функциональным особенностям конструкции, технологии изготовления, применяемым материалам, эргономическим требованиям;
3) выразительность объемно-пространственной структуры и пластики формы; выразительность и гармоничность цветового решения, фактуры и текстуры, графических элементов (знаков, указателей, текстовых таблиц);
4) тщательность выполнения видимых элементов формы (обработки поверхностей н выполнения художественно-графических элементов); качество защитно-декоративных покрытий.
При цветовом оформлении приборов необходимо учитывать их назначение, продолжительность н характер работы с ними, климатические условия, в которых они будут эксплуатироваться, условия их освещения.
Требования по безопасности труда
Конструкция приборов должна обеспечивать безопасность их обслуживания. Все составные части приборов, находящиеся под напряжением 36 В и более по отношению к корпусу прибора или объекту его установки, должны быть защищены от случайных прикосновений обслуживающего персонала во время их эксплуатации.
Конструкция приборов должна исключать возможность попадания электрического напряжения на наружные металлические части. Включение и выключение напряжения в приборах должно производиться устройствами, обеспечивающими безопасность обслуживающего персонала. В конструкции устройств питания приборов должна быть предусмотрена защита от перегрузок и коротких замыканий.
Полный объем требований безопасности труда изложен в системе стандартов безопасности труда.
Требования к составным частям приборов
Крепежные детали разъемных соединений следует предохранять от самоотвинчивания. Применяемые резьбы, их номинальные размеры, допуски и посадки должны соответствовать государственным стандартам.
На трущихся поверхностях механических деталей не допускаются пленки, раковины, трещины, заднры и другие подобные дефекты материала. Острые углы и кромки должны быть закруглены и притуплены фасками.
Поверхности деталей, которые могут дать рассеянный свет и блики, должны иметь черные матовые покрытия (гл. 17). Штрихи, надписи и оцифровка шкал должны быть четкими и сохраняться в течение срока службы прибора.
Движение подвижных частей прибора должно быть плавным без скачков и заеданий. Все трущиеся части должны быть смазаны смазкой (гл. 23). Все зазоры и места неподвижных соединений, через которые могут проникнуть внутрь прибора пыль и влага, должны быть уплотнены прокладками нли промазаны уплотнительными замазками (гл. 23).
Требования к оптическим деталям
Оптические детали, как правило, следует изготовлять из стекла I, II и III групп и, как исключение, IV группы химической устойчивости к пятнающим агентам по ГОСТ 13917—68. Изготовление деталей из стекол групп В и Д по химической устойчивости к влажной атмосфере допускается при условии применения надежных способов защиты.
Зеркальные покрытия должны удовлетворять требованиям Соответствующих стандартов. Металлические пленки зеркал должны иметь прочное сцепление с подложкой. В зеркалах, работающих в сходящихся пучках лучей, допускаются сквозные отверстия в виде пор диаметром ие более 0,05 мм, не имеющие характер скоплений. В зеркалах, отражающих параллельные пучкн лучей, кроме указанных выше дефектов, допускаются отверстия диаметром до 0,1 мм не более 2 шт. на 1 см? и иесквозные царапины суммарной длиной до 30 мм на 1 см2.
В зеркалах проекционных и осветительных систем допускаются сквозные отверстия диаметром не более 0,05 мм, ие имеющие характер скопления, отверстия диаметром до 0,1 мм не более 2 шт. на 1 см?, диаметром до 0,2 мм ие более 1 шт. на 1 см? и черные точки диаметром до 0,5 мм не более 1 шт. на 10 см? у алюминированных зеркал и иа 50 см? у хромированных.
Требования к оптическим деталям, находящимся в оптических системах
На поверхностях оптических деталей не должно быть жировых, водных и биологических налетов, обнаруживаемых при просмотре как в проходящем, так и в отраженном свете.
Возникающие при просветлении и обнаруживаемые в отраженном свете радужные пятиа иа оптических деталях допускаются, если они не ухудшают качество изображения и спектральное светопропускание. Видимые в проходящем свете мутные пятна, являющиеся результатом химического разрушения стекла, не допускаются.
Чистота просветленных поверхностей должна удовлетворять требованиям ГОСТ 11141—76.
В клеящем слое оптических деталей, совпадающем с плоскостью действительного изображения, расклейка и пузыри в пределах световых диаметров не допускаются. Расклейки допускаются, если клеящий слой не находится в плоскости действительного изображения и составляет общую площадь не более 0,5% площади светового диаметра.
При соединении деталей оптическим контактом ие допускается нарушение контактов у краев. Количество и размеры таких участков в других частях деталей устанавливаются в частных технических условиях (ЧТУ). При осмотре поля зрения невооруженным глазом через окуляр в сильном проходящем свете не должны быть видны загрязие-
ния, свили, налеты, царапины, пузыри « другие дефекты, кроме допустимых по технической документации.
В зависимости от числа оптических деталей прибора, находящихся в плоскостях действительных изображений или вблизи от них (в пределах ±10 дптр), в ЧТУ рекомендуется указывать допустимые дефекты чистоты поля для пространства изображения (за окуляром) согласно табл. 20.1.
Таблица 20.1. Допустимые дефекты чистоты поля (не более)
Число деталей, близких к плоскости действительного изображения Зоны поля
Центральная 1 Средняя 1 ^Гаевая
Точки Царапины Точки Царапины Точки Царапины
Диаметр, лг « Количество Ширина, • Общая длина, Мм Диаметр, - J Количество ! Ширина, • » Общая длина, мм 3 Диаметр, Количество 1 Ширина, // • • - - - d Общая длина, мм
1 30 2 20 0,2 90 3 40 0,2 120 6 40 0,3
2 3 4 0,3 9 0,4
3 5 10 0,5
4 0,3 6 0,4 12 0,6
5 4 13
6 7 15
Под деталью, близкой к плоскости действительного изображения (фокальной плоскости), следует подразумевать деталь, для которой лучн, исходящие из какой-либо ее точки в выходном зрачке, обладают сходимостью или расходимостью до D = ±10 дптр.
Нерезкие тени от дефектов поверхностей, расположенных вблизи фокальных плоскостей, допускаются в пределах общего количества указанных-в таблице дефектов при условии, что угловой размер этих дефекте® не превышает Г + 0,5'D. Данные табл. 20.1 действительны для приборов г окуляром, угловое поле которого 2© <70°, и с f* системы после плоскости изображения, не превышающим 40 мм. При большем окулярном поле и большем фокусном расстоянии приведенные допуски могут быть соответственно расширены.
Для приборов, у которых наблюдение за объектом осуществляется центром ноля, в центральной зоне не следует допускать никаких дефектов. На оптических деталях не допускаются следы смазки и замазки, видимые со стороны окуляра или объектива.
Т а б лиц а 20.2. Требования к оптической системе полевых телескопических приборов
Характеристика Допуск X ар актеристик а Допуск
Видимое увеличение гу, % Угловое поле 2<о, % Диаметр выходного зрачка D', % Удаление выходного зрачка от вершины задней поверхности окуляра s’% Предел разрешения для системы, с D' < 3,5 мм » с D' 3,5 мм Качество изображения Наклон изображения (у призменных систем), ...° Разность углов поворота изображения вокруг оптической оси у левой и правой частей бинокулярного прибора, ...' Наклон (разворот) сетки, ...° ±5 ±5 ±5 ±10 „ 120" г = К D „ 35" Гг Не ниже эталона 1 30 1 Непараллел ьность оптических осей за окулярами (у бинокулярных приборов с постоянным или переменным расстоянием между зрачками от 56 до 76 мм): в горизонтальной плоскости: схождение, ...' расхождение, « • й расхождение по вертикали, Резание по горизонту н вертикали Относительная разность увеличений правой и левой частей бинокулярного прибора: ПР« 2“оК = = 50°, %; ПРИ 2(0ок > > 50°, % 20 1 15 1/2 допуска на ошибку угла визиро- вания 2 1,5
Примечания: 1. К — численный множитель (см. табл. 20.3), 2. D — диаметр входного зрачка, мм. 3. Несовпадение плоскости изо* Сражения предмета с плоскостью сетки или параллактическое смещение изображения относительно измерительной или прицельной марки сетки при перемещении глаза в плоскости выходного зрачка (параллакс изображения) определяется разностью сходимостей пучков лучей (за окуляром), исходящих обычно из центрального знака сетки н из находящегося рядом изображения точки предмета.
Требования к телескопическим приборам
Требования к этой группе приборов приведены в табл. 20.2. Значения численного множителя К приведены в табл. 20.3.
Таблица 20.3. Значения множителя К
Виды приборов К
Простые оптические приборы с оптикой малого относительного отверстия и с малым увеличением Малые астрономические трубы, геодезические инструменты. Другие телескопические системы без оборачивающих систем, состоящие из несветосильных и неширокоугольных компонентов. Дальномеры. Точные измерительные приборы Приборы, содержащие одну линзовую оборачивающую систему Призменные бинокли. Приборы, содержащие одну призменную оборачивающую систему Приборы с тремя линзовыми оборачивающими системами с увеличением до бх Панкрэтические приборы при большом увеличении. Салтые сложные приборы. Приборы с несколькими линзовыми оборачивающими системами с большим количеством призм, зеркал и защитных стекол с увеличением на менее 15* 1,05 1,2 1,3 1,5 1,6 2,0 2,2
Ниже приведена допустимая разность сходимостей.
Диаметр выходного зрачка прибора, мм............. 1—2 2—3 3—4 4 — 5 Более 5
Допустимая разность сходимостей, дптр.......... 0,7 0,5 0,4 0,3 0,25
Требования к устойчивости приборов к внешним воздействиям при эксплуатации
Конструкция приборов должна обеспечивать достаточную прочность и устойчивость под воздействием механических факторов, встречающихся в процессе эксплуатации. При механических воздействиях ие должно быть повреждений приборов, нарушения регулировки рабочих механизмов, разъюстировки оптической системы, загрязнения оптики, смещения установок на шкалах и появления ошибок в показаниях, снимаемых со шкал. Указанные требования проверяются в действительных условиях или с помощью специального испытательного оборудования. Значения характеристик воздействующих факторов при испытаниях, виды и режимы испытаний назначаются в зависимости от назначения приборов и условий их эксплуатации. К наиболее часто назначаемым видам механических испытаний относятся испытания на устойчивость и прочность при воздействии вибраций и прочность при транспортировании.
Таблица 20.4. Категории изделий в климатических исполнениях в зависимости от места размещения при эксплуатации (по ГОСТ 15150—69)
Характеристика мест размещения изделия прн эксплуатации Категория
На открытом воздухе 1
В помещениях категории 4 и (кратковременно) в дру- 1.1
гих условиях, в том числе на открытом воздухе В помещениях, где колебания температуры и влажности 2
воздуха несущественно отличаются от колебаний на открытом воздухе и имеется сравнительно свободный доступ наружного воздуха В закрытых помещениях с естественной вентиляцией 3
без искусственно регулируемых климатических условий, где колебания температуры и влажности воздуха и воздействие песка и пыли существенно меньше, чем на открытом возду хе В помещениях с искусственно регулируемыми климати- 4
ческими условиями В помещениях с кондиционированным или частично 4.1
кондиционированным воздухом В лабораторных и капитальных жилых помещениях 4.2
В помещениях с повышенной влажностью 5
Конструкция приборов должна обеспечивать возможность выполне* ния ими их функций, сохранения параметров и внешнего вида в пределах установленных норм во время или после воздействия климатических факторов в процессе эксплуатации (табл. 20.4—20.8).
ГОСТ 15150—69 устанавливает следующие климатические исполнения изделий.
1. Изделия, предназначенные для эксплуатации на суше, реках и озерах в макроклиматических районах, климат которых:
У — умеренный (средняя из ежегодных абсолютных максимумов температура воздуха t < 40° С. а средняя из ежегодных абсолютных минимумов —45° С);
ХЛ — холодный (средняя из ежегодных абсолютных минимумов температура воздуха ниже минус 45° С);
ТВ — влажный тропический (сочетание температуры t 20° С и относительной влажности равной или выше 80% сохраняется в течение не менее 12 ч в сутки за непрерывный период не менее двух месяцев в году);
ТС — сухой тропический (средняя нз ежегодных абсолютных максимумов температура воздуха />40° С), который не отнесен к районам с влажным тропическим климатом;
Т — тропический (сухой и влажный).
Для изделий, предназначаемых для эксплуатации в любых районах на суше, установлено общеклиматнческое исполнение — О, в любых районах на море — ОМ и во всех районах на суше и на море — В.
Таблица 20.5. Классификация условий эксплуатации по коррозионной активности атмосферы для металлических изделий или деталей без покрытий, а также с металлическими и неметаллическими покрытиями
Группы условий эксплуатации Исполнения Категории изделий
Названия Обозначения
основные дополнительные
Легкая Л Все исполнения ХЛ, У, ТС 4.1 3 ♦; 4 (кроме 4.1)
Средняя с С1 С1 С1 С2 сз С4 ТВ, Т, М, ТМ, ОМ, О, в тс ТВ, Т, О, в тс У, ХЛ Все исполнения 4 (кроме 4.1) 2; 3; 1 * (кроме 1.1) 3 * 1 (кроме 1.1) 2; 3; 1 **; 1 * (кроме 1.1) 1.1
Жесткая ж Ж1 Ж1 Ж2 жз ТВ, Т, О В У, ХЛ М, ТМ, ом 2; 3; 1 **; 1 * (кроме 1.1) 3 1 (кроме 1.1) 2 ***
Особо жесткая ож ОЖ1 ОЖ2 ожз Все исполнения ТВ, Т М, ТМ, ОМ 5 1 (кроме 1.1) 1 (кроме 1.1); 2
ъ Только для внутренних деталей, размещенных в кожухах изделий с естественной или искусственной вентиляцией. ** Только для изделий, специально предназначенных для эксплуатации в атмосфере типа I. *** Только для деталей, защищенных от попадания брызг морской воды.
Таблица 20.6. Условия эксплуатации металлов, а также металлических и неметаллических неорганических покрытий в зависимости от исполнения и категории размещения изделий
(по ГОСТ 15150—69)
Категории изделий Группы условий эксплуатации для исполнений
У, ХЛ тс ТВ, т М, ТМ, ом о в
1 (кроме 1.1) СЗ**, Ж2 Cl *, С2 Ж1 **, ОЖ2 ЖЗ***, ОЖЗ |Ж1 **; ОЖ2 ЖЗ ***, ОЖЗ
1.1 С4 С4 С4 С4 С4 С4
2 сз С1 Ж1 ЖЗ***, ОЖЗ Ж1 ЖЗ ***, ОЖЗ
3 л *,сз Л *, С1 С1 *, Ж1 С1 *, Ж1 С1 *, Ж1
4.1 л л л л л л
4 (кроме 4.1) л л С1 С1 С1 С1
5 ОЖ1 ОЖ1 ОЖ1 ОЖ1 ОЖ1 ОЖ1
• Только jyisUдеталей, размещенных в кожухах изделий с естественной или искусственной вентиляцией. ** Только ' для изделий, специально предназначенных для эксплуатации в атмосфере типа I. *** Только для деталей, защищенных / от попадания брызг морской воды.
о Таблица 20.7. Группы условий хранения изделий в зависимости
So от места и климатических факторов (по ГОСТ 15150—69)
Группы условий хранения Место хранения Температура воздуха, °C (см. примечания) Относительная влажность воздуха Интенсивность дождя Пыль Плесневые н де-ревораз-рушаю-щие грибы
Названия Обозначения
основные допол-нн-тель-ные Верхнее значение Нижнее значение
Легкая Л —- Отапливаемые (или охлаждаемые) и вентилируемые склады, расположенные в любых климатических условиях +40 4~ 1 Такая же, как для категории 4.1 —
Средняя с Помещения с естественной вентиляцией без искусственно регулируемых климатических условий, где колебания температуры и влажности воздуха существенно меньше, чем на открытом воздухе в районах с умеренным и холодным климатом +40 —50 Такая же, как для категории 3 исполнений У, ХЛ
Жесткая ж Ж1 Открытые площадки в районах с умеренным и холодным климатом в ат- мосфере типа I 4" 50 • —50 Такая же, как для категории 1 исполнений у, ХЛ Такая же, как для исполнений У, ХЛ Есть —
6б9 1 - Ж2 ЖЗ Навесы, или помещения, где колебания температуры и влажности воздуха несущественно отличаются от колебаний на открытом воздухе в районах с умеренным и холодным климатом в атмосфере типа I Помещения с естественной вентиляцией без искусственно регулируемых климатических условий, где колебания температуры и влажности воздуха существенно меньше, чем на открытом воздухе в районах с тропическим климатом +50 +50 —50 —50 Такая же, как для категории 2 исполнений У, ХЛ Такая же, как для категории 3 исполнения Т Есть Есть
Особо жесткая ож ОЖ1 ОЖ2 Открытые площадки в любых климатических районах, в том числе в районах с тропическим климатом Навесы или помещения, где колебания температуры и влажности воздуха несущественно отличаются от колебаний на открытом воздухе в любых климатических районах +60 +60 —50 —50 Такая же, как для категории 1 исполнения Т Такая же, как для категории 2 исполнения Т Такая же, как для исполнения Т Есть Есть Есть Есть
Группы условий хранения Температура воздуха, °C (см. примечания) Плесне-
Обозначения Место хранения Относительная Интеиснв- Пыль вые и де ревор аз-ру тающие грибы
Названия основные допол-ни-тель-ные Верхнее значение Нижнее значение влажность воздуха ность дождя
Особо жесткая ож ОЖЗ ОЖ4 Открытые площадки в районах с умеренным и холодным климатом в атмосфере типов II и III Навесы или помещения, где колебания температуры и влажности воздуха несущественно отличаются от колебаний на открытом воздухе в районах с умеренным и холодным климатом 4-60 4-50 —50 —50 Такая же, как для категории 1 исполнений У, ХЛ Такая же, как для категории 2 исполнения ХЛ Такая же, как для исполнений У, ХЛ Есть Есть
Примечаниям 1. Среднегодовое значение температуры для условий хранения Л, С, Ж1. Ж2, ОЖЗ, ОЖ4 составляет 20° С, для условий хранения ЖЗ, ОЖ1, ОЖ1 равно 27° С. 2. Для условий Ж1 н ОЖЗ допускается кратковременное (до 3—4 ч в год) повышение верхнего значения температуры до 4-606 С. 3. Нижнее значение температуры для групп условий хранения Ж и ОЖ для изделий исполнений ХЛ, О, В принимается минус 60° С. Это же значение принимается для изделий других исполнений, у которых в стандартах или ТУ принято нижнее значение температуры при эксплуатации ниже минус 50° С. 4. Если изделие должно храниться в условиях ОЖ1 н ОЖ1 и не будет транспортироваться илн храниться на территории а умеренным и холодным климатом в зимнее время или транспортироваться самолетом в любое время года, допускается нижиее значение температуры принимать минус 20° С. 5. Для групп условий хранения Ж1, ОЖ1 н ОЖЗ верхнее рабочее значение интегральной плотности теплового потока солнечной радиации для высот до 15 км составляет 1125 Вт/м2. Аизлогичиое значение для высот выше 15 км составляет 1375 Вт/м2. 6. При хранении в условиях сухого тропического климата можно принимать группу условий хранения С, если обеспечена сохранность изделия при транспортировании. . .... _________ ___ _____________
Таблица 20.8. Виды испытаний, параметры и нормы режимов в зависимости от категории размещения изделий
Виды ясны- Наименование параметров Нормы испытательных режимов при эксплуатации приборов по категориям
таннй 4.1 4.2 2 5 1 1.1
Влагоустой-чивость Температура, °C Относительная влажность, % Продолжительность испытания при длительном выдерживании, сут 1 1 1 40 95—98 7 40 95- 100 21 40 95— 100 10 40 95- 100 40 40 95— 100 14
Теплоустойчивость Рабочая температура, °C Продолжительность, ч Предельная температура, °C Продолжительность испытания, ч 25 40 4 45 4 45 4 50 4 70 4 60 4 80 4 60 4 80 4 55 4 70 4
Холодоустойчивость Рабочая температура, °C Продолжительность, ч Предельная температура (при транспортировке), °C Продолжительность испытаний, ч III 1 3 4 —40 6 0 4 —40 6 —60 4 6 -10 4 —40 6 4 —40 6
Гр ибо устойчивость Температура, °C Относительная влажность, % Продолжительность испытания, сут 1 1 1 30 95— 100 30 30 95— 100 30 30 95— 100 30 30 95- 100 30 30 100 30
Воздействие солнечной^ радиации Интегральная плотность теплового потока излучения, кал/см3с (Вт/м2) Интенсивность ультр афиолетового излучения, кал/см2с (Вт/м2) Продолжительность облучения, ч Количество цик-лов 1 1 II II II II II 1 0,027 (1125) 0,0010 (42) 36 6 0,027 (1125) 0,0010 (42) 18 3
Виды испытаний Наименование параметров Норма испытательных режимов при эксплуатации приборов по категориям
4.1 4.2 2 б 1 1,1
Скорость воздушного потока, м/с 0,5— 1 0,5— 1 0,5— 1 0,5— 1
£ л s В >> о ч я a sr Продолжительность перемешивания, ч Продолжительность 2 2 2
с оседания ч, 1 1 1
<4 X Водность, г/м2 3 - - со 1 см со 1 2—3 со 1 сч
Р CJ “ Температура, °C Дисперсность, мкм —* 27 27 27 27
•К О Ф f-< 1—10 1—10 1—10 1—10
СТ О m м О о CQ Си О £ Продолжительность, сут 7 2 10 10
& о g Интенсивность, мм/мин — 5—8 §
m У» 3 g из S а Продолжительность, ч 2 2
2. Изделии, предназначенные для эксплуатации на морских судах в районах, климат которых:
М — морской умеренно холодный (мори и океаны, расположенные севернее 30° северной широты или южнее 30° южной широты);
ТМ — тропический морской (моря и океаны, расположенные между 30° северной широты и 30° южной широты).
К приборам всех климатических исполнений следует предъявлять требования по температуре внешней среды, сменам температуры, влажности и давлению воздуха. Требованиям по устойчивости к воздействию солнечной радиации и дождя должны задаваться только для приборов категории 1, а для приборов категории 1.1, — если это указано в ТЗ.
К приборам категории 1 исполнений ТС, О и В, имеющим подвижные части, следует задавать требования по работоспособности и пыленепроницаемости при статическом или динамическом воздейстиии пыли. Приборы (их узлы и детали) исполнений Т, ТВ, О, ТМ и В, кроме категории 4.1, должны быть устойчивыми к поражению плесневыми грибами.
Приборы категории 1 и 2, предназначенные для эксплуатации иа побережьях, а также приборы исполнений М, ТМ и ОМ должны выдерживать воздействие соляного тумана по нормам, установленным в ТЗ или в стандартах. Приборы исполнений ХЛ, О, В, М и ОМ, предназначенные для наружного монтажа переносных (кроме категорий 1.1,
3, 4 и 5) н передвижных устройств, должны быть работоспособны при выпадении на них инея.
В технически обоснованных случаях могут устанавливаться требования и по другим видам воздействия.
При оценке климатических факторов внешней среды различают три типа атмосфер, характеризуемых по содержанию коррозионно-активных агентов на открытом воздухе:
I — атмосфера примерно соответствует атмосфере сельской, лесной, горной местности вдали от промышленных объектов;
II — атмосфера примерно соответствует атмосфере промышленных районов;
III — атмосфера примерно соответствует морской.
Требования к приборам, предназначенным для работы в районах с тропическим климатом
Приборы в климатическом исполнении Т в зависимости от места размещения прн эксплуатации изготавливают по категориям 1; 1.1; 2; 4; 4.1; 4.2; 5 в соответствии с ГОСТ 15150—69 и отраслевым стандартом.
Общие указания по конструированию приборов. При конструировании приборов для работы в условиях тропического климата должны быть обеспечены следующие основные требования:
1) длительная эксплуатация приборов при номинальных температурах окружающей среды;
2) стойкость конструкционных и электроизоляционных материалов;
3) антикоррозионная защита и внешняя отделка;
4) защита от воздействия плесневых грибов;
5) защита на период транспортирования и хранения.
Обеспечение требуемой стойкости приборов для работы в условних тропического климата может быть достигнуто*
1) специальными конструктивными решениями — применением эффективных вентиляционных устройств, эффективного охлаждения, герметизации, исключением открытых невентилируемых полостей, зазоров, впадин и острых углов у деталей;
2) правильным выбором материалов, шероховатости поверхности деталей и способов их защиты;
3) выбором оптимальной технологии изготовления;
4) надлежащим уходом при эксплуатации, правильной консервацией и упаковкой на период транспортирования и хранения.
Общие решения по конструированию приборов и выбору конструкционных материалов и их защиты принимают в соответствии с ГОСТ 15150—59. Особое внимание нужно уделять мерам по обеспечению иысокого качества внешнего вида.
. Выбор материалов. Запрещается применять материалы, подвергающиеся интенсивному микробиологическому разрушению, без специальных средств защиты (антисептирование, введение фунгицидов и др.). В качестве конструкционных материалов для изготовления изделий должны применяться коррозионностойкие металлы и сплавы. Применение других металлов и сплавов допускается прн условии надежной защиты их от коррозии.
Углеродистые и низколегированные стали, а также чугуны всех марок следует применять только с противокоррозионной защитой, если изготовленные нз них детали не работают в полностью герметичных приборах. Алюминий и его сплавы должны применяться с защитными покрытиями. Применять для изготовления деталей цинковые н магние
вые сплавы не следует. Медь и медные сплавы, кроме коррозионно-стойких, должны применяться с защитными покрытиями. В отдельных конструктивно обоснованных случаях для иедекоративных деталей медь и медные сплавы можно применять без защитного покрытия, ио, как правило, с пассивированием.
Крепежные детали рекомендуется изготавливать из медиых сплавов с гальваническими покрытиями или из высоколегированных сталей без покрытий.
Пружины и пружинные шайбы следует изготавливать из бериллиевой, фосфористой или алюминиевой бронзы и из нержавеющей стали с последующим никелированием, если их толщина более 0,4 мм.
Стальные лепестки диафрагм затворов и объективов следует подвергать щелочному оксидированию с последующей обработкой в мыльном растворе и пропиткой маслом или кремнийорганическими жидкостями.
Заводские щитки и надписные таблички изготавливают из латуни с никелированным выпуклым изображением на черном оксидированном фоне, покрывают прозрачным защитным лаком (МЛ-92, ЭП-524, АК-113Ф или клеем БФ-2 или БФ-4) с последующей горячей сушкой. Таблички с делениями, цифрами и надписями рекомендуется делать из латуни или листового дюралюминия с последующим оксидированием, а также защитными гальваническими или лакокрасочными покрытиями. Таблицы можно делать способом офсетной печати или гравировкой. Металлические шкалы следует изготавливать из анодированного и покрытого грунтом ФЛ'ОЗЖ алюминия с последующей окраской лаком ФЛ-582 или ХСЛ или из фосфатированной и покрытой грунтом ФЛ-ОЗК стали.
Барабанчики счетных механизмов изготавливают из анодированного алюминия или оловянистых сплавов без покрытий. Оси, валы и червяки, не работающие в масляной среде, нужно выполнять из нержавеющих хромоникелевых и хромовых сталей с содержанием хрома ие менее 18% или из бронз.
Токоведущие детали рекомендуется изготавливать из меди и медных сплавов с последующим серебрением, лужением, покрытием родием или никелем с оловом. Применение золота, платины, палладия и их сплавов для контактов возможно при любых климатических условиях.
Из сплавов с высоким омическим сопротивлением рекомендуется применять нихром и константан. Применять молибден, сплавы ковар и инвар следует только с гальваническими или лакокрасочными покрытиями.
Пайку нужно вести серебросодержащими припоями, с обязательным удалением флюса.
При подборе металлов, сплавов и покрытий для контактирующих друг с другом деталей следует принимать во внимание электрохимические свойства металлов и пользоваться рекомендациями по их выбору, приведенными в отраслевом стандарте и в табл. 17.2.
В качестве электроизоляционных материалов рекомендуется применять: пластические массы на основе тепло- и влагостойких искусственных смол с неорганическими наполнителями (кварц, слюда, стеклянное волокно и ткань, асбестовое волокно и ткань), некоторые специальные материалы, в состав которых введены фунгисиды, синтетические материалы (полиэтилен, фторопласт, полиамид и др.) и керамические материалы с глазированной поверхностью или поверхностью, покрытой кремнийорганическими лаками. Не следует применять: хлопчатобумажные, шерстяные и шелковые ткани, бумагу, картон, фибру, дерево, пластмассы с древесными и целлюлозными наполнителями, аминопласты 634
и слоистые пластики с основами бумажной, хлопчатобумажной и из натурального шелка.
Текстиль, войлок, фетр, кожа и ее заменители, бумага, картон и резина при изготовлении деталей должны быть обработаны специальными составами, обеспечивающими их устойчивость от воздействия плесени, влаги, термитов и других факторов тропического климата. Детали из картона и бумаги следует обрабатывать в соответствии с требованиями ГОСТ 15158—78, защищать от воздействия влаги или при возможности заменять полиэтиленом, полихлорвинилом, фторопластом-4 или стеклотекстолитом. Детали из натуральной кожи рекомендуется изготавливать из хрома и полухрома. При сборке следует избегать их контакта со стальными деталями. Прокладки из коры пробкового дуба применяют без антисептирования, если пробка стерильна.
Защиту деталей из древесины осуществляют в соответствии с требованиями ГОСТ 15151—69 и ГОСТ 15155—79 или покрытием их тропико-стойкими лаками и эмалями. Хлопчатобумажные, льняные и полульняные ткани и изделия из них подлежат защите по ГОСТ 10776—78 и ГОСТ 15160—69 или по возможности замене синтетическими тканями (стеклопряжей, капроном, ацетатным шелком и др.). Антисептироваиие шерстяных и войлочных материалов и изделий из них должно производиться по ГОСТ 15159—76 и ГОСТ 16151—79.
Склеивать оптические детали следует клеями по ГОСТ 14887—69. Склеивание других материалов производят в соответствии с отраслевыми руководящими техническими материалами.
Резиновые технические изделия изготавливают по ГОСТ 15152—69.
При выборе масел и смазок следует руководствоваться ГОСТ 15156—69 и отраслевыми руководящими техническими материалами.
Для окраски торцов и фасок оптических деталей с целью устранения возможных бликов и снижения отражения проходящего света рекомендуется применять эмаль ХС-543.
При выборе основных материалов, рекомендуемых для изготовления деталей в тропическом исполнении, следует руководствоваться отраслевым стандартом.
ГЛАВА 21
ОСНОВНЫЕ ПРАВИЛА РАЗРАБОТКИ КОНСТРУКТОРСКОЙ ДОКУМЕНТАЦИИ
Стандарты, используемые в начальной стадии разработки конструкторской документации
При разработке конструкторской документации на оптико-механические приборы следует руководствоваться требованиями стандартов ЕСКД и ведомственных нормативно-технических документов.
ГОСТ 2.002—72.ЕСКД. Требования к моделям, макетам и темпле -там, применяемым при проектировании.
ГОСТ 2.101—68.ЕСКД. Виды изделия. В стандарте определяется понятие «изделие», приводится деление изделий в зависимости от назначения и наличия в них составных частей, устанавливаются виды изделий (детали, сборочные единицы, комплексы и комплекты), дается их определение и структура.
ГОСТ 2.102—68.ЕСКД. Виды и комплектность конструкторской документации.
ГОСТ 2.103—68.ЕСКД. Стадии разработки. Стандарт устанавливает этапы работы и следующие стадии конструкторской документации: техническое задание, техническое предложение (разрабатывается по ГОСТ 2.118—73), эскизный проект (разрабатывается по ГОСТ 2.119—73), технический проект (разрабатывается по ГОСТ 2.120—73).
• Стандарты, используемые
при разработке чертежей
ГОСТ 2.104—68.ЕСКД. Основные надписи. Стандартом устанавливаются формы, размеры, порядок заполнения основных надписей и дополнительных граф к ним.
ГОСТ 2.105—79.ЕСКД- Общие требования к текстовым документам.
ГОСТ 2.106—68.ЕСКД. Текстовые документы. Стандарт устанавливает формы и правила выполнения: ведомостей спецификаций, ссылочных документов, покупных изделий и технического предложения, ведомостей эскизного и технического проектов, пояснительной записки, программы и методики испытаний н расчетов.
ГОСТ 2.109—73.ЕСКД. Основные требования к чертежам. Приводятся основные требования к выполнению чертежей деталей, сборочных, габаритных и монтажных на стадии разработки рабочей документации. 636^
ГОСТ 2.113—75.ЕСКД. Групповые и базовые конструкторские документы.
ГОСТ 2.301—68.ЕСКД. Форматы.
Ниже приведены обозначения и размеры основных форматов.
Обозначение ...............
Размеры сторон, мм.........
Обозначение ...............
Размеры сторон, мм.........
44
11 69 X 841
24
594X 841
22 12 11
594 x420 297X420 297x210
Стандартом допускается применение дополнительных форматов, образуемых увеличением сторон форматов на величину, кратную размерам формата 11.
ГОСТ 2.302—68.ЕСКД. Масштабы. Стандарт устанавливает следующие масштабы изображений на чертежах: масштабы уменьшения 1:2; 1 : 2,5; 1:4; 1:5; 1 : 10; 1 : 15, 1 : 20; 1 : 25; 1 : 40; 1 : 50; 1 : 75; 1 : 100; 1 : 200; 1 : 400; 1 : 500; 1 : 800; 1 : 1000; масштабы увеличения 2 : 1; 2,5 : 1; 4 : 1; 5 : 1; 10 : 1; 20 : 1; 40 : 1; 50 : 1; 100 : 1.
ГОСТ 2.303—68.ЕСКД. Линии. Стандарт устанавливает наименование, назначение, начертание и толщину линий на чертежах по отношению к толщине основной линии. Толщина сплошной основной линии s должна быть в пределах 0,6 до 1,5 мм. Толщина сплошной тонкой, сплошной волнистой, штриховой и штрих-пунктирной тонкой и сплошной тонкой с изломами линий выбирается в пределах от s/2 до s/3. Толщина штрих-пунктирной утолщенной линии — от s/2 до 2s/3, а разомкнутой линии — от s до 3$/2.
ГОСТ 2.304—68.ЕСКД. Шрифты чертежные. Основные положения стандарта следующие. Наклон надписей к основанию строки должен быть примерно 75°; размеры шрифта (определяемые высотой прописных букв, мм): 2,5; 3,5; 5; 7; 10; 14; 20; 28; 40. Высота букв и цифр должна быть не менее 2,5 мм на чертежах, выполненных тушью, и не менее3,5 мм
Таблица 21.1. Расстояние между буквами, словами и строками, мм
Определяемое расстояние Размер шрифта, мм
2,5 3,5 5 7 10 14
Между буквами, цифрами и знаками 0.7 1 1.4 2 3 4
Между словами и числами Не меиее ширины букв текста
Между основаниями строк 3,8 5,3 7,6 10,5 15 21
на чертежах, выполненных в карандаше; расстояния между буквами, словами и строками должны примерно соответствовать значениям, приведенным в табл. 21.1.
ГОСТ 2.305—68.ЕСКД. Изображения — виды, разрезы, сечеиия.
ГОСТ 2.306—68.ЕСКД. Обозначения графических материалов и правила их нанесения на чертежах. Из приведенных в стандарте графических обозначений материалов при вычерчивании элементов оптико-механических приборов встречаются следующие: металлы и твердые сплавы (рис. 21.1, а), неметаллические материалы, в том числе волокнистые монолитные и плитные (рис. 21.1,6), древесина поперек волокон (рис. 21.1, в), древесина вдоль волокон (рис. 21.1, г), фанера (рис. 21.1, д) стекло и другие прозр ачные матер и алы (рис. 21.1, е), жидкости (рис. 21.1, ж).
ГОСТ 2.307—68. ЕСКД- Нанесение размеров и предельных отклонений.
ГОСТ 2.308—79. ЕСКД- Допуски формы и расположения поверхностей. Указания на чертежах (см. табл. 21.2).
Вид допуска формы и расположения следует обозначать на чертеже условным знаком согласно табл. 21.2. Для допусков формы и расположения поверхностей, не предусмотренных табл. 21.2, вид допуска может быть указан в технических требованиях. Прнэтом в тексте приводят: наименование допуска; указание поверхности, для которой задается допуск; числовое значение допуска в миллиметрах и, при необходимости, базу, относительно которой задается допуск.
Прн нанесении условных знаков и данных допуска следует соблюдать следующие правила:
1. Знак и числовое значение допуска или обозначение базы вписывают в прямоугольную рамку допуска, разделенную иа два или три поля (рис. 21.2, а, б), в которых помещают: в первом — знак допуска согласно табл. 21.2, во втором — числовое значение допуска в миллиметрах, в третьем — буквенное обозначение базы.
2. Рамки допуска вычерчивают сплошными тонкими линиями одинаковой толщины с цифрами. Размеры рамки допуска и его полей должны обеспечивать возможность четкого вписывания всех данных.
3. Высота цифр и букв, вписываемых в рамки, должна быть равна размеру шрифта размерных чисел. Рекомендуемое графическое изображение знаков и рамки допуска приведено в приложении к стандарту.
е)
изображение иа чертежах материалов
Таблица 21.2. Условные обозначения допусков формы и расположения поверхностен
Группа допусков Вид допуска Знак
Допуски формы Допуск прямолинейности Допуск плоскостности Допуск круглости Допуск цилиндр ичности Допуск профиля продольного сечения 1 О |
Допуски расположения Допуск параллельности Допуск перпендикулярности Допуск наклона Допуск соосности Допуск симметричности Позиционный допуск Допуск пересечения осей //-
Суммарные допуски формы и расположения Допуск радиального биения Допуск торцового биения - Допуск биения в заданном направлении
Допуск полного радиального биения Допуск полного торцового биения
Допуск формы заданного профиля Допуск формы заданной поверхности со
4. Рамку располагают горизонтально. В случае если рамка затемняет чертеж — допускается выполнить ее вертикально так, чтобы данные читались с правой стороны чертежа.
5. Пересекать рамку допуска какими-либо линиями ие допускаетси.
6. Рамку допуска соединяют при помощи прямой или ломаной линии, оканчивающейся стрелкой, с контурной линией (рис. 21.3, а) или выносной линией, продолжающей контурную линию (рис. 21.3, б). При этом стрелка должна быть обращена к контурной (выносной)
линии в направлении измерения отклонения.
7. Если допуск относится к поверхности или ее профилю (линии), а не к оси, то стрелку
// А
Рис. 21.2, Условное обозначение данных о предельных отклонениях формы и расположения поверхностей
располагают на достаточном расстоянии от конца размерной линии или стрелки (рис. 21.3, б). Если допуск относится к оси или плоскости симметрии, то конец соединительной линии дол-
жен совпадать с продолжением размерной линии соответствующего размера (рис. 21.3, в).
8. Перед числовым значением допуска необходимо вписывать: символ 0 или R в зависимости от того, указывает ли он круговое или цилиндрическое поле допуска; символ Т или 772 соответственно, если поля допуска симметричности, пересечения осей и позиционный допуск ограничены двумя параллельными прямыми или плоскостями в диаметральном или радиусном выражении; слово «сфера», если ноле допуска
шаровое.
Рис. 21.3. Выполнение рамки с данными о предельных отклонениях формы или расположения поверхностей
9. Числовое значение допуска действительно для всей поверхности или длины, если не задан нормируемый участок. Нормируемый участок обозначают штрих-пунктнрной линией, ограничив ее размерами. Для указания выступающего поля допуска расположения применяют символ р.
10. Надписи, дополняющие данные, следует вписывать над рамкой допуска или под ней.
Базы обозначают зачерненным равносторонним треугольником с высотой, равной размеру шрифта размерных чисел, который соеди-640
няют с рамкой допуска соединительной линией. Основание треугольника располагают на контурной линии или на выносной, продолжающей контурную линию элемента, образующего базу.
ГОСТ 2.309—73. ЕСКД. Обозначение шероховатости поверхностей. Стандарт устанавливает обозначения шероховатости поверхностей и правила нанесения их на чертежах. Структура обозначения шероховатости поверхности приводится на рис. 21.4.
ГОСТ 2.310—68. ЕСКД. Нанесение на чертежах обозначений покрытий, термической и других видов обработки.
п Вид обработки поверхности и (или)
Параметр (параметры)-------- -----
~ шероховатости по ГОСТ 2783-73 Знак
другие дополнительные указания Полка зща
базовая длина
по ГОСТ 2783-73
Условные обозначения
направления неровностей
W77777777777777777777777777777777,
Рис. 21,4. Структура обозначения шероховатости поверхности
ГОСТ 2.3И—68.ЕСКД. Изображение резьбы. Резьбу на стержне изображают сплошными основными линиями по наружному диаметру резьбы и сплошными тонкими линиями — по внутреннему диаметру. На изображениях, полученных проецированием на плоскость, параллельную оси стержня, сплошную тонкую линию по внутреннему диаметру резьбы проводят на всю длину резьбы без сбега, а на видах, полученных проецированием на плоскость, перпендикулярную к оси стержня, по внутреннему диаметру резьбы проводят дугу, приблизительно равную 3/4 окружности, разомкнутую в любом месте.
Резьбу в отверстии изображают сплошными основными линиями по внутреннему диаметру резьбы и сплошными тонкими линиями — по наружному диаметру.
На разрезах, параллельных оси отверстия, сплошную тонкую линию по наружному диаметру проводят на всю длину резьбы без сбега, а на изображениях, полученных проецированием на плоскость, перпендикулярную к оси отверстия, по наружному диаметру резьбы вцчерчивают дугу, приблизительно равную 3/4 окружности, разомкнутую в любом месте. Сплошную тонкую линию при изображении резьбы наносят на расстоянии не менее 0,8 мм от основной линии и не более шага резьбы. Штриховку в разрезах и сечениях проводят до линии наружного диаметра резьбы на стержне и до линии внутреннего диаметра в отверстии, т. е. во всех случаях до сплошной основной линии.
Размер длины резьбы на стержне и в отверстии, как правило, указывают без сбега. Сплошная тонкая линия изображения резьбы на стержне должна пересекать линию границы фаски.
ГОСТ 2.312—72.ЕСКД. Условные изображения и обозначения швов сварных соединений. Включает соединения, получаемые пайкой,
склеиванием, клепкой и сшиванием. Припой и клей в разрезах и на видах изображают линией толщиной 2s.
Для обозначения пайки (рис. 21.5) или склеивания (рис. 21.6) применяют условный знак, который наносят на наклонном участке линии-выноски, заканчивающейся окружностью диаметром 3—4 мм. При необходимости, на изображении паяного соединения указывают размеры шва, а также шероховатости (на линии-выноске).
Рис. 21.5. Изображение на чертеже неразъемных соединений получаемых пайкой
Обозначение припоя или клея по соответствующему стандарту или ТУ приводят в технических требованиях. При необходимости в том же пункте технических требований излагают требования к качеству шва. Ссылку на номер пункта помещают на полке линии-выноски, проведенной от изображений шва (см. рис. 21.5).
Рис. 21.6. Изображение на чертеже неразъемных соединений, получаемых склеиванием
На чертежах соединений, получаемых сшиванием, швы изображают штриховой линией толщиной s/З с наклонными штрихами в интервалах (рис. 21.7). Длина штрихов в линии — 10—30 мм, длина наклонных штрихов — 2—3 мм, угол наклона штрихов к линии — 45°.
Обозначение материала (ниток и т. п.) по соответствующему стандарту или ТУ приводят в технических требованиях чертежа. Ссылку на номер пункта помещают на полке линии-выноски, проведенной от изображения шва. При необходимости под полкой линии-выноски указывают количество рядов в шве и расстояние между рядами. Размещение заклепок на чертеже указывают условным знаком +.
ГОСТ 2.314—68.ЕСКД. Указания на чертежах о маркировании и клеймении изделий.
ГОСТ 2.315—68.ЕСКД. Изображения упрощенные и условные крепежных деталей.
ГОСТ 2.316—68.ЕСКД. Правила нанесения на чертежах надписей, технических требований и таблиц.
ГОСТ 2.401—68.ЕСКД- Правила выполнения чертежей пружин.
Рис. 21.7. Изображение иа чертеже соединений, получаемых сшиванием
ГОСТ 2.402—68.ЕСКД. Условные изображения зубчатых колес, реек, червяков и звездочек цепных передач.
ГОСТ 2.403—75.ЕСКД. Правила выполнения чертежей цилиндрических зубчатых колес.
ГОСТ 2.404—75. ЕСКД. Правила выполнения чертежей зубчатых реек.
ГОСТ 2.405—75.ЕСКД. Правила выполнения чертежей конических зубчатых колес.
ГОСТ 2.406—76.ЕСКД. Правила выполнения чертежей цилиндрических червяков и червячных колес.
ГОСТ 2.407—75.ЕСКД. Правила выполнения чертежей червяков и глобоидальных передач.
ГОСТ 2.408—68.ЕСКД- Правила выполнения рабочих чертежей звездочек приводных роликовых и втулочных цепей.
ГОСТ 2.409—74.ЕСКД. Правила выполнения чертежей зубчатых (шлицевых) соединений.
ГОСТ 2.412—68.ЕСКД. Правила выполнения чертежей й схем оптических изделий.
ГОСТ 2.413—72.ЕСКД. Правила выполнения конструкторской документации изделий, изготовляемых с применением электрического монтажа.
ГОСТ 2.414—75.ЕСКД. Правила выполнения чертежей"жгутов, кабелей и проводов.
ГОСТ 2.418—77.ЕСКД. Правила выполнения конструкторской документации упаковки.
ГОСТ 2.420—69.ЕСКД. Упрощенные изображения подшипников на сборочных чертежах.
ГОСТ 2.701—76.ЕСКД. Схемы. Виды и типы. Общие требования к выполнению.
ГОСТ 2.702—75.ЕСКД. Правила выполнения электрических схем.
ГОСТ 2.703—68. ЕСКД. Правила выполнения кинематических схем.
Стандарты, используемые при разработке технических условий
ГОСТ 2.114—70.ЕСКД. Технические условия. Правила построения, изложения и оформления. Технические условия выполняют на листах формата 11 по ГОСТ 2.301—68 с основной надписью по ГОСТ 2.104—68 (формы 2 и 2а). Схемы, чертежи и таблицы допускается составлять на листах форматов 12 и 22 по ГОСТ 2.301—68; при этом основную надпись выполняют по форме 2а ГОСТ 2.104—68. Остальные требования к выполнению ТУ — по ГОСТ 2.105—79.
Стандарты, используемые при разработке эксплуатационной документации
ГОСТ 2.601—68.ЕСКД. Эксплуатационные документы. Стандарт устанавливает комплектность и правила разработки эксплуатационных документов на изделия.
Как правило, подлежат разработке следующие эксплуатационные документы: техническое описание (ТО), инструкция по эксплуатации (ИЭ), инструкция по техническому обслуживанию (ИО), формуляр (ФО), паспорт (ПС) или этикетка (ЭТ) и ведомости ЗИП (ЗИ). Номенклатура эксплуатационных документов на изделия, предназначенные для самостоятельной поставки, должна быть согласована с заказчиком.
Литература: 168, 107, 108J.
ГЛАВА 22
ОПТИЧЕСКИЕ МАТЕРИАЛЫ
Оптическое бесцветное стекло
Оптическое неорганическое стекло поставляется по техническим условиям в соответствии с ГОСТ 3514—76 в заготовках размером (диаметром или с наибольшей стороной) не более 500 мм следующих типов: ЛК — легкий крон, ФК — фосфатный крон, ТФК — тяжелый фосфатный крон, К — крон, БК — баритовый крон, ТК — тяжелый крон, СТК — сверхтяжелый крон, ОК — особый (с особым ходом дисперсии) крон, КФ — крон-флинт, БФ — баритовый флинт, ТБФ — тяжелый баритовый флинт, ЛФ — легкий флинт, Ф — флинт, ТФ — тяжелый флинт, ОФ — особый (с особым ходом дисперсии) флинт.
Стекла изготовляют двух серий: обычные — с нумерацией марок от 1 до 99; серии 100— малотемнеющие под воздействием ионизирующего излучения, с нумерацией марок от 100 до 199 (табл. 22.1). Марки стекол и соответствующие им оптические физико-химические характеристики приведены в табл. 22.1 и 22.2. (ГОСТ 13917—68 и ГОСТ 13659—78). Стекла нормируются по следующим параметрам: показателю преломления пе, средней дисперсии °ДН0Р°Д’
ноет и партии заготовок по пе и — пс')> оптической однородности, двойному лучепреломлению, радиационно-оптической устойчивости (стекла серии 100), показателю ослабления вд, бессвильности и пузырности.
По отклонениям констант и других характеристик качества оптическое стекло разделяется на категории и классы (табл. 22.3—22.18). Оптическая однородность заготовок стекла размером до 250 мм оценивается по разрешающей способности 1 (табл. 22.5), а размером более 250 мм — по коэффициентам Кф, АК (определяемым при X = 550 нм) и Кх (табл. 22.8).
По двойному лучепреломлению 2—4-й категории поставляют стекла: СТК9, СТК12, СТК19, ТБФ4, ЛФ105, ЛФ9, ЛФ10, Ф9, Ф13, Ф113, ОФ4, остальные марки стекла — 1—4-й категории.
По бессвильности поставляют стекла 2-й категории: ЛК 105, ЛК7, СТК9, СТК12, СТК19, КФ7; остальные стекла— 1-й и 2-й категории.
По однородности партии по показателю преломления и средней дисперсии поставляют стекла классов А—Г: К8, К108; классов Б—Г— остальные марки стекла.
1 Определяется значеияем отношения <р/(р0, где <р0 — теоретический угол разрешения дифрактометра; <р — угол разрешения дифрактометра вместе с проверяемой заготовкой.
Таблица 22.1. Оптические постоянные, химические свойства, плотность стекол
Марка стекла Показатель преломления Средняя дисперсия Группа химической устойчивости по ГОСТ 13917—68 Плотность, г/см3
пе «01 ('Эи—Ж) 14 о о е 1 е к влажной атмосфере к пятнающим агентам
лкз, лкюз 1,4891 1,4874 700 696 А III 2,46
ЛК4 1,4922 1,4903 758 753 А I 2,33
ЛКЮ5 1,4799 1,4781 731 729 А I 2,27
ЛК6 1,4721 1,4704 708 704 А IV 2,30
ЛК7 1,4846 1,4828 732 728 А 1 2,30
ФК14 1,5821 1,5799 898 891 Д I 3,39
К8, К108 1,5183 1,5163 812 806 А I 2,52
К100 1,5237 1,5215 882 875 — —‘
К14, КИ4 1,5168 1,5147 856 849 А 1 2,53
К19, К119 1,5208 1,5187 848 841 А I 2,62
БК4, БК104 1,5324 1,5302 884 877 А I 2,76
Б Кб, БК 106 1,5421 1,5399 913 905 А I 2,86
БК8, БК 108 1,5489 1,5467 877 871 А III 2,85
БКЮ, БКПО 1,5713 1,5688 1024 1015 А III 3,12
БК13 1,5617 1,5594 992 915 А III 3,04
ТК2, ТК102 1,5749 1,5724 1005 996 А II 3,20
ТК4, ТК104 1,6138 1,6111 1105 1095 А III 3,58
ТК8 1,6168 1,6140 1125 1114 А III 3,61
ТК12 1,5710 1,5688 911 904 А III 3,06
ТК13 1,6063 1,6038 1004 996 А III 3,44
ТК14, ТК114 1,6155 1,6130 1020 1012 А III 3,51
ТК16, ТК116 1,6152 1,6126 1059 1050 А III 3,56
ТК17 1,6305 1,6279 1067 1058 А III 3,66
ТК20, ТК120 1,6247 1,6220 1107 1097 А III 3,58
ТК21, ТК121 1,6600 1,6568 1299 1285 А III 3,98
ТК23 1,5915 1,5891 970 962 А III 3,24
СТ КЗ 1,6622 1,6594 1160 1150 А IV 3,91
СТК9 1,7460 1,7424 1492 1478 а HI 4,11
СТК12 1,6950 1,6919 1268 1258 а III 3,46
CTKI9 1,7476 1,7440 1489 1476 а IV 4,09
КФ4 1,5203 1,5181 886 879 А I 2,57
КФ6 1,5027 1,5005 882 875 В I 2,52
КФ7 1,5200 1,5175 1022 1012 А I 2,51
БФ1 1,5271 1,5247 964 955 Б I 2,67
БФ6 1,5724 1,5696 1164 1152 А I 3,16
БФ7 1,5822 1,5795 1087 1076 А 111 3,23
БФ8 1,5857 1,5826 1269 1254 А 1 3,28
БФ11, БФ111 1,6251 1,6222 1183 1171 А III 3,66
БФ12, БФ112 1,6298 1,6259 1622 1601 А 111 3,67
БФ13, БФ113 1,6428 1,6395 1340 1325 А 111 3,82
БФ16 1,6744 1,6709 1435 1419 А III 4,02
БФ21, БФ121 1,6178 1,6140 1554 1534 А I 3,56
Показатель преломления Средняя дисперсия Группа химической устойчивости по ГОСТ 13917—68 09 2 о
Марка стекла а 4 О О и S о 2 S =1 О и? л н
пе nD О е ч Г, е г» ¥ О) е у Sg я s S Л ь ь К X Г"! fl) о о S о
С е н я я ч Е
БФ24 1,6386 1,6344 1750 1726 А I 3,67
БФ25 1,6108 1,6076 1333 1318 А I 3,47
БФ28 1,6687 1,6641 1900 1874 А I 3,96
ТБФ4 1,7836 1,7786 2072 2045 а IV 4,46
ЛФ5, ЛФ105 1,5783 1,5749 1409 1392 А I 3,23
ЛФ9 1,5837 1,5800 1547 1526 А I 2,61
ЛФ10 1,5509 1,5480 1209 1195 А I 2,73
Ф1, Ф101 1,6179 1,6138 1681 1659 А I 3,57
Ф102 1,6210 1,6169 1707 1684 А I 3,60
Ф4 1,6285 1,6242 1762 1738 А I 3,67
Ф104 1,6290 1,6247 1762 1738 А I 3,67
Ф6 1,6070 1,6031 1611 1590 А I 3,48
Ф9 1,6180 1,6137 1801 1775 А I 2,93
Ф13 1,6241 1,6199 1730 1706 А I 3,63
Ф113 1,6246 1,6204 1730 1706 А I 3,63
ТФ1, ТФ101 1,6522 1,6475 1940 1912 А II 3,86
ТФ2 1,6776 1,6725 2118 2087 А II 4,09
ТФЗ 1,7232 1,7172 2469 2431 А III 4,46
ТФ103 1,7237 1,7177 2469 2431 А III 4,46
ТФ4 1,7462 1,7398 2670 2628 А III 4,65
ТФ104 1,7462 1,7398 2662 2623 А III 4,65
ТФ5, ТФ105 1,7617 1,7550 2788 2743 А III 4,77
ТФ7 1,7343 1,7280 2611 2570 А III 4,52
^Ф8, ТФ108 1,6947 1,6893 2249 2215 А 11 4,23
ТФ10, ТФНО 1,8138 1,8060 3233 3178 А III 5,19
ОФ1, ОФ 101 1,5319 1,5294 1032 1022 А IV 2,56
ОФ4 1,6541 1,6505 1513 1497 а IV 3,48
Примечания: 1. Предпочтительно применять стекла марок» выделенных жирным шрифтом, 2. На стеклах JIKJ05 и ЛК.7 может образовываться невидимый разрушенный слой, обнаруживаемый после обработки при температуре свыше 400° С по помутнению, сморщиванию или растрескиванию.
Таблица 22.2. Категории марок стекла и термические свойства
Марка стекла Категории Приращение показателя преломления Роти • 107, град"1, в пределах температур от —60 до 4-20° С Коэффициент линейного расширения а. 107 в пределах температур
по показателю преломления реднен дисперсии «сг по показателю ослабления ед 1 по оптической однородности заготовок размером, мм
пе * * ДО 250 св. 2 50 от — 60 до + 20° С от 4-20 до 4- 120° С
о о с 1 к Ц. S?
лкз * 1- 4 4— -5 1- -3 4—5 1—3 II— IV —10 -9 —6 86 92
ЛК103 * 1- 4 4— 5 1- -3 4—5 1—3 II— IV —10 —9 —6 86 92
ЛК4 * 1 — 4 3- -5 1- -3 3—4 1—3 III— IV 37 38 42 50 52
ЛКЮ5 * 1- 4 3- -5 1- -3 7—8 2—3 III— IV “ — —
ЛК6 * 1- 4 3- -5 Ь -3 2-5 1—3 II— IV —3 —2 0 80 83
ЛК7 * 1- -4 3- -5 1- -3 5—6 2—3 III- IV 53 54 57 40 44
ФК14 3- -4 2- -3 2—4 1—3 —28 —26 —23 88 98
К8 1- -4 4- -5 1- -3 2—4 1—3 I— IV 22 24 28 68 76
КЮ8 1- 4 4- -5 1- -3 2-5 1—3 I— IV — — — —
кюо 2- -4 4- -5 2- -4 5—6 1—3 II— IV — — — — —
К14 2— -4 4— -5 1- -3 4—5 1—3 I— IV 38 40 44 62 69
К114 2— -4 4— -5 2- —4 4—5 1—3 I— IV —1 — — —
KI9 3- -4 4- -5 1- -3 3—4 1—3 I— IV 22 23 27 74 80
КИ9 3- -4 4- -5 Ь -3 4—5 1—3 I— IV — — — — —
БК4 2- -4 4— -5 1- -4 2-5 1—3 II — IV 17 18 23 74 80
БКЮ4 1- -4 4— -5 1- -3 4—5 1-3 II — IV — — — — —
Б Кб 2— -4 4— -5 ь -3 2—4 1—3 II — IV 16 18 22 74 82
БКЮ6 1- -4 4— -5 2- -3 4—5 1—3 II— IV — — — —
БК8 2- -4 4— -5 1- -3 2—4 1—3 II — IV 32 34 38 56 62
БКЮ8 2— -4 4— -5 2- -3 4—5 1—3 II— IV — — — — ——
БКЮ 2— -4 4— -5 2- -3 2—4 1—3 II— IV 35 37 42 65 71
БКПО 2— -4 4— -5 2- -3 LO 1 со 1—3 II— IV — — — — —
Б КЗ 2— -4 4- -5 2- -3 4—5 1—3 II — IV 24 26 29 62 69
ТК2 1- -4 4— -5 2- -3 3—4 1—3 II— IV 31 33 38 64 70
ТКЮ2 2- -4 4— “5 2- -3 4—5 1—3 II- IV — — — —
ТК4 2— -4 4— -5 2- -3 3—4 1—3 II- IV 40 42 47 59 66
ТК8 2— -4 4— -5 2- 4 ьо 1 СП 1—3 II- IV 34 36 42 62 71
TKI2 2— -4 4— -5 1- -3 3—4 1—3 II- IV 26 27 30 58 65
ТК13 2— -4 4— -5 2- 4 1—3 II- IV 23 24 28 61 67
ТК14 2— -4 4— -5 2- -3 2—4 1—3 II- IV 20 21 23 63 69
ТКН4 2— -4 4— -5 2- -3 4—5 1—3 II- IV — — — —
ТК16 2— -4 4— -5 2- -3 2—4 1—3 II- IV 18 20 24 66 72
ТК116 2— -4 4— -5 1- -3 3—5 1—3 II- IV — — — — —
ТК17 2— -4 2- -3 2—4 1—3 7 9 12 69 76
ТК20 2— -4 4— -5 Ь -3 3—5 ,‘~3 II- IV 21 23 27 66 73
648
I । I i I I
I
Марка стекла Категории Приращение показателя преломления Ротн • 107. град-1, в пределах температур от '-60 до 4-20° С Коэффициент линейного расширения а. Ю7 в пределах температур
по показателю преломления по средней дисперсии Пр' —nQf по показателю ослабления ед по оптической однородности заготовок размером. мм
* * пе До 250 св. 250 со. & от — 60 до + 20° С от +20 до +120° С
TKI20 2-4 4- -5 2—3 4-5 1—3 II -IV — -
ТК21 2—4 4— -5 2—3 3—4 1—3 II -IV 31 33 39 73 81
ТК121 2—4 4— -5 2—3 4—6 1—3 II -IV — — ——
ТК23 2—4 4— -5 1—3 2—5 1-3 II -IV 33 35 38 52 58
СТ КЗ 2—4 4— -5 1—3 2—3 1—3 II -IV 2 4 9 71 79
СТК7 2—4 4- -5 3—4 2-3 2—3 II -IV —14 — 13 -12 84 94
СТК9 2—4 2—3 4—7 2—3 55 57 64 51 57
CTKI2 2—4 4— -5 2—3 2—6 2—3 II -IV 33 35 39 57 67
СТК19 2—4 4— -5 1—3 3—4 2—3 II -IV — — — 1
КФ4 1—4 4— -5 3—4 4—5 1-3 II -IV 35 36 40 63 71
КФ6 1—4 1—4 4—5 1—3 29 30 34 62 68
КФ7 3—4 1—3 5—7 1—3 42 44 50 55 60
БФ1 2-4 4— -5 2—4 2—5 1—3 II -IV 32 34 39 66 72
БФ6 2—4 3- -4 2—3 4 1—3 II -IV 22 24 31 77 83
БФ7 3—4 4— -5 1—3 3—4 1—3 II -IV 38 40 46 68 75
БФ8 2—4 3- -4 1—3 3—4 1—3 II -IV 26 29 35 77 82
БФ11 2—4 3- -4 2—3 4—5 1-3 II -IV 40 42 48 63 70
БФ111 2—4 4— -5 2—3 4—5 1—3 II -IV — — —
БФ12 1—4 4— -5 2—4 3—5 1—3 II -IV 25 29 39 83 88
БФ112 2—4 4- -5 1—4 4—5 1-3 II -IV — — — ' ' ' —
БФ13 2—4 4— -5 2—4 2—5 1—3 II -IV 40 43 52 61 68
БФ113 3—4 4— -5 2—4 4—5 1—3 II -IV — — — Ч —
БФ16 2—4 4— -5 2—4 3—5 1—3 II -IV 22 25 32 78 84
БФ21 3—4 4— -5 3—4 4 1—3 II- -IV 44 47 55 71 77
6Ф121 3—4 4— -5 3—4 4—5 1—3 II- -IV —- —- — « — —
БФ24 3—4 4— -5 3—4 2—4 1—3 II -IV 48 52 62 74 79
БФ25 2—4 3- -4 2—4 2—5 1—3 II -IV 47 50 59 66 73
БФ28 2 4 3- -4 3—4 4—5 1—3 II -IV 79 84 97 59 65
ТБФ4 3—4 3—4 5—8 1—3 63 68 81 65 75
ЛФ5 2—4 3- -4 2—3 3—4 1—3 I -IV 38 42 50 67 72
ЛФ105 2—4 3- -4 2—3 4—5 1—3 II -IV — — 1 —
ЛФ9 2—4 2—4 6—7 1—3 — 3 6 14 81 89
ЛФ10 3—4 3—4 5—7 1—3 23 26 32 72 77
Ф1 2—4 3- 4 2—4 2—4 1—3 I -IV 45 49 59 71 74
Ф101 2—4 3- -4 2—4 3—5 1—3 I- -IV —— ——
Ф102 2—4 3- 4 2—4 4—5 1—3 I- -IV — — - — —
649
Категории Приращение показателя преломления В -107 ропт ’ град-1, в пределах температур Коэффн циент линейного расширения а-10’ в пределах
по показателю преломления S Сй К S S о» ю св по оптической однородности заготовок размером,
Марка стекла о. о» с и о О о мм от — 60 до -Ь 20° С температур
S t=c
пе * * пе средней ' -пс' н л СП 03 а о С До 250 св. 250 — 60 + 20° С + 20 + 120° С
о с е О С £ 02. £ от ДО н о о »=с
Ф4 2—4 4—5 2—4 4—5 1—3 I—IV 47 52 64 73 76
Ф104 3—4 4—5 1—4 4—5 1—3 I—IV — ——1 -—- —- —
Ф6 2—4 3—4 2 4 3—4 1—3 I—IV 40 45 56 70 74
Ф9 2—4 1 । 4 6—7 1—3 —5 —1 8 90 96
Ф13 2—4 4—5 । 4 2—4 1—3 II—IV 47 52 64 71 75
Ф113 1—4 4—5 2—4 3—4 1—3 II—IV -1 — — —— -—
ТФ1 1—4 3—4 2—4 2—4 1—3 II—IV 29 34 46 82 86
ТФ101 2—4 3—4 4—5 1—3 II—IV — — — —
ТФ2 2—4 4—5 2—4 2 4 1—3 II—IV 53 59 75 73 78
ТФЗ 1—4 4—5 2—4 2 4 1—3 II—IV 56 64 83 77 83
ТФ103 2—4 4—5 1—4 2—4 1—3 II—IV — —- — —— "
ТФ4 1—4 3—4 2—4 N3 1 СП 1—3 II—IV 65 74 97 77 82
ТФ104 2—4 2 4 3—4 7—8 1—3 II—IV — — — —
ТФ5 2—4 4—5 2—4 3—5 1—3 II—IV 69 78 102 78 84
ТФ105 2—4 4—5 3—4 7—8 1—3 II—IV — — — ——
ТФ7 2—4 4—5 2—4 2—5 1—3 II—IV 42 49 70 93 96
ТФ8 2—4 4—5 2-4 2—4 1—3 II—IV 53 60 78 77 82
ТФ108 2—4 4—5 3—4 5—6 1—3 II—IV —- —
ТФ10 2—4 4—5 2—4 ю 1 со 1—3 II—IV 87 97 125 75 81
ТФ110 2—4 4—5 2—4 7—8 1—3 II—IV — — — — —
ОФ1 2—4 3—4 3—4 4—5 1—3 II—IV 31 33 37 59 63
0ФЮ1 2—4 3—4 2—4 4—5 1—3 II—IV — —
0Ф4 3—4 5 3—4 2—3 1—3 II—IV 36 38 44 44 52
Примечание. Абсолютные значения изменений показателя преломления 0agc U°. X) в зависимости от температуры см, ГОСТ 73659—78.
* Допускается устанавливать требования к коэффициентам Дф
и ЛК отдельно от требований к коэффициенту К . ** Для заготовок, подвергнутых тонкому отжигу со скоростью менее 0,5 град/ч.
Т а б л и ц а 22.3.
Предельное отклонение Пе и (tip, —пс>)
Категория пе Пр? — П(у
1 ±2-10“4 ±2* 1(Т5
2 ±3-10“ 4 ±3-10-5
3 ±5-10-‘ + 5-10-6
4 ±10*10“4 + 10-10-5
5 ±20-10“ 4 ±20-1(Г5
Таблица 22.4.
Предельное отклонение по однородности в партии заготовок по Пе и [tipr —
Класс пе Пр'— Прр
А 0,2.1(Г*
Б 0,5-10~* —
В НО'4 1-10~б
Г В пределах задан-
ной категории
Таблица 22.5.
Оптическая однородность, оцениваемая по разрешающей способности
Категория Отношение (р/(р0. не более
1 и 2 3 4 5 1,0 1,1 1,2 1,5
Примечание. Для стекла 1-й категории дифракционное изображение точечной миры не должно иметь разрывов, хвостов и заметного на глаз отклонения от круга.
Таблица 22.G.
Категории бессвильности
Категория Характеристика бессвильности
1 Не допускаются свили, равные по оптическому действию контрольной свили 1-й категории
2 То же, 2-й категории
' Таблица 22.7. Классы бессвильности
Класс Направления, в которых заготовка должна удовлетворять заданной категории бессвильности
А Б Два взаимно перпендикулярных направления Одно направление
Примечание. Допускается в среднем ие более 10 узловых свилей длиной до 10 мм в 1 кг стекла.
Таблица 22.8. Допустимые отклонении по оптической однородности, характеризуемых коэффициентами Кф, дК и К*
Категория Яф АЛ
I До 0,25 * До 0,15 *
II Св. 0,25 до 0,70 Св. 0,15 до 0,25
III Св. 0,70 до 1,50 Св. 0,25 до 0,80
IV Св. 1,50 до 3,00 Св. 0,80 до 1,50
V Св. 3,00 Св. 1,50
«х
Свили, обнаруживающие двойное лучепреломление Допускаются одиночные свили Допускаются потоки свилей общей площадью от площади заготовки, %
на расстоянии друг от друга, мм общей длиной от размера заготовки
Не допускаются Св. 50 мм До одного диаметра —
Св. 30 мм До двух диаметров (диагонали) заготовки До 10
Св. 20 До 50
Не допускаются очень грубые одиночные свили и потоки свилей, обнаруживающие двойное лучепреломление св. 30 нм, расположенные в центральной трети толщины заготовки, и св. 10 нм при расположении их в крайних третях заготовки
* Для заготовок деталей интерференционных приборов Кф и ДК до 0,10. Бессвильность (см. табл. 22.6 и 22.7) н двойное лучепреломление (см. табл. 22.9) не указывают, так как качество стекла обеспечивают выполнением требований к коэффициентам Кф, ДК и Лх.
Т а б л и ц а 22.9. Двойное лучепреломление
Т а б л и ц а 22.10.
Показатель ослабления
Категория Двойное лучепреломление, им/см, ие более, при оптическом коэффициенте напряжения, 1 О12 1/Па
ДО 2,0 от 2,0 ДО 2,8 св. 2,8
1 1,5 2 3
2 4 6 8
3 7 10 13
4 10 15 20
5 35 50 65
Категория Показатель ослабления
Ел-'°4 , см-1
1 2— -4
2 5- -9
3 10- -17
4 18- -25
5 26- -35
6 36- -45
7 46- -65
8 66- -130
Таблица 22,12.
Классы пузырности
Т а б л и ц а 22.11.
Категории пузырности
Категория Диаметр наибольшего пузыря, мм
1 0,002
1а 0,05
2 0,1
3 0,2
4 0,3
5 0,5
6 0,7
7 1,0
8 2,0
9 3,0
10 5,0
Класс Число пузырей диаметром свыше 0,03 на 1 кг, не более
А 10
Б 30
В 100
Г 300
д 1000
Е 3000
Примечание. В стекле категорий 1а—10 (см. табл. 22.11) число пузырей размером не более 0,03 мм не должно превышать числа пузырей, допускаемых по соответствующему классу.
Таблица 22.13. Категории пузырности в зависимости от массы и класса пузырности стекла
Класс пуаыр-но’сти Масса заготовок, г, не более, для категории пузырности
1. 1а 2 3 4 5 6 7 8 9 10
А 300 500 700 1000 1500 3000 5000 20 000 Св. 20 000 Св. 20 000
Б 100 250 500 700 1000 2000 3000
В 50 100 200 300 500 1000 3 000 20 000 10 000
Г 30 50 100
д 10 30 50 Св. 10 000
Е-Ж — 5 10 30 100 300
Т а б л и ц а 22.14. Категории пузырности различных марок стекол в зависимости от массы заготовки
Марка стекла Масса заготовок, г, не более, для категории пузырности
1а 2 3 4 5 6 1 8 9 10
ТК4, ТК104, ТК8, TKI4, ТКП4, ТК16, ТКН6, ТК120, ТК21, ТК121, ТК23, СТ КЗ, СТК7, СТК12, БФ13, БФ113 100 200 700 1000 1500 3000 5000 20 000 Св. 20 000
СТК9, СТК19 30 50 100 200 300 500 1000 3 000 10 000 Св. 10 000
Таблица 22.15. Классы пузырности стекла, сваренного в керамическом и платиновом сосудах
Марка стекла Класс пузырности
К19, К119 А—Б
К8, К108, ЛФ6, Ф1, Ф101, Ф102, Ф4, Ф104, Ф13, ТФ1, ТФ101, ТФ2, ОФ1, 0ФЮ1 А—В
ЛКЗ, ЛКЮЗ, ЛК4, ЛК6, ЛК7, БК4, БК104, БК8, БКЮ8, КФ4, КФ6, БФ1, БФ6, БФ7, БФ8, БФ12, БФ112, БФ24, ЛФ105, ФИЗ, ТФЗ, ТФ103, ТФ8, (ТК4, ТКЮ4, ТК8, ТК14, ТКП4, ТК20, ТК21, ТК23, TKI21, СТК7, БФ16) Б—В
К14, КИ4, БК6, БК106, БК10, БКНО, БК13, ТК2, ЛФ6, ТФ4, ТФ104, ТФ108, (ТК16, ТК! 16, СТКЗ, СТК12, БФ13, БФ113) Б—Г
КЮ0. ТК12, БФ21, БФ121, Ф9, ТФ5, ТФ105, ТФ7, БФ28, ЛФ10 В—Г
К7, (СТК9, СТК19) в-д
ТК4, ТКЮ4, БФ25, ТБФ4, ОФ4, ТК12 г-д
ФК14 Г—Е
ТФЮ, ТФ110 д-ж
Примечания. 1. Марки стекла, заключенные в скобки, сварены в платиновом сосуде. 2. В стекле с показателем ослабления 1 — 3 категории число пузырей в 1 кг стекла соответствует наибольшему классу пузырности для стекла данной марки
Таблица 22.16. Радиационно-оптическая устойчивость, характеризующая приращение оптической плотности ДО на 1 см после облучении
Марка стекла ND, не более Марка стекла ND, не более
лкюз, ТФ103, ТФ110 БКНО, ТФ105, 0,040 БКЮ8, ТК120 ТК121 0,020 0,065
ЛКЮ5, 0ФЮ1 0,050 БФ111 0,060
К108, БК106 БК104, 0,015 БФ113 0,200
К100 0,030 БФ121 0,120
КИ4, БФ112 ТФ104, 0,045 ЛФ105 0,110
К119, ТК104, ТКЮ2, ТКИ4, 0,025 Ф101, Ф102, Ф104, Ф113 0,070
ТК116 ТФ101, ТФ108 0,080
Т а б л и ц а 22.17. Рекомендации по замене исключенных из ГОСТ 3514—76 марок стекол
Марка стекла Рекомендация по нх замене Марка стекла Рекомендация по нх замене
ФК1 ФКП КФ1 БФ1
К17 К8, К100 КФ8 ОФ1
БК9 Б КЮ БФ23 БФ4
ТК109 БФН1 ОФ2 ЛФ11
Примечание. Стекла марок ФК1, ФК 11 н БФ4 поставляются по нормативно-технической, документации.
Таблица 22.18. Группы химической устойчивости стекол (ГОСТ 13917—68)
Группа К в л аж н ой атмосфере Группа 1 К пятнающим агентам
А Б В а У д Силикатные стекла Неналетоопасные Промежуточные Налетоопасные Несиликатные стекла Устойчивые Промежуточные Нестойкие I II III IV Непятнающиеся Промежуточные Пятнающиеся Нестойкие стекла, требующие особо осторожного обращения при обработке
Примечание. Силикатные стекла содержат SiO2 > 30% мол.; несиликатные — SiO2 < 30% мол. (ТФК, ФК. СТК, ТБФ).
Таблица 22.19. Показатели преломления и дисперсии оптических стекол
Марка стекла ?0l pw— 1 1 Д к? п to nF~ne ng~nF nh~ng "С-"о, 7
nF~nc nF~nC Пр~пс nF~nC
ФК11 1,5199 752 0,701i 0,4539 0,5338 0,4407 0,158s
ТФК1 1,6084 933 0,703б 0,4564 0,54 0в 0,4472 0,153,
СТК20 1,7647 1522 0,7065 0,4593 0,550б 0,4604 0,152,
OKI 1,5222 684 0,704о 0,456, 0,5394 0,4449 0,1557
ТЬФ9 1,8083 1890 0,711о 0,4644 0,5642 0,4761 0,148e
СТФ2 1,9441 4626 О,726о 0,4824 0,632в 1 0,135o
СТФЗ 2,1696 6873 0,7298 0,4874 — — 0,1315
СТФ11 2,0557 6351 0,7307 0,4885 0,6588 — 0,1319
По классу бессвильности Б поставляют стекла: Л КЗ, ЛКЮЗ, ЛК4, ЛК105, ЛК6, ЛК7, ФК14, ТК12, ТК17, СТКЗ, СТК9, СТК12, CTKJ9, КФ6, КФ7, ТБФ4, Ф6, Ф9, ОФ1, 0ФЮ1, ОФ4; остальные стекла — по классу А—Б.
Вне рабочей зоны заготовки стекла требования к нормируемым параметрам, кроме двойного лучепреломления, не устанавливают.
Таблица 22.20. Категории и классы оптических стекол
Наивысшие категории по Классы по
Марка стекла nDf nF-nc прн размере заготовки, мм оптической однородности при размере заготовки, мм >му лучепрелом- телю ослабле-р ИЛИ k, CM-1 1 бес-евнль-ностн при размере заготовки, мм )дности партии X н О о X А НОСТИ
ДО 150 св, 150 до 150 св. 150 двойне ленню показа НИЯ До 150 св, 150 ДО 300 и Q. О X о X и о о си ко пузыр!
ФКП 4 4 1 2 1 4 2 2 В в Г—Е
ТФК1 5 — 2 — 2 7 2 — в в Е
СТК20 5 — 2 1 7 1 — в в г-д
OKI 5 5 1 1 2 5 2 2 А в Е
ТБФ9 5 - ' 2 — 2 8 2 А в Е
СТФ2 5 — 2 * 3 5% 2 — — — в Е
СТФЗ 4 3 —— 1 7,5% 1 — в в Е-Ж
СТФН 5 — — 3 7% 2 — — в Е
Стекла марок ЛК1, ЛК5, ФК13, KI, К2, К102, КЗ, К5, К15, К18, К20, БКП, ТК1, ТКЮ8, ТКН2, ТК123, СТК8, СТКЮ, КФ104, КФ5, БФ4, БФ106, БФ107, БФ108, БФ26, БФ27, ТБФЗ, ЛФ1, ЛФ7, ЛФ8, ЛФ11, ЛФ12, Ф2, Ф7, Ф8, Ф108, ТФ102, ТФ11, ТФ12, ОФЗ, ОФ5 не вошли в ГОСТ 3514--76 и изготовляются по нормативно-технической документации.
Появление новых марок стекол позволяет разработать оптические системы с меньшим числом линз. Они открывают широкие возможности в конструировании оптических систем, обладающих высокой степенью коррекции аберраций в широкой области спектра.
В табл. 22.19 и 22.20 приведены характеристики некоторых марок стекол, соответствующих отраслевому стандарту. Б ол ьшой иите рес представляет особый крон OKI, который обладает большим коэффициентом светопропускания в инфракрасной области спектра и в сочетании с особыми флинтами ОФ4 и ОФ5 дает отличную апохроматическую коррекцию.
Оптическое цветное стекло
Оптическое цветное неорганическое стекло, предназначенное для изготовления светофильтров, выпускается в заготовках размером (диаметром или с наибольшей стороной) не более 250 мм и не более 360 мм для стекла, окрашенного сульфоселенпдами или сульфидами металлов (ГОСТ 9411—75).
Таблица 22.21, Показатель преломления, химическая устойчивость и плотность цветного стекла
Ё о Группа t s Группа
химиче- о хнмиче-
Ч ской м ч ской со
0) Ct устой- Е и Ct устой- Е CJ
с чивости с чивости
Марка л Й н л Я Я 0) F-) ТЗ Марка Д гнаю-геиту
С ГС К Л d н с о я я а я н о стекл« Ч £ е О Я f-U
Показа лен j/я д Ч U « о S Я К ПЯ' щему а о я о ч с Показа ления 2-е- § Я Л К ПЯ’ щему а о я н о ч с
У л ь т р а ф И 0 Л е т о в о е ЗС10 1,535 д IV 2,83
с т е к л С ) ЗС11 1,550 в I 2,83
УФС1 1,540 д I 2,84 Же л т О - з е л ено е
УФС2 1,557 д 1 2,65 с т е к л с >
УФС6 1,520 в I 2,58 2,52
УФС8 С 509 А IV 2,46 ЖЗС1 1,522 В I
ЖЗС6 1,522 В I 2,50
Ф И О л е т о в о е стекло ЖЗС9 1,522 В I 2,50
ФС6 | 1,495 1 А I 2,40 ЖЗС12 ЖЗС13 1,527 1,527 В в I I 2,53 2,53
С р [нее с т е К Л О ЖЗС17 1,527 в I 2,53
ЖЗС18 1,534 д IV 2,84
СС1 1,520 В I 2,51
СС2 1,520 В I 2,51 Желтое с т е к л <
СС4 СС5 СС8 СС15 1,520 1,582 1,520 1,513 В в в в I II I I 2,51 3,25 2,52 2,48 жсз ЖС4 жсп ЖС12 1,536 1,632 1,523 1,523 В А В В IV I I I 2,78 3,69 2,64 2,64
С и н е - з еле н о е ЖС16 1,523 В I 2,64
с т е к Л о ЖС17 1,523 В I 2,64
СЗС7 ЖС18 1,523 В I 2,65
1,514 В I 2,57 ЖС19 1,502 В III 2,40
СЗС8 1,517 В I 2,59 ЖС20 1,540 д I 2,82
СЗС9 1,522 в I 2,61
СЗС16 1,515 А I 2,60 Opai н жев ое стекло
СЗС17 1,518 А I 2,50 1,523 2,55
СЗС20 1,477 В IV 2,27 ОС5 В I
СЗС21 1,535 а IV 2,86 ОС12 1,523 В I 2,64
СЗС22 1,535 а IV 2,93 ОС13 1,523 В I 2,64
C3C23 1,534 Д IV 2,84 ОС14 1,523 в I 2,65
СЗС24 1,516 а I 2,55 ОС17 1,523 в I 2,64
СЗС25 1,515 а 1 2,54
СЗС26 1,534 д I 2,84 Кр а с н о е ст е к л О
СЗС27 1,503 а IV 2,44 кси 1,523 в I 2,64
Зел е н о ( ; с т е к л о КС13 КС15 1,523 1,523 в в I I 2,64 2,64
зсз 1,523 В I 2,52 КС17 1,523 в I 2,64
ЗС7 1,535 д IV 2,85 КС18 1,523 в I 2,64
ЗС8 1,534 д IV 2,83 КС19 1,523 в I 2,67
Марка стекла Показатель преломления Пр Группа химической устойчивости Плотность d, г/см3 Марка стекла Показатель преломления Пр Группа химической устойчивости Плотность d, г/сма
к влажной атмосфере к пятнающему агенту к влажной атмосфере к пятнающему агенту
И н ф р а к р а С н о е НС6 1,502 А IV 2,42
с т е К Л С ) НС7 1,502 А IV 2,42
ИКС5 ИКС6 ИКС7 1,533 1,541 1,556 в В В I I I 2,73 2,74 2,82 НС8 НС9 нею НС11 1,503 1,505 1,509 1,514 А А А А IV IV IV IV 2,42 2,42 2,42 2,43
П у р п у р н о е стек л о НС12 1,527 А IV 2,46
ПС5 1,673 А I 4,09 Т е м н о е с т е к л о
ПС7 ПС8 ПС13 1,537 1,604 1,591 А А В I I IV 2,72 3,56 3,26 тез тсю 1,525 1,523 В А I I 2,53 2,51
ПС14 1,477 В IV 2,27 Бесцветн о е с т е к л о
ПС15 1,477 В IV 2,27 БСЗ 1,512 А I 2,52
Н е й т р а л ь н о е с т е К Л О БС4 1,502 Б I 2,38
НС1 НС2 нсз 1,521 1,523 1,526 В В В I I I 2,51 2,52 2,52 БС7 БС12 БС14 1 1,643 1,508 1,670 А А а I I IV 3,72 2,47 3,08
Примечание. Предпочтительно применять стекла марок, выделенных жирным шрифтом.
Т а б л и ц а 22.22. Категории пузырности цветного стекла (по ГОСТ 3514—76)
Марка стекла Масса заготовок, г, не более, для категорий
СЧ 00 СО 00 00 1 iO 00 1 CD 00 J. 8
CCl, СС2, СЗС20, ЗС1, ЗСЗ, ЖЗС1, ЖЗС5, ЖЗС6, ЖЗС9, жеи, ЖС12, ЖС16, ЖС17, ЖС18, ОСП, ОС12, ОС13, ОС14, ОС17, КС11, КС13, КС15, КС17, КС18, КС19, НС1, НС2, НСЗ, НС6, НС7, НС8, БСЗ, БС7, БС8, БС12, ПС5 30 50 100 300 500 1000 3000
Марка стекла Масса заготовок, г, не более, для категорий
7 00 1 СО 4—8 00 1 ю 6 — 8 7—8 8
СС9, СЗС7, СЗС8, СЗС17, СЗС21, СЗС22, C3C23, СЗС24, СЗС25, СЗС27, ЗС10, ЗС11, ЖС4, ЖС19, ПС14, ПС15, ТС6, БС4 10 30 50 300 500 1000 3000
СЗС5, СЗС9, C3CI5, C3CI6, СЗС26, ЗС6, ЗС8, ЖЗС18, ЖСЗ, ЖС20, ОС5, ОС6, ПС7 5 10 30 100 300 1000 1000
ТС7, БС14 — — 30 50 100 300 500
СС4, СС5, СС8, СС15, ЖЗС12, ЖЗС13, ПС8, ПОЗ, НС9, ТОО — 1 10 30 50 100 200
УФС1, УФС5, УФС6, УФС8, ФО, ФС6, ИКО, ИКСЗ, ИКС5, иксе, ИКС7, нею — — — 30 50 100 200
Примечание. Ввиду невозможности контроля ие устанав лнвается 2-я категория пузырности для заготовок марок СЗС9, СЗС20, СЗС21, СЗС22, C3C23, ЗС1, ЗС10, ОС5, ОС6, ПС5, ПС14, ПС15, НСЗ, НС8, ТС6, УФС2, УФС8, ФС7, ЖЗС17, НС11, НС12, ТСЗ.
Таблица 22.23. Спектральные характеристики стекла для нейтральных светофильтров
Марка стекла Показатель поглощения k up мм-1 ^ср ^тах
Номинальный Предельное отклонение по категориям %, не более, по категориям
1 2 1 2 1 2
НС1 0,07 ±0,01 ±0,02 10 15 20 25
НС2 0,24 ±0,03 ± 0,05
нсз 0,47 ±0,05 ±0,10 25 30
НС6 0,06 ±0,01 ±0,02 30 35
Марка стекла Показатели поглощения k ср мм-1 °ср ° шах
Номинальный Предельное отклонение по категориям %, не более, по категориям
1 2 1 2 1 2
НС7 0,12 ±0,02 ±0,04 7 10 17 23
НС8 0,37 ±0,03 ± 0,06 5 10 10 15
НС9 0,55 ±0,06 ±0,11 15 20
нею 0,90 +0,10 0,09 +0,20 —0,18 20 25
НС11 —* ±0,18 ±0,36
НС12 — ±0,35 ±0,66 10 15 30 35
Т а б л и ц а 22.24. Спектральные характеристики стекол, окрашенных сульфоселенндами нли сульфидами металлов
Марка стекла Длина волны X нм .Г Длина волны > нм Показатель поглощения , мм, ие более Крутизна кривой оптической плотности не ме- Р нее, при толщине светофильтра, мм
Но-мн-наль-ная Предельное отклонение по категориям
1 2 3 2 и 3 5 [ 1Э и 20
жен 420 ± 5 ± 10 ± 15 560 0,005 0,6 0,4 1
Ж12 450
Ж16 470 0,8 0,8
ЖС17 490 580 1,2 1,0
Ж18 510 600 0,8
осн 535 650 0,007 1,2 1,2
ОС12 550
ОС13 565
ОС14 580 680
Марка стекла Длина волны Хп нм Длина волны Хо, нм Показатель поглощения , мм, не более Крутизна кривой оптической плотности k0, не менее, при толщине светофильтра, мм
Номинальная Предельное отклонение по категориям
1 2 3 2 н 3 5 10 и 20
ОС17 540 ±5 ±10 ±15 650 0,007 0,2—0,6 для светофильтра толщиной 1; 2; 5 и 10 мм
КСИ 610 680 1.2 1,2 1,2
кс1з 630 700
КС15 650 720 1,0 1,0 —
КС17 670 750
КС18 685 800 0,02 0,68 0,8
КС19 700 0,03
Оптическое цветное стекло нормируется по следующим параметрам: физико-химическим свойствам, показателю поглощения, двойному лучепреломлению, пузырности, бессвильности, неоднородности. В табл. 22.21—22.24 приведены марки стекол, основные параметры и технические требования по ГОСТ 9411—75.
По показателю поглощения устанавливаются две категории цветного стекла, характеризуемые предельными значениями и отношением показателей поглощения.
Для стекла типа НС устанавливаются две категории по показателю поглощения &Ср, характеризуемые 0Ср и^тах(табл. 22.23), где &ср— среднее арифметическое значений показателя поглощения /гх> измеренного через каждые 20 нм в области спектра 440—660 нм для стекла марок НС1—НСЗ и в области 440—700 нм, для стекла марок НС6—НС 12; ОСр ~ среднее арифметическое абсолютных значений отклонения показателя поглощения k\ от измеренного значения /еср, выраженное в процентах от &ср; Отах— наибольшее из абсолютных значений отклонения показателя поглощения k\ от измеренного значения &ср, выраженное в процентах от &ср.
Стекло, окрашенное сульфоселенидами или селенидами металлов, нормируется по показателю поглощения Лпр и k для стекла толщиной, равной толщине светофильтра (табл. 22.24), где — показатель поглощения в области наименьшего поглощения; Хпр — длина волны, при которой оптическая плотность стекла превышает на 0,3 оптическую плотность стекла той же толщины при длине вотиы Хо; ky — крутизна кривой оптической плотности стекла, равная разности оптических плотностей стекла при длинах волн Хпр — 20 и Хпр, нм.
Категории двойного лучепреломления стекла — 3—5 по ГОСТ 3514—76. По бессвильности устанавливаются четыре категории стекла: 1-я и 2-я категории определяются по ГОСТ 3514—76; по 3-й категории не допускаются видимые в проходящем свете потоки свилей, но одиночные и узловые свили допускаются, а по 4-й категории допускаются свили, оставшиеся после перемешивания по установленному технологическому режиму для данной марки. Неоднородность окраски стекол сульфидами или сульфоселенидами металлов, характеризуемая наибольшей разностью значений Лпр в пределах одной заготовки диаметром (или наибольшей стороной) до 40 мм, не должна превышать ЛЛПр — 2, для заготовки размером свыше 40 мм до 90 мм —• ДА,пр = 3, размером свыше 90 до 180 мм — ДЛпр = 5, размером свыше 180 до 360 мм — ДЛпр “= 10.
Химический (синтетический) состав оптических цветных стекол регламентируется технической документацией, утвержденной в установленном порядке.
Оптические кристаллы
Искусственные оптические кристаллы имеют ряд ценных свойств, отсутствующих у оптического стекла: пропускание излучения в ультрафиолетовой области спектра; пропускание излучения в инфракрасной области спектра; значительная величина коэффициента дисперсии при малом показателе преломления (у фтористых соединений).
Оптические кристаллы вместе с тем имеют и недостатки, затрудняющие их применение. К ним относятся: оптическая и механическая
неоднородность в различных направлениях и наличие вредных включе-
Рис. 22.1. Спектральное ‘ пропускание пластинки из хлористого калия толщиной 12 мм
ний; гигроскопичность и растворимость в воде некоторых кристаллов; дороговизна и ограниченные размеры монокристаллов; малая твердость ряда кристаллов; ядовитость некоторых кристаллов.
В табл. 22.25 и 22.26 даны
характеристики наиболее часто применяемых для изготовления оптических деталей искусственно выращиваемых кристаллов. Все указанные кристаллы относятся к кубической системе,
обладают, следовательно, оптической изотропностью и поэтому не имеют двойного лучепреломления (при условии отсутствия в них внутренних натяжений).
NaCl — мягкий, с высокой степенью однородности кристалл, хорошо растворим в воде и гигроскопичен. Пригоден дли области спектра с длиной волны 0,25—15 мкм. Практически используемый интервал дисперсии в инфракрасной области спектра равен 8,5—15 мкм. В основном применяется для спектральных призм в инфракрасной области
спектра.
КС1 — очень мягкий достаточно однородный кристалл, хорошо растворим в воде и гигроскопичен. Практически используемый интервал пропускания 0,33—21 мкм (рис. 22.1). Применяется для конденсорных линз ультрафиолетовых микроскопов, призм и окошек спектральных приборов для инфракрасной области.
Т а б л и ц а 22.25. Характеристики оптических кристаллов
Наименование Химическая формула Показатель преломления пр Коэффициент дисперсии Vp Плотность, г/см3 Мнкротвер-дость прн нагрузке 0,3 Н, МПа Растворимость в воде, г/см3 Коэффициент линейного расширения а. 106
Хлор истый натр и й (каменная соль *) NaCl 1,54432 42,7 2,17 160 0,260 42
Хлористый калий (сил ьвин) КС1 1,49038 43,9 1,98 90 0,256 28
Фтористый литий L1F 1,3920 99,3 2,64 960 0,0026 41
Фтор истый натр и й (в иллиомит) NaF 1,3250 85,3 2,81 500 0,043 33
Фтор истый кальци й (флюорит или плавиковый шпат) * CaF2 1,4338 95,3 3,18 1680 1,7-10~5 19,5
Бромистый калий КВг 1,5599 33,5 2,76 — 0,394 37
Бромистый таллий (КРС-5) TIBr и T1J 2,6316 — 7,4 42 0,0005 70
о о СП Алюмокалиевые квасцы * Встречаются в eci KA1(SO4)2- 12H2O -ественном виде. 1,45620 58,5 1,75 0,115
G66
Т а б л и ц а 22.26. Показатели преломления кристаллов при t == 20° С [66, 89]
Л., нм CaF 2 KJ LiF NaF NaCl KCI KBr
1083,03 1,42839 1,6381 1,38657 1,32125 1,53116 1,47878 1,54355
768,20 1,43092 1,6494 1,38927 1,32307 1,53654 1,48349 1,55007
728,14 1,43141 1,6520 1,38978 1,32349 1,53777 1,48454 1,55160
556,28 1,43248 1,65809 1,39085 1,32436 1,54052 1,48700 1,55519
589,30 1,43383 1,66643 1,39204 1,32549 1,54416 1,49020 1,55995
587,56 1,43387 1,66654 1,39209 1,32552 1,54428 1,49028 1,56010
546,07 1,43496 1,67310 1,39300 1,32640 1,54730 1,49293 1,56405
486,13 1,43704 1,68664 1,39480 1,32818 1,55327 1,49818 1,57191
404,66 1,44151 1,71843 1,39851 1,33194 1,56660 1,50993 1,58989
366,31 1,44477 1,74416 1,40121 1,33482 1,57684 1,51889 1,60391
313,17 1,45163 1,80707 1,40669 1,34062 1,59915 1,53875 1,63607
302,15 1,45357 1,82769 1,40818 1,34232 1,60578 1,54468 1,64603
280,35 — 1,8837 1,41188 1,34645 1,62214 1,55939 1,67125
265,37 —‘ 1,9424 1,41504 1,34999 1,63680 1,57270 1,6950
253,65 1,46597 2,0116 1,41792 1,35325 1,65112 1,58569 1,7198
240,28 — 2,0548 1,41942 1,35500 1,65878 1,59265 1,7330
239,98 — — 1,42195 1,35793 1,6721 1,60500 1,7576
NaF — достаточно твердый, однородный кристалл, мало растворим в воде и негигроскопичен. Применяется для изготовления призм и окошек в инфракрасных спектрометрах. Пределы пропускания 0,2— 12 мкм. Практически используемый интервал дисперсии 0,4—11 мкм.
CaF2 — твердый, хрупкий кристалл, обладает выраженной анизотропностью механических свойств. Применяется для изготовления деталей ультрафиолетовой и инфракрасной микроскопии, для окошек и призм в ультрафиолетовой и инфракрасной спектроскопии. Область пропускания 0,18—10 мкм.
КВг — очень мягкий, достаточно однородный кристалл, хорошо растворим в воде, гигроскопичен. Применяется в инфракрасной спектроскопии для изготовления призм и окошек. Диапазон пропускания 0,21— 27 мкм. Практически используемый интервал дисперсии в инфракрасной области 15—27 мкм.
КРС-5 — очень мягкий кристалл, практически нерастворим в воде и негигроскопичен, ядовит. Диапазон пропускания приблизительно 0,5—40 мкм. Используемый интервал дисперсии 24—40 мкм.
KA1(SO4)2* 12Н2О — мягкий, однородный кристалл, хорошо раство
рим в воде, гигроскопичен апохроматических объективов микроскопов, предназначенных для видимой области спектра.
Оптическое кварцевое стекло (плавленое)
В зависимости от основной области спектрального пропускания ГОСТ 15130—69 устанавливает пять марок кварцевого стекла, предназначенного для деталей, работающих на пропускание света в одном направлении (табл. 22.27 и рис.
Применяется в основном в качестве линз для
Рис. 22.2. Спектральные кривые пропускания кварцевого стекла различных марок в слое толщиной 1 см:
1 — для КУ-1; 2 — для КУ-2; 3 — для
КВ-Р; 4 — для КВ; 5 — для КИ
22.2).
К нормируемым показателям качества стекла (табл. 22.28—22.34) относятся: оптическая однородность, двойное лучепреломление, бессвиль-
ность, мелкозернистая неоднородность, пузырность, люминесценция и пропускание в ультрафиолетовой части спектра (для КУ-1 и КУ-2), интегральное пропускание в видимой части спектра (для КВ и КВ-Р), пропускание в инфракрасной области спектра (для КИ), устойчивость к гамма-радиации (для КВ-Р).
По пропусканию в ультрафиолетовой части спектра устанавливается четыре категории, характеризуемые показателем поглощения прц длинах волн 170, 215 и 240 нм и две категории — на участке спектрд 2600—2800 им (табл. 22.28). Значение коэффициента светопоглощения в видимой части спектра в слое толщиной 1 см не должно превышать 0,1%
Таблица 22.27. Спектральная характеристика кварцевого стекла
Марка стекла Спектральная характеристика Основное назначение
КУ-1 Стекло, прозрачное в ультрафиолетовой области спектра, без заметных полос поглощения в интервале длин волн 170—250 нм, нелюмннесцирующее Защитные стекла, призмы спектрофотометров и другие оптические детали, работающие в вакуумной и ультрафиолетовой части спектра
КУ-2 Стекло, прозрачное в ультрафиолетовой области спектра, с зам етн ой полосой поглощения в интервале длин волн 170—250 нм Оптические детали, для которых полосы поглощения не важны
КВ Стекло, прозрачное в видимой области спектра, не свободное от полос поглощения в ультрафиолетовой области спектра и от полосы поглощения при 2720 нм Оптические детали, работающие в области спектра 0,25—2,5 мкм; детали, требующие низкого коэффициента расширения или высокой термостойкости
КВ—Р КИ Стекло с теми же свойствами, что и КВ, устойчивое к гамма-радиации Стекло, прозрачное в инфракрасной области спектра, без заметной полосы поглощения при 2720 нм Защитные стекла и другие оптические детали, работающие в инфракрасной области спектра (до 3,5— 4 мкм)
Т а б л и ц а 22.28. Категории стекла, характеризуемые показателем поглощения
Категория Показатель поглощения см~\ не более
прн длинах волн к, нм на участке спектра 2600 — 2800 нм
170 215 240
1 0,3 0,05 0,05 0,05
2 Не нормируется 0,10 0,05 0,10
3 Не нормируется 0,15 0,10 ——
4 Не нормируется 0,25 0,27 —
Т а б л и ц а 22.29. Допускаемые отклонения по оптической однородности
К атегория Наибольшее отношение Ф/Фо Качество дифракционного изображения точки
1 1 Без дефектов для заготовки длиной хода луча не свыше 20 мм
1а 1 Допускаются дефекты
2 1 Не нормируется
3 1,1
4 1,2
5 1.5
Таблица 22.30. Двойное лучепреломление в зависимости от категории оптической однородности для заготовок всех марок стекол (кроме К И)
Категория Разность хода, нм/см, не более Категория оптической однородности
I 30 1; 1а; 2
II 50 3—5
III 70 Не нормируется
Примечание. У стекла марки КИ двойное лучепреломление не должно превышать 100 нм/см.
I_______________________________________________________________________
Т а б л и ц а 22.31.
Категории и размеры пузырей
Т а б л и ц а 22.32. Категории по пузырям и количество пузырей размеров 0,05 мм
Категория Наибольший размер пузыря, мм
I 0,1
II 0,2
III 0,5
IV 1,0
V 2,0
VI 3,0
Марка стекла Среднее число пузырей на 1 кг стекла категорий
1 и II III и IV V и VI
КУ-1 КУ-2 кв КВ-Р До 100 До 500 До 1000
КН До 200 До 1000 До 2000
Таблица 22.33. Приращения показателей преломления при повышении температуры на ГС
Показатель преломления Приращение р.10’ при температуре, °C
— 100 — 70 — 50 -20 + 10 + 20 + 40 + 60
пА' 97 93 93 96 98 99 102 104
пс 99 95 95 98 99 100 103 107
nD 100 96 96 99 101 102 105 108
пе 101 98 98 100 102 104 107 ПО
nF 104 99 100 102 104 106 109 112
nG, 106 103 102 104 107 109 112 115
Таблица 22.34. Показатели преломлении при t = 20° С
X, нм "X X, им пк X, нм пк X, им пк
214,4 1,5341 700,0 1,45550 1300 1,44712 2400 1,4319
253,6 1,5053 766,5 1,45412 1400 1,4460 2500 1,4301
280,3 1,4942 800,0 1,45351 1500 1,4448 2600 1,4282
312,5 1,4847 863,0 1,45249 1600 1,4436 2700 1,4262
365,0 1,47472 900,0 1,45194 1700 1,4424 2800 1,4241
404,7 1,46980 950,8 1,45124 1800 1,4411 2900 1,4219
434,1 1,46708 1000 1,45061 1900 1,4398 3000 1,4196
486,1 1,46332 1050 1,44999 2000 1,4384 3100 1,4171
546,1 1,46028 1100 1,44940 2100 1,4369 3200 1,4146
589,3 1,45860 1150 , 1,44882 2200 1,4353 3300 1,4119
656,3 1,45657 1200 1,44825 2300 1,4336 3400 3500 1,4091 1,4062
Устойчивость _ к воздействию гамма-радиации характеризуется величиной (в см *), которая при длинах волн 300 и 540 нм после облучения дозой 106 рад составляет соответственно 0,150 и 0,025 и после облучения дозой 108 рад — не более 0,200 и 0,050.
По люминесценции, возбуждаемой УФ излучением устанавливаются две категории: по категории 1 люминесценция не допускается; по категории 2 интенсивность люминесценции не должна превышать интенсивности контрольного образца. Стекло всех марок должно быть устойчивым к гамма-радиации дозой не менее 104 рад.
Интегральное светопропускание в видимой области спектра, характеризуемое коэффициентом светопоглощения в слое 1 см, для стекла марок КУ-L КУ-2 и КИ составляет 0,1—0,2%.
Средняя термооптическая постоянная И = — 1) —а —
в пределах температуры от —60 до +20° С равна 213-10-7 град'1.
Средний коэффициент линейного расширения а в пределах температур:
От —60 до +20° с........................... 2. ю-’
> +20 * +50° С........................... 4- ю-7
» +20 » +120° С.......................... 5 * 10—7
» +20 » +420° С.......................... 6-10“7
Жаропрочность 1000е С Химическая устойчивость 1—А (по ГОСТ 13917—68).
Механические свойства: предел прочности при изгибе при 20° С — не ниже 40 МПа, при изгибе при 800° С — не ниже 70 МПа; при сжа-
тии — выше 600 МПа; при ударном изгибе — 0,2— 0,3 МПа; плотность при 20° С —2,21 г/см3.
Оптические ситаллы
Ситаллы — стеклокристаллический материал, состоящий из двух основных фаз — стекловидной связки и равномерно распределенных в ней кристаллов, образовавшихся в результате специальной термической обработки стекла опреде
Рис. 22.3. Пределы температурного удлинения ситаллов СО115М, СО156, СО21
ленного химического со
става, с малым или близким к нулю коэффициентом теплового линейного
расширения.
Ситаллы имеют повышенные по сравнению со стеклом термостойкость, механическую прочность и твердость. Они относятся к хрупким материалам, разрушающимся под воздействием ударно-вибрирующих нагрузок. По химической устойчивости по ГОСТ 13917—68 к воздействию влажной атмосферы ситаллы относятся к группе А, к пятнающим агентам к группе— 1.
СО115М применяется для изготовления изделий, в которых не допускается изменение формы поверхности с изменением температуры (астрозеркал, подставок для интерферометров и гироскопов и других изделий, не работающих в проходящем свете); выпускается в заготовках, имеющих форму дисков, квадратных или прямоугольных пластин диаметром до 2000 мм, шириной до 1000 мм и толщиной до 300 мм. По среднему коэффициенту теплового расширения аГср в интервале температур от —60 до +60° С для ситалла СО115М установлены три категории: 1-я соответствует ct/cp — 0± 1,5* 10“7; 2-я — а,ср =0±2,5* 10~7; 3-я — ot/cp — 0±4- 10"7.
По пузырности установлены две группы, характеризуемые числом пузырей определенного диаметра и расположением их в рабочей зоне заготовки. Число пузырей (камней, узловых свилей) диаметром менее 0,3 мм в рассредоточенном виде в обеих группах для заготовок не устанавливается. Для заготовок диаметром (или с наибольшей стороной) до 500 мм допускаются в 1 кг ситалла пузыри (камни, узловые свили)
Таблица 22.35. Физико-химические свойства ситаллов
Параметр Марки ситаллов
СО115М СО 156 СО21
Средний коэффициент линейного расширения а*107 град-1, в диапазоне температур 20—420° С От 2,5 ДО 6 От 7 ДО 10 От —2,5 до +0,5
Термостойкость, °C 545 ± 50 350± 50 650± 50
Коэффициент пропускания т* 10, %, в образце толщиной 10 мм Не менее 60 60—70 45—65
Показател ь прел омле-ния пе 1,538± ±4*10“4 1,548± ±2-10~3 1,556.10“4
Средняя дисперсия Пр > Ст 0,0103± ±3-10“ 4 0,0006± ±2-10“4 0,0110± ±2-10“ 4
Плотность, г/см3 2,46 2,49 2,52
Пузыри, камни, узловые свили диаметром: до 0,3 мм рассредоточенном виде от 0,3 до 2 мм, шт./кг более 2 мм Г [е нормируете Не более 500 Допускае' 0,001 по г всей площа/1 :я Не более 1000 гея не более 1ЛОЩЭДИ от щ заготовки
размером от 0,3 до 2 мм в количестве 50 шт. (1-я группа) и 100 шт. (2-я группа); для заготовок размером от 500 до 1200 мм допускается количество пузырей 60 шт. (1-я группа) и 200 шт. (2-я группа) указанных выше размеров. Пузыри диаметром свыше 2 мм допускаются в таком количестве, при котором их общая площадь не превышает 0,1% (1-я группа) и 0,2% (2-я группа) от рабочей площади заготовки. Коэффициент пропускания в слое 1 см (источник А по ГОСТ 7721—76)— не менее 60%; показатель ослабления £л — 0,22 см'1. Некоторые физико-химические свойства ситалла приведены в табл. 22.35 и на рис. 22.3.
СО156 отличается от СО115М повышенной прозрачностью в видимой части спектра и лучшей однородностью, но обладает меньшей термостойкостью, имеет более резкое изменение коэффициента линейного расширения с повышением температуры и значительно большую пузырность (см. табл. 22.35 и рис. 22.3). Ситалл применяется для изготовления пробных стекол и деталей измерительной техники.
С021 — ситалл с отрицательным коэффициентом линейного расширения от 0 до 350° С, что обеспечивает его высокую термостойкость (см. табл. 22.35 и рис. 22.3). Применяется для изготовления деталей типа обтекателей, смотровых люков и защитных экранов.
Оптическая керамика
Оптическая керамика — поликристаллические материалы, полученные методом прессования под большим давлением в вакууме, механически изотропны, по термомеханическим свойствам значительно превосходят аналоги соответствующих монокристаллов, хорошо обрабатываются и обладают высокой устойчивостью к тепловым ударам.
Оптическая керамика применяется для изготовления светорас-свивающих экранов, подложек интерференционных светофильтров, окон и обтекателей в приборах, работающих в ПК-области спектра, а также в условиях высоких механических и термических нагрузок.
К01 — поликристаллический материал, получаемый из порошкообразного фторида магния MgF2; обладает средней твердостью (585* 10 МПа), прозрачный в области спектра 2—7 мкм. Плотность 3,171 г/см3. Не растворяется в воде, разбавленных кислотах, щелочах и органических растворителях.
К02 — поликристаллический материал на основе сульфида цинка ZnS, мягкий (354* 10 МПа), прозрачный в области спектра 1,8—14 мкм. Плотность 4,09 г/см3. Не растворяется в воде и органических растворителях; незначительно растворяется в слабых растворах кислот и щелочей. Предел прочности при температурах 20, 200 и 400° С соответственно равен 7,9; 5,5; 6,6* 10 МПа.
К04 — поликристаллический материал на основе селенида цинка ZnSe, прозрачный в области спектра 0,546—14 мкм. Плотность 5,25 г/см3. Не растворяется в воде, растворяется в кислотах.
К05 — поликристаллический материал на основе окиси магния с добавкой фторида лития в количестве до 0,3% по массе. Прозрачный в области спектра 0,5—7 мкм. Плотность 3,578 г/см3.
Оптическая керамика нормируется по следующим показателям качества: пропусканию в ИК-области спектра; равномерности показателя ослабления; включениям. В табл. 22.36—22.50 приведены некоторые физико-химические свойства оптической керамики.
Т а б л и ц а 22.36. Показатели преломления К01
X, мкм X, мкм "X X, мкм X, мкм
1,0 2,0 2,2 2,4 2,5 2,6 1,3778 1,3720 1,3706 1,3692 1,3683 1,3675 2,8 3,0 3,2 3,4 3,6 3,8 1,3658 1,3640 1,3620 1,3598 1,3576 1,3551 4,0 4,2 4,4 4,6 4,8 5,0 1,3526 1,3499 1,3470 1,3439 1,3407 1,3374 5,2 5,4 5,6 5,8 6,0 6,5 7,0 1,3339 1,3301 1,3266 1,3221 1,3179 1,3063 1,2934
Интерполяционная формула — А + где L = (X2 — 0.028)-1; А = 1,37770; В = D =* —0,0015041; Е = — 4,41 - 10~«. BL + CL = 0,001348; 2 + Z)X2 + EX4, С = 0,000216;
Таблица 22.37. Коэффициент пропускания К01 различной толщины (потери на отражение не исключены)
Категория Длина волны, мкм Коэффициент пропускания %, ие меиее, для толщины заготовки, мм
6 7 8 9 10
1 2.4 3,0 3,5 4,0 4,5 59,6 (9,2) 66,5 (6,8) 74,5 (4,5) 79,0(4,1) 81,0 (1,2) 55,0 (10,6) 63,0 (8,0) 71,5 (6,3) 76,0 (4,7) 79,0 (1,9) 51,0(11,3) 59,0 (9,2) 68,5(7,1) 74,0 (5,4) 76,5 (2,5) 47,0 (13,0) 55,5 (10,2) 65,5 (8,0) 71,5(6,0) 74,5 (2,6) 43,5 (14,7) 52,0 (11,2) 63,0 (8,8) 69,0 (6,7) 72,5 (2,7)
2 2,4 3,0 3,5 4,0 4,5 52,5 (16,7) 63,0(11,7) 66,5 (10,5) 70,5 (9,2) 73,5 (5,3) 47,5 (19,2) 59,0 (13,5) 63.0 (12,1) 67,5 (10,3) 70,0 (6,4) 43,0 (21,3) 55,0 (15,3) 59,0 (13,7) 64,0(12,1) 67,5 (6,7) 39,0 (23,3) 51,0(17,0) 55,5 (15,3) 60,5 (13,5) 64,5 (7,6) 35,5 (25,4) 48,0 (18,7) 52,5 (16,8) 57,5 (14,9) 61,5 (8,9)
Примечание. В скобках приведена равномерность коэффициента пропускания, характеризуемая величиной (Tfflax“Tmln)/Tniax %, не более. ’
Т а б л и ц а 22.38. Коэффициент пропускании К01 слоя толщиной 1 см
X, мкм X, мкм тх- % X, мкм тх* % X, мкм
2,0 2,4 2,5 50 62 65 2,75 3,0 3,5 33 72 80 4,0 4,5 4,95 86 90 78 5,0 6,0 85 86
Т а б л и ц а 22.39. Показатели преломления К02
X, мкм пк Х,мкм пк X, мкм пк X, мкм пк
1,8 2,2658 5,0 2,2447 8,5 2,2162 12,0 2,1688
2,0 2,2631 5,5 2,2416 9,0 2,2107 12,5 2,1601
2,5 2,2589 6,0 2,2381 9,5 2,2048 13,0 2,1508
3,0 2,2558 6,5 2,2344 10,0 2,1985 13,5 2,1410
3,5 2,2551 7,0 2,2304 10,5 2,1918 14,0 2,1306
4,0 2,2504 7,5 2,2260 11,0 2,1846
4,5 2,2477 8,0 2,2213 11,5 2,1769
Интерполяционная формула = A -{-BL + CL2 + OX2 + EK4, где L = (V — 0.028)"1; A = 2,25698; В — 0,032586; С = 0,000679; D = —0,0005272; E = —6,04~7
Таблица 22.40. Коэффициент пропускания К02 различной толщины (потери на отражение не исключены)
Категория Длина волны, мкм Коэффициент пропускания %, не менее, для толщины заготовки, мм
2 4 8 10
1 5,0 12,0 71,0 (0,8) 67,5 (2,4) 69,5(1,9) 61,5 (4,4) 66,0 (3,6) 50,5 (8,9) 65,0 (4,5) 46,0 (10,8)
2 5,0 12,0 70,0(1,4) 66,5 (2,7) 68,0 (2,6) 60,0 (5,4) 64,0 (5,5) 48,0 (10,4) 62,0 (6,8) 43,0 (13,0)
Примечание. В скобках приведена равномерность коэффициента пропускания, характеризуемая величиной (Ттах—Tmin)/Tmax % (не более). *
Таблица 22.41. Коэффициент пропускания К02 слоя толщиной 1 см
К мкм ТХ’ % X, мкм т%> % К мкм % X, мкм тх* 0/о
2,0 2,5 3,0 3,5 62,0 70,0 74,0 78,0 4,0 5,0 6,0 7,0 82,0 87,0 87,0 86,5 8,0 9,0 10,0 11,0 86,0 85,5 82,0 61,0 11,5 12,0 13,0 68,0 61,0 32,0
Таблица 22.42. Показатели преломления К04
X, мкм X, мкм "X X, мкм X, мкм
0,5461 0,5876 0,6563 и 1,2 2,6684 2,6250 2,5779 2,4796 2,4720 1,4 1,8 2,2 2,6 3,4 2,4615 2,4502 2,4443 2,4406 2,437 4,6 5,0 6,0 7,0 9,0 2,432 2,430 2,427 2,423 2,414 10,0 12,0 14,0 2,408 2,395 2,379
Таблица 22.43. Коэффициент пропускания К04 различной толщины (потери на отражение не исключены)
Категория Длина волны, мкм Коэффициент пропускания %, не менее, для толщины заготовки, мм
2 4 6 8
8,0 63,0 (1,9) 57,5 (3,8) 52,0 (5,4) 48,0(7,1)
1 10,6 65,0 (1,4) 61,0 (2,7) 57,5 (4,2) 54,0 (5,4)
14,0 66,5 (1,0) 63,5 (1,9) 60,5 (2,7) 58,0 (3,7)
8,0 60,0 (4,0) 52,5 (7,9) 46,0(11,7) ' 40,0 (15,2)
2 10,6 62,0 (3,3) 56,0 (8,3) 51,0 (9,3) 46,0 (12,1)
14,0 64,0 (2,3) 59,5 (4,5) 55,0 (6,6) 51,0(8,8)
Примечание. В скобках приведена равномерность коэффициента пропускания, характеризуемая величиной — \/Tmav \ lildA 111111 // Шал * % (не более).
Т а б л н ц а 22.44. Коэффициент пропускания К04 слоя толщиной 1 см
к, мкм ТХ’ °/о X, мкм о/ Л, /о X, мкм т ТХ' /о X, мкм ТХ> %
1.0 35,6 8,0 81,7 12,0 88,3 17,0 52,9
3,0 65,2 9,0 78,7 14,0 87,5 18,0 46,5
5,0 77,3 10,0 89,1 15,0 84,3 20,0 8,0
7,0 79,4 11,0 88,7 16,0 64,3
П р и м е ч а н и е. Потери на отражение исключены.
Т а б л н ц а 22.45. Показатели преломления К05
X, мкм ч X, мкм X, мкм лх X, мкм "X
1,00 1,7227 2,75 1,6968 4,50 1,6536 6,25 1,5845
1,25 1,7188 3,00 1,6920 4,75 1,6455 6,50 1,5721
1,50 1,7156 3,25 1,6868 5,00 1,6368 7,00 1,5452
1,75 1,7123 3,50 ' 1,6811 5,25 1,6275 7,25 1,5307
2,00 1,7089 3,75 ' 1,6750 5,50 1,6177 7,50 1,5154
2,25 1,7052 4,00 1,6684 5,75 1,6072 7,75 1,4993
2,50 1,7012 4,25 1,6612 6,00 1,5962 8,00 1,4824
Т а б л н ц а 22.46. Коэффициент пропускания К05 различной толщины (потери на отражение не исключены)
Категория Длина волны, мкм Коэффициент пропускания %, ие менее, для толщины заготовки, мм
2 4 5
1 1,0 3,0 5,5 74,0 84,5 86,0 63,5 82,0 83,5 59,0 81,1 82,0
- 2 1,0 3,0 5,5 65,5 82,0 83,5 49,5 78,0 78,0 43,0 75,5 75,5
Таблица 22.47» Коэффициент пропускания тд, К05 слоя толщиной 1 см
К мкм К. мкм %
0,5 30,0 5,0 90,0
1,0 50,0 5,5 87,0
2,0 84,0 6,0 85,0
3,0 87,0 7,0 17,0
4,0 89,0
Т а б л и ц а 22.48. Коэффициенты линейного расширения в интервале температур, °C
Марка Коэффициент линейного расширения otp 107, град-4 (среднее значение) в интервале температур, °C
К01 100 От —60 до 20 113 От 20 До 120 117 От 20 до 180 123 От 20 до 280 135 От 20 до 500
К02 59 От —60 до 20 69 От 25 до 100 69 От 25 до 200 72 От 25 до 300 75 От 25 до 400
К05 90,4 От —60 до 20 109,9 От 20 до 120 114,4 От 20 До 180 120,7 От 20 до 280 126,8 От 20 до 420
К04 7,7-10 "в в интервале температур от 25 до 200
T а б л в ц а 22.49. Показатель ослабления в рабочей области свектра
Марка < Д,чмна волны, мкм Псклаавель «сляблення в^, см“л, »е белее, по категориям
1 2 '
код 2,4 3,0 3,5 4,0 4,5 0,34 (0,2) 0,26 (0,2) 0,18(0,2) (С 14 (0,2) 0,12 (0,2) 0,43 (0,3) 0,30 (0,3) 0,26 (0,3) 0,22 (0,3) 0,19 (0,3)
К02 • 5,0 12,0 0,07 (0,3) 0,26 (0,2) 0,10 (0,3) 0,30 (0,2) :
К04 8,0 10,6 14,0 0,19 (0,2) 0,13 (0,2) 0,10(0,2) 0,29 (0,3) 0,22 (0,3) 0,17 (0,3)
КОБ 1,0 3,0 5,5 0,33 (0,5) 0,06 (0,5) 0,07 (0,5) 0,60 (0,5) 0,12 (0,5) 0,14 (0,5)
Примечание. В скобках приведена равномерность (8max’“8niin)/eniax в пределах 4 диаметр а одной заготовки.
nrWitliHitb
Таблица 22.50. Размеры заготовок
Марка Диаметр диска, мм Толщина, мм Отношение диаметра к толщине
К01 От 30 до 200 От 4 до 10 От 5 : 1 до 20 : 1
К02 От 30 до 100 От 4 до 10 От 5 : 1 до 20 : 1
К04 От 25 до 80 От 3,0 до 3 От 10 : 1 д о 20 ; 1
. К05 От 30 до 50 От 3.5 до 7 От 10:1 до 20 : 1
Примечание. Для К01 поставляются заготовки с диаметром полусферы от 50 до 200 мм.
Оптические термопластичные полимерные материалы
Термопластические нодимерлые материалы используются для изготозления оптических деталей, работающих в видимой и близкой инфракрасной областях спектра. Согласно отраслевому стандарту из гцмимеров в зависимости от их назначения могут изготовляться оптические детали следующих типов:
В — растры, линзы Френеля, расположенные в плоскости воображения или вблизи нее;
Рис. 22.4, Спектральные кривые коэффициента пропускания пластин:
/ «*> полимета л мета крплата толщиной 0,6 мм;
2 А полистирола толщиной 0,6 мм; 3 —> полнкарч боната толщиной 1 мм
Г — детали приборов широкого потребления — фотоаппаратов, бииоклей, луп, очков и т. п.;
Д — детали осветительных систем;
Е — защитные стекла, матовые экраны.
В табл. 22.51 и на рис. 22.4 даны физико-мехаиические свойства термопластических полимеров типа пол н метилметакрилата, полистирола блочного марки «Д» и поликарбоната, используемых для изготовления оптических деталей. Детали из полимеров характеризуются следующими показателями качества: чистотой поверхности, величиной включен ний, а также габаритными размерами.
По величине включений детали из полимеров разделяются на четыре группы, характеризуемые диаметром и числам включений на определенном участке в пределах светового диаметра (табл, 22.52). В табл. 22,53 даны рекомендации по выбору требований по чистоте поверхности и включениям деталей в зависимости от назначения последних. Детали более высокого качества, а также детали других типов, изготовленные из полимеров марок, не указанных в отраслевом стандарте, изготавливаются по соглашению между заказчиком и изготовителем.
Таблица 22.51. Физико-механические свойства термопластичных полимеров
Характеристика Полнметнлметакрнлат Полистирол блочный «Д> (ГОСТ 9440—60) Смола поликарбонатная «Дифтон» (ТУ 6-16-1450—69)
£ 1 О О Ч ЛСО—Мб лпт (МРТУ 6-05-871-66)
ТУ 6-01-283 — 68
Показатель преломления пе (20° С) Коэффициент Коэффициент пропускания т Коэффициент расширения а-107 град-1 Рекомендуемая температура эксплуатации) °C Плотность, г/см3 Твердость по Бринеллю, МПа, не менее Усадка, % 1,49 См рис 600 ±60 1,19 130 0,6—0,8 1,49 . 22.4 | ± 50 1,19 130 1,49 кривая 1) 900 ±50 1,19± ±0,01 170—180 1,59 30,8 См. рис. 22.4 (кривая 2) 800 (0+50° С) ±40 1,05+0.ь 140—150 0,4—0,6 1,58 См. рис. 22.4 (кривая 3) 600 ±100 1,2 150—160 0,5—0,7
Таблица 22.52. Группы включений
Группа Диаметр участка, мм Диаметр включений Число включений, шт., не более Расстоиние между вклю-чениими, мм, не менее
0 5 До 0,01 Св. 0,01 до 0,02 » 0,02 Не учитываются 3 Не допускаются 1
1 10 До 0,05 Св. 0,05 до 0,10 » 0,10 » 0,30 » 0,30 Не учитываются 3 1 Не допускаются 5
Продолжение табл. 22.62
Группа Диаметр участка, мм Диаметр включений Число включений, шт., не более Расстояние между вклю-чениими, мм, не менее
2 15 До ОДО Св. ОДО до 0,30 » 0,30 » 0,50 » 0,50 Не учитываются 1 Не допускаются 5
3 г 15 До ОДО Св. ОДО до 0,50 » 0,50 » 0,70 » 0,70 Не учитываются 2 3
Таблица 22.53. Классы чистоты и группа по включениям в зависимости от типов деталей
Типы деталей Назначение детали как элемента оптической системы Класс чистоты поверхности по ГОСТ 11141-76 Группа по включениям
Детал и, находящиеся в фокальной плоскости и рассматриваемые под увеличением не менее 5х IV 0
В Растры, линзы Френеля (при расположении их в плоскости изображения или вблизи нее) IV 1
Г Лупы, очки, детали фотоаппаратов, биноклей н других приборов широкого потребления IV—VII 1—2
гт Детали осветительных систем 1 V—VII
Е Защитные стекла, экраны VI—VII о
О
Таблица 22.54. Некоторые физические свойства органических стекол
Марка стекла Плотность, г/см* Показатель преломления пе при температуре, °C Температура размягчения, °C • 1 Коэффициент линейного расширения а. 10е при температуре, °C
21 45 60 75 95 — 40 — 20 0 20 40 60 80 100
СОЛ 1,18 1,492 1,488 1,486 1,483 1,481 90 64 63 66 71 86 96 125
ст л 1,18 1,489 1,486 1,484 1,482 1,481 ПО 1 1 77 82 86 90 111
2-55 1,18 1,496 — 1 " 133 •и»»» 69 73 69 73 84
Т2-55 1,2 1,498 W — 130 ' ' 75,6 1 • 75,6 75,6 94,5
Т а б л и ц а 22.55. Спектральное свето про пускание органического стекла
Область сцектра
Ультрафиолетовая | Видимая | Инфракрасная
Марка Длина волны, им
стекла
300 320 '340 360 380 400 | 750 800 1000 1200 1400 1600 1800 2000 2200 2400 2600 2800 3000
Коэффициент светопропускаиня, %
СОЛ 11 53 76 86 88 89 92 90 90 61 60 70 45 49 7 0 2 12 0
СТ-1 0 0 11 85 89 90 80 92 92 90 60 69 42 49 5 1 8 20 0
• 2-55 0 0 0 67 85 88 90 88 88 82 50 49 25 20 — — — — —
Т2-55 0 0 0 45 74 80 90 89 90 80 60 49 33 21 — — — — —
Стекло органическое конструкционное
В зависимости от назначения конструкционное органическое стекло выпускается по ГОСТ 15809—70 следующих марок: СОЛ — пластифицированное, СТ — непластифицирован-цое, 2-55 сополимерное. В табл. 22.54 и $2.55 приведены некоторые физические Двойства и светопропускание органических стекол.
Светорассеивающие стекла
По своим свойствам и назначению светорассеивающие стекла разделены на три типа (табл. 22.56) [47]. Указанные стекла являются силикатными и по химической устойчивости по ГОСТ 13917—68 относятся к группе A-I (типы I и II) и A-III (тип III). Некоторые характери
кривые коэффициента отражения р (X) стекол МС20, ОНС1, ОНС2, ОНСЗ и ОНС4 в видимой области спектра
стики светорассеивающих стекол приведены в табл. 22.57 и 22.58. На рис. 22.5 показаны спектральные кривые коэффициентов отражения стекол. Индикатрисы рассеяния (рис. 22.6—22.11) представлены
Таблица 22.56. Классификации светорассеивающих стекол
Тип Марка стекла Показатель преломления nD Плотность, г/см8 Назначение
МС20 1,52 2,80 Изготовление непрозрачных
ОНС1 1,50 2,61 деталей, диффузно отражаю-
I ОНС2 1,50 2,61 щих направленный на них
ОНСЗ 1,50 2,61 свет (экраны, пластины, кю-
ОНС4 1,50 2,61 веты, сферы, образцы сравне-
ния и рабочие эталоны отра-
жения и белизны)
МС19 1,472 2,30 Изготовление деталей, пре-
II МС13 1,51 2,54 обр азующих иапр авленный
МС23 1,52 2,63 световой пучок в диффузный
МС12 1,49 2,45 при работе в проходящем свете
МС16 1,472 2,30 Изготовление образцов и
III МС17 1,472 2,30 рабочих эталонов мутности,
МС18 1,472 2,30 а также имитаторов различ-
МС19 1,472 £30 ных рассеивающих сред
Примечания: 1. МС — молочные, а также мутные стекла; ОНС — отражающие нейтральные стекла. 2. Стекло марки МС19 применяется как для преобразования проходящего направленного пучка света в диффузный, так и в качестве образца мутности, поэтому оно отнесено к типам П и III. 3. Стекло марки МС20 является заменителем стекла марки MCI4.
Таблица 22.57. Спектральные кривые коэффициента отражения р (Л) (рнс. 22.5)
Длина волны, им р
МС20 ОНС1 ОНС2 ОНСЗ ОНС4
400 0,935 0,690 0,450 0,290 0,170
440 0,945 0,715 0,485 0,300 0,165
480 0,960 0,735 0,515 0,300 0,155
520 0,970 0,740 0,530 0,295 0,155
560 0,970 0,740 0,530 0,290 0,150
600 0,970 0,740 0,525 0,285 0,150
640 0,965 0,735 0,525 0,280 0,150
720 0,965 0,735 0,525 0,275 0,165
Таблица 22.58. Зависимость интегрального коэффициента пропускания от толщины полированного стекла
Марка стекла Толщина образца, мм Коэффициент пропускания Марка стекла Толщина образца, мм Коэффициент пропускания
MCI 2 2 0,27 МС23 2 0,61
1 0,36 1 0,68
МС13 3 0,59 MCI 9 8 0,79
2 0,68 6 0,82
1 0,78 4 0,86
2 0 91
МС23 3 0,53 UjJ 1
Рис. 22.6. Индикатрисы спектрального коэффициента яркости Р (X) стекол МС20, ОНС1, ОНС2, ОНСЗ, ОНС4 при 8 = 0 (а) и 8 = 45 (б). Стрелкой отмечен угол падения освещающего пучка
Рис. 22.7. Индикатрисы спектрального коэффициента яркости Р (X) стекла MCI9 при е = 0; Р (Л) — 1 при угле наблюдения 5°
Рис. 22.8. Индикатрисы коэффициента яркости р (X) стекла марки MCI 2 толщиной 0,5—3,0 мм (штриховая линия) и марки МС13 (сплошные линии); р (%) = == 1 при угле наблюдения у = 0
Рис. 22.9. Индикатрисы коэффициента яркости р (Л) стекла марки МС23 (пунктирные линии) и марки МС19 (сплошные линии); р (X) = 1 при у — 0 (для стекла МС23) и при у=5° (для стекла
MCI 9)
Рис и 22.10. Индикатрисы рассеяния стекол MCI6, MCI7, MCI8;
Р (X) = 1 при у — 90°
графиками зависимости коэффициента яркости' ₽х светорассеивакмцего полированного стекла от угла наблюдения в одной плоскости. Цифры около кривых означают тол-
щииу образца в мм; 8 — угол падения освещающего пучка.
Стекло листовое малопузырное
Стекло листовое малопузырное марки СВВ предназначается для изготовления доступных чистке плоских оптических деталей, для которых оптические константы не нормируются. Физико-химические свойства: п = = 1,515=4=0,001; nF,— nc, = 0,0088. Коэффициент линейного расширения (при ^температуре 20—120° С) равен 85* 10~7±0,5* 10 ’.Плотность2,49г/см3. Площадь листа не более 1000 см2; наибольшая из сторон листа 50 см; толщина листа 3, 4, 5, б, 7, 8, 9, 10 и 12 мм. Допуск для толщины листа ±0,5 мм.
Стекло должно отвечать следующим техническим требованиим. Раз-
Рис. 22,11. Индикатрисы коэффициента яркости р (X) стекла МС19; значения
Р (X) = 104 при у = 5°
нотолщинность по краю ±0,1 мм для листов толщиной до 6 мм и ±0,2 мм — для листов толщиной более 6 мм. Кривизна (стрелка прогиба) не более 0,1 мм на длине 10 см. Допуск на кривизну всего листа изменяется пропорционально изменению его размера. Поверхность листа, полученная в процессе вытягивания стекла, должна быть гладкой. Допускается серый налет и отдельные царапины шириной не более 0,15 мм. В средней эоне листа, составляющей 75% его площади, пузыри диаметром до 0,15 мм в рассредоточенном виде ие нормируются. Для стекла толщиной до 6 мм допускается один пузырь диаметром от 0,15 до 0,5 мм на площади 20 см2 н в том числе диаметром свыше 0,3 до 0,5 мм иа площади 200 см2; для стекла толщиной свыше 6 мм допускается не более двух пузырей иа указанных площадях. Диаметры пузырей свыше 0,5 мм не допускаются. В краевой зоне пузыри не нормируются.
Двойное лучепреломление для листов толщиной до 6 мм не должно превышать 70 нм/см и стекла толщиной более 6 мм — 100 нм/см. Свили,
видимые невооруженным глазом в проходящем свете, не нормируются. Светопог лощение стекла не должно превышать 7% на 1 см слоя стекла; допускается слабая зеленоватая или голубоватая окраска. Светопро-пускание пластинок стекла толщиной 1 см— ие меиее 85%. Химическая устойчивость IB; после кремнеземно-восковой или кислотно-парафиновой защиты стекло удовлетворяет группе А.
Клеи для оптических деталей
Пихтовый бальзам (ГОСТ 2290—76) применяется трех типов: О — непластифицированныЙ, Оп — пластифицированный — для склеивания оптических деталей из силикатных стекол, точная центрировка которых обеспечивается за счет дополнительного крепления и фиксации я оправах; Н — непластифицированныЙ — для склеивания предметных стекол и других деталей, 686
пропускание иической
кремнийорга-смолы толщиной 13 мкм
Бальзам типов О и On в зависимости от числа пенетрации подразделяется на следующие марки: 5 (весьма твердый, только бальзам типа 0); 20 (твердый); 45 (средний); 75, 105 (мягкий); 145, 195 (весьма мягкий).
По внешнему виду бальзам — совершенно прозрачная масса желтоватого цвета. Показатель преломления при 20° С: nt~ 1,524-1,54. Коэффициент линейного расширения в интервале температур 0—25° С: а == (1,54-2,0)10^*. Светопропускание при толщине склеивающего слоя 0,01 мм и интервале длин волн 320—2700 нм — ие менее 99%. Допустимые разности коэффициентов термического расширении Да склеиваемых деталей ие более 30* 10'7, Условия склеивания — при нагревании до 120—130° С. Склеивание бальзамом применяется только для деталей, работающих при температуре не свыше 45° С.
Клей ОК‘72Ф — для склеивания оптических деталей, в том числе с различными покрытиями, а также деталей консольно подвешенных, работающих на удар; для склеивания деталей в тропическом исполнении; деталей с разностью коэффициентов Да > > 30* 10’7; деталей изтяжелых флинтов; для герметизации склеивающих слоев. Показатель преломления при 20° С: = 1,588±0,02. Условия склеивания — при температуре 18— 20° С. Клей ОК-72Ф токсичен. Клей ОК- 90 (пластифицированный) применяется в видимой области спектра для склеивания крупногабаритных оптических линз; может быть применен для
склеивания органического стекла с силикатным; латунных и дюралюминиевых коронок с рубином; пластин монокристаллического германия. Показатель преломлении при 20°С:Пе= 1,543±0,001. Условия склейки — при температуре 18—26° С.
Клей УФ235М — для склеивания деталей из ультрафиолетового стекла, кварца, флюорита, фтористого лития и других минералов, прозрачных в ультрафиолетовой области спектра от 220 им. Показатель преломления при 20°С: — 1,464±0,002, Условия склейки—при температуре 95° С.
Клей 0К-60 — для склеивания деталей, изготовленных из кристаллов (например, из флюорита, бромистого калия, хлористого натрия), прозрачных в инфракрасной области спектра до 8000 нм. Показатель преломления при 20°С: 1,517±0,002. Условия склейки — при
температуре 18—26° С.
Бальзамин применяется в видимой области спектра для склеивання оптических деталей с разностью Да не более 30* 10”7 и диаметром не более 80 мм. Склеивание линз с отношением наименьшей толщины к диаметру d/D > 0,10 производят при условии, что деформация ие влияет заметно на оптические свойства. Показатель преломления прн 20°С: п₽ = 1,521 ±0,002. Условия склеивания — прн нагревании до 70—80° С.
Бальзамин-м применяется в видимой области спектра для склеивания оптических деталей, линз любых размеров с разностью Да> > 30* 10‘7; деталей с любым отношением наменьшей толщины к
диаметру, призм, в том числе со светоделительными покрытиями; светофильтров, поляроидов всех размеров. Показатель преломления при 20° С: о пе = 1,520± 0,001. Условия склеивания — при температуре 18—26 С.
Акриловый клей применяется в видимой области спектра для склеивания поляризационных призм из кальцита; деталей из силикатного
/OU 44U bUU SUUV SfUU tjOO
Рис. 22.13. Спектральные кривые коэффициентов пропускания клеев при толщине слоя 0,01 мм:
I » бальзамин; 2 — бальзамин-м; 3 — акриловый клей: 4 « ОК-ЭО* 5 — ОК-72Ф и ОК-50П; 6 УФ?235-М; 7 « ОК-60
стекла диаметром до 30 мм; полироидов; светофильтров и клиньев с желатиновыми и поливиниловыми пленками; деталей из квасцов; силикатного стекла с металлом (кроме олова, хрома, инвара, ковара). Показатель преломления при 20° С: пе = 1,488± 0,001.
Клей ОК-50П применяется в видимой области спектра для склеивания оптических деталей, а также деталей консольно подвешенных, работающих на удар; деталей из силикатных стекол с различными покрытиями; стекол с металлами (за исключением хрома, олова, инвара, ковара). Показатель преломления при 20° С; пе = 1,582± 0,002. Условия склеивания — при температуре 18—26° С. Клей токсичен.
Указанные выше клеи (кроме бальзама) должны отвечать требова* ииям ГОСТ 14887—69, 688
Примеры условного обозначения клеев:
Бальзам пихтовый Оп—Т20 ГОСТ 2290—76 (твердый пихтовый бальзам типа Оп марки 20).
Бальзам пихтовый О—ВМ145 ГОСТ 2290—76 (весьма мягкий пихтовый бальзам типа О марки 145).
. , Клей ОК-72Ф ГОСТ 14887—69.
Морозостойкость до разрушения склеивающего слоя (при средних радиусах кривизны поверхностей склеиваемых деталей и с разностью ДаЗО-10~7) для клеев бальзамин, акриловый, УФ-235М и ОК-60 — не менее 60° С, для клеев ОК-50П, ОК-90, ОК-72Ф и бальзамин-м — не менее 90° С. Склеивающий слой указанных выше клеев плесневыми грибками не поражается. Бальзамин помимо влагостойкости обладает также устойчивостью к бензину, керосину и маслу.
Клеи бальзам, акриловый и УФ-235М не используются в деталях, работающих с перепадом температуры от +50 до —60° С.
Оптический клей, прозрачный в ИК-области спектра, представляет собой раствор кремнийорганической смолы и имеет интегральное пропускание, равное 82,1%, в интервале 1—8 мкм (рис. 22.12) [46].
На рис. 22.13 приведены спектральные кривые коэффициентов пропускания клеев при толщине слоя 0,01 мм (ГОСТ 14887—69).
Клей ММА используется для соединения детален из стекла диаметром до 900 мм, работающих в различных климатических условиях. Разность коэффициентов термического расширения соединяемых стекол допустима до 0,5* 10 7 град Полимеризуется при температуре 18— 20° С и деформации деталей не вызывает.
Сплав ТКС-1 — термопластичный клей, применяется для склеивания деталей из материалов с показателем преломления пе > 2 (кремний, германий, стекла ИКС-24, ИКС-26, ИКС-30и др.), допускающими нагрев до 170° С.
Литература; [46, 47, 66, 89].
ГЛАВА 2а
КОНСТРУКЦИОННЫЕ МАТЕРИАЛЫ
Стали углеродистые качественные конструкционн ые
Современный уровень техники предъявляет к оптико-механическим приборам требования обеспечения надежной и долговечной работы в различных условиях их эксплуатации. Поэтому применяемые для их изготовления конструкционные материалы должны обладать комплексом разнообразных свойств, физических н механических характеристик.
Из всех материалов лучшее сочетание прочности и долговечности имеет сталь. Содержание углерода в сталях составляет от 0,08 до 2,14%.
Качественная конструкционная сталь маркируется по химическому составу цифрами, которые указывают среднее содержание углерода и сотых долях процентов. С повышением содержания углерода прочность стали повышается, а пластичность уменьшается.
Для изготовления малоответственных деталей применяют автоматные стали — низкоуглеродистые стали с повышенным содержанием серы и фосфора. Недостатками этих сталей являются пониженная пластичность и вязкость, а также повышенная склонность к коррозии. Механические свойства углеродистой качественной конструкционной стали приводятся в табл. 23.1 и 23.2.
Легированные конструкционные стали
В легированной стали содержатся специальные легирующие элементы (хром, никель, вольфрам, молибден, ванадий, марганец, кремний, медь, кобальт и др.), повышающие ее механические и специальные свойства.
Хром — повышает прочность и твердость, увеличивает пр окал и-ваемость стали, одновременно понижая ее пластичность и вязкость. Содержание хрома — до 3%.
Никель — придает стали антикоррозионную устойчивость, прочность и пластичность, повышает сопротивление удару, повышает прокалнваемость и уменьшает коэффициент* теплового расширения. Содержание никеля — 1—5%.
Вольфрам — увеличивает твердость стали, препятствует росту зерен при нагреве, способствует уменьшению хрупкости при отпуске. Содержание вольфрама — до 1^5%.
Таблица 23.1. Мехатнескве свойства углеродистой качественной конструкционной стали; плотность 7,8 г/см® (по ГОСТ 1050—74)
арка ста-[ СГТ.1О-*, МПа СГв‘.10-«, МПа б, % % м 1 « О ЛЕ , ’ £ X 1—г ч *‘4 НВ Назначен не
Не менее
08 10 20 21 : 33 34 33 31 60 55 " 131 143 Детали, изготавливаемые штамповкой, холодной высадкой или сваркой. Цементируемые и цианируемые детали, не требующие высокой прочности сердцевины
20 25 42 % 55 163 Оправы к резьбовые кольца для оптических деталей. Корпуса для шарикоподшипников
30 30 50 21 50 8 179 Малойагруженные оси и валики-
35 40 32 34 54 58 20 19 45 45 7 6 187 197 Детали, обладающие достаточно высокой прочностью при средней вязкости: осн, валики, зубчатые колеса, детали муфт и кронштейны
45 36 61 16 40 5 J 207 Оси, валики, зубчатые колеса, рейки и болты
50 55 38 39 64 66 14 13 40 35 4 217 229 Детали высокой прочности: зубчатые колеса, рейки, муфты, оси, валики н иинты движения
60 41 69 12 35 —... 229 Кулачки и эксцентрики
65Г 70Г 44 46 75 80 ; 9 8 1 229 Дет ал и, р аботающяе на износ, пружинные шайбы, спиральные дружины, кольца и втулки
Примечания: 1. Сталь 45 м сталь 55 следует применять только как s вмените ли. 2. Нормы механических свойств приведены для нормализованной стали. 3. Здесь и далее в таблицах: ов — временное сопротивление разрыву (предел прочности при растяжении); предел текучести; 6 — относительное удлинение; гр — относительное сужение; д ударная вязкость; ИВ ** число твердости по Бринеллю. 0
Таблица 23.2. Механические свойства конструкционной горячекатаной стали (по ГОСТ 1414—75)
я и я Па б, % % иаметр гпечат-а, мм НВ Назначение
м а, е 2 RO W
Не меиее
АН 42 22 34 4,75 160 Для изготовления сложных
А12 42 22 34 4,75 160 по форме и трудных в обра-
А20 46 20 30 4,65 168 ботке мелких деталей (шестерни, винты, гайки, втулки, фланцы, малонагружеи-
ные оси, резьбовые оправы
дл я оптических деталей). Сталь А20 рекомендуется также для деталей, подвергаемых цементации и цианиро-
ванию
АЗО 52 15 25 4,45 185 То же, но для более нагру-
А35 А40Г 52 15 23 4,25 201 женных осей, деталей муфт и неотсчетных мелких шестерен
60 14 20 4,20 207 Для изготовления нагруженных неотсчетных осей, шестерен, деталей муфт
и т. п.
Примечание. Механические свойства приведены для термически необработанной стали.
Молибден — повышает твердость и прочность стали, уменьшает хрупкость, пластичность и вязкость. Содержание молибдена — 0,2— 0,6%.
Кремний — увеличивает прочность (не снижая вязкость), упругость и жаростойкость. Содержание кремния 1—2%.
Марганец — повышает прокаливаемость стали, увеличивает ее твердость и износоустойчивость и уменьшает магнитность. Содержание
Легированную сталь обозначают сочетанием букв и цифр. Первые две цифры показывают содержание углерода в сотых долях процента. Следующими за ними буквами обозначают содержащиеся в стали легирующие элементы: X — хром, В — вольфрам, М — молибден, С— кремний, Н — никель, Г — марганец, К — кобальт и т. д. Если содержание легирующего элемента больше 1%, то следующими за буквами цифрами указывают процент его содержания. Буква А в конце маркировки озна-692
Таблица 23.3. Механические свойства легированных конструкционных и подшипниковых сталей
Марка стали <тт-10“‘, МПа ’в-10'*-МПа д. % Ч>-% а .10-», Дж/м» Назначение
Не менее
15Х 50 70 12 45 7 Для деталей, подлежащих цементации (кольца насыпных шарикоподшипников, шестерни, валики, шариковые направляющие); мелких деталей, работающих в условиях износа при трении
40Х 80 100 10 45 6 Для аналогичных деталей, подвергаемых закалке
ШХ15 42 73 21 46 4,5 Отожженная. Для деталей, требующих высокой твердости и сопротивления истиранию, постоянства размеров (отсутствие поводок): кол ьца шар ико- подшипников, валики и диски фрикционных механизмов, направляющие. Твердость до HRC, 62—65
Примечания: L Приведены нормы свойств сталей 15Х. и 40Х после закалки и отпуска. 2. Стали 15Х» 40Х — по ГОСТ 4543—71; сталь ШХ15 — по ГОСТ 801—78.
чает, что сталь содержит менее 0,025% вредных примесей серы и фосфора и является высококачественной.
Пружины изготавливают из специальных пружинных сталей, обладающих повышенными упругими свойствами, которые достигаются действием легирующих элементов и термической обработки. Для изготовления деталей, работающих при высоких температурах, применяют жаропрочные стали.
В качестве коррозионностойких используют высокохромистые нержавеющие и хромоникелевые стали.
Для изготовления колец, роликов и шариков подшипников малых сечений применяют высокоуглероднстые хромистые стали, а для больших сечений — хромомарганцевую сталь. Эти стали хорошо сопротивляются контактной усталости и обладают высокой износостойкостью и твердостью.
. Механические свойства некоторых легированных сталей приводятся в табл. 23.3 и 23.4.
Таблица 23.4. Мехштеаше свойства нержавеющих сталей (вв РОСТ 54М9—75)
Марка стали •< 1 о —. « ' С t>eg сгтЛО-\ МЙа б, % * и» 1 •* О S ЯЛ Назначена©
Н< г менее
20X13 66 45 16 8 Для изготовления деталей с повышенной пластичностью, подвергающихся удар- . ным нагрузкам или действию слабо агрессивных сред. Наибольшая коррозионная стойкость достигается после закалки с отпуском и последующей полировки
’30X13 1''* •— 48 Для изготовления пружин.
40X13 — 1 50 Сталь применяется после за-калки и низкого отпуска со шлифованной и полированной поверхностью
12Х18Н9Т 55 20 40 Для изготовления свариваемых деталей (кожухов, каркасов и т. п.)
12Х18Н9 50 20 45 Для деталей и хохструк-Ш4Й, свариваемых точечно* сваркой
Литейные стали
Углеродистые и легированные стали, применяемые для изготовления деталей методом литья обозначаются так же, как обычные конструктивные стали с добавлением буквы Л. Механические свойства литейных сталей 35ХГСЛ, 45Л и 50Л приведены в табл» 23.5.
&М
Таблица 23.5. Мехашнескяб свойства литейных сталей; плотность 7,8—7,85 г/аН (ив ГОСТ 977—75)
Марка ' стали Состояние стали (Та-Ю*1. МПа б, % Дж/м* ф, % Назначение
Не менее
35ХГСЛ Нормализация или нормализация с отпуском 60 14 3,0 25 Для средне* габаритных отливок с тол-
Закалка и отпуск 80 10 4,0 20 щиной стенок до 4 мм
45Л Нормализация или нормализация с отпуском 55 12 3,0 20 Зубчатые венцы, зубчатые колеса,
Закалка и отпуск 60 10 2,5 20 шестерни
50Л Нормализация или нормализация с отпуском 58 11 2,5 20 Для тонкостенного литья по выплавляв-
Закалка и отпуск 75 14 3,0 20 мым моделям с минимальной толщиной стенок 2—4 мм
Сплавы алюминиевые для холодной обработки
Сочетание малой плотности с достаточно высокой прочностью, немагнитность, электропроводность, коррозионная стойкость, хорошие технологические свойства и обрабатываемость резанием обусловливают широкое применение алюминиевых сплавов в приборостроении.
Сплавы алюминия делят на группы: 1) деформируемые — для изготовления обработкой давлением полуфабрикатов (листов, прутков, труб и т. д.); 2) литейные — для изготовления фасонных отливок; 3) спеченные — для изготовления изделий из порошков.
Деформируемые сплавы делятся иа неупрочняемые термической обработкой и упрочняемые.
К неупрочвяемым сплавам относятся такие сплавы, как АМц, АМг; К упрочняемым относят дуралюмины Д1, Д16, высокопрочный сплав В95 и др.
По механическим свойствам деформируемые алюминиевые сплавы превосходят литейные. Механические свойства деформируемых алюминиевых сплавов приводятся в табл. 23.6.
Т а б л и ц а 23.6. Механические свойства алюминиевых сплавов для холодной обработки; плотность 2,7—2,8 г/см3 (по ГОСТ 21631—76)
Марка сплава Состояние сплава О'в10"’- МПа ат-ю-«, МПа б, % Назначение
Не менее
АМцМ Отожженный 9,0 — 18 Листовой ма-
АМЦ1/2Н Полунагартован-ный 15,0 - 5 тернал. Хорошо сваривает-
АМг2М Отожженный 17,0 16 ся. Приме-
АМг21/2Н J Полунагартован-ный 23,0 14,0 5 няется для футляров, металлических ящиков и коробок
Д1АМ Отожженный 15,0 II 12 Для деталей
Д1АТ Закаленный и естественно состаренный 37,0 19,0 15 средней прочности
Д16АМ Отожженный 15,0 — 10 Для несущих
Д16АТ Закаленный и естественно состаренный 41,5 27,5 10 и сильно нагруженных деталей
В95АТ1 Закаленный и искусственно состаренный 49,0 41 6 приборов
В95АМ Отожженный Не более 25,0 10
Сплавы алюминиевые литейные
Сплавы алюминиевые литейные используются для получения отливок сложной конфигурации, изготовление которых другими способами обработки нерационально. Наиболее распространенными являются сплавы алюминия с кремнием (силумины). Имеются сплавы алюминия и кремния с добавками меди, марганца и магния, а также сплавы алюминия с магнием.
Механические свойства наиболее часто применяемых в приборостроении алюминиевых литейных сплавов приведены в табл. 23.7. 696
Таблица 23.7. Механические свойства и примерное назначение цветных литейных сплавов
Марка сплава Способ литья Термообработка МПа в. % НВ Назначение
Не менее
ЦАМ10-5 Мл4 Мл5 Млб Сплав ци в Д С 3 3 3 [новый антифрик плавы магниевые Гомогенизация с закалкой на воздухе То же и старение Отжиг Гомогенизация с закалкой на воздухе То же и старение Гомогенизация с закалкой на воздухе То же и старение Ц И О Н 35 i (ПО П 16 22 23 15 15 23 23 15 22 22 н ы й 4 ЭСТ 28 3 5 2 2 2 2 2 1 4 1 (по ГО 90 56—68) СТ 21437—75) Для направляющих скольжения, корпусов малых диафрагм и рукояток Для корпусов и кронштейнов Для высоконагруженных деталей приборов — качалок, педалей, кронштейнов и др. Для высоко и средненагру-женных деталей приборов — корпусов, кронштейнов и др. Целесообразно применение для деталей, требующих повышенного предела текучести —
Марка сплава Способ литья Термообработка МПа в. % НВ Назначение
Не менее
БрО5Ц5С5 БрАЖ9-4Л БрАМЦ9-2Л БрБ2 мягкий БрБНТ1,9 мягкий ЛК80-ЗЛ ЛС59-1ЛД ЛС59-1Л Е к 3 к Б[ 3 к Б р Сплавы К 3 Д Ц • ) р О Н 3 ы оловянны о и з ы алюмин и ев онзы бериллиевь Закалка » медноцннковые— е (по ] 18 15 ы е (пс 50 40 40 •г е (по 40 40 лату 30 30 20 20 'ОСТ 6 4 6 > ГОСТ 12 10 20 ГОСТ 20 20 н и (гл 15 15 6 20 13—79) 60 60 493—S 100 100 80 1789—; 130 1 1201 э ГОС! НО 100 70 30 Антифрикционные детали, арматура 14) Для фасонного литья, подшипниковых втулок, черв яч-ных колес ?0) Для плоских пружин и пружинных шайб 17711—72) Антифрикционный сплав. Применяется для фасонного литья, изготовления шестерен н деталей, работающих в морской воде Для литья под давлением, а также для других видов литья Для фасонного литья, арматуры, втулок и сепараторов подшипников
Марка сплава Способ литья Термообработка ав-10->, МПа в, % НВ Назначение
Не мен( ?е
Сп лавы алюминиевые (по ГОСТ 2685— 75)
Группа /. Сплавы на осио-
ве системы алю-
мнний—кремний: Для тонкостенного ажурного
АЛ2 зм, ом, вм. taw 15 4 50
км литья. Изготовление деталей
к • 1^ 16 2 50 с повышенной герметичностью
д — 16 1 50 (корпуса приборов). Ввиду плохой обработки мелких резьб
зм, ом, вм, Т2 14 4 50
км не рекомендуется ' применять
к Т2 15 3 50 резьбы диаметром менее 3 мм
д Т2 15 2 50
АЛ9 3, о, в, к 16 2 50 Для корпусов, оправ, крон-
д 17 1 50 штейнов, направляющих с лег-
3, О, В, к, д Т2 14 2 45 ким трением и т. п. По обраба-
км Т4 19 4 50 тываемостн превосходит АЛ2.
3, О, в к, км Т4 18 4 50 Высокая коррозионная стой-
Т5 21 2 60 кость
3, О, в Т5 20 2 60
зм, ом, вм Т5 20 2 60
зм, ом, вм Тб 23 1 70
зм, ом, вм Т7 29 2 60
зм, ом, вм Т8 16 3 55
s
Продолжение табл. 23.7
Марка сплава Способ литья * Термообр аботка ав.1(Г>, МПа в, % нв Назначение
Не менее
Грута II.
Сплавы на осно-
ве системы алю-
миний—крем-
ний—медь:
АЛЗ к 17 0,5 65 Для изготовления деталей
средней нагруженности (кор-
3, О, в 14 0,5 65 пуса приборов). Удовлетвори-
тельиая обрабатываемость ре-
3, о, в, к Т1 17 —- 70 занием и свариваемость
з, о, в, к Т2 15 1,0 65
3, О, в Т5 22 0,5 75
к Т5 25 0,5 75
з, о, в, к Т7 21 1,0 70
з, о, в, к Т8 18 2,0 65
16 0,5 65
Продолжение табл. 23.7
Марка сплава Способ лнтья Термообработка * О < 6. % нв Назначение
Не менее
Г рута IV. Сплавы иа основе системы алюминий—магний: АЛ8 3, о, в, к Т4 29 9,0 60 Для изготовл ения деталей, требующих высокой коррозионной стойкости, а также несущи х повышенные вибр ациои-ные нагрузки. Отличная коррозионная стойкость и обрабатываемость резанием
Примечание. Для бериллиевых бронз число твердости по Виккерсу (ие более). Условные обозначения способов литья и видов термической обработки: 3 — лнтье в песчаные формы; О — литье в оболочковые формы; В — литье по выплавляемым моделям; К — литье в кокиль; Д — литье под давлением; М. — модифицирование. Т1 — искусственное старение без предварительной закалки; Т2 — отжиг; Т4 — закалка; Т5 — закалка и кратковременное (неполное) искусствеииое старение; Тб — закалка и полное искусственное старение; Т7 — закалка и стабилизирующий отпуск; Т8 закалка и смягчающий отпуск.
Сплавы алюминиевые спеченные
Спеченные алюминиевые сплавы (САС) представляют собой брикетированные, спеченные и деформированные порошки алюминия и легирующих элементов или порошки, из которых состоят стандартные алюминиевые сплавы.
Спеченные алюминиевые сплавы применяют в случаях, когда, их нельзя получить методом литья и обработки давлением. Методом спече-иия изготавливают САС, содержащие ряд легирующих элементов и обладающие особыми физическими свойствами.
Спеченный алюминиевый сплав САС1 кроме алюминия содержит 25—30% кремния и 5—7% никеля. Низкий коэффициент линейного расширения сочетается в этом сплаве с малой теплопроводностью. САС1 применяют для изготовления деталей, работающих в паре со сталью при температурах от 20 до 200° С.
Сплавы цветные литейные
Из цветных литейных сплавов в оптико-механическом приборострое-вни применяют: сплав цинковый антифрикционный, магниевые сплавы, бронзы оловянные, алюминиевые и бериллиевые, а также медноцинко-вые сплавы — латуни.
Магниевые сплавы обладают небольшой плотностью и достаточно высокой прочностью. Кроме магния они содержат алюминий, цинк, марганец и другие легирующие элементы. Магниевые сплавы надежно работают в услових вибрации и хорошо обрабатываются резанием. Недостатками их являются: низкая антикоррозионная стойкость, плохая деформируемость в холодном состоянии и легкая воспламеняемость.
Сплавы на основе медн с добавками олова, алюминия, свинца, кремния нлн бериллия называют бронзами. Бронзы обладают хорошими механическими, антифрикционными, литейными свойствами, антикоррозионной стойкостью и хорошо обрабатываются резанием. Бронзы обозначают буквами и цифрами соответственно входящим в них компонентам и нх процентному содержанию.
Латунями называют сплавы меди и цинка. Сплав обозначают буквой Л, буквенным обозначением основного легирующего элемента и цифрой, соответствующей содержанию меди и этих элементов.
Механические свойства н примерное назначение цветных литейных сплавов приводится в табл. 23,7.
Нейзильбер
Сплав ТБ — Нейзильбер МНЦ15-20 (ГОСТ 492—73) применяется для изготовления особо точных шкал с тонкими штрихами и характеризуется высокой коррозионной стойкостью, красивым серебристым цветом и хорошей обрабатываемостью в горячем и холодном состоянии.
Твердость по Бринеллю: мягкого металла НВ 700, твердого с наклепом НВ 1650. Химический состав: Zn — 18,0—22,0%; Ni-f-CO — 13)5— 16,5%; Си — остальное.
Титан и его сплавы
По сочетанию физико-механических свойств титановые сплавы являются универсальным конструкционным материалом, обладающим нехладноломкостью алюминия и сталей, высокой коррозионной стойкостью медноннкелевых сплавов и нержавеющих сталей, немагнит-иостью и прочностью большей, чем у большинства конструкционных материалов.
Электрохимическое поведение титана при контакте в морской воде с другими металлами аналогично поведению нержавеющей стали. Сам титан во многих случаях ускоряет процесс корродирования контактирующих с ним металлов.
Ниже приведены основные свойства титана.
Плотность при 20° С, г/см3................. 4,5
Коэффициент теплового расширения .... (8,15±г0,15) 10~’
Коэффициент теплопроводности.............. 0,057—0,055
Удельное электрическое сопротивление, 10~8 Ом,м.................................. 42,5
Модуль упругости, МПа ......... 112 000
Модуль сдвига, МПа ........................ 41 000
Коэффициент Пуассона ...................... 0,32
Титан хорошо обрабатывается давлением. Обрабатываемость титана и его сплавов резанием близка к* обрабатываемости нержавеющих сталей. Нарезание внутренних резьб на высокопрочных титановых сплавах затруднительно. Титановые сплавы поддаются газовой резке» резке вулканитовыми кругами, свариваются контактной н аргонодуговой сваркой и соединяются пайкой (припоем на основе серебра) со всеми сталями и цветными металлами. Механические свойства титана в сравнении с другими металлами приведены в табл. 23.8.
Характерным для титана и его сплавов является склонность к контактному схватыванию при трении, что затрудняет их обработку резанием и создает опасность заклинивания деталей в трущихся узлах механизмов. Среднее значение статического коэффициента трения для пары титан—титан 0,61, а динамического (прн скорости 1 см/с) — 0,47—0,49. При сухом трении цветных сплавов по титану коэффициент трения находится в пределах 0,2—0,5.
Существующие смазки не обеспечивают значительного повышения сопротивления схватыванию н снижению коэффициента трения и износа в узлах трения.
Вследствие низких антифрикционных свойств применять неупроч-ненный титан и его сплавы в узлах трення следует только прн низких параметрах трення. Упрочнение путем термического оксидирования, диффузионное упрочнение поверхности титана и его сплавов путем насыщения поверхностного слоя кислородом» азотом, бором, углеродом
Таблица 23.8. Механические свойства титана в сравнении со свойствами других металлов
Металл •’в-1’’*-МПа 6. % Ф, %,
Титан технической чистоты (ВТ1-00) Армко-железо Алюминий технический Никель Магний Медь Ванадий Цирконий 34,6 34,4 8,0 35,9 20,0 22,0 36,8 20,4 44,7 36,9 38,0 43,8 11,5 46,0 32,0 29,0 81,2 91,8 87,8 74,9 12,5 70,2 72,0
или кремнием и упрочнение применением гальванического хромирования или химического никелирования поверхности повышают их антифрикционные свойства.
Титан и его сплавы применяют для изготовления деталей приборов, к которым предъявляются требования высокой прочности, коррозионной и термической стойкости: деталей амортизаторов, втулок, валиков, кронштейнов, оснований, фланцев н стоек.
Пластические массы
Обладая комплексом ценных свойств, пластические массы являются хорошими конструкционными материалами.
В состав сложных пластмасс входят:
1) связующее вещество, которое придает пластмассе пластичность, способность формироваться и при затвердеваний сохранять полученную форму;
2) наполнитель, вводимый для упрочнения и придания пластмассе требуемых свойств. Неорганические наполнители повышают термическую и химическую стойкость и изменяют свойства пластмассы. Органические наполнители упрочняют пластмассу;
3) пластификатор, придающий пластмассе мягкость и пластичность;
4) красители, применяемые для окрашивания пластмассы в требуемый цвет;
5) стабилизаторы, препятствующие разложению под действием солнечного света или температуры.
Характеристика и области применения, физико-механические свойства и обозначения некоторых пластмасс приведены в табл. 23.9, 23.10 и 23.11.
Таблица 23.9. Общая характеристика и области применения пластмасс
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства и применение Способ перер а-ботки
03-010-02 А. I VOCX 5689—79 I. Фе н О! Тресспорошки Органиче- пл а с т ы общего наг Черный значения Температура эксплуатации от КП, лп
Э2-330-02 Б. Эл ГОСТ 5689—79 скнй ектроизоляцш Органиче- энные прес Черный —60 до +60° С. Для изготовления ненагруженных армированных и неармнрованных деталей и декоративных деталей (кнопки, маховички, патроны, столики микроскопов) спорошки Для изготовления армирован- f кп, лп
Э1-340-02 ЭЗ-340-65 В. £ ГОСТ 5689—79 с кий 'ысокочастотг-Ми нераль- или коричневый 1ые пресет От жел- ных деталей электрот ехнического назначения (платы, к орпуса патронов, колодки и др.) крошки Устойчин в условиях тропиче- КП
ный того до темнозеленого ского климата. Температура эксплуатации от —65 до +100° С. Для изготовления ненагруженных и слабоармированных деталей радиотехнического назначения, эксплуатирующихся на воздухе и в условиях повышенной влажности
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства я применение Способ переработки
Г. 4 Ударопрочные пресспорощки
У4-080-02 ГОСТ 5689—79 д. в Органический дагохимостой Черный кие пресет Для изготовления деталей, обладающих повышенной стойкостью к ударным нагрузкам. Температура эксплуатации до 2009 С эрошки КП
Вх4-080-34 ГОСТ 5689—79 Минеральный Черный Для изготовления деталей электротехнического назначения, обладающих повышенной водостойкостью к ударным нагрузкам. Пригоден для прессования в’ысокоар-мированных изделий сложной конфигурации. Нельзя применять серебряную арматуру. Устойчив в условиях тропического климата КП, лп *
Вх2-090-69 ГОСТ 5689—79 Органический и минеральный > Стоек к воде и кислым средам. Для изготовления деталей с повышенной кнслотостой костью КП, лп
Продолжение табл. 23.Й
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства и применение Способ переработки
Вх 1-090-34 ВхЗ-090-14 К-214-52ВХ (фенолит РСТ) К-214-52Э Ж1-010-40 Ж2-0Ю-60 КФ-3 ГОСТ 5689—79 ГОСТ 5689—79 МРТУ 6-05-1297—70 МРТУ 6-05-1297—70 р. Я ГОСТ 5689—79 ГОСТ 5689—79 Ж. ТУ 6-05-1625—73 Минеральный Органический Минеральный волокнистый То же Жаростойкие л Минеральный Органический и минеральный Фрикционные Асбест Желтый, коричневый О'ттемно-зеленого ДО черного ipeccnopotui Черный » 9 пресспорс Серо-фиолетовый Стоек к воде и кислым средам. Устойчив в условиях тропического климата. Для изготовления деталей с повышен НОЙ В0Д0 КИСЛОТНОСТЬЮ Работает в тропических условиях. Предназначается для изготовления деталей электротехнического назначения <и Устойчив в условиях тропического климата. Для изготовления электроустаиовочиых изделий, обладающих повышенной жаростойкостью пики Для изготовления изделий с высокой механической прочностью и фрикционных изделий КП КП КП, лп КП, лп КП кп КП, лп
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства и применение Способ переработки
У1-ЗО1-О7 У 2-301-07 Волокнит К-420-15 Электротехнический листовой: А, Г 3. ГОСТ 5689—79 ТУ 6-05-1466—71 ТУ 12-22—71 ГОСТ 2910—74 Волокнистые Органический Вискозное волокно И. Тексп прессмате} Серокор ячневый юлиты эиалы Обладает высокой механической прочностью н хорошими антифрикционными свойствами. Температура эксплуатации до 100° С. Для изготовления деталей с повышенной прочностью при изгибе и кручении (фланцы, рукоятки, стойки, кулачки, шестерни, направляющие втулки и т. п.) Для изготовления методом прессования изделий технического назначения различного профиля, к которым предъявляются повышенные требования в отношении механической прочности • Температура длительной эксплуатации от —65 до +105° С. Для изготовления деталей (клеммных плат и др.) с повышенными электроизоляционными показателями, работающих на воздухе и в трансформаторном масле в электрических полях частотой 50 Гц КП, ЛП МО, СК
Продолжение табл. ^3.9
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства и применение Способ переработки
Б — Температура эксплуатации та-
ЛТ кая же, как для марок А, Г. Для изготовления деталей с повышенными механическими показателями, работающих на воздухе в электрических полях частотой 50 Гц Температура длительной экс-
Конструкционный: ПТК и ПТ ГОСТ 5—78 плуатации от —65 до +120° С. Для изготовления изделий, работающих на воздухе с относительной влажностью 95±2% при частоте 50 Гц Температура эксплуатации 125—155° С. Текстолит ПТК по сравнению с текстолитом ПТ имеет более высокую прочность. Для изготовления силовых деталей — шестерен, втулок, подшипников скольжения, роликов, прокладок и т. п. Для изготовления вкладышей
ПТМ-2
- / подшипников. Можно эксплуатировать при температурах 125— 155° С
о
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства и применение Способ переработки
’ А и Б j Электротехнический листовой: I, II, V-l, V-2 III IV ТУ 6-05-898—71 ГОСТ 2718—74 К. Асботе Л. Геп кыполиты гинакс Для изготовления бензо- и маслостойких деталей с повышенными механическими показателями, работающих при температуре до 125° С (детали механизмов сцепления и тормозов) Работает в диапазоне температур от —65 до +105° С. Для изготовления деталей электротехнического назначения, предназначенных для работы на воздухе в нормальных климатических условиях при частоте 50 Гц и напряжении до 1000 В Применение то же, но для работы в условиях повышенной влажности То же, но для деталей, предназначенных для работы в условиях влажного тропического климата мо, m ГП, МО
Продолжение табл. 23.9
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства н применение Способ переработки
Стекло органическое термопластичное: Л-1 ЛСО-М ЛПТ Стекло органическое конструкционное; СОЛ СТ-1 2-55 Т-2-55 II. П о А ТУ 6-05-1344—71 ТУ 6-01-283—68 ТУ 6-05-871—66 ГОСТ 15809—70 ТУ 6-01-360—69 л и м е т и л . Прессованны Б. Листовые в — 1111 | III 5 » § 15 и л а Т Ы 1ЛЫ. Для изготовления изделий технического назначения (колпачки, шкалы, индексы) и оптических деталей неответственного назначения ы Для изготовления прозрачных деталей приборов. Надежно работает в интервале температур от —60 до +60° С ГП Ф,св, МО
*•4 to Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства в применение Способ переработки
Класс А, группы Al, А2 Группа АЗ Ориентированный прессматериал АГ-4С ГОСТ 9359—73 Г ГОСТ 10087—62 III. Амине Прессовочные Сульфитная целлюлоза /. Стекло А. Прессовоч । п л а с т 1 материал* Различный п л а с т и ныв матер Желтый Я Не имеет запаха, светостоек, может окрашиваться в любые тона. Основными недостатками являются: склонность к растрескиванию при эксплуатации и высокое водо-поглощение. Аминопласты А1 применяются для изготовления просвечивающих деталей; А2 — для непросвечивающих. Обладает высокой водо-и теплостойкостью, прочностью и способностью окр ашиваться в любые тона. Изделия не растрескиваются. Применяется для изготовления не-прссвечивающихся деталей приборов (главным образом светотехнических) к и шалы Для изготовл ения конструкционных и электротехнических деталей повышенной прочности, пригодных для работы в диапазоне температур от —60 до +200° С. Хорошо армируется гл, лп Ф, лп
, Панов и
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства и применение Способ перера-
Б. Стеклотекстолиты
КАСТ ТУ 401-433—74 Высокая тепло- и влагостойкость. Для изготовления конструкционных деталей гп
V. Поле [ о л е ф и и ы
А. Полиэтилен высокого давления (низкой плотности)
11402—70 11502—70 18202—055 12002—200 - 10702—020 10802—020 II102—020 11303—040 ГОСТ 16337—77 Белый или любой Малое вл аго поглощение, гибкость при низких температурах, высокая температура теплового разрушения, стойкость к действию агрессивных сред. Изделия нз полиэтилена склонны к растрескиванию под влиянием механических воздействий и окружающей среды. Для изготовления деталей приборов Ф, ЛД
Б. Полиэтилен низкого давления (высокой плотности)
20906—040 ГОСТ 16338—77 — ' Белый или любой Более высокая прочность, чем у полиэтилена высокого давления КП, ЛД
Марка ГОСТ, ТУ Наполнитель Цвет Основные свойства н применение Способ переработки
В. Пропилен
05П10/020 МРТУ 6-05-1105—67 VI. Фтор Белый или любой о п л а с' Высокая водо- и химическая стойкость. Меньше, чем полиэтилен, подвержен растрескиванию, ио более склонен к старению. Без эффективных стабилизаторов имеет малую стойкость к воздействию ультрафиолетовых лучей. Для изготовления деталей приборов г ы ЛП
Фторопласт-4 ГОСТ 10007—72 Белый Высокие диэлектрические свойства. Стоек в тропических условиях и не подвержен действию грибков. Стоек к агрессивным средам и к действию радиационного излучения. Обладает большим коэффициентом линейного расширения, тепло- и холодоустойчивостью. Нельзя нагружать даже при норм ал ьиой темпер атуре свыше 3 МПа. Для изготовления прокладок втулок и шайб КП, ш, св
Фторопласт-3 ГОСТ 13744—76 Белый Высокие прочностные показатели, хорошее сопротивление ползучести. Для изготовления уплотнительных деталей для высокого давления при температуре до 70° G КП, ЛД, МО
Продолжение табл. 33.9
сл
Мерка ГОСТ, ТУ * Н аполнитель Цвет Основные свойства и применение Способ перера-бо!ки
Блочный полистирол . д 1 т Эмульсионный полистирол А ПМ 67 ПМ*69 ГОСТ 20282—74 * ТУ П-622—69 ТУ П-729—70 VII. Поли VIII. Пол Графит, о кислы металлов, абразивы и др. стирол Бесцветный Различный Белый и а м и д ь Желтый Ы Стоек к щелочам и слабым кислотам, разрушается в нефтепродуктах. Разлагается прн темпёра-турах выше 220° С. Хрупок. При эксплуатации появляются поверхностные трещины, увеличивающиеся под действием нагрузок. Для изготовления электроизоляционных деталей, катушек и кассет для фото- и киноаппаратуры, футляров, а также неответственных оптических деталей I Высокая стойкость к истиранию, низкий коэффициент трения, высокая механическая прочность. Устойчив к окислению и ионизирующему излучению. Хорошо сопротивляется ползучести. Не горит на воздухе. Легко обрабатывается резанием. Для изготовле ння подшипников, винтов н шестерен ЛД ЛД, КП
Условные обозначения: ГП — горячее прессование; ЛП — литьевое прессование; МО — механическая обработка; Ф — формование; СВ — сварка; ЛД — литье под давлением; КП — компрессионное прессование; 1U — шТам-повка; СК — склеившие. % t
Oi
Плот- Разрушающее напряжение, 0,1 МПа Удар- Твер- Тепло-стой- В о долог ло- Масло-стой- Бен зо-ст ой-
Марка ность. г/см8, не более при растяжении при сжатии при статическом изгибе пая вязкость, кДж/м2, не менее дость по Бринеллю кость по Мартенсу, *С, не меиее щение за 24 ч, мг, не более кость за 24 ч, % кость за 24 ч, %
Не менее
Пресспорошки обе цего назнач ения
03-010-02 1,4 1 600 1 700 6,9 30—40 130 55 1 0,03 0,05
Э2-330-02 Э1-340-02 1 М 1 К4 1 = 1 Электроизоляционные пресспорошки 1 500 I 637 I 4,9 1 30—40 1 500 1 688 1 4,9 1 20 I 125 1 125 I 45 ] 55 I 0,03 | 0,03 I 0,05 I 0,05
ЭЗ-340-65 1,95 — Высок 1 100 о частотны 490 е пресспоро 3,4 шки 20 150 10 0,015 I 0,03
У4-080-02 I 1Л 1 " Уде 1 200— 1600 гропрочные 392 пресспорош | 8.8 ки | 20-45 I 130 1 65 1 ~ 1
Вк4-080-34 Вх2-090-69 Вх 1-090-34 ВхЗ-090-14 К-214-52 (Э и ВХ) 1,75 1,6 1,6 1,5 1,65 1' li I 1 1 Влаге. 1 200— 1 500 1 500 — 1 700 1 500 — 1 700 1 100— 1 700 1 400 — 1 700 )химостойк1 343 539 588 590 600 ие npeccnopt 7,8 4,4 4,4 5,9 6,0 ушки 30—40 30—40 27 — 31 30—32 120 125 125 125 ПО 20 20 15 15 15 0,012 0,02 0,016 Стоек 0,4 0,05 0,03 0,016 Стоек »
Продолжение табл. 23.10
Марка Плотность, г/см®, не более Разрушающее напряжение, 0,1 МПа Ударная вязкость, кДж/м2, не менее Твердость по Бринеллю Теплостойкость по Мартенсу, вС, не менее В одо-поглощен ие за 24 ч, мг, ие более Масло-стойкость за 24 ч, % Бензо-стойкость за 24 ч, %
при растяжении прн сжатии при статическом изгибе
Не менее
Жаростойкие пресспорошки
ЖЬО10-040 1,90 1 600 — 1 700 441 2,9 36—40 145 20 0,01 0,01
Ж2-010-060 1,75 Фри 539 кционные п 3,9 рессматери< 40 алы 140 35
КФ-3 У1-301-07 ч У2-301-07 1 I 1,85— 1 1,95 1 *- 700 Воле 1 800 пенистые п. 21 рессматерис 30 1ЛЫ 200 1.45% 0,1 0,1—0,3
Волокннт ? Элек тро тех н н ч е-ский листовой толщиной 1—9,5 мм: 1,45 1 200 784 Тексте 8,8 >литы 25 140 90 0,11 0,025
А, Б, Г 1,45 500 to— 12 — 17 135 3-9,0% —
ЛТ Конструкционный: 1,35 1000 1 » 25 0,45— 0,9%
птк 1,4 1000 1 500/2 500 1500 35 М 140 0,8 ж —-
ПТ 1,4 850 1 300/2 300 1400 35 140 0,9 — —-
ПТМ-2 * Только пар 1,4 аллельио с ЛОЯМ. 1 200 * 1200 30 1,0
Марка Плотность, г/см*, не более Разрушающее напряжение, 0,1 МПа Ударная вязкость, кДж/м8, не менее Твердость по Бринеллю Теплостойкость по Мартенсу , °C, не менее Водо-погло-щенне за 24 ч, мг, ие более Масло-стойкость за 24 ч, % Бензо-стойкость за 24 ч, %
при растяжении при сжатии прн статическом изгибе
Не менее
Асбо текс то лит ы
А —— ч» 1100 35 хх 2,0 1 .
Б 1 <1.7 — — 900 27 1 X. 2,0 tete
Гетинакс
Электротехниче-
скнй:
I, И Ш 1,45 800 1000 8—15 хм 150 - - -
1.4 700 1000 13 tete 150 - —
IV 1,38 600 600 4 — 5 150 - - -
V-l, V-2 1.4 600 — 800 8—10 150 — ха —-
Стекло органическое конструкционное
СОЛ 1,18 775/710 29 000 1195/990 25,5/13.0 21,1/21,5 Xte - .
СТ-1 1,18 830/780 32 100 1010/1180 33,3/13,8 23,7/23,7
2-55 1,18 1,2 1080/925 X* 1550/1210 32,0/14,8 23,7/29,9 -
Т-2-55 1055/1000 1760/1200 28,9/15,0 27,4 ♦♦ ха чм ха
Аминопласты
Класс А! группа А1 Пе менее 600 6,5 — 100 2%
0.3
» А2 Не менее X* 750 7,0 хм 100 2% X» -
0,3
* АЗ Не менее 700 6,0 120 1,5% -
0,3
С т еклотек столит ы
КАСТ 1,9 30 — 1 — ! 60,0 — 1 200 1,4 —2,5%1 “ 1
** Только для неориентированного стекла.
Продолжение табл. 23.10
Марка Плотность, г/см3, не более Разрушающее напряжение, 0,1 МПа < . Ударная вязкость, кДж/м8, не менее Твердость по Бринеллю Теплостойкость по Мартенсу, °C, не менее ..... —. Водо-погло-щенне за 24 ч, мг, не более Масло-стойкость за 24 ч, % * Бензо-стойкость за 24 ч, %
прн растяжении прн сжатии прн статическом изгибе
Не менее
Полиэтилен вы- 0,930 100 — 170 Полиол 120—170 ефины 1,4 —2,5 te*
сокого давления
Полиэтилен низ- 0,955 220 — 300 200 — 350 2 — 12 4,5-5,8
кого давления Полипропилен 05Г110/020 0,91 250 — 400 33 — 80 6,0 —6,5 160 tex tete
Фторопласт-4 2,02 140 — 350 100 Фтороп ласты 100 3 — 4 по
Фторопласт-3 2,16 350 — 400 2 000 — 600 (не ломается) 20 10—13 130 — - — te*
2 500 Полиса шролы
Блочный:
Д 1,06 420 — 400 1000 20 14—16 95
Т 1,06 420—400 — 1000 20 14—16 95 ^х —-
Эмульсионный А 1,07 400 — 450 1000 22 14 — 20 100 —
ПМ-67 1.41 1000— 2 000 — Полиа 1800 миды 60 18 — 28 280 0,29% tex tete
ПМ-69 1,41 1300 950 — 2 300 2 100 — 1800 60 20 — 27 280 0.30% X— •^tei
1250 2 400 1
Примечания:!. Разрушающее напряжение текстолитов н асбот^столитов прн растяжении дано по основе. Напряжение при сжатии в числителе параллельно слоям, в знаменателе — перпЯдикулярно. 2. По органическому стеклу в числителе приведены показатели свойств для ориентированного стекла, а в знаменателе — для неорнентирбванного. 3. Теплостойкость для полипропилена приводится по методу НИИПП, а дли фторопластов, полистиролов и полиамидов — по методу Вика. 4. Физико-механические свойства органических стекол ЛСО-Mj Л ПТ, приведены в Гл. 22.
По новым ГОСТам н ТУ По старым ГОСТам н ТУ
Пресспорошки и прессмате-риалы: 03-010-02 Э2-330-02 Э1-340-02 ЭЗ-340-65 Вх2-090-69 У1-301-07 У2-301-07 Текстолит конструкционный ПТМ-2 Гетинакс: I II 111 IV V-1 V-2 Аминопласт: Класс А, группа А1 Класс А, группа А2 Класс А, группа АЗ К-18-2 К-21-22 К-211-2 К-211-3 К-18-23 Волокнит » Текстолит марки 2 Гетинакс: В, Вс Г Б Аминопласт марки: А Б КМ-68 —
Смазки и масла
Смазки и масла (табл. 23.12 и 23.13) предназначаются для уменьшения износа трущихся поверхностей деталей, снижения трения, обеспечения плавности хода деталей и узлов и работы приборов в широком диапазоне температур, герметизации предохранения осыпки на оптические детали. В зависимости от назначения смазочные материалы подразделяют на антифрикционные, противоосыпочные, консервациои-вые пластичные смазки и смазочные масла.
Замазки
Замазки применяют в разъемных соединениях оптико-механических приборов для заполнения зазоров и уплотнения швов между деталями из стекла, стали и цветных сплавов, для обеспечения влаго- и пыленепроницаемости (табл. 23.14).
720
Т аблица 23.12. Смазочные материалы, рекомендуемые для применения и узлах приборов, непосредственно контактирующих с оптическими деталями
Обозначение Рабочий температурный интервал, °C; консистенция Температура каплепадения по ГОСТ 6793 — 74, °C, не менее Применение
Смазка АЦ1 ТУ 38-101383—73 Смазка АЦ2 ТУ 38-101383—73 Смазка АЦЗ ТУ 38-101383—73 Смазка СОТ ТУ 38-101382—73 Смазка КРОН 1 ТУ 38-001191—74 Смазка КРОН 3 ТУ 38-001191—74 Смазка ЛИТА ТУ 38-101214—72 А н т н ф ] От —50 до +65; высокая От —60 до +65; средняя От —60 до + 65; низкая От —10 до +85; высокая От —50 до +60; средняя От —60 до +60; низкая От —40 до +60; средняя р икционные 100 100 100 Не плавится 180 180 180 смазки Для резьб окуляров и объективов, в соединениях при зазорах свыше 50 мкм Для трущихся поверхностей и резьбовых соединений при небольших контактных нагрузках, в соединениях при зазорах 20— 50 мкм Для точных трущихся поверхностей, цилиндрических и конических осей, при больших контактных нагрузках, в соединениях с зазорами до 20 мкм Для трущихся поверхностей и резьбовых соединений с зазорами выше 50 мкм. Может применяться как противоосыпочная от —50 до +85° С Для окуляров с многозаходной резьбой н других с зазорами свыше 20 мкм Для точных трущихся соединений с зазорами до 20 мкм и малыми контактными нагрузками Для объективов киноаппаратов, зубчатых, червячных передач, подшипников скольжения, шарниров и других соединений с высокими контактными нагрузками
722
Продолжение табл. 23.12
Обиз.>зчение
Смазка Орион
ТУ 38-001188—74
Смазка ГОИ-54п
ГОСТ 3276—74 Смазка М3
ТУ 38-101213—72
Масло МС-6
ГОСТ 11552—76
М ас л о в е р е те в н ое /ХУ ГОСТ 1642—75
Масло МС-14
ГОСТ 21743—76
Масло ВНИИНП-6 ТУ 38-001168—74
Масло МБП-12 ГОСТ 7935—74
Рабочий температурный интервал, °C; консистенция Температура каплепадения по ГОСТ 6793 — 74. Применение
°C, не менее
Противоосы ночная смазка
От —60 до +80; высокая 180 Для внутренних полостей, в том числе и в условиях вакуума до 1,3* 10-3 Па
Консерванионные смазки
От —50 до +50; средняя 60 Для защиты наружных поверхностей при хранении изделий в укупорке до 10 лет
От —*50 до +80; средняя 100 Для защиты изделий в морских условиях и в приморских районах на сроки до 8 ле1
С м а з о ч ные масла
От —50 до +50 f Для механизмов с малыми нагрузками (шарикоподшипники, микровинты и др.)
От —30 до +40 Для подшипников скольжения, зубчатых передач, шарниров, валов и других механизмов при средних нагрузках
От —10 до +40 Для микровннтов фокусировки (на иглах), точечных соединении и т. п. с высокими контактными нагрузками
От —45 до +150 Для скоростных шарикоподшипников и узлов трения скольжения с высокими контактными нагрузками
От —10 до +50 Для шестерен, трибок типа часовых механизмов, фотоаппаратов (автоспуски, пс£ты замедления) пар трения сталь—сапфир и других механизмов с высокими нагрузками
Примечание. Смазки, удовлетворяющие по верхнему пределу рабочих температур требованиям ТУ йа изделия в тропическом исполнении, можно применять в тропических условиях с антнсептированием их 1%-иым раствором 4-капроил-рс?°рцина Ь смм'-ки АЦ,. КРОН и Орион следует добавлять 0,3% гексаэтилдистанрксаиа.
Т аблица 23.13. Смазочные материалы, применение которых допустимо в узлах приборов, не контактирующих с оптическими деталями и находящихся ие ближе 30 мм от и их
Обозначение рабочий температурный интервал, °C; консистенция Температура каплепадения по ГОСТ 6793 — 74, °C, ие менее Применение
Смазка ЦИАТИМ-201 ГОСТ 6267—74 Смазка ЦИАТИМ-221 ГОСТ 9433—60 Смазка ВНИИНП-228 ГОСТ 12330—77 Смазка ВНИИНП-267 ГОСТ 16105—70 Смазка ОКБ-122-7 ГОСТ 18179—72 А н т и ф р и От —60 до +90; низкая От —60 до +150; средняя От —45 до +150; средняя От —60 до +150; низкая От —60 до +120; средняя кционные см 170 200 175 180 160 а 3 к и Для подшипников качения, зубчатых зацеплений и других узлон с малыми контактными нагрузками. Не рекомендуется применять в условиях прямого контакта с водой и при относительной влажности воздуха более 80%, а также прн длительном (более 3 лет) контакте с цветными металлами Для подшипников качения, пар металл — резина при умеренных нагрузках Для высокоскоростных шарикоподшипников (до 60 000 об/мин), узлов трения гироскопов, подшипников качения чувствительных опор точных механизмов и т. д. Для шарикоподшипников (скорость до 30 000 об/мин), редукторов, резьбовых соединений, и том числе при остаточном давлении до 1,3* 10~6 Па Для подшипников качения и скольжения (в том числе гиромоторов до 25 000 об/мин), цапф шарниров, опор, зубчатых и червячных зацеплений и др.
Обозначение Рабочий температурный интервал, °C; консистенция Температура каплепадения по ГОСТ 6793—74, °C, не менее Применение
Смазочные масла
Масло смазочное 132-08 ГОСТ 18375—73 От —70 до +70 — Для подшипников качения и скольжения
Примечание. Смазки, удовлетворяющие по верхнему пределу рабочих температур требованиям ТУ иа изделия в тропическом исполнении, можно применять н тропических условиях при условии аитисептирования нх 1%-ным раствором 4-капроилрезорцина.
Таблица 23.14. Замазки, применяемые в оптико-механических приборах
Обозначение Цвет, группа твердости Рабочий температурный интервал, ®С Температура каплепадения, °C Назначение
Замазка 5 Замазка 30 Замазка 25 Замазка 50 Черный, мягкая Коричневый, мягкая То же Зеленый, __ мягкая От —50 до +50 От —60 до +130 От —60 до +130 От —50 до +50 +70 Не плавится » » г +70 Уплотнение узлов и изделий с жесткими фланцами, заливка и уплотнение винтов Уплотнение узлов и изделий с жесткими фланцами, заливка и уплотнение винтов Уплотнение тонких фланцев, несущих оптику
Продолжение табл. 23.14
Обозначение Цвет, группа твердости Рабочий температурный интервал, °C Температура каплепадения, °C * Назначение
Замазка 35 Коричневый, мягкая От —40 до +50 +65 Соединение на контакт больших поверхностей
Замазка 135 Коричневый, полутвердая От —60 до +130 Не плавится Уплотнение разъемных соединений, имеющих в стыке средние зазоры, уплотнение винтов
Замазка 140 Голубоватозеленый, полутвердая От —40 до +50 +65 Уплотнение зазоров более 0,5 мм, залнвка головок винтов
Замазка 230 Черный, твердая От —40 до +50 +70 Уплотнение зазоров не более 0,5 мм. Завальцовка оптических детален
Замазка 245 Черный, твердая От —60 до +130 Не плавится Уплотнение зазоров более 0,5 мм
Невысыхающий герметик 51 -Г-3 ТУ 38-405138—73 Черный, мягкая От —60 до +100 Герметизация разъемных соединений изделий
Замазка У-20А ТУ 38-105357—71 Зеленый, полутвердая От —50 до +70 Не плавится Герметизация заклепочных швов и разъемных соединений изделий. В условиях тропического климата применяют только в закрытых объемах
Примечание. Замазки, удовлетворяющие требованиям ТУ на изделия в тропическом исполнении по верхнему пределу рабочих температур, можно применять как тропикоустойчивые при положительном результате их испытания на грибоустойчивость. При отрицательном результате — в замазку необходимо ввести 1%-иый раствор 4-капроилрезорцина.
Адсорбенты для осушки приборов
В качестве адсорбента для постоянной осушки находящегося внутри прибора воздуха применяют технический силикагель (табл. 23.15). Технический силикагель представляет собой высушенный гель кремниевой кислоты пористого строения, с сильно развитой внутренней поверхностью. В зависимости от формы зерен силикагель бывает гранулированным илн кусковым, а в зависимости от величины пор — мелко- или крупнопористым.
Т а б л и ц а 23.15. Основные характеристики технического силикагеля (по ГОСТ 3956—76)
Сорт Внешний вид Размер зеренt мм Механическая прочность, % Насыпная плотность, г/дм’ Влагоемкость, %, прн относительной влажности
20% 40% 60%
Не менее
Высший Первый Стекловидные прозрачные или матовые зерна овальной или сферической формы Стекловидные прозрачные или матовые зерна овальной, сферической или неправильной формы. Цвет — от бесцветного до темного с черными включениями 2,8—7,0 2,8—7,0 * 98 94 780 720 9,5 9,0 17,0 16,0 27,0 25,0
Для заполнения патронов постоянной осушки рекомендуется применять гранулированный мелкопористый силикагель марки КСМГ высшего или первого сорта. Перед применением силикагель следует просушить горячим воздухом при температуре 150—180° С для удаления адсорбированной влаги.
Силикагель-индикатор представляет собой сухие зерна мелко* пори с; ого силикагеля, пропитанные раствором солей кобальта. Он приесняекя или только для контроля относительной влажности среды в замкнутом объеме прибора по йзмененню его окраски или одновременно в качсчтве адсорбента и для контроля относительной влажности. Ниже приводятся основные свойства силикагеля-индикатора (ГОСТ 8984—75);
Цвет зерен
От синего до светло-голубого
Содержание зерен размером 1,0—3,6 мм, %, не менее.................................... 06
Влагоемкость, %, не менее, при относительной влажности: ........................
20% 8
35% 13
50% 20
При изменении окраски силикагеля-индикатора (за счет его увлажнения) на сиреневую или розовую его следует перед применением просушить при температуре 120±5°С до окрашивания в светло-синий или голубой цвет.
Литература! [89, 90, 98, 108].
СПИСОК ЛИТЕРАТУРЫ
1. Апенко М. И., Дубовик А. С. Прикладная оптика. М., Наука, 1971. 392 с.
2 Бардин А. Н. Сборка и юстировка оптических приборов. М., Высшая школа, 1968. 325 с.
3. Бегунов Б« Н., Заказное Н, П. Теория оптических систем. М., Машиностроение, 1973. 488 с.
4. Бородачев Н. А. Обоснование методики расчета допусков и ошибок кинематических цепей. Ч. I. М.—Л., АН СССР, 1943. 88 с.
5. Бородачев Н. А. Обоснование методики расчета допусков и ошибок размерных и кинематических цепей. Ч. II. М*—Л., ДН СССР, 1946. 228 с.
6. Бородачев Н. А. Анализ качества и точности производства. М., Машгнз, 1946. 252 с.
7. Бородачев Н. А. Основные вопросы теории точности производства. М.—Л., АН СССР, 1950. 416 с.
8. Браславский Д. А., Петров В. В. Точность измерительных устройств. М., Машиностроение, 1976. 311 с.
9. Бруевич Н. Г. Точность механнзхмов. М., Гостехтеоретиздат, 1946. 352 с.
10. Бруевич Н. Г., Доступов Б. Г< Счетно-решающие устройства. М., Военно-воздушная Краснознаменная академия им. проф. Н. Е. Жуковского, 1954. 412 с.
11. Вейнберг В. Б., Саттаров Д. К* Оптика световодов. Л., Машиностроение, 1977. 319 с.
12. Волосов Д. С., Цивкнн М. В. Теория и расчет светооптнческих систем. М„ Искусство, 1960. 526 с.
13. Волосов Д. С. Фотографическая оптика. М., Искусство, 1978. 543 с.
14. Войшвнлло Н. А., Блинова Л. Д., Миронова Л, Р. Индикатрисы рассеяния стекол, применяемых для рассеяния проходящего направленного пучка света. — ОМП, 1974, № 2, с. 29.
15. Войшвилло Н. А., Демкина Л. И. Светорассеивающие стекла для изготовления образцов мутности и имитаторов светорассеивающих сред. — ОМП, 1972, № 2^ с. 35.
16. Вудсон У., Коновер Д. Справочник по инженерной психологии для инженеров и художников-конструкторов. Пер. с англ. М., Мир; 1968. 517 с.
17. Гальперн Д. Ю., Нефедов Б. Л. О возникновении рассеянного света в оптических приборах и способах его устранения. — ОМП, 1953, № 6, с. 36—44.
18. Герцбергер М. Современная геометрическая оптика. Пер. с англ. М., Изд-во иностр, лнт., 1962. 487 с, 728
19. Гершун А. А. Избранные труды по фотометрии н светотехнике. М.—Л., Гостехиздат, 1958. 548 с.
20. Городинский Г. М. Рассеивающие свойства восковых экранов. — ОМП, 1963, № 9, с. 7—9.
21. Городинский Г. М„ ПороховаТ. Г., Тоскуева Л. П. О чувствительности поперечных и продольных наводок в проекционных отсчетных устройствах. — ОМП, 1971, № 6, с. 3—7.
22. Городинский Г. М., Орещенко Л. П. Исследование оптической керамики КО1. — ОМП, 1977, № 8, с. 34—35.
23. Городинский Г. M.j Маленкова А. И. Рассеивающие свойства матовых экранов в ближней ИК-области спектра. — Прикл. спектр., 1972, т. XVII, № 2.
*24. Городинский Г. М., Закорнна Н. А. Рассеивающие свойства матовых стекол при отражении. — ОМП, 1961, № 7, с. 35—39.
25. Городинский Г. М., ПороховаТ. Г., Будин В. П. Разрешающая способность экранных отсчетных устройств. — ОМП, 1976, № 2, с. 51—56.
26. Городинский Г. М., Тоскуев Л. П. О некоторых фотометрических характеристиках иммерсионного экрана. — ОМП, 1972, № 3, с. 61—62.
27. Грейм И. А. Оптические отсчетные системы в приборостроении и машиностроении. М.—Л., Машгиз, 1963. 239 с.
28. Грейм И. А. Элементы проектирования и расчет механизмов приборов. Л., Машиностроение, 1972. 216 с.
29. Грейм И, А., Зальц А. Е. Зеркально-призменные системы, их расчет и элементы юстировки. Л., СЗПИ, 1978. 79 с.
30. Гришин Б. С. Юстировка геодезических инструментов. М., Геодезиздат, 1962, 184 с.
31. Гришин Б. С. Юстировка сложных оптических систем приборов. М., Машиностроение, 1976. 205 с.
32. Гуревич М. М. Введение в фотометрию. Л., Энергия, 1968. 244 с.
33. Данилевич Ф. М., Никитин В. А., Смирнова Е. П. Сборка и юстировка оптических контрольно-измерительных приборов. Л., Машиностроение, 1976. 255 с.
34. Джеррард А., Дж. М. Берч. Введение в матричную оптику. М., Мир, 1978. 342 с.
35. Днепровский Н. И», Каврайскнй В. В., Мусселнус М. М. Введение в практическую астрономию. М.—Л., ОНТИ, 1936. 408 с.
36. Долинский И. Мм Дюкачева О. В., Рагузин Р. М. Особенности механизмов для перемещения объектов в плоскости, перпендикулярной оптической оси микроскопа. — ОМП, 1969, № 5, с. 36—40.
37. Ельников Н. Т., Днтев А. Ф., Юрусов И. К* Сборка и юстировка оптико-механнческнх приборов. М., Машиностроение, 1974. 350 с.
38 , Ефремов А. А., Законников В. П., Подобрянский А. В. Сборка оптических приборов. М., Высшая школа, 1978. 296 с.
. 39. Журавлев А. Н. Допуски и технические измерения. М., Высшая школа, 1978. 251 с,
40. Захарьевский А. Н. Контроль оптических систем н приборов. Л., ЛИТМО, 1946, вып. 2. 90 с.
41. Захарьевский А. Н. Конспект сферической тригонометрии (с примерами из оптотехннки), Л„ ЛИТМО, 1948. 44 с.
42. Захарьевский А, Н. Интерферометры. М., Оборонгиз, 1952. 296 с.
43. Иванцов А. И. Основы теории точности измерительных устройств. М., Изд-во стандартов, 1972. 212 с.
44. Ильин Ф. С., Федоров Г. И., Федив Л. А. Лабораторные оптические приборы. М., Машиностроение, 1966. 496 с.
45. Импульсная фотометрия. Сборник статей, Л., Машиностроение, 1978, вып. 5. 264 с.
46. Ишматурова М. С., Сергеев Л. В. Оптический клей, прозрачный в инфракрасной области спектра. — ОМП, 1967, № 12, с. 43—45.
47. Каталог светорассеивающих стекол (оптических). Л.? ГОИ, 1975. 56 с.
48. Ксмпияский М. М. Проектирование механизмов измерительных приборов. М., Машгиз, 1961. 143 с.
49. Кемпинский М. М. Точность и надежность измерительных приборов. М., Машиностроение, 1972. 264 с.
50. Коротков В. П., Тайц Б. А. Основы метрологии я точности механизмов приборов. М., Машгиз, 1961. 400 с.
51. Коротков В. П., Тайц Б. А, Основы метрологии и теории точности измерительных устройств. Изд-во стандартов, 1978. 352 с.
52. Козлов М. П. Зубчатые передачи точного приборостроения. М., Машиностроение, 1969. 398 с.
53. Кожевников Ю. Г. Оптические призмы. М., Машиностроение, 1975. 192 с.
54. Кравков С, В» Глаз и его работа. М.—Л., АН СССР, 1951. 531 с.
55. Крылова Т. Н. Интерференционные покрытия. Л., Машиностроение, 1973. 224 с.
56. Кругер М, Я., Кулежиов Б. М. Конструирование оптико-механических приборов. М.—Л., Машгиз, 1948. 219 с.
57. Лебедев И. В. О некоторых свойствах систем плоских зеркал.— Труды ИФМ. Вып. 1. Минск, АН СССР, 1956, с. 125—151, 58. Литвин Ф. Л. Проектирование механизмов и деталей приборов. Л., Машиностроение, 1973. 696 с.
59. Максутов Д. Д. Изготовление и исследование астрономической оптики. М.—Л., ГИТТЛ, 1948. 280 с.
60. Мальцев М. Д. Расчет допусков на оптические детали. М., Машиностроение, 1966. 265 с.
61. Микроскопы. Л., Машиностроение, 1969. 511 с./Авт.: Г. Е. Скворцов, В. А. Панов, Н, И, Поликов, Л. А. Федин.
62. Михайлов Е. А. О повышении точности счетно-решающих приборов методом регулировки. М., Оборонгнз, 1958.
63. Нагибина И. М., Прокофьев В. К* Спектральные приборы н техника спектроскопии. Изд. 2-е, Л., Машиностроение, 1967. 324 с.
64. Нефедоа Б. Л. Методы решения Задач по вычислительной оптике. М.—Л., Машиностроение, 1966. 264 с.
65. Оптико-механические приборы. М., Машиностроение, 1965. 366 с./Авт.: С. Г. Бабушкин, М. Г, Беркова, К. Р. Гольдин, Н. Я. Крупп, К. А. Муниц, С. А, Сухопарое, К. И. Тарасов.
66. Оптические материалы для инфракрасной техники. М., Наука, 1965. 335 с./Авт.: Е. М. Воронкова, Б. Н, Гречушникова, Г. И. Дист-лер, И. П. Петров.
67. Оптические приборы в машиностроении: Справочник/Под ред. Н. П. Заказнова. М., Машиностроение, 1974. 238 с.
68. Орлов П, И. Основы конструировании’. Справочно-методическое пособие. М., Машиностроение, 1977. 357 с, 730
69. Ортоскопия фотограмметрических объективов. М., Недра, 1976. 176 с./Авт.: М. М. Русинов, В. Г* Афремов, А. Ш. Шахвердов, Е. Г. Шлим.
70. Основы инженерной психологии, М., Высшая школа, 1977.
334 с./Авт.: Б. А. Душков, Б. Ф. Ломов, В. Ф. Рубахин, Б. А. Смирнов.
71. Панов В. Ам Андреев Л. Н. Оптика микроскопов (Расчет и проектирование). Л., Машиностроение, 1976. 432 с.
72. Плотнвков В. С., Варфоломеев Д. И., Пустовалов В. Е. Расчет и конструирование оптико-механических приборов. М., Машгиз, 1972.
73. Погарев Г. В. Оптические юстировочные задачи: Справочное пособие. Л., Машиностроение, 1974 . 224 с.
74. Погарев Г. В. Юстировка оптических приборов. Л., Машиностроение, 1968. 292 с.
75. Проектирование механизмов и приборов/Под ред. К. И. Заблон-ского. Киев, Вища школа, 1971. 520 с.
76. Рагузин Р. М. Проектирование механизмов микроскопов. — ОМП, 1972, с. 36—39.
77. Рагузли Р. М. Предметные столики и препаратоводители микроскопов. — ОМП, 1973, с. 29—33.
78. Русниоа И. И. Габаритный расчет оптических систем. М., Геодезиздат, 1959. 258 с.
79. Русинов М> М, Техническая оптика. Л., Машиностроение, 1979. 488 с.
80. Русинов М. М, Несферические поверхности в оптике. М., Недра, 1973. 326 с.
81. Русинов М. М. Юстировка оптических приборов. М., Недра, 1969. 326 с.
82. Сакин И. Л. Инженерная оптика. Л., Машиностроение, 1976. 255 с.
83. Сапожников Р. А. Теоретическая фотометрия. Л., Энергия, 1967. 268 с.
84. Скворцов Г. Е. О влиянии некоторых ошибок юстировки пано-рамичёских систем на точность измерения углов. Сборник статей. — ЛИТМО, 1956, вып. 19, с. 66—74.
85. Слюсаре в Г. Г. Методы расчета оптических систем. Л., Машиностроение, 1969. 672 с.
86. Слюсарев Г. Г. Расчет оптических систем. Л., Машиностроение, 1975. 639 с.
87. Сокольский М. Н. Влияние аберраций оптической системы на точность нониального совмещения штрихов. — Опт. и спектр., 1970, т. XXIX, вып. 1, с. 183—189.
88. Сокольский М. Н. О точности продольных наводок в оптических приборах. — Опт. и спектр., 1970, т. XXIX, вып. 2, с. 401—406.
89. Справочник конструктора оптико-механических приборов. Изд. 2-е/Под ред. М. Я. Кругера и В. А. Панова. Л., Машиностроение, 1967. 760 с.
90. Справочник по пластическим массам. Изд. 2-е/Под ред. В. М. Катаева, В. А. Попова, Б. И. Сажных. М.» Химия, 1975, т. 1. 447 с.; т. 2. 567 с.
91. Справочник по военной онтике/Под ред. акад. С. И. Вавилова н проф. М. В. Савостьяновой. Л., Гостехтеорегиздат, 1945. 263 с.
92. Справочник конструктора точного приборостроения/Под ред. Ф. Л. Литвина. М.—Л., Машиностроение, 1964. 943 с.
93. Справочник конструктора точных приборов. Изд. З-е/Под ред. И, Я. Левина. М.» Машиностроение, 1967. 727 с.
94. Сухопарое С. А, Сборка и юстировка морских оптических дальномеров. М., Обороигиз, 1961. 180 с.
95. Сухопарое С. А., Долинский И. М. Методы расчета допусков на юстировку оптических систем с помощью передаточных коэффициентов. — ОМП, 1967, № 3, с. 1—5.
96. Сухопарое С. А., Долинский И. М. Передаточные коэффициенты оптических систем. — ОМП, 1967, № 4, с. 10—14.
97. Тарасов К. И. Спектральные приборы. Л., Машиностроение, 1977. 359 с.
98. Титановые сплавы в машиностроении/Под ред. Г. И. Капы-рина. Л., Машиностроение, 1977. 247 с.
99. Топорец А. С. Монохроматоры. М., Гостехиздат, 1955. 264 с.
100. Тудоровский А. И. Теория оптических приборов. М.—Л., АН СССР. Ч. 1, 1948. 661 с. Ч. 2, 1952. 567 с.
101. Турыгии И. А. Оптические части приборов. Справочная книга оптико-механика. Ч. 2. Под ред. Л. Г. Титова. М.—Л., ОНТИ, 1937, 117—180.
102. Турыгин И. А. Прикладная оптика. М., Машиностроение, Ч. 1, 1965. 362 с.; Ч. 2, 1966. 431 с.
103. Урмахер Л. С. Справочник по офтальмологической оптике и приборам. М., Медицина, 1971. 179 с.
104. Фабри Ш. Общее введение в фотометрию. М.—Л., ОНТИ, 1934. 175 с.
105. Федии Л. А., Барский И. Я. Микрофотография. Л., Наука, 1971. *220 с.
106. Фурман LU. А. Тонкослойные оптические покрытия, Л., Машиностроение, 1977. 263 с.
107. Ханзен Ф. Основы общей методики конструирования. Пер. с нем./Под ред. М. Я- Кругера. Л., Машиностроение, 1969. 165 с.
108. Цветные металлы и сплавы: Справочник. М., Металлургия, 1975. 216 с.
109. Цуккермаи С. Т. Точные механизмы. М., Оборонгиз, 1941. 304 с.
НО. Цурабо Д. Д. Детали и узлы приборов: Справочное пособие, М., Машиностроение, 1975. 557 с.
111. Чуриловский В. Н. Теория оптических приборов. М.—Л., Машиностроение, 1966. 564 с.
112. Чуриловский В. Н. Теория хроматизма н аберрация 3-го порядка. Л., Машиностроение, 1968. 312 с.
113. Шерклифф У. Поляризованный свет. М., Мир, 1965. 264 с.
114. Шнейдер Ю. Г, Образование регулярных микрорельефов на деталях и их эксплуатационные свойства. Л., Машиностроение, 1972. 240 с.
115. Шубников А. В. Оптическая кристаллография. М.—Л., АН СССР, 1950. 275 с.
116. Якушенков Ю. Г. Основы теории и расчета оптико-электронных приборов. М., Советское радио, 1971. 336 с.
117. HerzbergerM. Refractive Indices of Infrared Optical Materials and Color Correction of Infrared Lenses. JOSA, 1962, v. 52, N 4, p. 420—427.
ОГЛАВЛЕНИЕ
Предисловие ................................................ 3
Глава 1. Физическая оптика (Ф. А. Паноф..................... 5
Электромагнитная природа света.............. —
Электромагнитные волны. Спектр электромагнитных колебаний.................................. —
Уравнения волнового движения............... 6
Интерференция света. Основы теории интерферометров 7
Оптическая длина пути ................................. 8
Область и поле интерференции............... —
Входные и выходные зрачки и поле интерферометров —
Ширина щели при нелокализованных полосах.... 9
v Допустимый размер входного зрачка при локализованных полосах .......................................... —
Интерференция в пластинках ........................... 10
Кольца Ньютона ................................. 11
Принцип создании интерференционной картины в интерферометре ............................................ 12
Дисперсия света. Основы теории спектральных приборов 14
Принципиальная оптическаи схема спектральных приборов ................................... * « » Ц * *****
Светосила спектрального прибора ...................... 15
Линейная дисперсия призменных спектральных приборов —
Теоретическая разрешающая способность спектральных приборов.............................................. 17
Фрауигоферова дифракция от круглого отверстия .... 18
Увеличение прибора, имеющего спектральные призмы 19
Кривизна спектральных линий .......................... 20
Реальная разрешающая способность спектрального прибора ................................................. 21
Дифракционные решетки ................................. —
Угловая и линейная дисперсии решетки ................. 22
Разрешающая способность прибора с дифракционной решеткой.............................................. 23
Излучение и поглощение света............................ —
Монохроматическое и сложное излучение.................. —
Законы теплового излучения АЧТ........................ 25
Излучение тел, не являющихся абсолютно черными 30
Соотношение между энергетическими и светотехническими величинами ........................................... 31
Расчет световых свойств потока на основе кривой распределения энергии по спектру......................... 33
Светотехнические величины ............................ 34
Излучение равнояркостных поверхностей................ 38
Реакция приемников лучистой энергии на падающий поток излучения ...................................... 39
Отражение света ...................................... 41
Поляризация света при отражении....................... 42
Виды поляризации света ............................... 43
Потери света в оптических приборах.................... 44
Просветление стекол ................................... —
Расчет светопропускания и светопоглощения бесцветного стекла ............................................... 45
Потери света при отражении и поглощении в светофильтрах ................................................. 46
Расчет интегрального коэффициента пропускания светофильтра для видимой области спектра при сложном . излучении ............................................. —
Светофильтры переменной плотности (фотометрические клинья) .............................................. 47
Расчет коэффициента светопропускания оптических приборов ................................................ 48
Формулы для вычисления оптической плотности некоторых отдельных элементов оптической системы........... 51
Распространение света в анизотропной среде (кристаллы) 54
Двойное лучепреломление в одноосных кристаллах . . —
Положительные и отрицательные кристаллы. Волновые поверхности Френеля .................................. 55
Поляризаторы...................................... —
Поляризационные призмы........................... 56
Примеры расчета симметричного поля поляризации призм ................................................ 59
Оптические компенсаторы .............................. 60
Расчет интерференционной окраски кварцевой пластинки при параллельных николях ............................. 61
Глава 2. Геометрическая оптика (В. А. Панов) .............. 63
Основные понятия геометрической оптики.................. —
Строение пучка лучей................................... —
Основные законы геометрической оптики ................. —
Параксиальная оптика .................................. 65
Правила знаков ...................................... —
Главные точки, главные плоскости, фокусы и фокусные расстояния............................................ 66
Формулы, определяющие положение сопряженных точек.
Линейное увеличение в сопряженных плоскостях ... 67
Угловое н продольное увеличения ...................... 68
Узловые точки ....................................... 69
Построение изображения ............................. —
Построение изображения с помощью узловых точек 70
Преломление луча через сферическую поверхность . , . —
Преломление через несколько сферических поверхностей 71
Оптическая сила системы ............................ 72
Бесконечно тонкая лииза ............................... —
Система из нескольких линз, расположенная в воздухе 73
Линзы конечной толщины................................. —
Кардинальные величины системы, состоящей из двух частей ............................................... 74
ч/ Ограничение пучков лучей в оптических системах . ... 75
Геометрическое виньетирование ........................ 76
Положение зрачков и окон в основных типах оптических систем ............................................... 77
Соотношения между линейным полем и светосилой системы (инварианты Лагранжа—Гельмгольца) ...... 78
Видимое увеличение оптических приборов........ 79
Видимое увеличение лупы .............................. 80
Видимое увеличение лупы, работающей с аккомодирующим или аметропическим глазом.................. —
Телескопические или афокальные системы............. 81
Сложный микроскоп ................................... 82
Передача перспективы оптическими приборами .... 85
естественное впечатление ........................... 86
Общие формулы для светосилы оптического прибора —
Светосила оптического прибора при малой передней апертуре (объективы зрительной трубы, фотографические объективы для ландшафтных съемок и т. д.)............. 87
Светосила оптического прибора при малой задней апертуре (проекционные приборы, осветительные системы, прожекторы и др.) ..................................... —
Разрешающая способность оптических приборов........ 88
Согласование разрешающей способности прибора с разрешающей способностью глаза ........................... —
Дифракционная разрешающая способность прибора . . —
Глубина изображаемого н ростр аисте а ................. 90
Глубина резкости телескопической системы.............. 92
Глубина резкости лумы и микроскопа .................... —
Глубина резкости при аккомодации глаза................. —
Аберрации центрированных систем ....................... 93
Аберрации третьего порядка. Коэффициенты Зейделя — Коэффициенты аберраций третьего порядка бесконечно тонких компонентов ................................. 94
Сферическая аберрация................................. 96
Кома................................................. 97
Условие синусов ..................................... 98
Апланатические точки преломляющей поверхности ... 99
Формы апланатических менисков ......................... 100
Изоплапатическое изображение элементарной поверхности вблизи оптической оси................... 102
Астигматизм и кривизна изображения..................... —
Дисторсия ............................................. 101
Хроматические аберрации............................. 105
Зависимость между волновой и продольной аберрациями 108
Объективы из двух склеенных линз .................... 112
Особенности расчета окуляров .......................... 114
Линзовые конденсоры.................................... 115
Назначение асферических поверхностей................... 119
Выражение аберраций системы через аберрации ее компонентов .............................................. —
Формулы для вычислений аберраций системы после окуляра ........................................... 120
Анализ кривой широкого наклонного пучка в меридиональном сечении ..................................... 123
Отражение и преломление на плоских поверхностях оптических деталей ..... ............................... —
Преломление луча через плоскость ................... 123
Отражение от плоского зеркала ....................’ 125
Система зеркал....................................i —
Преломление пучка через плоскопараллельную пластинку или призму................................... 127
Графическое построение хода луча через плоскопараллельную пластинку (или любую ей эквивалентную призму) методом редуцирования ...................... 128
Преломление лучей через призму в ее главном сечении — Преломление луча, проходящего через призму вне плоскости главного сечения (внемериднональный луч) ... 129
Дисперсия призм................................ . 130
Ахроматические клинья............................... 133
Габаритный расчет зрительной трубы . * , ............. —
Условия н ер встраиваемости оптического прибора при изменении температуры .............................. 139
Определение значений показателей преломления оптических стекол . ................................ . 143
Интерполяционные формулы М. Герцбергера для вычисления показателя преломления в инфракрасной области спектра ................................... 146
Глава 3. Глаз как оптический инструмент (Л1. Я* Кругер) 147 Строение и свойства глаза .............................. —
Аккомодация глаза ..............................к . 148
Недостатки зрения ..............................У'» —
Влияние на остроту зрения условий освещенности . 149
Световые пороги ...................................... —
Контрастная чувствительность........................ 150
Разрешающая способность .............................. —
Бинокулярное зрение................................. 151
Цветоощущение....................................... 152
Воздействие невидимых излучений....................... —
Глава 4. Оптические детали и узлы (М. >7. Кругер, В. А. Панов) ........................................ . 154
Общие сведения ........................................ —
Условные обозначения, применяемые на чертежах и схемах — Требования к оформлению чертежей оптических деталей, узлов и схем......................................... 155
Общие требования ..................................... —
Оформление рабочих чертежей деталей................ 156
Оформление рабочих чертежей узлов.................. 162
Оформление оптических схем......................... —
Линзы ........................................... 165
Конструкция линз ...................................... —
Фаски на оптических деталях круглой формы (линзы, сетки, светофильтры и др.) ......................... 168
Зеркала ............................................... —
Призмы................................................. 169
Составные призмы ..................................... 181
Расчет размеров призм ................................ —
Призмы с одной отражающей гранью (тнп А).............. 183
Паразитные отражения в призмах ....................... 184
Призменные системы для раздвижки окуляров по расстоянию (базе) между глазами.................. 186
Призмы для разделения пучков лучей.............. 188
Призмы для соединения полей ....................... 188
Оборачивающие призменные системы .............. . 190
Оптические шарниры ................................ 192
Клинья .................... ............ .......... —
Фаски иа призмах и иекруглых пластинках.............. 193
Дифракционные решетки ............................... 194
Сетки ............................................... 198
Растровые (трансверсальные) сетки . ............. 201
Допуски на изготовление заготовок сеток и лимбов. Выбор марки стекла ............................... —
Методы и точность нанесения делений на сетках . * ♦ 202
Сетки с искусственной подсветкой .................. 206
Светофильтры...................................... 207
Стеклянные светофильтры для микроскопии ..... 209
Светофильтры для контрольно-измерительных приборов 210
Светофильтры поляризационные ...................... 211
Светорассеивающне экраны ............................ 212
Чувствительность визирования штрихов на просветных экранах ........................................... 214
Чувствительность визирования штрихов на непрозрачных отражающих экранах .................... 215
Разрешающая способность отсчетных устройств при дополнительных системах наблюдения на экране ... 216
Рассеиватели из оптической керамики КО1.............. 217
Люминесцирующие экраны ...................... —
Защитные стекла ....................................... 218
Требования к качеству и чистоте защитного стекла ... 219
Защитные стекла в бинокулярном телескопическом приборе ............................................. —
Защитные стекла с обогревом ....................... 220
Жгуты волоконно-оптические гибкие..................• 221
Объективы ........................................... 231
Окуляры.............................................. 244
Типы окуляров и их характеристики.................... —
Автоколлимационные окуляры ........................ 250
Уровни .............................................. 252
Пробные стекла для проверки радиусов сферических по-вер хностей оптических деталей интерференционным методом ............................................... 255
Допуски на чистоту поверхностей оптических деталей 257
Глава 5. Крепление оптических деталей (Я. А. Михайлов) 263 Общие положения ........................................... —
Крепление круглых оптических деталей............... 264
Крепление завальцовкой............................. 267
Крепление резьбовым кольцом........................ 269
Крепление пружинящими планками . .................. 273
Крепление проволочным кольцом...................... 275
Крепление приклеиванием.............................. —
Крепление зеркал ............................... 277
Крепление призм ..................................... 283
Крепление защитных стекол ........................... 301
Крепление линейных шкал ............................ 304
Глава 6. Типовые конструкции оптико-механических узлов (М. Д. Кругер, В. А. Панов, Р. М. Рагузин и И. М. Долинский) ........................................ 305
Узлы крепления защитных стекол ....................... 305
Системы визирования ................................... —
Объективы телескопических приборов ................... 311
Зеркально-линзовые объективы ......................... 312
Фото- и кинообъективы ......................... . 313
Микрообъективы ....................................... 316
Окуляры............................................... 320
Системы смены увеличении ,............................ 327
Светофильтры.......................................... 330
Механизм клинового компенсатора....................... 331
Коиденторы и коллекторы микроскопов................... 332
Выключающееся зеркало................................. 333
Крепление дифракционных решеток .................. ' —
Модуляторы света...................................... 334
Фокусировочиые механизмы ............................. 336
Глава 7. Диафрагмы, щели, бленды, иаглазиики и налобники (М. Д. К руге р, Б. Г. Резницкий, В. А. Панов) 338
Диафрагмы......................................... —
Расчет ирисовых диафрагм ............................. 345
Щелевые диафрагмы.............. 346
Наглазники и налобники ................................. 347
v Бленды и устройства для защиты от рассеянного света . . 352
Способы уменьшения вредного (рассеянного) света ... —
Глава 8. Расчет допусков на изготовление и сборку опти-
ческих деталей, узлов и приборов (Г. В. Погарев) 357
Критерии оценки качества изображения и допуски иа дефекты оптической, системы................... 358
Расчет допусков на оптические поверхности и детали, перпендикулярные оси системы.......................1 362
Расчет допусков на наклонные оптические поверхности н пластинки .......................................... 365
Влияние смещений и поворотов зеркально-призменных систем на положение н ориентировку изображения . . . 367
Расчет допусков на оптические детали с учетом требований к точности функционирования и к сборке приборов 376 Пример расчета допусков на оптические детали артиллерийской панорамы . ................................ 385
Глава 9. Методика структурного анализа механизмов приборов (И, М. Долинский)..................................... 396
Общие сведения .....................................
Основные определения ................................... —
Избыточные связи и местные подвижности в механизме 398
Методика структурного анализа ...................... 399
Определение общего числа подвижностей в кинематических парах анализируемого механизма и числа контуров в нем ................................................ 401
Таблица для структурного анализа механизмов ... —
Структурный анализ механизмов с упругими звеньями 406
Структурный анализ неподвижных соединений .... 407
Рекомендации по изложенной методике.................. 413
Глава 10. Расчет и конструирование подвижных систем оп-
тических приборов (В. В. Кулагин) ...... 414
Механические системы оптических приборов.......... —
Механизмы подвижных систем оптических приборов ' (ПСОП) ..............................................
Замечания к проектированию механизмов ПСОП , . « . 420
Характеристики точности механизмов ПСОП ...... 423
Причины и виды ошибок механизмов .................. 424
Определение ошибок механизмов ...................» 428
Расчетные формулы ошибок механизмов ....... 431
Расчеты на точность при проектировании (виды расчетов, исходные данные н условия) ................... 435
Критерии технологичности конструкций ....... 436
Критерии степени влияния ошибок.................... 442
Методы компенсации ошибок механизмов ....... 444
Проектный расчет механизмов на точность ...... 445
Проверочный расчет механизмов на точность........ 446
Примеры расчета механизмов на точность............. 447
Глава 11. Направляющие для прямолинейного и вращательного движения (Л4. Д. Кругер, М. И. Калинин) ................................................. 456
Общие сведения ....................................... —
Принципы коиструнровання направляющих............... 457
Направляющие для прямолинейного движения.......... —
Направляющие с треннем скольжения.................... —
Направляющее с трением качения .................... 468
Направляющие с внутренним (молекулярным) треннем 474
Направляющие для вращательного движения............. 475
Направляющие с трением скольжения ........ —
Направляющие дли вращательного движения с трением качения ........................................... 480
Конструкции н расчет специальных подшипников . . . 483
Крестообразный пружинный шариир .................. 485*
Определение моментов трення в опорах скольжения и качения .............................................. —
Глава 12. Винтовые механизмы (Л£ Д. Кругер^ В. А. Панов) 491
Винтовые механизмы точного движения .................. —
Расчет винтовых механизмов ........................ 492
Точность винтовых механизмов ...................... 494
Конструкции отсчетных иннтовых механизмов........... 495
Точность изготовления ............................... —
Материалы для винтовых пар........................ 499
Глава 13. Зубчатые передачи (Л1. Я. К руге р, М. И. Калинин) 500
Общие сведения........................................ —
Цилиндро-коническая передача с углом 90° между осями 502
Погрешности зубчатых-передач........................ 505
Расчет моментов и усилий ......................... 506
Расчет мертвых ходов .............................. 509
Глава 14. Отсчетные устройства (М. Д. К руге р, В. А. Панов) 512
Оптические отсчетные устройства....................... —
Оптические отсчетные устройства непосредственного от-. счета ........................................... .....
Оптические отсчетные устройства с микрометрами ... 513
Шкаловые отсчетные устройства ....................... —
Допуски на деления линейных и угловых шкал .... 515
Шкалы на металле . ................................ 517
V Размеры штрихов ................................ —
Точность шкал ................................... 518
Размеры цифр и знаков ............................. 519
Профиль штриха .................. —
Конструкции отсчетных устройств .................. . 519
Применяемые материалы .................................. 525
Точные фиксаторы ....................................... 526
Глава 15. Герметизация и осушка приборов (Л4. %, Кру-гер, Б, Г» Резницкий) ........................................ 529
Общие сведения ............................................. —
Конструкции корпусов приборов, сальников, патронов и клапанов осушки .......................................... 530
Расчет элементов уплотнения .............................. 531
Глава 16. Покрытия оптических деталей (Л4. Я» Кругер, В. А. Панов) ....................................... 541
Виды покрытий............................................... —
Основные характеристики и выбор покрытий.................. 556
Глава 17, Защита от коррозии. Покрытия деталей оптико-мехаиических приборов (А. 7И. Левинзон) . . . 558
Общие сведения о коррозии .................................. —
Металлы и сплавы, применяемые без покрытий........... —
Контактная коррозия ...................................... 559
Нанесение на чертежах обозначений покрытий ..... 562
Покрытия металлические и неметаллические неорганические ..................................................... —
Краткая характеристика покрытий .......................... —
Обозначения покрытий ................................... 563
Выбор покрытий ....................................... 564
Основные требования, предъявляемые к деталям, подвергающимся покрытию.................................... 567
Основные характеристики металлических покрытий . . ч 569
Основные характеристики неметаллических неорганических покрытий ............................... 572
Покрытия лакокрасочные ................................. 574
Краткая характеристика покрытий............... —
Обозначения лакокрасочных покрытий........... 575
Выбор лакокрасочных материалов для окраски деталей 576
Специфические лакокрасочные материалы, применяемые в оптико-механическом приборостроении ....... . 581
Требования к окрашиваемым деталям ................• —
Временная противокоррозионная защита изделий . . . 582
Глава 18. Источники и приемники света (В. А. Панов, Л4. Я* Кругер)...................................... 584
Лампы накаливания для оптических приборов......... —
Кинопроекционные лампы накаливания........ 585
Лампы накаливания с йодным циклом (галогенные) для оптических приборов .................................... 592
Лампы электрические светоизмерительные..............
Дуговые лампы высокого и сверхвысокого давления . . . Ртутно-кварцевые лампы .............................
Ксеноновые лампы с дуговым разрядом ................
Газоразрядные циркониевые лампы .................... 593
Газоразрядные спектральные лампы с линейчатым спектром излучения....................................... 598
Импульсные и стробоскопические лампы.................. —
Фотоэлектронные умножители ........................... —
Болометры .......................................... 612
Электронно-оптические преобразователи (ЭОП) • , • • 612
Фоторезисторы и фотодиоды.............................. —
Глава 19. Организация рабочего места и органы управления приборами (М. Я. Кругер, Л Рагузин) 613
Рабочее место оператора ............................... —
Органы управления..................................... 615
Расположение и мнемоничность органов управления 616
Средства отображения информации ..................... 617
Пульты управления ................................... 618
Глава 20. Технические требовании к оптико-механическим приборам (Б, Г. Резницкий) ................................ 619
Общие требования ...................................... —
Требования по стандартизации и унификации .... —
Требования к консервации и упаковке ................... —
Эргономические требования и требования технической эстетики ............................................. 620
Требования по безопасности труда ...................... —
Требования к составным частям приборов ................ —
Требования к оптическим деталям...................... 621
Требования к оптическим деталям» находящимся в оптических системах ....................................... —
Требования к телескопическим приборам ............... 624
Требования к устойчивости приборов к внешним воздействиям при эксплуатации ...................... —
Требования к приборам, предназначенным для работы в районах с тропическим климатом ..................... 633
Глава 21. Основные правила разработки конструкторской документации (Б, Г. Резницкий)............................. 636
Стандарты, используемые в начальной стадии разработки конструкторской документации..................... —
Стандарты, используемые при разработке чертежей —
Стандарты, используемые при разработке технических условий ............................................ 644
Стандарты, используемые при разработке эксплуатационной документации ................................ —
Глава 22. Оптические материалы (В. Л. Панов) .... 645
Оптическое бесцветное стекло ................ —
Оптическое цветное стекло .............. 658
Оптические кристаллы ................................ 664
Оптическое кварцевое стекло (плавленое)........ 667
Оптические ситаллы .................................. 671
Оптическая керамика ................................. 673
Оптические термопластичные полимерные материалы . . 679
Стекло органическое конструкционное ................. 683
Светорассеивающие стекла ............................ —
Стекло листовое малопузырное ........................ 686
Клеи для оптических деталей ........................... —
Глава 23. Конструкционные материалы (В. Г. Резницкий) 690
Стали углеродистые качественные конструкционные , . —
Легированные конструкционные стали..................... —
Литейные стали..................................... 694
Сплавы алюминиевые для холодной обработки........ 695
Сплавы алюминиевые литейные ...................... 696
Сплавы алюминиевые спеченные...................... 702
Сплавы цветные литейные............................. —
Нейзильбер........................................... —
Титан и его сплавы ................................ 703
Пластические массы ................................ 704
Смазки н масла .................................... 720
Замазки ............................................. —
v Адсорбенты для осушки приборов ...................... 726
Список литературы ................;...................... 726