Математические кружки в 8—10 классах. - Петраков И.С.

Author: Петраков И.С.
Tags: методика преподавания учебных предметов в общеобразовательной школе математика педагогика задачи по математике школьная математика
Year: 1987
Similar
Алгебра и начала математического анализа. Дидактические материалы. 10 класс
Сборник задач по физике, 8-10 класс.
Дидактические материалы по алгебре и началам анализа для 10 класса
Избранные вопросы математики. 10 класс. Факультативный курс.
Text
                    И.С.ПЕТРАКОВ
МАТЕМАТИЧЕСКИЕ
КРУЖКИ
.810
КЛАССАХ
И.С.ПЕТРАКОВ
МАТЕМАТИЧЕСКИЕ
КРУЖКИ
«810
КЛАССАХ
КНИГА ДЛЯ УЧИТЕЛЯ
МОСКВА
«ПРОСВЕЩЕНИЕ»
1987
ББК 74.262
ПЗО
Рецензенты:
доктор педагогических наук, профессор С. И, Шварцбурд\
ст. преподаватель Харьковского пединститута им. Г. С. Сковороды
Е. П, Нелин
Петраков И. С.
ПЗО Математические кружки в 8—10 классах: Кн. для учителя.—
М.: Просвещение, 1987.— 224 с.: ил.
В книге приводится содержание всех занятий математических кружков в 8—10 клас-
сах. Во второй части пособия к задачам, рассматриваемым на занятиях, даются ответы,
решения или указания к ним.
Книга написана на основе опыта работы учителей математики средней школы.
4306010000-508 _е ос	ББК 74.262
п~ioRoW-
© Издательство «Просвещение», 1987
ПРЕДИСЛОВИЕ
Основным видом внеклассной работы по математике в школе
являются математические кружки. Вызывая интерес учащихся к
предмету, кружки способствуют развитию математического круго-
зора, творческих способностей, учащихся, привитию навыков само-
стоятельной работы и тем самым повышению качества математической
подготовки учащихся. Их дополняют разовые мероприятия, прово-
димые как в школе (математические вечера, викторины, олимпиады,
КВН, соревнования команд и др.), так и вне школы (математичес-
кие конкурсы, проводимые отдельными газетами, журналами, заня-
тия в физико-математических школах при высших учебных заведе-
ниях, конкурсы по решению задач, проводимые радио и телевидением,
и др.).
В пособии приводится содержание всех занятий математических
кружков с разнообразным набором задач. Во второй части пособия
даются решения задач, указания к решению либо ответы. К темам,
выходящим за рамки школьной программы, предлагается теорети-
ческий материал (краткое изложение). Содержание и порядок рас-
смотрения материала примерные. Это ориентир для учителя. Ис-
пользуя литературу и собственный опыт, учитель конкретизиру-
ет содержание каждого занятия. Молодой учитель, не имеющий
еще достаточного опыта ведения кружковой работы, может принять
за основу работы кружка материал данного пособия.
По каждому классу математические кружки могут быть в основном
двух уровней: один—для более сильных учащихся, второй—для
средних. В пособии нет возможности привести содержание всего
материала для кружков каждого уровня. Учитывая, что значитель-
ная часть материала занятий этих кружков совпадает, в каждое
занятие включено на несколько заданий больше. Это дает возмож-
ность исключить более легкие упражнения в одном случае и более
сложные—в другом.
Занятие математического кружка может быть построено по сле-
дующему плану:
1)	доклад одного из участников кружка на 5—10 мин по исто-
рии математики; сообщение руководителя или участника кружка по
теме занятия;
2)	решение задач, в том числе повышенной трудности (*);
3)	решение задач занимательного характера (о) и задач на сме-
калку (Д);
3
4)	ознакомление участников кружка с задачами, предлагавшимися
на приемных экзаменах в вузы (к);
5)	ответы на разные вопросы учащихся.
Знакомство с конкурсными задачами (к) поможет учащимся со-
ставить конкретное представление о требованиях по математике при
поступлении в вуз. Эти задания взяты в основном из журналов
«Математика в школе» и «Квант». Они предлагались на экзаменах
в 1981 —1983 гг. С условиями таких задач целесообразно знакомить
участников в конце каждого занятия, а их решение можно пред-
лагать желающим для самостоятельной работы дома. Следует иметь
в виду, что выполнение домашних заданий не обязательно.
Материал по каждому классу располагается в порядке нараста-
ния его трудности. Первая тема в VIII классе «Различные системы
счисления» интересна сама по себе, а также важна для ознакомле-
ния учащихся с работой ЭВМ. На втором занятии рассматривается
график линейной функции и графическое решение систем линейных
уравнений. Этот материал тоже достаточно прост и постоянно ис-
пользуется в дальнейшем. Целесообразно познакомить участников
кружка с доказательством того, что графиком линейной функции
является прямая линия. Это покажет им, что кружок не является повто-
рением урока, и даст возможность получить первое знакомство с требо-
ваниями к поступающим в вузы на примере рассмотрения наиболее
простого вопроса курса математики средней школы. Третье занятие
отводится графику квадратичной функции и графическому решению
квадратных уравнений, четвертое — графическому решению систем
уравнений, пятое—знакомству с решением систем линейных урав-
нений методом определителей. На следующих занятиях решаются
алгебраические, а затем геометрические задачи. На десятом занятии
участники кружка знакомятся с жизнью и деятельностью известных
математиков Ф. Виета и Р. Декарта. Весь рассмотренный перед
этим материал является необходимой базой для темы указанного
занятия. Следующее занятие — «Формула расстояния между двумя
точками» — по существу посвящено вопросам приложения открытий
Ф. Виета и Р. Декарта. На следующих трех занятиях изучается
материал, связанный с понятием модуля числа, строятся графики
и решаются уравнения, содержащие знаки модуля. Далее учащиеся
знакомятся с жизнью и деятельностью женщин-математиков как
прошлого, так и настоящего времени. Это дает возможность сопо-
ставить условия жизни и деятельности женщин-ученых в разные
исторические эпохи. Занятие целесообразно провести накануне
Международного женского дня. На последних занятиях решаются
алгебраические и геометрические задачи.
При решении задач обращается внимание учащихся на отыскание
наиболее рациональных, оригинальных способов их решения. Так
же как и при выполнении учащимися экзаменационных работ в
школе, и на вступительных экзаменах в вузы или техникумы, выбор
способа решения—право учащегося. Оформление решения задачи и
4
используемая учащимися символика также могут быть различными,
лишь бы они были математически правильными.
Творческое начало должно преобладать и при решении геомет-
рических задач на построение. Здесь желательно проводить анализ,
который помогает наметить план решения. Если условие задачи до-
пускает разное число решений, то учащийся должен уметь проана-
лизировать возможное число решений, а иногда и обосновать, сколько
и конкретно каких решений будет, если он изменит данные в задаче
величины.
В действующих учебниках алгебры и начал анализа нет поня-
тия ОДЗ. И на кружке при решении алгебраических задач нет
смысла уделять особое внимание этому вопросу и требовать от уча-
щихся нахождения ОДЗ. Но в ряде случаев нахождение допустимых
значений буквенных параметров или переменных облегчает решение
задачи. В таких наиболее простых случаях полезно указать допу-
стимые значения. Отсутствие шаблона в подобных вопросах способ-
ствует развитию самостоятельности, творческого подхода при реше-
нии задач, развитию математического мышления учащихся.
В IX классе первое занятие отведено рассмотрению метода ма-
тематической индукции. На втором занятии решаются задачи на
применение метода математической индукции. Его значение в позна-
вательном и методическом отношении велико. К тому же этот
материал на уроках не изучается. А тема «Метод математической
индукции» не требует знания программного материала курса мате-
матики IX класса. На третьем занятии рассматривается материал,
относящийся к действиям над действительными числами и выполне-
нию тождественных преобразований. На четвертом занятии решаются
алгебраические и геометрические задачи. Следующие два занятия
посвящены рассмотрению числовых последовательностей. Этот ма-
териал связан с программой IX класса. Седьмое занятие проводится
накануне 7 Ноября. Оно знакомит учащихся с ведущими советскими
математиками, а значит и с достижениями советской математической
школы. Затем на трех занятиях решаются геометрические задачи.
Далее дается представление о комплексных числах и их приложе-
ниях к решению уравнений, в первую очередь двучленных и трех-
членных. На следующих занятиях рассматриваются графики функ-
ций, затем задачи на построение сечений многогранников. Двадцатое
занятие отведено знакомству с жизнью и научно-общественной
деятельностью Н. И. Лобачевского. Это занятие можно провести в
форме вечера. На заключительных занятиях отрабатываются навыки
преобразований тригонометрических выражений и доказательств
тригонометрических тождеств.
Первая тема X класса — «Комбинаторика и бином Ньютона».
Этот материал важен и полезен для дальнейшего изучения матема-
тики, тем более что программный материал еще не накоплен на
уроках для его использования на кружковых занятиях. На эту
тему можно отвести четыре занятия. На следующих двух заня-
тиях закрепляются навыки преобразований тригонометрических йы-
5
ражений и решаются тригонометрические уравнения. Далее решаются
геометрические задачи, причем в основном планиметрические. Это
является подготовкой к решению стереометрических задач. На за-
нятиях по теме «Уравнения и их системы» отрабатываются наиболее
рациональные приемы решения уравнений. Затем рассматриваются
уравнения и неравенства, содержащие показательную и логарифми-
ческую функции. Одно занятие отводится знакомству с жизнью и
деятельностью одного из крупнейших математиков всех времен —
Карла Гаусса. На заключительных занятиях решаются неравенства
и геометрические задачи с использованием векторов, а также стерео-
метрические задачи, предлагавшиеся на приемных экзаменах в вузы.
Подготовка к занятиям на исторические темы начинается за
3—4 недели до проведения. Весь материал темы необходимо раз-
бить на отдельные вопросы, каждый из которых представляет само-
стоятельный доклад одного из участников кружка.
Причем если доклад об ученом небольшой, то его делает один
ученик. Если большой, то один из кружковцев рассказывает о
жизни ученого, второй — о его научных открытиях, третий — о его
общественной деятельности. Число докладчиков может быть и гораздо
большим. Преподаватель заранее распределяет материал между
участниками вечера, указывает им на литературные источники.
Ответственные за занятие вместе с докладчиками подготавливают
иллюстративный материал. Решению задач, предусмотренных на
занятии, желательно придать игровую, занимательную форму. Можно
провести небольшой конкурс.
Занятие на историческую тему лучше проводить в конце какой-
либо четверти или в каникулы в форме вечера. В этом случае же-
лательно включить и художественную часть. На вечера пригла-
шаются все, в первую очередь учащиеся старших классов школы.
Порядок изучения тем на кружковых занятиях примерный.
Учитель вправе изменить его по своему усмотрению, исключить
некоторые темы, заменить другими. С целью более свободного
варьирования тематикой в пособии приведено по каждому классу
на 2—3 занятия больше, чем это необходимо. Проводится одно за-
нятие в 2 недели, с сентября по апрель включительно. Продолжи-
тельность каждого занятия—не более 1,5 ч. На первое занятие
кружка учителя приглашают всех желающих, и после этого уча-
щийся должен решить вопрос о его участии в работе кружка; на
нем же проводится вводная беседа, на которой руководитель кружка
знакомит учащихся с содержанием и с планом работы кружка.
Работу кружка по каждому классу целесообразно освещать в
математической газете, выпускаемой раз в месяц. В газете, как
правило, помещаются план работы кружка, задачи для проведения
заочного математического конкурса, заметки и др. Итогом работы
кружка являются математические олимпиады или конкурсы по ре-
шению задач.
6
VIII класс
Занятие 1. Тема. Различные системы счисления
Система счисления—это совокупность правил чтения и записи
чисел. Принятая нами система счисления называется позиционной
десятичной системой счисления. В ней за основание нумерации при-
нято число 10 и соответственно этому имеется 10 различных
знаков—цифр для записи чисел. Числа от 0 до 9 составляют про-
стые единицы. Десять единиц составляют один десяток—единицу
второго разряда. Десять десятков составляют одну сотню—единицу
третьего разряда и т. д. Значение цифры для чтения и записи числа
зависит от ее места, позиции в записи числа. Поэтому система
счисления и называется позиционной. Так, в числах 528, 352, 285
цифра 5 стоит на разных местах и в зависимости от этого имеет
различные значения: в первом числе она означает сотни, во вто-
ром—десятки, а в третьем—единицы.
Если за основание принять другое число, то получим другую
систему счисления: восьмеричную, если за основание принять чис-
ло 8; троичную, если за основание принять число 3, и т. д. Наи-
большее применение в вычислительной математике имеет двоичная
система счисления. В ней всего две цифры: 0 и 1. Числа, записан-
ные в двоичной системе счисления, удобно вводить в вычислитель-
ную электронную машину и производить над ними действия для
решения различных довольно сложных задач.
Действия над числами в любой системе счисления выполняются
аналогично действиям над числами в десятичной системе счисления.
Надо только помнить, что если в каком-то разряде получается число
единиц этого разряда, равное основанию системы счисления, то это
будет единица следующего разряда. Аналогично одна единица стар-
шего разряда при переводе в младший разряд равна числу единиц
в основании системы счисления.
Основой перевода чисел из любой системы счисления в десятич-
ную является запись их в виде многочлена, расположенного по
степеням основания системы.
Так, в десятичной системе счисления 1353 = 1000 + 300+ 50 +
+ 3 = 1 • 103 + 3.102 + 5 • 10 + 3.
Для того чтобы показать, в какой системе счисления записано
число, справа внизу записывают основание системы счисления.
Числа в десятичной системе счисления записываются без указания
основания системы счисления.
В восьмеричной системе счисления 13538= Ь8? + 3«8^+5*8 + 3.
7
В десятичной системе счисления это число равно: 512 + 192 4- 40 -[•
+ 3, т. е. 747.
ДлЙ перевода одного числа из десятичной системы счисления в
другую его Делят на основание системы счисления. Первый остаток
будет цифрой последнего разряда числа в новой системе счисления.
Полученное частное вновь делят на основание системы счисления.
Остаток даст следующую цифру числа и т. д., пока не получится
остаток, меньший основания системы счисления. Последнее частное
равно первой цифре в записи числа.
Примеры.
1. 183 = хб, 183|5 , 36|5 , 7|5 , х5 = 1213б.
33 36	1 7	2 1
3
Итак, 183= 1213б.
2. 163=х2, 163|2 , 8112 , 40|2' , 2012 , 10|2 , 5|2 , 2|2,
1 81	1 40	0 20	0 10	0 5	1 2	0 1
х2 = 101000112, 163= 101000112.
Задачи и упражнения
1.	Запишите числа в указанной системе счислений: а) 178 = х3;
б) 594 = х6; в) 898 = х7; г) 793 = х2; д) 21021123 = я10.
2.	Выполните действия: а) 21314 4- 3201б) 2313425 — 421235;
в) 25464-342б; г) 3245-325; д) 1412б:246.
3.	Найдите основание системы счисления: а) 43^ = 27; б) 324х—
= 89; в) 421^—143^ = 234/, г) 53^ 16х = 880*.
4Д. Докажите, что разность между трехзначным числом и числом,
записанным теми же цифрами, но в обратном порядке, не может
быть квадратом натурального числа в десятичной системе.
5°. Восстановите математическую запись примера
АННА
“ВАЛЯ
4 7 09,
где разные буквы обозначают разные цифры, а одинаковые буквы —
одинаковые цифры.
6°. Цена бриллианта пропорциональна квадрату его массы. Брил-
лиант массы т разделен на 2 части. В каком случае общая цена
двух частей будет наименьшей?
7К. На плоскости отмечены три точки, две из которых являются
серединами сторон треугольника, а третья — точкой пересечения его
медиан. Остальные элементы треугольника стерты. С помощью
циркуля и линейки постройте треугольник.
8К. За 3,5 ч работы один штамповочный пресс может изготовить
42% всех заказанных деталей. Второй пресс за 9 ч работы может
изготовить 60% всех деталей, а скорость выполнения работы на
третьем прессе относится к скорости выполнения на втором как
6:5. За сколько времени будет выполнен весь заказ, если все три
пресса будут работать одновременно?
8
Занятие 2. Тема. Линейная функция и ее трафик
Функция вида y — kx+b называется линейной. В этой зависи-
мости k и Ь—постоянные величины, х и у—переменные. Причем
х—-независимая переменная —аргумент, у—функция.
Линейная функция очень часто встречается в практической дея-
тельности. Длина стержня является линейной функцией температуры.
Длина рельсов, мостов также является линейной функцией темпе-
ратуры. Расстояние, пройденное пешеходом, поездом, автомашиной
при постоянной скорости движения, — линейные функции времени
движения. Объем работы, выполненной механизатором, рабочим
предприятия при постоянной производительности, являются линей-
ными функциями времени работы и т. п.
Графиком линейной функции является прямая линия. Докажем
это утверждение. Для этого возьмем две пары чисел (хх, yt) и (х2, у2),
удовлетворяющие зависимости y — kx + b. Построим на координатной
плоскости точки А(х1,у1) и В(х2, у2). Проведем через них прямую
(рис. 1). Покажем, что координаты любой точки М (х3, у3) этой пря-
мой удовлетворяют данной зависимости. Действительно,
Поэтому	, DO^b, СО==а. Отсюда у3 = х3 4- где ~ = k.
Значит, y3 = kx3 + b. Утверждение доказано.
Докажем справедливость обратного утверждения, т. е. покажем,
что любая пара чисел (хл, уп), удовлетворяющая зависимости уп =
= кхп + Ь, является координатами некоторой точки (хп, уп), при-
надлежащей построенной прямой.
Действительно, возьмем точку N1(xn9 0) и восставим из нее
перпендикуляр к Ох до пересечения с АВ в некоторой точке Af.
Тогда NN1\\DO9 поэтому	Откуда получаем A^Af =
т. е. yn = NiN. Значит, точка (хл, уп) принадлежит построенной
прямой. Утверждение доказано.
Для определенности точки А и В были взяты в первой четверти
координатной плоскости. Рассуждения сохраняют свою силу при
любом расположении точек А и В на плоскости.
Рис. 1
9
Так как положение прямой оп-
ределяется двумя точками, то для
ее построения, когда ни один из
коэффициентов в уравнении пря-
мой не равен нулю, эти точки луч-
ше брать на осях координат.
Если дана система линейных
уравнений, например:
/ Зх + %= 15
16х—5# = 12,
то координаты точек графика пер-
вого уравнения удовлетворяют
первому уравнению, а координаты
Рис- 2	точек графика второго уравнения
удовлетворяют второму уравнению.
Значит, координаты точек пересечения графиков (рис. 2) удовлетво-
ряют одновременно обоим уравнениям, т. е. являются решением дан-
ной системы уравнений. В рассматриваемом примере решением сис-
темы будет пара чисел (3; 1,2).
Задачи и упражнения
Постройте график функции:
9. 3x4-2z/ = 6. 10. z/===~x—3.
11. 5х —10 = 0. 12. 8 — Зу — Q.
13.	Прямая проходит через точки А (2; 3) и В(3; 10). Напишите
уравнение этой прямой.
14.	Прямая проходит через точку (5; 2) и начало координат.
Напишите уравнение этой прямой.
15.	Прямая проходит через точку А (4; 3) параллельно прямой
10х—5z/ = 8. Напишите уравнение этой прямой.
16.	Прямая проходит через точку (5; 0) параллельно оси ординат.
Какой вид имеет ее уравнение?
17.	Прямая, параллельная оси абсцисс, проходит через точку
(0; 7). Какой вид имеет ее уравнение?
Решите графически систему уравнений:
to /6х + ^ = 6	/х—12у=3
t 4x + 3//=lh	19‘ |х + 4#=19.
1 5x+7z/ = 64.	21- ) 15z/ = 28x—70.
99 f 15z/+4x = 25	J 3x+16r/= 12
I 2x—5 = 0.	Д 4y—6 0.
24A. На лужайке паслось 90 телят и гусей. Всего у них было
256 ног. Сколько было телят и сколько гусей?
ГО
25°. Восстановите цифры в примерах:
а) 4 # # • 3 * * б)
3 * * *
« # « 5
* * « 3 «
* * *	* :? 8 о
* *
# #
# # #
% & #
26к. Автомобиль выехал из города А в город В, расстояние
между которыми 234 км. Через 1 ч навстречу ему из города В вы-
ехал второй автомобиль, скорость которого на 12 км/ч больше пер-
вого. Определите скорость каждого автомобиля, если они встрети-
лись на расстоянии 108 км от города В.
27к. Бригада рабочих должна была за определенный срок изго-
товить 400 деталей. В течение первых пяти дней бригада перевы-
полнила норму на 20%, в последующие дни изготовляла ежедневно
на 15 деталей сверх плана и уже за два дня до срока изготовила
405 деталей. Сколько деталей должна была изготовлять ежедневно
бригада по плану?
Занятие 3. Тема. График квадратичной функции
Функция вида у = ах2- + Ьх + с, где а, Ь, с—постоянные, назы-
вается квадратичной. Графиком квадратичной функции является
парабола. Причем если а > 0, то парабола выпукла вниз, или, как
говорят, ветви параболы направлены вверх. Если а < 0, то парабола
выпукла вверх, т. е. ветви параболы направлены вниз. Парабола
имеет ось симметрии. Значит, точки пересечения параболы е осью Ох
симметричны относительно ее оси. Это используется при схематиче-
ском построении графика квадратичной функции. Для построения
точек пересечения графика с осью Ох выражение приравнивают
к нулю и находят значения х. Если дискриминант положителен
(Г»>0), то таких значений будет два. Затем находят абсциссу и
ординату вершины параболы.
По трем точкам с учетом направления ветвей параболы строят
схематический график параболы. Если 0 = 0, то можно найти коор-
динаты вершины параболы, а затем, взяв несколько значений х,
близких к абсциссе вершины, найти ординаты соответствующих точек
параболы и по этим точкам построить схематически график функ-
ции. При D < 0 необходимо выделить из трехчлена полный квадрат:
„ , ,	.	(	. Ь \? Ь2—4ас
y = ax2 + bx + c = a^x + ^j---
Отсюда ясно, что если а < 0, функция имеет наибольшее значение,
равное yQ = при *о == — , а если а > 0, функция имеет наи-
11
—b»	b r\
меньшее значение, равное t/0 =—при ^o = ~^- Значения xe
и yn являются координатами вершины параболы. Рассмотренный спо-
соб нахождения координат вершины параболы применим и при Р^О.
Задачи и упражнения
28, Постройте график квадратичной функции, выделив полный
квадрат. По графику определите наибольшее или наименьшее зна-
чение функции: а) у — х2 —2х—15; в) у ——5х24-6х—1;
б) у = Л'2 — Сх 4- 13;	г) х — ц2 - 4, где х—функция,
у—аргумент.
Постройте график функции:
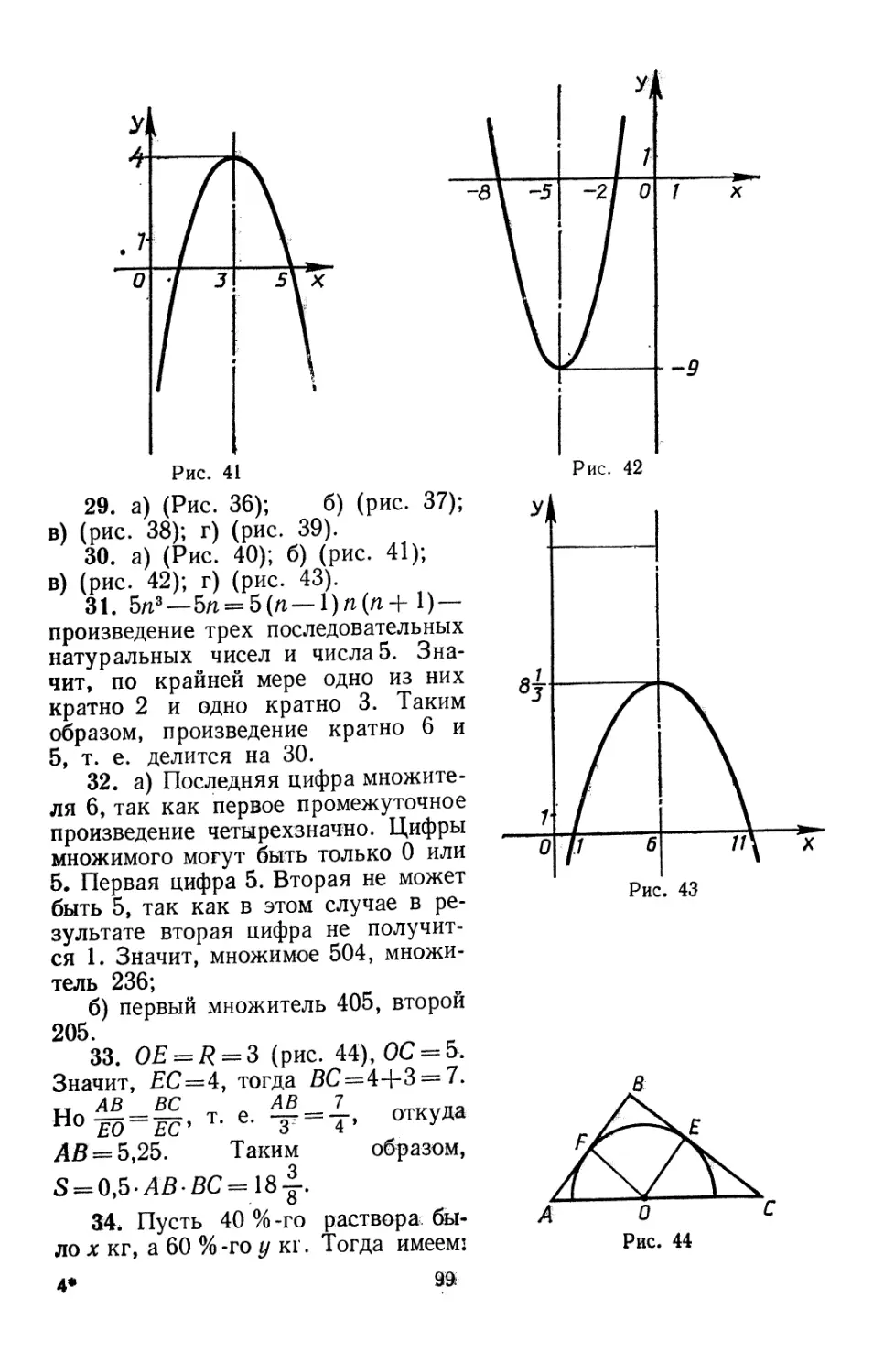
29. а)	у = х2 4-8х 4-7;	в) г/ — —0,5х24-4х—3,5;
б)	у — 0,5х2 + 5х-\- 8;	г) у — х2—7х-[-6.
30. а)	г/ = х2—8х-|-7;	в) г/ = х24- 10x4- 16;
6)	У~—х2-|-6х—5;	г) у — —^-х24-4х—3-|-.
и	о
31Л. Докажите, что при любом натуральном п выражение 5я3—5п
делится на 30.
32°. Восстановите цифры в примерах:
а) * * 4 б) * «• *
23*	2**
« * 2 4	2 » » 5
1 * * *	« » 0
1 * * *	8 3 •» * «•
«1 •»»*«
33к. Центр О окружности радиуса 3 лежит на гипотенузе АС
прямоугольного треугольника АВС. Катеты треугольника касаются
окружности. Найдите площадь треугольника, если известно, чго
длина отрезка ОС равна 5.
, 34к. 40%-ный раствор серной кислоты разбавили 60%-ным, после
чего добавили 5 кг чистой воды и получили раствор 20 %-ной кон-
центрации. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-ного
раствора серной кислоты, то получился бы раствор 70%-ной кон-
центрации. Сколько было 40- и 60%-ного раствора серной кислоты?
Занятие 4. Тема. Графическое решение систем уравнений
и квадратных уравнений
35.	Решите графически уравнение:
а)	х2—X—2 = 0;	в) 2х2—9x4-4 = 0;
б)	х24-2х—3 = 0; г) х2—2х = 0.
12
36.	Решите графически систему уравнений;
а) I х2 — I/ = 3	б) I у + х2 = 7
\у—х = —1;	( х + у = 1;
в) ( у — х2—4	г) J у2—х = 7
|х = (г/—2)2—6; I х + 0,5г/2 = 5.
37°. В следующем примере цифры заменены буквами. Причем
разные буквы обозначают разные цифры, одинаковые буквы обозна-
чают одинаковые цифры. Подберите значения букв так, чтобы были
верны все горизонтальные и все вертикальные равенства:
ААВ + СВ = БДС
BEA : КЕ = НН
СР—АС = НВ.
38°. Восстановите цифры в решении примера:
* 1 * * *
237
******
» »» » »
7 ***065
39Д. Три пионера одной школы—Коля, Дима и Наташа участ-
вовали в районной математической олимпиаде и получили одну пер-
вую, одну вторую и одну третью премии, но им не сообщили, кто
какую премию получил. Позже Таня сказала, что Дима получил
не первую, Коля — не вторую, Наташа получила вторую премию.
Потом оказалось, что из этих трех высказываний верным было только
одно, а два ложны. Какую премию получил каждый пионер?
40к. Решите уравнение + у = у.
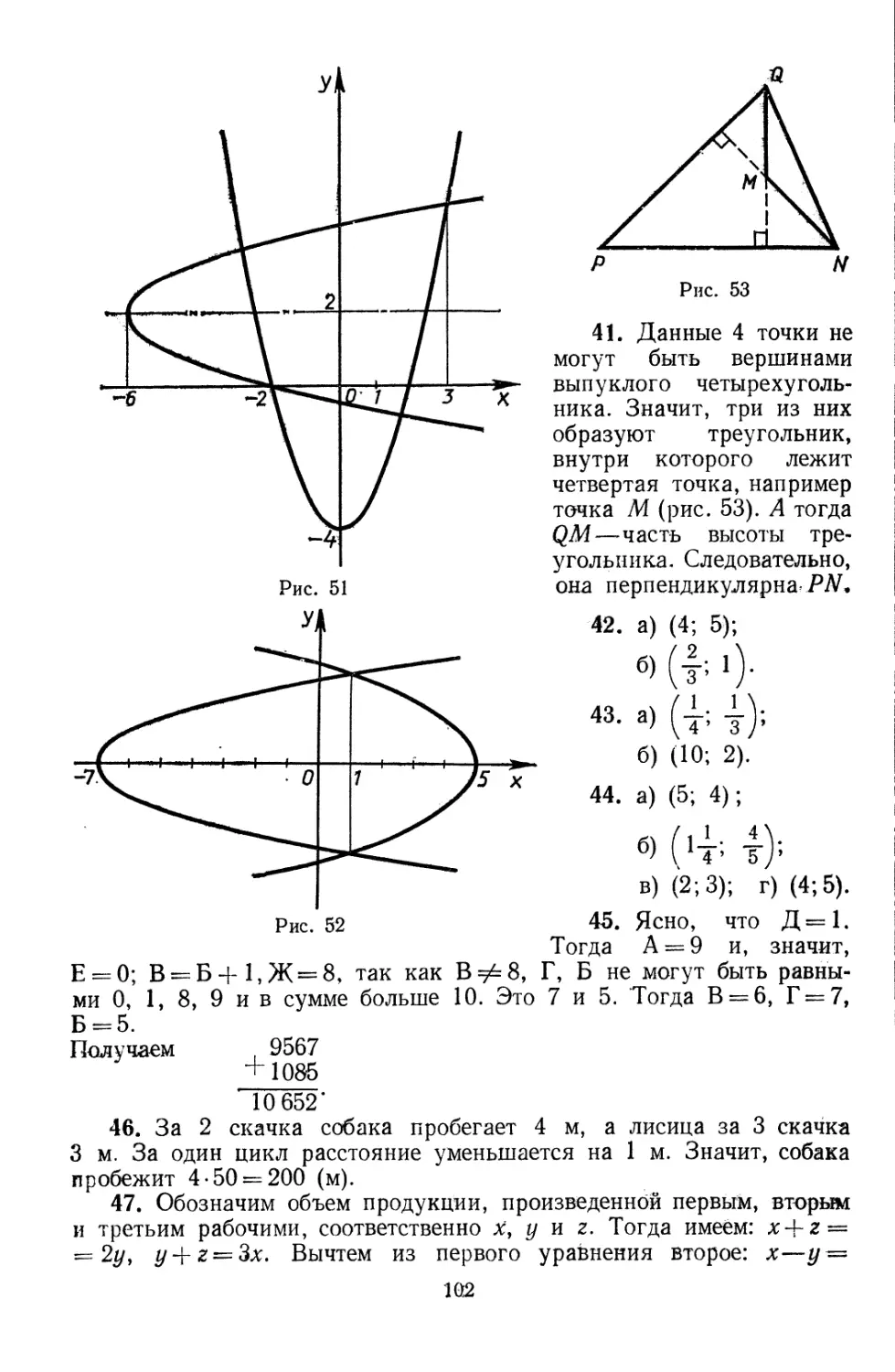
41к. Точки М, N, Р, Q расположены на плоскости так, что
MP I NQ, MN I PQ. Докажите, что MQ I NP.
Занятие 5. Тема. Определители
Пусть дана система двух линейных уравнений с двумя пере-
менными:
(a1x + b1y = ci
\ а^х + b2y = с2.
Умножив первое уравнение на Ь2, а второе на —bi и сложив
полученные уравнения, получим
(аД—аД)х—сД—сД.	(1)
13
Если —a2kt^0, то находим:
Y =	— ez’}i
а±Ь2—a2*4
(2)
Аналогично, умножив первое уравнение на —а2, а второе на а,
и сложив полученные уравнения, находим
(аД—аД) у = агс2 — a2ct.	(3)
Если а.Ь,2—то
и — П1С2—g2C*
«А—«2^1
(4)
Анализируя полученные выражения, замечаем, что при любых
значениях коэффициентов, удовлетворяющих условию —
легко сразу записать выражения для нахождения значений хну.
Они выражаются дробью, знаменатель которой равен разности про-
изведений коэффициента при х в первой строке на коэффициент
при у во второй строке и коэффициента при х во второй строке на
коэффициент при у в первой строке. Иначе говоря, из произведения
коэффициентов по первой диагонали надо вычесть произведение
коэффициентов по второй диагонали. Это правило удобно изобразить
так:
l+ч Л
Числитель в выражении для х находится аналогично, только надо
предварительно заменить коэффициенты при х на свободные члены.
Числитель в выражении для у находится по тому же правилу, но
с заменой коэффициентов при у на свободные члены. Выражения
для нахождения значений х и у удобно для применения указанного
Ci
#2 С2
01 &1
о2 ь2
правила записать в виде:
01 *11
02 *2 1
«1 *1I ’
02 *2
Каждую из таблиц в этих выражениях называют определителем.,
Определитель, стоящий в знаменателе, обозначают D. Это число,
равное:
fl2^2
= at&2—аД.
Определители, стоящие в числителях, соответственно обозначают
и Dy:
В* ~ । сг Ьг | =	— С2Й1'> Ч/ = | Д2 С2 । = а1С2 — fl2Cl-
Иногда определитель обозначается буквой греческого алфавита А
(дельта).
14
Через определители выражения для х и у запишутся так:
Из (1) и (3) равенств имеем: если £> = 0, a Dx^=0 и	то
система не имеет решений. Если D=^=0, то система имеет единст-
венное решение. Если все определители равны нулю, то система
имеет бесконечное множество решений. Но при этом следует иметь
в виду, что если мы возьмем какое-либо значение х, то у нельзя
уже брать произвольным, а его необходимо найти из одного из дан-
ных уравнений, т. е. решениями будут пары значений х и у, свя-
занных между собой.
Можно доказать, что если любые два из определителей равны
нулю, то и третий определитель равен нулю (доказательство можно
предложить желающим учащимся).
Пример:
/ 13х—15# = 35
| 7х + 3# = 41.
Решение. Вычислим все определители.
о=	I1?	— 15 3	= 13-3—(—15).7 = 39 + 105= 144,
Dx =	35 41	— 15 3	= 35-3—(—15) 41 = 105 + 615 = 720,
	13 7	35 41	= 13 • 41 — 7 • 35 = 533—245 = 288.
Следовательно,		х — -	s; Dj> 288 о D — 144“ ’ y~ D ~ 144	’
Задачи и упражнения
Решите с помощью определителей систему уравнений:
42.	a) .	J 10%—3# = 25 1 5x—9y = —25;	6).	J 3x+ 10# = 12 ( 12x—5# = 3.
43.	a) <	1 12x+ 15# = 8 ( 16x + 9# = 7;	6) .	j 7x-\-4y — 78 ( 5% +7# = 64.
44.	a)	(2,5x—1,25# = 7,5 ( l,2x+0,7# = 8,8;	6) J	[ 4x—2,5# = 3 [ 1,5*+ 0,75# = 2,475;
	в) <	j 0-x + 7,&y = 22,8 ( 7x—4y — 2;	0 .	J 2,5*+ 2,4# = 22 (1,5*—0-# = 6.
45°. Восстановите цифры в примере А Б В Г , если одинаковые
ДЕЖБ
ДЕВОЗ
буквы обозначают одинаковые цифры, а разные буквы—разные цифры.
46+ Собака погналась за лисицей. В то время когда собака
делает 2 скачка, лисица делает 3 скачка, но скачок лисицы равен
15
I м, а собак??---в 2 раза больше. Какое расстояние пробежит собака,
чтобы догнать лисицу, если первоначальное расстояние между ними
равно 50 м?
47*. Трое рабочих участвовали в соревновании. Первый и третий
из них произвели продукции, в 2 раза больше, чем второй, а второй
и третий — в 3 раза больше, чем первый. Какое место занял каж-
дый рабочий в соревновании?
48*. Найдите значение х, удовлетворяющее условию
(х2—4)Их + Т=^0.
Занятие. 6. Тема. Решение алгебраических задач
49.	Шофер грузовой автомашины рассчитал, что, дв'шаясь со
скоростью 40 км/ч, он прибудет в город М в назначенный срок.
Однако, пройдя — всего пути, он сделал вынужденную остановку
на 20 мин. Чтобы прибыть в город М в срок, остальной путь он
ехал со скоростью на 5 км/ч большей первоначальной. Найдите рас-
стояние до города Л4.
50.	Моторная лодка прошла от города М по течению реки до
города К за 8 ч, а от К до М за 12 ч. За сколько часов проплы-
вет плот от города М до города /б?
51.	Найдите два простых двузначных числа, состоящих из одних
и тех же цифр, если разность между этими числами равна полному
квадрату.
52^. У женщины в корзине лежали яблоки. Ее спросили, сколько
яблок у нее в корзине. Ока ответила, что не знает точно, но когда
дети их перекладывали по 2, по 4, по 5, по 6 и по 7, то всегда
одно яблоко было лишним. Какое наименьшее число яблок могло
быть у женщины в корзине?
53Д. Плывя ввеох против течения реки и проплывая мост, пло-
вец потерял спасательный круг. Потерю заметил он через 20 мин.
Сразу повернув обратно и плывя с тем же усилием, пловец догнал
спасательный круг в 2 км от моста. Определите скорость течения
реки и скорость пловца, если скорость пловца в 2 раза больше
скорости течения реки.
54°. Четырьмя гирями продавец может взвесить любое целое число
килограммов, от 1 до 40 включительно. Общая масса гирь равна
40 кг. Какими гирями располагает продавец?
2	'
55к. Решите неравенство —+ 3^|/ 41 —
16
х
56к. Найдите все действительные решения системы уравнений:
2и -J- v = 7
\и—v | = 2,
16
3 э?н я т и е 7. Тем а. Решение алгебраических задач
57.	Пассажир заметил, что поезд, в котором он едет, прошел
мимо стоящего поезда длиной 100 м за 5 с, а встречный поезд дли-
ной 60 м прошел мимо окна за 2 с. Найдите скорость поезда, в ко-
тором ехал пассажир, и скорость встречного поезда.
58.	Сумма, произведение двух чисел и разность их квадратов
равны между собой. Найдите эти числа.
59.	Сергею вдвое больше лет, чем Володе было тогда, когда
Сергею было столько лет, сколько Володе теперь. Когда Володе
будет столько лет, сколько Сергею теперь, тогда сумма их возрастов
будет равна 63 годам. Сколько лет каждому?
60д. Найдите двузначное число, равное сумме чисел его десятков
и квадрата числа единиц.
61&. Найдите двузначное число, которое равно удвоенному про-
изведению его цифр.
62°. Восстановите числа в примере:
% 1 &
1
«• К й Н
♦Х« * * I
8 -х- * 4 * »
63к. Из города А в город В, расстояние между которыми 120 км,
на мопеде отправился курьер. Через 1 ч после этого из А на мото-
цикле выехал второй курьер, который, нагнав первого и передав
ему поручение, немедленно с той же скоростью двинулся обратно
и возвратился в Л в тот момент, в который первый достиг города В,
Какова скорость первого курьера, если скорость второго равна
50 км/ч?
64к. В прямоугольном треугольнике АВС, где С = 30°, из веР"
шипы прямого угла В проведена медиана ВК. Найдите площадь
треугольника ВСК, если длина катета АВ равна 4 см.
Занятие 8. Тема. Решение геометрических задач*
65.	Постройте равнобедренный треугольник по высоте и медиане,
проведенной к боковой стороне.
66.	Из вершины тупого угла В ромба ABCD опущены перпен-
дикуляры BE и BF на стороны AD и DC, пересекающие диагональ
АС в точках М и N. Точка Е соединена с г. Определите площадь
фигуры MNFE, если диагонали ромба равны 160 см и 120 см.
* Занятия 8 и 9 можно отвести на решение в основном геометрических за-
дач. Эти задачи охватывают различные свойства треугольников, четырехуголь-
ников и окружности. Таким образом, в них используется теоретический материал,
уже изученный учащимися в школе.
17
67.	К окружности радиуса г из точки А, удаленной от центра
на расстояние 2г, проведена касательная AD. Радиус OD продол-
жен до точки В так, что В£> = уг, ВС ОА-, ВС и AD пересека-
ются в точке Е. Найдите площадь четырехугольника ODEC,
68.	В ромбе ABCD сторона является средним пропорциональ-
ным его диагоналей. Найдите углы ромба.
69.	Окружность с центром О касается прямой а в точке В. Че-
рез произвольную точку А этой окружности проведена вторая ок-
ружность, касающаяся первой, и прямая В А, пересекающая вторую
окружность еще в точке С, СЕ | а, где Е £ а. СЕ пересекает вто-
рую окружность в точке D. Докажите, что около четырехугольника
BADE можно описать окружность.
70Д. В классе 25 учащихся. Из них 8 занимаются в секции ве-
лосипедистов, 13—в секции плавания, 17—в лыжной секции. Ни
один из учеников не занимается в трех секциях. Все спортсмены
учатся только на 4 и 5 не в пример 6 ученикам, имеющим тройки
по математике. Сколько учеников имеет двойки по математике?
Сколько велосипедистов занимается в секции плавания?
71Д. Найдите все натуральные числа, оканчивающиеся на 91,
которые после вычеркивания этих цифр уменьшаются в целое число
раз.
72к. Найдите наибольшее значение функции у = (2—х)(х + 2).
73к. Морская вода содержит 5 % соли. Сколько килограммов
пресной воды необходимо добавить к 80 кг морской, чтобы содер-
жание соли в последней составило 4 %?
Занятие 9. Тема. Решение геометрических задач
74.	Докажите, что биссектрисы внешних углов прямоугольника,
пересекаясь, образуют квадрат.
75.	Диагонали прямоугольной трапеции ABCD пересекаются в
точке Р, через которую проведена прямая, параллельная основа-
ниям, до пересечения с боковыми сторонами в точках Е и F. До-
кажите, что EP — PF.
76.	На катетах прямоугольного треугольника АВС построены
квадраты, центры которых соединены между собой и с серединой
гипотенузы данного треугольника. Докажите, что получившийся
треугольник прямоугольный и его гипотенуза проходит через вер-
шину прямого угла данного треугольника.
77.	Равнобедренный треугольник АВС обладает тем свойством,
что центры вписанной и описанной окружностей симметричны отно-
сительно его основания АВ. Докажите, что в этом случае угол при
основании треугольника равен 36°.
78.	Стороны четырехугольника ABCD равны АВ =12 см, ВС =
= 18 см, CD = 6 см, А£)=14см, а диагональ АС = 10 см. Около
каждой из его вершин проведена окружность радиуса 2 см. Вычис-
лите площадь и периметр фигуры, ограниченной дугами проведен-.
18
ных окружностей и отрезками касательных, проведенных к этим
окружностям.
79*. Две окружности пересекаются в точках А и В, Прямая,
проведенная через центры окружностей ОА и О2, пересекает внеш-
ние дуги окружностей в точках М и V. К окружностям проведена
общая касательная TS. Через точки касания Т и S проведены пря-
мые MS и NT, пересекающиеся в точке Р. Докажите, что: а) точ-
ки Р, А и В лежат на одной прямой; б) PA-PB-MN~PM-PNx
xTS.
80А. На рисунке 3 показано 9 точек и 8 прямых, каждая из
которых проходит через 3 из этих точек. Измените положение дан-
ных точек так, чтобы можно было провести 10 прямых, каждая из
которых также будет проходить через 3 из данных точек.
81^. На рисунке 4 расположено 7 кругов в виде треугольника.
Расположите в этих кругах числа от 1 до 7 так, чтобы сумма чи-
сел ио каждой прямой, содержащей 3 круга, была одна и та же.
82А. 9 кругов расположены .так, как показано на рисунке 5.
Расположите в них числа от 1 до 9 так, чтобы сумма чисел, ле-
жащих в вершинах каждого из 7 изображенных на рисунке тре-
угольников, была одна и та же (задача Эйнштейна).
83к. Бригада рабочих должна была изготовить 360 деталей. Из-
готовляя ежедневно на 4 детали больше, чем предполагалось по
плану, бригада выполнила задание на один день раньше срока.
Сколько дней затратила бригада на выполнение задания?
84к. Решите неравенство- —> 2.
Занятие 10. Тема. Франсуа Виет и Рене Декарт
Франсуа Виет родился в 1540 г. во Франции в Фонтене-ле-Конт.
По образованию юрисг. Он много занимался адвокатской деятель-
ностью, а с 1571 по 1584 г. был советником королей Георга III и
Георга IV. Но все свое свободное время, весь свой досуг он отда-
вал занятиям математикой, а также астрономией. Особенно усиленно
он начал работать в области математики с 1584 г. после отстра-
нения от должности при королевском дворе. Виет детально изучил
труды как древних, так и современных ему математиков.
2*	19
Франсуа Виет по существу создал новую алгебру. Он ввел в нее
буквенную символику. Основные его идеи изложены в труде «Вве-
дение в аналитическое искусство». Он писал: «Искусство, которое
я излагаю, ново...» — и далее: «Все математики знали, что под их
алгеброй и альмукабалой были скрыты несравненные сокровища,
но не умели их найти: задачи, которые они считали наиболее труд-
ными, совершенно легко решаются с помощью нашего искусства».
Действительно, все мы знаем, как легко решать, например,
квадратные уравнения. Для их решения имеются готовые формулы.
До Ф. Виета решение каждого квадратного уравнения выполнялось
по своим правилам в виде очень длинных словесных рассуждений
и описаний, довольно громоздких действий. Даже само уравнение
в современном виде не могли записать. Для этого тоже требовалось
довольно длинное и сложное словесное описание. На овладение
приемами решений уравнений требовались годы. Общих правил,
подобных современным, а тем более формул решения уравнений не
было. Постоянные коэффициенты буквами не обозначались. Рассмат-
ривались выражения только с конкретными числовыми коэффици-
ентами.
Виет ввел в алгебру буквенную символику. После открытия
Виета стало возможным записывать правила в виде формул. Правда,
у Виета показатели степеней еще обозначались словами, и это соз-
давало определенные трудности в решении некоторых задач. Во вре-
мена Виета был еще ограничен запас чисел. Так, еще не нашли
своего признания отрицательные числа. Франсуа Виет очень под-
робно изложил в своих трудах теорию решения уравнений с первой
по четвертую степень.
Большой заслугой Виета было открытие зависимости между
корнями и коэффициентами уравнений приведенного вида произ-
вольной натуральной степени. Нам хорошо известна знаменитая
теорема Виета для приведенного квадратного уравнения: «сумма
корней квадратного уравнения приведенного вида равна второму
коэффициенту, взятому с противоположным знаком, а произведение
корней этого уравнения равно свободному члену». Эта теорема поз-
воляет устно проверять правильность решения квадратных уравне-
ний, а в простейших случаях устно находить и корни уравнений.
Отметим также, что Виет дал первое в Европе аналитическое
(с помощью формулы) представление числа л.
Умер Виет в возрасте 63 лет в 1603 г.
Рене Декарт родился в 1596 г. в городе Лаэ на юге Франции,
в дворянской семье. Отец хотел сделать из Рене офицера. Для этого
в 1613 г. он отправил Рене в Париж. Много лет пришлось Декарту
пробыть в армии, участвовать в военных походах в Голландии,
Германии, Венгрии, Чехии, Италии, в осаде крепости гугенотов
Ла-Рошали.
Но Рене интересовала философия, физика и математика. Вскоре
по приезде в Париж он познакомился с учеником Виета, видным
математиком того времени—Мерсеном, а затем и с другими мате-
20
матиками Франции. Будучи в армии., Декарт все свое свободное
время отдавал занятиям математикой. Он изучил алгебру немецких,
математику французских и греческих ученых.
После взятия Ла-Рошали в 1628 г. Декарт уходит из армии.
Он ведет уединенный образ жизни с тем, чтобы реализовать
намеченные обширные планы научных работ.
Философские взгляды Декарта не соответствовали требованиям
католической церкви. Поэтому он переселился в Голландию, где
прожил 2Q лет, с 1629 по 1649 г., но из-за гонений протестантской
церкви в 1649 г. переехал в Стокгольм. Но суровый северный кли-
мат Швеции оказался для Декарта губительным, и он умер от про-
студы в 1650 г.
Декарт был крупнейшим философом и математиком своего вре-
мени. В основе его философии лежал материализм. Самым извест-
ным трудом Декарта является его «Геометрия» Декарт ввел систему
координат, которой пользуются все и в настоящее время. Он уста-
новил соответствие между числами и отрезками прямой и таким
образом ввел алгебраический метод в геометрию. Эти открытия Де-
карта дали огромный толчок развитию как геометрии, так и дру-
гим разделам математики, оптики. Появилась возможность изобра-
жать зависимость величии графически на координатной плоскости,
числа —отрезками и выполнять арифметические действия над отрез-
ками и другими геометрическими величинами, а также различными
функциями. Это был совершенно новый метод, отличавшийся кра-
сотой, изяществом и простотой.
Задачи и упражнения
85.	Найдите корни уравнения, используя зависимость между
корнями и коэффициентами квадратного уравнения:
а) х2— 7х—30 — 0; б) х2+15х + 50 —0;
в) х2—12х + 32-0; г) х2+ 2х—48-0.
86.	Не решая уравнения, определите знаки корней:
а) х2 —25х + 37 — 0; б) х2 + 41х + 50 —0;
в) х2—17х— 8 — 0; г) х2 + 23х—51—0.
87.	Составьте квадратное уравнение, имеющее корни: а) 25 и 8;
б) —10 и —7; в) —13 и 5; г) 16 и —25.
88.	Выведите уравнение окружности, центр которой лежит в на-
чале координат и радиус равен 5 см. Запишите уравнение окруж-
ности радиуса 7? с центром в начале координат.
89.	Выведите уравнение окружности* с центром в точке 4 (2; 3)
и радиуса 6 см.
* Аналогично выводится уравнение эллипса как множества (геометрического
места) точек, сумма расстояний которых от двух данных точек —фокусов эл-
липса—равна данному числу, а также уравнение гиперболы как множества (гео-
метрического места) точек, разность расстояний которых от двух данных точек
рдвна данному числу, т. е. тоже постоянна.
21
/ J- + д' = 49
' I х + г/ = 7;
/ у—х2 = 0
Г) I х—у2 = 0.
90.	Постройте отрезок, длина которого равна: а) /3; б) /5;
в) /17; г) /35.
91.	Решите графически систему уравнений:
. / х2 + w2 = 25
аК 1
I у—х=1;
( у—х2 = 0
В) 1 /х=2;
Занятие 11. Тема. Формула расстояния между двумя точками
Пусть на координатной плоскости даны две произвольные точки
A Ui, У1) и В (х2, у2) (рис. 6, а, б). Выразим расстояние АВ между
этими точками через их координаты. Проведем из данных точек
перпендикуляры на ось Ох, а также отрезок АС, параллельный
Ох. Тогда получим прямоугольный треугольник АВС. В нем
ЛС = х2—xi> ВС — Уъ—У}. По теореме Пифагора имеем АВ2 =
— АС2-\-ВС2 или АВг — (х2 —хх)2 (у2 — уг)2. Следовательно, А В —
= К (*2—*i)2 + (у2—УгУ-
Полученная формула верна при любом расположении точек А
и В на плоскости. Действительно, как бы ни были расположены
точки А и В, выполнив указанные построения, мы всегда получим
прямоугольный треугольник АВС (за исключением случая, когда
они расположены на прямой, параллельной одной из осей, но легко
видеть, что формула верна и в этом случае). В треугольнике АВС
всегда АС==)х2—xi\, ВС=\у2—yj, но |х2—|2 — (х2—хг)2;
|у2—= У1У и. следовательно, АВ = /(х2 —хг)2 + (у2—У1)2-
Задачи и упражнения
92.	Выведите уравнение окружности радиуса R с центром в
точке М(а, Ъ).
93.	Выведите уравнение эллипса как множества точек, сумма
22
расстояний каждой из которых до двух точек, называемых фоку-
сами, равна 2а. (Расстояние между фокусами 2с и с2—а2 = 62.)
94.	Напишите уравнение окружности с данными центром и ра-
диусом:
a) ОДЗ: 4), /? = 6; б) Ot (—2; 5), 2? = 3;
в) ОД—4; 3), /? = 7; г) Ог (4; —2), R = 8.
95.	Напишите уравнение эллипса с данными полуосями а и b и
найдите расстояние от начала координат до его фокуса (половину
фокального расстояния):
а) а = 5, 6 = 3; б) а~ 2,5, 6 = 2;
в) <7=10, 6 = 8; г) а = 8, 6=10.
96. Решите графически систему уравнений:
а)
-	/ У2 и2
+ = = 1
-v-(/==12;	( x2 + z/2 = 64.
97. Выведите уравнение гиперболы как множества точек, разность
расстояний каждой из которых до двух данных точек, называемых
фокусами гиперболы, постоянна. (Расстояние между фокусами обо-
значьте 2с, постоянную разность 2а и с2 — а2 = Ь2Л
98°. На стоянке было 75 автомашин и мотоциклов, три из ко-
торых были с колясками, а остальные без колясок. Всего у них
было 259 колес. Сколько было на стоянке автомашин и сколько
мотоциклов без колясок?
99А. Докажите, что по крайней мере одно из трех чисел т-\-п,
т—п или та, где т и п—натуральные числа, кратно трем.
100к. Числа Ьх—у, 2х + Зу и х + 2у составляют арифметическую
прогрессию, а числа (у +1)2, ху+\ и (х—I)2 составляют геометри-
ческую прогрессию. Найдите х и у.
101к. Постройте прямоугольный треугольник по острому углу и
противолежащему катету.
Занятие 12. Тема. Модуль числа
Любое действительное число, можно изобразить точкой числовой
прямой. Расстояние этой точки от начала отсчета на этой прямой
равно положительному числу или нулю, если точка совпадает с на-
чалом числовой прямой.
Расстояние точки, изображающей данное число на числовой пря-
мой, от начала этой прямой называется модулем данного числа.
Модуль числа а обозначается |а|.
Например, |—3| = ЛО = 3, |4| = ОВ = 4, |0| = 0 (рис. 7).
Л	?
Чз ’	' о 1
Рис. 7
23
В
*4
К
Рис. 8
Геометрический смысл модуля удобно использовать при решении
некоторых уравнений.
Пример. Решим уравнение |х—6| = 9.
Решение. Если число 6 изобразить точкой А (рис. 8), то по
определению модуля следует, что точка х отстоит от точки А на
расстоянии 9 единиц. Но на числовой прямой таких точек две.
Одна имеет координату х = 6 + 9=15, вторая имеет координату
х — 6—9 = —3.
Следовательно, данное уравнение имеет два решения: х=15 и
х = —3.
При решении уравнений, содержащих несколько выражений со
знаком модуля, удобнее пользоваться алгебраическим определением
модуля числа:
модулем или иначе абсолютной величиной отрицательного числа
называется противоположное ему положительное число, модулем по-
ложительного числа и числа нуль называется само это число.
Определение кратко запишется так:
. , I	а, если а О,
\а = <	п
1 1 I —а, если а < 0.
Например, |—51 = 5, 171 = 7, |0| = 0.
Для решения уравнений, содержащих два и более выражений
со знаком модуля, сначала записываем уравнение без знаков мо-
дуля. Причем так как каждое выражение, записанное со знаком
модуля, может быть или отрицательным, или неотрицательным, то
при его записи без знака модуля надо рассмотреть оба случая от-
дельно. Для уравнений, содержащих два выражения со знаком мо-
дуля, получается четыре комбинации, а для уравнений, содержа-
щих три выражения со знаком модуля, получается восемь комби-
наций, т. е. надо решить восемь уравнений без знаков модуля.
Затем обязательно проверить, какие из найденных значений х yji&b-
летворяют данному уравнению.
Но можно упростить решение таких уравнений.
Пример. Решим уравнение |2х—121 + 16х + 481 = 160.
Решение. Найдем корни (нули) каждого выражения, содержа-
щего знак модуля: 2х—12 = 0, х = 6; 6х + 48 = 0, х = —8.
Найденные значения х разбивают числовую прямую на 3 про-
межутка: х<—8, —8^х<6, х^6 (рис. 9).
Решение данного уравнения рассматриваем в каждом промежутке
отдельно.
В промежутке х < —8 оба выражения, стоящие под знаком мо-
дуля, отрицательны. Поэтому в этом промежутке при записи урав-
24
—*-+
-в
н—I—I—I—i—  — >-
0 1	6 X
Рис. 9
нения без знаков модуля знаки этих выражений меняем на проти-
воположные. Получим уравнение — (2х — 12) — (6% + 48) = 160.
Откуда х =—24,5. Это значение принадлежит рассматриваемому
промежутку. Значит, оно является решением данного уравнения.
Во втором промежутке —8^х<6 первое выражение отрица-
тельно, а второе положительно. Следовательно, в этом промежутке
уравнение запишется так: —(2х—12) 4-(6x4-48) = 160. Откуда х =
= 25 не принадлежит промежутку.
В третьем промежутке х^б оба выражения положительны. Сле-
довательно, в этом промежутке уравнение запишется так: (2х—12) +
+ (6x4- 48) = 160. Откуда х=15,8. Значит, решением данного урав-
нения будут значения х =—24,5 и х=15,8.
Задачи и упражнения
Решите уравнение:
102.	а) | 3—х] = 7; б) |2х—51 = 39.
103.	а) | 84—5х| = 64; б) |28х—37j = 93.
104.	а) |56—8х| + |36x4- 1441 = 356;
б)	|2х—16| + | 5х + 20| 4-| Зх—301 = 300.
105.	a) J 15х—1051 4-112х—2881 = 535;
б)	136— 12х|—|5х + 20| — |7х— 351 = 240.
106.	|х2— 1 | + | 4—х21 = 2х.
107°. Как разменять 2 р. 25 монетами достоинством 50 к., 20 к.
и 5 к.?
108Л. Найдите двузначное число, равное квадрату числа его
единиц, сложенному с кубом числа его десятков.
-«ла< тт «	2х2 — 51 х 14-2	А
109х. Найдите все решения уравнения --- = 0, принад-
лежащие области определения функции у = 4хгТГf -
110к. Найдите первый член и знаменатель геометрической прог-
рессии, сумма первых трех членов которой равна 10,5, а разность
первого и четвертого членов равна 31,5.
Занятие 13. Тема. Графики функций, содержащих выражения
под знаком модуля
Для построения графиков функций, содержащих выражения под
знаком модуля, как и при решении уравнений, сначала; находят
корни выражений, стоящих под знаком модуля. Эти корни разби-
25
вают числовую прямую на промежутки. График строят в каждом
промежутке отдельно.
В простейшем случае, когда только одно выражение стоит под
знаком модуля и нет слагаемых без знака модуля, можно построить
график функции, опустив знак модуля, и затем часть графика, рас-
положенную в области отрицательных значений у, отобразить сим-
метрично относительно оси Ох. Это вытекает из определения мо-
дуля числа.
Примеры.
1.	Построим график функции г/ = |О,5х|.
Решение. Строим график г/==0,5^ и часть графика, располо-
женную ниже Ох, отражаем симметрично относительно оси Ох (рис. 10).
2.	Построим график функции г/ = /(0,5х—З)2.
Решение. ?t/ = j/(0,5x—З)2 = | 0,5х — 3|. Строим график у =
= 0,5х—3 и часть графика, расположенную ниже Ох, отображаем
симметрично относительно оси Ох (рис. 11).
26
3.	Построим график функции t/ = |2x —4| + |6 + Зх|.
Решение. Находим корни каждого выражения, стоящего под
знаком модуля: 2х—4 = 0, х = 2; 6 + Зх = 0, х =—2. В результате
ось Ох разбиваем на три промежутка. В каждом промежутке выра-
жение, стоящее под знаком модуля, имеет определенный знак. Опу-
скаем знаки модуля, беря выражение в каждом промежутке с соот-
ветствующим знаком:
1)	х<—2, у-—(2х—4)—(6-)-Зх) =—5х—2;
2)	—2<х<2, z/ = —(2х—4) + (6 + Зх) = х+Ю;
3)	х^2, у — 2х—4 + 6 +Зх = 5х + 2.
Получим в каждом промежутке выражение функции без знака мо-
дуля. Строим график функции в промежутке. При правильном построе-
нии в области определения график должен представлять непрерыв-
ную линию (рис. 12).
Задачи и упражнения
Постройте график функции:
111.	а) у = |ух + 2б) // = |1—2х|;
в) 1/ = |5 — г) У— \ Зх + 11.
112.	а) г/ = /(7+ТУ+/(х-1)2; б) // = |1х-2|-|1х4-2|.
113.	у = /(х + З)2- К(0,5х—I)3 + /(0,5х + 2)2.
114.	у = /(3—х)3 - К(0,5х + 3)2 — /(0,5x4- I)2• _
115.	a) f/= |ух—21 +13 + ух| —3; б)г/ = ^5^.
116Д. Найдите шестизначное число, начинающееся с цифры 2,
которое от перестановки этой цифры в конец числа увеличивается
в 3 раза.
117°. Сколько треугольников в фигуре, изображенной на ри-
сунке 13?
118к. Постройте график функции
у = \х— 11 + |х—21 + х.
119к. Решите систему уравнений:
(х—f/ = 6
I х3—ys= 126.
Занятие 14. Тема. Графики квадра-
тичных функций, содержащих знаки модуля *
Пример. Построим график функции
 у = |х3—2|.
* Порядок построения этих графиков аналогичен
построению графика линейной функции, содержащей
знаки модуля.
27
вую запись примера:
Решение. Строим график функции
t/==x?—2. Часть графика, расположенную
ниже оси Ох, отражаем симметрично отно-
сительно оси Ох (рис. 14).
Задачи и упражнения
Постройте график функции:
120. y = |9 — х2|.
121.	а) z/ = |x2— 5х+6|;
б)	у — \х2 + 2х—8|.
122.	а) г/ = |х2-|-Зх—13,751;
б)	у = 13 — 0,5х2|.
123.	у — х2—4Ц-3.
124.	у = |х2- 3|—2.
125.	= — х-|%|.
126Д. Число 30 запишите в виде четырех различных выражений,
из трех одинаковых цифр каждое. Цифры могут быть соединены
знаками действий.
127°. В данном примере одинаковыми буквами обозначены
одинаковые цифры, разными —разные цифры. Восстановите цифро-
МАША
КЛАША.
СЕСТРЫ
128к. Даны две окружности радиусов 12 см и 7 см с центрами
в точках Ог и О2, касающиеся некоторой прямой в точках М± и М2
и лежащие по одну сторону от этой прямой. Отношение длины от-
2
резка к длине отрезка ОХО2 равно —g—. Вычислите длину
отрезка Alj/vig.
129к. В прямоугольный треугольник, периметр которого равен
36 см, вписана окружность. Точка касания гипотенузы с окружно-
стью делит гипотенузу в отношении 2:3. Найдите стороны треуголь-
ника.
Занятие 15. Тема. Женщины-математики
Гипатия—дочь известного греческого математика Теона. Она
родилась и жила в Александрии с 370 по 415 г. Гипатия была пер-
вой женщиной математиком, философом, астрономом и врачом. Она
была настолько всесторонне образованна, что с ее мнением считались
все ученые того времени. Гипатия написала научный комментарий
к трудам по решению неопределенных уравнений первой степени
знаменитого ученого древности Диофанта и к трудам па коническим
28
сечениям не менее знаменитого ученого Аполлония, Благодаря Гипа-
тии до нас дошли многие рукописи Диофанта и Аполлония. К сожа-
лению, другие научные труды Гипатии не сохранились. Гипатия
прожила короткую жизнь. Она, как и ее предки, была язычницей.
А1 период ее жизни характеризовался распространением и усилением
христианства. Язычество стало подвергаться гонению. Поэтому, не-
смотря на то что у Гипатии было много друзей среди христиан,
руководители христианской общины Александрии натравили фана-
тичную толпу христиан на Гипатию, и эта толпа растерзала, а затем
сожгла знаменитую ученую. Такая- же толпа за 20 лет до этого
разгромила Александрийскую библиотеку—прекрасное и самое боль-
шое по тому времени собрание древних рукописей.
После смерти Гипатии в течение более тысячи лет мы не встре-
чаем женщин-математиков.
С. В. Ковалевская — замечательная русская женщина-математик,
родилась в 1850 г. в семье богатого помещика генерал-лейтенанта
Корвин-Круковского. Родители мало интересовались ее воспитанием.
Значительное влияние на Софью оказал ее дядя — Петр Васильевич.
Он не был математиком, но прочитал много математических книг
и любил с увлечением рассказывать Софье о разных вопросах мате-
матики. Его увлеченность передалась и племяннице. Математика
казалась Софье таинственной наукой, открывающей свои тайны только
посвященным в нее людям. А с диофантовым и интегральным исчи-
слением она познакомилась по листам книги, которыми была оклеена
одна из детских комнат. На общественно-политические взгляды Софьи
Васильевны большое влияние оказала ее старшая сестра—Анна,
которая впоследствии уехала в Париж. Там она стала активной
участницей Парижской Коммуны и вышла замуж за одного из ее
руководителей.
Софья решила всерьез заняться математикой. Но в то время
женщины не имели права учиться в университетах России. Высшее
образование она могла получить только за границей. Но ее отец
был человек консервативных взглядов и, естественно, не мог позво-
лить Софье поехать учиться за границу. Софья Васильевна вступает
в фиктивный брак с известным палеонтологом В. О. Ковалевским.
Правда, они вскоре полюбили друг друга — и их брак оказался
законным. В 1869 г. супруги Ковалевские уехали за границу.
Математическими занятиями С. В. Ковалевской руководил один из
крупнейших немецких математиков — Карл Вейерштрасс (1815—1897).
Его поражала быстрота и оригинальность математического мышле-
ния Ковалевской.
В 1874 г. за оригинальные математические работы Геттингенский
университет присвоил Ковалевской ученую степень доктора филосо-
фии. Ее работы относились к весьма тонким разделам высшей мате-
матики. Причем две из них были из области математического ана-
лиза. В них были изложены вопросы теории гироскопа, необходимые
29
для расчета устойчивости корабля. Третья работа относилась к астро-
номии. В ней рассматривался вопрос о кольцах Сатурна.
В 1874 г. Софья Васильевна вернулась в Россию, где продол-
жает активную научную деятельность, выступает с научными докла-
дами на съездах естествоиспытателей, публикует научные ci гьи
в журналах, одновременно ведет активную литературную работу.
К этому времени относится написание ею романа «Нигилистка».
Но преподавательскую работу в России Ковалевская получить не
может. Женщины не допускались к преподаванию в университетах
России. Весной 1883 г. скончался ее муж и она вынуждена была
уехать с малолетней дочерью в Швецию. Там Ковалевская получила
должность доцента Стокгольмского университета и вновь занялась
научной работой.
В 1884 г. она стала первой в мире женщиной-профессором. Лек-
ции профессора Ковалевской в Стокгольмском университете были
блестящими. Опа читала курсы по наиболее сложным разделам выс-
шей математики и теоретической механики.
1888 г. был триумфальным для С. В. Ковалевской. Ее научная
работа о вращении твердого тела была признана Парижской ака-
демией наук лучшей. Ковалевской была присуждена премия, причем
увеличенная почти вдвое по сравнению с обычной. В 1889 г. за
научную работу по той же теме Ковалевская получила премию
Шведской академии наук.
Научные исследования Ковалевской принесли ей мировую славу.
По предложению виднейших русских математиков в ноябре 1889 г.
С. В. Ковалевская была избрана членом-корреспондентом Академии
наук России. Но даже избрание в Академию не дало ей возможно-
сти получить соответствующую работу и вернуться на родину. Она
скончалась в Стокгольме в 1891 г.
Эмми Нетер родилась в 1882 г. в Германии в городе Эрланген
в семье видного математика Макса Нетер. Она была, пожалуй,
самой известной женщиной-математиком первой половины XX в., но,
несмотря на это, жизнь ее протекала очень тяжело. В 1907 г. она
защитила докторскую диссертацию. Первые научные работы Эмми
Нетер дали ей репутацию первоклассного математика. Но основные
ее научные достижения приходятся на период, начинающийся с 1920 г.
Она фактически создает так называемую общую, абстрактную алгебру.
Работы по абстрактной алгебре принесли Нетер мировую известность
и славу. Ее заслуги в математике признают ив Геттингенском уни-
верситете, куда она переехала в 1916 г. Но, несмотря на это, Эмми
не может получить работу в университете. Только в 1919 г. после
разгрома немецкой монархии она становится приват-доцентом универ-
ситета, в 1922 г. — сверхштатным профессором, но получила неболь-
шую зарплату, да и то с ежегодного утверждения министерством.
И несмотря на активную поддержку ее друзей—видных немецких
математиков, таких, как Д. Гильберт (1862—1943), Ф. Клейн
(1849—1925), Г. Вейль (1885—1955), Р. Курант (1888—1972), ее
30
так и не допустили на штатную должность. Основной официальной
причиной такого решения было то, что Эмми—женщина, а женщина
не могла быть допущена на заседания сената университета. Но не
менее важной причиной было то, что Эмми придерживалась передо-
вых социально-политических взглядов. Идеи и научные взгляды
Эмми Нетер оказали большое влияние на развитие многих отраслей
науки, на многих ученых-математиков. Но после прихода в Герма-
нию власти фашистов Эмми потеряла и тот небольшой заработок,
который имела, поэтому она вынуждена была переехать в Америку
в 1933 г., где и умерла в 1935 г.
Советские женщины-математики. Совершенно другая судьба, дру-
гие условия жизни и работы, другие возможности творчества и заня-
тий наукой имеют женщины в нашей стране. В наших университе-
тах, вузах и научных учреждениях работает немало женщин-про-
фессоров, докторов наук и еще больше доцентов, кандидатов наук.
Это академик ГТ. Я. Полубаринова-Кочина (род. в 1899 г.)—спе-
циалист по механике, работающая в области прикладной матема-
тики; профессор С. А. Яновская (1896—1966), внесшая большой
вклад в развитие математической логики, истории математики, раз-
вития кибернетики в нашей стране; профессор МГУ Н. К. Бари
(1901 —1961), известная своими работами в области теории функций
действительной переменной и теории рядов; профессор ЛГУ О. А. Лады-
женская (род. в 1922 г.), работающая в области дифференциальных
уравнений, и др.
Ольгу Арсеньевну Олейник, профессора МГУ им. Ломоносова
знают математики всего мира. Она родилась в 1925 г. в небольшом
городке Мату сове в Киевской области. В 1942 г. она окончила
X класс и поступила на физико-математический факультет Перм-
ского университета. В это время в Пермском университете работала
профессор МГУ Софья Александровна Яновская. Ольга Арсеньевна
посещала математический кружок Софьи Александровны. В 1943 г.
Московский университет вернулся из Свердловска в Москву, а вместе
с ним вернулась в Москву с группой своих кружковцев и Софья
Александровна. В их числе была и Олейник.
В МГУ Олейник участвовала в работе научного семинара, руко-
водимого академиком И. Г. Петровским. Занятия в семинаре и опре-
делили основное направление научных интересов Ольги Арсеньевны.
Уже в это время Ольга Арсеньевна пишет и публикует свои первые
работы, результаты которых впоследствии вошли во многие учебники
вузов. Часть этих работ выполнялась аспиранткой Олейник совместно
с ее учителем, академиком И. Г. Петровским. В 1950 г. она защи-
тила кандидатскую диссертацию и стала работать в Математическом
институте АН СССР им. Стеклова и преподавать в МГУ. В 1952 г.
она первой была удостоена премии имени знаменитого русского мате-
матика Н. Г. Чеботарева.
В 1954 г. Олейник защитила докторскую диссертацию, а в 1955 г.
ей было присвоено звание профессора Московского университета.
31
И после защиты докторской диссертации Ольга Арсеньевна продол-
жала разработку наиболее сложных вопросов математического ана-
лиза, и в частности дифференциальных уравнений различного вида,
имеющих большое практическое значение и применение в различных
вопросах физики и техники. В 1964 г. за свои научные работы
Олейник удостоена премии им. М. В. Ломоносова первой степени.
Ольга Арсеньевна ведет большую педагогическую работу и работу
по руководству аспирантами. Под ее руководством написали и защи-
тили кандидатские диссертации десятки молодых ученых. Она руко-
водит научным семинаром им. академика И. Г. Петровского. На засе-
даниях семинара выступают многие ученые из разных городов Совет-
ского Союза и зарубежных стран., В 1967 г. Олейник избрана ино-
странным членом Итальянской академии наук в Палермо. С 1973 г.
Ольга Арсеньевна возглавляет кафедру дифференциальных уравне-
ний Московского университета.
Олейник — непременный участник по существу всех международ-
ных симпозиумов, конференций и конгрессов по дифференциальным
уравнениям. Она выступала со своими научными сообщениями, докла-
дами во многих странах мира; читала курсы лекций по различным
видам дифференциальных уравнений во многих университетах: США,
Румынии, Франции, Италии и др. Олейник в настоящее время яв-
ляется одним из ведущих ученых мира по теории дифференциаль-
ных уравнений с частными производными и по теории действительных
алгебраических кривых и поверхностей.
Занятие 16. Тема. Решение алгебраических
и геометрических задач
130.	Докажите, что сумма расстояний от любой точки, взятой
внутри или на любой стороне правильного треугольника, до его
сторон равна высоте треугольника, т. е. величина постоянная.
131.	Постройте треугольник по данным медианам, проведенным
к боковым сторонам, и высоте, проведенной к основанию.
132.	Точки А и В расположены на диаметре симметрично отно-
сительно центра окружности. Докажите, что сумма квадратов рас-
стояний от любой точки окружности до точек А и В есть величина
постоянная.
133.	В круге радиуса R проведены два взаимно перпендикуляр-
ных диаметра. Докажите, что расстояние между проекциями любой
точки окружности на эти диаметры есть величина постоянная, не
зависящая от положения точки на окружности.
134.	Решите систему уравнений:
32
135.	Решите уравнение:
ч х2 . 36	16 / х 6 \ х2 48 1Л ( х	4 \
а) -пг4—г = у т—~ ’» б) - + -5-= 10.  ----------к
' 25 1 х2 5 \ 5 х /	7 3 х2 \ 3 х /
136°. Найдите все числа, которые уменьшаются в 12 раз при
зачеркивании в них последней цифры.
137Д. Сколькими нулями оканчивается произведение
1-2-3-4-5-6. ... .98-99.100?
138к. Решите уравнение К* = 6
__4 I
—ТТ > 2.
Занятие 17. Тема. Решение алгебраических
и геометрических задач
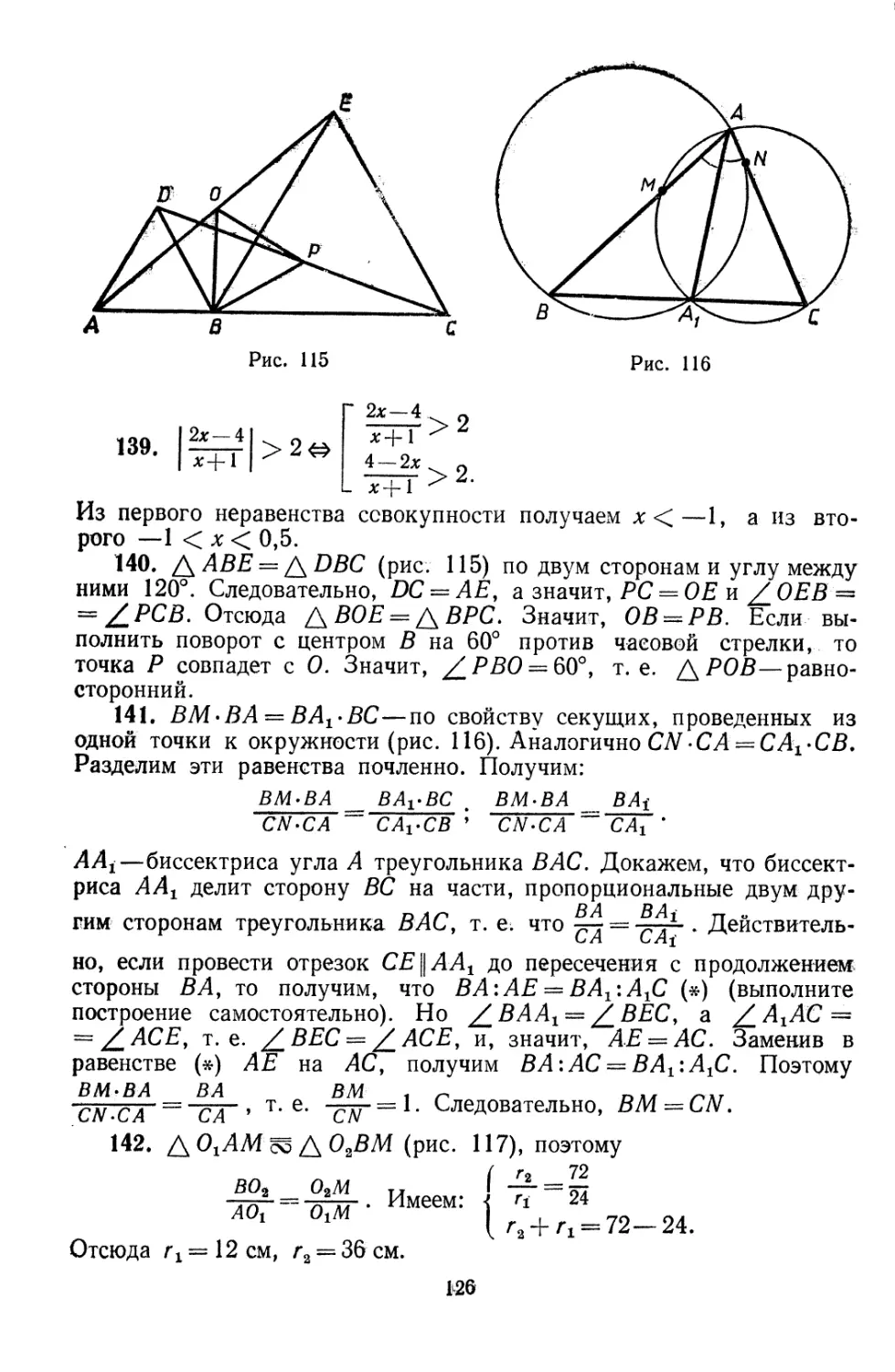
140.	На отрезках АВ и ВС, расположенных последовательно на
одной прямой, построены правильные треугольники ADB и ВЕС.
Точка А соединена с точкой Е, а точка D—с точкой С. Точка В
соединена с серединами О и Р отрезков АЕ и DC. Докажите, что
треугольник ВОР—равносторонний.
141.	В треугольнике АВС проведена биссектриса AAt угла А.
Около треугольников BAAt и АгАС описаны окружности, которые
пересекают стороны АВ и АС соответственно в точках М н N.
Докажите, что BM — CN.
142.	К двум касающимся окружностям проведена общая внешняя
касательная, которая пересекается с продолжением линии центров
в точке, удаленной от центров на 24 см и 72 см. Найдите радиусы
окружностей.
143.	Постройте треугольник по углу а при вершине А, отношению
высоты ha к основанию ВС, равному 1,5, и медиане та основания ВС.
144.	Решите в целых числах уравнение (х4- 1)(ж* + 1)=е/3.
145.	Решите систему уравнений:
f 1—х1х2==0
1 ~~~ х^х^ 9
1 —х3х4 = 0
1	•^'20'^21 — 9
1—х21х1 = 9.
146д. Докажите, что если из трехзначного числа вычесть число,
записанное теми же цифрами, но в обратном порядке, то получим
число, сумма цифр которого равна 18.
147°. На столе лежит 89. одинаковых по виду металлических
шариков. Один из них несколько легче остальных. Как найти этот
шарик не более чем четырьмя взвешиваниями на чашечных весах
без гирь?
2 № 3671	33
148к. Упростите выражение	_______
m-f-n . 7 m-j-n___п [ m \___________1//Г( 1 — У п
У/п + УТг \т—n п—У тп	т+Утп )	*
где /п > 0, п > 1.
149к. Решите систему уравнений:
{4х— у + 4z = О
х+ Ьу—2z = 3
— хЧ- &/—2z=±= 1.
Занятие 18. Тема. Решение геометрических
и алгебраических задач
150.	Из трех данных точек как из центров опишите три попарно
касающиеся окружности.
151.	Докажите, что сумма медиан треугольника меньше его
периметра.
152.	Докажите, что прямая, соединяющая точку пересечения про-
должения непараллельных сторон трапеции с точкой пересечения
ее диагоналей, делит основания трапеции пополам.
153.	Постройте прямоугольный треугольник по катету и сумме
гипотенузы с другим катетом.
154.	Сосуд, имеет четыре крана. Дели открыть все четыре .крана,
то сосуд наполнится за 4 ч. Первый, второй и третий краны напол-
няют его за 5 ч; второй, третий и четвертый —за 6 ч. За сколько
времени наполнится сосуд, если открыть первый и четвертый краны?
155.	Решите в целых числах уравнение
(х2+ 1)(у2 + 1) = (х +у)2Ч- 1.
156.	Докажите, что если медиана равна половине стороны, к ко-
торой она проведена, то треугольник прямоугольный.
157Д. Найдите двузначное число, равное удвоенному произве-
дению его цифр.
158Д. Два товарища живут в поселках А и Б. Один вышел из А
в Б в 8 ч 38 мин. Он может прибыть в Б в 13 ч 8 мин. Второй
вышел из Б в 4 в 10 ч 8 мин. Он может прибыть в Л в 13 ч 44 мин.
В какое время они встретились?
159к. Решите уравнение 14х-^2х2 = |х — 7|.
160к. Найдите первый член и разность d арифметической про-
( а2 + аь—а3 = 10
грессии, в которой	—17
Занятие 19. Тема. Решение геометрических
и алгебраических задач
161.	Постройте прямоугольный треугольник по гипотенузе и ме-
диане одного из катетов.
162.	Дан четырехугольник, площадь которого равна 90 см2. Его
34
диагонали делятся точкой пересечения в отношении 2:3 и; 4:о.
Найдите площадь каждого из четырех треугольников, на которые
диагонали разделили четырехугольник.
163.	В треугольник с основанием 30 см и высотой 10 см вписан
равнобедренный прямоугольный треугольник так, что его гипотенуза
параллельна основанию, а вершина прямого угла лежит на осно-
вании. Определите стороны вписанного треугольника.
164.	В треугольнике проведите прямую параллельно основанию
так, чтобы ее отрезок между боковыми сторонами треугольника был
равен сумме отрезков сторон, прилежащих к основанию треугольника.
f xy(x-\-y) = 3Q
165.	Решите систему уравнений: 1 3 , 3 ос
у Xй 4' У ===
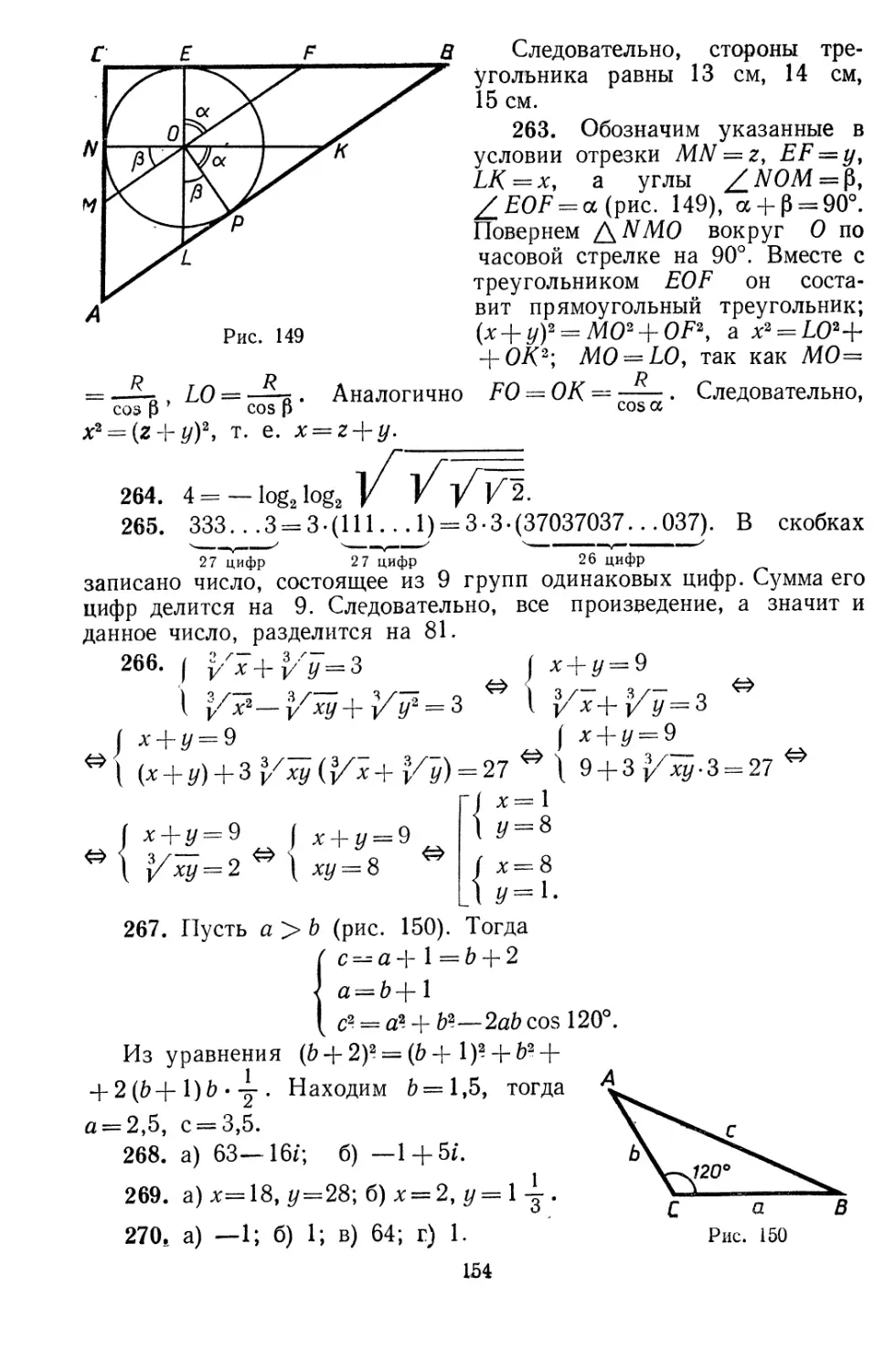
166.	Докажите, что	2а2—b2-\-2dl^ а2—Ь2 —	а2—2Ь]>/Г а2—Ь2—
г=а + Ь при а > b ]/2 > 0.
167Д. На покупку магнитофона ученик заработал в каникулы
52 р. Остальные деньги ему дали два старших брата и отец. Причем
отец дал 50% всех собранных денег без его денег, первый брат
дал ЗЗу % всех собранных денег без его денег и второй брат дал
25% всех собранных без его денег. Сколько денег дал каждый
йз них?
168Д. Найдите все двузначные числа, обладающие тем свойством,
что каждое из них в сумме с числом, записанным теми же цифрами,
но в обратном порядке, равно квадрату некоторого числа.
169к. В питомнике было 82 000 саженцев клена, что составляло
4% всех саженцев питомника. 85% всех саженцев составляла сосна.
Сколько саженцев сосны было в питомнике?
170*. Постройте график функции г/ = 3% + | 5х—10 |.
2*
IX класс
Занятие 1. Тема. Метод математической индукции
Индукция есть метод получения общего утверждения из частных
наблюдений, например любой человек наблюдает смену ночи утром,
утра—днем и т. д. На основе этих наблюдений он делает вывод
о смене времени суток как об общей закономерности. Вывод этот верен.
Аналогично можно сделать вывод о смене времен года.
Рассмотрим целые числа, определяемые формулой п(х)—х2+х+41.
Будем давать х значения 0, 1,2, .... Тогда п(0) = 41, п(1) = 43,
п(2) = 47, п(3) = 53, п(4) = 61.
Из этих частных наблюдений можно сделать вывод о том, что
формула п(х) = х24-х+ 41 дает только простые числа. Утверждение
это ошибочно. Такую ошибку в свое время допустил Леонард Эйлер.
Прих=40 п(40) = 4024-40 + 41—число составное, равное 1681 = 412.
Чтобы избежать подобных ошибок, надо или перебрать все
возможные случаи, что не всегда возможно, или справедливость
утверждения доказать методом, основанным на принципе (аксиоме)
математической индукции.
Суть принципа математической индукции заключается в сле-
дующем: если некоторое утверждение (формула) справедливо при
п==1 (или при другом значении и, при котором имеет смысл это
утверждение) и из предположения его справедливости для некоторого
натурального значения n = k следует справедливость утверждения
для следующего натурального значения n = k+l, то утверждение
справедливо для всех натуральных значений п.
Метод доказательства, основанный на применении принципа
математической индукции, носит название метода математической
индукции.
Способ доказательства методом математической индукции заклю-
чается в следующем:
1) доказывают или непосредственно проверяют справедливость
утверждения (формулы) для п=1;
2) предполагают справедливость утверждения для некоторого
натурального n = k. Исходя из этого предположения, доказывают
справедливость утверждения для п = k 4- 1.
Ясно, что метод математической индукции можно применять
только для доказательства утверждений, зависящих от натураль-
ного п. В основном он применяется для решения задач двух видов:
1) исходя из частных наблюдений устанавливают некоторую законо-
мерность и затем доказывают ее справедливость методом математи-
36
ческой индукции; 2) доказывают справедливость некоторой формулы
методом математической индукции.
Примеры.
1. Выведем формулу суммы первых п нечетных чисел натураль-
ного ряда.
Решение. S(l)=l,	S(2)=l +3 = 4, S(3)= I+3 + 5 = 9,
S (4) = 1 + 3 + 5 + 7 = 16, S (5) = 1 + 3 + 5 + 7 + 9 = 25. Замечаем,
что сумма первых п нечетных чисел натурального ряда равна п2,
т. е. S(n) = n2.
Докажем это.
1) Для и=1 формула верна.
2) Предположим, что она верна для какого-либо натурального
п = А, т. е. 5(й) = А2. Докажем, что тогда она будет верна и для
ti^k+1, т. е. S(k+ 1)-(^+ I)2:
5(^ + 1) = 1+3 + 5+... + (26—1) + (2й+ l) = S(fe) + (2Z?+l) =
= А+ + 2& + 1 =(А> + I)2.
Следовательно, формула верна для всех натуральных значений и,
т. е. S(n) = n2.
2. Докажем, что сумма квадратов первых п натуральных чисел
пятшя n(n+i) (2п+1)
JJ a D nd	g	•
Доказательство. 1) Проверим справедливость утверждения
для и = 1. При и=1 сумма состоит из одного члена, т. е. S2(l) = 1,
и по формуле имеем 32(1) =—*—!—— т, е. для п=1
формула верна.
2) Предположим справедливость формулы для некоторого /2 = -fe,
т. е.
S2(/e) = la + 23 + 32 + ... + ^= fe(fe+№+1) .
Исходя из этого предположения докажем справедливость фор-
мулы для п = k + 1. Действительно,
S2(k+ 1)= I2 + 22 + З2 + ... +fe2 + (А+1)2.
г.	о /м & (£ +1) (2А? +1)	q
Сумма первых k слагаемых равна 32(я)= —-——~. Значит,
sa (k +1)=s2 (k) + (k +1)2 = fe<fe+!L(2fe+1)+(k +1)2 =
(£+1) (2^2 + ^ + 6^ + 6) _ (& + I) (2£2 + + в) _
"6	“	6
__ (k + 1) (k + 2) (2k + 3) _ (k + 1) ((k +1) + 1) (2 (k +1) + 1)
""	6	6
Итак, мы доказали, что формула верна для n = Z?+l.
Мы получили ту же формулу. Следовательно, в силу принципа
математической индукции данная формула верна для любого нату-
рального п.
37
Задачи и упражнения
Докажите, что:
171.	2 + 6 + Ю+...+2(2п—1) = 2п2.
172.	2 + 10 + 24 + ... + (Зп2—и) = п2 (п + 1).
173.	1-2 + 2-5 + 3-8+... +n(3n—1) = п2(п + 1).
174.	Выведите формулу суммы S(n) =772+2^3+ • • • + п (J_|_ ij
Докажите, что:
175.	I3 + 23 + З3 + ... + п3 = п!,(п+Ц*..
176.	12 + 32 + 52+ ... +(2/г—1)2 = ”(2Аг-’^2п-+1).
177.	Найдите сумму 1 • 114-2-2! 4-3-31 4-... 4-п-п!
178.	Докажите, что сумма членов каждой строки таблицы
1
2, 3, 4
3, 4, 5, 6, 7
равна квадрату нечетного числа, номер которого в строке равен
номеру строки от начала таблицы.
179д. Сколько раз в сутки совпадают часовая и минутная
стрелки? Во сколько времени происходит первое совпадение? Вось-
мое совпадение?
180°. Если к некоторому двузначному числу приписать восьмерку
справа, а затем тройку слева, то первое трехзначное число будет
в 2 раза больше второгог Чему равно это двузначное число?
181к. На основаниях АВ и CD вне трапеции построены квад-
раты. Докажите, что прямая, соединяющая их центры, проходит
через точку пересечения диагоналей трапеции.
182к. Наименьший из углов прямоугольноготреугольника равена.
Через середину меньшего катета и середину .. гипотенузы проведена
окружность, касающаяся гипотенузы. Найдите отношение площадей
круга и треугольника.
Занятие 2. Тема. Решение задач методом
математической индукции
Докажите, что:
184 -4-—4-	4- " — 1__- и>2
2!-t-3! 4-• • • “Г п! —1 n! ,
185.	Докажите, что для любого натурального п справедливо
равенство
1 -а + 2{а+1) + 3(а + 2) + ... + п (а= М1±1Н^±2п-2),
где a£R.
186.	Докажите, что при любом натуральном п > 3 справедливо
1,1,1,	. 1	2м—1
неравенство -+-+-+...+—< —— .
187.	докажите справедливость равенства
т-|+4-у+• • • + (-D— •£-}•(»+ <-'Г‘ • ¥)•
188.	Найдите сумму ~	+	   + ,з.,_.2)'з„+„ 
Докажите справедливость равенства:
юп । (" + W । (^ + 2)! ,	, (м+/м)1 _ (п+т + 1)!
18У. П. +	1{	+	21	+ ••• +	•
ion	__!__l _|_______1____— - п
2-5 ‘5-8^8*11 ‘ *** ^(Зм—1)(Зм + 2)”“ 6м + 4‘
191 А. Можно ли из 36 спичек, не ломая их, сложить прямоуголь-
ный треугольник?
192°. В классе случилось происшествие. Учитель решил устано-
вить, как все было. Он пригласил трех мальчиков—Гену, Алика
и Славу—и попросил каждого рассказать, как все было. Каждый
рассказал свою версию. Затем учитель спросил, кто рассказал
верно. Гена сказал, что Алик рассказал неверно. Алик сказал, что
Слава рассказал неверно. Слава сказал, что Алик и Гена рассказали
неверно. После этого учитель сразу назвал мальчика, рассказ кото-
рого был верным. Кто из трех мальчиков рассказал верно о про-
исшествии?
193к. В окружности радиуса г на расстоянии •— от центра про-
ведена хорда. В меньший из образовавшихся сегментов вписаны
две равные окружности так, что они касаются одна другой и каж-
дая из них касается данной окружности и проведенной хорды.
Определите радиусы этих окружностей.
194к. Упростите выражение
V ху» I + V * * (.	9	, У '•
Занятие 3. Тема. Действительные числа, преобразование
выражений
195.	С помощью циркуля и линейки постройте на числовой
прямой точки х, такие, что а) x = J^3; б) x = j/7; в) х—у 13,
г)х = /87.
196.	Постройте квадрат, равновеликий данному прямоугольнику,
со сторонами 5 см и 2 см.______	‘
197.	Дано: S—i^20 + 14 V2 — 20—14К2 . Вычислите S2 и S*
и выразите S в виде рационального, числа, не прибегая к исполь-
зованию таблиц.
39
Докажите, что:
198; j/7 + УЖ—^V50 —7 = 2.
199.	Kill ... 1 — 222 ... 2 = 333 ... 3.
2п	п	п
I Л -2.	-2.
200.	Упростите выражение \(х + а)3-(х—а) 3+(х + а) Зх
.. JL
—	\	I д3
х(х—а) 'л — 2)	при х = а>	> где тп > 0.
201Д. Известно, что 2х+3у при некоторых натуральных значе-
ниях х и у делится на 17. Докажите, что при этих значениях
х и у выражение 9х + 5# также делится на 17.
202А. Дано 1989 положительных чисел. Известно, что произве-
дение любых 22 нз них больше 1. Докажите, что произведение всех
данных чисел больше 1.
203х. Моторная лодка прошла против течения реки 16 км и воз-
вратилась назад, затратив на обратный путь на 40 мин меньше, чем
на путь против течения. Найдите скорость лодки в стоячей воде,
если известно, что скорость течения реки равна 2 км/ч.
204к. Решите систему уравнений:
( х2 + 2ху + у2—-х—у=^6
t х—2у = 3.
Занятие 4. Тема. Решение алгебраических
и геометрических задач
205.	По окружности, имеющей длину 1350 м, в одном направ-
лении едут два велосипедиста. Первый обгонял второго каждые
27 мин. При движении в противоположных направлениях они встре-
чаются каждые 3 мин. Найдите скорости велосипедистов.
206.	Сколько 90 и 60%-ной серной кислоты надо взять, чтобы
получить 5,4 кг 80%-ной серной кислоты?
207.	Сплавили два слитка серебра: 600-й пробы 75 г и 864-й
пробы 150 г. Определите пробу сплава.
208.	В трапеции ABCD AD || ВС, AD = a, ВС~Ь, а>Ь. Высота
трапеции равна h. Найдите площадь четырехугольника, ограничен-
ного основанием AD данной трапеции, отрезками ее средней линии
и диагоналей.
209.	Постройте равносторонний треугольник, вершины которого
лежат на трех данных параллельных прямых.
210.	Постройте квадрат, три вершины которого лежат на трех
данных параллельных прямых.
211.	Постройте равнобедренный треугольник с данным углом а
при вершине так, чтобы его вершины лежали на трех данных па-
раллельных прямых.
40
212д. Докажите, что число п4 —4п3— 4п2+16«п, где п—нату-
ральное число, кратное 2 и большее 4, делится на 384.
213д. Не решая уравнения х2—21x4-47 = 0, найдите сумму
кубов его корней.
214к. Решите уравнение Кх2 + 8 = 2х 4-1.
215К. Решите неравенство | log* 4 4-11	3.
Занятие 5. Тема. Числовые последовательности
216.	Вычислите	5 К 3 V 5 ,,. ,
217.	Сумма трех последовательных членов арифметической про-
грессии в 5 раз меньше их произведения. Найдите эти члены, если
они являются целыми числами.
218.	Докажите, что 3 неравных между собой числа не могут
одновременно составлять арифметическую и геометрическую прогрес-
сии.
219.	Сумма членов бесконечной убывающей геометрической про-
грессии равна 15, а сумма квадратов ее членов равна 75. Найдите
сумму 6 членов этой прогрессии.
220.	В арифметической прогрессии сумма шестого, девятого,
двенадцатого и пятнадцатого ее членов равна 20. Найдите сумму
первых двадцати "членов этой прогрессии.
221.	Найдите сумму 1 4-11 4-111 + ... + 111... 1.
п
00.
222.	Найдите предел произведения
3	5 17 257	22"-1+1
2	4 1 6 256	22 1 г
223.	Докажите, что если стороны прямоугольного треугольника
составляют арифметическую прогрессию, то ее разность равна ра-
диусу вписанного круга.
224°. На шахматной доске с обычной раскраской проведите
окружность наибольшего радиуса, не пересекающую ни одного бе-
лого поля.
225Д. Найдите произведение п(п—1)(п—2)(и—3) ... (п—2п),где
n^N.
Решите уравнение:
226к. 1g 8—lg (x + 7) = lg2—1g /х + 7.
227K. ^±L + ^L. = 5.
X	Z.X -j- L
Занятие 6. Тема. Числовые последовательности
228. Найдите значение выражения
|/ 7 ]/'211/7/21..'.
41
3
229.	Найдите сумму и вычислите ее значение при х=-g-
1 4-3*+ 5х3 + 7х3 + 9х4 + ... .
230.	Найдите сумму 1 4- 2b 4- 362 4- 4&3 4- 5&4 + • • • +
231.	Дана таблица
1	2	3	... 99	100
101	102	103	... 199	200
201	202	203	... 299	300
• * •	• • •	• • •	• • • •	• • •
9901	9902	9903	...9999	10000
Берется произвольное число в этой таблице и вычеркивается
строка и столбец, в которых оно стоит. Затем из оставшихся
не вычеркнутыми чисел берется вновь произвольное число и вычер-
кивается столбец и строка, в которых оно стоит. Вся операция
повторяется до тех пор, пока не будут вычеркнуты все числа таб-
лицы. Докажите, что сумма выбранных чисел не зависит от порядка
их выбора, и найдите ее значение.
232.	Найдите значение суммы бесконечной числовой последова-
тельности
1-2‘3-4^2-3-4«5 ‘ 3-4-5-6 ' п («4-1) («4-2) («4-3)^ ’ * *
233д. Докажите, что при четном п число "pg + ”§~ +-gj"—целое.
234°. Как прямоугольник со сторонами 2 см и 10 см разрезать
на такие 5 частей, чтобы из них можно было составить квадрат?
235к. Решите уравнение Кбх—54-j/10x—5 = К15х—10.
Й36к. Рабочий А может закончить некоторую работу на 5 дней
позже, чем рабочий В, и на 9 дней позже, чем рабочий С. Рабочие
Л и В, работая вместе, могут закончить эту работу за столько
дней, за сколько ее может закончить рабочий С. За сколько дней
каждый рабочий в отдельности может закончить эту работу?
Занятие 7. Тема. Советские математики
Николай Николаевич Лузин родился в 1883 г. в Томске в семье
служащего. Дед его был крепостным крестьянином. В 1901 г. Лузин
закончил Томскую гимназию и поступил в Московский университет
ца математическое отделение. В гимназии у него был неудачный
учитель математики, который предпочитал бессмысленную зубрежку
осмысленному усвоению материала. У Лузина механическая память
была плохая, и он возненавидел математику. Поэтому в знаниях по
42
математике у него были серьезные пробелы. Но ум у юноши был
живой, пытливый. Он мечтал стать инженером, а для этого решил
получить предварительно хорошую математическую подготовку в
Московском университете. Блестящие лекции профессоров универси-
тета полностью изменили его планы и судьбу. Он стал активно за-
ниматься в кружке, на который приходили и профессора. На заня-
тиях рассматривались новые математические открытия. Его члены
занимались изучением новейших направлений в математических ис-
следованиях.
В 1905—1906 гг. Н. Н. Лузин был направлен в Париж, где
слушал лекции Э. Бореля (1871 —1956), А. Пуанкаре (1854—1912)
и других известных французских математиков того времени, изучал
новинки математической литературы. В 1906 г. он окончил университет
и был оставлен при университете для подготовки к профессорской
деятельности. В 1911 г. Лузина зачислили на должность доцента
кафедры чистой математики. В последующие годы основное свое
внимание он сосредоточил на изучении и разработке теории мно-
жеств и теории функций. Его научные статьи печатались как в па-
рижских, так и в московских научных изданиях. Он доказал одну
очень важную теорему интегрального исчисления и получил ряд
новых научных результатов. Лузин сделал важные открытия в об-
ласти степенных и тригонометрических рядов. Эти открытия сделали
его известным среди математиков всего мира.
По итогам своих научных исследований Н. Н. Лузин представил
ученому совету университета магистерскую диссертацию. Но резуль-
таты его исследований были столь значительны, что совет присвоил
ему сразу степень доктора чистой математики. В 1917 г. Лузин был
избран профессором. Его диссертация содержала весьма глубокие
результаты по различным вопросам теории функций и теории рядов.
Все основные исследования Лузина этого периода были изложены
в книге «Интеграл и тригонометрический ряд». Эта книга явилась
источником новых проблем для многих ученых на долгие годы.
Теорией функций и рядов Лузин занимался до конца своей
жизни и получил в этой области науки весьма значительные резуль-
таты. Он вел научные исследования по приближенным вычислениям,
дифференциальной геометрии/истории математики, написал учебник
по дифференциальному и интегральному исчислению.
В течение многих лет Н. Н. Лузин возглавлял советскую мате-
матическую школу. Его учениками являются большинство наших
выдающихся ученых-математиков. Своими идеями он охотно делился
с молодыми математиками, привлекая их к научным исследованиям.
Это была революция в методах научной работы. Научные беседы
продолжались и после работы, когда профессор возвращался домой
в окружении своих учеников. Лекции он читал превосходно, с вдох-
новением, как бы творя в аудитории новую теорию. К тому же у
него была прекрасно отработанная речь, красивый голос.
Но главной заслугой Лузина является создание им школы уче-
ных, которые развили его идеи и внесли большой вклад в другйё
43
области математики. К ученикам Н. Н. Лузина, впоследствии став-
шим видными учеными, относятся такие знаменитые советские мате-
матики, как член-корреспондент АН СССР А. Я. Хинчин (1894—1959),
член-корреспондент АН СССР Д. Е. Меньшов (род. в 1892 г.),
академик П. С. Александров (1896—1982), член-корреспондент
АН СССР В. В. Голубев (1884—1954), член-корреспондент АН СССР
И. И. Привалов (1891 — 1941).
Столь сильная научная школа Н. Н. Лузина оказала огромное
влияние на развитие советской математики и математики ряда за-
рубежных стран. Деятельность Лузина и математиков его школы
высоко оценивали математики всего мира. Он был избран членом
многих иностранных академий наук. Умер Н. Н. Лузин в 1950 г.
Иван Матвеевич Виноградов родился в 1891 г. в селе Милолюб
Великолукского района Псковской области в семье священника.
Окончив Великолукское реальное училище, он поступил в Псков-
ский университет. После его окончания Виноградов был оставлен
при университете для подготовки к профессорскому званию. Далее
он—профессор Псковского университета, профессор Ленинградского
политехнического института и Ленинградского университета, дейст-
вительный член АН СССР, а с 1932 г. директор Математического
института им. В. А. Стеклова АН СССР.
Научные работы И. М. Виноградова посвящены аналитической
теории чисел. Он создал методы исследования и решения проблем
теории чисел, оказавшие огромное влияние на развитие этой науки
и ряда смежных наук, например теории вероятностей. Им решены
проблемы, считавшиеся недоступными математикам начала XX в.
Результаты научных исследований, полученные Виноградовым, пре-
взошли достижения его предшественников и современников и вызва-
ли восхищение ученых всех стран мира. И. М. Виноградов был
избран членом многих иностранных академий наук и научных об-
ществ. Он удостоен Государственной премии СССР, звания Героя
Социалистического Труда, золотой медали им. Ломоносова и мно-
гих других медалей.
Почти все проблемы аналитической теории чисел довольно просто
формулируются на языке конечных сумм слагаемых вида
cosF(xn х2, ..., xn) + i sinf (xn х2, ..., ха),
где F—действительная целочисленная функция, a i — число, квад-
рат которого равен —1. Центр тяжести многих исследований был
перенесен на изучение таких сумм и, в частности, на задачу воз-
можно более точной оценки модуля указанных сумм. На основе ис-
пользования глубоких арифметических свойств рассматриваемых
сумм Виноградов получил исключительно сильные оценки модуля
широкого класса таких сумм. Этот метод позволил Виноградову
получить фундаментальные, близкие к предельно возможным резуль-
таты в целом ряде вопросов теории чисел.
Пользуясь созданным им методом аналитической теории чисел —
методом тригонометрических сумм, Виноградов решил очень важную
44
проблему теории чисел—проблему закономерности распределения
значений функции f(xlt x2f ..., хг) в точках с целочисленными
координатами.
Большой вклад он внес в решение проблемы распределения
вычетов и невычетов данной степени, в частности квадратичных вы-
четов, т. е. решений сравнений вида x2==a(modp), где р—простое
число, a а—остаток от деления х? на р. Он впервые дал оценку
величины квадратичного вычета, т. е. решения указанного сравнения.
Существенный вклад Виноградов внес в решение проблемы Ба-
ринга о представлении целого числа N в виде суммы М = х? +
+ х£ + ... + х?, где х19 х2, ..., xr—натуральные числа, а число
слагаемых г зависит от п. В 1937 г. Виноградов решил проблему
Гольдбаха о представлении натурального числа в виде суммы трех
простых чисел N = Pt + Р2 + Р3, над которой математики бились
с 1742 г. Это было сенсацией. А в 1938 г. он решил вопрос о пред-
ставлении натурального числа в виде, суммы степеней г простых
чисел N = Р” + Р”+ • • • + Р?, являющихся объединением проблемы
Баринга и проблемы Гольдбаха. Методы Виноградова подробно изло-
жены в его труде «Новый метод в аналитической теории чисел».
До последних дней своей жизни И. М. Виноградов продолжал
успешно развивать и совершенствовать свой метод, получая все
более глубокие и более значительные результаты. Умер И. М. Ви-
ноградов в 1983 г.
Андрей Николаевич Колмогоров родился в 1903 г. в Тамбове
в семье агронома. Еще в раннем детстве он увлекался математикой.
В 5-летнем возрасте он самостоятельно подметил такую закономер-
ность:
1 = Р, 1 + 3 = 22, 1 +3-|-5 = 32, 1+3 + 5 + 7-42, ... .
Тетушки Андрея Николаевича в то время открыли домашнюю
школу для десятка детей разного возраста. В школе издавался жур-'
нал «Весенние ласточки», в котором было опубликовано и «откры-
тие» Андрея. Он любил придумывать арифметические задачи, кото-
рые публиковались в журнале.
Семи лет Андрея определили в частную гимназию в Москве.
Учился в гимназии он с интересом. Но гимназия все время нахо-
дилась под угрозой закрытия. Ведь ее организовали прогрессивные
интеллигенты, и она была смешанной. Девочки и мальчики учились
вместе. Это по тому времени было дерзостью. На всех экзаменах
всегда присутствовал представитель учебного округа. Учащиеся все
это знали и старались показать отличные успехи. В гимназические
годы Андрей Николаевич увлекался и математикой, и естествозна-
нием, и историей, и социологией. Последнее увлечение было столь
серьезно, что первый научный доклад им был прочитан в универси-
тете в 1920 г. об исследовании новгородского землевладения в
XV—XVI вв. Правда, и в этом докладе при обработке данных
использовалась математика.
45
В 1918—1920 гг. Колмогоров участвует в строительстве желез-
ной дороги Казань—Екатеринбург (Свердловск) и самостоятельно
готовится к экзаменам экстерном за курс гимназии. В 1920 г. он
возвращается в Москву и получает без сдачи экзаменов аттестат за
курс гимназии. В этом же году Андрей Николаевич без экзаменов
поступил на математический факультет Московского университета и
• экзаменом по математике—на металлургический факультет инсти-
тута им. Менделеева. Сдав в первые месяцы все экзамены за первый
курс университета, он, как студент II курса, стал получать продо-
вольственный паек (16 кг хлеба, 1 кг масла в месяц), туфли на
деревянных подошвах смастерил себе сам. Но на жизнь все же не
хватало, и Андрей Николаевич параллельно с учебой в универси-
тете стал работать учителем математики и физики. Он активно уча-
ствовал в жизни педагогического коллектива. Был секретарем совета
и воспитателем в интернате.
В университете Колмогоров посещает только спецкурсы и семи-
нары. Тогда и решил он посвятить себя математике. Уже в возра-
сте 18 лет Андрей Николаевич написал первую выдающуюся науч-
ную работу, а в 19 лет—вторую. Обе из области теории функций
действительного переменного, но по совершенно различным направле-
ниям. Первая работа—об операциях над множествами, вторая —
элементарный пример суммирования функций с повсюду расходя-
щимся рядом Фурье. Это показывало, что его дарование обладает
редкой широтой. Во второй работе проявилась его конструктивная
сила, а в первой—сила абстрактного математического мышления.
Уже эти работы принесли Колмогорову мировую известность и
сыграли значительную роль в развитии теории функций. Андрей Ни-
колаевич создал первоклассные научные труды по математической
логике и геометрии с топологией. Его исследования по топологии
вошли во все учебники по этой науке. Но все же первое место в
научной работе Колмогорова занимают его труды по теории вероят-
ностей. В начале 30-х гг. возникла необходимость построения теории
вероятностей на новой основе. Система науки, выработанная еще в
XVIII столетии, устарела. Необходима была перестройка логиче-
ской основы науки и расширение ее применений. Обе эти задачи
были успешно решены Андреем Николаевичем. Он разработал новую
современную аксиоматику теорий вероятностей и по существу вновь
разработал всю систему изложения науки, описанную в его труде
«Основные понятия теории вероятностей», а также разработал новые
методы теории вероятностей. Они дали возможность применения
теории вероятностей в самых различных научных исследованиях.
По существу Колмогоров проложил* новые пути в развитии теории
вероятностей и ее приложений в области естествознания, техники,
механики, минералогии и др.
Андрей Николаевич—прекрасный организатор и руководитель
научной работы своих многочисленных учеников. Его учениками
являются видные ученые: академик^ А. И. Мальцев (1909*1967),
академик С. М. Никольский (род. в 1905 г.), академик М. Д. Ми-
46
лионщиков (1913—1973), член-корреспондент АН СССР А. М. Обу-
хов (род. в 1918 г.), академик И. М. Гельфанд (род. в 1913 г.),
академик Ю. В. Прохоров (род. в 1929 г.), действительный член
АН УССР Б. В. Гнеденко (род. в 1912 г.), действительный член
АПН СССР И. Я. Верченко (род. в 1907 г.) и др.
Андрей Николаевич—любознательный математик. Это* пожалуй,
основная движущая сила его научного творчества. Он—крупный
представитель тех областей математики, которые связаны с естест-
вознанием и техникой. В своих работах он является в той же мере
математиком, как и естествоиспытателем. Он утверждает, что мате-
матик, интересующийся естествознанием, должен понимать, в чем
состоит интересующая его естественнонаучная проблема, и уже затем
решать ее соответствующими математическими методами, может быть,
специально их разработав.
Ведя плодотворную научную работу, Андрей Николаевич всегда
принимал активное участие в общественной жизни, увлекался ту-
ризмом и альпинизмом, путешествовал по Северу, Уралу, Сибири,
Кавказу.
В начале 30-х гг. Андрей Николаевич стал профессором МГУ, а
затем и директором Математического института Московского уни-
верситета. В возрасте 36 лет Колмогоров был избран действительным
членом Академии наук СССР. А. Н. Колмогоров—член многих
иностранных академий наук и научных обществ (Франции, Англии,
США, Голландии, Венгрии, Румынии и др.); Многие иностранные
университеты избрали его своим почетным доктором.
Андрей Николаевич много внимания уделяет работе с учащими-
ся, проявляющими склонность к занятия^ математикой. При его
непосредственном участии были созданы физико-математические
школы в нашей стране, разрабатывались их программы, создавались
учебные пособия. Он сам много лет преподавал в физико-математи-
ческой школе-интернате при Московском университете. С момента
начала проведения всероссийских и всесоюзных математических, а
также и физико-математических олимпиад школьников он активно
участвует во всех мероприятиях по их проведению. Его работа в
оргкомитете и жюри, в методкомиссиях, встречи и беседы с участ-
никами олимпиад и членами жюри имеют неоценимое значение, в
деле воспитания юных математиков.
Андрей Николаевич-—лауреат Ленинской и Государственной пре-
мий, Герой Социалистического Труда. Он награжден пятью ордена-
ми Ленина, орденом Красной Звезды И другими наградами.
Занятие 8. Тема. Решение геометрических задач*
237. Окружность вписана в прямоугольный треугольник. Одна
из точек касания ее делит гипотенузу на части 6 см и 8 см. Най-
дите площадь треугольника.
* Занятия 8, 9, 10 отводятся на решение в основном планиметрических за-
дач. Сложность и тематика их различны., Но большинство задач нестандартны.
Они интересны и полезны с точки зрения развития геометрического кругозора.
47
238.	Через данную точку вну-
три круга проведите хорду наи-
меньшей длины.
239.	Определите площадь за-
штрихованной части полукруга
(рис. 15), радиус которого равен 7?.
240.	Три окружности радиусов
5 см, 10 см и 15 см касаются
внешне друг друга (рис. 16). а)
Найдите радиус окружности, про-
ходящей через центры окружнос-
тей. б) Найдите радиус окружности,
проходящей через точки касания
данных окружностей, имеющих
радиусы 14 см, 16 см, 18 см.
241.	Диагонали трапеции ABCD
взаимно перпендикулярны и равны
соответственно 12 см и 5 см. Най-
дите длину MN средней линии
трапеции.
242д. Найдите значение выра-
жения р—22+З2 —42 + 52 —62 +
+ ... Ч-9992—10002.
243°. Чтобы определить самого
смышленого из мальчиков А, Б, В,
Рис. 16
Г, им завязали глаза, положили каждому на голову либо зеленую,
либо желтую коробочку. Далее развязали глаза и сказали: «Пусть
каждый, кто видит больше зеленых Коробочек, чем желтых, встанет».
Все встали. «А теперь стойте до тех пор, пока кто-либо из вас не
определит, какого цвета коробочка у него на голове. Угадавший
будет считаться самым смышленым». Первым воскликнул А: «У меня
на голове зеленая коробочка!» Он оказался прав и сумел это дока-
зать. Какие коробочки были на голове у остальных и как А дока-
зал свое утверждение?
244\ Определите бесконечную геометрическую прогрессию,
в которой второй член равен 6, а сумма равна 0,125 суммы прогрес-
сии, составленной из квадратов членов данной прогрессии.
245к. Сумма третьего и девятого членов арифметической прогрес-
сии равна наименьшему значению трехчлена 2х2— 4х+10. Найдите
сумму одиннадцати первых членов этой прогрессии.
Занятие 9. Тема. Решение геометрических задач
246. В треугольнике АВС со сторонами АВ = 18см, ВС = 10см
и АС == 14 см из вершины С проведены высота, биссектриса и ме-
диана. Найдите отрезки, на которые они разделили сторону АВ.
247*. В круг радиуса R вписаны три равных круга, касающиеся
друг друга и данного круга, а также три равных круга, каждый
48
из которых касается двух вписанных кругов и данного круга, и
круг, касающийся трех первых вписанных кругов. Найдите радиусы
каждого из вписанных кругов.
248.	В окружность вписан четырехугольник, одна диагональ
которого проходит через центр окружности. Докажите, что проекции
противоположных сторон четырехугольника на другую диагональ
равны между собой.
249.	Внутри острого угла А дана точка В. Через эту точку
проведите прямую так, чтобы ее отрезок от В пересечения
с одной стороной угла был в два раза больше отрезка от В до пе-
ресечения с другой стороной.
250.	Постройте окружность данного радиуса R так, чтобы она
проходила через данную точку А и отсекала на данной прямой
отрезок данной длины а.
251.	На сторонах параллелограмма построены с внешней стороны
квадраты. Докажите, что их центры являются вершинами квадрата,
площадь которого равна части суммы площадей построенных
квадратов, сложенной с площадью данного параллелограмма.
252Д. Имеется лом двух сортов с содержанием никеля 5 и 40%.
Сколько нужно взять каждого из этих сортов, чтобы получить
140г сплава с содержанием никеля 30%?
253А. Докажите, что nV—5п3 + 4п делится на 120 при любом
натуральном п.
254к. Для уборки урожая было выделено несколько одинаковых ком-
байнов, которые могли убрать поле за 24 ч, если бы приступили
к работе одновременно. Но случилось так, что они приступали К ра-
боте один за другим через равные промежутки времени, а затем
каждый работал до окончания работы. За какое время было убрано
поле, если первый комбайн работал в 5 раз больше времени, чем
последний?
255к> При каких значениях параметра а неравенство ах2 + 2dx Jr
+ 0,5^0 выполняется на всей числовой прямой?
Занятие 10. Тема. Решение геометрических задач
256.	Постройте правильный треугольник АВС, если дана , его
сторона а и известно, что две стороны АВ, АС и биссектриса AD
проходят через три данные точки М, N, Р, лежащие на одной
прямой.
257.	Докажите, что если прямая проходит через середину одной
стороны треугольника и отсекает от второй стороны отрезок, рав-
ный третьей части этой стороны, считая от третьей стороны, то эта
прямая отсекает от продолжения третьей стороны отрезок, равный
этой стороне.
258.	Постройте четырехугольник по трем сторонам и двум углам,
прилежащим к четвертой стороне.
259.	В правильный треугольник со стороной а вписаны три
49
равные окружности, касающиеся друг друга и каждая двух сторон
треугольника. Найдите радиус окружности.
260.	В треугольнике проведена высота и в каждый из получив-
шихся треугольников вписана окружность. Докажите, что если ра-
диусы вписанных окружностей равны, то треугольник равнобедрен-
ный.
261.	Пятнадцать биллиардных шаров, диаметр каждого из кото-
рых равен 5 см, сложены так, что касательные к ним образуют
равносторонний треугольник. Определите стороны треугольника.
262.	Периметр треугольника равен 42 см, площадь его равна
84 см2, а радиус описанной около треугольника окружности равен
8,125 см. Найдите стороны треугольника.
263.	Докажите, что если через центр вписанной в прямоуголь-
ный треугольник окружности провести три прямые, параллельные
сторонам треугольника, то средний отрезок гипотенузы будет равен
сумме средних отрезков катетов, отсекаемых на них проведенными
прямыми.
264°. Запишите число 4 тремя двойками, используя математиче-
ские знаки и символы.
265Д. Докажите, что двадцатисемизначное число 333...3 делится
на 81.
266к. Решите систему уравнений: ( у/~У = 3
267к. В треугольнике с углом 120° стороны образуют арифмети-
ческую прогрессию с разностью 1 см. Найдите стороны треугольника.
Занятие 11. Т е м а. Комплексные числа
Решение многих задач физики и техники приводит к квадратным
уравнениям с отрицательным дискриминантом. Эти уравнения не
имеют решения в области действительных чисел. Но решение многих
таких задач имеет вполне определенный физический смысл. Значения
величин, получающихся в результате решения указанных уравнений,
назвали комплексными числами. Комплексные числа широко исполь-
зовал отец русской авиации Н. Е. Жуковский (1847—1921) при
разработке теории крыла, автором которой он является. Комплекс-
ные числа и функции от комплексного переменного находят приме-
нение во многих вопросах науки и техники.
Рассмотрим решение квадратного уравнения х2 + 1= 0. Отсюда
х2 =—1. Число х, квадрат которого равен —1, называется мнимой
единицей и обозначается i. Таким образом, i2 = —1, откуда / = К—1.
Решение квадратного уравнения, например х2—8х + 25 = 0, можно
записать следующим . образом: х — 4 ± И16— 25 = 4 + У —9 —
= 4 ± /9 • (—1) -= 4 ± 3 • У— 1 = 4 ± 3f.
Числа вида 4 + 3/ и 4 — 31 называются комплексными числами.
В. общем виде комплексное число записывается а + Ы,. где а и Ь —
действительные числа, а /-—мнимая единица. Число а называется
50
действительной частью комплексного числа, bi—мнимой частью
этого числа, b—коэффициентом мнимой части комплексного числа.
Сложение комплексных чисел. Суммой двух комплекс-
ных чисел z^a + bi и z2 = c + di называется комплексное число
z = (a -|-с) + (b + d)i.
Числа а -\-Ы и а—Ы называются сопряженными. Их сумма
равна действительному числу 2а, (а+ 6Z) +(a—Ы) = 2а.
Числа а-\-Ы и —а—bi называются противоположными. Их сумма
равна нулю.
Комплексные числа равны, если равны их действительные части
и коэффициенты мнимых частей: a + bi — C-\-di, если а —с, b — d.
Комплексное число равно нулю тогда и только тогда, когда его
действительная часть и коэффициент мнимой части равны нулю,
т. е. z — a-{-bi — 0, если а = 0 и 6 = 0.
Действительные числа являются частным случаем комплексных
чисел. Если 6 = 0, то а-\-Ы = а—действительное число.
Если а = 0, ab#=O, то а -\-Ы = Ы—чисто мнимое число.
Для комплексных чисел справедливы переместительный и соче-
тательный законы сложения. Их справедливость следует из того, что
сложение комплексных чисел по существу сводится к сложению
действительных частей и коэффициентов мнимых частей, а они яв-
ляются действительными числами, для которых справедливы указан-
ные законы.
Вычитание комплексных чисел определяется как дейст-
вие, обратное сложению: разностью двух комплексных чисел а + Ы
и с называется комплексное число x-{-yi, которое в сумме
с вычитаемым дает уменьшаемое. Отсюда исходя из определения
сложения и равенства комплексных чисел получим два уравнения,
из которых найдем, что х = а—с, у = Ь—d. Значит, (а-{-Ы)—
— (c + di) = (a— c) + (b— d) i.
Произведением комплексных чисел ^ = a + 6i и
z2 = c + di называется комплексное число z = (ac—bd) + (ad + be) it
(a + bi) • (c + di) = (ac~^ bd) + (ad + be) i.
Легко проверить, что умножение комплексных чисел можно вы-
полнять как умножение многочленов с заменой i2 на —1.
Для умножения комплексных чисел также справедливы перемес-
тительный и сочетательный законы, а также распределительный
закон умножения по отношению к сложению.
Из определения умножения получим, что произведение сопря-
женных комплексных чисел равно действительному числу:
(а + Ы) (а—Ы) = а2 + 62.
Деление комплексных чисел, кроме деления на нуль,
определяется как действие, обратное умножению. Конкретное пра-
вило деления получим, записав частное в виде дроби и умножив
числитель и знаменатель этой дроби на число, сопряженное со зна-
менателем:
z j ,.х #	-_(а+bi) (с— di)_(ac-j-bd) + (be—ad)i ___ ас-{-bd у be— ad
{a + oi):\cTai) — (c+dr) —	c2+d?	:
51
i.

Степень числа i является периодической функцией пока-
зателя с периодом 4. Действительно, i2 = —1, i3 —— i, i* = l,
=	=!«== 1, ^«+1 = 1, f4« + 2 = _li /4»+»=—j.
Задачи и упражнения
268.	Выполните действия над комплексными числами:
а) (5—12/)-(3 + 4г); б) (2 +Зг)-(1 +1).
269.	Найдите х и у, если:
а)	(5х—Зу) + (х—2у) i — 6 + (8—х—у) i;
б)	(5х—10) +(Зг/—4)1 = 0.
/ 1 уГ "о \з / 1	1/*"з М
270.	Выполните действия: а) (у—; б) (—fl—J ;
в) (1-1УЗ)»; г)	.
271	А. Найдите все двузначные числа, которые на 9 больше суммы
квадратов их цифр.
272д. В параллелограмме проведены биссектрисы углов между
диагоналями. Докажите, что их пересечения со сторонами паралле-
лограмма будут вершинами ромба.
273к. Найдите наибольшее и наименьшее значения функции
z/ = 2x?—39х34-252х+1 на [5; 8].
274к, В треугольнике ABC Z А = 45°, /	75°. На стороне АВ
как на диаметре построена окружность, которая пересекает стороны АС
и ВС в точках D и Е. Определите площадь треугольника АВС,
если DE = 1.
Занятие 12. Тема. Тригонометрическая форма
комплексного числа
Умножение, деление, возведение в степень и извлечение корня
удобно выполнять над комплексными числами, записанными в три-
гонометрической форме.
Пусть дано комплексное число z = a + bi. Проведем оси коорди-
нат (рис. 17). Действительную часть комплексного числа будем от-
кладывать на оси абсцисс, а коэффициент мнимой части — на оси
ординат. Тогда комплексное число z изобразится точкой А (а, в).
Длина радиуса-вектора ОА называется модулем комплексного
числа. Ее принято обозначать буквой г: г = | z | = а2 + Ь2. Угол АО В
называется аргументом комплексного числа: ф — argz, =
Очевидно, что а = г cos ф, b = г sin ср. Тогда число z запишется в виде
z = а + bi = г cos ф + ri sin ф — г (cos ф + i sin ф).
Такая запись комплексного числа называется тригонометрической
формой комплексного числа.
52
Умножение и деление комплексных чисел, запи-
санных в тригонометрической форме. Пусть
Zi = i\ (cos Фх + i sin фх), z2 = г2 (cos ф2 + i sin ф2),
тогда:
2i • z2 = (cos фх + i sin фг) • r2 (cos ф2 + i sin ф2) =
= rrr2 ((cos фг • cos ф2 — sin фх • sin ф2) + i (cos фх sin ф2 + sin фх • cos ф2)) =
= r±r2 (cos (фх + ф2) + i- sin (фх + ф2)),
т. e., чтобы перемножить два комплексных числа в тригонометри-
ческой форме, надо перемножить их модули, а аргументы сложить.
Для нахождения частного комплексных чисел, записанных
в тригонометрической форме, надо разделить их модули, а из аргу-
мента делимого вычесть аргумент делителя:
г 1 (cos cpi+г sin <рх): r2 (cos <p2+i sin <р2) = ~ (cos (<Pi—<p2)+i sin (<рх—<p2)).
Из правила умножения комплексных чисел в тригонометрической
форме получаем правило возведения комплексного числа в натураль-
ную степень:
(г (cos ф + i sin ф))" = rn (cos п ф + i sin пф).
Корнем из комплексного числа г (cos ф + i sin ф) на-
зывается такое комплексное число (cos фг + i sin фх), n-я степень
которого равна данному комплексному числу г(со5ф + i зтф):
У г (cos ф + i sin ф) = f\ (cos фх + i sin фх).
Из определения корня следует, что (г1(созф1+fsin^i))" ~
= г (cos ф + i sin ф), т. е. г? (cos n^t + i sin n фг) = r (cos ф + i sin ф).
Отсюда имеем rj = r, т. е.	/гф1 = ФЧ-2лй, ф1==2^^,Где
& = 0, 1, 2, 3, ..., (и—1) — всего имеем и различных значений
аргумента фх и соответственно п различных значений корня.
Пример. Найдем все значения корня третьей степени из еди-
ницы.
53
Решение. Сначала данное
число запишем в тригонометриче-
ской форме: z=l = cos 0 + i sin О,
Z — X3, х3 = 1,
х,= И =
з/--а 1 ♦  —а	0-{-2л& ,
= т/ cos 0 +1 sin 0 =cos --р
у	о
. . . О -4— 2л&	1 а 1 п
+ rsin—, 6 = 0; 1; 2.
о
Xt = cos 0 + i sin 0 = 1;
2л ... 2л 1 . .V* 3
х2 = cos -3-+1 sin-jj- = —2-4-1^-,
4л ... 4л 1	.1^*3
х3 = cos-3-4-1 Sin-y- = —J— 1~~ .
Замечание. При решении подобных примеров полезно исполь-
зовать геометрическую интерпретацию комплексного числа (рис. 18).
Практически для извлечения корня n-й степени из числа z надо
провести окружность радиуса У | г | с центром в начале координат,
разделить ее на п равных частей, начиная от точки, соответствующей
, и записать все комплексные числа, изображаемые полученными
точками окружности.
Задачи и упражнения
275.	Представьте в тригонометрической форме число:
a) 3 + 3*; б) 5—5i; в) Т +
Представьте в алгебраической форме число:
276.	12 (cos 330° + i sin 330°).
277.	15(cos( —у) 4-isin(—.
278.	Докажите, что | zx 4- z2|2 + |zt—z2|2 = 2|z1|2 + 2|z2|2,
12__5 ।
z~+5
/ i 1/л"з \48
280.	Найдите значение степени комплексного числа (-у ~Н -^-у )
записав предварительно это число в тригонометрической форме.
]- fl/" 3 Д« / _|
----2”^—)	/
равно 2, если п кратно .3, и равно —1,. если п некратно 3.
282Д. Найдите четырехзначное число, которое увеличивается
в 4 раза при перестановке его цифр в обратном порядке.
283°. Постройте множество точек, заданное уравнением | у | +1 х |—4.
54
(I . 2x—8	18—4x
X — V < “fi-'—ч—
/х—2	2 \	5
9—(—r-+ t*) >* —o-.
\ 4 1 3 /	3
285K, Исследуйте функцию у — x3—9x и постройте ее график.
Занятие 13. Тема. Решение двучленных
и трехчленных уравнений
Пример. Решим уравнение х4 + 1 = 0.
Решение. хк=у— ! = / cosn;+isinn.=cos——+tsin—,
k = 0, 1, 2, 3;
л ... л У"2 . . V"2
x$ = cos-^- + i sin-j-=+y- +i~2~
Задачи и упражнения
Решите уравнение:
286. а) хв+1=0; б) х8 —1=0.
287. а) х24 — 1 = 0; б) х24 + 1 = 0.
288. Вычислите г2* +	, если известно, что z + у = 1.
Решите уравнение:
289. xu + x10 + x9 + xs + x’ + xe + x5 + x* + x3 + x2 + x+ 1 =0.
290. х6 *—65х3 = —64.
291. а) Xе—33x3 + 32 = 0; б) 16х8—49х4 +3 = 0.
292Д. Даны окружность с центром О и точка М вне ее. С по*
мощью одной линейки проведите через точку окружности диаметр,
перпендикулярный касательной, проведенной к окружности из точ-
ки М, через ту же точку окружности
проведите хорду, перпендикулярную
ОМ.
293Д. По окружности длиной
800 м едут два велосипедиста снача-
ла в одном направлении, а потом в
противоположных. В первом случае
первый велосипедист обгоняет второ-
го через каждые 24 мин, а во втором
они встречаются через каждые 3 мин.
Найдите скорости велосипедистов.
294к. Постройте график функции
/(х) = х2 —|х|.
295к. Найдите координаты то-
чек касания, в которых касатель-
55
Рис. 19
равный 4.
Занятие 14. Тема. Построение графиков функции*
296.	Дан график функции y = f(x). Построим график у = — f(x).
Новый график (рис. 20) будет симметричен данному относительно
оси Ох.
297.	Дан график функции y = f(x). Построим график y=^f(—х).
Новый график (рис. 21) будет симметричен данному относительно
оси Оу.
298.	Дан график y = f(x). Построим график у = [(х) + а. Новый
график получается параллельным переносом данного графика па-
раллельно оси Оу на а единиц (рис. 22).
299.	Дан график y=zf(x). Построим график £/ = /(хЦ-6). Новый
график получается параллельным переносом данного вдоль оси Ох
на —b единиц (рис. 23).
* На занятиях 14—17 рассматриваются различны^ преобразования, позво-
ляющие строить графики довольно сложных зависимостей.
56
300.	Дан график z/ = /(x). Построим график y = f~1(x). Здесь
/~г(х) обозначает функцию, обратную данной. Для получения функ-
ции, обратной y — f(x), надо поменять ролями функцию и аргумент,
сделав функцию аргументом, а аргумент—функцией. Практически
в зависимости y=f(x) меняют местами обозначения х и у. Полу-
чают функцию, обратную данной, в неявном виде: x = f(y). Отсюда
выражают у через х и получают функцию, обратную данной, в явном
виде. Ее обозначают y = f~1(x}. Новый график симметричен данному
относительно биссектрисы I и III координатных углов (рис. 24).
301.	Дан график у = [(х). Построим график y = kf(x), где k > 0.
Новый график получается растяжением данного графика от оси Ох
в k раз (рис. 25).
302.	Дан график у —/(х). Построим график y = f(kx), где k > 0.
Новый график получается сжатием данного графика к оси Оу
в k раз (рис. 26).
Задачи и упражнения
303.	По графикам функций y = f(x) и у = <р(х) постройте гра-
фик функции: а) у==/(х)<р(х); б) У = ^', в) У = ц^ 1 г) y = f(x) +
+ <р(х); д) t/ = |f(x)|; е) у = /(|х|).
304°. Восстановите цифры в записи решения примера:
* 3 «•
» 7
* « *
*	0 * «
*	* » » 8
305д. Отец в 5 раз старше сына. Отец окончил институт в воз-
расте 22 лет. С тех пор прошло время, равное половине того,
которое требуется сыну, чтобы ему стало тоже 22 года. Сколько
лет сейчас сыну и сколько отцу?
57
306к. Решите систему уравнений:
х—z/4-Кх2— 4z/? = 2
xs Кх2—4у2 = 0.
307к. На плоскости лежит равнобедренный прямоугольный тре-
угольник, у которого катеты имеют длину а. Поворотом данного
треугольника вокруг вершины прямого угла на угол 45° получается
другой равнобедренный треугольник. Найдите площадь четырех-
угольника, являющегося общей частью этих двух треугольников.
Занятие 15. Тема. Построение графиков функций
308.	По графику функции У — ^ путем преобразования построй-
те график функции у = 3 (J—2) 4'
309.	Дан график функции iy = log2x. Постройте график:
а) у= — 4 log2(3x +3)4-3; б) у = 2 log2 х+ 1)— 3.
310.	Постройте график функции:
a) z/ = |-22*-2 + 3; б) у = -^.2~^ + 3;
в) у = х + ±-	Г) =	^=.
311Д. Найдите сумму всех чисел таблицы:
1,	2,	3,	4,	.......... 99,	100
2,	3,	4,	5................ 100,	101
100,	* 161,’ ’ 102, ’ ’ 103*, ' ’. *. *. ’.	198, ’ 199
312Д. Найдите двузначное число, которое при делении на цифру
единиц дает в частном цифру единиц, а в остатке цифру десятков.
313к. Дан прямой угол и окружность радиуса R, центр которой
лежит на продолжении (за вершину) одной из сторон угла на рас-
стоянии у от его вершины. Определите радиус окружности, вписан-
ной в данный угол и касающейся извне данной окружности.
314к. Площадь равнобедренной трапеции,- в которую можно
вписать окружность, равна 2 см2. Определите стороны трапеции,
если угол при основании равен 30°.
Занятие 16. Тема. Построение графиков функций
Постройте график функции:
315.	у = х1 —2х24-2.
316.	a) £ = log,i |х—3|; б) у = loga]х|.
317.	^ = £±+1.
* X
58
318.	По графику функции у — — х2 Ц- 1 постройте график функ-
ции у = —F+T-
1
319.	Постройте график функции t/=l°g2
320.	Определите, четна или нечетна функция
f (*)=1g (V 9tg2x+l + 3 tg х).
321°. Для игры школьники разбились на 2 партии: «серьезные»,
отвечающих правильно на любой вопрос, и «шутников», дающих на
любой вопрос только неправильный ответ. Учитель спросил Ива-
нова, серьезный он человек или шутник. Не расслышав ответа Ива-
нова, он спросил у Панькина и Демина: «Что ответил мне Иванов?»
Панькин сказал: «Иванов ответил, что он серьезный человек»,
а Демин сказал: «Иванов ответил, что он шутник». Кем были Пань-
кин и Демин?
322Д. Докажите, что число /г5 * * *—20/г3 + 64/г, где четное п > 4,
делится на 1920.
323к. В равнобедренную трапецию вписана окружность. Расстоя-
ние от центра окружности до точки пересечения диагоналей тра-
пеции относится к радиусу окружности как 3:5. Найдите отноше-
ние периметра трапеции к длине вписанной окружности.
324к. Решите неравенство ]/ 4—К1—х—У'2—х > 0.
Занятие 17. Тема. Графики тригонометрических функций
По данным графикам основных тригонометрических функций
постройте с помощью их преобразований график функции:
325. у = — lsin(2x—3) + 4. 326. у=Л cos ( — Тх + 2Нз.
327. y = |sin-i-х|.	-328. z/*=sin| i-d-
329. # = y tg —1)4-2.	330. z/ = jy cos 0,5x|.
331°. Двое продали гурт скота и выручили за каждую голову
столько рублей, сколько голов в гурте. Чтобы разделить выручку,
они стали поочередно брать из нее по 10 р. После того как первый
взял последние 10 р., второму осталось меньше Ю р. Сколько руб?
лей первый должен вернуть второму, чтобы .каждый получил по?
ровну?
3329. Восстановите цифры в записи решения примера:
5 *
5*1
5 * *
* * 5 *
* * * 5
* * * 5 * *
59
333к. Решите уравнение
lg(3-4x)
334к. Даны функции /(х) =
"4 — 15х2—2х3 и ф(х) = 2х3 +
4-18x4-1. При каких значениях
х будет выполняться неравенство
Занятие 18. Тема. Построе-
ние сечений многогранников*
Примеры
1. Построим сечение четыреху-
гольной призмы ABCDA^BfiJ)^
проходящее через данные точки
Л4, N, Р, где Me AA^N^DD^
PeCCt (рис. 27).
Решение. Используем метод следов. Суть метода следов заклю-
чается в том, что сначала находят линию пересечения секущей пло-
скости с плоскостью основания данного многогранника—след секу-
щей плоскости на плоскости основания многогранника. Затем про-
водят плоскость через определенные ребра многогранника и данные
точки. Получают на следе секущей плоскости точки пересечения
вспомогательной плоскости—следы, являющиеся одновременно точ-
ками пересечения прямых, проходящих через данные точки и лежа-
щие в секущей плоскости. Эти прямые позволяют найти другие
точки пересечения секущей плоскости с ребрами многогранника.
Для удобства рассуждений в данной задаче секущую плоскость
назовем а, а плоскость основания —|3. В плоскости грани AAJJJD
проведем прямую MN. Она пересечет прямую AD в точке Е.
В плоскости грани DDfifi проведем прямую PN. Она пересечет
прямую CD в точке Г; FE—линия пересечения плоскостей а и р.
Проводим плоскость BBJJJD и в ней прямую через точку N и точ-
ку Л— пересечения этой плоскости с EF. Эта прямая лежит в а
и пересекает ребро ВВ1 в некоторой точке R. Соединив R с М
и с Р, получим искомое сечение MNPR (см. рис. 27).
2. Построим сечение прямой четырехугольной призмы плоско-
стью, проходящей через точки 7И, N, Р, где М ^АВВ1А1, N£
^BBfifi. Р^ВВ1 (рис. 28).
Решение. Используем способ построения внутренних допол-
нительных плоскостей. Так как М^А^ВА и Р^Л^ВЛ, то
РМ(}АА1 = Е, где а — секущая плоскость. Аналогично Р и
N принадлежат BfifiB. Значит, PNczBfifiB и PN
* Учащихся можно познакомить с двумя способами построения сечений:
способом следов и использованием вспомогательных внутренних сечений.
60
Для нахождения точки пересече-
ния плоскости другим ребром про-
водим через параллельные ребра
ААг и ССГ плоскость р. В этой
плоскости лежат точки Е и К.
Значит, ВЛ ср. Через BBt и DDr
проводим плоскость у, pfly^OOf,
001П ЕК == R, т. е. EKcza.
Так как и 7?С<х, то PRcza,
PRnDD1 = F. Соединим точку F
с точками Е и Л, получим сечение
призмы плоскостью a: EPRF —
искомое сечение.
Задачи и упражнения
335.	В правильной четырех-	Рис- 26
угольной пирамиде проведите сече-
ние через середины двух ребер основания, выходящих из одной вер-
шины, и середину ребра, не имеющего общих точек с указанными
ребрами основания.
336.	В прямой пятиугольной призме проведите сечение через
две точки, лежащие в смежных боковых гранях, и точку, лежащую
в несмежной с ними боковой грани.
337.	В кубе ABCDA^fiJ)^ проведите сечение через вершину Л,
середину ребра ВС и центр грани DCCJ)V Вычислите площадь
сечения, если ребро куба равно а.	________
338А. Найдите целые значения х, при которых Их2—х+1—
целое число.
339°. Макс очень хотел пойти в кино. Билет стоил 1 марку
80 пенсов, а у Макса была сувенирная монета в 1 марку и еще
20 пенсов. Тогда он заложил ростовщику сувенирную монету и по-
лучил от него 80 пенсов и расписку о залоге. По пути в кинб он
встретил своего приятеля Генриха и предложил ему расписку ро-
стовщика за 80 пенсов. Генрих решил, что это выгодно, и купил
расписку. У Макса оказалось 1 марка и 80 пенсов. Он пошел
в кино. Кто и на сколько пострадал от этой операции?
340к. Основание AD трапеции ABCD вдвое длиннее основания
ВС и вдвое длиннее боковой стороны АВ. Найдите скалярное про-
изведение (ЛР-DC), если Л. В АС = а и площадь треугольника АВС
равна S.
341к. В основании треугольной пирамиды SABC лежит правиль-
ный треугольник АВС со стороной 1. Плоскости граней SAB и
АВС перпендикулярны, SA = SB, высота пирамиды равна 1. На ребре
5Л выбрана точка М так, что MA = 2SM, точка N— середина реб-
ра SC. Плоскость а проходит через точки В, /И, N. Найдите урав-
нение плоскости а.
61
Занятие 19. Тема. Решение задач
на сечения многогранников
342.	В прямоугольном параллелепипеде ABCDAlByC1D1 АВ —а,
AD = b, АА^с. Проведите сечение параллелепипеда плоскостью,
параллельной диагонали основания параллелепипеда и диагонали
параллелепипеда и пересекающей ось параллелепипеда в точке, от-
стоящей от верхнего основания параллелепипеда на расстоянии,
равном его высоты.
343.	Определите площадь сечения куба плоскостью, проходящей
через середины двух смежных ребер куба параллельно диагонали
дуба, пересекающей эти ребра, если ребро куба равно а.
344.	В* правильной четырехугольной пирамиде через вершину
нижнего основания проведите сечение перпендикулярно противопо-
ложному боковому ребру. Найдите площадь построенного сечения,
если боковое ребро пирамиды равно а и образует с основанием
угол а.
345.	В кубе с ребром а проведите сечение, проходящее через
центр куба и середины двух ребер куба, выходящих из одной вер-
шины. Вычислите площадь полученного сечения.
346.	В правильной шестиугольной пирамиде проведите сечение
через середины двух смежных сторон нижнего основания и середину
бокового ребра, выходящего из вершины противоположной той, из
которой выходят две первые стороны основания.
347°. Запишите произвольное целое число п с помощью трех
двоек, используя математические знаки и символы.
348°. Мужчины одной семьи, в которой было два отца, два сына,
дед и внук, за обед в ресторане должны были уплатить поровну
9 р. 90 к. Расплачивался каждый отдельно. Сколько пришлось каж-
дому заплатить за свой обед?
349к. Среди равнобедренных трапеций с острым углом 45° и сум-
мой длин высоты и большого основания, равной аг найдите трапе-
цию наибольшей площади.
350к. В правильной четырехугольной пирамиде плоский угол при
вершине равен 60°. Докажите, что один из двугранных углов этой
пирамиды вдвое меньше другого.
Зшнятие 20. Тема. Н. И. Лобачевский
Николай Иванович Лобачевский родился 1 декабря 1792 г.
в Нижнем Новгороде (ныне г. Горький) в семье мелкого чиновника.
В семилетием возрасте он лишился отца, и его мать Прасковья Ива-
новна переехала с тремя детьми в Казань, где она стала готовить
детей к поступлению в гимназию. В 1802 г. Николай и его братья были
зачислены в гимназию на казенное содержание. Успехи Николая
п1 гимназии по математике и древним языкам были феноменальны.
В 14 лет он был подготовлен для поступления в университет и
в 1807 г. был зачислен в Казанский университет.
62
В возрасте 18 лет Лобачевский получил степень магистра с отли-
чием, минуя ученую степень кандидата наук, и был оставлен при
университете. В 1814 г. он был утвержден адъюнктом чистой мате-
матики, а в 1815 г. в возрасте 23 лет ему было присвоено звание
профессора. Лобачевский читал лекции по математике, астрономий,
физике. Лектор он был блестящий. С 1827 по 1846 г. Лобачевский
был ректором Казанского университета, а с 1846 г.— заместителем
попечителя Казанского учебного округа.
Научная деятельность Н. И. Лобачевского. Откры-
тие неевклидовой геометрии. Более 2200 лет в мире гос-
подствовала единственная геометрия—геометрия Евклида. В основе
геометрии Евклида лежит система аксиом, т. е. первоначальных
истин, принимаемых без доказательства. Все остальные утвержде-
ния—теоремы—доказываются на основе этих аксиом и уже дока-
занных теорем. Во все времена у ученых вызывал сомнение пятый по-
стулат— аксиома о том, что через точку вне прямой можно провести
прямую, параллельную данной, и притом только одну. У Евклида
он сформулирован несколько иначе, сложнее. Но современная его
формулировка и формулировка Евклида в научном отношении рав-
носильны. У Евклида было сказано: «И если прямая, падающая на
две прямые, образует внутренние и по одну сторону углы, меньШйе
двух прямых, то продолженные эти две прямые неограниченно встре-
тятся о той стороны, где углы меньше двух прямых». Формулировка
этой аксиомы казалась больше похожей на теорему. Но попытки
ее доказательства приводили только к замене этой аксиомы другой,
ей равносильной. Правда, эти попытки часто давали значительный
толчок в развитии различных областей геометрии. Только Николай Ива-
нович Лобачевский показал, что пятый постулат нельзя доказать,
опираясь только на остальные аксиомы Евклида и следствия и? них.
Более того, он показал, что если пятый постулат заменить другим,
не эквивалентным евклидову, то получится новая геометрия... Лоба-
чевский предположил, что вполне правомерно допущение о том, что
через точку вне прямой можно провести к данной прямой две пря-
мые, ей параллельные: левую параллельную к данной прямой Я
правую параллельную прямую. Этой аксиомой он заменил пятый
постулат Евклида и развил на основе новой системы аксиом свою
геометрию. Она оказалась очень стройной и впоследствии нашла
свое практическое и научное, применение.
Впервые свое открытие Лобачевский дбложил на заседании совета
отделения физико-математических наук .Казанского, университета
в 1826 г., а опубликовал в 1829 г. Надо сказать, что создание
новой геометрии Лобачевским нанесло сокрушительный удар пр
философам-идеалистам. Их глава И. Кант утверждал, что единственно
возможной, раз и навсегда данной свыше является геометрия Евк-
лида. Лобачевский это опроверг. Причем открытие Лобачевского
повлекло за собой ряд новых открытий,ш в частности еще одрой гео-
метрии-—геометрии Римана, в которой вообще нет параллельных
и сумма углов любого треугольника больше 180°. Но современники
63
Лобачевского в своем большинстве не поняли его открытия. Един-
ственные ученые, которым было понятно это открытие, были К. Гаусс
и Я. Больяи. Гаусс независимо от Лобачевского пришел к анало-
гичным идеям, но, боясь критики современников, так и не опубли-
ковал их. Я. Больяи опубликовал свое открытие несколько позже
Лобачевского. Но описание было очень кратким и не содержало
изложения всей геометрии. Вероятно, ученые чувствовали величие
открытия Н. И. Лобачевского. Поэтому никто открыто против него
выступить не осмелился. В России в одном из журналов была
опубликована статья против Лобачевского, но и это была не науч-
ная статья, а пасквиль. Его автор даже не посмел указать свою
фамилию.
Аксиома Лобачевского не противоречит основным математическим
утверждениям. Ее непротиворечивость может быть разъяснена на
основе тех математических понятий, которые имеются у учащихся
IX—X классов, на основе понятия предела последовательности.
Действительно, пусть дана прямая а и точка А вне ее. Опустим
перпендикуляр AD на а. Будем откладывать на прямой а вправо
и влево от точки D точки на равных расстояниях друг от друга.
Обозначим их соответственно В1У В2, В31 ..., Вп, ... иСь С3, С3, ...
..., Сп, ... . Через точку А и каждую из построенных точек про-
водим прямые. Углы этих прямых с перпендикуляром AD обозначим
соответственно а1? а2., а3, ..., ап, ....... и р2,' Рз, • • •» Рл» • • • •
Каждая из этих последовательностей возрастающая. Они обе беско-
нечны и ограниченные, так как ни один из углов не может быть
больше прямого. Значит, по признаку Вейерштрасса каждая из
указанных последовательностей имеет предел. Обозначим эти пре-
делы а и р. Углы аир принято называть предельными углами.
Им соответствуют положения вторых сторон АВ и АС углов (первая
сторона АО). Эти прямые АВ и АС называются предельными пря-
мыми. Предельные прямые не могут пересекать прямой а, так как
в противном случае мы получили бы члены последовательности,
превосходящие аир, что невозможно. Предельные прямые АВ и АС
называются правой и соответственно левой прямой, параллельной а
и проходящей через точку А. Ниоткуда не следует, что эти прямые
должны совпадать. Если предположить, что они совпадают, получим
геометрию Евклида, а если предположить, что они не совпадают,
то получим геометрию Лобачевского. Обе геометрии одинаково верны
и непротиворечивы. В геометрии Лобачевского предельные углы а и
Р называются углами параллельности в точке А относительно пря-
мой а. Лобачевский показал, что с увеличением длины отрезка AD
угол параллельности уменьшается. В геометрии Лобачевского сумма
углов треугольника меньше 180°. Причем с увеличением длины
сторон треугольника она уменьшается. В геометрии Лобачевского
нет подобных фигур. Если углы одного треугольника равны углам
другого, то треугольники будут равны. При малых размерах фигур
угол параллельности практически не отличается от прямого, а сумма
углов треугольника мало отличается от 180°. Все теоремы и фор-
64
с
A	D	N	В
Рис. 29
мулы геометрии Лобачевского в этом случае совпадают с соответ-
ствующими теоремами и формулами геометрии Евклида. В ге-
ометрии Лобачевского углы треугольника однозначно определяют
длину его сторон.
В математике очень важна не только геометрия на плоскости,
но и на различных криволинейных поверхностях: на сфере, пара-
болоиде, гиперболоиде и др. Если на плоскости кратчайшее расстоя-
ние—длина отрезка прямой, соединяющей две точки, расстояние
между которыми мы находим, то на криволинейной поверхности две
точки чаще всего нельзя соединить отрезком прямой, лежащим на
этой поверхности. На криволинейной поверхности кратчайшее рассто-
яние между двумя точками измеряется отрезком геодезической линии,
т. е. линии, дающей кратчайшее расстояние между этими дву-
мя точками. Например, на сфере линиями, дающими кратчайшее
расстояние между двумя точками, являются дуги больших кругов,
проходящих через эти точки. Углами между ними будут углы, обра-
зованные касательными, проведенными в точке пересечения дуг. Ясно,
что сумма углов любого криволинейного треугольника, образован-
ного дугами больших кругов, будет больше 180°. Очевидно, что
через две точки, не лежащие на концах одного диаметра, можно
провести только один большой круг. Следовательно, расстояние
между двумя точками и здесь единственно.
Если мы начертим на плоскости трактрису — линию, определяе-
мую уравнением	—------У~ а2—у2^ (рис. 29), и
будем ее вращать вокруг оси Ох, то получим
поверхность, называемую псевдосферой (рис. 30). ЖЧ
Геометрия на псевдосфере является геометрией Ж -А
Лобачевского. В частности, сумма углов треу-	\
гольника на псевдосфере меньше 180°. С увели-
чением размеров треугольника сумма его углов '
уменьшается, с увеличением суммы углов его сто-
роны уменьшаются. При неограниченном умень-	~ ""3^
шении сторон треугольника сумма его углов стре-	•* у
мится к 180°. На псевдосфере верны все формулы	$
геометрии Лобачевского. На предельной поверх- W $
ности, получаемой вращением предельной пря- Ж/
мой вокруг перпендикуляра AD, справедлива
геометрия Евклида, если только заменить Рис. 30
3 № В671
65
прямые предельными линиями, являющимися на предельной поверх»
ности геодезическими линиями.
Рассмотрение предельной поверхности позволило Лобачевскому
вывести все формулы неевклидовой геометрии, разработать аналити-
ческую геометрию и другие вопросы из области открытой им геомет-
рии. Основные результаты по новой геометрии Лобачевский изложил
в трудах «О началах геометрии с полной теорией параллельных»
(1840), «Всеобщая геометрия» (иначе «Пангеометрия», 1855).
Н. И. Лобачевскому принадлежат серьезные исследования по
многим вопросам алгебры и математическому анализу. Многие из
его научных трудов в этих областях не потеряли своего значения
и в наше время.
Деятельность Н. И. Лобачевского на посту рек-
тора университета. Молодой Казанский университет нуждался
в налаживании учебного процесса, оснащении оборудованием и стро-
ительстве учебных и лабораторных зданий. До начала работы Лоба-
чевского в университете фактически не действовала научная библио-
тека, без которой невозможна самостоятельная исследовательская
работа студентов, да и не только студентов.
Лобачевский поднял на большую научную высоту преподавание
физико-математических наук и вообще естественных дисциплин. Он
развернул большие строительные работы. Была выстроена астроно-
мическая обсерватория, аналитический музей, физический кабинет,
прекрасная библиотека, клиника. Лобачевский изучил архитектуру
и сам участвовал в разработке проектов зданий университета и их
строительстве. В 1834 г. под руководством Лобачевского начали
издаваться «Ученые записки» Казанского университета. В бытность
ректором он оказывал большую помощь преподавателям математики
всех учебных заведений Казанского учебного округа. В Г&ЗО г. в
Казани разразилась эпидемия холеры. Она унесла огромное коли-
чество жизней. Чтобы спасти преподавателей и студентов, Лобачев-
ский поселил их вместе с семьями в университете. Это помогло
избежать трагедии, подобной той, которая постигла город. ’
К сожалению, царское правительство не проявило заслуженного
внимания к Лобачевскому как ученому. В 1846 г. исполнилось 30 лет
его педагогической деятельности. По положению он должен был
уйти в отставку. Лобачевский был в это время в расцвете творче-
ских и физических сил. Ученый совет университета единогласно
проголосовал за то, чтобы оставить его еще на 5 лет в должности
профессора университета, а значит и ректора. Это допускалось
положением, н^ решение должен был утвердить министр просвеще-
ния. Министр отказал в просьбе совету, Лобачевский был назначен
помощником попечителя Казанского учебного округа, человека
весьма недалекого, невежественного. Лобачевский фактически ли-
шился возможности ведения плодотворной научной работы^ повсе-
дневного общения, с учеными университета. Это был удар, который
подорвал здоровье Николая Ивановича. Вскоре умер его сын. Смерть
сына окончательно сломила Лобачевского. Он начал слепнуть и
60
вскоре совсем потерял зрение. Последний свой труд—«Пангеомет-
рию» он диктовал, будучи слепым. Здоровье его быстро ухудшалось»
и 24 февраля 1856 г. Лобачевского не стало.
Лобачевский уделял большое внимание постановке преподавания
математики в гимназиях и других средних учебных заведениях.
Его суждения по методике преподавания математики не потеряли
значения и в наше время. Николай Иванович построил полный кура
тригонометрии, исходя из своей геометрии.
Занятие 21. Тема. Преобразование
тригонометрических выражений
Докажите тождество:
. I 4. о	SIH2--FT1-
351.	1=-------Ц-.
„ . а 4- В cos a cos р
2tg—
352.	cos2 x + cos2 + 4-cos2	•
353.	log , (cos2 (a 4- P) + cos2 (a—P) — cos 2a cos 2P) = 0.
T
354.	1 + cos(n 4-3a) cos 2a—cos	л—За) sin 2a = 2 sin2
355.	Преобразуйте данное выражение в произведение
tga+ tg р + tg у
sin (a 4-Р +у)
cos a cos [J cos у '
Вычислите без таблиц:
356.	(tg 30° 4- tg 40° 4- tg 50° 4- tg 60°) sec 200° ctg 300°.
357.	tg 9°— tg 27°— tg 63° 4- tg 81°.
Докажите тождество:
358, 16 sin 10° sin 30° sin 50° sin 70° sin 90° = 1.
359. tg 4a 4-sec 4a= cos2a ~‘ sin 2a.
&	cos 2a —sin 2a
360. -s-----:---5—:----=— = 2 sin a-sin 2a.
2 cos a 4- cos 3a 4- cos 5a
361д. Решите уравнение V x2 у x2 у x2 ... = 49.
362Д. Найдите значение выражения | 23	53 j/^23 j/"5* ....
363Д. Найдите косинус угла между векторами а+b и а—Ь9
если |о| = 2, |b| = 1, а угол между а и b равен 60°.
х 4“ 2
364к. В какой точке касательная к графику функции у —
образует угол 135° с осью Ох? Найдите уравнение этой касательной.
67
365к. На кривой у = х3—Зх3 + 2 найдите точки, в которых каса-
тельная параллельна прямой у = 3х. Напишите уравнение каса-
тельной.
Занятие 22. Тема. Преобразование тригонометрических
выражений
366.	Преобразуйте в произведение сумму
cos х + 2 cos 2% + cos Зх + cos lx + 2 cos 8% + cos 9x.
Докажите равенство:
367.	8 cos 20° cos 40° cos 80° = 1.
368.	sin475°4-4sin375°sin 15°+6 sin2 75° sin215°-j-4 sin 75° sin315°+
+ sin415° =-J.
369.	cos 2a—cos8 a + sin8 a = 4- sin 2a sin 4a.
4
Упростите выражение:
370 sin a+sin 2a -|- sin 3a 4-...+ sin na
cos a + cos 2a + cos 3a4~ ... 4-cosna ’
371.	cos a cos 2a cos 4a ... cos 2n a.
372.	Докажите равенство
tg4 2Г + ctg4 £ + tg4 & + ctg4 = 3332-
373.	Преобразуйте сумму в произведение
sin2 a + sin2 0 + sin2 (a 4- 0)—2.
374°. Найдите наименьшее число, при делении которого на 2
получается точный квадрат, а при делении на 3 получается точ-
ный куб.
375А. Вычислите произведение tg 1 °. tg 2° • tg 3° •... • tg 88° • tg 89°.
376к. В трапеции ABCD диагональ AC перпендикулярна боковой
стороне CD, а диагональ DB перпендикулярна боковой стороне АВ.
На продолжениях боковых сторон за меньшее основание трапеции ВС
отложены отрезки ВМ и CN так, что получилась новая трапеция
BMNC, подобная трапеции ABCD. Найдите площадь трапеции ABCD,
если площадь трапеции AMND равна S, а сумма углов CAD и BDA
равна 60°.
377к. Напишите уравнения касательных к кривой у = х\х—1)
в точкам пересечения ее с осью Ох.
378к. Найдите наибольшее и наименьшее значения функции у =
= Зх3—9х?4-2 в промежутке [—1; 1J.
X класс
Занятие 1. Тема. Комбинаторика
В математике и ее приложениях часто приходится иметь дело
с различного рода множествами и их подмножествами: устанавливать
связь между элементами каждого из них, определять число множеств
или их подмножеств, обладающих определенными свойствами. Такие
задачи приходится рассматривать при определении наиболее выгод-
ных коммуникаций внутри города, при организации автоматической
телефонной связи, работы морских портов, при выявлении связей
внутри сложных молекул, генетического кода, а также в лингви-
стике, в автоматической системе управления, а значит, и в теории
вероятностей и математической статистике со всеми их многочислен-
ными приложениями.
Наука, изучающая способы составления и количество множеств
и их подмножеств, называется комбинаторикой.
Каждое конкретное подмножество, составленное из элементов
данного конечного множества, называется соединением.
Если во множестве введено отношение порядка, т. е. определено,
какой элемент множества за каким следует или какому предшест-
вует, то множество называется упорядоченным. Если в упорядочен-
ном множестве изменить расположение элементов, то мы получим
другое, отличное от первого множество.
Мы познакомимся с тремя основными видами соединений: разме-
щениями, перестановками и сочетаниями.
Размещениями из п элементов по т называются упорядо-
ченные подмножества, каждое йз которых содержит т элементов
из и элементов данного множества. Размещения отличаются друг
от друга либо порядком элементов, дибо самими элементами.
Если некоторые элементы данного множества могут повторяться
в размещении, то такие размещения называются кортежами или
размещениями с повторениями. Число элементов в размещении на-
зывается его длиной.
Примеры.
1.	Пусть дано множество М = {#1, а2, а3, ...,ап}. Сколько кор-
тежей длины т можно составить из элементов этого множества?
Решение. Первый элемент каждого кортежа мы можем выбрать
п способами, записав на первое место любой из п элементов. Вто-
рой элемент тоже можно выбрать п способами и т. д. Значит, общее
число кортежей из множества п элементов, по т элементов в каж-
69
дом, будет равно пт. Число кортежей из п по т обозначается А™,
т. е. Ап=пт.
2.	Сколько четырехзначных чисел можно составить из 9 цифр:
1, 2, 3, 4, 5, 6, 7, 8, 9?
Решение. Цифры в числах могут повторяться, и число зави-
сит от порядка цифр в его записи. Значит^это размещения с повто-
рениями, т. е. кортежи. Их число равно Ад = 94 = 6561.
3.	Пусть имеем множество М. = {at, а2, а3, ..., ап}< Сколько раз-
мещений без повторения элементов, по т элементов в каждом, можно
составить из элементов этого множества? (В дальнейшем размещения
без повторений мы будем называть одним словом—«размещения».)
Решение. На первое место можно записать любой элемент из
М. Значит, имеем п возможностей. На второе место—любой эле-
мент, кроме выбранного на первое место. Итак, при каждом выборе
первого элемента для выбора второго имеем (п—1) возможностей,
т. е. для выбора двух элементов имеем п(п—1) возможностей. При
каждом выборе первых двух элементов для выбора третьего элемента
имеем п—2 возможности и т. д. На последнее m-е место можно за-
писать любой элемент, кроме выбранных т—1 элемента на преды-
дущие места, т. е. для его выбора имеем п—(т—1) = м—mfl воз-
можностей. Следовательно, всего размещений из п по т элементов
будет:
А% = п(п—1)(п—2).. .(п—т+ 1).
Полученное выражение состоит из т последовательных натуральных
множителей, наибольший из которых равен п. Умножив и разделив
полученное выражение на (п—т)\, получим
Лт__
~~ (п—т)\ •
4. В чемпионате участвует 12 команд. Сколькими различными
способами могут быть распределены три различные медали?
Решение. Л^2 = 12-11 • 10 = 1320.
Перестановки. Размещения из п элементов по п принято
называть перестановками. Иначе, перестановки—это упорядоченные
множества из п элементов по п. Перестановки отличаются друг от
друг! только порядком элементов. Число перестановок принято обо-
значать Рп.
Общее число перестановок из п элементов равно
Рп = А% = п-(п— 1)(п—2).. .3-2.1 =п!
Пример. Сколькими способами можно разместить за круглым
столом 12 человек?
Решение. Одно размещение от другого может отличаться толь-
ко порядком размещения людей, т. е. имеем перестановки 12 эле-
ментов: Р12 = 12!
70
Сочетания. Сочетаниями из п элементов по т называются
соединения, каждое из которых содержит т элементов из данного
множества п элементов и отличается от других хотя бы одним эле-
ментом.
В сочетаниях нас интересуют только сами элементы множества
й не интересует их порядок. Важно, какие конкретно элементы мно-
жества входят в каждое соединение.
Число сочетаний, т. е. число всех различных подмножеств дли-
ны т из данного множества, содержащего п элементов, обозначает-
ся С%. Легко видеть, что если мы возьмем все сочетания из п эле-
ментов по т и в каждом из них упорядочим элементы всеми воз-
можными способами, т. е. из каждого сочетания получим все воз-
можные перестановки, то получим все размещения из п элементов
Ат	Р
по т. Значит, А™ = С™ • Рт. Отсюда С ™ = ~~ или С% ==	. Иначе:
Счп__
п т\ —	'
Из последней формулы имеем следствия:
1.
2. Сп=1 (пустое множество только одно).
3/^т	। ГЧп-1_Счп
• ^п-1 Т ^п-1 —Ьп.
Теорема. Общее число подмножеств множества
M = {ai, a2, а3...ап} равно 2", т. е. C®+Q-f-C^+...+С" = 2Л.
Доказательство проведем методом математической индукции.
1)	/1 = 1, Af={a}. Имеем два множества: Л1 = {а} и 0. Значит,
их число равно 2п — 21. Утверждение справедливо.
2)	Пусть теорема верна для n — k, т. е. если M = {ai,a2, ...,aj,
то число всех подмножеств множества М. равно 2к: С£-|-С£+... +С£=2*.
Докажем, что при этом предположении число всех подмножеств
множества, состоящего из k + 1 элемента, равно 2к+1.
Присоединим еще один элемент к нашему множеству М. Полу-
чим множество {а1( а2, ..., ак, ак+1}. Чтобы получить все его под-
множества, очевидно, достаточно к подмножествам множества М
присоединить все подмножества, получающиеся из них присоедине-
нием к каждому элемента ак+1. Таких подмножеств будет столько
же, сколько и первоначальных, т. е. 2к. Следовательно, общее чис-
ло подмножеств будет равно 2к-2 = 2к+1, т. е. С“+1 + Ск+1 + Ск+1+...
...Ч-С1+1 + ОД = 2*+1.
Задачи и упражнения
379А. Докажите, что любое шестизначное число, в котором три
последние цифры совпадают с тремя первыми цифрами, записанными
в том же порядке, делится на 7, 11 и 13.
380°. Отец привез из сада яблоки. Дети спросили, сколько штук
яблок он привез. Отец ответил, что он их не считал, но когда пе-
71
рекладывал по 2, по 3, по 4, по 5, по 6, по 7, то каждый раз ос-
тавалось одно яблоко. Какое наименьшее число яблок мог при-
везти отец?
381к. Решите уравнение
sinx—sin Зх-{-2 sinxsin2x + 4 sinxsin3xcos3x = 0.
382к. Решите уравнение 2 cos 2х+cos2-^- — 10cosf ~—х ) -|-~==~cosx.
Занятие 2. Тема. Решение задач
по комбинаторике
383.	12 друзей решили после окончания школы каждый год
встречаться в одном кафе. Они считали, что удобнее обмениваться
впечатлениями и беседовать за столиками по 4 человека. Сколько
лет им потребуется, чтобы каждый мог посидеть с каждым из ос-
тальных за каким-либо одним столиком?
384.	На шахматном турнире было сыграно 130 партий. Все уча-
стники играли друг с другом по одной партии, но два участника
турнира выбыли из соревнования после того, как сыграли по 5 пар-
тий каждый. Сколько было первоначально участников турнира?
385.	Сколько различных четырехзначных номеров автомашин
можно составить из 10 цифр?
386.	Сколько различных трехзначных чисел можно составить из
цифр 0, 1, 2, 3, 4, 5?
387.	В группе 30 человек учащихся. Надо выбрать 3 человека
для работы на ЭВМ. Сколькими способами можно это сделать?
388.	Сколько ? различных дятицветных флагов можно сделать из
5 полотен разных цветов так, чтобы каждое полотно занимало толь-
ко одну полосу?
389.	Упростите: а)	б) А^~^; в)	;
\ ‘ Лщй. + Хп+2
390.	Вычислите: s = Cioo 4“ -Ь ЗС^оо • • • И- lOOCJoo*
Решите уравнение:
39Г. |/ 2sin2^——l=2sinx.
392к. cosx-tg2-J = — у.
Занятие 3. Тема. Решение задач по комбинаторике
393.	Три юноши и семь девушек отправляются на двух лодках
по реке. Сколькими способами их можно разместить в лодках по-
ровну, чтобы в каждой был хотя бы один юноша?
394.	На плоскости даны 15 точек. Никакие три из них не лежат
72
на одной прямой. Сколько различных прямых и сколько окруж-
ностей определяют эти точки?
395.	Участники кружка решили для одной игры написать номера
из цифр трех цветов. На первом месте пишут три цифры красного
цвета, на втором—две цифры желтого цвета и на третьем месте
пишут 4 цифры зеленого цвета. Сколько всего можно написать
различных номеров, если красным цветом можно писать цифры 1,
2, 3, 4, 6, желтым—0, 2, 5, 7, зеленым—1, 3, 5, 6, 7, 8, 9?
Решите уравнение:
396.	а) ^±*- = 72; б) =
397.	СГ2 = 45.
398.	-р+2 - = 132.
Апх-Рх-П
QQQ Г’гх+з  1 Q дз
и 2х+8— 1OZ12x+6-
400.	СГ3 + Сх-2= 15 (х— 1).
ДП1 /°4(^+1)__КДЗ
Wl. b4x4f) —O/l4x+7.
402. Решите систему уравнений:
/ Дп
] ™т-2
I Сп
\ С*т—2
4Х+7»
. ДИ-1   Q	/ Д/1-2. Дп-3  О
•/1т-2 — °	| ™2Х *™2Х —°
.Г*Л-1 _ Л fi. 6) j . Г>П-3 ___ OjL
•^т-2 —	3 •
403к. Найдите наименьший положительный корень уравнения
cos х • cos Зх = cos 5х • cos 7х.
/ 3 •	\
404к. Решите уравнение sin4x—cos4x = cos ( у л—х 1.
Занятие 4. Тема. Бином Ньютона
При решении различных математических задач приходится стал-
киваться с необходимостью возводить двучлен (бином) в натураль-
ную степень, находить заданные члены разложения степени двучле-
на или члены, обладающие определенными свойствами. Эти вопросы
подробно исследовал для натуральной степени бинома И. Ньютон
и вывел формулу возведения двучлена в любую натуральную сте-
пень.
Рассмотрим треугольник Паскаля. Он имеет следующий вид:
1
Г 1
1 2 1
13 3 1
1 4 6 4 1
1 5 10 10 5 1
Треугольник Паскаля построен следующим образом. В первой
строке записана 1. Во второй — по бокам от нее по единице. В каж-
дой следующей строке — первое и последнее числа единицы, а ос-
73
гальные расположены между числами предыдущей строки и равны
-сумме этих двух чисел.
Члены каждой строки треугольника Паскаля являются коэффи-
циентами разложения степени двучлена, показатель которого равен
номеру строки треугольника Паскаля, причем первая строка соот-
ветствует нулевому показателю степени двучлена. Так,
(а + х)ъ = 4-	+ 10а3х2 + 1 Оа2х3 + 5лх4 4- х5.
В свою очередь члены треугольника Паскаля равны сочетаниям
из числа, равного показателю бинома по 0, 1,2, 3, ..., п, умножен-
ному на произведение соответствующих степеней слагаемых. Причем
степень первого слагаемого от члена к члену уменьшается на еди-
ницу от п до 0, а второго слагаемого увеличивается от 0 до п.
Принимаем CJ = 1.
CJ
С? Ci
СО	/°2
2
СО	Z>2 рЗ
3 U3 ^3	'“'3
СО pi р2	рп
п	....
Отсюда видим, что член разложения (а4-х)п, стоящий на k-\ 1-м
месте от начала разложения, имеет коэффициент С£, т. е. он ра-
вен Tk+1= Скпхкап^.
Сумма всех биномиальных коэффициентов разложения равна 2",
т. е.
СПС*+С*+...+С"==2\
Задачи и упражнения
405.	Найдите х, если третий член разложения [2 у
равен 240.
406.	При каком значении х четвертый член разложения бинома
/Юкvr + _L_\7 раВен 3500 000?
\	ю^/
х 1/* X Ь
407.	В разложении бинома I —?—|-	) найдите член, содер-
\ V X*J
жащий х5’5, если сумма биномиальных коэффициентов разложения
равна 256.
408.	Найдите средний член разложения бинома ( а “р/а— 1/	,
\	' у а/
если коэффициент пятого члена разложения относится к коэффици-
енту третьего члена как 14:3.
409.	Найдите член разложения {z уг'Ц ’ не с°ДеРжа'
щий z.
74
/	__ 2	__\m
410.	В разложении бинома	—а35-^/а)	коэффициент
третьего члена на 35 больше коэффициента второго члена. Опреде-
лите член разложения, содержащий а в первой степени.
411Д. В составе хоккейной команды 3 нападающих, 2 защитника
и 1 вратарь. Сколько различных команд может составить тренер,
если у него 6 нападающих, 4 защитника и 2 вратаря?
412А. Докажите, что 1 + 2С\ + 36^ + 4С3п 4-... +(п+ 1)С£ ==
= (n + 2)-2«-\
413к. Найдите коэффициент b в уравнении 5х24-&х—28 = 0, если
известно, что корни уравнения находятся в зависимости 5х! + 2х2=1
и b—число целое.
414к. При каких значениях k система уравнений
((k—2) х +27г/= 4,5
( 2х + (&4-1)у = —1
имеет бесконечное множество решений?
. 31л
sin-gj-.
. (2п— 1) л 2	..
.. »sm-- -где п ^N.
Занятие 5. Тема. Преобразование
тригонометрических выражений
Докажите, что:
415.	sin 20° sin 40° sin 60° sin 80° = 4-
lo
416.	a) tg20° + 4 sin20° = /3; 6) tg 7°30'=/б-Ь/2— /3—2.
Вычислите без таблиц:
л 4л 5л
417. cos-у cos-у cos-у-.
л л • л,	. Зл	• 5л
418.	Sin 77 • Sin 77- • Sin^r •
64	64	64
419.	Докажите, что
.л	.	Зл	.	5л
Sinr • Sin-7- • Sin-г- • ... - от--р-
4п	4п	4п	4п
420.	Докажите равенство
ап—ьп	(1	у cos х)п — (1 — К COS х)”	/	<>	,	1.	•>	~ _
..	~—т----75 , если известно, что (а?	+ b‘)	tg?	-у—
аа+Ь»	(l + /cosx)n + (l-Kcosx)rt	V	& 2
= 2ab, а > & > 0,
г>	*	*	1g 2 cos 15°
421.	Вычислите без таблиц —о. -ГгГо- •
ig z sin 10
422.	Докажите, что треугольник, углы которого удовлетворяют
sin2 А 4- sin2 В sin2 С о
равенству —тут—гвЯ—-^ = 2, прямоугольный.
r J cos2 А + cos2 В + cos-С	r J
423д. Докажите, что И10—1 делится на 100.
424°. Собака преследует зайца, который находится впереди нее
на 40 своих прыжков. Собака делает 7 прыжков в то время, за
которое заяц делает 9 прыжков, но 3 прыжка собаки равны 5 прыж-
75
кам зайца. Сколько прыжков нужно сделать собаке, чтобы догнать
зайца?
425к. Хорда параболы у = — а2х2 + Ъах— 4 касается кривой у =
= Т~х в точке х==2 и делится этой точкой пополам. Найдите а.
426к. Найдите экстремумы функции у = х3(8—х).
Занятие 6. Тема. Упрощение тригонометрических выражений,
решение тригонометрических уравнений
427. Докажите равенство tg3a— tg2a—tga = tg3atg2a tga.
Решите уравнение:
428. cosxcos5x+ cos 7x = 3.
sin4*-}-cos4*—1 __2
sin6 *-|-cos6 x—1	3
430.	cos x + 2 cos 2* + cos 3x + cos 7x + 2 cos 8x + cos 9x = 0.
пх 2пх	4 л*	1
431.	COS-77- COS —7T- cos -гг-==—.
У	У	У о
432.	cosхcos2xcos4x ... cos2nx = 2nl+1 .
433Д. Упростите выражение
т+’-'+тТ 4+tcost-
434A. Докажите, что 21984— 1 делится на 3.
435к. Число Ш представьте в виде суммы двух положительных
слагаемых так, чтобы сумма половины квадрата первого слагаемого
и куба второго была наименьшей.
436к. Решите уравнение (3 — 1g х)2 (3 + 1g х)2 =-- (4 — 1g2 х)2 —
— 7 1g2*4-50.
Занятие 7. Тема. Решение геометрических задач
437.	Докажите, что биссектриса прямого угла прямоугольного
треугольника является биссектрисой угла между высотой и медиа-
ной, проведенными из вершины прямого угла.
438.	Дан остроугольный треугольник АВС, внутри которого
взята точка М. Эту точку соединили со всеми вершинами треуголь-
ника. Получившиеся отрезки образуют с высотами треугольника
соответственно углы а, Р и у. Докажите, что сумма произведений
каждого из этих отрезков на косинус угла (соответственно а, р, у)
и на сторону треугольника (соответственно ВС, АС, АВ) равна
учетверенной площади данного треугольника.
439.	В прямоугольном треугольнике АВС ^/В = 90°, высота, про-
веденная из вершины В, равна а, медиана равна Ь. Найдите пло-
щадь треугольника АВС.
76
440.	Из концов отрезка AB — R проведены дуги радиуса R до
взаимного пересечения. Внутри получившейся фигуры на АВ по-
строены две равные полуокружности, касающиеся друг друга и по
одной из дуг, и окружность, касающаяся этих полуокружностей
и первых двух дуг. Найдите радиус этой окружности и расстояние
ее центра от АВ.
441.	Пусть ha, hb, hc1 ba, bb, bc соответственно высоты и биссек-
трисы треугольника ЛВС. Докажите соотношение
ha I h^ . he I ___су hahbhc
ь2с 'ЪмГ
442.	Три равных квадрата соединены в ряд и левая нижняя
вершина первого соединена с правыми верхними вершинами второго
и третьего квадратов. Докажите, что сумма углов этих отрезков
с верхними основаниями квадратов равна 45°.
443А. Сколькими нулями окайчйвается число, равное произведе-
нию 1-2-3«...-98-99-100?
444°. Восстановите цифры в записи решения примера:
******* |**1
* * * 8 * * * *
* * * *
* * 8 *
(х2-==(х—а) у
445к. Решите систему уравнений: 1 2	__Q
\У~ —Ху —• У(1Х •
п	3 cos 5х—2 (cos 6x4-cos 4х)	,
446к. Решите уравнение	"---тг 4—Л = tg 1lx.
J н	3 sin 5х—2 (sin 6x4-sin 4х)	ь
Занятие 8. Тема. Решение геометрических задач
447.	Около правильного треугольника описана окружность. До-
кажите, что сумма расстояний от произвольной точки окружности
до двух ближайших вершин треугольника равна расстоянию этой
точки до третьей вершины треугольника.
448.	В трапеции ABCD АВ || CD. Диагонали трапеции пересека-
ются в точке Л4, а непараллельные стороны — в точке S. Через
точку М проведен отрезок EF, параллельный основаниям трапеции,
и из S— перпендикуляр на основания трапеции, пересекающий верх-
нее основание в точке Л, а нижнее в точке L и EF—в точке О.
Докажите, что EF—биссектриса углов AOD и СОВ.
449.	Докажите, что окружности, проведенные через точку пере-
сечения высот треугольника и каждую пару его вершин, равны
между собой.
450.	Из точки О проведено три луча, образующие между собой
острые углы. На первом луче взята точка А и на О А как на диа-
метре построена полуокружность, пересекающая два других луча.
На третьем луче отложен отрезок ОВ — ОА и на ОВ построена
77
полуокружность, пересекающая два других луна. Докажите, что
сумма квадратов расстояний от А и В до среднего луча меньше
квадрата расстояния от А до ОВ.
451.	Внутри треугольника АВС взята произвольная точка М
и через нее проведены отрезки, параллельные сторонам треуголь-
ника: ЕТЦАВ, KLIIВС, PR || АС, где Е, F, К, L, Р, R принадле-
п	АР . BF , CL .
жат сторонам треугольника. Докажите, что -тб-+-бтг +-77г == 1.
/iZz	/iG
452к. Дан треугольник АВС, Построены точки, симметричные
относительно сторон треугольника точке пересечения высот. Дока-
жите, что все эти точки лежат на окружности, описанной около
треугольника АВС,
453. Высота, биссектриса и медиана, проведенные из одной вер-
шины треугольника, разделили угол при этой вершине на 4 равные
части. Докажите, что треугольник прямоугольный.
454А. В таблице 0 1 2 3... 1986 1987
135. . . . 3973
4 8......
каждый член последующей строки расположен между двумя членами
предыдущей строки и равен их сумме. Число членов от строки
к строке уменьшается на единицу. Докажите, что число, получив-
шееся в последней строке, делится на 1987.
455°. На столе лежат три одинаковых ящика. В одном из них
2 белых шара, в другом—белый и черный, в третьем—2 черных.
Аналогичные надписи сделаны на крышках ящиков, но ни одна из
них не соответствует действительности. Как, вынув только один
шар, определить, в каком ящике какие лежат шары?
456к. В полукруг радиуса R вписана трапеция ABCD так, что
ее основание AD является диаметром, а вершины В и С лежат на
окружности. Какова величина угла при основании у трапеции
ABCD, имеющей наибольший периметр?
457к. Вокруг квадрата, сторона которого равна а, описана ок-
ружность, а около окружности описан правильный шестиугольник.
Определите площадь шестиугольника.
Занятие 9. Тема. Решение геометрических задач
458.	Докажите, что если в треугольнике высота и медиана, про-
веденные из одной вершины, делят угол на три равные части, то
треугольник прямоугольный.
459.	Дан выпуклый четырехугольник ABCD. Его стороны про-
должены на такое же расстояние, что и их длина: АВ—за вершину
В, ВС — за вершину С, CD—за вершину D, DA — за вершину А,
Внешние концы получившихся отрезков последовательно соединены
между собой. Докажите, что площадь полученного четырехуголь-
ника в 5 раз больше площади данного четырехугольника.
460.	Внутри круга с центром О и радиусом R взята точка Л
на расстоянии а от центра. Через К проведены две взаимно перпен-
дикулярные хорды, одна из которых образует с диаметром, прохо-
дящим через Л, угол в 45°. Найдите площадь вписанного в круг
четырехугольника, диагоналями которого являются эти хорды.
461.	Впишите в данную окружность треугольник, если известны
точки пересечения окружности с продолжением высоты, биссектрисы
и медианы, проведенных из одной вершины треугольника.
462.	Докажите., что если через точку А пересечения двух окруж-
ностей провести секущую и через точки ее пересечения с окружно-
стями провести касательные к этим окружностям, то образуемый
ими угол не меняется при повороте секущей вокруг точки А.
463.	Дан правильный тетраэдр с ребром а. Постройте сечение
так, чтобы в сечении получился квадрат. Найдите площадь сечения.
464°. По улицам города, разбитого на квадратные кварталы,
движется автомобиль, сворачивая на каждом перекрестке налево
или направо. Квартал он проезжает за 15 с. Докажите, что, про-
ехав перекресток, автомобиль может вновь появиться на нем лишь
спустя целое число минут.
465А. Докажите, что р2— 1, где р—простое число, делится на 24.
Решите неравенство:
466к. /х2—4х>х—3.
у 2_______________________________ |	|
467к. /'(*) + <₽ (х) < 0, где /(х) = -7-=у, ф(х) = у-у.
Занятие 10. Тема. Нестандартные приемы
решения уравнений
Многие уравнения, и особенно системы уравнений второй и более
высоких степеней, при решении обычными способами, например
способом подстановки, приводят к весьма громоздким преобразова-
ниям и отсюда к большому числу ошибок, а часто и невозможности
получения окончательного результата. Вместе с тем эти уравнения
могут быть сравнительно легко решены, если применить более ра-
циональный, как говорят, нестандартный способ их решения.
Примеры	__________
1.	Решим уравнение 2х2 + 3х—5У 2х2 + 3x4-9+ 3 = 0.
Решение. Если это уравнение решать обычным способом как
иррациональное уравнение, то получится уравнение четвертой сте-
пени, которое без знания теоремы Безу мы не можем решить, а
часто и теорема Безу нам не поможет его решить, если оно имеет,
например, иррациональные или дробные корни. Замечаем, что сла-
гаемые, содержащие переменную под корнем и вне его, одинаковы.
Введем новую переменную у = j/2x? + 3x + 9, у^О. Тогда данное
уравнение примет вид у2—9 — 5у + 3 = 0. Откуда у==—1 или// = 6,
но г/^0, значит, К2х* + Зх + 9 = 6. Решив это уравнение, получим
79
х =— 4,5 или х==— з. Проверкой убедимся, что эти значения пе-
ременной удовлетворяют исходному уравнению.
Замечание. Рассмотренный способ применим даже для подоб-
ного вида уравнений, содержащих буквенные параметры. Однако
в случае наличия буквенных параметров необходимо исследовать,
какие значения могут принимать эти параметры в данном уравнении.
2.	Решим уравнение 12 + И12 +х =х.
Решение. Ясно, что х > 0. Введем новую переменную у =
= j/’12 4-x, где у > 0. Тогда 12 4-х = у2, а из данного уравнения
имеем |/12 4- у — х. Отсюда 12 4~ У = *2• Получаем систему уравне-
(у2—х = 12
ний: 1 g ig. Вычтем из первого уравнения второе. Получим
у2—х2 + у—х = 0. Разложим на множители: (у—х) (у 4-х 4- 1) = 0.
Так как х > 0, у > 0, то х4-у4-1>0. Значит, у—х = 0, т. е.
у = х. Подставим это во второе уравнение. Получим х2—х—12 = 0,
откуда х = 4 или х = — 3 < 0, значит, окончательно получаем х = 4.
3.	Решим уравнение 4 {/(2х —7)24- •г/(2х4~7)2 = 4 {/4х2 — 49.
Решение. Значение х = 3,5 не удовлетворяет уравнению. Зна-
чит, мы можем рассматривать решение уравнения на множестве
значений х=/=3,5. Разделим обе части уравнения на (2х — 7)2. По-
п /~ /2х4-7 \ 2 п /*2x4-7*
лучим 4 + ]/ I 2%_7 / =4у 2%_7 • Введем новую переменную у =
=	2х—1 ’ где У>°- Имеем у2—4у 4- 4 = 0, откуда у = 2. Значит,
Hit-2' ’ -
4. Решим уравнение 2а 2р{/xP+q = %/х+ Ух.
Решение. Заменим радикалы степенями с дробными показате-
P + Q	1	1
лями и перенесем все члены влево. Получим 2ах 2pq —хр—xq =0.
Все слагаемые содержат х. В подобных случаях неизвестное х
в наименьшей степени следует вынести за скобки и затем этот мно-
житель приравнять нулю. В рассматриваемом случае вынесем за
1 1
скобки X р ИЛИ X q .
1 / д-р д-р \
Уравнение примет вид xq • \2ах 2pq —х pq — 1) = 0, откуда
1	д-р д-Р
xq = 0, т. е. х = 0, или 2ах 2pq —х pq —1=0. Введем новую пе-
д-р
ременную у = х 2pq , тогда 2ау—у2—1=0, т. е. у2 — 2ay^ \=Q,
_____	д - р	____
откуда г/ = а±Ка2—1, где | а |	1, значит, x2pq = а+|/'а2 —1,
______2Р7
т. е. х=(а±К#2— l)z7“p. Таким образом х = 0, или х =
_____________2рд	_____ 2рд
— {а 4-Ио2 — 0ч~р > или х = (а — У а2 — где |а|> 1.
80
5. Решим уравнение у хп+п+1/anxll! + У ап +"+i//апгхп —Ь.
Решение. Заменим радикалы степенями с дробными показа-
телями и затем разложим левую часть на множители. Получим
Возведя обе части уравнения в степень получим
Откуда х”** =	— а~,
(п	п \п+1
bn+1— ап+1) п .
Уравнение имеет решение, если Ь^а>0.
Задачи и упражнения
468. Решите уравнение х2 + 2J/"*2 — 3x4-11=3x4-4.
469Д. Учитель и ученик измеряли шагами размеры школьного
участка. Первый раз учитель прошел вдоль большей стороны, а уче-
ник вдоль меньшей, и сделали они в общей сложности 350 шагов.
Второй раз ученик прошел вдоль большей стороны, а учитель вдоль
меньшей, и насчитали они всего 400 шагов. Найдите размеры участка,
если длина шага учителя равна 0,75 м, а ученика—0,5 м.
470А. Два пешехода идут вниз по движущемуся эскалатору
метро. Первый за время спуска насчитал 40 ступенек, а второй — 60.
Один из них идет s 2 раза быстрее другого. Сколько ступенек им
пришлось бы пройти, если бы эскалатор стоял?
471К. Векторы /, /—единичные, ортогональные. Докажите, что
треугольник АВС, где АВ = 41 4-2/, АС = 3/4-4/, прямоугольный,
и найдите его площадь.
472к. В прямой треугольной призме ABCAJB^ ABf = d и
АВ1В = а. На прямой, являющейся пересечением плоскости АВС
и плоскости симметрии призмы, содержащей прямую BBlt взята
точка О, которая удалена на одинаковое расстояние от точек Л,
В и С. Через точку О параллельно прямой А^ проведена пло-
скость, пересекающая отрезок ВВг в точке D, причем BJ) : DB = 1:2.
Определите площадь сечения призмы этой плоскостью, если известно,
что Z_ ЛВС = |3.
81
475.
Занятие 11. Тема. Решение систем уравнении
Решите систему уравнений:
473. 7х2 4- ху + у2 = 7
[х + ху + у = — 5.
474. 72 (х-\-у) = 5ху
(х3 + у3) = 65ху.
'ху = 6
yz — 12
zx — 8.
476-	[ху+уг = 8
< yz + zx = 20
\zxху — 14.
477.	(х2у—ху2 — 30
[ху2+х2у = 70.
478.	7x44~z/4—х2у2= 13
[х2—у2 + 2ху = 1.
4794. Найдите сумму ± 4-	+ • • • + 99^00 •
480°. Сто монет разложены в 10 стопок, по 10 монет в каждой.
В одной из стопок все монеты фальшивые. Масса каждой нормальной
монеты 5 г, а фальшивой—на 0,5 г меньше. Как при помощи одного
взвешивания на весах с разновесами определить, в какой стопке
находятся фальшивые монеты?
48Г. При каком а площадь фигуры, ограниченной параболой
о 2	«	20/"2.
у = 2х2 и прямой у —а, равна --g—?
482к. Вычислите площадь фигуры, ограниченной параболой
у = х\ касательной к ней в точке с абсциссой 2, и осью абсцисс.
Занятие 12. Тема. Решение нелинейных уравнений*
Решите уравнение:
483.	(%2—x+ I)4 — 10х2(х2—1) + 9х4 = 0.
484.	^х(х + 5)2 + б/х3 = 5?/х2(х4-5).
485.	Зх4 4-1 Зх3 4- 20х2 4- 13х 4- 3 = 0.
486.	^(х4-1)24-3/(х—1)2 = 4/х2 —1.
487.	х8 4- х4—2х3—2х2 4-2 = 0.
488.	а —Vа Л- х — х.
* На занятии рассматриваются в основном уравнения, при решении которых
целесообразно использовать замену переменных.
82
489.	Решите систему уравнений: (х 4- ху 4- у — 27
\хъу + ху2 = — 520.
49О.	д Постройте окружности с центрами в трех данных точках,
попарно касающиеся друг друга.
491д. Докажите, что при всяком нечетном натуральном п число
п12—п®—п4+1 делится на 512.	_
492к. Векторы а и b взаимно перпендикулярны, а вектор с обра-
зует с каждым из них угол в 60°. Зная, что |а| = 3, jj?| = 5 и
| с | = 8, вычислите скалярное произведение (За—2/?)-(fe + Зс).
493к. Известны координаты вершин треугольника АВС: 4(1; 1; 1),
В (2; 4; 2), С (8; 3; 3). Определите, является ли этот треугольник
прямоугольным или тупоугольным.
Занятие 13. Тема. Решение уравнений
и систем уравнений *
494. Решите уравнение хъ 4- Зх4— 17х3—27х2 4- 52х 4- 60 = 0.
Решите систему уравнений:
495.
496.
497.
498.
499.
-^- = 5
х + у
-^ = 4]
У + z	J
2гх п
г+х —
х(у + !) + ({/ + 1)2х2 = 12
у(х+1) + (х+1)2{/2 = 20.
х44- г/4 = 17
х+ У = 3.
—-4-2
-4-^-=12
у 1 х
±4-1=1.
X ~ У 3
500°. Докажите, что не существует дву-, трех- и четырехзнач-
ных натуральных чисел, которые увеличиваются в 2 раза от пере-
становки первой цифры в конец числа.
501Д. В шаре проведены три взаимно перпендикулярных диа-
метра, каждый из которых разделен на три равных отрезка и через
* На этом занятии можно сообщить учащимся теорему Виета для приведен-
ного уравнения произвольной степени и основную теорему алгебры, а также след-
ствие из них: если уравнение произвольной степени приведенного вида с целыми
коэффициентами имеет целые корни, то они являются делителями свободного члена
уравнения.
83
каждую точку деления проведена > плоскость, перпендикулярная
диаметру. На сколько частей эти плоскости делят поверхность шара?
502.	Решите уравнение cos х = tg х (1 + cos 2х).
503.	Исследуйте функцию у = 2х3 + Зх2— 12х + 5 на локальные
максимум и минимум.
Занятие 14. Тема. Решение уравнений и систем уравнений
504.	Решите в целых числах уравнение х8—z/5z = x5, где х, у,
г — простые числа.
505.	Решите систему уравнений:
f Х2-\- y2 = Z2~
< ху + у2-\-2Х = 47
(z—x)(z—y) = 2.
506.	Найдите действительные решения уравнения
3 (х2 + у2 + z2) = 2 (ху + yz 4 гх) + 8у + 16z —56.
Решите систему уравнений:
507.	( x + yzt=10
I y + ztx=10
] z+ txy — 10
( t + xyz=10.
508.	x2 + y2 + z = 8,
x + y + z2=12
xy+ yz + zx=l\, где x, у, z, t — целые числа.
509°. Собака погналась за лисой, которая была от нее в 30 м.
Скачок собаки равен 2 м, в лисицы—1 м, но в то время, за кото-
рое лисица делает три скачка, собака делает только два скачка.
Через сколько метров собака догонит лисицу?
510Л. Докажите, что числа вида п4 + 4, где п>1,
составные.
511к. Составьте уравнение касательных к кривой z/ = x2 + 2x—3
в точках ее пересечения с осью абсцисс.
512к. Найдите наибольшее и наименьшее значения функции
Дх) = -j-х! + 4х2 на отрезке [—1; 1].
Занятие 15. Тема. Решение иррациональных, показательных
и логарифмических уравнений
Решите уравнение:
513.	х—2 Их— 1 =1 +У^х+ 3—4 Их— 1.
514.	У х—4Их—4х + 5—6J/x—4 = 1.

515.	Докажите, что при 1<Са^2 справедливо равенство
]/" a + 2\f а— 1 + )/" а—2]/~а—1=2.
516.	Найдите значение выражения 3*—3~*, если известно, что
9*+ 9-* = 51.
Решите уравнение:
517.	(/2 + /з)Х+(]Л2-/7з)* = 4.
518.	2 (jA-Кз) J-G V 2 + Кз)* = 3-2*.
519.	Их2—р+2}/'х2—1—х, где р —действительное число.
520.	К2х2 + 8х + 7—х = 2.
521°. В турпоходе участвовало 20 мужчин, женщин и школьни-
ков. Масса их рюкзаков составила 20 пудов. Причем масса рюкзака
мужчины равна 2 пудам, женщины — 0,5 и школьника — 0,25 пуда.
Сколько участвовало в походе мужчин, женщин и школьников?
522Д. Найдите наименьшее число, которое при делении на 2, 3,
4, 5, 6, 7, 8, 9 дает в остатке 1.
523к. Решите уравнение 91g (*-«)-'о —З'е**-1).
524к. Найдите область определения функции
X2 + 2 X - 3
//=(% +0,5) g*+0’5 «2+«-з.
525.	к Решите систему уравнений:
f 4* =(4V • 1728
( 10g4* = y — log4y+log43.
Занятие 16. Тема. Решение показательных
и логарифмических уравнений
l°g6 (log6a)
526.	Докажите, что а ]0«ьа	= log6 а.
527.	Дано log108 N = a, log72 N = b.
а) Выразите log2 N и logsW через а и Ь; б) покажите, что
1	__ п	т
logxnum А “ logx Л + log9 Л ’
где А, х, уС(О; 1)U (1; °о), a, b, т, n£R.
Решите уравнение:
=ое log2(3x-H)	2
‘ 1 +log2 (Зх-1) ,3+log2.(3x=J)'
529.	х— 1— log7(| -Iх —1) = — log,(7* — 5).
. . . log's Vx-F 1—j-logs (х2;-1)	___
530.	\^\	=K2(x— 1).
531.	151о&>3-х|о8ь9* + 1 = 1.
85
532.	Решите систему уравнений:
Л log2 (х + $/)| +1 log2(x—у)\ = 3
I ху = 3.
533°. Возраст некоторого человека в 1989 г. равен сумме цифр
года его рождения. Сколько ему лет в 1989 году?
534Д. Сколько цифр имеет число 2100?
Решите неравенство:
log , I/ 4
535к. 1 log2(5*—4) + 4 log5^-4 2 < -	;29- .
.	8 — 12Х
536.	5 х~в > 25.
537.	Решите уравнение log2(9x“1 + 7) = 2-log2(3x~1+1).
Занятие 17. Тема. Карл Фридрих Гаусс
Карл Фридрих Гаусс является одним из величайших математи-
ков. Он родился 30 апреля 1777 г. в небольшом немецком городе
Брауншвейге. Дед Карла был крестьянином, а отец работал в го-
роде водопроводчиком. На умственное развитие юного Карла плодот-
ворное влияние оказал брат матери — Фридрих, поощрявший жи-
вую сообразительность мальчика.
У Карла очень рано обнаружились математические способности.
В последствии он говорил, что научился раньше считать, а потом
говорить. По поручению городских властей отец часто производил
различные арифметические расчеты. Однажды Герхард Гаусс—отец
Карла — вслух выполнял вычисления и, дойдя до конца рассчетов,
услышал с удивлением замечание трехлетнего Карла: «Папа, вычис-
ления неверны. Должно быть ...». Карл назвал результат. Про-
верка показала, что число, названное Карлом, было правильным.
Отец был против обучения сына, но настойчивость матери Кар-
ла—Доротеи — преодолела его упрямство. В возрасте семи лет он
начал посещать школу, в которой математика изучалась, начиная
с третьего класса. В школе быстро обнаружились математические
способности мальчика. В классе было около ста учащихся. Как-то
ребята очень расшалились, и, чтобы их чем-то занять, учитель пред-
ложил им сосчитать сумму 100 чисел: 81 297 +81 495 +81 693+...
...+ 100899, где каждое слагаемое на 198 больше предыдущего
числа. Думая, что это займет много времени, он занялся другими
делами. Дети действительно считали в течение часа, и никто, кроме
Гаусса, не дал верного ответа. Как только учитель кончил писать
задание, Гаусс положил свою грифельную доску ему на стол. После
этого учитель сказал, что он не сможет больше ничему научить
Гаусса. С Карлом начал индивидуально заниматься помощник
учителя Бартельс.
86
С Бартельсом Гаусс быстро освоил многие серьезные мате-
матические книги. По ходатайству Бартельса герцор Брауншвейгский
предоставил Гауссу материальную возможность для продолжения
образования. Из средств герцога Гауссу выплачивалась стипендия
вплоть до защиты докторской диссертации.
В 1795 г. Гаусс окончил гимназию и поступил в Геттингенский
университет. Он детально самостоятельно изучил труды таких зна-
менитых математиков, как Ньютон, Лагранж, Эйлер. Еще будучи
студентом, Гаусс сделал ряд открытий в математике. Наиболее
серьезные из них—доказательство возможности построения с по-
мощью циркуля и линейки правильного 17-угольника (1796). До
Гаусса были известны способы построения 3, 4, 5, 15-угольников,
а также многоугольников, получающихся из этих путем удвоения
числа их сторон. В том же году он рассмотрел все случаи, при ко-
торых возможно решение в квадратных радикалах двучленного
уравнения хп—1=0, и соответственно случаи возможности деления
окружности на соответствующее число равных частей с помощью
циркуля и линейки. Мы сейчас это уравнение легко решаем
с помощью единичной окружности и записи координат точек окруж-
ности, получающихся делением ее на п равных частей, на комп-
лексной плоскости. Тогда такой возможности не было, и метод
Гаусса произвел сенсацию.
Еще раньше Гаусс вывел и дал строгое обоснование формулы
разложения степени бинома в сумму для произвольных рациональ-
ных значений показателя. (И. Ньютон вывел формулу только для
натуральных значений показателя степени бинома.) Сумма полу-
чается при дробных показателях бесконечной, и ее значение не
всегда совпадает со значением степени данного двучлена. Тогдаш-
ние математики не всегда обращали внимание на необходимость со-
ответствующих исследований.
В 1797 г. Гаусс дал свое по существу первое точное и полное
доказательство основной теоремы алгебры о том, что всякое алгебраи-
ческое уравнение с действительными коэффициентами имеет корень,
действительный или мнимый, и эквивалентное утверждение о том,
что всякая рациональная алгебраическая функция одной перемен-
ной может быть разложена на действительные множители первой и
второй степени.
Из этих утверждений следует, что левая часть уравнения
хп + а1хп~1 + ... +ал = 0 может быть представлена в виде произве-
дения линейных множителей (х—Xf)(x—х2)(х—х3)... (х—хп) = 0,
где х{—корни данного уравнения. А если раскрыть все скобки, то
получим ал=(—l^XiXgXg.. .х„. Это даст возможность находить це-
лые корни уравнений подбором и проверкой делителей свободного
члена.
За эту работу Гаусс получил степень доктора.
Новые открытия в математике у Гаусса в эти годы шли непре-
рывно. Рассматривая вопрос о числе цифр периода при обращении
обыкновенной дроби в периодическую, Гаусс разработал очень важ-
87
яые вопросы аппарата теории чисел—-теорию сравнений — и развил
ее положения и весьма важные приложения, создал теорию квад-
ратичных вычетов, открыл закон взаимности квадратичных вычетов.
Это были весьма важные и трудные математические исследования.
Он нашел условия, при которых имеют решения в целых числах
двоичные и троичные квадратичные формы, т. е. неопределенные
уравнения вида ах2 + 2Ьху + су2 = т, где а, Ь, с, т—целые числа
и ах2 Ч 2ху + су2 + 2dxz ~\fz2 = m, где все коэффициенты целые числа.
Особенно детально он исследовал соотношения между коэффициен-
тами уравнений ах2 + су2 + fz2 = т и тх2 + ш/2 = Д, при которых
они имеют целые решения.
Теорией чисел Гаусс занимался всю свою жизнь и сделал много
открытий в этой области математики.
Большой вклад он внес в так называемую современную алгебру:
теорию групп, колец, полей. Он распространил законы теории чи-
сел на множество комплексных чисел, дал геометрическую интер-
претацию комплексных чисел, т. е. изображение комплексных чисел
точками плоскости. Гауссу принадлежит введение обозначения мни-
мой единицы / = К — 1 и современная запись комплексного числа
а + Ы. Он показал, что в математических исследованиях и практи-
ческих приложениях мнимая единица и мнимые числа имеют такое
же значение, как и действительные числа. Он ввел все операции
над комплексными числами.
Работы Гаусса в теории чисел и в арифметике дали толчок ис-
следованиям других ученых.
Значительны заслуги Гаусса и в развитии астрономии. В 1801 г.
Гаусс по нескольким наблюдениям рассчитал орбиту малой планеты
Цереры, открытой за год до этого и потерянной в лучах Солнца.
Гаусс точно предсказал ее местоположение, и астрономы нашли
в указанном месте планету. Это принесло триумф и славу Гауссу
как математику. Он написал труд «Теория движения небесных тел,
обращающихся вокруг Солнца». В нем не было новых открытий, но
были разработаны новые, более простые способы расчета орбит пла-
нет. Все это позволило Гауссу занять пост директора Геттингенской
обсерватории и по совместительству должность профессора универ-
ситета. Обсерваторией он руководил до конца своей жизни.
Большой вклад Гаусс внес в исследование функций комплекс-
ного переменного, в теорию эллиптических функций. С 1820 г. он.
руководил геодезическими работами по съемке плана Ганноверского
государства (королевства), Занятия геодезией послужили толчком
к разработке теории поверхностей. До Гаусса исследования про-
водились только на плоскости. Он разработал основы теории внут-
ренней геометрии произвольной поверхности (длины дуг кривых на
данной поверхности, углы между дугами, площадь поверхности фи-
гуры, геодезические линии на поверхности).
Гаусс открыл и доказал основную теорему геометрии поверх-
ностей о полной кривизне поверхности в данной точке. Полная
88
кривизна поверхности в данной точке ныне называется гауссовой
кривизной.
Серьезные исследования Гаусс провел по электричеству. В ча-
стности, он разработал и ввел понятие потенциала электрического
поля, сконструировал электрический телеграф.
Гаусс был жизнерадостный человек, интересовался литературой,
политикой, экономикой. Он хорошо знал ряд древних и европейских
языков. Но, пожалуй, отличительной чертой его характера была
целеустремленность и настойчивость в достижении поставленной
цели. Если он брался за решение какого-либо вопроса или задачи,
то не отступал, пока не доводил решение до конца. В случае за-
труднения в решении он мог одновременно начать решать и другую
задачу, но первую не бросал.
Гаусс любил работать один. У него не было учеников, и он ни
с кем не делился своими идеями. Все доводил до конца самостоя-
тельно.
С 1824 г. Гаусс стал иностранным членом Петербургской акаде-
мии наук и поддерживал с ней регулярные научные связи на про-
тяжении всего последующего периода жизни. В возрасте 62 лет он
изучил русский язык и всю переписку с Академией вел на русском
языке. Он любил читать Пушкина и других русских поэтов и пи-
сателей того времени.
Умер Гаусс 78 лет 23 февраля 1855 г. Уже при жизни его за-
служенно называли королем математиков. Труды Гаусса не потеряли
своего значения и в наше время.
Занятие 18. Тема. Доказательство неравенств
Существует большое разнообразие способов доказательства не-
равенств. Отметим наиболее часто встречающиеся способы их дока-
зательства.
1-й способ. Рассматривают разность между левой и правой
частями неравенства. Устанавливают ее знак, по которому и делаются
заключения о справедливости рассматриваемого неравенства.
2-й способ. Используя основные свойства неравенства и неко-
торые простейшие неравенства, например что среднее арифметическое
двух положительных чисел не меньше их среднего геометрического
или сумма двух взаимно обратных положительных чисел не меньше
двух, сводят данное неравенство к очевидному.
3-й способ. Путем перехода с помощью тождественных преоб-
разований от очевидного неравенства приходят к данному или, на-
оборот, от данного к очевидному.
4-й способ. Используют принцип усиления неравенства.
5-й способ. Используют метод математической индукции.
6-й способ. Используют уже доказанные неравенства.
89
Задачи и упражнения
Докажите неравенство:
538.	(а 4-64-с)	+ у + ^ ^9, где а > О, b > 0, с> 0.
коп а14-а24-аз+а4
ОоУ.	У	,
где а± 0; а2 0; я3 0; а4 0.
540. Докажите, что если я2-|-62==1, то |а-|-&|^К2.
541. Докажите неравенство
а2 Ь2	। с* 3
$*-|-с2 *	а24~6?	2
для любых отличных от нуля действительных чисел а, Ь, с.
542. Что больше: К8 + К17 или К10 + К15?
543. Какое число больше: 99! или 50"?
545. Докажите, что при любых натуральных значениях п^2
1,1,1,	,1' п — 1
справедливо неравенство 52 +32+ 42 + • • • +^ < ~7Г •
546. Докажите справедливость неравенства для любых нату-
ральных значений п:
. 1 . * 1 . । 1 . т.
$ n+l+n + 2^ ‘ ’ * +зп+1>1,
1 । 1 । , 1 1
°^n + l'tn + 2"t ’ ’ ’ ~^2п^ 2 *
547°. Постройте магический квадрат 3x3, в котором расположите
числа от 3 до 11 так, чтобы по всем строкам, столбцам и диагоналям
была одна и та же сумма.
548+ Один катет прямоугольного треугольника равен 13, а две
другие его стороны выражены целыми числами. Найдите стороны
этого треугольника.
549к. В основании прямой призмы лежит равнобедренный прямо-
угольный треугольник с катетом а. Диагональ большей боковой грани
и диагональ другой боковой грани, исходящие из одной вершины,
образуют угол а. Найдите объем призмы.
550к. Найдите площадь боковой поверхности правильной четырех-
угольной призмы, если площадь основания призмы равна S и диа-
гональ призмы образует с боковым ребром призмы угол а.
Занятие 19. Тема. Доказательство и решение неравенств *
Решите неравенство:
551- ЗХ2 + 17Х216 >0-
552.	|х—2|<5.
553.	(х+5)(х +3) (х—1) (х—7) > 0.
554.	а) (Х2+Д~51(Г7' > °;
(х + 5)3(* + 3)х2	п
(х+4)2(х—2)3
555.	а) х—J/T—х2^0;	в) К* + 8^Сх + 2;
б)	х+ИГ^х^О; г) /Зх—5<7—/х + 2.
556.
2х—Зх2 + 1
557. sinx + y sin2x + y sin Зх > 0.
558А. Докажите, что выражение п5— 5п3 + 4п, где п—четное
число, не делящееся на 3 и 4, делится на 1440.
559Л. Постройте треугольник по трем медианам.
560к. В тетраэдре ABCD двугранные углы при ребрах ВС, BD
и АС—прямые, а величина двугранных углов при ребрах АВ и CD
равна 15°. Найдите радиус шара, вписанного в тетраэдр, если CD==2.
561К. В шар вписан конус, образующая которого равна диаметру
его основания. Найдите отношение полной поверхности этого конуса
к поверхности шара.
Занятие 20. Тема. Решение геометрических задач
562.	Дана прямая I и отрезок АВ, не лежащий в одной пло-
скости с прямой I. Найдите на прямой / такую точку С, для ко-
торой площадь треугольника АВС наименьшая.
563.	В правильной четырехугольной пирамиде сторона основания
равна а, а угол между боковыми гранями равен а. Найдите объем
пирамиды.
564.	Правильный тетраэдр спроектирован на плоскость, парал-
лельную двум его несмежным ребрам. Докажите, что в проекции
получился квадрат.
565.	Три грани трехгранного угла со взаимно перпендикулярными
ребрами пересекают шар по трем кругам. Докажите, что сумма
площадей кругов не изменится, если трехгранный угол повернуть
вокруг его вершины так, чтобы его грани по-прежнему пересекали
шар.
* В начале занятия необходимо повторить основные свойства неравенств,
содержащих переменную. Особо отметить случай деления и умножения на отри-
цательное число. Напомнить решение неравенств методом интервалов. На первом
примере полезно проиллюстрировать аналитический и геометрический способы
решения неравенств второй степени, а также способ интервалов.
91
566.	Две правильные треугольные пирамиды имеют общую вы-
соту. Вершина каждой пирамиды лежит в центре основания другой.
Боковые ребра их попарно пересекаются и боковое ребро первой
пирамиды длины I образует с высотой угол а, а боковое ребро
второй пирамиды образует с высотой угол р. Определите объем
общей части обеих пирамид.
567.	Докажите, что в правильном тетраэдре сумма расстояний
от любой его внутренней точки и точек его поверхности до граней
тетраэдра есть величина постоянная. Чему равна эта величина?
568.	В правильный тетраэдр вписаны четыре равных шара, каж-
дый из которых касается трех других шаров и трех граней тетра-
эдра. Вычислите объем тетраэдра, если радиус каждого из указанных
шаров равен R.
569°. Докажите, что если sin (х + у) — cos(x—у) 4- 2 = 0, то
sin (х + у) + cos (х—у) = 0.
570А. Найдите все натуральные числа, разность квадратов кото-
рых равна 799.
571°. В пяти корзинах имеются яблоки. Из первой корзины пе-
рекладывают во вторую пятую часть того, что в ней есть. Затем из
второй в третью перекладывают пятую часть того, что в ней стало.
Далее из третьей в четвертую—пятую часть того, что в ней стало.
Из четвертой в пятую—пятую часть того, что в ней стало. Нако-
нец, из пятой в первую перекладывают пятую часть того, что стало
в пятой корзине. После этого в каждой корзине оказалось по. 48
яблок. По скольку яблок было в каждой корзине первоначально?
' ' 572к. В правильную треугольную пирамиду вписан шар радиуса 7?,.
Радиус окружности, проведенной через точки касания шара с бо-
1/"т" о
новыми гранями пирамиды, равен Найдите объем пирамиды.
573к. В прямом круговом конусе расположены два шара еди-
ничного радиуса, касающиеся основания конуса в точках, симмет-
ричных относительно центра основания конуса. Каждый из шаров
касается боковой поверхности конуса и другого шара. Найдите
угол между образующей конуса и основанием, при котором объем
конуса наименьший.
Занятие 21. Тема. Решение геометрических задач
574к. В некоторой неправильной пирамиде все внутренние дву-
гранные углы при основании равны а. Площадь основания равна S,
а периметр основания равен 2р. Найдите объем и полную поверх-
ность этой пирамиды.
575. Два соосных конуса имеют общее основание и расположены
один вне другого. Образующая одного конуса равна /, а угол осе-
вого сечения при вершине равен 2а. Угол в осевом сечении при
вершине другого конуса равен 2р. Найдите объем полученного тела.
576к. В правильную четырехугольную пирамиду, боковые грани
92
которой наклонены к плоскости основания под углом ф, вписан ци-
линдр. Одно основание цилиндра лежит в плоскости основания
пирамиды, а окружность второго основания цилиндра имеет по одной
общей точке с каждой гранью пирамиды. Радиус основания цили-
ндра и его высота равны г. Вычислите объем пирамиды. При каком
значении угла ф объем пирамиды наименьший?
577к. В прямой круговой конус с образующей / и высотой Н
вписана правильная шестиугольная призма так, что нижнее осно-
вание призмы лежит в плоскости основания конуса, а вершины
верхнего основания принадлежат конической поверхности. Найдите
площадь основания призмы, если известно, что площадь поверхно-
сти этой призмы наибольшая из всех возможных.
578к. В прямоугольном параллелепипеде точка пересечения ди-
агоналей нижнего основания соединена с серединой бокового ребра
отрезком длины т. Этот отрезок образует с основанием параллеле-
пипеда угол а и с боковой гранью угол 2а. Найдите объем па-
раллелепипеда.
579к. Определите размеры открытого бассейна объемом 32 м3 с
квадратным дном, на облицовку дна и стен которого затрачивается
наименьшее количество материала.
580А. Покажите, что 4317+ 1717 делится без остатка на 60.
581°. Один раджа имел п сыновей и оставил им в наследство
бриллианты. Завещание гласило, что первый получит 1/п часть всего
наследства, второй получит 1/п часть оставшегося наследства и еще
один бриллиант, третий 1/п часть оставшегося после этого наслед-
ства и еще два бриллианта, четвертый 1/п часть оставшегося и еще
три бриллианта и т. д. Каково было наследство, если в результате все
сыновья получили поровну?
582к. Найдите площадь фигуры, ограниченной линиями у = х.2 —
— 2х-|-2, у = х2 + 4х+5, у=1.
583к. Вычислите площадь фигуры, ограниченной линиями
у = х2 — Зх и у = х+1.
Занятие 22. Тема. Решение геометрических задач
584к. Докажите, что точки А(3; 0), В (0; 1), С (2; 7) и D (5; 6)
являются вершинами прямоугольника ABCD. Вычислите его пло-
щадь и укажите все перемещения плоскости, при которых он пере-
ходит в себя.	__ ________ _________
585к. В пирамиде ABCS даны | АВ| = 1, | АС| = 2, |AS| = 4. Углы
между АВ и АС, АВ и AS равны ~, угол между АС и AS равен ~ .
Найдите объем пирамиды.
586. Одно из оснований правильной треугольной призмы при-
надлежит большому кругу шара радиуса R, а вершины другого
основания принадлежат поверхности этого шара. Определите высоту
призмы, при которой ее объем будет наибольшим.
587. Боковые грани четырехугольной пирамиды — равные равно-
93
бедренные треугольники, а в основании пирамиды лежит ромб, одна
диагональ которого в 2 раза длиннее другой. Найдите объем пира-
миды, если известно, что площадь боковой поверхности равна 6, а
среди боковых ребер есть два ребра, составляющие тупой угол.
588к. Периметр равнобедренного треугольника равен 2р. Какой
длины должны быть его стороны, чтобы объем тела, образованного
вращением этого треугольника вокруг боковой стороны, был наи-
большим?
589°. Один древний римлянин, умирая, оставил беременной жене
2
и будущему ребенку завещание: «Если родится сын, то у наслед-
1	1
ства получает он и т мать; если родится дочь, то она получает
о	о
2
наследства, а мать -у наследства». Но вдова родила близнецов —
мальчика и девочку. Такого в завещании не предусматривалось.
Математическое решение задачи во многом зависело от юридического
толкования завещания. Римляне были большие специалисты в юри-
дических делах, и один юрист разделил наследство. Как он мог
разделить наследство и каково его толкование завещания? Какое
деление возможно еще?
590Д. Докажите, что выражение (2-57— 5-27)83—((2-57)83—
— (5-27)83) делится на 83.
591к. На кривой у = х3—6х2 + 12 найдите точки, в которых ка-
сательная параллельна оси Ох.
592к. Найдите площадь фигуры, ограниченной графиками функ-
ций у = — х2 + 3,5х+1, у — 2~х, х = 2(х^2).
Ответы, решения и указания
1. а) 178 = х3, 178|3 , 5913 , 19|3 , 6|3 , 178 = 20121,; 1 59	2 19	1602 б) 594 = х„ 594|6_, 99|6 , 1616 , 594 = 24306; в) 898 = х„ 0 99	3 16	4 2 89817 , 128|7 , 18|7 , 898 = 2422.; г) 793 = х2, 79312 , 39612 , 2128	2 18	4 2	1 396	0198 198|2 , 99|2 , 49|2 ,24|2 , 1212 ,6|2 ,3|2 ,793=1100011001,; 0 99	1 49 1 24 0 12	0 6 0 3 1 1 д) 21021123 = х, х = 2-3* 4-1-З5 4- 2-33 4- 1-З2 4- 1-3 4-2 = 1769.. 2. а) , 2131, б) 231342. в) , 254в. + 3201/	- 42123/	+342/ 11332,	134214,	1040, г) 324, . д) 1412,|24, Х 32, ’	-120 Ж'	
1203 2032 22023,	212 212 0
3. а) 43* = 27, 4x4-3 = 27, х=6;
б) 324* = 89, 3-х2 4-2х—85 = 0, х = 5 fx =— у не удовлетворяет
условию задачи 1;
в) 421*—143* = 234*, 4х2 4-2х 4-1 —л:2 —4х—3 = 2х24-3x4-4, х2 —
— 5х—6 = 0, х = 6 (х= — 1 не удовлетворяет условию задачи);
г) 53*-16* = 880*, (5х + 3) (х4- 6) = 8х24- 8х, 5х24- ЗЗх4-18 = 8х24- 8х,
Зх2—25х—18 = 0, или х = 9 (х=—к не удовлетворяет условию
задачи).
4.	Пусть трехзначное число будет abc, а разность d. Тогда d =»
= 100а 4- 10b 4-с—100с—10b—а = 99(а—с) = 9-11 (а—с). Так как
а—с < 11, то п2.
5.	Сначала определим соотношения между буквами (цифрами) в
примере. Так как А первая слева, то А^=0. Если А = 9, то Я = 0,
и тогда Н = Л, что невозможно. Значит, А < Я, А 4-10—Я = 9,
95
Ад-1=Я, Н — 1 = Л, А> 5. Значит,
Н<А, Н + Ю —А = 7, т. е. Н = А-3,
А—1—в = 4, таким образом, А = В + 5.
Далее рассмотрим возможные значения В:
если В = 1,	то	А = 6,	Н = 3,	Л = 2,	Я = 7;
если В = 2,	то	А = 7,	Н = 4,	Л = 3,	Я = 8;
если В = 3,	то	А = 8,	Н = 5,	Л = 4,	Я =9.
Других решений нет.
6.	Пусть масса первой части будет
1огда масса второй части — х.
тт	«	/т ,	\2	о	(т \2
Цена первой части	» иена втором части а ( —х\ , цена
двух частей бриллианта равна а + х\ — xj = 6zf-y + 2x2l.
Она будет наименьшей при х = 0, т. е. когда бриллиант разделят
на 2 равные части.
7.	Пусть данные точки В19 О (рис. 31). Проведем через точку
О отрезки А1А = 3-Аг0 и В1В = 3-В10. Точки А и В будут верши-
нами искомого треугольника. Третью вершину получим, проведя
через АВ± и ВА± прямые до пересечения в точке С.
Необходимо обосновать, что полученный треугольник искомый.
Это предоставим читателю.
8.	Найдем время выполнения всего заказа каждым прессом:
3,5:0,42 = 8-4 (ч), 9:0,6=15 (ч), 15:х = 6:5, где х—время выполне-
О
ния заказа третьим прессом. Значит, х=12,Й(ч). Искомое время
равно
i/l i1,	1 \	Q3/\
1:	(	1 + 15 + 12,5	3 4
V 3	7
13. 7х—i/=ll.	14. Ьу — Чх. 15. у — Чх—5.
16. х = 5.	17. у = 7.	18. (0,5; 3).
19. (15; 1). 20. (10; 2). 21. (10; 14).
22. (2,5; 1). 23. (— 4; 1,5). 24. 38 телят и 52 гуся.
25. а) 415-382 б) 1089708[12
830	108	90809
3320	97
1245	96
158530	108
108
Указание. При умножении делителя на 8 (третья цифра част-
ного) получается двузначное число. Значит, частное равно 90809,
а делитель 12.
96
26.
	км V — ч	S км	t ч
I автомобиль	X	126	126 X
II автомобиль	х+12	108	108 х -р 12
——х 4-1'2 ~ 1- П° условию задачи х#=0 и х^= —12. Решаем урав-
нение: 126х~!-1512—108х = х2 4~ 12х; х2— 6х—1512 = 0; х = 42 (х =
= —36 не удовлетворяет условию задачи). Таким образом, скорость
первого автомобиля 42 км/ч, а второго—54 км/ч.
27.	По плану ежедневно бригада должна выполнить х деталей.
Значит, 1,2х-54-(х+15)^^2—7) —495, где —7^ дней работа-
ла бригада, изготовляя 15 деталей сверх плана, откуда х=40.
28.	а) г/ = (х—I)2—16, ymin = —16 (рис. 32);
б)	У = (х—3)24-4, z/min = 4 (рис. 33);
в)	у= — 5-(х—0,6)24-0,8, г/тах = 0,8 (рис. 34);
г)	(рис. 35) xmin=—4.

Рис. 38
98
29.	а) (Рис. 36); б) (рис. 37)
в) (рис. 38); г) (рис. 39).
30.	а) (Рис. 40); б) (рис. 41);
в) (рис. 42); г) (рис. 43).
31.	5п3—5п = 5(п—1)и(и+1) —
произведение трех последовательны:
натуральных чисел и числа 5. Зна
чит, по крайней мере одно из ни:
кратно 2 и одно кратно 3. Такш
образом, произведение кратно 6 i
5, т. е. делится на 30.
32.	а) Последняя цифра множите
ля 6, так как первое промежуточное
произведение четырехзначно. Цифрь
МНОЖИМОГО МОГуТ быть ТОЛЬКО 0 ИЛ!
5. Первая цифра 5. Вторая не можел
быть 5, так как в этом случае в ре-
зультате вторая цифра не получит-
ся 1. Значит, множимое 504, множи-
тель 236;
б)	первый множитель 405, второй
205.
33.	О£ = 7? = 3 (рис. 44), ОС = 5.
Значит, ЕС=4, тогда ВС=4+3 = 7.
•-	--	АВ 7
-3-= V откуда
Таким образом,
5 = 0,5-АВВС — 18-I-.
О
34* Пусть 40 % -го раствора, бы-
ло х кг, а 60 % -го у кг. Тогда имеем:
и АВ __ ВС
И0 Е0~~ ЕС
АВ = 5,25.
в
О
Рис. 44
т. е.
4*
за
Решая эту систему, получим х—1 кг, у = 2 кг.
35.	а)х=—1 илих = 2 (рис. 45); б) — 3 или х— 1 (рис. 46);
в) х = 0,5 или х = 4 (рис. 47); г) х = 0 или х — 2 (рис. 48).
36.	а) ( — 1; —2), (2; 1) (рис. 49); б) (—2; 3), (3; —2) (рис. 50);
в) ( — 2; 0), (3; 5), (—2,8; 3,84), (1,8;—0,75) (рис. 51); г) (1;—2,8),
(1; 2,8) (рис. 52).
100
37.	Из первого столона А = В + 1,
далее С + Е = 10 4- А — 1. Из первой
строки Б == А + 1. Но Л <; 9. У бежда-
емся, что А 8, А 7, А /= 6, А =/= 5.
При Д = 4, В = 3, Б —5 и Е + С=13,
но 13 = 8 + 5 невозможно, так как 5
занято, тогда 13 = 7 + 6. Проверка по-
казывает, что Е = 7, С —6. Итак,
443 4 63 = 506
374:К7 = ЯЯ
6Р — 46 = НЗ '
Из последнего столбца ясно, чго Н = 2.
Тогда Р = 9, К — 1, т. е.
443 + 63 = 506
374:17 = 22
69 —46 = 23‘
38.	Последняя цифра множимого 5.
Чтобы получить в результате предпо-
следнюю цифру 6, надо при умножении
второй цифры на 7 получить число,
оканчивающееся на 8, т. е. предпослед-
няя цифра 4. Продолжая аналогичные
рассуждения, получим, что множимое
равно 31 245.
39.	Наташа получила первую, Ко-
ля—вторую, Дима—третью премию.
Указание. Рассмотрите три возмож-
ных предположения. В каждом случае
одно высказывание считайте верным, а
остальные ложными. Установите в каж-
дом случае возможные варианты распре-
деления премий.
40.	Введем новую переменную у —
= |/"где х > 0 и у > 0. Тогда
у + 1/ = у> 2у2—5у + 2 = 0, откуда
у = 0,5 или у = 2. Если у = 0,5, то
= 0,5, откуда х = — 1у (не удо-
влетворяет условию задачи). Если у = 2,
/1 -j-X 0	1
—= 2, т. е.
X	о
101
Рис. 52
41.	Данные 4 точки не
могут быть вершинами
выпуклого четырехуголь-
ника. Значит, три из них
образуют треугольник,
внутри которого лежит
четвертая точка, например
точка М (рис. 53). А тогда
QM—часть высоты тре-
угольника. Следовательно,
она перпендикулярна PN*
42.	а) (4; 5);
43.	а) (1; ±);
б)	(10; 2).
44.	а) (5; 4);
б)	(11; у);
в)	(2; 3); г) (4; 5).
45.	Ясно, что Д=1.
Тогда А = 9 и, значит,
Е = 0; В = Б + 1,Ж = 8, так как В =/=8, Г, Б не могут быть равны-
ми 0, 1, 8, 9 и в сумме больше 10. Это 7 и 5. Тогда В = 6, Г = 7,
Б = 5.
Получаем , 9567
+ 1085
10 652’
46. За 2 скачка собака пробегает 4 м, а лисица за 3 скачка
3 м. За один цикл расстояние уменьшается на 1 м. Значит, собака
пробежит 4-50 = 200 (м).
47. Обозначим объем продукции, произведенной первым, вторым
и третьим рабочими, соответственно X, у и z. Тогда имеем: х + г =
= 2у, y-\-z = 3x. Вычтем из первого уравнения второе: х—у~
102
= 2у—Зх, т. е. 4х = 3//. Следовательно, х = 0,75 у, т. е. z/>x;
z — —у + 2,25//, z— 1,25//. Значит, г > у >х. Итак, I место занял тре-
тий рабочий, И место—второй рабочий и Ш место—первый рабочий.
4». х не должен быть меньше —1. Имеем х =—1 или х==2.
	Расстояние, км	Скорость, км/ч	Время, ч
Расчетные	X	40	X 40
Фактические	0,4х	40	2х 200
	0,6х	45	Зх 225
Из уравнения 55 =	+ у находим х = 200 (км).
50.	Пусть скорость лодки в стоячей воде равна х км/ч, а ско-
рость течения реки у км/ч. Тогда условие запишется так:
	Скорость, км/ч	Время, ч	Путь, км
Лодки от М до К	х+у	8	(х-Н)-8
Лодки от К до М	(Х—у)	12	(х-у)-12
Плота	У	S У	S
8-U + t/)= 12(х—у), Ьу = х, s = 8-(x4-//) = 48//.
Таким образом, у = у^ = 48 (ч).
51.	I число: 10x4-//, 1^х, у ^9,
II число: 10//4-Х, 1 <у, х^9.
Составим уравнение (10x4- у)—(10//4-х) = п2, 9-(х—//)=«*.
Откуда х—у = 1 или х—у = 4. Если х—у=\, то одно двузначное
число будет четным и, следовательно, составным, значит, х—у —4.
Тогда х^5. Если х = 5, то //=1, но 51—составное число. Если
х = 7, то у — 3. Тогда одно число 73, второе 37. Их разность
73—37 = 36 = 62. Если х —9, то // = 5, но 95—составное число.
Итак, искомые числа 73 и 37.
52.	3-4-5-7 + 1=421.
103
53.	Пусть собственная скорость пловца х км/ч, а скорость тече-
ния реки у км/ч. Против течения скорость пловца (х—у) км/ч,
проплыл он (х—У)'~% км. По течению реки он проплыл ^(х—у)х.
хт+2;км за ——у—ч-Всего он плыл	ч*а
2
спасательный круг — ч. Отсюда получаем систему уравнений!
I 1 । (*-</)+6 г . 2
<3^3 (х + у) у
( х = 2у, откуда находим- собственная скорость пловца 6 км/ч, ско-
рость течения реки 3 км/ч.
54.	1 кг, 3 кг, 9 кг, 27 кг.
55.	Неравенство справедливо при всех х < 0. Рассмотрим его
решение при х > 0: ~ + 3:С ]/ 41—-у, что равносильно системе?
откуда х I.
Итак, х<0 или х>1.
56.
2м + о = 7
. .	Г 2м+ о = 7
-о| = 2, 0™УДа ^м—о = 2
или
2м + 0 = 7
о—м = 2,
2	2
т. е. м = 3, о=1 или м = 1 =, 0 = 3-5-.
О	о
100-3600	-70 /	, \	, 60-3600
57.	1ооо-5~==72 (КМ/Ч) (скорость поезда пассажира), 2-
= 108 (км/ч), 108—72 = 36 км/ч (скорость встречного поезда).
58.	Пусть первое число х, а второе у. Тогда имеем:
х + у = ху
х2 — у2 = х + у.
Одно решение х = у = 0. Найдем другие решения.
Если х + у = 0, то х = — у, и тогда х = у = 0. Поэтому рассмат-
риваем случай, когда х + у^О.
Сокращаем на х-\-у. ( х + у —ху
(х—«/= 1.
Первоначальную систему можно записать в виде;
( х = у +1
t2у + 1 = у3 + у.
104
Из второго уравнения находим у
или
т. е. другими решениями являются
59
1 ± к 5 ~
. Тогда:
i + Гб
У=~2—
х .3+Г5
х —	2	,
пары чисел
1-
	Теперь, лет	Было, лет	Станет, лет
Сергей	У	X	(у + (.У—х))
Володя	X	(х—(у — х))	У
и
(2(х—(у—х)) — у	( 4х—2у = у
|у4-(у—х) 4-У = 63	Зу—х = 63, откуда х = 21, у = 28, т. е.
Сергею 28 лет, Володе 21 год.
60.	10x4- у — ху2; 9х = у(у—1). Значит, х—четно. Отсюда
ясно, что х = 8, у —9, т. е. это число 89.
61.	10x4- у — 2ху. Отсюда у четно, у ^2. Вычтем из обеих час-
тей уравнения 4х, получим 6х4-у = 2х(у—2). Здесь у—2 > 0, зна-
чит, yi>4. Вычтем еще по 4х, получим 2x4-У = 2х(у—4). Здесь
2х + у>0, значит, и у—4 > 0, т. е. у ^6. Если у = 6, то 10x4-
4-6 = 2-6-х, х = 3. Тогда искомое число 36. Если у = 8, то 10x-j-
4~8=16х, откуда 6х = 8, что невозможно.
62.	По пятой строке имеем: последняя цифра первой строки 1,
вторая цифра в обоих множителях может быть только 9, иначе не
получится 1 в четвертой строке. Последняя цифра второго множи-
теля только 1. Первую цифру подбираем проверкой. Это только 4.
Итак, имеем:
4 19 1
1 9 1
4 19 1
3 7 7 1 9
4 19 1
800481
105
12Q-y
Рис. 54
63.	Пусть мотоцикл догнал мопед в пункте С. Обозначим рас-
стояние СВ = у. Тогда АС = 120—у (рис. 54). Запишем все отно-
шения в виде таблицы:
		V км/ч	S км	t ч
До встречи в С		X	(120—у)	120—у X
	Мотоцикл	50	(120—у)	120—у 50
После встречи в С	Мопед	X	У	У X
	Мотоцикл	50	(120—у)	120—у 50
z 120 -у	120—у_
х 50 ~
У _ 120—у
ч х 50
( у2 — 205// + 7200 = 0
( х= 120—2у.
Из первого уравнения имеем у = 45 (у =110 не удовлетворяет усло-
вии^ задачи). Значит, скорость первого курьера 30 км/ч.
64.	4С = 8 (рис. 55), ВС = /64=Й6=4КЗ. 5дВСК = 15длвс=
~ ± АВ ВС = 4'4 ^ = 4^3.
4	4 г
65.	Анализ. Высота h треугольника АВС определяет положение
прямой PL, параллельной основанию и являющейся геометрическим
местом вершин В треугольника АВС. Медиана определяет положе-
ние прямой, делящей высоту пополам и являющейся геометрическим
местом оснований D медиан AD. В равнобедренном треугольнике
высота одновременно является и медианой. Значит, однозначно
определяется положение точки их пересечения О.
Построение. Проводим произвольную прямую MN и к ней пер-
пендикуляр длины h (рис. 56). Делим его пополам. Через середину
перпендикуляра проводим прямую, параллельную MN. На ней
W6
берем произвольную точку D и из нее как из центра проводим
дугу радиусом т до пересечения с прямой MN. Полученная точка
есть вершина А искомого треугольника. Проводим прямую, парал-
лельную MAf, на расстоянии у h от MN. Через точку ее пересече-
ния с AD проводим высоту треугольника АВС, Получаем вершину
В. Через В и D проводим сторону ВС, Задача всегда имеет един-
. h
ственное решение, если т > у.
66.	EMNF—трапеция. Ее площадь S =	. ОК;
tXACD^EFD,
+	CD-100 (рис. 57);	,-<>.5• ,1Г/
xBD = CD-BF-, 0,5-160-120= 100 BF, BF = 96. Из треугольника
BCF CF2=BC-—BF2, СР= 1002 — 962, CF = 28. Значит, DF =
= CD—CF = 72;	115,2.
-Яу = -££-, (Ж =16,8; Д BMN cv Д BEF,	MN = 90.
Ou CU	br di\
SEMNF^ 90+2115’2.. 16,8= 1723,68.
67.	Eodec = S^ode + S^oec (рис. 58), S^oDe = -tOD' DE;
S^Oec = ~OC-EC- ^BDE^&OBC-. = /\ОВС: ОС* =
— OB*—ВС*; &OBA-. So/}A = EqA-BC = E0B-DA; отсюда ВС =
__ AD-OB
OA *
ДООД: AD2 = OA2 — OD2. Значит, AD = r]/^, тогда ВС =
r 3 • у Г	~	--- /Ч\2 /3 г — \ 2	Q
= ---—BC = 4r^3; OC2-(^-r ) — (4г/3) =^г2; ОС ==
2г ’	4	’	\ 2 )	\4	/	16’
167
1	3
j-^-; de
АС=ОА-ОС=2г—%-г=Лг,
6 b ’	4	4
Г(Г~"~48”;	— -^гУз.
1.-|.г4гГЗ; SAO£C = Ar2)/3; S^0DE
Q _"-b3. „	_r2/3, 5	,/--5 23г>Кз
Лдосе- 12	, &ODEC~ 12 + 32r ' 6~~	96
68. Обозначим AB = l, AC — dlt BD — d2 (рис. 59). Тогда имеем
B = di-d2, SpoM6a = y dj-d2 = -T/2. С другой стороны, 5ром6а = Л£>-BE,
где BE | AD, т. е. Sp0Mga = I• h. Таким образом, -^В — 1-h, откуда
/i=yZ. Следовательно, в тре-
угольнике АВЕ/_Е — 90°, / А =
=30°, /ЛВС= 180-° —30°= 150°.
69. Рассмотрим преобразование
подобия с центром А и коэф-
АС
фициентом k = -jg- . Окружность
О переходит в О^ радиус О А в
радиус О]А и Д ВО А в Л COtA
(рис. 60). При этом СОЛ ВО.
Следовательно, COL лежит на СЕ,
т. е. CD—диаметр окружности
Ор Значит, 2^СДЕ = 90о. В четы-
рехугольнике BADE Z-A — Z_E=
~ 90°. Поэтому около него мож-
но описать окружность. Ее диа-
метр BD.
108
4-
D£№^£
dC
DE
EC* = AE*-AO,
О
AE = AD—DE^z-УЗ-
25r2 25f2 25г2
— 12
ОЕС =
• -ТГ •
В	£
Рис. 60
11
8
6	17	2
Рис. 61
70.	Двоечников нет (рис. 61). В секции плавания занимаются 2
велосипедиста.
71.	Обозначим искомое число у, число сотен в этом числе х.
Тогда у — 1 ООх + 91. Далее х-п= 100x4- 91, х-(п —100) =91, иначе
х-(п—100) = 7-13. Отсюда имеем четыре возможности:
Г и—100 = 13	( п—100=7	1 п—100=1	( п—100 = 91
| х = 7,	|х=13,	( х = 91,	|х=1.
В первом случае г/ = 791, во втором у = 1391, в третьем у = 9191 и
в четвертом у =191.
72.	f/max = 4.
73.	Обозначим искомую величину х. Тогда 80 • 0,05 = (80 4- х) • 0,04.
Отсюда 400 = 320 4-4х, 4х = 80, х = 20.
74.	Это прямоугольник (рис. 62). А вследствии того что равно-
бедренные треугольники попарно равны, стороны прямоугольника
равны, т. е. он является квадратом.
75.	Д ВЕР со Д BAD. Следовательно, = -ff- (рис. 63).
/\CPF со &CAD. Отсюда=	. А так как	то
BE	ср	ЕР	FP
-й-г = 7гп. Сравнивая эти равенства, получим -тп=Тп’ т-е-
/1 2л	Л/	/11/	2*11-/
ЕР = FP.
76.	Отрезки ВО* и ВО2 составляют угол 180°. Значит, ОгВО2
прямая, т. е. отрезок OtO2 проходит через точку В. О—центр ок-
ружности, описанной около треугольника АВС. Следовательно,
перпендикуляры, проведенные из О к АВ и к ВС, делят эти от-
резки пополам. Делят их пополам и перпендикуляры, опущенные
из точки 01 и из точки О2. Значит, OOi I АВ и ООа I ВС. А так
109
как АВ I ВС, то 00^ I О0|, т. е. треугольник 00х02—прямоуголь-
ный (рис. 64).
77.	Пусть ^ВАС = х. Тогда ^/СВА—х и, следовательно, дуги
АС и ВС равны по 2х. Значит, ^.АОВ — 4х, £0AD = £0BD =
= у (рис. 65). В Л АО В сумма углов равна 5х=180°; х = 36°.
78.	Р = А В + ВС + CD + AD + 2л/? = 50 + 4л (рис. 66). S = Зд,+
+ % + Р • 2 + л/?2. Обозначим Рх = 20, Р2=15. Тогда по формуле
Терона: Зд, =/20(20—12) (20—18) (20—10) = 40/?, Зд, =
=/15-1-5-9= 15_/3. Далее /’•2=100, л/?2 = 4л. Таким образом,
S= 40 / 2+15 / 3+100 + 4л.
79.	Пусть Р — точка пересечения MS и АВ. Докажем, что PN
проходит через Т. а) Точку пересечения PN с окружностью Ох
обозначим Тх (рис. 67). Тогда по свойству: если из точки, взятой
вне окружности, провести несколько секущих, то произведение
каждой секущей на ее внешнюю часть есть величина постоянная,
равная квадрату касательной, имеем
PS-PM — PTi-PN = PA-PB.
С другой стороны, A SPT cv Д MPN (докажите, рассмотрев
углы). Значит, — Отсюда PT — PTit т. е. точки Т и Тг
совпадают. Значит, все три прямые проходят через точку Р.
б)	Из подобия треугольников PST и PMN имеем	=
= ~РЖ- Отсюда получаем	• Поэтому ST2 -PM-PN=
= MN2-PS PT (1). Из пропорции = имеем MN'PT =
= ST-PM (2), а по свойству секущих PS-PM = PA-PB (3). Пере-
множим равенства (1), (2), (3). Получим: ST2-PM-PN-MN-PT-PS*.
xPM = MN2 PSPT-ST-PM-PA-PB. Отсюда
ST-PM PN = MN-PA-PB.
80.	(Рис. 68).
81.	Xi “I- %2 “Ь ===	“1“ ^4 “1“ ^7 == ^2 "P ^3	^4 =- ^3 ""Ь *^6	^7	^3 I
4-x6. Обозначим сумму чисел трех кругов S. Тогда
Г х, + 2S = 28
{ 35—2x4 = 28.
Отсюда Xj = 4, 5=12, х2 выбираем произвольно, остальные находим ।
из уравнений (рис. 69, 70).
Ш
82.	(Рис. 71).
83.	Обозначим искомое время через х. Тогда условие задачи
можно записать в виде таблицы:
	Время выполне- ния задания, дни	Объем задания, детали	Количество деталей, изготовляемых в день
По плану Фактически	X	360 360	360 *+1 360 X
------гт = 4, х2 + х—90 = 0, х = 9 (х =—10 условию задачи не
удовлетворяет).
2—5% о х
84-	7+Т>2;7+1<0’ 0ТКУда
( х < 0	7 х > 0
( х-Т 1 >0 ИЛИ ( х+1 <0,
т, е. —1 <С х 0.
85.	а) (—3; 10); б) (—10; —5); в) (4; 8); г) (—8; 6).
86.	a) Xj >0, х2 > 0; б) хг <0, х2 < 0; в) хх <0, х2 > 0;
г) Xi <0, х2 > 0.
87.	а) х2 —ЗЗх + 200 = 0; б) х2+17х + 70 = 0;
в)х2 + 8х—65 = 0;	г)х2 + 9х—400 = 0.
88.	Проводим оси координат (рис. 72). Окружность—геометри-
ческое место точек, удаленных от центра на одно и то же расстоя-
ние, в данном случае на 5 см. Возьмем какую-либо произвольную
точку А окружности. Пусть ее координаты х и у. Соединим А с О
и проведем АВ _\_Ох. Треугольник АОВ—прямоугольный. По тео-
реме Пифагора имеем х2 + i/2 = 52. Так как точка А была произволь-
ной точкой рассматриваемого множества, то полученное соотноше-
ние верно для любой точки окружности.
Если радиус окружности равен R, то ее уравнение будет иметь
вид х2 + у2 = R2.
112
89.	(х—2)2 + (У—3)2 = 36.
90.	Рис. 73, 74, 75, 76. Можно решить иначе. Действительно,
(/п)2=Ьп. Значит |/ п есть среднее пропорциональное между 1 и
п, поэтому можно использовать свойство перпендикуляра, проведен-
ного из точки окружности на ее диаметр.
91.	а) (3; 4), (—4;—3) (рис. 77); б) (0; 7), (7; 0) (рис. 78);
в) (—1; 1), (2; 4) (рис. 79); г) (0; 0), (1; 1) (рис. 80).
92.	Возьмем произвольную точку А (х, у), принадлежащую ок-
ружности (оис. 81). Тогда 01А2 = (х—а)3 + (у—Ь)2, т. е. (х—а)2
+ (t/-^)2=>2.
ИЗ
93.	Малая полуось эллипса связана с а и.с формулой Ь2 — а2— с2.
Это следует из прямоугольного треугольника OEFa EF^ — a, OE=b,
OFt = с.
Возьмем произвольную точку А эллипса. Тогда (рис. 82) ЛГ2=
=К(х4~с)24~//2, AF-^y(х—с)2А-у2', AF^A-AF-l =2а, т. е. К(х+с)24-*/24-
4- К(х—с)2 4- у2 = 2а. Перенесем второй корень вправо и возведем обе
части равенства в квадрат: х2 + 2сх 4- с2 4- у2 = 4а2 — 4а V(х—с)2А-у2+
4- х2—2схА~ с2 4- у2- Далее последовательно получаем:
4а —с)2 4- у2 = 4a2—4сх, а]/\х—с)2 + у2 = а2—сх,
а2 (х2—2сх 4- с2 4- У2) = а4—2а2 сх 4- с2х2,
(а2 — с2) х2 + а2у2 = а4—а2с2; Ь2х2 А-а2у2 = а2Ь2.
94.	a) (x—3)2+(y—4)2 = 36; 6) (x+2)2 + (y—5)2 = 9; в) (x + 4)2+
+ (y—3)2 = 49; r) (x—4)2 + (y + 2)2 = 64.
95.	a) 4 + 4 = 1, . = 4; 6) §^+4 = 1,	1,5; в) 4+^ =
= l,C = 6;r) 4 + 4=1, C = 6.
96.	a) (4; 3), (3; 4), (—4; —3), (—3; —4) (рис. 83); б) прибли-
женно по графику имеем: (6,6; 4,5), (6,6; —4,5), (—6,6; 4,5),
(—6,6; —4,5) (рис. 84).
97.	Возьмем произвольную точку А гиперболы (рис. 85).
Тогда F±A = К(х + с)2 + у2, F2A = V(x—c)2 + У2', К (* + с)2 + У2 —
— К(х—с)2 + у2 = 2а. Выполняя преобразования, получаем:
х2 + 2хс + с2 + у2 = 4а2 + 4а И (х—с)2 + у2 + х2—2сх + с2 + у2,
4а К(х—с)2+ у2 = 4сх—4а2, а К(х—с)* + У2 = сх—а2,
а2(х2—2сх + с2 + у2) = с2х2—2а2сх + а4, (с2—а2)х2—а2у2 = а2(с2 — а2),
у2 »»2
Ь2х2—а2у2 = а2Ь2, 4—тг=1-
v	’ a2 bs
98.	53 автомашины и 19 мотоциклов без колясок.
99.	Если т или п кратны трем, то утверждение верно. Если ни
т, ни п. не кратны трем, то возможны 3 случая: 1) m — 3k + 1,
п = 3/?+1; 2) т = 3^4-2, п = Зу + 2; 3) /и — З/г+2, н = 3&4-1, где
k, pk.N. Случай /п = 3&+1, п = Зр4-2 аналогичен случаю 3).
В случаях 1) и 2) т—п будет кратно трем, а в случае 3) т + п
кратно 3.
100.	По свойству членов арифметической и геометрической про-
грессии имеем:
Г (5х—у) + (х+2у) = 2-(2х+3у)
\ (г/+1)2.(х-1)2 = (ху + 1)2.
П5
Из первого уравнения получим 6х + # =
5
= 4x4-6#, х = у#. Подставим это выраже-
ние во второе уравнение:
i)a=(-h1 2+1)?.
Если выражения, стоящие под знаком мо-
дуля, оба положительны или оба отрица-
5 n .5	4 Ю
тельны, то j#2 —#4-у#—#2+ь Откуда у = у , х = у .
(5	\
у#—1 J —
5	3	3
= у #2 4~ 1 • Тогда х = 0, # = 0 или х = — — , у =— .
Проверкой можно убедиться, что все найденные значения пере-
менных удовлетворяют условию задачи.
101.	Строим острый угол А, равный данному углу а. Из произ-
вольной точки В± его стороны проводим к АВг перпендикуляр и на
нем откладываем отрезок В^^ равный данному катету (рис. 86).
Через С\ проводим прямую, параллельную АВ±. Точку ее пересе-
чения со второй стороной угла обозначим С. Из нее опускаем пер-
пендикуляр СВ на ABi. Треугольник АВС — искомый.
102.	а) —4 или 10; б) 22 или —17.
103.	а) 29,6 или 4; б) —2 или 4^.
104.	а) Нули подмодульных выражений: —4; 7 (рис. 87): 1
Рис. 87
1) х< — 4; 56—8х—36х—144 = 356, х = —10д;
2) —4<х< 7; 56—8х+ 36x4-144 = 356, x = 5-i;
3)х^7;8х—56 + 36х+144 = 356, x = 6-i < 7 (не принадлежит
рассматриваемому промежутку). Значит, х = —10^ или х=5у.
б) Нули: —4, 8, 10 (рис. 88):
Рис. 88
116
1)	х <—4, —2х+16—5х—20—Зх-|-30 = 300, х =—27,4;
2)	—4^х<8,—2x4-16 + 5x4-20—Зх + ЗО = ЗОО, решения нет;
3)	8<х<10, 2х—164-5х + 20—Зх + ЗО = ЗОО, х = 66,5 (не при-
надлежит рассматриваемому промежутку);
4)х>10, 2х—16 + 5х + 20 + Зх—30 = 300, х = 32,6. Значит,
х =—27,4 или х = 32,6.
105.	а) Нули: 7, 24 (рис. 89):
*>
к
Рис. 89
1)	х С 7, — 15x4- 105—12х + 288 = 535, х = — 5 Ж
2)	7^х<24, 15х—105—12x 4-288 = 535, х = 117 Л- (не принад-
О
лежит рассматриваемому промежутку);
3)	%^24, 15%—105+12%—288 = 535, % = 34^. Таким образом,
г 7	о , 10
X = —5 27 или	.
б)	Нули: —4, 3, 5 (рис. 90):
О 3
Рис. 90
Д'
1)	%<—4, 36—12%+ 5%+ 20+ 7%—35 = 240, решения нет;
2)	— 4<%<3, 36—12%—5%—20 + 7%—35 = 240, х = — 25,9 (не
принадлежит рассматриваемому промежутку);
3)	3<х< 5,	—36 4-12х—5х—20 +7х—35 = 240, х = 23^
(не принадлежит рассматриваемому промежутку);
4)	х ^5, —36+12%—5%—20 — 7% + 35 = 240, % < 0 (не принадле-
жит рассматриваемому промежутку).
Итак, уравнение не имеет решения.
106.	%^0. Нули: —2, —1, 0, 1, 2 (рис. 91):
1)	0<%_<1, 1~%2 + 4—%2_ = 2%, 2%2 + 2% — 5 = 0,
—1 — К Н	--1 + КТ1 /
% =--— или ------------2 — \не пРиналлежат рассматриваемому
промежутку);
2)	1^%<2, %2 —1+4—%2 = 2%, 2% = 3, % =1,5;
3)	%>2, %2—1—4 +%2 = 2%, 2%2—2%—5 = 0,
-2 —7
Рис. 91
117
i+/ii / i-Vn
x =—-%----(x =----— не принадлежит рассматриваемому про-
\ „	,	. к 1 + /П
межутку 1. Таким образом, х=1,5 или х =———.
107.	Пусть х монет достоинством 50к., у монет—достоинством
20 к., тогда (25—х—у) монет—5 к. Запишем уравнение
50х + 20г/ + 5 • (25—х—у) = 200.
Далее 9х4~Зг/=15, 3x4-у = 5. Отсюда х=1, у = 2. Значит, 25 —
— х—у = 22.
108.	ab=10a + b, 1^а^9, 1 b s'' 9, 10а+ Ь = &2 +а3. Отсюда
10а + Ь^а3 + Ь, значит, а2 10, т. е. а^З. Значит, а=1,2илиЗ.
Проверим каждое из этих значений:
если а= 1, то 104-Z> = Z>24- 1, b(b—1) = 9, что невозможно;
если а = 2, то b(b—1) = Г2, & = 4, тогда искомое число 24;
если а = 3, то b(b—1) = 3, что невозможно.
109.	Данная функция определена при всех действительных зна-
чениях х#=±0,5. При х < 0, ху=—0,5, имеем 2х2 + 5х + 2 = 0,
х = —2 — не удовлетворяет уравнению 1х =— у не удовлетворяет
условию задачи). При х^0, х#=0,5, имеем 2х2—5х 4-2 = 0, х = 2
^х=у не удовлетворяет условию задачи). Значит, х = 2.
НО. ( ai 4-a2 + a3 = Ю,5	( ах axq axq2 = 10,5
( ах — a4 = 31,5	t Й1 — а1<?3 = 31,5
Г at (1 + q + q2) — 10,5
^(аД!—<?) (1 4~ <7 + </2) = 31,5, отсюда 1—</= 3, q = —2.
Из второго уравнения системы получаем ax (1 4-8) = 31,5, aj = 3,5.
111.	а) г/=|ух4-2| (рис. 92); б) у = |1—2х| (рис. 93); в) у=*
= 1б—у х I (рис. 94); г) у = | 3x4-1 | (рис. 95).
118
112.	а) Нули: —1, 1 (рис. 96):
1)	х <—1, у — — х—1—х + 1 = — 2х;
2)	—1	х < 1, у — х-^1 —х-|-1 = 2;
3)	х^1, у = х1 -\-х—1=2х.
б)	Нули: —4, 4 (рис. 97):
1)	х<—4, ^ = —ух + 2 + у х + 2 = 4;
2)	—4=Сх<4, у= — ух + 2—ух—2 = — х:
3)	х>4, у = ±х—2 — ух—2 = — 4.
113.	у = У(х+ З)2 —	(±х—1)2+ ]/"(уХ + г)2 = [х + 3[-
— |тх—1	+ ’ НУли: —4, —3, 2 (рис. 98):
1)х<—4, у = — х—3 + ух—1—ух—2.= — х—6;
2)	— 4<х<— 3, г/ = —х—3+уХ—1+у^ + 2 = —2;
119
3)	—3^х<2, у = х + 3 + х—1 + ух + 2 = 2х + 4;
4)	х^2, у = х -j- 3—х 1 Н—2* % "Ь 2 = х -}- 6*
114.	^ = /(3=7^+ )Л(|х + з)?- ]/(|х+1)2 = |3-х| +
+ |ух + з|—|ух4-1|. Нули: —6, —2, 3 (рис. 99):
1)	х 6, у — 3—X X—3 "ту" Л' _;1 —- — -V _|-1
2)	— 6<х<— 2, у = 3—х + 1х + 3 + -|х+1 = 7;
3)	—2^х<3, у = 3—х + -|-х + 3—-^-х—1= — х + 5;
4)	x^s3, у = —3 + х + -^-хЧ-3—-^х—1=х—1.
115.	a) z/ = |lx—2| + |з+|х|—3. Нули: —4,5, 6 (рис. 100);
1)	х<—4,5, z/ = — 1х + 2—3 — |х-3 = — х—4;
2)	—4,5<х<6, z/ = _±x + 2 + 3+4^—3 = 4х + 2’>
О	о	о
120
б) У= 1 х— 1'~ * X=?tl <рис’ 101)‘
1 \	1	—% ~F 1	1
1) х< 1, г/=-х-Д.= —1,
2) х> 1, t/ = l.
116. (2000004-х)-3=10х 4-2, 600000+ 3х= 10x4-2, 7х=599 998,
х — 85714. Искомое число равно 285 714.
117. 60 треугольников.
118. у = \х—114-1х—214-х- Нули: 1, 2 (рис. 102):
1) х <7 1, у = — х 4" 1 4" 2—х 4" х = — х 4- 5;
2) 1^х<2, у — х—14-2—х4-х = х4- 1;
3) х2>2, у = х—1—24-*4~х = Зх—3.
119. ( х—у = 6	( х — у = 6	( х—у = 6
( х3 — у3 = 126	( ха + ху 4- у2 3 = 21	\ (х—у)2 4- Зху = 21,
откуда х=1, у — —5 или х = 5, z/ =—1.
120. (Рис. 103.)
121. а) (Рис. 104); б) (рис. Ю5).
122. (Рис. 106); б) (рис. 107).
123. (Рис. 108.)
124. (Рис. 109.)
125. При х<0 у = х2, при х^0 у——х3 (рис. НО).
126. 6-6—6; 5-5.4-5; 384- 3; 33—3.
127. Ясно, что С=1, Е = 0, К = 9; Т—нечетно, Т = 6/4-1,
Ы—четно, Т — 3, 5 или 7. Проверим эти возможности.
1) Т = 3, тогда А = 1, что невозможно.
121
2) Т = 5, тогда А = 2 или 7, Ы = 4. При А — 2 будет М + Л=11,
Р—четно, т. е. Р = 6 или 8. Если Р = 6, то Ш — 3, но тогда нельзя
подобрать М и Л. Если Р = 8, то Ш — 4, что невозможно.
Проверим А — 7, тогда Ы = 4, Р — 3, III —6. Итак, имеем:
,	2 7 6 7
+98767
1 0 1 5 3 4*
Проверкой можно убедиться, что Т не может равняться 7.
122
128.	Введем обозначения O1O1 = d, М^.^ — 1 (рис. 111). Тогда
I d2 — l2 + 5?
имеем: 1 /	2 Кб" . Отсюда d = — ,	— Z2-Ь 25, /?= 100, I —
I ~d~	5~
— 10, т. е. Л4!Л12=10 см.
129.	Пусть AE = z, ЕВ —у, DC = x. Тогда ЛП=г, BF — y,
FC — x (рис. 112). Из условия можно записать:
2
' 2х-г 2г/+ 2г = 36
(*+ Z)2 = (х 4- у)2 + (у + г)2 &
3z = 2x
\
(	2
| г=з-х
У= 18-
I х2 + 45% -
z =
о
2
х + y + -jX= 18
У х2 = 2ху + 2г/2 + у ху
5
3 Х
-486 = 0.
123
Отсюда х~9, z/~3, z —6, и тогда стороны треугольника равны
12 см, 15 см и 9 см.
130.	Указание. Соедините данную точку со всеми вершинами
треугольника и сравните сумму площадей получившихся треуголь-
ников с площадью данного треугольника.
131.	Проведем к произвольной прямой MN перпендикуляр EF,
равный данной высоте h (рис. 113). Из его середины D проведем
медиану DA = rna и через точку О медианы такую, что OD:OA =
1:2, проведем вторую медиану тъ так, чтобы ОВ:О/< = 2:1. Че-
рез конец высоты проведем прямую, параллельную MN, и прове-
дем прямую через А и К до пересечения с прямой, параллельной
MN. Точка их пересечения будет вершиной С искомого треуголь-
ника. Соединив ее с В, получим искомый треугольник АВС. Пост-
роение можно выполнить и другим способом.
132.	Проведем оси координат, взяв центр окружности за начало
координат, ось Ох проведем через точки А и В, ось Оу—перпенди-
кулярно Ох (рис. 114).
Обозначим радиус окружности через 7?, а расстояние от каждой
из данных точек до центра окружности через а. Тогда имеем
А (—а, 0), В (а, 0), М(х, у). Используя уравнение окружности и
формулу расстояния между двумя точками, получим х2 + у2 = 7?2,
AM2 + ВМ2 = (х + а)2 + у2 + (х—я)2 + у2=2х2 + 2у2 + 2а2=2 (х2+у2)+
+ 2а2 = 2R2 + 2а2 = const.
133.	Взяв произвольную точку окружности и опустив из нее
перпендикуляры на указанные диаметры, получим прямоугольник.
Интересующее нас расстояние будет диагональю этого прямоуголь-
ника, она равна радиусу круга.
134.	Введем новые переменные: и = — , и = ——. Получим:
х у Z
{и + и = 6
и+ t = 4
t и = 5. Откуда и = 3,5, v = 2,5, t = 1,5, тогда х = 4 , у — z =4 
/	О	и
124
135.	а) Легко заметить, что квадрат выражения, стоящего в
скобках в правой части, равен левой части с точностью до постоян-
ного слагаемого. Поэтому это выражение удобно принять за новую
переменную. Найдя значение этой переменной, сведем решение дан-
ного уравнения к решению квадратного уравнения. Итак, -£—у —
= 4/. Тогда ^ = ^-4-———. Значит, - + — = у* + -. Данное
уравнение примет вид: у2 + у, 5у2—16^+12 = 0, « = -|- или
у —2. Следовательно, если ц = то ~—- = 4-, х#=0, х2-—6х—
^5’5x5
— 30 = 0, откуда х = 3—К39 или х = 3 + ]/39. Если у = 2, то
Л—~==2, х=/=0, х2—10х—30 = 0, откуда х = 5—55 или х = 5+
D X
+/55.
б)	Корни уравнения: —2, 6, 3—К21, 3 + К21.
136.	Искомое число #=10х + а, где а—число единиц, а х—де-
сятков. По условию задачи 10х + а=12х, 2х = я, 1^а^9, а —
четно. Значит,
если а = 2,	то	х=1,	а	#=12;
если а = 4,	то	х = 2,	а	у = 24;
если а = 6,	то	х = 3,	а	# = 36;
если я = 8,	то	х=4,	а	# = 48.
137.	Число нулей равно числу множителей 5, а их в каждом
десятке по 2, итого 2-10 = 20. Кроме того, еще по одной пятерке
в числах, кратных 25, т. е. всего 24.
138.	Так как одновременно должно быть х^0 и 6х—3^0,
.	1	. 1 т-г
т. е. х^у, то имеем х^у. Поэтому данное уравнение равно-
сильно уравнению 6х + Кбх—3• Кх = 3 (*). Отсюда И6х2 — Зх =
= 3—6х, 6х2 — Зх = 9—36x4-36х2. Решая это уравнение, получим
х = -|-; х = 4-. Проверкой убеждаемся, что х = ~ не удовлетворяет
О	Л	о
уравнению.
Следовательно, х = у .
Уравнение (*) можно решить иначе. Легко видеть, что х = у —
корень уравнения. При х > 6х > 3 и второе слагаемое больше
нуля, т. е. значения х>у не могут быть решениями уравнения.
Значит, уравнение имеет единственный корень х = ~.
125
2х—4.
Из первого неравенства совокупности получаем х <—1, а из вто-
рого —1 < х < 0,5.
140.	£±АВЕ = £\DBC (рис. 115) по двум сторонам и углу между
ними 120°. Следовательно, DC — AE, а значит, PC = ОЕ и ^/ОЕВ =
= / РСВ. Отсюда Л ВОЕ = Д ВРС. Значит, OB = РВ. Если вы-
полнить поворот с центром В на 60° против часовой стрелки, то
точка Р совпадет с О. Значит, ^/РВО = &0°, т. е. /\РОВ—равно-
сторонний.
141.	ВМ.-ВА = ВА1-ВС—по свойству секущих, проведенных из
одной точки к окружности (рис. 116). Аналогично CN-СА = CAf СВ.
Разделим эти равенства почленно. Получим:
ВМ-ВА	BAVBC . ВМ-ВА	ВА±
CN-CA “ CAt-CB ’ CN-CA	САг *
ААг—биссектриса угла А треугольника ВАС. Докажем, что биссект-
риса ААг делит сторону ВС на части, пропорциональные двум дру-
гим сторонам треугольника ВАС, т. е. что ~	. Действитель-
C Л С Л j’
но, если провести отрезок СЕЦАА! до пересечения с продолжением
стороны В А, то получим, что ВА\АЕ — ВАг\ (*) (выполните
построение самостоятельно). Но	а Z1AAC ~
~ j/ACE, т. е. ,/ВЕС = Х.АСЕ, и, значит, АЕ = АС. Заменив в
равенстве (*) АЕ на АС, получим ВА-.АС = ВА1:А1С. Поэтому
ёй'сА~ = "ТТ" ’ т* е’ ТУ’==^' Следовательно, BM = CN.
142.	Д01АМ ^ Д02ВМ (рис. 117), поэтому
( г2 72
_вог ОаМ Имеем: { ““24
ЛО, О,м-	|,;+fl = 72 - 24.
Отсюда гг = 12 см, га = 36 см.
126
143.	Отрезок С1В1 произвольной длины принимаем за основание
треугольника, подобного данному. Строим на нем часть окружности
так, чтобы вписанный в нее угол, опирающийся на Сг был ра-
вен углу а. Проводим прямую параллельно на расстоянии
yCiBi. Ее пересечение с окружностью даст две точки, любую из
которых можно принять за вершину А искомого треугольника. Из
А проводим медиану стороны C^Bi и на ней от А откладываем от-
резок AD, равный данной медиане та. Через D проводим прямую,
параллельную CtBlf до пересечения со сторонами угла а в точках
С и В. А АВС—искомый.
144.	Непосредственно видим, что пары чисел (0; 1) и (—1; 0)
являются решениями уравнения. Других решений нет, так как
х3 < (х + 1) (х2 4- 1) < (х + 1) (х Н- 1 )2 = (х + 1 )3, то (х + 1) (х2 + 1) А у1
ни для какого целого у (располагается между кубами последова-
тельных целых чисел).
145.	Xi ==х2= ... =х21== 1 и х1 = х2 = ... = х21 = — 1 являются
решениями системы.
Других решений нет. Действительно, мы можем рассматривать
положительные значения х, так как если какой-то набор х{ есть
решение, то набор противоположных значений xz тоже будет реше-
нием.
Пусть не все xf, удовлетворяющие системе уравнений, равны 1.
Тогда среди них есть больше 1 и есть меньше 1. Будем считать,
что Xj < 1. Тогда х2 > 1. Из системы уравнений следует, что все
xf с нечетными номерами будут меньше 1, ас четными номерами
будут больше 1. Но в последнем уравнении оба множителя имеют
одинаковую четность, и, значит, это равенство не может быть вер-
ным. Мы пришли к противоречию. Из этого следует, что наше
предположение о том, что не все хгравны 1, неверно.
Можно решить систему и иначе. Перенесем свободные члены
вправо. Затем разделим каждое уравнение на следующее за ним, а
127
последнее на первое. Тогда получим равенство всех переменных.
Поэтому каждое уравнение можно записать как равенство квадрата
переменной единице. В итоге получим тот же результат,
146.	abc— cba^lQQa^ 10b-У с—100с—106—а=99а—99с = 99х
х (а—с). Естественно считать а > с, (а—с) — число однозначное.
Произведение 99 на любое однозначнее число дает в произведении
число, сумма цифр которого равна 18. Это легко проверить непо-
средственно. Можно установить закономерность результата иным
путем, например, представив 99 как разность 100—1 и рассмотрев
произведение этой разности на однозначное число.
147.	Все шары сначала разделим на 3 части по 27, 27 и 26 ша-
ров и на весы положим по 27 шаров. Если одна из чашек весов
будет легче, то там и более легкий шар. Если чашки весов будут
в равновесии, то более легкий шар в партии, где 26 шаров. Это
первый этап. Далее берем часть шаров, содержащую более легкий
шар. В первом случае, т. е. когда более легкий шар содержится в
партии из 27 шаров, дальнейшая схема взвешивания такая: а) 9,
9, 9; б) 3, 3, 3; в) 1, 1, 1.
Во втором случае, т. е. когда легкий шар находится среди 26
шаров, на втором этапе шары распределяются на 3 части так: 9,
9, 8. На весы кладут по 9 шаров. Далее рассуждают аналогично
описанному вначале. Во всех случаях более легкий шар находится
четырьмя взвешиваниями.
148.	т > 0, п > 0, т н, п > 1.
т-\-п	/т-\-п п . т \ V (1—Уп)2 __________________
Уm-j- Уп \т — п	п — У тп У тп -{-т /	2
т-\-п m п +/г Д-К тп-\-т- У пт	1 — У п
'Ут-у Уп *	2
2 г 2
(Ут + V п ) • 2 (т + п) 2
__ У т — 2 У п Д- 1 * 1
2	’
149. Ко второму уравнению прибавим почленно третье, а к пер-
вому— учетверенное третье. Получим:
f 31 r/—4z = 4
1 13г/— 4з = 4
—х~\-8у—2z=l. Отсюда у = 9, z =—1, х=].
150. Постройте треугольник с вершинами в данных точках и
впишите в него окружность. Точки ее касания со сторонами тре-
угольника будут точками касания искомых окружностей.
128
151.	Продолжите медиану, например та (рис. 118), на такое же
расстояние за сторону АВ и соедините полученную точку с точками
Ви А. Тогда 2та<Ь + с. Аналогично 2ть<а + с, 2те<а + Ь.
Сложив почленно все три неравенства, получим 2-(та + ть + тс) <
< 2(я4-&4-£), откуда следует утверждение задачи.
152.	Обозначим МО — п\ МР — пг, ВК = сг, КС~Ь\ ЕО = х\
OF —у, где О—точка пересечения диагоналей трапеции, a EF^AD\
AE = k\ АВ = р-, FD^k^CD^pt (рис. 119). Д МОЕ cv Д МАР,
следовательно,	, т. е. i == —. Д MOF оо Д MPD, следо-
Л л	/VI1	с tn
OF МО	у п	х у . ч
вательно, 755- = -^ > т. е. f = —• Откуда получаем - =	(*),
A OFD со Д BCD, следовательно,	, т. е. —7-7 = — ,
dC СЫ	а-\-о pi
л л г4/^ л л	ЕО АЕ	х k
/\ АЕО съ /\АВС, следовательно,	т- е- —но
ZjG Л£?	а у—о	р
— — , Поэтому —т. е. х — у. Значит, из (*) имеем
Pi р	J a~yb а + 6 ’	' 7
c — d, т. е. AP — PD.
153.	Построим прямой угол С. От его вершины на одной сто-
роне отложим данный катет ВС —су на другой отложим отрезок,
равный сумме гипотенузы и второго катета CD — by-c. Соединим В
с D и проведем серединный перпендикуляр к BD. Точка его пере-
сечения с CD есть третья вершина искомого треугольника (рис. 120).
Можно решить задачу иначе. По теореме Пифагора имеем с2 =
= & + а2. Откуда а2 = (с + Ь) (с—Ь),	. Строим четвертый
пропорциональный отрезок с—Ь, а затем находим сумму или раз-
ность отрезков с + Ь и с—Ь, т. е. 2с или 2Ь, и далее находим с
или Ь. Строим искомый треугольник по катету и гипотенузе или по
двум катетам.
154.	Обозначим время наполнения сосуда первым, вторым, треть-
им и четвертым кранами соответственно х, у, z, t. Тогда из условия
5 № 3671	129
задачи получаем систему уравнений:
Умножив первое уравнение на 2 и
вычтя из него второе и третье, получим
1+1=А	=
х t 15’	15	2
Итак, четвертый и первый краны наполняют сосуд за 7 ч 30 мин.
Систему уравнений можно было решить заменой переменных
=	~~:==v'’ у —у =	Я33™ и, q, а затем хи/. Далее по
найденным значениям хи/ найти время наполнения сосуда первым
и четвертым кранами.
155.	Выполним преобразование в левой и правой частях: х2у2 +
+ х2 + У2 + 1 = *2 + 2ху + у2 + 1, далее ху (ху—2) = 0, откуда ху = 0
или ху = 2. В первом случае х = 0, y£Z или у = 0, x£Z. Во вто-
ром случае четыре возможности: х=1, у = 2; х = 2, у=1; х = —1,
у=—2\ х = — 2, у — ~ 1.
156.	Рассмотрим основание медианы (рис. 121). Оно удалено от
всех вершин треугольника на одно и то же расстояние, равное ме-
диане. Значит, если провести окружность с центром в этой точке
и радиусом, равным медиане, то она будет описанной около дан-
ного треугольника, причем его сторона будет диаметром этой окруж-
ности и, следовательно, угол, из которого проведена медиана, пря-
мой, т. е. треугольник прямоугольный.
157.	По условию задачи 1 Ой + b = 2аЬ, где 1^а^9, 1^/?^9,
причем b—четно. Значит, b может принимать значения 2, 4, 6, 8.
Проверим каждое из них:
если Ь = 2, то 10а4-2 = 4а, т. е. 6а = 2, что невозможно;
если Ь = 4, то 10а 4-4 = 8а, т. е. 2а = —4, что невозможно;
если й = 6, то 10а 4-6= 12а, т. е. а = 3, тогда искомое число 36;
если /? = 8, то 10а4-8= 16а, т.е. 6а = 8, что невозможно.
158.	Первый товарищ шел 4 ч 30 мин, значит, за 1 ч он про-
I 2
ходил —р = -д часть всего пути. Второй всего шел Зч 36 мин, зна-
^2
1	I 5	ТЭ	1
чит, за 1 ч он проходил	части всего пути. Вместе за 1 ч
3-5
2,51	гт
они проходили у + часть всего пути. Первый до встречи шел
2	3	1
на 1,5 ч больше второго. За это время он прошел —	часть
430
пути. Одновременно им останется пройти
1	2
1—часть пути. Для этого потре-
о о
2 1	1
буется у’- 2" = ly (ч)« Значит, встретятся
они в 10 ч 8 мин4-1 ч 20 мин=11 ч
28 мин.
159* Из условия следует, что 14%—
—2х?^0. Отсюда х-(7—х)^0, т. е. 0<С
Поэтому 14х—2х2 = 7—х, далее
2х? — 15x4-7 = 0, откуда х = 0,5 или х = 7.
160.	По определению арифметической
прогрессии имеем:
( су 4-	4- 4d—6^1—2d — 10 z
I б?* 4~ 4~ 4~ 3d =17
j су 4-3d = 10
^12^4-9^=17
161.	Фактически известны две медианы треугольника. Вторая
медиана, проведенная из вершины прямого угла, равна половине
гипотенузы. Постройте окружность на гипотенузе как на диаметре
(рис. 122). Постройте точку D пересечения медиан как вершину
1	2
треугольника 0DA, где ОЛ = 0,б£, OD — — OC и 4О = у/тга, продол-
жите OD до пересечения с окружностью. Полученная точка и будет
третьей вершиной треугольника.
162.	Пусть Е—точка пересечения диагоналей четырехугольника.
Обозначим z4£ = 4x, £С = 5х, DE = 3y, ЕВ — 2у (рис. 123). Проведем
высоты BF и DK треугольников АВС и ADC\ Д BEF со Д DKE,
Значит, BF*.DK = BE-.DE. Следовательно, BF\DK = 2:3. Обозначим
BF = 2г, тогда /Ж = 3г. Запишем:
S&abe ==у • 4х-2г,	= у . 4х-3г, 5дВЕС • 5х-2г,
1	45
S&deg • 5х-3г. По условию 90 = ухг, откуда хг = 4.
Следовательно, Зд аве = 16 см2, Зд aed = 24 см2, Зд beg = 20 см2,
Зд deg — 30 см2.
163.	Д FBK оо Д АВС (рис. 124). Отсюда следует, что Ду? =
5*
131
Рис. 125
проводим отрезок Е^ЦЛС. Он и
165. Введем новые переменные
вид;
-ЕМ т-г	Z7ZZ
=-----тп;--. Пусть FK = х, тогда
UD
ЕМ = FM = МК = и, следова-
х
тельно,	=—Гт,— . Откуда х =
oU J U
=30—х = 12. Таким образом,
ГК = 12 см. По теореме Пифагора
находим FE = КЕ = 6^2 см.
164. Проводим биссектрисы уг-
лов А и С (рис. 125). Они пере-
секутся в некоторой точке О внут-
ри треугольника. Через точку О
будет искомым отрезком.
j— v Тогда система примет
uv = 30
v (у2—3^) = 35
т. е.
ху = 6
v = 5
и ?= 6,
Решая последнюю систему, получим: (2; 3) и (3; 2).
166.	]Z2а2—Ь2 + 2а \^а2—Ь2 —jZa2—2b Ка2—62 =
=|Z (a2—b2) + 2aVa2—b2 + a2—jZа2—Ь2—2Ь]/га2—Ь2+Т2 =
= jZ (И^—62 + «)2 —|Z(|Za2—fe2—&)2 • - К а2— Ь2 + а—К а2— Ь2+
4-ft = а + Ь, так как по условию а > b К2 и, следовательно, К а2—&2>
>К2&2—й2 = &>0. Поэтому У а2—Ь2—b > 0.
167.	Пусть первый брат дал х рублей, второй дал у рублей,
а отец z рублей. Тогда из условия задачи имеем систему уравнений:
(52+(/+г)Зз1
О
х = ——
< и — (52+% + г) 25
у 100
(52+% + </) 50
100
(Зх = 52 + у + z
4у = 52 + х + г
2г = 52 + у + х.
Решая эту систему, получим: х = 60, у — 48, z = 80.
168.	Запишем искомое число ab. Тогда имеем: 10a+&+10Z>+a=n2,
11(а + 6) = п2, 1^а^9,	Значит, « + 6=11. Поэтому
2^«^9, 2^6^9 и, следовательно, искомым числом может быть
29, 38, 47, 56, 65, 74, 83, 92.
169.	—^:85 = 1 742 500.
132
170.	Найдем корень выражения, стоящего
под знаком модуля: 5х—10 = 0, х = 2,
1) х < 2, у = 3х—5х+ Ю = —2х +10;
й) x^2, z/ = 3x + 5x—10 = 8х—10 (рис. 126).
173. При /1=1 имеем 1-2= I2 (1 + 1),
т. е. для п=1 формула верна.
Предположим, что формула верна для
некоторого натурального /i = fe, т. е.
1-2 + 2- 5 + 3-8+ ... + k(3k— l) = fe2(fe + l).
Докажем, что тогда формула будет спра-
ведлива и для п = k +1:
1.2 + 2.5 + 3-8+ ... + k(3k—1) +
+(&+1) (36 + 2)-/г2 (k+1) + (k + 1) (3k + 2)=
= (k+ 1)(&2 + 3k + 2) = (k + 1)(£ + l)(Z> + 2) =
= (& + I)2 (fe + 2).
174.S(1) = 4, S(2) = l + gL = l S(3)=
==5(2) + з74=:;4 + з74=Т- сРавнивая слу-
ченные выражения, делаем предположение,
что S (п) =	. Докажем это. Для п — 1
формула верна.
Предположим, что формула верна для некоторого п = k, т. е.
5 (/г)	1.2 + 2.3+• • • + *(д+1) — й+1-
Исходя из этого предположения докажем справедливость формулы
для п = k 4-1:
S(fe+ 1) = 372 + 273+ • • • + k(k+Y) +’(’ft+0(^ + 2) =
= S^ + (й+1)(й+2) = FF1 + (fe+l)(fe+2) =
_ А2 + 2*+1 _	(й+1)?	_^+1
— (Jfe-f-1) (*+-2) — (ft+l)(fe+2) ~~ k + 2'
1 2. /1 I П2
175.	При и=1 имеем 13 = — '4	' » т-е- Для п—1 формула
верна.
Предположим, что формула верна для некоторого натурального
n = k,
т. е. S (fe) = I3 и- 23 4- З3 + ... + fe3 = fe2 (fe4+ -)2-.
133
Докажем, что тогда она верна и для п = ^+1:
S(/e+l)=l3 + 23 + 33 + .. .+^3 + (^ + l)3 = S(fe) +
+ + 1)з = fe2(fe+l)2 + (k + j jз _ (£+1)2 (^+4fe+4) = (fe4-W+2)*
тт	1	19 1-(2-1 — 1) (2-1 4-1)	< .
176.	При п—\ имеем 12 = —-----------j_2, т, е. для п=1 фор-
мула верна.
Предположим, что формула верна для некоторого натурального
п = k, т. е.
s(£) = Р4-3? + 52 + ... + (2fe—1 )2 = 	.
О
Докажем, что тогда она верна и для п = k 4- 1:
S(k + 1)=Р4- 32 4- 5?4- ... +(2/?—1)24-(2М-1)2==
= S(k\ + (2k + 1 )2 =	0(^+1) _j_ (2^ 4-1)2 =
_ (2*4-1) (2*? —*+2*-3 + 3) _ (2*+1) (2*?+5* + 3) _ (* +1) (2* 4-1) (2*4-3)
—	3	—	3	~	3	•
177.	1-1! = 1, 1+2.21=5, 1 • 1!+ 2-2! + 3-3! = 23, Ы! + 2-2! +
+ 3-3! + 4-4! = 119.
Замечаем, что 119=120—1=5! — 1, 23 = 24—1 =4! — 1, 5 =
=6—1=3! — 1, 1=2—1=2! — 1. Можно предположить, что S(n)==
= 1-1!+ 2-2! + 3-3!+ ...+»•«! = (« +—
Докажем это. Для п = 1 формула верна. Предположим, что она
верна и для некоторого натурального n = k, т. е.
S(fe)= 1-1!+2-2!+3-31 + ... + k-k\ = (k+V)l — 1.
Докажем, что тогда она будет верна и для п = k + 1:
S(k+ 1) = S(£) + (fe+l)(fe+l)! = (Z> + l)!-l+(Z:+1)^ + 1)! =
= (fe+ 1)! (1 +* + l)-1 =(fe+ 1)! (fc + 2)-1 =(^H-2)! — 1.
178.	Общий член последовательности, т. е. п-я строка, может
быть записан так: п, п+1, п + 2, ..., (п + (п—1)-2). Значит, по-
следний член в этой строке равен Зп—2. Надо доказать, что сумма
чисел этой строки равна S(n) = (2n—I)2.
Для п—1 формула верна. Предположим, что формула верна для
некоторого натурального значения п = k, т. е.
S (£) = £> + (&+1)+ (& +2)+...+(3£—2) = (26—I)2.
Докажем, что тогда она верна и для п = & + 1:
S (& + 1) = (£ +1) + (& + 2) + ... + (3k—2.) + (3k — 1) + 3k +
+ (3&+ !) = & + (& + 1) + (А> + 2)+ ...+ (3&—2) + (3£—1) +
+ 3k+(3k+l)—k^S(k) + (3k—l) + 3k + (3k+l)~k =
= (2k— I)2 + 8k = 4k2—4k + 1 + 8k = 4A2 + 4k + 1 = (2k + I)2.
134
Можно было дать и другое ре-
шение. Действительно, n-я строка
представляет собой арифметичес-
кую прогрессию с разностью 1,
первым членом и, последним чле-
ном Зп—2 и числом членов 2п—1.
Ее сумма равна (2/г—I)2.
179.	Первое совпадение стрелок
происходит в 1 ч 5^- мин, вось-
мое— в 8 ч 43 мин. Всего за сут-
ки, считая начальное совпадение,
будет 23 совпадения.
180.	ху=А0х + у, 100х + 10// +
+8 = (300 + 1 Ох + у) • 2, 80х + 8у =
=592, 1 Ох + у = 74, х// = 74.
181.	ДДОСооДЛОВ. Поэтому
OB АВ ,	1о_	О±В	АВ
OD ~~ DC (рИС’ 127)’ O2D	DC *
Значит, =	^ОВА =
и	зна-
чит, / 01В0=2/ O2DO. Следова-
тельно, Д ODO2 оо Л ОВОи откуда
^BOO^^/DOO^. Но точки D,
О, В лежат на одной прямой,
значит, и точки (\, О, О2 тоже на
одной прямой, т. е. точка О лежит
на прямой, соединяющей центры
квадратов.
182.	Пусть гипотенуза равна
с. Тогда DK = , DF = ~ cos а,
/? = О0 = _^_ = ££212., вс =
since 4 sin а
=c-sina, AC = c-cosa (рис. 128).
кр	16 sin? а ’
1 о .	*$кр л cos а
= -тг £2 sin а cos а, = т-т-s—.
2	’ Зд 8 sin3 а
Рис. 128
/	1 \	24-1
183.	При п — 2 имеем (1—> т. е. Для п = 2 формула
верна.
Предположим, что формула верна для некоторого натурального
n — k, т. е.

135
Докажем, что тогда она верна для п==^+1:
_ПНД (\	1	V-M’’ k2 + 2k+l-l _
1 'Д (*+l)2/	2£ *	(£4-1)2	—
_ £(£4-2) _ (£-i-l)4-l
~ 2£(£-)-1)	2 (£4-1) ’
184.	При п = 2 имеем = 1 —, т. е. для п = 2 формула верна.
Предположим, что она верна для некоторого натурального n—k,
т. е.
5 (^)	2! +" 3! + ' ‘	£! —
Докажем, что тогда она верна и для n = k+ 1:
5(fe4-l) = -2f4--3j-4-.-. +_feT- + (fe+i)! = S(^) + (й-pi)] =
__1	1 I k   1 k 1 — k	1	1
(Н-i)!	— ^’+1)! ’
185.	При n=l имеем a = a, т. e. для п=1 равенство верно.
Предположим, что оно верно для некоторого натурального
n = k, т. е.
S(k)=l-a + 2-(a+ 1) + 3-(а + 2) + ... + k-(a + k—1) =
__ £(&+1)(За + 2£—2)
~	6
Докажем, что тогда оно верно и при n = k+l:
S(k+l) = S(k) + (k+l)(a + k) = k{k+l} .(.fe+2fe-2) 4
4- (fe 4-1) (a 4- k) = Щ • (3ak 4- 2k*—2k 4- 6a 4- Ы) =
=	• (2Z4 4- За/г 4- 4k 4- 6а) =
_ (£ 4-1) (£4-2) (2£ 4- За) _ (£ 4-1) (£ 4- 2) (За 4- 2 (£ 4-1) — 2)
—	6	”	6
17	3
186.	При n — 4 имеем < 1-^-, т. e. для n=4 неравенство верно.
Предположим, что оно верно для некоторого натурального
n = k, т. е.
L+_L+J_+
1!	2!	3!	k ’
136
Докажем, что тогда оно верно и для п = £+ 1:
-L4.-L + -L+ I 1 I 1	<2*-» I	1	_
1!	2! ~ 3! т т k\ (*+1)1 k т (*+1)! —
о 1 ,	1	_2(*+1)	1,1 I ,
*1"(*+1)!	*+1	*+l’t~*+l k f
,	1	2(*+1)-1 , (	1____1_\
1" (*+!)!“'	*+1 ~Г\(*+1)! *(* + 1)/'4
WM	_1_______1_
k+\	’ *•	(^+1)!
Т-Т	1	1	1 /о , 3.1 +2\	.
187.	При п=1 имеем: у = -.(2-|-т. е. для п=1 ра-
венство верно.
Предположим, что равенство верно для некоторого натурального
п = &, т. е.
ад=|-4+4-4+---+<-1)*~*-4=:
= 1.(2 + (-1)*->.ЗЩ).
Докажем, что тогда оно верно и для n = fe+h
scfe+ij^l-A+A-A + ^i)^ .A + (_i)ft.*+L
=s (k) + (-1)*4Й = 4 • (2 + (-1)*-*	+
+ (-i)ft-^ = |(2 + (-i)ft-1-^ + 9-(-1)fc-feW) =
188.	S(l) = l, S(2) = y, S(3) = S(2) + 74o = 4 Можно пред™'
ЛОЖИТЬ, ЧТО ^(n)^3^“pp
Докажем это. Для п=1 формула верна. Предположим, что она
верна для некоторого натурального n = fe. Докажем, что тогда она
будет верна и для п = k + 1:
S(fe+ l) = S(fe) + (З^_|_р (3^ +4) = ЩП + (3^+1) (3^ + 4)
Ж + 4k +1	(& +1) (3&4-1) __ &+1 _	£4-1
~(3&+1)(3&+4)~(3£ + 1)(3£4-4)	3&Ч-4	3(£+1) + 1 *
189.	При доказательстве справедливости этого равенства индук-
цию надо проводить по т. При т= 1 в левой части равенства имеем:
, , (п + 1)!	,о\	« (я +2)1 м! (ti + 1) (ti -р 2)	, / । п \
п! +'---~7  = п\ (н + 2), в правой: 	’ =— ' ~/~1—— = п\ (п-^-2),
1!	Л ~I~ 1	Т1 "у- 1
т. е. для т = 1 равенство верно.
137
Предположим, что равенство верно при некотором натуральном
m = k, т. е.
„I , (п + 1)! , (п+2)! , (л+3)!	,(«+*)!	(п + 6+1)!
«! + —П----И—2j—+ —зГ~+ •••+—£!-- 6!(п + 1) ’
Докажем его справедливость для т = k + 1:
(п+1)! , (п+2)!	(п+3)!	(п+6)! , (п + 6+1)! _
П! Ч----— + —а)-----1-— + • • • + —kj ।	(Гр)!----
(п + 6+1)! . (п + 6+1)! _ (п + 6 + 1)! (6+1 +п + 1) _
"= 6! (п + 1) + (*4-1)1 ~	(6+1)! (п + 1)	-
_(п + й+1)!(п + й+2)_ (п + (й+1) + 1)!
(6+1)! (п+1)	(6+1)! (п + 1) •
190.	При п=1 имеем = т. е. для п=1 формула верна.
Предположим, что формула верна для некоторого натурального
n — k, т. е.
2.5Т5-8Т8.11 "г • ' г (36—1) (36 + 2) —66 + 4'
Докажем ее справедливость при п = А+1:
2.5г5-8г8-1Г	^(36—1) (36+2) ^(36+ 2) (36+5)
_	6	______1______________ 362 + 56 + 2	_
~ 66 + 4 + (36 + 2) (36 + 5)	2 (36 +2) (36 + 5) ~
(6+1)(36 + 2) _ 6+1	6+1
— 2(36 + 2) (36 + 5) — 66+10 “ 6 (6+1)+4'
191.	В прямоугольном треугольнике с2 = а2 + 62. В египетском
треугольнике стороны равны 5, 4 и 3. Их сумма равна 12. Увели-
чив каждую сторону в 3 раза, получим прямоугольный треугольник
со сторонами с — 15, а—12, Ь — 9. Взяв соответствующее число спи-
чек, сложим прямоугольный тре-
угольник.
192.	Верно рассказал Слава.
193.	В задаче не требуется опи-
сывать построение. Поэтому можно
считать, что построение выполнено
(рис. 129). Линия центров ОгО2 про-
ходит через точку касания А вписан-
ных окружностей. Эти окружности
касаются радиуса данной окруж-
ности, проведенного через точку А.
Треугольник OOjA— прямоугольный.
В нем Ot А — В А = х, АО = х + -$,
ООх = г—х. По теореме Пифагора
138
получаем:
(г—х)2 = № +	+-^у, г2—2гх + х2 =
= х2 + х2+ % + -£, 64х2+ 144гх—63г2 = 0,
4 1 64 ’
3	/ о5	\
откуда х = ^г\х =—2у г условию задачи не удовлетворяет).
+ /// -
\ V X— V у	/ ху /	\\ г X/ )
=/,//+|/7-. <7 /I)=|/^ • 771=wd -I- у.
195.	Последовательность построения определяется формулами:
а) х = /3 = /2^+; б) х =/7 =/З2—(/Р+Т)1; в) х = /13 =
= /З2 + 22; г) х = /87 = /102—(/32 + 22)2.
196.	Сторона квадрата равна длине перпендикуляра, восстав-
ленного из точки диаметра окружности, делящей егэша отрезки 2 см
и 5 см, до пересечения с окружностью.
197.	S8=20+14 /2+20—14/2+3 /(20+14 /2) (20—14 /2) х
х(/20+14/2+ V20—14/2), S3 = 40 + 3S /400—392; S3 =
=40 + 6S; S3—6S—40 = 0.
Найдем целые решения уравнения подбором: S—четно, но S=^2;
S = 4 — корень уравнения. Разделим левую часть уравнения на S — 4.
В этом случае деление всегда выполняется нацело. Получим S3 —
— 6S — 40 = (S2 + 4S+ 10)(S—4). Уравнение можно записать в виде
(S24- 4S+ 10)(S — 4)=^0. Приравняв нулю первый множитель, най-
дем остальные корни, если они существуют. В данном случае диск-
риминант уравнения S2 + 4S+10 = 0 отрицателен. Действительных
корней это уравнение не имеет. Таким образом, S = 4,S2— 16, S3=64.
198.	Выполнив преобразования, получим:
7 +/50—/50 + 7— з(/7+/50-//50—7) х
х (/7+/50— //50—7) = 8,
14—3 /50-49-2 = 8, т. е. 8 = 8.
Так как в итоге получилось верное равенство, то вследствие
равносильности всех преобразований верно и данное равенство.
Пример можно было решить аналогично предыдущему, обозначив
левую часть равенства буквой X и выполнив все те же самые пре-
образования.
139
199.	Kill ...1—222...2 = Kill-- - 1-(100- -О1 —2) =
2/2	П	n	/2+1
=K111. .. 1-999... 9 = K91H...12 = 3-111... 1 = 333... 3.
n	n	tl	n
200.	Ц(х + a)6 (x—a) 6—(x + tf) 6 (x—a)6 j J 2 =
/ i	j_\ ~1	1
__/ (x-\-d) 6	(x— a) 6 j	(x2— a2) 6
\(x—a)6	(x-}-fl) 6 ' (x-i-fl) 3—(x— fl)3
^2^ 4- fl2
При x^a———г имеем:
1	m3—n3
где m=0=n, x^a.
201.	Преобразуем данное выражение 9x + Ьу = 17 (x + у) —
— 4(2x + 3z/). Каждое слагаемое делится на 17. Значит, и их сумма
9х + 5у делится на 17.
202.	Разобьем все числа подряд на группы по 22 числа. Полу-
чим 90 групп. Произведение всех чисел в каждой группе больше
единицы. Кроме того, у нас осталось еще 9 чисел. Выберем в пер-
вых 9 группах по одному наибольшему числу. Каждое выбранное
число больше единицы. Объединим эти числа в группу. Их произ-
ведение больше единицы. Оставшиеся первоначально после объеди-
нения 9 чисел распределим в каждую из групп по одному. Так что
в них вновь станет по 22 числа. Значит, произведение чисел в каж-
дой группе больше 1. Таким образом, мы получили 91 группу чисел,
произведение чисел каждой из которых больше единицы. Значит,
и произведение всех групп больше 1. Но оно равно произведению
всех данных 1989 чисел. Следовательно, это произведение больше
единицы.
203.	10 км/ч.
204.	I (х+^-(х + г/) = 6	((3 +3z/)2—(3+3z/)—6=0
\x+y — 3-\-3y	&\х = 3 + 2у.	Получен-
ную систему можно решить введением новой переменной t = 3 + Зу,
(1	2 \
— т; —К > (3; 0)-
о	о j
140
05^1 + 0,05v2 = 1,35.
205.	Пусть скорость первого
велосипедиста км/ч, а второго
v2 км/ч. За 27 мин они проедут со-
ответственно 0,45 Vi км и 0,45 v2 км.
Причем первый проедет на длину
одной окружности больше второго,
т. е. 0,45^1—0,45у2=1,35.
За 3 мин первый проедет 0,05
км, а второй 0,05у2 км, а вместе
они проедут расстояние, равное
длине полной окружности, т. е. 0,
Объединим эти уравнения в систему, из которой найдем скоро-
сти велосипедистов. Скорость первого велосипедиста 15 км/ч, а вто-
рого 12 км/ч.
206.	Пусть 90%-ного раствора взяли х кг, тогда 60%-ного раст-
вора взяли (5,4—х) кг. Чистой серной кислоты в первом растворе
будет 0,9х кг, а во втором растворе 0,6 (5,4—х) кг. В смеси чистой
серной кислоты 0,8-5,4 кг. Отсюда получаем уравнение 0,9х+0,6х
х(5,4—х) = 0,8*5,4, из которого находим я = 3,6. Значит, 90%-ной
серной кислоты надо взять 3,6 кг, а 60%-ной—1,8 кг.
207.	Номер пробы показывает, сколько тысячных долей чистого
серебра находится в сплаве. Уравнение задачи запишется так:
75-0,6+ 150-0,864 = 225-я,
где х—число тысячных долей серебра в сплаве. Отсюда находим
я = 0,776.
208.	Samnd = ^(AD + MN)- 4 (рис. 130). MN=EF—EM—NF =
= Х.(АЯ + ВС)—ХвС—±ВС = ±(АЯ—ВС) = ±-(а—Ь), ЕМ —
средняя линия треугольника ABC, NF—средняя линия треуголь-
ника BCD.
________ 1 /3	1 <\ h  За—b <
^amnd “2” * (	& 2+ / * "2*	8 *
209.	На средней прямой в произвольной точке поместите верши-
ну А искомого треугольника. Поверните весь чертеж вокруг А на 60°.
Точка пересечения нижней и верхней прямых будет второй верши-
ной В треугольника. Вершину С после этого можно построить
с помощью циркуля.
210.	Смотри указание в задаче 209, но поворот выполните на 90°.
211.	Смотри указание к задаче 209, но поворот выполните на
угол а.
212.	п4— 4п3 — 4n2+ 16п = п(м3 — 4п2 — 4n+ 16) = м(п2(м—4) —
— 4(п—4)) = п(п—4)(п2 — 4) = п (п— 4)(п — 2)(п + 2) = (п — 4)х
х (n —2)п(п + 2) — получили произведение четырех последо-
вательных четных чисел. По крайней мере два из них делятся на 2,
одно — на 4 и одно—на 8. Кроме того, хоть одно делится на 3,
т. е. все произведение делится на 2-2-4.8-3 = 384.
141
213.	х2—21х + 47 = 0. По теореме Виета имеем:
Xj + х2 = 21
Х!-х2 = 47.
Значит, х| + х2 — (Xj + х2) (х2—XjX2 4- xf) = (Xj4-x2) ((хг 4- х2)2—3xjX2)=
= 21-(212 — 3-47) = 21 • (441— 141) = 21.300 = 6300.
214.	2x4-1^0, т. е. х^—у.
Тогда х24-8= 4х24-4x4-1, Зх24-4х—7 = 0, х=1 или х = —24-.
О
тт 1 t
Но	—-j , поэтому корень исходного уравнения х=1.
215. 7 log* 4 <2 1 log* 4 > —4 1 х > 0	откуда ’ [ Хф 1,	' log*4 <2	Г log* 4 <2 log* 4	—4 или < log* 4 —4 0 < х < 1	( 1 < х.
Решив эти системы, находим	у"2 < х < 1 или х 2.
216. Предполагаем, что значение этого выражения существует.
Введем обозначения
)/'5]/з/5/3...=х, У ЗУ 5/з/5...=«/,
где х > 0, у > 0. Тогда получим систему: ( 5у = х2
* ( Зх = у2.
Последовательно находим у =	, Зг =	, х3 = 75, х — р/75.
Пример можно решить иначе. Запишем множители в виде сте-
пеней. Получим
V зУзУ5/з/5777 = 5^. З^-5^.3^.5^
—	—+—4-—4-...
= 5 2 8 32	.3 4 16 64	=
1	1
2	4
= 5”т -З1” =5Т-3~=(52.3)“= /75.
В данном случае в показателях получались суммы бесконечно убы-
вающих геометрических прогрессий. Они существуют, поэтому пред-
положение о существовании значения выражения не требуется.
217.	Из условия задачи имеем:
7 5 («! 4-Оа 4-а3) = а А«з
I. а14-а3 = 2а2,
откуда 15а2 = о1о2о3, о1-о3=15. Значит, «1 = 1, о3=15, а2 = 8 или
ах = 3, а3 = 5, аа = 4. Числа можно взять и в обратном порядке.
142
218.	Если числа а, Ь, с составляют арифметическую и геометри-
ческую прогрессии, то имеют место соотношения:
=	, Ь — V ас.
Но	ас, если а^с. Тем самым утверждение доказано.
219.	Из условия задачи имеем:
( ai — 1 5
1-<7	/^ = 225(1 — q)*
____75	1 «2 = 75(1 —<?2).
1— q2. ~ ‘°
Приравняв правые части, последовательно получаем:
225(1— <?)2 = 75(1—<?2), 3(1—<?)= 1+ </, <7 = Т.
49
Находим «1=7,5, Se = 14g^.
220.	Из условия задачи имеем ав 4- а9 4- а±2 4- аг5 = 20. Далее
S2o = ++*2O = -++.2O = (2a14- 19а)-10,	«14-5d 4-«i 4-8d +
4-	«!-+- Hd4-«i4- 14d = 20, 4«i4-38d = 20, 2«i4-19d= 10. Таким
образом, S20= 10-10= 100.
221.	14-114-1114-.. .4-111... l=(14-104-1004-.. .4-1000.. .0)4-
4 n '	n
+ (1 + 10+ 100+.. . + 1000. ..0)+(l + 10+100+. .. + 1000..,0)+..
n~1	n-2
... 4-(l 4-10)4-1 = * 1^+~ 4-	• •  +++* 1 =
_10«—1 10"-1 — 1 10«~2— 1	102—1 . 10—1 _ 1 /10«+l—10
9 I 9	I 9	г • • • 4- 9 4-g — 9 I ~	nl-
= 1. (10n+1 —10—9n).
ol
9
9
9
• 992 n -2 А И 257	22”-1+i
2 • 4 • 16 • 256 • • •	22n~l
==(1+4)(1+т)(1+й)(1+25б) *” +(1+"2^)~
’ (1— 2O 0 + 2") (1 + t) (1 "I"ie) (1 '^25б)'' '(* +22""*)=
1	2
= 2-(!-+); lim П„ = 1йп2(1-±) = 2.
223. AF = AD = y,BD = BE = x,CF=CE=r (рис. 131). Из условия
задачи имеем:
1 d = AB—ВС f y = d + r
I d = BC—AC, J x = d-Fy
1 (x 4- y)2- = (x 4- r)2 4- (y 4- r)2-
143
Выразим х через d и г: x~2d+r. Далее (3d + 2r)2 = (2d + 2r)2 +
+ (d + 2r)2, 9d2 + 12dr + 4r? == 4d2 Н-8dr + 4r2 + d2 + 4dr + 4r2, 4d2-
== 4r2, откуда d = r.
224.	Ясно, что окружность радиуса ОА не пересекает белых
полей (рис. 132). Если точку А взять в более удаленной от О точке,
то окружность пересечет некоторые белые поля. Приняв длину
стороны клеточки поля за единицу, получим ОД = 0,5К10.
225.	Множитель (п—п) равен нулю. Значит, и все произведение
равно нулю.
226.	х > —7. Последовательно получаем:
1g 8—1g (х + 7) = 1g 2 — 1g Vx + 7, 1g 8 + 1g V x + 7 = 1g 2 4- 1g (x + 7),
1g 8 KT+7 = 1g 2 {x 4- 7), 8/x + 7==2(x + 7), 64 (x + 7) = 4 (x + 7)2,
16 = x + 7, x = 9.
2x4-1
227.	Введем новую переменную y = —-—(*)• Тогда уравнение
примет вид у 4- -у = 5, откуда z/2—5z/ + 4 = 0, z/=l или z/ = 4. Из (*)
получим х — —1 или х = 0,5.
228.	j/"7 V211^7 ]/21К7 /2ГГТ-7~-21~-7~-21«... =
1	1
2	4
111	1	1 , 1	________1_	1	2	1
8 + з2+’'’. 21 a +ie 64+'“	_ 7 1 4 . 21	4	=7 3	«21 3	=
= 7-3“ = 7 з/з.
229.	S=l+3x-|-5x2 + 7x34-9x4+ ...=(1+х+ х2 + х3+...) +
4~ 2х(1 +2х+ Зх2- + 4х3+ .. .). В первой скобке записана сумма
бесконечной убывающей геометрической прогрессии. Ее найдем по
формуле. Во второй скобке выражение тоже можно представить
в виде суммы нескольких бесконечных убывающих геометрических
144
прогрессий и найти их суммы. Получим:
S=r^+2x((l + x + xa+ ...)+(х + х2 + х3+ -	+
4-(х2+х3+х4+••)+••• )=7т^+2х(т^+к^+]Т^+т—;+ •
1	. 2х /it . о I q I	\	1 I	1
=—+1-^(1+^ + ^ + ^+ •••)=Т^+—•—Y=
__1 —х + 2х  1 4-Х
(1—х)2	(1 — Д')2 ’
230.	1 4 2Н-Зо2 + 4Ь3 4-5Ь4 + ... 4 пЬ"-1 = (1 +& + Ь2 4- Ь3 + ...
...+^-i)+(&4-^4-^4-&4+ ...4-^-1)44&24-&34-&44----4-&"~1)4-.  •
1__hn h___hn Л2___hn	hn~2__hn
... 4-(^-?4-^-1)4-^ = +^ + 4+ + +^+••+++-4-
+ bn\1^" = т^((1 4- b + b2 4- ... 4- b^-nb") =	=
1 - bn — nbn + nbn +1	1 — (1 + n) bn + nbn +1
-	(T=z+	-	(i_&)2
231.	В каждой строке числа представить в виде суммы числа
круглых сотен и остатка. Причем последнее число 10000=9900+ 100.
Тем самым фактически будет выбрано 100 слагаемых по одному из
каждой строки и каждого столбца. Следовательно, в них войдут
все числа первой строки и по одному первому слагаемому (сотни)
из каждой из остальных строк, т. е. от второй до сотой строки.
Первая группа слагаемых — арифметическая прогрессия: ах=1,
п = 100, а100 = 100. Вторая группа слагаемых — арифметическая
прогрессия:
^ = 100, я99 = 9900, п = 99.
Сумма всех слагаемых равна 500 050 = const.
232.	Разложим дробь в сумму четырех дробей со знаменателями
первой степени (метод неопределенных коэффициентов).
_____ __!---------— — _1——l _£—l  (1)
п (/1+1) (п + 2) (п + 3)-п *+ +1 * п + 2 ’ п + 3 '
где Л, В, С, D—постоянные числа. Для их нахождения осво-
бодимся в равенстве (1) от дробей. Получим: 1==Л(п3 + 6п2 +
+ 11п + 6) + В (п3 + 5п2 + 6п) + С (п3 + 4м2 + Зп) + D(n3 + Зм? + 2м).
Открыв скобки и приведя подобные члены, получим:
1 = м3(Л + В + С + О) + м2 (6Л+5В + 4С + 3£)) +
+ ti (11А + 6В + ЗС + 2D) + 6Л,
145
Приравняв коэффициенты в левой и правой частях равенства при
одинаковых степенях п, получим систему уравнений:
	( 6Л = 1 J Л + В + С + £) = 0 ] 6Л + 5В + 4С + ЗГ> = 0 ( 11Л + 6В + ЗС + 2О = 0,
из которой	найдем: Л = 4-, В — —С = Т > D — —4 • Значит, О	Z	Z	о 1	2 /2_1 (—	!	\
и (не- применим суммы:	1) (и 4- 2) (и 4- 3)	6 у и п 4“ 3 /	2 я -j- 1	4" 2 / эту формулу к каждому слагаемому рассматриваемой 1	1	/J	£\	£ М	И 1-2-3-4	6^1	4 J 2	\2	3/’ 1	1	/_1	1_\	1_ М	— И 2-3-4-5	6	\ 2	5 )	2	V 3	4 1	_	1	/ 1	1 \	_1_	( 1	1 'i 3-4.5-6	6	\ 3	6 )	2	\ 4	5 )' 1	1	/ 1	1 \	1/1	И 4.5-6-7	6	\ 4	7 )	2	\ 5	6 Г
________1________. / 1__________1\_____1_. / 1_____1\
(п-—2) (п— 1) п (и 4- 1)	6 ’	2 n-J-l J 2 \п —1 un J *
(и—1) п (п4-1) («4-2) “ 6 ’ \п—1	и 4-2 J 2 \ п n-4-l ) ’
_________1	= 2. Л L1 L. _______________L1
п (n-f-1) (п 4~2) (п-}-3)________________________6 \п n-\-3j	2 \и4"1	п4-2/
Сложив все равенства почленно, в левой части получим данную
в условии сумму:
ч 1	/i , 1 , 1	1	1	1 \	1/1	1 \
6 \ 1	2	3	«4-1	п4-2	п+3)	2 \2	п4-2/
е Нт S = lf 1-4-1-4-1V1 1-1 Н- 1
5 п™/”	6 \ 1 1 2 + 3 )	2*2	6 ’ 6	4	18*
9оо п , I П3 __2п + 3п2 4-п3 __п(п4-1) (п-1-2)
12-г 8 -г 24	24	24
Один из множителей числителя делится на 3, каждый множи-
тель пи п4~2 делится на 2, а один из них делится на 4. Следо-
вательно, все произведение этих множителей делится на 2-4-3 = 24,
т. е. дробь равна целому числу.
234.	Рис. 133, а, б.
235.	х=1.
236.	Рабочий А может выполнить работу за 15 дней, рабочий
В—за 10 дней, а рабочий С—за 6 дней.
237.	Обозначим радиус окружности г (рис. 134). По свойству
146
Рис. 133	Рис. 134
касательных, проведенных из одной точки к окружности, имеем
АЕ = AD = 6, BF = BD = 8. По теореме Пифагора (г + 6)2 + (г + 8)2=
= 142, откуда г = К97—7.
$давс — ^-АВ-ВС, т. е. 5д авс = -^ • (б + К97—7)х
X (8 +К97-7) = 48.
238.	Через данную точку проведите диаметр окружности, а затем
хорду, перпендикулярную этому диаметру.
239.	Проведем радиус ОА через центр Olt радиус ОВ—через О2,
О2С _1_ОА, радиус O2D (рис. 135). Введем обозначения: OA = R,
OOi= г = -у> 02О = 0С = Г1, Ofi — R — rlt O1O2 = r + ri, 02С = х,
OjC = r—гг. Из A 020jC и Д.020С имеем систему:
f (r + r^^fr—r^ + x2
1 (/?-Г1)2=(г2 + х2).
Последовательно получаем:
(г + rtf-tR-rJ2 = (г-Г1)2-г2,
г2 + 2rrt + г2 — R2 + 2Rrx—= г2—2ггх+ г2—г{,
4rr1 + 2Rr1 + R2, или 2Rrt + 2Rrr = R2, r1 = ^-R.
S = — nR2—лг2—2лг; = 4" nR2.
2	о
240.	а) Эта окружность описана около треугольника, стороны
которого равны попарным суммам радиусов трех данных окружно-
стей (см. рис. 16). Ее радиус можно найти по формуле R =	,
где а9 Ь, с—стороны треугольни-
ка, a S—его площадь.
Так как я = 25, & = 20, с=15,
р = 30, по формуле Герона нахо-
дим 8=150; Я = 2^0^= 12,5.
б) Окружность вписана в тот
же треугольник. Ее радиус можно
найти из формулы г = -|-, где8—
площадь треугольника, а р—его
полупериметр. Получим г = 6^7 см.	Рис. 135
1.47
241.	Проведем CF\\BD, (рис. 136). ^ЛСГ=90°, ЛР=4С2 + СР,
но CF = BD, ЛР = 4С2 + В£>2= 169, ЛР=13, AF=--AD + BC, AD+
+ ВС= 13, ALV = 6,5.
242.	12—22 + З2 — 42 + 52— 52+... + 9992 — 10002= (1 — 2) (1 + 2)+
+ (3 —4)(3 + 4) + (5—6)(5 + 6)+ ••• +(999—1000) (999+1000) =
= —3—7— 11 _	_ 1999 = _ 1+_L?99.5оо = —500500.
242.	1а—22+ 32—42+... +9992—10003=—1 • (1 +2)—1 -(3+4)—...
...— 1 -(999+ 1000) = —(3 + 7+ 11 + ... + 1999) = —3 + *999 ♦ 500=
= 500500.
243.	Предполагается, что на головах были как желтые, так и
зеленые коробочки. Значит, А видел две зеленые и одну желтую
коробочку. Он рассуждал так: «Если у меня желтая коробочка, то
двое, у которых зеленые коробочки, не встали бы, ибо они видели
желтые и одну зеленую коробочку. Но они встали. Значит, они
видят по две зеленые и одну желтую коробочку, которую вижу и я.
Следовательно, у меня зеленая коробочка».
244.	Из условия задачи следует, что рассматриваемые бесконеч-
ные суммы сходятся. Это возможно только при |^| < 1.
( aiq = 6	а1 = —
| ai — 1  д"	, I at
( \_q	8	I-?2	[
S(l + ?) = 4, 4</2 + 4<7—3 = 0, откуда 9 = 4 (q——1,5 не удовлет-
воряет условию задачи), «1=12.
245.	2х2—4х+10 = 2(х2—2х+1) + 8 = 2(х—1)2 + 8; min(2x2 —
— 4х+10) = 8.
«з + а9 = 8» 2^+104 = 8, flf + 5d = 4;
Sii = £i+£S-. П = .2а*+10< 11 = 4-11=44.
£ £
246.	Прежде всего надо установить вид треугольника. Угол
С—тупой, так как с2 > а24-62. Следовательно, все указанные отрез-
ки проходят внутри треугольника (рис. 137). Имеем
AF — FB, £АСЕ = /_ЕСВ. Обозначим АЕ = х, CD — h, AD = z.
АЕ _ АС х __14
Её"““св’ х~То*
148
откуда х=10,5. Таким образом,
АЕ = 10,5, ЕВ == 7,5; AF = FB = 9.
Далее
I г2 + /г2=142,
\ (18—z)2 +/г2= 102,
откуда г = 11	. Значит, AD =
= 11 |, DB = fj^-,EF—l,5,ED=
О	О
-1!-
247.	02Е = rt\ / EOfi = 30°;
002 = R — rlt Е0^~-00г =
= y(R— Г1) (рис. 138).
С
Рис. 138
(R - Г1)2 = 4 (R -- Г i)2 + rl- 4 (R - г О2 = г2;
V 3 р /з
2	2
/3 р. 5/з .
2	’ 1 2+КЗ ’
r1 = R (2/3-3).
05 = г3; r34-2r1 = R; r3 = R—2r1=R—2R_(2/3—3)=R—4R/34-
4-6R = R (7—4/3).
r3=R (7-4/3).
06С = г2; в Д00А ZO6OO2 = 60°; OO5 = R-r2;
002 = R —74; O5O2 = rx + r2.
По теореме косинусов
(0602)2 = (OOS )2 + (OO2)2 - 2 (OO6) • (OO2). cos Z O6OO2.
(G + r2)2 = (R— rtf + (R—rx)2—2 (R — r2) (R — rx) • 4;
rf+2r1ri 4- rf= R2—2Rr2 + r2 + R2—2Rrt + r{—R* + Rrt + Rr2—гггг;
3r2r1 + Rr2 = R2—Rri,
= R (R-rd = R(R-2R /3 4-35) = 5(4-2/3) =
Гг 3^4-5	65 /3— 954-5	2(3/з-4)
_ 5 (4—2 /3 ) (3 /3 4-4) _ 5-2 (2 /3 — 1) _ 5 (2 /3 -1)
2(27 — 16)	2-11	~~	11
248.	Пр. DC = DE, пр. AB = BF (рис. 139). ^BAC=Z_BDC=a.
^ABD = j/ACD = fi. D£' = DCcosa=2/?cospcosa, BF=XBcosP^
= 2R cos a cos p. Следовательно, DE = BF.
249.	Из произвольной точки С AN опускаем перпендикуляр
DtMt на AM (рис. 140). Берем на нем точку Ег, такую, что D^—
^=2-EtMv Соединяем В с А. Из Et проводим	до пересе-
149
х = 40.
чения с АВ. Через Вг проводим
DiCx, где С1^АМ. Тогда £>ХВХ =
= 2-В1С1. Через В проводим
DC\\D1C1. Отрезок DC будет иско-
мым. Доказывается это на основе
рассмотрения подобных треуголь-
ников.
250.	Расстояние от А до пря-
мой MN должно быть меньше R.
Отложим на MN от произволь-
ной точки В отрезок ВС длины а.
Найдем точку Ох, удаленную от
В и С на расстояние R. Через 0^
проведем прямую, параллельную
MN. Из А как из центра прове-
дем дугу радиуса R. Пересечение
ее с построенной прямой будег
центром искомой окружности. Она
пересечет Л4М в точках Е и F,
таких, что EF = a (рис. 141).
251.	Первое утверждение сле-
дует из симметрии фигуры относи-
тельно О и равенства треугольни-
ков с вершинами в точках О,
0g, О3, О4 (рис. 142). Второе из
равенства треугольников EFB и
ARL, MNC и PQD, а также тре-
угольников, расположенных внут-
ри квадратов (например, OJRE и
0JK).
Можно обосновать иначе, срав-
нив треугольники А0х04, С0203,
D0304 и ВОХО2.
252.	Пусть первого сорта на-
до взять х г. Тогда второго сорта
надо взять (140—х) г. Значит, чис-
того никеля в первом сорте будет
0,05 х г, а во втором сорте
0,4-(140—х) г и в их сплаве
0,3-140 г. Отсюда получаем урав-
нение 0,05x4-0,4-(140—х) = 0,3-140, решив которое, находим
253.	п$— 5п34- 4n = n-(/i4—5п2 4- 4) = п • (п2—4)-(п2—1)=(м—2)х
Х(п— 1)п(и4- 1)(п4-2).
Получилось произведение пяти последовательных натуральных
чисел. Значит, одно из них делится на 5, по крайней мере одно
делится на 3, одно на 2 и еще одно делится на 4. Следовательно,
15Э
все произведение делится
на 5-3-2-4 = 120.
254.	Пусть первый ком-
байн работал х ч, тогда
второй—0,8* ч, третий —
0,6* ч, четвертый — 0,4а: ч
и пятый —0,2* ч. Каждый
за время своей работы
выполнил соответственно
х 0,8* 0,6х 0,4* 0,2*
24^5’ 2475’ 24^5’ 2475’ 24-5
часть всей работы, тогда
х 0,8* . 0,6* . 0,4*
2475 + 24^5 2475 + 24.5
. 0,2* __ .
‘2475“
откуда *=40.
255.	( а>0,
I D<0, т. е,
I а > 0
1 4а2—4а -0,5^ 0, откуда
0 < а < 0,5.
Рис. 142
256.	Анализ. Дана сторона и точки М, N, Р (рис. 143). Кроме
того, X MAN = NAP — 30°. Если на отрезках MN и NP по-
строить сегменты, вмещающие углы в 30°. то пересечение их дуг
даст вершину А. Далее если от точки А отложить на лучах AM
и АР отрезки, длина каждого из которых равна а, то получим две
другие вершины В и С треугольника. Задача имеет решение и при-
том единственное при условии, что МР < а.
257.	Продолжим АС, так, чтобы AC —CD, соединим точку D
с точками В и Е (середина АВ). Тогда в треугольнике ABD ВС и
DE— медианы. Они пересекаются в точке F, отстоящей от С на
расстоянии, равном третьей части стороны треугольника (рис. 144).
Отсюда получаем, что если через Е и F провести прямую до пере-
сечения с продолжением стороны АС, то она пересечет это продол-
жение в точке, удаленной от С на расстояние, равное длине АС.
258.	Построение. На произвольной прямой MN берем точки А
и и строим при них данные углы аир (рис. 145). На боковых
сторонах этих углов откладываем данные стороны четырехугольника
АВ = с и — Через Ct проводим прямую, параллельную MN,
и из точки В радиусом а проводим дугу до пересечения с этой пря-
мой. Получаем третью вершину С искомого четырехугольника. Через
С проводим отрезок CDWCJ).^ Четырехугольник ABCD—искомый.
259.	Первый способ (рис. 146):
OiOi^O^ + OjE2, О1О2 = 2г, 02Е = И—ОЕ — В02,
= DE = r, ВО, = 2г, (2г)2 = (?-р—г—2r)a + r2,
откуда г = -2-(/3 — 1) (г = -^ (ИЗ +1) — невозможно).
Второй способ. Рассмотрим Д£ВО2:ГВ = —, FO2 = r, г =
= FB-tg3O°, r = 2гИЗ + 2г = а, г = -^—- = 4(/3 — 1).
6	’	2 КЗ	2(КЗ +1)	4
260.	Покажите, что О1О2||ЛС, KLWOfi^. Отсюда KB=BL (рис. 147).
Тогда и AK = LC, т. е. ДЛВС—равнобедренный (ОХЛ J_ ЛВ,
02L±BC).
261.	Рис. 148: £F = 5-4 = 20, ЕК = 2,5, Л£ = 5, АК =
= /Л£2—£№ = 2,5/3, ЛС = /<£ + 2-ЛЛ: = 20 + 5/3.
152
262.	Обозначим стороны треугольника а, Ь, с. Тогда имеем:
>' a-i-b + c — 42
. — = 84
4R
^21(21—а) (21—Ь) (21 —с) = 84.
Выполнив преобразование, получим:
{а-\- b = 42—с
ab = —
2730	°
+ с (42—с) = 587
и, следовательно, с3 — 42с2 + 587с—2730 = 0.
Решение этого уравнения основывается на обобщенной теореме
Виета и основной теореме алгебры. Из них следует, что если урав-
нение приведенного вида с целыми коэффициентами имеет действи-
тельные (в частности, целые) корни, то они являются делителями
свободного члена.
Разложим свободный член на множители и проверим, какой из
них является корнем уравнения. В нашем случае 2730= 1-2-3-5-7-13.
Множители можно брать в любой комбинации и с разными зна-
ками. Из вида нашего уравнения ясно, что корень может быть
только положительным. Причем маленькие числа в данном случае
не будут корнями уравнения. Начнем проверку с с =13. Подставим
это значение в уравнение. Получим 133—42 • 132 Ц-587 • 13—2730 =;
= 2197 — 7098 + 7631—2730 = 0, 0 = 0.
Разделив левую часть уравнения на с—13, получим с2—29с+ 210.
Значит, левую часть уравнения можно заменить произведением
(с—13) (с2—29с + 210) = 0. Случай, когда с = 13, нами уже рассмот-
рен, поэтому считаем, что с у= 13. Приравняв к нулю второй мно-
житель, найдем еще два корня уравнения: с=14 или с=15.
Найдем значения а и Ь:
1)	если с =13, то ( а + & = 29
| ай = 210,
откуда (2=14, b = 15 или а =15, &=14;
2)	если с =14, то ( а-'-Ь = 28
1 ab== 195,
откуда а =13, Ь=15 или а =15, &=13;
3)	если с =15, то J а + & = 27
| ab=182,
откуда а=14, Ь=13 или а=13, &=14.
153
Следовательно, стороны тре-
угольника равны 13 см, 14 см,
15 см.
263.
условии
LK = x,
__ R
COS Р
X2 = (z + у)2,
D
, LO = —я . Аналогично
cos р
т. е. x—z-}-y.
Обозначим указанные в
отрезки MN = z, EF = y,
а углы X.NOM==fi,
/ EOF = а (рис. 149), а + р = 90°.
Повернем /\NM.O вокруг О по
часовой стрелке на 90°. Вместе с
треугольником EOF он соста-
вит прямоугольный треугольник;
(х_|_у)2==д4О2 + ОР, a x2 = LO2+
+ ОК2; M0 = L0, так как МО=
%
FO = ОК —------. Следовательно,
cos а
264.	4= —log2log2
265.	333. . .3 = 3-(111... 1) = 3-3-(37037037.. .037). В скобках
27 цифр	2 7 цифр	26 цифр
записано число, состоящее из 9 групп одинаковых цифр. Сумма его
цифр делится на 9. Следовательно, все произведение, а значит и
данное число, разделится на 81.
266.	| Ух + Уу^З
I Ух2— Уху + У у2 = 3
J x+r/^9
I (x + У) + 3 y^xy ( yf x + y^ y) — 27
х + у-9	| х + у =
Уху = 2	\ хг/ = 8
( х + г/ = 9_
\ 9 + 3 р/ху-3 = 27
х~ 1
У = 8
х~ 8
г/= 1.
267. Пусть а > b (рис. 150). Тогда
' с == а -Г 1 = b -J- 2
, а==&4-1
+ &—2a&cosl20°.
Из уравнения (р + 2)2 = (Ь + 1)? + 62 +
Ч-2 (&-h 1) • у . Находим 6=1,5, тогда
а = 2,5, с = 3,5.
268. а) 63—16г; б) — 1 + 5г.
269. а) х=18, г/=28; б) х = 2, г/= 1 Т .
270е а) —1; б) 1; в) 64; г) 1.
154
271.	ав, 10а + &—(я2 + &2) = 9, l^tz^9, 0</?<9, а(10—а) =
^=b(b—1)4-9. Отсюда следует, что а — нечетно:
если a=it то Ь = 0, или fo= 1, искомое число 10 или 11,
если <7 = 3, то 3-7 = fe(b—1) + 9, b(b—1)=12, fe=4; искомое
число 34.
если а = 5, то 5-5 = b(b—1) + 9,
b(b—1)= 16, решений нет;
если а = 1, то 7-3 = b(b—1) + 9,
b(b—1) = 12, искомое число 74;
если а = 9, то 9• 1 = b (Ь—1) + 9, Ь=1 или Ь = 0, искомое число
91 или 90.
272.	KL^_EF (рис. 151), OK~OLy OE = OF, следовательно,
KELF—ртб.
273.	у' = 6х2— 78х + 252, у' = 0, 6х?—78х + 252 — 0. Отсюда х — 6
или % = 7; у (6) = 541; у (7) = 540.
Найдем еще значения функции на концах промежутка: /(5) = 536;
/(8) = 545. Сравнивая все полученные значения, приходим к выводу,
что на данном промежутке функция имеет наименьшее значение в
начале промежутка, а наибольшее в его конце.
274.	Соединим точку D с точками Е и В (рис. 152). Тогда
Z^DB = 90°,	/ ДВЕ» = 45° и, следовательно, /DBE = 30°,
ZDEB =135°,	а Z АСВ = 60°. Имеем:
5длвс = 4--AB-AC-smA, = АС = АВ-^,
2	’ sin В sin С ’	sin С ’
ОВ->.Ц±-ОВ = у-2,АВ-2;
о	1	. D9 sin B-sin Л D
8лАвс =-ту • AB2  -г-7;—. Выполнив вычисления, получим
2.	sin С/
е 14-^3
275.	а) ЗК2 ^cos 4 +j sin-^-) > б) 5 j/2(cos 4 л + i'sin 4 л) ;
ч л ... л
в) COS-Г-Д- I Sin-X- .
о	о
ж
276.	б/З—6i.
277.	7,5 —7,51 КЗ-
278.	Пусть = а 4- bi, z2 = c + di. Тогда Zi 4- z2 = (a 4- c) + (b 4- d) i,
2 j — z2 = (a—c) + (b—d) i, \Zi 4- z2 j2 = (a 4- c)2 4- (b 4- d)2 = a2 4- c2 +
4- 2ac + b2 + d2 + 2bd, \zr— z212 = (a—c)2- 4- (b—d)2 = a2 4- c2—2«c 4-
+ b2 + d2 — 2bd, | Zj + z2 p 4-12j—z2\2 = 2(a2 + b2 + c2-Vd2),	| Zj |2 =
= a2 + b2,	\z,\2 = c2 + d2. Следовательно, |zx4-z2124-1zr — z2|2 =
= 2112 | 21 Г2.
”»• Il+IP'KWO- |г-5|<|г + 5|.
(x—5)2 4- y2 (x 4- 5)2 4- y2, —lOx^lOx, x^O.
280. cos 16л 4- i sin 16л = 1.
281. Пусть n = 3m. Тогда
При n = Зт 4-1 имеем:
/ _1 + / уз V / _i-iVsF у _ ( — 14-i V"3 ym / —1-нУТ
\	2	/ + V 2	/	\	2	/	\	2
1 ( _i-( Уз Ym ( — l-i/з	—14-4 Уз , —1-j/lF
+ \	2	/	\	2	/	2'2“
При n = 3m 4- 2 имеем:
+	Y ,	у / —14-1 У^З" V"* /—14-1’Уз
\	2	/^\	2 J ~\	2	)	\	2
f—\-i уз у* /_1-(Уз\2 i_2iys-3 , i+аУз-з _
“r\i2/\2/“	4	'	4	“
282. 4abcd = dcba. Отсюда a—четно. Если a = 2, то d = 8. Других
значений and иметь не могут, так как при а > 2 после умноже-
ния получается пятизначное число, а при d=/=3 после умножения
на 4 не получается на конце цифры 2. Тогда b < 3, так как
иначе d > 8. Итак, 6=1 или 6 = 2.
Если 6=1, то 4-21с8 = 8с12. Отсюда
8000 + 400 4- 40с 4- 32 = 8000 4- Ю0с 4- 12,
60с = 420, с = 7. Искомое число 2178.
Если 6 = 2, то 4-22с8 = 8с22, 8000 4-
4~ 800 4~ 40с 4*32 = 800 4- 100с 4~ 88•— урав-
нение не имеет целых решений.
283.	Рис. 153.
284.	Система не имеет решения.
285.	Рис. 154.
156
286.	a) xk = j/cos л + i sin л=
= cos л+2л/:+г51пя+^ , 6 = 0, 1, 2, 3,
6	0
4, 5;
8 f C\ » • * (\	2 31^/ 
6)	xk = у cos 0 +1 sin 0 = cos -g—H
4-isin^ , 6 = 0, 1, 2, 3, 4, 5, 6, 7.
287.	a) xk = 2£/cos0 + i sin 0 = cos-^-4-
+ isin-^-, 6 = 0, 1, 2, 3,	23;
6)	xk = 2p/cos л 4- i sin n = cos	4-
+ i sin , 6 = 0, 1, 2, 3.....23.
288.	z4--|=l, z^O, z2—z+l = 0,
l-i/T	1-НКз
откуда z =------- или z =—-?----. тогда
Рис. 154
z21 -4- — ==
224
/1—i/з
V 2
24
==1 + 1=2
ИЛИ Z24 +
1	(l+iV3 \24
z24-\	2 J
1
l/-T\24
1 + 1=2.
289.	Умножим обе части уравнения на х— 1 Получим:
(х— 1) (х11 + х10 + х9 + ... + х + 1) = 0, откуда последовательно по-
лучаем: х12— 1 = 0, х12 = 1, х12 = cos 0 + i sin 0, xk = cos 0 + i sin 0=^
= cos + i sin , так как x #= 1, то k Ф 0, k = 1, 2, 3, ..., 11.
Для преобразования суммы в левой части уравнения можно
воспользоваться формулой суммы геометрической прогрессии.
290.	Введем новую переменную, у = х3, тогда у2—65z/ + 64 = 0.
Откуда у==1 и у = 64.
Корни исходного уравнения: хх=1; х2=—х3 =«
= -4+i-^-;x4 = 4;x5 = -2 + iK3; x„ = -2-i/3.
291.	а) х1 = 1, х2=—1—х3 = —4 + i-^-. х’ = 32,
х4 = 2 ^/4, х5 = — j/4—i	хй = —^/4 4- i yz4;
157
б) х1 = >/3, х2 = I р/3, х3 = — //3, х4 = —i р/З, х5 = у , х6 = Т«,
. _____1_ ________1_.
2 > *^в	21 *
292.	Через точку М и центр окружности проводим прямую ОМ.
Она пересекает окружность в точках А и В (рис. 155). Из точки
М проводим касательные к окружности СМ и DM. Соединяем точки
касания С и D, а также проводим диаметр через точки С и О.
Получаем АВ I CD, СЕ _]_ СМ.
293.	Из системы уравнений
| 24х—24г/= 800
| Зх + 3«/ = 800
находим х = 9 км/ч, у — 1 км/ч.
294,	График функции рассматриваем в двух промежутках:
1) при х < 0 f (х) = х3 + х;
2) при х^О /(х) = х3—х (рис.
156).
295^'(х)=етж;
^^-=4; (х+ 1)? = 1; |х+ 1| = 1.
Значит, х + 1 = 1, х = 0, f (0) = —2
или х + 1 — —1, х = —2, /(—2) = 6.
303. а) Рис. 157; б) рис. 158;
в) рис. 159; г) рис. 160; д) рис.
161; е) рис. 162.
30.4. По последней цифре ре-
зультата определяем, что послед-
няя цифра первого множителя —4.
Так как первое неполное произве-
дение трехзначно, то первая циф-
ра первого множителя— 1. Первая
Рис. 157
158
цифра второго множителя больше
7. Значит, это 8 или 9. Провер-
кой убеждаемся, что это не 9. Сле-
довательно, первая цифра второ-
го множителя —8, т. е. 13 4
8	7
9	3 8
10	7 2
11058 *
305.	Из условия задачи (рис.
163) запишем систему уравнений:
( 22 + -| = 5х
I x + z/ = 22, откуда х = 6, у =16,
значит, сыну 6 лет, отцу 30 лет.
306.	Из второго уравнения
системы получаем х5 Ух2 — 4у2 = 0,
откуда х = 0 или х2— 4у2 = 0. Ес-
ли х = 0, то из системы у = 0, что
невозможно. Значит, х2 — 4у2 = 0.
~ / х~~
Тогда \ п л или
I х—2у = 0
( х— у = 2
П + 2у = 0, 0ТКуДа
/ 1	2 \
(4; 2) и 1 -г ; —я- — решения
системы.
307.	&FCM = /\MCN (рис.
164), значит, Scpmn = 2S^fMC,
Safmc = ±MF.FC, fc = ^=,
MF = DF = a— Следователь-


Рис. 159
нп Q   1 . a (n a \ a2(l^ 2 О e ________________a<2, /i/*n 1)
но, oFMC~-у I a	------4----» ^cfmn — -2\V	—4*
308.	График функции y = — сдвинем вправо параллельно Ох на
2 единицы, затем выполним сжатие его к Ох в 3 раза и сдвинем
вверх на 4 единицы.
309.	а) Преобразуем данное выражение функции в выражение
у = — ~ log2 3 (х + 1) + 3. Г рафик функции у = log2 х сдвинем влево
параллельно Ох на 1, затем выполним сжатие к Оу в 3 раза, сжа-
тие к Ох в 2 раза и отразим симметрично Ох, поднимем вверх
параллельно Оу на 3 единицы;
09

Рис. 166
б) у — 2 log2 у (х + 2)—3. График функции y = log3x сдвинем
влево на 2 единицы, потом выполним сжатие к оси Оу в 0,5 раза,
т. е. растянем от Оу в 2 раза, затем растянем от Ох в 2 раза и
опустим вниз параллельно Оу на 3 единицы.
310.	У — -^- • 22<х—3> + 3. График функции у = 2* сдвинем вправо
параллельно Ох на 2 единицы, затем выполним сжатие к Оу в 2 раза,
к Ох в 3 раза и поднимем вверх параллельно Оу на 3 единицы;
б)	у = —1.2-2^+2> + 3. График у = 2х сдвинем влево парал-
лельно Ох на 2 единицы, выполним сжатие к Оу в 2 раза, затем
отразим симметрично относительно Оу, выполним сжатие к Ох в
3 раза, отразим симметрично относительно Ох и поднимем вверх
параллельно Оу на 3 единицы;
в)	построим в одних координатах графики функций у = х и
У — — . затем сложим соответствующие координаты у. Соединив полу 311 312
ченные точки непрерывной кривой, получим искомый график;
г) находим область определения функции: х^1, х#=0. у =
— -— == V — х + 1 + 1. По графику у = — х +1 строим график
y = ]f — х + 1, затем сдвигаем его вверх параллельно Оу на 1.
311. Сумма чисел в каждом столбце может быть найдена по
формуле суммы членов арифметической прогрессии. Тогда получим,
что общая сумма чисел таблицы будет равна: S = 101-50+103-50+
+ 105-50+ ... +299-50 = 50.(101 + 103+ 105+ ... +299) = 50 х
х 101+293 -100 = 2500 • 400 = 1 000 000.
312. \Oa + b = b‘b + а, 9a = b>(b—1), b и b—1 взаимно простые
и b—1 на 1 меньше Ь. Отсюда & = 9, а = 8. Искомое число 89.
6 № 36^1
161
313.	Обозначим точку касания окружностей А, а точки касания
вписанной окружйости со сторонами угла—В и С (рис. 165). Иско-
мый радиус обозначим Rt. Тогда из \Ofi±B имеем 0гВ2- + OJP- =>
= Ofil, так как Ofix = + ОХВ — Ri, то
я? + (я1 + т/?У==(/?+7?1)а’
2
откуда, выполнив преобразования, получим Ri — 2-^-R.
314.	Обозначим стороны трапеции ВС = а, AD = b, АВ = с, CD=d,
высоту BE = h, отрезок АЕ = т (рис. 166). Тогда имеем:
ci + b = c -4- d,
учитывая, что c — d, tn = b—^-, находим a-|-b = —, — —2c, c — 2,
£	c c
( a-~^b = 4
d = 2, т. e. получаем систему: -! m = J/" 3 из которой находим
I b—d = 2K3,
с = 2—1/3, fe = 2 + КЗ.
315,	Функция четна. Ее график симметричен относительно оси Оу.
Находим корни (нули) функции. О<0 Корней нет. График не
пересекает оси Ох. Он расположен выше оси Ох. Находим интер-
валы монотонности и экстремумы функции, у' = 4х3—4х —4х(х2— 1),
у' = 0, 4х(х2—1) = 0, откуда х = 0, или х = — 1, или х=1:
если х < — 1, х = — 2, у'(—2) = — 24 < 0, функция убывает,
если —1 < х < 0, х — — 0,5, у' (—0,5)== 1,5 > 0, функция воз-
растает;
Рис. 167	Рис. 168
162
если 0 < х < 1, № 0,5, у* (0,5) = — 1,5 < Q, функция убывает.
Следовательно, в точках х=—1 и х = 1 имеем минимум, а в
точке х = 0 максимум! ут1а =» 1, t/max = 2.
По найденным точкам с учетом того, что при х —оо, у —► оо,
строим график функции (рис. 167).
316.	а) Рис. 168, х=^3; б) рис. 169, х^=0.
317.	Рис. 170, х>—1, х^=0.
318.	Построим график у =— х?4-1, проведем прямую у — 1,
построим точки искомого графика, деля приближенно 1 (ординату
точек прямой) на соответствующие ординаты построенного графика
(рис. 171).
319.	Преобразуем данную функцию
У= l°ga	= 1о§2 (*+ О—(*?—Зх 4- 2).
Построим графики функций z/ = log2(x4-1) и y = log2(x?—3x4-2),
а затем построим искомый график, найдя ординаты его точек как
разность ординат соответствующих точек построенных графиков.
320.	Воспользуемся определением четной и нечетной функции.
Если функция нечетная, то /(х) = —f(—х). Отсюда f(x) + f(—х) = 0,
а для четной функции Дх)4-/(—х) = 2/(х).
Найдем в рассматриваемом случае сумму f(x)4-/(—х) =*
= 1g (K9tg?xH-l 4- 3 tg х) 4- Ig (/9tg?(—-x) 4-1 4- 3 tg (-X)) =
= Ig 0/9tg«x4-1 4- 3 tgx) 4- lg(K9tg2x4-1—3tgx) *==
= 1g((|/’9tg?x4-14-3 tgx) (/9tgSx4-l-3 tg x ))«
= 1g (9 tga x 4-1 —9 tg2 x) = 1g 1 = 0,
т. e. данная функция нечетна.
6»
163
Задачу можно решить иначе!
/(— x) = lg(/ 9tg?x+ 1— 3tgx)=s
= j (Kstg^+i-atgxHKgtggx+l + Stgx)_ . 9tg?x+l-9tg2x e
8	v9tg?x+l+3tgx	8 |/9tg*x + l+3tgx
'«ww-,.- |e(|/WT+i + 3tg,) = -/w -
функция нечетна.
321 • Если Иванов серьезный человек, то он так и сказало себе,
что он серьезный человек. Если он шутник, то он должен был ска-
зать о себе не то, что было в действительности, т. е. и в этом
случае он мог сказать только одно, что он серьезный человек. Зна-
чит, Демин сказал не то, что сказал Иванов. Следовательно, Демин
шутник, а Панькин серьезный человек.
322.	til—20п3 + 64п = п (п* — 20п2 + 64) = п (п2—4) (п2 —16)==
= (п — 4) (п—2) п (п + 2) (п + 4)—произведение пяти последователь-
ных четных натуральных чисел. Значит, по крайней мере одно из
них делится на 5, одно на 3, три на 2, два на 4, т. е. все произ-
ведение делится на 5-3-8-16= 1920.
323.	Проведем EF | AD через точку пересечения диагоналей
трапеции О, и	(рис. 172). По условию OO1 — -^R. Следо-
вательно, ЕО, = O,F = 4-7?.
О	о
Обозначим ВЕ~х, AF = y.
AB=z. Тогда из подобия треуголь-
ников ВЕОг и AFOX, из треуголь-
ника АВМ, из свойств сторон
описанного четырехугольника по-
лучим:
' х _ 2
(У—x)2 + 4/?2 = z2
z = x + y.
Из этой системы находим х = 0,5/?,
у = 2/?, z = 2,5/?. Следовательно,
P = 2-(z+ * + #)= 10/?, С = 2л/?
Р 5
и 7^ ==77-
С Л
324.	Область определения вы-
ражения 15 х , следовательно,
-5+Г~3 г .
2
164
325.	Рис. 173. 326. Рис. 174.
327. Рис. 175.
328.	(Рис. 176). 329. (Рис. 177).
330.	(Рис. 178).
331.	Выручка равна квадрату
числа. Причем квадрат этот содер-
жит нечетное число десятков, а
число единиц четно. Значит, число
единиц может быть либо 4, либо
6, а с учетом нечетности числа
десятков квадраты могут рав-
няться 36, 196, 256, 576, 676, ...
Значит, первый должен вер-
нуть второму 2 р.
332.	5 5 1
5 3 1
5 5 1
16 5 3
2 7 5 5
2 9 2 5 8 1
333. Область определения функ-
„	3	.1	9
ции 0<x<-j-,x=/=Y»T-e- х=1б‘
3341 —5 х 0.
335.	В плоскости основания пи-
рамиды проводим прямую через
две данные точки М и N (рис.
179). Продолжаем ребра CD и СВ
до пересечения с этой прямой в
некоторых точках К и R. Точки
Р и К лежат в грани SCD.
Значит, прямая РК, где Р—
данная точка ребра SC, пере-
секает ребро SD в некоторой
Рис. 176
Рио. 177
165
Рис. 179
точке Q. Аналогично прямая PR пересекает ребро SB в некоторой
точке Т. Соединяем последовательно точки М, N, Q, PtT. Пяти-
угольник MNQPT — искомое сечение.
336.	Пусть данные точки Ог, 02, О3 принадлежат соответствен-
но граням ABBiAi, ЛЕЕ^А^ CDD^Ci (рис. 180). Проведем че-
рез точки О2 и Oi плоскость а, а через точки О2 и О3—плоскость 0,
перпендикулярные основанию призмы. В этих плоскостях проведем
прямые ОгО2 и О203 до пересечения с плоскостью основания соответ-
ственно в точках Q и R. Точки Q и R лежат одновременно в плоскости
основания и в секущей плоскости. Значит, эти плоскости пересе-
каются по прямой QR. Плоскость грани ABBtAi пересекает QR в
точке 3. Точка 5 принадлежит секущей плоскости и OjS принадле-
жит секущей плоскости. Прямая Q^S пересекает ребра ААГ и BBt
соответственно в точках Z и L. Плоскость грани АЕЕ1А1 пересе-
кает QS в точке U. Прямая O2U пересекает ребра ААг и ЕЕг в
точках Z и X, принадлежащих сечению. Плоскость грани EDD^Ef
пересекает QS в точке Т. Прямая ТХ пересекает ребро DD2 в точке У,
принадлежащей сечению. Соединив последовательно полученные точки,
получим искомое сечение LZXYV, где V £УО.,пСС'1-
337.	Секущая плоскость пересекает основание куба по прямой
AOf (рис. 181). Прямые AOf и DC пересекаются в точке Е. Прове-
дем через Е и О2 прямую. Она пересекает ребро ССг в точке F й
ребро DDt в точке К. Эти точки принадлежат сечению. Искомое
сечение AOXFK.
Площадь сечения равна	5 = Здлх£—Здо,^	ЗдЛде =
= Vp (р—АЕ)(р—КЕ)(р—АК).
166
Из ДАРЛ АЛ = Ц^;ЕР=
= 2а; OiF = у А К =	, так
как OtF—средняя линия тре-
угольника АКЕ',_ АЕ —
= Ко2 + (2а)? = а К5. Из тре-
угольника	DKE	КЕ =
= DE^ + KD1. Так как
Д DKE ю Д O2LE, то ££ = ,
KS^La Li La
DK	2a	2
— =; DK = т а, значит,
a	3	3
T 2“a _________
KE=lf 4a? + 4«?
J	у о
Вычислив полупериметры и стороны ДАЛЕ, по формуле Герона
с 35a? /23
получаем г>дЛКЕ =—щ.
Так как /^O^Ezn&АК.Е с коэффициентом подобия 0,5, то
площадь /\OtFE равна одной четверти площади ДАЛЕ. Отсюда
5	35a? /23
338.	Ух1—x+l^n, х?—x-f-1 =/г2,
x?—x + 1—n? = 0,
t ±/4n?-3
x— 2
Чтобы x было целым числом, необходимо и достаточно, чтобы 4п?—3
было полным квадратом, т. е. 4п?—3 = 6?. При n = l fc = l. Тогда
х — 0 или х =s 1. Других значений быть не может, так как при уве-
личении и на 1 4п? увеличивается больше чем наЗ, т. е. расстояние
между соседними квадратами больше 3 и, следовательно, 4п?—3 не
может снова равняться квадрату натурального числа.
339.	Пострадал Генрих на 60 пенсов.
340.	Из рисунка 182 имеем Е = ЛД-f-BC.. ВЕ = 3~ sina.
Отсюда: АВ? = у-^-; DS = AC—AD^AB + BC—AD; AD-DC =
3sina
=AD • (AB + BC— Atf)=AS -AB + AD- BC—AD-AD=2- AB1. - cos a+
+ 2-AB1—4 AB? =. — 2 AB? (1 — cos a) - — 4AB2 sin2 J.
167
AD-DC — — 4-^-
3 sin a
2S.sin?-2-
sin* 4-----4-----------------2—
2	o n . a a
3*2 sin-g- cos у
AD-DC = -±Stg%.
341.	Введем систему координат. Ось Ох направим по ОС, ось Оу —
по ОВ, ось OZ—по OS (рис. 183). Найдем координаты точки А и
точек В, М, N: NN^Of, ON^^, ММг=~, MOi=±, ОВ =
= 0,5, ОА — 0,5, следовательно, А (0; — 0,5; 0), В (0; 0,5; 0),
n(^; 0; 0,5), Л1(о; —4; 4)-
Уравнение плоскости в общем виде можно записать так: ах + ЬуА-
4- cz+ 1 = 0. Найдем а, Ь, с, подставив координаты точек В, М, N-
0,5Ь+1 = 0, Ь = —2
1^<1+0,5с+1=0
_|(, + |с+1=0.
Уравнение плоскости будет —2у—2z+l=0.
342.	Искомое сечение параллельно BDt и Оно проходит
через точку О2, такую, что О1О2 — ^-ОО1 (рис. 184). В плоскости
168
BBJDJJ) через 02 проводим NM^D^, MN £a—искомое сечение;
M € BBi, N £ B2Dt. Так как a ||ДхСх, то a пересекает AjBiCiDt по
.E/'IdjCi. В плоскости диагонального сечения ДД^С проводим
через 02 КЦА-fii. Соединяем полученные точки Е, F, К, М, L. По-
лучаем искомое сечение EFKML.
343.	Пусть точки Е и F—середины смежных ребер. EF f]BD = N
(рис. 185). Проводим	NLfyOOi — O^. Через 03 проводим
М/СЦДС. Искомое сечение EFKLM.
Sce4 = Sefkm +*$дл1К£; Sefkm —	• 03N",
EF =1- ДС=1а/2, MN-=a^2, O3N = 1 В£П = 1 a/3 ,
c 3a? K"6
^EFKM = --jg- 5
S^mkl^^MK-02L- MK = aV2,
таким образом,
s	। 1 ац/б-7д-Г6
^сеч— ig + 4 ° V °— ig
344.	Искомое сечение AEFM (рис. 186).
Saefm = у ’ ME- AF;
в Д50С: ОС = SC-cosa, ОС — acosa, XC = 2acosa, SO==asina;
в /\ACF: AF -AC- sin a = 2a cos a sin a — a sin 2a;
169
в Л AOK'* AO~OC—acQ$a, /АКО~а, OK=АО -ctga=a cos a *ctga;
SK=* SO—OK = a sin a—a cos a ctg a,
SK -- a * sin^ a~C03^a  a cos 2a #
sin a	sin a *
в ДШ:/Ш = а, Ж==5/Сс1ёа = -а^2. ctga;
sin a
M£ = —2a^-^.ctga;
sin a ’
Saefm = 4- f— 2a C°s • ctg a) • a sin 2a = — 2a2 cos 2a cos a ctg a.
345.	В сечении получается правильный шестиугольник EFKLMN
(рис. 187).
е ___no	п NK-\-EF
0сеч = 4&efkn = * --2- ’	’
KN^aV"2, EF=-^a^2.
В треугольнике 00±Р 001 I BD,
00^, 01Р = |аГ2, 0Р = /00Ц-01Р5 =	+	=
fly-g _ За’^З
дсеч —	2	’	2	—	4
346.	Пусть Р и Q—середины ребер ED и CD данной пирамиды,
а Дх—середина ее ребра S4 (рис. 188). В диагональном сечении ASD
середину отрезка PQ точку 0^ соединим с At; А^са—искомому
сечению. X1OJriSO = O2, где SO—высота данной пирамиды. Через Ог
проведем LN^PQ, LN a: a; L и N лежат в гранях пирамиды. Точки
пересечения прямой PQ с прямыми EF и ВС обозначим соответст-
венно X и Y. Проведем LX и NY. Получим линии пересечения FJEi
170
и BxCj плоскости а с двумя гра-
нями пирамиды. Соединив Ег с Р,
Сг с Q и Р с Q, получим искомое
сечение AiBiC&PEJ^.
347.	При п > 0 п =
= — log2 log2	. К 2 ;
п радикалов
при п < О
п = log2log2 ]/"]/.. ./2 ;
п радикалов
при п = 0 п = log2 log3 2.
348.	Зр. 30 к.
349.	Площадь данной трапе-
ции будет равна 5 — —---------- BE
(рис. 189). Выразим S через
AD:BC = AD—2АЕ, АЕ = ВЕ,
BC — AD—2BE,	BE = a—AD,
BC = AD—2a + 2AD=3AD — 2cr, >
S = ЗЛР.-^а+Л£  (a—AD). Обо-
значим AD = x, тогда
S (x) =& (2x—a) (a—x) = — 2x2 + 3ax—
мум. Найдем его. S' (x) = — ^x-\-3a,
Рис. 190
а*. Эта функция имеет, макси-
S' (х) = 0, х - ~ a, smax-^-а2.
3	1
Трапеция наибольшей площади имеет стороны. AD^-^a, ВС =^-^а,
AB = CD = ^a^2.
350.	Обозначим сторону основания через а. Выразим двугранные
углы при основании и при боковой грани через a; SE = ytg60° =
а У~3 гуп а	ОЕ а а V 3 Л 3 ;	1ПЛЧ
= —,О£ = у, cosa===g^ = -2-: —j—= “- (рис. 190). Прове-
дем сечение пирамиды через BD перпендикулярно ребру SC.
£BMD^$—линейный угол двугранного угла SC. Так какASD=
— 60°, то /\,ASD—равносторонний, SD = а. В треугольнике
SDM DM=SD-s'm60°	в треугольнике ODM OD = a 2- ,
. р OD а]/"2 аУ"3	В	.г 0 _ ^3 а
Sln 2 — DM— 2 ’ 2 — 3 »cos 2 У 1 Sln 2	—, Т-е.
cosa=cos-|-; значит, а = у, т. е. Р = 2а.
171
sin (a + P)
tga + tgp	. cos a cos p	«
2tg-£±H	2Sln^
a + P
c°s—
o . a + P a+P a + P
2 sin —cos --г* 2 3- cos —+-L
_	Z	2.	2 J _____
2 sin cos a cos P
2 a + p	2 a + P	о
cos? —h-2-	cos2 ——cos a cos P
z ।	z	,
cos a cos P	cos a cos p
l+cos(a + P)
—!---—-—-i—cos a cos P
cos a cos p
___ 1 + cos a cos P — sin a sin P — 2 cos a cos P_
~~	2 cos a cos P
__1 — (cos a cos p + sin a sin p)
2 cos a cos p
2 sin2	sin2 a~~ft
l„cos(a-P) ^/Sln 2	== __2_
2cos a cos p 2 cos a cos P cos a cos P *
что и требовалось доказать.
352. cos2x+cos^f~ + x) + cos?fv—=
\ О /	\ О /
(2	\	/2
У n+2x) ( 1 + соз(дя-2х
“	2 'r	2	+	2
cos 2*+^ соз^~л + 2лу+ cos^~n — 2z j J
2
о cos 2x4-2 cos-й-л • соз 2x
__ 3 ,______J_____3__________3 , cos2x—cos 2x_ 3
” 2	2	— 2 +	2	~~2 '
353. logj_ (cos? (a 4- P) 4- cos? (a—(J)—
— cos 2a cos 20)=logj_ (
3 '
4-	—cos 2a cos2p^ =
= logA (1 + S°ill«-+P)+cos 2 <a-P>_Cos 2acos 2g) =
= iogj_ ( i 4-------------cos 2a cos201 = log j_l = 0.
3	3
172
(3	\
у л—За 1 sin 2а =
= 1 —cos За cos 2а + sin За sin 2а = 1 — cos 5а = 2 sin2 у а.
355. tg а + tg Р + tg у —sln (и+Р+у) _=
&	& г & Г COS а cos р cos у
__ sin а	.	sin р	.	sin у	sin(a + P+y) ____
cos a	‘	cos P	*	cos у	cos a cos flcos у
__sin a cos P cos y + sin P cos a cos y + sin у cos a cos fl— sin (a + fl + y)
cos a cos P cos у
__cos у «sin (a + p)+sin У cos a cos P — sin (a+fl) cos у—sin ycos(a+P)_
cos a cos P cosy
__sin у (cos a cos fl — cos a cos fl+sin a sin P)_
cos a cos fl cos у
sin a sin fl sin у ,	, Q .
=-----------L---L_ = tg a tg В tg y.
cos a cos P cos у	1	*
356. (tg 30° + tg 40° 4- tg 50° + tg 60°) • sec 200° ctg 300° =»
_ fV3 , sin 90°	,	К 3
\ 3 * cos 40° cos 50° v /' 3 cos 200° '
= ( j________1	\ . __O_ — (! 2 . КЗ ,
\	3	* cos 40° cos 50° / ’ 3 cos 20°	\	3 sin 80° / ’ 3 cos 20°
/4 КЗ ,	2 \ КЗ 4 '	2 КЗ _
\	3	+ cos 10°/	3 cos 20°	3cos20° + 3 cos 10° cos 20°
-	4 * &	/pndOU^k4^5104005 3^-
3 cos 10° cos 20° Д ’1" 2 /	3 cos 10° cos 20°
8 cos 20° cos 10°	8
3 cos 10° cos 20°	3
357. tg 9° — tg 27° — tg 63° + tg 81 ° = (tg 9° + tg 81 °) —
__/l cyio । f ________ sin 90________ sin 90__________
— (igz/ ig oo J — cos9ocos81o cos 27° cos 63° “
_	1	1	__	2	2	__
cos 9° sin 9° cos 27° sin 27° sin 18й sin 54°
—	2	__2 (sin 54° — sin 18°) _ 4 cos 36q sin 18°_ .
sin 18° cos 36° sin!8Qcos36° sin 18° cos 36°
358. 16 sin 10° sin 30° sin 50° sin 70° sin 90° =
16«2 cos 10° sin 10° sin30° sin 50° sin 70° _ 8 sin 20° sin 30° sin 50° cos 20°
2 cos 10°	cos 10°
— 4 sln 40° sin 30° CQS 40°	2 Sin 8°°‘~2 __ cos 10° = 1
““ cos 10°	cos 10° cos 10°
1	1 sin 4a __
359. tg 4a + sec4a = sl” n-----------------t—
&	cos 4a	cos 4a	cos 4a
1 + cos 4a
cos 4a
2 cos2 ( 2a
\ 4
cos 4a
173
ft . , n cos2a-|-cos ( -5-— 2a ) 2coscos ( ~ — 2a j
cos 2a-f-sin 2a ___ \ 2______J __	4	\ 4__£
cos 2a — sin 2a п / л o \	л o« \
cos 2a—cos I -7Г — 2a J	2 sin — sin I —— 2a )
\ 2 J	4	\ 4	/
2 cos? f -2- — 2a2cos2 f -7-— 2a
_______\ 4	)______\ 4_____) e
__	--	-	cos	4a	»
sin I -g- — 4a I
2cos2 2a^ 2cos2 f 2a
\ 4____)______\ 4____/
cos 4a	cos 4a
оsin? 4a_______________________sin2 4a_________sin2 4a___
’ 2 cos a + cos 3acos 5a 2cos a 4-2 cos 4a cos a 2cosa»(l+cos4a)
4 sin2 2a cos? 2a	sin 2a • 2 sin a cos a	n . o
= n----n—8=8-------------------- 2 sin 2a sin a.
2 cos a • 2 cos? 2a	cos a
222	222
361. Преобразуем уравнение: x3 -x 9 * * * *x27 •... = 49, x3 9 27 “ =
2
3
!_1_
=49, x 3 =49, откуда x = 49.
362. Преобразуем выражение:
з з з з	з з з j_________з э
22 «54 * «28 -516. ♦. ®1Р'+"5М‘ 32	* i6 + 64 + *“ —
з	з
__2	4
i __L 1 —-L
= 2 4 * * * *-5 4 ==22-5==20.
363. cosa = ^—
364. / = —(ТТгуР У’^к, fc = tgl35° = — 1, значит, —
=—1, откуда находим х=0 или х=4. Значит, имеем две точки
(0; —1) и (4; 3). Уравнения касательных: у ——х— 1 и у —— х4-7.
365. </_=Зх?—6х, y' = k = 3, Зх?—6х = 3, откуда х=1—1^2 или
х— 1 +И2. Еслих = 1 —«К2, то у — (1—V2.)*—3 (1 —}/Г2)г-(-2—^/Г2,
если х=1 + И2, то z/=(l+K2)3—‘3(1 + /2)?+2=12—И2.
Значит, имеем две точки (1—И2; И2) и (1 + И2; 12—К2).
Уравнения касательных: у = 3х—3 + 4^2 и г/ = Зх + 9—4рг2.
366. cos х + 2 cos 2х + cos Зх + cos 7х -|-2 cos 8х 4- cos 9х = (cos х 4-
4- cos 9х) 4- 2 (cos 2х 4- cos 8х) 4- (cos Зх 4- cos 7х) — 2 cos 5х cos 4х 4-
4- 4 cos 5х cos Зх 4- 2 cos 5х cos 2х = 2 cos 5х • (cos 4x4-2 cos Зх 4- cos 2х)=
= 2 cos 5х (2 cos Зх- cos х 4- 2 cos Зх) = 4 cos’5x cos Зх (cos х 4-1) ==
— 8 cos 5х cos Зх cos? у.
174
on'-? о пло лао оло 8 sin 20° cbs 20° соа 40° cos 80"
367. 8cos20 -cos40 -cos80
sin 20°f
4 sin 40° cos 40° cos 80°_2 sin 80° cos 803 _sin 160°_sin 20°
<йпЖ	sin 20°	— sin 20° ~~ sin 20°:
368. sin4 75°4-4 sin3 75° sin 15°4-6 sin* 2 75Ojsin215°4-4 s.in75°*sin315°4-
4- sin415° == (sin2 75° 4- sin215°)? 4- 4 sin 75° sin 15° (sin2 75° 4- sin215°) 4-
4- 4 sin2 75° sin215°= (sin2 75°4-cos275°)2 4-4 cos 15°-sin 15°(sin2 75°4-
4- cos2 75°) 4- 4 cos215° sin215° = 1 4- 2-sin30°. 1 4- sin2 30°«
= l + l + 4- = 21.
Примечание. В X классе данное выражение можно заменить
степенью бинома. Сумму синусов . заменить произведением, после
чего легко находится числовое значение полученного выражения.
369. cos2a—cos8a4-sin8a=cos2a4-(sin4a—cos4a)(sin4a4-cos4a)
— cos 2а 4- (sin2 а—cos2 а) (sin2 а 4- cos2 а) ((sin2 а + cos? а)2—
— 2sin2acos2 a) = cos 2a—cos 2a-^l —у sin2 2a =
— cos 2a f 1 —14-4 sin2 2a ) == 4- cos 2a • sin2 2a = 4 sin 4a sin 2a;
\	2 J 2	4
4 sin 4a sin 2a = 4" sin 4a sin 2a.
4	4
37Ф sin a-Hsin 2a4-sin 3a4- . •. 4~sin ла_
‘ cos a 4-cos 2a4-cos	3a4-••• +cos na
Л	.	a-j-^a a — na , n	. 2a4-(л—1) a	2a—(n—l)a	.
2	sin —%— cos —2---г 2 sin--------— cos—--- 2 T. —	; ’ *
n	a 4-ла a —na , n	2a + (л—0 a	2a —(n.—l)a	.
2 cos —— cos —£--[-2 cos--—~2----— cos----4" • • >
_ . a 4-ла f	a —na .	2a—(n — 1) a .	3a — (n — 2) a .	\
2 sin —2“ ( co$ —— 4- cos-------—4~ cos  --"y 4 4~ ... 1
~~ n а4-ла/	a—na .	2a —(n—l)a .	3a — (n — 2) a .	\
2 cos — ( cos - --4-cos-----2 4cos	^4.... 1
= <кЦ=.
Примечание. При чётном п преобразования очевидны. При
нечетном п средний член в числителебудет равен sin -2.., а сред-
нии член в знаменателе будет равен cos—и после вынесения
за скобки тех же самых множителей в скобках останутся тоже оди-
наковые выражения. Получим тот же самый результат.
371. cos a • cos 2a * cos 4a •... •cos2na =
_ 2 sin a cos a cos 2a cos 4a.. . cos 2Л a_2 sin 2a cos 2a cos 4a... cos 2n a __
2 sin a	2^ sin a
__ sin 4a cos 4a... cos 2” a  	_sin 2a+1 a
2? sin a	’ ’ ’ 2n +1 sin a ’
175
= (16.(2 + V 3)—2)2 + (16(2—К 3)—2)?—4 = (30+1бИз)2 +
+ (30 — 16 КЗ)2—4 = 900 + 2 • 30 • 16 /3 + 768 + 900—2 • 30 • 1 б^З +
+ 768 — 4 = 3332.
373.	sin2a + sin20 + sin2(a + 0)—2 =
_ 1 — cos 2a . 1 — cos 20 ,1 — cos 2 (a + 0) n_
$	| g I 2 Z —
= ——у (cos 2a + cos 20 + cos 2 (a + 0))=—у—
— у (2 cos (a + 0) cos (a— 0) + 2 cos? (a + 0) — 1) =
= —g-—cos (a+0) (cos (a—0)+cos (a+0))+y=—2cos(a+0)cosacos0.
374.	Обозначим искомое число буквой х. Тогда по условию за-
дачи имеем:
отсюда 2п2 = 3т3. Достаточно взять /г = 2-32, т = 2-3. Тогда 2п? =
= 23-34, 3/и3 = 23-34, т. е. х = 648.
375.	tg 1°•tg 2°•tg 3°-... • tg 88° • tg 89° = (tg I°.tg89°).(tg2°x
xtg88°).. .(tg44°.tg46°).tg45°=l.
376.	Так как в трапеции ABCD (рис. 191)^/ ABD = ^/ACD—900, то
около нее можно описать окружность с диаметром AD. Обозначим
радиус этой окружности через R, тогда легко видеть, что ABCD —
равнобедренная трапеция; поэтому / CAD — /_ BDA — 30°, значит,
дуги АВ, CD и ВС содержат по 60° и, следовательно, BC = R.
Трапеция BM.NC получается из трапеции ABCD гомотетией с цент-
ром в точке О пересечения продолжения боковых сторон трапеции
и коэффициентом k = ВС :AD — R: 2R = 0,5.
176
Обозначим площадь трапеции ABCD через	о
Sit а площадь трапеции BMNC—через S2.	Л.
Тогда S2’.Sl — k2, т. е.	S2+SX=S, м/ ^\n
но Х2 = -|-Зр Таким образом,-|-S1 = S, Sx=
_±с	/7>Х<\\
— 5	// s'
377.	у' — 2х—1. Уравнение касательной
в общем виде y — k(x—хй)-\-уй. В рассмат- д'	в
риваемом случае уо = О, хо = О или х0=1.
Найдем k-.k = у' (х0), k = —1 или Л=1.3на-	Рис- 191
чит, уравнение касательной будет иметь вид
у = — х или у = х—1.
378.	f (х) — №—18х. Наибольшее значение функции в проме-
жутке равно 2 при х = 0, наименьшее равно —10 при х ——1.
379.	abcabc = 100 000а + 100006 + 1000с + 100а + 106 + с =
= 100100а + 100106 + 1001с = 1001 (100а +106 +с); 1001 делится
нацело на 7, И и 13. Следовательно, и все произведение, т. е. дан-
ное число, делится на 7, 11 и 13.
380.	3.4-5.7+1 = 421.
381.	Преобразуем левую часть уравнения:
2cos2x-sinx + 2sinxsin2x + 4sinxsin3x.cos3x = 0; далее 2sinxx
X (cos 2х + sin 2х + 2 sin Зх cos Зх) = 0, откуда либо sin х = 0; х = пп,
n£Z', либо cos2x + sin2x + sin6x=0, cos2x + 2sin4xcos2x = 0,
cos2x(l+2 sin4x) = 0; либо cos2x = 0, 2x = y + nm, откуда x =
= -j-+y/n, mgZ; либо l + 2sin4x = 0; sin4x = — 4x =
= (_l)ft+i2L + nfct откуда х = (-1)*+^ + -£б, k£Z.
382.	Преобразуя правую и левую части уравнения, последова-
тельно имеем:
4 cos 2х + 2 cos? — 20 sin х + 7 = cos х,
4 cos2x+ 1 + cosx—20 sinx4-7 = cosx,
4(1 —2 sin?x)—20sinx + 8 = 0,
2—4sin2x—10sinx + 4 = 0,
2 sin? x + 5 sin x—3 = 0.
Введем новую переменную, получим 2t/? + 5у—3 = 0, откуда
У —----------— = —, у=0,5 или у==— 3 (невозможно). Итак,
sinx=0,5, х = (—1)"~ + л/г, n£Z.
177
383.	Всего имеется CJ2 четверок. А так как каждый год осущест-
вляются ровно 3 четверки, то число лет равно -|-С^ = 165.
384.	Пусть первоначально было х + 2 человека, а осталось х чело-
век. Они сыграли 130—10= 120 партий: х^х~ = 120, откуда х = 16
(х =—15 не удовлетворяет условию задачи).
385.	Это размещения с повторением, т. е. кортежи из 10 по 4:
а;0=ю4.
386.	п = А2—А| = 63 — 62 = 2 1 6—36= 180.
387.	С33 = ^^ = 4060.
388.	Р6 = 5! = 120.
а) (n-l)(n-2)	’	°' ~~ 4 ’ В' (л4-2)(л + 1)’
ч (т — п + 3) (т2 — 2тп	п2 — Зп 4)
Г)	^2	•
390. Преобразуем выражение /г-го слагаемого:
kc^oo = k • м (100_ = 100-^_1)( (99_(й_1^ — loo-Ch1. Тогда S„ =
= 100+ 100CU+юос29+.. .+ioocg=ioo(q9+Q9+c29+.. .+q»)=
= 100-2".
391. Преобразуем левую часть уравнения: * 392 393 394 * *
1 — cos^y—х) + cos2x—-!• —2sinx, гдез1пх + 0, далее cos2x—
— sinx = 4sin2,x, 1— 2.sin*x—sin4sitfix; 6sin-2x + sinx;— 1 =0,
откуда sin x = у или sinx = —0,5 < 0; sinx = -^- ,x = (—l)"arcsiny +
+ лп, n£Z.
x	3	*2”	3
392. cosx-tg2—== —-^ , x#=n + 2nfe, k^Z- cosx-----—
2	z	cos?-J	2
2cosxsin2 у+ 3cos2-j = 0, cosxfl — cosx) +-y (1 + cosx) = 0, 2cos2x—
— 5cosx—3 = 0, откуда cosx = — 0,5 или cosx = 3>l.
2
cosx = — 0,5, x = ±-x-л + 2nn, n£,Z.
О
393. CJ-C* + CS2C’ = 2-3.^1 = 210.
394. Прямых будет CJe=^7y = 105, а окружностей C^==
15-14-13
---ПГТ = 455’
178
395.	Д’-ДМ*«5».4?;7*.
396.	а) п = 7; б) решений нет.
397.	х = Ю.	398. х=10.
399.	Указание. Воспользуйтесь равенством	—Clx+i, х= 13.
400.	Указание. Воспользуйтесь равенством С^-3 + С£~г=»
= C1 + Q, х = 9.
401.	Указание. Воспользуйтесь равенством С^1’ — С«+»»
х = 4.
402.	а) Система преобразуется к виду!
( т—п — 1 =3
I иг—п —1=0,6п, откуда n = 5, т = 9;
б) система преобразуется к виду!
( 2х—п + 3 = 8
1 3(2х—п + 3) = 8(п—2), откуда х = 5, п = 5.
403.	Преобразуя левую и правую части уравнения последова-
тельно, имеем:
cos4x + cos2x = cos 12х+ cos2x, cos4x—cosl2x = 0, 2sin8xsin4x = 0,
откуда sin8x = 0, или sin4x = 0; x = -^-m, m£Z, x = ^n, n£Z.
Наименьший положительный корень у.
404.	Преобразуя левую и правую части уравнения последова-
тельно, имеем:
sin’ х— cos? х = — sin х,
2sin4x + sinx—1 = 0,"откуда sin х — — 1 или sinx = y, значит, х =
= —y-f-2nn или х = (—1 )га + лиг, п, m£Z.
,	,____ 4 v ( ixl it’V
405.	.^2 4/ 2~х + —J =\2 х +4X+4 J . По формуле имеем:
(х+3\ а / *-1 \ 4	4Х+12 4Х-4	/Х+3
4х+«у ^2 х ) .далее 15-2 х+* .2 х =240,2 х = 2‘.
Решив последнее уравнение, находим х = — 1—К5 или х= — 1 +Кб.
406.	7\ = С,(10 *8») .(101е х)4. Из уравнения С’-10 18 Хх
1
х 104,8*2 =3500000, 1ех#=0; х=/=1, х>0, находим х = или
ь	у- 10
х=1000.
/jci<7 ь \т ( -	-—\т
407.	(LL2 + -2—=(x2&-1+fex »J ,	2« = 256,	т = 8;
179
(jAfc / 3	\8-Л	Ji. 3	.
bx~ « J .{x2i-1)	= C^x"3 Х2	ЙЛ~8 =
= C^2*-8x"“*+’2; -'-h + 12 = 5-1 & = з; т.«= C\Wx^x’%“» =
= сз^=5б^.
408.	(а~Уа— |Z-11Y = (а~— а~“) ,
\	r V а /
Сп _ 14 п(п—1)(п —2)(п-3)-1-2_ 14
Сп ~ 3 ’	l-2-3-4(n— 1) п “ 3*
Решив это уравнение, находим: п=10 или п — — 5 < 0, Tt =
(i \s ( 1 V
а~ ! ) Ла 2 / =С«-
409.	fz-yZz-x+y-=Y = \z3 +z 7) ,Тк+1 — С^г 7 -z3	=
\	|/ г2 /
= qcz-^A+^<10"l -2^ + |(10-Л) = 0, откуда £ = 7;78 = С70 =
==С’« = ТТТ==120-
[	___ 2	/ _2
410.	уУа^—а^-уа) = \а 7 — а^) -,^—^=35, Ь2 —
^-k
— m = 35, откуда m=10 или m = — 7 < 0. 7\+1 = (—1)*С&а38 х
ха 7 (1° k) = (—l)ftCJ0a35* 7 (1° k} —1(10—£)=1. Решив
последнее уравнение, находим k = N. Значит, члена, содержащего
а в первой степени, в разложении нет.
411.	Cl-Cl-C^ 111115 = 240.
412.	1 + 2С7+ЗС2 + 4С2+ ... +(п+ 1)C" = (1+Q + C2+C2+...
• • • + £n) + ((^h + 2С,г 4- ЗС3п + . •. + яСл) = 2" + (яСд_1 +	+•••
... + nCnnz\) = 2" + п• 2"-1 = 2й”1 (2 + п).
413.	Из системы
28
—	5
“g”== <^14“ аг2
> 5xi 4- 2х2 = 1
12	3
находим х2 = 4 или х2 = — Зу, Xf = —1у или Xi=ly. Так как
9 >
b = 5 (хх4-х2), то 6=13 или Ь = —1-jq^Z.
180
—1 ’
414.	=’^77 = 221. откуда k = — 7.
415.	sin20°• sin 40°• sin60°• sin 80° =	п-20°g-V18.9°H2sln40° sin60°)
4
(cos 60°—cos 100°) (cos 20° — cos 100°)_
~	4	~
__2 (cos 60° cos 20°—cos 60° cos 100°—cos 100° cos 20°+cos? 100°)
__cos 80°+cos 40° — cos 160°—cos 40°—cos 120°—cos 80° +1 + cos 200°
- . —
__cos 20° +cos 60° +1 —cos 20°_T +1__3
"	~ ~ ~8~~	16*
416.	a) tg 20°+ 4 sin 20° = ?*”20°+4 sin 2 * 4 * * *f‘cos 20°==
' °	cos 20°
sin 20° 4- 2 sin 40°  sin 20° + sin 40° -{- sln 40°  2 sin 30е cos 10° -(-cos 50е
cos 20°	cos 20°	~~
cos 10° + cos 50°_2 cos 30° cos 20° iZo.
cos 20°	~ cos 20°	~ г o,
8
cos 20°
2—
3 (2-K2+K з)/2+К 3
.	"ь/ 1 ”4“ cos 30
6М8 7°Ж = Ц^5°
1 — cos 30°
2
417
n . л л 4л / 2л \
4л 5л 2sln 7 'С03 7-cos -у • Г — cos—у—у
COS -= • COS -=- • COS -я- =---------------i------—L =
7	7	7	. л
2 sin у
n s 2л 2л 4л o 4л , 4л t 8л л
— 2 sin — cos —-cos —	2 cos-у sin— sin-у- sin у
4 sin у	8 sin у	8 sin у 8 sin у 8
418. Преобразуем произведения пар множителей, равноотстоящих
. л .31л .л	л
от концов данного	произведения’	sin ^7 • sin-77-= 31077	• cos	~ =
4	04 o4 64	64
1 . Л
— TS,n32 ‘
Аналогично можно преобразовать каждую пару указанных множи-
телей.
181
_	1	. я . Зя . 15л	.1	1 . я . Зя
Тогда подучим: ^--sin -^ ... sin-gg- = sin^ • sin-^-..
. 7я _ 1	1	1 . я . Зя _ 1	1	1	1 . я _ V 2
Sin 16 ~ 28 ’ 24 * * * ’ 2? Sin 8 'Sin 8 — 28 * 24' 2? * 2 ’81П 4 —’ 218
419. См. решение примера 418.
420. Так как (а2 4- Ь2) ig2 | = 2ab, то ^ = ctg21
---	----- х .	/ о 2	; ’ 2ab ° 2 ’ 1 — cos а
Обозначим у = х1( ± = х, Тогда xrx2=l, Xj4-x2 =
= 2 •, cos ' Поэтому и х2 являются корнями уравнения х2—2х
х ,* l + cosax+1 =0. Решив его, находим: ->4 —-1—XCOSOi	х2
1 —cosa	l-/cosa 2 3
1 — У cos a
1 + У cos a
г---------	f—V—1
1 — у cosa b	an—bn	\bj
к KaK 1 + V cosa ~ T° a^+b^~
(* + К cos: a V __ ।
\l~Kcosa/ ==(1 + Kcosa)n —(1 —Kcosa)n
/ 1-4-'У Cdisa V । ।	(14- У cos a)w -J- (1 — У cos a)n
\ 1 — У cos a /
.	1 4~ cos 30°	
Ig2cosl5°_ -r 2	;	lgl/2-|-Fz"3
• Ig2sinl5° 1£2y 1-cos 30° lgK2~K3
lg|/~2+r^  lg/2 + /3 
422. Преобразуем левую часть равенства:
1 — cos 2Л 4-1 — cos 26 1 — cos 2C____„
1 + cos 2Л 4~ 1 + cos 2B 4* 1 + cos 2C
Далее последовательно получаем:
3—cos2(B4-C)—cos2B—cos2C=6-|-2cos2(B4-C)4-2cos2B4-2cos2Ct
3 cos 2 (B 4- C) 4- 3 cos2B 4- 3 cos2C = —3,
cos 2 (B 4- C) 4* cos 2B 4- cos 2C = —1,
2 cos? (B 4- C)— 1 4- 2 cos (B 4- C) cos (B—C) = —1,
cos (B 4- C) (cos (B 4- C) 4- cos (B—C)) — 0.
Отсюда либо cos (В 4- С) = 0, тогда / В 4- / С = 90° и, значит,
22^ = 90°, либо 2 cos В cos С = 0, т. е. cosB = 0, либо cosC = 0,
тогда либо / В = 90°, либо / С = 90°.
423.	11«— 1 =(10 + I)10 — 1 = 1010 + C}0• 10’ + ... + Go• 10 +
4-	10*— 1 = 10lo+GolO’ + ... + 10-10—каждое слагаемое делится
на 100, значит, и вся сумма разделится на 100.
424.	Собаке надо пробежать х прыжков. За это время заяц еде-
О
9	4о+7х х
лает ух прыжков. Решив уравнение —g— = у, находим х— 105.
425. Уравнение хорды в общем виде у—yQ — k(x—х0). В точке
х0 = 2, у0 = —1; / =	 /(2)=1» т- е- k=l. Итак, уравнение
хорды у = х—3. Из системы
у = — а2х? 4- 5ах—4
У = х—3
имеем уравнение а2х2—(5а—1)х4~1=0. Найдем промежутки зна-
чений а, в которых это уравнение имеет решения. О=(5а—1)?—4а2 =
=21а2—10а4-1, D > 0, 21а?—10а4-1> 0, откуда а = 4- или а = ~,
i	О
т. е. и > 0 при а < у или а > у .
Определим искомое значение а: —у-*? = 2, но х* + хг = — ~
следовательно, 5**у- = 4, откуда а=1 или а = у (невозможно).
426.	ушах = у(6) = 216.2 = 432.
427.	tg За — tg 2а — tg а = —-------—
ь ь ь cos За cos а cos 2а
_ —_sin.fe------(cos (За—а)—cos За cos а) =
соз За cos 2а cos а ' v '	'
_----- sin 2а---, s сод а	sjn за sjn а—cos Зд cos а\ =
cos За cos 2а cos а'	'
sin За sin 2а sin а	За { 2а f
cos За cos 2а cos а	& о о
428.	Так как |cosx| 1, то данное уравнение равносильно си-
стеме:
' cosx= l
cos? х = 1
cos7x= 1,
’ из которой находим х = 2лй, fegZ.
429.	Преобразуем левую часть уравнения
sin4 х—sin2 X (1 + cos2 х) _ sin2 х- (sin2 х— 1 — cos2 х)_
sin6 х —sin?х (1 + cos2 x + cos4x)	sin2 x-(sin4 x—1 —-cos?x—cos4 x)
_________—2 cos2 x_______—2 cos? x , 2
sin2x—cos?x—1 — cos?x	—3cos?x	3’
e. v —Здесь мы полагаем sinx=/=0, cosx^O, т. e.
0-0
где n 6 Z.
183
430.	Преобразуем левую часть уравнения
+ (cos Зх 4- cos 7х) 4- 2 (cos 2х 4- cos 8х) = 0, далее
имеем:
2 cos 5х cos 4х +2 cos 5х  cos 2х 4- 4 cos 5х • cos Зх = 0;
cos 5х (cos 4х 4- cos 2х 4- 2 cos Зх) = 0;
cos 5х (2 cos Зх • cos х 4- 2 cos Зх) = 0;
cos 5х • cos Зх • (cos х 4-1) = 0, откуда
cos5x = 0, или cos3x = 0, или cosx = —1.
гтъ	«гк ।	л । лш
Таким образом, х = 77: + -^-, или х = т- + -^-, или
1V о	О О
k, tn, п£ Z.
431.	Преобразуем левую часть уравнения:
лх лх 2лх 4лх
2sin	-cos-g-cos-g-cos —g—	J
---------—----------------= -§-. Здесь sin -g- Ф 0,
2Sin —
далее, поскольку при sin-^ = 0 получаем jcos
2лх n 9 лх	<	, 4лх o 9 2лх
COS -5- = 2 COS2 --1 = 1 и COS -3- = 2 cos2
У	У	У
лх 2лх 4лх < , 1
куда cos—cos-g-cos уу = 1 =4= у.
. 2лх 2лх 4лх 1
Sin —g- • COS —g- • COS
. 4лх 4лх 1
Sin—g—COS — =
. 8лх . лх
Sin-g- = Sin—,
_ лх . 7лх
2 cossin —jg-=
Значит, x=14-2n или x = -y^, где n, tn£,Z.
Так как -д-=#лй, т. е. х=#9я, то — =A9r, -у=5^я,	k^Z.
Итак, х= 14-2п или х=^, где	п, m, k$Z.
1	JT
432.	Если п = 0, то cos х =-77, х = ± -^-\-2nm, т£ Z. Если п>0,
Z	О
то sinx#=0. Поэтому умножим обе части уравнения на 2sinx. По-
лучим уравнение, равносильное данному:
2 sinx-cosx.cos2x«cos4x-... .cos2nx = ^sinx.
Далее последовательно получаем:
sin 2х cos 2х cos 4х ... cos 2”х = sin х,
(cos х + cos 9х) +
последовательно
х = п + 2пп, где
-у-| = 1. а тогда
_---1=2-1 —1 = 1, от-
. лх
“9 TSin~9" ’
. лх
у Sin—;
. 8лх	. лх п
sin-g---sin — = 0,
0, откуда cos-^ = 0 или sin-^y = 0.
sin2“+xx = sinx, sin2n+1x—sinx = 0,
184
2л + 1лг4-х . 2п+1х—Х А
2 cos------• sin---—- = О,
(2л+1+1)х n . (2"+1—1) х ~
откуда cos-----—— = 0 или sin  -—— = 0,
2«+1+1 л .	. 2п + 1--1
следовательно,   — лг = у + лй или —— х ~ ппг-
гг	л	2nk	2лт
Таким образом, x = 2^+1J|_y + 2n+i+1 или	1 ’
2Z? -I— 1	.	/ t.	т /	1
2» + 1+1'^Р’ 2^-\^Г’ k' т’ П' Г' P$Z’ П=£—L
433.	]/~ 4+4]/^ 4+4]/' 4+- - -+4 V 4+4cosf=
/1 , 1	/ 1 , 1	/ 1 ,	। 1 а	а
Т + у]/ 2 + 2 г 2 + • • • + 2 cos 2a — • • • — COS 2^+Г-
434. 21984— 1 = 4992 — 1 =(3 + I)992 — 1 =(s+ 1)—1,
где s—сумма первых 992 членов разложения бинома, каждый из кото-
рых делится на 3. Следовательно, и все данное выражение делится на 3.
435. Пусть первое слагаемое равно х, тогда второе слагаемое
будет (10—х). По условию имеем: у — 4х2 + (10—х)3;
у' = х + 3(10—х)?-(—1), у' = 0, х—3(10—х)2 = 0, откуда х = в+
или х— 12 > 10.
Если х<в4, х = 8, у' (8) = 8—3-4 = —4 < 0.
о
Если х>8±, х = 9, «/'(9) = 9—3 = 6>0. у	= Ут\п- Итак,
х = 8+, Ю—х=1у-
436.	Преобразуем левую и правую части уравнения
(9—1g2 х)? =16—81g-х-f- 1g1 х—7 Ig2х+ 50,
далее
81 —181g? х + Ig4 х = 16—8 Ig2 х + Ig4 x—7 Ig2 x 4- 50,
31g2x=15; lg2x = 5, откуда lgx = K5 или lgx =— Кб.
Итак, x=10~1'6 или x=10,/5.
437.	Пусть в Д АСВ / С = 90°, CD J_AB, АО = ОВ и / ЛСЕ=
= /_ ЕС В (рис. 192). Докажем, что £DCE = £ ECO; /_ACD=s
= / DBC как углы со взаимно перпендикулярными сторонами.
/ ОС В = / О ВС, так как О В = ОС, следовательно, / DCE = / ОСЕ.
438.	Соединим точку М с вершинами треугольника АВС и опу-
стим из М перпендикуляры на высоты треугольника (рис. 193).
Тогда 5двмс = -гг • ВС • А'МЛ = -^-ВС^АА' — АМ^) = S^abg ~~
А	А
185
Рис. 192
— -у ВС- АМа. Аналогично $д слм =$д лва—у • СА-ВМв, S^AMB—
— S& лес—2 ' АВ-СМс.
Сложим полученные равенства почленно. Получим, что площадь дан-
ного треугольника равна ,4BG = 3SA лвс—у (ВС.АМа+САх
хВМв+ АВ-СМс). Отсюда получим, что
ВС• АМд + СА*BM.fi -j- АВ *СМс == 45д лв<*«
Но = AM cos а, 23Л4Д = ВМ cos Р, СМс » CM cos у, откуда
имеем AM • ВС cos а + ВМ • AC cos fi + CM> АВ cos у = 45ЛЙС.
439.	ВЕ = ±АС = Ь (рис. 194). DBJ_AC, BD = a,	ABQ =
= 1- BD-AC = ±-a-2b = ab.
2r
440.	AB = R, AO = OB = 4’ ^ = 0,0 = 4, ОяЕ = га, A03 =
— R—r9, 00t — x (рис. 195). Из треугольников A090 и
получаем:
pR-r,)>»x>+(4y
1('-+4)МЯ+Л
186
Вычтем из первого уравнения
/ R \ 2
второе: (/? — r^— I G + -4J =
~ (т-)2 — (jr}2' ^ьшолнив Да"
лее преобразования, находим
г3=0,37?, тогда x^—(R—0,37?)2—
— (т-)2’ откУда = 0.27? Кб.
441.	Пусть DAJ_BC,
/_ВАЕ = /_ЕАС,	DA = hA,
АЕ^Ъа, Z_ BAD = р, / DAE=a
(рис. 196). Тогда а = +>-—13,
Z4 = 180°-C/S + ZQ- ₽ =
=90°-ZB,.:a ^18K-ZB-ZC
— 90° + 7 в= С ; Ф =
2 Ра
с
Рис. 197
Рис. 196
В—С
= cos-^2-
Аналогично записав другие два
соотношения, получим систему:
На
~ = COS
Ьа
в—с
2
hft
-7^- = cos
1>В
С—А
2
hc
7— = COS
be
A-В
2 *
Возведем каждое равенство в квадрат, а затем сложим почленно
эти равенства. Получим:
Й > Й । hc <>В—С , 9С — А f „А — В
-4- + -4- +	“ cos -+ COS2—+ COS2 •.-
Ьд Ьв bl	2	*	2 Г 2
Г 4- cos (В —- С) 4-1 -Ь cos (С—А) 4~ 1 + cos (А—В)
2
О1П В-A В-\-А—2С	2А — В
24-2 cos ——cos---£----4*2cos-—2—
==>	2
t ,	B — A(	B+A — 2C , A — B\
= 1 4- COS —— ( COS -------b COS-1 =3
- , o А —В A—C B—C
= 1 + 2 cos—j- • cos —j-" • cos —F” ’ T’ e’
. he . he 1 __ 2 • кл'Ьв'кс
Ьд Ьв be	Ьа'Ьв*Ьс
442. Приведем тригонометрическое доказательство утверждения.
Имеем (рис. 197): sina = -^!=-,cosa==-^= , sinP = yl=-, cosfl =	;
187
13	2	1
sin (a + 6) = sin a cos 6 + cos a sinB = —7=- • •	4-	=s
'	'	К 5 Кю	Кб	Кю
3	2	5	1
=7F5 + sFT-571"VT' с-’«',оа|“ы"'. «+₽-«’
443.	Число нулей в произведении равно числу множителей 5,
а оно равно 20+4 = 24. Значит, число, полученное в произведении,
оканчивается 24 нулями.
444.	При умножении делителя на последнюю цифру частного
получилось четырехзначное число, а при умножении на 8—первую
цифру частного—получилось трехзначное число. Значит, последняя
цифра частного 9, а три средние—нули. Первая цифра делителя 1,
иначе при умножении на 8 получилось бы четырехзначное число.
Вторая цифра 2 и последняя 1. Отсюда находим делимое:
9681089 1 121
9б8	80009’
1089
1089
445.	При а = 0 решением будет х = # = с, где c£R. Пусть а=£0.
Тогда разделим первое уравнение на второе, предварительно пре-
образовав их к виду:
I х(у~х)~ау
1 у (у—х) = 9ах.
Т-Т	х ! у	X 1	у	1	о
Получим —•-г-, откуда или ~ =. т. е. у==3х или
У У X	у о	X	О
у —— Зх. Тогда х-2х==а«3х, откуда x«=l,5a, i/«=4,5a; х-(—4х) =
о	3	о 1
=—Зах, откуда х = уа, следовательно, у =—2у а.
446» Преобразуем левую часть уравнения:
3 cos Ьх—4 cos 5х cos х . . 7
3 sin 5х — 4 sin 5х cos х 8
Поскольку 3—4 cosx7^= 0, то, сократив дробь на 3—4 cosx, получим:
cos5x sin 17х cos 22х Л	Л
-r-g..«а---7=-, -т—=---rx- = 0, cos22x==0;
sin 5х cos 17х * sin5xcosl7x ’	*
22х = у4-ЛИ, ^ = 44+ -22 ’
Легко видеть, что найденное множество значений х входит в область
определения данного уравнения и, следовательно, является решением
данного уравнения.
447.	Обозначим радиус описанной около треугольника окружно-
сти через /?, ^/Z?0M = 2a, ^/ЛЮСя=2р, £АОМ~2у (рис. 198),
188
Рис. 199
а расстояния от М до А, В, С соответственно х, у, z. Выразим
х, у, z через R и a: z/ = 2/?sina, 2р=120°—2а, р = 60°—а, z =
= 2R sin (60°—а); у + г = 2R (sin а + sin (60° — а)) = 4R sin 30° х
X cos (а—30°) = 2R cos (а—30°).
2т=120°+2а; у = 60° + а; x^2R sin (60° + а) = 2R cos (30°—а) =
= 27? cos (а—30°), т. е. у + г — х.
448.	Л DMC со Л АМВ (рис. 199). Следовательно, =	=
=	= /\SDC со Л SAB и Л SDK со Л SAL. Следовательно,
=	=	=	. Из этих пропорций и перпендикулярности SL
zlZ-/	rXtj Ld
к DC и к АВ следует, что Д КОС со Д BOL, а тогда /_КОС =
= j/_LOD, а значит, /_СОЕ = £ВОЕ. Аналогично доказывается,
что / DOF = / AOF.
449.	Построим вневписанный треугольник А1В1С1 (рис. 200).
Получим три треугольника А1ВС, В^АС, СгАВ и соответственно три
четырехугольника OBAtC, OCBtA, ОАСгВ. Около каждого из этих
четырехугольников можно описать окружность, так как в каждом
из них имеется по два противоположных прямых угла. Эти окруж-
ности будут одновременно описанными около указанных треуголь-
ников и проходить через точку О. Но треугольники равны между
собой, так как каждый из них равен данному треугольнику. Сле-
довательно, и окружности, описанные около этих треугольников,
будут равны окружности, описанной около данного треугольника.
450.	Обозначим AAu = d, AA1 = dt, BB1 — d2, AO — OB — 2R
(рис. 201). Тогда d = 2R sin (а 4-Р), d1 = 27?sina, da = 27?sinp. Рас-
смотрим разность d2—(dj 4- d%) = 4R2 (sin3 (a 4- P)—(sin2 a 4- sin3 P)) =
= 4/?2(sin3acos?P 4- 2sinacosPcosasinP 4- cos3asin3P—sin2a—sin2P) =
== 47?3 (2 sin a cos P cos a sinp—sin3 a sin2 P—sin2 a sin2 P) =
= 8/?2 sin a sin p (cos a cos P—sin a sin p) = 8R2 sin a sin p cos (a 4- P) > 0,
так как все множители положительны. Следовательно, d?>d,4-d2.
451.	х — АВ 4- вс 4- Ас — дВ +	+ дС (рис. 202). Умножим
числитель и знаменатель каждой дроби на высоту, проведенную на
n	ME-hi . KM-h2 , MR-ha
соответствующую сторону. Получим х= AB.h 4~ вс'.Н + ~AC-h '
Знаменатель каждой дроби равен 25д лве. В числителе каждой дроби
высоты представим в виде суммы двух отрезков: от вершины до
прямой, проведенной через точку Л4, и от этой прямой до парал-
лельной ей стороны треугольника. Получим ME-h^ME-h^A-
4-МВ-/ц = £лтв4-25д£МЛ 4-SM/?cz? Аналогично KM-h2 = SK3FM +
4* 25д дл! р 4- $дрмв< MR -h3 — Smrcl 4- 25д м fr 4- $кврм> тогда х =
_ АВС ।
23д АВС
452.	Продолжим высоты треугольника АВС до пересечения
с описанной окружностью в точках М, К, N (рис. 203). Соединим
С и К\ ^.CFE = £ВАС как углы с взаимно перпендикулярными
сторонами. /ВКС — /_ВАС, они измеряются половиной дуги ВС.
Следовательно, ^CFE = ^EKC, а значит, CF — CK, CEJ_FK.
Значит, FE = EK, т. е. точка К, симметричная с точкой пересече-
Рис. 202
190
ния высот треугольника, лежит
на окружности, описанной около
треугольника АВС,
А налоги чно доказываете я,
что точки М и N симметричны
точке F относительно сторон ВС
и АВ.
453.	Пусть высота h = CD,
биссектриса Ь = СЕ, медиана
m = CF (рис. 204). Тогда
AD = h tg a, DF = Л tg 2а, FB =
=DB — DF = A tg 3<х— h tg2a,
но AF — FB, иначе AD +
+DF=^DB—DF или /itga +
4-/i tg 2a = h tg 3a—h tg 2a, h=^=6.
Отсюда получаем: tga + tg2a=
a =—-----
cos 3a cos a
sin 2a	2 sin 2a
ИЛИ ——x— ~
cos 2a
= tg 3a— tg 2a, 2 tg 2a = tg 3a— tg
-—5------. Откуда 2 cos 3a cos a — cos 2a = 0; cos 4a + cos 2a —
COS oCt cos ot
— cos2a = 0, cos4a = 0, 4a = ry, t. e. £ACB=^.
454.	В каждой строке сумма членов, равноотстоящих от концов
строки, делится на 1987. В предпоследней строке будет два числа.
Их сумма делится на 1987, т. е. полученное в последней строке
число делится на 1987.
455.	Надо вынуть один шар из ящика с двойной надписью «бч»
или «чб». Если он окажется белым, то в ящике оба белых шара.
Тогда в ящике с надписью «чч» окажутся разного цвета шары,
а в третьем ящике будут черные шары. Если первый вынутый шар
окажется черным, то в ящике с надписью «бб» окажутся шары раз-
ного цвета, а в третьем ящике будет 2 белых шара.
456.	Обозначим боковую сторону трапеции через а, верхнее осно-
вание—/?, угол боковой стороны с основанием—х (рис. 205). Тогда
У = R cosx, a = 2/?cosx, = 7? cos (л— 2x), b = — 2/?cos2x, P(x) =
= 2R 4- 2a + b = 2/?+4/?cosx—2/?cos2x; P' (x) = — 4/?sinx+4/?sin2x;
P' (x) = 0, sin 2x—sin x = 0, sin x (2 cos x— 1) = 0, t откуда sinx = 0,
х = пп (невозможно) или 2cosx—1=0, cosx = 4-, x = ~. Тогда
4	0
А	О
Рис. 205
P(x) = 2/? + 4/?.l-2/?. (_|) = 5/?.
457.	Обозначим сторону шестиугольника
через b, а радиус окружности — через/? (рис.
206). Тогда площадь шестиугольника будет
Д равна 5 = 6-	4 = 7? tg 30° = -£=;
г	4’2	° 1Л 3
191
& = а = /?/2, /?=«;& =
У о	У
_ 2а ^а/~2. g„6 а2-2/3
К2-КЗ ” V 3 ’	3-4 ~
= а2|/3.
458.	DC±AB и \/ACD = ^DCE
(рис. 207). Значит, AD — DE, АЕ — ЕВ.
Следовательно, DB — 3-DE. В треуголь-
DE
нике CDE tg а =	, в треугольнике
CDB tg2a = ^^. Отсюда tg2a = 3tga.
Найдем а: 2	- = 3 tg a, tga#=0,
Т-1Т- = 3; 2 = 3-3 tg2a; 3 tg2a= 1;
i	V”3
tg2 a = -=, откуда tg a = -Ц—, следова-
тельно, a = y, а ^/ACB —За —
459.	Вся фигура разбивается на 4 вида различных по площади
треугольников. Причем ABCD покрывается двойным слоем таких
треугольников (рис. 208). 2S^gc.D = S1 + S2H-S3 + S4, SJiBtCi£>i =
•= 3SX + 3S2 -]- 3S8 + 3S4 — ^abcd = 3 (“-*1	^2 4* *->s 4" ^*) ^abcd ~
^^ABCD $ABCD~ 5SABCD-
460.	Так как диагонали четырехугольника ABCD взаимно пер-
пендикулярны (рис. 209), тоSABCD = у • АС-BD. Но АС — BD. Значит,
192
Sabcd — ~2"	В треугольнике AOE
OA=R, OE=d, AE = ^R^d^-,
AC = 2AE, ЛС = 2//??—da, d = -^-,
К2
Sabcd-2 (R*-d*) =2 [R2-^\
461.	Анализ, Предположим, что за-
дача решена. Тогда ВЛб и СЛб равны
между собой. Как бы мы ни перемеща-
ли вершину треугольника, его основа-
ние будет оставаться параллельным ВС,
Построение. От точки Лб отложим
ВхЛб, проведем хорду ВГСА (рис. 210).
Через точку Ah проведем прямую, пер-
пендикулярную В^С^ Точка Л — Пересе
вершина искомого треугольника. Соединим ее с Ат и из О опус-
тим перпендикуляр на В^С^ Точку его пересечения с ААт обозна-
чим Е. Это —пересечение медианы с основанием искомого треуголь-
ника. Через нее проведем хорду ВС || ВгСг и соединим точки В и
С с точкой Л. Треугольник АВС — искомый.
462.	Повернем секущую CD на угол а. Точка С переместится
В
В
Лб
Рис. 210
окружностью, Л —
с
по окружности на угол 2а, точка D также переместится по второй
окружности на угол 2а. Значит, углы Е и F равны (рис. 211),
Рис. 211
193
7 № 3671
Рис. 212
а поэтому и углы К и L равны, так как
в сумме соответственно с углами Е и F
они составляют 180°—р.
463.	Проведем секущую плоскость
через середины ребер /4S и АС—точки
L и Е, а также через середину F ребра
ВС. Она пересечет грань SBC по прямой
KF, где точка К—середина ребра SB. По-
лучившееся сечение—параллелограмм (рис.
212), так как его стороны попарно па-
раллельны ребрам SC и АВ. Все стороны
этого параллелограмма равны между собой
и каждая равна половине ребра тетраэдра,
а так как скрещивающиеся ребра АВ и SC тетраэдра взаимно пер-
пендикулярны, то сечение есть квадрат. Его площадь равна 0,25а2.
464. Покажите, что число горизонтальных и вертикальных звеньев
одинаково, причем число тех и других четно. Действительно, вслед-
ствие попарной параллельности улиц если автомобиль проехал квар-
тал влево, то он должен проехать и квартал вправо (учитывая
перпендикулярность параллельных улиц двух направлений), чтобы
вернуться на параллельную улицу, проходящую через тот же пере-
кресток. Аналогично вверх и вниз. Отсюда получим, что общее число
кварталов кратно четырем.
465.	р2— 1 = (р— 1) (р + 1) — произведение двух последовательных
четных чисел. Значит, одно из них кратно 2, а другое—четырем.
Если рассмотреть произведение (р—1) р(р+ 1), то один из этих трех
последовательных натуральных множителей делится на три; р—про-
стое число, большее трех, оно не может делиться на три. Значит,
на три делится либо р—1, либо р+1. Отсюда произведение
(р—1)(р+ 1) делится на 2-4-3 = 24.
466.	х2 — 4x^0, отсюда x<JO или х^4. Решение рассмотрим
при х^4, так как при х^О неравенство справедливо для всех
значений х этого промежутка. Имеем х2 — 4х>х2 — 6х + 9, откуда
х>4,5. Таким образом, х<10 или х > 4,5.
467.	0 < х < 3 или 3 < х < 6.
468.	y = j/x2—Зх+11, у^О, у2 + 2у—15 = 0, у = 3. Корни
исходного уравнения х=1 или х = 2.
469.	Длина участка х м, а ширина—у м. Тогда имеем:
|о75 + й = 350
1б^ + оТ5 = 400’
откуда х=150м, у = 75м.
470.	Пусть скорость первого пешехода х ступенек в минуту.
Тогда скорость второго пешехода 2х ступенек в минуту. Первый
пешеход спускался — мин, а второй —д- = — мин< Скорость эс-
X	X
194
калатора у ступенек в минуту.
За время движения первого пеше-
40
хода эскалатор опустится на у- —
ступенек и длина его будет рав-
на 40 + -^ ступенек, а за время
движения второго пешехода он
зо
опустится на у~ ступенек и дли-
на его будет равна 60 + ступе-
нек. Отсюда получаем уравнение
40 12^ == 60 +	, откуда у = 2х.
Значит, пешеходам пришлось бы
пройти по 120 ступенек.
471.	Найдем стороны треуголь-
ника: ДВ = К1бТ4-2/5, АС =
= ¥9+ 16 = 5, BC = V(4—3)2 + (2 — 4)2 = К1 + 4 = /5.
ДВ2 + ВС2 = 20 + 5 = 25, т. е. ЛВ2 + ВС2 = ЛС2.
прямоугольный. Его площадь равна
Откуда
Значит, Д АВС —
5 = 1.ДВ.ВС = 1.2/5./5 = 5.
472.	Поскольку у призмы имеется плоскость симметрии, прохо-
дящая через ВВХ, то ВС —В А. По условию AB^d, ^^451В = а.
Из условия следует, что О — центр окружности, описанной около
/\АВС, ОеВЕ, BE А. AC, СЕ = АЕ, BJ)-.DB=\-.2 (рис. 213).
>lB = dsina, BBt = dcosa. Значит, ВО =-|-d cos а. Проводим
OF А_ АВ. Тогда ОВ — ОА как радиусы описанной около треуголь-
ника АВС окружности. BF = ^- ЛВ = у dsina; в треугольнике BOF
/л BF	d sin ос	л»-) ту л гг л п 1	d sin ос . В
ОВ  ----тг =------; в треугольнике ОВК ОК = ОВ tg =-------3-• tg ;
cos 2 cos£	2 cos -B-
KL — 2 • OK =	• tg -у ; в треугольнике BDO DO = КBD2. + OB2. =
p z
cos 5-
/4	9	. d2 sin2 a c	1 „т	1 dsinoc . В
yd2cos2a +-------g-; S^dkl = ^-KL-DO =y------------X
4 cos2	cos ~
o
— d2 sin2 a sin -E-	------------—p-----
X *1/ d2 cos2a + d =-----------------g---у 16 ctg2 a cos2 ~ + 9.
F	4cos2— 12 cos3-~
7*
195
473.
х2 4-2хг/4-/ 4-х 4- г/ = 2	((х+г/)2+(х-Ь #) = 2
х + ху 4- у = — 5	t (х + у) + ху = —5.
Выполним замену переменных и = х + у, v = xy. Получим:
ы24-и—2 = 0
_ J	Ги= — 2
т. е.
( х + у= —
\ху = —3
2
или
х+ у — 1
хг/ = — 6.
(1>-1
Е = — 6,
Эти системы можно решить или способом подстановки, или
используя свойство корней квадратного уравнения, путем составле-
ния и решения нового квадратного уравнения. В результате полу-
чим х=—3, у=1, или х=1, у ——3, или х =—2, у = 3, или
х = 3, у — —2.
474.
( 2 (х + у) = 5ху ( 2 (х + у) = Зху
8 (х3 + у3) = 65ху 18 (х + у) ((х 4- z/)2 — Зху) = 65хг/.
Одно решение системы х = у — 0. Найдем другие решения. Пусть
х=/=0, тогда и у Выполним замену переменных х + у = и,
„	( 2« = 5и
xy = v. Тогда 1 о . , „ . сс . n . _	13
^8м(м2—Зи) = 65к;	о=И=0, откуда v =—или
1	13
v = 1,	—уф или
Г7	13
Если и = —
( 	13
*+У= —io
13
ху~ 25
5
«--j •
13
v =—то из системы
— 13—/377	-134-/377
находим х =-----, у=---------------
-134-/377	—13—/377
или х =----------, у =------------.
Если zz = -|-, v—1, то из системы f х+ У = у находим х =
[ху = 1
у = 2 или х = 2, У = у-
47е»	хУ'2х__6«8	2__ л qv xy*yz__6*12	2__Q. оч yz-zx__12-8
4/О- yz ~ 12 ’ Х	zx	S 'У	ху ~ 6	’
z2—16. Все переменные должны быть одного знака. Следовательно,
система имеет два решения: х = 2, у = 3, z = 4 или х=—2, у — —3,
__4.
476.	Сложив два и вычтя третье уравнение, заменим данную
196
систему ей равносильной: f ху—\
j yz = 7
I zx = 13. Ее решением будет
z/ = -]/Z = -K9l или х= ]/у, у —
г = К91.
477.	х = 5, у —2.
478.	Выполним замену переменных х* 2—у2 —и, xy = v. Тогда
( ы24-и2=13 I и=1— 2v
I ы + 2и=1 I 1 — 4и + 4и2 + и2= 13,
6	17	0	2
откуда v = —г , и = -г- или и 2, и = —3.
D	О
Г7	6	17
Если v = —f, = то из системы
5	5 ’
2	2	17
У2 = у
6
ху =— у находим у=
=	^/10(/433+17) „л, у-
х=-1/Ю(Г433+ 17).
Если v = 2, и ——3, то из системы I х2— у2=-—3
I xz/ = 2 находим у =
= —2, х——1 или у = 2, х=1.
480. Пронумеруем стопки. Из первой положим на весы одну
монету, из второй—две монеты и т. д. Всего 55 монет. Вычислим,
на сколько полграммов масса 55 монет меньше 275 граммов.
В стопке с таким номером и будут фальшивые монеты.
481. у = 2х\ у = а, 2х2 = а, х = ± j/~.
S= С (a-— 2x2)dx = ( ах—— х3
20 V*” 3 si г\(\	3 з /1 rxs\
—L— 6Z2 = 100—o’, а = -5-« i/lOO.
Z	о	Z
482. у = х2, ха = 2, уй = 4, у'= 2х, k = 4, у—4 = 4(х — 2),
у = 4х—4 при у —0, х—1.
2	2	2	2
S = Jx2dx—J (4х— 4)dx = -^x? — (2х2 — 4х) =’!’•
0	1	0	1
197
483.	В данном уравнении можно выполнить преобразование, ко-
торое приведет его к виду с одной новой переменной. Для этого
разделим все его члены А на х2(х2—х + 1). Получим уравнение
--------—Ю +Г2------тгп2 = 0. Оно равносильно данному, так как
х2(х2—х + 1) #= о.
„	/х2-х+1\2
Введем новую переменную	—х/ ’ 1°гДа получим £/ —
g
— 10 + —= 0. Откуда у —9 или у=1. Возвращаясь к переменной
х, получим 4 значения х: х——1, х=1, х = 2—V 3, х = 2 + |/"3.
484.	Если все члены уравнения содержат искомую переменную
или общее выражение с переменной в качестве множителя, то эти
члены надо перенести в одну сторону уравнения и вынести общий
множитель за скобки. Затем приравнять полученные множители к
нулю и решить записанные уравнения. В рассматриваемом случае
решение запишется так:
l/x({/(x+ 5)2 + 6 -р/х2—5 ^/х(х + 5)) = 0, откуда {/х==09 т. е.
х=0, или р/(х+5)2 +6 ^/х2—5 р/х(х+ 5) = 0. Так как х = 0 не
удовлетворяет этому уравнению, разделим все его члены на р/х2?
Получим уравнение, ему равносильное:
^i^4-6==0. Введем новую переменную у =
= |/^~~х“* Тогда уравнение примет вид у2 — 5г/ + 6 = 0, откуда
z/ = 3 или у = 2. Окончательно получим х = 0, или х==-^ , или х = -|-.
485.	Разделив все члены уравнения на х2=/=0, получим уравне-
1 з
ние, равносильное данному: Зх2 + 13x4-20+ 13-—= откуда
3 ( х + — ] +13(х+у 1+14 = 0. Введем новую переменную у =
= х + у. Тогда уравнение примет вид Зу2+13у+14 = 0, откуда
у
z/ =——- или z/ =—2. Окончательно получаем х= — 1, или х =
—1— /Тз	—7 + КТз
о	о
486. Перенесем все члены уравнения влево и разделим на
у/(х—I)2. Получим уравнение, равносильное данному:j/"(7737)*+
+ 3—4|/"ji-p = 0. Введем новую переменную =	Тогда
уравнение примет вид у2—4z/+ 3 = 0, откуда у = 3 или у=1.
Окончательно получаем х = ?
198
487.	Уравнение запишем в виде (х3— Г)2 + (х?—1)2 = 0, которое
равносильно системе: J х3—1=0
I —1=0, откуда х = 1.
488.	Введем новую переменную у = V а + х. Данное уравнение
при х^О, z/^О равносильно системе
J /а—у = х	(а — у — х3-
\]fa + x — y, т. е. \а + х = у3.
Вычтем из второго уравнения почленно первое. Получим х + у =
= (у—х)(у + х), откуда х=—у или у—х=1, но х=—у только
при х=у=а=0 (поскольку х^О, у^О). Если у—х=1, то
/о"+х = х+1, откуда х2 + х+1—а = 0, следовательно, х =
— 1 + К4а —3	— 1 — /4а —3 , Л	п
=----L------- или х —-----------<0. Но х^О, поэтому послед-
нии корень отпадает и окончательно получаем х = --%---- при
а^ 1.
489.	Выполните замену переменных а = х + у, v = xy. Тогда
(х-\-у = —13	[ х + у = 40
1	(А	ИЛИ 4	1Q
(ху = 40	(ху ——13.
Решения данной системы: (8; 5), (5; 8), (—20—J/^413; —20 + /413),
(— 20 + /ЙЗ; — 20—/443).
490.	Впишите окружность в треугольник с вершинами в данных
точках. Точки ее касания со сторонами данного треугольника будут
точками касания искомых окружностей.
491.	n12—n8—n4 + 1 = п8(п4— 1)—(я4— 1) = (я4 — 1)(п8—1) =
= (n2 + l)(n4 + 1)(я+1)(я—1)(п2+ 1)(« + 1)(п—1). Все множители
четны. Так как п— 1 и п +1 —последовательные четные числа, то одно
из них делится на 4. Значит, все произведение делится на 2М? = 512.
492.	(За—2Ь)  (Ь 4- Зе) = За • b + 9а • с—2Ь • b—Qb-c =
= 0 + 9-3-8 cos 60°—2-5-5—6-5-8-cos 60° = 108—50—120= —62.
493.	Вычислим длины сторон данного треугольника:
АВ = /(2 —1)2 + (4 —1)2 + (2 — I)2 = /1+9 + 1 = /ТГ,
АС = /(8 —1)2 + (3—1)2 + (3—1)^ = /49 + 4 + 4 = /57,
ВС = /(8—2)2 + (3—4)2 + (3—2)2 = /36+1+Т = /38.
(/57)2 > (/38)2 + (/ТТ)2, т. е. АС3> ВС3 + АВ2.
Следовательно, треугольник тупоугольный.
494.	Свободный член уравнения имеет делители ±1, ±2, ±3
и др. Проверка показывает, что х = + 1 не удовлетворяет уравнению,
х =—1 удовлетворяет уравнению. Разделив левую часть уравнения
199
на *4-1, получим х44-2*3—19*2 — 8х + 60. Значит, левую
часть уравнения можно представить в виде произведения
(х 4- I) (х4 + 2х3—19х2—8х4-60) = 0. Приравняв нулю первый мно-
житель, получим уже найденный корень. Приравняв нулю второй
множитель, получим уравнение, из которого найдем остальные корни
данного уравнения. Проверяем х = 2. Получаем 0 = 0. Разделив ле-
вую часть уравнения на х—2, получим х34~4х2—Их—30. При-
равниваем нулю частное: х34-4х2—Их—30 = 0. Проверяем х — — 2.
Получаем 0 = 0. Разделив левую часть уравнения на х4~2, получим
х2 4 2х—15.
Приравниваем нулю новое частное и решаем полученное квад-
ратное уравнение х24~2х—15 = 0. Откуда находим еще 2 корня:
х = — 5 и х = 3. Итак, уравнение имеет корни: —5; —2, 1; 2; 3.
495.	Ни одна переменная не может равняться нулю. Поэтому
все дроби можно заменить обратными. Получим систему, равносиль-
ную данной:
(1+1=£
У X 5
U+-L = l
z ' у 4
1 + 1 = 2
X 2	3 ’
1 59	10	~ 6
решив которую, находим х=1^, у = Юрр z = 6jg.
496.	Выполним замену переменных: z = x(z/ + l), / = г/(х+1).
Тогда система примет вид:
(z2 + z —12 = 0
4 + /—20 = 0.
Решая эту систему, получим г — — 4 или г = 3, t — — 5 или 1 = 4.
В результате получим четыре системы уравнений с переменными
х и у:
1)1х(г/+1) = 3	2) |х(у+1) = -4
\i/U+l) = 4,	\z/(x4-l) = —5,
3)	(х(у+1) = 3	4) Jx(z/+l) = -4
4(*+1) = —5,	(г/(х+1) = 4.
Решив системы по правилу сложения, получим:
(1; 2), (-3; — 2), (- 9-/Я \ (7 + ^' ;	Y
/—9—Кбб . 7 — Кб5 \ (— 9+К65 . 7-|->/'б5>
\	2	’	2	/’ \	2	’	2	/
497.	Преобразуйте систему к виду:
J(x2 + z/2)2—2x2z/2= 17
U^+t/2) + 2xz/ = 9.
200
Выполните замену переменных: « = +	v — xy, где «^>0.
Решения системы (1; 2), (2; 1).
498.	В этой системе х=#0 и г/=#0, х и у имеют одинаковые
знаки.
В данном виде в системе ни подстановка, ни замена переменных
невозможны. Во втором уравнении в левой части вынесем за скобки
У х2у2 = Уху. Система примет вид:
{ /f + /f-V= + 2
Сделаем замену переменных t = j/*, t > 0; v = Уху, v > 0f
получим:
г fz+4-У=~+4
' v(/-bl) = 3/2 IV (* + y) = 3/2.
r>	, , 1	3/2
Решив последнюю систему с помощью подстановки ‘ + — = —-—«
т/~"2'	у—
находим t = - 2. или t = y 2, v = 2. Далее имеем:
или
Решения исходной системы: (1; 4), (—1; —4);	2/2J,
(--^;-2/2),(4;1),(-4;-1),(2/2; Х^-), (-2/2;
499.	Систему преобразуйте к виду:
< х+#__ 1
ху ~~ з * Решение системы (6; 6).
500.	Предположим обратное. Тогда имеем abcd~2dabc, т. е.
1000а + 100й + 10с + d = 2000d + 200а + 206 + 2с. Отсюда 800а + 80&+
4-8c=1999d, или, иначе, 8(100а+10й + с)= 1999d. Значит, d де-
лится на 8, т. е. d = 8. Тогда 100а+10Z? + c= 1999, что невозможно.
Значит, наше предположение о существовании указанного в условии
четырехзначного числа неверно. Такое число не существует. Анало-
гично решается вопрос о трех- и двузначных числах.
501.	Проведем плоскости, перпендикулярные первому диаметру.
Они разделят поверхность шара на 4 части. Затем проведем плоскость
201
©большого круга, перпендикулярную второму
диаметру. Она разделит каждую часть по-
верхности пополам. Получим 8 частей. Затем
проведем две другие плоскости, перпендику-
лярные этому диаметру. Число частей еще
удвоится. Получим 16 частей. Это ясно из
рисунка 214, на котором изображено сечение
шара плоскостью большого круга, перпен-
дикулярного третьему диаметру. Эта плос-
кость разделит каждую часть сферы попо-
п П1Л	лам. Получим 32 части. Две оставшиеся
Рис. 214	J
плоскости позволят еще удвоить число час-
тей сферы. Всего получится 64 части.
Примечание. Желающие могут попробовать свои силы в ре-
шении аналогичной задачи с большим числом плоскостей, указанных
в задаче. При решении этих задач важным будет вопрос о пересе-
чении крайних плоскостей. Они не все пересекаются.
502.	cos х 0, т. е. х^^ + яп, где и = 0; ±1; ± 2; ... .
Тогда
cosх —	*  • 2cos2x<=> cosх = 2sinх• cosх,
COS x	’
1	ЭТ
откуда 2sinx=l, t. e. sinx = y, следовательно, x =
m = 0; +1; ±2; ±3; ... .
503.	z/raax = z/(—2) = 25, z/min = у (1) = — 2.
504.	x5(x3—l) = y5z. Если x, y, z—простые числа, то x = у,
z — x3— 1 (z=/=x?, так как z—простое число). Из последнего уравне-
ния z = (x—1)(х? + х+1). Чтобы z был простым, необходимо, чтобы
х—1 = 1, т. е. х — 2. Тогда у = 2, z — 1. При х—1=—1 получаем
х = у — 0. Но 0 не относится к простым числам. Итак, х = у = 2, z — 1.
505.	Сложим все три уравнения почленно, раскрыв в последнем
скобки. Получим (х+у)2 = 49. Следовательно, х + у — 1 или
х + у — —7.
1) х+ у-1- Тогда второе уравнение будет иметь вид: ху + 7z=47.
Умножим обе части этого уравнения на 2 и прибавим к первому.
Получим:
(х + у)3 + 14г = 94 + г2.
Учитывая, что х + у = 1, находим г = 5 или г = 9. Тогда имеем
две системы:
{г = 5 f г = 9
х + у = 7 или < х + у = 7
ху=12	( ху ——16.
Решение первой системы (3; 4; 5), (4; 3; 5), второй системы
/7—^113. 7 + Г113. Q\ /7+1<113. 7—КПЗ .. Q\
\	2	’	2	’ У/’ \	2	’	2	’ У/'
202
2) х + у ——7. Тогда ху—7z = 47. Аналогично предыдущему
имеем (х+«/)* 2 * 4—14z = 94+z2, откуда z =—5 или z — —9. Откуда
z = —5	( г — —9
х + У — —7 или , х + у = —7
ху=12	ху=—16.
Решение первой системы (—3; —4; —5); (—4; —3; —5), решение
о (— 7+/"ПЗ —7—/НЗ	п\ /—7— V113 — 7+V113	Q\
второй (—f; -9), {-----------------§; -------2--; -9).
506.	Перенесем все члены влево, раскрыв при этом скобки.
Получим:
Зх2 + Зг/2 + Зг2—2ху—2уг—2хг—8у— 16z + 56 = 0.
Левую часть уравнения преобразуем к сумме трех квадратов
многочленов:
(х + у — г—2)2 + (х—г/ + z—4)2 + (—% + «/ + z—6)2 = 0.
Так как х, у, z—действительные числа, то равенство возможно
только при одновременном обращении в нуль каждого из трех сла-
гаемых, т. е. это уравнение будет равносильно системе трех урав-
нений:
' х + у—z—2 = 0
,	х—y+z—4 = 0
—x+y + z— 6 = 0, откуда х = 3, у = 4, z = 5.
507.	Вычтем первое уравнение из каждого из остальных. Полу-
чим систему уравнений, равносильную данной:
( х + yzt = 10
I (х—z)(l— yt) — O
j (x—y)(l—z/) = 0
I (x—0(1— yz) = 0.
Эта система равносильна 8 системам, в каждую из которых вхо-
дит по одному множителю из уравнений этой системы. Но вследствие
симметрии переменных решения многих из них могут быть записаны
по аналогии с другими. Итак, рассмотрим новые системы уравнений
и их решения:
1)
<
х + yzt — 10
х—z = 0
х—у —9
х—t =0,
4) [ x + yzt= 10
I 1 —z// = 0
। x—г/ = 0
x—(=0,
2) Г x + yzt = 10
I x—z = 0
I	x—y = 0
I 1—#z = 0,
5) C x + yzt= 10
I 1— yt = O
।	x—y — 0
( 1 —z/z = 0,
203
3) 7	x + yzt = 10
J	x—z = 0
J	1—z/ = 0
(	x—/ = 0,
6)	( x +yzt —iO
| 1—yt — O
| 1— zt = O
( 1—z/z = O,
7)	( x + yzt = 10	8) | x + yzt = 10
j x—z = 0	I 1—yt = O
] 1— zt^O	| 1—z/ = 0
| 1— yz = O,	x—t = 0.
Из первой системы x = y = z = t, и тогда имеем х + х* —10,
(х3 — 8) + (х—2) = 0, (х—2)(х2 + 2х + 5) = 0, откуда х~2 = 0, т. е.
х = 2, и тогда х = у — z = t — 2. Второй множитель не может рав-
няться нулю, так как его дискриминант отрицателен.
Из второй системы x = y = z. Тогда имеем из первого уравнения
х+х2/—10, а из четвертого уравнения 1—х^ = 0. Отсюда х=1 или
х = —1, t = 0 или t = 11. Итак, в этом случае система имеет два
решения: х = ^/= г = 1, / = 9 или x = y = z = — 1, /=11.
Решение системы 3) аналогично системе 2): x = z — t=l, у — 0
или X—Z~t=— 1, у = 11.
Решение системы 4) аналогично системе 2): х = £/ = / = 1, z = 0
или х = у — t ~ — 1, z= 11.
Из пятой системы имеем yt = yz, у=^0, t=-z\ у = х, тогда
х + х/2=10 и 1—xt — 0. Из уравнения х2+1 = 10х находим
x = z/=5±2l/'6, Z = z = 5±2/6.
Из шестой системы yt=^zt = yz. Откуда следует, что у = z = t — ± 1.
Если y = z = t = +\, то х = 9, если y-=z = t = — 1, то х=Н.
Остальные случаи рассматриваются аналогично.
Из седьмой системы получим x = z, у = t, х + х/2 = 0 и 1—х/ = 0.
Далее х2—10х+1=0, х=5±К25— 1 ^5 ± 2 Кб и х-гу = 10. От-
сюда получаем x = z = 5 + 2Кб, y = t = 5 — 2 Кб или x = z = 5—
—2Кб, y = t = 5 + 2l/6.
Из восьмой системы получаем y — z, x-=-t, х + у2х =10, х2 + у2х2 =
= 10х, 1—ух = 0. Поэтому х2 — 10х+ 1 =0; х — 5 ±2 Кб.
Из первого уравнения x+z=-10, г=10—х.
Если х = / = 5 + 2 У 6, то y = z = 5—2 К6, если х = t = 3—2 К6,
то z/ = / — 5 + 2J/6.
508.	Если умножить третье уравнение на 2 и сложить все урав-
нения почленно, то получим уравнение (х + у + z)2 + (х н- у + z) — 42
= 0, Отсюда найдем, что (1) x-\-y + z = —7 или х + уz = 6 (2). Из
второго уравнения данной системы и уравнений (1) и (2) найдем г,
а затем из этих уравнений и третьего уравнения данной системы
найдем х и у. Получим х^2, у=1, z = 3 или х= 1, у = 2, г —3.
Остальные решения иррациональны.
509.	Обозначим искомое расстояние х м. Тогда расстояние, прой-
денное лисицей, будет (х—30) м. Примем за единицу время двух
скачков собаки и, значит, трех скачков лисицы. Тогда за единицу
времени собака пройдет 4 м, а лисица — 3 м. Значит, время погони
„	х	х — 30	гл
собаки равно , а время бега лисицы равно ——. Они равны
между собой:	= *~30, откуда х=120.
204
510.	ft4 4- 4 = п* 4- 4/i2 + 4 —W = (ft2 4- 2)2—4ft2 = (n2 4- 2—2n)x
x (ft2 4-2 +2«). Оба множителя — натуральные числа, не равные еди-
нице. Значит, ft4+ 4 — число составное.
511.	у = —4х—12, у = 4х—4.
512.	ymax = z/(—2) = 91-, //min = у (0).= 0.
513.	Преобразуем левую и правую части уравнения
Y(X—1) —2/Г=7Г+ 1 = 1 + ]/ (х— 1)— 4|/х=Т+4,
далее
/ (К^=Т-1)2 = 1+]/ (УУ^Т-2)2,
откуда
I1 1 = 1 +| >/7=4-2 |.
Рассмотрим три промежутка:
1)	Кх—1^2, Кх—1 — 1 = 14->/х—1—2, т. е. х2>5;
2)	<2, /7-Г-1 = 1+2-Г^Т, х = 5, 0;
3)	Кх^=Т < 1, 1— Кх7ГГ=1 4-2 — УУ-i, 0.
514.	Преобразуем левую часть уравнения (х^4):
у (х —4)—4/х^4 + 4 4- )Ах—4) —6/х=^4 4-9 = 1,
далее / ух_4_2)2 + / (Гх-4— 3)2== 1,
откуда |Их—4—214-1Ух—4—3| = 1.
Решая аналогично упр. 513, находим 8^х^13.
515.	1 <7=72; а 4- 2 У а—1 4-	а—2 У а—1 =:
= ]/(а— 1) 4- 2 Уа^-1 4- 1 + V(а— 1)—2 /о=+4- 1 =
= ]/ (К^-Г+ ОЧУ4 (К^=Т-1)2=| /7=Т+1|4-|К^Т-1|=
— У а —14- 1 + 1— У а—1=2.
516.	32х—2 + 3~2Х = 49; (3х—3~х)2 = 49; 3х —3~х = 7 или 3х —
— 3~х = —7.	_____
517.	Введем новую переменную z/= (у^ + Кз) , где у>0.
Уравнение примет вид: # + у = 4, откуда у = 2 + К3 или у = 2 —1^3.
Далее получим х = 2 или х = —2.
518.	Перепишем уравнение в виде:
2 + (2-/2+Кз)2х-3 (2]/2 + /з)х = 0,
поскольку тЛ2—V 3 = - у_L=r .
Г	|/2+Кз
205
Введем новую переменную: у= (2]/^2 + Кз) , тогда у2.—3«/ + 2 = 0,
откуда у = 1 или у — 2.
Далее находим х — —-—М2	•, х = 0.
Jg(2 V 2 + К3)
519.	Из условия следует, что xi>0. Далее
V х2—р = х—2J/х2— 1, х2—р = х-—4хК*2— 1 + 4х2—4;
4хКх2— 1 = 4х2—4 + р;
16х2(х2— 1)— 16х4 + 16+ р2—32х2 + 8х2р—8р,
„	16+р2-8р	(4—р)2
о^уда =	=
где р < 2. Следовательно, х =	К2 (2—р).
520.	х = — 1.
521.	8 мужчин, 4 женщины, 8 школьников.
522.	5-7-8-Э+ 1 =2521.
523.	х>а, х>1,	21g(x—а) — 1g 4 = 1g (х—1), 1g (х—а)2 =
= lg4 (х— 1), (х—а)2 = 4(х— 1), х2—2ах + а2—4х + 4 = 0, х2—(2а +
+ 4) х +а^ +4 = 0, откуда х = (J/а ± 1)2 + 1 > а^0. Легко видеть,
что при любом а += 0 выполняется неравенство х > 1.
Проверим выполнение первого ограничения на параметр а и тем
самым уточним возможные значения параметра а:
если (К«+ 1)2 + 1 > а, то а~^ 0, а С /?;
если (Ка— 1)2 + 1 > а, то Vа < I, а < 1.
Итак, при Ог+а+31 х = (рГй+ 1)2+ 1 и х=(Ка—1)2+ 1; при
й>1 х=(|/га+1)2+1.
524.	Решив неравенство
няется при —1,5<х<0,5
< х < 0,5 и х > 1.
525.	Из первого уравнения имеем 12*=123, т. е. х = 3, значит,
1og43 = 4~log4y + log«3’ т-е- 1о§4У = 4’ у = 2-
log&('°g&a)
526.	а х°8ьа =а
527.	а) 108 = 22-33; 72 = 23-32. Запишем систему-
Z _	1
° ~ logjV(22-З3)
’ h- 1
log^23.32)’
I _	_3
ГТ_Г2---5 > 0, находим, что оно выпол-
и х > 1, а так как х > —0,5, то —0,5 <
10ga (1о+ а)
loga * logj,а = al°ga (l°g6 а) = log() a<
далее имеем:
: 2 logjv 2+ 3 logyv 3 f а ~ 2 log'V 2 + 31°§Л' 3
1 1
3106^2+2108^3	T=31og7V2+ 21ogA, 3,
206
откуда
SlogjyS-- g-,	]o&jV	,	logsW— 36_2a ,	2a =£36;
51ogw2 = 4—”. tAv	=-3a~2Z>	,	log^ = -o 5ao<,	26#= 3a;
syv b a * log2 N ab ’	6,2	3a— 2b ’	'
6) logx»»» A = —1 „	;	n—!—г	= n log» x + m log» x =-; n . 4-
7	6 y log/ Xnym	’	lOg^B, A	&A > &A	logj, A
, m
+ logj, A •
113
528.	x>y, х=/=у, x=/=-g. Указание. Введите новую пере-
менную у — log2 (Зх—1).
В ответе получите х — 1, х =	.
529.	log, 7х-1—log, (3 - 7х-1—1) = — log, (7х—5),
log, 7х-1 + log, (7х—5) = log, (3-7Х-1 —1),
7Х-Х-(7Х—5) = 3-7Х~*—1. Введем новую переменную у = 7х-1, у>0.
Тогда из уравнения у(7у—5) = 3у—1 находим у —у или у = 1,
откуда х = 0 или х = 2.
, Vx+1	о,	1
.....  г-...	.. .-	—2 logs .	-1
530.	х> 1; (З-2)	^2-i =/2.(х— 1) ; 3	Гх-‘=2/х—I;
3iogs (х-1 > j/"2 (х—1) , х—1 = К2(х—1) , откуда х = 3.
531.	Прологарифмируем обе части уравнения по основанию 5.
Получим:
log5 3 • 1 Og515 + (logs 9х + 1) logs X = О,
logs3 (logs з + 1) + (2 logs 3 + logs x + 1) logs X = o.
Введем новую переменную «/ = log5x, тогда logs3 + log53 + 2t/log53-l-
+ у* + у=о,
y2 + (2 logs 3 + l)y + log| 3 + logs 3 = 0,
откуда y= (21og53+l) ±Jт e t/ = —lOg515 или y== — log53.
1 1
Следовательно, x = те" или x = -y .
532.	(|log2(x + t/)| + |log2(x—1/)| = 3	(1)
lxy = 3.	(2)
Из равенства (2) следует, что х и у имеют одинаковые знаки,
а тогда из области определения log2 (х + у) следует, что х > 0 и у > 0,
а из области определения log2(x—у) следует, что х > у.
1)	Если log,(x—у) > 0, то
J logg (х2—У2) = 3 „ f х2 —у2 = 8
( ху = 3	I ху = 3
х = 3
У=1
207
2)	Если log2(x—у) < 0, a log2 (х 4 у) > О, то
(log2^-
, Ь2 х — у
I ху = 3
3	=
О j X — У
\ху = 3
/ 9у=7х р- 7 ^21
\ХУ^3	\y=±V"2A.
t о
3)	log2(х + у) не может быть меньше нуля, так как х4#>1.
533.	Пусть возраст человека в 1989 г. равен ab—lOa + b. Год
его рождения будет 19(8—а) (9—Ь). По условию имеем 10а-'-Ь =
— 1 +9 4-(8—о)4(9—Ь), 11а42& = 27. Так как 2Ь четно, а 27 не-
четно, то 11 -а нечетно, т. е. а нечетно и меньше 3. Значит, а = 1.
Тогда 2Ь=16, Ь = 8, т. е. 18 лет.
534.	210» = х, lgx= 100 lg2 = 100-0,3010 = 30,1. Число имеет 31
цифру.
535.	log2 (5* —4) + 3 logsx-4 2 < 2 log .у- jj/4 ,
Q
log2 (5* —	—t~ < 4.
to2 x ' * log2 (эх — 4)
Введем новую переменную у~ log2 (5х — 4), тогда из неравенства
0 + у<4 находим 0 < у < 1 или у > 3. Имеем:
1) 0< log2(5x — 4) < 1, 1 <5*-—4 <2, 5 <5* <6, Ig5<xlg5<
<lg6, 1 <x<-J||.
2) 3 < log2 (5х—4), 8<5Х—4, 5х > 12, х >	.
536.	5'0g;c~~ > 25, log/^ >2, где 4 < х < 6.
х—и	3
п	1	8— 12,-;	„	8— i2.v — л-846ха	„ (х-2)3
При х > 1 имеем ------т- > х\----------------> 0,	- < 0,
г	X — 6	X— 6	X — 6
откуда х—2 >0, х > 2, значит, 2 < х < 6.
о 2	.	8—12х а (х— 2)3 п	п
При у < х < 1 имеем — — 6 ~ < Л > х~'~б~ > откуда х—2 < 0,
т. е. х < 2.
2
Таким образом, -^-<х<1, 2<х<6.
о •
537.	9х"14 7 = (3х"14-1)2, 32х~2-J-7 = 32х~24 2-Зх-14 1, 2-Зх~1 =
= 6, 3х’1 = 3, х = 2.
538.	Преобразуем левую часть неравенства: (а4&4с)-^4 + 4" +
4—^ = 1 4 — 4 — 4 — 4 14 — 4 — л~ — 4 1 = 3 4 ( — 4 — -1- f — 4
с )	' Ь с а'^ с Ла' >>^	'\Ь ^а) ‘\с^
Q \	[ Ь С \
\ ~ + "у )	+ 2 + 2 4- 2 = 9, так как сумма в каждой скобке
больше или равна 2.
208
539.	Два раза примените сравнение среднего арифметического
и среднего геометрического двух положительных чисел.
540.	Из условия следует, что | а (1 и	причем так как
то а и b можно заменить на синус и косинус: а = sin а,
fc = cosa. Тогда а-гЬ — sin a 4-cos a = sin a + sin	=2-sinyX
xcos —a) =K2cos —a) . cos —a) 1- Значит, |aД-Z?| C
Рассуждая иначе, получаем: 1 — д2-|-&2	2 Иа2Ь2 = 2|ab|; 2^
^a2H-b2-i-2|ab|=(|a| + |Z>|)2; K2>|a| + |&|>|a + &|, что и тре-
бовалось доказать.
541.	Введем новые переменные: x = a24-b2, z/ = b2 + c2, z = a2-|-c2.
т,	,	>,	,	, x+z—у ,, х+у—г „
Выразим через них а2, Ь2, с2:а2 =—Ь2 =—, с2—
_У+г—х
~	2
Преобразуем неравенство:
x+z—у . x-j-y—г	y + z—x  1 f х_ z_ ] , х, _у 1 I £ I £ _
-1)=М(1 + ^) + (7 + ^) + (т + 7)-3)>4 (2 + 2 + 2-3).=
2 ’
542.	Докажем, что К*8 + К17 < И 10 + V15 (можно сделать и
обратное предположение, тогда придем к противоречию, которое и
будет доказывать справедливость записанного неравенства). Возводим
в квадрат: 25 + 2 К136 < 25 + 2 V150, откуда V136 < Y150.
543.	99! =(1 -99).(2-98).(3-97). . .(49-51)-50< ((2+98)3х
х(Ц^)2---(^т^)2,50=502'502’502'-,-'502'50=5()99’ т- е-
99! < 50".
544.	Преобразуем левую часть неравенства, а затем восполь-
зуемся свойством суммы двух взаимно обратных положительных
чисел:
fl2+2 -fl2+1+1-r^+~i+-1
/а24-1	/а24-1 V ^Ка2 + 1
545.	При п = 2 неравенство справедливо: f < j • Предположим,
что оно справедливо при некотором натуральном n = k, т. е. S(k) =
14 № 2939
209
б	11	4
5	7	9
10	3	8
Рис. 215
Докажем его справедливость для n — k 4-1.
s(*+i)=4-+-i-+--
= S(^)+	<
 (£-1)(£+1)2 + £
+JL+.. 2_=
* £2 * (£_|-1)2
k— 1	1
k +(£-1-1)2 —
(£2—1) (£+1) + £
£(&+1)2 “ £(£+1)?
£3_L£2__£_1+^ _ £3 + £2_1
£(А;+1)2	"" £(£+1)2 <
&3 + #? £
£(£+1)2	£+1
1
следовательно, неравенство справедливо при любом, 2.
546.	Используйте метод математической индукции.
547.	Рис. 215.
548.	Обозначим длину гипотенузы через а. а второго катета
через Ь. Тогда а2— 62= 132, (а—Ь) (а + Ь)= 169, 169=13-13 или
169=1-169, а — Ь-=£а-]-Ь. Следовательно, а—6=1, аа + 6=169.
Отсюда а = 85, 6 = 84.
549.	Объем призмы равен V = S0CH-6, S0CH = ~«2, где h—высота
призмы, а—катет основания призмы (рис. 216).
BrC = a ctg a, h = B^B — V^ ВгС2— ВС2 = K^2ctg2a—а2 =
= j/cos2a—sin2 а =—^—• К cos 2а ; V = ~а-^'cos 2а .
sin а	sin а	2 sin а
550.	Обозначим ребро основания призмы через а, ЛД = а(рис. 217).
Тогда АС = аК2 , ЛЛТ = AC-ctgа = #И2-ctgа, S0CH = S = a2, а =
= j/s ; S6oK = 4a-tfJ/r2-ctgа = 4а2 2 ctgа.
551.	1) Аналитический метод решения неравенства. Неравенство
равносильно совокупности систем:
/2х2 — 15х—50 > 0	/2х2— 15х—50 < 0
|3х2+17х—6 > 0 или (Зх2+17х—6 < 0.
210
Решаем каждую систему отдельно, найдя предварительно корни
трехчленов.
Решением первой системы будут значения х<—6 или л: > 10
(рис. 218).
01	Ю х
Рис. 218
Решением второй системы будет—2,5<х<Т (рис. 219).
jm\\\\w	^^/////////////^^^^
-5	-2~5	61	to х 3
Рис. 219
Таким образом,, решением данного неравенства будут значения
х<—6, —2,5 < х< у , х> 10.
2) Графический способ решения неравенства.
Строим в осях координат (на одной координатной плоскости)
графики трехчленов, стоящих в числителе и знаменателе данного
неравенства. Построение выполняем схематически. Важно, чтобы
точно были указаны корни трехчленов и правильно выбрано направ-
ление ветвей парабол. Через точки пересечения графиков с осью Ох
проводим вертикальные прямые (рис. 220). Теперь легко увидеть
значения х, при которых знаки значений трехчленов совпадают и
при которых они противоположны. В рассматриваемом случае знаки
трехчленов совпадают при х<—6, при —2,5<х< у, х> 10. Это
и будет решением неравенства.
3) Способ интервалов.
Разложим трехчлены на множи-
тели. В данном случае используем
уже найденные корни трехчленов*
2 (х + 2,5) (х- 10) > 0
3 (x-j-б) (х—
\ /
Отметим корни на оси Ох (рис.
221). В самом левом интервале все
множители положительны. Значит,
вся дробь положительна. Далее
при движении по оси вправо при
переходе от интервала к интервалу,
т. е. при переходе через каждый
корень, знак всего выражения ме-
няется на противоположный. Таким
14*
2П
образом, в данном случае решением неравенства будут значения
х <—6, — 2,5<х<у, х> 10.
При определении знака выражения методом интервалов безраз-
лично, являются ли двучлены множителями в числителе или в зна-
менателе дроби. Разница только в том, что корни двучленов, сто-
ящих в знаменателе дроби, не могут быть решениями неравенства,
а корни двучленов, стоящих в числителе, могут быть решениями
неравенства, когда это неравенство нестрогое, т. е. когда оно
включает знак равенства. При решении неравенств методом интерва-
лов нет необходимости и в изображении, хотя бы и примерном,
графика функции. Достаточно только указать знак всего выражения,
как это сделано на рисунке 221.
552.	—3 <х<7.
553.	Рис. 222.
ч . г	о	1 о	(*+5)3 (х+3) х2
554.	а) х <—5, или — 2 < х < 1, или 3 < х < 7; б) j—>
> 0 <=>	> о, x —4, х о Следовательно, —5 < х <—4,
или —4 < х <—3, или х > 2.
i/“2
555.	а) ——	б)-----в) х^1; г) неравен-
ство равносильно системе:
' Зх—5 <49 —14/7+2 + % +2
Зх— 5>0
х + 2^0
7 — /7Т2>0.
2
Решив ее, находим 1 -у х 7.
О
556.	2sin3x—4<0 при любых значениях х. Следовательно, дан-
ное неравенство равносильно неравенству 2х—Зх2+1>0, откуда
557.	Приведем неравенство к виду:
sinx + sinхcos* + -|- sinx(4 cos? x— 1) > 0,
212
далее
sin х (3 + 3 cos x -г 4 cos2 x— 1) >0,
Q
sin x (2 -p 3 cos x + 4 cos2 x} > 0, sin x > 0,
о
так как дискриминант квадратного трехчлена, стоящего в скобках,
отрицателен и поэтому знак трехчлена при любом знаке cos % сов-
падает со знаком старшего члена. Следовательно, трехчлен положи-
телен при любом значении х.
Итак, 2пп < х < л Ч- 2лл, п g Z.
558.	и5— 5п3Н-4п = (п — 2) (/г 4- 1)/2 (п—1)(п4-2). Получили про-
изведение пяти последовательных натуральных чисел. Два из этих
чисел делятся на 3, одно на 5, по крайней мере одно делится на 2
и два на 4. Значит, все произведение делится на 9-5-2-16= 1440.
559.	Анализ, Пусть треугольник АВС построен. АЕ, BF, CD —
данные медианы (рис. 223). Если BF продолжить до Blt такой, что
OF^=B}F, то получим параллелограмм АОСВ,. Причем в £\AOBV
2
стороны равны у длины соответствующей медианы данного тре-
угольника. Отсюда ясен порядок построения.
Построение. Строим ДЛОВП каждая сторона которого равна --
длины соответствующей медианы. Делим ОВГ пополам, проводим AF
и продолжаем его на такое же расстояние. АС — основание искомого
треугольника. OF продолжаем до точки В, такой, что BO=^OBY.
/\АВС — искомый.
Задача имеет решение и притом единственное, если для медиан
выполнено неравенство треугольника.
560.	Так как шар вписан в тетраэдр, то объем тетраэдра можно
вычислить по формуле V = yr-S, где г — радиус вписанного шара,
a S — площадь полной поверхности тетраэдра. Из этой формулы
можно будет найти г. С другой стороны, V = ~DC-BC-AB, где DC,
ВС и А В — взаимно перпендикулярные ребра тетраэдра (докажите)
(рис. 224); DC -2, ВС = DC-ctg 15°, ВС = 2-ctg 15°, АВ = ВСЛ<& 15°'
213
AB = 2, отсюда находим V = y • (2+Кз).
лг— вс _ 2 ctg 15° _	2	. nR DC 2
cos 15° cos 15° sin 15°’ UD ~ sin 15° — sin 15° ’
M. ^2-2-ctg 15" + 2 • -^. + 2ctg l5°-2 + 2 .	_
= 4 ( ctg 15°-I_!_= 4 . t+cos lS0
Vg +sinl5°_/	sin 15°
1 л 1/1 + cos 30°	______
= 4----£	= 4 •	= 4 (2/2+^3+ 2+/3).
у 1 ~~cos 30	V 2~У 3	Г
Подставив найденные значения V и S в формулу 7 = -^-r-S,
найдем r = 4(3j/6 + K2—2)/3—3).
561.	Обозначим^ радиус шара буквой R. Выразим все величины
через R: =	3, где а3 — сторона правильного треугольника;
ЛВ = / = /?ИЗ; О1С = г = ^ = -Ц^(рис. 225). SK0JJ = лг2 + лг/=
= л(^+^р-.7?Гз) = |лЯ2; 5ш=4лЯ2, 5к0н:5ш = (| л£2):
:(4л/?0 = й-
562.	Анализ. Пусть h—расстояние между прямыми I и АВ (рис. 226),
и пусть С—такая точка на прямой /, расстояние от которой до пря-
мой I равно h. Тогда S^ABC = уAB-h, так как h—перпендикуляр,
опущенный из С на прямую АВ, т. е. h—высота треугольника АВС.
Если С'—другая точка на Z, то расстояние от С' до / (обозначим его й')
больше Л, и поэтому S&ABC, AB-hr > ~ AB>h.
Построение. 1) Проводим через произвольную точку прямой I
прямую Г, параллельную АВ, а затем плоскость а через прямые /
и I'. 2) Проводим прямую АВ. 3) Из произвольной точкй D пря-
мой АВ опускаем на плоскость а перпендикуляр DD', 4) Через
точку D' проводим прямую Г, параллельную АВ. 5) Находим точку
пересечения Г и /. Точка С—искомая: расстояние от С до прямой АВ
равно h — расстоянию между прямыми I и АВ. Таким образом,
авс == у АВ • h = Smin.
563.	V = ~a2-H, BE±~AS. Тогда ED^_AS, следовательно,
о
BED = а (рис. 227). В треугольнике ВОЕ В0 = а^ 2 , ЕО = ВОх
Xctg| • ctg|; ^ASOco^EOS, , Д5= Н2 + £ ,
• а 2 .------------------------------------------------------%
-----и-------- —	. Из соотношения ctg %- • 1/ Н2 +	= Н
Н---------------------------------------------------------------ау 2	te 2 К '2
—ctg а
a sin
находим Н —  г —	, тогда
У — 2 cos а
. а
о лг-о	Sin —
у а3 У 2 _________2
6	У cos (л — а)
564.	Проекции несмежных ребер произвольного тетраэдра при
указанном его расположении взаимно перпендикулярны и равны
этим ребрам, т. е. равны между собой. Кроме того, плоскости про-
ектирования, проведенные через данные ребра перпендикулярно
плоскости проекции, будут плоскостями симметрии данного тетраэдра
и, значит, будут делить пополам как другое ребро, так и его про-
екцию. Таким образом, проекции ребер точкой пересечения будут
делиться пополам. Значит, в проекции получится квадрат.
565.	Обозначим радиусы кругов пересечения шара с гранями
трехгранного угла через г1ч г.2, г3. Тогда сумма площадей этих кру-
гов будет равна S = л ++г|). Но O'O1 = dli O'O2 = d2, O'O3 = d3,
где dlf d2i d3— расстояния от центра шара О' до соответствующих
граней трехгранного угла (рис. 228), Тогда rl = R2—df; rl = R2—d22;
r2 = R2—d2, S = n(3R2—(d21 + d2 + d23)) = n(3R2—d2), где d = OO'f
t. e. S — величина постоянная.
566.	Пересечением двух пирамид будет многогранник, состоящий
из двух пирамид с общим основанием А2С2В2 (рис. 229). Обозначим
высоту одной из них О1О2 = х9 тогда высота другой будет ОО2 = Н—х,
где Н—общая высота пирамид. Искомый объем будет равен
„	1 а2Кз 1 а2/з	а2уз
^ = “3 4—*+у—£—(Н—х) = —где я—сторона
треугольника А2В2С2. Л2О2 = /?, Z/ = O1O = /cosa, /? = xtga,
215
Рис. 228
Рис. 229
7? = (/ cos а—х) tg р. Из системы
=	„ D sin 2а cos р
< + Q , г» найдем R = 1о-• .—,
|xtgP = /cosa — R	2sm(a + p)’
ni/'o /i/о sin 2a cos В	/31Л 3
далее a = RV 3 = /|/3	, тогда V =
sin2 2a cos2 fl cos a
sin2 (a + p)
567. Разбейте данный тетраэдр на четыре тетраэдра, вершина
каждого из которых лежит в выбранной точке, а основаниями яв-
ляются грани данного тетраэдра. Сумма объемов этих тетраэдров
равна объему данного тетраэдра.
568. Данный тетраэдр будет гомотетичен тетраэдру с вершинами
в центрах вписанных шаров с центром гомотетии в центре шара,
вписанного во внутренний тетраэдр. Значит, для нахождения объема
данного тетраэдра достаточно найти объем
внутреннего тетраэдра и умножить его на
куб коэффициента гомотетии. Часть внутрен-
него тетраэдра с вершинами в центрах впи-
санных шаров изображена на рисунке 230.
Ребро этого тетраэдра равно a = 2R, высота
боковой грани равна h = =zR]f 3.
Радиус вписанного в него шара обозна-
чим г:
г = 00'= 00",
00" О4О"
O'D “ О'О4 ’
216
— — . в треугольнике О'О J)
Hh
Н — -^- РУ 6, тогда г = -Д.
У 6
v 1 9 V 3 гг 1 4Я2К 3
Объем внутреннего тетраэдра равен Уг =у а2  Н = -$ • —j—х
2R /б _2К3/2
х 3	~	3
Коэффициент гомотетии k = —, где d—расстояние от О до грани
данного тетраэдра: d = R + 00'= R + r — R + рД =	, k =
= ^(l + <6)/6_1 ,z-g
V б-'R
Значит, К = /-Л3 =	. (1 +/6)3= 2R3^2 (19+ 9/б) =
О	о
= ^(19/2	18/3).
569.	Из равенства sin (х 4 -у)— cos (%—у) + 2 = 0 следует, что
sin (x + i/) = —1, cos(x—у)=1, а тогда sin(x + y) +cos(x—y)=^Q.
570.	Обозначим искомые числа т и п. Тогда имеем т2— м2 = 799»
(т + п) (т—п) =17-47.
/ m + п = 47	( т + п = 799
Отсюда <	или <	.
\ т — п= 17 I т — п = 1.
Значит, т = 32, п =15 или т = 400, /г = 399.
571.	Пусть в первой корзине было k яблок, во второй—/, в треть-
ей— т, в четвертой — п и в пятой—р яблок. Когда из первой пе-
1	4
реложили во вторую у часть яблок, то в первой осталось -g-й,
а во второй стало Z + -—P яблок. Из второй в третью переложили
v- часть яблок. Значит, в ней осталось т /+т-Н а в третьей
О	О \ о /
стало ~ ^1 +	+ т яблок. После очередного перекладывания
в третьей осталось "5"("5'Н4"5"^)+т), а в четвертой стало
+	^осле всех перекладываний в первой
корзине оказалось у + у I р + у м + у ( Ц- у U + 5" ) ) )) »
во второй—-|-^/+~/г^,в третьей—-g- (^1+	+ т), в четвер-
ТОЙ---5 [д + y	+^J и в ПЯТОЙ — -g-^tt+y X
х (т + +/ + у/г))) +р) •
217
По условию в каждой корзине стало по 48 яблок. Значит,
4(/ + ^) = 48
! T(l(Z+T^) + m)=48
+ l(z+!*))+“)= 48
,4(l(n+l(m+l(z+l*)))+/’)=48-
Решив эту систему, найдем, что т = 48, и = 48, р = 48, k = 45,,
/ = 51.
572.	У = ^Р3/3. (рис. 231).
573.	Обозначим искомый угол через х (рис. 232). Объем конуса
равен Р = -^л7?2Я, R = АО = АС 4- СО, СО=1, 4C = ctg-J,
R = 1 +ctgy, Н = 40-tgx = (1 + ctgy) • tgx.
1 f	x \3
Таким образом, V = -g- л •( 1 4-ctg у j • tgx. Найдем V'(x) =
= -i- л • f3 ( 1 + ctg 4-V • f- -\ • tg x(1 4- ctg 4-) • —y— ,
3	\ \ to 2 j	„ . , x ° ‘I 1	& 2 / cos2x 7’
44	7	2 sin? -g- j	v	7	7
V (x) = 0.
Преобразуем выражение для производной:
sirr -j	4	7
14-ctg |=/= 0,	тогда	— ytgx--------+ f1+ctg4')=°.
. о Л	LUo Л \	£» 1
sm-T
218
sin у#; 0, cosx=/0, тогда	—3 cos х • cos у 4- sin у 4- cos у = О,
—3 fcos-5-—sin-к-') fcos £- + sin-£) • cos4-4-sincos4 = 0>
. X .	/ f\	i о (	%	• X \	r\
sin у 4~ cos у =£ О, значит, 1—31 cos у—sin у \ • cosy = 0.
Далее получаем:
sin2 у + cos23 cos2y 4- 3 sin| cos | = 0, tg2 ± 4- 3 tg y- 2=0,
, x /17-3	o . /17—3
откуда tgy = -?_-—, т. e. x = 2arctg—.
574.	Объем пирамиды равен V = у50сн-Я, 50СН = уР-/', где Р —
периметр основания пирамиды, а г—радиус вписанного в основание
круга (докажите, что в основание пирамиды можно вписать круг);
Р = 2р. Поэтому S — pr, г~~^- Высота пирамиды Н = МО, H=r tg а,
// = y*tga (рис. 233). Значит, V = y S~ • tga; V = y-ytga.
2Scos2f 1 S2
^ПОЛН '— "^осн 4“ ^бок —• coTa ’	— "3 ~p ' tg a’
575.	Осевое сечение образованного тела показано на рисунке 234.
^^^конояз+^конгяв = у nR\DO+OE) = у n£2(/cosa4-/sina-ctgP)=
= JL ЛР2/. sin(« + P) _ _L Я/3. sin2 «sin (а 4-Р) .
3	sin р 3	sin р
576.	Из того, что боковые грани пирамиды наклонены под одним
и тем же углом к основанию, следует, что высота пирамиды яв-
ляется ее осью симметрии и высота вписанного цилиндра лежит на
высоте пирамиды; ОгС~CD — r (рис. 235); DN = г-ctgср, MN
=2 (г4- r ctg<p) = 2r (l 4-ctg(p); V = у • S0CH• И; ^1 = 00^0^ =
=r(l + tg<p); 50СН = 7ИЛГ2 = 4г?-(1 4-ctgф)?; V = y • 4r?-(l 4-ctg<p)2x
4
Xг(1-J-tg<р). Таким образом, V = r3(l + ctg<p)3-tgcp.
r = lf..(-3(1+ctgW._aJL + _L_.(|+ctg<p).);
-з. (1 + ctg ,f)..	. (1 + ctg T). = 0,
так как ср	< у,	cos ср #= 0,	sin ср О, то 1 + ctg ср =/= 0;
----:—-----1------— • (1 + ctg ср) = О,
Sin ф COS ф	COS2 ф v to т/ ,
—3	cos ср	+	sin ср + cos ср = 0; tgcp = 2, т. е. qp = arctg2.
577.	Ось призмы лежит на оси конуса (рис. 236). Обозначим
М0~Н, ВМ = l,jOO1 = h. Тогда полная поверхность призмы будет
а2Г 3
равна 5 = 6-------1- 6ah, где а — сторона основания призмы. Она
равна радиусу описанного круга. ОА=а, ВА—ВО—ДО=КВ-—ЕВ—а,
h   У12 — Н2 — а ,  rj УI2— И2 —а
в “ ур.-н* ’ ~ К /2—//? ’
5 = 4 а2 /з + ба  ——• (К/2—//2—а) =
2	У 12~ И2	'
= 4 а2 3 + 6а//---— • а2;
2	У12-Н2
S' = За J/3 + 6/7-. • а, За !/3 + 6/7----J--— а= О,
У 12-н2	У п-т
ему 12-Н2	2НУI2 — Н2
откуда а —--------г : г; а =-----'		—;
3	\2Н — ЗУЗ(12 — Н2)	4Н—У3(12. — Н2)
„	бН2(12-н2)У~з
осн ~ (4Н--У3(12~Н2)У
578.	Обозначим AD = a, АВ = Ь, ВВх=с (рис. 237). Тогда
V — a-b-c; ВВХ = 2BF — 2т sin a; AD — 2EO = 2т sm2a.\ АВ = 2ВЕ,
220
ВЕ=УEF2—FB2, EF=m cos2a, значит, BE=Vm2 cos2 2a—m2sin22a=
=mKcos4a. Итак, V = 8m3 sin 2asinaKcos 4a.
579.	Пусть высота бассейна равна //, а длина стороны основания
равна х. Тогда V = x2-H, Н — S = x2 + 4H-x, S = x24--^~;
с, о 4V	л
S =2х------—, приравняв производную к нулю, находим х = 4, тогда
Я = 2.
Итак, сторона основания бассейна 4 м, а высота бассейна 2 м.
580.	4317+ 1717 делится на 43 + 17 = 60. Мы воспользовались тем,
что при нечетном п ап-\-Ьп делится на а-\-Ь.
581.	Пусть все наследство составляет х бриллиантов. Тогда пер-
вый получил второй —	1 ~~—“~ + 1- Эти величины
равны: + = +• —-^-+h откуда х = п2, т. е. каждый получил п брил-
tT /2-	72-
лиантов.
582.	При определении площади фигуры, ограниченной кривыми,
важно правильно определить взаимное расположение линий, левую
и правую точки их пересечения, какая линия расположена выше,
какая ниже. Поэтому необходимо схематически, но принципиально
правильно построить график этих линий, а значит и интересующую
нас фигуру в одних осях координат (рис. 238). В данном случае
фигура, площадь которой мы находим, разбивается на два криво-
линейных треугольника ABD и BCD. Абсциссы точек А и С соот-
ветственно равны —2 и 1. Найдем абсциссу точки В: х2 — 2x4-2==
=х24- 4х+5, х = — 0,5.
-0,5	1
S = J ((х24-4х + 5)—l)dx+ J ((х2 —2x4-2) — l)dx.
-2	— 0,5
Выполнив вычисления, найдем S = 2,25.
221
1	, 1
У = — у Х+ I;
583.	6 4 Кб.
584.	Напишем уравнения прямых — границ четырехугольника'
ABCD (рис. 239).
АВ- Х~~Х1 __ У—У1  х 3 У—°
х2 — *1	У2—У1 ’ 0 — 3	1—о
ВС: Й = У = Зх+1;
У = Зх-9-
С0:й=&> y—ix+7l-
Сравнивая угловые коэффициенты, заключаем, что АВ || CD.
AD || ВС, ABA..AD. Значит, ABCD—прямоугольник. S — 20.
585.	V = • -г • ЛС-Л5-sin СЛ5-Я (рис. 240). Находим И:
о А
BO_1_ASC, в треугольнике ABM AM = АВ -cos 4 = 4- АВ, в тре-
угольнике АМО £МА0 = ^, ^АМ0 = ^, МО = ^, АО=^--
в треугольнике ABO Н = ВО = У АВ2—АО2 — •
..	I? 2V 2
Итак, выполнив вычисление, находим V =——.
О
586.	Перпендикуляр к плоскости	проведенный из центра
описанного около этого треугольника круга, проходит через центр
шара. Обозначим ОВ1 = 7?, OB — Rlt BBl — h = x, тогда Rx —х2,
ВС = 7?! УЗ, ВС = И3(7?2—х2), S0CH ==
Рис. 240	РиС. 241
222
(рис. 241), V = S0(.„h = 3 '3 • х. Найдем производную и при-
R К"з
равняем ее к нулю, получим х — —.
587.	Обозначим BD — 2x, АС==4х, OD — x, SO = H (рис. 242).
Тогда AD = x]f5, AS = AD = xVr5. Из условия задачи следует, что
противоположные боковые ребра попарно равны между собой и два
из них равны ребрам основания пирамиды. В треугольнике ДЗО,
ЗО2 = ЗД2—ОД2, SO = x; SD2 = SO2 + OD2, SD^xV'Z. Проведем
ДЕ.LSD, AD = AS- ED=^\ AE* = AD* — ED\ AE = ^^-,
Збок = 4- D-£~-, S6OK = 6x2, T. e. 6x2 = 6, отсюда x= 1;
5осн = |.ДС-ВР, т. e. SOCH = 4x2, К = 1.4х2.х = |.
588.	Обозначим AB~BC=x, OC=R, тогда AC=2p—2x=2(p—x)
(рис. 243). V — -j nR2‘AB. Из соотношения OC-AB= BD-AC naxo-’
n 2 (p~x) У~2рх~р2	r7 4	(p‘—x)2 (2x — p)
дим R = ——, тогда V = -^np —---------------— -
X	О	X
Найдем производную и приравняем ее к нулю, откуда х =	.
Значит, АВ = ВС —АС~^7^.
О	т:
589.	Римлянин разделил наследство в отношении м:с:д = 2:4:1.
Это выгодно для матери. Можно поделить наследство, например,
в отношении м:с:д = 5:8:1. Воспроизведите рассуждения деливших.
590.	(2 • 5’ — 5 • 2’)83—((2 • 57)83—(5 • 2?)83) = 1083 • (5е—26)83— 1083 х
Х((56)83—(2e)83)=1083-((5e—26)83—(58)83 + (26)83). Если (56 — 26)83 раз-
ложить по формуле Ньютона, то первый и последний члены разло-
жения уничтожатся с членами, идущими за степенью бинома. Коэф-
фициенты всех остальных членов кратны 83. Значит, все выражение
делится на 83.
591.	(0; 12) или (4; —20).
592.	5 = 4 у.
223
СОДЕРЖАНИЕ
Предисловие............................................3
VIII	классы................‘......................... 7
IX	классы........................................	36
X	классы.......................................... 69
Ответы, указания к решению задач, решения ....	95
ИВАН СЕМЕНОВИЧ ПЕТРАКОВ
МАТЕМАТИЧЕСКИЕ КРУЖКИ В 8-10 КЛАССАХ
Зав. редакцией Р. А. Хабиб
Редактор Л. В. Туркестанская
Младшие редакторы Е. Л. Козырева, Л. И. Заседателева
Художник Б. Л. Николаев
Художественный редактор Е. И. Карасик
Технический редактор Р. С. Невретдинова
Корректоры Г. В. Хрусталева, О. В. Ивашкина
ИВ № 9593
Сдано в набор 18.08.86. Подписано к печати 31.03.87. Формат
oOxOOVie- Бум. кн.-журн. отечеств. Гарнитура «Литератур-
ная». Печать высокая. Усл. п. л. 14 + форз. 0,25. Усл. кр.-отт.
14,69. Уч.-изд. л. 14,16 + форз. 0,36. Тираж 210 000 экз.
Заказ 3671. Цена 60 коп.
Ордена Трудового Красного Знамени
издательство «Просвещение» Государственного комитета РСФСР
по делам издательств, полиграфии и книжной торговли.
129846, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано с матриц ордена Октябрьской Революции
и ордена Трудового Красного Знамени
МПО «Первая Образцовая типография» имени А. А. Жданова
в областной типографии управления издательств, полиграфии
и книжной торговли Ивановского облисполкома, 153628,
г. Иваново, ул. Типографская, 6.
Школьные учебники (((Р
SHEBA.SPB.&U/SHKOLA