йзйяг
50 40 з'о
:-~ S2 S
Kb
ПРОСВЕЩЕНИЕ

СООТВЕТСТВИЕ МЕЖДУ ПУНКТАМИ УЧЕБНИКА И ЗАДАЧАМИ ТЕТРАДИ
Номера
пунктов
учебника
1
3
4
5
6
7, 8
9
11
12
14, 15
16
17
18
19
20
21
22, 23
24
25
27, 28
29
30
31
32
33
34
35
37
38
Тема
Точки, прямые, отрезки
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков и углов
Длина отрезка. Единицы измерения.
Измерительные инструменты
Градусная мера угла
Смежные и вертикальные углы
Перпендикулярные прямые
Треугольник. Первый признак равенства
треугольников
Перпендикуляр к прямой
Медианы, биссектрисы и высоты треугольника
Свойства равнобедренного треугольника
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой. Примеры
задач на построение
Определение параллельности прямых
Признаки параллельности двух прямых
Об аксиомах геометрии. Аксиома параллельности
прямых
Теоремы об углах, образованных двумя
параллельными прямыми и секущей
Теорема о сумме углов треугольника
Остроугольный, прямоугольный и тупоугольный
треугольники
Теорема о соотношениях между сторонами и
углами треугольника
Неравенство треугольника
Некоторые свойства прямоугольных треугольников
Признаки равенства прямоугольных треугольников
Расстояние от точки до прямой. Расстояние
между параллельными прямыми
Построение треугольника по трем элементам
Номера
задач
тетради
1—8
9—11
12—16
18, 19
20—24
25—31
32—40
41—46
47—49
50—59
60—62
63—65
66—70
71, 72
73—76
77, 78
79—83
84—86
87—104
105—108
109—115
116—124
125—129
130—134
135—137
138—145
146—149
150—155
156, 157

ГЕОМЕТРИЯ
РАБОЧАЯ
ТЕТРАДЬ
КЛАСС
Пособие
для учащихся
общеобразовательных
учреждений
13-е издание
Москва
«Просвещение»
2010

УДК 373.167.1:514
ББК22.151я72
Г36
Авторы:
Л. С. Атанасян, В. Ф. Бутузов, Ю. А. Глазков, И. И. Юдина
Рабочая тетрадь является дополнением к учебнику «Геометрия, 7—9»
авторов Л. С. Атанасяна и др. и предназначена для организации решения
задач учащимися на уроке после их ознакомления с новым учебным
материалом. На этом этапе учащиеся делают первые шаги по осознанию нового
материала, освоению основных действий с изучаемым материалом.
Поэтому в тетрадь включены только базовые задачи, обеспечивающие необходимую
репродуктивную деятельность в форме внешней речи. Наличие текстовых
заготовок облегчает ученику выполнение действий в развернутой письменной
форме, а учителю позволяет осуществлять во время урока оперативный
контроль и коррекцию деятельности учащихся. Использование данной
тетради для организации других видов деятельности (самостоятельных
работ, повторения, контроля и т. д.) малоэффективно.
Учебное издание
Атанасян Левон Сергеевич
Бутузов Валентин Федорович
Глазков Юрий Александрович
Юдина Ирина Игоревна
ГЕОМЕТРИЯ
Рабочая тетрадь
7 класс
Пособие для учащихся
общеобразовательных учреждений
Зав. редакцией Т. А. Бурмистрова. Редактор Л. В. Кузнецова. Младший редактор
Н. В. Ноговицына. Художники В. А. Андрианов, О. П. Богомолова, В. В. Костин.
Художественный редактор О. П. Богомолова. Компьютерная верстка Е. А Стрижевской.
Корректоры Л. С. Вайтман, И. Б. Окунева
Налоговая льгота — Общероссийский классификатор продукции ОК 005-93—953000.
Изд. лиц. Серия ИД №05824 от 12.09.01. Подписано в печать 23.03.10. Формат 7OX1OO716-
Бумага писчая. Гарнитура Школьная. Печать офсетная. Уч.-изд. л. 2,47.
Доп. тираж 60 000 экз. Заказ №29847.
Открытое акционерное общество «Издательство «Просвещение».
127521, Москва, 3-й проезд Марьиной рощи, 41.
Отпечатано в ОАО «Саратовский полиграфкомбинат».
410004, г. Саратов, ул. Чернышевского, 59. www.sarpk.ru
ISBN 978-5-09-023709-3 © Издательство «Просвещение», 1998
© Художественное оформление.
Издательство «Просвещение», 2004
Все права защищены

Глава I
Начальные геометрические
сведения
Прямая и отрезок
1
Какие точки на рисунке лежат и
какие не лежат на прямой Ы Ответ
запишите, используя знаки е и i.
Ответ.
К
Через какие точки на рисунке
проходит прямая т и через какие
не проходит? Ответ запишите,
используя знаки £ и i.
Ответ.
а) Отметьте на рисунке точки Т,
О и Р так, чтобы выполнялись
условия: Теп, Оеп, Pin. Запишите,
как читаются эти условия.
б) Запишите, как еще можно
обозначить прямую п.
Ответ.
а) Точка Т лежит на прямой
точку . Точка О
или прямая п проходит через
б) Прямую п можно обозначить еще так:
или

а) Проведите прямые а и & так,
чтобы выполнялись условия:
А € а и В е а;
б) Каково взаимное расположение
прямых а и &?
Ответ.
б) Прямые а и &
Прямые тип пересекаются в точке С, а точка Ну отличная
от точки С, лежит на прямой т. Лежит ли точка Н на
прямой п?
Объясните ответ.
Решение. Н п, так как по условию задачи прямые т
и п имеют общую точку С, а двух общих точек две прямые
иметь
Ответ.
Точка Н на прямой п.
Отметьте на прямой МК две
точки: точку А, лежащую на отрезке
МК, и точку Б, которая не лежит
на отрезке МК. Какая из точек — А М
или В — лежит между точками М
vlKI
Ответ.
Между точками М и К

Пересекаются ли на рисунке:
а) отрезки ЕН и АВ, ЕН и ВС,
НК и АВ;
б) отрезок ЕН и прямая ВС,
отрезок НК и прямая АВ?
Ответ.
а) Отрезки Ei/ и АВ ;
отрезки ЕН и ВС ;
б) Отрезок ЕН и прямая ВС
8
Выпишите все отрезки, изображенные на рисунке к задаче 7:
а) на которых точка В лежит, но не является их концом;
б) концом которых является точка В.
Ответ.
а)
б)
Луч и угол
а) Какие точки на рисунке,
отличные от точки Т, лежат на луче ТР1
б) Какие лучи совпадают с лучом
ТР1
в) Какой луч является
продолжением луча ТР1
Ответ.
а) На луче ТР лежат точки
б)
О
м
в)

10
а) Отметьте на прямой НК
точки А и Б так, чтобы
выполнялись условия: точка А лежит между
точками Н и К и точка К лежит
между точками Н и В.
б) Напишите, какой луч
совпадает с лучом АК и какой луч
является продолжением луча АК.
Ответ.
б) С лучом АК совпадает луч ;
продолжением луча АК является
луч
Н
11
Отметьте на луче h точку М, а
на продолжении луча h — точку С.
Используя форму записи, введенную
в задаче 10, опишите взаимное
расположение точек А, М и С.
Ответ.
12
а) Запишите обозначения всех
углов, изображенных на рисунке.
б) Какой из этих углов является
развернутым?
Ответ.
a)Z.ABZ),
б) Развернутым является угол

13
Проведите лучи Лире началом
в точке О так, чтобы угол kp был
развернутым. Запишите обозначения
всех получившихся углов.
Ответ.
Акр,
14
а) Закрасьте цветным карандашом
внутреннюю область угла М.
б) Какие точки лежат на сторонах
угла М; внутри угла М; вне угла Ml
Ответ.
б) На сторонах угла М лежат
точки ; внутри угла М
; вне
D
М
15
Какой луч на рисунке делит угол
ABC на два угла? Объясните ответ.
Решение. Луч делит угол на
два угла, если он:
1) исходит из угла;
2) проходит угла.
Луч ВМ угол ABC
на два угла, так как он
из вершины угла ABC и проходит
угла ABC.
Луч ВК угол ABC
на два угла, так как он
из вершины угла ABC, но
Ответ.
Луч
делит угол ABC на
М
два угла.

16
Проведите луч КО, который
делит угол МКТ на два угла, и луч
КС, который не делит угол МКТ на
два угла.
Сравнение отрезков и углов
17
С помощью прозрачной пленки выясните, какие фигуры на
рисунке равны фигуре Ф.
Ответ.
Фх = Ф,
18
На луче, исходящем из точки А,
отмечены три точки К, М и Р так,
что точка М лежит между точками
А и Р и точка К лежит между
точками А и М. Сравните отрезки АК и АР.
Сделайте чертеж и объясните ответ.
Решение. По условию задачи
А—М—Р, поэтому отрезок AM— часть
отрезка . Аналогично А—К—М,
поэтому отрезок АК — часть
AM. Следовательно, АК АР.
Ответ.
8

19
а) С помощью циркуля сравните
отрезки АВ и CD, AB и BD, АС и
CD. Запишите результат сравнения
и выясните, какая из точек — В
или С — служит серединой отрезка
AD. А С В
б) На прямой AD отметьте точку
М так, чтобы точка С была
серединой отрезка DM.
Ответ.
а)АВ CD, АВ BD, AC CD;
середина отрезка AD — точка
20
Точка М — середина отрезка ОТ. Можно ли наложением
совместить отрезки:
а) ОМ и МТ;
б) ОМ и ОТ;
в) МТ и ОТ?
Объясните ответ.
Решение.
а) Точка М — середина отрезка ОТ, поэтому ОМ = , а
равные отрезки совместить наложением
б) Точка М — отрезка ОТ, поэтому ОМ ОТ,
а неравные отрезки ОМ и
в).
Ответ
а)
б)
в)

21
На рисунке отрезки НК, КР9 РО
и ОТ равны друг другу.
а) Укажите отрезок, серединой
которого служит точка О.
б) Укажите середину отрезка НТ.
в) На прямой КО отметьте точку
А так, чтобы точка Т была
серединой отрезка РА.
Ответ.
а) ; б)
Н К Р О Т
22
Луч AM делит угол ВАС на два
угла. Сравните углы ВАМ и ВАС.
Сделайте чертеж и объясните ответ.
Решение. Углы ВАМ и ВАС
имеют общую сторону , луч AM
делит угол на два угла,
поэтому луч AM проходит внутри угла
ВАС, значит, угол ВАМ — часть
угла , поэтому /.ВАМ /.ВАС.
Ответ. /.ВАМ /.ВАС.
23
Три луча Л, k и m исходят из
точки О, луч h является продолжением
луча k. Сравните углы hk и km.
Сделайте чертеж и объясните ответ.
Решение. По условию задачи
луч h является
луча ft, значит, угол

развернутый. Угол km — неразвернутый,
поэтому он составляет часть угла ,
т. е. /. hk /. km.
Ответ, /.hk Z. km.
10

24
На рисунках а и б Z. km = Z.kn.
На каком из этих рисунков луч k —
биссектриса угла тп? Объясните
ответ.
Решение. Луч называется
биссектрисой угла, если он:
1) исходит из угла;
2) делит угол
На рисунке а луч k исходит из
угла тп и делит
. Следовательно,
луч k — угла тп.
На рисунке б луч k исходит из
угла тп, но
угол пополам.
Следовательно, луч k
биссектрисой угла тп.
Ответ.
Луч k является биссектрисой
угла на рисунке
т
Измерение отрезков
25
На рисунке отрезки АВ, ВС, CD
и DE равны.
Найдите длину отрезка AD, если
за единицу измерения принят
отрезок: а)АВ; б) АС; в)АЕ.
Ответ.
sl)AD =
6)AD =
в)
D Е
11

26
Точка А лежит на отрезке ВС. Каким из чисел: -2; -0,5; 0;
0,3; 1,5 — может выражаться длина отрезка ВА, если за
единицу измерения принят отрезок ВС?
Решение. Длина любого отрезка может выражаться только
числом. По условию задачи точка А
лежит между точками Б и С, следовательно, ВА < ВС, поэтому
длина отрезка ВА может выражаться только числом
Ответ.
Длина отрезка ВА может выражаться только числом
27
На рисунке с помощью
масштабной линейки отметьте на прямой АВ
точку М так, чтобы ВМ = 20 мм.
а) Сколько таких точек можно
отметить на прямой АВ?
б) Измерьте в миллиметрах длину
отрезка AM в каждом из случаев.
Ответ.
а)
б) AM = или AM =
28
Точки К, Р и О лежат на одной
прямой. Каким может быть
расстояние КО, если КР = 3 см, РО = 1,5 см?
Решение. Расстоянием между
точками К и О называется длина
. Возможны два
случая:
а) Точка О лежит на луче РК
(сделайте чертеж). В этом случае КО +
+ ОР = , т. е. КО + 1,5 = ,
откуда КО = см.
12

б) Точка О лежит на продолжении
луча (сделайте чертеж). В этом
случае КР + РО = , т. е. КО =
см.
Ответ.
КО=
см или КО =
см.
29
Длина отрезка ВС на рисунке
равна а. Известно, что точка М —
середина отрезка ВО, точка К — середина
отрезка ОС. Отметьте точки М и К
на рисунке. Найдите расстояние МК.
Решение. По условию
задачи точка М — середина отрезка ,
поэтому МО = ~оВО; точка К —
середина отрезка , поэтому ОК =
= I мк = мо+ =
ОС
2 2
Ответ.
МК =
■>-£
30
Измерьте длину и ширину рабочей тетради и выразите их в
миллиметрах, сантиметрах, дециметрах, метрах и километрах.
Ответ.
Длина:
Ширина:
31
Выразите метр в аршинах и саженях.
Ответ.
13

Измерение углов
32
Измерьте с помощью
транспортира данные углы БАЙТ, ВАМ, КАМ и
САМ.
Ответ.
К
33
Углы ABC и КОР можно совместить наложением, Z.ABC = 15°.
Какова градусная мера угла КОР?
Решение. Так как по условию задачи углы ABC и КОР
можно совместить наложением, то они , а равные
углы имеют Следовательно,
АКОР =
Ответ.
34
Не измеряя углы КАС и САМ на рисунке к задаче 32,
сравните их градусные меры.
Объясните ответ.
Решение. Угол САМ составляет часть угла КАС,
следовательно, угол САМ меньше угла , а меньший угол
имеет градусную меру.
Ответ.
/LCAM Z.KAC.
14

35
С помощью транспортира
отложите от луча ОА угол АОС, равный 35°.
а) Сколько таких углов можно
отложить от луча ОА?
б) Измерьте угол СОВ в каждом
из случаев.
Ответ.
а)
б) АСОВ =
или /LCOB =
36
Луч АВ делит угол КАР на два
угла так, что угол КАВ тупой.
Сделайте чертеж. Может ли угол ВАР
быть тупым или прямым?
Решение. Так как луч АВ
делит угол КАР на два угла, то

Предположим, что угол ВАР тупой или
прямой. Тогда /.КАР 180°, что
невозможно.
Значит, угол ВАР
Ответ.
37
Луч МН делит угол АМС на два угла.
Найдите /.АМС, если /.АМН = 15°23', Z.HMC = 84°57'.
Решение. Так как луч МН делит угол АМС на два
угла, то /.АМС =/.АМН + , т.е. /.АМС = +
+ =
Ответ.
/.АМС =
15

38
Луч СЕ — биссектриса угла РСТ, АЕСТ = 37°37'. Найдите АРСТ.
Решение. Так как луч СЕ — биссектриса угла РСТ, то
Ответ. АРСТ
39
С помощью транспортира
постройте биссектрисы углов КМС и СМТ.
Измерьте угол, образованный
построенными биссектрисами, и запишите
результат измерения.
Ответ.
К
М
40
С помощью транспортира
разделите угол АОВ на три равных угла.
Перпендикулярные прямые
41
На каком из рисунков а — г углы
1 и 2 смежные? Объясните ответ.
Решение. Смежными
называются два угла, у которых одна
сторона общая, а две другие являются
продолжением
Углы 1 и 2 имеют общую сторону
на рисунках а, Две стороны
углов 1 и 2 являются продолжением
одна другой на рисунках Оба
условия выполняются на рисунке ,
т. е. углы 1 и 2 являются
смежными на рисунке
Ответ. Смежные углы — на рисунке
в)
г)
16

42
а) Проведите луч ОС так, чтобы
углы АОВ и СОВ были смежными,
и луч ОМ так, чтобы углы АОВ и
МОА были смежными.
б) Вычислите градусные меры
углов СОВ и МОА, если /.АОВ =
= 100°.
Ответ.
б) /.СОВ =
43
Сумма углов ABC и АВО равна 160°. Являются ли они
смежными?
Решение. Если углы ABC и АВО смежные, то
выполняется равенство Z.ABC + Z.ABO = , что противоречит
условию задачи.
Следовательно, углы ABC и АВО
Ответ.
44
На каком из рисунков а — г углы
1 и 2 являются вертикальными?
Объясните ответ.
Решение. Два угла
называются вертикальными, если стороны
одного угла являются
сторон другого. Это условие
выполняется на рисунке
Ответ.
Вертикальные углы изображены
на рисунке
в)
2 Геометрия, 7 кл

45
На рисунке Z.ABC = 83°, Z_ABK =
= 65°. Найдите Z.PBM.
Решение. /. РВМ = Z. ,
так как эти углы ;
Z. = 83°- =
. Следовательно, /LPBM
Ответ.
46
Прямые АВ и ОТ пересекаются
в точке С, /-АСО = 40°. Сделайте
чертеж. Найдите Z.BCT, A. ACT,
АВСО.
Решение.
1) Z ВСТ = zl , так как эти
углы ,
поэтому /-ВСТ =
2) A ACT + ZACO = ,
так как эти углы ,
поэтому Z. ACT =
3) /. ВСО = Z.
, так как.
следовательно, Z. ВСО =
Ответ.
47
С помощью транспортира и
линейки проведите через точку А прямую
6, перпендикулярную к прямой т.
т
18

48
Прямые КМ и ВС пересекаются в точке О, /- СОМ = 89°.
Перпендикулярны ли прямые КМ и ВС? Объясните ответ.
Решение. Две пересекающиеся прямые называются
перпендикулярными, если они образуют
. По условию задачи Z. СОМ = , т. е. он не
Ответ.
, поэтому прямые КМ и ВС
49
Прямая Ъ пересекает стороны угла С в точках А и В. Могут ли обе
прямые СА и СВ быть перпендикулярными к прямой Ы
Решение. Предположим, что СА 1Ь и СВ _1_ 6, тогда две
прямые, перпендикулярные к прямой Ь, в точке
С, что невозможно. Следовательно, обе прямые СА и СВ быть
перпендикулярными к прямой Ъ
Ответ.

Глава II
Треугольники
Первый признак равенства
треугольников
50
а) Запишите все возможные
обозначения данного треугольника.
б) Укажите: сторону, лежащую
против угла С; угол, лежащий против
стороны СМ; углы, прилежащие к
стороне ЕС; угол между сторонами ЕС и ЕМ.
в) Измерьте меньшую сторону данного треугольника и его
больший угол и запишите результат измерений.
Ответ.
а) АСЕМ,
б) Против угла С лежит сторона ; против стороны СМ
лежит ; к стороне ЕС прилежат углы ; между
сторонами ЕС и ЕМ — угол
в) ЕМ = см; /-СЕМ =
51
а) С помощью масштабной
линейки закончите построение
треугольника ABC, если АВ = 5 см, АС = 4 см.
б) Измерьте градусные меры углов
Б и С построенного треугольника ABC
и запишите результат измерений.
в) Измерьте сторону ВС и
найдите периметр треугольника ABC.
Ответ.
б) Z. В =
в) ВС = см и РАВС = см.
20

52
При наложении треугольника ABC на треугольник МКН
сторона АВ совместилась со стороной МК, сторона АС — со
стороной МН.
Совместилась ли сторона ВС со стороной КН1 Объясните
ответ.
Решение. Так как стороны АВ и АС совместились со
сторонами , то точки Б и С совместились
соответственно с точками . Следовательно, концы
отрезков ВС и совместились, а значит, отрезки ВС и
КН
Ответ.
53
На рисунке изображены равные
треугольники ABC и РОТ.
а) Укажите соответственно равные В Т
элементы этих треугольников.
б) Измерьте стороны и углы
треугольника ABC и запишите
результат измерений.
в) Не измеряя, найдите длины сто- А СО
рон и градусные меры углов
треугольника РОТ.
Ответ.
б)
в)
21

54
Заполните пропуски в
формулировке и доказательстве первого
признака равенства треугольников.
Теорема. Если две стороны
и угол между ними одного
треугольника соответственно равны
другого треугольника, то такие
треугольники
Д ано : ААВС и АНКР, АВ = НКУ АС = НР,
Доказать: Л ABC=
Доказательство.
1) По условию теоремы /_А = АН, поэтому треугольник ABC
можно наложить на так, что вершина А
совместится с вершиной Н, а стороны АВ и АС наложатся
соответственно на лучи НК и
2) По условию АВ = , АС = , следовательно,
сторона АВ совместится со стороной , а сторона АС — со
стороной , в частности, совместятся точки В и , С и
Поэтому совместятся стороны
3) Итак, треугольники ABC и НКР полностью совместятся,
значит, они Теорема доказана.
55
На рисунке точка О — середина
отрезков АВ и РТ. Докажите, что
ААОТ = АВОР.
Доказательство.
1)АО = , ОТ = , так
как по условию задачи точка О —
середина отрезков и
2) Z. АОТ = , так как эти
углы вертикальные.
22

3)Итак, АО = ОВ, ОТ =
тельно, ААОТ =
/L АОТ =
следова-
(по двум сторонам и
56
На рисунке к задаче 55 точка О — середина отрезка АВ,
АТ = ВР, /_ОАТ = АОВР. Докажите, что точка О — середина
отрезка РТ.
Доказательство.
1) АО = ОВ, так как точка О — середина отрезка
2) Л АОТ = , так как АО = , AT = , /.OAT =
= (по двум сторонам ).
Поэтому ОТ =
, т. е. точка О — середина
57
На рисунке Z.CAD = AACB, AD =
= ВС. Докажите, что АВ = CD.
Доказательство.
1)АС — общая сторона
треугольников и
2) ACAD = по двум
сторонам и
(АС — общая сторона, AD = и
Z. CAD = по условию).
Поэтому АВ =
58
Дано: АВ = СВ, Z.ABH = Z.CBH
(см. рисунок).
Доказать: АН = НС.
Доказательство. Л АВН =
= по двум
(ВН—
_). Поэтому АН =
23

59
Дано: AABH = Z_CBH, АВ = СВ
(см. рисунок).
Доказать: Z.AHB = 90°.
Доказательство.
1) Л АВН = по двум
(ВН — общая сторона,
и /_АВН =
АВ =
по условию).
2) Так как Л АВН = ,
то ААНВ = Z. Но углы
АНВ и смежные, поэтому
= , т. е.
2Z_AHB =
Z_AHB =
, следовательно,
Медианы, биссектрисы и
высоты треугольника
60
а) Выясните с помощью
чертежного угольника, какой из отрезков
МР, МТ, МОУ изображенных на
рисунке, является перпендикуляром,
проведенным из точки М к прямой
АС.
б) Проведите из точки М
перпендикуляр к прямой ВС.
Ответ.
а) Перпендикуляром, проведенным
из точки М к прямой АС, является
отрезок
М
24

61
Через точку О, не лежащую на
прямой ВС, проведены прямые ОМ,
ОК и ОА, пересекающие прямую ВС.
Какой из отрезков ОМ, OK, OA
является перпендикуляром,
проведенным из точки О к прямой ВС, если:
а) ОМ _1_ ВС и MiBC;
б)КеВС и АВКО* 90°;
в)ОА±ВС иАеВС?
Сделайте чертеж.
Р е hi e н и е .
а) По условию ОМА и М__ ВС, поэтому отрезок ОМ
перпендикуляром, проведенным из точки О к
прямой
б)КеВС и /-ВКО*
, следовательно, отрезок ОК
перпендикуляром, проведенным
в) OA
и
поэтому отрезок ОА
Ответ. Отрезок
62
Даны прямая а и три точки В, С,
Н, такие, что Bia, da, Hea, BC1. а.
Сделайте чертеж и докажите, что
/.ВНС * 90°.
Доказательство.
1)По условию Bia, ВС ,
С , поэтому отрезок ВС —
перпендикуляр, проведенный из точки
Бк
2) Из точки В, не лежащей на
прямой а, можно провести к этой
прямой только
перпендикуляр, следовательно, АВНС
25

63
С помощью чертежных
инструментов найдите на рисунке:
а) медиану;
б) биссектрису;
в) высоту
треугольника МКТ.
Решение.
а) Медианой треугольника называется отрезок, соединяющий
вершину треугольника с
Серединой стороны треугольника МКТ является
_, значит, отрезок — медиана треугольника МКТ.
точка
б) Биссектрисой треугольника называется отрезок
угла треугольника, соединяющий вершину треугольника
стороны. Биссектрисой
треугольника МКТ является луч , поэтому
— биссектриса треугольника МКТ.
угла
отрезок _
в) Высотой треугольника называется
проведенный из вершины треугольника к
ром на рисунке является отрезок
высота треугольника МКТ.
Ответ.
а) Медиана — отрезок
б) Биссектриса — отрезок
в) Высота —
. Таким перпендикуля-
поэтому отрезок —
64
На рисунке с помощью чертежных
инструментов проведите:
а) медиану треугольника ВСЕ из
вершины Е;
б) биссектрису треугольника из
вершины С;
в) высоту треугольника из
вершины В.
Е
26

65
На стороне КС треугольника ВКС
отмечена точка М так, что Z.BMK =
= /.ВМС. Сделайте чертеж.
Докажите, что отрезок ВМ — высота
треугольника ВКС.
Доказательство.
По условию Z.BMK = Z. .
Но эти углы смежные,
следовательно, АВМК = /. = 90°.
Поэтому отрезок ВМ — перпендикуляр,
проведенный из вершины В
треугольника ВКС к прямой,
содержащей противоположную
треугольника, т. е. отрезок ВМ —
треугольника ВКС.
а) С помощью масштабной
линейки выясните, какой треугольник на
рисунке является равнобедренным и
какой равносторонним.
б) Запишите, какие стороны
равнобедренного треугольника
являются боковыми, а какая сторона —
основанием.
Ответ.
а) Равнобедренным является
треугольник , равносторонним —
треугольник
б) В треугольнике

боковыми сторонами являются стороны
, основанием — сторона
О
27

67
Является ли равнобедренным треугольник НОТ, если его
периметр равен 47 см, НО = 19 см, ОТ = 9 см? Объясните ответ.
Решение. Треугольник называется равнобедренным, если
РНОТ = НО + + = 47 см, откуда НТ = см, т.е.
НТ НО у поэтому треугольник НОТ
Ответ.
68
Определите вид треугольника ABC, если АВ + ВС = АВ + АС =
= ВС+АС.
Р е hi e н и е .
1) По условию АВ + ВС=АВ + , значит, ВС =
2) АВ + АС = ВС + , значит, АВ =
3) Итак, АВ = и ВС = , т. е. все стороны
треугольника ABC Следовательно, треугольник ABC
Ответ.
Является ли треугольник равнобедренным, если его углы
равны 35°, 45° и 100°?
Решение. В равнобедренном треугольнике два угла
В данном треугольнике равных углов ,
поэтому он
Ответ.
70
Найдите биссектрису AM, проведенную к основанию ВС
равнобедренного треугольника ABC, если периметр треугольника
ABC равен 32 см, а периметр треугольника АВМ равен 24 см
(сделайте чертеж).
28

Решение.
1) По условию треугольник ABC —
, ВС — его
поэтому АВ =
2) AM — биссектриса
равнобедренного треугольника, проведенная к
основанию ВС, значит, AM является
и треугольника ABC,
т. е. ВМ =
^Р^с = АВ + ВС
= 2(АВ +
АВ + БМ = см.
4)РАБМ = АБ + ВМ +
= + AM.
Итак, 16+АМ=
тельно, AM = см.
Ответ.
AM = см.
) = 32 см. Отсюда
следова-
Второй и третий признаки
равенства треугольников
71
На рисунке
СМ = 5 см.
Найдите DM.
Решение. Л АМС =
по стороне и двум
= /.В9
(Z.AMC =
как вертикальные углы, AM =
и £А = по условию). Поэтому
DM = = 5 см.
Ответ.
DM =
29

72
Биссектриса ВН треугольника ABC
совпадает с его высотой. Сделайте
чертеж и докажите, что ABAC =
Доказательство.
1) По условию ВН — биссектриса
треугольника ABC, т.е. Z.ABH =
= ; ВН — высота
треугольника ABC, т. е. ААНВ = /_ = 90°.
2) Л АВН АСВН по стороне и
(ВН — общая сторона,
_ , Z.AHB =/. ).
следует, что Z. ВАН =
Отсюда
т.е. ABAC =
73
Даны равнобедренные треугольники ABC и МКО с
основаниями ВС и КО у АВ = МК. Какое условие достаточно добавить,
чтобы данные треугольники были равны:
а) по первому признаку равенства треугольников;
б) по третьему признаку равенства треугольников?
Ответ.
а)
б)
74
Даны равнобедренные треугольники ABC и МКО с
основаниями ВС и КО, ВС = КО. Какое условие достаточно добавить,
чтобы данные треугольники были равны:
а) по второму признаку равенства треугольников;
б) по третьему признаку равенства треугольников?
Ответ.
а)
б)
30

75
На рисунке AB = CD, AC = BD.
Докажите, что Z.ACB =Z. DBC и Z ABD =
= Z.DCA.
Доказательство.
1)ДАВС ADCB по
сторонам (АВ = , АС = ,
ВС — общая ). Поэтому
ААСВ Z.DBC и /_АВС = /.
2)ZABZ) = A ABC - Z ,
Z.DCA = ADCB - Z. Поэтому
/.ABD ADCA.
Итак, Z.ACB =
и Z.ABD =
В С
76
На рисунке АВ = CD, ВС = AD.
Докажите, что точка О — середина
отрезков АС и BD.
Доказательство.
1)AABD ACDB по
сторонам (АВ = и AD = по
условию задачи, сторона
щая). Поэтому Z. ABD = Z _
об-
2) Л ABC = ACDA по трем
сторонам (
). Поэтому /_ВАС = /-
3) Л АОВ ACOD по
углам (АВ =
Z ВАО =Z. _
_ , Z ABO = Z ,
_). Поэтому АО =
и ВО = , т. е. точка О —
отрезков АС и BD.
31

Задачи на построение
77
а) Измерьте диаметр окружности с
центром в точке В. Чему равен ее
радиус?
б) Какие точки лежат на данной
окружности и какие принадлежат
дуге АМС1
в) Как называется отрезок AMI
г) Проведите хорду через точки Н
и В. Как называется такая хорда?
Ответ.
а) Диаметр окружности равен см, радиус
б) На окружности лежат точки
АМС — точки
в) Отрезок AM называется
г) Самая большая хорда проходит через
и называется
Н
см.
на дуге
окружности
78
Докажите, что диаметр
окружности, перпендикулярный к хорде,
делит эту хорду пополам.
Доказательство.
1)АО= (радиусы окружности),
следовательно, Л АОВ —
2) По условию CD±AB, т.е.
ОНА , значит, ОН —
треугольника АОВ.
3) Итак, Л АОВ — ,
ОН — его , а поэтому и
(свойство
равнобедренного треугольника), т. е. АН =
32

79
Постройте луч ОС так, чтобы луч
ОА был биссектрисой угла ВОС.
Решение.
1) Проведем окружность
произвольного радиуса с центром О. Она
пересечет лучи ОА и ОВ в точках
А и в,.
2) Проведем окружность радиуса
АХВХ с центром Av Она пересечет
первую окружность в точках С и
3) Проведем луч ОС. Докажем,
что луч ОС искомый.
Действительно, AOAJi^ по трем
, поэтому Z.AOB =
= /_.
, т. е. луч ОА —
_ угла ВОС.
80
Отложите от данного луча АВ
угол, равный 45°.
Решение.
1) Отложим от луча АВ прямой
угол ВАС, для чего построим
прямую АС,
к прямой АВ.
2) Построим биссектрису AM угла
Угол ВАМ искомый, так как
АВАМ= V
= 45°.
81
Постройте высоты АН и ВК
треугольника ABC.
33

82
Постройте медиану ВМ данного
треугольника ABC.
Решение. Построим середину
стороны — точку М. Проведем
отрезок Отрезок ВМ искомый,
он является
треугольника ABC.
83
Постройте биссектрису АЕ
треугольника ABC и биссектрису угла
CAT, смежного с углом А
треугольника.

Глава III
Параллельные прямые
Признаки параллельности
двух прямых
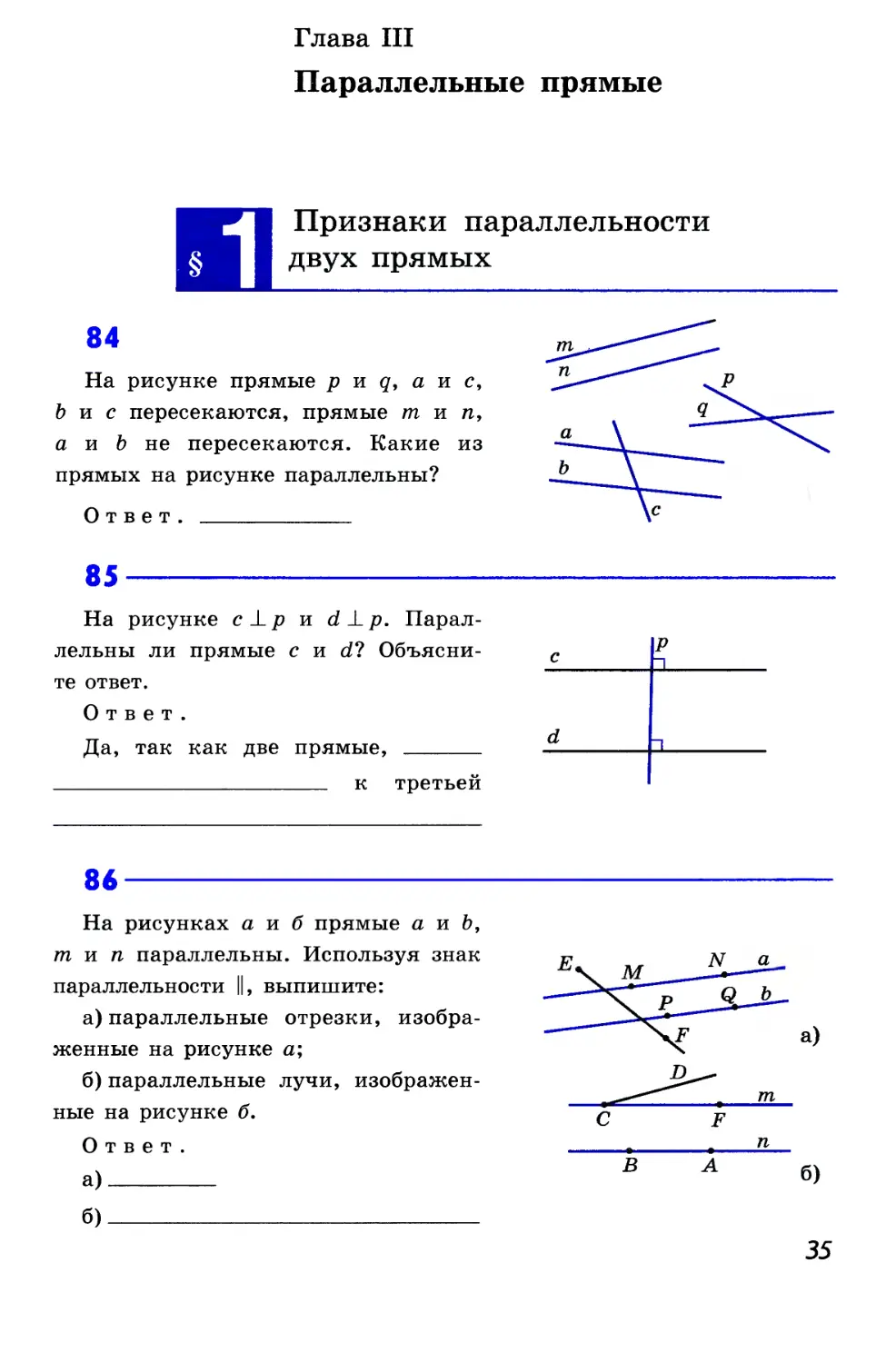
84
На рисунке прямые р и q, а и с,
Ъ и с пересекаются, прямые тип,
а и Ъ не пересекаются. Какие из
прямых на рисунке параллельны?
Ответ.
85
На рисунке с±р и d_Lp.
Параллельны ли прямые end?
Объясните ответ.
Ответ.
Да, так как две прямые,
к третьей
86
На рисунках а и б прямые а и Ь,
тип параллельны. Используя знак
параллельности ||, выпишите:
а) параллельные отрезки,
изображенные на рисунке а;
б) параллельные лучи,
изображенные на рисунке б.
Ответ,
а)
б)
В А
т
п
35

87
Какая прямая на рисунке
является секущей по отношению к двум
другим прямым?
Ответ.
Прямая а — секущая по
отношению к прямым бис; прямая Ь —
; прямая с —
88
На рисунке прямые тип
пересечены секущей р. Из восьми
образовавшихся углов, обозначенных
цифрами, выпишите все пары углов:
а) накрест лежащих;
б) односторонних;
в) соответственных.
Ответ.
a) Z3 и Z5;
б)
в)
89
На рисунке прямые AF и AM
пересечены секущей DE в точках В и
С. Назовите угол, который
составляет с углом ABC пару углов:
а) односторонних;
б) накрест лежащих;
в) соответственных.
Ответ.
а)
б)
в)
36
п
2\1

90
На рисунке
a) Z.4 =
= zL5. Докажите, что:
Доказательство.
а) Z.4 = Z.6, так как эти углы
смежные с равными углами 3 и 5;
б) Z.1 = Z.5, так как
в) Z3 + /-6 = 180°, так как
а \<
Теорема. Если при
пересечении двух прямых секущей накрест
лежащие углы , то
прямые
Дано: прямые а и 6 и их
секущая АВ9 углы 1 и 2 накрест
лежащие, zll = ZL2 (рисунок а).
Доказать: а \\ Ь.
Доказательство. Если углы
1 и 2 прямые, то a LAB, Ъ ±АВ,
поэтому а || Ь. Рассмотрим случай,
когда углы 1 и 2 не прямые. На
рисунке б точка О — середина
отрезка АВ, ОНА. а, ВНг=АН.
1)АОНА = АОН1В по
поэтому ZL3 = Z4 и
2) Из равенства углов 3 и 4 следует, что точка Нх лежит на
продолжении луча ОН, т. е. точки Н, О и Нх лежат
3) Из равенства углов 5 и 6 следует, что /-6 =
Х Ь.
4) Итак, прямые а и Ъ к прямой
поэтому они . Теорема доказана.
т. е.
37

92
На рисунке Z.l = 47°, Z.2 = 133°.
Докажите, что d \\ e.
Доказательство.
1) Z. 3 = 180° - = ,
т.е. Z1
2) Равные углы 1 и 3 —
, поэтому d || е.
93
На рисунке MN = NPy PF = FE.
Докажите, что MN \\ FE .
Доказательство.
1) /Л = Z.2 и zL3 = Z4, так как в
равнобедренном треугольнике
так как эти углы
. Следователь-
М<
4 —
но, Z.1 = Z2 = Z.3 = Z4.
3) Равные углы 1 и
при пересечении
прямых MN и F22 секущей ,
поэтому MN || FE .
94
На рисунке MN = PQ, MQ = PN.
Докажите, что MQ \\ PN, MN \\ PQ.
Доказательство.
1) AMNP = APQM по
следовательно, /l± = Z.z
2) Равные углы 1 и 2 —
прямых
поэтому MQ
3) Равные углы 3 и 4 —
при пересечении
_ секущей ,
, поэтому MN || PQ.
38

95
На рисунке Z_l = Z.2, DN = DF.
Докажите, что MN \\ DF.
Доказательство.
1) ADFN — ,
поэтому /- = Z , а так как ZL2 =
= ZL по условию, то zL3 = Z.I.
2) Равные углы 1 и 3 —
прямых
поэтому MN
при пересечении
секущей ,
М
D
96
Теорема. Если при
пересечении двух прямых секущей
соответственные углы , то
прямые
Дано: прямые а и 6 и их
секущая с, углы 1 и 2 соответственные,
Доказать: а\\ Ь.
Доказательство.
1) Z.1 = Z.2 по
, Z.2 = Z13, так как эти углы
, следовательно, Z.1 = Z.3.
2) Равные углы 1 и 3 —
, поэтому а || Ъ. Теорема доказана.
97
На рисунке /_1 = 125°, Z.2 = 55е
Докажите, что k \\ f.
Доказательство.
39

98
На рисунке /Л = 70°, A.DEF = 140°,
луч ЕМ — биссектриса угла DEF.
Докажите, что CD || ЕМ.
Доказательство.
1) Z.2 = 70°, так как
D
2) Z.1
= 70е
эти углы —
_ при пере-
и се-
Е
сечении прямых
кущей , поэтому CD || ЕМ.
99
На рисунке /_1 = 38°, Z2 = 71°,
луч РМ — биссектриса угла EPN.
Докажите, что РЕ II MN.
Доказательство.
1) AEPN = 2 -Z.2 = 142°, так как
2)/. EPN
/.!=.
= , т. е. сумма односторонних
углов ЕРЛГ и 1, образованных при
пересечении прямых и
секущей , равна
Поэтому РЕ || MN.
Е
100
На рисунке точка Q — середина
отрезков CD и EF. Докажите, что
ЕС || DF.
Доказательство.
1)ACEQ = ADFQ по
,
следовательно, углы 1 и равны.
2) Равные углы и —
, поэтому ЕС || DF.
40

101
На рисунке MQ = NPy /_1 = Z2.
Докажите, что МЛ^ || PQ.
Доказательство.
102
На рисунке AB = DE, BC = EF,
AD = CF.
Докажите, что АВ \\ DE.
Доказательство.
l)AC = DF, так как
Е
2)AABC =
по
следовательно, /.ВАС = /LEDF, а эти
углы
, поэтому АВ || DE.
юз
С помощью чертежного
угольника и линейки проведите через
точку М прямую, параллельную данной
прямой т.
М
т
41

104
С помощью циркуля и линейки
постройте прямую DE, параллельную
данной прямой MF.
Указание. Постройте угол
PDE, равный углу FPD, так, чтобы
углы PDE и FPD были накрест
лежащими при пересечении прямых
MF и DE секущей CD.
М
Аксиома параллельных прямых
105
На рисунке BD || АС, прямые АЕ
и АС не совпадают. Докажите, что
прямая АЕ пересекает прямую BD.
Доказательство. Прямые
АС и BD параллельны по условию,
прямая АЕ
прямую АС, поэтому, согласно
следствию 1° из аксиомы параллельных
прямых, прямая АЕ
и прямую BD.
106
Прямые а, 6 и с пересечены
секущей d; а || 6, Zl = 54°, Z2 = 126°.
Докажите, что Ъ || с.
Доказательство.
1) а || с, так как zll + zL2 = ,
а углы 1 и 2 при
пересечении прямых и
секущей
42

2) Итак, а || с и а\\Ъ (по
_), поэтому, согласно
следствию 2° из аксиомы параллельных прямых, прямые и
параллельны.
107
На рисунке Z. 3 = Z. 4 = 138°, Z5 =
= 42°. Какие из прямых т, п и р
являются параллельными?
Решение.
1) /-2 = ZL4, так как эти углы
, Z.3 = Z.4 по
, поэтому zL2 = zl
Равные углы 2 и 3 —
при пересечении прямых
и секущей , поэтому т \\ п.
2) Углы 1 и 5 , поэтому /_1 = 180° - Z. =
= , а так как ZL3 = по условию, то Z_1 = Z_3.
Равные углы 1 и 3 — при
пересечении прямых и секущей , поэтому т \\ р.
3) m || /г и m || р, поэтому, согласно следствию 2° из аксиомы
параллельных прямых, п || р.
Ответ.
108
На рисунке АВ || NC, точка Б
середина отрезков DC и PQ.
Докажите, что АВ \\ MQ.
Доказательство.
по
м
D
Q
2) Из равенства треугольников ВСР и BDQ следует равенство
углов 1 и 2, а эти углы — при
пересечении прямых и секущей , поэтому
прямые NC и параллельны.
3) Итак, АВ || NC, NC
, следовательно, АВ \\ MQ.
43

109
Теорема. Если две
ны секущей,
углы
прямые пересече-
то накрест лежащие
а
Дано: а || 6, MN — секущая,
углы 1 и 2 накрест лежащие.
Доказать: zll = zL2.
Доказательство.
Допустим, что zll ^ ZL2.
1) Построим угол NMP, равный углу 2, как показано на
рисунке. Так как Zl ^ ZL2, то прямые МР и а не совпадают.
Равные углы NMP и 2 — при
пересечении прямых МР и Ъ секущей MN, поэтому || 6.
2) Мы получили, что через точку М проходят две прямые:
а и , параллельные прямой 6. Но это противоречит
Значит, наше допущение
доказана.
но
и /Л = Z2. Теорема
На рисунке а || 6, с — секущая,
zL4 + ZL6 = 78°. Найдите все углы,
обозначенные цифрами.
Решение.
1) По условию Z.4 +Z.6 = 78°, а эти
углы
поэтому Z4 Z6 =
2) zL2 = Z.4, zL8 = Z6, так как эти Ь
углы ,
поэтому /-2 = и /.8 =
так как
3 и Z.4, Z.5 и Z.6 —
4)zLl = zL3 и Z7 = zl5, так как эти углы
Ответ.
44

Ill
На рисунке т \\ п9 р — секущая,
угол 1 в три раза больше угла 2.
Найдите ZL3.
Решение.
так как эти углы
, следовательно, угол 3 в
три раза больше угла 2.
2) Углы 2 и 3 —
поэтому их сумма равна , т. е.
Z.2 + 3 • /.2 = , откуда Z.2 = ,
а Z.3 =
Ответ.
1.3 =
т
п
112
На рисунке MN \\ PQ, АВ —
секущая, угол 1 на 110° больше угла 2.
Найдите ZL3.
Решение.
1) Zl = zL3, так как
, поэтому угол 3
на 110° больше угла 2, т.е. ZL3 =
и /_2 —
при пересечении
прямых MN и PQ
секущей АВ, а потому ZL3 + /-2 =
3) Итак, Z.2 +110°+zl2= ,
откуда /-2 = , следовательно,
Z3 = Z.2 + =
Ответ.
45

113
На рисунке треугольник MNP
прямоугольный, Z.N = 90°, PF \\ MN,
Найдите Z.MPN и Z.M.
Решение.
1) PN1.PF, так как прямая PN,
перпендикулярная к одной из
параллельных прямых MN и PF,
перпендикулярна и к другой, поэтому
Z.FPN =
2) Z.MPN = Z.FPN - Z. = 90° -
3) Z.M Z.MPF = 42°, так как
М\
N
Ответ.
Z.MPN =.
114
На рисунке MN \\ CD, MN = MD.
Докажите, что DN — биссектриса
угла D.
Доказательство.
1)zL1 = zL2, так как
2) Z.2 = ZL3, так как эти углы
М
N
Е
3)Итак, Z.l = Z.2 и Z.2 = Z3,
поэтому zl = zl , т. е. луч DN —
биссектриса угла D.
46

115
На рисунке DM \\ СЕ, луч DE —
биссектриса угла CDM, Z.4 = 108°.
Найдите углы треугольника CDE.
Решение.
D М
1) Z.CDM = Z4 = 108°, так как
3)zl3 = /Lb = 54°, так как
4) Z.2 = 180° — Z4 = , так как
Ответ. /-С = , /-D =
Z.E =
С Е
2) /Л = £.Ь = 54°, так как

Глава IV
Соотношения между сторонами
и углами треугольника
EL
Сумма углов треугольника
116
В равнобедренном треугольнике MNP с основанием МР
Z.M = 43°. Найдите углы N и Р.
Решение.
1) Z.P =/_
, поэтому ZP =
2) L.M + ZP + Z.N = по теореме о
, поэтому /-N = -
Ответ.
117
На рисунке треугольник ABC
равнобедренный с основанием АС,
Z.DAC = 117°. Найдите углы
треугольника ABC.
Решение.
1)ADAC и /.ВАС —
углы, поэтому ABAC = - Z-DAC =
= - 117°=
2) Треугольник ABC
равнобедренный, поэтому /-С = Z. =
3)Так как ZB + ZA + Z.C =
(по теореме о
), то Z.B =
Ответ.
48

118
В треугольнике ABC угол С в два раза меньше угла А, а
угол В в три раза больше угла С. Найдите углы треугольника.
Решение. Пусть Z.C = хс', тогда Z.A = 2х°у Z.B = Зх°.
1) /_А+ Z.B + /.С = по теореме о
, т.е. 2х + Зх + х = , 6х = ,
х = , поэтому /-С = 30°.
2) АА = 2х° =
Ответ.
/_А = , АВ = , /.С =
119
В треугольнике ABC угол А на 25° больше угла С, а угол С
в три раза меньше угла В. Найдите углы треугольника.
Решение. Пусть /.С = х°, тогда Z.A = х° + , Z.B = Зх°.
1) /.А + /-В + /-С = по теореме о
, т. е. = ,
= , х = , поэтому /.С = 31°.
2) Z.A = + = , Z.B = 3
Ответ.
/_А = , /LB = , Z.C =
120
В треугольнике MNP отрезок NQ —
биссектриса, ZM=74°, Z3=112°.
Найдите углы N и Р треугольника MNP.
Решение.
1) Угол 3 — внешний угол при
вершине Q треугольника MQN>
поэтому ZL3 = /- + ZL1, откуда
Z.1 = Z.3-Z.M= 112°- = ;
AN = , так как NQ —
2) Z.P = 180°- ( + ) =.
Ответ.
49

121
Найдите углы равнобедренного треугольника, если один из
них равен 72°.
Решение, Рассмотрим два случая.
1) Пусть угол А при основании АС равнобедренного
треугольника ABC равен 72°, тогда Z.C = zl = . Согласно теореме
о Z.B = -2- =
2) Пусть угол Б, противолежащий основанию АС
равнобедренного треугольника ABC, равен 72°, тогда Z.A + Z.C = -
-72° = , а так как Z.A и Z.C — углы,
то Z. А Z.C = : 2 =
Ответ.
или
122
Биссектрисы AD и BE
треугольника ABC пересекаются в точке О,
Z.A=78°, Z.B = 38°. Найдите угол
АОЕ.
Решение.
+
)=
2) Z.AOE —
_, угол
треугольника АОВ, поэтому /LAOE =
= Z. + Z. =
Ответ.
Z.AOE =
123
На рисунке CF — биссектриса
равнобедренного треугольника CDE с
основанием СЕ, /LCFE = 102°.
Найдите углы треугольника CDE.
Решение.
1) Пусть /Л = х°, тогда /.3 = 2х°,
так как
Е
50

2) Z2 + Z.3 + Z.CFE =
куда Зх =
3) Z.D =180° -
Ответ.
по
., поэтому х +2x4-102° =
. Таким образом, /_С = Z.E = 2х° =
, от-
= 9v° =
Z.
-) =
124
На рисунке биссектрисы ME и
треугольника MNP пересекаются в
точке О, /.РОЕ = 52°.
Найдите ZJV.
Решение.
1) /.РОЕ — угол
треугольника МОР, поэтому /.РОЕ =
= /. 4- /. , т. е. /Л 4- /_2 =
2) AN = 180°- (/_М 4- /_Р) = 180°-
- 2 • = 180° - =
Ответ.
/.N =
М
Е
F N
125
Могут ли два внешних угла треугольника при разных его
вершинах быть:
а) острыми;
б) прямыми?
Объясните ответ.
Ответ.
а) Нет, так как тогда треугольник имел бы два тупых угла,
а это невозможно.
б) Нет, так как тогда треугольник
51

126
Могут ли углы при основании равнобедренного
треугольника быть прямыми или тупыми? Объясните ответ.
Ответ.
Нет, так как в треугольнике только один угол может быть
или
127
Может ли угол при основании равнобедренного треугольника
быть равным 93°?
Ответ.
Нет, так как углы при основании равнобедренного
треугольника
128
Найдите углы равнобедренного треугольника, если один из
его углов равен 98°.
Решение. Угол при основании равнобедренного
треугольника равным 98°, так как углы при основании
равнобедренного треугольника острые. Пусть ABC —
равнобедренный треугольник с основанием АС и углом при вершине Б,
равным 98°, тогда АА + АС = - /.В = -98° = ,
а так как углы А и С , то /-А Z.C =
Ответ.
98°, ,
129
Проведите высоту АН
треугольника ABC и укажите катеты и
гипотенузу в треугольниках АВН и АСН.
Ответ.
В треугольнике АВН и
— катеты, — гипотенуза.
В треугольнике АСН
52

Соотношения между сторонами и
углами треугольника
130
а) В треугольнике MNP выполняется следующее соотношение:
MN < NP < РМ. Может ли угол М этого треугольника быть
прямым?
б) В треугольнике CDE выполняется следующее соотношение:
СЕ < DC = DE. Может ли угол D этого треугольника быть
тупым?
Решение.
а) Предположим, что в треугольнике MNP угол М
прямой. Тогда гипотенуза NP прямоугольного треугольника
MNP будет больше катета РМ, что противоречит условию
NP <РМ.
Значит, предположение неверно, и Z.M ^ 90°.
б)
Ответ.
а)
б)
131
Докажите, что в тупоугольном треугольнике сторона,
лежащая против тупого угла, больше каждой из двух других
сторон.
Доказательство. Пусть в треугольнике ABC угол В
тупой, тогда углы А и С острые, поэтому zLB>zLA, /LB> AC.
Следовательно, AC > ВС и АС>АВ, так как в
треугольнике против большего угла
53

132
На рисунке угол В тупой, точка
F лежит на стороне АВ. Докажите,
что АО FC.
Доказательство.
1) Угол AFC — внешний угол
треугольника , поэтому Z.AFC =
= /LB + ABFC, т.е. Z.AFC ZS, а
так как угол В тупой по условию, то
и угол AFC
2) В треугольнике AFC угол AFC
тупой, поэтому Z.AFC Z.A и,
следовательно, АС FC, так как в
треугольнике против большего угла
133
На рисунке MN = NP, точка Q
лежит на стороне МР. Докажите,
что NQ < MN.
Доказательство.
1) /-М /-Р как углы при
основании равнобедренного треугольника
2) Угол NQP — внешний угол
треугольника , поэтому Z.NQP =
М О
т.е. /LNQP Z.M,
а значит, Z.NQP Z.P.
3) В треугольнике NPQ Z.P
Z.NQP, поэтому NQ NP.
Итак, NQ NP, следовательно,
NQ MN.
134
AD — биссектриса треугольника ABC, /LB> Z.C. Докажите,
что DODB.
54

Доказательство.
В треугольнике ABC AC>ABy так как

Поэтому, если на луче АС отложить отрезок АЕ, равный отрезку АВ,
то точка Е будет лежать на отрезке АС (см. рисунок).
1) AABD = AAED по
следовательно, DB = DE и Z3 = Z4.
2)zL5 = zL6, так как эти углы —
смежные с равными углами 3 и 4.
3) zL5 > /-C, так как угол 5 —
внешний угол треугольника ,
следовательно, ZL6 > /-С.
4) В треугольнике DCE Z6 > ZC,
поэтому DC > DE, а так как DE =
= DB, то DC > DB.
135
В равнобедренном треугольнике одна сторона равна 15 см,
а другая — 7 см. Какая из них является основанием?
Решение. Если предположить, что основание равно 15 см,
то сумма двух боковых сторон будет равна см, т. е.
сумма двух сторон будет третьей стороны
треугольника, что противоречит неравенству треугольника.
Ответ.
Основанием является сторона, равная
136
Найдите третью сторону равнобедренного треугольника, если
две его стороны равны 10 см и 20 см.
Решение.
Ответ.
Третья сторона треугольника равна
55

137
Существует ли треугольник со сторонами:
а) 3 см, 4 см, 7 см; б) 2,1 дм, 3 дм, 0,9 дм?
Решение.
а) Если предположить, что треугольник со сторонами 3 см,
4 см, 7 см существует, то сумма двух его сторон (3 см + 4 см)
будет равна третьей стороне (7 см), что противоречит
неравенству треугольника. Значит, такого треугольника не существует.
б)
Ответ, а) ; б).
Прямоугольные треугольники
138
Один из острых углов прямоугольного треугольника на 24°
больше другого. Найдите острые углы треугольника.
Решение. Пусть углы А и В — острые углы
прямоугольного треугольника ABC, тогда Z.A + /LB = .
Предположим, что угол А на 24° больше угла В. Тогда
24°, АА + АВ = (Z. + 24°) + Z.B = ,
откуда АВ= |( -24°)= , a
Ответ. ,
139
Один из острых углов прямоугольного треугольника в 4 раза
меньше другого. Найдите эти углы.
Решение.
Ответ.
56

140
На рисунке треугольник ABC —
прямоугольный с прямым углом С,
СН — высота, /- А = 52°. Найдите
Z.1, £2, /-3.
Решение.
1) Треугольник АСН
прямоугольный с прямым углом , так как
СН — треугольника
ABC у поэтому 1А + /.А = ,
откуда /А = - Z. А = - 52° =
2) Z.1 + /.2 = 90°, так как
, поэтому Z.2 = 90° - Z.1 = .
3) Z.2 + A3 = 90°, так как
-Z.2 =.
Ответ.
поэтому
= 90° -
141
На рисунке CD — высота
прямоугольного треугольника ABC,
проведенная к гипотенузе. Докажите, что
А А = /.BCD.
Доказательство.
1) /-А + Z.B = , так как
2) Углы BCD и В — острые углы
прямоугольного треугольника ,
поэтому /.BCD + /.В =
3) Из 1) и 2) следует, что /.А =
D
57

142
В прямоугольном треугольнике
ABC, изображенном на рисунке, угол
А в два раза меньше угла В, а
гипотенуза АВ равна 18 см. Найдите
катет ВС.
Решение.
1) Углы А и В — острые углы
прямоугольного треугольника ABC,
поэтому /LA + /-B =
2) По условию /-В = 2 • АА, поэтому
откуда /-А =
3) Так как в прямоугольном треугольнике ABC /.A =
то катет ВС, лежащий против этого угла, равен
гипотенузы АВ, т. е. ВС =
Ответ. ВС=
В
/.А + 2 • АА = .
143
На рисунке в равнобедренном
треугольнике ABC с основанием АС
угол В равен 120°, а высота,
проведенная из вершины В, равна 13 см.
Найдите боковую сторону треуголь- A D С
ника ABC.
Решение.
1) В равнобедренном треугольнике ABC углы при основании
, поэтому ZA = Z = |(180°-Z_ ) =
2) Так как в прямоугольном треугольнике ABD угол А равен
, то катет равен гипотенузы АВ,
откуда АВ = 2
см.
Ответ.АВ=
см.
144
На рисунке CD — высота прямоугольного треугольника ABC,
АС = 90°, /.В = 60°, BD = 8 см. Найдите AD.
58

Решение.
1)В прямоугольном
треугольнике BCD ZS = 60°, поэтому Z.BCD =
= и, следовательно, ВС =
= 2- = см.
2) В прямоугольном
треугольнике ABC АА = , поэтому АВ =
= 2- = см.
3)AD=AB - BD =
(см).
Ответ. AD= см.
145
В прямоугольном треугольнике MNP
MP + PN = 27 см. Найдите МР и PN.
Решение.
1) Z.M + Z.P = , откуда АМ=
= 2-
2) По условию МР + PN = 27 см, следовательно,
+ PN = 27 см, откуда PN = см, МР = см.
Ответ. МР = см, PN = см.
= 90°, zLP =
и поэтому МР =
+
146
Гипотенузы МР и NF
прямоугольных треугольников MNP и FPN
пересекаются в точке К, MN = FP.
Докажите, что:
а) треугольник NKP равнобедренный;
Доказательство.
1) AMNP = AFPN по двум (MN = FP по
условию, NP — катет), следовательно, /- MPN = Z.
2) В треугольнике NKP два угла равны: Z. = Z. ,
поэтому треугольник NKP
3)
59

147
На рисунке АВ=АС, DP1.AB, DF1.AC, ВР = CF.
Докажите, что точка D — середина стороны ВС.
Доказательство.
1) Треугольник ABC
равнобедренный с основанием ВС, поэтому
Z. = Z.
2) Прямоугольные треугольники
BPD и CFD по катету
(ВР = CF по условию) и
прилежащему острому углу (Z.S = zL ).
Следовательно, BD = и, значит,
точка D — стороны ВС.
D
148
На рисунке МВ±АВ, МС±АС, МВ = МС. Докажите, что
луч AM — биссектриса угла А.
Доказательство.
ААВМ = ААСМ по
Из равенства этих треугольников
следует, что Z.1 = zl , т. е. луч
AM — угла А.
149
На рисунке точка D — середина стороны ВС
треугольника ABC, DP±AB, DF±AC, DP = DF. Докажите, что
треугольник ABC равнобедренный.
Доказательство.
Л BPD = ACFD по
, следовательно,
Z.B = /L , и поэтому треугольник
ABC
60

Построение треугольника
по трем элементам
150
В треугольнике АВС
выполняются условия: АВ = ВС= 20 см, ААВС =
= 120°.
Найдите расстояние от вершины
В до прямой АС.
Решение. Пусть ВН± АС (см.
рисунок), тогда длина
перпендикуляра ВН — расстояние от точки В
до прямой АС. В прямоугольном
треугольнике ВНС Z.C = 30°, так
как
Следовательно,
=fBC =
Ответ.
151
На рисунке BD — биссектриса
прямоугольного треугольника АВС
с прямым углом С. Докажите, что
точка D равноудалена от прямых ВС
и АВ.
Доказательство.
Проведем из точки D перпендикуляр DF
к стороне АВ (см. рисунок).
Прямоугольные треугольники BCD и BFD
равны по
. Отсюда следует,
что DC = , т. е. расстояния от
D
точки D до прямых ВС и АВ равны.

152
Докажите, что в равнобедренном
треугольнике середина основания
равноудалена от боковых сторон
(сделайте чертеж).
Доказательство.
153
На рисунке CF — биссектриса
треугольника CDE, DH — высота, Z.C =
= 60°, СО = 12 см. Найдите
расстояния от точки О до прямых СЕ и CD.
Решение.
Н
Е
Ответ.
154
На рисунке т || п. Расстояние от
точки М до прямой т равно 3,8 см,
а до прямой п — 12,2 см. Найдите
расстояние между прямыми тип.
Решение.
М
т
п
Ответ.
62

155
На рисунке АВ \\ CD, CB = 24 см,
/-BCD = 30°. Найдите расстояние
между прямыми АВ и CD.
Решение.
Ответ.
156
Постройте треугольник по стороне, прилежащему к ней углу
и биссектрисе треугольника, проведенной из вершины этого
угла. (Задача 286 учебника.)
Решение. Даны отрезки PXQV P2Q2 и угол hk (рисунок а).
Требуется построить треугольник ABC, у которого одна из
сторон, например АС, равна данному отрезку PXQV угол А
равен данному углу hk, а биссектриса AD этого треугольника
равна данному отрезку P2Qr
Построение (рисунок б). Pi Qi
1) Построим угол XAY, равный Р2 9г
данному углу hk.
2) На луче AY отложим отрезок
AC, равный данному отрезку РгЯг.
3) Построим биссектрису AF угла
XAY.
4) На луче AF отложим отрезок
AD, равный данному отрезку P2Q2-
5) Искомая вершина В — точка
пересечения луча АХ с прямой CD.
Построенный треугольник ABC
удовлетворяет всем условиям задачи:
AC = PlQv /_A = /-hk, AD = P2Q2, где
AD — биссектриса треугольника ABC.
а)
63

157
Постройте треугольник по двум
сторонам и медиане, проведенной к
одной из этих сторон.
Решение. Даны отрезки PXQV
P2Q2y P3Q3 (рисунок а). Требуется
построить треугольник ABC, у
которого одна из сторон, например АВ,
равна данному отрезку PXQV еще
одна сторона, например АС, равна
данному отрезку P2Q2, а медиана,
проведенная к одной из этих сторон,
например ВМ, равна данному
отрезку PSQS (рисунок б).
Построение.
1) Проведем прямую а и отметим
на ней точку А (рисунок в).
2)
а)
б)
а
в)

ОГЛАВЛЕНИЕ
Глава I. Начальные геометрические сведения
§1. Прямая и отрезок 3
§2. Луч и угол 5
§3. Сравнение отрезков и углов 8
§4. Измерение отрезков 11
§5. Измерение углов 14
§6. Перпендикулярные прямые 16
Глава II. Треугольники
§1. Первый признак равенства треугольников 20
§2. Медианы, биссектрисы и высоты треугольника 24
§3. Второй и третий признаки равенства треугольников 29
§4. Задачи на построение 32
Глава III. Параллельные прямые
§1. Признаки параллельности двух прямых 35
§2. Аксиома параллельных прямых 42
Глава IV. Соотношения между сторонами и углами
треугольника
§1. Сумма углов треугольника 48
§2. Соотношения между сторонами и углами треугольника 53
§3. Прямоугольные треугольники 56
§4. Построение треугольника по трем элементам 61