Author: Половко А.М. Маликов И.М. Жигарев А.Н. Зарудный В.И.
Tags: электротехника задачи по теории надежности
Year: 1972
Text
СБОРНИК
ЗАДАЧ
ПО ТЕОРИИ
НАДЕЖНОСТИ
СБОРНИК ЗАДАЧ
ПО ТЕОРИИ НАДЕЖНОСТИ
Под редакцией
А. М. ПОЛОВКО и И. М. МАЛИКОВА
МОСКВА
«СОВЕТСКОЕ РАДИО»
1972
УДК 621.3.019.076
Сборник задач по теории надежности. Под ред. А. М. П о-
ловко и И. М. Маликова. М„ Изд-во «Советское радио»,
1972, 408 стр., т. 25 000 экз., ц. 1 р. 44 к.
Авторы: А. М. Половко, И. М. Маликов, А. Н. Жи-
гарев, В. И. Зарудный.
«Сборник задач по теории надежности» содержит задачи по
всем основным разделам теории надежности. В него включены за-
дачи по расчету надежности невосстанавливаемых и восстанавли-
ваемых изделий при основном и резервном соединении элементов,
а также задачи по оценке надежности изделий по данным об их
отказах, полученным по результатам испытаний или эксплуатации.
В каждой главе приведены краткие сведения из теории надежности,
иллюстрируемые типовыми примерами, а также большое число задач
с ответами. В отдельных случаях даны краткие указания, позволяю-
щие читателю найти наиболее простой путь решения. В сборнике
помещены как простые задачи, полезные читателю при первоначаль-
ном изучении теории надежности, так и сложные, решения которых
будет способствовать углублению знаний теории и выработки прак-
тических навыков.
Сборник задач рассчитан на широкий круг инженеров и науч-
ных работников, занятых решением проблемы надежности техниче-
ских устройств различного назначения. Он также предназначен для
студентов высших и средних технических учебных заведений.
108 табл. 116 рис., библ. '20 назв.
Авторы
А М. ПОЛОВКО, II. М. МАЛИКОВ, А. Н. ЖИГАРЕВ, В. И. ЗАРУДНЫЙ
3-3-14
58-72
ПРЕДИСЛОВИЕ
Наилучшим методом изучения теории является реше-
ние практических задач. Между т»м в отечественной и
зарубежной литературе еще нет задачника по теории
надежности — науке, имеющей большое практическое
значение.
Авторы решили восполнить этот пробел и составили
746 задач по основным разделам теории надежности.
Для облегчения решения задач приведены основные
сведения из теории, расчетные формулы, вспомогатель-
ные таблицы и графики, а также 119 типовых примеров
с решениями. К задачам приводятся ответы, а иногда
также указания, позволяющие читателю, найти наиболее
рациональный путь решения задачи.
Книга содержит пять глав. В каждой главе три па-
раграфа. В первом из них даются сведения из теории и
расчетные формулы, во втором -типовые примеры с ре-
шениями, а в третьем — задачи с ответами. Числовые
ответы являются приближенными, как правило, получен-
ными при расчетах с помощью логарифмической линейки
и таблиц, приведенных в приложениях к сборнику за-
дач.
Цель «Сборника задач по теории надежности» — по-
мочь заинтересованному читателю изучить теорию на-
дежности и приобрести навыки применения ее результа-
тов к решению различных прикладных вопросов. Поэто-
му при подборе задач и методов их решения основное
внимание было обращено на прикладное содержание
книги. Решение примеров, формулировка задач и описа-
ние способов их решения осуществлены по методикам,
применяемым в промышленных предприятиях, конструк-
торских бюро и н аучно-иоследовательских институтах.
Книга рассчитана на широкий круг инженеров, зани-
мающихся проектированием, созданием и эксплуатацией
различных технических устройств. Она также будет по-
лезной студентам высших и средних технических учебных
заведений. Так как в настоящее время учебные програм-
мы различных учебных заведений существенно отлича-
" ; 3
ются по объему й содержанию, даже дЛя одинаковых
специальностей, то выбор конкретных задач для студен-
тов лежит на обязанностях преподавателей.
В книге помещены задачи различной трудности — от
простых до весьма сложных. Простые задачи могут ре-
шаться студентами техникумов и вузов при первоначаль-
ном изучении теории надежности. К простым задачам
относятся задачи первой и второй глав, за исключением
тех, в которых используются неэкспоненциальные законы
распределения отказов и преобразование Лапласа.
Сложные задачи, приведенные в третьей и четвертой гла-
вах, рассчитаны на читателя, владеющего основами тео-
рии надежности в объеме известных книг [1—17]. Задачи
пятой главы не трудны. Однако они требуют знания ма-
тематической статистики, которая в необходимом объеме
в ряде вузов не изучается.
В «Сборнике задач по теории надежности» имеются
трудные и весьма трудные задачи. К числу таких задач
относятся задачи, в которых требуется учитывать после-
действия отказов, а также задачи с временной избыточ-
ностью.
Задачник, конечно, не охватывает всех разделов тео-
рии надежности. В нем не содержатся оптимальные за-
дачи, задачи контроля и технической диагностики, оцен-
ки надежности систем по результатам испытания ее ком-
понентов.
Здесь также не описаны и не применяются логикове-
роятностные методы и методы статистического моделиро-
вания.
Сборник задач преследует учебные цели. Поэтому
примеры и задачи носят гипотетический характер.
В книге по просьбе издательства используется терми-
нология ГОСТа 13377—67. Однако авторы считают не-
удачными термины «интенсивность отказов» и «параметр
потока отказов». Называть характеристику 7(0 интен-
сивностью отказов не следовало бы, так как 7(0 харак-
теризует поведение изделия до первого отказа и при ее
получении никакого потока отказов, который можно ха-
рактеризовать интенсивностью потока, нет. Другое дело,
что k(t) численно равна интенсивности потока в частном
случае, когда поток отказов простейший.
Невосстанавливаемая система не допускает отказов,
но всегда имеется некоторая вероятность, отличная от
единицы, того, что в изделии возникнет отказ. Наиболее
4
удачным для Л>(/) был бы термин «опасность возникно-
вения отказа» или просто «опасность отказа». Тогда
ю(0 целесообразно называть не параметром потока,
а интенсивностью отказов, так как a(t) является харак-
теристикой потока отказов восстанавливаемой системы
и совпадает с понятием интенсивности потока в теории
массового обслуживания.
В ГОСТе 13377—67 не отражена плотность распреде-
ления .времени до отказа. Эта характеристика случайной
величины — времени исправной работы — является коли-
чественной характеристикой надежности. По мнению
авторов, ее было бы целесообразно называть частотой
отказов.
Авторы благодарны всем, кто способствовал изданию
настоящего сборника задач, и будут признательны ли-
цам, приславшим замечания о всех недостатках, имею-
щихся в книге.
Особую благодарность мы выносим рецензентам за-
дачника профессорам И. А. Рябинину и Н. А. Шишон-
ку, чьи советы помогли улучшить первоначальную ре-
дакцию, а в ряде случаев избежать неточностей и даже
ошибок.
Авторы
ГЛАВА ПЕРВАЯ
КОЛИЧЕСТВЕННЫЕ ХАРАКТЕРИСТИКИ
НАДЕЖНОСТИ
§ 1.1. КРИТЕРИИ И КОЛИЧЕСТВЕННЫЕ
ХАРАКТЕРИСТИКИ НАДЕЖНОСТИ
Критерием надежности назовем признак, мерило, по
которому оценивается надежность различных изделий.
К числу наиболее широко применяемых критериев
надежности относятся:
—• вероятность безотказной работы в течение опреде-
ленного времени
: —средняя наработка до первого отказа Тср;
1 —наработка на отказ tcp;
— частота отказов а(/);
— • интенсивность отказов Z)(0;
— параметр потока отказов и(/);
— функция готовности Кг(0;
— коэффициент готовности Кг.
\ Характеристикой надежности будем называть количе-
ственное значение критерия надежности конкретного из-
! делил.
Выбор количественных характеристик надежности за-
висит от вида изделия.
Основные критерии надежности можно разбить на две
группы:
— критерии, характеризующие надежность невосста-
навливаемых изделий;
— критерии, характеризующие надежность восстанав-
ливаемых изделий.
Невосстанавливаемыми называются такие изделия,
которые в процессе выполнения своих функций не допу-
скают ремонта. Если происходит отказ такого изделия,
то выполняемая операция будет сорвана и ее необходи-
мо начинать вновь в том случае, если возможно устра-
6
иение отказа. К таким изделиям относятся как изделия
однократного действия (ракеты, управляемые снаряды,
искусственные спутники Земли, усилители системы под-
водной межконтинентальной связи и т. п.), так и изделия
многократного действия (некоторые системы навигацион-
ного комплекса судового оборудования, системы ПВО,
системы управления воздушным движением, системы уп-
Рис. 1.1. Временной график работы невосстанавливаемых и восста-
навливаемых изделий:
а — изделия невосстанавливаемые — время непрерывной работы, Н. О. —
начало операции, К. О. — конец операции); б — изделия восстанавливаемые
(?р — время исправной работы, — время вынужденного простоя).
равления химическими, металлургическими и другими
ответственными производственными процессами и т. д.).
Восстанавливаемыми называются такие изделия, ко-
торые в процессе выполнения своих функций допускают
ремонт. Если произойдет отказ такого изделия, то он вы-
зовет прекращение функционирования изделия только на
j период устранения отказа. К таким изделиям относятся:
телевизор, агрегат питания, станок, автомобиль, трактор
I и т. п.
I На рис. 1.1 представлен временной график работы не-
i восстанавливаемых и восстанавливаемых изделий.
! 1. КРИТЕРИИ НАДЕЖНОСТИ НЕВОССТАНАВЛИВАЕМЫХ
S ИЗДЕЛИИ
Рассмотрим следующую модель испытаний.
Пусть на испытании находится No изделий и пусть
испытания считаются законченными, если все они •отка-
зали. Причем вместо отказавших образцов отремонти-
рованные или новые не ставятся. Тогда критериями на-
дежности данных изделий являются:
— вероятность безотказной работы
— частота отказов ШЦ);
7
•— интенсивность отказов Z(0;
— средняя наработка до первого отказа Т1Г.
Вероятностью безотказной работы называется вероят-
ность того, что при определенных условиях эксплуатации
в заданном интервале времени или в 'пределах заданной
„наработки не произойдет ин одного отказа.
Согласно определению
P(t)=P(T>t), (1.1)
где t — время, в течение которого определяется вероят-
ность безотказной работы; Т — время работы изделия от
его включения до первого отказа.
Вероятность безотказной работы по статистическим
данным об отказах оценивается выражением
(1.2)
где No — число изделий в начале испытания; n(t) — чис-
ло отказавших изделий за время t; P(f) —статистиче-
ская оценка вероятности безотказной работы. При боль-
шом числе изделий No статистическая оценка P(t) прак-
тически совпадает с вероятностью безотказной работы
P(t). На практике иногда более удобной характеристи-
кой является вероятность отказа Q(t).
Вероятностью отказа называется вероятность того,
что при определенных условиях эксплуатации в заданном
интервале времени возникнет хотя бы один отказ. Отказ
и безотказная работа являются событиями несовмест-
ными и противоположными, поэтому
Q(t)=P(T^t), Q(t) =n(t)/No, Q(t) = l—P(t). (1.3)
Частотой отказов называется отношение числа отка-
завших изделий в единицу времени к первоначальному
числу испытываемых изделий при условии, что все вы-
шедшие из ст’роя изделия не восстанавливаются.
Согласно определению
£а(0=п(Л0МШ (1-4)
где н(Д£) —число отказавших образцов в интервале вре-
мени от t—kt/2 до t+lNt/2.
Г~~ Частота отказов есть плотность вероятности (или за-
j кон распределения) времени работы изделия до первого
I 8
отказа. Поэтому
t
a(t) = — Pf(t)=Q'(f), Q(t)=^a(t)dt,
о
t
P(/)=l — ^a(t)dt.
6
(1-5)
Интенсивностью отказов называется отношение числа
отказавших изделий в единицу времени к среднему чис-
\ лу изделий, исправно работающих в данный отрезок вре-
i мени.
L _ Согласно определению
У’ = (1.6)
где Ncp=‘(Ni + Ni+i)l2 — среднее число исправно рабо-
тающих изделий в интервале A/; Ni— число изделий, ис-
правно работающих в начале интервала At; Ni+l — число
изделий исправно работающих в конце интервала А/.
Выражение (1.6) есть статистическое определение ин.
тенсивности отказов. Вероятностная оценка этой харак-
теристики находится из выражения
K(t)=a(t)/P(t). (1.7)
Интенсивность отказов и вероятность безотказной ра-
боты связаны между собой зависимостью
о
Р(0=е • (1.8)
Средней наработкой до первого отказа называется
математическое ожидание времени работы изделия до
отказа.
Как математическое ожидание, Тср вычисляется че-
рез частоту отказов (плотность распределения времени
безотказной работы):
+ 00
М [/] -= Тср == J ta (0 dt.
(1-9)
Так как t положительно и Р(0)=1, а Р(оо) = 0, то
\ о
(1-10) ’
9
По статистическим данным об отказах средняя нара-
ботка до (первого отказа вычисляется по формуле
(No \ /
7ср = IX ] О-В)
\z=i / /
где ti — время безотказной работы t-го образца; No —
число испытуемых образцов.
Как видно из формулы (1.11), для определения сред-
ней наработки до первого отказа необходимо знать мо-
менты выхода из строя всех испытуемых элементов. По-
этому для вычисления Тср пользоваться указанной фор-
мулой неудобно. Имея данные о количестве вышедших
из строя элементов tii в каждом i-м интервале времени,
среднюю наработку до первого отказа лучше определять
из уравнения
(тп \ I
No. (1.12)
j=i JI
В выражении (1.12) tcpi и m находятся ою следую-
щим формулам:
^cpi= (^i-i + ^)/2> m=tk№H,
где ti-i — время начала i-ro интервала; — время конца
i-ro интервала; tk— время, в течение которого вышли из
строя все элементы; islt~ti-4—ti — интервал времени.
При изучении надежности технических устройств наи-
более часто применяются следующие законы распределе-
ния времени безотказной работы: экспоненциальный, усе-
ченный нормальный, Релея, Гамма, Вейбулла, логариф-
мически-норм альный.
В табл. 1.1 (приведены выражения для оценки коли-
чественных характеристик надежности изделий при ука-
занных законах распределения времени их безотказной
работы.
Из выражений для оценки количественных характе-
ристик надежности видно, что все характеристики, кро-
ме средней наработки до первого отказа, являются
функциями времени. На рис. 1.2 приведены типичные
зависимости количественных характеристик надежности
изделий различного назначения от времени.
Рассмотренные критерии надежности позволяют до-
статочно полно оценить надежность невоестанавливае-
мых изделий. Они также позволяют оценить надежность
восстанавливаемых изделий до первого отказа. Наличие
10
Рис. 1.2. Типичные зависимости количественных характеристик на-
дежности от времени:
а — экспоненциальный закон; б — усеченный нормальный закон; е — закон
Релея: г-Гамма-распределение: д — закон Вейбулла; е — логарифмически-
нормальный закон.
11
ТАБЛИЦА I. t
м
Основные соотношения для количественных характеристик надежности при различных законах
распределения времени до отказа
Наименование закона распре- деления Частота отказов (плотность распределения) Вероятность безотказной ра- боты Интенсивность отказов Средняя наработка до первого отказа
Экспоненци- альный Xe~W . е-м ' >=const 1 X
Релея t 2сз ~С __ 2з2 е t в2
Гамма (при k целом) №*~> е_у л° (fe— 1)! й-1 e-vV<^. /=0 х„ (Х^-1 k Xq
IIJII I .!«.! ЙИ1
Наименование закона распре- деления Частота отказов (плотность распределения) Вероятность безотказной ра- боты
Вейбулла 1 А е °'
Усеченный нормальный (t-тр 1 2а’- / т р (—— 3 ]/~2тс \ ° '(*)
Логарифмы- чески-нор- мальный 1 1 2 /=, е о/ у 2л Пп t-у. у 1 ' и. — In t \ , 2 +Ф о ) L. т-гл-д-. - -w 4 1-»- . а...л.
Продолжение таблицы 1.1
Интенсивность отказов
Средняя наработка до пер-
вого отказа
Г
2а*
е
Т?
V 2ticF —
2а»
~ 2
е
(In t—yY*
2.2
о/ /2л
р.— In t \
с
е
dt
О
o.i
нескольких критериев вовсе не означает, что всегда нуж-
но оценивать надежность изделий по всем критериям.
Наиболее Полно надежность изделий характеризуется
частотой отказов a(t). Это объясняется тем, что частота
отказов является плотностью распределения, а поэтому
несет 'в себе всю информацию о случайном явлении —
времени безотказной работы.
Средняя наработка до первого отказа является до-
статочно наглядной характеристикой надежности. Одна-
ко применение этого критерия для оценки надежности
сложной системы ограничено в тех случаях, когда:
— время работы системы гораздо меньше среднего
времени безотказной работы;
— закон распределения времени безотказной работы
не однопараметрический и для достаточно полной оценки
требуются моменты высших порядков;
— система резервированная;
— интенсивность отказов непостоянная;
— время работы отдельных частей сложной системы
разное.
Интенсивность отказов — наиболее удобная характе-
ристика надежности простейших элементов, так как она
позволяет более просто вычислять количественные ха-
рактеристики надежности сложной системы.
Наиболее целесообразным критерием надежности
сложной системы является вероятность безотказной ра-
боты. Это объясняется следующими особенностями веро-
ятности безотказной работы:
— она входит в качестве сомножителя в другие, более
общие характеристики системы, например в эффектив-
ность и стоимость;
— характеризует изменение надежности во времени;
— может быть получена сравнительно просто расчет-
ным путем в процессе проектирования системы и оцене-
на в процессе ее испытания.
2. КРИТЕРИИ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ
ИЗДЕЛИИ
Рассмотрим следующую модель испытания.
Пусть на испытании находится N изделий и пусть от-
казавшие изделия немедленно заменяются исправными
(новыми или отремонтированными). Испытания счита-
ются законченными, если число отказов достигает вели-
14
чины, достаточной для оценки надежности с определен-
ной доверительной вероятностью. Если не учитывать
времени, потребного на восстановление системы, то ко-
личественными характеристиками надежности могут
быть параметр потока отказов «(/) и наработка на от-
каз /ср-
Параметром потока отказов называется отношение
числа отказавших изделий в единицу времени к числу
испытываемых изделий при условии, что все вышедшие
из строя изделия заменяются исправными (новыми или
отремонтированными).
Согласно определению
ш (/) = п (Д/)/(ММ),
(1-13)
где п (А/) —число отказавших образцов в интервале вре-
мени от t—А//2 до Z+IA//2; N — число испытываемых об-
разцов; А/— интервал времени.
Выражение (1.13) является статистическим определе-
нием параметра потока отказов.
Параметр потока отказов и частота отказов для орди-
нарных потоков с ограниченным последействием связаны
интегральным уравнением Вольтерра второго рода
t
= (1.14)
о
По известной a(t) можно найти все количественные
характеристики надежности невосстанавливаемых изде-
лий. Поэтому (1.14) является основным уравнением, свя-
зывающим количественные характеристики надежности
невосстанавливаемых и восстанавливаемых изделий при
мгновенном восстановлении.
Уравнение (1.14) можно записать в операторной
форме:
ш (х) = . —a (s) = т “ Ц (1.15)
' ' 1 —- a (s) ' ' 1 + ы (s) ' '
Соотношения i(1.15) позволяют найти одну характе-
ристику через другую, если существуют преобразования
Лапласа функций a(s) и ы(х) и обратные преобразова-
ния выражений (1.15).
Параметр потока отказов обладает следующими важ-
ными свойствами:
15
1) для любого момента времени независимо от зако-
на распределения времени безотказной работы параметр
потока отказов больше, чем частота отказов, т. е. ы(/)>
>а(0;
2) независимо от вида функции a(f) параметр пото-
ка отказов о>(/) при t—>оо стремится к \/Тср. Это важ-
ное свойство параметра потока отказов означает, что при
длительной эксплуатации ремонтируемого изделия поток
его отказов независимо от закона распределения вре-
мени безотказной работы становится стационарным. Од-
нако это вовсе не означает, что интенсивность отказов
есть величина постоянная;
3) если Х(0—возрастающая функция времени, то
если МО—убывающая функция, то
и(0>М0>а(0;
4) при ?.(Z)^const параметр потока отказов системы
не равен сумме параметров потоков отказов элементов,
т. е.
N
l№c (0 ¥= У,(0- (1-16)
; г=1
Это свойство параметра потока отказов позволяет -
утверждать, что при вычислении количественных харак-
теристик надежности сложной системы нельзя суммиро-
вать имеющиеся в настоящее время значения интенсив-
ностей отказов элементов, полученные по статистиче-
ским данным об отказах изделий в условиях эксплуата-
ции, так как указанные величины являются фактически
параметрами потока отказов;
5) при Х(/) =X=const параметр потока отказов равен
интенсивности отказов & =2i»(0 =&,.
Из рассмотрения свойств интенсивности и параметра
потока отказов видно, что эти характеристики различны.
В настоящее время широко используются статистиче-
ские данные об отказах, полученные в условиях эксплуа-
тации аппаратуры. При этом они часто обрабатываются
таким образом, что приводимые характеристики надеж-
ности являются не интенсивностью отказов, а парамет-
ром потока отказов m(Z). Это вносит ошибки при расче-
тах надежности. В ряде случаев они могут быть значи-
тельными.
Для получения интенсивности отказов элементов из
статистических данных об отказах ремонтируемых систем
необходимо воспользоваться формулой (1.6), для чего
16
необходимо знать предысторию каждого элемента прин-
ципиальной схемы. Это может существенно усложнить
методику сбора статистических данных об отказах. По-
этому целесообразно определять Z(/) по параметру по-
тока отказов а>(£). Методика расчета сводится к следую-
щим вычислительным операциям:
— по статистическим данным об отказах элементов
ремонтируемых изделий и по формуле (1.13) вычисляет-
ся параметр потока отказов и строится гистограмма
ю,(0;
— гистограмма заменяется кривой, которая аппрокси-
мируется уравнением;
— находится преобразование Лапласа иг(«) функции
©г (0;
— по известной соДв) на основании (1.15) записы-
вается преобразование Лапласа щ(х) частоты отказов;
— по известной a;(s) находится обратное преобразо-
вание частоты отказов щ (0 ;
— находится аналитическое выражение для интенсив-
'ности отказов по формуле
2г(/)=аг-(/) / / 1 — |; (Ы7)
I \ о J
— строится график
Если имеется участок, где Ki(t) =X;=const, то посто-
янное значение интенсивности отказов принимается для
оценки вероятности безотказной работы. При этом счи-
тается справедливым экспоненциальный закон надежно-
сти.
Приведенная методика не может быть применена, ес-
ли не удается найти по a(s) обратное преобразование
частоты отказов a(t). В этом случае приходится приме-
нять приближенные методы решения интегрального урав-
нения (1.14). Решение наиболее просто можно получить
сдюмощыо ЭЦВМ.
\ Наработкой на отказ называется среднее значение
^времени между соседними отказами.
Эта характеристика определяется по статистическим
данным об отказах по формуле
где ti — время исправной работы изделия между (i—1)-м
и i-м отказами; п—число отказов за некоторое время t.
2—1086 17
Из формулы (1.18) видно, что в данном случае нара-
ботка на отказ определяется по данным испытаийя-од-
ного образца изделия. Если на испытании находится
N образцов в течение времени t, то наработка на отказ
вычисляется по формуле
^ср —
N
(119)
где — время исправной работы /-го образца изделия
между (i—1)-м и z-м отказом; tij— число отказов за
время t /-го образца.
Наработка на отказ является достаточно наглядной
характеристикой надежности, поэтому она получила ши-
рокое распространение на практике.
Параметр потока отказов и наработка на отказ ха-
рактеризуют надежность ремонтируемого изделия и не
учитывают времени, потребного на его восстановление.
Поэтому они не характеризуют готовности изделия к вы-
полнению своих функций в нужное время. Для этой це-
ли вводятся такие критерии, как коэффициент готовности
и коэффициент вынужденного простоя.
Коэффициентом готовности называется отношение
времени исправной работы к сумме времен исцравной|ра-
боты и вынужденных простоев изделия, взятых за один
и тот же календарный срок. Эта характеристика обозна-
чается Кт-
Согласно данному определению
Kr=Wp+k), (1.20)
где —суммарное время исправной работы изделия;
tn — суммарное время вынужденного простоя.
Времена и tn вычисляются по формулам
(1-21)
где /Рг —время работы изделия между (i—1)-м и г-м
отказом; tn г — время вынужденного простоя после t-ro
отказа; п — число отказов (ремонтов) изделия.
Выражение (1.20) является статистическим определе-
нием коэффициента готовности. Для перехода к вероят-
ностной трактовке величины t# и /п заменяются матема-
18
тическими ожиданиями времени между соседними отка-
зами и времени восстановления соответственно.
Тогда
/<г='М(^+^в) (1-22)
где fap — наработка на отказ; /в—среднее время восста-
новления.
Г~ Коэффициентом вынужденного простоя называется
отношение времени вынужденного простоя к сумме вре-
мен исправной работы и вынужденных простоев изделия,
дззятых за один и тот же календарный срок.
Согласно определению
Kn—'t-a! (^p+'Ai)
(1-23)
или, переходя к средним величинам,
Кп—rfB/ (^ср+'^в) •
(1.24)
Коэффициент готовности и коэффициент вынужденно-
го простоя связаны между собой зависимостью
Кп=1-Кг. (1.25)
При анализе надежности восстанавливаемых систем
обычно коэффициент готовности вычисляют по формуле
Кг=Тср/(7’ср+'М. (1-26)
Формула (1.26) верна только в том случае, если по-
ток отказов простейший, и тогда tcp=TCVl.
Часто коэффициент готовности, вычисленный по фор-
муле (1.26), отождествляют с вероятностью того, что
в любой момент времени восстанавливаемая система
исправна. На самом деле указанные характеристики не-
равноценны и могут быть отождествлены при определен-
ных допущениях.
Действительно, вероятность возникновения отказа ре-
монтируемой системы в начале эксплуатации мала. С ро-
стом времени t эта вероятность возрастает. Это означает,
что вероятность застать систему в исправном состоянии
в начале эксплуатации будет выше, чем по истечении
некоторого времени. Между тем на основании формулы
(1.26) коэффициент готовности не зависит от времени
работы.
2* 19
Для выяснения физического смысла коэффициента го-
товности /Сг запишем формулу для вероятности застать
систему в исправном состоянии. При этом рассмотрим
наиболее простой случай, когда интенсивность отказов н
интенсивность восстановления есть величины постоян-
ные.
Предполагая, что при t = Q система находится в ис-
правном состоянии (7-’(0) = 1), вероятность застать систе-
му в исправном состоянии определяется из выражении
СН-р.) t
Рх {t) = -JL-+ е~
Рг(0 = Яг + (1-Яг)е~
где
__ 1 . 1 . Др
, Р* • , Л г "т । у •
7 ср Гв 'срТЧ
Это выражение устанавливает зависимость между ко-
эффициентом готовности системы и вероятностью застать
ее в исправном состоянии в любой момент времени /.
Из (1.27) видно, что Pr(t)—при t—>оо, т. е.
практически коэффициент готовности имеет смысл веро-
ятности застать изделие в исправном состоянии при уста-
новившемся процессе эксплуатации.
В некоторых случаях критериями надежности восста-
навливаемых систем могут быть также критерии надеж-
ности невосстанавливаемых систем, например: вероят-
ность безотказной работы, частота отказов, средняя на-
работка до первого отказа, интенсивность отказов. Такая
необходимость возникает всегда, когда имеет смысл оце-
нить надежность восстанавливаемой системы до первого
отказа, а также в случае, когда применяется резервиро-
вание с восстановлением отказавших резервных устройств
в процессе работы системы, причем отказ всей резерви-
рованной системы не допускается.
§ 1.2. ТИПОВЫЕ ПРИМЕРЫ И ИХ РЕШЕНИЯ
Задачи, которые встречаются при определении коли-
чественных характеристик надежности, могут быть раз-
биты на следующие группы:
1) определение количественных характеристик на-
дежности по статистическим данным об отказах изде-
лия;
20
2) определение количественных характеристик на-
дежности изделия при известном аналитическом выра-
жении одной какой-либо характеристики.
При решении задач первой группы используются ста-
тистические определения количественных характеристик
надежности, при решении задач второй группы — веро-
ятностные определения характеристик и аналитические
зависимости между ними.
В настоящей главе при определении количественных
характеристик надежности технических устройств по
статистическим данным об их отказах не учитывается до-
стоверность полученных результатов. По этой причине
иногда в примерах и задачах исходные данные о числе
испытуемых образцов и количестве отказов приводятся
без учета требований достоверности получения количест-
венных характеристик надежности. Вопросы достоверно-
сти результатов испытаний рассматриваются в пятой
главе.
Следует иметь в виду, что частота, интенсивность от-
казов и параметр потока отказов, вычисленные по фор-
мулам (1.4), (1.6) и (1.13), являются постоянными в диа-
пазоне интервала времени АС а функции a(t), X(Z),
со(0—ступенчатыми кривыми или гистограммами. Для
удобства изложения в дальнейшем при решении задач на
определение частоты, интенсивности и параметра потока
отказов по статистическим данным об отказах изделий
ответы относятся к середине интервала А/. При этом ре-
зультаты вычислений графически представляются не
в виде гистограмм, а в виде точек, отнесенных к 'Середи-
не интервалов АС и соединенных плавной кривой.
Рассмотрим типовые примеры.
Пример 1.1. Допустим, что на испытание- поставлено
1000 однотипных электронных ламп типа 6Ж4. За
3000 час отказало 80 ламп. Требуется определить вероят-
ность безотказной работы и вероятность отказа элек-
тронных ламп в течение 3000 час.
Решение. По формулам (1.2) и (1.3) определяем
Р (3000) = - =0,92,
С(з«ю)=г1й=-^=о,о8
ИЛИ
(>(3000) = 1— Р (3000) = 1—0,92=0,08.
21
Пример 1.2. На испытание было поставлено 1000 од-
нотипных ламп. За первые 3000 час отказало 80 ламп,
а за интервал времени 3000—4000 час отказало еще
50 ламп. Требуется определить частоту и интенсивность
отказов электронных ламп в промежутке времени 3000—
4000 час.
Решение. По формулам (1,4) и (1,6) находим
M3^=^=Tinnw=5-1'’',i
2(3500) == 1000.(920 + 870J/2 ~ 5.6-10 1 —.
Пример 1.3. На испытание поставлено №=400 изде-
лий. За время #=3000 час отказало п(#)=200 изделий,
за интервал времени Ai#=100 час отказало n(\At) =
= 100 изделий (рис. 1.3). Требуется определить Р(3000),
Р(3100). Р(3050), а(3050) Д(3050).
t-0 t = 3000 час At = 100 час
n(t)-ZOO n(&t)-1OO t
'' j , *£,=200 *1^ = 100
Рис. 1.3. Временной график к примеру 1.3.
Решение. 1. По формуле (1.2) найдем вероятность
безотказной работы:
для #н = 3000 час (начало интервала)
Р (3000)
Nq — п (3000)
№
400 — 200 п _
№оо—=0’5’
для tK = 3100 час (конец интервала)
Р (3100) = =^-^° =0,25.
№ - ' 400
Определим среднее число исправно работающих образ-
цов в интервале At:
Ncp=J5 + A^=2™ + ™=150.
'4^,, Число отказавших^изделий за время # = 3050 час
п (3050) = № — Уср = 400—150 = 250,
22
йяяй» wwsaaed
тогда
р (3050) = - = 4004bd2^° = °’375-
2. По формуле (1.4) определяем частоту отказа:
i"(3o5°> = fW=ToS» =2.5'10-
3. По формуле (1.6) определяем интенсивность отказа
£730'SOI — п ______— fi 7 -1 О '3 —
Z(dUt>U)—• 100 (200 + 100)/2 °’' 1U час'
Интенсивность отказа можно также определить по фор-
муле (1.7):
Z (30501__ «(3050) _ 0,0025 — 6 7-Ю'3 — •
Z(30t>U)— ,0(3050) —0,375 1U час
Пример На испытании находилось No= 1000 об-
разцов перемонтируемой аппаратуры. Число отказов
п(Д/) фиксировалось через каждые 100 час работы (А(=
= 100 час). Данные об отказах приведены в табл. 1.2.
Требуется вычислить количественные характеристики на-
дежности и построить зависимости характеристик ог
времени.
ТАБЛИЦА 1.2
Данные об отказах к примеру 1.4
Д^, час П (Aff) Д^, час « (Aft) Д^, час п (MJ
0—100 50 1000—1100 15 2000—2100 12
100—200 40 1100—1200 14 2100—2200 13
200—300 32 1200—1300 14 2200—2300 12
300—400 25 1300—1400 13 2300—2400 13
400—500 20 1400—1500 14 2400—2500 14
500—600 17 1500—1600 13 2500—2600 16
600—700 16 1600—1700 13 2600—2700 20
700—800 16 1700—1800 13 2700—2800 25
800—900 15 1800—1900 14 2800—2900 30
900—1000 14 1900—2000 12 2900—3000 40
Решение. Аппаратура относится к классу невосста-
навливаемых изделий. Поэтому критериями надежности »
будут P(t), a(/),W(0, Тср.
23
Рис. 1.4 Зависимость Р от t (к примеру 1.4).
Вычислим Р(0- На основании формулы (1.2) имеем
₽(100) = «.-ДОС*» =‘g^=0.95.
Р (200) =!?®=j“= 0,91,
Рис. 1.5. Зависимость а и Л от t (к примеру 1.4)
Для расчета характеристик a(t) и Л(/) применим фор-
мулы (1.4) и (1.6), тогда
а (50)— _____50 —пк in-3 1
U' N^t ~1000-100 10 час'
й(150)=тет=°.4'10-^,
а(295°)-ттао-=о«4.1о-«Х;
2 (5°) ~ AWcp~‘= 100 (1000 + 950)/2 ~0,514’ Ю 3 —,
24
Z(150)— 100(950 + 910)/2 0,43‘10 3 Wc>
2 (2950) — 100 (465 4.425)/2 °’9’10 3 Wc-
Значения P(Z), «(/) и <%(/), вычисленные для всех
\ti, приведены в табл. 1.3, а их зависимости от време-
ни— на рис. 1.4 и 1.5.
_ _ _ ТАБЛИЦА 1.3
Вычисленные значения P(t), a (t) и Ц1) к примеру 1.4
Д/1> час Р(0 а (/), 10“М/»/ас 7(0, 10“М/«ас
0—100 0,950 0,50 0,514
100—200 0,910 0,40 0,430
200—300 0,878 0,32 0,358
300—400 0,853 0,25 0,289
400—500 0,833 0,20 0,238
500—600 0,816 0,17 0,206
600—700 0,800 0,16 0,198
700—800 0,784 0,16 0,202
800—900 0,769 0,15 0,193
900—1000 0,755 0,14 0,184
1000—1100 0,740 0,15 0,200
1100—1200 0,726 0,14 0,191
1200—1300 0,712 0,14 0,195
1300—1400 0,699 0,13 0,184
1400—1500 0,685 0,14 0,202
1500—1600 0,672 0,13 0,192
1600—1700 0,659 0,13 0,195
1700—1800 0,646 0,13 0,200
1800—1900 0,632 0,14 0,220
1900—2000 0,620 0,12 0,192
2000—2100 0,608 0,12 0,195
2100—2200 0,595 0,13 0,217
2200—2300 0,583 0,12 0,204
2300—2400 0,570 0,13 0,225
2400—2500 0,556 0,14 0,248
2500—2600 0,540 0,16 0,290
2600—2700 0,520 0,20 0,376
2700—2800 0,495 0,25 0,490
2800—2900 0,465 0,30 0,624
2900—3000 0,425 0,40 0,900
Следует иметь в виду, что в табл. 1.3 данные Р(/)
приведены для концов интервалов А/г-, а данные для
я (0 и Х(/)—для середины интервалов А/,-. Поэтому
25
определение P(f)_no формуле (1.7) и данным табл. 1.3
не даст значений P(t), указанных в таблице.
Вычислим среднее время безотказной работы, пред-
положив, что на испытании находились только те образ-
цы, которые отказали.
По формуле (1.12), учитывая, что в данном случае
т=Д/А/=3000/100=30 и Л?0=575, имеем
т
гр i~l ___
у ср ~
__ 50-50+ 40-150+ 32-250+... + 30.2850 4-40-2950 _
— 575 —
---1400 час.
Полученное значение средней наработки’ до первого
отказа является заниженным, так как опыт был прекра-
щен после отказа 575 образцов из 1000, поставленных на
испытание.
Пример 1.5. В течение некоторого периода времени
производилось наблюдение за работой одного экземпля-
ра радиолокационной станции. За весь период наблю-
дения было зарегистрировано 15 отказов. До начала на-
блюдения станция проработала 258 час, к концу наблю-
дения наработка станции составила 1233 час. Требуется
определить среднюю наработку -на отказ /Ср-
Решение. 1. Наработка радиолокационной станции
за наблюдаемый период равна
/ = ^ — ^=1233 — 258 = 975 час.
п
2. Принимая £ = 975 час, по формуле (1.18)’нахо-
дим среднюю наработку на отказ:
п
/=1 975
tCD =---= —=-=65 час.
1 п 15
Пример 1.6. Производилось наблюдение за работой
трех экземпляров однотипной аппаратуры. За период на-
блюдения было зафиксировано по первому экземпляру
аппаратуры 6 отказов, по второму и третьему—11 и
26
Ь отказов соответственно. Наработка первого экземпляра
составила 181 час, второго — 329 и третьего — 245 час.
Требуется определить наработку аппаратуары на отказ.
Решение. 1. Определяем суммарную наработку трех
образцов аппаратуры:
Лг щ
h = S S = 181 + 329 4- 245 = 755 час.
J-=l i~\
2. Определяем суммарное количество отказов:
N
= Ju ,li ~ 6 -ф- 11 + 8 = 25 отказов.
/=1
3. Находим среднюю наработку на отказ по форму-
ле (1.19):
Л’ щ
^ = 4^- =1^1 = 30,2^.
2 пз
i=i
Пример 1.7. Система состоит из 5 приборов, причем
отказ любого одного из них ведет к отказу системы. Из-
вестно, что первый прибор отказал 34 раза в течение
952 час. работы, второй—-24 раза в течение 960 час. ра-
боты, а остальные приборы в течение 210 час. работы
отказали 4, 6 и 5 раз соответственно. Требуется опреде-
лить наработку на отказ системы в целом, если справед-
лив экспоненциальный закон надежности для каждого из
пяти приборов.
Решение. Для решения данной задачи воспользуем-
ся следующими соотношениями:
Л'
Яс = Лг- и fcp =
1=1
1. Определим интенсивность отказов для каждого
прибора:
4 = — —0,0357 —, 4 0,025 —,
952 час 2 960 час
г
4 + 6 + 5
210
= 0,0714 —.
27
2. Интенсивность отказов системы будет
N
яс = J и = Я, + + 4- Я3> 4.5 = 0,0357 + 0,025 +
/=;!
+ 0,0714 = 0,1321 —.
‘ час
3. Средняя наработка на отказ системы равна
132Г* -7’57 Ча£-
Пример 1.8. За наблюдаемый период эксплуатации
в аппаратуре было зафиксировано 8 отказов. Время вос-
становления составило: /1=12 мин; /2=23 мин; t3—-
= 15 мин; tt=9 мин; /5=17 мин; te=28 мин; /7 = 25 мин;
/g = 31 мин.
Требуется определить среднее время восстановления
аппаратуры.
Решение:
п
Ё tt
, _t-=i ___12 + 23 + 15 + 9 + 17 + 28 + 25+31 _
— “ 8 —
160 пг.
=-—=20 мин.
8
Пример 1.9. При эксплуатации системы было зарегист-
рировано п=40 отказов. Распределение отказов по груп-
пам элементов и время, затраченное на восстановление,
приведены в табл. 1.4. Необходимо найти величину сред-
него времени восстановления систем.
Решение. Определяем среднее время восстановле-
ния аппаратуры по группам элементов.
Для полупроводниковых приборов
пг 8
(=1 z=jl
Аналогично:
— для резисторов и конденсаторов 76 мин;
— для реле, трансформаторов, дросселей ИЗ мин;
— для ЭВП 50 мин;
— для прочих элементов 120 мин.
28
ТАБЛИЦА 1.4
Количество зарегистрированных отказов по группам
элементов и время, затраченное на восстановление
аппаратуры (к примеру 1.9)
Группа элементов Количество отказов по группе Вес отказов по группе пг пъ " г п Время восста- новления tit мин Суммарное время восста- новления по группе ta, мин
ппп 8 0,2 80 59 110 91 45 43 99 73 600
Резисторы и конденсаторы 10 0,25 61 73 91 58 44 112 82 54 91 94 760
Реле, транс- форматоры, дроссели 4 0,1 102 98 124 128 452
эвп 14 0,35 60 64 56 36 65 44 42 33 32 23 86 75 61 23 700
Прочие эле- менты 4 0,1 125 133 115 107 480
29
Рассчитаем среднее время йосстановления системы по
формуле
т
+. с ^вг^г,
i=l
где tBi — среднее время восстановления элементов z-й
группы; trii-—вес отказов по группам элементов.
Подставляя значения данных в формулу, получим
7В с = 0,2 75+0,25 76 + 0,1 • 113+0,35 • 50+
+ 0,1 120 = 75 мин.
Пример 1.10. Аппаратура имела среднюю наработку
на отказ /<р:=65 час и среднее время восстановления
= 1,25 час. Требуется определить коэффициент готов-
ности.
Решение. По формуле (1.22) имеем
К ~_________—_____1___=_____1___=0 98
Аг + А 1 + <вАср 1 + 0.019 и,эо-
Пример 1.11. Пусть время работы элемента до отказа
подчинено экспоненциальному закону распределения
с параметром 7.=2,5- 10~5 1/час.
Требуется вычислить количественные характеристики
надежности элемента P(t), о(/), 7’<р, если Т=500, 1000,
2000 час.
Решение. Используем формулы для P(t), a(t) и
Тср, приведенные в табл. 1.1.
1. Вычислим вероятность безотказной работы:
п. —X/ — 2,5-10--/
Р (I) = е = е
Используя данные табл. П. 7.14, получим:
Р(500) = e“2,510's’500= е-*’0,26= 0,9875;
Р (1000) = е—2.5-ю-=.1ооо = е- о,о2й = 0,9753;
Р (2000) = е~2,5-ю~5-2ооо _ е-о,о6 = о,9512.
30
2. Вычислим частоту отказа:
a (t) = Я (О Р (0 = 2,5- Ю-’-е-2'510^.
а (500) = 2,5- io-5 - e~2’5 10'5-590 =
= 2,5-10”5-0,9875 = 2,469-10“5 ~
а(1000)==2,5-1О-5-е-2’51о'мооо==
= 2,5-10 ~5-0,9753 = 2,439-10-s
а (2000) = 2,5-1О"5-е“2,5',о’5’2°оо =
= 2,5-IO’6-0,9512 = 2,378-10“5 —•
3. Вычислим среднюю наработку до первого отказа:
Тср = 4^2,5.П)-^^40000 ча£'
Пример 1.12. Пусть время работы элемента до отка-
за'подчинено усеченному нормальному закону с парамет-
рами Т1 = 8000 час,, о = 2000 час. Требуется вычислить
количественные характеристики надежности P(t), a(t),
‘h(t),Tcp для /=4000, 6000, 8000, 10 000 час.
Решение. Воспользуемся формулами для P(t), a(t),
Z(/), Тср, приведенными в табл. 1.1.
1. Вычислим вероятность безотказной работы:
/ 8000--М
F ( о ) F ( 2000 J
P /л — < — —1___________Д.
F (11Д F <4>
( 0 /
По данным табл. П. 7.16 найдем:
F ,8000 — 4000
Р(4000) = J_____2000 1 _^(2)_ 0.97725 _
’ F (4) F (4) 1 ~ ’
/8000 — 6000 \
Р(6°00) ---------С=_.701^0,8413;
/8000 — 8000
Р (8000) = —у 2000____о 5-
' ' F (4) F (4) ’ ’
31
Р (10 000) =
8000— 10 000 X
Fooo j
HP
— F(4) F(4) 0,1687.
График Р (t), построенный по полученным данным, по-
казан на рис. 1.6.
2. Определим частоту отказа:
1
a (t) =---------— e-O-'WzA
Вычисления удобно производить, используя табл. П. 7.17
функции <р(л) = e~~xS/2. В нашем случае л=—
Имея в виду, что F (TJz) = F (8000/2000) = F (4) 1,
найдем a (t) = <? (л)/з. Тогда:
/4000 — Г]
О
о
/4000 — 8000 \
? 2000 )
2000
а (4000) =
у (-2) у (2) 0,05399 ,,) 5 J_-
~ 2000 ~~ 2000 2(00 ’ ’ и час’
f 6000 —8000 \
а (6000) - V I 2000 ' _т 0 — ? 0)_.
оцоиии; — 2000 2000 — 2000 —
^°WoL1 12’Ь1СГГ' — >
2000 час
/8000 — 8000 \
а (8000) = —-__=1121—2:.3989—20 • 10 ~5 — •
(Ноиии; 2000 2000 2000 “ 1и члс’
/ 10 000 — 8000 \
а (10000)=___-___2000______12 1 • 10~5 —
ацииии; 2(Ю0 iz,i w
График a(t), построенный по полученным данным, по-
казан на рис. 1.7.
3. Рассчитаем интенсивность отказов 7(/).
Подставляя найденные значения о(/) и Р(Г) в выра-
жение Z(Z) —a(f)IP(t), определяем:
32
Рис. 1.6. Зависимость Р от I
(к примеру 1.12).
Рис. 1.7. Зависимость а и X от
t (к примеру 1.12).
I(4000)- а М — 2-7- j°~5 2 76• Ю-5 -1-
к (WW) —, р (4000) — 0 97725 Z’/D <МС’
я (6000)=тан- =14,4 1 о 5 —;
' ' Р (6000) 0,8413 час
я (8000) = —-20'10 5 40. io-6 — •
Л(оиии)— р(8000) 0>5 -4U 1U адс,
,/ЩЛЛПТ «0 0 000) __ 12,1-10-* 1
2 (1° 000) = +(10066)------0 Л 587— 76>4’10 5^с-
График Я (/), построенный по полученным данным, при-
веден
4.
на рис. 1.7.
Вычислим среднюю наработку до первого отказа:
Тер = ЛЧ
f(~
2 2
.e-rj/20 —8000 +
2000
8000 \ ’е
F 2000)
= 8000 +
о
2
2000 е~8 оппп ос
+ ==-==- = 8000,26 час.
F (4) К2я
Из графиков и найденных результатов видно, что
данном случае усеченный нормальный закон распреде-
ления близок к нормальному.
В—1086
33
Пример 1.13. Пусть время работы до отказа подчине-
но усеченному нормальному закону распределения с па-
раметрами Л = 8000 час и сг= 1000, 2000, 3000, 4000 час.
Требуется вычислить количественные характеристики на-
дежности Р(/), a(t), Тср для /=4000, 6000, 8000.
10000 час.
Решение. Используя формулы табл. 1.1 и порядок
решения, приведенный в .примере 1.12, сведем найденные
данные в табл. 1.5.
ТАБЛИЦА I.
Вычисленные значения P(t), a(t), Л (t) и Т,.р
(к примеру 1.13)
Количественные характеристик и а, час t, час
4 0TJ 6 0)0 „8 000 10 009
1 ОСО 1 0,977 0,5 0,023
Р(0 2 С00 0,977 0,841 0,5 0,159
3 000 0,908 0,749 0,5 0,251
4 000 0,857 0,705 0,52 0,317
«(/), 1 1 000 0,013 5,4 39,89 5,4
2 000 2,7 12,1 20 12,1
10-5 — 3 000 5,5 10,7 13,3 10,7
час 4 000 6,5 8,8 10 8,8
Mt). 1 1 000 0,013 6,24 79,78 235
2 000 2,76 14,4 40 76
105 3 000 6,05 14,3 23,6 42,8
час 4 000 7,6 12,5 19,2 28,7
^срс» 1 000 2 000 3 000 4 000 1 8 000 8000,26 8 035 8 220
Графики Р(/), построенные по полученным данным,
приведены на рис. 1.8, а графики a(t) и Х(/)—на
рис. 1.9.
Из рисунков и данных таблицы можно сделать сле-
дующие выводы:
— надежность изделия до / = Т1 = 8000 час тем выше,
чем меньше щ;
— интенсивность отказов растет тем быстрее, чем
меньше oi, что свидетельствует о более интенсивном ста-
рении элементов;
34
Рис. 1.8. Зависимость Р от l (к примеру 1.13).
— параметры Л, о усеченного нормального распре-
деления не являются соответственно средней наработкой
до первого отказа и дисперсией подобно случаю нор-
мального закона распределения.
Пример 1.14. Время работы изделия до отказа (на-
пример, некоторых электровакуумных приборов) подчи-
няется закону распределения Релея. Требуется вычи-
слить количественные характеристики надежности изде-
лия P(t), a(t), %(/), Тср для / = 500, 1000, 2000 час, если
параметр распределения о=1000 час.
3* 35
Решение. Воспользуемся формулами, приведенны-
ми в табл. 1.1. Для £ = 500 час:
5002
2-1000я
t*
~ 2а2"
Р (500) = е = е
___/»
/г„„ч t 2а» 500
а (500) о2 е ч-ооо2 е
= е~°’125 = 0,88;
5Э02
=0,44-10——;
’ час
Я(5ОО)=4г=-^=О,5.1О-^;
Тср^ У ~ а=У^ 100° = 1253 час-
Для t = 1000 час:
1000*
Р(1000) = е~ 2 10002 =е-°.5 = 0,606;
1000»
/1ПППХ 1000 -2-10Ю2 А «ПЛ 1П-3 1 .
я(1ОО°) = Доб№ е =0,606-10
2(1000)=-^= 10 3 —
' ’ 1С002 час
Для £ = 2000 час:
F 2300*
Р(2000) = е 2 1 )002 —-е~а = О,1353;
2J002
zonnn\ 2000 п 07 1П-3 1
а (2000)=-== е -0,27-10 ----------------
х ’ 10002 час
>’(2000) = '-S-= 2 -10'3 —.
’ ЮОО2 час
Из примера видно, что данные электровакуумные
приборы имеют низкую надежность и практически могут
работать в течение времени /<500 час.
Пример 1.15. Время безотказной работы элементов
подчинено экспоненциальному закону с Х=3-10-5 \/час,
а время работы изделия /==20 000 час. Требуется вычи-
слить количественные характеристики надежности резер-
вированного изделия при общем ненагруженном резер-
вировании замещением с кратностью т = 3.
36
решение. Вычислим количественные характеристи-
ки надежности по формулам, приведенным в табл. 1.1.
В нашем случае 7.о = /-=3 10~5 l/час, k=m+l=4. Тогда
вероятность безотказной работы будет
1=0
Найдем вначале значение М:
^ = 3-10"5-2-104 = 0,6.
Подставляя это значение в выражение для P(t), полу-
чим
Р (20 000) =е ~°-6 (1 + 0,6 + =0,908.
' Частота отказов будет
„ их 7 P-v_; (W)m P-w
=Z-;;?r-e .
Подставляя численные значения в a(t), находим
<7.(20000)= 3-е~°-е= 5,4-10 ~5~—.
Вычислим интенсивность отказов:
-/оплопч в (20 000) 0,54-10-» „ 5 1
a(2°000) = ^7^ = --ouf-=6-10 .
Средняя наработка до первого отказа изделия будет
^cp=V = ~~A”“ ~ 'З Ю-5 133000 ‘1ас-
Пример 1.16. Время безотказной работы гироскопи-
ческого устройства с шарикоподшипниками в осях рото-
ра гироскопа подчиняется закону Вейбулла с парамет-
рами &=1,5 Zo=10-4 1/чос, а время его работы (=100чис.
Требуется вычислить количественные характеристики на-
дежности такого устройства.
Решение. Определим вероятность безотказной ра-
боты по формуле (см. табл. 1.1)
P(0 = e-v\
37
Подставляя значения Я„, t и k из условий задачи, по-
лучим
Р(100) = е'10" 1031 '5= 0,9.
Частота отказов определяется по формуле
«(0 = 1 •
Тогда
«(100) = 10 4-1,5- 100'|Г- 0,9 = 1,35- 10л —,
' час
Я (100) = = 1 ’5 • 1 о ’3 — •
' ’ Р (100) 0,9 час
Вычислим среднюю наработку до первого отказа по
формуле
гСр=г^4-1)/^й-
Вначале вычислим значение гамма-функции, восполь-
зовавшись табл. П.7.18.
В нашем случае х='(1/&) +1 = (1/1,5) + 1 ~ 1,67, тогда
Г(х) =0,9033. Подставляя в выражение для Тср значение
гамма-функции и параметры распределения Я и /г, полу-
чим
7’ср = 0,9033/(10-4)1/1’5 ^ 418 час.
Пример 1.17. Допустим, что в результате анализа дан-
ных об отказах аппаратуры частота отказов получена
в виде
а (/) = ^Де^ Д- «42e~w .
Требуется определить все количественные характери-
стики надежности.
Решение. 1. Определим вероятность безотказной
работы. На основании формулы (1.5) имеем
t
P(t) = 1 — ^a(t)dt = \ —
б
t
4~ c2Z3e~wi#
о
= 1 — [—cte + с. — с2е Kt + с2] =
= !—(<?,+ с2) 4- п,е v 4- с2е и .
38
co
Вычислим сумму с,+с2. Так как ^a(t)dt=l, то
о
С с Де^ dt + J с^е'^ dt = ct + c2=l.
0 0
Тогда It
P(t)^c,e-llt + c2e 1 •
2. Найдем зависимость интенсивности отказов от вре-
мени по формуле (1.7):
, й<0 .ДЛ.е~^ +
А^>-~Р(Г) Cle-^ +
3. Определим среднюю наработку до первого отказа.
На основании формулы (1.10) будем иметь
со со
ТСр =[^(0^ = 0 Je-Vd/ +
О о
со
I С —72/ 11__ | ^2
+ o2je dt=^-\-^.
о
4. Вычислим зависимость параметра потока отказов
от времени. Воспользуемся формулой (1.15), для чего
найдем преобразование Лапласа частоты отказов a(t):
4
оо оо
a(s) — Ja(t) e~stdt— e'8t dt 4-
о b
co co
+ Jo2Z2e“we-s1^ = o,2, Je-/ (>1+s)dt Д
0 0
co
+ ^A f e~'
' J A, + s 1 A2 + s
о
Подставляя полученное значение в формулу (1.15), на-
ходим
a (s)
s (с,А, + с2А2) + А,Х2
со (si =----------------------------------------
V ’ 1— a(s) s[s + X, (I - c,) + X2(l-c2)J
c.X, |— c2A2
s + A] (1 — Cj) + A2 (1 — c2)
_________________a,a2_________________
s Is T- A, (1 — c,) +A2 (1 - c2)J ’
39
Для отыскания <о(1) найдем обратное преобразова-
ние Лапласа функции oj(s).
Корнями знаменателей будут
s1==0, s2 = — ЯД1 — ct) — 2а(1— c2).
Тогда
co (/) = (сД + с/2) e“111 + * +
[ X, (1 — C,) + Ml — c2)
— [\ (1-—£t) + ^2 1
MO --- Cl) + ^2 0 - c2) J
После преобразований окончательно получим
ш(0 = т—— ГМг +
7 ЛуС2 + ^2С1 2
-J-c^, (2, — 2,)2 е~(Va+ХаС1)' .
Пример 1.18. В результате эксплуатации Лг= 100 вос-
станавливаемых изделий получены статистические дан-
ные об отказах, сведенные в табл. 1.6.
ТАБЛИЦА 1.6
Статистические данные об отказах восстанавливаемых
изделий (к примеру 1.П)
п 46 40 36 32 30 28 26 24 24 22 22 20 20 20
Ы, 10г час 2 2 2 2 2 2 2 2 9 2 2 2 2 2
<о, 10~5- 1/члс 23 ‘20 18 16 15 14 13 12 12 11 11 10 10 10
Необходимо найти среднюю наработку до первого
отказа изделия Дг, вероятность безотказной работы
P{t) и интенсивность отказов 2(0-
Решение. 1. В нашем случае эксплуатируются из-
делия восстанавливаемые, поэтому они работают в ре-
жиме смены отказавших элементов. Основной характе-
ристикой таких изделий при условии мгновенного ре-
монта является параметр потока отказов. Значения
сн(/), вычисленные по формуле (1.13) и данным об от-
казах, полученным из эксплуатации, приведены
в табл. 1.6, а гистограмма — на рис. 1.10.
49
Рис. 1.10. Гистограмма ы(/) (к примеру 1.18).
2. Аппроксимируем кривую . ю(/), полученную в ре-
зультате сглаживания гистограммы рис. 1.10, уравне-
нием
ш(>/) =a+be~ht.
Найдем значения коэффициентов а, b и k:
ш(0) =a + Z> = 25-10-5 1/час при / = 0,
ш(оо) =а—10~4 \/час при t—>оо,
тогда & = со(О)—а=25*10-5—10^4= 15 • 10”3 1/час.
Определить коэффициент k можно по любой точке
гистограммы. Выберем значение со при /=9000 час; по
кривой ш(9000) = 1,5-10-4 \/час. Тогда
1,5.1О- 4=а + 6е~мооо= 10~4+ 1,5 • 10“4e-ft9000.
Из этого равенства путем очевидных вычислений по-
лучим к — 1,22-10-4 \1час.
Таким образом, параметр потока отказов можно ап-
проксимировать уравнением
ю (/) = 10-4 4-1,5- 10-^е“1,22'1(™.
3. Вычислим среднюю наработку до первого отказа
изделия. Наиболее просто ее найти, используя следую-
щее свойство функции со(/):
lim «>(/)= 1/Тср.
/—>со
В нашем случае lira«>(/) = а= 10~4 \]час.
Тогда Тср=1/а = 10000 час.
41
4. Найдем вероятность безотказной работы как
функцию времени.
Чтобы рассчитать P(t) или любую другую характе-
ристику надежности, необходимо вначале найти по из-
вестной частоту отказов a(i). Наиболее удобно
здесь воспользоваться выражениями (1.15):
Г /а 10-4 । 1,5-10--*
<»(S) = J<o(Oe 122 10_4
и
Тогда
, <0 (s) 10~5 . 2,4-10 4
O(S)—1 +aj(s) — s + о,36-10~4 * s -p 3,36-10-4 ‘
Обратное преобразование Лапласа
a (0 = 10-VAS6-,:r4 + 2,4- 10~4e-3-36-,tr‘f.
Вероятность безотказной работы изделия будет
P(/) = l— \a(t)dt=\ — 10'5 Ге-о-зб-'о-4^—
о б1 *•
— 2,4-10~4 е~3,36'10'4?гй = 0,28e~(l’36'1(r‘z +
б
5. Интенсивность отказов легко находится при из-
вестных P(t) и a (it) по формуле (1.7):
10 - 5 е-0’36',(гЛ + 2,4.10- 4е~-3-36-10~4*
0,28е-°-36'10-4/ + 0,72е-3’36' 10~4/
Зависимость Л(/) приведена на рис. 1.10. Как видно
из рисунка, оэ(0 и Л(/) не совпадают, а интенсивность
отказов на нормальном участке работы изделия, когда
приработка закончена, равна 0,36-1 (К41 /час.
Пример 1.19. Известно, что интенсивность отказов
/. = 0,02 1/час, а среднее время восстановления /п==
= 10 час. Требуется вычислить функцию и коэффициент
готовности изделия.
42
Решение. В нашем случаё средняя наработка до
первого отказа Tcv = 1/7 = 1/0,02 = 50 час. Тогда коэффи-
циент готовности будет
Кг = ^=^нГ = 0’83-
Функцию готовности легко вычислить по формуле
(1.27):
Кт (о = Кт + (1 — Кт) е //Л'Г <в = 0,83 +
4- (1 — 0,83) е~//0-83'10 = 0,83 + 0,17е-°’,г‘ .
§ 1.3. ЗАДАЧИ
В настоящем параграфе приведены задачи по расчету количест-
венных характеристик надежности, предлагаемые для самостоятель-
ного решения. Эти задачи легко решить, используя типовые примеры,
приведенные в предыдущем параграфе.
1.1. Допустим, что на испытание поставлено 1 000 однотипных
электронных ламп типа 6Ж4. За первые 3 000 час отказало 80 ламп.
За интервал времени 3 000—4 000 час отказало еще 50 ламп. Тре-
буется определить частоту и интенсивность отказов ламп в проме-
жутке времени 3 000—4 000 час.
Ответ: я(3 500) =5 • 10~5 1/час; 7.(3500)--5,6• 10-5 \)час.
1.2. Используя данные задачи 1.1, определить вероятность без-
отказной работы и вероятность отказа электронных ламп за первые
3 000 час. _ _
Ответ: Р(3 000) =0,92; (5(3 000) =0,08.
1.3. Используя данные задачи 1.1, найти вероятность безотказ-
ной работы и вероятность отказа электронных ламп за время
4 000 час. _ _
Ответ: Р (4 000) =0,87; Q (4 000) =0,13.
1.4. На испытание поставлено 100 однотипных изделий. За
4 000 час отказало 50 изделий. За интервал времени 4 000—4 100 час
отказало еще 20 изделий. Требуется определить частоту и интенсив-
ность отказов изделий в промежутке времени 4 000—4 100 час.
Ответ: «(4 050) =2 • 10~3 l/час; Х(4 050) =5 - К)3 1/чсс.
1.5. Используя данные задачи 1.4, определить вероятность без-.
отказной работы и вероятность отказа изделий за первые 4 000 час.
Ответ: Р(4 000) =0,5; (5(4 000) =0,5.
1.6. Используя данные задачи 1.4, вычислить вероятность без-
отказной работы и вероятность отказа изделий за время 4 100 час.
Ответ: Р(4 100) =0,3; (5(4 100) =0,7.
1.7. В течение 1 000 час из 10 гироскопов отказало 2. За интер-
вал времени 1 000—1 100 час отказал еще один гироскоп. Требуется
найти частоту и интенсивность отказов гироскопов в промежутке
времени 1 000—1 100 час.
Ответ: ё(1 050) =10~3 1/чсс; Ц1 050) = 1,3 10~3 1/чсс.
1.8. На испытание поставлено 400 резисторов. За время нара-
ботки 10 000 час отказало 4 резистора. За последующие 1 000 час
43
ТАБЛИЦА 1.7
Задачи 1.10—1.100
Номер задачи Исходные данные Ответы
А'о t, час д/, час МО п (Af) 1 (час V Л ДЛ ( л)’ 1 /час
1.10 400 3 000 103 230 100 0,5 0,25 2,5-Ю'з 6,7-10’3
1.11 1 003 3 000 1 000 80 59 0,92 0,87 5.10-5 5,6-10’5
1.12 103 8 000 100 53 10 0,5 0,4 1-Ю-з 2,22-10-8
1.13 10 1 000 100 3 2 0,7 0.5 2-Ю-з 3,33-19’3
1.14 10 1 000 100 3 1 0,7 0,6 ЫО-з 1,54-10-з
1.15 1 003 0 1 000 0 20 1,0 0,98 0,2.10-1 0,202-10’4
1.16 1 033 1 000 1 033 23 25 0,98 0,955 0,25-10-1 0,258-10’’
1.17 1 000 2 000 1 030- 45 35 0,955 0,92 0,35-10-‘ 0,373-10-*
1.18 1 000 0 100 0 5Т 1,0 0,95 0,5-10-з 0,514-Ю-з
1.19 45 75 5 44 1 0,022 0 4,44-Ю-з 1 200-10-5
1.20 45 0 10 0 19 1,0 0,578 4,22-10-2 5,07-IO"2
1.21 1 000 5 003 1 000 *60 50 0,84 0,79 5-Ю-’ 0,13-10’5
1.22 1 003 4 000 1 000 'зо 30 0,87 0,84 3-10’3 3,5-10’5
1.23 1 003 100 100 Б0 40 0,95 0,91 0,4-Ю-з 0,43-10-з
1.24 1 030 200 103 90 32 0.91 0,878 3,2.10-> 3,6-10-4
1.25 45 Ю 10 19 13 0,578 0,289 2,89-10-2 6,67-10’2
1.26 45 60 10 44 1 0,022 0 0,22.10-2 20-10’2
1.27 45 5 5 1 5 0,978 0,867 22-IO'3 24-10’3
1.23 1 000 зоо 100 122 25 0,878 0,853 2,5-10-1 2,9-10-4
1.29 1 030 2 903 100 535 40 0,465 0,425 0,4-10-з 0,9-10’3
1.30 1 003 2 00Э 100 380 12 0,62 0,638 0,12-Ю’з 0,2-10’3
1Л1 1 033 1 500 100 315 13 0,685 0,672 1,3-10-4 1,92-10-4
1.32 1 003 25 000 1 000 980 29 0,02 0 2-Ю-з 200-10-5
1.33 1 000 9 000 1 003 349 30 0,66 0,63 Р-10-3 4,6-10-3
1.34 1 030 12 030 I 000 453 59 0,55 0,5 5-Ю-з 9,5-10“3
1.1*6 1 000 6 000 1 009 210 49 0,79 0,75 4-Ю-з 5,2-10’5
1.36 1 003 23 000 1 003 925 25 0,075 0,05 2,5-10-5 40-10’5
1.37 1 003 16 030 1 003 бзо 59 0,37 0,32 5-IO"3 14,5-10-5
1.38 1 000 2 800 103 5)5 30 0,495 0,465 ’3-10-4 6,24-10’4
1.39 1 000 400 100 147 23 0,853 0,833 0,2-Ю-з 0,24-10"а
1.40 1 000 1003 103 245 15 0,755 0,74 1,5-10-* 2-10’4
1.41 1 000 700 100 230 16 0,8 0,784 16-10-5 2Э-10-5
1.42 1 оээ 2 200 100 495 12 0.595 0,583 1,2-10-1 2-Ю’1
1.43 1 оээ 1 7)0 109 341 13 0,659 0,646 0,13-10’3 0,2-10-з
1.44 45 20 10 32 8 0,29 0.11 1,8.10’2 8,9-Ю"2
1.45 45 0 5 0 1 1,0 0.978 4,4-10’3 4,5-10-=
1.46 45 30 5 27 4 0,4 0,31 1,88.10-2 5,1-IO’2
1.47 45 70 5 41 3 0,089 0,022 1,3-10’2 2,4-10’2
1.48 1 000 7 000 1 000 250 4) 0,75 0,71 4-10’5 5,5-10-5
1.49 1 030 22 000 1 000 893 35 0,11 0,075 3,5-10-5 38-10’5
1.5Э 1 030 13 000 1 003 533 40 0,5 0,46 4-10’5 8,3-IO’3
1.51 45 30 10 40 3 0,11 0,044 6,67.IO’5 5.7-10"2
1.52 1 030 500 100 167 17 0,833 3,816 0,17-10-= 0,21-Ю-з
1.53 1 030 1 юэ 100 233 14 0,74 0,723 1.4-10-’ 1,9-IT4
1.54 1 00) 603 100 184 16 0,816 0,8 1,6-10’ 1,98-1О’1
1.55 45 50 10 43 1 0,044 0,022 0.002 0,067
1.56 45 10 5 6 8 0,867 0,687 3,5-13-* 4,6-10’-’
1.57 45 35 5 31 3 0,31 0,245 1,3-13-2 4,8-10’2
1.58 1 000 8 000 10)0 233 53 0,71 0,66 5-10-5 7,3-10-5
1.59 1 000 14 000 1 000 54) 53 0,46 0,41 5-Ю’5 •11,5-10’5
1.63 100 5 030 100 10 10 0,9 0.8 1-Ю’з 1,18-10-=
1.61 100 4 00) 230 20 2) 0,8 0,6 1-10’3 1,43-10’3
1.62 103 3 000 1 000 23 23 0,8 0,6 2-Ю’4 2,86-Ю-1
1.63 1 000 803 100 216 15 0,784 0,769 0.15-Ю-з 0,193-Ю’з
1.64 1 оээ 2 300 100 417 13 0,583 0,570 0,13-10-= 0,225-10’3
1.65 1 000 1 200 100 274 14 0,726 0,712 1,4-Ю"4 1,95-10’4
1.66 1 003 900 100 231 14 0,769 0,755 0,14-Ю-з 0,184-10'3
1.67 1 000 10 000 1 000 370 40 0,63 0,59 4-10’5 6,55-10-5
1.68 1 000 15 003 1 009 590 40 ' 0,41 0,37 4-10-5 10,3-10-5
1.69 1 000 21 000 1 033 840 5) 0,16 0,11 5-19’5 .37-10’5
1.70 1 000 11 003 1 000 410 40 0,59 0,55 4-10-5 7-IO'2
44
Продолжение табл. 1.7
Номер I задачи Исходные данные Ответы
Л'о 1, час Ы, час «(0 п (Л/) P(t) 1 (час 1 / ч ас
1.71 1 000 1 300 109 288 13 0,712 0,699 1,3-10-* 1,84-1О"4
1.72 1 000 1 900 100 36S 12 0.632 0,62 1,2-10-* 1,92-10--»
1.73 1 000 2 700 100 480 25 0,52 0,495 2,5- Кг’ 4,9-Ю"4
1.74 45 15 5 14 9 0.687 0,643 8,9-10-з 13,3-10-8
1.75 45 45 5 34 1 0,245 0,223 4,44-10-3 19-Ю-з
1.76 45 63 5 35 3 0,223 0,153 13,3-10-з 70,8-10-з
1.77 10Э 6 000 530 53 20 0.5 0,3 4-Ю-* 1-Ю-з
1.78 юэ 4 000 1 000 10 6 0,9 0,84 6-10-5 6,9-IO’5
1.79 100 10 000 1 000 25 5 0.75 0,7 5-Ю-з 6,9-10-5
1.80 1 000 1 400 100 301 14 0,699 0,685 0,14-10-а 0,2-Ю-з
1.81 1 000 2 400 100 430 14 0,57 0,556 0,14-Ю-з 0,25-Ю-з
1.82 1 000 17 0ЭЭ 1 000 680 40 0,32 0,28 4-Ю-5 13,3-10-5
1.83 10 3 000 25 4 2 0,6 0,4 8-Ю-з 16-Ю-з
1.84 2Э 8 000 100 4 4 0,8 0,6 2-Ю-з 2,86-10-3
1.85 10 003 5 000 1 000 18 2 0,9982 0,998 2-10"’ 2,04-Ю"7
1.86 63 3 000 100 15 5 0,75 0,667 0,83-Ю-з 1,18-Ю-з
1.87 1 000 20 003 1 000 805 35 0,195 0,16 3,5-10’5 19,7-Ю-з
1.88 1 000 1 800 100 354 14 0,646 0,632 0,14-Ю-з 0,22-Ю-з
1.89 1 000 2 600 100 460 20 0,54 0,52 0,2-Ю-з 0,38-Ю-з
1.90 1 000 19 000 1 000 770 35 0,23 0,195 3,5-10'= 16,4-10-5
1.91 100 1 000 10 1 10 10 0,9 0,8 1-Ю-з 1,18-Ю-з
1-92 100 100 100 1 1 0,99 0,98 МО-4 1,015-Ю-* 1 *
1.93 10 100 100 1 1 0,9 0.8 1.10-? 1,17-Ю-з
1.94 10 1 000 100 6 2 0,4 0,2 2-Ю-з 6,67-Ю-з
1.95 1 000 1 600 100 328 13 0,672 0,659 0,13-Ю-з 0,195-Ю-з
1.96 1 000 2 500 100 444 16 0.555 0,540 0,16-Ю-з 0,29-Ю-з
1.97 1 000 18 000 1 000 720 53 0,28 0.23 5-10-5 19,6-IO'5
1.98 5 1 003 100 1 2 0,8 0,4 4-Ю-з 6,67-Ю-з
1.99 20 1 000 100 16 2 0,2 0,1 1-10’3 6,67-Ю’3
1.100 1 000 2 100 100 392 13 0,698 0,595 1,3-10’“ 2,17-Ю-1
отказал еще 1 резистор. Определить частоту и интенсивность отка-
зов резисторов в промежутке времени 10 000—11 000 час.
Ответ: «(10 500) =0,25 • 10~5 Цчас; 1(10 500) =0,253 • I0 5 Цчас.
1.9. Используя данные задачи 1.8, найти вероятность безотказ-
ной работы и вероятпость отказа резисторов за время 10 000 час.
Ответ: Р(10 000) =0,99; (>(10000) =0,01.
1.10—1.100. На испытание поставлено No изделий. За время
t час вышло из строя n(t) штук изделий. За последующий интервал
времени At вышло из строя n(At) изделий. Необходимо вычислить
вероятность безотказной работы за время t и t+At, частоту отказов
и интенсивность отказов на интервале At.
Исходные данные для решения задачи и ответы приведены
в табл. 1.7.
1.101. Допустим, что на испытании находилось 1 000 однотипных
ламп 6Ж4. .Число отказавших ламп учитывалось через каждые
1 000 час работы. Данные об отказах ламп сведены в табл. 1.8. Тре-
буется определить вероятность безотказной работы, частоту отказов
и интенсивность отказов в функции времени, построить графики этих
функций. Необходимо также найти среднюю наработку до первого
отказа.
Ответ: P(t), a(t), X(Z) см. табл. 1.9 и рис. 1.11 и 1.12; 7Ср =
= 12 895 час.
45
ТАБЛИЦА IЛ
Данные об отказах к задаче 1.101
Д/р час п(Ыг) Д/р час Д/р час «(Ч)
0—1 000 20 9 000—10 000 30 18 000—19 000 50
1 000—2 000 25 10 000—11 000 40 19 000—20 000 35
2 000—3 000 35 11 000—12 000 40 20 000—21 000 35
3 000—4 000 50 12 000—13 000 50 21 000—22 000 50
4 000—5 000 30 13 000—14 000 40 22 000—23 000 35
5 000—6 000 50 14 000—15 000 50 23 000—24 000 25
6 000—7 000 40 15 000—16000 40 24 000—25 000 30
7 000—8 000 40 16 000—17 000 50 25 000—26 000 20
8 000—9 000 50 17 000—18 000 40 — —-
ТАБЛИЦА 1.
Вычисленные значения
Р (t), а (/), X (/) к задаче 1.101
Д/р час PW Q С
0—1 000 0,98 2,0 2,02
1 000—2 000 0,955 2,5 2,58
2 000—3 000 0,92 3,5 3,73
3 000—4 000 0,87 5,0 5,6
4 000—5 000 0,84 3.0 3,5
5 000—6 000 0,79 5,0 6,15
6 000 -7 000 0,75 4,0 5,2
7 000—8 000 0,71 4,0 5,5
8 000—9 000 0,66' 5,0 7,3
9 000—10 000 0,63 3,0 4,65
10 000 11000 0,59 4,0 6,55
11 000—12 000 0,55 4,0 7
12 000—13 000 0,50 5,0 9,5
13 doo—14 000 0,46 4,0 8,3
14 000—15 000 0,41 5,0 11,5
15 000—16 000 0,37 4,0 10,25
16 000—17 000 0,32 5,0 14,5
17 000—18 000 0,28 4,0 13,3
18 000—19 000 0,23 5,0 19,6
19 000—20 000 _Д, 195 3,5 16,4
20 000—21 000 0,16 3,5 19,7
21 000—22 000 0,11 5,0 37
22 000—23 000 0,075 3,5 38
23 000—24 000 0,05 2,5 40
24 000—25 000 0,02 3,0 85,7
25 000—26 000 0,00 •2,0 200
Рис. 1.11. Зависимость Р от t
(к задаче 1.101).
Рис. 1.12. Зависимость а и А
от t (к задаче 1.101).
46
ТАБЛИЦА 1.10
Исходные данные к задаче 1.102
Д/4, час час п(Д^) Д^, час „(Мг)
0—5 1 30—35 4 60—65 3
5—10 5 35—40 3 65—70 3
10—15 8 40—45 0 70—75 3
15—20 2 45—50 1 75—80 1
20—25 5 50—55 0 .—• .—
25—30 6 55—60 0 — —
1.102. В результате наблюдения за 45 образцами радиоэлектрон-
ного оборудования получены данные до первого отказа всех 45 об-
разцов, сведенных в табл. 1.10. Требуется определить вероятность
безотказной работы, частоту отказов и интенсивность отказов в функ-
ции времени, построить графики этих функций, а также найти сред-
нюю наработку до первого отказа TTp-
Ответ: P(t), a(t), Х(1) см. табл. 1.11 и рис. 1.13 и 1.14; 7’ср =
=31,7 час.
ТАБЛИЦА 1.11
Вычисленные значения
P(t), a(t), 7.(1) к задаче 1.102
час p(t) 5(')- 10“31/чос 10"31/час
0—5 0,978 4,44 4,5
5—10 0,867 22,2 24,1
10—15 0,687 35,5 45,7
15—20 0,643 8,9 13,3
20—25 0,531 22,2 37,7
25—30 0,4 26,6 57,1
30—35 0,311 17,8 50
35—40 0,245 13,3 48
40—45 0,245 0 0
45—50 0,223 4,44 19
50—55 0,223 0 0
55—60 0,223 0 0
60—65 0,156 13,3 70,8
65—70 0,089 13,3 109,1
70—75 0,022 13,3 240
75—80 0 4,44 1 200
1.103. В результате наблюдения за 45 образцами радиоэлектрон-
ного оборудования, которые прошли предварительную 80-часовую
приработку, получены данные до первого отказа всех 45 образцов.
47
ТАБЛИЦА 1.12
Исходные данные к задаче 1.103
н
V
1
fl
1
I
Д/4, час час л(«4) час п(Д^)
0—10 19 30—40 3 60—70 1
10—20 13 40—50 0 .— —
20—30 8 50—60 1 — -—
сведенные в табл. 1.12. Необходи-
мо найти вероятность безотказной
работы, частоту отказов и интен-
сивность отказов в функции вре-
мени, построить графики этих
функций, а также найти среднюю
наработку до первого отказа.
Ответ: P(t), a(t), Х(1) см.
табл. 1.13 и рис. 1.15 и 1.16,
7’ср.~|5.9 час.
Рис. 1.14. Зависимость а
и 7. от t (к задаче 1.102).
Рис. 1.13. Зависимость Р от t
(к задаче 1.102).
ТАБЛИЦА 1.13
Вычисленные значения Р (/), «(/), А (0 к задаче 1.103
час Р(0 a(t), 10“2 1/ час X (Г), 10-2 1/час
0—10 0,578 4,22 5,07
10—20 0,289 2,89 6,67
20—30 0,111 1,78 8,89
30—40 0,044 0,667 5,71
40—50 0,044 0 0
50—60 0,022 0,222 6,67
60—70 0 0,222 20,0
48
Рис. 1.15. Зависимость Р от t
(к задаче 1.103).
Рис. 1.16. Зависимость а и X
от t (к задаче 1.103).
1.104. На испытание поставлено Л' = 1 000 элементов. Число отка-
зов фиксировалось в каждом интервале времени испытаний А/ —
= 500 час. Данные об отказах сведены в табл. 1.14. Требуется опре-
Т АБЛ ИЦ А 1.14
Исходные данные к задаче 1.104
час n(Af4> Д/4, час и(Д1() Д/4, час п(ду
0—500 145 3 000—3 500 51 6 000—6 500 60
500—1 000 86 3 500—4 000 45 6 500—7 000 75
1 000—1 500 77 4 000—4 500 41 7 000—7 500 62
1 500—2 000 69 4 500—5 000 37 7 500—8 000 42
2 000—2 500 62 5 000—5 500 33 8 000—8 500 16
2 500—3 000 56 5 500—6 000 35
делить вероятность безотказной работы, частоту отказов и интенсив-
ность отказов в функции времени, построить графики этих функций
и найти среднюю наработку до первого отказа элементов.
Ответ: P(t), a(t) и Х(/) см. табл. 1.15 и рис. 1.17, 1.18; Tcv =
=3562,5 час.
Рис. 1.17. Зависимость Р от t
(к задаче 1.104).
Рис. 1.18. Зависимость а и Л
от t (к задаче 1.104).
4—1086
49
ТАБЛИЦА 1.16
Вычисленные значения Pit), a(t), \(f) к задаче 1.104
Д^, час Р (0*) 5(0. IO'5— час nt), 10-5— час Д/г-, час Р (0*) « (0. 10-s— ч ас Ц0. 10-5— час
0—500 0,855 29 31,3 4 500—5 000 0,331 7,4 21,2
500—1 000 0,769 17,2 21,2 5 000—5 500 0,298 6,6 21
1 000—1 500 0,692 15,4 21,1 5 500—6 000 0,263 7,0 25
1 500—2 000 0,623 13,8 21 6 000—6 500 0,203 12,0 51,5
2 000—2 500 0,561 12,4 21 6 500—7 000 0,128 15,0 90,7
2 500—3 000 0,505 11,2 21 7 000—7 500 0,066 12,4 127,8
3 000—3 500 0,454 10,2 21,3 7 500—8 000 0,024 8,4 186,7
3 500—4 000 4 000—4 500 0,409 0,368 9,0 8,2 20,9 21,1 8 000—8 500- 0,008 3,2 200
*) t—конец интервала.
1.105. Имеются статистические данные об отказах трех групп
одинаковых изделий, приведенные в табл. 1.16. В каждой группе
ТАБЛИЦА 1.16
Исходные данные к задаче 1.105
ДГ4, час I группа л(Д/р II группа п(Д^) III группа
0—25 4 6 5 15
25—50 8 9 8 25
50—75 6 5 7 18
75—100 3 4 5 12
100—150 5 5 6 16
150—2С0 4 3 3 10
200—250 1 3 — 4
250—300 2 2 -—- 4
300—400 3 4 7
400—550 5 -— — 5
было по 100 изделий и их испытания проводились по I группе
550 час, по II группе 400 час и по III группе 200 час. Необходимо
вычислить количественные характеристики P(t), a(t), 7(1) и по-
строить графики этих функций.
Ответ: P{t), aft), 7.(1) см табл 1.17 и рис. 1.19 и 1.20.
50
Рис. 1.19. Зависимость Р от t (к за-
даче 1.105).
ТАБЛИЦА 1.17
Вычисленные значения
P(t), a(f), X (t) к задаче 1.105
Д/г-, час /'(0 a(t), 10“з 1/час >(/), 10"г 1/час
0—25; 0,95 2 2,05
25—50 0,867 3,3 3,67
50—75 0,807 2,4 2,87
75—100 0,767 1,6 2,03
100—150 0,713 1,1 1,44
150—200 0,68 0,67 0,957
200—250 0,67 0,40 0,588
250—300 0,65 0,40 0,606
300—400 0,615 0,35 0,553
400—550 0,59 0,33 0,542
3*
1.106— 1.115. В течение времени А/ производилось наблюдение
за восстанавливаемым изделием и было зафиксировано n(At) отка-
зов. До начала наблюдения изделие проработало G [час], общее вре-
мя наработки к концу наблюдения составило t2 [час]. Требуется
найти наработку на отказ.
Исходные данные для решения задачи и ответы приведены
в табл. 1.18.
ТАБЛИЦА 1.18
Задачи 1.106—1.115
Номер задачи Исходные данные Ответ /ер. час
t3, час ta, час п(Д/)
1.106 350 1 280 15 62
1.107 400 1 600 3 400
1.108 1 000 6 400 9 600
1.109 770 4 800 7 575
1.110 1 200 5 558 2 2 179
1.111 300 540 12 20
1.112 540 1 200 5 132
1.113 300 3 200 8 362,5
1.114 12 184 16 10,75
1.115 570 2 000 27 53
1.116— 1.130. В течение некоторого времени проводилось наблю-
дение за работой Д'о экземпляров восстанавливаемых изделий.
Каждый из образцов проработал [час] и имел п, отказов. Требу-
ется определить наработку на отказ по данным наблюдения за ра-
ботой всех изделий.
Задачи
Исходные
задачи «1 tlt час п3 t3, час Г* <з, час ts, час
1.116 1 300 3 600 2 400 .— —_
1.117 3 90 6 270 4 140 5 230
1.118 12 960 15 1 112 8 808 7 1 490
1.119 6 144 5 125 3 80 8 176
1.120 8 176 5 150 4 112 8 216
1.121 6 144 5 125 3 80 •—- -—
1.122 10 1 020 18 2 700 26 3120 32 4 000
1.123 32 4 000 24 3 480 16 2 080 —
1.124 10 1 020 26 3 120 24 3 480 18 2 700 3
1.125 18 2 700 32 4 000 24 3 480 16 2 080
1.126 3 720 4 1 040 2 500 6 1 800
1.127 1 300 3 600 6 2 300 7 2 450
1.128 5 1 500 8 1 920 3 180 4 680
1.129 3 1 650 2 1 200 4 2 300 .—_ •—
1.130 5 72 4 60 7 92 8 96
52
Исходные данные для решения задачи и ответы приведены
в табл. 1.19.
1.131— 1.140. Система состоит из Л' приборов, имеющих разную
надежность. Известно, что каждый из приборов, проработав вне
системы ti [час], имел отказов. Для каждого из приборов справед-
лив экспоненциальный закон надежности. Необходимо найти нара-
ботку на отказ всей системы.
Исходные данные для решения задачи и ответы приведены
в табл. 1.20.
1.141— 1.145. Электронная аппаратура состоит из k групп эле-
ментов. В процессе эксплуатации зафиксировано п отказов. Коли-
чество отказов в j-ft группе равно и-ц среднее время восстановления
элементов j-й группы равно tj. Требуется вычислить среднее время
восстановления аппаратуры.
Исходные данные и ответы приведены в табл. 1.21.
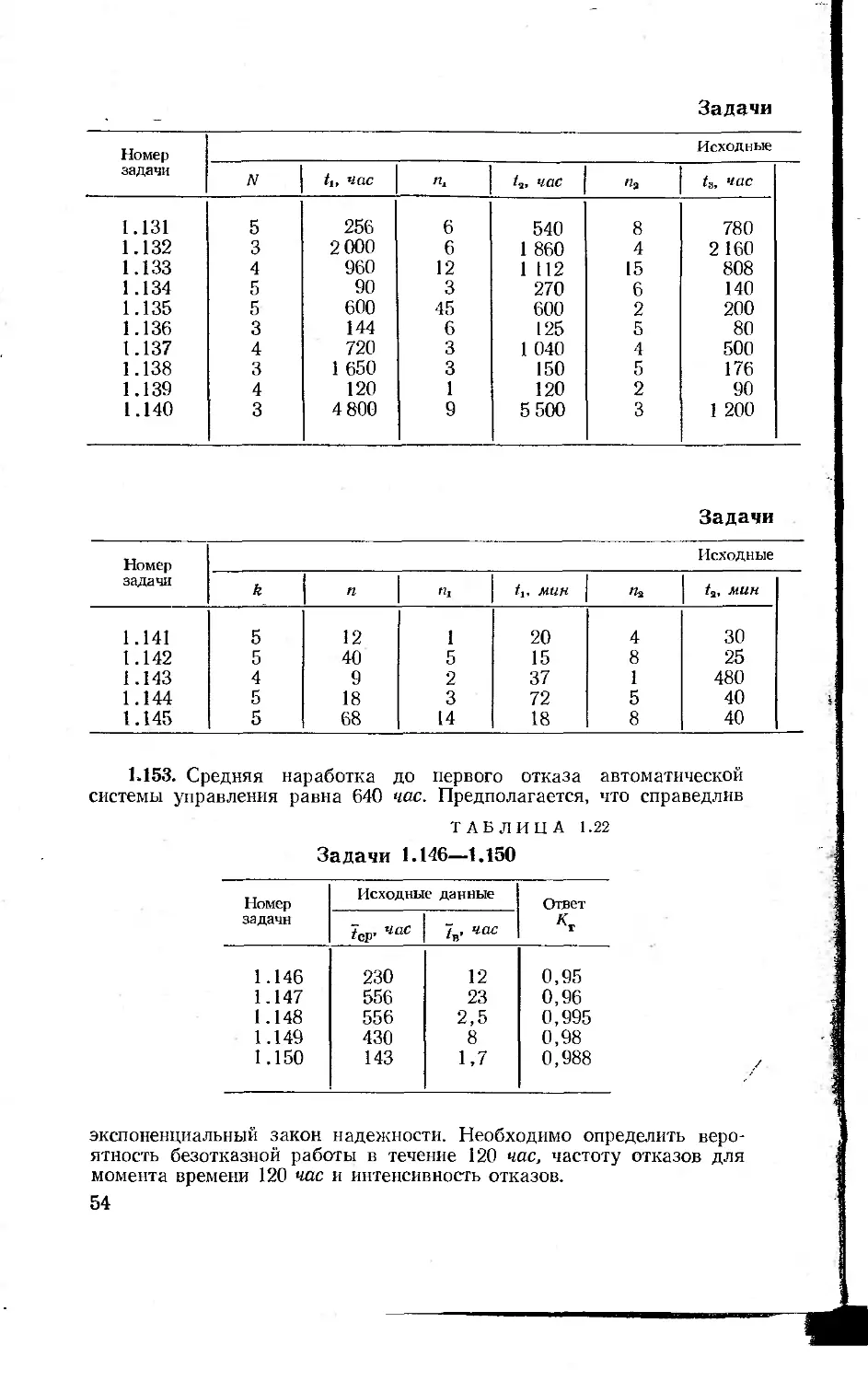
1.146— 1.150. Изделие имеет среднюю наработку на отказ tCp и
среднее время восстановления tB. Необходимо определить коэффи-
циент готовности изделия.
Исходные данные и ответы приведены в табл. 1.22.
1.151. Интенсивность отказов изделия 7=0,82 • 10-3 l/'z<zc=const.
Необходимо найти вероятность безотказной работы в течение 6 час
полета самолета /’(6), частоту отказов <2(100) при 1=100 час и сред-
нюю наработку до первого отказа ТСр.
Ответ: Р(6)=0,995; а(100) =0,75 • 10~3 Цчас; Тср = 1220 час.
1.152. Вероятность безотказной работы автоматической линии
изготовления цилиндров автомобильного двигателя в течение 120 час
равна 0,9. Предполагается, что справедлив экспоненциальный закон
надежности. Требуется рассчитать интенсивность отказов и частоту
отказов линии для момента времени 120 час.
Ответ: 7=0,83-10"3 Цчас; с(120) =0,747• 10 3 l/час; Тс? =
= 1 200 час.
ТАБЛИЦА 1.19
1.116—1.130
данные Ответ
«5 t5, час t6, час п7 /7, час 7Ср. час
216
3 180 — .— — — 43
_—. -—— -— — -—- 104
5 150 4 112 8 216 25,7
— —- -— —- .—. —- 26
— —- -—. —- . .... — 25
24 3 480 16 2 080 — — 130
— .—. -— —• —- -—- 133
-— — — — —- -— 132
— .—. — -— —- •— 136
.—_ .—- 271
5 1 200 2 540 4 770 291
3 1 290 2 2 200 10 1 500 265
_—. .—- 572
4 50 3 42 6 78 13,2
53
Задачи
Номер Исходные
задачи N tit час п, 4» час /в. час
1.131 5 256 6 540 8 780
1.132 3 2 000 6 1 860 4 2 160
1.133 4 960 12 1 112 15 808
1.134 5 90 3 270 6 140
1.135 5 600 45 600 2 200
1.136 3 144 6 125 5 80
1.137 4 720 3 1 040 4 500
1.138 3 1 650 3 150 5 176
1.139 4 120 1 120 2 90
1.140 3 4 800 9 5 500 3 1 200
Задачи
Номер Исходные
задачи k п «1 tA, мин 4» мин
1.141 5 12 1 20 4 30
1.142 5 40 5 15 8 25
1.143 4 9 2 37 1 480
1.144 5 18 3 72 5 40
1.145 5 68 14 18 8 40
1.153. Средняя наработка до первого отказа автоматической
системы управления равна 640 час. Предполагается, что справедлив
ТАБЛИЦА 1.22
Задачи 1.146—1.150
Номер задачи Исходные данные Ответ
7ср- час 7В. час
1.146 230 12 0,95
1.147 556 23 0,96
1.148 556 2,5 0,995
1.149 430 8 0,98
1.150 143 1,7 0,988
экспоненциальный закон надежности. Необходимо определить веро-
ятность безотказной работы в течение 120 час, частоту отказов для
момента времени 120 час и интенсивность отказов.
54
ТАБЛИЦА 1.20
1.131—1.140
данные Ответ
п3 [ t4, 4UC t5, час | «S fcp. час
10 250 4 900 12 12,5
3 — — — — 153
8 1 490 7 — -— 24,6
4 230 5 180 3 8,2
4 200 6 200 2 7,25
3 — .— — — 8,4
2 1 800 6 .— — 65,4
10 — .— _— -— 10,9
8 700 1 .— .— 8,7
3 — — — — 203
ТАБЛИЦА 1.21
1.141—1.145
данные Ответ
«3 /3, мин п. tit ми 1 п5 /5, мин 7В» мин
3 16 2 36 2 40 28,3
12 60 6 40 9 20 35,4
2 60 4 25 .—- .—. 86
4 36 2 120 4 60 57,8
27 20 6 30 13 15 21,9
Ответ: Р(120)=0,83; а(120) = 1,3- 10-s {[час; Х=1,56- К) '1 1/час.
1.154. Время работы изделия подчинено усеченному нормальному
закону с параметрами 7'1=8000 час, сн=1 000 час. Требуется найти
вероятность безотказной работы изделия в течение 8000 час.
Ответ: Р(8 000) =0,5.
1.155. Используя данные задачи 1.154, вычислить частоту отка-
зов для / = 6 000 час.
Ответ: о(6 000)=5,4-10-5 1/час.
1.156. Используя данные примера 1.154, определить интенсив-
ность отказов для /=10 000 час.
Ответ: 7.(10000) =2,35- IО'3 1/час.
1.157. Используя данные примера 1.154, вычислить среднюю на-
работку до первого отказа.
Ответ: 7'Ср = 8000 час.
1.158. Время безотказной работы электровакуумного прибора
подчинено закону Релея с параметром о=1 860 час. Требуется рас-
считать вероятность безотказной работы электровакуумного прибора
в течение времени /=1 000 час, частоту отказа «(1 000), интенсив-
ность отказов 7.(1 000) и среднюю наработку до первого отказа.
Ответ: Р(1 000) =0,87; «(1 000) =0,25 • 10~3 1/час; 7.(1000) =
= 0,29- 10-3 1/час; 7'ср = 2 320 час.
55
Рис. 1.21. Зависимость X от /
(к задаче 1.159).
исправной работы подчинено
1.159. При проведении форси-
рованных испытаний изделия полу-
чена зависимость Х(/), приведенная
на рис. 1.21. Необходимо найти ве-
роятность безотказной работы в те-
чение /= 1 000 час, частоту отказов
для /=1000 час и среднюю нара-
ботку до первого отказа изделия.
Ответ: Р(1 ООО) = 0,9;
о(1 ООО) = 1,98-10-4 1/час; Тсг =
= 2 680 час.
1.160. Вероятность безотказ-
ной работы изделия в течение t=
= 1000 час Р(1 ООО) =0,95. Время
закону Релея. Требуется опреде-
лить количественные характеристики надежности a(t), ?.(/), Тер.
Ответ: а(1 000) =0,95 • 10~4 1/час; Х(1 000) = 10-4 1/час; Гср =
=4 000 час.
1.161. Средняя наработка изделия до первого отказа равна
1 260 час. Время исправной работы подчинено закону Релея. Необ-
ходимо найти его количественные характеристики надежности для
/= 1 000 час.
Ответ: Р(1 000) =0,61; Х(1 000)=10~3 1/час; а(1000) =
=0,61 • 10-3 1/час.
1.162. Время исправной работы изделия подчинено гамма-рас-
пределению с параметрами k = 3 и Хо=1,5-10~4 1/час. Необходимо
определить вероятность безотказной работы изделия в течение
10 000 час.
Ответ: Р( 10 000) =0,81.
1.168. Используя данные задачи 1.162, вычислить частоту отказа
для /=5 000 час.
Ответ: а(5 000) =3,75 • 10~4 1/час.
1.164. Используя данные задачи 1.162, найти интенсивность отка-
за для /=5 000 час.
Ответ: Х(5 000) =4 • 10~4 1/час.
1.165. Используя данные задачи 1.162, определить среднюю на-
работку до первого отказа изделия.
Ответ: Тер с = 2000 час.
1.166. Время исправной работы скоростных шарикоподшипников
подчинено закону Вейбулла с параметрами /г=2,6, Хо=1,65-1О-7 1/час.
Необходимо найти вероятность безотказной работы шарикоподшип-
ника в течение 150 час.
Ответ: Р(150) =0,92.
1.167. Используя данные задачи 1.166, вычислить частоту отка-
зов шарикоподшипников для времени /=150 час.
Ответ: а(150) = 11,9-10~4 1/час.
1.168. Используя данные задачи 1.166, рассчитать интенсивность
отказов шарикоподшипников для /=150 час.
Ответ: Х( 150) = 12,9 • 10-4 1/час.
1.169. Используя данные задачи 1.166, вычислить среднюю нара-
ботку до первого отказа шарикоподшипников.
Ответ: Гер—350 час.
1.170. Вероятность безотказной работы гироскопа в течение
/=150 час равна 0,9. Время исправной работы подчинено закону
Вейбулла с параметром 6=2,6. Необходимо определить опасность
56
отказов гироскопов для /=150 час и среднюю наработку до первого
отказа.
Ответ: 7.(150) =0,38• 10'6 1/'/ос; Тср = 27О час.
1.171. Известно, что параметр потока отказов аппаратуры выра-
жается формулой <о(/)=0,2-10-3 (1—е—о.б.Ю =/). Необходимо найти
среднюю наработку до первого отказа аппаратуры.
Ответ: ТСР = 5 000 час.
1.172. Преобразование Лапласа параметра потока отказов аппа-
ратуры при раздельном резервировании с кратностью т=1 выража-
ется зависимостью co(s) = 2X2/.s(.s'+3X). Требуется вычислить среднюю
наработку до первого отказа, если интенсивность отказов Х=
= 1,5 • 10‘3 1/час.
Ответ: 7'CI, = 1 000 час.
1.173. В результате анализа данных об отказах изделия установ-
лено, что частота отказов имеет вид я (/) = 2Хе—W (1 — е—W). Не-
обходимо определить количественные характеристики надежности P(t),
Х(/), ГсР, «(/).
Ответ:
Р (t) = 2e-W — e~2W;
7<,Р = 3/2Х; <о (/) =-|-X (1 — e“3W).
1.174. В результате анализа данных об отказах изделий установ-
лено, что вероятность безотказной работы выражается формулой
Р (/) = Зе-w— 3 -|-е—3W . Требуется найти количественные ха-
рактеристики надежности «(/), X (/), со{/), Тер.
Ответ:
а (/) = ЗХ e-’^l — е“м)2;
X (/) = X (1— e“w)2 / ( 1 —'e~w+-4- е
w (/) =-jj-р — J/ -у-е 3W sin ^К2 X/ 4- arctg —j •
11
^ср= 6?1 •
1.175. Известно, что частота отказов изделия аппроксимируется
формулой a (t) = 6Х e~~2lt (1 — е”-^). Необходимо определить сред-
нюю наработку до первого отказа.
Ответ: 7ер = 5/6Х.
1.176. Интенсивность отказов изделия зависит от времени и вы-
ражается функцией X (<) = k (1 — e~kt) /( 1 e~k/ j Требуется
57
определить количественные характеристики надежности р (t), a(t),
(0> Т’ер-
Ответ:
Р (t) = 2е-*‘ —е"2*'; а (/) = (1 — e~kt);
2 / \ з
o(/)=y/Jl^e-3^l; rcp=-2fe
1.177. Интенсивность отказов изделия зависит от времени и вы-
ражается функцией Л(/) =k2t/(l+kt). Необходимо найти P(t).
Ответ: P(t)=e~ht(l+kt).
1.178. Используя данные задачи 1.177, определить частоту отка-
зов изделия a(t).
Ответ: a(t)=k2te~ht.
1.179. Используя данные задач 1.177 и 1.178, найти среднюю
Наработку до первого отказа.
Ответ: 7'сР=2/К
1.180. Частота отказов изделия a(t)=k2te~hi. Требуется опреде-
лить параметр потока отказов b>(t).
k
Ответ: <о(/) = -2-(1—е 2М).
1.181. Интенсивность отказов Лс сложной восстанавливаемой
системы есть величина постоянная и равная 0,015 Х/час. Среднее
время восстановления /в = 100 час. Необходимо вычислить вероят-
ность застать систему в исправном состоянии в момент времени
1 = 10 час.
Ответ: Кг( 10) «0,867.
1.182. Коэффициент готовности сложного восстанавливаемого
изделия Кг=0,9. Среднее время его восстановления К =100 час.
Требуется найти вероятность застать изделие в исправном состоянии
в момент времени /=12 час.
Ответ: Кг (12) =0,987.
Рис. 1.22. Зависимость X от t
(к задаче 1.183).
1.183. В процессе эксплуатации Ко = 1ОО восстанавливаемых изде-
лий возникали отказы, которые фиксировались в интервалах времени
Д/=100 час. Число отказов п за время эксплуатации в течение
1 000 час приведено в табл. 1.23. Требуется определить интенсивность
отказов и построить график.
Ответ: график Х(0 рис. 1.22.
58
ТАБЛИЦА 1.23
Исходные данные к задаче 1.183
Д^, час 0—100 100—2Э0 200—300 300—400 400—500
п 2 4 6 7 8
“г час 5Э0—60Э 600—700 700—800 800—900 900—1 000
п 9 9 10 10 10
1.184. Используя данные задачи 1.183, определить вероятност!
безотказной работы изделия в течение / = 1 000 час.
Ответ: Р(1 ООО) «0,4.
ГЛАВА ВТОРАЯ
РАСЧЕТ ХАРАКТЕРИСТИК НАДЕЖНОСТИ
НЕВОССТАНАВЛИВАЕМЫХ ИЗДЕЛИЙ
ПРИ ОСНОВНОМ СОЕДИНЕНИИ ЭЛЕМЕНТОВ
§ 2.1. МЕТОДЫ РАСЧЕТА
СЕсли отказ технического устройства наступает при
отказе одного из его элементов, то говорят, что такое
устройство имеет основное соединение элементов. При
расчете надежности таких устройств предполагают, что
отказ элемента является событием случайным и неза-
висимым.
Тогда вероятность безотказной работы изделия в те-
чение времени t равна произведению вероятностей без-
отказной работы ее элементов в течение того же време-
ни. Так как вероятность безотказной работы элементов
в течение времени t можно выразить через интенсив-
ность отказов в виде (1.8), то расчетные формулы для
вероятности безотказной работы технического устрой-
ства при основном соединении элементов можно запи-
сать следующим образом:
N
Рс (0 = Pi (О А (0 • • • PN (0 = П
1=1
(t \ ( / \
— Я1 (/)dt I exp I —j22(/)d/j... (2.1)
б / \ о /
/ t \ /Nt \ ~1
...exp/—(f) dtU-cxp / — J] J Xi (t) dt j. /
\ 0 / V z' - l 0 -J
Выражения (2.1) наиболее общие. Они позволяют
определить вероятность безотказной работы изделий до
первого отказа при любом законе изменения интенсив-
ности отказов во времени.
60
Йа практике наиболее часто интенсивность отказов
изделий является величиной постоянной. При этом время
возникновения отказов обычно подчинено экспоненци-
альному закону распределения, т. е. для нормального
периода работы аппаратуры справедливо условие 2v=
= const.
В этом случае выражения для количественных ха-
рактеристик примут вид: н
\ Рс (/) = e~V = е“'/Гср с, Яс = S К,
V <=1
(2-2)
ac(t) = Xce T’cpc = l/Ac.
Если все элементы данного типа равнонадежны, ин-
тенсивность отказов системы будет
Лс = £лГЛ, (2.3)
<=1
где Ni — число элементов i-ro типа; г — число типов
элементов.
На практике очень часто приходится вычислять ве-
роятность безотказной работы высоконадежных систем.
При этом произведение Kat значительно меньше едини-
цы, а вероятность безотказной работы P(t) близка к еди-
нице. В этом случае, разложив е с в ряд и ограни-
чившись первыми двумя его членами, с высокой сте-
пенью точности можно вычислить P(t).
Тогда основные количественные характеристики на-
дежности можно с достаточной для практики точно-
стью вычислить по следующим приближенным форму-
лам:
Рс (0 ~ 1 -1 £ дгл = 1 - Kt, К = S NiK,
i=l i=l
(2.4)
Гс = 1 i МЛ=1/К, a(t) ~ Лс(1 - Kt).
I <=>
Вычисление количественных характеристик надежно-
сти по приближенным формулам не дает больших оши-
бок для систем, вероятность безотказной работы кото-
рых превышает 0,9, т. е. для 0,1.
61
При расчете Надежности систем часто приходится
перемножать вероятности безотказной работы отдель-
ных элементов расчета, возводить их в степень и извле-
кать корни. При значениях P(i), близких к единице, эти
вычисления можно с достаточной для практики точно-
стью выполнять по следующим приближенным форму-
лам:
Рг (0 Рг (!) PN (0 ~ 1 — S qi (0>
b ^'(0=l-W(0, (2.5)
где qi(t) —вероятность отказа i-ro блока.
В зависимости от полноты учета факторов, влияю-
щих на работу изделия, различают прикидочный, ори-
ентировочный и окончательный расчет надежности.
; ПРИКИДОЧНЫИ РАСЧЕТ НАДЕЖНОСТИ
Прикидочный расчет основывается на следующих до-
пущениях:
— все элементы изделия равнонадежны;
— опасности отказов всех элементов изделия не за-
висят от времени, т. е. %,= const;
— отказ любого элемента приводит к отказу всего
изделия.
Прикидочный расчет надежности применяется в сле-
дующих случаях:
1) при проверке требований по надежности, выдви-
нутых заказчиком в техническом задании (ТЗ) на про-
ектирование изделия;
2) при расчете нормативных данных по надежности
отдельных блоков, устройств и приборов системы (рас-
чет норм надежности отдельных частей системы);
3) для определения минимально допустимого уровня
надежности элементов проектируемого изделия;
4) при сравнительной оценке надежности отдельных
вариантов изделия на этапах предэскизного и эскизного
проектирования. 9
62
Прикпдочный расчет надежности позволяет судить
о принципиальной возможности обеспечения требуемой
г надежности изделия.
Характеристики надежности рассчитываются по фор-
мулам (2.2) или (2.4), при этом kc = N‘k3KB, где /,Э1ш—
эквивалентное значение интенсивности отказов элемен-
тов, входящих в изделие.
ОРИЕНТИРОВОЧНЫЙ РАСЧЕТ НАДЕЖНОСТИ
Ориентировочный расчет надежности учитывает вли-
яние на надежность только количества и типов приме-
ненных элементов и основывается на следующих допу-
щениях:
— все элементы данного типа равнонадежны, т. е.'
величины интенстивности отказов (Лг) для этих элемен-
тов одинаковы;
— все элементы работают в номинальном (нормаль-
ном) режиме, предусмотренном техническими условия-
ми;
— интенсивности отказов всех элементов не зависят
от времени, т. е. в течение срока службы у элементов,
входящих в изделие, отсутствует старение и износ, сле-
довательно, %,- (/) = const;
— отказы элементов изделия являются событиями
случайными и независимыми;
— все элементы изделия работают одновременно.
Для определения надежности изделия необходимо
знать:
1) вид соединения элементов расчета надежности;
2) типы элементов, входящих в изделие, и число эле-
ментов каждого типа;
3) величины интенсивности отказов элементов %,-, вхо-
дящие в изделие. Выбор %, для каждого типа элементов
производится по соответствующим таблицам.
Таким образом, при ориентировочном расчете на-
дежности достаточно знать структуру системы, номен-
клатуру примененных элементов и их количество.
Ориентировочный метод расчета надежности исполь-
зуется на этапе эскизного проектирования после разра-
ботки принципиальных электрических схем изделий.
Этот-расчет позволяет определить рациональный состав
элементов изделий и наметить пути повышения надеж-
ности изделия на стадии эскизного проектирования и
проводится по формулам (2.2) — (2.4).
63
РАСЧЕТ НАДЕЖНОСТИ С УЧЕТОМ РЕЖИМОВ РАБОТЫ
ЭЛЕМЕНТОВ (ОКОНЧАТЕЛЬНЫЙ РАСЧЕТ)
Окончательный расчет надежности изделия выпол-
няется тогда, когда известны реальные режимы работы
элементов после испытания в лабораторных условиях
макетов и основных узлов изделия или после тщатель-
ного расчета схемы.
Элементы изделия находятся обычно в различных
режимах работы, сильно отличающихся от номинальной
величины. Это влияет на надежность как изделия в це-
лом, так и отдельных его составляющих частей1_Выпол-
нение окончательного расчета надежности возможно
только при наличии данных о коэффициентах нагрузки
отдельных элементов и при наличии графиков зависи-
мости интенсивности отказов элементов от их электри-
ческой нагрузки, температуры окружающей среды и
других факторов, т. е. для окончательного расчета не-
обходимо знать зависимости
Эти зависимости приводятся в виде графиков либо
их можно рассчитать с помощью так называемых попра-
вочных коэффициентов интенсивности отказов
Д/.т, позволяющих учесть влияние различных факторов
на надежность изделия.
I Для определения надежности изделия необходимо
знать:
1) число элементов е разбивкой их по типам и режи-
мам работы;
2) зависимости интенсивности отказов элементов Кг
от электрического режима работы и заданных внешних
условий;
. ...3) структуру системы^
! В общем случае Ki зависит от следующих воздейст-
вующих факторов: электрического режима работы дан-
ного элемента; окружающей температуры; вибрацион-
ных воздействий; механических ударов; линейных уско-
рений; влажности; воздействия морской воды; воздейст-
вия биологических факторов (грибок, плесень, насеко-
мые); давления; реактивного облучения и ряда других
возможных факторов-J
Знание зависимости интенсивности отказов Кг от воз-
действующих факторов является необходимым для пра-
64
вильного использования элементов с целью получения
заданной вероятности исправной работы за время t.
Наиболее существенными воздействующими фактора-
ми являются: окружающая температура и скорость ее
изменения; электрическая нагрузка; механические пере-
грузки, вызванные вибрациями, ударами и линейными
ускорениями.
При разработке и изготовлении элементов обычно
предусматриваются определенные, так называемые «нор-
мальные» условия работы: температура +25±10°С, но-
минальный электрический режим, относительная влаж-
ность 60 ±20%, отсутствие механических перегрузок и
т. д. Интенсивность отказов элементов в номинальном
режиме эксплуатации называется номинальной интен-
сивностью отказов Лот.
Интенсивность отказов элементов при эксплуатации
в реальных условиях Л, равна номинальной интенсивно-
сти отказов Лот, умноженной на поправочные коэффици-
енты а, и ki. Поправочный коэффициент интенсивности
отказов aj=/(/°, ХЕ) учитывает влияние окружающей
температуры и электрической нагрузки, поправочный
коэффициент интенсивности отказов = <р)—тип
воздействия, главным образом механические перегрузки
и относительную влажность окружающего воздуха.
Графики = Ки) приведены в приложении 4.
Значения поправочных коэффициентов k, приведены
в табл. 2.1—2.3.
.Окончательный расчет надежности применяется на
этапе технического проектирования изделия"?"Он обычно^
возможен тогда, когда на изделие заполнила так назы-
ТАБЛИЦА 2.1
Поправочные коэффициенты kt в зависимости от
воздействия механических факторов
на неамортизированную аппаратуру
Условия эксплуатации аппаратуры Вибрация Ударные нагрузки *2 Суммарное воздействие ^2
Лабораторные 1,0 1,0 1,0
Стационарные (полевые) 1,04 1,03 1,07
Корабельные 1,3 1,05 1.37
Автофургонные 1,35 1,08 1,46
Железнодорожные 1,4 1,1 1,54
Самолетные 1 ,46 1,13 1,65
5—1086
65
ТАБЛИЦА 2.2
Поправочные коэффициенты
^3
ТАБЛИЦА 2.3
Поправочные коэффициенты
К
Влажность, % Темпера- тура, °C Поправоч- ный коэф- фициент Л3 Высота, км Поправоч- ный коэф- фициент /?4 Высо- та, км Поправоч- ный коэф- фициент kt
60—70 20—40 1,0 0—1 1,0 8—10 1,25
1—2 1,05 10—15 1,3
90—98 20—25 2,0 2—3 1,1 15—20 1,35
3—5 1,14 20—25 1,38
90—98 30—40 2,5 5—6 1,16 25—30 1,4
6—8 1,2 30—40 1,45
ваемая ведомость (карта) режимов работы элементов.
Этот расчет ведется по известным характеристикам на-
дежности деталей, узлов, блоков, механизмов, приборов
и т. и., входящих .в изделие. Как правило, при расчете
изделие расчленяется на отдельные конструктивно само-
стоятельные части путем деления системы на приборы,
приборов на крупные узлы и блоки, блоков и крупных
узлов на более мелкие узлы и т. д. При этом расчет про-
изводится последовательно от простого к сложному.
Например, при расчете надежности системы следует
определить вначале количественные характеристики от-
дельных приборов по известным количественным харак-
теристикам их узлов п деталей, затем вычислить коли-
чественные характеристики системы по рассчитанным
количественным характеристикам отдельных приборов.
Будем называть каждое устройство, имеющее количе-
ственную характеристику надежности, элементом рас-
чета надежности. Тогда элементами расчета надежности
могут быть детали (резистор, конденсатор, электрова-
куумный прибор и так далее), узлы (электронный уси-
литель, триггерная ячейка), блоки (приемник, передат-
чик), приборы (вычислительный, счетно-решающий) и
даже системы, если вычисляется надежность комплекса
систем.
При расчетах полезно применять интервальную оцен-
ку характеристик надежности. При этом интенсивности
отказов элементов рассматриваются как случайные ве-
личины, взятые из нормальной генеральной совокупно-
сти. Тогда при доверительной вероятности у верхний
66
pn(i) и нижний Pn(t) доверительные пределы P(t) на-
ходятся из равенств
Рв(0-Л(0+г(1+7)/2ар(О, (2.6)
^и(0 = ^е(0— г(1_ (2-7)
где Po(ii)—средняя вероятность безотказной работы,
определяемая по средним значениям интенсивности от-
казов элементов; ор«> — среднее квадратическое откло-
нение; — квантиль уровня р нормального распределе-
ния.
Для верхнего доверительного предела рв= (1+у)/2,
для нижнего рв= (1—у)/2.
При у=0,9 имеем:
(2-8)
Здесь ='Ягог-, где пг-— коэффициент вариации (0<
щ<1).
Аналогично находятся доверительные пределы и для
других характеристик надежности.
Таблицы величин интенсивностей отказов и попра-
вочные коэффициенты для некоторых элементов приве-
дены в приложении 3.
В приложении 2 приведены данные по интенсивности
отказов элементов, опубликованные в трудах симпози-
умов США.
Методика расчета надежности, как правило, включа-
ет в себя следующие моменты:
— определение типа элемента и его характеристики;
— выбор метода расчета с последующим подбором
определенных номограмм, таблиц, графиков или попра-
вочных коэффициентов;
— определение электрических нагрузок и влияния
внешней среды на каждый элемент;
— определение по соответствующей таблице или
графику интенсивности отказа каждого элемента;
— суммирование всех интенсивностей отказов для
определения интенсивности отказов всего изделия.
5* 67
При практическом определении интенсивности отка-
зов изделия данные об интенсивностях отказов отдель-
ных элементов рекомендуется заносить в определенном
порядке в так называемые рабочие таблицы, формы ко-
торых приведены в приложении 5.
[Расчет надежности изделия целесообразно прово-
дить в следующем порядке//
1. Формулируется понятие отказа1
От понятия отказа изделия зависит выбор числа эле-
ментов, которые должны учитываться при расчете на-
дежности. Часто в сложных системах имеются элемен-
ты, выход из строя которых приводит лишь к ухудше-
нию некоторых характеристик системы (точности,
качества переходного процесса и т. д.). Выход из строя
других элементов приводит к нарушению работоспособно-
сти системы, т. е в смысле надежности эти элементы
системы не равнозначны. Поэтому необходимо учиты-
вать только те элементы, выход из строя которых при-
водит к отказу. Таким образом, -прежде чем приступить
к расчету надежности, необходимо четко сформулиро-
вать, что следует понимать под отказом изделия, а затем
уже выбирать число элементов, которое должно быть
учтено при расчете вероятности исправной работы или
при расчете других количественных характеристик на-
дежности.
^2. Составляется схема расчета надеж-
ности /
СхелГу расчета надежности удобно составить таким
образом, чтобы элементами расчета были конструктив-
но оформленные блоки. Может оказаться, что в расчет-
ных блоках имеются элементы, работающие не все вре-
мя .в течение работы блока, а только некоторую часть
времени. В этом случае целесообразно такие элементы
распределить по времени их работы на группы и обра-
зовать из этих групп самостоятельные элементы расче-
та. На схеме расчета надежности целесообразно указы-
вать время работы каждого элемента расчета.
/3. Выбирается метод расчета надеж-
но с т и
В соответствии с видом расчета выбираются расчет-
ные формулы и для определения интенсивности отказов
изделия по соответствующим таблицам определяются
величины интенсивности отказов элементов.
При наличии ведомостей (карт) режимов работы
68
элементов определяются коэффициенты нагрузки и по
графикам или по поправочным формулам вычисляются
%,- для всех элементов.
Если в течение времени работы аппаратуры элемент
имеет не постоянную интенсивность отказов, но суще-
ствуют четко выраженные временные интервалы, в тече-
ние которых интенсивность отказов элемента в основном
постоянна, то для расчета надежности используется так
называемая эквивалентная интенсивность отказов эле-'}
мента. Допустим, что интенсивность отказов элемента}
за период времени ti равна за период tz равна Д и]
т. Д- Тогда интенсивность отказов такого элемента за
период времени / = /1+1/2+^ + ... будет
А'ЭКВ ~ (W1+W2+W3+ - - -)А- (2.9)
14. Составляется таблица расчета интен-
сивности отказов и з д е л и я.д
Для расчета интенсивности отказов изделия обычно
используются формы таблиц, приведенных в приложе-
нии 5, например: для ориентировочного расчета надеж-
ности применяется табл. П. 5.1; для окончательного рас-
чета надежности в случае использования графиков Лг"
=,f(Kn,T0)—табл. П. 5.2; для окончательного расчета
надежности при использовании поправочных коэффици-
ентов— табл. П. 5.3.
Интенсивность отказов данного типа элемента в ре-
альных условиях работы вычисляется по формуле
п
—- ^20^1^2 • * ^20 | ^2» (2- 10)
/-1
где До— интенсивность отказов элемента, работающего
в нормальных условиях при номинальной электрической
нагрузке; си, аг,.. ., ап —поправочные коэффициенты,
зависящие от различных воздействующих факторов.
5. Р а с с ч и т ы в а ют с я количественные ха-
рактеристики надежности./
Данные расчета заносятся в Итоговые таблицы или
приводятся в виде графиков. {^Расчеты оформляются
в виде технического отчета.J
щОтчет должен содержать:
а) структурную схему надежности системы с крат-
ким объяснительным текстом;
б) формулировку понятия отказа системы;
69
в) расчетные формулы для количественных характе-
ристик надежности;
г) расчет количественных характеристик надежности,
итоговые таблицы и графики;
д) оценку точности расчета; __
е) выводы и рекомендации.'^' Д-р? /-7 п£
§ 2.2. ТИПОВЫЕ ПРИМЕРЫ
Пример 2.1. Система состоит из 12 600 элементов,
средняя интенсивность отказов которых ХСр=0,32-10-6
\1час.
Необходимо определить вероятность безотказной ра-
боты в течение / = 50 час.
Решение. Интенсивность отказов системы по фор-
муле (2.3) будет
ЛС=Й,С1Л=О,32 • IO-8 • 12 600=4,032 • Ю~3 Цчас.
Тогда на основании (2,2)
Р (50) = e-V = е-4.032.Ю-з.БО 0,82
Пример. 2.2 Используя данные примера 2.1, вычис-
лить среднюю наработку до первого отказа.
Решение. Средняя наработка до первого отказа
Тер с вычисляется по формуле (2.2). Подставляя в фор-
мулу значение Хс, пз примера 2.1 получим
Т’ере — 4,032-10-’ ~ 2^0 ЧОС.
Пример 2.3. Система состоит из N=5 блоков. Надеж-
ность блоков характеризуется вероятностью безотказной
работы в течение времени t, которая равна: pi(f)=0,98;
р2(/)=0,99; р3(0=0,97; p^t) =0,985; p5(i) =0,975.
Требуется определить вероятность безотказной рабо-
ты системы.
Решение. На основании формулы (2.1) имеем
n \
Рс (/) = П Л (0 = 0,98 0,99 0,97-0,985-0,975?
i=i
70
Вероятности pi, рг,.. р$ близки к единице, поэтому
вычислить pc(t) удобно, использовав приближенную фор-
мулу (2.5).
В нашем случае </1=0,02; <72=0,01; </з=0,03; </4=0,015;
</5=0,025. Тогда
5 5
?=1 i—1
= 1 — (0,02 +;o,oi -К0,03;+'0,015 + 0,025) = 0,9.
Пример 2.4. Система состоит из трех устройств. Ин-
тенсивность отказов электронного устройства равна Zi=
= 0,16-IO-3 l/«ac=const. Интенсивности отказов двух
электромеханических устройств линейно зависят от вре-
мени и определяются следующими формулами:
Лг=0,23 • 10~4/1 /час, Л3=0,06 • 10”6 /2>6 1 /час.
Необходимо рассчитать вероятность безотказной ра-
боты изделия в течение 100 час.
Решение. На основании формулы (2.1) имеем
J \dt 4- J Я2 (0 dt + J Я3 (0 dt
.0 0 б
Г / /2 ,
= ехр — (Я/ + 0,23-10-4~4'
4-0,06-10-’
Для t = 100 час
Рс(100) = ехр
0,16- IO'3-100 + 0,23-IO’4
1002
2
4-0,06^^- - ю-Л I о,зз.
Пример 2.5. Система состоит из трех блоков, средняя
наработка до первого отказа которых равна Т\= 160 час,
= час, 7'з=600 час. Для блоков справедлив экспо-
ненциальный закон надежности. Требуется определить
среднюю наработку до первого отказа системы.
71
Решение. Воспользуемся формулой (2.2) для сред-
ней наработки до первого отказа системы. В нашем слу-
чае
== + К + ^3= у-by--=
1 1 ' 2 1 3
.—LJ ]—L ~ о pi I ±_
~ 160^320^600 U’U11 час '
Тогда
^СРС=ТГ~67О1Т 91 час- :
Пример 2.6. Система состоит из двух устройств. Ве-
роятности безотказной работы каждого из них в течение
времени /=100 час равны: pi(100) =0,95; р2( 100) =0,97.
Справедлив экспоненциальный закон надежности. Необ-
ходимо найти среднюю наработку до первого отказа си-
стемы.
Решение. Найдем вероятность безотказной работы
изделия: Рс(100) =/?i(100) -p2(100) =0,95-0,97=0,92.
Найдем интенсивность отказов изделия, воспользо-
вавшись формулой
Рс (100) = 0,92 = e~V = e“V100 .
По табл. П. 7. 14 имеем
Хс • 100 = 0,083 или Хс = 0,83- 10 -’ 1/час.
Тогда
Тс» с== ' Оз:То=г ~1209 час'
Пример 2.7. Вероятность безотказной работы одного
элемента в течение времени t равна p(t) =0,9997. Требу-
ется определить вероятность безотказной работы систе-
мы, состоящей из ^ = 100 таких же элементов. V
Решение. Вероятность безотказной работы систе(
мы равна Рс(/) =pN(t) = (0,9997) 10°. Вероятность РЛ1)
близка к единице, поэтому для ее вычисления восп- иь-
зуемся формулой (2.5). В нашем случае <у(/) = 1—p(i) —
= 1—0,9997 = 0,0003. Тогда Рс(0 « 1—Nq(t) ~ 1 — 100Х
X 0,0003 = 0,97.
Пример 2.8. Вероятность безотказной работы систе-
мы в течение времени t равна Рс(/)=0,95. Система
состоит из А'=120 равнонадежных элементов. Необходи-
мо найти вероятность безотказной работы элемента.
72
Решение. Очевидно, что вероятность безотказной
работы элемента будет pi(() = (/ Рс (/). Так как p(t)
близка к единице, то вычисления p(t) удобно выполнить
по формуле (2.5).
В нашем случае qc (^) = 1 — Рс (0 = 1 — 0,95 = 0,05.
Тогда
Р if) = У О) = 1 - 1 - ЛДГ ~ °-9996-
Пример 2.9. В системах могут быть использованы
только элементы, интенсивность отказов которых равна
Z,i=10~5 1/час. Системы имеют число элементов Лт=500
и 7V2 = 2 500. Требуется определить среднюю наработку
до первого отказа и вероятность безотказной работы
в конце первого часа Рс(1).
Решение. Интенсивность отказов систем соответ-
ственно будет
Ad=NAi = 500-10 г’=0,5-1О2 1 /час,
Лс2=Лиг = 2 500 • 10-5=0,025 1/час.
Тогда
РС1 = е41' = е0’5'10’2'1 =0,995;
РС2 = е-0,025'1 = 0,975;
Тс$с1 Х01 0,5- 10~г 200 Ч0С'
Tcpcs ЛС2 0,025 —40 Ч<К'
Задачу можно легко решить, используя номограмму
приложения П. 1. 1.
Пример 2.10. По аналогии с ранее разработанными
системами предположено, что сложность проектируемой
системы не должна превышать Л’с=2 500 элементов. Не-
обходимо при обсуждении проекта технического зада-
ния на новую систему выяснить, насколько реально вы-
полнимы предъявленные требования без использования
специальных способов повышения надежности. Допу-
стим, что требуется определить, может ли быть спроек-
тирована система, к которой предъявлено требование
Рср с= 120 час.
73
Решение. Пользуясь номограммой П. 1.1, на левой
шкале находим риску 120 и восстанавливаем из нее пер-
пендикуляр. На верхней шкале, где указано количество
элементов в системе, находим риску 2 500 и опускаем из
нее второй перепендикуляр до пересечения с первым.
Точка 'пересечения обоих перпендикуляров на номограм-
ме показана кружком.
Уровень надежности элементов, соответствующий
точке пересечения перпендикуляров, может быть опреде-
лен методом экстраполяции. Пользуясь рисками шкалы
интенсивности отказов и проводя через них дополнитель-
ные уровни, определим, что требуемая интенсивность
отказов элементов должна быть равна ^ = 3,6-10“® 1/час.
Если продолжить перпендикуляр, восстановленный
из точки 120 левой шкалы ТСрС, до пересечения его
с правой шкалой, то на последней найдем, что вероят-
ность исправной работы системы в конце первого часа
будет равна
Рс(1) =99,1 %.
Просматривая данные об интенсивности отказов эле-
ментов, обеспечиваемых современным состоянием про-
мышленности, увидим, что предъявленные в данном при-
мере требования к надежности системы выполнимы.
Пример 2.11. В системе Afc=2500 элементов и веро-
ятность безотказной работы ее в течение одного часа
Рс(1)=98°/о. Предполагается, что все элементы равно-
надежны. Требуется вычислить среднюю наработку до
первого отказа системы ТСрс и интенсивность отказов
элементов X.
Решение. На правой шкале номограммы П. 1. 1
находим риску 98 и проводим через нее перпендикуляр
до пересечения с перпендикуляром, опущенным из точки
2 500 верхней шкалы. На номограмме пересечение пер-
пендикуляров обозначено квадратиком с точкой в цент-
ре. Тогда точке пересечения перпендикуляров будет со-
ответствовать интенсивность отказов элементов %=8,4Х
X Ю-6 \1час. /
Продолжив перпендикуляр по горизонтали д/ пере-
сечения с левой шкалой ТСрС, найдем, что этому значе-
нию параметров соответствует Тсрс = 50 час.
Пример 2.12. Система состоит из пяти приборов, ве-
роятности исправной работы которых в течение времени
/=100 час равны: pi( 100) =0,9996; р2(Ю0) =0,9998;
р3( 100) =0,9996; р4( 100) =0,999; р6( 100) =0,9998. Тре-
74
буется определить частоту отказов системы в момент
времени /=100 час.
Предполагается, что отказы приборов независимы
и для них справедлив экспоненциальный закон надеж-
ности.
Решение. По условию задачи отказы приборов не-
зависимы, поэтому вероятность безотказной работы си-
стемы равна произведению вероятностей безотказной
работы приборов. Тогда по формуле (2.5) для случая
высоконадежных систем имеем
6
Рс (100) 1 — v Q. (100) = 1 — (0,0004 +
/=1
Д- 0,0002 + 0,0004 + 0,001 + 0,0002) = 0,9978.
Так как вероятность безотказной работы близка к еди-
нице, то в соответствии с формулой (2.4) для P(t) ин-
тенсивность отказов можно вычислить из выражения Ас =
1—Pe(Q Подставляя значения Рс (100) и время / =
= 100 час, получим
* 1 -— 0,9978 Q о 1 н - 5 1/
Яс==----Гоо---=2,2-10 5 1/час.
Тогда частота отказов в соответствии с формулой (2.4)
будет
(1 — V) = 2,210'6(l — 2,2-10“®-100) =
= 2,195-10~5 1/час.
Пример 2.13. Изделие состоит из 14 маломощных низ-
кочастотных германиевых транзисторов, 4 плоскостных
кремниевых выпрямителей, 56 керамических конденса-
торов, 168 резисторов типа МЛТ мощностью 0,5 вт, 1 си-
лового трансформатора, 2 накальных трансформаторов,
6 дросселей и 3 катушек индуктивности. Необходимо
найти вероятность безотказной работы изделия в тече-
ние /=260 час и среднюю наработку до первого отказа
Др с-
Решение. Для выполнения ориентировочного рас-
чета надежности составим и заполним табл. П. 5. 1, вы-
числив величину интенсивности отказов изделия. Третья
графа таблицы не заполняется, так как при ориентиро-
75
вечном расчете можно осуществлять расчет без наличия
схемы. Значение интенсивностей отказов Л, элементов
(пятая графа) выбирается из таблиц приложения 3.
Заполненная табл. 2.4 приведена ниже.
ТАБЛИЦА 2.4
К примеру 2.13.
Наименование и тип элемента Обозначе- ние по схеме Количество элементов Ni Интенсив- ность от- казов, 10“5 ]/час IO-5 IIчас Примеча- ние
Транзистор маломощ- ный низкочастотный германиевый Выпрямитель плос- костный кремниевый Конденсатор керами- ческий "фб 1 1 < ' /'-.с Резистор МЛТ, 0,5 вт Трансформатор си- ловой Трансформатор на- кальный Дроссель Катушка индуктив- ности 02 / 1 . (д И 14 4'1 -да 168 1 2 6 3 0,3 0,5 о,л* 0,05 0,3 0,2 0,1 0,05 Т 4 Тг84 8,4 0,3 0,4 0,6 О','Тб Табл. И. 3.5 Табл. И. 3.5 Табл. П. 3.3 Табл. П. 3.1 Табл. П. 3.7 Табл. И. 3.7 Табл. П. 3.7 Табл. П. 3.7
, о о Ц' /0! О О s ХУг = 254 Хс=^УДг = 23,89-10--5 1/час г=1 Цц *=I
По данным таблицы- и формулам (2.2) находим
Рс (260) = e~V = е-23-89' 10’ъ-260 ъ 0,94,
т ____!_____—д I ул час
с₽с Ас 23,89-Ю-5
Пример 2.14. Все элементы электронного усилителя
работают в нормальный период эксплуатации, т. е. Х =
= const. Усилитель должен непрерывно работать в тече-
ние 10 час. Из схемы известно, что усилитель состоит из
2 ламп, 8 резисторов и 6 конденсаторов; режимы рабо-
ты всех элементов известны и указаны в табл. 2.5. Тре-
буется рассчитать вероятность безотказной работы Рс('/)
и среднюю наработку до первого отказа Тс,рус.
76
Рис. 2.1. Зависимость интен-
сивности отказов объемного ре-
зистора (1 вт) от окружающей
температуры и коэффициента
нагрузки.
Рас. 2.2. Зависимость интенсив-
ности отказов керамических
конденсаторов от окружающей
температуры при различных
коэффициентах нагрузки.
Решение. Определим интенсивность отказов усили-
теля, для чего заполним таблицу расчета П. 5. 2.
На основании данных о режиме работы электроэле-
ментов определяем интенсивность отказов, используя
зависимости ki = f(Kn, Т°) (рис. 2. 1 и 2.2). Значение ин-
тенсивности отказов записываем в соответствующую
графу таблицы расчета (табл. 2.5).
Вероятность безотказной работы усилителя в тече-
ние 10 час непрерывной работы
^ус(Ю) —ехр
= ехр (—10-19,32-10-5) = ехр ( 19,32-101) = 0,998.
Средняя наработка до первого отказа усилителя
равна
I _ 1
СРУС“' Хус ~ k
X NiU
1
19,32 10-6
— 5000 час.
77
Таблица расчета интенсивности отказов X к г ТАБЛИЦА 2.5 римеру 2.14
Режим работы
Наимено- ванне и тип] элемента Обозначе- ния по ^схеме Количество элементов Hi ! Коэффициент нагрузки /Сн । Температура, °C Интенсив- ность от- казов 10"5 1/ час 10"5 1/чаС | Примечание
Резистор R1, «2 2 0,5 40 0,09 0,18
Резистор Я3, 2 0,5 80 0,12 0,24
Резистор R$> R6 2 0,8 60 0,10 0,20
Резистор Rv Kg 2 1,0 50 0,10 0,20
Конденса- G, G 2 0,2 50 о,оз 0,06
тор Конденса- тор G» C4 2 0,4 60 0,13 0,26
Конденса- G> G 2 0,2 80 0,09 0,18
тор Лампы tZZi, JJz 2 1,0 — 9 18
k £
16 1 ХД = Н ),32-10-s 1/час
i~Y 1
Пример 2.15. Электронное устройство непрерывно ра-
ботает в течение 500 час. Число входящих в него эле-
ментов и их режимы работы приведены в табл. 2.6. Не-
обходимо вычислить вероятность безотказной работы
РСО.
Решение. Для определения надежности вычислим
интенсивность отказов элементов для заданных темпе-
ратурных условий и в определенных электрических ре-
жимах, используя графики, приведенные в приложе-
нии 4.
Интенсивность отказов элементов с учетом электри-
ческой нагрузки и температуры окружающей среды оп-
ределяется выражением
— 'Ди Пт.
Заполним табл. П. 5. 3 расчета интенсивности отка-
зов устройства. Значения Ди взяты из таблицы приложе-
ния 2, коэффициенты нагрузки электроэлементов — из
ведомости режимов работы, обычно прилагаемой к тех-
ническому заданию на расчет надежности. Поправочные
78
ТАБЛИЦА 2.&
Таблица расчета интенсивности отказов X к примеру 2. 15
Наименование и тип элемента Обозначе- ние по типовой схеме Количество элементов *1 Интенсивность отказов при номинальном режиме 10*в \/час Режим работы Поправоч- ный коэф- фициент Интенсивность отказов Ьго элемента \iaf 1 0"s ! 1чаС Интенсивность отказов'изде- лия из-за эле- ментов 1-ГО типа Nt\(au 10"» 1/час
Коэффи- циент на- грузки К* Темпера - тура, °C
Конденсатор бумажный С, 1 0,05 0,6 50° С 0,77 0,0385 0,0385
Конденсатор слюдяной Сг-г-С5 4 0,075 0,8 То же 0,8 0,0600 0,248
Резистор углеродистый Ri 1 0,045 0,7 Я 0,95 0,0430 0,043
Резистор композицион- ный 1 0,053 0,6 я 1,2 0,0636 0,0636
Резистор металлопле- ночный ^12 10 0,04 0,7 я 0,8 0.032 0,32
Трансформатор анодный —Трз 3 0,025 1,0 я 1,0 0,025 0,075
Трансформатор силовой Тр4 1 1,04 1,0 я 1,0 1,04 1,04
Пайки 100 0,004 — я — 0,004 0,4
т
S'Vt = 121
1=1
Хо= =2,22.10-» {/час
1=1
ТАБЛИЦА 2.7
00
Таблица расчета интенсивности отказов X к примеру 2.16
Наименование и тип элемента Обозначения по схеме Количество эле- ментов Интенсивность отказов при номинальном режиме , 10"s 1/час Режимы работы Поправоч- ный ко- эффициент ai ог г’ 1/час Nt\iav 10“6 1 час
Коэффици- ент на- грузки 7<н 1емиерату- ра среды, °C
Резистор МЛТ, 1 вт -Rs 5 1 0,2 50 0,4 0,4 2
Резистор МЛТ, 0,5 вт Re- -Re 4 0,5 0,8 65 1,86 0,93 3,72'
Резистор ПЭВ, 10 вт ^ю " ^14 5 3,2 0,2 80 0,14 0,45 2,25
Резистор СПО, 2 вт 7? 15 1 1,8 0,8 50 1,38 2,48 2,48
Конденсатор МБМ с\- -С7 7 2 0,3 50 0,38 0.76 5,32
Диоды кремниевые (вы- прямительные точечные) D,- -Он 11 2 0,5 50 1,05 2.1 23,1
Трансформаторы вые СИЛО- Tp-U Тр-З 3 3 1 50 5,2 15,6 46,8
Дроссель D- -1 1 1 0,8 60 4,1 4,1 4,1
37
£л^о4Й4 = 89,77-1О-в Х/час
8
IX = 37
коэффициенты а< определены по графикам приложе-
ния 4: рис. П. 4.8 для конденсаторов бумажных,
рис. П. 4. 12 — для слюдяных, рис. П. 4. 5 для резисто-
ров углеродистых, рис. П.4.4 — для металлопленочных
и рис. П. 4. 6. — для композиционных.
Рассчитанные Л.с приведены в табл. 2.6.
Вероятность безотказной работы блока для t=
500 час будет
р (500) = ехр | —t | = ехр (—500-2,22- 10~с) =
\ <=1 J
= 0,9989.
Пример 2.16. Блок питания состоит из элементов, но-
менклатура и режим работы которых приведены
в табл. 2.7. Требуется определить среднюю наработку
до первого отказа и вероятность безотказной работы
в течение 240 час.
Решение. Определим эксплуатационные значения
интенсивностей отказов элементов по формуле (2.10),
для чего номинальные значения интенсивностей отказов
Хог элементов возьмем из таблиц приложения 3: для ре-
зисторов— из табл. П. 3. 1; для конденсаторов — из
табл. П. 3. 3; для полупроводниковых приборов — из
табл. П. 3. 5; для трансформаторов и дросселей — из
табл. П. 3. 7. Поправочные коэффициенты аг выберем из
табл. П. 3. 2, П. 3. 4, П. 3. 6 и П. 3. 9 соответственно.
Для .определения интенсивности отказов блока пита-
ния заполним таблицу по форме П. 5. 3. Величины ин-
тенсивности отказа блока питания приведены в табл.2.7.
По данным таблицы и формулам (2.2) находим
Рс (240) = e~V = е-89’77-240'7 В * 10'6 ~ 0,98,
7'СР с~ТГ = 89,77-ю-6 ~11ЧаС'
§ 2.3. ЗАДАЧИ
В настоящем параграфе приведены задачи на расчет надеж-
ности невосстанавливаемых изделий при основном соединении эле-
ментов. Эти задачи легко решить, используя типовые примеры, рас-
смотренные в § 2.2.
2.1. Аппаратура связи состоит из 2000 элементов, средняя интен-
сивность отказов которых Лср=0,33 • 10-6 1/час. Необходимо опре-
делить вероятность безотказной работы аппаратуры в течение
1 = 200 час и среднюю наработку до первого отказа.
Ответ: Р(200) =0,27; Тср с = 151,5 час.
6—1086
81
2.2. Невосстанавливаемая В процессе работы майшна coctoHT
из 200 000 элементов, средняя интенсивность отказов которых
7=0,2 • 10~6 1/час. Требуется определить вероятность безотказной
работы электронной машины в течение /=24 час и среднюю нара-
ботку до первого отказа.
Ответ: /’(24) =0,383; Тер с =25 час.
2.3. Используя данные задачи 2.2, определить А (24) и Герс при
условии, что 7=0,2- 10 7 1/час.
Ответ: Р(24) =0,908; Тер с=250 час.
2.4. Система управления состоит из 6 000 элементов, средняя
интенсивность отказов которых 7ср=0,16 • 10~6 1/час. Необходимо
определить вероятность безотказной работы в течение / = 50 час и
среднюю наработку до первого отказа.
Ответ: А (50) =0,953; ТСрС = 1 040 час.
2.5. Невосстанавливаемая в процессе работы радиоаппаратура
сантиметрового диапазона состоит из 1 000 элементов. Требующееся
время непрерывной работы /=200 час. Определить вероятность без-
отказной работы и среднюю наработку до первого отказа, если
7=0,1 • 10—’ 1/час.
Ответ: А (200) =0,82; Тсрс = 1000 час.
2.6. Невосстанавливаемый портативный радиоприбор состоит из
500 элементов, средняя интенсивность отказов которых 7ср=
=0,2 10~5 1/час. Найти вероятность безотказной работы в течение
200 часов и среднюю наработку до первого отказа.
Ответ: Р (200) =0,8187; Тср с = 1 000 час.
2.7. Система состоит из 4 000 элементов, средняя интенсивность
отказов которых 7ср=0,25 10-6 1/час. Необходимо определить ве-
роятность безотказной работы в течение 5, 10, 20, 30 и 50 час и
среднюю наработку до первого отказа.
Ответ: Р(5) =0,995; Р(10)=0,99; Р (20) =0,98; Р(30) =0,97;
Р(50) =0,95; Тср С = 1 000 час.
2.8. Невосстанавливаемая в процессе работы аппаратура состоит
нз 2 000 элементов, средняя интенсивность отказов которых 7СР=
=0,05 • 10 г' 1/час. Время непрерывной работы аппаратуры 7=200 час.
Определить вероятность безотказной работы и среднюю наработку
до первого отказа.
Ответ: Р(200) =0,82; Тср с-= 1 000 час.
2.9. Аппаратура состоит из 3 000 элементов, средняя интенсив-
ность отказов которых 7ср=0,5-10-6 1/час. Необходимо найти ве-
роятность безотказной работы в течение 100 час и среднюю нара-
ботку до первого отказа.
Ответ: Р(100) =0,86; 7’срс=665 час.
2.10. Используя данные задачи 2.9, определить Р(100) и 7’ср е,
если 7ср=0,5-10~7 1/час.
Ответ: /'( 100) =0,985; 7’сре=6 665 час. ’’
2.11— 2.40. Изделие состоит из N элементов, средняя интенсив-
ность отказов которых 7ср. Требуется вычислить вероятность безот-
казной работы в течение t и среднюю наработку до первого отказа.
Исходные данные для решения задачи и ответы приведены
в табл. 2.8.
2.41. Система состоит из N—20 приборов. Надежность приборов
характеризуется вероятностью безотказной работы в течение вре-
мени t, которая равна: pi(/)=0,98; 02(0 = 0,94; дз(О—0,99; p4,s,e(O =
=0,997; р7 8,9(7/=0,965; р1о(//=О,95; Pll(t) =0,997; pn(t)=0,975;
Р1з(7) =0,985; pit(/)=0,97; p15,i6,i7(0 =0,96; pla,ls(t) =0,995; p2o(/) =
82
ТАБЛИЦА 2.8
К задачам 2.11—2.40
Номер задачи Исходные данные Ответ
N \р. 1/ч«С t, час Pit) Гср. час
2.11 5 200 0,16-Ю-5 200 0,19 , 120
2.12 3 600 0,210-» 50 Д698- 139
2.13 2 500 0,35-10-6 100 0,916 1 143
2.14 2 500 0,5-10-5 100 0,2865 80
2.15 1 000 0,5-10-5 100 0,6065 200
2.16 750 0,5-10-5 100 0,6873 266
2.17 500 0,5-10-5 100 0,7788 400
'2.Т8 250 0,5-10-5 100 0,8825 800
2.19 20 500 2-Ю-8 2 0,44 2.44
2.20 1 000 0.5-10-» 0,5 0,7788 2
2.21 2 000 5-Ю-6 10 0,905 100
2.22 95 000 0,5-10-5 2 0,91 21
2.23 150 000 0,25-10-в 4 0,86 26.7
2.24 45 000 0,5-10-5 2 0,6376 4,4
2-25 300 000 0,2-10-’ 8 0,953 166,7
2.26 50 000 0,2-10-5 5 Ю,95 100
2.27 170 000 0,7-10-е 3 0,7 8,4
2.28 189 000 1,4-10-6 2 0,59 3,8 .
2.29 547 000 0,4-10-6 2 0,65 4,57
2.30 35 1-Ю-5 1 000 0,7 2 860
2.31 175 0,5-10-5 480 0,9588 1 143
2.32 1 750 0,1-10-5 40 0,93 571,4
2.33 21 000 0,1-10-6 100 0,81 475
2.34 88 000 0,1-10-’ 50 0,957 1 136
2.35 600 000 0,6-10-8 20 0,93 278
2.36 600 000 0,5-10-’ 10 0,74 33,3
2.37 890 0,7-10-5 25 0,86 160
2.38 15-Ю6 1-10-» 24 0,6977 66,7
2.39 1,5-10» 1-ю-8 2 0,97 66,7
2.40 15-104 1-10-’ 20 0,74 66,7
=0,945. Необходимо определить вероятность безотказной работы
системы.
Ответ: (О=0,595.
2.42. Аппаратура состоит из Л'-11 блоков. Надежность блоков
характеризуется вероятностью безотказной работы в течение вре-
мени t, которая равна: pi,z,s(t) =0,997; р4,5 в(7) =0,965; pt,8,s(7_) = 0,96;
Pio,it(t) =0,995. Требуется найти вероятность безотказной работы
аппаратуры.
Ответ: Pc(t)=0,78.
2.43. Прибор состоит из N—5 узлов. Надежность узлов характе-
ризуется вероятностью безотказной работы в течение времени t.
которая равна: pi (7)—0,98; р2(Т) = 0,99; р3(7) = 0,998; р4 (7) = 0,975;
р6<7> 0,985. Необходимо определить вероятность безотказной рабо-
ты прибора.
Ответ: Pup(t) =0,93.
6!
83
К задачам
Исходные
Номер задачи N Pi (0 А (0 А (0 А (0 А (0
2.46 3 0,97 0,98 0,99
2.47 5 0,9996 0,9998 0,9996 0,999 0,998
2.48 6 0,998 0,98 0,975 0,96 0,95
2.49 10 0,9999 0,9998 0,9996 0,9994 0,9992
2.50 10 0,9998 0,9998 0,9998 0,996 0,996
2.51 9 0,996 0,996 0,996 0,994 0,994
2.52 9 0,95 0,95 0,95 0,955 0,955
2.53 9 0,9999 0,9999 0,9999 0,9998 9,9998
2.54 9 0,9994 0,9994 0,9994 0,9992 0,9992
2.55 9 0,998 0,998 0,998 0,996 0,996
2.56 8 0,992 0,992 0,992 0,99 0,99
2.57 8 0,986 0,986 0,986 0,984 0,984
2.58 8 0,98 0,98 0,975 0,975 0,97
2.59 7 0,97 0,97 0,97 0,965 0,965
2.60 7 0,995 0,995 0,955 0,955 0,95
2.61 6 0,945 0,945 0,95 0,955 0,96
2.62 7 0,922 - 0,922 0,93 0,93 0,94
2.63 5 0,922 0,93 0,94 0,945 0,95
2.64 6 0,95 0,96 0,97 0,97 0,975
2.65 7 0,98 0,98 0,982 0,982 0,984
2.66 8 0,984 0,984 0,986 0,986 0,988
2.67 5 0,992 0,994 0,996 0,998 0,999
2.68 6 0,922 0,93 0,94 0,945 0,948
2.69 5 0,95 0,955 0,96 0,965 0,97
2.70 8 0,9998 0,9998 0,9996 0,9996 0,9994
... ------—________________ ^.^г. й ,, „ ...nr , iiirtiwifittii
2.44. Изделие включает четыре устройства, надежность которых
характеризуется вероятностью безотказной работы в течение време-
ни t, равной: р1(7) = 0,94; рг(7)=0,95; р3(?) = 0,97; p^t) =0,945. Поль-
зуясь формулами (2.1) и (2.5), необходимо вычислить вероятность
безотказной работы изделия.
Ответ: P(2.i)(f) = 0,82; P(2.s)(0 =0,805. •
2.45. Комплекс состоит из N—Z систем. Надежнс^ш' отдельных
систем характеризуется вероятностью безотказной работы в течение
времени I, которая равна pi(7) = 0,78; рг(7)=0,93; р;<(7) = 0,82. Опре-
делить вероятность безотказной работы комплекса.
Ответ: PE(t)=0,595.
2.46— 2.70. Изделие состоит из N частей. Надежность каждой
части изделия характеризуется вероятностью ptft) безотказной рабо-
ты в течение времени I. Необходимо найти вероятность безотказной
работы изделия.
Исходные данные для решения задачи и ответы приведены
в табл. 2.9.
84
ТАБЛИЦА 2.9
2.46 — 2.70
данные
Ре (О Р-, (0 Рей) Ре (0 Рю (0 Ответ (/)
— .— 0,94
— — — — — 0,996
0,94 — .— — — 0,82
0,999 0,998 0,996 0,994 0,992 0,977
0,996 0,998 0,998 0,998 0,994 0,976
0,994 0,992 0,992 0,992 .— 0,956
0,955 0,960 0,960 0,960 — 0,661
0,9998 0,9996 0,9996 0,9996 — 0,998
0,9992 0,999 0,999 0,999 — 0,993
0,996 0,994 0,994 0,994 — 0,974
0,99 0,988 0,988 — — 0,923
0,982 0,982 0,982 — — 0,875
0,97 0,965 0,965 — — 0,797
0,96 0,96 .— — — 0,783
0,95 0,95 — — — 0,772
0,96 — — — — 0,747
0,94 0,95 — — > 0,617
— — .— .— — 0,693
0,98 .— -— — — 0,822
0,984 0,98 — — — 0,873
0,988 0,99 0,99 — .—. 0,904
.— .— -— — — 0,978
0,949 .—. -— —„ — 0,685
— .— — — — 0,815
0,9994 0,9992 0,9992 —. — 0,996
2.71— 2.75. Изделие состоит из N групп приборов. Отказы при-
боров первой группы подчинены экспоненциальному закону с ин-
тенсивностью отказов отказы приборов второй группы — нормаль-
ному закону с параметрами h и ст, отказы приборов третьей груп-
пы — закону Вейбулла с параметрами /.<, и k. Требуется определить
вероятность безотказной работы в течение времени t.
Исходные данные для решения задач и ответы приведены
в табл. 2.10.
2.76— 2.80. Изделие состоит из N групп приборов. Отказы пер-
вой группы подчинены экспоненциальному закону с интенсивно-
стью отказов X, отказы приборов второй группы — закону Релея
с параметром о п отказы приборов третьей группы — закону Вей-
булла с параметрами /.о и k. Необходимо найти вероятность без-
отказной работы в течение времени t.
Исходные данные для решения задач и ответы приведены
в табл. 2.11.
2.81. Система состоит из пяти приборов, средняя наработка до
первого отказа которых равна: 7’1 = 83 час; Тг=220 час; 73 = 280 час;
85
ТАБЛИЦА 2.10
К задачам 2.71—2.75
Номер задачи Исходные данные Ответ F (0
N групп X, 10“4 1}час Ti, час а, час Ю-s 1/ час k t
2.71 3 1 7 200 2 000 0,1 1,5 100 0,89
2.72 2 — ’6 000 J4 000 0,3 1,5 1 000 0,87
2.73 2 3,2 — — 0,2 1,3 500 0.45
2.74 2 0,93 8 000 3 000 —- — 2 000 0,82
2.75 3 0,6 4 000 4 000 0,16 1,4 2 400 0,67
74=400 час; Т6 = 700 час. Для приборов справедлив экспоненциаль-
ный закон надежности. Требуется найти среднюю наработку до пер-
вого отказа системы.
Ответ: Тср с=41,5 час.
ТАБЛИЦА 2.11
К задачам 2.76—2.80
Номер задачи Исходные данные Ответ Pit)
N групп X, 10_з {/час а, час Хо, 10"4 \[час k час
2.76 3 0,2 1 000 0,1 1,5 500 0,7
2.77 3 0,1 1 200 0,03 1,5 1 000 0,54
2.78 2 — 1 000 1,6 1,3 500 0,53
2.79 2 0,09 —. 1,3 1,3 120 0,93
2.80 2 0,06 800 — — 200 0,96
2.82. Система состоит из двух блоков, средняя наработка до пер-
вого отказа которых равна Ti = 200 час; Т-> = 40 час. Для блоков
справедлив экспоненциальный закон надежности. Необходимо опре-
делить среднюю наработку системы до первого отказа.
Ответ: Тсрс = 33,3 час.
2.83— 2.90. Система состоит из Л' блоков, средняя наработка до
первого отказа которых равна Т,-. Для блоков справедлив экспонен-
циальный закон надежности. Требуется найти среднюю наработку
до первого отказа системы.
Исходные данные для решения задачи и ответы приведены
в табл. 2.12.
2.91. Система состоит из трех устройств. Вероятность безотказ-
ной работы каждого из них в течение времени /=100 час равна:
Р1(100) =0,95; /?2(100) =0,96; /?з(Ю0) =0,97. Справедлив экспонен-
циальный закон надежности. Необходимо вычислить среднюю нара-
ботку до первого отказа системы.
Ответ: Тер с =830 чес.
86
ТАБЛИЦА 2.1
К задачам 2.83—2.90
Номер задачи Исходные данные 4 Ответ ^ерс- ч“с
N Л г» Л т. 7. Т6 Г,
2.83 5 2 000 1 850 1 600 1 750 1 650 352
2.84 7 160 320 600 220 /280 400 700 50
2.85 3 150 750 500 — .— — -—- 100
2.86 6 10 000 18 000 12 000 14 000 16 000 15 000 — 2280
2.87 4 1 600 1 800 2 000 2 200 —~ -— — 468
2.88 7 600 800 100 500 770 870 625 87,2
2.89 5 20 30 40 50 60 —. -— 6,9
2.90 7 75 000 80 000 40 000 50 000 60 000 87 000 1оо;ооо 9175
2.92. Прибор состоит из пяти блоков. Вероятность безотказной
работы каждого блока в течение времени /=50 час равна: pi (50) =
=0,98; р2 (50) =0,99; р3 (50) =0,998; р4 (50) =0,975; р5(50) =0,985.
Справедлив экспоненциальный закон надежности. Требуется найти
среднюю наработку до первого отказа прибора.
Ответ: Тср с =675 час.
2.93. Используя данные задачи 2.92, определить среднюю нара-
ботку до первого отказа прибора, если время непрерывной работы
/ = 200 час, вместо 50 час, принятых в предыдущей задаче.
Ответ: ТСР с=2 700 час.
2.94— 2.100. Система состоит из N блоков. Вероятность безотказ-
ной работы каждого блока в течение времени t равна Спра-
ведлив экспоненциальный закон надежности. Необходимо найти
среднюю наработку до первого отказа системы.
Исходные данные для решения задачи и ответы приведены
в табл. 2.13.
К задачам 2.94—2.100
ТАБЛИЦА 2.13
Номер задачи Исходные данные Ответ Т ср е» час
N 1, час А(О Ра (0 Ра(0 р»(П р.(О р»(0 Рв(П
2.94 3 1 000 0,97 0,98 0,96 _ 10 640
2.95 8 100 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,97 185
2.96 5 240 0,9 0,8 0,85 0,7 0,75 — -— — 210
2.97 4 10 0,94 0,95 0,97 0,98 — .—- — .— 62,5
2.98 6 50 0,7 0,75 0,8 0,76 0,72 0,78 — — 29,5
2.99 5 120 0,99 0,9 0,85 0,95 0,8 -—- — — 218
2.100 8 500 0,9 0,8 0,7 0,75 0,85 0,95 0,72 0,92 312
87
2.101— 2.110. Система состоит из N элементов. Вероятность без-
отказной работы одного элемента в течение времени / равна
Требуется определить вероятность безотказной работы системы.
Исходные данные для решения задачи и ответы приведены
в табл. 2.14.
ТАБЛИЦА 2.14
К задачам 2.101—2.110
Номер задачи Исходные данные Ответ Номер задачи Исходные данные Ответ Рс (0
р (/) N pW N
2.101 0,999 100 0,9 2.106 0,9997 50 0,985
2.102 0,9999 1 000 0,9 2.107 0,99995 1 000 0,95
2.103 0,9998 50 0,99 2.108 0,995 15 0,925
2.104 0,9996 100 0,96 2.109 0,996 20 0,92
2.105 0,9995 75 0,96 2.110 0,9997 250 0,925
2.111— 2.120. Вероятность безотказной работы системы в течение
времени t равна Система состоит из N равнонадежных эле-
ментов. Необходимо найти вероятность безотказной работы элемента.
Исходные данные для решения задачи и ответы приведены
в табл. 2.15.
К задачам 2.111—2.120
ТАБЛИЦА 2.15
Номер задачи Исходные данные Ответ Номер задачи Исходные данные Ответ ре
р (/) N pH) N
2.111 0,96 100 0,9996 2.116 0,95 50 0,999
2.112 0,97 200 0,99985 2.117 0,97 100 0,9997
2.113 0,95 300 0,99983 2.118 0,98 500 0,99996
2.114 0,98 1 000 0,99998 2.119 0,98 100 0,9998
2.115 0,99 120 0,99992 2.120 0,96 50 0,9992
2.121— 2.150. В изделии могут быть гЛгользованы только те эле-
менты, средняя интенсивность отказов которых равна Лср. Изделие
имеет число элементов N. Требуется определить среднюю наработку
до первого отказа и вероятность безотказной работы в конце первого
часа.
Исходные данные для решения задачи и ответы приведены
в табл. 2.16.
2.151. Необходимо выполнить ориентировочный расчет надеж-
ности усилительного каскада, содержащего 2 маломощных германие-
вых транзистора, 2 керамических конденсатора и 6 резисторов типа
МЛТ мощностью 0,5 вт. Требуется вычислить вероятность безотказ-
ной работы каскада в течение 1=1000 час и среднюю наработку до
первого отказа.
Ответ: Тс(1 000) =0,988; ТсРе==85 000 час.
88
ТАБЛИЦА 2.16
К задачам 2.121—2.150
Номер задачи Исходные данные Ответ
\р> /V ₽с(1) 7сР- час
2.121 1 -10-5 500 0,995 200
2.122 1-ю-5 2 500 0,975 40
2.123 1-Ю-3 100 0,905 10
2.124 I -10—4 100 0,99 100
2.125 1-ю-5 100 0,999 1 000
2.126 1 -10—4 1 000 0,905 10
2.127 3,5-10-5 200 0,993 143
2.128 2-Ю-6 700 0,9986 714
2.129 2-10-5 10 000 0,8187 5
2.130 2-Ю-6 50 000 0,905 10
2.131 4-Ю-4 500 0,8187 5
2.132 2-10_6 2 500 0,995 200
2.133 2-Ю-’ 8 000 0,9984 625
2.134 1-Ю-5 50 0,9995 2 000
2.135 4-Ю-6 60 0,99976 4 166
2.136 2,5-Ю-3 20 0,95 20
2.137 2,5-Ю-5 100 0,9975 400
2.138 2.5-10-5 400 0,999 100
2.139 2,5-Ю-5 1 000 0,975 40
2.140 2,5-Ю-5 40 0,999 1 000
2.141 0,5-10~5 1 000 0,995 . 200
2.142 0,5-10-5 3 000 0,985 66,7
2.143 0,5-Ю-5 10 000 0,95 20
2.144 0,5-10-5 800 0,996 250
2.145 0,5-10-5 1 000 0,995 200
2.146 2-Ю-3 30 0,94 16,7
2.147 2,5-Ю-3. 10 0,975 40
2.148 5-Ю-5 800 0,96 25
2.149 2-Ю-5 250 0,995 200
2.150 2-10-3 80 0,852 6,25
2.152. Необходимо выполнить ориентировочный расчет надеж-
ности изделия, содержащего 100 маломощных низкочастотных гер-
маниевых транзисторов, 10 плоскостных кремниевых выпрямителей,
260 керамических конденсаторов, 1 350 резисторов типа МЛТ мощ-
ностью 0,5 вт, 1 силовой трансформатор, 2 накальных трансформа-
тора, 6 дросселей и 3 катушки индуктивности. Необходимо найти
вероятность безотказной работы изделия в течение 360 час и сред-
нюю наработку до первого отказа.
Ответ: Рс (360) =0,6; ГСрс = 715 час.
2.153. Требуется выполнить ориентировочный расчет надежности
телевизора, который согласно принципиальной электрической схеме
содержит следующие элементы: электровакуумные приборы [Xi =
= (0,08:0,11) • 10 I/час] - 20 шт.; приемная трубка (Хг=
= 0,23-10“" Цчас) — 1 шт.; резисторы угольные (Z3 = 0,35-i0“5 Цчас)—
89
К задачам
Номенклатура и колн
Номер задачи [Резисторы /? Конденсаторы С Диоды D
тип ШТ. тип ШТ. тип шт.
2.154 (2.186) МЛТ-0,25 МЛТ-0,5 13 10 Керамичес- кие Танталовые 18 3 Точечные германиевые 5
(2.206) ГЖВ-2 2 • выпрями- тельные
2.155 (2.187) МЛТ-0,25 ГЖВ-2 25 5 Керамичес- кие Танталовые 27 6 Точечные кремниевые 10
(2.207)
2.156 (2.188) (2.208) ВС-0,25 ВС-0,5 ВС-1 20 6 3 Бумажные 8 Плоскост- ные выпрями- тельные 16
2.157 (2.189) ВС-0,25 МЛТ-1 16 10 Керамичес- кие Танталовые 6 6 Точечные импульсные 16
(2.209) МЛТ-2 3
2.158 (2.190) (2.210) МЛТ-0,5 МЛТ-1 24 8 Слюдяные Танталовые ,5 13 Плоскост- ные выпрями- тельные 5
2.159 (2.191) (2.211) МЛТ-0,25 МЛТ-0,5 МЛТ-1 22 12 6 Керамичес- кие Танталовые 8 14 Плоскост- ные выпрями- тельные 4
90
ТАБЛИЦА 2.17
2.154—2.173
чество элементов Время работы Ответ
Транзисторы Т | Силовые | Тр-ры 1 Дроссели L Электрические машины
tt час Р (О Гср- час
тип шт. кол. ШТ. шт. тип шт.
Маломощные низкочастот- ные германиевые 6 1 3 2 — — 250 0,98 13 400
Мощные высокочас- тотные германиевые 10 2 3 5 500 0,932 7 900
Мощные низкочас- тотные 7 4 4 — — — 1 000 0,84 5 700
Маломощные низкочас- тотные германиевые 7 3 3 2 — — 320 0,96 7700
Маломощные низкочастот- ные кремниевые 9 1 — 4 — — 260 0,97 8 300
Маломощные низкочас- тотные германиевые 9 1 1 2 Двигатели пос- тоянного тока, п = 3 000 об/мин 1 300 0,96 8 700
91
Номенклатура и коли
Номер задачи Резисторы Р Конденсаторы С Диоды D
тип UIT. тип HIT. тип ШТ.
2.160 (2.192) (2.212) ВС-0,25 ВС-0,5 ВС-1 20 14 6 Слюдяные Танталовые 10 12 Точечные германиевые выпрями- тельные 6
2.161 (2.193) (2.213) МЛ Т-0,5 МЛТ-1 МЛТ-2 32 19 4 Керамичес- кие Танталовые 8 15 Точечные германиевые выпрями- тельные 9
2.162 (2.194) (2.214) МЛ Т-0,25 МЛТ-1 40 2 Слюдяные Керамичес- кие Танталовые 30 49 6 Выпрями- тельные плоскостные 2
2.163 (2.195) (2.215) МЛТ-0,5 МЛТ-1 МЛТ-2 ВС-0,25 1 200 300 140 500 Керамичес- кие Бумажные Слюдяные Танталовые 1 140 256 244 160 Выпрями- тельные плоскостные 40
2.164 (2.196) (2.216) МЛ Т-0,25 МЛТ-0,5 МЛТ-1 21 5 3 Слюдяные 8 Точечные кремниевые выпрями- тельные 16
2.165 (2.197) (2.217) МЛТ-0,25 МЛТ-0,5 МЛТ-1 СПО-2 ПЭВ-10 ПЭВ-25 8 5 2 1 3 2 Бумажные 17 Плоскост- ные выпрями- тельные 11
92
Продолжение табл. 2.17
чество элементов Время раб оты Ответ
Транзисторы 7 1 Силовые тр-ры Дроссели L Электрические машины
t, час р (?) гср.час
тип шт. кол. • шт. шт. тип шт.
Мощные низкочастот- ные Маломощные низкочастот- ные германиевые 5 4 1 1 2 Двигатели пос- тоянного тока, /2 = 4 000 об-мин 1 650 0,92 8 100
Маломощные низкочастот- ные германиевые Мощные низкочастот- ные 11 4 2 2 4 260 0,96 6 500
Маломощные низкочастот- ные кремниевые 10 2 — 40 — — 5 000 0,35 4 700
-— 12 40 — Двигатели пос- тоянного тока, п —3000 об/мин Сельсины бесконтактные 8 12 200 0,4 218
Маломощные низкочастот- ные кремниевые 7 5 2 — 2 000 0,82 10 000
Мощные низкочастот- ные 8 3 2 2 400 0,67 6 200
93
Номер задачи Номенклатура и коли
Резисторы /? Конденсаторы С Диоды D
тип ШТ. тип шт. ТИП шт.
2.166 (2.198) (2.218) МЛТ-0,25 МЛТ-0,5 МЛТ-1 МЛТ-2 27 625 12 300 638 37 Керамичес- кие 62 000 Выпрями- тельные точечные германиевые 11 262
2.167 (2.199) (2.219) МЛТ-0,25 МЛТ-0,5 МЛТ-1 42 17 7 Бумажные 16 Точечные кремниевые выпрями- тельные 5
2.168 (2.200) (2.220) МЛТ-0,25 МЛТ-0,5 МЛТ-1 210 50 30 Слюдяные 76 Точечные кремниевые выпрями- тельные 158
2.169 (2.201) (2.221) МЛТ-0,25 МЛТ-0,5 ПКВ-2 136 96 12 Керамичес- кие Танталовые 176 32 Точечные германие- вые выпрями- тельные 47
2.170 (2.202) (2.222) МЛТ-0,25 МЛТ-0,5 МЛТ-1 217. 123 64 Керамичес- кие Танталовые 83 136 Выпрями- тельные плоскостные 44
2.171 (2.203) (2.223) МЛТ-0,25 МЛТ-0,5 МЛТ-1 МЛТ-2 2 760 1 216 64 14 Керамичес- кие 6 136 Точечные германиевые выпрями- тельные 1 126
94
Продолжение табл. 2.1?
чество элементов Время работы Ответ
Транзисторы Т Силовые тр-ры I Дроссели L Электрические машины
t, час PW
тип | шт. кол. ШТ. шт. тип ШТ.
Маломощ- ные низкочас- тотные германие- вые 1637 16 896 324 — — 6 0,49 8,4
Маломощные низкочас- тотные кремниевые 21 7 — — — — I 000 0,84 5 700
Маломощные низкочастот- ные германиевые 73 16 20 16 Вращающиеся трансформаторы Асинхронные короткозамкну- тые двигатели 96 10 24 0,966 670
Маломощные низкочас- тотные германиевые 63 7 37 21 — — 25 0,98 1 370
Маломощные низкочас- тотные германиевые 93 164 11 17 24 Двигатель пос- тоянного тока, п=3 ООО обjмин 4 24 0,97 820
Маломощные низкочас- тотные германиевые 3 93 32 — — 60 0,32 53
Номенклатура и коли
Номер задачи Резисторы R Конденсаторы С Диоды D
тип ШТ. тип ШТ. ТИП шт.
2.172 (2.204) (2.224) МЛТ-0,5 СПО-2 ПЭВ-10 146 3 5 Бумажные 176 Выпрями- тельные кремниевые повышенной мощности 116
2.173 (2.205) (2.225) МЛТ-0,5 МЛТ-1 240 86 Слюдяные Танталовые 53 13 Плоскостные выпрями- тельные 57
Примечание. Ответы Р (/) и Т даны для задач 2.154—2.173.
80 шт.; резисторы проволочные (Х4 = 1,25 • 10“® 1/час)—4 шт.; кон-
денсаторы керамические (Х6 = 0,23 • 10“5 1/час)—27 шт.; конденса-
торы бумажные (Хв = 0,16 • 10-s 1/час)—25 шт.; конденсаторы
переменной емкости (М= 1,86 10“= 1/час)—4 шт.; конденсаторы
электролитические (Xs = 8,0-10“5 1/час)—8 шт.; конденсаторы дру-
гих типов [Ха= (0,124-0,2) • 10“5 1/час]—12 шт.; катушки индуктив-
ности [Xio= (0,14-0,15) • 10~5 1/час] — 51 шт.; трансформаторы [Лц =
= (0,44-0,6)-10“® 1/час]—6 шт.; дроссели i[Xi2= (0,14-0,15)-10“5 1/час]—
6 шт.; плавкие вставки (Х1з=1-10“5 1/час)—3 шт. Требуется рас-
считать зависимость P(t) и среднюю наработку до первого отказа
телевизора для минимального и максимального значений интенсив-
ностей отказов, а также построить график P(t).
Ответ; Р (t) = е“Т3.1 •з,/5)-10 3, Гср с 323 ~ 267 час, гра-
фик приведен на рис. 2.3.
Рис. 2.3. Зависимость вероятно-
сти безотказной работы от вре-
мени телевизионного приемни-
ка (задача 2.153).
«6
Продолжение табл. 2.17
2.154— 2.173. Необходимо выполнить ориентировочный расчет
надежности системы, состоящей из N элементов различного типа.
Требуется вычислить вероятность безотказной работы системы в те-
чение времени t и среднюю наработку до первого отказа Тср с-
Расчет следует выполнять по данным о надежности элементов, при-
веденным в приложении 3.
Исходные данные для решения задачи и ответы приведены
в табл. 2.17. X
2.174— 2.185. Необходимо выполнить ориентировочный расчет
надежности системы, состоящей из N элементов различного типа.
Требуется вычислить вероятность безотказной работы в течение
времени непрерывной работы изделия t и среднюю наработку до
первого отказа, а также построить график P(t) для максимальных
и минимальных значений интенсивностей отказов элементов до зна-
чения P(t) sZtip,. Расчет выполнить по данным о надежности элемен-
тов, приведенным в приложении 2.
Исходные данные для решения задачи приведены в табл. 2.18.
2.186— 2.205. Произвести окончательный расчет надежности изде-
лия, используя данные задач 2.154—2.173. Режимы работы элемен-
тов указаны в табл. 2.19. Расчет выполнить по данным о надежности
элементов, приведенным в приложении 3. Номера задач указаны
в табл. 2.17 в скобках.
2.206— 2.225. Произвести окончательный расчет надежности изде-
лия, используя данные задач 2.154—2.173. Режимы работы элементов
указаны в табл. 2.19. Расчет выполнить, используя данные о значе-
ниях номинальных интенсивностей отказов, приведенных в приложе-
нии 3 (табл. П.3.1, П.3.3, П.3.5, П.3.7, П.3.8), и графики для попра-
вочных коэффициентов, приведенные в приложении 4. При расчете
7—1086 Х 97
Z. 1 / У ОУО 2.180 30 2.181 30 000 2.182 65 2.183 29 2.184 41 2.185 53 2.174 82 2.175 260 2.176 2 520 2.177 18 2.178 868 gx со 2 Резисторы Номенклатура и количество элементов ТАБЛИЦА 2.18 оо К задачам 2.174—2.185
/О иии | 33 10 31 000 10 000 27 7 8 16 87 2 54 3 30 24 143 -'• 1 286 32 63 32 386 132 Конденсаторы Диоды
12 118 86 138 10 7 10 16
Транзисторы
59 10 7 725 8 Электронные лампы
18 19 19 64 112 31 Реле
1 1 1 1 1 1 1 1 Батареи
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 3 - 12 — 9 12—9 42 — — — 3 4 Выключатели Гироскопы Электродвигатели
1 1 1 1 1 1 1 1 о 1 1 1 Генераторы
«—4^ I 00 *— -Р* ел о 1 Дроссели
1 18 24 5 1 726 Катушки
10 10 16 8 22 260 5 12 4 Переключатели (чис- ло контактных групп)
1 1 1 1 1 1 о ю 1 со со о Пот ен циометры
1 1 1 1 1 1 1 со Преобразователи
1111 I I — ьэ ьо ю 1 1 1 1 СО 1 1 СП СП о О нР» Раз'ьемы
NO сл 1 NO <£*• —* О NO ьР» СО 1 0OGOK0 Трансформаторы
100 24 120 200 10 1 000 5 000 10 10 000 1 000 10 000 5 000 Вемя непрерывной рабо- ты час
ТАБЛИЦА 2.19
Режимы работы электроэлементов
Элементы Режим работы
Коэффи- циент наг- рузки, Темпера- тура, *С
Резисторы МЛТ-0,25 0,9 70
МЛТ-0,5 0,8 80
МЛТ-1 0,7 90
МЛТ-2 0,5 100
ВС-0,25 0,9 70
ВС-0,5 0,8 90
ВС-1 0,7 100
ПКВ-2 0,5 80
СПО-2 0,1 60
ПЭВ-10 0,8 90
ПЭВ-25 0,6 90
Конденса- Бумажные 0,6 80
торы Керамические 0,6 80
Слюдяные 0,7 70
Танталовые 0,5 60
Диоды Точечные германиевые 0,7 50
Точечные кремниевые 0,6 55
Плоскостные 0,7 60
Транзисто- Г ерманиевые 0,7 60
ры Кремниевые 0,6 50
Трансформаторы 0,8 60
Дроссели 0,7 50
Катушки индуктивности 0,8 45
Электрические машины 0,9 60
поправочные коэффициенты для трансформаторов, дросселей, кату-
шек индуктивности и электрических машин принять равным единице.
Номера задач указаны в табл. 2.17 в скобках.
Т
ГЛАВА ТРЕТЬЯ
РАСЧЕТ ХАРАКТЕРИСТИК НАДЕЖНОСТИ
XI4HHVflOdHfld3£3d ХНМЗУЯИЕЯУНУЕЭЭОЯЗН
ИЗДЕЛИЙ
§ 3.1. МЕТОДЫ РАСЧЕТА
Резервированным соединением изделий называется
такое соединение, при котором отказ наступает только
после отказа основного изделия и всех резервных изде-
лий.
На практике применяются способы резервирования,
приведенные на рис. 3.1. Схемные обозначения различ-
ных способов резервирования приведены на рис. 3.2.
Общим резервированием называется метод повышения
надежности, при котором резервируется изделие в целом
(рис. 3.2,а). Раздельным резервированием называется
Рис. 3.1. Способы резервирования.
100
Рис. 3.2. Схемные обозначения различных способов резервирования:
а — общее постоянное с целой кратностью; б — раздельное постоянное с целой
кратностью; в — общее замещением с целой кратностью; г — раздельное за-
мещением с целой кратностью; д — общее постоянное с дробной кратностью:
е — раздельное замещением с дробной кратностью.
метод ’повышения надежности, при котором резервиру-
ются отдельные части изделия (рис. 3.2,6).
Основным параметром резервирования является его
кратность. Под кратностью резервирования т понимает-
ся 'Отношение числа резервных изделий к числу резерви-
руемых (основных).
Различают резервирование с целой и дробной крат-
ностью. Схемные обозначения обоих (видов резервирова-
ния при (постоянном включении резерва одинаковы. Для
их различия на схеме указывается кратность резервиро-
вания т.
При резервировании с целой кратностью величина
т есть целое число, при резервировании с дробной
кратностью величина т есть дробное несокращаемое
число. Например, т=4/2 означает наличие резервиро-
вания с дробной кратностью, (при котором число резерв-
101
ных элементов .равно четырем, число основных — двум,
а общее число элементов равно шести. Сокращать дробь
нельзя, так 'как если ш = 4/2 = 2, то это означает, что
имеет место резервирование с целой кротостью, при ко-
тором число резервных элементов равно двум, а общее
число элементов равно трем.
По способу включения резервирование разделяется
на постоянное и резервирование замещением. Постоян-
ное резервирование — резервирование, при котором ре-
зервные изделия подключены к основным в течение все-
го времени работы и находятся в одинаковом с ними ре-
жиме. Резервирование замещением—резервирование,
при котором резервные изделия замещают основные
после их отказа.
При включении резерва по способу замещения ре-
зервные элементы до момента включения в работу мо-
гут находиться в трех состояниях:
— нагруженном резерве;
— облегченном резерве;
— ненагруженном резерве.
Приведем основные расчетные формулы для указан-
ных выше видов резервирования,
1. Общее резервирование с постоянно включенным
резервом и с целой кратностью (рис. 3.2,а):
1 —
п 1т+1
1 ~ П мо
/=1 j
(3.1)
где pi(t) —вероятность безотказной работы i-ro элемен-
та в течение времени /; п—число элементов основной
или любой резервной цепи; m — число резервных цепей
(кратность резервирования).
При экспоненциальном законе надежности, [когда
X(0 = e“V,
Pc(f)=l“—[1 — e~vlm+1,
1 (3-2)
J m m ,
т — 1 V 1 — т ЛП 1
срс~ л0 2ji+1 cp°s2j*+ •’
1=0
n
где = S — интенсивность отказов нерезервированной
i=l s
системы или любой из ш резервных систем; Гсро — сред-
102
нее время (безотказной работы нерезервированной систе-
мы или любой из т резервных систем. При резервиро-
вании неравнонадежных изделий
рс (о=1 -:п 9/(о-l - п 11 - а (01. (з.з)
Z—О 1=0
где ?г(0> Pi{t)—(вероятность отказов и вероятность
безотказной работы в течение времени t i-ro изделия
соответственно.
2. Раздельное резервирование с постоянно включен-
ным резервом и с целой кратностью (рис. 3.2,6):
рс (о - п о - п -а (0]и<-Г (М
— /=1
где pi(t)—вероятность безотказной работы i-ro эле-
мента; т,—'кратность резервирования i-ro элемента;
п — число элементов основной системы.
При экспоненциальном законе надежности, когда
A(0 = e-V,
^с(0 = П{1-11-е-^Г+,}.5 (3.5)
/=1
При равнонадежных элементах и одинаковой кратности
их резервирования
- Рс(0=={1— ’[1— e“w]m+1}«, (3.6)
оо m
ТСр с = ^Рс (0 dt = J Vf (Vi + i)...(Vf + „_1).
о /=0
(3-7)
где v,= (i+l)/(m+1).
3. Общее резервирование замещением с целой крат-
ностью (рис. 3.2,в):
П
Pm+, ®=rpmw+ j Pi(t - T)VW dt, ;з.8)
о
где Pm+i(t), Pm(f)—вероятности безотказной работы
резервированной системы кратности т + 1 и т соответ-
ственно; Р«-т) — вероятность безотказной работы ос-
новной системы в течение времени (i—т); ат(г)—час-
тота отказов резервированной системы кратности т в
момент времени т.
103
Рекуррентная формула (3.8) .позволяет получить рас-
четные соотношения для устройств любой кратности ре-
зервирования. Для получения таких формул необходимо
выполнить интегрирование в правой части, подставив
вместо P(t—т) и пт(т) их значения в соответствии
с выбранным законом распределения и состоянием ре-
зерва.
При экспоненциальном законе надежности и нена-
груженно'м состоянии резерва
т
Pc(/) = e-vyj-^, (3.9)
7'(.р(.-7'сР(.И-|.1), (3.10)
где Ло, Tf.po — интенсивность отказов и средняя наработ-
ка до первого отказа основного (нерезервированного)
устройства.
При экспоненциальном законе и недогруженном со-
стоянии резерва
tn
где д.г = ]]
1=о
tn
(ЗЛ2>
/=0
. , ?(1 \ , \ -
/ - ); /г= Я, —интенсивность отка-
1 71 ) Хо
зов резервного устройства до замещения.
При нагруженном состоянии резерва формулы для
P"(t) и Др с совпадают с (3.2).
4. Раздельное резервирование замещением с целой
кратностью (рис. 3.2,а):
\ = (3-13)
1 1=1
где Pi{t) —.вероятность безотказной работы системы
из-за отказов элементов 7-го типа, резервированных по
способу замещения. Вычисляется P-i(t) по формулам
общего резервирования замещением {формулы (3.8),
(3.9), (3.11)].
104
5. Общее резервирование с дробной кратностью и по-
стоянно включенным резервом (рис. 3.2,д):
PC(O = Z (3.14)
i=0 j=0
^.-vErh-- <з-15>
i=i)
где Po(t) —вероятность безотказной работы основного
или любого резервного элемента; I — общее число ос-
новных и резервных систем; /г—число систем, необхо-
димых для нормальной работы резервированной сис-
темы.
В данном случае кратность резервирования
m=(l—h)lh. (3.16)
6. Скользящее резервирование:
Рс (0 = Рп (0 + п рп -1 (О J а (т) р (t - г) ch +
о
I /1— г л
4- п‘р -1 (/) а (т) J а. (т,) р (t — т1) cht I ch ...
О ( б J
t (t—т ' f i—т.
4-//>•" ’ fa(T)J f f c(z2)...
6 16 I 6
/_T(w0—2)
f a i) P Ц — t"’0”1) ch ,
] ' m0—If r \ f ???0—1
6
ch A ch, (3.17)
где г1 = т 4-1,; т11 = т 4-Tj 4-t2 ...; -t"0 1 — г 4- + ... 4-
4“'I,„0_i; n—число элементов основной системы; т0—чис-
ло резервных элементов; р (t — — вероятность безотказ-
ной работы одного элемента в течение времени t — tp,
— x,t — тто~1; a(tz) — частота отказов одного из
основных элементов в момент времени тг-,
т7- — т, т,,..., т ,
1 ’ 1 ’ '«о—1
105
При экспоненциальном законе надежности
Рс (0 = [1 + пи + -^ + - + =
т0 т0
= е-м = е-* £ ; (3.18)
i=o i=U
Т'ср с = Т'ср о (^По+1) ,
где Хо=п% — интенсивность отказов нерезервированной
системы; X — интенсивность отказов элемента; п. — число
элементов основной системы; Теро— среднее время без-
отказной работы нерезервированной системы; т0 — чис-
ло резервных элементов.
В этом случае кратность резервирования
т=то/п. (3.19)
Приведенные выше формулы (кроме (выражений (3.8),
(3.11), (3.12)] могут быть использованы только в тех
случаях, когда справедливо допущение об отсутствии
последействия отказов.
Последействие отказов имеет место практически
всегда при постоянном включении резерва, а также
в случае резервирования замещением при недогружен-
ном состоянии резерва.
Выражение (3.8) является основным при получении
расчетных формул в случае учета влияния последейст-
вия отказов. При этом члены p(t—т) и ат(т) должны
быть записаны с учетом последействия отказов, вида
резервирования и его кратности.
Элементы резервированных устройств в ряде слу-
чаев могут иметь два вида отказов — «обрыв» и «корот-
кое замыкание». В этом случае вычислять вероятность
безотказной работы следует, суммируя вероятности всех
благоприятных (не приводящих к отказу) гипотез, т. е.
/>.(0=2 ^(0. (3.2С)
/=1
где pj(t) —вероятность j-й благоприятной гипотезы, вы-
численной с учетом двух вадов отказов; k — число бла-
гоприятных гипотез.
106
При 'вычислениях p,(t) следует иметь ib виду, что
для элементов сложной системы справедливы выраже-
ния
/?(0 = ехр
t q
— J Я (/)<# , ?0 + ?3 = 1,
о J
(3.21)
где Х(/) —интенсивность отказов элемента; <ро, <р3— ве-
роятность возникновения «обрыва» и «короткого замы-
кания» соответственно.
При экспоненциальном законе надежности
'’« = еЛ?.= т^г,%= (3.22)
где Хо, Хз — интенсивность отказов элемента по «обрыву»
и «короткому замыканию» соответственно.
Остальные количественные характеристики надежно-
сти в случае необходимости вычисляются через Р<(1)
по известным аналитическим зависим остям, приведен-
ным в гл. 1.
Расчет надежности резервированных систем иногда
полезно выполнять, используя схему «гибели» («чистого
размножения»), В соответствии с этой схемой преобра-
зование Лапласа вероятности возникновения п отказов
вычисляется по формуле
pn(s) —(s + Xc)(s + X,)--(s + X„) •
(3.23)
При неравных корнях знаменателя обратное преоб-
разование'Лапласа Рп($) будет
п 8к*
рп (t) = М, ... Яп_, J • (3.24)
k—о
В формулах (3.23) и (3.24) приняты обозначения:
Хс — интенсивность отказов системы до выхода из строя
первого элемента; Xi — интенсивность отказов системы
в промежутке времени от момента отказа первого эле-
мента до второго; 2.2 — интенсивность отказов системы
в промежутке времени от момента отказа второго эле-
мента до третьего и т. д.; п— число отказавших элемен-
тов; Sk=—%!<—k-й корень знаменателя выражения
(3.23); B'(sk) — производная знаменателя в точке sj,.
107
При одинаковых опасностях отказов X/, т. е. Хо= /
= Х1='...=ХП, расчетные формулы имеют вид I Л
-" '-1 <» + £*' • р»<0 = -^^. (3.25)/ 1
При расчетах надежности по формулам (3.23) —
(3.25) следует 'помнить, что они не определяют вероят-
ности безотказной работы (или вероятности отказа)
резервированной системы, а определяют лишь вероят-
ность п-го состояния системы, т. е. вероятность того, что
в системе откажут п элементов. Для .вычисления вероят-
ности безотказной работы необходимо находить вероят-
ности 0, 1, ..., п отказов, когда система еще находится
в работоспособном состоянии (исправна), и суммиро-
вать полученные вероятности.
Среднее время безотказной работы системы при ис-
пользовании схемы «гибели» вычисляется по формуле
п—1
(3‘26)
1—0
где 2.; — интенсивность отказов системы до выхода из
строя Сго элемента.
При схемной реализации резервирования в ряде слу-
чаев конкретные технические решения не приводятся к
логическим схемам расчета надежности (рис. 3.2).
В этих .случаях следует для получения аналитичес-
ких выражений для (количественных характеристик на-
дежности использовать метод перебора благоприятных
гипотез. Вероятность безотказной работы в этом случае
вычисляется по выражению (3.20).
При анализе надежности резервированных устройств
на этапе проектирования приходится сравнивать раз-
личные схемные решения. В этом случае за критерий
качества резервирования принимается выигрыш надеж-
ности. Выигрышем надежности называется отношение,
количественной характеристики надежности резервиро-
ванного устройства к той же количественной характе-
ристике нерезервированного устройства или устройства
с другим видом резервирования.
Наиболее часто используются следующие критерии
качества резервированных устройств: Gq(t) —выигрыш
надежности в течение времени t по вероятности отказов;
108
Qp (/) — выигрыш надежности в течение времени t по
вероятности безотказной работы; GT— выигрыш надеж-
ности по среднему времени безотказной работы.
При резервировании элементов электроники (рези-
сторов, 'конденсаторов, контактов реле, диодов и т. п.)
всегда произведение интенсивности отказов элемента на
время его работы значительно меньше единицы, т. е.
Поэтому при вычислении Gq(t) и Gp(t) целесо-
образно функции вида e~kV (экспоненциальный случай)
разложить в ряд:
e~ftW= 1 —Ш -[- k (при небольшом k).
Если система исправна при отказе т элементов, то
необходимо (брать не менее чем ш + 2 членов разложе-
ния.
§ 3.2. ТИПОВЫЕ ПРИМЕРЫ
Пример 3.1. Дана система, схема расчета надежно-
сти 'которой изображена на рис. 3.3. Необходимо найти
вероятность безотказной работы системы при известных
Рис. 3.3. Схема расчета надежности (к примеру 3.1).
вероятностях безотказной работы ее элементов (значе-
ния вероятностей указаны на рисунке).
Решение. Из рис. 3.3 видно, что система состоит
из .двух (I и II) неравненадежных устройств.
Устройство I состоит из четырех узлов:
а— дублированного узла с постоянно включенным
резервом, причем каждая часть узла состоит из трех
последовательно соединенных (в смысле надежности)
элементов расчета:
109
б—дублированного узла по способу замещения;
в — узла с одним нерезервированным элементом;
г — резервированного узла с кратностью т = 1/2 (схе-
ма группирования).
Устройство II представляет собой нерезервированное
устройство, надежность которого известна.
Так как оба устройства неравнонадежны, то на осно-
вании формулы (3.3) имеем
т
Л(0 -1 - ПI1 ~ А (01 = 1-11 (01 [1 - Рп (01-
;=о
Найдем вероятность pi(t). Вероятность безотказной
работы устройства I равна произведению вероятностей
безотказной роботы всех узлов, т. е. Р1=РаРбРврг-
В узле а число элементов основной и резервной цепи
п = 3, а кратность резервирования т = 1. Тогда на осно-
вании формулы (3.1)
ра= 1 —
! —П А (0
i=l
= 1— 11—0,97^0,93.
В узле б кратность общего резервирования замеще-
нием т=\, тогда на основании формулы (3.9) имеем
т
рб (t) = e"w £ = e"v (1 4- М ~
1=0
~ 0,9(1 4- 0,1) = 0,99.
В узле г применено резервирование с дробной крат-
ностью, когда общее число основных и резервных систем
/=3, число систем, необходимых для нормальной ра-
боты, h=2. Тогда на основании формулы (3.14)
l—h 1 1 I
рг=^с1Л1^
1=0 f=0 i=0 f=0
= 3j4— 2р\ = 3 (0,9)’ - 2 (0,9)3 = 0,972.
Вероятность безотказной работы устройства I будет
pt = рарбрврв = 0,93 • 0,99 0,97 • 0,972 ~ 0,868.
ПО
Т 7
\ Тогда вероятность безотказной работы резервирован-
( ной системы будет
\ Рс=1— (1—Pi) (1—рп) = 1—(1—0,868) (1—0,9) =0,987.
\ Пример 3.2. Вероятность безотказной работы преоб-
I разователя постоянного тока в переменный в течение
\ /=1000 час равна 0,95, т. е. Р (1000) =0,95. Для повы-
\ шения надежности системы электроснабжения на объек-
те имеется такой же преобразователь, который включа-
ется .в работу при отказе первого. Требуется рассчитать
вероятность безотказной работы и среднюю наработку
до первого отказа системы, состоящей из двух преобра-
зователей, а также построить зависимости от времени
частоты отказов ас (/) и интенсивности отказов /.< (/) си-
стемы.
Решение. Из условия задачи видно, что имеет ме-
сто общее резервирование замещением кратности т=1.
Тогда на основании формулы (3.9) имеем
Рс (/) = e-v V = e~W (1 + М-
/=о
Из условия задачи е ’°* = 0,95, тогда Д/ 0,05. Под-
ставляя значения Р(ЮОО) и полученное значение fat
в выражение для P0(t), получим
Рс (t) = (1 + V) ^0,95 (1 + 0,05) = 0,9975.
Средняя наработка до первого отказа системы на
основании формулы (3.10) будет
Тер с = Тер o(tn + 1) =2Тср о.
Так как в течение времени t— 1000 час 2с/ = 0,05,
. 0,05 0,05 п г 1П_4 . ,
то х0 = —-— — =0,5-10 4 \[час, а средняя нара-
ботка до первого отказа нерезервированного преобразова-
теля Тср0 = -А- = 0 5 у.,- = 20000 час.
Тогда средняя наработка до первого отказа резерви-
рованной системы будет
Тер с = 2Тср о=40 000 час.
Ill
Для Построения графиков ac(t) и Хс('/) найдем ана-
литические выражения этих функций по известной ве-
роятности безотказной работы 'системы:
ас (/) =- Р'с (/) = 20e~w (1 -ВоО - =
= = 0,25 • 1 О’8 /е~0’5'10'4/
, гл — «»(/) — Х«/е W — $
cU Рс(0 е^(1+м 0+М '
_ 0,25-10~Е/
1 + 0,5-10—‘
Графики ac(t) и &<.(?) приведены на рис. 3.4.
Рис. 3.4. Зависимость ас и лс от t
(к примеру 3.2).
Пример 3.3. Система состоит из 10 равнонадежных
элементов, средняя наработка до первого отказа ТСр
элемента равна 1000 час. Предполагается, что справед-
лив экспоненциальный закон надежности для элементов
системы и основная и резервная системы равнонадежны.
Необходимо найти среднюю наработку до первого от-
каза Тсрс системы, а также частоту отказов ac(t) и
интенсивность отказов /.<(/) в момент времени /==50 час
в следующих случаях:
а) нерезервированной системы,
б) дублированной системы при постоянно включен-
ном резерве,
в) дублированной системы три включении резерва по
способу замещения.
Решение. По условию задачи справедлив экспонен-
циальный закон надежности для элементов, поэтому
112
средняя наработка до первого отказа Теро основной си-
стемы будет
т _ 1 _ 1 _ 1 _ г _
7 ср О — hi — ? — 10 1ОХ 10
IX
1=1
1000
10
100 час.
Тогда на основании формулы (3.2) для средней нара-
ботки до 'первого отказа при постоянно -включенной
одной резервной системе имеем
т
Тср с = тб =Тср 0£ = тсро (1 + 4) = 150 час.
1=0
При дублировании системы по методу замещения
Тер с = Те= (/тт+1) Тср о = 2ТСр о = 200 час.
В случае нерезервированной системы интенсивность
отказов не зависит от времени и равна сумпие интенсив-
ностей отказав элементов.
Найдем интенсивность и частоту отказов системы
в момент / = 50 час для случая а:
ю ю
(50) = £ я, = 2 Щ = 0.01 ,
____\ (5Э)-5Э
(50) = Лп (50) Р (50) = 2П (50) е
= О,О1е_о’о1'59^6-1О"3—— .
В случае дублированной системы интенсивность и
частота отказов могут быть найдены по известной веро-
ятности безотказной работы системы. В рассматривае-
мом случае число элементов нерезервированной системы
п=10, кратность резервирования ш=1. Тогда на осно-
8—1086 113
вании формул (3.2) и (3.9) имеем
Р6 (0 == 1 — [1 — e~w ]«+1= 2е“’” — e-2V,
рв (0 = e~w £ = e"w (1 + М),
, £-0
где Zo=^ = 0,01^L .
Найдем частоту и интенсивность отказов для случаев
«б (0 = - Р'б ® = 220е-^ (1 - e~v),
, /А —a6(Z) _2Xoe-V(i_e-V) 2X0(l —e-V)
dU Рб(0 Зе-^-е-2^ ~ 2-е-^ ’
ав(0 = -Л(О = ^/е-^,
2 /А-Йв(<) -
° ' ’ ~~ Рв (0 " e-V (1 - Х.0 1 + м •
Подставляя в полученные выражения исходные дан-
ные, будем иметь:
аб (50) ~ 4,8- КН3 1/час, 5,7-10-* \/час,
ав(50) = 3-10~3 \!час, 2в = 3,33-10-’ \/час.
Пример 3.4. Для повышения надежности усилителя
все его элементы дублированы. Предполагается, что
элементы подвержены лишь одному виду отказов и по-
следействие отказов отсутствует. Необходимо найти ве-
роятность безотказной работы усилителя в течение
(=5000 час. Состав элементов нерезервированного уси-
лителя и данные по интенсивности отказов элементов
приведены в табл. 3.1.
Решение. В нашем случае имеет место раздельное
резервирование с кратностью Шг = 1, число элементов
нерезервированного усилителя н=11. Тогда, используя
114
ТАБ Л ИЦ A 3.1
Данные по интенсивности отказов элементов
(к примеру 3.4)
Элементы Количество элементов Интенсивность от- казов элемента X, 10"5 \}час
Транзисторы 1 2,16
Резисторы 5 0,23
Конденсаторы 3 0,32
Диоды 1 0,78
Катушки индуктивности 1 0,09
данные табл. 3.1, на основании формулы (3.5) получим
Рс (5 000) = J] {1 - {1 - е-^500°]в}.
i=i
Так как Яг-<1, то для приближенного вычисления по-
казательную функцию можно разложить в ряд и ограни-
, —5001».
читься первыми двумя членами разложения 1 — е ~
50002/. Тогда
п н
Рс (5000) « J] I1 — (5000Я/)2] 1 — £ (5000Яг)2 =
1=1 1=1
п
= 1 - 5000’ S 1 — 25-10’ |2,16\+ 5-0,232 +
z=i
+ 3-0.323 + 0,78\Ч- 0,092] 10-‘° 0,985.
Пример 3.5. Схема расчета надежности устройства
приведена на рис. 3.5. Предполагается, что последейст-
Рис. 3.5. Схема расчета надеж-
ности (к примеру 3.5).
вие отказов отсутствует и все элементы расчета равно-
надежны. Интенсивность отказов элемента 7.= 1,35-10~3
\j4ac. Требуется определить наработку до первого от-
каза резервированного устройства.
8* 115
Решение. В данном 'случае имеет .место раздельное
резервирование равнонадежных устройств ic постоянно
включенным резервом. Для вычисления средней нара-
ботки до первого отказа целесообразно воспользоваться
формулой (3.7). По условию задачи число элементов не-
резервированной системы и = 2, .кратность резервирова-
ния т = 1. Тогда
т — (,г1>! V________________i___________
7 с ?. (m-|1) 2jv4(v*+ !) (*« + «—1) ~
S1 = 1 Г 1 I 1 .
Vi(Vi+ 1) 2Л I-J0(v(, p 1) ' V, (v,-pl)
7=0
Так как
1 .
то v0 = — , V, = 1.
Тогда
Т — 1 Г 1 1 1 1— 11
'ср С— 2Л [ 1Д.ЗД ф 2 J- 12Л “
11
12-1,35-Ю-3
680 час.
Пример 3.6. Схема расчета надежности резервиро-
ванного устройства приведена на рис. 3.6. Интенсивно-
сти отказов элементов 'имеют 'следующие значения:
Рис. 3.6. Схема расчета надежности (к примеру 3.6).
Х1 = 0,23-10“3 1/адс, А2=0,5-10“4 \/час, Хз=0,4• 10<!\]час.
Предполагаем, что последействие отказов элементов от-
сутствует. Необходимо найти среднюю наработку до
первого отказа устройства и построить зависимость ин-
тенсивности отказов устройства от времени.
116
Решение. Готовой формулы для средней наработ-
ки до первого отказа в рассматриваемом случае нет.
Поэтому необходимо воспользоваться соотношением
Герс^рсЮ^-
О
Найдем выражение для вероятности безотказной ра-
боты Рс(0 устройства. Очевидно, Pc(t)=p1(t) р{] (t) рт (t),
где 1 — [1 —А(01а = 2А(0 — р\ (0.
Рш (0 = 1 - [1 - р3 (/)]2 - 2А (0 - р\ (t).
Тогда, подставляя значения р{ (t) и //]1Г (/) в выраже-
ние для Рс (f), получим
Рс (0 = [2р, (0 - р* (01 А (0 |2/;3 (0 -pl (/)] =
= 4р> (0 р2 (0 р3 (0 — 2р\ (t) р2 (t) р3 (/) — 2/2, (f) р2 (t) X
XpI (0 + rf (0 A (0^3 (0-
Так как р1 (/) = e~v, p2 (f) — e~^, ps (t) = e-7^, то
p —(2Д { 2-|-23)1 2^.— (Х+\ + 2Г3)? ।
। e— (21i + \+223)f 4e~0,68-10-s/ 2e—°.O1-10-=/
o —i,o8-io-3f . — 1,31-ю-ч
— 2e Xе
Tcp c = f Pc (0 dt = =—ГД-Ц-Д------—i~i—FT--------
CP J 1 M + A-2 + кз 2Л, + X2 + x3
0
_________2_______-I---1____________
Л, + X, + 2X3 ' + X2 + 2X3
Подставляя в выражение для Тср с значение интенсив-
ности отказов из условия задачи, получаем
7 — 4 2
СРС — ю-з (0,23 + 0,05 + 0,4) io-3 (0,40 +0,05 + 0,40) '
______________1________ _|___________1____________
10--’ (0,23 + 0,05 + 0,8) ~ 10-3 (0,46+ 0.05 + 0,8) ~
2590 час.
117
Воспользовавшись соотношением (1.7), найдем зависи-
мость
М0 =
(О
PC(Z)
Р'е (О _
Ре(0 —
10-* (2,72е—0’6810'а/— 1,82е—0,9,'1()'з; —2,lGe—1,08'10’s<
4е—0,68- Ю-’Z _ 2е—0.91.10'4 _ 2е—1.08-10-4 .
+ 1,31е—1,31 |O'S/)
। е—1,31-10-4
Функция Хс(7) приведена на рис. 3.7. Заметам, что
интенсивность отказав резервированной системы при
1=0 равна 0,5 10-4 1/час, т. е. равна интенсивности от-
казов 7,2 нерезервированного элемента. При больших I
Рис. 3.7. Зависимость 7.с от t
(к примеру 3.6).
интенсивность отказов стремится к величине 7л+7.2+Яз=
=6,8-10”4 \/час, т. е. к интенсивности отказов нерезер-
вированной системы. Это свойство справедливо для
сколь угодно сложных систем с любьИм видом резерви-
рования.
Пример 3.7. Радиопередатчик имеет интенсивность
отказов Zo = O,4- 10_3 \/час. Его дублирует такой же пе-
редатчик, находящийся до отказа основного в режиме
ожидания (в недогруженном состоянии резерва). В этом
режиме интенсивность отказов передатчика Xi —
0,06 • 10'3 \/час. Требуется вычислить вероятность безот-
казной работы передающей системы в течение
7= 100 час, а также среднюю наработку до первого от-
каза и интенсивность отказов, построив зависимость
ЛсЮ.
Решение. В нашем случае кратность резервирова-
ния т=\, тогда на основании формулы (3.11) для слу-
118
чая общего резервирования при недогруженном состоя-
нии резерва имеем
Рс(0 = е-*
1=1
= e-v|l+at(l-e-v)l,
где
или окончательно
Рв (t) = e“w (1 + --е~^).
Подставляя в эту формулу значения неизвестных из
условия задачи, получим
D 1ХПГЛ —0,410-3.100 Л . 10,4-10-’
Рс (100) = е + 0 06.10_,--
0,4-10-*
0,06-10-’
—0,06-10-3-100
е
= 0,998.
На основании формулы (3.12) средняя наработка до
первого отказа будет
1
1 + k
Так как й = Я,/Яс, то окончательно
Т —
1 ср с---
Ло
Подставляя в эту формулу значения интенсивностей
отказов, получим
гр 1 /"« । 0,4 • 10 $ \
1 срс = 0,4-10-’ • 0,4-10-’ + 0,06-10-’ J “4(10'
Найдем зависимость интенсивности отказов системы
от времени, воспользовавшись соотношениями (1.5),
(1-7):
119
Р'е (0 _ (1 - e~V;
Г>е(О " . К -
* 1 IIе
0,4-10-3 (1 е~~0,06'|0~3/)
1 — 0,87e~w
График функции Хс(/)
сунка 'видно, что при / = 0
Рис. 3.8. Зависимость Лс от t
(к примеру 3.7).
приведен на рис. 3.8. Из ри-
пнтенсивность отказов лс = 0.
Это общее свойство всякого
резервирования и объясня-
ется ординарностью потока
отказов элементов 'системы.
При t—>оо интенсивность
отказов системы стремится
к величине 0,4 10~3 1/час,
т. е., как и следовало ожи-
дать, к интенсивности отка-
зов нерезервированной си-
стемы.
Пример 3.8. Цифровая
вычислительная машина со-
стоит из 10'24 однотипных
ячеек и сконструирована так,
что имеется (возможность заменить любую из отказав-
ших ячеек. В составе ЗИП имеется 3 ячейки, каждая из
которых (может заменить любую отказавшую. Требуется
определить вероятность и среднюю наработку до пер-
вого отказа ЦВМ в течение 10000 час, если известно,
что интенсивность отказов ячейки равна 0,12- 10 fi \/час.
Под отказом (будем понимать событие, (когда ЦВМ не
может работать из-за отсутствия ЗИПа, т. е. когда весь
ЗИП израсходован и отказала еще одна ячейка памяти
ЦВМ.
Решение. Так как любая ячейка из состава ЗИПа
может заменить любую отказавшую ячейку ЦВМ, то
имеет место «скользящее» резервирование. Вероятность
безотказной работы может быть вычислена по формуле
(3.18).
В нашем случае число элементов основной системы
/’.= 1024, интенсивность отказов нерезервированной си-
стемы /,(| = /?4.= 1024 0,12 • 10(i~ 1,23 • 104 1/час, число
резервных элементов т0=3. Подставляя полученные
120
данные в формулу (3.18), находим
то /
Рс (/) = ev = е~ v И + V
г=;0
-l-2310"!01^ +1,23-10~1-WJ +
Средняя наработка до первого отказа на основании
(3.18) будет
’ГСрС = ТСр0(1П1)-\- 1) = ^(т„ + 1) =
1,23-10-* (3+1)^ 32 500 час.
Пример 3.9. Две аккумуляторные батареи работают
на -одну нагрузку. Интенсивность отказов -каждой из них
Z = 0,l 10~4 1/час. При повреждении (отказе) одной из
батарей интенсивность отказов исправной возрастает
вследствие более тяжелых условий работы и равна
/.1 = 0,8-10~'4 1/час. Необходимо найти вероятность без-
отказной работы системы в течение времени /=1000 час,
а также среднее время безотказной работы.
Решение. Решим задачу двумя способами.
Способ 1. В нашем случае имеет место общее резер-
вирование с постоянно включенным резервом. Так как
при отказе одной батареи ,интенсивность отказов другой,
исправной, изменяется, то имеет место последействие
отказов. Дублированная система исправна в течение
времени t при следующих' благоприятных ситуациях:
А— ни одна из батарей за время t не отказала;
Б — аккумуляторная батарея 1 отказала, проработав
время т</, а батарея 2 оставалась исправной в течение
времени /;
В — аккумуляторная батарея 2 отказала, проработав
время т</, а батарея 1 оставалась исправной в течение
времени /.
121
Принимая указанные ситуации за гипотезы, можно
найти вероятность безотказной работы системы
как сумму (вероятностей благоприятных (гипотез, т. е.
Рс(0=рл(0+р£(0+рв(0.
Гипотезы А и Б одинаковы, поэтому рБ (t) = рв (f), и тог.
да
^с(0 = Рл(0 + 2/?£(0.
Так как рл(1) есть вероятность того, что за .время t ни
одна из батарей не откажет, то
РАЧ) = *~™. 1
Вероятность гипотезы Б можно вычислить, восполь-
зовавшись выражением
t
Р£ (0 = f «. (т) А СО A (t — О
о
где а, (т) dx — вероятность отказа первой батареи в мо-
мент т (вернее, в течение малого промежутка dx);
а, (х) = Ле-— частота отказов первой батареи в момент т:
Pz(t) —вероятность безотказной работы аккумулятор-
ной батареи 2 ,в течение времени т, т. е. до отказа пер-
вой батареи, очевидно, р2(т) = е—1х; p2(t—т)—вероят-
ность безотказной работы батареи 2 за промежуток вре-
мени от т до t. Так как в этом промежутке интенсив-
ность отказов батареи равна Xi, то
А«-х) = е-^-х>.
Подставляя все значения вероятностей в выражение
для /?£(0 и интегрируя, получаем
t
рБ (t) = J te-^-^e-W-^dx = J) e-V _
о
122
Тогда вероятность безотказной работы (резервирован-
ной системы будет
(0 = МО + 2р£ (0 == e~2W+
2Х
X, — 2Х
{е_(2х_м<_1]е_ М==
X, — 2М 2Х _ v
—--------р------------р
X,— 2Х X, — 2Х
Подставляя в эту формулу значения времени t и зна-
чения интенсивностей отказов из условия задачи, полу-
чаем
р _______ 0,8-10~4 -2.0,1-10—4-10®
rcV) 0,8-1G4 — 2-0,1-Ю'4 е
2-0,1 -104
0.8-10-4— 2-0,1-Ю"4
—0,8-10—4-10’
е
0,999.
Средняя наработка до первого (Отказа определяется
из соотношения
СО оо
Гер с = j Г’с (/) dt = j ( — 2Х е
о о
—v
2Х
Л-2Л
dt =
1 I 1
2Х "Г X, •
е
Подставляя значения Я и Я, в эту формулу, имеем
Гсрс— 2-0,1-Ю 4 о,8-ю-4 62500 час.
Следует помнить, что при вычислении Т(;рс предпо-
лагалось, что 2.—const. Если же окажется, что в течение
времени /<62500 интенсивность отказов непостоянна, то
наше решение неверно.
Способ 2. Используем для решения задачи схему
«гибели». В нашем случае интенсивность отказов систе-
мы дю выхода из строя первой батареи Ло=2Х=
= 0,2 • 10-4 1/час, интенсивность отказов системы в проме-
жутке времени от момента отказа первой батареи до
второй Xi=0,8-10~4 \/час.
Тогда вероятность возникновения отказа системы рав-
на вероятности возникновения двух отказов. На осно-
123
ваиии 'формулы (3.23) преобразование Лапласа вероят-
ности отказа 'будет
р (s) —_______________
(s + SXHs + XJs •
В нашем случае корни знаменателя равны s0=—22;
51=—Ац s2=0. Тогда
B'(s0) =22(22—2i), В'(sj 22), В'(s2) =2221.
Подставляя значения интенсивностей отказов, корней
S/t и производных B'(sh) в (3.24), получим
eSkt
Ж)
_ 222, | 2? (2Х _ „ 22)
, А] —2W . 22 —V
= 1--ХГ^зГе +л—2Ге •
Так как вероятность безотказной работы Рс (/) = 1 —
— Р2(0. т0
что совпадает с решением, полученным по первому спо-
собу.
Среднюю наработку до первого отказа можно вычис-
лить по формуле (3.26). В нашем случае
что совпадает с решением по первому способу.
Пример 3.10. Система электроснабжения постоянным
током состоит из трех источников 1на'пряжения: промыш-
ленной сети с преобразователем переменного тока в по-
стоянный, автономного маломощного источника и акку-
муляторной батареи. При ’исправной промышленной се-
ти потребители питаются только от преобразователя.
При отказе промышленной сети или преобразователя
подключается автономный маломощный источник сов-
местно с буферной батареей.
124
Система электроснабжения не обеспечивает пита-
нием потребителей в том -случае, если все три источника
отказали или отказала сеть и автономный источник
(одна аккумуляторная батарея не может обеспечить
питанием потребителя). Необходимо найти вероятность
безотказной работы системы -электроснабжения, если
известны следующие данные:
Xi = 0,25 10-3 \)час—суммарная интенсивность отка-
зов промышленной сети и преобразователя;
Хг=0,8- 10 3 \)час — интенсивность отказов автоном-
ного источника при совместной параллельной работе
с аккумуляторной батареей;
А'г=5,8- 1(Г3 \1час — -интенсивность отказов автоном-
ного источника при отказе аккумуляторной батареи;
Л,з = 0,1 • 10 3 \1час — интенсивность отказов аккуму-
ляторной батареи при параллельной работе с автоном-
ным источником;
./=100 час—необходимое время непрерывной рабо-
ты системы электроснабжения (потребители допускают
перерыв в работе лишь
на короткое время под-
ключения автономного
источника с аккумулятор-
ной батареей в случае от-
каза сети). До включения
в работу автономный ис-
точник и аккумуляторная
батарея не расходуют на-
дежность и отказать не
могут (Х2 = Хз='О).
Решение. Здесь
сложный случай резерви-
рования источников элек-
троснабжения, когда не-
возможно привести схему
расчета к классическим
случаям. Поэтому соста-
вим все благоприятные
Рис. 3.9. График функциониро-
вания системы (к приме-
ру 3.10):
/ — промышленная сеть и преобра-
зователь; 2 — автономный источник;
3 — аккумуляторная батарея.
гипотезы, вычислим веро-
ятности их появления и затем воспользуемся формулой
Благоприятные ситуации, не 'приводящие к отказу
системы электроснабжения, следующие (рис. 3.9):
125
Л—'промышленная сеть и 'преобразователь исправны
в течение времени
Б — промышленная сеть или преобразователь отка-
зали в момент х, а в оставшееся время t—х исправны
автономный источник с аккумуляторной батареей;
'В—промышленная сеть или преобразователь отка-
зали в момент т, >в момент £>т отказала аккумулятор-
ная батарея, а в течение времени t—т автономный ис-
точник исправен. Принимая эти ситуации за благопри-
ятные гипотезы, найдем вероятности их появления. Оче-
видно, что Ла(0 Так как момент отказа про-
мышленной сети есть событие случайное, то вероятность
гипотезы Б можно определить из выражения
t
РБ® = рт W А .з (у — г)
О
где at (%) = \ е-7'~ — частота отказов промышленной сети
в момент i; p2,3(t — -t) = е— (t~'t)—вероятность того,
что за время t—т не откажет ни автономный источник,
ни аккумуляторная батарея. Подставляя О1(т) и
Р2,з(^—т) в выражения для pE(t) и интегрируя, полу-
чаем
t
РБ ® (’) А.» (Z — г) dx =
О
t
— е~(>*+ м ~ ”ch ~
О
= 5—гф—г- e-w [1 —е~
По аналогии с гипотезой Б вероятность гипотезы В
можно получить из выражения
t
Рв (0 = Jai (с) А .3 (5. t — "О dx,
о
где р2,з(£, t—т)—вероятность того, что аккумуляторная
батарея в момент g откажет, а автономный источник бу-
126
дет работать исправно в течение времени t—т. Эта ве-
роятность может быть получена из выражения
А.з W = J«3 (5) Р.
Здесь «з (£) = Я3 е~м — частота отказов аккумуляторной
батареи в момент 6; р2 (£, t — £) = е~г*(t-T> е-’1'* <Л~Л) — ве-
роятность того, что автономный источник исправен в те-
чение времени t—т при условии, что аккумуляторная
батарея отказала в момент
Подставляя значения a3(g), /Mg, t—т) и /?2,з(|, t—т)
в выражение для рв(1) и интегрируя, получаем
t t
Рв (0 = (т) рз ® & Z — 5) =
О т
t t
= j Я, e~v j z3 е~г‘ (^’ e~Vs (,~и dtdz =
О 1
— [ е~(ЛОз) 1 1е~ (>’"Ла) 1 — ч _
^2--^-2 ^3 V ^-2
— (Ъ+^з) t е—1
Г
На основании (3.20) вероятность безотказной работы
системы электроснабжения будет
Рс(0=рл(0+р£(0+Рв(0.
Подставляя значения интенсивностей отказов в выра-
жения для рд, рБ и рв и делая очевидные^ вычисления,
получаем Рс (100) 0,999.
Пример 3.11. Система электроснабжения состоит из
четырех генераторов, номинальная мощность каждого
из которых №=18 кет. Безаварийная работа еще воз-
можна, если система электроснабжения может обеспе-
чить потребителя мощностью 30 кет. Необходимо опре-
делить вероятность безотказной работы системы элек-
троснабжения в течение времени /=600 час, если интен-
сивность отказов каждого из генераторов Х=
= 0,15-10~3 1/час. Необходимо также найти среднюю на-
работку до первого отказа системы электроснабжения.
127
Решен,не. Мощности двух генераторов достаточно
для питания потребителей, так как их суммарная мощ-
ность отставляет 36 кет, а по условию задачи достаточ-
но лишь 30 кет. Это значит, что отказ системы электро-
снабжения еще не наступит, если откажут один или два
любых тенератора. Здесь имеет место случай резервиро-
вания с дробной кратностью, (когда общее число
устройств / = 4, число устройств, необходимых для нор-
мальной работы, h = 2, а кратность резервирования
/72 = 2/2. На основании формулы (3.14)
2 I
pc(o = Xc>47'(oS (-1)е7У(о-
= 6/? — 8/У 4- 3/У = 6с^7 — 8e~3W + Зе~4М.
Для данных задачи М = 0,15-10 3- 600 = 0,09. Тогда
Рс (600) = бе — 8e-°'S7 + Зе~°’34^ 0,997.
Средняя наработка до первого отказа на основании
формулы (3.15) будет
2
т - 1 V 1 _ 1 f 1 д_ 1 । 1 13 —
7 ср с — X 2л 2 + 1 ~~ К К2""- 3, Г 4 ) Ш
7=0
Пример 3.12. Для повышения точности измерения не-
которой величины применена схема группирования 'при-
боров из пяти по три, т. е. результат измерения счита-
ется верным по показанию среднего (третьего) прибора.
Требуется найти вероятность п среднюю наработку до
первого отказа такой системы, если интенсивность отка-
зов каждого прибора 7=0,4 • 10~3 1/час, последействие
отсутствует, а время, в течение которого система изме-
рения должна быть исправна, /=500 час. Необходимо
также построить зависимость интенсивности отказов си-
стемы от времени.
Решение. Решим эту задачу тремя способами.
Способ 1. В данном случае измерительная система
отказывает в том случае, если откажут из пяти прибо-
ров три и более, т. е. имеет место общее резервирование
дробной кратности, когда общее число приборов / = 5,
число приборов, необходимых для нормальной работы,
й.=3, а кратность .резервирования т = 2/3.
128
Используя формулу (3.14), получаем
₽««=yс, р'~‘ (о у <- и1 ю=
1 U
2 i
=S с*, <- =6/- 15Р> юр’.
;=э /=о
Так как вероятность безотказной работы одного при-
бора в течение времени / = 500 час будет
ро (500)=e~v = е-°-4'10“3-5Э0 =е°,2 0,82,
то
Рс (/) = 6^— 15/Л|- 10р3о = 6 • 0,825 - 15- 0,824 +
10-0,823 0,95.
Средняя наработка до первого отказа системы вы-
числяется но формуле (3.15):
т 1 V 1 — 1 V 1 — 1 ' 1 -I- 1 j.. 1 V-
ср с С Л + 1 ' Ao L 3 + * > 0 V 3'1 Г 5 /
/=0 z=o
47 47 1ПСО
“"“ббХ-’ G0-0,4 10-3 —1958 час-
Интересно отметить, что при рассматриваемом .виде
резервирования средняя наработка до первого отказа
системы ниже, чем одного нерезервированного прибора
в 47/60 раза.
Способ 2. Благоприятными ситуациями в рассматри-
ваемом случае являются следующие:
А — все пять приборов исправны, вероятность этой
гипотезы рА (/) = р® (/);
Б — один любой прибор отказал, а остальные
исправны; так как приборов пять и каждый может
отказать с равной вероятностью q„=^ 1—р0, то pb{t) —
= 5<7оР = 5р4-5^;
В — два любых прибора из пяти отказали (таких ситуа
Ций может быть С/.—-10), а остальные три исправны,
9—1085 . 194
вероятность этой гипотезы будет
= 10Х-20/о+10/А
Вероятность безотказной работы измерительной си-
стемы на основании (3.20) будет
= бро5(0-15^(0 + 10/73о(0,
что совпадает с решением по формуле (3.14).
Средняя наработка до .первого отказа вычисляется
в данном случае путем интегрирования Рс(0 по всей
временной оси:
оо оо
Гср с = ре (0 dt = J [6^ (0 - 15/?4 (0 + 10р3( 0] dt =
о о
оо оо оо
6 J &~^dt — 15 J e~4W dt + 10 J e“3W dt =
о о 0
_/ 6 15 , 10 1 47
Д 5 4 T 3 j - 60/.'
что совпадает с ответом, полученным при первом спосо-
бе решения.
Способ 3. Воспользуемся схемой «гибели». В нашем
случае отказ системы наступит при отказе не менее трех
приборов. Вычислим вероятность отказов п=0, 1, 2 при-
боров.
В нашем случае интенсивность отказов системы до
выхода из строя одного прибора Xo=5Z, в промежутке
времени от момента отказа первого прибора до второго
Xi=4X, а от момента отказа второго прибора до треть-
его х2=зх.
Тогда на основании формулы (3.23)
Ро = s + K0 ’ P1 & = (s + Ло) (s + М ’
А (S) = (s + M (s+\) (s + X2) ’
130
Обратное |Преобразавание Лапласа этих 'Вероятно-
стей на основании (3.24) 'будет
Г с^о/ । е~г‘( ।
рг (t) =2.0\ L (К) _ Хо) {Ха _ Ко) н- -р^-х^-х,) +
e“w I
+(х„ - Х2) (X, - Х2) J
Подставляя в эти выражения вместо Ao. М и Х2 их
значения, получаем
pAi) = t , А(о = —5е + 5е
р2 (f) = 10e-5W —20е—4W -f- 10e-3W.
Так как отказа системы не 'будет при n = 0, 1, 2, то
вероятность безотказной работы системы равна сумме
вероятностей р0, pi и Рг, т. е.
лс(0 = а(0+а(0 + а(0 =
= 6 e-5U — 15 е~4М + 10 е "",
что совпадает с решением по первым двум способам.
Средняя наработка до первого отказа на основании
формулы (3.26) будет
Т — V 1 -= V—=—+— +—=
ср с “ ZJ V Zj Xi х„ x, r х2
i=0 /—О
1 । 1 . 1 _ 47
5X ' 4X * ЗХ ~ 60X ’
что совпадает с решением, полученным первыми двумя
способами.
Построим зависимость /.<(/), воспользовавшись со-
отношением
э ^е(0_ 30Х(1-е^)2
cU Ре (/) 6е-2И - 15е--)7 |- 10 “
__ 0,012 (1—e~°-4'10~3f )2
~ бе“°'8-10-3/ - 15 е"°-4‘ 10~3/ + 10
9-
131
Зависимость Xc/X=f(X/) приведена на рис. 3.10. Из
рисунка видно, что кривая /.< (/) .начинается с нуля,
а затем пересекает, ось Хс/Х = 1 и асимптотически
стремится к интенсивности отказов ХС = ЗХ нерезерви-
рованной системы. Таким образом, интенсивность отка-
Рис. 3.10. Зависимость Лс/Л от W
(к примеру 3.12).
I
зов резервированной системы при />т выше, чем нере-
зервированной.
Пример 3.13. Для повышения надежности электрон-
ной схемы все конденсаторы зарезервированы путем
последовательного их соединения, как показано на
Рис. 3.11. Схема соединения конденса-
торов (к примеру 3.13).
рис. 3.11. Необходимо найти вероятность безотказной
работы соединения и построить графики Рс(/) и вы-
игрыша надежности Gq(t) по вероятности отказов, если
известно, что интенсивность отказов конденсатора
А=0,3-10~с 1/час, а вероятность возникновения отказов
типа обрыв <ро = 0,2. Предполагается, что электронная
схема .не критична к изменению емкости цепи конден-
саторов и последействие отсутствует.
Решение. Благоприятные ситуации, не приводящие
к отказу схемы рис. 3.11, возникают в том случае, если:
А — не откажет ни один из конденсаторов;
Б—пробит один любой конденсатор, а два других
не откажут;
В—пробиты два любых конденсатора, а один ис-
правен.
Принимая эти ситуации за гипотезы, найдем вероят-
ности их появления.
Вероятность того, что не откажет ни один из конден-
саторов, будет равна произведению вероятностей p(t)
132
безотказной работы всех трех конденсаторов, Т. е.
ра(0=р3(0-
Вероятность того, что два конденсатора исправны,
а один пробит, равна p2q3. Но вероятность пробоя кон-
денсатора q3 равна произведению вероятности того, что
отказ возникнет, на вероятность того, что возникший от-
каз будет типа пробоя, т. е. <7з=<рз<7-
Так как в схеме три конденсатора, то возможен про-
бой любого из них, поэтому вероятность гипотезы Б будет
рБ (0 = Зр2 (О Ъ>4 (О = &?3Р2 (0 [1 — Р (01 -
Вероятность того, что пробиты два конденсатора, а один
исправен, равна pq\ Но так как по-прежнему qa = (f3q и
таких ситуаций в схеме рис. 3.11 возможно ровно С2 =
— 3, то
рв (о=?>р (о = 3v (о [1 — р со]2-
Суммируя вероятности всех гипотез, получим
= ps (0 + 3<p3jt7=(o11 - Р (01 + з¥> (0 [I - р (0]в-
Так как <р3 = 1 — <ро = 1 — 0,2 = 0,8, а р (f) = е—\ то
Рс (/) = е~зг/+2,4е~2ХГ (1 — e~w) +
+1,92 е~”(Г— e“v)2 = 0,52е“ж — 1,44 е~2Н + 1,92 е~м.
Выигрыш надежности по вероятности отказа будет
1 — Рс (0 1 — 0,52 e-?w +1,44 e“2W —1,92 е~м
1-р(0~ 1-е-м
Зависимости Рс(1) и Gq(t), а также вероятность
безотказной 'работы нерезервированного конденсатора
при Х=0,3-10-6 1/час приведены на рис. 3.12. Из рисун-
G,(0 =
Рис. 3.12. Зависимость G9 и Рс
от t (к примеру 3.13).
133
ка .видно, Что |резер|Вирбванйе .в Данном случае выгодно
для любого времени работы схемы.
Пример 3.14. На рис. 3.13 изображены две схемы
резервирования диодов. Известно, что интенсивность от-
казов диода Х=0,5-10"6 1/час, вероятность отказов типа
«пробой» <р3=0,85, а'время непрерывной работы схемы
/ = 5 000 час. Предполагается, что 'последействие отказов
отсутствует. Необходимо выяснить, какая схема лучше и
какой выигрыш надежности по вероятности отказов она
дает.
Решение. Найдем вероятность безотказной работы
схем рис. 3.13. Благоприятные ситуации схемы
рис. 3.13,а, не приводящие к отказу, возникают в сле-
дующих случаях:
А —все диоды исправны; вероятность этой гипотезы
равна р4(./);
Б — один любой диод отказал (либо обрыв, либо
пробой), а остальные исправны; вероятность гипотезы
равна 4<7(/)р3(/);
Рис. 3.13. Схемы резервирования диодов:
а - последовательно-Параллельное соединение; б — параллельно-последователь-
ное соединение (к примеру 3.14).
В—один любой диод отказал по обрыву, а другой
по замыканию, остальные два диода исправны; вероят-
ность гипотезы будет 12фофз^26/)р2(0;
Г — два диода отказали по обрыву, а остальные ис-
правны; вероятность гипотезы 2^3 (Z) рг (/);
Д — два диода отказали по пробою, а остальные
исправны; вероятность гипотезы (С2 — 2) ?2 (f (t) р2 (/) =
Е — один диод исправен, два отказали по обрыву,
а один — по пробою; вероятность гипотезы 4'р2|р3<73(0 p(t)‘,
134
_________один диод исправен, два отказали по пробою,
а один —по обрыву; вероятность гипотезы Д) р (t).
Суммируя вероятности гипотез, получим вероятность
безотказной работы диодной схемы рис. 3.13,а:
Ра (0 = Р' (0 + 4<7 (О PS (0 + 1 2'Ро?з<73 (0 Р2 (0 +
+ 2<рУ + 4?У(0/72(0 +
+ 4<р^ (о р (0 + 8<Ро?У (О Р (О-
Подставляя значения ф3 и <р0=1—дъ—1—0,85=0,15,
получаем
Ра(Р) = 0,5215р4—2,0995р3+ 1,6345р2 +0,9435р.
Схема рис. 3.13,6 не откажет в тех же ситуациях,
что и схема рис. 3.13,а, только число гипотез Г, Д, Е
и Ж будет иное. Теперь вероятности этих гипотез будут
иметь вид:
4'Р^2 (0 Р2 (0 (гипотеза Гу,
2<р2</! Г (0 (гипотеза Д);
B'f’o'iM’3 (0 р (t) (гипотеза £);
4'Ро'Рз<73 (0 р (t) (гипотеза yW).
Рб (0 = Р4 V) + 4с/ (0 Р3 (0 + 1(0 р3 (0 +
+ 4?у (0 р2 (0 + (0 рг (0 + 8<р2о?^ (0 р (0 +
+ 4оУ (0 Р (0 = — 0,5215р4 — 0,3705р3
4- 1,3055р3 4- 0,5865р.
Выигрыш надежности схемы рис. 3.13,а по сравнению
со схемой рис. 3.13,6 будет:
__ 1 — 0,5215р4 + 2,0995р3 — 1,6345рг — 0,9435р
1 + 0,5215р4 + 0,37057?3— 1,3055ра —0,5865/7 '
Найдем вероятность безотказной работы одного диода
в течение 5000 час работы:
р (5000) = е^71’5300 — g-o.s.io-f’-sooo^ 0,9975.
135
Подставляя значение р(5000) в выражение для Gq(t)
и делая очевидные вычисления, получаем Gg (5000) —0,5,
т. е. схема рис. 3.13,а более выгодна, чем схема
рис. 3.13,6, и число ее отказов в течение 5000 час будет
примерно в 2 раза меньше, чем схемы рис. 3.13,6.
§ 3.3. ЗАДАЧИ
3.1. Схема расчета надежности приведена на рис. 3..14. Необхо-
димо найти вероятность безотказной работы изделия, если известны
вероятности отказов элементов. Хр
Ответ: = 1— [1—(1 (1—/?2)]3 = 0,997.
3.2. Схема расчета надежности показана на рис. 3.15, .где приве-
дены данные о вероятностях безотказной работы элементов. Требует-
q=o,O5 qz = o,f Pt=o,9 рг=о,в
Рис. 3.14. Схема расчета на-
дежности (к задаче 3.1).
Рис. 3.15. Схема расчета надеж-
ности (к задаче 3.2).
ся определить вероятность безотказной работы и вероятность
отказа Qc изделия.
Ответ: Рс = [1—(1—pi)3][l—(1—р2)3]«0,991; Qc = l—Рс = 0,009.
3.3. Схема расчета надежности показана на рис. 3.16. Необхо-
димо найти по известным вероятностям отказов элементов qi и </2
вероятность безотказной работы изделия.
Ответ: /%=(! — q]) (I—<?|) = 0,95.
р^0,3 Pt = O,B
Рис. 3.16. Схема расчета надеж-
ности (к задаче 3.3).
р = 0,85 р, =О.дч
'з 4
Рис. 3.17. Схема расчета надеж-
ности (к задаче 3.4).
4t = °>'
3.4. Схема расчета надежности показана на рис. 3.17, на кото-
ром приведены вероятности безотказной работы элементов. Требует-
ся вычислить вероятность безотказной работы изделия.
Ответ: Рс = 1—(1—Р1Р2) (1—Pspi) —0,944.
136
3.5. Схема расчета надежности показана па рис. 3.18. Интенсив-
ности" отказов элементов имеют следующие значения: >-i = 0,3X
Х10-3 1/час, 7.2 = 0,7 • 10 3 1/час. Необходимо определить вероят-
ность безотказной работы изделия в течение времени t—100 час,
среднюю наработку до первого отказа, частоту отказов и интенсив-
ность отказов в момент времени /=100 час.
Ответ:
Рс (/)1[ 1 - е~ ()'+>а) z]s;
3
I/ (100) = 0,99; Тср с = -2 + х = 1500 час;
ае (t) = 2 (Хг + ?.2)е‘р'+1“> 4 [1 — е~Р>+Мf ];
ас (100) = 1,8-10-“ 1/час;
«.(100)
Хс (100) = -р1рщ-^л(100) = 1,8-10-“ 1/час.
3.6. Схема расчета надежности изделия показана на рис. 3.16.
Интенсивности отказов элементов имеют значения: Xt = 0,3-10-3 1/час,
Х2=0,7 • 10 3 1/час. Требуется найти вероятность безотказной рабо-
Г,
Рис. 3.19. Схема расчета на-
дежности (к задаче 3.9).
Рис. 3.18. Схема расчета надеж-
ности (к задаче 3.5).
ты изделия в течение времени (=100 час, среднюю наработку до пер-
вого отказа, частоту отказов и интенсивность отказов в момент
времени /=100 час.
Ответ:
Рс (/) = [1 - (1 -е-у>‘ )*] [1 - (1-е-^ )2];
4,5
Ре (100) 0,994; Тща— Х2)
“ 2 ( 2Х, + Х2 + X, + 2Х2 )- 1760 адс:
ае (0 = 2e-(>i+*a) 4 [ (X, 4- Х2) (2 + —
- (2Х, + Х2) е~114 - (X. + 2Ха) е-^];
ae(100)AsXe(100) = 0,108.10-s 1/час.
137
3.7. Средние наработки до первого Отказа элементов схемы
рис. 3.18 равны Ti и Т2. Справедлив экспоненциальный закон надеж-
ности для элементов. Необходимо найти среднюю наработку до пер-
вого отказа схемы.
Ответ: 7'ср e = 37’i7’2/2(7’i + 7’2).
3.8. Средняя наработка до первого отказа схемы рис. 3.18
7’ср с = 1 ООО час и 7’1 = 27’2- Необходимо найти вероятность безотказ-
ной работы схемы в течение 100 час.
Ответ: Рс( 100) - 0,98.
3.9. Средние наработки до первого отказа элементов схемы
рис. 3.19 равны Т, и Т2. Найти среднюю наработку до первого отка-
за системы.
Ответ: 7’срС = 7\ + 7’2—T’lT^/fT’i + T’a).
3.10. Средние наработки до первого отказа элементов схемы
рис. 3.17 равны Tlt Т2, Тз и 7’4. Найти среднюю наработку до пер-
вого отказа системы.
т Ге__________ ' T,T2T3Tt
Ответ. Т^срс — (Г, + Т2) (Г, + Т4) с
где с=Л7’2(7’3+7’4)+7’з7’4(7’1+7’2).
3.11. Средние наработки до первого отказа элементов схемы
рис. 3.14 равны Т± и Т2. Найти среднюю наработку до первого отка-
за системы.
Ответ: Тср с = 11TiT2/6(Ti + T2).
3.12. Средние наработки до первого отказа элементов схемы
рис. 3.15 равны 7"i и Т2. Найти среднюю наработку до первого отка-
за системы.
Ответ:
т -Т Г 3(^ + 6д+11) 3(4^ + 12д+П) ,
вр с “ 1 L (! + «) (2 + «) (3+«) (1 +2а) (2-+2«) (3+2а)
9а2 + 18« + 11
•"(I + За) (2 +За) (3 +За)
где a=Ti/T2.
3.13. Схема расчета надежности изделия приведена на рис. 3.20.
Вероятность безотказной работы нерезервированного устройства
в течение 300 час равна 0,74, резерв ненагруженный и интенсивность
Рис. 3.20. Схема расчета надежности
(к задаче 3.13).
отказов устройств X=const. Необходимо найти его вероятность и
среднее время безотказной работы.
Ответ: Рс(300)«0,995; Т'«3 000 час.
3.14. Изделие состоит из двух элементов, менее надежный эле-
мент дублирован путем замещения при ненагруженном состоянии
резерва. Средние наработки до первого отказа элементов равны
138
Т =100 час и 7’2=200 час. Найти среднюю наработку до первого
отказа изделия, если для элементов справедлив экспоненциальный
закон надежности.
Ответ:
7’ср е = 7’1+7'2 = 300 час.
3.15. Предложено конструктором три варианта схем построения
изделия (рис. 3.21):
а) изделие нерезервировано и средние наработки до первого
отказа элементов равны 7^ = 7г = 300 час;
б) один элемент дублируется путем замещения при ненагружен-
ном состоянии резерва, а второй, как и в схеме ри£. 3.21,с, нерезер-
вирован, причем средние наработки до первого отказа дублирован-
ного узла и нерезервированного элемента те же;
в) один элемент дублирован путем постоянно включенного
резерва, а второй нерезервирован, причем, как и в схемах рис. 3.21,а
и б, средние наработки до первого отказа дублированного узла и
нерезервированного элемента равны 300 час.
Какой из вариантов более предпочтителен с точки зрения надеж-
ности, если надежность изделия оценивать средней наработкой до
первого отказа?
500
Ответ: Та=150час, Тб = —167, Тд = 165.
Лучшим вариантом является схема рис. 3.21,6, а наихудшим —
схема рис. 3.21,а.
Рис. 3.21. Варианты по-
строения изделия (к зада-
че 3.15).
6)
3.16. Интенсивность отказов изделия 1=0,016 1/чсс. Для повы-
шения надежности имеется возможность либо облегчить режимы
работы элементов и тем самым снизить интенсивность отказов изде-
лия вдвое, либо дублировать изделие при постоянно включенном
резерве без облегчения режимов работы элементов.
Какой способ более целесообразен, если надежность изделия
оценивать средней наработкой до первого отказа?
Ответ: Более целесообразно облегчить режимы работы элемен-
тов, так как при этом среднее время безотказной работы изделия
возрастет вдвое, а при дублировании — только в 1,5 раза.
1'39
3.17. Используя -данные задачи 3.16, установить, какой способ
повышения надежности изделия из предложенных в задаче 3.16 бо-
лее целесообразен, если надежность оценивать вероятностью без-
отказной работы в течение времени непрерывной работы изделия
/ = 20 час.
Построить график Pc(t) и объяснить, почему ответы в задачах
3.16 и 3.17 не совпадают.
Ответ: Более целесообразно дублировать изделие, так как при
дублировании вероятность безотказной работы Рс (20) =0,93, а при
облегченном режиме работы элементов Р, (20) —0,85.
На рис. 3.22 приведены
и с облегченными режимами
что при /<^62 час, точнее,
кривые Рс (?) дублированного изделия
работы элементов. Из кривой видно,
2 2
при t <Z In —j—, целесообразно
дублирование изделия, а при />62 час — облегченный режим рабо-
ты элементов. Площади под кривыми P(t) на всей временной оси
являются средними временами безотказной работы. Этими обстоя-
тельствами и объясняется кажущееся противоречие в ответах задач
3.16 и 3.17.
3.18. Для повышения надежности изделия применена схема груп-
пирования из трех по два (гп^Уг). При каких значениях вероят-
Рис. 3.22. Зависимость Ре от t (к задаче 3.17).
ности р безотказной работы нерезервированного изделия схема
группирования приводит к повышению надежности?
Ответ: Рс = 'Лрг—2ps, при р>0,5 схема группирования приво-
дит к повышению надежности.
3.19. Время непрерывной работы измерительной системы t=
= 100 час. Какова должна быть интенсивность отказов устройства,
чтобы схема группирования, примененная для повышения точности
измерения, также способствовала повышению надежности системы?
Ответ: Х<(1п2)/100 1/час.
3.20. При каких значениях вероятности р безотказной работы
схема группирования из пяти по три (т=2/3) дает выигрыш в на-
дежности по сравнению с нерезервированным изделием?
Ответ: р>0,5.
3.21. Интенсивность отказов измерительного прибора Х=
=0,83 • 10~3 {/час. Для повышения точности измерения применены
две схемы: а — схема группирования из трех по два (^='/2), б —
140
схема группирования из пяти по три (т = 2/з). Необходимо опреде-
лить: 1) какая схема имеет большее среднее время безотказной
работы? 2) вероятность безотказной работы какой схемы выше, если
время непрерывной работы измерительной системы /=100 час?
Ответ: 1) средняя наработка до первого отказа системы при
т=Ч2 равна 1 000 час, а средняя наработка до первого отказа си-
стемы при т=2/3 равна 940 час.
2) Pm=2iz> ?т=Ц2-
3.22. Автомобильный двигатель имеет /=4 свечи зажигания, по
одной на каждый цилиндр. Интенсивность отказов свечи Л= 10~3 Х/час,
а длительность работы двигателя в течение всего путешествия
/=20 час. Предполагается, что автомобиль может ехать также при
одном неработающем цилиндре. Какова вероятность того, что авто-
мобиль доставит туристов в пункт назначения без замены свечей?
Ответ: Ре (/)=4 e~3W — 3 e ~w; ре (20) = 0,9977. *
3.23. Машина состоит из I 024 стандартных ячеек и множества
других элементов. В ЗИПе имеется еще две однотипные ячейки,
которые могут заменить любую из отказавших. Все элементы, кроме
указанных ячеек, идеальные в смысле надежности. Известно, что
интенсивность отказов ячеек есть величина постоянная, а средняя
наработка до первого отказа машины с учетом двух запасных ячеек
Тсрс = 60 час. Предполагается, что машина допускает короткий пере-
рыв в работе на время замены отказавших ячеек. Требуется опреде-
лить среднюю наработку до первого отказа одной ячейки.
Ответ: То=20 480 час.
3.24. Система состоит из двух одинаковых элементов. Для повы-
шения ее надежности конструктор предложил два .следующих
варианта (рис. 3.23): а — дублирование системы по способу замеще-
tz) б)
Рис. 3.23. Варианты резервирования (к задаче 3.24).
ния с ненагруженным состоянием резерва; б — скользящее'резервн-
рование при одном' резервном элементе, находящемся в неиагружен-
ном состоянии. Какой из. вариантов более целесообразен с точки
зрения надежности, если интенсивность отказов элемента X?
Ответ: Ра (/) = Р- (/) = e~2W (1 2Kt), т. е. варианты" рав-
ноценны.
3.25. Система состоит из N однотипных элементов, каждый из
которых имеет среднюю наработку до первого отказа, равную
П>кв= 1/Хакв. Для повышения надежности применено скользящее
резервирование, при котором т резервных элементов находятся
в ненагруженном режиме. Необходимо найти среднюю наработку
До первого отказа.
Ответ: ГСр с = Ганв(ш+1)/Л/.
141
3.26. Предложены следующие три системы электроснабжения
промышленной сети:
а — один генератор мощностью 300 000 кет;
б- три генератора, каждый мощностью 100 000 кет;
в — пять генераторов, каждый мощностью 60 000 кет.
Какая система электроснабжения более надежна, если, она не
допускает восстановления и перерыва в работе и предназначена для
непрерывной работы в течение t = 1 000 час? Интенсивности отказов
генераторов растут пропорционально убыванию их мощности. Интен-
сивность отказов генератора мощностью 300 000 кет Л=3- IO ’5
Предполагается, что в системе электроснабжения б допустим отказ
одного генератора, а в системе электроснабжения в — двух генера-
торов. Предполагается также, что последействие отказов отсутствует.
Ответ: Ра (1 000) =0,97; Рб (1 000) =0,98; Ре (1 000) =0,981.
3.27. Какая из систем электроснабжения, указанных в задаче
3.26, более надежна, если интенсивность отказов генераторов не за-
висит от мощности и равна 3- 10 5 1/час? Каков выигрыш в надеж-
ности по вероятности отказов имеют резервированные системы по
сравнению с нерезервированными?
Ответ:
Ра (1000) = 0,97; Рб (1000) = 0,997; Ре = 0,9997;
G6
да
'Чб
G.
Ча
че
Если оценивать надежность по вероятности отказов, то вариант б
в 10 раз, а вариант в в 100- раз надежнее нерезервированной систе-
мы электроснабжения.
3.28. Для повышения надежности схемы резисторы, имеющие
сопротивление R, решено резервировать путем параллельного их
соединения. Схема допускает изменение величины сопротивления не
более чем на 25%, поэтому для защиты схемы от одного отказа
параллельно приходится включать не менее четырех резисторов.
Необходимо определить выигрыш в надежности Ge схемы из четырех
параллельно включенных резисторов по сравнению с одним нерезер-
вированным резистором. Интенсивность отказов резистора 7.=
=0,25 • Ю |: \!час, а время непрерывной работы схемы / = 40, 400,
4 000 час.
Ответ: Сч(40) G8(400)=sx-| • 10“4; Gq (4000)=^
1
sss-x- -103.
6
3.29. По данным примера 3.28 построить функцию выигрыша
надежности от времени и сделать выводы о целесообразности резер-
вирования. Найти время работы схемы т, до которого целесообразно
применять резервирование резисторов путем параллельного включе-
ния четырех элементов.
Ответ: График G8(f) приведен на рис. 3.24; резервирование
целесообразно при Хт-^1п[6/(1 -К К13)] или при~т<-П06 час. Так как
142
с кратностью ш=1/з для всего времени
спок службы современных резисторов меньше чем т, то можно сде-
Лать вывод, что резисторы, у которых Zsg0,25 • IO fl \!час, целесооб-
разно резервировать по схеме с кратностью ш=1/з для всего времени
их срока службы.
Рис. 3.24. Зависимость Gq от
(к задаче 3.29).
3.30. Для повышения надежности схемы резисторы резервиро-
ваны путем параллельного их соединения. Схема допускает измене-
ние сопротивления на 33%, поэтому для защиты схемы от одного
отказа параллельно включено три резистора. Необходимо определить
выигрыш в надежности резервированной схемы по сравнению с на-
дежностью нерезервированного резистора, если интенсивность отка-
зов резистора Z=0,25 10~6 1{час, а время непрерывной работы /=40,
400, 4 000 час. Предполагается, что последействие отказов отсутст-
вует.
Ответ: Gg(40) = -|--10-5;£Ggr(400) =^-.10-“; Gg»(4000)=
1
= .у- io-s.
3.31. По данным примера 3.30 установить условия, при которых
резервированная схема нецелесообразна по сравнению со схемой
с одним резистором.
Ответ: Резервированная схема нецелесообразна при условии
С>10,; In 16 час.
3.32. Предложены следующие две схемы резервирования рези-
сторов: а — три параллельно соединенных резистора; б — шесть па-
раллельно соединенных резисторов. Обе схемы допускают изменение
общего сопротивления на '/3.
Какая схема более надежна, если интенсивность отказов одного
резистора Д=0,5 • 10-е {/час, а время непрерывной работы / = 40, 400,
4 000 час? Сравнительную оценку провести по средней наработке до
первого отказа и вероятности отказа, предложив, что последействие
отказов отсутствует.
Ответ:
q /а _ _fdfl=-^-.10-‘ при Z=40 час,
т Та 50 3
4
Gg (t) = -g- -10“3 при t — 400 час,
4
Gg (f) = -у- • 10~2 при t = 4000 час.
143
3.33. По данным примера 3.32 построить зависимости Pa(t) и
‘ Из кривых найти область значений времени т, при которых
схема 6 более надежна, чем схема а. Объяснить, почему средняя
наработка до первого отказа схемы б всегда ниже, чем схемы а (см.
ответ задачи 3.32), а вероятность безотказной работы выше, если
/<Т.
Ответ: Зависимости Pa(t) и P6(t) приведены па рис. 3.25. Схе-
час. Средняя наработка до пер-
Рис. 3.25. Зависимость Ра и Рб
от t (к задаче 3.33).
вого отказа является интегральным критерием, она равна площади
под кривой P(t) при изменении t от 0 до оо. Этим и объясняется
кажущееся противоречие в ответах задачи 3.32.
3.34. Конструктором предложено два варианта повышения на-
дежности резисторов в электронной схеме: а — облегчение режимов
работы резисторов вдвое; б — резервирование путем параллельного
включения трех резисторов (схема не критична к изменению сопро-
тивления цепи на '/з). Какой из вариантов целесообразно исполь-
зовать для повышения надежности электронной схемы, если интен-
сивность отказов резистора до облегчения режима Л=0,5-10-6 \/час,
после облегчения уменьшается вдвое, а время непрерывной работы
/ = 5 000 час? Задачу решить в предположении, что в резервирован-
ной схеме последействие отказов отсутствует.
Ответ: Ge(5 000) = qa(5 ООО) / <7^(5 000) = 67, т. е. более целесо-
образно резисторы резервировать.
3.35. Правильно ли поступил конструктор, решив выбрать луч-
ший из вариантов повышения надежности резисторов, предложен-
ных в задаче 3.34, оценивая надежность средней наработкой до пер-
вого отказа?
Ответ: Средняя наработка до первого отказа схем будет
Та=4 -10е час, Тб = 5/3.10° час, т. е. Тб <Та. Конструктор неверно
выбрал вариант повышения надежности. Это объясняется тем, что
он не учел времени непрерывной работы электронной схемы.
3.36. Для повышения надежности системы управления решено
создать две системы, основанные на разных физических принципах,
и применить дублирование замещением при ненагруженном резерве.
Интенсивности отказов систем имеют значения: ?и=0,4 10-3 \!час,
/.а—0,25 • 10~2 1/час, а время непрерывной работы системы управ-
ления /=100 час. Какая из систем должна быть основной, а какая
резервной, чтобы надежность всей резервированной системы управ-
ления была максимальной?
Ответ: С точки зрения надежности оба варианта равноценны,
вероятность безотказной работы резервированной системы управле-
ния равна примерно 0,995.
144
3.37. Схема расчета надежности изделия приведена на рис. 3.26.
Необходимо найти интенсивность отказов изделия при f=0 и
t........—>-оо.
Ответ:
। Х3 при t = О,
Хс — )
(X, + Х2 + Х3 при t -> со.
Рис. 3.26. Схема расчета надежности (к задаче 3.37).
3.38. Схема расчета надежности изделия приведена па рис. 3.14.
Требуется определить интенсивность отказов изделия при t—100 час,
если интенсивности отказов элементов имеют следующие значения:
Xi=0,23- IO-3 1/чсгс> Х2=0,17- IO-3 1/час.
О г в е т:
ЗХе~х/ (1 — е'Л/Г
МО • м100) 19’2’10'7 |/,/яс-
1 ПЛ )
3.39. Схема расчета надежности изделия приведена на рис. 3.16.
Необходимо построить график зависимости интенсивности отказов
изделия от времени, если известны интенсивности отказов элементов:
Xi = 0,3- 10~3 l/час, Хг = 0,7- 10-3 1/час.
Ответ: График Kc(t) изображен на рис. 3.27.
Рис. 3.27. Зависимость Хс от t Рис. 3.28. Зависимость Хс от t
(к задаче 3.39). (к задаче 3.40).
3.40. Схема расчета надежности изделия изображена на
рис. 3.23,6. Требуется построить график зависимости интенсивности
отказов изделия от времени, если известно, что интенсивность отка-
зов элемента Х=0,3-10-6 i/час.
Ответ; График Xcf/J изображен на рис. 3.28.
3.41. Машина состоит из большого числа элементов, среди кото-
рых имеется 512 однотипных ячеек. Интенсивность отказов ячейки
Х= 1,97-К)-5 1/час. Предполагается, что машина допускает перерыв
в работе на короткое время замены отказавших ячеек, а ячейки не
10—1086 145
восстанавливаются и при хранении не отказывают. Сколько необхо-
димо иметь запасных ячеек, чтобы вероятность безотказной рабо-
ты машины из-за отказов ячеек была не ниже 0,98 в течение време-
ни /=100 час?
Ответ: Не менее трех ячеек.
3.42. Для повышения надежности системы, состоящей из N—
=5600 элементов, решено применить дублирование каждого элемен-
та с постоянно включенным резервом. Какова должна быть средняя
интенсивность отказов элемента, если требуется, чтобы вероятного,
безотказной работы системы в течение времени /=300 час была не
ниже 0,99?
Ответ:
Лср = 1/300 In [1— ]/1—530^/(К99].
3.43. Система построена таким образом, что отказ одного любого
элемента не ведет к отказу системы, а отказ любых двух элементов
и более приводит к нарушению ее работоспособности. Известны
число элементов N, интенсивности отказов всех элементов и время /
непрерывной работы системы *. Требуется получить формулу для
вероятности безотказной работы системы.
Ответ:
/ N j —\ / N \
Ре (0 = I 1 + ут----------- ) exp I — / I,
' <=1 ' «=1
где Z, — интенсивность отказов i-ro элемента.
3.44. Система электроснабжения самолета состоит из четырех
параллельно работающих однотипных генераторов. При отказе двух
и более генераторов наступает отказ системы электроснабжения,
так как мощности двух исправных генераторов недостаточно для пи-
тания всех потребителей и часть из них отключается. Интенсивность
отказов генератора при всех исправных генераторах Х=0,25Х
ХЮ-2 1/час, а при отказе одного из них 7=0,5 • 10~2 \!час. Необ-
ходимо найти вероятность безотказной работы в течение времени
полета /=8 час и среднюю наработку до первого отказа системы
электроснабжения.
Ответ:
р /а________3____ [4М _______4____ -3V.
ГоЩ— з_4ХД1 е 4 —ЗЛ./Л
Р (8) = 0,995; TcV е = -^-+= 167 час.
3.45. Для повышения надежности схемы резисторы резервиро-
ваны путем параллельного соединения. Схема допускает изменение
сопротивления на 1/3, поэтому параллельно включено три резистора.
Известно, что интенсивность отказов резистора при параллельном
соединении трех резисторов /.=0,25-10“6 \1час, при отказе одного
из них интенсивность отказов каждого из исправных возрастает
вдвое, т. е. 7.1=0,5 • Ю"6 Х/час. Интенсивность отказов одного нере-
* Подобная задача возникает при расчете надежности электрон-
ных схем с дублированием всех элементов.
146
нервированного резистора также равна Х=0,25-10-6 \/час, а время
1 - »-.nrr\TLI PVTlTlILr Т Л RAf) 1-4С1Г\Л vri т-ттл n.I/A Anna Па ПТЛТ'Г.
непрерывной работы схемы < = 3 500 час. Необходимо определить
выигрыш в надежности резервированной схемы по сравнению с не-
резервированной, если надежность оценивать вероятностью отказа
и средним временем безотказной работы.
Ответ:
1 — [2Х,/(2Х, — 3?.)] e-3’z— [ЗХДЗХ — 2Х,)] e“.2V .
G? (0 = 1 _’
7
Gg (3500) 5-10~3; GT=-j^.
3.46. Для повышения надежности системы управления на объек-
те установлены два прибора с разными физическими принципами
действия. Первый прибор имеет интенсивность отказов М. Второй
прибор состоит из двух одинаковых устройств, каждый из которых
имеет интенсивность отказов Z2; они образуют прибор с общим по-
стоянным резервированием (дублированием). Установить, какой из
двух приборов должен быть основным, а какой резервным, если
применить резервирование замещением с ненагруженным резервом.
Ответ: Оба варианта равноценны, вероятность безотказной ра-
боты в обоих случаях выражается формулой
2Х,е-^ Л,е-2^ 2Х2е~^
Рс - Xj — Х2 + 2Х2 — X, + (Х2 — X,) (2Ха — X,)’
3.47. Для измерения некоторой физической величины использует-
ся схема из пяти однотипных приборов, результат измерения выда-
ется по показаниям среднего (третьего) прибора. Известно, что Х=
= 0,25 • 10-2 1/час— интенсивность отказов каждого прибора при всех
исправных; Xi=0,4-10~z \/час— интенсивность отказов каждого из
исправных приборов, если один из пяти приборов отказал; Хг=
=0,65-Ю”2 1/час — интенсивность отказов каждого из исправных
приборов, если два из них отказали; <=100 час — время непрерыв-
ной работы схемы. Необходимо определить вероятность и среднюю
наработку до первого отказа схемы.
Ответ:
12Х,Х2е“ш 15XX2e~4W
(4Xj — 5Х) (ЗХ2 — 5Х) +(5Х —4Х,) (ЗХ2 —4ХД +
, 20XXt e"3V
+ (5Х —3X2)(4Xt—ЗХ2) ’
Рс (100) = 12,8е-’2.5— 19,8 е~’.6 ф-8 е~
е= 5х + 4х;+“зх; 193 час'
3.48. Машина состоит из большого числа элементов, в том числе
она имеет 512 однотипных ячеек. Известно, что: 1=0,36 • 1О"4 Л/час—
интенсивность отказов одной ячейки; лг=2-= число запасных ячеек;
10* 147
Xi = 0,18 10 5 1/час — интенсивность отказов запасной ячейки при
хранении; /=100 час — время непрерывной работы машины.
Предполагается, что машина допускает перерыв в работе на
короткое время замены отказавшей ячейки, но ремонт ячеек невоз-
можен. Требуется найти вероятность безотказной работы машины н
среднюю наработку до первого отказа машины из-за отказов ячеек.
Ответ:
•°с (0 = е“<512х р + (1 - e-V ) +
+
512Х / 512Х>
2Х, + X,
, Л —j— VJK ~г~ Л.
Рс (100) =5= 0,4; Тср с = (ГцГЩГ+26)’ k = '512Х ’
3.49. Система электроснабжения автомобиля состоит из генера-
тора и аккумуляторной батареи. Без аккумуляторной батареи езда
на автомобиле невозможна, так как нельзя запустить двигатель. При
отказе генератора езда возможна в течение очень короткого време-
ни (единиц часов). Известно, что интенсивность отказов генератора
>4 = 0,25-Ю-2 1/час; интенсивность отказов аккумуляторной батареи
при параллельной работе с генератором Хг=0,15 • 10-2 1/час, а при от-
казе генератора Х3 = 1,6-10~2 \1час. Необходимо получить формулу
для вероятности безотказной работы Pc(i} системы электроснабже-
ния и вычислить эту вероятность при / = 2 час.
Ответ:
Р (ft----—--——е—(Х+Х>)< J-----------е—W • р —0 987
~ X, +X2~ -Xs Xi+хг—Х,е ’
3.50. Автомобилист-любитель для повышения надежности осве-
щения установил дополнительные фары. Известны следующие исход-
ные данные: Х1=0,35 • 10~2 1/час — интенсивность отказов основных
фар; Х2=0,75-10-2 \1час—интенсивность отказов дополнительных
резервных фар во включенном состоянии; Хз=0,1 • 10-2 1/час —
интенсивность отказов дополнительных фар в выключенном состоя-
нии; /=5 час —время движения автомобиля со включенными фа-
рами.
Предполагается, что при /=0 все освещение исправно, а допол-
нительные фары включаются только после отказа основных. Какой
выигрыш в надежности он получил, если надежность оценивать ве-
роятностью отказов и средней наработкой до первого отказа?
Ответ: Ge(/)~X3f; (5) =0,5 • 10 2; G\=2,4.
3.51. Для повышения надежности используется схема группиро-
вания однотипных приборов из трех по два (т=1/2) с четвертым
таким же резервным прибором, находящимся в ненагруженном ре-
жиме и могущим заменять любой из отказавших. Известно, что:
Х=0,2 • 10~2 1/час — интенсивность отказов одного прибора при ис-
правных приборах схемы группирования; Xi=0,36-10-2 \/час —
интенсивность отказов одного прибора при работе схемы группиро-
вания с одним отказавшим прибором; /=100 час — время непрерыв-
148
ой работы схемы. Найти вероятность безотказной работы схемы И
среднюю наработку до первого отказа.
Ответ:
4„/4Xf — 12ХХ, 6ХХ,/ V
Рс (0 = е (2Х, — ЗХ)г~ + 2Х, — ЗХ J +
(ZKi—S'ky
2 1
Ра (100) 0,7; + 2^=5=472 аде.
3.52. Решить задачу 3.51 при условии, что четвертый резервный
прибор находится в нагруженном режиме и его интенсивность отка-
юв в этом состоянии равна X.
Ответ:
8Х, е~зм 6Х, e-4W .. 12Х2 e-2V
Рв ® — ЗХ ~ 2Х, — 4Х + (4Х — 2Х,) (ЗХ - 2Х,) ’
7 , 1
Ре (100) 0,62; 7’срс = -12г+‘72Х~':=43 ‘iac'
3.53. Решить задачу 3.51 при условии, что четвертый резервный
прибор находится в облегченном режиме и в этом состоянии его
интенсивность отказов Х2=0,1 • 10~2 1/час.
Ответ:
6ХХ, (ЗХ + Х2) е~(а+>з) z 2Х, (ЗХ + Х2)
Р° W = Х2 (ЗХ+Х2) (Х2+ЗХ — 2Хх) + Х2 (ЗХ — 2XJ +
. ЗХ (ЗХ + Х2)е~2>1/
(2Xj —ЗХ) (ЗХ + Х2 —2Xj)’
Рс (100) = 0,68;
Pope— зх + х2 +ЗХ+ 2Х, 470 час.
3.54. Решить задачу 3.26, исключив предположение об отсутст-
вии последействия отказов при следующих дополнительных исходных
Данных: Xi = 3-10^4 1/час — интенсивность отказов генератора мощ-
ностью в 100 000 кет в режиме работы системы электроснабжения,
когда отказал один генератор; Х2 = 3-10"4 1/час — интенсивность
отказов генератора мощностью 60 000 кет в режиме работы системы
электроснабжения, когда отказал один генератор; Хз=10~3 1/час—’
интенсивность отказов генератора мощностью 60 000 кет в режиме
работы системы электроснабжения, когда отказали два любых гене-
ратора.
Ответ: Ра (1000) =0,97; Рб (1000) =0,96; Ре (1000) =0,94.
3.55. Решить задачу 3.26, исключив предположение об отсутст-
вии последействия отказов, при следующих дополнительных исход-
ных данных: интенсивность отказов генераторов не зависит от их
мощности и равна Х=3-10“5 1/час; Х1=7,5-10^5 1/час — интенсив-
ность отказов генератора мощностью 100 000 кет в режиме работы
149
системы электроснабжения, когда отказал один генератор; Л2=
=4.10-5 1/час—интенсивность отказов генератора мощностью
60 000 кет в режиме работы системы электроснабжения, когда отка-
зал один генератор; 7.з=104 [/час — интенсивность отказов генера-
тора мощностью 60 000 кет в режиме работы системы электроснаб-
жения, когда отказали два любых генератора
Ответ: РД1000) = 0,97; Рб (1000) = 0,988; Рв (1000)=0,993.
3.56. Решить задачу 3.32, сняв предположение об отсутствии по-
следействия отказов при следующих дополнительных исходных дан-
ных: Л.1 = 0,75 • 10-в Х/час—интенсивность отказов резистора в схеме
а при отказе одного любого из трех параллельно соединенных; Л2 =
=0,6-10-6 1/час — интенсивность отказов резистора в схеме б при
отказе одного любого из шести параллельно соединенных; Хз=
= 0,75 • 10~6 1/час — интенсивность отказов резистора в схеме б при
отказе двух любых из шести параллельно соединенных резисторов.
Ответ:
GT = Тб/Та = 0,75; Gg= 1,6-10-* при / = 40 час.
Gg= 1.6-10-’ при /= 400 час, Gg = l,6-10 2 при/=4000 час.
3.57. Решить задачу 3.34, сняв предположение об отсутствии по-
следействия отказов. Известно, что интенсивность отказов резистора
в схеме б возрастает в 1,5 раза, если произойдет отказ одного из
трех параллельно соединенных резисторов
Ответ: Gg (5000) = qa (5000)/<уб (5000) 45, т. e.J резисторы
целесообразно резервировать.
3.58. Для повышения надежности конструктором предложено
два варианта схем резервирования резисторов:
а — параллельное соединение двух элементов;
б — параллельное соединение трех элементов.
Интенсивности отказов последних имеют следующие значения:
Х=0,3-10-6 \.)час — интенсивность отказов резистора в схеме а
или б при всех исправных элементах схемы; 7.1 = 27.— интенсивность
отказов исправного резистора в схеме а после отказа одного из двух
параллельно соединенных резисторов; 7.2=1,57. — интенсивность отка-
зов любого из исправных резисторов в схеме б после отказа одного
элемента; Хз=ЗЛ — интенсивность отказов исправного резистора
в схеме б после отказа любых двух резисторов.
Время непрерывной работы схемы /=5000 час. За критерий це-
лесообразности применения схемы следует выбрать выигрыш в на-
дежности по вероятности отказов в течение времени /. Какой из
вариантов следует принять, если схема не критична к изменении
сопротивления цепи резисторов?
Ответ: Gg’(5000) — qa (5000)/</б (5000) = 296, т. е. следует
принять вариант б.
3.59. Имеется дублированная система при общем резервирова-
нии с постоянно включенным резервом Интенсивность отказов одной
системы Zi, а другой 7.2. При отказе первой системы интенсивность
отказов второй возрастает и становится равной Х'2>Лг, при отказе
второй системы интенсивность отказов первой также возрастает и
становится A'i>A.i. Требуется получить формулу для вероятности
безотказной работы системы
150
Ответ:
Ag С
Р‘« = Х+И
^1 4" ^2 ---2
(X.X\ — У,Л'2 + LA't) e~(*‘+Xa) 1 -
(Xj + Л2 h'1) (^1 + ^2 h'2)
3.60— 3.73. Известны: /.— интенсивность отказов конденсатора;
Хо> %з=М— интенсивность отказов конденсатора соответственно по
обрыву и замыканию (пробою); фо = Ло/(Хо + м)—вероятность того,
что возникший отказ конденсатора произойдет из-за обрыва; t —
время непрерывной работы схемы. Предполагается, что последействие
отказов отсутствует. Найти вероятность безотказной работы схем
соединения конденсаторов (диодов, контактов реле), показанных
в табл 3.2.
Ответы приведены в табл. 3.2.
3.74— 3.87. Найти среднюю наработку до первого отказа схем
соединения конденсаторов (диодов, контактов реле), прнзеденных
в табл. 3.2, при исходных данных, указанных в задачах 3.60—3.73.
Ответы даны в т.абл. 3.2.
3.88. Найти условия, при которых параллельное соединение двух
конденсаторов (диодов, контактов реле) и последовательное соеди-
нение двух конденсаторов (диодов, контактов реле) дает выигрыш
в надежности по сравнению с одним нерезервированным конденса-
тором. Предполагается, что последействие отказов отсутствует и схе-
ма некритична к изменению емкости.
Ответ: Параллельное соединение двух конденсаторов целесо-
образно, если (ро >0,5; последовательное соединение целесообразно,
если ф3>0,5.
3.89. Определить условия, при которых параллельное (последо-
вательное) соединение трех конденсаторов целесообразно по сравне-
нию с одним нерезервированным конденсатором, если известно, что
вероятность безотказной работы конденсатора равна р и схема не-
критична к изменению емкости.
Ответ:
—3/Н- И12 —3/>2
¥о> 6(1—70
саторов;
„ -374-/12-3^
¥э> 6(1-р)
денса торов.
при параллельном соединении конден-
при последовательном соединении кон-
3.90. Найти условие, при котором диодная схема рис. 3.13,а бо-
лее надежна, чем схема рис. 3.13,6, если последействие отказов
отсутствует.
Ответ: Диодная схема рис. 3.13,а более надежна при <p3><p0.
3.91. Для повышения надежности реле его контакты дублирова-
ны путем параллельного соединения. Интенсивность отказов контак-
та /.=0,36 • Ю ’5 1/час, <ро=0,1; 0,3; 0,5, а время непрерывной' рабо-
ты t~lQO час. Предполагается, что последействие отказов отсутст-
151
Таблица 3.2
Номер ' задачи Схема соединения конденсаторов Ответы
P(t) reP
3.60
(3.74) *“ II и [2k, (k0 + X,) e-w+ (kg-kg) е“2^ k" = (4X,k„ + kg + 3kf)/2k3
3.61 1—il—1
(3.75) *—II— [2k0 (k0 + k,) e (k2;— kg) e“k-2 (4k, k0 + k2 + 3kg)/2k3
3.62 II 11 II п [3k2 (k„ + k,) eyw + 3k, (k2 - k2) e~2«+ (i8kfk0 + svg+iik^kgvek4
(3.76) 1|... || It -4 + (k3 + k3) e“2WJ k-’
3.63 U [3kg (k0 + k,) e v 4- 3k0 (kj — kg) e—“W+ (18kgk, + 9kok2+iug+2kf)/6k*
(3.77) •- й * + (\S +IX?) e-3VJ k-3
—II—
3.64 и [Xi (4Xq + + Xj) e (2Xq — ^0^1 — (21kgk,+ 24k0k? + 7k? +
(3.78) — 1г II— — 2k0kf + kf) e-2>f - (kg + Xf) e-3^] k-3 + 4kg)/6k*
Продолжение табл. 3.2
Номер задачи Схема соединения конденсаторов Ответы
Pit) Tcp
3.65 (3.79) —11— —II—II— —• [Хо (4Х2 + 5Х]Хо + Хо) е->'+ Н - Х1 Хо - - 2X,Xg + Х30) e~2W - (X3 + X3) e-3w] X-3 (21xfXo+ 24XiXq + 7Xq + + 4X|)/6X“
3.66 (3.80) —IHHHh [4Х3 (Х„+ ХО е- « + 6Х2 (Х2 _ е-2Н+ + 4Хх (Х3+ X3) e~3W + (X* — Xf) е~4Ч Х-* (48k|X0 + 36X^2 -j- 16X]Xq-|- + + 3k^)/12X5
3.67 (3.81) —II— —II— —II— —II— [4Х§ (Xi + Х„) e~w + 6X2 (?2_ X2j е-2М+ + 4Х0 (X3 + X3) e~3W + (X4 - X4) е~ш] Х-« (48XgXt + 36X^X[ + 16X„X? + + 25Xg + 3X|)/12X5
3.68 (3.82) с - f~T I Т [X? (6X2 + 8Х0Х, + 2Х2) е-^+бХоМХрХ^е-2^ + 4-(2Х0Х3 — 2ХдХ, + 2Xg - 2Xf) -(X4-X4) e-4W]X-< (72XgX? + 68X0X3 + 28XgX, + + 19Xf -J- 5X£)/12XS
Продолжение табл. 3.2
Номер задачи Схема соединения конденсаторов Ответы
Р(0 ГеР _
3.69 .(3.83) - п , —41— лг [X, (8Х30+ 9Х2Х, + 3XfX0 + X3) е-«+3(Х31Х0-Х1Х^- -^о + ^о) e-2W+ (Х§Х,-ЗХ3Х0+X4-3X4)e~3W+ + (X4-Xf) е~4М] X- (82XqX, -1- 90XqX] + 4X0X? + 13X) + 9Xj)/12Xs
•" II 11 —II—
3.70 (3.84) иа_ ! ^XqXJXq + ЗХ0Х; + 2Х[) е (2Xg + 4X3Xj — „ 6X2/2 _ 4Л3Хо+ 4?ф е-2М _ 4Xi (K3_X3)e-3W _ — (Xq —X4) e-4WJX-^ (88XgXt + 56X^Xf + 72X0Xf+ + 9Xq + 11X4)/12X=
—-•
!Г" II
3.71 (3.85) О f4AoXj (X] 4- SXqXj-)- 2Xq) e (2X4 -f- 4X3X0 — - 6X2X2 - 4Xfl3X1+ 4Xq) e-2«- 4X0 (X3 - X3) — (Xf —Xq) е-ш]Х-4 (88X„Xf + S6X2Xf + 72XSX^ + + 9X4 + 1 1Xq)/12X5
3.72 (3.86) чннн JI [Xo(8Xf+J9XoX2 + SXqXj+Xq) e ^-f_8X1(X3— X0Xj — -X^X, + X3) e-2V+:(XoXf’- 3X30x7+LX4- -3Xf)e~3W+ (X| — X4) е“ш] X-* (82X0X3 + 90X;Xq + 42XgXx + + 13Xq+9X4),/12X5
3.73
(3.87)
[Л, (2Х3 + 9ЛЛ0.+ 8Х?Х0 + 4Х1) e“W+ (5Мо -
— 8XfXg — 5Х3Х0 + 2Х4 + Xq) е (Х3Х0 —
- ЗХ,Х3 - ЗХ4 + Л4) е"^+ (Х| - X4) e~4W] X -*
(42XgXi + SOX^Xf + 62Х„Х3 4-
+ 15Х4 +7Xq)/12X5
вует. Необходимо вычислить выигрыш в надежности (sq(t) lie*
сравнению с нерезервированными контактами.
Ответ:
Gg (0
2уо —Х/(1 — Зро) .
1 — Л//2
Gg(100) = 0,2 при у0= 0,1, Gq (100) = 0,6 при ?о = 0,3,
Gg(I00)= 1 при <ро = 0,5.
3.92, Для повышения надежности схемы диоды дублированы
путем их последовательного соединения. Интенсивность отказов дио-
да Л=О,25 10 *' \!час; сра = 0,1; 0,25; 0,5, а время непрерывной рабо-
ты /=1000 час. Предполагается, что последействие отказов отсутст-
вует. Требуется определить выигрыш в надежности Gq(t) по вероят-
ности отказа по сравнению с нерезервированным диодом.
Ответ:
г /п 2¥з —(1 — Зу3)
Gs (0 1 . _ х//2
Gg(1000)=0,2 при <р3=0,1, Gg( 1000) =0,5 при <р3=0,25, Gg(1000) =
= 1 при <р3=0,5.
3.93. Интенсивность отказов конденсаторов Л настолько низка,
что для времени непрерывной работы порядка нескольких тысяч
часов всегда выполняется условие МС1. При этом условии необ-
ходимо найти выигрыш в надежности Gq(t) схемы рис. 3.13,а по
сравнению со схемой рис. 3.13,6.
Ответ:
Г /Л ?а(0 _3~2Уз-¥о-61Ро¥з
Ч()~ МО 3-2¥2-¥*-6№ '
3.94. Для повышения надежности конденсаторы дублированы
путем последовательного и параллельного соединений. Известно,
что вероятность того, что возникший .отказ конденсатора будет типа
замыкания, равна Требуется определить выигрыш в надежности
схемы GT по средней наработке до первого отказа в сравнении
с одним нерезервированным конденсатором.
Ответ:
1
Gr=<f3-|--2--при последовательном соединении,
3
Gt=~2----<р3 — при параллельном соединении.
3.95. Для повышения надежности применены следующие две
схемы резервирования конденсаторов путем последовательного и
параллельного соединения трех конденсаторов. Известно, что вероят-
ность того, что возникший отказ конденсатора будет типа замыка-
ния, равна <р3. Необходимо найти выигрыш в надежности схем по
среднему времени безотказной работы в сравнении с одним нерезер-
вированным конденсатором.
155
Ответ:
1 9
GT = -g- + 0,5<p3 + fg — при последовательном Соединений,
11 г 2
Gj- = —g— — 2,5<р3 + <р3 — при параллельном соединении.
3.96. Для повышения надежности контакты реле дублированы
путем их последовательного соединения. Известны следующие дан-
ные: X — интенсивность отказов одной пары контактов; <ра — вероят-
ность того, что возникший отказ контакта будет типа замыкания;
Xi — интенсивность отказов одной пары контактов после отказа дру-
гой пары; t — время непрерывной работы реле. Требуется определить
вероятность безотказной работы дублированной схемы.
Отв ет:
Ре= e-2W (1 — 2Х—х, ^ТгГ^^хГ ¥зe~V'
3.97. Для повышения надежности диоды дублированы путем
параллельного их соединения. Известны следующие данные: X —
интенсивность отказов диода; Xi — интенсивность отказов исправ-
ного диода после возникновения отказа типа обрыва в одном из
двух диодов; фо — вероятность того, что возникший отказ диода
будет отказом типа обрыва; t — время непрерывной работы схемы.
Необходимо найти вероятность безотказной работы дублированной
схемы.
Ответ:
_f ‘2К \ , 2Х _л .
Рс(0 = е (1— 2Х- Х, ¥oj+ 2Х —X, ¥ое ’ •
3.98. Схема двухполупериодного выпрямления резервирована
так, как показано на рис. 3.29,а и б. Известны следующие данные:
X — интенсивность отказов диода; фо, фа — вероятности того, что
Рис. 3.29. Схемы Двухполупериодного выпрямления (к задаче 3.98).
156
возникший отказ в диоде будет соответственно тийа «обрыв» иЛН
типа «замыкание» (пробой); t — время непрерывной работы схемы.
Предполагается, что последействие отказов отсутствует, а отказ
схемы наступает при отказе любого одного плеча. Требуется полу-
чить формулы для вероятности безотказной работы схем.
Ответ:
Ра (/) = e-4W [b + е~и (а — Зй) 4- e~2W (4 — 2а 4-Зй) +
+ е“;ш (а — Ь — 3)]*;
Ръ (/) = е"ш [d + e~w (с — 3d) + e~zw (4 — 2с + 3d) +
+ e-3W (с — d — 3) J*;
я — 2 (1 -f- <р3 -f- З?оу3); Ь = 4уоу3 (1 <р3);
с = 2 (1 4- <р0 4- 3¥о¥з); d = 4<ро<р3 (1 — <ро)•
3.99. Известно, что все элементы равнонадежны, имеют два типа
отказов (обрыв и короткое замыкание) и последействие отсутствует.
Известны также следующие данные: р — вероятность безотказной
работы элемента; ф0, <р3'—вероятности возникновения отказов эле-
ментов соответственно типа «обрыв» и «замыкание». Необходимо
найти формулу для вероятности безотказной работы резервирован-
ной схемы рис. 3.2,а.
Ответ:
/5а={1—[(1--Фо) (1—р)]и}'"+1—{1—[1—фо(1—p)]”}m+1.
3.100. Необходимо получить формулу для вероятности безотказ-
ной работы резервированной схемы рис. 3.2,6, если известны те же
данные, что и в задаче 3.99.
Ответ:
Рв = {1—1[фо(1— р)]т+,}п— {1— [(1—фо)р]™+1}"-
ГЛАВА ЧЕТВЕРТАЯ
РАСЧЕТ НАДЕЖНОСТИ ВОССТАНАВЛИВАЕМЫХ
ИЗДЕЛИЙ
§ 4.1. МЕТОДЫ РАСЧЕТА
К восстанавливаемым относятся такие изделия, кото-
рые после отказов могут быть отремонтированы и снова
выполнять свои функции. Восстановление возможно
с прекращением выполнения изделием своих функций и
без нарушения выполнения своих функций.
При разработке сложной электронной аппаратуры,
цифровой техники и систем автоматического управления
практически встречаются следующие случаи восстанав-
ливаемости изделий.
1. Резервирование с восстановлением, т. е. такое ре-
зервирование, когда отказавшие блоки восстанавливают-
ся и снова включаются в состав резервированной груп-
пы. Существенной особенностью конструкции аппаратуры
является возможность осуществлять ремонт отказавших
блоков во время выполнения аппаратурой своих функ-
ций.
2. Изделия с временной избыточностью, т. е. изделия,
располагающие для выполнения поставленной задачи ре-
зервом времени.
Основной круг задач, рассматриваемых при расчете
надежности восстанавливаемых изделий, относится к сле-
дующей ситуации. Исправное изделие начинает эксплуа-
тироваться в момент Y=0 и, проработав случайное время
Xi, выходит из строя. На ремонт требуется случайное
время Уф Этот процесс продолжается в течение всего
срока службы изделия, причем величины X, и У$ (i=l,
2, ...) независимы. В случайные или заранее установ-
ленные моменты времени tj (j=l, 2,...) могут прово-
диться профилактические работы случайной или постоян-
ной длительности Zi. Этот процесс усложняется в основ
ном последующим причинам:
158
— наличие резервных устройств и, как следствие это-
го, наличия переходов из одного уровня избыточности
на другой;
— дискретность работы изделия с заранее запланиро-
ванными или случайными 'моментами начала и окончания
работы;
— ограниченность числа восстановлений (например,
в тех случаях, когда восстановление заключается в про-
стой замене, а запасных устройств конечное число);
— наличие очереди на обслуживание;
— наличие ложных восстановлений исправных изде-
лий из-за отказа схемы, контроля;
— невозможность начать восстановление изделия сра-
зу же после его отказа из-за неполноты схемы контроля.
Рассмотрим наиболее распространенные эффективные
методы расчета надежности восстанавливаемых изделий.
А. МЕТОДЫ, ОСНОВАННЫЕ НА ИСПОЛЬЗОВАНИИ
КЛАССИЧЕСКОЙ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Рассмотрим основные положения этих методов.
Если любые отказы непрерывно работающей системы
устраняются мгновенно (все Уг = О), профилактика от-
сутствует, число восстановлений неограниченно, а все Xi
являются независимыми одинаково распределенными слу-
чайными величинами с одной и той же плотностью рас-
пределения
ft (*)=/(*) =Е'(х),
(4-1)
то моменты отказов образуют простой процесс восста-
новления.
Частным случаем простого процесса восстановления
является пуассоновский процесс, для которого
f(A-) = Xe->x,
Е(х) = 1 — е~\ Я>0.
(4-2)
Если все условия для простого процесса восстановле-
ния выполнены за исключением того, что длительность
от начала работы до первого отказа имеет плотность
распределения
ft(x)=#f(x), (4.3)
159
го такой процесс называется общим процессом восста-
новления. Общий процесс восстановления, для которого
fA И) = П - F (Л-)] / \xf (х) dx, (4.4)
/ о
называется стационарным процессом восстановления.
Если в условиях простого процесса восстановления
величины У, =А 0 и распределены одинаково с плотностью
распределения
g(/) = G/(Z), (4.5)
то такой процесс называется процессом восстановления
с конечным временем восстановления.
В рассматриваемых случаях большую роль играет
среднее число отказов за время t, называемое функцией
восстановления, или среднее число замен Я(/), причем
для всех приведенных выше случаев имеем
Я(0 = £фп(0- (4.6)
11=1
При п=1 получим:
— для простого процесса восстановления
Ф1(0=Л(/)=Е(/); (4.7)
— для общего процесса восстановления
Ф1(0 = ^.(0 = {А(г)^. (4-8)
б
При мгновенном восстановлении и п ^2
t
(0 = Fn{t) = \Fn ^(t-z)dF (г). (4.9)
б
В частном случае для стационарного процесса
Н (t) = t / p-f (х) dx — t IM [x]. (4.10)
i б i
Из (4.6) следует, что при простом процессе восста-
новления H(t) удовлетворяет интегральному уравнению
Вольтерра 2-го рода
/
Н (t) = F (0 4- (И (t — х) dF (х). (4.11)
б
160
Переходя к преобразованию Лапласа, получаем
H(s)=F(s)/[l—sF(s)], (4.12)
где
Н (s) = Je-Sttf (0 dt\ F (s) = Je-sfF (t) dt.
б о
Важную роль играет функция плотности восстановле-
ния, имеющая вид
ОО оо
h (t) = И' (t) = 2 ф n (0=S fn (0- (413)
n=l п=Л
При простом процессе восстановления из (4.11) сле-
дует, что
t
h (t) = Н’ (0 = f (0 +J/i (t — x)f (х) dx. (4.14)
о
В теории надежности эта функция называется пара-
метром потока отказов, т. е. /г(/) =ю(/).
Вероятность безотказной работы системы на участке
t, t+Ait при Atf—>0 равна
Р(/, t+iM) = l~h(t)M+G(M). (4.15)
Таким образом, h(t) приблизительно равна безуслов-
ной вероятности отказа за единицу времени $(£), а ин-
тенсивность отказов
4t)-f(t)/V-F(t,)] (4-16)
равна условной вероятности отказа за единицу времени
при условии, что до момента t отказов не было.
В частности, для стационарного процесса восстанов-
ления
h(ty ='Х(0 =const. (4.17)
Известно, что если f(t)—>0 при t—>оо, то
Нт/г(/) = 1/Тср, (4.18)
/-5-00
т. е. с течением времени процесс восстановления стано-
вится стационарным.
При нахождении через f(t) можно воспользо-
ваться приведенным в гл. 1 уравнением связи между пре-
11—1086 161
образованием Лапласа для частоты отказов и средней
частоты отказов, т. е.
Ms)=f(s)/[l-f(s)]. (4.19)
В случае конечного времени восстановления
t
Фп (0 = — z) dGn (z),
о
где
G(t), n=l.
Gn(t) =
t
^Gn_t(t — z)dG(z),
.0
(4.20)
(4.21)
Из (4.20) с учетом (4.9) и (4.21) следует, что
(0 = Ф и (о = J fn (t — х) gn (х) dx, (4.22)
б
где
(0 = F'n = (X) dx- (4.23)
о
gn (0 = G' (0 = (t-x)g (x) dx. (4.24)
Используя теорему нахождения преобразования Лапласа
свёртки функций, получаем
Оо
Тп («) = j'Pn (0 е "8 * dt = fn (s) gn (s), (4.25)
0
где
co
fn (S) = f fn (0 e-^dt=fn^ (s) f (s)= [f (S)]«; (4.26)
0
co
gn (s) = Jg„ (0 e~st dt = gn^, (s) g (s) = [g (s)]n. (4.27)
6
Различные предельные выражения для процесса вос-
становления можно найти, используя теорему Смита, со-
162
гласно которой
lim JQ (t — x) dH (x) = -^-Jq (x) dx, (4.28)
о 0
где Q(x) —любая невозрастающая, интегрируемая функ-
ция на участке (0, оо).
Изложенные элементы теории позволяют найти функ-
цию готовности /Сг(/),—равную, по определению, 'вероят-
ности того, что в момент t система исправна.
Система будет исправна в момент 7/ при осуществле-
нии одного из следующих несовместимых событий:
1) за время t система не отказала;
2) за время система отказывала и восстанавлива-
лась ровно п раз (п=1, 2,...), причем последний ремонт
произошел на участке х, х+Дх (x^jt) и за оставшееся
время t—х система больше не отказывала.
Вероятность первого события равна
’ Р($) = 1-Р(0,
а второго — порядка
Ф',г (х) ДхР (£—х) =<рп (х) ДхР (t—х).
Устремим Дх к нулю и просуммируем по всем х от О
до t и по всем /г от 1 до оо. В итоге получаем, что веро-
ятность безотказной работы системы в момент t при на-
личии отказов и ремонтов равна
t СО t
^Р (t —х)£ <р„ (х) rfx=JP (t — x)h (х) dx,
О /г=1 О
ОО
где h (х) = У, <р„ (х) есть плотность процесса,
п=1
ного моментами
\=1Ж+п).
.1
Следовательно,
t
(f) = P(t) + \P(t—x)h(x)dx.
о
(4.29)
образован-
(4.30)
11
163
Стационарное значение функции готовности (коэффй*
циент готовности) можно найти с помощью теоремы
Смита.
Так как limP(Z)=O, а математическое ожидание Т
t -*00
случайной величины Xn + Yn (расстояние между сосед-
ними точками рассматриваемого случайного процесса)
при любых п равно
Т = У xdF (х) ф- \tydG (у) = Тср + тв,
о о
то по теореме Смита имеем
t оо
Ar = Iim ( Pty— х) h (х) dx = —f-—,--[р (t)dt==~^~—.
J 7 ГСр + Ч 1 ' 7 Тер + %
о о
(4.31)
Аналогично определяется вероятность 'P(t, т) того, что
система проработает безотказно на заданном участке (Л
f+т). Имеем
t
P(t, т) = Р(^ + т)+ — x)h(x)dx. (4.32)
о
• В стационарном случае
(т) = lim Р (t, т)
ОО
!----f Р (х) dx =
ОО
= к Г Р (х) dx -.
1 J
(4.33)
Рассмотрим очень важный для теории надежности
случай, когда
F (t) = 1 — е"\ f (0 = F’ (0 = Ze-M,
(4.34)
G (0 = 1 - е^7, g (0 = G’ (/) = ре-'*,
где р — интенсивность восстановления.
164
В данном случае
(4.35)
g («) = J p.e-1Vsft# =
Тогда, используя (4.13), (4.25) — (4.27), получаем
h(s)= j h (t) e-sttft — (s) =
0 п=Л
co
=S [<x+X + s)T=^TO-
Аналогично, из уравнения (4.30) следует:
Ar (s) = Р (s) + Р (s) h (s) = Р (s) [1 + h (s)J. (4.37)
Так как Р (/) = 1 — F (/) = е—w, то
Р (s) = [ Л е ~^dt = —Ц-,
Аг (S) = -L- Г1 + , Л , J =- / S,+/,........V (4.38)
г'/ s + X [ 1 s (s + X + р.) J s (s + X + р.) v ’
Отсюда
Аг (0 =4—U-?—еГ-(,'"х) г. (4.39)
1 4' л р р. 1 -Л + р. ' '
Положив в (4.33)
Р (t + т) = (Z+T) == е~^Р (t),
получаем, что вероятность безотказной работы на задан-
ном участке (/, t+т) равна
Р = Г ГТ------------ е ~(Х+Н ‘ I (4.40)
7 [Л + Л 4- j v 7
При t—>оо получаем стационарное значение этой ве-
роятности:
(4.41)
165
При решении большого класса задач удобно исходить
из вероятностей нахождения системы в том или ином со-
стоянии. В общем случае число таких состояний будет
больше двух, но при решении задач теории надежности
обычно приходится иметь дело с конечным или по мень-
шей мере со счетным числом состояний.
Пусть в момент t система находится в состоянии i.
Если вероятность Pij(t, т) .перехода системы за время г
из состояния i в состояние j не зависит от поведения си-
стемы до момента t, то такой случайный процесс назы-
вается марковским процессом. Если эта вероятность не
зависит также от момента t, то имеет место однородный
марковский процесс.
Для этого случая можно найти характеристики на-
дежности путем решения различный интегральных, диф-
ференциальных и интегро-дифференциальных уравнений.
Например, пусть по-прежнему требуется найти коэф-
фициент готовности Кг(/). Если система исправна, будем
говорить, что она находится в состоянии «О», если неис-
правна и восстанавливается — в состоянии «1». Обозна-
чим вероятности нахождения системы в момент t в этих
состояниях через До(0 и Pi(t) соответственно. Естест-
венно, что
АЛ) + А (0 = 1- (4-42)
При экспоненциальном законе распределения времени
безотказной работы Е(/) = 1—е~м и произвольном за-
коне распределения времени восстановления G(t) веро-
ятность Pi(t) можно представить в виде
t
Pt (t) = Х j‘ Ро (t — X) [1 — G (x)] dx. (4.43)
6
Подставляя (4.43) в (4.42), получаем
t
Ръ (?) + я J P„ (t ~ x) [1 — G(x)]dx=l
0
или
. (4.44)
°' ’ A-f-sfl—AG (s)] ' '
Так как /^o(^) =/Сг(^), то выражение (4.44) принципи-
ально позволяет вычислить /Сг(0 при любом законе рас-
пределения времени восстановления.
166
При произвольном законе распределения времени без-
отказной работы F(t) и экспоненциальном законе рас-
пределения времени восстановления G(fj = l—е—р/ ве-
роятность Ро (f) можно представить в виде
i
Ро (t) = 1 — F (t) + р. J Pt (t — х) [1 — F (x)] dx. (4.45)
о
Заменяя в (4.45) Px(t—x) на 1—PG(t—x) и переходя
к преобразованию Лапласа, получаем
р —(S + P-) [1 — sF (s)l
° ' ' sfs-j-p. — sp-F (s)l‘
(4.46)
Если в (4.44) и (4.46) подставить G(s) = l/s—l/(s +
-f-p,) и F(s) = l/s—l/(s+/l) соответственно, получим уже
известное выражение (4.38).
При экспоненциальном законе распределения и нали-
чии ряда исправных состояний наиболее распространен-
ный метод нахождения KT(f) состоит в составлении и ре-
шении дифференциальных уравнений. Методика их со-
ставления описана в разделе Б. Однако при неэкспонен-
циальном законе распределения сложность решения за-
дач резко возрастает. В этих случаях на практике в ос-
новном нашли применение методы, связанные с решением
интегральных и интегро-дифференциальных уравнений.
Вероятность Pm+1(t) безотказной работы восстанав-
ливаемой системы, состоящей из основного и т ненагру-
женных резервных устройств, может быть 'вычислена пу-
тем решения следующего уравнения:
t
Рт+1 (0 = (0 — J (t — X) dPm (х), (4.47)
О
где х) при т = 1, 2,... есть функция, удовлетво-
ряющая интегральному уравнению Вольтерра 2-то рода:
t
(0 = (t) — у G (х) <рт (I — х) d(pm_1 (х). (4.48)
О
Значение вероятности Pm+l(t), как видно из (4.47) и
(4-48), находится рекуррентно. При этом <{эд(/) =Pi(t) =
=p(t) —вероятность безотказной работы одного устрой-
ства; G(x) — функция распределения времени восстанов-
ления.
167
При выводе (4.48) предполагалось, что (время вос-
становления не зависит от того, сколько проработало
устройство.
При отсутствии восстановления
фт(0=фт-1(0= ••• =<Р0(О =А(0=^(0- (4.49)
В случае дублирования (т=1) и экспоненциального
закона распределения, г. е. при
Р, (t) G (0 == 1 —е“< (4.50)
функция ф1(г) удовлетворяет дифференциальному урав-
нению
ф"1+(2%+р)ф/1+1Хг<р1—0. (4.51)
Решая это уравнение при начальных условиях <рц (0) =
=фо(0)==1>ф'1(0)=<р'о(0) = —Z, получаем
W&x,t ~ <4-52)
Л*2 ”
где
„ _ (2Л + н) ±
-S.2 2
Подставляя (4.52) в (4.47), получаем
(0 = ^Xlt - А>с^- <4-53>
В общем случае решение уравнений (4.47) и (4.48)
возможно лишь приближенными методами с применени-
ем цифровых вычислительных машин-или путем пред-
ставления в виде бесконечного ряда.
В практически важном частном случае, когда т=1
(дублирование), а средняя наработка до первого отказа
(Тер) и время восстановления (тв) устройства удовлет-
воряют соотношению
Тв/ТСр<1, (4.54)
величину Р2(0 можно найти по приближенной формуле
Р2(0^е“^Г\ (4-55)
где
оо
а = -Ц1-С(0ИЛ(0. (4.56)
О
168
частности, при выполнении (4.50) и (4.54), полу-
чаем
а
f e~^e~vdt = ; 7\ ==
J jx + Л р. ’ 1 Л
о
т. е.
Р2 е-м/(н-+>)
(4.57)
В общем случае расчет надежности резервированных
восстанавливаемых систем при экспоненциальном законе
распределения времени безотказной работы и времени
восстановления рекомендуется проводить методами, из-
ложенными ниже в разделах Б и В.
Однако в различных случаях временной избыточности
составление интегро-дифференциальных и интегральных
уравнений даже при экспоненциальном законе распреде-
ления, как правило, является основным способом нахож-
дения количественных характеристик надежности.
При временной избыточности, когда допустимы пере-
рывы в функционировании на постоянное время т, веро-
ятность выполнения поставленной задачи P(t, т) можно
искать или в виде
P[t — х — y,t]dG(y), t>x, (4.59)
Р(/, ^) = 2/Ш T)Gft(-0, (4.58)
k-Л
или
P(t, t) = 1 — F(t — -t) +
V
0
где P^it, t)—вероятность того, что за время t будет
ровно k отказов, при условии, что длительность восста-
новления в каждом случае была меньше т; Г{х) —функ-
ция распределения времени безотказной работы; G(x) —
функция распределения времени восстановления.
При мгновенном восстановлении и экспоненциальном
законе распределения времени безотказной работы
F(x) = l- (4.60)
вероятность Pk (t, 0) подчиняется закону Пуассона
0)==^-е“\ (4.61)
169
Зависимостью (4.61) можно воспользоваться и при не
СО
мгновенном восстановлении, если t > т, t > тв = J [ 1 —
о
— G (х)| dx, а 1 /2 есть величина того же порядка, что
и t. Тогда
Pk (О т) « Рк (t, 0) = е“м- (4.62)
С учетом (4.62) из (4.58) получаем
СО
Р (t, т) e-w l^l11 = e-Wf,-G . (4.63)
k—0
В частности, если
G(T)=1— е”^, (4.64)
то
Р (/, т) « (4.65)
В случае выполнения и (4.60), и (4.64) точное значе-
ние вероятности Р(1, т) проще искать в виде
P(t, т) = Р0(Л т) +Pi(t, т),
где P0(t, т), Pi(t, т)—условные вероятности того, что
в момент t система соответственно функционирует или
находится на восстановлении при условии, что за время
t длительность каждого восстановления не превышала т.
Вероятности P0(t, т) и Pi(t, т) при находятся путем
решения численными методами системы интегро-диффе-
ренциальных уравнений:
Р'о(0 = -ярс(0 + рЛ(0>
2 (4.66)
Р, (0=2 Г Ро (/ — х) е-1ХЛ dx.
о
Аналогичная система уравнений может быть состав-
лена и при сочетании этого вида временной избыточно-
сти с аппаратурной.
Средняя наработка до первого отказа может быть
найдена из соотношения
7cpc=Jn*. i)dt =
О
= J 1 -dt + ^P(t, T)dt=i+^P(t, т).
От т
170
В частности, интегрируя от 0 до оо обе части системы
(4.66), получаем
В случае временной избыточности, связанной с нали-
чием излишка времени, расчетные соотношения зависят
от характера влияния отказа на результаты проделанной
работы.
Если после восстановления работу приходится начи-
нать сначала, то вероятность P(t, т) того, что задача,
требующая для своего выполнения непрерывной работы
изделия в течение т, будет решена за время />т, опреде-
ляется выражением
P(t, г) =
О, t < -С.
1— F(t) + J j P(t — х — у, dF (х) dG (у),
О о
(4.68)
f Xp(t-x-y, dF (х) dG (у),
о о
t 2т.
В практически важном частном случае, когда избы-
ток времени не очень велик (г^'/=С2т), значение P(t, т)
проще искать из выражения
P(t,
т) = [1-Е(т)]
оо
i + SOntf—O
/г—1
= [1-Е(т)] {1+Я(^-г)},
(4.69)
где Ф„(|/—т) определяется из выражения (4.20); —
—т) —функция восстановления.
Если отказ вызывает задержку в выполнении задачи,
равную длительности восстановления изделия, то задача
будет выполнена, как только суммарная полезная нара-
ботка достигнет заданной величины т. Обозначим эту на-
работку в произвольный момент времени t через St. Тог-
да вероятность P(t, т) того, что задание длительностью
171
т будет выполнено в течение времени вычисляется
из соотношения
P(t, T) = P(St>T) = l [Gn(^-T)-Gn+1(^-T)]Fn(T),
n=0
(4.70)
где Gn(t—r), Gn+i(t—т) и Fn(t) <при н^1 определяются
выражениями (4.9) и (4.21), a Go(t—т) =77о(т) 1.
При экспоненциальном законе распределения, когда
F, (х) = F (х) = 1 — е~1х , G, (х) = G (х) = 1 — е-^,
имеем
P(t, т)=1— е
[р- (< —т)Р~
(4-71)
р.т + |1(/—-и)]
/=0
При больших t величина St независимо от законов
распределения асимптотически нормальна со средним
Si=[TJ(TM--Ts)]t
и дисперсией
2 __ ^Tl^/Tl + 4/Tl)
(Л+,Л)3
(4.72)
(4.73)
где Tlt Oj — среднее время наработки до первого отказа
2
и его дисперсия; тв, а2 — среднее время восстановления
и его дисперсия.
Следовательно, при больших t
Pit, т)^-*- е (4.74)
У ZTzaQ 1
Б. МЕТОД, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ
ТЕОРИИ МАССОВОГО ОБСЛУЖИВАНИЯ
Метод состоит -в следующем:
1) составляются уравнения массового обслуживания;
2) выбираются начальные условия решения задачи;
3) определяются вероятности застать изделие в ис-
172
нравном состоянии в любой момент времени и вероятно-
сти безотказной работы;
4) определяются в случае необходимости другие 'ко-
личественные характеристики надежности по аналитиче-
ским зависимостям, приведенным в гл. 1.
Составление уравнений массового обслуживания
Перенумеруем возможные состояния изделия. В про-
стейшем случае таких состояний будет два: изделие ис-
правно («состояние «О») и изделие неисправно (состоя-
ние «1»). При m-цратном общем резервировании изделия
число возможных состояний равно т+2. Будем говорить,
что имеет место i-e состояние, если неисправны i изде-
лий (/ = 0, 1, 2,..., m+'l).
Для составления искомых уравнений должны быть
заданы: Z;-i, i— интенсивность перехода из (г—1)-го со-
стояния в i-e; рг-, i-i — интенсивность обратного перехода
из /’-го состояния в (i—1)-е.
Для краткости будем в дальнейшем писать
А—1, г=|Яг—Pi, г—1“Рг*
Пусть pi(t) — вероятность того, что в момент t имеет ме-
сто i-e состояние. Сравнивая эти состояния в моменты I
и по формуле полных вероятностей получаем
—У.. Ы —l-M — и. Л/
= а-ЛОП —е • ]+А(01е е 1 +
+ A-U0I1 - е ,1‘+’"]+0(ДО =
= A-i (О IV ,Д* + О (ДО] + А (0 [ 1 — (Я/ + !Ч-)Д/+0 (Д01+
+ а+х &ч+1Д* + о (ДО] + О (ДО-
Здесь через О (ДО обозначены величины второго по-
рядка малости по сравнению с Д/.
В пределе при At—>0 приходим к системе дифферен-
циальных уравнений:
A(0=-Vo(0+f4M0.
Р г (t) — (0 —* (Яг- -|- рг) Pi (0 -|- Рг+1А+1 (0
(t= 1, 2,... , 7П),
/Лп+1(0^ VaUO — P^Ab-UO-
(4.75)
173
Процесс изменения состояний рассматриваемой систе-
мы изделий можно 'проиллюстрировать с помощью гра-
фа, представленного на рис. 4.1. Узлам графа соответст-
вуют состояния системы (0, 1, 2,..., т + 1), а ветвям —
возможные переходы из одного состояния в другое.
Искомая система дифференциальных уравнений мо-
жет быть составлена с помощью графа совершенно меха-
нически. Для этого необходимо при всех
О] значениях i слева написать производную
от вероятности pi(t), а справа просумми-
Л ровать вероятности состояний, из кото-
0 1 рых возможен переход в t-e состояние,
предварительно умножив их соответствен-
’ но на интенсивности этих переходов, и
отнять вероятность pi(t), умноженную на
сумму интенсивностей переходов из i-ro
состояния во все другие.
* Приведенный на рис. 4.1 граф есть
• простой неветвящийся граф. Примером
простого ветвящегося графа состояний
Рис. 4.1. Граф переходов системы
при. m-кратном общем резервиро-
вании.
системы массового обслуживания может служить граф,
приведенный на рис. 4.2, где приняты обозначения:
Xij — интенсивность перехода из i-ro состояния в состоя-
ние j; — интенсивность обратного перехода из j-ro со-
стояния в состояние i.
Тогда система дифференциальных уравнений массо-
вого обслуживания будет иметь вид:
Р'о (0 = — А> (t) + (О,
Р\ (0 = ЧРо (0 — (^2 + ^3 + Рю) pt (0 + Р2, А(0 + Р31Рз(0>
(4.76)
Р 2 (О == ^IzPt (0 V“2iP2 (О’
р,з(0 = я18а(0 — Р31М0-
.174
Так как при любом t сумма вероятностей всех (Воз-
можных состояний системы равна единице, то сумма чле-
нов правых частей систем (4.75) и (4.76) должна рав-
няться нулю.
Система дифференциальных уравнений типа (4.75) и
(4.76) может использовать-
ся при определении следую-
щих показателей:
— вероятности безотказ-
ной работы (резервирован-
ных восстанавливаемых и не-
восстанавливаемых ремонти-
руемых систем;
— функции и коэффици-
ента готовности восстанав-
Рис. 4.2. Простой ветвящийся
граф переходов системы.
ливаемых резервированных
и 'нерезервированных систем
при различных способах об-
служив ания;
— вероятности нахождения в данный момент времени
на восстановлении k элементов;
— среднего времени пребывания системы в любом со-
стоянии.
Выбор начальных условий решения задачи
, Надежность восстанавливаемого изделия, как прави-
ло, определяется при условии, что >в момент включения
все элементы исправны. Тогда
Pi (0) —
( 1, х = 0,
(о,
(4.77)
В общем случае в момент / = 0 изделие может нахо-
диться в некотором состоянии j.
Тогда
А(0) =
1, i==j,
0, i =4= j.
(4.78)
175
Определение вероятности застать изделие в исправном
состоянии в любой момент времени
Вероятность застать изделие в исправном состоянии
в любой момент времени находится путем решения урав-
нений типа (4.75) и (4.76). Ограничимся рассмотрением
системы типа (4.75).
При заданных начальных условиях эта система имеет
единственное решение, причем для любого начального
состояния существуют пределы
lira Pi (0 = Рг = 0/ I S 0/, (4.79)
I «=о
где
I
00-1; 0т= П-чг2- <4-80)
/=1
- Искомая вероятность Кт (t) находится из выражения
Кг(П=Ел(0',
f~0
(4.81)
гдеп—последнее исправное состояние изделия (n=Cm).
При т=0 (резервирование отсутствует) решение си-
стемы (4.75) (приводит к уже известному выражению
(4.39), полученному ранее с помощью функции восста-
новления.
Часто число состояний, в которых изделие неисправ-
но, меньше, чем число состояний, в которых изделие ис-
правно. В этом случае удобно вначале находить вероят-
ность застать изделие в неисправном состоянии Кп(£) по
формуле
т+1
Ки(о= £ А-(0.
(4.82)
а затем — функцию готовности из выражения
Kr(t) = l— (4.83)
176
Если изделие считается отказавшим только при на-
хождении егов состоянии иг,+ 1, то
т
Кт (0 = S Pi (0 = 1 - pm+i (0- (4.84)
<=о
Коэффициент готовности находится из (4.81) как
установившееся значение Лг(/), т. е.
Лг = ПшЛг (/). (4.85)
>00
Определение вероятности безотказной работы
и средней наработки до первого отказа
Вероятность безотказной работы находится путем ре-
шения системы дифференциальных уравнений типа (4.75)
и (4.76) при заданных начальных условиях. При этом
в системах (4.75) и (4.76) исключаются в правой части
те члены, которые содержат интенсивности переходов
из отказовых состояний.
На практике иногда целесообразнее находить вероят-
ность отказа изделия, так как отказовых состояний обыч-
но меньше, чем исправных. Далее по известной вероятно-
сти отказов находят вероятность безотказной работы.
Ограничимся рассмотрением системы (4.75) при усло-
вии, что отказ наступает при выходе из строя всех т+'1
устройств. В этом случае в системе (4.75) необходимо
положить pm+i='O, а искомая вероятность безотказной
работы есть вероятность того, что рассматриваемый слу-
чайный процесс изменений состояний изделия за время
ни разу не окажется в поглощающем состоянии m+'l.
Обозначим решение этой новой системы уравнений через
3 tit). Тогда
т
Рс (0 = i (0 = 1 — S- т+, (0. (4.86)
1=0
Если в начальный момент времени система находится
в состоянии fe = O, то средняя наработка до первого от-
каза есть среднее время перехода из нулевого состояния
в состояние m+'l и определяется выражением
т / k \
Гсрс = 2 £0г/Ш • (4.87)
*=0 \/=0 )
12—1086
177
В ряде 'прикладных задач теорий надёжности йербят-
ность безотказной работы системы довольно точно опре-
деляется через Тсрс по приближенной формуле
Pc(t)^e~tlTcVe. (4.88)
В. МЕТОД, ОСНОВАННЫЙ НА ИСПОЛЬЗОВАНИИ
ТЕОРИИ ГРАФОВ
Не составляя и не решая дифференциальных или ин-
тегральных уравнений, можно получить количественные
характеристики надежности восстанавливаемых резерви-
рованных устройств.
Непосредственно по известному графу состояний за-
писываются выражения для установившегося значения
коэффициента готовности, а также выражения в преобра-
зованиях Лапласа для вероятности безотказной работы
и вероятности застать устройство в исправном состоянии
в любой момент времени.
Рассмотрим эту методику на частном примере.
Пусть дано некоторое устройство (элемент, узел,
блок, система и т. п.), для повышения надежности ко-
торого применено общее постоянное резервирование. Из-
вестны:
— интенсивности перехода устройства из i-ro состоя-
ния в состояния i—1 и /4-1;
— необходимое время работы устройства;
— кратность резервирования;
— число обслуживающих бригад.
Необходимо вычислить вероятность безотказной ра-
боты P(t) в течение времени / и вероятность Кг(/) того,
что резервированное устройство будет исправно в любой
момент времени 4
Решение. Сделаем следующие допущения:
— длительность безотказной работы и время восста-
новления отдельных элементов подчиняются экспоненци-
альному закону;
— при отказе одного из устройств оно сразу же от-
правляется на восстановление и ожидает очереди на об-
служивание, если все ремонтные бригады заняты, или
178
немедленно начинается процесс восстановления, если
очереди на обслуживание нет.
При указанных выше допущениях функционирование
резервированного устройства можно представить уже
известным графом, изображенным на рис. 4.1.
В дальнейшем для конкретности предположим, что
кратность резервирования т=2, все устройства равно-
Рис. 4.3. Граф переходов
системы при двухкратном
общем резервировании.
З-ot - Ло
надежны, каждое из них имеет интенсивность отказов Z,
а при отказе любого из устройств надежность исправ-
ных не меняется. Предположим, что резервированная си-
стема обслуживается одной бригадой, а интенсивность
восстановления равна pi. Тогда граф рис. 4.1 преобра-
зуется в граф, показанный на рис. 4.3.
Из нулевого состояния (все устройства исправны)
возможен переход в состояние 1, когда одно устройство
отказало и отправлено в ремонт, а два других исправны.
Интенсивность перехода будет 7ioi=lXo=3k Из состояния
1 возможен переход либо в состояние 0 с интенсивностью
восстановления ц10=р, либо в состояние 2 с интенсив-
ностью отказов Л.12=|Л.1=2Л. В состоянии 2 одно устройст-
во исправно, одно ремонтируется и одно ожидает ре-
монта.
Из состояния 2 вновь возможны два перехода: в со-
стояние 1 с интенсивностью восстановления pi2i=pi (так
как имеется только одна ремонтная бригада) и в состоя-
ние 3 с Интенсивностью перехода 7.2з=^2=^- В состоянии
12* 179
3 все устройства отказали, поэтому возможен переход
только в состояние 2 с интенсивностью восстановления
Р32= Р-
Если имеется несколько бригад обслуживания, то вид
графа не меняется, а изменяются лишь интенсивности пе-
рехода р,г. Так, например, если имеется две бригады об-
служивания, то pio=p, р.21 = рз1=2р. Если число бригад
k=3, то pio=p, |Ц21=2р, <pS2=3p. Вид графа также не из-
меняется, если имеет место резервирование замещением.
В этом случае Л,1о=Л21=^з1=Л, (в предположении, что ин-
тенсивности отказов резервных устройств до включения
в работу равны нулю).
Если отказ одного из устройств вызывает изменение
интенсивности отказов устройств, оставшихся исправны-
ми, то вид графа вновь не изменяется. В этом случае
7.01=37., Л12=2Л(1), 2.2.з=2.(2), где 2.— интенсивность отказов
любого из устройств, когда все
они исправны; 2Я— интенсив-
ность отказов каждого из исправ-
ных устройств при отказе любого
одного; 2Я—интенсивность от-
казов исправного устройства при
отказе двух любых устройств.
Рассмотрим, как деформиру-
ется приведенный на рис. 4.3 граф
в случае резервирования по схе-
ме группирования (с дробной
кратностью, когда т=1/2). Так
как отказ наступает, когда отка-
зывают любые два устройства, то
Ар/ - 5Л.
Рис. 4.4. Граф перехо-
дов системы при общем
резервировании с крат-
ностью т=1/г-
при одной бригаде обслуживания
2щ=32., 2.i2 = 2/., 2^23=0, |iio=-
=H2i=p, Цз2=0. Очевидно, что
в этом случае граф будет иметь
вид, показанный на рис. 4.4. Не-
зависимо от вида графа ясно, что для нахождения коли-
чественных характеристик надежности перечисленных в
нашем примере случаев достаточно было бы получить фор-
мулы для вычисления вероятностей состояний устройст-
ва в зависимости of интенсивностей переходов Хц и fiji.
Получим расчетные формулы для коэффициента го-
товности, вероятности застать систему в исправном со-
стоянии в любой момент времени и вероятности безот-
казной работы системы.
180
Составим систему дифференциальных уравнений, опи-
сывающих поведение такого устройства:
= hlPo (0 - (*,2 + Рю) Pl Ю + Р21Р2 (0>
(4.89)
^ = \2А(0-(^з + ^>)а(0 + ^а(0>
^=W2(0-^a(0-
Начальные условия: ро(0) = 1; /?1(0) =/?2(0) =/?з(0) =0.
Решая эту систему уравнений с помощью преобразо-
вания Лапласа, приходим к следующей системе линейных
алгебраических уравнений:
(S + *о>) Ро («) — РюР, (s) = 1,
*О1Ро (s) 4" (s 4" *12 4" Рю) Pl (®) Р21Рг (®) 0, gg.
— *laPi (s) 4“ (s Ч~ *23 4" Pai) Ps (s) — P32P3 (s) = 0,
— *a SPs[(s) 4- (« 4- P32) Ps (s) = °>
где pi(s)—.преобразования Лапласа вероятности pi(t).
Правило Крамера дает нам решение такой системы
в виде Рг (х)'= Д//Д, S 4“ ^01 Р*1О — Aoi S + Xia+Pno ' —^21 (4.91)
Д 0 —Л12 S + ^23 +р*21 ^23 0 0 Х2д S 4“ №32 ’ (4.92)
где А — главный определитель системы; А, — частный
определитель, который находится из (4.92) заменой /-го
столбца коэффициентами, стоящими в правых частях
уравнений (4.90).
Раскрывая Д по степеням s, получаем
Д — s [s5 Ч~ (*oi 4" *12 4" *23 4". Рю 4" Pai 4" Рза) s2 4“
4" (*01Р21 4“ *01*23 4“ *O1PS2 Ч" *01*18’4" Р10Р21 Ч"
4" Pio*2s 4" РюРза 4“ *12*23 4“ *1аРза Ч" PaiPsa) ® Ч*
Ч- PitPaiPja 4" *<iPsiP«s 4" *oi*iaPis 4“ *01*12*2»] (4.93)
181
Анализируя вид коэффициентов в определителе Л,
можно заметить, что они построены следующим образом.
Свободный член равен 0. Это является необходимым
условием существования стационарных решений для
Pi (s), так как
(оо) — lim spi (s) = const.
Коэффициент при s4 равен 1. Коэффициент при s3 пред-
ставляет собой сумму всех 'интенсивностей переходов пра-
фа рис. 4.3. Коэффициент при s2 есть сумма попарных
произведений интенсивностей переходов, за исключением
произведений вида и iXv, i+igi, j-i. Наконец, коэффи-
циент при s есть сумма произведений интенсивностей пе-
реходов, взятых по три, за исключением тех, в которых
встречаются те же произведения 'кгЩц и Хг, г-i, т. е.
остаются только произведения интенсивностей переходов
из каждой крайней точки графа состояний в данную
(ЩЩЩЗ —в точку 0, 7.(||Л2|1й — в точку 1, %oWs—в точку 2,
Ws — в точку 3).
В нашем случае имеется только одно отказовое со-
стояние— состояние 3. Поэтому вероятность р3 есть ве-
роятность простоя Кп, причем
где
s 4* ^01
^01
о
о
Кп(5) =Ps(s) =Д3/А,
-Р-1 0
8 + Ma4-Pio — Pai
•—’^12 8—рЛ23 + р-21
0 -- А-23
о
— Рза
8 4- Р-32
’ (4.94)
Из выражения для Аз видно, что этот определитель пред-
ставляет собой произведение интенсивностей переходов
из всех возможных исправных состояний в неисправное
состояние 3.
Таким образом, для нашей задачи вероятность пре-
бывания резервированной системы в состоянии 3 или ве-
роятность простоя в преобразовании Лапласа будет
иметь вид
(s) = + Л + ^2 + ^3 4" Pl + Рг + Рз) S2 +
+ (Я4Р24*ЯЛ 4“ Лр-s + 4- p-iPa 4~ рЛ 4"
4* Р1Р» 4* я2яа 4- ЯдРз 4" РаРз)s 4- (PiPaPs 4-.МЛ 4“
4- *Лр» 4- Яичр»)!} -1-
(4.95)
182
Если известно Kn(s), то вероятность застать систему
в исправном -состоянии находится из выражений
. Кг(4) = 1—Кп(0, /Cr(s) = l/s—Kn(s) =
= 1/х^А3/А. (4.96)
Установленное нами правило для системы, граф со-
стояний которой соответствует рис. 4.3, оказывается спра-
ведливым для системы с произвольным числом состоя-
ний, граф которой изображен на -рис. 4.1, т. е.
A = Asft + As't-1+... + As, (4.97)
где
k—2 k—2
Ai = I? Аг — X ^г.г'+i X P-z’+i.zl
i=0 i~0
Ai (i=3, 4, ...,&)—сумма произведений интенсивностей
переходов, взятых по I—1, за исключением тех членов,
в которых содержатся произведения вида i+i, pj+i, г и
i4-lj Pi, г—1 (i = 0, 1, 2, . . ., k 2),
k—1
Afc
i=0
Доказать сформулированное выше правило легко мето-
дом математической индукции.
Граф состояний резервированной восстанавливаемой
системы может иметь более сложный вид, чем показан-
ный на рис. 4.1. Сложные ветвящиеся графы получаются
при раздельном резервировании, учете двух характеров
отказов, отсутствии контроля моментов отказов отдель-
ных устройств резервированной системы, резервировании
неравнонадежных устройств и т. п.
В этих случаях может быть несколько отказовых со-
стояний. Тогда вероятность того, что резервированная
система будет неисправна в любой момент времени I,
равна
N
Кп(О = Ха(0, (4-98)
i—i
где pi(t) —вероятность того, что система в момент вре-
мени t находится в i-м отказовом состоянии; У— число
отказовых состояний.
183
Очевидно, что преобразование Лапласа для Pi(i) на-
ходится из выражения
р,(«)=Д{(в)/Д(5), (4.99)
где Д(«) = s'jAoS/l“1+As'1~2+ ... +A7i_i] — главный опреде-
литель системы; A, (s) =Bos’1+BiS’1~1+ ... +Вп — частный
определитель; п — число, зависящее от уровня отказового
состояния; k — число состояний системы.
Нами установлено, что независимо от вида графа ре-
зервированной восстанавливаемой системы коэффициен-
ты Аг определителя A(s) находятся по указанному выше
правилу.
Оказывается, что число п и коэффициенты Вг частно-
го определителя Aj(s) легко находятся, непосредственно
из графа и выражений для коэффициентов А при соот-
ветствующих степенях s определителя А. Степень поли-
нома числителя определяется из выражения
n=k—1—I,
где k — число состояний устройства, равное числу узлов
графа; I — номер уровня i-ro отказового состояния, чис-
ленно равный количеству неисправных устройств резер-
вированной системы, находящейся в отказовом состоя-
нии i.
Коэффициент В, определителя Ai(s) находится непо-
средственно из коэффициента At при той же степени s
определителя A(s). Оказывается, что Вг содержит те
члены коэффициента Аг, в которых имеются произведе-
ния всех интенсивностей переходов из состояния 0 (все
элементы исправны) в отказовое состояние i по кратчай-
шему пути, т. е. без восстановления.
Описанная методика .позволяет особенно легко найти
установившееся значение функции готовности — коэффи-
циент готовности. Так как
Кп — lim sKu (s), Кг = lim sKT (s), KT = 1 — Ka, (4.100)
s->0 s->0
то очевидно, что
.. + ...+ ВЯ Bn
A>sft-‘ + Asft-2 + ..-+A-I A-
KT = 1 - Ka = (Ak_t -
184
Для нашего примера
. ^оА12^23
П “^h-l ^01^12^23 + ХoiK12ps2 ~Р K01p-2ip32 + Р40Р12Р32
По известной функции готовности легко также найти
вероятность безотказной работы. Очевидно, что в графе
состояний теперь будут отсутствовать переходы из отка-
зовых состояний всего устройства в исправные. Тогда для
отыскания преобразования Лапласа вероятности отказа
достаточно в выражении для 7Cn(s) вычеркнуть члены,
которые содержат интенсивности переходов из отказо-
вых состояний системы в исправные во всех коэффици-
ентах Ai и Вг. В нашем примере необходимо вычеркнуть
члены, в которых содержится коэффициент ц32- Тогда из
выражения для Kn(s) получим
Q (s) = 202j22 {s [s3 (Яо + 4~ ^2 4“ Hi 4~ H2) s2 4“
4" (pVo 4“ Уг 4“ Vi 4" H1H2 4- 4“ s 4- УА} 1
p ____ 1 q /„\__ s2 + (Ko T Ki -p X2 -p pi -p Рг) s -p
s —s’-MKo + M+Ks+Pi+P^) s2 +
T KqXi T- X(l7.a -p Х1Л2 T- Л0р2 -p Pipa ~P PiKg
T (KoK-i + X0X2 -p KxZ.2 -p XoP-2 + P'lKa T P1P2) s T KoKj X2
Зная P(s), легко найти среднюю наработку до первого
отказа. Так как
Р (s) = ( Р (f) е stdt,
о
(4.101)
то
P(Q}^P(t)dt=:Tcv,
S
(4.102)
т. е. для определения средней наработки до первого от-
каза достаточно найти преобразование Лапласа P(s) и
затем, подставляя в него s = 0, записать выражение для
средней наработки до первого отказа.
Для нашего примера из выражения для P(s) имеем
Т ____ -|- Х0Л2 -р Л,Л2 + КоР*2 -р Р-1К-2 -р РчРг
СР'~"
185
Описанный метод расчета надежности резервирован-
ных восстанавливаемых устройств позволяет найти рас-
четные соотношения непосредственно из графа состояний
системы, не составляя и не решая уравнений массового
обслуживания. Его недостаток ib том, что для определе-
ния Kr(t) и P(t) необходимо находить обратные преоб-
разования Лапласа от функций Kr(s) и P(s), представ-
ляющих собой дробно-рациональные функции.
§ 4.2. ТИПОВЫЕ ПРИМЕРЫ
Пример 4.1. Резервирование осуществлено по методу
замещения с ненагруженным резервом. Время работы до
отказа работающего канала описывается экспоненциаль-
ным законом с параметром Z, а микромодульный усили-
тель заменяется после отказа всех т каналов. Предпола-
гается, что переключающие устройства идеальны в смыс-
ле надежности. Требуется найти за время t среднее чис-
ло замен микромодульного усилителя, состоящего из
основного и т—1 резервных каналов.
Решение. Так как число замен за время t равно
количеству отказов, то, по определению, среднее число
замен есть функция восстановления H{t). Воспользуем-
ся выражением (4.12):
H(s) =F(s)/[l—sF(s)],
где F(s) —есть преобразование Лапласа закона распре-
деления суммы т независимых случайных величин с за-
коном распределения 1—е каждая.
Преобразование Лапласа от плотности распределения
этой суммы определяется соотношениями (4.26) и (4.35)
и равно
f (s) =Р7(*+'МГ.
Z
Так как F (?) = (х) dx, то
о
F(s) = Xf(s)
Следовательно,
Н {s) = A^/s [(s + F)m — Л'1].
186
Отсюда Н (I) равняется сумме вычетов функции
Zmesi/s [(s + ^),n — '-,п] по полюсам s = 0 и s = sfe =
= 2(eh — 1), /? —О, — 1, где e = e2"‘/m, I—}/—1.
Так как s0 = 0, то полюс s = 0 есть полюс второго по-
рядка. Следовательно, Н (s) можно представить в виде
-•п— 1
//(s)==Zm/s2 [! (s —sfe).
Й=1
По правилам перехода от
имеем
V k=\
изображения к оригиналу
т—1
+У mIrSJ-
'=1 S2
k=i
т~1
Заметим, что (s 4- ^)7П— /Lw = s (s—sft). Следовательно,
/г-1
m—1
П (s — Sr) I s=o = lim + =
Л=1
Аналогично,
.. (s + X)m — Xm — sm(s + X)m-’ m— 1
i^+x^-x^F — 2Wx«-
Так как
S—Sj
П (s—s»)
fe=l
__ 1
~~ m—1
di Ibs-s*)
S~Sj k= 1
187
л S—
a s0 = и, то -- m—j------- можно представить в виде
S2 П (s ~ Sr)
S=SJ
1 1
S m—l
k=O s=s3
1
A[(s + X)m_Am]
m).m ei — 1
Подставляя полученные значения в выражение для
Н (t), получаем
m—1
H(0==_L Л_'2ЦД_|_у;^ЦеМ(е/-!) .
v' т -2 1 /Д е3 — 1
/=1
Среднее число замен в единицу времени равно
f т—1
h (/) = Н’ (/) = А- < 1 + £ Siew (г'~1) .
' /=1
Пример 4.2. По условиям предыдущего примера най-
ти среднее число замен усилителя за время /ив единицу
времени при т=1 и экспоненциальном законе распреде-
ления длительности замены усилителя с параметром
р, = 0,5 {/час. Интенсивность отказов работающего кана-
ла равна 0,01 1/час, t=50 час.
Решение. По определению (см. формулу 4.6), сред-
нее число замен есть
/7(0 = 1 Ф«(0>
п=1
где согласно (4.7), (4.9), (4.20) и (4.21)
Ф„(0= \Fn(t-Z)dGn(2)-
6
(0 = IJ pn . __ z} dpn (2)j n 2;
G(0, n=l,
t
J if — 2) dGn (2), /z > 2.
0
188
При решении предыдущего примера было показано,
что функция распределения безотказной работы дубли-
рованного усилителя F(t) подчиняется закону Эрланга:
t
F (f) = j f (t)dt=\ — e—w (1 + M)-
о
Tак как Fn (s) = Fn _, (s) sF (s) ~sn~1Fn (s), имеем
Fn (s) — sn 1 s s + x (s -|- /.)2 j s (s лр» •
Аналогично, если G (/) — 1 — e то Gn (s) = pn/s (s -|- p)'n.
По теореме нахождения преобразования Лапласа
свертки функций получаем
Ф„ (s) = Fn (s) sGn (s) = . , S'? ,
n V / n \ I n\ / S (s + X)2n (s + р*)и
00
Так как //(0 = X T0
1 A2p
5 z _ Z [ K2P I
(s + 2)2 (s + p) 1 - (s + A)2 (s + p) J
____________________7.2P_______________
s2 [s2 (22 4- p.) .S' A2 -|- 2Xp]
По формулам перехода от изображения функции к ее
оригиналу находим
Н (f\ — — lJ-<2Z + ^ I Ре~(2Х+>х) V2
U А+2ц (X + 2p42 । 2 (X + 2р.)2 j/> — 4Ap. A
x {[2я2 4- p.a + (22 4- p.) Xp.2 —W]
— [2Я2 4- p.3 — (22 4- p.) V p2 —42p] e~ ti2y
Отсюда
ip. Xu.e~ (2Х+^ z/2
h (t) = H' (0 = ---------F -- -,;z X
' 2+2p 2 (2 + 2p) Kp2 — 4Xp
X {[22 4- p 4- j/'X^/p] t/2 __
. — [22 4- p — Xp2—42;4 c~ #/2|
189
Подставляй исходные Данные из условия задачи, По-
лучаем: Н (50 час) — 0,156 замен, ft (50 час) —
« 0,0033 замен/адс.
Пример 4.3. Длительность безотказной работы каж-
дого устройства и суммарная длительность восстановле-
ния обоих устройств подчиняются экспоненциальному
закону с параметрами Лиц соответственно. Необходи-
мо определить функцию готовности дублированной си-
стемы с ненагруженным резервом, восстанавливаемой
после отказа основного и резервного устройства.
Решение. Воспользуемся выражением (4.37), свя-
зывающим Kr(s) cft(s):
7Cr(s) =/?(s)'(l+ft(s)].
Как было показано в гл. 3, вероятность безотказной ра-
боты дублированной системы с ненагруженным резервом
равна
/2(0 = e-w(l +Z0-
Следовательно,
p(s) = 1/(s+Л) +Л/ (s+Л)2.
При нахождении ft(s) воспользуемся результатами при-
мера 4.2. Было показано, что
Н (s) =Л2ц/52|7>2+ (2Л+ц)£+Л2+2Лц].
Так как ft(7) =Н'(t), а /7(0) =0, то
ft (s) = sH (s) —H (0) = Л2ц/$[«2+ (2Л + p )s + Л2+2Лц].
Подставляя найденные значения p^s) и h(s) в выраже-
ние для Кт($), получаем
Kr (S) — • I -1 4-1 -L1V2-Ь
г ' ’ s + \ 1 (s + X)2 1
I_________________Х2ц___________.
s (s + Л) [s2 ~р (2Х + ц) s + X2 + 2Хц] '
I_______________Х5ц______________
Т" s (s + X)2 [s2 + (2Х + ц) s + X2 + 2Хц] '
Отсюда
к , . _ 2р. Ху (я, 4- 2Х) sj_____
'г'‘' Х+2р' Sj (s, + X)2 (s, — ss)
______Х2Ц (^2 ~Ь 2Х)_^sat
S2 (s2 + X)2 (Sj — s2)
где sn s — [— (2Я + p>) Kp2 — W]/2>
190
Пример 4.4. По условиям предыдущего примера найти
вероятность безотказной работы на участке (/, ?+т).
Определить стационарное значение этой вероятности.
Решение. Воспользуемся выражением (4.32).
Имеем
t
р (/, t —т) --- р (t —т) —р (Л-|- т — л?) h (x) dx.
о
Здесь p(i+t) —вероятность безотказной работы дублиро-
ванной системы с ненагруженным резервом в течение
времени £+т, т. е.
^(^ + т) = е-и^)[1+2(^ + т)Ь
Плотность восстановления h(x) для данного случая
была определена в примере 4.2 и имела вид
h ix\___ fy- I pSif______
—А + 2р.-Г S1(S1_S2) L s2(s,-s2) е ’
где
„ ____[— (2Л + ц) ± Ир.г — ]
*1,2 '
2
Подставляя найденные значения p(t+r), р(4+'т—х) и
h(x) в исходное выражение, после интегрирования и
алгебраических преобразований получаем
Г S] + 2к
111 ^2IJ>
Ит е — •——тяг— X
J (s, s2) (s2 -р Z.)
Стационарное значение искомой вероятности имеет вид
Аггац (х) — Р (t, /Д-т) = е =—ц-=-(2Ят).
t-^oo Л ~Г ZIJ'
Значение /2стац(т;) можно найти, не зная вероятности
P(t, /-Н) из выражения (4.34):
Pew СО = Кг f р (x)'dx,
—г ср J
т
191
где в рассматриваемом случае
т _________ 2 iz .__. Уер 2/Л 2р
с₽ ~ X ’ Лт ~ +Р + Ч ~~ 27Г+1Л1—Х+2р.*
Следовательно,
со
Л,„(х) = ^4 Je^(l +М&= ^"^(2 + 2,).
"Е
Пример 4.5. Основным ненадежным элементом непре-
рывно работающей следящей системы является усили-
тель. Восстановление устройства заключается в простой
замене усилителя из числа имеющихся т запасных.
Время работы до отказа и время замены усилителя рас-
пределены по экспоненциальному закону с параметрами
лир соответственно. Требуется найти вероятность за-
стать систему в момент i в исправном состоянии. Иссле-
довать поведение этой вероятности при р—>оо.
Решение. Решение поставленной задачи связано
с рассмотрением случайного процесса x(t) состояний си-
стемы с конечным временем восстановления. Пусть t{ и
t'i есть соответственно моменты i-го отказа и i-ro восста-
новления, причем по условию после наступления т+1
отказа (вышли из строя основной и все резервные уси-
лители) система не восстанавливается. Система будет
исправна в момент t в тех случаях, когда момент t нахо-
дится на интервале (t'i, fi+j), где i~0, 1, ..., m, a t'Q=0.
Следовательно, искомую 'вероятность можно получить
в виде
т
Кг (0 = S {* (0 &f'i, +
i~0
т *t
1=1 о
где Фг(х)—функция распределения случайной величи-
ны t'i, определяемая с помощью рекуррентного соотно-
шения (4.20), т. е.
t
Ф? (х) = J Fi (t — х) dGi (л).
о
192
Законы Fi(x) и G/(x) определяются через Исходные
законы F{ (х) — 1 — е~и и G (х) — 1 — е~р'х с помощью
выражений (4.9) и (4.21). Используя преобразование Лап-
ласа, получаем
Фг- (s) = Fi (s) sGt- (s);
m
f=l
m
1=1
_L_?L_ V si- 1 Г X 1i si 1 !'______i * =
‘ s + X 2Ы | 4 X) | j « (« + ,IJ‘' j
i=l
_____1 I VI (Xp-P
s + X“r2j (s + Mi+1 (s + F)4’
i=l
Переходя от изображения к оригиналу, находим
e-M +
т £+1
г--о k=i
где
д __ 1 d*-’ г 1 | . J-1)'1 ’ДХг .
(й-i)! rfs*-i[ {s + F)i р=_г ’
_____1 cl'^1 Г 1
(k—1)! dsfe-1 [ (s-pX)i + 1
(-IV-’CU-I
(F-— X)i+fe ‘
При p—>oo (мгновенная замена) остаются только т?
члены первой двойной суммы, которые соответствуют Л-~
= 1. При этом в пределе имеем
т
1=0
13—1086
193
что совпадает с выражением для вероятности безотказ-
ной работы при m-кратном ненагруженном резерве. .
Пример 4.6. Система состоит из основного и резерв-
ного усилителей. Восстановление отказавшего усилителя
сводится к простой его замене на запасной. Длитель-
ность восстановления постоянна и равна т. Требуется
определить вероятность безотказной работы системы
в случае ненагруженного резерва.
Решение. Принципиально решение может быть най-
дено с помощью выражений (4.47) и (4.48), где G(x) = l
при х^т и G (х) = 0 при х>т.
Однако при этом возникают большие трудности, свя-
занные с отысканием <pi(0- Значительно проще задача
решается с помощью изложенных методов составления
дифференциальных уравнений массового обслужива-
ния.
Действительно, для того чтобы в момент t+At систе-
ма была исправна, необходимо выполнение одного из
следующих несовместимых событий:
1) в течение времени I система была исправна и
в промежутке t, t+At отказов не было;
2) в течение времени t—т система была исправна,
в промежутке времени от t—т до t отказов не было,
а в промежутке t, t+At работающий усилитель отказал.
Если обозначить искомую вероятность через p(t), то
с точностью до бесконечно малых о (At) второго порядка
малости по сравнению с At вероятность первого события
есть p(t)(l—KAt), а вероятность второго события равна
2.Ate~ир (t — т).
Следовательно,
р (t 4- AZ) = р (0 (1 — ЛДО + (t — т) 4- о (ДО-
При At—>-0 приходим к следующему дифференциально-
разностному уравнению:
р'[(0 = - хр (0 4- ^Р (t - т).
Будем искать решение в виде
p(t)=e*u(t).
Подстановка этого выражения в искомое дифферен-
циальное уравнение дает
и'(t) =Au(t—т).
194
Так как при восстановление невозможно, то
p(t) определяется по известной формуле для дублиро-
ванной системы с ненагруженным резервом:
р (t) = е~*г (1 — It),
т. е. при ()++++ u(t) = 1+77. Следовательно, при
т<С^<2т
u(t—т)='1+1Х(/—т), u'(t) =Л[1 +2.(/—т)].
Интегрируя последнее уравнение по I от т до t, получа-
ем, что при т^/^2т
t
и (0 = м (т) + Z j [1 + 2 (х — т)] dx—
2
= 1 JJ.КУ-^У=JI U[^ — 1)
*=о
Методом полной индукции можно доказать, что при лю-
бом п>0 на отрезке (п—имеет место равен-
ство
u(o-y{X[f-g—
я.
k=Q
Таким образом,
/г=0
Пример 4.7. Каждый комплект оборудования имеет
интенсивность отказов ,7.=0,02 1/час, интенсивность вос-
становления ц=1 1/час, систему обслуживает одна бри-
гада, а в начальный момент времени все комплекты
исправны. Для обеспечения непрерывности работы ре-
зерв должен быть нагруженным. Необходимо, чтобы си-
стема управления и контроля имела высокую надеж-
ность для .всего периода своей работы. Сколько резерв-
ных комплектов оборудования т потребуется для дости-
жения вероятности безотказной работы системы pm+t (/)
^0,98 в течение /=360 час?
Решение. Рассматриваемая задача сводится к изу-
чению однородного марковского процесса с т+2 состоя-
ниями. Обозначим через Pk(t) вероятность того, что
в момент t неисправно k комплектов оборудования (си-
13* 195
Стема находится в состоянии k). Состояние т+'1 являет-
ся поглощающим. Для решения поставленной задачи
воспользуемся системой дифференциальных уравнений
(4.75):
Р'ь (О — (4 + М Рк (0 + . А+> (0.
k — 0, 1,..., т -J- 1,
где
Яй (tn -|- 1 — k) Я, k = 0, 1,... , т Д- 1;
Р-л = Р-= 1/т=тз. k=\, 2,..., nt',
Я_ ] = Р-о -=“ Pm+i ==
Так как система исправна, если работает хотя бы
один комплект, то
Р (t, т) = S Рк (0 — 1 — Рт+1 (0-
fe=o
Рассмотрим последовательно случаи m = 0, 1, 2, ...
При т = 0 (резервирование отсутствует)
A(0 = e~w,
р1 (360) = е-°’02 3* = е"7'2 0,0007466,
т. е. при отсутствии резервирования надежность системы
не удовлетворяет заданным требованиям.
При воспользуемся методикой, изложенной
в разделе В, и графом, приведенным на рис. 4.1. Было
показано, что преобразование Лапласа от вероятности
Pm+i имеет вид
п /,Л ___ ($) _____ ^т+1 ($)
Pm + i V) - - д (S) — зД0 (S) ’
где Ao(s) = Д1 + AiS*-2 + ... + Ah-t, hm+t(s) = sn +
+BiSn_1+...k — число состояний системы; п =
=k—1—/; I — количество неисправных устройств систе-
мы, находящейся в отказовом состоянии т+1.
В нашем случае k=m+2, l=m + 1; п = т+2—1—(т +
+1) = 0. Следовательно,
Ao(s) =sm+1+^is’"'-|- ... +Дто+1, A,n+i(s)=Bo-
Пользуясь изложенными правилами нахождения
коэффициентов А и В через интенсивности переходов,
получаем, что
Bo=An+i= (tn+ 1)7 • тЯ ... Я= (т+1) !7m+1.
196
Таким образом, преобразование Лапласа Для вероят-
ности безотказной работы равно
Р (*) = (s) = J-
_ Ч- ... + Ат
s™+' + Ats™ + + Ат+1 •
Можно показать, что в случае нагруженного резерва
уравнение До(«)=О имеет т + 1 различных действитель-
ных (отрицательных) корней s1; s2, ..., sm+i, т. е. A0(s) =
= (s—Si) (s—s2) ... (s—sm+1). Отсюда
m+1 f
p(t)= ,
f=I
где Ci= (s Sj)p(s) | £=«*-
Так как Лто+1=«1, «2, • sm+i (из теории алгебраиче-
ских уравнений), а
\+АС + - + Ап =
__ ['5Г^~1 + ^lsT + ••• + ^mS4] _ _Лт+1
Si Si ’
получаем
m + 1 "
С*=П •
J=i
Таким образом, задача определения p(t) свелась
к нахождению корней уравнения Ao(s)=O. Пусть т=\.
Тогда
Aq.(s) = s2+Л15+Л2 = 0.
Согласно доказанному в § 4.1 правилу есть сумма
всех интенсивностей переходов, т. е.
= 2/.+Л.+р,=ЗЛ.+(i, Л2==2Х • X—2Z,2.
Следовательно,
— (ЗХ + р.) + СХ2 + 6Ху. + у.2
Подставляя заданные значения X и ц, получаем
0,000755, s2«—1,059245, р2(360) ^1,000713 е-®-2718»
~ 0,7626, что также меньше требуемой величины
0,98.
197
Пусть m = 2. Тогда
Ao(s) — 53 + Л152+Л2х+-43 = О.
Согласно доказанным правилам имеем:
Л1=ЗХ+2Х-|-Х-Нц+1ц=2 (ЗХ+!ц),
Аг —ЗХ • 2Х+ЗХ • Л+2Х • X+ЗХр +Хр + ц2=
= 1 1Х2+4Хц4-1ц2,
Л3=ЗХ-2Х-Х=6Х3.
После подстановки численных значении X и ц находим:
Si-—0,00004820, 52^—0,86185268,
s3~—1,25809912, .
Р,(360) ~ (g е36°*~ °’9829’
что больше заданного значения 0,98.
Следовательно, необходимая кратность резервирова-
ния т — 2.
Пример 4.8. Имеется непрерывно работающая двух-
канальная линия передачи информации. Восстановление
отказавшего канала требует выключения всей линии.
Доля информации, теряемой в единицу времени при про-
стое г каналов (г=1, 2), равна hr. Время безотказной
Рис. 4.5. Графы состояний линии
передачи информации (к примеру
4.8).
работы и время восста-
новления капала имеют
экспоненциальное распре-
деление с параметрами X
и ц соответственно. Тре-
буется найти, при каком
количестве отказавших г
каналов остановка линии
на восстановление будет
обеспечивать минимум
потерь информации?
При остановке линии
после отказов обоих ка-
налов рассмотреть слу-
чаи:
а) каналы .восстанав-
ливаются поочередно;
б) одновременно мо-
гут восстанавливаться
два канала.
198
Решение. Составим граф состояний линии. Если
г— 1, то линия может находиться только в двух состоя-
ниях: «О» — оба канала работают; «1» — оба канала про-
стаивают, но восстановления требует только один. Сле-
довательно, искомый граф будет иметь вид, приведенный
на рис. 4.5,а.
При г=2 линия может находиться в трех состояниях:
«О» —оба канала работают; «1» — один канал работает,
второй простаивает; «2» —линия простаивает до оконча-
ния восстановления обоих каналов.
Граф состояний линии представлен на рис. 4.5,6.
Обозначим среднее время пребывания линии в z-м со-
стоянии через 7\r (z=0, 1, 2). Тогда средняя продолжи-
тельность цикла работы до возвращения в исходное со-
Г
стояние равна У} Тг>г, г = 1, 2.
1=0
Величины Т?-,г легко находятся с помощью приведен-
ных графов. Действительно, так как из каждого состоя-
ния возможен переход только в одно последующее, то
за исключением Гад значение Tit т есть просто величина,
обратная интенсивности перехода из z’-ro состояния, т. е.
Величина Т2,2 зависит от числа персонала, производяще-
го восстановление. Если отказавшие каналы восстанав-
ливаются поочередно, то в среднем длительность восста-
новления каждого канала по условию равна 1/ц, т. е.
(X • (X {X
Если отказавшие каналы восстанавливаются одновре-
менно, то интенсивность ремонта равна 2ц, пока не-
исправны оба канала, и ц — с момента завершения ре-
монта одного из каналов.
Следовательно,
Т — 1 4- 1 — 3
Js'2 2р. р. 2р."
Найдем величину потерь информации Нпот за один
чикл работы. Так как при нахождении линии в i-м со-
199
стоянии (i=l, ..., г) в единицу времени теряется hitT
единиц информации, то
Hnoi = ЛдЛщ при г— 1,
Киот = А,2^1,2 + 2^2,2 При Г = 2,
где из условия задачи следует, что /?1,1=/г2,2=/г2, Л1,2=/ц.
Рассмотрим неравенство
^0,2 + ?1,2 + ^2.2 7о.1+71,1
В левой части неравенства стоит ожидаемая средняя
величина потерь информации в единицу времени при
г=2, в правой — то же самое при r= 1.. Подставляя сюда
значения Ti<r и решая относительно >Х/р, получаем
Л 1
ц h2/h1 — 2 ’
если каналы восстанавливаются поочередно, и
ц З/га/2/jj — 2 ’
если одновременно могут восстанавливаться оба канала.
При соблюдении указанных неравенств остановка ли-
нии на восстановление после отказа одного из каналов
обеспечивает минимум потерь информации.
Пример 4.9. Имеется непрерывно работающая систе-
ма, которая производит автоматическую обработку по-
ступающей информации и-запись результатов. Контроль
и профилактика системы осуществляются через опреде-
ленные промежутки времени Т, после каждого возвра-
щения системы в исходное состояние. Длительность про-
филактики исправной системы равна То, неисправной Ть
Во время профилактики и от момента отказа до начала
профилактики информация теряется.
Необходимо определить оптимальный период контро-
ля Гопт, при котором теряется минимум информации,
если интенсивность отказов системы X постоянна.
Вычислить Топт при 1/Х=50 час, то=1 час.
Решение. Ищем вначале коэффициент готовности
Кг в виде отношения М[Л]/М[У], где М[Х] — математиче-
ское ожидание времени работы системы за период меж-
ду двумя последовательными моментами профилактиче-
ского обслуживания, а М[У] — математическое ожидание
200
длительности интервала между двумя последовательны-
ми моментами профилактического обслуживания.
По определению, математическое ожидание
т т
М ]Х]= j xf (х) dx -ф- Ге” w = Л J хс~>хdx-\-T
о о
Так как интервал между двумя последовательными
моментами профилактического обслуживания состоит из
периода Г и случайной длительности профилактики, то
М [У] - Г + Че~хг + т. (1 ~
Отсюда
к • _
г М[К] + ’
-^-=0 = ^ [Г + тое -фтД!—е )] —
- (1 - е;/) [ 1 - Ятое“*г + Че~Х7’].
Величина Гопт находится путем решения (графически
или численными методами) уравнения
e-*rUr + 4 + l)=l-
При Г=0,02 \1час и т0=1 час имеем ГОПТ~9,7 час.
Пример 4.10. Восстанавливаемая система состоит из
п основных и одного нагруженного резервного приборов.
При переходе на резерв допускается перерыв в работе
на постоянное время тдоп одного из основных приборов.
При отказе резервного и одного из основных приборов
система считается отказавшей независимо от длительно-
сти пребывания в этом состоянии.
Найти среднюю наработку до первого отказа Гср,.
при экспоненциальном законе распределения времени
безотказной работы прибора, времени восстановления
и длительности перехода на резерв с параметрами X, ц
и у соответственно. Рассмотреть случай /1 = 2, Х=
201
—0,1 1/чос, р,= 1 Х/час, у=10 Х/час, тДОп=5 мин й
сравнить со случаем мгновенного перехода на резерв.
Решение. Составляем систему интегро-дифферен-
циальных уравнений типа (4.66). В момент t система
считается исправной, если она находится в одном из
следующих состояний: «0»—.исправны все приборы;
«1» — неисправен один из основных приборов; резервный
еще не подключен, а с момента отказа прибора прошло
время меньше г; «2» — неисправен прибор, находящийся
в резерве.
Обозначим условную вероятность нахождения систе-
мы в i-м состоянии (i=0, 1, 2), при условии безотказной
работы .в течение времени /, через
Сочетая методы составления уравнений массового
обслуживания типа (4.75) и интегральных уравнений
типа (4.43), (4.45) при />т, получаем:
p'o(t) =— («+ 1)'%ГМ(/) +рра(О,
р, (/) = гй. J р9 (/ — х) х dx,
о
Р’г (0 = *Ро (0 + YA (0 — («я + Р-) А (0-
Искомую величину Тсрс согласно (1.10) можно искать
в виде
Т’ср С = J [А (0 + Р> (0 + А (01 dt = т. + Л + Г2.
о
Интегрируя обе части системы уравнений от 0 до оо
(при /<?т необходимо в написанном уравнении для /ц(/)
заменить т на /), находим
-1=-(« + 1)Л7в + Р7’а,
о=-йгрг I1 - е"("Ж) ’ Л,
Решая полученную алгебраическую систему по прави-
лу Крамера, получаем
Ус— (Ао+1Д'1+'Л2)/А,
202
где
д=_ Г-4Т-+« («+1)^+4?-e-(nX+7>' 1 ;
[ лХ + т ’ ' 1 ’ 1 nX + тГ J
д0= — (р- -Н
Д, = - [1 - е—<пХ+т) Ч (р + /U);
Д2 = - {2 + ^[1 - е-('л+7>1: ]}.
При заданных значениях н, "к, р, у и тдоп имеем:
До= —1,2 1/час; Д)^—0,01346 1/чпс;
Д2=—0,2122 1/час; Д^—0,1477 1/час; ТсРс~9,6 час.
При мгновенном переходе на резерв (у—>-оо) имеем:
До=—(ц+пХ); Д1=0; Д2=—(/i + l)X; Д=—п(п+1)Х2.
Следовательно,
Т
J ср с
р. + (2/г + 1) X
п (л + 1) X2
25 час.
Пример 4.11. Цифровая вычислительная машина
имеет экспоненциальное распределение времени работы
без сбоев с параметром Х=0,06 1/час. Найти вероятность
p(t, т) того, что задача длительностью т=10 час будет
решена за время £=15 час, если при сбое машины реше-
ние приходится начинать сначала. Длительностью устра-
нения сбоя можно пренебречь.
Решение. Из выражения (4.69) находим
p(t, t) = e-b(l+//(/-<
Так как восстановление мгновенное, то для нахождения
H(t—т) можно воспользоваться выражением (4.12):
H(s) =F(s)/[\- sF(s)l
где в нашем случае F(s) =X/s(s + X). Отсюда H(s)^=
Следовательно,
p (£,т) = е-ь [1 -|- я {t — x)J, p (15,10) = e~’-e-1,3 0,713.
203
§ 4.3. ЗАДАЧИ
4.1. Имеется дублированная система с ненагруженным резервом.
Каждая из подсистем состоит из двух последовательно соединенных
приборов с постоянными интенсивностями отказов Xi=l-10-2 1/час
и Л2=3-10“2 1/час, Система восстанавливается после отказа обеих
подсистем. Длительностью восстановления можно пренебречь. Тре-
буется вычислить среднее число отказов за время /=100 час. По-
строить график зависимости среднего числа отказов в единицу време-
ни от времени работы.
Ответ:
И (100)= + 4- е 2М3^2,75 отказов,
где X = Xj -|— Ху. ,
Зависимость /г(0 = '4(1 — е 2)7) от времени работы приведена
на рпс. 4.6.
4.2. По условиям задачи 4.1 найти среднее число восстановлений
за время t при экспоненциальном законе распределения суммарной
Рис. 4.6. Зависимость h от X/ Рис 4.7. Зависимость h от t
(к задаче 4.1). (к задаче 4.2).
длительности восстановления обеих подсистем с параметром ц=
= 1 \/час. Построить график зависимости среднего числа восстанов-
лений в единицу времени от времени работы.
Ответ: /7(100) «1,70 восстановлений. Зависимость h(i) от
времени работы приведена на рис. 4.7.
4.3. По условиям задачи 4.1 определить среднее число восстанов-
лений за время /ив единицу времени при экспоненциальном законе
распределения длительности восстановления каждой подсистемы
с параметром ц=1 \/час, если подсистемы восстанавливаются пооче-
редно.
204
138-2--,
О т в е т: (
н (л __ _ У1*7____(Х L2?X_;___________(X + н) />
10 ~ 2 (А + р) 4(Л-|-р)2 Г2(М-Р)г
Х2р2 Г es‘Z eSa< 1
(s, s2) s, (Sj + X p) s| (s2 + X + p) J ’
где
s1t2 = [— (X+ p) + КХ^=6Хр + p2 ~]/2;
X = Xt +X2 = 4-10~2 1/час;
H (100) 1,65 восстановлений;
h (100) 0,0192 восстановлений/час;
h (t) = 3^ [1 — e~ (7' + p,) z] + ———X
' ' 2 (X + p) 1 J Sj — s2
x Г es‘f__________________e^ 1 .
L Si (Si + X + p) s2 (s2 Ц- X -f- p) J
4.4. По условиям задачи 4.1 рассмотреть случай двух резервных
подсистем. Построить зависимость среднего числа отказов в единицу
времени от времени работы.
Ответ:
Н (!) = ^(Х, + Х2) t— 1 + е—3 Z/2 X
к/ Г (А, 4- Аг) t V3 1 (X, + Уз 11
X [ cos-------sin-----------------------------] f >
_J1 + А2 I 3(X1 + X2)f/2 Г (Х1 +М1У3__________________________
— 0 11 — с I соэ 2 *
+ УЗ sin
(X, + Х2)/Кз
2
I
I'
При /=100 час, Л1=10-2 1/час и Аг=3- 10-2 1/час, от-
каз, h(t) ~ 0,0133 отказ/час.
Зависимость h(t) от времени приведена на рис. 4.8.
Рис. 4.8. Зависимость h от t
(к задаче 4.4).
205
4.5. Найти среднее число восстановлений за врсмй /ив еди-
ницу времени при скользящем резервировании двух основных
устройств двумя ненагруженными резервными. Интенсивности от-
казов основных устройств постоянны и равны Х=у2,5 • 10-2 \/час,
/=40 час, а восстановление начинается после отказа/трех устройств.
Длительностью восстановления можно пренебречь.
Ответ:
Н (0 = [2Х/ — 1 + е“31/ (cos Х//3~+ sin Х//Г)],
Н (400) =5:0,34 восстановлений,
h (/) = [1 — e-3W (cos И УЗ~ + J/Tsin X/ КЗИ,
Л (500) «0,0154 восстановлений/час.
4.6. Вычислить функцию готовности и коэффициент готовности
при скользящем резервировании п однотипных усилителей одним
ненагруженным резервным, если восстановление проводится после
отказа двух усилителей. Суммарная длительность восстановления
подчиняется экспоненциальному закону с параметром ц. Интенсив-
ность отказов каждого усилителя постоянна и равна Х=0,0005 \ j4ac,
ц=40Х=0,2 1/час, /=30 час, п=10.
Ответ:
8 ( 1 пХ/ \
Kr(0=-g-+(-9-+^-)e-3'iW.
• ^(30) =5:0,8956, Kr = 8/9.
4.7. По условиям задачи 4.6 найти функцию готовности и коэф-
фициент готовности при экспоненциальном законе распределения
длительности ремонта каждого усилителя с параметром ц, если уси-
лители ремонтируются поочередно. Рассмотреть случай произвольных
значений X, р, t и п.
Ответ:
к м _ + „-(ЛД+И) t ,
Лг W — «X + р. 2р. (пХ + р.)
. п2Х2р.а (s, + пХ)_______ Sit _
"«1 (si + /г^)2 (si + пХ + Р-) (s> — s2) е
__________игХгр-г (s2 + nX)_______
S2 (s2 + nX)a (s2 + rik p.) (Sj — s2)
где
— (nX + p.) + Vn2X2 — 6nXp. + p.2 .
«1,2 — 2 ’
Ar = P'/(«X + p.).
4.8. По условиям задачи 4.7 вычислить функцию готовности в мо-
мент /=1О час для трех случаев:
1) пХ=0,475 1/час; ц=1 1/час;
2) пХ=|л=0,157 1/час;
206
к
\
3) пХ = р^З — 2^2)^0,157 i/чМ.
Ответ: '
1) Kr (t)=^ 0,9991;
2) Kt (t) — -у- [1 + е~пУл cos nM], Kt (10) = 0,5;
2 + К2 ЗК2 —4 -2(2+V2)nlt
3) Kt W = ~------+-----4----e
nkt ] e- <2+ ’
Kr (10) 0,74.
4.9. Найти среднее число восстановлений изделия за время t
и в единицу времени при экспоненциальном законе распределения
времени безотказной работы с параметром X и постоянной длитель-
ности восстановления т.
Ответ:
H0-S t>(^r
k—\
k=l /=0
где п — целое положительное число, удовлетворяющее неравенству
nrC/^fn+l)?.
4.10. По условиям задачи 4.9 рассмотреть случай, когда время
безотказной работы подчиняется закону Эрланга вида
Ответ;
f (0 =
h (0 = е~г <'“/гг)
Й=1
X2ft —
(2Й-1)!
п
J]
£=i
е-
2k—1
Х< (t — kzy
И
где п — целое положительное число, удовлетворяющее неравенству
«</<(«+1)т.
4.11. По условиям задачи 4.3 найти вероятность безотказной
работы системы на участке (t, /+т) при т=5 час. Вычислить ста-
ционарное значение этой вероятности.
207
Ответ:
/-L-Д
| X + м.
*___I
2 (X 4- I1) J
е—(X + |л) /_]_
।______________________________________Г gi + 2?- . I я,/ _
r (s> (s, - S2) (S, + X) (S1 4- X + н [ S1 + X + Хт | е
-------------------*___________________Г ^+2Х , I I ,
•S'2 (S’! — s2) (s-2 + A) (s2 + А Н') l 52 + A J |
Iх ( Ат \
Ретин (’) = Х + р,' ( 1 + ~Т] 6 ’
где
s1>2 = [— (X + Р1) + Дх2 * * — 6Хр 4“ р-2]/2-
4.12. Время работы до отказа подчиняется закону Вейбулла
г / ч *А ______|/2 —х
с плотностью распределения / (х) = ~2~% 1 е , а длительность
восстановления описывается логарифмически-нормальным законом с
плотностью распределения
g (*) = " i/V-
х V 2л с
е-(1п ахП2о^
где Х=0,1 \1час, с=0,4, а~0,5 час. Требуется определить стацио-
нарное значение вероятности безотказной работы системы Рстац(х)
при т=0,25 час.
О т в е т:
I 2 , ех2'2 Д’2 (1 4- ХЮ)
Рстац (т) = А2 + д J е
Рстац (0,25) Sfe0,988.
4.13. Найти функцию готовности изделия, длительность ремонта
которого постоянна и равна т, а длительность безотказной работы
подчиняется экспоненциальному закону с параметром X.
Ответ:
t < t,
Кт (0 =
1=0
где г=1[//т] — целая часть отношения t/x-
4.14. Непрерывно работающая система допускает перерывы
в функционировании на постоянное время т, необходимое для под-
включения резерва. Во время срабатывания переключающий автомат
208
\
может отказать\с вероятностью 1—а. Найти вероятность безотказной
работы системы \при а=1 и среднюю наработку до первого ее отка-
за при т-кратпом пенагруженном резерве и экспоненциальном зако-
не распределения', длительности безотказной работы отдельной под-
системы.
С т в е т:
Ре (0 =
1, t -С (m + 1) т,
т
у, е-> , /в (,„+ 1к.
1—0
Л® С -
4.15. По условиям предыдущей задачи найти Pc(t) и ТСр с при
однократном нагруженном резерве и а=^=1.
Ответ:
е -W-П + а е —>(#—2х)| !+/ (/ _ 2т) - -, />2т;
(1 + и).
4.16. По условиям предыдущей задачи определить Гсрс при
Ш-кратном нагруженном резерве. Контроль за состоянием резерва
отсутствует, поэтому при замене может быть подвключена неисправ-
ная подсистема, что приводит к отказу системы в целом.
Ответ:
(1 \ Р^Лхе-11 а=е~ЗЪ ат е-т(т +1)^/2 |.
гсрс==^-у-+1Д1 + -2т+—3j F--+ (И + i)j j'
4.17. По условиям задачи 4.14 найти Герс при двукратном на-
груженном резерве при условии, что система контроля позволяет
подключать из резерва только исправнные подсистемы.
Ответ:
14—1086
209-
-Д15
4.18. Для повышения надежности прибора используется второй
резервный прибор, работающий в нагруженном режиме. Длитель-
ность безотказной работы и время восстановления прибора подчи-
няются экспоненциальному закону с параметрам^/ Аир соответст-
венно. При каких значениях Аир для фиксированного t будет обес-
печена требуемая вероятность безотказной работы 0,98?
Ответ: А/ « 0,01 р/А.
4.19. По условиям задачи 4.18 найти связь между Аир при
ненагруженном состоянии резервного прибора.
Ответ: М « 0,02 р/А.
4.20. Для повышения надежности п однотипных следящих систем
используется резервный усилитель, который может быть мгновенно
подключен вместо любого отказавшего основного усилителя, пока
тот не будет заменен из числа имеющихся г запасных. Построить
граф изменений состояний системы в целом, если время работы до
отказа и время замены усилителя распределены по экспоненциально-
му закону с параметрами Аир соответственно.
Ответ: См. рис. 4.9.
На рисунке символы п, i, j означают, что имеется п основных,
i резервных (;--0,1) и j запасных (/=0, 1, .... г) усилителей.
4.21. Применительно к условиям задачи 4.20 найти вероятность
застать систему в момент t в исправном состоянии, если г=2.
Ответ:
1 2
Д. (0 = X X Pn.t.1 (0>
1=0 1=0
где
Рпад(0 = е-<п-,>";
р m Х е~(й+‘> v— Х е“(гЛ+|х) *'
е р —А е
210
„ /л ' Г (П + !) ХрЛ —+ 0 Xp 1 („q-П It
р, —X (p — X)*Je
(n-J-l)Xp -QA+IX) t.
(p-X)2 e
(n + 1)2X2^ 2(« + 1)2XV
(p_X)2 (p-X)3
e — (n+I)M _|_
(n + l)2X2p< 2 (n + l)2X2p
(p-X)2 + (p-X)3
e—(nX+|x) i't
Г («+1 )2X2p2/2 2 (n + l)2X2p2/ 3 (n + l)2X2p2 I
A»,i,o (0 — 2» (p„x)2 (и.—X)3 + (p—X)4 J
v P-(«+D W_ r(n + l)W* 3 (n + l)2X2p21 („х+и) t.
x L (p--*)3 (p-*)4 J
i г Х2р-2/2
Pn.o.o (0 = (n + O’ L 2! (p.__X)2
, Xp.2 (tx - 3X) f p.2 (p.2- 4X}X + 6Л2) ] („+1)x t ,
+ (P-X)3 + (P-X)4 J
Г хзр.г
L (p-X)3
X3 (4р. — X) I („1+}1> Д
(p-x)4 Je f
4.22. Применительно к условиям задачи 4.20 найти среднюю на-
работку до первого отказа системы и сравнить со случаем неогра-
ниченного числа запасных усилителей.
Ответ:
Т 1 /14- пХ + ,Л Г1 ( * -У + 1Р
уер«-„х |*+(п + 1)х L1-v^+pJ Jf
при г -» со
т -|- 1) X 4- р.
'еро— П(и+1)Х2
4.23. Длительность безотказной работы каждого из устройств
подчиняется экспоненциальному закону с параметром X, а длитель-
ность восстановления отказавшего устройства постоянна и равна т.
Найти вероятность безотказной работы системы, состоящей из основ-
ного и резервного устройства в нагруженном режиме.
И* 211
I
Этвет: у
/е=0
п—1 х
+ e~yt j e y (t~k^-x) [X (t — kt — x)]hdx =
k=Q 0
e-2M S|2eb? (t^b)1*+
k—O
n—1
+ e-'* 2л+*[ал+2 (2W - 2kU) — p^2 (2M - 2Kki — 2?.t)],
k=O
1
где /,2h+2 (й) = yi<+i/a!
a
yKe~~t,l:2,dy — интегральная функция хи-квад-
o
рат распределения с 2k + 2 степенями свободы; п — целое число,
удовлетворяющее неравенству (п—1) 1 <m.
4.24. По условиям задачи 4.23 и примера 4.6 сравнить вероят-
ность безотказной работы невосстанавливаемой и восстанавливаемой
системы для случая Х=0,1 1/час, т=1 час, 1=2 час.
Ответ:
Резерв нагруженный: Рв (2) —0,96714 — без восстановления,
Рс (2) =0,97481 —при восстановлении.
Резерв ненагруженный: Рв (2) =0,98247—без восстановления,
Рс (2) =0,98657 — при восстановлении.
4.25. Имеется вычислительная машина, состоящая из п блоков
с интенсивностями отказов z.i, 7.2, ..., 7.и и интенсивностями восста-
новления ръ р,2, -. 1U- Найти коэффициент готовности, если во
время восстановления одного из блоков остальные находятся в на-
груженном режиме и также могут отказать. Количество персонала
неограниченно.
Ответ:
к.-П(т^
i~ 1
4.26. Определить коэффициент готовности непрерывно работаю-
щей радиолокационной станции, если после каждого второго отказа
проводятся капитальные ремонты с интенсивностью ц2. Интенсив-
ность отказов после капитального ремонта равна 7ч, а после просто-
го 7.2 (7.2>7ч). Интенсивность восстановления простого ремонта рав-
на ju (p.i>p,2). Ji
Ответ: 54
к__________1+Х,Да «
А' - 1 + Л>/Х2 + Xj/h
212
4.27. По условиям предыдущей задачи определить, при каких
соотношениях Хь Х2, Pi и р,2 предпочтительнее проведение капиталь-
ного ремонта после каждого отказа.
Ответ: При условии, что (Xi/X2) (pi/p2) <1.
4.28. Радиопередатчик радиолокационной станции может или
понизить свою мощность до 50% от номинальной (с интенсивностью
отказов Xi), или отказать полностью (с интенсивностью отказов Х2_).
В первом случае потребуется на его профилактику в среднем 1/jii
часов, во втором — на ремонт 1 /р2 часов.
В каких случаях следует проводить профилактику, если при ра-
боте радиопередатчика на номинальную мощность вероятность обна-
ружения цели есть /:0, а при работе на пониженной мощности она
равна Л1?
Ответ: Профилактику следует проводить, если Р, > Р2, где
Р1Р2 ,
Р, = —-——-—р ,---------Пп — есть вероятность оонаружения цели в
« Р-2 (^2^0 Ч-
случае проведения профилактики: P2= XJ7+Х^2 + Х2 -есТЬ
вероятность обнаружения цели при отсутствии профилактики.
4.29. По условиям задачи 4.48 сравнить Pi и Рг, если:
a) Xj=0,05 1/час, Х2=0,01 1/час, Ц1=2 1/час, j(2=l 1/час, h0=
= 0,99, /i! = 0,70;
б) Хг=Л2=Х, M.1 = }i2=g.
Ответ:
а) А = 0,957, Р2=0,75, t. е. Pi>P-t,
б) Pi>Pz, если ц/(ц+2Х) >Л1/Ло-
4.30. Имеется система, конструктивно выполненная в виде двух
приборов: счетно-решающей части и устройства ввода — вывода. Для
повышения надежности применено раздельное дублирование, при-
чем каждая группа приборов восстанавливается своей ремонтной
бригадой. Как распределить отношение Х/р между приборами, чтобы
коэффициент готовности системы Кг был не менее, чем Ко?
Ответ:
X, 1 — Ко + — Kg
Pi 2К0
Х2 < I + 2Х,/р, - Ко (1 - 2Х,/р, + 2х2/р2) +
1X2 " 2Ко (1 + 2Х,/н +
^/~ 1 ф- 2Х1/р.1 -|- 2Х^ /р2
+ 2Х| /р.2)
4.31. Информационная система допускает непрерывный контроль
по сигнальным лампочкам без отключения системы для проверки.
Система контроля может дать ложный сигнал с интенсивностью от-
213
казов Ль тогда как интенсивность отказов самой системы есть Л2.
Найти коэффициент готовности системы, если интенсивности восста-
новлений ложных и действительных отказов есть соответственно щ
и |12.
Ответ:
__________1_________
1 + А|/р-| + Л2/р2
4.32. По условиям предыдущей задачи определить область до-
пустимых значений отношений Ai/pi и Лг/рг. при которых коэффи-
циент готовности Кт не меньше заданного Ко-
Ответ:
Pl Ра Ко
4.33. Вычислить коэффициент готовности и среднюю наработку
до первого отказа дублированной системы, допускающей непрерыв-
ный контроль, если резерв нагруженный, а в остальном сохраняются
условия задачи 4.31. При нахождении коэффициента готовности рас-
смотреть случаи двух и одной восстанавливающих бригад, причем
в последнем случае обслуживание идет в порядке наступления от-
каза.
Ответ:
„ (Ai А2 4- Р-i) (А, 4- А2 4- р2) + 2Л, (Л, 4- А2 4- р2)4-
Фр с —
2 (X) Л2) [Л2 (^i 4- А2 4~ Pi) +
4- 2А? (Л, 4- Л2 4 ~ р-3
4- Aj (А] 4- А2 4- Ps) J
При одной восстанавливающей бригаде
1 + 2А,/р, + 2А2/р-9
2А,
Р-i
2А2
Р-2
2Л? 2Л,
+—2-+-О-4-2АЛ
Р1 Рг
При двух восстанавливающих бригадах
„____________________1 4~ 2Л,/рч 4- 2А2/р2_________
г 1 4- 2^/Рч 4- 2А2/|а2 4- (Ai/p-i 4- Аг/р-г)2
4.34. По условиям задачи 4.33 рассмотреть случай ненагружен-
ного состояния резерва.
Ответ:
~ (Ai 4~ А2 4~ Pi) (Ai 4~ А2 4~ р2) 4- А, (А, 4- А2 4- Ра) 4~
(А] 4*.Аг): [А] (Aj'-ф А2 + р2) 4-
* 4~~ А2 (А, 4~ А2 4~ Pi)
4"^а (А| 4-4- Р»)]
214
При Одной восстанавливающей бригаде
1 I ^-2 + Р-г)
^1Р1 ~Ь Х2Рг 4~ PiPa
X, (?Ч Ч~ Ха Ч~ Pi) (X] 4~ Х2 Ч~ Ре) .
Pi (Mpi + Х2р2 + Р1Рг)
Х2 (X] ~Ь Х2 4~ Pi)
Xipi 4* Х2р2 + Р1Р2
. Х2 (Х-i 4 Х2 4~ Pi) (^-1 Ра)
Ра (X] Pi 4~ Х2р2 4 Р1Р2)
При двух восстанавливающих бригадах
1 4~ X, /p i 4~ Х2/р2
^'г 1 4- X, /р-i 4~ Х2/р2 + 2 (Xi/2pI4-X2/2p2)2
4.35. По условиям задачи 4.33 найти область допустимых зна-
чений отношений Xi/gi и Х2/Р2, при которых коэффициент готовности
Кг не меньше заданного Ко-
От в е т: При одной ремонтной бригаде
Xj/p, < (а 4- Vа2 4- 2а)/2,
^а ) Г X] 7 р2 . Pi \ 1
Ра 2 Pi Pi Ра J J
При двух ремонтных бригадах
(Xj /p, 4~ Х2/р2) <= а 4~ V я2 4- а,
1
где « = -р— — 1.
*\©
4.36. По условиям задачи 4.34 найти область допустимых значе-
ний отношений Xi/gi и X2/p2. при которых коэффициент готовности
Кг не меньше заданного Ко, если имеются две ремонтные бригады.
Ответ:
'.М , Х2 ,-----------------
-^+^<а+^а2+2а>
где а=(1/Ко)—I.
4.37. Аппаратура встроенного контроля радиолокационной стан-
ции (РЛС) сигнализирует об отказе только в 100у% случаев. Не-
выявленные отказы устраняются после выхода из строя контроли-
руемых элементов или средств контроля и после полной проверки
станции специальной аппаратурой, при этом РЛС и средства кон-
троля восстанавливаются поочередно. Требуется составить граф воз-
можных состояний РЛС и систему дифференциальных уравнений,
215
позволяющих найти функцию готовности РЛС при экспоненциальных
законах распределения времени работы до отказа и времени восста-
новления РЛС и контрольного устройства с параметрами X, Х(|, ц
и у,, соответственно. Длительность ложной проверки исправной стан-
ции описывается экспоненциальным законом с параметром Т).
Ответ: Система дифференциальных уравнений имеет вид:
Р'ч(1) =— (Х|Х/,)у(,(ф4-цу1(() + г|р.Д/9,
Р'1 (0 =уЛро (0 —HPi (0 + уХр2 (/) + Т]рв (0,
p'z(t)=(i—y)hp(l(T)^('\’k+'kh)p2(t),
p,3(t) = 'kkpo(t)—llkps (/),
p',,(t) ='Р1,рз(()~^( t),
Ps(t) = \hP2(t)--\^p5(t),
P'e(t) =ili,Pb(t)—l]pe(t).
Граф состояний РЛС приведен на рис. 4.10
Рис. 4.10. Граф состояний РЛС (к задаче 4.37).
4.38. Имеется одноканальная стабилизирующая система лета-
тельного аппарата, позволяющая компенсировать параметрические
отказы канала с помощью блока самонастройки. Найти вероятности
возможных состояний системы, если поток параметрических отказов,
поток внезапных отказов канала и блока самонастройки и поток
автоматических восстановлений канала являются простейшими с па-
раметрами Хь Ха, Х3 и у соответственно.
Ответ:
« __. —— р— Да + Хз) t ।____^2 р (X, -г Ха + Хз ф р) (
„ (/\ .--—— р — (X,+ Хз) t------^2— р— (X, + Ха + Х3 + р) t
Pl V) - X, _|_.р.е Х,ф-уе - ’
Ла (Хо —I- Хч —Н Р4)
Рг (/) = (ХГ+х3) (Xt + Х2 ф х3 4-р)
--------------1__________р - (Ха + Хз) t
(Х2 ф- Х3) (X, ф- у)
________________^3_____________ р — (Ха 4- Ха ф Хз -I- |х) t
(X, ф- у) (X, ф- Х2 ф- Х3 ф- у.)
... _ Х,Х3 (Х2 -|- Х3 ф- у) /______
Рз ' (^2 + X,) (X, ф- Х2 ф- Х3 ф- у)
216
A,X3 [X] (A2 4~ А») - p- (M H A2 -|~ A3 Д t1) 1 I
* (X2 + X3)2 (A, + A2 + A3 + P-)a
А, Аз(p — A2 — A3) - (13 + X3) t I
^(A2 + A3)2(A,+|x)
, ^'Хз + A2 + Аз + P) _ (X, + x 4- X, + |X) t
(Ai + A2 + A3 -|- p.) (X, +p)
...________A2 (X2 —|— Aa —|— p)________
Рь (A2 + A3) (X, + X2 + A3 4- p)
----------__________e - (Ъ + M t _
(A2 -|- A3) (X, -|- p)
_ ____________„ - (’. + >2 + >3 + Ю t
(Xj + X2 Ц- X3 + p) (X! + p)
где pv(t) — вероятность того, что в момент / система исправна;
pi(t)— вероятность того, что в момент t имеет место параметриче-
ский отказ; р%(t) — вероятность того, что в момент t отказал блок
самонастройки; ps(t) — вероятность того, что в момент t имеет ме-
сто параметрический отказ и отказ блока самонастройки; pt(t) —
вероятность того, что в момент t система отказала.
4.39. По условиям задачи 4.38 найти вероятность застать систему
в момент t в исправном состоянии, если мгновенное значение пара-
метра потока параметрических отказов после каждого восстановле-
ния
Ai (/) — Хо //(1 + W).
Рассмотреть случай: Хо = 24,91 1/час’, Л2 = 0,01 \/час; Хз=
=0,005 \pLac; pi=100 1/час; 7=10 час.
Ответ:
р _ е-(Д + Ь) t (__________________ь (sa + P) (^г + 2Хс) t_
( X2 + 2Xop ' s2(s2-s3)
__(s3 4~ p) (Л'з 4~ 2X0) ^st ।
s3 (s2 Ss) j
где _________
- (2A„ + p) ± Vp2 + 4X0p
s2,3 — 2
Pe (10) ^0,765.
4.40. Электроэнергетическая система питания состоит из пяти
одновременно работающих турбогенераторов. При отказе любого из
турбогенераторов начинается его восстановление с постоянной ин-
тенсивностью ц. Длительность безотказной работы турбогенератора
подчиняется экспоненциальному закону с параметром X. Необходи-
мо найти вероятность безотказной работы системы и среднюю нара-
ботку до первого отказа, если один из турбогенераторов является
резервным,
217
Ответ:
Ро (0 = у—*- у- [х2еХ1' — х,еХа<],
— (9Х + р) ± Кх24~ 18Хр4~Р2
Xita — 9
_ __ -Xi 4~ х2 9Х 4~ Р
2<* х,х2 ~ 20Х2 ‘
4.41, Для повышения надежности системы используется резерв-
ный прибор, работающий до отказа основного в облегченном режи-
ме. Имеется устройство контроля и переключения, отказ которого
приводит к одной из следующих ситуаций:
— производится ложное переключение (с постоянной интенсив-
ностью т]); если при этом резервное устройство уже восстанавлива-
ется или проверяется, то происходит отказ системы;
— выдается ложный сигнал о неисправности резервного прибора
(с постоянной интенсивностью g);
— не будет подключен резерв при действительном или ложном
отказе основного прибора (с постоянной вероятностью 1—а).
Найти вероятность безотказной работы системы и среднюю на-
работку до первого отказа, если интенсивность отказов прибора
в основном и резервном режимах постоянна и равна Xi и Хг соот-
ветственно, интенсивность восстановления постоянна и равна рь ин-
тенсивность проверки после ложного переключения или ложного
сигнала о неисправности резерва постоянна и равна Рг-
Ответ:
р ... __ — (X, 4-тда) (Х,а -|- Х2 4~ 4~ Е) ___
° ~ (х2 — Х1) (Хз — X,) е
— (М ~4~ тух) 4~ A.g -р ту* 5)
еХз/+
(%2 Xj) (^3 ' ' -Хг)
Х,Х2 — (Л, + ту*) (Xja + + тух + Е)
(Хз Х2) (х3 Xi)
где хп х2, х3 есть корни уравнения
X3 *4~ X2 (2А-1 "4~ Зт}а -J- рч *4“ Р*г) *4~
+> [(М + 4“ + Pi) (*i + Vх + Рг) + + £) (2X1 + 2i)a -|- р.,) +
+ (Х.« + Х2) (2X1 + 2tj<x + |Л2)] -|- (Xi + трт) [(т;а + 5) X
X (Xi + т)<х + р.,) + (Xjti + Хг) (Xi + т)а 4- р.2)] = 0;
7'oi'e== Х144-7]а" {* +
_|___________(Х1 4- У) (X, 4- У 4- Pl) (X, 4- У 4~ Рг)
(трт 4- g) (X. т)<х 4- p.j) 4- (Xia 4~ Х2) (Х1 4- Ч1* 4" Рг)
218
4.42. По условиям предыдущей задачи вычислить 7срс при про*
извольных законах распределения времени восстановления и време-
ни проверки с функциями распределения F\(x) и F2(y) соответст-
венно.
Ответ:
Гсро== +
,__________________X, +тух___________________)
“М + h + -fp + & — W-i + М bi — (’rft + 6) b2 | ’
где
Ь> = j’ е~ (1,*+ dFj (%); Ь2 = ( е“(’“ + Чи) у dF2 (у).
о о
4.43. По условиям задачи 4.42 найти Тср с, если Xi=X2=0,l [/час,
1]=|=0,01 i/час, а=1, а времена восстановления и проверки постоян-
ны и равны соответственно ti=30 мин и т2=15 мин.
Ответ:
bi = е~ <*» + 1“) т* = е-°.055 =5= 0,9465, Ь2 == е“01 + ’>“>т* =
= 6-0.02’5^о,9732, Тсрй=^175 час.
4.44. По условиям задачи 4.42 определить Тсрс, если вероят-
ность того, что отказ резервного устройства будет обнаружен сразу
же после его возникновения, равна ,р (резервный прибор контроли-
руется неполностью).
Ответ:
Г«Ро= |1 +
,______________________а (>ч + ''О________________Д
«А, + А2 + 7)а + (аХ, + |5X2) bi — (т)а -|- b2 | ’
где bl = J е-<г,+’!‘х) * dFi (х); b2 = j e-f^+^l у dF2 (у).
о о
4.45. По условиям задачи 4.44 найти 77 Р с при проведении про-
филактических проверок резервного прибора с интенсивностью у.
Длительность проверки описывается функцией распределения Fs(z).
Проверка заканчивается после выяснения истинного состояния
резервного прибора.
Ответ:
о X] 4- т]а
, _____________________а (>ч + ~4)____________________
«Aj-J-Xg+Tx-HP-1-7 (1—*,)—(oXi+PAg) bi—ОзМ-ЭД *2—
уХа (1 — Р) bib2
+ >)« + 7
219
Где
06 6б
b3 = j е"^ xdF} (х); b2 = j VdF2 (y);
о о
b3 = ^e-~^ + ^zdFs(z).
о
4.46. По условиям задачи 4.45 выяснить оптимальную частоту
профилактики уОпт, максимизирующую 7’ср с. Выяснить, при каких
условиях проведение профилактики дает увеличение 7’ср с.
Ответ:
1/M1—Р) (*i+V) п , .
Tout — (К + V)-
Профилактика с любой частотой дает увеличение"7’ср с только тогда,
когда
^2 (1 -- Р) 1 Ь3
К +ч“ ' btb3
4.47. По условиям предыдущей задачи определить оптимальную
частоту профилактики, если (х) = 1 — с~'|11Л, F3 (?) = 1 — е—|±зг.
Ответ:
Аг (1 — Р) Рч.»-з
X] 4- 7J“ + Н
7опт —
(Х1 + 7-и) .
4.48. Структурная схема расчета надежности автопилота само-
лета представлена на рис. 4.11. Найти вероятность Pc(nt) безотказ-
Рис. 4.11. Схема расчета надежности (к задаче 4.48).
ной работы автопилота при п полетах длительностью t каждый и
среднее время безотказен работы 7’ср с для случаев:
а) восстановление» отсутствует;
б) проводится проверка и восстановление отказавших узлов по-
сле каждого полета.
Ответ:
а) Ре (nt) = е-пУ-'{ (2е-'Да/ —
4_____________4_______| 1
с _|_ 2/;х, /гЛ] -|- ЗпХ2 ’* nkt + 4пЛ2 ’
б) Рс (nt) = fe-’1' (2e“laf — e-2V)2]’*,
7cpc — ПК, + (2/2 + P) К '
д=о
220
4.49. Имеется непрерывно работающая треХкайаЛьЙая линия Пе-
редачи информации. Ремонт отказавшего капала требует выключе-
ния всей линии. Необходимо определить, при каком количестве от-
казавших каналов г остановка линии на ремонт будет обеспечивать
минимум потерь информации, если доля информации, теряемой
в единицу времени при простое г каналов (/'=1, 2, 3), равна hr. Вре-
мя безотказной работы и время восстановления канала имеют экспо-
ненциальное распределение с параметрами Л. и р соответственно.
Рассмотреть случаи:
а) каналы восстанавливаются поочередно;
б) одновременно могут восстанавливаться два канала;
в) одновременно могут восстанавливаться три канала.
Ответ:
а) г = 1, если
X hj/hs
Р 1 3/Zj//Zj
г = 2, если
hilhz A
1 — 3ft,//«3 < V < 7 + S/ij/Лз — 12/z2/ft3 ’
г = 3, если
X 5ft2//z3 — ‘ih-Jha
Р > 7 + ‘3ht/h3- 12ft2/ft3 *
б) г = 1. если
р 2 —Зй,//г3 ’
X 1О/г2//г3 — (>hl/h3
г = 2, если
ht/h3
2 —3ft,/ft3 р 13 4-3ft,/ft3 — 18ft2/ft3 ’
в) г = 1, если
г = 2, если
hjh3
2 — 3hi/h3
k h, /ha
p. 2 — ’3>Их]1гъ '
3 (5/z2//z3 — 3/z, //z3)
22 -j- 3/z,/ft3 — 27йг/й3 ’
г = 3, если
X 3 (5/г2//?3 —3ft,/7г3)
р > 22 -|- ‘3hl/ha — 27ft2/ft3
4.50. В дублированной восстанавливаемой системе длительность
подключения ненагруженного резервного устройства взамен отказав-
шего основного есть случайная величина, распределенная по экспо-
ненциальному закону с параметром у. Система считается отказавшей,
если длительность перехода на резерв превысит допустимое время т
или одновременно будут неисправны оба устройства. Требуется най-
ти среднюю наработку до первого отказа системы при экспоненци-
альных законах распределения времени безотказной работы и вре-
мени восстановления устройства с параметрами X и р соответст-
венно.
221
Ответ.
(X+p.)Y + X(X+p. + Y)(l-e“^)
0,10 №+<”)
4.51. По условиям предыдущей задачи вычислить Тср с, если
Х=0,1 Х/час, ц=1 Х/час, Тдоп=0,1 час, а переход на резерв может
осуществляться автоматически (1/'у=0,02 час), полуавтоматически
(1/у=0,04 час) и вручную (1/у=0,1 час).
Ответ:
Гсрс = П2 час — автоматический переход; Гер с=66 час — полу-
автоматический переход; ГСрс=25 час — ручной переход.
4.52. По условиям задач 4.50 и 4.51 вычислить Герс, если дли-
тельность допустимого перерыва в работе есть случайная величина,
распределенная по экспоненциальному закону с параметром т]=
= 10 Х/час.
Ответ:
т _ (A+p-)(X + y + -4) + Xy
®«— MMy + ч) + м]
ГСр с=44 час — автоматический переход; ГСрс = 30 час — полу-
автоматический переход; ГСрс='19 час — ручной переход.
4.53. Требуется, исправная работа прибора в течение 20 час. При
этом допускается Однократный перерыв в работе на время не более
чем т=1 час. Какова вероятность того, что задание будет выполне-
но, если интенсивность отказов прибора постоянна и равна Л=
=0,01 Х/час, а интенсивность восстановления также постоянна и рав-
на ц—2 Х/час.
Ответ:
Ре(t. -t) = е->[1 -е-<^>’] е^ .
Ре (20,1) 0,962.
4.54. Цифровая вычислительная машина должна выполнить боль-
шой объем вычислительных работ за время /=400 час. При отказе
результаты предыдущей работы сохраняются. Какова вероятность
Pe(t, т) того, что задача будет выполнена, если при отсутствии
отказов работа была бы закончена за время т=350 час? Законы рас-
пределения времени безотказной работы и времени восстановления
ЦВМ являются экспоненциальными с параметрами Х=0,1 Х/час и
р.= 1 Х/час соответственно.
От в е т: P(t, т) «0,96.
4.55. По условиям предыдущей задачи найти искомую вероят-
ность при постоянном времени восстановления тв = 1 час.
Ответ: Р(400, 350) «0,9935.
4.56. Имеется машина, перерабатывающая в час 10 кг некото-
рого сырья. За время /=12 час требуется переработать 100 кг сырья.
Какова вероятность того, что машина справится с поставленной за-
дачей, если время работы до отказа машины и длительность восста-
новления подчиняются экспоненциальному закону с параметрами
7.=0,1 Х/час и ц=1 Х/час соответственно?
Ответ: Рс (/) «0,606.
222
4.57. По условиям задачи 4.56 определить, сколько в среднем
потребуется времени на переработку всего сырья?
Ответ:
100
Йер— 10
X \
1 + — —11 час.
в- j
4.58. Цифровая вычислительная машина имеет экспоненциальное
распределение времени безотказной работы с параметром Х=
=0,06 \/час и экспоненциальное распределение времени восстанов-
ления с параметром [1=1 \/час. Найти вероятность Pe(t, т) того, что
задание длительностью т=10 час будет решено за время £=15 час,
если допускается только одно восстановление, после которого реше-
ние приходится начинать сначала.
Ответ:
Ре (f, т) = е-^ Г 2 - -Ц- е-+ <^>1,
с' ’ I р. — X р. — X J
Ре(15, 10) =5x0,667.
4.59. По условиям предыдущей задачи вычислить l\(t, т), если
восстановление мгновенное. Сравнить со случаем отсутствия времен-
ной избыточности.
Ответ:
Ро (t, т) = e~>T [2 — е“х х)],* Ре (15, 10) 0,691. Если t = т, то
Рс (т) = е“' х =%= 0,549.
4.60. При значениях ,Х и т, приведенных в задаче 4.58, выяснить,
что выгоднее: параллельное решение поставленной задачи двумя
ЦВМ при отсутствии временной избыточности или решение той же
задачи одной ЦВМ при наличии избытка времени t—т=10 час.
Ответ: При простом дублировании
Ре (т) = 1 — (1 — е"^)2 =5х 0,796.
При временнбй избыточности одной ЦВМ
Ре (£, т) = е“[1 + Н (£ — г)] =%= 0,878.
4.61. Исследуется надежность блока питания, состоящего из по-
нижающего трансформатора, дросселя и двух конденсаторов с ин-
тенсивностями отказов ХТр = Х1=9 10-е \/час, Хдр = Хг=0,2Х
ХЮ-6 \/час, Хс=Хз=5-10-6 1/час и средними временами замены
Т1=тТр=1,5 час; Т2=тдр = 1 час и тз=Тс=0,5 час. Пробой любого
из конденсаторов приводит к перегоранию трансформатора. Для по-
вышения надежности блока конденсаторы зарезервированы путем
последовательного подсоединения к каждому из них еще одного кон-
денсатора, при этом из-за уменьшения нагрузки по напряжению
вместо Хс имеем Х,з=Х'с=0,ЗХс. Блок обслуживает один человек.
Конденсатор может отказать только из-за пробоя.
Найти Pe(t), ТСр с, Те и Кг, если £=2000 час, ремонт может
начаться только после отказа всего блока в целом и ведется до пол-
ного восстановления блока.
223
Ответ:
Ре (2000) = е-».»2’6 (2,5e-».»os — Обе"».1”5) 0,9727,
т ( К \2 1_____________4Х3Х'3
'еРо-^х3-2Х'3J Ъ+\2 + Ы3 (Х3-2Х'3)зЛ
X_________!__________+ )2______1_________,
Xi 4~ Х2 4~ Х3 4“ 2Х'3 О3 2Xf3 I X, -f- Х2 -j- 2Х3
?ер с = 92 320 час,
,______Xtt, -)- Х2т:2 4X;Xf3 (т. 4~ ^з) 4~ 4Х2Х'3 (т2 -|~ т3)
в X, 4~ Х2 4- 4Х'3 (X, -|- Х2 4- 4Х'3) (X, -|* Х2 ~Ь ЗХ^э"—J— Х3)
_________8Х, (Х'3)2 (т, 2т3) -|- 8Х2 (Х'3)2 (т2 (- 2т3)_
(X] 4- Х2 4~ 4Х'3) (X, 4- Х2 4- 2Х'3 4- Х3) (X; 4- Х2 4- 2Х3)
[8Х3Х% (X, + Х2 4- 2Х3) 4- 12X3 (Xi ~Ь Х2)] '’з
(Xi 4- Х2 4- 2Х'3 4- Х3) (Х3 4- Х2 4- 4Х'3) (X, 4- Х2 4~ 2Х3) ’
Гв=5= 1,79 час,
К* = Тер С/(ГСР с 4- ЛО 0,99998.
4.62. Восстановление отказавшего прибора, состоящего из п
равнонадежиых блоков, ведется путем поочередной замены каждого
блока новым до тех пор, пока не будет обнаружен неисправный
блок. Длительность замены блока постоянна и равна т. Требуется
вычислить вероятность р/, того, что придется заменить k блоков и
ожидаемое время восстановления тв.
п
г, 1 ' VI , («'+1) ’
Ответ: рк=~, тв = т: kph =-------.
«««
*=1
4.63. По условиям предыдущей задачи прибор состоит из блоков
разной надежности. Вероятность отказа прибора из-за отказа /г-го
блока есть qk, а длительность замены k-ro блока постоянна и рав-
на Ть Найти такую стратегию восстановления прибора, при которой
ожидаемое время восстановления будет минимальным, и вычислить
для этой стратегии рь и тв.
Ответ: Необходимо проверять блоки поочередно, предвари-
тельно занумеровав их таким образом, чтобы выполнялось условие
Ч. Як
'’R+1 'Zk+l
k= 1, 2..../1—1;
- 7’k = '7k.
п
% = X СЧ + 't2 4" • • • + "hi) Як-
k=\
224
4.64. По условиям предыдущей задачи /г = 2, </1 = 0,7, </2=0,3,
Ti = 30 мин, Тг=Ю мин. Найти оптимальную очередность замен бло-
ков и вычислить для этой очередности тв. Сравнить со случаем, ког-
да очередность замен не устанавливается и равновероятна замена
любого блока.
Ответ: В первую очередь заменяется второй блок, при этом
тв = 31 мин. При равновероятной замене любого блока имеем
1 1
= у ['71 xi + <7г fri!+ хг) j + -у + <7i СЧ + Ч)1 = 32 мин.
4.65. Система, состоящая из N одинаковых блоков, считается
исправной, если в ней отказало не более п блоков. Считается, что
отказы блоков независимы, время безотказной работы каждого бло-
ка распределено по закону F(t), во время профилактики все отка-
завшие блоки мгновенно заменяются, а моменты tn надо выбирать
так, чтобы вероятность отказа блока на каждом участке равнялась
одной и той же величине. Выбрать моменты профилактики /|<^<
<t3<. ..<tk<... таким образом, чтобы вероятность безотказной ра-
боты системы на участке времени между соседними профилактпками
равнялась заданной величине 1—f>.
Ответ: Моменты 6 находятся путем решения системы уравне-
ний
m—1
Ре (4n) + a Р ~ /г) = 1 — а, т = ], 2, ,
1=1
где Pc(tm)=l—F(tm), а — вероятность отказа каждого блока на
участке между соседними профилактпками.
Значение а определяется из выражения
1
4.66. По условиям задачи 4.65 можно доказать, что с течением
времени система войдет в стационарный режим, т. е. t,—tj-\ = h =
= const при любых достаточно больших I. Найти приближенное вы-
ражение для h, если вероятность отказа блока а мала, а средняя
наработка до первого отказа блока равна Тср.
Указание. Найти точное выражение для вероятности безотказ-
ной работы блока на участке между профилактпками как сумму ве-
роятностей благоприятных событий, после чего вычислить прибли-
женно
ТСР = J Рс (0 dt,
6
используя формулу трапеций.
Ответ:
Л«аТср/(1—а/2).
15—1086
ГЛАВА ПЯТАЯ
ОЦЕНКА И КОНТРОЛЬ НАДЕЖНОСТИ
ТЕХНИЧЕСКИХ УСТРОЙСТВ ПО РЕЗУЛЬТАТАМ
ИХ ИСПЫТАНИЙ
§ 5.1. ОСНОВНЫЕ ПОЛОЖЕНИЯ
ВЫБОРОЧНЫХ ИСПЫТАНИЙ
Испытания технических устройств на надежность про-
изводятся 'с целью определения реального уровня их
надежности. Естественно, что испытаниям подвергается
выборка из генеральной совокупности. По результатам
испытаний выборки судят о надежности всей генераль-
ной совокупности.
Для устройств, работающих дискретно, непосредст-
венно из опыта определяется вероятность безотказной
работы (вероятность отказа) по методике описанной
ниже.
Исчерпывающей характеристикой надежности
устройств с непрерывным характером работы служит за-
кон распределения времени безотказной работы. Если
известен вид закона и его параметры, то легко опреде-
лить любую, интересующую нас характеристику надеж-
ности. Статистическое определение закона распределе-
ния времени безотказной работы связано с большими
затратами сил и средств. Техническая сторона этого во-
проса хорошо описана в учебной литературе, посвящен-
ной испытаниям, и поэтому в данной книге не рассма-
тривается.
В ряде случаев вид закона распределения времени
безотказной работы бывает известен. В таком случае
опытным путем находятся оценки параметров закона и
затем необходимые характеристики надежности, в част-
ности вероятность безотказной работы как функция рас-
пределения, т. е.
(5-1)
226
где P(t) — оценка вероятности безотказной работы за
время t; 0i, 62 -.. — оценки параметров распределения.
ОПРЕДЕЛЕНИЕ ВИДА И ПАРАМЕТРОВ ЗАКОНА
РАСПРЕДЕЛЕНИЯ ВРЕМЕНИ ИСПРАВНОЙ РАБОТЫ
(ВРЕМЕНИ ДО ОТКАЗА)
В результате испытаний можно получить точечные
значения оценки параметра (которые будем обозначать
теми же символами, что и математические ожидания, но
с черточкой сверху, например 0) и интервальные оцен-
ки. При интервальных оценках определяется, какой
интервал оценок с заданной доверительной вероятностью
а накрывает математическое ожидание оцениваемого
параметра. Границы такого интервала называются до-
верительными границами. Можно записать
а=Вер(0в=С0^0в), (5.2)
где 0Н, 0в — нижняя и верхняя доверительные границы
параметра 0.
Вероятность того, что значение 0 выйдет из интервала
[0н, 0в], называют уровнем значимости 0;
0 =Вер (0Н>',0>'0В) = 1—а. (5.3)
Наиболе часто значения доверительных вероятностей
принимают равными 0,90; 0,95; 0,99 или уровни значи-
мости соответственно 0,10; 0,05; 0,01.
Доверительная вероятность а, определяемая соотно-
шением (5.2), характеризует степень достоверности ре-
зультатов двусторонней (т. е. с определением двух гра-
ниц) оценки. Но часто <в практических целях достаточно
установить одну из границ интервала, нижнюю или верх-
нюю, отвечающих доверительным вероятностям щ, или
а2. Тогда
ai=Bep(0^0H), (5.4)
«2=Вер(О^10в). (5.5)
Вероятности а, щ й а2 связаны между собой уравне-
нием
a=iai+ta2—1. (5.6)
Первоначально рассмотрим определение вида закона
распределения.
15* 227
Наиболее распространенными законами распределе-
ния отказов изделий являются:
— экспоненциальный;
— усеченный нормальный;
— логарифм ически-нормальный;
— Вейбулла;
— гамма.
Поэтому при определении вида закона распределе-
ния рекомендуется аппроксимировать эксперименталь-
ные характеристики этими законами в топ последова-
тельности, которая указана выше.
При выявлении закона распределения целесообразно
соблюдать следующий порядок:
— подготовка опытных данных;
— построение гистограммы какой-либо количествен-
ной характеристики надежности;
— проверка допустимости предполагаемого закона
распределения отказов, используя определенные крите-
рии согласия (Колмогорова, Пирсона и. др.).
Подготовка опытных данных включает выборку
исходных результатов из отчетных документов, составле-
ние вариационного ряда и заполнение таблицы отка-
зов.
При составлении вариационного ряда исследуемого
времени безотказной работы (или времени восстановле-
ния) это время записывается в порядке возрастания ве-
личин, причем одинаковые значения не исключаются,
а повторяются друг за другом. По полученным данным
заполняется таблица, образец которой приведен в виде
табл. 5.1. В ней приняты следующие обозначения: xf —
значение члена вариационного ряда (наработка до от-
каза, наработка между соседними отказами); щ — число
ТАБЛИЦА 5.1
Таблица исходных данных для определения
графическим способом закона распределения
xi пг Нг 0) Нг 1- _д_ («>
1 2 3 4 5
228
наблюдаемых однозначных отказов /-го интервала вре-
мени; 2п,-— общее число отказов; //,-—накопленное чис-
(<)
ло отказов, являющееся суммой п, отказов второго
столбца, начиная с первого числа th и кончая i-м чис-
лом n,-; HiHLrii — частость отказов.
(О
Приведенная таблица предназначена для определе-
ния закона распределения графическим способом при по-
мощи координатной сетки. При таком способе вид зако-
на распределения оценивается, как это следует из
табл. 5.1, по виду кривой вероятности безотказной ра-
боты
/1 — Hi / S /7г \
\ / (О J
Координатные сетки для различных законов распре-
деления приведены в приложении 6.
Если вид закона распределения оценивается не гра-
фическим способом, то удобно применять табл. 5.2, в ко-
торой обозначено: ДЛ— длина /-го интервала времени;
ТАБЛИЦА 5.2
Таблица исходных данных для определения
закона распределения аналитическим сдосэбом
", л(3/г) /з(Д? ) й(0= Л(0
1 2 3 4 5
н(А/,) —число отказов на участке Ai,-; No—число образ-
цов, первоначально установленных на испытание; Ncv—
среднее число исправно работающих элементов в про-
межутке Ai,; P(t), a(t), —вероятность безотказной
работы, частота отказов, интенсивность отказов соответ-
ственно.
По данным табл. 5.2 строятся гистограммы для коли-
чественных характеристик надежности (либо P(t), либо
o(i), либо X(i)] и аппроксимируются кривой, по виду ко-
торой можно установить ориентировочно закон распре-
деления отказов путем сравнения с соответствующими
теоретическими кривыми.
Проверка допустимости принятого закона распреде-
ления отказов осуществляется по критериям согласия.
2’
(5.8)
интер-
стати-
(5.9)
Наиболее употребительными критериями являются кри-
терий х2 Пирсона и критерий Колмогорова.
При использовании критерия %2 Пирсона вычисляется
вероятность следующего вида:
Р (X2 < Д < °°) = рг (и) du, (5.7)
где А— мера расхождения; %2—функция плотности рас-
пределения, вычисляемая из выражения
k
(щ — ПА) .
Л 1л npi ’
i=l
п — общее число опытов; pi=tiiln — частость i-ro
вала статистического ряда; k — число интервалов
стического ряда;
г 2Г/2 Г (г/2)
r—k—1—число степеней свободы распределения.
Для вычисления вероятности (5.7) используются таб-
лицы.
Если вероятность Д(х2^Д<о°) <0,1, то следует счи-
тать неудачным выбранное теоретическое распределение.
В противном случае следует считать, что взятое нами
теоретическое распределение согласуется с эксперимен-
тальным и может быть принято.
На основании критерия согласия Колмогорова экспе-
риментальное распределение согласуется с выбранным
теоретически, если выполняется условие
ПфГ<1, (5.10)
где D — наибольшее отклонение теоретической кривой
распределения от экспериментальной; k — общее количе-
ство экспериментальных точек.
После установления вида распределения можно при-
ступить к определению его параметров. Законы распре-
деления могут быть однопараметрические и многопара-
метрические.
Рассмотрим методы оценки параметров различных
законов распределения отказов.
230
ЭКСПОНЕНЦИАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Экспоненциальное распределение характерно для вне-
запных отказов элементов и систем. Плотность вероят-
ности экспоненциального распределения задается урав-
нением
f(f) = Xe-w, (5.11)
где X — интенсивность отказов есть величина, обратная
средней наработке до отказа /==\/Т.
Оценки параметра X экспоненциального распределе-
ния могут быть получены по формулам, соответствую-
щим планам испытаний [3] и приведенным в табл. 5.3. Во
втором столбце этой таблицы располагаются условные
трехбуквенные обозначения планов, которые расшифро-
вываются следующим образом:
первая бука п означает объем выборки, подвержен-
ной испытаниям;
второй буквой Б или В обозначены планы без восста-
новления выборки или с восстановлением ее соответст-
венно;
третья буква (и, или /0, или d) в условном обозначе-
нии плана указывает на признак окончания испытания.
Планы, предусматривающие испытания до отказа всех
испытываемых элементов выборки, обозначены буквой и;
планы с окончанием испытаний через заданное время
обозначены буквой /0; буквой d обозначены планы
с окончанием испытаний после появления установленно-
го числа d отказов.
Таким образом, символом [и, В, /0], например, обозна-
чен план с восстановлением выборки объема п и оконча-
нием испытаний по истечении времени /0. Символ [и, Б,
d] относится к плану без восстановления выборки с окон-
чанием испытаний после d отказов. Кроме указанных
выше символов в таблице приняты также следующие
обозначения:
td — время от начала испытаний до d-ro отказа;
t-s.— суммарная наработка.
Формулы, содержащиеся в табл. 5.3, удобно обозна-
чать двузначными числами, у которых первая цифра —
номер строки (план), а вторая — номер столбца. Напри-
мер, в таблице формула, обозначенная номером (14),
записывается в виде
231
ТАБЛ И II А 5.3
Пл-аны испытаний для случая экспоненциального распределения (оценка параметра /.)
Номе? плана План испыта- ний Суммарная наработка Оценка интенсив- ности отказов X Нижняя граница X Верхняя граница
2 3 4 5 6
1 [16 и п i= 1 n 17 2 X(l—-x,) (2n) ,,2 /.(e.j) (27) 2/v
2 [п5/0] rf ф 0 d X, -i + ('i — ф ?t> i = l d Б л,2 Xfl-cc,) (Z-') 2/s „2 X(a8) (2 •) 2/s
3 [н5/0] d =0 «'o __ 0 To /v
4 \иБ.Ц 1 4- r> .![ d — 1 V2 (2 ) 2 X(a2) (2 ) 2/v
fs
5 [пВЦ nte d .,2 X(l-7,) (20 2tv 2 %(a2) (2 ’-j-2) 2fv
6 [nBdj rd a rf— 1 .,2 Afl-r.,) (27) 2/, уЛ8) (2 ') 2/£
Для определения доверительных границ .X при d^O
необходимо пользоваться таблицей квантилей хы-квад-
рат распределения (табл. П.7.1), в которой параметрами
являются вероятность Р(1—сц или «2) и число степеней
свободы k. равное 2п, 2d или 2d+2, в зависимости от
плана.
Для определения при d=0 в плане [л, Б, /] нужно
определить коэффициент г0 по табл. П.7.8.
Учитывая, что при экспоненциальном распределении
P(0 = e-w, а
получим:
-//г
= е
= е
Рв(/) = е
ГН=1ДВ, Тъ=Ша.
(5.12)
в
Для этих целей можно воспользоваться и непосредст-
венно табл. 5.3.
В том случае, когда число степеней свободы k (2п
в планах [и, Б, п] или 2d в других планах) более 100.
формулы для определения доверительных границ, приве-
денные в табл. 5.3, не могут быть реализованы ввиду
ограниченности табл. П.7.1. При таких объемах испыта-
ний выборочная оценка средней наработки на отказ рас-
пределена нормально и поэтому могут быть использова-
ны формулы для границ Т при нормальном распределе-
нии времени безотказной работы, в соответствии с кото-
рыми
Т’в.н = T±ta {n_^Siyn. (5.13)
Получение значения S при этом может оказаться за-
труднительным и в ряде случаев невозможным. Тогда сле-
дует воспользоваться свойством экспоненциального рас-
пределения, у которого о=Т, а следовательно, S—T.
При планировании объема испытаний для случая
экспоненциального закона распределения времени без-
отказной работы необходимо определить, сколько экзем-
пляров и сколько времени нужно испытывать, чтобы по-
лучить из опыта интенсивность отказов с ошибкой, не
превосходящей заданную. Если заданная предельная
233
Ошибк5 выражена в процентах и равна 6, то можно за-
писать
= 1 + ' (5Л4>
Тогда для плана [«, Б, п\ имеем
* = (5-15)
Это соотношение при заданных k и .щ позволяет опре-
делить объем испытаний п с помощью табл. П.7.1. Для
удобства решения этой задачи составлена табл. П.7.2
для значений Г1=/г, в которой входами являются d=n и
а—щ. Табл. П.7.2, очевидно, может быть использована
для определения п в планах [п, Б, п].
При планах [п, Б, /0] объем испытаний определяется
величинами п и /0. При испытаниях регистрируется чис-
ло отказов d. Очевидно, что между d и t0 существует
неявная связь. Поэтому по величине k~Rlt пользуясь
табл. П.7.3, составленной для вероятности а=0,95, на-
ходим d. Затем но числу d и заданному значению дове-
рительной вероятности определения объема испытаний
оо с помощью табл. П. 7.4 находим коэффициент rs и по
формуле получаем примерный объем испытаний
nt0=dr3rk0, (5.16)
где Ло — ожидаемое значение X. Если п или to задается
заранее, то из произведения nt0 легко определить иско-
мое.
Для планов [п, Б, d] объем испытаний определяется
значениями п и d. Число отказов d можно определить по
табл. П.7.2, исходя из заданного k=rt и доверительной
вероятности «1. Величина п влияет только на длитель-
ность испытаний: чем больше п, тем скорее будет достиг-
нуто число отказов d и, следовательно, время испытаний
будет меньшим;
В случае планов типа [и, В, 4] испытанию подлежат
п объектов -в течение времени 4- Время t0 косвенно свя-
зано с числом отказов d при испытаниях, которое опре-
делим по табл. П.7,2 для заданных k и щ. Для того
чтобы по числу d найти необходимые п и t0 с вероят-
ностью «о, воспользуемся вспомогательным коэффициен-
том г3, определяемым из табл. П.7.4 по известным d и .а0-
234
Наконец, установив предполагаемое значение «о, нахо-
дим по формуле (5.16) произведение nt0.
Для планов типа [и, В, d] объем испытаний опреде-
ляется величинами п и d, которые находятся так же, как
и в случае планов типа [п, Б, dj.
УСЕЧЕННОЕ НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Нормальный закон распределения наиболее часто
используется для оценки надежности изделий при нали-
чии постепенных отказов. Плотность вероятности нор-
мального распределения задается уравнением
<517>
где Т — средняя наработка до отказа; <г — среднее квад-
ратическое (стандартное) отклонение времени безотказ-
ной работы.
Так как при нормальном распределении случайная
величина может принимать любые значения от —оо до
+ оо, а время безотказной работы может быть только
положительным, нужно рассматривать усеченное нор-
мальное распределение с плотностью
= (618)
где с — нормирующий множитель.
Нормирующий множитель с определяется из выра-
жения
c°^f\t}dt=\ (5.19)
О
и равен
' <520>
г,/а
где F У е—3(1,2 dx— табулированная интеграль-
—00
/ Г \
ная функция нормального распределения; Фо -у- =
d~x‘12dx — нормированная функция Лапласа.
о
235
Средняя наработка до отказа и параметр 1\ усечен-
ного нормального распределения связаны зависимостью
7’=7’1+——е 1 . (5.21)
\ 3 J
При что имеет место'в абсолютном большин-
стве случаев при оценке надежности устройств с нор-
мально распределенными отказами, коэффициент с мало
отличается от единицы и усеченное нормальное распре-
деление достаточно точно аппроксимируется обычным
нормальным законом.
При 'испытании -выборки объемом в п изделий с на-
работкой ti, t2, .tn параметры распределения Т и о
оцениваются по формулам
(5.23)
С целью экономии времени и уменьшения ошибок
при подсчетах S, когда п велико, а — большие или
нецелые числа, следует использовать тождество
(5.24)
Доверительные границы Т определяются по уравне-
ниям:
— S
Т’н = Т — (/г_,} нижняя граница, (5.25)
+fas(«-i) Уп
верхняя граница,
(5.26)
где — квантиль распределения Стьюдента для ве-
роятности а или уровня значимости р = 1 —а и числа сте-
пеней свободы f — n — 1; величина t , находится по
табл. П.7.5.
В случае двустороннего определения доверительных
границ
^ = ^ = (1 — «)/2.
236
Доверительные границы о определяются с помощью
формулы
(/2-1)5 = (/2-l)S*
2 " 3 2
Х(1—3/2) (л-1) %(₽/2) (лг-1)
(5.27)
где Х(1~?/2) (п-i) — квантиль xu-квадрат распределения при
вероятности р=1—ф/2 и числе степеней свободы k~
= — п—то же для вероятности /? = р/2.
Значения у?.. . находятся по табл. П.7.1.
Если время безотказной работы устройств имеет нор-
мальное распределение, то оценка вероятности безотказ-
ной работы за время t определяется по формуле
, Д(0 = 1-[фо(-<Л)+фо(^)],
(5.28)
где Фо(х) —нормированная функция Лапласа, получен-
ная по П.7.13:
Z
Фс(г)=-—[e~^v.
о
(5.29)
При этом следует учитывать, что функция Фо нечет-
ная, т. е.
Фо(—z) =— Фо(г).
Нижняя доверительная граница для P(t) может быть
приближенно найдена по формуле
(5.30)
где иа — квантиль нормального распределения (при 7 = 0
и о= 1), определяемый по табл. П.7.7; — оценка стан-
р
Дартного отклонения оценки Р (t);
(5.31)
(5.32)
237
Если рассматриваются постепенные отказы и надеж-
ность определяется вероятностью того, что выходная ха-
рактеристика Y не выйдет за допустимые пределы Уи,
Ув, иначе УИ^У^УВ, то оценка Р(У) производится по
формуле
(5.33)
Нижняя доверительная граница Р(У) приближенно
определяется по формуле, аналогичной (5.30), но диспер-
сия оценки находится при помощи уравнения
-МЛ(1 + -1-М.)1. (5 34)
где
ki = 0,4 exp -g z^,
?г- = (Уг—F)/S
при i = 1; 2.
Часто при оценке надежности устройств с нормаль-
ным распределением отказов требуется определить гра-
ницы (пределы) интервала, в котором будет находиться
нормально распределенная случайная величина с дан-
ной вероятностью Р. Гранины Ун и Ув и интервалы ча-
сто называются толерантными (допустимыми предела-
ми).
Толерантные пределы запишутся следующими выра-'
жениями:
верхний предел Ув—
[—оо, У+Л5], (5.35)
нижний предел УГ1—
[У—kS, + оо], (5.36)
двусторонний интервал
[У—kS, У+ftS],
(5.37)
где У — выборочное среднее случайной величины; S —
оценка стандартного отклонения.
238
Так как толерантные ^пределы определяются на осно-
ве выборочных данных У и S, то они устанавливаются
с вероятностью а.
Константа k, являющаяся функцией объема выборки
п, вероятности Р и доверительной вероятности а, при-
ближенно выражается формулой
. . «а , 5«а + Ю \ „
k — гР^1 + ^+ 12/г J' (5’38)
где zp и иа определяются из табл. П.7.6 для р=Р и
для р=а соответственно.
Полученные таким образом толерантные пределы
будут более широкими, чем их точные значения, вычис-
ление которых громоздко и поэтому здесь не приво-
дится.
Объем испытаний для определения Т с ошибкой не
более е часов с доверительной вероятностью а прибли-
женно может быть получен при помощи уравнения
n~ (ZpCTo/e)2, (5.39)
где zp-—квантиль нормального распределения, опреде-
ляемый по табл. П.7.6, для вероятности р = а; его —ори-
ентировочное значение о.
В случае усеченной выборки, когда в результате ис-
пытаний объектов получены г возрастающих значений
наработки (г<н) для отказавших объектов Л, /2, •••, tr,
а п—г объектов по истечении некоторого времени ta^tr
остались исправными, параметры Тио можно оценить
по (методу квантилей следующим образом.
Считаем, что за время t.t вероятность выхода из строя
испытываемых объектов составляет pi^i]n. Для этой
вероятности ,по табл. П.7.6 определяем квантили ир и
составляем г уравнений:
(5.40
Т + ир° = 11’
Т — ^2»
Полученную систему уравнений решаем по методу
наименьших квадратов, для чего умножим левую и праву1
части каждого из уравнений системы (5.40) на ир
UPa""' ир соответственно и все г уравнений сложи
в результате .получим первое, так называемое нормаль-
ное уравнение
Т Е Upt + 3 Ё % = Ё (5-41)
1=1 1=1 1=1
Второе нормальное уравнение получим суммировани-
ем уравнений системы (5.40):
Гг + 3Ё^=Е?г- <5’42)
/=1
Уравнения (5.41) и (5.42) решаем относительно не-
известных Т и о и находим, таким образом, их оценки.
Точность полученных значений Т и о может быть
оценена с помощью уравнений
°4T)^f2(k), (5.43)
з2(3)-^М^). <5’44)
где k=(T—to)/с, f2(&) и fs(k)—вспомогательные функ-
ции, определяемые по табл. П.7.7.
ГАММА-РАСПРЕДЕЛЕНИЕ
Данное распределение в практике оценки надежно-
сти технических устройств имеет большое значение, так
как время безотказной работы систем с ненапруженным
резервом, каждый компонент которых имеет экспонен-
циальное распределение отказов, подчиняется этому за-
кону. С помощью гамма-распределения можно также
оценить наработку при определенном числе отказов вос-
станавливаемых устройств.
Плотность вероятности наработки в случае гамма-
распределения имеет вид
= <5’45)
где m — параметр формы распределения; % — масштаб-
ный параметр.
Обычно параметр m известен как число компонентов
резервированном устройстве или как число отказов во
СЭ
23.
время испытаний устройств с экспоненциальным распре-
делением. В таком случае, в результате испытаний необ-
ходимо оценить параметр К который в данной интер-
претации гамма-распределения является интенсивностью
отказов. Параметры т .и X легко определить
моментов, исходя из того, что
/Л '
ti
методом
Л1(0 = 7=^-
п,
(5.46)
(« -1),
(5.47)
п
где ti — наработка до /n-го отказа при одном испытании;
п — число испытываемых устройств.
Совместное решение уравнений (5.46) и (5.47) позво-
ляет получить оценки т и X. При известном т оценкой
параметра X является опытное значение X, определяемое
по уравнению
1 = тп I ti- (5.48)
I /-I
Доверительные границы для X, отвечающие довери-
тельным вероятностям си и а2, определяются по уравне-
ниям
Ян = (2т.г) /2тп, (5.49)
= ^Х(о2) (2тп'№ПГ1' (5.50)
где и } — квантили распределения лтг-квадрат
с 2тп степенями свободы для вероятности 1 —а, и а2.
Учитывая уравнение (5.48), можно (5.49) и (5.50)
записать в более удобном виде:
^-Н = Я1) (2тп) ti, (5.51)
(=1
j.= 4,|2„„,/2S l„ (5.52)
(=1
Следовательно, при определении доверительных гра-
ниц X нужно пользоваться таблицей хи-квадрат распре-
деления (табл. П.7.1).
16—1086 241
В том случае, .когда испытываются п однотипных
устройств, наработка которых подчиняется гамма-рас-
пределению с одинаковым параметром X, но различны-
ми известными параметрами оценка параметра ).
Производится по формуле
__ п
i=l
(5.53)
При этом уравнения для определения доверительных
границ Л остаются в силе при условии
У, Шг = тп.
/=1
Оценка вероятности безотказной работы устройств
с гамма-распределением отказов производится по фор-
муле
(5.54)
k=m
где к и т — оценки масштабного параметра и парамет-
ра вида закона соответственно.
Для подсчета P(t\) можно использовать таблицы сум-
марных значений функции Пуассона (табл. П.7.9). В тех
случаях, когда т не является целым числом, нужно при-
бегать к интерполированию.
При отсутствии таблиц для малых, но больших еди-
ницы значений т, а также при значениях М,<0,1 можно
воспользоваться формулой
т— 1 _
IP(0 = j]
k=0
(5.55)
Для определения доверительных границ P(t) при
гамма-распределении нет приемлемого для практики ре-
шения.
Объем испытаний п для оценки параметра к при
известном параметре т можно определить, если задана
242
относительная ошибка 6 (в процентах). Обозначив через
ri — 1 + юо х„ ’
находим то табл. П.7.2 для заданного п и доверитель-
ной вероятности а'=(1+а)/2 (а— вероятность довери-
тельного интервала) число степеней свободы mn=k.
Тогда
n=klm.
НЕПОСРЕДСТВЕННАЯ ОЦЕНКА ВЕРОЯТНОСТИ
БЕЗОТКАЗНОЙ РАБОТЫ (ВЕРОЯТНОСТИ ОТКАЗА)
Если три испытаниях невозможно или нецелесообраз-
но регистрировать наработку испытываемых объектов,
но могут быть зарегистрированы факты отказов, то
оценка вероятности безотказной работы (вероятности от-
каза) при независимых испытаниях производится непо-
средственно с помощью частотьцпо формулам
Р= (п—d)]n,Q=d]n (5.56)
где Р и () —оценка вероятности безотказной работы и
вероятности отказов соответственно; п—объем выбор-
ки; d — число зарегистрированных отказов.
В большинстве случаев удобнее первоначально оце-
нивать вероятность отказа, а затем, при необходимости,
определять вероятность безотказной работы.
Доверительные границы вероятности отказа вычис-
ляются по следующим формулам:
Qa —-------(2^-----------------, (5.57)
2/г — cl + 1 4- Х(1—а,) (27)
V2
QB =-------у.2-»-----------, (5.58)
2/г — d + -g- (2т+2)
Где 7(1~К1) (2<о—квантиль распределения xu-квадрат с k—
~2d степенями свободы для вероятности а,; х2Кз) (2rf+2) —
квантиль того же распределения с k = 2 (сЦ-1) степенями
свободы для вероятности аа.
Значения у2 (2а) и yJM (2а+2) определяются по
табл. П.7.1.
*6* 243
При определении двустороннего доверительного ин-
тервала с вероятностью а нужно исходить из уравнения
а=«1 + аг—1. (5.59)
При cti = ct2=a'
а=2а'—1. (5.60)
Если число отказов d=0, то
Q^l/(/z + l), QH = 0, QB==l-(/r^;. (5.61)
При ограниченных .генеральных совокупностях при-
веденные выше 'формулы дают хорошие результаты при
условии
n/W<0,l, (5.62)
где N — число .экземпляров устройств в испытываемой
партии (объем генеральной совокупности).
Объем потребных испытаний п для оценки Q с пре-
дельной абсолютной ошибкой е при доверительной веро-
ятности а приближенно находится из уравнения
z2
n = ~-Qe(i-Qe), (5-63)
где Qe — ориентировочное значение вероятности отказа.
Величину za для р — а. находим из табл. П.7.6.
Если испытываются несколько выборок из одной и
той же генеральной совокупности, то оценка вероятно-
сти отказа производится по формуле
Q = X di I S Пг = (5.64)
i=l / <=1
где г — число выборок.
Доверительные границы определяются также по фор-
мулам (5.57) и (5.58), но и для определения квантилей
xw-квадрат распределения нужно брать следующие чис-
ла степеней свободы: &=2о^. —для нижней границы,
k=Q (ds+ 1) —для верхней границы.
Основным критерием надежности устройств с цикли-
ческим характером работы является вероятность отказа
<7о (вероятность безотказной работы р0=1—<?о) в каж-
дом отдельном цикле, которая определяется по формуле
(5.56) при г/=^=0, где п— число циклов работы при испы-
таниях, а d — число циклов с отказами. Когда d=0,
оценка Q производится по формуле (5.61).
244
Производными критериями от q0 являются:
i) вероятность получения т последовательных цик-
лов безотказной работы
(5.65)
2) вероятность отказа на m-м цикле
(5-66)
3) вероятность т и более последовательных циклов
безотказной работы
т
^т = 1-£(1-Л; (5.67)
1=0
4) 'Среднее число (математическое ожидание) циклов
безотказной работы
<5-68)
1 Чо Чо
5) среднее число циклов гзго отказа восстанавливае-
мых устройств
М (5.69)
^=l-r qa - ' ’
Оценки этих критериев могут быть получены по при-
веденным выше формулам с подстановкой вместо qo его
оценки до, полученной опытным Путем.
КОНТРОЛЬ НАДЕЖНОСТИ
Контроль надежности имеет своей целью проверить
гипотезу о том, что надежность не ниже установленного
уровня. При этом конечным результатом, как правило,
является одно из двух решений: принять партию, считая
надежность изделий удовлетворительной, или забрако-
вать контролируемую партию изделий как ненадежную.
Так как контроль надежности производится на осно-
ве испытаний выборки, то при принятии решений воз-
можны два вида ошибок:
а) ошибка первого рода — когда хорошая партия
бракуется;
б) ошибка второго рода — корда плохая партия при-
нимается.
' 245
Вероятность ошибки первого рода называется риском
поставщика и обозначается буквой а. Вероятность ошиб-
ки второго рода называется риском заказчика и обозна-
чается буквой р.
Существуют три основных статистических метода
контроля надежности:
— метод однократной выборки (одиночный кон-
троль) ,
— метод двукратной выборки (двойной контроль),
— последовательный метод.
Каждый из этих методов имеет свои достоинства и
недостатки и может быть оптимальным в том или ином
конкретном случае.
Контроль по методу однократной выб.орки легче пла-
нируется и осуществляется. Однако это наименее эко-
номичный метод, так как он требует относительно боль-
шого объема контроля, особенно для партий с высокой
или .низкой надежностью.
Контроль по методу двукратной выборки более эко-
номичен, чем одиночный. Но это его главное преимуще-
ство проявляется лишь при контроле больших партий
с очень низкой или очень высокой надежностью. При
промежуточном уровне надежности нет выигрыша в по-
требном объеме выборки. Расчеты, связанные с осуще-
ствлением двойного контроля, более сложные, чем при
одиночном контроле. Кроме того, увеличивается время,
потребное для контроля. Поэтому метод двукратной вы-
борки применяется для целей контроля надежности
крайне редко.
Самым экономичным методом контроля надежности
является последовательный метод. Средний объем вы-
борки обычно составляет 50—65% объема при одиноч-
ном .контроле для партий с высокой надежностью. Тех-
ническое осуществление последовательного контроля не
связано с какими-либо трудностями. Единственный не-
достаток этого метода заключается в большем времени
контроля, чем при предыдущих методах. Однако этот
недостаток можно свести к минимуму рациональной
организацией испытаний.
В связи с тем, что в практике контроля надежности
пользуются главным образом одиночным и последова-
тельным методами, рассмотрим лишь эти два метода.
Совокупность условий испытаний контролируемых
изделий и правил принятия решений называется планом
246
контроля. Под совокупностью условий испытаний пони-
маются условия браковки и приемки, заданные значения
аир, установленный объем испытаний ,и др. Правила
принятия решений определяются методами контроля. Так
как число сочетаний различных условий испытаний и
правил принятия решений может быть значительным, то
и количество различных планов весьма большое.
По целевому назначению планы статистического кон-
троля надежности можно подразделить на две группы:
— планы контроля вероятности отказа (вероятности
безотказной работы) или числа дефектных изделий
в партии;
— планы контроля уровня параметров законов рас-
пределения отказов.
КОНТРОЛЬ НАДЕЖНОСТИ НО МЕТОДУ ОДНОКРАТНОЙ
ВЫБОРКИ
Метод однократной выборки заключается в том, что
из контролируемой партии объема N изделий берется
одна случайная выборка, объема п экземпляров. Исходя
из N, п и а или р устанавливаются оценочные нормати-
вы Ао и Аг, если выборочное значение контролируемого
параметра меньше или равно Ао, то партия признается
надежной; если больше или равно At, то партия бра-
куется.
Если контролируется число дефектных изделий (ве-
роятность отказа) в партии объема N изделий и при
наличии в ней О0 дефектных изделий [qo—Do/N), надеж-
ность партии считается высокой, а при наличии Z)t де-
фектных изделий (q1 = Di/N)—низкой, то при заданных
а и р оценочные нормативы До и Л1 устанавливаются из
соотношении
(5.70)
(5-71)
где d— число дефектных изделий в выборке; а' — риск
поставщика,' близкий к заданному а; р'— риск заказчи-
ка, близкий к заданному р.
247
В общем случае а'^а и из-за диокрётности
гипер геометрического распределения, используемого
в формулах (5.70) и (5.71). Величины сочетаний, приме-
няемые в этих формулах, могут быть взяты из
табл. П.7.10.
Практическое использование формул (5.70) и (5.71)
при «>100 весьма затруднительно. При <7о<О,1 и qt<
<0,1 хорошее приближение к (5.70) и (5.71) дают фор-
мулы
а' = 1 - £ ClDo (l-f)D“~< (5.72)
(5-73)
<?=0
где f—nIN.
Соотношения (5.72) и (5.73) целесообразно исполь-
зовать для партий объемом N^. 500.
Когда объем партии Лг>500, а также при испытани-
ях восстанавливаемых изделий или когда п^0,1Л\ мож-
но пользоваться биномиальным законом распределения,
в соответствии с которым
а'=1-£ C^(l-<7o)*-d, (5-74)
d=0
(5-75>
</=0
Для подсчета Ао и Д при «<;50 можно пользоваться
табл. П.7.11.
Если соблюдаются условия
n^0,lN; гд>0,1, <7^0,1;
то, пользуясь распределением Пуассона, получим
<?=Л0+1
а=А,
(5.76)
(5-77)
где cio~q0n; a^q^n.
248
Ошибка, возникающая при замене биномиального
распределения распределением Пуассона, имеет порядок
q2n. Формулы (5.76) и (5.77) целесообразно использо-
вать для контроля надежности ,кру1пиосер'ий'ных (п2>50)
высоконадежных устройств. Для облегчения определе-
ния А. и Ai служит табл. П.7.9.
Очень удобной таблицей для построения .планов кон-
троля, основанных на распределении Пуассона, является
табл. П.7.12, с помощью которой .при заданных а или р
и Ло или Ai можно определить a0=nq0 или При
этом легко определить объем выборки, если известны </о
или qi, а также решить обратную задачу — найти c/o(r/i)
при заданном п.
При .контроле больших партий (SOsgCnsgCOJK) со
сравнительно невысокой надежностью (по9оД4) можно
пользоваться приближенными .формулами
• а = 0,5 — Фо Г(5.78)
1 Vnq0 (1 - ?„) J
р' = 0,5 — Фо
Гnq, Д- 0,5 — 4, 1
L Кл?, (1 — </,) J’
(5.79)
где Фо — функция Лапласа, значения которой находятся
по табл. П.7.13.
Контроль надежности по наработке сводится к срав-
нению средней наработки до отказа со значениями до-
верительных границ, определенных с вероятностями
cti=l—а и 02=1—Р-
ПОСЛЕДОВАТЕЛЬНЫЙ МЕТОД КОНТРОЛЯ НАДЕЖНОЕ! И
Последовательный .метод контроля не предусматри-
вает предварительного определения объема выборки.
Информация о надежности испытываемых устройств
накапливается при последовательно возрастающем объ-
еме испытаний (т). На каждом этапе испытаний отно-
шение правдоподобия 1т сравнивается с заранее опре-
деленными оценочными нормативами
А=(1—₽)/а, (5.80)
В = р/(Ь-а). (5.81)
При этом .могут быть приняты три решения:
249
если lm^B — партия принимается;
если — партия бракуется;
если B<zlm<A—испытания продолжаются.
При последовательном методе контроля возможны
два способа контроля — контроль числа дефектных из-
делий и контроль по наработке.
Контроль числа дефектных изделий
В том случае, когда необходимо произвести контроль
числа дефектных изделий в малосерийной партии, со-
стоящей из W экземпляров, 1т можно подсчитать по
формуле
С1”1 ст
<1 fn—d
Г m Г t
^Do \M—Dt
(5.82)
где dm — число дефектных изделий в выборке объемом
в т экземпляров; Do — число дефектных изделий в пар-
тии хорошей надежности, Di — число дефектных изде-
лий в партии плохой надежности.
Формула (5.82) практически может быть использова-
на только для очень малых партий (W^150). Но и при
этих условиях расчеты 1т .громоздки, что усложняет
контроль.
Более удобной и достаточно точной является форму-
ла
(5.83)
где с==С§»; ст = С°°_^. r = D,-DB.
Для облегчения процедуры контроля можно заранее
подсчитать для определенных значений dm=0, 1, 2, 3, ...
приемочные (тПр) и браковочные («бр) объемы испы-
таний:
fnap^N[l-(cmB/c)llr], (5.84)
тебр<Лф - (стА!с)'1г]. (5.85)
Рассчитанный таким образом план контроля может
быть представлен в табличной или графической форме.
На рис. 5.1 показан график контроля, где область П,
лежащая ниже линии J, —область приемки, область Б,
250
ле',ащая выше линии 2,— область браковки, область
ПИ, заключенная между линиями 1, 2 и осями коорди-
нат, — область продолжения испытаний.
Графики контроля можно строить по трем характе-
ристическим точкам:
a)Jro = 0, /n0 = N(l-B1/,);1 1
б) dm = £>„ т = N (1 — (A/c)1/rj; [ (5'86)
в) dm = (D0-{-Dl)[2,^m = N. J
Для контроля надежности больших партий изделий
(М_>1 ООО), а также восстанавливаемых изделий целе-
Рис. 5.1. График контроля.
dm
а пт
сообразно пользоваться биномиальными планами, по-
лучаемыми из соотношения
(5.87)
где — вероятность отказа в каждом одиночном испы-
тании для партии с хорошей надежностью; q\— то же
для партии с плохой надежностью.
Из (5.87) вытекают формулы для приемочных (dnp)
и браковочных (^бр) чисел дефектных изделий из числа
т испытаний:
<7ир < -j- ms, d6f) > А2 -|- ms, (5.88)
где
^ = (lgB)/[lgf-+lg jEy).
I \ VO 1 41/
л2 = (1ёЛ) / (1g ^-4-ig
I \ 40 1 41/
(5.89)
Приемочные и браковочные числа для ряда значений
т могут быть подсчитаны заранее и представлены в виде
таблиц плана. Для практических целей удобнее пред-
251
ставЛять план контроля в виде графика (рис. 5.2). Из
(5.88) следует, что приемочные (dnp) и браковочные
(dep) числа линейно зависят от объема испытаний, при-
чем /ц и й2 определяют отрезки на оси ординат, as —
тангенс угла наклона прямых .к оси абсцисс. Если вели-
чина риска поставщика а и риска заказчика р равны,
то й1 = й2- При построении графика плана полезно опре-
Рис. 5.2. План контроля.
делить минимальное число испытаний, при котором
можно принять партию, когда число отказов d=0. Из
(5.88) получаем
/По=—hi/s.
(5.90)
Вычисли® т0, можно построить график плана по трем
характеристическим точкам:
a) dm = 0, тс = — hjs;
б) dm = ht, т = 0-
в) dm — h„, т — 0. «
(5.91)
Если контролируется надежность большой партии
изделий (N^\ ООО) или изделий, восстанавливаемых
в процессе контроля,-при условии <71^0,1, то, исходя из
распределения Пуассона, имеем
(5.92)
252
Тогда исходные величины для построения графика
контроля определяются соотношениями
h2 = -**~
s=_ 0,4343 (д -д)
(5.93)
Vo
Все остальные положения последовательного контро-
ля остаются такими же, как и в биномиальном плане.
Контроль по наработке
Последовательный контроль надежности по наработ-
ке в случае экспоненциального распределения времени
безотказной (работы изделий осуществляется в соответ-
ствии с правилами:
— партия принимается, если
hy -ф
— партия бракуется, если
й2 ] “
— испытания продолжаются, если
^2 ~4~ dms 17 /д ] - dms,
(5.94)
(5.95)
(5.96)
где — суммарная наработка всех испытываемых изделий;
й1 = - 2,303 (lg B)/(2j — 2С);
/г2 = — 2,303 (1g A)/(F — 20);
s = 2,303 ( IgM I
\ ло J
(5.97)
Xo — интенсивность отказов надежной партии; Zi— ин-
тенсивность отказов ненадежной партии.
Следует отметить, что при неусеченных последова-
тельных испытаниях невосстанавливаемых устройств на
каждом этапе испытаний
dm
С = S h, (5.98)
z=i
где ti — наработка до отказа i-го экземпляра.
253
При одновременном испытании N невосстанавЛййае-
мых экземпляров на каждом этапе испытаний, отмечен-
ных временем I*,
“п
+ (5.99)
Если на испытании находится N восстанавливаемых
устройств, замена которых осуществляется практически
мгновенно, то на каждом этапе
ts = M*. (5.100)
Очевидно, что при испытаниях в (5.99) и (5.100)
можно взять постоянным /*, a N последовательно уве-
личивать, что удобно в приемочном последовательном
контроле.
График последовательного контроля наработки изо-
бражен на рис. 5.3. Характеристическими точками гра-
фика являются:
a) dm = — hjs ^ = 0; I
б) dm = 0, = ? (5.101)
в) dm = 0, tz — ht. J
Контроль наработки устройств с нормальным рас-
пределением времени безотказной работы при извест-
Рнс. 5.3. График последовательного контроля.
ном среднем квадратическом отклонении осуществляет-
ся с помощью следующих условий:
— партия принимается, если
/Е > й, ф- sm,
— бракуется, если
iy <й2ф-5/н,
254
(5.102)
(5.103)
— испытания продолжаются, если
К + sm^>ty~J>hz-\^ sm,
(5.104)
где
4=Ste
i=l
л, = —2,303-У1ё т ;
—2,303 ~~lg^ :
г0 —А
*=(т;+л)/2
(5.105)
То — средняя наработка до отказа в партии с хорошей
надежностью; Ti—средняя заработка до отказа в пар-
тии с плохой надежностью.
Характеристические точки графика плана:
а) т = — hjs, ty = 0; 'J
б) т = 0, = hz- ?
в) т = 0, ty~hl. I
(5.106)
График контроля соответствует рис. 5.4.
Следует отметить, что иногда точное построение гра-
фика плана только по характеристическим точкам за-
труднительно. В таком случае следует воспользоваться
Дополнительно одной или двумя точками, лежащими на
продолжении линии, или увеличить масштаб графика.
255
§ 5.2. ТИПОВЫЕ ПРИМЕРЫ И ИХ РЕШЕНИЕ
Задачи, которые встречаются при оценке надежности
по результатам испытаний могут быть разбиты на сле-
дующие группы:
— определение вида и параметров законов распре-
деления времени исправной, работы (времени до отка-
за) ;
— определение количественных характеристик на-
дежности;
— контроль .надежности на соответствие техническим
условиям;
— определение числа испытуемых изделий и време-
ни испытания для получения характеристик надежности.
Рассмотрим типичные примеры в указанной последо-
вательности.
Пример. 5.1. В результате опыта получен следующий
вариационный ряд времен исправной работы изделия
в часах:
2; 3; 3; 5; 6;
7; 8; 8; 9; 9;
13; 15; 16; 17; 1'8;
20; 21; 25; 28; 35;
37; 53; 56; 69; 77;
86;, 98; 119.
Требуется установить закон распределения времени
безотказной работы.
Решение. 1. Используя данные и .вычислив =
=28, заполняем табл. 5.4 но форме табл. 5.1.
2. Проверяем согласие экспериментального распреде-
ления с экспоненциальным распределением. Наносим
экспериментальные данные на координатную сетку
(рис. П.6.1). Получаем расположение точек, показанное
на рис. 5.5.
3. Проводим через отметки прямую линию таким об-
разом, чтобы отклонения точек от прямой были мини-
мальными. Убеждаемся в возможности линейной интер-
поляции. Находим и снимаем наибольшее отклонение.
В нашем случае D=0,09.
4. Рассчитываем критерий согласия Колмогорова:
D|//7^0,0'i j/28 = 0,48,
0,48 <1,00.
256
Г АБЛ ИЦ A 5.4 Т АБ Л ИЦ А 5.5
Таблица экспериментальных Исходные! данные к
данных к примеру 5.1 примеру 5.2
6 ni Нг *4 Ч ni nt Hi
2 1 1 0,04 0,96 115 1 1 0,04 tl 0,96
3 2' 3 0,11 0,89 232 1 2 0,08 0,92
5 1 4 0,14 0,86 328 1 3 0,12 0,88
6 Г 5 0,18 0,82 368 1 4 0,16 0,84
7 1 6 0,21 0,79 393 1 5 0,21 0,79
8 2 8 0,29 0,71 404 1 6 0,25 0,75
9 2 10 0,36 0,64 421 1 7 0,29 0,71
13 1 И 0,39 0,61 457 1 8 0,34 0,66
15 1 12 0,43 0,57 483 1 9 0,39 0,61
16 1 13 0,47 0,53 511 1 10 0,44 0,56
17 1 14 0,50 0,50 527 1 11 0,50 0,50
18 1 15 0,54 0,46 540 1 12 0,54 0,46
20 1 16 0,57 0,43 544 1 13 0,58 0,42
21 1 17 0,61 0,39 572 1 14 0,62 0,38
25 1 18 0,64 0,36 598 1 15 0,66 0,34
28 1 19 0,68 0,32 605 1 16 0,70 0,30
35 1 20 0,72 0,28 619 1 17 0,74 0,26
37 1 21 0,75 0,25 633 1 18 0,78 0,22
53 1 22 0,79 0,21 660 1 19 0,83 0,17
56 1 23 0,82 0,18 681
69 1 24 0,86 0,14 1 20 0,87 0,13
77 1 25 0,89 0,11 736 1 21 0,91 0,09
86 1 26 0,93 0,07 791
98 1 27 0,96 0,04 1 22 0,95 0,05
119 1 28 1,00 0,00 942 1 23 1,00 0,00
В соответствии с формулой (5.10) считаем, что закон
распределения времени безотказной работы не противо-
речит экспоненциальному.
Пример 5.2. В результате опыта получен следующий
вариационный ряд времен безотказной работы изделия
в часах:
115; 232; 328; 368; 393;
404; 421; 457; 483; 511;
527; 540; 544; 572; 598;
605; 619; 633; 660; 681;
736; 791; 942.
Нужно определить закон распределения времени без-
отказной работы.
17—1086 257
258
Решение 1. Используй дайнме, заполняем Табл. 5.5,
предварительно вычислив значение У, гц = 23.
(')
2. Проверяем согласие экипе|римещтальн'ого распре-
деления с экспоненциальным распределением. В резуль-
тате 'Проверки получен отрицательный ответ. Проверяем
согласие экспериментального распределения с усечен-
ным нормальным распределением. Наносим эксперимен-
тальные данные на координатную сетку (рис. П.6.2). По-
лучаем расположение отметок, показанное на рис. 5.6.
3. Проводим через отметки прямую линию и убеж-
даемся .в возможности линейной интерполяции. Находим
и снимаем наибольшее отклонение: 0 = 0,03.
4. Рассчитываем критерий согласия:
D |7/г = 0,03 (/23=0,14, 0,14>1,00.
В соответствии с формулой (5.10) считаем, что ис-
следуемый закон распределения .времени исправной ра-
боты подчиняется усеченному нормальному.
Пример 5.3. В результате опыта получен следующий
вариационный ряд времен восстановления в минутах:
10; 20; 35; 35; -35;
35; 35; 35; 45; 45;
45; 53; 60; 60; 60;
60; 70; 70; 70; 75;
75; 85; 85; 90; 95.
Требуется установить закон распределения времени
восстановления.
Решение. 1. Исполь-
зуя данные, заполняем
табл. 5.6.
2. Нанесем эксперимен-
тальные данные на коор-
динатную сетку (рис.
П.6.1). Получаем распо-
ложение отметок, пока-
занное на рис. 5.7. Из ри-
сунка видно, что линей-
ная интеполяция невоз-
можна. Это свидетельст-
вует о том, что экспери-
ментальные данные не
подчиняются экспоненци-
альному закону.
17*
ТАБЛИЦА 5.6
Исходные данные к
примеру 5.3
5 «г "i Нг «I с” £ я Д
10 1 1 0,04 0,96
20 1 2 0,08 0,92
35 6 8 0,32 0,68
45 3 11 0,44 0,56
53 1 12 0,48 0,52
60 4 16 0,64 0,36
70 3 19 0,76 0,24
75 2 21 0,84 0,16
85 2 23 0,92 0,08
90 1 24 0,26 0,04
95 1 25 1,00 0,00
£59
Проверка на соответствие экспериментального рас-
пределения усеченному нормальному также не дает по-
ложительного результата. Тогда .в соответствии с приня-
той последовательностью законов производим проверку
подчинения экспериментального распре деления логариф-
мичес.ки-н'ормальному закону. Для ©того наносим экспе-
риментальные данные на координатную сетку
(рис. П.6.3). Получаем расположение отметок, показан-
ное на рис. 5.8.
3. Проводим через отметки прямую линию и убеж-
даемся в возможности линейной 'интерполяции.
Находим и снимаем наибольшее отклонение: £) = 0,07.
4. Рассчитываем критерий согласия:
D ]/k = 0,07 /25 = 0,35;
ТАБЛИЦА 5.7
Исходные данные к
примеру 5.4
час Х(Д/Г) }[час
0—20 16 0,0400
20—40 5 0,0263
40—60 2 0,0167
60—80 2 0,0250
80—100 2 0,0500
100—120 1 —
0,35< 1,0.
В соответствии с формулой (5.10) считаем, что ис-
следованный закон распреде-
ления времени восстановления
подчиняется логарифмически-
нормальному.
Пример 5.4. Используя дан-
ные примера 5.1 путем постро-
ения гистограмм и их аппро-
ксимации аналитическими вы-
ражениями, установить закон
распределения времени исправ-
ной работы.
Решение. 1. Заполняем
табл. 5.7 по форме табл. 5.2.
2. Строим гистограмму Х(/) (рис. 5.9).
3. Находим среднее значение Лср и наибольшее от-
клонение:
. 0,0400 + 0,0263 + 0,0167 + 0,0250 + 0,0500 _
Л ср — 5 —
= 0,0316-^-,
час
D — 0,0184.
4. Проверяем соответствие закона по критерию со-
гласия Колмогорова
D yk = 0,0184 /28 = 0,097 < 1.
260
Рис. 5.7. График к примеру 5.3 (экспоненциальный закон).
Рис. 5.8. График к примеру 5.3 (логарифмически-нормальный).
261
Рис. 5.9. Гистограмма Л (Д#,) (к примеру 5.4).
В соответствии с формулой (5.10) считаем, что за-
кон распределения экспоненциальный. ’
Пример 5.5. При испытании десяти механических эле-
ментов, отказы которых распределены нормально, полу-
чены следующие значения времени безотказной работы
в часах: 150, #2=100, Z3=70, #4=200, #5= 100, t6= 100,
#7=150, #8=200, #9=80, #ю=150.
Требуется оценить Т и о и определить для них дву-
сторонние доверительные интервалы с вероятностью а=
= 0,90.
Решение. 1. По формуле (5.22) определяем Т:
Т = (150 + 100 4-70 + 200 + 100 + 100 + 1504-
+ 200 + 80 + 150) = 130 час.
2. Для определения S производим предварительные
ТАБЛИЦА 5.8
Предварительные вычисления для определения $
(к примеру 5.5)
#1- -т 20 30 60 70 30 30 20 70 50 20
(ti- -Г)2 400 900 3600 4900 900 900 400 4900 2500 400
вычисления, сведенные в табл. 5.8, и суммируем квад-
раты разностей #„—Т:
10
£ (#г — 7)2 = 19800.
Z=:l
262
Подставляя полученную величину в уравнение (5.23),
получаем
S=/'§™=47.
3. Чтобы определить доверительный интервал для Т,
подсчитываем
——-^L- = 14,8.
п Ию
С помощью табл. П.7.5 находим / = f(0 и) (в) =
= 1,83.
Воспользовавшись уравнениями (5.25) и (5.26), по-
лучаем
Тн=130 -1,83-14,8=130—27 = 103,
7',,= 130 + 27= 157.
Следовательно, можно утверждать с вероятностью не
ниже чем 0,9, что интервал времени 103—157 час на-
крывает параметр Т.
4. Для определения доверительного интервала о по
табл. П.7.1 находим
. 2 __ 2 _ о оо
Z(3/2) («—1) - /(о.Оо) (s)
Т — 1 =16 9
/-(1-3/2) (и—1) — /-(о,»5) (о) 1и,;7-
В соотв-тствит с формулой (5.27) получаем
9-47г ^_г.^ 9-47г:
16.9 +,:Г~
или 1100 < 72 < 5660.
Откуда
33,5 час О <2 75 час.
Пример 5.6. В результате испытаний 15 экземпляров
электрохимических элементов были получены следую-
щие значения наработки в часах: 10,2; 12,3; 17,1; 18,4;
20,3; 22,7; 23,1; 25,5; 26,4; 28,9; 30,3; 32,5; 33,3; 38,1; Jl,0.
Определим оценку средней наработки до отказа (7) и
дисперсию (о2), а также нижнюю границу Т и верхнюю
границу ц с вероятностью а=0,95.
263
Решение. 1. Находим
п
= (10,2 +12,3 +17,1 +18,4 +
«=1
+ 20,3 + 22,7 +;23,1 + 25,5 + 26,4 + 18,9 + 30,3 +
+ 32,5-1^33,3 + 38,1 4-41,0)==--380,1 =25,34 час.
2. Определяем S2, используя тождество (5.24), для
чего значения наработки возводим в квадрат и сум-
мируем:
Е = 104,04 + 151,29 + 292,41 + 338,56 + 412,09 +
i=i
+ 515,29 + 533,61 + 650,25 + 696,96 + 835,21 +
+ 918,09 + 1056,25 + 1108,89 + 1451,61 +
+ 1681,00= 10745,55;
— / =-]L.380,l2=-1^^=9631,73;
п I J / 15 15
£ (ti — Т)2 = 10745,55 — 9631,73 = 1113,82.
1=1
По формуле (5.23) находим S2 и затем X:
S2 = ~ 1113,82 = 79,56; S = 8,92 час.
3. Для определения нижней границы Т подсчитываем
величину
5 8,92 „ о
—г— 1’ Z.’J
Ун
и по табл. П.7.5 находим квантиль распределения Стыо-
дента для вероятности 0,95 и числа степеней свободы
/=14:
^(0,в5)(14) = 1,76.
По формуле (5.25) находим
Тн=25,34— 1,76 • 2,3=25,34—4,05=21,29 час.
264
Следовательно, можно утверждать с вероятностью
0,95, что средняя наработка до отказа будет не менее
21,29 час.
4. Верхняя граница а определяется из соотношения
(w-l)-S2
° < „2
%(!-«,) (п-1)
По табл. П.7.1 находим , = 6,57, тогда
'ЧО.Об) (141
з 14*79,56 < j-л -« q
з < ——= 169,50; а < 13 час.
< 0,0/
Пример 5.7. Определить приближенно объем п испы-
таний для оценки средней наработки до отказа с ошиб-
кой е не более 25 час при вероятности а=0,90, если со
ориентировочно равно 50 час.
Решение. По табл. П.7.6 для а = 0,9 находим za=
= 1,64.
Из уравнения (5.39) находим
Пример 5.8. Испытания 100 ламп накаливания про-
должались 4=500 час. За время испытаний вышло из
строя 5 ламп с наработкой до отказа в часах соответ-
ственно 0=50, 4=150, 4=250, 4=300 и 4=450. Опре-
делить среднюю наработку до отказа ламп и среднее
квадратическое отклонение, полагая, что срок службы
ламп подчиняется нормальному закону.
Решение. Для вероятностей 0,01; 0,02; 0,03; 0,04;
0,05 по табл. П.7.6 находим квантили ир :
и =2,33; и = — 2,05; и = — 1,88;
Pi Ра Ра
и = — 1,75 и и = —1,64.
Pi Ръ
Составляем уравнения:
Т — 2,33а = 50,
Г —2,05а = 150,
Г—1,88а = 250,
Г—1,75а = 300,
Т— 1,64а=450.
265
Для решения данной системы уравнений складываем
их и получаем 5Т—9,65о= 1 200.
Затем, умножая исходные уравнения на коэффици-
енты при о* и суммируя, получаем 9,657’—48,90о=2 160.
Решая нормальные уравнения, находим Т~ \ 140 час,
о=465 час.
Для оценки точности полученных значений Т и S = s
определяем
k —
1140 — 500
465
= 1,38.
По табл. П.7.7 находим /г(1,38) =23,65, /З(1,38) =9,11.
Тогда
(Т) - f2 (£)=^--23,65 = 51000,
(^-^-9,11 = 19,60.
Откуда о(Т’) =230 час, о(сг) =45 час.
Как видно, точность определения параметров распре-
деления в условиях данного примера невысокая. Дове-
рительные интервалы величиной ±2о, что соответствует
вероятности приблизительно 95%, в данном случае со-
ставляют
7’±2о!(7’) = 1 140±2- 230=1 140±460 час,
о±2о((т) =465±2-45=465 час±90 час.
Пример 5.9. План [п, Б, п]. При испытании п=10
устройств до выхода их из строя получены следующие
значения наработки в часах: /i=30, tz=35, 4=50, 4=85,
4=100, 4=150, 4 = 250, 4= 300, 4=400, 4о=600.
Требуется определить:
1. Оценку К интенсивности отказов %.
2. Верхнюю доверительную границу с доверитель-
ной вероятностью «2=0,90.
3. Двусторонний доверительный интервал для X при
а=0,90 и 01=02=0,05. _
4. Оценку средней наработки до отказа Т и его ниж-
нюю границу с вероятностью 0,90.
266
Решение. На основании табл. 5.3 имеем:
ю
= 2000 ^ас.;
1=1
1=^-=^=5.10- 1/шс;
г=1
„,2
, __ Л(0,9) (20)
Ав~~ 2-2000 *
Пользуясь табл. П.7.1, определяем
у? ., . = 28,4.
А(о,э) (20)
Тогда
Zb=^-=7’1-10’’ 1 час-
Из табл. 5.3 следует, что
2 2
г, _ 7(0,95) (20) . j 7(0,05) (20)
в4000 ’ н 4000
Пользуясь табл. 11.7.1, находим
у2 .. . = 31,4 у.2 .. .= 10,9.
/ч-(0,95) <20/ л0,051 (20)
Тогда
2в=тббб~=7’85’10-3
10 о
Ян = Т5бГ^2’72’10"3 Хчас-
Учитывая соотношения Т=1/Я и 7,Н=1/ЯВ, определяем
= 2000 ппп ™ 2-2000 1ЛП
Т = -JQ- — 200 час-, Тп = -28 4 = 140 час.
Пример 5.10. План [п, Б, Ц. За время испытаний по
плану [п=50, Б, /о=500 час] отказало d=6 устройств,
причем отказавшие устройства проработали до выхода
из строя соответственно 50, 150, 200, 300, 350, 450 час.
Требуется определить оценку X и двусторонний довери-
тельный интервал для а=0,8 при Pi=P2=0,10.
267
Решение. На основании табл. 5.3 (план № 2) име-
ем
б
^ = S j+ (50 — 6)-500 = 50+150 4-200 + 300 + 350 4-
i=l
+ 450 + (50 — 6) • 500 = 1500 + 22000 = 23500 час,
х=Т7“2+=2.85'10-'
2 2
, __ Х(0.9) (12) . , _ Х(0,10) (12)
в^“ 2-23500 ’ в 2-23500 '
Из табл. П.7.1 находим
Уч н ч=18,5; у? .. — 6,3.
•о.эМПЗ) ’ z"(0,I0)(12)
Тогда
».=‘S=3.95-10- l/vu:-,
i- = B®=1-34'20
Пример 5.11. План [п, Б, /0]. При испытаниях п=50
устройств в течение времени t0=500 час не зарегистри-
ровано ни одного отказа. Определить верхнюю довери-
тельную границу интенсивности отказов X с вероятно-
стью 02=90.
Решение. Суммарная наработка подсчитывается по
формуле (см. табл. 5.3)
tL — nt0=50 • 500=25 000 час.
Для определения воспользуемся формулой
+ = г0/ts.
Из табл. П.7.8 для а=0,90 определяем г0=2,3. Тогда
я-= й-0»'10'1 У™
Пример 5.12. План [п, Б, d]. При испытаниях по пла-
ну [«=50, Б, d=6] получены следующие значения нара-
ботки отказавших устройств: 50, 150, 200, 300, 350
и 450 час. Отказавшие устройства не восстанавливаются.
268
Требуется найти оценку л и доверительный интервал
с вероятностью а=0,90 при |3i= р2 = 0,05.
Решение. Подсчитаем суммарную наработку всех
испытываемых устройств (см. табл. 5.3):
6
/, = £ ti 4- (50 — 6)-450 = 50 + 150 + 200 -ф 300 -ф
-ф 350 + 450 + (50 — 6) - 450 = 1500 -ф 19800 = 21300 час.
Определяем Я:
Значения Лн и Яв будут:
2 2
- _ Х(1—0,95)(12) . п _ Х(0,95)(12),
н ~ 2-21300 ’ ®—' 2-21300
Пользуясь табл. П.7.1, находим
Х(1—0,95) (12) = 5,23, Х(0,95)(12) = 21,0.
Тогда
Ч=^г=4.9Б.10-1/<М<!.
Пример 5.13. План [п, В, /0]. При испытаниях «=100
устройств в течение времени /0=Ю0 час зарегистрирова-
но 5 отказов. Отказавшие устройства мгновенно заменя-
ются исправными. Требуется определить оценку интен-
сивности отказов, верхнюю доверительную границу %
с вероятностью 0,99 и доверительный интервал для X
с а=0,90 при Pi= [12=0,05.
Решение. Для оценки 7с воспользуемся формулой
Суммарная наработка определяется по формуле
= nt0 = 100-100 = 10000 час.
Тогда
— ч
юооо =5-10 г\]час.
269
Односторонняя верхняя доверительная граница будет
2
/в — 2Ц
Из табл. П.7.1 определяем
-/2 = 26 2
/>(0,99)(12) z'u,z'’
яв = -|^=13,1-10-41/^.
Для получения доверительного интервала воспользуемся
формулами табл. 5.3:
, %(0,05)(10) ; лв= %(0.95)(12)
н — 20000 20000'
Из табл. П.7.1 находим
v2 — о од. -у2 ___ О1 f)f)
>0(0,05)(10)J Л(0,95)(12)-4,’ии1
Таким образом,
Лв~ ^=1,97-10-4/^; 2В = iy.^10,5- час.
Cj " 1 kJ Z * 1U
Пример 5.14. План [п, В, d], При испытаниях п=
= 100 устройств до <7=10 отказов отмечено время td =
= 90 час десятого отказа.
Необходимо определить оценку интенсивности отка-
зов и верхнюю доверительную границу Лв с вероятностью
«2=0,95.
Решение. Оценка Л производится по формуле
где согласно табл. 5.3 (план № 6) tY = ntd= 100-90 =
= 9000 час.
Следовательно,
Я= 9000 =1’10 31]час.
Верхняя доверительная граница определяется по фор-
муле
2
, _ %(0,95)(20)
ъ~~ 2-9000 ’
270
По табл. П.7.1 находим для
Z(0.9S)(20) = 31,4,
Яв=-21А-= 1,75-\0~3Х/час.
Пример 5.15. При эксплуатации 240 невосстанавли-
ваемых объектов в течение года с общей наработкой
480 000 час выбыло из строя 80 объектов. Найти верхнюю
границу интенсивности отказов с вероятностью «2 = 0,95,
если известно, что отказы распределены по экспонен-
циальному закону.
Решение. В данном случае имеет место план
[п, Б, /о]. Определяем
ж (е _ 480000 еллл
7 = — - —— — 6000 час.
d 80
Затем, предполагая S — T и определяя по табл. П.7.5
/(о,95)(79)= 1,665, находим по формуле (5.13)
6000
~=- - 4900 час.
оо
Та = 6000-1,665-
контрольно-измерительном
Откуда Лв = 2,04- Ю4 Х/час.
Пример 5.16. Испытания
аппаратуры проводились по плану {н=20, В, t0= 1000 час].
За время испытаний зарегистрировано 62 отказа, кото-
рые немедленно устранялись. Оценить Z и найти ее дву-
сторонний интервал с вероятностью 0,90, если распреде-
ление отказцв аппаратуры экспоненциальное.
Решение. Находим Я, используя формулы табл. 5.3
(план № 5):
Я = = 31 10-4 Х/час.
ntB 20-1000 '
Для определения доверительного интервала нельзя
воспользоваться формулами табл. 5.3, так как число сте-
пеней свободы 2н=124>100, а табл. П.7.1 рассчитана на
число степеней свободы 100 и менее, поэтому восполь-
зуемся формулой (5.13), для чего по табл. П.7.5 находим
^(о,9о)(б1)= 1,295. _
Определив 7= 1/Я=323 час и положив S — T, получаем
7’BB«323±1,295-?L=323 ±51 час,
Кб2
?в = 374 час, Тп~27‘2час. Откуд а Я ~ (2,7 = 3,7) • 10-3 Х/час.
271
Б,Н
Пример 5.17. Для плана [п, Б, п] определить объем
испытаний, если необходимо оценить 7, с ошибкой, не
превосходящей 25% от истинного значения с вероят-
ностью ао = О,9О.
Решение. По формуле (5.14) находим й=л=1,25.
Пользуясь табл. П.7.2, для ri = l,25 и ао = О,9О находим
п 40.
Пример 5.18. Для плана [п, Б, /0] найти объем испы-
таний с вероятностью ао=0,80, если требуется оценить .7
таким образом, чтобы действительное значение не пре-
вышало с вероятностью а=0,95 более чем в 2 раза ниж-
нюю ее границу; если предполагаемое значение Хо=
= 2,5- 10“4 !/час
Решение. По табл. П.7.3 для k=Ri = 2 определяем
d = 8. Для ао=0,80 и rf = 8 по табл. П.7.4 определяем
коэффициент г3=0,78. Затем, предполагая Д>=2,5Х
X 10~4 1/час, по формуле (5.16) находим
/ 8-0,78 л с 1Л4
— 2 5-102< = 2,5-10
Пример 5.19. По плану [п, Б, d] необходимо организо-
вать испытания таким образом, чтобы с вероятностью
а=0,90 истинное значение 7 не превышало опытное бо-
лее чем в 2 раза.
Решение. Для /г = 2 и а=0,95 по табл. П.7.2 нахо-
дим d=8.
Пример 5.20. Для плана [п, В, /0] необходимо оценить
объем испытаний с вероятностью cto=O,9 при условии,
что истинная X не должна превышать опытную более
чем в 2,5 раза с а=0,95, если ориентировочно 7о =
= 5-10~4 11час.
Решение. Для k = 2,5 и а=0,95 по табл. П.7.2 опре-
деляем d—5. Затем пз табл. П.7.4 для d=5 и <хо=О,9О
находим г3=0,б2. Предполагая 7о=5-1О-4 {/час по фор-
муле (5.16) находим
, 5-0,62 conn
nt^ = ~5.10—4- —6200 час.
Пример 5.21. Известно, что число компонентов в си-
стеме ш=3, а а=0,9. Необходимо определить потреб-
ный объем испытаний аппаратуры с гамма-распределе-
нием отказов для оценки параметра с относительной
ошибкой не более 50%.
272
Решение. Определяем rt= 1+50/100.
По табл. П.7.3 для г, = 1,5 и а' = —~^-=0,95 на-
ходим число степеней свободы k = 20. Отсюда п =
20 „
ЭКЗ.
О
Пример 5.22. При испытаниях 5 электрогенераторов
с отказами, имеющими гамма-распределение, зарегист-
рированы значения наработок до отказа 100, НО, 130,
160 и 200 час. Оценить параметры т и Л.
Решение. По формулам (5.46) и (5.47) определяем
5
™ 140,
Л 5 &i5
5
ЕОг-ИО)2
™ --------------= 1650.
Откуда получаем Л = 0,0851 /час, иг =11,8.
Пример 5.23. Шесть экземпляров резервированной
системы с двукратным ненагруженным резервом и иде-
ально надежными переключающими устройствами испы-
тывались до наступления отказов. В результате испыта-
ний получены следующие наработки систем в часах: 200,
250, 300, 450, 600 и 780. Требуется оценить параметр Л
и найти его доверительный интервал с вероятностью
а=0,90, исходя из экспоненциального распределения от-
казов основного и резервных компонентов системы.
Решение. Из условия задачи вытекает, что нара-
ботка до отказа резервированной системы имеет гамма-
распределение с ш=3. Оценку параметра Л производим
по формуле (5.48):
Пользуясь табл. П.7.1, для
0,9 + 1 п
а, = а2 =---------------—=0,95
18—1086
273
и числа степеней свободы k = Чти = 2 3 6 = 36 находим
яи=-йй-=4’5-10’31/^-
2в=-^ = 9,9-10“31/адс.
Пример 5.24. Испытания 8 электронных устройств
производились до 5 отказов каждый. Суммарная нара-
ботка всех устройств составила 4 600 час. Оценить сред-
нюю наработку до отказа 7’ср, если закон распределения
отказов испытываемых устройств экспоненциальный.
Решение. В соответствии со свойством экспонен-
циального закона и формулой (5.48)
тср= * ±±_=1^.= 115 час_
ср Л тп 5-8
Пример 5.25. В ходе эксплуатации 3 однотипных вы-
числительных устройств: первое устройство до 3-го отка-
за наработало 85 час, второе до 5-го отказа наработало
15 час и третье до 2-го отказа — 40 час.
Наработка данных вычислительных устройств до ш-го
отказа имеет гамма-распределение. Оценить параметр Л
и найти его верхнюю доверительную границу с вероят-
ностью а2=0,95.
Решение. В соответствии с формулой (5.53) нахо-
дим
1— 3 + 5+2 — 10______4-10-21/чйс
85+ 115 + 50 250 ~4 Ш 1/ЧОС.
По табл. П.7.1 для а = 0,95 и £ = 2-10 = 20 находим
Х(0,9Б) (20) = 31,4.
Пользуясь формулой (5.52), определяем
V-=|2^6,28-10-2l/wx
Пример 5.26. При испытаниях 10 объектов по плану
[/г, Б, и] определено Г=50 час. Оценить P(t) для
/=100 час и найти верхнюю границу с вероятностью
а=0,90.
274
Решение. 1. Определяем
J____100 _о
Т 50 Z'
Пользуясь табл. П.7.14, находим р (100) = 0,1353.
2. Для получения Д, (100) по формуле РБ (t) =
-11
= е н необходимо найти 1Н. В соответствии с табл. 5.3
z„ определяется по формуле
„2
2 Х(1—а)(2«)
Из табл. П.7.1 находим yjr. = 12,4. Значение
-(и,Ш/
ищем как Тп. Таким образом,
19 4
2и = ДпЙ^=0-°124 1Л«с.
Для Д /= 0,0124 100= 1,24 Рв(100) на основании
табл. П.7.14 будет Рв (100) =0,2894.
Пример 5.27. При испытаниях 12 экземпляров аппа-
ратуры по плану \п, Б, /0] получена суммарная наработка
4 =1 500 час при отказе 6 экземпляров. Требуется оце-
нить время, в течение которого аппаратура будет рабо-
тать безотказно с вероятностью а = 0,95.
Решение. По формуле Т = tjd находим
Исходя из условия задачи и учитывая, что Р (/) =
= е~™ 1 — М, получаем 0,95 =1 — //250, откуда t =
=12 час.
Пример 5.28. Было испытано ряд электродвигателей,
наработка которых имеет гамма-распределение, и полу-
чены оценки параметров: т=11,8, .Х=0,085. Нужно оце-
нить вероятность безотказной работы электродвигателей
для времени /=100 час.
Решение. Для Pt—0,085-100=8,5 и А = т=11,8 по
табл. П.7.9 при помощи интерполирования находим сум-
му в соответствии с формулой (5.54): 2 — 0,17. Тогда
/>(/)« 1—0,17=0,83.
18* 275
Пример 5.29. После испытания партии устройств
с двойным ненагруженным резервом подсчитано, что
7 = 0,007. Требуется оценить P(t) для времени / = 50 час.
Решение. В данном случае т = 3, а Х/ = 0,007-50 =
= 0,35. Для определения P(t) воспользуемся форму-
лой (5.55):
2
fe=0
По табл. П.7.14 находим е °-35=0,705.
Тогда
р (50) = 0,705 <1 4- 0,35 4- = 0,705 -1,411 0,995.
к 2 J
Пример 5.30. При испытаниях механических деталей
с нормальным распределением отказов получены сле-
дующие оценки параметров распределения: 7’=2 500час;
5=1 000 час. Определить вероятность безотказной рабо-
ты за время /=500 час.
Решение. 1. Находим
500 - -2500 _ о. 2500 о е
1000 1000 — 2,0
2. По табл. П.7.13 определяем Фо (2,5) =0,494;
ф0 (—2) =0,477.
3. По формуле (5.28) получаем Р=1—0,017=0,983.
Пример 5.31. Используя данные примера 5.30, опре-
делить 90%-ную нижнюю доверительную границу P(t),
если дополнительно известно, что испытывалось n= i
= 100 изделий.
Решение. 1. Определяем коэффициент k по фор-
муле (5.32):
/г = 0,4е-2=0,054.
2. По формуле (5.31) получаем
'°l=2^-3=87'10-.
откуда а- — 0,0093.
3. Из табл. П.7.6 определяем ио,эо= 1,282 и, пользуясь
(5.30), окончательно находим
Ра=0,977— 1,282 • 0,0093=0,965.
276
Пример 5.32. По техническим условиям рабочее на-
пряжение генератора должно составлять 220 в ±10%.
После испытания 10 шт. генераторов получены значения
среднего У = 230 в и 5 = 20 в. Оценить вероятность
выполнения технических условий работы генератора и
найти нижнюю доверительную границу для P(v) са = 0,90.
Решение. 1. По формуле (5.33) и табл. П.7.13 на-
ходим
- ,, /242 —2304 ./198 — 2304
РО ) = ф« { —20 —J - Ф»(^0 —) =
= Фо (0,6) — Фо (— 1,6) = 0,226 + 0,452 = 0,678.
2. Для определения доверительной границы вычисляем
198 — 230 . с 242 — 230 п„
= 20 = -1.6; г2 = 20 - 0,6;
kt = 0,4 exp =0,11;
/г2 = 0,4 ехр (— °'6 = 0,33;
-г =тЦо,1Р(1 + -Ц^+о.зз* (1 + Т)-
— 2 • 0,11 • 0,33 1 _1_ о, 11 - 0,33> = 0,009.
3. В соответствии с формулой (5.30) находим
Рн=0,678— 1,28 • 0,09 = 0,563.
Пример 5.33. При испытании о = 25 химических источ-
ников тока получены выборочное среднее рабочего на-
пряжения й = 24,5 в и стандартное отклонение S = 0,5 в.
Определить с доверительной вероятностью а=0,95 гра-
ницы двустороннего толерантного предела, накрываю-
щего 90% (Р = 0,90) значений рабочего напряжения всей
генеральной совокупности.
Решение. 1. Из табл. П.7.6 определяем
zp =4,645; иа = 1,645.
2. Применяя (5.38), получаем
1,645 । 5-1,6452 + 10
/±25 *" 12-25
277
3. В соответствии с формулой (5.37) находим толе-
рантные пределы
izE,H=24,5 ± 2,14 • 0,5 = 24,5 ± 1,07,
ив = 25,57; пн = 23,43.
Пример 5.34. Испытано п = 32 вала двигателя и полу-
чены оценки средней наработки до отказа 7=800 час,
стандартного отклонения S = 50 час. Найти нижний толе-
рантный предел времени работы вала, при котором веро-
ятность безотказной работы Р будет не менее 0,98 и
достоверность решения а = 0,90.
Решение. Соблюдая последовательность решения
примера 5.33, находим
1. zp = 2,33, и = 1,280;
2. А = 2,33 Л1 4- -L^-|-51’^2 + 10^ = 2,80;
V ' К2-32 12-32 J
3. ta = 800 — 2,8-50 = 660 час.
Пример 5.35. При испытании /г = 50 предохранителей
отказало 4. Оценить вероятность отказа Q и найти дове-
рительные границы с вероятностью а = 0,95.
Решение. 1. По формуле (5.56) получаем Q =
= 4/50=0,08.
2. Для определения QH и QB из табл. П.7.1 находим:
для pi= 1—а= 1—0,95=0,05 и k=2d=8
Xo.O5='2J3;
для
А = 0,95 и k = 2(d + 1) = 2(4+ 1)= 10
Хо.95= 18,3.
3. По формулам (5.57) и (5.58) получаем
^н== 2-50 — 4+1 4-0,5 — 2,73 ~0,028’
18,3
Q —_______________________—о 174
Чв 2-50 — 4 + 0,5.18,3
Следовательно, с вероятностью а=2-0,95—1 = 0,90
имеем Q = 0,028+0,174.
278
Пример 5.36. При испытании « = 40 электронных ламп
на ударную нагрузку ле произошло ни одного отказа.
Найти доверительные границы для вероятности отказа
при а = 0,90.
Решение. QH=0. Для определения QB формулу
(5.61) преобразуем к виду
lg (1 - Qb)
Отсюда lg(l—QB) = 1,975; QB = 0,066.
Пример 5.37. Ориентировочно вероятность отказа ис-
следуемого типа устройств Q0=0,l. Определить пример-
ный объем испытаний, при котором с вероятностью
а = 0,90 предельная ошибка оценки е составит 0,03.
Решение. По табл. П.7.6 находим zo,9o= 1,645. Поль-
зуясь уравнением (5.63), получаем
0Л О-0’1) = 270-
Пример 5.38. Неудачная попытка запуска дизельной
электростанции в ограниченное время расценивается как
отказ. В процессе эксплуатации г = 3 электростанций
были получены следующие данные запусков:
1) удачных — 28, неудачных — 3;
2) удачных — 64, неудачных — 5;
3) удачных — 57, неудачных — 2.
Нужно оценить вероятность отказа дизельной элек-
тростанции при запуске в установленное время и опре-
делить доверительные границы с «1 = 0,90 и «2=0,99.
Здесь «1=31, «2=69, «з=59, rfi = 3, с?2=5, d3=2.
Решение. 1. По уравнению (5.64) находим
q___ 3 + 5-f-2 _ Ю___о Q63
""31 4-69 4-59"" 159 ~u>utKS-
2. Для определения Q„ и QB из табл. П.7.1 находим
квантили xu-квадрат распределения для pt = 1—а,=
= 1—0,90 = 0,10; /г, = 2с/г = 20 и для /?2 = а2 = 0,99,
^ = 2(dE4-l) = 2(10+l) = 22:
^(0,10)(20)----12,4 И Х(0>99)(22) — 40,-
279
3. По формулам (5.57) и (5.58) находим
Qa =-----------------т----=^4 = 0,039,
2-159—10+1+-^ ,2’4
QB =--------------------=5т=0’ I23-
2-159 — 10 +-д-40,3
Пример 5.39. В результате испытаний шасси самоле-
тов при 99 посадках не произошло пи одного отказа.
Оценить вероятность отказа при каждой посадке, а так-
же найти оценки критериев надежности, выраженных
формулами (5.65) — (5.68), если т=10.
Решение. 1. По формуле (5.61) определяем
2. Пользуясь формулой (5.65), находим вероятность
безотказной работы на 10-й посадке: Р(р=10) =
= (1—0,01)10=0,904.
3. Определяем вероятность отказа на 10-й посадке,
пользуясь формулой (5.66):
Q(ii=9) = (l — 0,01)9-0,01 =0,009.
4. Вероятность того, что шасси выдержит не менее
10 циклов вычислим по формуле (5.67):
ю
Л^ю> = 1 - S (1 - 0,01)^ 0,01 = 0,956.
i=;0
5. Среднее число циклов безотказной работы опреде-
ляем по формуле (5.68):
Пример 5.40. При испытании прерывателя тока на
10 000 циклов 8 циклов было с отказами. Найти среднее
число циклов безотказной работы при двух ремонтах.
1. По формуле (5.56) определяем .
‘ Q— . 8-т==8-10~4.
4 10000
2. По формуле (5.69) находим М при г = 0:
м=3?-та^2^3‘те^-=3750 циклов-
280
Пример 5.41. Партия изделий, надежность которой
нужно проконтролировать, состоит из 50 экземпляров.
Партия считается хорошей, если в ней содержится не
более 10% дефектных изделий, и плохой — при содержа-
нии 20% дефектных изделий. Риск поставщика и риск
заказчика приняты равными и составляют а=,р = 0,10.
Определить приемное (Ло) и браковочное (Л1) числа
дефектных изделий в выборке объемом п = 20 экземпля-
ров.
Решение. Так как партия малая (7V<100), а отно-
сительный объем выборки велик (n/N=0,4), то контроль
нужно осуществлять, исходя из гипергеометрического
распределения.
1. Число дефектных изделий при 10% дефектных
изделий в партии составляет Do=Nqo=50‘ 0,10=5; при
20% дефектных изделий Di = M/i = 50 • 0,20= 10.
2. Для определения приемочного числа дефектных
изделий воспользуемся формулой (5.70), суммирование
вероятностей гипергеометрического распределения про-
изводим до тех пор, пока накопленная вероятность не
приблизится к 1—а, т. е.
R(d^A0) ~ l /z = 1—0,10=0,90.
Таким образом,
р/л . Щ — С50=° _!-3169870830126 _nnfi7
"Щ —— 20 47129212243360 — и>ио/-
Величины сочетаний (биномиальные коэффициенты)
определяем с помощью табл. П.7.10:
п /л _ п _ С5-С50~°5 _5-2438362177020 „
П— „23 — 47129212243960 —
с50
d/л ох Qi'^50—5 10-1715884494940. „ Q„.
(rf = 2) = -20 = 47129212243960 = °’364’
с50
р/д_ч\_ С5-С50=! _ 10-1103068603890 _ „ „.
А (Я —о)— с2Э ~ 47129212243960 —
R (d < 3) = 0,067 + 0,258 + 0,364 + 0,234 = 0,923.
Полученная величина близка к 1—а=0,90, т. е. фак-
тический риск поставщика близок к принятому: а'~
= 1—0,923 = 0,077.
Поэтому приемочное число можно взять равным трем
(/40=3). Если принять Ло=2, то риск поставщика стал
281
бы неприемлемо велик: а'=1—(0,067-4-0,258+0,364) =
= 1—0,689=0,311.
3. Аналогичным образом может быть рассчитано
браковочное число Ли Для этого по формуле (5.71) на-
капливаем вероятности /? до тех пор, пока выполняется
условие p/ = /?(d<Ai) «гр:
R(d^= 0) = г0 г-20—0 ь10’ ь50—10 Л-2:) с50 _ 1-137846528820 47129212243960 0,003,
R(d — 1) = rl /--20—1 с10’ ’“'50—10 г-20 ь50 10-131282408400 _ 47129212243960 0,028,
R(d = 2) = г2 г20—2 с10* с50—10 г-20 с50 __ 45-113380261800 _ 47129212243960 0,096,
Я (d< 2) = 0,003+0,028 + 0,096 = 0,127.
Следовательно, с риском р'=0,127, близким к перво-
начально установленному (р = 0,10), при di = 2 дефект-
ным изделиям в выборке партию можно принять, а при
di = 3 дефектным изделиям — нужно браковать.
В данном примере приемочное и браковочное числа
получились одинаковыми A0=At = 3. Это значит, что оди-
ночный контроль не может производиться одновременно
в интересах поставщика и заказчика.
Защита интересов потребителя может привести
к требованию браковочного числа меньшего, чем при-
емочное число при контроле в интересах поставщика.
Обоюдно малый риск при браковочном числе, на единицу
превышающем приемочное, может быть получен в том
случае, когда Di существенно больше D(l, в чем можно
убедиться при решении задач данного параграфа.
Пример 5.42. Контролю надежности подлежит партия
ич А = 200 изделий. Необходимо определить приемочное
(. I») и браковочное (+) числа дефектных изделий в вы-
борке из п = 40 изделий. Партия считается хорошей, если
в ней содержится 5%, и плохой — если 10% дефектных
изделий. Риск поставщика принят равным 0,20, а риск
за казчика — 0,10.
Решение. Учитывая относительно большой объем
контролируемой партии и небольшие значения доли де-
фектных изделий, целесообразно производить решение,
исходя из /-биномиального распределения, в соответст-
вии с формулами (5.72) и (5.73).
и:
1. Рассчитываем величины f, Do и D^
/-^-=^=0,2; А> = М7о=Ю; А = Ж = 20.
2. Приемочное число Ао определяется суммированием
вероятностей /-биномиального распределения [форму-
лы (5.72)] до величины а', близкой к а:
R(d^A0) = 1—а = 1—0,20=0,80.
Вычисляем вероятности R (d) и суммируем их:
R(J = O) = C°o-O,2°-(l — 0,2)10 = 1 -1 -0,107 = 0,107,
R(d= 1) = С}0-0,21(1 — 0,2)" = 10-0,2-0,134 = 0,268,
R(d = 2) = Cfo-O,22-(l — 0,2)8 = 45-0,04-0,168 = 0,320,
R {d = 3) = Cio- 0,23 • (1 — 0,2)’ =120- 0,008-0,210 = 0,202,
R (d < 2) = 0,107 + 0,268 -f- 0,320 = 0,695,
R (d < 3) = 0,107 + 0,268 + 0,320 + 0,202 = 0,897.
Таким образом, можно принять приемочное число
/10 = 2 с риском поставщика а/=1—0,695=0,30 или Ло=3
с риском поставщика а'=1—0,897 = 0,10.
Если требуется фактический риск приблизить к за-
данному, то это можно сделать при постоянных объеме
партии и доле дефектных изделий в ней, варьируя объе-
мами выборки и приемочными числами.
3. Браковочное число Ai определяется аналогично
приемочному числу, с той лишь разницей, что в данном
случае нужно руководствоваться формулой (5.73) и сум-
мировать вероятности /-биномиального распределения
до величины [7~ 0,10.
Итак,
R (d = 0) = С°о • 0,2° • (1 — 0,2)2° = 1 -1 • 0,010 = 0,010,
R (d = 1) = С*о • 0,2 0,819 = 20 • 0,2 • 0,0144 = 0,058,
R (d = 2) = С2() • 0,22 • 0,818 = 190 • 0,04 • 0,18 = 0,137,
Так как
R (d< 1) = 0,010+0,058 = 0,068,
R(tZ<2) =0,010+0,058+0,137 = 0,205,
283
то, очевидно, целесообразно считать браковочным числом
Д1=2, тогда риск заказчика будет более близким к уста-
новленному.
Пример 5.43. С целью контроля надежности проведе-
ны испытания 20 (н = 20) восстанавливаемых объектов,
при этом зарегистрировано 2 отказа. Необходимо решить,
принять партию или забраковать, если контроль произ-
водится в интересах заказчика. Партия считается пло-
хой, когда вероятность отказа в каждом одиночном испы-
тании составляет Решение должно быть при-
нято с риском р = 0,08.
Решение. Исходя из условия задачи, контроль
может быть произведен по биномиальному плану с по-
мощью формулы (5.75).
Процедура решения сводится к накапливанию веро-
ятностей до тех пор, пока кумулятивная вероятность не
станет близкой к заданному риску. Сравнение числа
отказов d, полученных при испытании, с вычисленным
браковочным числом At позволит принять решение:
если d<Au то партию можно принять;
если d^Ai> то партию нужно забраковать.
Вычисления в значительной степени облегчаются при
использовании табл. П.7.11, параметрами которой явля-
ются объем выборки /г, заданная вероятность q (в дан-
ном случае qt) и число дефектных изделий d.
Для /г = 20, <7 = 0,10 и Д=2 по табл. П.7.11 находим
|У=0,68, что значительно превышает заданный риск,
следовательно, партия должна быть забракована.
Из этой же таблицы видно, что при п = 20, </1 = 0,10
при Д = 0 вероятность составляет 0,12. Значит, принимая
партию при Д=0, риск приемки плохой партии будет ра-
вен 0,12.
Пример 5.44. Из неограниченно большой партии изде-
лий извлечена выборка'’объе'мом п = 50 изделий, которая
испытана с целью контроля надежности в интересах
поставщика. Партия может быть принята с риском
а=0,15, если вероятность отказа каждого изделия со-
ставляет </о=0,05.
Определить приемочное число Ао.
Решение. Так как партия неограниченно большая,
то испытания независимы, это позволяет пользоваться
биномиальным законом распределения и определять Ло
по формуле (5.74) или табл. П.7.11.
284
Пользуясь таблицей, определяем, что при п = 50,
7=7о=О,О5О вероятность 3 или меньшего количе-
ства дефектных изделий составляет 0,76, а для с?^4—
0,90. Следовательно, приемочное число можно взять
До=3, при этом риск поставщика составит а/=1—0,76 =
= 0,24, или взять Ло=4, тогда а'=1—0,90=0,10.
Пример 5.45. Определить, какой объем выборки в би-
номиальном плане нужно испытать в интересах заказ-
чика, чтобы забраковать партию с вероятностью безот-
казной работы каждого изделия 0,85 и менее, если бра-
ковочное число Ai=1, а риск заказчика ориентировочно
равен 0,10.
Решение. С помощью табл. П.7.11 определяем, что
при 7=71 = 0,15 и 7 = 0 объем выборки п =15, при этом
р'=0,09.
Пример 5.46. Из большой партии изделий (N> 1 000)
извлечена выборка в 60 экземпляров с целью контроля
надежности в интересах поставщика. Предполагаемая
вероятность отказов изделий, при которой партия долж-
на быть признана хорошей, составляет 7О=0,02. Опреде-
лить приемочное число Ао с риском а=0,10.
Решение. По условиям данного примера для его
решения целесообразно воспользоваться распределением
Пуассона, отраженного в формуле (5.76). Реализацию
этой формулы удобно произвести с помощью табл. П.7.9.
Для этого определяем
W = Oo=7oH = 0,02 • 60= 1,2.
В соответствии с табл. П.7.9 при m = d==3 суммарная
вероятность составляет 0,120. Следовательно, Л0=2.
Пример 5.47. Установлены следующие параметры
плана контроля. Приемочное число Ао=О, риск постав-
щика а=0,10 и вероятность безотказной работы ^о=0,01.
Определить объем выборки, потребный для осуществле-
ния контроля по плану, основанному на распределении
Пуассона.
Решение. 1. По табл. П.7.12 для Ло=0 и а=0,10
находим а = 0,10536.
2. По формуле n=afq0 и заданному qQ определяем
объем выборки
285
Пример 5.48. Для контроля надежности в интересах
заказчика выделена выборка объемом п = 40 экземпля-
ров. Установлены значения .0 = 0,05 и браковочное число
Л1 = 2. Определить верхнее значение вероятности отказа
в случае приемки партии при d= 1.
Решение. 1. По табл. П.7.12 для Л1 = 2 и р = 0,05
определяем о = 4,74.
2. По полученному значению а и заданному п нахо-
дим
Пример 5.49. Партия проверяется в интересах постав-
щика с допустимым риском а = 0,10. Приемлемая вероят-
ность отказов изделий q0 составляет 0,15. В результате
испытаний получено d=8 отказов. Требуется произвести
контроль большой партии изделий, выборка из которой
объемом в /г=100 экз. составляет незначительную долю
(/г/Л^<0,1).
Решение. Для определения пригодности партии
в данном примере можно воспользоваться формулой
(5.78), полученной исходя из нормального закона.
Подсчитаем величину г, подставив в формулу (5.78).
значения d вместо До-'
d — -f- 0,5 _ 8— 100 0,15 + 0,5 _ ।
““ V nq„ (Т^Т^Г ЙТЖо,15(1~Т+о?15)
С помощью табл. П.7.13 определяем значение функ-
ции Лапласа для 2 =—1,85: Ф0(1,85) =—0,468.
По формуле (5.78) находим а7=0,5+ 0,468=0,968.
Следовательно, при A0 = d=8 браковка партии приво-
дит к риску поставщика, значительно превышающему
данный. Для уменьшения риска нужно брать Ло3>8, т. е.
при d = 8 в данном примере партия может быть принята.
Нетрудно подсчитать (см. пример 5.51), что До=2О.
Пример 5.50. Объем испытаний п =‘200, верхняя гра-
ница вероятности отказа <71 = 0,10, а браковочное число
Л1 = 15. Определить риск заказчика, исходя из нормаль-
ного распределения числа дефектных изделий в выборке.
Решение. Исходя из условий задачи, для опреде
ления 0' воспользуемся формулой (5.79).
Определяем
/ид + 0,5—И, 200-0,1 +0,5— 15 5,5 . „о
//7^(1 — q.) у 200-0,1 (J—0,1) 4’25
286
По табл. П.7.13 находим значение функции Ф0(1,28),
тогда [’/=-0,5—0,4 = 0,10.
Пример 5.51. Испытаниям подвергнута опытная пар-
тия подъемных механизмов, для которых удовлетвори-
тельной вероятностью безотказной работы в каждом
цикле считается Ро = О,98. Требуется найти приемочное
число отказов Ло с допустимым риском а~ 0,05 при объе-
ме испытаний /г = 500 циклов.
Решение. Учитывая большой объем выборки, ре-
шим данный пример с использованием нормального за-
кона распределения частостей, т. е. применим форму-
лу (5.78).
Так как заданная величина риска поставщика состав-
ляет 0,05, то нужно получить
ФО(?) = Ф[
!А — + 0,5
Р nq0 (1 — <7„)
= 0,45.
Из табл. П.7.13 определяем для Ф0(Х) = 0,45, г=1,6. ,
Следовательно, можно записать равенство
1 А —500-0,02 + 0,5 _Л — 9,5
' 500-0,02-0,98 ~ 3,14 ’
откуда Ао= 15.
Пример 5.52. Последовательному контролю надеж-
ности подлежит партия, состоящая из 7V= 100 невосста-
навливаемых изделий. Партия считается хорошей при
доле дефектных изделий ф)=0,05 и плохой— при <71 = 0,10.
Риск поставщика равен риску заказчика и составляет 0,1.
Требуется определить приемочные (тпр) и браковоч-
ные (тор) числа испытаний при числе дефектных изде-
лий rfm=0, 1, 2, 3, 4 и 5, а также построить график кон-
троля по характеристическим точкам и принять решение
в случае появления четырех отказов при 25 испытаниях.
Решение. Так как общий объем исследуемой сово-
купности мал, необходимо осуществлять контроль по
/-биномиальному плану. Для определения приемочных
и браковочных чисел и построения графика контроля не-
обходимо произвести следующие вычисления.
1. Определяем число дефектных изделий в партии
при нулевой и альтернативной гипотезах:
Др= 100-0,05 = 5, £>1=100-0,10=10.
267
2. Находим значения оценочных нормативов А и В:
л_ 1 —р _ 1 —0,10 п. » Р _ 0,10 _он
Л а 0,10 ~У’ 1—а 1—0,10 U’11-
3. Для определения характеристических точек графика
плана подсчитываем сиг (используется табл. П.7.10):
с = Сд*=С^0 = 252; г = — Do= 10 —5 = 5.
4. Приемочные числа определяем по формуле (5.84),
в которую подставляем постоянные величины N, В, с, г
и переменную для каждого числа дефектных изделий
величину.
Таким образом,
d = 0; £„, = 0^ = 252;
- inn Ь / 252-0,11 X1/5 1 o_
^пр' Ю0 I 1 • ( \ I—36,
^=1; сто = С^ = 126;
_1ппГ1 / 252-0,11
10011 ( j 2g
И T. Д.
Для подсчета браковочных чисел используется фор-
мула (5.85). Очевидно, что эта формула имеет смысл при
On ~г==—что в соответствии с таблицей би-
номиальных коэффициентов имеет место при dm>3. Для
d - 3 ст - 21 ;Т/пбр < Ю0[ 1 - (--J1)'7" ] = 7 и
т. д.
После расчета всех приемочных и браковочных чисел
таблица плана может быть представлена в виде табл. 5.9.
Т A Б]Л J1 Ц А 5.
Расчет плана к [примеру 5.52
0 1 2 3 4 5
тпр не менее 36 44 53 61 69 78
т$ не более —• — — 7 27 49
28 8
5. Определяем характеристические точки графика
плана:
a) dm = 0, 7тг0 = 2V (1 — В1/г)= 100(1 — 0,111/5) = 36;
б) dm — D0 = 5, ;/г = Л^1 — ] =
= 100[1-^)1/5]=49;
в) dm = D°+D'-=A±lg-=7,5; т = N = 100.
Для построения графика плана (рис. 5.10) строим
прямоугольные оси координат с ординатами <2т=04-10
Рис. 5.10. График контроля (к примеру 5.52).
и абсциссами т=0-е-100 и отмечаем точки а, бив. За-
тем точку в соединяем с точками а и б.
Заданная по условию примера рабочая точка d=4,
7П = 25 (на рис. 5.10 отмечена крестиком) попадает
в область браковки. Следовательно, партию можно за-
браковать и испытания прекратить.
Правильность решения можно проверить по правилу
браковки:
1га>А.
С этой целью подсчитаем
1т= —(1 — 0,25)5 = 14,9.
Так как 14,9>9, то партия бракуется.
Пример 5.53. Партия считается хорошей при /?о=О,99
в одном цикле, а плохой — при /ц = 0,88. Контроль дол-
жен осуществляться с риском а=0,08 и р = 0,06. Требует-
ся построить план последовательного контроля вероят-
19—1086 289
пости безотказной работы восстанавливаемых изделий
в табличной и графической формах до dm.= 10. Принять
решения для трех рабочих точек: d=l, т=46; d=4,
т = 50; d = 5, т = 100.
Решение. Учитывая независимость испытаний,
строим биномиальный план, пользуясь формулами
(5.88), (5.89), (5.90) и (5.91).
1. Для построения плана нужно предварительно
определить оценочные нормативы А и В и константы
плана hi, h2 и s:
а 0,08 ’ 1—а I—0,08
1g В 1g 0,065
<7, 1— qB~ , 0,12 0,99
1П q<> + lg 0,01 + lg 0.88
__ 1,18/ _ , 050
1,079 + 0,051 ~~ 1,W’
_ lg 11,75 __ 1,07
h =______= 1-u' —Q95Q
2 qx 1 q„ 1,130 1,130
ig v”+lgr~;г
Vo 1 Vi
. 1 — Qo
lgr^
/7i
, 1 1 ~~
<7o g 1 —
0,051
1,130
0,045.
2. Для вычисления таблицы плана используем форму-
лы (5.88), которые лучше представить в следующем виде:
Тогда при d = 0
_ — /г, ___ 1,05
Ицр — —“—— 0 045
. Q 95
тбр — —~~ о 0’45 = — 21 — браковка не осуществля-
ется,
при d = 1
2,05 .г
/?^Р^_'0+45 =="6’
1-0,95 ,
ит- А-
290
Результаты расчета могут быть представлены в виде
табл. 5.10.
ТАБЛИЦА 5.10
Расчет плана к примеру 5.53
0 1 2 3] 4 5 6 7 8 9 10
тпр не менее 23 45 67 91 112 134 156 179 201 228 245
/и6Р не более — 1 23 45 68 90 112 134 156 179 201
3. График плана (рис. 5.11) наиболее просто строит-
ся по трем характеристическим точкам:
a) dm = 0, т0 = 23;
б) dm — = —1,05, т = 0;
в) dm = h2 — 0,95, m —0.
4. Точка d=l, т=4(з определяет приемку партии;
точка d=4, гп = 50 позволяет принять решение о браков-
Рис. 5.11. График плана контроля (к примеру 5.53).
ке и точка d = 5, m=100 соответствует правилу продол-
жения испытаний.
Пример 5.54. Для контроля надежности большой
партии (TV>2 000) телевизоров требуется построить
в табличной (до d=10) и графической формах план
последовательного контроля с риском поставщика а = 0,05
и риском заказчика |3 = 0,10. Надежность партии счита-
ется высокой при <70=0,02 и низкой при <74 = 0,10. Принять
решения для трех рабочих точек: d=0, m = 40; d=3,
ш = 20; d=2, m=100.
Решение. По условию примера построение после-
довательного плана возможйо с применением распреде-
ления Пуассона. Решение примера производим в той же
последовательности, что и предыдущего.
19* 291
1. Определяем А, В, hi, h2 и S.
л 1-0,10 R. R 0,10
1g ~ Чо _ 1g 0,01 __ — 2 _ 0,10 0,699 ’ОО’ lg 0,02
_ Ш -4 __ 1g 18 1.255 __ .
— с, ~ 0,699 “"0^99
lg ~~
Чо
s 0,4343 (у, -^0) = 0,4343-0,08 _ Q 05
, <?! 0,699 ' ’
lg---
Яо
2. Вычисляем таблицу плана (табл. 5.11) по формулам:
d — h, d 4-2,88
^пр== - = 0 05 ;
d — h, d — 1,80
3. Графики плана (рис. 5.12) строятся по характери-
стическим точкам:
a) d = 0, !т = 58;
б) d = hx = — 2,88, 1^ = 0;
в) d = h3 = 1,80, 'tn = 0.
ТАБЛИЦА 5.11
Расчет плана к примеру 5.54
d 0 1 2 3 4 5 6 7 8 9 10
тПр не менее 58 28 98 118 138 158 178 198 218 238 258
/ивр не более — — 4 24 44 64 84 104 124 144 164
4. Из таблицы и графика видно, что при положении
рабочей точки d — Q, m = 40 испытания нужно продол-
жать, при положении точки d = 3; m=20 партию’следует
браковать, при положении точки d=2; m=100— прини-
мать.
Пример 5.55. Надежность электронных преобразова-
телей, выпускаемых большой серией, считается высокой
при интенсивности отказов Zo=2-lO~4 \)час и низкой —
292
Рис. 5.12. График плана контроля (к примеру 5.54).
при л4=1 • 10~3 \1час. Риск заказчика и поставщика оди-
наков и составляет а=р = 0,05. Требуется рассчитать
последовательный план выходного контроля надежности
таких преобразователей. План контроля необходимо
представить в табличной и графической формах до d=
=m=10. Принять решения для трех рабочих точек:
d=0, =5 000 час, d — 1, — 5000 час; ? ~'d — 2,
t = 300 час.
Решение. 1. Для построения плана необходимо
определить его константы, для чего вычисляем:
/]_ 1-0,05 о________ 0.05 — q 053-
7 — 0,05 1У’ — 0,05 U’UM’
5 = - 2,303 +2,303 (^^+- = 0,367.10";
O = -2'303s^4;=- 2.303(-геТ^ =-0.367.10<;
lg + L *
- __ 9 ОАО _ 2,303-0,699 п,
s — ~8: Гб-4 -'1и •
2. Таблицу плана вычисляем исходя из формул (5.94)
и (5.95). Так, минимальная величина наработки при
соответствующем числе дефектных изделий для приемки
293
и браковки подсчитывается по соотношениям соответст-
венно
^hi+dms=0,367 • 104-НД, • 2 • 103,
= —0,367-104+2- 103rfm.
Подсчитанные по этим формулам данные заносятся
в табл. 5.12.
ТАБЛИЦА 5.1
Расчет плана к примеру 5.55
3. График плана (рис. 5.13) можно построить с по-
мощью полученной таблицы или по трем характеристи-
ческим точкам:
а) </„ = -^=^„1,83, (,=0;
б) dm==0, /г2= —3670;
в) dm—0, Л, = 3670.
Для точного построения графиков по вычисленным
точкам необходимо выбрать соответствующие масштабы
ДЛЯ dm И
Рабочей точке с/ 0,7. =5000 час соответствует реше-
ние о приемке контролируемой партии преобразователей.
Рис. 5.13. График плана
контроля (к приме-
ру 5.55).
294
Если рабочая точка имеет положение d=l, 4 =5000 час,
то испытания нужно продолжить. При d = 2 и /Е==
= 300 час принимается решение о браковке.
Пример 5.56. В эксплуатации находится 50 непрерыв-
но и одновременно работающих восстанавливаемых тех-
нических устройств, замена которых при отказе произ-
водится практически мгновенно. Надежность устройств
считается высокой и доработка не требуется при средней
наработке до отказа 7о=4ОО час, а при наработке 71=
=200 час необходима доработка. Закон распределения
отказов принят экспоненциальным. Для выявления не-
обходимости доработки эксплуатируемых технических
устройств нужно осуществить контроль их надежности
по наработке. Решение должно быть принято со значе-
ниями риска а = 0,05 и ₽ = 0,10. План контроля нужно
представить в табличной форме.
Решение. Так как распределение отказов исследуе-
мых устройств экспоненциальное, то 7о = 1/70= 1/400 =
= 2,5.10-3 1/час, 71=1/71=1/200 = 5-10-3 \/час.
Контроль производится по правилам, описанным
формулами (5.94), (5.95). Но имея в виду одновремен-
ную работу N=50 устройств и возможность их восста-
новления, целесообразно строить таблицу и график пла-
на с учетом времени эксплуатации t*, которое определя-
ется из формулы (5.100):
Константы плана ht, hz и s находятся по формулам
(5.97), для чего предварительно нужно определить А, В,
Xi/Ло и их логарифмы:
/I 1 0»10в .о г, 0,10 л 1 лс '^1
Л==“(Г0Г ’==:18’ В==~ПГщо5 =0,105;^=
5-Ю-3
2,5-10“3
2;
1g А= 1,255; 1g В = — 0,979; 1g 2 ==0,301;
^~2’3f^=90°; ^=-2'324^=-
1160;
5==2’32ДИСРГ=276-
Л , <7 Л 17
295
Пользуясь формулами (5.94) и (5.95), а также учиты-
вая (5.100), составляем таблицу плана, округляя время
эксплуатации до часа (табл. 5.13).
ТАБЛИЦА 5.13
Расчет клана к примеру 5.56
dm 0 1 2 3 4 5
i*up, час не менее 18 24 29 35 40 45
t№, час не более — — — — — 4
Пример 5.57. На испытание поставлено N—20 экземп-
ляров, 7.о = 7,5-1О 4 \/час, Zi = 2-10"'3 1/час; а=0,10;
₽ = 0,03. Требуется составить план контроля надежности
по наработке невосстанавливаемых устройств до d=5
и принять решения в случаях, когда:
а) произошло два отказа при наработках отказав-
ших экземпляров 0 = 55 час, /2=100 час и испытания
приостановлены;
б) после отказов, указанных в пункте а, все осталь-
ные устройства продолжали работать до момента кон-
троля /* = 250 час,
в) после трех отказов устройства наработали 5, 15
и 20 час.
Решение. План контроля в данном случае опреде-
ляется так же, как и в примере 5.55:
в-т^=°’0334;
1gЛ = 0,987; lgB = 1,476; 1g-^=0,426;
Л, = 2,3 12^= 2720; _2,3^^= - 1860;
s — 9 Q 0,426 _yoj-
S 2,3 12.5-10'4 ~Z°b-
По полученным данным строится табл. 5.14.
Для определения положения рабочей точки и приня-
тия решения в процессе контроля необходимо подсчиты-
296
Таблица 6.u
Расчет плана к примеру 5.57
0 1 2 3 4 5
ZEnp> час не менее 2 720 3 505 4 290 5 075 5 860 6 645
/1бр, час не более — — __ 495 1 280 2 065
вать наработку по формуле (5.99). Так, для первой рабо-
чей точки
d
f 4- + (У — dm)/* = 55 + 100 +(20 — 2)100 =
= 1955 < 4290.
В соответствии с условием (5.96) испытания нужно
продолжить. Для второй рабочей точки наработка со-
ставляет
Zj. = 155 + 18-250 = 4655 > 4290.
В соответствии с условием (5.94) партию нужно при-
нять. Для третьей точки:
= 5 +15 + 20 + (20 — 3)-20 = 380 < 495.
По условию (5.95) испытания прекращаются и партия
бракуется.
Пример 5.58. В процессе приемки изделий завода
представителями заказчика проверяется их функциони-
рование в течение /*=20 час. Необходимо использовать
информацию, получаемую при контроле функционирова-
ния, для контроля наработки, если, как и в предыдущем
примере, Лю=7,5-10“4 1/час; Xi = 20-10“4 1/час; а=0,10;
Р=0,03. Изделия после отказа не восстанавливаются.
Требуется принять решение в случае, когда испытано
Л?=125 изделий, из них отказало 5 с общей наработкой
отказавших изделий
5
^4=75 час.
i=i
Решение. Для построения таблицы и графика при-
меняются планы, рассмотренные в примере 5.55. Нара-
ботка в процессе контроля определяется по формуле
297
(5.99), но в качестве t* берется установленное время
функционирования.
5
Так, для /’=20, Л?=125, d—Ь и J] ti =75 определяем
t=i
tz = 75 + (125 — 5) 20 = 2475 час.
Обращаемся к таблице плана (см. пример 5.57) и
устанавливаем, что при d=5 полученная наработка боль-
ше требуемой для браковки и меньше требуемой для
приемки, т. е. 2 065<2 475<6 645, что соответствует
условию продолжения испытаний.
Пример 5.59. Надежность устройств с нормальным
законом распределения отказов считается высокой при
средней наработке до отказа То >150 час и низкой при
7\^100 час. Требуется рассчитать план последователь-
ного контроля средней наработки до отказа, если стан-
дартное отклонение известно и составляет o'=20 час.
Риск поставщика равен риску заказчика и состав-
ляет 0,05.
Решение. 1. Для расчета констант плана восполь-
зуемся формулами (5.105):
/z, = — 2,3
°21g В
т0-1\
0,05
L204g i__0j05
— 2,3 150—100 ~23,6;
/г2 = —2,3
о21g А
т.-т.
= — 2,3
202lg
1—0,05
0,05
150— 100
23,6;
s = + —150+ 100_ j 25
2
2. Характеристические точки графика плана опреде-
ляются по (5.106):
а) =-^-=^=0,198, /т=0;
б) /72 = 0, = — 23,6;
в) т = 0, /£ = ht = 23,6.
3. Таблица плана строится по соотношениям (5.102)
и (5.103).
298
§ 5.3. ЗАДАЧИ
В настоящем параграфе приведены задачи на оценку и контроль
надежности технических устройств по результатам их испытаний,
предлагаемые для самостоятельного решения.
Задачи легко решить, используя типовые примеры, приведенные
в § 5.2.
5.1. В результате обработки данных по испытаниям получен сле-
дующий вариационный ряд значений времени безотказной работы
изделия в часах: 2; 2; 3; 3; 5; 6; 7; 8; 9; 9; 13; 15; 16; 17; 18; 20; 21;
25; 27; 35; 38; 53; 56; 69; 77; 86; 98; 120. Требуется выявить закон
распределения времени безотказной работы.
Ответ: Экспоненциальный.
5.2. В результате проведения испытания системы получен сле-
дующий вариационный ряд времени безотказной работы в часах:
60; 100; 150; 170; 240; 300; 430; 650; 1100. Требуется установить
закон распределения времени безотказной работы.
Ответ: Экспоненциальный.
5.3. В результате обработки экспериментальных данных получен
следующий ряд времени безотказной работы аппаратуры при уско-
ренных испытаниях в час: 12; 25; 34; 34; 34; 34; 34; 34; 45; 45; 45; 53;
61; 61; 61; 61; 69; 69; 69; 75; 75; 84; 84; 92; 95. Требуется выявить
закон распределения времени безотказной работы.
Ответ: Логарифмически-нормальный.
5.4. Обработкой исходных данных получен следующий вариаци-
онный ряд времен восстановления изделия в минутах: 1; 3; 3; 6; 6;
7; 8: 12; 12; 14; 17; 18; 21; 23; 24; 26; 27; 28: 32; 34; 37; 37; 44; 47.
Требуется выяснить закон распределения времени восстановления.
Ответ: Логарифмически-нормальный.
5.5. На испытаниях получены следующие времена безотказной
работы изделия в часах: 11; 34; 35; 62; 63; 77; 86; 124; 129; 148; 178;
182; 213; 235; 241; 264; 275; 281; 323; 340: 372; 372; 443; 478. Тре-
буется установить закон распределения времени безотказной работы.
Ответ: Логарифмически-нормальный.
5.6. В результате обработки данных на испытаниях получен сле-
дующий вариационный ряд значений времен безотказной работы
однотипных изделий в часах: 22: 31: 35: 50; 67; 74; 80: 84; 91; 93;
138: 152; 166; 171. Необходимо выявить закон распределения време-
ни безотказной работы.
Отв е т: Экспоненциальный.
5.7. В результате проведения испытаний изделии получен сле-
дующий вариационный ряд 'Времен безотказной работы в часах:
82; 89; 116; 124; 132; 197; 431; 1027. Требуется установить закон
распределения времени безотказной работы.
О.т в е т: Экспоненциальный.
5.8. На испытаниях произведено 15 замеров времени восстанов-
ления, значения которых в минутах равны: 1; 3; 4; 6; 7; 12; 13; 15;
18; 18; 23; 24; 26; 32; 44. Нужно установить закон распределения
времени восстановления.
Ответ: Логарифмически-нормальный.
5.9. В результате опытной эксплуатации однотипных систем по-
лучены данные по отказам, которые сведены в следующий вариа-
ционный ряд: 3; 4; 5; 5; 6; 6; 7; 7; 7; 7; 7; 8; 9; 10; 10; 11; 12; 42; 12;
12; 12; 14; 14; 15; 15; 15; 16; 17; 18; 20; 20; 20; 21; 21; 22; 22; 23;
299
29; 30; 32; 33; 37; 38; 40; 40; 40; 42; 45; 46; 48; 49; 50; 53; 55; 55;
73; 86; 90; ПО; 129. Необходимо выяснить закон распределения вре-
мени безотказной работы систем рассматриваемого типа.
Ответ: Экспоненциальный.
5.10. В результате испытания партии трансформаторов получен
вариационный ряд времени безотказной работы- 19; 28; 28; 32; 36;
36; 50; 51; 71; 124; 126; 138; 163; 231; 246; 260; 300; 302; 320; 341;
380; 384; 468; 477; 603; 807; 895; 920 ; 937; Требуется установить за-
кон распределения времени безотказной работы изделия.
Ответ; Экспоненциальный.
5.11. В результате испытания двигателей постоянного тока по-
лучен вариационный ряд времени безотказной работы в часах: 15;
28; 29; 29; 54; 61; 71; 73; 76; 77; 91; 102; 103; 117; 145; 150; 470; 196;
200; 204; 245; 249. Необходимо выявить закон распределения вре-
мени безотказной работы изделия до первого отказа.
Ответ: Логарифмически-нормальный.
5.12. В результате испытания партии электромеханических срав-
нивающихся устройств получен следующий вариационный ряд вре-
мен безотказной работы до первого отказа в часах: 19; 62; 92; 102;
121; 193; 200; 200; 215; 229; 245; 384; 385; 462; 486; 538; 576; 631;
680; 715. Нужно выявить закон распределения времени безотказной
работы изделия до первого отказа.
Ответ: Логарифмически-нормальный.
5.13. При испытании партии датчиков импульсного питания по-
лучен вариационный ряд наработки до первого отказа изделия в ча-
сах; >17; 18; 57; 134; 160; 160; 174; 198; 200; 225; 279; 370; 420. Тре-
буется выявить закон распределения отказов.
Ответ: Нормальный.
5.14. В результате испытания партии часовых механизмов полу-
чен следующий вариационный ряд наработки до первого отказа из-
делия в часах: 61; 64; 92; 149; 150; 150; 178; 179; 200; 200; 250; 252;
255; 255; 312; 340; 341; 359; 362; 378; 600; 600. Необходимо выявить
закон распределения наработки до первого отказа.
Ответ: Нормальный.
5.15. В результате обработки данных по отказам изделий, полу-
ченных из эксплуатации, составлен следующий вариационный ряд
наработки до первого отказа в часах: 699; 724; 794; 799; 810; 935;
997; .1115; 1120; 1174; 1190; 1300; 1353; 1500; 1534; 1573; 1800; 1800;
1900; 2000; 2166; 2278; 2301; 2400; 2444; 2447; 2500; 2700; 2700;
2850; 2950. Нужно выявить закон распределения наработки до пер-
вого отказа.
Ответ: Экспоненциальный.
5.16— 5.25. В результате исследования пульта контроля с высо-
кой плотностью информации осуществлялся контроль комплекса па-
раметров путем считывания показаний со шкал пульта. При считы-
вании стократно фиксировалась длительность операции контроля
в секундах. Требуется на основании полученного вариационного ряда
длительности операций контроля выяснить соответствие полученных
данных определенным законам распределения.
Исходные данные для решения задач и ответы приведены
в табл. 5.15.
5.26. В результате опытной эксплуатации однотипных изделий
получены данные по отказам в часах, которые сведены в следующий
300
ТАБЛИЦА 5.5
Задачи
Исходные данные
Номер задачи Длительность операций 11, zzt—число операций равной длительности Огвет
5.16 1 (2); 1,8; 2,1; 2,2 (3); 2,3; 2,4; 2,5; 2,6; 2,8 (6); 3,0 (2); 3,2 (4); 3,4 (4); 3,6 (2); 3,7; 4,0 (3); 4,1; 4,2 (3); 4,4 (3); 4,6 (4); 4,7; 4,8 (2); 5,0 (6); 5,2 (4); 5,4 (3); 5,5 (3); 5,6 (2); 5,7 (2); 5,8 (5); 6,0 (2); 6,1 (2); 6,2 (2); 6,6; 6,8; 7,0 (2); 7,2 (2); 7,4; 7,8; 7,9; 8,0; 8,1; 8,7; 8,8; 10,8; 11,0; 11,4; 11,8; 12,0; 13,2; 13,4; 14,1; 18,8 Логарифмиче- ски-нормаль- ный
5.17 4,6; 7,8 (2); 9,7 (2); 10,4 (4); 11,2; 11,4 (3); 11,5 (3); 11,8; 12 (3); 12,6(5); 13,2; 13,6 (2); 13,8 (2); 14,0 (3); 14,2 (4); 14,7 (3); 15,6 (3); 16,2 (2); 16,4 (5); 16,8 (4); 17,9 (3); 18,4 (3); 18,9 (3); 19,4 (2); 19,6 (4); 19,9 (3); 20,6 (3); 21,3 (4); 22,4 (2); 23,5 (3); 24,2 (2); 25,5 (2); 26,3 (4); 27,2 (4); 30,2; 31,8; 35,6; 39,0 Логарифмиче- ски-нормаль- ный
5.18 4,7 (2); 6,4; 7,3 (3); 8,4 (2); 9,6 (2); 10,0 (2); 10,4 (2); 10,7 (3); 11,2 (7); 11,8 (2); 12,0 (4); 12,3 (3); 13,0 (5); 13,6 (6); 14,2 (5); 14,8 (2); 15,6 (8); 16,5(2); 17,4 (5); 18,0 (3); 18,4 (3); 19,0 (3); 20,2 (3); 20,7 (2); 22,5 (2); 23,4 (2); 24,6 (2); 25,0 (3); 25,8; 26,4; 28,3; 29,6; 31,9; 32,6; 34,0; 37,0; 37,9; 42,6; 52,6 Логарифмиче- ски-нормаль- ный
5.19 1,9 (4); 3,4 (3); 4,3 (5); 4,8 (4); 5,5 (7); 6,2 (4); 6,7 (4); 7,2 (7); 7,8 (8); 8,2(4); 8,6(4); 9,5(8); 10,5 (3); 11,5 (5); 12,0(4); 12,2 (4); 13,4 (3); 14,7; 15,5 (2); 16,2; 17,6; 18,5 (3); 20,1; 22,2; 24,0; 26,4 (2); 27,2 (2); 31,6; 36,0; 45,3; 57,0 Логарифмиче- ски-нормаль- ный
5.20 6,6; 8,0; 10,7 (2); 11,3 (3); 12,4 (4); 13,2 (3); 13,8 (2); 14,3 (6); 15,0 (3); 15,8 (3); 16,0 (4); 16,3' (4); 16,8 (2); 17,7 (3); 18,6 (4); 18,8 (2); 19,0 (2); 19,4 (3); 19,8 (3); 20,4 (5); 21,2 (4); 21,8 (3); 22,2 (3); 22,4 (4); 22,8; 23,6; 24,4; 24,6 (2); 26,3 (3); 27,5 (2); 28,7; 29,3 (2); 30,2 (2); 31,6; 35,2; 36,4; 41,8; 42,0; 45,4; 49,4; 53,2; 54,0; 60,8; 79,2 Логарифмиче- ски-нормаль- ный
301
Продолжение табл. 5.15
Номер задачи Исходные данные Ответ
Длительность операций — число операций равной длительности
5.21 1,8; 2,2 (2); 2,7 (2); 3,2; 3,8 (3); 4,2 (6); 4,7 (2); 5,6 (4); 6,0 (2); 6,3 (6); 6,8 (3); 7,0 (3); 7,4 (6); 7,7 (4); 8,1 (4); 8,2 (7); 8,3 (3); 9,3 (4); 9,8 (4); 10,3 (3); 10,8 (2); 11,6; 12,4 (4); 13,4 (3); 14,4 (3); 15,4 (2); 16,5 (3); 17,4 (2); 19,4 (2); 20,8 (2); 22,4; 23,6 (2); 24,6; 27,0; 32,4 Нормальный
5.22 2,5; 3,7; 4,8 (2); 5,6; 6,7; 7,1 (3); 8,3 (4); 8,7 (4); 9,2 (5); 10,0 (4); 10,4 (7); 10,8 (6); 11,4 (9); 11,8 (4); 12,1 (4); 12,6 (7); 13,4 (3); 14,1 (7); 14,6 (5); 15,4 (4); 16,1 (3); 17,4 (2); 18,4; 19,0; 19,4 (3); 19,8; 21,0; 25,2; 26,0; 30,2; 31,8; 40,4; 51,6 Нормальный
5.23 4,9; 5,8; 6,0; 6,2; 7,7; 8,9; 9,4; 10,2; 12,4; 12,6; 12,7; 13,0; 14,4; 15,2; 15,4; 16,0 (3); 16,8 (2); 17,2 (2); 17,4; 18,2 (2); 18,4; 18,6 (2); 19,8; 20,0(2); 20,8; 22,0; 22,2(3); 22,6(2); 23,2; 23,4; 23,6; 24,6(2); 25,0 (2); 25,6; 26,0; 26,6; 29,0; 30,3; 31,2; 31,8; 33,0; 33,2; 33,6; 33,8 (2); 34,7 (3); 38,6 (5); 40,2 (2); 42,4; 43,5 (3); 44,9; 47,2 (5); 49,6 (2); 50,8; 52,5 (2); 53,8 (2); 57,6 (2); 61,3 (3); 64,7 (4); 70,2 (2); 73,1 (2); 74,2; 76,2; 85,1 Нормальный
5.24 0,6 (3); 1,5 (6); 2,3 (9); 3,1 (4); 3,5 (10); 3,8 (5); 4,1 (8); 4,2 (6); 4,6 (9); 5,4 (9); 6,5 (7); 7,2 (6); 7,7 (4); 8,8 (2); 9,1 (2); 10,3 (2); 11,8; 12,6; 14,4; 15,4 (2); 16,2; 22,6; 37,0 Нормальный
5.25 0,5 (2); 1,2 (3); 1,8 (4); 2,3 (3); 2,6 (3); 3,2 (6); 4,1 (6); 4,5 (9); 4,9 (3); 5,4 (5); 5,7 (2); 6,2 (10); 6,8 (7); 7,6 (9); 8,0 (3); 8,6 (3); 9,1 (3); 9,9 (2); 11,1 (2); 11,7 (2); 12,3 (4); 13,1 (2); 14,4 (2); 15,6; 16,5 (2); 21,0; 24,4 Нормальный
302
Вариационный ряд: 200; 232; 328; 368; 393; 404; 421; 4S7; 483; 611;
527; 540; 544; 572; 598; 605; 619; 633; 660; 681; 736; 791; 942. Необхо-
димо выяснить закон распределения времени безотказной работы
изделий рассматриваемого типа.
Ответ: Вейбулла.
5.27. В результате проведения испытаний изделия получен сле-
дующий вариационный ряд времени безотказной работы в часах:
780; 2000; 3000; 4273; 4474; 4500; 5000; 5100; 5200; 5300; 5395;
5900; 5940; 6000; 6320; 6390 ; 6600; 6760; 6870; 7250; 7500; 7550;
7655; 7870; 8100; 8520; 8600; 9000; 9100; 9110; 9200; 9700; 9730; 9760;
9860; 40130; 10870; 12400; 12550; 12840; 13870; 15350 (п=42). Требует-
ся установить закон распределения времени безотказной работы.
Ответ: Вейбулла.
5.28. В результате обработки данных по испытанию изделий по-
лучен следующий вариационный ряд времен безотказной работы
в часах: НО; 260; 460; 520; 520; 530; 665; 945; 965; 995; 1050;
1115; 1255; 1315; 1315; 1320; 4370; 1455; 1500; 1540; 1540;
1565; 1565; 1580; 1650; 4700; 1705; 1725; 1730; 1755; 1820; 1860, 1875;
1900; 1925; 1935; 2000; 2070; 2130; 2180; 2210; 2230; 2300; 2335; 2430;
2460; 2520; 2540; 2540; 2545; 2545; 2560; 2720; 2860; 3040; 3040; 3050;
3385; 3385; 3515; 3520; 3540; 3545; 3580; 3635; 3705; 3845; 3870; 3970:
4015; 4060; 4605; 4705; 5030; 5700 (п=.75). Нужно выявить закон
распределения времени безотказной работы.
Ответ: Вейбулла.
5.29. В результате обработки экспериментальных данных полу-
чен следующий вариационный ряд времени наработки до первого
отказа в часах: 3; 5; 7; 10; 43; 25; 38; 42; 51; 52; 72; 80; 85; 90; 105;
120; 123; 128; 136; 160; 170; 187; 195; 195; 205; 215; 225; 235; 245;
245; 265; 275; 280; 280; 282; 285; 305; 310; 310; 315; 315; 345; 355; 365;
372; 378; 390; 390; 395; 418; 418; 428; 428; 436; 436; 440; 465; 470;
475; 490; 495; 495; 515; 535; 560; 575; 595; 610; 625; 645 (п=70).
Необходимо выявить закон распределения наработки до отказа.
Ответ: Вейбулла.
5.30. На испытаниях получена следующая наработка до отказа
изделия в часах: 10; 16; 30; 35; 40; НО; 118; 122; 435; 150; 165; 230;
240; 240; 275; 300; 325; 350; 355; 370; 395; 460; 490; 495; 540; 555;
565; 575; 620; 620; 675; 680; 730; 760; 780; 785; 785; 805; 810; 810;
825; 825; 870; 880; 890; 905; 910; 945; 985; 1040; 1045; 1050; 1075;
1090; 1115; 1120; 1140; 11175; 1195; 11205; 1225; 1235; 1245; 1260; 1270;
1270; 1330; 1345; 1345; 1365; 1410; 1420; 1430; 1445; 1525; 1540;
1635; 1660; 1745; 1760; 1795; 4855; 2095; 2095 (п=84). Требуется
установить закон распределения наработки до отказа.
Ответ; Вейбулла.
5.31. В результате испытаний восьми электродвигателей на дол-
говечность получены следующие значения наработки до отказа в ча-
сах: 156; 201; 348; 370; 400; 480; 520 и 605. Нужно определить оцен-
ки средней наработки до отказа и стандартного отклонения, предпо-
лагая закон распределения отказов нормальным. Найти также дове-
рительные интервалы для Т и о с вероятностью а=0,80.
3080
Ответ: Т=>—g—=385 час, S=153 час, 7’в=308,5 час, Тв =
=461,5 час, 117<о<241 час.
5.32. Выборка объемом 25 экземпляров из партии механических
устройств подверглась испытаниям с целью определения доверитель-
303
ного интервала для средней наработки до отказа. По результатам
испытаний найдены 7=1000 час и S = 100 час. Найти доверительные
границы для доверительной вероятности а=0,99, если закон распре-
деления отказов принят нормальным.
Ответ: Гн=944 час, Гв = 1056 час.
5.33. После испытаний десяти экземпляров аккумуляторных ба-
тарей короткого срока службы определено среднее время разряда
Т~3а мин и дисперсия времени разряда 0=25 мин.
Определить нижнюю доверительную границ)? математического
ожидания времени разряда Гн для доверительной вероятности <ti =
= 0,95 и доверительный интервал для Т с той же вероятностью.
Ответ: 7Н = 32,1 мин; 31,4 ж//и<Г<38,6 мин.
5.34. Испытано на надежность 9 гироскопических узлов до из-
носа, при этом зарегистрированы следующие значения наработки
в часах: 5; 10; 25; 50; 75; 100; 125; 150; 160.
Нужно определить Т, S и нижнюю границу для Т с вероят-
ностью а=0,99, считая распределение наработки нормальным.
Ответ: 1=77,8 час-, S=95 час. Доверительные границы не мо-
гут быть определены, так как предположение о нормальном распре-
делении отказов неверно.
5.35. Известно, что распределение наработки до отказа нор-
мальное с Сто =150 час. Требуется оценить объем испытаний изде-
лий, необходимый для оценки средней наработки до отказа с ошиб-
кой не более 75 час при доверительной вероятности а=0,80. (Срав-
ните результат решения с условием и решением примера 5.5.)
Ответ: п~7.
5.36. Известно, что ожидаемая дисперсия равна 10 000 час. Оце-
нить объем испытаний, потребный для оценки средней наработки
до отказа с ошибкой, не превосходящей 50 час при доверительной
вероятности а=0,99. (Сравните результат решения с условием и ре-
шением примера 5.6.)
Ответ: п~22.
5.37. Ориентировочно известно, что в среднем наработка состав-
ляет около 1 000 час, закон распределения отказов нормальный и
коэффициент вариации v=T/o составляет приблизительно 0,1. Опре-
делить ориентировочно минимальный объем испытаний для точной
оценки параметров закона распределения износовых отказов щеток
электромашин. Относительная ошибка при оценке Т и о не должна
превышать 5% с доверительной вероятностью равной 0,99.
Ответ: п=22.
5.38. Из 50 (п=50) гироскопических узлов, испытанных в тече-
ние 100 час (7о=100) отказало 4 штуки. Наработки отказавших
узлов в часах составили: 51, 74, 90, 95. Предполагается, что отказы
распределены нормально. Нужно оценить параметры закона распре-
деления с доверительной вероятностью не ниже 0,95.
Ответ: Т=227 час± 134 час, о=88 час±80 час.
5.39. При испытании 8 дизельных электростанций по плану [п,
Б, п] получены следующие значения наработки в часах: 8; 9; 15; 28;
36; 54; 102 и 148. Предполагается экспоненциальный закон распре-
деления отказов. Необходимо определить X и верхнюю границу Хв
при доверительной вероятности «2=0,95.
Ответ: Х=2-40~2 1/час; Хв=3,3-10~2 1/час.
5.40. Испытанию были подвержены 15 трансформаторов. В ре-
зультате испытаний, при которых не было замены отказавших
экземпляров, получены наработки в часах: 2; 5; 8; 16; 19; 25; 43; 67;
304
94; 116; 159; 201; 332; 400 и 418. Определить двусторонний довери-
тельный интервал для интенсивности отказов с доверительной ве-
роятностью а=О,99.
Ответ: Х= (0,364= 1,41)-НО-2 1/час.
5.41. По плану [п. Б, п] испытано 12 изделий с общей наработ-
кой 1464 час. Требуется оценить среднюю наработку до отказа и
определить ее нижнюю границу с вероятностью ai=0,9, исходя из
предположения о экспоненциальном законе распределения отказов.
Ответ: 7=122 час; 7В=88 час.
5.42. По план)' [и, Б, п] испытано 10 изделий с экспоненциаль-
ным законом распределения отказов. Суммарная наработка испы-
танных изделий составляет 8 000 час. Определить с вероятностью
а='0,97 доверительный интервал для средней наработки до отказа,
причем нижняя доверительная граница должна быть определена
с вероятностью сц=0,995.
Ответ: 7=400=1480 час.
5.43. За время испытаний 10 изделий (я=10) по плану '[п, Б, 7о]
отказало 4 изделия, наработки которых были 50, Н'00, 150 и 200 час.
Испытания продолжались 250 час. Нужно оценить интенсивность от-
казов и определить ее доверительный интервал с вероятностью а=
=0,95.
Ответ: %=2 • 10~3 1/час; Л= (5,5=44) • 10-4 1/час.
5.44. При испытаниях 100 электродвигателей по плану [п, Б, /о]
в течение 1 000 час отказало 8 шт. Суммарная наработка составила
92 400 час. Оценить среднюю наработку до отказа и найти ее ниж-
нюю доверительную границу с вероятностью ai=0,99, исходя из
экспоненциального закона распределения отказов.
Ответ: Т—1'1 500 час; Тв~5 775 час.
5.45. На испытания поставлено 50 невосстанавливаемых изделий.
Время испытаний ограничено 1 000 час. За это время отказало 10
экземпляров изделий, которые показали следующую наработку в ча-
сах: 4; 27; 69; 118; 182; 222; 293; 385; 602; 887. Определить верхнюю
доверительную границу интенсивности отказов с доверительной ве-
роятностью «2=0,99 и двусторонний доверительный интервал с ве-
роятностью ia=0,95.
Ответ; Л.в=0,44-10-3 1/час; 7= (0,11 =0,40) • IO”3 1/час.
5.46. При испытаниях 50 изделий по плану [п, Б, /о] в течение
1 000 час отказов не было. Необходимо найти верхние доверительные
границы интенсивности отказов с доверительной вероятностью «1=
=0,99 и «2=0,95.
Ответ: 7в=0,92• 10~4 1/час и Хв=0,60-10-4 1/час.
5.47. По плану [п, Б, /о] было испытано 20 редукторов в тече-
ние 1 500 час. За время испытаний отказов не было. Определить
нижнюю границу средней наработки до отказа с вероятностью «1=
=0,95, исходя из предположения о экспоненциальном законе рас-
пределения отказов.
Ответ: 7H=il0 000 час.
5.48. При испытаниях п=60 двигателей по плану {и. Б, d] до
11-го отказа, происшедшего на 40-м часу работы, зарегистрированы
следующие значения наработки отказавших экземпляров в часах:
1; 2; 4; 8; 10; 22; 28; 29; 32; 40. Требуется оценить 7 и найти их
доверительные -Интервалы с вероятностью 0,95.
Ответ: 7=4,57-10-® 1/час; 7=218 час; 7= (2,29=7,8) X
Х10-’ 1/час; 7='128= 456 час.
20—1086 305
5.49. По плану [п. Б, d] было испытано п=30 изделий до 6-го
отказа, наступившего через 50 час после начала испытаний. Нара-
ботка остказавших изделий в часах составила: 7, 13; 26; 30; 36; 38
и 50. Требуется определить нижнюю доверительную границу Т с ве-
роятностью Hi- -0,999 и его выборочную оценку.
Ответ: 7’н=89 час; 7=280 час.
5.50. По плану '[я, Б, а] испытано 50 редукторов. После 10-го
отказа наработка отказавших экземпляров составила 1 000 час. Де-
сятый отказ произошел па 200 час с начала испытаний. Найти дове-
рительный интервал для интенсивности отказов с вероятностью ы=
=0,95.
Ответ: Х= (0,53= 1,9) • 10~3 1/час.
5.51. За 500 час эксплуатации 15 генераторов произошло 7 от-
казов, отказавшие генераторы немедленно заменялись, время отка-
зов не регистрировалось. Оценить среднюю наработку до отказа ге-
нераторов и найти его нижнюю границу с вероятностью «1=0,99.
Ответ: 7’=1070 час; 7н=470 час.
5.52. Испытано 8 экземпляров цифровой вычислительной маши-
ны по плану [п, В, 7о]. Испытания продолжались 7о=100 час и при
этом зарегистрировано 8 отказов. Отказы машин мгновенно устра-
нялись. Найти доверительный интервал значений интенсивности от-
казов с доверительной вероятностью для нижней границы «1 = 0,90
и для верхней «2=0,995; определить доверительную вероятность для
двустороннего интервала.
Ответ: Х= (0,58=2,33) 10-2 1/час; «=0,895.
5.53. В эксплуатации находилось 29 связных радиостанций. За
год круглосуточной эксплуатации произошло 249 отказов, которые
устранялись в короткое время. Оценить наработку до отказа (Т)
и найти ее нижнюю границу с вероятностью си=0,95.
Ответ: 7=1000 час; 7в=900 час.
5.54. По плану [п, В, d] были испытаны 20 электродвигателей.
После 6-го запланированного отказа, наступившего через 180 час
после начала испытаний, испытания приостановлены. Требуется оце-
нить интенсивность отказов и найти ее верхнюю границу с вероят-
ностью «2=0,95.
Ответ: Х=1,39-10~3 1/час; Хи=2,92• 10-3 1/час.
5.55. При осуществлении плана (п=50, <7=101) испытаний элек-
тронных приборов 101-й отказ наступил через 696 час испытаний,
время наступления предыдущих отказов не регистрировалось. Опре-
делить среднюю наработку до отказа и найти его нижнюю границу
с доверительной вероятностью ai=0,99, исходя из экспоненциального
закона распределения отказов.
Ответ: 7=348 час; 7В=266 час.
5.56. Для осуществления испытаний по плану [п. Б, п] необходи-
мо ориентировочно установить количество объектов, которое нужно
подвергнуть испытаниям, чтобы с вероятностью 0,95 истинное зна-
чение Л отличалось от оценки не более чем на 50%.
Ответ: п=-20.
5.57. Определить количество изделий, которые нужно испытать
по плану [п, Б, п], если нужно оценить X так, чтобы оценка не пре-
вышала математическое ожидание более чем в 2,3 раза с вероятно-
стью a=0,99.
Ответ: п~13 шт.
306
5.58. Установить объем испытании для плана [п, Б, п] так, чтобы
оценка средней наработки до отказа с вероятностью 0,975 не отли-
чалась от верхней доверительной границы более чем в два раза.
Ответ: п='1О.
5.59. Найти объем испытаний с вероятностью ао=О,8О для плана
[п, Б, £о], если предполагаемая интенсивность отказов составляет
.3 - J0 •; 1/час. Полученная оценка не должна превышать нижнюю
границу с вероятностью 0,95 более чем в 3 раза.
Ответ: п/о=1000 час.
5.60. Для осуществления испытаний для оценки среднего вре-
мени безотказной работы по плану [п , Б, /о] определить объем ис-
пытаний с вероятностью 0,90, при котором оценка не должна отли-
чаться от верхней границы с вероятностью 0,95 более чем в два ра-
за, если предполагается, что Го»’1000.
Ответ: nte « 4800 час.
5.61. Для организации испытании по плану [п, Б, Д нужно най-
ти d так, чтобы оценка -X не отличалась от нижней границы более
чем 1,5 раза с вероятностью 0,90.
Ответ: rf=15.
5.62. Испытание для определения Т предполагается производить
по плану '[и, Б, d], Нужно определить cl так, чтобы оценка Т не от-
личалась от математического ожидания с вероятностью а=0,95 бо-
лее чем в два раза.
Ответ: d = 8.
-5.63 . При планировании испытаний типа [п, В, /о] с целью оцен-
ки X нужно с ”о = О,95 определить ориентировочный объем испыта-
ний nto, при котором с вероятностью а=0,90 оценка не будет отли-
чаться от нижней границы более чем на 40%, если ориентировочно
Хо=4О~2 1/час.
Ответ: nl<,= 1400 час.
5.64. Рассчитать ориентировочно с вероятностью а=0,80, за ка-
кое .время эксплуатации можно оценить интенсивность отказов 15
объектов' восстанавливаемой электронной аппаратуры, если предпо-
ложительно Хо=1-10—3 1/час. Точность оценки должна быть такова,
чтобы она с вероятностью 0,99 не отличалась от нижней границы
более чем в 3 раза.
Ответ: Л>=36О час.
5.65. Для организации испытаний 20 двигателей внутреннего
сгорания по плану [п, В, d] необходимо оценить d так, чтобы оценка
X не превышала истинного значения с вероятностью а=0,95 более
чем в два раза.
Ответ: d—8.
5.66. Для оценки средней наработки до отказа с ошибкой не
более 50% при доверительной вероятности 0,99 определить ориенти-
ровочное количество отказов, которое потребуется для испытания
п = 50 восстанавливаемых изделий.
Ответ: d=30.
5.67. По плану [п, В, /о] испытано п=100 изделий в течение вре-
мени i0 = 100 час. При этом возникло 48 отказов. Оценить нижнюю
доверительную границу средней наработки до отказа с вероятностью
«1=0,95, используя формулы табл. 5.3 и формулу (5.13).
Ответ: Тн= 158 час.
5.68. При испытаниях по плану {и, В, rf] п=200 изделий 50-й
запланированный отказ произошел через td= 100 час испытаний.
20* 307
Определять с вероятностью а4 = 0,95 нижнюю границу средней нара-
ботки до отказа по табл. 5.3 и формуле (5.13).
Ответ: Гня325 час; Тв = 360 час.
5.69. Испытано 6 экземпляров электронных усилителей, отказы
которых подчинены гамма-распределению. Время безотказной работы
усилителей в часах следующее: 215; 95; 360; 260; 370 и 500. Оценить
параметр in и 7..
Ответ: к—1,62 • 10~2 1/час; т=4,85.
5.70. При испытаниях 10 электронных ламп получены следующие
результаты: математическое ожидание времени безотказной работы
М(/) = 1000 час, дисперсия Л(/) = 105 час. Оценить параметры рас-
пределения, исходя из предположения о гамма-распределении отка-
зов.
Ответ: %='1 • 10-2 1/час, т= 10.
5.71. Приняв в условии задачи 5.70 £>(/) = 106 час, оценить к
и т.
Ответ: Х=11 • 10-3 1/час, т=1, т. е. распределение отказов
экспоненциальное, что согласуется с равенством стандартного откло-
нения математическому ожиданию.
5.72. Определить примерно необходимое количество k запасных
блоков на каждый находящийся в эксплуатации блок, с тем чтобы
обеспечить наработку в среднем по 1000 час, если интенсивность от-
казов к составляет 4- 10-3 1/час.
Ответ: /г = 3.
5.73. На испытания поставлено 8 экземпляров резервированной
аппаратуры с трехкратным ненагруженным резервом и идеально на-
дежным переключающими устройствами. Все устройства работали до
полного отказа, показав наработку в часах: 156; 184; 201; '252; 302;
366; 405 и 503. Наработка имеет гамма-распределение. Нужно оце-
нить параметр к и найти его верхнюю границу с доверительной ве-
роятностью «2=0,99.
Ответ: 7.= 1,35 • 10‘2 1/час; 7.,.. = 2,2 • 16 2 1/час.
5.74. Двадцать экземпляров однотипной резервированной аппа-
ратуры с гамма-распределением наработки до отказа при испыта-
ниях наработали в сумме 5100 час. В аппаратуре применено одно-
кратное ненагруженное резервирование с практически безотказными
переключающими устройствами. Требуется найти с вероятностью
0,95 нижнюю доверительную границу средней наработки на отказ
основного компонента системы.
Ответ: Гв=100 час.
5.75. Десять экземпляров электронных преобразователен тока
многократно испытывались на наработку с восстановлением после
отказов. Количество испытаний /и,- распределилось по экземплярам
следующим образом: 3, 1, 2, 4, 3, 1, 4, 3, 2, 2. Общая наработка со-
ставила 2500 час. Оценить среднюю наработку на отказ и найти ее
доверительный интервал с вероятностью 0,90, исходя из гамма-рас-
пределения наработки до т-го отказа.
Ответ: 7’=100, 7’в=74 час, 7’в = 144 час.
5.76. Четыре экземпляра цифровой вычислительной машины ис-
пытывались до 10-го отказа каждого экземпляра и показали нара-
ботку 210; 240; 250 и 300 час. Оценить параметр к, исходя из гам-
ма-распределеппя наработки.
Ответ. 7.=0,04 1/час.
,308
5.77. В паспортных данных 5 поверочных установок, .направлен-
ных в ремонт, указаны следующие величины чисел отказов и нара-
боток за время предшествующей эксплуатации:
l-й экземпляр — 6 отказов с общей наработкой 323 час;
2-й экземпляр — 5 отказов с общей наработкой 441 час;
3-й экземпляр — 8 отказов с общей наработкой 948 час;
4-й экземпляр—2 отказа с общей наработкой 352 час;
5-й экземпляр — 4 отказа с общей наработкой 511 час.
Оценить интенсивность отказов и найти ее верхнюю границу
с вероятностью «2=0,95, если предположить гамма-распределение
наработки до т-го отказа.
Ответ: Х=9Д • 10~s 1/час; Хв = 1,31 • 10-2 1/час.
5.78. Определить примерное количество экземпляров аппаратуры,
необходимое для испытаний, чтобы оценить параметр X с относи-
тельной ошибкой не более 30% при доверительной вероятности а —
= 0,8, если отказы этой аппаратуры имеют гамма-распределение
с известным параметром т=2.
Ответ: и=15.
5.79. Определить, до какого числа отказов (т) нужно испыты-
вать каждый из пяти экземпляров аппаратуры с постоянной интен-
сивностью отказов, чтобы оценить X с относительной ошибкой не бо-
лее 30% при доверительной вероятности «=0,8.
Ответ: т = 6.
5.80. Найти объем (тп) испытаний восстанавливаемых устройств
с постоянной интенсивностью отказов, потребный для оценки X с от-
носительной ошибкой не более 25% с доверительной вероятностью
а=0,95.
Ответ: mn=W0.
5.81. Известно, что X = 1,03 • 10 3 1/час, Xв = 1,96 • ГО 3 \/час,
Хн = 0,68-10~3 1/час. Оценить вероятность безотказной работы в те-
чение / = 20 час и найти доверительный интервал.
Ответ: Р(20) =0,979; Рн(20) =0,961; Рв (20) =0,986.
5.82. При испытаниях надежности партии изделий получена
оценка средней наработки до отказа 7=120 час. Оценить по точным
и приближенным формулам P(t) и найти абсолютную и относитель-
ную ошибку при приближенных расчетах для времени наработки
50, 30 и 20 час.
Ответ: См. табл. 5.16.
ТАБЛИЦА 5.16
Ответ к задаче 5.82
t 5Э час 30 час 20 час
Р (0 (точное) -Р (/) (приближенное) ДР ДР, »/о 0,657 0,585 0,072 И 0,779 0,750 0,029 3,8 0,845 0,833 0,012 1,4
5.83. В результате испытаний 15 экземпляров аппаратуры по
плану [п, Б; п] получена суммарная наработка Р =1200 час. Оценить
309
P(t) при £=10 час и найти нижнюю границу для вероятности а=
=0,99.
Ответ: Р(10) =0,883; Р„(10) =0,81'1.
5.84. В результате испытаний по плану ![га=50, Б, £о = 500] полу-
чена суммарная наработка £к =20000 час при отказе 5 изделий..
Найти доверительный интервал P(f) для £=240 час, если « = 0,90.
О т в ет: Ри=0,895; Рв = 0,976.
5.85. При испытаниях по плану 1[га, Б, d] и 10 запланированных от-
казах (d=10) .получена суммарная наработка £s =1890 час. Оценить
Р(/) при £=60 час и найти верхнюю границу с вероятностью а=
=0,99.
Ответ: Р (60) =0,655; Рв:(60) =0,88.
5.86. В результате испытаний 30 изделий в течение 100 час не
отмечено ни одного отказа. Определить нижнюю доверительную гра-
ницу с вероятностью «=0,95 для Р(£) за время £=90 час.
Ответ: Рн(90)=0,91.
5.87. В ходе .испытаний по плану [п=20, В, £7 =100 час] отмечено
9 отказов. Оценить Р(£) и найти нижнюю границу с вероятностью
а=0,95 для времени работы £=8 час.
Ответ: Р(8) =0,964; РЕ(6) =0,942.
5.88. В результате испытаний по плану (п, В, d], где d='15, сум-
марная наработка составила 52 000 час. Требуется оценить Р(£) за
время £=100 час и найти доверительный интервал с 'а=0,90.
Ответ: P(il00) =0,973; Р„=956; Рв=0,99'1.
5.89. В ходе эксплуатации контрольно-измерительной аппарату-
ры установлено ее среднее время между отказами (наработка на
отказ) 7'ср=120 час. Определить, в течение какого времени аппара-
тура будет работать безотказно с вероятностью Р(£)=0,99.
Ответ: £=1,2 час.
5.90. Верхняя граница вероятности отказа аппаратуры за время
£='10 час должна быть 0,02 с .вероятностью « = 0,95. Найти верхнюю
границу интенсивности отказов аппаратуры.
Ответ: Лв=2- 10-3 1/час.
5.91. Испытание надежности радиоламп с_гамма-распределенпем
отказов дало следующие результаты: т=1,5; Х=10-4 1/час. Оценить
вероятность безотказной работы радиоламп для времени £=
= 1000 час. _
Ответ: Р(1000) =0,95.
5.92. В результате испытаний аппаратуры с гамма-распределе-
нием отказов получены следующие оценки параметра распределения:
щ=2; Х=10~6 1/час. Нужно оценить время, при котором вероят-
ность безотказной работы будет равна 0,95.
Ответ: £=4 • 105 час.
5.93. Резервированная аппаратура с однократным ненагружен-
ным резервом имеет интенсивность отказов Х=2-10-5 1/час. Опре-
делить вероятность отказов за £=500 час.
Ответ: Р (500) =0,9999.
5.94. Интенсивность отказов Х=5 10~4 1/час, а требуемая веро-
ятность безотказной работы за 1000 час не менее 0,98. Найти крат-
ность невосстанавливаемого ненагруженного резерва аппаратуры.
Ответз т—2.
5.95, Испытано на износ 200 шт. шарикоподшипников гироско-
пов и получена Т=1240 час, S=180 час. Оценить вероятность без-
310
отказной работы подшипников на протяжении 1000 час и опреде-
лить «пжнюю границу с доверительной вероятностью а = 0,99.
Ответ: Р=0,9'1; Рн=0,86.
5.96. В результате испытании 100 ламп накаливания получены
значения выборочной средней наработки до отказа 7 = 2000 'час и
стандартного отклонения 5=400 час. Найти нижнюю доверительную
границу вероятности безотказной работы для / = 800 час и а=0,999.
Ответ: Рн = 0,995.
5.97. При входном контроле партии резисторов испытана выбор-
ка и получены следующие результаты: выборочное среднее Р =
= 5050 ом, стандартное отклонение S = 60 ом. Оценить долю рези-
сторов в партии, у которых параметр выйдет за установленные до-
пуска 5000±2%, что равносильно отказу.
Ответ: 1—Р=21%.
5.98. Измерительный прибор не имеет систематических ошибок,
а случайные ошибки распределены нормально. После ряда измере-
ний получены оценки измеряемой величины х ='10,57 и стандартного
отклонения о = 2,05. Определить вероятность надежности измерений,
заключающейся в том, что абсолютное значение ошибки в опреде-
лении истинного значения измеряемой величины не превысит 20%
ОТ X-
Ьтъет. Р = 68111о.
5.99. Исполнительный орган системы работает надежно при вы-
ходном сигнале 100±20 мв. В результате 80 измерений получены
оценки среднего значения сигналами стандартного отклонения: Т =
= 105 же; 5=10 же. Найти оценку Q и с доверительной вероятностью
а=0,99 верхнюю границу вероятности отказа исполнительного
органа за счет_входного сигнала.
Ответ: <2= 0,074; QB=0,121.
5.100. В результате старения при годичном хранении среднее
значение выходной характеристики аппаратуры У составляет 85 же.
Стандартное отклонение осталось неизменным и составило S=6 же.
Эти данные получены в результате проверки 16 экземпляров аппа-
ратуры. Найти оценку вероятности безотказной работы аппаратуры
после годичного хранения и ее нижнюю границу с вероятностью
ai=0,95, если аппаратура считается исправной при выходной харак-
теристике У=75 =100 же.
Ответ: Р=0,946; Р,-.~ 0,885.
5.101. Исходя из условия задачи 5.95, найти гарантийное время
безотказной работы (нижний толерантный предел) шарикоподшип-
ников с гарантийной вероятностью «=0,90 и достоверностью расчета
Р=0,99.
Ответ: 910 час.
5.102. Исходя из условия задачи 5.96, найти гарантийное время
безотказной работы ламп с гарантийной вероятностью Р—0,996 и
a=0,999.
Ответ: 550 час.
_ 5.103. При испытании на износ н=50 шт. редукторов получено
7=1500 час, 5=1100 час. Найти нижний толерантный предел вре-
мени безотказной работы с вероятностью /’=0,95 при доверительной
вероятности a=0,90.
Ответ: 1270 час.
5.104. В результате переменных факторов выходная характери-
стика системы подвержена флюктуации и имеет среднее значение
У=200 мв и стандартное отклонение £=15 мв. Эти данные иолу-
311
ЧёнЫ по 160 измерениям. Определить тблерантнЫе пределы измене-
ния выходной характеристики при Р = 0,98 и а=0,95.
Ответ: Уи =160 мв\ Ув = 240 мв.
5.105. Из партии сухих электробатарей, находившихся «а хра-
нении, взята выборка 60 шт. и проверено напряжение. Установлено,
что среднее выборочное и=24,22 в и стандартное отклонение 0,31 в.
Найти с достоверностью а=0,995, в каком диапазоне будет нахо-
диться напряжение у 95% изделий.
Ответ: нн = 23,4 в; нв=25 в.
5.106. Проведено га=500 испытаний механизмов катапультиро-
вания и зарегистрировано d—'2 отказа. Определить верхнюю довери-
тельную границу вероятности отказа механизма катапультирования
с доверительной вероятностью «2=0,975.
Ответ: QB = 0,014.
5.107. При испытании на ударную нагрузку п=65 блоков элек-
тронной аппаратуры отмечено 5 отказов. Найти двусторонний дове-
рительный интервал вероятности безотказной работы с а=0,95.
Ответ: Р=0,830=0,975.
5.108. Испытано 4 экземпляра поверочной аппаратуры цикличе-
ского характера работы:
1-й экземпляр в 118 циклах имел 6 отказов;
2-й экземпляр в 87 циклах имел 5 отказов;
3-й экземпляр в 121 циклах имел 4 отказа;
4-й экземпляр в 59 циклах имел 1 отказ.
Определить оценку вероятности безотказной работы аппаратуры
в одном цикле п нижнюю границу с доверительной вероятностью
ai=0,99. _
Ответ: Ро=0,958; Рн=0,928.
5.109. При испытании 12 подъемных механизмов по 50 циклов
работы каждого не зарегистрировано ни одного отказа. Оценить
ь доверительных границах с вероятностью «=0,95 вероятность без-
отказной работы подъемного механизма в одном цикле.
Ответ: Рв=1; Рн=0,995.
5.110. Предполагается, что вероятность отказа затворов около
0,01, а ошибка при ее оценке ® не должна превышать 0,001 с веро-
ятностью 0,95. Найти примерный требуемый объем .испытаний за-
творов.
Ответ: п=38000.
5.111. Предельно допустимая ошибка в оценке вероятности от-
каза составляет 0,01 с вероятностью а=0,96 и предполагаемая веро-
ятность отказа равна 0,01. Определить примерный объем испытаний.
Ответ: га=380.
5.112. Из партии изделий объемом в Д'=40 экземпляров извле-
чена выборка, объем которой равен 10 экземпляров. При испыта-
ниях выборки с целью контроля надежности, в интересах заказчика,
обнаружено 2 дефектных изделия. Следует решить, можно ли при-
нять партию с риском аas0,12, если при числе дефектных изделий
в партии Di^5 партия должна быть забракована.
Ответ: Партия бракуется.
5.113. В эксплуатации находится 20 невосстанавливаемых объек-
тов и 30 таких же объектов хранится на складе. К заданному сроку
эксплуатации 1 объект вышел из строя. Допустимая доля дефектных
изделий всей партии за данное время эксплуатации составляет 6%.
Определить с риском 0,20 возможность дальнейшей эксплуатации из-
делий без профилактических мер.
Ответ: Профилактика должна быть произведена.
5.114. Заводом изготовлено 45 специальных автомашин. Допу-
стимое число неисправных машин в партии £>о = 4 шт. Найти при-
емочное число Ао, если испытаниям будет подвергнуто 15 машин.
Решение должно быть принято с риском, не превышающим 0,10.
Ответ: Ло = 2; а'=0,098.
5.115. Заводом изготовлена серия автоматов в количестве 120 шт.
Для выходного контроля .выделено 20 автоматов. Для признания
серии надежной в ней должно быть не более 5% дефектных изде-
лий. Определить приемочное число с риском а ~ 0,05.
Ответ: Ло=2; «'=0,06.
5.116. На складе хранится 200 изделий однократного действия.
При испытании 50 изделий, взятых из общего числа случайным об-
разом, зарегистрировано 2 отказа. Требуется найти с риском 0,20
соответствие требованиям к надежности всей партии изделий, если
допустимая вероятность безотказной работы должна быть не менее
0,95.
Ответ: Партия должна быть забракована, так как Д, = 1.
5.117. Для контроля надежности в интересах заказчика взята
выборка п=30 из Л,=300 устройств однократного действия. Кон-
тролируемая партия устройств допускает максимальную вероятность
отказов менее 0,12. Определить браковочное число с риском Р = 0,1С.
Ответ: Л1=2.
5.118. Для выборки п=10 изделий из партии М=100 шт. уста-
новлено приемочное число Ло=1. Найти риск поставщика при с/о =
= 0,05 с использованием формул гипергеометрпческого и ^биноми-
ального распределений.
Ответ: При гипергеометрическом распределении а'=0,077; при
/-биномиальном </=0,081.
5.119. Из партии объемом Л,= 1000 изделий взята выборка п=
= 100 экземпляров. Установлены приемочное и браковочное числа:
.4о = 3, At = 4. Определить риск поставщика и риск заказчика, если
<7о=0,02, а <71=0,2, с использованием формул гипергеометрического
и f-бпномиального распределения.
Ответ: Для гипергеометрпческого распределения а'=0,131;
Р'=0,030; для /-биномиального распределения а'=0,133, Р'=0,035.
5.120. Используя селения задачи 5.119, найти риск поставщика
и риск заказчика, исходя из биномиального распределения.
Ответ: «'=0,141; Р'=0,037.
5.121. Используя условия задачи 5.118, пользуясь биномиальной
аппроксимацией, определить риск поставщика. Сравните с ответом
задачи 5.11-8.
Ответ: а'=0,086.
5.122. По условию задачи 5.115 вычислить приемочное число и
риск поставщика; исходя из биномиальной аппроксимации, сравнив
результат с ответом задачи 5.115.
Ответ: Ло = 2; а'=0,075.
5.123. Для контроля надежности в интересах заказчика прове-
дено 50 испытаний восстанавливаемой электронной аппаратуры, ве-
роятность отказов которой должна, быть меньше 0,10. При испыта-
ниях зарегистрировано 2 отказа. Найти риск заказчика.
Ответ: Р'=0,112.
5.124. Вычислить объемы выборок биномиального плана контро
ля надежности в интересах заказчика при браковочном числе Ai — l
при рисках р ~ 0,05; 0,10; 0,20; и </1 = 0,05; 0,10.
313
Ответ: См. табл. 5.Г7.
ТАБЛИЦА 5.17
Ответ к задаче 5.124
qY = 0,05 п — 50 [7 = 0,077 п = 40 Р' = 0,128 п ~ 30 [7 = 0,215
= 0,10 п = 30 ₽' = 0,042 п = 20 Р' = 122 п — 15 [7= 0,206
5.125. Рассчитать браковочные числа при испытании выборки
объемом 50 изделий с целью контроля в интересах заказчика, если
установить q-L равным 0,04; 0,08 и 0,15, а «0,10.
Ответ: См. табл. 5.18.
ТАБЛИЦА 5.18
Ответ к задаче 5.125
<71 0,04 0,08 0,15
А, 1 2 5
Г 0,130 0,083 0,112
5.126. Для выходного контроля надежности заводской продукции
взята .выборка п=100 экз. невосстанавлпваемых устройств. Изделия
считаются надежными при <?(><:0,02. Найти приемочное число с ри-
ском изготовителя и ~0,10 п фактический риск, исходя из распреде-
ления вероятностей по закону Пуассона. Сравнить результат с усло-
вием и ответом задачи 5.119.
Ответ: Л0=3; а'=0,143.
5.127. Выборка объемом п=И00 устройств подлежит испытанию
в интересах заказчика. Браковочное число принято Ai='4, a <?i = 0,08.
Определить риск ['/, исходя из распределения.^Пуассона, и сравнить
результат с ответом задачи 5.119.
Ответ: р,=0,042.
5.128. При контроле надежности с применением распределения
Пуассона установлено: приемочное число Ло=1, риск поставщика
а=0,05 .и значения вероятности ^о=0,01; 0,02; 0,03 п 0,05. Вычислить
объемы испытаний для соответствующих значений qo.
Ответ: См. табл. 5.19.
ТАБЛИЦА 5.19
Ответ к задаче 5.128
<7о 0,01 0,02 0,03 0,05
п 35 18 12 7
314
5.129. Для Выходного контроля заказчиком продукции заводй
установлен риск р~0,10, вероятность отказа <71=0,05. Рассчитать
потребные объемы выборок при браковочных числах от 1 до 10.
Ответ: См. табл. 5.20.
ТАБЛИЦА 5.20
Ответ Ънзадаче 5.129
А, 1 2 3 4 5 6 7 8 9 10
п 60 95 126 155 183 210 223 263 289 301
5.130. При испытании устройств многократного действия в тече-
ние 10 000 циклов, требуемая вероятность безотказной работы кото-
рых составляет А = 0,995, решено установить приемочные числа
Ло=5О пли Л0=60. Определить риск изготовителя в том и другом
случае.
Ответ: При Ло = 5О, «' = 0,472; при Ло=6О, а'=0,056.
5.131. Вероятность отказов стартерного механизма дизеля долж-
на быть менее 0,08. Найти браковочное число А с риском заказ-
чика Р = 0,10при 1000 запусков двигателя.
Ответ: А=70.
5.132. Система зажигания двигателя внутреннего сгорания испы-
тывалась в течение 2000 циклов, при этом отмечено 40 отказов.
Определить, можно ли принять данную систему, если число отказов
считать приемочным числом при риске р=0,05 и предельной веро-
ятности отказа <7 = 0,02.
Ответ: //=0,532. Следовательно, партия не может быть при-
нята.
5.133. Построить f-биномиальный график последовательного кон-
троля, исходя из параметров #=200; <7о = 0,03; </1 = 0,08; «=0,10;
Р=0,05. Принять решение при положениях рабочей точки <7=4; т=
=40; d=3; m=60; d=0; m=58. Проверить решение сравнением от-
ношения правдоподобия 1т с оценочными нормативами А и В.
Ответ: Характеристические точки графика:
a) d=0, т=50-
б) d=6, m=98;
в) d=ill, m=200.
Положение рабочей точки d=4, m=40 соответствует браковке
/=13>Л=9,5. Положение рабочей точки d=3, m=60 соответствует
правилу продолжения испытаний В = 0,056</т=0,79<Л=9,5. Поло-
жение рабочей точки <7=0, m=52 соответствует приемке, так как
то=50.
5.134. Для партии объемом #=400 изделий, когда риск постав-
щика равен риску заказчика и составляет «=1р=0,10, а число де-
фектных изделий в партии при нулевых гипотезах (£>о) составляет
6, 4, 2 шт., число дефектных изделий при альтернативных гипоте-
зах одинаково и составляет ьОш 'Ю шт. Требуется .рассчитать табли-
цы /-биномиального последовательного плана контроля доли дефект-
ных изделий.
315
Ответ: См. табл. 5.21.
ТАБЛИЦА 5.21
Ответ к задаче 5.134
Номер плана Приемочные и браковоч- ные числа испытаний d
0 I 2 3 4 5 6
[ р. не менее 42 49 56 64 70 78 87
т6р не более — — — — 11 32 54
II тир не менее 28 41 50 61 72 — —
гп6р не более — — — 18 75 — —
ш 2 /?7пр не менее 26 38 53 —- — — —
т№ не более — — 18 — — -—• —
5.135. Определить константы hi, h2 и 5 пЛана периодического
последовательного контроля надежности полупроводниковых прибо-
ров при пх‘ серийном производстве, если за заданное время испыта-
ний 9о='1 10 91 = 5- 10~4; а=Р=0,05.
Ответ: Л±=—1,83; /z2=l,83; S=2,5-104.
5.136. Известны <Д = 2 • 1(Ц5, г/1 = 12 • 105, а=0,02, р=0,01. Вы-
числить константы плана контроля неограниченно большой партии
изделий.
Ответ: hi~—2,58; /г2 = 3,46; S = 0,56-10-4.
5.137. Используя условия примера 5.53, определить константы
плана, применяя закон Пуассона; составить таблицу -плана п срав-
нить ее с табл. 5.10 примера 5.53.
Ответ: hi = —1,10; й2 = 0,99; 5 = 0,044 ц см. табл. 5.22.
ТАБЛИЦА 5.22
Ответ к задаче 5.137
т d
0 1 2 3 4 5 6 7 8 9 W
25 48 71 94 116 138 164 185 207 230 253
'«бР — — 23 46 69 92 114 136 158 181 204
5.138. Рассчитать константы биномиальных планов -последова-
тельного контроля вероятности отказов при а='Р = 0,10 п данных, по-
мещенных в табл. 5.23.
ТАБЛИЦА 5.23
Исходные данные к задаче 5.138
Номер плана I II 1П IV V
«7» 0,06 0,05 0,04 0,03 0,02
91 0,10 0,11 0,12 0,13 0,14
316
Ответ: См. табл. 5.24.
Таблица 5.24
Ответ к задаче 5.138
Номер плана I II III IV V
й, —4 —2,6 — 1,9 —1,4 —1,06
/г2 4 2,6 1,9 1,4 1,06
S 0,071 0,069 0,073 0,067 0,063
5.139. Для контроля доли дефектных изделий в партии объемом
М=1000 изделий построить таблицы гппергеометрического и биноми-
ального последовательных планов при а = |3 = 0,10; 01=10 (91 = 0,10)
и Do —5; 4 и 2 (<уо = О,О5; 0,04 и 0,02). Сравнить эти планы с экви-
валентными f-бпномиальными (см. пример 5.52 и задачу 5.134).
Ответ: См. табл. 5.25.
таблиц г 5.25
Ответ к задаче 5.139
Номер плана Do (<7о) План Приемочные и браковочные числа испы- таний d т
0 1 2 3 4 5
I 5 (0,05) Г илергео- метрическии /?7пр не ме- нее /7?бр не ме- нее 33 42 51 60 8 69 27 78 50
Биномиаль- ный /??пр не ме- нее /лбр не бо- лее 46 61 77 92 107 16 122 31
II 4 (0,04) Гиьергео- метрический не ме- нее /??бр не бо- лее 29 39 50 60 20 71 42 —
Биномиаль- ный /ипр не ме- нее тбР не бо- лее 33 48 62 78 11 92 26 —
III 2 (0,02) Гипергео- метрический /т?пр не ме- нее /77бР не бо- лее 22 37 53 19
Биномиаль- ный /??пр не ме- нее тбр не бо- лее 26 46 65 14
317
S.140. Определить плай последовательного контроля интенсив-
ности отказов невосстанавливаемых устройств в табличной и гра-
фической формах до d=8, если Ло = 0,5-||0‘2 1/час, Z.i=^3-102 1/час
и а = р = 0,10.
Ответ: 1) Таблица плана (см. табл. 5.26).
2) Характеристические точки графика плана:
a) dm = 1,22, tL= 0;
6)dm=0, /Е = — 88;
в) dm = 0, /v = 88.
Ответ к задаче 5.140
ТАБЛИЦА Б.26
dm 0 1 2 3 4 5 6 7 8
ZSnp, час не менее 84 160 232 304 376 448 520 592 664
i'vfip. час не более __ — 56 128 200 272 344 416 488
5.141. Определить план последовательного контроля интенсивно-
сти отказов, изменив в условии задачи 5.140 величины риска постав-
щика п заказчика, приняв их равными 0,05.
Ответ: 1) Таблица плана (см. табл. 5.27).
2) Характеристические точки плана:
a) dm — 1,63, = 0;
6)dm = 0, /х =/г2 = — 118;
в) dm = 0, /Е - й] — 118.
ТАБЛИЦА 5.27
Ответ к задаче 5.141
5.142. На испытания -одновременно поставлено М=400 изделий,
восстановление которых производится практически мгновенно. Тре-
буется осуществить контроль интенсивности отказов при условии,
что партия испытываемых изделий может быть принята, если Ло =
= 3 - 10 5 1/час, и должна быть забракована при 10~s 1/час.
Риск поставщика и риск заказчика составляет а=1Р=0,03. План кон-
троля нужно представить в табличной и графической формах в виде
зависимостей времени испытаний от числа отказов при максималь-
ном количестве отказов d=20.
318
Ответ: 1) Таблица плана (см. табл. 5.28).
2) Характеристические точки плана:
a) </т = 1,92, /*=0;
б) rfm=0, /*=—345;
в) rfm=0, /*=345.
ТАБЛИЦА Б.28
Ответ к задаче 5.142
d т 0 1 2 3 4 5 6 7 8 9 10
t* час не ме- пР нее 345 525 705 885 1 0Б9 1 245 1 425 1 605 1 785 1 965 2 145
час не более 6Р — 15 195 375 555 735 915 1 095 1 275 1 455
d т 11 12 13 14 15 16 17 18 19 20
/*пр, час не ме- нее 2 325 2 505 2 685 2865' 3 045 3 225 3 405 3 585 3 765 3 945
час не более 6Р 1 635 1 815 1 995 2175 2 355 2 535 2 715 2895 3 075 3 255
5.143. Представителем заказчика проверяется в течение /* =
= 10 час функционирование каждого экземпляра выпускаемой заво-
дом аппаратуры. Возникающие при этом отказы устраняются прак-
тически мгновенно путем замены функциональных блоков. Известно,
что отказы исследуемой аппаратуры подчиняются экспоненциальному
закону. По техническим условиям при средней наработке до отказа
Го = 2ОО час надежность аппаратуры считается хорошей и не тре-
буется никаких изменений в технологии производства; при 7\ =
=100 час надежность аппаратуры считается плохой и технология ее
производства должна быть улучшена. Риск заказчика установлен
в размере (3=0,05, а риск поставщика а = 0,20. Требуется использо-
вать испытания на функционирование для контроля надежности по
наработке. План представить в табличной и графической формах до
d=8.
Указание к решению задачи. В данном случае при
наработке /£ =t*N время испытаний /* является постоянным, а чис-
ло испытываемых объектов — переменным. Поэтому таблица и
график плана должны отражать зависимость W от d. Все остальные
действия аналогичны примеру 5.57.
Ответ: 1) Таблица плана (см. табл. 5.29).
Т АБЛ ИЦА 5.29
Ответ к задаче 5.143
0 1 2 3 4 5 6 7 8
/Vnp не менее 55 69 83 97 111 125 139 153 167
N6p не более — — — 11 25 39, 53 ,67 81
319
2) Характеристические ючкп:
a) drn = 2,2l, Л?=0;
б) rfm=O, N=~31;
в) rfm=O, W = 55.
5.144. В двух организациях находятся в эксплуатации однотип-
ные изделия, не подлежащие восстановлению после отказа. В пер-
вой организации из 56 изделий за 100 час эксплуатации отказалт
3 изделия с общей наработкой 120 час. Во второй организации из
74 изделий за 140 час эксплуатации отказало 7 изделий с общей
наработкой 508 час. Надежность изделий считается хорошей, если
средняя наработка до отказа 7о = ЗООО час, и плохой, если средняя
наработка Ti=2000 час. Составить план последовательного контроля
надежности эксплуатируемых устройств для а=0,03 и |3=О,О6 и при-
нять решение о целесообразности дальнейшей эксплуатации рассмат-
риваемых устройств.
Ответ. hy = 16650; h2 = — 20 600; S = 243С; = 15588.
Решение не может быть принято, так как при d= 10
3700<15588<40300.
5.145. При приемке заказчиком продукции завода каждое изде-
лие проверяется на функционирование и соответствие параметров
установленным нормам в течение t*—2 час. Изделия поме отказа
не восстанавливаются. Составить таблицу последовательного плана
контроля надежности по наработке до 10-го отказа, если /.(,=0,002'.
>4=0,005; а=0,10; р=0,05, и принять решения в трех случаях:
1. Испытано 1000 устройств, из них отказало при проверке in
функционирование 4 экземпляра с общей наработкой 5 час.
2. Испытано 500 устройств, из них ни одно не отказало.
3. Испытано 250 устройств, из которых 5 отказало с общей на-
работкой 6 час.
Ответ: Таблица плана (см. табл. 5.30).
ТАБЛИЦА 5.30
Ответ к задаче 5.145
d т 0 1 2 3 4 5 6 7 8 9 10
^пр> час не ме- нее 965 1 270 1 575 1 880 2 185 2 490 2 795 3 100 3 405 3 700 4 015
час не бо- лее — — — 165 470 775 1 080 1 385 '1 690 1 995 2 30
Для рабочей точки 7V = 1000, d=4 решение не может быть при-
нято, так как
775<5+996 • 2<2490.
Для рабочей точки Л’=500, d=0 принимается .решение о соот-
ветствии надежности требованиям, так как
500 • 2> 965.
Для рабочей точки Л'=250, d=5 принимается решение о браков-
ке, так как
6+245 • 2<775.
320
5.146. Вычислить константы плана последовательного контроля
средней наработки до первого отказа устройств с нормально распре-
деленными отказами при условии: То = 1000 час, 71 = 750 час, с=
= 100 час, а='Р = 0,03.
Ответ: /?i = 139; ft2=139; s=875.
5.147. Требуемое значение средней наработки до первого отказа
партии подшипников должно составлять не .менее 25 000 час при
дисперсии, равной 1 • 106 час. Если оно окажется равным 20 000 час
и менее при той же дисперсии, то партия должна быть забракована.
Определить константы плана контроля с риском поставщика а = 0,10
и риском заказчика р = 0,20.
Ответ. /14 = 302; й2=—416; «=22500.
5.148. Испытания изделия закончены на отказе. Общая наработ-
ка 798 час. Количество отказов «=28. Известно, что закон распре-
деления отказов экспоненциальный. Определить доверительные гра-
ницы средней наработки до отказа.
Ответ: 21,9 час<Т<37,3 час.
5.149. Испытания изделия закончились спустя некоторое время
после отказа. Общая наработка 815 час. Количество отказов «=28.
Закон распределения отказов экспоненциальный. Требуется опреде-
лить доверительные границы средней наработки до отказа.
Ответ: 22,4 час<Т<37,5 час.
5.150. На испытаниях не было отказов образцов. Общая мара-
ботка 4000 час. Закон распределения отказов изделий данного типа
экспоненциальный. Определить доверительные границы средней -нара-
ботки до отказа.
Ответ: Т> 1740 час.
5.151. При испытаниях общая наработка изделия составляет
12160 час. Количество отказов «=23. Закон распределения отказов—
усеченный нормальный. Требуется определить доверительные грани-
цы средней наработки до отказа Т.
Ответ: 477 час<Т<581 час.
5.152. Используя данные задачи 5.5, определить доверительные
границы средней наработки до отказа.
Ответ: 159,4 чсс<7<350,8 час.
5.153. Используя данные задачи 5.151, найти доверительные гра-
ницы средней наработки до отказа изделия, считая закон распреде-
ления неизвестным.
Ответ: 432 час<Т<626 час.
5.154. Используя данные задачи 5.149, определить доверительные
границы для интенсивности отказов.
Ответ: 2,67-Ю-2 1/час <7.<4,47 10~2 1/час.
5.155. Используя данные задачи 5.150, определить доверитель-
ную границу для интенсивности отказов.
Ответ: Х<5,74 • 10~4 1/час.
5.156. Используя данные задачи 5.151, определить интенсивности
отказов для времен 100 и 500 час.
Ответ: 7 (100) =2,4 • 10 е 1/час, 7(500) =5,4 • 10"3 1/час.
5.157. Используя данные задачи 5.5, определить интенсивности
отказов для времен 100 и 300 час.
Ответ: 7(100) =6,0 • 10“3 1/час, 7(300) =3,3 10~3 1/час.
5.158. Используя данные задачи 5.149, определить доверительные
границы вероятности безотказной работы при временах работы 2,
10 и 15 час.
21—1086 321
Ответ: 0,915<Р(2)<0,948; 0,625<Р(10)<0,763; 0,549<Р(15)<
<0,670.
5.159. Используя данные задачи 5.1'50, определить нижнюю до-
верительную границу вероятности безотказной работы за время ра-
боты 100 час.
Ответ: Р( 100) =0,945.
5.160. Используя данные задачи 5.151, определить доверительные
границы вероятности безотказной работы за время работы 100, 200
и 300 час.
Ответ: 0,999>7>( 100) >0,974; 0,999>7>(200) >0,924; 0,991>
>Р (300) >0,821.
5.161. Используя данные задачи 5.5, определить доверительные
границы вероятности безотказной работы за время работы 50 и
300 час.
Ответ: 0,970> Р (50) >0,732; 0,352 > Р (300) > 0,209.
5.162. В результате обработки данных испытания изделий полу-
чены следующие значения времен безотказной работы в часах: 2;
3; 3; 5; 6; 7; 8; 8; 9; 9; 13; 15; 16; 17; 18; 20; 21; 25; 28; 35; 37;
53; 56; 69; 77; 86; 98; 120. Требуется определить доверительные гра-
ницы вероятности безотказной работы изделия данного типа за вре-
мя работы 5 и 20 час, считая закон распределения неизвестным.
Ответ: 0,7<Р(50) <0,95; 0,27<Р('20) <0,6.
5.163. На испытаниях изделие проработало без отказов по 5 час
более 25 раз. Определить нижнюю доверительную границу вероят-
ности безотказной работы в течение 5 час работы. Закон распреде-
ления отказов неизвестен.
Ответ: Р(5)>0,832.
5.164. В процессе испытаний произведено 14 замеров времен вос-
становления изделия, значения которых в минутах равны: 22; 31; 35;
50; 67; 74; 80; 84; 91; 93; 138; 152; 166; 171. Известно, что они под-
чиняются экспоненциальному' закону распределения. Требуется опре-
делить доверительные границы среднего времени восстановления.
Ответ: 62 лшн<тср<132 мин.
5.165. Используя данные задачи 5.8, найти доверительные гра-
ницы среднего времени восстановления.
Ответ: 11 л»н<тСр<34 мин.
5.166. В тактико-техническом задании дано значение средней на-
работки до отказа 7=20 час. На испытаниях получено 25 отказов
(п=25) при суммарной наработке изделия /Е = 1000 час. Испытания
закончились спустя некоторое время после отказа. Известно, что от-
казы подчинены экспоненциальному закону распределения. Требуется
определить, удовлетворяет ли предъявленному требованию среднее
время безотказной работы.
Ответ: Испытанное изделие предъявленному требованию удов-
летворяет.
5.167. В технических условиях задано 7=500 час. По результа-
там испытаний получено: средняя наработка до первого отказа 7* =
=727 час, От = 146 час и число отказов п=22. Известно, что отказы
подчинены нормальному закону распределения. Установить удовлет-
воряет ли предъявленному требованию средняя наработка до пер-
вого отказа.
О т в е т: Испытанное изделие предъявленным требованиям удов-
летворяет.
5.168. В ТТЗ задано Р(2)=0,92. На испытаниях получено: О =
= 800 час, п = 2О. Испытания закончились па отказе. Имеет место
322
экспоненциальный закон. Требуется определить, удовлетворяет ли
предъявленному требованию вероятность безотказной работы изде-
лия?
О т в е т: Испытанное изделие предъявленному требованию удов-
летворяет: Р(2)=0,935>0,92.
5.169. В ТТЗ задано Р(100) =0,95. На испытаниях получено:
7 = 529 час, о=145 час, п=23. Имеет место нормальный закон.
Установить удовлетворяет ли предъявленному требованию вероят-
ность безотказной работы изделия?
Ответ: Испытанное изделие предъявленному требованию удов-
летворяет: Р{ 100) =0.972>0,950.
5.170. В результате наблюдения за эксплуатацией 5 экземпляров
однотипной аппаратуры было зарегистрировано 11 отказов за время
суммарной наработки 6475 час. Требуется определить доверительный
интервал средней наработки на отказ с доверительной вероятностью
1-« = 0,9.
Ответ: 382</Ср<1053 час.
5.171. В ходе эксплуатации 25 образцов однотипной аппаратуры
были найдены значения средней наработки на отказ для каждого
образца. Затем определено значение средней наработки на отказ для
всей группы, равное 48 час. При этом среднее квадратическое от-
клонение равно 7,35 час. Требуется определить доверительный интер-
вал, в котором с вероятностью 1—с=0,9 находится средняя нара-
ботка на отказ аппаратуры данного типа.
Ответ: 45,49 </’<50,51 час.
21
ЛИТЕРАТУРА
I. Астафьев А. В. Окружающая среда и надежность радио-
технической аппаратуры. Изд-во «Энергия», 1965.
2. В е и т ц е л ь Е. С. Теория вероятностей. Физматгиз, 1968.
3. Гнеденко Б. В., Беляев Ю. К., Соловьев А. Д. Мате-
матические методы в теории надежности. М. Изд-во «Наука», 1965.
4. Г л у з м а и Г. Л., П а д е р н о И. П. Надежность установок и
систем управления. Изд-во «Машиностроение», 1966.
5. Дружи ни и Г. В. Надежность систем автоматики. Изд-во
«Энергия», 1967.
6. Кузнецов В. А. Основные вопросы надежности радиоэлек-
тронной аппаратуры. Изд-во «Энергия», 1965.
7. Маликов И. М„ П о л о в к о А. М. Количественные харак-
теристики надежности. Изд-во ЛДНТП, 1968.
8. Маликов И. М., П о л о в к о А АЕ, Романов Н. А.,
Ч у к р е е в П. А. Основы теории и расчета надежности. Судпромгиз,
1960.
9. М а л и к о в И. М. Надежность судовой электронной аппара-
туры и систем автоматического управления. Изд-во «Судостроение»,
1967.
10. Мал и ков И. М., За й д е н б е р г М. Г., П а и т е л е е в П. М.
Организация работ по расчетам надежности. Изд-во ЛДНТП, 1966.
11. Маликов И. М. Надежность элементов электронной аппа-
ратуры. Изд. ЛЭТИ, 1967.
12. По ловко А. М. Основы теории надежности. Изд-во
«Наука», 1964.
13. Сотсков Б. С. Основы теории и расчета надежности эле-
ментов и устройств автоматики и вычислительной техники. Изд-во
«Высшая школа», 1970.
14. Рябинин И. А. Основы теории и расчета надежности су-
довых электроэнергетических систем. Изд-во «Судостроение», 1967.
15. Широков А. М. Основы надежности и эксплуатации элек-
тронной аппаратуры. Изд-во «Наука и техника», Минск, 1965.
16. Шашонок Н. А., Репкин В. Ф., Барвинский Л. Л.
Основы теории надежности и эксплуатации радиоэлектронной техни-
ки. Изд-во «Советское радио», 1964.
17. Шор Я- Б. Статистические методы анализа и контроля ка-
чества и надежности. Изд-во «Советское радио», 1962.
18. Шор Я. Б., Кузьмин Ф. И. Таблицы для анализа и кон-
троля надежности. Изд-во «Советское радио», 1968.
19. Янко Я. Математико-статистические таблицы. Пер. с чешек.
Госстатиздат, 1964.
20. Янко Е., Э м д е Ф. Таблицы функций с формулами и кри-
выми. Гостехиздат, 1948.
ПРИЛОЖЕНИЯ
326
Рис. П.1.1. Номограмма, определяющая зависимость вероятности и
среднего времени исправной работы от сложности системы и вели-
чины интенсивности отказов элементов.
327
ПРИЛОЖЕНИЕ 2
ИНТЕНСИВНОСТИ ОТКАЗОВ И УСЛОВНЫЕ ДОЛГОВЕЧНОСТИ
ИЗДЕЛИЙ [12, 9]
(по данным седьмого, восьмого и девятого симпозиумов США)
ТАБЛИЦА П.2.1
Интенсивность отказов
Изделия Интенсивность отказов X, 10"е 1/час
макси- мальная средняя мини- мальная
Автопилоты 30,11 18,38 7,35
Аккумуляторы 19,3 7,2 0,35
Акселерометры 7,5 2,8 0,35
Акселерометры тензометрические 21,4 8,0 1,00
Амортизаторы кольцевые 0,057 0,037 0,002
Амперметры -— 0,29 .—-
Антенны 3,25 0,36 0,2
Антенные переключатели 5,38 4,0 3,23
Антенны следящие 10,04 5,7 1,36
Арматура осветительная 0,71 0,1 0,04
Батареи:
— заряжаемые 14,29 1,40 0,50
— одноразовые (сухие) 300 30 10
— кислотно-свинцовые 12,1 1,1 0,5
Вентиляторы вытяжные Вибраторы: 9,0 0,295 0,21
— разные 1,6 0,875 0,2
— несинхронные 1,84 1,15 0,92
— синхронные 0,8 0,5 0,4
Воздуходувки 3,57 2,4 0,342
Волноводы:
— гибкие 4,54 2,64 1,133
— жесткие 1,92 1,1 0,59
Выводы:
— высокочастотные 4,22 2,63 1,131
— электрические 0,08 0,045 0,02
Выключатели:
•— быстродействующие 2,1 0,4 0,09
— автоматические 0,4 0,1375 0,045
— рычажные типа „Тумблер" 0,123 0,06 0,015
— автоматические тепловые 0,50 0,30 0,25
Выпрямители:
— разные 0,75 0,6 0,20
— селеновые 1,6 0,76 0,26
328
Продолжение табл. П.2.1
Изделия Интенсивность отказов
макси• мяльная 10“6 1/час
средняя V' мини- мальная
Генераторы: — звуковой частоты 0,56 0,35 0,14
— опорные 2,5 0,9375 0,045
— постоянного тока 6,27 0,9 0,30
•—-переменного тока 2,94 0,7 0,033
Гироскопы: 11,45 7,5 3,95
— высокоскоростные
— компасные —- 3,82 —-
— особо точные (эталонные) 25 10,0 2,5
Гнезда (на один контакт) 0,02 0,01 0,002
Головки записи (магнитные) 0,26 0,18 0,13
Двигатели: 11,2 8,6 4,49
— асинхронные
— вентиляторов 5,5 0,2 0,05
— гидравлические 7,15 4,3 1,45
— синхронные 6,25 0,359 0,159
— шаговые 0,71 0,37 0,22
Держатели плавких предохранителей 0,10 0,02 0,008
Детекторы кристаллические 0,371 0,20 0,03
Диоды:
—• германиевые 0,678 0,157 0,002
— кремниевые 0,452 0,2 0,021
— кремниевые карбидные 0,55 0,1 0,002
— селеновые 0,6 0,2 0,11
— мощные 3,0 1,42 0,018
Дифференциалы 1,58 1,0 0,012
Дроссели:
— анодные ' 0,09 0,02 0,005
—- высокой частоты • 4,75 2,1 0,056
— низкой частоты 0,280 0,175 0,070
— с насыщением 0,320 0,14 0,12
— зарядные 2,220 1,3875 0,555
Зажимы 0,0009 0,0005 0,0003
Изоляторы 0,08 0,05 0,03
Искатели линейные проверочные 0,082 0,05 0,02
Кабели 2,2 0,475 0,002
Клапаны:
— поплавковые 11,2 8,0 5,6
— сервомеханизмов 56,0 30,0 16,8
Катушки:
— дроссельные 0,100 0,02 0,01
— обмоток моторов 0,045 0,03 0,01
— высокой частоты 0,05 0,01 0,005
— настроечные 0,2858 0,15 0,0142
— индуктивности 0,031 0,02 0,011
329
Продолжение табл. П.2.1
Интенсивность отказов X,
10"6 \/час
изделия макси- мальная средняя мини- мальная
—"индуктивности высокого напря- 0,73 0,40 0,07
жения
— индуктивности соленоидные 0,091 0,04 0,02
Компасы магнитные — 8,66 .—
Конденсаторы:
— бумажные 0,29 0,05 0,003
—• бумажные до 600 в 0,04 0,025 0,01
— бумажные свыше 600 в 0,235 0,09 0,0083
— бумажные нейлоновые 0,014 0,01 0,006
•— воздушные переменные 0,082 0,034 0,01
— керамические 0,213 0,1 0,063
-— керамические повышенной на- 0,29 0,06 0,011
дежности
— керамические до 600 в 0,133 0,0625 0,04
— керамические переменные 0,35 0,155 0,008
— масляные 1,95 0,3 0,12
— постоянной емкости до 600 в 0,018 0,01 0,001
— постоянной емкости свыше 600 в 0,486 0,27 0,027
— постоянной емкости свыше 2,385 0,325 0,1325
1000 в
— слюдяные 0,132 0,075 0,005
— слюдяные до 600 в 0,066 0,0375 0,009
— слюдяные пуговичные 0,068 0,03 0,003
— слюдяные с посеребренными 1,41 0,083 0,025
пластинами
— слюдяные фольговые повышен- 0,076 0,045 0,014
ной надежности
— стеклянные 0,87 0,06 0,0005
— танталовые 1,934 0,6 0,103
— танталовые фольговые 0,5 0,117 0,001
— фарфоровые высоковольтные 1,02 0,09 0,04
— электролитические 0,513 ,0,035 0,003
— электролитические алюминиевые 0,425 0,135 0,02
Контакты прерывающиеся 0,8 0,5 0,31
Контакторы (на контактную группу) 0,4 0,25 о,1
Коробки соединительные 0,58 0,4 0,28
Крепежные детали монтажные 0,55 0,012 0,003
Кристаллы:
— кварцевые высокочастотные 0,6 0,03 0,025
— генератора колебаний 1,1 0,6 0,1
— селеновые 0,42 0,3 0,12
— кремниевые 0,28 0,2 0,08
— магнезиевомедносульфидные 0,07 0,05 0,02
К ристал лодержат ели 0,1 0,02 0,01
330
Продолжение табл. П.2.1
Изделия Интенсивность отказов 10“6 1/час
макси- мальная средняя мини- мальная
Лампы.
— накаливания 32,0 8,0 5,0
— неоновые тлеющего разряда 18,8 10,25 4,50
Линии:
— задержки постоянного тока 0,25 0,1 0,08
— задержки переменного тока 4,62 3,00 0,22
Магниты 7.11 5,65 2,02
Манометры 7,8 4,0 0,135
Муфты:
— управления переключающие 3,2 1,69 0,065
— фрикционные предохранительные 0,94 0,3 0,07
— электромагнитные 0,93 0,6 0,24
Насосы 24,3 13,5 2,7
Насосы вакуумные 16,1 9,0 1,12
Ограничители 0,783 0,35 0,165
Оси 0,62 0,35 0,15
Отметчики времени:
— электромеханические 2,57 1,5 0,79
— электронные 1,8 1,2 0,24
— механические (счетчики) 2,57 0,24 0,04
Охладители 7,0 1,67 0,156
Панели:
— модульные (на одно гнездо) — 0,0244 —
— электронных ламп (на одно 0,009 0,005 0,002
гнездо)
Передачи:
— зубчатые цилиндрические 4,3 2,175 0,087
— зубчатые секторы 1,8 0,9125 0,051
— зубчатые винтовые 0,098 0,05 0,002
— зубчатые редукторные . 0,36 0,2 0,11
Переключа тели:
— блокировочные (на одну кон- 1,0 0,5 0,25
тактную группу) '
— кнопочные 0,11 0,7 0,043
— кулачковые 0,12 0,075 0,048
— быстродействующие 5,38 4,0 0,476
— волноводные 0,71 0,48 0,26
— микроминиатюрные 0,5 0,25 0,09
— плунжерные = 0,112 0,054 0,041
— с приводом от двигателя 0,292 0,19 0,128
— чувствительные большие 0,072 0,045 0,121
— чувствительные малые 0,124 0,06 0,045
Поводки сельсинные — 0,24 —
331
Продолжение табл. П.2.1
Изделия Интенсивность отказов X, 10~6 1/«/СС
макси- мальная средняя мини- мальная
Подшипники:
— шариковые высокоскоростные 3,53 1,8 0,072
тяжелой серии — шариковые низкоскоростные 1,72 0,875 0,035
легкой серии — роликовые 1,0 0,5 0,02
— скольжения 0,42 0,22 0,008
Потенциометры:
— композиционные 0,3 0,1 0,04
-— проволочные 2,0 1,2 0,72
— проволочные миниатюрные 1,92 1,19 0,53
(/? ~ Ю ком) — проволочные миниатюрные 2,02 1,21 0,81
(R = 20 ком) ‘— проволочные миниатюрные 2,04 1,23 0,88
(R 20 ком) — с приводом от двигателя 12,60 5,485 1,71
— угольные 4,44 0,25 0,1
•— счетно-решающих механизмов 14,7 5,0 1,18
Предохранители:
— плавкие 2,75 0,5 0,001
— проволочные 0,83 0,5 0,38
Преобразова тели 52,2 15,0 7,0
Прерыватели (зуммеры) Приводы: 1,3 0,6 0,05
•— следящих систем 33,6 12,5 0,86
— общего назначения, крупногаба- 18,5 6,9 0,6
ритные — общего назначения малогаба- 9,6 3,6 0,17
ритные — ременные 15,0 3,875 0,142
Провода соединительные (между эле- 0,12 0,015 0,008
ментами) Прокладки:
— шайбы 0,015 0,001 0,0005
— пробковые 0,077 0,04 0,003
—^пропитанные 0,225 0,137 0,05
— сеточные 0,908 0,05 0,0022
кольцевые 0,035 0,02 0,01
феноловые 0,07 i 0,05 0,01
— резиновые 0,03 0,02 0,011
Пружины:
— калиброванные 0,42 0,22 0,09
— возвратные 0,022 0,012 0,001
Пускатели, стартеры 16,1 10,0 3,03
332
Продолжение табл. П.2.1
V V Изделия Интенсивность отказов \ 10“Б 1/час
макси- мальная средняя мини- мальная
Разъемы: — штепсельные банановые (на один штырек) — штепсельные коаксиальные (на один штырек) — штепсельные переменного тока (на один штырек) — штепсельные со скользящим плоским контактом (на один штырек) — штепсельные телефонные (на один штырек) Регуляторы напряжения угольные, ав- томатические Резисторы: • —угольные, композиционные — композиционные, переменные — металлопленочные — нелинейные (тириты) — пленочные — постоянные — постоянные многоватные — проволочные — проволочные точные — проволочные мощные . — проволочные переменные — угольные Реле: — электромагнитные (на одну кон- тактную группу) — с соленоидными катушками (на одну контактную группу) — герметически закрытые (на од- ну контактную группу) — малогабаритные (на одну кон- тактную группу) — миллисекундные (на одну кон- тактную группу) — миниатюрные (на одну контакт- ную группу) - — миниатюрные быстродействую- щие (на одну контактную группу) —- мощные (на одну контактную группу) 1,11 0,193 0,05 0,03 0,04 13,16 0,297 0,533 0,4 0,153 0,058 0,07 0,065 0,165 0,191 0,076 0,807 0,898 0,5 0,81 0,19 0,54 0,84 0,25 1,13 4,10 0,062 0,003 0,003 0,002 0,002 9,65 0,043 0,053 0,04 0,10 0,03 0,03 0,028 0,087 0,091 0,04. 0,09 0,045 0,3 0,5 0,04 0,25 0,44 0,06 0,7 0,30 0,025 0,001 0,001 0,0011 0,001 6,09 0,005 0,007 0,004 0,047 0,0017 0,01 0,009 0,046 0,052 0,021 0,02 0,005 0,11 0,30 0,02 0,145 0,18 0,03 0,42 0,15
333
/
Продолжение табл.' П.2.1
Изделия Интенсивность отказов 10"в 1/час
макси- мальная средняя мини- мальная
высокочувствительные (на одну 0,89 0,40 0,22
контактную группу)
•— задержки времени (на одну 0,749 0,39 0,156
контактную группу)
— термические (на одну контакт- 1,0 0,4 0,12
ную группу7)
Реле времени:
— электронные 1,80 .. 1,20 0,24
— электромеханические 2,57 1,50 0,79
— пневматические 6,80 3,5 1,15
Реостаты 0,19 0,13 0,07
Серводвигатели 5,61 1,51 0,101
Сельсины:
— синхронных передач 0,61 0,35 0,09
— решающих устройств 1,14 1,113 0,29
Соленоиды 0,55 0,05 0,036
Соединения:
— гибкие 1,348 0,6875 0,027
— гидравлические 2,01 0,03 0,012
— механические 1,96 0,02 0,011
— пневматические 1,15 0,04 0,021
— паяные 0,005 0,004 0,0002
— шарнирные 4,0 2,4 0,80
— жесткие 0,049 0,025 0,001
Схемы задержки импульсов 0,96 0,6 0,24
Счетчики электрические:
— переменного тока 0,035 0,026 0,021
— постоянного тока 0,40 0,036 0,017
Стабилизаторы напряжения: *
— угольные 13,16 9,65 6,09
— магнитных усилителей 0,69 0,5 0,37
Тахометры 0,55 0,3 0,25
Тензометры 15,0 11,6 1,01
Термовыключатели (на одну контакт- 0,261 0,161 0,114
ную группу
Транзисторы:
— германиевые 1,91 0,3 0,04
— германиевые мощные 1,4 0,6 0,33
— кремниевые 1,44 0,5 0,27
— усилители 0,84 0,5 0,31
— переключатели 0,71 0,4 0,1
1/ Трансформаторы:
* — анодные 0,052 0,025 0,012
— входные 2,08 1,09 0,12
— выходные 0,2 0,09 0,04
_ ... _
334
Продолжение табл. П.2.1
Изделия Интенсивность отказов У., 10~е 1/час
макси- мальная средняя мини- мальная
—- высокочастотные 0,062 0,045 0,019
— звуковой частоты 0,04 0,02 0,01
— импульсные 0,235 0,17 0,03
— импульсные высокого напряже- ния 0,235 0,15 0,065
— магнитных усилителей 0,485 0,152 0,052
-— накала 0,06 0,027 0,013
— промежуточной частоты 0,31 0,08 0,02
— развязывающие 0,093 0,03 0,011
— силовые 2,08 1,04 0,46
v — силовые высокого напряжения 1,88 0,94 0,407
Умформеры Уплотнения: 5,46 2,8 1,15
— вращающиеся 1,12 0,7 0,25
— скользящие у Фильтры: 0,92 0,3 0,11
— электрические 3,0 0,345 0,140
— механические 0,80 0,30 0,045
— световые 0,80 0,20 0,12
Шарики' термометров 3,30 1,0 0,05
Шестереночный зуэ, кулачок, палец, соэачка 0,004 0,002 0,001
Штифт Щетки электрические: 2,6 1,625 0,65
— вращающихся устройств 1,Н 0,1 0,04
— соединенные с зажимами 1,02 0,063 0,01
— щеткодержатели Электродвигатели: 4.И 1,3 0,87
— переменного тока 9,36 5,24 1,12
— постоянного тока -—• 9,36 .—.
— вентиляторов 5,5 0,2 0,05
— шаговые Электронные лампы: 0,71 0,37 0,22
— приемно-усилительные 2,6 1,7 1,1
— приемно-усилительные мощные 9,45 7,05 2,17
— генераторные импульсные 43,0 30,0 20,0
— микроволновые 32,0 20,0 9,7
— миниатюрные 15,0 1,9 0,55
— мощные 13,5 10,0 3,8
— сантиметровых волн 9,0 5,0 2,8
—{передающие 175,0 58,2 3,8
— приемные 3,24 2,0 1,5
— приемные миниатюрные 5,7 3,08 2,1
— приемно-передающие 7,93 5,0 2,1
— субминиатюрные 4,31 1,15 0,36
335
Продолжение табл. П.2.1
Изделия Интенсивность отказов X, ИГ6 \{час
макси- мальная средняя мини- мальная
субминиатюрные (регуляторы напряжения) 6,5 1,7 0,47
усилители мощности 40,0 20,0 12,0
— диоды одиночные 2,5 0,8 0,24
.— диоды двойные 2,0 0,8 0,32
— диоды связанные 1,89 1,0 0,38
-— клистроны 6,0 3,0 1,2
— магнетроны 1000,0 100,0 8,0
— магнетроны без подстройки 350 ,150,0 75,0
—‘ магнетроны с подстройкой ча- стоты 5500,0 3000,0 450,0
— триод одиночный 3,86 1,3 0,67
— двойной триод 1,74 1,0 0,52
.— двойной триод связанный 3,88 2,0 1,17
— триод субминиатюрный одиноч- ный 2,91 1,75 0,53
— двойной триод суоми ниат юркий 2,29 1,34 0,41
— двойной триод связанный суб- миниатюрный 4,31 2,6 0,78
-— тетроды 3,90 1,8 0,88
— тетроды субминиатюрные 3,62 2,15 0,69
— пентоды 3,86 2,5 0,73
— пентоды субминиатюрные 3,62 2,15 0,69
— газонаполненные приемные 6,5 3,9 2,7
ТАБЛИЦА П.2.2
Условная долговечность
Изделия Условная долговечность £0, 10"е
мини- мальная средняя макси- мальная
Аккумуляторы 0,002 0,008 вкл. 0,1
Акселерометры 0,02 0,1 изм. 0,5
Амперметры — 1,0 изм. —
Антенны 0.0С004 0,008 0,04
Волноводы 0,012 0,015 0,02
Выключатели быстродействующие 0,00005 0,0001 выкл. 0,0005
Выключатели рычажные типа 0,0032 0,05 выкл. 0,1
„Тумблер"
336
Продолжение табл П.2.2
Изделия Условная долговечность 10, 10"6
мини- мальная средняя макси- мальная
Генераторы 0,002 0,01 0,02
Генераторы постоянного тока 0,002 0,006 0,02
Гироскопы высокоскоростные 0,0001 0,002 0,04
Г незда — 0,001 вкл. —
Двигатели вентиляторов 0,002 0,007 0,02
Катушки индуктивности — 0,15 —
Конденсаторы 0,002 0,015 0,06
Конденсаторы керамические 0,002 0,016 0,02
Конденсаторы слюдяные 0,0025 0,015 0,02
Контакты прерывающиеся 0,0012 0,005 0,008
Контакторы 0,02 0,05 вкл. 0,1
Лампы накаливания -— 0,01
Лампы неоновые тлеющего разряда — 0,03 —
Линии задержки 0,001 0,005 0,025
Отметчики времени пневматические — 0,0025
Отметчики времени счетчики 0,005 0,03 цикл. 2,0
Передачи, редукторы 0,002 0,005 0,08
Переключатели 0,01 0,03 цикл. 20,0
Переключатели кнопочные 0,01 0,05 цикл. 1,0
Подшипники калиброванные 0,002 0,007 0,02
Подшипники калиброванные для
тяжелого режима использования 0,0001 0,002 0,003
Потенциометры 0,0025 0,02 0,03
Потенциометры счетно-решающгх 0,001 0,04 0,06
механизмов
Потенциометры проволочные — 0,002 —
Прерыватели (зуммеры) 0,01 0,1 цикл. 1.0
Разъемы штепсельные в печатных 0,00015 0,0003 вкл. 0,0015
схемах
Разъемы штепсельные коаксиаль- 0,00005 0,0001 цикл. 0,0005
ные
Резисторы композиционные 0,011 0,014 0,04
Резисторы пленочные 0,0135 0,0145 0,06
Резисторы проволочные 0,011 0,014 0,05
Резисторы переменные 0,014 0,016 0,017
Резисторы угольные 0,012 0,015 0,05
Реле высокочувствительные 0,02 0,2 цикл. 0,3
Реле малогабаритные 5,0 10,0 цикл. 100,0
22—1086
337
Продолжение табл. /П.2.2
Изделия Условная долговечность Lq, 10"®
мини- мальная средняя макси- мальная
Реле миниатюрные 0,05 0,25 цикл. 0,5
Реле общего назначения 0,02 0,2 цикл. 0,7
Серводвигатели 0,001 0,008 0,02
Счетчики 0,1 0,3 цикл. 0,6
Счетчики электрические 0,005 0,009 0,0135
Тахометры 0,005 0,01 0,016
Трансформаторы 0,004 0,01 0,03
Фильтры электрические 0,008 0,012 0,02
Шарикоподшипники 0,0005 0,006 0,016
Щетки электрические, вращаю- 0,001 0,003 0,01
щихся устройств
Электродвигатели переменного тока — 0,03 -—
Примечания к таблицам П.2.1 и П.2.2.
1. Если в графе 3 после чисел величина не указана, то показате-
ли имеют размерность' [час]. Иногда проставлены следующие размер-
ности: вкл. (включений); выкл. (выключений); изм. (измерения);
цикл, (циклов); конт. (контакт); шт. (штырек); гн. (гнездо); к. г.
(контактная группа); выв. (вывод).
Например, в позиции «Гнезда» показатели следует читать так:
среднее значение Х5=0,01 • 10"6, 1/гн. (/.« дана на одно гнездо),
а среднее значение условной долговечности
Lc=O,OOl • 10е= 1000 включений.
Если среднее значение имеет именованную величину, то она же
подразумевается и для минимального и максимального значений по-
казателя (в этом случае сокращенные обозначения равномерности
ввиду недостатка места около них опущены).
2. Абсолютные значения показателей надежности приведены для
условий испытаний в лаборатории, т. е. при нормальных значениях
атмосферного давления, температуры, влажности, без учета влияния
вибрации и ударных воздействий и для номинальной нагрузки.
ПРИЛОЖЕНИЕ 3
ИНТЕНСИВНОСТИ ОТКАЗОВ ЭЛЕМЕНТОВ ЭЛЕКТРОННОЙ
АППАРАТУРЫ И ПОПРАВОЧНЫЕ КОЭФФИЦИЕНТЫ [11]
ТАБЛИЦА П.3.1
Номинальная интенсивность отказов резисторов
при Т° = +20 °C и ZCH=1
Номинальная мощность рассеяния ^Еом- вт
Тип рези- сторов 0,25 0,5 ! 2 5 10 15 20 25 30 50 60 75 10°
Интенсивность отказов Хо, 10е i/час
| Непроволочные МЛТ ТВО МОУ МУН УНУ КЭВ ВС УЛИ БЛП СПО СП 0,4 0,5 1,0 1,6 — — — — — — 0,4 0,45 0,8 1,4 2,2 3,0 — 4,0 — 6,0 0,5 0,55 1,1 1,5 2,3 3,1 — — 4,2 — 5,5 10 0,6 0,6 1,2 2,0 — — — 0,6 0,7 1,2 1,7 2,3 3,0 — — 4,8 — 8,0 12 0,6 0,75.1,3 1,75 2,4 3,1 — — 5,0 0,7 0,8 1,35 1,8 2,5 3,3 — 0,6 0,65 1,3 — —— — — 0,7 0,75 1,4 — - — — — 0,6 0,7 1,15 1,8 — — — 0,7 0,8 1,3 2,0 — — — — — —
| Проволочные ПТН ПКВ ПЭВ ПТП РП — 1,1 1,4 1,8 — — — — , 1 2 15 20 2 5 - - - - — — 1’б 2,0 2,'б 2,9 3,2 3,5 — 4,55,05,6 — 8,012 — — 2,2 2,6 3,0 — -- — — — — 3,0 — — — — 4,7 8,5 —
Обозначения резисторов;
МЛТ —металлепленочные, лакированные, теплостойкие
тво — теплостойкие, влагостойкие, объемные
МОУ — металлоокисные, ультра высокочастотные
МУН — мета.плопленочные, ультравысокочастотные, незащищенные
УНУ —углеродистые, незащищенные, ультравысокочастотные
КЭВ — композиционные, эмалированные, влагостойкие
ВС •— углеродистые
УЛИ — углеродистые, лакированные, измерительные
БЛП—бороуглеродистые, лакированные, прецизионные
СПО — переменные, объемные
СП — переменные, композиционные
ПТН—проволочные, точные, нихромовые
ПКВ— проволочные, на керамическом основании, влагостойкие
“ЭВ проволочные, эмалированные, влагостойкие
СТП потенциометры теплостойкие, прецизионные
"П — потенциометры регулируемые
22* 339
ТАБЛИЦА П.3.2
Поправочные коэффициенты 04 = f (Кв, Т®)
для определения >.о резисторов
Тип рези- сторов т°, с к*
0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,00
и
ч
g
я
к
о
Г
щ
6
£
20 5Ц5А20 0,26 0,35 0,42 0,50 0,60 0,72 0,84 1,00
25 0,18 0,23 0,30 0,39 0,46 0,56 0,67 0,79 0,94 1,10
30 0Д1 0,27 0,34 0,43 0,51 0,62 0,75 0,88 1,07 1,26
<35) L 6,2^0,30 0,38 0,47 0,56 0,69 0,84 0,99 1,22 1,47
^40 0,27 0,33 0,42’ 0,51 0,60 0,76 0,94 1,11 1,38 1,71
45 0,30 0,36 0,46 0,55 0,66 0,84 1,05 1,24 1,57 1,95
50 0,34 0,40 0,50 0,59 0,71 0,92 1,17 1,38 1,76 2,22
55 0,37 0,44 0,54 0,63 0,76 1,00 1,30 1,54 1,96 2,51
60 0,40 0,47 0,57 0,67 0,82 1,08 1,43 1,70 2,17 2,81
65 0,43 0,50 0,60 0,71 0,88 1,17 1,57 1,86 2,41 3,14
70 0,46 0,54 0,64 0,75 0,94 1,26 1,72 2,04 2,69 3,52
75 0,50 0,58 0,68 0,79 1,00 1,35 Г,88 2,25 2,99 3,94
80 0,54 0,61 0,71 0,84 1,07 1,46 2,05 2,48 3,31 4,40
85 0,57 0,66 0,75 0,88 1,14 1,55 2,20 2,73 3,65 4,86
90 0,60 0,70 0,79 0,92 1,20 1,66 2,40 2,99 2,04 5,40
95 0,64 0,74 0,82 0,96 1,26 1,76 2,58 3,27 4,46 6,05
100 0,69 0,78 0,87 1,00 1,32 1,88 2,77 3,60 4,90 6,70
20 0,01 0,02 0,02 0,05 0,10 0,20 0,34 0,51 0,73 1,09
25 0,02 0,03 0,03 0,07 0,12 0,22 0,39 0,55 0,77 1,05
30 0,02 0,04 0,04 0,08 0,14 0,26 0,43 0,60 0,81 1,10
35 0,03 0,05 0,05 0,09 0,16 0,29 0,48 0,64 0,86 1.19
40 0,04 0,06 0,06 0,11 0,19 0,32 0,53 0,69 0,92 1,29
45 0,05 0,07 0,07 0,12 0,22 0,36 0,57 0,75 0,99 1,41
50 0,06 0,08 0,08 0,14 0,25 0,39 0,63 0,81 1,06 1,55
55 0,07 0,09 0,09 0,15 0,27 0,43 0,68 0,88 1,16 1,71
60 0,08 0,10 0,10 0,17 0,30 0,47 0,73 0,95 1,27 1,91
65 0,09 0,11 0,11 0,18 0,32 0,51 0,79 1,04 1,43 2,18
70 0,10 0,12 0,12 0,20 0,35 0,56 0,85 1,14 1,60 р,51
75 0,11 0,13 0,14 0,21 0,37 0,61 0,91 1,24 1,80 2,89
80 0,12 0,14 0,15 0,22 0,40 0,67 8,98 1,36 2,01 3,25
85 0,13 0,16 0,17 0,24 0,43 0,73 1,07 1,50 2,26 3,65
90 0,14 0,17 0,18 0,26 0,46 0,80 1,15 1,65 2,51 4,05
95 0,15 0,18 0,19 0,28 0,49 0,88 1,24 1,82 2,80 4,49
100 0,16 0,18 0,20 0,30 0,52 0,96 1,33 2,00 3,15 5,00
340
ТАБЛИЦА И.3.3
Номинальные интенсивности отказов конденсаторов
при 7°= +20 °C и /Сн=1
Тип конденсатора Интенсивность отказов Хо, 10’в 1]час
Бумажные 1,8
Металлобумажные 2,0
Слюдяные 1,2
Стеклянные 1,6
Керамические 1_л
Пленочные 2,0
Электролитические алюминиевые 2,4
Электролитические танталовые 2,2
ТАБЛИЦА П.3.4
Поправочные коэффициенты «2 = f (Кш Т°)
для определения Хэ конденсаторов
Конденсаторы Т, °C
0,14-Э.З | 0,4 | 0,5 | 0,6 | 0,7
Бумажные 20 0,06 0,08 0,10 0,18 0,23
Керамические 25 0,07 0,08 0,10 0,21 0,25
Слюдяные негерметичные 30 0,07 0,08 0,11 0,22 0,27
1 35 0,07 0,09 0,12 0,24 0,31
40 0,07 0,09 0,13 0,28 0,35
45 0,08 0,09 0‘, 14 0,33 0,40
50 0,08 0,10 0,15 0,36 0,46
60 0,10 0,12 0,20 0,45 0,62
65 0,11 0,13 0,23 0,55 0,66
70 0,13 0,15 0,26 0,60 0,83
75 0,15 0,17 0,33 0,73 1,13
80 0,17 0,22 0,43 0,92 1,46
85 0,25 0,30 0,65 1,14 1,88
90 0,33 0,38 0,82 1,70 2,40
95 0,43 0,47 1,08 2,40 2 90
100 0,55 0,57 1,36 3,00 3,40
Слюдяные герметичные 20 0,28 0,36 0,49 0,18 0,23
25 0,29 0,37 0,49 0,21 0,25
30 0,30 0,38 0,50 0,22 0,27
35 0,32 0,39 0,51 0,24 0,31
40 0,34 0,42 0,54 0,28 0,35
45 0,36 0,45 0,59 0,33 0,40
50 0,38 0,49 0,63 0,36 0,46
55 0,42 0,54 0,67 0,40 0,53
341
Продолжение табл. П. 3.4
Конденсаторы т, °C
0,1-=-0,3 0,4 0,5 0,6 0,7
Слюдяные герметичные 60 0,46 0,61 0,75 0,45 0,62
65 0,51 0,68 0,85 0,55 0,66
70 0,58 0,76 0,96 0,60 0,83
75 0,66 0,86 1,14 0,73 1,13
80 0,75 0,97 1,40 0,92 1,46
85 0,85 1,13 1,95 1,14 1,88
90 0,98 1,30 2,80 1,70 2,40
95 1,12 1,50 3,50 2,40 2,90
100 1,30 1,70 4,50 3.00 3,40
Металлобумажные, стек- 20 0,28 0,36 0,49 0,64 0,80
лянные, пленочные 25 0,29 0,37 0,49 0,66 0,88
30 0,30 0,38 0,50 0,70 0,94
35 0,3?' 0,39 0,51 0,75 1,00
40 0,34 0,42 0,54 0,80 1,10
45 0,36 0,45 0,59 0,86 1,25
50 0,38 0,49 0,63 0,95 1,43
55 0,42 0,54 0,67 1,06 1,70
60 0,46 0,61 0,75 1,19 2,00
65 0,51 0,68 0,85 1,37 2,10
70 0,58 0,76 0,96 1,58 2,30
75 0,66 0,86 1,14 1,87 2,50
80 0,75 0,97 1,40 2,10 2,80
85 0,85 1,13 1,95 2,30 3,40
90 0,98 1,30 2 80 2,70 3,80
95 1,12 1,50 3,50 3,00 4,40
100 1,30 1,70 4,50 3,50 5,00
Электролитические с алю- 20 0,65 0,48 0,40 0,48 0,65
миниевым анодом 25 0,72 0,54 0,44 0,54 0,72
30 0,82 0,60 0,48 0,60 0,82
35 1,00 1,73 0,56 0,73 1,00
40 1,24 0,90 0,64 0,90 1,24
45 1,48 1,12 0,80 1,12 1,48
50 1,73 1,40 1,17 1,40 1,73
55 1,95 1,70 1,38 1,70 1,95
60 2,30 2,Ю 1,80 2,10 2,30
65 3,50 2,80 2 26 2,80 3,50
70 4,30 3,60 2,90 3,60 4,30
75 5,50 4,60 4,00 4,60 5,50
80 7,00 5,60 4,40 5,60 7,00
85 8,80 6,80 5,50 6,80 8,80
90 п,о 8,00 6 50 8,00 и,0
95 14,0 9,50 7,70 9,50 14,0
100 18,0 И,4 9,00 Н.4 18,0
342
Продолжение табл. П.3.4
1 Конденсаторы т, ес
О,1-5-Э,3 0,4 0,5 0,6 0,7
Электролитические с тан- 20 0,39 0,20 0,20 0,20 0,39
таловым анодом 25 0,40 0,21 0,21 0,21 0,40
30 0,41 0,22 0,22 0,22 0,41
35 0,43 0,26 0,26 0,26 0,43
40 0,47 0,30 0,30 0,30 0,47
45 0,53 0,35 0,35 0,35 0,53
50 0,57 0,40 0,40 0,40 0,57
55 0,64 0,45 0,45 0,45 0,64
60 0,70 0,50 0,50 0,50 0,70
65 0,78 0,57 0,57 0,57 0,78
70 0,86 0,65 0,65 0,65 0,86
75 0,94 0,72 0,72 0,72 0,94
80 1,05 0,80 0,80 0,80 1,05
85 1,17 0,90 0,90 0,'90 1,17
90 1,30 1,00 1,00 1,00 1,30
95 1,45 1,12 1,12 1,12 1,45
100 1,65 1,25 1,25 1,25 1,65
ТАБЛИЦА П.3.5
Номинальные интенсивности отказов полупроводниковых
приборов при 7°= +20 °C и ЛГН==1
Полупроводниковые приборы Интенсивность отказов 10”6 11час приборов
герма- ниевых кремние- вых
[Транзисторы Диоды । Выпрямительные точечные Выпрямительные микроплоскостные Выпрямительные плоскостные Выпрямительные плоскостные повышенной на- дежности Выпрямительные повышенной мощности Импульсные точечные Импульсные плоскостные мезадиоды Импульсные сплавные Управляемые Стабилитроны Варикапы Выпрямительные столбы Микромодульные Маломощные низкочастотные Мощные низкочастотные Маломощные высокочастотные Мощные высокочастотные Микромодульные 0,7 3 2 4,2 3 4,6 2,6 5 1 2 • 0,7 5 2,5 5 2,5 0,6 5 5 5 5 4,5 4 1,7
343
ТАБЛИЦА П.3.6
Поправочные коэффициенты «» = f (Ян» 1 °)
для определения Хэ полупроводниковых приборов
Пол у про- *н
ВОДНЙКО-
вые при-
боры 0.1 0,2 0,3 0,4 0,5 0,6 0,7 0,8
20 0,09 0,15 0,22 0,30 0,39 0,50 0,62 0,74
ф 25 0,10 0,16 0,24 0,32 0,42 0,52 0,64 0,76
3 со 30 0,12 0,19 0,26 0,35 0,45 0,55 0,66 0,79
ф к 35 0,13 0,20 0,29 0,38 0,47 0,58 0,70 0,85
Д го 40 0,15 0,23 0,32 0,41 0,51 0,63 0,76 0,91
S 4b 0,17 0,26 0,37 0,49 0,62 0,77 0,94 1,15
ф' 50 0,20 0,32 0,45 0,60 0,76 0,95 1,15 1,41
55 0,31 0,42 0,54 0,70 0,89 1,13 1,40 1,73
о 60 0,42 0,53 0,66 0,86 1,13 Г,40 1,75 2,13
20 0,77 0,77 0,78 0,79 0,81 0,83 0,85 0,88
25 0,80 0,80 0,81 0,83 0,84 0,87 0,89 0,92
ф 3 30 0,85 0,85 0,85 0,86 0,88 0,’90 0,92 0,97
со ф 35 0,88 0,88 0,88 0,90 0,92 0,95 0,97 1,03
S S 40 0,92 0,92 0,92 0,94 0,97 1,00 1,04 1,08
S ф 45 0,94 0,95 0,96 0,98 1,00 1,04 1,08 1,13
Он 54 50 0,96 0,98 1,00 1,02 1,05 1,09 1,13 1,19
55 0,98 1,01 1,04 1,07 1,11 1,16 1,22 1,29
60 1,00 1,04 1,08 1,11 1,16 1,22 1,30 1,39
20 0,20 0,23 0,26 0,35 0.42 0,50 0,70 0,74
25 0,20 0,24 0,29 0,40 0,47 0,57 0,75 0,83
30 0,21 0,27 0,32 0,45 0,52 0,65 0,83 0,95
Ф 35 0,23 0,29 0,36 0,50 0,58 0,73 0,93 1,07
Ф 40 0,25 0,32 0,40 0,55 0,66 0,81 1,04 1,22
Ф 45 0,27 0,36 0,45 0,61 0,74 0,94 1,17 1,36
LL, ГО 50 0,30 0,42 0,50 0,68 0,84 1,08 1,31 1,50
Он 55 0,34 0,46 0,56 0,76 0,96 1,23 1,47 1,68
ф 60 0,39 0,52 0,63 0,86 1,10 1,38 1,65 1,90
65 0,44 0,57 0,71 0,98 1,25 1,55 1,84 2,13
70 0,49 0,63 0,80 1,11 1,40 1,73 2,05 2,35
о 75 0,54 0,69 0,91 1,25 1,57 1,92 2,24 2,59
S со Д 20 0,06 0,16 0,18 0,20 0,35 0,43 0,52 0,63
ГО 25 0,С6 0,16 0,18 0,21 0,36 0,44 0,53 0,65
Е—1 30 0,06 0,16 0,19 0,22 0,37 0,46 0,55 0,67
ф 35 0,07 0,16 0,19 0,22 0,39 0,49 0,57 0,70
40 0,07 0,17 0,20 0,23 0,40 0,51 0,59 0,72
ф 45 0,07 0,17 0,20 0,23 0,42 0,53 0,62 0,75
к 50 0,08 0,18 0,21 0,24 0,45 0,55 0,65 0,78
ф 55 0,08 0,18 0,21 0,25 0,47 0,58 0,68- 0,81
Он о 60 0,08 0,19 0,22 0,26 0,50 0,61 0,71 0,85
65 0,09 0,19 0,22 0,26 0,53 0,65 0,76 0,90
70 0,09 0,20 0,23 0,27 0,56 0,70 0,81 0,97
75 0,09 0,20 0,23 0,28 0,60 0,74 0,87 1,04
344
ТАБЛИЦА П.3.7
Номинальная интенсивность отказов трансформаторов
и моточных изделий (дроссели, катушки
индуктивности и др.) при 7'®=4-20*С и Кн=1
Трансформаторы и моточные изделия Интенсивность отказов Хо, 10"6 1/час
Автотрансформаторы 5,0
Силовые 3,0
Высоковольтные 4,0
Накальные анодные 2,0
Импульсные 0,5
Дроссели 1,0
Катушки индуктивности 0,5
ТАБЛИЦА П.3.8
Номинальные интенсивности отказов электрических машин
и машинных электроэлементов при Т°= +20 °C и Кн=1
Электрические машины и их элементы Интенсивность отказов Хо, 10-в \{час
Двигатели постоянного тока Коллекторные Стабилизированной скорости 8 10
Машины пере- менного тока Асинхронные короткозамкнутые Синхронные Асинхронные с полым ротором 5 7 6
Сельсины Бесконтактные Контактные Дифференциальные 5 6 5
Вращающие трансформа- торы Линейные, синусно-косинусные (ВТ, ЛВТ, СКВТ) Масштабные (МТ, МВТ) 6 5
Машинные электро- элементы Электромагнитные муфты Регуляторы напряжения Фазорегуляторы Тахогенераторы Двигатели генераторы Электромеханические усилители 4 8 8 8 10 12
345
ТАБЛИЦА П.3.9
Поправочные коэффициенты а4 = f Т°) для определения 1.»
моточных изделий, трансформаторов и обмоток
электрических машин
Т, °C
0,3 0,4 0,5 • 0,6 0,7 0,8 0,9 1,о
20 0,1 0,1 0,1 0,2 о,3 0,6 0,8 1,0
25 0,1 0,1 0,2 0,3 0,5 0,8 1,2 1,3
30 0,1 0,1 0,2 0,3 0,6 1,0 1,4 1,6
35 0,1 0,1 0,2 0,4 0,9 1,3 1,9 2,5
40 0,1 0,2 0,2 0,5 1,2 1,8 2,4 3,0
45 0,2 0,2 0,3 0,6 1,4 2,3 3,2 4,2
50 0,2 0,2 0,3 0,8 1,8 2,8 4,0 5,2
55 0,2 0,2 0,3 1,0 2,2 3,5 5,2 6,9
60 0,2 0,3 0,4 1,2 2,5 4,1 6,4 8,6
65 0,2 0,3 0,5 1,6 3,4 5,7 8,5 11,5
70 0,3 0,4 0,6 2,0 4,2 7,2 10,7 14,0
ТАБЛИЦА П.3.10
Поправочные коэффициенты (дополнительная интенсивность
отказов) AZ. электрических машин в зависимости
от скорости вращения
П, об 1 мин Дополнительная интенсивность отка- £зсв дХ, Ю"6 \[час п, об 1 мин Дополнительная интенсивность отка- зов ДХ, 10"6 1[час
без щеток со щетками без щеток со щетками
До 1000 0,04 0,5 6 000 1,4 2,9
2 000 0,15 0,7 7 000 1,8 4,3
3 000 0,35 1,0 8 000 2,3 5,7
4 000 0,6 1,5 9 000 2,8 7,0
5 000 0,9 2,2 10 000 3,5 8,5
Примечания:
1. Таблицы П.3.1, П.3.3, П.3.5, П.3.7 и П.3.8 содержат значения
интенсивности отказов, используемые для ориентировочного расчета
надежности.
2. Определение эксплуатационных значений интенсивности отка-
зов элементов производится по формуле:
Л8=Хоа1 (1/час],
где А.0 — номинальное значение интенсивности отказов резисторов,
конденсаторов, полупроводниковых приборов, трансформаторов и
моточных изделий и машинных электроэлементов, взятых из
табл. П.3.1, П.3.3, П.3.5, П.3.7 или П.3.8 соответственно.
31 j
Здесь поправочный коэффициент для резисторов щ определяется
по табл. П.3.2, для конденсаторов аг — по табл. П.3.4, для полупро-
водниковых приборов а3 — по табл. П.3.6, для моточных изделий,
трансформаторов и обмоток электрических машин — по табл. П.3.9.
3. Определение эксплуатационных значений интенсивности отка-
зов электрических машин производится по формуле
Лэ — 1Л0О.4 “Г'Л'Л,
где Ло— номинальное значение интенсивности отказов электрических
машин, взятое из табл. П.3.8, at — поправочный коэффициент, взя-
тый из табл. П.3.9, ЛХ — дополнительная интенсивность отказов, взя-
тая в зависимости от скорости вращения и наличия щеток из
табл. П.3.10.
ПРИЛОЖЕНИЕ 4
ГРАФИКИ ПОПРАВОЧНЫХ КОЭФФИЦИЕНТОВ cn=f(t°C, К») [10]
Рис. П.4.1. Зависимость а от t и Кв для проволочных
сопротивлений.
Рис. П.4.2. Зависимость а от t и Кв для сопротивлений
типов ПЭВ и ПТМН.
су Рис’ П.4.3. Зависимость а от i и Кп для переменных
ё проволочных сопротивлений.
Рис. П.4.4. Зависимость а от t и Кв для сопротивлений
типов ОВС, ОМЛТ, МТ, СПО, УЛИ, УЛМ и др.
350
Рис. П.4.5. Зависимость а от / и для пленочных Рис. П.4.6. Зависимость а от t и Кв для композицион
углеродистых сопротивлений. ных сопротивлений.
Рис. П.4.7. Зависимость а от t и Кп для объемных
(типа ТВО и подобных) сопротивлений.
Рис. П.4.8. Зависимость а от t и /<н для конденсаторов
с металлобумажной изоляцией типов БМТ, БМ, МБМ,
КБГ, МБГ, БГТ, МБГЦ, МБГЧ, МБГТ, МБГО.
CjD
ел
to
Рис. П.4.9. Зависимость а от t и Кп для конденсаторов Рис. П.4.10. Зависимость а от 1 и Ля для конденсато-
с бумажной изоляцией. ров слюдяных типов КСОТ, КСО.
23—1086
Рис. П.4.11. Зависимость а от I
и Ли для конденсаторов стекло-
керамических типов СКМ.
Рис. П.4.12. Зависимость а от t
и Л’н для слюдяных конденса-
торов.
Рис. П.4.13. Зависимость а от t и /<н
для конденсаторов с керамической
изоляцией.
Рис. П.4.14. Зависимость а от t и Кв для электрических
танталовых конденсаторов.
Рис. П.4.15. Зависимость а от t и Кв для алюминие-
вых конденсаторов типов К50-ЗБ, ЭГЦ, К-53-1.
Рис. П.4.16. Зависимость а от t и Ан для электро-
вакуумных приборов (диоды и триоды).
Рис. П.4.17. Зависимость а от t и Ан для электроваку-
умных приборов (тетроды и пентоды).
Рис. П.4.19. Зависимость а от t и Кя для точечных
микромодульных германиевых диодов типа ДММ-1,3.
‘Рис. П.4.18. Зависимость а от t и К-a для электронно-
лучевых трубок и СВЧ приборов (разрядники, клистро-
ны, магнетроны и тиратроны).
ДГ-Ц21+27
Д75+Ж
Рис. П.4.20. Зависимость а от t и 7(н для плоскостных
германиевых диодов.
Рис. П.4.21. Зависимость а от t и /<и для точечных
кремниевых диодов.
358
Рис. 4.22. Зависимость а от t и Кн для плоскостных
кремниевых диодов.
Рис. П.4.23. Зависимость а от t и Кк для германиевых
транзисторов. -
Рис. П.4.24. Зависимость а от t и К,, для кремниевых
транзисторов.
Рис. П.4.25. Зависимость а от t и Кв для германиевых
высокочастотных транзисторов.
360
Рис. П.4.26. Зависимость а от t и Дн для кремниевых
высокочастотных транзисторов.
Рис. П.4.27. Зависимость а от t и
Лн для микросопротивлений.
Рйс. П.4.28. Зависимость а от t
и Ка для микроконденсаторов.
Рис. П.4.29. Зависимость а от t и Кк для микромодуль-
ных транзисторов типа ТМ-5 и др.
Рис. П.4.30. Зависимость а от t и Кн для микромодуль- Рис. П.4.31. Зависимость а от t и Кв для микромо-
ных транзисторов типа ТМ-10. дульных транзисторов типа ТМ-11.
Рис. П.4.32. Поправочный коэффициент интенсивности
отказов, учитывающий влияние температуры окружаю-
щей среды и время (относительно) нахождения обмот-
ки под напряжением для реле типа РЭС.
Рис. П.4.33. Поправочный коэффициент интенсивности
отказов, учитывающий влияние температуры окружаю-
щей среды и время (относительно) нахождения обмот-
ки под напряжением для реле типов ТКЕ, ТКД, ТКС и
РЭС-6, ТВЕ, СПЕ, ЭР-З-Н, 8Э11-14, РЭС-22.
ПРИЛОЖЕНИЕ 5
ФОРМЫ ТАБЛИЦ ДЛЯ ОПРЕДЕЛЕНИЯ
ИНТЕНСИВНОСТЕЙ ОТКАЗОВ
ТАБЛИЦА И.5.1
Определение интенсивности отказов
при ориентировочном расчете надежности
№ п/п Наимено- вание и типы эле- ментов Обозна- чение по схеме Количество элементов шт. Интен- сивность отказов X, 10"5 II час Произведение \,лгг’ I0"5 1/час Приме- чание
1 2 3 4 5 6 7
1 2 3 4 т
т i=! т ;=1
ТАБЛИЦА П.5.2
Определение интенсивности отказов при окончательном расчете
надежности с использованием графиков Х4—f (Кв, t°C)
№ п/п Наиме- нование и типы элемен- тов Обоз- наче- ние По схеме Количе- ство эле- ментов л^, шт. Режим работы Интен- сивность отказов X, 10“5 1/час \NV 10"5 1/час Приме- чание
коэф- фици- ент на- грузки, К темпе- ]ратура,
1 2 3 4 5 6 7 8 9
1 2 3 т
1 еМ.« т 1=1
364
ТАБЛИЦА П.5.3
Определение интенсивности отказов при окончательном расчете надежности
с использованием графиков at — f (Кп, t ’С)
№ п/п Наимено- вание и типы эле- ментов Обозначе- ние по схеме Количество эле- ментов шт. Интенсив- ность отка- зов при номиналь- ном режи- ме \i- 1/час Режим работы Поправоч- ный коэф- фициент а1 Интенсив- ность отка- зов г'-го элемента ^ot'aV 10"5 1/час Интенсивность отка- зов Z-Й группы эле- ментов 10“s \/час
коэффи- циент нагрузки к* темпера- тура 0, °C
1 2 3 4 5 6 7 8 9 10
1 2 3 т •
365 т KvO-tNi, z = l
ПРИЛОЖЕНИЕ 6 КООРДИНАТНЫЕ СЕТКИ
Рис. П.6.2. Координатная сетка 2.
X
ПРИЛОЖЕНИЕ 7
МАТЕМАТИЧЕСКИЕ ТАБЛИЦЫ
ТАБЛИЦА И.7.1
Квантили распределения хи-квадрат
Вероятность Р
о Д t=t 2 ф о К £ о 0,001 0,005 0,010 0,025 0,05 0.100 0,200 о.зоо
J34 о о
1 0,16-10-5 0,39-10-* 0,16.10'3 0,93-10“3 0,39-10'3 0,016 0,064 0,148
2 0,20-10'2 0,010 0,020 0,051 0,103 0,211 0,446 0,713
3 0,024 0,072 0,115 0,216 0,352 0,584 1,00 1,42
Ш 0,091 0,207 0,297 0,484 0,711 4,06 1,65 2,19
5 0,210 0,412 0,554 0,831 1,15 1,61 2,34 3,00
6 0,381 0,676 0,872 1,24 1,64 2,20 3,07 3,83
7 0,598 0,989 1,24 1,69 2,17 2,83 3,82 4,67
8 0,857 1,34 1,65 2,18 2,73 3,49 4,59 5,53
9 1,15 1,73 2,09 2,70 3,33 4,17 5,38 6,39
10 1,48 2,16 2,56 3,25 3,94 4,87 6,18 7,27
И 1,83 2,60 3,05 3,82 4,57 5,58 6,99 8,15
12 2,21 3,07 3,57 4,40 5,23, 6,30 7,81 9,03
13 2,62 3,57 4,11 5,01 5,89 7,04 8,63 9,93
14 3,04 4,07 4,66 5,63 6,57 7,79 9,47 10,8
15 3,48 4,60 5,23 6,26 7,26 8,55 10,3 11,7
16 3,94 5,14 5,81 6,91 7,96 9,31 11,2 12,6
18 4,90 6,26 7,01 8,23 9,39 10,9 12,0 14,4
20 5,92 7,43 8,26 9,59 10,9 12,4 14,6 16,3
22 6,98 8,64 9,54 11,0 12,3 14,0 16,3 18,1
24 8,08 9,89 10,9 12,4 13,8 15,7 18,1 19,9
26 9,22 11,2 12,2 13,8 15,4 17,3 19,8 21,8
28 10,4 12,5 13,6 15,3 16,9 18,9 21,6 23,6
30 11,6 13,8 15,0 16,8 18,5 20,6 23,4 25,5
35 14,7 17,2 18,5 20,6 22,5 24,8 27,8 30,2
40 17,9 20,7 22,2 24,4 26,5 29,1 32,3 34,9
45 21,3 24,3 25,9 28,4 30,6 33,4 36,9 39,6
50 24,7 28,0 29,7 32,4 34,8 37,7 41,4 44,3
55 28,2 31,7 33,6 36,4 39,0 42,1 46,0 49,1
60 31,7 35,5 37,5 40,5 43,2 46,5 50,6 53,8
65 35,4 39,4 41,4 44,6 47,4 50,9 55,3 58,6
70 39,0 43,3 45,4 48,8 51,7 55,3 59,9 63,3
75 42,8 47,2 49,5 52,9 56,1 59,8 64,5 68,1
80 46,5 51,2 53,5 57,2 60,4 64,3 69,2 72,9
85 50,3 55,2 57,6 61,4 64,7 68,8 73,9 77,7
90 54,2 59,2 61,8 65,6 69,1 73,3 78,6 82,5
95 58,0 63,2 65,9 69,9 73,5 77,8 83,2 87,3
100 61,9 67,3 70,1 74,2 77,9 82,4 87,9 92,1
368
Продолжение табл. П.7.1
Число степени свободы k Вероятность Р
0,700 0,800 0.90Э 0,953 0,975 0,990 0,995 0,999
1 1,07 1,64 2,71 3,84 5,02 6,63 7,88 10,8
2 2,41 3,22 4,61 5,99 7,38 9,21 10,6 13,8
3 3,67 4,64 6,25 7,81 9,35 11,3 12,8 16,3
4 4,88 5,99 7,78 9,49 11,1 13,3 14,9 1875
5 6,06 7,29 9,2.4 ТГ.Т 12,8 15,1 16,7 20,5
6 7,23 8,56 10,6 12,6 14,4 16,8 18,5 22,5
7 8,38 9,80 12,0 14,1 16,0 18,5 20,3 24,3
8 9,52 11,0 13,4 15,5 17,5 20,1 22,0 26,1
9 10,7 12,2 14,7 16 л 19,0 21,7 23,6 27,9
10 11,8 13,4 16,0 18,3 20,5 23,2 25,2 29,6
11 12,9 14,6 . 17,3 19,7 21,9 24,7 26,8 31,6
12 14,0 15,8 х 18,5 21,0 23,3 26,2 28,3 32,9
13 15,1 17,0 19,8 '22,4 24,7 27,7 29,8 34,5
14 16,2 18,2 21,1 23,7 26,1 29,1 31,3 36,1
15 17,3 19,3 22,3 25,0 27,5 30,6 32,8 37,7
10 18,4 20,5 23,5 26,3 28,8 32,0 34,3 39,3
18 20,6 22,8 26,0 28,9 31,5 34,8 37,2 42,3
20 22,8 25,0 28,4 31,4 34,2 37,6 40,0 45,3
22 24,9 27,3 30,8 33,9 36,8 40,3 42,8 48,3
24 27,1 29,6 33,2 36,4 39,4 43,0 45,6 51,2
26 29,2 31,8 - 35,6 38,9 41,9 45,6 48,3 54,1
28 31,4 34,0 37,9 41,3 44,5 48,3 51,0 56,9
30 33,5 36,3 40,3 43,8 47,0 50,9 53,7 59,7
35 38,9 41,8 46,1 49,9 53,2 57,3 60,3 66,6
40 44,2 47,3 51,8 55,8 59,3 63,7 66,8 73,4
45 49,5 52,7 57,5 61,7 65,4 70,0 73,2 80,1
50 54,7 58,2 63,2 67,5 71,4 76,2 79,5 86,7
55 60,0 63,6 68,8 73,3 77,4 82,3 85,7 93,2
60 65,2 69,0 74,4 79,1 83,3 88,4 92,0 99,6
65 70,5 74,4 80,0 84,8 89,2 94,4 98,1 106,0
70 75,7 79,7 85,5 90,5 95,0 100,4 104,2 112,3
75 80,9 85,1 91,1 96,2 100,8 106,4 110,3 118,6
80 86,1 90,4 96,6 101,9 106,6 112,3 116,3 124,8
85 91,3 95,7 102,1 107,5 112,4 118,2 123,3 131,0
90 96,5 101,1 107,6 113,1 118,1 124,1 128,3 137,2
95 101,7 106,4 113,0 118,8 123,9 130,0 134,2 143,3
100 106,9 111,7 118,5 124,3 129,6 135,8 140,2 149,4
ТАБЛИЦА П.7Л
Значения коэффициента гх
Число отказов Вероятность Р (а)
0,999 о;99о-' 0,975 0,950 0,900 0,800
1 1 000 100 40 19,5 9,50 4,48
2 44,0 13,5 8,26 5,63 3,77 2,42
3 15,7 6,88 4,84 3,66 2,73 1,95
4 9,33 4,85 3,67 2,93 2,29 1,74
5 6,76 3,91 3,08 2,54 2,05 1,62
6 5,43 3,36 2,73 2,29 1,90 1,54
8 4,06 2,75 2,31 2,01 1,72 1,43
10 3,38 2,42 2,08 1,83 1,61 1,37
15 2,59 2,01 1,78 1,62 1,46 1,28
20 2,23 1,81 1,64 1,51 . 1,37 1,24
25 2,02 1,68 1,55 1,44 1,33 1,21
30 1,89 1,60 1,48 1,39 1,29 1,18
40 1,72 1,50 1,40 1,32 1,24 1,16
50 1,61 1,43 1,35 1,28 1,21 1,14
60 1,56 1,38 1,31 1,25 1,19 1,12
80 1,47 1,32 1,26 1,21 1,16 1,10
100 1,40 1,28 1,23 1,19 1,14 1,09
150 1,31 1,22 1,18 1,15 1,12 1,07
200 1,26 1,19 1,16 1,13 1,10 1,06
250 1,23 1,17 1,14 1,11 1,09 1,06
300 1,21 1,15 1,12 1,10 1,08 1,05
400 1,18 1,13 1,11 1,09 1,07 1,04
500 1,16 1,11 1,09 1,08 1,06 1,04
600 1,14 1,10 1,08 1,07 1,05 1,04
-> 800 1,12 1,09 1,07 1,06 1,05 1,03
1 000 1,11 1,08 . 1,06 1,05 1,04 1,03
ТАБЛИЦА П.7.3
Значения коэффициента Rx при а=0,95
d d/n=R, d dln—Rt d d ln~Px
1 19,5 25 1,44 300 1,10
2 5,63 30 1,39 400 1,09
3 3,66 40 1,32 500 1,08
4 2,93 50 1,28 600 1,07
5 2,54 60 1,25 800 1,06
6 2,29 80 1,21 1 000 1,05
8 2,01 100 1,19
10 1,83 150 1,15
15 1,62 200 1,13
20 1,51 250 1,П '
370
Таблица n.7.4
Значения коэффициента г3
d «8
0,999 0,990 0,975 0,950 0,900 0,800
1 0,14 0,22 0,27 0,33 0,43 0,62
2 0,22 0,30 0,36 0,42 0,51 0,67
3 0,27 0,36 0,42 0,48 0,57 0,70
4 0,31 0,40 0,46 0,52 0,60 0,73
5 0,34 0,43 0,49 0,55 0,62 0,75
6 0,36 0,46 0,52 0,57 0,65 0,76
8 0,41 0,50 0,56 0,61 0,60 0,78
10 0,44 0,53 0,58 0,64 0,70 0,80
15 0,50 0,59 0,64 0,68 0,74 0,83
20 0,54 0,63 0,67 0,72 0,77 0,85
25 0,58 0,66 0,70 0,74 0,79 0,86
30 0,60 0,68 0,72 0,76 0,80 0,87
40 0,64 0,71 0,75 0,78 0,83 0,88
50 0,67 0,74 0,77 0,80 0,84 0,89
60 0,70 0,76 0,79 0,82 0,86 0,90
80 0,73 0,78 0,81 0,84 0,87 0,91
100 0,75 0,80 0,83 0,86 0,88 0,92
150 0,79 0,84 0,86 0,88 0,90 0,93
200 0,81 0,86 0,88 0,89 0,92 0,94
250 0,83 0,87 0,89 0,90 0,92 0,95
300 0,84 0,88 0,90 0,91 0,93 0,95
400 0,86 0,89 0,91 0,92 0,94 0,96
500 0,88 0,90 0,92 0,93 0,94 0,96
600 0,89 0,91 0,92 0,94 0,95 0,97
800 0,90 0,92 0,93 0,94 0,96 0,97
1 000 0,91 0,93 0,94 0^95 0,96 0,97
I*
ТАБЛИЦА П.7.5
Квантили распределения Стьюдента
Число степеней свободы k V, Вероятность Р
0,6 0,7 0.8 0.9 0,95 0,975 0,990 0.995 0,999 0.9995
1 0.325 0,727 1,376 3,078 6,314 12,71 31,82 63,66 318,3 636,6
2 ,289 ,617 ,061 1,886 2,920 4,303 6,965 9,925 22,33 31,60
3 ,27? ,584 ,978 1,638 2,353 3,182 4,541 5,841 10,22 12,94
4 .271 ,569 ,941 1.523 2,132 2,776 3,747 4,604 7,173 8,610
5 ,267 ,559 ,920 1,476 2,015 2,571 3,365 4,032 5,893 6,859
6 ,235 ,553 ,9Э6 1,440 1,943 2,447 3,143 3,707 5,238 5,959
7 ,263 ,549 ,893 1,415 1,895 2,365 2,998 3,490 4,785 5,405
8 ,262 .546 ,889 1,397 1,860 2,306 2,893 3,355 4,501 5,041
9 ,231 .543 ,833 1,383 1,833 2,262 2,821 3,250 4,297 4,781
371
Продолжение табл. П.7.5
Вероятность Р
Число степен< свобод! 0,6 0,7 0,8 0,9 0,95 0,9/5 0,990 0,995 0,999 0.9995
19 ,230 ,542 ,879 1,372 1,812 2,228 2,764 3,161 4,144 4,587
11 ,260 ,540 ,876 1,363 1,793 2,2)1 2,718 3,106 4,025 4,437
12 ,253 ,539 .873 1,356 1,782 2,17) 2,681 3,055 3,930 4,318
13 ,259 ,538 ,870 1,350 1,771 2,169 2,653 3,012 3,852 4,221
14 ,258 ,537 ,868 1,345 1,761 2,145 2,624 2,97.7 3,787 4.140
• 15 ,258 ,533 ,856 1,341 1,753 2,131 2,602 2,947 3,733 4,073
16 .258 ,535 ,835 1,337 1,743 2,129 2,583 2,921 3,686 4,015
17 ,257 ,534 ,8)3 1,333 1,740 2,110 2,567 2,898 3,646 3,965
18 ,257 ,534 ,862 1,330 1,734 2,101 2,552 2,878 3,611 3,965
19 ,257 ,533 .8)1 1,328 1,729 2,093 2,539 2,861 3,579 3,883
29 ,257 ,533 ,860 1,325 1,725 2,086 2,528 2,845 3,552 3,850
21 ,257 ,532 ,'859 1,323 1,721 2,080 2.518 2,831 3,527 3,819
22 ,256 ,5'<2 ,858 1,321 1,717 2,074 2,538 2.819 3,535 3,792
23 ,253 ,532 .858 1,319 1,714 2,039 2,530 2,807 3,485 3,767
24 ,235 ,531 ,857 1.318 1,711 2,064 2,492 2,797 3,467 3,745
25 ,251 ,531 ,856 1,316 1,708 2,060 2,485 2,787 3,450 3,725
23 ,256 ,531 ,853 1,315 1,70'5 2,056 2,479 2,779 3,435 3,707
27 ,253 ,531 ,855 1,314 1,703 2.052 2,473 2,771 3,421 3,690
28 ,256 ,530 ,855 1,313 1,701 2,048 2,457 2,763 3,408 3,674
2Э ,253 ,530 ,854 1,311 1,699 2,045 2,462 2,756 3,396 3,659
30 0,253 0,530 1,854 1,310 1,6V 2,042 2,457 2,753 3,385 3,646
40 ,255 .529 ,851 1,303 1,6)4 2,021 2,423 2,704 3,307 3,551
5Э ,255 ,523 ,849 1,2)8 1,676 2,002 2,433 2,678 3,262 3,495
61 ,251 ,527 ,848 1,296 1,671 2,000 2,390 2,660 3,232 3,4)0
80 ,254 ,527 ,846 1,292 1,6)4 1,993 2,374 2,639 3,195 3,415
100 ,254 ,525 ,845 1,200 1,630 1,984 2.365 2,626 3.174 3,389
20Э ,251 ,525 ,843 1,236 1,653 1,972 2,345 2,601 3,131 3,330
530 ,253 ,525 ,842 1,283 1,648 1,935 2,334 2,586 3,106 3,310
со ,253 ,524 ,842 1,282 1,645 1,930 2,326 2,576 3,090 3,291
а1 0,2 0,4 0,6 0,8 0,9 0,95 0,98 0,99 0,998 0,999
₽1. % 40 30 20 10 5 2,5 1 0,5 0,1 0,05
₽2. % 80 60 40 23 10 5 1 2 1 0,2 0,1
ТАБЛИЦА П.7.6
Квантили нормального распределения
р— ~ —^р
р ы р гр р ир гР
0,50 0 0,674 0,82 0,915 1,341
0,51 0,025 0,690 0,83 0,954 1,372
0,52 0,050 0,706 0,84 0,994 1,405
0,53 0,075 0,722 0,85 1,036 1,440
0,54 0,100 0,739 0,85 1,080 1,476
372
Продолжение табл. 11.7.6
р % zp р °р zp
0,55 0,126 0,755 0,87 1,126 1,514
0,56 0,151 0,772 0,88 1,175 1,555
0,57 0,176 0,789 0,89 • 1,227 1,598
0,58 0,202 0,806 0,90 1,282 1,645
0,59 0,228 0,824 0,91 1,341 1,695
0,60 0,253 0,842 0,92 1,405 1,751
0,61 0,279 0,860 0,925 1,440 1,780
0,62 0,305 0,878 0,93 1,476 1,812
0,63 0,332 0,896 0,94 1,555 1,881
0,64 0,358 0,915 0,95 1,645 1,960
0,65 0,385 0,935 0,96 1,751 2,054
0,66 0,412 0,954 0,97 1,881 2,170
0,67 0,440 0,974 0,975 1,960 2,241
0,68 0,468 0,994 0,980 2,054 2,326
0,69 0,496 1,015 0,990 2,326 2,576
. 0,70 0,524 1,036 0,99'1 2,366 2,612
0,71 0,553 1,058 0,992 2,409 2,652
0,72 0,583 1,080 0,993 2,457 2,697
0,73 0,613 1,103 0,994 2,512 2,748
0,74 0,643 1,126 0,995 1,570 2,807
0,75 0,674 1,150 0,996 2,652 2,878
0,76 0,706 1,175 0,997 2,748 2,968
0,77 0,739 1,200 0,9975 2,807 3,024
0,78 0,772 1,227 0,9980 2,878 3,090
0,79 0,806 1,254 0,9990 3,090 3,291
0,80 0,842 1,282 0,9995 3,291 3,480
0,81 0,878 1,311 0,9999 3,719 3,885
ТАБЛИЦА П.7.7
Вспомогательные функции
k fi (*) f2(*) fM k M*) Uk)
—2,0 2,373 1,003 0,519 —1 1,525 1,042 0,643
— 1,9 2,285 1,004 0,524 —0,9 1,446 1,054 0,671
—1,8 2,197 1,005 0,530 —0,8 1,367 1,069 0,702
— 1,7 2,110 1,006 0,537 —0,7 1.290 1,089 0,740
—1,6 2,024 1,009 0,546 —0,6 1,215 1,114 0,783
373
Продолжение табл. П.7.7
k /.(*) fM k tM h(k)
— 1,5 1,939 1,011 0,556 —0,5 1,141 1,147 0,833
— 1,4 1,854 1,015 0,568 —0,4 1,069 1,189 0,891
—1,3 1,770 1,019 0,583 —0,3 0,9982 1,243 0,959
—1,2 1,688 1,025 0,600 —0,2 0,9294 1,312 1,039
—1,1 1,606 1,032 0,620 —0,1 0,8626 1,401 1,132
0 0,7979 1,517 1,241 1 0,2876 8,448 4,561
0,1 0,7353 1,667 1,370 1,1 0,2520 10,90 5,408
0,2 0,6751 1,863 1,523 1,2 0,2194 14,22 6,462
0,3 0,6172 2,119 1,704 1,3 0,1897 18,73 7,780
0,4 0,5619 2,453 1,919 1,4 0,1629 24,89 9,442
0,5 0,5092 2,893 2,178 1,5 0,1388 . 33,34 11,55
0,6 0,4592 3,473 2,488 1,6 0,1174 44,99 14,24
0,7 0,4119 4,241 2,863 1,7 0,0984 61,13 17,71
0,8 0,3676 5,261 3,319 1,8 0,0819 83,64 22,19
0,9 0,3261 6,623 3,876 1,9 2,0 0,0676 0,552 115,2 159,7 28,05 35,74
ТАБЛИЦА П.7.8
Значения коэффициента rD
a 1,0 0,999 0,990 0,975 0,950 0,900 0,800
Го 0 6,91 4,60 3,69 3,00 2,30 1,61
ТАБЛИЦА П.7.5'
Суммарные значения функции Пуассона
11 т\ е
т 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0
0 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000
1 ,095133 ,181269 ,259182 ,329680 ,393469 ,451188 ,503415 ,550671 ,593430 ,63212V
2 ,004679 ,017523 ,036936 ,061552 ,090204 ,121901 ,155805 ,191208 ,227518 ,26424!
3 ,000155 ,001149 ,003600 ,007926 ,014388 ,023115 ,034142 ,047423 ,062857 ,080301
4 ,000004 ,000057 ,000266 ,000776 ,001752 ,003358 ,005753 ,009080 ,013459 ,018988
5 —- ,000002 ,000016 ,000061 ,000172 ,000394 ,000786 ,001411 ,002344 ,00366(7
6 — — ,000001 ,000004 ,000014 ,000039 ,000090 ,000184 ,000343 ,000594-
7 — — — — ,000001 ,000003 ,000009 ,000021 ,000043 ,000083
8 — — — — — — ,000001 ,000002 ,000005 ,000010
9 — —-• — — — — — — — ,000001
376
Продолжение табл. П.7.9
т
1,1 1.2 м 1,4 1.5 1,6 1,7 1,8 1,9 2,0
0 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,оооооо 1,000000 1,000000
1 ,667129 ,698806 ,727468 ,753403 ,776870 ,798103 ,817316 ,834701 ,850431 ,864665
2 ,300971 ,337373 ,373177 ,408167 ,442175 ,475069 ,506754 ,537163 ,566251 ,593994-
3 ,099584 ,120513 ,142888 ,166502 ,191153 ,216642 ,242777 ,269379 ,296280 ,323324
4 ,025742 ,033769 ,043095 ,053725 ,065642 ,078813 ,093189 ,108708 ,125298 ,142877
5 ,005435 ,007746 ,010663 ,014253 ,018576 ,023682 ,029615 ,036407 ,044081 ,052653-
6 ,000968 ,001500 ,002231 ,003201 ,004456 ,006040 ,007999 ,010378 ,013219 ,016564-
7 ,000149 ,000251 ,000404 ,000622 ,000926 ,001336 ,001875 ,002569 ,003446 ,004534-
8 ,000020 ,000037 ,000064 ,000107 ,000170 ,000260 ,000388 ,000562 ,000793 ,001097
9 ,000002 ,000005 ,000009 ,000016 ,000028 ,000045 ,000072 ,000110 ,000163 ,000237
10 — ,000001 ,000001 ,000002 ,000004 ,000007 ,000012 ,000019 ,000030 ,000045
11 — — — — ,000001» ,000001 ,000002 ,000003 ,000005 ,000008
12 — — — — — — — — ,000001 ,000001
25—1086
т
2,1 2.2 2,3 2,4
0 1,000000 1,000000 1,000000 1,000000
1 ,877544 ,889197 ,899741 ,909282
2 ,620385 ,645430 ,669146 ,691559
3 ,350369 ,377286 ,403961 ,430291
4 ,161357 ,180648 ,200653 ,221277
5 ,062126 ,072496 ,083751 ,095869
6 ,020449 ,024910 ,029976 ,035673
7 ,005862 ,007461 ,009362 ,011594
8 ,001486 ,001978 ,002589 ,003339
9 ,000337 ,000470 ,000642 ,000862
10 ,000069 ,000101 ,000144 ,000202
11 ,000013 ,000020 ,000029 ,000043
12 ,000002 ,000004 ,000006 ,000008
13 — ,000001 ,000001 ,000002
14 — — — —
15 — — — —
Продолжение табл. П.7.9
2,5 2,6 | 2.7 2,8 2,9 3,0
1,000000 1,000000 1.000000 1,000000 1,000000 1,000000
,917915 ,925726 ,932794 ,939190 ,944977 ,950213
,7’12703 ,732615 ,751340 ,768922 ,785409 ,800852
,456187 ,481570 ,506375 ,530546 ,554037 ,576810
,242424 ,263998 ,285908 ,308063 ,330377 ,352768
,108822 • ,122577 ,137092 .152324 ,168223 ,184737
,042021 ,049037 ,056732 0,65110 ,074174 ,083918
,014187 ,017170 ,020569 ,024411 ,028717 ,033509
,004247 ,005334 ,006621 ,008131 ,009885 ,011905
,001140 ,001487 ,001914 ,002433 ,003058 ,003803
,000277 ,000376 , 000501 ,000660 ,000858 ,001102
,000062 ,000087 ,000120 ,000164 ,000220 ,000292
,000013 ,000018 ,000026 ,000037 ,000052 ,000071
,000002 ,000004 ,000005 ,000008 ,000011 ,000016
— ,000001 ,000001 ,000002 ,000002 ,000003
— — — — — ,000001
Продолжение табл. П.7.9
GJ
ОО
т 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0
0 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000
1 ,954951 ,959238 ,963117 ,966627 ,969803 ,972676 ,975276 ,977629 ,979758 ,981684
2 ,815298 ,828799 ,841402 ,853158 ,864112 ,874311, ,883799 ,892620 ,900815 ,908422
3 ,598837 ,620096 ,640574 ,660260 ,679153 ,697253 ,714567 ,731103 ,746875 ,761897
4 ,375160 ,397480 ,419662 ,441643 ,463367 ,484784 ,505847 ,526515 ,546753 ,566530
5 ,201811 ,219387 ,237410 ,255818 ,274555 ,293562 ,312781 ,332156 ,351635 ,371163
6 ,094334 ,105408 ,117123 ,129458 ,142386 ,155881 ,169912 .,184444 ,199442 ,214870
7 ,038804 ,044619 ,050966 ,057853 ,065288 0,73273 ,081809 ,090892 ,100517 ,110674
8 ,014213 ,016830 ,019777 ,023074 ,026739 ,030789 ,035241 ,040107 ,045402 ,051134
9 ,004683 ,005714 ,006912 ,008293 ,009874 ,011671 ,013703 ,015984 ,018533 ,021363
10 ,001401 ,001762 ,002195 ,002709 ,003315 ,004024 ,004848 ,005799 ,006890 ,008132
И ,000383 ,000497 ,000638 ,000810 ,001019 ,001271 ,001572 ~,001929 ,002349 ,002840
12 ,000097 ,000129 ,000171 ,000223 ,000289 ,000370 ,000470 ,000592 ,000739 ,000915
13 ,000023 ,000031 ,000042 ,000057 ,000076 ,000100 ,000130 ,000168 ,000216 ,000274
14 ;000005 ,000007 ,000010 ,000014 ,000019 ,000025 ,000034 ,000045 ,000059 ,000076
15 ,000001 ,000001 ,000002 ,000003 ,000004 ,000006 ,000008 ,000011 ,000015 ,000020
16 — — — ,000001 ,000001 ,000001 ,000002 ,000003 ,000004 ,000005
17 — — — — — ,000001 ,000001 ,000001
379
т
4,1 j 4,2 4,3
0 1,000000 1,000000 1,000000
1 ,983427 ,985004 ,986431
2 ' ,915479 ,922023 ,928087
3 ,776186 ,789762 ,802645
4 ,585818 ,604597 ,622846
5 ,390692 ,410173 ,429562
6 ,230688 ,246857 ,263338
7 ,121352 ,132536 ,144210
8 ,057312 ,063943 ,071032
9 ,024492 ,027932 ,031698
10 ,009540 ,011127 ,012906
11 ,003410 ,004069 ,004825
12 ,001125 ,001374 ,001666
13 ,000345 ,000431 ,000534
14 ,000098 ,000126 ,000160
15 ,000026 ,000034 ,000045
16 ,000007 ,000009 ,000012
17 ,000002 ,000002 ,000003
18 > — ,000001
19 •— —• -—
Продолжение табл. П.7.9
4.4 4,5 4,6 4,7 4,8 4,9 5,0
1,000000 1,000000 1,000000 1,000000 1,000000 1,000000 1,000000
,987723 ,988891 ,989948 ,990905 ,991770 ,992553 ,993262
,933702 ,938901 ,943710 ,948157 ' ,952267 ,956065 ,959572
,814858 ,826422 ,837361 ,847700 ,857461 ,866669 ,875348
,640552 ,657704 ,674294 ,6900316 ,705770 ,720655 ,734974
,448816 ,467896 ,486766 ,505391 ,523741 ,541788 ,559507
,280088 ,297070 ,314240 ,331562 ,348994 ,366499 ,384039
,156355 ,168949 ,181971 ,195395 ,209195 ,223345 ,237817
,078579 ,086586 ,095051 ,103969 ,113334 ,123138 ,133372
,035803 ,040257 ,045072 ,050256 ,055817 ,061761 ,068094
,014890 ,017093 ,019527 ,022206 ,025141 ,028345 ,031828
,005688 ,006669 ,007777 ,009022 ,010417 ,011971 ,013695
,002008 ,002404 ,002863 ,003389 ,003992 ,004677 ,005453
,000658 ,000805 ,000979 ,001183 ,001422 ,001699 ,002019
,000201 ,000252 ,000312 ,000385 ,000473 ,000576 ,000698
,000058 ,000074 ,000093 ,000118 ,000147 ,000183 ,000226
,000016 ,000020 ,000026 ,000034 ,000043 ,000055 ,000069
,000004 ,000005 ,000007 ,000009 ,000012 ,000015 ,000020
,000001 ,000001 ,000002 ,000002 ,000003 ,000004 ,000005
— — ,000001 ,000001 ,000001 ,000001
ТАБЛИЦА П.7.10
Таблица числа комбинаций из 7V элементов по п
(биномиальные коэффициенты)
/N\f N \ _ М
у п J —п ] п \(N—и)!
п N
12 3 4 5 6 7 8 9 10 в 12 13 14
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1
1 1 2 '3 4 5 6 7 8 9 10 11 12 13 14
2 1 3 6 10 15 21 28 36 45 55 66 78 91
3 1 4 10 20 35 56 84 120 165 220 286 364
4 1 5 15 35 70 126 210 330 495 715 1 001
5 1 6 21 56 126 252 462 792 1 287 2 002
6 1 7 28 84 210 462 924 1 716 3003
7 1 8 36 120 330 792 1 716 3 432
8 1 9 45 165 495 1 287 3 003
9 1 10 55 220 715 2 002
10 i И 66 286 1 001
11 1 12 78 364
12 1 13 91
13 1 14
14 1
Продолжение табл. П.7.10
N
п 15 16 17 18 19 20 21 22 23
0 1 1 1 1 1 1 1 1 1
1 15 16 17 18 19 20 21 22 23
2 105 120 136 153 171 190 210 231 253
3 455 560 680 816 969 1 140 1 330 1 540 1 771
4 1365 1 820 2 380 3 060 3 876 4 845 5 985 7 315 8 855
5 3 003 4 368 6188 8 568 11 628 15 504 20 349 26 334 33649
6 5 005 8 008 12 376 18 564 27 132 [38 760 54 264 74 613 100 947
7 6 435 11 440 19 448 31 824 50388 77 520 116 280 170 544 245 157
8 6 435 12 870 24 310 43 758 75582 125 970 203 490 319 770 490 314
9 5 005 48 620 92 378 167 960 293930 497 420 817190
10 3 003 184 756 352 716 646 646 1 144 066
11 1 365 705 432 1 352 078
12 455
13 105
14 15
15_ 1
380
Продолжение табл. П.7.10
п N
24 25 26 27 28 29
0 1 1 1 1 1 1
1 24 25 26 27 28 29
2 276 300 325 351 378 406
3 2 024 2 300 2 600 2 925 3 276 3 654
4 10 626 12 650 14 950 17 550 20 475 23 751
5 42 504 53130 65 780 80 730 98 280 118 755
6 134 596 177 100 230 230 296 010 376 740 475 020
7 346 104 480 700 657 800 888 030 1 184 040 1 560 780
8 735 471 1 081 575 1 562 275 2 220 075 3 108 105 4 292 145
9 1 307504 2 042 975 3124 550 4 686 825 6 906 900 10 015 005
10 1 961 256 3 268 760 5 311 735 8 436 285 13123110 20 030 010
И 2 496 144 4 457 400 7 726 160 13 037 895 21 474 180 34 597 290
12 2 704 156 5 200 300 9 657 700 17 383 860 30 421 755 51 895 935
13 10 400 600 20 058 300 37 442160 67 863 915
14 40 116 600 77 558 760
Продолжение табл. П.7.10
п N
30 31 32 33 34
0 1 1 1 1 1
1 30 31 32 33 34
2 435 465 496 528 561
3 4 060 4 495 4 960 5 456 5 984
4 27 405 31 465 35 960 40 920 46 376
5 142 506 169 911 201 376 237 336 278 256
6 593 775 736 281 906 192 1 107 568 1 344 904
7 2 035 800 2 629575 3 365 856 4 272 048 5 379616
8 5 852 925 7 888 725 10 518 300 13 884156 18 156 204
9 14307 150 20 160 075 28 048 800 38 567 100 52 451 256
10 30 045015 44 352 165 64 512 240 92 561 040 131 128 140
11 54 627 300 84 672 315 129 024 480 193 536 720 286 097 760
12 86 493 225 141 120 525 225 792 840 354 317 320 548 354 040
13 119 759 850 206 253 075 347 373 600 573 166 440 927 983 760
14 145 422 675 265 182 525 471 435 600 818 809 200 1 391 975 640
15 155117520 300 540 195 565 722 720 1 037 158 320 1 855 967520
16 601 080 390 1 166 803 110 2 203 961 430
17 2 333 606 220
381
Продолжение табл. П.7.10
п /V
35 3G 37 38
0 1 1 1 1
1 35 36 37 38
2 595 630 666 703
3 6 545 7 140 7J70 8 436
4 52 360 58 905 66 045 73 815
5 324 632 376 992 435 897 501 942
6 1 623 160 1 947 792 2 324 784 2 760 681
7 6 724 520 8 347 680 10 295 472 12 620 256
8 23 535 820 30 260 340 38 608 020 48 903 492
9 70 607 460 94 143 280 124 403 620 163 011 640
10 183 57§396 254 186 856 348 330 136 472 733 756
11 417 225 900 600 805 296 854 992 152 1 203 322 288
12 834 451 800 1 251 677 700 I 852 482 996 2 707 475 148
13 1 476 337 800 2 310 789 600 3562 467 300 5 414 950 296
14 2 319 959 400 3 796 297 200 6 107 086 800 9 669 554100
15 3 247 943 160 5 567 902 560 9 364 199 760 15 471 286 560
16 4 059 928 950 7 307 872 НО 12 875 774 670 22 239 974 430
17 4 537 567 650 8 597 496 600 15 905368 710 28 781 143 380
18 9 075 135 300 17672 631 900 33 578 000 610
19 35 345 263 800
Продолжение табл. П.7.10
п 39 40 41 42
0 1 1 1 1
1 39 40 41 42
2 741 780 820 862
3 9 139 9 880 10 660 11 480
4 82 251 91 390 101 270 111 930
5 575 757 658 008 749 398 850 668
6 3 262 623 3 838 380 4 496 388 5 245 786
7 15 380 937 18 643 560 22 481 940 26 978 328
8 61 523 748 76 904 685 95 548 245 118 030 185
9 211 915 132 273 438 880 350 343 565 445 891 810
10 635 745 396 847 660 528 1 121 099 408 1 471 442 973
11 1 676 056 044 2 311 801 440 3 159 461 968 4 280 561 376
12 3 910 797 436 5 586 853 480 7 898 654 920 11 058 116 888
13 8 122 425 444 12 033 222 880 17 620 076 360 25 518 731 280
14 15 084 504 396 23 206 929 880 35 240 152 720 52 860 229 080
15 25 140 840 660 40 225 345 056 63 432 274 896 98 672 427 616
16 37 711 260 990 62 852 101 650 103 077 446 706 166 509 721 602
17 51 021 117 810 88 732 378 800 151 584 480 450 254 661 927156
18 62 359 143 990 113 380 261 800 202 112 640 600 353 697 121 050
19 68 923 264 410 131 282 408 400 244 662 670 200 446 775 310 800
20 137 846 528 820 269 128 937 220 513 791 607 420
21 538 257 877 440
382
Продолжение табл. П.7.10
Л'
47
48
383
п 43 44 45 46
0 1 1 1 1
1 43 44 45 46
2 903 946 990 1 035
3 12 341 13 244 14 190 15 180
4 123 410 135 751 148 995 163 185
5 962 598 1 086 008 1 221 759 1 370 754
6 6 096 454 7 059 052 8 145 060 9 366 819
7 32 224 114 38 320 568 45 379 620 53 524 680
8 145 008 513 177 232 627 215 553 195 260 932 815
9 563 921 995 708 930 508 886 163 135 1 101 716 330
10 1 917 334 783 2 481 256 778 3 190 187 286 4 076 350 421
11 5 752 004 349 7 669 339 132 10 150 595 910 13 340 783 196
12 15 338 678 264 21 090 682 613 28 760 021 745 38 910 617 655
13 36 576 848 168 51 915 526 432 73 006 209 045 101 766 230 790
14 78 378 960 360 114 955 808 528 166 871 334 960 239 877 544 005
15 151 532 656 696 229 911 617 056 344 867 425 584 511 738 760 544
16 265 182 149 218 416 714 805 914 646 626 422 970 991 493 848 554
17 421 171 648 758 686 353 797 976 1 103 068 603 890 1 749 695 026 860
18 608 359 048 206 1 029 530 696 964 1 715 884 494 940 2 818 953 098 830
19 800 472 431 850 1 408 831 480 Оьб 2 438 362 177 020 4 154 246 671 960
20 960 566 918 220.1 761 039 350 070 3 169 870 830 126 5 608 233 007 146
21 1 052 049 481 860 2 012 616 400 080 3 773 65.5 750 150 6 943 526 580 276
22 2 104 098 963 720 4 116 715 363 800 7 890 371 113 950
23 8 233 430 727 600
П родолжение табл. П.7.10
N
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
1
47
1 081
16 215
178 365
1 533 739
10 737 573
62 891 499
314 457 495
1 362 649 145
5 178 066 751
17417133617
52 251 400 851
140 676 848 445
341 643 774 795
1
48
1 128
17 296
194 580
1 712 304
12 271 512
73 629 072
377 348 994
1 677 106 640
6 540 715 896
22 595 200 368
69 668 534 468
192 928 249 296
482 320 623 240
Продолжение табл. П.7.10
п N
47 48
15 751 616 304 549 1 093 260 079 344
16 1 503 232 609 098 2 254 848 913 647
17 2 741 188 875 414 4 244 421 484 512
18 4 568 648 125 690 7 309 837 001 104
19 6 973 199 770 790 11 541 847 896 480
20 9 762 479 679 106 16 735 679 449 896
21 12 551 759587422 22 314 239 266 528
22 14 833 897 694 226 27 385 657 281 648
23 16 123 801 841 550 30 957 699 535 776
24 32 247 603 683 100
25
Продолж е н и е табл. П.7.10
п 49 50
0 1 1
1 49 50
2 1 176 1 225
3 18 424 19 600
4 21Ц876 230 300
5 1 906 884 2 118 760
6 13 983 816 15 890 700
7 85 900 584 99 884 400
8 450 978 066 536 878 650
9 2 054455 634 2 505 433 700
10 8 217 822J536 10 272 278 170
11 29 135 916 264 37 353 738 800
12 92 263 734 836 121 399 651 100
13 262 596 783 764 354 860 518 600
14 675 248 872 536 937 845 6561300
15 1 575 580 702 584 2 250 829 575 120
16 3 348 108 992 991 4 923 689 695 575
17 6 499 270 398 159 9 847 379 391 150
18 11 554 258 485 616 18 053 528 883 775
19 18 851 684897584 30 405 943 383 200
20 28 277 527 346 376 47 129 212 243 960
21 39 049 918 716 424 67 327 446 062 800
22 49 699 896 548 176 88 749 815 264 600
23 58 343 356 817 424 108 043 253 365 600
24 63 205 303 218 876 121 548 660 036 300
25 126 410606 437 752
4
*’(*
У*
*
Примечание. Коэффициенты до ('rjpj опубликованы в кни-
ге Т. Фрай „Теория вероятностей для инженеров", ОНТИ, 1934.
384
385
ТАБЛИЦА П.7.11
Вероятность d или меньшего количества дефектных изделий для биномиальных распределений
<? d Объем выборки п d
5 6 7 8 9 10 15 20 25 30 40 50
0,001 0 1 0,9950 0,9940 0,9930 0,9920 0,9910 0,9900 0,9851 0,9802 0,9753 0,9704 0,9608 0,9512 0,9999 0,9998 0,9997 0,9996 0,9992 0,9988 0 1
0,0027 0 1 2 0,9866 0,9839 0,9813 0,9786 0,9760 0,9733 0,9603 0,9474 0,9346 0,9221 0,8975 0,8736 0,9999 0,9999 0,9998 0,9998 0,9997 0,9997 0,9993 0,9987 0,9979 0,9970 0,9947 0,9918 0,9999 0,9998 0,9996 0 1 2
0,005 0 1 2 3 0,9752 0,9704 0,9655 0,9607 0,9559 0,9511 0,9276 0,9046 0,8882 0,8604 0,8183 0,7783 0,9998 0,9996 0,9995 0,9993 0,9991 0,9989 0,9975 0,9955 0,9931 0,9901 0,9828 0,9739 0,9999 0,9999 0,9997 0,9995 0,9989 0,9979 0,9999 0,9999 •0 1 2 3
0,01 0 1 2 3 4 0,9510 0,9415 0,9321 0,9227 0,9135 0,9044 0,8601 0,8179 0,7778 0,7397 0,6690 0,6050 0,9990 0,9985 0,9980 0,9973 0,9966 0,9957 0,9904 0,9831 0,9742 0,9639 0,9393 0,9106 0,9999 0,9999 0,9999 0,9996 0,9990 0,9980 0,9967 0,9925 0,9862 0,9999 0,9998 0,9993 0,9984 • 0,9999 0 1 2 3 4
0,02 0 1 2 3 4 5 6 1 0,9039 0,8858 0,8681 0,8508 0,8337 0,8171 0,7386 0,6676 0,6035 0,5455 0,4457 0,3642 0,9962 0,9943 0,9921 0,9897 0,9869 0,9838 0,9647 0,9401 0,9114 0,8795 0,8095 0,7358 0,9999 0,9998 0,9997 0,9996 0,9994 0,9991 0,9970 0,9929 0,9868 0,9783 0,9543 0,9216 0,9998 0,9994 0,9986 0,9971 0,9918 0,9822 0,9999 0,9997 0,9988 0,9968 0,9999 0,9995 0,9999 0 1 2 3 4 5 6
Продолжение табл. П.7.11
Объем выборки п
Q d 5 6 7 8 9 10 15 20 25 30 40 50 d
0,03 0 0,8587 0,8330 0,8080 0,7837 0,7602 0,7374 0,6333 0,5438 0,4670 0,4010 0,2957 0,2181 о.
1 0,9915 0,9875 0,9827 0,9777 0,9718 0,9655 0,9270 0,8802 0,8280 0,7731 0,6615 0,5553 1
2 0,9997 0,9995 0,9991 0,9986 0,9980 0,9972 0,9906 0,9790 0,9620 0,9399 0,8822 0,8108 2
3 0,9999 0,9999 0,9999 0,9992 0,9973 0,9938 0,9881 0,9686 0,9372 3
4 . . . 0,9999 0,9997 0,9992 0,9982 0,9933 0,9832 4
5 , . . 0,9999 0,9998 0,9988 0,9963 5
6 . . , . . . . . . . . . . 0,9998 0,9993 6
7 ... •.. •.. ... 0,9999 7
0,04 0 0,8154 0,7827 0,7514 0,7214 0,6925 0,6648 0,5421 0,4420 0,3604 0,2939 0,1954 0,1299 0
1 0,9852 0,9784 0,9706 0,9619 0,9522 0,9418 0,8809 0,8103 0,7358 0,6612 0,5210 0,4005 1
2 0,9994 0,9988 0,9980 0,9969 0,9955 0,9938 0,9797 0,9561 0,9235 0,8831 0,7855 0,6767 2
3 . . . 0,9999 0,9998 0,9997 0,9996 0,9976 0,9926 0,9835 0,9694 0,9252 0,8609 3
4 0,9998 0,9990 0,9972 0,9937 0,9790 0,9510 4
5 0,9999 0,9996 0,9989 0,9951 0,9856 5
6 . . . 0,9999 0,9990 0,9964 6
7 . . . 0,9998 0,9992 7
8 *• • ’ 0,9999 8
0,05 0 0,7738 0,7351 0,6983 0,6634 0,6302 0,5987 0,4633 0,3585 0,2774 0,2146 0,1285 0,0769 0
1 0,9774 0,9672 0,9556 0,9428 0,9288 0,9139 0,8290 0,7358 0,6424 0,5535 0,3991 0,2794 1
2 0,9988 0,9978 0,9962 0,9942 0,9916 0,9885 0,9638 0,9245 0,8729 0,8122 0,6767 0,5405 2
3 . . . 0,9999 0,9998 0,9996 0,9994 0,9990 0,9945 0,9841 0,9659 0,9392 0,8618 0,7604 3
4 . . . . . . . . . 0,9999 0,9994 0,9974 0,9928 0,9844 0,9520 0,8964 4
5 . . . . . . . . . 0,9999 0,9997 0,9988 0,9967 0,9861 0,9622 5-
6 ... ... ... ... ... ... 0,9998 0,9994 0,9966 0,9882 6
Продолжение табл. П.7.11
Объем выборки п
d 5 6 7 8 9 10 15 23 25 30 40 50
0,05 7 8 9 0,9999 0,9993 0,9968 0,9999 0,9992 0,9998 7 8 9
0,06 0 1 2 3 4 5 6 7 8 9 10 0,7339 0,6899 0,6485 0,6096 0,5730 0,5386 0,3953 0,2901 0,2129 0,1563 0,0842 0,0453 0,9681 0,9541 0,9382 0,9208 0,9022 0,8824 0,7738 0,6605 0,5527 0,4555 0,2990 0,1900 0,9980 0,9962 0,9937 0,9904 0,9862 0,9812 0,9429 0,8850 0,8129 0,7324 0,5665 0,4162 0,9999 0,9998 0,9996 0,9993 0,9987 0,9980 0,9896 0,9710 0,9402 0,8974 0,7827 0,6473 0,9999 0,9998 0,9986 0,9944 0,9850 0,9685 0,9104 0,8206 0,9998 0,9991 0,9969 0,9921 0,9691 0,9224 0,9999 0,9995 0,9983 0,99090,9711- 0,9999 0,9997 0,9977 0,9906 0,9995 0,9973 ’ 0,99990,9993 0,9998 0 1 2 3 4 5 6 7 8 9 10
0,07 0 1 2 3 4 6 6 7 8 0,6957 0,6470 0,6017 0,5596 0,5204 0,4840 0,3367 0,2342 0,1630 0,1134 0,0549 0,0266 0,9575 0,9392 0,9187 0,8965 0,8729 0,8483 0,7168 0,5869 0,4696 0,3694 0,2201 0,1265 0,9969 0,9942 0,9903 0,9853 0,9791 0,9717 0,9171 0,8390 0,7466 0,6487 0,4625 0,3108 0,9999 0,9997 0,9993 0,9987 0,9977 0,9964 0,9825 0,9529 0,9064 0,8450 0,6937 0,5327 0,9999 0,9998 0,9997 0,9972 0,9893 0,9726 0,9447 0,8546 0,7290 0,9997 0,9981 0,9935 0,9838 0,9419 0,8650 0,9997 0,9987 0,9961 0,9802 0,9417 ' 0,9998 0,9992 0,9942 0,9780 0,9999 0,9985 0,9927 0 1 2 3 4 5 6 7 8
Продолжение табл. П.7.11
Объем выборки п
0 d 5 6 7 8 9 10 15 20 25 30 40 50 d
0,07 9 10 11 0,9997 0,9978 0,9999 0,9994 0,9999 9 10 11
0,08 0 1 2 3 4 5 6 7 8 9 10 11 12 0,6591 0,6064 0,5578 0,5132 0,4722 0,4344 0,2863 0,1887 0,1244 0,0820 0,0356 0,0155 0,9456 0,9227 0,8974 0,8702 0,8417 0,8121 0,6597 0,5169 0,3947 0,2958 0,1594 0,0827 0,9955 0,9915 0,9860 0,9789 0,9702 0,9599 0,8870 0,7879 0,6768 0,5654 0,3694 0,2260 0,9998 0,9995 0,9988 0,9978 0,9963 0,9942 0,9927 0,9294 0,8649 0,7842 0,6007 0,4253 0,9999 0,9999 0,9997 0,9994 0,9950 0,9817 0,9549 0,9126 0,7868 0,6290 0,9993 0,9962 0,9877 0,9707 0,9033 0,7918 0,9999 0,9994 0,9972 0,9918 0,9624 0,8918 0,9999 0,9995 0,9980 0,9873 0,9562 0,9999 0,9996 0,9963 0,9834 0,9999 0,9990 0,9944 0,9998 0,9983 0,9995 0,9999 0 1 2 3 4 5 6 7 8 9 10 11 12
0,09 0 1 2 3 4 5 6 7 0,6240 0,5679 0,5168 0,4703 0,4279 0,3984 0,2430 0,1516 0,09*46 0,0591 0,0230 0,0090 0,9326 0,9048 0,8745 0,8423 0,8088 0,7746 0,6035 0,4516 0,3286 0,2343 0,1140 0,0532 0,9937 0,9882 0,9807 0,9711 0,9595 0,9460 0,8531 0,7334 0,6063 0,4855 0,2894 0,1605 0,9997 0,9992 0,9982 0,9966 0,9942 0,9912 0,9601 0,9007 0,8169 0,7175 0,5092 0.3303 0,9999 0,9997 0,9995 0,9990 0,9918 0,9710 0,9314 0,8712 0,7103 0,5277 0,9999 0,9987 0,9932 0,9790 0,9519 0,8535 0,7072 0,9998 0,9987 0,9846 0,9848 0,9361 0,8404 0,9998 0,9989 0,9959 0,9758 0,9232 0 1 2 3 4 5 6 7
Продолжение табл. П.7.11
389
Объем выборки п
(?) d 5 6 7 8 9 10 1S 20 25 30 40 S0 d
0,09 8 9 ; io : н 12 13 0,9998 0,9990 0,9919 0,9672 0,9998 0,9976 0,9875 0,9994 0,9957 0,9999 0,9987 0,9996 0,9999 ’ 8 9 10 11 12 13
0,10 0 1 2 3 4 5 6 7 8 9 10 И 12 13 14 0,5905 0,5314 0,4783 0,4305 0,3874 0,3487 0,2059 0,1216 0,0718 0,0424 0,0148 0,0052 0,9185 0,8857 0,8503 0,8131 0,7748 0,7361 0,5490 0,3917 0,2712 0,1837 0,0805 0,0338 0,9914 0,9842 0,9743 0,9619 0,9470 0,9298 0,8159 0,6769 0,5371 0,4114 0,22280,1117 0,9995 0,9987 0,9973 0,9950 0,9917 0,9872 0,9443 0,8670 0,7636 0,6474 0,4231 0,2503 ... 0,9999 0,9998 0,9996 0,9991 0,9984 0,9874 0,9568 0,9020 0,8245 0,6290 0,4312 0,9999 0,9999 0,9978 0,9887 0,9666 0,9268 0,7937 0,6161 0,9997 0,9976 0,9905 0,9742 0,9005 0,7702 0,9996 0,9977 0,9922 0,9581 0,9779 0,9999 0,9995 0,9980 0,9845 0,9421 0,9999 0,9995 0,9949 0,9755 0,9999 0,9985 0,9906 0,9996 0,9968 0,9999 0,9990 ’ 0,9997 0,9999 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
0,15 0 1 2 0,4437 0,3771 0,3206 0,2725 0,2317 0,1969 0,0874 0,0388 0,0172 0,0076 0,00150,0003 0,8352 0,7765 0,7166 0,6572 0,5995 0,5443 0,3186 0,1756 0,0931 0,0480 0,0121 0,0029 0,9734 0,9527 0,9262 0,8948 0,8591 0,8202 0,6042 0,4049 0,2537 0,1514 0,04860,0142 0 1 2
Продолжение табл. П.7.11
390
Объем выборки п
Q d 5 6 7 8 9 10 15 20 25 30 40 50 d
0,. 15 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0,9978 0,9941 0,9879 0,9786 0,9661 0,9500 0,8227 0,6477 0,4711 0,3217 0,13020,0460 0,9999 0,9996 0,9988 0,9971 0,9944 0,9901 0,9383 0,8298 0,6821 0,5245 0,2633 0,1121 0,9999 0,9998 0,9994 0,9986 0,9832 0,9327 0,8385 0,7106 0,4325 0,2194 0,9999 0,9964 0,9781 0,9305 0,8474 0,6067 0,3613 0,9994 0,9941 0,9745 0,9302 0,7559 0,5188 0,9999 0,9987 0,9920 0,9722 0,8646 0,6681 0,9998 0,9979 0,9903 0,9328 0,7911 0,9995 0,9971 0,9701'0,8801 0,9999 0,9992 0,9880 0,9372 0,9998 0,9957 0,9699 0,9986 0,9868 0,9996 0.9947 0,9999 0,9981 0,9993 0,9998 0,9999 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
0,20 0 1 2 3 4 5 0,3277 0,2621 0,2097 0,1673 0,1342 0,1074 0,0352 0,0115 0,0038 0,0012 0,0001 0,7373 0,6554 0,5767 0,5033 0,4362 0,3758 0,1671 0,0692 0,0274 0,0105 0,0015 0,0002 0,9421 0,9011 0,8520 0,7969 0,7382 0,6778 0,3980 0,2061 0,0982 0,0442 0,0079 0,0013 0,9933 0,9830 0,9667 0,9437 0,9144 0,8791 0,6482 0,4114 0,2340 0,1227 0,02850,0057 0,9997 0,9984 0,9953 0,9896 0,9804 0,9672 0,8358 0,6296 0,4207 0,2552 0,0759 0,0185 ... 0,9999 0,9996 0,9988 0,9969 0,9936 0,9389 0,8042 0,6167 0,4275 0,1613 0,0480 0 1 Ь 4 5
Продолжение табл. П.7.11
Объем выборки п
Q d 5 6 7 8 9 10 15 20 25 30 40 50 d
0,20 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 . . 0,9999 0,9997 0,9991 0,9819 0,9133 0,7800 0,6070 0,2859 0,П)34 0,9999 0,9958 0,9679 0,8909 0,7608 0,4371 0,1904 0,9992 0,9900 0,9532 0,8713 0,5931 0,3073 ... 0,9999 0,9974 0,9827 0,9389 0,73180,4437 0,9994 0,9944 0,9744 0,8392 0,5836 0,9999 0,9985 0,9905 0,9125 0,7107 0,9996 0,9969 0,9568 0,8139 ... 0,9999 0,9991 0,98060,8894 ' 0,9998 0,9921 0,9393 0,9999 0,9971 0,9692 ... 0,9990 0,9856 ... 0,9997 0,9937 . ... 0,9999 0,9975 ... 0,9991 ’ ... 0,9997 0,9999 6 7 8 9 10 11 12 13 14 15 16 17 18’ 19 20' 21
ТАБЛИЦ А П.7.1
Значения a = nq для заданных вероятностей распределения
Пуассона /
а
0,01 | 0,05 I' 0,10 | 0,90 | 0.9S 0,99
^0 А
0,99 | 0,95 I 0,90 0,10 0,05 0,01
0 1 0,01005 0,05129 0,10536 2,3026 2,9957 4,6052
1 2 0,14856 0,35536 0,53181 3,8897 4,7439 6,6384
2 3 0,43604 0,81770 1,1021 5,3223 6,2958 8,4060
3 4 0,82324 1,3663 1,7448 6,6808 7,7536 10,045
4 5 1,2791 1,9702 2,4326 7,9936 9,1535 11,605
5 6 1,7853 2,6130 3,1519 8,2747 10,513 13,108
6 7 2,3302 3,2853 3,8948 10,532 11,842 14,571
7 8 2,9061 3,9808 4,6561 11,771 13,148 16,000
8 9 3,5075 4,6952 5,4324 12,995 14,435 17,403
9 10 4,1302 5,4254 6,2213 14,206 15,705 18,783
10 11 4,7712 6,1690 7,0208 15,407 16,962 20,145
11 12 5,4282 6,9242 7,8294 16,598 18,208 21,490
12 13 6,0990 7,6896 8,6460 17,782 19,443 22,821
13 14 6,7824 8,4640 9,4696 18,958 20,669 24,139
14 15 7,4768 9,2463 10,300 20,128 21,886 25,446
ТАБЛИЦА П.7.13
Нормированная функция Лапласа
_ 1 Г 2 е dz
Сотые доли для г
Z 0 1 > 2 3 4 'Э 1 6 7 1 8 9
’ 0,0 0,0000 040 080 120 160 199 О', :Z279'' 319 359
. 0,1 398 438 478 517 557 596 взг 675 714 753
793 832 871 910 948 <Ф87У -,026 064 103 141
0,3 0,1179 217 255, 293 331 368' ' 406 443 480 517
, 0,4 554 591 628 664 700 736 772 808 844 879
0,5 915 \950 '985 019 054 088 123 157 190 224
0,6 o,W 291 324 357, 389 422 .454_, 486 517 549
0,7 580 611 642 673 703 734 764 '79? 823 852
392
Продолжение табл. П.7.13
Сотые доли для £ \ : :
Z г 0 2 3 4 3 6 7 8 9
0,8 881 910 939 967 995 023 051 078 106 133
0,9 0,3159 186 212 238 264 289 315 340 365 389
1,0 413 437 461 485 508 583 554 577 599•> 621
1,1 643 665 686 708 729 749 770 790 810 830
1,2 849 869 888 907 925 944 962 980 997 015
1,3 >0,«)32 049 066 <^2) 099 115 131 147, 162 . 177
1,4 . 192 207 222 236 251 265 279 292 306 319
1,5 332 345 357 370 382 394 406 418 429 441
1.6 452 463 474 484 Z$9^ 505 515 525 535 545
1,7 554 564 573 582 53Т 599 608 616 625 633
1,8 641 649 656 664 671 678 686 693 699 706
1,9 713 719 726 732 738 744 750 756 761 767
2,0 772 778 783 <788 793 798 803 808 812
2,1 821 826 830 834 838 842 846 850 854 857
2,2 860 864 867 871 874 877 880 883 886 889
966 474 906 263 545 755 894 962 962 893
2,3 892 895 898 900 903 906 908 911 913 915
2,4 918 920 922 924 926 928 930 932 934 936
025 237 397 506 564 572 531 493 309 128
2,5 937- 039 941 942 944 946 947 949 950 952
903 634 323 969 574 139 664 151 600 012
2,6 0,4953 954 956 957 958 959 960 962 963 964
388 729 035 308 547 754 930 074 189 274
t л 965 966 967 968. 969 970 971 971 972 973
330 358 359 333 280 202 099 972 821 646
2,8 974 975 975 976 977 978 979 979 980 980
449 229 988 726 443 140 818 476 116 738
2,9 981 981 982 983 983 984 984 985 985 986
342 929 498 052 589 111 618 НО 588 051
3,0 986 986 987 987 988 988 988 989 989 989
501 938 361 772 171 558 933 297 650 992
3,1 990 990 990 991 991 991 992 992 992 992
324 646 957 260 553 836 112 378 636 886
3,2 993 993 993 993 994 994 994 994 994 994
129 363 590 810 024 230 429 623 810 991
3.3 995 995 995 995 995 996 996 996 996 996
166 335 499 658 811 959 103 242 376 505
26—1086
393
Продолжение табл. 11.7.13
Z Сотые доли для z >
0 । 1 2 3 4 5 6 7 /8 9
3,4 966 996 996 996 997 997 997 997 997 997
631 752 869 982 091 197 299 398 493 585
3,5 997 99ZJ > 997 997 997 998 998 998 998 998
674 759 842 992 999 074 146 215 282 347
3,6 998 998 998 998 998 998 998 998 998 998
409 469 527 583 637 689 739 787 834 879
.^3,7 998 998 999 999 999 999 999 999 999 999
922 964 004 043 080 116 150 184 216 247
3,8 999 999 999 999 999 999 999 999 999 999
274 305 333 359 385 409 433 456 478 499
3,9 999 999 999 999 999 999 999 999 999 999
519 539 557 575 593 609 625 641 655 670
4,0 999 999 999 999 999 999 999 999 999 999
683 696 709 721 733 744 755 765 775 784
4,1 999 999 999 999 999 999 999 999 999 999
793 802 811 819 826 834 841 848 854 861
4,2 999 999 999 999 999 999 999 999 999 999
867 872 878 883 888 893 898 902 907 911
4,3 999 999 999 999 999 999 999 999 999 999
915 918 922 925 929 932 935 938 841 943
4,4 0,^9 999 999 999 999 999 999 999 999 999
946 948 951 953 955 957 959 961 963 964
4,5 999 999 999 999 999 999 999 999 999 999
5,0 966 999 997 968 969 971 972 973 974 976 977 978
Примечание. В таблице заданы лишь три последних деся-
тичных знака из четырех; первый из них записан в графе „0“ данной
строки или выше данной. Если перед последними тремя десятичными
знаками стоит точка, то это означает, что первый десятичный знак
надо смотреть в графе „0“, следующей строки. Например, для
z=0,53 имеем ф0 (0,53) = 0,2019 (а не 0,1019).
Для значения 2,2^z<50 под основными четырьмя десятичными
знаками функции Фо (z) даются еще три десятичных знака. Например,
при z = 3,51 находим (3,51) = 0,4997, т. е. ф0 = 0,4997759
Пример. Требуется определить вероятность того, что нор-
мально распределенная нормированная величина z имеет значение в ин-
тервале от 0 до 3,28. Имеем Р (0<z<3,28), Фо (3,28) = 0,4994810.
394
X
0 0,001 |
0,00 1,0000 0,9990
0,01 0,9900 0,9891
0,02 0,9802 0,9792
0,03 0,9704 0,9695
0,04 0,9608 0,9598
0,05 0,9512 0,9502
0,06 0,9418 0,9408
0,07 0,9324 0,9315
0,08 0,9231 0,9222
0,09 0,9139 0,9130
0 0,01
0,1 0,9048 0,8958
0,2 0,8187 0,8106
0,3 0,7408 0,7334
0,4 0,6703 0,6637
ТАБЛИЦА П.7.14
Таблица значений функции е-*
0,002 0,003 0,004 0,005 0,006 0,007 0,008 0,003
0,9980 0,9970 0,9960 0,9950 0,9940 0,9930 0,9920 0,9910
0,9881 0,9871 0,9861 0,9851 0,9841 0,9831 0,9822 0,9812
0,9782 0,9773 0,9763 0,9753 0,9743 0,9734 0,9724 0,9714
0,9685 0,9675 0,9666 0,9656 0,9646 0,9637 0,9627 0,9618
0,9588 0,9579 0,9570 0,9560 0,9550 0,9541 0,9531 0,9522
0,9493 0,9484 0,9474 0,9465 0,9455 0,9446 0,9436 0,9427
0,9399 0,9389 0,9380 0,9371 0,9361 0,9352 0,9343 0,9333
0,9305 0,9226 0,9287 0,9277 0,9258 0,9259 0,9250 0,9240
0,9213 0,9204 0,9194 0,9185 0,9176 0,9167 0,9158 0,9148
0,9121 0,9112 0,9103 0,9094 0,9085 0,9076 0,9066 0,9057
0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,8869 0,8781 0,8694 0,8607 0,8521 0,8437 0,8353 0,8270
0,8025 0,7945 0,7866 0,7788 0,7711 0,7634 0,7558 0,7483
0,7261 0,7189 0,7118 0,7047 0,6977 0,6907 0,6839 0,6771
0,6570 0,6505 0,6440 0,6376 0,6313 0,6250 0,6188 0,6126
Продолжение табл. П.7.14
х
X 0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,5 0,6065 0,6005 0,5945 0,5886 0,5825 0,5769 0,5712 0,5655 0,5599 0,5543
0,6 0,5488 0,5434 0,5379 0,5326 0,5273 0,5220 0,5169 0,5117 0,5066 0,5016
0,7 0,4966 0,4916 0,4868 0,4819 0,4771 0,4724 0,4677 0,4630 0,4584 0,4538
0,8 0,4493 0,4449 0,4404 0,4360 0,4317 0,4274 0,4232 0,4190 0,4148 0,4107
0 0,01 0,02 0,03 0,04 0,05 0,06 0,07 0,08 0,09
0,9 0,4066 0,4025 0,3985 0,3946 0,3906 0,3867 0,3829 0,3791 0,3753 0,3716
1,0 0,3679 0,3642 0,3606 0,3570 0,3535 0,3499 0,3465 0,3430 0,3396 0,3362
1,1 0,3329 0,3296 0,3263 0,3230 0,3198 0,3166 0,3135 0,3104 0,3073 0,3042
1,2 0,3012 0,2982 0,2952 0,2923 0,2894 0,2865 0,2837 0,2808 0,2780 0,2753
1,3 0,2725 0,2698 0,2671 0,2645 0,2618 0,2592 0,2567 0,2541 0,2516 0,2491
1,4 0,2466 0,2441 0,2417 0,2393 0,2369 0,2346 0,2322 0,2299 0,2276 0,2254
1,5 0,2231 0,2209 0,2187 0,2165 0,2144 0,2122 0,2104 0,2080 0,2060 0,2039
1,6 0,2019 0,1999 0,1979 0,1959 0,1940 0,1920 0,1901 0,1882 0,1864 0,1845
1,7 0,1827 0,1809 0.-1791 0,1773 0,1755 0,1738 0,1720 0,1703 0,1686 0,1670
1,8 0,1653 0,1637 6,1'620 0,1604 0,1588 0,1572 0,1557 0,1541 0,1526 0,1511
1,9 0,1496 0,1481 0,1466 0,1451 0,1437 0,1423 0,1409 0,1395 0,1381 0,1367
2,0 0,1353 0,1340 0,1327 0,1313 0,1300 0,1287 0,1275 0,1262 0,1249 0,1237-
2,2 0,1108 0,1097 0,1086 0,1075 0,1065 0,1054 0,1044 0,1033 0,1023 0,1013
X X
° 0,01 0,02 0,03 0,04
2,3 0,1003 0,0993 0,0983 0,0973 0,0963
2,4 0,0907 0,0898 0,0889 0,0880 0,0872
2,5 0,0821 0,0813 0,0805 0,0797 0,0789
2,6 0,0743 0,0735 0,0728 0,0721 0,0714
2,7 0,0672 0,0665 0,0659 0,0652 0,0646
2,8 0,0608 0,0602 0,0596 0,0590 0,0584
2,9 0,0550 0,0545 0,0539 0,0534 0,0529
0 0,1 0,2 0,3 0,4
3 0.0498 0,0450 0,0408 0,0368 0,0334
4 0,0183 0,0166 0,0150 0,0136 0,0123
5 0,0067 0,0061 0,0055 0,0050 0,0045
6 0,0025 0,0022 0,0020 0,0018 0,0017
7 0,0009 0,0008 0,0007 О; 0007 0,0006
8 0,0003 0,0003 0,0002 0,0002 0,0002
Продолжение табл. П.7.14
0,05 0,05 0,07 0,08 о,оэ
0,0954 0,0944 0,0935 0,0926 0,0916
0,0863 0,0854 0,0846 0,0837 0,0829
0,0781 0,0773 0,0765 0,0758 0,0750
0,0707 0,0699 0,0693 0,0686 0,0679
0,0639 0,0633 0,0627 0,0620 0,0614
0,0578 0,0573 0,0567 0,0561 0,0556
0,0523 0,0518 0,0513 0,0508 0,0503
0,5 0,6 0,7 0,8 0,9
0,0302 0,0273 0,0247 0,0224 0,0200
0,0111 0,0101 0,0091 0,0082 0,0074
0,0041 0,0037 0,0033 0,0030 0,0027
0,0015 0,0014 0,0012 0,0011 0,0010
0,0006 0,0005 0,0005 0,0004 0,0004
0,0002 0,0002 0,0002 0,0002 0,0001
Степени некоторых
X рх
1 0,999 0,9975 0,995 0,99 0,98 0,97
2 0,99800 0,99461 0,99002 0,9801 0,9604 0,9409
3 0,99700 0,99192 0,98507 0,97030 0,94119 0,91267
4 0,99601 0,98924 0,98015 0,96060 0,92237 0,88529
5 0,99501 0,98657 0,97525 0,95099 0,90392 0,85873
6 0,99401 0,98391 0,97037 0,94148 0,88584 0,83297
7 0,99302 0,98125 0,96552 0,93207 0,86813 0,80798
8 0,99203 0,97860 0,96069 0,92274' 0,85076 0,78374
9 0,99104 0,97596 0,95589 0,91352 0,83375 0,76023
10 0,99004 0,97333 0,95111 0,90438 0,81707 0,73742
20 0,98019 0,94736 0,90461 0,81791 0,66761 0,54379
30 0,97043 0,92209 0,86038 0,73970 0,54548 0,40101
40 0,96077 0,89750 0,81832 0,66897 0,44570 0,29571
50 0,95121 0,87356 0,77831 0,60501 0,36417 0,21807
100 0,90479 0,76310 0,60577 0,36603 0,13262 0,04755
X рх
1 0,90 0,89 0,88 0,87 0,86 0,85
2 0,8100 0,7921 0,7744 0,7569 0,7396 0,7225
3 0,72900 0,70497 0,68147 0,65850 0,63606 0,61412
4 0,65610 0,62742 0,59970 0,57290 0,54701 0,52201
5 0,59049 0,55841 0,52773 0,49842 0,47043 0,44371
6 0,53144 0,44698 0,46440 0,43363 0,40457 0,37715
7 0,47830 0,44231 0,40868 0,37725 0,34793 0,32058
8 0,43047 0,39366 0,35963 0,32821 0,29922 0,27249
9 0,38742 0,35036 0,31648 0,28554 0,25733 0,23162
10 0,34868 0,31182 0,27850 0,24842 0,22130 0,19687
20 0,12158 0,09723 0,07756 0,06171 0,04897 0,03876
30 0,04239 0,03032 0,02160 0,01533 0,01084 0,00763
40 0,01478 0,00945 0,00602 0,00381 0,00240 0,00150
50 0,00515 0,00295 0,00168 0,00095 0,00053 0,00030
100 0,00003 0,00001 . . . . . . . . .
398
ТАБЛИЦА П.7. 1
десятичных дробей
X р X
1 0,96 0,95 0,94 0,93 0,92 0,91
2 0,9216 0,9025 0,8836 0,8649 0,8464 0,8281
3 0,88474 0,85738 0,830458 0,80436 0,77869 0,75357
4 0,84935 0,81451 0,78075 0,74805 0,71639 0,68575
5 0,81537 0,77378 0,73390 0,69569 0,65908 0,62403
6 0,78276 0,73509 0,68987 0,64699 0,60636 0,56787
7 0,75145 0,69834 0,64848 0,60170 0,55785 0,51676
8 0,72139 0,66342 0,60957 0,55958 0,51322 0,47025
9 0,69253 0,63025 0,57299 0,52041 0,47216 0,42793
10 0,66483 0,59874 0,53862 0,48398 0,43439 0,38942
20 0,44200 0,35849 0,29011 0,23424 0,18869 0,15164
30 0,29386 0,21464 0,15626 0,11337 0,08197 0,05905
40 0,19537 0,12851 0,08416 0,05487 0,03561 0,02300
50 0,12989 0,07694 0,04533 0,02656 0,01547 0,00896
100 0,01687 0,00592 0,00205 0,00071 0,00024 0,00008
Продолжение табл. П.7.15
X
1 0,84 0,83 0,82 0,81 0,80 0,79
2 0,7056 0,6889 0,6724 0,6561 0,6400 0,6241
3 0,59270 0,57178 0,55137 0,53144 0,51200 0,49304
4 0,49787 0,47458 0,45218 0,43047 0,40960 0,38950
5 0,41821 0,39390 0,37074 0,34868 0,32768 0,30771
6 0,35130 0,32694 0,30401 0,28243 0,26214 0,24309
7 0,29509 0,27136 0,24929 0,22877 0,20972 0,19204
8 0,24788 0,22523 0,20441 0,18530 0,16777 0,15171
9 0,20822 0,18694 0,16762 0,15009 0,13422 0,11985
10 0,17490 0,15516 0,13745 0,12158 0,10737 0,09468
20 0,03059 0,02407 0,01889 0,01478 0,01153 0,00896
30 0,00535 0,00374 0,00260 0,00180 0,00124 0,00085
40 0,00094 0,00058 0,00036 0,00022 0,00013 0,00008
50 0,00016 0,00009 0,00005 0,00003 0,00001 0,00001
100 . . . . . . • . .
399
X рх
1 0,78 0,77 0,76 0,75 0,74 0,73
2 0,6084 0,5929 0,5776 0,5625 0,5476 0,5329
3 0,47455 0,45653 0,43898 0,42188 0,40522 0,38902
4 0,37015 0,35153 0,33362 0,31641 0,29987 0,28398
5 0,28872 0,27068 0,25355 0,23730 0,22190 0,20731
6 0,22520 0,20842 0,19270 0,17798 0,16421 0,15133
7 0,17566 0,16049 0,14645 0,13348 0,12151 0,11047
8 ' 0,13701 0,12357 0,11130 0,16011 0,08992 0,08065
9 0,10687 0,9515 0,08459 0,07508 0,06654 0,05887
10 0,08336 0,07326 0,06249 0,05631 0,04924 0,04298
20 0,00695 0,00537 0,00390 0,00317 0,00242 0,00185
30 0,00058 0,00039 0,00024 0,00018 0,00012 0,00008
40 1 0,00005 0,00003 0,00002 0,00001 0,00001
50 . . .
X
1 0,66 0,65 0,64 0,63 0,62 0,61
2 0,4356 0,4225 0,4096 0,3969 0,3844 0,3721
3 0,28750 0,27462 0,26214 0,25005 0,23833 0,22698
4 0,18975 0,17851 0,16777 0,15753 0,14776 0,13846
5 0,12523 0,11603 0,10737 0,09924 0,09161 0,08446
6 0,08265 0,07542 0,06872 0,06252 0,05580 0,05152
7 0,05455 0,04902 0,04398 0,03939 0,03522 0,03143
. 8 0,03600 0,03186 0,02815 0,02482 0,02183 0,01917
9 0,02376 0,02071 0,01801 0,01563 0,01354 0,01169
10 0,01568 0,01346 0,01153 0,00985 0,00839 0,00713
20 30 0,00025 0,00018 0,00013 0,00010 0,00007 0,00005
Продолжение табл. П.7.15
X Рх
1 0,54 0,53 0,52 0,51 0,50
2 ; 0,2916 0,2809 0,2704 0,2601 0,2500
3 0,15746 0,14888 0,14061 0,13265 0,12500
4 0,08503 0,07890 0,07312 0,06765 0,06250
5 0,04592 0,04182 0,03802 0,03450 0,03125
6 0,02479 0,02216 0,01977 0,01760 0,01562
7 0,01339 0,01175 0,01028 0,00897 0,00781
8 0,00723 0,00623 0,00535 0,00458 0,00391
9 0,00390 0,00330 0,00278 0,00233 0,00195
10 0,00211 . 0,00175 0,00145 0,00119 0,00098
20 . . .
Примечание. Многоточие указывает на то, что значение рх
меньше 0,00005.
400
Продолжение табл. П.7.15
X Рх
1 0,72 0,71 0,70 0,69 0,68 0,67
2 0,5184 0,5041 0,4900 0,4761 0,4624 0,4489
3 0,37325 0,35791 0,34300 0,32851 0,31443 0,30076
4 0,26874 0,25412 0,24010 0,22667 0,21381 0,20151
5 0,19349 0,18042 0,16807 0,15640 0,14539 0,13501
6 0,13931 0,12810 0,11765 0,10792 0,09887 0,09406
7 0,10031 0,09095 0,08235 0,07446 0,06723 0,06061
8 0,07222 0,06458 0,05765 0,05138 0,04572 0,04061
9 0,05200 0,04585 0,04035 0,03545 0,03109 0,02721
10 0,03744 0,03255 0,02825 0,02446 0,02114 0,01823
20 0,00140 0,00106 0,00080 0,00060 0,00045 0,00033
30 0,00005 0,00003 0,00002 0,00001 0,00001 0,00001
40 ... ...
50 . . . . . . . . . . . .
Продолжение табл. П.7.15
X Рх
1 0,60 0,59 0,58 0,57 0,56 ' 0,55
2 0,3600 0,3481 0,3364 0,3249 0,3136 0,3025
3 0,21600 0,20538 0,19511 0,18519 0,17562 0,16638
4 0,12960 0,12117 0,11316 0,10556 0,09834 0,09151
5 0,07776 0,071449 0,06564 0,06017 0,05507 0,05033
6 0,04666 0,04218 0,03807 0,03430 0,03084 0,02768
7 0,02799 0,02489 0,02208 0,01955 0,01727 0,01522
8 0,01680 0,01468 0,01281 0,01114 0,00967 0,00837
9 0,01008 0,00866 0,00743 0,00635 0,00542 0,00461
10 0,00605 0,00511 0,00431 0,00362 0,00303 0,00253
20 0,00004 0,00003 0,00002 0,00001 0,00001 0,00001
30 . . . . . .
ТАБЛИЦА П.7.16
Значения функции FB (х)
X 0 I 2 3 4 5 6 7 8 9
0,0. 0, 5 000 5 040 5 080 5 120 5 160 5 199 5 239 5 279 5 319 5 359
0.1 0, 5 398 5 438 5478 5 517 5 557 5 596 6 536 5675 5 714 5 753
0,2 0, 5 793 5 832 5 871 5 910 5 948 5 987 6 026 6 064 6 103 6 141
0,3 0, 6 179 6 217 6 255 6 293 6 331 . 6 368 6 406 6 443 6 480 6 517
0,4 0, 6 55! 6 594 6 628 6 664 6 700 6 736 6 772 6 808 6 844 6 879
0,5 0. 6 915 6 950 6 985 7 019 7 054 7 088 7 123 7 157 7 190 7 224
0,6 о» 7 257 7 291 7 324 7 357 7 389 7 422 7 454 7 486 7 517 .7 549
0,7 о, 7 581 7 611 7 642 7 673 7 704 7 734 7 764 7 794 7 823 7 852
0^8 о. 7 881 7 910 7 939 7 967 7 995 8 023 8 051 8 078 8 106 8 133
0,9 о, 8 159 8 186 8 238 8 212 8 264 8 389 8 315 8 340 8 365 8 389
1,0 о, 8 413 8 438 8 461 8 485 8 508 8 531 8 554 8 577 8 599 8 621
1.1 0, 8 643 8 665 8 686 8 708 8 729 8 749 8 770 8 793 8 810 8 830
1.2 0, 8 849 8 869 8 888 8 907 8 925 8 944 8 9Ё2 8 980 8 997 9 015
1,3 0.9 0 320 0 490 0 658 0 824 0 988 1 149 I 308 1 466 1 621 1 774
1.4 0,9 1 924 2 073 2 220 2 364 2 507 2 647 2 785 2 922 3 056 3 189
1,5 0,9 3 319 3 448 3 574 3 699 3 822 3 943 4 062 4 179 4 295 4 408
1.6 0,9 4 52Э 4 630 4 738 4 855 Ч95Э 5 053 5 154 5 254 5 352 5 449
1.7 0,9 5 543 5 637 5 728 5 818 5 907 5 994 6 080 6 164 6 246 6 327
1,8 0,9 6 407 6 485 6 562 6 637 6 712 6 784 6 856 6 926 6 995 7 062
1.9 0,9 7 128 7 193 7 257 7 320 7 381 7 441 7 500 7 588 7 615 7 670
2,0 0.9 7 725 7 778 7 831 7 882 7 932 7 982 8 030 8 077 8 124 8 169
2.1 0,9 8 214 8 257 8 300 8 341 8 382 8 422 8 461 8 500 8 537 8 574
2-2 0,9 8610 8 645 8 679 8 713 8 745 8 778 8 809 8 840 8 870 8 899
2.3 0,9 8 928 8 953 8 983 9010 9 036 9 051 9 086 9 111 9 134 9 158
2’4 0,99 1 802 2 024 2 240 2 451 2 656 2 857 3 053 3 244 3 431 3 613
2.5 0,99 3 790 3 963 4 132 4 297 4 457 4 614 4 766 4 915 5 Обо 5 201
2>6 0,99 5 339 5 473 5603 5 731 5 855 5 975 6 093 6 2Э7 6 31g 6 427
2’7 0,99 6 533 6 636 6 736 6 833 6 928 7 020 7 110 7 197 7 282 7 365
2-8 0,99 7 445 7 523 7 599 7 673 7 7*'4 7 814 7 882 7 948 8 012 8 074
2’9 0.99 8 134 8 193 8 250 8 305 8 359 8 4П 8 462 8 511 8 55g 8 605
3’0 0,99 8 650 8 694 8 736 8 777 8 817 8 856 8 893 8 930 8 965 8 999
3’1 0,9з 0 324 0 646 0(57 1 260 1 553 1 836 2 112 2 378 2 636 2 886
3>2 0,9з 3 129 3 363 3 590 3 810 4 022 4 230 4 42?! 4 623 4 810 4 991
3’3 0,9з 5 166 5 335 5 499 5 658 5811 5 959 6 103 6 242 6 376 6 505
3’4 0.9з 6 631 6 752 6 869 6 982 7 091 7 197 7 299 7 398 7 493 7 585
3.5 0,93 7 674 7 760 7 842 7 922 7 999 8 074 8146 8 215 8 282 8 347
3.6 0,93 8 409 8 469 8 527 8 583 8 637 8 689 8 739 8 787 8 834 8 879
3.7 0,9з 8 922 8 964 9 004 9 043 9 080 9 116 9 150 9 184 9 216 9 247
3.8 0,£4 2 765 3 052 3 327 3 593 3 848 4 094 4 331 4 558 4 777 4 988
3.9 0,9» 5 ISO 5385 5 573 5 753 5 926 6 092 6 252 6 406 6 554 6 696
4.0 0,9“ 6 833 6 964 7 090 7211 7 327 7 439 7 546 7 649 7 748 7 843
4,1 0,9» 7 934 8(22 8 106 8 186 8 264 8 338 8 409 8 477 8 542 8 606
4,2 0,94 8 665 8 723 8 778 8 832 8 882 8 931 8 978 9 023 9 066 9 107
4,3 0,95 1 460 1 837 2 198 2 544 2 876 3 193 3 497 3 788 4 066 4 332
4,4 0,95 4 588 4 832 5 065 5 288 5 502 5 706 5 902 6 089 6 268 6 439
4,5 0,95 6 602 6 759 6 908 7 051 7 187 7 318 7 44'2 7 561 7 675 7 784
4,6 0,95 7 888 7 987 8 081 8 172 8 258 8 340 8 419 8 494 8 566 8 634
4,7 0,9& 8 699 8 761 8 821 8 877 8 931 8 9831 9 032 9 079 9 124 9 166
4,8 0,9е 2 067 2 454 2 8(2 3 173 3 508 3 827 4 131 4 420 4 696 4 958
4,9 0,9е 5 238 5 446 5 673 5 888 6 094 6 289 6 475 6 652. 6 821 6 981
5,0 0,9е 7 134 7 278 7 416 7 548 7 672 7 791 7 904 8 011 8 ИЗ 82>0
5,1 0,9е 8 302 8 389 8 472 8 551 8 626 8 698 8 765 8 830 8 891 8 949
5,2 0,97 004 056 105 152 197 240 280 318 354 388
5,3 0,97 421 452 481 509 539 560 584 606 628 648
5.4 0,97 667 685 702 718 734 748 762j 775 787 799
5,5 0,97 810 821 831 840 849 857 865 873 880 886
5,6 0,97 893 899 906 910 915 920 924 929 933 936
5,7 0,98 40 44 47 50 53 55 58 60 63 65
5,8 0,9s 67 69 71 72 74 75 77 78 79 81
5,9 0,9е 82 83 84 85 86 87 87 88 89 90
6,0 0,98 90 — — — —
40?
ТАБЛИЦА П.7.17
1
Значения функции <f (х)=
-ла/2
Г2^е
X 0 1 2 3 4 5 6 7 8 9
0,0 0, 3 989 3 989 3 989 3 988 3 986 3 984 3 982 3 980 3 977 3 973
0,1 0, 3 970 3 965 3 961 3 956 3 951 3 945 3 939 3 932 3 925 3918
0,2 0, 3 910 3 902 3 894 3 885 3 876 3 867 3 857 3 847 3 836 3 825
0,3 0, 3 814 3 802 3 790 3 778 3 765 3 752 3 739 3 725 3 712 3 697
0,4 0, 3 683 3 668 3 653 3 637 3 621 3 605 3 589 3 572 3 555 3 538
0,5 0, 3 521 3 503 3 485 3 467 3 448 3 429 3 410 3 391 3 372 3 352
0,6 0, 3 332 3 312 3 292 3 271 3 251 3 230 3209 3 187 3 166 3 144
0,7 0, 3 123 3 101 3 079 3 056 3 034 3 011 2 989 2 966 2 943 2 920
0,8 0, 2 897 2 874 2 853 2 827 2 803 2 780 2 756 2 732 2 709 2 685
0,9 0, 2 661 2 63/ 2 613 2 589 2 555 2 541 2 516 2 492 2 468 2 444
1,0 о, 2 420 2 396 2 371 2 347 2 323 2 299 2 275 2 251 2 227 2 203
и о. 2 179 2 155 2 131 2 107 3 083 2 059 2 036 2012 1 989 1 965
1,2 0, 1 942 1 919 1 895 1 872 1 849 1 825 1 804 1 781 1 758 1 736
1.3 о, 1 714 1 691 1 669 1 647 1 626 1 634 1 582 1 551 1 539 1 518
1.4 о. 1 497 1 476 1 456 1 435 1 415 1 394 1 374 1 354 1 334 1 315
1.5 о, 1 295 1 276 1 257 1 238 1 219 1 200 1 182 1 163 I 145 1 127
1.6 0, 1 109 1 092 1 074 1 057 1 040 1 023 1 006 0 989 0 973 0 957
1.7 0,0 9 405 9 246 '9 089 8 933 8 780 8 628 8 478 8 329 8 183 8 038
1,8 0,0 7 895 7 754 7 614 7 477 7 341 7 206 7 074 6 943 6 814 6 687
1,9 0,0 6 562 6 438 6 316 6 195 6 077 5 959 5 844 5730 5 618 5 508
2,0 0,0 5 399 5 292 5 186 5 082 4 980 4 879 4 780 4 682 4 586 4 491
2.1 0,0 4 398 4 30/ 4 217 4 128 4 041 3 955 3 871 3 788 3 706 3 626
2,2 0,0 3 547 3 470 3 394 3 319 3 246 3 174 3 103 3 034 2 965 2 898
2,3 0,0 2 833 2 768 2 705 2 643 2 582 2 522 2 463 2 406 2 349 2294
2,4 0.0 2 239 2 186 2 134 2 083 2 033 1 984 1 936 1 888 1 842 1 797
2,5 0,0 1 753 1 709 1 667 1 625 1 585 1545 1 506 1 468 1 431 1 394
2,6 0,0 1 358 1 324 1 289 1 256 1 223 1 191 1 160 1 130 I 100 1 071
2,7 0/,0 1 042 1 014 0 987 0 961 0 935 0 909 0 885 0 861 0 837 0 814
2,8 0,00 7 915 7 696 7 483 7 274 7 071 6 873 6 679 6 491 6 307 6 127
2,9 о, ио 5 952 5 782 5 616 5 454 5 296 5 143 4 993 4 847 4 705 4 567
3,0 0,00 4 432 4 301 4 173 4 049 3 928 3 810 3 695 3 584 3 475 3 370
3, 0,00 4 432 3 267 2 384 1 723 1 232 0 873 0 612 0 425 0 292 0199
4, 0,03 1 338 0 893 0 589 0 385 0 249 0 160 0101 0 064 0 040 0 024
5, 0,0° 1 487 0 897 0 536 0317 0 186 0 108 0 062 0 035 0 020 ООН
ТАБЛИЦ'А П.7.18
Значения гамма-функции
X Г(х) ч-Л X Г Г(х) X ГЦ) X Г(х)
1,00 1 1,00000 1,25 0,90640 1,50 0,88623 1,75 0,91906
1 о 0,99433 6 0,90440 1 0,88659 6 0,92137
Z о 0,98884 7 0,90250 2 0,88704 7 0,92376
о л 0,98355 8 0,90072 3 0,88757 8 0,92623
4 0,97844 9 0,89904 4 0,88818 9 0 92877
1, иь 0,97350 1,30 0,89747 1,55 0,88887 1,80 0,93138
b 0,96874 1 0,89600 6 0,88964 1 0,93408
о 0,96415 2 0,89464 7 0,89049 2 0,93685
о п 0,95973 3 0,89338 8 0,89142 3 0,93369
У 0,95546 4 0,89222 9 0,89243 4 0,94261
403
Продолжение табл. П.7.18
X г (X) X Г(Л) X X г (Л)
1,10 0,95135 1,35 0,89115 1,60 0,89352 1,85 0,94561
1 0,94740 6 0,89018 1 0,89468 6 0,94869
2 0,94359 7 0,88931 2 0,89592 7 0,95184
3 0,93993 8 0,88854 3 0,89724 8 0,95507
4 0,93642 9 0,88785 4 0,89864 9 0,95838
1,15 0,93304 1,40 0,88726 1,65 0,90012 1,90 0,96177
6 0,92980 1 0,88676 6 0,90167 1 0,96523
7 0,92670 2 0,88636 7 0,90330 2 0,96877
8 0,92373 3 0,88604 8 0,90500 3 0,97240
9 0,02089 4 0,88581 9 0,90678 4 0,97610
1,20 0,91817 1,45 0,88566 1,70 0,90864 1,95 0,97988
1 0,91558 6 0,88560 1 0,91057 6 0,98374
2 0,91311 7 0,88563 2 0,91258 7 0,98768
3 0,91075 8 0,88575 3 0,91467 8 0,99171
4 0,90852 9 0,88595 4 0,91683 9 2,00 0,99581 1,00000
ОГЛАВЛЕНИЕ
Предисловие................................. . 3
А Глава первая
' Количественные характеристики надежности 6
§ 1.1. Критерии и количественные характеристики надежности
§ 1.2. Типовые примеры и их решения ....... 20
§ 1.3. Задачи...........................................43
Глава вторая
Расчет характеристик надежности невосстанавливаемых
изделий при основном соединении элементов
§2.1. Методы расчета.......................... . . 60
§ 2.2. Типовые примеры .................................70
§ 2.3. Задачи......................................... 81
( Главатретья
Расчет характеристик надежности невосстанавливаемых
резервированных изделий
§3.1. Методы расчета..................................100
§ 3.2. Типовые примеры ............................ . 109
§ 3.3. Задачи......................................... 136
Глава четвертая
Расчет надежности восстанавливаемых изделий
§ 4.1. Методы расчета . .........................158
§ 4.2. Типовые примеры .........................186
§ 4.3. Задачи........................................ 204
___ Главапятая
Оценка и контроль надежности технических устройств
по результатам их испытаний
§ 5.1. Основные положения выборочных испытаний .... 226
§ 5.2. Типовые примеры и их решение....................256
§ 5.3. Задачи..........................................299
Литература.............................................324
Приложение 1. Номограмма для расчета надежности . 326
Приложение 2. Интенсивности отказов и условные дол-
говечности изделий [12, 9]...................... 328
Таблица П.2.1. Интенсивность отказов...................328
Таблица П.2.2. Условная долговечность..................336
Приложение 3. Интенсивности отказов элементов элек-
тронной апапартуры и поправочные коэффициенты [11] 339
405
Таблица П.3.1. Номинальная интенсивность отказов резисторов
при Т°= +20 °C и Кн=1................................339
Таблица П.3.2. Поправочные коэффициенты tai=f(Ks, Т°) для
определения Хэ резисторов............................340
Таблица П.3.3. Номинальные интенсивности отказов конденса-
торов при Т°= +20° С и /<н 4.........................341
Таблица П.3.4. Поправочные коэффициенты !«2=!7(Л'и, Т°) для
определения конденсаторов .......................... 341
Таблица П.3.5. Номинальные интенсивности отказов полупро-
водниковых приборов при 7’°=+20сС и Кп=1 . . . 343
Таблица П.3.6. Поправочные коэффициенты аз=/(Кп, Т°) для
определения полупроводниковых приборов . . . 344
Таблица П.3.7. Номинальная интенсивность отказов трансфор-
маторов и моточных изделий (дроссели, катушки, ин-
дуктивности и др.) при Т°=+20°С и Кн=1 . . . 345
Таблица П.3.8. Номинальные интенсивности отказов электри-
ческих машин и машинных электроэлементов при Т°=
= +20°C и Кн=1.......................................345
Таблица П.3.9. Поправочные коэффициенты щ=/(/<н, Т°) для
определения Ла моточных изделий, трансформаторов и
обмоток электрических машин..........................346
Таблица П.3.10. Поправочные коэффициенты (дополнительная
интенсивность отказов) ДХ электрических машин в за-
висимости от скорости вращения.......................346
Приложение 4. Графики поправочных коэффициентов о; =
=/(/°С, Кв) [10].....................................348
Приложение 5. Формы таблиц для определения интенсив-
ностей отказов.......................................364
Таблица П.5.1. Определение интенсивности отказов при ориен-
тировочном расчете надежности..........................364
Таблица П.5.2. Определение интенсивности отказов при окон-
чательном расчете надежности с использованием графи-
ков Хг=НКн, ГС)......................................364
Таблица П.5.3. Определение интенсивности отказов при окон-
чательном расчете надежности с использованием гра-
фиков ai=f(Kn, ГС) . . . ..........365
ПР иложение 6. Координатные сетки..........................366
Приложение 7. Математические таблицы.......................368
Таблица П.7.1. Квантили распределения хи-квадрат . . . 368
Таблица П.7.2. Значения коэффициента ц.....................370
Таблица П.7.3 Значения коэффициента Ri при а = 0,95 . . 370
Таблица П.7.4. Значения коэффициента г3 .... 371
Таблица П.7.5. Квантили распределения Стыодента . . 371
Таблица П.7.6. Квантили нормального распределения Ui~P =
=—иР . . : : 372
Таблица П.7.7 Вспомогательные функции 373
Таблица П.7.8. Значения коэффициента го....................374
Таблица П.7.9 Суммарные значения функции Пуассона
со
SM”1 ,-М
ml .......................
m
406
Таблица П.7.10. Таблица числа комбинаций из N элементов
... f N \
по п (биномиальные коэффициенты I ) = I N____ 1=
N\
~n\(N — n)\.......................................... 380
Таблица П.7..11. Вероятность d или меньшего количества де-
фектных изделий для биномиальных распределений . . 385
Таблица П.7.12. Значения a=nq для заданных вероятностей
распределения Пуассона................................392
Таблица П.7.13. Нормированная функция Лапласа
2 2а
1 О ~~2 ,
фо<2) = ' Iе dz...................................... 392
У 2л J
О
Таблица П.7.14. Таблица значений функции е~х . . •. 395
Таблица П.7.15. Степени некоторых десятичных дробей . . 398
Таблица П.7.16. Значения функции Ро(х)...................402
Таблица П.7.17. Значения функции <р(х) = ' ' е~. 403
Таблица П.7.18. Значения гамма-функции...................403
СБОРНИК ЗАДАЧ ПО ТЕОРИИ НАДЕЖНОСТИ
Под редакцией
А. М. Половко и И. М. Маликова
Редакторы А. А. Александрова, Э. М. Горелик
Художественный редактор 3. Е. Вен дрова
Технический редактор Г. 3. Кузнецова
Корректоры: Н. М. Давыдова, Н. М. Кухтяева
Сдано в набор П/1 1972 г. Подписано в печать 15/IV 1972 г. Т-05162
Формат 84X108/8а Бумага типографская машииомелованная
Объем 21,42 усл. п. л. Уч.-изд. л. 22,744
Тираж 25 000 экз. ' Зак. 1086 Цена 1 р. 44 к.
Издательство .Советское радио", Москва , Главпочтамт, п/я 693,
Московская типография № 10 Главполиграфпрома
Комитета по печати при Совете Министров СССР,
Москва, Шлюзовая наб., 10.