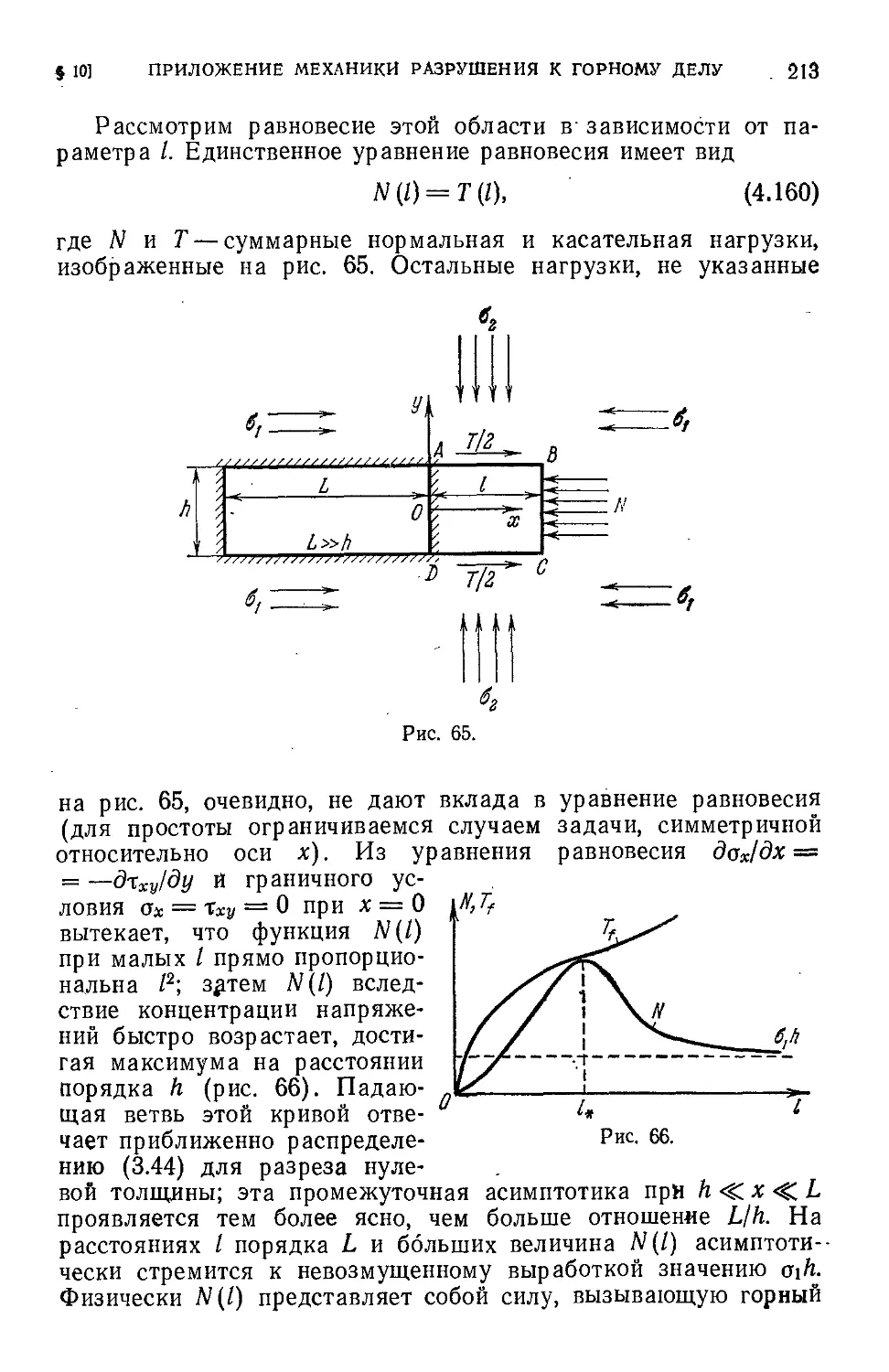
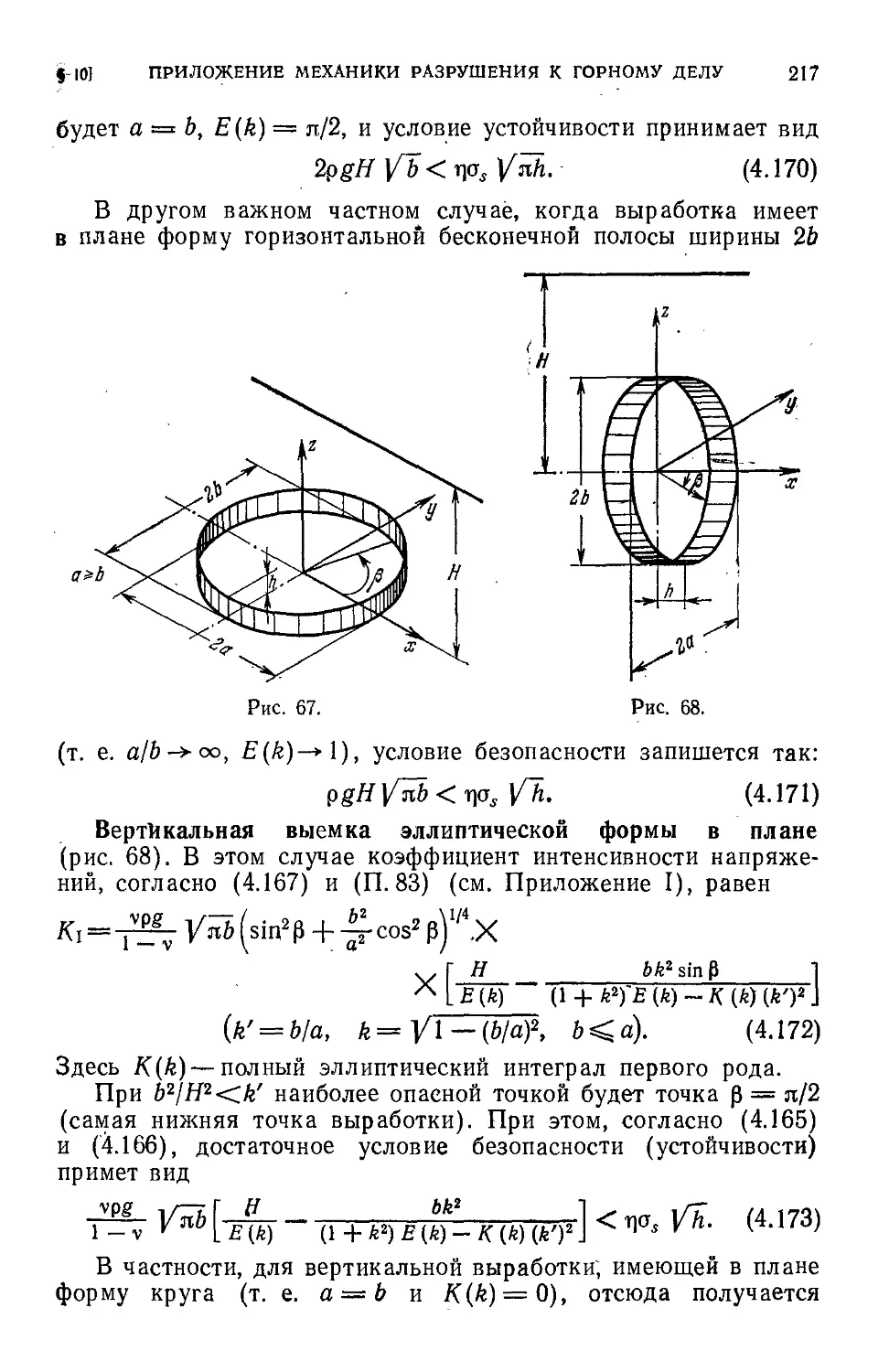
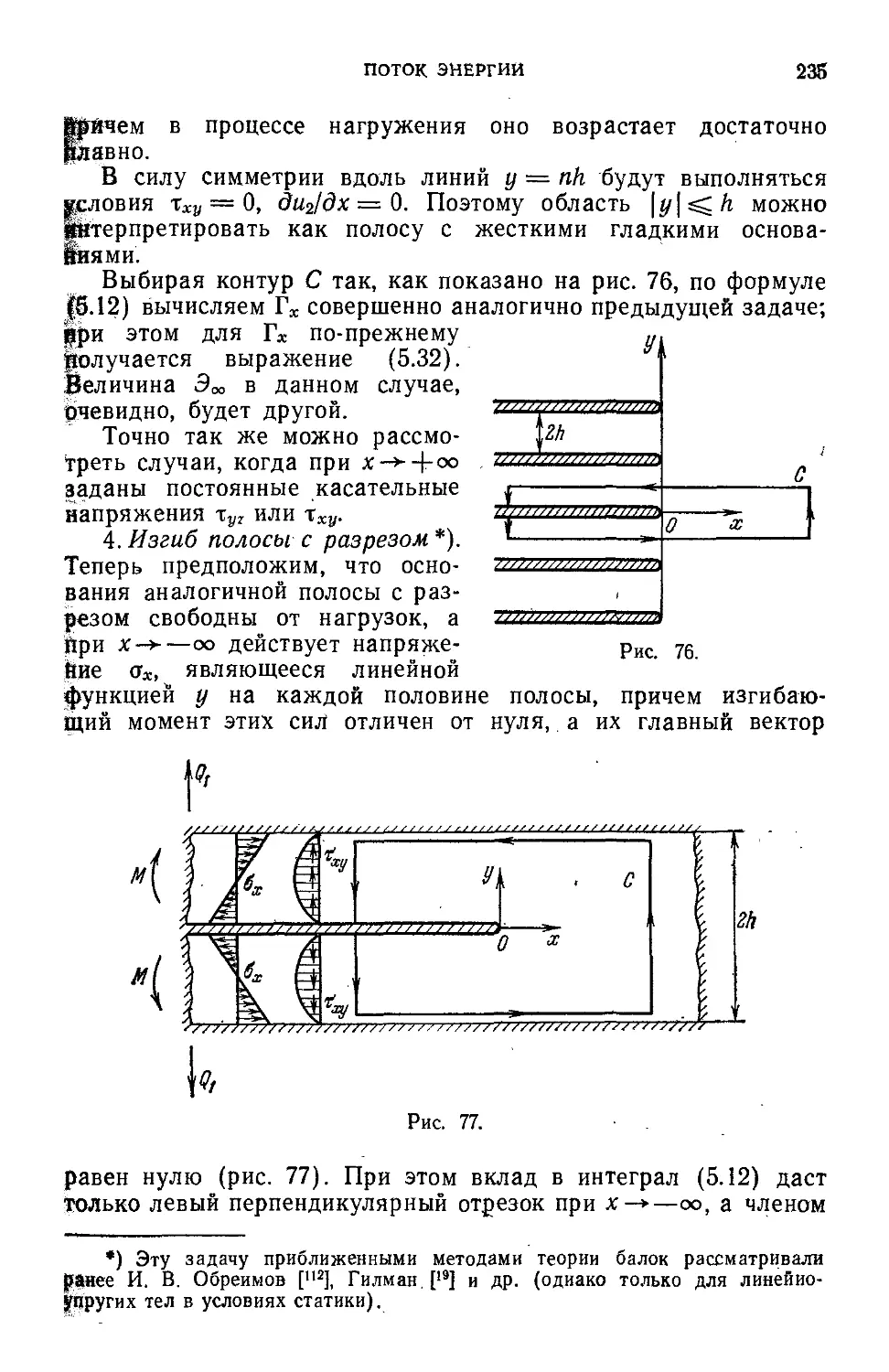
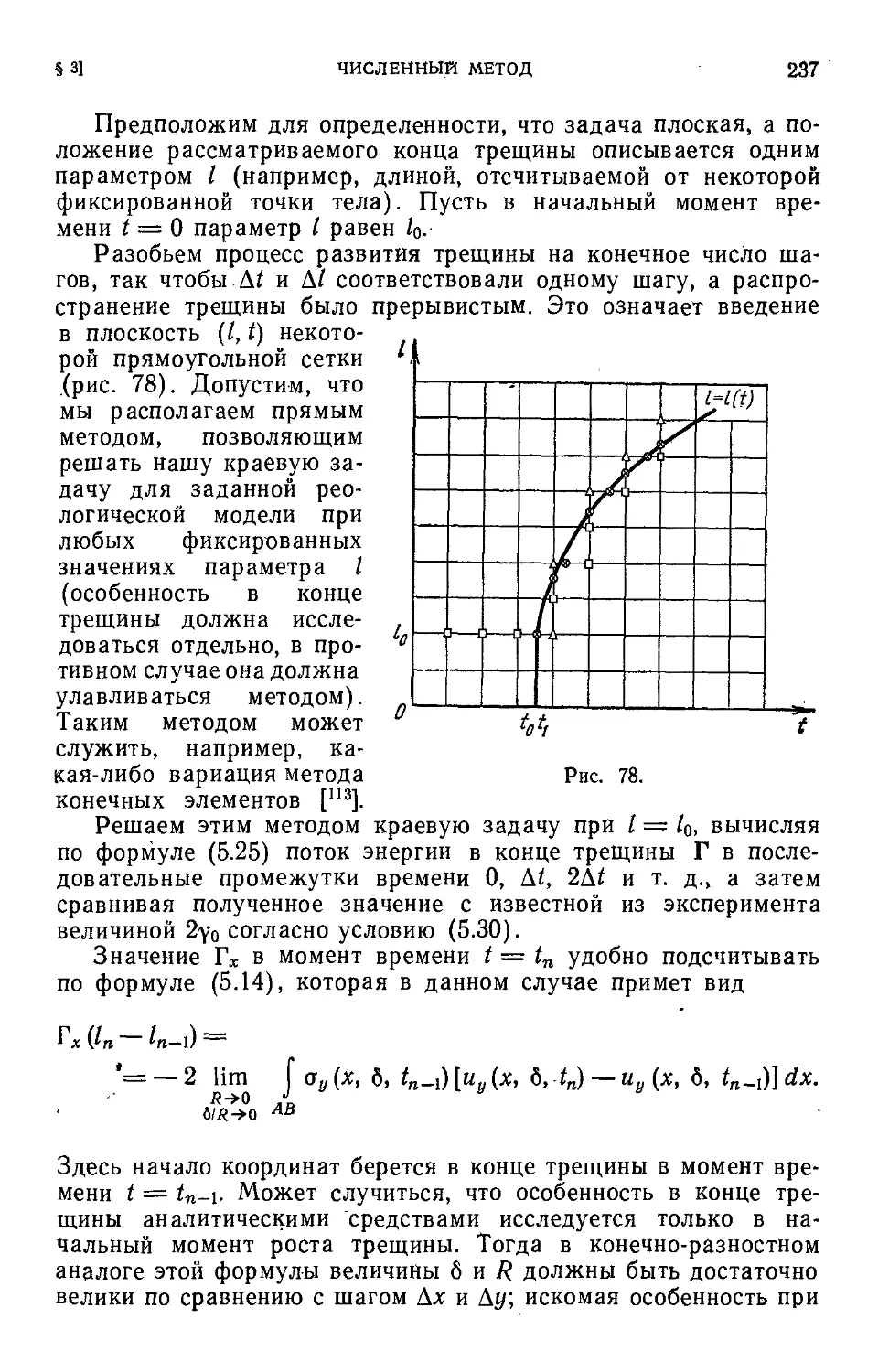
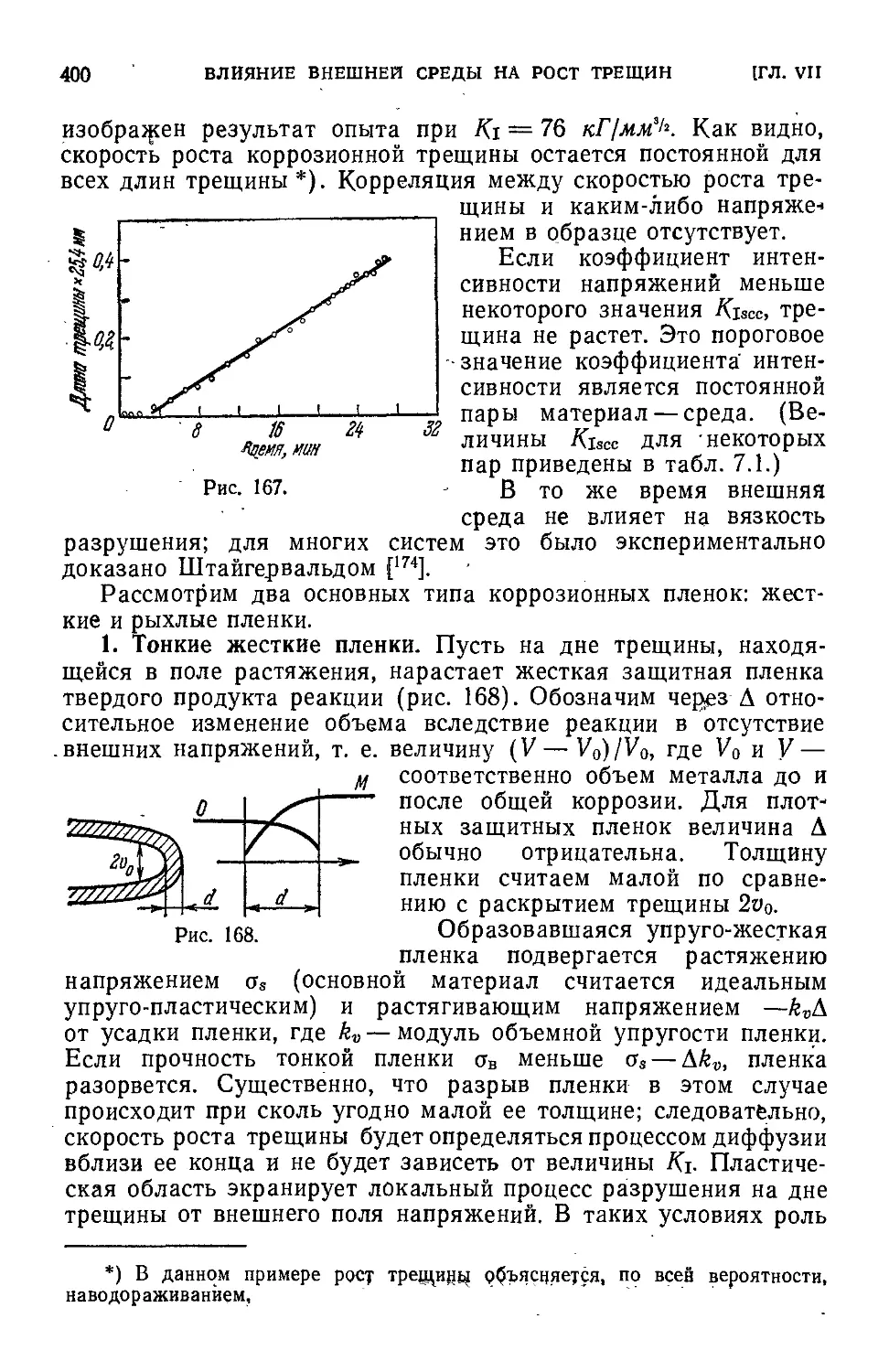
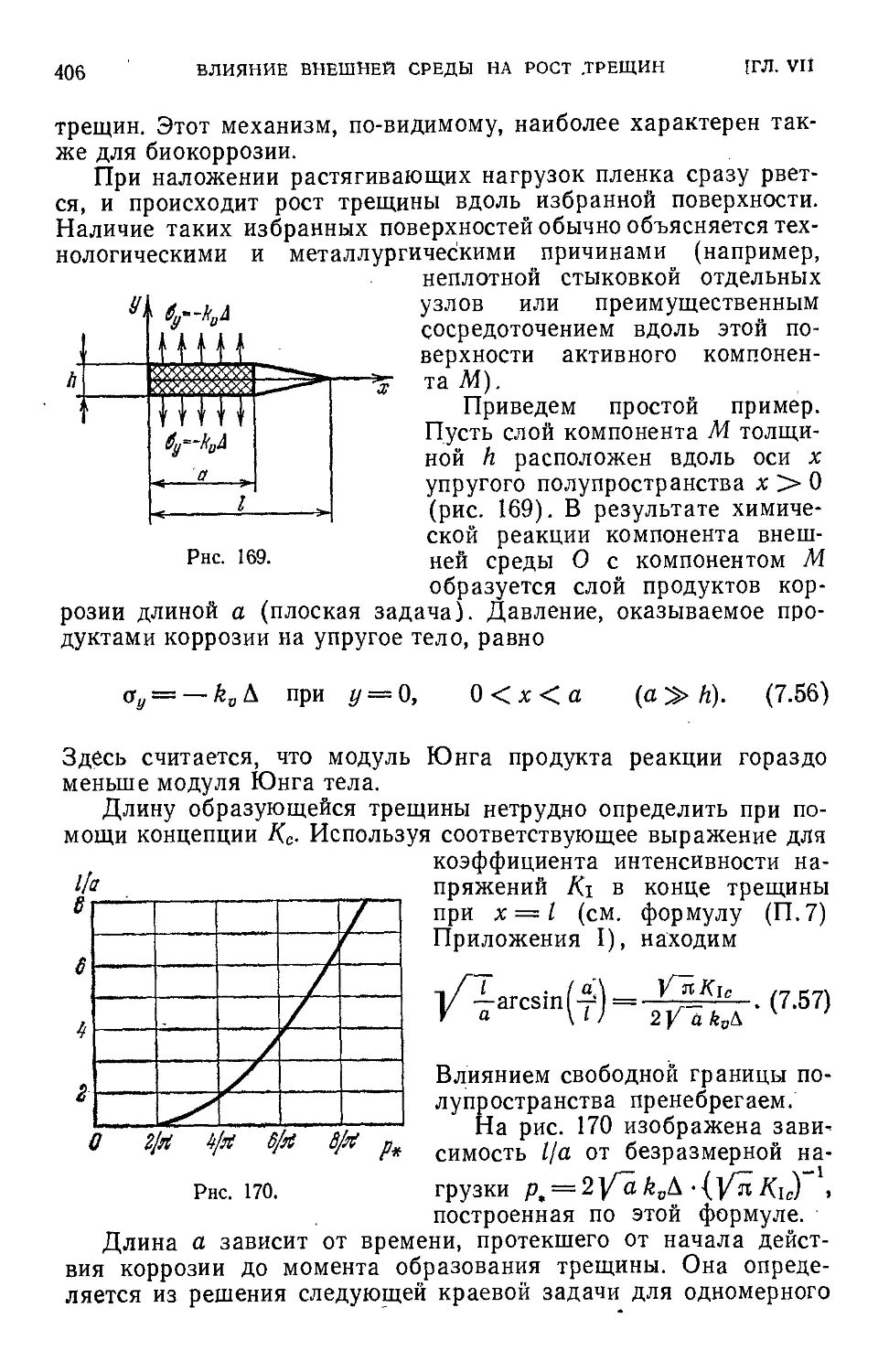
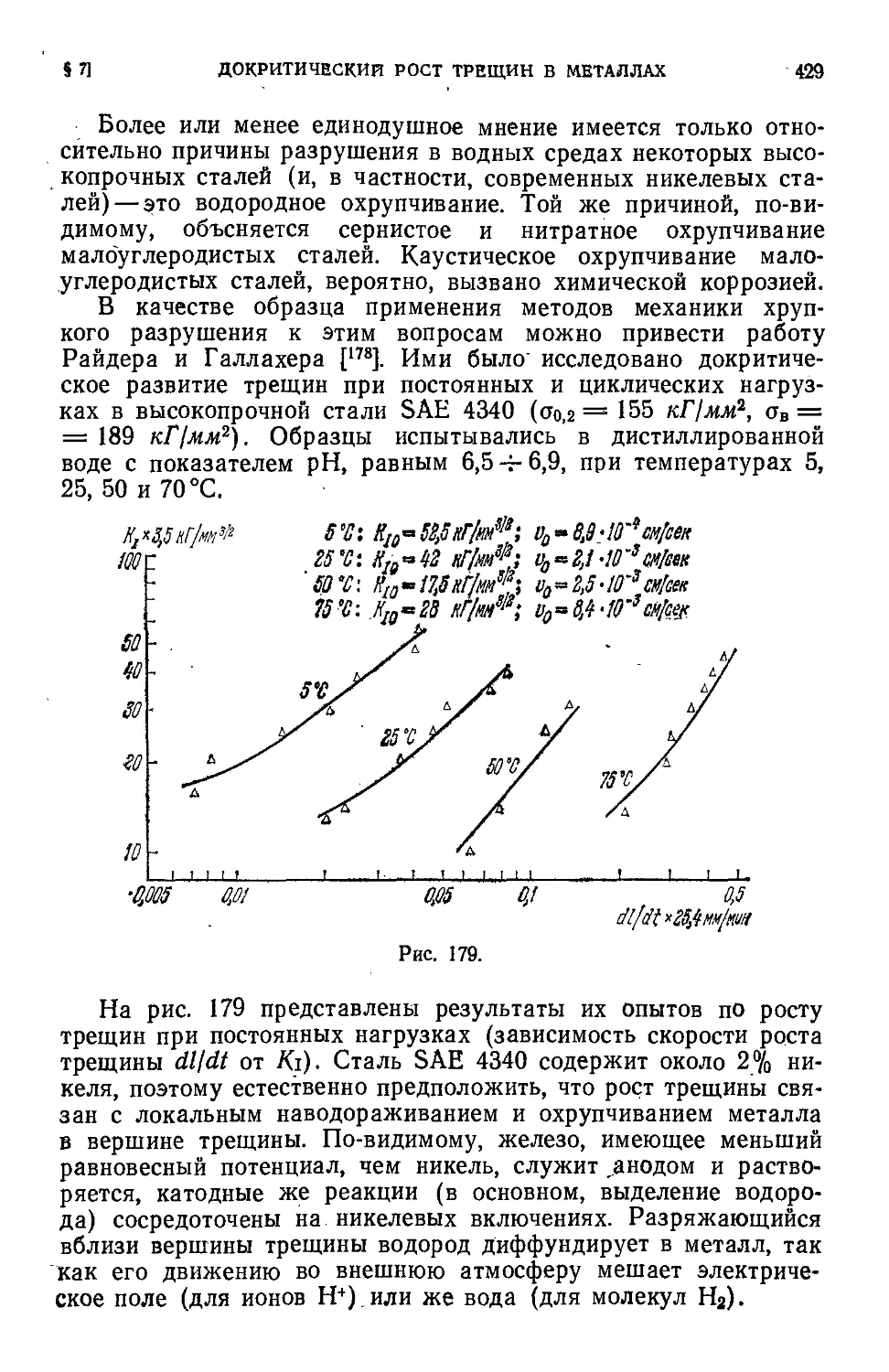
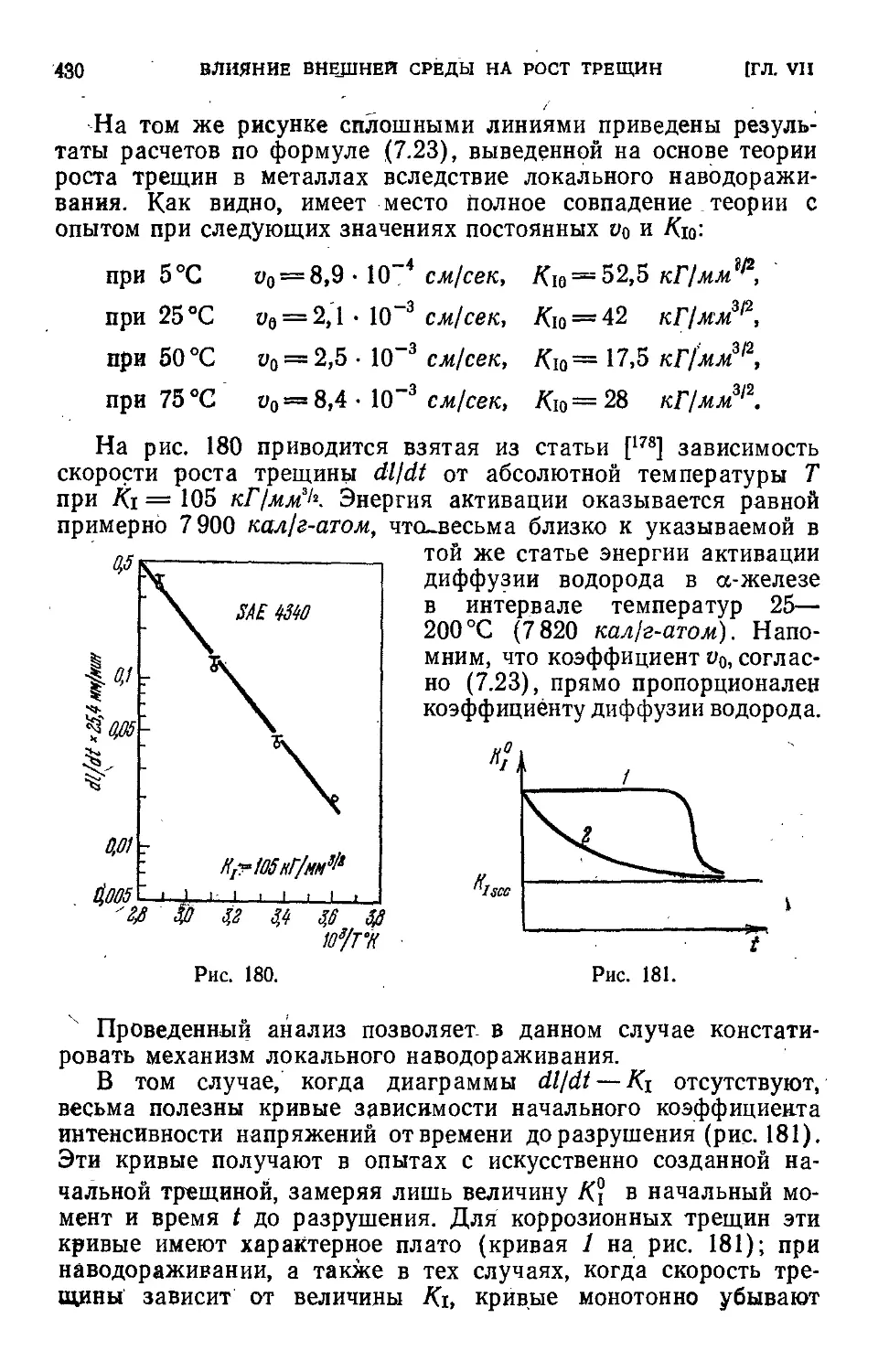
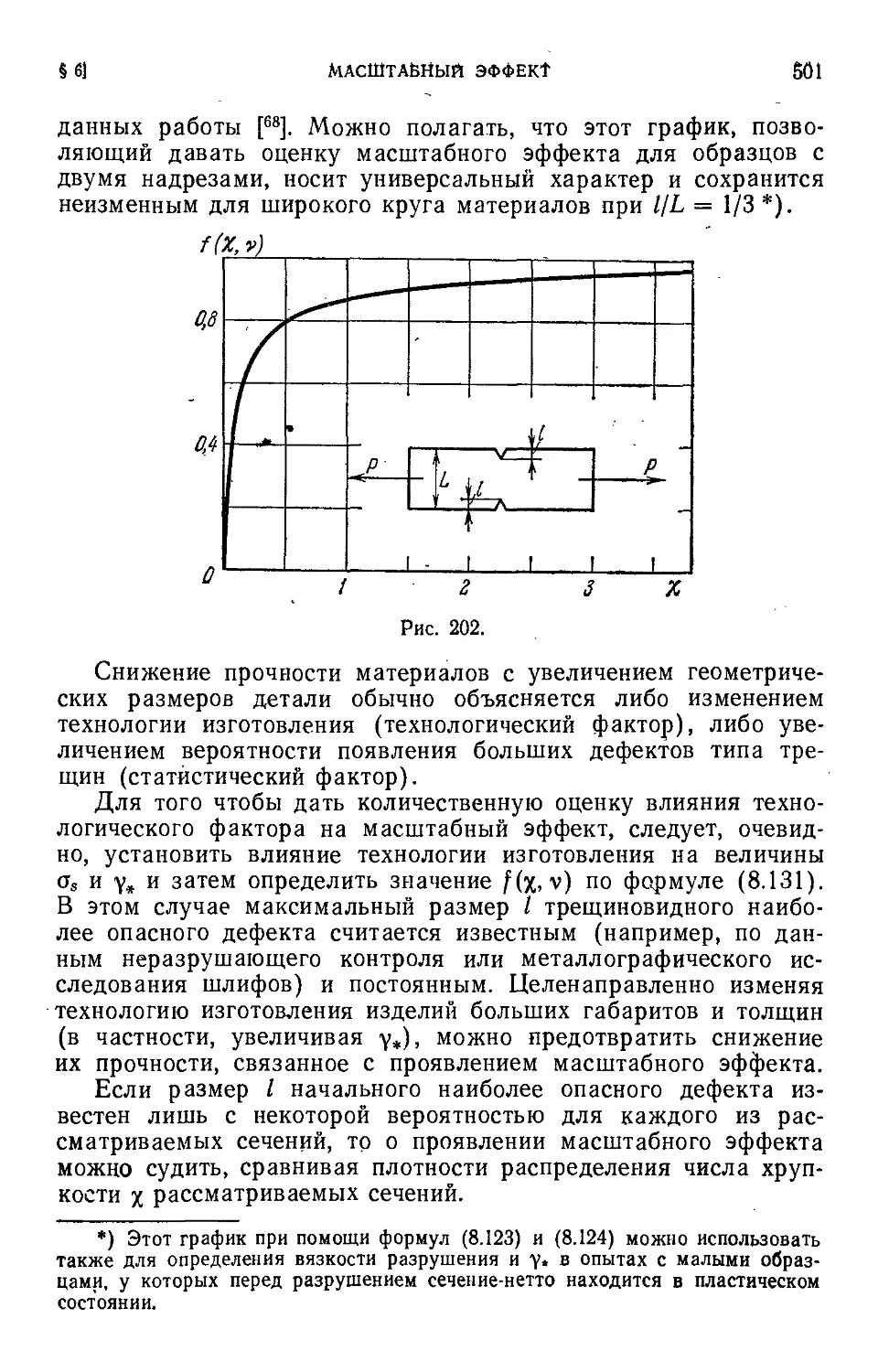
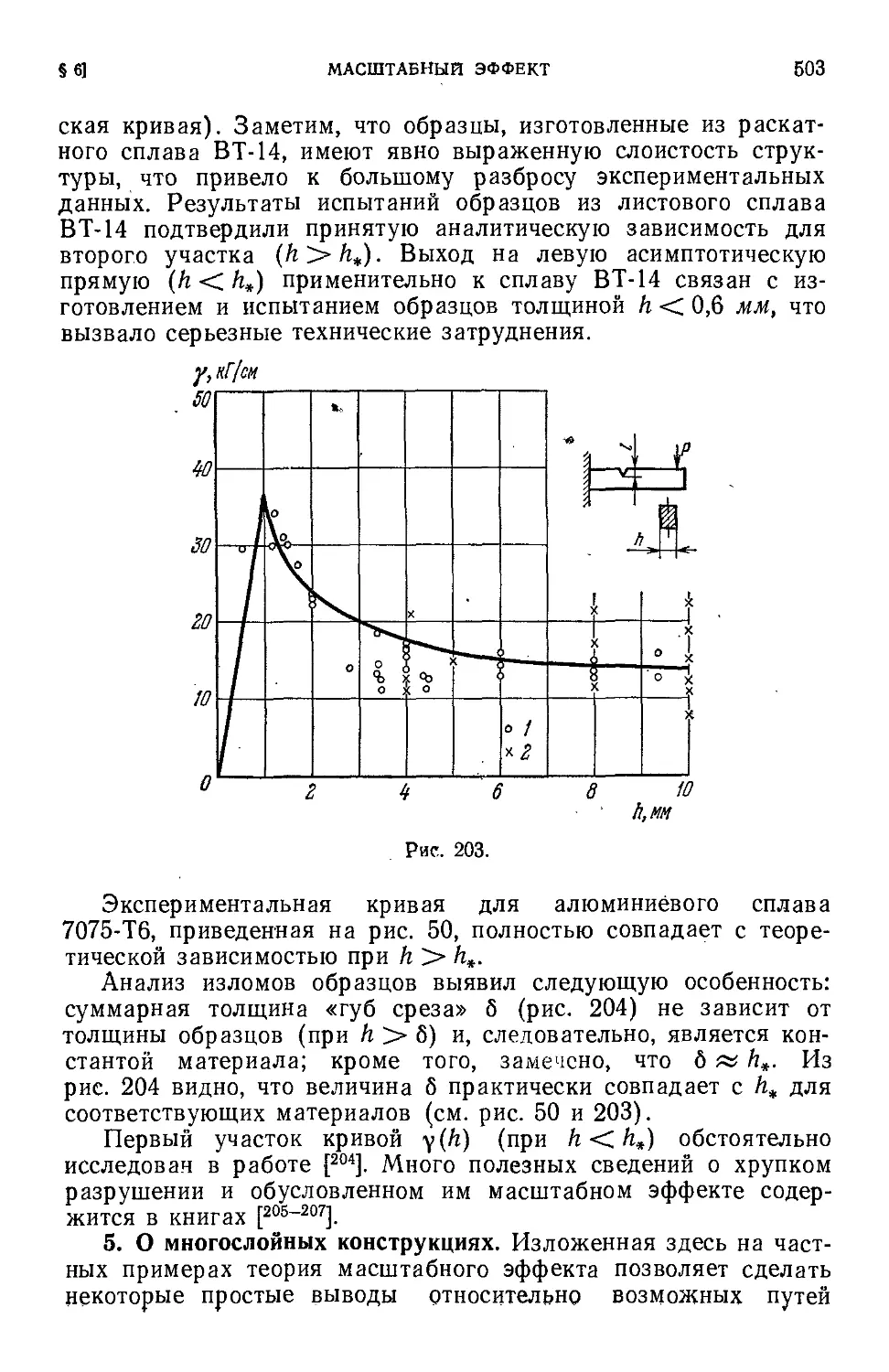
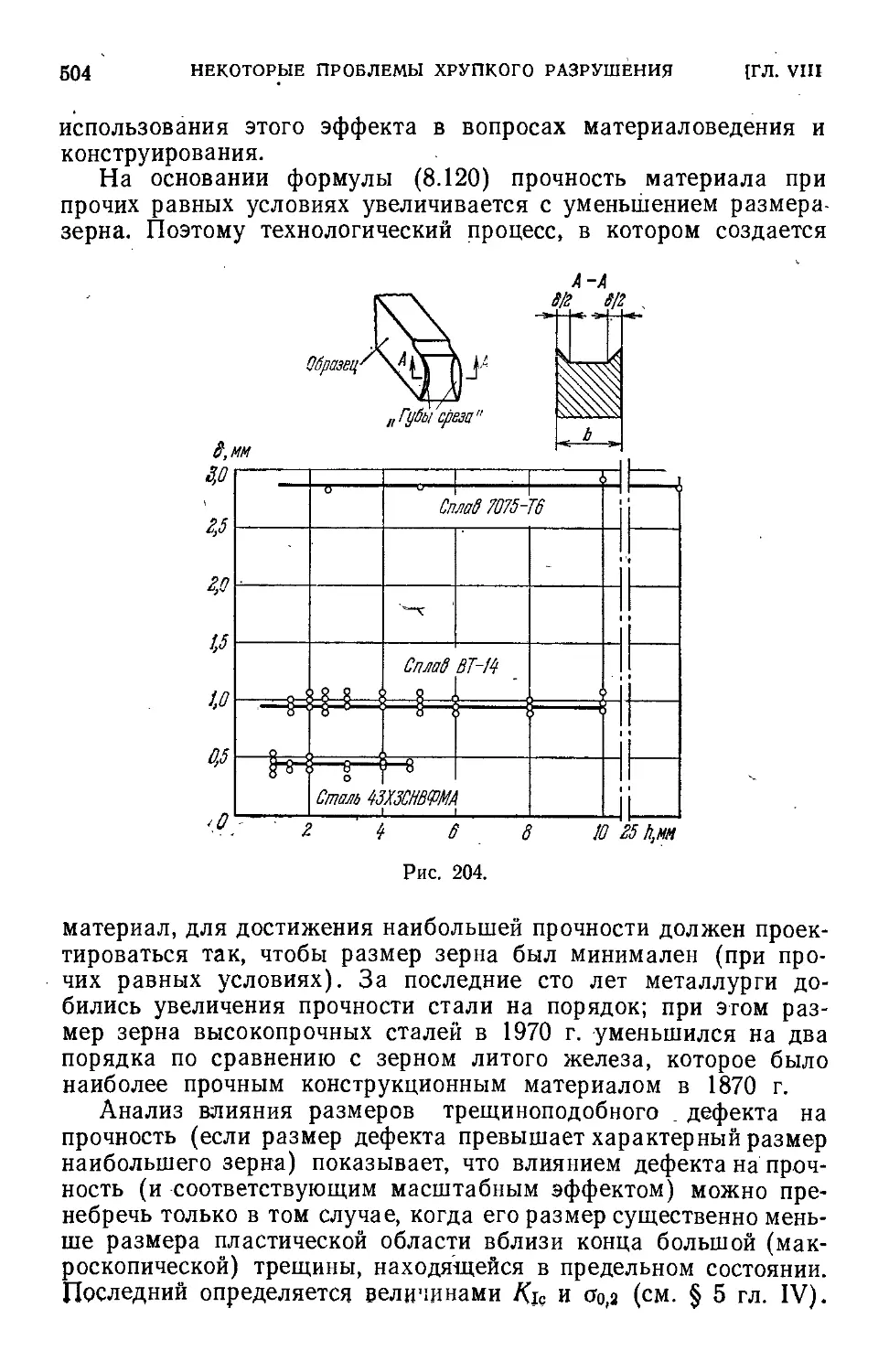
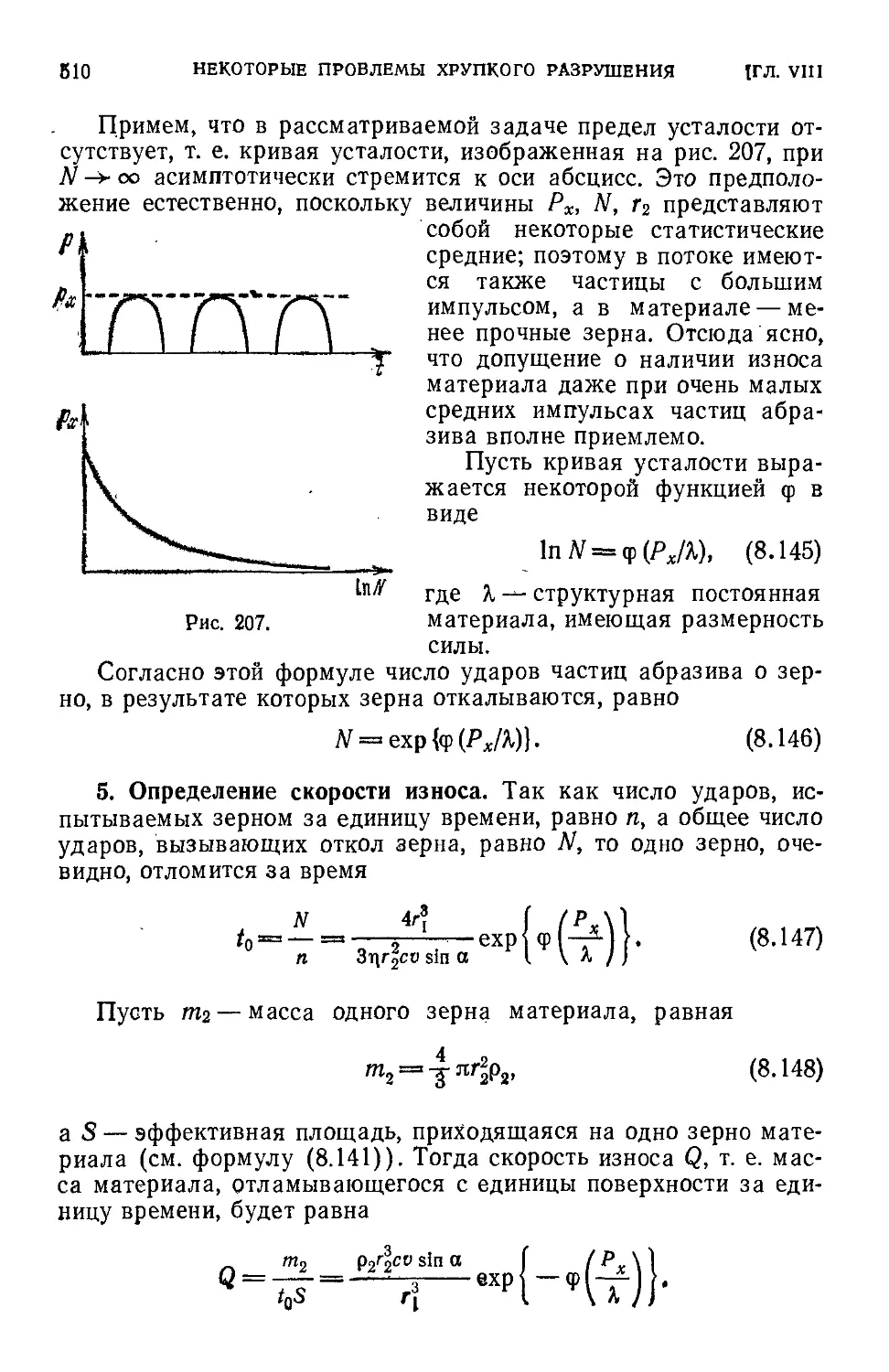
Author: Черепанов Г.П.
Tags: общая механика механика твердых и жидких тел физика механика механика деформируемых тел
Year: 1974
Text
Г. П. ЧЕРЕПАНОВ
МЕХАНИКА
ХРУПКОГО
РАЗРУШЕНИЯ
ИЗДАТЕЛЬСТВО «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1974
S31
4-46
УДК 531
Механика хрупкого разрушения, Г. П. Черепанов,
Издательство «Наука», Главная редакция физико-
математической литературы, М., 1974, 640 стр.
Непредвиденные разрушения конструкций, как
правило, являются хрупкими, т. е. вызываются посте-
постепенным или быстрым развитием трещин. В последние
годы был достигнут значительный прогресс как в об-
области теоретического осмысления этих вопросов, так
и в области инженерных приложений теоретических
результатов для расчета и прогнозирования хрупкого
разрушения.
В книге излагаются основные идеи и методы ме-
механики хрупкого разрушения, а также некоторые
наиболее важные практические вопросы их прило-
приложений. В частности, изложены следующие вопросы:
теория Гриффитса — Ирвина, теория роста усталост-
усталостных трещин, теория водородного охрупчивания, кор-
коррозия под напряжением, теория действия взрыва,
адсорбционный эффект, теория огневого бурения,
оптическое разрушение, масштабный эффект и т. д.
Предназначена4 для научных работников, инже-
инженеров, преподавателей, аспирантов и студентов, за-
занимающихся проблемами прочности- и разрушения.
Илл. 329. Библ. 361.
Геннадий Петрович Черепанов
Механика хрупкого разрушения
М., 1974 г., 640 стр. с илл.
Редактор В. М. Сафрай
ГеКн. редактор Й. Ш. Аксельрод . Корректоры О. А. Бутусова, Н. Б. Румянцева
Сдано в набор 26/11 1974 г. Подписано к печати 9/VI11 1974 г. Бумага 60Х90'/16. тнп. № 2-
Физ. печ. л. 40. 'Услозн. печ. л. 40. Уч.-изд. л, 41,01. Тираж 5900 экз. Т-14535-
Цена книги 2 р. 70 к. Заказ № 110
Издательство сНаука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Ордена Трудового Красного Знамени Ленинградская типография № 2 имени Евгении
Соколовой Союзполиграфпрома при Гбсударственном комитете Совета Министров СССР
по делам издательств, полиграфии и книжной торговли.
198052, Ленинград, Л-52, Измайловский проспект, 29.
Главная РеДакЦия .
физико-математической литературы
Н 1974
igQ^ фк
053@1)-74 издательства «Наука», 1974.
ОГЛАВЛЕНИЕ
Предисловие . б
Глава I. Введение 9
§ 1. Классификация реологических моделей . 9
§ 2. Теории прочности 14
§ 3. Вязкое разрушение 16
§ 4. Работа Гриффитса «Явление разрушения и течения твердого
тела» : 18
§ 5. Некоторые замечания 21
Глава II. Прочность идеально-периодических структур . 25
. § 1. Точный квантовомеханический метод ... . 25
§ 2. Приближенные методы 32
§ 3. Некоторые оценки 40
§ 4. Метод теплового смещения 42
Глава III. Сингулярные задачи теории упругости 4 ..... 51
§ I. Классификация особых точек 51
§ 2. Основные теоремы . 54
§ 3. Плоская задача теории упругости 58
§ 4. Цилиндр 68
§ 5. Поле упругих напряжений и смещений в малой окрестности края
произвольной трещины 71
§ 6. Налегающие трещины и влияние включений , . . 76
§ 7. Анизотропное тело ......... 86
§ 8. Кусочно-однородное тело 93
§ 9. Влияние конечности деформаций . . 101
§ 10. Влияние физической нелинейности и размеров начальной по-
полости ПО
§ 11. Динамические эффекты 118
Глава IV. Основные положения механики хрупкого разрушения ... 135
§ 1. Критерий локального разрушения 135
| 2. Энергетический метод 144
,§ 3, Обобщенный нормальный разрыв 149
1*
4 ОГЛАВЛЕНИЕ
§ 4 Устойчивость роста хрупких трещин ... . « . ... . . . 158
§ 5. Концепция квазихрупкого разрушения. Структура- конца тре-
трещины .->... ;..."- • ¦ 160
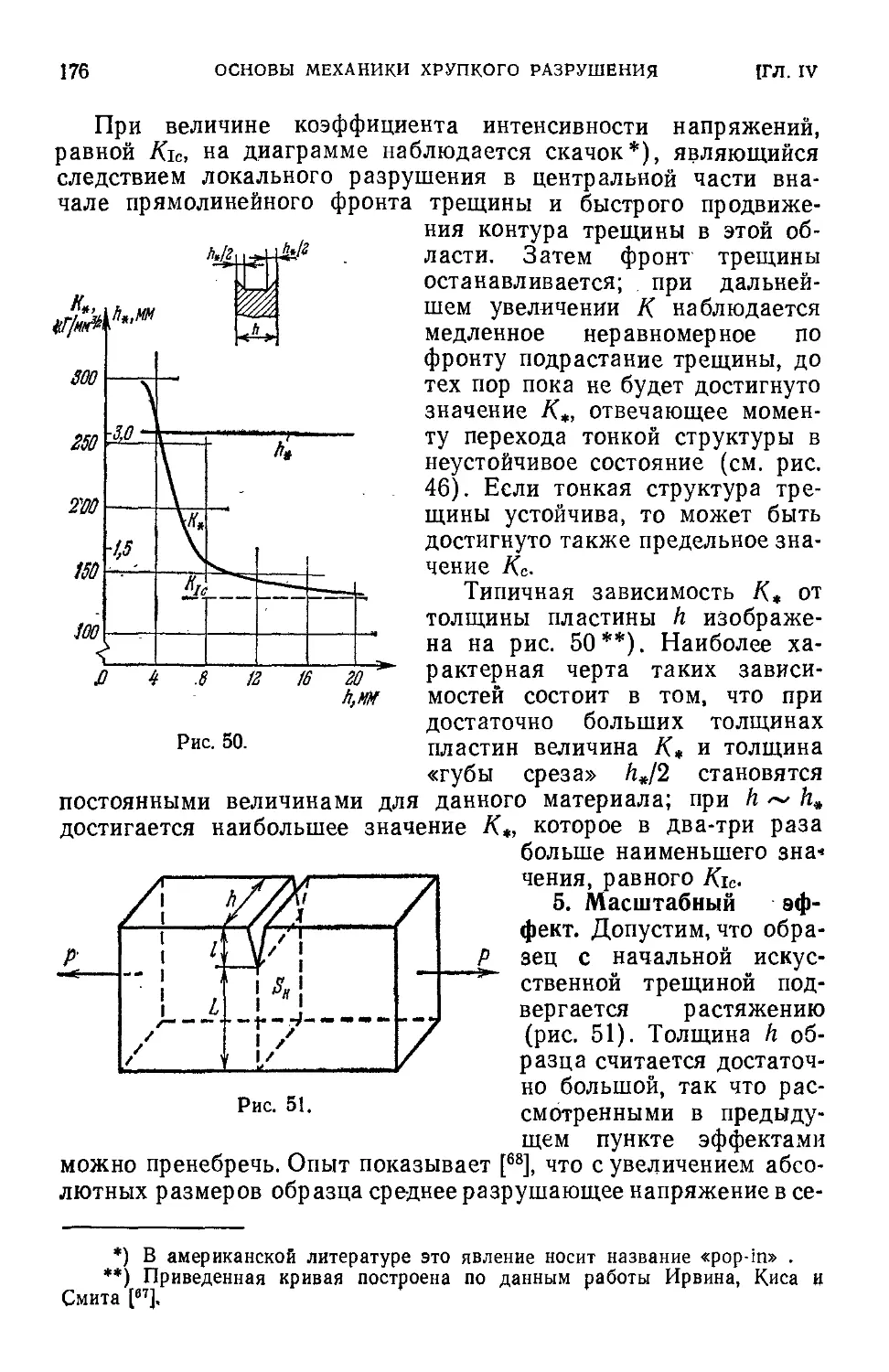
§ 6. Некоторые основные эффекты процесса разрушения .170
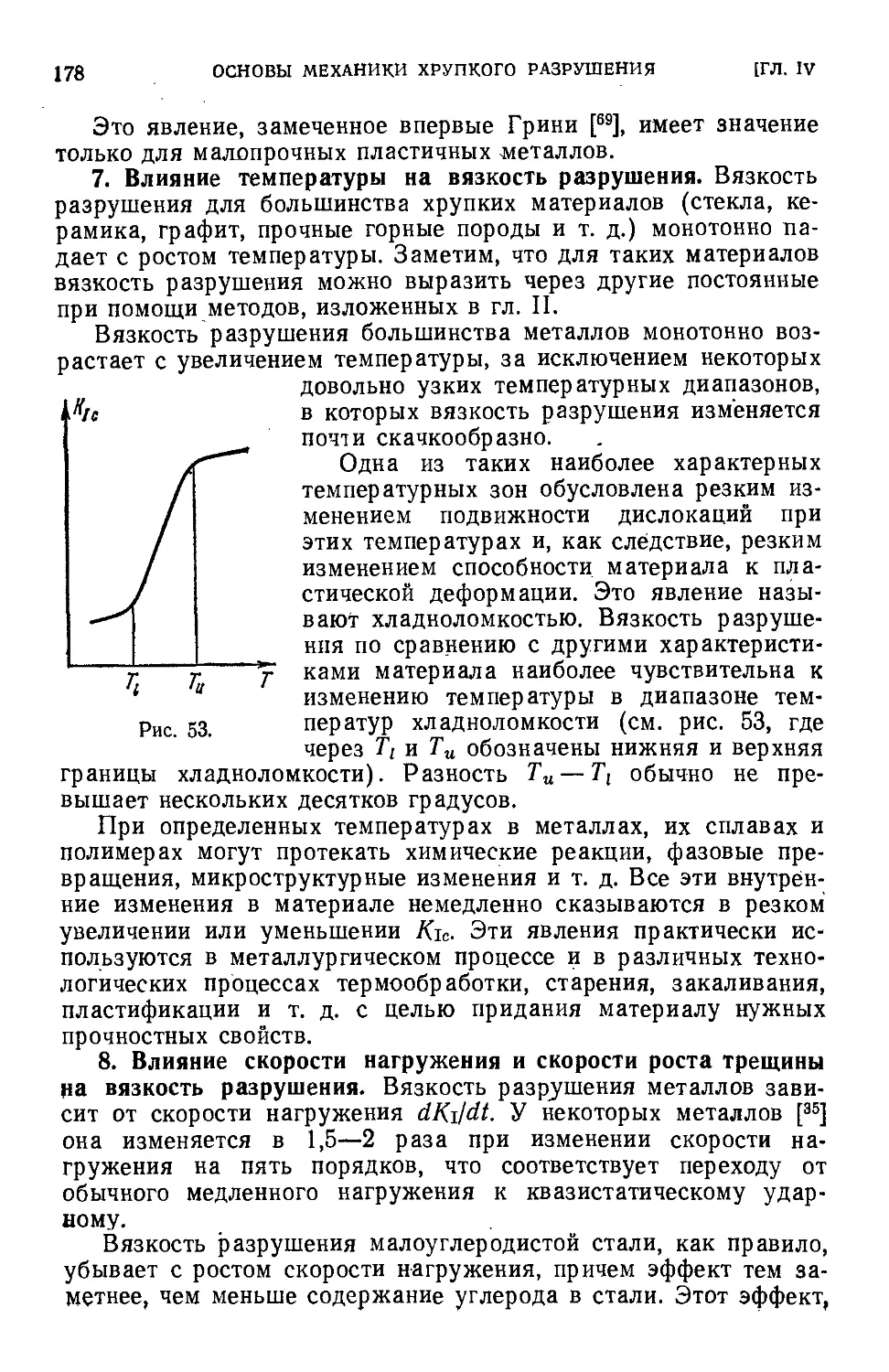
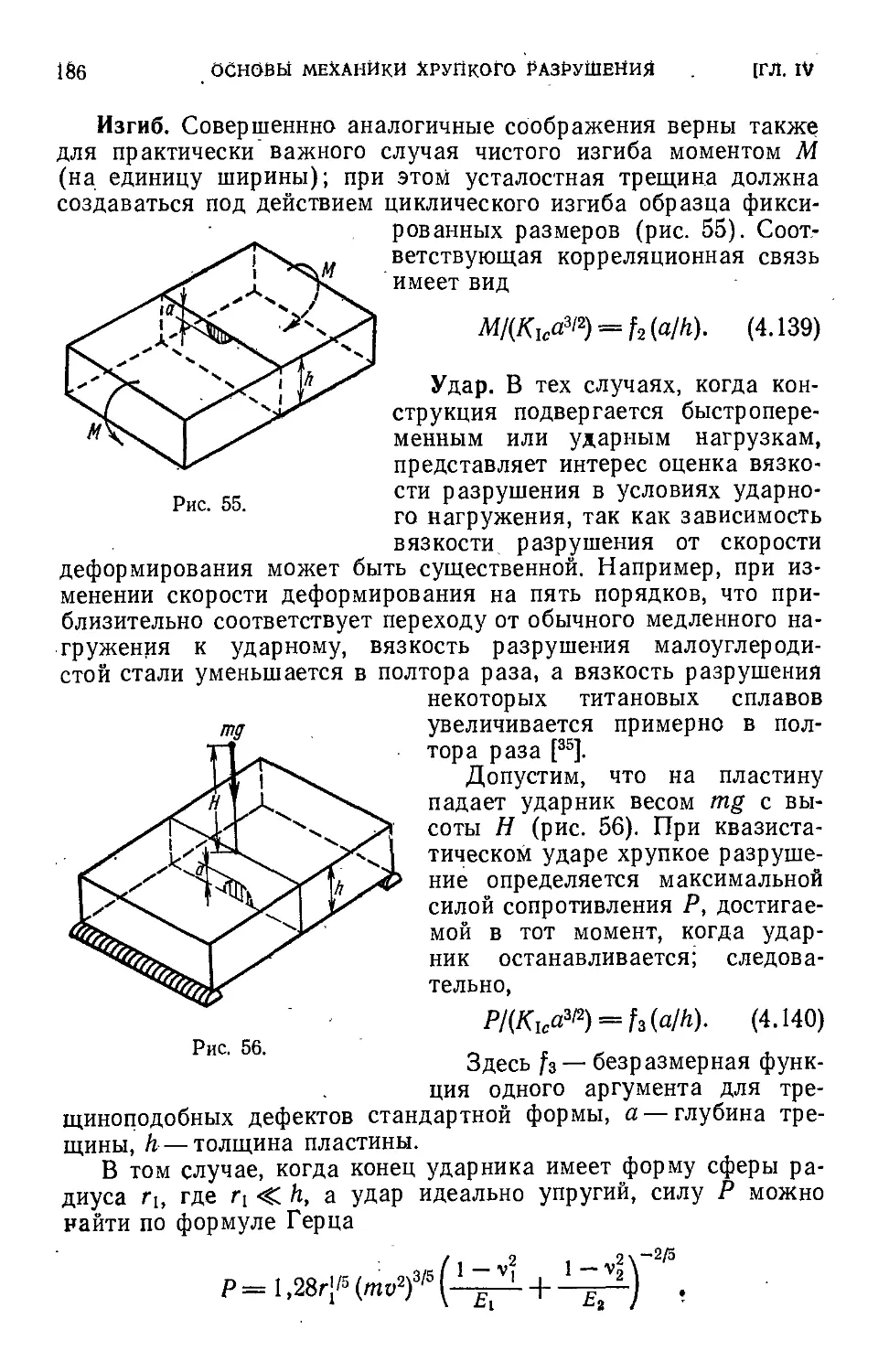
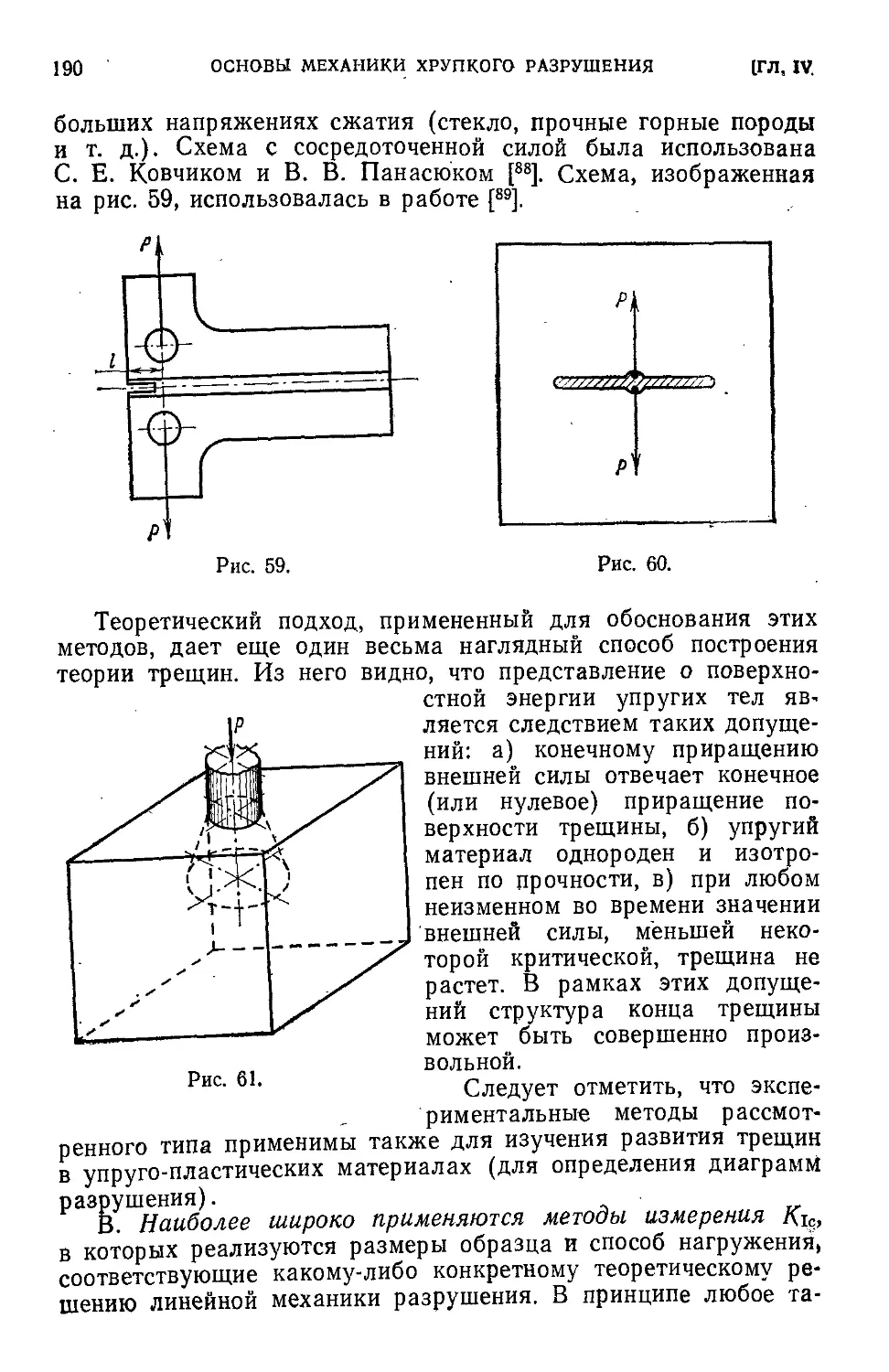
§ 7. Методы определения вязкости разрушения .183
§ 8. Оценка технической ..прочности и вязкости разрушения некоторых
материалов ....197
§ 9/ Другие критерии локального разрушения 208
§ 10. Одно приложение механики разрушения к горному делу . . .211
Глава V- Некоторые общие вопросы механики разрушения . . . . < 220
§ I. Уравнение энергии .- . . . 220
§ 2. Поток энергии . . ; 228
§ 3. Численный метод ................... 236
§ 4. Упругое тело .' . ' 239
§ 5. Упруго-пластическое тело 257
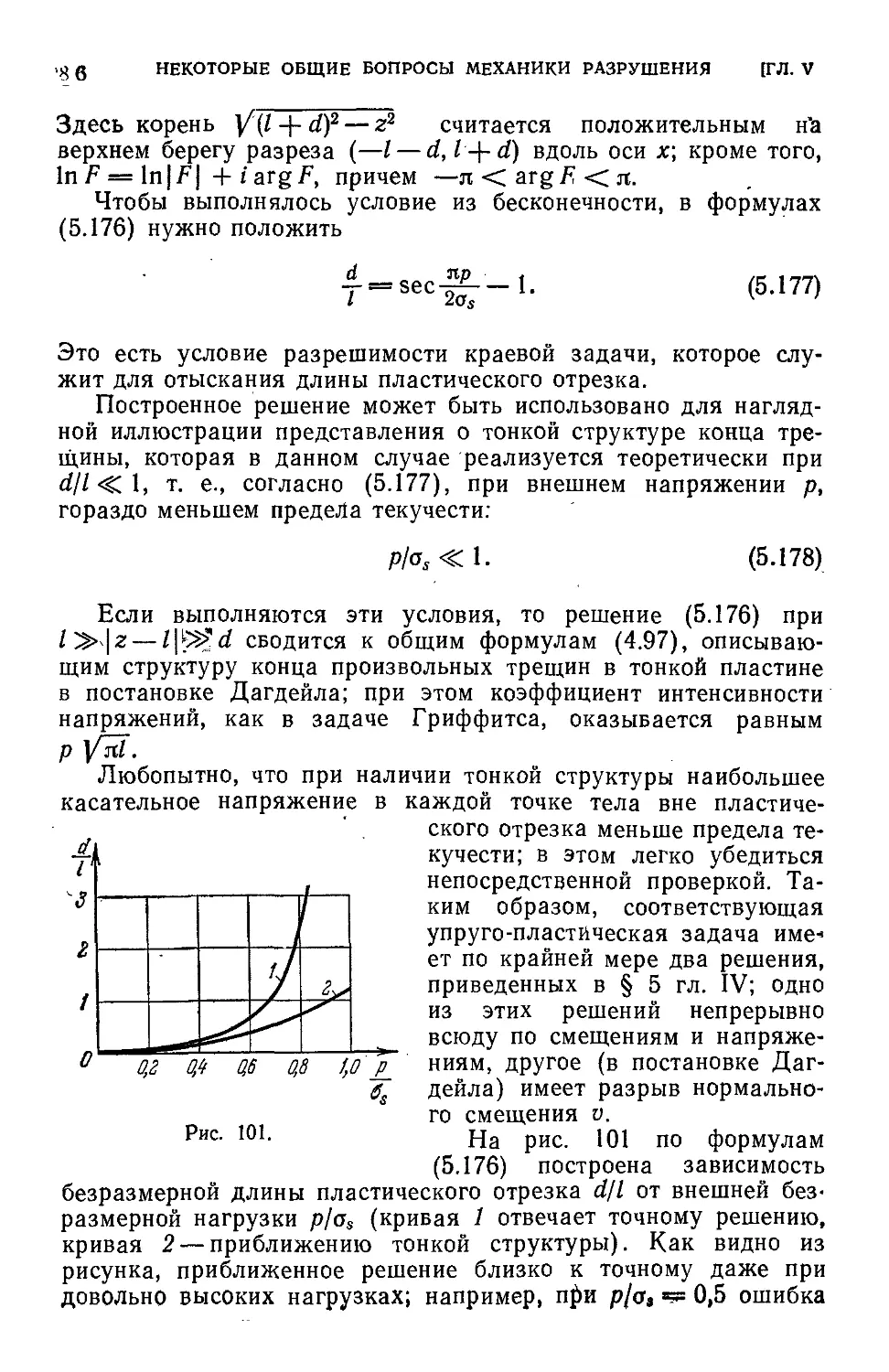
§ 6. Один упруго-пластический аналог задачи Гриффитса 283
§ 7. Вязкоупругое тело , ., 293
§ 8. Развитие полостей при конечных деформациях 300
Глава VI. Рост усталостных трещин 307
§ 1. Введение . . .307
§ 2. Подрастание трещины при монотонном нагружении 310
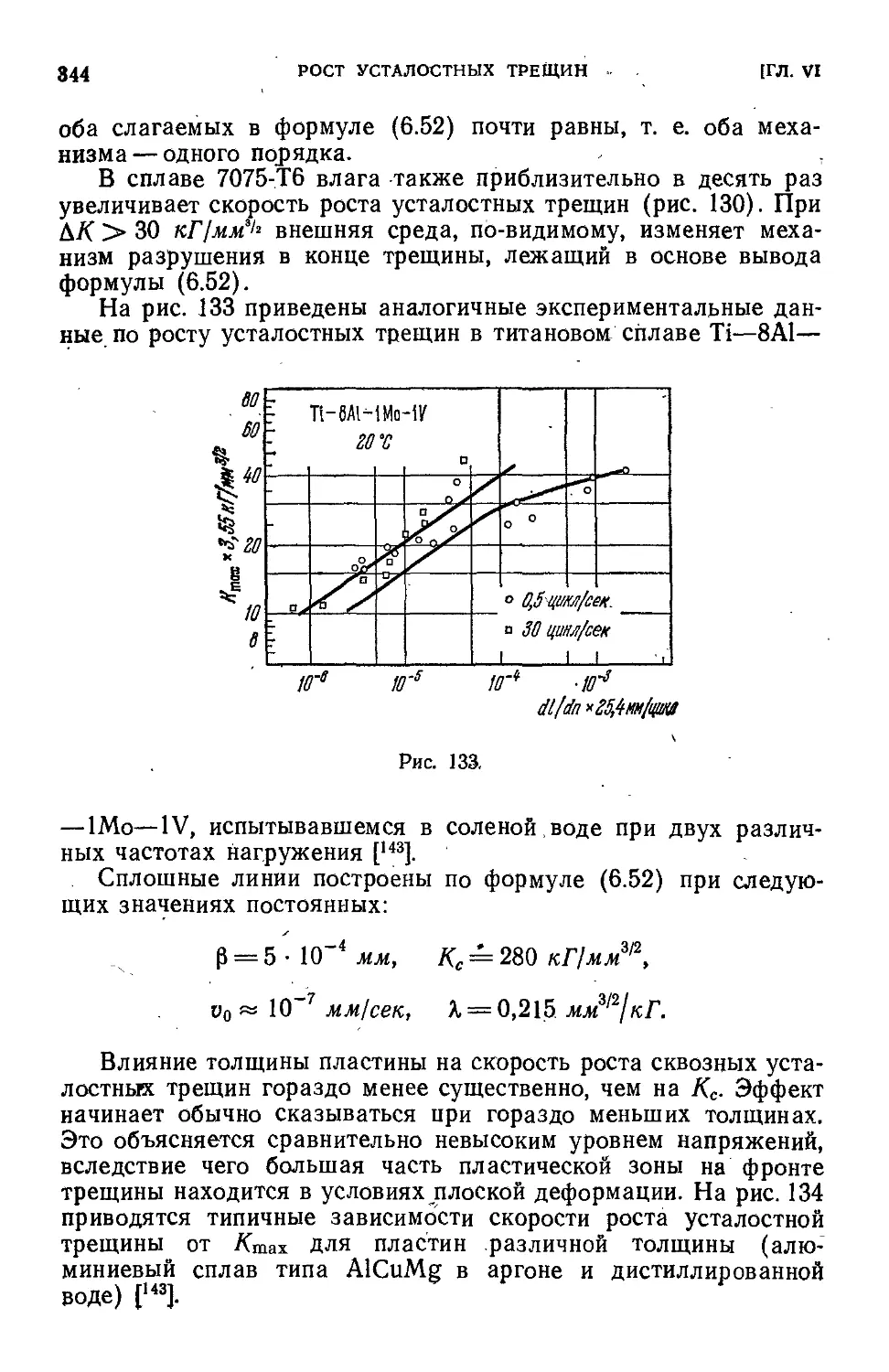
§ 3. Рост усталостных трещин (теория) - .-.. . . . 322
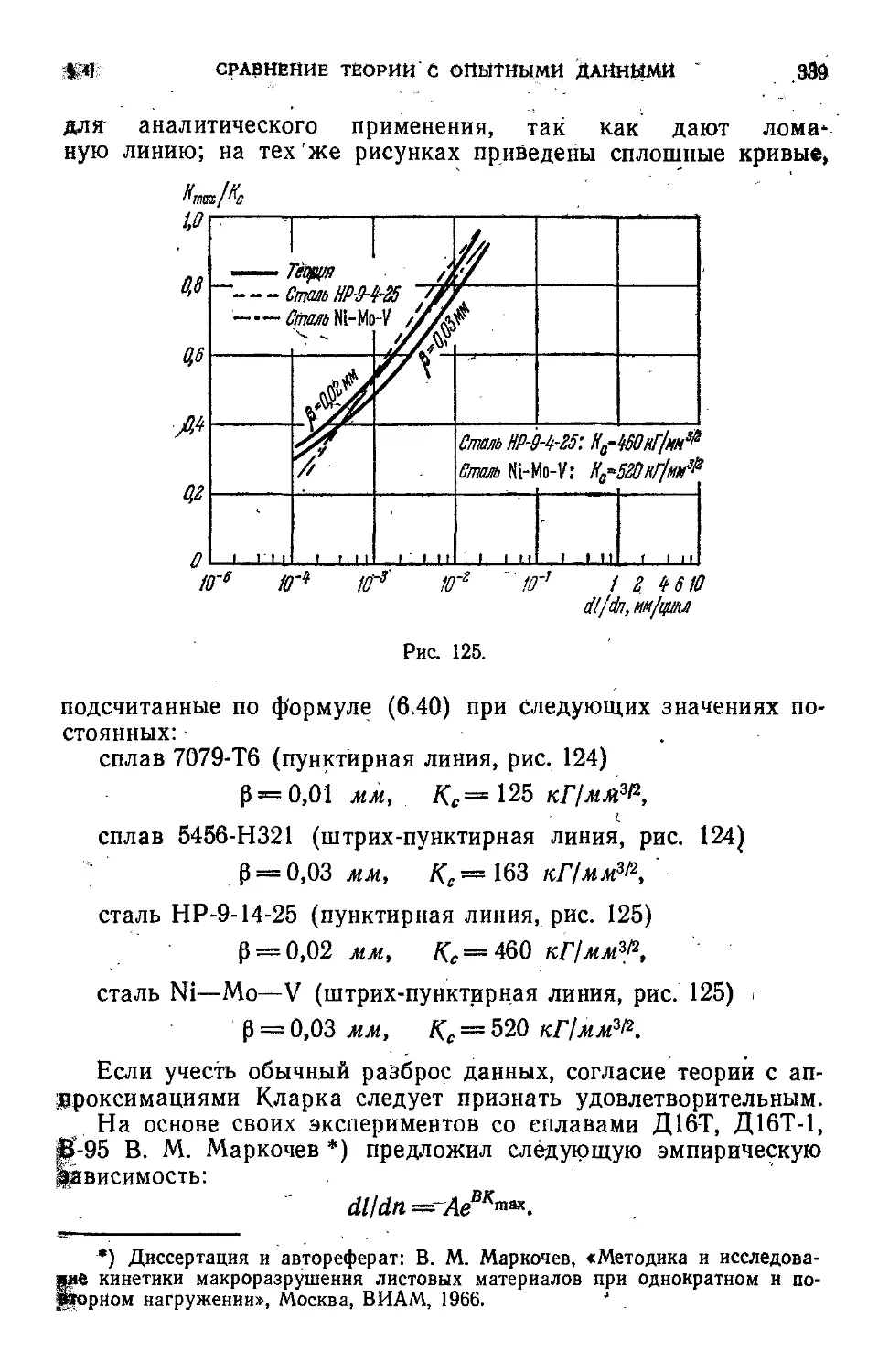
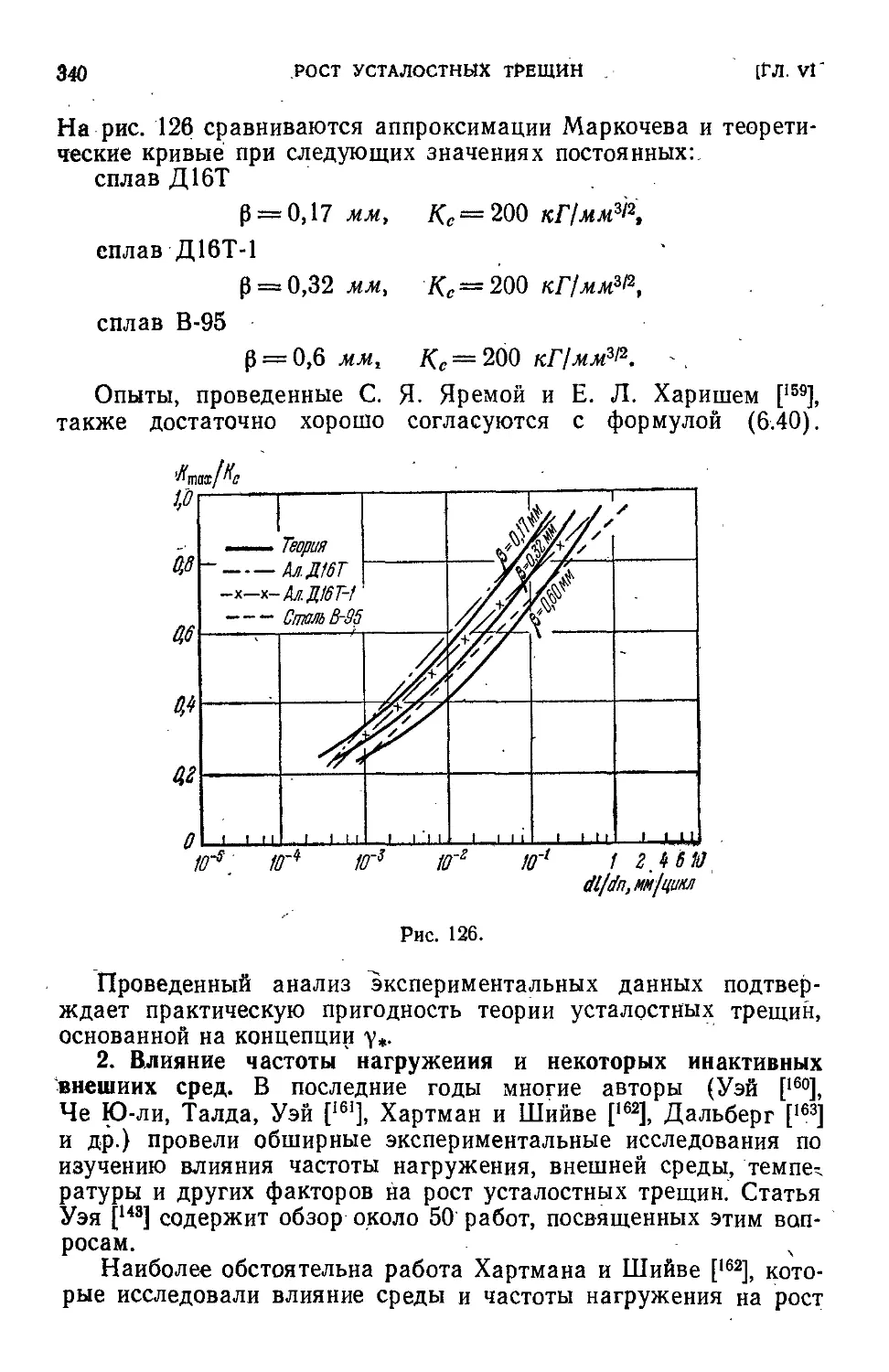
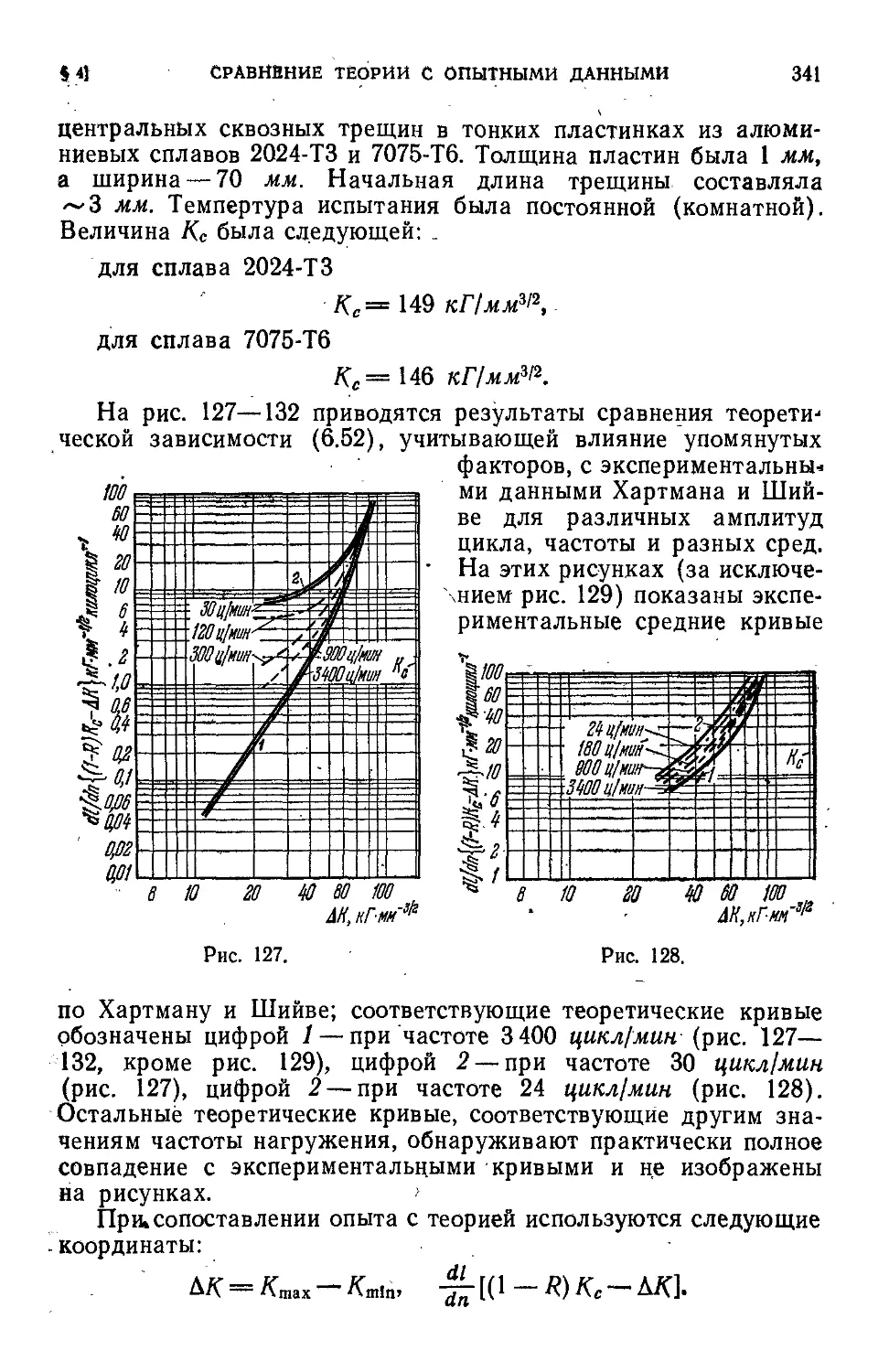
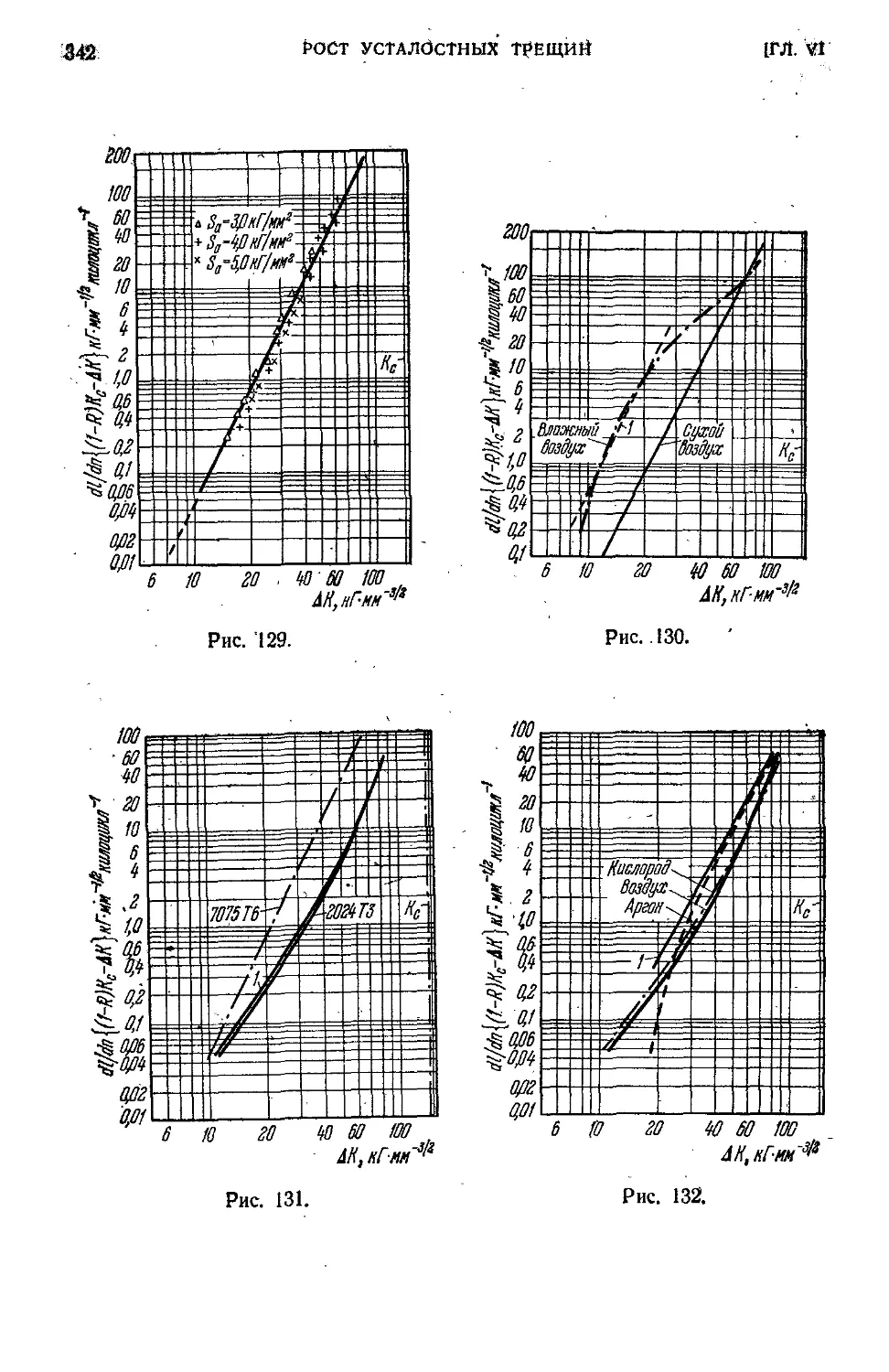
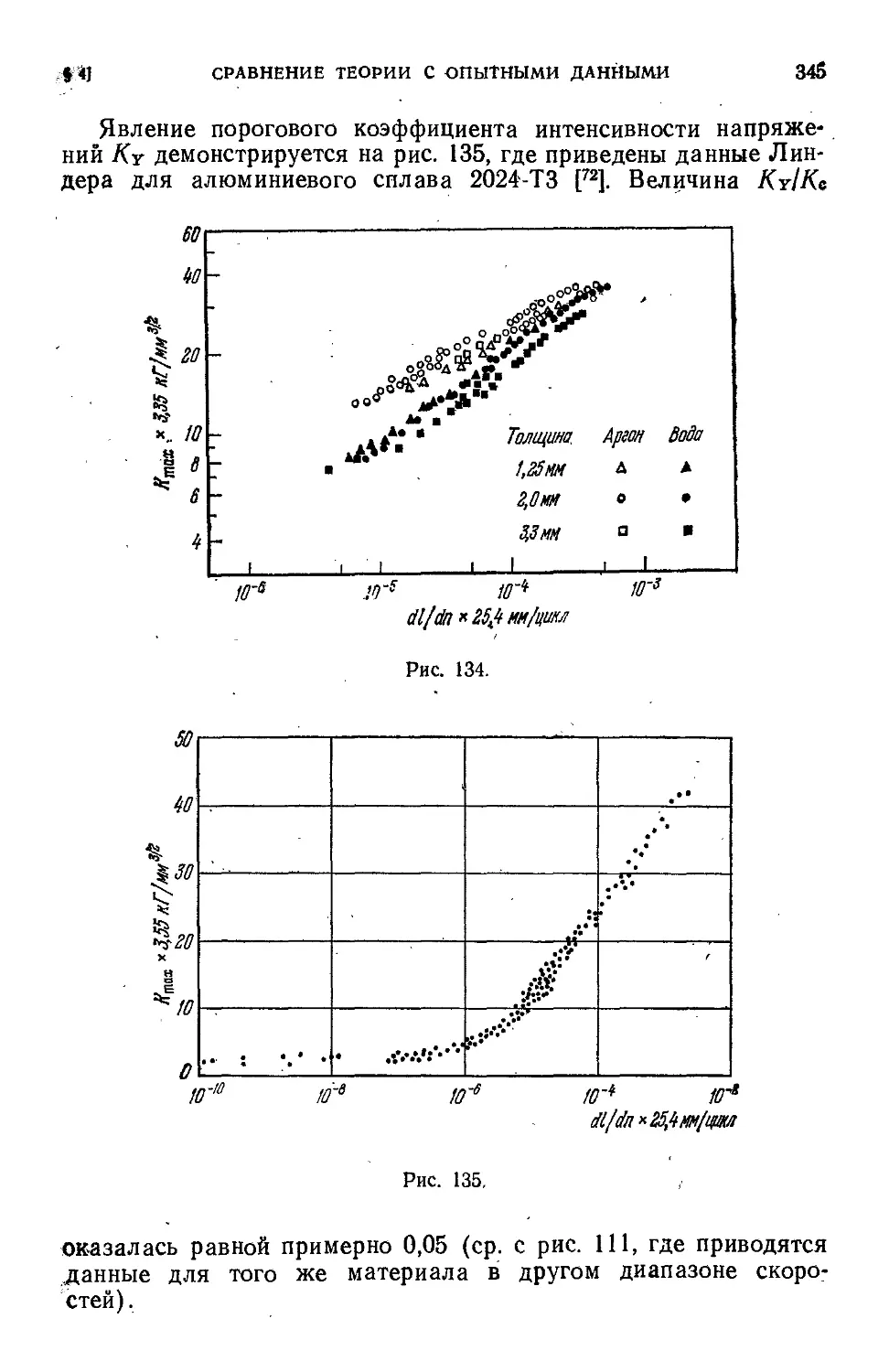
§'4. Сравнение теории с опытными данными . 333
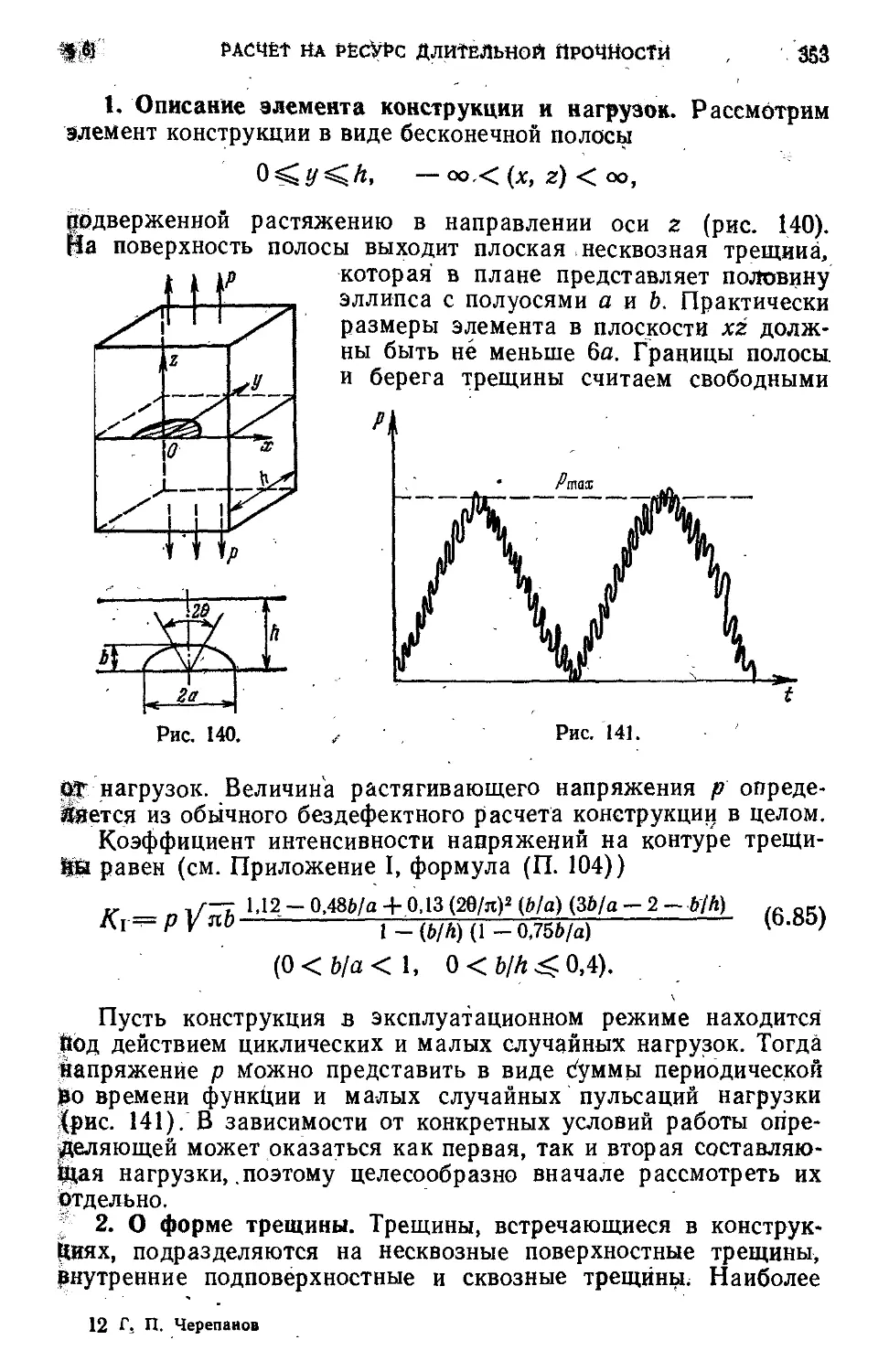
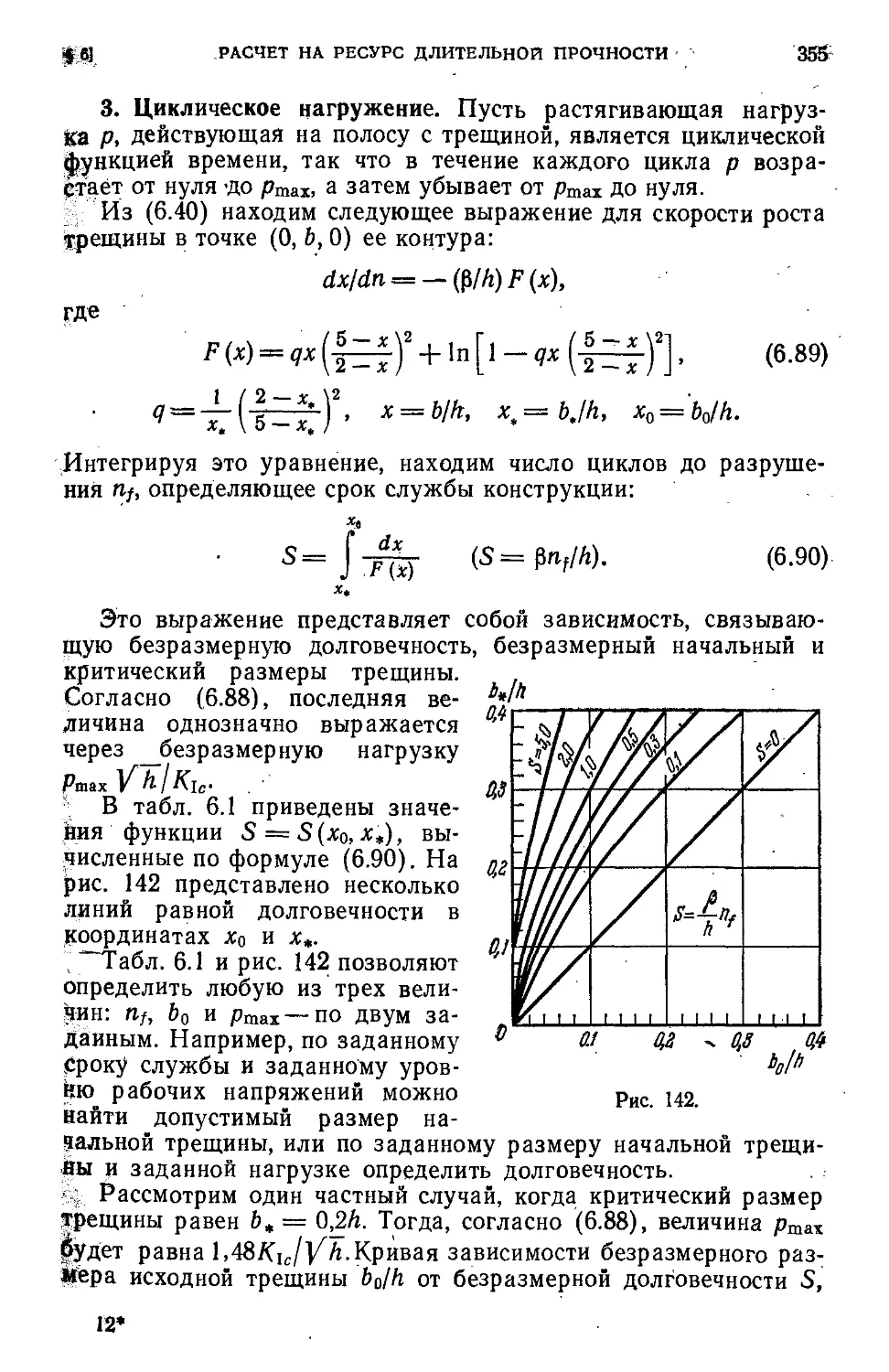
§ 5. Некоторые конкретные задачи 346
§ 6. Пример расчета на ресурс длительной прочности при усталостном
разрушении . . 352
Глава VH. Влииние внешней среды на рост трещин ....... 364
§ 1. Введение 364
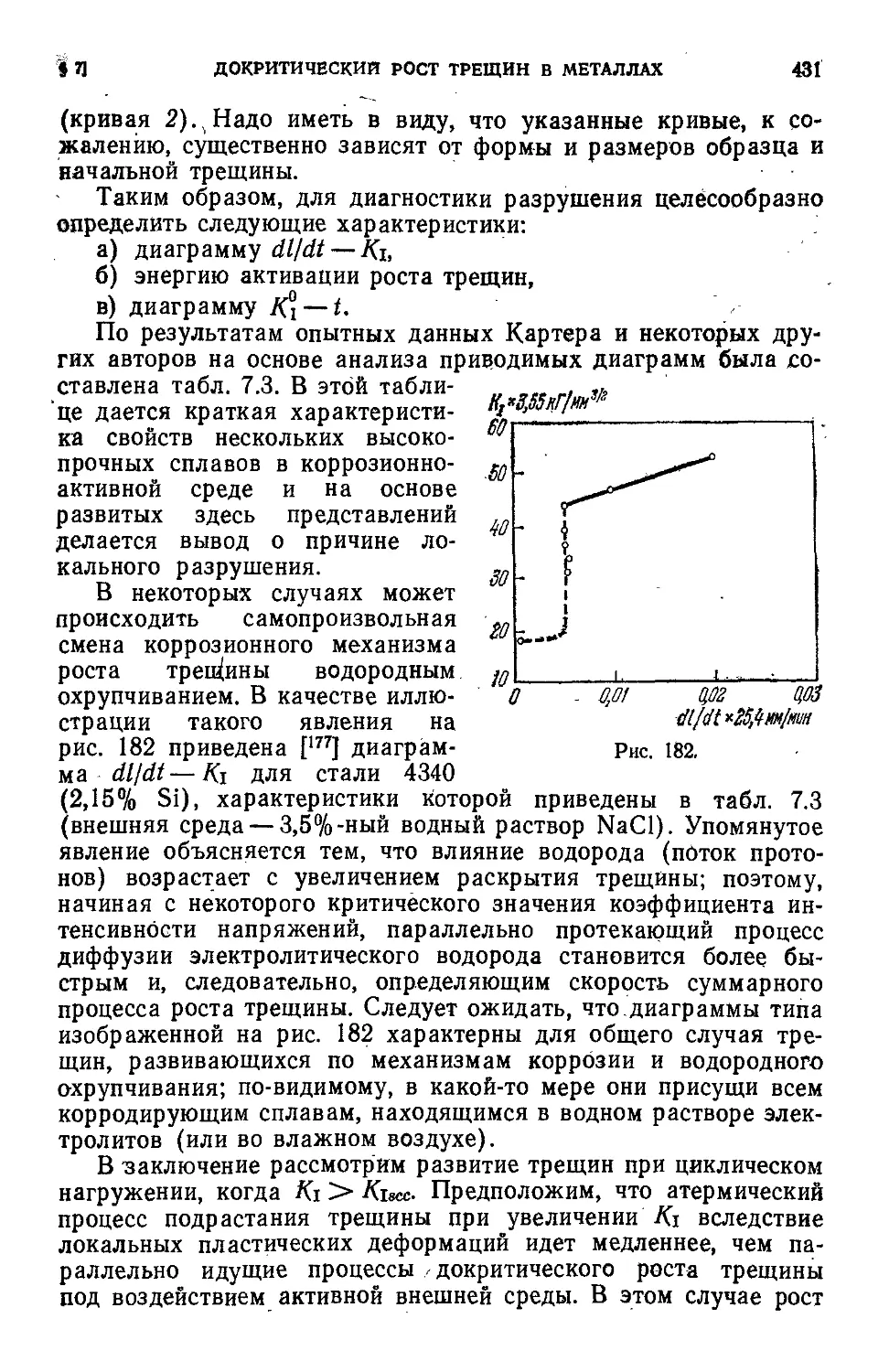
§ 2. Влияние водорода и влагн на рост трещин в металлах (опытные
данные 366
§ 3. Рост трещин в металлах под действием водорода (теория) . ч . 3-73
§ 4. Адсорбционный эффект 388
§ 6j Развитие коррозионных трещин (химическая коррозия под напря-
напряжением 398
§ 6. Электрохимический механизм роста трещин 408
§ 7. Сравнительный анализ основных механизмов докритического роста
трещин в металлах 426
§ 8. Влияние воды на разрушение стекла и горных пород ...... 435
§ 9. Разрушение горящих порохов . - 441
Глава VIII. Некоторые проблемы хрупкого разрушения ...... 449
§ 1. Разрушение при взрыве ....'.:..; 449
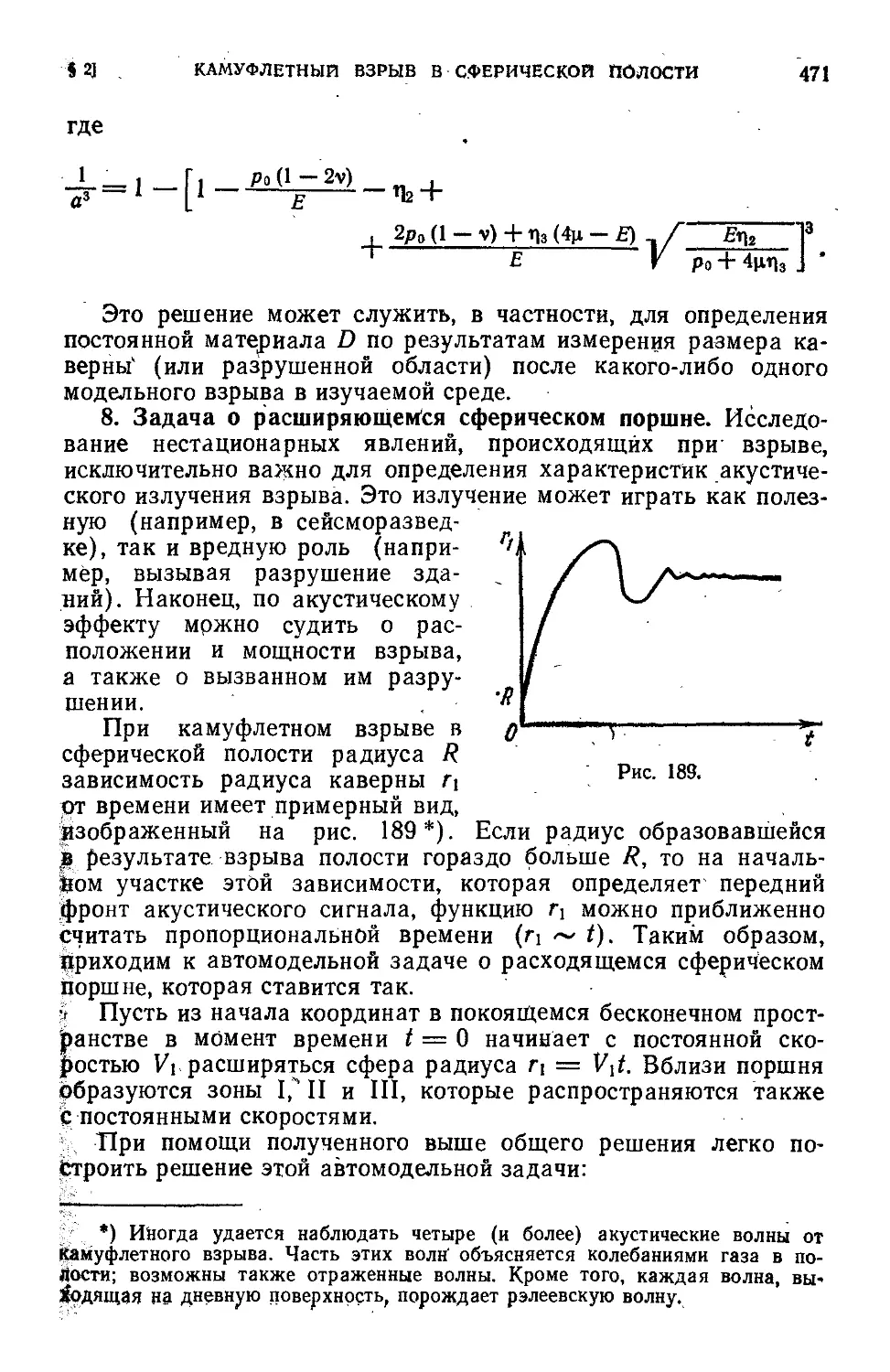
§ 2. Камуфлетный взрыв в сферический полости ........ 459
§3. Самоподдерживающееся разрушение ' 473
§ 4. Теория огневого бурения , 480
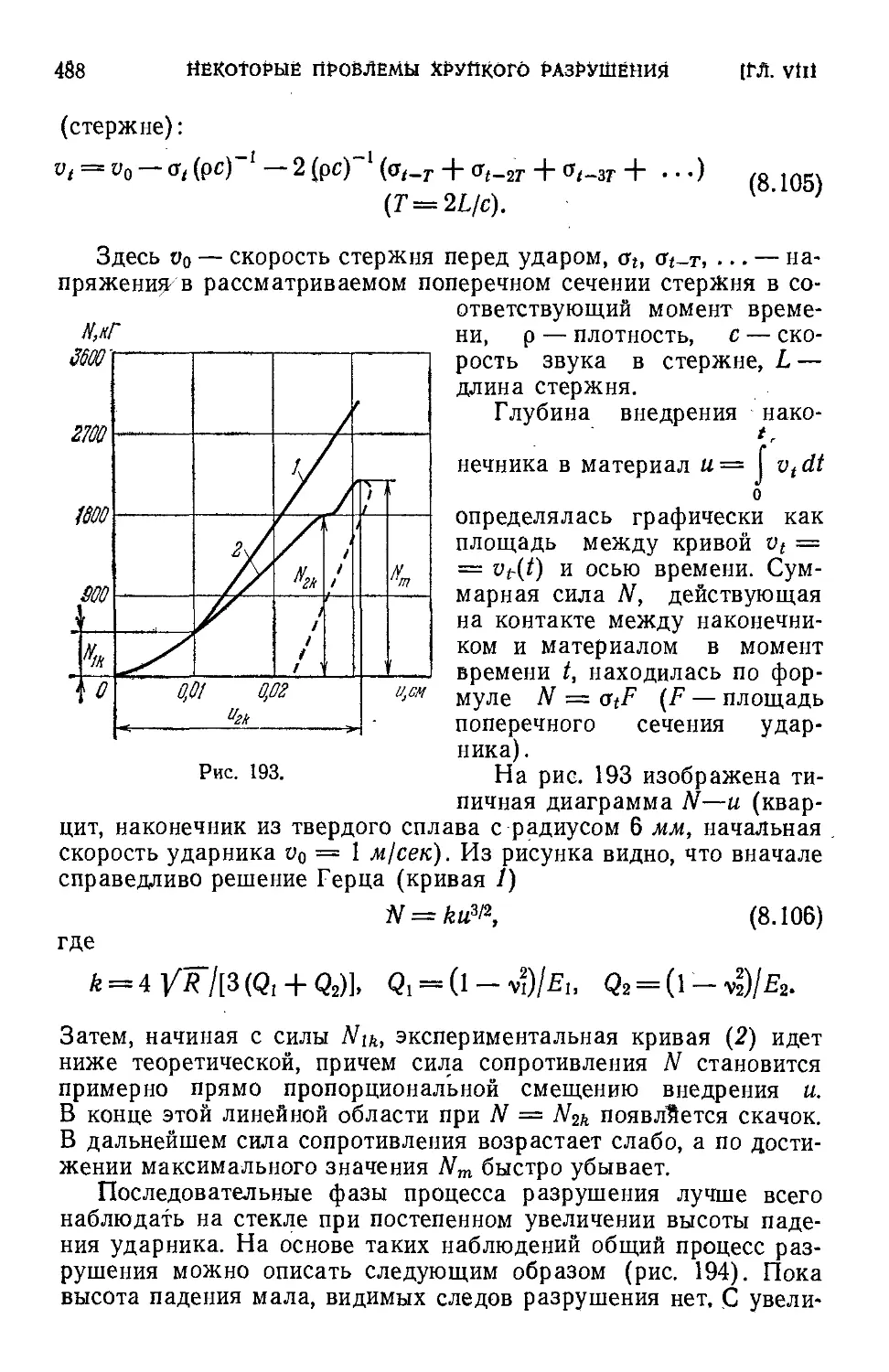
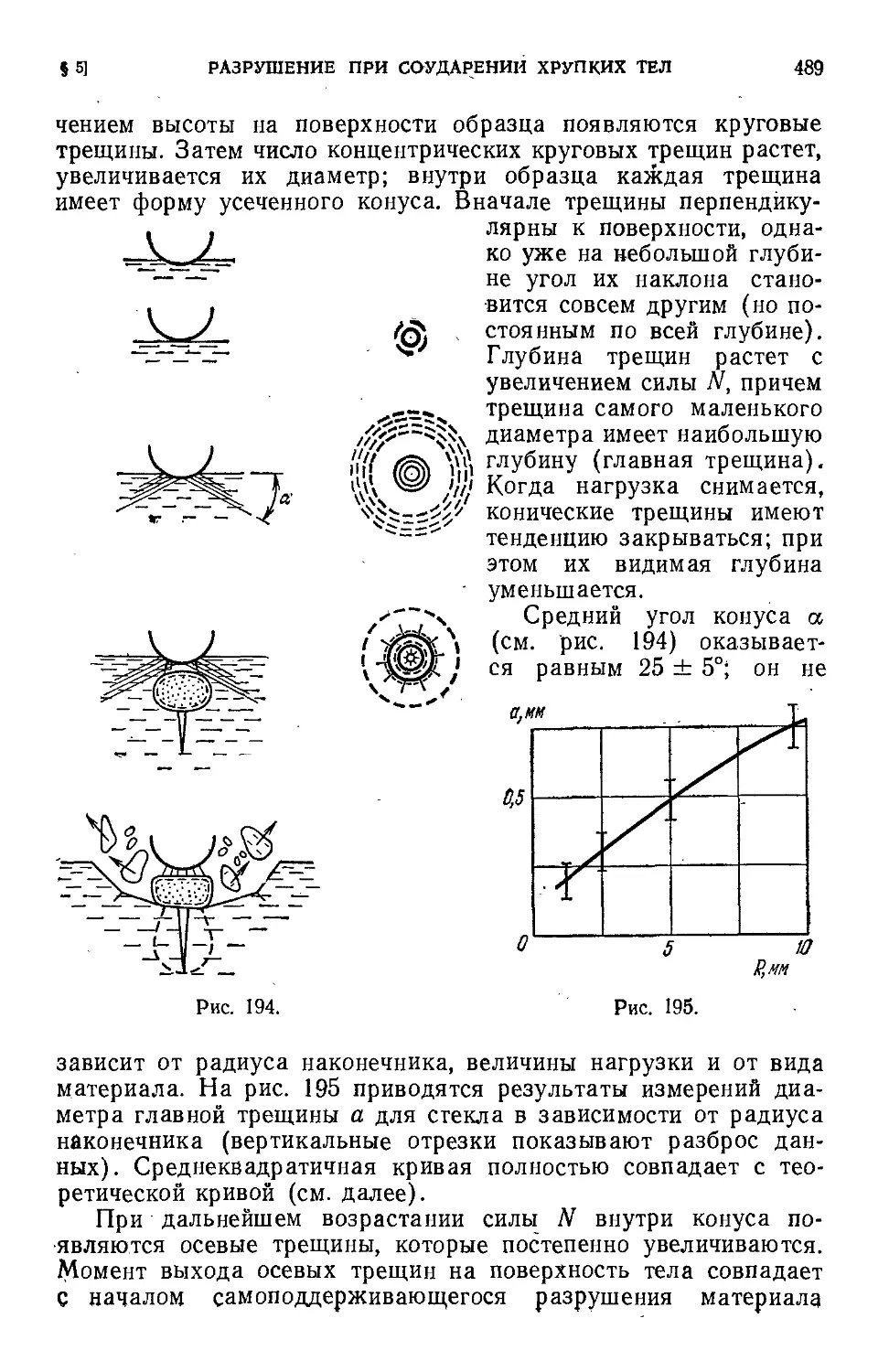
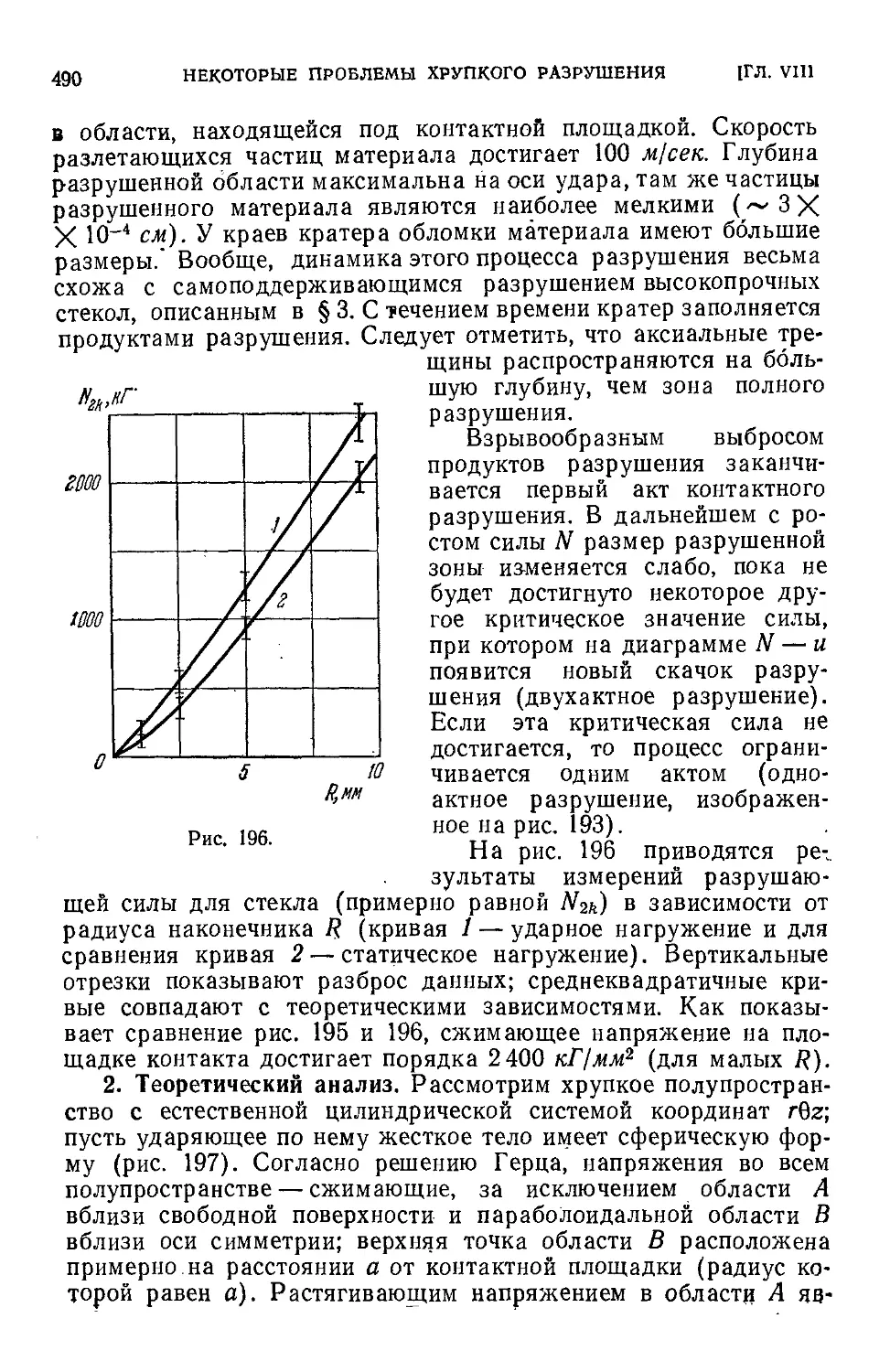
§ 5; Разрушение при соударении хрупких тел .' 486
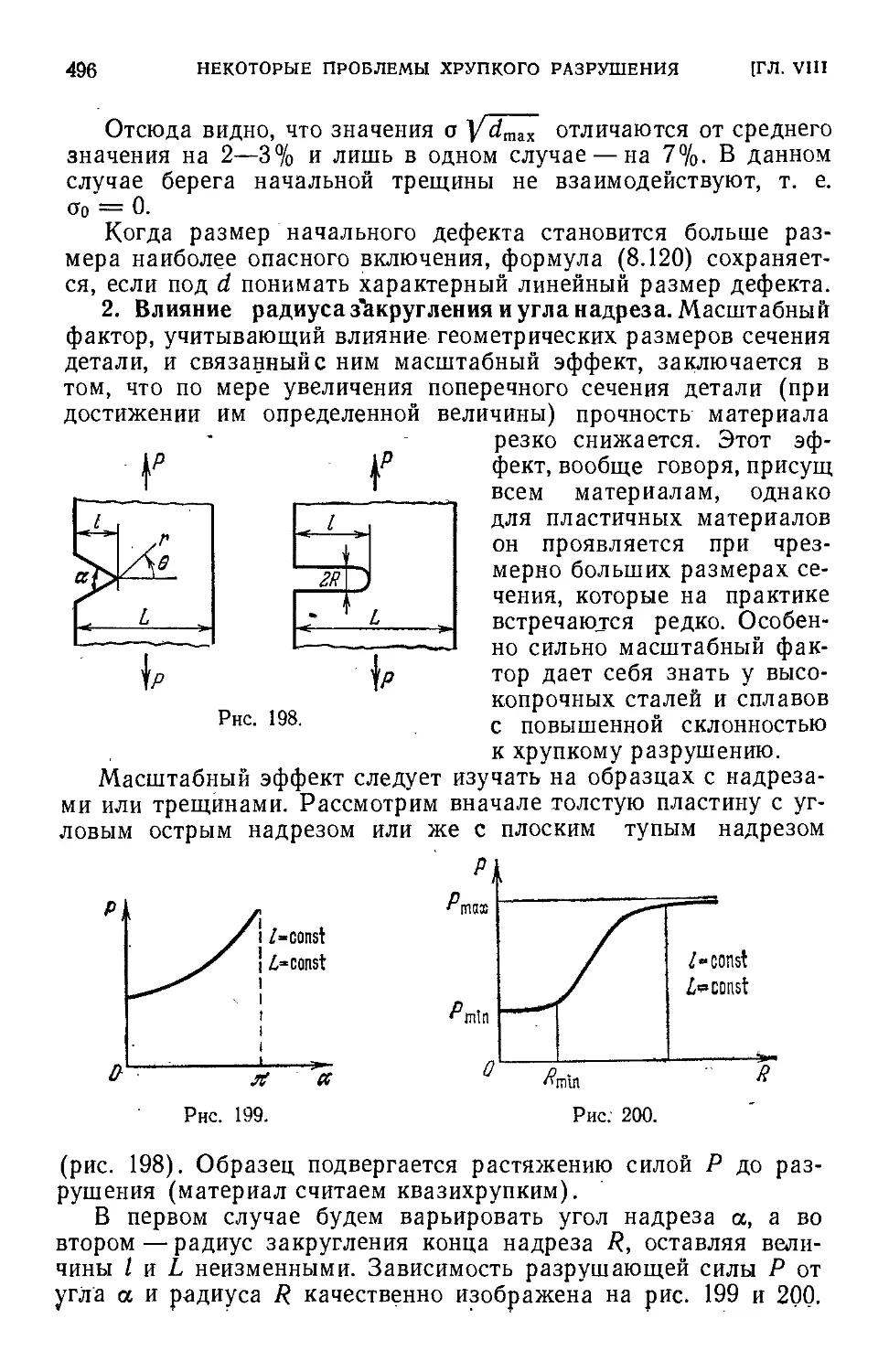
,,.§6. Масштабный эффект 495
§ 7: Некоторые проблемы эрозии твердых тел в потоке жидкости или.
' газа . . 505
§ 8,'Оптическое разрушение .512
ОГЛАВЛЕНИЕ 5
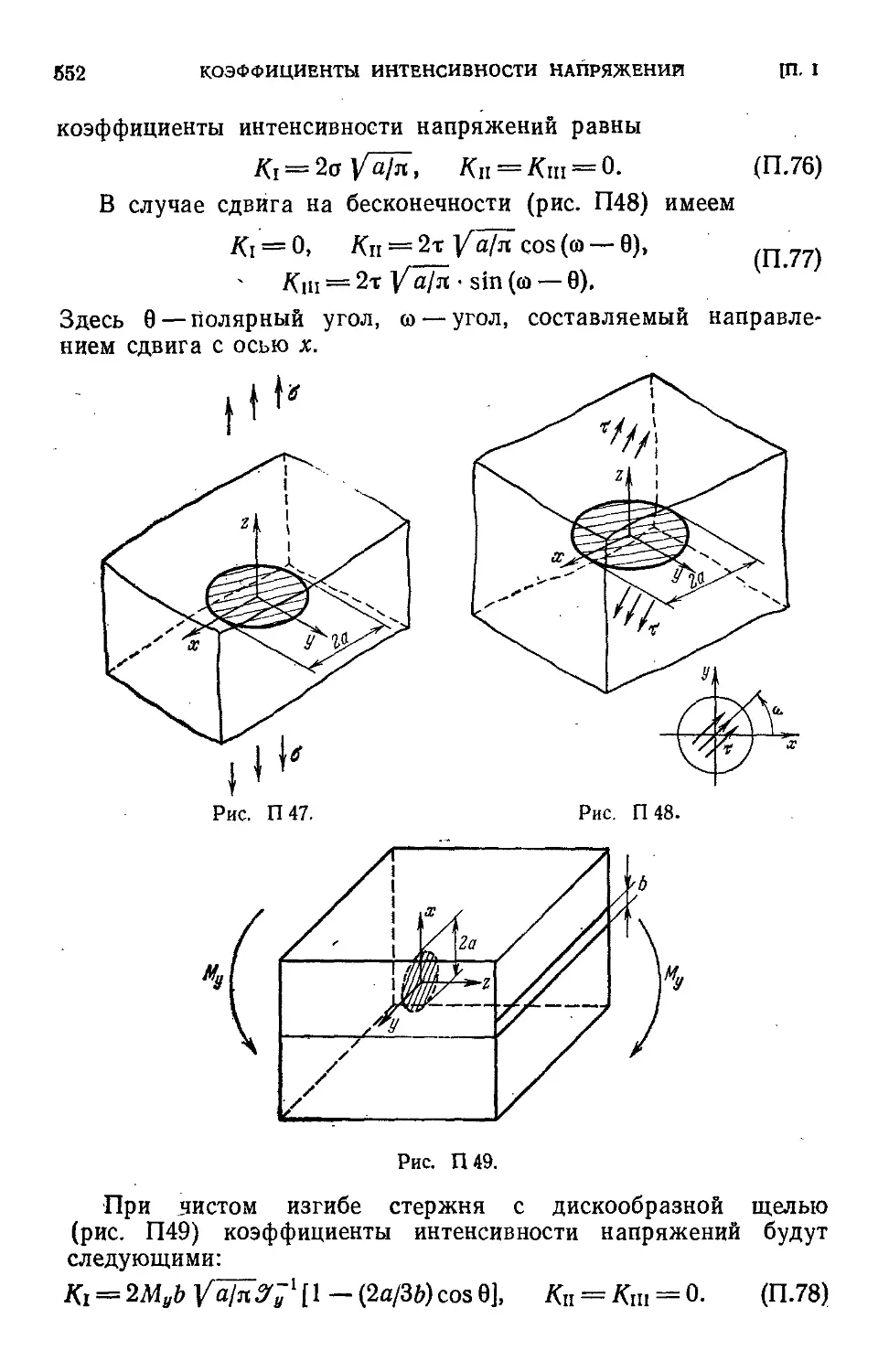
Приложение I. Коэффициенты интенсивности напряжений., . . .519
§ 1. Плоские статические задачи 1521
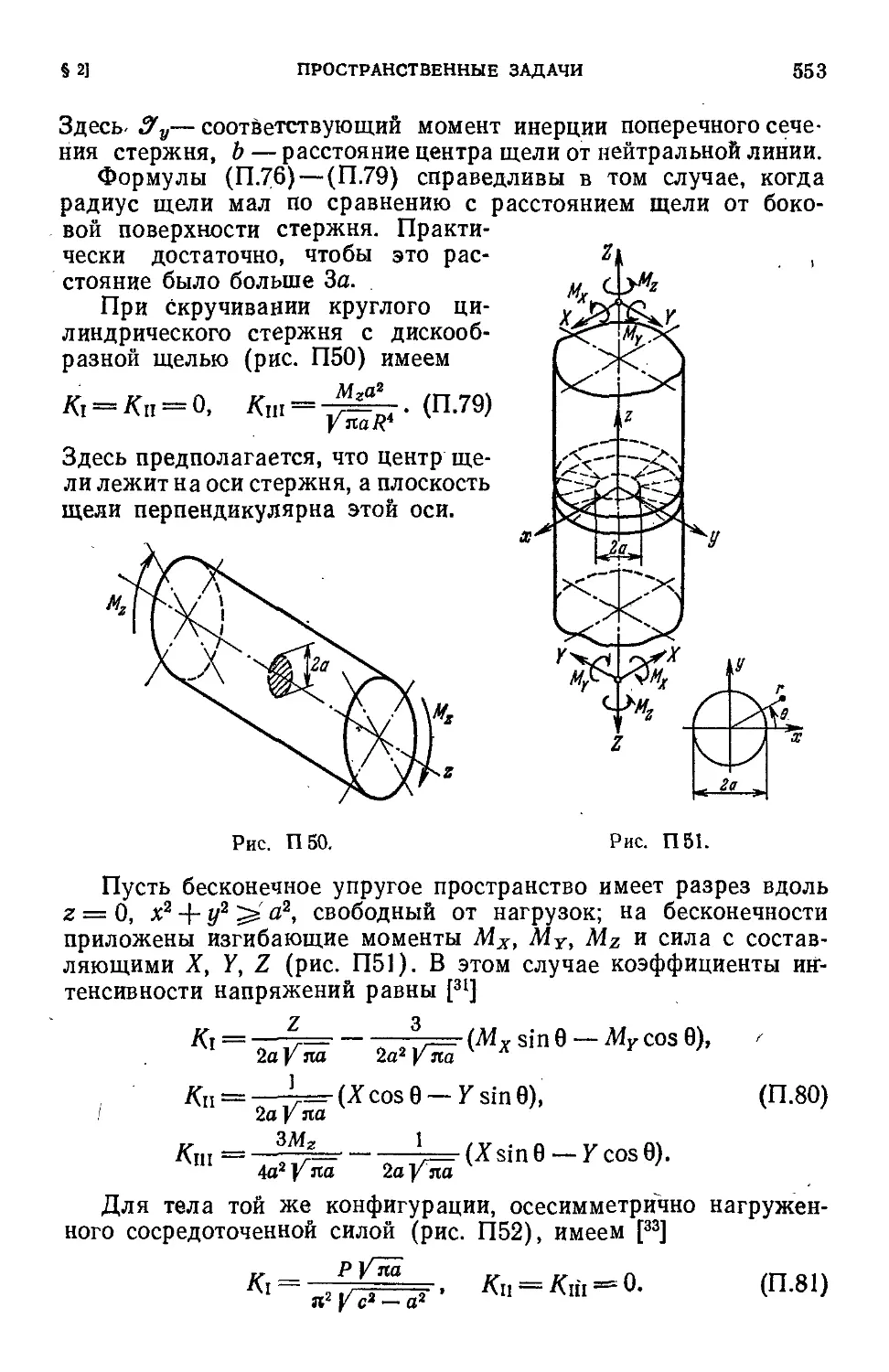
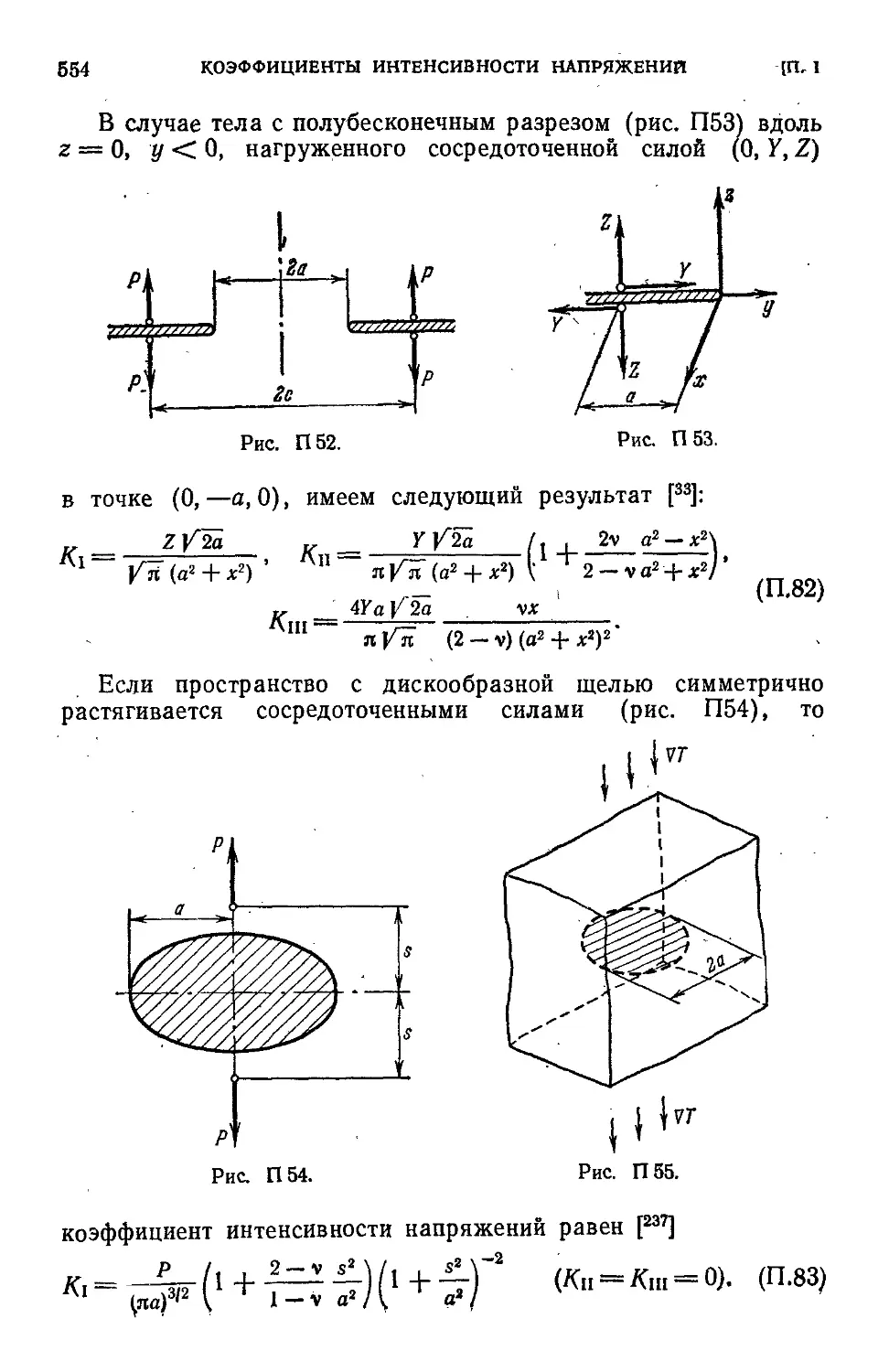
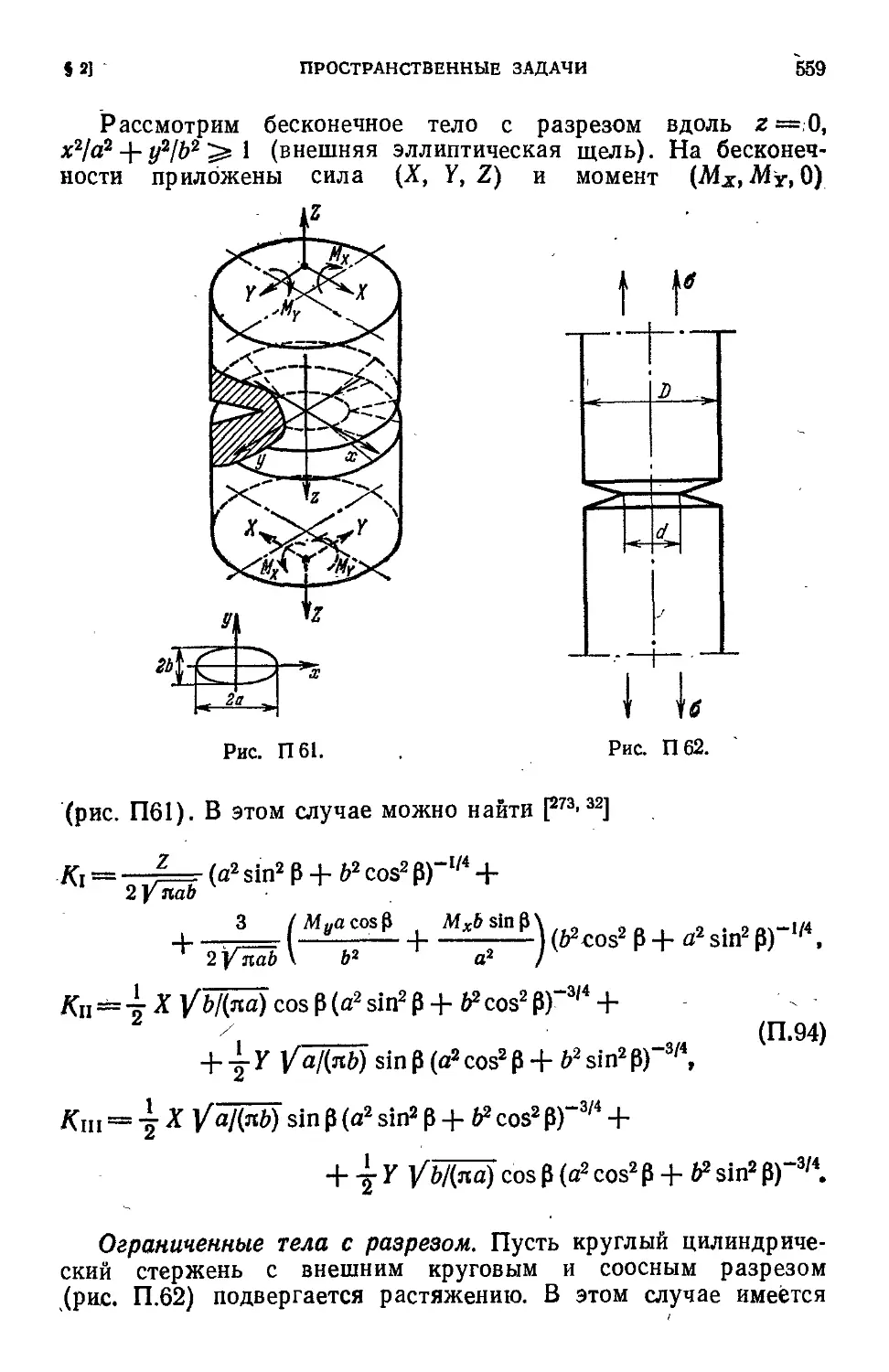
§ 2. Пространственные задачи 548
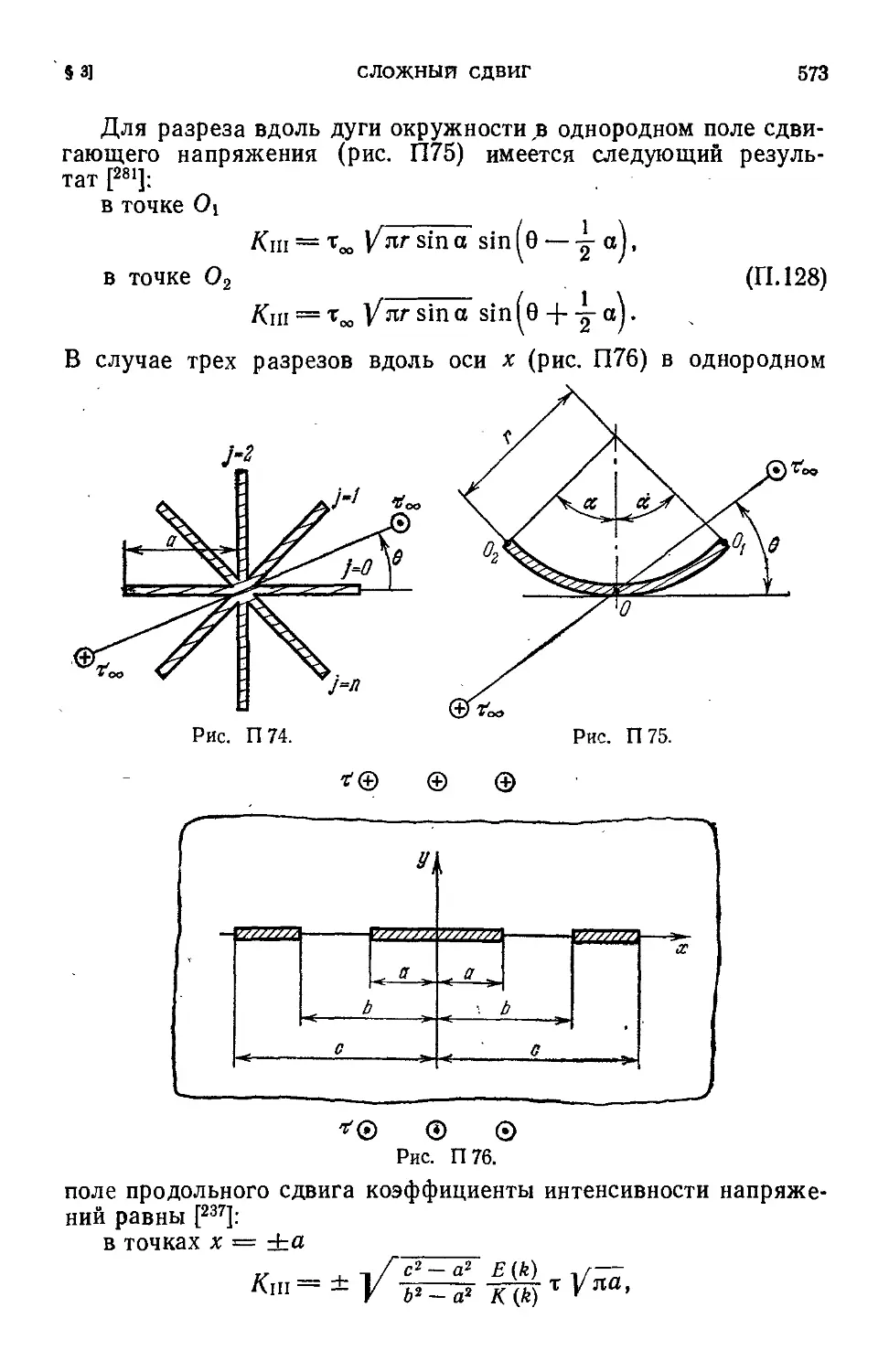
§ 3.-Сложный сдвиг 568
§ 4. Динамические задачи . - . . 577
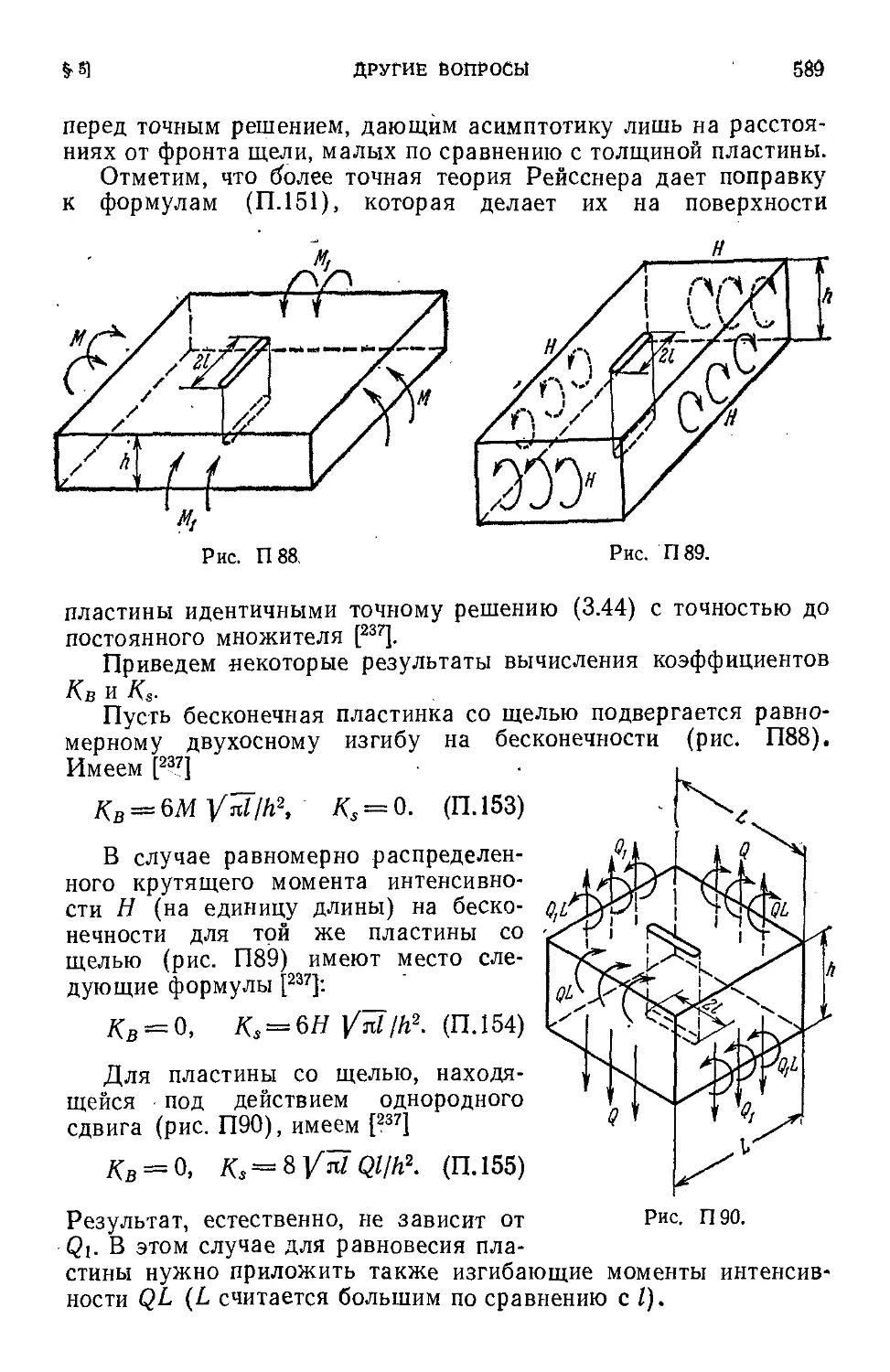
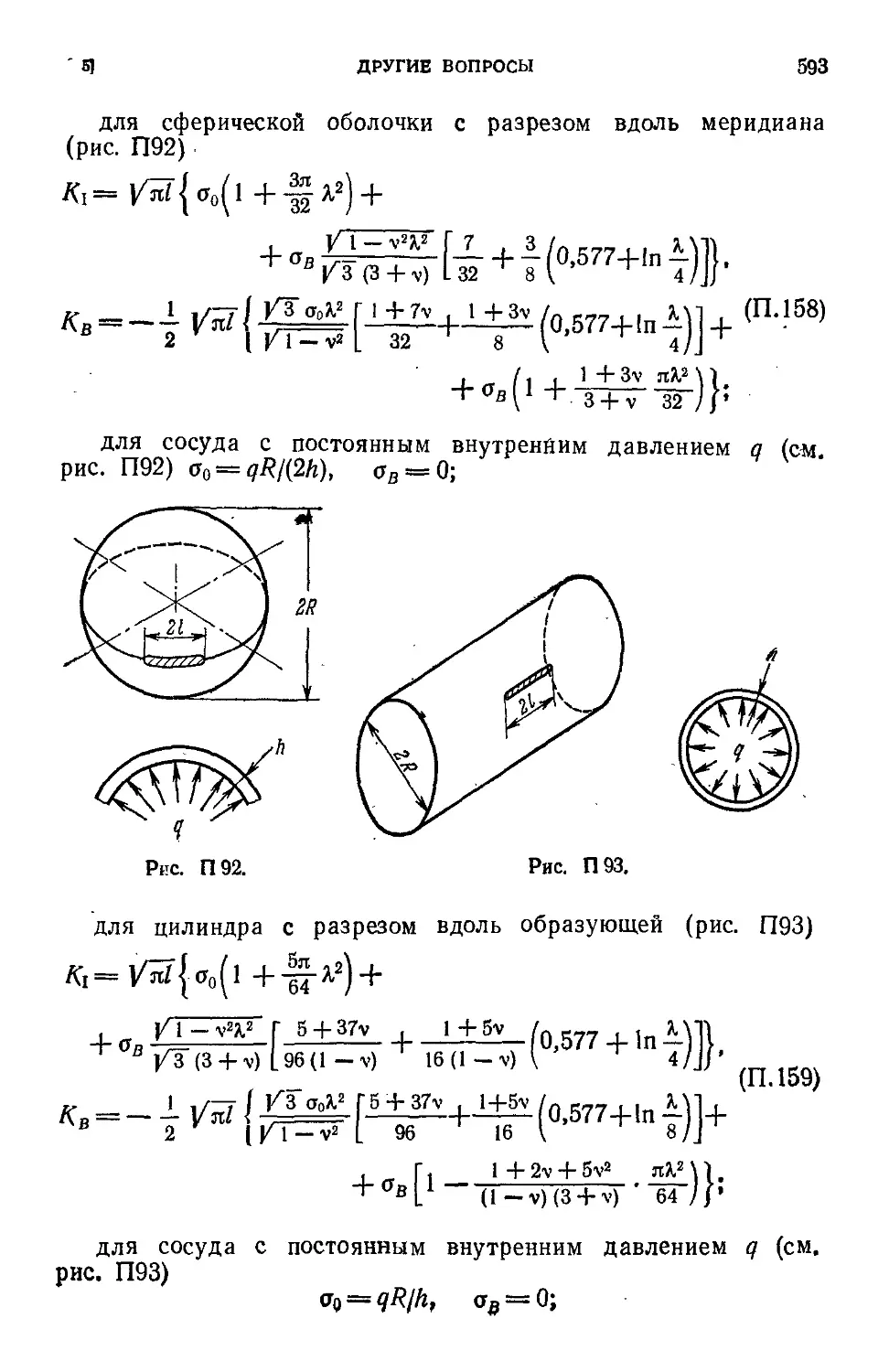
§ 5. Другие вопросы * -.........._ 586
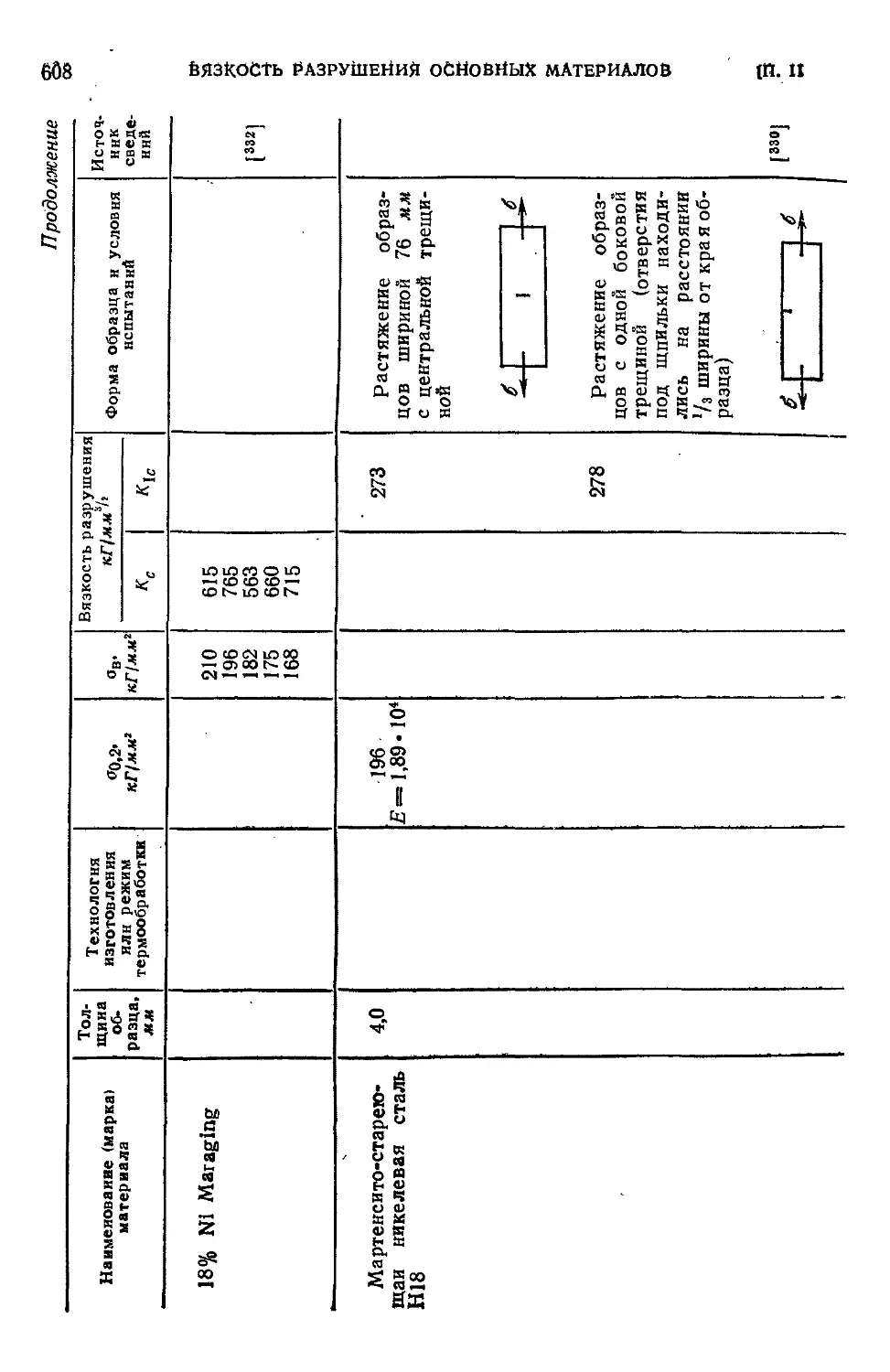
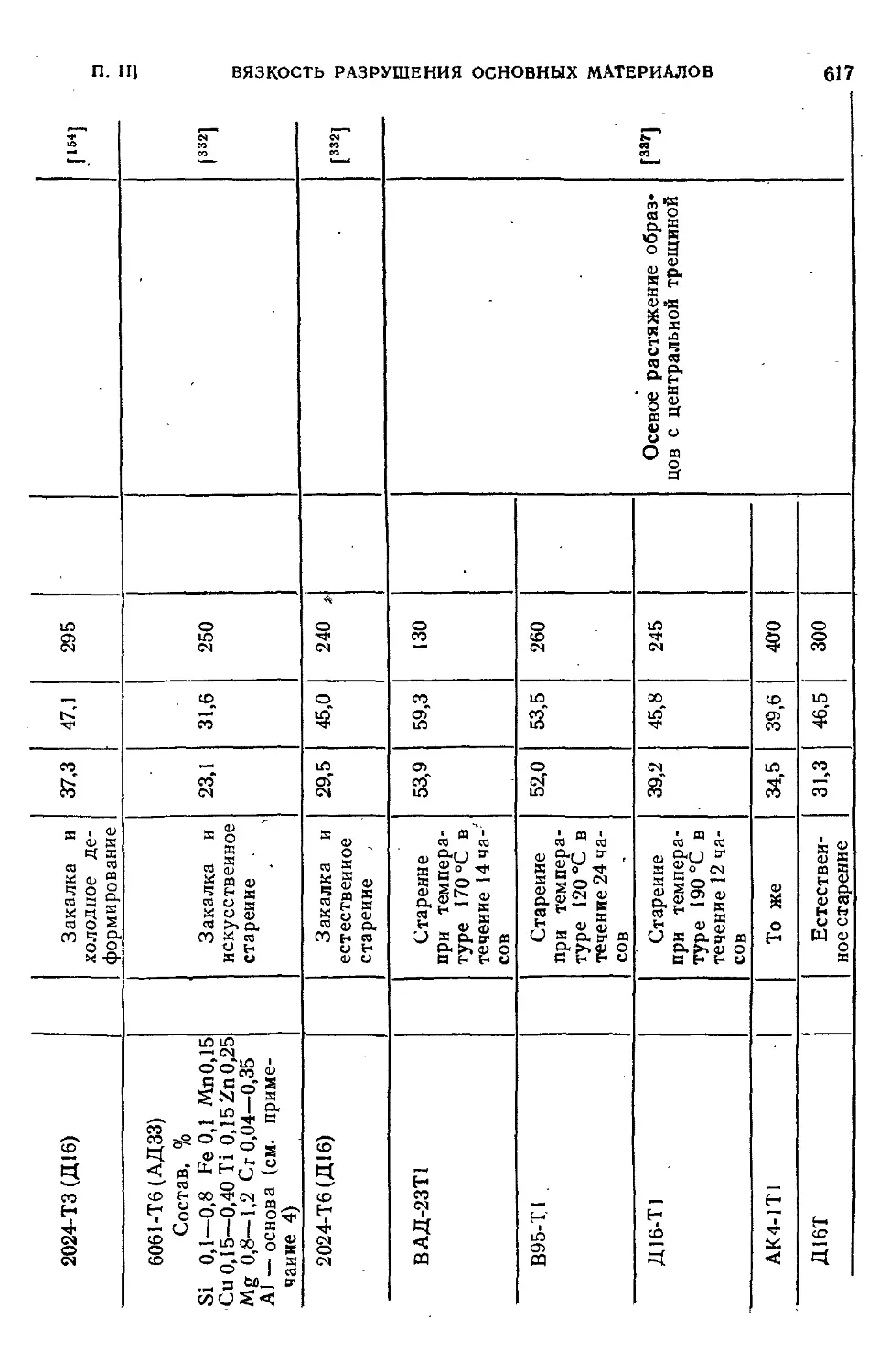
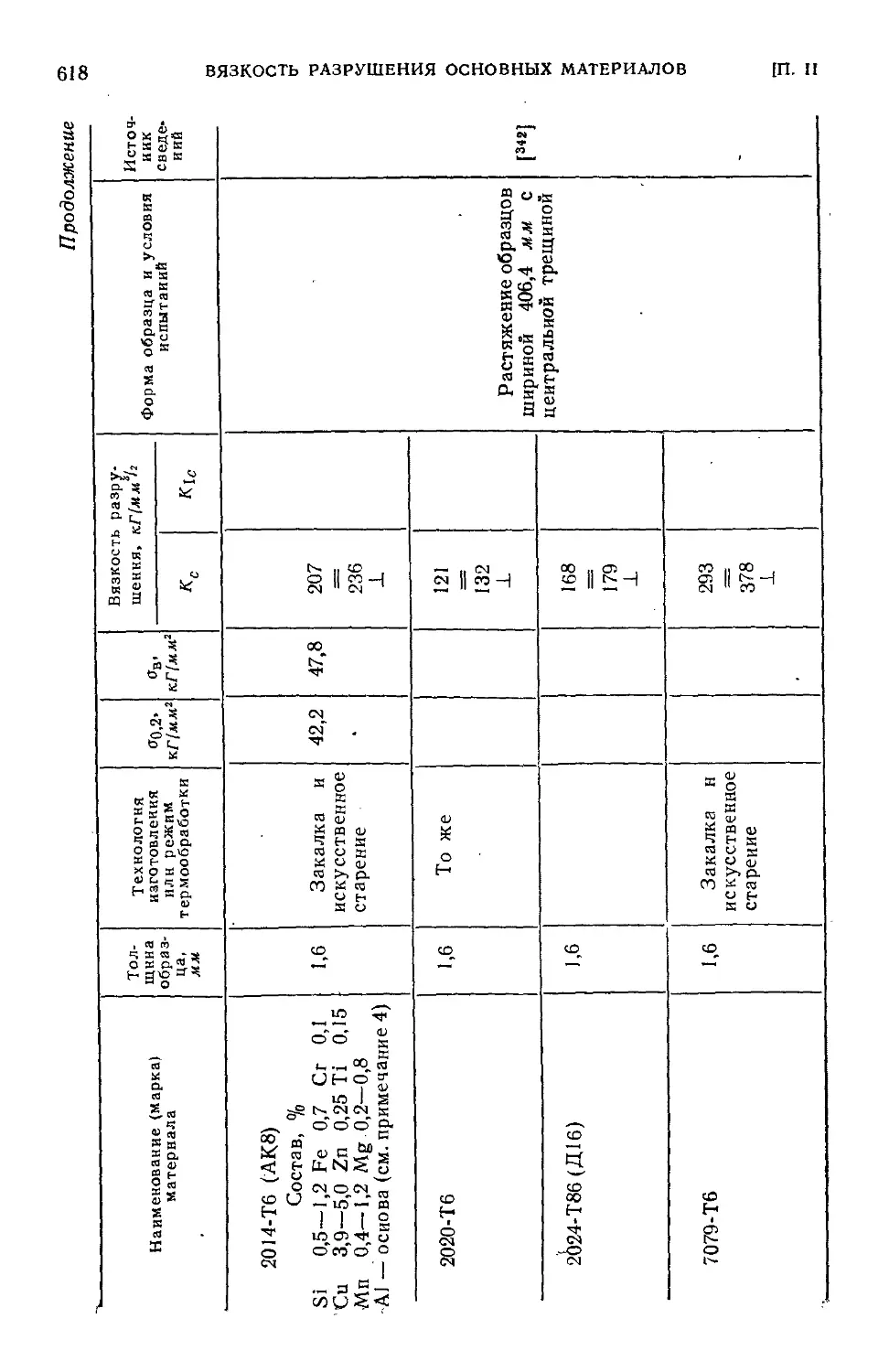
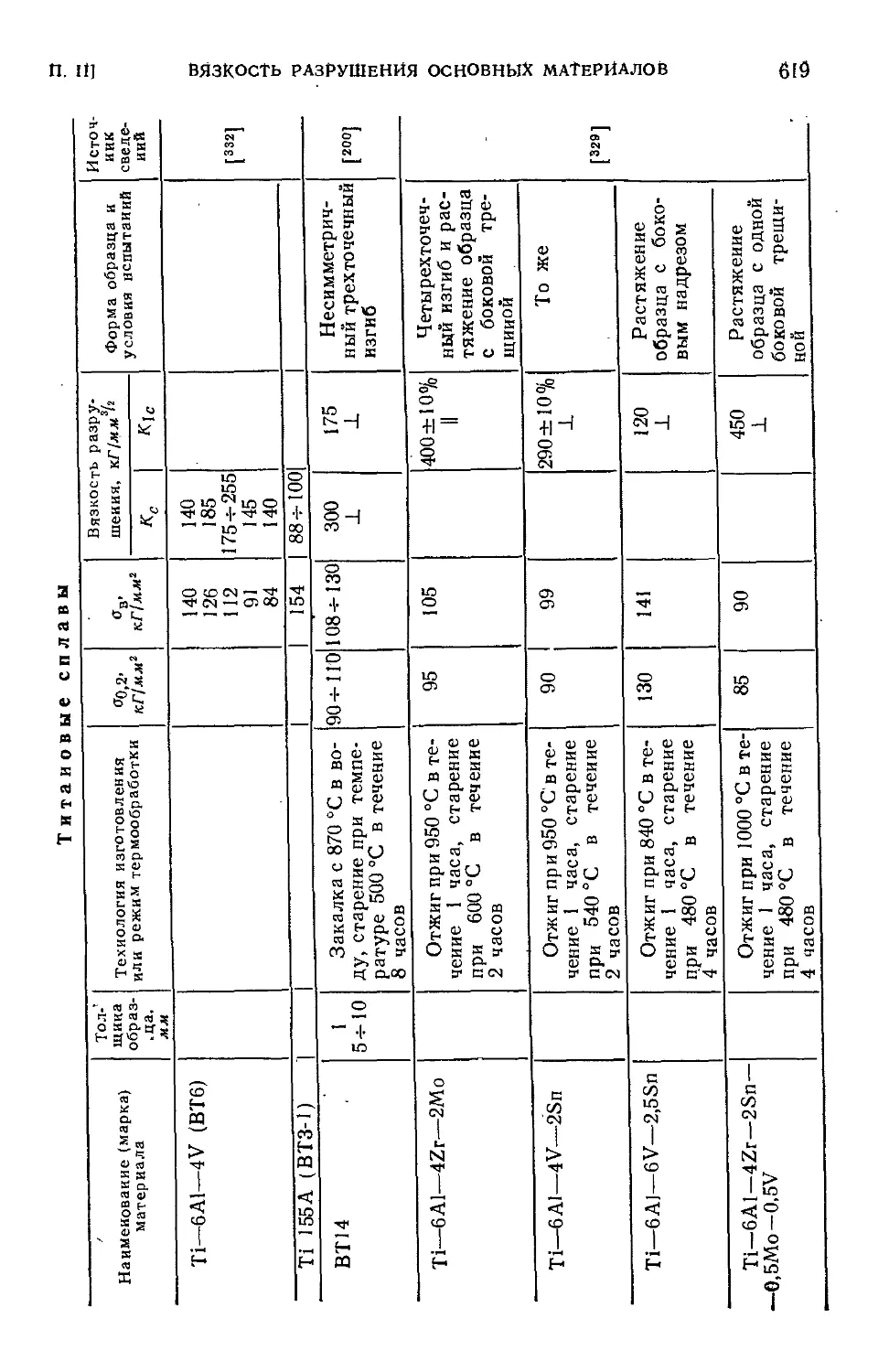
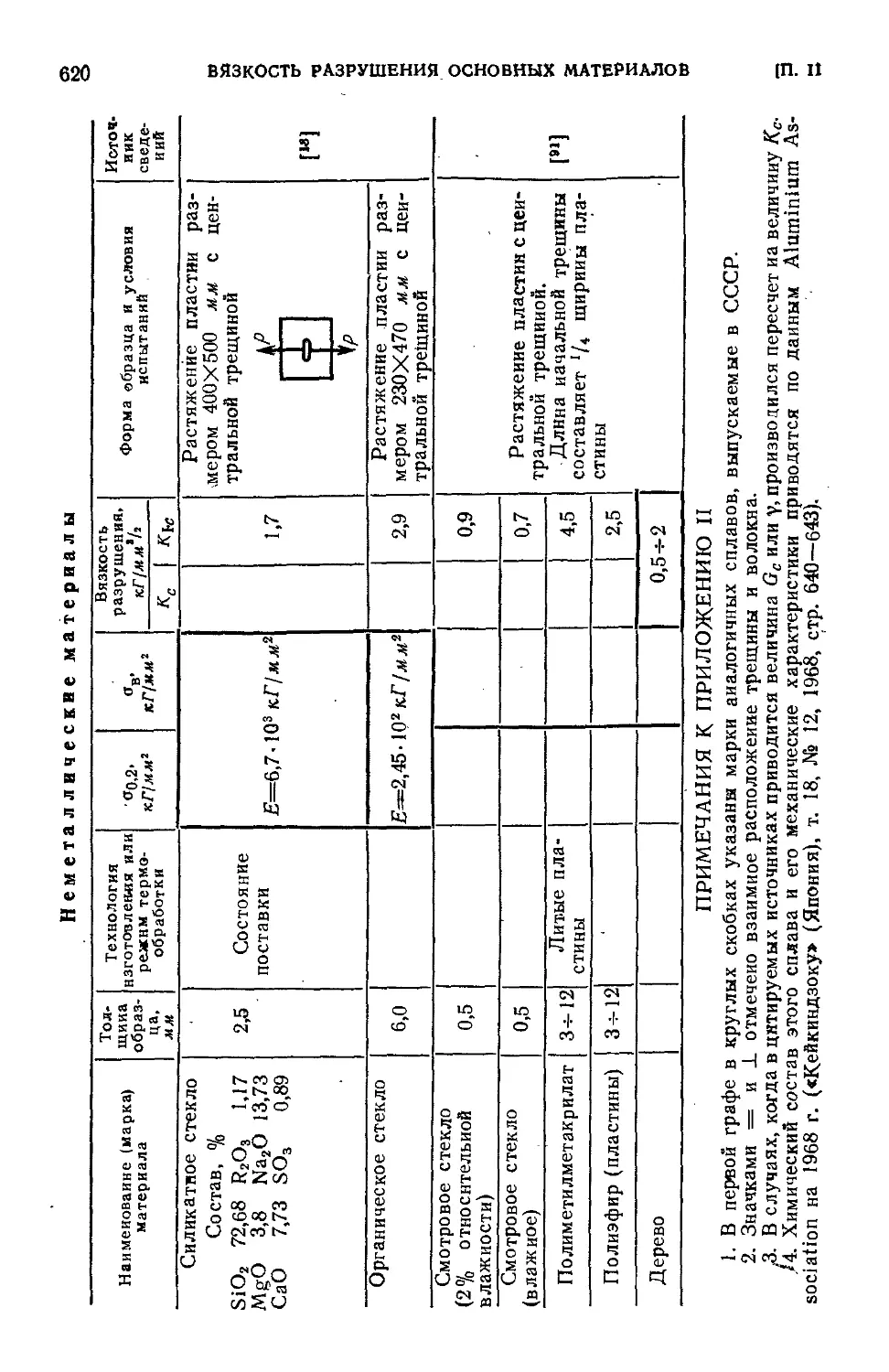
Приложение П. Вязкость разрушения основных конструкционных
материалов ....:.•...........- 607
Приложение III. Некоторые пары, металл — среда, для которых на-
наблюдается хрупкое разрушение материала, подверженного растяги-
растягивающим вапряжением 621
Литература . ' . 626
ПРЕДИСЛОВИЕ
Непредвиденные разрушения конструкций, как правило, яв-
являются хрупкими, т. е. объясняются постепенным или быстрым
развитием трещин. Механика хрупкого разрушения занима-
занимается изучением развития трещин в -хрупких и квазихрупких
телах*).
' Термин «механика разрушения», появившийся несколько лет
назад, употребляется в двояком смысле. К механике разруше-
разрушения в узком смысле слова относят исследования по распростра-
распространению трещин; за два последних десятилетия они получили ши-
широкий размах как в СССР, так и за рубежом. В более широком
смысле механика разрушения включает в себя тот раздел науки
о сопротивлении материалов, который изучает заключительную
стадию процесса деформирования. Тем самым, проблемы проч-
прочности сооружений входят в механику разрушения как ее важная
составная часть.
Хотя людям с древнейших времен приходилось строить раз-
различные, порой весьма сложные сооружения, знания о прочности
и разрушении материалов раньше приобретались эмпирически и
в значительной степени случайно, передаваясь из поколения в
поколение как некое искусство. У истоков научного подхода
к вопросам прочности и разрушения стоят такие корифеи, как
Леонардо да Винчи и Галилео Галилей. Леонардо да Винчи
первым начал проводить опыты по определению несущей спо-
способности (эксперименты с железной проволокой). Ему приписы-
приписывают открытие явления, которое называют теперь масштабным
эффектом. .Однако достижения Леонардо да Винчи остались
неизвестными последующим поколениям и поэтому не оказали
влияния на развитие механики разрушения. Основоположником
*) Тело называется хрупким, когда материал сохраняет свойство линейной
упругости вплоть до разрушения. Если характерный линейный размер области
около контура трещины, где материал отступает от свойства линейной упру-
упругости, мал по сравнению с длиной трещины (или с другим характерным раз-
размером тела), то такое, тело называют квазихрупким. В соответствующих слу-
случаях говорят о хрупком или квазихрупком разрушении, хрупкой или квази*
хрупкой трещине.
ПРЕДИСЛОВИЕ 1
механики разрушения по праву может считаться Галилей, уста-
установивший, что разрушающая нагрузка растягиваемого бруса
прямо пропорциональна площади его поперечного сечения и не
зависит от его длины. Этот вывод, модифицированный на
неоднородное напряженное состояние, до сих пор играет
основную роль в практических инженерных расчетах на проч-
,ность.
С именами Ш. Кулона, А. Сен-Венана, О. Мора, А. Гриффитса
связано дальнейшее развитие механики разрушения. Кулон, Сен-
Венан и Мор положили начало теории предельного равновесия,
а Гриффите — теории хрупкого разрушения. Обе эти теории, в
дальнейшем доведенные многочисленными последователями до
совершенства, составляют фундамент современной механики
разрушения.
В последние годы был достигнут значительный прогресс как
в области теоретического осмысления вопросов прочности и раз-
разрушения, так и в области инженерных приложений теоретиче-
теоретических результатов.
В этой книге излагаются основные идеи и методы- механики
хрупкого разрушения, а также некоторые их обобщения. Первая
глава имеет вводный характер, во второй и третьей главах изло-
.'жены физические и математические основы теории хрупкого раз-
разрушения. Главное внимание уделяется наиболее принципиаль-
принципиальным вопросам, относящимся к формулировке дополнительных
условий на фронте трещин и к постановке физически коррект-
корректных математических задач о разрушении твердых тел (четвер-
(четвертая— восьмая главы). В Приложении I для справок приведены
наиболее значительные результаты вычислений коэффициентов
интенсивности напряжений для тел с разрезами. Изложение
_ориентировано не только на научных работников и студентов,
но и на инженеров, в связи с чем в Приложениях II и III по-
помещены некоторые экспериментальные данные, относящиеся
к основным конструкционным материалам.
Частичное изложение некоторых из .упомянутых вопросов
можно найти во втором томе известного курса Л. И. Седова
«Механика сплошной среды» и в книге В. В. Панасюка «Пре-
«Предельное равновесие хрупких тел с трещинами». Весьма интерес-
интересный материал регулярно публикуется в двух международных
журналах по механике разрушения. Недавно в США вышло
семитомное энциклопедическое издание. «Разрушение», охваты-
охватывающее широкий круг вопросов механики разрушения. Однако
очень большой объем этого руководства, отсутствие единого
подхода1 и к тому же недостаточное освещение некоторых наи-
наиболее принципиальных вопросов распространения трещин
отнюдь не способствует усвоению читателем методов механики
разрушения.
8 ПРЕДИСЛОВИЕ
В настоящей монографии в основном содержатся резуль-
результаты, полученные автором. Литература по вопросам разрушения
столь обширна, что автор при всем своем желании не смог
уделить достаточного внимания многим весьма интересным и
важным исследованиям. Поэтому в данной книге в список ра-
работ вошел лишь необходимый минимум источников.
Автор выражает искреннюю признательность лицам, ока-
оказавшим помощь при подготовке книги: В. Д. Кулиеву, X. Хал-
манову, А. Б. Каплуну, В. М, Мирсалимову, В. М. Смольскому,
Г. Г. Кузьмину.
30 сентября 1971 т. Автор
ГЛАВА I
ВВЕДЕНИЕ
§ 1. Классификация реологических Моделей
В природе и человеческой практике встречается великое
многообразие материалов, процесс разрушения которых харак-
характеризуется различными свойствами. Прежде всего это металлы
и их сплавы, имеющие главное значение в инженерных кон-
конструкциях. Далее идут полимеры, биологические ткани и кости,
горные породы и грунты, сыпучие тела, стёкла и керамика, по-
пористые материалы, композиты, лед и т. п. Многообразны также
внешние условия, типы нагрузок, конфигурации конструкций,
температура и др. Исследованием разрушения отдельных мате-
материалов или некоторых их классов в определенных условиях
'занимаются в рамках различных дисциплин целые научные
направления. .
Для механики характерно стремление к описанию основных
черт явления разрушения в рамках строго сформулированных
и достаточно' общих математических моделей. Поскольку, по-
видимому; в настоящее время еще рано говорить о построении
какой-то общей теории разрушения, более предпочтительным
представляется развитие частных теорий, более или менее хо-
хорошо описывающих поведение некоторых классрв материалов
в определенных условиях. В связи с этим возникает необходи-
необходимость достаточно полной и общей классификации основных
типов поведения твердых тел и соответствующих им многочис-
многочисленных теорий.
Вначале дадим классификацию реологических моделей*).
Рассмотрим элементарный объем dxdydz, нагруженный по
поверхности напряжениями ац как некий «черный я,щик», на
вход которого подаются напряжения оч> а на выходе сни-
снимаются деформации etj. Будем считать, что если в число пара-
параметров, описывающих эту систему, ввести температуру Т, то
система будет замкнутой. Согласно этому феноменологиче-
феноменологическому допущению, деформации etj должны вполне опреде-
определиться величинами оц, Г и их эволюцией. При этом бесконечно
*) Основы классификации в рамках термодинамического подхода и
описание основных моделей сплошной среды можно найти в курсе Л. И. Се-
Седова [М. . '
10 ВВЕДЕНИЕ • [ГЛ. I
малые приращения выходных величин могут быть записаны
через соответствующие приращения damn, dt и dT в следую-
следующем виде:
dzi} = Ailmn damn + Ви dt + С{} dT A.1)
(t — время). Здесь Ацтп, Вц, Сц— некоторые функционалы от
параметров ъц(х,у,z, t), aij(x,y,z,t), T(x,y,z,t) в области, за-
занятой, телом.
Введем гипотезу «близкодействия». Согласно этой гипо-
гипотезе, параметры, определяющие уравнения A.1) для произ-
произвольного элементарного объема, не зависят от состояния лю-
любого другого элементарного объема, даже сколь угодно близко
расположенного. Кроме того, предполагается, что в уравнения
A.1) не входят объемные силы (в частности, инерционные и
гравитационные). Эта гипотеза основана на том физическом
факте, что силы взаимодействия элементарных частиц весьма
быстро убывают с увеличением расстояния между ними, так
что на расстояниях порядка Д (Д — характерный линейный
размер элементарного объема) их можно не учитывать. Систе-
Системы, удовлетворяющие этой гипотезе, будем называть систе-
системами с близко действием. Почти все известные в механике реоло-
реологические модели относятся к системам с близкодействием*).
Если силы, сцепления — дальнодействующие {таковы, на-
например, кулоновские силы в некоторых физических систе-
системах), то и в этом случае ввиду произвольного характера Д
его можно, вообще говоря, выбрать достаточно большим, что-
чтобы была справедлива гипотеза близ ко действия. Таким обра-
образом, учет взаимного влияния объемов тела в определяющих
уравнениях A.1) существен лишь тогда, когда размер Д из
каких-то дополнительных физических соображений не может
быть взят достаточно большим; последнее обстоятельство мо-
может иметь место, например, в тех случаях, когда характерный
размер тела сравним с радиусом «угасания» сил сцепления
(в однородных материалах) или с размером зерна (в неодно-
неоднородных материалах).
Функционалы Ацтп, Вц, Сц по t,x,y,z в определяющих
уравнениях A.1) в случае систем с близкодействием вырож-
вырождаются в функционалы только по t от параметров eij, оц, Т и
их производных по x,y,z любого конечного порядка.
Реологические модели для систем с близкодействием мож-
можно разбить на градиентные и безградиентные. В последнем
*) Заметим, что гипотеза «бдизкодействия» по существу равносильна до-
допущению о том, что элементарный объем с заданной системой параметров
можно считать замкнутой системой.
$1] . КЛАССИФИКАЦИЯ РЕОЛОГИЧЕСКИХ МОДЕЛЕЙ 11
случае в определяющие уравнения не входят производные по
x,y,z от Eij, вц, Т. Большинство рассматриваемых в механике
моделей являются безградиентными, однако в теории упруго-
упругости был предложен также ряд градиентных моделей. Заметим,
что физические теории микронеоднородного упругого тела при-
приводят к необходимости учета градиентных членов, когда про-
производные достаточно велики [2].
Если функционалы А^тп, Bjj, Сц не инвариантны относи-
относительно сдвига во времени*), то соответствующие системы на-
называют системами «со старением»; реологические свойства
таких систем изменяются с течением времени. Мы будем рас-
рассматривать только безградиентные модели, инвариантные от-
относительно сдвига во времени, для систем с близкодействием.
Дальнейшую классификацию таких систем естественно
провести по характеру реакции системы на внешние возмуще-
возмущения. Заметим, что в нашей системе (элементарном объеме)
роль реакции играют деформации е,ц, а роль внешних возму-
возмущений — нагрузка оц и температура Т на поверхности элемен-
элементарного объема. В данном случае вопрос о том, в каком
смысле понимаются, вообще говоря, конечные деформации ец
элементарного объема, не имеет принципиального значения.
Мы предполагаем, что, начиная с некоторого момента времени
t = 0, эволюция внешних возмущений ац и Г в точности из-
известна; считается известным также распределение Eij, оц и Т
в начальный момент t = 0. Элементарный объем состоит из
одних и тех же материальных частиц (х, у, z—'лагранжёвы
координаты). Требуется определить реакцию системы eij во
времени.
Реакция системы на внешнее возмущение может быть мгно-
мгновенной и с последействием (соответствующие системы будем на-
называть системами с мгновенной реакцией и с последействием).
Для систем с мгновенной реакцией Вц =. 0, а функционалы
Ацтп и Сц не зависят от времени (в том числе от производ-
производных определяющих параметров по t любого порядка). В таких
системах реакция на мгновенное возмущение появляется мгно-
мгновенно и в дальнейшем, вообще говоря, остается неизменной,
если Oij и Г не изменяются. В произвольных системах есте-
естественно представить полную реакцию (полное приращение де-
деформаций) в виде суммы мгновенной реакции и последействия.
Последнее по определению представляет собой ту часть полной
реакции, которая возникает с течение^ времени.
Предположим, что внешнее возмущение исчезает с течением
времени. При этом реакция системы также может исчезнуть.
*) Начальный момеш времени t = 0 считается фиксированным.
12 ВВЕДЕНИЕ [ГЛ. I
Системы, в которых реакция на исчезнувшее возмущение
также исчезает (хотя бы за бесконечно большое время), будем
называть системами с обратимой реакцией. Таким, образом,
полную реакцию произвольной системы на исчезнувшее-внеш-
исчезнувшее-внешнее возмущение в некоторый конечный момент времени можно
представить в виде суммы обратимой реакции и необратимой,
которая остается даже по истечении сколь угодно большого
промежутка времени. В свою очередь, каждое слагаемое со-
состоит из мгновенной реакции и последействия. Остаточные де-
деформации характеризуют «память» системы об исчезнувшем
внешнем возмущении. . '
Основные реологические модели па типу реакции можно
классифицировать следующим образом.
Термоупругое тело относится к системам с мгновенной
обратимой реакцией. Мгновенность и обратимость полной
реакции означает, что eij представляют собой некоторые одно-
однозначные функции Gij и Т. Таким образом, в этом случае коэф,-
фициенты Ацтп, Cn(Bij = 0) в определяющих уравнениях
A.1) представляют собой некоторые обычные функции от ац
и Т, удовлетворяющие, кроме того, условию существования
полного дифференциала. К тому же выводу можйо прийти, ис-
используя термодинамический подход. Уравнения A.1) допу-
допускают дальнейшие упрощения/ при наличии физической или
геометрической симметрии системы (например, изотропии), ма-
малости деформаций, линейности соотношений A.1),' изотермич-
ности процесса.
Упруго-пластическое тело принадлежит к системам с мгно-
мгновенной реакцией (Bjj = O). Введение дополнительной гипотезы
о существовании поверхности нагружения и применение ква-
квазитермодинамического постулата Драккера позволяют, по-ви-
по-видимому,' наиболее просто получить ассоциированный закон
течения, лежащий в основе современной теории упруго-пласти-
упруго-пластических сред. Вместо постулата Драккера^ можно использовать
также следующие два допущения: а) вся^ необратимая работа
переходит в тепло, б) скорость приращения энтропии макси-
максимальна; можно принять и некоторые другие допущения. Со-
Согласно ассоциированному закону, роль эксперимента, помимо
определения термоупругих констант, сводится к определению
поверхности нагружения и ее изменения при необратимых про-
процессах деформирования. Использование дополнительных физи-
физических принципов дает возможность найти в специальной
форме функционалы Aiimn и Сц из меньшего числа опытов.
Тела называют идеально упруго-пластическим, если соответ-
соответствующая поверхность нагружения не изменяется, при любом
процессе деформирования (в этом случае ее называют также
поверхностью текучести или условием текучести). Наиболее
Ij'ti: • КЛАССИФИКАЦИЯ РЕОЛОГИЧЕСКИХ МОДЕЛЕЙ 13
вдвестны варианты теорий течения, применяемые к металлам
и их сплавам, а также к грунтам.
Если имеет место простое нагружение, т. е. в каждой точке
тела параметры состояния -возрастают прямо пропорционально
параметру нагружения, то уравнение A.1) (при Вц = 0) ин-
интегрируется. То же самое справедливо для малой частицы при
любом фиксированном пути нагружения в пространстве (ац,
Т). Так подходят к изучению упруго-пластических сред в де-
деформационных теориях пластичности. -
Теории предельного состояния (идеальное жестко-пластиче-
жестко-пластическое тело, сыпучее тело, тело, не выдержквающее^растягиваю-
щих напряжений, и др.) можно рассматривать как предельные
случаи соответствующих теорий идеальной • упруго-пластиче-
упруго-пластической среды, когда в уравнениях опускаются члены с упругой
компонентой деформации.
Вязкое тело относится к системам с последействием (с ну-
нулевой мгновенной реакцией) и с полной необратимой реакцией;
в этом случае в уравнениях ¦ A.1) /4ijmn = Ci;= 0. При этом
естественно считать Вц обычными функциями ац, ы$ и Т.
В простейшем случае, когда В,, представляют собой линейные
функции о*;, получается классическая модель вязкой жидкости.
Если учесть также мгновенную деформацию, определяемую
согласно теории упруго-пластических сред, и считать Btj неко-
некоторыми функциями . аг, ег — г?-, и Т, то из A.1) получится
наиболее распространенный вариант теории ползучести метал-
металлов (г°и — необратимые мгновенные деформации). В основу
этой теории положено допущение о существовании потенциала
скоростей ползучести.
Наследственное тело с последействием и с полностью обра-
обратимой реакцией описывает поведение многих полимерных мате-
материалов. Весьма общее описание таких систем дается при по-
помощи обобщенной теории Вольтерра
г. t-f, amn(t')]dt' +
о
t f
+ J J KilHlmAT,t-t',t-t",akl(t'),amn(t")\dt'dt"+ .... A.2)
0 0
где -
Kltmn\T, t—t', СТт„(О1 = 0 при t'>t0,
' Ktjkimn\T, t—t', t—t", akt {f), ann (t")\ = 0 при /' >.4 t" > f»
KiimnlT.t, amn)^0 при t-*oo, A.3)
oo, f —* oo.
Kilmn(T, t, emn)-+0 при t-
КцЫтп{Т, t, t', akh dmn)->0 При t-
14 ВВЕДЕНИЕ !ГЛ. I
Здесь Кцтп, Kijkimn,... — непрерывные однозначные функции
аргументов Т, атп, аы,... и, вообще говоря, обобщенные функ-
функции /.
Если отказаться" от условий A.3), то появится также оста-
остаточная компонента деформаций, и уравениями A.2) можно
будет описывать также необратимую реакцию (ползучесть).
Наиболее широко распространен вариант линейного вязко-
упругого тела или наследственного тела Больцмана, содержа-
содержащийся в A.2).
Вязко-пластическое тело относится к разновидности нели-
нелинейно-вязких сред. Предполагается, что в пространстве (ац, Т)
существует поверхность, такая, что по одну сторону от этой
поверхности реакция на внешнее возмущение отсутствует, а по
другую сторону от нее среда ведет себя как вязкое тело. Про-
Простейшими моделями такого типа описывается поведение густых
смазок, металлов при высоких температурах и т. д. ,
Поведение рассматриваемой системы бписывается указан-
указанными основными типами реологических моделей (упруго-пла-
(упруго-пластическое, вязкое и наследственное тела) или некоторой их
комбинацией, если только в системе нет каких-либо скрытых
параметров (описывающих, например, химические реакции, фа-
фазовые переходы, электромагнитные эффекты и т. д.). В конкрет-
конкретных исследованиях важно не столько знание общей теории,
сколько искусство подбора наиболее простой модели, дающей
объяснение и описание наблюдаемого на опыте реологического
явления.
Правильный выбор реологической модели является опреде-
определяющим при решении проблемы разрушения и прочности; за-
задачи механики разрушения невозможно решать без предвари-
предварительного исследования деформативных свойств тел.
§ 2. Теории прочности
В расчетах на прочность обычно предполагается, что раз-
разрушение тела происходит, как только в некоторой точке его
определенная комбинация параметров ац, гц, Tut достигнет
критического значения. При этом сам процесс разрушения не
рассматривается. Ясно, что при таком подходе проблема проч-
прочности решается подбором той или иной реологической модели
и критерия разрушения (последний в сопротивлении материа-
материалов обычно называют теорией прочности).
Этот подход является прямым логическим следствием при-
принятого феноменологического рассмотрения в рамках указанных
параметров. Физически он оправдывается тем, что развитие
дефектов материала, приводящих к потере несущей способно-
способности, весьма часто происходит в узкой околокритической обла-
§ 21 ТЕОРИИ ПРОЧНОСТИ . 15
сти, так что детальное знание самого процесса разрушения
имеет второстепенное значение. При этом определяемый экспе-
экспериментально критерий разрушения отражает сложные микро-
микрофизические процессы разрушения, происходящие в масштабе
структурной ячейки вплоть до молекулярного уровня и приво-
приводящие к образованию макродефекта. Кроме того, поведение
макродефекта (понимаемого феноменологически как -некото-
-некоторый разрыв смещения) зависит от типа разрыва. Например,
образование дислокаций и линий скольжения, даже перерезы-
перерезывающих тело, как правило, не приводит к его разрушению.
В качестве критериальной величины обычно берут наиболь-
наибольшее главное ' напряжение, наибольшее главное относительное
удлинение, наибольшее главное касательное или октаэдриче-
ское напряжение, удельную энергию формоизменения, полную
удельную энергию деформации*). Каждый из критериев при-
применим при вполне определенных условиях для некоторого
класса материалов. Правильное использование этих критериев
существенно зависит от практического опыта исследователя.
^Накоплению такого опыта посвящено большинство эксперимен-
экспериментальных работ по прочности.
Заметим, что в разное время этим критериям придавали
различное значение, иногда абсолютизируя тот или иной кри-
критерий. Например, Ляме и Рэнкин принимали в качестве крите-
критерия прочности наибольшее главное напряжение, а Понселе и
Сен-Венан — наибольшую деформацию.
Приведем два наиболее ярких примера использования кри-
критерия 'наибольшего главного относительного удлинения.
1) При растяжении стержня под действием постоянного
напряжения о, вообще говоря, возникают необратимые дефор-
деформации ползучести (наиболее существенные для металлов при
высоких температурах и полимеров). При этом большую часть
времени до разрушения т стержень «ползет» с постоянной ско-
скоростью деформации ёс (установившаяся ползучесть). Таким
образом, имеем
тё(, = е0, A.4)
где во — наибольшее относительное удлинение. Если считать
величину ео постоянной материала и учесть эмпирическую за-
зависимость скорости установившейся ползучести от нагрузки а
Ьс — С^ или гс = С2ап A.5)
(Ci, Сг, К, п — постоянные материала), то формула A.4) позво-
позволяет найти время до разрушения (долговечность) в зависимо-
зависимости от приложенного напряжения.
*) Часто применяют также условие сухого трения со сцеплением (Кулоч)
Щ ?Eфбщенную теорию прочности Мора.
16 ВВЕДЕНИЕ [ГЛ. I
Получающаяся зависимость для долговечности действи-
действительно наблюдается для.широкого класса полимеров и метал-
металлов и даже для таких материалов, которые до разрушения
практически не обнаруживают необратимых деформаций и раз-
разрушаются хрупко. (Для последних приведенные выше сообра-
соображения теряют смысл.)
2) Пусть на металлический стержень действует периодическое
во времени напряжение 0 = 0(/) (циклическое нагружение).
Обозначим наибольшую величину растягивающего, напряжения
в течение цикла через 0Шах, а наименьшую — через —0Шах-
. Так как структура металлов существенно неоднородна, то
даже при сравнительно малых напряжениях в местах локаль-
локальной концентрации напряжений возникают местные пластиче-
ческие зоны, соответствующие определенным структурным из-
изменениям. Это приводит к накоплению необратимой пластиче-
пластической деформации Аер за цикл, величина которой обычно очень
мала. Предполагая ее не зависящей от числа предшествующих
циклов, можно найти необратимую деформацию стержня е0 за
п циклов до разрушения:
п-.Дер = е0. . .A.6)
Если теперь считать е0 постоянной материала и допустить,
что по аналогии с накоплением необратимых деформаций пол-
ползучести справедлива формула
Дер = С3е^ах . A.7)
(С3, % — постоянные материала), то по формуле A.6) можно
найти число циклов до разрушения в- зависимости от макси-
максимального напряжения за цикл (кривая Велера). Получаю-
Получающаяся зависимость действительно наблюдается для металлов
в том случае, когда величина 0max больше предела усталости.
При меньшей нагрузке, по-видимому, вследствие эффекта
микроприспособляемости становится неприемлемым допущение
о накоплении пластических деформаций.
Эти примеры нетрудно обобщить на произвольный трехмер-
трехмерный случай, если взять в качестве критериальной величины,
например, второй инвариант девиатора напряжений (октаэд-
рическое напряжение) ввиду сдвиговой природй необратимых
деформаций в металлах.
§ 3. Вязкое разрушение
Изучение критериев разрушения (теорий прочности) в рам-
рамках указанного подхода до сих пор сохраняет основное практи-
практическое значение при расчетах на прочность/ Однако исследова-
исследований только в этом направлении недостаточно по целому ряду
причин.
§3]
ВЯЗКОЕ РАЗРУШЕНИЕ
17
Прежде всего, многие материалы в достаточно широком
интервале изменения внешних условий и параметров системы
способны испытывать значительную пластическую деформацию
до разрушения. Для таких материалов более правильным ока-
оказывается предположение о том, что разрушению тела соответ-
соответствует постепенный переход наиболее опасного .сечения тела
в пластическое состояние, когда в некоторой окрестности этого
сечения выполняется условие пластичности, т. е. определен-
определенная комбинация параметров aij и Т достигает критического зна-
значения. Этот тип разрушения будем называть вязким разру-
разрушением. .
Следует отметить, что в однопараметрических" задачах
(растяжение, изгиб или кручение одним моментом и т. п.) вы-
выбор критерия разрушения или условия пластичности не имеет
существенного значения, так как в любом случае момент раз-
разрушения будет определяться некоторым критическим значением
<0
,р
о
Рис. 1.
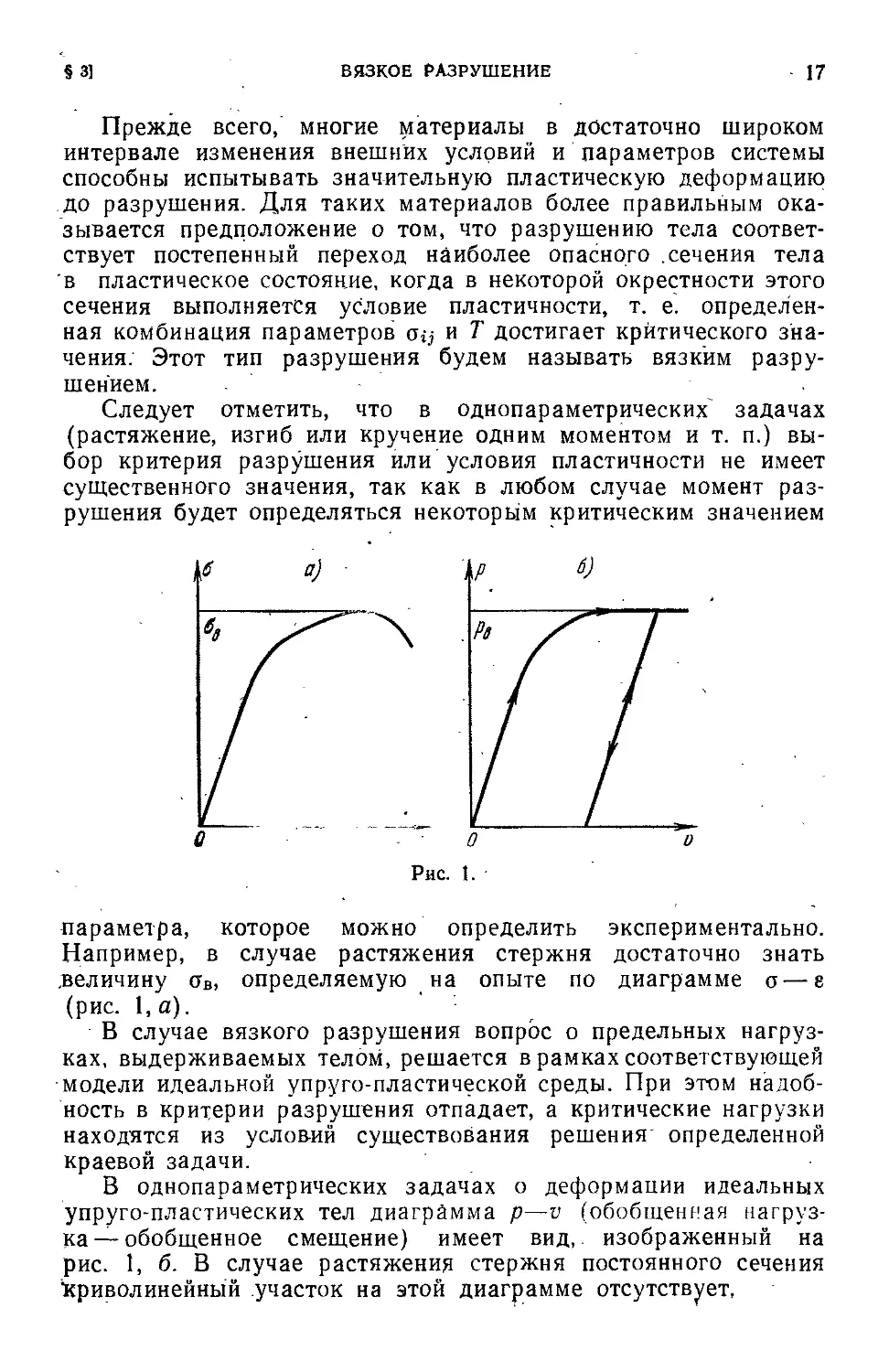
параметра, которое можно определить экспериментально.
Например, в случае растяжения стержня достаточно знать
.величину 0в, определяемую на опыте по диаграмме a—е
(рис. \,а).
В случае вязкого разрушения вопрос о предельных нагруз-
нагрузках, выдерживаемых телом, решается в рамках соответствующей
модели идеальной упруго-пластической среды. При этом надоб-
надобность в критерии разрушения отпадает, а критические нагрузки
находятся из условий существования решения определенной
краевой задачи.
В однопараметрических задачах о деформации идеальных
упруго-пластических тел диаграмма р—v (обобщенная нагруз-
нагрузка—обобщенное смещение) имеет вид, изображенный на
рис. 1, б. В случае растяжения стержня постоянного сечения
'Криволинейный участок на этой диаграмме отсутствует,
18
ВВЕДЕНИЕ
!ГЛ.
Если в уравнениях идеальной упруго-пластической модели
опустить члены с упругой деформацией, то получатся уравне-
уравнения соответствующей теории предельного состояния. Приме-
Применение теории предельного состояния позволяет значительно
упростить определение верхней и нижней оценок для разру-
разрушающих нагрузок, а в ряде случаев получить совпадение верх-
верхней и нижней оценок, т. е. точно найти предельные нагрузки
в случае вязкого разрушения, не решая сложной упруго-пла-
упруго-пластической задачи.
Изложение хорошо развитых к настоящему времени теорий
вязкого разрушения можно найти, например, в монографиях
Надаи [3], Ю. Н. Работнова [4], Хилла [5], Койтера [6], В. В. Со-
Соколовского [7], Д- Д- Ивлева [8] и др.
§ 4. Работа Гриффитса «Явление разрушения
и течения твердого тела»
Существует широкий круг явлений хрупкого разрушения,
для которых представление о критериях разрушения (теориях
прочности) неприменимо. Еще Фохт, проведя серию экспери-
экспериментов х; хрупкими материалами, пришел- к отрицательному
заключению относительно возможно-
А А | | | | сти применения к ним критериев проч-
111111, ности. Бриджмен обнаружил явление
«пинч-эффекта», которое невозможно
объяснить с позиций теорий прочности.
Открытый А. Ф. Иоффе эффект уве-
увеличения прочности кристалла камен-
каменной соли при растворении его поверх-
поверхностных слоев, многочисленные случаи
разрушения металлических конструк-
конструкций при напряжениях, меньших услов-
условного предела текучести о0,2, а также
многие другие явления разрушения,
принципиально необъяснимые с точки
зрения теорий прочности, заставили
ряд исследователей отказаться от га-
лилеева представления о прочности ов
как о некоторой константе материала.
Это направление в механике разруше-
разрушения основано на изучении самого про-
процесса разрушения. Оно берет начало от работы Гриффитса [9],
опубликованной в 1920 г. В этой работе была рассмотрена сле-
следующая задача.
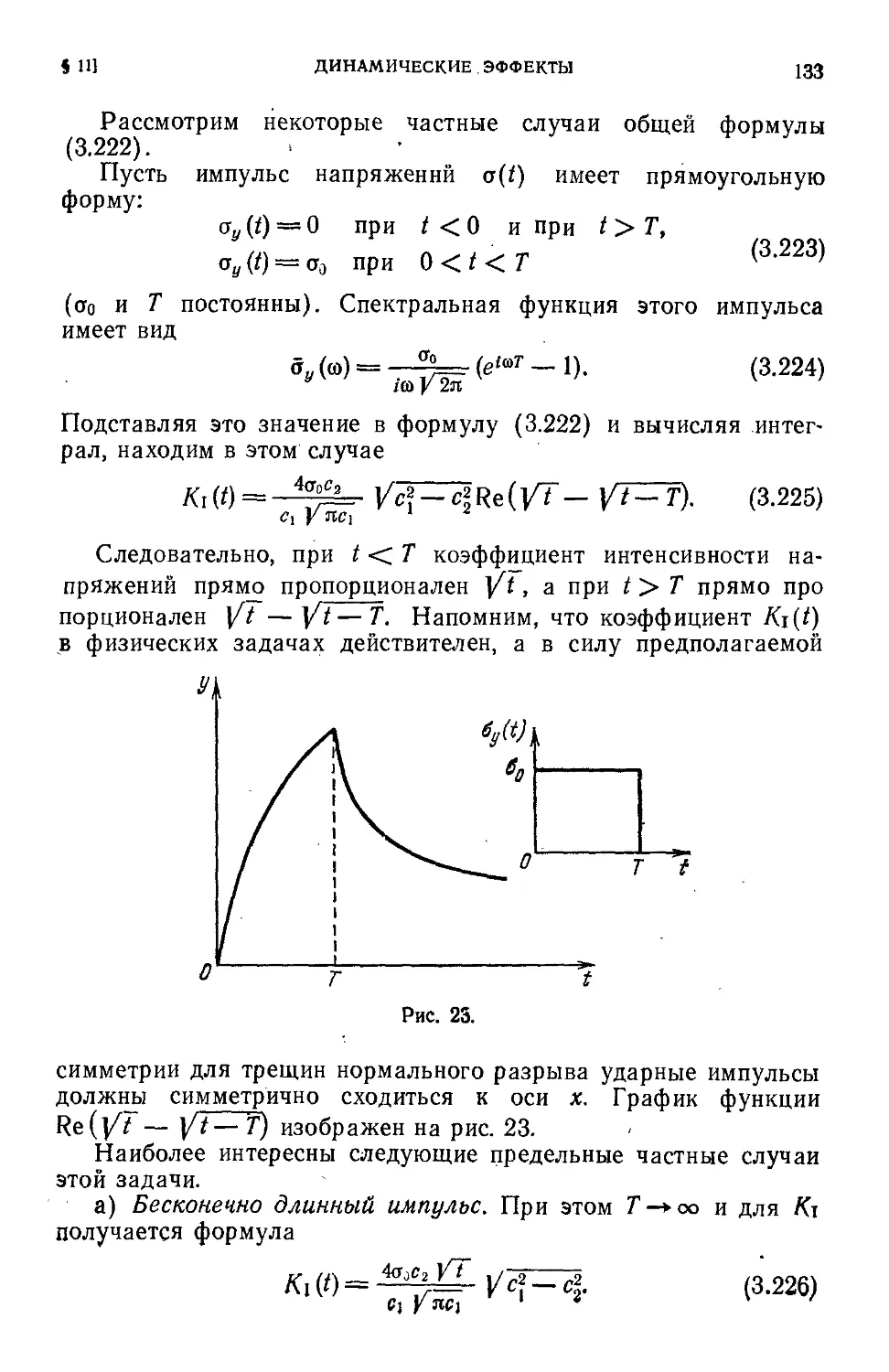
Пусть тонкая хрупкая пластина равномерно растягивается в
одном направлении напряжениями р в своей плоскости (рис.2).
mill
Рис. 2.
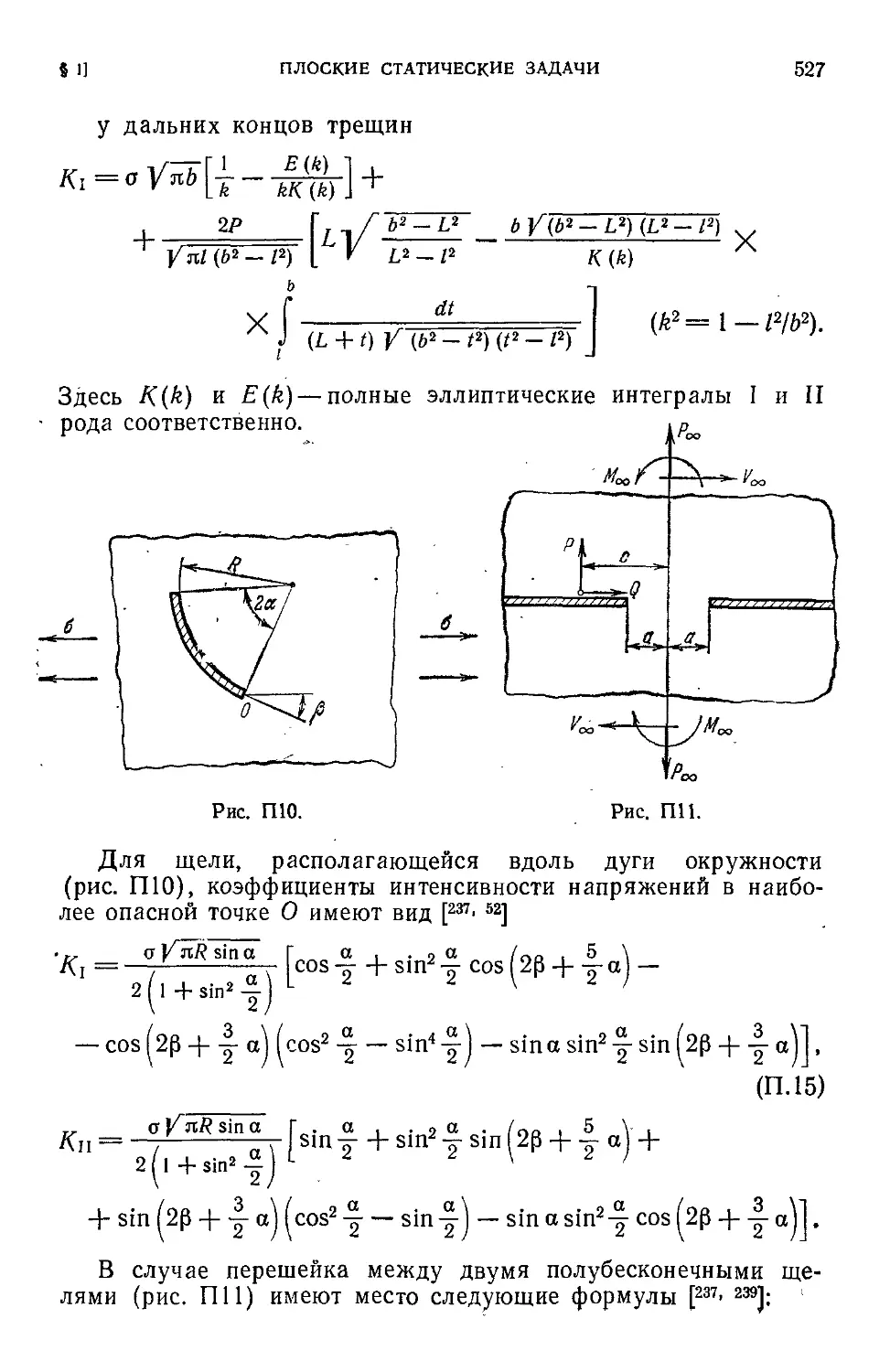
§ 4] РАБОТА ГРИФФИТСА Ш
В пластине имеется сквозная трещинагдлины 21, ориентирован-
ориентированная перпендикулярно направлению растяжения. Длина тре-
трещины считается малой по сравнению с размерами пластины
(/<о, I <.b). Опыт показывает, что, начиная с некоторого р,
происходит развитие трещины, сопровождающееся увеличением
свободной поверхности. Поэтому Гриффите ввел поверхностную
энергию хрупкого тела и сформулировал принцип, согласно
которому существующая трещина станет лавинообразно рас-
распространяться, если только скорость освобождения энергии
упругой деформации превзойдет прирост поверхностной энер-
энергии.трещины, т.-е. если
dAU/dl>4y. A.8)
Здесь AU— изменение упругого потенциала пластины вслед-
вследствие наличия трещины, у— поверхностная энергия единицы
свободной поверхности.
Упругая энергия U пластины с трещиной равна^ Uo —.AU,
где Uo — упругий потенциал пластины без трещины. Величина
AU равна произведению средней площади области концентра-
концентрации напряжений (пропорциональной Р), на среднее значение
плотности упругого потенциала (пропорциональной р2/Е, где
Е— модуль Юнга)
AU = X0l2p2/E, U=U0 — AU. A.9)
Здесь множитель Яо может зависеть только от коэффициента
Пуассона*).
Так как величина Uo не зависит от /, то, согласно A.9) и
A.8), находим в критическом состоянии
2Еу = %0рЧ. A.10)
Таким образом, из A.10) получается следующая зависи-
зависимость нагрузки от длины трещины:
p = %i VEy/l. A.11)
Здесь Я1 — множитель порядка единицы **).
Формула A.11), которая представляет собой выражение
для разрушающей нагрузки в зависимости от длины начальной
трещины, является основным достижением теории Гриффитса.
*) р своей основополагающей работе [9] Гриффите провел точный рас-
расчет на основе решения Инглиса и нашел значение константы Ко, однако сде-
сделал это неверно. Правильное значение этой постоянной (равное 2л для тон-
тонкой пластины) было указано им впоследствии.
**) Для плоского напряженного состояния Ai =
20 ВВЕДДНИ? ' 1ГЛ. t
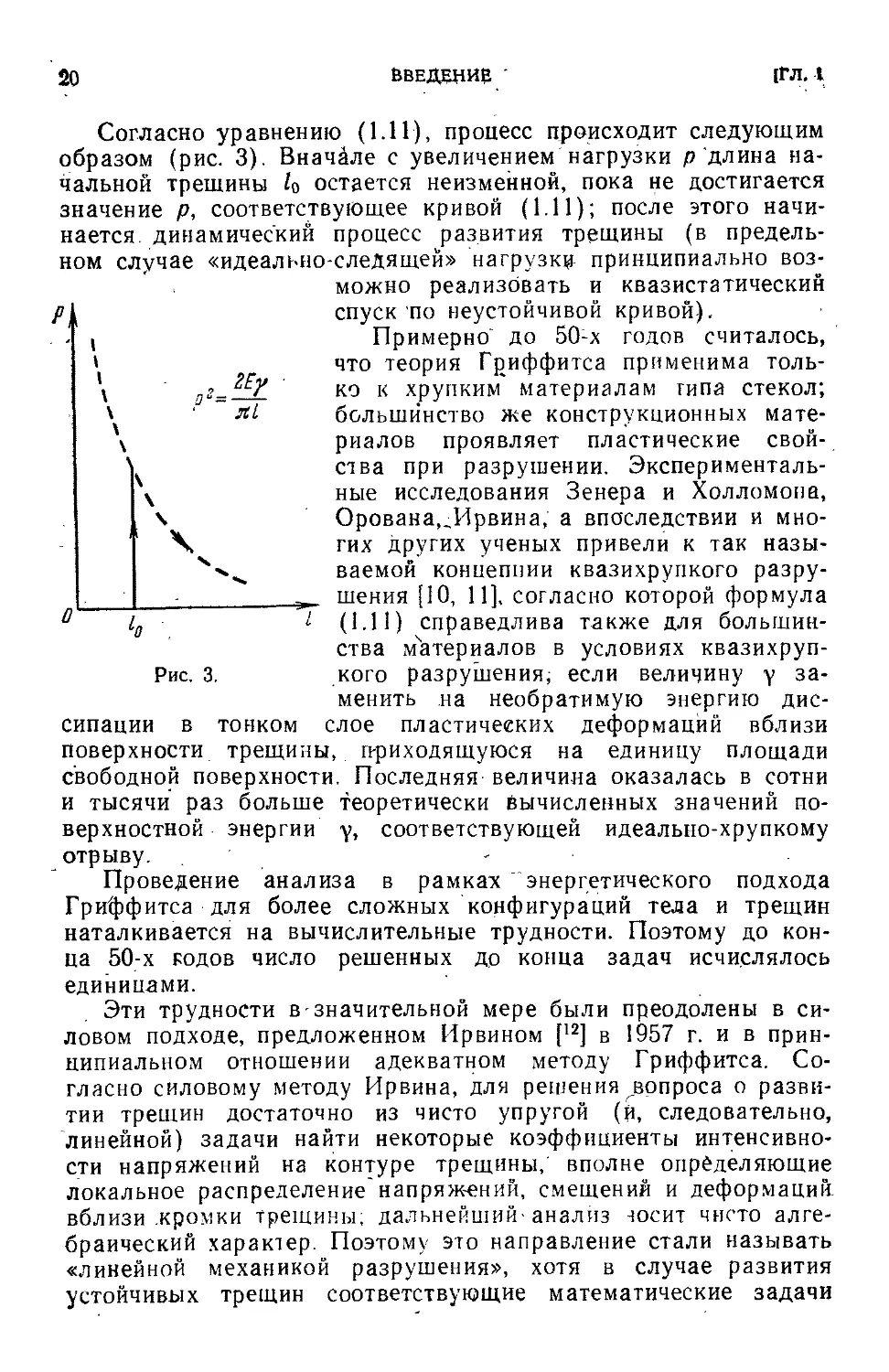
Согласно уравнению A.11), процесс происходит следующим
образом (рис. 3). Вначале с увеличением нагрузки р длина на-
начальной трещины А) остается неизменной, пока не достигается
значение р, соответствующее кривой A.11); после этого начи-
начинается динамический процесс развития трещины (в предель-
предельном случае «идеально-следящей» нагрузку принципиально воз-
возможно реализовать и квазистатический
спуск по неустойчивой кривой).
Примерно" до 50-х годов считалось,
i что теория Гриффитса применима толь-
\ /;?=_? ко к хрупким материалам типа стекол;
\ ' я1 большинство же конструкционных мате-
материалов проявляет пластические свой-
свойства при разрушении. Эксперименталь-
Экспериментальные исследования Зенера и Холломона,
ч Орована,.Ирвина, а впоследствии и мно-
\ гих других ученых привели к так назы-
ч>.^ ваемой концепции квазихрупкого разру-
разрушения [10, 11], согласно которой формула
l0 ^ A.11) справедлива также для большин-
большинства материалов в условиях квазихруп-
Рис. 3. кого разрушения, если величину у за-
заменить на необратимую энергию дис-
диссипации в тонком слое пластичееких деформаций вблизи
поверхности трещины, п-риходящуюся на единицу площади
свободной поверхности. Последняя величина оказалась в сотни
и тысячи раз больше теоретически вычисленных значений по-
поверхностной энергии у» соответствующей идеально-хрупкому
отрыву. -
Проведение анализа в рамках энергетического подхода
Гриффитса для более сложных конфигураций тела и трещин
наталкивается на вычислительные трудности. Поэтому до кон-
конца 50-х родов число решенных до конца задач исчислялось
единицами.
Эти трудности в-значительной мере были преодолены в си-
силовом подходе, предложенном Ирвином [12] в 1957 г. и в прин-
принципиальном отношении адекватном методу Гриффитса. Со-
Согласно силовому методу Ирвина, для решения ^вопроса о разви-
развитии трещин достаточно из чисто упругой (и, следовательно,
линейной) задачи найти некоторые коэффициенты интенсивно-
интенсивности напряжений на контуре трещины, вполне определяющие
локальное распределение напряжений, смещений и деформаций
вблизи .кромки трещины; дальнейший-анализ -юсит чисто алге-
алгебраический характер. Поэтому это направление стали называть
«линейной механикой разрушения», хотя в случае развития
устойчивых трещин соответствующие математические задачи
НЕКОТОРЫЕ ЗАМЕЧАНИЯ 21
относятся к классу нелинейных задач, с неизвестной заранее '
|раницей. - ¦ -
fc Наиболее серьезное возражение против теории Гриффитса
|остоит в том, что она чрезмерно упрощает ряд гораздо более
Вложных явлений разрушения. Некоторые из таких явлений
|писаны ниже (§ 6 гл. IV, а также главы V—VII): Однако
Существование явлений-, для "объяснения которых теория Гриф-
(|йтса не годится, подчеркивает ее значение как некоторого;
Универсального предельного случая более общих, но зато и
|Ьлее сложных теорий, В этом смысле механика хрупкого раз-
разрушения, основанная, по существу, на теории Гриффитса, за-
занимает в механике разрушения место, аналогичное тому, кото-
которое занимает теория упругости в механике твердого деформи-
деформируемого тела.
" Величину у по традиции часто называют пов'ерхностной
Энергией; на самом деле она представляет собой необратимую
работу (на единицу площади), так как трещины всегда необ-
необратимы. Для ее обозначения применяются также следующие
термины: удельная энергия диссипации, энергия разрушения,
эффективная поверхностная энергия, скорость освобождения
упругой энергии (последний термин—-для величины, рав-
равной 2у). ¦ ¦
Следует подчеркнуть, что под необратимостью трещин пони-
понимается их неспособность «залечиваться» мгновенно, сразу после
снятия внешних нагрузок. «Залечивание? трещин, происходящее
пр диффузионному (например, сращивание двух кусков металла
Ври сжатии)* или биологическому (например, заживление по-
пореза) механизмам и протекающее во времени, здесь не рас-
рассматривается.
§ 5. Некоторые замечания
В современной механике разрушения, берущей начало от
работ. Гриффитса, Дж. Тейлора, Орована, Ирвина, -в качестве
исходных обычно используются следующие соображения.
Разрушение твердого тела почти всегда происходит вслед-
вследствие развития в нем некоторых поверхностей разрыва смеще-
смещений. При этом, если реализуется разрыв нормального к поверх-
поверхности смещения, то говорят о трещине нормального разрыва
^отрыва) или просто трещине; если же реализуется разрыв ка-
касательного к поверхности смещения, то говорят о трещине
сдвига, полосе скольжения или дислокации. Роль указанных
двух типов разрывов различна в различных конкретных усло-
условиях. С уменьшением прочности материала, увеличением тем-
йературы при сжатии, как правило, возрастает роль трещин
Сдвига и дислокаций. С увеличением прочности, уменьшением
Температуры, при наличии циклических нагрузок, агрессивных
22 . ВВЕДЕНИЕ |ГЛ. !
сред, облучения, как правило, возрастает роль трещин нормаль-
нормального разрыва.
Развитие поверхностей разрыва начинается с несовершенств
структуры материала, которые приходится рассматривать в
начальный момент как некоторые заданные конечные возмуще-
возмущения, всегда присутствующие в системе. Эти возмущения обычно
рассматривают в виде некоторых начальных трещин или дисло-
дислокаций, что хорошо согласуется с прямыми наблюдениям».
Дальнейшее развитие начальных возмущений при нагружении
может происходить по-разному.
Для роста дислокаций характерно почти одновременное и
стабильное развитие "сразу многих дислокаций, образующих по-
полосы скольжения и целые пластические области. Поэтому тео-
теория дислокаций яйляется физической основой феноменологиче-
феноменологической теории пластичности. Как уже отмечалось, модель идеаль-
идеального упруго-пластического тела и теории предельного состояния
(типа теорий Мора) дают ответ на вопрос о предельных на-
нагрузках и несущей способности конструкции в рамках самой
реологической модели без привлечения каких-либо дополнитель-
дополнительных критериев прочности.
Для роста трещин характерно преимущественное развитие
одной, наиболее опасной трещины (однако есть исключения,
например, рост трещин в условиях сжатия), ее способность к
быстрому неустойчивому росту, обычно приводящему к разде-
разделению, тела на части. При составлении критерия прочности на
основе теории трещин в большинстве случаев получаются обыч-
обычные теории прочности, однако фигурирующие в них константы
следует считать уже зависящими от размеров начальной тре-
трещины, а также от ее формы и места расположения. Впрочем,
для широкого круга явлений разрушения микронеоднородных
тел прочность не зависит от величины начального возмущения
(начальной трещины) и определяется характерными парамет-
параметрами структуры тела, например, величиной зерна [13].
Таким образом, формально к теории трещин можно подойти
как к простейшему*обобщению обычных теорий прочности пу-
путем введения одного дополнительного внутреннего структурного
параметра, не участвующего в формулировке реологической мо-
модели. Такой подход созвучен идее о введении дополнительных
структурных параметров в уравнения состояния, развиваемой
Л. И. Седовым и Ю. Н. Работновым.
Не следует забывать также о том, что исследование про-
процесса разрушения весьма часто представляет самостоятельный
интерес, вне связи с вопросом о несущей способности.
Исторически теория дислокаций и теория трещин складыва-
складывались отдельно; различие формального аппарата этих теорий
объясняется тем обстоятельством, что в теории дислокаций рас-
§ 51 НЕКОТОРЫЕ ЗАМЕЧАНИЯ 23
сматривают непосредственно разрывы смещений и потому в ли-
линейной теории имеют дело с логарифмическими особенностями,
а в теории трещин на поверхности разрыва обычно задают си-
силовые условия и потому имеют дело со степенными особенно-
особенностями. Однако между этими теориями имеется глубокое внут-
внутреннее сходство, заключающееся в том, что коэффициентам при
этих особенностях в обеих теориях придается смысл основных
параметров системы. Заметим так-
также, что зависимость характерной
нагрузки р от характерного смеще-
смещения v для идеально-хрупкого тела
с трещинами имеет вид, изображен-
изображенный на рис. 4. Криволинейный уча-
участок диаграммы отвечает устойчи-
устойчивому росту трещин, стрелки указы-
указывают направления, по которым раз-
разрешается движение изображающей
точки.
В теории трещин наиболее прин-
принципиальным моментом является р .
формулировка условия локального
разрушения в рассматриваемой
точке контура трещины. Для решения вопроса о развитии тре-
трещины это так же важно, как, например, выбор правильного
условия текучести в случае вязкого разрушения.
Теория предельного состояния и теория хрупких трещин со-
составляют основу современной механики разрушения. Это мате-
математически завершенные теории, на основе которых было решено
много проблем большого практического значения. Эти теории
дают идеализированное описание"свойств вязкого и хрупкого
разрушения (пластичности и хрупкости), которые в разной мере
присущи всем твердым телам.
В реальных условиях прочность твердого тела может.зави-
может.зависеть от следующих основных факторов: а) вид материала,
б) форма и размер тела, в) время, г) число циклов нагрузки
(в случае циклического нагружения), д) температура, е) сте-
степень агрессивности внешней среды, ж) скорость и предыстория
деформирования, з) внешнее излучение и электромагнитное
поле. Оказывается, существует некоторая переходная зона из-
изменения указанных параметров, которая отделяет область вяз-
вязкого разрушения от области хрупкого разрушения, в которой
эксплуатация конструкции обычно считается недопустимой.
В области вязкого разрушения расчет прочности производят или
по теории предельного состояния, или по теориям прочности.
Перечислим основные факторы, способные вызвать охрупчи-
вание и, как следствие, ослабление конструкции:
24 ВВЕДЕНИЕ [ГЛ. I
— увеличение содержания углерода в стали;
— близость напряженного состояния к равномерному все-
всестороннему растяжению;
— увеличение прочности металла при термообработке (не
всегда); - -
— увеличение габаритов конструкции;
— наличие концентраторов напряжения;
— увеличение числа циклов нагрузки;
— понижение температуры;
— наличие водорода во внешней среде;
— коррозионная и адсорбционная активность внешней среды;
— наличие жидкого металла в контакте с конструкцией (не
всегда);
— увеличение скорости нагружения (не всегда);
— наличие влаги в окружающей среде (не всегда);
— радиационное издучение (в особенности-^ потоки про-
протонов).
Вывод о недопустимости работы конструкции в области
хрупкого разрушения связан с трудностью "обнаружения зара-
заранее, методами неразрушающего контроля, трещиноподобных де-
дефектов, могущих привести к разрушению и фигурирующих в
формулах хрупкой прочности. Следует иметь в виду, что типы
таких дефектов многообразны; Зто могут быть, например,, раз-
различного рода непровары в сварных конструкциях, зоны окислен-
окисленного или охрупченного металла, загрязнения, инородные вклю-
включения металлургической или технологической природы и т. д.
К сожалению, во многих ответственных конструкциях не удает-
удается избежать даже весьма больших по^размерам дефектов.
Внезапные хрупкие поломки конструкции при напряжениях,
меньших предела текучести, связаны прежде всего с общей тен-
тенденцией использования все более прочных (и, как правило, бо-
более хрупких) материалов, со специфическими условиями работы
некоторых конструкций, вызывающими рост усталостных и кор-
коррозионных трещин (например, в химически активных средах).
Нет сомнения, что вывод о недопустимости работы конструкции
в области хрупкого разрушения имеет временный характер, и
в будущем, по-видимому, его придется- пересмотреть.
Отметим в заключение два важнейших круга задач, когда
вопрос о предельных нагрузках может быть в принципе решен
без привлечения механики разрушения, на основе решения за-
задачи в рамках реологической модели: а) задачи, в которых тело
способно испытывать произвольные конечные деформации,
б) задачи на'потерю устойчивости.
ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ
СТРУКТУР
. § 1. Точный квантовомеханический метод
Все тела представляют собой совокупность атомных ядер и
электронов; объем, занимаемый этими частицами, ничтожно
мал по сравнению с объемом образуемого ими твердого тела.
Каждая из частиц представляет собой некоторый сгусток мате-
материи, являющийся носителем массы, энергии и заряда. Заряд
ядра всегда положителен и равен Ze, где Z — порядковый номер
соответствующего химического элемента в таблице Менделеева,
е — абсолютная величина (отрицательного) заряда электрона
(е = 4,8-10~10 электростатических единиц). Масса покоя элек-
электрона те = 9,1-10~28 г, а масса ядра почти точно равна Ата,
где А — массовое число (атомный вес) соответствующего хи-
йического элемента или некоторого его изотопа, та—атом-
яая единица массы (та = 1,66 • 10~24 г). Радиус ядра имеет по-
порядок 10~13—10~12 см, а межатомное расстояние — порядок
ТО'8 см. ¦ . '
Пока еще не существует теории, которая объясняла бы ато-
атомистическую природу материи; последняя принимается как не-
некоторый исходный (по существу, чисто эмпирический) факт во
рсех физических теориях. Процесс разрушения твердых тел в
©бычных условиях представляет собой весьма слабое (химиче-
(химическое) взаимодействие указанных элементарных частиц. Каждая
вз частиц создает вокруг себй электромагнитное поле и, в свою
ряередь, находится в силовом поле, созданном всеми другими
Частицами (при изучении процессов разрушения в большинстве
«еЛучаев можно пренебречь ядерным и гравитационным взаимо-
Й?йствием). Кроме того, сами элементарные частицы можно
считать материальными точками, не имеющими размеров. Почти
бегда можно пренебрегать также релятивистскими эффектами,
явственными лишь при скоростях движения элементарных
астиц, близких к скорости света. Заметим, что в некоторых
яучаях, кроме обычных пространственно-временных координат,
г 4ементарным частицам следует приписывать дополнительную
Яезавиеимую переменную — спиновое число.
26 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР {ГЛ. II
В основе теории твердого тела, объясняющей, в частности,
его .дефармативные и прочностные свойства, лежит квантовая
механика. Используя квантовомеханический подход, все эмпи-
эмпирические постоянные, фигурирующие в феноменологических тео-
теориях упругости, пластичности, ползучести, разрушения и т. д.,
можно, в принципе, точно вычислить, коль скоро известны
строение и химический состав тела. Более того, в принципе
можно заранее (до опыта) определить все наиболее устойчивые
или наиболее прочные структуры элементарных частиц; можно
также предсказать поведение любой структуры ,при изменении
внешних условий.
Однако по целому ряду причин возможные рамки таких вы-
вычислений (и любых других, основанных на атомистических
представлениях) ограничены, по существу, ситуациями, близ-
близкими в некотором смысле или к идеальному беспорядку, или
к идеальному порядку в расположении частиц. Первая ситуа-
ситуация реализуется в идеальных газах, вторая — в идеальных кри-
кристаллах. В остальных случаях приходятся привлекать допол-
дополнительные сведения и эмпирические факты; поэтому соответ-
соответствующие теории имеют частный характер и пригодны для
описания только вполне определенных свойств системы в неко-
некоторых границах изменения внешних параметров. Это обстоя-
обстоятельство объясняется не столько математическими трудностями
решения задач квантовой механики для многих частиц (а они
весьма велики), сколько тем, что точная структура любого твер-
твердого тела заранее неизвестна.
Большинство конструкционных материалов состоит из мно-
множества нерегулярно расположенных мелких кристаллов (поли-
(поликристаллические тела). Таковы, например, металлы и их спла-
сплавы. В лучшем случае при описании структуры таких тел можно
надеяться на определение функций распределения кристаллов
по величине, форме, расположению и т. д., на определение ме-
места расположения и размера наиболее крупных кристаллов
или дефектов типа трещин, дислокаций, инородных включений
и т. п. ' ¦
В полимерах роль таких зерен играют различного рода над-
надмолекулярные образования, в аморфных телах типа стекол —
начальные флуктуации структуры, имеющие технологическое
происхождение (например, трещины). Опыт показывает, что
прочность твердого тела существенно зависит от характера и
величины таких образований, размеры которых значительно
больше среднего межатомного расстояния.
В рамках классической электродинамики определение поня-
понятия твердого тела как некоторой системы электрических заря-
зарядов вызывает существенные затруднения.
§ П ТОЧНЫЙ КВАНТОВОМЕХАНИЧЕСКИИ МЕТОД 27
Действительно, запишем уравнения Максвелла для точечных
зарядов, движущихся в пустоте [1, 14]:
=-i-^, div#=0,
if+±LJ, • B.1)
Здесь Е и Я — векторы напряженностей электрического и маг-
магнитного полей соответственно, / — вектор плотности тока, t —
время, р — плотность заряда (представляемая, в нашем случае
суммой дельта-функций), с — скорость света в вакууме (с =
=3-1010 см/сек). Величина каждого точечного заряда кратна е.
Сначала покажем, что при отсутствии внешних полей любое
расположение покоящихся зарядов неустойчиво, т. е. стабиль-
стабильные структуры из покоящихся электрических зарядов невоз-
невозможны. Действительно, допустим, что существует некоторое
расположение покоящихся точечных зарядов в пространстве. Из
соображений анализа размерностей энергия взаимодействия
равна ае2/г, где а — некоторое число, свое для каждого распо-
расположения зарядов, г — характерный линейный размер (например,
кратчайшее расстояние между зарядами). Поэтому сила вза-
взаимодействия, возникающая при всестороннем равномерном рас-
растяжении, будет равна производной по г от энергии взаимодей-
взаимодействия и всегда отлична от нуля, так что состояние покоя
неустойчиво.
Теперь покажем, что при отсутствии внешних полей не су-
существует решений уравнений Максвелла, отвечающих устано-
установившимся периодическим движениям точечных зарядов в конеч-
конечном объеме. Опять-таки допустим, что существует некоторое
такое движение; при этом движении, очевидно, каждый точеч-
точечный заряд должен описывать замкнутую траекторию в про-
пространстве. Скорость изменения кинетической энергии Тп произ-
произвольно фиксированной частицы с зарядом е равна
dTJdt = eEv, ¦ B.2)
уде v — вектор скорости частицы.
Из первого и третьего уравнений B.1) легко получить сле-
следующее соотношение:
-в4?- + -Я-~-= — — JE — HrotE + Etotff. B.3)
!Гак как
u{EXH) HiE — ErotH,
равнение B.3) можно записать в виде
jJL f B.4)
28 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР [ГЛ. II
Проинтегрируем B.4) по некоторому конечному объему V,
включающему в себя установившиеся траектории всех частиц,
которые согласно предположению образуют рассматриваемое
твердое тело; используя теоремуч Остроградского, получаем
BXmdZ. B.5)
Так как ток, создаваемый зарядом- е, равен ev6(r — г0) (где
г0-*-'радиус-вектор заряда), то интеграл JEdV можно запи-
записать в виде суммы "LevE по всем зарядам и при помощи B.2)
прийти к следующему уравнению:
J j B-6)
Здесь Т — кинетическая энергия всех частиц, образующих твер-
твердое .тело.
Уравнение B.6) выражает закон сохранения энергии. Слева
стоит изменение полной энергии рассматриваемого твердого
тела, а справа — количество энергии поля, протекающее в еди-
единицу времени через его поверхность. Воображаемое твердое
тело либо излучает энергию (при этом правая часть B.6) отри-
отрицательна), либо не излучает ее. В первом случае полная энер-
энергия твердого тела будет уменьшаться, стремясь к нулю при
rf—>оо, что, очевидно, невозможно. .
В другом случае при t —*¦ оо имеем
+ T\ = 0; B.7)
т. е. полная энергия твердого тела сохраняется постоянной.
Ввиду произвола в выборе объема V (напомним, что он дол-
должен включать в себя траектории всех частиц) отсюда вытекает,
что поле может быть отличным от нулевого только вдоль траек-
траектории частиц, а вне траекторий поле отсутствует. Так как это
невозможно, остается признать, что исходные допущения были
неверными. .
Следовательно, построение теории твердого тела и, в част-
частности, объяснение его прочностных и деформативных свойств в
рамках классической физики невозможно, и необходимо при-
привлекать квантово-механические представления.
Рассмотрим идеально-периодическую пространственную
структуру, состоящую из ядер и электронов. Согласно кванто-
вомеханическому методу, все возможные стационарные со*
*$ 1J ТОЧНЫЙ КВАНТОВОМЕХАНИЧЕСКИЙ МЕТОД 29
стояния системы определяются из решения уравнения Шредин-
гера [15] -
Wj anl>, B.8)
где *ф — волновая функция, до—полная энергия системы; опе-
оператор W определяется так:
—fiT
Здесь Шг и ?i — масса и заряд i-й элементарной Частицы соот-
соответственно; Хи уи zt — координаты i-й частицы (спиновым вза-
взаимодействием частиц пренебрегается), Ь — постоянная Планка
{Ь = 1,05-107 эрг-сек), N — число частиц в системе.
Первый член в формуле B.9) описывает кинетическую энер-
энергию частиц, второй — кулоновское взаимодействие частиц.
В силу идеальной периодичности можно выбрать такую наи-
наименьшую по размерам область V в пространстве (элементар-
(элементарную ячейку), чтобы состояние в любой фиксированной точке
пространства описывалось состоянием в соответствующей точке
элементарной ячейки, причем соответствие точек определялось
0ы только векторной операцией периодического продолжения.
^Очевидно, элементарная ячейка всегда представляет собой не-
некоторый правильный многогранник; условимся выбирать его
|аким образом, чтобы на гранях S выполнялось граничное ус-
условие локальной симметрии
= -Ц- = 0 на 5 (i=l, 2, .... АО, B.10)
Ше tii — нормаль к соответствующей грани (п* — Щ(хиУи
Тогда можно ограничиться изучением одной указанной эле-
йентарной ячейки; N будет равно числу частиц в одной ячейке,
^.условие нормировки запишется в виде
^ (*i. Уи «1 %. #*>• *n) f dxx dyx dzx ... dxN dyN dzN = \.
Запомним, что выражение
I iH*i> У\, Zi xN, yN, zN) f dxx dyx dz{ ... dxN dyN dzN
pier вероятность того, что первая частица находится в элементе
щ^ма-dxi dyi dzi с центром в точке (xuyuzi), вторая частица
Йроднтся в элементе объема dx2 dy2 dz2 с центром в точке
Щз» Уг, ?г) и т. д., т, е. |ij)|2 представляет собой плотность ве-
|ЮЯТНОСТН.
30 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР 1ГЛ. Н
Дуализм квантовомеханических представлений заключается
в том, что, несмотря на наличие в уравнении Шредингера ко-
координат частиц, в результате его решения можно определить
только вероятность нахождения совокупности частиц в том или
ином объеме пространства (частицы «размазаны» в некоторое
«облако»). Примерные размеры этого «облака» Ад:, Ау, Дг свя-
связаны с размером соответствующего «облака» в пространстве
импульсов Д/?ж, &Pv> bpz соотношением неопределенностей
Ах ¦ Арх ~Н, Ду • Ару ~ ft, Дг • Арг~ И. B.12)
Кроме того, неопределенность в величине полной энергии частиц
Aw связана с характерным «временем жизни» в нестационарном
состоянии Д/ соотношением
Aw-At~h. B.13)
В стационарном состоянии At == оо и Aw = 0.
Согласно квантовомеханическим представлениям, мир имеет
статистическую природу; при задании начального состояния си-
системы дальнейшее ее развитие можно определить лишь с неко-
некоторой вероятностью.
Краевая задача B.8) — B.10) представляет задачу на соб-
собственные числа, где роль собственного числа играет полная
энергия элементарной ячейки w. Поэтому решение задачи су-'
шествует только для вполне определенного множества значе-
значений w. Если это множество дискретно, то говорят о дискретном
спектре; если множество непрерывно, то говорят, что спектр —
сплошной. Оператор W — самосопряженный, поэтому для конеч-
конечной области V собственные числа да образуют действительное
счетное множество. Для механики разрушения наибольший ин-
интерес представляет состояние с наинизшей энергией Доо', в этом
состоянии система может находиться сколь угодно долго. Дру-
Другие стационарные состояния системы, соответствующие боль-
большим w, обычно квазистационарны, так как под действием внеш-
внешних электромагнитных волн система через определенное конеч-
конечное время с вероятностью, близкой к единице, переходит в
более устойчивое состояние с меньшей энергией. Вблизи точки
w = w0 на основании соотношения B.13) нет других возмож-
возможных стационарных состояний системы.
Из соображения анализа размерностей энергия w0 равна
-=•)• B-14>
Здесь г — характерный линейный размер элементарной ячейки;
функция / — своя для каждого заданного набора N ядер и элек-
электронов.
fjU| ТОЧНЫЙ КВАНТОВОМЁХАНИЧЕСКИЙ МЕТОД 31
Знание функции w0 позволяет отыскать все величины, харак-
характеризующие реакцию идеальной решетки на внешние возмуще-
возмущения, например, ее сопротивление деформации,, прочность, хими-
химическую активность и т. д.
Указанная постановка задачи довольно неопределенна, по-
поскольку не приведены дополнительные данные для выбора раз-
размера и формы элементарной ячейки. По существу, факт суще-
существования, а также размер и форма этой ячейки для заданного
набора ядер4 и электронов должны определяться из решения
самой задачи при помощи граничного условия B.10) и условия
абсолютного минимума полной энергии ячейки w. Получаю-
Получающаяся обратная задача чрезвычайно сложна; решение ее
открыв бы грандиозные перспективы в создании новых кри-
кристаллических материалов (или некоторых модификаций уже
Известных кристаллических форм), обладающих, например, по-
повышенной прочностью.
Некоторые предварительные соображения, основанные на
принципе максимального перекрывания и принципе Паули [15],
позволяют полагать, что для соединений с ковалентной связью
более прочные на разрыв материалы, чем углерод со структурой
алмаза, невозможны (особенно если иметь в виду удельную
прочность).. Действительно, среди элементов с двумя энергети-
энергетическими уровнями углерод имеет наилучшее число валентных
электронов (четыре), так как при ковалентной связи у каж-
каждого атома углерода на втором уровне оказывается максималь-
максимально возможное число электронов D + 4 = 8); «обобществление»
большего числа электронов (большего 4 на втором уровне) не
допускается принципом Паули. Для металлов этот вопрос го-
гораздо более сложен; в первом приближении, по-видимому, мож-
можно "считать, что прочность структуры тем больше, чем больше
янсло валентных электронов и число ближайших соседей у
каждого иона.
Приведем вариационный принцип, получающийся умноже-
умножением обеих частей уравнения B.8) на ф и интегрированием по
объему ячейки V. На основании B.11) и условия стационар-
стационарности энергии системы w получаем
б J ij>Wi|> dxi dyl dzi ... dxN dyы dzH = 0. B.15)
v
Вариационный принцип B.15) открывает возможность при-
применения прямых методов типа метода Ритца. Вариационная
оцедка дает верхнюю границу, вообще говоря, для наинизшего
значения энергии w0.
ч р 0
^Форма и размеры элементарной ячейки кристаллов, встре-
встречающихся в природе, весьма точно определяются эксперимен*
щ Йрочйость идеально-Периодических стрдаур [гл. и
таяьно. При использовании таких дополнительных данных за-
задача'значительно упрощается, однако все еще остается весьма
сложной. В случае простых элементов для определения элемен-
элементарной ячейки нужно построить плоскости, проходящие через
середины отрезков между соседними ядрами и перпендикуляр-
перпендикулярные к этим отрезкам. Для получения численных результатов
наряду с использованием вариационного принципа применяют
различные варианты метода возмущений, который подробно
описан в книгах по квантовой механике. Следует отметить, что
большие возможности, открывающиеся в применении точного
квантовомеханического метода,, пока не реализованы из-за вы-
вычислительных сложностей, и поэтому в дальнейшем будут рас-
рассмотрены только приближенные полуэмпирические методы, поз-
позволяющие дать оценку прочности некоторых идеально-периоди-
идеально-периодических структур.
§ 2. Приближенные методы
В классической физике идеально-периодическая структура
(ее называют также идеальной решеткой или идеальным кри-
кристаллом) представляется [16] состоящей из упакованных частиц
конечных размеров, между которыми при растяжении действуют
силы притяжения, а при сжатии — силы отталкивания (урав-
(уравновешивающиеся в состоянии покоя).
Частицами, образующими кристалл,, могут быть разноименно
заряженные ионы (как в каменной соли), положительно заря-
заряженные ионы (как в металлах), ней-гральные атомы одного и
того же элемента (как в алмазе), нейтральные атомы различ-
различных элементов (к^к в карборунде), молекулы (как в, кристал-
кристаллах льда). Соответственно, по характеру сил притяжения
различают ионную, металлическую, ковалентную и межмолеку-
межмолекулярную (ван-дер-ваальсову) связь. В металлах валентные элек-
электроны свободно перемещаются в решетке, образуя «электронный
газ». Сила притяжения в случае металлической и ковалентной
связи объясняется обменным взаимодействием валентных элек-
электронов и носит существенно квантовомеханический характер.
Сиды отталкивания во всех случаях — квантовомеханического
происхождения. '
С точки зрения -квантовой механики представление о таких
частицах оправдывается тем, что> в большинстве случаев об-
область, в которой, в основном, распределена плотность, |я|)|2,
представляет собой совокупность некоторых . повторяющихся
зон, сравнительно слабо связанных друг с другом и характер-
характерных для отдельного иона, атома или молекулы того или иного
химического вещества (волновые функции которых в кристалле
§ i\ ¦ ПРИБЛИЖЁННЫЕ МЕТОДЫ 33
«перекрываются» обычно лишь в небольшой пограничной об-
области).
Наиболее существенным недостатком классических представ-
представлений является предположение о том, что все частицы в кри-
кристалле имеют сферическую форму и между любыми двумя ча-
частицами имеет место центральное взаимодействие. Однако это
упрощение дает возможность наглядного и эффективного ко-
количественного . описания. В большинстве
материалов обычно так или иначе пред- ил
ставлены все типы связей, и доминирую-
доминирующую связь, характеризующую прочность
на разрыв, иногда выделить нелегко.
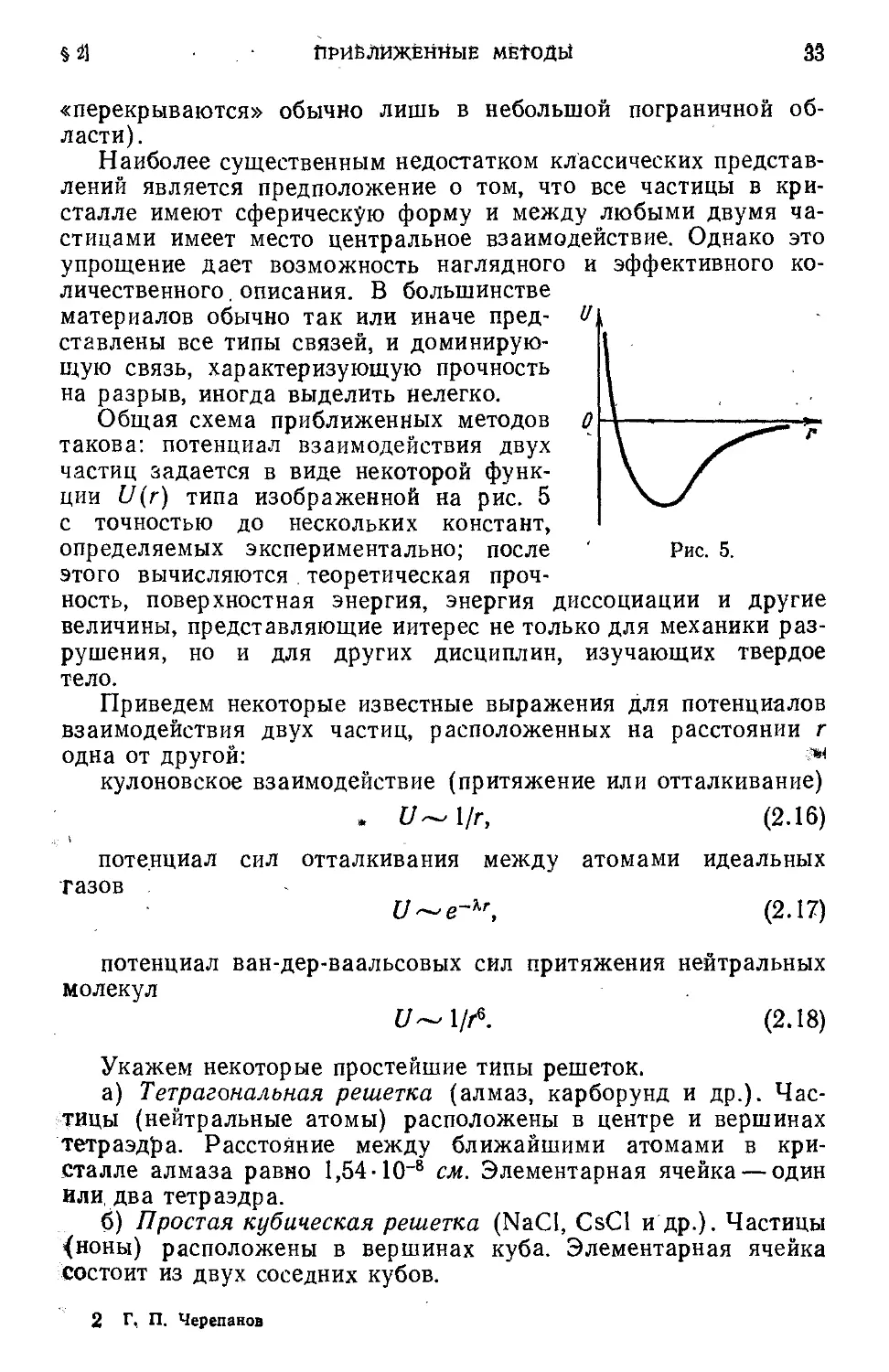
Общая схема приближенных методов О
такова: потенциал взаимодействия двух
частиц задается в виде некоторой функ-
функции U(г) типа изображенной на рис. 5
с точностью до нескольких констант,
определяемых экспериментально; после ' Рис. 5.
этого вычисляются теоретическая проч-
прочность, поверхностная энергия, энергия диссоциации и другие
величины, представляющие интерес не только для механики раз-
разрушения, но и для других дисциплин, изучающих твердое
тело.
Приведем некоторые известные выражения для потенциалов
взаимодействия двух частиц, расположенных на расстоянии г
одна от другой: *
кулоновское взаимодействие (притяжение или отталкивание)
. ?/~1/г, B.16)
потенциал сил отталкивания между атомами идеальных
газов
?/~е-*г, B.17)
потенциал ван-дер-ваальсовых сил притяжения нейтральных
молекул
С/— 1/гб B.18)
Укажем некоторые простейшие типы решеток.
а) Тетрагональная решетка (алмаз, карборунд и др.). Час-
Частицы (нейтральные атомы) расположены в центре и вершинах
тетраэдра. Расстояние между ближайшими атомами в кри-
кристалле алмаза равно 1,54-10"8 см. Элементарная ячейка — один
или два тетраэдра.
б) Простая кубическая решетка (NaCl, CsCl и др.). Частицы
.<{ноны) расположены в вершинах куба. Элементарная ячейка
состоит из двух соседних кубов.
2 Г, П. Черепанов
34
прочность идеально-периодических структур
[ГЛ. П
в) Объемно-центрированная и гранецентрированная кубиче-
кубическая решетка. В первой, помимо вершин куба, в центре куба
имеется еще одна частица (элементарная ячейка — октаэдр); во
второй, помимо вершин куба, частицы расположены в центре
каждой грани (элементарная ячейка — додекаэдр).
г) Гексагональная решетка. Каждая элементарная ячейка
представляет собой додекаэдр с расположенной в центре ча-
частицей, соседние частицы касаются друг друга в серединах гра-
граней (всего 12 пятиугольных граней). Большинство металлов
кристаллизуется по типам в) иг).
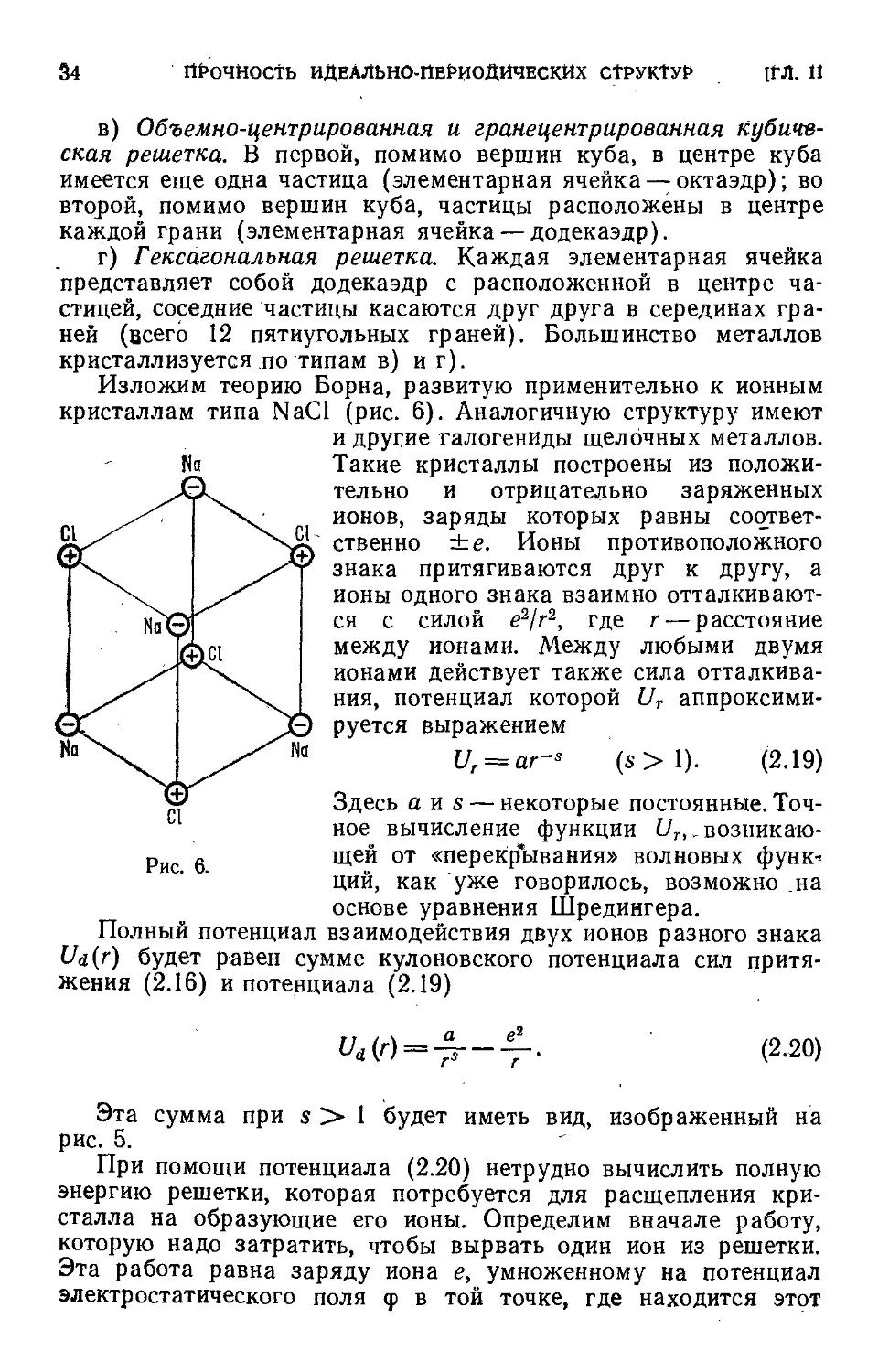
Изложим теорию Борна, развитую применительно к ионным
кристаллам типа NaCl (рис. 6). Аналогичную структуру имеют
и другие галогениды щелочных металлов.
Такие кристаллы построены из положи-
положительно и отрицательно заряженных
ионов, заряды которых равны соответ-
соответственно ±е. Ионы противоположного
знака притягиваются друг к другу, а
ионы одного знака взаимно отталкивают-
отталкиваются с силой е2/г2, где г — расстояние
между ионами. Между любыми двумя
ионами действует также сила отталкива-
отталкивания, потенциал которой Ur аппроксими-
аппроксимируется выражением
Ur = ar~s (s>l). B.19)
Cl
Рис. 6.
Здесь а и s — некоторые постоянные. Точ-
Точное вычисление функции Ur,r возникаю-
возникающей от «перекр*ывания» волновых функ-
функций, как уже говорилось, возможно .на
основе уравнения Шредингера.
Полный потенциал взаимодействия двух ионов разного знака
Ud(r) будет равен сумме кулоновского потенциала сил притя-
притяжения B.16) и потенциала B.19)
г
B.20)
Эта сумма при s > 1 будет иметь вид, изображенный на
рис. 5.
При помощи потенциала B.20) нетрудно вычислить полную
энергию решетки, которая потребуется для расщепления кри-
кристалла на образующие его ионы. Определим вначале работу,
которую надо затратить, чтобы вырвать один ион из решетки.
Эта работа равна заряду иона е, умноженному на потенциал
электростатического поля ф в той точке, где находится этот
5 2] ПРИБЛИЖЕННЫЕ МЕТОДЫ
ион, от действия всех остальных ионов. Суммируя, находим
—оо /=—оо
(i, /,
Здесь г — кратчайшее расстояние между ионами противополож-
противоположного знака, ам — сумма тройного ряда. Прямое вычисление [16]
дает ам= 1,7476.
Следовательно, электростатическая, энергия взаимодействия,
приходящаяся на пару ионов, равна —а,ме2/г.
При вычислении сил отталкивания обычно предполагают, что
эти силы убывают с расстоянием так быстро, что достаточно
учесть только ближайшие ионы. В рассматриваемой структуре
у каждого иона имеется шесть ближайших соседей, поэтому
энергия перекрывания, приходящаяся на пару ионов, равна 6Ur,
а полная энергия решетки, приходящаяся на пару ионов, равна-
„(,) = _¦? + ?. . B.22)
В отсутствие внешнего давления состояние устойчивого рав-
равновесия, реализующееся в кристалле, очевидно, будет отвечать
точке минимума функции U(r) при г = г0 («дно потенциальной
ямы»). Отсюда (dU/dr)r=r = 0 и
«лАо — 6sa- B-23)
Значение второй производной d2U/dr2 в точке минимума оп-
определяет объемную сжимаемость и частоту колебаний ионов
вблизи положения равновесия.
Действительно, разложение потенциала в окрестности точки
минимума имеет вид
(^Ц(ЛгJ. B.24)
Обозначим модуль всестороннего сжатия через k. Приравни-
Приравнивая упругую энергию сжатия —ke2r^N, образующуюся в объеме
Nr^ (N — число ионов в этом объеме, е = ЗАг/г0), величине
-^N(U — C/min) соответствующего изменения полной энергии ре-
решетки из N ионов, получаем
2*
36 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР [ГЛ. II
Используя выражение B.22), отсюда находим
0 rs-l
rO
Таким образом, если воспользоваться экспериментальными
значениями г0 и k, из системы уравнений B.23) и B.26) можно
определить постоянные а и s. Находим
Вычислим величины, представляющие для нас основной ин-
интерес: прочность и поверхностную энергию рассматриваемой
структуры.
Представим себе, что решетка, изображенная на рис. 6,
подвергается всестороннему растяжению усилием а, отнесен-
отнесенным к единице площади. При этом прира-
приращение внешней работы 3a{Nr3yibN'lsdr, оче-
очевидно, равно изменению полной энергии ре-
решетки у N dr (dUjdr) в объеме Nr3. Отсюда
получаем выражение
справедливое также для конечных дефор-
г маций решетки. Функция а (г) имеет вид,
качественно изображенный на рис. 7. Мак-
Рис. 7. симальное сопротивление всестороннему
растяжению атах достигается в точке г=г#,
где da/dr обращается в нуль. Окончательно при помощи формул
B.22), B.27) и B.28) находим
B.29)
s—1 аме2
B>30)
Величину Ощах называют теоретической прочностью идеального
кристалла. При а > атах равновесное состояние ионов невоз-
невозможно; при г> г* равновесие неустойчиво, что отвечает, во-
вообще говоря, динамическому протеканию процесса разрушения.
Отметим, что разрушение идеального* кристалла соответствует
расщеплению его на отдельные ионы, т. е. полной диссоциации.
Теория Борна, несмотря на кажущуюся простоту и стро-
строгость, вызывает серьезные возражения. Как видно, она основана
J Я ПРИБЛИЖЕННЫЕ МЕТОДЫ 37
на суммировании кулоновских взаимодействий во всем про-
пространстве (см.. ряд B.21)). Этот ряд, как нетрудно заметить,
является условно сходящимся. Следовательно, его сумму в за-
зависимости от порядка суммирования членов можно сделать рав-
равной любому наперед заданному числу*). Отметим, что в фи-
физической постановке задачи нет каких-либо дополнительных
условий, позволяющих отдать предпочтение какому-то опреде-
определенному способу суммирования. Поэтому даже в силах притяже-
притяжения для ионных кристаллов, по-видимойу, необходимо учиты-
учитывать обменное взаимодействие. В рамках же излагаемого под-
подхода Борна наиболее правильно выбирать константу ам на
основании дополнительных экспериментальных данных. Напри-
Например, при помощи цикла Борна — Габера можно найти из опы-
опытов величину Umm и, сравнивая ее с теоретическим значением,
определить ам- Полученное таким способом значение ам совпа-
совпадает с приведенным выше.
Метод Борна, обычно применяемый для вычисления поверх-
поверхностной энергии ионных кристаллов и приводящий к необходи-
необходимости суммирования некоторых дополнительных условно сходя-
сходящихся рядов, представляется еще более ненадежным, так как
лока что отсутствуют надежные опытные данные по поверхно-
поверхностной энергии. Поэтому при вычислении поверхностной энергии
будем применять приближенный метод, считая, что связи су-
существуют лишь между ближайшими частицами, так что энер-
энергия каждой связи равна -^ Umin, а сила натяжения каждой
связи равна F. Таким образом, энергия решетки, приходящаяся
на объем r-j, т. е. —у(^),._Г|>, равна поверхностной энергии
где у — поверхностная энергия структуры, приходящаяся
на единицу свободной поверхности. Отсюда получаем
Эта величина характеризует, очевидно, геометрически наи-
наименьшую величину поверхностной энергии. Возможно также
образование свободных плоскостей, проходящих под углом 45°
к граням кубов; соответствующие значения поверхностной энер-
энергии также нетрудно подсчитать. Заметим, что величина (— Щг=и
по своему физическому смыслу представляет энергию диссоциа-
диссоциации, приходящуюся на пару ионов.
*) В работах Борна, Штерна, Маделунга, Френкеля и многих других
авторов этот ряд именуется «плохо сходящимся», причем всюду подразуме-
подразумевается,, что сумма этого ряда не зависит от порядка суммирования,
38 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР [ГЛ. II
Для решетки каменной соли NaCl имеем
г0 = 2,8 ¦ 10~8 еж, k = 3 ¦ 105 кГ/см2.
В этом случае вычисление по формулам B.27) — B.31) дает
s = 9,4, — (?/)г=Го = 182 ккал/г ¦ атом,
г, = 3,2 • 10~8 см, атах = 420 кГ/мм2, B.32)
Y = 1350 дн/см, Fmax = 4,3 • 10 дн.
Экспериментально наблюдались значения прочности кри-
кристаллов каменной соли, достигающие 160 кГ/мм2. В этих опытах
А. Ф. Иоффе и его сотрудники испытывали на односторонний
разрыв образцы в воде, после того как поверхностные дефект-
дефектные слои кристалла растворялись [Ц]. Измеренная многими ис-
исследователями величина у кристалла каменной соли [18] колеб-
колеблется примерно от 200 до 500 дн/см, т. е. приблизительно в три
раза меньше теоретического значения. Указанные опыты про-
проводились в условиях естественной атмосферной влажности;
ввиду сильной гигроскопичности каменной соли и полярности
молекул воды поверхностные слои ионното кристалла находи-
находились в условиях, далеких от теоретической схемы (подробнее
об этом см. § 8 гл. VII).
Изложенная теория удовлетворительно описывает прочность
галогенидов щелочных металлов и серебра, а также силикатных
стекол (см. § 8 гл. VII). Для более прочных структур с метал-
металлической и ковалентной связью эта теория не годится, по-
поскольку силы притяжения в этих случаях оказываются гораздо
более короткодействующими. Однако общую схему метода рас-
расчета можно использовать, если задаться более точным выра-
выражением для потенциала взаимодействия.
Примем следующие допущения:
а) каждая частица взаимодействует только с п ближайшими
частицами, причем потенциал всех парных взаимодействий оди-
одинаков и не зависит от других взаимодействий;
б) полная энергия взаимодействия пары частиц описывается
потенциалом
^о = -7Г- тг, B.33)
где по и а\ — некоторые постоянные.
Первое допущение ограничивает круг рассматриваемых ве-
веществ и, строго говоря, допускает только простые соединения
(т. е. состоящие из одного химического элемента). При этом
элементарная ячейка может представлять собой правильный
многогранник только одного из четырех типов: тетраэдр, куб,
приближенные методы
39
октаэдр, додекаэдр (предполагается плотная упаковка частиц).
Величина г (расстояние между ближайшими ядрами) будет
равна удвоенному расстоянию от ядра до грани ячейки. Второе
допущение надо рассматривать как некоторую аппроксимацию
реального потенциала (степень первого члена, характеризую-
характеризующего силы отталкивания заполненных электронных оболочек,
взята под влиянием предыдущего расчета для структуры NaCl).
В металлах кулоновское взаимодействие частиц (положитель-
(положительных ионов) экранируется электронными оболочками, так что
им можно пренебречь.
, В силу указанных допущений полная энергия решетки, при-
приходящаяся на пару частиц, равна
U (г) = -р pj- B.34)
(п — число ближайших соседей в решетке).
Вычисления, аналогичные предыдущим, позволяют опреде-
определить значения а0, аь г*, атах через эмпирические значения г0
и k. Опуская эти вычисления, приводим окончательный ре-
результат:
ао
2k%
.12
Зп 'с
;=1,1Ого,
kkr0
а, =
kXr20
Здесь ^тах — предельная сила натяжения одной связи.
Значения Я и ц приводятся в табл. 2.1.
Таблица 2.1
Значеняя параметров I яц, входящих
в формулы B.35), для разных типов
элементарных .ячеек
B.35)
Я
V-
п
Тетраэдр
1.73
10.39
4
Куб
1
6
6
Октаэдр
0.86
5,20
8
Додекаэдр
, ,0.69
4.17
12
Подчеркнем, что в формулах B.35), как и везде ранее в
этом параграфе, речь идет о всестороннем растяжении и о наи-
наименьшем значении поверхностной энергии. -
40 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР [ГЛ. II
Отметим одно обстоятельство, которое обычно не учитывает-
учитывается. «Кажущаяся» поверхность излома кристаллов представляет
собой некоторое геометрическое осреднение действительной по-
поверхности, обычно имеющей различные неровности, впадины и
пики. Площадь действительной свободной поверхности всегда
больше площади «кажущейся». Кроме того, как было показано
выше, на различных участках действительной поверхности по-
поверхностная энергия может быть существенно различной. Поэ-
Поэтому экспериментально замеряемые величины поверхностной
энергии всегда характеризуют некоторый средний для данной
поверхности рельеф. Это обстоятельство может иметь сущест-
существенное значение при сравнении экспериментальных данных с
результатами теоретического расчета.
§ 3. Некоторые оценки
Прочность и поверхностную энергию идеально-периодических
структур оценивают обычно при помощи одного дополнитель-
дополнительного допущения (как правило, не оговариваемого), которое су-
существенно упрощает расчет на одноосное растяжение. А имен-
именно, считают, что деформации и разрушению подвергаются лишь
связи, пересекаемые некоторой плоскостью, перпендикулярной
к направлению растяжения, а все остальные связи считаются
абсолютно жесткими недеформируемыми. При этом атомная
структура учитывается только в выражении для сил сцепления
двух полупространств путем использования некоторых приемов,
которые рассматриваются ниже. Указанное допущение дает
возможность весьма просто оценивать теоретическую прочность
и поверхностную энергию тел любой структуры (например,
аморфных и поликристаллических тел); точность получающихся
результатов зависит от удачной аппроксимации разрывающих-
разрывающихся связей.
Метод Френкеля. В 1926 г. Я- И. Френкель оценил макси-
максимальную величину касательного напряжения, возникающего
при относительном сдвиге двух полупространств. Если тело
имеет периодическую атомную структуру, то силы сцепления
должны представлять собой периодическую функцию взаимного
смещения полупространств с периодом bo (характерным для
границы). Френкель аппроксимировал эту функцию синусоидой
и использовал закон Гука для малых смещений, считая, что
границы полупространств отстоят одна от другой на расстояние
ао. Тогда для напряжения сдвига т получается выражение
где ц, — модуль сдвига.
НЕКОТОРЫЕ ОЦЕНКИ 41
Отсюда максимальное напряжение сдвига равно
W = ^. B.37)
Например, в случае гранецентрированной кубической решет-
решетки (плотная упаковка) для плоскости A11) имеем ao — boY~2,
ТЭК ЧТО Ттах «0,1 Ц,.
Совершенно аналогичный метод применил Гилман [19] для
оценки теоретической прочности при одностороннем растя-
растяжении напряжением ст. Была взята синусоидальная аппрокси-
аппроксимация
а = 3± sin 22- @ < v < bo). B.38).
Здесь Е — модуль Юнга, v — взаимное смещение полупро-
полупространств по нормали к плоскости разрыва, а0 — среднее меж-
межатомное расстояние, Ьо — «радиус угасания» сил сцепления, ко-
который Джиллмэн принял равным диаметру атома.
Отсюда для теоретической, прочности на одностороннее рас-
щщёййе Отах и поверхностной энергии у имеем
По-видимому, Джиллмэн сильно преувеличивал значение наи-
наибольшей деформации решетки (для алмаза, например, он счи-
считает справедливыми оценки bo/ao ~ 1 и сттах ~ Е/п).
Метод Гриффитса. Формула Гриффитса для прочности упру-
грго тела с трещиной длинц / позволяет оценить теоретическую
Прочность, если экстраполировать формулу на трещины до раз-
размеров порядка среднего межатомного расстояния: / ~ а0. При
этом из A.25) получаем
Отах = Л, УЕ\/п0. B.40)
Как будет показано в дальнейшем, согласно методу Гриф-
фйтса прочность хрупкого тела на одностороннее и всесторон-
яее растяжения одинакова.
Другие аппроксимации. Для простейшей аппроксимации
«треугольником»
a = Ev/d0 при 0<w<60/2, B.41)
ст —Д (Ьо — v)/a0 при 60/2 < v < Ьо
следующие выражения для стШах и у.
Отп = EbJBa0), у = Eblmaj). B.42)
42
ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР
[ГЛ. II
Для аппроксимации типа B.33) зависимость сил сцепления
о от расстояния между плоскостями (v -\- а0) будет следующей:
Величина ffmax и y Для силы сцепления B.43) будет равной
<W = 0,043? (при v ~ 0,125а0), B.44)
Y = a0?/108.
§ 4. Метод теплового смещения
Получающиеся оценки довольно разноречивы (ср., напри-
например, B.39) и B.44)), поэтому представляет интерес оценка
«радиуса угасания» сил сцепления из
каких-либо дополнительных сообра-
. жений.
а* До сих пор в расчетах нигде не
учитывались колебания атомов и ио-
ионов решетки вблизи положения равно-
равновесия. Это объясняется тем, что при
. обычных температурах энергия коле-
' баний решетки, приходящаяся на пару
частиц, равна примерно 10~2—10~' эв,
в то время как энергия химической
связи, определяющая прочность ре-
.] шетки, для твердых тел обычно со-
' ставляет 1—10 эв.
С увеличением температуры тепло-
тепловое движение частиц (атомов, ионов,
молекул) усиливается, пока не дости-
достигается такая температура, при кото-
которой энергия колебаний решетки стано-
t) вится сравнимой с энергией химиче-
химической связи и близлежащие частицы
обретают способность в той или иной
степени преодолевать взаимное притя-
притяжение. В процессе нагревания тела
происходит его тепловое расширение.
Эти явления можно увязать в следующей простой модели [Щ
(рис.8).
Допустим, что при абсолютном нуле температуры эффектив-
эффективный радиус частицы равен с0, а расстояние между центрами
двух соседних частиц равно а0 (рис. 8,а). Эффективный размер
частицы несколько больше геометрического размера самой ча-
частицы (области, где ф-функция ire равна нулю) вследствие слу-
случайных колебаний ее вблизи положения равновесия. Величина
Рис. 8.
§4] МЕТОД ТЕПЛОВОГО СМЕЩЕНИЯ 43
Со представляет собой некоторую среднюю величину (осредне-
(осреднение производится или по одной фиксированной частице за до-
достаточно большой промежуток- времени, или же по многим ча-
частицам в один и тот же момент времени; в силу стационарно-
стационарности процесса эти средние совпадают). Соотношение между Со
и а0 зависит от характера связи; в случае ионной и молекуляр-
молекулярной связи обычно 2с0 « а0, так как ф-функции частиц почта
«не перекрываются», а в случае ковалентной и металлической
связи обычно ао < 2со вследствие перекрывания ф-функций и
обобществления валентных электронов. Колебания частиц при
абсолютном нуле температуры имеют квантовый характер и объ-
объясняются тем, что каждая частица в устойчивом стационарном
состоянии находится на дне некоторой «потенциальной ямы».
Предположим, что к решетке быЯа приложена некоторая
внешняя растягивающая сила, под действием которой соседние
частицы разошлись вначале на расстояние (ao-f и»), соответ-
соответствующее максимальному значению силы сопротивления связи
(теоретической прочности), а затем на расстояние (ао-{-Ьо), где
силы взаимного притяжения двух частиц пренебрежимо малы
(рис. 8,6).
С увеличением температуры энергия колебаний частиц рас-
растет, вследствие чего увеличивается эффективный средний ра-
радиус частиц и происходит тепловое расширение тела (рис. 8, в,
где увеличенными кружками изображены эффективные размеры
частиц; с определенной конечной вероятностью частица может
находиться в любой точке этого кружка).
Наконец, достигается такое состояние (рис. 8,г), в котором
при отсутствии внешней нагрузки расстояние между наиболее
дальними точками двух соседних зон (в каждой из зон одна
из двух рассматриваемых частиц испытывает случайные ко-
колебания) достигает величины а0 + и,. Как только это расстоя-
расстояние будет превзойдено, возникает конечная вероятность «пере-
«перехвата» одной из двух рассматриваемых частиц некоторой со-
соседней частицей (не изображенной на рис. 8), так что частицы
могут менять своих соседей. Вероятность «перехвата» становит-
становится больше вероятности сохранения своего постоянного «соседа»,
как только среднее расстояние между рассматриваемыми части-
частицами (среднее межатомное расстояние) превысит величину
а0 + и,. Последнее свойство характерно для жидкости, поэтому
температура тела, равная температуре плавления, характери-
характеризует тот момент, когда среднее межатомное расстояние Aв от-
отсутствие внешней силы) р-авно ао + и*- Следовательно,
Tf
' B.45)
44 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР [ГЛ. II
Здесь Tf — абсолютная температура плавления материала,
Р(Г) —коэффициент линейного температурного расширения (на
рис. 8 и, = г, — г0).
Разумеется, теоретическая прочность жидкости при всесто-
всестороннем растяжении будет иметь порядок теоретической проч-
прочности соответствующего твердого тела, так как она опреде-
определяется осреднением по очень многим связям на элементарной
площадке, а в любой заданный момент времени доля связей,
для которых межатомное расстояние меньше,- чем а0 -\- v*, от-
отнюдь не мала.
Состояние жидкости можно охарактеризовать плотностью ве-
п=п2
роятности р(п), считая, что величина iV 2 Р(п) (гДе N — об-
щее число частиц в системе) равна числу частиц в системе,
имеющих за бесконечное время от rt\ до щ разных «соседей».
Под «соседями» подразумеваются частицы, центры которых в
некоторый момент времени отстояли один от другого на рас-
расстояние, меньшее по -j- и*- При нагревании жидкости максимум
плотности р(п) сдвигается вправо, до тех пор пока не будет
достигнуто предельное распределение
0 при пф N,
1 при n — N, v '
характеризующее идеальный газ (абсолютно хаотическое дви-
движение частиц).
Температура жидкости, равная температуре кипения, харак-
характеризует тот момент, когда среднее межатомное расстояние
(в отсутствие внешней силы) становится равным а0 -\- Ьо. Сле-
Следовательно,
Tv
B.47)
Здесь Tv — абсолютная температура кипения материала.
Ход рассуждений не изменится, если его проводить не от аб-
абсолютного нуля, а от некоторой началяной температуры тела То;
при этом, очевидно, нижний предел интегрирования в B.45) и
B.47) будет равен То.
Следует отметить, что вследствие случайных колебаний ча-
частиц для твердого тела также существует определенная вероят-
вероятность перескока частицы из стационарного узла в решетке в не-
некоторое другое положение (именно этим объясняется образова-
образование «вакансий» и междоузлий в идеальной решетке, а также
диффузия в твердых телах), однако эта вероятность чрез-
чрезвычайно мала. Идеальной решетке (колебания частиц
lU метод теплового смещения 45
полностью отсутствуют) соответствует предельное распределение
0 при п ф «л,
, B-48)
1 при п = по,
где щ — некоторая постоянная решетки (число «соседей» у каж-
каждой частицы). Когда энергия тепловых колебаний становится
существенной (особенно вблизи точки плавления), диффузион-
диффузионные процессы в твердом теле могут играть значительную роль.
Всем промежуточным состояниям (от идеальной решетки до
идеального газа) соответствуют некоторые распределения, про-
промежуточные между B.46) и B.48).
Составим уравнение энергии. Для определенности положим,
что единичный объем рассматриваемого твердого тела нагре-
нагревался от Т = То до Т = Tv при постоянном внешнем давлении
(например, атмосферном). Внутреннюю энергию этого объема
представим в виде суммы энергии связи Uc (потенциальной энер-
энергии взаимодействия частиц) и энергии колебаний решетки Uk
(средней,кинетической энергии движения частиц). Электронной
составляющей, обусловленной движением и спином электронов,
пренебрегаем. Тогда закон сохранения энергии в любой момент
процесса нагревания запишется в виде
Ue(T) - Uе (Го).+ Uk\T) - Uk (То) =
г ,
dT. B.49)
)
¦•о То
Здесь р и V — внешнее давление и объем тела соответственно,
Ир — теплоемкость при постоянном давлении.
Все предыдущие методы вычисления поверхностной энергии
.были основаны на мысленном процессе разрыва, в котором
Т = const, Uk = 0, так что энергия св,язи изменялась только за
.Счет последнего члена в правой части уравнения B.49), т. е.
за счет внешней работы. Если внешние нагрузки малы (гораздо
меньше теоретической прочности), то этим членом можно пре-
йебречь.
Предположим, что
Uk(To)<Ve(To). B.50)
Как уже говорилось выше, для большинства твердых тел в
йбычных условиях это условие выполняется.
Тогда из уравнения B.49) получаем
т
= - J cp(T)dT + Uk(T) + UC{T). B.51)
и
4в прочность идеально-периодических структур [гл. и
При температуре кипения T=TV будет [/сG\,)=0, а
Uk(Tv) будет равно средней кинетической энергии частиц при
давлении р и температуре Tv (т. е. внутренней энергии газа,
образовавшегося из рассматриваемого единичного объема твер-
твердого тела). Окончательно получаем
Uс (T0) = -\cp(T)dT + ^g^-. B.52)
Здесь ро — плотность твердого тела при Т = То, гп0 — масса од-
одной частицы, Na = 6,02-1023 моль~1 — число Авогадро, R =
= 1,987 кал/(град-моль)—универсальная газовая постоянная.
Последний член в формуле B.52), равный Uk(Tv), полу-
получается следующим образом. В единице объема твердого тела
находится 'роМо частиц, которые после превращения твердого
тела в газ при Т = Tv приходят в хаотическое движение. Со-
Согласно кинетической теории газов, средняя кинетическая энер-
энергия этих частиц равна
<2-53)
где Afi — число частиц в единице объема газа. Это число равно
(pNa)/(RTv), так как в одном моле газа, занимающем объем
Vm (pVm = RTV), согласно закону Авогадро, содержится Na ча-
частиц. Отсюда и находится окончательное выражение для Uh(Tv).
В первом члене правой части B.52) (энергия сублимации),
разумеется, должна быть учтена скрытая теплота плавления и
испарения, а также скрытая теплота других возможных фазо-
фазовых превращений.
Формула B.52) представляет интерес для механики разруше-
разрушения, так как поверхностная энергия твердого тела прямо про-
пропорциональна энергии связи UC(TO), которая на основании
B.52) может быть вычислена довольно точно из опытных дан-
данных по нагреванию и испарению твердого тела.
Отметим еще один метод, которым весьма точно (особенно
для простых элементов) можно определить энергию связи. До-
Допустим, что решетка подвергается облучению потоком частиц
(например, протонов или а-частиц). Если кинетическая энергия
атома после соударения с одной из этих частиц превышает
энергию связи, приходящуюся на атом, то он вырывается из ре-
решетки.
Законы сохранения импульса и энергии при ударе нереляти-
нерелятивистских частиц записываются в виде
moVo = mi (У» — Vlk), m0V20 = пц (i4— V\k). B.54)
§ 4] МЕТОД ТЕПЛОВОГО СМЕЩЕНИЯ 47
Здесь /щ, Vik, Fio —масса, конечная и начальная скорости ле-
летящей частицы соответственно; /щ—чиасса вырываемой части-
частицы, -получающей после удара скорость Vo. Отсюда можно опре-
определить энергию связи по минимальной, кинетической энергии
летящих частиц, требуемой для начала радиационного повреж-
повреждения.
Следует упомянуть также чисто химический метод измерения
энергии связи по реакционной способности твердого тела, осно-
основанный на измерении его химического потенциала.
Поверхностную энергию можно вычислить из энергии связи
U? следующим способом.
Допустим, что разрьиз твердого тела образовался вдоль не-
некоторой поверхности. Пусть на единицу этой поверхности при-
приходится sQ разорвавшихся связей. Будем учитывать взаимодей-
взаимодействие только близлежащих частиц твердого тела (связь можно
изображать черточкой, которая соединяет любые две соседние
частицы и которая стирается, если через нее прошла поверх-
поверхность разрыва). Считаем, что энергия всех связей одинакова.
Тогда поверхностная энергия у на единицу площади опреде-
определяется формулой
- Ро«
Действительно, общее число связей в единице объема равно
p0n/Bm0), так что для разрыва одной связи требуется энергия
2Ucm0/(p0n); отсюда легко получить- формулу B.55), если
учесть, что свободная поверхность тела, образовавшаяся после
разрыва, по площади в два раза больше соответствующего гео-
геометрического сечения в сплошном теле.
По формулам B.52) и B.55) можно определить также зави-
зависимость поверхностной энергии тела от его температуры То. Как
видно, с ростом температуры поверхностная энергия убывает,
причем в не слишком широком интервале температур эту зави-
зависимость можно считать линейной.
Приведенные в этом параграфе расчеты можно модифици-
модифицировать также на случай неравнозначных частиц и связей, если
ввести статистические функции распределения соответствующих
величин. Однако эти вычисления ввиду их громоздкости опу-
опускаем; полученные ранее формулы будем применять и к этому
более сложному случаю, используя осредненные характе-
характеристики.
Применяемый подход (как и статистический подход) не учи-
учитывает перераспределения усилий, возникающего при обрыве
лишь некоторых связей. Учет этого обстоятельства, как будет
показано в гл. IV, приводит к величине прочности, значительно
меньшей теоретической и хорошо согласующейся с эксперимен-
48 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР [ГЛ. II
тальными данными по прочности большинства обычных мате-
материалов. Значение изложенного метода заключается прежде всего
в том, что он позволяет определить «потолок» возможной проч-
прочности твердых тел. В будущем, с улучшением структуры (а тем
самым и прочности) конструкционных материалов роль этого
метода, а также требования, предъявляемые к его точности,
будут возрастать. В настоящее время область его практического
применения ограничена в основном кристаллами, близкими
к идеальным. Для хрупких материалов (стекло, плавленный
кварц и т. д.) представляют интерес также расчеты поверхност-
поверхностной энергии.
Знание энергии связи позволяет более точно рассчитать тео-
теоретическую прочность. Для этого аппроксимируем полную энер-
энергию взаимодействия пары частиц в решетке U следующим вы-
выражением:
• V(r)=^~--^-. B.56)
Здесь г — расстояние между частицами, Ао, А\, t—некоторые
постоянные, которые будем определять на основании экспе-
экспериментальных измерений сжимаемости, периода решетки
и энергии связи в состоянии равновесия (в отсутствие внеш-
внешних сил).
Принимая допущения а) и б) § 2 и проводя расчеты, совер-
совершенно аналогичные вычислениям § 2, нетрудно получить сле-
следующие результаты:
_
/in
0 я (9-0 ' "' nf (9-0 '
12
j. г U
у =
г.
B.57)
Обозначения в этих формулах совпадают с принятыми в соот-
соотношениях B.35). Знание предельной силы натяжения одной свя-
связи Fmax позволяет оценить прочность идеальной структуры
также при одностороннем растяжении (точный расчет оказы-
оказывается слишком сложным из-за различного натяжения связей, за
исключением некоторых простейших случаев, например, растя-
растяжения простой кубической решетки в направлении ее ребра).
Поверхностная энергия на любой площадке разрыва вычисляет-
§fl
МЕТОД ТЕПЛОВОГО СМЕЩЕНИЯ
49
ся весьма просто: для этого достаточно просуммировать энер-
энергию связей, оборвавшихся на данной площадке.
Формулы B.57) позволяют определить теоретическую проч-
прочность и поверхностную энергию твердого тела, по-видимому,
с наибольшей точностью. ,
Отметим, что разрушение всегда должно сопровождаться
акустическим и электромагнитным излучением. Действительно,
в процессе разъединения атомных плоскостей (или некоторых
участков, больших по сравнению с межатомным расстоянием,
Таблица 2.2
Теоретические значения поверхностной энергии н прочности
некоторых материалов
№
п/п
1
2
3
4
5
6
7
8
9
10
и
12
13
14
15
16
Кристалл
MgO
LiF
NaCl
NaBr
KC1
KBr
KJ
Стекло
Cu
a-Fe
v-Fe
Al
Au
Лед
Алмаз
Алмаз
Расстояние
между
ближайшими
соседями
в решетке
га X Ю~8 см
2,10
2,00
2,81
2,97
3,14
3,29
3,53
2,30
2,55
2,58
2,57
2,86
2,88
' 2,76
1,54
1,54
Модуль
сжимаемости
1 см2
к ' кГ
0,70 • 10
1,50-10"?
3,30 • 10"'
5,20 • 10~°
5,51 • 10-°
6,30 • 10 "'
8,60 • 10"'
2,03 • 10"'
0,719 «10"'
0,587 • 10"'
0,587 • 10"'
1,33-10"'
0,584 • 10"'
0,5 • 10
0,6-10
0,6 - 10~7
Поверхност-
Поверхностная
энергия V,
дн/см
3 300
3 400
1350
1 120
950
830
620
2 320
980
1200
1200
600
1400
15
5 500
7 100
Энергия
связи 11С,
икал/гратом
186
236
182
167
162
159
145
213
76
137
95
58
98
3
170
212,6
Теоретиче-
Теоретическая
прочность
при всесто-
всестороннем
растяжении
<ттах, кГ/мм'
1730
1 140
420
310
260
225
160
800
1470
1800
1800
800
1800
21
11600
17660
ПРИМЕЧАНИЯ К ТАБЛ. 2.2
1. Кристаллы 1—7 ямеют простую кубическую решетку типа NaCl.
Величины у, Uc и атах вычислялись по формулам B.22), B.30), B.31).
2. Химический состав стекла и метод расчета указаны в § 8 гл. VII.
3. Кристаллы металлов Си, А1, Аи, ^-Fe имеют структуру гранецентриро-
ванного куба, a-Fe — объемноцентрированного Куба. Величины у. Uc и атах
для этих кристаллов вычяслены по формулам B.35).
4. Молекулярная решетка льда считалась тетрагональной. Величины у,
Uc и атах для льда и алмаза A6) вычислены по формулам B.35).
5. Данные для алмаза A5) рассчитаны по формулам B.67), причем энер-
энергия связи была взята из работы [324].
6. Величины г0 и k были взяты из следующих источников: кристаллы
1-7 [325.326,19], кристаллы 9-13 [19.327], дед [328] алмаз [324]
50 ПРОЧНОСТЬ ИДЕАЛЬНО-ПЕРИОДИЧЕСКИХ СТРУКТУР (ГЛ. II
как в концевой части трещины) практически невозможно осу-
осуществить медленный спуск по неустойчивой ветви (см. рис. 7).
Поэтому процесс разрушения — всегда динамический (в малой
окрестности конца трещины); некоторая часть работы внешних
сил переходит в энергию звуковых и электромагнитных волн.
Эта энергия мала, однако она может иметь большое значение
для контроля за процессом разрушения. Мощность излучения,
очевидно, прямо пропорциональна площади вновь образовав-
образовавшейся поверхности трещины и обратив пропорциональна вре-
времени ее образования.
В табл. 2.2 приводятся результаты вычислений \, Отах и Uc
для некоторых материалов.
Г Л А В А III
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
§ 1. Классификация особых точек
Прочность большинства хрупких тел определяется дефек-
дефектами типа трещин, размеры которых велики сравнительно
с межатомным расстоянием. Такие дефекты в десятки и сотни
раз снижают прочность материала по сравнению с теоретиче-
теоретическим значением для идеально-периодической структуры. По-
Постановка задачи, учитывающая атомную структуру материала
в явном виде, настолько усложняет решение, что почти всегда
приходится отказываться от нее и прибегать к модели сплош-
сплошного деформируемого тела. Для хрупких материалов такой мо-
моделью является модель линейно-упругого тела при малых де-
деформациях.
Как будет показано в гл. IV, для решения проблемы проч-
прочности хрупкого тела нужно уметь находить решение соответ-
соответствующей математической задачи теории упругости для тела
с разрезами нулевой толщины. Эти задачи относятся к так на-
называемым сингулярным краевым задачам, т. е. к граничным
задачам с особыми точками. Такими точками являются, напри-
например, бесконечно удаленная точка, угловая точка, коническая
точка, точка разрыва граничных условий, точка приложения
сосредоточенной силы и т. д. Появление таких точек обычно
связано с некоторой идеализацией исходной физической задачи.
При этом в линейных задачах решение (или его производные,
начиная с некоторого порядка) стремится к бесконечности при
приближении к особой точке. Поскольку граничная задача
в особой точке не определена, встает вопрос о формулировке
физически осмысленного дополнительного условия в такой
точке, т. е. о постановке корректной сингулярной краевой
задачи.
Особый интерес представляет исследование бесконечно уда-
удаленной точки; общепринятый подход основан на применении
эвристического принципа, сформулированного впервые Сен-Ве-
наном для кручения и изгиба тонких стержней и обобщенного
Буссинеском и Томсоном на пространственные задачи и на
пластинки. В последние десятилетия в основном усилиями Ми-
зеса, Штернберга, Розенталя, Койтера,- Белоносова были
52 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (ГЛ. Ш
найдены некоторые (правда, довольно экзотические) примеры,
противоречащие принципу Сен-Венана, а формулировка самого
принципа была уточнена. Однако указанным авторам не уда-
удалось получить законченных результатов в этом направлении.
В этой главе излагается общий подход к решению проблемы
особых точек, основанный на понятии корректной краевой за-
задачи и теореме об однородных решениях [21]. В сочетании с про-
простейшими инвариантно-групповыми соображениями предлагае-
предлагаемый подход позволил достаточно полно изучить наиболее ин-
интересные случаи в плоской статической задаче теории упругости,
а также случай цилиндрической точки.
Используя предложенный подход и теорему Клапейрона, уда-
удалось доказать классический принцип Сен-Венана в его перво-
первоначальной формулировке, т. е. для кручения и изгиба цилиндри-
цилиндрических (призматических) тел.
Показано, что для плоских задач теории упругости все мно-
множество сингулярных упругих задач с бесконечно удаленной
точкой можно разбить на два эквивалентные по мощности*)
класса: класс S, для которого выполняется принцип Сен-Ве-
Сен-Венана, и класс N, для которого принцип Сен-Венана несправед-
несправедлив. Например, к классу N принадлежит упругая задача для
тела с бесконечно удаленной точкой типа клина с углом рас-
раствора, большим я. Для постановки корректной краевой задачи
в классе /V оказывается необходимым ввести дополнительное
условие на бесконечности. В качестве иллюстрации рассмот-
рассмотрены решения некоторых конкретных задач. Показано, напри-
например, что известные решения задач о действии сосредоточенной
силы и момента в вершине бесконечного клина некорректны
при угле раствора, большем я.
Задачи теории упругости для тел с разрезами типа трещин
оказываются принадлежащими классу N. Упомянутый метод по-
позволил, в частности, строго вывести закон распределения на-
напряжений и деформаций в малой окрестности края трещины
любой гладкой формы для различных наиболее часто встречаю-
встречающихся случаев (с учетом анизотропии, неоднородности, сил
инерции, физической и геометрической нелинейности, различных
вариантов граничных условий на трещине и т. д.).
Рассмотрим классическое линейно-упругое тело, ограничен-
ограниченное поверхностью F(x,y,z) = О, где х, у, z — прямоугольные де-
декартовы координаты. Для простоты тело вначале считаем одно-
однородным и изотропным; учет неоднородности или анизотропии
вносит в анализ усложнения, не имеющие принципиального ха-
характера. Объемными силами пренебрегаем. Вся граница упру-
*) Два множества эквивалентны по мощности, если каждому элементу
одного множества соответствует один элемент другого множества, и обратно.
§ 1] КЛАССИФИКАЦИЯ ОСОБЫХ ТОЧЕК 53
гого тела разбита на фиксированные области, в каждой из ко-
которых заданы или нагрузки, или смещения, или краевые условия
типа контактной задачи. Контуры этих областей считаются за-
заранее заданными и неизменными в процессе деформации. Гра-
Границу тела предполагаем всюду гладкой, за исключением конеч-
конечного числа особых линий и точек.
Кроме того, граничная поверхность может содержать беско-
бесконечно удаленную точку; считается, что в окрестности этой точки
поверхность допускает группу подобия или переноса (клин, ко-
конус, цилиндр, полоса и т. д.). Для определенности предположим,
что граница тела в окрестности бесконечно удаленной точки
свободна от нагрузок. (Применяемый ниже подход годится и
для более общих однородных граничных условий.) Напомним,
что принцип Сен-Венана формулируется именно для таких граг
ничных условий. Этот принцип утверждает, что если некоторая
совокупность внешних сил, действующих на некотором участке
поверхности тела, будет заменена другой системой внешних сил,
статически эквивалентной предыдущей и распределенной на том
же участке, то напряжения, соответствующие этим двум нагруз-
нагрузкам, будут одинаковыми на достаточном удалении от места при-
приложения сил.
Требуется найти решение уравнений статической теории
упругости в указанной области, удовлетворяющее заданным гра-
граничным условиям в регулярных точках границы и некоторым
дополнительным условиям в сингулярных точках. Общий вид
дополнительных условий в особых точках устанавливается
ниже.
Итак, поставленная краевая задача имеет особые линии и
точки следующих типов:
а) бесконечно удаленные точки;
б) линии разрыва первых производных функций F(x, у, z);
в) точки пересечения линий разрыва и конические точки;
г) линии разрыва граничных условий;
д) точки приложения сосредоточенных сил, моментов и т. д.
к границе тела.
Во всех случаях предполагается, что поверхность в малой
окрестности изолированной особой точки допускает или группу
подобия
0), /=1,2,3, C.1)
или группу переноса
*[ === #j -J- Kj> Х2 = Х2 ~\- И2» #3 == Х3>
9 в малой окрестности точки, находящейся'на особой линии,—
следующую группу подобия:
*{ = **,, x'2 = tx2, x'3 = x3 (t>0). C.3)
54 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. ill
Здесь Х{ — локальные декартовы координаты с началом в осо-
особой точке, t и %i — произвольные параметры (параметры
групп). В формулах C.3) ось х3 направлена вдоль особой
линии.
§ 2. Основные теоремы
Определим вначале некоторые понятия.
Канонические сингулярные задачи. Краевую задачу теории
упругости будем называть канонической сингулярной задачей,
если удовлетворяются следующие требования:
1) граничная поверхность тела F(x, у, г) =0 представляет
собой или двугранный угол, или совокупность двух параллель-
параллельных плоскостей (слой), или цилиндрическую поверхность (в част-
частности, бесконечный круговой цилиндр и бесконечная призма),
или коническую поверхность (в частности, многогранный угол
и круглый конус);
2) линии раздела граничных условий в случае смешанной
краевой задачи допускают одну и ту же группу, соответствую-
соответствующую граничной поверхности;
3) граничные условия однородны и относятся, например,
к одному (или к некоторой совокупности в случае смешанной
задачи) из следующих типов: а) внешние нагрузки отсутствуют,
б) ректор смещения равен нулю, в) нормальная нагрузка и ка-
касательное смещение равны нулю, г) нормальное смещение и ли-
линейная комбинация касательной и нормальной составляющих
вектора внешней нагрузки обращаются в нуль (кулоново
трение). ,
Можно поставить также много других корректных, однород-
однородных граничных условий, имеющих физический смысл.
Решения канонических сингулярных задач будем называть
однородными решениями. Относительно однородных решений
имеет место следующее предложение.
Теорема 3.1. Каждой канонической сингулярной задаче со-
соответствует некоторое трансцендентное уравнение, каждому
корню которого отвечает определенное однородное решение;
число произвольных действительных постоянных в этом реше-
решении равно кратности корня. . v
Трансцендентное уравнение, его корни и соответствующие им
однородные решения представляют собой своего рода характе-
характеристическое уравнение, собственные числа и собственные функ-
функции рассматриваемой канонической сингулярной задачи. Число
собственных функций бесконечно, так как число корней транс-
трансцендентного уравнения бесконечно; каждый корень непрерывно
зависит от коэффициента Пуассона (и коэффициента трения
при наличии кулонова трения), вообще говоря, входящего в
трансцендентное уравнение. Модуль Юнга, очевидно, не может
jf 2] ОСНОВНЫЕ ТЕОРЕМЫ 55
входить р трансцендентное уравнение для указанных выше
типов граничных условий.
Общее решение канонической сингулярной задачи равно
произвольной линейной комбинации собственных функций.
Теорема 3.1 доказывается в следующих параграфах для наи-
наиболее типичных канонических задач. В число однородных реше-
решений, естественно, входят решения Сен-Венана, которыми мы бу-
будем в общем случае называть однородные решения, дающие
конечные главный вектор и главный момент. Эти решения полу-
получаются из обычной теории изгиба, растяжения и кручения
стержней, а также отвечают решениям задач о сосредоточенной
силе и сосредоточенном моменте в вершине клина и в вершине
конуса (в случае слоя решение Сен-Венана соответствует чи-
чистому изгибу и однородному растяжению). Однородные реще-
ния, не являющиеся решениями Сен-Венана, по определению
дают главный вектор и главный момент, равные или нулю, или
бесконечности.
Всюду в дальнейшем, когда производится сравнение различ-
различных собственных функций, подразумевается, что они относятся
к одним и тем же физическим величинам (например, напряже-
напряжениям или смещениям) и, следовательно, все произвольные по-
постоянные имеют одинаковую размерность.
Если левая часть трансцендентного уравнения представляет
собой аналитическую функцию, то корни уравнения (вообще го-
говоря, комплексные) будут дискретными («дискретный спектр»).
Корректная краевая задача теории упругости. Исходную
краевую задачу теории упругости будем называть корректной,
если 1) существует единственное решение этой задачи (решение
предполагается непрерывным в смещениях всюду в конечной
области при отсутствии сосредоточенных воздействий), 2) ре-
решение устойчиво по отношению к малым возмущениям гранич-
граничных условий и формы тела в следующем смысле: если форма
тела и граничные условия претерпели изменения на некотором
малом участке, такие, что разность главных векторов и главных
моментов возмущенной и невозмущенной внешних нагрузок
равна нулю, то при стремлении всех размеров этого участка
к нулю отношение характерных возмущенных напряжений к со-
соответствующим невозмущенным будет всюду как угодно близко
к единице. Под характерными понимаются компоненты тензора
напряжений, не равные тождественно нулю в возмущенном или
невозмущенном состоянии. л
Принципиальную в'ажность исследования однородных реше-
решений показывает следующая
Теорема 3.2. В бесконечно малой окрестности особой точки
решение корректной краевой задачи теории упругости ведет
себя как асимптотически наибольшая по абсолютной величине
бб СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
собственная функция соответствующей канонической сингуляр-
сингулярной задачи. Собственная функция, естественно, должна быть
или решением Сен-Венана, или удовлетворять одному из сле-
следующих условий: а) смещения непрерывны в конечной особой
точке, б) напряжения затухают в окрестности бесконечно уда-
удаленной точки типа клина или конуса, в) напряжения ограни-
ограничены в окрестности бесконечно удаленной точки типа слоя или
цилиндра.'
На первом этапе доказательства теоремы 3.2 покажем, как
вопрос об исследовании поведения решения в окрестности осо-
особой точки приводится к определенной канонической сингуляр-
сингулярной задаче теории упругости.
Рассмотрим малую окрестность х\ + х\ < г\, х\ < ъ\, г\ <С е|
некоторой точки О, находящейся на особой линии (линии раз-
разрыва граничных условий или первых производных функции
F(x,y,z), или тех и других вместе). Напомним, что поверхность
тела в малой окрестности рассматриваемой точки допускает
группу подобия C.3).
Запишем уравнения Ляме
«М/ + Т=27<им).'=0 (U=l,2,3), C.4)
где щ — составляющие-вектора смещения по осям х{. Перейдем
в них к новым переменным х\ согласно C.3). Получим
а 1+ \-2чдх[^ t2[d{4J
JL 4. _L
, , "Г л
. 1
где
l-2v дх'2 t2[d(x3f l-2v дх'3дх'2
_L Г д2цз . t д__ t ди\ , ди2 . 1 диЛ'
t2 [d(x3f 1 - 2v 3^3 \3^ ^2 1~д73)
= 0, C.5)
= 0,
q 3«l . 3«2
В новых переменных рассматриваемая область будет сле-
следующей:
Примем значение параметра t равным {z2l&if и перейдем к сле-
следующему пределу в формулах C.5) и C.6):
8[-*0, е2->-0, ejE2-+Q, f->oo. C.7)
В результате получим уравнения
Д"' + 7^;^"==0' А = 0 (/==1'2) C.8)
§ 21 ' бСНОВНЫЕ ТЕбРЁМЫ Ы
в бесконечной области, заключенной внутри двугранного угла,
образованного касательными плоскостями к поверхности тела
в точке О. Уравнения C.8) представляют собой уравнения Ляме
в случае плоской задачи теории упругости (первые два урав-
уравнения соответствуют обычной плоской деформации, последнее —
сложному сдвигу). При предельном переходе C.7) в однород-
однородных граничных условиях указанного выше типа в новых пере-
переменных получаются те же условия, если в них формально по-
положить д/д*з = 0.
Таким образом, вопрос об исследовании поведения решения
в окрестности точки, лежащей на особой линии, сводится к ка-
канонической сингулярной задаче плоской теории упругости для
двугранного угла.
Если заранее предположить выполненными условия плоской
задачи, то совершенно аналогичное преобразование к тем же
новым переменным при t = е~2 и предельный переход е —¦ оо
позволяют свести к той же канонической задаче вопрос об
исследовании решения в окрестности бесконечно удаленной
точки типа клина.
Пользуясь аналогичным приемом*), нетрудно установить
сводимость к соответствующей канонической сингулярной за-
задаче всех случаев особых точек, указанных в первом пара-
параграфе.
Теперь для доказательства теоремы 3.2 осталось лишь пока-
показать, что для условия корректности краевой задачи теории упру-
упругости следует выбирать наибольшее по абсолютной величине
однородное решение, соответствующее одному из собственных
чисел.
Предположим, что выбрана некоторая собственная функция,
не являющаяся асимптотически наибольшей по модулю. Изме-
Изменим на некотором малом участке форму граничной поверхности
и приложим к ней некоторую нагрузку, статически эквивалент-
эквивалентную нулю и отвечающую собственной функции, наибольшей по
модулю. Тогда при приближении к особой точке возмущенное
решение будет по порядку величины превосходить невозмущен-
невозмущенное решение, что противоречит предположению о корректности
краевой задачи. Теорема доказана.
Классы S а N краевых задач теории упругости. Будем го-
говорить, что краевая задача теории упругости с бесконечно уда-
удаленной точкой принадлежит классу S, если для нее справедлив
принцип Сен-Венана, и классу N, если принцип Сен-Венана для
нее не выполняется.
*) Этот прием иногда называют «принципом микроскопа» (соответ-
(соответственно «принципом телескопа» при <->-0). Разумеется, эти «принципы» не
имеют физического содержания; они дают лишь наглядное представление
о соответствующем математическом преобразовании и предельном переходе.
88 сингулярные задачи tеорий yrtpyrocfи (гл. пт
На основании теоремы 3.2 принцип Сен-Венана можно сфор-
сформулировать так: асимптотически наибольшая по модулю соб-
собственная функция канонической сингулярной задачи (удовлет-
(удовлетворяющая условию затухания или ограниченности напряжений)
всегда представляет собой решение Сен-Венана.
Отсюда получаем следующий признак принадлежности крае-
краевой задачи теории упругости к классу N или 5.
Теорема 3.3. Если существует собственная функция (удовлет-
(удовлетворяющая условию затухания или ограниченности напряжений)
более высокого порядка по сравнению с решением Сен-Венана,
то соответствующая краевая задача теории упругости принадле-
принадлежит классу N. Если такой собственной функции не существует,
то соответствующая упругая задача относится к классу S.
Для доказательства второй половины теоремы 3.3 Нужно
быть уверенным в том, что, если некоторая собственная функция
имеет тот же порядок, что и решение Сен-Венана, то эта соб-
собственная функция с точностью до множителя есть решение Сен-
Венана. Это утверждение доказывается ниже для наиболее ти-
типичных случаев.
Дополнительное условие в бесконечно удаленной точке для
упругих задач класса N. Из теорем 3.2 и 3.3 следует, что решение
упругой задачи, относящейся к классу N, зависит от произволь-
произвольных-постоянных, которые входят в наибольшую по модулю соб-
собственную функцию и которые в отличие от решения Сен-Венана
не зависят от граничных условий в конечной части тела. По-
Поэтому в постановку корректной краевой задачи теории упруго-
упругости, относящейся к классу N, следует включить задание ука-
указанных постоянных. Физический смысл этого дополнительного
условия будет выяснен в дальнейшем. Аналогичное дополни-
дополнительное условие требуется также в некоторых задачах класса S
(см., например, далее задачу о гиперболе).
< § 3. Плоская задача теории упругости
Допустим, что поле упругих смещений и деформаций не за-
зависит от одной из прямоугольных декартовых координат х, у, г,
например, от г. В этом весьма общем и важном случае все
смещения и напряжения можно представить через функции
Ф(г), W(z) и j(z), являющиеся аналитическими функциями
комплексного переменного *) г = х + iy в области, занятой те-
телом. Первые две из них часто называют потенциалом Коло-
Колосова — Мусхелишвили.
*) Применение одной и той же буквы г для обозначения комплексной
переменной н декартовой координаты, очевидно, не должно привести к пу-
путанице.
§8J
ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ
59
Приведем основные представления, которые в дальнейшем
будут часто использоваться (вывод их. можно найти в моногра-
монографии Н. И. Мусхелишвили [23]):
<т„ - <х, + 2irtn = 2е««* [гФ' B) + Т B)],
2ц (ы + lv) = щ (г) — 2ф' (г) —1|) B),
w = Re / B), тй + /т„г = цГфе-,
?5j* j Xn + ^Т„) ds,
АВ
C.9)
f
1
3 — 4v (плоская деформация, ez = 0),
C — v)/(l+v) (плоское напряженное состояние, <х2 = 0).
t
Здесь Ы — произвольная прямоугольная декартдва система ко-
координат в плоскости ху, а—угол между осями х и t (направ-
(направление отсчета — от х к t), и, v, w — составляющие вектора сме-
смещения по осям х, у, z соответственно, at, on, oz, ttn, ttz, tnz —
компоненты тензора напряжений, ц и v — модуль сдвига и ко-
коэффициент Пуассона-соответственно.
Наиболее часто формулы C.9) применяются при а = О,
тогда индексы t и п заменяются соответственно на х и у. Далее,
символ [ ]д обозначает приращение выражения, заключен-
заключенного в скобки, при перемещении по, дуге АВ из А в В; Хп и Yn —
компоненты усилия, действующего на дугу в данной точке, по
осям х и у.
Как видно, плоское поле распадается на два независимых
поля, одно из которых соответствует сложному сдвигу
0,
xtz
ф0, и = v = 0,
а другое — плоской деформации
ифО, v-фО, апф0, а{ф0,
dw/dz = 0, xtz = xnz--
т,„ Ф 0, oz Ф 0,
= 0,
ИЛИ плоскому напряженному состоянию
ифО, уф 0, апф0, а{ф0, хмф0,
dw/dz фО, аг = хи = хпг = 0.
В плоской задаче теории упругости Г. В, Колосовым и
Н. И. Мусхелишвили были развиты мощные методы [23]. Еще
более широкий круг эффективных решений может быть получен
60 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
методами, предложенными сравнительно недавно С. М. Белоно-
совым [34].
Рассмотрим одну каноническую сингулярную задачу теории
упругости для двугранного угла (клина).
Двугранный угол. Пусть (в полярных координатах) тело за-
занимает область 0 < г < оо, 6i < 9 < вг. Границы свободны от
нагрузок.
Напряжения вв и тге при помощи потенциалов Колосова —
Мусхелишвили можно представить так:
~ (z = re'e). C.10)
Согласно C.10), если Ф(г) и W{z) удовлетворяют гранич-
граничным условиям, то Ф(С[2) и xF(Ciz) (Ci — произвольное действи-
действительное число) также им удовлетворяют. Вследствие линейно-
линейности и однородности краевой задачи функции С2Ф(г) и C2W(z)
(С2— произвольный действительный параметр) также будут
решениями. Следовательно, общее решение, порожденное неко-
некоторыми решениями Ф(г) и W(z), имеет вид соответственно
С2Ф{Схг) и C2W(Ciz); иначе говоря, множество искомых функ-
функций допускает группу подобия (автомодельные решения). Со-
Согласно определению группового свойства [25], функции Ф(г) и
^(z) должны удовлетворять функциональному уравнению
C2f(ClZ) = f(z). C.11)
Допустим, что решение этого уравнения представляет собой
некоторую дифференцируемую функцию. Подставляя ее в урав-
уравнение C.11), найдем, что С2 будет функцией Ct и, вообще го-
говоря, некоторых постоянных, входящих в решение. Если под-
подставить эту функцию С2 = C2(Ci) в уравнение C.11), оно пре-
превратится в тождество, которое можно дифференцировать по Си
В результате дифференцирования получим
0*^-0. C.12)
Введя постоянную Я'== d ^ с" , это уравнение можно запи-
записать так:
Л^- =-К. C.13)
d In z v '
Его Общее решение, очевидно, имеет вид
f (z) = C3z-* (Я - In Ca/In С,), C.14)
где Сз — произвольная постоянная.
Можно показать, что решение функционального уравнения
C.11) в классе любых непрерывных функций также дается фор-
формулой C.14),
§ 3] ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ 61
Таким образом, решение исходной граничной задачи имеет
следующий вид:
Ф(г)*=Аг-\ ^{z) = Bz-\ C.15)
где А, В, Я —некоторые (вообще говоря, комплексные) по-
постоянные.
Дальнейший ход решения таков: подставляем C.15) в гра-
граничные условия при 9 = 6i и 8 = 8г, полученные при помощи
(ЗЛО); сокращение одного и того же множителя г~х приводит
к линейной однородной алгебраической системе, состоящей из
четырех уравнений (вместе с комплекснр-сопряженными)_и слу-
служащей для определения неизвестных коэффициентов Л, А, В, В.
Условие обращения в нуль определителя системы приводит
к следующему характеристическому уравнению задачи:
sin2 Р = ЬУ, C.16)
где
р = (А-0F,-6,), б^9!.-90.
Каждому корню уравнения C.16) соответствует некоторое
решение C.15); число неопределенных постоянных, входящих
в него, очевидно, равно кратности корня. Число корней беско-
бесконечно, мнимая часть корня с наибольшей действительной частью
равна нулю.
Наличие комплексного корня с наибольшей действительной
частью свидетельствовало бы о некорректности физической по-
постановки задачи, так как решения с бесконечно частым изме-
изменением знака на конечном интервале не имеют физического
смысла; тем не менее, и в этом случае, который представится
далее при изучении кусочно-однородных тел, постановка мате-
математических задач имеет определенный смысл при выполнении
некоторого общего условия, накладываемого на физические па-
параметры. Отметим некоторые частные решения.
а) Сосредоточенная сила (решение Мичелла р6])
А— 1, о— л, л
-9')<х + 'г> +1^Щ~е2г9')Iх- iY)
4[(в2 — 602 — sin2 (в2 — es)]
C.17)
где X, Y — составляющие вектора силы.
б) Сосредоточенный момент М (решение Карозерса [27])
, = 2, А = — 2 [sin (9г _ в)) _ (е2 _ 6i j cos (е2 _ 9i)] . C.18)
tg (в, - в,) - (в, - в,)
62
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. III
в) Сосредоточенный момент п-го порядка (X = п — целое
число, больше двух) существует только при 82 — Oi = я и
Э2 — 01 = 2я;
г) Решение, непрерывное в смещениях при z -> 0 и соответ-
соответствующее корню характеристического уравнения с наибольшей
действительной частью • (решение Вильямса [28]). Указанный ко-
корень Vmx кратности единица (в данном случае мнимая часть
его равна нулю) с ростом (92 — 9i) монотонно увеличивается;
приведем график этой зависимости (рис. 9). В частности,
при 02— 81->0 %-*¦ — оо (полоса),
при 82— Э1 = я К=0 (полуплоскость),
при 82 — 0! = 2я К = 1/2 (щель).
C.19)
Решения а) и б) представляют собой решения Сен-Венана,
по нашей терминологии. Приведенные результаты анализа ха-
характеристического уравнения
C.16) на основании теорем
3.2 и 3.3 позволяют сформу-
сформулировать следующие предло-
предложения.
А. Краевая задача плоской
-теории упругости для тела с
бесконечно удаленной точкой
типа клина принадлежит клас-
классу S, если угол раствора кли-
клина изменяется в пределах 0 <
< 82 — 0i < я, и классу N,
если выполняется неравенство
я < 8г — 0i ^ 2я. В частности,
решения C.17) и C.18) не
имеют физического смысла
(некорректны) при я < 02 —
— 01<2я.
Рис. 9. Б. В корректной краевой
задаче для тела с бесконечно
удаленной точкой типа клина, угол раствора которого удовлетво-
удовлетворяет условию я'< 02 — 0i ^ 2я, должны быть заданы постоян-
постоянные Л и Б в формуле C.15), определяющие асимптотический
характер затухания напряжений в бесконечно удаленной точке.
В. В случае конечной угловой точки при z = 0 (некоторая
окрестность границы которой свободна от нагрузок) при я <
<С 02 — 0i ^ 2я в корректной краевой задаче должно быть по-
поставлено следующее условие:
при
1 = 0A), C.20)
§ 3] ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ 63
где К—корень уравнения C.16) с наибольшей Действительной
частью.
Г. Множества краевых задач класса S и класса N эквива-
эквивалентны по мощности*).
Предложение Г легко доказывается; если заметить, что каж-
каждой краевой задаче класса 5 взаимно однозначно соответствует
некоторая задача класса N, которая получается из первой рас-
рассмотрением области, дополняющей область, занятую телом, до
полной плоскости.^ Это предложение разрушает распространен-
распространенную иллюзию, что принцип Сен-Венана не справедлив только
в исключительных случаях.
Случай 02 — 8i->0 (полоса) нужно рассматривать как осо-
особый, он изучается в следующем параграфе.
Некорректность представления о сосредоточенной силе или
моменте, приложенных в угловой точке при л < 82 — 9i <; 2я,
математически состоит в том, что результат предельного пере-
перехода, соответствующего некоторому возмущению границы тела
или нагрузок в окрестности угловой точки, существенно зависит
от способа предельного перехода. Решения C.17) и C.18) в этом
случае представляют собой результат лишь некоторого опреде-
определенного способа перехода, при других предельных переходах мо-'
гут получиться совершенно другие решения. Физически это
означает, что упругое поле на расстояниях, больших по сравне-
сравнению с характерным радиусом закругления в «угловой» точке, но
малых по сравнению с характерным линейным размером тела,
в этом случае существенно зависит от характера распределения
нагрузки по закруглению.
Предложения А — Г завершают решение проблемы угловой
точки. Решения а) — г) были найдены ранее как некоторые
частные решения теории упругости вне связи с общими предло-
предложениями А —Г. Например, Вильяме не приводит каких-либо
соображений при выборе корня с наибольшей действительной
частью (см. также статью Каландия [29]). Штернберг и Кой-
тер [30], используя некоторую частную систему возмущающих
нагрузок, показали, что решение б) не имеет физического
смысла при 02 — 0i > 1,43л. В отличие от условия C.20) усло-
условия в угловой точке, накладываемые на искомые функции для
обеспечения единственности решения, обычно получаются фор-
формально из некоторых математических требований, физический
смысл которых неясен (см., например, [и>24]).
Рассмотрим два примера неканонических сингулярных за-
задач теории упругости, наглядно иллюстрирующих предложения
А и Б.
*) Т. е., грубо говоря, случаи, когда принцип Сен-Венана выполняется,
встречаются так же часто, как и случаи, когда он нарушается.
64
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ
(ГЛ. Ш
Парабола. Пусть упругое тело занимает область х2^
^ 4а2 (у + а2), т. е. часть плоскости не со стороны фокуса па-
параболы; ось параболы направлена по оси у, вершина распо-
расположена в точке х = 0, у = —а2, а фокус —в начале координат
(рис. 10). На границе тела считаем заданными нагрузки. При
помощи конформного отображе-
у ния на нижнюю полуплоскость
0
z^i&-iaJ (a>0) C.21)
легко найти общее решение одно-
однородной задачи
C>22)
(С
~ la)*
—]•
Рис. 10.
Здесь С — произвольная комп-
комплексная постоянная.
Частное решение неоднород-
неоднородной задачи получено Н. И. Мус-
хелишвили Р3]; при z -* оо оно ведет себя как О A/z), если
главный вектор внешних нагрузок отличен от нуля. Общее ре-
решение поставленной задачи, очевидно, равно решению Мусхели-
швили плюс решение C.22). Согласно C.22) и C.19), при
z —* оо это решение ведет себя так, как если бы тело представ-
представляло собой внешность полубесконечного разреза вдоль оси у,
что хорошо согласуется с «принципом телескопа». Рассматри-
Рассматриваемая задача, очевидно, принадлежит классу N, и величина С
должна быть задана при ее постановке. При любых С Ф 0 реше-
решение Мусхелишвили неустойчиво по отношению к малым воз-
возмущениям границы тела и внешней нагрузки.
Параметр С определяется из решения более общей задачи,
в которой рассматриваемая парабола будет конечным элемен-
элементом. Рассмотрим пример.
Пусть полуплоскость с глубоким вырезом в форме параболы
растягивается на бесконечности постоянными напряжениями р
в направлении, перпендикулярном оси параболы (последняя
нормальна к границе полуплоскости (рис. 11)). Предполагается,
что глубина выреза / гораздо больше радиуса кривизны пара-
параболы в ее вершине, т. е. / S> 2a2. Граница тела свободна от на-
нагрузок. Решение этой задачи «склеивается» из двух решений,
первое из которых представляет собой решение соответствую-
соответствующей упругой задачи для полуплоскости с щелью длины /, а вто-
5 31
ПЛОСКАЯ- ЗАДАЧА ТЕОРИИ УПРУГОСТИ
65
tttttt
рое — решение C.22); первое решение описывает упругое поле
на расстояниях от вершины параболы, больших по сравнению
с радиусом-кривизны в этой точке, а второе решение — в остав-
оставшейся окрестности конца выреза. Параметр С определяется из
условия асимптотического склеивания этих решений при
I Э> г ^> а2, где г — расстояние от вер-
вершины параболы. Решение первой за-
задачи приводится в Приложении I
(см. формулу (П.22)). Используя его
асимптотику при г-*~1, можно най-
найти С:
С = 0,79рУТ. C.23)
Существенно подчеркнуть, что
склеиваемые асимптотики этих двух
решений обязаны быть одними и теми
же, так как они отвечают одной и
той же канонической сингулярной за-
задаче.
Число примеров решения задач для
различных тел с глубокими вырезами
параболической и более сложной фор-
формы можно значительно увеличить, ис-
используя аналогичный метод. \^
Как видно, в задачах класса N напряжения, вызванные на-
нагрузками, приложенными в окрестности конца выреза, вообще
говоря, затухают как 1/г, а напряжения от внешнего поля за-
затухают как 1/г\ где 0 < Ж 1/2, т. е. гораздо медленнее, так
что внешнее поле нельзя не учитывать.
Гипербола. Пусть упругое тело занимает область (рис. 12)
1, C.24)
c2cos260 с2 sin2 6,, ^= '
т. е. часть плоскости, расположенную между ветвями гиперболы
Bс— расстояние между фокусами, ±tg60 — угловые коэффи-
коэффициенты асимптот). Границы тела считаем свободными от на-
нагрузок. Рассматриваемая задача, очевидно, принадлежит клас-
классу S; искомое решение при z -* <х> ведет себя так, как если бы
тело представляло собой клин с углом раствора я — 28о, где
О < 8о < я/2. Своеобразие этой задачи заключается в том, что
в ней имеется две бесконечно удаленные точки, и поэтому, не-
несмотря на принадлежность к классу S, существует нетривиаль-
нетривиальное решение однородной задачи. Это решение отвечает конеч-
конечным главному вектору и главному моменту нагрузок, приложен-
приложенных в каждой из бесконечно удаленных точек.
3 Г. П. Черепанов
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. Ш
Краевую задачу на основании формул C.9) можно запи-
записать так:
VJ (zs=L) C.25)
(бо = 0 при х < О, 60=1 при л:>0). Здесь (X, У) —главный
вектор нагрузок, приложенных в бесконечности при у-*—оо
Рис. 12.
(из условия равновесия в другой бесконечно удаленной точке —
при у-* со — главный вектор равен (—X,—Y)).
При помощи конформного отображения
z = -^\e X -\- е % ) (<х=(я — 2Э0)/я), C.26)
где ?а = exp[a(ln|?|-f- i arg?)], перейдем на верхнюю полу-
полуплоскость параметрического переменного ?; при этом стремле-
стремлению у->оо соответствует ?->со, стремлению у—*—со соответ-
соответствует ?->0, левая ветвь гиперболы переходит в действительную
полуось (—со, 0), а правая часть — в полуось @, оо).
Краевая задача C.25) на > плоскости ? примет следую-
следующий вид:
при
C.27)
Здесь
F='sin па/(па)).
C.28)
§ 3] ПЛОСКАЯ ЗАДАЧА ТЕОРИИ УПРУГОСТИ 67
Согласно C.27), если ф*(?) и г|)*(?,) удовлетворяют гранич-
граничным условиям, то (p,(Ci?) + С2 и г|э*(С3?) + С4 соответственно
-также будут решениями краевой задачи, и множество искомых
функций допускает группу (Сь Сз— произвольные действитель-
действительные, а С2, С4 — произвольные комплексные числа, С2 + С4 = 0).
Согласно определению группового свойства функции ф*(?) и
•ф*(?) должны удовлетворять функциональному уравнению
+ C2 = f@, C.29)
общее решение которого нетрудно найти при помощи метода,
подробно рассмотренного ранее на примере функционального
уравнения C.11):
f(O = _C5lnE + C6 (C8 = C2/InC,). C.30)
Таким образом, решение сингулярной краевой задачи C.27)
должно иметь вид
+ D, C.31)
где А, В, С, D — некоторые постоянные. Подставляя C.31)
в C.27), находим эти постоянные:
X + iLVX^lY) ' B = -A, C + D=i(X + iY). C.32)
Постоянные С и D не влияют на напряженное состояние.
При ?-*оо и ?—>-0 решение C.31), C.32) переходит в ре-
решение Мичелла C.17), как это и должно быть на основании
«принципа телескопа».
В случае, если X = Y = 0, краевая задача C.27) допускает
группу, которой соответствует функциональное уравнение типа
C.11); поэтому ее решение должно иметь вид
Ф.(» = ОГ\ *.(?) = ^ГХ (ReA>0), C.33)
где %, G и N\ — некоторые постоянные.
Подставляя функции C.33) в C.27), находим, что характе-
характеристическое уравнение в точности совпадает с уравнением
C.16), в котором нужно положить р = пК (б определено в
C.27)). Это уравнение в данном случае (т. е. при 0 < а < 1)
имеет единственный корень, удовлетворяющий условию Re?->0:
Х = а (при этом Ni = — G). C.34)
Это решение отвечает конечному главному моменту нагрузок,
приложенных на бесконечности. Обозначая величину момента че-
через М, из уравнения равновесия окончательно находим
д ' Мге~г9° C 35)
с cos rax (tg па — па)
68 " СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (ГЛ. Ш
в полном соответствии с решением Карозерса C.18) при ?—>0 и
С —оо. "
Частное решение общей неоднородной задачи для гиперболы
(описывающее поЛе местных возмущений от приложенных нагру-
нагрузок) найдено С. М. Белоносовым [24]. Общее решение, очевидно,
равно сумме полученного решения C.31) — C.35) (общего ре-
решения однородной задачи) и решения Белоносова.
Как видно, из-за наличия двух бесконечно удаленных точек
в однородной задаче при ее постановке следует задавать вели-
величины М, X и Y, определяющие интенсивность внешнего поля.
Полученные решения представляют также практический ин-
интерес в задаче о концентрации напряжений в образцах с двумя
симметричными глубокими выточками, форма каждой из кото-
которых близка к клиновидному вырезу с закругленным основанием
(образец подвергается растяжению и изгибу). Однородная за-
задача другим методом была решена ранее Нейбером [31]. Умест-
Уместно отметить, что её не удается решить общими методами, изло-
изложенными в монографиях [23>24]. Например, использование ме-
метода С. М. Белоносова приводит к расходящимся интегралам.
§ 4. Цилиндр
Пусть упругое те'ло ограничено бесконечной цилиндрической
(призматической) поверхностью, свободной от внешних нагру-
нагрузок. Ось г прямоугольной декартовой системы координат xyz
направим вдоль образующей.
Рассмотрим систему уравнений в напряжениях
<*/./ = О
= 0, (/,/=1,2,3). (8.36)
Здесь индексам 1, 2, 3 соответствуют х, у, г; принимаются обыч-
обычные соглашения о немых индексах, за исключением одного слу-
случая: при i = / во втором уравнении ви означает соответствую-
соответствующую компоненту тензора напряжений.
Пусть Oth(x, у, z) представляют собой некоторое решение по-
поставленной канонической сингулярной задачи. Тогда, очевидно,
будут решением также функции CiOik(x, у, z-f C2), т. е. мно-
множество искомых функций обладает групповым свойством, со-
согласно определению которого функции а,к(х, у, z) должны удов-
удовлетворять функциональному уравнению
(х, у, z + C2) = aik (x, у, г). C.37)
Здесь С2 — произвольная действительная постоянная, а
произвольная комплексная постоянная.
Щщ цилиндр 69
(Убщее решение функционального уравнения C.37) можно
райти совершенно аналогично предыдущему; оно имеет следую-
следующий вид:
о1к = Re [Fik (х, у) е^}. (я. = -~ 1п ±). C.38)
Здесь % — произвольное комплексное число, Fik (х, У) — произ-.
Вольные комплексные функции хну.
,: Подставляем общее решение C.38) в систему уравнений
1C.36) и граничные условия; после сокращения общего множи-
'теля еи получаем на плоскости ху однородную краевую задачу
в области S для функций F{h(x,y), где S—поперечное сечение
цилиндра. Решение этой задачи существует только при неко-
некоторых (собственных) значениях к и определяется, очевидно,
с точностью до произвольных множителей. Таким образом, мы
приходим к типичной задаче на собственные значения.
Легко убедиться непосредственной проверкой, что число
X = 0 является собственным значением краевой задачи, а со-
соответствующее ему решение зависит от четырех неопределенных
действительных постоянных (при этом используется теорема
существования и единственности в классических теориях пло-
плоской деформации, изгиба и кручения). Эти постоянные выра-
выражаются через величину суммарной растягивающей силы и три
составляющих вектора-момента от нагрузок в поперечном се-
сечении S. Получается классическое решение Сен-Венана (рас-
(растяжение, кручение и чистый изгиб стержня). Естественно, сюда
не входит решение об изгибе поперечной силой стержня конеч-
конечной длины.
Учитывая этот результат, принцип Сен-Венана в рассматри-
рассматриваемой задаче можно сформулировать так: значение "к = О
представляет собой единственное чисто мнимое собственное
число полученной выше краевой задачи. Действительно, соглас-
согласно C.38) любое решение при ЯекфО дает главный вектор и
главный момент, которые стремятся или к нулю, или к беско-
бесконечности при z-*±oo; по определению, такое решение не мо-
может быть решением Сен-Венана*).
Характеристическое уравнение для определения собственных
чисел X нетрудно составить в случае, если можно произвести
разделение переменных в краевой задаче, когда, например, об-
область S представляет собой круг, полосу или клин. Для первых
двух случаев соответствующие характеристические уравнения и
исследование их корней имеются в книгах А. И. Лурье [32] и
Я. С. Уфлянда [33]. В частности, там показано, что единственным
*) По той же причине невозможны кратные чнсто мнимые собствен-
собственные числа.
70 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. HI
чисто мнимым корнем этих уравнений является нуль. На
основании предыдущего, этот результат завершает строгое
доказательство принципа Сен-Венана для кругового цилинд-
цилиндра и слоя.
Дадим доказательство принципа Сен-Венана для произволь-
произвольного сечения цилиндра. Будем доказывать от противного. Пусть
существует решение однородной краевой задачи теории упруго-
упругости для бесконечного цилиндра с чисто мнимым собственным
числом % = iy, отличным от нуля (y^=0)- Согласно C.38), на-
напряжения и деформации, отвечающие этому решению, будут
периодическими функциями z с периодом 2я/у. Покажем, что
соответствующие им смещения также будут периодическими
функциями z (с точностью до смещения и вращения тела как
жесткого целого). Для этого выпишем следующие три кинема-
кинематических соотношения:
-^ = ег, *L+to^ *L+*L==2evz. C.39)
дг г' дг ' дх гх дг ' ду Уг v '
Здесь и ниже ех, еу, ez, exz, eyz, exy — деформации. Интегрируя
по порядку C.39), убеждаемся в периодичности по z функций
и, v, w.
Рассмотрим теперь два поперечных сечения цилиндра z = 0
и z~2nnl\, где п — некоторое целое число, и применим тео-
теорему Клапейрона к конечной части цилиндра, ограниченной
этими сечениями. Напомним, что теорема Клапейрона является
следствием уравнений теории упругости; теорема утверждает,
что
(Xnu + Ynv + Znw)dS,
S
Здесь V — область, занятая телом, S — поверхность тела,
(Xn,Yn,Zn) — вектор внешней нагрузки, W — потенциальная
энергия деформации, заключенная в единице объема. В нашем
случае боковая поверхность цилиндра свободна от нагрузок, и
S будет совпадать с поверхностью торцов 2 = 0 и z = 2лп/у,
а компоненты внешней нагрузки Хп, У„, Zn будут равняться на-
напряжениям %xz, tyz, oz соответственно, взятым с обратным зна-
знаком. Левая часть равенства C.40) вследствие периодичности де-
деформаций (а, следовательно, и W) по z будет равна пЭ, где
Э — упругий потенциал цилиндра длины 2я/у, т. е. величина,
всегда положительная. Правая часть равенства C.40) вслед-
ЩЩ НАПРЯЖЕНИЯ СМЕЩЕНИЯ У КРАЯ ТРЕЩИНЫ 71
ртвие периодичности по z напряжений и смещений будет пред-
представлять собой величину, не зависящую от п. Ввиду произволь-
произвольности п, очевидно, всегда можно выбрать такое п, чтобы тео-
теорема Клапейрона не выполнялась, что невозможно.
Таким образом, исходное допущение о существовании чисто
мнимого собственного числа X — iy, отличного от нуля, не-
неверно. Принцип Сен-Венана доказан.
Анализируя доказательство, нетрудно заметить, ч^то оно
справедливо для конечного поперечного сечения S любой связ-
связности, при наличии угловых точек на контуре сечения, а также
в кусочно-однородном случае, когда стержень составлен из
призматических (цилиндрических) тел, сделанных из различ-
различных материалов и спаянных между собой вдоль боковых по-
поверхностей.
Решение однородной краевой задачи определяется с точно-
точностью до произвольных множителей, которые находятся только
из решения более сложной задачи с учетом краевых эффектов.
Во всяком случае, на основании C.38) краевой эффект (раз-
(разность между строгим решением и решением Сен-Венана) за-
затухает экспоненциально при z-*oo, при этом существенно, что
показатель при экспоненте вполне определяется формой попе-
поперечного сечения S и не зависит от граничных условий на торце.
Упругое поле напряжений и деформаций вблизи торца про-
произвольного тонкого стержня постоянного поперечного сечения
или тонкой упругой оболочки постоянной толщины согласно
«принципу микроскопа» определяется из решения следующих
канонических задач: а) для криволинейного стержня — задача
о прямолинейном полубесконечном цилиндре того же самого
поперечного сечения; граничные условия на его торце в точ-
точности соответствуют граничным условиям на изучаемом торде
исходного стержня; б) для тонкой оболочки — задача о полу-
полубесконечной полосе; граничные условия на ее основании в точ-
точности соответствуют граничным условиям на исследуемом краю
исходной оболочки.
§ 5. Поле упругих напряжений и смещений
в малой окрестности края произвольной трещины
Для механики разрушения большой интерес представляет
изучение асимптотического распределения напряжений, дефор-
деформаций и смещений вблизи свободного от нагрузки края щели
в однородном и изотропном упругом теле.
Малая окрестность каждой точки контура щели является
двугранным углом, рассмотренным в § 3 при Q2 — 0i = 2я и
% = 1/2; поэтому можно непосредственно использовать оконча-
чательные формулы C.15) и представления C.9). Однако,
п
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
1гл, m
ввиду важности для дальнейшего этого частного случая, изучим
его отдельно.
Рассмотрим малую окрестность произвольно фиксированной
точки О на гладком контуре щели, выбранной в качестве
начала декартовых координат' xyz (рис. 13). Путем двойного
предельного перехода, ана-
аналогичного «принципу микро-
микроскопа», в этом случае мож-
можно прийти к следующей
канонической сингулярной
задаче теории упругости:
при у = 0, — оо <* <0,
— OO.<Z<+OO C.41)
Передняя . °у = %ху = Хуг = °-
кромка трещины _
Эта задача принадлежит
классу N, т. е. для нее прин-
принцип Сен-Венана не выпол-
Рис 13. няется. Согласно общим по-
положениям А, Б и В (см. § 3)
корректное решение этой задачи в напряжениях при г-*-О и
при z -> оо (z = х + iy) должно иметь порядок О (| z | ~1/2),
причем коэффициенты в асимптотике при z-»-oo должны быть
заданы.
Выясним смысл этих результатов в данном, случае. При
помощи представлений C.9) граничные условия C.41) запи-
запишем так:
при у — О, х < О
= 0r ImQ(z) = 0,
C.42)
Нетрудно заметить, что краевая задача C.42) имеет беско-
бесконечное множество решений вида Czn, где С — произвольная дей-
действительная постоянная, а п равно 0, ±1/2, ±1, ±3/2, ±2, ...
Условия корректности из этого множества выделяют единствен-
единственное значение л = —1/2, причем соответствующие постоянные С
должны быть заданы заранее. Действительно, значения п, рав-
равные 0, +1/2, +1, +3/2, +2, ..., недопустимы вследствие усло-
условия затухания напряжений на бесконечности (тривиальный слу-
случай простого растяжения в направлении осей z или х, соответ-
соответствующий п = 0, не рассматривается), а при п, равных —1,
—3/2, —2 смещения в конце щели оказываются бесконеч-
, НАПРЯЖЕНИЯ СМЕЩЕНИЯ У КРАЯ ТРЕЩИНЫ
73
ршми, что не допускается в отсутствие сосредоточенных воз-
воздействий.
Решения с п,= —1 и п =.—2 отвечают сосредоточенной
Силе и моменту соответственно, приложенным в конце трещины;
Эти решения некорректны.
Итак, общее корректное решение зависит от трех действи-
действительных параметров, которые участвуют в решении в качестве
множителей при различных членах асимптотики и которые сле-
следует считать заданными в локальной постановке задачи (на
самом деле они определяются из решения задачи в целом).
а
ш
Каждый из указанных трех членов асимптотического разложе-
разложения соответствует одному из трех основных типов трещин, ко-
которые изображены на рис. 14. Решение можно записать так:
if G\
C.43)
Ki — //Си = 2 Mm |
при 0 = 0 0Й -f /тед = {Ki
Ф (г)],
где
(угол 0 отсчитывается от продолжения трещины).
Действительные параметры Ki, Кц, Km носят название ко-
коэффициентов интенсивности напряжений. Они зависят от формы
74 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
тела, внешних нагрузок, расположения и длины трещин. Ко-
Коэффициенты интенсивности напряжений имеют размерность
силы, деленной на длину в степени три вторых.
Рассмотрим некоторые частные случаи.
I. Нормальный разрыв или отрыв (при Ки = Km = О,
КгФО). '
Трещина локально представляет собой разрыв нормального
смещения и, симметричный относительно плоскостей xz и ху;
остальные смещения {и и ш) на разрезе равны нулю.
II. Поперечный сдвиг (при Ki = Km = О, Кц Ф 0).
Толщина вблизи края представляет собой разрыв касатель-
касательного смещения и, симметричный относительно плоскости ху и
кососимметричный относительно плоскости xz; смещения v и w
на разрезе равны нулю.
III. Продольный сдвиг (при Ki = Kii = 0, КтФО).
Трещина вблизи края представляет собой разрыв касатель-
касательного смещения w; смещения и и v на разрезе равны нулю.
Этим типам разрывов в теории дислокаций отвечают клино-
клиновые, краевые и винтовые дислокации соответственно. Для тре-
трещин произвольного типа все величины Ki, Ku, Km. отличны от
нуля.
По формулам C.9) при помощи C.43) найдем распределе-
распределение напряжений и смещений вблизи края произвольной хрупкой
трещины для указанных основных типов разрывов.
Нормальный разрыв:
ох = -jk= cos 1 A - sin -5- • sin 1 б),
]/2яг 2 I 2 2 /
cos-5-/1 + sin^--sin-2-
2 \ 2 2 }
. e e з n
sin — • cos — cos — 0,
Ш 2 2 2
a = v(a -t- a \ т =т =0 C-44)
при г/ = 0, л;>0, ax = ay =
при г/ = 0, х < 0, о = ^-=^- Ki \Гг1Щ), и = 0,
i 5] НАПРЯЖЕНИЯ СМЕЩЕНИЯ У КРАЯ ТРЕЩИНЫ 75
. Поперечный сдвиг:
ах = ^L-sin-f2 + cos-cos-?- б),
/Си ¦. в е з Q
Ф sinTcos 7cos 1 '
хху = -ДУ=г cos|/1 - sin-5- sin -i в),
** ^ 2 ^ 2 2 I' C<45)
ог = v (стл + a y), xxz = туг = О,
при у —0, х > О, ах = а
при у = О, х<0, о = 0
Продольный сдвиг:
т =--?lli-sin-
xz Y 2nr 2
cos — ,
2 C.46)
при y = Q, x>0, xxz = 0, Xyz = /Cm
при // = 0, x<0, Ш
Формулы C.44) и C.45) были получены для случая плоской
деформации; в случае плоского напряженного состояния нужно
взять в них аг = 0 и заменить v на v/(l+v). Эти формулы
можно получить также из решения частных задач, разлагая ре-
решение по г в малой окрестности края щели и ограничиваясь
наибольшим членом разложения. Слова «в малой окрестности
края» означают физически, что г считается малым по сравнению
с характерным линейным размером тела, например, длиной тре-
трещины или расстоянием ее конца от свободной границы. Именно
таким способом — из точного решения различных частных за-
задач—были найдены асимптотические формулы C.44) —C.46)
?6 СИНГУЛЯРНЫЙ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 1ГЛ. Ш
различными исследователями (Снеддон, Ирвин, Вильяме). Ир-
Ирвин и Вильяме первыми поняли общий характер этого распреде-
распределения, однако строгого доказательства его общности они не дали.
Приведенный анализ упругого поля вблизи края трещины,
как нетрудно сообразить, используя «принцип микроскопа» или
соответствующий ему предельный переход, годится также для
произвольных неоднородных тел, если зависимость модуля
Юнга и коэффициента Пуассона от координат точки представ-
представляет собой дифференцируемую функцию. В этом случае слова
«вблизи края» означают также, что расстояние от контура тре-
трещины г считается малым по сравнению с величинами ЕО1Е'О и
Vq/vq, где Ео, v0, Е'о и v'o — значения упругих постоянных и
их градиентов в рассматриваемой точке О. Случай анизотроп-
анизотропных тел и тел, у которцх упругие постоянные представляют со-
собой разрывные функций координат (например, случай кусочно-
однородных тел), требует специального изучения.
Замечание. Допустим, что в некоторой окрестности конца
полубесконечного разреза заданы некоторые нагрузки. Общее
решение этой неоднородной задачи, очевидно, равно некоторому
частному решению неоднородной задачи плюс общее решение
однородной задачи,-выражаемое формулами C.43).
Например, в частном случае граничных условий
при у«= 0, *<0, %Xy = xyz = 0, Oy = p(x),
при г/=А х>0, i:xy = xyz = Q, dvJdx = 0,
где функция р(х) обращается в нуль при х <—d, решение
имеет вид
Jd х-г 2]/nz
и, следовательно, при z-^oo не зависит от нагрузок р(х). Это
свойство решения, типичное для всех задач класса N, суще-
существенно используется в дальнейшем.
В конце разреза при z = Отрешение может обращаться в бес-
бесконечность или- быть ограниченным; это не влияет на его асим-
асимптотику при \z\ S> d.
§ 6. Налегающие трещины и влияние включений
. При действии сжимающего напряжения в направлении, пер-
перпендикулярном к поверхности трещины, а также в некоторых
других случаях противоположные берега ее смыкаются, налегая
друг на друга. Эффект налегания берегов трещины в окрестно-
окрестностях точки О контура трещины приводит к перераспределению
I в] НАЛЕГАЮЩИЕ ТРЕЩИНЫ И ВЛИЯНИЕ ВКЛЮЧЕНИЙ 77
сингулярного поля напряжений и деформаций вблизи точки О.
Результирующее поле можно отыскать, пользуясь общими мето-
методами нахождения сингулярных решений.
В данном случае граничные условия соответствующей кано-
канонической сингулярной задачи теории упругости имеют следую-
следующий ВИД1
при у = 0, — оо.<;с<0, — oo<z<oo
Здесь F(ay) — некоторая заданная функция. Первая группа
условий C.47) означает непрерывность нормального смещения
на разрезе и условия равновесия; вторая группа условий вы-
выражает условия взаимного скольжения противоположных бере-
берегов трещины (условие предельного равновесия и условие ко-
аксиальности вектора касательного напряжения и вектора
скачка смещения в каждой точке поверхности трещины). В про-
простейшем случае в качестве условия предельного равновесия
можно взять условие сухого кулонова трения со сцеплением
F = (—k -\- рбуJ, где k — постоянная сцепления, р — коэффи-
коэффициент трения.
Если предельное равновесие не достигнуто и, таким образом,
взаимное проскальзывание берегов отсутствует,' то граничные
условия C.47) заменятся следующими:
при у==0, —oo<jc<0, —оо<г< + оо
KI = [*хв] = [*гв] = 0, [и] = [v] = И = 0. C.48)
В этом случае все напряжения и деформации будут, очевид-
очевидно, ограничены в точке О (сосредоточенные воздействия исклю-
исключаются из рассмотрения).
Найдем- решение нелинейной граничной задачи C.47).
При помощи основных представлений C.9) и функции
Q(z) = гФ'(z)-\-^?(z) условия непрерывности можно записать
в виде
-/'(*)] = 0,
[ (х) — Щх)] = 0 при х<0.
Последнее уравнение получается из продифференцирован-
продифференцированного по х представления для смещений и и v.
Из граничных условий C.49) для Ф(г) и п{г) видно, что
при х < 0
[Im Q (*)] = [1га Ф (*)]=* 0, {ЯеBФ(*) + О(*))] = 0. C.50)
78 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ill
Отсюда следует, что функция 2Ф(z) + Q(z) на разрезе
у = 0, х < О непрерывна, а поэтому аналитична во всей пло-
плоскости г. Поэтому в классе ограниченных функций
+ Q(z) = o0 + /C,. C.51)
Здесь 0о представляет собой, согласно C.9), напряжение оу
при у = 0, действительная постоянная С\ несущественна. От-
Отсюда,, в частности, вытекает, что в малой окрестности точки О
контура налегающей трещины (на ее поверхности и на продол-
продолжении трещины) напряжение ау ограничено; величина, сто опре-
определяется из решения задачи в целом.
При помощи C.51) и C.9) для смещений и касательных на-
напряжений при у = 0 можно получить следующие формулы:
a=Reco(x), т,„ = —-^J
, tyz — — \ilmf'(x),
где
<»(z) = —
Используя C.52), оставшиеся граничные условия C.47)
можно записать так:
при у = 0, х < 0
-—^ {Im©'(*)}2 + (Im/'(х)}2 = ±F
lX + lj4 Im со' (*) ~ Re со (х) '
Первое граничное условие C.53), очевидно, может выпол-
выполняться только в том случае, когда Im «/(*)* и \mf'(x) постоянны
на разрезе. Отсюда нетрудно найти общее решение краевой за-
задачи C.53) в классе функций, ограниченных на бесконечности,
а в нуле имеющих особенность (по напряжениям) более слабую,
чем 1/г:
f (г) = ^iiLL- + / Ь. , ГШЕ + с2, C.54)
Здесь /Сц, /Cm, Сь Сг — произвольные действительные постоян-
постоянные, определяемые из решения задачи в целом.
§ 6] НАЛЕГАЮЩИЕ ТРЕЩИНЫ И ВЛИЯНИЕ ВКЛЮЧЕНИЙ 79
. Сравнивая решение C.54) с соответствующими формулами
C.43) для свободной вблизи точки О трещины, легко заметить,
что сингулярная часть решения C.54) в точности отвечает фор-
формулам C.43) при Ki = 0. Следовательно, распределение напря-
напряжений, деформаций и смещений вблизи точки О контура тре-
трещины с налегающими берегами такое же, как для трещин про-
продольного и поперечного сдвига со свободными берегами, т. е.
оно определяется формулами C.45) и C.46).
Полученное решение представляет интерес также для трещин
«с заполнителем». Допустим, что некоторая трещиновидная по-
полость плотно заполнена материалом, более пластичным, чем
основной материал. Тогда при увеличении внешних нагрузок
вначале будет достигнуто некоторое предельное состояние пла-
пластического материала в полости, и только затем в основном
материале будет расти концентрация напряжений вблизи края
полости согласно формулам C.45) и C.46).
Можно показать, что вторая группа граничных условий
C.47) является следствием уравнений пластического течения
«заполнителя» при таких допущениях:
а) «заполнитель» представляет собой произвольное несжи-
несжимаемое идеально-пластическое тело;
б) между поверхностью полости и «заполнителем» нет про-
проскальзывания;
в) выполняются условия /i<L, |grad/i|<Cl, где h(x,z) и
L — поперечный и характерный продольный размеры полости;
г) нагружение — пропорциональное.
Действительно, для «тонкого» несжимаемого «заполнителя»
можно считать, что его напряженное состояние в каждой точке
(х, z) описывается суммой напряжения всестороннего сжатия
или растяжения ау и вектора касательного напряжения в сре-
срединной поверхности (по толщине полости напряжения не изме-
изменяются). Далее, вектор скорости сдвига Y в каждой точ$е равен
V = [u]lh, C.55)
где [и]—скачок вектора скорости противоположных берегов по-
полости в соответствующих точках. Согласно ассоциированному
закону течения, из C.55) следует, что
[йУххд = [хЬУтуг. C.56)
Отсюда для пропорционального нагружения [u] = A,[tw] полу-
получается соотношение, фигурирующее в C.47).
От условия пропорциональности нагружения можно отказать-
отказаться, взяв в качестве граничного условия уравнение C.56). В этом
случае, проверив ход решения, нетрудно убедиться в том, что
Д80 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 1ГЛ. Ill
формулы C.54) будут по-прежнему верны, если взять Ко
равным
4к . C.57)
¦
На практике трещины с «заполнителем» встречаются весьма
часто. Роль «заполнителя» играют, например, графитовые про-
прослойки в чугуне, инородные включения или зоны окисленного
м,еталла в сплавах, слои малопрочной глины или песка в текто-
тектонических трещинах, сварные швы и т. д.
Следует подчеркнуть, что приведенный анализ влияния «за-
«заполнителя» на напряженно-деформированное состояние в окрест-
окрестности края полости годится только для случая непрерывного
течения несжимаемого «заполнителя»; при наличии разрывов
или упругости «заполнителя» вблизи края трещины, вообще го-
говоря, появляется также ненулевая компонента Ki нормального
разрыва.
Исследуем влияние упругого «заполнителя» на поле напря-
напряжений и деформаций вблизи края трещины. В математическом
отношении этот вопрос эквивалентен вопросу об упругом поле
вблизи конца линии «утонения» в тонкой пластине.
Граничные условия соответствующей канонической сингуляр-
сингулярной задачи теории упругости имеют следующий вид:
при t/ = 0, — oo<*<0, — oo<z< + «>
x = K[w]
Здесь Я.1, fa, "кг— функции, определяемые соотношениями
f C.59)
где h--толщина слоя, Еи ц2, цз— модуль Юнга и модули
сдвига упругого слоя, характеризующие его работу на нормаль-
нормальный разрыв, поперечный и продольный сдвиг соответственно (по
аналогии с винклеровским основанием). Толщина слоя, а тем
самым и величины К\, ^2. ta представляют собой заданные функ-
функции х.
Решение граничной задачи C.58) можно представить в виде
суммы решений следующих трех задач:
1) oy = 2Xl\v\, т^ = тгг, = 0; C.60)
2) хху = 2к2\и\, оу = туг = 0; C.61)
3) ryz = 2%3\w\, <xy = T^ = 0. C.62)
Эти граничные задачи отвечают соответственно нормальному
разрыву, поперечному -и продольному сдвигу, причем первое
§6) НАЛЕГАЮЩИЕ ТРЕЩИНЫ И ВЛИЯНИЕ ВКЛЮЧЕНИЙ 81
граничное условие в каждой задаче выполняется при у = О,
х < 0, а второе — на всей оси х.
При помощи представлений C.9) для соответствующих слу-
случаев можно получить следующие формулы:
„, Р C.63)
при г/ = 0 <т* = ofj, = 2ReФ(г), и = -^—1т<р(г);
2)
' ' v "' C.64)
при г/ = 0, Txy=lmQ (z), u = —*J~ Re(o(z);
3) Ф B) = п (z) = 0,
при г/ = 0, xzy = — film/'(z), ai = Re/(z). C>65)
При получении представлений C.63) — C.65) было исполь-
использовано лишь условие исчезновения напряжений в бесконечно
удаленной точке, поэтому эти формулы годятся для произволь-
произвольных плоских задач, когда,граничные условия заданы вдоль оси
х. Указанный прием разбиения любой краевой задачи такого
типа на сумму трех задач (для нормального разрыва, продоль-
продольного и поперечного сдвига) особенно удобен при решении кон-
конкретных задач, так как встающие математические проблемы для
каждой из этих задач эквивалентны. Достаточно получить ре-
решение, например, для нормального разрыва; решения для дру-
других случаев получаются при помощи очевидных подстановок.
Поэтому можно ограничиться решением краевой задачи
C.60). Используя формулы C.63), из условий C.60) получаем
краевую задачу для отыскания функции ф(г):
при -у = 0, х<0 ^
при у = 0, х>0 Im<p(z) = 0. Cl66)
Решение краевой задачи C.66) для произвольной функции
%\(х) весьма сложно и в замкнутом виде недостижимо. По-ви-
По-видимому, впервые с задачами такого типа столкнулся А. Пуан-
Пуанкаре при решении некоторых проблем гидродинамической тео-
теории приливов.
Ограничимся решением некоторых классов краевых задач
C.66); эти решения можно найти в замкнутом виде, и они охва-
охватывают практически наиболее важные случаи*).
1. Упругое включение в форме тонкого клина. Пусть толщина
упругого «заполнителя» меняется по закону
h (х) = — 2ак (а < 1), C.67)
*) Далее в этом параграфе для простоты предполагается, что при у = О,
х-+ оо будет Ох =:= Оц.
82
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. III
где 2а — угол раствора клина. В этом случае функция ki(x)
имеет вид
Т, ( v\ ~j /О C:Q\
а соответствующая краевая задача C.66) допускает следующую
группу преобразований:
х' = Схх, ф' = С2ф, C.69)
где Ci и Сг — произвольные действительные параметры.
Поэтому в рассматриваемом случае решение граничной за-
задачи C.66) имеет вид
<p(z)=Az\ . C.70)
где А— произвольный действительный коэффициент. Подставляя
C.70) в C.66), нетрудно получить характеристическое уравне-
уравнение для определения к:
Корни уравнения C.71), как нетрудно видеть из графического
представления решения, находятся на сегментах (Г/2, 1),
C/2,2), ..., (—1/2,—1), (—3/2,—2), ... действительной оси, по
/г/л
Рис. 15.
одному на кйждом из этих сегментов. Как следует из теоремы
3.2, решению корректной краевой задачи отвечает единственный
корень, расположенный на отрезке A/2, 1). Зависимость вели-
величины этого корня от безразмерного коэффициента упругости
«заполнителя»
C-72)
изображена на рис. 15. Коэффициент А, как всегда в задачах
класса N, считается заданным заранее.
§ 61 НАЛЕГАЮЩИЕ ТРЕЩИНЫ И ВЛИЯНИЕ ВКЛЮЧЕНИЙ 83
Легко видеть, что аналогичное автомодельное решение
имеет место для упругого включения в форме клина с произ-
произвольным углом раствора 2а, а также для любого числа раз-
различных включении такого типа. В каждой из этих задач полу-
получается свое трансцендентное уравнение для определения
числа к.
2. Упругие включения специального вида. Пусть толщина
упругого включения меняется по закону
h{x)=iMu (x<0)- C-73)
Здесь Р(х) и Q(x) —произвольные полиномы с действительны-
действительными коэффициентами.
Введем новую аналитическую функцию F(z):
F (z) = <р' (z) - (к + 1) Е, VzQ (z) Ф (z)/[2M/> (г)]. C.74)
Согласно C.66) и C.73), эта функция должна удовлетворять
следующим граничным условиям:
при z/ = 0, x<0 ReF(z) = Q,
при у = 0, х > 0 Im F (z) = 0. ^3^
Из выражения C.74) вытекает, что функция F(z) анали-
тична всюду в верхней полуплоскости, за исключением нулей
полинома P(z), в которых она имеет полюсы соответствующего
порядка, и, быть может, бесконечно удаленной точки.
Решение краевой задачи C.75) имеет вид
F(z)= L(z\-. C.76)
w P(z)Vz K '
Здесь L(z)—некоторый полином с действительными коэффи-
коэффициентами.
Решая дифференциальное уравнение первого порядка C.74)
относительно функции <$(z), получаем
Ык^й- <3'77)
где
Порядок полинома L(z) легко определяется из граничного
условия на бесконечности при помощи формул C.76) и C.74).
Функция (f(z) согласно формуле C.77) имеет особенности в ну-
нулях полинома Р{г), что исключается физической постановкой
задачи. Уничтожение этих особенностей приводит к некоторой
$4 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
линейной однородной системе уравнений относительно неопреде-
неопределенных коэффициентов полинома L(z).
Полученная однородная система, очевидно, будет Действи-
Действительной, так как все аналитические функции, фигурирующие
в формуле C.77), удовлетворяют условию типа ф(г)=ф(г).
Поэтому решение линейной системы существует и определяется
с точностью до произвольного действительного множителя.
Этот множитель аналогичен коэффициенту интенсивности
напряжений Ki для обычных трещин нормального разрыва со
свободными от нагрузок берегами вбл«зи кромки; он опреде-
определяется из решения задачи в целом, а в данной сингулярной
задаче (принадлежащей классу N) его следует ''задавать при
постановке корректной краевой задачи.
Функцией типа. C.73). можно с любой точностью аппрокси-
аппроксимировать произвольную непрерывную функцию h(x) на любом
конечном интервале; поэтому решение рассмотренного класса
задач можно использовать в качестве приближенного эффектив-
эффективного метода решения и в общем случае.
В качестве простейшей иллюстрации приведем окончатель-
окончательные формулы для тонкого упругого включения параболической
формы:
где р и Ki — заданные действительные постоянные. В пределе
при z -* О будет ф (z) = К\ \'zj{2n).
3. Упругое включение постоянной толщины. Пусть включе-
включение имеет постоянную толщину
h (х) = h = const (Л, = ?,//г). C.79)
В этом случае можно дать точное решение краевой задачи
C.66) при помощи интегральных преобразований. Однако этот
метод приводит к чересчур сложным выражениям, к тому же
он годится только для полубесконечных областей. Поэтому при-
приведем лишь одну оценку поведения решения вблизи конца
включения и укажем схему решения задач такого типа при по-
помощи асимптотических разложений.
Введем безразмерный параметр е:
ee*?±]L C.80)
Решение граничной задачи будем искать в виде следующего
асимптотического разложения:
при е-»0 Ф(г) = фо(г) + вф,B) + е2ф2(г)+ ... C.81)
Здесь фо, фь ф2» — — искомые аналитические функции.
§ 6) НАЛЕГАЮЩИЕ ТРЕЩИНЫ И ВЛИЯНИЕ ЙКЛЮЧЁНЙЙ 85
Подставляя C.81) в граничное условие, нетрудно получить
следующую цепочку стандартных краевых задач:
@) при у = 0, х<0 Req>?(z) = 0,
при у = 0, х>0 1тфо(г) = О;
A) при у = 0, *<0 Неф[B) = -^-1тфо(г),
при 0 = 0, х>0 Imq>,(z) = 0; C>82)
B) при у = О, х<0 Re<p5(z) = llmqiJ(z),
при г/ = 0, х > 0 1т ф2 (г) — О
и т. д.
Для рассматриваемого случая полубесконечной области не-
непосредственное решение краевых задач C.82) приводит к рас-
расходящимся интегралам. Поэтому необходимо прибегнуть к ус-
условному интегрированию, оставляя в формальна вычисленном
расходящемся интеграле лишь его конечную часть, а слагаемые,
стремящиеся в бесконечность, полагая равными нулю. Такое ус-
условное понимание интеграла соответствует выделению в реше-
решении для конечной области, когда расходящихся интегралов не
возникает, главных членов вблизи конца включения. В этом
можно убедиться, составляя указанным методом решения раз-
различных частных задач.
Функция ф'(г) вблизи конца включения ведет себя следую-
следующим образом:
^ > -Inz)].' C.83)
Здесь /Ci—некоторая постоянная, фо — алгебраическая функция
своих аргументов. Естественно, при этом предполагается, что
\г\ >Л. -
Когда модуль Юнга включения Е\ велик по сравнению с мо-
модулем Юнга основного материала, т. е. е >¦ 1, естественно
искать решение граничной задачи в виде асимптотического раз-
разложения по малому параметру 1/е. При этом получается це-
цепочка легко решаемых стандартных задач Дирихле.
Для нахождения решения при промежуточных значениях е
следует применить склеивание различных асимптотических
разложений при малых и больших е. Практически хорошие
(т. е. весьма близкие к точным) результаты получаются уже,
если ограничиться только первыми двумя-тремя членами разло-
разложений по е и 1/е. Отметим, что аналогичные методы широко
распространены в теории течений вязкой жидкости (теория по-
пограничного слоя).
Замечания. 1. Задачи о тонком упругом включении в об-
общем случае не допускают какой-либо группы преобразований,
S6 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
поэтому они не принадлежат к каноническим сингулярным за-
задачам и для них не существует конечного характеристического
уравнения.
2. Задача о тонком упругом включении представляет инте-
интерес также в том случае, когда имеется некоторый заданный
скачок смещения вдоль этой же линии. При этом\ краевая за-
задача становится неоднородной; методы ее решения в основных
чертах аналогичны только что изложенным.
§ 7. Анизотропное тело
Рассмотрим некоторые сингулярные задачи для анизотроп-
анизотропного однородного линейно-упругого тела.
Предварительно найдем общее решение уравнений плоской
задачи анизотропной теории упругости, аналогичное представ-
представлениям C.9) для изотропного тела.
В плоской задаче напряжения, деформации и смещения не
зависят от координаты г; при этом полная система уравнений
для произвольного анизотропного тела имеет следующий вид:
уравнения равновесия
дох дхху дхху деу дтхг дгу1_
~~ '
закон Гука
ех = апах + ai2ay + ai3xxy + аиххг + а15хуг,
C.85)
а52ау + асзтху + амхХ2 + a55xyz,
кинематическая связь деформаций со смещениями
д,и do dw p.
&х~~~д7' &у~~ду' e2~~"ai"~Uj
— J*l _i_ iL — ^!_ — JE. C.86)
yxy~ ду -г дх ' Vxz — -^-, Ууг— ду •
При записи закона Гука C.85) было учтено, что гг = 0; это
равенство служит для определения напряжения oz через осталь-
остальные напряжения. Матрица упругих постоянных о.ц симметрична
(т. е. ац = ац). Таким образом, число существенных упругих
постоянных в самом общем случае анизотропной плоской зада-
задачи равно 15.
Частный случай плоской задачи, когда отличны от нуля
только 6 постоянных an, ai2, а\г, а22, а23, а3з, подробно изучен
С. Г. Лехницким [34]. В этом случае упругие свойства в каждой
§ 7] АНИЗОТРОПНОЕ ТЕЛО 87
точке тела симметричны относительно любой плоскости, перпен-
перпендикулярной ОСИ 2.
Из соотношений C.86) вытекают следующие условия сов-
совместности:
дЧу
Ihj2'+ ~dx~2~ ~~ Wdy ' ~ду~~~Ш~' [-'>
Общее решение уравнений равновесия можно представить
через две произвольные функции так:
д2и __ д2и
_ д2и _dF_ __iL ( '
Х*У— дхду' Ххг~~ ду' ХУг~~ дх'
Подставляя выражения C.88) в закон Гука, а полученные
выражения для деформаций — в условия совместности C.87),
получаем следующую систему уравнений для функций U и F:
21 + 22
Здесь
д1
i2 + «зз)
¦ _ I _ д* i I \
¦42 — L21 — а2Ь -flZT "Т" \а2\ ~Г а35>
d2
Согласно C.89), функции if и F должны удовлетворять
уравнениям
LU = 0, LF = 0. C.90)
Здесь
L - L,,L22 - L12 = 6, ^^ + b
Й6 Й6 Й6 Й6
x — a22a55 — a25,
2 = 2a25 (a24 + a35) — 2a23a55 — 2a45a22,
= a22a44 + 4a45a23 + a55 Ba12 + а3з) — (a2i + %;J — 2a25 (a,5 + a34),
= 2a14a25 + 2 (a24 + a35) (a15 + a34) —
— 2a23a44 — 2a13a55 — 2a45 Ba12 + a33),
5= 0,11^55 + 4ai3a45 + a44 Ba12 + a33) — (a15 + a34J + 2^14(^24 + «as).
= 2aH («15 + «34) — 2а4ба„ — 2а13а44,
88 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Нетрудно показать, что все смещения, напряжения и дефор-
деформации также удовлетворяют уравнению C.90).
Оператор L можно представить в виде
Здесь 2i, 22, zi — следующие комплексные переменные:
z3 = x — \i3y, C.92)
где постоянные величины \i\, ц2, Из суть корни характеристиче-
характеристического уравнения
b7\i6 + hn5 + htf + b4ix» + 63Ц2 + Ь2\х + 6, = 0. C.93)
Так как коэффициенты этого уравнения действительны, то
его корни представляют собой комплексные числа, встречаю-
встречающиеся только сопряженными парами (т. е. корнями будут ць Дь
Р2> Ц2. Цз. Дз)- Чисто действительные корни, по-видимому, не-
невозможны из физических соображений, однако строгое доказа-
доказательство этого факта в общем случае затруднительно; для слу-
случая плоской деформации такое доказательство получено
С. Г. Лехницким [34]. Дальнейшее изложение относится только
к случаям комплексных (или чисто мнимых) корней.
При помощи разложения C.91) легко найти общее решение
уравнений C.90); могут представиться три случая:
1. Все корни различны, т. е. цг ф ц2, Цгт^Цз» M^i =Н= из»
U = фц (Zi) + <Pl4 Bi) + ф12 (Z2) + <Pl5 (Z2) + Ф13 (z3) + <Pl6 (Z3)>
F = q>21 (Zi) + qp24 (г,) + Ф22 (z2) + ф25 (z2) + ф23 (z3) + ф^ (z3).
2. Два корня одинаковы, т. е. ц2 = ц3> V-i Ф ц2» C.94)
U = ФП (z,) +. ф14 B0 + ztz{ [ф12 (z2) + ф15 B2)] +
+ [22ф13 B2) + 22ф,6 B2)] ZtZu
F — ф21 (Zi) + Ф24 Bl) + 2,2, [фга B2) + ф25 B2)] +
+ [22ф23 B2) + 22ф26 B2)] ZiZi.
3. Все три корня одинаковы, т. е. Ц[ = \i2 = \х3,
U = Ф„ B.) + Ф14 B,) + 2,ф12 B,) + 2,ф15 B,) + ф13 B,) + 2?ф16 B,),
Ф24 B,) + г^^ B,) + 2,?25 B,) + 2^ (г,) + zjq^ B,).
Так как ?/ и F — действительные функции, то аналитические
функции <$ц должны удовлетворять очевидным соотношениям
(г = 1, 2). C.95)
§71 , АНИЗОТРОПНОЕ ТЕЛО 89
После этого общее решение C.94) можно записать в более ком-
компактной форме:
L ^1=7^2. ^2^3. ILtl^f^
(U, F) = Re [qpn B,)
(при / = 1 правая часть этого равенства дает U, а при
i = 2-F).
(U, F) = Re [фп B,) + г&мп (z2) + z2z{z^a (z2)). C.96)
3. ^,==^2 = ^3.
(U, F) = Re [Фп B,) + 2,Фг2 (z,) + 2f?i3 B,)].
Между функциями ф*3- существуют некоторые зависимости,
вытекающие из уравнений C.89). Подставляя общее решение
C.96) в C.89), после простых преобразований нетрудно найти
эти соотношения:
Случай 1 (hi Ф ц2, ц2 Ф ц3> ^1 ^ Цз)
«„ + «зз) I*? + 2^f + «J-
+ ^^ + К + ^^ + а»] С3-97)
(/=1,2,3);
эти зависимости верны также для случая 2 (при i = 1,3) и для
случая 3 (при i = 3). 4
Случай 2 ({Х2 = ц3, Ц|=7^Ц2)
2) [«22 + 2М2з + »\ Bа
12
.= - Ф^ B2) [«25 + ^2 («24 + fl35) + ^2 (flU + «34)
¦ + <Й Ы [~ За25 - ц2 (а24 + а35) + м| (а15 + а34) +
Формулы для случая 3 не будем выписывать ввиду их гро-
громоздкости.
Таким образом, в каждом случае 6 функций фг-3- оказывают-
оказываются связанными посредством трех линейных зависимостей. По-
Поэтому общее решение определяется тремя аналитическими
функциями, которые могут быть выбраны из указанных шести
произвольно..
В дальнейшем ограничимся наиболее общим случаем трех
различных корней. При помощи C.96) и C.97), переобозначая
90 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ ?ГЛ. Ш
аналитические функции, находим следующие основные пред-
представления:
U= S Re[pub(Zi)], F= 2 Re^fr)]. C.98)
Здесь
р2. = аиц* + 2аац] + Bа12 + «зз) I*? + 2«2з1** + «22-
Для напряжений отсюда, согласно C.88), получаются фор-
формулы
,= SRe[|i,pn<p7(zf)], C.99)
Аналитические функции ф1, ф2 и ф3 должны находиться из
решения граничных задач. Смещения, как обычно, восстанавли-
восстанавливаются по деформациям интегрированием зависимостей C.86);
находим.
<1 О 3 '
и=21 Re[9,^B,)]. o=SRe[92M(zi)]. ш = 21 Re[Wt(z*)]-
C.100)
Здесь
Как видно, в общем случае плоская задача не расщепляется
на плоскую деформацию и сложный сдвиг; расщепление имеет
место только в том случае, когда постоянные аи, ai5, a2i, a25,
«34, «35 равны нулю. Этот вырожденный случай требует отдель-
§ 7] АНИЗОТРОПНОЕ ТЕЛО 91
ного рассмотрения; для него представления C.98) — C.100) не
годятся. При этом уравнения C.89) упрощаются:
L,,C/*=O, L22F = 0 (L12=L21 = 0). C.101)
Решения уравнений C.101) для плоской деформации, а так-
также соответствующие представления для напряжений и смеще-
смещений записываются в следующем виде [34]:
Числа Hi, p.], ц2, jl2— корни уравнения
' йцН4 — 2д1з}г3 + B^12 + %?) ^2 — 2я23ц + я22 = 0. C.103)
Далее, для сложного сдвига будет
*«&-**«¦?%+ <Ь%-?0 C.104)
w = Re ф3 («а), Bз = *^
где (i3 и Д3~КОРНИ уравнения
2 % = 0. C.106)
В частном случае плоской деформации, когда щ = ^2, имеют
место представления
U — Re [ф,(г,)
«х = ^е [Й?ФГ (^,) + 2ц, Й,Ф2' ()]
«, = «е К C^ + ^^O + W (*.)].
т„ = Re [|*.фГ (z.) + A*1 + А) ф' («О + i*s< (*)]
и = Re [р,Ф; (z,) + Р2Ф2 (z.) 4- /»,г,ф^ (z,)],
о = Re [- qyt (z,) + ?2Ф2 (z,) - ^z1?j (z,)],
92 ' СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
где р, = anv\ + ai2 + ц^, р2 = BД,— Ц^Ц^ц + Яю + Мю»
2 '. 23> Mi L 12 \ni / ^2 J 23J"
Приведенные представления практически исчерпывают все
возможные случаи плоской задачи анизотропной теории упру-
упругости.
Теперь рассмотрим задачу о распределении напряжений и
деформаций вблизи произвольной точки О контура трещины в
анизотропном однородном упругом теле.
Применяя «принцип микроскопа», приходим к следующей
канонической сингулярной задаче (см. рис. 13):
при у = 0, х<0 ау = хху = хуг = 0, C.108)
которая при помощи C.99) формулируется так:
при у = 0, х< 0
з
2 Re[Pi^7(z)] =
3 3
= 2 Re [Miitf Щ = 2 Re [- Р2|< (г)] = 0. C.109)
Корректное решение краевой задачи C.109) запишется сле-
следующим образом:
з
?=1
3
t=l
3
1=1 2i l 3
Здесь Ки К2, Кз — заданные действительные постоянные, ана-
аналогичные коэффициентам интенсивности напряжений; они опре-
определяются из решения задачи в целом. -
Отсюда легко определить функции ф", ф2', ф" и, подставив
их в C.99) и C.100), найти искомое поле напряжений и смеще-
смещений вблизи конца трещины. Получающиеся формулы ввиду их
громоздкости в общем случае выписывать не будем; приведем
эти формулы только для случая расщепления поля на плоскую
S 8] КУСОЧНО-ОДНОРОДНОЕ ТЕЛО
деформацию и сложный сдвиг [35]:
_ __ __^1_ р„ / _HiH2_ Г Иг
°х — _/-=— ке <
I Hi¦— Иг L
93
— и? sin 9 /cos 9 — |i] sin 9
" /2лг
V2nr
Hi — Иг L V cos 9 — |i2 sin 9
_J Г и.
Hi — Иг L
— Hi sin 9
— n2sin9 /cos 9— Hi sin 9 J J
— ^s sine J J (зли)
l
— u? sin 9
Ku
t hi — Иг L
x = K11L Г
— n2sin9 /cos 9 — njsin9
Иг
9JJ
/cos9 —Hisinejj'
Нз
V^cos 9 — Нз sin 9 '
V2n?
/cos 9 — Цз sin 6
при 6 = 0 ay + ixxy = (Ki + iKu)l 1
Здесь Ki, /Си, Km — действительные постоянные (коэффициен-
(коэффициенты интенсивности напряжений), определяемые из решения за-
задачи в целом.
§ 8. Кусочно-однородное тело
Рассмотрим задачу о распределении напряжений и деформа-
деформаций вблизи края щели, выходящей на границу раздела двух од-
однородных изотропных полупро-
полупространств с различными упру-
упругими постоянными. Эта задача /
представляет интерес также
для механики разрушения ком-
композитных материалов, приме-
применительно к клеевым соедине-
ниям, в вопросах развития -^
сквозных трещин вблизи сту-
ступенчатого утолщения пластин
и т. д.
Применяя «принцип микро-
микроскопа», приходим к следующей
канонической сингулярной задаче теории упругости (рйс. 16):
при у = 0, х < 0 ау = хху — %уг = О,
Рис. 16.
2.
94 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Условия на границе двух различных упругих полупро-
полупространств (y = xtga) означают отсутствие скачка смещения и
отсутствие внешних нагрузок.
При помощи основных представлений C.9) отсюда получаем
следующую краевую задачу:
при у = 0, х<0 f'{ = j't,
Ф* + Ф/ + гФ'г + гр, = 0 (г =1,3);
при y — xiga и t>0
Ф,-+ Ф1 + е21а (гФ{ + ?,) = Ф2 + Фа + е2
— Ф1 — е~ПагФ[ — е-2НР,) =
= ц, (х2ф2 - Ф2 -е
при y = xtgaut<0
Фг + Ф2 + e2ia (гФ2 + ^г) = Фз + Фз + е21а (гЩ +
фз - ф"з - е-"а*®3 ~ е~Ш%) =
= ц, (х2Ф2 — Ф2 — e~2iaz% —
Здесь индексы 1, 2, 3 относятся к соответствующим секто-
секторам, указанным на рис. 16; в секторах 1 и 3 упругие постоян-
постоянные одинаковы и равны \ii и %\.
Краевая задача C.113) допускает группу преобразований
подобия; следовательно, ее решение, согласно § 3, имеет сле-
следующий вид:
Oi(z)=Aiz\ Wi(z) = Biz\
П(г) = С^ (/=1,2,3) C.114)
tz\—.e\(\a\z\ + i argz); Z6 __ g6(In | z | + < arg г))_
Здесь Ait Bit Ci — некоторые комплексные постоянные, А. и
б — собственные числа, отвечающие соответственно плоской де-
деформации и сложному сдвигу (плоская задача, как видно, рас-
расщепляется на плоскую деформацию и продольный сдвиг).
Функции z% и z6 аналитичны вне разреза у — 0, х < 0.
§ 8] КУСОЧНО-ОДНОРОДНОЕ ТЕЛО 95
Легко заметить, что указанное групповое свойство имеет
место также в том случае, когда в точке О сходится произволь-
произвольное число секторов с различными упругими постоянными, при-
причем каждый из секторов однороден и анизотропен, а вместо
трещины может быть «пустой» сектор. Поэтому применяемый
метод решения годится и в этом более общем случае.
В том случае, когда число X (или 5) комплексно (Я =
= Я,о + ф, где ко и р— вещественные числа), искомые функции
(например, OiB)) ведут себя как О (A sin pin г) или О (rx° cos р In г).
Функции типа sin (pinr) на любом участке вблизи конца тре-
трещины испытывают бесконечное число перемен знака, поэтому
напряжения при приближении рассматриваемой точки к концу
трещины также меняют знак бесконечное число раз. Этот ре-
результат говорит о том, что решение с комплексным Я, вообще
говоря^ не имеет физического смысла, а появление комплексного
Я свидетельствует о некорректности математической постановки
задачи.
Тем не менее, решениям с комплексным собственным числом
Я можно придать совершенно четкий смысл, если физические па-
параметры таковы, что комплексность Я в некотором смысле
«слаба». Выясним в общем виде это ограничение, накладывае-
накладываемое на физические параметры.
Неопределенные коэффициенты Аи Ви С* в C.114), очевидно,
должны содержать множитель типа ехр (—t'p/nL), где L — не-
некоторая постоянная размерности длины. В рассматриваемой по-
постановке сингулярной канонической задачи величины размерно-
размерности длины отсутствуют, поэтому точное значение множителя,
как и самих коэффициентов Л,-, Bit CV может быть определено
только из решения задачи в целом.
По своему физическому смыслу величина L представляет
собой характерный линейный размер тела (например, длину
трещины или расстояние ее конца от границы тела). При этом
размер области А, в которой напряжения меняют знак и реше-
решение некорректно, определяется соотношением
lpin(A/L)|« 1, C.115)
т. е.
Согласно «принципу микроскопа», решение с комплексным
Я имеет физический смысл на расстояниях г, больших по срав-
сравнению с А, т. е." при
r/L » е-1/ IPI. C.116)
Покольку при постановке сингулярной канонической задачи
предполагалось, что г ¦< L, то отсюда вытекает необходимое
96 СИНГУЛЯРНЫЕ ЗАДАЧИ ^ТЕОРИИ УПРУГОСТИ [ГЛ. «1
условие корректности рассматриваемой краевой задачи
' , I»*-1/!?!, C.117)
налагающее ограничения на значения физических параметров
системы.
Строго говоря, эти рассуждения справедливы лишь при бес-
бесконечно малых |р|; поэтому для малых, но конечных |р| реше-
решение типа C.114) имеет смысл приближенной асимптотики не-
неизвестного строгого решения на расстояниях г, удовлетворяю-
удовлетворяющих условию 1 > .4- > е~111p (.
Если выполняется условие корректности задачи C.117), то
fH3 C.116) следует, что в указанном асимптотическом прибли-
приближении будут справедливы следующие соотношения:
р In (r/L) « 0, cos(p in r) » 1, sin (p In r) » 0. C.118)
Используя C.118), подставляем функции C.114) в гранич-
граничные условия C.113); после сокращения общего множителя
гл» (или г8») получаем следующую однородную систему линей-
линейных уравнений относительно постоянных А{, В\ и С,:
A +Л) Л,+ 1,6-^+6, = 0,
A + Л) Л, + А{е-2Ш + Я,е«« = A+Я) A2+A2e-u«l+B2e2ia,
A + К) Аг — к, А1е~2Ш + Bie2ia =
= k [A + А) Л2 — %2А^-2Ш + Я2е2<«],
A + Л) А2 + Л2еш («-«* -f B2e2ia = ' ¦
= A + к) А3 + ~А#2и <*-»> + Bse2'"»
еш<я-а) + б3е2га= (ЗЛ19)
== k [A + Л) Л2
, | , = С2е + 2
k [С, — С,е2'« ('+«)] = С2 — С2е2га (•+«,
= С3е2«' <«
С2 — Сгв2'0^«'<а-") = k [С3 —
$'81
КусоЧйо-ОДноРоДное тело
9?
Всего имеется 6 комплексных уравнений для 6 комплексных
постоянных Ах и В{, а также 6 действительных уравнений для
трех комплексных постоянных d(i = 1, 2,3).
Собственные числа X и б удовлетворяют характеристическим
уравнениям, получающимся из условия разрешимости этой од-
однородной системы линейных уравнений. Согласно теореме 3.2,
интерес представляют в данном случае только те корни харак-
характеристических уравнений, которые лежат в области
— KRe6<0, — KReA<0.
C.120)
Искомые корни будут представлять собой некоторые (вооб-
(вообще говоря, комплексные) функции к, щ, к2, а.
Характеристические уравнения в общем случае довольно
громоздки; поэтому ограничимся двумя важнейшими частными
случаями рассматриваемой задачи, когда а = 0 и а = я/2.
Трещина на границе раздела различных упругих сред *).
В этом случае а = 0, и третий сектор исчезает; для величин
Ah A2, В и В2 остается система первых четырех уравнений из
системы C.119) (во втором уравнении А3 и 53 заменяются на
А2 и В2). Система для Ci и С2 состоит из четырех действитель-
действительных уравнений (два последние уравнения в C.115) пропадают,
а С3 заменяется на С2).
Характеристические уравнения оказываются следующими:
k A
— е-ая1
+ е2Ш)
= 0. C.121)
Решение этих уравнений, удовлетворяющее C.120), име-
имеет вид
6=»—'1/2, Л=-1/2±/р
. C.122)
Проверим выполнимость общего условия корректности
C.117) в,рассматриваемом случае. Простой анализ выражения
C.122) для р показывает, что максимум |р| в случае плоской
деформации равен 1пЗ/2я (при vi = 0, ц,2=°°), т. е.
ехр(—1/|р|) ^ 0,0007, что гораздо меньше 1. Поэтому найден-
найденное сингулярное решение имеет физический смысл.
Представляет интерес вопрос о причинах физической некор-
некорректности «в малом», казалось бы, классической краевой
*) Задачи такого типа рассматривались в работах Вильямса, Черепа-
Черепанова, Эрдогана и др.
4 Г. П. Черепанов
§8 Сингулярные задачи теории УпруГОстй [ГЛ. ш
задачи, сравнительно хорошо изученной для гладких областей.
В настоящем примере это объясняется невозможностью удовлет-
удовлетворить граничным условиям отсутствия нагрузок вблизи края
щели; если материалы различны, то всегда вблизи края щели,
оказывается, существуют участки, на которых противоположные
берега щели «взаимно проникают» один в другой, что невоз-
невозможно. Поэтому решения поставленной краевой задачи, строго
говоря, не существует; тем не менее, когда комплексность соб-
собственных чисел «слаба» в указанном ранее смысле, формальное
математическое решение имеет определенный физический смысл.
Постоянные Ль Л2, Ви В2 определяются с точностью до двух
действительных параметров следующей цепочкой формул:
В, = — A + М Л,— Л,е-2Ляг, C.123;
В2 = — A + I) Л2 —
Напряжения, вычисленные по формулам C.9) при
= —1/2 +/р, имеют вид (с учетом условия C.118))
*i ( р (9-д) Г3 cos 1 _ 2р Sin 9 • cos — -
2 ch яр • Vinr I L 2 2
-sine-sin—1 —ер(е-я)-соз-2-1 Ku ,— (eg'9-"'sin-+
2 J 2 / 2 ch Я0 • f2nr \ 2
-Y-—2psine-sin-y-]},
os
vT=fe)[cos + 2Psine-cos + sine-sin-l
2chnp-j/2n7 I L ¦ 2 2 2J
(esin +
2 / 2сЬяр-К2я/- I 2
в-Р(в-я) Jsin| _ sine • cos -y- + 2p sine • sin-f-] }, C.124)
«) fsin- +sine-cos--2p sine sin-1-
L 2 2 V 2 J
2с
2 ch яб ¦ V~2nr I "~ 2
Kn (-еР(в-Я).'С051
2
§ 8] КУСОЧНО-ОДНОРОДНОЕ ТЕЛО 99
при 0 = 0
(z = relf>).
Здесь /Ci, /Си, /Cm — действительные параметры (коэффи-
(коэффициенты интенсивности напряжений), которые должны опреде-
определяться из решения задачи в целом. При у < 0 и при X =
= —1/2 — ф соответствующие формулы получаются при помо-
помощи очевидных переобозначений.
Трещина, перпендикулярная к границе раздела различных
упругих сред*). В этом случае а = л/2, и для трещин продоль-
продольного сдвига при помощи C.119) можно найти
б = — 1 arctg l/jiL . C.125)
Соответствующие напряжения и смещения имеют вид
*шУ]±гве-™ при 1 в |< я/2,
У 2яц,
» при л/2 < 1 6 |< я,
XSO =
Ж
191<я/2) (ЗЛ26)
_яб] При f
Здесь /Сщ — коэффициент интенсивности напряжений от
продольного сдвига.
В случае трещин нормального разрыва, когда на продолже-
продолжении трещины при у = 0, х > 0 будут выполняться условия
v = 0, тжу = 0, являющиеся следствием симметрии относительно
плоскости трещины, искомое собственное число К будет также
действительным. При этом величины А2 и В2, как легко видеть,
будут действительными, и в силу симметрии достаточно рас-
рассмотреть область #>0; в системе C.119) останется всего три
комплексных уравнения (первое, третье и четвертое).
*) Эту задачу рассматривали Зак и Вильяме [зе] при помощи другого,
более частного метода
100 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ {ГЛ. III
В результате их решения получим:
fei (ЗЯ + 2) - fe2О
_;cos JiX*+JL [k
2О + 2Я).+ Я+П
Г+1 J~
- C.127)
(ЗЛ 4- 2) — ^a A Ч- 2Л.) + Я, 4-
(Л + 2) (ft, + 1)
+ /cos
JJ'
__. Ki (Я + 1)
I &1(ЗЯ + 2) — А21
Здесь /Ci—коэффициент интенсивности напряжений, kx=-. _—г,
i 1 — Vo . / , Ц| \
k2=-, —k йе^-1— ; для плосконапряженного состояния Vi
надо заменить на Vi/A +v<).
Число Я представляет собой единственный действительный
корень характеристического уравнения
[(к+ lJD&i&2— 4ft?)+ 2Л? —2*1*2 + 2^ — ^2 +
+ 1— cos яЯ Bftifts —2ft? —2fti + 2ftj)] sin яЛ, = О, C.128)
лежащий в интервале (—1, 0). Зависимость этого корня от ве-
величины k при vi = V2 == 0,3, взятая из работы Зака и Вильямса
[36], приводится на рис. 17 (при ft—>oo имеет место асимптотика
X = —1+0,88 ft~1/2). Качественно зта зависимость имеет вид,
аналогичный соответствующей функции C.125) для продольного
сдвига.
Рассмотренный пример замечателен тем, что в данном слу-
случае напряжения в конце трещины имеют особенность порядка
г\ причем Я., вообще говоря, отлично от —1/2. Поэтому размер-
размерность коэффициентов интенсивности напряжений Кг и Km от-
отлична от размерности коэффициентов интенсивности напряже-
напряжений в однородном теле. Существенно, что, если трещина пере-^
It]
ВЛИЯНИЕ КОНЕЧНОСТИ ДЕФОРМАЦИЙ .
V
с
—II —
•
*¦' :т
л
ходит из более твердой среды в более мягкую (т. е. k цц
> 1), то порядок особенности больше, чем в однородном теле
(т. е. А.< —1/2), н наоборот.
Не нужно думать, что эта сингулярность имеет преходящий
характер, не существенный для механики разрушения, посколь-
поскольку при сколь угодно малом
приращении длины трещины Ы
конец ее оказывается уже окру-
окруженным однородной средой, и
напряжения будут по-прежне-
по-прежнему иметь особенность О (г-'1').
Дело в том, что последняя
особенность реализуется на
расстояниях, малых по сравне-
нию с А(; на расстояниях же,
больших по сравнению с А1
(но по-прежнему малых срав-
сравнительно с характерным ли-
линейным размером тела), будет ^
реализоваться только что изу-
изученная промежуточная асимп- Рис- 17-
тотика, характерная для ку-
кусочно-однородного тела. Поэтому коэффициенты интенсивности
напряжений, характеризующие упругое поле на расстояниях,
малых по сравнению с А/, будут вполне определенными функ-
функциями коэффициентов Къ Кп, Km промежуточной асимптотики
кусочно-однородной среды. Все эти заключения становятся со-
совершенно очевидными, если применить «принцип микроскопа»..
§ 9. Влияние конечности деформаций
Обращение физических величин в бесконечность при реше-
решении задачи говорит об идеализации математической постановки
физической проблемы. Наиболее часто такие особенности воз-
возникают вследствие линеаризации задачи. Не следует думать,
что эти особенности представляют собой что-то патологическое
и потому мало интересны для приложений. Наоборот, иссле-
исследование этих особенностей представляет наибольший интерес
при изучении линейных задач, так как в них заложены ос-
основные свойства и возможности решений линеаризованных
задач.
Особенности напряжений и деформаций в конце трещинь^
возникающие при решении корректно поставленной задачи в
рамках классической линейной теории упругости, неизбежны.
Они говорят о том, что полученное решение в непосредственной
окрестности конца трещины не годится и нужно привлекать
102 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ш
более точную постановку задачи для определения физических
величин вблизи конца трещины.
При любом уточнении постановки задачи особенность приб-
приближенного решения будет играть уже роль некоторой промежу-
промежуточной асимптотики уточненного решения в том смысле, что
уточненное решение очень близко к приближенному на рас-
расстояниях г от конца трещины, удовлетворяющих условию / 3>'
^> г ^> Д, где / — характерный линейный размер тела (напри-
(например, длина трещины), Д — характерный линейный размер обла-
области вблизи конца трещины, в которой приближенная постановка
задачи по тем или другим причинам незаконна.
Однако если свойство линейной упругости в какой-то мере
присуще всем твердым телам, то отклонения от нее при доста-
достаточных деформациях для различных типов материалов имеют
различную природу и описываются в рамках различных мате-
математических теорий. Поэтому распределение напряжений и де-
деформаций в области размером Д и сама величина Д различны
в разных материалах, а линейно-упругая асимптотика, всегда
реализующаяся при достаточно больших размерах I, с точно-
точностью до некоторых множителей будет одной и той же для всех
материалов.
Этот факт, как будет видно из дальнейшего, лежит в осно-
основе построений линейной механики разрушения и объясняет ее
основной интерес к сингулярным решениям теории упругости.
Отметим основные причины появления сингулярности реше-
решения в конце трещины:
а) незаконность вблизи конца трещины применяемых при
решении приемов в рамках линеаризованной постановки (на-
(например, снесение граничных условий со стенок начальной тре-
щиноподобной полости с конечным радиусом закругления в ее
конце или неучет участков перекрывания берегов в случае тре-
трещин на границе различных упругих сред);
б) пренебрежение конечностью деформаций (эффект гео-
геометрической нелинейности);
в) пренебрежение влиянием пластических деформаций (эф-
(эффект физической нелинейности);
г) пренебрежение дискретным (атомным) строением твер-
твердого тела.
В каждом реальном материале представлены все указанные
факторы, однако весьма часто доминирует одна из этих причин.
В металлах и их сплавах, во многих полимерах доминирующим
является пластическое течение; в низкомодульных материалах
типа резин и в некоторых полимерах — фактор высокоэластиче-
высокоэластических (конечных) деформаций; в хрупких материалах типа стек-
стекла, плавленного кварца и др. — атомная природа тела (непри-
(неприменима модель сплошной среды). Следует отметить также при-
§ 9] ЁЛИЯНИЁ KOHE4H0CfH ДЕФОРМАЦИЙ ЮЗ
сущую всем телам микронеоднородность структуры, которая во
многих случаях существенно влияет на распределение напряже-
напряжений и деформаций в области размером А.
Учет любого из указанных эффектов приводит к «размазы-
«размазыванию» упругой особенности, которое является следствием ре-
решения математической задачи в уточненной теории. Следует
подчеркнуть, что сингулярность в конце трещины обычно
остается даже в уточненной (геометрически или физически не-
нелинейной) теории; однако она существенно изменяется и имеет
силу на значительно меньших расстояниях, чем упругая асимп-
асимптотика. Этот факт говорит о приблизительном характере всякой
«строгой» теории.
Рассмотрим эффект конечности деформаций. Пусть Х\, х2,
х3 — некоторая декартова система отсчета. Тройка чисел (хи
х2, Хз) задает положение некоторой материальной точки, испы-
испытавшей смещение (мь и2, м3) из недеформированного состояния.
Смещения иь и2, щ будем считать функциями х\, х2, Хз, при
этом начальные координаты точки в недеформированном со-
состоянии jfOi определятся соотношением хт = х* — щ.
Между напряжениями ai} и деформациями етп в упругом
теле существует взаимно однозначная зависимость [37], которую
можно записать так:
(n, v,, v2, .,.). C.129)
Здесь
„ L ( дит 1 dUn L диа ди
6 \- Г +
2. \~охп ахт
Б, vi, V2, ... — упругие постоянные, первая из них имеет размер-
размерность напряжения, а остальные безразмерны, /'¦>' — некоторые
ограниченные безразмер-
безразмерные функции.
Допустим, что в не-
деформированном теле
имелся разрез нулевой /fo х АО В
толщины; при приложе- ///z^^
нии нагрузки разрез пре- в
вращается в полость (рис. Рис. 18.
18). Пусть имеет место
нормальный разрыв, а длина начального разреза достаточно ве-
велика (или приложенные нагрузки достаточно малы), так что
разрез можно считать полубесконечной плоскостью у = 0, х<0;
образующаяся полость близка к этому разрезу в том смысле,
что деформации на бесконечности бесконечно малы, а распреде-
распределение напряжений и деформаций при г->-оо такое же, как в ли*
нейной теории упругости (формулы C.44)). Реальность такой
ситуации следует из «принципа микроскопа».
J04 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (ГЛ. Ш
Отметим следующие свойства решения этой задачи, харак-
характерные для любых конечных упругих деформаций:
а) угловые точки и точки возврата на контуре недеформиро-
ванного. тела исчезают при сколь угодно малых нагрузках;
б) напряжение ау в,конце полости (в точке О на рис. 18) не
зависнет от Ki (и, тем самым, от приложенных нагрузок) и
равно
a» = ?X,(v,, v2> ...); C.130)
в) характерный линейный размер области А, в которой су-
существенны эффекты конечности деформаций, равен
A = -§-Mv" v2, ...)• C-131)
Здесь Ху и Я2 — некоторые безразмерные функции своих ар-
аргументов.
Первое свойство непосредственно следует из сингулярности
напряжений и деформаций в угловой точке (и точке возврата)
при сколь угодно малых внешних нагрузках в линейной теории
угругости, которую можно рассматривать как теорию малых
возмущений точной (геометрически нелинейной) теории упруго-
упругости. Разумеется, имеются в виду угловые точки класса N.
Второе и третье свойства становятся очевидными, если
учесть, что в поставленной задаче нет характерного линейного
размера и единственным внешним .параметром является коэф-
коэффициент интенсивности напряжений Къ определяющий требуе-
требуемую на бесконечности/асимптотику.
При получении формулы C.130) существенно использована
также ограниченность функций рк Если pi нёограничены, то
возможна также зависимость типа
5-, v,, v2, ...J (при r->0 A3-*oo),
где т — расстояние от конца полости.
¦Найдем точное решение поставленной задачи для следую-
следующей модели несжимаемого упругого тела при конечных дефор-
деформациях (плоская деформация):
3
Ееху — -^х
C.132)
ау).
Здесь
е* ~~~-дх ' еУ ~ ду ' вх« ~~ 2 \ ду + дх
точка над буквой означает полную производную по времени.
§ 9]' ВЛИЯНИЕ КОНЕЧНОСТИ ДЕФОРМАЦИЙ 105
Соотношения C.132) представляют собой обычный закон
Гука, записанный в скоростях напряжений и деформаций. Оче-
Очевидно, что таким образом можно записать закон бесконечно
малого деформирования в окрестности произвольной конечной
деформации любого несжимаемого упругого тела, однако мо-
модуль Юнга будет, вообще говоря, зависеть от величины ко-
конечной деформации (точнее говоря, от трех инвариантов тен-
тензора деформации, так как тело считается изотропным). Пред-
Предположение о постоянстве Е означает, что реакция выбранной
модели упругого тела на малые возмущения не зависит от
величины конечной деформации.
Следует иметь в виду, что полное соответствие модели, опи-
описываемой уравнениями C.132), некоторому геометрически нели-
нелинейному упругому телу имеет место в случае только одного
параметра нагружения. При наличии нескольких параметров
нагружения конечные деформации этой модели, вообще говоря,
будут^зависеть от пути нагружения (гипоупругое тело).
Общее решение уравнений C.132) и уравнений равновесия
"лГ+"^Г==0> ~dT"^~df===0 C.133)
можно представить при помощи формул, аналогичных соотно-
соотношениям Колосова — Мусхелишвили C.9) в плоской задаче ли-
линейной теории упругости:
ох + ду =А Re Ф (г, t) (z = х + iy),
ду — ох + 2ixxy = 2 [гФ' (z, f) + W (z, t)],
у?(п + п)) = ф(г, *) —zq>'(z, О-* (г. 0.
[Ф(z, t) + гЩг~Т) + <ЙгГО]д =1 \ (К + Яп) ds, C.134)
АВ
t) — d(f (z't]
Здесь /^время, y(z, t) и i|)(z, t)—однозначные аналитические
функции z в области, занятой телом; другие обозначения иден-
идентичны принятым в формулах C.9).
Следует отметить, что уравнения C.133) —не точные, а при-
приближенные; в них пренебрегается членами вида grad ii-grada*
по сравнению с членами типа -=T-grad(rx. Строго говоря, это
верно только для малых деформаций. Приближенность такой
постановки задачи вполне искупается возможностью ее полного
аналитического исследования. Кроме тога, решение этой задачи
позволяет проиллюстрировать некоторые моменты, характерные
для проблемы конечной деформации в целощ,
106 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
На неизвестной границе полости L, уравнение которой имеет
вид F(x,y, t) = 0, должно выполняться условие кинематической
совместности
3F . . 3F . . dF n /o 1Qr\
-дГ + иЖ + и^^° (ЗЛ35)
(F (х, у, 0)— заданная функция).
Граница полости L в любой момент времени свободна от
внешних нагрузок; отсюда при помощи представлений C.134)
находим следующее граничное условие:
, 0 = 0 (ze=L). C.136)
В бесконечно удаленной точке функции ф(г, t) и i|>(z, t), со-
согласно C.43), ведут себя так:
" при z—> сю
Ф(г, t) = KlVm^ + o{zW),
C.137)
Таким образом, поставленная задача свелась к краевой за-
задаче C.135) — C.137) с неизвестной границей от одной ком-
комплексной и одной действительной переменных.
Перейдем на верхнюю полуплоскость параметрической пло-
плоскости ? при помощи отображения 2 = со(?, t); аналитическая
функция со(?, t) конформно отображает область Im^^O на об-
область, занятую телом и ограниченную контуром L, со взаимно
однозначным соответствием начала координат и бесконечно
удаленных точек (см. рис. 18). Следовательно,
ш(?. <) = —сЮС + ой8) при ?->оо, C.138)
где c(t) —действительная положительная функция.
При этом краевые условия C.136), C.137) на плоскости ?
запишутся в виде
Ф. E. « = - Kill V^f)№t + о (О,
Здесь
% (I, t) = Ф [<а (;, о, fl, if. (?, 0 = 1|> [ш (;, 0,
§8]
ВЛИЯНИЕ КОНЕЧНОСТИ ДЕФОРМАЦИЙ
107
где соо(?)—задаваемая функция. Точка над буквой означает
производную по комплексной переменной. Функции ф*(?, t),
•ф. (?, t) и со (?, t) подлежат определению.
Условие кинематической совместности удобно записать та-
таким образом:
при Im? = О
2п, [ да> (С, t)
у ? lm [
да Д. О 1 _
1 _
J —
Это условие получается из следующих соображений
(рис. 19). Каждой точке М контура L в любой момент времени
t соответствуют две скорости: а)
скорость материальной частицы, на-
находящейся в момент времени / в
точке М; комплексный вектор этой
скорости и + iv определяется фор-
формулой C.134); б) кинематическая
скорость перемещения точки М са-
самого контура L (daldt), соответ-
соответствующая одному и тому же значе-
значению параметра ?, задающего поло-
положение точки М на кривой L в любой
момент времени, Как следует из
рис. 19, на котором сравниваются два близких положения кон-
контура L в малой окрестности точки М в моменты времени / и
t + dt, проекции указанных двух векторов скорости на нормаль
пг к контуру L в точке О должны быть равны между собой. Те-
Теперь для доказательства C.140) осталось лишь найти-выражение
для комплексного вектора единичной нормали пг на контуре L:
„ _ dz _ ю'(Е. 0 # __, ">'(?¦*)
t+it
Рис. 19.
\dz\
I «>'(?. 01
C.141)
и составить скалярное произведение а„ комплексного вектора
а = |a|exp(uxi) на комплексный вектор nz = exp(ia2):
ап = | a |cos (ai — a2) = Re (aiiz). C.142)
Формулы C.138) —C.140) завершают постановку краевой
задачи для верхней полуплоскости комплексного переменного
?. Рассмотрим класс решений этой краевой задачи, в котором
выполняется условие
|*^|4py--*^0 (ЗЛ43)
»' (С 0
при
108 , сингулярные задачи теории упругости [гл. т
представляющее собой векторное равенство кинематической
скорости и скорости материальной частицы на границе полости.
При этом условие C.140) выполняется тождественно. Как будет
видно из дальнейшего, исходная задача, в которой начальная
полость представляет собой полубесконечный прямолинейный
разрез нулевой толщины, входит в этот класс.
Сложив C.143) и C.139), получим
^- = 3cp.(S, t) при Im? = 0. C.144)
В силу принципа непрерывного продолжения соотношение
C.144) должно выполняться также в полной плоскости ?.
Подставляя функцию ф*(?, t) согласно C.144) в C.143) или
в C.139) и преобразуя, можно найти
= — Зо^ю' при Im? = 0 C.145)
или
Т1ГНС. *)<»'«, 01 = -¦.«, <)ffl'<C t) при
Введем вспомогательную аналитическую функцию Г E, t):
Г«' /) = —^hr\ h'& ^)W'(S> <)л+го@ • C-146)
Функция Г<>(?) несущественна, и ее можно считать равной
нулю. При помощи функции Г(?, t) краевое условие C.145)
можно записать так:
=»Г(С, t) при ImS = 0. C.147)
Решение краевой задачи C.147) -в классе функций, имею-
имеющих на бесконечности заданный порядок О(?2) и удовлетворяю-
удовлетворяющих условиям симметрии, запишется в виде
»E, *) = —сфС2 —ЭД?, Г«, 0 = --g-^I
C.148)
Действительные положительные функции c(t) и b{t) должны
определяться из условий C.139) на бесконечности для функций
$91 ЁЛИЯМИВ К0НЕЧН6СТИ ДЕФОРМАЦИЙ Ю9
Ф.С?,0 и т|з*(С, 0; при помощи C.146), C.148) и C.144) нахо-
находим следующие дифференциальные уравнения, которым долж-
должны удовлетворять функции c(t) и b(t):
de 1 db
dt ' 3 dt
Таким образом^ функция c(t) равна постоянной, которую без
ограничения общности можно считать равной единице. Оконча-
Окончательно получаем
Ь = 3Kil{E V^2jT) + b0, с = 1, C.150)
где bo — произвольная постоянная.
Искомые функции o>(g, /), <р*(?, /) и i|)*(?, t) запишутся
в виде
В начальный момент нагружения Ki = 0 и b = bo, т. ё. по-
постоянная 60 определяет форму начальной ^полости. Согласно
C.151), контур полости в любой момент нагружения представ-
представляет собой параболу
W C.152)
Как видно, величина 62/2 равна 'радиусу кривизны в вер-
вершине параболы. В интересующем нас случае начального разре-
разреза нулевой толщины Ьо = 0.
Найдем исходные функции в физической плоскости г;
К, 2z + b Yb2 + 4г — Ь2
¦
C.153)
(Ь2 + 4г)
3/2
1 К) СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ (ГЛ. И!
Из формул C.134), интегрируя по времени, определяем поле
смещений и напряжений
— 4? Рр In
3
_ АЕ Г 6 + /б2 + 4г 32 +
3 L uJ 0
C.154)
u+lv =±R[V7T Vl& ](b2®
b + fW+H 1 ,
— Z In . -{ Z In
bo+Vbl+& 2
Формулы C.154) позволяют определить также конечные де-
деформации тела в любой точке и при любом значении параметра
нагружения Ki (или Ь, согласно C.150)).
В случае начального разреза нулевой толщины, когда
60 = 0, напряжения в вершине параболы ведут себя следующим
образом:
при 2->0
ах^0> хх,^0, ау = ^-\п~ + ОA), C.155)
т. е. напряжение ау имеет логарифмическую особенность. Появ-
Появление этой особенности связано, по-видимому, с тем обстоятель-
обстоятельством, что в используемой модели упругого тела допустимы
бесконечно большие напряжения и деформации; последнее пред-
представляет собой некоторую идеализацию. Следует отметить так-
также, что на применяемой диаграмме а — е нет каких-либо харак-
характерных точек; поэтому граница области, в которой существенны
эффекты конечности деформаций, имеет условный характер.
§ 10. Влияние физической нелинейности
и размеров начальной полости
В рамках теории малых деформаций отклонения от закона
Гука при достаточно больших деформациях, а также отличие
начального трещиноподобного дефекта от математического раз-
разреза нулевой толщины приводят к перераспределению напряже-
напряжений и деформаций в непосредственной окрестности контура тре-
трещины. Рассмотрим эти эффекты на простейших примерах.
§ !0] ВЛИЯНИЕ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ 111
1. Нелинейно-упругое тело*). Пусть нелинейно-упругое од-
однородное и изотропное тело содержит в себе трещины нормаль-
нормального разрыва. Будем считать, что среда несжимаема и подчи-
подчиняется произвольной степенной зависимости между интенсивно-
интенсивностью касательных напряжений / и интенсивностью деформаций
сдвига Г. Эту зависимость можно рассматривать в качестве
удобной аппроксимации произвольной связи между / и Г в ин-
интервале величин, характерных для окрестности контура тре-
трещины.
На основании теоремы Ильюшина р2] поведение рассматри-
рассматриваемого тела идентично поведению упрочняющейся несжимае-
несжимаемой упруго-пластической среды со степенной зависимостью
между интенсивностью касательных напряжений и интенсивно-
интенсивностью скоростей деформаций сдвига, если внешние нагрузки
возрастают прямо пропорционально одному параметру на-
гружения. /
Следует указать еще на одно счастливое обстоятельство:
в случае степенной зависимости переменные в соответствующих
уравнениях нелинейной теории упругости разделяются, по край-
крайней мере, в декартовых и полярных координатах. Это позво-
позволяет найти эффективное решение некоторых конкретных задач
для рассматриваемого тела.
Приведем основные соотношения в полярных координатах г8:
уравнения равновесия
0 ^rL iifl o^L-o (
+ г ае + г ~"и> дг ^ г ае + z г — и> \
условие совместности деформаций
д I дегв \ д2ег дег д* (гее)
2 IF у ~Ш~!:==~т2 Г1Г + Г аг2 ' C-157)
соотношения между деформациями и напряжениями
ег = — se == т aI* (°r — ffe). ere = al\e,
C.158)
2/=1/K_ffeJ + 4T2e> r =
Здесь а и к — упругие постоянные. Величины / и Г в данном
случае равны максимальному касательному напряжению и
наибольшей деформации сдвига в каждой точке.
Согласно «принципу микроскова» вопрос о распределении
напряжений и деформаций вблизи края трещины нормального
*) Решение этой задачи впервые было получено в работе автора C81.
Позже тем же методом, но без ссылки на работу [38J эта задача была решена
Райсрм и Розенгреном [39].
112 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
разрыва сводится к решению следующей однородной краевой
задачи для системы уравнений C 156)— C.158):
при 0=±я, 0<г<оо {г9 = тг9 = 0. C.159)
. Кроме того, решение должно быть симметрично относитель-
относительно оси абсцисс, так как рассматриваются трещины нормального
разрыва.
Поставленная краевая задача допускает группу преобразо-
преобразований /' = С\1, 8' = 6, г' = С2г, где под / подразумеваются на-
напряжения (или деформации), С] и С2 — параметры группы.
Можно показать, что такую же группу допускает аналогич-
аналогичная краевая задача для произвольного сектора, занятого рас-
рассматриваемым материалом; в вершине сектора могут быть при-
приложены сосредоточенная сила и момент. Граничные условия
могут быть любого из четырех типов, указанных в § 2 при
определении канонических сингулярных задач. Кроме того, сам
сектор может быть кусочно-однороден и кусочно-анизотропен;
линии разрыва упругих постоянных должны совпадать с радиу-
радиусами. Качественное и количественное исследование указанного
класса нелинейных задач может быть проведено при помощи
излагаемых здесь методов.
Следует отметить, что получающиеся качественные резуль-
результаты для рассматриваемого нелинейно-упругого тела оказы-
оказываются теми же, что и для тела Гука; в частности,' в, случае
свободных от внешних нагрузок границ s будут справедливы
утверждения, аналогичные предложениям А — Г § 3.
Из группового свойства и из общего решения уравнений
равновесия при помощи функции Эри вытекает, что сингуляр-
сингулярное решение краевой задачи должно иметь вид
Or = - (А + I) ^ [Г (в) + d + 2)f @I,
Ч г*П6)
Здесь /@)—произвольная функция, % — собственное число.
Подставляем выражения C.160) в формулы C.158) для де-
деформаций, затем последние подставляем в условие совместности
C.157); окончательно получаем следующее обыкновенное диф-
дифференциальное уравнение относительно функции /@):
[ ] [Ф* W - (/О2] • C.161)
Здесь
4Ф2 = 4 (/'J + [(А + 2) / - (Я + I) (Г + Ч + 20JV
S 10] ВЛИЯНИЕ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ ИЗ
Граничные условия C.159) запишутся в виде:
при 6= ±л / F) = /' (в) = 0. C.162)
Вследствие симметрии тге, дог/дд и двв/dQ должны обра-
обращаться в нуль при 6 = 0; отсюда:
при 6 = 0 /'@) =/"'@) = 0. C.163)
Таким образом, на сегменте [0, л] для уравнения четвёртого
порядка C.161) получается двухточечная краевая задача на
собственные значения. Для любого заданного значения упругой
постоянной к можно получить численное решение этой задачи
на ЭВМ.
В случае разрезов нулевой толщины (как в данной задаче)
собственное число К может быть найдено [38] из физических со-
соображений, на основании общих положений механики разру-
разрушения. В гл. V будет показано, что во всякой физически кор-
корректной модели упругого тела характерные напряжения и де-
деформации на краю математического разреза (в рамках теории
малых деформаций) должны обращаться в бесконечность так,
чтобы их произведение имело особенность вида 1/г. В предель-
предельных- случаях допускается ограниченность напряжений или де-
деформаций: идеально-пластическое тело (напряжения ограниче-
ограничены, деформации имеют порядок О A/г)), идеально-отвердеваю-
идеально-отвердевающее тело (деформации ограничены, напряжения имеют порядок
0A/0).
Согласно C.160) и C.158), деформации имеют порядок
О(г%+Ы), а напряжения — порядок О (г1). Тогда из указанного
условия находим
Х=-1/(х + 2). C.164)
В частности, для тела Гука х = 0 и К = —1/2, что уже было
получено ранее другими методами.
Таким образом, на краю разреза в подчиняющемся степен-
степенному закону нелинейно-упругом теле напряжения имеют поря-
порядок О (г-^н-2»), а деформации — порядок О (г-<*+1>/<*+2>).
Знание собственного числа Я значительно облегчает задачу
численного интегрирования уравнения C.161), так как для за-
заданного v. оно вполне определено. Заметим, что функция /(9)
находится из граничной задачи с точностью до неопределенного
множителя, который, играет роль коэффициента интенсивности
напряжений и определяется внешним полем. Как и вообще в
задачах класса N, он должен быть задан при постановке за-
задачи. Без потери общности функцию f@) можно считать равной
1 при 0 = 0; при этом простейший метод решения краевой.за-
краевой.задачи C.161) — C.163) состоит в том, чтобы, задавая еще /"@)
при 6 = 0 и решая стандартную задачу Коши для уравнения
114 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
C.161), стремиться к тому, чтобы /F) обращалась в нуль при
б = я. Последовательное задание /"F) при 6 = 0 удобно осу-
осуществлять, например, способом, аналогичным методу Ньютона
при отыскании корня уравнения.
Отметим наиболее примечательный результат численного
анализа: при увеличении к От нуля до бесконечности (что соот-
соответствует переходу от диаграммы Гука к диаграмме Прандтля)
происходит притупление конца трещины от упругой параболи-
параболической формы до прямоугольной, с конечным скачком смещения
2v0 в конце трещины, что отвечает идеальному упруго-пласти-
упруго-пластическому телу.
2. Полости. Реальные дефекты, служащие причиной разру-
разрушения, в большей или меньшей степени отличаются от мате-
математических разрезов нулевой толщины, обычно фигурирующих
в теории.
Пусть S — срединная поверхность, представляющая собой
геометрическое место точек, равноотстоящих от противополож-
противоположных берегов начальной трещиноподобной полости. Обозначим
через h(x\, х2) толщину полости (пара чисел (хи х2) задает
положение точки на поверхности 5).
Допустим, что выполняются условия
h(xux2)<l, lgrad/ф,, х2)\< 1, ' C.165)
где / — характерный линейный размер полости в продольном
направлении. В этом случае для приближенного решения за-
задачи можно применить следующий прием: снесем граничные
условия со стенок полости на поверхность S, опуская в гра-
граничных условиях малые величины, и решаем задачу так, как
если бы полость была математическим разрезом вдоль S. При-
Прибавляя к начальным координатам материальной точки ее сме-
смещение, полученное из приближенного решения, находим поло-
положение соответствующей точки в деформированном состоянии.
Этот прием соответствует нулевому приближению в решении
задачи асимптотическим методом, когда искомые функции пред-
представляются в виде асимптотического разложения по малому
параметру е = max h/l:
оо
/ (хи х2, х3) = /о (*i, х2, х3) + 2 ft (хи х2, х3) ф,- (е) -3 j
(фг(е)-*0 при е-*0).
Здесь координата х3 выбрана так, чтобы при х3 = 0 получа-
получалась поверхность S.
Представляет интерес вопрос о степени близости приближен-
приближенного решения f0 к точному при е—*0 в рамках линейной теории
упругости. Можно показать, что, если во всех точках поверхно-
поверхности § эьшолняются условия C.165) и, кроме того, полость на
§ Ю] ВЛИЯНИЕ ФИЗИЧЕСКОЙ НЕЛИНЕЙНОСТИ 115
конце (на контуре поверхности S) имеет точку возврата, то
приближенное решение во всех точках Х\, х2, хг близко к точ-
точному по абсолютной величине. Если же полость на конце (на
контуре поверхности S) имеет угловую точку или, тем более,
плавное закругление, то о близости этих решений можно гово-
говорить только в пространстве Lp *). В малой- окрестности точек
контура поверхности S эти решения значительно отличаются по
модулю при сколь угодно малых е. Асимптотическое разложе-
разложение C.166) годится только на расстояниях, больших по сравне-1
нию с характерным размером полости в ее конце (для случая
плавного закругления таким размером служит радиус закруг-
закругления).
Таким образом, решение, получаемое путем снесения гра-
граничных условий на поверхность S, близко к точному на расстоя-
расстояниях от контура поверхности S, больших по сравнению с радиу-
радиусом закругления полости А. На расстояниях порядка Д задачу
следует решать в точной постановке (метод асимптотического
разложения не годится).
При / ^> А на основании «принципа микроскопа» для поло-
полостей имеет смысл представление о коэффициентах интенсивно-
интенсивности напряжений, задающих поле напряжений и деформаций на
расстояниях от края полости, больших по сравнению с А и
определяемых внешним полем.
Концевая часть любой плавно закругляющейся полости с
ограниченным радиусом кривизны при е-*0 представляет со-
собой параболический цилиндр; поэтому распределение напряже-
напряжений и деформаций в непосредственной окрестности края полости
определяется потенциалами C.22) для параболического цилин-
цилиндра, которые удобно записать так:
*) Lp — пространство функций, заданных при а ^ х < Ь, для которых
b
Г [f(x)]pdx принимает конечное значение.
116 сийг^лйрнЫё задачи теории уйругос*и [гл. Ш
Здесь уравнение контура параболического цилиндра принято
в виде Ь2х = —у2, так что срединная поверхность полости бу-
будет совпадать с полуплоскостью у = О, х ¦< 0.
В частности, для максимальных напряжений в конце поло-
полости получаются формулы
Приведем два конкретных примера (для эллиптической по-
полости и двух глубоких гиперболических вырезов).
Пусть контур полости представляет собой эллипс
а упругая плоскость растягивается на бесконечности напряже-
напряжением оу = р (задача Колосова). В этом случае, воспользовав-
воспользовавшись указанным приближенным приемом, легко определить ко-
коэффициент интенсивности напряжений (см. гл. IV), а по фор-
формуле C.168) — максимальное растягивающее напряжение в
конце полости. Находим
Ki = Р V^R, оу = 4р/( 1 - т). C.170)
Согласно точному решению Колосова [23], максимальное на-
напряжение при произвольных т равно
3 — 2/и — /п2 /
Отношение максимальных напряжений, согласно формулам
C.170) и C.171), равно
(стк)точн ,1 / 1 \ /о 1 то\
_-_=1—-е 8=1— т). C.172)
• \ау)прибл- *
Как видно, даже для круговой полости, когда т = 0, ошибка
приближенного решения не превышает 25%.
Пусть теперь упругое тело занимает область, расположен-
расположенную- между ветвями гиперболы (см. формулу C.24) и рис. 12),
причем Э «С 1 (задача Нейбера). В этом случае также можно
воспользоваться приближенным приемом снесения граничных
условий на ось абсцисс и без труда определить коэффициенты
интенсивности напряжений.
Находим (в точке z = с)
L ™ * =-?=' C-173)
У пс
.. У пс с у пс у пс У пс
Здесь приняты обозначения рис. 12, добавлены лишь сосре-
сосредоточенные силы Z на бесконечности от продольного ^двига,
действующие перпендикулярно плоскости чертежа.
iioi влияние ФизйЧбской нелинейности и?
По формулам C.168) отсюда можно найти максимальные
напряжения в конце глубокого тонкого гиперболического выре-
выреза при х = с, у = 0:
(Д = с02). C.174)
Согласно точному решению (см. § 3), для гиперболы с про-
произвольным углом раствора Эо напряжение атах при х = с, у = 0
равно
_ -2/ ¦ AM ctg 80
тах с sin 90 (яа + sin яа) "" с2 cos яа (tg яа — яа)
(яа = я — 2во). C.175)
Отношение максимальных напряжений при М = 0 полу-
получается равным
(вшах/точи ^9("
• (я — 290 + sin 2B0) *
Даже для равнобочной гиперболы, когда Эо = я/4, ошибка
приближенного решения не превышает 35%.
Таким образом, указанный приближенный прием с исполь-
использованием промежуточных сингулярных решений C.167) полезен
также при определении концентрации напряжений в наиболее
опасных точках вырезов и отверстий различной формы. Это
особенно важно в тех случаях, когда точное решение задачи
представляет большие трудности.
Если известно точное решение задачи о концентрации напря-
напряжений при произвольном радиусе закругления А в конце по-
полости, то при помощи C.167) легко определить соответствую-
соответствующие коэффициенты интенсивности напряжений при А—»0, на-
например, по асимптотике решения C.167) при z-*0 (т. е. при
Находим
Ki — iKn= Hm
г , ft,\ — ftn\-\ C.177)
: = — film lim
г/Д-»0, .
Здесь ф(г) и f(z) — потенциалы точных решений.
Например, коэффициенты интенсивности напряжений Ki и
Кш можно определить по максимальным напряжениям
118 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 1ГЛ. III
в наиболее опасной точке 2 = 0:
/<¦]= lim М—-отах , Кщ= Vim [УпК %тлх\
A-»OL л J Д->0
famax = Оу lz-0. ^тах = *zy Iz-o)> C-178)
Отметим, что случай полостей, концы которых не имеют
плавного закругления, требует специального рассмотрения.
§11. Динамические эффекты
Учет сил инерции приводит к перераспределению напряже-
напряжений и деформаций в окрестности края хрупкой трещины. Наи-
Наиболее просто анализируются эти эффекты в следующих слу-
случаях, являющихся в известном смысле предельными случаями
общего динамического решения:
а) фронт трещины распространяется в упругом теле с боль-
большой скоростью, сравнимой со скоростью звука, причем упругое
поле стационарно в малой окрестности кромки трещины в дви-
движущейся системе координат, связанной с концом трещины;
б) фронт трещины неподвижен; внешние нагрузки, помимо
постоянной составляющей, имеют компоненту, которая изме-
изменяется во времени с большой частотой по закону синуса (уста-
(установившиеся колебания).
Изучим эти случаи, считая упругое тело для простоты од-
однородным и изотропным.
1. Локально стационарное поле. В плоской стационарной
динамической задаче теории упругости имеют место следую-
следующие основные представления, полученные впервые Л. А. Гали-
ным [40]:
" ^ 7^17Im
— Req>3(z2),
- 2v) [P,fW (.) + Ы N].
op (-5.1/У)
7
(l+vOl-2v)
fg») ReЖ
'§11] ДИНАМИЧЕСКИЕ ЭФФЕКТЫ 119
Здесь:
m =
С\ и с2 — скорости распространения волн расширения и сдвига
соответственно, р — плотность. Функции cpi(zi), 92B2) и фз(гг)
представляют собой аналитические функции комплексных пере-
переменных
Zx = x—Vt+ihy, z2 = x-Vt + i$2y. C.180)
Представления C.179), C.180) описывают плоское упругое
поле, стационарное в системе координат % = х— Vi, т) = у, дви-
движущейся в направлении неподвижной положительной оси х со
скоростью V, меньшей с2. Это поле, как и в статическом случае,
расщепляется на два независимых поля, дающих соответственно
плоскую деформацию (функции cpi и фг) и сложный сдвиг
(функция фз).
Приведем также следующие зависимости:
2nER(m,x)
+ v) A - 2v) [- р^,, (га) + ф4р1Ш2 (г2)]
(ш, v)
Здесь ш(B) и ш2(г) — аналитические функции (потенциалы
Галина), которые определяются следующими интегралами
Коши:
+ 0
+00
} ЫЛ-ОТ#7. C.182)
120 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
Отметим еще соотношение
?М _ 1+у Гр?(Р4 —1) г" dt
д% /п_о "" ER (я, v) я J lCVi-o l _
U ¦ —оо
C.183)
Теперь рассмотрим задачу о распределении напряжений и
деформаций в малой окрестности произвольной точки О дви-
движущегося фронта трещины, причем направление скорости V
перемещения фронта в этой точке лежит в плоскости, касатель-
касательной к поверхности трещины в той же точке.
Упругое поле считаем локально стационарным в рассмат-
рассматриваемый момент времени относительно системы координат,
движущейся вместе с концом трещины. На основе «принципа
микроскопа» приходим к следующей канонической сингулярной
задаче для упругого пространства с полубесконечным разрезом:
при т) = 0, |< 0 CTtl = T5r)=Ttl2-=0. C.184)
Подвижные координаты |тJ, связанные с фронтом трещины, —
те же, что и координаты xyz на рис. 13.
При помощи C.179) и C.182) граничные условия C.184)
запишутся в виде
при т) = 0, |<0 ImWj (z) = lm w2(z) = Im <$'3(z) = 0. C.185)
Корректное решение этой сингулярной краевой задачи по
аналогии со статическим случаем имеет следующую форму:
У „ , ^ . V C-186)
Здесь Vz — однозначная аналитическая функция в плоско-
плоскости z, разрезанной вдоль положительной полуоси | (|Лг ^0
при г = х + /О).
Коэффициенты интенсивности напряжений Ki, Kn, Km в об-
общем случае зависят от времени, граничных условий, конфигура-
конфигурации тела и трещины, скорости и ускорения роста трещины
и т. п.; эта зависимость определяется из решения задачи в це-
целом. Если упругое поле стационарно в целом, то эти коэффи-
коэффициенты, очевидно, не будут зависеть от времени и от скорости
трещины.
§ ill Динамические эффекты 121
Напряжения и деформации вблизи конца трещины легко оп-
определяются по формулам C.179), C.181) и C.186). Приведем
получающийся результат, ограничившись наиболее важным
случаем трещин нормального разрыва, когда Кп = Кш = 0:
ч
* . . . I — 8184 cos -pr arctg (pi tg 9)
ди д i A -г v) I 2 ^ ,
~д% ~~ ER (m, v) У~Ъп L (cos29 + p^sin29I/4
|- arctg (p2tg 9I
.I ' I» I j I -4 1 Л/I
3 + P|sin29I/4 J
P1P2 «OS -5- i
dv
Cl + v> f~P?sinTarCtg(P2tg9) P4P? sin -I aretg (p
L
~д$~~ ER(m,s)^bTr L (cos2e+Pisin2ey/4 ~ (cos2 9 + tfx sin2 9)
_ Kx \ PP
П ~ R (m, v) f*Tr L
g (p, tg в) 1 '
sin2 9I'4 J'
(cos2 9 + P2 sin2 e)
2sin29I/4
P,P3p4cosYarctg(P1tg9) 1
~ (cos29+p2sin29I/4 J'
_ Ki Г P^cos^rctg^tgg)
Gi)~ R (m, v) K^ L (cos2 9 + E2 sin2 9) ' ~
p2p2cos-^-arctg(P2tg9) 1
(cos29+p2sin2eI/4 J'
(P2tg9) 1
sin29) J'
sini-arctg(p,tg9) siniarctg
Xlr]== R{m,v)f2^r [ (co^e+pfsta'eI'* "" (cos29+($2sin29)
fb —^=0, (Tc^V^s + a,,).
Примерный график функции arctg(ptgG) указан ниже на
рис. 79.
Выясним, при каких условиях.упругое поле вблизи конца
движущегося разреза будет локально стационарным. Вначале
напишем уравнения динамической теории упругости для плос-
плоской задачи, когда д/dz = 0:
122 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЁОС ИИ УПРУГОСТИ [ГЛ. lit
Напряжения и смещения выражаются через волновые потен-
потенциалы у(х, у, t) и ty(x, у, t) так:
В этих формулах xyz — неподвижная декартова система ко-
координат. Допустим, что скорость V распространения разреза
в рассматриваемой точке О фронта трещины представляет со-
собой непрерывную функцию времени. Тогда в течение бесконечно
малого промежутка времени ее можно считать постоянной.
В подвижной системе координат | = х—Vt, r\ = у волновой
оператор ? на этом промежутке времени запишется следую-
следующим образом:
U дх2 """ ду2 с2 dt2 ~
~ d|2 ^ дт\2 с2 д%2 ^ с2 dldt с2 dt2 ' \
Таким образом, необходимым и достаточным условием ло-
локальной стационарности упругого поля вблизи точки О является
ограниченность вторых производных d2/d?,dt и d2/dt2 волновых
потенциалов в точке О, рассматриваемых как функции |, г\ и t.
Действительно, при выполнении этого условия двумя послед-
последними членами в выражении оператора ? можно пренебречь в
малой окрестности точки О по сравнению с первыми тремя син-
сингулярными членами.
Следует отметить, что в некоторых (например, автомодель-
автомодельных) задачах условие локальной стационарности не выполняется.
2. Установившиеся колебания. Рассмотрим стационарный
волновой процесс в плоскости ху, считая, что зависимость всех
переменных физических величин от времени выражается мно-
множителем ехр(—шО» гДе ** — частота колебания. При этом
S 11] ДИНАМИЧЕСКИЕ ЭФФЕКТЫ 123
уравнения C.188) примут вид
— 0, kW + klw = O, C.191)
Ф (*, у, t) = Ф (л:, у) е-'«", Мр (х, y,t) = V (х, у) е~ш,
w(x, y,t) = W(x, у)е~ш.
Здесь ki и k2 — волновые числа для продольной и попереч-
поперечной волн. Отметим известные соотношения для монохроматиче-
монохроматической волны
C.192)
где Т — период колебания, с — скорость распространения волны,
К — длина волны, k — волновое число.
В соотношения C.189) время не, входит, поэтому они оста-
останутся справедливыми также для соответствующих предэкспо-
ненциальных множителей при искомых функциях.
Пусть в упругом теле имеется трещина-разрез с характер-
характерной длиной /; фронт трещины предполагается неподвижным.
Качественная картина изменения упругого поля в окрестности
трещины в зависимости от частоты будет следующей. При ма-
малых частотах колебаний, пока длина волны велика по сравне-
сравнению с /, упругое поле будет квазистатическим; в частности, за-
зависимость коэффициентов интенсивности напряжений на фрон-
фронте трещины от времени будет выражаться только множителем
ехр(—iat). С увеличением частоты колебаний, когда длина
волны X становится сравнимой с /, упругое поле будет пере-
перестраиваться, а предэкспоненциальны» множители в коэффициен-
коэффициентах интенсивности напряжений будут уже зависеть от со.
Наконец, при больших частотах, когда длина волны X мала
по сравнению с характерной длиной трещины /, вблизи фронта
трещины обосабливается область, характерный линейный раз-
размер которой мал по сравнению с / (своеобразный пограничный
слой). При этом вне этой области решение легко находится
(оно соответствует решениям геометрической оптики), а для
определения краевого эффекта нужно решать сингулярную гра-
граничную задачу для волновых уравнений C.191) на полубеско-
полубесконечном прямолинейном разрезе, свободном от внешних на-
нагрузок.
Существенно подчеркнуть, что при больших частотах, когда
К -С I, коэффициенты интенсивности напряжений на фройте^
трещины вполне определяются характеристиками падающей
волны (угол падения, частота, интенсивность) и коэффициен-
коэффициентом Пуассона; конфигурация тела и трещины не влияет на их
величину. Действительно, при любых частотах, очевидно, рас-
распределение напряжений и деформаций в достаточно малой ок-
окрестности фронта трещины при г <^; % будет квазистатичееким
|24 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
(т. е. определяется формулами C.44) — C.46)), так как вблизи
фронта трещины инерционные члены в уравнениях C.191) пре-
пренебрежимо малы по сравнению со статическими (на самом
фронте волновые потенциалы ограничены, а их вторые произ-
производные по координатам сингулярны). При Я «С / квазистатиче-
квазистатическое упругое поле имеет место в области г <С Я, а на расстоя-
расстояниях г ~ Я поле вполне определено характеристиками падаю-
падающей волны.
Поэтому на основании анализа размерностей нетрудно найти
следующие асимптотические формулы для коэффициентов ин-
интенсивности напряжений (модуль сдвига, очевидно, входит в
решение только через посредство с\ или с2):
при Я < / (или при и > с/1)
Ки = Ли (8. v) тутах ]Г^ е-Ч. (ЗЛ93)
Km = Лш (9. v) тгтах У с Jet е~ш.
Здесь t)i, т)п, Лш — некоторые безразмерные функции коэффи-
коэффициентов Пуассона и направления излучения на бесконечности;
Рис. 20.
х, Тутах и tzmax — наибольшие значения напряжений ау,'хху
и tzn, соответственно, для волны на бесконечности (п — нормаль
к фронту волны).
В пределе при и->оо (т. е. при Я-*0) решение легко стро-
строится для трещин произвольной формы, причем концентрация
напряжений на контуре трещины, согласно C.193), исчезает.
В качестве иллюстрации на рис. 20 построено решение этой
предельной задачи для изолированной прямолинейной трещины
I 111 ДИНАМИЧЕСКИЕ ЭФФЕКТЫ 125
длины 21. Предполагается, что плоская монохроматическая вол-
волна расширения
<ро<—'exp{?[(fe, г)—e>t]), ¦фо==О (|fe| = co/c,) C.194)
излучается из бесконечности на трещину под углом 0, опреде-
определяемым вектором k.
Потенциалы отраженных волн имеют вид:
в области ABB"А"
\Lf J •^^fc' CA.L7 1^1 \**1 > ' / J J VI I I "" ***/ ^11 IJC ^~~ «v Jg> -1Ы У/1
C.195)
в области ABCD
¦ф, — exp ft Г(Л„, г) — ©Ш
LV Ji , C.196)
I I f» I . — f{\ I f b -"' ¦ о о — т- I/ (itfi114 ^— ?** 1
\ rt-n | Ш/ I'nj /vn,, №vj /Vn.. —"" У W /l/q *v v I*
\ | Z [ ' L AX, A ^y • ' л */
В области A'ABB' возмущение отсутствует («тень»); линии
АА\ ВВ', АА", ВВ", AD и ВС представляют собой линии раз-
разрыва потенциалов.
Амплитуды отраженных волн легко находятся из граничных
условий на трещине. Для определения коэффициентов х\\, х\а
и т)ш в асимптотических форму-
формулах C.193) необходимо найти У
решения сингулярных задач о па-
падении монохроматических пло-
плоских волн на полубесконечный
прямолинейный разрез, свобод-
свободный от внешних нагрузок (см.
рис. 21). <»»»)>ш»/»,гт
В случае плоской деформации ч *'
эту задачу изучал Мауэ D1]; в Рис- 21.
случае продольного сдвига реше-
решение этой задачи (точнее, математически эквивалентной ей опти-
оптической задачи о дифракции волны на экране) <>ыло получено
Зоммерфельдом [42].
Как вытекает из предыдущего, решение динамических задач
теории упругости об установившихся колебаниях однородного
изотропного тела со свободным от нагрузок разрезом должно
удовлетворять следующему условию (условию на ребре):
при r-»0 aik = О (r-Ч2), ф~Чг~г3/2. C.196а)
Рассмотрим сингулярную граничную задачу для полубес-
полубесконечного разреза, ограничившись для простоты наиболее
126
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[ГЛ. Ш
важным случаем нормального разрыва:
при у = 0, х < 0 а у = хху = О,
при у = 0, л; > 0 t^ = 0, у = О,
при г->оо Ф0(л;, г/) =
C.197)
1 = 0 (у>0).
Таким образом, монохроматическая волна сжатия (или рас-
растяжения) с максимальным напряжением Отах падает на полу-
полубесконечный разрез вдоль отрицательной полуоси х под углом
6 = я/2 (см. рис. 21).
Введем новый потенциал <Di = Ф — Фо; при этом согласно
условию на бесконечности потенциал Ф] должен стремиться к
нулю при г-*оо.
Решение задачи ищем в виде [41], который легко находится
методом разделения переменных;
ФЛх,у) = - ]~R (Я) A kl - Я2) е1
W (Х, у) = fR (Я) Я Vk\ - Я2 e
\-%2у)
dh (у>0),
C.198)
(у>0).
Здесь #(Я)—неизвестная функция; функция j/&2 — я2 ана"
литична в комплексной плоскости Я с двумя полубесконечными
разрезами вдоль действительной оси (—оо, —k{) и (k\, оо); под-
подразумевается ветвь этой функции, действительная и положи-
положительная при —ki <. Я< ku т. е. положительно мнимая на верх-
верхнем берегу левого разреза и на никнем берегу правого разреза.
Контур интегрирования в C,198) показан на рис. 22.
Будем пользоваться следующими соотношениями, легко по-
получаемыми из C.189) и C.191):
дФ
дх '
C.199)
дхду '
(
2ц ~ дх ду \дх2
(множитель е~т здесь опущен).
,§ и! динамические эффекты 12?
Решение в форме C.198) удовлетворяет дифференциальным
уравнениям C.191) и граничному условию %ху = 0 при у =? 0.
Условия излучения для принятой временной зависимости
ехр(—Ш) также выполняются [43].
Выберем функцию R(K) так, чтобы удовлетворить остав-
оставшимся граничным условиям, нулевому условию на бесконеч-
бесконечности и условию на ребре.
Решение будем строить методом Винера — Хопфа, точнее,
при помощи его модификации, предложенной Джонсом (см.
книгу Нобла [43]).
Согласно формулам C.198) и C.199), находим при у = 0
величины оу и v, соответствующие потенциалам Ф{ и Ч':
где
_оо —оо
(при г/ = 0),
а (л) = я2 V{k] - л2) (kl - я2) + A *? - я2 J,
Отсюда, используя обратное преобразование Фурье, по-
получаем
+°о
А (Я)
В'(Я)
Г ,
1 (О
J v
— oo
+ 00
f (о
y/2\i)y=0 e l x dx = Q
)y^oe-ilxdx=V+(b
!+(Я)
¦)+v
+ Q"
/¦— /л \
\ / *
(Я),
C.201)
где
C.202)
128
СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ
[гл: m
Искомые функции О~(к) и V+(l) аналитичны соответственно
в нижней и верхней полуплоскости комплексного переменного X.
Напомним, что граница, разделяющая эти полуплоскости, про-
проходит так, как показано на рис. 22 (в частности, точки X = О,
Х =—k\ и X = — k2 принадлежат нижней полуплоскости, а
точки X = k\ и X = k2 — верхней полуплоскости).
Оставшиеся неудовлетворенными граничные условия C.197)
при помощи величин (ау)у = о и (и)„ = о, отвечающих потенциа-
потенциалам <X>i и Ч?, запишутся так:
(On \
2ц /j,_0
СТщах
C.203)
(при у = 0, х<0), (при у = 0, х > 0).
Подставляя эти значения в Q+ (X) и V~ (X), находим
i2 '
C.204)
Ири вычислении бралась конечная часть расходящегося ин-
интеграла, как обычно в теории волн [43].
Подставляя найденные функции в соотношения C.201), ис-
исключая из них R(X) и вводя обозначение
*!-*?_
2 —
C.205)
приходим к следующему уравнению Винера — Хопфа:
F (X) V+ (Я) - О" (Я,):
4пцХ
Функции F(X) и
(факторизация):
= /1+(Л)^-(Л),
(l—~) Vkl — X2 F (Я). C.206)
представим в виде произведении
C.207)
Здесь ^(Я) и F~(Я.) — функции, аналитические соответствен-
соответственно в верхней и нижней полуплоскостях Я. Согласно выбору
ветви функции Ykl X2 и контура, разделяющего нижнюю и
верхнюю полуплоскости X (см. рис. 22), Yk2-\-X будет анали-
аналитической функцией в верхней полуплоскости (разрез вдоль
§ il]
ДИЙАМИЧЕСКЙЕ ЭФФЕКТЫ
= 0, —оо <; Я < — k2), а У k2 — Я — аналитической функ-
функцией в нижней полуплоскости (разрез вдоль Im Я = 0, k2 < Я<
Задачу факторизации функции F{X) решил Мауэ [41]; вос-
воспользуемся его результатом
г, г,\2
±Я
2 —
~ { arctg
2 2
rfz
(KR = <a/cR). C.208)
Здесь ся — скорость распространения поверхностных волн Рэлея
(cR < c2); в формуле C.208) берутся только верхние или толь-
только нижние знаки.
С учетом факторизации уравнение Винера — Хопфа C.206)
можно записать так:
l(Tmax
C.209)
f- (Я) v k2 - х
Так как второй член в правой части этого уравнения имеет
полюс при Я = 0, а точка Я = 0, согласно рис. 22, принадлежит
нижней полуплоскости, преобразуем этот член следующим об-
образом:
_
@) Vk2 - F~ (Я) /fe2 - Я,]
4яцЯ/?~ (я; Vk2 — я
"Ттах
@) V^ 4jthXF" (Я) fki-XF' @)
Здесь значение функции F~ (%) в точке Я = 0 равно [44]
f-(Q) = /?+(Q) = . ^^«=.= с'^с' =, (з.2Ц)
Учитывая это преобразование, уравнение Винера^ Хопфа
можно записать в форме
C 212)
F (Я) /ft2 — Я 4яцЯ/?~ (Я) /fta — Я F~ @) |^ '
Левая часть этого уравнения представляет собой функцию,
аналитическую в верхней полуплоскости, а правая часть —
5 Г, П. Черепанов
130 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. Ill
функцию, аналитическую в нижней полуплоскости %. Согласно
принципу непрерывного продолжения, левая и правая части
этого уравнения являются аналитическим продолжением друг
друга. Осталось выяснить поведение определенной таким об-
образом функции, аналитической во всей плоскости Я, в беско-
бесконечно удаленной точке.
Для этого воспользуемся следующим известным соотноше-
соотношением [43].
Если при — 1 < б < 0
U-*oo
то C.213)
A->0
Здесь Q (%) = J a (x) e~Xx dx, Г (б + 1) — гамма-функция. _
о
В этих формулах нужно брать либо верхние, либо нижние
предельные переходы.
Согласно условию на ребре C.196а) и формулам C.123),
единая аналитическая функция, определенная уравнением Ви-
Винера— Хопфа C.211), стремится к нулю на бесконечности. Сле-
Следовательно, по теореме Лиувилля она тождественно равна нулю
во всей плоскости %. Таким образом, получаем
1/+ (J.\ =
OVnax
C.214)
При помощи преобразования Фурье и формул C.204) вос-
восстанавливаем напряжение ау на продолжении разреза и сме-
смещение его берегов о, отвечающие исходной граничной задаче
C.197) и описываемые потенциалами Фи?:
о = — I-
C.215)
Контур интегрирования показан на рис. 22.
IPJ ДИНАМИЧЕСКИЕ ЭФФЕКТЫ 131
Теперь определим коэффициент интенсивности напряжений
Ifi и тем самым коэффициент rji(n/2, v.) в формуле C.193). На-
Ц сначала, используя C.213) и C.208),
~'/2. C.216)
Так как при х-> + 0 ay = Ki/V^nx > то при помощи формул
C.211), C.213) и C.202) отсюда можно окончательно найти
(с учетом опущенного ранее экспоненциального множителя)
?
*! = (!+0 атах^ИЕ1 /ie-. C.217)
Как уже говорилось, эта формула годится не только для по-
полубесконечных разрезов, но также для конечных трещин -при
наличии пограничного слоя, т. е. когда со >¦ с/1 (I — характерная
длина трещин)..
Воспользовавшись решением Зоммерфельда (см. также [43])
и формулой C.213), нетрудно вычислить и коэффициент интен-
интенсивности напряжений для трещины продольного сдвига
Km = V 1 ~ cos 9 тгтах Y*tA + 1) е~Ш- C'218)
В случае трещин-разрезов конечных размеров наиболее
эффективным является метод асимптотических разложений иско-
искомого решения уравнений C.191) по малым и большим волно-
волновым числам. Разложение по малым параметрам kl и k\ при-
приводит к цепочке стандартных граничных задач статической
теории упругости с объемными силами, определяемыми преды-
предыдущим приближением. При больших волновых числах (малый
параметр при старшей производной) вблизи фронта трещины
возникает описанное явление пограничного слоя, где требуется
точный анализ задачи для полубесконечного разреза; вне по-
пограничного слоя решение строится элементарно. Склеивание
асимптотических разложений при малых и больших частотах
позволяет получить эффективное решение для всей области
частот.
3. Ударные нагрузки. Для решения динамических задач
о воздействии произвольных ударных (импульсных) нагрузок
(например, ударных волн) на неподвижные разрезы наиболее
эффективен следующий метод. Ударный импульс a{t), движу-
движущийся в упругом теле, представляет собой, «пакет» монохрома-
132 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ [ГЛ. III
тических волн, которому соответствует комплексная спектраль-
спектральная функция (т(<й):
+°°
а (о) = —у J a (t) еш dt. C.219)
—оо
Ширина спектра Аи и длительность импульса А/ связаны
соотношением неопределенностей, аналогичным принципу Гей-
зенберга в квантовой механике:
Ао • А/ ~ 2я. C.220)
Следовательно, чем более «размазан» импульс a(t), тем бо-
более компактен спектр, и наоборот.
Величина ст(о))^о)/]/2л представляет собой амплитуду моно-
монохроматической волны е~ш в этом «пакете»; она создает коэф-
коэффициент интенсивности напряжений Ki{(o)da>e-iat на фронте
трещины. При этом Ri(u>), отвечающий монохроматической
волне с частотой ©, определяется из решения задачи об уста-
установившихся ^колебаниях, рассмотренной выше. Отсюда, приме-
применяя принцип суперпозиции, находим коэффициент интенсивно-
интенсивности напряжений Ki(t) в вершине трещины при произвольном
динамическом ударе:
Ki(t) = f7L- Г &Ие-'*<*©. C.221)
— оо
Таким образом, распределение'напряжений и деформаций в
достаточно малой окрестности конца неподвижного разреза в
упругом теле будет всегда статическим, т. е. в любой динами-
динамической задаче также будет иметь вид C.44) — C.46).
Рассмотрим, например, задачу о воздействии произвольных
ударных нагрузок на полубесконечную трещину нормального
разрыва, расположенную вдоль у = 0, х < 0, используя при
этом полученное выше точное решение этой задачи в случае
установившихся колебаний с произвольной частотой и. Огра-
Ограничимся лишь выражением для коэффициента интенсивности
напряжений, представляющим наибольший интерес для меха-
механики разрушения; формулы для напряжений и смещений в уп-
упругом пространстве опустим. При помощи C.217) получаем
-1-ОО
-1-ОО
~^=^- f /-5-а>)в-'«>. C.222)
—оо
Здесь функция ду(а>) определяется через заданный импульс
ov(t) посредством формулы C.219).
* 111
ДИНАМИЧЕСКИЕ ЭФФЕКТЫ
133
Рассмотрим некоторые частные случаи общей формулы
C.222).
Пусть импульс напряжений o(t) имеет прямоугольную
форму:
ау @ = О ПРИ t < О и при t > Т,
оу @ = <т0 ПРИ 0<t<T
@0 и Т постоянны). Спектральная функция этого импульса
имеет вид
?шт _ i)# C.224)
Подставляя это значение в формулу C.222) и вычисляя интег-
интеграл, находим в этом случае
Ki(t) =
Ж=ЦRe(VT- \П=
C.225)
Следовательно, при t <; Г коэффициент интенсивности на-
напряжений прямо пропорционален Yt, а при t > Т прямо про
порционален \/t —Yt—Т. Напомним, что коэффициент Kj(t)
в физических задачах действителен, а в силу предполагаемой
Рис. 23.
симметрии для трещин нормального разрыва ударные импульсы
должны симметрично сходиться к оси х. График функции
(Y — Vt— Т) изображен на рис. 23.
Наиболее интересны следующие предельные частные случаи
этой задачи.
а) Бесконечно длинный импульс. При этом Г—>оо и для К\
получается формула
C.226)
134 СИНГУЛЯРНЫЕ ЗАДАЧИ ТЕОРИИ УПРУГОСТИ 1ГЛ. Ш
Этот случай физически соответствует мгновенному образо-
образованию полубесконечного разреза в бесконечной упругой плос-
плоскости, подвергнутой однородному растяжению напряжением о0.
Непосредственное решение этой автомодельной динамической
задачи теории упругости D4] оказывается достаточно утоми-
утомительным.
б) Мгновенный импульс. При этом Т—>0, так что oqT-*P,
где Р — величина суммарного импульса, и тогда
Это соотношение справедливо также для произвольного им-
импульса при больших временах t >• At, где /it — продолжитель-
продолжительность импульса.
Из предыдущего изложения вытекает, что трещины, присут-
присутствующие в упругом теле, «срезают» частоты <а^ С\\1 (/ — ха-
характерная длина трещин). Трещина длины / полностью отра-
отражает колебания с частотой й> cjl (см. рис. 20), являясь для
них своеобразным «зеркалом». Трещиноватое упругое тело, та-
таким образом, непроницаемо для звуковых частот w ^ Ci/l; поэ-
поэтому оно модулирует ударные импульсы, «срезая» высокоча-
высокочастотную часть их спектра. В силу соотношения неопределенно-
неопределенностей наибольшей модуляции подвергаются короткие импульсы
с крутыми фронтами. При прохождении через трещиноватое
тело форма импульса сглаживается и округляется.
Эти свойства трещин-полостей и трещиноватых тел могут
представлять интерес, например, для следующих приложений:
а) обнаружение внутренних дефектов типа трещин в напря-
напряженных конструкциях посредством звукового облучения высо-
высокой частоты, * '
б) создание искусственных полостей-«зеркал» в горном мас-
массиве в целях облегчения сейсморазведки,
в) определение средней трещиноватости горных пород,
г) защита сооружений от взрывов путем создания искус-
искусственных трещинообразных полостей и т. д.
Замечание к главе III. Методы решения конкретных
задач для полубесконечных разрезов, рассмотренные в §§ 5—7,
позволяют получить эффективное решение этих задач также для
случая произвольного числа разрезов, расположенных вдоль
одной и той же прямой.
t Л А Ъ А IV
ОСНОВНЫЕ ПОЛОЖЕНИЯ МЕХАНИКИ
ХРУПКОГО РАЗРУШЕНИЯ
§ 1. Критерий локального разрушения
В этой главе рассматриваются основные методы механики
хрупкого разрушения (общефункциональный и энергетический),
Криволинейные трещины, структура края квазихрупкой тре-
трещины, указываются основные эффекты явления разрушения, вы-
выходящие за рамки классической теории, и приводятся различ-
различные оценки физических характеристик прочности.
Рассмотрим трещину произвольной формы в однородном и
изотропном хрупком теле, подвергнутом растяжению. Предпо-
Предположим, что при определенной внешней нагрузке в бесконечно
малой окрестности некоторой точки О контура трещины произо-
произошло местное разрушение, в результате которого контур тре*
щины переместился в новое положение. Встает вопрос о том,
как сформулировать критерий локального разрушения.
Напряжения, деформации и смещения вблизи точки О до
разрушения описывались формулами C.44) — C.46), в которые
входят в качестве параметров коэффициенты интенсивности на-
напряжений Къ Кп, Km- Задание этих параметров полностью
определяет напряженно-деформированное состояние вблизи
точки О. Поэтому простейшее предположение о локальном раз-
разрушении состоит {45] в том, что начало-разрушения определяется
только этими параметрами, т. е. существует замкнутая поверх-
поверхность
f(Ku Кп, Кт) = 0, D.1)
охватывающая начало координат, такая, что, как только конец
вектора {Ki, Кп,,Кт) попадает на эту поверхность, в соответ-
соответствующей точке О контура трещины происходит локальное раз-
разрушение. Если конец вектора находится внутри области, огра-
ограниченной поверхностью D.1), то разрушения не происходит, а
положение конца вектора вне этой области считается невозмож-
невозможным. Из простых соображений очевидно, что любой луч, исходя-
исходящий из начала координат, может пересекать поверхность D.1)
только в одной точке.
Физически реализуется случай Ki 5& 0. так как при Ki < 0
вследствие налегания противоположных берегов трещины
136 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. tV
происходит перераспределение напряжений вблизи контура тре-
трещины*).
Указанное предположение в рамках идеально-упругого тела
тривиально, поскольку состояния вблизи любых двух точек кон-
контура трещины в таком теле при одном и том же векторе
{#ъ Кп, Km} совершенно не различимы, если тело однородно и
изотропно, и не зависят ни от времени, ни от предшествующего
роста трещины.
В дальнейшем под однородными и изотропными телами бу-
будут подразумеваться такие тела, у которых не только упругие,
но и прочностные свойства однородны и изотропны. Более стро-
строго, тело однородно, если поверхность D.1) не зависит от поло-
положения в теле точки О контура трещины; тело изотропно в дан-
данной точке О контура трещины, если поверхность D.1) не зави-
зависит от ориентации плоскости трещины в этой точке.
Поэтому можно говорить о телах, которые неоднородны и
анизотропны по прочности (в указанном смысле), но одно-
однородны и изотропны по своим упругим свойствам. Этот случай
реализуется на практике весьма часто в клеевых соединениях,
в образцах и заготовках из металлов и сплавов, где всегда ма-
материал в большей или меньшей степени анизотропен и неодно-
неоднороден по прочности вследствие предшествующих технологиче-
технологических процессов (например, проката, термообработки и т. п.).
Для произвольных неоднородных по прочности тел функция
D.1) будет зависеть также от трех координат точки О; для
произвольных анизотропных по прочности тел в функцию D.1)
войдут еще два аргумента, определяющие ориентацию вектора
нормали к плоскости трещины в точке О. Таким образом, в са-
самом общем случае неоднородного и анизотропного по прочно-
прочности хрупкого тела в функцию D.1) будут входить еще пять
независимых переменных. В случае плоской задачи число до-
дополнительных аргументов снижается до трех, а если тело одно-
однородно— до одного.
Для общего случая неоднородного и анизотропного по проч-
прочности идеально-упругого тела физическое допущение, содержа-
содержащееся в закономерности D.1), состоит лишь в том, что процесс
локального разрушения считается не зависящим от предысто-
предыстории развития трещины.
Функцию f(Ki,Kii,Km) можно определить из эксперимен-
экспериментальных данных или из дополнительных физических соображе-
соображений. Для трещин основных типов критерий локального разру-
разрушения D.1) принимает следующий вид:
нормальный разрыв
Ki"BtKiCt Kn = Km — 0> D.2)
*) Для полостей физический смысл имеет также случай Кг < О,
s I]
КРИТЕРИЙ ЛОКАЛЬНОГО РАЗРУШЕНИЯ
137
поперечный сдвиг
Кп = Кп
Ki = Km = 0;
продольный сдвиг
Km = Km с> Ki = Кп = 0.
D.3)
D.4)
Здесь Kic, Kiic, Ктс — некоторые постоянные материала. Ве-
Величина Kic называется вязкостью разрушения.
Наибольшую важность для механики разрушения представ-
представляет изучение трещин нормального разрыва. В этом случае, со-
согласно критерию локального разрушения D.2), на той части
контура трещины, где происходит локальное разрушение и тем
самым продвижение трещины, коэффициент интенсивности на-
напряжений постоянен и равен Kic, а на неподвижной части кон-
контура трещины он меньше Kic-
Это условие играет роль дополнительного граничного усло-
условия на контуре трещины нормального разрыва в хрупком теле.
Оно позволяет замкнуть постановку задачи о. развитии таких
трещин в упругом теле, если из каких-либо соображений зара-
заранее известно направление распространения трещины. Например,
если задача обладает симметрией относительно некоторой пло-
плоскости (т. е. тело и внешние нагрузки симметричны относитель-
относительно этой плоскости, а начальная трещина — плоская и ее пло-
плоскость совпадает с плоскостью симметрии), то естественно до-
допустить, что плоскость симметрии останется таковой и в процессе
развития трещины, так что трещина останется плоской. Это до-
допущение оправдывается в теории криволинейных трещин нор-
нормального разрыва; в боль-
шинстве случаев оно под-
подтверждается на опыте, хотя
есть и исключения, объяс-
объясняющиеся различными усло-
усложняющими факторами (в
основном, влиянием пла-
пластичности и инерционными
эффектами).
Рассмотрим некоторые
конкретные задачи.
Пусть прямолинейная изолированная трещина у = 0, а <
< х < Ь в бесконечной упругой плоскости подвергается воздей-
воздействию нагрузок
Рис. 24.
¦Р(х),
, = о,
D.5)
приложенных к ее берегам симметрично относительно оси х
(рис. 24). Напряжения на бесконечности предполагаются нуле-
нулевыми. Задача считается плоской.
J38 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
При помощи основных представлений C.9) и условия сим-
симметрии задачи относительно оси х находим
при # = 0, a<x<b, Q(z) = 0, ЯеФ(г)*=±р{х), D.6)
при z->oo Ф(г) = оA), Q(z) = o(l). D.7)
Согласно условиям C.43), функция Ф(г) на концах разреза
имеет особенность порядка z~1/2
Решение задачи Дирихле D.7) для разреза (а, Ь) оси х
в этом классе функций находится по формулам Келдыша — Се-
Седова [46-47]:
/
Q(z) = O, Ф(г) = - г - . =¦
2я/]^(z — a) (z — 6) J * —z
Здесь при z-> оо
Корень под знаком интеграла представляет собой значение вет-
ветви соответствующей аналитической функции, выделяемой усло-
условием D.9), на верхнем берегу разреза.
Используя решение D.8), D.6) и формулы C.43), нетрудно
найти коэффициенты интенсивности напряжений:
в точке х = а
ь
= ^-ff—г f p W Yt=1 dx' ^n^Km = 0; D.10)
У л (Ь — a) J г х — а
в точке х — Ь
= *»1=0- DЛ1)
Сделаем одно замечание. Используя принцип линейной су-
суперпозиции, нетрудно рассмотреть также случай, когда напря-
напряжения ох и оу на бесконечности не обращаются в нуль. В дан-
данном случае этот принцип гласит: напряженное состояние в за-
задаче о трещине с ненулевыми напряжениями на бесконечности.
ох—в%(х, у), оу=о™(х, у), ^=0 является суперпозицией двух
напряженных состояний, одно из которых отвечает напряже-
напряжениям на бесконечности для пространства без трещины,
т. е. ох=о™(х, у), оу—о™(х, у), *ху=0, а другое — напряжениям
в только что рассмотренной задаче с нулевым напряженным
состоянием на бесконечности и нагрузкой
ау = Р М ~ °Г (*. °)' х*у = ° D.12)
S ij Критерий локального разрушения 139
на берегах трещины. Коэффициенты интенсивности напряжений
в исходной задаче, очевидно, соответствуют второму напряжен-
напряженному состоянию.
Разберем простейшие примеры.
а) Задача Гриффитса (см. рис. 2). В этом случае в форму-
формулах D.8) — D.11) надо положить
a = ~l, b = l, р (я) = р = const, D.13)
где 21 — длина трещины, р — величина растягивающего напря-
напряжения ау на бесконечности.
Величина другого главного напряжения (ах) на бесконечно-
бесконечности не входит в р{х), поэтому на развитие хрупкой трещины
в этом случае оказывает влияние только та нагрузка, которая
перпендикулярна к плоскости трещины.
По формулам D.10) — D.13) находим
Ki = pV^l, /Сп = /Сш = 0. D.14)
Используя критерий локального разрушения для трещин
нормального разрыва D.2), находим зависимость разрушаю-
разрушающей нагрузки р от длины I:
p^KijVrt. DЛ5)
Таким образом, при увеличении нагрузки трещина вначале
стоит, до тех пор пока не будет достигнуто критическое значе-
чение ру после чего трещина начинает расти (см. рис. 3). Как
видно, величина нагрузки р уменьшается с ростом размера тре-
трещины I; из элементарных соображений*) следует вывод о не-
неустойчивости равновесия трещины в этом случае.
Формула D.15) совпадает с полученным ранее результатом
Гриффитса AЛ1), если положить Kic—^i YnEy для плоского
напряженного состояния. Отметим, что формулу D.15) легко
получить также из соображений анализа размерностей (с точ-
точностью до численного множителя).
" По формулам D.8) и C.44) нетрудно определить потенциал
Ф{г) и форму трещины при р(х) = р = const:
D.16)
= 0, \х\<1 v =
при j/ = 0, \x\>l oy=
*) Строгая теория устойчивости, основанная на общей закономерности
A.10), излагается в § 4 для произвольных хрупких трещин.
140 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ (ГЛ. IV
Следовательно, трещина Гриффитса имеет форму сплюсну-
сплюснутого эллипса.
б) Задача о сосредоточенной силе (рис. 25). Пусть к проти-
противоположным берегам трещины в точке х = с приложены две
равные и противоположно направленные сосредоточенные силы
Р, расширяющие начальную трещину. В этом случае
р(х) = -Рд(х-с), , D.18)
где Ь{х — с) — дельта-функция Дирака. По формулам D.8) —
D.11) находим
ф(г)== РУ(с--а)(Ь-с)
v ' 2п(с-г)Уг(г-а)(г~Ь) ) '
в точке х = а
4p/A^ 0; D.20)
у n{b — а) ' с — а
в точке х= Ь
Ь — с
D.21)
Допустим вначале, что размеры начальной трещины удов-
удовлетворяют условию &о + ао < 2с. В этом случае предельное
значение коэффициента интенсивности напряжений, равное Ки,
при увеличении Р достигается впервые в точке х = bo при зна-
значении силы Р = Р., определяемом из уравнения D.21):
D.22)
Поэтому трещина начинает развиваться своим правым кон-
концом х = Ь, а левый конец остается неподвижным (см. рис. 25).
При значении силы Р = Р**, где
P» = KicVn(c-ctQ), D.23)
предельное значение коэффициента интенсивности напряжений
достигается т'акже в точке х = а^, в этот момент правый конец
трещины находится в точке
Ь = 2с — ай. D.24)
При дальнейшем увеличении силы Р оба конца трещины
симметрично растут, причем
i D.25)
где 21 — длина трещины.
Случай Ьо + по ^ 2с рассматривается аналогично.
КРИТЕРИЙ ЛОКАЛЬНОГО РАЗРУШЕНИЯ
141
В этой задаче росту трещины отвечает увеличение силы Р\
это свидетельствует об устойчивом квазистатическом разви-
развитии трещины.
в) Комбинация сосредоточенной силы и растяжения на бес-
бесконечности (рис. 26). Пусть в центре трещины длины 21
действуют равные и противеположно направленные силы Р,
\
Р**
о-ао 0 bo-c 2c-an
-I
\
Р1
Рис. 25
иг
Р
Рис. 26.
которые стремятся сомкнуть трещину, а на бесконечности
приложены постоянные разрывающие нагрузки р, как в задаче
Гриффитса.
Комбинируя формулы D.16) и D.19), D.14) и D.25), со-
согласно принципу линейной суперпозиции получаем в этом
случае:
Ф(г) = *L-(l—g-).
Согласно D.26) и D.2) величина разрывающей нагрузки р*
равна
f--4-- D.27)
Развитие трещины неустойчиво, как и в задаче Гриффитса.
Пусть, например, сила Р, подкрепляющая трещину, осущест-
осуществляется посредством сварного шва или приклепанного стрин-
стрингера, поперечное сечение которого равно S, а прочность на
142
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
разрыв — йь. При этом будет иметь место неравенство Р ^ сть5;
знак равенства соответствует разрушению стрингера. Подста-
Подставив в D.27). Р = ObS, в этом случае можно найти предельную
нагрузку, не решая сложной задачи о предшествующем про-
процессе деформирования стрингера.
Рассмотрим еще один интересный частный случай, содержа-
содержащийся в D.26). Пусть нагрузка р будет сжимающей, а сила
II
1
t
р
р
ч
И!
р
Рис. 27.
Р — разрывающей (рис. 27). В этом случае с увеличением Р
трещина развивается устойчиво, причем
р=яр/ + Ки V^i ¦ D-28)
Если прочность материала пренебрежимо мала по сравне-
сравнению с действующими на тело нагрузками, точнее, ¦ если
Ки ^ Р V^l то из D.28) получается зависимость
P — npl, D.29)
которая соответствует контактной задаче о сжатии двух упру-
упругих полупространств (сжатию противодействуют сосредоточен-
сосредоточенные силы).
г) Изгиб на бесконечности (рис. 28). Пусть издали от трещи-
трещины, поверхность которой свободна от нагрузок, действуют на-
напряжения
. ох = хху = 0, D.30)
§ 1]
КРИТЕРИИ ЛОКАЛЬНОГО РАЗРУШЕНИЯ
143
возникшие, например, от чистого изгиба моментом М полосы
шириной 2h, причем начальная трещина мала сравнительно с
шириной полосы, т. е. Ь — a <g. h.
По формулам D.10) и D.11), используя принцип суперпози-
суперпозиции, находим
в точке х = Ъ
зУп л л
= ;=г М
^2
D.31)
в точке х= а
_ -ь* — 2аЪ
A3 Vb - a
Км = Кщ = 0.
Разрушение начинается с правого конца начальной трещины
при х = Ь; медленное развитие трещины неустойчиво, как в за-
задаче Гриффитса.
д) Влияние1 прочностной неоднородности- Допустим, что в
задаче Гриффитса при росте трещины вязкость разрушения Ки
меняется от точки к точке, т. е.
Kic = Kic(l)- Наглядно это можно
представить себе как случай неод-
неоднородного по прочности клея, соеди-
соединяющего два одинаковых упругих
полупространства. Пусть, например,
функция Kic(l) монотонно возрас-
возрастает: при малых / — прямо пропор-
пропорционально /, а при достаточно боль-
тих / достигает некоторой постоян— р*
ной насыщения.
Соответствующая зависимость
«нагрузка — длина трещины», кото-
которая определяется по формуле D.15),
изображена на рис. 29. Как видно, о
в этом случае трещина растет ус-
устойчиво при 0 < / <С /*, а с мо-
момента- достижения наибольшей
нагрузки р=р* начинается неустойчивый рост трещины, причем
Рис. 29.
/.)
D.32)
Существенно подчеркнуть, что в этом случае разрушающая
нагрузка рч не зависит от размера начальной трещины U (если
U <¦ '•)'. разрушение происходят, даже если начальной трещины
нет вовсе. . '
Рассмотренная задача может служить моделью, дающей
объяснение одному из возможных механизмов образования
144 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
начальных трещин в процессе нагружения. Этот механизм, по-ви-
по-видимому, имеет место в металлах и сплавах при возникновении и
развитии внутризеренных трещин, когда макропластические
процессы не развиты, и следовательно, вязкость разрушения
существенно меньше, чем для макротрещин (размер которых
велик по сравнению с величиной зерна).
§ 2. Энергетический метод
Пусть в упругом однородном и изотропном теле имеется
хрупкая трещина; форма тела и трещины совершенно произ-
произвольны. Предположим, что локальное разрушение в процессе
развития трещины всегда происходит в плоскости, касающейся
поверхности трещины в точке разрушения, так что результирую-
результирующая поверхность трещины не имеет угловых линий и точек.
В этом случае некоторое обобщение метода Гриффитса позво-
позволяет определить функцию f(Ki,Kn,Km), фигурирующую в об-
общем критерии локального разрушения D.1).
Запишем закон сохранения энергии для упругого тела с тре-
трещинами
J ,da=U—TS + 2Y1 D.33)
Здесь вц и «г — составляющие тензора напряжений и вектора
смещения на поверхности тела Б (включая трещины), U —
внутренняя энергия тела, Я; —компоненты внешней нормали
к поверхности Б, у~~повеРхностная энергия, приходящаяся на
единицу свободной поверхности тела, Т и S — температура и
энтропия тела соответственно. Точка над буквой означает про-
производную по времени.
Закономерность D.33) нужно дополнить еще условием не-
необратимости роста трещины
S>0. D.34)
Существенно, что условие D.34) должно выполняться также
для любой части рассматриваемого тела. При этом, естественно,
не учитывается изменение поверхности, обусловленное малыми
деформациями тела.
По теореме Остроградскбго — Гаусса и вследствие уравне-
уравнений равновесия имеем
J or,/«i«/rf(T=J (ei,ui)l,tdv=j oitBittdv,eil~=j(uttl^-uht), D.35)
2 V ,V
где V — объём, занятый телом,
S 2] ЭНЕРГЕТИЧЕСКИЙ МЕТОД 145
Поэтому уравнение D.33) можно записать также в виде
J (ачё{, — Uа — TS0) dv = 2уЁ D.36)
(u=j.Uodv, TS=JTSodv\.
\ v v )
Здесь Uo и So — объемная плотность внутренней энергии и
энтропии соответственно.
Отсюда вытекают обычные уравнения теории упругости
.. =|-г— {rn=Un — ТЬп) D.37)
ае. / \ уе., /
2=const 2=const
и обобщенное условие Гриффитса
дН_\ _
12 As<f=const
S0const
u~const
где
H = U— J aijUitijda, F=U—TS, G = U — TS—
Уравнения D.37) и D.38) вместе с условием необратимости
D.34) представляют собой наиболее общую замкнутую форму-
формулировку задач о распространении трещин в упругих телах. Эта
формулировка годится для произвольных неоднородных анизо-
анизотропных тел, в том числе нелинейно-упругих; поверхность тре-
трещины может быть произвольно криволинейной и может иметь,
например, угловые линии.
Изучение локального поля напряжений и деформаций
вблизи контура трещины во всех этих случаях принципиально
позволяет при помощи D.38) и сингулярного решения найти
связь между y и предельными комбинациями из коэффициентов
интенсивности, фигурирующих в сингулярном решении. Найдем
эту связь в частном случае линейно-упругого однородного и
изотропного (по упругим свойствам) тела, считая поверхность
растущей трещины всегда гладкой.
Применяя «принцип микроскопа», приходим к уже рассмат-
рассматривавшейся сингулярной задаче для полубесконечного разреза
(см. рис. 13). Считая процесс адиабатическим, используем пер-
первую формулу D.38) и сингулярное решение C.44).
146
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV_
Пусть вначале К\ ф О, Ки = Km = 0. При этом напряжение
Оу вблизи рассматриваемой точки О контура трещины на ее
продолжении равно
Oy*=KilV*u (хху = хгу = 0), D.39)
а упругие смещения v берегов трещины вблизи ее конца, опре-
определяющие форму трещины вблизи точки Q, таковы:
i>=±2(l — v)/Ci
D.40
AL
Рис. 30
Процесс распространения конца трещины из положения О
в положение О\, находящееся на расстоянии А/ от точки О
(рис. 30), можно представить
себе так *). В тот момент, когда
конец трещины находится в точ-
точке О, сделаем мысленный раз-
разрез вдоль ОО\ и приложим к про-
противоположным берегам разреза
ОО\ равные и противоположно
*?¦ (направленные нагрузки K\J V2nx,
дающие такие же напряжения,
которые имеют место в нераз-
неразрезанном теле в момент ло-
локального разрушения. Затем будем монотонно уменьшать эту
нагрузку до нуля. В результате снятия нагрузки берега разреза
ОО\ будут расходиться, и в тот момент, когда нагрузка ста-
станет равной нулю, смещения берегов достигнут наибольшей
величины, очевидно, равной ±2A—v) К\с V&l — xf(Y2n\i).
Изменение внутренней энергии Д?/ рассматриваемой полу-
полубесконечной области за счет представляемого таким образом
возрастания длины трещины на А/, при 5 = const и щ =.const
(щ — в данном случае смещения на бесконечности), легко оп-
определить по формуле D.33), используя теорему Клапейрона.
Находим:
м
Д?/
=— ^~К\ J
о
при и, = const. D.41)
Вычисляем интеграл в D.41), переходим к пределу при
Д/-+0 и используем первую формулу D.38). В результате по-
получим, считая, что U относится к единице длины вдоль оси z:
— V
¦2Y)/ = 0.
D.42)
*) Этот прием впервые применил Ирвин в 1957 г. [1Z].
§•21 . ЭНЕРГЕТИЧЕСКИЙ МЕТОД , 14?
Отсюда вытекает, что для неподвижной трещины (/ = 0)
выражение в квадратной скобке, вообще говоря, отлично от
нуля, а для растущей трещины (/ > 0) выражение в квадрат-
квадратной скобке должно обращаться в нуль.
Окончательно получаем:
Y == /Сic A — v2)/B?) (плоская деформация). D.43)
Точно такой же расчет в случае плоского напряженного со-
состояния приводит к следующей формуле:
у = К.ЫBЕ) (плоское напряженное состояние).
В общем случае Ki ф 0, Кп Ф 0, /Cm Ф 0, применяя анало-
аналогичные рассуждения, вместо D.41) нетрудно получить следую-
следующее уравнение:
м
= — J
о
Здесь напряжения ау, хху, тгу берутся из сингулярного ре-
решения C.44) — C.46) при 0 = 0, г = х\ смещения и, v, w отве-
отвечают смещениям кончика трещины, взятым из того же решения
при 0 = я, г = А/ — х.
При помощи условия Гриффитса D.38) отсюда получаем
такой локальный критерий разрушения:
f (Кь /Си, Km) = 4hy - A - v) (/Ci + /Cri) - Km = 0. D.45)
Совершенно аналогичный результат можно получить, рас-
рассматривая другие процессы, например, при Т = const, ы* = const
или при 5 = const, Oijtij = const. При этом отличие будет со-
состоять лишь в том, что упругие постоянные* ц и v должны со-
соответствовать этим процессам. Из опыта известно, что длЪ
большинства- упругих тел различие между адиабатическими и
изотермическими константами упругости очень мало, так что в
большинстве случаев им можно пренебречь.
Таким образом, в случае трещин основных типов (нормаль-
(нормальный разрыв, поперечный сдвиг, продольный сдвиг) между соот-
соответствующими константами Kic, Kiic, Кшс и поверхностной энер-
энергией у существует прямая зависимость; поэтому энергетический
метод в этом случае не дает ничего принципиально нового по
уравнению с простым общим подходом, изложенным в преды-
предыдущем параграфе.
148 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
Для трещин произвольного типа с гладкой поверхностью
предположение о постоянстве у позволяет, найти [*8] критерий
локального разрушения D.45) и тем самым замкнуть поста-
постановку соответствующего класса задач линейной механики раз-
разрушения. Этим же методом можно получить аналогичные кри-
критерии для случая анизотропных и кусочно-однородных, а также
нелинейно-упругих тел.
Приведем некоторые из полученных таким образом резуль-
результатов:
анизотропное тело C.85) с девятью отличными от нуля кон-
константами [35] аи, ai2, аи, a22, а2з, «зз, «44, а55, ai5:
(Hi и ц2— корни уравнения C.103));
ортотропное тело, когда три из указанных девяти констант
обращаются в нуль: а\г = а2ъ = «45 = 0 [35]:
4Y =
+ Ки Van Ba22 + 2a12 + a33) +
трещина на границе раздела двух различных изотропных
упругих сред: v
(обозначения здесь в точности такие же, как в формулах
C.124)).
Однако практическое значение этих результатов, по-види-
по-видимому, невелико. Это объясняется следующими двумя обстоя-
обстоятельствами:
а) трещины смешанных типов в неоднородных или анизо-
анизотропных телах чаще распространяются неплоско, с образова-
образованием угловых линий на своей поверхности;
б) когда трещина смешанного типа распространяется без
образования угловых линий (это имеет место в тех случаях,
когда развитие трещины происходит по заранее известной из
конструктивных соображений гладкой поверхности, например,
в клеевых соединениях), пользование критерием типа D.45)
без дополнительных экспериментальных данных представляется
|3) ОБОБЩЕННЫЙ НОРМАЛЬНЫЙ РАЗРЫВ 149
неразумным, так как величина у, вообще говоря, зависит от
отношений Ki/Kn, Ki/Km- Действительно, из опыта известно,
что для большинства хрупких и квазихрупких тел величина у
при нормальном разрывэ существенно меньше, чем при сдвиге.
§ 3. Обобщенный нормальный разрыв
Гораздо больший практический интерес представляют тре-
трещины обобщенного нормального разрыва.
Вначале заметим, что величины
[Vu] D.46)
г->0
(оц — напряжения вблизи точки О контура трещины, г — рас-
расстояние от точки О) представляют собой компоненты симмет-
симметричного тензора интенсивности напряжений, зависящего от 0.
Согласно свойствам симметричных" тензоров, существуют три
взаимно перпендикулярных направления |, ц и ?, таких, что
Кн = Кя = Кг& = 0. D.47)
На каждой из площадок, перпендикулярных к одному из
главных направлений, действует только нормальное напряже-
напряжение, а касательные напряжения обращаются в нуль.
Естественно было бы считать, что локальное разрушение
происходит в тот момент, когда в условии
тах(Кц,Кт,К&ХКгс D.48)
впервые будет достигнут знак равенства, а само разрушение
имеет место вдоль площадки, перпендикулярной к главному на-
направлению, отвечающему наибольшей из величин Кц, /Cw K&.
Однако эта площадка обычно не лежит в плоскости трещины,
поэтому условие D.48) не годится для определения магистраль-
магистрального направления развития трещины.
В опытах наиболее часто имеет место другой тип локального
разрушения, который будем называть обобщенным нормальным
разрывом; более подробно рассмотрим его для - того случая,
когда Кш = 0. При этом напряжение ав в малой окрестности
некоторой точки О контура трещины ведет себя так:
D.49)
где /Се(9) — некоторая функция полярного угла. Развитие тре-
трещины происходит по направлению, определяемому углом 0 = 0».
Величина 0» является корнем уравнения
. D.50)
ISO йсновы меХАнИки хрупкого разрушений [гл. iv
где /CicF)—вязкость разрушения. Для изотропных по прочно-
прочности тел Kic не зависит от угла 8, а для'однородных по прочности
тел /Cie не зависит также от положения точки О в теле. Локаль-
Локальное разрушение происходит в тот момент, когда в условии
Кв(ВХКи(в) - D-51)
впервые будет достигнут знак равенства.
Обобщенный нормальный разрыв реализуется в большинстве
хрупких и квазихрупких тел. У кусочно-однородных тел и в не-
некоторых других случаях порядок особенности, вообще говоря,
будет уже отличен от 1/2; соответствующее определение поня-
понятия обобщенного нормального разрыва на этот случай не вы-
вызывает затруднений.
Аналогично можно определить обобщенный сдвиг как та-
такой тип локального разрушения на контуре трещины, который
удовлетворяет критерию
г->о
где К.в — некоторая постоянная. При этом разрушение происхо-
происходит на площадке, ориентированной под углом 8, к плоскости
трещины. Такие трещины можно назвать трещинами обобщен-
обобщенного сдвига.
В случае статических плоских трещин в однородных и изо-
изотропных телах, когда Кп — Km = 0. наибольшее значение
Кв(8), согласно C.44), достигается при 8 = 0, а условие D.51)
совпадает с критерием локального „разрушения D.2) для тре-
трещин нормального разрыва; поэтому обобщенный нормальный
разрыв совпадает с обычным нормальным разрывом.
Рассмотрим произвольные криволинейные трещины обоб-
обобщенного нормального разрыва в однородных и изотропных
телах.
В этом случае постоянная Kie не будет зависеть от 8, а функ-
функция /Се(8) будет дифференцируемой. Поэтому условия D.50)
и D.51) можно записать так (Б0]:
. D.52)
Дополнительное условие в точке излома поверхности трещи-
трещины. Пусть вследствие несимметрии, исходной задачи в окрестно-
окрестности некоторой точки О контура трещины возникло напряжен-
напряженное состояние, характеризуемое коэффициентами интенсивности
напряжений Ki и Ки (Дш = 0). Согласно C.44) и C.45), на-
напряжение се определяется формулой ^
Г 1 ¦ 3 ~\
аа = —L= Re |3 (Ki - iKu) e"? "" + (Ki + ЗВД e? "J. D.53)
4 у ZJtr
S3]
ОБОБЩЕННЫЙ НОРМАЛЬНЫЙ РАЗРЫВ
161
Максимальное значение ое достигается по направлению
8 = 8», которое определяется из условия 09F,) = 0, приводя-
приводящего к следующему уравнению:
in -^ + sin-|-) + Кп (Зсоз-^ + cos f-) = 0. D.54)
Решение этого уравнения, удовлетворяющее условию 9* = О
при К = О, можно привести к виду
8. = 2 arctg [A - Vi+ 8А2)/DА)] (А = KxxIKi). D.55)
Зависимость 8. = 8*(Х) представлена на рис. 31.
о
-0,2
>-0,6
-1,0
Ж OJL
\
Рис. 31.
О 0,2 Cfi ' W
Рис. 32.
Подставляя угол 8* из D.55) в выражение D.53) и исполь-
используя второе условие D.52), можно найти критерий локального
разрушения в следующем виде:
где
D.56)
Ш-4/2А3-
При 1~>оо /0(А,) = 2А//3, 8, = —69°, 2/Си=
График функции fo(^) изображен на рнс. 32.
Рассмотрим конкретную задачу.
Пусть бесконечная упругая плоскость разрезана вдоль от-
отрезка (—/, -\4) оси х; к верхнему и нижнему берегам разреза
152
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. JV
приложены нагрузки <т+, т+ и а~, х~ соответственно. На бес-
бесконечности действуют главные напряжения JVi и А/2, причем
ось, соответствующая Nu составляет угол а с осью Ох. При
помощи представлений C.9) эта граничная задача сводится
к задаче Дирихле во внешности разреза для функций Ф(г)
и Q(z).
Решение ее имеет вид [23]
Ф(г) =
1 Г ЧоМ
Здесь
D.57)
+1 . +1
^l2 J t — z 2ni J /_
+
|
- (Nt - N2) e*«] -
. D-58)
^bu j
= T К ~ <V) - T (T^ ~ T^)'
D.59)
— I2 = z -j- О (z~x) при г-*оо,
/|/г2 —/2| при Imz = 0, —/<Re2</,
(X, Y) — главный вектор нагрузок, приложенных к разрезу.
Разлагая решение D.57), D.58) в ряд вблизи концов раз-
разреза и используя асимптотические формулы C.43), находим
коэффициенты интенсивности напряжений;
S3]
ОБОБЩЕННЫЙ НОРМАЛЬНЫЙ РАЗРЫВ
153
при х
К\ — i
-(Ni - N2)e**] - -pL J pQ (t) ^TTt
при x =
dt
±±JL\, D.60)
-iNi- M2) e^] - pL
j
При х= ± I находим
= р sin a • cos a Y~nl. D.63)
Используя критерий D.56) и формулы D.60), D.61), не-
нетрудно определить минимальные нагрузки, а также направле-
направление самого разрушения по
формуле D.55).
Пусть, например, берега
трещины свободны от нагру- у
зок, а на бесконечности плос-
плоскость растягивается одноосным
напряжением р под углом а к
оси х (рис. 33). В этом случае
в формулах D.60) и D.61)
надо положить *)
Ро(О = О, N{ = p,
N2=*0. D.62)
¦О
21
Рис. 33.
Подставляя значения Ki и Кп согласно D.63) в формулы
D.55) и D.56), получаем разрушающую нагрузку /?* и угол 0»
*) Эта задача была рассмотрена в работах Эрдогана и Си [51], В. В. Па-
насюка и Л. Т. Бережницког.о [52].
1в4
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЙ
[ГЛ. IV
в зависимости от а:
р, V~nl _ tg а A2 ctg2 а + 1 - )Л + 8 ctg2 аK/2
Кю 4 }/2cos2аA + 3 j/"l+8ctg2a)
9e = 2arctg
+ 8ctg2 a
D.64)
4 ctg а
Графики этих функций изображены на рис. 34 и 35. Как
видно, угол 9* — а, составляемый начальным направлением
распространения трещины с на-
направлением растяжения, ме-
меняется в пределах я/2 ± 0,1я; при
я/4 ",<: а < я/2 разрушающая на-
нагрузка почти не отличается от
9ш,
0
цгя
П/iif
i
Ы
/
не -
/
а
Рис. 34.
Рис. 35.
гриффитсовой, соответствующей углу а = я/2. Любопытно, что
минимальная разрушающая нагрузка, составляющая 0,97, от
х гриффитсовой, достигается при
щ ' а «70°.
*~ ' *- В качестве еще одной простой
| иллюстрации рассмотрим тот
* случай, когда на бесконечности
¦ плоскость сдвигается касательны-
i,,,r, ,ш,,, ми напряжениями т параллельно
1 плоскости трещины (рис. 36).
"' ' В этом случае в формулах D.60)
и D.61) надо положить
Рис. 36.
<х = я/4. D.65)
При xi= ± I находим
i(, = 0, Ки = т V*i. . D.66)
В этом случае X — Kn/Ki -*«» и, совершая предельный пе-
переход а формулах D.55), D.56), получаем
6 = — 2 arctg (l/]/2) м — 69°, Ки = (УЩКи- D.67)
§ 3] ОБОБЩЕННЫЙ НОРМАЛЬНЫЙ РАЗРЫВ 155
Согласно D.66) и D.67), разрушающая нагрузка т, име-
имеет вид
т в Щм-. D:68)
2/я/
.. Рассмотрим в заключение случай трещин продольного
сдвига, когда Кг = Кп = 0. Допустим, что 'Произвольный ци-
цилиндрический стержень, скручиваемый некоторым моментом,
имеет начальный разрез (или щель), края которого параллельны
образующей цилиндра. Поверхность разреза представляет со-
собой цилиндрическую поверхность, соосную с поверхностью
стержня. Напряженно-деформированное состояние вблизи края
щели будет продольным сдвигом; оно описывается формулами
C.46). Легко видеть, что максимальное растягивающее напря-
напряжение будет равно KmlV^nr вблизи края щели; оно дей-
действует на площадке, направленной под углом 45° к оси стержня
и к поверхности щели в рассматриваемой точке контура. В слу-
случае обобщенного нормального разрыва локальное разрушение
на этой площадке произойдет в тот момент, когда коэффи-
коэффициент Km достигнет величины Kic- Дальнейшее развитие тре-
трещины проследить трудно, так как плоскость образовавшегося
разрыва не совпадает с плоскостью начальной трещины и за-
задача становится трехмерной.
Дополнительное условие на контуре гладкой криволинейной
трещины. Угол излома 6* может быть конечным только в том
случае, если внешняя нагрузка изменяется во времени скачко-
скачкообразно, или же положение конца трещины в точке О соответ-
соответствует начальному несимметричному состоянию. В случае не-
непрерывного изменения нагрузки и непрерывного развития тре-
трещины поверхность трещины будет гладкой, без изломов; при
этом, согласно D.52), в любой момент роста трещины каса-
касательная плоскость к ее поверхности в любой точке -контура бу-
будет представлять собой площадку, на которой величина Кв
максимальна, а Кгв обращается в нуль.
В малой окрестности произвольной точки О контура тре-
трещины упругое поле будет симметрично относительно этой пло-
площадки, так что рассматриваемая трещина будет относиться
к трещинам нормального разрыва. Таким образом, состояние в
каждой точке контура трещины нормального разрыва (т. е. Бри
/Си = Km = 0) аналогично одноосному растяжению стержня
в силу аналогии, существующей между тензором интенсивности
напряжений Кц и тензором напряжений а^-.
Поверхность криволинейной трещины неизвестна заранее и
должна быть определена в процессе решения. Найдем дополни-
дополнительное условие, определяющее радиус кривизны поверхности
трещины в каждой точк~е [*Б].
156 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
Обозначим параметр внешней нагрузки через р, а длину
трещины, измеряемую от некоторой фиксированной точки, че-
через I. Для определенности ограничимся плоской задачей. Пусть
х = хоA), у = г/о@ будут уравнениями линии трещины. Пред-
Предположим, что значениям пара-
метров I, p n I -\- Al, p + Ар со-
соответствует положение конца
трещины в точках О и О] со-
соответственно (рис. 37).
rOt(L+M, р+Ар) Разобьем мысленно процесс
развития трещины на конечное
число шагов так, чтобы Ар и
Д7 соответствовали одному
шагу, а распространение тре-
0A,р) л щины было скачкообразным.
При этом ломаная линия тре-
Рис- 37- щины будет состоять из отрез-
отрезков прямых. В пределе при
Др->0 и Д/->0 должно получиться постепенное развитие иско-
искомой гладкой трещины.
На каждом шаге малому углу излома линии трещины
Д8 = 6* соответствует некоторая малая величина АК\\\ обе эти
величины удовлетворяют общему уравнению D.54). Совершая
в нем предельный переход Д9-*0, АКп—>О, находим для глад-
гладкой трещины
-2(^L) =*,. D.69)
Здесь dKn — приращение Ки в точке О, соответствующее уве-
увеличению нагрузки на dp при фиксированной длине трещины.
Напомним, что для гладкой растущей трещины нормального'
разрыва, согласно D.52), имеют место соотношения
КЛР,1) = Ки, /Си (р, 0 = 0. D.70)
Пусть функция 1 = 1(р) представляет собой искомую зави-
зависимость длины трещины от нагрузки. Подставляем ее в первое
уравнение D.70) и дифференцируем получившееся тождество;
находим
dp dp I dl
Уравнения D.69) и D.71) позволяют определить радиус кри-
кривизны гладкой трещины в любой точке:
I 3) ОБОБЩЕННЫЙ НОРМАЛЬНЫЙ РАЗРЫВ 157
Примененный конечно-разностный метод удобен также для
численного решения задачи о развитии криволинейных тре-
трещин; условия D.70) и D.72) играют в этих задачах роль допол-
дополнительного граничного условия на контуре гладкой трещины
нормального разрыва.
Рассмотрим один пример.
Допустим, что в рассмотренной выше задаче об изолирован-
изолированной трещине действующие нагрузки близки к симметричным от-
относительно оси х, т. е. величины а, X, У, qo{t) близки к нулю.
При этом контур криволинейной трещины будет близок к пря-
прямолинейному отрезку вдоль оси х. В первом приближении, снося
граничные условия на ось х, форму слабо искривленной тре-
трещины можно определить следующим образом.
Обозначим через (I, у) координаты конца трещины ((/</).
Величина I соответствует условию Кц = 0в конце трещины, т. е.
а = 0, q — 0. Величина у определяется из решения обыкновен-
обыкновенного дифференциального уравнения
xc^W)' D#73)
полученного согласно дополнительному условию D.72). Здесь
правая часть представляет собой некоторую функцию I, свою
для каждого пути нагружения; величины Ki и Кц берутся со-
согласно формулам D.60) и D.61), причем Ki соответствует
а = 0, q — 0, а Кц отвечает малым отклонениям от симметрии.
Пусть, например, действующие нагрузки близки к случаю
нагружения двумя симметричными сосредоточенными силами
(АР<Р). D.74)
В этом случае, согласно D.61),
Kl~W Ktt—W+4VW D>75)
В силу симметрии задачи относительно оси у достаточно огра-
ограничиться рассмотрением правого конца трещины.
В случае пропорционального нагружения
D.76)
имеем
дК\ _ Ао дКи _ _ (х— 1)ДД) ,4 77ч
dp ]/lTl ' dp 2A+х)/я7*
а дифференциальное уравнение D.73) принимает вид
(х-1)дл,\ D78)
158
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
{ГЛ. IV
Решение этого уравнения, удовлетворяющее начальным усло-
условиям
при l = l0, y = 0 dy/dt = Q^, D.79)
имеет вид
y = Al[lln(l/lo) — l + l()] + e.(l — to)- D-80)
Здесь 0» — угол отклонения трещины от оси х в начальный мо-
момент развития; его нетрудно найти при помощи формулы D.69):
(х+1)Л0 • <4>й1^
Параметры р и / связаны между
собой, согласно условию /Ci=/Cic,
так:
1 = ^~- D-82)
32
16
8
У
-
Зависимость D.80) в безразмер-
безразмерных переменных
в
Рис. 38.
10 t
изображена на рис. 38.
Формулы D.80)—D.82) определяют размер и форму кри-
криволинейной трещины в любой момент нагружения.
Весьма существен тот факт, что форма криволинейной тре-
трещины зависит от пути нагружения.
§ 4. Устойчивость роста хрупких трещин
Рассмотрим вопрос о -локальной устойчивости развития
конца хрупкой трещины по отношению к малым возмущениям
внешних нагрузок, сопровождающимся малым увеличением по-
поверхности трещин 6Е.
Будем исходить из следующего общего соотношения:
— 2y 62.
D.83)
Здесь 6f/, 6«i> 6S, 6Е—бесконечно малые возмущения соответ-
соответствующих величин; знак равенства отвечает состоянию равно-
равновесия (ср. с формулой D.33)). Это соотношение справедливо
для всего тела или любой его части, причем в силу необрати-
необратимости роста трещин 6Е ^ 0. Заметим, что в функцию U входит
также некомпенсированное тепло, образующееся при развитии
трещины (см. гл. I).
S 4] УСТОЙЧИВОСТЬ РОСТА ХРУЙКИХ ТРЕЩИН 1S9
Знак неравенства в соотношении D.83) обусловлен необра-
необратимостью бесконечно малых возмущений (правая часть больше
левой на величину кинетической энергии и некомпенсированного
тепла в объеме тела,'соответствующих этим возмущениям).
Рассмотрим случай линейно-упругого однородного и изотроп-
изотропного (по упругим свойствам) тела, считая поверхность разви-
развивающейся трещины гладкой, без изломов. Изучим процесс де-
деформирования и разрушения, как обычно, в малой окрестности
произвольной точки О контура -трещины. Применим «принцип
микроскопа» и придем к канонической сингулярной задаче для
полубесконечного разреза (см. рис. 13).
Для определенности -ограничимся процессом щ = const,
Т = const. Согласно общему соотношению D.83), в рассматри-
рассматриваемой системе самопроизвольно могут протекать только такие
процессы, которые сопровождаются уменьшением функции F:
F = U—TS +2yZ, т. е. 6F<0. D.84)
Следовательно, в состоянии устойчивого равновесия функ-
функция F должна быть минимальна, т. е.
dF==0, d2F>0. D.85)
Применяя прием Ирвина совершенно аналогично тому, как
это сделано в § 2 этой главы, при помощи D.85) легко полу-
получить следующие соотношения:
D.86)
(Ж
Соотношение D.86) представляет собой уже полученное ра-
ранее условие локального равновесия упругого тела с трещинами;
неравенство D.87) является условием локальной устойчивости
этого равновесия.
Следует подчеркнуть, что полученные условия устойчивого
равновесия являются локальными в том смысле, что они отно-
относятся к некоторой точке контура трещины при определенных
значениях внешних нагрузок. Решение вопроса о развитии тре-
трещины и о характере этого развития (устойчивом или неустой-
неустойчивом) в целом требует изучения конкретной задачи, т. е. зна-
знания зависимости коэффициентов интенсивности напряжений от
нагрузок и длины трещины. Последнее представляет собой за-
задачу классической теории упругости, и коль скоро она решена,
решение вопроса о развитии трещин на основе условий D.86)
и D.<87) может натолкнуться разве что на трудности алгебраи-
алгебраического характера.
160 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
В наиболее важном случае трещины нормального разрыва
условия устойчивого равновесия сводятся к следующим:
Ki = Kxc, dKi/dl<0. D.88)
Здесь было принято, что величина у не зависит от / (однород-
(однородное по прочности тело).
Пусть р и / — параметры внешней нагрузки и длины тре-
трещины соответственно, а Кг представляет собой некоторую функ-
функцию этих параметров Ki(p,l), причем дКт/др > 0. Тогда на
основании D.88) и D.67) условие устойчивости равновесия
можно записать также так:
^ = _f/^>0. D.89)
dp dp I dl v '
Условие устойчивости в этой форме хорошо согласуется с ин-
интуитивным представлением об устойчивости равновесия хруп-
хрупкой трещины.
Если хрупкая трещина растет устойчиво, скорость роста
трещины / прямо пропорциональна скорости увеличения на-
нагрузки /):
'—'^-/Ф- с-90»
В случае неустойчивого равновесия имеет место неравенство
D.91)
так что после достижения предельного состояния равновесия
режим развития трещины становится динамическим.
§ 5. Концепция квазихрупкого разрушения.
Структура конца трещины
Концепция квазихрупкого разрушения формулируется так:
величина необратимой работы у, затраченной на образование
единицы площади свободной поверхности тела при развитии
трещины, является постоянной материала, не зависящей от на-
нагрузок, формы и размеров тела.
Эта эмпирическая закономерность была установлена на
основании многочисленных экспериментов, с различными ма-
материалами в широком диапазоне изменения внешних условий.
Впервые наиболее четко сформулировали ее Ирвин и Орован
в конце 40-х — начале 50-х годов. Установление этой законо-
закономерности явилось крупнейшим достижением механики хрупкого
разрушения после работы Гриффитса.
Чтобы понять физический смысл этой концепций, рассмотрим
конкретный пример. Пусть полоса с краевой трещиной растяги-
i 5|
КОНЦЕПЦИЯ КВАЗИХРУПКОГО РАЗРУШЕНИЯ
161
вается на бесконечности напряжением р (рис. 39). Допустим,
что нагрузка монотонно увеличивается, начиная с нуля, в ре-
результате чего в конце трещины образуется пластическая область,
размер которой растет с увеличением р. Возможны два исхода:
или пластическая область будет расти неограниченно при до-
достаточно больших / и L (при этом разрушение будет связано
с тем, что все сечение перед
трещиной перейдет в пластиче-
пластическое состояние, т. е. с исчерпа-
исчерпанием способности тела к пла-
пластическому деформированию),
или же рост пластической об-
области будет происходить до не-
некоторого предельного размера
d, после чего будет иметь ме-
место локальное разрушение в
конце трещины, и она будет
развиваться.
Согласно концепции квази*
хрупкого разрушения, для всех
материалов при достаточно
больших / и L считается реа-
реализующейся вторая возмож-
возможность, т. е. существует пре-
предельный размер d. Тогда для
любого материала существуют такие достаточно большие раз-
размеры тела и трещины L и I, что о нем можно говорить, как о
хрупком материале. Действительно, пусть I a L настолько ве-
велики, что на расстояниях г от конца трещины О, удовлетворяю-
удовлетворяющих условиям
d < г <С /, d < г < L, D.92)
распределение напряжений и деформаций будет описываться
упругой асимптотикой C.44). То, что для любых конечных d
и достаточно больших I тл L такая асимптотика существует, вы-
вытекает из «принципа микроскопа». Будем говорить, что у тре-
трещины реализуется тонкая структура, если на некоторых рас-
расстояниях г от конца трещины (d <С «С I, d<g r <g^ L) осуще-
осуществляется упругая асимптотика C.44). При наличии тонкой
структуры можно провести все энергетические рассуждения,
которые привели к формулировке критерия локального разру-
разрушения на контуре хрупкой трещины (см. § 2 этой главы).
,При этом для трещин нормального разрыва условие локаль-
локального разрушения по-прежнему формулируется в виде К\ = A'ie
(для любых нагрузок имеет место неравенство Ki^Kic)- Из
Рис. 39.
в Г, П. Черепанов
162 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ 1ГЛ. IV
общефункционального метода § 1 вытекает, что величина Kic
представляет собой некоторую функцию предыстории нагруже-
ния (в частности, времени, скорости роста трещины и т. п.). На
основании концепции квазихрупкого разрушения функциональ-
функциональной зависимостью Kic от предыстории нагружения пренебре-
пренебрегаем, и величина Kic считается постоянной характеристикой ма-
материала (концепция Kic).
Концепция квазихрупкого разрушения позволяет полностью
перенести все установленные для хрупких тел закономерности
на квазихрупкие тела, т. е. такие упруго-пластические тела
с трещинами, для которых реализуется тонкая структура. В этом
случае пластическая область перемещается вместе с концом
трещины как жесткое целое, не изменяя своей формы; форма и
размер этой области не зависят от нагрузок и конфигурации
тела с трещинами.
Указанная концепция позволяет также подойти к объясне-
объяснению хрупкого и вязкого разрушений как к некоторым предель-
предельным случаям квазихрупкого разрушения при d—>0 и d-»oo со-
соответственно.
Само название константы Kic (вязкость разрушения) озна-
означает, что при одинаковых геометрических размерах образцов
с трещиной из различных материалов (с одинаковым времен-
временным сопротивлением) разрушение будет тем ближе к вязкому,
чем больше Kic, и наоборот, чем меньше Къ, тем ближе раз-
разрушение к хрупкому.
Существенно подчеркнуть, что в рамках теории квазихруп-'
кого разрушения распределение напряжений и деформаций на
расстояниях порядка d от конца трещины может быть самым
различным; сила и общность механики хрупкого разрушения
как раз и заключается в том, что ее закономерности не зависят
от характера этого распределения.
Однако для различных уточнений и обобщений механики
хрупкого разрушения знание такого распределения (будем го-
говорить— знание структуры конца трещины) представляет боль-
большой интерес.
Структура конца сквозной трещины в тонкой пластине. Рас-
Рассмотрим тонкую пластину с произвольной сквозной трещиной
нормального разрыва, подвергающуюся воздействию растяги-
растягивающих усилий. Материал пластины будем считать идеальным
упруго-пластическим и удовлетворяющим условию пластичности
Мизеса. Рассмотрим окрестность конца трещины, малую срав-
сравнительно с характерным линейным размером пластины, но
большую по сравнению с характерным размером пластической
области. На плоскости ху трещина представится полубесконеч-
полубесконечным разрезом вдоль отрицательной полуоси х, свободным от
внешних нагрузок (рис, 40).
§б]
КОНЦЕПЦИЯ КВАЗИХРУПКОГО РАЗРУШЕНИЯ
163
Численное решение этой упруго-пластической задачи конеч-
конечно-разностным методом [53] показало, что уравнение контура L,
разделяющего упругую и пластическую области, можно запи-
"сать приближенно в следующем виде:
^-. D.93)
Здесь as — предел текучести на растяжение.
Соответствующая пластическая область
рис 40 в безразмерных координатах
изображена на
). D.94)
Как видно, она довольно близка к приближенному решению
Дагдейла; согласно гипотезе Дагдейла [54], пластические де-
деформации сосредоточены на продолжении трещины вдоль уз-
узкого слоя нулевой толщи-
толщины (рис. 40), так что пла- У*
стическую линию можно
считать просто линией
разрыва упругого смеще-
смещения, а само решение ис-
искать в классе разрывных
решений теории упруго-
упругости. Напряжения на пла-
пластической линии разрыва
@, d) будут равными
, = 0. D.95)
Рис. 40.
При помощи основных представлений C.9) и условия тонкой
структуры C.43) находим
/ (г) = 0, при 2 -> оо ф (г) =
{ 0 при у=*0, х < 0,
D.96)
-5-a.s при г/ = 0, 0<x<d.
Ограниченное всюду решение краевой задачи D.96) име-
имеет вид
ni
D.97)
Для сравнения с точным решением отрезок d показан на рис. 40
жирной линией.
¦Jfl4 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
Приведем еще формулу для наибольшего скачка смещения
на пластической линии разрыва 2ио, достигаемого в точке О
(конец трещины) согласно D.97) и определяющего раскрытие
трещины в этой точке:
2vo=-gf. D.98)
Формулы D.97) и D.98) позволяют определить наибольший
размер пластической линии d и наибольший скачок смещения
2v0 в момент локального разрушения*), т. е. при К = Кс-
Заметим, что
oydv = — J Gy-^-dx = osv0 = -?§-. D.99)
о о
Как видно, физически величина у может рассматриваться
не только как необратимая работа образования единицы по-
поверхности трещины, но и как равнодействующая внешних сил,
приложенных к пластическому слою @, d) и направленных
вдоль оси х. Последнее оправдывает в данном случае силовое
рассмотрение у как некоторого эффективного поверхностного
натяжения материала в конце трещины.
Следует отметить, что экспериментальные данные в некото-
некоторых случаях (тонкие пластины из малоуглеродистой стали, не-
некоторые полимерные и композитные материалы) лучше согла-
согласуются с гипотезой Дагдейла, чем точное решение. По-видимому,
это связано с особенностями распространения пластических зон
в материалах- с задержкой текучести и с ориентационным
упрочнением.
Структура конца трещины в плоскодеформированном состо-
состоянии. Гораздо больший практический интерес представляет
изучение структуры конца трещины нормального разрыва в наи-
наиболее типичном для нее состоянии плоской деформации. Мате-
Материал тела будем по-прежнему считать идеальным упруго-пла-
упруго-пластическим и удовлетворяющим условию пластичности Мизеса.
Численное решение этой упруго-пластической задачи для
квазихрупкого тела конечно-разностным методом [55] с приме-
применением деформационной теории пластичности показало, что
*) Для пластин величина Кс в случае сквозных трещин иногда суще-
существенно зависит от толщины пластины, а для весьма тонких пластин из пла-
пластичных материалов трещина часто распространяется как трещина продоль*
ного сдвига, причем поверхность трещины становится наклоненной к лло»
скости пластины под углом 45° (косой срез). Пластическая линия разрыва
физически реализуется как локальная «шейка» в пластине на продолжении
трещины (см. § 7 этой главы).
КОНЦЕПЦИЯ КВАЗИХРУПКОГО РАЗРУШЕНИЯ
165
уравнение контура L, разделяющего упругую и пластическую
„области, можно записать приближенно так;
¦(—У
D.100)
Соответствующая пластическая область изображена на
рис. 41 в безразмерных координатах D.94). Она представляет
собой внутренность эллипса с центром
в конце трещины.
Как видно, пластические деформа-
деформации в этом случае сосредоточены вдоль
сравнительно узкого слоя, исходящего
из конца трещины перпендикулярно к
ее поверхности.
Поэтому представляет интерес при-
приближенное решение этой задачи в по-
постановке, которая в некотором смысле
аналогична постановке Дагдейла. Бу-
Будем считать пластическую зону отрез-
отрезком вдоль оси у, а решение искать в
классе разрывных решений теории уп-
упругости (см. рис. 41).
На линии разрыва, представляю-
представляющей собой при таком подходе линию
пластического скольжения, должны
выполняться условия
при х = 0, —d<y<d
X
D.101)
Здесь скобки [ J означают скачок со-
соответствующей величины. Для просто-
простоты принято условие Треска. Укажем
простое приближенное решение этой задачи, аппроксимировав
скачок смещения v на линии скольжения линейной функцией
координаты у и удовлетворив условию хяу =» as/2 в среднем, т. е.
считая, что
при х = 0, \у\
[ах + 1тху] = 0,
D.102)
jgg " ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
При помощи основных представлений C.9) отсюда можно по-
получить следующую граничную задачу для аналитических функ-
функций Ф(г) и Q(z):
при х = 0, | у |.< d
[ф(г)] = -2цР0/(к+1), [Q(z)] = -4hPo/(k+1); D.103)
при у = 0, х<0,
Im Q = 0, Re BФ + Q) — 0;
при г -» то
Решение краевой задачи D.103) запишется так:
с'
ln Z + W
_ _
?l_ + -!^- f
О
F{x)dx
— oo
Постоянные Ро и d находятся из условия на бесконечности и
условия для среднего касательного напряжения на линии сколь-
скольжения. Постоянные Ci и С2 вычисляются из условия отсутствия
сосредоточенной силы и скачка смещения в точках z = ±id.
После вычисления интегралов получаются следующие уравнения:
Р 1n Z-'d | ?} |_
, j
2n/ A + к) У г + l^^iJ 2 K=U (KF + V^ld) ' D.105)
- 5,4р0Ц » я A + х) а„ - цРо /5" = /я A +
Есть основания полагать, что для материалов с задержкой
текучести построенное разрывное решение ближе к истине, чем
непрерывное решение упруго-пластической задачи.
Окончательно для величин р0 и d, определяющих мощность
и размер линии скольжения, получаются следующие выражения?
d = 0,2WCj/oJ, Po = 2,3 A - v) сг,/ц. D.106)
.15]
Концепций Квазихрупкого разрушения
16?
Приведем еще формулу для раскрытия трещины в ее конце:
2и0 = 0,58 A — v2) K^j(Eas). D.107)
Задача о структуре конца трещины в плоскодеформирован-
ном состоянии для идеального упруго-пластического материала
с условием Мизеса (по теории течения) была изучена Райсом
с сотрудниками [56]. Для численного расчета на ЭВМ был при-
применен метод конечных элементов;
коэффициент Пуассона был взят
равным 0,3.
Полученные результаты для кон-
. тура L, а также напряжения ау на
продолжении трещины приведены на рис. 42 и 43. Напряжение
можно приближенно аппроксимировать следующими выраже-
выражениями:
«У** = [Vr^'-(VrJW./8 + 0,l _ о, is)],
или, более грубо, с погрешностью 20%
D.108)
Контур L, разделяющий упругую и пластическую области,
4 в координатах х* и у* имеет приблизительно форму эллипса с
большой-осью длины 0,43, малой осью длины 0,35 и с центром
в точке х-, « 0,05, у* «0,18, причем большая ось наклонена
к оси х* под углом 70° и контур L пересекает ось х* в точке
*, « 0,1.
Раскрытие трещины в ее конце оказывается равным
D.109)
168
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[гл, iv
Структура конца трещины продольного сдвига. В случае тре-
трещин продольного сдвига может быть найдено точное решение
упруго-пластических задач р7]. Ограничимся изучением распре-
распределения напряжений и деформаций в окрестности такой тре-
трещины, когда реализуется тонкая структура (рис. 44). Решение
этой задачи было впервые получено Халтом и Мак-Клинтоном
[58]. Приведем здесь простое решение, данное в работе [57].
В этом случае в пластической области имеют место соот-
соотношения
дхи
дх
dw
= 0
dw
xz~bJ~
(уравнение равновесия),
(условие текучести),
(уравнение Генки).
D.110)
Здесь k = os/2 по условию Мизеса, k=as/Y3 по условию
Треска — Сен-Венана.
Представим напряжения в виде [3]
Здесь функция %(х,у) удовлетворяет уравнению
cos 6 -~ sin 6-^— =0.
Характеристики этого уравнения представляют собой семей-
семейство прямыХ у = xtgQ-\- С, 0 = const, совпадающих с линиями
скольжения и ортогональ-
B'
ных вектору х = rxz-\-ityz
в каждой точке. На осно-
основании уравнения Генки
D.110) вдоль линии сколь-
скольжения имеет место так-
также условие w = const.
Линии скольжения, оче-
очевидно, представляют со-
собой перпендикуляры, вос-
восставленные из точек
контура свободной от на-
нагрузок границы тела в
пластической области. На
границе упругой и пластической областей L напряжения и сме-
смещения непрерывны.
Напомним общее представление напряжений и смещения в
упругой области через аналитическую функцию f(«):
D.111)
Рис. 44.
% 51 КОНЦЕПЦИЯ КВАЗИХРУПКОГО РАЗРУШЕНИЯ 169.
Заметим, что контур L не может охватывать точку О, так
как в противном случае на некоторой части контура L, согласно
граничному условию, будет f'(z) = const, что невозможно.
Если представить себе конец трещины (точку О) как пре-
предел некоторого выпуклого овала, стягивающегося в эту точку,
то становится ясным, что линии скольжения должны представ-
представлять собой радиальные прямые («веер»), т. е. в пластической
области, согласно D.109),
гхг + пуг = Ш*. D.112)
При этом в конце трещины смещение w будет терпеть ска-
скачок 2ш0, а деформация будет иметь особенность порядка 1/л
Таким образом, для функции f(z) получается следующая
краевая задача:
при у = 0, л:<0 Imf (z) = 0,
. на L |/'(z)|=*/ii, arg[z/'(z)] = -ji/2, D.113)
при z->oo /'(z) =
На плоскости годографа ?
? Г (г) D.114)
Г
упругой области соответствует верхняя половина единичного
круга. На плоскости Z, на основании D.113) получаем краевую
задачу
при ImC = 0 Imzft)-0,
при 1С 1=1 С*2(С) + 2@ = 0,
При С"*0 Z@ = ——illy.
Продолжим аналитически функцию z(?) в нижний полукруг при
помощи соотношения z(?) = z(?); получим следующую гранич-
граничную задачу для единичного круга:
при | С 1= 1
D.116)
Продолжим еще раз аналитически функцию z(?) на всю
плоскость ? при помощи соотношения
z(l/C) =-С8* (С). D-П7)
Получившаяся функция z(?) аналитична во всей плоскости
С» за исключением точки Z, = 0, где она имеет полюс второго
§. 6] НЕКОТОРЫЕ ЭФФЕКТЫ ПРОЦЕССА РАЗРУШЕНИЯ 171
времени, предыстории, внешней среды и др. (некоторые из них
подробнее рассмотрены в главах VI—VIII).
1. Устойчивое подрастание трещины при монотонном нагру-
жении*). В большинстве материалов, проявляющих в какой-то
мере пластические свойства перед разрушением (например, ме-
металлы, полимеры и др.), трещина устойчиво подрастает в про-
процессе монотонного нагружения, прежде чем перейти в динами-
динамический режим или в режим контролируемого устойчивого роста,
характерные для хрупких и квазихрупких трещин и изученные
выше. Средняя величина докритического подрастания для ме-
металлов составляет КН— 10 см в условиях плоской деформа-
деформации, а в тонких пластинах значительно больше. Это подраста-
подрастание нельзя объяснить в рамках концепции квазихрупкого раз-
разрушения неоднородностью прочностных свойств материала, так
как оно зачастую значительно больше среднего размера зерна.
Величина подрастания зависит от остроты искусственного
надреза (трещины): для более острой трещины подрастание на-
начинается раньше, а величина подрастания, как правило, больше;
для тупого надреза подрастание может вовсе отсутствовать.
Механизм такого докритического роста трещины состоит
в исчерпании способности к пластическому деформированию в
некоторой области вблизи конца трещины, малой по сравнению
со всей пластической зоной в конце трещины, задолго до на-
наступления предельного состояния всей тонкой структуры.
В основе этого механизма лежит локальная концентрация де-
деформаций на контуре трещины.
Если реализована тонкая структура, то из соображений
анализа размерностей скорость роста трещины при монотонном
нагружении должна выражаться формулой вида
DЛ22)
dKx о* v
Здесь Ф — некоторая безразмерная функция своих аргументов,
Y — необратимая работа образования единицы поверхности тре-
трещины.
Наиболее простое теоретическое описание этого явления
представляется следующим [б0]. Пусть в упруго-пластическом
теле рост трещины происходит в процессе локального нагру-
нагружения при любых Къ меньших Къ- Напомним, что при выводе
критерия локального разрушения D.1) для хрупких трещин
считалось, наоборот, что при достаточно малых К\ трещина не
растет.
.•) По-видимому, первая (неудавшаяся) попытка теоретического объяс-
объяснения этого явления была предпринята Я. И. Френкелем [*»].
170 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
порядка с заданной интенсивностью; при ?—»-оо согласно D.И6)
и D.117) она равна постоянной KuiK^nk2).
Таким образом, получаем
г @ = Али A - Г*)l{2nk*). . D.118)
Отсюда
f(z)= _^HI=r, D.119)
ц V К?„ - Ink2г
Контур L, разделяющий упругую и пластическую области, пред-
представляет собой окружность
- d/2f = d2/4, d == Kmlink2). D.120)
Отметим еще формулу для раскрытия трещины в ее конце
и формулы для распределения деформаций в пластической
области
Напряжения в упругой области, согласно D.119) ,и D.111),
оказываются такими же, как если бы конец трещины был рас-
расположен в центре пластического круга x = d/2, j = 0 и тело
было идеально-упругим.
Все полученные в этом параграфе решения упруго-пластиче-
упруго-пластических задач найдены для того случая, когда в процессе нагру-
жения коэффициент интенсивности напряжений в данной точке
О контура трещины монотонно возрастает.
Отметим одно общее свойство всех изученных здесь реше-
решений: при значительном разнообразии свойств структуры конца
трещины форма трещины вблизи ее конца оказывается во всех
случаях прямоугольной с некоторым характерным раскрытием
в этой точке.
§ 6. Некоторые основные эффекты процесса разрушения
Основная концепция механики хрупкого разрушения (вяз-
(вязкость разрушения Kjc является постоянной характеристикой ма-
материала) не в состоянии- объяснить многие весьма важные яв-
явления процесса разрушения. Хотя бы беглое знакомство с ними
представляется целесообразным прежде всего для того, чтобы
оценить границы применимости указанной основной концепции
механики хрупкого разрушения, а также для того, чтобы иметь
представление об основных направлениях научных поисков в
этой области. В этом параграфе рассматриваются основные
эффекты, связанные с влиянием пластичности, температуры,
172
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
Можно показать [в0], что в этом случае для идеальных упру-
упруго-пластических сред необратимая работа у, расходуемая при
образовании единицы свободной поверхности трещины нормаль-
нормального разрыва, равна
Y «=» —7L /С? 4- &к\ (а 19ч\
Здесь р — некоторая постоянная материала.
При этом процесс развития трещины представляется таким,
как он изображен на рис. 46. Пластическая область в процессе
нагружения не только расширяется, но и смещается как жест-
жесткая в направлении роста
трещины вместе с ее кон-
концом; концепция квази-
квазихрупкого разрушения реа-
реализуется асимптотически
при достаточно больших
приращениях длины тре-
трещины как выход на ста-
Рис. 45. ционарный режим рас-
распространения пластиче-
п „ ской области.
Простейшее допущение о том, что Y является постоянной
материала, позволяет при помощи D.123) получить простую
аналитическую зависимость подрастания трещины Д/==/_/о
от Ki в процессе монотонного на-
нагружения *)
«1
1
Г"
1 '
>
а*2
Klc
и
0,2
dl.
Рис. 46.
изображенную на рис. 46. Эта
зависимость хорошо описывает
имеющиеся экспериментальные
данные [35>61-62].
Существенно подчеркнуть, что
величина Ки, соответствующая
обычно переходу в неустойчивую область и, тем самым за-
замеряемому на опыте моменту разрушения, оказывается меньше
предельной величины, достигаемой при Д/-»со (различие этих
величин исчезает только при хрупком разрушении, когда нет
подрастания и пластической области).
рушения ЩВИСИМ0СТЬ на?-ывают Диаграммой Ki-Al или диаграммой раз-
§ 6] НЕКОТОРЫЕ ЭФФЕКТЫ ПРОЦЕССА РАЗРУШЕНИЯ 173
Если тонкая структура трещины устойчива, т. е. dKi/dl < О,
то на опыте может быть достигнуто также значение Kic-
Концепция о постоянстве y пРи Д/-*°° переходит в концеп-
концепцию квазихрупкого разрушения,.а при А/—>0 — в концепцию
Гриффитса для хрупких тел. Таким образом, концепция Гриф-
фитса и концепция Ирвина — Орована представляются различ-
различными предельными случаями данной теории.
2. Рост усталостных трещин при циклическом нагружении.
Допустим, что к упруго-пластическому телу прикладываются на-
нагрузки, являющиеся периодическими функциями времени. Со-
Согласно основной концепции механики хрупкого разрушения,
трещина нормального разрыва расти не будет, если всюду на
ее контуре максимальная величина коэффициента интенсивно-
интенсивности напряжений за цикл нагружения меньше вязкости разру-
разрушения Kic. Это не соответствует многочисленным опытным дан-
данным по усталостному разрушению, причиной которого является
{часто весьма значительное) докритическое развитие трещин.
Если реализована тонкая структура, то анализ размерностей
дает [60]
^*Ц (* i ^ Л D.124)
dn as \ Ey /Cimax Е
Здесь dl/dn — скорость роста трещины, п — число циклов,
и /Cimin — наибольшее и наименьшее значения коэффициента
интенсивности напряжений за один цикл.
Наиболее характерная особенность развития усталостной
трещины заключается в ее устойчивом подрастании в процессе
монотонного нагружения за каждый цикл и в необратимости
трещины при разгрузке (dl^O). Концепция о постоянстве y
на основе уравнения энергии D.123) позволила найти следую-
следующую зависимость [60]:
dl
¦ = — ay
dn 4 2?Y/(l-v2)
2?у-A-У2)^тах 1
22?V-6(l-v2)/C2miJ'
D.125)
1 При Kl mln > 0,
~ 0 При Kl min < 0.
Здесь a — некоторая постоянная материала'(а > 0).
При /Cimin = 0, /С2тах^-Еу из зависимости D.125) полу-
получается следующая простая формула:
dl _ a(l -v2J „4
dn ~~ av2"
174
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. tv
Эту формулу впервые получил Пэрис [63] на основании анализа
экспериментальных данных по многоцикловым усталостным
трещинам. Зависимость D.125) подтверждается опытом прак-
практически во всем диапазоне числа циклов до разрушения [64>65].
3. Скачкообразный рост трещины. В некоторых упруго-пла-
упруго-пластических материалах наблюдается скачкообразное развитие
трещин в условиях локальной плоской деформации, когда в
процессе плавного нагружения этапы медленного роста трещины
чередуются с промежутками весьма быстрого развития.
Предлагались различные объяснения этого явления, осно-
основанные на введении зависимости у от скорости роста трещины
dl/dt [66] и от скорости нагружения dKi/dt [60].
4. Зависимость вязкости разрушения от толщины пластины
для сквозных трещии. Распространение сквозных трещин в пла-
пластинах из упруго-пластического материала имеет некоторые
Рис. 47.
особенности, которые затрудняют применение к ним общей тео-
теории, основанной на предположении о плоском деформированном
или плоском напряженном
состояниях. На рис. 47 и 48
показаны обычные виды из-
изломов, характерные для раз-
разрушения пластин, и схема-
схематически пунктирными линия-
линиями изображены последова-
последовательные положения фронта
трещины для полностью
«косого» излома и для сме-
смешанного излома [35].
Как видно из этих рисун-
рисунков, в пластической области
вблизи конца трещины, при-
прилегающей к свободной по-
поверхности пластины, механизм пластического деформирования
и разрушения аналогичен тому, который характерен для косых
изломов в тонких пластинах, и близок к продольному сдвигу.
В области прямого излома поле пластических деформаций
л
Vs"
\\
1 J
\''
\
\
/
/
/
*~ /
/
t /
N ч
>
/
1
г
N
\
/
/
Ч
\
\
;
у
Рис. 48.
f 6]
НЕКОТОРЫЕ ЭФФЕКТЫ ПРОЦЕССА РАЗРУШЕНИЯ
175
вблизи края трещины близко к плоскодеформированному со-
состоянию.
Допустим, что длина трещины гораздо больше толщины пла-
пластины и реализована тонкая структура конца трещины в том
смысле, что линейный размер пластической области вблизи
конца трещины (и толщина пластины) гораздо меньше харак-
характерного размера в плане (например, длины трещины). Тогда
-коэффициенты интенсивности напряжений в рассматриваемом
конце трещины будут по-прежнему теми единственными внеш-
внешними параметрами, через которые могут быть выражены зако-
закономерности локального разрушения и, в частности, особенности
структуры конца трещины.
Поэтому все результаты механики хрупкого разрушения,
основанные лишь на представлении о коэффициентах интенсив-
интенсивности напряжений в конце трещины, целиком переносятся и на
рассматриваемый случай. Однако при этом соответствующие
константы и прежде всего соответствующая вязкость разруше-
разрушения, будут зависеть уже от толщины пластины.
Рис. 49.
Чтобы отразить эту зависимость для трещин нормального
разрыва, будем обозначать через К и Кс коэффициент интен-
интенсивности напряжений и вязкость разрушения соответственно.
Подчеркнем, что в определение понятия «нормальный разрыв»
входят лишь условия Кп = Km = 0 на расстояниях, больших
по сравнению с размером пластической зоны и толщиной пла-
пластины; реализующийся на самом деле тип разрыва может быть
весьма далек-от нормального разрыва, в особенности в области
вблизи свободной поверхности пластины.
Диаграмма К — А/ для пластин имеет характерный вид [35],
Изображенный на рис. 49. В качестве приращения длины тре-
Щнны Д/ берется средняя по толщине пластины величина.
176
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
1ГЛ. IV
К..
При величине коэффициента интенсивности напряжений,
равной Kic, на диаграмме наблюдается скачок*), являющийся
следствием локального разрушения в центральной части вна-
вначале прямолинейного фронта трещины и быстрого продвиже-
продвижения контура трещины в этой об-
области. Затем фронт трещины
останавливается; при дальней-
дальнейшем увеличении К наблюдается
медленное неравномерное по
фронту подрастание трещины, до
тех пор пока не будет достигнуто
значение /С*, отвечающее момен-
моменту перехода тонкой структуры в
неустойчивое состояние (см. рис.
46). Если тонкая структура тре-
трещины устойчива, то может быть
достигнуто также предельное зна-
значение Кс-
Типичная зависимость К* от
толщины пластины h изображе-
изображена на рис. 50**). Наиболее ха-
характерная черта таких зависи-
зависимостей состоит в том, что при
достаточно больших толщинах
пластин величина К* и толщина
«губы среза» hJ2 становятся
постоянными величинами для данного материала; при h ~ /г*
достигается наибольшее значение К*, которое в два-три раза
больше наименьшего зна«
чения, равного Kic.
5. Масштабный эф-
эффект. Допустим, что обра-
р зец с начальной искус-
искусственной трещиной под-
подвергается растяжению
(рис. 51). Толщина h об-
образца считается достаточ-
достаточно большой, так что рас-
рассмотренными в предыду-
предыдущем пункте эффектами
можно пренебречь. Опыт показывает [68], что с увеличением абсо-
абсолютных размеров образца среднее разрушающее напряжение в се-
12
16 го
h,MM
Рис. 50.
Рис. 51.
*) В американской литературе это явление носит название «pop-in» .
**) Приведенная кривая построена по данным работы Ирвина, Киса и
Смита [<"],
§ 6] НЕКОТОРЫЕ ЭФФЕКТЫ ПРОЦЕССА РАЗРУШЕНИЯ 177
чении с трещиной («сечении-нетто») падает (рис. 52). При этом
его наибольшее значение равно ов (в модели идеального упруго-
пластического тела значение ав аппроксимируется величиной as)
я соответствует малым размерам образца, когда характерный
линейный размер предельной пластической области в конце
трещины при /Ci = /Cic гораздо больше
L и /. Это условие при помощи D.100) ,pj$H
можно записать так: *
Эффект уменьшения прочности наи-
наиболее ясно проявляется при достаточ-
достаточно больших размерах образца, когда
на конце трещины формируется тон-
тонкая структура; в этом случае
Рис-52'
и соответствующее значение прочности может быть вычислено
методами механики хрупкого разрушения.
Опытные данные [35] позволяют уточнить границу примени-
применимости механики хрупкого разрушения, вытекающую из D.128).
Согласно этим данным, результаты, полученные методами ме-
механики хрупкого разрушения, т. е. на основе концепции Kic,
удовлетворительно согласуются с экспериментальными резуль-
результатами вплоть до среднего разрушающего значения напряже-
напряжения в «сечении-нетто», равного*) О,8(Хо,2, если вместо длины
трещины I в формулы для прочности подставить величину
I + А/, где поправка
А/ «* PK2idao,2 (р —некоторое число) D.129)
учитывает подрастание трещины и пластическую зону (раз-
(разность Kic и Ки).
6. Эффект Грини. Если образец с трещиной, изображенный
на рис. 51, подвергнуть сначала сжатию, а затем растянуть до
разрушения, то вязкость разрушения получится несколько мень-
меньшей. Этот эффект объясняется двумя основными причинами:
а) предварительное сжатие уменьшает остроту трещины и при-
приводит к появлению остаточных растягивающих напряжений в
пластической области вблизи конца трещины, б) предваритель-
предварительное сжатие уменьшает прочность пластически деформирован-
деформированного металла на растяжение вследствие эффекта Баушингера.
*) Напомним, что условный предел текучести иа растяжение Сто.г равен
тому значению напряжения, при котором в гладком растягиваемом стержне
Появляется необратимая пластическая деформация величиной 0,2%.
178 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
Это явление, замеченное впервые Грини [б9], имеет значение
только для малопрочных пластичных металлов.
7. Влияние температуры на вязкость разрушения. Вязкость
разрушения для большинства хрупких материалов (стекла, ке-
керамика, графит, прочные горные породы и т. д.) монотонно па-
падает с ростом температуры. Заметим, что для таких материалов
вязкость разрушения можно выразить через другие постоянные
при помощи методов, изложенных в гл. II.
Вязкость разрушения большинства металлов монотонно воз-
возрастает с увеличением температуры, за исключением некоторых
довольно узких температурных диапазонов,
в которых вязкость разрушения изменяется
почти скачкообразно.
Одна из таких наиболее характерных
температурных зон обусловлена резким из-
изменением подвижности дислокаций при
этих температурах и, как следствие, резким
изменением способности материала к пла-
пластической деформации. Это явление назы-
называют хладноломкостью. Вязкость разруше-
разрушения по сравнению с другими характеристи-
характеристиками материала наиболее чувствительна к
изменению температуры в диапазоне тем-
рис 53. ператур хладноломкости (см. рис. 53, где
через TL и Ти обозначены нижняя и верхняя
границы хладноломкости). Разность Ти — Г, обычно не пре-
превышает нескольких десятков градусов.
При определенных температурах в металлах, их сплавах и
полимерах могут протекать химические реакции, фазовые пре-
превращения, микроструктурные изменения и т. д. Все эти внутрен-
внутренние изменения в материале немедленно сказываются в резком
увеличении или уменьшении К\с. Эти явления практически ис-
используются в металлургическом процессе и в различных техно-
технологических процессах термообработки, старения, закаливания,
пластификации и т. д. с целью придания материалу нужных
прочностных свойств.
8. Влияние скорости нагружения и скорости роста трещины
на вязкость разрушения. Вязкость разрушения металлов зави-
зависит от скорости нагружения dKi/dt. У некоторых металлов [35]
она изменяется в 1,5—2 раза при изменении скорости на-
нагружения на пять порядков, что соответствует переходу от
обычного медленного нагружения к квазистатическому удар-
ударному.
Вязкость разрушения малоуглеродистой стали, как правило,
убывает с ростом скорости нагружения, причем эффект тем за-
заметнее, чем меньше содержание углерода в стали. Этот эффект,
§ 6] некоторые эффекты Процесса разрушения 179
по-видимому, объясняется явлением задержки текучести [70],
наблюдающимся у малоуглеродистых сталей.
Более общим следствием увеличения скорости нагружения
является локальное увеличение температуры вблизи края тре-
трещины. Это в какой-то мере присуще всем упруго-пластическим
материалам, например, металлам и полимерам.
Верхнюю оценку величины локального теплонагрева для
движущейся трещины можно произвести следующим простым
способом. Будем считать, что вся необратимая работа y> затра-
затраченная на образование единицы площади свободной поверхно-
поверхности трещины, переходит в теплоту, выделяющуюся в пластиче-
пластическом слое единичной длины; толщина слоя, -согласно D.100),
равна
(влиянием остаточных напряжений на толщину слоя пренебре-
пренебрегаем) . Допустим, что процесс нагружения весьма быстрый (ло-
(локально адиабатический), так что утечкой тепла из пластиче-
пластического слоя можно пренебречь. Тогда среднее увеличение тем-
температуры в слое AT будет равно
Здесь р — плотность, с — теплоемкость.
При аналогичных допущениях можно найти верхнюю оценку
величины локального повышения температуры в пластической
области вблизи края трещины для неподвижной трещины. Пусть
коэффициент интенсивности напряжений очень быстро увеличи-
увеличивается от нуля до максимально возможной величины Kic. За
это время в пластической области диссипируется энергия, имею-
имеющая порядок
l (Гр~<г,/?). D.131)
Здесь 5 — площадь пластической области, Гр — интенсивность
пластических деформаций сдвига. Отсюда находим максимально
возможное повышение средней температуры
ДГ = D/(pcS) « аЦ(рсЕ). D.132)
Формулы D.130) и D.132) дают, как видно, примерно одина-
одинаковые значения.
У сталей, даже самых высокопрочных, разогрев оказывается
незначительным и не превышает 10—20 °С; у титановых спла-
сплавов разогрев может достигнуть уже нескольких сот градусов.
По-видимому, именно локальное повышение температуры
180 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ IV
объясняет наблюдающееся на опыте увеличение вязкости разру-
разрушения некоторых титановых сплавов с увеличением скорости
нагружения [35].
Следует отметить, что скорость роста трещины dl/dt и ско-
скорость нагружения dKildt в случае постоянных внешних нагру-
нагрузок связаны очевидным соотношением
Поэтому в этом случае указанные параметры равнозначны
с точки зрения оценки их влияния на вязкость разрушения.
9. Влияние времени. Замедленное разрушение. Если обра-
образец с трещиной подвергнуть нагружению постоянной во времени
нагрузкой, меньшей критической, то, вообще говоря, через не-
некоторое время т образец разрушится (предполагается, что
dKi/dl>0). Этот эффект также не описывается классической
концепцией механики хрупкого разрушения D.1).
Общее время до разрушения можно представить в виде
суммы
т = Т1 + т2. D.134)
Здесь xi — продолжительность инкубационного периода, в те-
течение которого исходная трещина не развивается, тг — время
роста трещины от начальной до критической величины. По-
Последняя отвечает тому моменту, когда коэффициент интенсив-
интенсивности напряжений в конце трещины достигает величины вяз-
вязкости разрушения данного материала.
Если реализована тонкая структура конца трещины, то из
общих соображений теории флуктуации для времени п полу-
получается следующее соотношение [20]:
U-?Kl . D.135)
Здесь R—универсальная газовая постоянная, Т — абсолютная
температура, т0, U и г] — постоянные материала, которые зави-
зависят также от окружающей среды. В работе [71] эта зависимость
была подтверждена для некоторых алюминиевых сплавов.
Если реализована тонкая структура конца трещины, то ско-
скорость докритического роста трещины dl/dt хорошо коррелирует
[72] с коэффициентом интенсивности напряжений Ki, т. е.
dl/dt = f(Ki), D.136)
где / — некоторая функция. Кинетические соображения приво-
приводят к следующей зависимости [20]:
^ ^^. D.137)
§6] НЕКОТОРЫЕ ЭФФЕКТЫ ПРОЦЕССА РАЗРУШЕНИЯ 181
Здесь у0) ?, U— постоянные материала, зависящие от окружаю-
окружающей среды.
Соотношения типа D.136) позволяют определить время до-
критического развития трещины т2. Формула D.137) в перемен-
переменных «логарифм времени тг — приложенное напряжение р» при-
.водит к характерной линейной зависимости, подтвержденной,
например, для некоторых закаленных хромокремнистых сталей
в работе [74] (см. также [7б'76]).
Относительная роль указанных двух этапов (инкубацион-
(инкубационного периода и периода роста трещины) зависит от условий
испытания и от материала.
Практически, если коэффициент интенсивности напряжений
/Ci меньше некоторой «пороговой» величины Късс, трещина не
развивается. Зависимости D.135) и D.137) не описывают этого
«порога».
Формулы типа D.135) или D.137) позволяют объяснить
большинство экспериментальных данных по временной зави-
зависимости прочности в инактивных средах. Однако общность этих
формул иллюзорна; это объясняется тем, что эти формулы
имеют структуру вида 0-оо. Действительно, множители то и Vo
очень малы (например, то ~ 10~12 сек), а множитель exp(U/RT)
чрезвычайно велик (напомним, что Т/ -— 104 кал/моль, R л;
« 2кал1'{град• моль)). Поэтому относительно небольшим изме-
изменением постоянных т, U, ц, лежащих в пределах опытных дан-
данных, можно получить любое требуемое значение ti или dl/dt
(своеобразная неустойчивость, вызванная неопределенностью
произведения типа 0-сю). По этой причине указанные формулы
.не годятся для практического применения (т. е. для прогноза
долговечности при заданных эмпирических константах т0, U, ?),
так как они требуют недостижимо высокой точности определе-
определения этих эмпирических постоянных, чтобы добиться точности
предсказания хотя бы по порядку величины.
Однако те же самые формулы становятся пригодными для
расчета, если их записывать в виде
т, = Al exp (— aiKJT), dl/dt = v2 exp (a2KJT),
где Аи аи v2, a2 — некоторые эмпирические константы (для опре-
определения А\ и v2, на основании изложенного, требуются допол-
дополнительные опыты, так как их нельзя определить по to, v0, U).
При этом указанные формулы проигрывают в общности, но
зато выигрывают в содержании. Именно в таком смысле сле-
следует понимать формулы D.135) и D.137).
10. Влияние внешней среды. Коррозионный и адсорбцион-
адсорбционный механизмы. Наиболее сложным является вопрос о влиянии
внешней среды на развитие трещины. Экспериментальные дан-
данные р, 7б, 7г, 78] свидетельствуют о том, что водород, жидкие
182 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
металлы, влага, поверхностно-активные вещества обычно способ-
способствуют росту трещин в металлах (и уменьшают «пороговый»
коэффициент интенсивности напряжений Кыс)\ в то же время
кислород, добавленный даже в очень небольших количествах
в водородную среду, практически останавливает в некоторых
случаях развитие трещин.
Форма зависимости скорости докритического развития тре-
трещины dl/dt от коэффициента интенсивности напряжений Ki мо-
может быть весьма различной, характеризуя тот или иной домини-
доминирующий механизм разрушения в конце трещины [72-75].
По-видимому, наиболее полно изучено прямое адсорбцион-
адсорбционное воздействие активной внешней среды на материал, сказы-
сказывающееся непосредственно в уменьшении истинной поверхност-
поверхностной энергии материала yt. Последняя может быть выражена ме-
методами гл. II через постоянные других физических процессов.
Некоторые соображения [79] приводят к выводу о том, что yt
имеет порядок yoJE. Поэтому вдякое изменение y* вызывает
пропорциональное изменение необратимой работы у и соответ-
соответствующее изменение вязкости разрушения материала.
В то же время известный эффект Иоффе [17]> при котором
происходит растворение поверхностных слоев материала вместе
с трещинами (или, по крайней мере, затупление конца тре-
трещины), приводит к упрочнению материала под воздействием
внешней среды.
В отличие от физической (обратимой) адсорбции, влияние
химической (необратимой) адсорбции, как и коррозионного воз-
воздействия, изучено гораздо менее полно.
Вопросы докритического развития усталостных и коррозион-
коррозионных трещин имеют основное практическое значение; исследо-
исследование их занимает центральное место в современной механике
хрупкого разрушения.
11. Влияние горения твердого тела. Если твердое тело пред-
представляет собой взрывчатое вещество, то при некоторых условиях
в теле может произойти бьштрое развитие начальных трещин,
что вызовет резкое изменение нормального режима горения [80].
12. Вторичные звуковые и электромагнитные эффекты. При
развитии трещины ее край является источником звукового и
электромагнитного излучения; эти эффекты представляют
интерес, в частности, для методов неразрушающего контро-
контроля [81-82].
13. Самоподдерживающееся разрушение. Разрушение мате-
материалов с прочностью, близкой к теоретической, должно быть
в какой-то степени близким к теоретической диссоциации, т. е.
в результате разрушения должно образовываться большое коли-
количество мелких частиц. Это явление действительно наблюдается,
например, при разрушении высокопрочных стекол [83]. Разру-
f 7J МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ 183
Шение таких материалов происходит в волне разрушения, ана-
аналогичной в некотором смысле детонационной волне во взрывча-
взрывчатых веществах [84].
Самоподдерживающееся разрушение может иметь место так-
также в обычных хрупких телах (например, в стекле, прочных гор-
горных породах и т. д.), если предварительное нагружение тела
или некоторого его объема близко к всестороннему сжатию.
Это условие реализуется, например, в приконтактной зоне при
соударении хрупких тел [85], на продолжении выработки в гор-
горной породе [86] и т. д.
14. Влияние двуосности напряженного состояния. Согласно
концепции /Cic, прочность тела определяется лишь составляю-
составляющей внешней нагрузки, обеспечивающей растяжение по нор-
нормали к трещине, а растяжение вдоль трещины не влияет на
предельную нагрузку, так как не вызывает концентрации на-
напряжений на фронте трещины.
Это заключение противоречит многочисленным эксперимен-
экспериментальным данным для пластичных металлов и полимеров, со-
согласно которым опасность хрупкого разрушения возрастает
с увеличением растяжения в плоскости трещины. Для некото-
некоторых неориентированных полимеров предельная нагрузка при
всестороннем растяжении пластины с трещиной на порядок
ниже, чем при одностороннем растяжении.
Это наиболее типичный эффект, который не может быть
объяснен в рамках представления о тонкой структуре; он объ-
объясняется тем, что растяжение в плоскости трещины по разным
причинам «загоняет» пластическую область в конец трещины.
У металлов причина кроется в сдвиговой дислокационной при-
природе пластичности, у полимеров — в ориентационном характере
пластического течения, приводящего к существенно анизотроп-
анизотропной пластичности.
§ 7. Методы определения вязкости разрушения
При экспериментальном определении вязкости разрушения
/Cic (или Кс Для сквозных трещин в пластинах малой толщины)
встают следующие основные проблемы:
а) выбор наиболее рациональной формы и размера образца,
а также схемы нагружения;
б) создание искусственных трещин;
в) регистрация длины трещины и нагрузок.
В зависимости от вида материала и от экономических воз-
возможностей исследователя эти вопросы в применяемых на прак-
практике методах решаются по-разному. Универсального метода, ко-
который наилучшим образом решил бы эти вопросы для всех ма-
материалов, по-видимому, указать нельзя.
184
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
Наиболее существенные ограничения связаны с выбором
размера образцов, поскольку в небольшом образце из хрупкого
материала трудно создать трещину, а у пластичных материа-
материалов существует некоторый минимальный размер образца, ниже
которого разрушение становится преимущественно вязким (на
опыте последнее сказывается в том, что формально определяе-
определяемые величины Kic, у, Кс становятся зависящими от размеров
образца).
Применяемые на практике экспериментальные методы мож-
можно условно разбить на следующие три группы:
A. Методы, в которых используется корреляция вязкости
разрушения с другими, более легко измеряемыми величинами.
Б. Прямые методы измерения необратимой работы у.
B. Методы, основанные на решении конкретных задач линей-
линейной механики разрушения.
Рассмотрим каждую из этих групп в отдельности.
А. Наиболее заманчивыми представляются методы первой
группы. Действительно, наличие надежной корреляции, напри-
например, между Kic и значениями твердости, ударной вязкости, 0В,
0о,2 и др., позволило бы весьма быстро находить вязкость раз-
разрушения при помощи стандартной аппаратуры. Хотя в суще-
существование такой корреляции для всех материалов трудно по-
поверить, для некоторых классов материалов она вполне воз-
возможна. На образцах определенной формы с трещинами такие
корреляционные зависимости в некоторых случаях можно на-
находить опытным путем. Такие корреляции особенно полезны и
надежны, потому что позволяют
определять вязкость разрушения
в условиях, максимально прибли-
приближенных к условиям разрушения
конструкции. Приведем три лри*
мера.
Растяжение. Пусть разруше-
разрушение металлической конструкции
происходит из-за наличия пло-
плоской краевой трещины под дей-
действием растяжения, перпендику-
перпендикулярного к плоскости трещины
(рис. 54). Чувствительность материала к дефектам такого типа
и вязкость разрушения можно найти, не прибегая к теоретиче-
теоретическим решениям. Для этого берется образец любой удобной из
конструктивных соображений формы (например, в форме пря-
прямоугольного параллелепипеда), в котором под действием цик-
циклического растяжения создается краевая усталостная трещина;
затем образец растягивается до разрушения и замеряется раз-
разрушающая нагрузка 0, соответствующая созданной трещине.
Рис. 54.
|'7] МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ 185
Размер образца должен быть таким, чтобы была реализована
тонкая структура конца трещины.
На основании анализа размерностей корреляционная связь
должна иметь вид
oVa/Kic = h(a/h). D.138)
Здесь /i — некоторая безразмерная функция своего аргумента,
а и h — характерные линейные размеры трещины и образца со-
соответственно.
Теперь заметим, что скорость роста усталостной трещины,
чрезвычайно чувствительна к величине коэффициента интенсив-
интенсивности напряжений (см. формулу D.125)). Поэтому трещина раз-
развивается так, чтобы распределение коэффициента интенсивности
напряжений вдоль ее контура выравнивалось; последнее харак-
характерно такжг для хрупкой трещины при монотонном нагружении
в некотором диапазоне начальных трещин [87]- Вследствие этого
можно говорить о практически достаточно точном соответствии
формы развитой усталостной трещины и развитой хрупкой тре-
трещины в начале ее нестабильного роста для некоторого множе-
множества начальных трещин различной формы.
Аналогичное стремление к некоторой стандартной форме
краевой трещины будет иметь место также у коррозионных тре-
трещин и трещин замедленного разрушения, так как скорость ро-
роста таких трещин также весьма чувствительна к величине ко-
коэффициента интенсивности напряжений*).
Из соображений анализа размерностей форма усталостной
трещины, созданной в результате растяжения, при заданной на-
нагрузке не будет зависеть от свойств материала (если не считать'
коэффициента Пуассона), а будет вполне определяться формой
и размерами образца. Поэтому функция /i в D.12) для образца
заданных размеров и формы будет зависеть лишь от одного
аргумента, и ее можно определить экспериментально на осно-
основании таких же опытов по разрушению с искусственно создан-
созданной усталостной трещиной для некоторого контрольного мате-
материала с уже известной вязкостью разрушения Къ (в качестве а
можно взять, например, глубину трещины, а в качестве h —
толщину образца).
Коль скоро функция /i определена, формулу D.138) можно
использовать для определения вязкости разрушения других
материалов из аналогичных экспериментов с образцами той же
формы и размеров (по разрушающей нагрузке о и глубине тре-
трещины а).
' *) Возможны исключения (например, для коррозионных трещин, разви-
развивающихся по электрохимическому механизму, см. гл. VII).
186
Основы механики Хрупкого разрушений
[ГЛ. IV
Рис. 55.
Изгиб. Совершеннно аналогичные соображения верны также
для практически важного случая чистого изгиба моментом М
(на единицу ширины); при этом усталостная трещина должна
создаваться под действием циклического изгиба образца фикси-
фиксированных размеров (рис. 55). Соот-
Соответствующая корреляционная связь
имеет вид
M/(Kica3l2)^f2(a/h). D.139)
Удар. В тех случаях, когда кон-
конструкция подвергается быстропере-
менным или ударным нагрузкам,
представляет интерес оценка вязко-
вязкости разрушения в условиях ударно-
ударного нагружения, так как зависимость
вязкости разрушения от скорости
деформирования может быть существенной. Например, при из-
изменении скорости деформирования на пять порядков, что при-
приблизительно соответствует переходу от обычного медленного на-
нагружения к ударному, вязкость разрушения малоуглероди-
малоуглеродистой стали уменьшается в полтора раза, а вязкость разрушения
некоторых титановых сплавов
тд увеличивается примерно в пол-
полтора раза [35].
Допустим, что на пластину
падает ударник весом mg с вы-
высоты Н (рис. 56). При квазиста-
квазистатическом ударе хрупкое разруше-
разрушение определяется максимальной
силой сопротивления Р, достигае-
достигаемой в тот момент, когда удар-
ударник останавливается; следова-
следовательно,
W) = h{alh)- D.140)
Рис. 56. _ , ,. ,
Здесь ]г — безразмерная функ-
функция одного аргумента для тре-
щиноподобных дефектов стандартной формы, а — глубина тре-
трещины, h — толщина пластины.
В том случае, когда конец ударника имеет форму сферы ра-
радиуса гь где rx < h, а удар идеально упругий, силу Р можно
найти по формуле Герца
§ 7] МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ 187
Здесь v — скорость ударника в момент, предшествующий на-
началу контакта, Vj и ?j (? = 1, 2) — коэффициенты Пуассона и
модули Юнга материала ударника и образца.
Если же форма ударника такова, что площадка контакта
не изменяется в процессе упругого удара, то силу Р легко опре-
определить по упругому коэффициенту постели k так:
В других случаях требуется непосредственное измерение
силы Р.
Рассмотренная задача представляет интерес также в связи
с распространенным методом испытания материалов на удар-
ударную вязкость (рис. 57). Пусть
образец Шарпи с V-образным
сквозным надрезом глубины
/о и усталостной трещиной дли-
длины /, развившейся из дна над-
надреза в глубину образца, под-
подвергается удару. В этом слу-
случае величина разрушающей
кинетической энергии ударни-
ударника, приходящейся на единицу
нетто-площади (ударная вяз- Рис 57.
кость), определяется при помо-
помощи формулы D.140), где нужно положить а = 10 + I. Определив
на контрольном материале функцию f3, на основании этой фор-
формулы имеем корреляцию ударной вязкости с вязкостью разру-
разрушения для любых материалов. Еще раз подчеркнем, что этакор--
реляционная связь будет различной для образцов разной формы
и условий закрепления. При этом методе испытаний, очевидно,
усталостная трещина может быть создана различными спосо-
способами, лишь бы фронт ее был параллелен дну надреза.
Во всех изложенных примерах для получения корреляцион-
корреляционных зависимостей был применен метод моделирования разру-
разрушения .на образцах одних" и тех же размеров из разных мате-
материалов, однако, очевидно, можно использовать также геометри-
геометрически подобные образцы с геометрически подобными трещи-
трещинами. При этом нужно следить лишь за соблюдением условия
тонкой структуры; практические границы соблюдения этого
условия, а тем самым, границы законного применения представ-
представлений механики хрупкого разрушения оказываются удивитель-
удивительно широкими, особенно если использовать эмпирическую по-
поправку на подрастание трещины и наличие пластической зоны
(см. формулу D.129)).
Указанный метод моделирования можно использовать и во
многих других практически часто встречающихся случаях
188 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ..IV
.разрушения; следует иметь в виду, что хотя используемое пред-
представление о наличии некоторых стандартных форм простран-
пространственной трещины в момент начала ее нестабильного развития
достаточно универсально и охватывает наиболее важные прак-
практически случаи, тем не менее возможны исключения, относя-
относящиеся к начальным трещинам продолговатой формы. В послед-
последнем случае возникают осложнения, связанные с трудностями
создания трещины заранее заданной формы и с появлением
в корреляционной зависимости других параметров моделирова-
моделирования, описывающих форму трещины.
Б. В методах второй группы экспериментально измеряется
величина необратимой работы у. Рассмотрим теоретические
основы этих методов.
Пусть на упругое тело действует некоторая внешняя сила Р;
смещение v точки приложения силы вследствие деформации
тела и развития трещины равно
и = ЯР, . D.141)
где X — податливость упругой системы, которая зависит от ее
конфигурации и в том числе от размера трещины. Чтобы избе-
избежать возникающего в теории упругости парадокса расходимо-
расходимости, связанного с действием сосредоточенной силы, нужно пред-
представлять себе силу Р приложенной
к некоторому абсолютно жесткому
телу конечных или бесконечных
размеров, которое давит на упругое
тело; при этом v будет равно сме-
смещению жесткого тела. Зависимость
D.141) схематически изображена
на рис. 58 кривой ОАВС. Трещина
начинает расти от точки А; участок
О А — прямолинейный, что соответ-
соответствует неподвижной начальной тре-
трещине. В случае хрупкой трещины
при разгрузке все напряжения и
Рис. 58. смещения в упругой системе долж-
должны исчезать, а трещина вследствие
необратимости оставаться неизменной; поэтому на диаграмме
Р — v участок разгрузки будет представляться прямолинейным
отрезком, проходящим через начало координат под углом к оси
v, меньшим соответствующего угла наклона начального прямо-
прямолинейного участка нагружения. Последнее вытекает из того оче-
очевидного факта, что при развитии трещины податливость упругой
системы всегда увеличивается.
Необратимая работа, затраченная на образование новой
поверхности трещины вследствие ее роста, равна площади гй-
5 7] МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ 189
стерезисной петли, образовавшейся в процессе «нагружение —
разгрузка» (на рис. 58—площадь заштрихованного криволи-
криволинейного треугольника ОАВ). Отсюда величина у будет равна
указанной площади, деленной на приращение площади поверх-
поверхности тела.
Возможны два случая: а) развитие трещины неустойчиво
с самого начала, б) развитие трещины устойчиво.
В первом случае реализуется лишь (теоретически) беско-
бесконечно малая гистерезисная петля, так как точка В бесконечно
близка к концу прямолинейного участка нагружения (к точке
А). Вычисляем эту площадь, используя D.141)t
ОАВ ОАВ
= j § P2dK = \PAdh D.142)
ОАВ ОАВ
(РА — величина силы Р в момент разрушения).
Здесь dk и d2 — бесконечно малые приращения податливо-
податливости -и поверхности одного берега трещины, соответствующие
участку АВ. Так как К для данного тела и условий нагружения
представляет собой однозначную функцию 2, отсюда находим
2y = jP2AdWZ. D.143)
Изложенный подход, по существу, эквивалентен энергетиче-
энергетическому методу, на основании которого Ирвин впервые получил
формулу D.143) и предложил использовать ее для измерения
у. Этот метод называют методом податливости или смещения
[35]. Осуществление этого метода на практике требует весьма
точных измерений смещения v и изменения поверхности тре-
трещины 2.
В случае устойчивого развития трещины величины Я и 2 мо-
могут претерпевать конечные изменения; в этом случае у можно
определять непосредственным изменением конечной площади
гистерезисной петли на диаграмме Р — v. При этом требования
К точности измерения и и 2 значительно меньше, так что этот
метод можно использовать даже для измерения у у хрупких
материалов типа стекол, графита, кристаллов и т. д.
Некоторые наиболее удобные типы образцов и схемы нагру-
нагружения, применяемые на практике для осуществления контроли-
контролируемого устойчивого роста трещин, изображены на рис. 59—61,
Вдавливание плоского осесимметричного индентора (рис. 61)
целесообразно применять лишь для хрупких материалов, прак-
практически не испытывающих пластических Деформаций при
190
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
1ГЛ, IV.
больших напряжениях сжатия (стекло, прочные горные породы
и т. д.). Схема с сосредоточенной силой была использована
С. Е. Ковчиком и В. В. Панасюком [88]. Схема, изображенная
на рис. 59, использовалась в работе [89].
Рис. 59.
Рис. 60.
Теоретический подход, примененный для обоснования этих
методов, дает еще один весьма наглядный способ построения
теории трещин. Из него видно, что представление о поверхно-
поверхностной энергии упругих тел яв-
ляется следствием таких допуще-
допущений: а) конечному приращению
внешней силы отвечает конечное
(или нулевое) приращение по-
поверхности трещины, б) упругий
материал однороден и изотро-
изотропен по прочности, в) при любом
неизменном во времени значении
I внешней силы, меньшей неко-
некоторой критической, трещина не
растет. В рамках этих допуще-
допущений структура конца трещины
может быть совершенно произ-
произвольной.
Следует отметить, что экспе-
экспериментальные методы рассмот-
рассмотренного типа применимы также для изучения развития трещин
в упруго-пластических материалах (для определения диаграмм
разрушения).
В. Наиболее широко применяются методы измерения Кц,
в которых реализуются размеры образца и способ нагружения,
соответствующие какому-либо конкретному теоретическому ре-
решению линейной механики разрушения. В принципе любое та-
Рис. 61.
§ 7] МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ . 191
кое решение можно использовать для определения вязкости
разрушения.
В табл. 4.1 приведены некоторые достаточно простые схемы
нагружения и указаны типы образцов, позволяющие наиболее
экономно расходовать материал с использованием образцов
сравнительно небольших размеров. Там же даются формулы,
по которым нужно определять К\с, используя полученные экспе-
экспериментально значения разрушающей нагрузки. Формулы эти
можно применять практически даже тогда, когда среднее на-
напряжение в сечении-нетто достигает 0,8 Оо,2 (т. е. почти все се-
сечение образца под трещиной переходит в пластическое состоя-
состояние), если использовать' в этих формулах эмпирическую по-
поправку Р5]. Поправка* состоит в следующем: начальное значение
/Cico получают по упомянутым формулам, затем по тем же фор-
формулам вычисляют следующее приближение Kid," причем вместо
длины I в этих формулах берут 1 + &1, где kl — pK\cQl<5% 2; да-
далее по тем же формулам вычисляют Kic2> причем вместо / бе-
берут / + А/, где А/ = pKlci/o$ 2, и т. д. Полученное таким методом
последовательных приближений предельное значение Къ прини-
принимают за вязкость разрушения.
Величина поправочного коэффициента р выбирается из сле-
следующих соображений. Аппроксимируем напряжение ау на про-
продолжении трещины в упругой области функцией вида
ay = KilV2n(x — M) при у = 0 D.144)
(х—расстояние от конца трещины).
Эта функция описывает распределение напряжения ау в фик-
фиктивном идеально-упругом материале с вязкостью разрушения
изучаемого реального материала, причем конец фиктивной тре-
трещины сдвинут на расстояние А/ относительно конца реальной
трещины. Если возможна такая аппроксимация, то границы тон-
тонкой структуры для фиктивного материала и трещины в нем
можно сдвинуть до края пластической области.
Напомним, что для трещин продольного сдвига, согласно
D.119), указанная аппроксимация оказывается точной, если А/
взять равным радиусу пластического круга на продолжении
трещины:
Al = K2mfBnk2). D.145)
Поскольку в тонких пластинах из упруго-пластического ма-
материала тип разрушения вблизи конца трещины разрыва бли-
близок к продольному сдвигу, было предложено [35] на основа-
основании D.145) брать в этом случае'коэффициент р равным 1/2п,
гчто оказалось в хорошем согласии с экспериментальными
данными Р5].
192
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
¦Ч"
га
83
о
в
я
я
4)
в
IS
I
?
к
а
к
t
5
В"
В
к
к
в
V
ч
о
5
о,
13
о
а
8
i
as
в
о
I
S
8
I
I
о
О
со
о
-С
II
+
V/
V
-с
V
>я
о
я
л
я
9
га
р.
ю
О)
s
я
и
§71
МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ
193
О
•I-
СО
о
г
•а
со
о
I
•а
о сГ
+ +
со со
о" о
I I
¦с -е
О)
s
X
S
S
о.
с
О
<и
s
к
в
В1
!U
S '
о.
с
О
я
к
в
В1
О)
S
S.
в
U
«о
Е
7 Г. П. Черепанов
194
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
«2
g
a
s
4)
S
0}
О
я
" f-
o
0>
о
льн
има
G
О
л
о Я
о ч
огреш
форм
Ч
S
«
?-
0}
В*
о
«I
ft
Схема
к
S
га
сил
Я
сосредоточен
я
3
&
я
о.
<м
о
1
•е
»-»
т
1B:
0,5
•я V/
,I<N Я
^ * '
О.
II
J
1
!
О)
о
а
зе:
га
о.
ю
О
ю
II °
" II
«э "
(N — о —"
II II II 11
1! II II II
о^ оз oq oq
^ !С !? "в
1
«3
—1
—^,
-*
СО л
о> о
+ v
х g v
^-
О.
о,
КЗ <N
»¦ А,
к X
ч
\
f Ч
(Ь rdr
t
с»
и
S
Щ
S
к
XT
и
<?
S
а
С
я
ч
ф
а
•S
ш
g
г
>,
а
(-
а>
а
s
о
и
га
ю
S
и
п
S
о
чистог
№
Ч
СО
Я
о
о
а;
Ч
S
фор
о
с
№
и
S-
ляе
преде
о
!^
гина
¦j
к
ч
о>
и
CD
4-
га
с;
о
О
<и
со
О.
\о
о
га
Е-
S
и
<**
00
га
S
X
и
ляется
и
№
га
Ч
га
SS
тер:
СЯ
S
к
к
•4J
юно:
ч
смыс
и
II 4
II о
^а
а
я я
11
si
2 ч
га о
хо «о
к к
и га
S
CD
S
схе
ется
X
ч
и
№
ени!
а
о
0TI
еском
в-
s
т
npai
и
той
црос
<и
.—. О)
Е|
га
ь X
о .
га
о.
$ 7] МЕТОДЫ ОПРЕДЕЛЕНИЯ ВЯЗКОСТИ РАЗРУШЕНИЯ 195
Для толстых пластин (т. е. для плоскодеформированного
состояния) число р получается совершенно другим. Из формулы
D.108), аппроксимирующей решение Раиса с сотрудниками [56],
вытекает, что в этом случае
Д/«— 0,015/i(]/as2. D.146)
Следовательно, для плоскодеформированного состояния р =
= —0,015. При этом формула D.108) аппроксимирует истинное
распределение ау вплоть до конца реальной трещины.
Наличие сложной структуры конца сквозных трещин в плас-
пластинах и большая легкость протекания пластического деформи-
деформирования в этом случае создает дополнительные трудности изме-
измерения Kic на образцах конечной толщины со сквозной трещи-
трещиной. Бойл, Салливен и Краффт предложили метод скачка [90],
который позволяет определять Kic на пластинах, толщина
которых меньше, чем это требуется для полностью прямого из-
излома. Этот метод основан на том, что первое заметное распро-
распространение сквозной трещины происходит скачкообразно; в этот
момент иногда слышен слабый треск. Во время скачка прямо-
прямолинейный фронт трещины искривляется, при этом центральная
часть его продвигается вперед, а часть, прилегающая к свобод-
свободным поверхностям пластины, почти не изменяет своего положе-
положения (см. рис. 48). Скачок, очевидно, происходит в тот момент,
когда коэффициент интенсивности напряжений на фронте тре-
трещины достигает величины Kic (напомним, что в центральной ча-
части фронта осуществляется плоскодеформированное состояние).
Момент скачка определяют или на слух, или при помощи при-
приборов, следящих за длиной трещины.
Для регистрации длины трещины применяют следующие
основные методы:
а) визуальный метод,
б) фото- и киносъемка,
в) измерение электросопротивления (образца с трещиной
или тонкого слоя, наклеиваемого на образец),
г) анализ разрывов тонких проволочек, наклеенных на пути
распространения трещины,
д) использование красящих жидкостей, загоняемых в тре-
трещину,
е) наблюдение цвета побежалости металла,
ж) метод вихревых токов,
з) применение датчиков смещения, ¦ фиксирующих разность
смещений в некоторых точках, расположенных по обеим сто-
сторонам пути распространения трещины,
и) акустический метод с применением пьезоэлектрических
датчиков,
к) фрактографический метод.
196 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
Каждый из упомянутых методов имеет свои достоинства и
недостатки, определяющие область его применения.
Искусственные трещины создаются следующими основными
способами:
а) локальным охлаждением области вблизи конца надреза
до температур, меньших температуры хладноломкости, с после-
последующим надрывом или ударным инициированием;
б) созданием усталостных трещин; •
в) применением нагрузок, приводящих к контролируемому
развитию устойчивых трещин из начального разреза (раскли-
(расклинивание, сосредоточенные силы и т. д.).
Следует отметить, что в некоторых случаях (пластичные ме-
металлы и полимеры) роль трещины может играть надрез, полу-
полученный обычным механическим способом, т. е. надрез с до-
довольно большим радиусом кривизны в конце. Это возможно в
тех случаях, когда раскрытие конца естественной трещины в
момент разрушения столь велико, что достигает размеров, при-
примерно равных размерам рабочей части инструмента (например,
толщины фрезы). Раскрытие конца трещины можно оценить по
формулам D.98) и D.107).
Максимально возможное раскрытие в ряде случаев можно
оценить практически из серии экспериментов по разрушению
одинаковых образцов с разрезами одинаковой глубины, но
различного радиуса кривизны дна надреза; существует такая
критическая величина радиуса надреза, что при радиусах кри-
кривизны, меньших этой величины, разрушающая нагрузка прак-
практически не зависит от радиуса дна надреза. Эта критическая
величина примерно равна наибольшему раскрытию естествен-
естественной трещины в ее конце. Для искусственных надрезов в этом
случае, разумеется, будет отсутствовать стабильное подрастание
конца трещины.
В некоторых случаях для определения вязкости разрушения
можно использовать следующий способ. Определяются средние
величины вязкости разрушения при нескольких значениях ра-
радиуса г искусственного надреза (серия образцов для каждого г)
и по этим опытным данным строится аппроксимирующая их
аналитическая "зависимость; распространение этой зависимости
вплоть до точки г = 0 позволяет найти наименьшую вязкость
разрушения, соответствующую максимально острому надрезу—¦
трещине.
Для любых г формула для вязкости разрушения берется
на основании решений механики хрупкого разрушения, полу-
полученных в предположении, что надрез представляет собой ма-
математический разрез нулевой трещины. Этот способ особенно
полезен в тех случаях, когда возникают трудности с созданием
трещины. В случае хрупких пористых тел (керамика, графиты,
J8] ТЕХНИЧЕСКАЯ ПРОЧНОСТЬ И ВЯЗКОСТЬ РАЗРУШЕНИЯ 197
горные породы и т. д.) экспериментально удается легко выхо-
выходить на горизонтальную асимптотику г-*0, применяя доступ-
доступные инструменты для создания надрезов с радиусом надреза
порядка наибольшего характерного размера пор.
Применяемые методы позволяют определять вязкость разру-
разрушения с точностью, примерно соответствующей точности изме-
измерения условного предела текучести ао,2-
Полученные различными методами значения вязкости разру-
разрушения некоторых материалов приводятся в Приложении II.
Величина Kic для стекол имеет порядок 1—2 кГ/мм\ для ме-
металлов 50—600 кГ/мм\ для хрупких горных пород 2—4 кГ/мм'Ь,
для некоторых полимеров 2—5 кГ/мм'Ь.
§ 8. Оценка технической прочности и вязкости
разрушения некоторых материалов
Одной из основных проблем материаловедения и металлур-
металлургии является создание материалов с наибольшей вязкостью
разрушения и наибольшей прочностью. Последнее требование
выражено не вполне четко, так как прочность не является кон-
константой материала. Поэтому будем различать два понятия: ме-
металлургическую прочность и конструкционную прочность. Под
первой понимается (обычно приводимое в справочниках по ма-
материалам) значение прочности, полученное на гладких лабора-
лабораторных образцах определенных размеров из материала в со-
состоянии поставки. Прочность изделия из этого же материала
(конструкционная прочность) иногда оказывается существенно
меньшей. Особенно часто это происходит при приближении к
области хрупкого разрушения.
Дефекты, служащие причиной разрушения образца или
конструкции, можно условно разделить на дефекты, образую-
образующиеся в металлургическом процессе (или в каком-либо другом
процессе создания заготовок материала), дефекты, создаваемые
в технологическом процессе сборки конструкции, и дефекты,
которые могут возникать или развиваться в процессе эксплуа-
эксплуатации конструкции (например, коррозионные или усталостные
трещины).
Наличие опасных дефектов технологического и эксплуата-
эксплуатационного происхождения как раз и объясняет обычно кажу-
кажущуюся преждевременной поломку конструкции.
Прочность конструкции всегда представляет собой некото-
некоторую случайную величину, так как, во-первых, точное располо-
расположение всех дефектов заранее неизвестно, а, во-вторых, если бы
это расположение и было точно известно, решение соответ-
соответствующей математической задачи было бы невозможно из-за
ее сложности.
198 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
При построении статистической теории прочности можно
идти двумя путями:
а) на основании опыта или интуиции выделить один или
несколько наиболее опасных дефектов, а остальные дефекты как
-бы равномерно «размазать», считая свойства получившейся
сплошной среды строго известными из макроэксперимента;
длина и, может быть, некоторые другие параметры, определяю-
определяющие расположение наиболее опасного дефекта, считаются слу-
случайными величинами с заданными функциями распределения;
б) все без исключения дефекты «размазать» по объему, счи-
считая получившуюся усредненную среду сплошной и «бездефект-
«бездефектной»; локальная прочность этой среды, а также напряжения
считаются некоторыми случайными функциями координат с за-
заданными функциями распределения в каждой точке тела (сред-
(средние значения напряжений и прочности определяются, соответ-
соответственно, из макротеории и макроопыта). При этом подходе
для получения окончательных выражений требуется еще ряд
дополнительных допущений.
Первый подход ближе к теории трещин (в нем подчерки-
подчеркивается физическая природа прочности); второй подход более
формален, он ближе к теориям прочности в сопротивлении ма-
материалов. Указанные подходы имеют несколько различные об-
области применения.
Допустим, что в процессе изготовления или эксплуатации
конструкции в ней не возникли более опасные дефекты, чем
металлургические, а характерный линейный размер конструк-
конструкции вел-ик по сравнению с размером зерна материала и раз-
размером дефекта. В этом случае применимость второго подхода
не вызывает сомнения. Именно этот подход разрабатывается
в большинстве исследований, посвященных статистическим воп-
вопросам прочности.
Теперь допустим, что при технологическом процессе или в
ходе эксплуатации в конструкции могут возникнуть более
опасные дефекты, чем металлургические. Для получения функ-
функций распределения согласно второму подходу требуется пред-
представительная выборка из некоторого числа п соответствующих
конструкций (минимально необходимое число п определяется
доверительным интервалом), при этом прогноз относительно
прочности одной конкретной конструкции оказывается уже ве-
вероятностным. Поэтому практически указанный подход может
быть применен лишь к сравнительно малоценным изделиям
массового производства; для уникальных или дорогих кон-
конструкций его использовать нельзя. В этом случае первый подход,
позволяющий, например, путем анализа сравнительно неболь-
небольшого числа поломок установить примерную величину и рас-
расположение дефектов, вызывающих разрушение, может оказать-
§ 8]. ТЕХНИЧЕСКАЯ ПРОЧНОСТЬ И ВЯЗКОСТЬ РАЗРУШЕНИЯ 199
ся единственно возможным. В дальнейшем в этом параграфе
дефекты технологического и эксплуатационного происхождения
исключаются из рассмотрения, и под прочностью будет пони-
пониматься обычная металлургическая прочность.
Представляют интерес оценки величины вязкости разруше-
разрушения и прочности, имеющие смысл для определенных классов
материалов в определенных условиях.
Тонкие пластины. Сквозные трещины «среза». В достаточно
тонких пластинах из упруго-пластического материала сквозные
трещины распространяются как трещины «среза», так что по*
верхность излома оказы-
оказывается наклоненной под
углом 45° к поверхности Р . —
пластины (косой излом, -* _
рис. 62). Рассмотрим сна-
сначала тот случай, когда
h <<¦ K\cjo2QiV т. е. толщи- —
на пластины значительно -=
меньше размера пласти- Р ~
ческой области вблизи
конца трещины, харак-
характерного для полностью Рис. 62.
прямого излома. При этом
пластическую область в конце трещины можно приближенно
считать плоскостью скольжения на продолжении трещинй
(см. рис. 40). В результате деформации пластины и разви-
развития трещины пластина теряет устойчивость в некоторой
окрестности трещины, причем с одного берега трещины пла-
пластина выпучивается в одну сторону, а с другого берега — в
другую сторону, в соответствии с рис. 62. Результат исчерпания
способности материала к пластическому течению ограничен
ситуацией, изображенной на нижнем рисунке, реализующейся
в конце трещины. Из геометрических соображений следует, что
при этом раскрытие трещины в ее конце 2v0 в момент продви-
продвижения конца трещины равно
2vo = h, D.147)
где h — толщина пластины. Это соотношение позволяет при по-
помощи формулы D.98) оценить вязкость разрушения /Сс тонких
пластин
Кс = V^Jh, V = josh. D.148)
Например, для алюминиевого сплава 7075-76 в случае, ис-
исследованном Ирвином с сотрудниками [67], толщина h при пол-
полностью «косом» изломе составляла 3 мм. Величина as для этого
200
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
сплава имеет порядок 50 кГ/мм2; отсюда по формуле D.148)
получаем у = 75 кГ/мм. Согласно опытам Ирвина, в этом слу-
случае у — 65 -т- 70 кГ/мм.
Полученная оценка Кс, строго говоря, справедлива только
для материалов, способных к неограниченному пластическому
течению вплоть до окончательного разделения образца. Для
большинства материалов ситуация, изображенная на нижнем
рисунке, не реализуется; поэтому формула D.145) дает завы-
завышенную оценку.
В некоторых материалах косой срез имеет место даже в
том случае, когда
К\с1
\ 2>
т. е. когда толщина пластины
значительно превышает размер пластической области вблизи
конца трещины, характерный для полностью прямого излома.
В этом случае разрушение можно считать квазихрупким; вели-
величина предельного раскрытия 2vu гораздо меньше толщины пла-
пластины h. Как вытекает из рис. 62, при этом на фронте трещины
возникает сложное напряженное состояние, которое о.твечает
комбинации продольного сдвига, и нормального разрыва с оди-
одинаковыми коэффициентами интенсивности напряжений К\ =
=/(ш=/<Уул2.Так как локальное разрушение при этом опреде-
определяется нормальным разрывом, то /Ci = /Cic в момент разруше-
разрушения, т. е. Кс = /2 К\с.
В общем случае в зависимости от значений безразмерного
параметра 1 = К\сОалЬ~Х величина вязкости разрушения Кс для
полностью косого излома изменяется от ]/2 /С1с до ]/ст4?/г.
Практически для большинства металлов и обычно применяемых
размеров образцов величина Кс при полностью косом изломе
изменяется в сравнительно узком диапазоне A,5 —- 2,5) Kic-
Сквозные трещины смешанного типа. Если сквозная трещи-
трещина в пластине вблизи свободных поверхностей пластины ведет
себя как трещина «среза» (косой излом), а в центральной
Рис. 63.
части — как трещина отрыва (прямой излом), то для приближен-
приближенной оценки можно пренебречь влиянием одной из поверхностей
пластины на другую, считая, что толщина «губ среза» равна
hj2, т. е. некоторой постоянной материала, отвечающей весьма
толстой пластине (рис. 63). Суммируя выражения для удель-
§8]
ТЕХНИЧЕСКАЯ ПРОЧНОСТЬ И ВЯЗКОСТЬ РАЗРУШЕНИЯ
201
ной необратимой работы образования каждой из этих двух ча-
частей новой поверхности трещины, получаем [20] следующее вы-
выражение для эффективной (средней по толщине пластины)
величины у:
К , 1 - v2
¦Kic
—г)
DЛ49)
Рис. 64.
Здесь величина ycv значительно меньше максимальной вели-
величины D.148) вследствие неспособности поверхностного слоя к
выпучиванию.
Зависимости D.148) и D.149) охватывают'весь диапазон
толщин от нуля до бесконечности (рис. 64). Этот вид функции
Y«=y(^) качественно хорошо
описывает имеющиеся экспери-
экспериментальные данные, однако вряд
ли всегда можно ожидать хоро-
хорошего количественного совпаде-
совпадения при всех h, поскольку теоре-
теоретические соображения, лежащие
в основе вывода этих формул,
справедливы, строго говоря, лишь
при очень малых и очень боль-
больших толщинах. Однако, если по-
постоянные os, Yep, К, фигурирую-
фигурирующие в формулах D.148) и
D.149), выбирать из условий наилучшего согласия с опытом, то
полученные зависимости дают также хорошее количественное
описание опытных данных при всех h.
Следует подчеркнуть, что критерием, характеризующим тол-
толщину пластины, помимо параметра | = КиОо^~\ является
также безразмерный параметр Д = h/l, где / — длина трещины
(или какой-либо другой характерный линейный размер поверх-
поверхности пластины). Именно этот параметр характеризует выпу-
выпучивание пластины, т. е. переход от решения, обладающего той
же симметрией, что и граничные условия, к несимметричному
решению. Трещины «среза» реализуются теоретически при
А->0, а чисто отрывные трещины — при А—> оо. Так как вели-
величина / не является локальным параметром, диаграммы типа
изображенной на рис. 64 в общем случае имеют смысл только
применительно к тому или другому кругу изучаемых конструк-
конструкций и материалов; они не имеют универсального характера
(в отличие от концепции Kic).
Наибольший интерес (и наибольшую сложность) представ-
представляет оценка величины Kic, для этого необходимо учитывать
внутреннюю структуру материала. Выделим следующие основ-
основные группы материалов: композитные гетерогенные мятр.пиялн
202 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
(в том числе металлы и их сплавы), хрупкие пористые мате-
материалы, гомогенные хрупкие материалы, полимеры.
Композитные гетерогенные материалы. Большинство важ-
важнейших конструкционных материалов относится к композитным
материалам, состоящим из нескольких компонентов и имеющим
весьма сложную внутреннюю структуру (неоднородную, анизо-
анизотропную, со сложным распределением внутренних напряжений).
В этот класс материалов нужно, прежде всего, включить ме-
металлы и их сплавы, затем металлопласты, стеклопластики, ком-
композиты на основе металла и углерода, металла и кремния и т.д.
Введем понятие структурной ячейки. Структурной ячейкой
будем называть минимальное по размерам образование мате-
материала, такое, что любое тело из данного материала можно счи-
считать склеенным из большого числа таких периодически повто-
повторяющихся в пространстве образований. Свойства материала в
структурной ячейке меняются от точки к точке, однако в соот-
соответствующих точках любых двух ячеек одинаковы.
Структурную ячейку можно определить, например, так, что-
чтобы граница ее (или область контакта ячеек) была наиболее
прочной.
Реальный композитный материал в лучшем случае состоит
из некоторого распределения более или менее подобных по
свойствам образований, поэтому представление о стандартной
для данного материала структурной ячейке с характерным раз-
размером d0 является некоторой идеализацией, оправдываемой
лишь простотой получающихся выводов и оценок.
В сплавах такими ячейками чаще всего являются зерна ос-
основного металла и химически активных примесей, образовав-
образовавшиеся из центров кристаллизации при отвердевании расплава;
роль прочностных барьеров на границах ячеек в некоторых слу-
случаях играют межкристаллитные пленки, образовавшиеся из хи-
химически неактивных атомов примесей, которые были оттеснены
к границе в процессе роста зерен.
Если представление о структурной ячейке применимо к дан-
данному материалу, то его вязкость разрушения из соображений
анализа размерностей должна быть такой:
*1в = ЛогвУ^. D.150)
Здесь о"в — средняя прочность на разрыв структурной ячейки с
характерным размером do, I — примерно постоянный множитель
порядка единицы.
Величина ов в разных классах материалов имеет разное зна-
значение вследствие масштабного эффекта. В высокопрочных ста-
сталях с очень мелким зерном порядка нескольких микронов вме-
вместо d0 можно брать средний диаметр зерна, а вместо ав — тео-
теоретическую прочность, равную приблизительно 0,1 Е.
ТЕХНИЧЕСКАЯ ПРОЧНОСТЬ И ВЯЗКОСТЬ РАЗРУШЕНИЯ
203
При этом, например, для стали СП 43 число X получается
равным примерно 1,6 (Ки « 7000 кГ/см\ do « 5 мкм, <тв да
« 160 кГ/мм2, Е да 2X104 кГ/мм2).
В крупнозернистых титановых и алюминиевых сплавах
(с величиной зерна порядка нескольких миллиметров) в фор-
формулу D.150) надо подставлять вместо ав временное сопротив-
сопротивление, определяемое из макроопыта, а вместо do— по-преж-
по-прежнему средний размер зерна. Приведем имеющиеся данные для
двух сплавов (титановый сплав ВТ 14 и алюминиевый сплав
Д20):
Материал
ВТ 14
Д20
К\с, кГ/см3/2
7000
3500
d,, мм
1-4-2
3
ав, кГ/мм2
104
40
1,7
1,6
В двухкомпонентных композитах, состоящих из достаточно
вязкого связующего, армированного прочными нитями (напри-
(например, металл — нити углерода, полимер — стеклянные волокна
и т. д.), на основании представления о структурной ячейке ве-
величины d0 и о"в будут выражаться через другие структурные
постоянные так:
Здесь Рвп — средняя прочность одной армирующей нити (или
стержня), п — среднее число нитей, приходящееся на единицу
поверхности излома (нити рвались, когда трещина их перере-
перерезала), о"вс — прочность связующего, е — объемная концентрация
армирующей компоненты (нитей).
В большинстве случаев вторым слагаемым в первой фор-
формуле D.151) можно пренебречь. При этом выражение для вяз-
вязкости разрушения, согласно D.150), принимает вид
Kia = ^PBnnm. D.152)
Прочность композита имеет порядок KiJVd . где d — ха-
характерный диаметр наиболее опасного трещиноподобного де-
дефекта.
В некоторых (в основном, крупнозернистых) металлах на-
начальный трещиновидный дефект в процессе нагружения устой-
устойчиво развивается примерно до контролируемых заранее разме-
размеров зерна, так что в момент разрушения величина d примерно
равна диаметру наибольшего зерна [13]. Это поясняет тот
факт, что прочность некоторых даже весьма хрупких сплавов
204
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
меняется в относительно небольшом диапазоне по сравнению с
прочностью аморфных материалов типа стекла.
В то же время существует много сплавов (в основном, вы-
высокопрочных сталей), для которых размеры трещиноподобных
дефектов металлургического?- происхождения существенно (на
несколько порядков) превышают средний размер зерна. Приве-
Приведем, например, данные для двух марок стали (СП 43 и Н 18,
см. Р5]).
Материал
СП 43
Н18Ц
К1с, кПсм'Ь
7000
9300
Размер
зериа,
мкм
~5
~4
<тв, кГ/мм2
160
190
Размер
критической
трещины, мм
~2
~2
В связи с этими оценками встает вопрос, всякие ли искус-
искусственные надрезы или трещины снижают прочность материала
по сравнению с сгв? Разумеется, в какой-то степени такое сни-
снижение происходит всегда, однако оно пренебрежимо мало, если
глубина вносимого надреза мала по сравнению с размером наи-
наиболее опасного дефекта, уже присутствующего в материале.
В этом смысле, если выполняется последнее ^условие, можно
говорить о том, что вносимый дефект не влияет на прочность
материала, имея в виду обычное трещиноватое тело. Для
идеального материала любой дефект вызывает уменьшение тео-
теоретической прочности.
Эти соображения должны быть определяющими при разра-
разработке нормативов на допуски при технологических операциях
с готовыми материалами. При этом следует помнить о таких
важнейших усложняющих факторах, как, например, коррозия,
цикличность нагрузок и т. д.
Хрупкие пористые материалы. Такие материалы можно
представить себе в виде окаменевшей губки со случайным и
однородным распределением пор, заполненных газом. К этому
типу материалов можно отнести многие горные породы типа
песчаников, графит, керамику, материалы, получаемые спека-
спеканием порошков, и т. д.
Из представления о структурной ячейке в этом случае вы-
вытекает следующая оценка для вязкости разрушения:
/Cie = А,! A — в
Здесь е — пористость (объем пор в единице объема простран-
пространства), Kico — вязкость разрушения монолитного материала, сгв —
теоретическая прочность монолитного материала, d0 — средний
диаметр пор, Ki и %2 — коэффициенты.
ТЕХНИЧЕСКАЯ ПРОЧНОСТЬ И ВЯЗКОСТЬ РАЗРУШЕНИЯ 206
Прочность пористого материала определяется формулами
} а (в, v)KiJVd^ при d<dQ, ,„ ,„„,
ffB={ I r— D.154)
I 4(v)KiJVd при d>d0.
Здесь dmax — наибольший диаметр одной поры, d — характер-
характерный линейный размер трещиновидного дефекта, а(е, v) и
«o(v) — некоторые безразмерные функции своих аргументов.
Аморфные хрупкие материалы. К таким материалам отно-
относятся стекла, плавленый кварц и др. Линейный размер струк-
структурной ячейки в этих материалах равен среднему межатомному
расстоянию. Поэтому для оценки вязкости разрушения (или
связанной с ней удельной необратимой работы у) можно при-
применить методы, рассмотренные в гл. II для идеально-периоди-
идеально-периодических структур. Они дают значения вязкости разрушения, со-
согласующиеся с экспериментальными.
Прочность таких материалов существенно зависит от раз-
размеров начальных трбщин, всегда присутствующих в этих мате-
материалах.
Например, прочность силикатного стекла на разрыв изме-
изменяется [92] примерно от 0,5 кГ/мм2 до 600 кГ/мм2. Нижняя
граница отвечает оконному стеклу с дефектным поверхностным
слоем, верхняя граница найдена при испытаниях в вакууме на
стеклянных образцах, полученных из хорошо гомогенизирован-
гомогенизированной стекломассы и обработанных плавиковой кислотой для уда-
удаления дефектного поверхностного слоя.
Так, например, в опытах, описанных в работе [83], был про-
произведен, изгиб пуансоном квадратной пластинки из такого
стекла; максимальное растягивающее напряжение при этом со-
составляло более 450 кГ/мм2. Многие исследователи [92] считают
достижимой прочность стекла порядка 1200 кГ/мм2.
Эти величины соизмеримы со значением теоретической проч-
прочности, отвечающей диссоциации тела на отдельные атомы.
Напомним, что для силикатных стекол модуль Юнга Е =
= E-г-7)-103 кГ/мм2. Как уже упоминалось ранее, разруше-
разрушение сверхпрочных стекол в какой-то степени напоминает такую
происходящую «со взрывом» диссоциацию, хотя размер обра-
образовавшихся осколков значительно больше межатомного рас-
расстояния (порядка 10~4—10~2 см).
Приведем оценку прочности силикатного стекла, считая, что
у = 2,Ы03 дн/см, Е = 6,7-103 кГ/мм2, v = 0,33. Среднее меж-
межатомное расстояние в стекле примем равным 4-10~8 см; напом-
напомним, что постоянные решетки натрия и кремния — основных
компонентов силикатного стекла — равны соответственно 3,2Х
XIО"8 см й 5,4-Ю-8 см.
206
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. IV
Прочность о хрупкого тела с круглой дискообразной трещи-
трещиной диаметром d определяется по формуле (см. Приложение I)
а =
D.155)
Для стекла получаем отсюда следующие данные:
d, см
а/Е
4- КГ8
0,6
2,6 ¦\0~7
0,2
ю-6
0,1
4-10~6
0,05
ю-6
0,01
ю-3
0,001
Представляет интерес также оценка размеров области вбли-
вблизи конца трещины, где тело уже нельзя считать сплошной сре-
средой. Согласно C.44), напряжение ау на продолжении конца
трещины в момент разрушения равно
0 у =
Еу
— V2
\2)лх
D.156)
Для стекла отсюда получаем:
X, СМ
Оу/Е
4-Ю-8
0,15
ю-7
0,1
4-10
0,06
Радиус кривизны конца трещины, определенный формально
по формулам C.44), равен
R = 8y(l — v2)/(nE). D.157)
Для стекла он примерно равен 0,5-10~8 см, т. е. гораздо меньше
среднего межатомного расстояния.
Приведенные оценки показывают, что используемый аппа-
аппарат механики сплошных сред не в состоянии описать структуру
конца трещины в аморфных хрупких материалах, так как на
расстояниях от конца трещины порядка межатомного дости-
достигается значение теоретической прочности, а радиус закругления
гораздо меньше межатомного расстояния, так что материал
нельзя считать сплошной средой. Поэтому вывод об эллипти-
эллиптической форме хрупкой трещины в ее конце и-о бесконечности
напряжений в этой же точке неверен, поскольку эти вопросы
не могут быть рассмотрены в рамках применяемой теории. Бо-
Более того, вопрос о структуре конца трещины становится бес-
бессмысленным для несплошной среды; решение же вопроса о точ-
точном определении области несплошности требует отказа от при-
S 8] ТЕХНИЧЕСКАЯ ПРОЧНОСТЬ И ВЯЗКОСТЬ РАЗРУШЕНИЯ 207
менения концепции сплошной среды. Простейшее предположе-
предположение состоит во введении разрывных решений уравнений теории
упругости, однако выбор таких решений в данном случае ни-
ничем не определен и может быть весьма произвольным (ср., на-
например, D.97) и D.104)). . -
Полимеры. Исчерпание способности к пластическому дефор-
деформированию полимерного материала вблизи конца трещины свя-
связано со способностью отдельных молекул или пачек молекул
(надмолекулярных образований) - к наибольшей вытяжке без
разрыва. Опыт показывает, что на продолжении трещины в по-
полимерах образуется узкая клиновидная область, противополож-
противоположные берега которой скреплены невзаимодействующими между
собой нитями; нити образовались вследствие значительной вы-
вытяжки надмолекулярных образований.
В этом случае вязкость разрушения Kic наиболее естествен-
естественно оценить, используя формулу D.98)
Kic=VosEb. D.158)
Здесь А — наибольшая величина линейной вытяжки до разрыва
надмолекулярного образования.
Эта оценка годится также для некоторых композитных ма-
материалов (полимерное связующее плюс кристаллический за-
заполнитель), когда силы адгезии составляющих малы. К таким
материалам относится, например, твердое ракетное топливо.
Надежность конструкции с трещиной. Механика -хрупкого
разрушения, основываясь на опытных данных, исходит из воз-
возможности существования трещин в любой конструкции. Сравни-
Сравнительная оценка надежности работы различных конструкций с
трещинами представляет большой интерес.
Если размер d начального трещиновидного наиболее опас-,
ного дефекта можно обнаружить с вероятностью 100% мето-
методами неразрушающего контроля, то сравнительной оценкой на-
надежности различных конструкций будет служить, очевидно, сле-
следующее число х (при одинаковых предельных нагрузках) [60'87]:
Х = /ЗДЧ). D.159)
Чем больше число %, тем разрушение более вязкое; чем
меньше число %, тем разрушение ближе к хрупкому: Предпо-
Предполагается, что d гораздо меньше характерного линейного раз-
размера конструкции.
Величина os получается аппроксимацией реальной диаграм-
диаграммы а — е диаграммой Прандтля. Надежнее брать ее равной ве-
величине (То,2; для высокопрочных материалов, у которых Сто,2 и
ав близки, этот вопрос не имеет значения.
208 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
Пусть величины Kic, os и, в особенности, d известны лишь
с некоторой вероятностью. Тогда при аргументированном вы-
выборе коэффициента запаса нужно прежде всего задать довери-
доверительную вероятность надежной работы конструкции (скажем,
90, 95 или 99%—это зависит от назначения изделия), затем
по формулам, определяющим хрупкую прочность (см. Прило-
Приложение I), подсчитать коэффициент запаса, требующийся для
обеспечения заданной вероятности. Дальнейшее сравнение двух
конструкций (с одинаковым коэффициентом запаса и предель-
предельной нагрузкой) производится сравнением функций распределе-
распределения числа %.
Практически может оказаться удобнее по проектируемому
коэффициенту запаса определить критические размеры дефектов,
а затем на основании имеющейся статистики разрушений (или
анализа металлургического и технологического процессов, при
которых образуются дефекты) оценить вероятность наличия в
конструкции сверхкритических трещин.
Отметим изящный экспериментальный метод (метод «про-
«провокаций») определения критических размеров трещин в метал-
металлических конструкциях при заданных стационарных рабочих на-
нагрузках. Для этого надо подвергнуть знакопеременному цикли-
циклическому нагружению часть конструкции, содержащую наиболее
опасное место, в котором делается искусственный надрез или
насечка; максимальная амплитуда циклических напряжений
вдали от надреза должна равняться рабочим напряжениям.^
После разрушения (вследствие развития усталостной трещины
из надреза) край критической трещины, соответствующей дан-
данным рабочим нагрузкам, легко визуально определить как гра-
границу, разделяющую блестящую поверхность медленного разви-
развития усталостной трещины и шероховатую поверхность быстрого
роста трещины.
Данная оценка представляет интерес, в особенности, при
сравнении конструкций одинакового назначения, но разного га-
габарита и из различных материалов.
§ 9. Другие критерии локального разрушения
Формулировка критерия локального разрушения D.2) для
трещин нормального разрыва не зависит от структуры конца
трещины. Например, в случае внутренних трещин структура
конца трещины совершенно не похожа на структуру конца
сквозной трещины в пластине (см. § 5 этой главы), однако кон-
концепция механики хрупкого разрушения справедлива в обоих
случаях, если реализована тонкая структура. Впервые наиболее
четко это было понято Ирвином [12>9I], исходившим из общих
энергетических еоображений, аналогичных изложенным ранее.
;| S] ДРУГИЕ КРИТЕРИИ ЛОКАЛЬНОГО РАЗРУШЕНИЯ 209
Некоторые исследователи приходили к аналогичным крите-
критериям на основе некоторых частных представлений о структуре
конца трещины. Перечислим наиболее известные концепции.
Концепция Нейбера: вблизи конца трещины имеется пласти-
пластическая область, размер d которой является структурной по-
постоянной материала. Эта концепция «пластической частицы»
была выдвинута Нейбером еще в 1935 г. [31]. При помощи фор-
формул типа D.97) ее легко переформулировать в виде критерия
локального разрушения Ki^Kic, составляющего основу меха-
механики хрупкого разрушения для трещин нормального "разрыва.
Только несовершенство применяемого математического аппа-
аппарата помешало Нейберу достичь этого.
Концепция Вильямса: локальное разрушение происходит в
момент достижения радиусом кривизны конца трещины некото-
некоторого предельного значения, своего для каждого материала [93].
Концепция Уэллса: локальное разрушение отвечает некото-
некоторому максимальному раскрытию трещины в ее конце [94], харак-
характерному для каждого материала (С. О. D.) *).
Концепция Мак-Клинтока: локальное разрушение происхо-
происходит, как только средняя деформация на некотором малом расстоя-
расстоянии ps от кромки трещины в пластической зоне достигнет неко-
некоторого постоянного для данного материала значения [95] (ps —
постоянная материала).
Концепция Леонова и Панасюка: на некотором участке на
продолжении трещины напряжение ау, а также раскрытие тре-
трещины в ее конце равны некоторым постоянным материала [96].
Эту концепцию можно считать также относящейся к некоторым
случаям упруго-пластического деформирования (ср. с гипотезой
Дагдейла для тонких пластин из идеального упруго-пластиче-
упруго-пластического материала).
, Все эти концепции заслуживают дальнейшего изучения, так
как они не основаны на представлении о тонкой структуре и
могут представлять собой возможные пути обобщения механики
хрупкого разрушения.
Недавно новый подход к проблеме хрупкого разрушения с
общих позиций устойчивости упругих систем был развит
В. В. Новожиловым [97- 98].
При наличии тонкой структуры конца трещины концепции
всех указанных выше авторов естественно приводят к критерию
D~.2) и в этом смысле эквивалентны [45> 62]. Следует отметить,
что в рамках линейной механики разрушения можно предло-
предложить много эквивалентных-моделей конца трещины; некоторые
из таких моделей позволяют наглядно представить основную
концепцию линейной механики разрушения.
*) Crack opening displacement.
210 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ (ГЛ. IV
Обобщенный критерий локального разрушения. До сих пор
в этой главе рассматривались только трещины (т. е. математи-
математические разрезы начальной нулевой толщины) в однородных и
изотропных по деформативным свойствам телах. Однако не-
нетрудно рассмотреть также гораздо более общие случаи.
Действительно, основной общефункциональный метод меха-
механики хрупкого разрушения, изложенный в § 1 этой главы, легко
обобщить следующим образом. Пусть решение задачи о дефор-
деформации некоторого твердого тела в малой окрестности точки О
определяется с точностью до нескольких независимых парамет-
параметров d, С2, ..., Сп. Тогда критерий локального разрушения в
точке О формулируется так: существует функция f(C\, C2, ...
..., Сп) такая, что пока f < 0, разрушения не происходит, а
как только достигается значение f = 0, происходит разрушение
в точке О.
В регулярных точках параметры Си С2, ..., Сп представ-
представляют собой просто независимые комбинации первых членов
разложения в ряд Тейлора напряжений и деформаций в малой
окрестности точки О. В этом случае формулировка критерия
совпадает с принятой в сопротивлении материалов формули-
формулировкой теорий прочности. Напомним, что в линейно-упругом
однородном и изотропном теле регулярными точками являются
все внутренние точки и точки на гладкой поверхности тела.
Аналогичный смысл имеют параметры Си С2, ..., Сп в цилинд-
цилиндрической особой точке. В особых точках класса S напряжения
и деформации обращаются в нуль (если нет сосредоточенных
воздействий); роль Сь С2,..., Сп играют независимые коэф-
коэффициенты при главных членах асимптотического разложения.
В особых точках класса N напряжения и деформации имеют
особенности; параметры Cj, С2, ¦ ¦ ¦, Сп представляют собой не-
независимые коэффициенты при главных членах асимптотического
разложения, т. е. некоторые аналоги коэффициентов интенсив-
интенсивности напряжений. Наиболее часто встречающиеся случаи та-
таких сингулярных точек были изучены в гл. III (налегающие
трещины, включения, анизотропия, кусочно-однородные и нели-
нелинейно-упругие тела, полости и т. д.).
Если число независимых параметров равно единице, что
весьма часто бывает на практике, то критерий локального раз-
разрушения сводится к неравенству вида С\ < С\с, и остается
лишь провести соответствующие эксперименты для определения
константы Сic. Функция f(ChC2, ..., Сп), вообще говоря, ме-
меняется от точки к точке; кроме того, она зависит от типа и рас-
расположения особой точки.
В такой формулировке критерий локального разрушения
справедлив на любом этапе идеализации задачи, причем имеет-
имеется в виду не только приближение к свойствам реального тела
$ 10] ПРИЛОЖЕНИЕ МЕХАНИКИ РАЗРУШЕНИЯ К ГОРНОМУ ДЕЛУ 211
в рамках конкретной математической модели, но и возможное
упрощение, связанное с выбором приближенного метода реше-
решения. Существенно подчеркнуть, что при таком подходе всякое
уточнение постановки задачи не изменит первоначального кри-
критерия, а только представит фигурирующие в нем постоянные
через другие постоянные, относящиеся к структурам меньшего
масштаба.
Приведем простой пример. Пусть образец растягивается мо-
нотонно возрастающим напряжением а. Согласно сформулиро-
сформулированному критерию, разрушение произойдет, как только а до-
достигнет предельной величины ас. Дальнейшее уточнение этой
задачи, диктуемое экспериментом, состоит в том, что в струк-
структуре материала стержня учитываются трещиноподобные де-
дефекты и, возможно, берется более точная модель среды. Это
позволяет выразить константу ос через другие постоянные типа
Kic, характеризующие предельную локальную интенсивность на-
напряжения в окрестности некоторых наиболее опасных точек
стержня, через размеры дефектов и через физические макро-
макроконстанты. Следующий этап состоит в более детальном изуче-
изучении малой окрестности опасных точек (тонких структур); он
приводит к выражению постоянных типа Kic через структурные
и физические постоянные материала, относящиеся к структурам
еще меньшего масштаба (сверхтонкие структуры). В пределе
такой подход должен привести к атомным масштабам и к вы-
выражению величины ас через атомные константы.
Отметим, что функция f может существенно зависеть также
.от других параметров (время, температура, скорость роста тре-
трещины, концентрация активного реагента и т. д.). Учет предысто-
предыстории приводит к тому, что в самом общем случае f является
функционалом по времени (в простейших случаях функционал
вырождается в обычную функцию от dl/dt, Си С2, ..., Сп и их
производных по времени до некоторого порядка). Отказ от ги-
гипотезы локального начального разрушения вызывает дальней-
дальнейшее усложнение: в этом случае / должна представлять собой
некоторый функционал по пространственным координатам.
В конечном счете необходимость учета того или другого из
усложняющих факторов диктуется опытом.
§ 10. Одно приложение механики разрушения
к горному делу
Одной из важнейших инженерно-технических проблем,
встающих при проведении выработок в горном массиве, являет-
является проблема безопасности. Рассмотрим возможные пути анализа
этой проблемы, основанные на развитых представлениях меха-
механики разрушения. При этом для определенности остановимся
212 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. IV
лишь на наиболее опасном и таинственном явлении — горном
ударе [86]..
Горным ударом называют взрывообразное внезапное раз-
разрушение породы в окрестности выработки, происходящее без
выделения газа; оно преставляет собой одно из проявлений
горного давления и тем опаснее, чем больше глубина горных
работ и прочность породы.
Горные удары происходят при прохождении подготовитель-
подготовительных выработок в их действующих забоях, еще более часты гор-
горные удары в целиках различного назначения, в забоях очистных
выработок., В подготовительных выработках гориые удары, с
выбросом в последних горной массы, происходят в забоях,
стенках выработок и в почве. Горные удары происходят в ста-
старых выработках, в старых целиках, и удары эти, как правило,
весьма большой мощности. Часто горные удары не сопровож-
сопровождаются выбросом массы в выработки, а их проявление выра-
выражается в виде сейсмической волны, аналогичной землетрясе-
землетрясению*).
. Сила толчка способна в этих случаях травмировать людей,
повредить оборудование и т. д. Достаточно полное представле-
представление о состоянии этой проблемы и ее связи с другими аспектами
горного дела- можно получить из трудов ["• 10°].
Возникновение горного -удара. Механизм горного удара
моЖно уяснить из следующей простейшей теоретической схемы
[101]. Пусть в горном массиве, который представим для простоты
однородным и изотропным телом, проводится горизонтальная
выработка высоты h (рис. 65). Считаем, что выработка имеет
прямоугольную форму и находится в поле горного давления
(в\ — боковое, а2~вертикальное давление); будем считать, что
размеры выработки в плане существенно превышают h^ при
этом все процессы деформирования и разрушения будут рас-
рассматриваться в плоскости чертежа (плоская задача).
Мысленно вырежем прямоугольную область ABCD длины /
на протяжении выработки (см. рис. 65) и приложим к грани-
границам этой области А В, ВС и CD нормальные и касательные на-
нагрузки, равные соответствующим" напряжениям в сплошном
теле.
*) В связи с особенностями роста трещин в сжатых телах [101>102] гор-
горному удару всегда предшествует устойчивое квазистатическое развитие тре-
трещин, что используется для обнаружения угрозы горного удара путем реги-
регистрации звуковых импульсов. Согласно имеющимся наблюдениям [103], для
горных ударов в прочных породах наиболее характерной является частота
звуковых импульсов (при числе «щелчков» меньше 20 в час горного удара
не бывает; при 30 и более горный удар возможен, а при 80 импульсах в час
горный удар неизбежен). Любопытно, что примерно за час до наступления
горного удара наступает тишина и звуковые импульсы полностью отсут-
отсутствуют.
5 Ю]
ПРИЛОЖЕНИЕ МЕХАНИКИ РАЗРУШЕНИЯ К ГОРНОМУ ДЕЛУ 213
Рассмотрим равновесие этой области в-зависимости от па-
параметра /. Единственное уравнение равновесия имеет вид
N(l) = T{l), D.160)
где N и Т — суммарные нормальная и касательная нагрузки,
изображенные на рис. 65. Остальные нагрузки, не указанные
L»h
D
Т/2
Рис. 65.
на рис. 65, очевидно, не дают вклада в уравнение равновесия
(для простоты ограничиваемся случаем задачи, симметричной
относительно оси х). Из уравнения равновесия дох/дх =
= —дхху/ду и граничного ус-
условия ах = хХу = 0 при х = 0 iN
вытекает, что функция NA)
при малых / прямо пропорцио-
пропорциональна /2; з^тем NA) вслед-
вследствие концентрации напряже-
напряжений быстро возрастает, дости-
достигая максимума на расстоянии
порядка h (рис. 66). Падаю-
щая ветвь этой кривой отве-
чает приближенно распределе-
нию C.44) для разреза нуле-
нулевой толщины; эта промежуточная асимптотика при h <* <с L
проявляется тем более ясно, чем больше отношение L/h. На
расстояниях / порядка L и больших величина NA) асимптоти-
асимптотически стремится к невозмущенному выработкой значению o\h.
Физически NA) представляет собой силу, вызывающую горный
.
Рис 66.
214 ' ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. [V
удар; она равна
N{l) = f,{l/h)pgHh. D.161)
Здесь р — безразмерный коэффициент концентрации напря-
напряжений, зависящий от формы выработки, а также от расположе-
расположения и типа крепи (он определяется из решения соответствую-
соответствующей задачи теории упругости или опытным путем), pg— сред-
средний удельный вес горной породы, Н — глубина заложения
выработки.
Величина ТA) физически представляет собой суммарную
силу сопротивления горному удару (разрушению); очевидно,
она не может превосходить некоторой предельной величины
Tf(l), характеризующей прочность породы. Функция Tt{l) мо-
монотонно возрастает с увеличением / и имеет вид (см. рис. 66)
Tf(l) = a(l/h)l<jc. D.162)
Здесь а — безразмерная функция l/h, зависящая также от фор-
формы выработки и прочих факторов, ае — предел прочности по-
породы на одноосное сжатие.
При малых l/h механизм разрушения может быть связан
только с раздавливанием тонкого слоя вследствие одноосного
сжатия; поэтому при малых l/h будет а да 1. При l/h ~ 1 раз-
разрушение происходит вследствие сдвига вдоль А В и CD, поэтому
соответствующие значения коэффициента а будут меньше еди-
единицы. Сопротивление сдвигу будет особенно малым, если вдоль
А В и CD имеются малопрочные прослойки или трещины, что
часто встречается на практике.
Из указанного характера кривых следует, что явление гор-
горного удара объясняется первоначальным касанием кривых NA)
и Tf(l) не в начале координат, а при некотрром I > 0. Если бы
равенство N (l)= Tf(l) впервые достигалось при / = 0, то про-
проблемы горного удара не существовало бы, так как происходило
бы явление, аналогичное смыканию (обрушению) кровли.
Управление процессом обрушения кровли не представляет труд-
трудностей вследствие его равномерности и маломощности.
Таким образом, условие возникновения горного удара в
произвольных выработках можно записать так:
$pgHh>aljac. D.163)
Усложняющие факторы: а) неоднородность и неизотроп-
неизотропность горной породы, б) естественная трещиноватость, в) неуп-
неупругость деформационных свойств породы, г) различные формы
выработок и применение крепи — значительно затрудняют ко-
количественное описание возникновения горного удара, но не
влияют на указанную выше качественную картину.
5 10] ПРИЛОЖЕНИЕ МЕХАНИКИ РАЗРУШЕНИЯ К ГОРНОМУ ДЕЛУ 215
Локальный критерий безопасности. Рассмотрим теперь слу-
случай, когда в некоторой окрестности края выработки реализует-
реализуется промежуточная асимптотика, характерная для концов раз-
разрезов нулевой толщины. Теоретически такая асимптотика имеет
место при условии L > h на расстояниях г от края таких, что
h <C r <C L. Точный расчет для случая эллиптического отвер-
отверстия (гл. III, § 10) показывает, что с приемлемой точностью
это условие можно считать выполняющимся уже при значениях
B)Л
()
Выработки или выемки часто таковы, что размеры выемки
в плане значительно больше ее высоты. Это связано с тем, что
полезные ископаемые, в особенности уголь, обычно залегают
в виде пластов или слоев.
Для выработок указанного типа сила, вызывающая горный
удар, описывается коэффициентами интенсивности напряжений
промежуточной асимптотики, которые определяются из решения
соответствующей упругой задачи при h = 0. Они зависят от
размеров выработки в плане, от положения точки на контуре
соответствующего разреза, от положения выработки в массиве,
от приложенных внешних нагрузок и т. п., но не зависят от h.
Сила сопротивления горному удару определяется, наоборот, де-
деталями структуры породы и пласта вблизи рассматриваемой
точки контура (т. е. в некоторой окрестности края выработки
порядка h). Однако независимо от этих деталей и механизма
разрушения локальный критерий безопасности запишется так:
f(Ku Ки, /СшХО. D.164)
Здесь f — некоторая функция (или функционал по времени, если
существенна предыстория образования полости), определяемая
экспериментально.
В случае Кп = Кха = 0 (аналогичном, с точностью до знака
напряжений, трещинам нормального разрыва) этот критерий
особенно прост:
\KiKKl D.165)
Здесь К* — величина, аналогичная вязкости разрушения для
трещин; она характеризует сопротивление разрушению системы
пласт — порода в рассматриваемой окрестности края выработки.
Величина Ki зависит от h, от прочности породы и пласта,
от механизма разрушения и других локальных факторов. Если
существенна ползучесть, то Кг будет зависеть также от вре-
времени. На основе анализа размерностей из предложенного ме-
механизма горного удара вытекает следующая формула:
D.166)
216 ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ 1ГЛ. IV
Здесь а8—абсолютная величина наименьшего сопротивления
сдвигу в системе пласт — порода (это может быть пласт, по-
порода и, чаще всего, контакт пласта с породой), к\ — безразмер-
безразмерный коэффициент, зависящий от внутренней структуры пласта
и окружающих пород в рассматриваемой окрестности тупика
выработки, а также от отношения упругих и прочностных ха-
характеристик пласта, прослоек и породы. Коэффициент ц имеет
порядок , единицы (точное его значение определяется опытным
путем).
Подчеркнем, что -если пласт имеет мощность порядка h
я достаточное сцепление с породой, то при вычислении коэф-
коэффициента интенсивности напряжений Ki все пространство
вне выработки-разреза можно считать заполненным одной
породой.
Рассмотрим некоторые конкретные случаи выработок, для
которых условие безопасности имеет особенно простой вид [104].
Вначале отметим, что для тяжелого однородного и изотропного
упругого полупространства z <C H поле напряжений вдали от
выработки определяется следующими формулами:
ах = oy = — [v/(\ — v)] pg (H — z), .
ог = — ?g{H — г), хху = хуг = ххг = 0.
Здесь мы пренебрегаем внутренними (тектоническими) на-
напряжениями в горном массиве. Внешние нагрузки на стенки
выемки учитывать не будем, высоту выемки h считаем по-
постоянной.
Горизонтальная выработка эллиптической формы в плане
(рис. 67). В этом случае коэффициент интенсивности напряже-
напряжений, согласно D.167) и (П.82) (см. Приложение I), равен
Ki = pgH Vnb [Е (?)Г1 • (sin2p + -¦?- cos2 p)'/4 D.168)
{k = V\-{blaf).
Здесь E(k) — полный эллиптический интеграл второго рода.
Наиболее опасные точки контура, т. е. точки, в которых Кг
максимально, согласно D.168) будут при 0 = ±п/2 (эти точки
лежат на малой оси эллипса). Используя локальный критерий
безопасности в виде D.165) и D.166), отсюда получаем следую-
следующее достаточное условие безопасности (устойчивости) данной
выработки;
pgH Vnb < цЕ (k) as УЪ. D.169)
В частности, когда выработка имеет в плане форму круга,
ПРИЛОЖЕНИЕ МЕХАНИКИ РАЗРУШЕНИЯ К ГОРНОМУ ДЕЛУ
217
будет а = Ь, E{k)= п/2, и условие устойчивости принимает вид
2pgH V~b < r\os Vnh. D.170)
В другом важном частном случае, когда выработка имеет
в плане форму горизонтальной бесконечной полосы ширины %Ь
•И
Рис. 67. Рис. 68.
(т. е. a/b-+oo, E{k)—*\), условие безопасности запишется так:
pgH Vnb < \]os ]/~h. D.171)
Вертикальная выемка эллиптической формы в плане
(рис. 68). В этом случае коэффициент интенсивности напряже-
напряжений, согласно D.167) и (П. 83) (см. Приложение I), равен
Ъкг sin P
' = b/a, к=У\—
D.172)
Здесь K(k) — полный эллиптический интеграл первого рода.
При Ь2/Я2</г' наиболее опасной точкой будет точка р = л/2
(самая нижняя точка выработки). При этом, согласно D.165)
и D.166), достаточное условие безопасности (устойчивости)
примет вид
в щ-
DЛ73)
В частности, для вертикальной выработки, имеющей в плане
форму круга (т. е. а = b и /С(&) = 0), отсюда получается
Sis
ОСНОВЫ МЕХАНИКИ ХРУПКОГО РАЗРУШЕНИЯ
|ГЛ. IV
следующее условие:
D.174)
Когда выработка имеет в плане форму бесконечной вер-
вертикальной полосы ширины 26, простирающейся горизонтально
(т. е. а/b—юо, E{k)—> 1), условие безопасности будет иметь вид
1 —'
D.175)
Формула D.172) становится непригодной при b > а. В этом
случае ограничимся только наиболее интересным случаем вы-
выработки (рис. 69), имеющей в плане форму бесконечной полосы
ширины 2а и простираю-
простирающейся вертикально (т. е.
Ь/а-»-оо). Предположим,
что z > а. Тогда в каж-
каждом сечении z = const
распределение напряже-
напряжений и деформаций по х и
у будет, очевидно,плоско-
деформированным (т. е. z
будет входить как пара-
параметр в боковое горное да-
давление) . Следовательно,
Рис. 69. можно использовать ус^
ловие D.171) с боковым
горным давлением; таким образом, получаем условие безопас'
ности (устойчивости) в следующем виде:
t ¦
z
X
-^— pgz
<
D.176)
Как видно, на большой глубине горные удары становятся
неизбежными, если не применять специальных подкреплений
(при наличии подкреплений на краю выработки коэффициент т]
увеличивается).
Приведем численный пример для случая горизонтального
бесконечного туннеля ширины 26, равной ~3/г(т] ~ 1, pg ~
~ 3 Г/см3, as ~ 100 кГ/см2). При помощи D.171) находим ус-
условие устойчивости неподкрепленной выработки: Н <<; 1 500 м.
Полученные условия безопасности выемок позволяют дать
оценки также для более сложных форм выработок. Например,
используя некоторые соображения, аналогичные приводимым в
контактной задаче [40], можно ожидать, что ошибка в опреде-
определении наибольшего коэффициента интенсивности напряжений
§ 10] ПРИЛОЖЕНИЕ МЕХАНИКИ РАЗРУШЕНИЯ К ГОРНОМУ ДЕЛУ 219
на контуре разреза прямоугольной формы в плане не превысит
нескольких процентов, если прямоугольник заменить равнове-
равновеликим эллипсом с соотношением осей, равным отношению сто- ¦
рон прямоугольника.
Найденные условия легко обобщить также на тот случай,
когда величина Ki переменна вдоль контура выработки. Это
может иметь место или вследствие переменной мощности пла-
пласта, или же из-за изменения локальной структуры и прочности
породы и пласта.
В работе [86] предложены некоторые способы использования
энергии взрыва в целях управления горным ударом. Следует
отметить принципиальную возможность добычи полезного иско-
ископаемого на достаточно глубоких круто падающих пластах в
самоподдерживающемся режиме горного удара (начинающе-
(начинающегося с нижней кромки пласта и распространяющегося вверх),
если достаточно быстро выбирать снизу падающую породу.
В горизонтальных выработках порода, выброшенная горным
ударом, образует естественный подпор кровле и тем самым
снижает коэффициент интенсивности напряжений.
Защита сооружений от разрушения. При проведении горных
работ или же в силу естественных причин (например, вслед-
вследствие землетрясения) в породе возможно образование и раз-
развитие поверхностей разрыва смещений (трещин). Достигая фун-
фундамента здания, они могут вызвать его разрушение. Трещины
особенно опасны потому, что многие применяемые на практике
строительные материалы (кирпич, бетон и т. п.) имеют весьма
низкую вязкость разрушения (порядка вязкости разрушения
стекла). Поэтому для предотвращения разрушений обычно идут
по пути увеличения вязкости разрушения строительного мате-
материала (например, применяя железобетонные конструкции).
Недавно был предложен оригинальный способ защиты со-
сооружений, который заключается в том, что в породе вокруг
здания создается искусственный трещиноподобный слой, кото-
который заполняется каким-либо пластичным материалом с боль-
большой вязкостью разрушения (например, глинистой пастой). Та-
Такой слой представляет собой непреодолимое препятствие для
трещин. В результате здание как бы плавает на «пластической
подушке». Применение этого способа требует исследования во-
вопросов устойчивости, родственных проблеме остойчивости ко-
корабля.
ГЛАВА V
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ
МЕХАНИКИ РАЗРУШЕНИЯ
§ 1. Уравнение энергии
Ниже рассматриваются подвижные поверхности разрыва
типа трещин в неупругих сплошных средах*). Основное вни-
внимание будет уделено изучению поля напряжений и деформаций
на фронте таких поверхностей в условиях монотонного нагру-
жения. Излагаются общефункциональный и энергетический
подходы, служащие для формулировки локальных критериев
разрушения. Всюду (за исключением § 8) трещина считается
математическим разрезом нулевой тол-
толщины; тем самым, предполагается, что
деформации среды малы. Отметим, что
для тел с начальными математическими
разрезами эти два допущения равносиль-
равносильны; при учете конечности деформаций
трещина превращается в полость**).
Пусть сплошное деформируемое тело
содержит поверхности разрыва смещений
(трещины). Ограничимся рассмотрением
процессов, в которых достаточно учиты-
учитывать лишь механическую и тепловую
энергию [38]. Обозначим через 2 произ-
произвольную замкнутую поверхность, ограни-
ограничивающую некоторую область D тела
(рис. 70). (В области D могут находиться трещины, к которым
не приложены внешние нагрузки или внешние потоки тепла; по-
поверхность таких трещин не входит в 2.)
Рис. 70.
*) Широкий круг вопросов прочности и разрушения материалов рас-
рассмотрен в весьма доступной форме Мак-Клинтоком и Аргоном [105]. Их книга
может служить прекрасным введением в современную науку о сопротивлении
материалов.
**) Можно решать задачи и в более точной (нелинейной) постановке,
считая деформации малыми, а граничные условия — удовлетворяющимися на
текущей (а не на начальной, как обычно) поверхности тела. Получающаяся
при этом ошибка имеет порядок той, которая отвечает пренебрежению квад-
квадратичными членами в выражении для компонентов тензора конечной дефор-
деформации.
§ 1] УРАВНЕНИЕ ЭНЕРГИИ 221
Согласно закону сохранения энергии, работа Л, совершенная
за единицу времени поверхностными силами на 2 и объемными
силами в D, плюс тепловая энергия Q, подведенная к телу D
за единицу времени через 2, равняются скорости возрастания
суммы кинетической К и внутренней энергии U тела в области
D плюс энергозатраты в единицу времени П, идущие на увели-
увеличение поверхности трещин S:
, E.1)
А= J Oifuitijdl + J pFititdv,
2
Здесь <7г и Fi — компоненты вектора теплового потока и объ-
объемной силы соответственно; щ — компоненты единичного век-
вектора внешней нормали к поверхности 2; р — массовая плот-,
ность; Yo — энергозатраты, приходящиеся на единицу площади
вновь образующейся поверхности трещин (величина Yo> вообще
говоря, зависит от положения точки на контуре трещин L); / —
скорость распространения края трещины в каждой точке кон-
контура L по нормали к контуру. Остальные обозначения уже при-
применялись выше (например, в формуле D.33)). Точка над бук-
буквой обозначает полную производную по времени t. Как будет
видно из дальнейшего, величина Yo существенно зависит от того,
какой моделью аппроксимируется рассматриваемая сплошная
среда.
По теореме Остроградского — Гаусса в силу произвольности
области D из уравнения E.1), как обычно (см., например, [106]),
вытекает локальный закон сохранения энергии
?u = #о B«i/= «I. / + «м). E-2)
если предположить, что справедлив закон Ньютона
оц. i + pFi = рй*. E.3)
Уравнение E.2) выполняется в каждой точке сплошной среды,
не лежащей на L. Заметим, что если предположить справедли-
справедливость локального закона сохранения энергии E.2), то из урав-
уравнения E.1) будут вытекать уравнения движения E.3),
2
L
222 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
Воспользуемся теоремой Остроградского — Гаусса
Г Г
J qinid2 = j qlAdv. E.4)
2 D
Отсюда, на основании E.2), уравнение E.1) можно предста-
представить в удобном виде, содержащем лишь смещения и на-
напряжения:
Y0J ds =
= ацй^п^Ъ -f- \pFiuidv—j -^¦(giiiU^dv— ЧцЪцйь. E.5)
2 D D D
Члены в правой части уравнения E.5) физически представ-
представляют собой соответственно работу поверхностных сил, работу
объемных сил, кинетическую энергию и работу внутренних сил.
При выводе E.5) предполагалось, что область D не зависит
от времени. В некоторых задачах (например, в задачах о го-
горении твердых тел) целесообразно выбирать D зависящей от
времени; при этом в правой
части E.5), очевидно, нуж-
нужно добавить следующий
член:
s
Здесь Vn — скорость движе-
движения поверхности Б в направ-
направлении нормали к поверхно-
поверхности в каждой точке.
Рис 71. Рассмотрим окрестность
произвольно выбранной точ-
точки О контура трещины, малую сравнительно с характерным ли-
линейным размером тела и трещины. Сплошная среда в малой
окрестности каждой точки гладкого контура трещины находится
в условиях плоской задачи, т. е. щ, о^, уо, I и т. д. не зависят
от z (см. рис. 13). Поэтому процессы деформирования и разру-
разрушения тела в рассматриваемой малой области вблизи точки О
можно изучать на плоском чертеже (рис. 71), считая трещину
полубесконечной, прямолинейной и имеющей всюду свободную
от внешних нагрузок поверхность, а размер в направлении нор-
нормали к чертежу — равным единице длины. При этом во всей
области, и в том числе в бесконечно удаленной точке, все функ-
функции, характеризующие напряжения, омещения, температуру
§ Ц УРАВНЕНИЕ ЭНЕРГИИ 223
и т. д., будут определяться некоторым асимптотическим распре-
распределением соответствующих величин в малой окрестности точ-
точки О исходного тела.
Обозначим через С\ и С% произвольные контуры, охваты-
охватывающие точку О и являющиеся границами соответствующих об-
областей D\ и D2 (см. рис. 71). На основании уравнения E.1)
в точке О будет
2Yo/= Лс_ + Qc, -KDi - UDi = АСг + QCi-KD- UD. E.6)
Второе равенство в E.6) является следствием закона сохране-
сохранения энергии для тела, занимающего область D2 — Di и не со-
содержащего в себе конца трещины.
Таким образом, величина Yo не зависит от выбора контура
С, охватывающего конец трещины; она вполне определяется
свойствами материала и характером процесса разрушения (на-
(начальными условиями, временем от начала нагружения, скоро-
скоростью роста трещины и т. д.). Поскольку край развивающейся
трещины из физических соображений представляет собой энер-
энергосток П > 0, то yo всегда положительна.
Допустим, что в некоторой сплошной среде, описываемой
определенной реологической моделью, распространяется мате-
математический разрез с заданным законом Движения его конца
l = l(t), l(t)^0. Чему равна величина удельных энергозатрат
Yo = Yo(O B этом случае? На этот вопрос можно ответить при
помощи E.1) и E.6); для расчета достаточно одного главного
члена асимптотического разложения решения вблизи края раз-
разреза. Вид этого члена обычно можно найти заранее, не решая
задачи в целом, методом сингулярных решений (гл. III); он
определяется с точностью до нескольких произвольных констант
или произвольных функций (последнее имеет место, например,
для некоторых уравнений гиперболического типа). Эти кон-
константы (или функции) могут быть найдены только из решения
задачи в целом. Предположим, что первый член асимптотиче-
асимптотического разложения известен, и будем стягивать контур С в точ-
точку О. Как следует из E.6), форма контура С несущественна,
поэтому ее можно выбирать произвольно, руководствуясь сооб-
соображениями удобства.
Обозначим через ху подвижную систему координат с цент-
центром в точке О и с осью х в направлении роста трещины (си-
(система Х\Х2 неподвижна и выбрана так, как показано на рис. 71).
Так как величины Ас, Qc, Kd, UD в E.6) представляет собой
некоторые функции t и l(t), то уравнение E.6) можно записать
так:
/4r(Ac + Qc-KD~VD)+jf(Ас + Qc~KD~VD). E.7)
224 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
Второй член в правой части этого уравнения равен нулю в силу
закона сохранения энергии для неподвижной трещины. Формула
E.7) принимает вид
(Б.8)
D D
Здесь и в дальнейшем контур С обходится против часовой
стрелки
Находим
дГ дх ' dt дх '
+ j рщщ) dv = — §(uo+~ рщщ) пх ds.
С
Здесь все функции, снабженные дополнительным индексом О,
отвечают первому члену асимптотического разложения реше-
решения в точке О в подвижных координатах ху, т. е., например,
Щ (хи х2, I, t) = ию (х, у, t) (х, — / == х). E.9)
Окончательно получаем следующее уравнение для определе-
определения величины Yo по первому члену асимптотического разложе-
разложения решения в точке О (дополнительный индекс 0 для простоты
опущен):
2Yo = j> [(Uo +1 рй,й| ~н)пх- {atl ^•¦b^f) «/] ds. (б. 10)
с
Следует отметить, что это уравнение можно сразу получить
из E.1), если главный член асимптотического разложения ре-
решения в точке О, например, функция Що в E.9), не зависит
от / (условие стационарности); однако, как видно из преды-
предыдущего, оно верно и в общем случае.
Каждое из слагаемых в подынтегральном выражении E.10)
на контуре трещины должно иметь особенность типа 1/г, чтобы
вклад от него в общую сумму был конечным. Особенность
большего порядка не допускается, так как это вызвало бы на-
нарушение закона сохранения энергии. Члены с особенностью
меньшего порядка, очевидно, выпадают из уравнения E.10).
§1]
УРАВНЕНИЕ ЭНЕРГИИ
22S
Уравнение E.10) можно представить также в другом виде,
когда в него входят распределения лишь для смещений и на-
напряжений в окрестности точки О. Преобразуем, используя
E.2):
У,
= llk(uo-9)dxdy=§{Uo-9)nxds. E.11)
D С
Здесь Э = J ац deif — плотность энергии деформаций. Подста-
Подставляя E.11) в E.10), получаем
2Yo = §[(Э + | рщщ -Н)пх- ач ^ и;] ds. E.12)
с
Подчеркнем, что при выводе уравнений E.10) и E.12) со-
совершенно не затрагивались механические свойства сплошной
среды, использована лишь ее непрерывность. Более того, урав-
уравнение E.10) в лагранжевых координатах справедливо, очевид-
очевидно, также для произвольных
конечных деформаций тела.
Следует отметить, что урав-
уравнения E.10) и E.12) в усло-
условиях плоской задачи законны
для любого замкнутого кон« 6
тура С, охватывающего точку
О (а не только для контура,
бесконечно близкого к точке
О); при этом в общем случае
участвующие в них функции Рис- 72- -
отвечают решению в целом,
записанному в координатах ху. Это обстоятельство будет ис-
использовано в дальнейшем.
Формулы E.12) принимают особенно простой вид, если в ка-
качестве С взять узкий прямоугольный, контур вдоль оси х
(рис. 72):
u-^-n,ds, E.13)
2R
В
Действительно, вклад в общую сумму от интегралов по от-
отрезкам ВС и DA будет пренебрежимо мал, так как б «С R,
а вдоль отрезков АВ и CD величина пх равна нулю.
8 Г. П. Черепанов
Ш некоторые общиж вопросы механики разрушения fuf
В наиболее важном случае трещин нормального разрыва
поле напряжений и смещений (а, следовательно, и некомпенси-
некомпенсированных тепловых потоков) локально симметрично относитель-
относительно плоскости трещины, так что уравнение E.13) принимает вид
Yo = — Hm J ву-^-dx, E.14)
АВ
R-+0, 6/R-+0.
Из уравнения E.13) следует, в частности, что если yo ко-
конечно, то произведение напряжений и деформаций на контуре
трещины в рамках теории малых деформаций должно иметь
особенность типа 1/г.
До сих пор рассматривалась задача об определении yo(t)
в рамках заданной реологической модели и теории малых де-
деформаций, когда известен закон движения конца разреза
I =з l(t). Фактически же стоит обратная (более сложная) задача
определения закона развития трещины / = l(t). Наиболее есте-
естественный подход, к решению этой задачи состоит в следующем.
Определим из специально поставленного эксперимента вели-
величину yo. воспользовавшись ее инвариантностью относительно
контура С. Если материал однороден и изотропен, то yo не бу-
будет зависеть от положения конца трещины в теле и от направ-
направления плоскости трещины. Если, кроме того, пренебречь старе-
старением материала, а также локальными времешшми процессами
и считать, что удельные энергозатраты на образование новой
поверхности не зависят от /, \ и т. д., то /уо будет представлять
собой некоторую константу материала, не зависящую от времени
и процесса разрушения.
Концепция постоянства yo является логически простейшей
возможностью последовательной и непротиворечивой поста-
постановки общей задачи о развитии поверхностей разрыва смеще-
смещений (трещин) в сплошной среде, описываемой сложной реологи-
реологической моделью. При этом уравнения E.10) или E.12) служат
дополнительным условием на контуре растущей трещины (если
правая часть этих уравнений меньше 2yo, to трещина не рас-
растет). Закон развития трещины l = l(t) определяется в каждом
конкретном случае из решения соответствующей краевой задачи.
В некоторых случаях поток энергии yo(t), вычисленный для
заданного движения математического разреза, оказывается
равным нулю или бесконечности. В этих случаях можно гово-
говорить об определенной неадекватности математической задачи
и- физического процесса; истолкование такой неадекватности -
зависит от конкретной задачи (см. ниже).
Выясним более подробно физический смысл величины yo-
Для этого проделаем следующий мысленный эксперимент. Со-
УРАВНЕНИЕ ЭНЕРГИИ 227
|вршим цикл «нагружение — разгрузка» над некоторым объе-
|{ом тела так, чтобы трещина подросла на малую величину А/
^задачу считаем* плоской). Необратимая работа за цикл АА,
Очевидно, равна теплу AQ, выделившемуся в объеме вследствие
$иссипативных процессов, плюс скрытая внутренняя энергия
Остаточных напряжений Ш, плюс истинная поверхностная энер-
энергия 2YiA/ новой поверхности трещины (кинетической энергией и
Объемными силами для простоты пренебрегаем):
АЛ— AQ.+ A?/ + 2y<A/. E.15)
Теперь допустим, что расчет соответствующих величин на осно-
основе решения краевой задачи в рамках заданной реологической
модели и теории малых деформаций дал значения AQi и AUU
AA = AQl + AU1 + 2y0Al. E.16)
Предположим, что реологическая модель тела точна в об-
области малых деформаций. Разности A(Q — Q\) и A(U—U{),
очевидно, будут равны теплу, выделившемуся непосредственно
вблизи новой поверхности трещины в слое толщиной порядка
величины раскрытия трещины в ее конце (в этом слое дефор-'
мации конечны и решение на основе теории малых деформаций
йе годится), плюс скрытая внутренняя энергия остаточных на-
напряжений в этом же слое.
Сравнивая E.15) и E.16), находим 2Yo:
E.17)
В идеальном случае, когда математическая постановка за-
задачи о деформировании тела точна вплоть до момента разру-
разрушения, имеем Q = Qi и U = Uu так что Yo будет равна по-
поверхностной энергии тела (см. гл. II). В общем случае Yo равна
сумме удельной необратимой работы деформаций в окрестности
края трещины (не учитываемых в принятой постановке задачи)
и поверхностной энергии. Например, для упругой модели Yo
равняется эффективной поверхностной энергии.
Таким образом, физический смысл Yo оказывается тесно свя-
связанным с точностью постановки задачи деформирования сплош-
сплошного тела. В рамках заданной модели величину Yo можно счи-
считать некоторой фиктивной поверхностной энергией, определяе-
определяемой из опыта.
Этот подход приводит к тем же результатам, что и обще-
общефункциональный подход, описанный в конце предыдущей главы,
если особенность подынтегрального выражения в формуле E.13)
можно описать с помощью одного параметра (коэффициента
интенсивности сверхтонкой структуры). В случае многих
8*
228 " НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
параметров и наличия усложняющих факторов функциональный
подход является более общим.
Замечание. Плотность энергии деформаций Э является
функцией деформаций в данной точке тела только для упругих
сред. В случае тел с необратимыми (пластическими, вязкими
и т. д.) деформациями величина Э, согласно E.2), представляет
собой некоторый функционал, зависящий от скорости и от исто-
истории процесса нагружения и разрушения всего тела, а также от
его теплового режима (Э = ?/о — Qi, %)¦
§ 2. Поток энергии
В объеме пространства, занятом сплошной средой, выделим
некоторую незамкнутую поверхность 2, ограниченную замкну-
замкнутой кривой С (рис. 73). Поверхность Е и кривая С могут произ-
произвольно двигаться в пространстве или же оставаться неподвиж-
неподвижными. Рассмотрим вектор с компонентами ГЦ:
Л]Е E.18)
= J al} deu, Н = J pF^ k d
Вектор П(Пь ГЬ, Пз) физически представляет собой поток
энергии через поверхность 2 в момент времени t, приходящийся
на единицу длины. Физический
смысл этой величины раскры-
раскрывается при рассмотрении движу-
движущихся источников или стоков
энергии.
Докажем следующее основное
свойство: векторный поток энер-
энергии П одинаков для всех незамк-
незамкнутых поверхностей Е, ограни-
ограниченных одной и той же кривой С.
Рис. 73. Для доказательства, очевидно,
достаточно показать, что для
замкнутой поверхности 2-f2i имеет место равенство
f [( уO/] E.19)
2+2,
где 2i — произвольная незамкнутая поверхность, ограниченная
кривой С (см. рис. 73).
ПОТОК ЭНЕРГИИ 229
Преобразуем поверхностный интеграл E.19) в объемный:
г
2+2,
+ 2
Н) k ~~ {°1>Щ-fe)-'] dv' El20)
где Di — объем, ограниченный поверхностью E + 2i-
Теперь преобразуем подынтегральные члены в E.20):
д
(dui)
\ дх. I
dxk dxk 2 "'/ [ dxk \ дх. I ' 5xfe
а /аИ/\ a / dut\ dau
dx.
(здесь использованы соотношения Оц = ац и 2eij = uiij + ujti),
ди, 1 дй. ди.
л,А = Р^г-^-, j9(uiul\k = pui-^- = pui-g^-. E.21)
В последнем преобразовании была использована малость
компонент тензора деформаций ъц и вектора ротации шу =
= у (««. / — «/. /)•
Собирая вместе преобразованные члены E.21), получаем,
что величина
] v E.22)
равна нулю в силу уравнений движения E.3), что и требовалось
доказать.
Как видно, инвариантное свойство вектора потока энергии
П в форме E.18) справедливо для произвольных сплошных сред
только при условии малости компонент %ц и юц. Укажем дру-
другое выражение для составляющих вектора потока энергии:
П* = J [(г/0 + \ РЩЩ - Я) nk - (ачщ, k + q,, k) nj dS. E.23)
s
Доказательство его инвариантности относительно выбора по-
поверхности 2 совершенно аналогично предыдущему.
Выражение для потока энергии в форме E.23), как легко
видеть, годится также для произвольных конечных деформаций
и углов поворотов, если под хи х2, х3 понимать лагранжевы ко-
координаты, «вмороженные» в деформируемую среду. При этом
230 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЕ 1ГЛ. V
компоненты тензоров и векторов берутся уже в соответствую-
соответствующей криволинейной системе координат.
Доказательство инвариантности вектора П справедливо
только в том случае, когда в области D\ нет каких-либо сосредо-
сосредоточенных источников или стоков энергии. В противном случае
напряжения и деформации будут обращаться в бесконечность
в сингулярных точках, и применяемые преобразования потеряют
в них смысл.
Необходимым и достаточным условием отсутствия подобных
сосредоточенных "источников и стоков энергии в области D яв-
является выполнение равенства E.19) для любой замкнутой по-
поверхности, расположенной в D.
Рассмотрим типы движущихся энергетических источников и
стоков: точечные, линейные, поверхностные и объемные. Будем
предполагать далее, что скорость движения источника или стока
энергии в любой точке совпадает со скоростью движения зам-
замкнутой поверхности или контура, охватывающих эту точку.
Можно считать также, что поверхность 2 и контур С непо-
неподвижны; при этом решение, фигурирующее в подынтегральном
выражении, надо брать в системе координат, движущейся вме-
вместе с источником или стоком как единое целое (как в предыду-
предыдущем параграфе).
Мощностью движущегося энергоисточника (или энерго-
энергостока) в точке О будем называть вектор Гр с компонентами Tph:
Г-р* = Нт | [(э + -j 9ШЩ — H}nk — atftifUi. *] dS E.24)
S(S0)->0.
Здесь 2о—произвольная замкнутая поверхность, охватываю-
охватывающая точку О, SBo) — площадь поверхности 20. Отметим, что
мощность точечного энергоисточника имеет размерность силы.
Пусть теперь энергосток распределен вдоль некоторой изме-
изменяющейся со временем пространственной кривой L. Линейной
плотностью движущегося, энергоисточника (или энергостока) в
точке О кривой L будем называть вектор Г с компонентами IV
Tk = lim <f \(э + у рщщ — н)пк — atjttjUit Jds,
сf u У J ч E.25)
е/Д->0, Д-»0.
Здесь Д — высота произвольно малой трубки, соосной с кривой
L в окрестности точки О, е — наибольшее расстояние точек бо-
боковой поверхности трубки от кривой L в сечениях, перпендику-
перпендикулярных кривой L, С — замкнутая кривая, получившаяся от пе-
пересечения поверхности этой трубки с плоскостью, перпендику-
Tsk = lim [(з + -i рщщ — я) nk —
ПОТОК ЭНЕРГИИ 231
jmofi к L в точке О, ttj — компонентьцзектора единичной нор-
(ыш к боковой поверхности трубки в точках кривей С.
рПлотность движущегося линейного энергоисточника имеет
^мерность силы, деленной на длину; вектор Г, очевидно, всегда
рпендикулярен кривой L в точке О.
Теперь распределим энергосток вдоль некоторой изменяю-
ся со временем поверхности S. Поверхностной плотностью
вргоисточника (или энергостока) в точке О движущейся по-
jxhocth S будем называть вектор Г8 с компонентами Т8й:
^ А и В — произвольно выбранные точки на перпендику-
перпендикуляре к поверхности S в точке О (по разные стороны от точки О),
!f(AO) и 1(ВО) — длины соответствующих отрезков [Х]\в озна-
означает разность X(А) — Х(В).
Вектор Г8 всегда перпендикулярен к поверхности S в точке
О; плотность движущегося поверхностного энергостока имеет
размерность силы, деленной на квадрат длины.
Наконец, распределим движущиеся энергостоки в некотором
объеме V. Объемной плотностью подвижного источника (стока)
Энергии в точке О объема V будем называть вектор Г„ с ком-
компонентами Гг*:
Г„к = lim i- J [E + ~ рщщ — я) nk ~ otjtijti,, k] dS,
S(E0)->0.
^десь 2o — произвольная замкнутая поверхность, охватываю-
охватывающая-точку О, S(So) — площадь поверхности So, о — объем за-
заключенной внутри нее области, щ — единичная внешняя иор-
маль к So. Величина Г„ имеет размерность силы, деленной на
куб длины.
Заметим, что во всех приведенных формулах можно брать
в качестве потока энергии выражение E.23). Уравнение E.27)
Можно записать также в следующих эквивалентных формах:
J
D
j рщщ - Я) nk ~ оцпрь k] d2 E.28)
ИЛИ
+ qt, i = Uo + pE, pE=V^vi, E.29)
Ще V — скорость движения источника (стока) энергии в точке
©г Рв — скорость поглощения энергии в единице объема.
232 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ (ГЛ V
Таким образом, удельная скорость поглощения энергии равна
скалярному произведению вектора Г„ на скорость движения
источника V.
Второе соотношение E.29) позволяет также понять физиче-
физический смысл идеализированных точечных, линейных и поверхно-
поверхностных источников (или стоков) энергии, если мысленно «раз-
«размазать» эти сосредоточенные источники в объемах, весьма близ-
близких к соответствующей точке кривой или поверхности. При этом
величина E# в формуле E.29) будет представлять собой
усредненную по этому объему удельную скорость поглощения
энергии.
След, оставляемый движущимся сосредоточенным источни-
источником энергии, представляет собой: незамкнутую кривую (точеч-
(точечный источник), незамкнутую поверхность (линейный источник),
ограниченный объем (поверхностный источник). Границы этих
областей являются источниками (или стоками) энергии в из-
изучаемый момент времени.
Развитый формализм относится к любым сплошным средам.
Конкретный физический смысл движущихся сосредоточенных
источников (стоков) энергии различен в разных физических си-
системах. Назовем, например, ударные волны в сжимаемых иде-
идеальных средах, которые представляют собой движущиеся по-
поверхностные стоки энергии; тонкое осесимметричное тело, дви-
движущееся с большой скоростью в сжимаемом идеальном газе
вдоль своей оси и имитируемое движущимся точечным энерго-
энергоисточником в головной части тела; различные тепловые источ-
источники и стоки и т. д. Теория этих явлений излагается в учебниках
по механике сплошной среды (см. курс Л. И. Седова [']).
Фронт движущейся поверхности разрыва смещений типа тре-
трещины представляет собой, как легко видеть, линейный сток
энергии, причем из сравнения формул E.12) и E.25) можно
заключить, что величина 2уо представляет собой проекцию век-
вектора Г на направление роста трещины в точке О (в плоскости
ху, перпендикулярной к фронту трещины в этой точке).
Рассмотрим несколько простых иллюстративных приложений
полученных результатов.
1. Криволинейные трещины. Теорию криволинейных трещин
в произвольных сплошных телах можно построить на основе со-
соотношения E.25) по аналогии с концепцией уо Для гладких
трещин.
Проведем из точки О контура трещины вектор потока энер-
энергии Г (рис. 74). Окружность, построенная на этом векторе как
на диаметре, представляет собой геометрическое место концов
векторов, проведенных из точки О, длина каждого из которых
ГF) равна потоку внешней энергии в точку О фронта трещины
в том случае, если направление вектора совпадает с направле-
ПОТОК ЭНЕРГИИ
233
ем роста трещины. Обозначим через 2уо@) величину удель-
энергозатрат, характеризующих локальные свойства ма-
ряала при развитии трещины из точки О под углом Э.
Сформулируем основные положения концепции у0, представ-
цяющей собой естественное обобщение соответствующей концеп-
|рм для хрупких тел.
В произвольной точке О контура трещины всегда выпол-
выполняется соотношение
E.30)
Причем трещина не развивается, если Г@)<2уо(9), и растет,
если Г (9) = 2уоF). Угол 0», под которым происходит рост тре-
трещины в точке О, является кор-
корнем уравнения *) У
= 2Yo@). E.31)
Рис. 74.
В частности, для изотроп-
изотропного тела величина 2уо не бу-
будет зависеть от 0, полярная
Диаграмма 2уо@) будет пред-
представлять собой окружность с
центром в точке О, так что рост
трещины будет происходить в
направлении вектора потока
энергии Г (при этом абсолют-
абсолютная величина вектора Г в
момент роста равняется 2уо).
Дальнейшие упрощающие допущения заключаются в том,
что величина 2уо считается не зависящей от положения точки О
в теле, от предыстории и скорости развития трещины. В общем
случае величину 2уо следует полагать экспериментально опре-
определяемой и зависящей от положения точки О в теле, от ориен-
ориентации плоскости трещины в этой точке, от предыстории и ско-
скорости развития-трещины.
Развитая энергетическая теория криволинейных трещин, как
будет видно из дальнейшего, не совпадает с теорией трещин
обобщенного нормального разрыва, однако экспериментальных
данных пока недостаточно, чтобы отдать предпочтение той или
другой теории.
Вычислим поток энергии Гж для нескольких простых конфи-
гураций в условиях плоской задачи, считая растущую трещину
прямолинейной. Объемными силами пренебрегаем.
*) Аналогичный подход развивали Л. В. Ершов и) Д. Д. Ивлев [""J,,
В. И, Моссаковский и М. 'Г. Рыбка [108].
234 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
"• 2. Полоса с защемленными основаниями*). Пусть полоса
<; основаниями у = ±h содержит полубесконечный разрез у=0,
х < 0 (рис. 75). Разрез свободен от нагрузок, а основания по-
полосы защемлены, так что вектор смещения и постоянен вдоль
каждого основания (но различен для у = —h и для y=+h).
Воспользовавшись основным свойством потока энергии, сде-
формируем контур С из бесконечно малой кривой, окружаю-
окружающей точку О, в контур, по-
показанный на рис. 75. Он со-
составлен границами полосы и
,У
2h ^лу/уу/У/улу/УлуЛ > 1 разреза, а также отрезка-
0 я Т ми, перпендикулярными к
оси х и отстоящими далеко
от точки О по сравнению с
шириной полосы.
¦ Воспользуемся формулой
E.12). Интеграл по берегам
разреза равен нулю вследствие того, что яж=0 и Oijtij—O. Вдоль
оснований полосы интеграл также обращается в нуль, так как
ди/дх = 0, пх = 0. Вдоль правого отрезка при я->--|-оо имеет
место однородное поле, так что ди/дх = 0 (пх = 1), и интеграл
вдоль него равен 29<x,h, где Э», — плотность энергии деформаций
при х—*-\-оо. Левый отрезок при х—*¦—оо возьмем достаточно
далеко не только от точки О, но и от той точки, в которой на-
находился конец разреза в начале нагружения. Тело будем счи*
тать ненапряженным и недеформированным до начала нагру-
нагружения; поэтому интеграл вдоль левого отрезка исчезает.
Член с кинетической энергией также не дает вклада, если
считать, что смещение границ полосы возрастало достаточно
плавно вплоть до заданного значения; при этом можно прене-
пренебречь кинетической энергией свободных колебаний полосы при
X—>—оо и при X—*-\-оо.
Окончательно получаем
1 х — "^оо"-1 (O.OZ)
3. Полоса с гладкими основаниями **). Пусть бесконечное
тело имеет периодическую систему разрезов вдоль у = 2nh,
х < 0, где п = 0, ±1, ±2, ... (рис. 76). Разрезы свободны от
внешних нагрузок, а напряжение ау при х—>-+оо равно ох,
*) Примеры 2 и 4 для упругих тел в условиях статики впервые рассмот-
рассмотрел Дж. Раис [ш'ш], который независимо, но несколько позже автора
(ср. t38]) развивал аналогичный подход, однако применительно лишь к упругим
статическим задачам (/ic-approach).
.**) Аналогичную задачу рассмотрел Койтер [1П] для лииешю-упругога
тела в условиях статики,
ПОТОК ЭНЕРГИИ
235
Шйчем в процессе нагружения оно возрастает достаточно
(равно.
В силу симметрии вдоль линий у = nh будут выполняться
келовия хху = 0, ди2/дх = 0. Поэтому область |г/|^Л можно
рйтерпретировать как полосу с жесткими гладкими основа-
Йиями.
Выбирая контур С так, как показано на рис. 76, по формуле
р. 12) вычисляем Гж совершенно аналогично предыдущей задаче;
|ри этом для Гж по-прежнему
Получается выражение E.32).
^Величина Эх в данном случае,
рчевидно, будет другой.
Точно так же можно рассмо-
рассмотреть случаи, когда при *->-|-оо
заданы постоянные касательные
напряжения %уг или %ху.
4. Изгиб полосы с разрезом *).
Теперь предположим, что осно-
основания аналогичной полосы с раз-
разрезом свободны от нагрузок, а
Йри х-*—оо действует напряже- Рис 76
йие ах, являющееся линейной
функцией у на каждой половине полосы, причем изгибаю-
изгибающий момент этих сил отличен от нуля, а их главный вектор
у
Zh
1
V
с
0 х
К/
Рис. 77.
равен нулю (рис. 77). При этом вклад в интеграл E.12) даст
только левый перпендикулярный отрезок при х—>—оо, а членом
•) Эту задачу приближенными методами теории балок рассматривали
ранее И. В. Обреимов [112], Гилман,[19] и др. (однако только для линейио-
|цругих тел в условиях статики).
236 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ.-V
с кинетической энергией по-прежнему можно пренебречь, если
нагружение весьма плавное. В итоге получаем
h h
Г* = -2 lim f b-cx^-)dy=2 lim f {-9+ox*x)dy. E.33)
Совершенно аналогично рассматривается тот случай, когда
полоса слева не бесконечна, а ограничена прямой, перпенди-
перпендикулярной основаниям полосы и отстоящей на расстоянии / от
конца разреза, причем к этому участку границы с каждой сто-
стороны полосы по параболическому закону приложено касатель-
касательное напряжение хху, создающее перерезывающую силу. Резуль-
Результат, очевидно, будет следующим:
J
о
л
= 2 J (-Э + ахвх + 2ххуеху) \x==_tdy + 2QlB,.f E.34)
о
так как
h . h h
ft
J xxy ^j-dy= ххущ — j щ dxxy = — J u, dxxy = — a,.Q,.
0 ° 0
°- 0
Здесь Qi — перерезывающая сила, mu — некоторая средняя ве-
величина щ при х = —I. В силу малости деформаций величина
uu при h^> h, очевидно, пренебрежимо мала по сравнению с и2.
Конфигурации, изображенные на рис. 75—77, принципиально
можно рассматривать как экспериментальные схемы определе-
определения величины Yo для трещин, растущих в конкретных материалах
при различных условиях. Действительно, правая часть формул
E.32) — E.34), дающих yo в этих случаях, легко определяется
из параллельных измерений в соответствующих точках (или же
вычисляется, если реологическая модель тела уже известна).
§ 3. Численный метод
Уравнения энергии в виде E.1) и E.5) (а также уравнения
для потока энергии в конце трещины в форме E.25)) на основе
физической концепции о постоянстве Yo (cm. E.30) и E.31))
позволяют указать численный алгоритм решения общей задачи
о распространении трещин в сплошном теле, описываемом за-
заданной реологической моделью.
I 3]
ЧИСЛЕННЫЙ МЕТОД
237
Предположим для определенности, что задача плоская, а по-
положение рассматриваемого конца трещины описывается одним
параметром / (например, длиной, отсчитываемой от некоторой
фиксированной точки тела). Пусть в начальный момент вре-
времени t = О параметр I равен V
Разобьем процесс развития трещины на конечное число ша-
шагов, так чтобы At и Д/ соответствовали одному шагу, а распро-
распространение трещины было прерывистым. Это означает введение
в плоскость (/, t) некото-
некоторой прямоугольной сетки
(рис. 78). Допустим, что
мы располагаем прямым
методом, позволяющим
решать нашу краевую за-
задачу для заданной рео-
реологической модели при
любых фиксированных
значениях параметра /
(особенность в конце
трещины должна иссле-
исследоваться отдельно, в про-
противном случае она должна
улавливаться методом).
Таким методом может
служить, например, ка-
какая-либо вариация метода Рис. 78.
конечных элементов [из].
Решаем этим методом краевую задачу при / = k, вычисляя
по формуле E.25) поток энергии в конце трещины Г в после-
последовательные промежутки времени О, Д*. 2М и т. д., а затем
сравнивая полученное значение с известной из эксперимента
величиной 2yo согласно условию E.30).
Значение Гж в момент времени t = tn удобно подсчитывать
по формуле E.14), которая в данном случае примет вид
'= — 2 lim J ау (х, б, *„_,) [иу (х, б, Q — иу (х, б, *„_,)] их.
в/й-»о Ав
Здесь начало координат берется в конце трещины в момент вре-
времени t — tn-i. Может случиться, что особенность в конце тре-
трещины аналитическими средствами исследуется только в на-
начальный момент роста трещины. Тогда в конечно-разностном
аналоге этой формулы величины б и R должны быть достаточно
велики по сравнению с шагом /±.х и Ду; искомая особенность при
$%& НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ ' [ГЛ. V
этом улавливается асимптотически при достаточно малых ша-
шагах Дх и Ау.
Аналогичная формула имеет место для компоненты Ту по
вытянутому вдоль оси i/прямоугольному контуру. Узловые точки,
в которых'Г < 2уо, будем снабжать на рисунке квадратом, а те
точки, в которых Г ^ 2уо, обозначим треугольником (см.
рис. 78).
Счет ведем шаговым методом при / = const или при
t == const до первого узла, в котором Г ^ 2^0, после чего ме-
меняем направление. Более точные значения / или t, соответствую-
соответствующие равенству Г = 2уо, определяем линейной интерполяцией
между соседними прямоугольным и треугольным узлами (на
рис. 78 интерполяционные значения, I и t обозначены крести-
крестиком). Параллельно на каждом шаге в узле, где Г ^ 2уо, опре-
определяем отклонение направления роста трещины по формуле
E.31). Таким образом, плоскость (t,t) играет роль двумерного
времени, а условия E.30) и E.31) определяют правила обра-
обращения с ним.
Допустим, что в узловой точке А при / = t\ впервые ока-
оказалось Г ^ 2уо (рнс. 78). Интерполяцией определяем момент
времени t = t0, в который начинается рост трещины; по фор-
формуле E.31) находим угол 8». При t=t\ трещине дадим мгно-
мгновенное приращение А/; при этом все величины, характеризующие
поля смещений, скоростей, напряжений и т. д., получат неко-
некоторые приращения, которые, очевидно, можно определить тем
же прямым методом, что и прн счете вдоль / = const. Вычис-
Вычисляем в этой точке величину Г, сравнивая ее с 2уо согласно
E.30), и т. д. При Д7->0, Aif-»"O приближенное решение будет
стремиться к точному.
Это построение показывает, что задачи о развитии трещин
(в частности, об определении их траектории) носят существенно
инкрементальный характер; каких-либо принципов, которые
связывали бы начальное и конечное состояния, не существует.
Исключение составляет лишь тот случай хрупких трещин, когда
положение всех точек их контуров описывается единственным
параметром (и тем самым, в частности, траектория трещин за-
заранее известна из каких-либо дополнительных условий).»
Допустим, что внешние нагрузки на тело описываются сово-
совокупностью некоторых параметров /?i, р2, ..., рп (ограничимся
хрупкими трещинами). Из указанного построения вытекает
также следующее: не существует (за упомянутым исключением)
такой поверхности в пространстве р\, р2, ..., рп, которая разде-
разделяла бы недостижимые состояния (в которых равновесие тела
с трещинами невозможно) от допустимых. Последнее ограничи-
ограничивает возможности применения теорий предельного состояния
к телам с трещинами.
§ fl УПРУГОЕ ТЕЛО 239
Указанный метод годится также при использовании обще-
общефункционального подхода к развитию трещин. При этом вместо-
E.30) и E.31) правила движения по плоскости (/, t) будут
определяться некоторой экспериментально определяемой ком-
комбинацией из коэффициентов интенсивности сверхтонкой струк-
структуры конца трещины.
§ 4. Упругое тело
Рассмотрим вначале вопрос о развитии трещин в однород-
однородных и изотропных упругих телах, пренебрегая объемными си-
силами, а также взаимным превращением тепловой, и механиче-
механической энергии. В этом случае величины у и Yo совпадают.
1. Динамические, трещины. Пусть в линейно-упругом теле
распространяется некоторый математический разрез со свобод-
свободными вблизи кромки берегами. Поверхность разреза в любой
момент времени считаем гладкой, так что вектор скорости роста
разреза лежит в плоскости, касательной к поверхности разреза
в соответствующей точке. Под скоростью движения контура
(кривой) в пространстве, как обычно, понимается скорость по
нормали к контуру.
Вычислим поток энергии Гж в произвольную точку О кон-
контура разреза в направления"его роста. Ограничимся наиболее
важным случаем трещин нормального разрыва.
Нам понадобится следующий интеграл (простые, но громозд-
громоздкие выкладки опускаем):
? sin-|-arctg(fe2tg6)-cosy arctg(fe,tg6)
f (cos2e + felsm2еI/4sme dB=V E>35)
(cos2е + febin2ef (cos2e + felsm2е)
Заметим, что в формулах C.187), так же как и в E.35), функ-
функция у = arctg(&tg6) в интервале (—п,п) ведет себя примерно
так, как показано на рис. 79.
По формулам C.187)-, E.14) и E.35) находим
+R ¦
E.36)
:
(m = i/c2<mR).
Соотношение E.36) выражает линейную плотность энерго-
сгока на фронте движущейся трещины через локальный
240
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ
1ГЛ. V
коэффициент интенсивности напряжений Кь В частности, в ква-
квазистатическом случае т-»-0 получается снова формула Ирвина
B)tf
()
Знаменатель правой части E.36) обращается в нуль при
= mR. Напомним, что уравнение Рэлея R(m, v) = 0 или
R(m, v) = |/(l-
-(l-i-m2J=0. E.37)
имеет единственный положительный корень, который меньше
единицы и который определяет скорость распространения неза-
незатухающих волн по свободной поверхности упругого тела [1М].
i ¦
J
У,
я
J
0
-Я
J
.6
t"
Рис. 79.
Рис. 80.
Приведем несколько значений корня mR в зависимости от
коэффициента Пуассона v:
mR 0,87 0,90 0,92 0,94 0,95 0,96
v 0 0,1 0,2 0,3 0,4 0,5
Согласно E.36), поток энергии Тх в конец трещины растет
с увеличением скорости, обращаясь в бесконечность при рэлеев-
ской скорости; при m > mR величина Тх меняет знак; это озна-
означает, что конец трещины должен излучать энергию, чтобы рас-
распространяться с такой скоростью. Поскольку это физически
невозможно, рэлеевская скорость представляет собой недости-
недостижимую верхнюю границу скорости распространения трещин
нормального разрыва.
В однородных материалах максимальная скорость ограни-
ограничена еще раньше величиной m = m», при которой происходит
ветвление трещины и вместо одного фронта трещины появ-
появляются два или даже больше (рис. 80). Уравнение, определяю-
определяющее значение /и*, легко получить следующим образом. При по-
помощи формул (ЗЛ87) найдем напряжение ста(8) вблизи конца
трещины. Исследование функции <тв(Э) показывает, что
существует значение т — шч такое, что при т<^т^ макси-
§ 4] УПРУГОЕ ТЕЛО 241
мум этой функции, как и для квазистатических трещин
нормального разрыва, имеет место при 8 = 0, а при т> т*
у нее появляются два симметричных максимума при 9= ±9*
(точка 9 = 0 становится локальным минимумом). Таким
образом, согласно теории криволинейных трещин обобщен-
обобщенного нормального разрыва прямолинейное распространение тре-
трещины при т>т* невозможно*). Точка m = m,, определяет
момент слияния двух максимумов, т. е. находится из условия
при 9 = 0 -^f = 0. E.38)
Отсюда при помощи C.187) получаем искомое уравнение
+![(¦ -М- /о -«ч(¦-
•??
E.39)
Приведем несколько значений корня т* в зависимости от
коэффициента Пуассона v:
т.
V
0,51
0
0
0
,56
,1
0,60
0,2
0,
0
,62
,25
0,
0,
65
,3
0,71
0,4
0
0
,76
,5
Экспериментально наблюдались значения предельной скоро-
скорости роста трещин в интервале @,4-г-0,6) с2 Для различных ме-
металлов, полимеров, стекол (см., например, работу Ирвина [91]).
Зависимость сге (в) весьма сильно выполаскивается уже при т,
значительно меньших /и*; поэтому в опытах практически невоз-
невозможно достичь значения /и*.
Если прямолинейность распространения трещины заранее
обеспечена (например, благодаря анизотропии прочности мате-
материала), то максимальная скорость распространения трещины
совпадает с рэлеевской скоростью**).
Отметим следующее обстоятельство. При стационарном рас-
распространении конца трещины в поле напряжений, не зависящих
*) Этот результат впервые получен Э. Иоффе [П6].
**) К этому результату почти одновременно и независимо пришли многие
авторы (Стро Г116], Крэгс [117], Бейкер [118], Броберг [11в], Г. И. Баренблатт
и Г. П. Черепанов [120] и др.).
242 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
от расположения конца трещины, величина К* будет неизмен-
неизменной в процессе роета трещины. При этом процесс распростране-
распространения трещины будет самоускоряющимся, так как согласно E.36)
поток энергии извне в конец трещины'возрастает с увеличением
скорости. Самоускорение, очевидно, должно продолжаться
вплоть до двойникования трещины. Если постоянная предельная
скорость распространения трещины в этом случае наблюдается
на значительном интервале длины, то это явление можно объ-
объяснить только тем, что; начиная с этого значения скорости, вели-
величина энергозатрат, требуемых для ускорения развития трещины,
превышает поток энергии Тх в конец трещины.
Вычислим коэффициент интенсивности напряжений Ki в ди-
динамическом случае для конфигураций тела, изображенных на
рис. 75—77. Напомним, что для рассматриваемого идеального
линейно-упругого тела энергия деформаций Э дается формулой
E.40)
Используя это соотношение, при помощи формул E.32) —
E.34) нетрудно найти коэффициент интенсивности напряжений
и поток энергии Тх для указанных конфигураций.
' Полоса с защемленными основаниями (см. рис. 75). В случае
растяжения на бесконечности при^д: -> +°° будет
Eve™ oo_ (i-v)?e^ E.41)
a7 — aT — (i + v) A - 2v) • a7~ (i+v)(l-2v) '
а Гх определяется формулой
(l-v)E(CY ,
Сравнивая это выражение с формулой E.36), находим коэф-
коэффициент интенсивности напряжений
-4A- У) * (вуУ .(/С- т^ - jzjpf ~ (l ~ -j-
A + vJ A - 2*) m* |/l - i^g- m*
E.43)
В частности, при m—>0 находим
§ 4} УПРУГОЕ ТЕЛО 243
В квазистатическом случае поперечного и продольного сдвига
на бесконечности при помощи E.32) и D.45) аналогично по-
получаем
2(J
)()
9F2h(p°°Y
А ш — —A -j. vJ — zn \xxz) •
Формулы E.43) — E.45) останутся справедливыми также и
для бесконечной плоскости с периодической системой полубеско-
полубесконечных разрезов, изображенных на рис. 76. Из выражения E.43)
видно, что с увеличением скорости распространения разрезов
коэффициент интенсивности напряжений монотонно падает, об-
обращаясь в нуль при рэлеевской скорости т = mR\ при т> тп
коэффициент интенсивности напряжений становится мнимым.
Изгиб полосы с разрезом (см. рис. 77). Для линейно-упругого
тела в случае чистого изгиба соотношение E.34) приобретает
следующий вид:
Г* = 2 | Э№ dy = | <т?е? dy. E.46)
о о
Напряжения и деформации при я-> — оо равны
?A+v) E.47)
При помощи E.46) и E.47) находим
г _ 12A-vW E4g)
Сравнивая эту формулу с выражением E.36), получаем коэф-
коэффициент антенсивности напряжений
. E.49)
ttl2
2 —2v
В частности, при т-*0 находим
а-?=12М2М3. E.50)
Полученное точное решение позволяет найти приближенное
решение многих других задач, когда нагрузка приложена к бере-
берегам трещины и к торцу х = —/, если, воспользовавшись теорией
244 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
балок, вместо М в формулу E.50) подставить суммарный мо-
момент этих нагрузок относительно конца трещины. При этом
требуется, чтобы выполнялось условие I ^> h; практически доста-
достаточно, чтобы кратчайшее расстояние приложенных нагрузок от
конца разреза в три-четыре раза превосходило ширину полосы h.
2. Нелинейно-упругое тело. Сверхтонкая структура конца
трещины. Рассмотрим нелинейно-упругое тело с трещинами.
В предположении, что объемные деформации линейно-упруги,
связь напряжений с деформациями можно записать в следую-
следующем виде [*]:
2I
-±еккЪи), E.51)
—y \aij ~~ ~2
Здесь /(/)—заданная функция, удовлетворяющая условию
f'(/) > 0, 8{j — символ Кронекера.
Уравнения E.51) вместе с уравнениями равновесия и кинема-
кинематическими' соотношениями между деформациями и смещениями
теории малых деформаций составляют замкнутую систему урав-
уравнений. Можно показать, что эта система принадлежит к "эллипти-
"эллиптическому типу, если выполняется условие /'(/) > 0.
Решение указанной системы уравнений, как правило, всегда
сингулярно в конце разреза по напряжениям и деформациям.
Действительно, это вытекает, например, из уравнения E.10),
если учесть, что величина y конечна, поскольку для разделения
тела на части нужно затратить конечную работу. Случай огра-
ограниченного решения, как и в линейно-упругом теле, отвечает не-
некоторым частным значениям внешних нагрузок (когда компен-
компенсируются особенности противоположного знака от различных
внешних нагрузок).
В силу сингулярности решения в конце трещины его асимпто-
асимптотическое поведение определяется характером функции /(/) при
/—* оо. Применяя «принцип микроскопа» и результаты исследо-
исследования особенностей в конце трещины для линейно-упругого и
степенного тел (см. §§ 5 и 10 главы 3), приходим к следующим
выводам.
Линейно-упругая асимптотика. Если зависимость f(I) при
/->оо стремится к линейной:
f (Л = (/ — Щ-ico при / -> оо, E.52)
где ц,х> и /0 — постоянные материала, то поведение напряжений
и деформаций непосредственно -вблизи конца трещины опреде-
§ 4] УПРУГОЕ ТЕЛО 245
ляется формулами C.44) —C.46), в которых ц нужно заменить
на (ioo, а вместо v подставить Voo, где
2 _ ?-2^A-2v) __.
Соответствующие коэффициенты интенсивности напряжений
будем обозначать/ через kj, kn, km. Размерность этих величин
совпадает с размерностью коэффициента Кь Для формули-
формулировки условия локального разрушения можно применить, оче-
очевидно, методы гл. IV. В простейшем случае трещин нормального
разрыва, если не учитывать влияние предыстории на локальное
разрушение, получается следующий критерий:
k\^kic, где ki = lim (У2яхоу). E.54)
Х->0
Здесь kic — некоторая постоянная материала, которая связана
с величиной у зависимостью, аналогичной формуле Ирвина
E.55)
Формула E.55), очевидно, останется справедливой, если за-
заменить в- ней 2y на Гх, a k\c на k\. Она позволяет определить
коэффициент интенсивности напряжений kj для указанной мо-
модели тела в случае конфигураций, приведенных на рис. 75—77.
Сравнивая E.55) с формулами E.42) и E.48) и исклю-
исключая у, находим:
для полосы с защемленными основаниями или периодиче-
периодической системы полубесконечных разрезов (см. рис. 75 и 76)
I ~~ A - v») A + v) A - 2v) ' {О-ОО)
для чистого изгиба полосы с полубесконечным разрезом (см.
¦ рис. 77) .
'и2_
В случае полубесконечного прямолинейного разреза в беско-
бесконечной упругой плоскости, приравнивая потоки энергии у, полу-
получаем зависимость kj от Ki'.
.2 _ A-у)цю К2
При выводе формул E.56) — E.58) существенно использова-
использовалось свойство инвариантности вектора потока энергии при де-
деформировании контура, охватывающего конец трещины. Особен-
Особенно важна формула E.58); она дает связь коэффициента интен-
интенсивности тонкой структуры К\ с коэффициентом интенсивности
Ш НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
сверхтонкой структуры k\. Подчеркнем, что постоянные v, ц, v«>,
Ноо представляют собой коэффициенты Пуассона и модули
сдвига на участках упругой диаграммы «напряжения — дефор-
деформации» только при бесконечно малых и бесконечно больших де-
деформациях (все это, разумеется, в рамках теории малых дефор-
деформаций, поэтому на самом деле здесь речь идет о некоторых про-
промежуточных асимптотиках).
Понятие сверхтонкой структуры края трещины уточняется
ниже. Формула E.58) справедлива также для критических (пре-
(предельных) значений коэффициентов интенсивности. Она позво-
позволяет определять вязкость разрушения Kic по эксперименталь-
экспериментальным значениям ⁣ последнее представляет большой практиче-
практический интерес, так как для определения kie годятся образцы
малых размеров, на которых тонкая структура края трещины не
реализуется.
Из формулы E.53) вытекает одно интересное следствие. По-
Поскольку для всех твердых тел ц*, <С Е, то v«> « 1/2, т. е.-с уве-
увеличением деформации Коэффициент Пуассона возрастает, так
что при больших деформациях, характерных для сверхтонкой
структуры, все тела приближенно можно считать несжимаемыми.
Разумеется, этот вывод верен лишь до тех пор, пока объемную
сжимаемость можно считать линейно-упругой. Из формул E.58)
и E.53) следует, что величина kic примерно в ty^n/[2(l —v)^]
раз меньше вязкости разрушения Kic- В пределе при [ico->0
величина kic также стремится к нулю, т. е. напряжения на краю
трещины становятся конечными.
Степенная асимптотика. Несжимаемое тело. Если зависи-
зависимость /(/)_при /-> оо стремится к степенной и при этом тело
можно считать несжимаемым, т. е.
) , v=l/2 при /->оо, E.59)
где es, as и к — постоянные материала, то поведение напряжений
и деформаций непосредственно вблизи конца трещины описы-4
вается соотношениями C.160) — C.164). В частности, напряже-
напряжения имеют порядок Н*^2). Обозначим соответствующий коэф-
коэффициент интенсивности напряжений в рассматриваемом случае
через k\, для случаев поперечного и продольного сдвигов — че-
через &2 и кг- Размерность этих величин равна силе, деленной на
длину в степени Bк + 3)/(и + 2). Для формулировки критерия
локального разрушения используем общефункциональный метод
гл. IV. В случае трещин нормального разрыва, если пренебречь
влиянием предыстории на локальное разрушение, критерий бу-
будет следующим:
где ki = lim [Bях)Шк+\]. E.60)
х-Ю
УПРУГОЕ ТЕЛО
247
Здесь kic — некоторая постоянная материала. Из соображений
Анализа размерностей (учитывая, что в уравнениях участвуют
йищь esas~K-1 и х) или же непосредственно из уравнения энергии
^5.10) видно, что величина k\ связана с
величиной у зависимостью
E.61)
Где Ао(и) —безразмерная функция к.
Сравнивая эту формулу с формулой 6
ррвина и исключая y> находим связь
Шг с Кг- ' g
иг2 —
AI —
E.62)
\
0 Ofi
¦*.—
15 0,010
X
Найдем приближенно функцию А0(х),
используя известный предельный случай
при х->0, а также некоторые числен-
численные результаты, полученные в работах
[39, i2i] для значений х = 2,33, к = 4,
к = 9.
На рис. 81 приведены графики напря-
напряжения ау на продолжении трещины для
этих значений х в зависимости от безраз-
безразмерного расстояния до конца трещины;
величина as задает масштаб напряжений, ее конкретное значе-
значение несущественно. Графики взяты из работы [122]; они построе-
построены при условии, что asl(esE)= 1/3, v = 1/2. При этих условиях
согласно E.60) и E.62) для весьма малых х имеем следующую
зависимость:
\Х+2
/LA I К, ¦ / Л. I I Ъ
E.63)
Рис. 81.
16я
При помощи этой формулы и рис. 81 находим следующие
значения Хо(х):
х 0 2,33 4 9
Я0(х) 8 165 1020 256 000
Последние три точки хорошо аппроксимируются функцией
Л0(х)= 12,8-3* B
E.64)
Погрешность этой аппроксимации составляет несколько процен-
процентов. Диапазон к от двух до десяти охватывает большинство
встречающихся на практике материалов, если их диаграммы
«напряжение — деформация» аппроксимировать прямой до
248 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
условного предела текучести 00,2, а затем применять степенную
аппроксимацию E.59). Формула E.64) хороша еще тем, что со-
согласно E.63) при % ->¦ °о<вблизи конца трещины на ее продолже-
продолжении получается ov = 3crS) что примерно отвечает идеальному
упруго-пластическому материалу (с условием пластичности Ми-
зеса) с пределом текучести на растяжение, равном as-
Подставляя E.64) в E.62), получаем окончательную зависи-
зависимость, связывающую k\ и К\'.
^ Ю). E.65)
Эта формула годится также для предельных значений коэф-
коэффициентов интенсивности напряжений, поэтому она позволяет
определять вязкость разрушения путем измерения k\c на малых
образцах. Подчеркнем, что постоянные v, E и es, crs> % относятся
к тонкой и сверхтонкой структурам соответственно.
Уточним понятие сверхтонкой структуры. Распределение на-
напряжений и деформаций непосредственно вблизи края трещины
в материале, не являющемся линейно-упругим, будем называть
сверхтонкой структурой конца трещины, если это распределение
получено в рамках теории малых деформаций. Физически сверх-
сверхтонкая структура конца трещины представляет собой, так же
как и тонкая структура, некоторую промежуточную асимптотику;
а именно, она реализуется на расстояниях г от края трещины,
удовлетворяющих условиям
p<r<d, p<r<L. E.66)
Здесь L — характерный линейный размер тела, d — характерный
линейный размер области вблизи края трещины, в которой свой-
свойства материала нельзя считать линейно-упругими, р — характер-
характерный линейный размер конца трещины в предельном состоянии
(например, радиус кривизны или раскрытие трещины).
Представление о сверхтонкой структуре, как видно, имеет
смысл для любых тел с трещинами, если под трещиной пони-
понимать, как обычно, математический разрез. Это представление
позволяет перенести все основные результаты по формулировке
локальных критериев разрушения для линейно-упругих тел
(гл. IV) на произвольные и в том числе неупругие материалы,
если вместо коэффициентов К\, Кп, Km использовать соответ-
соответствующие коэффициенты интенсивности напряжений сверхтон-
сверхтонкой структуры.
В случае квазихрупкого разрушения наряду со сверхтонкой
структурой реализуется также тонкая структура (на расстоя-
расстояниях г, удовлетворяющих условиям d <S r < L). Для нелинейно-
упругих тел последняя определяется характером функции f(/)
§41
УПРУГОЕ ТЕЛО
249
при / -> 0; соответствующие решения для линейно-упругой и сте-
степенной асимптотики были уже получены ранее в гл. III.
Приведем один конкретный пример. Пусть на границу полу-
полуплоскости перпендикулярно к поверхности выходит трещина
длины I (плоская деформация). На бесконечности тело подвер-
подвергается однородному растяжению напряжением р; поверхность
тела и трещины считается свободной от нагрузок. Кривую f(I)
аппроксимируем следующим выражением (материал считаем
несжимаемым):
3I/E при /<<то.2> ._с_.
ч*+1 , . E-67)
) т ПрИ /><То,2-
Используя, анализ размерностей и критерий локального раз-
разрушения E.60), нетрудно найти величину разрушающего напря-
напряжения р* в предельных случаях:
при
при
E.68>
Здесь Ai — число, Яг (и) — безразмерная функция и. В случае об-
образца конечной ширины они зависят также от отношения длины
трещины к ширине образца. Точное решение показывает (см.
Приложение I), что %\ = 0,516.
3. Концентрация напряжений в выточках. Используя инвари-
инвариантное свойство вектора потока энергии Г (см. E.18) или
E.23)), можно давать эффек-
эффективную оценку концентрации
напряжений и деформаций на
дне разнообразных выточек в
нелинейно-упругих телах в
наиболее опасных точках.
Рассмотрим окрестность
дна выточки, считая, что ее
верхняя и нижняя поверхно-
поверхности — плоские и параллельные
вплоть до некоторых точек А и
В, так что дуга АВ образует
дно выточки (рис. 82). Выточ-
Выточка предполагается близкой к
щели в том смысле, что
раскрытие 2/г мало по сравнению с глубиной выточки. Рас-
Рассмотрим цилиндрические поверхности- 2 с образующими, па-
параллельными оси г; каждая поверхность 2 ограничена обра-
образующей, лежащей на О'А и О"В. Поток энергии Тх через
Рис. 82.
260 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ {ГЛ. V
любую такую поверхность, приходящийся на единицу длины
вдоль z, равен *)
Гя =\3dy. E.69)
ВА
Действительно, согласно E.18) вдоль О'А и О" В имеет место
пх = 0 и, кроме того, вся поверхность выточки свободна от на-
нагрузок, т. е. Oijtij =* 0. С другой стороны, если поверхность Б вы-
выбрать достаточно далеко от начала координат в той области, где
реализуется тонкая структура, то величина Гж будет равной
E.70)
При этом предполагается, что нелинейно-упругое тело при
/ -> 0 ведет себя как линейно-упругое и, кроме того, что нагрузки
достаточно малы,' так что имеет место тонкая структура.
В нелинейно-упругом теле E.51) энергия деформаций равна
/ /
= Jade+1 |/<Ю = -4^(<^J + |J П'№1 E.71)
о о о
о
Предположим вначале, что напряжения и деформации вдоль
дуги АВ распределены равномерно, не изменяясь - от точки
к точке. Выточки с такими закругленными дугами АВ будем на-
называть равнопрочными. Они не имеют на дуге АВ каких-либо
точек, предпочтительных для разрушения, и потому по сравне-
сравнению со всеми другими выточками, имеющими отличную от равно-
прочных^орму закругления дна вдоль дуги АВ, обладают наи-
наибольшей прочностью. Определение формы равнопрочных выто-
выточек представляет самостоятельную задачу, решенную пока
только для нескольких частных случаев**). Для таких выточек
энергия деформации Э в формуле E.69), равная 5min. не будет
зависеть от у; поэтому при помощи E.69) и E.70) можно найти
(для условий плоской деформации)
^/d E.72)
Для всех остальных выточек на дуге АВ, очевидно, всегда
найдется такая точка, в которой энергия деформации Э будет
больше 5min- Поэтому величина Эцип представляет собой точную
нижнюю оценку наибольшей энергии деформации на дне вы-
выточки.
*) Райе tlos), ие знакомый с работой автора [м], предложил выражение
для» потока энергии в нелинейно-упругих телах именно в таком виде.
**) Одно решение ее дана, по-видимому, впервые в работе автора [1И].
УПРУГОЕ ТЕЛО
251
Используя формулу E.71), легко найти также величины на-
наяжений и деформаций, соответствующих значению Этщ- Наи-
олее важны два случая:
a) az = О (тонкая пластина); при этом
/; E.73)
б) ег = 0 (локальная плоская деформация); при этом согласно
р.51) и E.71) будет
2/ ffz 3
9 =
ff'4 2/ ? J'
E.74)
6?
I I t
I
2h
II
"Здесь ot — тангенциальное напряжение4 в точках дуги АВ. Пер-
Первое соотношение E.74) позволяет определить отношение аг1ой
например, для несжимаемых тел
v = 1/2 и 2ffz = at.
Таким образом, при помощи
.формул E.72)—E.74) легко най-
найти точную нижнюю оценку мак-
максимального напряжения на дне
выточки, если известен коэффи-
коэффициент интенсивности напряжений
Ki для математического разреза,
соответствующего данной выточ-
выточке при h = 0. Точной верхней
оценки, очевидно, не существует,
так как наличие, например, угло-
угловой точки класса N на дуге АВ
приводит к локальной сингулярно-
сингулярности напряжений и деформаций.
Приведем некоторые примеры.
а) Пусть выточка выходит за границу полуплоскости, растя-
растягиваемой на бесконечности однородным напряжением р в усло-
условиях плоской деформации (рис. 83). Поверхность полуплоскости
•н выточки считается свободной от нагрузок. Функцию /(/) аппро-
аппроксимируем выражением E.67), материал для простоты считаем
несжимаемым. В этом случае коэффициент интенсивности на-
йряжений Kj равен (см. Приложение I)
E.75)
Рис. 83.
252 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
При этом предполагается, что область нелинейных деформаций
мала по сравнению с глубиной выточки /.
Величина Э, согласно E.74) и E.67), равна
чИ+2
„„„ у С_11л п \ I 4i
| °-2 17
(v=il/2, ст2=1/2(Т„ / = <r,
Сравнивая E.75) и E.76), согласно E.72) получаем точную,
нижнюю оценку для максимального напряжения (с*)max на дне
выточки
V2<
E.77)
б) Оценим форму равнопрочной выточки, аппроксимировав
дугу АВ отрезком параболы 2Дх = —у2, где А — радиус кри-
кривизны дуги А В в вершине выточки (см. рис. 83). Материал счи-
считаем линейно-упругим, тогда на дуге АВ
Э = -2р-, (Tz = 0 (плоское напряженное состояние),
1 _ V2 E.78)
Э = —2/Г~ аЬ az = vat (плоская деформация).
При помощи E.72) и E.78) находим напряжение at в точках,
дуги АВ равнопрочной выточки
ot = KxlVh. E.79)
Напомним, что согласно C.168) напряжение в вершине соот-
соответствующей чисто параболической выточки равно 2/Ci/ ]/яД.
Считая оба напряжения примерно равными, находим оценку для
искомого радиуса кривизны дна равнопрочной выточки
А ~ 4А/я. E.80)
В действительности эта оценка, очевидно, несколько завы-
завышена; поэтому радиус кривизны дна равнопрочной выточки мож-
можно считать примерно равным h.
в) Сравним концентрацию напряжений в наиболее опасных
точках эллиптической выточки C.169) и равнопрочной выточки
IЯ
УПРУГОЕ ТЕЛО
253
рлины 2(l'-f m)R с раскрытием, равным радиусу кривизны эл-
Здипса в наиболее опасной точке х = A + *n)R, у = 0, т. е. при
tf(lJ(l+)'
"(рис. 84).
Так как величина /Ci
отвечает трещине Гриф-
фитса длины 2A + m)R,
при помощи E.79) .на-
.находим
I Ы
I г
E.81)
I I
гA*т)й
Рис. 84.
Используя точное ре-
решение Колосова для эл-
эллипса C.171), получаем отсюда отношение максимальных на-
напряжений в сравниваемых случаях
К тах)эллипс ^ 3 - 2/П - ОТ2
at fn A - т2)
E.82)
4. Криволинейные трещины. Применим энергетическую тео-
теорию криволинейных трещин (§ 2 этой главы) к линейно-упругим
телам в наиболее важном случае, когда /Cm = 0, а остальные
коэффициенты интенсивности напряжений /Ci и /Си отличны от
нуля.
Вычислим вначале вектор потока энергии Г = Yxi + Tyj
в произвольно выбранной точке О фронта трещины (система ло-
локальных декартовых координат xyz выбирается, как обычно, см.
рис. 13). Общие формулы E.25) в данном случае можно за-
записать так:
Г х = ¦
С'
E.83)
Здесь контуры Ci и Сг выбраны так, как показано на рис. 85
и 86. Действительно, в рассматриваемом случае q, = 0, а вклад
в общую сумму от интегралов по отрезкам длины 26 пренебре-
пренебрежимо мал вследствие того, что б < R,
25.4
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ ' 1ГЛ. »Г
Используя представления Колосова -г- Мусхелишвили C.9),
нетрудно получить следующие формулы:
E.84)
dv , ди к-г i T ,
'-д7 + ^у^х- = -^Г1т\
' ду ^ х» Эу 2ц '
y) Ф (г)].
Действительно, из формул C.9) вытекает следующее выра-
выражение для потенциала Ф (z):
В частности,
^-); E.85)
= ^ + 2^+'К-2^). E.86)
Подставляя Ф(х) из E.86) в E.84), убеждаемся в справедли-
справедливости соотношений E.84).
У
1 *
\П
\п
У
J
и
2R
С,
X
п
Рис. 85.
Рис. 86.
Отметим также следующие формулы, легко получаемые
из C.9):
о у - hxy = Ф (г) + Ф (г) + гФ' (г) + ? (г),
х + пху = Ф B) + Щг) — zWJz) - WJz).
E.87)
t$ WiPyroB тело 253^
На Основе соотношений E.84) и E.87) выражения для со-
составляющих вектора потока энергии E.83) примут вид
* ¦ (б<88)
_ __ __
г •=_ -?±I lim $1т(ФФ + & —гФФ' —ФУ) (n-i)ds.
Согласно C.43) функции Ф(г) и W(z), определяющие син-
сингулярное решение вблизи конца трещины, имеют вид
' УB)=/С1 + 3-^". E.89)
W 4/2H2 V
Подставляя функции Ф(г) и W(z) из E.89) в E.88) и опу-
опуская простые выкладки, находим в результате
Г,—=?¦(*? + *?,). Т^^-КгКп- E.90)
Таким образом, вектор потока энергии в конец трещины
равен
^=-2L^L[{K2l + Kn)i-2KiKid}- E-91)
В частности, для трещин нормального разрыва, когда Ки =0,
получается выражение
r = --?i±!^. , E.92)
Допустим, что трещина при своем развитии отклоняется на
угол 8 от своего первоначального положения в точке О. При
этом величина потока энергии, расходуемой на" такое развитие
"трещины, будет равна проекции вектора Г на направление роста
трещины (см. рис. 74)
г(Э) = —^[(к1+Кп) cose- 2/Ci/Cn sine]. E.эз)
Используя условия E.30) и E.31), находим отсюда критерии,
определяющие начало развития трещины и угол 8:
(/Ci + /С?,) cos в — 2/Ci/Cn sin 9 < ^у Yo (в). E.94)
Здесь Yo(9)—экспериментально определяемая функция в..В слу-
случае изотропного по прочности тела величина yo не будет зависеть
от 0; при этом из E.94) легко определить угол 0 и критерий ло-
локального разрушения (ем. рис. 74):
+ Kn), E.95}
Knf + 4/C?Ai, < 256ц2уо7A + кJ. E.96)
256
НЕКОТОРЫЕ ОБЩИН ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ 1ГЛ.,У
Так как 16цуо/A +«) = К21с, то поверхность разрушения,
согласно критерию E.96), можно записать в стандартном виде
D.1)
f (Ki, Kn) = Ки - ATifo (Я) = 0, E.97)
где
График функции /0(Я) приведен на рис. 87; для сравнения
там же нанесена пунктирной линией соответствующая функция
/о(Я) из теории трещин обобщенного нормального разрыва (см.
формулу D.56) и рис. 32).
График зависимости угла от-
отклонения 0 от Я,
0 = — arctg [2Я/A + Я2)], E.98)
приведен на рис. 88 вместе с соот-
соответствующей пунктирной кривой
0,8
-0,2
f.2
/у
У
-Ofi
-0,6
О 0,2 Ofi 0,6 0,3 _ 1,0 Л
Рис. 87.
\
\
\
\
\
\
\
•-¦—
Рис. 88.
для трещин обобщенного нормального разрыва (см формулу
D.55) ирис. 31). v v н у у
Как показывает сравнение, энергетическая теория дает ре-
результаты, весьма близкие к тем, которые получаются для тре-
трещин обобщенного нормального разрыва, если А.<;1. Серьезное
расхождение этих теорий получается только при Я » 1, т. е. для
трещин поперечного сдвига. Существующих к настоящему вре-
времени опытных данных в последнем случае пока еще недоста-
недостаточно, чтобы четко разграничить области приложения этих тео-
теорий к тем или другим классам материалов.
В случае криволинейных трещин нормального разрыва е
гладкой поверхностью, когда угол 0 в любой момент развития
трещины равен нулю, можно применить метод бесконечно малых
скачков, изложенный в § 3 гл. IV. Поскольку, согласно E.98),
при Я <& 1 0 = —2Я, энергетическая теория в этом случае при-
§5]
УПРУГО-ПЛАСТИЧЁСКОЁ
2S?
водит к точно таким же результатам, что и теория трещин обоб-
обобщенного нормального разрыва (см. формулы D.69) и D.72)).
Уместно подчеркнуть, что согласно энергетической теории
E.30) развитие трещины таково, что удельные энергозатраты на
образование новой поверхности в каждый момент развития тре-
трещины минимальны.
§ 5. Упруго-пластическое тело
Изучим сверхтонкую структуру конца трещины.в упруго-пла-
упруго-пластических средах. Вначале изложим основные представления
о развитии трещин в таких телах.
Допустим, что в упруго-пластическом теле сделан физически
абсолютно острый полубесконечный разрез (например, вынуты
одна или две атомных полуплоско-
полуплоскости, так что взаимодействием про-
противоположных берегов разреза мож-
можно пренебречь). Затем на бесконеч-
бесконечности тело нагружается; при этом
параметр нагружения —'¦ коэффи-
коэффициент интенсивности напряжений —
монотонно увеличивается (рис. 89).
В момент начала движения раз-
разреза коэффициент интенсивности
напряжений &,(=/Ci) достигает
критического значения, равного kic:
klc= У4цУA — v). E.99)
Здесь yt — наименьшее значение
эффективной поверхностной энергии
тела.
Величина yt близка к теоретиче
ским оценкам поверхностной энер-
энергии твердого тела (см. гл. II), так как при K\<.Kic пласти-
пластические деформации в теле отсутствуют. Поэ/гому yt будем назы-
называть истинной поверхностной энергией.
Момент начала движения разреза совпадает с моментом на-
начала движения и развития дислокаций вблизи его конца, т. е.
с моментом образования и роста пластической области вблизи
конца разреза (см. рис. 89). Поэтому при Ki > &ic происходит
«расщепление» структуры конца трещины на тонкую структуру,
которая реализуется на расстояниях, больших по сравнению с
размером пластической зоны вблизи конца трещины, на сверх-
сверхтонкую структуру, имеющую место непосредственно вблизи края
трещины (на расстояниях, малых сравнительно с размером
пластической области), и на переходную зону, занимающую
Рис. 89.
9 Г, П. Черепанов
258 Некоторые общие вопросы механики разрушения 1ГЛ. v
промежуточное положение между тонкой и сверхтонкой струк-
структурами. В рамках теории малых деформаций свертонкая струк-
структура соответствует асимптотике, устанавливающейся на беско-
бесконечно малых расстояниях от конца математического разреза.
При К\ < k\c обе структуры совпадают.
Вследствие увеличения коэффициента интенсивности напря-
напряжений тонкой структуры происходит дальнейшее продвижение
конца разреза вглубь тела, которое сопровождается еще более
интенсивным движением и развитием дислокаций (и пластиче-
пластической области). Дислокации блокируют сверхтонкую структуру
конца трещины, оставляя неизменным уровень ее напряжен-
напряженности, т. е. сохраняя коэффициент интенсивности напряжений
сверхтонкой структуры k\ постоянным и равным kic. Более быст-
быстрое развитие пластической области приводит к тому, что движе-
движение конца разреза является устойчивым на этом этапе. Предста-
Представление о постоянстве коэффициента интенсивности напряжений
сверхтонкой структуры при росте трещины будем называть кон-
концепцией kjc.
Наконец, достигается предельное (критическое) состояние
напряженности тонкой структуры, характеризуемое следующей
величиной коэффициента интенсивности напряжений:
/Ci = Кю (Kl = I*Y/A - v)). E.100)
Здесь Kic — вязкость разрушения, y — эффективная поверхност-
поверхностная энергия трещины в данный момент нагружения. При
Ki = Kic все локальные характеристики в конце разреза (ха-
(характерное раскрытие его конца, характерный размер пластиче-
пластической области и т. д.) также достигают своего критического зна-
значения.
При /Ci = Kic в конце разреза на его продолжении обра-
образуется острый надрыв; в силу перенапряженности состояние
сверхтонкой структуры в конце этого надрыва будет теперь не-
неустойчивым, и разрез будет при постоянной нагрузке продви-
продвигаться вглубь тела с большей скоростью, чем пластическая об-
область. у
Таким образом, момент потери устойчивости при Ki = Kic
физически объясняется образованием более острого разреза-тре-
разреза-трещины в сверхтонкой структуре (т. е. локального хрупкого разру-
разрушения).
Во многих случаях такого локального хрупкого надрыва не
происходит; при Ki = К\с тонкая структура насыщается и ста-
стационарно перемещается в пространстве при продвижении конца
трещины вместе с пластической зоной и сверхтонкой структурой.
Такой процесс соответствует классической концепции квазихруп»
кого разрушения.
S 6] УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО 259
Характер дальнейшего распространения разреза зависит от
устойчивости или неустойчивости состояния тонкой структуры
(определяемого внешним полем, см. § 4 гл. IV). Если состояние
тонкой структуры неустойчиво, то скорость движения разреза
будет возрастать, приводя к неустойчивому динамическому ре-
режиму роста трещины. Если же состояние тонкой структуры
устойчиво, то распространение разреза вскоре прекратится (так
как его конец попадает в менее напряженную область) и возоб-
возобновится только после возрастания внешней нагрузки и увеличе-
увеличения коэффициента интенсивности напряжений до значения, близ-
близкого к Kic- Следует подчеркнуть, что это значение не будет
равно Kic в силу зависимости напряженно-деформированного
состояния окрестности конца трещины в упруго-пластической
среде от предшествующей истории деформирования.
В большинстве случаев вязкость разрушения Kic в упруго-
пластической среде характеризует начало локально неустойчи-
неустойчивого (нестабильного) развития трещины. Если состояние тонкой
структуры устойчиво, то развитие трещины в таких случаях бу-
будет скачкообразным (т. е. вслед за интервалом быстрого разви-
развития трещины при постоянной внешней нагрузке следует период
стабильного роста трещины при увеличении внешней нагрузки
и т. д.). Если число скачков достаточно велико, т. е. велик ли-
линейный размер подросшей трещины при выполнении условия
тонкой структуры, то устанавливается некоторое среднее влия-
влияние предыстории, так что можно говорить о том, что коэффи-
коэффициенты интенсивности напряжений в момент начала нестабиль-
нестабильного движения трещины и в момент ее остановки постоянны для
данного материала (но, вообще говоря, различны, причем Кг
в начале движения, очевидно, больше, чем Ki в момент оста-
остановки).
Предположим теперь, что раскрытие конца начального искус-
искусственного разреза гораздо больше межатомного. Отметим, что
в металлах наиболее острые разрезы, которые удается создавать
искусственно, отвечают усталостным трещинам. Раскрытие в их
конце может быть почти на два порядка меньше предельного
раскрытия, отвечающего моменту наступления нестабильности?
Однако это раскрытие на несколько порядков больше среднего
межатомного расстояния, поэтому критическое значение коэффи-
коэффициента интенсивности Ki в момент наступления неустойчивости
при монотонном нагружении будет отлично от величины вяз-
вязкости разрушения Kic, соответствующей абсолютно острому на-
начальному разрезу. В 1958 г. Ирвин [9I] предположил, что влияние
величины раскрытия начального разреза и способа его образо-
образования на вязкость разрушения Kic пренебрежимо мало, если на-
начальное раскрытие гораздо меньше предельного. Эта гипотеза
подтвердилась экспериментально; она послужила основой
260
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ
[ГЛ. V
допущения, что вязкость разрушения /Cic является константой
упруго-пластического материала, характеризующей чувствитель-
чувствительность материала к росту трещин.
Как видно, несмотря на существенные качественные и коли-
количественные отличия развития трещин в упруго-пластических сре-
средах и в хрупких телах, аппарат механики хрупкого разрушения
годится для предсказания начала нестабильного роста трещин
в упруго-пластических материалах, если имеет смысл предста-
представление о тонкой структуре конца трещины. Если тонкая струк-
структура неустойчива (что чаще всего встречается на практике), то
этого предсказания достаточно, чтобы судить о прочности тела
с трещиной.
Если же тонкая структура устойчива, то необходимо еще рас-
рассмотреть вопрос о дальнейшем развитии трещины в процессе
монотонного возрастания внешней нагрузки. При рассмотрении
последнего вопроса механика хрупкого разрушения также мо-
может оказаться достаточной, если число скачков достаточно ве-
велико и при исследовании ставится ограниченная задача об опре-
определении приблизительного местонахождения конца трещины
после большого числа скачков. Для решения последней задачи
нужно взять некоторое среднее значение вязкости разруше-
разрушения Kie для устойчивой тонкой структуры и приравнять его ра-
расчетному коэффициенту интен-
интенсивности напряжений Ki\ при
этом движение конца трещины
будет монотонным и устойчи-
устойчивым. Следует подчеркнуть, что,
вообще говоря, среднее значе-
значение вязкости разрушения для
устойчивой тонкой структуры
отлично от вязкости разруше-
разрушения, соответствующей началу
нестабильного роста трещин,
поэтому для ее измерения не-
необходимы дополнительные экс-
эксперименты.
На рис. 90 приведен характерный график зависимости длины
трещины от нагрузки для металлов в ситуациях с устойчивой
тонкой структурой; монотонная кривая отвечает теоретическому
решению, полученному на основе механики хрупкого разру-
разрушения.
Если пластическая область в конце трещины велика, так что
тонкая структура не реализуется, то методы механики хрупкого
разрушения становятся неприменимыми. Обобщение этих мето-
методов приводит к необходимости изучения сверхтонкой струк-
структуры.
Рис 90.
4 Б] УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО 561
В дальнейшем рассматриваются лишь процессы с монотонно
возрастающей (растягивающей) внешней нагрузкой. Для опре-
определенности ограничимся наиболее важным случаем трещин нор-
нормального разрыва в условиях плоской деформации.
Опыт показывает, что подрастание трещины в процессе уве-
увеличения коэффициента интенсивности напряжений от kjc до Кю
происходит лишь за счет локальных конечных пластических де-
деформаций вблизи фронта -трещины и обычно не сопровождается
локальными надрывами; поэтому докритическое подрастание
трещины имеет порядок раскрытия ее конца. Этот вывод под-
подтверждается также фрактографическими исследованиями по-
поверхности усталостной трещины (см., например, статью Бичема
и Пеллу в книге [35]). Следует подчеркнуть, что в случае сквозных
трещин в тонких пластинах (т. е. когда А = h/l малы) иногда
наблюдается весьма значительное докритическое подрастание
трещин (например, на несколько сантиметров, см. [61]); это объ-
объясняется локально неоднородной пластической деформацией на
фронте трещины.
Следовательно, докритическим подрастанием трещины можно
пренебречь, если ограничиться монотонным нагружениём и пло-
плоской деформацией. Это упрощение приносит наиболее эффектив-
эффективные результаты при изучении сверхтонкой структуры в рамках
модели несжимаемого упруго-пластического тела со степенным
упрочнением.
1. Упрочняющееся упруго-пластическое тело. Уравнения тео-
теории упрочняющихся упруго-пластических сред возьмем в виде [4]
1 + у . v , . , и'(/) ; / 1
при />0 (нагружение), E.101)
jY при /<0 (разгрузка). -
Здесь 8ц — символ Кронекера, ©(/)—заданная функция упроч-
упрочнения, которая определяет поверхность нагружения
X = «>(/) («/(/) >0), E.102)
где
= У \°11 — j
Для определения функции.«(/) достаточно одной экспери-
экспериментальной диаграммы растяжения о— et
262
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ
[ГЛ. V
t-0
Рис. 91.
Уравнения E.101) представляют собой один из наиболее
распространенных и хорошо проверенных вариантов изотерми-
изотермической теории пластичности металлов. В них предполагается
изотропное упрочнение, описываемое одним параметром. Вместе
с уравнениями равновесия и кинематическими соотношениями
эти уравнения составляют замк-
замкнутую систему.
При помощи «принципа мик-
микроскопа» изучение сверхтонкой
структуры фронта трещин нор-
нормального разрыва в такой среде
в рамках теории малых деформа-
деформаций сводится к следующей зада-
задаче: требуется найти решение ука-
указанной системы уравнений во
внешности движущегося полубес-
полубесконечного разреза вдоль у = 0,
x<Cl(t) в условиях плоской де-
деформации для произвольной мо-
монотонно возрастающей функции
l{t) (рис. 91).
Так как деформации сингу-
сингулярны в конце разреза, а наклон
кривой а — е к оси абсцисс при больших е гораздо меньше, чем
в начале координат (см. рис. 91) ¦, то упругая компонента ско-
скорости деформации ke{j' в сверхтонкой структуре будет пренебре-
пренебрежимо малой по сравнению с пластической составляющей Щ.
при нагружении, т. е.
По той же причине е^ > ee{j. Тогда, если диаграмма сг—е имеет
вид е = е(а), то функция со(/) будет следующей:
E.104)
В предположении E.103) согласно E.101).тело будет несжи-
несжимаемым. При этом для плоской деформации будут иметь место
соотношения
е2=0, d/dz = 0, oz = j(ax + oy), ех + ва = 0. E.105)
Примем, что диаграмма растяжения а — е при больших е
имеет асимптотически линейный участок (рис. 91)
при
E.106)
I S) УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО . 263
Постоянные ?<» и Цоо характеризуют наклон этого участка.
Вследствие сингулярности решения в конце разреза именно эта
часть диаграммы реализуется в сверхтонкой структуре.
На основе соотношений E.101) — E.106) получаем следую-
следующие уравнения плоской деформации сверхтонкой структуры: .
дй ___дд_ 3 / , ,
дх ду 4?0О / ^°х Оу''
дй , дЬ 3/ ; л ,к л Л7ч
-яТ + -я7==-ГТх*у ПРИ />0' <5Л07>
Здесь
ПРИ
= 3//B?J).
Предположим вначале, что разрез неподвижен и во всех точ-
точках сверхтонкой структуры происходит нагружение, В этом слу-
случае сингулярное решение уравнений E.107) (плюс уравнения
равновесия) будет иметь вид
I Щ 6 . k\ sin 9 , . лч
а + а==7шСО51 /==TF^" (^>0)>
, E.108)
й+г'°=~tt V^sin2 т ¦em {ki > 0)-
Здесь k\ — коэффициент интенсивности напряжений сверхтонкой
структуры, являющийся монотонно возрастающей функцией вре-
времени (при нагружении).
Согласно концепции k\c, как только будет достигнуто значе-
значение коэффициента k\, равное k\c, начнется движение разреза.
При бесконечно малом изменении нового параметра нагруже-
ния I на 81 все функции приобретают бесконечно малые изме-
изменения (бм, 8у, 8ах, 6ау, 8хху). На основании E.107) и E.108) си-
система уравнений, служащая для их определения, имеет вид
дЬи dbv зуТ ., . 39
при б/>0; Eл09)
= бе^ = 6&ху = 0 при б/
(sign^ = + 1 при ^>0, sign#= — 1 при у < 0).
264 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
Здесь
sign у ¦ Ы = -pL- sin-^ (вв, - 6<rx) + /2 cos -f- • вт,„. E.110)
Кроме того, должны удовлетворяться уравнения равновесия
- Введем функцию тока if (х, у) при прмощи соотношений
. 3]/Т 3* . 3^2" <Эф /е , 1О\
6«=-irif-' ба=—fc-~sr- EЛЬ2)
При этом, согласно первому уравнению E.109), будет
d?h EЛ13)
Подставляя E.112) и E.113) в E.109), получаем следующее
уравнение относительно функции тока:
Преобразуем его к полярным координатам г9:
32ф 2 79 / . 9 \"' д2^ 1 д2й 1 М 2,9
-7F^-_71^-7rctgY- ^- = 0
F1 > 0). E.115)
Дискриминант уравнения E.114), равный
-l-(ctg-fJ, . E.116)
всегда меньше нуля. Поэтому уравнение принадлежит к гипер-
гиперболическому типу. Два семейства его характеристик представ-
представляют собой интегральные кривые следующих уравнений:
dy_ ± 1 - cos C9/2) /с 117ч
dx — sin C9/2) [ОЛИ)
Решения этих уравнений имеют вид
[±1-cos C9/2I rf9 /еПЯч
_ tg 9 (± [ _ cos C9/2))] •
Поле интегральных кривых изображено на рис. 92.
fS]
УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО
265
Через каждую точку плоскости проходят две взаимно ортр-
гональные кривые разных семейств (начало координат является
особой точкой типа центра). В системе криволинейных орто-
ортогональных координат ?т], образованных этими семействами,
уравнение E.11.4) приводится к простому виду д^/д^дц = 0.
Поэтому нетрудно найти об-
общее решение этого уравне-
уравнения, выраженное через две
произвольные функции. По-
Последние должны находиться
из граничных условий на
разрезе. При этом гранич-
граничные данные на любом отрез-
отрезке границы единственным
образом определяют реше-
решение внутри криволинейного
треугольника, основанием
которого является данный
отрезок, а сторонами — ха-
характеристики разных се-
семейств, исходящие из кон-
цов отрезка (рис. 92). Одна-
Однако в связи с рассматривае-
рассматриваемыми далее особенностями
этой задачи изберем другой
путь Решение уравнения
E.115) с однородными граничными условиями автомодельно;
оно имеет вид
ф __ rA.\jr @) E.119)
Подставляя его в E.115), получаем дифференциальное уравне-
ние относительно ^(б)
хр» (9) + 2 [ctg (9/2) + Я cos G9/2) cosec (9/2)] V (9) —
= 0 F/>0). E.120>
Рис. 92.
Величина б/, согласно E.113), будет равна
sign у • Ы =
?" (9) + 2 (Я + 1) ctg 29 • Ч" (9) - (Я - 2) Ш (9)].
(и. 12Л )
Найдем собственное число Я, используя энергетические сооб-
соображения. Величина потока энергии в конец трещины при ег<э
266 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
продвижении на 81, согласно E.14), равна
Yo б/ = — lim \oubvdx. E.122)
6/R->0 I
Так как величина уо конечна р отлична от нуля, а напряже-
напряжение оу, согласно E.108), имеет особенность порядка г/2, то из
E.122) вытекает, что собственное число X равно 1/2. При этом
из E.120) и E.121) для функции W(Q) получается следующая
краевая задача:
' W" + [2 ctg (9/2) + cos G9/2) cosec (9/2)] Ч" +1- ^ = 0
/ 3 \ (
sin29 • [sin C9/2)]-' \W" + 3ctg29 ¦ 4" -f -J Wj > 0,
при 9 = 0 W = 0. :
Граничное условие при 9 = 0 отвечает условию симметрии
8v = 0.
Покажем, что возможно лишь тривиальное решение краевой
задачи E.123) в классе ограниченных непрерывных функций.
Дифференциальное уравнение E.123) при бесконечно малых 0
имеет вид
?" + -§¦ У + -|ч? = 0. E.124)
Допустим вначале, что ^"(О) неограничена; тогда и ^'(О)
будет неограничена согласно E.124). При этом будет Y = С?И,
что неприемлемо. Теперь допустим, что W"@) и ^'(О) рграни-
чены. Разлагая функцию ^(Э) в ряд Тэйлора
? @) = а0 + а,в + а292 + ... . E.125)
и подставляя это разложение в E.124), находим
+ -Jflo = O. ••• E.126)
Если ЧЧО) = а0 = 0, то все коэффициенты разложения об-
обращаются в.нуль.
Таким образом, одно из двух линейно независимых решений
уравнения E.123) неограничено при 9 -*• 0, а другое ограничено
при 9 -*• 0, однако является тождественным нулем, если функ-
функция Y равна нулю в особой точке 9 = 0.
Так как тривиальное и неограниченное решения не отвечают
физическому смыслу задачи, остается допустить, что Чг@)^=0,
т. е. &v ф 0 при 9 = 0. При этом на продолжении трещины до-
допускается разрыв вариации перемещения §р,
51
упруго Пластическое тело
2-'
Следовательно, в данном случае развитие трещины можно
представить как результат последовательного разрыва локаль-
локальных связей непосредственно вблизи конца трещины; при k\ = kic
разрушение охватывает сразу некоторую область на продолже-
продолжении трещины, причем конец трещины продвигается мгновенно на
расстояние, равное вариации длины трещины (единственного
параметра нагружения в данной задаче).
Поскольку сингулярное решение определяется с точностью
до произвольного множителя, без ограничения общности можно
положить
?=1 при 8 = 0. E.127)
Получающаяся краевая задача (дифференциальное уравне-
уравнение E.123) и граничное условие E.127)) имеет единственное
решение, которое легко построить в виде ряда E.125) или же
численно, используя стандартные методы решения задачи Коши
(задача Коши ставится так: при б = А8 Ф = 1, W = 0, где Д9
достаточно мало). Дифференциальное неравенство в E.123)
играет роль фазового ограничения.
Приведем результаты численного анализа, ограничившись
для краткости вторым знаком после запятой (см. табл. 5.1).
Значения функций V (9) и — V (в)
Таблица 5.1
е
0
0.11
0.21
0.31
0.41
0.51
0,61
0.71
0.81
0.91
1.01
чг
1
1.00
1.00
0.99
0.99
0.98
0.97
0.96
0.95
0.93
0.91
-Ч"
0
0.01
0.02
0,04
0,05
0.07
0.10
0,13
0,16
0,20
0,23
в
1.11
1.21
1,31
1.41
1.51
1.61
1.71
1.81
1.91
2.01
2,11
ЧГ
0.88
0.86
0.83
0.80
0.78
0.75
0,73
0.71
0.69
0.67
0,65
0,25
0,27
0,27
0,26
0,25
0,24
0.22
0,21
0,21
0,21
0.22
е
2,21
2.31
2.41
2,51
2.61
2.71
2.81
2.91
3.01
з.п
чг
0.62
0.60
0.57
0.54
0.50
0.46
0.42
0.36
0.30
0.24
-ЧГ'
0.24
0.26
0.29
0.33
0.39
0.44
0.51
0.56
0.61
0.65
Условие нагружения выполняется при всех 0.
Вариации напряжений определяются из уравнений E.110) и
E.111). Введя функцию напряжений, нетрудно привести их
к уравнению E.115) относительно функции напряжений с из-
известной правой частью. Автомодельное решение последнего урав-
уравнения находится совершенно аналогичным способом.
Рассмотренная краевая задача интересна ещё тем, что она
имеет единственное решение, хотя есть лишь одно граничное
268 НЕКОТОРЫЕ ОВЩИВ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ 1ГЛ. V
условие E.127) (напомним, что дифференциальное уравнение —
второго порядка). Роль второго граничного условия в данном
случае играет условие ограниченности решения. Неопределен-
Неопределенный множитель в решении аналогичен коэффициенту интенсив-
интенсивности напряжений; из соображений анализа размерностей он
пропорционален k\U.-
Совершенно аналогично в рамках сверхтонкой структуры
можно поставить и исследовать задачу о начале движения тре-
трещины в упруго-пластическом теле с асимптотически степенным
упрочнением. При этом также оказывается, что рост трещины
можно представить как результат последовательного разруше-
разрушения материала непосредственно вблизи конца трещины.
2. Несжимаемое степенное тело. Модель несжимаемого сте-
степенного упруго-пластического тела получается из уравнений
E.101), если в них пренебречь упругими компонентами, а функ-
функцию ш'(/) считать степенной
(о'(/) = а/х+1, E.128)
где а и к — некоторые постоянные материала, которые полу-
получаются аппроксимацией эмпирических диаграмм а — е степенной
функцией. Постоянная а имеет размерность длины в степени
2(и+1)> деленной на размерность силы в степени (и+1); ве-
величина •& безразмерна.
Отметим основные свойства несжимаемого степенного тела.
Допустим, что на его границе заданы нагрузки. Тогда
1) напряжения в каждой точке несжимаемого степенного
тела не зависят от постоянной а;
2) если внешние нагрузки изменяются пропорционально па-
параметру нагружения, то и все напряжения в каждой точке тела
изменяются пропорционально тому же параметру [6];
3) напряжения и деформации в каждой точке этого упруго-
пластического тела такие же, как в степенном нелинейно-упру-
нелинейно-упругом теле, описываемом уравнениями E.51) и E.59), если все
внешние нагрузки изменяются пропорционально одному и тому
же параметру {6].
Первое свойство становится очевидным, если обе части урав-
уравнений E.101) разделить на а и учесть линейность условий со-
совместности. Второе свойство является следствием однородности
системы уравнений в напряжениях. Третье свойство не менее
очевидно, если проинтегрировать уравнение E.101) по пара-
параметру нагружения и учесть, что напряжение в каждой точке та-
такого 'тела пропорционально тому же самому параметру. При
этом получаются уравнения E.51), в которых нужно положить
x+\ v=l/2. E.129)
«61'
УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО
Отмеченные свойства делают особенно плодотворным прило-
приложение концепции &ic к несжимаемым степенным телам, так как
позволяют перенести на них все результаты, полученные для
напряжений и деформаций степенных нелинейно-упругих тел
с трещинами (в условиях пропорционального нагружения и в
пренебрежении подрастанием трещины).
ar=const
¦1 „
¦< " -'¦'
__. L >
L. ...
Рис. 93.
М
Рассмотрим несколько конкретных задач для несжимаемого
степенного тела.
Растяжение перешейка с разрезом (рис. 93). Пусть пере-
перемычка, образованная свободной границей тела и перпендикуляр-
перпендикулярным к ней полубесконечным разрезом,
также свободным от внешних нагрузок,
растягивается на бесконечности силой Р
в условиях плоской деформации.
Коэффициент интенсивности напряже-
напряжений k\ в конце разреза, определяемый
формулой E.60), в случае монотонного
возрастания силы Р зависит лишь от ши-
ширины перемычки L, силы Р и постоянной
¦к. Следовательно,
i
М
(a = const). E.130)
4 Рис. 94.
Здесь -Hi (>c)—безразмерная функция к.
Изгиб перешейка с разрезом (рис. 94). Пусть для конфигу-
конфигурации предыдущего примера на бесконечности действует моно-
монотонно возрастающий изгибающий момент М. В этом случае
270
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ
1ГЛ. V
величина k\ зависит лишь от L, М и и. Следовательно,
ТГГ
E.131)
Здесь Т12(и)— безразмерная функция и.
Условия в перемычке, весьма близкие к рассматриваемым
в этих двух примерах, реализуются, например, при растяжении
или изгибе полосы с глубоким надрезом, когда глубина надреза
превышает половину ширины полосы
(см. рис. 93). При этом случай растяже-
растяжения всегда сопровождается локальным
изгибом.
Растяжение полупространства с крае-
краевым дефектом (рис. 95). Пусть полупро-
полупространство имеет плоский краевой разрез
эллиптической формы в плане. Дефекты
такой формы с примерно постоянным
отношением полуосей (приблизительно
равным 2/3) наиболее часто встречаются
в конструкциях и служат источником
разрушения. Приблизительное постоян-
постоянство их формы объясняется условиями
докритического роста коррозионных и усталостных трещин в
процессе сборки или эксплуатации конструкции, приводящими
к выравниванию коэффициента интенсивности напряжений
вдоль контура разреза. Полупространство растягивается на бес-
бесконечности монотонно возрастающим напряжением р, нормаль-
нормальным к плоскости разреза. Граница полупространства и берега
разреза считаются свободными от нагрузок.
В рассматриваемом случае коэффициент интенсивности на-
напряжений k\ зависит лишь от глубины разреза Ь, от нагрузки р,
от постоянной и и от эксцентриситета эллипса. Следовательно,
E.132)
Рис. 95.
Здесь т]з — безразмерная функция и и отношения полуосей.
Критическая комбинация разрушающего усилия и размера
трещины получается приравниванием коэффициента k\ предель-
предельному значению, равному постоянной материала k\c.
Функции t]i, т]2 и Т1з в рассмотренных примерах определяются
или из точного расчета или на основании модельных эксперимен-
экспериментов с разрушением. В последнем случае для отыскания абсолют-
абсолютного значения klc можно использовать формулу E.65), связы-
связывающую коэффициенты интенсивности тонкой и сверхтонкой
структур. Для предельного состояния она примет вид
E.133)
§51 УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО 271
При помощи этой формулы можно определить kie по извест-
известной вязкости разрушения и наоборот. Таким образом, доста-
достаточно провести серию испытаний какого-либо контрольного мате-
материала с известной вязкостью разрушения на разрушение в
пластической области, чтобы затем из опытов по вязкому раз-
разрушению малых образцов из других материалов находить их
вязкость разрушения. Это одно из возможных приложений кон-
концепции k\c и найденных решений.
Непосредственное определение вязкости разрушения по стан-
стандартным схемам весьма часто требует нереально больших раз-
размеров образцов.
Схемы, изображенные на рис. 93 и 94, могут быть рекомен-
рекомендованы как наиболее удобные для определения значения kic.
При этом необходимо, чтобы в опыте соблюдались два основных
условия:
1) все (или почти все) сечение-нетто должно перейти в пла-
пластическое состояние перед разрушением; например, при растя-
растяжении среднее напряжение в этом сечении должно превы-
превышать 00,21
2) излом должен быть прямым.
Эти условия можно соблюсти при достаточно малой ширине
перемычки. Они обеспечивают требования плоской деформации
и степенной аппроксимации, наиболее хорошо описывающей
свойства материала в пластической области.
3. Идеальное упруго-пластическое тело. Модель идеального
упруго-пластического тела с условием пластичности Мизеса
определяется следующими уравнениями:
при Я > 0 (нагружение)
1+v. v.. .;/ 1, \
вг/ = —?— о1} — -gr OijOkk + *- 1о[} —¦jo^akkj,
EЛ34)
22
[ 1 \/ 1
Р = [oif — j Okk&ii) [Oi, — -g-
при К = 0, / < Y^xs (разгрузка)
1 + v . v
Здесь xs — предел текучести на сдвиг, к—новая неизвестная
функция: Я = х/BтЗ) = Лр/BтЗ)>0.
Нужно отметить следующее. В случае любой неподвижной
системы координат под ёц и дц в уравнениях E.134) нужно по-
понимать обычные частные производные по времени от компонент
Eij и Оц (ввиду предполагаемых малых деформаций). В случае
движущейся системы координат положение изменяется. Если
272 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. У
система координат декартова и движение ее происходит в на-
направлении оси х со скоростью V, то точка над буквой будет
означать полную производную от соответствующей величины,
равную d/dt — Vd/дх.,
Если же система координат криволинейна, то при ее движе-
движении базис в каждой точке изменяется; поэтому в этом случае
под 6ц и k,tj нужно понимать соответствующие компоненты пол-
полных тензорных производных от тензоров напряжения и дефор-
деформации. Последние следует находить по обычным правилам диф-
дифференцирования тензоров [124].
Будем предполагать далее, что контур, отделяющий упругую
область от пластической в плоскости 2 = 0 (см. рис. 91)г цели-
целиком охватывает конец трещины и в сверхтонкой структуре нигде
не происходит разгрузки*). Кроме того, упруго-пластическое
тело будем считать несжимаемым (v = 1/2). При таких допу-
допущениях изучение сверхтонкой структуры конца трещины нор-
нормального разрыва согласно E.134) сводится к решению следую-
следующей системы уравнений для движущегося полубесконечного раз-
разреза, свободного от внешних нагрузок:
дах [ дхху _п дхху | дау _ п E.135)
~ 2t \ду + дх Е Х*у) ~ a a [ дх
ду + дх Е Х*у) ~ ax - ay [ дх 2Е
HLj--EiL — n E,136)
дх "Г dy u*
Здесь подвижная декартова система координат ху связана с кон-
концом трещины (см. рис. 91), точка над буквой обозначает опера-
операцию d/dt — уд/дх, где V = dl/dt.
Поле напряжений определяется системой уравнений E.135)
и граничными условиями на разрезе независимо от поля смеще-
смещений. Как видно, напряжения в сверхтонкой структуре, в отличие
от смещений, одинаковы для движущейся и неподвижной тре-
трещины. Как нетрудно заметить, этот вывод является следствием
допущения об отсутствии разгрузки в сверхтонкой структуре.
Математическая задача о напряжениях совпадает с ситуа-
ситуацией вблизи угловой точки штампа в известной задаче Пранд-
тля, решенной им задолго до возникновения общей теории пла-
*) Точное численное решение для неподвижной трещины при иаличиа
тонкой структуры [56] подтвердило это допущение.
УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО
273
стичности. Поэтому воспользуемся решением Прандтля, изло-
изложенным во всех учебниках по теории пластичности:
при 0 < | 6 |< л/4
при л/4 <| 6 |< Зл/4
, тгв = т, E.137)
• *ху = xs cos 26, \
о = тД1 + Зл/2 — 26) j;
при Зл/4 < ] 6 К л
Поле линий скольжения в сверхтонкой структуре изображено
на рис. 96.
У
Л
х
Рис. 96.
В области |6| < л/4 и |6| > Зя/4, согласно E.137), вели-
величина хХу равна нулю; следовательно, на основании E.136) будет
dv п дй , at г {5Л38)
дй
дх
ду ' дх
Общее решение этих уравнений, удовлетворяющее условию
симметрии v (у) =—v(—y), и (у) =«(—«/), имеет вид
й = /«(х -y,t) + ft (x + У, t), v = ft(x-ry, t)-f, (x+y, t) E.139)
(t = l при | в |< лс/4; i = 2 при Зл/4<|6[<я).
Здесь U и h — произвольные функции, определяемые из условия
непрерывности смещений и скоростей на границе раздела упру-
упругой и пластической зон. Из формул E.139) вытекает, в част-
частности, что в конце трещины при |6|<л/4 смещения и скорости
можно считать равными нулю, а при Зл/4<|0|<я — ограни-
ограниченными.
274 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
Осталось изучить область я/4 < |0| < Зя/4 (см. рис. 96).
Девиатор напряжений в ней, согласно E.137), равен
Ъ = х3(ЭгЭв + ЭвЭг). E.140)
Здесь Эг и Эв—орты системы полярных координат г0 (см. рис. 91).
Так как
^ ^ ^ ^„ E.141)
то полная производная тензора D по времени равна
4yV(eA+w
Уравнения E.134) при v= 1/2 в тензорной записи имеют вид
^- (ЭвЭв - ЭГЭГ). E.142)
ют вид
E.143)
d "•
Здесь -тг-г — тензор скорости деформаций; его компоненты
в полярных координатах ёг, ёв и ёгв выражаются через ком-
компоненты вектора скорости йг и йв так:
Из полученных соотношений вытекают следующие уравнения:
дйг _ svxs sme i дйв йг _ svxs sine
~дГ е ~» 7^Г+Т~ — ~е
Последовательно интегрируя их, находим
+ F(B),
E.146)
Здесь /*" и f3 — произвольные функции, определяемые из условия
непрерывности скоростей на границе упругой и пластической
зон, г0 — характерный линейный размер.
Из условия непрерывности скорости йв при 0 = л/4 следует,
что функция /з(/\ t) и ее первая производная по г обращаются
в нуль при г—*0. Поэтому при изучении сверхтонкой структуры
ее можно опустить без потери общности,
$ 6] УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО 275
В случае неподвижной трещины (когда V = 0) деформации
ег и ее равны нулю, а сдвиговая деформация еге и смещения
таковы:
t
E.147)
ur = JF'(B,t)dt, ue = -JF(e,i)dt.
Как видно, деформация еге имеет в сверхтонкой структуре
особенность порядка 1/г, которая определяется функцией FF, t).
В конце трещины при деформации образуется скачок смещения
(см. рис. 96).
Случай движущейся трещины более сложен. Из E.136) сле-
следует, что
-1^+1^ = 0. E.148)
Так как
то вектор скорости а в каждой точке можно представить так:
u~ dt v dx — at ~ v V dx ^~i~dx~)~
E.150)
{tUf = u cos 0 + у sin 9, «e = — « sin 9 + v cos 9).
Таким образом, для смещений и и v получаются следую-
щие уравнения:
= --^ sine-In-?-
276 Некоторые общие вопросы Механики разрушения 1ГЛ. V
Исключая dufdt, находим
до _-_ it dv
dt v дх~~
=- Щ5- [cos 8 [cos 8 ~ Ч~) +1п т;{1 ~ Ч~cos e)] + Q <*• У' ')•
E.152)
где
Q (х, У, 0 = F' (в, 0 sin в — F (в, *) cos в.
Общее решение этого уравнения имеет вид *)
+ F0(x+Vt,y). E.153)
Здесь Fa—произвольная функция, которая определяется из на-
начальных условий в момент начала движения трещины.
Аналогичное выражение для составляющей смещения и легко
получить при помощи условия несжимаемости E.148).
По формулам E.14) и E.152) поток энергии в конце движу-
движущегося разреза равен
г ^_2_ lim Г
1 * V 6/R+O J
R-Ю -R
у=Ь
E.154)
так как функции ау и Q ограничены при *->0, г/->0, а член
с логарифмической особенностью не дает вклада в интеграл.
Таким образом, согласно теории малых деформаций поток
энергии в конец движущегося разреза в идеальной упруго-пла-
упруго-пластической среде равен нулю. На самом деле на расстояниях по-
порядка А от конца трещины, где А — характерное раскрытие тре-
трещины в ее конце, деформации конечны, и теория малых дефор-
деформаций не годится. Поэтому, строго говоря, предельный переход
R -* 0 в формулах E.154) неправилен, так как трещину в ее кон-
конце нельзя считать математическим разрезом. Учитывая конечный
размер А и формулу D.109), оценим величину Тх
2 1* °Г
Г* ~ у J oyi)dx ~ -?¦ J ln| r/r0 \dr
J J
-д , -д
)^^к^1 E.155)
-д
*) Частный случай этого решения (для установившегося развития тре-
трещины, когда d/dt = 0) изучен Райсом Г1101. Решение Раиса совпадает с пер-
первым членом формулы E153)"
щины, когда d/dt = 0) изуче
вым членом формулы E.153).
§ SJ УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО 27?
Здесь учтено, что согласно E.152)
v ~ (VaJE) In (r/ru) (ey~es) E.156)
на расстояниях г ~ Д от фронта трещины.
, Согласно энергетической концепции Г* = 2уо, где величина
Yp равна сумме удельной необратимой работы деформаций вбли-
вблизи края трещины (не учитываемых моделью идеальной пластич-
пластичности) и поверхностной энергии. Идеальная пластичность лучше
других моделей сплошной среды описывает свойства твердых
материалов- непосредственно перед разрушением, поэтому в дан-
данном случае можно считать, что величина уо имеет порядок ис-
истинной поверхностной энергии. При этом на основании E.155)
получаем следующую оценку, связывающую эффективную и ис-
истинную поверхностные энергии твердого тела:
oJE. E.157)
Согласно этой оценке, величина у« на два-три порядка мень-
меньше, чем у> что хорошо согласуется с опытными данными (см.
табл. 2.2 и Приложение II).
Из энергетического анализа также вытекает, что теория ма-
малых деформаций идеальных упруго-пластических тел недоста-
недостаточна для изучения роста трещин. По-видимому, трещина в та-
таких средах не может расти за счет постепенных локальных раз-
разрывов в ее конце, а расширяется, как полость. Развитие трещин
нормального разрыва в идеальных упруго-пластических средах
можно объяснить только нелокальными разрывами,, выходя-
выходящими за рамки сверхтонкой структуры. Изучения одной сверх-
сверхтонкой структуры в данном случае недостаточно для формули-
формулировки критерия разрушения.
С этим выводом, полученным на основе энергетической кон-
концепции, согласуется также общефункциональный подход. Дей-
Действительно, в рассматриваемом случае сверхтонкую структуру
конца трещины нельзя описать посредством какого-то одного
или нескольких промежуточных "параметров типа коэффициентов
интенсивности напряжений; следовательно, критерия локального
разрушения не существует. Поэтому при наличии тонкой струк-
структуры концепция Кс описывает разрывы в конце трещины, мас-
масштаб которых значительно превышает размеры сверхтонкой
структуры.
Следует отметить, что некоторыми авторами были предло-
предложены ранее критерии локального разрушения сверхтонкой струк-
структуры. Наиболее известны критерии, предложенные Уэллсом и
Мак-Клинтоком (см. § 9 гл. IV). Как вытекает из предыдущего
изложения, приложение этих критериев к идеальному упруго-
пластическому телу в рамках теории малых деформаций в об-
общем случае лишено физического смысла.
278
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ 1ГЛ. V
4. Энергетические соотношения. Остановимся на некоторых
следствиях, вытекающих из энергетической концепции и общих
для всех упруго-пластических сред.
Примем следующее выражение для скорости изменения
удельной внутренней энергии Uq:
ct. E.158)
Здесь с—удельная теплоемкость, е?.;— обратимая (упругая) со-
составляющая деформации. При этом локальное уравнение энер-
энергии E.29) примет вид
Величина рЕ в рассматриваемом случае всюду (кроме конца
трещины) равна нулю, поскольку учитываются только механи-
механические и тепловые процессы. Из
п уравнения E.159) получается обыч-
' ное уравнение теплопроводности
?. Т1 i • Р г* Т1 /С 1 С±Г\\
HI, ц -\- Oij&ij = el, (о. lbU)
если воспользоваться законом Фурье
q. = kTii. E.161)
Здесь k — коэффициент теплопро-
теплопроводности, &ptj — необратимая (пла-
(пластическая) составляющая деформа-
деформации. Второй член б уравнении теп-
теплопроводности представляет собой удельную мощность объем-
объемного теплового источника.
Вследствие инвариантности вектора потока Г (см. формулу
E.25)) величина
Рис- 97-
-(°il^ + ~f)n]]ds E.162)
не зависит от того, где проведен контур С, охватывающий ко-
конец трещины. В частности, можно взять контур С\, проходящий
б тонкой структуре (рис. 97). Действительно, вдоль берегов
разреза между Ci и С2 величина Г* будет равна нулю, так как
пх = 0, оу = хХу — 0 и в силу отсутствия тепловых источников
Ш = о.
Если взять, например, контур Ci в виде узкого прямоуголь-
прямоугольника, изображенного на рис. 72, то согласно E.122) имеем
= — 2 lim
в
E.163)
§ 5] УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО 279
Пусть материал сверхтонкой структуры несжимаем и обла-
обладает упрочнением, которое характеризуется в среднем касатель-
касательным модулем Цоо (см. формулу E.106) и рис. 91). Для про-
простоты будем считать, что величины ау и dv/dl в сверхтонкой
структуре в начале движения трещины такие же, как в соответ-
соответствующем нелинейно-упругом теле. Правая часть в уравнении
E.163) зависит только от коэффициента интенсивности напря-
напряжений сверхтонкой структуры k\ и модуля JW Поэтому, исходя
из соображений анализа размерностей, получаем зависимость
Г, = г^/Цоо. F.164)
Здесь у\ — численный коэффициент (в случае нелинейно-упру-
нелинейно-упругого тела, согласно E.55), г\ = 1/4).
В формуле E.164) пренебрегаем тепловыми напряжениями
и деформациями, возникающими вследствие локального разо-
разогрева. Последние могут иметь существенное значение (особен-
(особенно при локально адиабатических процессах), так как мощность
тепловых источников равна о?/ё^ и, тем самым, Т в конце тре-
трещины имеет порядок 1/л Заметим, что температурные напря-
напряжения будут сжимающими, и поэтому они будут снижать дей-
действие внешних растягивающих нагрузок, т. е. эффект тепловых
напряжений приводит к увеличению вязкости разрушения. Тем
не менее, для большинства металлов этим эффектом можно
пренебречь из-за хорошей теплопроводности и сравнительно ма-
малого теплового расширения. '
Кроме того, локальный разогрев приводит к уменьшению
величины \ioo, так что при этом вязкость разрушения также уве-
увеличивается. Этот эффект количественно более существен; его
легко учесть в формуле E.164), считая указанную постоянную
известной функцией температуры.
Деформируя контур С в контур С2, для величины Гж можно
получить выражение через коэффициент интенсивности тонкой
структуры. При этом в отличие от упругих тел в общем случае
нужно учитывать тепловые потоки q, и объемные силы с по-
потенциалом Н, возникающие от самоуравновешенных термиче-
термических напряжений.
Рассмотрим подробно два простейших предельных случая
локально адиабатического и изотермического процессов.
При локально адиабатическом процессе выделяемое тепло
консервируется в источниках и не распространяется, т. е.
q{ 4 = о, а вдоль контура С2 в тонкой структуре будет Н = 0
и dqj/dl = 0. При этом поле напряжений и деформаций вдоль
С%, очевидно, будет таким же, как и в упругом теле. Таким
280 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
образом, находим, ограничившись для простоты статическим
-случаем,
Г* = -Ц^ К\. E.165)
Согласно конценпции уо, в момент локального разрушения
(появления локального хрупкого надрыва в сверхтонкой струк-
структуре) величина Тх становится равной некоторой постоянной
материала 2^о- Отсюда на основании E.165) следует, что
величина эффективной поверхностной энергии у при локально
адиабатическом процессе равна постоянной у<ь вязкость раз-
разрушения Kic при этом связана с у0 следующим образом:
K?e = 4|iYo/(l-vJ (Y = Yo> E.166)
Кроме того, согласно E.164), в момент разрушения имеем
EЛ67)
Сравнивая E.164) и E.99), находим следующее соотноше-
соотношение между уо и yt:
E.168)
Yo 2т) ц
Эта зависимость (для упрочняющихся упруго-пластических
сред) согласуется с опытными данными и с соответствующей
оценкой E.157) для идеального упруго-пластического тела.
Напомним, что в основе вывода формулы E.168) лежит кон-
концепция kjc, подробно изложенная в начале этого параграфа для
растущих трещин.
В том случае, когда докритическим подрастанием трещины
можно пренебречь, концепция kjc особенно проста и наглядна.
Согласно этой концепции, насыщение сверхтонкой структуры
происходит, когда поток энергии Гж достигает величины 2у*
(с этого момента вблизи конца трещины начинается движение
дислокаций, появляется пластическая область, а диаграмма за-
зависимости некоторого среднего напряжения о в сверхтонкой
структуре от соответствующей средней деформации е стано-
становится нелинейной). В дальнейшем с ростом Гж величина kj не
изменяется, т. е. k\ = kic, величина dajde в сверхтонкой струк-
структуре уменьшается, а пластическая область растет, пока не до-
достигается предельное состояние тонкой структуры, характери-
характеризуемое величиной потока энергии Г* — 2уо- Последовательные
этапы этого процесса изображены на рис. 98; стрелка указы-
указывает направление процесса.
Зависимость E.168) показывает, что предельные состояния
тонкой и сверхтонкой.структур тесно связаны. При помощи диа-
$5)
УПРУГО-ПЛАСТИЧЕСКОЕ ТЕЛО
281
граммы рис. 98 величины цх и уо легко увязать также с неко-
некоторой предельной деформацией сверхтонкой структуры е,», при
которой течение этой структуры становится невозможным и
возникает локальный хрупкий надрыв. Существенно при этом,
что любая конкретная физическая модель разрушения сверх-
сверхтонкой структуры, не учитывающая временные процессы, при-
приводит к концепции k\c. В этом смысле можно говорить об уни-
универсальности концепции kic. В частности, теория Мак-Клинтока
с
л * as
Рис. 98.
[95] и теория Уэллса*) [Э4] в рассматриваемом случае приводят
к концепции kic. Вследствие E.164) концепции уо в рассматри-
рассматриваемом процессе эквивалентна концепции k\c.
Локально адиабатический процесс реализуется, если мате-
материал обладает специальными свойствами (плохая теплопровод-
теплопроводность, большая теплоемкость), или же при весьма быстрых
процессах (ударное нагружение для случая неподвижной тре-
трещины, быстрое продвижение фронта'трещины).
Температурное лоле в пластической области при таком про-
процессе определяется из уравнения
cf —
E.169)
В упругой области температура не меняется.
В формуле E.167) следует учитывать зависимость ц^, от
локальной температуры сверхтонкой структуры. Так как с увели-
увеличением Т величина \ix уменьшается, то значения \0 и вязкости
Концепция С. О. D. (см. подстрочное примечание к стр. 209).
282 некоторые общие йооросы механики разрушения [гл. v
разрушения Kic возрастают. Величину ftIc можно считать не за-
зависящей от температуры, так как постоянные ц и yt, через ко-
которые она выражается, слабо зависят от температуры.
Рассмотрим теперь изотермический процесс, когда выделяе-
выделяемое тепло мгновенно распределяется по всему телу. Он реали-
реализуется в материалах с хорошей теплопроводностью и малой
теплоемкостью при медленных процессах. Условия начала раз-
разрушения в металлах в большинстве случаев близки к условиям
изотермического процесса.
При изотермическом процессе согласно E.159) имеем
17n'ds =T J iinids=T J Ji<'<dv =
Л* = -7" EЛ70)
J cTnxds=cT J nxds = 0, Q= J J a^dv, J Hnxds = O.
C2 C2 Dp C2
Здесь Dp — пластическая область, Q — мощность тепловыделе-
тепловыделения в пластической области.
Поле напряжений и деформаций в тонкой структуре будет
таким же, как для идеально-упругого тела (случай стационар-
стационарного движения трещин здесь не рассматривается, зависимостью
упругих постоянных от характера процесса пренебрегаем). По-
Поэтому, интегрируя E.162) вдоль С2 и используя E.170) и
E.92), находим
г* ^r^1—w EЛ71)
Таким образом, вязкость разрушения Ки и эффективная по-
поверхностная энергия у при изотермическом процессе связаны
с yo следующим образом:
$) =Yo+^- EЛ72)
Для определения величины dQ/dl можно использовать или
прямой эксперимент', или же решение нестационарной упруго-
пластической задачи о начале движения трещины; при этом
следует применять' уравнения теории пластичности в скоростях
деформаций.
В общем случае процессов, не являющихся ни изотермиче-
изотермическими, ни локально адиабатическими, формулы E.172) оста-
останутся по-прежнему справедливыми, если пренебречь интегра-
§ 6] ОДИН УПРУГО-ПЛАСТИЧЕСКИИ АНАЛОГ ЗАДАЧИ ГРИФФИТСА 283
лами J Tnxds и \Hnxds,обозначить через Q,согласно E.159),
Ci С?
величину Q= Г J (<х^ё?;—cf) dv и учесть зависимость ц» от
температуры.
При этом вязкость разрушения, согласно E.167) и E.172),
будет равна
^e=sl T^Tlii. (Г) +~дГГ <5Л73)
Формула E.173) позволяет выявить два различных (и дей-
действующих в противоположные стороны) механизма влияния
скорости нагружения на вязкость
разрушения упруго-пластических
материалов.
С увеличением скорости нагру-
нагружения или скорости роста трещины
первое слагаемое в E.173) возрас-
возрастает, так как вследствие разогрева
уменьшается величина ц», а второе
слагаемое убывает вследствие
уменьшения теплоотвода из пласти- угк
ческой зоны. При очень больших
скоростях можно пренебречь вто- Рис 99.
рым слагаемым, а в весьма пластич-
пластичных телах при очень малых скоростях — первым. Поэтому зави-
зависимость вязкости разрушения от скорости приобретает харак-
характерный вид, изображенный на рис. 99. Различные участки этой
диаграммы могут иметь разное значение в зависимости от усло-
условий испытания и от материала.
,§ 6. Один упруго-пластический аналог задачи Гриффитса
Проиллюстрируем основные особенности роста трещин в
упруго-пластических телах на конкретной задаче.
1. Задача Дагдейла. Пусть тонкая пластина из идеального
упруго-пластического материала имеет прямолинейную сквоз-
сквозную щель длиной 21, находящуюся в однородном поле растя-
растягивающего напряжения ау = р (рис. 100). Начало декартовых
координат ху возьмем в середине щели, ось х направим вдоль
щели. Пусть берега щели свободны от нагрузок.
Дагдейл [54] предложил следующую гипотезу: пластические
области около концов щели представляют собой прямолинейные
ртрезки длины d, расположенные на продолжении щели.
284
Некоторые общие вопросы механики разрушения
1ГЛ. У
Проведенные Дагдейлом [54] эксперименты на пластинах из мало1
углеродистой стали с большой точностью подтвердили эту ги-
гипотезу. Примерная диаграмма а — е испытанной им мягкой
стали приведена на рис. 100 (нижний предел текучести равен
примерно 20 кГ/мм2). В опытах Дагдейла было показано также,
что краевая щель длины I и внутренняя щель длины 2/ (см.
рис. 100) имеют*), пластические отрезки одинаковой длины d.
'I I f
ч
1
V
I,.
7771
Hft
l+d y.
\\р
Рис. 100.
Пластические области реализуются в виде локальных шеек на
протяжении щели; скольжение в них происходит под углом 45°
к плоскости пластины.
Дальнейшие эксперименты на различных материалах (ста-
(сталях, алюминиевых и титановых сплавах, полимерах) показали,
что гипотеза Дагдейла выполняется достаточно хорошо лишь
для весьма мягких сталей; в других материалах наблюдаются
более или менее систематические отклонения. Тем не менее,
количественные расчеты, проводимые на основе гипотезы Даг-
Дагдейла, оказываются для тонких пластин в достаточно хорошем
согласии с опытными данными даже тогда, когда гипотеза
Дагдейла не выполняется. Этот факт объясняется на основе
точных теоретических расчетов тем, что пластическая область
вблизи конца сквозной трещины в тонкой пластине имеет
сплюснутую форму (см. § 5 гл. IV).
В случае несквозных трещин гипотеза Дагдейла^дает удоб-
удобную для вычислений качественную схему.
*) Это объясняется, по-видимому, локальным выпучиванием пластины
вблизи щели (см. Приложение I, § 6).
5 6] один упруго-пластический аналог задачи гриффитса $85
Пусть материал пластины удовлетворяет условию пластич-
пластичности Треска — Сен-Венана, которое в данном случае имеет вид
тах{|<Т] |, |(Г21> I <*i — o2\} = as, E.174)
где ffi и 02 — главные напряжения. Напомним, что максималь-
максимальное касательное напряжение в каждой точке упруго-пластиче-
упруго-пластического тела, согласно условию Треска — Сен-Венана, не может
превышать предела текучести на сдвиг. Как известно, макси-
максимальное касательное напряжение равно абсолютной величине
наибольшей из полуразностей главных напряжений; в пластине
одно из трех главных напряжений (по нормали к поверхности
пластины) равно нулю.
Вследствие симметрии главные напряжения на продолжении
трещины равны ах и ау, причем из физических соображений,
проверяемых a posteriori, будет ау > ах- Следовательно, на
основании E.174) и гипотезы Дагдейла краевая задача примет
следующий вид:
ву = <
о = (
ву
3 при у
as при t
3 при t.
-*"/'» <** "
г=0
/ = С
^ = 0
->о,
. с
1, -/.
|, | j
"^Ху
f = (
<u
->O
) при
|</ +
+ d,
при |
t/ = O,
d,
>x + iy\-
\x\<
-> oo.
/,
..E.
175)
Величина d должна быть определена из решения задачи. За-
Заметим, что согласно условию пластичности E.174) в пластине
невозможны бесконечно большие напряжения.
Граничная задача E.175), аналогично более общему случаю
(см. § 1 гл. IV), сводится к задаче Дирихле для разреза
(—l — d,l-{-d), решение которой дается формулой Келдыша—¦
Седова.
Вычисляя интеграл D.8) в данной задаче, нетрудно найти
ее решение (в классе ограниченных функций). Это решение
можно записать так:
dtl , . <JV 1 u v Лч /^^ rf4 /~\ » -, О.'-.Лл//~\ /C 1yg\
os ln fT
~Ш fd B/ + d)
'8 6
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ
[ГЛ. V
Здесь корень Y(l + df — z2 считается положительным н'а
верхнем берегу разреза (—/ — d,l-{-d) вдоль оси х\ кроме того,
In F = \n\F\ + i argF, причем —n<argF<.n.
Чтобы выполнялось условие из бесконечности, в формулах
E.176) нужно положить
E.177)
Это есть условие разрешимости краевой задачи, которое слу-
служит для отыскания длины пластического отрезка.
Построенное решение может быть использовано для нагляд-
наглядной иллюстрации представления о тонкой структуре конца тре-
трещины, которая в данном случае реализуется теоретически при
d/l4Z.l, т. е., согласно E.177), при внешнем напряжении р,
гораздо меньшем предела текучести:
P/os
E.178)
Если выполняются эти условия, то решение E.176) при
l~^>\z — l\^?d сводится к общим формулам D.97), описываю-
описывающим структуру конца произвольных трещин в тонкой пластине
в постановке Дагдейла; при этом коэффициент интенсивности
напряжений, как в задаче Гриффитса, оказывается равным
у
Любопытно, что при наличии тонкой структуры наибольшее
касательное напряжение в каждой точке тела вне пластиче-
пластического отрезка меньше предела те-
текучести; в этом легко убедиться
непосредственной проверкой. Та-
Таким образом, соответствующая
упруго-пластйческая задача име->
ет по крайней мере два решения,
приведенных в § 5 гл. IV; одно
из этих решений непрерывно
всюду по смещениям и напряже-
напряжениям, другое (в постановке Даг-
Дагдейла) имеет разрыв нормально-
нормального смещения и.
На рис. 101 по формулам
E.176) построена зависимость
безразмерной длины пластического отрезка d/l от внешней без-
безразмерной нагрузки p/as (кривая 1 отвечает точному решению,
кривая 2 — приближению тонкой структуры). Как видно из
рисунка, приближенное решение близко к точному даже при
довольно высоких нагрузках; например, при р(а, =з= 0,5 ошибка
Рис. 101.
*«]
ОДИН УПРУГО-ПЛАСТИЧЁСКИЙ АНАЛОГ ЗАДАЧИ Г^ЙФФЙТСА
287
о
составляет всего 25%. Эта ошибка существенно уменьшается,
если взять эмпирическую поправку Ирвина.
На рис. 102 в условиях тонкой структуры приведена кривая
зависимости безразмерного напряжения oy/as на продолжении
трещины от безразмерного расстояния x/d до конца трещины;
для сравнения показана также соответствующая кривая для
идеально-упругого тела.
Как видно, решение упруго-пластических задач в постановке
Дагдейла существенно упрощается, так как сводится к отыска-
отысканию разрывных решений в рамках теории упругости. Метод
Мусхелишвили [23] позволяет на-
находить эффективное замкнутое
решение таких задач в общем
случае произвольного числа тре-
трещин, расположенных вдоль одной
прямой в бесконечной пластине,
если разрывы расположены вдоль
той же прямой. При этом линей-
линейные размеры пластических от-
отрезков определяются из условий
разрешимости краевой задачи в
классе ограниченных функций
(напряжений).
Согласно E.174) в упругой
области должно выполняться
неравенство \a.i— or21 <C ors, иначе гипотеза Дагдейла становится
неверной. В действительности, начиная с некоторых значений
параметров нагружения, это неравенство нарушается; тогда
вблизи концов трещин возникают вторичные пластические об-
области (боковые полосы пластического скольжения [125]), сколь-
скольжение в них происходит по плоскостям, нормальным к плоско-
плоскости пластины.
2. Подрастание трещины. В отличие от условий плоской де-
деформации трещины в тонких пластинах из упруго-пластиче-
упруго-пластического материала обнаруживают тенденцию к (иногда весьма
значительному) устойчивому докритическому развитию. Рас-
Рассмотрим это явление в задаче Дагдейла на основе обобщенной
энергетической концепции [79].
В отличие от предыдущего пункта, где длина щели 2/
предполагалась неизменной, будем считать, что величина I
зависит от нагрузки р и должна быть определена из реше-
решения задачи. Естественно, длина начальной щели считается из-
известной.
Используя решение E.176), вычислим смещение и и у на
пластической линии разрыва
Рис. 102.
288 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
при у = 0, l<\ x\<l-\- d
— E.179)
Например, раскрытие трещины в ее конце при ? = 1 будет
равно
>(l,l, p)=—
^. E.180)
На рис. 103 изображена зависимость безразмерного раскры-
раскрытия конца трещины nEvo/Dosl) от безразмерной нагрузки p/as,
найденная при помощи формулы E.180). Для сравнения на
этом же рисунке нанесена кривая /, соответствующая прибли-
приближению тонкой структуры.
1,5
1,0
0,5
се
46SL
i
/
/
/
о,г
o,8
Рис. 103.
Рис. 104.
Пусть в некоторый момент времени, соответствующий зна-
значениям параметров / и р, разрыв смещения v на отрезке
(/, l-\-d) изображается условным треугольником A0CqB0
(рис. 104); через некоторое время, соответствующее прираще-
приращению параметров / и р на Д/ и Др\ рассматриваемый отрезок
займет сдвинутое в направлении роста трещины положение, ко-
которое условно изображается треугольником Л1С1В1. Точки Со
-и С\ отвечают концу пластической линии; точка Ао, А\ и Во.
В\ — концу трещины на различных берегах пластической линии
разрыва.
461 ОДИН «З^ОЛЛАСТИНЕСКИЙ АНАЛОГ ЗАДАЧИ ГМ1ФФЙТСА 289
Согласно E.176) напряжения в пластической области та-
таковы:
___ _____ ____ Л /р" 1 ft 1 \
При продвижении конца трещины на А/ напряжение произ-
произведет работу на соответствующем смещении; эта работа, оче-
йидно, равна полной диссипации энергии, которую обозначим
через \ФА1. Величина у* представляет собой полную диссипацию
энергии, приходящуюся на единицу длины трещины.
Вычислим величину у» в нашей задаче, считая длину тре-
трещины заданной функцией нагрузки. Имеем:
i+d
Y. А/ = J оу [v (х, I + М, р + Ар) — v (х, 1, р)] dx + AS. E.182)
i+м
При малых А/ справедливы следующие оценки:
J Oy [v (х, I + Д/, р + ДР) - v (х, I, p)] dx * (оу ¦%)¦_, (АО2.
J oy [v (х, I + М, р + ДР) — v'(x, I, P)] dx «* E.183)
A5«O[(A/J].
Разложим функцию v (x, I + Д/, p -f- Ар) в выражении E.182)
в ряд Тейлора по А/ и устремим Д/ к нулю, учитывая оценки
E.183). Получим
В частности, когда смещение v на пластическом отрезке
(/, l-\-d) стационарно в системе координат, движущейся вме-
вместе с рассматриваемым концом трещины, т. е. v = v(x-y-l), бу-
будут справедливы соотношения
dt»/ap = O, Qv/dt = dv/dx E.185)
Ю Г, П. Черепанов
290 Некоторые общие вопросы Механики разрушений if л. v
и выражение E.184) перейдет в следующее уравнение:
l+d l+d
dv ,
— osvQ. E.186)
i
Это уравнение совпадает с формулой D.99); оно отвечает
концепции квазихрупкого разрушения (см. § 5 гл. IV).
Используя формулы E.179), находим (простые, но громозд-
громоздкие выкладки опускаем)
I l (fi 11 In (f-Ofonpyi-f'coa'p + fcos'p+Ol ,, ,n
+ 2V ' ((+l)(sinpVl-^cos^-(cos2P+l)J ( Щ-
E.187)
При помощи E.187) находим
l+d l+d
l+d
dv (I, I,
Ji_ Г _эи_ _
i
*=^Г [2 (ln cosр + рtg Р) + /(рsec2р-tgр)~]. E.188)
Использованный прием вычисления у» аналогичен приему
Ирвина (§ 2 гл. IV). Покажем, как можно найти у*, применяя
метод Гриффитса.
Рассмотрим упругую среду, занимающую фиксированную
область |z[sSC/?, где радиус R велик по сравнению с длиной
трещины. Состояние этой системы определяется двумя парамет-
параметрами: / и р. Согласно закону сохранения энергии, мощность
внешних сил, приложенных на внешнем контуре |z| = /?, равна
скорости изменения упругой энергии тела W плюс скорость
диссипации энергии. В качестве параметра, заменяющего время,
может служить /. Имеем
6А/Ы = dW/dl + 4у.. E.189)
Распределение смещений и напряжений при больших R, со-
согласно E.176), определяется следующим потенциалом Коло-
Колосова— Мусхелишвили:
) при z->oo. E.190)
§ 6] ОДИН УПРУГО-ПЛАСТИЧЕСКИЙ АНАЛОГ ЗАДАЧИ ГРИФФИТСА 291
Вычисляем по формулам E.189), E.190) и E.176), исполь-
используя также теорему Клапейрона; получаем
2я
-^ = R J [К cos 6 + ххя sin в)-§-
Й" { 2 E +
cos 9 + оа sin 8) ж\ dQ = -^- р ? +
/ ^ [E + v) p sec2 p_C—v) tg p]}.
2д E.191)
^-jRJ [К cos 8 + хху sin в) и- +
о
+ (т*,, cos 8 + ау sin Э) v]dB — 2<rs J у (х, I, р) й?лг =
+ -^- [— 8 In cos р + (v — 3) р tg p].
Считая / независимым параметром, из E.189) и E.191)
легко найти
-tgP)-§-]. E.192)
На основе полученного уравнения энергии определим зави-
зависимость длины трещины от нагрузки. Будем исходить из кон-
концепции у* I45]; согласно этой концепции, величина у» является
постоянной материала. Концепция квазихрупкого разрушения,
принадлежащая Ирвину и Оровану, справедлива только для
стационарного поля E.185); в этом случае (согласно E.186))
она вытекает из концепции у*- Таким образом, концепция у*
представляет собой естественное обобщение концепции Ирвина
и Орована на нестационарный случай. Она дает весьма удовлет-
удовлетворительное количественное описание различных опытных фак-
фактов, имеющих важное практическое значение. Это, прежде всего,
рост усталостных трещин [65], стабильное докритическое подра-
подрастание трещин [20] и др. (см. также § 2 гл. VI).
Введем безразмерную длину X:
0 E.193)
Согласно концепции у* и уравнению E.192), искомая зави-
зависимость между р и % запишется окончательно в виде следующего
10*
292
НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ
дифференциального уравнения первого порядка:
dP I — 2Л. (In cos Р + Р tg P)
dX ~~ ^s(P2ptP)
[ГЛ. V
E.194)
На рис. 105 изображено поле интегральных кривых уравне-
уравнения E.194) в области 0 < X < оо, 0 < р < л/2. Сплошными
тонкими линиями обозначены устойчивые участки кривых, тон-
тонкими штрихами — неустойчивые участки. Кривая, определяе-
определяемая уравнением
1 = 2Я (In cos P + Э tg р), E.195)
разделяет всю область изменения переменных на область устой-
устойчивого развития трещины из некоторой начальной (в этой обла-
области dfildX > 0) и область неустойчивости (в которой dfi/dX < 0).
iff
Рис.
1,5
105.
&5
A •
US: W
Рис.
1,5
106.
Таким образом, трещина вначале монотонно растет с увели-
увеличением нагрузки.; максимальная нагрузка достигается в точке
пересечения с кривой E.195), после чего трещина попадает в
область неустойчивости.
Легко показать, что в области неустойчивости все интеграль-
интегральные кривые при больших X асимптотически стремятся к кривой
Гриффитса — Ирвина — Орована
E.196)
Кривые E.195) и E.196) изображены жирными линиями на
рис. 105. На рис. 106 приведен график зависимости безразмер-
безразмерной максимальной нагрузки р. от безразмерной длины на-
начальной трещины Хо, полученный при помощи рис. 105. Для
сравнения на этом рисунке дана также кривая E.196).
17J ВЯЗКОУПРУГОЕ ТЕЛО 293
§ 7. Вязкоупругое тело
Рассмотрим изотропное и однородное линейное вязкоупругое
тело с трещинами нормального разрыва. В условиях плоской
деформации связь напряжений и деформаций в таком теле мо-
может быть представлена следующим образом:
гх = Е~1ах — Е-1х(оу + ог), еу = Е~'ау — Е~1\(ах + аг),
Г . E.197)
eE-'O + v)^ Е-1[вх( + )] 0
Здесь Е~1 и v — линейные коммутирующие операторы по вре-
времени /. Для наследственного тела Больцмана они имеют вид
" E.198)
v/ = vf+Jvo(f-T)f(T)dT.
о
Здесь считается, что при / •< 0 деформации тела равны нулю,
а внешние нагрузки начинают действовать с момента времени
t — 0.
Первые слагаемые в этих соотношениях описывают мгно-
мгновенную реакцию (в данном случае она предполагается линей-
линейной, величины Е и v представляют собой соответственно модуль
Юнга и коэффициент Пуассона мгновенной деформации). Вто-
'рые слагаемые описывают последействие; функции E0(t) и
Vo(O характеризуют ,«память» системы. Будем считать, что они
удовлетворяют следующим физически очевидным условиям:
* t
а) (Eo(t)dt-^O, J vQ(t)dt-»O при /->0;
о о E.199)
б) E0(t) и vo(t) могут иметь лишь разрывы 1-го рода
при t>0.
Допустим, что к границе тела на некоторое время были при-
приложены (и затем сняты) внешние нагрузки. Тогда, если
при /->оо ?<,(*)-> 0, v0@->0. E.200)
то согласно E.198) за бесконечно большое время деформации
в, теле исчезают и тело принимает ту форму, которую оно имело
вначале. Таким образом, вязкоупругое тело, удовлетворяю-
удовлетворяющее условию E.200), обладает способностью к релаксации
294 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ 1ГЛ. V
деформаций. Большинство применяемых на практике твердых
полимеров удовлетворяет этому условию при не слишком вы-
высоких нагрузках.
Допустим теперь, что граница тела была продеформирована
заданным образом (т. е. на границе заданы смещения, кото-
которые, начиная с некоторого момента времени, постоянны). Тогда
из обращения соотношений E.197) видно, что если условие
E.200) не выполняется, то за бесконечно большое время напря-
напряжения в теле исчезают. Таким образом, вязкоупругое тело, не
удовлетворяющее условию E.200), обладает способностью к
релаксации напряжений. Большинство жидких полимеров, встре-
встречающихся в различных технологических процессах, относится к
таким телам.
В зависимости от того, выполняется условие E.200) или нет,
будем говорить соответственно о твердом теле или жидкости.
Обозначим через Т характерное время релаксации (дефор-
(деформаций— для твердого тела, напряжений — для жидкости).
В качестве Т для твердого тела можно взять характерный интер-
интервал изменения функций E0(t) и vo{t); для жидкости можно
взять аналогичную величину для функций, являющихся ядрами
обращенных операторов E.197). При этом для моделей упругого
тела и вязкой жидкости будет Т = 0.
В зависимости от времени действия внешней нагрузки ма-
материалы могут вести себя совершено различно. Например, вода,
которая при обычных временах приложения нагрузок ведет себя
как жидкость с весьма малой вязкостью, при весьма кратковре-
кратковременных нагрузках подобна упругому телу и может разрушаться
хрупко с образованием и развитием трещин [126]. Наоборот,
оконное стекло, которое обычно можно считать упругим телом,
близким к идеальному, при весьма длительных нагрузках течет
подобно вязкой жидкости. Если эти материалы моделировать
уравнением тела Максвелла
t
6 = JL 4-1 Г а (т) dx, E.201)
о
ограничившись для простоты одномерным случаем, то с этой
точки зрения стекло и вода будут отличаться лишь значениями
вязкости т] и времени релаксации Т (модуль Юнга у них одного
порядка). При этом, если t<^T, тело можно считать упругим,
а если t^T, — вязкой жидкостью.
1. Вязкоупругая аналогия. Задачи о распределении напря-
напряжений и деформаций в вязкоупругих телах с движущимися по-
поверхностями разрыва смещений являются весьма трудными при
граничных условиях общего типа. Однако имеется два доста-
§ f] ВЯЗКОУПРУГОЕ fЕЛО 295
точно общих случая, когда квазистатические напряжения и де-
деформации в вязкоупругом теле легко определить из соответ-
соответствующего статического упругого решения.
Первый случай. Если
а) тело конечно и односвязно,
б) оператор v равен постоянной,
в) на границе тела и на движущихся поверхностях разрыва
смещений заданы нагрузки,
то напряжения в вязкоупругом теле совпадают с напряжениями
в соответствующей упругой задаче.
. Второй случай. Если
а) оператор v равен постоянной,
б) на границе тела заданы смещения, а на движущихся по-
поверхностях заданы разрывы смещений (как в теории дисло-
дислокаций),
то смещения в вязкоупругом теле совпадают со смещениями
в соответствующей упругой задаче.
Эти результаты становятся очевидными, если уравнения
статической теории вязкоупругости записать в напряжениях
(или соответственно в смещениях) и сравнить результат с со-
соответствующими уравнениями теории упругости. В указанных
случаях в формулировку упругой задачи модуль Юнга не вхо-
входит, а уравнения вязкоупругости представляют собой результат
применения оператора Е-1 к соответствующим уравнениям тео-
теории упругости.
В силу теоремы единственности обращения оператора типа
свертки подынтегральные выражения можно положить равными
нулю, и таким образом, для напряжений (или смещений) вязко-
упругого тела получаются типичные краевые задачи теории
упругости. Заметим, что уравнения вязкоупругости, в отличие
от уравнений упругости, существенно изменяют свой вид в за-
зависимости от того, подвижна или неподвижна используемая си-
система координат.' Здесь предполагается, что применяется не-
неподвижная система координат; в подвижных координатах про-
произведение операторов свертки и дифференцирования становится
некоммутативным.
Для плоской деформации и плоского напряженного состоя-
состояния имеет место более сильное предложение, которое доказы-
доказывается аналогично. Если
а) главные векторы внешних усилий, приложенных к каж-
каждому из граничных контуров многосвязного (может быть, бес-
бесконечного) тела, в отдельности равны нулю,
б) на границе тела и движущихся поверхностях разрыва
смещений заданы нагрузки,
то напряжения в вязкоупругом теле равны напряжениям в со-
соответствующей упругой задаче.
296
HEKOf ОРЫЁ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ {ГЛ. V
В частности, поле напряжений вблизи фронта трещины пол-
полностью совпадает с упругим полем.
Деформации легко определяются при помощи E.197), коль
скоро напряжения известны. Отсюда вытекает, что смещения
вблизи фронта неподвижной трещины даются формулами
C.44) — C.46), в которых ц и v нужно заменить соответствую-
соответствующими операторами.
Случай движущейся трещины еще более прост: поле дефор-
деформаций вблизи ее фронта точно такое же, как в упругом теле,
упругие константы которого рав-
равны соответствующим постоянным
мгновенной деформации вязко-
упругого тела. Действительно,
рассмотрим рис. 107. Пусть
Xiyi — произвольная неподвиж-
неподвижная система координат с нача-
началом в некоторой трчке Oi, распо-
расположенной на пути распростране-
распространения трещины. Напряжения в
этой точке ограничены, пока в
момент времени t конец трещи-
трещины не достигнет точки О]. При
этом напряжения обратятся в
бесконечность по закону (например, для трещин нормального
разрыва)
t-At
Рис. 107.
Ох = О и = -
+ 0A) при Д*->0.
E,202)
Согласно неравенству Кощи — Буняковского
t t t
\\f(x)\dx E.203)
и условиям E.199), E.202), сингулярные деформации в конце
трещины описываются первым членом оператора свертки
E.198), т. е. равны мгновенным упругим деформациям, а вклад
второго члена с последействием конечен, и в достаточно малой
окрестности конца трещины им можно пренебречь.
Таким образом, вблизи фронта трещины, движущейся в вяз-
коупругом теле, поле напряжений и деформаций можно считать
чисто упругим. Следовательно, поток энергии в конец трещины,
движущейся в вязкоупругом теле, в точности такой же, как и
в соответствующем упругом теле. В частности, для трещин нор-
нормального разрыва
— v ) Ki/E-
E.204)
§ 1) ВЯЗКОУПРУГОЕ ТЕЛО 297
Упругая область вблизи фронта трещины имеет размер
D~VT, E.205)
где V — скорость роста трещины, Т — характерное время релак-
релаксации.
Допустим, что рассматриваемое- вязкоупругое тело при до-
достаточно высоких напряжениях проявляет также свойства пла-
пластичности или выеокоэластичности, не зависящие от времени.
Выясним, в каких случаях для такого тела справедливо пред-
представление о вязкости разрушения (концепция Кс)> которое, как
было обнаружено ранее, при определенных условиях имеет
,смысл для любых упруго-пластических моделей. Обозначим че-
через Os характерный предел текучести, а через d— характерный
линейный размер пластической области вблизи конца трещины,
равный
22. E.206)
Очевидно, что, если характерный линейный размер пласти-
пластической области мал по сравнению с упругой областью, т. е.
d < D (или К\в < a2sVT), E.2Q7)
то концепция Кс справедлива, и все локальные критерии > раз-
развития трещины будут такими же, как в соответствующем упру-
упруго-пластическом (иг в. частности, упругом) теле. Например, при
обычных условдях нагружения эта концепция годится для
стекла, представляющего собой жидкость Максвелла с весьма
большим временем релаксации 'Т\ для стекла условие E.207)
заведомо выполняется. Для воды это условие может выпол-
выполняться только для околозвуковых трещин, если положить as рав-
равным-, теоретической прочности при мгновенном нагружении
0,1 Е. Приведем соответствующие оценки. Для воды при ком-
комнатной температуре имеем примерно следующие значения физи-
физических постоянных: вязкость ц = 10~5 кГ-сек-см'2, плотность
р = Ю~6 кГ-сек2-см~4, скорость звука с=1,4-10~5 см/сек, по-
поверхностная энергия у — 10~4 кГ/см. Отсюда находим
модуль Юнга Е ~ с2р = 2,5-104 кГ-смг2,
время релаксации Т ~ \i/E — 4-10~10 сек,
характерный размер пластической области d~$c/e2:~
~ Ey/(lO~2E2) = 4 • 10~7 см.
Следовательно, если трещина распространяется в воде со
скоростью V, гораздо большей, чем величина d/T = 10 м/сек
(т. е. FS>'10 м/сек), то вблизи конца трещины имеется об-
область, которая деформируется, как упругое тело, и' разрушается
хрупко, как стекло. Например, при скорости V = 500 м/сек
298 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
упругая область вблизи конца трещины имеет примерный размер
D ~ VT = 2-10~5 см, т. е. достигает порядка микрона.
Условие E.207) для данного материала можно рассматри-
рассматривать как основное органичение, накладываемое на минимально
необходимую скорость роста трещины V, чтобы выполнялась
.концепция Кс- Если условие E.207) не выполняется, то концеп-
концепция Кс теряет физический смысл и формула E.204) уже не имеет
места.
Допустим, что в некотором вязкоупругом теле имеется на-
начальный математический разрез, а нагрузки приложены мгно-
мгновенно и затем остаются неизменными. В этом случае приведен-
приведенный анализ будет исчерпывающим, если вязкоупругое тело яв-
является жидкостью, т. е. способно к неограниченной деформации.
Действительно, если в процессе мгновенного приложения на-
нагрузки на фронте трещины не будет достигнуто условие хруп-
хрупкого разрушения Кг =S^ Kic, то в дальнейшем острый край тре-
трещины станет расплываться, и трещина превратится в полость,
способную лишь к расширению в поперечном направлении и не-
неспособную развиваться как трещина вследствие неограниченного
течения материала. Если же условие хрупкого разрушения на
фронте трещины будет достигнуто в процессе мгновенного при-
приложения нагрузки, то начальный разрез будет распространяться,
как хрупкая трещина. После того как растягивающие нагрузки
сняты, трещина в жидкости существует в течение некоторого
времени порядка времени релаксации Т и затем, очевидно, ис-
исчезает.
2. Медленное развитие трещин в твердых вязкоупругих телах.
Для медленно растущих трещин в твердых телах, когда условие
E.207) не выполняется, механизм локального разрушения в кон-
конце трещины совершенно отличен от чисто энергетического меха-
механизма распространения хрупких трэщин.
Рассмотрим механизм, связанный со старением материала.
Процесс старения протекает тем быстрее, чем выше уровень на-
напряжений. Поэтому для достаточно больших трещин, когда об-
область пластических или высокоэластических деформаций мала
по сравнению с длиной трещины или каким-либо другим харак-
характерным линейным размером тела, локальное разрушение в конце
трещины вполне контролируется коэффициентами интенсивности
напряжений. Изучение же тех случаев, когда размер пластиче-
пластической области около трещины соизмерим с длиной трещины, пред-
представляется преждевременным до тех пор, пока не будет построе-
построена достаточно надежная теория, описывающая напряжения и
деформации в вязкоупругих телах без трещин при высоком уров-
уровне напряжений, близких к разрушающим.
Предположим, что развитие трещины стационарно в том смы-
смысле, что размер d малой пластической области э ее конце не из-
7]
ВЯЗКОУПРУГОЕ ТЕЛО
99
меняется при увеличении длины трещины и не зависит от прило-
приложенных нагрузок. Это допущение по своему физическому смыслу
аналогично концепции квазихрупкого разрушения для растущих
"трещин в упруго-пластических средах. Среднее растягивающее
напряжение о в пластической области, согласно вязкоупругой
аналогии, таково:
ст = Л/Cjcf , • E.208)
где X — некоторое (безразмерное) число, которое можно считать
постоянным для данного материала.
Согласно эмпирическим данным по длительной прочности,
стержень, подвергаемый растяжению постоянной нагрузкой а,
разрушается через время
т = Лехр(— уа/Т). E.209)
Здесь А и у — постоянные материала, Т — абсолютная темпера-
температура. Эта зависимость обосновывается также некоторыми физи-
физическими соображениями о термоактивационном разрушении. Для
сквозных трещин в тонких пластинах величины Л и у зависят
также от толщины пластины.
Представляя развитие трещины последовательным скачкооб-
скачкообразным разрушением малых пластических областей в ее конце,
нетрудно видеть, что средняя скорость роста трещины равна
d\x. Отсюда при помощи формул E.208) и E.209) получаем сле-
следующее выражение для скорости роста трещины dl/dt в зависи-
зависимости от коэффициента интенсивности напря-
напряжений Ki'. (
dl/dt = voexp(t,Ki/T). E.210)
l
o _
И
'Р
Рис. 108.
Здесь v0 и ? — некоторые постоянные мате-
материала.
Следует подчеркнуть, что при этом специ-
специфические свойства вязкоупругого тела в ос-
основной массе, вне пластической1 области, не
влияют на развитие трещины; поэтому зави-
зависимость E.210) годится, в,частности, для до-
критического роста трещин в упругих телах. Разумеется, здесь
не учитываются коррозионные эффекты.
В качестве примера рассмотрим развитие краевой прямоли-
прямолинейной трещины длины / в бесконечной пластине, растягиваемой
перпендикулярно к направлению трещины (рис. 108). В рассма-
рассматриваемом случае коэффициент интенсивности напряжений К.х
равен (см. Приложение I)
E.211)
300 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
При помощи формул E.210) и E.211) получаем сл'едующее
дифференциальное уравнение для определения зависимости
длины трещины от времени:
(при * = Q f = /0). E.212)
Решение этого уравнения при постоянной нагрузке р имеет вид
' Т(\,Щр Ул)~1] X
E.213)
Наибольший интерес представляет отыскание времени до
разрушения. На основании E.213) это время не превышает ве-
величины т, равной
т = Лехр(-ур/Г), E.214)
где
А =
При / ^> h время до разрушения очень близко к т. Последнее
условие обычно выполняется в опытах на долговечность.
Точно такая же эмпирическая зависимость долговечности от
нагрузки найдена для многих материалов — как металлов, так
и полимеров I76]. Это служит косвенным подтверждением условия
E.210) и достаточной общности механизма докритического роста
трещин за счет процессов локального старения в конце трещины.
§ 8. Развитие полостей при конечных деформациях
Пусть к вязкоупругому телу'с некоторой начальной полостью
мгновенно приложены нагрузки, которые впоследствии не изме-
изменяются; тогда (см. § 7) хрупкое разрушение возможно лишь в
стадии приложения нагрузок, если пренебречь старением мате-
материала. Если хрупкого разрушения не произошло, начинается те-
течение материала, которое со временем существенно изменяет
форму начальной полости. Возникающие при этом эффекты
естественно изучить на предельном случае вязкой жидкости.
1. Основные соотношения. Рассмотрим вязкое тело, подчи-
подчиняющееся закону Ньютона и занимающее бесконечную область
во внешности некоторого контура L (задача считается плоской).
Внутренность контура L представляет собой некоторую полость,
форма которой известна лишь в начальный момент приложения
нагрузок. Предполагается следующее: а) стенки полости подвер-
подвержены постоянному давлению p(t); б) на бесконечности имеет
S..8] РАЗБИТИЕ ПОЛОСТЕЙ ПРИ КОНЕЧНЫХ ДЕФОРМАЦИЯХ 301
место однородное напряженное состояние^ = а~(/), а — a™(t),
тед = 0 (f-t- время); в) контур полости в любой момент вре-
времени имеет две оси симметрии, совпадающие с осями непо-
неподвижной декартовой системы координат; г) течение — медлен-
медленное и квазистационарное, так что в уравнениях Навье — Стокса
можно пренебречь инерционными членами. Для простоты огра-
ограничимся случаем несжимаемого тела, однако это допущение не-
несущественно для дальнейшего изложения.
В рассматриваемом случае составляющие тензора напряже-
напряжения ох, оу, txy и компоненты вектора скорости' й, и в системе
координат ху могут быть представлены при помощи формул,
аналогичных соотношениям Колосова — Мусхелишвили . в пло-
плоской задаче теории упругости
ax + or, = 4Re<D(z, Q (г = х + 1у),
<Уу-ох + Шхху = 2[гФ'(г, *) + W(г, /)],
_ -—,.— — (о..21 о)
+ш) = ф(г, 0 — г<р'(г, t) — y(z, t)
Здесь 2ц — коэффициент сдвиговой вязкости, ф(г, t) и г|? (г, t) —
однозначные аналитические функции г в области, занятой телом;
штрихом будем обозначать производную по соответствующей
комплексной переменной.
На неизвестной границе полости, уравнение которой имеет
вид F(x,y,t) =0 (F(x,y,0)~заданная функция), должно вы-
выполняться условие кинематической совместности
Кроме того,-на контуре L должно выполняться условие
Ф (г, 0 + 2фА(г, 0 + «(г, 0 = - р (t) г (ге L). E.217)
В бесконечно удаленной точке функции ф(г, t) и г|зB, t) ве-
ведут себя так:
при г-> то
Ф (г, 0 - т К W + °7 Щ г + ° B~') •
, F.218)
« (г, 0 = | К @ - °Г Щ г + О B"'>-
Таким образом, поставленная задача сводится к краевой за-
задаче E.216) — E.218).
Перейдем на внешность единичного круга параметрической
плоскости ? при помощи отображения 2 = (о(?, t); аналитиче-
аналитическая функция со (С, t) конформно отображает область |?| > 1 на
302 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
внешность контура L со взаимно однозначным соответствием
бесконечно удаленных точек, а также соответствующих участков
действительных и мнимых осей. Следовательно,
©(?, t) = с(t)?, + О(t,'1) при ?->оо, E.219)
где c(t) — действительная функция.
При этом краевые условия E.217) и E.218). на плоскости ?
запишутся в следующем виде:
при 1Б1=1,
при ?->оо ' ' E.220)
Ф, (Б. 0 = т с W К @ + <? @] Б + О (Г').
Ф. (Б, 0 = т с @ [а- @ - а» ЩI + О (Г1)-
Здесь
ф. (Б. 0 = Ф [© (Е. 0. *]. Ф. (Б.') = Ф [© (Б. 0- 'L
где юо(^)—задаваемая функция. '
Функции ф*(Б>0> ф»(?, 0 и ©¦(?,/) подлежат определению.
Условие кинематической совместности
удобно записать таким образом:
2JiRe[sf-co'(?,0] =
= Re { б*»' (Б, 0 [фЛР) -
при 1Б1=1.
Условие E.221) получается из следующих
соображений (рис. 109).
Рис. 109. Каждой точке О контура L в любой мо-
момент времени t соответствуют две скоро-
скорости: а) скорость материальной частицы, находящейся в момент
времени t в точке О; комплексный вектор этой скорости
(u + iv) определяется формулой E.215); б) кинематическая
скорость перемещения точки О самого контура (da/dt), соот-
соответствующая одному и тому же значению параметра ?, задаю-
задающего положение точки О на контуре L в любой момент времени.
Как следует из. рисунка (на котором сравниваются два бес-
§ 8] РАЗВИТИЕ ПОЛОСТЕЙ ПРИ КОНЕЧНЫХ ДЕФОРМАЦИЯХ 303
конечно близких положения контура L в малой окрестности
точки О в моменты времени / и t + dt), проекции указанных
двух векторов скорости на нормаль пг к контуру L в точке О
должны быть равны между собой. Теперь для доказательства
E.221) осталось лишь найти выражение для комплексного век-
вектора единичной нормали пг на L:
_ dz __ &' (g, t) dt, _ щ' (S, t)
n*— \dz\ ~ |«D'(t,OI \dU —fi|<D'(b0l
и составить скалярное произведение ап комплексного вектора
а = \а\ exp (i<x\) на пг = ехр (/аг):
ап = I a I cos (aj — а2) = Re (anz).
Формулы E.219) — E.221) завершают постановку краевой за-
задачи на плоскости ?.
2. Эллиптическая полость. Рассмотрим класс решений этой
краевой задачи, для которого выполняется условие
1=0. E-222)
представляющее собой векторное равенство кинематической ско-
скорости и скорости материальной частицы на границе полости. При
этом условие E.221) выполняется тождественно.
Сложив E.222) и E.220), получим
- р @ со (С, 0 + 2ц -f- = 2cp. ft, 0 при | g | = 1.. E.223)
В силу принципа аналитического продолжения соотношение
E.223) должно выполняться также в полной плоскости С» т. е.
<р. (?, *) = (i -g— у Р @ «(?, /). E.224)
Подставляя E.224) в E.222) и преобразуя, можно найти
•^-5Г(СТ7) + «(С, 0-^-=~*ЛсЛ)^(сТ7) E-225)
или
Введем вспомогательную аналитическую функцию Г(?, /):
Г «' ') = - 17tbr{ I ** К. 0 «' (?• 0 <« + Го (С) I • (?226)
304 НИКОТОРЫЕ ОВИрЙЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
Функция Го(?) несущественна, и ее можно считать равной
нулю. При помощи функции Г(?, t) краевое условие E.225) мож-
можно записать так:
|Ш(?, t)=TWb при|и=1. E.227)
Решение этой краевой задачи в классе функций, имеющих
заданный порядок 0(?) на бесконечности и удовлетворяющих
условиям симметрии, будет следующим:
со (?, /) = с (t) 5 + Ь №, Г (С, 0 = ц [& № ? + с (О/?]. E.228)
Действительные функции с(/) и 6(<) должны удовлетворять
условиям на бесконечности для функций ф(?, /) и г|э (?,?); ис-
используя эти условия, находим следующую систему дифферен-
дифференциальных уравнении первого порядка по t относительно c(t)
и b(t):
^±[с @ ь (t)] + [о; (t) - o~ щ [с (tw = о,
- [2p @ + a? @ + a» (*)] с @ = 0.
При t = 0 будет c(f) = c0, 6(^) = b0, где 60 и c0 — заданные
постоянные, определяющие форму полости в начальный момент
нагружения; последняя, согласно E.228), представляет собой
эллипс
*2/A + mf + уг/( 1 - mf - cl (m = 60/с0). E.230)
Решение системы, удовлетворяющее начальным условиям, за-
запишем в виде
ct-cez \U x dx]
c@-Coexp|JMtdtJ.
6@ = j bo — c0 J Y(*)exp 2 J X{xl)dxl driexp — J k(x)dx
\ о L о J j L о
Здесь
V @ = [о; (t) ~ o~ Щ1Bц), X (t) =* [2p @ + a» @ + о
Отсюда получаем искомые функции <р, (?,, t) и i|), (?, f):
ф, (С 0 = К М + аГ W]с ^ ^4~ Bс (f) К W - a? W] +
. + Ь(*)[4р@ + о?(/) + а-(*)]}/D?), E.232)
,., № л— и@(с3-г1)-ев«)
S 8J РАЗВИТИЕ ПОЛОСТЕЙ ПРИ КОНЕЧНЫХ ДЕФОРМАЦИЯХ 365
Здесь
А @ = цу (t) [с № В @ = 2ц {Я (/) [б2 (/) + с2 @] + Ъ (t) с @ у (/)] •
Решение задачи о развитии полости из начальной эллиптиче-
эллиптической найдено; точные формулы, учитывающие сжимаемость ма-
материала и несимметрию задачи, легко получить совершенно ана-
аналогичным методом.
Напомним, что соответствующая линейная задача была ре-
решена [23] Г. В. Колосовым и Инглисом для различных частных
случаев, а в общем виде — Н. И. Мусхелишвили.
Как видно, контур полости в любой момент времени пред-
представляет собой эллипс с центром в начале координат
*2Д 1 + т (OF + У2! [1 - m(t)Y = с2 (t) (m - Ь/с). E.233)
Рассмотрим некоторые наиболее интересные частные случаи
общего решения.
Осесимметричная задача. Пусть в любой момент времени вы-
выполняется равенство а* = ар Тогда
Y @ = m @ = 0, М/) = И*) + о«@]/Bц). E.234)
Полость представляет собой круг
I
E.235)
Одноосное растяжение начальной круговой полости. Пусть
будет р (/) = а~ (/) = 0, bo = O, o°° (t) = а = const. Тогда
/я<0 = — l-fexp[— <rf/Bn)l, c(/) = c0exp[a//D|i)]. E.236)
Контур полости сужается в направлении оси х и расширяется*
в направлении растяжения, стремясь при t-± oo к разрезу вдоль
оси у.
Одноосное растяжение начального разреза. Пусть выпол-
выполняются соотношения
h^cv o™ = p = 0, a~(/) = a = const,
т. е. тело подвергается одноосному растяжению вдоль оси у по-
постоянным напряжением; в начальный момент в теле имеется
разрез нулевой толщины длины 4со вдоль оси х. Согласно общим
формулам E.231) и E.233) получаем
m = 2exp[— at/Bn)]~ 1, с = с0ехр[а//Dц)]. E.237)
Таким образом, разрез превращается в эллипс, который с те-
течением времени сужается в направлении х и расширяется в
306 НЕКОТОРЫЕ ОБЩИЕ ВОПРОСЫ МЕХАНИКИ РАЗРУШЕНИЯ [ГЛ. V
направлении растяжения, стремясь при t-*-oo к разрезу вдоль
оси у. Приведем еще значение напряжения в наиболее напря-
напряженной точке х = (\ -\-т)с, у = 0:
<r, = <rcth[<rf/D|i)]. E.238)
Интересно, что в этой точке напряжение при малых относи-
относительных временах не зависит от приложенной внешней нагрузки
oy = 4]i/t при <rf<4fi. E.239)
Распределение напряжений и скоростей в окрестности конца
разреза на расстояниях-, больших по сравнению с радиусом кри-
кривизны эллипса в точке х = A -\- т)с, у = 0, но малых по срав-
сравнению с длиной начального, разреза 4со, при малых относитель-
относительных временах нагружения at «С 4ц — такое же, как распределе-
распределение соответствующих напряжений и смещений в линейной теории
упругости.
Чтобы найти смещения и деформации, нужно, как обычно,
проинтегрировать систему дифференциальных уравнений
dx/dt = u{x, у, t), dy/dt = v(x, у, t)
i \ j. r> E.240)
(u = x-—x0, v = y — yQ), при ^ = 0 x = x0, y = y0-
Правые части в эти уравнения подставляются из найденного ре-
решения.
Ясно, что в конце разреза в несжимаемом вязком теле де-
деформации не имеют особенности; поэтому поток энергии Г в ко-
конец трещины равен нулю. Аналогичное обстоятельство имеет ме-
место для несжимаемых идеальных упруго-пластических тел, как
легко видеть из оценок E.155). Начальная трещина в таких те-
телах неспособна распространяться; она всегда расширяется, как
полость.
Г Л А В А VI
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
§ 1. Введение
Наиболее частой причиной разрушения конструкций является
развитие в них усталостных и коррозионных трещин. С этим
связаны так называемые проблемы замедленного разрушения,
которое объясняется тем, что небольшие начальные трещины
растут в ходе эксплуатации конструкции, достигают критиче-
критической величины и приводят к внезапному хрупкому разрушению
конструкции при сравнительно низких рабочих напряжениях.
«Продолжительность жизни» изделия с развивающейся трещи-
трещиной обычно занимает значительную часть всего времени до раз-
разрушения.
В этой главе излагается теория роста усталостных трещин
ро, 65, 127-129^ приводится сравнение ее с экспериментальными
данными и рассматриваются различные конкретные задачи. Всю-
Всюду предполагается выполняющимся условие тонкой структуры.
Явление усталости металлов было обнаружено немецким уче-
ученым Велером более ста лет назад. Последующие исследования
позволили найти причину преждевременного хрупкого разруше-
разрушения конструкций при циклических нагрузках: медленное разви-
развитие трещин в процессе эксплуатации конструкции.
Картину разрушения образца под воздействием циклической
нагрузки, меньшей предела текучести, можно представить себе
в общих чертах так [13°-13s]. Вначале в образце нет каких-либо
видимых изменений; затем, начиная с некоторого числа циклов,
в материале обнаруживаются дислокации, субмикротрещины,
которые растут с увеличением числа циклов, материал разрых-
разрыхляется; далее появляются микротрещины и продолжается про-
процесс разрыхления и местного течения; заключительная стадия
характеризуется ростом одной макротрещины, приводящим к
хрупкому разрушению образца. Фрактографическое исследова-
исследование позволяет обнаружить после разрушения на поверхностях
трещины характерные бороздки, которые на снимках выглядят
как годичные кольца деревьев [136- ш]. Эти бороздки представ-
представляют собой следы подрастания трещины в течение каждого
цикла.
Процесс усталостного разрушения удобно разбить на два
этапа. На первом этапе размер образующихся микротрещин или
308 РС>СТ УСТАЛОСТНЫХ ТРЕЩИН [ГЛ. VI
дислокаций сравним с характерным линейным размером прочно-
прочностной неоднородности (зерна), поэтому на этом этапе необхо-
необходимо учитывать микроструктуру материала (инкубационный пе-
период или период зарождения трещины). К инкубационному пе-
периоду будем относить также то время, в течение которого уже
существующая трещина не растет. Второй этап характеризуется
ростом наиболее опасной трещины; размер этой трещины велик
сравнительно с размером зерна, поэтому при исследовании ско-
скорости роста трещины на этом этапе можно пренебречь неодно-
неоднородностью материала и считать его однородным и изотропным
(период роста трещины). В инкубационном периоде трещина
обычно развивается с постоянным взаимодействием берегов как
трещина сдвига (полоса пластичности), во втором периоде
взаимодействием берегов можно пренебречь (на полуцикле рас-
растяжения), а трещина обычно ведет себя как трещина нормаль-
нормального разрыва.
В дальнейшем рассматривается лишь второй период, однако
предлагаемый подход легко переносится также на случай вну:
тризеренных (или межзеренных) микротрещин; при этом,соог;
ветствующие физические постоянные (например, предел текуче-
текучести или энергия диссипации), естественно, принимают другие
значения, отвечающие материалу внутри зерна (или между
зерен).
За последние 15 лет значительное и все возрастающее вни-
внимание уделяется изучению докритического роста искусственно
созданных трещин нормального разрыва под действием цикли-
циклических нагрузок. Согласно общефункциональному методу, ско-
скорость роста усталостной трещины представляет собой некоторый
функционал по времени от коэффициента интенсивности напря-
напряжений в рассматриваемой точке контура трещины, если только
выполняется условие тонкой структуры. В простейшем случае,
при обычных дополнительных предположениях, функционал вы-
вырождается в функцию:
,x,Klmln). F.1)
Здесь п — число циклов, dl/dn — скорость роста трещины, Кг max
и Kifain — наибольшее и наименьшее значения коэффициента ин-
интенсивности напряжений за цикл. Поскольку п очень велико, а
приращение длины трещины за один цикл весьма мало, с / и п
можно обращаться как с непрерывными переменными.
Результат F.1) в явном виде впервые был сформулирован
в работе Пэриса, Гомеса и Андерсона [138], а затем получил осно-
основательное экспериментальное подтверждение в работе Доналд-
сона и Андерсона [139]. Мак-Ивили и Иллг [140] еще раньше при-
пришли к эквивалентным выводам в рамках подхода Нейбера. От-
Отметим также работы Халта [141] и Мак-Клинтока [142], в которых
Si]
ВВЕДЕНИЕ
309
была сделана попытка применить точный упруго-пластический
анализ к изучению роста усталостных трещин продольного
сдвига.
Из множества опытных доказательств корреляции F.1), по-
появившихся за последнее десятилетие [72- ш], приведем лишь два
примера, о которых сообщает-
сообщается в статье [72].
Свенсон испытывал на цик-
циклическое растяжение пластин-
пластинки из алюминиевого сплава с
центральной сквозной трещи-
трещиной, причем максимальная на-
нагрузка за цикл с ростом трещи-
трещины изменялась так, чтобы все
время оставалось постоянным
W гл sft Щ
Длина трещины * В,5Ц см
Рис. ПО.
5,0
или среднее напряжение в сече-
нии-нетто или коэффициент ин-
интенсивности Напряжений ftlmax
(величина К\-атх равнялась ну-
нулю). При этом в случае
Ki max = const скорость роста трещины оказалась не зависящей
от длины трещины (рис. 110'), а в случае постоянного среднего
50
\го
ю
. • =
¦ И
о
t ¦ t-
-
• У
•
10
-7
1O'S 10'* 10'*
dl/dn x z$fi им/цикл
Рис. 111.
напряжения в сечении-нетто скорость изменялась с увеличением
длины трещины.
На рис. 111 приводятся результаты экспериментов по росту
усталостной трещины в пластине из алюминиевого сплава
Зю рост усталостных трещин [гл. vi
7075-Т6 при нагружении пластины односторонним растяжением
на бесконечности или сосредоточенными силами, приложенными
к берегам трещины. В обоих случаях скорость роста трещины хо-
хорошо коррелирует с коэффициентом интенсивности напряжений
Ках (в ЭТИХ опытах значение Kmin было близко к нулю).
В 1965 г. Пэрис предложил эмпирическую формулу [63]
dl/dn = G0(Klm,,-KlmlnL F.2)
(Go — постоянная материала), дающую хорошее описание мно-
многих экспериментальных данных для разнообразных материалов
при не очень высоких нагрузках. Интересно толкование этого
закона, данное Джонсоном и Пэрисом [72] тремя годами позже;
«Тот факт, что такой простой закон может описать данные для
разных материалов, резко отличных по микроструктуре, любо-
любопытен сам по себе! Вероятно, механизм, управляющий ростом
трещины, для всех этих материалов одинаков и не зависит от
особенностей микроструктуры».
Излагаемая в этой главе теория, предложенная в работе [60],
подтверждает эту догадку. В простейшем случае она приводит
к зависимости
= _р + 1п 2 2 F.3)
dn \ Кс Кс —Arain /
(Р — постоянная материала), достаточно хорошо согласующейся
с опытом.
§ 2. Подрастание трещины при монотонном нагружении
Согласно'концепции Кс, трещина в упругом теле начинает ра-
расти только после того, как коэффициент интенсивности напряже-
напряжений на контуре трещины достигает величины вязкости разруше-
разрушения, причем в процессе квазистатического роста выполняется ра-
равенство Ki = Kic- В рамках этой концепции внешняя среда
может изменить лишь величину вязкости разрушения. Ясно, что
концепция Кс не может объяснить докритического развития
трещин.
Рассмотрим некоторую произвольно взятую точку О контура
трещины; будем считать, что тонкая структура в окрестности
этой точки подвергается монотонному нагружению, вполне опи-
описываемому коэффициентом интенсивности напряжений Къ Бес-
Бесконечно малое приращение длины трещины dl может зависеть
только от соответствующего приращения dKi, приращения вре-
времени dt, от мгновенных значений К\, t и предыстории развития
трещины. Согласно общефункциональному подходу, искомая за-
зависимость без потери общности может быть записана так:
F.4)
§2) ПОДРАСТАНИЕ ПРИ МОНОТОННОМ НАГРУЖЕНИИ 311
Здесь ф1. и фг — функционалы по времени, которые, помимо Кь
могут зависеть также от температуры, параметров внешней сре-
среды, концентрации отдельных компонентов среды и т. п. Первое
слагаемое в правой части F.4) характеризует мгновенную реак-
реакцию системы на внешнее возмущение (изменение Kj), а второе
характеризует последействие. Первое из них объясняется конеч-
конечными пластическими (необратимыми) деформациями самого
конца трещины, на расстояниях порядка радиуса кривизны кон-
конца; поэтому мгновенное приращение длины трещины имеет по-
порядок раскрытия трещины в ее конце. Второе слагаемое объяс-
объясняется действием разнообразных физических и химических про-
процессов в конце трещины (диффузия и массообмен, химические
реакции, фазовые переходы и т. п.), приводящих к локальным
разрывам видоизмененного материала с ухудшенными прочност-
прочностными свойствами. Эти процессы могут быть весьма неожиданной
природы, так как протекают в условиях максимально разрых-
разрыхленной внешней нагрузкой структуры материала на свежей по-
поверхности; эти условия практически невозможно воспроизвести
в опыте с большими кусками металла и на значительной пло-
площади.
В дальнейшем эти слагаемые рассматриваются отдельно.
1. Влияние пластичности. Пренебрежем вначале временными
эффектами. При этом в правой части формулы F.4) второе сла-
слагаемое обратится в нуль. Рассматриваемое тело будем считать
идеальным упруго-пластическим (os — предел текучести на рас-
растяжение) .
В предполагаемых условиях существования тонкой структуры
размер пластической области d вблизи конца трещины может за-
зависеть только от Кь <*s, Е и v.
Анализ размерностей дает
Здесь ai — некоторая безразмер-
безразмерная функция. Если пластические
свойства тела описываются не- Рис. [12.
сколькими константами размер-
размерности напряжения, то функция а\ будет зависеть также от отно-
отношения этих констант. Это замечание относится ко всем возни-
возникающим в дальнейшем безразмерным функциям.
При монотонно возрастающей внешней нагрузке коэффи-
коэффициент интенсивности напряжений Ki будет также монотонно воз-
возрастать в окрестности каждой точки контура трещины и, в
частности, вблизи рассматриваемой точки О (рис. 112). Предпо-
Предполагается, что в начале нагружения напряжения в теле отсутство-
отсутствовали. С ростом Ki трещина, вообще говоря, также будет расти.
312 РОСТ УСТАЛОСТНЫХ ТРЕЩИН [ГЛ. VI
Обозначим через у* диссипацию энергии вследствие роста тре-
трещины, приходящуюся на единицу площади вновь образующейся
поверхности. Приращение длины трещины А/, очевидно, может
зависеть лишь от Къ os, v, v* и Е. Анализ размерностей дает
Здесь Ф — некоторая безразмерная функция.
Составим уравнение энергии (см. рис. 111). При приращении
длины трещины на бесконечно малую величину Ы полная дисси-
пирующаяся энергия 2^*6/, очевидно, складывается из двух сла-
слагаемых:
2y,8l = 8At + 6Ap. F.7)
Слагаемое 6At равно по величине высвобождающейся упру-
упругой энергии; оно соответствует тому, что в процессе увеличения
длины трещины на 81 коэффициент интенсивности напряжений
(а следовательно, и d согласно F.5)) оставался неизменным.
Величина 8At может зависеть только от Къ Е, as, 81, v. На осно-
основании анализа размерностей получаем
f-fi/. F.8)
Заметим, что средняя величина интенсивности пластических
деформаций в пластической области зависит лишь от oJE й v,
но не зависит от Ki, так как в рассматриваемой задаче нет ха-
характерного линейного размера. Поэтому формула F.8) может
быть получена также при помощи F.5) из тех соображений, что
6At представляет собой необратимую работу пластических де-
деформаций вследствие смещения пластической области как жест-
жесткого целого в направлении роста трещины (см. рис. 112).
Второе слагаемое 8АР представляет собой необратимую ра-
работу пластических деформаций, вызванную увеличением пласти-
пластической области в процессе нагружения и не связанную с ростом
трещины; оно соответствует тому, что в процессе увеличения ко-
коэффициента интенсивности напряжений на fi/Ci длина трещины
оставалась неизменной (см. рис. 112). Величина 8АР равна
IDpbS, где / — интенсивность касательных напряжений, 8$—
приращение объема пластической области (приходящегося на
единицу толщины в направлении нормали к плоскости рис. 112),
Dp — среднее значение интенсивности пластических деформаций
в 65. Так как / ~ as, 8S ^ rfSrf, Dp ~ as/?, то при помощи F.4)
можно найти
R
F.9)
ill ПОДРАСТАНИЕ ПРИ МОНОТОННОМ НАГРУЖЕНИИ
Здесь «з — некоторая -безразмерная функция. (Учитывая, что ве-
величина 8АР может зависеть только от as, Ki, S/Ci, ? и v, формулу
F.9) легко получить также из анализа размерностей.)
Окончательно получаем следующее уравнение энергии:
Уравнение F.10) должно быть справедливым, в частности,
для идеально-упругого тела; при этом второй член в правой ча-
части обращается в нуль. В этом предельном случае величина у*
совпадает с интенсивностью эиергостока у, а величину аг можно
найти при помощи D.43):
11/2 (плоское напряженное состояние),
уA — v2) (плоская деформация).
Уравнение F.10) можно записать в виде, напоминающем
формулировку закона течения упрочняющегося упруго-пласти-.
ческого тела:
Сравнивая эту формулу с общей зависимостью F.4), нахо-
находим фь
Согласно уравнению F.12), величина¦ .Ki монотонно растет
при возрастании/ и асимптотически стремится к значению Кь,
если только Kie ограничено. Асимптотически, когда К\ = Kic,
реализуется энергетическая концепция квазихрупкого разруше-
разрушения, принадлежащая Ирвину и Оровану.
Введем следующее допущение: величина у» является констан-
константой материала (при одинаковых внешних условиях и темпера-
температуре) . Это предложение будем называть концепцией v«- -®но
представляет собой обобщение концепции Ирвина — Орована
на случай нестационарного развития трещины.
Концепция y* является ^логически простейшей возможностью,
позволяющей последовательно и непротиворечиво построить тео-
теорию роста трещин при циклическом нагружении. Полученные на
ее основе результаты хорошо согласуются с многочисленными
опытными данными (см. далее § 4). Разумеется, в самом общем
случае величина y* зависит от приращения трещины А/ и от на-
начальных условий (например, от раскрытия начальной трещинг
РОСТ УСТАЛОСТНЫХ ТРЕЩИМ
(ГЛ. VI
и способа ее образования). Однако сравнение с опытом показы-
показывает, что эти аргументы являются второстепенными и зависи-
зависимостью от них величины у* можно пренебречь.
Так как в предельном случае стационарного режима у* = Y»
то это равенство согласно концепции у* останется справедливым
и в случае нестационарного режима. Поэтому всюду в дальней-
дальнейшем звездочка у у опускается, так как у» равна константе ква-
квазихрупкого разрушения у.
С учетом концепции у» можно проинтегрировать дифферен-
дифференциальное уравнение F.12) и найти
(*,-0при / = /о). F.14)
Кривая F.14) в безразмерных переменных
А/. = —о—, К = —
F.15)
изображена на рис. 113 сплошной линией.
Условие F.14) играет роль дополнительного граничного ус-
условия на контуре трещины в упруго-пластическом теле; опреде-
определив из упругого анализа напряжений функцию Xi = Ki{p, I),
где р — параметр внешнего нагруже-
ния, можно затем при помощи F.14)
найти зависимость / от р в каждой
конкретной задаче.
Как видно из рис. 113, в упруго-
пластических телах рост трещин про-
происходит также при значениях коэффи-
коэффициента интенсивности напряжений,
меньших Kic, условие Ki = Kic выпол-
выполняется асимптотически при Д/^>1,
когда перестает сказываться влияние
начальных условий (практически уже
при Д/* > 2 трещина во всяком упру*
го-пластическом теле начинает вести
себя как идеально-хрупкая согласно
рис. 113).
Если при I = h будет Ki = /Сю ф 0, то вместо F.14), оче-
очевидно, получится такое соотношение:
2ofs L Alc AIc— AI0J
Кривые этого семейства получаются из кривой рис. 113 сдви-
сдвигом вдоль оси абсцисс.
Рис. 113.
§ 2] ПОДРАСТАНИЕ ПРИ МОНОТОННОМ НАГРУЖЕНИИ 315
Зависимость Ki от приращения трещины А/ = I — /о будем
называть диаграммой разрушения*). Диаграмма Кг— А/ по
своему физическому смыслу аналогична диаграмме о — е и со-
согласно F.6) может быть найдена непосредственно из экспери-
эксперимента, без привлечения каких-либо дополнительных физических
концепций. Однако практически это можно осуществить' лишь
для сквозных трещин в тонких пластинах, когда подрастание
трещины достаточно велико; в условиях плоской деформации А/
так мало, что его весьма трудно измерить в обычных условиях
макроопыта. .
Концепция y* достаточно хорошо описывает плавный рост
трещин в упруго-пластических телах. Однако существует эффект
второго порядка — явление скачкообразного роста трещин в не-
некоторых упруго-пластических материалах, который не может
быть объяснен в рамках этой концепции. Это явление соответ-
соответствует наличию горба на диаграмме Ki—А/ (на рис. 113 обо-
обозначен пунктирной линией). В случае сквозных трещин в пласти-
пластинах физической причиной такого горба является неоднородность
пластических деформаций вблизи конца трещины («pop-in»);
это доказано экспериментально (см., например, [35]). В слу-
случае плоской деформации горб может быть объяснен структур-
структурными микронеоднородностями материала, а также неоднознач-
неоднозначной зависимостью скорости пластических деформаций от скоро-
скорости нагружения, т. е. от dKi/dt.
2. Устойчивость роста трещин при монотонном нагружении.
Обозначим через р параметр внешней нагрузки, а через / —
параметр длины трещины, являющийся некоторой функцией от
р. Пусть с увеличением р внешняя нагрузка возрастает, а с уве-
увеличением I трещина растет. Тогда условие параметрической ус-
устойчивости роста трещины будет иметь вид
dp/dl>0. F.16)
(При перемене знака в F.16) получается условие неустойчиво-
неустойчивости.) Так как функция Ki—Ki(p,l) определена из упругого ана-
анализа напряжений, то формула F.14) дает в неявном виде зави-
зависимость р от /. Дифференцируя ее по / и используя F.16), полу-
получаем следующее условие устойчивости:
F.17)
Условие неустойчивости получается переменой знака в F.17).
Неравенство F.17) позволяет на основании упругого анализа
*) Это удачное название впервые встречается в работах Я. Б. Фридмана
с сотрудниками,
316 РОСТ УСТАЛОСТНЫХ ТРЕЩИН [ГЛ. VI
задачи заранее выделить на плоскости (р, /) области устойчи-
устойчивого и неустойчивого роста трещин.
В частности, при /Ci = Ku отсюда получается условие устой-
устойчивости роста хрупкой трещины
dKi/дКО. . F.18)
Из сравнения формул F.18) и F.17) вытекают следующие
выводы. Если хрупкая трещина устойчива, то соответствующая
трещина в упруго-пластическом теле будет также устойчива.
В случае же неустойчивой хрупкой трещины, которая вообще не
развивается до достижения предельного состояния, поведение
соответствующей начальной трещины в упруго-пластическом
теле будет совершенно другим, а именно, вначале ее развитие
всегда устойчиво, и только после достижения достаточно высо-
высокого уровня нагрузок наступает неустойчивое состояние. Из
условия F.17) вытекает, что момент наступления неустойчивого
режима нельзя охарактеризовать посредством одного только ко-
коэффициента интенсивности напряжений, и в критическое усло-
условие обязательно должны войти также неинвариантные перемен-
переменные I или р.
Следовательно, критический коэффициент интенсивности на-
напряжений, определяющий начало нестабильности трещины, стро-
строго говоря, согласно концепции y*> зависит также от / или р. По-
Поэтому для упруго-пластического тела подход, основанный на
предположении о постоянстве указанного коэффициента незави^
симо от длины трещины, и энергетическая концепция приводят
к различным разрушающим нагрузкам. Однако это различие не-
несущественно, если докритическое подрастание трещины мало по
сравнению с ее длиной (см. рис. 113). В большинстве случаев
это условие хорошо выполняется.
3. Тонкая пластина. В лредыдущих формулах фигурируют по-
постоянные ад, аг, аз,. о&4, которые,остались неопределенными; для
их отыскания можло использовать опыты или точный расчет на
основе решения упруго-пластической задачи. Последний особен-
особенно легко провести в рамках схемы Дагдейла, близкой к реально-
реальности в случае сквозных трещин в тонких пластинах. Предыдущая
теория, очевидно, годится также для сквозных трещин;' более
того, она вообще не зависит от деталей механизма разрушения
в конце трещины. В дальнейшем будем обозначать Kic через Кс,
чтобы отразить зависимость этой постоянной от толщины пла-
пластины.
В постановке Дагдейла комплексные упругие потенциалы
тонкой структуры конца трещины .даются формулами D.97).
При их помощи, используя общие представления плоской задачи
C.9), нетрудно найти смещение v противоположных берегов
пластической линии разрыва у = 0, 0 < х < d (сама щель
$2] ПОДРАСТАНИЕ ПРИ МОНОТОННОМ НАГРУЖЕНИИ
расположена вдоль отрицательной полуоси х):
' V~ ±~пЁ
317
F.19)
Сравнивая с F.5), находим, что ai = я/8.
Удельная энергия диссипации у* при помощи F.19) нахо-
находится следующим образом:
Y,== lim
^j[v (x — Д/, Ki + АКО - v (х, КО) dx } =
о J -
d
dK, Г да
4a?
nE
/ff
12O2SE dl
F.20)
F.21)
Сравнивая F.20) с F.10), находим
a2=l/2, а3 = яа,/A2?)
Таким образом, в рамках схемы Дагдейла и концепции у*
для упруго-пластического тела при монотонном нагружении по-
получаются следующие результаты:
условие в конце растущей тре-
трещины
/ — /о —
,о„2 ^2 "г П ^2 ^2
«а^ L ас лс — л,0 J
(/Ci = /Cio при / = /о),
условие неустойчивости
ю-
F.22)
t t Г
¦ж
It
Рис. П4.
(dK1jdp>0, K\ =
Подчеркнем, что эти результаты от- _ „ _.
носятся только к достаточно острым | » Т/
начальным трещинам, раскрытие
конца которых гораздо меньше пре-
предельного. Рассмотрим пример.
4. Трещина в полосе. Пусть в тонкой пластине, занимающей
в плоскости ху полосу |л'| < Л, —оо < у < +оо, имеется сквоз-
сквозная поперечная трещина длины 21, свободная от нагрузок
(рис. 114). Полоса подвергается монотонно возрастающей растя-
растягивающей нагрузке р, действующей на бесконечности,
318 РОСТ УСТАЛОСТНЫХ ТРЕЩИН [ГЛ. VI
В этом случае коэффициент интенсивности напряжений равен
(см. Приложение I, формула (П. 26))
К\ = р /jt/sec[jt//B/i)]. F.23)
Согласно F.19), длина пластических отрезков на продолже-
продолжении трещины определяется формулой
'~^~5- <6-24)
При помощи общих критериев F.22) в данном случае полу-
получаются такие результаты:
зависимость длины трещины от нагрузки
где
область неустойчивости на плоскости (/„, р.)
^ (i|-)] F.26)
(при /, = /,„ р, = 0),
На рис. 116 изображена типичная кривая р* = р*(/«) при
Я= 1 и /*о = О,1, построенная на основе уравнения F.25) (кри-
(кривая I). Там же приведена нейтральная кривая II, разделяющая
области устойчивости и неустойчивости, и кривая III, отвечаю-
отвечающая идеально-хрупкому разрушению.
5. Временные эффекты. Пренебрежем теперь влиянием пла-
пластичности, т. е. мгновенной реакцией системы на изменение Кь
При этом в правой части общего уравнения F.4) останется лишь
второй член, характеризующий последействие. Очевидно, это бу-
будет иметь место при достаточно плавном изменении коэффи-
коэффициента интенсивности напряжений.
Рост трещины при постоянных нагрузках можно представить
себе как результат некоторой химической реакции, происходя-
происходящей в конце трещины. Возможны различные случаи: а) в реак-
реакции (разложения) участвуют лишь компоненты рассматривае-
рассматриваемого твердого тела, а внешняя среда играет роль катализатора
(или ингибитора) или же совсем не влияет на скорость реакции,
б) в реакции участвуют компоненты среды и материала, в) сме-
смешанный случай.
Всюду в дальнейшем принимается гипотеза квазистационар-
квазистационарности, которая приводит к тому, что скорость роста трещины
должна быть некоторой функцией коэффициента интенсивности
ПОДРАСТАНИЕ ПРИ МОНОТОННОМ НАГРУЖЕНИИ
319
напряжений (см. формулу F.3)). Следует подчеркнуть, что эта
гипотеза справедлива только в том случае, когда активный ком-
компонент внешней среды (являющийся катализатором или реаген-
реагентом) присутствует в конце трещины в избытке. В противном
случае скорость химической реакции в конце трещины будет ли-
лимитироваться концентрацией этого компонента; это приведет к
зависимости скорости
роста трещины от ско- Р*
рости транспортировки
компонента в конец
трещины, определяе-
определяемой процессом диффу-
диффузии в самой трещине,
и, в конечном счете, к
зависимости dl/dt от
длины трещины. При
этом гипотеза о локаль-
локальном характере процес-
процесса разрушения в конце
трещины (а эта гипо-
гипотеза лежит в основе
вывода формул F.1) —
F.4)) становится не-
неверной. В закономер-
закономерностях типа F.4) при-
придется учитывать также
неинвариантные пере-
переменные, зависящие от
геометрии конкретного
тела.
Практические гра-
границы применимости ги-
гипотезы квазистационарности устанавливаются, как обычно, или
экспериментально или же на основе более общей теории, учи-
учитывающей диффузионно-обменные процессы в трещине и при-
приводящей к некоторой зависимости dl/dt от /.
В рамках гипотезы квазистационарности рассмотрим пока
только случай а), когда внешняя среда играет роль катализа-
катализатора или же вообще не участвует в реакции (т. е. химический со-
состав среды в устье трещины и вдали от тела один и тот же).
В' этом случае в реакции участвуют только компоненты твер-
твердого тела; скорость реакции (пропорциональная скорости роста
трещины), согласно закону Аррениуса, прямо пропорциональна
ехрг U(a)/{RT)], где U — энергия активации реакции, завися-
зависящая от напряжения о реагирующего структурного элемента
в конце трещины, Т — абсолютная температура тела. Теперь
О
Рис. 115.
РОСТ УСТАЛОСТНЫХ Т№ЩШ
(ГлГу!
аппроксимируем функцию U(e) линейной зависимостью ?/(а)*=
xfUxs — atd, что достаточно хорошо согласуется^ опытом, и
учти*, что напряжение о пропорционально Ki Vd (CM-> напри-
например, формулу F.5)), где d — характерный размер структурного
элемента, который можно считать константой материала, следуя
идее Нейбера.
Таким образом, в рассматриваемом случае получается сле-
следующая зависимость:
(v0 ~ ехр [—
R ~ 2 калЦград • моль)).
F.26)
Здесь vo и ? — некоторые постоянные материала. Следовательно,
функция / в F.1) (или фг в F.4)), отвечающая данному меха-
механизму локального разрушения, записывает-
записывается в виде
F.27)
it.
Ряс. И 6.
Формулу F.26) можно получить также
из общих соображений теории необратимых
флуктуации следующим образом. Разрыв
структурного элемента размером d в кон-
конце трещины можно представлять себе как
некоторую гигантскую тепловую флуктуа-
флуктуацию продолжительности ю. Вероятность
этой флуктуации равна ехр[—U(o)l(RT)].
Следовательно, разрыв структурного эле-
элемента с вероятностью единица произойдет
за время т, равное тоехр[— U(a)/(RT)].
Представляя себе развитие трещины как
последовательный разрыв структурных эле-
элементов на ее пути, получаем скороеть роста
трещины в виде
dl/dt -»djx = (й/т0) ехр IU (a)/(RT)]. F.28)
Дальнейший ход рассуждений аналогичен предыдущему.
Рассмотрим пример. Пусть упругое тело, занимающее полосу
О < у < h, —оо < (х, z) < оо и имеющее краевую полуэллип-
полуэллиптическую трещину при z = 0, подвергается на бесконечности
растяжению напряжением аг = р (рис. 116). Границы тела и
берега щели будем считать свободными от нагрузок. Будем счи-
считать также, что коэффициент интенсивности напряжений одина-
одинаков вдоль фронта щели; этому условию отвечает отношение по-
полуосей эллипса bja fa 1,5. В процессе докритичёского роста фор-
форма такой трещины (т. е. отношение Ь/а) будет оставаться неиз-
неизменной, а коэффициент интенсивности напряжений с ошибкой
§2] ПОДРАСТАНИЕ ПРИ МОНОТОННОМ НАГРУЖЁМИИ . 32i
примерно 10% равен (см. Приложение I, формула (П. 106))
Д", = 1,47руХ F.29)
(Здесь предполагается, что в критическом состоянии, когда на
фронте трещины достигается значение Къ равное Kic, выпол-
выполняется условие bfh .<; 0,4.) , '
Из элементарных соображений ясно, что начальная трещина
произвольной формы в плане с течением времени должна приоб-
приобретать такую «равнопрочную» форму с равномерным распреде-
распределением Ki вдоль контура щели. Это вытекает из того, что ско-
скорость dljdt монотонно увеличивается с ростом Ki (см., например,
формулу F.26)).. Определение трещин «равнопрочной» формы
представляет собой одну из важных задач обратной теории уп-
упругости.
Согласно F.26) и F.29), имеем следующее уравнение в точке
@, Ь, 0) контура трещины:
dbfdt = v0 exp [ 1 ,Щр V~b[(RT)] (b = b0 при t = 0). F.30)
Решение этого уравнения имеет следующий вид:
Vot = 2АГ2/Г2[A + Я,р Vh)ехр(-Л,/» VK) -
). F.31)
На основании F.31) долговечность полосы с трещиной не
превышает величины т, равной
. (А = 2 A + %хР VbdlWftfy, я2 = Ai Vh = ищ V^liRTj),
F.32)
При b >• b0, что обычно выполняется в опытах, долговечность
очень близка к т.
Формула F.32) впервые была найдена эмпирически
А. П. Александровым и С. Н. Журковым [145]; последующие экс-
эксперименты показали ее применимость для многих металлов и
полимеров [76].
6. Инкубационный период. Пусть в теле, подвергнутом ста-
стационарной нагрузке, имеется, надрез или щель и пусть по истече-
истечении некоторого времени т от начала нагружения щель начинает
развиваться. Согласно общефункциональному методу и гипо-
гипотезе локальности разрушения, это время (инкубационный пе-
период) выражается формулой вида
- F.33)
11 Г. П. Черепанов
322 РОСТ .УСТАЛОСТНЫХ ТРЕЩИН (ПК VI
Если внешняя среда играет роль катализатора или же в реак-
реакции не участвует, то на основании соображений, совершенно ана-
аналогичных предыдущим, можно найти
т = ВехрТО(ЯГ)], F.34)
где В и ?— некоторые постоянные материала.
7. Общий случай монотонного нагружения. Допустим те-
теперь, что в процессе монотонного нагружения и соответствую-
соответствующего монотонного подрастания трещины в правой части фор-
формулы F.4) существенны оба слагаемых. Будем считать, что ме-
механизм конечной пластической деформации конца трещины
действует независимо от термоактивационного химического
механизма последовательного обрыва связей в конце трещины.
Тогда на основании формул F.12) и F.26) находим
рт+oo {dim > )
dt Kc^Ki at . F.35)
§ 3. Рост усталостных трещии (теория)
Явление роста трещин в твердых телах при циклических и
случайных нагрузках объясняется монотонным подрастанием
трещины в течение каждого цикла нагружения и необратимо-
необратимостью роста трещин. На основе общей зависимости F.35) най-
найдем скорость роста трещин при нестационарном нагружении,
когда нагрузки представляют собой периодические или случай-
случайные функции времени.
1. Скорость роста трещины. Рассмотрим вначале квазиста-
тическое развитие трещин в упруго-пластических телах _ при
циклическом нагружении, пренебрегая временными эффектами.
При выполнении условия тонкой структуры скорость распро-
распространения конца трещины dl/dn может зависеть только от наи-
наибольшего и наименьшего значений коэффициента интенсивно-
интенсивности напряжений в течение одного цикла /Cimax и /Cimm, от числа
циклов п, от энергии у*, диссипируемой при образовании еди-
единицы поверхности трещины, и от постоянных материала E,as, v.
Анализ размерностей дает
^I ^) F.36)
K,
,max
Здесь Ч*1 — некоторая безразмерная функция. Эта функция мо-
может быть определена на основе соображений, совершенно ана-
аналогичных изложенным в предыдущем параграфе (где предпола-
Щ РОСТ УСТАЛОСТНЫХ ТРЕЩИН (ТЕОРИЯ) 323
далось, что в начале нагружения деформации и напряжения
отсутствуют).
Изучим теперь процесс роста конца трещины при увеличе-
увеличении Ki от /Cimin до ^Cimax, предполагая, что начальному состоя-
состоянию при /Ci = /Cimin предшествовал некоторый процесс дефор-
йирования, в результате которого в теле возникли остаточные
Напряжения и деформации. Нетрудно видеть, что все рассужде-
рассуждения, при помощи которых были получены формулы F.5),
1F.8) — F.10) и F.12), непосредственно переносятся и на рас-
рассматриваемый случай; однако величины он, «2 и аз теперь за-
зависят от истории деформирования, "предшествовавшего началь-
начальному МОМеНТу TjCi = Кщя- "
Обозначим через <т0 параметр, характеризующий величину
начальных напряжений, ответственных за предысторию нагру-
нагружения и развития трещины (a0<os). Как и при выводе F.5)
И F.-12), получим ' •
(Здесь постоянные материала <т„, Е, Кс и v, вообще говоря, за-
зависят от предварительного деформирования (разрыхления ма-
материала). Однако в дальнейшем для простоты такой зависи-
зависимостью пренебрегаем,)
Зависимостью функций а\ и,а4 от аргумента gq/Е можно пре-
пренебречь. Это следует из того, что <т0 ^ а„, а величина <т„/? для
всех конструкционных материалов мала (~0,01). Кроме того,
из предыдущего параграфа известно, что при <то—*0 существуют
конечные пределы непрерывных функций ai {oo/E, aJE, \) и
04((То/?, Gs/E, v). Эти пределы'соответствуют монотонному на-
гружению при равных нулю начальных напряжениях. Таким
образом, допущение о том, что влиянием остаточных напряже-
напряжений на рост трещины можно пренебречь, оправдывается воз-
возможностью замены, непрерывной функции f(e) на f@), так как
|@) конечно, а е мало.
Обозначим через р следующую постоянную материала:
§-. F.38)
В том случае, когда^ применима схема Дагдейла (так что
пластическая область представляет собой прямолинейный отре-
|qk на продолжении трещины), постоянную Р можно найти при
|омощи F.21):
11*
324 РОСТ УСТАЛОСТНЫХ ТРЕЩИН • [ГЛ. VI
Эта формула полезна в случае весьма тонких пластин, когда
докритическое подрастание трещины при монотонном- нагруже-
нии до разрушения значительно.
Весьма естественным является допущение о том, что при
разгрузке от Кш&х до /Cimin длина трещины не изменяется. Ис-
Используя это допущение и интегрируя F.37) от Kimn до Кшах,
находим приращение длины трещины А/ в течение одного
цикла:
/ к2 —к2 к? — К2\
A/ el 'шах "м min 1 1 •S'e "Ч max I /с <>n\
А/ = — Р -г -+1пТг—Т2 ]• F-39)
Переходя к непрерывным переменным, получаем искомую
скорость роста трещины
р( + igfH, F>40)
an \ Кс Кс — Кх min /
Если Kimia < 0, то в этой формуле следует полагать /Cimm = О,
так как при-сжатии трещина закрывается (за исключением,
быть может, малой области вблизи конца трещины) и концен-
концентрация напряжений в конце трещины исчезает.
В окончательное выражение F.40), кроме постоянной Кс,
воиша только одна новая постоянная р, которая должна опре-
определяться из опыта. Величина {$ имеет размерность длины и ха-
характеризует прирост длины трещины при циклическом нагруже-
нии (по порядку величины она равна приросту длины трещины
при возрастании Кг от нуля до Кс, см., например, формулу
F.14) и рис. ИЗ). Величина Кс близка к вязкости разрушения
Kic, за исключением, возможно, тех случаев, когда разрушение
происходит в течение небольшого числа циклов, или же случая
сквозных трещин в тонких пластинах (в последнем случае Кс
зависит от толщины пластины).
Следует подчеркнуть, что при усталостном разрушении ус-
условие тонкой структуры нарушается гораздо реже, чем при раз-
разрушении от однократного нагружения, поэтому усталостное раз-
разрушение твердых тел, как правило, бывает хрупким, без замет-
заметных пластических деформаций. Это объясняется более низким
уровнем напряжений при усталостном разрушении (а, тем са-
самым, меньшей величиной Ал) и сильной зависимостью размера
пластической области d вблизи конца трещины от Кг (согласно
F.5), d~ Kb-
Уравнение F.40) играет роль дополнительного граничного
услЪвия на контуре трещины в упруго-пластическом теле при
циклическом нагружении; зависимость / от параметра внеш-
внешнего нагружения /?шах и /?min в каждой конкретной задаче на-
S si
РОСТ УСТАЛОСТНЫХ ТРЕЩИН (ТЕОРИЯ)
325
ходится после подстановки коэффициентов интенсивности на-
напряжений /Cimax и /Cimin в дифференциальное уравнение F.40)
и его решения относительно 1{п). Это уравнение, очевидно, поз-
позволяет рассмотреть также тот случай, когда рлах и ршш изме-
изменяются от цикла к циклу. Условие устойчивости развития уста-
усталостной трещины, очевидно, по-прежнему дается неравенством
F.17).
Рис 117.
Если р и /Се известны, то из диаграммы на рис. 117, иллю-
иллюстрирующей формулу F.40), легко определить dl/dn.
В ряде случаев удобно пользоваться разложением правой
части F.40) в ряд Тейлора
I max
min
,
min
Ч max
4min
F.41)
326 РОСТ УСТАЛОСТНЫХ ТРЕЩИН [ГЛ..у1 '¦
Изложенный подход легко обобщается также на (принципиаль-
(принципиально возможный) случай зависимости величины у* от Kimax и
Ktmln-
2. Нераспространяющиёся усталостные трещины. Экспери-
Эксперименты показывают [И6-149], что иногда при .достаточно малых
нагрузках усталостные трещины не распространяются, незави-
независимо от Числа, циклов нагружения. Это явление, по-видимому,
связано с микрЪнеоднородностыо и зернистостью реальных ма-
материалов, а "также со свойством приспособляемости упруго-пла-
стлческого материала*).
Согласно общефункциональному методу условие нераспро-
нераспространения конца усталостной трещины за бесконечно большое
число циклов нагружения имеет следующий вид:
^Cl max ^ Kyf (Ki mlJKl max)> F.42)-
если только выполняется условие тонкой структуры. Здесь f —
некоторая безразмерная функция (будем считать, что f@) = 1),
Ky — постоянная материала @ sg /Су ¦< Кс) ¦ Если Ky ФО, то у
материала, очевидно, будет отличный от нуля предел усталости
(при Ky'= Кс предел усталости будет, равен временному со-
сопротивлению). Функция / и критический коэффициент интен-
интенсивности Ky должны определяться экспериментально.
Заметим, что согласно концепции у* рост усталостных тре-
трещин происходит при любых /Ci (см. F.40)). Фактическое по-
построение зависимостей максимальной нагрузки за цикл от числа
циклов до разрушения показывает, что при достаточно низких
нагрузках,скорость трещины очень мала, а число циклов, тре-
требуемое для разрушения тела, становится нереально большим.
Поэтому, если дополнительно к концепции y* ввести ограниче-
ограничение на возможные скорости роста усталостных трещин
f при /CImIn = 0, F.43)
то при помощи F.40) можно jafiTH величину Ky:
Kr = 2(v№)K*e. F.44)
Здесь Vf — некоторая структурная постоянная материала. При
выводе F.44) было учтено, что К? существенно меньше Кс,
поэтому можно воспользоваться первым членом разложения в
F.41).
Большую экспериментальную работу по определению усло-
условия нераспространения трещины проделал Фрост [147> И9]. В его
опытах трещина выходила на свободную прямолинейную гра-
границу полубесконечной пластины перпендикулярно к границе;
на бесконечности пластина подвергалась однородному цикли-
- *) На роль последнего фактора внимание автора обратил В. В. Болотин.
fc$ РОСТ УСТАЛОСТНЫХ ТРЕЩИН .(ТЙОРИЯ) 32?
ческому растяжению напряжениями р при постоянном коэффи-
коэффициенте асимметрии цикла. Им было найдено следующее эмпи-
эмпирическое условие нераспространения трещины: р\лу1<С* где
С — постоянная материала, / — длина трещины. Так как Ki=
•в 1,12р ]Лт/,то в данном случае строгое условие нераспростра-
нераспространения трещины, согласно F.42), запишется б виде
PLJ < 0.254/С2, (если *, mIn = 0). F.45)
Совпадение с данными Фроста cлeдyet признать удовлетво-
удовлетворительным, особенна если принять во внимание, что в опытах
Фроста при малых I усуювие тонкой структуры выполнялось
юГлохо.
3. Чистое последействие. Рассмотрим теперь квазистатиче*
лкое развитие трещин в упруго-пластических телах при цикли-
циклическом нагружении, пренебрегая влиянием первого слагаемого
в правой части формулы F.35) на монотонное подрастание
трещины в течение каждого цикла. В данном случае скорость
роста конца трещины будет существенно зависеть от частоты
Яагружения © и от формы цикла.
Для определенности примем следующее выражение дли
внешней нагрузки;
F.46)
Здесь рт — среднее значение нагрузки, ра — ее амплитуда. Тог*
да коэффициент интенсивности напряжений примет вид
Ki =*= 4i (Pm+ Pa
1 tv _l к \ n «f x IK К \ ^А1^
Рт ==~2^r~'Al шах Т Al mlij> Pa ==s ^T~ \ AI max Al m!n/>
Здесь т)i -^ некоторая функция, зависящая от длины трещины и
От геометрии тела, но не зависящая от нагрузки.
Ограничимся наиболее простым и часто встречающимся слу-
случаем, когда форма и размеры растущей трещины характери-
характеризуются одним параметром /; в этом случае х\\ будет функцией /,
*»е зависящей явно от времени. Подставляя F.47) в F.35) (где
учитывается лишь второе слагаемое), находим
Л/Л =»oexp[&T|i(Pm +Pa sin»/)] (при * = 0 7 = /0). F.48)
Так как / в течение одного цикла изменяется мало, урав-
Еие F.48) можно интегрировать от нуля до Т (где Т — пе-
д циклического нагружения), считая t)i постоянным в тече-
этого времени. Таким образом, получаем приращение
328 РОСТ УСТАЛОСТНЫХ ТРЕЩИН . [ГЛ. VI
длины трещины А/ в течение одного цикла
г
Ы = v0 J ехр [Атц {рт + ра sin ©01 dt =
о
= Bя/ш) оо ехр [(А/2) (*, max + *i mm)] /о [(Л/2) (ff, тах - tfi тш)]
(Г = 2я/со). F.49)
Здесь /o(jc) равна &o(ix)—функции Бесселя нулевого порядка
от мнимого аргумента [1Б0]. Напомним, что /0(л:) является чет-
четной, монотонно возрастающей (при х > 0) функцией, причем
при *->0
) +Ш +
при х->оа F.50)
Ё[ )]
Таким образом, учет одного последействия согласно F.49)
приводит к следующей зависимости для скорости роста уста-
усталостной трещины при синусоидальной нагрузке:
dlldn = Bя/«>) г»0 ехр [(А/2) (tf, max + tf i mm)] A. i
F.51)
(л — число циклов).
4. Общий случай циклического нагружения. В самом общем
случае, когда слагаемые, входящие в выражение F.35), имеют
одинаковый порядок, а механизм пластичности и временные
эффекты действуют независимо, из F.40) и F.51) получаем
следующую формулу для скорости роста трещины:
г2 if2 тг2 ь> 2
^1 шах I min i i *с ¦ I max i [
+ Bя/й>) Оо ехр [(А/2) (К, тах + Кх mta)] /0 [(A/2) (Kl max ~ Kl mln)]
F.52)
(/ = /o при л = 0). .
Это уравнение играет роль дополнительного граничного ус-
условия на контуре трещины. В него входят четыре опытных кон-
константы: /Сс, р, v0, А. Все они слабо зависят от температуры, од-
однако на интервале хладноломкости Кс, v0 и А, согласно F.26),
зависят от. абсолютной температуры так:
(R « 2 калЦград ¦ моль)). F.53)
S 3] РОСТ УСТАЛОСТНЫХ ТРЕЩИН (ТЕОРИЯ) 329
Здесь ?,, Vqo и Uo — некоторые постоянные (?/о — энергия акти-
активации).
Следовательно, решение общего уравнения F.52) в каждом
конкретном случае позволяет учесть влияние следующих фак-
факторов на усталостную прочность тела (перечисляются в порядке
их важности для -металлов и сплавов): а) амплитуда и сред-
среднее значение нагрузки за цикл, б) структура тела и, прежде
всего, расположение и величина начального дефекта /о, в) гео-
геометрия тела, г) частота цикла, д) температура тела*). В слу-
случае сквозных трещин в тонких пластинах можно учесть также
толщину пластины h, Подставляя вместо Кс известную из опыта
функцию Kc(h) (см., например, формулу D.149)).
5. Малоцикловое усталостное разрушение. До сих пор всюду
предполагалось выполнение условия тонкой структуры. При
достаточно высоком уровне напряжений это условие может
иногда не выполняться, и разрушение может происходить за
сравнительно небольшое число циклов нагружения. Концепция
Y» позволяет рассмотреть и этот случай, исходя из точного ре-
решения упруго-пластической задачи. Наиболее просто произво-
производятся расчеты в рамках схемы Дагдейла: вначале составляется
уравнение энергии (см., например, уравнение E.194) для ана-
аналога задачи Гриффитса), которое при условии y* = const и для
любой заданной нагрузки будет дифференциальным уравнением
первого порядка относительно длины трещины, затем это урав-
уравнение численно интегрируется в предположении dl/dt^O. В ра-
работах [т<152] таким способом были рассмотрены случаи одной
трещины и. периодической системы трещин (вдоль одной и той
же прямой), находящихся в однородном поле циклического рас-
растяжения.
6. Случайные нагрузки. Рассмотрим развитие фронта трещи-
трещины под действием случайных пульсаций нагрузки. Учтем вна-
вначале только пластичность, пренебрегая временными эффектами.
Выделим поизвольную пульсацию нагрузки, в течение которой
коэффициент интенсивности напряжений в рассматриваемой
точке фронта трещины изменяется от Kimm до Kimax- Уровень
напряжений считаем невысоким, т. е. К\ •< Кс, так что формулу
F.37) можно применять в таком виде:
(l F.54)
Интегрируя F.54), находим приращение".длины трещины А/
в течение рассматриваемой пульсации нагрузки
ax ^ Ki min)lKi F.55)
J. *) Если влияние внешней среды сказывается лишь в изменении кон-
ргант Кс, Р, »о и ?. такую среду будем называть инактивной. Инактивные
внешние среды не изменяют механизмов, лежащих в основе вывода фор*
1»улы F.52),
330 POCT усталостных трещин [гл. V»
Осредним это выражение за некоторое время А*, содержа-
содержащее достаточно большое количество пульсаций, но гораздо
меньшее общего времени роста трещины:
<A/>=-P</C!max-/Cim.n>/B/d). F.56)
Пусть средний период пульсации за это же время равен (т).
Тогда скорость роста усталостной трещины запишется в виде
Kl). F.57)
Формула F.57) имеет весьма общий характер. Допустим, что
имеется только один случайно изменяющийся параметр нагруз-
нагрузки размерности напряжения; обозначим его через р. Тогда
имеет место равенство
<*f шах ~ *\ m.n> « Л <Р^ах ~ Pmin>> F-58)
где ртах и ртш — н-аибольшее и наименьшее значения р в тече-
течение одной пульсации, ц—: детерминированная функция, не за-
зависящая от р. Средние величины (т) и (pmax — P^in) можно
определять непосредственно по реализации случайного про-
процесса.
Пусть внешняя нагрузка представляет собой квазистацио-
квазистационарный случайный процесс. Под квазистационарным ' случай-
случайным процессом понимается процесс, удовлетворяющий следую-
следующему условию: для любого момента времени t существует та-
такой интервал (/ — At, t-\-At) „(где At <C t), внутри которого слу-
случайный процесс можно считать стационарным. Напомним, что
все числовые характеристики стационардого случайного про-
процесса— математическое ожидание, дисперсия и т. д. — не зави-
зависят от времени. Кроме того, на основании эргодической гипо-
гипотезы для стационарного процесса средние по времени и по
множеству реализаций будут совпадать. В данном случае ртах
и pmin будут "представлять собой внутри каждого интервала At
случайные величины с некоторыми функциями распределения;
параметры, входящие в эти функции, для квазистационарных
процессов будут слабо зависеть от времени.
Общая формула F.57) годится для произвольногр квазиста-
квазистационарного процесса, схематически изображенного на рис. 118.
ДЛЯ ПРОСТОТЫ будем «ЧИТаТЬ, ЧТО ВеЛИЧИНЫ Ртах И Pmin ПОДЧИ-
ПОДЧИНЯЮТСЯ нормальным законам с плотностями вероятности /(ртах)
(Ртах - (Ртах)J
(Pmln —
121
F.59)
POCt УСТАЛОСТНЫХ ,Т1>Е1ЦЙН (ТЕОРИЯ)
331
Здесь crmax и ffmin — дисперсии случайных величин ртах и pmlt
соответственно. Имеем
F-60)
(Ртах - Pmin) = (Ршах) -
При помощи F.57) и F.58) отсюда находим окончательное
выражение, наиболее удобное для практических расчетов:
it=Тюк*[<Ртах>4"<PminL
+ 3<1ax-3<inj (PmIn>0). F.61)
В простейшем случае, когда случайная функция p{i) пред-
представляет СОбоЙ «беЛЫЙ Шум», а ВеЛИЧИНЫ (pmln) =.—(Ртах).
ffmin = tfmax не зависят от времени, формула F.61) принимает вид
Здесь правая часть не зависит от / и t. Во многих случаях ве-
величина т) представляет собой некоторую функцию /, определяе-
определяемую из упругого анализа и не зависящую явно от t (см.
?(*)
<Ртх>
Рис. 118.
Приложение I). В таких случаях решение дифференциального
уравнения F.62) находится сразу в виде '
i
'-T.Jw' F>63)
постоянная Л дается формулой
А ~ tmf [<Pmax>4+6с4ах (Pmax>2
832 Poet Усталостных трещин Р"Л. vi
рассмотрим теперь влияние чистого последействия, прене-
пренебрегая первым слагаемым в формуле F.35). Для определен-
определенности будем считать, что внешняя нагрузка представляет собой
следующую случайную функцию времени:
F.64)
Здесь рт, Ра и со — независимые случайные величины с задан-
заданными функциями распределения.
Выделим одну произвольную пульсацию нагрузки; в течение
этой пульсации за время Т == 2я/со подрастание трещины опи-
описывается следующей закономерностью:
dl/dt = оо-ехр (Я/Cj) = v0 ехр [Хг\ (рп + ра sin at)]. F.65)
Отсюда находим приращение длины трещины Д/ в течение од-
одной пульсации:
М = Tv0 ехр [(Я/2) п (ртах + praln)] • /0 [(Я/2) r\ (ртах - рт1п)]
/ \ {0.00)
(Ртах = Рт + Ра. Pmln = Ртах ~ Ра)-
Осредняя это выражение по времени и используя независимость
случайных величин ртах, Ршп и Т, находим скорость роста
усталостной трещины
dl/dt = {М)/(Т) =
= v0 (ехр [(Я/2) т] (ртах + pmln)] /0 [(Я/2) ц (ртах — рт1п)]>
(Ртт>0). ' F.67)
В случае стационарного случайного процесса функции рас-
распределения случайных величин рШах и pmin не зависят от t;
если к тому же функция ц (I) не зависит явно от времени, ре-
решение дифференциального уравнения F.67) имеет вид
dl F.68)
где
F(l) = (ехр [(Я/2) л (/) (ртах + рт1п)] • /0 [(Я/2) ц (I) (ртах - рга1„)]).
Если пластичность и временные эффекты соразмерны и про-
проявляются независимо, то скорость роста усталостной трещиЛы
при случайных нагрузках находится суперпозицией формул
F.61) и F.67). Если pmin < 0, то в этих формулах, как и в
случае циклического нагружения, следует положить pmin = 0.
Замечание. Как легко заметить, теория, изложенная в
§§ 2 и 3 этой главы и основанная на представлении о тонкой
структуре, целиком переносится на случай тел, которые являют-
$ fl СРАВНЕНИЕ ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ 333
-ся линейно-вязкоупругими, за исключением малой области
вблизи фронта трещины. Для таких тел коэффициент, интен-
интенсивности напряжений Кг сохраняет свой смысл, а упругие кон-
константы заменяются соответствующими постоянными мгновенной
деформации (см. § 7 гл. V).
§ 4. Сравнение теории с опытными данными
Несмотря на большое число экспериментов по усталостной
прочности, изучением роста фиксированных усталостных тре-
трещин занимаются лишь последние 15 лет. Первые исследователи
(Орован, Хэд, Фрост, Вейбулл) еще не понимали локального
характера закономерностей разрушения в конце трещины и
потому формулировали свои результаты в неинвариантных пе-
переменных (скорость роста трещины в зависимости от напряже-
напряжения). После работ Ирвина это стало очевидным. Ниже рассмат-
рассматриваются только те опыты, результаты которых обработаны в
инвариантных переменных. Все они выполнены в последнее де-
десятилетие.
Следует подчеркнуть, что в корректно поставленном опыте
по развитию усталостных трещин должны фиксироваться пара-
параметры внешней среды, так как она сама может служить причи-
причиной докритического роста трещин.
1. Опытная проверка концепции у*- Факторами, определяю-
определяющими скорость роста усталостной трещины в металлах, яв-
являются амплитуда и среднее значение нагрузки, а также ге-
геометрия тела и, в частности, длина трещины. Все эти факторы
влияют на коэффициент интенсивности напряжений Кг и через
него — на скорость трещины. Теоретическая зависимость, выве-
выведенная из концепции у* в пренебрежении временными эффек-
эффектами, дана формулой F.40), которая и подлежит эксперимен-
экспериментальной проверке. На рис. 119 приведены построенные согласно
этой фор муле кривые KmSlx(Kc==f(dt/dn) для различных значе-
значений р при Кып = 0. Эта система кривых используется в даль-
дальнейшем для эффективного определения |} методом наложения.
Большой экспериментальный материал по развитию уста-
усталостных трещин в сплавах алюминия 2024-ТЗ и 7075-Тб содер-
содержится в работе Доналдсона и Андерсона [139]. На рис. 120 пред-
представлены результаты обработки их опытов. Пунктирная кривая
проведена по осредненным экспериментальным данным для
сплава 7075-Тб, пунктирные отрезки показывают примерный
разброс точек, отвечающий К == const для каждой серии испы-
испытаний и соответствующий доверительной вероятности 0,98.
Штрих-пунктирная кривая относится к сплаву 2024-ТЗ, разброс
Точек показан штрих-пунктирными отрезками при той же
доверительной вероятности. На . том же рисунке сплошными
334
PQGT УСТАЛОСТНЫХ ТРЕЩИН
[ГЛ. VI
"max I "с
№
<1
///А//////
Qfi
1O
» til I lit I fit t 111 I It
ИГ* I0-2 W1 t 2 46fff
dl/dn, им/цикл
Рис. 119.
1,0
?
0,6
44
7
^, д
. t
— ;л
i fit
еория
Л.7075-Т6
1Ш-ТЗ
' Ml
f
l_ ! 11
f
1 111
/
-
Ю
-¦ lfl-3
10'' lO'4 10- /2 4.
I2 4 10
dl/dntM/n/mi
Рис. 120,
$ 4] .. СРАВНЕНИЕ ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ 335
линиями. нанесены соответствующие кривые, построенные до
формуле F.40) при следующих значениях постоянных:
для сплава 7075-Т6
* 0 = 0,15 мм, /С, = 140
для сплава 2024-ТЗ
0 = 0,10 мм, Кс = НО к
В указанных опытах отношение /(min/Kmax изменялось, глав-
главным' образом, от 0,2 до 0. При построении теоретических кри-
кривых этим отношением пренебрегали, т. е. считали, что Ктт = 0.
На основании разложения F.41) такое пренебрежение вполне
допустимо. Как видно, теоретическая зависимость в пределах
указанной доверительной вероятности хорошо согласуется с
опытом.
Следует подчеркнуть, что в такого рода зависимостях
сравнение кривых должно проводиться по быстро меняющейся
переменной, т. е. в данном случае по dl/dn.
В работах Пэриса [63] и Пирсона [153] было изучено большое
число сплавов алюминия, молибдена, титана и др. Свои резуль-
результаты, в отличие от предыдущих авторов, они представили в
виде некоторых эмлирических зависимостей. Пэрйс предложил
зависимость
, й?//й?П == Go (/Crnax — /*CmlnL (Go ~ ПОСТОЯННая),
Которая хорошо аппроксимирует экспериментальные точки для
сплавов алюминия 2024-ТЗ и 7075-Т6 в интервалах скорости от
10~5 до 10~2 мм/цикл. Для тех же материалов Пирсон предла-
предлагает аппроксимацию вида
щ интервала скоростей 10~4—10~3 мм/цикл. - '
^ Формула Пэриса при Kwin = 0 может быть получена из тео-
теоретической зависимости. F.41), если в разложении отбросить
члены высших порядков малости:
d//rf« = p/CLx/B^). F.69)
При Ктах/Кс ^ 0,5 ошибка не превышает 15%. Заметим, что
разброс опытных данных по развитию усталостных, трещин
обычно намного превышает эту цифру.
В дальнейшем формула Пэриса была проверена на многих
Других материалах р]; она оказалась справедливой при не
очень высоком уровне напряжений, если /*Сдиц/^Сщах достаточ-
достаточно мало. . _
336
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
[ГЛ. VI
Еще точнее оказалась эмпирическая формула, предложен-
предложенная Форманом [154]:
\\~R)
= Ктах ~Xmln)- F.70)
Формула Формана содержит три постоянные: С3, п, /Сс*).
На рис. 121 приведены результаты сравнения формулы Фор-
Формана с зависимостью F.40) при С3 = 2,13-10'13, п = 3,21 в
t,o
0,8
0,6
0,8
Теорий
По ср-ле Формана
n-3,Zl
. 1 mi
*
,/
1 III
Кс-№я1
R-0',5
i i 11
-/мм3"
\ in
п-г
, мм/цикл
Рис. 121.
уравнении F.70) и при р = 0,02 лж в уравнении F.40). Вели-
Величины Кс н R равны 140 кГ/мл?ь и 0,5 соответственно. Эти циф-
цифры взяты нз работы [155]. Максимальное относительное .отклоне-
.отклонение этих кривых не превышает 20—30%.
Когда коэффициент интенсивности напряжений близок к
значению Кс, наблюдается существенное отклонение экспери-
экспериментальных данных от формулы Пэриса; это объясняется воз-
возрастанием роли отброшенных членов в разложении F.41).
К. Карман и Кэтлин {156] провели эксперименты на образцах
из мартенсито-стареющих. сталей 250 и 300. На рис. 122 круж-
*) Чем большее количество неопределенных постоянных входит в эмпи-
эмпирическую или теоретическую зависимость, тем меньше ее практическая польза.
Это объясняется тем, что каждая новая константа для своего определения
требует увеличения объема экспериментальной работы, тем более, значитель-
значительного, чем больше разброс данных. С этой точки зрения едва ли не един-
единственное преимущестио рациональной аналитической теории над чисто' эмпи-
эмпирическим подходом состоит в разумном ограничении числа новых констант,
СРАВНЕНИЕ ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ
337
ками изображены экспериментальные данные для стали 250,
треугольниками — для стали 300. Сплошные, линии отвечают
1,0,
0,8
D,B
Ofi
о,г
о
1
—— Теория
t. Сталь 800
" Стиль 250
h Hr"f>7/} яГ/м
i i 11
,*7WлГ/м
Л
1 111
i in
/
1.1.11
\
1 III
1 III
10
s
W"
10''
Рис. 122.
/О'1
1 г 4бю
dl/dn,mlnm
кривым, построенным по формуле F.40) при следующих зна-
значениях постоянных:
для стали 250
Р = 0,2 мм, /Се = 710 кГ/мм*!2,
для стали 300
К. 5|нг [157] исследовал некоторые сплавы алюминия и стали.
Его экспериментальные результаты приведены на рис. 123
(кружки относятся к алюминиевому сплаву 2024-Т6, треуголь-
треугольники—к стали 310, черные точки —к стали 301). Теоретиче-
Теоретические кривые построены при следующих значениях постоянных:
для сплава 2024-Тб
0 = 0,34 мм, Кс= 192 кГ/мм3!2,
для стали 301
Р = 4,00 мм, /(с = 700 кГ/mmW,
для стали 310
Р=1,0лш, Кс — 463 кГ/мм?!2.
На основе этих данных Янг предложил эмпирическую фор-
формулу
338
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
[ГЛ. VJ
с показателями степени п = 5 для сплава алюминия и п — 7
для сталей.
i,0
0,8
US
— Теория
а Сталь 310
• Сталь 301
о
А
/ - 0,34м
У
/ /
кГ/мм3/г
р = 1,6 им, Ке-№ кГ/ми3/г
р - 4,0ии, Кй~700 нГ/мм3/г
.. ' 1,4
\ III
1 1 11
//
У-/
1 I II
t 1 И
Г* Ю~3 Ю'в
Рис. 123.
10'
г г 4 б ш
dlldn,mjcim
0,8
. Теория'
•Ал.7079-Т5
•Ал.5456Ч№1/
t
¦ Ал.7079-Т6:
Ал5456-Н3г1:. Кс'1ВЗнГ/ш!
II I I Y\ I I 1
w! w* . ю'! ю'г ю-' . / г ьбю
dl/dn, км/цикл
Рис. 124.
• На рис. 124 и 125 представлены результаты опытов Кларка
[158] (пунктирные и штрих-пунктирные кривые). Эмпирические
формулы Кларка содержат четыре постоянных и неудобщ
Ipl СРАВНЕНИЕ ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ " 339
дл$г аналитического применения, так как дают лома'
ную линию; на тех же рисунках приведены сплошные кривые,
1,0
0,8
0,5
JA
Ц2
О
Сталь НР^-'
СтшШ-Ш
i ] \\
S
! Ill
А
щ
t
г
Сталь НР-Н-25: К„-
Сталь Ni-Mo-V: HB-
1 1 М
i in
ШнГ/мм®
lullH/fMM
\ III
n-S
IT3'
ю-1
1 2 *6
dl/dn, мм/цш
Рис. 125.
подсчитанные по формуле F.40) при следующих значениях по-
постоянных: .
сплав 7079-Т6 (пунктирная линия, рис. 124)
р = 0,01 мм, /Сг== 125 кГ/мм3Р,
сплав 5456-Н321 (штрих-пунктирная линия, рис. 124)
; р == 0,03 мм, Кс = 163 кГ/мм3*2,
сталь НР-9-14-25 (пунктирная линия, рис. 125)
р = 0,02 мм, К, = 460 кГ/мм3®,
сталь Ni—Mo—V (штрих-пунктирная линия, рис. 125) <
р = 0,03 мм, Кс = 520 кГ/мм3!2.
Если учесть обычный разброс данных, согласие теории с ап-
Яроксимациями Кларка следует признать удовлетворительным.
На основе своих экспериментов со еплавами Д16Т, Д16Т-1,
Ю-95 В. М. Маркочев *) предложил следующую эмпирическую
Цависимость:
•) Диссертация и автореферат: В. М. Маркочев, «Методика и исследова-
6 кинетики макроразрушения листовых материалов при однократном и по-
эрном нагружении», Москва, ВИАМ, 1966. '
340
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
[ГЛ. VI"
На рис. 126 сравниваются аппроксимации Маркочева и теорети-
теоретические кривые при следующих значениях постоянных:
сплав Д16Т
$ = 0,17 мм, Кс = 200 кГ/мм3К
еплав Д16Т-1
0 = 0,32 мм, /Сс = 200 кГ/мм3®,
сплав В-95
Р = 0,6 мм, /Сс = 200 кГ/mmW. -.
Опыты, проведенные С. Я. Яремой и Е. Л. Харишем [159],
также достаточно хорошо согласуются с формулой F.40).
0,8
0,6
т
42
Теория
АЛ.Д16Т
-Х-Х-АЛ.ДЮГ-/
Сталь В-95
i ill
А
А
\ II'
S
/i
м
V
i til
1 f t I
-
1 111
Iff* КГ
10
.-г
Ю'1
f 2J6M
Рис. 126.
Проведенный анализ Экспериментальных данных подтвер-
подтверждает практическую пригодность теории усталостных трещин,
основанной на концепции у*.
2. Влияние частоты нагружеиия и некоторых инактивных
внешних сред. В последние годы многие авторы (Уэй [160],
Че Ю-ли, Талда, Уэй [161], Хартман и Шийве [162], Дальберг [163]
и др.) провели обширные экспериментальные исследования по
изучению влияния частоты нагружения, внешней среды, темпе-
температуры и других факторов на рост усталостных трещин. Статья
Уэя [143] содержит обзор около 50 работ, посвященных этим воп-
вопросам.
Наиболее обстоятельна работа Хартмана и Шийве [162], кото-
которые исследовали влияние среды и частоты нагружения на рост
СРАВНЕНИЕ ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ
341
центральных сквозных трещин в тонких пластинках из алюми-
алюминиевых сплавов 2024-ТЗ и 7075-Т6. Толщина пластин была 1 мм,
а ширина — 70 мм. Начальная длина трещины составляла
~3 мм. Темпертура испытания была постоянной (комнатной).
Величина Кс была следующей: _
для сплава 2024-ТЗ
149 кГ/мм3'2,
для сплава 7075-Т6
/Сс=146 кГ/мм3'2.
На рис. 127—132 приводятся результаты сравнения теоретик
ческой зависимости F.52), учитывающей влияние упомянутых
факторов, с экспериментальны*
й , 1,11.11 i.i i I, ми данными Хартмана и Ший-
ве для различных амплитуд
цикла, частоты и разных сред.
На этих рисунках (за исключе-
исключением рис. 129) показаны экспе-
экспериментальные средние кривые
¦ ЗОиЫин
- IWhIhuiP^
- З/Юн/нт- ^
А
¦¦-/.
#
г
t
34
щ
л\
щ
мТ
Щ„1ыт
а
ц
iMiih
-
в 10 20
Рис. 127.
'ff-JZ
- Шц/мт'¦<
z JWn/mff-Ш
1
¦ж)
Ко
в 10
Ш 100
Рис 128.
по Хартману и Шийве; соответствующие теоретические кривые
обозначены цифрой / — при частоте 3 400 цикл/мин (рис. 127—
132, кроме рис. 129), цифрой 2 — при частоте 30 цикл/мин
(рис. 127), цифрой 2 — при частоте 24 цикл/мин (рис. 128).
Остальные теоретические кривые, соответствующие другим зна-
значениям частоты нагружения, обнаруживают практически полное
совпадение с экспериментальцыми кривыми и не изображены
на рисунках. >
При» сопоставлении опыта с теорией используются следующие
i координаты:
~^ [A — R)KC
РОСТ УСТАЛОСТНЫХ ТрЕЩИЙ
[гл.
го
W 60 100 ,
АН,нГ-мм'3/г
гоо
Я
6
тж
Щ
\ /
/
1
1/
i
*
Ваз
И
п
г
(
б 10
W 60 100
Рис. 129.
Рис. .130.
ю го
w w too
АК,кГ-ии'1'г
100
60
% го
I ю
f 4
^ иг
§006
--¦¦
- -
¦-¦Кислороду
Вошух^
Apeoi
п
/?
н~
Г"
И
б @
20
40 60 100
АК.кГмм'®
Рис. 131.
Рис. 132.
I 41 СРАВНЕНИЕ'ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ 343
Это позволяет одновременно сравнить опытные данные с наибо-
наиболее универсальной эмпирической формулой Формана F.70), не"
учитывающей лишь влияния частоты и температуры.
Были найдены следующие значения постоянных:
сплав 2024-ТЗ, сухой воздух (рис. 127)
р=»5- 10~3 мм, X — 0,04 мм3'2\кГ, о0=» 0,15 мм/мин-,
сплав 2024-ТЗ, влажный воздух (рис. 128)
р= И . 10~3 мм, X = 0,04 ммш1кГ, о0 —0,19 мм/мин;
сплав 2024-ТЗ, аргон (рис. 132)
Р = 9 • 10~3 мм, А, = 0№~мм3121кГ, vQ = 0,22 мм/мин;
сплав 2024-ТЗ, кислород (рис. 132)
р = 5 • 10~3 мм, X = 0,04 ммзр1кГ, v0 = 0,45 мм/мищ
сплав 7075-Т6, сухой воздух (рис. 129)
р = 1 . ю~2 мм, X — 0,15 ммш1кГ, vQ = 0,009 мм/мищ
" \
сплав 7075-Тб, влажный воздух (рис. 130) >
Р = б,5 • 10~2 мм, X = 0,15 мм312/кГ, vQ = 0,046 мм/мин.
Рис. 127 демонстрирует влияние частоты нагружения для ~
сплава 2024-ТЗ в сухом воздухе. Как видно, уменьшение частоты
от 3400 цикл/мин до 30 цикл/мин при А/С « 30 кГ/мм3'* ведет
К увеличению1 скорости роста трещины приблизительно в десять
раз. При А/С — 30 кГ/мм*1* наличие влаги в воздухе в десять раз
увеличивает скорость роста трещины при частоте 3400 цикл/мин
И почти не сказывается при частоте 30 цикл/мин (см. рис. 128).
у Рис. 129 демонстрирует влияние амплитуды цикла Sa на ско-
скорость роста усталостной трещины в сплаве 7075-Т6 при частоте
3400 цикл/мин (сухой воздух). В данном случае зависимость
;{6.52) приводит к результатам, совпадающим с формулой Фор-
Формана (в остальных случаях, как видно из рисунков, формула
Формана не годится). Оказывается, что при низком уровне на-
Яряжений в формуле F.52) преобладает первый член, т. е. при
росте трещины доминирует механизм пластичности, а при высо-
высоких напряжениях основным становится влияние последействия.
Ш диапазоне
0,25/Ср
344
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
1ГЛ. VI
оба слагаемых в формуле F.52) почти равны, т. е. оба меха-
механизма— одного шэрядка.
В сплаве 7075-Т6 влага также приблизительно в десять раз
увеличивает скорость роста усталостных трещин (рис. 130). При
АК > 30 кГ/мм*1' внешняя среда, по-видимому, изменяет меха-
механизм разрушения в конце трещины, лежащий в основе вывода
формулы F.52).
На рис. 133 приведены аналогичные экспериментальные дан-
данные по росту усталостных трещин в титановом сплаве Ti—8А1—
80 т
I
40
7 Ti-6AlHMo-W
1 го°о
Г D
-
Г
У
о
о °
. о
а 30 цикл/сен
1 ¦,'
10'" 10~5 W* -W3
dt/dn-
Рис. 133.
— IMo—IV, испытывавшемся в соленой воде при двух различ-
различных частотах нагружения [ш].
Сплошные линии построены по формуле F.52) при следую-
следующих значениях постоянных:
л-4
3/2
р = 5 • 10 мм, Кс = 280 кГ/мм
v0 « 10~7 мм/сек, А = 0,215 ммт\кГ.
Влияние толщины пластины на скорость роста сквозных уста-
усталостных трещин гораздо менее существенно, чем на Кс- Эффект
начинает обычно сказываться при гораздо меньших толщинах.
Это объясняется сравнительно невысоким уровнем напряжений,
вследствие чего большая часть пластической зоны на фронте
трещины находится в условиях плоской деформации. На рис. 134
приводятся типичные зависимости скорости роста усталостной
трещины от /(max Для пластин различной толщины (алю-
(алюминиевый сплав типа AlCuMg в аргоне и дистиллированной
воде) ['«].
СРАВНЕНИЕ ТЕОРИИ С ОПЫТНЫМИ ДАННЫМИ
345
Явление порогового коэффициента интенсивности напряже-
напряжений Ky демонстрируется на рис. 135, где приведены данные Лин-
Линдера для алюминиевого сплава 2024-ТЗ [72]. Величина KyIKc
dl/dn * 2ifi мм/цикл
Рис. 134.
50
^10
D
¦ •¦ • • * •
.Ktitt''"''
у.
if*
.'.У
v :'•"•'¦'
• •
10
-ю
w
10'1
/О-*
dl/dn
Рис. 135.
оказалась равной примерно 0,05 (ср. с рис. 111, где приводятся
данные для того же материала в другом диапазоне скоро-
скоростей) .
VetАлостны* +*>ёщйй * [гл. vt
§ 5. Некоторые конкретные задачи
Если наибольшее и наименьшее значения нагрузки за цикл
ртах и рт1л не зависят от времени, измеряемого числом циклов,
а форма и размеры трещины определяются одним параметром /,
то решение дифференциального уравнения F.1), описывающего
рост усталостных трещин, можно записать сразу в явном виде:
i
п= f ,,„ dlK •¦ F.71)
У ' (*I max- *I rain)
h
Здесь функцию f в общем случае можно брать в форме F.52);
если же частотные эффекты несущественны, можно использо-
использовать более простую формулу F.40).
Если в качестве верхнего предела интегрирования в F.71)
подставить критическое значение / = /», определяемое как наи-
наименьший корень уравнения •
/Climax (Ртах, О = Кс, , F.72)
то формула F.71) определит общее число циклов нагружения,
требующихся для разрушения конструкции*). Эта величина
представляет наибольший практический интерес; как видно, в
каждом конкретном случае она вполне определенным образом
зависит от параметров цикла ртах и /?min, от частоты со, от раз-
размера и формы начальной трещины, от конфигурации тела, от
температуры и от внешней среды, от характеристик материала
/Сс'Р, wo и Я (или I, см. формулу F.53)).
Заметим, что при наличии временных эффектов, согласно
F.35), трещина будет всегда неустойчива в классическом смыс-
смысле, т. е. при / -> оо будет I —*¦ оо, если только lim Ki > 0 при
*->-оо. Однако и в общем случае определение параметрической
устойчивости или неустойчивости по р и I имеет физический
смысл качественной характеристики реакции системы на мгно-
мгновенное изменение нагрузки (коэффициента p(t) в дифферен-
дифференциальном уравнении F.35)). Соответствующее условие устой-
устойчивости по отношению к мгновенным изменениям p(t), как легко
видеть, совпадаете F.17).
Рассмотрим некоторые наиболее типичные задачи о развитии
усталостных трещин.
1. Аналог задачи Гриффитса. Пусть прямолинейная сквоз-
, ная трещина длины 21 находится в неограниченной пластине,
растягиваемой на бесконечности одноосным "напряжением ау ==
*) Вообще говоря, момент потери устойчивости наступает несколько
раньше, однако в большинстве случаев это можно не учитывать.
#51
НЕКОТОРЫЕ КОНКРЕТНЫЕ ЗАДАЧИ
347
= р (рис. 136). Направление растяжения перпендикулярно ли-
линии трещины, берега которой свободны от нагрузок. В "этом слу-
чае коэффициент интенсивности напряжений равен Ki — р Ynl.
Представим себе, что нагрузка р является синусоидальной фуню-
цией времени и рш&х ^ Р ^ рты- Согласно F.52) скорость роста
трещины будет равной
Р«а-*>)/ +In[(i-a/)/(l-
+ Bф) v0 ехр [УТ(С + d)} • /о
- d)]. F.73)
где
^(/) =
Здесь
Йри /?mln < 0 следует считать Ь — d = 0. _
Подставляя Kimax и дК\ тлЛд1 = рт&х /я/B yi) в условие
F.17), находим критическую длину трещины /* в момент потери
устойчивости (по отношению к малым
мгновенным возмущениям Нагрузки)Т "
\-i
F.74)
Если ра <С 1, Т. е. постоянна^ р го-
гораздо меньше критической гриффитсовой
длины трещины 1/а, отвечающей идеаль-
ао-хрупкому разрыву, то критическая ве-
дичина /* будет раана 1/а.
¦ Число циклов до момента потери
устойчивости П] определяется из решения
уравнения F.73)
F.75)
t t.t-t
II \ \ I
Решение уравнения F.73) существует рИс 136.
ри 1о < / <Z сг1; соответствующие зна-
1ия п заключены в области 0 •< 秊< пс, где максимально
зможное число циклов пс определяется^ уравнением F.75),
1и в качестве верхнего предела интегрирования вместо /» под-
1вить а-1. При пс > п > tif трещина будет расти в неустойчи-
режиме, поэтому «/ в данном случае следует считать числом
нов до разрушения всей пластины. Функция 1 = 1(п) соглас-
F.73) монотонно возрастает от l = k до 1 = сг1 — 1(пс),
ричем /'(«с) = оо.
348
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
[ГЛ. VI
Приведем некоторые результаты .вычислений, проведенных
в пренебрежении временными эффектами (при этом в формулах
F.73) » F.75) можно положить у0 = 0, а рост трещины не зави-
зависит от формы цикла). Пусть, например,
т. е. начальная длина трещины в десять раз меньше ее критиче-
критического, гриффитеова значения, а наименьшая величина нагрузки
в течение цикла равна-нулю. Результаты численного расчета
уравнения F.73) для этого случая приведены ниже для несколь-
нескольких значений числа циклов:
фп
al
0
0,01
6,12
0.15
9,06
0.20
10,76
0,30
Ш1
0,40
13,80
0,50
14,20
0,60
14,45
0,70
14.61
0,80
14.70
0.90
14.75
1,00
Здесь
0,1
Л= J
al
Приведем также некоторые значения максимальной нагрузки
за цикл ртах в зависимости от числа циклов tij до разрушения:
л,
ар
0
9
0,232
8
0,528
7
0,920
6
1,462
5
2.266
4
3,586
3
6.18
2
13.79
1
28.8
0,5
147
0.1
1475
0.01
оо
0
Здесь
о,1
1
Кривые ртах = Ртах.(щ) называют кривыми Велера.
Величина разрушающей нагрузки р* при монотонном нагру-
жении для упруго-пластического материала будет в данном слу-
случае равна
P.^SKJV^ (а/о = 0,1. ар = 9).
Заметим, что в общем случае задачи Гриффитса разрушаю-
разрушающая нагрузка р# при монотонном нагружении находится из
«5 5]
НЕКОТОРЫЕ КОНКРЕТНЫЕ ЗАДАЧИ
349
уравнения F.74) при i» == 10; она оказывается равной
F.76)
При р -С /о_эта зависимость переходит в формулу Гриффитса
р, = KclV^h- (Напомним, что эти формулы справедливы только
при выполнении условия тонкой структуры.)
Известно, что результаты испытаний материалов на усталост-
усталостную прочность имеют ярко выраженный статистический харак-
характер. Это объясняется влиянием начального размера дефекта, ко-
который, очевидно, в значительной степени является случайной
структурной характеристикой материала. Таким образом, стати-
статистическая природа усталостной прочности аналогична статисти-
статистической природе хрупкой прочности.
2. Краевая трещина. Пусть на прямолинейную свободную
границу полупространства выходит прямолинейная трещина
длины I перпендикулярно к границе (рис. 137). Предполагаются
Н
Рта
Рис. 137.
выполненными условия плоской деформации или плоского на-
напряженного состояния.
Считается, что берега трещины свободны от нагрузок, а на
бесконечности приложены циклические напряжения р, действую-
действующие параллельно границе тела. В этом случае коэффициент ин-
интенсивности напряжений равен (см. Приложение I, формула
(П. 22)) _
Ki=\,\2pVnl F.77)
Как нетрудно заметить, все формулы и заключения, получен-
таые для предыдущей задачи, остаются в силе и в данном случае,
если всюду р заменить на 1,12р.
3. Трещина под действием сосредоточенной силы. Пусть
К противоположным берегам прямолинейной сквозной трещины
длины 21 в безграничной пластине приложены равные и противо-
850
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
[гл. VI
положно направленные сосредоточенные силы Р (рис 138).
Силы действуют в середине трещины перпендикулярно к ее по-
поверхности. На бесконечности напряжения отсутствуют. В этом
случае коэффициент интенсивности напряжении равен (см. При-
Приложение 1, формула (П. 3))
Ki^PlVnl. I F.78)
Пусть Р представляет собой синусоидальную функцию вре-
времени, причем Ртах ^ Р ^ 0. Согласно F.52), для скорости роста
усталостной трещины имеем
dl/dn = F(l),
где
[ ()] ^^(^) F.79)
Согласно условию F.17), рост трещины в данном Случае бу-
будет всегда устойчив по отношению к малым мгновенным измене-
изменениям нагрузки. Решение уравнения
Р\
F.79) можно представить в виде
Ртх
dl
a). (§.80)
Рис. 138.
-•j- При />/о функция F(l) с воз-
возрастанием / монотонно убывает,
. стремясь к некоторому положитель-
положительному пределу при Z->oo (при wo==O
этот предел равен нулю). Поэтому
решение I = 1(п) представляет со-
собой монотонно возрастающую функ-
функцию, причем при я-»-то I-+00.
В пренебрежении временными- эффектами, т. е. при Vo = 0,
длина трещины при больших п будет выражаться асимптотиче-
асимптотической формулой
/ = (C/2)ра2пI/3. F.81)
Приведем некоторые значения функции I = 1{п) при 1>0=0и
10 = а, вычисленные при помощи F.80):
: Ча
0
1
0,0465
1,1
0,132
1,2
0,628
1.5
2,461
2,0
11.65
3,0
31,50
4,0
119,0
6.0
НЕКОТОРЫЕ КОНфЕТНЪПЗ ЗАДАЧИ
351
Здесь
a/1
$п[а = J Г2[t -f In A — /)Г! d/.
4. Трещина в балке прямоугольного сечення. Пусть балка
прямоугольного поперечного сечения подвергается знакоперемен-
знакопеременному чистому изгибу моментом М, приходящимся на единицу
толщины балки (в направлении нормали к плоскости рис. 139),
так что Мтах ^ М ^ — Мшах. Пусть трещины длины I разви-
развиваются симметрично с краев полосы шириной L (предполагаются
выполненными условия плоской задачи теории упругости). Счи-
Считаем, что при сжатии трещина закрывается. В этом случае коэф-
коэффициент интенсивности напряжений равен/М.
(см. Приложение I, формула (П. 30))
*¦¦«=
i = 4,2Ш1.-3/2 V A - 1/L)-3 - A — t/Lf,
F.82)
.1,15-60 (Z/LJ при
1 при
0 < Z/L < 0,05,
0,05 < ЦL < t. '
Ограничимся случаем &о = 0. Согласно
F.52), скорость роста усталостной трещи-
трещины равна . .
-а%4 (//!)]},
F.83)
а=D,2JМ2тах/
И
Рис. 139.
Качественные особенности поведения трещины — те же, что
й в аналоге задачи Гриффитса: вначале трещина растет моно-
монотонно и устойчиво, а по истечении некоторого числа циклов до-
ётигается неустойчивое состояние и происходит быстрое динами-
динамическое развитие трещины (разрушение).
Критическая длина /* идеально-хрупкой трещины, опреде-
определяемая условием Кх = Кс, согласно F.82), является корнем
уравнения .
tfL F.84)
Приведем результат численного расчета для начальной тре--
1дины длины /0 = 0,01L. Считая для простоты критическую
352
Р06Т УСТАЛОСТНЫХ ТРЕЩИМ
[ГЛ. Vt
длину /* предельно возможной, находим зависимость числа цик-
циклов до разрушения п/ от максимальной нагрузки Мтах:
PV
0
0,05
2
0,06
5
0,08
¦7
0,11
8
0,15
9
0,25
9,5
0,36
Здесь
¦¦ J {аЯ2а(;
0,01
— %2ao.{x)\\~x dx,
Зависимость IJL от а дается уравнением F.84).
§ 6. Пример расчета на ресурс длительной прочности
при усталостном разрушении
Фрактографические исследования показывают, что неодно-
неоднородность конструкционных материалов, являющаяся практически
неизбежной, в процессе металлургической и технологической
обработки приводит к образованию трещин и дефектов, с кото-
которыми в дальнейшем конструкция вступает в эксплуатацию. Оча-
Очагом разрушения служат именно трещины и дефекты, медленно
растущие в процессе эксплуатации.
При достаточно больших размерах начальной трещины раз-
разрушение может произойти в течение нескольких циклов нагру-
жения или даже при первом же" нагружении. Если же размеры
начальной трещины ^достаточно малы, то конструкция выдержи-
выдерживает много циклов нагружения при значительных напряжениях,
прежде чем трещина вырастет до критических размеров и про-
произойдет окончательное разрушение. Поэтому задача определения
допустимых размеров исходных трещин и допустимого уровня
рабочих нагрузок при заданных условиях работы конструкции
(определение ресурса прочности) является очень важной при
проектировании конструкции.
Долговечность конструкции определяется размером началь-
ной трещины, скоростью докритического роста трещины, харак-
характером и величиной приложенных нагрузок, геометрией тела,
свойствами материала и внешней среды. Пользуясь изложен-
изложенными выше результатами, проведем иллюстративный расчет на
ресурс длительной прочности и долговечности типичного эле-
элемента конструкции, работающего в условиях растяжения. Вре-
Временными эффектами пренебрегаем.
РАСЧЁТ ЙА
ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
353
1. Описание элемента конструкции и нагрузок. Рассмотрим
элемент конструкции в виде бесконечной полосы
0<:У<Н, — оо.< (*, z)< оо,
рдверженной растяжению в направлении оси г (рис. 140).
На поверхность полосы выходит плоская несквозная трещина,
которая в плане представляет половину
эллипса с полуосями а и Ь. Практически
размеры элемента в плоскости xz долж-
должны быть не меньше 6а. Границы полосы
и берега трещины считаем свободными
Ртах
Чту
Рис. 140.
Рис. 141.
ИГ нагрузок. Величина растягивающего напряжения р опреде-
определяется из обычного бездефектного расчета конструкции в целом.
Коэффициент интенсивности напряжений на контуре трещи-
ны равен (см. Приложение I, формула (П. 104))
Г~г Ы2 - 0.48&/а + 0.13 B9/я)а (ft/a) C6/а -2—ЬЩ
nb = l-F/A)(l-0.75ft/a)
@<6/a< 1, 0 < b/h ^ 0,4).
Пусть конструкция в эксплуатационном режиме находится
йод действием циклических и малых случайных нагрузок. Тогда
напряжение р можно представить в виде с'уммы периодической
во времени функции и малых случайных пульсаций нагрузки
(рис. 141). В зависимости от конкретных условий работы опре-
определяющей может оказаться как первая, так и вторая составляю-
составляющая нагрузки, .поэтому целесообразно вначале рассмотреть их
отдельно.
2. О форме трещины. Трещины, встречающиеся в конструк-
конструкциях, подразделяются на несквозные поверхностные трещины,
внутренние подповерхностные и сквозные трещины. Наиболее
12 Г. П. Черепанов
3g4 Poet усталостных и>ещИй ifA. vt
опасными являются поверхностные и внутренние трещины, кото-
которые способны достичь критических размеров до прорастания че- .
рез всю толщину детали, и потому развиваются без сопутствую-
сопутствующих явлений (например, появления течи в сосудах хранения),
предупреждающих о разрушении.
Изучение конструкций, разрушившихся в процессе эксплуа- ,
тации, показывает, что если разрушение происходит до образо-
образования устойчивых сквозных трещин, то трещина в момент по-
потери устойчивости обычно имеет форму полуэллипса с осью,
расположенной на границе тела. Отношение полуосей Ь/а кри-
критической трещины часто бывает близко к 2/3.
Эти факты объясняются особенностями докритического роста
пространственных трещин. Скорость распространения фронта
трещины весьма быстро возрастает с увеличением локального
коэффициента интенсивности напряжений (см., например, фор-
формулу F.52)). Поэтому; если коэффициент интенсивности напря-
напряжений распределен неравномерно вдоль контура начальной тре-
трещины, то в процессе докритического развития вначале будут из-
изменяться лишь те участки контура, на которых коэффициент
интенсивности максимален. Изменение формы трещины вызовет
перераспределение коэффициента интенсивности напряжений
вдоль контура. Если процесс развития фронта трещины локаль-
локально устойчив в каждой точке фронта, то коэффициент интенсив-
интенсивности будет выравниваться, пока не станет одним и тем же для
всех точек фронта трещины. При дальнейшем устойчивом раз-
развитии трещины форма ее все время будет такой, чтобы вдоль
всего контура выполнялось условие /Ci = const.
•В целях упрощения нашей задачи предположим, что коэф-
коэффициент интенсивности постоянен вдоль контура начальной по-
луэллиптической в плане трещины, а усталостная трещина в
процессе своего развития подобна начальной, так что пере-
перераспределения интенсивности напряжений вдоль ее контура не
происходит. Из формулы F.85) видно, что для этого необходимо
выполнение условия
Ь/а = 2/3 + 6ДЗА), F.86)
что хорошо согласуется с опытом. При этом условии для коэф-
коэффициента интенсивности напряжений получается выражение
Ki = 0,32р V^b E - b/h)/B - b/h) (О < b/h ^ 0,4). F.87)
Отсюда на основании критерия разрушения Ki = Kjc находим
зависимость максимального .напряжения ршях от глубины кри-
критической трещины &»:
Kic 2 — bjh
0.32
Fl88)
РАСЧЕТ НА РЕСУРС ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
35&
3. Циклическое нагружение. Пусть растягивающая нагруз-
Ка р, действующая на полосу с трещиной, является циклической
функцией времени, так что в течение каждого цикла р возра-
возрастает от нуля -до ртах, а затем убывает от ртах до нуля.
Из F.40) находим следующее выражение для скорости роста
трещины в точке @, Ь, 0) ее контура:
где
\n[l-qx [т
F.89)
Интегрируя это уравнение, находим число циклов до разруше-
разрушения щ, определяющее срок службы конструкции:
(S=$nflh).
F.90)
Это выражение представляет собой зависимость, связываю-
связывающую безразмерную долговечность, безразмерный начальный и
критический размеры трещины.
Согласно F.88), последняя ве-
величина однозначно выражается
через безразмерную нагрузку
0,4
W
о,г
0,1
1 ///
Ш
у/
V
V
1 1 1 1
У
/
1 I I I
•
1111
¦ В табл. 6.1 приведены значе-
значения функции 5 = S(x0, х*), вы-
вычисленные по формуле F.90). На
рис. 142 представлено несколько
линий равной долговечности в
координатах х0 и х*.
, ~™Табл. 6.1 и рис. 142 позволяют
определить любую из трех вели-
величин: Щ, Ьо И jOmax —ПО Двум ЗЭ-
даиным. Например, по заданному
Сроку службы и заданному уров-
йю рабочих напряжений можно
найти допустимый размер на-
начальной трещины, или по заданному размеру начальной трещи-
трещины и заданной нагрузке определить долговечность.
Рассмотрим один частный случай, когда критический размер
трещины равен Ъ„ = 0,2h. Тогда, согласно F.88), величина ртах
будет равна 1,48#1с/]/7г.Кривая зависимости безразмерного раз-
Цера исходной трещины bD/h от безразмерной долговечности S,
Ш
о,г
Рис. 142.
0,3
12*
356
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
[гл.4 vi
Таблица 6.1
Значения функции S(x0, ж,), вычисленные по формуле F.90)
0,04
0,08
0.12
0,16
0,20
0,24
' 0,28
,0,32
0,36
0,40
0,04
0,08
0.12
0.16
0,20
0.24
0,28
0,32
0,36
' 0!40
0,01
0.1661
0.964S
2,5 63^
5.058С
8,653/
13,8397
20,8751
27.909S
37,672*
50,5445
0,20
0
0,0311
0.1015
0.1920
0.3326
0,5369
0.02
0.0396
0,3452
f 1.0195
) 2,1120
' 3.7215
' 6,0736
9,2943
12.5364
! 17,0550
23,0358
0,22
0,0110
3,0601
3,1290
},2389
3,4020
0,04
0
0,0816
0;3220
0,7478
1,4022
2,3880
3,7616
5,1629
7,1316
9,7481
0,24
0
0.0311
0,0828
0,1684
0,2987
0,06
0,0064
0,1273
0,3473
0,7040
1,2580
2,0456
2,8604
'4,0140
5,5622
0,26
0,0117
0,0493
0,1152
0,2190
0,08
0
0,0489
0,1736
0,3908
0,7407
1,2498
1,7848
2,5491
3.5833
0.28
0
0,0254
0,0751
0,1572
0,10
*
0,0138
0,0854
0,2241
0,4584
0,8087
1,1837
1,7244
2,4623
0.30
0,00
0,04
0,10
92
52
93
0.3.
0
0.12
0
0,0375
0,1273
0,2888
05386
0,8119
1,2100
1,7587
0,0235
0,07
24
.0,14
0,0117
0,0683
0,1808
0,3625
0,5667
0,8677
1,2868
0,34
0,008
5
0,0443
0,36
0
0,0235
0,16
0
0,0321
0,1098
0.2432
0,3979
0,6294
0,9556
0.38
0,0088
0.18
0,0106
0,0625
0,1601
0,2784
0,4583
0,7153
0,40
0
построенная при помощи табл. 6.1, приведена на рис. 143. Диа-
Диаграмма долговечности позволяет по заданной долговечности
определить величину исходного дефекта и наоборот.
Пусть, например, толщина полосы h = 20 мм, постоянная ма-
материала конструкции р = 0,02 мм. Предположим, что конструк-
конструкция должна выдержать щ = 500 циклов нагружения.после чего
трещина вырастает до критического размера Ь* = 4 мм и про-
происходит разрушение. Пользуясь диаграммой рис. 143, опреде-
определяем допустимый размер начальной трещины Ьо = 1,4 мм.
4. Случайные нагрузки. Рассмотрим рост той же полуэллип-
тическои треццины в полосе под действием только случайных
пульсаций нагрузки, представляющих стационарный случайный
процесс
p(t) = J F((o)
F.91)
где F{(a)—случайная величина, являющаяся, вообще говоря,
РАСЧЕТ НА РЕСУРС ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
357
^общенной функцией ю, причем ее математическое ожидание
|вно нулю, а дисперсия' не зависит от © (белый шум). Белый
"рл чаще всего реализуется на практике; соответствующая
4
3
г
кг'
8
6
Л
3
2
.
\
S
Ч
# 6 610'' г 4 6 81 2
Рис. 143.
56
S
Рис. 144.
реализация p(t) изображена на рис. 144. Отметим, что на рост
Пущины влияет лишь положительная часть нагрузки, поэтому
|рЬбщих формулах F.58) и F.61) все величины с индексом min
«адо положить равными нулю. По формулам F.58) и F.87)
Рысодим
<К1тах> = 0,0105</4
F.92)
368 РОСТ УСТАЛОСТНЫХ ТРЕЩИН. [ГЛ. VI
Скорость роста усталостной трещины, согласно F.62) и
F.92), равна
F.93)
Это выражение, собственно говоря, представляет собой скорость
роста трещины лишь в одной точке ее контура при х = 0, у = Ь,
2 = 0. Однако его вполне достаточно, чтобы судить о форме
всей «равнопрочной» трещины.
В формулу F.93) в качестве характеристик случайного про-
процесса p(t) входят лишь среднее время пульсации(т), математи-
математическое ожидание (pmar) и дисперсия omar случайной величины
pmar, которая считается имеющей нормальный закон распределе-
распределения. Последними двумя слагаемыми в квадратной скобке F.93)
можно пренебречь по сравнению с первым слагаемым, если ди-
диапазон значений, принимаемых случайной величиной рШаг, не
слишком широк. Напомним, что примерная ширина этого диапа-
диапазона для нормального закона распределения составляет 5amar-
Например, если omar ^ 0,13(pmar), то ошибка, связанная с пре-
пренебрежением упомянутыми слагаемыми, не превышает 10%- По-
Поэтому в практических расчетах вместо формулы F.93) можно
применять более простую формулу
?L = 0,0052 J&». (|5^-L (АиахУ @ < Ык « 0,4). F.94)
Следовательно, с приемлемой для инженерных целей точностью
стационарную случайную функцию p(t) в данном случае можно
заменить периодической функцией с периодом (т) и ампли-
амплитудой {ртах).
Решение уравнения F.94) запишем в следующем виде:
Г. = 19,5 JB — хLE — *Г4х-*Лс. F.95)
*°
Здесь
;DШ) xo=ba/h, x. = bjh,
Т — общее время докритического развития трещины (срок слу-
службы конструкции).
Так как в формуле F.95) предполагается, что х* C$0,4, то
- подынтегральную функцию B — лсLE — д;) можно разложить
в ряд по малым х и, ограничившись первыми членами разложе-
разложения, получить следующее простое замкнутое выражение для
безразмерной долговечности:
2'Г. = Шо - Их, - 1,2 In (xJxQ) + 0,3 (х. - xQ). F.96)
РАСЧЕТ НА РЕСУРС ДЛИТЕЛЬНОЙ ПРОЧНОСТИ
359
§ значение интеграла отличается от точного меньше чем
на 1%.
Так как согласно F.88)
in \— ^1с 2~ *»
то, подставляя это выражение в F.96), нетрудно получить для
t" формулу
V
о
м
F.97)
в большинстве встречающихся на практике случаев уро-
уровень случайных нагрузок весьма мал по сравнению с предель-
предельными; при этом сами случайные &J/,
нагрузки не могут вызвать разру- Ofi
шения конструкции даже за весь-
весьма продолжительное время. Их
влияние в основном сказывается 0$
в том, что они" вызывают подрас-
подрастание усталостных трещин и тем
еамым ослабляют конструкцию.
В связи с этим рассмотрим
следующий режим работы эле-
элемента конструкции (рис. 140). Ш
Пусть в течение некоторого вре-
времени он подвергается малой слу-
случайной нагрузке р@» а затем
включается большая постоянная
нагрузка р0. Требуется опредв'
лить наибольшее время fmax та
4°"i'-mJ
iiii
0,1
0,2
Рис 145.
0,3 т
bo[h
р max
кое, чтобы нагрузка р0 не вызвала мгновенного хрупкого разру-
разрушения конструкции. Введем параметр е, характеризующий сред-
средний уровень случайных напряжений (pmar) относительно на-
нагрузки р0, которой отвечает критический размер трещины 6.:
F.98)
Белкина р0 как функция Kic, Ь„ и А дается выражением
|Р»88), в котором ртах нужно заменить на ро-
-Для рассматриваемого режима нагружения аналогично пре-
предыдущему нетрудно получить
Гг 0,0256^ (-|^J-J [L - ±
1п д.
,з (,. - ^1, F.99)
через Т обозначена величина е4р*тах/BА(т)).
На рис. 145 представлено несколько линий равной долго-
ности Т = const в координатах *. и х0. Пусть, например,
pout усталостных трегцйн
[ГЛ. Vt
критический размер трещины'6, равен 0,2Л. Построим при по-
помощи F.99) график зависимости Т от дг0 (рис. 146). Положим
е = 0,05, 60=0,07Л, Л = 20 мм, ?=0,02 мм.
Тогда на основании • рис. 146 величина fmax будет равна
1,3-108(т) (напомним, что при циклическом нагружении с ам*
плитудой ро для такого же подрастания трещины требуется
500 циклов).
S
- ^ч
= z :
^.-
\
\
353
S
\
\
W* 2 4 6 SIS'' 2 4 S3/ 2 4 10 '
Г
Рис. 146.
5. Сложное нагружеиие. Рассмотрим общий случай квазиста-
квазистационарного случайного процесса нагружения, считая, что слу-
случайную нагрузку можно представить в виде суммы детермини-
детерминированной функции p(t) и малой случайной нагрузки (белого
шума). Таким образом, имеем (см. рис. 118)
. (Ртах) = Р(!) + Ар, {рт1а) = р @ — Ар, " F.100)
где
<
< Р, огщ1п < р.
Величина Ар не зависит от i. Кроме того, для простоты будем
считать, что уровень нагрузок p(t) не слишком высок, чтобы
можно было воспользоваться приближенной формулой F.54)
вместо точного выражения F.37). Это условие обычно выпол-
выполняется в условиях длительного нагружения. Тогда можно при-
применить общую фбрмулу F.61) для скорости роста усталостных
трещин при квазистационарном случайном нагружении. Под-
Подставляя в нее выражения F.100), нетрудно получить
F.101)
§6}- РАСЧЕТ НА РЕСУРС ДЛИТЕЛЬНОЙ ПРОЧНОСТИ 361
Рассмотрим подробнее случай периодической функции p(t)
вида . :.
p(t) —р0 sin &t. F.102)
Отметим, что учет малой случайной составляющей нагрузки
приводит к зависимости скорости роста трещины от формы
основного цикла в отличие от чисто детерминированного цикли-
циклического нагружения.
Рост трещины будет происходить лишь в те промежутки вре-
времени, когда нагрузка p(t) положительна. Интегрируя уравне-
уравнение F.101) по времени от нуля до t = njat и считая, что прира-
приращение длины трещины А/ за это время весьма мало по сравне-
сравнению со всей длиной трещины, находим
я/в
А/ == 40т) Ар (<т> KIT' ¦ J Pi (sin ©О3 dt= вир-* Д/7о/C(о <т> ffj).
F.103)
Отсюда, вводя число циклов п = a>t(Bn), получаем скорость
роста усталостной трещины:
dl/dn = 8Р$ Арт]/C© (г) К% F Л 04)
Сравним это выражение с формулой, получаемой из F.41)
для аналогичного случая чисто циклического нагружения:
F.105)
Как видно, наложение малой случайной нагрузки увеличивает
скорость роста усталостной трещины в 16А/?/(Зсоро(т)) раз.
Согласно F.104) и F.92), скорость роста трещины в рассма-
рассматриваемом примере будет определяться уравнением
— blh \*
М т*0А- F106)
'Аналогично тому, как было найдено выражение F.96), нахо-
находим из решения этого уравнения число циклов до разрушения щ:
] F.I07)
Ч J
(х. ^ 6,4),
где jc» = bjh, Xq = bQlh.
Выражение F.88) дает связь р<> и Ь», если в нем ршах заме-
заменить на р0.
362
РОСТ УСТАЛОСТНЫХ ТРЕЩИН
1ГЛ. VI
6. Влияние вибраций. Рассмотрим еще следующий режим
нагружения (рис. 147):
Р @ = Ро + Ар sin ©f (Ар < ро), F.108)
\.
где ро, Ар и со не зависят от времени.
По-прежнему пренебрегая последействием, воспользуемся об-
общим уравнением F.40), в котором нужно положить
К: шах = /С10 + А/С, /CImln = /Cio-A/C> F.109)
где
А/С </Сю-
Величины /Сю и А/С соответствуют нагрузкам р0 и Ар. С уче-
учетом F.109) формула F.40) приобретает вид
dl 4p/cf0 AJC
^=^-4)" FЛ10)
Это выражение для скорости роста усталостной трещины спра-
справедливо в общем случае произвольной малой циклической на-
нагрузки, накладываемой на стационарную.
В рассматриваемом примере (см. рис. 140) величины /Сю и
Д/С даются формулой F.87), в которую вместо р нужно подста-
подставить ро или Ар соответ-
соответственно. Таким образом,
получаем
db _ 4$а2 Apf2 (b/h)
dn ~ pa[\ - af (b/h)] '
F.111)
где
а = @,32Jл,
Рис. 147.
Интегрируя это уравнение, находим число циклов до разру-
разрушения tif.
i = f[l-af(x)]f-2(x)dx F.112)
Согласно F.88) имеем
F.113)
§6] РАСЧЕТ НА РЕСУРС ДЛИТЕЛЬНОЙ ПРОЧНОСТИ 363
Так как х* <^. 0,4, то, разлагая подынтегральную функцию в
F.112) в ряд и ограничиваясь первыми членами разложения,
можно найти следующую простую замкнутую формулу:
>а2 Apnf/(poh) = 6,4 • 1(Г3[A/*о) -(l/xt) - A,2 + 6,25а) In (*,/*„) +
+ A.5 + 3,75а)(х,-*ь)]. F.114)
Приведем численный пример. Пусть
jc. = 0,2, h = 20 мм, р = 0,02лш, хо = О,О7, Ар/ро = О,О5.
По формулам F.113) и F.114) находим а = 0,70, nf=1000.
Напомним, что в аналогичном случае чисто циклического
нагружения при ртах = Ро и pmia = 0 (см. выше п. 3) щ равня-
равнялось 500.
Этот пример дает одно из возможных объяснений наблюдае-
наблюдаемому иногда на практике парадоксально резкому уменьшению
времени до разрушения некоторых полимеров и металлов под
действием вибраций.
В заключение отметим, что наиболее сложна и не изучена об-
область низких напряжений, в которой влияние внешней среды
может привести к значительному ускорению роста усталостных
трещин по сравнению с теорией. Так, для некоторых высоко-
высокопрочных сталей показатель п в соотношении dl/dt~Kimax ока-
оказался в этой области существенно меньше полученного выше
теоретического значения, равного 4 (наблюдались значения п
до 1,4). Однако анализ этих опытов показывает, что влияние
внешней среды в них не учитывалось, хотя высокопрочные стали
обычно весьма чувствительны к атмосферной влаге. Поэтому
исследование роста усталостных трещин обязательно должно
сопровождаться определением частотных характеристик и реги-
регистрацией параметров среды, в частности, влажности. Кроме того,
в условиях испытаний с малыми напряжениями возрастает роль
неучитываемых внешних вибраций («внешний фон»).
Диагностика причин разрушения является одним из наибо-
наиболее интересных и трудных вопросов механики разрушения.
В. этой связи следует указать на возможную неоднозначность
истолкования результатов опыта. Например, в случаях, приве-
приведенных на рис. 130, 132—134, можно ожидать также активного
воздействия внешней среды на металл (см. следующую главу).
ГЛАВА VII
влияние Внешней среды на рост трещин
§ 1. Введение
Вопросы влияния внешней среды на прочность материалов
относятся к наиболее важным и слабо изученным проблемам ме-
механики разрушения. Многообразны и сложны явления локаль-
hofo разрушения в конце трещины, вызывающие докритическое
развитие начальных трещин и замедленное разрушение кон-
конструкции. Основная задача теории заключается в обособлении
отдельных механизмов локального разрушения и создании до-
достаточно простых и надежных математических моделей.
Уже давно было замечено, что прочность и деформируемость
твердых тел завися! от той среды, в которой находится тело.
Под влиянием внешней среды тело может становиться более
пластичным или более хрупким, прочность его может умень-
уменьшаться или возрастать. Иногда достаточно микроскопических
добавок некоторых веществ во внешнюю среду, чтобы суще-
существенно изменить прочность тела.
Изменение внешних условий наиболее сильно сказывается
на процессах локального, разрушения в конце трещины. Поэтому
зависимость скорости роста трещин от внешних параметров яв-
является наиболее чувствительной и точной характеристикой
свойств системы материал ^- среда.
Только в очень редких случаях эту характеристику можно
описать в рамках концепции Кс, т. е. просто как изменение вяз-
вязкости разрушения материала под воздействием среды *). В боль-
большинстве случаев внешняя среда не влияет на вязкость разруше-
разрушения Kic, а влияет на скорость докритического роста трещин.
Видимо, гораздо чаще влияние внешней среды можно свести к
каталитическому или ингибирующему воздействию на хнмиче-
*) Отметим, что под воздействием среды вязкость разрушения может как
уменьшаться, так и увеличиваться. Например, во влажной атмосфере вяз-
вязкость разрушения силикатных стекол несколько снижается (см. ниже § 8).
В металлах под воздействием влаги вязкость разрушения обычно увеличи-
увеличивается (иногда до 50%, в связи с чем в некоторых американских работах
вязкость разрушения в среде обозначают специальным символом Kfc; при
этом время выдержки образца с трещиной в среде должно быть достаточно
большим). Это увеличение объясняется уменьшением эффективной остроты
усталостной трещины вследствие коррозионного воздействия среды.
р|) ВВЕДЕНИЕ 365
Шую реакцию разложения .материала тела в вершине трещины
щк. гл. VI). При таком представлении кинетики роста трещин
Киль коэффициента интенсивности напряжений- состоит в умень-
уменьшении активационного барьера, а роль внешней среды — в из-
изменении кинетических констант материала (v0, X, р или U и ?)".
Однако существуют явления, которые не могут быть объяс-
объяснены в рамках этой офщей кинетической концепции. Вот наибо-
наиболее известные из них:д
а) рост трещин в металлах под действием водорода,
б) адсорбционный эффект, .
в) развитие коррозионных трещин под действием двух
основных механизмов (электрохимическое растворение металла
в вершине трещины и локальное разрушение тонких хрупких
пленок).
Эти явления рассматриваются в дальнейшем. Всюду в теоре-
теоретических моделях предполагается выполняющимся условие тон*
кой структуры. Заметим, что в реальных системах могут одно-
одновременно действовать не один, а несколько механизмов. -
Для простоты рассматривается лишь случай стационарного
Погружения. Следует подчеркнуть, что в условиях циклического
нагружения внешняя среда иногда не оказывает влияния на ско-
скорость роста усталостных трещин, в то время как в аналогичных
условиях стационарного нагружения воздействие среды может
Оказаться весьма существенным. Это объясняется тем, что меха-
механизм конечной пластической деформаций вблизи конца трещины
В таких случаях превалирует над специфическим механизмом
локального разрушения при воздействии среды. Поэтому можно
сформулировать следующее простое правило: . если скорость
роста трещины в условиях стационарного- нагружения и воздей-
воздействия некоторой активной среды гораздо меньше скорости роста
трещины в условиях циклического нагружения в инертной среде,
то эта активная среда не окажет заметного влияния на развитие
усталостных трещин, и наоборот. (Уровень нагрузок при стацио-
стационарном нагружении, очевидно, должен соответствовать средним
^растягивающим нагрузкам за цикл.)
Процесс докритического разрушения под напряжением удоб-
Ш разбивать на два периода: инкубационный период (промежу-
(промежуток времени, в течение которого зарождается трещина или же
Яе растет начальная трещина) и период докритического роста
^Ррещины.^В дальнейшем, как правило, рассматривается лишь
Йбслёдний период.
В последние пять лет был собран значительный опытный ма-
материал по докритическому развитию трещин в условиях стацио-
||йрного и циклического нагружения (см., например, уже упоми-
Вйвшуюся обзорную статью Джонсона и Пэриса ['2] и обзор
[143]). Опыты на образцах с искусственно созданными
366 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН . [ГЛ. Vtl
трещинами в заданной внешней среде совершенно необходимы
для того, чтобы судить о стойкости материала к определенной
внешней среде. Дело в том, что инкубационный период суще-
существенно зависит от характера начальной нарушенности (дефект-
(дефектности) поверхности" и объема образца, которую чрезвычайно
трудно воспроизвести в том же виде, как в натуре, при эксплуа-
эксплуатации материала. Поэтому рекомендации, основанные на лабо-
лабораторных исследованиях только гладких образцов, недостаточны.
§ 2. Влияние водорода и влаги
на рост трещин в металлах (опытные данные)
Охрупчивание металлов водородом известно давно в связи
с металлургической проблемой образования флокенов *). Влия-
Влияние влаги на металлы, приводящее к их коррозии и разрушению,
было замечено уже тогда, когда люди еще только научились вы-
выплавлять металлы. В последнее время эта старая проблема при-
приобрела особенно большое значение в связи с катастрофическим
охрупчивающим воздействием влаги на высокопрочные стали.
По современным представлениям [72> ш], природа этих явлений
в случае высокопрочных сталей одинакова: локальное наводора-
живание металла в малой области вблизи конца начальных тре-
трещин и последовательные разрушения, приводящие к докритиче-
скому росту трещин. В то же время нельзя сбрасывать со счетов
окислительно-восстановительные реакции на свежей поверхно-
поверхности металла в вершине трещины; эти реакции, помимо выделе-
выделения электролитического водорода, приводят к растворению ме-
металла или к нарастанию коррозионной пленки окислов металла.
Отметим, что для усталостных трещин при циклическом на-
гружении влияние влаги может оказаться также весьма суще-
существенным. Например, в опытах Хартмана и Шийве [162] в неко-
некоторых случаях наблюдалось десятикратное увеличение скорости
роста усталостных трещин под действием влаги.
В отличие от других соединений, водород способен к хемо-
сорбции и диффузии во всех металлах [ш]. Водород находится
в металле в атомарном состоянии в виде протонов (протонный
газ). Растворимость водорода в металлических блоках не превы-
превышает 1—10 см3 на 100 г при нормальных температуре и давле-
давлении, а в металлических порошках может достигать 100—1000 еж3
на 100 г металла. С ростом температуры и внешнего давления
растворимость увеличивается. Способность водорода к растворе-
*) Флокены представляют собой (белые по цвету) сфероидальные объе-
объемы металла, обогащенного водородом и в высокой степени восстановленного
(в молекулы); в результате внедрения протонов (водорода) атомы металла
приобретают иную структуру электронных оболочек. Флокены образуются при
быстром охлаждении стали вследствие уменьшений растворимости водорода.
Щ !i ВЛИЯНИЕ ВОДОРОДА И ВЛАГИ (ОПЫТНЫЕ ДАННЫЕ) 367
яию и диффузии в металлах существенно тормозится адсорбцией
кислорода, наличием окисных пленок и т. п.
Коэффициент диффузии водорода в металлах D зависит от
абсолютной температуры Т так:
G.1)
Здесь U — энергия активации процесса, А> — некоторая по-
постоянная металла. Величины DQ и U для всех металлов изме-
изменяются в пределах
Do= КГ1 -4- 10~3 см21сец, U=3 -ь 25 ккалЦг ¦ атом),
а для стали
А, = 1(Г2 -ь 10~3 см2/сек, и = Ъ 4-9 ккалЦг • атом).
Водород охрупчивает все металлы, всегда уменьшая их пла-
пластичность и прочность (причем чем больше концентрация водо-
водорода, тем меньше прочность). Например, в стали явление охруп-
чивания наблюдается уже при концентрации водорода 0,2 см3 на
100 г металла при нормальных условиях (I атом водорода на
105 атомов металла). В пять раз большая концентрация счи-
считается опасной. Существует "нижняя граница температур водо-
водородной хрупкости; эта граница совпадает с минимально возмож-
возможной температурой хемосорбции. Например, у стали она рав-
равняется примерно —200 °С. После обезводораживания свойства
металла полностью восстанавливаются, если только в металле
не произошли необратимые структурные изменения.
Водород может поступать в металл не только путем физиче-
физической адсорбции молекулярного водорода на поверхности ме-
металла, но и путем осаждения атомарного водорода Н+, который
в чистом виде или связанный с нейтральными молекулами со-
содержится, например, в растворах электролитов и воде. Кроме
того, водород может выделяться при химических и электрохими-
электрохимических реакциях, происходящих на поверхности металла. Наи-
Наиболее благоприятные условия для протекания процессов погло-
поглощения водорода имеются в конце трещины, на малом участке
поверхности свежего металла, не покрытого защитной окисной
пленкой. Поэтому влияние влаги и водорода наиболее суще-
существенно в процессе докритического роста трещины; инкубацион-
инкубационный период весьма существенно зависит от состояния поверх-
поверхности гладкого образца, а при наличии надреза — от его
остроты.
Скорость докритического развития трещины dl/dt является
некоторой функцией коэффициента интенсивности напряжений
. G.2)
368
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
ГГЛ. VII
Таблица 7.1
Пороговый коэффициент интенсивности напряжение для некоторых пар
п/п
1
2
3
4
5
6
7
8
9
10
11
12
Материал
Мартеиситная леги-
.рованная сталь 4340
Мартенситная леги-
легированная сталь ДбА
Мартенситная леги-
легированная сталь, раскис-
раскисленная кремнием
Легированная сталь
18Ш-9Со-5Мо
Ti-7Al-2Co-lTa
Ti—8A1— IMo- IV
Ti-6A1-4V
TJ—5A1—2,5Sn
Ti-6Al-4V-lSn
Tl-6Al-6V-2,5Sn
Ti-6Ak-2Mo
Ti-7Al-3Mo
материал — среда
Предел
прочности
"в.
кГ/мм'
186
163
145
191
163
195
158
206
—
!
—
—
—
—
82,5
Предел
теку чести
°Ь,2'
кГ/мм'
156
• 147
137 •
170
153
169,5
144
197
71,5
71.5
73,5-77
74,3
79,0
92
75,7
84
91 •
81.3
87
116
78
80
92
130
88,5
89
73
Вязкость
разруше-
разрушения к1с,
кГ/мм'1'
146
171
376
210
338
149
178
231
390
373
355
376
145
461
398
320
192
312
410
227
462.
398
398
195
412
437
465
Пороговые
коэффициент
интенсивности
напряжен ни
Klscc
кГ/мм'1'
35
35
117
25
164
42,5
55
135
138
224
124
153
142
312
100
81,7
64
248
337
195
256
139
149
74,5
270
362
160
Источ-
Источник
сведе-
иив
[US]
ВЛИЯНИЕ ВОДОРОДА И ВЛАГИ (ОПЫТНЫЕ ДАННЫЕ)
369
Лрадолжение табл. 7.1
№
п/п
13
14
15
16
17
18
Материал
Мартенситная леги-
легированная сталь 4340
Мартенсито-старею-
щая сталь 250 A8% N1)
Мартенсито-старею-
щая сталь 250 A8% Ni)
Сплав алюминия
7079-Т6
Ti—7A1— 2Со-1Та
Ti—7A1—2,5Мо
Предел
прочности
ав- .
кГ/мм1
—
—
190
56
—
—
Предел
текучести
,2-
кГ/мм'
158
151
. 181,5
50'
77,7
85,1
1
Вязкость
разруше-
разрушения к/с>
кПмм'Ь
B24
408
240
71
422'
362
Пороговый
козффицнент
иитеисивиости
напряжение
Klscc-
kTImm'I'
18
248
130
19,5
159
283
Источ-
Источник
сведе-
сведений
[345J
1Ш1
[347]
ПРИМЕЧАНИЯ К ТАБЛИЦЕ 7.1
1. Для материалов 1—4 испытания проводились в нециркулирующей
дистиллированной воде; для остальных материалов — в морской воде.
2. Краткая характеристика схемы испытания: образец с краевой тре-
трещиной подвергался изгибу. . .
Эта функция равна нулю при Ki ^ KiSCc, а при Ki > /CiSCc она
монотонно возрастает с увеличением Кь Отношение KucdKic для
пластичных металлов обычно близко к единице, а для высоко-
высокопрочных и хрупких сплавов гораздо меньше единицы.
Величина Kiscc называется пороговым коэффициентом интен-
интенсивности напряжений. Значения /Ciscc для некоторых пар мате-
материал— среда приводятся в табл. 7.1. Диаграмма dl/dt — Ki
играет основную роль в изучении докритичеекого роста трещин.
На рис. 148 показана зависимость Кхс и Късс от относитель-
относительной влажности водяного пара для высокопрочной хромистой
инструментальной стали Н-11 E% Сг), у которой значение ао,2
равно 160 кГ/мм2. Как видно, величина /Ciscc одинакова для воды
и для влажного водяного пара. Это явление можно объяснить Р2]
капиллярной конденсацией воды в конце трещины для весьма
влажных газообразных сред, в результате чего локальный про-
процесс разрушения в конце трещины протекает в условиях полного
увлажнения,
370
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VII
Капиллярной конденсацией объясняется также [п] характер-
характерное насыщение зависимости скорости роста трещины от относи-
относительной влажности при Ki = const (рис. 149). Это же явление
имеет место для усталостных трещин [160].
Зависимость скорости роста трещин dl/dt от абсолютной тем-
температуры имеет характерный для термоактивационных процессов
Рис. 148.
, 1
•
/ •*
Те же
значения
в Воде
А
г
-
-
0,5
0,3
ofil
0,005
40 80
тя Платою,
Рис. 149.
а Относительная
блажшшьЮО'/-
Г II I I
40 44 46
//Г, Т'*Ю3
Рис. 150.
вид (см., например, рис. 150), причем энергия активации этого
процесса близка к энергии активации процесса диффузии водоро-
водорода в соответствующем металле [72]. Величины Kic и Kiscc менее
чувствительны к температуре, чем скорость роста трещины.
Газообразный водород обычно сильнее влияет на скорость
роста трещины и величину KiSCc, чем влага. Этот факт вытекает
из опытных данных для стали Н-11 при нормальном атмосфер-
1 влияние Водорода и влаги (опытные данные?
371
ном давлении (см. рис. 151, где приведена зависимость прираще-
приращения длины трещины Д/ от времени). На этом рисунке квадра-
квадратами изображены данные для чистого водорода при Ki'=
= 66 к?/мм31й, а кружками — для аргона с относительной влаж-
влажностью 100% при Ki = 80 кГ/мм312. Указанные опыты провели
t,mia
Хэнкок и Джонсон [165]. В их работе было проведено также, ин-
интересное исследование влияния малых добавок кислорода в раз-
различные сухие и увлажненные газы (водород,' аргон, азот) на
рост трещин в стали Н-11.
¦О
Рис. 15г.
^•Влажный а/вон ¦
птк нислород
(рцдные объёмы)
тйто
длажный аргон
плюс жлород
1№ны& (родные объёмы)
у fin пи *Г /
15 20
Время, ман
25
Риа 153.
На рис. 152 и 153 изображены некоторые результаты этих
экспериментов. Как видно, достаточно 0,6% кислорода, чтобы
практически мгновенно остановить докритический рост трещин.
372
ВЛИЯНИВ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ."*УП
Ингибирующее действие кислорода в водородных и водных сре-
средах объясняется гораздо большей химической активностью пары
кислород — металл по сравнению с парой водород — металл.
h - толщина пластины
? Средний уровень Яс или К1с
™
Я/ или Я/с в%5%растворе• NoCl;
Ti-dA\-1№-\V Г Tl—6Д1-4У
.$}
— Теория К1ОгПнф»д1,
о Эксперимент при&'?
Двойной отжиг Заводской отжиг
Рис. 154.
Поэтому на свежей поверхности металла в конце трещины обра-
образуется тонкая окисная пленка, защищающая металл от проник-
проникновения в него водорода. Когда подача кислорода прекращается,
начинает преобладать процесс
восстановления кислорода водо-
водородом или же-растворение плен-
пленки водой [72]. •
Влияние внешней среды го-
гораздо более существенно в усло-
условиях плоской деформации, чем
в условиях плоского напряженно-
напряженного состояния. Это эксперимен-
экспериментально доказали Пайпер, Смит и
Картер [72] для двух титановых
сплавов (см. диаграмму на рис.
154). БелЫе столбики на этой диа-
диаграмме дают значения Кс в возду-
воздухе, а заштрихованные столбики —
величины Kscc в 3,5%-ном водном
растворе NaCl (определяемые
при выдержке б часов). .
Отметим, что на полимеры влага оказывает иное действие по
сравнению с металлами: она обычно пластифицирует полимер-
полимерные материалы.
На рис. 155 и 156 представлены характерные зависимости
скорости роста трещины от коэффициента интенсивности напря-
Cfil
Стт H-tt 6 доде
t..,.j... i
COS
f
OJ
Рис. 155.
¦131
росттрейшн под действием водорода (теорий)
373
жений (Джонсон и Пэрис \J2], Смит, Пайпер и Дауни [ш\). Пер-
Первый рисунок относится к стали Н-11 в воде при 27 °С (Къ =
= 140 кГ/мм3/2, /С^сс = 60 кГ/мм3'2, сто,2 = 160 кГ/мм2), вто-
второй — к -титановому сплаву Ti—8A1— 1Мо— IV в 3,5%-ном вод-
водном растворе NaCl) (Късс = 72 — 84 кГ^мм3'2, Ки = 184, 320 и
390 кГ/мм*2).
30
Образец/И! д
Образец^
1-е испытание •
2-е испытание °
mi ы VvflvfliiUItVv
Образец Л'З
f-Buenmums ¦
2-е шпытшие °
-
: а д
i . * *'
о
#
•' а
о •
«о
s ••
¦ ° па
й "о
10
10s
Рис. 166.
Скорость роста трещины в стекле, находящемся во влажной
среде, также хорошо коррелирует с коэффициентом интенсивно-
интенсивности напряжений [72].
§ 3. Рост трещин в металлах
под действием водорода (теория)
Пусть идеальное упруго-пластическое тело имеет трещины
нормального разрыва. Тело будем считать однородным и изо-
изотропным; это допущение обычно всегда принимается при изуче-
изучений физических явлений, в которых неоднородность и анизотро-
анизотропия играют второстепенную роль. Встает вопрос о том, в какой
мере количественные результаты теории, основанной на этом до-
допущении, можно переносить на реальные материалы, предста-
представляющие собой обычно поликристаллические образования со
случайным распределением в пространстве деформационных и
прочностных характеристик. Этот вопрос особенно остро стоит
в механике разрушения, так ках характерное раскрытие трещи-
трещины в ее конце, а иногда и размер пластической области, срав-
сравнимо или даже значительно меньше среднего размера зерна.
Изучение же роста трещины основаГно на изучении процессов,
протекающих вблизи конца трещины. Теоретические результаты
374 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА POCt ТРЕЩИН [ГЛ. VII
в этом случае, очевидно, следует понимать как некоторое сред-
среднее (по множеству реализаций) описание процесса (т. е. среднее
по многим образцам одинаковой геометрии, с одной и той же
длиной трещины и из одного и того же материала). В этом
смысле теория годится для любых трещин, в том числе, для
микротрещин, длина или приращение длины которых сравнимы
или гораздо меньше размера зерна (но гораздо больше меж-
межатомного расстояния). Применение теории к одной единственной
реализации случайного процесса на основании эргодической ги-
гипотезы вполне законно в том случае, когда приращение длины
трещины и сама эта длина значительно больше среднего раз-
размера зерна (распределение деформационных и прочностных ха-
характеристик материала от точки к точке можно считать стацио-
стационарным случайным процессом).
В том случае, когда длина тре-
трещины (или соответственно при-
приращение длины) сравнима или
гораздо меньше размера зерна,
становится существенным ста-
статистический разброс.
Рассмотрим малую окрест-
окрестность конца трещины в упруго-
Рис. 157. пластическом теле (рис. 157).
~ч Обозначим через 2v0 раскры-
раскрытие трещины в ее конце (вследствие конечности деформаций но-
носик трещины будет не обрублен, как это следует из теории ма-
малых деформаций, а размыт). Пусть полость трещины заполнена
жидкой или газообразной средой, содержащей водород; атомы
водорода поступают в материал в основном через поверхность
свежего металла вблизи точки О. Пластическая область не изо-
изображена на рис. 157, ее размеры значительно больше 2v0. На
бесконечности тело подвергнуто стационарному растяжению,
которое вполне описывается положительным коэффициентом ин-
интенсивности напряжений Кь
Обозначим через с концентрацию протонов (водорода), ме-
меняющуюся от точки к точке тела. Наибольшее значение концен-
концентрации, равное-Со, будет, очевидно, в вершине трещины (в точ-
точке О). На бесконечности концентрацию водорода будем считать
равной нулю.
Диффундирующий водород оказывает двоякое действие. С
одной стороны, он «закрепощает» дислокации, охрупчивая мате-
материал и уменьшая его способность к деформации, тем самым
уменьшая и вязкость разрушения. С другой стороны, водород
«распирает» атомную решетку твердого тела; вследствие нали-
наличия градиента концентрации возникают концентрационные на-
напряжения. Эти внутренние напряжения, очевидно, будут ежи-
§ 3] РОСТ ТРЕЩИН ПОД ДЕЙСТВИЕМ ВОДОРОДА (ТЕОРИЯ) 375
мающими вблизи точки О, а на некотором расстоянии от точки
О вдоль оси х должны менять знак, причем равнодействующая
напряжения ау вдоль х должна быть равна нулю.
В связи с этим принципиально возможны следующие меха-
механизмы локального разрушения: а) разрушение от внутренних
сжимающих напряжений, б) разрушение охрупченной пластиче-
пластической области от внешней нагрузки, в) разрушение от растяги-
растягивающих напряжений в упругой области. Во всех случаях разви-
развитие трещины будет скачкообразным, причем величина скачков
определяется механизмом разрушения. При разрушении от сжи-
сжимающих напряжений величина скачков будет малой по сравне-
сравнению с раскрытием трещины 2v0, так как максимальное сжимаю-
сжимающее напряжение достигается на границе тела, в точке О; по-
поэтому при реализации первого механизма рост трещины можно
считать непрерывным.
Охрупчивающее действие водорода проявляется лишь в пла-
пластической области, где влияние внутренних растягивающих на-
напряжений минимально. Поэтому при разрушении по второму,
диффузионному, механизму величина скачков будет гораздо
больше 2г>о, но меньше размера пластической области вдоль
оси х.
Растягивающие напряжения в упругой области могут вместе
с растягивающим напряжением от внешнего поля приводить
к образованию локальных разрывов, расположенных на продол-
продолжении магистральной трещины. В этом случае величина скачков,
очевидно, будет больше размера пластической области.
Указанные механизмы локального разрушения в конце тре-
трещины существенно зависят от значения концентрации с0 в точ-
точке О: чем больше с0, тем больше градиенты концентрации, тем
ближе к точке О образуются локальные разрывы и тем меньше
скачок магистральной трещины за один цикл процесса. При ма-
малой (но опасной) концентрации Со величина скачка может значи-
значительно превышать не только 2v0, но и размер пластической об-
области. Теоретический анализ особенно прост в следующих трех
предельных случаях: а) величина скачка мала по сравнению
с раскрытием трещины 2v0, б) величина скачка гораздо больше.
2v0, но меньше размера пластической области, в) величина скач-
скачка значительно больше размера пластической области вдоль
оси х. Эти предельные случаи рассматриваются в дальнейшем.
I. Предельно большие градиенты концентрации. В этом слу-
случае развитие трещины можно считать непрерывным, а скачки
трещины — бесконечно малыми. Рассмотрим окрестность точ-
точки О, малую по сравнению с раскрытием трещины 2v0, в усло-
условиях квазистационарного роста трещины со скоростью V. По-
Подвижные координаты | и ц связаны с координатами начального
положения трещины соотношениями § = х — Vt, tj = у.
376 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
Пренебрегая влиянием градиентов напряжения на распреде-
распределение концентрации протонов, запишем уравнение диффузии
dt ~ дх*'
Это уравнение справедливо в полупространстве х ^ Vt, со-
соответствующем локальной окрестности точки О. В данном случае
протоны находятся в узкой полоске вдоль поверхности тела, в
лобовой части трещины; поэтому градиентами концентрации в
тангенциальном направлении можно пренебречь по сравнению
с. градиентами по нормали к поверхности. Граничные условия
будут следующими:
при х—Vt — O Ddcldx — —q,
при х — Vt->oo с->0. G-4^
Здесь q — приходящийся на единицу площади поток атомов во-
водорода через, поверхность металла вблизи точки О за единицу
времени. Если принять на поверхности контакта различных
сред закон массообмена, аналогичный закону теплопроводности
Ньютона
. ' D-^^hAco-cJ, G.5)
где hc— коэффициент массообмена, с\ — концентрация водорода
в окружающей среде, то, поскольку обычно с\ >• с0, получаем
G.6)
Эта формула для q, по-видимому, не годится, если водород до-
доставляется в металл путем промежуточной химической реакции
на свежей поверхности металла.
Стационарное решение краевой задачи G.3), G.4) имеет вид
"G.7)
Перемещение трещины происходит вследствие непрерывного
'разрушения тела в точке О и раздвигания поверхности слоя
тела в тангенциальном направлении. Скорость роста трещийы
dl/dt, согласно G.7), можно выразить через предельную концен-
концентрацию Со в точке О:
' G.8)
Как видно, в рассматриваемом режиме роста трещины "скорость
не зависит от коэффициента интенсивности напряжений. По-
Постоянную Со нетрудно связать с локальной прочностью тела на
сжатие ас: ^
Cg = (l-vKAaf?). ' G.9)
j 3} POCt ТРЕЩИМ ПОД ДЕЙСТВИЕМ ЙОДОР6ДА <f ЁбРЙЯ) 37?
Здесь осе — коэффициент линейного расширения металла под
действием водорода. «
Отметим, что физически локальное разрушение в точке О не
обязательно понимать как механическое разрушение; это может
быть также локальное растворение металла, при этом формула
G.8) останется по-прежнему справедливой.
2. Диффузионный механизм. Рассмотрим теперь развитие
трещины последовательными скачками, величина которых значи-
значительно больше раскрытия трещины в ее конце 2v0. При этом
трещину можно считать математическим разрезом (нулевой тол-
толщины). Таким образом, для определения концентрации с при-
приходим к следующей краевой задаче математической физики:
в конце неподвижного полубесконечного прямолинейного раз-
разреза в твердом теле вдоль у = О, х < О в начальный момент
времени /¦= 0 включается постоянно действующий точечный
источник протонов интенсивности Q. Предполагается, что вели-
величина Q не зависит от времени, а берега разреза свободны от
нагрузок. Требуется найти распределение концентрации прото-
протонов в теле.
¦ Уравнение, описывающее процесс диффузии протонов, име-
имеет вид
при 0<V<oo, 0
Здесь пренебрегаем влиянием градиентов напряжения и дефор-
деформации на поле концентрации; это влияние обычно сравнительно
мало [167]. Концентрация не зависит от полярного угла 8, по-
поэтому разрез не оказывает влияния на распределение с.
Уравнение сохранения массы
оо 2л оо
Qt= J jrcdrdQ = 2n \rc{r,t)dr G.11)
•000 » •
играет роль дополнительного условия (г -> оо величина с стре-
стремится к нулю).
Решение этой задачи автомодельно; как нетрудно проверить,
оно имеет следующий вид:
х
Здесь Ei(jt)= j -j-e'etf—интегральная показательная функ-
.—оо'
ция. Напомним, что функция —Ei(—х) при положительных х
378
ВЛИЯНИЕ. ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VI»
монотонно убывает, причем имеют место следующие асимптоти-
асимптотические формулы:
при д;->0 —Ei(—х) =— 1пд; — С,
при х -*¦ оо — Ei (— х) == е~*1х
G.13)
(С « 0,577— постоянная Эйлера).
Вследствие диффузии протонов вблизи конца трещины внутри
пластической области образуется круговая область охрупченного
металла, который ведет себя как упру-
упругое тело («упругое ядро», рис. 158).
Охрупчивающее действие протонов на
металл определяется их концентра-
концентрацией; поэтому будем считать для про-
простоты, что, пока концентрация с мень-
меньше некоторой критической величины
се, металл остается в пластическом со-
состоянии, а как только величина с пре-
превысит значение се, металл переходит
в упруго-хрупкое состояние. Величина
се является некоторой-постоянной ма-
материала в данной модели. При этом
радиус охрупченного кругового ядра de находится по формуле
G.12) из условия
Рис. 158.
Отсюда
при r =
Се-
AnDcJQ = — Ei [— dll(ADt)].
G.14)
G.15)
Таким образом, величина de монотонно растет во времени.
Пренебрежем внутренними концентрационными напряжения-
напряжениями по сравнению с пределом текучести as идеального упруго-пла-
упруго-пластического материала. При аппроксимации диаграммой Прандт-
ля реальной диаграммы о — е лучше всего брать некоторое сред-
среднее значение между ао,2 и ав. В принятом допущении роль
протонов заключается в «замораживании» пластических дефор-
деформаций упругого ядра; поле напряжений и деформаций вне упру-
упругого ядра и в том числе в пластической области остается таким
же, каким оно было до включения источника протонов.
В упругом круговом ядре поле напряжений полностью пере-
перестроится; появится также соответствующее поле упругих дефор-
деформаций, малых по сравнению с начальными пластическими де-
деформациями. (Возникающее перемещение на границе упругого
ядра, очевидно, будет также весьма малым, так что его влия-
влиянием на поле пластических деформаций можно пренебречь.) Так
как радиус упругого ядра гораздо больше раскрытия трещины,
§ 3] РОСТ ТРЕЩИН ПОД ДЕЙСТВ-HEM ВОДОРОДА (ТЕОРИЯ) 379
вблизи конца трещины формируется структура, характерная для
математических разрезов в упругих телах. Эта- сверхтонкая
структура вполне характеризуется локальным коэффициентом
интенсивности напряжений k\. Отметим, что градиенты началь-
начальных пластических напряжений, которые входят в уравнения
упругости в виде некоторой объемной силы, не изменяют харак-
характера этой структуры; они влияют лишь на величину k\.
Важно подчеркнуть, что локальный коэффициент интенсив-
интенсивности ki (как и все поле в упругом ядре) совершенно не зависит
от внешнего поля нагрузок, которое описывается коэффициентом
интенсивности напряжений Кг на расстояниях, больших по срав-
сравнению с размером пластической области. Пластическая область
вне упругого ядра полностью экранирует его от внешних на-
нагрузок.
Найдем локальный коэффициент интенсивности k\. Он опре-
определяется из решения плоской задачи теории упругости для кру-
круговой области радиуса de с радиальным разрезом; на границе
круга заданы нормальные 'и касательные нагрузки, зависящие
только от параметра ors (для простоты теория пластичности пред-
предполагается одноконстантной типа теории Губера — Мизеса или
"Треска — Сен-Венана). Объемные силы в упругом1 ядре также
зависят только от параметра ors. Следовательно, коэффициент k\
из соображений анализа размерностей равен
fti = 4i<T,V2".. " GЛ6)
Здесь Tii — некоторое постоянное число (в принятой постановке
задачи оно не зависит обычно даже от коэффициента Пуассона
или отношения as/?" и в принципе всегда может быть найдено,,
если известно решение соответствующей упруго-пластической за-
задачи).
Согласно формуле G.16), наряду с ростом упругого ядра уве-
увеличивается локальный коэффициент интенсивности ki, пока не
достигается некоторое предельное значение kjc (вязкость разру-
разрушения наводороженного металла). Отсюда находим максималь-
максимальный размер deo упругого ядра- в момент t = т, когда начинается
локальное разрушение':
G.17)
Трещина скачком распространяется на расстояние d^, оста-
останавливаясь на границе упругого ядра; затем процесс повторяет-
повторяется. Цикличность процесса развития трещины вполне характери-
характеризуется величиной скачка deo и периодом цикла т. Согласно G.17),
значение dU является некоторой постоянной пары металл — сре-
среда. Период цикла т определяется формулой G.15) при de = deCj;
0н существенно зависит от интенсивности источника протонов Q.
380 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТДРЕЩИН [ГЛ. VII
ч ¦
Интенсивность Q прямо пропорциональна величине раскры-
раскрытия трещины в ее конце:
Q^nv0, G.18)
так как свежая поверхность обнажающегося вследствие пласти-
пластической деформации металла, очевидно, пропорциональна vq.
Коэффициент т) зависит от среды и от адсорбционной активно-
активности по отношению к водороду контакта свежий металл — среда.
В случае, когда внешняя среда представляет собой смесь
идеальных газов, коэффициент ц будет, прямо пропорционален
числу ударов N водородосодержащих молекул за единицу вре-
времени, приходящихся на единицу поверхности. Коэффициент про-
пропорциональности определяется вероятностью того, что молекула,
находящаяся на поверхности металла, оставит протон.
Согласно кинетической теории газов число ударов N равно
GЛ9)
причем ,
»н = 3Рн/Рн-
Здесь рн, рн, у 1>н, пн — соответственно парциальные давле-
давление, плотность, среднеквадратичная скорость и число молекул
в единице объема, относящиеся к водородосодержащим моле-
молекулам. .
Исключая ofj, получаем
<Ч~Л0. G.20)
Этачформула вместе с выражением G.18) определяет зави-
зависимость интенсивности потока протонов от физических парамет-
параметров внешней среды в полости трещины вблизи ее вершины.
Коэффициент i\, вообще говоря, зависит от давления газа, так
как при достаточно высоких давлениях наступает адсорбцион-
адсорбционное насыщение поверхности. Коэффициент ц связан также с про-
процессами переноса внешней среды вдоль полости трещины в об-
область вблизи ее вершины. Эти процессы в зависимости от внеш-
внешних условий могут быть весьма разнообразными (вязкое течение,
капиллярная конденсация, кнудсеновская диффузия и т. д.).
Раскрытие трещины v0 равно (см. § 5 гл. IV)
) G.21)
2 — некоторое число).
Сравнивая с G.18), получаем
G.22)
РОСТ ТРЕЩИН ПОД ДЕЙСТВИЕМ ВОДОРОДА (ТЕОРИЯ)
381
Таким образом, величина Q прямо пропорциональна квадрату
коэффициента интенсивности напряжений Кл
Средняя скорость докритического роста трещины dt/dt,' со-
согласно формулам G.15), G.17).и G.22), равна
G.23)
Здесь функция у = F{x) определяется соотношением
— Ei(—«/) = Цх G.24)
(рис. 159).
Как видно, в выражение для скорости докритического роста
трещины при стационарном нагружении входят лишь две кон-
константы системы материал — среда: /Сю и щ. Эти постоянные
/ (ft
Todt
1,6
0,д
у
/
8 ю
РисЛ159.
можно определять из прямых экспериментов по докритическому
развитию трещин (см. ниже § 9).
На рис. 155 сплошной линией проведена теоретическая кри-
Зая, построенная при помощи формулы G.23) при v0 =
|= 3,4-10 см/сек и Кю = 77 кГ/мм3/2. Налицо полное совпаде-
совпадение с экспериментальными результатами Джонсона и Пэриса |72].
*Это позволяет думать, что докритическое развитие трещин в
стали Н-11 в водной среде происходит по описанному механизму
фокального охрупчивания вследствие наводораживания.
382 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ, VII
. Отметим, что в титановом сплаве Ti—8А1—1Мо—IV (см.
рис. 156) механизм роста трещин, очевидно, совсем иной, так
как опытные точки в этом случае не подчиняются закономерно-
закономерности G.23). В дальнейшем будет показано, что наиболее вероят-
вероятным механизмом здесь является электрохимический механизм.
3. Внутренние напряжения. Диффузионный механизм докри-
тического роста трещин имеет наибольшее практическое значе-
значение, так как внутренние напряжения, возникающие в металлах
вследствие градиента концентрации протонов, в большинстве
случаев сравнительно невелики. Практически, по-видимому,
весьма трудно разрушить металлический образец лишь за счет
режима наводораживания (не прикладывая к нему внешних на-
нагрузок). Во всяком случае, автору неизвестно, чтобы такие слу-
случаи отмечались в литературе. Тем не менее, оценка внутренних
напряжений представляется полезной, по крайней мере в пре-
предельном случае идеально-хрупкого тела, когда влияние внутрен-
внутренних напряжений на рост трещины будет наибольшим.
Поле внутренних упругих напряжений, возникающее вслед-
вследствие наличия градиентов концентрации, описывается [167] обыч-
обычными уравнениями теории упругости с объемной силой, компо-
компоненты которой равны
,у. аоЕ дс - acEQ* схп( г' \
рл~ l-2v дх 2jt(l-2v)?>r2 ехр \ ADt )' -
_ acEQy l G25>
Р1 ~ 1 - 2v ду ~ 2я A - 2v) ?r2 exp [ 4Dt
Здесь ас — коэффициент линейного расширения, равный ДУ/(Зс},
где ДV — приращение единицы объема в отсутствие внешних
напряжений за счет концентрации чужеродных атомов с.
Искомое решение упругой задачи представим в виде суммы
двух решений, одно из которых отвечает безграничному про-
пространству с объемной силой G.25), а другое — пространству без
объемной силы с разрезом вдоль у = 0, х < 0, нагруженным
нормальным напряжением ау, равным по величине и обратным
по знаку напряжению ста в первой задаче.
Первая задача, очевидно, осесимметрична; ее уравнения
имеют вид
d"ur I duT и, acQ A + v) eYn / « г* V n
.@<r<oo), G.26)
л dur
gfl=(l+v)(l-2v) LAV)+V^T
§ S) Рост трещин Под Действием водорода (теория) 383
Здесь tir— (единственное отличное от нуля) радиальное пере-
перемещение.
Решение уравнения G.26), как легко проверить, имеет вид
i • ^ ШEi (-
где
Отсюда находим напряжение ае в первой задаче
G.28)
Напряжения во второй задаче легко находятся в квадратурах
для произвольной нагрузки на разрезе (см. замечание к § 5
гл. III). Наибольший интерес представляют напряжения <уу на
продолжении разреза при у = 0, х > 0. Имеем
V~roAr)
_ 2у) /2 (g)]_ " 0 ~ Ду) 1
7 2l6/J |*j J
- (при f/=0, л;>0).
Здесь
uu
J
0
oo
= _ J (e-P - 1) ^^|L_ d - ,/B
Последнее слагаемое в G.29) отвечает сингулярному потен-
потенциалу Ф(г) ~ z~2; оно получается, или непосредственно, при вы-
вычислении расходящегося интеграла G.29) по правилу «конечная
часть расходящегося интеграла» (см. § 6 гл. III) или же после
предварительного вычитания этого сингулярного потенциала из
искомого решения (в результате чего получающиеся интегралы
будут сходящимися).
ВЛИЯНИЙ 8ЙЕШНЕЙ СРЕДЫ ЙА РОСТ ТРЕЩИН
Приведем некоторые значения, функций/i(|) и/г
[ГЛ. Vil
6.
h
h
0
2,02
1,98
0,5
0,74
1,04
1
0,48
0,76
1,5
0,36
0,61
2,5
0,23
0,44
5
ОЛЗ
0,27
10
0,07
0,16
15
0,05
0,11
20
0,04
0,09
30
0,03
0,06
40
0,02
0,05
100
0,008
0,0015
Функции /i(|) и /г(|) при больших I ведут себя так:
/,(8=0,816/1, /2(|) = 0,153/| (&-¦ оо).
Складывая выражения G.28) и G.29), находим искомое рас-
распределение*) внутреннего концентрационного напряжения ау
на продолжении трещины вдоль у = О, х > 0:
Заметим, что рассмотренная задача в математическом плане
идентична аналогичной задаче термоупругости о внутренних на-
напряжениях в пространстве с полубесконечным разрезом с. ис-
источником тепла постоянной интенсивности Q, расположенным
в конце разреза. Последняя задача представляет, в частности,
интерес при больших скоростях нагружения, когда тепло, выде-
выделяемое в конце неподвижного разреза вследствие локальных
пластических деформаций, создает градиенты температуры вбли-
вблизи конца разреза. ¦
Приведенный анализ внутренних напряжений можно исполь-
использовать для нахождения зависимости средней скорости роста тре-
трещин dl/dt от коэффициента интенсивности напряжений Ki, если
рост трещины происходит скачками, большими по сравнению
с размером пластической области в конце трещины.
4. Пороговый коэффициент интенсивности напряжений **).
Медленный рост трещин происходит только при значениях Ki,
изменяющихся от Kiscc до Kie-
*) Изложенный метод решения соответствует отбрасыванию некоррект-
некорректного моментного решения и выделению корректного решения с характерной
.корневой особенностью, представляющей интерес для механики разрушения.
**) Естественной нижней границей значения Кисе, очевидно, является
вязкость разрушения наводороженного металла k\c. Однако величина k\c,
по-видимому, очень мала, так как она отвечает почти полному отсутствию
пластических деформаций металла, т. е. теоретической вязкости разрушения,
которая в 10—100 раз меньше наблюдаемой (см. табл. 2.2 в гл. II, а также
Приложение 11).
S3] ' РОСТ ТРЕЩИН ПОД ДЕЙСТВИЕМ ВОДОРОДА (ТЕОРИЯ) 385
Наличие порогового коэффициента интенсивности напряже-
напряжений KiSCc в рамках описанной математической модели можно
объяснить так. С уменьшением коэффициента Ki уменьшается
раскрытие трещины 2v0 {vo~ Ki) и уменьшается поток прото-
протонов Q, поступающих в металл (Q = r\v0). С уменьшением рас-
раскрытия трещины становится существенной вязкость газа (или
жидкости). Напомним, что расход вязкой жидкости через узкую
плоскую щель прямо пропорционален кубу ширины щели и об-
обратно пропорционален длине щели. Как только раскрытие тре-
трещины 2v0 становится сравнимым с длиной свободного пробега
молекул окружающего газа, механизм движения газа.в полости
трещины резко изменяется (вместо гидродинамического меха-
механизма— кнудсеновская диффузия разреженного газа).
Напомним, что когда ширина канала меньше длины свобод-
свободного пробега молекул, число молекул, проходящих через канал
в единицу времени, убывает с увеличением длины канала обрат-
обратно пропорционально длине канала и прямо пропорционально
квадрату его ширины. Молекулы газа движутся независимо
друг от друга, причем компоненты смеси протекают так, как
если бы они были взяты'в отдельности и других компонентов не
было. Течение определяется парциальным давлением компонента
и не зависит от общего давления газовой смеси.
В случае воды или влажных газов непосредственно вблизи
вершины трещины, по-видимому, всегда имеется слой газа *), за
которым следует жидкий мениск. Действительно, вода обычно не
смачивает металл, поэтому капиллярная сила будет противодей-
противодействовать движению воды в узкую щелв. Критическая ширина
щели имеет порядок у/р, где у — коэффициент поверхностного
натяжения жидкости, ар — давление жидкости в мениске. При
нормальных условиях (температура 300 °К, давление 1 атм) эта
величина для воды имеет порядок 10~4 см. В этом случае водо-
водород доставляется в вершину трещины из насыщенной водяным
паром прослойки газа.
Например, в случае стали Н-11 имеем (см. рис. 148)
Kic= 140 кГ/ммт, /СЬсс = 60 кГ/мм3'2
(as= 160 кГ/мм\ E = 2- 104 кГ/мм2).
По формуле D.109) отсюда находим
при Ki==Kic 2ио = 3-1О~4 см,
при Ki==KiscC 2у0 —5- 10~5 см.
*) В случае смачивания этот слой газа отсутствует.
13 Г, П. Черепанов
386 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
Вычислим величину свободного пробега к молекул водорода
при нормальных условиях (диаметр молекулы s — 10~8 см):
У~ф _ ysRT/ц — 1840 м1 сек, R^2 калЦград ¦ моль),
п = ЪрЦтп?) = 3 • 1019 \/см3, А = 0,2/(ras2) = 7 • 10~5 см.
Здесь ц = 2 — молекулярный вес водорода; /п = 3,4-10-24 г —
масса молекулы водорода. Как видно, длина свободного пробега
получается близкой к величине раскрытия трещины при Кг =
= Klscc-
На основе сформулированной математической модели явле-
явления оценим время т, прошедшее от момента включения источ-
источника протонов до первого скачка трещины на расстояние deo (ин-
(инкубационный период); формула G.15) дает
х=а2ео[40Р(к\!кШ~\ G.31)
Здесь функция F определяется соотношением G.24) (см.
рис. 159).
Так как F(x) убывает с уменьшением х, то инкубационный
период, согласно G.31), возрастает с уменьшением коэффи-
коэффициента интенсивности напряжений. Существует критическое зна-
значение коэффициента интенсивности напряжений Кг* такое, что
при Кг > Кг* раскрытие трещины достаточно велико и газ (жид-
(жидкость), текущий в полости трещины, можно считать идеальным;
в этом режиме расход газа будет прямо пропорционален ширине
щели, и коэффициент ц в формуле G.18) не зависит от раскры-
раскрытия трещины и коэффициента интенсивности напряжений. При
Кг < Кг* механизм движения газа меняется (вязкое течение,
кнудсеновская диффузия и т. п.); при этом расход газа будет го-
гораздо сильнее зависеть от ширины щели, и коэффициент ц будет
уменьшаться с уменьшением v0 и Кг. В последнем режиме с
уменьшением Кг инкубационный период, согласно G.31), возра-
возрастает гораздо быстрее, чем в первом режиме; например, в про-
простейшем случае вязкого течения будет
т] ~ vq ~ /Сь т ~ \/F (х), где х ~ Кь
Таким образом, если время опыта меньше инкубационного
периода т, то соответствующий коэффициент интенсивности на-
напряжений будет зафиксирован как пороговый, т. е. как Късс-
В реальных системах во внешней среде всегда имеются ве-
вещества (например, кислород), способные вступать в реакцию
с металлом и образовывать твердые окисные пленки. Поэтому
параллельно с процессом диффузии водорода всегда идет кон-
конкурирующий процесс нарастания коррозионной пленки в вер-
вершине трещины. Как только пленка достигает критической тол-
§ 3] РОСТ ТРЕЩИН ПОД ДЕЙСТВИЕМ ВОДОРОДА (ТЕОРИЯ) 387
щины, доступ водорода в металл через вершину трещины пре-
прекращается. Для нарастания пленки необходимой толщины тре-
требуется определенное время, которое, очевидно, тем меньше, чем
меньше окислителя содержит внешняя среда.
Отсюда следует, что если инкубационный период, определяе-
определяемый формулой G.31), больше времени, требуемого для нара-
нарастания коррозионной пленки критической толщины, то механизм
распространения трещины будет иным, например, трещина мо-
может зарасти коррозионной пленкой и вообще не развиваться в
дальнейшем. Смешанный механизм, по-видимому, является наи-
наиболее общим. Влияние коррозионных пленок на рост трещин
рассматривается далее, в § 6.
На основе развитых представлений легко понять также кар-
кардинальное различие в докритическом поведении сквозных тре-
трещин в толстых и тонких пластинах (см., например, рис. 154).
Действительно, сравним основные параметры докритического
развития трещин (скорость роста трещины и инкубационный пе-
период) для случаев плоской деформации и весьма тонкой пла-
пластины при одном и том же коэффициенте интенсивности напря-
напряжений.
Уровень растягивающих напряжений в пластической области
в случае плоской деформации примерно в три раза выше, чем
в случае плоского напряженного состояния (напомним, что на-
напряжение ау в вершине трещины равно as для тонких пластин и
3<js для плоской деформации). Поэтому внешние нагрузки, при-
приложенные к границе кругового упругого ядра вблизи конца тре-
трещины, будут примерно в три раза выше в случае плоской де-
деформации; следовательно, коэффициент интенсивности напряже-
напряжений ki и число гц (см. формулу G.16)) для плоской деформации
будут приблизительно в три раза больше, чем для плоского на-
напряженного состояния. Отсюда, согласно G.17), следует, что по-
постоянная de0 для плоской деформации примерно в десять раз
меньше соответствующей постоянной для плоского напряженного
состояния.
Согласно формулам D.98) и D.109), величина vq (а также
Tfc и /Сю2 в формулах G.21) и G.23)) для тонкой пластины
примерно в два раза больше, чем для плоской деформации. Со-
Соответственно функция F, фигурирующая в формулах G.31) и
G.23), на основании рис. 159, будет как минимум в несколько
раз меньше для плоской деформации по сравнению с плоским
напряженным состоянием.
Собирая вместе эти оценки, из формул G.31) и G.23) полу-
получаем следующие результаты: а) инкубационный период в слу-
случае плоского напряженного состояния как минимум на два — три
порядка больше, чем в случае плоской деформации, б) скоро-
скорости докритического развития трещин в обоих случаях будут
18*
388 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
примерно одного порядка. За столь (относительно) длительный
инкубационный период конкурирующий коррозионный процесс
может свести к нулю диффузию водорода в металл через конец
трещины.
Таким образом, докритический рост трещин вследствие диф-
диффузии водорода гораздо более опасен в условиях плоской дефор-
деформации, чем в случае сквозных трещин в тонких пластинах. Из-
Изложенная теория может описывать также, в принципе, охрупчи-
вающее действие других сред, например азота.
§ 4. Адсорбционный эффект
Некоторые жидкие и газообразные среды существенно
влияют на прочность и пластичность твердого тела при одном
лишь поверхностном взаимодействии (при полном отсутствии
объемной диффузии и коррозионных явлений). После удаления
такой среды материал обычно восстанавливает свои прочностные
и деформативные свойства (если только в нем не появились тре-
трещины). Явление такого чисто поверхностного взаимодействия
твердого тела со средой называют адсорбционным эффектом.
Внешнюю среду, вызывающую адсорбционный эффект, назы-
называют поверхностно-активной (по отношению к данному телу).
Адсорбционный эффект начали изучать свыше пятидесяти лет
назад. В настоящее время по этому вопросу имеется богатая ли-
литература, содержащая много эмпирических данных (отметим ос-
основные монографии [16870]).
1. Опытные данные. Остановимся вначале на принципиаль-
принципиальных результатах экспериментов, которые будут положены в ос-
основу теоретической модели.
Некоторые поверхностно-активные среды могут пластифици-
пластифицировать твердое тело, т. е. уменьшать предел текучести (при рас-
растяжении образца с постоянной скоростью), либо увеличивать
скорость ползучести (при испытаниях с постоянной нагрузкой).
К таким средам относятся, например, растворы органических
кислот, спиртов и т. п. по отношению к олову, свинцу, алюминию
и другим металлам. Другие среды вызывают охрупчивание тела,
т. е. способствуют развитию в нем трещин и уменьшению проч-
прочности. По отношению к твердым металлам такими средами яв-
являются, например, расплавы некоторых других, более легкоплав-
легкоплавких металлов. В некоторых случаях среда способна вызвать
самопроизвольное диспергирование твердого тела на мелкие ча-
частицы (например, олово в присутствии жидкого галлия).
В дальнейшем для определенности будем рассматривать
лишь охрупчивающиеся системы твердый металл — жидкий ме-
металл, которые наиболее изучены.
Приведем основные опытные факты [170]..
АДСОРБЦИОННЫЙ ЭФФЕКТ
889
а) Смачивание твердого металла расплавом. Если на поверх-
поверхность растягиваемого металлического образца поместить каплю
поверхностно-активного расплава, то охрупчивающий эффект
проявляется тем сильнее, чем меньше краевой угол смачивания.
Вся поверхность разрушения оказывается всегда покрытой рас-
расплавом.
б) Избирательность действия жидких металлов. Охрупчива-
ние наблюдается лишь для определенных пар жидкий металл —
твердый металл. Некоторые такие пары приводятся в табл, 7.2,
взятой из книги [17°].
Таблица 7.2
Охрупчивание в некоторых системах металл — металл
Конструкцион-
Конструкционные сплавы
Сплавы алю-
алюминия
Сплавы маг-
магния
Сталь
Сплавы титана
Hg»)
30
X
0
0
X
Ga
50
X
0
0 .
0
Жидкие металлы и температура
Na
J25
X
X
0
0
In
180
X
0
X
0
Li
210
0
0
X
0
Se
250
0
0
0
0
Sn
260
X
0
0
0
BI
300
0
0
0
0
испытания, °С
Tl
325
0
0
0
0
Cd
350
0
0
X
X
Pb
380
0
0
0
0
Zn
450
X
X
X
0
Те
475
—
—
><
*) амальгама Hg — 3% Zn, X — возникновение охрупчивания, 0 — от-
отсутствие охрупчивания.
в) Характер явления. Возникновение" трещин под воздей-
воздействием жидких металлов обусловлено не диффузией или проник-
проникновением жидкого металла по границам зерен*), а процессами,
развивающимися на первоначальном участке непосредственного
контакта твердого и жидкого металла.
г) Закономерности развития трещин. Скорость распростра-
распространения трещин определяется характером течения жидкого метал-
металла по поверхности твердого тела и в трещине под действием сил
поверхностного натяжения; конечный размер образующихся тре-
трещин (точнее, их общая поверхность) определяется количеством
жидкого металла.
*) Межкристаллитное проникновение жидкого металла встречается край-'
не редко; оно вызывает весьма сильное охрупчивание (пример: система алю-
алюминий—жидкий галлий).
390
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VII
6.,иПт
д) Влияние локальных напряжений и деформаций. Возникно-
Возникновение трещин в твердом металле в некоторой точке контакта
жидкий металл — твердый металл не зависит от локальных на-
напряжений и деформаций твердого металла в этой точке. В част-
частности, скорость роста трещины и локальное разрушение в ее
конце не зависят от коэффициента интенсивности напряжений
в вершине трещины.
е) Влияние внешних нагрузок. Трещины, начинающиеся все-
всегда в том месте, где находится калля расплава, возникают лишь
после того, как приложенная нагрузка достигнет некоторого кри-
критического значения. Трещины обычно образуются в области рас-
растягивающих напряжений, причем чем больше (растягивающая
или изгибающая) внешняя нагрузка, тем меньшая область твер-
твердого металла вблизи капли расплава будет пронизана трещи-
трещинами (зато тем больше число трещин). Если приложенная на-
нагрузка меньше критической, разрушение происходит лишь через
некоторое время, как в испытаниях на длительную прочность.
С увеличением скорости деформи-
деформирования охрупчивающий эффект
уменьшается.
Особенно поразительны факты
д) и е), которые представляются
противоречивыми и взаимоисклю-
взаимоисключающими. Поэтому в подтвержде-
подтверждение их проанализируем результаты
соответствующих опытов, описан-
описанных в книге [17°].
Опыт 1 (гл. 4 книги [170]). Листо-
Листовые образцы толщиной 2 мм из
алюминиевого сплава 2024-Т4 под-
подвергались одностороннему однород-
однородному растяжению. Образцы с обеих
сторон имели V-образные выточки,
расположенные на оси, перпенди-
перпендикулярной к направлению растяже-
растяжения; глубина выточек была одина-
одинаковой, разными были лишь радиу-
радиусы кривизны при их вершинах. Перед испытанием в районе вы-
выточки наносилась ртутная амальгама (температура испытаний
была 100 °С). На рис. 160 приведены результаты измерения
разрывающего напряжения ав на бесконечности в зависимости
от радиуса кривизны вершины выточки г. Светлые кружки
соответствуют опытам без- ртутного покрытия, темные круж-
кружки— опытам в присутствии ртутного покрытия (точки при
г = сю представляют результаты опытов с образцами без вы-
выточек).
го-
Ш о,1
г, мм
Рис. 160.
§4]
АДСОРБЦИОННЫЙ ЭФФЕКТ
391
Напряжения и деформации в вершине выточки, очевидно, су-
существенно превышают соответствующие величины вдали от вы*
точки, однако, как видно, разрушение совершенно не связано
с наличием выточки, а определяется лишь величиной напряже-
напряжения на бесконечности (выводы д) и е)).
Опыт 2 (гл. 7 книги [170]). Полосы отожженной латуни
70/30% размером 0,5X300X400 мм подвергались одноосному
растяжению. Ртуть наносилась в центре поверхности образца
широкой поперечной полосой, направление которой перпендику-
перпендикулярно оси растяжения. В центре полосы наносилось углубление,
из которого начинала расти трещина, распространяющаяся в обе
стороны к краям образца. Измерялись длина трещины и необхо-
необходимая для ее развития нагрузка; в случае необходимости разви-
развитие трещины приостанавливали, уменьшая нагрузку на образец.
На рис. 161 приведены результаты измерений растягивающей
нагрузки а, необходимой для развития трещины, в зависимости
от /-'/» (/ — длина трещины) при нане-
нанесении ртути с обеих сторон пластины.
б, нГ/мм2 -
16 [ i i i i I ' i i .
13
о
О О О ~ .
о * °
О°оп8 о ° ° о о п
I 1 | | i i [_
OftB ОД * 0,22
в, нГ/ммг
14
13
12
II
10
i
-
-
о
0
0
о
о
1
1
е
-
-
1
42
й*
Рис 161.
Рис. 162.
На рис. 162 приведены результаты аналогичных измерений
при нанесении ртути на одну сторону пластины. Отмечалось, что
в этом случае вблизи конца трещины с той стороны образца, ко-
которая не смачивалась ртутью, были заметны пластические де-
деформации.
Данные рис. 161 полностью подтверждают выводы д) и е).
Результаты, приведенные на рис. 162, слегка расходятся с этими
выводами (с увеличением длины трещины от 6 мм до 160 мм
внешняя нагрузка, необходимая для распространения трещины,
уменьшилась с 14 кГ/мм2 до 10 кГ/мм2, т. е. примерно на 30%).
Это расхождение, очевидно, объясняется некоторым влиянием
392 ' ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
на локальное разрушение концентрации напряжений и деформа-
деформаций с той стороны пластины, которая не была смочена ртутью.
Общепринятое объяснение адсорбционного эффектарсновано
на теории Гриффитса. Оно состоит в следующем: жидкий рас-
расплав, проникая в вершину трещины, понижает поверхностную
энергию и вязкость разрушения материала, вследствие чего про-
происходит локальное охрупчивание и преждевременное хрупкое
разрушение при низких напряжениях. Описанные опыты и сфор-
сформулированные на их основе выводы д) и'е) показывают, что
применение теории Гриффитса к этому явлению неправомерно;
теория Гриффитса и все излагаемые до сих пор вопросы меха-
механики хрупкого разрушения основаны на том соображении, что
развитие трещины и разрушающая нагрузка полностью опреде-
определяются локальной концентрацией напряжений и деформаций
в вершине трещины*).
2. Теоретическая модель. Будем исходить из модели твердого
тела, основанной на следующих представлениях.
Рассмотрим совокупность материальных точек (атомов), в
которой взаимодействие любых двух точек описывается некото-
некоторым потенциалом, зависящим только от расстояния между этими
точками (включающим силы отталкивания на малых расстоя-
расстояниях и силы притяжения на больших расстояниях, см. рис. 5).
Если потенциал всех парных взаимодействий задан, то (посколь-
(поскольку каждая равновесная конфигурация этих частиц отвечает оп-
определенной точке минимума общего потенциала системы) в
принципе можно найти все возможные устойчивые структуры.
В частности, если число частиц бесконечно, можно определить
возможные периодические структуры (т. е. элементарную ячейку
идеального кристалла). Если число частиц конечно, то устойчи-
устойчивая структура будет занимать некоторый объем в пространстве,
причем периодическое расположение частиц уже невозможно.
В приповерхностном слое частицы -будут расположены менее
плотно, и связи в тангенциальном направлении будут растянуты
сильнее, чем в глубине тела.
Обозначим через Fm8LX предельную силу натяжения одной свя-
связи в поверхностном слое. Для простоты ее можно считать такой
*) Авторы книги [|то] тоже анализируют свои опыты с позиций теории
Гриффитса. Они считают, что наклон прямой, проведенной через опытные
точки на рис. 161 и 162, с точностью до постоянного множителя представляет
собой вязкость разрушения; исходя из этого, они оценивают ее величину в
присутствии ртути. Однако это недоразумение, так как, согласно формуле
Гриффитса D.15), указанная прямая должна проходить через начало коор-
координат (сГ, /"'/2). В силу этой формулы пря увеличеяии длины / в 26 раз (что
имело место в опытах) нагрузка должна была бы уменьшиться в 5 раз. По
более точной формуле, учитывающей краевой эффект, уменьшение нагрузки
было бы еще более значительным.
§ 4] АДСОРБЦИОННЫЙ ЭФФЕКТ 393
же, как для идеальной решетки (см. гл. II). Например, на осно-
основании формул B.35) можно ориентировочно принять
F «* 0, \Ea\, G.32)
где Е — модуль Юнга, по — межатомное расстояние. Если счи-
считать толщину поверхностного слоя равной а0, отсюда можно по--
лучить следующую оценку для величины предельного натяжения
слоя, отнесенного к единице длины (вдоль поверхности):
уП = FmiX/a0 « 0,1 Еа0. G.33)
Эта оценка годится также для жидкостей. Отметим, что поверх-
поверхностный слой жидкости в силу ее текучести всегда находится в
предельном состоянии; поэтому формула G.33) дает оценку по-
поверхностного натяжения жидкости.
У твердых тел предельное натяжение связи реализуется толь-
только в момент разрыва поверхностного слоя. В докритическом со-
состоянии натяжение поверхностной связи существенно меньше
^шах (в противном случае на поверхности твердого тела само-
самопроизвольно, т. е. в отсутствие внешних сил, могли бы образовы-
образовываться разрывы-трещины).
Натяжение поверхностной связи F зависит не только от при-
природы тела, но и от природы внешней среды, с которой рассма-
рассматриваемое тело находится в контакте. Наличие любой среды
всегда разгружает поверхностный слой и уменьшает натяжение
связей по сравнению с вакуумом. Сама по себе разгрузка по-
поверхностного слоя может лишь увеличивать
прочность твердого тела, так как часть внешней
нагрузки берет на себя адсорбционный слой
внешней среды.
В некоторых случаях силовое влияние внеш- ___.„______
ней среды может выходить далеко за пределы ' '
границы поверхностного слоя. Пусть, например,
полость трещины, выходящей на поверхность
тела перпендикулярно к направлению растяже-
растяжения, целиком заполнена жидкостью (рис. 163).
Так как модуль Юнга жидкостей значителен, PliCt 163-
жидкая среда примет на себя часть растягиваю-
растягивающих нагрузок и может существенно уменьшить коэффициент ин-
интенсивности напряжений в конце трещины. Если модуль Юнга
жидкости, полностью смачивающей полость трещины, равен мо-
модулю Юнга твердого тела и плоскость трещины является пло-
плоскостью симметрии задачи, то коэффициент интенсивности на-
напряжений должен, в принципе, исчезать, и трещина как бы
закрывается. Таким образом, в данном гипотетическом случае
эффект разгрузки связей внешней средой приводит к много-
многократному увеличению прочности тела.
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VII
В этом рассуждении не была учтена прочность контактирую-
контактирующей внешней среды. Посмотрим, к чему приводит учет этого
фактора.
Если на боковую поверхность растягиваемого цилиндриче-
цилиндрического образца нанести твердое покрытие (например, лак, краску
и т. п.), более жесткое и хрупкое, чем основной материал, то в
покрытии возникнут преждевременные трещины, которые могут
служить источником разрушения всего образца. Более мягкое и
пластичное твердое покрытие может лишь упрочнить тело.
Прочность жидкостей в реальных уловиях обычно во много
раз меньше прочности твердых тел. Источниками разрушения
жидкости служат микроскопические полости, образующиеся
вследствие тепловых флуктуации молекул; однако разрыв (тре-
(трещина) в жидкости может существовать лишь очень короткое
время, порядка времени релаксации. Следовательно, в адсорб-
адсорбционном слое жидкости, подвергающемся некоторому растяже-
растяжению вместе с твердым телом от внешних нагрузок, будут воз-
возникать разрывы-трещины; частота их появления существенно за-
зависит от энергии активации этого флуктуационного процесса Uo,
от величины растягивающего напряжения в жидкости о/ и от аб-
абсолютной температуры Т. Среднее время между разрывами
равно
т = т0 ехр [(?/0 — yOf)/(RT)]
(т0 «« 10~12 сек, R «* 2 кал/(град • мо^ь)). '
Вычислим величину о> Обозначим через 5 площадь общего
контакта жидкого покрытия с твердым телом до приложения
внешних нагрузок (рис. 164).
Вследствие деформации по-
после приложения растягиваю-
растягивающих нагрузок к твердому
телу площадь области кон-
контакта станет равной 5 + AS
(при вычислении А5 влия-
влиянием тонкого адсорбционно-
адсорбционного слоя жидкости можно
пренебречь).
Рис. 164. Адсорбционную пленку
будем представлять себе
двумерной упругой жидкостью, т. е. телом, занимающим некото-
некоторую поверхность в пространстве; упругое натяжение пленки у/
в каждой точке одинаково (у/ = hof, где h — толщина адсорб-
адсорбционного слоя, Of — среднее напряжение в слое на площадке,
нормальной к поверхности}. Такое представление отражает ос-
основные особенности реального адсорбционного слоя, для кото-
которого характерны большие градиенты механических свойств по
§ 4] АДСОРБЦИОННЫЙ ЭФФЕКТ 395
нормали к поверхности и неизменность этих свойств вдоль по-
поверхности слоя.
Исходя из этой модели, получаем
G.35)
Здесь ks — упругая постоянная адсорбционного слоя, аналогич-
аналогичная модулю объемной упругости жидкости.
Например, в случае, когда жидкое покрытие нанесено на бо-
боковую поверхность растягиваемого призматического образца,
имеем
и of = ksa/E, G.36)
где а — растягивающая нагрузка. Если образец имеет, выточку
или трещину и жидкое покрытие нанесено в районе выточки (на-
(например, как на рис. 164), то влияние выточки на величину о> ска-
скажется только в том случае, когда весь расплав расположен вбли-
вблизи вершины выточки. Если же область контакта велика или даже
сравнима с глубиной выточки, то без большой ошибки можно
пользоваться формулой G.36). В случае малой области контакта
около вершины необходим точный расчет, основанный на реше-
решении соответствующей упругой или упруго-пластической задачи.
В случае, когда жидкость заполняет полость трещины, распо-
расположенной перпендикулярно к направлению растягивающего на-
напряжения а (рис. 163), в жидкой среде возникает напряжение
всестороннего растяжения а/, которое нетрудно вычислить. Про-
Проведем такой расчет, для простоты ограничившись случаем задачи
Гриффитса (см. гл. IV, § 1, формулы D.17)). Согласно этим
формулам, увеличение объема Аи полости трещины, приходяще-
приходящегося на единицу длины в направлении нормали к плоскости ри-
рисунка, равно
Av = ^2±±L(o-of)E G.37)
Так как
of = kvAv/V0, G.38)
где kv — модуль объемной упругости, т. е. vdp/dv, то отсюда и
из G.37) находим
я (к +
Здесь Vo — начальный объем полости (в расчете на единицу дли-
длины вдоль оси z).
Величина растяжения жидкости в трещине согласно G.39) и
G.36) значительно больше растяжения адсорбционной пленки
(примерно в l/v раз, где / и v — длина и среднее расстояние ме-
между берегами трещины). Поэтому разрывы жидкости в этом
.366 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
случае согласно G.34) будут происходить весьма часто (так как
величина Uo — yof мала). Следовательно, процесс роста трещины
можно считать атермическим.
Изучим теперь влияние разрыва, происшедшего в жидкости,
на твердое тело. Если жидкость не смачивает твердое тело, то
острая трещина разрыва, достигнув поверхности твердого тела,
сразу закрывается, так как краевой угол а в состоянии равнове-
равновесия больше я/2. Если же жидкость смачивает твердое тело, то
после того как фронт трещины дойдет до поверхности тела, бе-
берега трещины вблизи поверх-
поверхности раскроются, образуя
клин с углом я— 2а (рис. 165).
а{ ^у ^s Y Величина угла а примерно
А ¦ в равна краевому углу смачива-
смачивания, меньшему я/2.
Рис- 165- Обозначим через y величи-
величину поверхностного натяжения
жидкости. Если у достаточно велико, а а достаточно мало, то
может произойти разрыв связи АВ. Условие разрыва связи за-
запишется в следующем виде:
аоу cos a > Fmix — F. G.40)
Напомним, что Fmax и F означают предельное и равновесное
натяжения поверхностной связи твердого тела. Значение F
уменьшается с увеличением температуры и с ростом растягиваю-
растягивающих нагрузок, поскольку и то и другое приводит к увеличению
среднего межатомного расстояния (и к ослаблению связей). Од-
Однако, если температура далека от температуры плавления, изме-
изменение F будет сравнительно мало (примерно на два порядка
меньше, чем изменение поверхностного натяжения жидкостей в
том же диапазоне температур, так как температурное расшире-
расширение жидкостей приблизительно на два порядка ниже, чем у твер-
твердых тел). Это замечание тем более справедливо для внешних
нагрузок.
На основании G.40) и G.33) можно получить также следую-
следующую оценку:
Y cos а > цЕа0, G.41)
где т| — некоторый коэффициент, меньший 0,1 и зависящий от
структуры поверхностного слоя.
После разрыва поверхностной связи образовавшаяся микро-
микрополость заполняется молекулами жидкости, которые окажутся
под действием еще больших растягивающих напряжений; в ре-
результате частота разрывов жидкости в этом месте увеличится.
Полость превращается в трещину, растущую по атермическому
механизму последовательного разрыва связей в ее конце (на-
.41
АДСОРБЦИОННЫЙ ЭФФЕКТ
397
пример, по двухэтапной схеме, как изображено на рис. 166). Ча-
Частота разрывов жидкости вблизи конца трещины так велика, что
рост трещины практически происходит сразу же, как только
жидкость достигает конца трещины; поэтому скорость развития
трещины-определяется (наиболее медленным) процессом гидро-
гидродинамического и миграционного движения жидкости в полости
трещины.
Рис. 166.
Количественное описание перемещения жидкости в данном
случае затрудняется тем, что наряду с большой и быстро расту-
растущей трещиной, выросшей от первоначального разрыва в наибо-
наиболее слабом месте, огромное число трещин должно Возникать на
берегах трещины (и поверхности тела). Это вытекает из изло-
изложенной теоретической схемы, поскольку для разрыва поверх-
поверхностных связей твердого тела достаточно растянутой пленки
смачивающей жидкости. Очевидно, что чем выше уровень на-
нагрузок, тем большее число трещин возникает в твердом теле.
При этом будут развиваться только такие трещины, плоскость
которых перпендикулярна направлению растягивающих напря-
напряжений.
Если нагрузку существенно уменьшить, скорость роста тре-
трещины может упасть весьма значительно, так как трещина закры-
закрывается и, кроме того, согласно G.34), увеличивается время
между последовательными разрывами жидкости.
Естественно, что никакой корреляции с коэффициентом интен-
интенсивности напряжений в данном случае нет.
В идеализированных случаях одиночной трещины или же од-
одной большой трещины с берегами, равномерно покрытыми боко-
боковыми трещинами, конечная длина основной трещины будет
прямо пропорциональна исходной массе расплава (однако коэф-
коэффициент пропорциональности будет различным в этих двух слу-
случаях). Если боковые трещины расположены неравномерно
(обычно они сгущаются к концу магистральной трещины), то за-
зависимость получится более сложная.
393 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
Данная теоретическая модель позволяет объяснить все ука-
указанные выше особенности хрупкого разрушения металлов под
действием расплавов*). Остановимся лишь на влиянии выточек
и трещин (опыты 1 и 2). Так как ртутная амальгама наносилась
широкой полосой, то напряжение а/ в адсорбционном слое мало
отличалось от соответствующего напряжения в отсутствие выточ-
выточки; поэтому при одной и той же скорости нагружения разрыв
адсорбционного слоя происходил при- одинаковом уровне внеш-
внешних нагрузок. При малых размерах площадки контакта влияние
локальной концентрации напряжений должно сказываться, од-
однако в этом случае следует ожидать большого статистического
разброса данных.
Формула G.34) позволяет с единой точки зрения объяснить
замедленное разрушение и влияние скорости нагружения. При
этом на основании излагаемой теории на диаграмме длительной
прочности In т — ев общем случае следует ожидать двух харак-
характерных участков с различными U и у (отвечающих разрывам
жидкого покрытия при малых а и разрывам самого металла при
достаточно больших а).
Модель годится также для объяснения адсорбционного
эффекта газообразных внешних сред в силу близкого сход-
сходства свойств их адсорбционных слоев с адсорбционным слоем
жидкости.
В том (более частном) случае, когда условие G.40) не вы-
выполняется, внешняя среда оказывает пластифицирующее дей-
действие. При этом разрыв связи АВ может произойти лишь тогда,
когда к ней подойдет достаточно мощная дислокация (так что
вследствие концентрации напряжений величина F увеличится и
условие G.40) окажется выполненным).
§ 5. Развитие коррозионных трещин
(химическая коррозия под напряжением)
Все твердые тела находятся в контакте с жидкой или газооб-
газообразной средой, как правило, содержащей активные компоненты,
вступающие в химическую реакцию с активными компонен-
компонентами твердого тела. С течением времени тело покрывается плен-
пленкой, состоящей из твердых продуктов реакции [171> 172]. Физиче-
Физические и химические свойства этой пленки существенно отличны
от свойств тела (в частности, прочность ее обычно мала по срав-
сравнению с прочностью металла). В результате равномерного нара-
нарастания коррозионной пленки фактическое рабочее сечение метал-
*) Для точного ответа на вопрос о возможности хрупкого разрушения
достаточно определить для данной пары константы До, Y> &> •fmax и F в'фор-
муле G.40).
S 5] РАЗВИТИЕ КОРРОЗИОННЫХ ТРЕЩИН 399
лической конструкции уменьшается до такого уровня, когда оно
перестает выдерживать приложенную нагрузку. Эта проблема
сравнительно проста, так как подобную общую коррозию обычно
нетрудно заметить и рассчитать. Гораздо коварнее в этом отно-
отношении избирательная коррозия и коррозия под напряжением.
В поле растягивающих напряжений фронт коррозии обычно не-
неустойчив, поэтому коррозия под напряжением развивается в виде
межкристаллитных или внутрикристаллитных трещин почти без
всяких видимых признаков образования продуктов коррозии.
Развиваясь, трещины достигают критического размера и приво-
приводят к хрупкому разрушению конструкции.
Способность металлов к коррозионному растрескиванию под
напряжением имеет существенно избирательный характер, т. е.
один и тот же материал корродирует в одних средах и не корро-
корродирует в других. В Приложении III приведены некоторые пары
материал ¦— среда, в которых возникает растрескивание мате-
материала под напряжением. Впервые подобная таблица была со-
составлена Джонсоном, использовавшим материалы более 50 пуб-
публикаций (см. книгу Логана [172] *)). Чувствительность металлов
к коррозионному растрескиванию под напряжением зависит во
многих случаях от наличия примесей и от термической обработ-
обработки материала. Толщина пленок колеблется в пределах 10~7 —
10~5 см. Чаще всего встречаются окисные пленки, образую-
образующиеся под воздействием кислорода и других окислителей, или
же под воздействием электрического тока. Однако могут быть
пленки совсем другой химической природы.
Согласно общефункциональному методу, скорость роста кор-
коррозионной трещины представляет собой некоторый функционал
по времени от коэффициента интенсивности напряжений в рас-
рассматриваемой точке контура трещины, если только выполняют-
выполняются условие тонкой структуры и гипотеза локальности разруше-
разрушения. При обычных предположениях получается зависимость
dl/dt = f(Ki), G.42)
где f — некоторая функция.
Наличие корреляционной связи G.42) получило к настоя-
настоящему времени основательное экспериментальное подтверждение
[72]. Упомянем лишь один наглядный опыт Джонсона и"Вилнера
[173], которые подвергли растяжению пластину из стали Н-11 с
центральной сквозной трещиной, помещенной в воду (темпера-
(температура испытания была 27 °С, сго,2 = 160 кГ/мм2). В процессе раз-
развития трещины нагрузка изменялась так, чтобы коэффициент
интенсивности напряжений оставался постоянным. На рис. 167
*) В книге Логана [172] содержится обзор около 700 работ по коррозион-
коррозионному растрескиванию, относящихся в основном к 1955—1965 гг, ""
400
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VII
Щемя, мин
Рис. 167.
изображен результат опыта при Кг = 76 кГ/мм'Ь. Как видно,
скорость роста коррозионной трещины остается постоянной для
всех длин трещины *). Корреляция между скоростью роста тре-
трещины и каким-либо напряжен
нием в образце отсутствует.
Если коэффициент интен-
интенсивности напряжений меньше
некоторого значения Кг$сс, тре-
трещина не растет. Это пороговое
значение коэффициента' интен-
интенсивности является постоянной
пары материал — среда. (Ве-
(Величины Кгкс для -некоторых
пар приведены в табл. 7.1.)
В то же время внешняя
среда не влияет на вязкость
разрушения; для многих систем это было экспериментально
доказано Штайгервальдом [174].
Рассмотрим два основных типа коррозионных пленок: жест-
жесткие и рыхлые пленки.
1. Тонкие жесткие пленки. Пусть на дне трещины, находя-
находящейся в поле растяжения, нарастает жесткая защитная пленка
твердого продукта реакции (рис. 168). Обозначим через-Д отно-
относительное изменение объема вследствие реакции в отсутствие
внешних напряжений, т. е. величину (V — Vo)/Vo, где Уо и У —
соответственно объем металла до и
после общей коррозии. Для плот-
плотных защитных пленок величина Д
обычно отрицательна. Толщину
пленки считаем малой по сравне-
сравнению с раскрытием трещины 2v0.
Образовавшаяся упруго-жесткая
пленка подвергается растяжению
напряжением as (основной материал считается идеальным
упруго-пластическим) и растягивающим напряжением — kvA
от усадки пленки, где &„ —модуль объемной упругости пленки.
Если прочность тонкой пленки ав меньше as — Akv, пленка
разорвется. Существенно, что разрыв пленки в этом случае
происходит при сколь угодно малой ее толщине; следовательно,
скорость роста трещины будет определяться процессом диффузии
вблизи ее конца и не будет зависеть от величины Кь Пластиче-
Пластическая область экранирует локальный процесс разрушения на дне
трещины от внешнего поля напряжений. В таких условиях роль
Рис. 168.
*) В данном примере рост трецущц р^ьясняется, по всей вероятности
наводораживанием, .... г
§ Ы РАЗВИТИЕ КОРРОЗИОННЫХ ТРЕЩИН 401
внешних напряжений (и коэффициента Ki) сводится к поддер-
поддержанию местной пластической зоны и к последовательному раз-
разрыву жесткой пленки на две трещины.
Обозначим через с0 концентрацию компонента О внешней
среды, участвующего в реакции с твердым телом, а через См —
концентрацию активного компонента М материала. Реакция про-
проходит в диффузионном слое с характерной толщиной d (см.
рис. 168). Считаем, что d ¦< 2v0; при этом задачу можно счи-
считать одномерной.
Запишем уравнения диффузии
nmx=Vt с„=сл-- r^J = n. dr.Jdt=ht*rt. G-44)
и граничные условия
при х -> — оо , с0 = сО0,
при х ->-+оо со = 0, -^ = ^0.
см*> [со\ = °> di
при л; < Vt cM = 0.
Здесь Z)o и Dm—коэффициенты диффузии компонентов О и М
соответственно, а и р — кинетические коэффициенты реакции,
k — константа скорости реакции, и — стехиометрический коэффи-
коэффициент, V — скорость роста трещины," со, и см, — начальные кон-
• центрации компонентов О и М, см* — концентрация компонента
М на границе твердого тела при х = Vt (на дне трещины).
Например, если происходит процесс нарастания окисной
пленки на металлической меди (М) под действием кислорода
воздуха (О) в соответствии с уравнением 2Си + Ог = 2СиО,
то согласно закону действующих масс а = 1, р = 2..
Грамм-атом меди составляет 64 г, а грамм-молекула кисло-
кислорода — 32 г. Так как, согласно уравнению химической,*реакции,
/на 1 г кислорода расходуется 4 г меди, то стехиометрический
коэффициент к в данном случае равен 4 (под концентрацией
понимается масса соответствующего компонента в единице объ-
объема). Ионы меди диффундируют к поверхности металла, моле-
молекулы кислорода — вглубь металла; твердый окисел меди обра-
образуется в диффузионном слое, относительная концентрация окис-
окисла возрастает с приближением к поверхности.
Однако следует иметь в виду, что закон действующих масс,
строго говоря, действителен только для гомогенных газовых сме-
смесей, поэтому под аир обычно понимают некоторые эмпириче-
эмпирические коэффициенты; при этом выражения для скорости реакции
; (последние члены в уравнениях G.43)) представляют собой не-
некоторую аппроксимацию скорости течения реальной "реакции,
402 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
которая может быть весьма сложной и многоэтапной. Так как
при х <CVt реакция не протекает, то k = 0 при х < Vt.
В такой постановке задачи имеются две трудности: а) зави-
зависимость коэффициентов диффузии от относительного содержания
металла и твердого продукта реакции в каждой точке (напри-
(например, величина Do в металле гораздо меньше, чем вблизи поверх-
поверхности коррозионной пленки), б) бесконечная протяженность
диффузионного слоя.
От этих недостатков можно избавиться, если ввести неизвест-
неизвестную подвижную границу при х = х\ (t) и искать разрывное при
х = Х\ решение задачи. Тогда вместо граничного условия при
х—> +оо в прежней задаче нужно поставить следующие краевые
условия на скачке:
при x = d d
(уравнения химической-кинетики),
(смо — См) dxi/dt = %Dodcoldx G.45)
(закон сохранения массы).
При х > х\ имеем с0 = 0, см = сМо-
Последнее условие G.45) служит для определения неизвест-
неизвестной функции Х\ (t); точно так же одно из лишних граничных ус-
условий при х = Vt в G.44) служит для отыскания неизвестной
скорости роста трещины V(t). В такой более точной постановке
задачи коэффициенты диффузии в диффузионном слое можно
считать постоянными.
Остановимся еще на определении концентрации см* на гра-
границе тела (см. G.44)). Если бы тело было ненапряженным, то
См* было бы равным нулю, так как в таком случае ничто не ме-
мешает полной коррозии компонента М. При наличии внешних на-
нагрузок упруго-пластический материал вблизи конца трещины
всегда находится в пластическом состоянии (в условиях конеч-
конечной плоской деформации растягивающее напряжение оу на дне
трещины приблизительно равно as). Пленка полностью прокор-
родировавшего металла, как предполагалось, не выдерживает
такого напряжения и разрывается; то же самое имеет место для
пленки с достаточно малым содержанием компонента М. Хими-
Химическая реакция приводит к замене прочного компонента М на
малопрочный продукт реакции ОМ.
Прочность сгв частично прокорродировавшего материала яв-
является некоторой функцией концентрации см:
Св = /Ы, G.46)
монотонно возрастающей с ростом сМ- В частности, при х = хи
когда см = ст, имеем crB > crs, а при см = 0 будет ав < а„.
§ 5] РАЗВИТИЕ КОРРОЗИОННЫХ ТРЕЩИН 403
Функцию Цсм) будем считать известной из дополнительно по-
поставленного опыта или же из дополнительных соображений. На-
Например, если компонент .М несет основную прочностную нагрузку
в исходном материале (так что влиянием других компонентов
на прочность можно пренебречь), то наиболее естественно в ка-
качестве функции / взять линейную зависимость
/ (см) = (вв)м см1р + (ав)ом WP> G-47)
где р — плотность среды, сОм — концентрация продукта реакции
ОМ (масса в единице объема), (оъ)м и (сгв)одг— прочность ком-
компонентов М и ОМ соответственно.
Таким образом, прочность волокон при удалении от поверх-
поверхности возрастает (рис. 168), так что на дне непрерывно расту-
растущей трещины должно выполняться условие предельного равно-
равновесия (с учетом усадки пленки)
as-k^ = f(cMf). G.48)
Это уравнение служит для определения величины см*- В про-
простейшем случае, пренебрегая усадкой и прочностью (сгв)одг, из
G.46) — G.48) находим
см* = posf(eB)M. G.49)
Итак, зависимость скорости роста трещины V от физико-хи-
физико-химических параметров среды находится из решения краевой за-
задачи G.43) — G.45). При помощи численных методов и ЭВМ
это решение в принципе всегда может быть получено с любой
точностью, если известны числовые значения параметров, входя-
входящих в задачу.
Напомним основные допущения, лежащие в основе развитой
'модели: а) Уо ^> d, б) разрыв пленки полностью прокорродиро-
вавшего металла на дне трещины происходит сразу после ее об-
образования. Первое допущение выполняется, по-видимому, в боль-
большинстве случаев, по крайней мере для металлов, так как в
металлах Уо^Ю^Ч-Ю см, a d~10-74-10-5 см. Можно пола-
полагать, что второе допущение для данной пары материал — среда
также выполняется, если в опыте на общую коррозию равно-
равномерно растягиваемого гладкого образца (без надрезов и тре-
трещин) наблюдается резкое увеличение скорости общей коррозии
при напряжениях, больших сго,2, по сравнению со скоростью кор-
коррозии образца в ненапряженном состоянии.
Наибольший интерес представляет стационарное решение
этой задачи, зависящее только от координаты
404 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
В этом случае скорость V должна определяться из решения
следующей краевой задачи:
при 0 < |< d
d2c dc dP'C dc
Do-W+V4T = k°aoCM> Dm-2F+V-?=> *44> G-50)
при | = 0
при g = d
При остальных g, очевидно, имеем
при | <0 со = ст
Ограничимся решением этой задачи в одном простом, но до-
достаточно важном случае, когда
<х=1, р = 0. G.51)
Этот случай реализуется для весьма малопрочных пленок и
высокопрочных металлов, когда (cfB)oM^tfs, a as близко к
(сгв)м, так что, согласно G.49), концентрация компонента М в
диффузионном слое меняется мало и скорость реакции можно
считать зависящей лишь от концентрации компонента О (реак-
(реакция первого порядка, т. е. а = 1,0 = 0).
Приведем получающееся в этом случае решение краевой за-
задачи G.50); при этом в целях простоты примем первоначальную
упрощенную постановку задачи и вместо граничного условия
при х = d будем требовать выполнения следующего условия на
бесконечности:
при|-> + оо со = 0, см = см0.
Так как градиенты, концентраций в диффузионном слое весь-
весьма велики, можно полагать, что это не скажется сколь-нибудь
существенно на величинах V и d, представляющих основной ин-
интерес. В результате получим
со = Соф-К1, см = ст - Ae-^ + {см* - ст + A) e~vllDM. G.52)
Здесь
2DQ
¦| 51 ¦ - РАЗВИТИЕ КОРРОЗИОННЫХ ТРЕЩИН 405
Скорость роста трещины V определяется следующим уравне-
уравнением: ¦
V (V + VV2 + AkD0) = 2kD0. G.53)
Единственный корень этого уравнения равен
V = 0,708 VkD0. G.54)
В Качестве толщины d диффузионного слоя (и коррозионной
пленки) примем то значение |, при котором концентрация ком-
компонента О уменьшится в е2 раз по сравнению с концентрацией
на границе; находим
d = 2/Л = 1,414 Y~Ddk. G.55)
Таким образом, в принятых допущениях скорость роста тре-
трещины, согласно формуле G.54), определяется константой скоро-
скорости реакции- k и коэффициентом диффузии Do- Аналогично мож-
можно рассматривать и более сложные случаи.
2. Толстые рыхлые пленки. До сих пор предполагалось, что
коррозионная пленка, образовавшись, сразу разрывается. Это не
так в том случае, когда прочность жесткой пленки больше as
(что, вообще говоря, маловероятно) или же если пленка более
податлива (рыхла), чем основной материал.
Допустим теперь, что по тем или другим причинам тонкая
пленка не разрывается. Тогда, очевидно, более толстые пленки
тем более не разрушаются*). В этом случае трещина не будет
развиваться при стационарных внешних нагрузках.
;! В предельном случае абсолютно податливой пленки все на-
напряжения в коррозионной пленке обращаются в нуль. При этом
роль коррозии сводится к расширению поперечных размеров по-
полости трещины и, в частности, к уменьшению остроты конца тре-
трещины. Это приводит к увеличению вязкости разрушения и, тем
самым, к упрочнению тела.
Однако рыхлые пленки в некоторых случаях могут значи-
значительно ослабить тело и даже при определенных условиях вы-
вызвать образование и рост трещин в отсутствие внешних нагру-
нагрузок. Дело в том, что в случае рыхлых пленок объем материала
после общей коррозии больше, чем до коррозии (при отсутствии
внешних нагрузок). Поэтому, если внутри тела имеются некото-
некоторые поверхности, вдоль которых происходит диффузия компо-
Вента О из внешней среды, то продукты реакции подобно клино-
Ьым дислокациям распирают тело и могут вызвать образование
*) В случае хрупких коррозионных пленок, толщина которых значительно
больше характерного раскрытия трещины, возможен также механизм роста
трещины, совершенно аналогичный описанному в § 3 этой главы (водородное
охрупчивание) и приводящий к характерной линейной диаграмме.
406
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ .ТРЕЩИН
[ГЛ. VII
трещин. Этот механизм, по-видимому, наиболее характерен так-
также для биокоррозии.
При наложении растягивающих нагрузок пленка сразу рвет-
рвется, и происходит рост трещины вдоль избранной поверхности.
Наличие таких избранных поверхностей обычно объясняется тех-
технологическими и металлургическими причинами (например,
неплотной стыковкой отдельных
узлов или преимущественным
сосредоточением вдоль этой по-
поверхности активного компонен-
компонента М).
Приведем простой пример.
Пусть слой компонента М толщи-
толщиной h расположен вдоль оси х
упругого полупространства х > О
(рис. 169). В результате химиче-
химической реакции компонента внеш-
Рис- 16Э- ней среды О с компонентом М
образуется слой продуктов кор-
коррозии длиной а (плоская задача). Давление, оказываемое про-
продуктами коррозии на упругое тело, равно
при у = 0, 0 < х < а (а » А). G.56)
Здесь считается, что модуль Юнга продукта реакции гораздо
меньше модуля Юнга тела.
Длину образующейся трещины нетрудно определить при по-
помощи концепции Кс- Используя соответствующее выражение для
коэффициента интенсивности на-
напряжений Ki в конце трещины
при х — I (см. формулу (П. 7)
Приложения I), находим
На
S
/
/
/
/
/
f
—arcsinl~
V^iKu
'^^-. G.57)
О Zjrt 4/a 6ft 6/rt
Влиянием свободной границы по-
полупространства пренебрегаем.
На рис. 170 изображена зави-
Р* симость l/а от безразмерной на-
Рис. 170. грузки р, = 2 \Га &0Д • (|/я Xic)~ ,
построенная по этой формуле.
Длина а зависит от времени, протекшего от начала дейст-
действия коррозии до момента образования трещины. Она опреде-
определяется из решения следующей краевой задачи для одномерного
§5]
РАЗВИТИЕ КОРРОЗИОННЫХ ТРЕЩИН
407
уравнения диффузии:
дс.
д2с
?¦ @<x<a), co = 0
dt ° дх2
При ?=0 со — 0,
ПрИ X — U Cq —; 00*
при л: = а — Do дсо/дх = %ст dafdi, dcoldt =
G.58)
— kc0.
Здесь предполагается, что. реакция протекает в узком диффу-
диффузионном слое вблизи точки х — а; толщина этого слоя мала по
сравнению с а и моделируется скачком решения при х = а, ко-
который перемещается с некоторой у
заранее неизвестной скоростью
вглубь тела. Последнее гранич-
граничное условие интегрируется:
со = соае~ы при х= а. G.59)
Ограничимся лишь рассмотре-
рассмотрением асимптотического поведения
решения при больших t. Соглас- Рис 17)
но G.59), при /->-оо будет
со = 0 на скачке х = а, и краевая задача G.58) становится ав-
автомодельной (задача Стефана).
Приведем окончательный результат:
при t -> оо а —2%
где функция 1 — ?(соо!смо) определяется уравнением
5
G.60)
Условие t—>оо в данном случае означает, что ka2/D0^> 1.
Давление продуктов коррозии при некоторых условиях мо-
Жет обусловить докритический рост трещин. Рассмотрим тонкую
структуру конца трещины, находящейся в поле растяжения, оп-
определяемом коэффициентом K.i (рис. 171). С течением времени
на берегах трещины нарастает коррозионная пленка, которая с
некоторого момента начинает производить давление на берега
(сначала только вблизи самого конца). Это вызывает локальное
разрушение в конце трещины и ее рост.
При стационарном развитии трещины с постоянной скоростью
dljdt в любой момент времени будет выполняться условие
К\ + К\ =
G.61)
408 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
где Ki — дополнительный коэффициент интенсивности напряже-
напряжений, вызванный давлением продуктов коррозии. Величина пло-
площадки контакта d из соображений анализа размерностей равна
^ G-62)
где % — некоторое число, зависящее от отношения ст/см0.
Действительно, в стационарном режиме постоянная k выпа-
выпадает из уравнения диффузии, и в нем остаются лишь Do, dl/dt,
соэ и см0; кроме того, расширение объема коррозионной пленки
прямо пропорционально А.
Коэффициент Кл равен
/Cf = ruMV3. G.63)
где г]4 — некоторое число, зависящее от отношения kJE и коэф-
коэффициентов Пуассона.
Согласно формулам G.61) — G.63), скорость роста трещины
зависит от Кг так:
Здесь tj и Kia — постоянные данной пары материал — среда.
Таким образом, вследствие нарастания и разрушения тонких
коррозионных пленок на дне трещины скорость ее роста постоян-
постоянна; она не зависит от внешних нагрузок и конфигурации тела.
При этом величина Кг должна быть достаточной для того, чтобы
обеспечить необходимое раскрытие трещины (и тем самым при-
приток реагента в устье трещины и пластические деформации на ее
дне). Нарастание податливых толстых пленок может вызвать
образование и развитие трещин.
Градиенты напряжений и деформаций, вообще говоря, вызы-
вызывают в твердом теле тепловые и диффузионные потоки: Однако
для большинства материалов эти эффекты пренебрежимо малы
и потому здесь не учитываются.
§ 6. Электрохимический механизм роста трещин
Исключительно большую роль в коррозионном разрушении
и развитии трещин играют электрохимические процессы. Как из-
известно, химические реакции, происходящие на границе металл —
раствор электролита, сопровождаются возникновением некоторой
разности потенциалов, характерной для данной системы; поэто-
поэтому, если два различных металла, находящихся в контакте, по-
поместить в электролит, то в цепи металл — электролит возникнет
электрический ток (гальванический элемент). При этом один из
§ 6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 409
металлов (анод) будет переходить в раствор в виде ионов и тем
самым растворяться, а другой (катод) будет восстанавливаться.
Отметим, что в большинстве случаев коррозионно-активная сре-
среда является раствором электролита (см. Приложение III).
Конструкционные металлы представляют собой сплавы многих
рдзнородных металлов. Поэтому при соприкосновении с раство-
раствором электролита на поверхности металла возникает множество
Микроскопических гальванических элементов разного типа, при
работе которых растворяются некоторые из компонентов спла-
сплава*). Это приводит к образованию «ям», «колодцев» и т. п. на
поверхности металла, которые выступают как концентраторы
напряжений. При наличии внешних растягивающих нагрузок в
конце концов возникает трещина, которая может развиваться
в дальнейшем за счет электрохимического механизма растворе-
растворения анодного металла на дне трещины и локального разрушения
ослабленного материала. В дальнейшем ограничимся лишь рас-
рассмотрением процесса развития трещины.
Металл будем считать идеальным упруго-пластическим те-
телом. Примем два основных допущения: а) в каждой точке ис-
исходного материала имеются анодные компоненты, причем све-
свежеобнаженную поверхность металла в среднем можно считать
анодной по сравнению с участками поверхности, уже подверг-
подвергшимися воздействию внешней среды, б) коэффициент интенсив-
интенсивности напряжений достаточно велик, чтобы обеспечить мгновен-
мгновенный разрыв ослабленного вследствие коррозии слоя на дне тре-
трещины сразу после его образования.
Первое допущение можно обосновать следующим образом.
^Гальванический элемент обычно видоизменяется со временем;
чаще всего это связано с выделением водорода или других ме-
металлов на катоде (катодная поляризация), а также с выделе-
выделением газообразного хлора или кислорода на аноде (анодная
поляризация). В результате этих процессов э. д. с. микроэле-
микроэлемента постепенно падает и ток прекращается, пока вследствие
локального разрыва не произойдет обнажения свежего металла,
.после чего процесс повторяется.
Второе допущение позволяет считать рост трещины непрерыв-
непрерывным (скачки трещины малы по сравнению с размером пластиче-
пластической области в конце трещины). Коррозионный слой полностью
окружен пластической зоной, которая экранирует его от внеш-
внешнего поля, так что скорость роста трещины не зависит от
коэффициента интенсивности напряжений. При этом из всей
совокупности явлений наиболее медленным процессом, опре-
*) В первую очередь растворяются те компоненты, которые расположены
выше в ряду напряжений, т. е. (с учетом знака) имеют меньший равновесный
Плтоитгио тт
потенциал.
410
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VII
деляющим кинетику роста трещин, будет электрохимический
процесс движения ионов в полости трещины. Ниже в п. 3 бу--
дет показано, каким образом можно отказаться от второго до-
допущения.
Существование скачкообразного режима роста трещин (со
скачками больше размера пластической области) по электрохи-
электрохимическому механизму является маловероятным, так как это тре-
требует чрезмерно большого времени работы одного и того же галь-
гальванического микроэлемента, которое на самом деле ограничено
естественными процессами поляризации (прежде всего катод-
катодной). Явление порогового коэффициента интенсивности напря-
напряжений объясняется именно этой причиной. Очевидной нижней
оценкой величины /CiSCc будет величина вязкости разрушения ме-
металла, из объема которого мысленно удалены все активные
анодные области, вызывающие рост трещины.
1. Основные уравнения движения ионов электролита в щелях.
Пусть две поверхности металла образуют узкую щель, запол-
заполненную раствором электролита. Обозначим через 5 срединную
поверхность, т. е. поверхность, равноудаленную от поверхностей
металла (берегов щели). Ширина щели считается малой по
сравнению с радиусом кривизны поверхности 5 в каждой точке.
Пусть и, v — неподвижные ортогональные гауссовы координаты
точки на 5. В растворе присутствуют ионы п сортов, концентра-
концентрация каждого сорта равна с{(и, v). Под сг будем понимать число
ионов i-ro сорта в единице объема, усредненное по толщине
щели.
Вблизи берегов щели имеется тонкий слой, в котором потен-
потенциал ф и истинные концентрации испытывают резкие изменения
(двойной слой); условимся вели-
величиной h обозначать ту часть ши-
ширины щели, в которой ф, а также
истинные концентрации можно
считать постоянными вдоль нор-
нормали к поверхности 5 (рис. 172).
Под ф(и, v) будем понимать
именно это постоянное значение
потенциала. Скорость течения
жидкости v(u, v) считается задан-
заданной (под v понимается средняя по сечению скорость, т. е. объ-
объемный расход, деленный на К). Толщина двойного слоя прене-
пренебрежимо мала по сравнению с h.
Будем изучать движение ионов в слое А толщины h (в с,- вхо-
входят лишь ионы из этого слоя, заштрихованного на рис. 172).
В тонком слое металл — электролит между границами слоя А
-и берегами щели происходят химические реакции; поэтому на
границах слоя А в направлении нормали к поверхности S, во-
h-
Рис. 172.
5 6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 411
обще говоря, существует поток ионов (и, значит, электриче-
электрический ток).
Закон сохранения вещества в слое А можно записать в виде
следующих уравнений на поверхности S:
| 5|^lGf(cp, ct) G.64)
(/=1, 2, ..., n).
Здесь Di и Zi — соответственно коэффициенты диффузии и ва-
валентности (с учетом знака), ионов i-ro сорта, ^ = 9,65-104 к —
число Фарадея, Gt((p, c{) —количество ионов г'-го сорта, перехо-
переходящих в двойной слой за единицу времени в расчете на единицу
площади срединной поверхности.
Функции Gj(cp, Ci) определяются поляризационными кривы-
кривыми, которые зависят от кинетики протекания химических реак-
реакций и фазовых превращений в двойном слое*). Будем считать
их известными, например, из полярографических измерений.
Отметим выражение для суммарной плотности тока на границе
металл — электролит
я
i = 2 ezkGk (e — заряд электрона). G.65)
Первый и второй члены в правой части уравнения G.64)
означают скорость изменения числа частиц, приходящихся на
единицу площади поверхности 5, вследствие диффузии и мигра-
миграции ионов под действием кулоновских сил [176]. Второе слагае-
слагаемое в левой части уравнения G.64) дает скорость изменения
концентрации вследствие конвективного переноса ионов потоком
2КИДКОСТИ.
Условимся потенциал металла на берегах трещины считать
равным нулю. Тогда ф(и,v) представляет собой скачок потен-
потенциала на границе металл — раствор при переходе через двойной
слой от металла к электронейтральному раствору. Через ф0 бу-
будем обозначать потенциал слоя А на дне трещины (ф0 — задан-
заданная эмпирическая постоянная рассматриваемой системы). При
этом автоматически учитывается также контактный потенциал
на границе различных металлов.
Уравнения G.64) получаются из строгих трехмерных урав-
уравнений движения электролитов следующим образом. Вначале точ-
точные уравнения (они совпадают с G.64), если в них положить
Gi = 0 и векторные операции подразумевать по всем простран-
*) Толщина двойного слоя в равновесном состоянии примерно соответ-
соответствует дебаевскому ионному радиусу. Для неравновесных процессов, которые
здесь рассматриваются, его толщина может быть гораздо больше. Для нас
этот вопрос несуществен.
412 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
ственным переменным) записываются в ортогональной криво-
криволинейной системе координат (u,v,n), так чтобы поверхность 5
совпадала с поверхностью п = 0. Затем вводятся следующие
два допущения: а) вектор v в каждой точке слоя А не зависит
от я, причем его компонента по нормали к поверхности S равна
нулю, б) производные дц/ди и дц/dv в. каждой точке слоя А не
зависят от п. С учетом этих допущений точные уравнения инте-
интегрируются по п в пределах слоя А от —Л/2 до -\-hJ2 и вводятся
средние концентрации по толщине слоя. Величины G,- равны
-ft/2
dct
ft/2
-ft/2'
Они представляют собой потоки соответствующих реагентов в
двойной слой (при G,- > 0).
Предполагая, как обычно, что раствор в слое А электроней-
электронейтрален, запишем еще одно уравнение:
J^ztct = 0, G.66)
Уравнения G.64) и G.66) представляют собой замкнутую
систему относительно искомых функций Ci(u, v) и ф(ы, v). К ним
нужно присоединить еще начальные и граничные условия.
На фронте трещины в любой момент времени должны удо-
удовлетворяться уравнения электрохимической кинетики
дс, D,z,F dm
Скорость роста трещины V определяется из закона сохранения
массы
epF дс.. z.,F д<в
—l—==,DM—~--\-DM-^—cM——. G.68)
Здесь т — масса иона металла, растворяющегося на дне тре-
трещины, р — плотность металла, DM, cM и zM — соответствующие
величины, относящиеся к ионам растворяющегося металла, п —
направление нормали к фронту трещины на поверхности S, е —
объемная доля в металле анодного компонента, растворяюще-
растворяющегося в результате анодной реакции на дне трещины (ионы М-го
сорта относятся к одному из п сортов). Функции /,- известны из
опыта или же из теории, относящейся к конкретной анодной
-реакции (в частности, если поток ионов i-го сорта через фронт
трещины равен нулю, то /4 = 0). Если трещина не развивается
(или развивается по какому-либо другому механизму), условие
G.68), очевидно, не выполняется.
~ Рассматриваемый процесс предполагается изотермическим-;
при наличии существенных градиентов температуры к получен-
§ 6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 413
иым уравнениям надо присоединить еще уравнение теплопро-
теплопроводности
^ + (vgrad) r = r,(r-rM) + Q. G.69)
Здесь г\—коэффициент теплообмена на границе металл — жид-
жидкость, Тм — температура металла в соответствующей точке по-
поверхности S, Q — доля суммарного теплового эффекта реакции
в двойном слое, приходящаяся на раствор. Ввиду хорошей теп-
теплопроводности металла и контакта металл — раствор тепловыми
потоками вдоль поверхности S можно пренебречь по сравнению
с потоком тепла в направлении нормали к этой поверхности.
В случае плоской щели и одномерного изотермического про-
процесса уравнения принимают вид
де' 4V dCi - п d4i 4- D^F д
G.70)
Пусть, например, в основном металле (Си) имеется цинко-
цинковое включение в виде тонкой пластины толщины h (рис. 173).
В серной•кислоте эта пара метал-
металлов образует гальванический эле-
элемент в соответствии с химической
реакцией
Zn + H2SO4^ZnSO4 + Н
2.
Си
H3SO4
Zn
Медь растворяется в серной кис-
кислоте гораздо слабее, так что ее рас- Рис' 173-
творимостью можно пренебречь.
G течением времени образуется щель ширины h, фронт которой
в установившемся режиме растет с постоянной скоростью.
Работа этого элемента аналогична работе элемента Вольта:
ионы Н+ движутся к берегам щели (катод), рекомбинируют там
в молекулы BН++ 2е —>¦ Н2), нейтрализуя электроны, и обра-
образуют газообразный слой; ионы SOi связывают в растворе
ионы Zn++, которые переходят в раствор, оставляя свои элек-
электроны на цинковом аноде.
Будем относить индексы 1, 2, 3 к ионам Zn++, H+ и SO"
соответственно. Потоки ионов Zn++ и SOi^ на катод и потоки
ионов Н+ и SO" на анод будут равны нулю; следовательно,
в данном случае
2, = + 2, z2=+l,.
414
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
[ГЛ. VII
В установившемся режиме левая часть уравнений G.70) об-
обращается в нуль (скорость роста трещины весьма мала, так что
членом VdCifdx можно пренебречь)-, а трещину можно считать
полубесконечной (х<С0). В этом случае на бесконечности при
д:->—оо должны быть заданы концентрации с* и потенциал ф.
Получающаяся краевая задача в каждом конкретном случае
может быть решена численно на ЭВМ.
2. Скорость роста коррозионной трещины. В случае бинар-
бинарных электролитов расчет стационарного режима можно прове-
провести аналитически. В качестве модели процесса рассмотрим рас-
растворение цинкового включения в меди, помещенной в сульфат
л
• so;
Рис. 174.
цинка (рис. 174). Под действием э. д. с. гальванического эле-
элемента ионы цинка переходят в раствор и точно такое же коли-
количество ионов цинка разряжается на меди, анодируя берега
щели. Растворимостью меди как более благородного металла
можно пренебречь. В этом случае
с1 = с2 = с, 2, = + 2, z2 = — 2, G2 = 0, e=l.
Здесь индекс 1 относится к ионам Zn++, а индекс 2 — к ионам
SO".
Для бинарных электролитов краевая задача, согласно G.70)
и G.67), записывается в следующем виде:
d4 .JhziF d I dy\ 1 r , v
dx*
при х =
при
RT dx V dx,
(— oo < x < 0)
OO C= С ф = (
RT
Здесь положено ^^с, с2=. — c2,/22.
Интегрируем второе уравнение, используя граничные условия:
с„ ехр —
Ф»)]-
G.72)
I 6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕ1ЦИН 41§
Подставляя это с в левую часть первого уравнения G.71),
получаем уравнение для потенциала:
DlFС^г' " Z2) Ж [?е~^~ ^^^ ~ Т °- С Ф)-
Пусть акту разряда отвечает уравнение М+г -{- Zie = М, где
M+z — частицы, находящиеся в растворе и подвергающиеся раз-
разряду с присоединением Z\ электронов, а М — частицы, образую-
образующиеся непосредственно после разряда и связанные с поверхно-
поверхностью электрода адсорбционными (или иными) силами. В рас-
рассматриваемом примере роль М играет Zn, a Z\ = 2.
Общее уравнение теории замедленного разряда для тех слу-
случаев, когда можно пренебречь влиянием структуры двойного
электрического слоя, имеет вид [176]
Gi (с, ф) = k{ce RT —&2cAie RT (уравнение Фольмера).
G.74)
Здесь с'ш— концентрация частиц М, а — эмпирическая по-
постоянная (коэффициент переноса), изменяющаяся в пределах
от нуля до единицы, но чаще всего близкая к 1/2, k\ и k2 — кон-
константы катодной реакции, зависящие от температуры так:
где Ui и Ui — энергии активации соответственно процессов раз-
разряда и ионизации в отсутствие скачка потенциала между ме-
металлом и раствором, &ю и k2u — некоторые постоянные.
Первое слагаемое в G.74) отвечает разряду, второе — об-
обратному процессу ионизации. Формула G.74) годится для про-
процессов выделения водорода и металлов (на катоде); она хорошо
описывает также анодную поляризацию. Потоку частиц G\ со-
соответствует электрический ток с плотностью Z\eG\. Часто на
катоде можно пренебречь ионизацией и ограничиться первым
слагаемым в G.74).
Уравнение G.73) при помощи G.74) и G.72) можно запи-
записать в виде
? Ч4г) ). G.76)
Здесь
__ ф —фор ._ Z2F (ф0 — фю)
Ф-' Л ~Ш '
D,PCooh (г, - г2) (фо -
416 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН 1ГЛ. VII
Величина ф<х> представляет собой равновесный потенциал на
границе металл — раствор электролита.
Обозначим
G.76)
Преобразуем уравнение G.75) к переменным риф:
kp2 = G(O). G.77)
Обозначим
У = р*. G.78)
В переменных у, Ф получаем линейное уравнение первого
порядка
dldQ + 2 2G{Q) G.79)
Решение этого уравнения, удовлетворяющее граничному ус-
условию: при Ф = 0 у = 0, запишем в виде
о
J G{x)etK*dx. G.80)
ф
Вспоминая G.76) и G.78), находим окончательное решение
уравнения G.75), удовлетворяющее граничному условию Ф= 1
при х = 0:
ф
0 G.81)
Q(x)enxdx
При помощи формул G.68), G.72) и G.80) получаем искомую
скорость роста трещины
_ Dxm Idc . ZiF_ d<p\I _
eo \dx-r RT1- dx)\nawx.
ер \dx ¦ кг dxl\apnx=s>
D\tnF B1 — z2) ^ф
при x=Q
epRT dx
. G.82)
В том случае, когда ионизацией на берегах щели можно пре-
пренебречь (т. е. &2 = 0), величина б(Ф), согласно G.75), имеет
вид
- г3) (Фо - Фоо)
Ф
§ 6) ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 417
В этом случае выражение G.82) принимает следующий про-
простой вид:
V = mc°° e~aziF<»JVRT) i / 2feiA (z2 — z{) Г j _ g\ B+aZjZ2 l)j ^ _ g4j
ер У zji B+ az^^)
Величина Я, < 0, так как ф0 — ф» < 0. При ф0 ^* фте > О, когда
катод и анод меняются местами, скорость становится мнимой,
что отвечает физическому смыслу задачи.
Величина aZxFy*, играет роль энергии активации рассмат?
риваемого процесса. Зависимость равновесного потенциала ф»
от стандартного потенциала, температуры и активностей ионов
определяется формулой Нернста [176].
Э. д. с. гальванического элемента фо — ф<х> нетрудно найти из
полученного решения и из общего уравнения G.74) в случае
анодной поляризации при помощи следующего условия:
при х = О
G.85)
(&га — константа анодной реакции, аа — соответетвующий коэф-
коэффициент переноса). Здесь учитывается лишь ток ионизации на
аноде, а разрядом пренебрегаем, что справедливо для условий,
достаточно далеких от равновесия.
При помощи G.80), G.85) и G.72) находим
ЕD, Bi —;
у 2e-
G.86)
Отсюда на основании G.83) получаем следующую формулу для
безразмерной э. д. с. гальванического элемента Я:%
. G.87)
Таким образом, с увеличением ширины щели э. д. с. моно-
монотонно убывает.
Подставляя найденное X в G.84), находим
еР V 22 B + аг122 ')
14 Г. П. Черепанов
G.88)
418 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ, VII
Здесь
2z2+az, | rl RT
2z2-
b - z,B-a-2aa) '
В случае растворения цинкового включения в сульфате
цинка (см. рис. 174) скорость трещины при а — оса = 1/2, со-
согласно G;88), будет равна
|/^/|[, _(?)"]. G.89)
где
Из G.88) видно, что скорость трещины тем больше, чем
меньше ширина щели (функция /0 монотонно убывает с увели-
увеличением h, обращаясь в нуль при h =¦ h0, когда потенциал qpo
становится равным равновесному потенциалу фте). Физически
этот результат совершенно естествен, так как с уменьшением
Ширины щели увеличивается плотность анодного тока, которая
определяет скорость роста трещины.
Изучим теперь структуру зоны, в которой происходит элек-
электрохимическая реакция. Ширина этой зоны х0 конечна; ее легко
определить при помощи формулы G.81):
и
-А!
Q(x)e2Udx
Ф
В пренебрежении ионизацией на катоде, когда G(x) имеет вид
G.83), отсюда получаем
Хо_
где 6 = 2 + o2,/22.
Как нетрудно сообразить, ширина зоны х0 монотонно убы-
убывает с уменьшением безразмерной э. д. с. гальванического эле-
элемента Я, обращаясь в нуль при ф0 = фте. На основании формул
G.72), G.81) и G.83) можно также заключить, что электриче-
электрический потенциал и концентрация ионов монотонно растут в зоне
— II 1 1 —
х0
9»
X
S в] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 419
реакции с увеличением х. Качественная структура зоны изо-
изображена на рис. 175.
3. Обсуждение результатов решения. Полученное решение
при е = 1 отвечает избирательной коррозии, при которой рас-
растворяется один из компонентов сплава, залегающий сплошным
слоем в основном металле. Такая модель применима, по-види-
по-видимому, также к распространению меж-
кристаллитных коррозионных трещин,
когда растворению подвергаются в ос-
основном интерметаллические соединен
ния, расположенные преимущественно
между зернами.
Приведенный выше анализ пока-
показывает, что в этом случае существует
механизм самоподдерживающегося
развития трещины, который может
привести к разрушению тела даже Рис- 175-
при отсутствии внешних нагрузок.
Однако катодные и анодные реакции не всегда можно счи-
считать пространственно разделенными: часто они в среднем совме-
совмещаются на одном и том же участке. Из-за того, что условия
протекания электродных реакций могут быть различными на
разных участках поверхности тела, возникает неравномерность
тока и преимущественная «катодность» или «анодность» уча-
участков.
Необходимым условием развития трещины по электрохими-
электрохимическому механизму в отсутствие внешних нагрузок является
резко выраженная анодность ее дна по сравнению с берегами;
при этом реакция ионизации металла (или некоторых его ком-
компонентов) на дне трещины должна протекать параллельно с
реакциями на берегах трещины, имеющими преимущественно
катодное направление.
При наличии внешних нагрузок в том случае, когда ширина
щели вблизи ее конца примерно равна раскрытию трещины 2v0,
скорость роста трещин на основании G.88) будет монотонно"
убывающей функцией коэффициента интенсивности напряжений
(так как уо~К]), Такие трещины вначале (пока Ki мало) ра-
растут быстро; затем, когда Ki увеличивается (при постоянных
внешних нагрузках), а трещина становится более тупой, ско-
скорость роста замедляется, и трещина может вовсе остановиться
(при 2v0 ~ ho). Это явление, на первый взгляд кажущееся
парадоксальным, наблюдалось в опцтах с коррозионными
трещинами при неизменных растягивающих нагрузках (см., на-
например, книгу Логана [172]). Для трещин такого типа харак-
характерно одновременное и устойчивое развитие сразу многих тре-
трещин в отличие от обычного случая монотонно возрастающей
14*
420 ВЛИЯНИЕ ВНЕШНИЙ СРЕДЫ НА РОСТ ТРЕЩИН 1ГЛ. VII
функции f(Ki) (dl/dt ~ f(Ki)), когда развивается преимуще-
преимущественно только наиболее опасная трещина.
Важнейшими электродными реакциями, наряду с иониза-
ионизацией и выделением металлов, являются выделение водорода и
кислорода, а также окисление металлов кислородом. Водные
среды всегда содержат чрезвычайно активные ионы водорода
и гидроксила и, как правило, растворенный кислород. Отсюда
вытекает весьма опасная роль любых водных сред как воз-
возбудителей электрохимической коррозии. Общая коррозия изу-
изучена весьма полно (см., например,
курс[178]).
Рассмотренную модель нетрудно
обобщить на тот случай, когда рост
трещины нельзя считать непрерыв-
непрерывным и анодные участки залегают
не сплошным слоем.
Вначале выведем общие уравне-
уравнения движения растворов электро-
Рис. 176. литов в туннелях; под туннелем бу-
будем понимать выемку (со всюду
одинаковым поперечным сечением), длина которой гораздо боль-
больше характерного линейного размера поперечного сечения
(рис. 176).
Введем ортогональную декартову систему координат xyz так,
чтобы плоскость yz совпадала с плоскостью какого-либо попе-
поперечного сечения туннеля Sj? (см. рис. 176). В этой системе ко-
координат запишем трехмерные уравнения движения раствора
электролита (они совпадают с G.64), если в них положить
Gj =« 0 и векторные операции подразумевать по всем простран-
пространственным переменным). Введем следующие допущения: а) ско-
скорость жидкости v в каждой точке сечения Sf не зависит от у
и z, причем компоненты вектора v по осям у и г равны нулю,
б) производная dyldx в каждой точке сечения SP. не зависит
от у и z, К общим уравнениям применим оператор
где через SF обозначена как область (поперечное сечение), так
и площадь этой области, что не должно приводить к путанице.
Введем ереднюю по сечению величину концентрации
-j-j jctdydz
и обозначим через Gtпоток ионов 1-го сорта в двойной слой щ
единицу времени, приходящийся на единицу площади бековой
S 6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 42!
поверхности туннеля SB
Здесь PF — замкнутый контур поперечного сечения SF и длина
этого контура (периметр), п — нормаль к контуру PF в плоско-
плоскости сечения. Функции Gild,ф) считаются известными.
Используя формулу Грина, получим в результате следующие
уравнения:
? G92)
= 0 (ct = ct (х,. t), Ф = ф (х, *)).
Здесь координата х отсчитывается вдоль образующей боковой
поверхности туннеля, а символ с* сохранен за средней по се-
сечению величиной концентрации.
Свободный член в уравнениях G.92) определяет величину
катйдного тока: чем он больше, тем больше анодный ток и
скорость роста туннеля. Поэтому при прочих равных условиях
с увеличением отношения Pp/Sp скорость коррозии должна воз-
возрастать.
Полученное ранее решение полностью относится также к
развитию туннелей; при этом в соответствующих формулах
нужно только заменить h на отношение SF/Pp.
Введем следующее естественное предположение: средняя ве-
величина отношения Sf/Pf в условиях естественной коррозии тех-
технических металлов является некоторой постоянной данной си-
системы, зависящей от химического состава металла и электро-
электролита, а также от структуры металла. Это допущение позволяет
обобщить предлагаемую модель роста трещин на произвольное
скачкообразное распространение трещин и произвольное зале-
залегание анодных участков. Действительно, при выполнении этого
условия развитие трещины полностью определяется ростом мик-
микротуннелей на дне трещины, характерных для дайной системы;
скорость их роста не зависит от внешних нагрузок и коэффи-
коэффициента интенсивности напряжений. Однако нагрузки должны
быть достаточно велики, чтобы разорвать ослабленный микро-
микротуннелями металл вблизи конца трещины (т. е. Ki > Kiacc).
4. Электростатический режим. Для растворов электролитов,
не являющихся бинарными, аналитический расчет стационарной
задачи можно провести в том случае, когда диффузионным пе-
ренддряжёнием Можно пренебречь. Это предположение обыч-
обычно принимается при расчетах »лектролизеров. В этом случае
422 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
в общих уравнениях нужно положить с{ = const, и для потен-
потенциала в растворе остается одно уравнение
Рассмотрим развитие туннеля в стационарном режиме; при
этом можно считать, что туннель расположен при —оо < х < О
(см. рис. 176). На основе общей кинетической теории Фольмера^
для двойного, электрического слоя (см. G.74)) граничные усло-
условия формулируются следующим образом;
на боковой поверхности туннеля Sb
= т]кЛф, G.94)
на дне туннеля при х = 0
= — т]аЛф. G.95)
Здесь т]к, Як, т]а, К'— кинетические постоянные данной системы,
описывающие соответственно суммарную катодную реакцию на
Sb (чаще всего разряд ионов водорода) и суммарную анодную
реакцию при х = О (ионизацию металла). Через Ф обозначен
безразмерный потенциал
Ф = (ф-Фм)/(Фо-фте) @<Ф<1), G.96)
где фоо — равновесный потенциал на контакте «катод — раствор»,
<ро — потенциал анода (потенциал металла считается нулевым).
При этом граничное условие на бесконечности запишется так:
при х -> — оо Ф = 0. G.97)
Функция Ф, очевидно, тоже удовлетворяет уравнению Лапласа.
Применим оператор -j- \ \ dydz к уравнению Лапласа
р sP
G.93). Для простоты сечение туннеля будем считать круговым
с. радиусом г, а функцию Ф — приблизительно постоянной в
каждом поперечном сечени туннеля (за исключением двойного
слоя). В результате, применяя формулу Грина и граничное ус-
условие G.94), находим
*?_^Д* = 0 (-оо<*<0). G.98)
Уравнение G.98) физически выражает баланс зарядов меж-
между двумя бесконечно близкими сечениями туннеля (первый
член — изменение потока заряда вдоль оси х, второй член-
сумм арный ноток к боковой поверхности),
$6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 423
Решение нелинейной краевой задачи G.98), G.95) и G.97)
находится совершенно аналогично решению уравнения G.75).
В итоге получаем
Vt\KK/r х = arctg VЛф — 1 — arctg УЛ— 1. G.99)
Из граничного условия G.95) находим уравнение, опреде-
определяющее э. д. с. гальванического элемента:
'Ма==Че~2Че*К-0- G.100)
Напомним, что согласно G.94) и G.95) коэффициенты т|а и
т|к прямо пропорциональны ]<р0 — ф»!, а коэффициенты К и
%& прямо пропорциональны | фо — ф» |.
Из решения G.99), G.100) находим ширину х0 зоны реакции
(при х = х0 Ф = 0):
arctg У?Г=ТВ
При помощи G.68) и G.95) определяем скорость роста туннеля
mDMzMFcM(d<?\ _.mDMzM
рГакой же будет скорость роста трещины при Ki > Kiscc (если
пренебречь искривлением анодных путей).
5. Диффузионный режим. Весьма часто взаимодействие
твердого тела со средой можно описывать, пренебрегая элек-
электрическими явлениями (например, если жидкость не обладает^
ионной проводимостью или твердое тело представляет собой
диэлектрик). В этом случае в общих уравнениях G.64) можно
положить ф = const; функции Gi(ct) будем считать известными
из уравнений кинетики гетерогенных реакций на берегах тре-
трещины или туннеля (если Gi > 0, то частицы i-ro сорта перехо-
переходят из жидкости в твердую фазу, если же G(<0, то частицы
твердого тела растворяются в жидкости).
Распространение трещин или туннелей в данном случае, оче-
очевидно, возможно лишь тогда, когда в твердом теле имеются
Непрерывно связанные области, растворимость которых в жидко-
жидкости по каким-либо причинам значительно превышает раство-
растворимость остальных областей (избирательное растворение). Рас-
Рассмотрим основные случаи, считая, что кинетика реакции рас-
растворения описывается уравнением
dc/dt=k(cu — c). G.103)
424 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
Здесь с — концентрация растворяющегося вещества, св — кон-
концентрация насыщенного раствора, k — константа скорости ре-
реакции.
Пусть растворяющийся компонент залегает тонким слоем
или в виде стержня перпендикулярно" к поверхности тела
(рис. 177). В этом случае имеем краевую задачу
-И—0!? при 0 <*<*(*)
при* = 0 с = 0, при / = 0 с = 0, G.104)
при x = l dc/dt=k(ca — c), pdl/dt = — Ddc/дх
(р— плотность растворяющегося компонента).
Интегрируя G.103), получаем
с = снA— е-**). G-105)
При t-*oo величина с стремится к сн на границе х = I, и за-
|дача G.104) становится автомодель-
: ^ у—^ ной (задача Стефана).
: ~ г Приведем окончательный ре-
зультат:
~*7
О ¦ - ¦ Ъ 7 .
* при /->оо . 1 = 21УТ>1, G.106)
lit)
где функция | = |(св/р) опреде-
определяется уравнением G.61), если
Рис. 177. Соо/(ксмо) заменить на cjp.
При сн < р имеем |= l/cH/Bp).
Установившегося режима роста трещины или туннеля в дан-
данном случае не существует. Однако стационарный режим стано-
становится возможным в том случае, когда частицы растворяюще-
растворяющегося на дне туннеля, вещества переходят затем в твердую фазу
на боковой поверхности. Это может происходить, например, в
тех случаях, когда жидкость содержит катализатор, способ-
способствующий реакции между растворимым и нерастворимым ком-
компонентами твердого тела с образованием нерастворимых соеди-
соединений. Рассмотрим установившееся развитие туннеля, считая,
что его дну соответствует координата х = 0 (см. рис. 176).
Краевая задача, согласно G.92), запишется в виде
^ ^ при-оо<д;<0, G.107)
при х->— оо с = 0,
при х = 0 с = сн.
Функция G(c) определяется кинетикой реакции на боковой по-
поверхности (G > 0).
f 6] ЭЛЕКТРОХИМИЧЕСКИЙ МЕХАНИЗМ РОСТА ТРЕЩИН 425
Решение этого уравнения, удовлетворяющее условию на бес-,
конечности, имеет вид (см. G.75))
G.108)
X
G (a) da
о
Скорость роста туннеля равна
Ширина зоны реакции х0, согласно G.108), равна
G.110)
(при х = —х0 с = 0).
В частности, если гетерогенная реакция — первого порядка,
так что G = квс, имеем
G.111)
Ширина зоны реакции в данном случае бесконечна.
Рассматриваемое твердое тело представим себе как неко-
некоторую пористую структуру, скелет которой образован нерас-
нерастворимым компонентом, а «поры» — растворимым компонентом.
Под воздействием жидкости в поверхностном слое тела появ-
появляются многочисленные микротуннели, развивающиеся во вре-
времени согласно закономерностям G.106) или G.109). Естествен-
Естественно, что отношение SfIPf для этих микротуннелей является не-
некоторой постоянной данной системы, зависящей от химического
состава жидкости и твердого тела (а также от структуры твер-
твердого тела), но не зависящей от внешних нагрузок и конфигу-
конфигурации тела. Тогда рост трещины при К\ > Ku<x полностью
определяется развитием микротуннелей на дне трещины, а сред-
средняя скорость трещины не зависит от коэффициента интенсив-
интенсивности напряжений и примерно равна скорости роста туннелей
426 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
{если пренебречь их искривлением). При этом рост трещины,
вообще говоря, будет скачкообразным; длина одного скачка
будет тем больше, чем меньше коэффициент интенсивности
напряжений. Пороговый коэффициент интенсивности Kiscc при-
приблизительно равен вязкости разрушения пористого тела, обра-
образованного лишь нерастворимым компонентом.
Развитие трещины во всех рассмотренных случаях пред-
представляет собой термоактивационный процесс, так хак скорость
трещины оказывается пропорциональной или коэффициенту
диффузии, или константе скорости реакции (т. е. термоактиви-
руемым величинам). , •
В случае однородного растворения, когда G» < 0, жидкость
оказывает упрочняющее действие, так как рост трещин и тун-
туннелей невозможен, причем конец начальной трещины в резуль-
результате растворения притупляется, а ее длина уменьшается (эф-
(эффект Иоффе [17]).
§ 7. Сравнительный анализ основных механизмов
докритического роста трещин в металлах
Правильный диагноз причин разрушения является "первоос-
"первоосновой возможных приложений теории и, конечно, совершенно
необходим для принятия оптимальных мер. безопасности. В не-
некоторых случаях для этой цели достаточно анализа изломов;
однако гораздо чаще, в особенности когда причина разрушения
связана с воздействием внешней среды, одного анализа изло-
изломов оказывается недостаточно. Наиболее точным методом ди-
диагностики разрушения является метод механики хрупкого раз-
разрушения, который заключается в изучении докритического роста
искусственно созданных трещин. При этом установление веду-
ведущего механизма развития трещин, вызвавших разрушение, име-
имеет большое значение.
Перечислим основные механизмы в порядке их практической
значимости:
1) наводораживание,
2) электрохимическая коррозия под напряжением,
3) химическая коррозия под напряжением,
4) общий кинетический механизм,
5) адсорбционный механизм.
Все эти механизмы, за исключением адсорбционного, яв-
являются локальными, т. е. основаны на процессах, протекающих
в вершине трещины. Для них зависимость скорости роста тре-
трещины от коэффициента К\ и абсолютной температуры Т имеет
следующую структуру:
G.112)
i D ¦ ДОКРИТИЧЕСКИЙ РОСТ ТРЕЩИН В МЕТАЛЛАХ 42?
Энергия активации U соответствует конкретному физико-химиче-
физико-химическому процессу в вершине трещины. Это следующие процессы:
1) диффузия водорода в металле; . ' -
2) диффузия ионов в растворе электролита, химические ге-
гетерогенные реакции (разряд ионов водорода и металлов, реком-
рекомбинация водорода, восстановление, кислорода, ионизация метал-
металлов и т. д.); -
3) диффузия,кислорода в окисной пленке, химическая реак-
реакция окисления металла и т. п.;
" 4) химическое разложение самого материала.
В реальных условиях обычно протекает сразу несколько
различных процессов. При этом надо иметь в виду, что ско-
скорость суммарного процесса (т. е. скорость роста трещины)
определяется скоростью наиболее медленного процесса при
последовательном протекании процессов и скоростью наиболее
быстрого процесса — при одновременном протекании процессов.
Функция f(Ki) в G.112) имеет существенно разную форму
для каждого из указанных механизмов.
* В случае наводораживанияэта функция в практически зна-
значимой области с ростом /Ci сначала примерно пропорциональна
Kv затем Ki и, наконец, при больших значениях /Ci пропорцио-
пропорциональна ln/Ci (см. формулу G.23) и рис. 159). Режим насыще-
насыщения (формула G.8)), по-видимому, практически не достигается.
Рост трещины — скачкообразный. Нераспространение трещин
при Ki < Кисе объясняется ухудшением условий доставки во-
водорода в вершину трещины и образо-
образованием защитных окисных пленок
вследствие конкурирующего процесса
окисления металла. Переход от нерас-
нераспространения к распространению —
сравнительно плавный. Как показыва-
показывает рис. 159, наиболее значителен
й
сток линейности ~ ,0 ^^ ^
dl/dt=a(Ki-KQ). G.113) рис 178
Здесь постоянные а и /Со нетрудно вы-
выразить через величины /Сю и v0, фигурирующие в формуле
G.23). Именно этот участок реализуется обычно в опытах ["*].
В случае коррозионных трещин функция f(Ki) обычно резко
переходит от нуля к режиму насыщения, характеризуемому по-
постоянной скоростью роста трещины (рис. 178 и формулы G.54),
G;84)). Рост трещин может быть скачкообразным или непре-
непрерывным, однако величина скачков меньше, чем в предыдущем
случае. В отличие от других случаев коррозионные трещины в
режиме насыщения имеют тенденцию к ветвлению и к образо-
образованию разветвленных систем.
428 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН рЛ. Vtl
Согласно представлениям об электрохимической и химиче-
химической коррозии, развитым в предыдущих параграфах*), рост
коррозионных трещин не зависит от коэффициента Кг, роль ко-
которого сводится к разрыву поверхностной пленки вблизи конца
трещины (эта пленка пронизана микротуннелями и потому ме-
менее прочна, чем исходный материал). Следовательно, при до-
достаточно больших Ki (меньших вязкости разрушения) разрыв
пленки может происходить одновременно по разным направле-
направлениям, что и является причиной ветвления трещины. Поэтому
условие ветвления коррозионной трещины можно охарактери-
охарактеризовать некоторым критическим значением KiB коэффициента
интенсивности напряжений [177]. Величина Ki в концах малых
трещин, отходящих от вершины основной трещины, уменьшает-
уменьшается вследствие взаимодействия трещин («звездообразная» тре-
трещина, см. Приложение I), так что ветвление новых трещин про-
происходит лишь после достижения ими достаточно большой дли-
длины. По этой причине ветвление трещины упрочняет образец, так
что его прочность на разрыв может быть существенно (напри-
(например, в два раза [177]) больше, чем в случае одной магистраль-
магистральной трещины. Соответственно увеличивается и кажущаяся
величина вязкости разрушения. Этим же обстоятельством объ-
объясняется характерная древообразная форма коррозионных тре-
трещин.
В случае общего кинетического механизма функция f(Ki)
характеризуется отсутствием режима насыщения, а также от-
отсутствием ярко выраженного порога распространения трещины
(т. е. отсутствием Kiscc). С ростом Ki она возрастает быстрее,
чем во всех других случаях. Рост трещин в этом случае непре-
непрерывный. Этот механизм развития трещин имеет наибольшее
значение для полимерных материалов; для металлов он, по-ви-
по-видимому, гораздо менее существен.
Несмотря на огромное количество экспериментальных работ,
механизм разрушения пока удалось установить лишь для очень
небольшого числа систем металл — внешняя среда. Это объяс-
объясняется тем, что точнце методы механики хрупкого разрушения
зародились совсем недавно и еще не. успели получить призна-
признание специалистов по коррозии и физико-химической механике
материалов. Поэтому большинство работ имеет описательный
характер, а их результаты обычно допускают различное тол-
толкование.
*) В этом случае принципиально возможно также коррозионное охрупчи-
вание с линейной диаграммой (см. сноску к стр. 405), однако вероятность
этого механизма в водных средах, по-видимому, мала по сравнению с вероят-
вероятностью водородного охрупчивания. Последнее объясняется значительно боль-
большей величиной коэффициента диффузии водорода в металлах по сравнению
с другими компонентами.
ДОКРИТИЧЕСКИЙ РОСТ ТРЕЩИН В МЕТАЛЛАХ
429
Более или менее единодушное мнение имеется только отно-
относительно причины разрушения в водных средах некоторых высо-
высокопрочных сталей (и, в частности, современных никелевых ста-
сталей)— это водородное охрупчивание. Той же причиной, по-ви-
по-видимому, объсняется сернистое и нитратное охрупчивание
малоуглеродистых сталей. Каустическое охрупчивание мало-
малоуглеродистых сталей, вероятно, вызвано химической коррозией.
В качестве образца применения методов механики хруп-
хрупкого разрушения к этим вопросам можно привести работу
Райдера и Галлахера [178]. Ими было" исследовано докритиче-
ское развитие трещин при постоянных и циклических нагруз-
нагрузках в высокопрочной стали SAE 4340 (ао,2 = 155 кГ/мм1, ов =
= 189 кГ/мм2). Образцы испытывались в дистиллированной
воде с показателем рН, равным 6,5 -т- 6,9, при температурах 5,
25, 50 и 70 °С.
К,Ц5 нГ/т®
SO
40
SO
?0
to-
to•O,0Q5
№
Рис. 179.
OJ
0,5
На рис. 179 представлены результаты их опытов по росту
трещин при постоянных нагрузках (зависимость скорости роста
трещины dl/dt от Ki). Сталь SAE 4340 содержит около 2% ни-
никеля, поэтому естественно предположить, что рост трещины свя-
связан с локальным наводораживанием и охрупчиванием металла
в вершине трещины. По-видимому, железо, имеющее меньший
равновесный потенциал, чем никель, служит ,анодом и раство-
растворяется, катодные же реакции (в основном, выделение водоро-
водорода) сосредоточены на никелевых включениях. Разряжающийся
вблизи вершины трещины водород диффундирует в металл, так
как его движению во внешнюю атмосферу мешает электриче-
электрическое поле (для ионов Н+) или же вода (для молекул Н)
430
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
{ГЛ. VII
На том же рисунке сплошными линиями приведены резуль-
результаты расчетов по формуле G.23), выведенной на основе теории
роста трещин в металлах вследствие локального наводоражи-
вания. Как видно, имеет место полное совпадение теории с
опытом при следующих значениях постоянных vQ и Кю:
~4
при 5°С wo = 8,9 • 1О~* см/сек, Кю = 52,5 кГ/мм1
при 25°С we = 2,1 • 10~3 см/сек, Кю = 42 кГ/мм3'2,
при 50 °С wo = 2,5 • 10~3 см/сек, /Сю = 17,5 кГ/'мм312,
при 75 °С «0 = 8,4 • 10~3 см/сек, /Сю = 28 кГ/мм3'2.
На рис. 180 приводится взятая из статьи [178] зависимость
скорости роста трещины dl/dt от абсолютной температуры Т
при /Ci=105 кГ/мм\ Энергия активации оказывается равной
примерно 7900 кал/г-атом, что-весьма близко к указываемой в
той же статье энергии активации
диффузии водорода в а-железе
в интервале температур 25—
200 °С G 820 кал/г-атом). Напо-
Напомним, что коэффициент vu, соглас-
согласно G.23), прямо пропорционален
коэффициенту диффузии водорода.
Рис. 180.
Рис. 181.
4 Проведенный анализ позволяет в данном случае констати-
констатировать механизм локального наводораживаиия.
В том случае, когда диаграммы dl/dt — Ki отсутствуют,
весьма полезны кривые зависимости начального коэффициента
интенсивности напряжений от времени до разрушения (рис. 181).
Эти кривые получают в опытах с искусственно созданной на-
начальной трещиной, замеряя лишь величину К.1 в начальный мо-
момент и время t до разрушения. Для коррозионных трещин эти
кривые имеют характерное плато (кривая / на рис. 181); при
наводораживании, а также в тех случаях, когда скорость тре-
трещины зависит от величины Ki, кривые монотонно убывают
'1Я ДОКРИТИЧЕСКИЙ РОСТ ТРЕЩИН В МЕТАЛЛАХ 431
(кривая 2). Надо иметь в виду, что указанные кривые, к со-
сожалению, существенно зависят от формы и размеров образца и
начальной трещины.
Таким образом, для диагностики разрушения целесообразно
определить следующие характеристики:
а) диаграмму dt/dt— /Ci,
б) энергию активации роста трещин,
в) диаграмму K\ — t.
По результатам опытных данных Картера и некоторых дру-
других авторов на основе анализа приводимых диаграмм была до-
доставлена табл. 7.3. В этой табли-
це дается краткая характеристи-
ка свойств нескольких высоко-
прочных сплавов в коррозионно-
активной среде и на основе
развитых здесь представлений
делается вывод о причине ло-
локального разрушения.
В некоторых случаях может
происходить самопроизвольная
смена коррозионного механизма
роста трешдаы водородным
охрупчиванием. В качестве иллю-
страции такого явления на
рис. 182 приведена [177] диаграм- рис. ig2.
ма dl/dt — Кг для стали 4340
B,15% Si), характеристики которой приведены в табл. 7.3
(внешняя среда — 3,5%-ный водный раствор NaCl). Упомянутое
явление объясняется тем, что влияние водорода (поток прото-
протонов) возрастает с увеличением раскрытия трещины; поэтому,
начиная с некоторого критического значения коэффициента ин-
интенсивности напряжений, параллельно протекающий процесс
диффузии электролитического водорода становится более бы-
быстрым и, следовательно, определяющим скорость суммарного
процесса роста трещины. Следует ожидать, что.диаграммы типа
изображенной на рис. 182 характерны для общего случая тре-
трещин, развивающихся по механизмам коррозии и водородного
охрупчивания; по-видимому, в какой-то мере они присущи всем
корродирующим сплавам, находящимся в водном растворе элек-
электролитов (или во влажном воздухе).
В ¦заключение рассмотрим развитие трещин при циклическом
нагружении, когда Ki > Kisec- Предположим, что атермический
процесс подрастания трещины при увеличении /Ci вследствие
локальных пластических деформаций идет медленнее, чем па-
параллельно идущие процессы / докритического роста трещины
под воздействием активной внешней среды. В этом случае рост
432
ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН
1ГЛ. VII
о,
О
1
тив
к
«а
1
1
о
Я
8.
кор
В)
В)
о
в
ч
а
О
S
в
«в
т
•)
s
о
в
J
ill
HI
Скорость
роста
грещины
dl/dt
8 *
л ¦
я
ill!
юбработк!
о
Н
и
I
№
со
О
а.
а.
о
const
3
т
§
314
о
; 6 час.
я"а
о ё"
2
П1
стар(
о §
t-1 СО
ж ч
0) Я
ь ь
о. о
я
я
I
—1
314
Ё
«
«о
я
к
аО
t4 cjD
я
Р. Я
to р.
о в
45С
о
о
I
А
g
410
и отпус
°с
я о
Ч *^Э
Sb
DOS
о
И—4Со-
А
7
Й
§8
365
8
и отпус
°С
SS
4(N
cs
US SS
Я О.
со В
30V
со
А
g
294
S
!<;
и отпус
-426 °С
я о
Я в
ИЛИ
40 @,540;
Уо Si)
3g
л
2
го
244
со
со
и отпус
К СО
Ss
со С
л
Ч
я
«°
я-*
ртенситн
-4Со—0,
sz
от
А
СП
со
127
о
я
В1
«о
0) °
woo
@ г**
Я*К
ею-
стар
6S
артенсит
сталь 31
< я
Я
А
ГО
149
Ю
ся
; 3 часа
°С
S О
я*«
S в
ею-
стар
артенсит
сталь 3,
< я
Я
О S <0
О. ш 0) ES
Pih о v
С? Я X «
g« S.S?
Я К О Q.
gm«g
182
о
к
о.
S
о
со
183
ю
и отпус
°с
я о
МО
Ч
SS.
(IS
40 B,15 °Л
§7]
ДОКРИТИЧЕСКИП РОСТ ТРЕЩИН В МЕТАЛЛАХ
433
i
i
5
1
S
Й
i
i
коррозия
A
1
150
. 326
174
старение З часа
при 480°С
Мартенсито-старею-
щая сталь 250
водородное
охрупчивание
$
1
$?
а
ветвления
иет
о
ю
262
142
закалка и отпуск
при 205°С
4340 @,05% Si)
А
А
Л
195
-
152
закалка и отпуск
при 205°С
4340 @,54% Si)
А
А
А
58
190
169
закалка и отпуск
при 260 °С
4340 A.08% Si)
л
со
ю
195
167
А
4340 A,58% Si)
л
л
л
со
ю
187
170
А
4340 B,15% Si)
А
А
106
191
132
закалка и отпуск
при 595 °С
1
X
А
t>
106
210
старение 8 час.
при 426°С
Мартенсито-старею-
щая сталь 350
А
А
л
ю
аз
1
155
старение 2 часа
при 260°С
SAE 4340**)
А
А
Л
О
СО
142
162
1
*
*
1
и
с
f
о
о
о
Я
ж
ж
я
t
434 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН {ГЛ. VII
трещины при произвольном нагружении определяется при по-
помощи диаграммы dl/dt — Ki, полученной для соответствующей
внешней среды. В качестве иллюстрации рассмотрим рост тре-
трещины под действием водородного охрупчивания; соответствую-
соответствующую диаграмму аппроксимируем линейной зависимостью {7.113).
Пусть циклическая нагрузка синусоидальна, т. е.
Ki = K«+AKsinfirf. G.114)
где Km, A^C и о не зависят от времени. В этом случае прира-
приращение трещины А/ за один цикл равно
Отсюда находим среднюю скорость роста трещины dlfdt при
синусоидальном нагружении:
dl/dt = Д//Bя/ш) = а (К„ — Ко)- G.115)
Этот же результат, очевидно, будет справедлив для любой фор-
формы цикла, если условиться под средней величиной Km подразу-
подразумевать то значение ординаты, которое делит цикл на две равные
по площади области.
Таким образом, скорость роста усталостной трещины при
водородном охрупчивании равна скорости роста трещины при
постоянной нагрузке, если величину Ki в G.113) заменить на
среднее значение Кт за цикл нагружения. В качестве опытного
подтверждения этого результата можно сослаться на работу
Райдера и Галлахера [178].
Скорость роста коррозионной трещины при /Cib > Ki> Kiscc
не зависит от режима нагружения во времени. Наиболее слож-
сложны и мало изучены явления усталостного развития трещин при
циклическом нагружении в области Ki <. /Ciscc', в этой области
происходит взаимное наложение и усиление-соизмеримых пла-
пластических и коррозионных эффектов.
С уменьшением температуры атермический механизм раз-
развития усталостной трещины играет все большую "роль по
сравнению с термоактивационными механизмами. Начиная с
некоторой критической температуры, он определяет скорость
суммарного процесса роста усталостной трещины. При темпе-
температуре ниже некоторой критической скорость роста усталостной
трещины не зависит от внешней среды.
iS 8] ВЛИЯНИЕ ВОДЫ НА РАЗРУШЕНИЕ СТЕКЛА 435
§ 8. Влияние воды иа разрушение стекла
и горных пород
Ввиду широкой распространенности воды в природе вопрос
о ее воздействии на прочность твердых тел имеет большое прак-
практическое значение. Молекула воды состоит из ядра атома кис-
кислорода, двух протЬнов и десяти электронов. Ее можно предста-
представить себе в виде правильного тетраэдра, в центре которого
расположено ядро атома кислорода (расстояние от центра до вер-
вершин тетраэдра равно @,95-Ь 0,99) • 10~8 см). Две вершины тет-
тетраэдра (в которых находятся протоны) несут положительный
заряд, а двум другим вершинам можно приписать отрицатель-
отрицательный заряд. Ковалентная связь О—Н весьма прочна, ее энергия
равна 109 ккал/моль. Исключительная полярность молекулы
воды и наличие двух положительных водородных ионов (прото-
(протонов) Н+ объясняет многочисленные аномалии в поведении воды и
ее способность к образованию довольно прочных соединений с
другими полярными молекулами. Вследствие того, что у иона Н+
отсутствует электронная оболочка (и потому его размеры в ты-
тысячи раз меньше, чем у всех остальных ионов), он притяги-
притягивается электронами других молекул и может внедряться в их
электронные оболочки. Таким образом, водородная связь ослаб-
ляет связи, присутствующие в твердом теле; поэтому вода всег-
всегда уменьшает прочность твердых тел и способствует их разру-
разрушению. (Энергия водородной связи для полярных молекул рав-
равна примерно 6—12 ккал/моль.)
Рассмотрим подробнее три основных механизма воздействия
воды на рост трещин.
1. Развитие трещии в стекле. Стекло можно считать идеаль-
идеально-хрупким телом, так что раскрытие трещины в ее конце имеет
порядок межатомного расстояния г0. Энергию, затраченную на
разрыв одной связи в идеально-хрупком материале, легко оп-
определить из макроопыта по распространению трещин. Действи-
Действительно, так как поверхностная энергия у представляет собой
суммарную энергию, затраченную на разрыв связей, приходя-
приходящихся на единицу площади поверхности, то энергия U разрыва
одной связи, очевидно, равна
G.116)
Эта формула годится не только для идеальных кристаллов, но
и для аморфных тел (например, стекол); в последнем случае
величины U, г0 и у будут представлять собой осреднения по
множеству частиц.
В стеклах преобладают ионные связи, поэтому для теорети-
теоретического определения энергии связи можно использовать тео-
теорию Ворна (см. § 2 гл. II). Стекло заменяется эквивалентной
436 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
идеально-периодической решеткой, имеющей структуру NaCl
(см. рис. 6) и одинаковые со стеклом плотность, сжимаемость,
прочность, энергию связи и поверхностную энергию. По химиче-
химическому составу стекла и его плотности легко определить атомный
вес и межатомное расстояние эквивалентной решетки. Для про-
простой кубической решетки энергия связи (в расчете, как обычно,
на пару частиц) равна &U, где U — энергия, затраченная на раз-
разрыв одной связи. Отсюда по формулам B.31) и B.27) находим
U (в этих формулах энергия связи обозначается через (^)г=Го).
Таким образом, в стеклах с преобладающими ионными свя-
связями поверхностную энергию, максимальную прочность И энер-
энергию связи можно определить теоретически' по химическому со-
составу стекла, его плотности, модулю Юнга и коэффициенту
Пуассона. Для иллюстрации рассмотрим конкретный пример.
Для силикатного стекла с составом (в %): 72,7 SiC>2, 14,05
Na2O, 7,6 CaO, 3,73 MgO и др. величина y в воздухе, опреде-
определенная экспериментально на основе методов механики хрупкого
разрушения [18], в комнатных условиях равна 2 400 эрг/см2. При
таком составе стекла на 1 атом Са приходится примерно 4 ато-
атома Na, 10 атомов Si и 24 атома О. Мысленно заменим стекло
простой кубической решеткой, состоящей из одинаковых частиц
и имеющей одинаковые со стеклом плотность и сжимаемость;
атомный вес каждой частицы считается равным среднему атом-
атомному весу
1 -40 + 4-23 + 10- 28+24- 16 0„
1+4+10 + 24 ~ 2U Э- е'
Так как плотность стекла равна 2,6 г/см3, то отсюда для стекла
данного химсостава можно найти межатомное расстояние- /"о в
идеальной решетке; оно равно 2,3-10~8 см.
Теперь при помощи формул B.31), B.27), B.30) и G.116)
находим энергию связи, поверхностную энергию, максимальную
прочность на разрыв и величину U:
(?/)г=Гв = 213 ккал/г-атом,
U = 35,7 ккал/г-атом = 2,7 • 10~12 эрг/атом,
Y = 2 320 эрг/см2, amax = 800 кГ/мм2.
(Модуль Юнга и коэффициент Пуассона были приняты рав-
равными ? = 6,5 • 103 кГ/мм2, v = 0,28.) Величина у весьма близка
к указанному выше экспериментальному значению.
Когда полость трещины заполнена водой, водородные связи
молекул воды (их энергия примерно 6—12 ккал/г-атом) экра-
экранируют межатомные взаимодействия в стекле; в результате
энергия U в конце трещины должна уменьшиться примерно на
6—12 ккал/г-атом, т. е. на 20—30%. Согласно G.116), поверх-
5 81 ВЛИЯНИЕ ВОДЫ НА РАЗРУШЕНИЕ СТЕКЛА 437
ностная энергия стекла в воде должна уменьшиться также на
20—30%. Эта цифра очень хорошо согласуется с эмпирическими
данными для стекла того же состава [18].
Силовую схему такого адсорбционного воздействия воды на
стекло можно представить следующим образом (рис. 183). Ион
водорода Н+ притягивается в вер-
вершину трещины электронными обо-
оболочками атомов стекла; в результа-
результате тетраэдр молекулы воды, как
клин, расширяет боковыми гранями - - -
берега трещины. Указанное взаимо- Рис. 183.
действие можно трактовать также
как реакцию обмена ионами водорода между двумя фазами —
водой и стеклом (как это принято в теории стеклянного элек-
электрода в электрохимии [176]).
Из этого анализа вытекает, что понижения поверхностной
энергии твердого тела можно ожидать также в случае поляр-
полярных молекул среды и твердых тел с преимущественно ионными
связями. Оценку этого понижения легко произвести аналогич-
аналогичным методом, если знать энергию соответствующей полярной
связи.
Как видно, адсорбционный эффект для стекол, в отличие от
металлов, можно описать в рамках концепции /Сс.
Если внешние нагрузки, приложенные к стеклу, меньше пре-
предельных, то докритический рост трещин происходит вследствие
локальных разрывов из-за тепловых флуктуации его атомов и
молекулы воды, расположенных в конце трещины (вместо воды
может быть другая жидкость с полярными молекулами или не-
ненасыщенными водородными связями). Вследствие капиллярной
конденсации влажный воздух оказывает такое же действие, как
и вода.
В результате приходим к следующему выражению для ско-
скорости роста трещин в стекле:
dt то ехр RT \
(т0 « 102Ч-Ю 3 сек, R л; 2 кал/(град-моль), yi—структур-
yi—структурная константа материала).
Роль поверхностно-активной среды заключается в уменьше-
уменьшении энергии активации Ux (примерно на величину энергии со-
соответствующей полярной связи).
Практически величина максимально возможной скорости
роста трещин ограничена предельными скоростями кнудсенов-
ской диффузии молекул воды в узких щелях приблизительно
межатомной ширины (вблизи конца трещины).
438
влияние вйеШней среды на рост трещин
[ГЛ. VI1
2. Разрушение горных пород." Объем воды при замерзании
в обычных условиях увеличивается почти на 10%. Это свой-
свойство воды является основной причиной' разрушения горных по-
пород в местностях с холодным климатом. Дождевая вода летом
попадает в расщелины скал, зимой замерзает, и образовавший-
образовавшийся лед распирает берега трещины, в результате чего она про-
продвигается на некоторое расстояние. Через год этот процесс по-
повторяется и т. д.
Рассмотрим теорию этого явления при некоторых естествен-
естественных допущениях (рис. 184), Пусть вода занимает перед замер-
i
1
/
}
d
. г У
Al«L
Рис. 184.
занием некоторую область — d < х <С 0 вблизи конца трещи-
трещины в произвольно взятый момент времени (измеряемого года-
годами). Для простоты будем предполагать выполненными условия
плоской деформации. Размер d зависит, в основном, от клима-
климатических условий данного района Земли: температуры, коли-
количества осадков, влажности воздуха. Эти условия, осредненные
по достаточно большому промежутку времени, можно считать
неизменными в пределах, скажем, определенного геологиче-
геологического периода Земли. Размер d можно считать также постоян-
постоянным для данного района Земли. В целях простоты и общности
анализа будем предполагать, что d мало по сравнению с глу-
глубиной трещины и размерами скалы.
После замерзания происходит продвижение трещины на Д/.
Так как модуль Юнга скалы гораздо больше модуля упругости
льда,- то напряжение, действующее на стенки трещины, можно
считать равным
<sy = x\kvk при у = 0, —d<x<0. G.118)
Здесь k-o— модуль объемной сжимаемости льда, Д — относитель-
относительное объемное расширение воды при замерзании (Д«0,1),
tj — некоторый коэффициент, меньший единицы, который учи-
учитывает уменьшение давления вследствие продвижения трещины.
S 8] ВЛИЯНИЕ ВОДЫ НА РАЗРУШЕНИЕ СТЕКЛА 439
Коэффициент интенсивности напряжений в конце полубеско-
полубесконечной трещины у — О, х < А/ с нагрузкой G.118) можно найти,
например, при помощи формулы (П.З) (см. Приложение I):
/ft = B/V«) Л*0А (Vd + М — V5J). /G.119)
Отсюда, используя условие локального разрушения.в конце
трещины Ki = Kic, находим приращение трещины за один цикл
(один год):
M = (d-do?JDdo), <7.120)
где
Так как d0 n d постоянны в пределах достаточно большого про-
промежутка времени, средняя скорость развития трещин в горных
породах постоянна. Если учесть, что вблизи конца волосяных
трещин всегда имеется капиллярная вода, можно оценить сред-
среднюю величину d по наибольшему радиусу капли, необходимому
для капиллярной конденсации.
Приведем некоторые конкретные оценки. Для горных пород
(мрамор, гранит, песчаники и т. д.) Kic изменяется в пределах
1—3 кГ/мм'Ь; пусть для определенности Kic = 2 кГ/мм\ Зна-
Значение kv, как и для воды [ш], возьмем равным 200 кГ/мм2; кро-
кроме того, будем считать А = 0,1, х\ = 1. Согласно [72], максималь-
максимальное значение радиуса капилляра, при котором происходит кон-
конденсация влаги в нормальных условиях, порядка 10~5 см. Такому
расстоянию между берегами трещины по формулам C.44) со-
соответствует величина d порядка 10~3 см (Е и v взяты равными
3-Ю3 кГ/мм2 и 0,25 соответственно). По формуле G.120) вели-
величина d0 имеет порядок 10~3 см, следовательно, приращение воло-
волосяных трещий за 1 год имеет также порядок 10~3 см. Скала
толщиной порядка 1 км (или гора такой же высоты) будет
полностью разрушена примерно за 100 млн. лет; такой порядок
имеет возраст старых гор (Урал, Хибины и т. п.), определен-
определенный радиоактивным методом.
3. Разрушение пористых материалов. Продвигаясь по капил-
капиллярам пористого тела под действием капиллярных сил, вода
быстро насыщает поры и в некоторых случаях может оказывать
существенное влияние на прочность, особенно тогда, когда
силы, связывающие отдельные частицы тела, имеют электроста-
электростатическую природу. Так как сила взаимодействия электрических
зарядов в воде в 81 раз меньше, чем в воздухе, то в соответ-
соответствующее число раз должна уменьшиться также вязкость раз-
разрушения полностью насыщенного водой материала с ионными
связями между частицами *). ,
*) Таковы, например, сахар, глииа, кристаллы большинства 'солей и кис-
кислот, некоторые горные породы.
440 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
Кроме того, фильтрация жидкости в пористом теле оказы-
оказывает силовое воздействие на скелет, которое сводится к неко-
некоторой объемной силе. Поле внутренних упругих напряжений,
возникающих вследствие фильтрации, описывается обычными
уравнениями теории упругости с объемной силой, равной
gradp, где р — среднее давление фильтрующейся жидкости в
порах.
Можно показать, что имеет место следующая аналогия: если
выполняется закон Дарси, то в стационарных задачах теории
фильтрации внутренние напряжения в упругом скелете полу-
получаются из решения классической теории термоупругости, если
в решение вместо аЕТ/{\—2v) подставить р (а — коэффициент
температурного расширения, Т — температура). На основе этой
аналогии при помощи каталога решений для термоупругих ко-
коэффициентов интенсивности напряжений, приведенных в При-
Приложении I, можно получить решение ряда задач о разрушении
пористых тел.
Рассмотрим конкретный пример.
Пусть в бесконечном пористом пространстве имеется диско-
дискообразная щель х2-{-у2^а2, z = 0. В щели под постоянным
давлением ро находится жидкость (давление может поддержи-
поддерживаться при помощи специальной скважины, в которую нагне-
нагнетается жидкость). Давление жидкости'в порах вдали от щели
считаем равным рх- При помощи формулы (П. 87), воспользо-
воспользовавшись сформулированной аналогией, находим коэффициент
интенсивности напряжений Ки в конце щели за счет объемных
сил:
^ GЛ21)
Коэффициент интенсивности от внешней нагрузки определяется
по формуле (П.76). Складывая эти выражения согласно прин-
принципу суперпозиции, находим искомый коэффициент
G'122>
Как видно, коэффициент интенсивности напряжений в по-
пористом теле по сравнению с непроницаемым телом уменьшается
в 2A—v) раз (например, при v = 0,25 — в полтора раза).
Используя теперь условие локального разрушения /Ci = Ки,
можно найти давление в щели, необходимое для разрыва (Kic —
вязкость разрушения насыщенного жидкостью пористого тела).
Подобные решения представляют интерес, например, для
теории гидроразрыва нефтяного пласта.
§9]
РАЗРУШЕНИЕ ГОРЯЩИХ ПОРОХОВ
441
§ 9. Разрушение герящих порохов
Иногда при работе двигателей на твердом топливе происхо-
происходит выход на нерасчетный режим, приводящий к взрыву. Одна
из наиболее распространенных причин этого явления состоит
в том, что в твердом топливе имелись недопустимо большие
трещиноподобные полости (возникшие, в основном, при техно-
технологическом процессе). Когда фронт горения подходит к краю
такой полости, то вследствие повышенного давления в камере
сгорания горение быстро охватывает всю полость. При достаточ-
достаточно узкой и длинной полости вследствие затрудненного газоот-
газоотвода давление в ней достигает столь большой величины, что
происходит выход системы на неустойчивый режим. В зависи-
зависимости от типа топлива неустойчивость может иметь два со-
совершенно различных физических меха-
механизма: а) локальное объемное горение в
конце полости, б) локальное разруше-
разрушение топлива. Ниже предлагается тео-
теоретическое описание указанных явле-
явлений [80].
1. Постановка задачи. Пусть горящее
твердое тело в момент времени t = 0 за-
занимает полупространство х ~> О, на гра-
границе которого при х = О происходит
реакция горения. В теле имеется трещи-
новидная полость в плоскости у = О, по-
поверхность которой также горит (рис. 185).
Обобщение дальнейшего изложения на
случай тела и трещины произвольной
формы не вызывает принципиальных
затруднений. Считаем, что все реагенты
равномерно распределены в твердой
фазе, а продукты реакции газообразны.
Будем пренебрегать толщиной зоны ре-
реакции, считая, что фронт горения совпа-
совпадает с поверхностью всего тела.
Имея в виду 'практические приложе-
приложения, ограничимся временами, малыми
по сравнению с характерным временем релаксации напряжений
в теле и с характерным временем нагревания тела вследствие
теплопроводности. При этом тело можно считать упруго-пласти-
упруго-пластическим, а его температуру — постоянной. Рассмотрим только
квазистатический процесс деформирования твердого тела, тем
самым считая, что характерные времена протекания процесса
велики по сравнению с характерным временем распространения
упругих волн в твердом теле.
442 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
-Запишем уравнения теории малых деформаций твердого
тела в упругой области:
уравнения равновесия
^/./ = 0 (/,/=1,2,3), 'G.123)
закон Гука для однородного изотропного тела
а„ = 2це1{ + Ябг/9 (9 = в«), G.124)
кинематическая связь деформаций со смещениями
.в*/=т К/+«/.')• <7Л25)
Здесь щ, ец, оц — смещения, деформации и напряжения соот-
соответственно; X и ц — постоянные Ляме; индексам 1, 2 и 3 со-
соответствуют х, у и z.
Будем учитывать только пластические эффекты в окрестно-
окрестности края полости. Применим приближенную схему Дагдейла,
согласно которой пластическая область сосредоточена* в неко-
некоторой узкой области D на продолжении трещины; размер этой
области должен быть определен из решения задачи. Для про-
простоты ограничимся случаем симметрии относительно плоскости
у = 0; при этом пластические деформации будут сосредоточены
в этой же плоскости в некоторой окрестности контура трещины/
(рис. 185), причем
Oy = os, xxg = rzy = 0 (y = 0,(x,z)(=D). G.126)
Здесь as — предел текучести на растяжение (реальная диаграм-
диаграмма в—е аппроксимируется диаграммой Прандтля). Всюду в
дальнейшем граничные условия с поверхности полости и обла-
области О будем сносить на плоскость у = 0 точно так же, как это
делается, например, в теории тонкого крыла в аэродинамике.
Схема Дагдейла получила удовлетворительное эксперимен-
экспериментальное подтверждение для композитных материалов с поли-
полимерным связующим, когда адгезионная прочность меньше
прочности полимера. В последнем случае в области D сконцен- .
трированы, собственно говоря, не пластические, а высокоэласти->
ческие деформации, однако, как нетрудно видеть, это несуще-
несущественно в рамках разрывных решений теории малых упругих
деформаций. Заметим, что смесевое ракетное топливо обычно
состоит из кристаллических частиц, распределенных в поли-
полимерном связующем.
Обозначим через 2А неизвестную заранее толщину полости,
через 2о — взаимное смещение противоположных стенок поло-
полости, через hc — толщину сгоревшего слоя на одной стенке.
Все эти величины, очевидно, представляют собой некоторые
:$9J ' РАЗРУШЕНИЕ ГОРЯЩИХ ПОРОХОВ . 443
искомые функции х, г и t. Они связаны между собой следую-
вдим равенством: '
ft = ftc-fo. G.127)
2. Уравнения течения газа в полости. Течение газа в полости
считаем локально-изэнтропическим и безвихревым, а газ —
идеальным. В каждой точке х, у, г имеет место замкнутая
система уравнений
" -f+ pdivV = 0, -^ = _-LgradP) 4"^ = 0' GЛ28)
at at p at р
Здесь р, р, V—'давление, плотность и вектор скорости газа со-
соответственно; к — показатель адиабаты.
При упрощении уравнений G.128) с учетом условия h<g.L,
где L — характерный линейный размер полости в плане, встре-
встречаются затруднения, родственные тем, которые имеют место
в теории упругих оболочек и в теории турбулентности. По-
Поскольку эти трудности не отражены в литературе, имеет смысл
остановиться подробнее на выводе основных уравнений течения
газа в полости.
Возможны два точных подхода. Первый из них основан на
операции усреднения, применяемой с целью замыкания системы
уравнений для средних значений искомых функций:
<р)=-ш $ pdy> <v>=iJv^ <7Л29>
-ft -h
а также моментов более высокого порядка. Однако в силу не-
нелинейности уравнений G.128) достичь этой цели не удается
(проблема замыкания, аналогичная той, которая имеет место
в теории турбулентности). Второй подход основан на введении
в искомые функции физического малого параметра (например,
hjL) и разложении функций в ряд по у и по малому параметру;
при этом для последовательных членов разложения получаются
замкнутые системы уравнений, которые в. принципе могли бы
быть решены поочередно в порядке возрастания индекса. Од-,
нако вследствие того, что граничные условия в краевых задачах
с различным индексом связаны между собой, возникающие труд-
трудности оказываются непреодолимыми в рамках точных методов
(не говоря уже о трудностях суммирования асимптотических
рядов).
Таким образом, при замыкании системы уравнений или форму-
формулировке граничных условий приходится делать некоторые физи-
физические допущения, упрощающие задачу (теория Кирхгофа для
упругих пластин, теории Тейлора и Прандтля в турбулентности
444 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [ГЛ. VII
и др.). Следуя указанному полуэмпирическому методу, примем
«гипотезу плоских сечений»:
Vy = 0, p = p(x,z,t), p = p(x,z,t),
Vx=Vx(x,z,t), Vz=Vz(x,z,t). GЛ30)
Тогда из G.128) для компонент Vx и Vz легко получить сле-
следующую систему уравнений (к уравнению неразрывности при-
применяется операция усреднения):
Здесь vn — скорость истечения газа по нормали к поверхности
полости. Напишем уравнение сохранения массы на фронте го-
горения
где ps— плотность твердой фазы. Так как ps ~> р, то
dhjdt G.132)
Приведем еще уравнение состояния идеального газа
p = pgRT/m (R**2 калЦград • моль)). G.133)
Здесь т — молекулярный вес газа, Т — его температура, g —
ускорение силы тяжести в данной точке пространства.
Скорость горения возьмем в виде некоторой эмпирически
определяемой зависимости
dhjdt« / (р) A + b Vl + b Vl), G.134)
где b — эмпирическая константа (при отсутствии эрозии b = 0),
f(p) — некоторая функция.
Полученная система, уравнений, как нетрудно проверить,
замкнута.
3. Критерий локальной неустойчивости. При определенных
критических условиях скорость изменения линейных размеров
полости в плане может быть гораздо больше скорости измене-
изменения толщины полости. Это происходит из-за действия следую-
следующих физических факторов: а) локального разрушения топлив.а
в концевой части полости (за счет концентрации напряжений),
б) резкого увеличения скорости горения в концевой части по-
полости вследствие локального разрыхления материала и увели-
увеличения поверхности горения (локальное объемное горение).
f в) РА8РУШЕНИЕ ГОРЯЩИХ ДОРОХОВ 445
Последний фактор обусловлен также местной концентрацией
деформаций.
Указанные физические механизмы локальной неустойчиво-
неустойчивости, играющие неодинаковую роль в различных материалах,
имеют общую природу: они связаны с локальной концентрацией
деформации. Это позволяет сформулировать следующий крите-
критерий предельного равновесия: в рамках схемы Дагдейла взаим-
взаимное смещение противоположных стенок полости на ее контуре
L всегда меньше или равно 2S:
о(х, z, f)<6 {x, zsL). G.135)
Здесь S — некоторая константа горящего твердого топлива; из
физических соображений ясно, что она может зависеть только
от температуры топлива и давления газа в соответствующей
точке контура L.
Согласно G.135), при v < б процесс локально устойчив и
размеры полости в плане не изменяются (подрастанием по-
полости, происходящим, в частности, вследствие устойчивого го-
горения, пренебрегаем, что вполне допустимо лишь для доста-
достаточно малых времен, когда /г ¦< L); как только хотя бы в одной
точке контура L будет достигнуто равенство v = б, в малой
окрестности этой точки начинается локально неустойчивый
процесс «горения — разрушения». Следует иметь в виду, что
в некоторых случаях система в целом может еще оставаться
устойчивой (т. е. конфигурация контура полости меняется в точ-
точках, где v = б, «не катастрофически быстро»). Такой случай
вполне реален. Поэтому вопрос об устойчивости системы в це-
целом должен изучаться отдельно.
Если схема Дагдейла неприменима, т. е. пластические де-
деформации «размазаны» в некоторой области, следует исполь-
использовать локальный критерий на основе коэффициента интенсив-
интенсивности напряжений сверхтонкой структуры.
В том случае, когда имеет смысл представление о тонкой
структуре конца полости, все эти критерии эквивалентны условию
Ki<Ku Шо = 2osE6). G.186)
Здесь Ki — коэффициент интенсивности напряжений, Къ — $яз-
кость разрушения горящего пороха, соответствующая aJisco
в сЛучае коррозии. Практически наиболее характерным призна-
признаком формирования тонкой структуры является: проявление
масштабного эффекта.
Для определения констант б и К\с наиболее удобна следую-
следующая схема эксперимента. В пластинке из исследуемого мате-
материала делается сквозной разрез, имитирующий дефект. Тол-
Толщина пластинки не должна быть слишком малой, чтобы не про-
проявилась зависимость б и /Cic от толщины пластину. По той же
446 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН . (ГЛ. VII
причине радиус надреза не должен быть слишком большим.
Эти границы для каждого материала свои и определяются прак-
практически; для смесевых твердых топлив они необременительны
. (разрез можно наносить стальной бритвой); Затем пластинка
с разрезом подвергается нагружению и поджигается в камере
с соответствующим давлением. Схемы нагружения могут быть
различными (наиболее просто осуществить центральный из-
изгиб). Предложенный способ удобрен тем, что при достаточно
малой толщине пластины давление в сквозной полости будет
таким же, как в камере; при этом величины v и Ki можно срав-
сравнительно легко вычислить в виде определенных функций внеш-
внешней нагрузки и геометрии пластины, а также Постоянных ма-
материала. Замеряя предельную нагрузку, по ним нетрудно опре-
определить S и Kic-
4. Плоская стационарная задача. Рассмотрим важный слу-
случай плоской стационарной заДачи, когда в приведенной выше
общей системе уравнений можно положить
= Q, dp/dt=O, dVJdt^Q. G.137)
В плоскости ху полость представляется вырезом длиньг /
вдоль оси х; толщина выреза h гораздо меньше I. На продол-
продолжении i выреза имеется пластический слой нулевой толщины
с длиной d, подлежащей определению.
В данном случае систему уравнений п. 1 в пренебрежении
эрозией можно свести к следующей:
VI' * Р ¦
2 ^ к — 1 р —Г««
id
+' ¦ G.138)
jD#±frf
t+d -I
I 9] РАЗРУШЕНИр ГОРЯЩИХ ПОР0Х0В 447
Здесь ji, v — модуль сдвига и коэффициент Пуассона соответ-
соответственно; <т" — рабочее напряжение ау вдали от полости; ро, Ро
и ~ри pi — давление и плотность газа в камере сгорания при
х = О ив конце полости при х = / соответственно (величины
с индексом 1, очевидно, подлежат определению); К(х)— задан-
заданная толщина начальной полости.
Последние два соотношения G.138) представляют собой ре-
результат решения плоской задачи теории упругости для разреза
у = 0, |*|</ + d в бесконечной плоскости с граничными усло-
условиями
при x-\-iy-+oo вд~>а7> хху-*®> ах->0,
при г/ = 0, l<\x\<l + d ay = as, txy = 0, G.139)
при {/ = 0, \х\<1 вут= — р, xxy = Q.
Для учета граничного условия на основном фронте горения
лри х = 0 вводится поправочный коэффициент г\, который равен
примерно 1,2.
Система G.138) служит для отыскания следующих величин:
d, p(x), p(x), Vx(x), v(x), h(x). Нетрудно свести ее к одному
интегро-дифференциальному уравнению относительно р(х). Для
численного решения этого уравнения (а только такое представ-
представляется возможным в общем случае) наиболее рационально при-
применить следующий метод: функция р{х) ищется в виде поли-
полинома с неизвестными коэффициентами (например, в виде ли-
линейной функции), а уравнение удовлетворяется приближенно в
смысле наибольшей близости к нулю среднеквадратичной на-
навязки. При этом неизвестные коэффициенты определяются из
условия минимума получившейся функции.
Для оценки величин проведем приближенный аналитический
расчет в предположении, что -
hQ (х) = ho = const, h0 > v, h0 > hc,
f . G-140)
f(p) = a + Ьр, j p(x)dx = \l(px
где а и b — эмпирические константы. При вычислении смеще-
смещения v в конце полости -при х-/ и величины d для простоты
также будем считать, что на стенкн полости действует постоян-
постоянное давление -г (pi + Ро)«
448 ВЛИЯНИЕ ВНЕШНЕЙ СРЕДЫ НА РОСТ ТРЕЩИН [IVL
В результате из уравнений G.138) получим
Ы<* + *>] {7Л41)
2 к-1 р, 2 к-1 р0
о = - л 2 A ~E v2) / Bg, + Pi + Po) In cos p, G.142)
d / я Bo
— = secp—1 IP == 9/9
Соотношения G.141) служат для определения ри pi, Ужь
Vxo- Формула G.142) на основании G.135) позволяет найти
достаточное условие устойчивости системы:
- Л/ Bg. + Pi + Po) In cos ft< 2 A"ffv>) . G.143)
Здесь величина pi представляет собой -корень следующего урав-
уравнения:
Полученное простое решение можно использовать в каче-
качестве нулевого приближения,
ГЛАВА VIII
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
§ 1. Разрушение при взрыве
В этой главе рассматриваются некоторые прикладные воп-
вопросы механики хрупкого разрушения, имеющие большое прак-
практическое значение. По большинству из этих вопросов имеется
обширная специальная литература*), поэтому здесь рассмат-
рассматриваются только наиболее принципиальные проблемы матема-
математического моделирования, а фактические сведения используются
лишь в той мере, в какой они необходимы для построения или
проверки теории. Для решения задач этой главы по тем или
иным причинам часто бывает недостаточно развитого выше ап-
аппарата, и необходимо построение новых математических моде-
моделей. Одной из таких задач является задача о разрушении твер-
твердых тел при взрыве.
Очень быстрое выделение большого количества энергии в не-
некотором объеме твердого тела сопровождается различными
процессами разрушения, характер которых существенно зави-
зависит от общего количества выделяющейся энергии и ее концен-
концентрации, от источника и способа выделения энергии, от физико-
' механических свойств твердого тела.
Назовем некоторые из источников взрывообразного выделе-
выделения энергии. Это ядерные реакции (атомные и ядерные взры-
взрывы), химические реакции (большинство взрывов ВВ), сильные
электрические разряды (например, атмосферная молния), мощ-
мощные световые импульсы (получаемые в квантовых генераторах).
Аналогичные явления имеют место, например, при соударении
быстро движущихся тел, при горных ударах и землетрясениях,
при разрушении высокопрочных стекол или сильно сжатых
хрупких материалов, при взрывах баллонов со сжатым газом
и т. д. В этом параграфе рассматривается, в основном, разру-
разрушение под действием химических и ядерных ВВ, когда в очаге
взрыва образуется газ, находящийся под большим давлением и
производящий деформацию и разрушение твердого тела.
*) Для первоначального ознакомления с этими и некоторыми другими
вопросами механики разрушения можно обратиться к обзорной статье [180].
Проблемы прочности конструкционных материалов весьма обстоятельно изло-
изложены в монографии Тетелмана н Мак-Ивнли [181].
15 Г. П. Черепанов
460 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ fftf, VI»
1. Законы подобия. Практика взрывного дела основана на
.законе подобия, согласно которому объем разрушенной породы
(а также объем полости, образующейся после взрыва) прямо
пропорционален объему заряда ВВ. Коэффициент пропорцио-
пропорциональности зависит от физико-механических свойств породы, ха-
характеристик ВВ, формы и расположения зарядов, устройства
зарядной камеры и способа взрывания.
Закон подобия получается из следующих соображений:
а)" характерные размеры заряда и зарядной камеры малы
по сравнению с характерным размером разрушенной обла-
области R; - ,
б) разрушение тела описывается некоторой теорией предель-
предельного состояния (типа теории Галилея — Кулона — Мора илн
Треска — Мизеса) с характерным напряжением os;
в) при одинаковых породе и ВВ, одной и той же геометрии
и способе взрывания размер R разрушенной области зависит
только от внутренней энергии заряда Э.
Величины R, Э и as могут образовывать лишь следующие
безразмерные комбинации:
точечный заряд линейный заряд
| = Э/(а,#3), t = 9l(osR*). (8.1)
Число | представляет собой параметр моделирования дей-
действия взрыва. Так как энергия Э пря*мо пропорциональна
объему заряда*), то закон подобия вытекает из (8.1). Коэф-
Коэффициент | определяется из модельных экспериментов со взры-
взрывами меньшего масштаба.
Указанный закон подобия нарушается только для весьма
мощных взрывов из-за сравнительно большого влияния силы
тяжести и для хрупких материалов, к которым, строго говоря,
неприменимы теории предельного состояния. Разрушение
идеально-хрупких тел под действием взрыва в общем случае
описывается тремя константами Ки, Кпс и Кпи, размерность
которых отлична от размерности напряжения. Сам процесс
разрушения можно представить себе как процесс развития и
размножения динамических трещин вследствие ветвления. На-
Начальные трещины, выходящие на границу зарядной камеры и
служащие очагом разрушения, не влияют на размер R разру-
разрушенной области, так как их длина значительно меньше R. По-
Поэтому для идеально-хрупких тел вместо допущения б) можно
принять следующее предположение, ограничившись лишь тре-
трещинами нормального разрыва:
*) Для химических ВВ величина Э прямо пропорциональна массе заряда,
а для ядерного горючего — общему дефекту массы.
i 1] : . РАЗРУШЕНИЕ ПРИ ВЗРЫВЕ 451
г) разрушение хрупкого тела описывается его характерной
вязкостью разрушения Kic-
Величины R, Э и Kic могут образовывать лишь следующие
безразмерные комбинации:
точечный заряд линейный заряд
3'2)- (8.2)
Согласно допущениям а), в) иг) число т] представляет со-
собой параметр моделирования действия взрыва [182- ш] в идеаль-
идеально-хрупких телах (например, в прочных горных породах, стекле
и т. п.)- Коэффициент tj, как и |, должен определяться из мо-
модельных экспериментов со взрывами меньшего масштаба.
Для упруго-пластической модели тела с трещинами примем
следующее допущение:
д) разрушение тела описывается характерными константами
материала as и Kic
В этом случае согласно допущениям а), в) и д) парамет-
параметрами моделирования действия взрыва будут числа ? и т).
Величины R, фигурирующие в формулах (8.1) и (8.2), имеют
различный физический смысл. Для идеально упруго-пластиче-
упруго-пластического тела R представляет собой, по существу, характерный ли-
линейный размер области необратимых пластических деформаций,
а для идеально-хрупкого тела — характерный размер разру-
разрушенной зоны вблизи очага взрыва, пронизанной трещинами,
образовавшимися вследствие взрыва. В последнем случае под
разрушенной зоной для определенности будем понимать область
тела, образованную несвязанными между собой кусками ма-
материала.
Размер разрушенной зоны гораздо больше размера пласти-
пластической области, если "выполняются следующие условия (полу-
(получаемые при помощи (8.1) и (8.2)):.
для точечного заряда для линейного заряда
a*9»/tfc, о1Э->К\с. (8.3)
Из этих оценок вытекает, что для достаточно моцщых взры-
взрывов поведение любого упруго-пластического тела с трещинами
приближается к идеально-хрупкому (когда пластическая зона
пренебрежимо мала по сравнению с разрушенной).^ В част-
частности, для достаточно мощных взрывов в любых твердых телах
размер разрушенной области значительно превосходит размер
образовавшейся каверны (размер каверны в момент непосред-
непосредственно после взрыва завиеит лишь от пластических свойств
породы и определяется параметром %). Поэтому размер раз-
разрушенной зоны определяется параметром т|.
15*
452 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
Этот вывод хорошо согласуется с экспериментальными дан-
данными, например, по подземным ядерным взрывам [184~186]. По-
Полость, сформировавшаяся после камуфлетного взрыва, имеет
форму конуса с вертикальной осью; радиус основания конуса
примерно равен радиусу каверны, образовавшейся непосред-
непосредственно после взрыва, а высота имеет порядок радиуса разру-
разрушенной области. Конус образуется вследствие обрушения раз-
разрушенного материала с купола каверны на ее дно под дей-
действием силы тяжести. Высота каверны достигает пяти — шести
радиусов основания [185> 186].
Трещинообразованием можно пренебречь только при выпол-
выполнении следующих условий:
для точечного заряда для линейного заряда
«*Э<К\С, ¦ о]Э<КЪ. (8.4)
Условие (8.3) выполняется практически всегда, в то время как
условие (8.4) может иметь смысл лишь для микровзрывов или
же для очень вязких тел (Kic весьма велико, a. os мало).
Во взрывном деле разработано мното интересных приемов,
позволяющих управлять действием взрыва. Для получения опти-
оптимального эффекта варьируют пространственное расположение
зарядов, времена их последовательного взрывания, конструк-
конструкции зарядов и зарядных камер. Весьма перспективным методом
управления действием взрыва является создание специальных
искусственных полостей с помощью взрывов малой мощности
[187]. Такие полости могут использоваться в качестве экрана,
предохраняющего от разрушения полезные объекты, а также
с целью отражения волны сжатия (и направления отраженной
волны растягивающих напряжений в заданный объем, подле-
подлежащий разрушению).
2. Общая теория действия взрыва. Для строгого количествен-
количественного расчета процесса разрушения под действием взрыва не-
необходимо, прежде всего, сформулировать математическую мо-
модель, описывающую поведение элементарных объемов твердого-
тела. Наиболее рациональной представляется теоретическая
схема, основанная4 на следующих представлениях.
а) Элементарный объем может находиться только в двух со-
состояниях: разрушенном и неразрушенном (в дальнейшем нераз-
неразрушенное состояние будем называть О-состоянием, а разрушен-
разрушенное — ^-состоянием).
б) В каждом из этих состояний материал ведет себя как
некоторое (в общем случае упрочняющееся) упруго-пластиче-
упруго-пластическое тело, причем свойства таких упруго-пластических тел, во-
вообще говоря, различны*).
*) Одномерная диаграмма а — е предлагаемой модели изображена на
рис. 186 вместе с правилами перехода, указанными стрелками,
S 1]
РАЗРУШЕНИЕ ПРИ ВЗРЫВЕ
453
в) Возможны лишь переходы из 0-состояния в ^-состояние,
обратные переходы невозможны.
г) Переход из 0-состояния в F-состояние происходит на не-
некоторой поверхности разрушения в физическом пространстве,
которая является поверхностью, сильного разрыва для напря-
напряжений и деформаций (поверхность
разрушения перемещается в про-
пространстве, разделяя 0- и F- состоя-
состояния) .
д) В каждой точке поверхности
разрушения выполняются следую-
следующие соотношения:
уравнение сохранения массы
>--.
Рис. 186.
три скалярных уравнения
сохранения
— vnF),
Ti0 — *tF = Po (»no — Vn) (vl0 — viF) (/=1,2),
уравнение сохранения энергии
импульса
D = j(Vn-vnOy+Uo~^f-^(Vn-vnFY-UF+^. (8.7)
Здесь xi, x2, n — локальная система декартовых координат в рас-
рассматриваемой точке поверхности разрушения (п — внешняя нор-
нормаль к этой поверхности), индексы 0 и F относятся к 0- и
F-состояниям соответствующих величин, риг; — плотность и
скорость материальных частиц соответственно, оп, п, х% — ком-
компоненты вектора напряжения на рассматриваемой площадке
поверхности, Vn — скорость распространения поверхности раз-
разрушения, U — упругий потенциал единицы массы, D — диссипа-
диссипация энергии на поверхности разрушения, приходящаяся на еди-
единицу массы (тепло, энергия остаточных микронапряжений, по-
поверхностная энергия трещин и др.).
Исключая из (8.7) при помощи (8.5) и (8.6) скорости Vn
и vn, нетрудно получить также соотношение*)
е) Величина D представляет собой некоторую постоянную
материала, если скорость распространения поверхности разру-
разрушения меньше скорости переднего фронта возмущения.
*) Это уравнение называют ударной адиабатой или адиабатой Гюгоиио,
Обычно его пишут, не выделяя в явном виде энергию диссипации D, а вклю-
включай ее во внутреннюю энергию е* = Ur + D,
464 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
Если скачок плотности на поверхности разрушения прене-
пренебрежимо мал, то уравнения (8.5) и (8.6) сводятся к обычным
условиям непрерывности нормальной скорости vn и вектора
напряжения (ап, ть^г). Уравнение сохранения энергии (8.7)
в этом случае примет вид ?/0 — Up = D, т. е. упругий потен-
потенциал терпит заданный скачок на поверхности разрушения.
Это условие по аналогии с критерием Гриффитса можно
сформулировать так: минимально необходимое количество
упругой энергии, высвобождающейся вследствие хрупкого раз-
разрушения (и приходящейся на единицу массы), есть постоянная
материала. Для определения этой постоянной, аналогичной по
физическому смыслу величине у в теории трещин, необходимы
специально поставленные эксперименты со взрывом.
Эти представления позволяют указать общую замкнутую
систему уравнений для описания процесса разрушения под дей-
действием взрыва. Согласно этим представлениям, разрушение
фиксированной материальной частицы под действием взрыва
происходит так.
Если ударная волна сжатия имеет достаточно большую ин-
интенсивность, то разрушение (дробление) частицы происходит не-
непосредственно на переднем фронте волны возмущения. В этом
случае поверхность разрушения совпадает с фронтом ударной
волны. Такую волну будем называть волной дробления. Заме-
Заметим, что для металлов и прочных горных пород ударные волны
Вплоть до давлений порядка 105 кГ/см2 можно считать звуко-
звуковыми. Если же интенсивность ударной волны недостаточно ве-
велика, то' скорость распространения поверхности разрушения
меньше скорости переднего фронта возмущения (ударной вол-
волны) и определяется дополнительным условием е). В этом слу-
случае вначале частица в 0-состоянии подвергается некоторому
возмущению, находящемуся в упругой (или упруго-пластиче-
упруго-пластической) области; затем начинается постепенное разрушение (т. е.
развитие трещин), которое, наконец, достигает такого уровня,
.что, если бы дальнейшее развитие трещин внезапно остано-
остановилось, то эту частицу все равно можно было бы отделить от
тела*). Этот момент разделения рассматриваемого объема тела
на несвязанные между собой части соответствует переходу из
0-состояния в F-состояние. В дальнейшем продолжается дроб-
дробление частицы, которое достигает тем большей степени, чем
ближе она расположена к месту взрыва. Таким образом, по-
поверхности разрушения в рассматриваемой модели придается
геометрический смысл (как некоторой границы возможной по-
полости в теле). Граница фактической полости реализуется как
*),При этом сами трещины могут быть расположены и вне рассматри»
ваемой частицы.
I 1] РАЗРУШЕНИЕ ПРИ ВЗРЫВЕ 455
предельное положение поверхности разрушения. Поверхность
разрушения, очевидно, имеет толщину порядка характерного
максимального размера отделившихся частиц материала; по-
поэтому фронт (поверхность) разрушения может быть весьма
размытым. Величина D равна необратимой работе пластических
деформаций плюс приращение поверхностной энергии трещин
на фронте разрушения. По существу, уравнение (8.7) при D=/=0
надо рассматривать как определение поверхности разрушения
в нашей модели. -
Следуя работам [188> 189], запишем систему основных уравне-
уравнений в неподвижной декартовой системе координат для общего
случая:
уравнения сохранения импульса
P-W = аЧ- / + Х< (*' Iв 1> 2> 3)'
уравнение сохранения массы
|e O, (8.9)
соотношения, выражающие компоненты тензора скорости де-
деформаций ец через компоненты скорости vt материальной ча-
частицы, - '' " .
ei/ = l(Oi/ + O/ii), (8.10)
общие уравнения упруго-пластической модели в случае од-
«ого параметра упрочнения %
(8.11)
1 = 1@^, ф(а(/) = 0. (8.12)
Здесь
1) со > 0, если только Ф = 0, -^—ди = 0, в остальных слу-
aaii
чаях со = О;
2) h > 0, если только Ф < 0 и д'— атп > 0, в остальных
случаях h = 0.
Здесь U, f, Ф, h — некоторые функции, определяемые экспе-
экспериментально A1 — упругий потенциал единицы массы, / — по-
поверхность нагружения, Ф — поверхность текучести, h{%)—функ-
h{%)—функция упрочнения), Xi — объемная сила, Оц — компоненты тензора
напряжений, со — новая неизвестная функция. Первое слагаемое
4&б Некоторые йроблеМы хрупкого разрушения [гл. vm
в правой части (8.11) представляет собой полную (тензорную)
производную упругой сотавляющей тензора деформаций; второе
и третье слагаемые описывают две пластические составляющие
(пластическое упрочнение и идеальную пластичность соответ-
соответственно). В случае изотропного тела функции U, f и Ф могут
зависеть только от трех независимых инвариантов тензора на-
напряжений.
Деформируемые системы, состоящие из твердых частиц, об-
обладают следующими особенностями:
1) тело может быть нелинейно-упругим даже при сколь угод-
угодно малых деформациях [188].
2) необратимые пластические деформации обусловлены не-
несколькими различными механизмами, из которых важнейшими
являются сдвиг, переупаковка частиц пористого тела и потеря
контактов между частицами при растяжении (в металлах по-
последние два механизма обычно несущественны).
Эти особенности в общем виде математически представлены
уравнениями (8.11), которые получены следующим образом:
скорость деформации записана в виде суммы трех слагаемых
(одно из которых отвечает упругой деформации, другое — пла-
пластической дефорации с упрочнением, а третье — предельному
состоянию); затем для каждой из пластических составляющих
пишется ассоциированный закон течения согласно общей теории
пластичности [190> 124]. Пластические составляющие не зависят
друг от друга, так как соответствуют различным областям про-
пространства напряжений.
Представления, сформулированные в [188> 189], позволяют так-
также учесть эффект интенсивной фильтрации газа в промежутках
между частицами разрушенного тела вблизи полости. Этот эф-
эффект влияет на условия расширения газа в полости, приводит
к появлению дополнительной объемной силы в теле и может
иметь самостоятельное значение, в особенности на заключитель-
заключительных стадиях процесса разрушения. Однако эти вопросы здесь
не рассматриваются, так как имеют второстепенное значение
для формулировки собственно проблемы разрушения.
Деформации тела ец выражаются через смещение и при
помощи обычных кинематических соотношений механики сплош-
сплошной среды [124], а смещения определяются из решения диффе-
дифференциальных уравнений
= v(r,t), u = r — r0. (8.13)
(Функции U, f, Ф и h, вообще говоря, различны для 0- и F-co-
стояний тела.)
Уравнения (8.8) — (8.12) составляют замкнутую систему; со-
соотношения на фронте разрушения даются формулами (8.5) —
(8.7).
S И РАЗРУШЕНИЕ ПРИ ВЗРЫВЕ 457
Наиболее полная теория действия взрыва (из предложен-
предложенных ранее) принадлежит С. С. Григоряну [191]*). В обзорной
статье [180] можно найти изложение ряда других, гораздо ме-
менее точных, теорий того же типа. Теория Григоряна основана
на представлении о том, что на поверхности разрушения со сто-
стороны неразрушенного материала выполняется условие типа кри-
критериев прочности (см. § 2 гл. I), т. е. существует некоторая
функциональная зависимость между напряжениями**):
fi(o(,) = 0. (8.14)
Эта зависимость должна определяться экспериментально. В мо-
модели Григоряна удельная диссипация энергии D на фронте раз-
разрушения определяется в каждой конкретной задаче из урав-
уравнения энергии (8.7). Имеются и некоторые другие отличия от
излагаемой здесь теории, однако они менее существенны.
Как показано в предыдущих главах, условие (8.14) прин-
принципиально не может описать разрушения хрупких тел, так как
для хрупких материалов в него входит еще скрытый структур-
структурный параметр — длина трещины (точнее, это соотношение бу-
будет зависеть от размеров, количества и расположения наиболее
опасных трещин).<Прочность хрупких материалов в зависимости
от значений этого неучитываемого скрытого параметра может
изменяться на несколько порядков (например, прочность обыч-
обычного силикатного стекла, как показывает опыт [92], может изме-
изменяться на три порядка). Поэтому вследствие развития трещин
разрушающие напряжения на поверхности разрушения в хруп-
хрупком теле могут изменяться на несколько порядков, если началь-
начальное давление газов в зарядной камере достаточно велико: от
весьма больших значений в начальные моменты времени N(боль-
N(больших, чем в статических условиях) до очень малых значений
(существенно меньших, чем в статических условиях испытания)
при больших временах, когда фронт разрушения приближается
к границе конечной полости. Например, в случае периодиче-
периодической системы полубесконечных хрупких трещин (см. рис. 76)
*) Следует отметить также близкую по постановке теорию распростра-
распространения динамических воли в упруго-пластических материалах с задержкой те-
текучести (малоуглеродистых сталях). Эта теория развита Ю. Н. Работновым
[70]; она основана, по существу, на тех же представлениях а) —д) (вместо
условия е) требуется, чтобы некоторый функционал во времени от определен-
определенной комбинации напряжений достигал критического значения). Представления
а) — д) были использованы также в теории псевдоожижения двухфазных
(дисперсных) систем, развитой автором [!88>189] применительно к вопросам
химической технологии.
**) На одномерной диаграмме рнс. 186 это соответствует тому, что поло-
положение точки М задается заранее, т. е. оно считается некоторой постоянной
характеристикой материала. В нашей модели положение этой точки опреде-
определяется условием на фронте (8.7), ""
458 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
развитие трещин согласно точной зависимости E.32) прекра-
прекращается лишь при напряжениях, удовлетворяющих условию
Uо < y/h, т. е. при весьма низких напряжениях.
Поэтому предлагаемая теория представляется более точной
и к тому же принципиально более простой (вместо эмпириче-
эмпирической функции от трех переменных в (8.14) — одна константа D).
В логическом отношении она является развитием общего энер-
энергетического подхода (§ 2 гл. V), родственного энергетическому
методу в теории трещин, применительно к данным задачам, в
которых энергосток распределен вдоль движущейся поверхно-
поверхности разрушения. ~
Наиболее правильным в принципиальном отношении уточне-
уточнением и обобщением предлагаемой модели по аналогии с тео-
теорией трещин является анализ структуры фронта разрушения,
который позволит установить возможную зависимость D от
Vn — vn0, an0 и р.
3. Некоторые упрощения. Как обычно, эффективные анали-
аналитические решения можно получить лишь для простейших слу-
случаев. Для получения таких решений сделаем следующие упро-
упрощения в общей модели:
1) тело линейно-упруго в 0-состоянии (т. e. pU представ-
представляет собой квадратичную функцию напряжений),
2) упрочнение тела в F-состоянии отсутствует, т. е. h = О,
3) поверхность текучести Ф(оц) = 0 является границей об-
области в пространстве напряжений, определяемой неравенствами
(8Л5)
(8.16)
Здесь 01, 02, аз — главные напряжения; оп и %п — соответ-
соответственно нормальное.и тангенциальное напряжения на площадке
с вектором нормали я; & и б — коэффициент сцепления и угол
внутреннего трения (в законе Кулона) ч Условие (8.15) выра-
выражает отсутствие сцепления между частицами разрушаемого ма-
материала при растяжении.
Определенная таким образом поверхность текучести является
сингулярной, т. е. имеет ребра и угловые точки. Заметим, что
уравнения (8.11) справедливы только для регулярных тонек
этой поверхности, однако на основе сформулированных пред-
представлений и общей теории пластичности для сингулярных по-
поверхностей текучести [19°-124] нетрудно получить соответствующие
уравнения также для сингулярных точек поверхности. Это пре-
предоставляется читателю.
Условие разрушения (8.14), которое ставится на поверхно-
поверхности разрушения в теории Григоряна, в некоторых наиболее
.важных случаях можно получить из (8.7), если ввести дополни-
IЯ КАМУФЛЕТЙЫЙ ВЗРЫВ В СФЕРИЧЕСКОЙ ЙОЛОСТЙ 4Й§
тельное допущение, что все члены в (8.7), кроме Uo — Up, малы
по сравнению с D. Тогда,, например, из предположения о сдви-
сдвиговом характере трещин на фронте разрушения следует, что
Vq — Up зависит в основном от второго инварианта тензора на-
напряжений; следовательно (так как D = const), на фронте раз-
разрушения этот инвариант должен достигать некоторого предель-
предельного значения (в 0-состоянии тела). Из предположения об от-
отрывном характере разрушения вытекает, что Uo—Up зависит
в основном от максимального растягивающего напряжения,
предельное значение которого должно достигаться на фронте
разрушения, так как D = const.
Следует подчеркнуть, что в отличие от традиционных упруго-
пластических моделей, в данной модели выполнение условия
(8.15) в некоторой точке не обязано сопровождаться выполне-
выполнением также условия (8.16). В упругой области могут нару-
нарушаться все условия (8.15) и (8.16). Переход из пластического
состояния (8.15) в другое состояние (8.16) может происходить
скачком. .
Условие (8.16) выполняется в ближней зоне взрыва, где
имеют место большие деформации, а твердое тело раздроблено
на мелкие частички, которые, перемещаясь, могут непрерывно
заполнять пустоты и радиальные разрывы, образовавшиеся при
расширении. Условие (8.15) выполняется в промежуточной зоне,
где деформации тела можно считать малыми, а размер частиц
велик по сравнению с радиальными просветами между ними,
так что проникновение частиц в пустоты становится невозмож-
невозможным. Поэтому примем также следующие упрощения:
4) деформации тела в состоянии (8.16) конечны, а тело не-
несжимаемо,
5) деформации тела в О-Состоянии и в состоянии (8.15)
малы, а упругие деформации линейны.
Заметим, что Ар «С р для металлов и прочных горных пород
вплоть до давлений порядка 10s кГ/см2. Для мягких грунтов и
пористых тел в некоторых.случаях эти допущения также можно
принять, если учесть скачок плотности только на ударной волне.
§ 2. Камуфлетный взрыв в сферической полости
Пусть в бесконечном однородном и изотропном пространстве
имеется сферическая полость радиуса R, заполненная заря-
зарядим ВВ, который после детонации превращается в газ с началь-
начальным давлением /?оо. Горное давление для простоты будем считать
гидростатическим и равным р0.
Пренебрежем волновыми процессами в газообразных продук-
продуктах детонации *), считая процесс расширения газа в полости
•) Это предположение недопустимо в начальные моменты времени.
460 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ 1ГЛ. VH1
квазистатическим и политропным:
pV" = PooVZ (8-17)
или
Здесь ri(t)—радиус полости в момент времени t, p — давле-
давление газа, и — показатель политропы.
Соотношение (8.17) является граничным условием задачи
о разрушении твердого тела (при г = г{).
В силу сферической симметрии задачи имеем *)
а единственными отличными от нуля компонентами вектора сме-
смещения и скорости материальной частицы будут радиальные со-
составляющие и (смещение) и v (скорость). Будем использовать
эйлерову координату г и начальную координату материальной
частицы г0. Отметим следующие тождества:
в эйлеровых координатах
, / ,ч ди . ди
r = rQ+u(r,t), v = w + v-3F,
в лагранжевых координатах (8.18)
г = го-\- и (г0, t), v = dr/dt = ди/dt.
Закон Кулона (8.16) в рассматриваемом случае сводится
к следующему линейному соотношению между напряжениями ат
и ств:
сте = авг + р @<б<я/2), (8.19)
где
1 — sin б - 2fecos6
а 1 + sin б ' " 1 + sin б '
Здесь использовано также условие \ar\ ^ |^е|, вытекающее
из физических соображений. При этом предельное условие (8.15)
в данной задаче означает, что ав ^ 0. Область допустимых на-
напряжений для материала в f-состоянии изображена на рис. 187.
*) Вообще говоря, сферическая симметрия обычно нарушается вследствие
развития нескольких трещии, растущих быстрее поверхности разрушения.
Этим эффектом здесь пренебрегаем, хотя и принципе его можно учесть в рам-
рамках предлагаемой теории. Заметим, что в рамках модели Григоряна его
учесть трудно, так как в конце трещины всегда нарушается условие предель-
предельного состояния (8.14). Учет этого эффекта приводит к появлению безразмер-
безразмерного параметра моделирования т) (см. (8.2)), в то время как в исходной
модели параметром моделирования является | (см. (8.1)). Действительно,
как легко видеть, в уравнения (8.5) — (8.16) входят лишь постоянные размер-
размерности напряжений.
.5]
КАМУФЛЕТНЫЙ B3t>bIB В СФЕРИЧЕСКОЙ ЙОЛОСТЙ
461
Рнс. 187.
В частности, если ar ^> k, тело будет идеально-сыпучим в F-co-
стоянии (свободный член в (8.19) можно опустить). Отметим
также три предельных случая, содержащихся в (8.19): а) при
6 = 0, k = 0 будет сте = Рг (идеальная жидкость); б) при
б = л/2 будет ое = 0; в) при 6 = 0,
k ф 0 будет сте — от = 2k (условие
Треска).
Введем следующие обозначения: //_
зона I — область сте— асТг=Р, стг<
< сте *< 0 в плоскости напряжений
(«re и соответствующая ей область F-
состояния в физическом пространстве,
зона II — область сте == 0 в плоско-
плоскости напряжений и соответствующая
ей область F-состояния в физическом
пространстве,
зона III — область возмущенного физического пространства,
где среда находится в 0-состоянии; соответствующая ей область
в плоскости напряжений неизвестна заранее и должна быть
определена из решения задачи.
Непосредственно вблизи полости, очевидно, зона II существо-
существовать не может, так как на границе полости ar ^> k. Следователь-
Следовательно, зоны I, II и III располагаются в
порядке их удаления от полости (рис.
188), причем с увеличением г движе-
движение изображающей точки в плоскости
напряжений происходит в направле-
направлении, указанном на рис. 187 стрелкой *).
Отметим, что зоны II может не быть
вовсе (например, в начальные момен-
моменты времени); об этом можно будет су-
судить уверенно только после анализа
решения задачи. Поверхность разру-
разрушения находится на границе зон II и рис |88.
Ill при г = rs(t).
Согласно ассоциированному закону течения (см. формулы
(8.11)), вектор скорости пластической деформации e(gP, eg)
перпендикулярен к границе области на плоскости напряжений
(см. рис. 187). Следовательно,
ав — ао/. = р,
сте = 0,
в зоне I,
в зоне II
(8.20)
er = dv/dr, ee =
*) Вообще говоря, возможны и другие комбинации зон.
462" Некоторые проблемы хрупкого, разрушения (гл. vtn
Найдем общее решение исходных уравнений последовательно
для зон I, II и III. '
1. Зона I. Система уравнений имеет вид
уравнение движения
Р [-W + v IF) = IF" + 2 ^ ~ «) ^г ~ 2^ <8'21>
уравнение сохранения массы
r-2d(r2v)/dr = 0. ' (8.22)
Условие несжимаемости позволяет обойтись в данном случае
без ассоциированного закона пластичности.
Согласно (8.22) имеем
о^МО/", (8.23)
где /i — произвольная функция. Подставляя v в (8.18) и (8.21),
находим
где fю и /го — произвольные функции.
При помощи граничного условия (8.17) находим /ю; в ре-
результате получим
(8.25|
Так как при t — 0 и г = i? было ы == 0, a /i @) без ограни-
ограничения общности можно положить равной нулю, то из перво-
первоначального соотношения (8.24) можно найти /го; в результате
имеем
(8.26)
Формулы (8.23), (8.25) и (8.26) дают общее решение задачи
в зоне I. Оно содержит две произвольные функции: r^t) и fi(t).
2. Зона 11. Система уравнений имеет вид:
уравнение движения
^ ^1г (*е = 0). (8.27)
" КАМУФЛЕТНЫИ ВЗРЫВ В СФЕРИЧЕСКОЙ ПОЛОСТИ 463
закон Гука
0Г = - />0 + А («* + 2е|)
(Я, ц —коэффициенты Ляме),
ассоциированный закон пластичности (см. (8.20))
ер = 0 (er = eP + e?=:dv/dr). (8.29)
Исключив е| из (8.28) и воспользовавшись (8.29), найдем
<тг = Е ди/дг — р0 A — 2v). (8.30)
Подставляя (8.30) в (8.27)г получим
^^ ^^Н^ (8.31)
Общее решение (8.31) имеет вид [191]
и = г-1 [U (cj -r) + fz (Clt + г)] + rpo(l- 2v)/E, (8.32)
где f2 и fз — произвольные функции.
Скорость и напряжение будут следующими:
Формулы (8.32) и (8.33) дают общее решение задачи в
зоне II, выраженное через две произвольные функции.
.3. Зона III. Запишем систему уравнений:
уравнение движения
закон Гука
/ ди , 2и \ . п ди
Подставляя (8.35) в (8.34), приходим к волновому уравнению
со-2-Ж = -0- + 2г~'-|--2г~2" (Ро<3 = *+2ц). (8.36)
Общее решение этого уравнения, соответствующее расходя-
расходящейся волне, имеет вид
-%ф-г), (8.37)
464 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
где /4 — произвольная функция. Отсюда при помощи (8.35) и
(8.18) получаем
v = сог~ Г: (cQt -г) + сог~% (cot - г),
= -pQ-(X + 2ц) Г% ip4 - г) -
- 4цг-*[гГ< (С</ - г) + U (cQt - г)],
= - р0 - kr-Г; (cot - г) + 2^г-з [rf \ (cot ~r) + U (cot - г)}.
Случай несжимаемого тела (коэффициент Пуассона ра-
равен 1/2), когда Я-»оо, а ди/дг + 2и/г -> 0, так что Х(ди1дг +
-\-2u\r) -> —р, требует самостоятельного исследования. В этом
случае система уравнений (8.29), (8.30) примет вид
u dt2 — дг ч и/
4-2 —
(8.39)
ов = — Ро — Р + 2ц ~,
ди_ . 2и_ q
Общее решение этой системы уравнений можно записать так:
Здесь U — произвольная функция. В несжимаемом теле упру-
упругая волна мгновенно уходит на бесконечность (напряжения на
бесконечности по условию равны — ро).
Решения, полученные в зонах II и III для малых деформа-
деформаций, будут справедливы также для коненных деформаций, если
вместо г всюду подставить лагранжеву координату Го [191].
4. Упругий режим. Построенные выше для отдельных зон
общие решения нужно склеивать вдоль разделяющей их гра-
границы, удовлетворяя следующим условиям склеивания: 1) смеще-
смещение непрерывно, 2) потоки массы и импульса при переходе через
границу сохраняются. На поверхности разрушения, кроме того,
должно еще выполняться условие (8.7) при заданном D.
В зависимости от давления газа в полости p(t) могут реали-
реализоваться самые различные сочетания зон в возмущенной об-
области. Перечислим простейшие формально возможные варианты
сочетаний (каждая зона указана в порядке ее удаления от по-
полости): I, II, III, I II, I III, II III, I II III, I U IIII и т. Д,
5 2] КАМУФЛЕТНЫЙ ВЗРЫВ В СФЕРИЧЕСКОЙ ПОЛОСТИ 465
По-видимому, подбором р (/) можно реализовать любое сколь
угодно сложное сочетание зон. Мы рассмотрим только первые
семь из перечисленных выше вариантов; из физических сообра-
соображений можно полагать, что они дают достаточно полную кар-
картину явления.
Начнем с чисто упругого режима, когда вся возмущенная об-
область занята зоной III. Рассмотрим случай несжимаемого тела
и общий случай малых деформаций.
Несжимаемое тело (общее решение (8.40)). Функцию /4@
находим из граничного условия на полости г = R:
/4-ро#-7Г- (841)
Искомое решение этого уравнения, удовлетворяющее нуле-
нулевым начальным условиям и = v = 0 при / = 0, имеет вид
f* W = ~ "fr{рж ~ Ро) A - cos ad) (со2 = WiPoR2)). (8.42)
Таким образом, несжимаемое упругое пространство со сфери-
сферической полостью испытывает незатухающие синусоидальные ко-
колебания с частотой со.
Учтем сжимаемость газа в полости согласно (8.17). Ограни-
Ограничимся при этом линейным приближением
при г = R аг = —р00A — Зки/R). (8.43)
Тогда вместо (8.41) получим следующее уравнение:
^ = Poo-Po- (8-44)
Его решение дается той же формулой (8.42), в которой нужно
положить
а2 = Dц + Зкроо) (роЯТ1. (8.45)
Общий случай малых упругих деформаций. Функцию /4 в об-
общем решении (8.37), (8.38) находим из граничного условия на
полости (8.43), которое приводит к следующему дифференциаль-
дифференциальному уравнению:
q/ -R) + ±f3 (cQt - R)] = Роо-р0. (8.46)
Решение этого уравнения, удовлетворяющее нулевым началь-
начальным условиям и = v = 0 при / = 0, имеет вид
' ^ (8.47)
466 НЕКОТОЕЫЕ ПРОБЛЕМЫ ХРУПКОГСГРАЗРУШЕНИЯ- 1ГЛ, УВД
Здесь
2/? ' ?, (Я. — Я) A
Таким образом, амплитуда синусоидального колебания в
каждой точке сжимаемого упругого пространства будет прямо
пропорциональна множителю ехр[—Z,i(cot — r)/BR)].
Отметим, что в рамках предложенной модели одного упругого
решения недостаточно, чтобы указать границы его существова-
существования (и, в частности, начало разрушения); для этого нужно рас-
рассмотреть решение с зоной разрушения (или с трещинами).
5. Режим чистого разрушения (волна дробления). Пусть те-
теперь вся возмущенная область занята зоной I, так что граница,
разделяющая возмущенную и невозмущенную зоны, является по-
поверхностью разрушения. В этом случае, согласно формуле (8.26),
смещение терпит разрыв на поверхности разрушения, что не до-
допускается вследствие непрерывности смещения. Следовательно,
волна лщэбления_.невр_зможна. Однако в других задачах при
определенных условиях волны дробления могут все же суще-
существовать; некоторые из таких задач рассматриваются в дальней-
дальнейшем (§4).
Варианты Пчи III, очевидно, также невозможны, так как в
зоне II возмущение распространяется со скоростью С]; которая
меньше скорости распространения ударной волны с0 в зоне III
(за исключением случая v = 0, кбгда С\ = с0).
6. Смешанный режим. Перейдем к исходной зад аде, соответ-
соответствующей варианту IIIIII (см. рис. 188). Будем пренебрегать
скачками плотности на границах раздела различных зон; тогда
граничные условия примут вид
при / = г2@ и' r = r3(t) [v] = 0, [or] = 0, (8.48)
при r = fzit) U0—UF = D. - (8.49)
К ним нужно присоединить еще условие кинематической со-
совместности:
на границе полости при r = ri(t) и = /11(/) — R. (8.50)
На границе раздела зон I и II упругий потенциал изменяется
непрерывно, т. е. эта граница не является поверхностью разру-
разрушения. Следовательно,
при г = г, @ [Ur} = 0, (8.51)
I 2] ^ КАМУФЛЕТНЫЙ ВЗРЫВ В СФЕРИЧЕСКОЙ ПОЛОСТИ 467
Нетрудно заметить, что общую модель, описанную в предыду-
предыдущем параграфе, можно было бы обобщить на случай нескольких
поверхностей разрушения (каждая со своей константой D), од-
однако это существенно усложнило бы расчет.
В рамках развиваемых представлений непрерывное дробле-
дробление тела1 в данном случае наиболее естественно описать зависи-
зависимостью *) -
— — — м — (8 Ч2\
Здесь U — упругий потенциал, к — некоторая постоянная ма-
материала, п — параметр, характеризующий степень дробления
(например, число несвязанных частиц материала или общая по-
поверхность трещин в единице объема).
В простейшем случае, когда принимается допущение о всюду
непрерывном характере дробления, величину D в (8.49) следует
положить равной нулю.
Потенциал Uq будет, очевидно, иметь вид
X [A + v + Sv2) ol - 4v C - v) eQer + B + 6V2) og]. (8.53)
Функция UF будет различной для зон I и II:
в зоне I
X [A + v + 2V2) а2г - 4v C - v) ar (авг + р) + B + 6v2) (авг +
в зоне II * <8-54)
Если в зонах II и III использовать решение для конечных де-
деформаций (в лагранжевых координатах), то вместо условия
[v] = 0 на границах раздела, различных зон надо брать условие
] 0 /
]
Таким образом, для определения семи неизвестных функ-
функций rt(t) (I = 1, 2, 3) и fm(t) (т¦= 1, 2, 3", 4) имеется семь
условий (8.48) — (8.51). Приведем получающуюся систему
*) В произвольном трехмерном случае эта зависимость примет вид
Unfit ш —-к grad U.
4бЙ ЙЁКОТбРЫЁ VlPOfcflEMbl ХРУПКОГО РАЗРУШЕНИЯ №Л. Vlll
функционально-дифференциальных уравнений: .
f[{t) = r2{t)cx{f'2(cf-r2(t)) + f'3(cxt + ra(t))\,
v2oy22 - 2v C - v) or2 (аап + P) + A + 3v2) (<xar2 + pJ = 0,
°n = [*/',Щ ¦ Щ(c~t + r2Щ- f2(ctt-r2Щ-
- [Щ Щ • If2 W - h Щ + П W + r2 @)] =
-a) Г p
L l-a
P Pff @ p(fi@)
1 - a r2 @ + 2 (г, @L '
(8.55)
- '"a @) + K/r3 (<)] /J (cot - r3 (t))
- [Elr3 Щ [f2 (c/ ^ r3 @) + U (*,' +
- - p0r3 (t) - {% + 2ц) ft (cQt - r3 (t)) -
- [4»lrl Щ ¦ [r3 @ f4 (cot - r3 (t)) + U (с? - r3 @)],
V2ff2 _ 2v C — v) ffecrr + A + 3v2) a| = A + v) pED.
Здесь аг и ae даются формутами (8.38) при г = r3(t).
Уравнения (8.55) содержат семь безразмерных параметров,
которые перечисляются в порядке их значимости: роо/ц, pD/ц, к,
б, ро/ц, ^/м, v. Эти параметры для прочных горных пород и хи-
химических ВВ имеют следующий порядок: v«0,3; роо/м-~ 10~'-М,
х ~ 3 -г- 1,5, pD/ц ~ Ю-6 ^- Ю-2, б - 10° -г- 60°, po/ii - 0 Ч- Ю,
А/ц - Ю-4 4- ЮЛ
Систему (8.55) удобнее всего решать конечно-разностным
методом как задачу Коши, на кажд nm шаге отыскивая решение
нелинейной алгебраической системы четырех уравнений (началь-
(начальные условия — нулевые- при t = 0u = v = 0).
Так как р сравнительно мало, то из условия [U] = 0 на гра-
границе зон I и II (второе уравнение (8.55)) следует, что <rr2 также
мало. Таким образом, из допущения о том, что граница зок I
и II не является фронтом разрушения (т. е. поверхностью раз-
разрыва упругого потенциала U), вытекает, что зона II при доста-
i 2J КАМУФЛЁТНЫЙ ВЗРЫЁ б СФЕРИЧЕСКОЙ ПОЛОСТИ 46§
точно мощных взрывах возникает на сравнительно поздних ста-
стадиях процесса и на достаточном удалении от полости. Для
взрывов малой мощности зоны I может не быть вовсе. Поэтому
численный анализ задачи следует начинать с вариантов IIII и
IIIII. Соответствующие системы функционально-дифференци-
функционально-дифференциальных уравнений для этих вариантов выводятся совершенно
аналогично системе (8.55). Например, для варианта IIII и не-
несжимаемого упругого тела получается система, состоящая из
двух нелинейных дифференциальных уравнений второго порядка
относительно функций r\{t) и r2(t) = r3(t).
7. Определение размеров каверны и разрушенной области
после взрыва. Для практики наибольший интерес представляет
знание окончательных размеров полости и разрушенной зоны,
образовавшихся после взрыва. Пренебрегая фильтрацией газа
из полости, определим основные параметры-задачи, установив-
установившиеся за достаточно большой промежуток времени (когда инер-
инерционными силами можно пренебречь).
При t-* оо произвольные функции fm (т = 1, 2, 3, 4) в об-
общем решении превращаются в постоянные, так что на основании
формул (8.25), (8.26), (8.32), (8.33), (8.37) и (8.38) решение
принимает следующий вид:
в зоне I (/ < г < г2)
и = г-го = г-(Гз- ЗС,)'/3 (<ге = аог + р),
в зоне II (r2<f<r3)
и = С2/г + гр0 A - 2v)/? + С4,
в зоне III (r3<r< оо)
u = CJr\ стг=-ра — 4цСз/Л сте = - рй
Здесь Ch (k = I, 2, 3, 4), гг (I = 1, 2, 3)— постоянные, подле-
подлежащие определению. Показатель х соответствует заключитель-
заключительному этапу расширения газа.
Граничные условия:
при г = Г\ u = rx — R,
при г = г2 [ы] = 0, [оу] = 0, [U] = 0, (8.57)
при r = r3 [u] = 0, [ar] = 0, [U] = D
470 некоторые проблемы хйуйкбгб разрушений {Рл, vllf
приводят к следующей алгебраической системе уравнений от-
относительно искомых постоянных:
Po(l-2v)', С2 , С< _ . (.¦ „ С,
Е Г2 Г2 \ Г2
l-a+ ft
г-эи
(8.58)
С2 ¦ po(l-2v) _ С3 С4
г
'
,
4цС3
v2/^ + ^%-Y — 2vC — v)f-^-
I* - г
Решение этой системы уравнений запишем в следующем
виде: - ¦ ~
Здесь t]2 и ть — положительные корни следующих квадрат-
квадратных уравнений: , ,
2v C - v) л2 (| - arj2) + A + 3v2) (-| - ац2J = 0,
а Я — корень уравнения
= а20""' [A -а)
@ < Я< 1),
5 2]. КАМУФЛЕТНЫЙ ВЗРЫВ В СФЕРИЧЕСКОЙ ПОЛОСТИ 471
где
%+
f Ец2 ]
Это решение может служить, в частности, для определения
постоянной материала D по результатам измерения размера ка-
каверны4 (или разрушенной области) после какого-либо одного
модельного взрыва в изучаемой среде.
8. Задача о расширяющемся сферическом поршне. Исследо-
Исследование нестационарных явлений, происходящих при взрыве,
исключительно важно для определения характеристик акустиче-
акустического излучения взрыва. Это излучение может играть как полез-
полезную (например, в сейсморазвед-
сейсморазведке), так и вредную роль (напри-
мёр, вызывая разрушение зда-
зданий). Наконец, по акустическому
эффекту мржно судить о рас-
расположении и мощности взрыва,
а также о вызванном им разру-
разрушении.
При камуфлетном взрыве в
сферической полости радиуса R
зависимость радиуса каверны Т\ Рис- 183>
*>т времени имеет примерный вид,
изображенный на рис. 189*). Если радиус образовавшейся
в результате взрыва полости гораздо больше /?, то на началь-
начальном участке этой зависимости, которая определяет передний
фронт акустического сигнала, функцию Т\ можно приближенно
считать пропорциональной времени (Т\ ~ t). Таким образом,
приходим к автомодельной задаче о расходящемся сферическом
поршне, которая ставится так.
v Пусть из начала координат в покоящемся бесконечном прост-
пространстве в момент времени t = 0 начинает с постоянной ско-
скоростью V\ расширяться сфера радиуса r\ = V\t. Вблизи поршня
образуются зоны I," II и III, которые распространяются также
с постоянными скоростями.
При помощи полученного выше общего решения легко по-
построить решение этой автомодельной задачи:
*) Иногда удается наблюдать четыре (и более) акустические волны от
камуфлетного взрыва. Часть этих волн' объясняется колебаниями газа в по-
полости; возможны также отраженные волны. Кроме того, каждая волна, вы-
выводящая на дневную поверхность, порождает рэлеевскую волну.
472 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
в зоне I (IV < г < V2t)
в зоне U(V2t<r< V3t)
(8.60)
в зоне III (V3t<r<cot)
и = у C4 {cQt - rf + r-2C, (cot - /f,
ar = — A) - r-'C4 (c0^ - r) [6 (Я + 2(x) + 4(xr (co# — r) Br + c0^)],
ae = - Po + r~lC, (cot — r) [2(xr-2 (cot — r) Br + c00 - Щ.
Здесь CA (^ = 1, 2, 3, 4), V2, V3 — постоянные, подлежащие
определению.
Граничные условия
[О] = 0 [a] = 0 [C/] = 0,
D {G- }
приводят к следующей алгебраической системе уравнений отно-
относительно искомых постоянных:
= Зс0С4 (Со -
- 2v C - v) ar2 (p + aar2) + A + 3V2) (ao^ + PJ = 0,
2a2? - 2v C - v) ащог^ + A + 3v2j a^ = A + v) pED,
§ 3] САМОПОДДЕРЖИВАЮЩЕЕСЯ РАЗРУШЕНИЕ 4?3
где
Решение этой системы уравнений легко найти при помощи
любого счетно-решающего устройства. Скорость V\ можно свя-
связать с данными реальной задачи" каким-либо дополнительным
условием, например,
при t=RIVu r=*R ar = Poo-
Для варианта I III соответствующая система уравнений, слу-
служащая для определения трех неизвестных постоянных Сь С4 и
V2, может быть решена весьма просто; приведем ответ:
2Aa) „ Р ,
(8.63)
Здесь постоянная V2 является корнем следующего алгебраи-
алгебраического уравнения:
A + 3 v2) [в* - (аог + рJ] - 2 v C - v) ar (ae-aar-p) = A + v) pED,
где
§ 3. Самоподдерживающееся разрушение
Явление самоподдерживающегося разрушения хрупкого тела
[83,84j заключается в следующем. Представим себе кусок хруп-
когд материала, находящийся в поле сжимающих напряжений,
таких, что развития начальных сдвиговых микротрещин не про-
происходит. Если поверхность образца внезапно освободить от на-
нагрузок, то вглубь материала начнет распространяться волна
разгрузки. Если запасенная телом потенциальная энергия упру-
упругого сжатия достаточно велика, то сдвиговые микротрещины, на-
находящиеся во фронте разгрузки, становятся неустойчивыми. Их
динамическое развитие приводит к разрушению тела. В случае
очень большого числа таких неустойчивых микротрещин можно
474 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIH
говорить о волне разрушения (дробления), подразумевая под
этим границу, разделяющую разрушенный материал от нераз-
неразрушенного. Следует сразу подчеркнуть, что скорость распростра-
распространения волны разрушения не зависит от скорости распростране-
распространения отдельных трещин и, в частности, не определяется предель-
предельной скоростью распространения изолированной трещины, равной
скорости волн Рэлея. Самоподдерживающийся механизм разру-
разрушения, состоящий в переходе потенциальной упругой энергии
хрупкого тела в поверхностную и кинетическую энергию от-
отдельных частиц-пылинок разрушенного тела, напоминает само-
самоподдерживающийся механизм распространения детонационной
волны, когда ударная волна подпитывается за счет запаса хи-
химической энергии в теле. Самоподдерживающееся разрушение
хрупкого тела сопровождается сильным звуком и разбрасыва-
разбрасыванием частиц разрушенного вещества, что внешне напоминает
слабый взрыв. -
Таким образом, основным фактором, определяющим способ-
способность хрупкого тела к самоподдерживающемуся разрушению,
является запас потенциальной упругой энергии в неразрушен-
неразрушенном теле. Наибольший запас упругой энергии в теле (практи-
(практически неограниченный) можно создать при всестороннем сжатии
или по некоторому пути нагружения,. .близкому к всестороннему
сжатию, когда тело остается не разрушенным трещинами попе-
поперечного сдвига. Важную роль в возможности создания запаса
потенциальной упругой энергии в хрупком теле играет проч-
прочность материала. Удаление поверхностных микротрещин или их
сжатие внутренними напряжениями, гомогенизация материала
в результате некоторых технологических операций увеличивают
прочность (при прочих равных условиях) и тем самым позво-
позволяют достигнуть большей величины упругой энергии тела до его
разрушения. У прочных стекол, характеризующихся отсут-
отсутствием поверхностных микротрещин или большими внутренними
сжимающими напряжениями в поверхностном слое, а также
весьма однородной объемной структурой, удается наблюдать са-
самоподдерживающееся разрушение не только при сжатии, но и
при изгибе и даже при растяжении.
Необходимый запас упругой энергии в теле может быть соз-
создан технологически («батавская слезка»). В местах концентра-
концентрации сжимающих напряжений также может быть достигнут боль-
большой запас упругой энергии (горный удар).
1. Динамический процесс. Самоподдерживающееся разруше-
разрушение хрупкого тела рассмотрим на следующей одномерной мо-
модели. Пусть в бесконечном упругом пространстве, находящемся
в однородном поле сжимающих главных напряжений ЛГЬ' N% и
N3, внезапно образовалась плоскость х = О, свободная от напря-
напряжений. Рассмотрим хрупкое полупространство х > 0. Считаем,
«J3J САМОПОДДЕРЖИВАЮЩЕЕСЯ РАЗРУШЕНИЕ 475
что напряжения Ni, N2 и N3 таковы, что не вызывают распро-
распространения сдвиговых микротрёщин и тем самым разрушения
сплошного тела (собственно говоря, это накладывает ограниче-
ограничение в основном на разность главных напряжений). Однако пред-
предполагаем, что напряжения Nit N2, N3 достаточно велики для того,
чтобы поддержать распространение стационарной волны разру-
разрушения. Тогда в полупространстве х i> 0 с некоторой скоростью V
пойдет волна разрушения (дробления), которую мы будем пред-
представлять себе в виде плоскости разрыва х = VL разделяющей
разрушенный материал от неразрушенного (х >Т/). Разрушен-
Разрушенный материал представляет собой множество отдельных частиц,
Движущихся со скоростью v относительно покоящейся неразру-
неразрушенной части тела. Волна разрушения, очевидно, имеет толщину
порядка характерного размера частиц. Запишем законы сохра-
сохранения массы и количества движения на скачке разрушения.
Имеем
— oOK (8.64)
• pQVvt = т0.
Здесь со — нормальное напряжение, действующее на пло-
площадке, параллельной плоскости разрушения, то — наибольшее
касательное напряжение на той же площадке. Величины vx и vt
представляют собой нормальную и касательную составляющие
ректора скорости v. ¦
Стационарный режим распространения волны разрушения
возможен лишь в том случае, когда скорость V равна скорости
распространения продольных упругих волн с0. Действительно,
У не может быть меньше с0, так как тогда волна разгрузки об-
обгонит волну разрушения, а самопроизвольное разрушение раз-
разгруженного материала невозможно (напомним, что фронт —
плоский). Величина V, очевидно, также не может быть больше
скорости распространения возмущений с0, которые подготавли-
подготавливают материал к разрушению. Заметим, что эти соображения
Совершенно аналогичны тем, которые приводят к гипотезе Чеп-
-Меиа — Жуге в теории стационарной детонации.
Рассматриэаемая волна разрушения (дробления) является
«екоторым аналогом волны разрежения в сжимаемом газе.
Из граничных условий следуют соотношения
- (N ,а2 + Ntf + Ntf)\
Здесь а, р, у — косинусы углов, которые ось х составляет
К главными осями напряжения (соответственно с первой, второй
476 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ 1ГЛ. VIII
и третьей). Таким образом, из уравнений сохранения массы и им-,
пульса получаем значение плотности разрушенного материала pF
и составляющих скорости движения его частиц vx и vt:
(8.66)
Росо/ Росо
В данном случае скорость V равна с0, поэтому согласно об-
общей теории динамического разрушения хрупких тел (см. допу-
допущение е) § 1 этой главы), удельная диссипация энергии на
фронте разрушения П будет больше константы материала D,
т. е.
±(l) 0^> (8.67)
Po PW Spfc
где
Uo = [A + v) {n\ + Ml + Nf) - v (Af, + N2 + #3J] BEPo)-1.
Согласно (8.67) при самоподдерживающемся разрушении
хрупкого тела в поверхностную энергию переходит лишь некото-
некоторая часть упругой энергии тела, а остальная часть переходит
в кинетическую энергию осколков.
Зная величину П, можно на основе соображений физиче-
физического и вероятностного характера вычислить геометрические
размеры частиц разрушенного вещества. Будем считать все ча-
частицы сферическими. (Отметим, что шаровидная форма энерге-
энергетически наиболее выгодна.) Эффективная поверхностная энергия
шаровидной частицы радиуса г равна Апуг2.
Радиус частицы г является случайной величиной с некото-^
рой плотностью распределения р(г). Поверхностную энергию
единицы массы разрушенного материала П, очевидно, можно
записать в виде
+°° +°°
n = 3Y J r*p(r)dr/9o J r3p(r)dr. (8.68)
Здесь предположено, что плотность каждой частицы разрушен-
разрушенного вещества равна плотности материала перед волной разру-
разрушения. Таким образом, в самом общем виде уравнение энергии
дает линейную связь второго и третьего моментов распределе-
распределения р{г). Конкретные предположения относительно функции
р(г) позволяют получить более определенные результаты: На-
Например, наиболее грубое предположение
р (г) = 6 (г-го), (8.69)
S 3] САМОПОДДЕРЖИВАЮЩЕЕСЯ РАЗРУШЕНИЕ 477
где 6 (г—г0)—дельта-функция, позволяет дать приближенную
оценку характерного размера частиц г0:
го = Зу/(роП). (8.70)
Если допустить, что распределение р(г) является нормаль-
является нормальным:
» Г?^1 (8.71)
то на основании (8.68) дисперсия распределения Л выражается
через средний размер частиц г0 следующим образом:
дя =
= 3v ~
г (8 72}
Зр0г0П - 3Y Го- \°-1?1
' Таким образом, уравнение энергии позволяет оценить сред-
средний размер частиц разрушенного вещества и параметры их рас-
распределения.
Самоподдерживающееся разрушение было обнаружено, на-
например, на образцах оконного стекла, полученного методом вер-
вертикального вытягивания [83]. Образцы имели форму квадрата
со стороной 60 мм и нарезались алмазом из листов стекла раз-
размером 500 X 500 мм. Толщина образцов была от 1,7 до 3,2 мм
в разных сериях опытов. Стекло имело приблизительно следую-
следующий химический состав: 72% SiO2, 15% Na2O, 3% MgO,8% CaO,
1,5—2% A12O3. Упрочнение образцов производилось путем обра-
обработки их поверхности вспененной плавиковой кислотой на лабо-
лабораторной установке, в результате чего удалялся дефектный по-
поверхностный слой толщиной 100 мкм. Измерения прочности на
симметричный изгиб производились на машине типа РМ с пре-
предельной нагрузкой 10 000 кГ. Для испытания образцов применя-
применялась квадратная опора с квадратным отверстием размером
50 X 50 мм и дисковый пуансон диаметром 6 мм. На опору по-
помещалась мягкая изоляция.
Образцы вынимали из ванны с плавиковой кислотой, промы-
промывали водой и, не высушивая, испытывали на центральный сим-
симметричный изгиб. Разрушение большинства образцов сопрово-
сопровождалось звуком, напоминающим звук выстрела, причем весь
^испытуемый образец разлетался на мелкие осколки, имеющие
вид иголок со средней толщиной от нескольких микрон до десят-
десятков микрон в зависимости от величины разрывного напряжения.
Если образцы высушивали, то подобное разрушение происхо-
происходило значительно реже. Следует отметить, что разрушение «со
Взрывом» имеет место только для стекол, полученных из хорошо
Кшогенизированной стекломассы.
, 2. Возникновение волны разрушения. Пусть образец подвер-
подвергается одноосному сжатию. Согласно условию (8.67), волна раз-
||ушения возникнет только в случае, если удельная упругая
478 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ {TJ
энергия образца превзойдет величину D, т. е. если будет Uo > 1}
(так как в данном случае ао = 0). При этом образец полностью
разрушится на мелкие части. В условиях одноосного сжатия
практически это условие достигается весьма редко, так как при
гораздо меньших U происходит разделение образца на две части.
Пусть теперь хрупкое тело имеет сложную форму и нахо-
находится в _ неоднородном напряженном состоящий. В этом случае
местное разрушение на контуре тела, вообще говоря, может не
вызвать разрушения всего тела. Рассмотрим условия самопроиз-
самопроизвольного разрушения хрупкого тела, ограничившись квазистати-
квазистатическим приближением. Это приближение всегда выполняется в
начале разрушения, так как внешние нагрузки предполагаются
квазистатическими.
В принятом приближении условие разрушения можно запи-
записать так:
%¦>!>• (8.73)
' Здесь 6U — изменение упругой энергии тела вследствие изме-
изменения его объема на 8v. Заметим, что величины 8v и 8U могут
быть как конечными, так и бесконечно малыми. Если до беско-
бесконечно,мало, то условие (8.73) будет необходимым и достаточ-
достаточным. Если же 8v есть некоторая конечная вариация объема тела,
то условие (8.73) как условие самопроизвольного разрушения
части тела, соответствующей вариации 8v, будет, вообще говоря*
лишь необходимым. Для того чтобы разрушение этой части тела
произошло, достаточно, например, чтобы (8.73) выполнялось
также для любой части 8v. (Под 8v понимается вариация обла-
области пространства, занятого телом, и объем этой вариации; оче-?
видно, это не может привести к путанице.) ;
Условие (8.73) является естественным обобщением условия
Гриффитса на объемное разрушение. Определение функционала
„ 8U/bv для произвольных ва-
вариаций границы упругого те-
тела является невыполнимо
Zb
S-
21 Т М
сложной задачей, однако
при некоторых ограничениях
на возможные вариации,
. подсказываемых опытом, ее
рис (до иногда удается решить. Тео-
Теория разрушения полостей,
развитая как обобщение теории Гриффитса и приводящая к ус-
условию (8.73), принадлежит Л. В. Ершову и Д. Д. Ивлеву [107].
Рассмотрим пример. Пусть бесконечное однородное упругое
пространство, находящееся в условиях плоской деформации,
имеет эллиптическую полость, свободную от нагрузок (рис. 190),
13J САМОПОДДЕРЖИВАЮЩЕЕСЯ РАЗРУШЕНИЕ 479
На бесконечности действует всестороннее сжимающее напряже-
напряжение р. Нетрудно подсчитать изменение упругой энергии тела
вследствие наличия полости; оно оказывается равным
U = лр2 A - v2) (If + 12)/Е, (8.74)
где Ь и / — полуоси эллипса, причем / > Ь.
Самопроизвольное разрушение, естественно, начинается в на-.
правлении большой оси эллипса, - где имеет место наибольшая
Концентрация упругой энергии (предполагается, что тело одно-
однородно по своим прочностным свойствам, т. е. постоянная D не
Зависит от координат). .
Допустим, что контур полости в процессе разрушения остает-
остается эллиптическим, причем изменяется лишь величина /, а Ь
остается неизменной. В результате увеличения I на Ы самопод-
самоподдерживающемуся разрушению подвергается область, объем ко-
которой (на единицу толщины) равен 8S = пЬЫ. Упругая энер-
энергия, высвободившаяся вследствие такого изменения контура
тела, согласно (8.74) равна
E. (8.75)
Йри этом предполагается, что частицы разрушенной области
удаляются, не оказывая давления ца стенки полости (и вообще
не изменяя граничных условий).
f Общее условие самопроизвольного разрушения (8.73) в дан-
данном случае дает
р2 B/+ 60 >&??>/( 1 — v2) (Ы>0). -(8.76)
Для конечных 81 это условие является необходимым, но мо-
Жет оказаться недостаточным (физически это объясняется тем,
%ro D может в принципе зависеть, например, от х, причем при
йалых 6/ величина D больше, чем при больших). Самопроиз-
Самопроизвольное разрушение охватит тем большую область, чем для
больших 81 выполняется условие (8.76). В случае однородных
тел, когда D не зависит от координат, локальное разрушение
произойдет, как Только величина рЧ достигнет критического зна-
значения, равного
'. (8.77)
Дальнейшее разрушение, согласно (8.76), будет продолжаться
самопроизвольно при. любых 81.
Заметим, что для сильно вытянутого эллипса (/ > Ь), когда
даиеет смысл понятие коэффициента интенсивности напряжений
Дописывающего некоторую промежуточную асимптотику), разви-
^йемый подход, основанный на введении константы D, приводит
щ- результатам, которые полностью совпадают с результатами,
ЦЬлученными на основе общефункционального подхода (см.
480 некоторые проблемы Хрупкого разрушения {гл. vtit
теорию горного удара, § 10 гл. IV). Между константами, фигу-
фигурирующими в этих теориях, на основании (8.77) существует
следующая связь:
*i=/w^r (8-78)
Однако излагаемый здесь подход предпочтительнее, так как он
применим к телам любой конфигурации. ¦»
Практическое использование общего условия (8.73) состоит
в том, что вначале на основе опытных данных определяется
форма области самопроизвольного разрушения (с точностью до
нескольких независимых параметров Аь Яг, .-., Яп). Затем на
основе решения соответствующей упругой задачи подсчиты-
вается изменение упругой энергии тела 8U, соответствующее не-
необратимым бесконечно малым изменениям параметров б^4 (т. е.'
таким изменениям, которые отвечают условию необратимости
разрушения, см. допущение в) § I этой главы). Высвобождаю-
Высвобождающуюся вследствие разрушения упругую энергию 8U и прираще-
приращение объема 6v можно представить в виде
бС/ = Лг6Я;) bv = Bib%t, (8.79)
где Аг и Bi — некоторые функции формы тела, внешних нагру-
нагрузок и параметров Я*. Тогда условие локального разрушения на
основании (8.73) запишется так: %
Ai = DBi (г=1, 2, .... п). (8.80)
Получается система п уравнений для определения значений п
независимых параметров %и описывающих равновесную /т. е.
находящуюся на грани между разрушением и отсутствием раз-
разрушения) форму тела.
Предлагаемая теория пригодна, в частности, для количествен-
количественного описания условий возникновения горных ударов, выбросов
угля, газа и т. п. в выработках произвольной формы. В послед-
последнем случае при вычислении SC/ нужно учитывать также объем-
объемную силу, вызванную фильтрацией газа.
§ 4. Теория огневого бурения
- Одним из перспективных способов проходки скважин, осо-
особенно при бурении прочных пород, является воздействие на по-
породу высокотемпературной струей газа. В местах интенсивного
нагрева происходит разрушение породы под действием темпера-
температурных напряжений. Наиболее эффективным режимом огневого
бурения, очевидно, будет режим, при котором происходит хруп-
хрупкое разрушение (раздробление) породы на мелкие куски и по-
порода не оплавляется.
§ 4] Теория огневого bvpеНиЯ 481
Ниже излагается теория этого явления, развитая в работе [194].
1. Постановка задачи. Представим себе неограниченное од-
однородное и изотропное упругое тело с осесимметричной полостью
в виде полубесконечнога цилиндра с закругленным основанием
(рис. 191). На дно полости направлена высоко-
высокотемпературная струя газа, исходящая из некото-
некоторого резервуара с соплом А. Под действием
разогрева в теле возникают термоупругие напря-
напряжения, подчиняющиеся закону Дюамеля — Ней-
Неймана. Внешние нагрузки считаем пренебрежимо
малыми сравнительно с характерными темпера-
температурными напряжениями. При достаточно боль-
больших внутренних напряжениях происходит разру-
разрушение приповерхностной области тела, и части-
частицы разрушенного материала уносятся струей рис 191.
газа. Разрушение тела считается хрупким; опла-
оплавление отсутствует. Эти условия налагают некоторые ограниче-
ограничения на температурный режим чисто хрупкого разрушения.
Введем следующее основное предположение:
). (8.81)
Здесь и — температуропроводность, k — теплопроводность,
р — плотность, с — теплоемкость, d — характерный линейный
размер тела (например, радиус кривизны закругления или ра-
радиус цилиндра), v — нормальная скорость бурения, т. е. ско-
скорость перемещения границы тела (в результате удаления разру-
разрушенного материала) по нормали к его поверхности.
Предположение (8.81) означает, что поле внешней темпера-
температуры в каждой точке границы тела проникает на глубину, малую
сравнительно с характерным линейным размером участка гра-
границы, подвергающегося интенсивному нагреву. Выполнимость
условия (8.81) обеспечивается весьма малыми значениями тем-
температуропроводности для большинства прочных скальных пород.
Приняв, например, d ~ 10 см и учитывая реальные значения к
для горных пород (и = Ю~3 -г- 10~2 см2/сек), из условия (8.81)
получаем следующее ограничение скорости бурения:
v » 1(И -г- 1(Н см/сек. Имея, в виду средние скорости про-
ходкк скважин, это условие следует считать не слишком обре-
обременительным.
На основании указанного предположения нормальная ско-
скорость бурения в рассматриваемой точке поверхности тела будет
полностью определяться локальными характеристиками потока
и самого тела в окрестности этой точки. Выберем декартову си-
систему координат хуг с'началом в некоторой точке О поверх-
поверхности тела; ось z направим по нормали к поверхности вглубь
тела. Тогда поля напряжений, деформаций и температур
16 Г. П. Черепанов
482 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. Vltl
в точке О будут медленно изменяющимися функциями х и у, но
быстро меняющимися функциями z. Рассматриваемые поля об-
образуют своеобразный пристеночный слой. Для вектора упругих
смещений (и, v, w) и для температуры Т в окрестности точки О
вследствие (8.81) будем иметь в обычном приближении
и = о = 0,' w = w(z,t), T=T(z,t). (8.82)
Уравнение Ляме в пренебрежении силами инерции при-
примет вид
(Я + 2ц) Ц - (ЗА, + 2ц) а ¦§- = 0. (8.83)
Здесь а — коэффициент линейного температурного расшире-
расширения, X и ц — постоянные Ляме. Упругие и термические постоян-
постоянные тела для простоты считаем не зависящими от температуры.
Температура ненагретого тела всюду принимается нулевой.
Из условия на бесконечности
dw/dz = 0, 7 = 0 при 2->оо (8.84)
и из уравнения Ляме находим
На основании закона Гука для главных напряжений ах, ау и
а2 получаем
— v), o2=0. (8.86)
Таким образом, приповерхностные области тела находятся в
условиях плоского напряженного состояния с всесторонним сжа-
сжатием, причем сжимающее напряжение максимально на поверх-
поверхности тела и быстро .убывает с глубиной. Температура тела удо-
удовлетворяет уравнению теплопроводности (в неподвижных коор-
координатах)
при z>0 %?L=dL (t — время) (8.87)
и граничному условию теплообмена
при z = 0 —kdT/dz = h(T0 — T). (8.88)
Здесь То — температура потока газа в точке О, h — коэффи-
коэффициент теплообмена.
Следует отметить, что если уравнения (8.82) —(8.88) спра-
справедливы для стационарного разрушения, то они, очевидно, тем
более будут выполняться для соответствующего нестационар-
нестационарного режима.
$ 4] ТЕОРИЯ ОГНЕВОГО БУРЕНИЯ 483
2. Стационарный режим бурения. Определим сначала нор-
нормальную скорость стационарного бурения. Пусть граница полу-
полупространства перемещается с постоянной скоростью v по нор-
нормали к своей плоскости, а температура газа То и коэффициент h
постоянны на границе. Для отыскания температуры тела имеем
следующую краевую задачу:
-k<*=hiTQ-T) (z-vt), (8-89)
Т = 0, dT/dz = 0 при z — of->oo.
Стационарное решение этой краевой задачи имеет вид
' <8-90)
Перемещение границы происходит вследствие непрерывного
разрушения тела и удаления частиц тела потоком газа. Напря-
Напряженное состояние тела описывается формулами (8.86). Примем
на свободной границе полупространства следующее дополни-
дополнительное граничное условие разрушения (crg — прочность тела на
двустороннее сжатие):
ox — Oy = —<!s ПРИ z==vt. (8.91)
Это условие вытекает из общего условия на фронте волны раз-
разрушения, так как в данном случае волна разрушения — квази-
квазистатическая (см. формулу (8.67)). Величина as весьма просто
связана с константой данного процесса D.
При помощи формул (8.86) и (8.90) из граничного условия
(8.91) получаем выражение для нормальной скорости бурения
v = hxk~l {aET0[(l — v) о,Г' — 1}. (8.92)
Используя решение задачи (8.90) и (8.92), нетрудно найти
условие отсутствия оплавления материала
(l-vW(a?7n)<l (8.93)
(Та — температура плавления).
Следует подробнее остановиться на механизме разрушения
в приповерхностном слое. Возможны два механизма разрушения
при сжатии: один из них связан с распространением трещин
сдвига и отрыва, другой — с потерей устойчивости и локальными
неоднородностями материала. В рассматриваемой задаче на на-
начальной стадии развития трещин, по-видимому, реализуется пер-
первый механизм, а на заключительной стадии — механизм потери
устойчивости, так как температурные напряжения сосредоточены
16*
484 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
в узком слое вблизи поверхности, причем тонкая пластинка ма-
материала, мысленно вырезанная из этого слоя, находится под дей-
действием двух одинаковых главных сжимающих напряжений. По-
Поэтому частицы разрушенного материала будут представлять со-
собой тонкие пластины толщины б, которая значительно меньше
характерного линейного размера сечения пластины в плане Ь.
3. Нестационарная задача. Перейдем к исходной осесиммет-
ричной задачи бурения (см. рис. 19*1). Рассмотрим режим ста-
стационарного бурения, когда температура тела и форма полости
зависят лишь от переменных ? = Z\ — vj и р, где р, Z\ — цилин-
цилиндрические координаты (р = 0 — ось симметрии задачи), и*—
скорость бурения. В данном случае температура и скорость по-
потока газа, а следовательно, и коэффициент теплообмена в каж-
каждой точке поверхности каверны различны, так что нормальная
скорость бурения в каждой точке v будет связана с неизвестной
формой полости ? = ?(р) зависимостью
f==f.{l + [S'(p)]2rI/2. (8.94)
В точке торможения потока газа, расположенной на оси сим-
симметрии поверхности тела (? = 0, р = 0), нормальная скорость
бурения v равна скорости бурения полости к*. Используя фор-
формулу (8.92) для нормальной скорости бурения, получаем пред-
представляющую основной интерес в рассматриваемой задаче зави-
зависимость для скорости бурения:
¦" о. = К (рс){аЕТ. [A - v) a,] - l). (8.95)
Таким образом, скорость бурения а* полностью определяется
следующими параметрами: коэффициентом теплообмена потока
газа с твердым телом в точке торможения /г*, температурой тор-
торможения газового потока Г*, плотностью материала р, теплоем-
теплоемкостью тела с, модулем Юнга Е, коэффициентом температурного
расширения твердого тела а, коэффициентом Пуассона v и проч-
прочностью тела на сжатие os.
Форма полости в квазистационарном приближении Должна
быть определена из решения газодинамической задачи. Допол-
Дополнительными граничными условиями для температур на неизвест-
неизвестном контуре служат условия (8.94) и (8.88). Для определения
коэффициента теплообмена h можно воспользоваться фор-
формулой Имая [106], полученной из рассмотрения уравнений погра-
пограничного слоя. Укажем прием, при помощи которого можно полу-
получить приближенное решение задачи об определении формы ка-
каверны. Температуру То и скорость потока UQ на поверхности тела
(на внешней границе пограничного слоя) аппроксимируем не-
некоторыми функциями параметра s (s — длина дуги):
rp = <p(s), ?/0 = *(s), (8.96)
5 4] ТЕОРИЯ ОГНЕВОГО БУРЕНИЯ 485
которые выбираются из соображений удобства решения уравне-
уравнений пограничного слоя и задаются с точностью до нескольких
постоянных. Из решения уравнений пограничного слоя при усло-
условиях (8.96) на внешней границе и условия для температуры газа
Т на границе с телом
T = (l-v)aJ(aE) (8.97)
(получаемого на основании (8.86) и (8.91)) находим коэффи-
коэффициент теплообмена
h = co(s) (8.98)
также зависящий от нескольких постоянных.
Исключая v из формул (8.92), (8.94), в квазистационарном
приближении получаем следующее соотношение, связывающее
форму каверны ? = ?(р) с коэффициентом теплообмена h и тем-
температурой То:
1 __ h [аЕТр - A - у) os] ,899ч
fl+W(p)]2 h,[aET.-(l-v)as]'
Перейдем к параметрической переменной s (длина дуги) и
используем формулы (8.96) и (8.98); тогда
?=Л VI -0»(S) ds,
о о (8.100)
я /<л == ш 00 [«?ф 00 - О - у) Qs)]
ик> <o@)[a?q>@)-(l-v)orj] '
Уравнения (8.100) представляют собой искомые уравнения
контура каверны в параметрическом виде.
По найденной (с точностью до нескольких постоянных)
форме полости можно определить течение газа в полости и найти
неопределенные постоянные. Таким образом, все три задачи (те-
(течение идеального газа в полости, течение вязкого газа в погра-
пограничном слое, разрушение твердого тела под действием темпера-
температурных напряжений) оказываются тесно связанными. Указанный
метод решения комбинированной задачи может быть иепользо-
ван также для получения точного решения (разумеется, при по-
помощи вычислительных машин).
Следует знать еще ошибку, допускаемую при замене фактиче-
фактически нестационарной (вследствие криволинейное™ каверны) за-
задачи о разрушении твердого тела квазистационарной задачей.
Для этого нужно оценить характерное время т выхода на ста-
стационарный режим. Тогда условие квазистзционарности может
быть записано в виде
%v<%.d. (8.101)
486 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
Здесь v — нормальная скорость бурения, d — характерный
линейный размер каверны. Время т на основании (8.87), (8.88)
определяется из решения краевой задачи
Г = 0 при * = 0, (8.102)
— k дТ/dz = h (To — Г) при г == 0, 0 < t < *„
= Q при z = v(t)t (v (t) > 0, t > *,),
Из соображений: анализа размерностей имеем
t^PTi/^Q2) при*,<т (8.103)
(р — некоторый постоянный множитель).
Используя формулы (8.92) и (8.103), выражение (8.101)
можно привести к виду
МЫ)< 1. (8.104)
Как видно, это условие квазиетационарности вытекает из основ-
основного предположения (8.81).
В заключение отметим, что совершенно аналогичный меха-
механизм поверхностного разрушения (шелушения) вследствие мест-
местных тепловых напряжений имеет место в ряде других физических
явлений, например, при воздействии интенсивных электро-
электромагнитных полей высокой частоты на хрупкие диэлектрики. Раз-
Разрушение метеоритов в земной атмосфере в некоторых случаях,
несомненно, также относится к этому классу явлений.
§ 5. Разрушение при соударении хрупких тел
В 1881 г. Генрих Герц решил проблему квазистатического
соударения двух различных упругих эллипсоидов [195]. Впослед-
Впоследствии А. Н. Динник [196] проверил экспериментально это решение;
он показал, что для хрупких материалов решение Герца пере-
перестает быть справедливым, как только на площадке контакта по-
появляются первые (окружные) трещины. Следует заметить, что
величина нагрузки в этот момент составляет примерно 0,2—0,3
максимального ее значения, отвечающего полному разрушению
материала в зоне контакта.
В начальной стадии контактного разрушения наблюдаются
устойчивые конические трещины, которь/е впервые наблюдали
Реслер [197] и Бенбоу [198]. Хоек и Бенявский [102] изучили некото-
некоторые особенности развития трещин в условиях сжатия, близких
РАЗРУШЕНИЕ ПРИ СОУДАРЕНИИ ХРУПКИХ ТЕЛ
487
к условиям контактного разрушения. Заключительный, динами-
динамический этап процесса протекает по механизму самоподдержи-
самоподдерживающегося разрушения, рассмотренному в § 3.
Исследование процесса контактного разрушения представляет
интерес, в частности, для горного дела в связи с широко рас-
распространенным способом ударного бурения крепких пород. Ниже
излагаются некоторые результаты экспериментального и теоре-
теоретического анализа этой проблемы, проведенного на основе пред-
представлений механики хрупкого разрушения [199]. Для определен-
определенности рассматривается удар жесткой сферы по хрупкому полу-
полупространству.
1. Экспериментальные результаты. В опытах тяжелый удар-
ударник (стержень) падал на образцы из хрупкого материала (серый
гранит, кварцит и оптическое стекло в блоках). Приведем зна-
значения модуля Юнга и коэффициента Пуассона для этих мате-
материалов, а также для материала жесткого наконечника (шарико-
(шарикоподшипниковая сталь или специальный твердый сплав):
Модуль Юнга Е, кГ/см2
Коэффициент Пуассона v
Гранит
Eч-6) Ю5
0.24
Кварцит
(8-5-10) 105
0,22
Стекло
E+6) 105
0,28
Наконечник
E+6) 10е
0.18-н0,22
•f-
v/
2
T
7
На рис. 192 показан блок испытываемого материала (/) и ци
линдрический стальной ударник B) с приваренным к нему на
конечником в форме полусферы C). Ра-
Радиус R этой полусферы был следующим
(в мм):
1,25; 2,25; 5,0; 9,5; 17,5; 100 (стальной
наконечник),
4,25; 6; 10 (наконечник из твердого
сплава).
Высота падения ударника постепенно
увеличивалась до тех пор, пока не проис-
происходило контактное разрушение. Спе-
циальные проволочные тензодатчики D)
прикреплялись к цилиндрической поверхности ударника вблизи
наконечника. Датчики размещались равномерно вдоль всего по-
поперечного сечения ударника.
Скорость vt ударника в поперечном сечении с датчиками
вблизи наконечника в момент времени t находилась по показа-
показаниям тензодатчиков с учетом волновых процессов в ударнике
У////////////////////7///7/,
1
Рис. 192.
488
НЕКОТОРЫЕ ПРОВЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
(ГЛ. Vtli
(стержне):
Vt = vQ — at (рс) — 2 (рс) (ot_T + ot_2T
(8.105)
Здесь vQ — скорость стержня перед ударом, сгь сгг_т, ... — на-
напряжения-в рассматриваемом поперечном сечении стержня в со-
соответствующий момент време-
времени, р — плотность, с — ско-
скорость звука в стержне, L —
длина стержня.
2700
1/1ПП
1QVU
опп
"т
-¦ 0
^у
Ух
у
«и,
i
i
i
0,0/ о,ог
"гк
/
/
\—
и,сн
внедрения нако-
Глубина
нечника в материал ы== vtdt
определялась графически как
площадь между кривой vt =
= vt(t) и осью времени. Сум-
Суммарная сила N, действующая
на контакте между наконечни-
наконечником и материалом в момент
времени t, находилась по фор-
формуле N = atF (F — площадь
поперечного сечения удар-
ударника).
На рис. 193 изображена ти-
типичная диаграмма N—и (квар-
(кварцит, наконечник из твердого сплава с радиусом 6 мм, начальная
скорость ударника vQ = 1 м/сек). Из рисунка видно, что вначале
справедливо решение Герца (кривая 1)
N = ku?l\ (8.106)
где
Рис. 193.
Затем, начиная с силы Nik, экспериментальная кривая B) идет
ниже теоретической, причем сила сопротивления jV становится
примерно прямо пропорциональной смещению внедрения и,
В конце этой линейной области при N = N2h появляется скачок.
В дальнейшем сила сопротивления возрастает слабо, а по дости-
достижении максимального значения Nm быстро убывает.
Последовательные фазы процесса разрушения лучше всего
наблюдать на стекле при постепенном увеличении высоты паде-
падения ударника. На основе таких наблюдений общий процесс раз-
разрушения можно описать следующим образом (рис. 194). Пока
высота падения мала, видимых следов разрушения нет, С увели-
55]
РАЗРУШЕНИЕ ПРИ СОУДАРЕНИИ ХРУПКИХ ТЕЛ
489
W
чением высоты на поверхности образца появляются круговые
трещины. Затем число концентрических круговых трещин растет,
увеличивается их диаметр; внутри образца каждая трещина
имеет форму усеченного конуса. Вначале трещины перпендику-
1 ; лярны к поверхности, одна-
т^^^^ ко уже на небольшой глуби-
не угол их наклона стано-
становится совсем другим (но по-
/ф , стоянным по всей глубине).
^ Глубина трещин растет с
увеличением силы N, причем
^=»N трещина самого маленького
///^^ЩЪ диаметра имеет наибольшую
({({ /!§ь V,|\ глубину (главная трещина).
^чч ^^ /'"/ Когда нагоузка снимяртгя
Когда нагрузка снимается,
конические трещины имеют
тенденцию закрываться; при
этом их видимая глубина
уменьшается.
Средний угол конуса а
(см. рис. 194) оказывает-
оказывается равным 25 ± 5°; он не
а, мм
0,5
т У
Рис. 194.
5 Ш
Рис. 195.
зависит от радиуса наконечника, величины нагрузки и от вида
материала. На рис. 195 приводятся результаты измерений диа-
диаметра главной трещины а для стекла в зависимости от радиуса
наконечника (вертикальные отрезки показывают разброс дан-
данных). Среднеквадратичная кривая полностью совпадает с тео-
теоретической кривой (см. далее).
При дальнейшем возрастании силы N внутри конуса по-
появляются осевые трещины, которые постепенно увеличиваются.
Момент выхода осевых трещин на поверхность тела совпадает
С началом самоподдерживающегося разрушения материала
490
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
1ГЛ. VIII
№0
в области, находящейся под контактной площадкой. Скорость
разлетающихся частиц материала достигает 100 м/сек. Глубина
разрушенной области максимальна на оси удара, там же частицы
разрушенного материала являются наиболее мелкими (~ЗХ
X Ю~4 см). У краев кратера обломки материала имеют большие
размеры." Вообще, динамика этого процесса разрушения весьма
схожа с самоподдерживающимся разрушением высокопрочных
стекол, описанным в §3. С течением времени кратер заполняется
продуктами разрушения. Следует отметить, что аксиальные тре-
трещины распространяются на боль-
большую глубину, чем зона полного
разрушения.
Взрывообразным выбросом
продуктов разрушения заканчи-
заканчивается первый акт контактного
разрушения. В дальнейшем с ро-
ростом силы N размер разрушенной
зоны изменяется слабо, пока не
будет достигнуто некоторое дру-
другое критическое значение силы,
при котором на диаграмме N — и
появится новый скачок разру-
разрушения (двухактное разрушение).
Если эта критическая сила не
достигается, то процесс ограни-
ограничивается одним актом (одно-
(одноактное разрушение, изображен-
изображенное на рис. 193).
На рис. 196 приводятся ре-_
зультаты измерений разрушаю-
разрушающей силы для стекла (примерно равной N2h) в зависимости от
радиуса наконечника R (кривая 1 — ударное нагружение и для
сравнения кривая 2 — статическое нагружение). Вертикальные
отрезки показывают разброс данных; среднеквадратичные кри-
кривые совпадают с теоретическими зависимостями. Как показы-
показывает сравнение рис. 195 и 196, сжимающее напряжение на пло-
площадке контакта достигает порядка 2 400 кГ/мм2 (для малых R).
2. Теоретический анализ. Рассмотрим хрупкое полупростран-
полупространство с естественной цилиндрической системой координат rQz;
пусть ударяющее по нему жесткое тело имеет сферическую фор-
форму (рис. 197). Согласно решению Герца, напряжения во всем
полупространстве — сжимающие, за исключением области А
вблизи свободной поверхности и параболоидальной области В
вблизи оси симметрии; верхняя точка области В расположена
примерно на расстоянии а от контактной площадки (радиус ко-
которой равен а). Растягивающим напряжением в области А яв-
Рис. 196.
$ 5] РАЗРУШЕНИЕ ПРИ СОУДАРЕНИИ ХРУПКИХ ТЕЛ 491
ляется ог; на краю площадки контакта оно достигает максиму-
максимума, равного примерно 0,13 от величины максимального сжимаю-
сжимающего напряжения в центре контактной площадки. В области В
растягивающими напряжениями являются сгг и ore; они дости-
достигают своего максимума на оси, на глубине A,5 -т- 2) а, причем ве-
величина максимума равна примерно 0,01— „
0,015 от наибольшего сжимающего напря-
напряжения в центре контактной площадки.
Ограничимся рассмотрением одноакт- А+
ного квазистатического процесса разру-
разрушения. В соответствии с эксперименталь-
экспериментальными наблюдениями процесс разрушения
схематично можно представить себе так.
Вначале контактная площадка увеличи- Рис. 197.
вается с ростом N, и все величины можно
найти из решения Герца. Первые окружные трещины появляют-
появляются вдоль контура площадки контакта, как только сгг достигает
прочности материала на разрыв; они еще весьма малы, так как
область растягивающих напряжений и их величина малы. Кроме
того, эти первые трещины закрываются растущей площадкой
контакта.
Следовательно, требуется некоторый запас упругой энергии
в области Л, чтобы могла возникнуть достаточно глубокая кони-
коническая трещина, которая росла бы непрерывно с возрастанием N.
Стадия быстро растущих конических трещин, очевидно, сооответ-
ствует малому переходному периоду между упругой и линейной
областями на диаграмме нагружения N — и (см. рис. 193). Бы-
Быстрый и значительный рост конических трещин ведет к обособле-
обособлению конического объема под контактной площадкой. Края обла-
области А вблизи контура контакта обламываются, и почти вся сила
N начинает действовать на характерную площадку контакта с
радиусом а» (от которой отходит главная коническая трещина).
Впоследствии процесс развивается так, как если бы сфера да-
давила только на фиксированную площадку контакта (радиуса я*).
Кроме того, можно принять, что приращение длины конических
трещин на этом этапе относительно мало. Этой стадии разруше-
разрушения, очевидно, соответствует линейная область на диаграмме на-
нагружения (см. рис. 193).
Дальнейшее увеличение силы N вызывает быстрый рост осе-
осевых трещин в области растягивающих напряжений В. Трещины
развиваются также в области сжатия С непосредственно под
контактной площадкой. Развитие трещин в условиях сжатия об-
обладает некоторыми характерными особенностями, которые объ-
объясняются тем, что в малой окрестности конца такой трещины с
налегающими берегами упругое поле полностью совпадает с тем,
которое имеет место в случае поперечного сдвига (см. § 6 гл. III).
4§2 Некоторые проблемы хрупкого разрушения [гл. vtit
Поэтому хотя трещина находится в условиях, близких к всесто-
всестороннему сжатию, вблизи ее конца имеется малая область растя-
растягивающих напряжений, причем максимум растягивающего на-
напряжения а9 достигается на площадке, наклоненной под углом
70° к плоскости трещины. Вследствие этого в хрупких материа-
материалах трещина нормального разрыва растет под таким же углом
к плоскости первоначальной трещины, причем рост трещины,
очевидно, будет устойчив, так как область растягивающих напря-
напряжений очень мала. Чем "больше уровень сжимающих нагрузок,
тем большее число начальных трещин начинает развиваться.
В условиях контактного разрушения максимальные сжимающие
напряжения на порядок превышают характерную прочность ма-
материала на одноосное сжатие (например, для стекла наибольшее
напряжение равно 1000—2000 кГ/мм2).
Таким образом, создается запас упругой энергии, необходи-
необходимый для возникновения самоподдерживающегося разрушения.
Излом на диаграмме N — и (при N = N2k), по-видимому, отве-
отвечает началу массового роста трещин.в условиях сжатия; при
N = Nm возникает самоподдерживающееся разрушение.
Этот анализ позволяет количественно описать процесс разру-
разрушения с помощью анализа размерностей [144]. Рассмотрим ста-
стадию развития конических трещин. Сначала предположим, что
длина трещин достаточно велика, чтобы игнорировать влияние
кривизны сферы на распределение напряжений вблизи конца
трещин. Тогда диаметр d конической трещины будет зависеть
лишь от a, N, Kic и v; модуль Юнга в граничные условия не вхо-
входит, поскольку мы пренебрегли кривизной штампа. Следова-
Следовательно,
"-{¦^J «[-&¦••)¦ . (8Л07)
где ф1 — произвольная функция своих аргументов.
При d %> а влиянием первого аргумента на функцию ф! мож-
можно пренебречь, и тогда из (8.107) получаем
!/3, (8.108)
где фг — произвольная функция.
Те же самые соображения для угла конуса а дают
д-2/З \
^. v], (8.I09)
где фз — произвольная функция.
Следовательно, при d >> а угол а зависит только от коэффи-
коэффициента Пуассона, который мало изменяется для всех материа-
§ 6] . РАЗРУШЕНИЕ ПРИ СОУДАРЕНИИ ХРУПКИХ ТЕЛ 493
лов. Поэтому произвольные функции коэффициента Пуассона
практически можно считать постоянными.
Строго говоря, формула (8.108) получена для асимптотиче-
асимптотического случая очень больших трещин. Оддако опыт показывает,
что вывод о точно конической форме трещин справедлив вплоть
до величин d, близких к а. Имея в виду этот опытный факт, при
помощи (8.108) получаем
3. (8.110)
Согласно решению Герца, радиус площадки контакта равен
1/31/31/3. (8.111)
Здесь а может быть равно, в частности, своему предельному
значению а*. Используя (8.110) и (8.111), находим
a. = ZK]'?E-2'3R213, Nlk = ZK2cE-lR, (8.112)
где ? и g — численные коэффициенты.
Обработка опытных данных для стекла по этим формулам
позволила получить следующие значения констант: ? » 50; | «
« 1,7.10s (при этом была использована величина поверхностной
энергии для стекла у = 2-10~3 кГ/см). Следует отметить, что
поверхностная энергия многих прочных горных пород, опреде-
определенная по экспериментальным данным на контактное разруше-
разрушение при помощи формул (8.112), оказалась в 4—10 раз больше,
чем у стекла.
Рассмотрим теперь стадию процесса, соответствующую ли-
линейному уч-астку диаграммы нагружелия. На этой стадии можно
пренебречь развитием трещин. Кроме того, так как d >> а*, про-
процессы деформации и разрушения будут развиваться так же, как
в случае удара плоским торцом прямого кругового цилиндра
диаметром 2а*. В таких предположениях смещение и — U\k мо-
может зависеть лишь от N— Nik, a, E и v. Так как тело линейно-
упруго, получаем
где ц — численный коэффициент. Обработка опытных данных
для стекла позволила найти т) ^= 1,2.
Таким образом, диаграмма нагружения N — и при ударе
жесткой сферы по хрупкому полупространству имеет следующий
вид:
NJ 1TtS)/ "P« «<«u. (8.114)
i Nlk + l,2?a. (u — uik) при и > ulk.
494 Некоторые проблемы хрупкого разрушения [гл. viit
Наконец, рассмотрим заключительную стадию перехода к
самоподдерживающемуся разрушению. Эта стадия быстротечна,
однако очень важна, так как она определяет наибольшую вели-
величину силы Nm при одноактном разрушении. Величина Nm может
зависеть лишь от a*, Kic, v и от структурной постоянной мате-
материала /о (начальная длина трещины или средний размер зерна).
Как и раньше, кривизной индентора (а следовательно, и моду-
модулем Юнга) можно пренебречь. Таким образом, имеем
Nm = Klcal^(l0K, v), (8.115)
где г|з — произвольная функция. В области значений а*, пред-
представляющих практический интерес, ее можно аппроксимировать
функцией вида
г|> = с2+С1(а,//оI/2. (8.116)
где ei и с2 — численные постоянные (cj « 240, с2 ~ 75).
Окончательно силу Nm можно представить выражением
. (8.117)
Второй член в этой формуле описывает масштабный эффект.
Для точного определения силы Nm нужно использовать точ-
точный подход, основанный на общем условии возникновения само-
самоподдерживающегося разрушения (8.73). При этом необходимо
учесть предшествующее развитие стабильных трещин (кониче-
(конических и осевых), изменяющих формулу тела и существенно ус-
усложняющих расчет. Считая силу Nm известной, оценим при по-
помощи формулы (8.73) объем v разрушенной области:
v=W/D. (8.118)
Здесь X — числовой конэффициент, U — полная упругая энер-
энергия тела, которая согласно диаграмме нагружения (8.114) равна
площади под кривой N(u):
щ
U = J JV du = 8Е VR [ 15 A — v2)] и%2 +
+ Nlk (u2k - ulk) + QfiEa. {щк - ulkf. (8.119)
Полученная формула вместе с зависимостями (8.112), (8.114) и
(8.117) позволяет давать количественные характеристики кон-
контактного разрушения, происходящего при соударении хрупких
тел. Они позволяют также решать ряд интересных задач о вза-
взаимном движении ударяющихся хрупких тел при наличии разру-
разрушения.
МАСШТАБНЫЙ ЭФФЕКТ
§ 6. Масштабный эффект
495
Масштабным эффектом называют влияние характерного ли-
линейного размера тела на его прочностные характеристики. Ниже
рассматриваются некоторые основные проявления масштабного
эффекта [13-200'201'202].
1. Влияние структуры материала. Структурную неоднород-
неоднородность конструкционных материалов можно описать при помощи
представления о структурной ячейке (см. § 8 гл. IV). Пусть ха-
характерный размер наиболее опасного дефекта меньше харак-
характерного линейного размера структурной ячейки d (это чаще все-
всего размер наиболее опасного зерна или включения, входящего
в структурную ячейку). В этом случае прочность материала не
зависит от размеров начального дефекта, а определяется формой
и размерами Наиболее опасного включения или зерна.
Это весьма важное заключение трудно доказать в сколь-ни-
будь общем виде, однако оно очевидным образом вытекает из
различных простейших моделей развития трещин в неоднород-
неоднородных телах (см., например, задачу д) из § 1 гл. IV или задачи,
рассмотренные в статьях {13- 202]). Общий вид зависимости проч-
прочности материала от размера наиболее опасного включения d
легко установить из соображений анализа размерностей *)
(8.120)
Здесь -0о — предельное напряжение, характеризующее взаи-
взаимодействие противоположных берегов начальной трещины (на-
(например, сухое трение или пластическое течение в заполнителе),
Ti — коэффициент, зависящий от формы включения и ячейки и от
безразмерных комбинаций из упругих констант (т. е. х\ можно
считать постоянной материала).
Проверим теоретическую зависимость (8.120) на иллюстратив-
иллюстративном примере опытов Ставермана Р3], который изучал композит,
состоящий из резины с 42% объемным содержанием кристаллов
поваренной соли. Приводим данные, взятые из его работы:
d X Ю 4 см
аъ, кГ/см2
<*Ь V rfmax
300—480
4
87,5
210—300
5,2
90
90-105
9
92
50-60
12
93
33-40
13
82,5
*) Эта формула хорошо известна в металловедении (формула Петча —
Стро — Коттрелла), но сейчас уже трудно установить, кто предложил ее
первым. Во всяком случае, некоторые авторы применяли ее раньше указан-
указанных. Истоки формулы (8.120) лежат в теории Гриффитса.
496
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. VIII
Отсюда видно, что значения а У dmux отличаются от среднего
значения на 2—3% и лишь в одном случае — на 7%. В данном
случае берега начальной трещины не взаимодействуют, т. е.
(То = 0.
Когда размер начального дефекта становится больше раз-
размера наиболее опасного включения, формула (8.120) сохраняет-
сохраняется, если под d понимать характерный линейный размер дефекта.
2. Влияние радиуса закругления и угла надреза. Масштабный
фактор, учитывающий влияние геометрических размеров сечения
детали, и связанный с ним масштабный эффект, заключается в
том, что по мере увеличения поперечного сечения детали (при
достижении им определенной величины) прочность материала
резко снижается. Этот эф-
эффект, вообще говоря, присущ
всем материалам, однако
для пластичных материалов
он проявляется при чрез-
чрезмерно больших размерах се-
сечения, которые на практике
встречаются редко. Особен-
Особенно сильно масштабный фак-
фактор дает себя знать у высо-
высокопрочных сталей и сплавов
с повышенной склонностью
к хрупкому разрушению.
Масштабный эффект следует изучать на образцах с надреза-
надрезами или трещинами. Рассмотрим вначале толстую пластину с уг-
угловым острым надрезом или же с плоским тупым надрезом
Р
' mace
i /-const
i i-const
< /
¦
L
Рис. 198.
Рис. 199.
Рис. 200.
(рис. 198). Образец подвергается растяжению силой Р до раз-
разрушения (материал считаем квазихрупким).
В первом случае будем варьировать угол надреза а, а во
втором — радиус закругления конца надреза R, оставляя вели-
величины / и L неизменными. Зависимость разрушающей силы Р от
угла а и радиуса R качественно изображена на рис. 199 и 200.
§ 6] МАСШТАБНЫЙ ЭФФЕКТ 497
Обратимся сначала к рис. 199. Согласно решению Вильямса
(см. § 3 гл. III), поле напряжений и деформаций в малой окрест-
окрестности конца углового надреза в данном случае полностью харак-
характеризуется одним коэффициентом интенсивности напряжений Ка,
равным
Ка= Нт [Bяг)*<гв]- (8-121)
г-»0, 6=0
Здесь X— наибольший корень уравнения C.16), зависящий
лишь от а. Зависимость X от а изображена на рис. 9 (X соответ-
соответствует Яшах, а 02 — 8i отвечает 2я— а). Согласно общефункцио-
общефункциональному методу механики хрупкого разрушения, каждому зна-
значению угла а соответствует некоторая константа материала Кас,
которая имеет размерность кГ-см%~2. Эту константу можно опре-
определить, например, при помощи опытной кривой рис. 199 на ос-
основе решения упругой задачи для конфигурации, изображенной
на рис. 198. *
Как видно, наличие ненулевого угла а изменяет показатель X
масштабного эффекта при хрупком разрушении (равный 7г при
ее = 0). Например, при L ^$> I разрушающая нагрузка, очевидно,
будет такой:
\ (8.122)
где постоянная | может зависеть только от а.
Рассмотрим теперь рис. 200. Величина /?min, очевидно, имеет
порядок наибольшего раскрытия конца трещины. Наибольшее
значение силы Ртах соответствует прочности гладкого образца
с сечением L — I, а наименьшее значение ?Vn — прочности об-
образца с трещиной. Зависимость критического коэффициента ин-
интенсивности напряжений в момент разрушения от радиуса R
имеет такой же вид, при этом минимум соответствует вязкости
разрушения Kic- Кривую рис. 200 часто можно аппроксимировать
ПрЯМОЙ на отрезке (^mim #max).
3. Влияние ширины образца. Рассмотрим пластину со сквоз-
сквозной трещиной в условиях плоской деформации (см., например,
рис. 51). Будем варьировать ширину пластины, сохраняя подо-
подобие всех геометрических размеров тела в плане (толщина пла-
пластины в данном случае предполагается неизменной и весьма
большой). Для количественного описания масштабного эффекта
в случае идеальных упруго-пластических тел наиболее удобно
воспользоваться концепцией уя (см. § 2 гл. VI). Изложим ме-
метод исследования на примере растяжения полосы с боковой тре-
трещиной (рис. 51). Следует только иметь в виду, что в других
случаях y*. вообще говоря, может иметь другую величину, если
пластическая область соизмерима с поперечным сечением,
498
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
1ГЛ. VIII
Из варьируемых параметров Е\%, as и L можно составить
единственную безразмерную комбинацию
% = EyJ(alL). (8.123)
Безразмерный параметр % назовем «числом хрупкости». Фи-
Физически он определяет отношение максимально возможного ли-
линейного размера пластической области в конце изолированной
трещины к расстоянию L, задающему геометрический масштаб
образца при l/L = const и h = const.
Среднее разрушающее напряжение а в рабочем сечении об-
образца с учетом влияния масштабного эффекта можно записать
в виде
o = asf(x, v), (8.124)
где /(%, v)— некоторая безразмерная функция. Очевидно, про-
проявление масштабного эффекта, т. е. снижение прочности с уве-
увеличением размеров сечения, имеет место при /(%, v)< 1.
Поскольку число хрупкости х определяет пластический или
хрупкий характер разрушения, его можно считать критерием.
Если, например, для данного материала и при данной толщине
стенки конструкции % ~Э> 1, то тело ведет себя
как идеально жестко-пластическое. В случае
X -С 1 тело ведет себя как идеально хрупкое.
Для рассматриваемых двух предельных
случаев хй>11 и л«1) функцию f(%,v) в
формуле (8.124) можно легко определить.
а) Пусть %~^> 1, т. е. максимально возмож-
возможный размер пластической области гораздо
больше L. При этом
v)=l. (8.125)
Рис. 201..
Уравнение (8.125) следует из разрывного
решения жестко-пластической задачи, изобра-
изображенного на рис. 201, в двух предельных слу-
случаях: h~^> L (плоская деформация) и h <C L
(плоское напряженное состояние). При h > L
и h ~ L линии разрыва тангенциальной компоненты скорости
ОА и ОА' разделяют жесткие части тела (такая кинематическая
картина наблюдалась неоднократно, например, в экспериментах
Орована и Работнова). Заштрихованные и незаштрихованные
области соответствуют разрывному статически допустимому со-
состоянию, дающему ту же предельную нагрузку. При h <C L
обычно реализуется линия разрыва нормальной компоненты ско-
скорости ОВ (шейка), разделяющая жесткие части образца. Стати-
Статически допустимое состояние — то же самое. В этом случае мас-
масштабный эффект отсутствует.
§ 65 МАСШТАБНЫЙ ЭФФЕКТ 499
б) Пусть % <С 1, т. е. максимально возможный размер пла-
пластической области гораздо меньше величины L. Для образцов
с одним боковым надрезом концепция у* при помощи формулы
(П.22) позволяет получить следующее значение предельного
напряжения о при I <C L и %L/l «С 1:
1М. (8Л26)
После подстановки соотношения (8.123) в это уравнение имеем
а = 0,71 уТ A + ЦЦ aj VJjL. (8.127)
Отсюда значение /(%, v) будет
Ах. v) = 0,71 У%у==-. (8-128)
Найдем функцию /(%, v) для другого широко распространен-
распространенного типа образцов — образцов с двумя противоположно распо-
расположенными боковыми подрезами. Используя решение Бови
(П.26), напишем формулу для предельного значения растяги-
растягивающего напряжения о, приложенного на бесконечности:
<8-129)
В этом случае среднее напряжение, действующее в сечении-
нетто между надрезами, равно
f
+ f/L / Еу, /я
шту я/ • (8
2 (/ + L)
В этих формулах <p(l/L) — поправочный коэффициент, учиты-
учитывающий влияние свободной границы образца.
После подстановки значения Еу* из выражения (8.123) в
формулу (8.130) получим
(ЦЦ /
* L g 2 (L
откуда
Г 1 + L
1/ я/
* L g 2 (L +
2 (L + I)
Формулы (8.128) и (8.131) дают количественное описание
масштабного эффекта в рассматриваемых частных случаях.
500 Некоторые проблемы хрупкого разрушения [гл. vnt
Для экспериментальной оценки границ применимости фор-
формулы (8.131) используем данные С. В. Серенсена и Н. А. Маху-
това {68] о зависимости разрушающих напряжений для образцов
с двумя боковыми надрезами от площади поперечного сечения-
нетто при отношении сторон поперечного сечения h/(L-\-l) =0,4;
l/L = 1/3.
По известным размерам образцов рассчитываем величину
/(х,v). Затем сравниваем ее с экспериментально полученной в
работе [68] величиной снижения прочности образцов при увели-
увеличении их размеров (материал образцов — сталь 22К)- Для этого
необходимо определить величину % для используемых образцов,
что, в свою очередь, требует знания величин as и у* Для мате-
материала образцов.
Для стали 22К при нормальной температуре величина as,
определенная по данным, приведенным в работе [68], составляет
55 кГ/мм2. Для нахождения значения у* были использованы
результаты испытаний на растяжение образцов с площадью
поперечного сечения 0,7-105 мм2. Результаты испытаний обра-
обрабатывали по уравнению (8.130), решив его относительно у*.
Величины L и I определяли из следующих условий: отношение
сторон прямоугольного поперечного сечения равно 0,4; среднее
значение относительной глубины острого надреза 1/L = 1/3.
Значение модуля Юнга принималось равным 2,1 -104 кГ/мм2.
В этих испытаниях было получено оя = 0,7 as (считалось, что
os — оъ)- Поправку на пластичность металла в вершине надреза
вводили путем увеличения расчетной длины начального над-
надреза I на величину А:
/, = / + Д. (8.132)
Поправку А для условий плоской деформации в вершине
надреза определяли по эмпирической формуле Ирвина .
Д = (*1С/*ЛFя). (8-133)
Вычислив по уравнению (8.130) величину у*, определим за-
затем значение 1\, а потом заменим I па 1\ в (8.130) и снова вы-
вычислим у*- В результате получим у* = 4,2 кГ/мм. В этом случае
для образцов с площадью поперечного сечения 0,7-105 мм2 чис-
число хрупкости х = 0,24.
Расчет величины масштабного эффекта для аналогичных об-
образцов с площадью поперечного сечения МО5 мм2 (% = 0,21)
дал значение /(х, v) = 0,63, что удовлетворительно согласуется
с опытной величиной стн = 0,66 as. Для образцов, имеющих число
хрупкости х > 0,25, расчетные значения f(%, v) не совпадают
с экспериментальными значениями ан.
На рис. 202 представлена функция f(%, v).'B интервале
0 < х < 0.25 она построена по уравнению (8.131), в интервале
0,25 < х < 4 — по результатам обработки экспериментальных
«61
МАСШТАЁНЫЙ ЭФФЕКТ
501
данных работы [68]. Можно полагать, что этот график, позво-
позволяющий давать оценку масштабного эффекта для образцов с
двумя надрезами, носит универсальный характер и сохранится
неизменным для широкого круга материалов при 1/L = 1/3 *).
ffX, >)
0,8
/
/
1
,
- -
\
)f
¦ 1
\
1
/
¦¦¦¦¦—
7
и 12 J X
Рис. 202.
Снижение прочности материалов с увеличением геометриче-
геометрических размеров детали обычно объясняется либо изменением
технологии изготовления (технологический фактор), либо уве-
увеличением вероятности появления больших дефектов типа тре-
трещин (статистический фактор).
Для того чтобы дать количественную оценку влияния техно-
технологического фактора на масштабный эффект, следует, очевид-
очевидно, установить влияние технологии изготовления на величины
as и у* и затем определить значение /(%, v) по формуле (8.131).
В этом случае максимальный размер / трещиновидного наибо-
наиболее опасного дефекта считается известным (например, по дан-
данным неразрушающего контроля или металлографического ис-
исследования шлифов) и постоянным. Целенаправленно изменяя
технологию изготовления изделий больших габаритов и толщин
(в частности, увеличивая y*)> можно предотвратить снижение
их прочности, связанное с проявлением масштабного эффекта.
Если размер / начального наиболее опасного дефекта из-
известен лишь с некоторой вероятностью для каждого из рас-
рассматриваемых сечений, то о проявлении масштабного эффекта
можно судить, сравнивая плотности распределения числа хруп-
хрупкости х рассматриваемых сечений.
*) Этот график при помощи формул (8.123) и (8.124) можно использовать
также для определения вязкости разрушения и Y* в опытах с малыми образ-
образцами, у которых перед разрушением сечение-нетто находится в пластическом
состоянии.
502 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VItt
4. Влияние толщины пластины. Рассмотрим снова пластину
из упруго-пластического материала со сквозной трещиной (см.
рис. 51) и будем варьировать толщину пластины к, считая, что
величины / и L велики по сравнению с размером пластической
области. В этом случае изменение толщины пластины скажется
лишь в изменении Кс и соответствующей величины у. Количе-
Количественное описание масштабного эффекта в этом случае дается
следующей формулой (ем. § 8 гл. IV):
_(ych/h, при h<ht,
У~\Ъс + (Ус-'Ъс)Г1.1к при h>ht. (
Величина h% представляет собой толщину, соответствующую
максимальному значению у = ус, величина у\с — наименьшее
значение у (для толстых пластин). С дальнейшим увеличением
толщины при h > h* значение у и связанная с ним величина
хрупкой прочности начинает уменьшаться. Величины ус и yic
можно рассматривать как характеристики материала, опреде-
определяющие максимальное и минимальное значения хрупкой проч-
прочности. Отметим, что величина /гж может представлять особый
интерес, поскольку пластины толщиной /г* обладают наиболь-
наибольшей удельной прочностью.
Для экспериментальной проверки этого уравнения исполь-
используем данные [200], полученные на высокопрочном титановом
сплаве ВТ 14 в термоупрочненном состоянии, а также данные
Сроули и Брауна [351 Для алюминиевого сплава 7075-Т6.
Образцы, изготовленные из сплава ВТ-14, находились в сле-
следующих исходных состояниях: 1) вырезались из листов толщи-
толщиной 10 мм, полученных холодной прокаткой (направление роста
трещины — вдоль волокна), 2) вырезались из заготовок, полу-
полученных методом раскатки (сплав со слоистой структурой). Для
всех образцов упрочняющую термообработку выполняли по од-
одному и тому же режиму: закалка с температуры 870 °С в воду,
старение при Температуре 500 °С в течение 8 час.
Высота L-\-1 всех образцов составляла 20 мм, длина —
72 мм, толщина h менялась от 0,65 до 10 мм путем фрезерова-
фрезерования боковых поверхностей. После термообработки на образцах
создавалась сквозная боковая усталостная трещина длиной
/ = 6 мм. Образцы нагружали консольным изгибом по схеме,
приведенной на рис. 203. Результаты испытаний обрабатывали
по формуле (П.29). При испытании образцов средние напря-
напряжения в сечении-нетто не превышали предела текучести ма-
материала. Учет пластичности металла производили так же, как
и ранее.
Результаты испытаний образцов, выполненных из сплава
ВТ-14, представлены на рис. 203 (сплошная линия — теоретиче-
F1
МАСШТАБНЫЙ ЭФФЕКТ
603
екая кривая). Заметим, что образцы, изготовленные из раскат-
раскатного сплава ВТ-14, имеют явно выраженную слоистость струк-
структуры, что привело к большому разбросу экспериментальных
данных. Результаты испытаний образцов из листового сплава
ВТ-14 подтвердили принятую аналитическую зависимость для
второго участка (ft>ft*). Выход на левую асимптотическую
прямую (ft < ft») применительно к сплаву ВТ-14 связан с из-
изготовлением и испытанием образцов толщиной h < 0,6 мм, что
вызвало серьезные технические затруднения.
у, «Г/си
50
40
30
го
/о
7
/
\
V
\
к
0
"*>
0 ]
0 ;
X
<Ъ
0
:i
j
1
Л
¦'¦
1
t
A
h,m
w
Рис. 203.
Экспериментальная кривая для алюминиевого сплава
7075-Т6, приведенная на рис. 50, полностью совпадает с теоре-
теоретической зависимостью при h > h*.
Анализ изломов образцов выявил следующую особенность:
суммарная толщина «губ среза» 5 (рис. 204) не зависит от
толщины образцов (при h > 5) и, следовательно, является кон-
константой материала; кроме того, замечено, что б fa /г*. Из
рие. 204 видно, что величина 5 практически совпадает с ft* для
соответствующих материалов (см. рис. 50 и 203).
Первый участок кривой yW (пРи ft < ft») обстоятельно
исследован в работе [204]. Много полезных сведений о хрупком
разрушении и обусловленном им масштабном эффекте содер-
содержится в книгах р05-207].
5. О многослойных конструкциях. Изложенная здесь на част-
частных примерах теория масштабного эффекта позволяет сделать
некоторые простые выводы относительно возможных путей
604
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. VIII
использования этого эффекта в вопросах материаловедения и
конструирования.
На основании формулы (8.120) прочность материала при
прочих равных условиях увеличивается с уменьшением размера-
зерна. Поэтому технологический процесс, в котором создается
А-А
В/г t/г .
10 25h,MH
материал, для достижения наибольшей прочности должен проек-
проектироваться так, чтобы размер зерна был минимален (при про-
прочих равных условиях). За последние сто лет металлурги до-
добились увеличения прочности стали на порядок; при этом раз-
размер зерна высокопрочных сталей в 1970 г. уменьшился на два
порядка по сравнению с зерном литого железа, которое было
наиболее прочным конструкционным материалом в 1870 г.
Анализ влияния размеров трещиноподобного дефекта на
прочность (если размер дефекта превышает характерный размер
наибольшего зерна) показывает, что влиянием дефекта на проч-
прочность (и соответствующим масштабным эффектом) можно пре-
пренебречь только в том случае, когда его размер существенно мень-
меньше размера пластической области вблизи конца большой (мак-
(макроскопической) трещины, находящейся в предельном состоянии.
Последний определяется величинами Ки и 0о,з (см. § 5 гл. IV).
I f] ЭРОЗИЯ ТВЕРДЫХ ТЕЛ В tlOtOKE ЖИДКОСТИ ИЛИ ГАЗА S05
Анализ диаграммы y(h) показывает (см., например,
рис. 203), что существует оптимальная толщина пластины й„,
при которой вязкость разрушения (а следовательно, и проч-
прочность) будет максимальной при прочих равных условиях. По-
Поэтому, если, например, монолитный образец толщины h, изо-
изображенный на рис. 51, заменить многослойным образцом той
же толщины (толщина каждого слоя равна ft», число слоев
равно hjh*, слои склеены каким-либо малопрочным связую-
связующим), то для заданной толщины h будет достигнута максималь-
максимально возможная прочность. Таким образом, создание многослой^
ных конструкций является одним из путей повышения удельной
прочности и надежности:1"
Следует подчеркнуть, что в спроектированных таким обра-
образом конструкциях достигается наибольшее сопротивление рас-
распространению трещин (при прочих равных условиях). Если
создание многослойной конструкции технологически невозмож-
невозможно или дорого, а материал и толщина h могут варьироваться
(величина суммарной нагрузки задана), то при отыскании ми-
минимума комбинации р/г также полезно иметь в виду этот мас-
масштабный эффект.
§ 7. Некоторые проблемы эрозии твердых тел
в потоке жидкости или газа
Срок службы изделия весьма часто определяется скоростью
его постепенного поверхностного разрушения. Причины поверх-
поверхностного изнашивания материала (эрозии) многообразны.
В конечном счете оно объясняется силовым и химическим воз-
воздействием на поверхность данного тела других твердых тел,
а также жидкостей и газов*).
Если локальные нагрузки невелики, то скорость эрозии ме-
металлов определяется усталостным отколом частиц материала
под действием локально нестационарного нагружения. Пусть
v — характерная скорость роста усталостной трещины в течение
цикла нагружения, п — характерное число циклов нагрузки в
единицу времени. Тогда объем материала Q, разрушенного за
единицу времени (приходящегося на единицу поверхности),
равен
Q = x\vn, , (8.135)
где т) — численный коэффициент. Параметр п зависит в свою
очередь, например, от рельефа поверхности, от числа Струхаля
или от скорости относительного движения тел и т. п. Параметр v
*) Общее представление о состоянии этого вопроса можно получить по
обзору [180]. По различным частным аспектам этой общей проблемы читателе
может обратиться, например, к монографиям рм-ш].
806 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЙ (ГЛ.
зависит от уровня нагрузки, химического состава внешней среды,
размера и формы зерен и т. п.
Выведем количественную зависимость скорости эрозии от
указанных факторов для случая обтекания твердых тел пото-
потоком жидкости или газа, содержащим мелкие твердые' частицы
(абразив) B1а].
Расчеты выполним применительно к малым скоростям дви-
движения, наблюдающимся, например, в нефтяных и газовых сква-
скважинах (скорость движения жидкости около 1 м/сек, а скорость
газа — до 100 м/сек). При этом обтекаемое тело считается ме-
металлическим, а следовательно, имеющим резко выраженную
микронеоднородность прочностных свойств (зернистость).
Поверхность металла всегда шероховата, поэтому каждый
отдельный бугорок поверхности испытывает многочисленные си-
силовые воздействия от ударов частиц абразива, от гидродинами-
гидродинамических сил сопротивления (особенно срыва вихрей), от схлопы-
вания кавитационных пузырь-
пузырьков (в случае жидкости). По
границам зерен от шероховато-
шероховатостей отходят усталостные тре-
трещины, развитие которых при-
приводит к откалыванию зерен на
поверхности (рис. 205). При
малых скоростях движения
влиянием гидродинамических
Рис- 205- сил и схлопыванием кавита-
кавитационных пузырьков можно
пренебречь по сравнению с воздействием частиц абразива.
Гидродинамические силы довольно стационарны. Воздействие
твердых частиц носит циклический характер. Усталостное
разрушение чувствительно к переменным составляющим на-
нагрузки, а от постоянной составляющей нагрузки усталостная
кривая зависит довольно слабо. Примем, что распределение ско-
скоростей и концентрации твердых частиц вблизи поверхности об-
обтекаемого тела известно и постоянно, абразивные частицы
имеют шарообразную форму, удар частиц о поверхность метал-
металла— идеально упругий. Влияние таких факторов, как микроше-
микрошероховатость поверхности абразивных частиц, температура, кор-
коррозия и т. п., учитывать не будем. Полученные при этом резуль-
результаты следует считать среднестатистическими.
1. Вспомогательная задача об ударе шара о полупростран-
полупространство. Пусть упругий шар радиуса г\ из материала плотно-
плотности pi движется по нормали к границе покоящегося упругого
полупространства со скоростью v. О характере соударения сде-
сделаем следующие два допущения: а) удар чисто упругий, т. е.
диссипацией энергии (вязкой или пластической) можно пре-
§ 71 ЭРОЗИЯ ТВЕРДЫХ ТЕЛ В ПОТОКЕ ЖИДКОСТИ ИЛИ ГАЗА 507
небречь по сравнению с потенциальной энергией упругих дефор-
деформаций; б) энергия упругих волн мала по сравнению с энергией
упругих деформаций. Согласно решению Герца (применительно
к нашему случаю удара упругого шара о полупространство),
наибольшая сила Р упругого сопротивления, действующая на
шар со стороны полупространства (в момент остановки), равна
|()( ) (8136)
Здесь
Ei и Е2 — модули Юнга шара и полупространства; vj и V2 — со-
соответствующие коэффициенты Пуассона.
2. Расчетная схема. При расчете скоростей износа металла
будем считать, что
1) поверхность металла состоит из множества плоских мик-
микроплощадок, случайно ориентированных по отношению к пло-
плоскости металла;
2) каждая частица абразива (трактуемая как шар радиуса
Г]) идеально упруго соударяется с одной из микроплощадок
только один раз;
3) откалывание кусков металла с поверхности (в виде зерен
размером г2) происходит вследствие роста усталостных трещин.
Величины Г\ и г2, а также скорость и угол атаки частиц абра-
абразива в некоторых условиях могут быть случайными величинами.
Скорость износа металла представляет собой определенный
функционал от указанных параметров задачи, конкретизируемый
при некоторых естественных допущениях о функциях распреде-
распределения случайных величин.
3. Расчет интенсивности силового воздействия на одно зерно.
Пусть твердая частица (упругий шар радиуса г{) ударяется о
микроплощадку, угол наклона
которой к поверхности тела
Ох (средняя линия микрорель-
микрорельефа) равен р (рис. 206). Пусть
ось у направлена по нормали к
поверхности тела; обозначим
Через а угол, составляемый
вектором скорости шара v с
осью Ох, через хп — систему Рис- 206-
прямоугольных декартовых ко-
координат, связанную с наклонной микроплощадкой (ось т направ-
направлена вдоль площадки, ось п — по нормали к ней).
Следует иметь в виду следующее. Микрорельеф поверхности
тела вырабатывается в процессе взаимодействия твердого тела
С абразивом (и, в общем случае, — о потоком жидкости)} он н$
608 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
зависит от начальных условий (в частности, степени шлифовки
поверхности) и, вообще говоря, определяется не только физиче-
физическими характеристиками материала, но и величинами Г\, pi, v, a,
характеризующими поток абразива [2М]. Поэтому величину, угла
Р следует понимать как некоторую среднестатистическую харак-
характеристику микрорельефа. В наших условиях скорость потока
жидкости и частиц абразива весьма мала, так что можно прене-
пренебречь эффектами вязкого и пластического течения материала з
поверхностном слое и считать разрушение квазйхрупким (уста-
(усталостным), происходящим вдоль слабых мест материала с отко-
отколом некоторых частиц (зерен); размер г2 последних можно рас-
рассматривать как некоторую среднестатистическую характеристику
структуры материала. При этом микрорельеф поверхности (и, в
частности, величина р) полностью определяется структурой ма-
материала и не зависит от величин гь рь v, а, характеризующих
поток абразивных частиц. Таким образом, величину р можно
считать структурной постоянной материала.
Определим силовое воздействие, испытываемое зерном мате-
материала при идеально упругом ударе одной частицы абразива. Из
рис. 206 нетрудно найти составляющие импульса рх и ру, полу-
полученные телом;
рх = 2mv cos V sin Р = 2mv sin (a + p) sin p,
py = — 2mu cos y cos P = — 2musin(a +P)cosp, '
где т и v — масса и скорость частицы абразива соответственно.
Наибольшую величину силы Р, действующей на тело во вре-
время удара и соответствующей, очевидно, прямому удару того же
шара со скоростью v cos y, находим по формуле (8.136):
Р = 4 г? A0яр,K/5 (9, + е2)/5 (v cos yN/5 • (8.138)
Эта сила направлена по нормали к микроплощадке. Составляю-
Составляющая ее Ру в среднем будет вызывать в теле только сжимающие
напряжения, а составляющая Рх вызовет также растягивающие
напряжения (вследствие изгиба). Поскольку усталостные тре-
трещины растут в основном от растягивающих нагрузок, ясно, что
ответственной за усталостное разрушение зерна является лишь
составляющая силы Рх, которая будет равна
Рх = -| г\ A0яР1K/5 (9, + 92)/5 [v sin (a + P)f/5 sin p. (8.139)
Теперь подсчитаем число ударов, испытываемых в среднем
одним зерном материала (шар радиуса г2) за единицу времени.
Пусть объемная концентрация твердых частиц абразива равна с.
§ 71 ЭРОЗИЯ ТВЕРДЫХ ТЕЛ В ПОТОКЕ ЖИДКОСТИ ИЛИ ГАЗА 509
Отсюда расход абразива G через площадь S за единицу времени
равен
G=j^c9lvndS, (8.140)
s
где vn — составляющая скорости частиц по нормали к площадке.
Площадь 5, приходящаяся на одно зерно материала, равна
S = r\nrl (8.141)
Здесь коэффициент ц показывает, какая часть наибольшего
поперечного сечения зерна проектируется на плоскую поверх-
поверхность тела. Из соображений непрерывности процесса разруше-
разрушения очевидно, что коэффициент ц в среднем равен единице. Из
формул (8.140) и (8.141) находим
G = wr22cptv sin a. (8.142)
При этом пренебрегаем изменением vn и cpi в масштабах зерна.
Так как каждая частица абразива имеет массу
а общая масса частиц абразива, ударившихся о зерно за еди-
единицу времени, равна G, то число ударов п, испытываемых в сред-
среднем одним зерном материала за единицу времени, будет равно
(fU44)
> 4. Единичный акт усталостного откола. Используем кривую
усталости (кривую Велера) для одного зерна. Эта кривая опре-
определяет зависимость предельного числа циклов N (после которого
происходит разрушение) от максимального напряжения (или на-
нагрузки) в течение пульсирующего цикла. Напомним, что под
пульсирующим понимается цикл, минимальное напряжение в ко-
котором равно нулю. Форма цикла и частота слабо влияют на пре-
предельное число циклов. Характерная кривая усталости изобра-
изображена на рис. 207.
В нашем случае (поскольку удар каждой частицы абразива
можно считать в среднем идеально упругим и квазистатическим)
каждое зерно будет нагружаться по схеме пульсирующего цикла
(каждый удар — цикл нагружения). При этом максимальная на-
нагрузка за цикл равна Рх (см. формулу (8.139)), а число циклов
за единицу времени равно п (см. формулу (8.144)).
610
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
1ГЛ. VIII
0*
Примем, что в рассматриваемой задаче предел усталости от-
отсутствует, т. е. кривая усталости, изображенная на рис. 207, при
N-*¦ оо асимптотически стремится к оси абсцисс. Это предполо-
предположение естественно, поскольку величины Рх, N, г2 представляют
собой некоторые статистические
средние; поэтому в потоке имеют-
имеются также частицы с большим
импульсом, а в материале — ме-
менее прочные зерна. Отсюда ясно,
что допущение о наличии износа
материала даже при очень малых
средних импульсах частиц абра-
абразива вполне приемлемо.
Пусть кривая усталости выра-
выражается некоторой функцией ф в
виде
1п# — <р(/ул), (8.145)
ТТ7Т7Т
Рис. 207.
где Я — структурная постоянная
материала, имеющая размерность
силы.
Согласно этой формуле число ударов частиц абразива о зер-
зерно, в результате которых зерна откалываются, равно
(8.146)
5. Определение скорости износа. Так как число ударов, ис-
испытываемых зерном за единицу времени, равно п, а общее число
ударов, вызывающих откол зерна, равно N, то одно зерно, оче-
очевидно, отломится аа время
N
п
Зцг^м sin a
ехр
Пусть т.ч. — масса одного зерна материала, равная
(8.147)
(8.148)
a S — эффективная площадь, приходящаяся на одно зерно мате-
материала (см. формулу (8.141)). Тогда скорость износа Q, т. е. мас-
масса материала, отламывающегося с единицы поверхности за еди-
единицу времени, будет равна
tQs
Л
ехр -Ф —
*»]
эрозия тйеРДых тел в потоке жидкости или газа
511
Используя формулу (8.139) для Рх и вводя новую постоянную
размерности силы
получим следующую окончательную формулу для скорости
износа:
Q = p2cy(r2/r,Ksinaexp{ — <p(g)}, (8.149)
/
4- &)]615 В U\ v^'P1 -J-''1 .Л/р 1~2/5
где
Постоянные В, р и функцию <р(|) следует находить из вспо-
вспомогательных опытов по эрозии металлов. Так, величину р мож-
можно определить по наблюдениям угла отражения частиц абразива
от выработанной поверхности металла, а потоянную В и вид
функции ф(|) можно найти из анализа кривых усталости, по-
полученных при испытании цилиндрических образцов из данного
металла на изгиб.
В первом приближении кривая -усталости может быть аппрок-
аппроксимирована прямой линией. Тогда ф(|) = а — |, а основная
формула (8.149) примет вид
cv sin a
-5— expX
т,ие
50'|—
X
Ь'
1-vf
-v?^2/5
(8.150)
/О
7
г
\
\
Здесь через Л обозначена новая
структурная постоянная разрушаемого
материала, имеющая размерность мас-
массы и равная А = р2ф~а.
6. Сравнение с экспериментом. Ос-
Основная теоретическая зависимость
(8.150) для скорости износа качествен-
качественно хорошо согласуется с эксперимен-
экспериментальными кривыми, полученными
А. А. Антоновым при иследовании ста-
сталей и чугуна воздушной абразивной струей [215]. А при подходя-
подходящем выборе структурных постоянных А, В, $ эта формула хо-
хорошо согласуется с опытами и количественно. Так, при всех по-
постоянных, принятых в работе [215], и подходящем подборе струк-
структурных постоянных формула (8.150) для общей массы износа
30
Рис. 208.
812 Некоторые гФоёлемы хрупкого Разрушений ff\ft. vitt
металла принимает вид
m=16sinctexp{l,7[cos(a—15°)]6/5}.
Кривая, соответствующая этому уравнению, представлена на
рис. 208 (сплошная линия); она почти совпадает с эксперимен-
экспериментальными данными (крестики), приведенными в работе [215].
§ "8. Оптическое разрушение
Бурное развитие техники ставит перед механикой разрушения
ряд новых задач. К ним относится, например, проблема влияния
на прочность твердых тел облучения (пучки нейтронов, мощное
фотоизлучение, электромагнитные волны высокой частоты и т. д.).
Остановимся весьма кратко на тех аспектах этой проблемы,
которые наиболее важны для механики хрупкого разрушения.
1. Нейтронное облучение. Как известно, ядерные реакции
сопровождаются потоками элементарных частиц (у-кванты, р-лу-
чи, потоки нейтронов и протонов и т. д.), энергия которых го-
гораздо больше энергии связи атомов - твердого тела. Попадая
в тело, они вызывают каскад других частиц и в итоге приводят
к некоторым локальным нарушениям структуры тела. При до-
достаточной интенсивности или продолжительности действия они
могут привести к полной деструкции тела или к потере его ра-
работоспособности. Наибольшее влияние оказывают пучки нейтро-
нейтронов и у-квантов, которые не несут электрического заряда и по-
потому обладают наибольшим проникающим действием. Не имею-
имеющие массы у"кванты воздействуют в основном на электронные
оболочки; при не слишком высоких энергиях и интенсивностях
их действие сводится к нагреванию тела. Нейтроны способны
искажать решетку, непосредственно воздействуя' на ядро атомов.
Нейтронное облучение вызывает ослабление пластических
свойств тела, уменьшение вязкости разрушения Ки и ведет к
образованию дефектов, что также охрупчивает материал. Кроме
того, в металлах важную роль играет тепловая диффузия про-
протонов и нейтронов, вызывающих охрупчивание совершенно ана-
аналогично влиянию водорода (см. §§ 1, 2 гл. VII); протоны могут
попадать в тело через поверхность из внешних протонных пучков
или же возникать в объеме тела при столкновении нейтронов
с ядрами.
При наличии только тепловых протонов и нейтронов их влия-
влияние можно полностью описать в рамках механики хрупкого раз-
разрушения при помощи экспериментально замеряемой зависимости
вязкости разрушения от концентрации протонов и нейтронов.
Кроме того, нужно учесть докритический рост начальных тре-
трещин под действием растягивающих напряжений и локальной
концентрации этих частиц в конце трещины. Механизм этого яв-
§ 8] ОПТИЧЕСКОЕ РАЗРУШЕНИЕ 513
ления аналогичен рассмотренному в § 2 гл. VII диффузионному
механизму.
При более значительных энергиях (и количестве) протонов и
нейтронов необходимо учитывать старение материала (зависи-
(зависимость Kic от времени), а также докритический рост начальных
трещин вследствие вызываемого непосредственно частицами ло-
локального разрушения в конце трещины (см. § 2 гл. VII, рост
трещин при предельно больших градиентах концентрации).
2. Электромагнитные волны. Распространение электромаг-
электромагнитных волн в диэлектриках сопровождается поляризацией ма-
материала, в результате которой асимметрия (полярность) элек-
электронного облака внутри элементарной ячейки увеличивается и
появляются внутренние деформации. Тензор деформаций ец в
первом приближении линейно связан с вектором поляризации Р<
*U*=AlJkPk. , (8.151)
Здесь A{jh — постоянные материала, образующие тензор
третьего ранга (линейный пьезоэффект или электрострикция).
Уравнения Максвелла плюс уравнения теории упругости и
уравнения (8.151) образуют замкнутую систему, которой нужно
пользоваться для решения задач о деформации и хрупком раз-
разрушении. Такой подход для обычных интенсивностей и частот
электромагнитных волн необходим лишь при изучении пьезо-
кристаллов, у которых постоянные Л^ь относительно велики.
Для большинства твердых тел указанным эффектом обычно
можно пренебречь. Гораздо более существенными для них ока-
оказываются гистерезисные потери, имеющие место в течение ка-
каждого цикла поляризации и вызывающие нагревание тела. Для
таких тел задача о хрупком разрушении решается в два этапа.
Сначала из решения уравнений Максвелла определяется погло-
поглощение электромагнитной энергии в среде, причем'диэлектриче-
причем'диэлектрическая постоянная и коэффициент поглощения считаются извест-
известными из опыта. Коэффициент поглощения связан с шириной
резонансной кривой или же с шириной спектральной линии. Зату-
Затухание волн можно учесть также, задавая связь между напря-
напряженностью Е и поляризацией Р в виде
Здесь т, xi и Х2 — некоторые постоянные. Согласно экспери-
экспериментальным данным, коэффициент линейного поглощения прямо
пропорционален квадрату частоты. -Затем ищутся решение соот-
соответствующей задачи термоупругости с найденным распределе-
распределением тепловых источников и термоупругие напряжения.
Этот эффект становится существенным для всех диэлектриков
при достаточно высоких частотах, так как гистерезисные потери
17 Г. П. Черепанов
g]4 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. Vllt
быстро возрастают с увеличением частоты. При этом в случае
прозрачных или полупрозрачных тел возникает возможность
фокусировать энергию волн на расстоянии и внутри заданного
объема тела, добиваясь избирательного разрушения. Непрозрач-
Непрозрачные диэлектрики под действием электромагнитного излучения
разрушаются с поверхности совершенно аналогично хрупкому
разрушению при огневом бурении (см. § 4 этой главы).
В металлах электромагнитное поле вызывает, кроме того,
электрические токи и нагревание за счет джоулева тепла. В фер-
ферромагнетиках существенно также намагничивание тела под дей-
действием электромагнитных волн.
3. Воздействие света на непрозрачные тела. Вследствие по-
поглощения фотонов электронами непрозрачные материалы под
действием света нагреваются с поверхности. Термический эффект
преобладает вплоть до весьма высоких интенсивностей световых
пучков', создаваемых в современных оптических устройствах.
И только когда напряженность электрического поля в световой
волне становится сравнимой с напряженностью внутреннего
поля (порядка 107—109 вольт/см), созданного электронами и
ядрами атомов тела, начинают играть роль процессы прямой
ионизации атомов материала в световых пучках. На языке меха-
механики разрушения это соответствует достижению в теле предель-
предельно больших напряжений, сравнимых с теоретической прочностью.
Напомним, что отрыв от атома наиболее слабо связанных с ним
электронов, обеспечивающих химическую связь атомов, означает
диссоциацию тела на ионы, т. е. теоретическое разрушение.
Поэтому энергия химической связи близка к потенциалу иони-
ионизации.
Квантовые генераторы света мощностью до 108 вт могут соз-
создавать тонкие пучки света (с диаметром фокуса до 10~3 —
10~4 см) на длине волн 10~4—10 см длительностью 10~9 —
10~7 сек (гигантские импульсы лазеров с модулированной доб-
добротностью) .
Плотность мощности в фокусе луча достигает 1012 вт/см2 и
более, что сравнимо с плотностями мощности энергии, выделяе-
выделяемой вблизи очага атомного взрыва. При воздействии импульсами
такой интенсивности на непрозрачное тело происходит мгновен-
мгновенная ударная ионизация и оплавление материала в месте удара;
образовавшаяся плотная плазма, пар и осколки материала раз-
разлетаются с большой скоростью (до 100 км/сек), а в месте удара
образуется кратер [216]. При уменьшении мощности импульса
роль термических эффектов возрастает.
Представляет интерес вопрос о размерах кратера. Согласно
упрощенной теории точечного взрыва в твердом теле (см. § 1
этой главы), объем кратера прямо пропорционален общей энер-
энергии импульса (количество движения светового импульса прене-
§8] ОПТИЧЕСКОЕ РАЗРУШЕНИЕ 515
брежимо мало). Более строгое решение этой задачи дополни-
дополнительно к модели разрушения § 2 требует учета ионизации, испа-
испарения и оплавления тела. В соответствии с этим к упругой зоне
и двум зонам разрушения (для хрупких тел) нужно добавить
зоны жидкого и газообразного состояния, а также зону ионизо-
ионизованной плазмы. Судя по описанию опытов в работе [216], в ре-
режиме свободной генерации размер кратера для многих материа-
материалов, по-видимому, можно оценить, учитывая в качестве первого
приближения лишь сублимацию (т> е. считая, что вся энергия
импульса расходуется на сублимацию объема кратера). При
увеличении длительности импульса и уменьшении энергии хи-
химической связи материала глубина кратера возрастает, и он в
результате прожигания превращается в туннель. Глубину тун-
туннеля также можно оценить, в простейшем случае учитывая лишь
сублимацию.
4. Воздействие света на прозрачные тела. При не слишком
высоких интенсивностях световой волны поглощение света, как
и других электромагнитных волн, в прозрачных диэлектриках
очень мало; оно объясняется гистерезисными потерями в течение
цикла поляризации. Термодинамическая природа такого погло-
поглощения аналогична природе поглощения акустических волн в
(почти) упругом теле. Когда напряженность поля в световой
волне становится сравнимой с напряженностью внутреннего
поля в данном теле (а в некоторых случаях и еще раньше), всту-
вступают в игру разнообразные .микрофизические процессы, которые
в зависимости от конкретных условий могут играть различную
роль*). Дадим весьма краткое описание некоторых возникаю-
возникающих при этом нелинейных процессов с феноменологической точки
зрения.
а) В большинстве материалов диэлектрическая постоянная
(и коэффициент преломления) увеличивается с возрастанием на-
напряженности электрического поля. В результате в интенсивном
световом поле возникает самофокусировка луча, если его мощ-
мощность превышает некоторую критическую величину; луч создает
себе диэлектрический волновод и распространяется в нем, не ис-
испытывая дифракции. Диаметр волновода составляет несколько
длин волн; в некоторых случаях он на два порядка меньше, чем
диаметр фокуса в приближении линейной оптики [220]. Благодаря
самофокусировке концентрация энергии в луче возрастает во
много раз.
В математическом плане возникающие оптические проблемы
совершенно аналогичны динамическим проблемам нелинейной
теории упругости в случае продольного сдвига.
*) Многообразные явления нелинейной оптики и результаты их теорети-
теоретического изучения излагаются в книгах [*»-"»].
17*
516 НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ [ГЛ. VIII
Фактически при достаточно высоких интенсивностях поля у
вектора поляризации появляется необратимая составляющая, и
поэтому вместе с нелинейностью необходимо учитывать также
необратимость. Теорию необратимых явлений нелинейной оп-
оптики наиболее естественно строить на основе принципа макси-
максимума скорости возрастания энтропии аналогично общей теории
пластичности. Напомним,, что существует термодинамическая
аналогия этих различных физических явлений, причем вектору
поляризации в оптике соответствует в теории пластичности век-
вектор деформации (для продольного сдвига), а вектору электриче-
электрической напряженности в оптике соответствует вектор'напряжения
(для продольного сдвига).
Учет необратимых составляющих вектора поляризации, за-
зависящих от времени и частоты, приводит к теории, совершенно
аналогичной теории вязкоу пру гости. Соответствующие состав-
составляющие диссипации (поглощения) энергии отвечают линейному
(тело Кельвина) и нелинейному поглощению.
б) .Предыдущий (чисто оптический) подход не учитывает
взаимодействия света с веществом (точнее, учитывает это взаи-
взаимодействие посредством эмпирических зависимостей коэффи-
коэффициента преломления от напряженности поля, посредством эмпи-
эмпирического коэффициента затухания и т. п.). Более строгий, но и
более громоздкий подход заключается в явном учете этого вза-
взаимодействия; он состоит в совместном исследовании уравнений
деформирования твёрдого тела (на основе теории пластичности
и вязкоупругости) и уравнений Максвелла, связанных друг с
другом (в уравнения движения вводится объемная сила, завися-
зависящая от напряженности поля, а диэлектрическая постоянная счи-
считается зависящей от деформаций). В рамках такого- подхода,
очевидно, можно получить большинство эффектов, наблюдае-
наблюдаемых на опыте р21]: генерацию звуковых волн, модуляцию свето-
светового сигнала, вынужденное рассеяние и т. д. При приближении
к резонансу мощность звуковых и вторичных электромагнитных
волн нарастает, т. е. поглощение первичного электромагнитного
излучения увеличивается (вследствие нелинейности уравнений
положение резонанса существенно зависит от интенсивности
этого излучения). Критическое состояние неустойчивости рас-
рассматриваемой оптико-механической системы в точке резонанса
соответствует разрушению; поэтому определение этой точки и
соответствующей плотности мощности дает одновременно пре-
предельную оценку момента разрушения.'
Отметим, что такой подход к отысканию критических условий
разрушения аналогичен подходу, применяемому для оценки опас-
опасности разрушения упругой конструкции при приближении к
условиям-резонанса, когда значительная часть работы внешних
сил перекачивается в кинетическую энергию; в положении ре-
§ 8] . ОПТИЧЕСКОЕ РАЗРУШЕНИЕ 617
зонанса апмлитуда внешней силы, требуемая для разрушения,
минимальна.
Этот механизм разрушения реализуется в хрупких диэлек-
диэлектриках для импульсов света высокой интенсивности и малой
длительности A(И— 10~9 сек).
в) В обоих рассмотренных выше подходах нужно принять
во внимание также уравнение энергии (уравнение теплопровод-
теплопроводности), так как от температуры зависят все эмпирические кон-
константы (диэлектрическая постоянная, коэффициент преломле-
преломления, упругие и прочностные константы и т. д.). Относительная
роль тепловых эффектов возрастает с увеличением длительно-
длительности импульса. В режиме свободной генерации для большинства
материалов они имеют основное значение.
Соответствующий механизм разрушения заключается в том,
что поглощение энергии луча вызывает образование очага газо-
газообразной плазмы, находящейся под большим давлением и про-
производящей разрушение. Этот механизм как основная причина оп-
оптического разрушения был предложен впервые Брюэром и Рик-
хофом р2], а затем подтвержден экспериментально для многих
материалов (см., например, [223-225]). Он совершенно аналогичен
механизму разрушения при атомном взрыве, и поэтому для ко-
количественного расчета области разрушения и акустических волн
в хрупких материалах можно применить общую теорию дей-
действия взрыва (§§ 1 и 2 этой главы).
Общая картина разрушения хрупких тел представляется сле-
следующей [224> 226]. Если луч сфокусирован на передней поверхно-
поверхности образца, то с увеличением плотности мощности разрушение
(кратер глубиной порядка 10~4 см) появляется впервые на пе-
передней поверхности (самофокусировка и самоканализация луча
происходят еще раньше); в дальнейшем с увеличением плотно-
плотности мощности появляется кратер порядка 10~3 — 10~2 см на вы-
выходной поверхности образца. Затем следы разрушения появ-
появляются внутри образца (их порог разрушения выше, чем у
первичного поверхностного разрушения). Вдоль волновода, обра-
зованногр лучом, образуется нитевидная каверна, на которую
нанизана система пузырьков* и дискообразных трещин. При даль-
дальнейшем увеличении энергии импульса толщина нити слегка воз-
возрастает, а число и размер дисков растут значительно быстрее.
В некоторых случаях нитевидных следов разрушения не об-
образуется, а разрушение возникает только в области фокуса.
Для практики весьма важно знать пороювые значения плот-
плотности мощности (оптическую прочность), при которой впервые
возникает разрушение. Превышение этого значения приводит к
нарушению расчетного режима работы некоторых оптических
устройств. В табл. 8.1 приведены значения порога разрушения
для некоторых материалов, взятые из книги [219]. Эта таблица
518
НЕКОТОРЫЕ ПРОБЛЕМЫ ХРУПКОГО РАЗРУШЕНИЯ
[ГЛ. VIII
демонстрирует также влияние на прочность длины импульса и
диаметра фокуса. Влияние диаметра фокуса (и диаметра
волновода) на прочность представляет собой масштабный эф-
эффект, связанный с различной вероятностью встретить неоднород-
неоднородность или дефект, которые играют весьма существенную роль
в поглощении энергии.
Таблица 8.1
Оптическая прочность некоторых материалов
Оптическая
прочность,
sr/см2
2-Ю9
2 • 108-5 • 109
109
10"
101г
2-Ю9—2-Ю10
Dч-7)-10"
Материал
кристаллы NaCl
оптические стекла
алмаз
алмаз, карбид крем-
кремния
алмаз
силикатные стекла
кронглас и кварце-
кварцевые стекла
Длина
импульса,
сек
7-Ю-9
з-ю-8
3-Ю"8
ш-3
4 • 10~8
7-Ю"8
7-Ю-8
Диаметр фокуса,
см
5-Ю-3
0,01
0,1
5 • Ю-3
8-Ю-4
диаметр фокуса
варьировался
—
По мощности лазерного луча W и его диаметру D нетрудно-*
определить напряженность электрического поля Е в однородном
световом поле, так как
W =±
(с = 3 • Ю1Осм/сек). (8.163)
Здесь п — коэффициент преломления. Эту формулу и данные
табл. 8.1 можно использовать также для оценки напряженности
роля в момент разрушения, .
приложение t
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
Вопросы прочности конструкций и сооружений представляют
собой одно из важнейших (но отнюдь не единственное) прило-
приложений механики разрушения. Расчет на прочность, предлагае-
предлагаемый механикой хрупкого разрушения, включает в себя следую-
следующие основные моменты:
а) выбор формы, размера и местоположения наиболее опас-
опасного трещиноподобного дефекта;
б) определение коэффициентов интенсивности напряжений
на фронте трещины с учетом внутренних напряжений металлур-
металлургического, технологического или эксплуатационного происхо-
происхождения;
б) выбор критерия локального разрушения на фронте тре*
щины, изучение докритического развития трещины и отыскание
критического (предельного) состояния, которое соответствует
выходу конструкции на нерасчетный режим (например, разру-
разрушению).
Первый из этих вопросов решается на основе натурных и ла-
лабораторных наблюдений и во многом пока зависит от интуиции
инженера. Быстро развивающаяся техника неразрушающего
контроля сулит большие надежды, однако состояние этого во-
вопроса нужно признать еще весьма далеким от желаемого. В то
же время накопленный к настоящему времени эксперименталь-
экспериментальный и теоретический материал убеждает в том, что без реше-
решения указанного вопроса нельзя надеяться и на решение практи-
практической проблемы прочности. Казалось бы, методы статистиче-
статистических теорий хрупкой прочности позволяют обойти эту трудность,
так как они приводят к зависимостям типа ств ~ Vn (V — объ-
объем тела, (тв — среднее значение временного сопротивления, и —
эмпирический коэффициент), в которые не входит размер де-
дефекта, являющегося причиной разрушения. Коэффициент п из-
изменяется от 6 для идеально хрупких материалов типа стекол до
50—100 для пластичных металлов. Однако оказывается, что в
процессе эксплуатации пластичных металлов, например, при
циклическом нагружении, коэффициент п может меняться от
100 до 6, а в случае весьма хрупких материалов случайный раз-
разброс аи так велик, что делает невозможным расчет конкретной
конструкции с позиций теорий прочности. Механика хрупкого
520 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ [it t
разрушения объясняет эти факты тем, что при расчете не был
учтен скрытый параметр — размер трещины. Поэтому коэффи-
коэффициент п на самом деле зависит от размера наиболее опасной
трещины. Более детальное рассмотрение этих вопросов чита-
читатель может найти в статьях рэт-229].
Второй вопрос решается на основе методов классической тео-
теории упругости. Ниже приводятся некоторые основные резуль-
результаты вычислений коэффициентов интенсивности напряжений для
различных тел с заданными разрезами — трещинами. За под-
подробностями вычислений читатель отсылается к цитируемой ли-
литературе. В рамках линейной теории упругости этот вопрос раз-
разработан в настоящее время наиболее полно. В этом случае при-
приведенные результаты вычислений имеют физический смысл
только тогда, когда выполняется условие тонкой структуры, что
и предполагается в дальнейшем.
На последнем этапе расчета на прочность вычисленное зна-
значение наибольшего коэффициента интенсивности напряжений
Кг (как определенной функции нагрузок, размеров тела и дли-
длины начальной трещины) приравнивается некоторому критиче-
.скому значению этого коэффициента, характеризующему сопро-
сопротивление материала отрыву на фронте трещины нормального
разрыва. Получается критериальная зависимость, связывающая
допускаемые величины внешних нагрузок, длин трещин, внут-
внутренних напряжений, температурных градиентов и т. д. В случае
устойчивого развития хрупких трещин эта зависимость служит
для определения длины трещины.
Практически наиболее важную роль играют следующие кри-
критические коэффициенты интенсивности напряжений:
а) вязкость разрушения Ки (при монотонном нагружениидо
начала локально нестабильного разрушения в условиях стеснен-
стесненной плоской деформации),
б) величина Кс (при монотонном нагружении пластин со
сквозными трещинами),
в) величина Ky (при циклическом нагружении),
г) величина Късс (в условиях длительного нагружения по-
постоянной нагрузкой в коррозионно-активной среде).
Величина Кс изменяется в пределах (l-r-3)Kic- Величина
/Су представляет собой практический предел усталости; соглас-
согласно имеющимся данным I72- 230], она равна примерно @,1 -f-
-f-0,05)/Cic- Пороговый коэффициент интенсивности напряжений
Kiacc существенно зависит от внешней среды; согласно опытным
данным (см. табл. 7.1) он может меняться в пределах @,1-^-1)
от вязкости разрушения. Значения Кс и Kic для некоторых ма-
материалов приведены в Приложении II.
Если коэффициент интенсивности напряжений Ki меньше
(или соответственно Кисе), то трещина не растет. На самом
§ 1] ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ 521
деле это заключение,'вообще говоря, справедливо только для
некоторой фиксированной базы испытания, играющей роль га-
гарантийного срока (в приведенных выше цифрах менее 108 —
109 циклов для Ky и менее года для Късс)- Это нужно иметь
в виду при оценке промежутка времени между профилактиче-
профилактическими осмотрами конструкции (в особенности для усталостных
трещин Р2]).
Указанный метод расчета хрупкой прочности по критическим
коэффициентам интенсивности напряжений нельзя считать впол-
вполне удовлетворительным, так как он не учитывает медленного до-
критического развития усталостных и коррозионных трещин.
Однако ясно, что этот фактор идет в запас прочности, поэтому
в ряде случаев бывает достаточно получаемых оценок.
Приведем основные результаты вычислений коэффициентов
интенсивности напряжений. Подчеркнем, что для линейно упру-
упругих тел при определении Кг, Kn и Km можно применять прин-
принцип суперпозиции.
§ 1. Плоские статические задачи
В задачах о плоской деформации и плоском напряженном
состоянии коэффициенты интенсивности напряжений опреде-
определяются по асимптотике комплексного потенциала Ф(г) в конце
разреза (см. формулы C.43)). Для этой цели может служить
также любая из формул C.44) и C.45), дающих асимптотику
упругого поля вблизи края разреза.
Разрезы вдоль одной и той же прямой или вдоль одной и
той же окружности я бесконечной упругой плоскости. Если со-
совокупность математических разрезов расположена вдоль одной
и той же прямой или вдоль одной и той же окружности и дру-
других границ упругое тело не имеет, то в квадратурах могут быть
решены следующие краевые задачи:
а) на разрезах произвольно задана касательная и нор-
нормальная нагрузка (Д. И. Шерман [231], Н. И. Мусхелишвили
[232,23]).
б) на разрезах заданы произвольные смещения (Н. И. Мус-
Мусхелишвили [232> 23]) ;
в) на одном берегу разрезов задаются смещения, а на дру-
другом берегу — нагрузки (Д. И. Шерман f233], H. И. Мусхелишвили
р32,«3]);
г) участки с произвольно заданными смещениями или на-
нагрузками чередуются любым образом вдоль нижнего и верхнего
берегов разрезов (Г. П. Черепанов р34-235]);
д) берега разрезов взаимодействуют, причем касательное на-
напряжение взаимодействия произвольным образом зависит от
нормального давления (Г. П. Черепанов [101]);
522
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
[П. i
е) касательное напряжение на разрезах обращается в нуль,
участки с произвольно заданным нормальным смещением (глад-
(гладкие штампы) или с нормальной нагрузкой расположены произ-
произвольно на берегах разрезов; эта задача легко приводится к
проблеме Римана — Гильберта для соответствующей совокуп-
совокупности разрезов (Г. П. Черепанов [23в]).
В последнем случае, если трещины расположены вдоль од-
одной и той же прямой, яв'ляющейся линией симметрии краевой
задачи, на штампах можно
учесть также кулоново трение;
при этом задача сводится к
проблеме Римана — Гильберта
для полуплоскости [46> 47].
Для указанных типов задач
можно найти коэффициенты
интенсивности напряжений; не-
=»?- которые случаи • рассмотрены
ниже. -
Если ,в упругой плоскости
имеется один прямолинейный
разрез, свободный от нагрузок,
а в некоторой точке (х0, Уо)
действуют сосредоточенная си-
сила (Р, Q) и сосредоточенный момент М (рис. Ш), то на правом
конце щели коэффициенты интенсивности напряжений будут сле-
следующими [237]:
'//////////////////77.
Уо
Рис. Ш.
I (Р - iQ) (г0 - г0) + U {\+к)М
(ПЛ)
где г0 == х0 + iy0, zo~xo — iy0; корень Ух2 — I2 положителен
при х > I, а х — постоянная плоской теории упругости (см.
етр. 59).
Это выражение можно использовать в качестве функции
Грина для отыскания коэффициентов интенсивности напряже-
напряжений в случае одной изолированной трещины при любом распре-
распределении объемных и поверхностных нагрузок (включая распре-
распределенные моментные нагрузки).
В частности, если сосредоточенные сила и момент приложе-
приложены к верхнему берегу щели, т. е. za = х + Ю, имеем следующие
§1]
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ .
523
формулы:
АI =
Д'п ——
2(%+\)Vnl 2
(x-l)Q , Я (/ + *„) '
/ - х0
(П.2)
Если сосредоточенные сила и момент приложены симметрич-
симметрично к верхнему и нижнему берегам щели (рис. П2), то при по-
помощи формул (П.2) получаем
Кг = -7=4== [Q (I
Д'п = ¦
При соблюдении тех же условий симметрии, что и на рис. П2,
для произвольных распределенных нагрузок на щели при
L
N P
С f )
к////////////
1
к I >
X
Рис. П2.
Рис. ПЗ.
помощи формул (П.З) и принципа суперпозиции находим
j, (l-x)Vt2-x* j'
+1
(П. 4)
/я/ _J
Здесь m (ж) — плотность распределенной на щели моментной
нагрузки
m{x) = dM/dx. (П. 5)
Когда постоянные нагрузки приложены на некотором участ-
участке верхнего берега щели (рис. ПЗ), при помощи формул (П.2)
624 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ \П. t
можно найти f237]
_ о (с — 6) х — 1
I Т (С ~ 6) К — 1
2 )/"пГ х + 1
V/77////////7,
/777/.
W
/77777/7/77777,
Рис. П4.
Рис. Пб.
В случае, изображенном на рис. П4, имеем
-farcsin-), /С„ = 0.
(П.7)
В частности, при а = 0 (трещина Гриффитса) получим
/Ci = ffVnT. Л"п = 0. (П.8)
Для примера, показанного на
рис. П5, можно найти
на правом конце
у//////////////7/л
U- и А
на левом конце (П.9)
/Сн-=0.
Рис. П6.
При косом растяжении пластины с прямолинейной щелью
(рис. П6) имеем
^ JT (П. 10)
§1]
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
S25
Для бесконечного ряда щелей (размеры и нагрузки указаны
на рис. П7) в наиболее опасных точках коэффициент интенсив-
интенсивности равен Р37]
2a/Fsir,-g-
т/cos^-
У 26
nc
/, . nl I . nl , . nc
ftsm_^sm_+sm_
В частности, когда с = l, интенсивность напряжений на обоих
концах щелей одинакова:
Т/ b sin
ПС
~Ь
(П. 12)
Для случая поперечного сдвига (рис. П8) получается сле-
следующий результат:
tg-g- , /Ci = 0. (П.13)
Вообще, при любом числе разрезов, расположенных вдоль
одной и той -же прямой в упругой плоскости, математические
, I
. I ..
2b
V//.
в
v////7\
-4
Рис. П7.
задачи, соответствующие нормальному разрыву и поперечному
сдвигу, тождественны (см. § 6 гл. III). Поэтому коэффи-
коэффициенты /Си получаются из величин К\ простой подстановкой
526
Коэффициенты интенсивности напряжений
[П. I
соответствующих касательных нагрузок вместо нагрузок, перпен-
перпендикулярных к линии трещин, и наоборот (при этом моментные
нагрузки исключаются из рассмотрения).
и
21
Y/////////
.<,—.
26
с 2l XI
Г/////////Л
V//////////1
Рис. П8.
Имея в виду это обстоятельство, в указанных случаях будем
приводить только значения К\.
\ f Р
p
r ".. • I
/////////////Л
1
< b
. I
i
////
p
¦I I \t
Рис. П9.
В случае двух одинаковых трещин (рис. П9) имеются сле-
следующие результаты f237' 238]:
у ближних концов трещин
n b2E (k) — 12K (k)
i к (k) Уь2 - /2
|/я&(&2-/2) [К &2_L2
bV(b2
aJ
J (t + /)^D«-<»)(/«-,
(П.14)
1] ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
у дальних концов трещин
527
I
2P
L2-/2
dt
Ь У(Ь2 - L2) (L2 - Р)
K{k)
X
1
- /2) (t2 -12) J
(L + о У (b2
Здесь K{k) и E(k) — полные эллиптические интегралы I и II
рода соответственно.
Рис. П10.
Рис. ПИ.
Для щели, располагающейся вдоль дуги окружности
(рис. П10), коэффициенты интенсивности напряжений в наибо-
наиболее опасной точке О имеют вид [237> б2]
• „ a V~nR sin а
2(l+sin2-|)
Mcos-f
sin2f
— cosBp + ¦«- a) (cos2 -^ — sin4-^-) — sinasin2-~sinBp + — a) 1,
(П.15)
,5
2 I 1 + sin2 ¦
+ sin Bp + v а I (cos2 4 ~ sin "TI — sin а si "T cos BP + T aI •
В случае перешейка между двумя полубесконечными ще-
щелями (рис. ПИ) имеют место следующие формулы [237- 239J:
528
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. I
у левого конца перешейка
Р Yc2 - a2
Л1 =
2/ла(с.-а) Y™
2У"па(с-а)
у правого конца перешейка
(П.16)
Kv
(с + а)
Q Ye2 - a2
+ ¦
+ ¦
I ОО
При расклинивании тонким абсолютно жестким клином бес-
бесконечной упругой плоскости (рис. П12) справедливы такие со-
соотношения [120>2S4]:
= . /Си-О
*1==7Г+*)
(трение на границе клина с упругим телом отсутствует),
(П.17)
/Си == О (П. 18)
(трение на границе клина с упругим
телом очень велико; практически
Рис. П12. коэффициент трения должен быть
больше 0,5); ц — модуль сдвига.
Эти формулы отвечают плоской деформации. Для плоского
напряженного состояния после обычной замены я вместо (П.17)
получается простое выражение Ki = ]f2Eh{nl)~m.
2а
| |
Р
Рис. П13.
Для периодической системы трещин под действием сосредо-
сосредоточенных сил (рис. П13) имеем [238]
-G-х) &ch&A+2^2)]
ЛЩ A "f" Л ) J /1-1 1 q\
—¦ — —- - — ¦-¦ ". A1.1У1
г{\ + Л2) sin (я///,)
„,.
§ 11
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
529
где
, = shF/m), 6 = na/BL), m = sin[nl/BL)].
21
-Z
Некоторые другие аналогичные примеры рассмотрены л ра-
работе Р40].
Если температура упругого тела зависит от координат, то в
нем возникают термические напряжения. Поле этих напряжений
находится из обычных уравне-
уравнений теории упругости с объем-
объемной силой, определяемой после
решения чисто температурной
задачи [106]. Поэтому распре-
распределение напряжений и дефор-
деформаций вблизи фронта хрупкой
трещины в неизотермическом
случае дается общими форму-
формулами C.44) —C.46).
Пусть пластина с одной-
прямолинейной сквозной тре-
трещиной подвергается воздей-
воздействию однородного теплового
потока с постоянным темпера-
температурным градиентом VT, напра-
направленным под углом р к трещине (рис. П14). Предполагается, что
по нормали к плоскости пластины температура не имеет гра-
градиента; кроме того, считается, что Щель не-
непроницаема для теплового потока. Тог-
Тогда [2371
чт
Рис. П 14.
к- — 1
лн — т
sin p,
Km = 0, (П.20)
где а — коэффициент температурного рас-
расширения.
Пусть изолированная щель является рас-
распределенным источником тепла, а вектор
теплового потока лежит в плоскости пла-
Рис. П15.
стины и на щели перпендикулярен к ее поверхности (рис. П15).
В этом случае [237]
— aEq V1
/Сн-О.
(П.21)
Здесь Я, — коэффициент теплопроводности, q — количество теп-
тепла, выделяющееся на поверхности щели за единицу времени и
приходящееся на единицу площади (величина q считается по-
постоянной вдоль щели).
630
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. I
Разрез в полуплоскости. Задача о растяжении упругой полу-
полуплоскости с краевой щелью (рис. П16) рассматривалась мно-
многими авторами. Ее решение получено многими способами — как
точными аналитическими, методами р41> ш], так и приближен-
приближенными р43' VA\ Приведем результат:
TS 1 inrf л/*тг? w к i\ (^~\ 99^
Коэффициент 1,12 вычислен с погрешностью 1%. Как видно,
влияние свободной границы тела приводит к увеличению коэф-
коэффициента интенсивности напряжений на 12%.
//////,/////1
. 1
\ \ \i
Рис. П 16.
////////////
ч
1
////.
Л
S
6
s///////////\
ъ
1
Роо
Poo
Рис. П 17.
Рис. П 18.
Используя это решение и результаты Бюккнера [245], можно
найти также коэффициент К\ в задаче, изображенной на
рис. П17:
Ki = 0,68сг |^7, Ки = Km = 0. ' (П.23)
(Коэффициент 0,68 вычислен с ошибкой 3%-)
В случае полубесконечного разреза, приближающегося к сво-
свободному краю полуплоскости (рис. П18), коэффициент интен-
интенсивности напряжений равен Р37]
f— 4Я— 12 Ра
Я2 - 8 VI
4я - 8 М
я2 —8
(П.24)
Щель в полосе. Задачу о растяжении бесконечной полосы с
центральным разрезом (рис. П19) рассматривали Исида [24в] и
Феддерсен р47], причем первый дал численное решение с погреш-
погрешностью до 1%, а второй указал весьма простую аппроксимирую-
§1]
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
631
Таблица П1
Значения функций F (t/b) и ^sec lnt/Bb)]
Hb
F (ЦЬ)
¦л/ ™l
V S6C2F
0
1
1
0,1
1.006
1,006
0,2
1,025
1,026
0,3
1,058
1,059
0,4
1,109
1,112
0,5
1,187
1,189
0,6
1,303
1,304
0,7
1,488
1,484
0,8
1.811
1.799
0,9
2,470
2.528
щую формулу. Приведем их результаты (см. также сравнитель-
сравнительную табл. Ш):
Ki = a VnJF(Ub) (Исида),
/Ci = or /л/ sec[n//B6)] (Феддерсен), (П.25)
Приведем также численные результаты, полученные недавно
[248] для прямоугольной пластины конечной длины 2L (см.
табл. П2 и рис. П19). .
\\\
< 2Ь >
гь
ти
Рис. П 19.
II
Рис. П20.
Для случая растяжения прямоугольной пластины с двумя
одинаковыми боковыми разрезами (рис. П20) было найдено
Г249, 2371
/Ci^ffjAfttg-g-tif-i, у), tfn = 0. (П.26)
632
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ [П. t
Таблица П2
Значения функции F(l/b) [МЦ
Ы1
1/6 = 1
ЦЬ = Ч
1/6 = 3
10,0
1,01
1.01
1,01
5,0
1,06
1,03
1,03
2,5
1,22
1,11
1,11
2,0
1.33
1.19
1.19
1,5
-1,60
1,42
1,41
1,35
1,78
1,60
1,59
1,25
2,00
1.82
1,81
1,20
2,1ft
2,00
1,99
1,175
2,27
2,12
2,11
1,150
2.41
2,27
2,26
1,125
2,60
2,46
2,42
1,10
2,87
2,72
2,72
Значения функции ц в некоторых точках приводятся в сле-
следующей таблице:
Значения функции tj I— -r-
Таблица ПЗ
ць
1/6=1
L/b = 3
L/b-+oo
0
1
1
1
0,1
1,13
1,12
1,12
0.2
1,13
1,11
1,12
0,3
1,14
1,09
1.13
0.4
1,16
1,06
1.14
0,5
1,14
1.02
1.15
0.6
1,10
1,01
1,22
0.7
1,02
1,00
1,34
0,8
1.01
1,00
1,57
0.9
1,00
1,00
2,09
Последняя строка в этой таблице, вычисленная с погрешно-
погрешностью 1 %, относится к растяжению бесконечной полосы. Для этого
случая Ирвин указал простую аппроксимирующую формулу [237]
(П.26а)
которая с погрешностью 1% совпадает с численными резуль-
результатами.
Для растяжения полосы с одним боковым разрезом
(рис. П.21) имеет место такая зависимость [237]:
tf« = 0. (П.27)
Значения функции t(l/b) приводятся в следующей таблице:
Таблица П4
1/Ь
I (Hb)
0
1.12
0.1
1.14
Значения
0.2
1.19
0.3
1.29
функции |
0.4
1,37
0.5
1.50
(ЦЬ)
0,6
1,66
0,7
1,87
0,8
2,12
0.9
2.44
1.00
2,82
Ill
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
533
В работе [87] была указана простая зависимость
лГ1 1.П+5 (//26)* т9Яч
1\1 = оул1 1 — //B6) ' \ll.4o)
которая с ошибкой 1 % аппроксимирует приведенные численные
результаты.
6
Рис. П21. Рис. П22.
Для изгиба полосы с одним боковым разрезом (рис. П22)
имеются численные расчеты [245>237]:
Кх = 6М B6 - /)/2 ? [//B6)], ffn = О (П.29)
(значения функции ? l/Bb)] приведены в табл. П5).
Таблица Пб
Значения функции ? [//B6)]
//Bft)
0,05
0,36
0,1
0,49
0,2
0,60
0,3
0,66
0,4
0,69
0,5
0,72
0,8
0,73
1,0
0,73
Эти численные результаты аппроксимируются (с наибольшей
ошибкой менее 4%) следующей зависимостью [35- 87]:
4.2М BЬГ312 /"A - -4-) - A —if .
(П.ЗО)
где
1,15 — 60 [ДО)]2 при 0 <//B6) < 0,05,
1 при 0,05 < //B6) < 1.
834
КОЭФФИЦИЕНТЫ ИНТЕНСИВЙОСТИ НАПРЯЖЕНИЙ
Щ. I
Для случая изгиба полосы с продольной щелью (рис. П23)
имеет место следующая формула:
(/ > К). (П.31)
Задача о растяжении полосы с продольной симметрично
1
1
II
II
\
1
21
\\
II
t
1
Рис. П23.
Рис. П24.
расположенной щелью конечной длины (рис. П 24) была изу-
6 чена Б. И. Сметаниным [250]. Он получил
к к к k к формулу
(П.32)
O777
\
\
\
\
\
\
\
\
\
\
\
\
\
6
t
6
21
\
\
\
\
\
777) г
\
± '
1
Функция -ф (///г) зависит от граничных
условий на боковых поверхностях полосы.
Было рассмотрено три варианта*): 1) кон-
контакт с абсолютно жесткими гладкими пли-
плитами (это условие выполняется также в за-
задаче о периодической системе параллель-
параллельных разрезов одинаковой длины, рис. П25),
2) условия жесткого сцепления (смещения
обращаются в нуль), 3) границы свободны
от нагрузок.
Приведем результаты вычислений функ-
функции г|э(^/Л) для этих граничных условий, основанные на ра-
работе [250] (см. табл. П6).
Рис. П.25.
*) Следует отметить, что первый и третий варианты были несколько
раньше рассмотрены в работах [2М>25г] (см. также книгу Снеддона и Ловен-
груба Р3]).
«11
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
535
Таблица П6
W
Гладкий кон-
контакт
Сцепление
Границы сво-
свободны от наг-
нагрузок
0,05
0.997
0,996
1,003
Значенш
0,10
0,998
0,983
1,011
0,15
0,973
0,963
1,025
¦ функции 1|)
0,20
0,955
0,937
1,045
0,25
0,933
0,906
1,069
Wh)
0,30
0,911
0,873
1,098
0,35
0,893
0,838
1,131
0,40
0,884
0,801
1,169
0,45
0,892
0,762
1,209
0,50
0,930
0,712
1,253
При 1/2<//Л<оо для задачи рис. П24 в работах [250,254,255]
были получены такие зависимости:
1-й вариант (см. рис. П25)
(П.ЗЗ)
(П.34)
(см. также [237]),
2-й вариант (жесткое сцепление)
„ __ 2ayr2(%-\)h
3-й вариант (границы свободны от нагрузок)
I = а УШ @,1267 + 0.6733Д,-1 + 0,5Я~2 + С),
(П.35)
С=@,0104 - 0,1267Л - 0,5034*,"*) @,6733 + Х~1) ' (А, = hit).
Ошибка в формулах (П.32) — (П.35) значительно меньше 1%.
Разрезы, исходящие из круглого отверстия. В работе [256]
было изучено влияние щели на концентрацию напряжений в
точке О круглого отверстия (рис. П26). Приведем результаты
вычислений напряжения со в точке О:
Таблица П7
Значения напряжения а0
d/(d + t)
«То/а
0,05
10,44
0,1
7,64
0.15
6,34
0,3
4,74
0,4
4,20
0,5
3,83
При d/l —*¦ 0 имеет место следующая формула [256]:
сто/а = 3 + 2,115
(П.36)
536
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
[П. I
Отсюда легко вывести асимптотическое соотношение для
максимального напряжения в очень малой круглой выточке в
коние трещины
.o0=l,69KilVd (<*-</). (П.37)
Эта зависимость справедлива для тел и разрезов любой формы,
если круглый вырез достаточно мал по сравнению с характер-
характерным линейным размером тела и разреза. Круглые выточки ино-
иногда применяют на практике, чтобы снять бесконечную концен-
концентрацию напряжений в конце острой трещины и остановить или
задержать ее развитие. Если напряжение сто в точке О считать
(—
к
\ 1
j
* '¦ ¦¦¦ у
—¦—_
• >
1
t f
г
2г
\
J
¦' ' ' ¦«
)
Рис. П26.
Рис. П27.
равным некоторой постоянной характеристике материала в мо-
момент разрушения (например, временному сопротивлению ав),
то формула (П.37) позволяет определить критическое значение
коэффициента интенсивности напряжений Ки в рассматривае-
рассматриваемом конце трещины с выточкой:
Ки = 0,59crB Yd. (П.38)
При /Ci < /Ci# разрушения не происходит, при К\ = Ки начи-
начинается разрушение (по меньшей мере, локальное). Величина К\
определяется из решения соответствующей упругой задачи для
тела с разрезом без выточки.
Задача о всестороннем и одностороннем растяжении плоско-
плоскости с одной и двумя щелями, исходящими из кругового отвер-
отверстия (рис. П27), была рассмотрена в работе [257]. Имеем
(П.39)
Результаты расчета функции F(t/r) приведены в табли-
таблице Ш.
Ill
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
53?
Таблица П8
Иг
0.
0,1
0,2
0,3
0,4
0,5
0,6
0,8
1,0
1.5
2,0
3,0
5,0
10,0
оо
Для
одноосное
растяжение
3,36
2,73
2,30
2,04
1,86
1,73
1,64
1,47
1,37
1,18
1,06
0,94
0,81
0,75
0,707
Значения функции
одной щели
всестороннее
растяжение
2,24
1,98
Г,82
1,67
1,58
1,49
1,42
1,32
1,22
Г.06
1,01
0,93
0,81
0,75
0,707
F (Иг)
Для двух
одноосное
растяжение
3,36
2,73.
2,41
2,15
1,96
1,83
1,71
1,58
1,45
1,29
1,21
1,14
1,07
1,03
1,00
щелей
всестороннее
растяжение
2,24
1,98
1,83
1,70
1,61
1,57
1,52
1,43
1,38
1,26
1,20
1,13
1,06
1,03
1,00
Задача о всестороннем растяжении плоскости со звездооб-
звездообразной щелью (рис. П28) была изучена в работе [258] (см. также
книгу I253]). Приведем окончательный результат:
Д-, = ? (я) а |/я7. (П.40)
Зависимость функции Ъ(п) от числа разрезов п дается
табл. П9 (п предполагается четным).
Таблица П9
Значения функции \ (п)
п
1(п)
2
1
4
0,894
6
0,778
8
0,705
При п ^ 10 справедлива формула
(П.41)
Как видно, влияние соседних разрезов в данном случае сво-
сводится к взаимному ослаблению интенсивности напряжений в
концах щелей.
538
Коэффициенты интенсивности напряжений
[П. I
Раздавливание круглого диска с внутренней щелью двумя
сосредоточенными силами (рис. П29) было рассмотрено в ра-
работе р59]. Было найдено
Кх = (Р/ У^Ю VW [ 1 + C/2) (IIRf + C/4) {URf + C/64) {URf].
(П.42)
Тела сложной формы. В работах В. В. Панасюка, А. А. Ка-
Каминского, Л. Т. Бережницкого и других авторов были изучены
многие случаи различных криволинейных отверстий со щелями.
Частичное изложение этих
работ имеется в монографии
В. В. Панасюка [18]; подроб-
подробную библиографию можно
Рис. П29.
найти в обзорной статье Г. Н. Савина и В. В. Панасюка [260].
Приведем только некоторые простейшие результаты.
В случае всестороннего растяжения упругой плоскости с ги-
поциклоидальным отверстием, контур которого описывается ура-
уравнениями
х —
-3Mcose + -cos«eV
rt + 1 \ ' П )
{a>0, 0<9<2я), (П.43)
где п — целое положительное число, коэффициенты интенсивно-
интенсивности напряжений равны [18]
2а У пап
АГп==О.
(П.44)
Гипоциклоида имеет п'-\- I точку возврата, каждая из кото-
которых с точки зрения концентрации напряжений эквивалентна
концу трещины (на рас. ПЗО изображена астроида с я = 3).
Дефекты такого типа могут определять прочность хрупких по-
§ 1]
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
539
ристых материалов типа графита или чугуна, если нет более
крупных трещин.
При одноосном растяжении пластины с отверстием в фор-
форме астроиды (см. рис. ПЗО) в направлении оси симметрии, про-
проходящей через пару точек возврата, имеем [18]
l -стУ%ш/8. (П.45)
Здесь Kimto соответствует двум точкам возврата, лежащим на
оси растяжения, a /Cimax — остальным точкам возврата.
Рис. ПЗО.
Рис. П31.
В случае одноосного растяжения пластины с круговым от-
отверстием и двумя равными щелями в направлении, перпендику-
перпендикулярном линии щелей (см. рис. П27), А. А. Каминский нашел
простую приближенную формулу [260]
Кг — or У я (г + 0 {1 — [г/(г -f О]4}' (П. 16)
В концах одного изолированного разреза с налегающими
берегами, находящегося в однородном поле сжимающих нагру-
нагрузок (рис. П31), коэффициенты интенсивности напряжений будут
следующими [1°1]:
#1 = 0. (П.47)
Здесь был принят следующий закон взаимодействия берегов
разреза;
•*#* — — Ь-\-роу (сг„<0, а<я/2), (П.48)
540
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. I
где k и р — постоянные сухого (кулонова) трения. Метод ра-
работы [1Ш] позволяет вывести аналогичные выражения для любой
нелинейной зависимости хху = хху {ау) и для любого числа ще-
щелей вдоль одной и той же прямой.
В работе [2613 рассмотрена плоская задача теории упругости
для тела, границами которого являются любое число отрезков
оси х и прямые, перпенди-
перпендикулярные к оси х (рис.
П32). На границах, па-
параллельных оси у, зада-
задаются нормальное смеще-
смещение и касательная нагруз-
нагрузка или тангенциальное
смещение и нормальная
нагрузка, а на участках
границы вдоль оси х ста-
ставится любая комбинация
s " из трех основных краевых
задач теории упругости или контактная задача. Этот случай
можно привести к краевой задаче для двух аналитических функ-
функций Ф(г) и Q(z), в которую не входят производные.
Этот вывод основан на следующих формулах, которые мож-
можно получить из общих представлений C.9):
Рис. П32.
¦?-• (п-49)
*У
дхХу
-4ЦУ-3-Г , (П.50)
Q(z) = z<D'(z) + iF(z).
При у = 0 xxy=lmQ(z), a,
Поэтому конформное отображение позволяет существенно
упростить рассматриваемую область, не усложняя краевой за-
задачи (в отличие от общего случая).
6 частности, если касательное напряжение всюду на границе
тела обращается в нуль и, кроме того, задано нормальное сме-
смещение на границах, параллельных оси у, краевая задача рас-
расщепляется, так что для функции Q (г) получается задача Ди-
Дирихле. После отыскания Q(z) для функции Ф(г) получается
смешанная краевая задача, эффективное решение которой
всегда можно найти при помощи формул Келдыша — Седова,
S 1]
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
541
если известно конформное отображение на полуплоскость (в
случае односвязного тела). Этот последний частный случай
представляет собой расширение класса решений, найденных ра-
ранее Вестергардом [262]. Метод Вестергарда годится лишь для
такого тела, граница которого расположена,только вдоль оси х,
причем касательное напряжение
должно обращаться в нуль на всей
границе.
Приведем результаты решения
некоторых простейших задач о ще>
лях указанного типа.
Для полосы со щелью под дей-
действием сосредоточенной силы (рис.
ПЗЗ) имеем [i6i]
Ki
Р cos [nl/{2h)]
У
Р
Р
_ 21
2h
X
Vhsin(nl/h) •• ч
Эта задача позволяет оценить влия-
влияние подкреплений границ полосы на Рис. ПЗЗ.
развитие внутренней трещины.
Пусть на отрезке х = 0, \у\<.а упругой плоскости имеется
клиновая дислокация, которая возникла вследствие того, что
вначале вдоль этого отрезка был сделан разрез, затем с обоих
берегов разреза убрали некоторое коли-
количество материала, так что в ненапряжен- У,
ном пространстве образовалась тонкая
полость толщины 2ы:
(П.52)
а затем противоположные берега этой по-
полости склеили. Такой клиновой дислока-
дислокацией иногда можно схематизировать по-
поле остаточных напряжений, возникаю-
возникающих, например, в окрестности сварного
шва, при ковке и в других технологиче-
технологических процессах обработки металлов. По-
Постоянная а может быть легко оценена по Рис П34.
коэффициенту температурного расшире-
расширения сварного металла и по ширине шва. Предположим, что
сварной шов прошел по центру трещины (рис. П34). Тогда в
конце трещины от остаточных напряжений возникнут разрываю-
разрывающие напряжения такой интенсивности [261]:
2а {а2-
0
-у
2)
при
при
\У\
\У
К
|>
а,
а,
(П.53)
542
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
[П. I
Еще опаснее внутренние напряжения, если сварной шов про-
проходит параллельно плоскости трещины вблизи ее вершины. Не-
Нетрудно решить эту задачу для произвольного расположения
клиновой дислокации и трещины.
Отметим, что одной из наиболее существенных трудностей
технологического освоения высокопрочных металлов (в первую
очередь высокоуглеродистых сталей) является развитие трещин
«¦-'
2h „
и
21
Рис. П35.
x
21
Рис. П36.
при сварке, приводящее иногда к разрушению уже в процессе
сваривания.
Для конфигурации, изображенной на рис. П35, коэффи-
коэффициенты интенсивности равны |50]
2 yh V
B -
2 A-6*)
где | и т) — действительные корни следующих уравнений:
|f B - л2) = 1/л2^ГТ+ B - т]2) arcsin |
(П.54)
(Ц.Б5)
При l/h-*оо получается простая формула (ср. D.25))
(П.56)
Для сдвига периодической системы параллельных разрезов
(рис. П36) было найдено [ш]
_ | яхЧ [1 + лЧ2/№2)] при hit > 0,5,
Кп I Зт2/2/» A + 0.570Л// + 0.082Л2//2) при h/l < 0,5, . (Ut57'
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
543
Эти формулы при t/h « 0,5 дают наибольшую ошибку ме-
менее 1%. ' . . '
Кусочно-однородные тела*). Общая упругая задача для про-
произвольного числа разрезов вдоль одной и той же прямой или
1
tt
21
V-
t "-^
11 Vt
Рис. П37.
вдоль одной и той же окружности, разделяющих различные
упругие среды, была решена в работе р63] в квадратурах. При
этом были рассмотрены
следующие краевые за-
задачи:
а) на разрезах заданы
произвольные смещения;
б) на разрезах произ-
произвольно задаются каса-
касательная и нормальная на-
нагрузки;
в) на одном берегу
разрезов заданы смеще-
смещения, а на другом берегу —
нагрузки.
Впоследствии различные частные случаи из этого класса за-
задач были рассмотрены независимо Грилицким, Райсом, Си,
- Эрдоганом и другими авторами.
Для случая, изображенного на рис. П37, имеем
Al—Оу у nl, Лц = Хху уЯ1. \И.ио)
Для сосредоточенной силы, действующей в произволь-
произвольной точке z = 2о (рис. П38), были получены следующие
Рис П38.
*) Здесь приняты такие же обозначения, как в § 8 гл. III.
544
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
m.
формулы Р64]:
Ki — iKn = —
[?)(/, го)
Здесь
(П.59)
2я
В частности, если сила (Р, Q) приложена в середине верх-
верхнего берега разреза, эти формулы дают
[Р A + к,) е~лР —
-2^ — 1)],
(П.60)
Используя выражения (П.59) в качестве функции Грина, в
^рассматриваемом случае можно найти коэффициенты интенсив-
интенсивности напряжений для произвольно
jl распределенных поверхностных и
Mcof f-V-K» объемных сил.
Если перешеек, соединяющий
два различных упругих простран-
пространства (рис. П39), подвергается
Iй!' Vl
ZL
Рис. П39.
Рис. П40.
воздействию сосредоточенной силы и момента, приложенных на
бесконечности, то коэффициенты интенсивности напряжений
оказываются равными
К — Рос 2^сс
Al K55 iVi'
If , " со
Kll~W
S П
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
545
В случае одного изолированного симметрично нагруженного
разреза (рис. П40), когда
= fay — i*xy)z-x-to ~ Р (х),
(П.61)
а напряжения на бесконечности обращаются в нуль, коэффи-
коэффициенты интенсивности напряжений будут следующими:
dx. (П.62)
1 ^
Для конфигурации, изображенной на рис. П41, в точках
х = ±а имеем
Kl + iKu ^
(П.б3)
В случае периодической системы разрезов (рис. П42) на-
находим
-g-. (П.64)
Следует напомнить, что понятие коэффициента интенсивно-
интенсивности напряжений вблизи края трещины на границе различных
9к
-b
-а
+а
+6
21
гь
21
21
гь
Рис. П41.
Рис. П42.
упругих сред имеет физический смысл только при выполнении
условий C.118); эти условия накладывают ограничение на ха-
характерный размер тонкой структуры. При выводе формул для
коэффициентов интенсивности напряжений указанные условия,
обычно не принимавшиеся во внимание, были учтены.
В рассматриваемых задачах некоторое своеобразие пред-
представляет задание условий на бесконечности (рис. П37). Вслед-
Вследствие условий сцепления на границе сред напряжения
18 Г, П. Черепанов
Й46 Коэффициенты интенсивности напряжений rn. i
в бесконечно удаленной точке нельзя задавать производьно, они
должны удовлетворять следующему соотношению:
+ 1)а~2]. (П.65)
Напряжения о~ и х™у в обоих полупространствах равны
в силу уравнений равновесия, а напряжение а™, вообще го-
говоря, может быть различным в верхнем и нижнем полупро-
полупространствах, т. е. поле напряжений на бесконечности кусочно-
однородно. Величина т^ не входит в условие (П.65) и может
быть задана произвольно (некоторое ограничение она наклады-
накладывает только на значения вращении верхнего и нижнего полупро-
полупространств, что несущественно для поля напряжений). Если на
бесконечности задается еще условие однородности а?} = о^> то
величина а?>, согласно (П.65), вполне определяется значением о~.
Анизотропные однородные, тела*). В самом общем случае
плоской задачи анизотропной теории упругости в квадратурах
можно решать следующие типы задач-для тел с разрезами:
а) любое число разрезов расположено вдоль одной и той же
прямой в неограниченной упругой плоскости, на разрезах про-
произвольно заданы или нагрузки, или смещения;
б) любое число разрезов расположено вдоль одной и той же
прямой, касательные напряжения всюду на разрезах обра-
обращаются в нуль, на берегах разрезов чередуются участки с за-
заданным нормальным смещением (гладкие штампы) и с задан-
заданной нагрузкой.
Действительно, обратимся к общему представлению решения
плоской задачи через три аналитические функции (формулы
C.99) и C.100)). В случае а) для трех линейных комбинаций
этих функций (в,силу того, что при у = 0 Zi—Z2 = z3) полу-
получаются стандартные задачи Дирихле для внешности указанных
разрезов [46-47]. После решения задач Дирихле сами функции
легко находятся из получающейся системы трех линейных ал-
алгебраических уравнений.
В случае б) два условия обращения в нуль касательных на-
напряжений дают возможность совершенно аналогично случаю а)
определить две линейные комбинации из трех неизвестных ком-
комплексных потенциалов. Используя найденные комбинации, все
потенциалы можно выразить чере.з какой-то один потенциал,
выбираемый из соображений удобства. Оставшиеся граничные
условия позволяют составить для этого потенциала смешанную
краевую задачу для внешности разрезов, разрешимую в квад-
квадратурах [236].
•) Здесь всюду используются обозначения § 7 гл. III.
ПЛОСКИЕ СТАТИЧЕСКИЕ ЗАДАЧИ
547
Конкретные расчёты проводились в основном для того слу-
случая, когда упругие свойства материала симметричны относи-
относительно любой плоскости ху, перпендикулярной к оси г, а внеш-
внешние нагрузки и граничная поверхность не зависят от г. При
этом краевая задача расщепляется на плоскую деформацию и
сложный сдвиг, так что можно пользоваться основными соот-
соотношениями C.102) и C.105). В этом
р случае оказывается справедливым
< i >
Рис. П43.
Рис. П44.
следующий вывод [265>237]: если внешние касательные и нормаль-
нормальные нагрузки, приложенные к берегам разрезов вдоль од-
одной и той же прямой, симметричны относительно линии ще-
щелей*), то коэффициенты интенсивности напряжений Къ Ки и
Km, определяемые асимптотикой C.111), будут в точности
совпадать с соответствующими ко-
коэффициентами Кь Ки и Km для
изотропного тела.
Приведем результаты решения
'некоторых других примеров.
В случае, изображенном на
рис. П43, имеем [266]
_ Р Г,/"аТ7 1 а„1
Здесь
(П.66)
< а >
оо
а
Р~,
-
а0 — /р0. Д2 «¦ — ао — 'Ро.1
Рис. П45.
где ць Дь цг, Дг —корни уравнения C.103) при а13 = а2з = 0.
Тем самым предполагается, что рассматриваемое тело орто-
тропно. Это решение можно использовать в качестве функции
Грина для определения коэффициентов интенсивности напря-
напряжений при произвольном распределении нормальной нагрузки
вдоль берегов щели.
*) Т. е. выполняется соотношение (П. 61).
18*
848 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ [П. I
В задаче о расклинивании ортотропного тела жестким глад-
гладким клином постоянной толщины (рис. П44) получается сле-
следующая формула Р65]:
2M ii==Q б7)
«22 lt»l + [*2 I Г 2я/
(направление трещины совпадает с линией упругой симметрии).
Для конфигурации рис. П45 находим
^^ „ Д^. (П.68)
па а у па у па
§ 2. Пространственные задачи
При решении трехмерных задач теории упругости обычно
применяют представления Буссинеска — Папковича — Нейбера
через четыре гармонические функции {32'40].
Пусть граница тела расположена вдоль плоскости г =а 0, т. е.
тело представляет собой пространство с плоскими щелями вдоль
одной плоскости или полупространство. Если на границе заданы
произвольные нормальные и касательные нагрузки, то эту об-
общую задачу теории упругости можно свести к суперпозиции
трех отдельных задач Дирихле для гармонических функций,
применяя специальные представления через одну функцию.
Приведем эти удобные представления Р7]:
а317,
вувг2 ' ~Ър~Х дхдг2 '
дхду +Z дхдудг'
s 21 ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ 549
2)
3)
OV d*U* -\.~ ^з Ог _z д*Ц3
2ц дудг ^ л дх2ду ' 2ц •*—¦••
а* . д2и, д3ия
24
Задача Дирихле для пространства с разрезами вдоль пло-
плоскости г = 0 допускает, точное решение в тех случаях, когда
фронт разреза в этой плоскости представляет собой а) окруж-
окружность, б) две концентрические окружности, в) одну или две
параллельные прямые, г) два луча, исходящие из одной
точки.
В случае, если фронт плоского разреза представляет собой
эллипс х2/а? + У2/Ь2 = 1 в плоскости z = 0 и на разрезе при
z = ±0 задано граничное условие dy/dz = ±2шт(х, у) (где
ф(х, у, г) — функция, гармоническая вне разреза, а а(х, у) — не-
некоторая заданная функция), имеет место весьма сильное, но
полузабытое предложение, которое носит название теоремы
Дайсона [268-269]. Приведем ее без доказательства.
650 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЯ [П. I
Теорема Дайсона. Если
а (х, у) = A - х*1сР - yWf~m f (х, У) (А > 0), (П.72)
где f(x,y) — любая функция, которая может быть представлена
в виде сходящегося ряда по положительным целым степеням х
и у, то упомянутая выше функция q>(*, у, z) равна
ЯГ (Я) Г A/2)
Здеоь
00
J fu (а» + и) (^
Ь'у
у2
хг у2
Л (и) == 1 — а2 + в - 62 + в - —
D
1)...(* + «, B.
е представляет собой положительный корень уравнения R (в) =0,
Г (Я)—гамма-функция. Для точек на разрезе, где z = 0 и
х2/а2 + у2/Ь2 ^ 1, е равно нулю. Теорема остается справедливой
при % — 0; в этом случае ЯГ(Я) нужно положить равным еди-
единице.
Если f(x,y) представляет собой полином степени п по х
и у, то бесконечный ряд под интегралом обрывается. Если,
кроме того, А, — целое положительное число, тогда на разрезе
(где е = 0) функция ф будет представлять собой полином сте-
степени 2Л -(- п по х и у. Отсюда следует, что, если ф на разрезе
представляет собой полином степени п по х и у, то а будет,
очевидно, функцией вида
a^(l-x2la2-y2l^-ll2f(x, у),
где f — полином степени п по х и у.
Последние предложения были установлены независимо, но
позже Л. А. Галиным {270], Кассиром и Си [2П].
Этими случаями, по существу, исчерпываются возможности
замкнутого решения указанных пространственных задач теории
упругости. Во всех остальных случаях приходится прибегать
к приближенному решению.
Приведем окончательные результаты вычисления коэффи-
коэффициентов интенсивности напряжений в пространственных за-
задачах,
«21
Пространственные задачи
5S1
Дискообразная щель (рис. П46). В общем осесимметричном
случае дискообразного разреза вдоль 2 = 0, х2 + у2 < а2 в без-
безграничном пространстве имеем [237]
а
X 2_ Г roz(r)dr
V Q V
а
к- 2 f r*rz (r) dr -n _..
*и=7^7^тГ' ( }
а
„ _ 2 Г rrze(r)dr
~ 'Vna' J iAa2_r2 '
Здесь предполагается, что нагрузки
симметрично приложены к верхнему
и нижнему берегам щели, а на беско-
бесконечности напряжения исчезают.
Допустим, что к противоположным
берегам того же дискообразного раз- -^
реза приложена произвольная нор-
нормальная нагрузка az(x, у) симме-
симметрично относительно плоскости 2 = 0, Рис. П46.
а касательная нагрузка равна нулю
(на бесконечности напряжения по-прежнему считаются исчезаю-
исчезающими). При помощи давно известных результатов теории потен-
потенциала [40] эта задача легко решается. Когда в некоторой точке
х = |, у = ц дискообразного разреза приложены разрывающие
сосредоточенные силы Р, т. е. az(x, у, 0) = — РЬ{х —1)8(у — ц)
на обоих берегах разреза, коэффициент интенсивности напряже-
напряжений К\ на контуре щели определяется из функции Зоммерфель-
да и оказывается равным (рис. П46)
л/na (acos6 —
(П.75)
Исцользуя его в качестве функции Грина, для произвольного
распределения az(x,у) находим
П
s*
(область S — круг |2 + tj2 ^ a2).
Недавнее решение этой же задачи в рядах [272] весьма гро-
громоздко и труднообозримо.
Для однородного растяжения бесконечного тела со сво-
свободной от нагрузок дискообразной щелью (рис. П47-)
652 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
коэффициенты интенсивности напряжений равны
= 0. (П.76)
В случае сдвига на бесконечности (рис. П48) имеем
Km — 2т У а/я • sin (© — 9).
Здесь 9 — полярный угол, и — угол, составляемый направле-
направлением сдвига с осью х.
(П.77)
' У
г.
{ />
V
1
X
Рис. П47.
Рис. П48.
мв\
/ 1
/ У
///
/
Рис. П49.
При листом изгибе стержня с дискообразной щелью
(рис. П49) коэффициенты интенсивности напряжений будут
следующими:
1 [I — Bа/ЗЬ)cos 9], /Си == Km = 0. (П.78)
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
553
Здесь. &у—соответствующий момент инерции поперечного сече-
сечения стержня, Ь — расстояние центра щели от нейтральной линии.
Формулы (П.76) — (П.79) справедливы в том случае, когда
радиус щели мал по сравнению с расстоянием щели от боко-
боковой поверхности стержня. Практи-
Практически достаточно, чтобы это рас-
расстояние было больше За.
При скручивании круглого ци-
цилиндрического стержня с дискооб-
дискообразной щелью (рис. П50) имеем
Здесь предполагается, что центр ще-
щели лежит на оси стержня, а плоскость
щели перпендикулярна этой оси.
Рис П50.
Рис. П51.
Пусть бесконечное упругое пространство имеет разрез вдоль
z = О, х2 -\- у2^. а2, свободный от нагрузок; на бесконечности
приложены изгибающие моменты Мх, MY, Mz и сила с состав-
составляющими X, У, Z (рис. П51). В этом случае коэффициенты ин-
интенсивности напряжений равны [31]
Z 3 ¦ (М х sinQ —My cos Q), '
(П.80)
/Си = ¦ ' (X cos 9 - Y sin 9),
2a у па
(X sin 9 — Y cos 9).
4а2 У~па
Для тела той же конфигурации, осесимметрично нагружен-
нагруженного сосредоточенной силой (рис. П52), имеем [33]
„ _ РУНЕ
Кп = Km = О»
(П.81)
554
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЯ
В случае тела с полубесконечным разрезом (рис. П53) вдоль
= 0, у <. 0, нагруженного сосредоточенной силой @, У, Z)
,8а .
Рис. П52.
Рис. П53.
в точке @, —а, 0), имеем следующий результат [33]:
^* iA^" /_9 _|_ Х2\ ' ^ лУ^зг (а2-\-х2) \ 2 va2 + xi
VX
(П.82)
nfn B - v) (а2 + х1J'
Если пространство с дискообразной щелью симметрично
растягивается сосредоточенными силами (рис. П54), то
Рис. П55.
коэффициент интенсивности напряжений равен [237]
«2]
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
555
Пусть бесконечное тело содержит дискообразную щель, пло-
плоскость которой перпендикулярна к градиенту температуры VT
вдали от щели (рис. П55). Если щель свободна от нагрузки, то
коэффициенты интенсивности напряжений будут следующими
Р87]:
Ki = EaaWVT/[3n A - v)], Кп = Km = О, (П.84)
где а — коэффициент температурного расширения. Щель счи-
считается непроницаемой для теплового по-
потока.
. Пусть изолированная дискообразная
щель z = 0, г < а является распределен-
распределенным источником тепла (рис. П56)
a-'Q(r/a) при 0 < г < a, z = 0,
0 при r> a, z = 0,
а температура в любой точке тела равна
grad Г
1
1
J
grad Г
2а
\
\ ¦
: >
Рис. П56.
где Т^ — стационарная температура тела вдали от щели.
Тогда [253]
Кг = - [A + v)/(l - v)] aT. У^ц J sQ (s)ds, (П.85)
о
(Кп = Km = 0).
В частности, если Q(r) = — Qo, имеем
iCi = (iy2)[(l + v)/(l-v)]areeQ0l/^|i, (Ku = Km = 0). (П.86)
Если на щели задана постоянная температура, т. е.
8 = — 0О при 0 < г < a, z = 0; dQ/dz = 0 при r>a, z = Q,
то
Q (р) = 2QQ/(n /Г^р5) при 0 < р < 1
и коэффициент интенсивности напряжений равен [253]
Ki = - 2 A + v) [я A - V)] аГ^Оо /я?ц {Кп = Km = 0). (П.87)
Эллиптическая щель. Пусть безграничное тело с разрезом
вдоль z = 0,. х2/а2 -(- y2/b2 ^ 1 подвергается однородному рас-
растяжению в направлении оси z напряжением а на бесконечности
(рис. П57). В этом случае {237]
(si°2 Р + $¦cos2 Р
556
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
ГП. I
Здесь E(k) — эллиптический интеграл II рода:
я/2
Е (k) = j 1/1 — /fe2sin29 йв
= 1 —
P— параметр эллипса, задаваемого уравнениями * =
у = b sin p.
Вместо точной формулы (П.88) можно пользоваться про-
простой приближенной формулой [*7] (обеспечивающей погрешность
не более 1 %)
— 0,366/а) (sin2 p + ^а cos2 P)I/4 (П.89^
На
шинах
основании этих формул максимум Ki имеет место в вер-
вермалой оси эллипса. Следовательно, локальное разруше-
разрушение вначале произойдет только в
этих точках контура щели, так
что трещина будет развиваться,
стремясь к круговой форме с диа-
диаметром, равным большой оси
начального эллипса 2а. Изучим
развитие хрупкой трещины, имев-
имевшей вначале эллиптическую фор-
форму, принимая упрощающее допу-
допущение о том, что трещина в про-
процессе своего развития сохраняет
форму эллипса. При помощи
формулы (П.89), используя кри-
критерий локального разрушения в
точке р = 0 и принятое допуще-
допущение, можно найти
— О,ШЫа) = Ки- <П.9О)
Это уравнение служит для оты-
отыскания параметра Ь, определяю-
Рис. П57. щего форму текущего эллипса.
На рис. П58 изображена зави-
зависимость безразмерной нагрузки a ValKic от безразмерного па-
параметра b/а, построенная по формуле (П.90). Как видно, если
для начальной трещины b/а < 0,80, то развитие трещины будет
всегда неустойчивым. Если же 0,80 < b/а < 1, то началу быст-
быстрого динамического развития всей трещины предшествует мед-
медленное стабильное подрастание хрупкой треЩины, в процессе
которого форма трещины стремится к круговой с диаметром 2а.
S2]
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
557
Дальнейшее развитие дискообразной трещины будет динамиче-
ским.
Указанное устойчивое подрастание хрупкой трещины в одно-
однородном поле напряжений является характерной особенностью
пространственных трещин.
Формулу 1
(П.91)
можно рекомендовать в качестве расчетной для определения
хрупкой прочности тела с начальной эллиптической трещиной
при 0,80^ b/a ^ 1, если наименьшее расстояние точек контура
наиболее опасного трещи-
0,950
0,910
0,870
>
—L
\
\
Ч
¦"¦>
новидного дефекта от
свободной поверхности
тела или от соседнего
дефекта не менее За.
0,5 0,6 0,7
0,9 1,0 Ь[а
Рис. П58.
Рис. П59.
Пусть бесконечное тело с плоским эллиптическим разрезом
подвергается сдвигу на бесконечности напряжениями
= — qcosm,
Согласно принципу суперпозиции, эти напряжения можно сне-
снести на щель z = 0, х2/а2 -{-у2/Ь2^. 1 (рис. П59) при вычислении
коэффициентов интенсивности напряжений. Имеем {271]
Кп = ~
(П.92)
sin p - ЬС cos P)
558
Здесь
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. 1
cos e>
"~ (k2~v)E(k)+vk'K{k) '
р ab2kzq sin ш
(k2 + vb2a-2) E (k) — \b2a~2K (k) '
k2=\ — bPja2, k' = b/a, b< a,
K(k) и E(k) — полные эллиптические интегралы первого и вто-
второго рода соответственно; уравнения эллипса здесь и в даль-
дальнейшем берутся в виде х = a cos р, у = b sin p.
Пусть призматический стержень со щелью подвергается чи-
чистому изгибу моментами Мх и Му (рис. П60). Будем считать,
Рис. П60.
что плоская щель эллиптической формы в плане расположена
' в поперечном сечении стержня, причем центр эллипса нахо-
находится в центре тяжести поперечного сечения. Оси х и у выбраны
совпадающими с большой и малой осью эллипса соответствен-
соответственно. В этом случае A04]
Ь2
¦CDS'1
Af и
(b/aJK{k) + {
b Vnb sin P
+
Зх B~b2/a2)E(k)-(b/aJK(k)
¦], (П.93)
Здесь K(k) и E(k) определены выше, Эх и 2fy — моменты инер-
инерции поперечного сечения стержня относительно осей х и у. При
выводе формул (П.93) предполагалось, что щель расположена
достаточно далеко от боковой поверхности стержня.
Случай, когда центр эллипса не лежит в центре тяжести се-
сечения, получается суперпозицией формул (П.88) и (П.93).
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
559
Рассмотрим бесконечное тело с разрезом вдоль г = О,
х2/а? + г/2/62 ^ 1 (внешняя эллиптическая щель). На бесконеч-
бесконечности приложены сила (X, Y, Z) и момент (Мх, Му, 0)
Рис. П61. . Рис. П62.
(рис. П61). В этом случае можно найти [273-32]
Кг = -
(a2 sin2 Р + б2 cos2 p)~1/4 +
±=jX Vb/(na) cosР(а2sin2p + ^cos2P)'4 +
+ jY \ГфЩsinр(а2cos2р + б2sin2p)
-3/4
(П.94)
Km = y X Va/W) sin P (a2 sin2 р + б2 cos2 P)/4 +
+ \ Y Vbj№) cos р (а2 cos2 р + й» sin2 P)/4.
Ограниченные тела с разрезом. Пусть круглый цилиндриче-
цилиндрический стержень с внешним круговым и соосным разрезом
(рис. П.62) подвергается растяжению. В этом случае имеется
560
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
[П. I
приближенное решение [237] (с относительной погрешностью
около 3%).
Ki = a VnDF (d/D) (П.95)
(см. табл. П10).
Таблица П10
Значения функции F (d/D)
d/D.
F(d/D)
0
0
0,1
0,111
0,2
0,155
0,3
0,185
0,4
0,212
0,5
0,240
0,6
0,255
0,707
0,259
0,8
0,251
0,9
0,210
0,95
0,162
0,97
0,130
1
0
В случае растяжения круглого стержня с внутренним диско-
дискообразным разрезом (рис. П63) имеем [253]
ttf
= 2а Vajn F Ba/D)
(П.96)
"itt
(см. табл. П11).
Таблица П11
Значения функции F Ba/D)
2a/D
F Ba/D)
0,2
1,005
0,3
1,013
0,5
1,072
0,7
1,259
0,8
1,479
0,9
2,002
В приведенных случаях предполагалось, что
боковая поверхность цилиндрического стержня
Рис. П63 свободна от нагрузок. Предположим теперь, что
стержень находится в жесткой гладкой матрице,
т. е. при г = D, иг = 0, тГ2 = 0. При этом для конфигурации
рис. П63 будем иметь [253]
Ki — 2а У~ф, F [ОЦ2а)] (П.97)
(см. табл. П12).
Таблица П12
Значения функции F [D/Ba)J
D/Ba)
F \D/Ba)}
1,05
2,40
1,10
1,88
1,20
1,42
1,30
1,27
1,667
1,095
2,5
1,023
5,0
1,003
S 21
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
561
Пусть дискообразная щель расположена симметрично в по-
полосе (рис. П64). К берегам щели приложена нормальная на-
нагрузка интенсивности о. В этом случае имеет место следующая
формула t250]:
Ki = 2а Vahii.1 + cok~3 + Э.б^/Г5 -f c^~6)
(K = h/a, 2<Я<оо). (П<98)
Погрешность формулы (П.98) не превышает 1%. Коэффици-
Коэффициенты с0 и С! в зависимости от граничных условий на гранях
слоя имеют следующие значения:
1) грани слоя свободны от на- -
грузок
с0 = 0,906, с, = —0,179;
2) на гранях слоя все смещения
равны нулю
со = — 0,824, с, = 0,115 (v = 0,3);
ш
ТУТ
т \'\
т
3) слой зажат между двумя
гладкими жесткими основаниями,,
силы трения между основаниями и
слоем отсутствуют (эти условия от- Рис- П64-
вечают также периодической си-
системе дискообразных разрезов вдоль z = 2nh, x2 + у2 < а2, где
п — целое число)
с0 = — 0,512, С! = 0,0585.
Если k = h/a^.2 (см. рис. П64), имеют место следующие
формулы (с погрешностью не более 1%):
1) грани слоя свободны от нагрузок Р54]
^ = а УЖ @,1267 + 0,6733 • /Г1 + 0,5 • /Г2 + С),
С = @,0104 —х0,1267Л,-1 -0,5034/Г2) @,6733 + /Г1)"' (П"99)
(ср. с формулой (П.35));
2) смещения равны нулю на границах слоя [255]
(СР. с (П.34,,;
(П.100)
3) нормальное смещение и касательные напряжения на гра-
гранях слоя равны нулю
(ср. с (П.ЗЗ)).
(П. 101)
662
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. I
Формулы (П.99) — (П. 101) на основании «принципа микро-
микроскопа» годятся также для плоских разрезов произвольной фор-
формы в плане, если они расположены посредине между гранями
слоя (с соответствующими граничными условиями на гранях)
и характерный линейный размер разрезов в плане велик по
сравнению с толщиной слоя. Соотношения, в которых нормаль-
нормальные смещения на гранях слоя считаются обращающимися в
нуль (и задается нормальная постоянная нагрузка на разрезе),
При помощи принципа суперпозиции легко пересчитать также
на тот случай, когда нагрузка
i б на разрезе обращается в нуль,
^^ТН^А ' а ноРмальное смещение вдоль
5L ' 1г\. каждой грани слоя постоянно.
Рис. П65.
В работе Смита, Эмери и Кобаяши [274] рассмотрены весьма
интересные для приложений случаи плоских полукруглых ще-
щелей, выходящих на свободную границу слоя перпендикулярно
к свободной поверхности (щель в плане имела форму окруж-
окружности с центром на границе тела).
В случае однородного растяжения слоя с полукруглой крае-
краевой щелью (рис. П65) имеем [87]
/Ci = 20 Vajh [1 + 0,2 B0/яJ] @ <ra/h < 0,2). (П. 102)
Для чистого изгиба того же слоя с полукруглой щелью
(рис. П66) коэффициенты интенсивности напряжений будут
следующими [87]:
Я, = 6,8М/Г3/2 \Гф [1-1,4а/А + BЭ/яJ @,2 + а/А)] (П. 103)
@<а/А<0,5).
пространственные задачи
563
Здесь момент М приходится на единицу ширины пластины (как
это обычно принято в плоских задачах).
Формулы (П.102) и (П. 103) представляют собой аппроксима-
аппроксимацию (с погрешностью примерно 3%) точного численного реше-
решения работы [274]. Эти формулы годятся, очевидно, также для слу-
случая полупространства с краевой трещиной, когда на бесконеч-
бесконечности действуют растягивающие напряже-
напряжения, являющиеся линейными функциями
расстояния от свободной границы тела.
Аналогично случаю эллиптической тре-
трещины в безграничном теле развитие полу-
полукруглой краевой трещины будет вначале
происходить с краёв, прилегающих к сво-
свободной границе, при этом рост трещины бу-
будет устойчивым до тех пор, пока интенсив-
интенсивность напряжений не станет постоянной
вдоль всего контура трещины. Затем начнет-
начнется нестабильный динамический процесс раз-
разрушения. В процессе устойчивого развития
трещина принимает овальную форму, кото-
которую приближенно можно считать эллипти-
эллиптической. На основании экспериментальных
данных можно принять, что контур крае-
краевой трещины с равномерным распределе-
распределением коэффициента интенсивности напря-
напряжений примерно соответствует эллипсу с
•центром на свободной границе тела и с от- Рис- П67.
ношением осей, равным 3/2 (т. е. Ь/а=2/3).
В общем случае краевой полуэллиптической щели в полосе
(рис. П67) имеется [87] следующее приближенное выражение для
коэффициента интенсивности напряжений (с погрешностью ме-
менее 10%):
растяжение
(П. 104)
изгиб
к, -
а \ а
@<Ь(а< 1,
т ± т D - о,4+o,6j
@<b/a< I,
(П. 105)
564 ' КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ [П. 1
Здесь
f 1,15 — 60 (b/hf при - 0<b/h< 0,05,
Л==1 1 при 0,05<6/Л< 1.
Суперпозиция позволяет при помощи этих формул рассмот-
рассмотреть также совместное действие изгиба — растяжения.
Соотношения (П. 104) и (П. 105) позволяют изучить развитие
краевой пространственной трещины и найти оценки для разру-
разрушающих нагрузок. Если отношение полуосей контура начальной
щели (рис. П.67) находится в пределах 2/3 с<: Ь/а <<: 2, то не-
неустойчивому развитию трещины предшествует медленное ста-
стабильное подрастание трещины. Примем упрощающее допущение,
что в процессе стабильного развития трещина сохраняет эллип-
эллиптическую форму; это позволяет использовать формулы (П. 104)
и (П. 105) при анализе докритического роста трещины.
Возможны два случая.
а) Начальная трещина имеет такие размеры, что коэффи-
коэффициент при 02 положителен. Тогда трещина начинает развиваться
вдоль кромки, прилегающей к поверхности слоя, а глубина тре-
трещины b не изменяется (Ь/а уменьшается). Предельное состояние,
предшествующее переходу в динамический режим, достигается
в момент обращения в нуль коэффициента при 82.
б) Начальная трещина имеет такие размеры, что коэффи-
коэффициент при б2 отрицателен. Тогда трещина начинает развиваться
вглубь, а длина трещины на поверхности 2а не изменяется (Ь/а
возрастает). Вследствие такого изменения формы трещины про-
происходит перераспределение интенсивности напряжений вдоль ее
контура в сторону выравнивания. Предельное состояние будет
достигнуто в момент обращения в нуль коэффициента при 02,
если только b/h <<C 0,4.
В случае b/h ^, 0,4 динамическое распространение трещины
может перейти вновь на устойчивый режим, как только трещина
станет сквозной, вследствие увеличения вязкости разрушения
для сквозной трещины.
Приведем окончательные формулы, полученные на основании
(П. 104) и (П. 105), определяющие предельные нагрузкл для не-
несквозных трещин при наличии стабильного подрастания:
растяжение
а = @,68 ± 0,04) Kj Vb (b/h ^ 0,4), (П. 106)
изгиб
М = 0,12Дуг2//уТ (Ь/А^0,4), ЛП.107)
где
1±0,1 при 0 < &/Л < 0,1,
1,1 — 1,2Ь/й±0,1 при 0,1<&/Л<0,4,
$ 2] ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ 565
растяжение-изгиб при о = C-н 10) ат
1,4а УЬ A + b/2h) + 8,ЗМ Vbglh2 < Kic, (П. 108)
где
gz=\ 0,8 ±0,05 при 0,2<6/Лс<:014.
/ 1 — 6/Л±0,05 при 0 <b/h< 0,2,
'~10,8±0,С
Здесь ат — максимальное напряжение от изгибающего момента
(в пограничном волокне); знак равенства в (П. 108) соответ-
соответствует разрушающей комбинации нагрузок. Функции f и g ап-
аппроксимируют более сложные выражения, полученные из (П. 104)
и (П. 105).
В случае неустойчивого развития несквозной трещины с са-
самого начала следует использовать соотношения (П. 104) и
(П. 105).
Приведем еще взятые из работы р74] результаты вычисления
коэффициента интенсивности напряжений на контуре краевой
полукруглой щели г = 0, х2 -\- у2 ^ а2 в пластине 0 <С х <С h
(см. рис. П65), находящейся в неравномерном неустановив-
неустановившемся температурном поле. Были рассмотрены следующие
случаи.
а) Трещина находится у поверхности полупространства (т. е.
Л->оо); температура поверхности считается постоянной и рав-
равной Tw, начиная с момента времени t = 0. Внешние нагрузки от-
отсутствуют.
Имеем
Если к поверхности трещины приложена нагрузка
Р (г, в) = рй + Pit cos 6 + р2 erf [r cos в/B
то коэффициент интенсивности напряжений Ki можно вычислить
по следующей формуле:
Ki = Е \Гф A + V) • (р0г|>0 + ptf, + р2ф2). (П. 110)
б) Поверхность пластины с трещиной свободна от нагрузок.
При х = h (на противоположной от трещины стороне пластины)
температура равна нулю, а при х = 0 (на той стороне пластины,
где имеется трещина) температура постоянна и равна Тш,
566 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЯ
начиная с момента времени t = 0. Тогда
[П. I
2ft3 t
Максимум /Ci достигается в точке 6 = я/2 при ft*/a2 = 0,25,
если hja лежит в интервале от 2 до 4. Когда Л/а = 10, максимум
Ki имеет место при ktja2 = 0,50.
в) Поверхность пластины с трещиной свободна от нагрузок.
При х — h температура постоянна и равна Tw при t ^ 0, а при
•# = 0 температура равна нулю, т. е. нагревание происходит
с противоположной от трещины стороны пластины. Тогда
=n2aE^r- Tw( Ь[erf А - -^B + е-*2
2Л2 tioJ ' ¦¦\h2Vn 2ft3 щ
(величина Ki отрицательна).
Приведенные формулы справедливы для интервала времени
от 0 до Л2/Dft).
Поясним обозначения, принятые в формулах (П. 109) —
(П.П2):
erf х
СО
= -!=¦ Г е~° dt, ч\ ч=
уп J
k = Л/(рс)-
Здесь ^ — коэффициент температуропроводности, a — коэффи-
коэффициент линейного теплового расширения, Я — коэффициент тепло-
теплопроводности, р — плотность, с — удельная теплоемкость.
Таблица П13
Значения функций % (в), % F), \|>2 @, kt/a2)
2 в/я
ь
ь
ktla?=O
kt/a2 =0,25
Af/a2 = 0,50
0
1,02
0,72
1,02
0,68
0,54
0,2
1,03
0,68
!,02
0,66
0,52
0,4
1,04
0,60
1,03
0,60
0,46
0,6
1,08
0,48
1,08
0,52
0,38
0,8
1,13
0,34
1,114
0,40
0,30
1.0
1,20
0,19
1,24
0,22
0,16
ПРОСТРАНСТВЕННЫЕ ЗАДАЧИ
567
E,,vt
Функции i|)o(e), i|)i(e) и $2(Q,kt/a2) приводятся в табл. ШЗ,
построенной по графикам работы [274].
В. И. Моссаковский и М. Т. Рыбка
[275] решили осесимметричную задачу
о растяжении безграничного прост-
пространства, состоящего из двух различных
упругих полупространств г > О и
г < О и имеющего дискообразный
разрез на границе их раздела вдоль
г = 0, х2 + у2<а2 (рис. П68). Предпо-
Предполагалось, что на остальной границе
раздела справедливы условия сцепле-
сцепления, а направление растяжения пер-
перпендикулярно к плоскости раздела;
щель считалась свободной от внешних нагрузок. Приведем их
результаты.
Напряжения на продолжении щели равны
Рис. П68.
о, — -
A + v,) A - 2v2) - Е2 (I
о
v,) A - 2v,)]
X
0
-2v2) -
!13)
1 I
sin
2 -
1 . Jg, (I + v») C - 4v2)
2я m ?, A + v,) + E2 A + v,) C - 4v,)
Потенциальная энергия тела, вычисленная в предположении,
что на стенки щели действует постоянное давление р, а на бес-
бесконечности напряжения исчезают, оказывается равной [Эт5]
8,J5| +
v2) A
A + v2) A -2v2) -E,(l+ v,) A -2v,) *
(П.114)
668 коэффициенты интенсивности напряжений pi. i
Здесь
J(
(?=1,2),
912 = A - 2v,) A - 2v2) + 4 A - v,) A - v2).
Кэссир [276] нашел коэффициент интенсивности напряжений
/Ci для плоского разреза эллиптической формы в плане z = О,
х = a sin р, г/ = b cos p, находящегося в стационарном темпера-
температурном поле в безграничном теле:
щ- VT (a2 cos2 р+ft2 sin2
Здесь а — коэффициент линейного расширения, Т — температура
поверхности эллиптической щели (на бесконечности температура
принимается равной нулю).
§ 3. Сложный сдвиг
В случае сложного сдвига отличен от нуля только один из
трех комплексных потенциалов, f(z), общей плоской задачи (см.
формулы C.9)). Дри вычислении коэффициента интенсивности
напряжений Кха используются асимптотические соотношения
C.4.3) и C.46).
Сложный сдвиг представляет собой простейшее сложно-на-
сложно-напряженное состояние. Математически он совершенно аналогичен
плоской гидродинамике идеальной жидкости, причем несжимае-
несжимаемой жидкости соответствует линейно-упругое тело Гука, а сжи-
сжимаемой баротропной жидкости — нелинейно-упругое тело. Един-
Единственное отличное от нуля смещение w соответствует при этом
потенциалу скорости, а вектор напряжения т = xxz + ixyt соот-
соответствует вектору скорости. Вихри в идеальной жидкости мате-
математически идентичны винтовым дислокациям в упругом теле.
Поэтому при отыскании коэффициента Km во многих случаях
можно воспользоваться готовыми решениями плоской гидроди-
гидродинамики B77J.
Этот тип напряженного состояния, несмотря на сравнительно
малое практическое значение, представляет интерес вследствие
простоты математического аппарата и возможности эффектив-
эффективного исследования. Отметим, что сложный сдвиг реализуется в
некоторой окрестности любой точки скручиваемого стержня,
если характерный линейный: размер этой окрестности мал по
сравнению с характерным линейным размером поперечного се-
сечения стержня.
Пусть бесконечное тело находится в условиях сложного
сдвига и нагружено на бесконечности постоянным касательным
СЛОЖНЫЙ СДВИГ
569
напряжением too = т<х>е'е. В теле имеется вырез произвольной
формы, имеющий конечные размеры, поверхность которого сво-
свободна от нагрузки. Такая задача соответствует задаче о бесцир-
бесциркуляционном обтекании контура в плоской гидродинамике иде-
идеальной несжимаемой жидкости. Согласно известным решениям
Р77'278], имеем в этом случае
/(z)=*n-'T,e-'eg(z)+ Xoof{^ . (П.116)
Здесь g(z)—функция, осуществляющая конформное отображе-
отображение внешности контура в физической плоскости z на внешность
круга радиуса R, такая, что g'(oo) = 1.
Рассмотрим для примера случай, когда вырез представляет
собой окружность с одним или двумя одинаковыми разрезами
<1 »
О
б)
Рис. П69.
(рис. П69), перпендикулярными к вектору напряжений на бес-
бесконечности too = xxeiIt/2. Имеем, соответственно, для одной и
двух щелей р79]
Кщ = тте V2^F Я~1/2 B + ЯГ3/2 A + АГ3/2 [A + ЯL - 1],
/Cm == тгто УягA+Л)[1— A+Я)] (Я = //г).
В частности, при Я -> оо получаются асимптотические фор-
формулы
соответствующие изолированной щели длиной 21 и / в однород-
однородном поле напряжений. При К -> 0 получаем асимптотическую
формулу
совпадающую с формулой для краевой щели длины / в поле на-
напряжения 2тоо, соответствующего максимальной концентрации
напряжений вблизи кругового выреза.
670
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. I
Пусть на некоторой части —b ^ х ^ b поверхности изолиро-
изолированного прямолинейного разреза —/ ^ х ^ / задано постоянное
смещение w = ±Л (знаки плюс и минус отвечают верхнему и
нижнему берегам щели). Остальная часть поверхности разреза
свободна от напряжений. Эта задача для трещин нормального
разрыва соответствует задаче о расклинивании клином конечной
длины Р80]. Имеем *¦
(ft» е- l-.fi»//>).
(П.118)
Здесь E(k)—полный эллиптический интеграл второго рода.
В частности, при b -> оо получаем аналог решения для полубес-
полубесконечного клина.
В случае плоского напряженного состояния соответствую-
соответствующая формула для К\ получается из (П.118) заменой ц на Е.
21
*Л—*-
с
(
)
)
21 ,
Рис. П70.
В случае периодической системы разрезов, находящихся в
однородном поле напряжений (рис. П70), имеем следующие ре-
результаты [279]:
одинаковые разрезы вдоль одной и той же прямой
(П. 119)
одинаковые параллельные разрезы, имеющие общие перпен-
перпендикуляры в соответствующих точках,
Km = тю V2Lth[nl/BL)].
(П. 120)
Взаимодействие трещин существенно различно при различ-
различном их расположении. Наличие трещин вдоль одной и той же
линии уменьшает прочность тела, уменьшая критический раз-
размер трещин при данной нагрузке. Наличие параллельных тре-
13]
СЛОЖНЫЙ СДВИГ
571
|щин, наоборот, упрочняет тело, увеличивая критический размер
|рещин при данной нагрузке. В пределе при / -> оо для полу-
оесконечных параллельных разрезов имеем
/Сш = тм |/2Т. (П. 121)
Для любого числа разрезов вдоль оси х и произвольной на-
нагрузки, симметричной относительно этой оси, коэффициент Km
|ролучается из соответствующего выражения для Ki в случае
формального разрыва заменой внешних нагрузок <зу на щелях
Напряжением xyz (ср., например, (П.114) и (П.12) при Р = 0).
| Пусть прямолинейная трещина, выходящая на свободную
границу полуплоскости под углом а, поддерживается двумя
Противоположно направленными сосредоточенными силами Pi
и Pi, приложенными по разные стороны трещины в точке вы-
Рис. П71.
Рис. П72.
|6да трещины на свободную поверхность (рис. П71). Оказы-
Оказывается [2Г9], существует единственное значение угла а, равное
а = яУр1/A/Л + УР~я) (П.122)
й такое, что по направлению трещины напряжение tZ9 макси-
максимально. При этом значении угла а коэффициент интенсивности
Напряжений равен
Km =
(П.123)
Следовательно, когда отношение сил Р\ и Pi постоянно в про-
fcecce нагружения, развитие хрупкой трещины продольного сдви-
|а происходит по прямой под углом а к свободной поверхности,
Определяемым формулой (П. 122).
Для аналогичного случая трех сосредоточенных сил
{рис. П72) получены следующие зависимости йй
Km-
[ 2 )
(П.124)
572
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
[П. I
Для ломаного разреза, находящегося в однородном поле
сдвигающих напряжений (рис. П73), имеем [281]:
в точке О\
НЬ sin [у - Р - m (a + Зя/2)]
sin •
в точке О2
(П. 125)
„ т.»/да sin [у + Р —ш(а + Зя/2) ]
Alii = -
COS ¦
cos-
o-l
Здесь параметры аир выражаются через а и 6 по формулам
a = 4^os^±PI-m(c--a-^l+m
6 = 4i?(sin-^
sinP=msma. (П. 126)
В случае п одинаковых разрезов, исходящих из одной и той
/
(cos
(sm —2^)
sim
Рис. П73. .
же тачки под равными углами друг к другу, — «звездообразная
трещина» (рис. П74) — имеем [281]
/С,„ = (—1I+/ 2Cп-4)/2лТоо У^ф sin @ + 2я//л) (П. 127)
в конце /-го разреза (/ = 1, 2, 3 п).
СЛОЖНЫЙ СДВИГ
573
Для разреза вдоль дуги окружности,в однородном поле сдви-
сдвигающего напряжения (рис. П75) имеется следующий резуль-
результат [281]:
в точке О\
/Сш = -«¦„, V яг sin a sin(e — -i-a),
в точке О2
(П. 128)
Km = тте У яг sin a sin (в + \ а).
В случае трех разрезов вдоль оси х (рис. П76) в однородном
© ©
Рис. П76.
поле продольного сдвига коэффициенты интенсивности напряже-
напряжений равны [237]:
в точках х = ±а
Б74 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ 1П. I
в точках х = ± Ь
¦ 2 _ 2 1 . г _ г „ ,. ( т |/ло, A1. ЫУ;
в точках х=±с
-./"с2 —а2 Г, E(kI
Пусть круглый цилиндрический стержень с продольным ра-
радиальным разрезом (рис. П77) подвергается кручению моментом
Рис. П78.
М и изгибу поперечной силой Р. Коэффициенты интенсивности
напряжений при этом будут следующими [237]:
/С, = Кп = 0, Km = 0,%9Mr-W - F,95 + 6,47v) A + v) Pr-W.
(П. 130)
В случае скручивания профиля, изображенного на рис. П78,
имеем [237]
0
Здесь
а=1— l/r,
а-A-
9 3]
СЛОЖНЫЙ СДВИГ
678
В. М. Мирсалимов [ш] рассмотрел задачу о влиянии малого
отверстия эллиптической формы, высверливаемого в конце тре-
трещины продольного сдвига (рис. П79). Приведем его результаты
(взятые из его диссертационной работы):
/w—^
z+ Vz2-4mR2 -2/?
Vz + yz2 — 4m/?2
где уравнение эллипса записывается в виде
**/A + тJ + у2/A - тJ = R2 {z=*x + iy).
При 8 = 0, r~^(l -\- m) R
. *ш r+Vr2- 4mR2 + 2/?
(П.132)
Tr» = l
я у г2 - 4m/?2
в частности, при г =A + m)R
При 6 = л/2,
Y.9
+ ^2 - 4/п/?2
- m)R
г+Vr2+4mR2)
=
4/2
г2 + 4т/?2 У г + ]/г2 + 4т/?2
-2/?)
2 ylsiVr* + 4т/?2 /г +
в частности, при г={\ — т)R
4т/?2
На контуре круглого отверстия \z\ = R, т. е. при /и = 0
будет
тг6 = B/Cui/ 1/2я/?) cos (9/2);
в случае, когда эллипс вырож-
вырождается в отрезок длины 4R, пер-
перпендикулярный полубесконечному
разрезу (т. е. при т = —1), име-
имеем в конце дополнительного раз-
разреза _
Рис. П79.
Здесь заданный коэффициент Km
определяет поле на бесконечно-
бесконечности (при г >•/?).
Райе [283] решил задачу о продольном сдвиге плоскости с
изолированным разрезом из нелинейно-упругого материала
576
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ
[П. I
с произвольной зависимостью т — Y (рис. П80):
toy/Yo при y < Yo>
т (y) при y > Yo»
т =
Здесь то, Yo определяют начальную точку нелинейного поведе-
поведения, t(y)—функция упрочнения. Связь напряжений с деформа-
деформациями имеет вид
(yфу
циями имеет вид
Для случая полубесконечного разреза решение имеет вид:
в пластической области
y = R(y)sm2q> при y > Yo!
в упругой области ' (П. 133)
х = X(yo) + R(Y) cos2ф, y = R(y)sin2q при y < Yo-
Здесь
Таким образом, линии постоянных thy представляют собой
окружности радиуса R(y) с центрами, расположенными на рас-
расстоянии Х(у) от конца щели на ее
продолжении. Как и в случае иде- '
альной пластичности, поле в упру-
упругой области не зависит от поля
i
г
Рис. П 80.
в пластической области; оно совпадает с идеально-упругим
решением, сдвинутым на A'(yo) вправо (см. рис. П80). Задавае-
Задаваемый коэффициент /Cin характеризует поле на бесконечности?
S 41 ДИНАМИЧЕСКИЕ ЗАДАЧИ 5??
в конце щели поле напряжений и деформаций вполне опреде-
определяется асимптотическим поведением функции т(\) при у-> <х>,
В частном случае степенного упрочнения
при Y>Yo
получаются следующие результаты:
§ 4. Динамические задачи
Инерционные эффекты могут быть существенны при движе-
движении трещин с околозвуковыми скоростями и при действии крат-
кратковременных или высокочастотных нагрузок. Ниже используются
обозначения § II гл. III.
Неподвижный разрез. Методы интегральных преобразований
и асимптотических оценок в сочетании с методом Винера —
Хопфа позволяют находить решение динамических задач тео-.
рии упругости для бесконечного однородного тела с фиксирован-
фиксированными плоскими разрезами, имеющими в плане форму круга (или
внешности круга), полосы' или бесконечного сектора, при зада-
задании на разрезе произвольных внешних нагрузок. При этом вслед-
вследствие принципа суперпозиции основное значение имеет по-
построение аналога решения Лэмба (в за-
задаче о воздействии мгновенного сосредо-
сосредоточенного импульса на границу полупро- А*0
странства) для соответствующей конфи- I
гурации тела. »>Л»>>>гтт.
Приведем результат решения одной | О х
задачи такого типа, принадлежащей I
Фройнду [285]. Пусть бесконечное упругое \Р
однородное и изотропное тело,'занимаю- рис> П81.
щее внешность разреза у = О, х < О,
вначале покоится (рис. П81). В начальный момент времени
t = О на обоих берегах разреза в точке х = —/ мгновенно
прикладываются две разрывающие сосредоточенные силы Р, ко-
которые в дальнейшем при t > 0 остаются неизменными. Задача
считается плоской. Коэффициент интенсивности напряжений
в этом случае будет следующим:
Ki^-PVWHcxW при КЦСЮ
A1.134)
/(, = р ]/2/л1 при t > l/cR.
Здесь функция f положительна; при <,<;0,9//сд она близка к
нулю (f<0,l), а при t ^ 0,91/cr она быстро увеличивается,
19 Г, П. Черепанов
g?8 Коэффициенты интенсивности напряжений Ш. 1
стремясь к бесконечности при t -> ljcR по закону квадратного
корня.
Таким образом, до прихода рэлеевской волны коэффициент
интенсивности напряжений отрицателен; как только рэлеевская
волна достигает конца трещины, коэффициент интенсивности
принимает свое статическое значение. Последний результат, по-
видимому, справедлив также в общем случае произвольных
конфигураций трещин и произвольных динамических нагрузок.
Следовательно, если в рассматриваемой задаче берега тре-
трещины сомкнуты в начальный момент, то раскрытие трещины
будет распространяться с рэлеевской скоростью, пока не достиг-
достигнет конца трещины, так что вплоть до этого момента коэффи-
коэффициент интенсивности напряжений равен нулю, а затем сразу
принимает статическое значение. Если сила Р возрастает посте-
постепенно в течение некоторого промежутка времени At, то коэф-
коэффициент интенсивности напряжений вначале равен нулю (при-
(примерно при t^.l,U}cB), а затем в течение времени, примерно
равного OJAt, быстро увеличивается до своего статического зна-
значения, которое в дальнейшем остается неизменным [285].
Стационарные динамические задачи. Мощный метод, разви-
развитый Л. А. Галиным в плоской стационарной задаче динамиче-
динамической теории упругости [40], позволяет легко получить следующий
результат: если упругое однородное и изотропное тело представ-
представляет собой внешность любого числа разрезов вдоль одной и той
же прямой, движущихся с одной и той же скоростью вдоль этой
прямой, а внешние нагрузки симметричны относительно этой
прямой и перемещаются вдоль нее с той же скоростью, то коэф-
коэффициенты интенсивности напряжений в концах разрезов будут
такими же, как и в соответствующей статической задаче. Коэф-
Коэффициент Ki определяется в соответствии с формулами C.187).
Этот результат распространяется также на произвольные
анизотропные тела [265], для которых линия разрезов будет ли-
линией упругой симметрии, если под коэффициентом Кг понимать,
как обычно, Нт(|/2лг ау) при г->0, 8 = 0, под коэффициентом
/Си — Нт (У2га- хХу) и под коэффициентом #ш — \im{V^nr т^),
см. рис. 13 (г — расстояние от конца щели).
Приведем результат решения несколько более сложной за-
задачи.
Пусть упругое тело расклинивается в условиях плоской де-
деформации тонким абсолютно жестким бесконечным клином, дви-
движущимся с постоянной скоростью V в направлении отрицатель-
отрицательной оси Хи Перед клином образуется свободная трещина, на
поверхности соприкосновения клина с расклиниваемым телом
действуют силы кулонова трения (рис. П82). Считается, что на-
напряжения на бесконечности имеют порядок ОA/г), т, е. внешнее
§4]
ДИНАМИЧЕСКИЕ ЗАДАЧИ
579
поле отсутствует. В этом случае в силу симметрии задачи лишь
один коэффициент Ki будет отличен от нуля; он равен [120]
Kl
Здесь
| tf- [с0 - рsin яе J nt-hwr
9 = A/я) arctg [ \l(kq)], m = V/c2,
v)m2
-2v
! —2v
tri'
1 = 1*'
!-2v
1.135)
й — коэффициент кулонова трения на щеках клина (хху = ^(Ту).
2f(t — li)—толщина клина (равная постоянной величине 2h на
бесконечности).
Между величинами h и /г су- 1 \
ществует одно соотношение, вы-
вытекающее из условия конечности
напряжений в точках схода |==/г
для клина гладкой формы:
Если положение точки схода
известно заранее, то это условие Рис. П82.
обычно не выполняется.
Постоянная Со в (П. 130) определяется следующим соотноше-
соотношением:
ярАГ A/2) llfe
T(e)r(i/2-e)cosiie
cos я8 [*-/(/,-/,)] Г A/2)
ГA/2-в) Г (9)
19*
580 ¦ коэффициенты интенсивности напряжений [п. I
Здесь Г(х)—гамма-функция, S(t,0)—главное значение инте-
интеграла
S(t, 9) = J
Сопротивление трения движению клина равно
00
-2J
h
оно не зависит от коэффициента трения и формы клина. При от-
отсутствии сил трения на щеках клина k = 0 и 0 = 1/2; для клина
постоянной толщины будет f'(t — 1\) = 0.
Приведенное решение годится также для ортотропного тела
с плоскостями упругой симметрии, параллельными осям хх и х2;
при этом величины р и q определяются упругими константами
ортотропного тела; эта зависимость имеется в статье [265].
Нестационарные динамические задачи для подвижных разре-
разрезов. Укажем класс автомодельных плоских задач динамической
теории упругости, решение которых при помощи комплексных
переменных Zi и 2г, где
zk=Xt~ly ^у, +У - (k=l,2),
сводится к краевым задачам теории аналитических функций од-
одной комплексной переменной (в простейших случаях — к задаче
Дирихле или к задаче Келдыша — Седова). Этот класс опреде-
определяется следующими условиями: 1) бесконечное упругое про-
пространство имеет любое число разрезов вдоль оси х, концы раз-
разрезов xh перемещаются с постоянными скоростями Vh, так что
xh = Vht (в частности, это может быть полупространство);
2) в начальный момент времени t = 0 пространство покоится;
3) нормальные и касательные напряжения на разрезах пред-
представляют собой произвольные линейные комбинации следующих
функций:
dmfn (х) dkh (t)
dxm ' dtk '
где
0 при |< 0,
? при | > 0.
Здесь k, I, m, n — произвольные целые положительные числа.
При тп~> п первый сомножитель с точностью до численного
коэффициента представляет собой (пг — п+1)-ю производную
5 4]
ДИНАМИЧЕСКИЕ ЗАДАЧИ
581
дельта-функции; это же замечание относится ко второму сомно-
сомножителю с очевидным соответствием индексов т -*• k, n-* I. Тип
автомодельности определяется парой индексов (т — п, k — /);
для каждого типа удобно выводить вначале общие представле-
представления через аналитические функции, а затем уже решать конкрет-
конкретные краевые задачи. Ниже даются общие представления для
трех наиболее употребительных типов автомодельности; а) с па-
парой индексов A, 1), когда потенциалы смещения являются одно-
однородными функциями координат и времени нулевого измерения;
б) с парой индексов A, 0), когда
смещения представляют собой одно-
однородные функции координат и време-
времени нулевого измерения; в) с парой
индексов @,0), когда напряжения
являются однородными функциями
координат и времени нулевого изме-
измерения.
Пусть бесконечное однородное и
изотропное идеально-упругое про-
пространство находится в условиях пло-
плоской деформации. В этом простран-
пространстве в обе стороны по оси х в
момент времени t = 0 начинает рас-
распространяться с постоянной скоро-
скоростью V разрез, поверхности которого свободны от нагрузок
(рис. П83). Скорость V считается меньше рэлеевской скорости.
Приведем некоторые имеющиеся решения для одного разреза.
Пусть разрез распространяется в однородном поле односто-
одностороннего растяжения, т. е. при х2 + y2~^c2t2 ау = а0, ах = т =0.
В этом случае коэффициент Къ определяемый, как обычно,
формулой Ki= Hm аи Ул (х — Vt), равен [119'288]
Рис. П83. •
Здесь
Кг — 4(j0 YnVt R (m, k)/G (m, k).
(П.136)
R(m, k)=Y(l-m2)(l-k2tn2)-(l -1 m2J,
G(m, k)=
— Am2(I — k2m2) К(У1 — m2) + 8A — k2m2)
m=V/c2> k = cs/ci = 1/A — 2v)/B — 2v) < 1,
E(x) и K(x) — полные эллиптические интегралы второго и пер*
вого рода соответственно, / — время.
582 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИИ [П. I
Само решение можно записать так *):
2B2_у-2ГусГ2_22
Лг*ус2-2_22
А 2сГог к'
- •
Аг3
(П. 137)
где
* 2сГо V к
ЦЦГ.
В любой момент времени щель имеет форму сплюснутого эл-.
липса ( как в задаче Гриффитса, но с другим эксцентриситетом,
зависящим от скорости V). Решение этой задачи более громозд-
громоздким методом было получено впервые Бробергом [119]. Аналогич-
Аналогичная задача для ортотропного тела решена Аткинсоном [289]; при
этом щель оказалась также эллиптической формы.
Пусть теперь разрез распространяется в покоящемся про-
пространстве, причем импульс (см. рис. П83)
dv
у>о
конечен и равен Р в любой момент времени t > 0. Задача пред-
предполагается симметричной относительно оси х. По своей физиче-
физической постановке она аналогична задаче Седова о сильном взры-
взрыве [290]. В этом случае имеем р87] **)
. <р (*, у, t) = Re Ф (г,), Ч> (*. У> 0 = Re ? (z2),
Ус,2-? (ПЛ38)
•) Представление справедливо для любых задач типа в).
**) Представление справедливо для любых задач типа а),
Динамические Задачи
583
Коэффициент интенсивности напряжений К\ равен
» 2PR (m, k)
Ai = '
(П. 139)
t A - k2)YnVt A - k2m2)
Наконец, пусть разрез распространяется в покоящемся про-
пространстве, причем нормальная сосредоточенная сила Р, дей-
действующая в начале координат, постоянна в любой момент вре-
времени t > 0. В этом случае имеем [287] *) *
и (х, у, t) = Re [?/, (z,) + U2 (z2)], v (x, y, t) = Re [ Vl (z,) + V2 (z2)],
i(z)~
(П.140)
Коэффициент интенсивности напряжений равен
Pi? {k, т)
Л",.
2тг A -
(П.141)
Фройнд [66] решил следующую плоскую задачу динамической
теории упругости для произвольной непостоянной скорости дви-
движения разреза. Пусть в неко-
некотором произвольном статиче-
статическом поле в начальный момент
времени имеется полубесконеч-
полубесконечная трещина нормального раз-
разрыва, которая распространяет-
распространяется в дальнейшем с произволь-
произвольной скоростью (рис. П84).
Предполагается, что с течени-
течением времени внешние нагрузки
не изменяются, поэтому дина-
динамические возмущения вызваны Рис. П84.
лишь ростом трещины. В этом
случае коэффициент интенсивности напряжений для произволь-
произвольной скорости трещины l(t) равен [66]
К(I, /) = k(I) \ [p(s)lVl(t)~s]ds. 0ПЛ42)_
*) Представление справедливо для любых задач типа б).
€84
Здесь
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
?П. Г
k(l) =
1 —•
1 —-
*?я — скорость рэлеевской волны, ci — скорость продольной вол-
волны, p(s)—нормальная нагрузка на отрезке 0 ^ х ^ /(/) (см.
рис. П84); эта нагрузка равна по вели-
величине и противоположна по знаку на-
напряжению оу на продолжении разреза,
получившемуся из решения статической
задачи в начальный момент времени.
Эта постановка задачи годится
5" лишь для того момента времени, пока
не придет возмущение от другого края
трещины или от границы тела, или от
динамических нагрузок. Будем счи-
считать, что динамический импульс возму-
возмущения симметричен относительно оси х, т. е. сохраняется нор-
нормальный разрыв. Пусть импульс растягивающего напряжения
задается функцией a = a(t). Тогда возникает дополнительное
динамическое поле напряжений; это поле описывается следую-
следующим коэффициентом интенсивности напряжений Ki{t,l,t) вблизи
конца трещины, движущейся с произвольной непостоянной ско-
скоростью l(t) (рис. П85):
Рис. П85.
(/, /, t)
A f
0
a' (s) YT^l ds. (П. 143)
Решения Фройнда охватывают, по существу, все наиболее значи-
значительные случаи динамического развития трещин с переменной
скоростью.
Приведем результат решения аналога задачи Броберга для
случая продольного сдвига. Следуя [292], находим
Здесь К и П — полные эллиптические интегралы соответственно
первого и третьего рода. Коэффициент Km равен
Bт0/ Vn) VVt(l-m2) К (/я).
(П. 144)
8 4] ДИНАМИЧЕСКИЕ ЗАДАЧИ 585
В случае продольного сдвига можно построить решение для
переменной скорости распространения щели, используя метод,
развитый в теории сверхзвукового обтекания тонкого крыла.
Пусть на разрезе вдоль у = О, 0 < х < /(/) в безграничном
пространстве задано произвольное напряжение хуг = —х(х, t)
при t ^ 0 (начальные условия — нулевые). В этом случае коэф-
коэффициент интенсивности напряжений Km выражается форму-
формулой [293]
f
f
J
о
« (П. 145)
(при *<0 / = 0).
Отметим простейшие частные случаи:
а) при х(х, t) = x0
Km = 2т0 VB/n)(c2-t)t, (П. 146)
б) при т (х, t) = Рб (х + х0), где б {х) — функция Дирака,
Осесимметричный аналог задачи Броберга (распространение
дискообразной щели с постоянной скоростью V в однородном
поле растяжения Оо) был рассмотрен в работах [294>295]. Условия
задачи оказалось возможным удовлетворить, выбрав форму
разреза в виде сплюснутого эллипсоида (по аналогии с резуль-
результатом Броберга). Аналогичное обстоятельство было удачно ис-
использовано также при решении соответствующей задачи для
анизотропной среды [286]. Приведем получающийся результат для
смещения берегов трещины в изотропном случае [294]:
— г2, А = 5 . (П. 147)
Здесь
СО
3-00 = /
¦rfv.
При V-+0 имеем 2f (V) « п(с2 — c2)/DFc|).
В работах [297-298] задача Броберга была обобщена на случай
произвольно заданной на щели нормальной нагрузки, сохраняю-
сохраняющей автомодельность задачи. Были рассмотрены плоская и осе-
симметричная задачи. Приведем один результат, относящийся к
динамической плоской упруго-пластической задаче в постановке
586 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ [П. I
Дагдейла (рис. П86). В этом случае величина V—Vo, опре-
определяющая размер пластической зоны — отрезка, находится из
следующего уравнения:
8** [е{УГ=И?) - Е (/l-
hi _-. t yi — nr
(П.148)
_ -П1-—t, Vl-m2i =
m0 1^A-m2)(m2~m2)
(m — V/c2, m0 = VJc2, k — c2lc{). ¦
Здесь E(x), U(x,y)—полные эллиптические интегралы второго
и третьего рода соответственно. Длина пластического отрезка
убывает с ростом скорости тре-
t| кР щины Vo, обращаясь в нуль при
| I рэл'еевской скорости.
§ 5. Другие вопросы
Рассмотрим некоторые вопро-
вопросы, не освещенные в предыдущих
параграфах, однако представляю-
представляющие значительный интерес.
Сквозные разрезы в изгибае-
il I мых пластинах. Иногда работа
у |/7 некоторых тонкостенных кон-
конструкций допускается даже при
Рис. П86. наличии в них устойчивых сквоз-
сквозных трещин больших размеров,
сравнимых с радиусом кривизны оболочки или с каким-либо дру-
другим характерным линейным размером конструкции.
Согласно теории Кирхгофа, смещение в жесткой упругой
пластине, находящейся под действием одной только поперечной
нагрузки, удовлетворяет следующему уравнению [299]:
(П.149)
Здесь w — смещение точек пластины по нормали к ее поверх-
поверхности, D — цилиндрическая жесткость пластины, q (x, у) — попе-
поперечная нагрузка.
|61 ДРУГИЕ ВОПРОСЫ 587
Имеют место следующие формулы [299]:
и
Здесь ?, га — произвольная система декартовых координат, Mt и
Мп — изгибающие моменты, Mtn — крутящий момент, Qt и Qn —
перерезывающие силы.
Существует математическая аналогия рассматриваемой за-
задачи изгиба пластин по теории Кирхгофа с плоской задачей тео-
теории упругости (с объемными силами). Действительно, пусть объ-
объемная сила (X, Y) имеет потенциал F(x,y), так что X = дР/ду,
Y = dF/dx.
Уравнения плоской задачи имеют вид
~дГ
, д(хху + Р) _п д(чху + Р) f дау
Отсюда получаем
2 d2F
1 — v дх ду '
причем
ах = дЧЦду*, 0У = д2и/дх*, хху + F (х, у) = - d*U/dx ду.
Таким образом, функции Эри U соответствует смещение w,
а функции —2Fxyl(\—v) — нагрузка q. В частности, там, где
q[x, у) = 0, имеют место следующие представления [23]:
Здесь Ф(г) nW(z)— аналитические функции.
Однако граничные условия на берегах разрезов уже ие имеют
такого соответствия, поэтому требуется самостоятельное иссле-
исследование. Вильяме [300] первым изучил поле напряжений вблизи
конца сквозного разреза в изгибаемой пластине, Он получил
588
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
trt i
следующие формулы (рис. П87), приводимые в соответствии со
статьей [237]:
7 + v
2C + -
v) V2nr Л \ 7
+ •
6 36
cos cos —
2C+v)
0Й
6
7 + v
2 C + v
7 + v
3v
KB z/5+3v 6 . 38 \
===— cos —\- cos — —
0 Vinr A V 7 + v 2 2 )
v
3v
2 C + v) УШ h\ 2
(П.151)
2 C + v)
Кв г I 1 —v 6 36 \
В j gjj, |_ д|ц J _|_
^2я7 А\ 7+v 2 2)
6 , 36 \
COS-+COSYJ.
1 —v
5 + 3v
2C + v) У2яг
Здесь Кв и Ха — коэффициенты интенсивности напряжений, ко-
которые можно найти из асимптотического выражения для ком-
комплексного потенциала Ф(г) вблизи конца щели г = 0 по фор-
формуле
У (г)]. (П. 152)
Упругое поле вблизи конца щели, согласно (П.151), отли-
отличается от точного распределения в общем случае, которое дается
формулами C.44) и C.45). Это объ-
объясняется тем, что теория Кирхгофа
(как и всякая другая двумерная
теория пластин) носит приближен-
приближенный характер и не может учитывать
подробности распределения напря-
напряжений на расстояниях от конца
щели, меньших или равных по по-
порядку толщине пластины. Формулы
(П.151) дают промежуточную асим-
асимптотику упругого поля на расстоя-
расстояниях от конца щели, больших по
сравнению с толщиной пластины, но
малых сравнительно с длиной щели
или каким-либо другим характерным линейным размером пла-
пластины в плане. Эти формулы не зависят от подробностей струк-
структуры фронта трещины вблизи ее конца (например, в случае пря-
прямолинейного фронта не зависят от наклона прямой к плоскости
пластины); в этом заключается их общность и преимущество
Рис. П87.
ДРУГИЕ ВОПРОСЫ
589
перед точным решением, дающим асимптотику лишь на расстоя-
расстояниях от фронта щели, малых по сравнению с толщиной пластины.
Отметим, что более точная теория Рейсснера дает поправку
к формулам (П.151), которая делает их на поверхности
Рис. П88.
Рис. П89.
пластины идентичными точному решению C.44) с точностью до
постоянного множителя [237].
Приведем яекоторые результаты вычисления коэффициентов
Кв и К,-
Пусть бесконечная пластинка со щелью подвергается равно-
равномерному двухосному изгибу на бесконечности (рис. П88).
Имеем [237]
= 6Л*
= 0. (П. 153)
В случае равномерно распределен-
распределенного крутящего момента интенсивно-
интенсивности Н (на единицу длины) на беско-
бесконечности для той же пластины со
щелью (рис. П89) имеют место сле-
следующие формулы [237]:
/Св = 0, Ks = bH Vnl/h2. (П. 154)
Для пластины со щелью, находя-
находящейся под действием однородного
сдвига (рис. П90), имеем [237j
(П.155)
Рис. П90.
Результат, естественно, не зависит от
Qi. В этом случае для равновесия пла-
пластины нужно приложить также изгибающие моменты интенсив-
интенсивности QL (L считается большим по сравнению с /).
590
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
[П. Т
. В случае сосредоточенной пары сил произвольного направле-
направления на поверхности щели в бесконечной пластине (рис. П91)
коэффициенты интенсивности напряжений в наиболее опасной
точке О равны
ЗМ
I
н
I
м-
и
Рис. П91.
На рис. П91 показаны направления соответствующих вектор-
моментов (изгибающего М и крутящего Я). Это решение можно
использовать в качестве функции Грина
для отыскания коэффициентов интенсив-
интенсивности напряжений при произвольно рас-
распределенных вдоль щели моментах.
В самом общем случае растяжения
и изгиба пластин со сквозными разре-
разрезами, кроме Кв и /Cs, появляются также
коэффициенты Кг и Кц. Условие локаль-
локального разрушения на фронте трещины
определяется некоторой критериальной
комбинацией из этих четырех параметров. Наиболее надежным
способом ее определения является эксперимент.
Если размер пластической области вблизи фронта трещины
мал по сравнению с толщиной оболочки и, кроме того, условия
локального разрушения в точках фронта трещины близки к усло-
условиям локальной плоской деформации, то критериальная комби-
комбинация в принципе может быть определена из решения сингуляр-
сингулярной задачи для полубесконечного разреза в пластине и критерия
локального разрушения в условиях плоской деформации. Пояс-
Поясним это на простейшем случае, когда фронт разреза прямоли-
прямолинеен и перпендикулярен к плоскости пластины. Сингулярная за-
задача на основании «принципа микроскопа» ставится так: тре-
требуется найти решение уравнений теории упругости в полосе
|г| < /г/2 с разрезом вдоль у = 0, х < 0 при всюду свободных
от нагрузок границах (см. рис. П87). Поле на бесконечности за-
задается суперпозицией формул C.44), C.45), (П. 151).
Решение этой сингулярной задачи даст зависимость локаль-
локальных коэффициентов интенсивности напряжений К[Л), КиК Knl
на фронте трещины от четырех параметров поля на бесконеч-
бесконечности в виде
тг-Щ t tic. v v v\
5 5] ДРУГИЕ ВОПРОСЫ 591
где U, /2, h — функции, определяемые из решения указанной син-
сингулярной задачи. Отсюда по известному критерию локального
разрушения fOcf11» КиК /(ш) = 0можно найти искомую крите-
критериальную комбинацию. В частности, в наиболее важном для
практики случае трещин нормального разрыва, когда K\f=Kn\=s
= 0, критериальная комбинация, описывающая начало разру-
разрушения, будет иметь вид
Для рассматриваемой частной конфигурации фронта, очевидно,
достаточно рассмотреть лишь случай чистого изгиба на бесконеч-
бесконечности (решения C.44) и C.45) в данном случае годятся для
всей области). Вообще говоря, в данном случае начальное раз-
развитие фронта трещины будет устойчивым; поэтому для нахожде-
нахождения критериальной комбинации, характеризующей начало не-
неустойчивости всего фронта, нужно решить также задачу об
устойчивом росте трещины и изменении ее фронта вплоть до до-
достижения неустойчивой для всего фронта ситуации (ср. с.про-
с.пространственной трещиной эллиптической формы в плане, § 2 При-
Приложения I).
Экспериментальному изучению разрушения анизотропных
пластин со сквозными трещинами в условиях плосконапряжен-
плосконапряженного состояния посвящена работа By [301]. На исследованных им
материалах (армированный пластик и бальза) конструктивно
была обеспечена прямолинейность развивающейся трещины. Был
получен следующий эмпирический критерий локального разру-
разрушения:
(/С,//С,сJ + (/С„//С„сJ=1, (П. 157)
причем величина /Спс оказалась в 2,5—3,5 раза больше, чем Kic
(ср. с замечанием в конце § 2 гл. IV).
Экспериментальная проверка основной концепции механики
хрупкого разрушения применительно к задачам изгиба пластин
была произведена в работах [302>303]. Изгиб неоднородных и ани-
анизотропных пластин со щелями изучали Янг, Вильяме, Си, Пэрис,
Эрдоган и др.
Сквозные щели в оболочках. Рассмотрим жесткие упругие
оболочки со сквозными щелями при следующих допущениях:
а) прогибы оболочки малы по сравнению с ее толщиной, б) тол-
толщина оболочки мала по сравнению с радиусом кривизны обо-
оболочки, в) длина щели велика по сравнению с толщиной обо-
оболочки. Все эти допущения необходимы для применения класси-
классической линейной теории оболочек. Из «принципа микроскопа»
692 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ 1П. I
непосредственно вытекает, что в этом приближении поле упругих
напряжений и деформаций вблизи конца сквозной щели (т. е. на
расстояниях от конца щели, малых по сравнению с ее длиной и
радиусом кривизны оболочки, но больших по сравнению с тол-
толщиной оболочки) в самом общем случае дается суперпозицией
формул (П.151) и C.44), C.45) для плоского напряженного со-
состояния. Первые описывают изгиб относительно нейтральной по-
поверхности, а вторые — растяжение.
Из «принципа микроскопа» также вытекает, что критериаль-
критериальная комбинация из коэффициентов интенсивности напряже-
напряжений Ki, Kn, Kb, Ks, характеризующая локальное разрушение
в конце сквозной трещины в оболочке, совпадает с соответ-
соответствующей критериальной комбинацией из тех же параметров для
упругих жестких пластин из того же материала и той же тол-
толщины.
В работах Фолиаса, Эрдогана и Килбера, Дункана изучены
поля напряжений и деформаций в пологих цилиндрических и
сферических оболочках со сквозными плоскими разрезами нор-
нормального разрыва, т. е. при Ks = Кц = 0. Приведем их резуль-
результаты, взятые из обзорной статьи [304].
Введем обозначение [304]
X = Ehl*/(DR2) = 12 A—v2) l4/(R2h2).
Здесь R — радиус цилиндрической или сферической оболочки,
h — ее толщина, / — полудлина разреза (вдоль нейтральной по-
поверхности).
Воспользовавшись принципом суперпозиции, каждое напря-
напряжение в оболочке с разрезом, свободным от внешних нагрузок,
представим в виде суммы двух слагаемых, одно из которых
представляет собой соответствующее напряжение в сплошной
оболочке, подверженной внешним нагрузкам, а другое — напря-
напряжение в свободной от внешних нагрузок оболочке с разрезом,
нагруженным разрывающими усилиями, перерезывающими си-
силами и изгибающими моментами. Последние величины берутся
из решения задачи для сплошной оболочки (с обратным зна-,
ком). Коэффициенты интенсивности напряжений, очевидно, впол-
вполне определены вторым напряженным состоянием.
Обозначим через а0 давление от разрывающих усилий, а че-
через Ов — максимальное давление от чисто изгибающего момента
(в волокне, прилегающем к поверхности оболочки). Далее рас-
рассматривается толькЪ тот случай, когда величины а0 и ав на раз-
разрезе постоянны вдоль разреза.
При X < 1 коэффициенты интенсивности напряжений будут
выражаться следующими формулами [304];
ДРУГИЕ ВОПРОСЫ
593
для сферической оболочки с разрезом вдоль меридиана
(рис. П92)
у i _ у2
и +1 (°'577+!п t)J) '
Н
(П. 158)
для сосуда с постоянным внутренним давлением а (ал
рис. П92) o0 = qR/Bh), aB = 0;
Рис. П93,
для цилиндра с разрезом вдоль образующей (рис. П93)
В
Г 5 + 37v , 1
(.96A-v) 16A-'
(П. 159)
для сосуда с постоянным внутренним давлением q (см.
рис. П93)
594 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ- [П. I
для цилиндра с разрезом вдоль окружности (рис. П94)
+ vK2(l-v)
64
(П.160)
-v) 64J
для сосуда с постоянным внутренним давлением q (см.
рис. П94)
При ов = 0 и h^ 1 коэффициенты
интенсивности напряжений для всех
случаев можно представить следую-
следующим образом:
^&М
Значения функций ЦК) и
приведены в табл. П14.
Данные для последних двух столб-
столбцов табл. П14 были сняты с графика,
приведенного в работе [304], и потому
менее точны.
В работах [305>306] рассмотрены аналогичные задачи для по-
пологих и эллипсоидальных оболочек. В статье [306] вычислены
Рис. П94.
Рис. П 95.
коэффициенты /Ci и Кв в следующем случае (рис. П95).
Пусть радиус-вектор точки срединной поверхности оболочки
t «1
ДРУГИЕ ВОПРОСЫ
595
Таблица П 14
0.2
0.4
0,6
0,8
1,0
1,2
1,4
1.6
1,8
2,0
2,2
2,4
2,6
2,8
3,0
3,25
3,50
3,75
4,00
4,25
4,50
5,00
5,50
6,00
6,50
7,00
7,50
8,00
Сфера
/<м
1,0112
1,0422
1,0887
1.1479
1.2174
1.2956
1,3812
-4731
1.5706
1.6729
.7795
1,8899
2,0038
2,1208
2,2408
2,3947
2,5526
2,7143
2,8796
3,0485
3,2208
3,5750
3,9446
_
—
Значения
(рис. П92)
& <м
0,00611
0,01693
0,02919
0,4186
0,05448
0,06685
0,07886
0,09045
0,10155
0,11216
0,12223
0,13172
0,14058
0,14879
0,15630
0,16463
0,17172
0,17751
0,18194
0,18483
0,18644
0.18493
0,17802
—
—
—
—
—
функций 1(к) и 3(Ц
Цилиндр
/ (М
1,0096
1,0371
1,0795
1,1344
1,1993
1,2723
1,3519
1,4367
1,5256
1,6177
1,7122
1,8085
1,9060
2,0045
2,1035
2,2276
2,3519
2,4761
2,5999
2,7232
2,8459
3,0895
3,3303
3,5681
3,8029
4,0347
4,2637
4,4895
(рис. ,П93)
& (А.)-0,54
0,00410
0,01124
0,01902
0,02659
0,03359
0,03985
0,04529
0,04990
0,05368
0,05664
0,05883
0,06018
0,06090
0,06083
0,06014
0,05832
0,05549
0,05172
0,04700
0,04154
0,03512
0,02012
0,00234
0,02222
0,04130
0,06622
0,09350
0,12279
Цилиндр
—
—
—
1,05
1,072
1,094
1,116
1,138
1,16
1,188
1,216
1,244
1,272
1,30
1,335
1,37
1,405
1,44
1,475
1,51
1,58
1,65
1,72
1,79
1,86
1,93
2,00
(рис. Л94)
& <*>
0,009
0.018
0,027
0,036
0,045
0.053
0,060
0,065
0,069
0,071
0,069
0,065
0,06
0,053
0,046
0,034
0,021
0,06
-0,010
-0,015
-0,02
-0,04
-0,06
-0,08
-0,10
—0,12
-0,14
-0,16
равен ,_
г (|, л) = bli - foi/ + * А- в У к
(p2 = ^ + Ti2, г = Ыа, \1\<\, 1л1<1).
Это — уравнение эллипсоида вращения с полуосями а и Ь, при-
причем Ъ < а. Берега сквозного разреза вдоль -л = Ло, || — Ъ\ < А,
нагружены нормальным давлением ао; Других нагрузок нет. Ко-
Коэффициенты интенсивности равны
УШ [ 1 - е2А2 A ± 2|0/Я)],
Здесь предполагалось, что е •< 1, т. е. эллипсоид сильно вытянут.
Щели в мембранах. Допустим, что оболочка не допускает из-
гибных и сжимающих напряжений. Если в такой оболочке!
S96
КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ
т.
находящейся в некотором безмоментном напряженном состоянии,
сделать сквозной разрез (или отверстие), то вблизи него, как
правило, возникнет область, в которой оболочка выпучится; все
напряжения в этой области иногда обращаются в нуль [307].
Форма и размеры выпучен-
| j ной области неизвестны
заранее и подлежат опреде-
определению; в этом смысле рас-
рассматриваемая задача анало-
" гична некоторым упруго-
пластическим задачам для
- идеально-пластического тела.
Локальное закритиче-
ское выпучивание приводит
к увеличению коэффициен-
коэффициентов интенсивности напряже-
напряжений в концах щели.
Оценим этот эффект
ро7,308j на ПрИМере двусто-
двустороннего растяжения плоской
мембраны с прямолинейным
разрезом (рис. П96). Точное исследование показывает, что в
этом случае при <х~< а~ выпучивания не происходит, а при
1 ^о°°1в™^5граница выпученной области представляет собой
плавную кривую, имеющую следующее представление;
S
.1
X
¦и \
Рис. П 96.
y = A(l-t2f2
Л
~°х
?=/1-2
(П. 163)
Коэффициент интенсивности напряжений равен
при 1 ^ ог°°/ог~ <Л 5
1
при а~ > о~
00 »
(П. 164)
Как видно, увеличение коэффициента Ki вследствие выпучи-
выпучивания не превосходит 10%- По-видимому, более существенное
влияние локального выпучивания состоит в облегчении пластиче-
пластических деформаций вблизи вершины трещины, приводящем к
¦S]
Другие вопросы
697
уменьшению Кс- Эффект погранслоя приводит к размыванию об-
области выпучивания и в первую очередь к размыванию точек
возврата на ее контуре.
Образование складок на мембранах. Пусть в точках х = ±1,
у = 0 бесконечной плоской мембраны, подверженной всесторон-
всестороннему растяжению о на бесконечности, действуют сосредоточен-
сосредоточенные силы, равные по величине X и направленные навстречу одна
другой (рис. П97). В этом случае образуется зона локального
'¦ ¦ ¦
Рис. П97.
закритического выпучивания, которая представляет собой вну-
внутренность эллипса [309]
х2 + у2№ = 12 A = Х/(ло1)). (П. 165)
При а -> О эта область стремится к полосе |*|< /, —оо <
'< у •< оо. Влияние весьма малой, но конечной изгибной жест-
жесткости приводит к эффектам типа пограничного слоя. В данном
случае оно приводит к тому, что и при а = 0 выпученная об-
область будет иметь конечную протяженность; на мембране обра-
образуется складка, продольный размер которой 2L гораздо больше
поперечного (равного 21).
Решение проблемы закритического складкообразования на
основе уравнений теории гибких пластин представляет собой
весьма сложную нелинейную задачу [310]. Между тем, на осно-
основании «принципа микроскопа» очевидно, что поле напряжений
и деформаций в окрестности конца складки такое же, как вблизи
конца трещины (с точностью до знака). При этом имеется в виду
асимптотика на расстояниях от конца складки, больших по
сравнению с радиусом ее кривизны, но малых по сравнению с
длиной складки (L~^> r ^> I). Следовательно, сопротивление вы-
выпучиванию в конце складки, определяющее ее продольный
S98 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ [П. Т
размер 2L, описывается в терминах коэффициентов интенсивно-
интенсивности напряжений. Поэтому критерий локального выпучивания в
конце складки формулируется так: существует некоторая функ-
функция коффициентов интенсивности напряжений, одна и та же для
всех мембран данной толщины, сделанных из одного и того же
материала. В частности, если складка аналогична трещине нор-
нормального разрыва, этот критерий сводится к следующему: ко-
коэффициент интенсивности напряжений Kj в конце складки равен
некоторой постоянной материала, зависящей от толщины мем-
мембраны. Эту постоянную можно найти с точностью до числового
коэффициента из анализа размерностей. Действительно, в точ-
точные уравнения теории упругих гибких пластин входят лишь сле-
следующие постоянные: модуль Юнга Е, коэффициент Пуассона v,
толщина пластины /г. Из Е и h можно составить только комби-
комбинацию Е Л/h размерности /С/. Окончательно, в наиболее важном
частном случае критерий локального выпучивания имеет такой
вид: _
Ki=*a(s)EVh, (П. 166)
где функция a(v) вполне универсальна. Для ее определения до-
достаточно одного эксперимента с какой-либо мембраной.
В нашем примере с сосредоточенными силами (см. рис. П97)
коэффициент Ki равен Х/угяГ, поэтому длина складки равна
L = {n[a{v)}2E2h}-lX2. (П. 167)
Очевидно, приведенные рассуждения имеют вполне общий ха-
характер, так что все результаты, относящиеся к решению конкрет-
конкретных задач о сквозных трещинах в пластинах и оболочках, авто-
автоматически переносятся также на проблему образования складок
в мембранах.
Как видно, теория складкообразования в мембранах предста-
представляет собой (несколько неожиданное) приложение общего асим-
асимптотического метода механики хрупкого разрушения.
Пинч-эффект. Бриджмен [зи] описал ряд явлений, характер-
характерных для разрушения твердых тел при больших давлениях. Одно
из этих явлений, названное «пинч-эффектом», заключается в
следующем. «Сплошной цилиндр подвергается давлению, дей-
действующему только на наружную цилиндрическую поверхность;
торцы же остаются не подверженными давлению. Когда давление
достигает величины, численно равной примерно пределу проч-
прочности при чисто растягивающей нагрузке, цилиндр обычно раз-
разрывается на части, где-то около середины и очень редко в зоне,
примыкающей к сальникам. Создается такое впечатление, будто
цилиндр разорван растягивающей силой, приложенной непосред-
непосредственно к его выступающим концам... Если прут сделан из хруп-
S 5] ДРУГИЕ ВОПРОСЫ 599
кого материала, например, стекла или стали, обладающей твер-
твердостью стекла, разрыв образует-ясно выраженную плоскость,
перпендикулярную к оси, но если прут сделан из материала, ко-
который до разрыва обладает текучестью (например, из мягкой
стали), то получается значительное сужение площади в месте из-
излома; вообще, вид излома очень похож на тот, который полу-
получается при обыкновенном испытании на разрыв» ([зи], стр. 96).
Объяснение «пинч-эффекта», данное Бриджменом и основанное
на критерии максимального удлинения, представляется неудо-
неудовлетворительным. Рассмотрим это явление подробнее.
Главные упругие напряжения в цилиндре, очевидно, равны
ar = —p, ore = — P, of2 = °-
Здесь г, 9, z — цилиндрические координаты (ось z совпадает
с осью цилиндра), р — боковое давление.
Цилиндр из идеально-пластического материала, очевидно,
разрушится при давлении р, равном as, где as — предел текуче-
текучести, так как именно при этом давлении он переходит в пластиче-
пластическое состояние Bтахт= | сгг — сгг j =as). Эта величина
разрушающего давления, а также направление площадок сколь-
скольжения совпадают с соответствующими величинами для случая
растяжения стержня напряжением аг = as.
Будем теперь считать материал цилиндра идеально хрупким
или квазихрупким. Характерным свойством таких материалов
является наличие на их поверхности большого числа микротре-
микротрещин-дефектов. Согласно механике хрупкого разрушения, проч-
прочность стержня на растяжение равна
.... «„)• _ (П.168)
Здесь R — радиус цилиндра. Функция / зависит от безразмер-
безразмерных геометрических параметров ai, ..., а„; она полностью опре-
определяется геометрией поверхностных микротрещин. При этом
наибольшую роль играют максимальные по размерам и нор-
нормальные к поверхности стержня трещины. В опытах Бриджмена
давление на боковую поверхность цилиндра передавалось по-
посредством жидкости или газа. Очевидно, жидкость или газ
проникали в поверхностные микротрещины и производили давле-
давление на их стенки, равное давлению на боковую поверхность ци-
цилиндра. Решая соответствующую задачу теории трещин, нетруд-
нетрудно сообразить, что по крайней мере в том случае, когда все ми-
микротрещины нормальны к поверхности стержня, разрывающее
давление будет совпадать с величиной а, определяемой форму-
формулой (П.168). Строго говоря, функция f(ai, ..., ап) для стержней
одинаковой длины и радиуса, но из разных материалов будет
различной; однако для стрежней из одинакового материала
с одной и той же технологией изготовления и одинаковой
600 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ Щ. I
предысторией ее можно считать примерно одинаковой. Отсюда
получается результат Бриджмена о примерном равенстве пре-
предельного давления пределу прочности на растяжение [312].
Бриджмен описал также другой случай разрушения, когда
удлинение не определяет разрыва, а каждое отдельное напряже-
напряжение и деформация являются сжимающими. Стальной цилиндр
конечной длины был плотно пригнан внутрь эбонитовой трубки
той же длины. Полученная система подвергалась гидростатиче-
гидростатическому давлению, действовавшему на всю внешнюю поверхность.
Разрыв происходил так, как если бы в трубку был введен конуе,
растягивающий ее до точки разрыва. Объяснение этого явления
аналогично объяснению «пинч-эффекта» и основано на том, что
напряжение 09 в трубке по абсолютной величине всегда меньше
внешнего давления. Нетрудно найти величину разрушающего
внешнего давления р, используя высказанные ранее соображе-
соображения: ,
р = [A -2v2)?, -(I -2v,)?2r' ?,св. (П.169)
Здесь 0в — прочность на растяжение материала трубки (эбо-
(эбонита); vi, V2—^коэффициенты Пуассона, Е\, Е2 — модули Юнга
(индекс 1.относится к материалу сплошного цилиндра (стали),
индекс 2 — к материалу трубки (эбониту)).
Моментные напряжения. Один из наиболее известных вариан-
вариантов моменгной теории упругости принадлежит Миндлину [313]
(см. тчкже В. В. Новожилов [2]). Моментные напряжения, по-
видимому, существенны в тех явлениях, при описании которых
элементарный объем нельзя выбрать достаточно большим, так
что начинают сказываться осбенности микроструктуры. Учету
этих, эффектов в окрестности щели посвящены работы pn-3i6j
Согласно работе [зи], поле сингулярных напряжений вблизи кон-
конца трещины нормального разрыва будет следующим:
1 - 2v КГ> /91 36 \
a, = r= cos sin Э • sin—)•
3 — 2v V2nr V 2 2 2 /
/2ra
a»* == — - ,„ "„' - 77==^ Sin 9 • COS -^,
Kf Г 6 l-2v 391
= r cos sin 9 • sin — ,
/2га- I 2 2 C - 2v) 2 J
1 - 2v Kf . 39
rsin 9 cos ,
2C-2v) Vi*T 2 (П.170)
M2) 391
j
SSI
ДРУГИЕ ВОПРОСЫ
GO I
Здесь к\} и К.? — коэффициенты интенсивности напряжений, \ix
и \iv — моментные напряжения.
В случае прямолинейной щели длины 2/ (рис. П98) в одно-
однородном поле растягивающего напряжения р (аналог задачи Гриф-
фитса) коэффициенты интенсивности напряжений таковы [314]:
у9Г ((-1,2). (
111
21
Здесь Г» — некоторые функции а/1, представленные в [зи] весьма
сложными интегральными выражениями, а — дополнительная
постоянная в моментной теории
упругости [313], имеющая размер-
размерность длины.
Трещины в жидкости. При воз-
воздействии кратковременных интен-
интенсивных растяжений в жидкости воз-
возможно быстрое развитие трещин.
Трещины существуют некоторое
время порядка характерного време-
времени релаксации и затем исчезают.
Экспериментально наблюдались
трещины даже в воде [126}. В работе
[2921 дана постановка задач о разви-
развитии трещин в идеальной жидкости
и получено эффективное решение
некоторых конкретных задач.
Пусть идеальная жидкость, покоящаяся в начальный момент,
подвергается воздействию интенсивных массовых сил и отрица-
отрицательных давлений в течение некоторого промежутка времени Д/.
Допустим, что v < с, v&t -С L. Здесь v — характерная скорость
частиц жидкости после действия давления р и массовых сил, с —
скорость звука в теле, L — его характерный линейный размер.
При выполнении этих условий для скорости частиц жидкости v
м
непосредственно после удара и для импульса давленияР= Гpdt
Р\
\ I \
Рис. ПЭ8.
имеют место основные соотношения
v = grad ф,
(П. 172)
Здесь F — импульс массовых сил, U — потенциал, Д — оператор
Лапласа, р — плотность.
Для плоской задачи эти соотношения удобно записать так:
' = PRe/(z),
(П. 173)
602 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ {П. 1
Здесь f(z) — аналитическая функция г = х -f Щ (предполагает-
(предполагается, что импульс массовых сил равен нулю).
Допустим, что выполняется условие
VM->1. (П. 174)
Здесь V — скорость распространения трещины, / — длина тре-
трещины, образующейся после удара. Это условие означает, что
время неустановившегося развития трещипы мало по сравнению
со временем действия интенсивных давлений. Заметим, что ха-
характерная скорость распространения динамической трещины
имеет порядок скорости звука, поэтому условие (П. 174) согла-
согласуется с условием vAt ^ /.
Предполагается, что зависимость давления от времени имеет
характерный вид, изображенный на рис. П99.
В малой окрестности конца произвольной щели в жидкости
со свободными от нагрузок берегами поле скоростей и импульса
давления будет следующим (рис. П99):
Kf I 39 39\ (П.175)
vx + ivy = J_ ¦ cos (-/sin-— .
* 2р]А2я r'2 \ 2 2 /
Здесь Kf — коэффициент интенсивности импульса давления,
имеющий размерность кГ-сек-см.-*1*. При помощи общефункцио-
общефункционального метода механики хрупкого разрушения можно уста-
„. новить, что существует постоянная Kfc,
* которая характеризует сопротивление
жидкости развитию трещин, так что
критерий предельного состояния на
S" фронте трещины имеет вид
Kf<Kfe. (П. 176)
р
* Если предположить, что величина
/С/с зависит лишь от поверхностного
натяжения у, от сжимаемости жидко-
жидкости с2р и продолжительности импуль-
^_ са Д?, то из соображений анализа раз-
i мерностей получим
К(с = цсЫ]/ру, (П.177)
Рис. П99. , ,
где ц — числовой коэффициент.
В статье р92] указан также прием для приближенного опре-
определения статического коэффициента Kj в упругих телах с раз-
разрезами по коэффициенту Kf соответствующей задачи в рассма-
рассматриваемой постановке, если касательные нагрузки на поверхно-
поверхности упругого тела и разреза равны нулю.
§5]
ДРУГИЕ ВОПРОСЫ
603
Оценим размер трещины, образующейся в условиях опыта
Кольского (касательный удар пули по поверхности воды, см.
схему рис. Ш00). Контур фронта образующейся трещины будем
считать дугой окружности радиуса а с центром в точке удара
(величина импульса равна F). Ради простоты схематизируем
2F
га
Рис. пюо.
эту задачу осесимметричной задачей о сосредоточенных импуль-
импульсах величины 2F, действующих на берегах дискообразного раз-
разреза радиуса а в безграничном пространстве.
Таким образом, при помощи (П. 172) приходим к следующей
задаче теории потенциала:
при 2 = 0, г <а
при 2 = 0, г > а
(г =
а
2я J rb(r)dr=\,
дфг = 0
у2, 6 (г) — дельта-функция).
(П.178)
Решение этой задачи, согласно (П. 175), следует искать в
Классе функций ср, имеющих на контуре г — а особенность типа
Г(г — а)~чк Заметим, что в классе ограниченных на контуре
^функций решения этой задачи не существует (например, нет ре-
решения соответствующей контактной задачи теорди упругости,
|когда функция ср при z = 0 представляет собой составляющую
Смещения по оси г).
" Введем новую функцию i|>(r, г):
|пр(г, г) dr.
(П. 179)
Функция ф(г, г), как нетрудно проверить, также явля-
является гармоничеекой. Для нее, согласно (П.178), имеют место
604 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ [П. I
следующие граничные условия:
при 2 = 0, г < a ip = 2F/р,
= 0 (П. 180)
Функция ty(r, z) ограничена на контуре z = 0, г = а. Реше-
Решение краевой задачи (П. 180) нетрудно получить различными спо-
способами. Для наших целей достаточно следующего результата,
вытекающего из ее решения [40]:
при z — 0, г < а
dj, _ 4F (П. 181)
дг яр /а2 — л2 '
Согласно (П. 179)
<РС-'2> = -2я717- (
Используя две последние формулы, находим
при z = 0, г < а
dcp/dz = 2/7[я2р (а2 - г2K/2]. (П> 183)
При помощи этого результата и формул (П. 175) получим коэф-
коэффициент Kf в исходной задаче:
Kf = 2F/(nafp. (П. 184)
Пользуясь критерием (П. 176), отсюда находим формулу для ра-
радиуса трещины, образующейся в опытах Кольского:
а = A/я)-B/^J/3. (П. 185)
Другие примеры решения задач в рассматриваемой поста-
постановке можно найти в работе [292].
Меры борьбы с развитием трещин в конструкциях. При ана-
анализе причин разрушения конструкции существенными могут ока-
оказаться многообразные факторы, которые целесообразно разбить
на несколько групп.
1) Механические факторы (фрактографический анализ из-
изломов, установление очага разрушения, определение напряжен-
напряженно-деформированного состояния в районе очага и влияния на
него различного рода подкреплений, приклепанных или прива-
приваренных стрингеров, выточек, сварных швов и т. д., анализ цик-
циклических напряжений). Рассмотрение этих факторов обычно
приводит к необходимости некоторого изменения конструкции,
которое должно быть минимальным с точки зрения экономии
§ 5J ДРУГИЕ ВОПРОСЫ 605
средств или времени при условии обеспечения безопасности и
работоспособности конструкции. Чаще других при этом прово-
проводят следующие мероприятия:
а) сведение до минимума циклических и случайных напря-
напряжений (в частности, конструкция должна быть спроектирована
или изменена так, чтобы исключалась возможность ее работы в
режиме, близком к резонансному),
б) присоединение дополнительных ребер жесткости и нало-
наложение сварных швов или заклепок,
в) просверливание разгружающих выточек (например, от-
отверстия в конце развившейся сквозной трещины в пластине или
оболочке).
Теоретический расчет этих способов борьбы с развитием тре-
трещин достаточно сложен, а успех его существенно зависит от
удачной схематизации. Для знакомства с применяемыми при
этом приемами читатель отсылается к литературе [239> 317-321,
256, 257, 2821
2) Химические факторы (химический анализ поверхности
очага разрушения, определение механизма химической реакции
и локального разрушения в конце коррозионной трещины, уста-
установление возможностей и причин локального наводораживания
и т. п.). Для борьбы с ростом трещин в этих случаях приме-
применяют
а) устранение активного компонента из внешней среды (на-
(например, водорода),
б) использование защитных пленок и покрытий,
в) ингибирование.
3) Физические факторы (физический анализ свойств мате-
материала в очаге разрушения и прежде всего его вязкости разру-
разрушения, определение остаточных внутренних напряжений, оты-
отыскание охрупченных зон и трещиноподобных дефектов в струк-
структуре материала). Для устранения или уменьшения опасности
хрупкого разрушения применяют следующие меры:
а) замену материала конструкции или некоторой ее части,
б) устранение внешних физических причин охрупчивания
(например, изменение режима термообработки или уменьшение
радиационного облучения),
в) изменение технологического процесса, приводящего к об-
образованию слишком больших дефектов и растягивающих оста-
остаточных напряжений в районе очага разрушения,
г) введение дополнительных технологических операций для
локальной обработки зоны очага разрушения (например, спе-
специальная термообработка с целью локальной пластификации
материала и увеличения его вязкости разрушения Кш проковка
или обработка взрывом с целью создания внутренних сжимаю-
сжимающих напряжений и локального упрочнения материала).
606 КОЭФФИЦИЕНТЫ ИНТЕНСИВНОСТИ НАПРЯЖЕНИЙ [П. I
Замечание. В настоящем приложении рассмотрены ос-
основные результаты решения конкретных задач математической
теории упругости для тел с разрезами*). Большинство из них
получено аналитическими методами, требующими на заключи-
заключительной стадии сравнительно небольшого объема вычислитель-
вычислительной работы. Применение ЭВМ и прямых вычислительных мето-
методов типа метода конечных элементов [ш] в принципе позволяет
получить решение практически любой задачи такого типа (в том
числе — с учетом любых пластических деформаций).Достаточно
сказать, что прямое решение трехмерной упруго-пластической
задачи для слоя с полуэллиптическим краевым разрезом f323] до-
доступно современным вычислительным машинам с умеренным
быстродействием. Поэтому успехи будущей механики разруше-
разрушения связаны с разработкой более принципиальных вопросов до-
критического разрушения (прежде всего усталостного и корро-
коррозионного).
*) Большой список работ по механике хрупкого разрушения и их обстоя-
обстоятельный анализ читатель может иайти в обзорной статье Д. ДЛИвлева [ш].
П. It]
ЁЯЗКОСТЬ РАЗРУШЕНИЙ ОСНОВНЫХ МАТЕРИАЛОВ
60?
OQ
О
ч
<
s
a
щ
x
3
E
E
О
s
« a
W
ы
S
о,
с
и
E
о я
X ?
I"
OQ
О
s
и
о
s
E
UJ
S»
a.
m
л
и
о
m
Of;
a
tr*
0
S
*^
к
s
я
i
Я <U Я
я « я
°
к
н условн
«ни
&?
а с
та
S
Фор
а
СЧ
cd
fi.
A
3K0CT
к
г>
к,
а
«Л
й
X
» * * *
с
с
I
<
1 Тол- !
i (- я о
; о g S
Я Щ
щнна
об-
образца,
мм
п
г*
« я
я я
И р.
сз щ
я
2
ю
НЫЙ НЗГ»
СИ
В1
о
р.
редр
СОС!
со
&5
оо
1 173 !
а
<и
s
ф
II
II
1ча-
а. к
СО ш
н
и
1 19,1 1
¦ста-!
о
LH3H3Xd
а
(D
В1
CU
ь
i
м
—'
ос
с^
сг
о
ео
со
ю
8?
' о
1§
а:
184
тем-
s
Си
с ьО
п
о
о
эо
ая ни
таль Н
реющ
вая с
со о
Q.O
си О)
В -Ч"
•*"оо"оо"о*о"
остав.
,03 Mi
,06 Ni
,005 Сс
01 Ti
10 Al
о о о о о"
с
t
со
се р,
о. <и
т
о
Я"
со
се
а.
ю
о
И
мм спов
со
V
>*¦ ю
Раст
со
¦ч*
210
1
209
a
си
s
си
в
S
3
f-.
«
ером
)СТН0
S
m
се
ч
_c_
$ча-
O-S
со аз
Ь
О
со
со"
ста-
о
ХИЭНЭХС
со
CU
3"
CU
ь
се
Ь
№
се
S
m
"•I
1
м
1
1
CQ ё^
зет1
тем-
S
О-
а
а
о
о
о
1
Ni—Со
Э^2
О,-ч
CU
Си
?<J
СЗ 0
ОчСЧ
д
остав.
звка 1 п.
:
се
И
о
Си ГГ
П CJ
_о.1О °о "^
°Я ?
s X си
ц Ю Си
CUCO Ь
о *3 S
СО О ^
1
og-oo giN
° 5 «Й 5 со
ЗЗСОСОООООО
N. 00* Ч* о" О* О* О О* О
8,63 I
со ю-зчп
ЭСОСОООООО
3) -Ч" О О О О"О О
J5;H<UG
aw
бЯЗКОСТЬ РАЗРУШЕНИЙ ОСНОВНЫХ МАТЕРИАЛОВ
{П. II
5
« 5 к
CO S и
о. я
°?&
CU «S <8
Я О О
х х а
II S |J
W A)
а, «а*
а о и
аз-
оковой
ерстия
аходи-
га
о.
>о
о g шя
и о
ss I
СО 3
0,9 ш Ч
О О.О
ЯНЕ
IS
К №
О со
8 &
со ь
О.О
3
its s
gio
- «СО
&
Ч^Р-
R
о
2
СО ^
л оо
И Ь
§?li
Н ?3 Я о.
4,0
а ш
2
П. Ill
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
609
1
а
>
г «о
3 я сцу
S m
('К
-
<1 .„
Чистый изгиС
1 «у
-
я..
-
СО
300
700
210
Вакуумная
плавка
Мартенсито-старею-
Мартенсито-стареющая никелевая сталь
Н18
[332]
-
00 Tf
Ю 00
СО О)
О> 00
ЗООМ [181]
Состав, %
С 0,007 Ti , 1,33
Мп <0,02 Ni 17,6
Si 0,001 Al 0,095
Mo 4,93 Fe—основа
Co 9,01
[332]
-
IN
i Ю-О0
¦1 — со со
0!0<NOO
— cn oo to
Hll I181]
Состав, %
С 0,4 Mo 1,4
Мп 1,35 V 0,45
Si 1,0 Fe—основа
Cr 5,0
20 Г. П. Черепанов
610
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
(П. П
{Г
omos
t- as ш я
и и о щ
К *<
rt tfi<S
«ss
n ca S3
Соя
О t? E-
Форм;
и у
исп
к
к
к
уше
2
¦й *
О
ы
т
К
W
u
й
о к,
ехнология
готовлен Hs
ли режим
мообработ]
Н « я о-
t-l
Тол-
Толщина
об-
образца.
а.
я
3 я
Ss
5 в
аименован
матер
134
CD CS OJ Ю СЧ-OJ
—' 00 Ю CD 00 С^-
ЛЛ
00 00 Ю О О- CD
СО О00 00 CD -Ч"
00 О С^- CD C75 CD
Я о о «G~
куумная
ка с рас
:ым элей
Темпе
отпуска
149
204
260
316
371
427
та ш g • со
CQ CO <D S С1^
2,54
i
СО
я
о
к
ю о
g° О|00_ О
О— I
1—' о
§ U rcoooitG
¦* о'о'о'о"
1 1
¦—<
СО -^ *Р
о о со
СО t^ CD
CD О» 00
СП 00 CD
JSJ 4340
<
ш
OONO
00 00 00 ^
OOtNOO
— aioo cd
о
s
irsteel X
<
| |
to
I—<
•1-
220
166
2,0
О
8
irsteel X
<
i—¦
c^-oo oo ^
—• (N CM О
00 ^ "^ C^-
O CD CM 00
—i СП 00 CD
cs — —¦ —н
MS 6434
<
'—'
о
CO
300
168
о
of
000
ascojet 1
П. II]
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
611
N
со
со
120
210
Vascojet 1000
C32]
211 -s- 270
208 ¦*¦ 246
345
458
о со oq оо
— СП 00 CD
Ladish D6AC
[335]
•1-
.О
ю
то
168
O'S
Ladish D6AC
[332]
271
168
РН15-7МО [ш]
Состав, %
С <0,09 Мп <1,0
Si <l,0 Сг 15,0
Мо 2,5 Ni 7,0
А1 1,0 Fe—основа
[332]
Ч"
о
•1-
СП
AM 355
[332]
сч — о
CN CN CN
то t-^ -ч1
ТО Ч" Ю
17-7РН [ш]
Состав, %
С <0,09 Мп <1,0
Si < 1,0 Сг 17,0
Ni 7,1 Fe—основа
AI 1,0
[332]
in
о
oin
00 CD
Super Ну Tuf
[332]
160 ¦*¦ 205
125
160
185 ¦*- 265
210
ооюоп
СП СП t"^ CD 1П
,.
20*
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
[П. II
О x ч«
«ВШИ
к
ш
о
ч
и
к*
м§
м|
«S
03
X
&
е ¦
к
в
аз
о
а Д.
о
о
1
О
4
г-!
о С
К
К К
«SJI-
?5*8
Тол-
шина
об-
образца,
мм
арка
г«
«5
овани
атери;
Г
а
X
«о
250
200
246
282
О Оэ 1Л —< ^
^D 00 t4^ Ю 1Л
Я—' —'—'—•
S3
со
005
180
5^-
ёо
04
О [^ СП <М
00 00 <МС0
— " <М (М
О5 00 с?> Ю
( |
со
ю
со
а.о
Ей
о
1-8
о о ex
S я я
¦—¦«
" ^ о
"* о-"ё
И о :
W « |
я.©
1Л
И
о
о
W
СО
^^^
м
rt
Ю Ю
COCO
•1- -1-
о ю
in t^-
ш ю
:В40
a
л
(Л
840
•1-
о
00
00
•1-
g
S
2,0
я- с ._ о
ь
о
t^ о ...
GCX-
С
0,38
1,65
0,014
1,78
П. II]
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
613
ц
|8
ю
¦I-
о
н
S
S
S
ь u я
Onfi1
Ss-2
ss
"I
О
CO
ю
11
11
О.
С9
а
я
V
ш
к
a
а
s
V
go
га —_
1
33
S
614
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
[П. II
V
D
о к ч^
р аз о к
У К cq К
К у
К
К
ш
:ло
^е
а к
я
Я"
S
1
? 3
fs
о
BJ
р.
О
©
ь разру-
кГ/мм ¦"
с; о:
Вязко
шени
о" .$
А**
нология
товления
[ режим
обработки
Тех
НЗГО'
или
термо
^§ ¦ in
н 5° S3 ^
^ а
СХ
Наименование (м;
материала
лка
°С, охла-
Зака
930
Сталь ВЛ-1Д
о
Состав, %
е на воз-
Отпуск в
е 3 часов
мпературе
s s ш
о
(N
О СО СП
0} 1О ^"
о'о" о"
С 0,30 Si
Мп 0,92 Сг
Ni 1,0 Mo
W 1,07
m m
га о
D- CQ
\о м
о <->
а а
в«
си о
R S
||
Is
д
UJ U
U
О ш
а
со
со
S
о
а
о
о.
f"
i
о 1
а ч>Т
ю оо ю
СП СО Ю (N
ююйю
— МОП
г-ю —
•-^ w^ w^
«—1
о оо оо со
rf (N СП ТР
оос
г
отпуска
без
|лка
Зака
Сталь ВКС-1
"С, охла-
е на воз-
940
сдени
о я
Отпуск в
е 3 часов
ухе.
ечени
ч t~
о
мпературе
<и
ш
00 —ЮСО
O_O_t^_lC
-о-
-о
(N —
ю-*
00 1-—
— (N
t^ сп
ю со
270
отпуска
без
Состав, %
С 0,39 Si
Мп 0,83 S
Р 0,008 Сг
Ni 0,65 Mo
V 0,07
en a
га qj
о. а
д О
а^
3^
Q.1N
Ю V
°S
ojoB
lx
Is
к со
о S
га о
В
S
1лка
С в масло,
So
«55
и
О_
<N
00
Л
ч
га
Углеродистая ст
а
я
а
0J
о.
«я
о
в
га
о.
:при190°С
тпуск
о
ft. ill
S#3JCOCfb РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
615
[338]
Осевое растяжение образ-
образцов размером 75X19X9 мм
с односторонним расположе-
расположением усталостной трещины
/=+40°С
>=+20°С
у-
5» Ей*-.
9,0
Мп—Сг—Мо—V
(сталь, содержащая
1,5% Мп)
[339]
226
142
Сталь 40 ХН
[339,
182
Сталь 35 ГС
[339]
$ $ 2
Горячая про-
прокатка и естест-
естественное старение
Отжиг 950 °С
2 часа
ММТО (четы-
(четырехкратное де-
деформирование на
длину площадки
текучести при
комнатной темпе-
температуре с проме-
промежуточным старе-
старением при 100°С
в течение 6 ча-
часов)
Сталь Ст. 3
[339]
^* о
Горячекатан-
ная
М'МТО
Сталь 20
616
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
[П. II
о.
т
ь
<п
К
СП
о*
.\
о
¦ В
sS
S3
о *
ев
сх
S
©
К
шени
т
сч а*
^и
Технология
«готовления
или режим
рмообработки
У-
*
Тол-
Толщина
образ-
образца,
JKJK
"с?
а.
аименован
матер
а
in -ф
•* со
00 Ч ^** *
В О
240
со
58
со
ю
Закалка и
скусственное
тарение на
аксимальную
s о г
,5
,3
-0,35
,20
00
ю г? о*
7075-Т6
Со ста
0,40
1,2—2,0 1
2,1—2,9
5,1-6,1
рочность
с
яме-
о.
- основа
ние 4)
<
а
5разцо1
о
<и
S
03
(U
к
га
238
о
S
Закалка и
а
7075-Т6 (
т
5 а
ч о.
центра
с в ве
3 мм
ко
? «. .,
—Тога
«II
1
X X X Ч»|
197
О)
00
,
см"
скусственное
гарение
к о
см
со
см см
СО СМ
ССО>
С3> t^
о» —
см"-"
1Л 1С
со" см"
7075-Т65
та
СО
¦1-
О
см
S3
ю
о
Отжиг
д
t
S
о
бразцо
Ч)
я
к
f?
229
со
оо"
ю
СО
•—
Закалка и
S
га
7075-Т6
?*
со
d.
К
ст
о
° 1
03*
О. 03
4
скусственное
тарение
я о
П. II]
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
617
*
in
295
47,1
37,3
Закалка и
холодное Де-
Деформирование
2024-ТЗ (Д16)
04
250
31,6
23,1
Закалка и
искусственное
старение .
6061-Т6(АДЗЗ)
Состав, %
Si 0,1—0,8 Fe 0,1 MnO,15
Си 0,15—0,40 Ti 0,15Zn0,25
Mg 0,8—1,2 Cr 0,04—0,35
Al — основа (см. приме-
примечание 4)
04
{О
240 >
45,0
29,5
Закалка и
естественное
старение
2024-Т6(Д16)
п
Осевое растяжение образ-
образцов с центральной трещиной
130
59,3
53,9
Старение
при темпера-
температуре 170 °С в
течеиие 14 ча-'
сов
ВАД-23Т1
260
53,5
52,0
Старение
при темпера-
температуре 120 °С в
течение 24 ча-
часов
В95-Т1
245
45,8
39,2
Старение
при темпера-
температуре 190 °С в
течение 12 ча-
часов
Д16-Т1
о
39,6
34,5
То же
АК4-1Т1
300
46,5
те
со
Естествен-
Естественное старение
618
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
[П. II
о
Источ
ник
сведе-
сведений
Форма образца и условия
испытаиий
Вязкость разру-
разрушения, кГ1ммъ1*
*
•Л
Технология
изготовления
илн режим
термообработки
Тол-
Толщина
образ-
образца,
мм
Наименование (марка)
материала
СО
Растяжение образцов
шириной 406,4 мм с
центральной трещиной
о II со Н
47,8
42,2
Закалка и
искусственное
старение
«5
20I4-T6 (АК8)
Состав, %
Si 0,5—1,2 Fe 0,7 Cr 0,1
Cu 3,9—5,0 Zn 0,25 Ti 0,15
Mn 0,4—1,2 Mg 0,2—0,8
Al — основа (см. примечание 4)
То же
3-
2020-Т6
8.SH
да.
to
оо
н
а.1н
Закалка и
искусственное
старение
1,6
7079-Т6
П. I1J
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
619
лавы
в
и
2
«
о
Т итаи
|
ник
веле-
иий
рма образца и
овия нспытаиий
о ч
&•
со
«
1 Вязкое
f
шения,
в с
М-Л.
а
5 °
g«
°i
СО Р.
f-
Sa
олоп
|ежи
я "•
х а
н а
СО А
Ч К =0 ю
с
ь
а сиг»
а о
Я
о.
я
5=0
ш я
? IS
К О.
Я dJ
я <-
§ я
2
S
СО
я
о m
-5-00
[332]
ю
175-5-25
145
140
1 ЯЯ-=-10
О COIN —-*
¦*СМ —О5 00
сВ
ffl
I
н
[оог]
1есимметрич-
i трехточечный
иб
а
го
о
го
оо
о
ср
о
О 0)
<а с 870 °С в в
гние при темп
ч о-
га л
го о
>ч
4
о
^— 1
ю
ffl
S
0>
S
ЮО °С в течен
?8
t- В1
га
р. оо
[етырехточеч-
i изгиб и рас-
хение образца
боковой тре-
иой
j »5 а
в f о я
о
+1 ==
400:
105
S
i <L) UJ
L^ S S
- при 950 °С в 1
часа, старен
) °С в течен
*"О В
S со о
? си о
Ogag
3 о.
В1 С СМ
о
1
N
со
н
То же
о
+|-
290:
8
о
о>
t
0)
¦при950°Свт
'ЖИГ
О
С
Т
со
[329 J
а
часа, старен
"С в течен
~
в
0)
в1
^ а
а ?
о.
сем
астяжение
азца с боко-
t надрезом
О. О- ?
О ffl
см —|
141
S
¦ при 840 °С в те
часа, старени
"С в течени
« о
а — оо я
м ¦* о
? си с
5 о.9
В1 ЕГ-*
С
ю
см"
1
1
со
I
н
астяжеиие
азца с одной
эвой треши-
О ю И
о
ю
00
1
со си си
Ь м я
при 1000 °С в
часа, старен]
°С в течен]
« •*? о
я а а
AS га
О в я з-
So-
В1 С ¦*
Sn —
СМ
N
со
¦Ц
О
620
ВЯЗКОСТЬ РАЗРУШЕНИЯ ОСНОВНЫХ МАТЕРИАЛОВ
1П. 11
алы
тери
неметаллические ма
Источ-
Источник
сведе-
НИИ
Форма образца и условия
испытаний .
Вязкость
разрушения,
кГ/мм'Ь
*
.'*
к
¦ а
Технология
изготовления или
режим термо-
термообработки
Тол-
щииа
образ-
образца,
мм
Наименование (иарка)
материала
ластин раз-
мм с цен-
той
8 1 **¦
.а ю Ь
Растяже
.мером 400
тральной 1
n
о
f
Состояние
поставки
Силикатное стекло
Состав, %
SiO2 72,68 R2O3 1,17
MgO 3,8 Na2O 13,73
CaO 7,73 SO3 0,89
Растяжение пластин раз-
размером 230X470 мм с цен-
центральной трещиной
2,9
а;
о
|"
6,0
Органическое стекло
Растяжение пластин с цен-
центральной трещиной.
Длина начальной трещины
составляет '/4 ширины пла-
пластины
0,5
Смотровое стекло
B% относнтельной
влажности)
0,7
0,5
Смотровое стекло
(влажное)
4,5
Литые пла-
пластины
Зн-12
Полиметилметакрилат
2,5
СО
Полиэфир (пластины)
ю
о*
Дерево
С га ^
л) о m «
* I s s .
я e a я °°
ПРИЛОЖЕНИЕ III
НЕКОТОРЫЕ ПАРЫ МЕТАЛЛ — СРЕДА, ДЛЯ КОТОРЫХ
НАБЛЮДАЕТСЯ ХРУПКОЕ РАЗРУШЕНИЕ МАТЕРИАЛА,
ПОДВЕРЖЕННОГО РАСТЯГИВАЮЩИМ НАПРЯЖЕНИЯМ
Сплав
Алюминиевые сплавы:
Al-Zn
Al-Mg
Al-Mg- 1
Al-Cu-Mg }
AI-Mg-Zn J
Al-Zn-Cu
Al-Zn—Mg—Mn )
Al—Zn—Mg—Cu—Mn I
Al—Cu—Mg—Mn
Al-Cu
Al-Mg
Al-Zn-Mg
Al—Zn—3Mg-
Чистый алюминий
Магниевые сплавы:
Mg-Al
Mg-Al-Zn—Mn
Mg
Mg—Zn—Zr
Среда
Воздух
Растворы NaCl + H2O2) NaCl, воз-
дух
Морская вода
Растворы NaCl, NaCl + Н2О2
Морская вода
Растворы NaCl + Н2О2
Растворы NaCl + H2O2, NaCl,
NaCl + NaHCO3, KC1, MgCl2
Растворы СаС12, NH4CI, CoCl2
Дистиллированная вода, СН3ОН,
CCL4
1 % раствор NaCl в воде
В растворах-. NaCl, NH4C1, BC12,
СаС12, MgCl2, ZnCl2, KF, N2SO4,
A12(SO4K) NaNO3, KNO3, A1(NO3K>
NaHPO4) Na3PO4, Na2CO3) NaHCO3,
(NH4JCO,, Na2B4O7, Na2Cr04)
K2Cr207, Na2SiF6, Na2SO3, Na2S2O7,
(NH4JS2O5> Na2S2O4, KMnO4, H2O2
Растворы HNO3, NaOH, HF, ди-
дистиллированная вода
Растворы NaCl + H2O2, NaCl +
+ KjCrO4) влажный воздух + SO2 +
+ CO2
Раствор KHF2
Раствор NaCl
Источник
сведений
l172l
[848]
[349]
[350]
[172]
[Ml]
622
НЕКОТОРЫЕ ПАРЫ МЕТАЛЛ - СРЕДА
[П. 111
Продолжение
Сплав
Mg—Mn—Ge
Mg-Mn-Ge-Al
Mg-Mn-Nb-Ni
Mg-Al-Cd-Ag—Mn
Mg-Sn
Mg-Al
Mg-AI-Zn-Mn
Медные сплавы:
Cu—Zn )
Си—Zn—Sn }
Cu-Zn-Pb J
Си—Sn—P
Си—Zn
Си—Zn—Ni 1
Си—Sn j
Cu-Zn-P 1
Cu-As |
Си—Р, Си—As, Си—Sb, 1
Cu-Ni, Cu-Al, Си-Si \
Си—Zn, Си—Si—Mn J
Си—Si—Mn
Си—Zn—Sn—Mn
Си—Аи
Си—Zn,
Си—Zn—Mn
Cu-Mn
Си—Zn с небольшими до-
добавками AI, As, Be, B, Cd,
Co, Au, Pb, Mn, Ni, Pd,
Ag, Sr, Tm, Sn, Sb, Ba,
Bi, Ca, Ce, Cr, Fe, Mg, P,
Si, Те, Ti, Zr, Li, Nb, Mo,
K, Se, Na, S, Та
Cu—Ni—Si
Cu-Al—Fe
Cu—Be
Cu—AI
Среда
Раствор NaCl, влажная атмосфера
Растворы NaCl + K2Cr04, Na2SO4,
H2SO4, Na2CO3, воздух
Растворы CH3COOH, NaCl, KC1,
вода, воздух
Пары и растворы NH3
Концентрированный NH4OH
Амины
Пары и растворы NH3
Воздух
Влажная атмосфера NH3
Пары воды
Вода
Растворы NH4OH, FeCl3, HNO3
Влажный SO2, растворы Cu(NO2J
Влажный SO2) Cu(NO2J, H2SO4>
HC1, растворы HNO3 '
Влажная атмосфера NH3
Влажная атмосфера NH3
Пар
Влажная атмосфера Н3
Пары NH3, растворы NH3
Источник
сведений
[171]
[.72]
[.72]
[Ш]
П. III]
НЕКОТОРЫЕ ПАРЫ МЕТАЛЛ - СРЕДА
623
Продолжение
Сплав
Сплавы на основе железа:
Малоуглеродистая сталь
Fe—Cr—С
Fe—Ni—Cr
Fe—Co—Cr
Fe—Ni-C
Fe—Cr—Ni—С
Сплавы на основе никеля:
Ni
Ni-Cr—Fe
Среда
NaOH+ Na2Si03, Ca(NO3J,
NH4NO3 и растворы NaNO3, HCN +
+ SnCl2 + AsCl2 + CHC13.
Раствор Na3PO4.
Раствор чистого NaOH, NH3 +
+ CO2 + H2S + HCN.
Растворы NaOH, КОН; раствор
моноэтаноламина + H2S + CO2.
Fe(A!O2K + A12O3 + раствор СаО,
HNO3 + H2SO4, MgCl2 + раствор
IN dr.
Безводный жидкий NH3.
Среда H2S.
Раствор FeCl3.
Растворы KNO3, LiNO3, NaNO3+
+ HC1, NaNO3 + HNO3, MnCl +
+ NaNO3, NaNO3 + MnSO4,
KMnO4 + NaNO3
NH4CI, MgCl2, (NH4)H2PO4.
Растворы Na2HPO4.
H2SO4 + раствор NaC].
NaCl + раствор Н2О2, морская
вода.
Растворы H2S
Раствор H2SO4
HC1+H2SO4, пар, растворы H2S
NaCl + раствор Н2О2, морская
вода.
H2SO4 + раствор CuSO4, MgCl2,
СоС12.
NaCl, растворы ВаС12, СН3СН2С1+
+ вода, LiCl, ZnCl2, СаС12 растворы
NH4C1, (NH4JCO3, NaCl, NaF, NaBr,
Nal, NaH2PO4, Na3PO4, Na2SO4,
NaNO3, Na2SO3, NaC103, раствор
NaC2H3O2.
Пар + хлориды, растворы H2S.
Раствор NaCl + NH4NO2,- раствор
NaCl + NaNO2.
Политионовые кислоты
Растворы NaOH, КОН, расплав
NaOH.
NaOH + сульфидный раствор, пар
Источник
сведений
[.72]
[171J
[362]
[.72]
[.72]
624
НЕКОТОРЫЕ ПАРЫ МЕТАЛЛ — СРЕДА
[П. III
Продолжение
Сплав
Ni—Си
Ni—Си—А1 1
Ni—Си
Ni-Al
Ni-Cr—Fe
Ni—Cr—Fe—Ti
A1S1 4340
300M \
D6Ac )
vioooj
300M
Ni—Co—Mo
Сплавы титана
Ti—6A1—4V
Ti
Ti_13V— llCr-3Al
Ti—5A1—2.6A1
Ti-8-Al-lMo-lV
Другие сплавы
Аи—Си—Ag
Си—Аи
Ag—Аи
Ag-Pt
Pb
V—Zr—Cr
V—Ti-Cr
Среда
Расплав NaOH, раствор H2SiFe,
хромовая кислота, сульфированное
масло, пар
Пары HF
Морская атмосфера, вода, СС14
NaCl, NaNO3, Na2SO4) NaPO3
Чернила, дистиллированная вода,
амиловый спирт, бутиловый спирт,
бутилацетат, ацетон, смазочное ма-
масло, бензол
Дистиллированная вода, соленая
вода, индустриальная и приморская
атмосфера, трихлорэтилен,
6% NaCl + 1,5% Na2Cr207
NaCl в твердом состоянии при
290 "С, электролиты при комнатных
условиях
N2O4 в жидком состоянии
Красная дымящаяся азотная кис-
кислота, 10%-ные растворы НО
В искусственной морской воде
C,5% NaCl +0,5% MgCl2)
В 10%-ном растворе соляной кис-
кислоты
В случае нанесения смеси LiCl,
КС1 при 335 °С
Растворы FeCl2
HNO3 + HCI, HNO3, FeCls, рас-
растворы NH4OH
NHO3 + НС1, HNO3, растворы
FeCl3.
Растворы FeCl3.
Растворы Pb(OAcJ + HNO3, воз-
воздух
Жидкий натрий с незначительной
концентрацией кислорода
Источник
сведений
С72]
[171]
[,72]
[¦72]
[¦72]
[353]
П. Ill]
НЕКОТОРЫЕ ПАРЫ МЕТАЛЛ — СРЕДА
625
Продолжение
Сплав
Среда
Источник
сведений
Мп—Си—Ni
Zr
Хромо-никелевые сплавы
Cr.-Ni
Аустенитная сталь
0Х17Н7М2, 0Х17Н7М2Б,
0Х17Н7М2Ю, 0Х17Н7Д2Б;
Х21Н5Т, Х18Н10Т
0XI8H9, 1Х18Н9,
Х23Н23МЗДЗ
ЗОХГСНА
Х17Н2, Х17Н5МЗ
A1S1 304
18Сг—10Ni
Воздух, Н2О, растворы NaCl
Растворы FeCl3
Вода, водяной пар, H2SO4, 25%
NaCl+0,5% K2Cr207, в кипящем
HNO3> Ш HNO3 + 2% HF
5% HNO3 + 0,3% FeCl3) CHCI3, CC14,
C2H6C1, MgCl2,
CaCl2, ZnCl2, NaCl, KC1, NH4Cl,
CrCl3, FeCl3, HgCl2
В кипящем растворе 42% MgCI2 +
+3% FeClj
В кипящем ' растворе CuSO4 +
+ 5Н2О, HiSO4
В 20% H2SO4 + NaCl C0 г/л),-
20% H2SO,, 3% NaCl, 3% NaCl +
+ 0,1% H2O2
В 20% растворе NaCl (кипящем)
FeCl3l CuCl2, NaOH, H2Cr04
В растворах хлоридов ZnCl2, NaCl
(насыщенный), 20% NaCl +
+ FeCl3.6H2O, FeCl3-6H2O,
CuSO45H2O, Cr2(SG4KI8H2O,
уксусно-кислый натрий, Na2SO4,
NaCO3, Na2HPCvl2H2O, K2Cr04,
Na2Cr207 • 2H2O, NaNO2, NaNO3,
3% NaCl + Na2Cr207 • 2H2O,
3% NaCl + KC1 (насыщенный),
NH4C1, CaCl2-2H2O, NaCl, KC1
I171]
[1721
I354]
[3.1]
[355]
[355]
[357]
f.72]
ЛИТЕРАТУРА
1. Седов Л. И., Механика сплошной среды, т. I и II, «Наука», М., 1970.
2. Новожилов В. В., О связи между напряжениями и упругими дефор-
деформациями в поликристаллах, в сб. «Проблемы гидродинамики и механики
сплошной среды» (к 60-летию академика Л. И. Седова), «Наука», М.,
1969.
3. Н а д а и А., Пластичность и разрушение твердых тел, перев. с англ., т. I,
ИЛ, 1954, т. II, «Мир», М., 1969.
4. Р а б о т н о в Ю. Н., Ползучесть элементов конструкций, «Наука», М.,
1966.
5. X и л.л Р^ Математическая теория пластичности, перев. с англ., Гостех-
издат, М., 1956.
6. Койтер В. Т., Общие теоремы упруго-пластических сред, ИЛ, 1961.
7. С о к о л о в с к и й В. В., Теория пластичности, «Наука», М., 1966.
8. И в л е в Д. Д., Теория идеальной пластичности, «Наука», М., 1966.
9. Griffith A. A., The phenomenon of rupture and flow in solids, Phil.
¦ Trans. Roy. Soc. A221, 1920, pp. 163—198.
10. I г win G. R., Fracture dynamics, в книге «Fracturing of Metals», ASM,
Cleveland, 1948, pp. 147—166.
11. Orowan E. O., Fundamentals of brittle behavior of metals, в книге
«Fatigue and, Fracture of Metals» (Murray W. M., ed.), Wiley, New York
1950, pp. 139—167.
12. Irwin G. R., Analysis of stresses and strains near the end of a crack
traversing a plate, J. Appl. Mech. 24, 1957, pp. 361—364.
13. Черепанов Г. П., О прочности композитов, ПМТФ № 3, 1967.
14. Ландау Л. Д., Лифшиц Е. М., Теория поля, «Наука», М., 1967.
15. Мотт Н., С не д дон И., Волновая механика и ее применения, перев.
с англ., «Наука», М., 1966.
16. Лейбфрид Г., Микроскопическая теория механических и тепловых
свойств кристаллов, перев. с нем., Физматгиз, М., 1963.
17. И о ф ф е А. Ф., Физика кристаллов, Госиздат, М., 1929.
18. П а н а с ю к В. В., Предельное равновесие хрупких тел с трещинами,
«Наукова думка», Киев, 1968.
19. Gilman J. J., Cleavage, ductility and tenacity in crystals, в сб. Fracture,
Wiley, New York, 1959 (русский перев.: Гилман Дж., Скол, пластич-
пластичность и вязкость кристаллов, в сб. «Атомный механизм разрушения», Ме-
таллургиздат, М., 1963).
20. Ch e rep a n о v G. P., On crack propagation in solids, Int. J. Solids &
Structures 5, 1969, pp. 863—871.
21. Черепанов Г. П., О сингулярных решениях в теории упругости, веб.
«Механика твердого деформированного тела» (к 60-летию академика
В. В. Новожилова), «Судостроение», Л., 1970.
22. Ильюшин А. А., Пластичность, Изд-во АН СССР, М., 1965. '
23. Мусхелишвили Н. И., Некоторые основные задачи математической
теории упругости, изд. 5-е, «Наука», М., 1966.
ЛИТЕРАТУРА 627
24. Б е л о н о с о в С. М., Основные плоские статические задачи теории упру-
упругости для односвязных и двусвязных областей, Изд-во Сиб. отд. АН
СССР, Новосибирск, 1962.
25. К у р ош А. Г., Теория групп, «Наука», М., 1967.
26. Michell J. H.,'Elementary distributions of plane stress, Proc. London
Math. Soc. 32, 1901.
27. Car others S. D., Plane strain in a wedge, Proc. Roy. Soc. 23, Edin-
Edinburgh, 1912.
28. ,W i 11 i a m s M. L, Stress singularities resulting from various boundary
conditions in angular corners of plates in extension, J. Appl. Mech 19,
№ 4, 1952.
29. Кала нд и я А. И., Замечание об особенности упругих решений вблизи
углов, ПММ 33, вып. 1, 1969.
30. Sternberg E., Ко Her W. Т., The wedge under a concentrated couple:
a paradox in the two-dimensional theory of elasticity, J. Appl. Mech. 25,
№ 4, 1958 (русский перев.: Штернберг Е., Койтер В., Клин под
действием сосредоточенного момента, парадокс в плоской теории упру-
упругости, «Механика», сб. переводов, № 3 E5), ИЛ, 1959).
31. Нейбер Г., Концентрация напряжений, перев. с нем., Гостехиздат, М.,
1947.
32. Лурье А. И., Теория упругости, «Наука», М., 1970.
33. У ф л я н д Я. С, Интегральные преобразования в задачах теории упру-
упругости, «Наука», Л., 1967.
34. Лехницкий С. Г., Теория упругости анизотропного тела, Гостехиздат,
М., 1950.
35. Fracture Toughness Testing and Its Applications, Sympos. Chicago 1964,
Philadelphia 1965 (Amer. Soc. Test. Mat.) (русский перев.-. Прикладные
вопррсы вязкости разрушения, сб. переводов, «Мир», М., 1968).
36. Z a k A. R., Williams M. L., Crack point stress singularities at bima-
terial interface, Trans. ASME, ser. E, J. Appl. Mech. 30, № 1, 1963, p. 142.
37. Новожилов В. В., Теория упругости, Судпромгиз, Л., 1958.
38. Черепанов Г. П., О распространении трещин в сплошной среде,
ПММ 31, вып. 3, 1967.
39. Rice J. R., R ose n g r e n G. F., Plane strain deformation near a crack
tip in a power law hardening material, J. Mech. Phys. Solids 16, 1968, p. 1.
40. Галин Л. А., Контактные задачи теории упругости, Гостехиздат, М., 1953.
41. Майе A. W., Die Beugung elastischer Wellen an der Halbebene, ZAMM
33, H. 1/2, 1953, S. 1—10.
42 Sommerfeld A., Vorlesungen iiber theoretische Physik, Bd. IV, Optik,
Wiesbaden, 1950.
43. Нобл Б., Метод Винера — Хопфа, ИЛ, 1962.
44 Майе A. W., Die Entspannungswelle bei plotzlichem Einschnitt eines
gespannten elastischen Korpers, ZAMM 34, H. 1/2, 1954, S. 1—12.
45 С h e г e p a n о v G. P., Cracks in solids, Int. J. Solids & Structures 4,
1968, pp. 811—831.
46 Мусхелишвили Н. И., Сингулярные интегральные уравнения, изд.
3-е, «Наука», М., 1967.
47. Г а х о в Ф. Д., Краевые задачи, Физматгиз, М., 1963.
48. Б а р е н б л а т т Г. И., Черепанов Г. П., О конечности напряжений
на краю произвольной трещины, ПММ 25, вып. 4, 1961.
49. Mechanics of Fracture. Series edited by G. С Sih, Lehigh Univ. Press,
vol. 1. «Methods of Analysis and Solution of Crack Problems», 1973.
50. Черепанов Г. П., Одна задача о вдавливании индентора, ПММ 27,
вып. 1, 1963.
51. Erdogan F., Sih G. С. On the crack extension in plates under plane
loading and transverse shear, Trans. ASME, ser. D, 85, № 4, 1963,
pp. 519—527.
628 ЛИТЕРАТУРА
52. Панасюк В. В., Бережницкий Л. Т., Определение предельных
усилий при растяжении пластины с дугообразной трещиной, в сб. «Во-
«Вопросы механики реального твердого тела», вып. 3, «Наукова думка»,
Киев, 1964.
53. К у др явце в Б А., Партон В. 3., Песков,Ю. А., Черепа-
Черепанов Г. П., О локальной пластической зоне вблизи конца щели МТТ
№ 1, 1970.
54. D u g d a I e D. S., Y i е 1 d i n g of steel sheets containing slits, J. Mech.
. Phys. Solids 8, № 2, 1960.
55. Кудрявцев Б. А., Партон В. 3., Песков Ю. А., Черепа-
Черепанов Г. П., О локальной пластической зоне вблизи конца щели (плоская
деформация), МТТ № 5, 1970.
56. Levy N.. Marcal P. V., Ostergren W. J., Rice J. R., Small scale
yielding near -a crack in plane strain: a finite element analysis Techn.
Report NASA NGL 40-002-080/1 to the National Aeronautics and Space
Administration, Nov., 1969.
57. Черепанов Г. П., Упруго-пластическая задача в условиях антипло-
антиплоской деформации, ПММ 26, вып. 4, 1962.
58. Ни It J. A. H., McClintock F. A., Elastic-plastic stress and strain
distributions around sharp notches under repeated shear, 9th Intern. Congr.
for Appl. Mech., Brussels 1957, vol. 8, pp. 51—58 (русский перев. в сб.
«Механика» № 5, ИЛ, 1959).
59. Френкель Я. И., Теория обратимых и необратимых трещин в твердых
телах, ЖТФ 22, 1952, стр. 1857—1866.
60. Черепанов Г. П., О росте трещин при циклическом нагружении,
ПМТФ № 6, 1968.
61. Д роздовский Б. А., Маркочев В. М., Фридман Я- Б., Диа-
Диаграммы разрушения твердых тел, ДАН СССР 174, № 4, 1967.
62. Галин Л. А., Фридман Я- Б., Черепанов Г. П., Моро-
Морозов Е. М., П а р т о н В. 3., Об условии в конце трещины, ДАН СССР
189, № 3, 1970.
63. Paris P. С, The fracture mechanics approach to fatigue, в сб. «Fatigue»,
Proc. 10th Sagamore Army Mater. Res. Conf., 1963, Syracuse Univ. Press,
1964.
64. Халманов Х., Черепанов Г. П., Анализ экспериментальных дан-
данных по развитию усталостных трещин, ПМТФ № 6, 1970.
65. Cherepanov G. Р., Н а 1 m a n о v H., On the theory of fatigue crack
growth, Engng Fracture Mech. 4, № 2, 1972.
66. Freund L. В., Crack propagation in an elastic solid subjected to general
loadings, J. Mech. Phys. Solids 20, 1972, pp. 129—152.
67. I r w i n G. R., К i e s J. A., Smith H. L, Fracture strength relative to
onset and arrest of crack propagation, Proc. Amer. Soc. Test. Mater. 58,
1958, p. 640.
68. С е р е н с е н С. В., М а х у т о в Н. А., Механические закономерности
хрупкого разрушения. Автоматическая сварка, № 8, 1967.
69. О р о в а н Е., Классическая и флокационная теория хрупкого разруше-
разрушения, в сб. «Атомный механизм разрушения», Металлургиздат, М., 1963.
70 Р а б о т н о в Ю. Н., Модель упруго-пластической среды с запаздыванием
текучести, ПМТФ № 3, 1968.
71. Зенкова Э. К., Крапотин В. Н., Мальцев М. В., Кинетика
распространения трещин в сплаве АЦМ при замедленном разрушении.
Физико-химическая механика материалов 6, № 1, «Наукова думка»,
Киев, 1970.
72 Johnson H. H., Paris Р. С, Sub-critical flaw growth, J. Engng
Fracture Mech. 1, № 1, 1968, pp. 3—45.
73. 4 e p e n а н о в Г, П., О развитии трещин в вязких телах, МТТ № 1,
1969.
ЛИТЕРАТУРА 629
74. Р о м а и и в О. Н.( Д у д и н В. А., 3 и м а Ю. В., Некоторые особенности
распространения трещин в закаленных сталях при замедленном разруше-
разрушении, Физико-химическая механика материалов 6, № 1, «Наукова думка»
Киев, 1970.
75. Чувствительность механических свойств к действию среды, сб. статей,
перев. с англ., «Мир», М., 1969.
76. Z h u r k о v S. N., Kinetic concept of the strength of solids, Int J Frac-
Fracture Mech. 1, № 4, 1965.
77. Л и x т м а н В. И., Ребиадер П. А., Карпенко Г. В., Влияние по-
поверхностно-активной среды на процессы деформации металлов, Изд-во
АН СССР, М., 1954.
78. Лихтман В. И., Щукин Е. Д., Ребиндер П. А., Физико-химиче-
Физико-химическая механика металлов, Изд-во АН СССР, М., 1962.
79. Черепанов Г. П., О квазихрупком разрушении, ПММ 32, вып 6
1968.
80. Черепанов Г. П., О горении в узких полостях, ПМТФ № 2, 1970.
81. D une g an H. L, Tetelman A. S., Non-destructive characterization of
hydrogen-embrittlement cracking by acoustic emission techniques, Engng
Fracture Mech. 2, № 4, 1971.
82. D u n e g a n H. L., Harris D. O., T a t г о С. A., Fracture analysis by
use of acoustic emission, Engng Fracture Mech. t, № 1, 1968, pp. 105—
123.
83. Галин Л. А., Рябов В. А., Федосеев Д. В., Черепанов Г. П.,
О разрушении высокопрочного стекла, ДАН СССР 169, № 5, 1966.
84. Галин Л. А., Черепанов Г. П., О самоподдерживающемся разруше-
разрушении напряженного хрупкого тела, ДАН СССР 167, № 3, 1966.
85. Черепанов Г. П., Соколинский В. Б., О разрушении хрупких
тел при соударении, Труды конференции по контактным задачам, «Ма-
«Машиностроение», М., 1969.
86. А вершин С. Г., Мосинец В. Н., Черепанов Г. П., О природе
горного удара, ДАН СССР 204, № 3, 1972.
87. Черепанов Г. П., Хрупкая прочность сосудов под давлением, ПМТФ
№ 6, 1969.
88. Панасюк В. В., Ко.вчик С. Е., Влияние поверхностно-активной
среды на поверхностную энергию хрупкого тела, ДАН СССР 146, № 1,
1962.
89. Черепанов Г. П., Каплун А. Б., Карасе в Л. П., К у т е п о-
в а Л. И., Рабочая методика определения энергии разрушения металла,
Физико-химическая механика материалов 6, № 1, «Наукова думка»,
Киев, 1970.
90. Boyle R. W., Sullivan А. М., К г a f f t J. M., Determinations of pla-
plane-strain fracture toughness with sharply notched sheets, Amer. Weld. J.
Res. Supplement 41 (9), 428S, 1962.
91. I r win G. R., Fracture, Handbuch der Physik, Bd. 6, Springer-Verlag,
Berlin, 1958, S. 551—590.
92. Прочность стекла, сб. статей, перев. с англ., «Мир», М., 1969.
93. Williams M. L., Some observations regarding the stress field near the
point of a crack, Proc. Crack Propagation Symp., Cranfield (England),
Cranfield College Aeronaut. 1, 1962.
94. Wells A. A., Application of fracture mechanics at and beyond general
yielding, Brit. Weld. J. 10, № 11, 1963.
95. M с С 1 i n t о с k F. A., Ductile fracture instability in shear, J. Appl. Mech.
25, № 4, 1958.
96. Леонов М. Я., Панасюк В. В., Розвиток найдрибшших трицин b
твердому тш, Прикладна механша, вып. 5, 1959.
97. Новожилов В. В., О необходимом и достаточном критерии хрупкой
прочности, ПММ 33, вып. 2, 1969.
630 ЛИТЕРАТУРА
98. Новожилов В. В., К основам теории равновесных трещин в упругих
телах, ПММ 33, вып. 5, 1969. *
99. Авершин С. Г., Горные удары, Углетехиздат, М., 1955.
100. Труды V Международного горного конгресса, «Недра», М., 1968.
101. Черепанов Г. П., О развитии'трещин в сжатых телах, ПММ 30,
вып. 1, 1966.
102. Н о е k E., В i e n i a w s к i L. Т., Brittle fracture propagation in rock
under compression, Int. J. Fracture Mech. 1, № 3, 1965.
103. Исследование горного давления геофизическими методами «Наука» М
1967.
104. Черепанов Г. П., Смольский В. М., Напряжение в окрестности
эллипсоидальной выработки в горном массиве, в сб. «Проблемные во-
вопросы механики горных пород», «Наука», Алма-Ата, 1972.
105. Макклинток Ф., Аргон А., Деформация и разрушение материалов,
«Мир», М., 1970.
106. Боли Б., Уэйиер Дж., Теория температурных напряжений, «Мир»,
М„ 1964.
107. Ершов Л. В., И в л е в Д. Д., Об условиях квазихрупкого разруше-
разрушения, ПММ 31, вып. 3, 1967.
108. Мо с с а ко веки й В. И., Рыбка М. Т., Попытка построения теории
прочности хрупких материалов, основанной на энергетических соображе-
соображениях Гриффитса, ПММ 29, вып. 2, 1965.
109. Rice J. R., A path independent integral and the approximate analysis of
strain concentration by notches and cracks, Trans. ASME, J. Appl. Mech.,
1968, pp. 379—386.
110. Rice J. R., Mathematical analysis in the mechanics of fracture, Treatise
on Fracture, vol. II, Academic Press Inc., New York, 1968, pp. 191—311.
111. Кой тер В. Т., Бесконечный ряд параллельных трещин в упругой пло-
плоскости, в сб. «Проблемы механики сплошной среды» (к 70-летию ака-
академика Н. И. Мусхелишвили), «Наука», М., 1961, стр. 202.
112. Obreimov I. V., The splitting strength of mica, Proc. Roy. Soc. A127i
1930, pp. 290—297.
113. Zienkiewicz O. C, Chung Y. K-, The finite element method in
structural and continuum mechanics; McGraw-Hill, New York, 1967.
114. Соболев С. Л., Некоторые вопросы теории распространения колеба-
колебаний, в кн.: Франк Ф., М и з е с Р., Дифференциальные и интегральные
уравнения математической физики, ОНТИ, М., 1937.
115. Yoffe Ё., The moving Griffith crack, Philos. Mag., VII ser., 42, 1951,
pp. 739—750.
116. Stroh A. N., A theory of the fracture of metals, Advances in Physics 6.
1957, p. 418.
117. Craggs I. W., On the propagation of a crack in an elastic-brittle ma-
material, J. Mech. Phys. Solids 8, 1960, p. 66.
118 Baker B. R., Dynamic stresses created by a moving crack, Trans. ASME,
ser. E, J. Appl. Mech. 29, № 2, 1962.
119 В rob erg К. В., The propagation of a brittle crack, Arkiv for Fysik 18,
1960, p. 159.
120 Баренблатт Г. И., Черепанов Г. П., О расклинивании хрупких
тел, ПММ 24, вып. 4, 1960.
121. Hutchinson J. W., Singular behavior at the end of a tensile crack in
a hardening material, J. Mech. Phys. Solids 16, 1968, p. 13.
122. Rice J. R., Johnson M. A., The role of large crack tip geometry chan-
changes in plane strain fracture, Technical Report № 38, Contract
№ AT C0-1)-2394, US Atomic Energy Commission, Sept. 1969.
123. Черепанов Г. П., Обратная упруго-пластическая задача в условиях
плоской деформации, Изв. АН СССР, ОТН, Механика и машиностроение,
№ 1, 1963,
ЛИТЕРАТУРА 631
124. Седов Л. И., Введение в механику сплошной среды, Физматгиз, М.,
1962.
125. Леонов М. Я-, В и т в и ц к и й П. М., Ярема С. Я., Полосы пластич-
пластичности при растяжении пластин с трещиновидным концентратором, ДАН
СССР 148, № 3, 1963.
126. Ко 1 sky H., Rader D., Stress waves and fracture, в сб. «Fracture»,
ed. by ft. Liebowitz, vol. 1, Academic Press, New York — London, 1969.
127. Черепанов Г. П., Халманов X., К теории роста усталостных тре-
трещин, Труды Всесоюзного рабочего симпозиума по вопросам малоцикло-
малоцикловой усталости, Каунас, 1971.
128. Черепанов Г. П., Кулиев В. Д., Влияние частоты нагружения и
неактивных внешних сред на рост усталостных трещин, Проблемы проч-
прочности, № 1, 1972.
129. Черепанов Г. П., Некоторые основные вопросы линейной механики
разрушения, Проблемы прочности, № 2, 1971.
130. Сервисен С. В., Когаев В. П., Шнейдерович Р. М., Несущая
способность и расчеты деталей машин на прочность, Машгиз, М., 1963.
131. Работнов Ю. Н., Сопротивление материалов, Физматгиз, М., 1962.
132. Ратнер С. И., Разрушение при повторных нагрузках, Оборонгиз, М.,
1959.
133. О д и н г И. А., Допускаемые напряжения в машиностроении и цикличе-
циклическая прочность металлов, Машгиз, М., 1962.
134. Иванова В. С, Усталостное разрушение металлов, Металлургиздат,
At, 1963.
135. Усталость и выносливость, металлов, сб. статей, ИЛ, 1963.
136. For'syth P. J. Е., A two stage process of fatigue crack growth, Proc.
Crack Propagation Symp., Cranfield (England), Cranfield College Aero-
Aeronaut. 1, 1962, p, 76.
137. Grosskreutz J. C, A critical review of micromechanisms in fatigue,
в сб. «Fatigue», Proc. 10th Sagamore Army Mater. Res. Conf., 1963, Sy-
Syracuse Univ. Press, 1964.
138. Paris P. C, Gomez M. P., Anderson W. E., A rational analytic
theory of fatigue, The Trend in Engineering, vol. 13, (January 1961).
139. Donaldson D. R., Anderson W. E., Crack propagation behavior of
some airframe materials, Proc. Crack Propagation Symp., Cranfield (Eng-
(England), Cranfield College Aeronaut. 2, 1962, p. 375.
140. M с E v i 1 у A. J., Jr., 111 g W., The rate of crack propagation in two alu-
aluminium alloys, NASA Tech. Note № 4394, 1958.
141 Hult J. A. H., Fatigue crack propagation in torsion, J. Mech. Phys.
Solids 6, № 1, 1957, pp. 47—52.
142. McClintock F. A., On the plasticity of the growth of fatigue cracks,
в сб. «Fracture of Solids», Proc. Int. Congr. Metallurgy, 1962, vol. 20,
Washington, 1963.
143 Wei R P , Some "aspects of environment enhanced fatigue crack growth,
' Engng Fract. Mech. 1, № 4, 1970, pp. 633—651.
144 Седов Л. И., Методы подобия и размерности в механике, изд. 5-е,
«Наука», М., 1967.
145 Александров А. П., Журков С. Н., Явление хрупкого разрыва,
ГТТИ, М. 1933.
146. Frost N. Е., D u g d a 1 е D. S., Fatigue tests on notched mild steel
plates with measurements of fatigue cracks, J. Mech. Phys. Solids 5, № 3,
1957, pp. 182—192.
147. Frost N. E., Hoi den J., Phillips С. Е., Experimental studies into
the behavior of fatigue cracks, Proc. Crack Propagation Symp., Cranfield
(England), Cranfield College Aeronaut. 1, 1962, p. 166.
148 О s g о о d С. С, A basic course in fracture mechanics, Machine Design 43,
№ 18—23, 1971.
632 ЛИТЕРАТУРА
149. Frost N. Е., Significance of non-propagating cracks in the interpretation
of notched fatigue data, J. Mech. Engng Sci. 3, № 4, 1961, p. 299.
150. Градштейн И. С, Рыжик И. М., Таблицы интегралов, сумм, рядов
и произведений, Физматгиз, М., 1963.
151. Кудрявцев Б. А., Партон В. 3., Черепанов Г. П., Упруго-пла-
стическая задача для плоскости с прямолинейными щелями, МТТ № 3
1969.
152. Р ы б а к и н а О. Г., Распространение трещин при повторно-статическом
растяжении, Труды Всесоюзного рабочего симпозиума по вопросам ма-
малоцикловой усталости, Каунас, 1971.
153. Pearson S., Fatigue crack propagation in metals, Nature 211, № 5053
1966, p. 77.
154. Forma n R. G., Kearney V. E., Engle R. M., Numerical analysis of
crack propagation in cycle loaded structures, Trans. ASME, ser. D, 89,
№ 3, 1967.
155. Hudson С M., Scardina J. Т., Effect of stress ratio on fatigue-crack
growth in 7075-T6 aluminium alloy sheet, Engng Fracture Mech. 1, № 3,
1968.
156. Carman C. M., Katlin J. M., Low cycle fatigue crack propagation
characteristics of high strength steels, Trans. ASME, ser. D, J. Basic
Engng 88, № 4, 1966.
157. Yang С. Т., A study of the low-cycle crack propagation, Trans. ASME,
ser. D, J. Basic Engng 89, № 3, 1967.
158. Clark W. Q., Jr., Subcritical crack growth and its effect upon the fati-
fatigue characteristics of structural alloys, Engng Fracture Mech. 1, № 3,
1968.
159. Ярема С. Я., Хариш Е. Л., Зависимость длительности периода раз-
развития трещины при повторно-ударном нагружений от температуры испы-
испытания, Проблемы прочности, № 8, 1970.
160. Wei R. P., Fatigue-crack propagation in a high-strength aluminium alloy,
Int. J. Fracture Mech. 4, № 4, 1968.
161. Che-Yu-Li, Та Ida P. M., Wei R. P., The effect of environments on
fatigue-crack propagation in an ultra-high-strength steel, Int. J. Fracture
Mech. 3, № 1, 1967.
162. Hart man A., Schijve J., The effects of environments and load fre-
frequency on the crack propagation law for macro fatigue crack growth in
aluminium alloys, Engng Fracture Mech. 1, № 4, 1970, p. 615.
163. Dahlberg E. P, Fatigue-crack propagation in high-strength 4340 steel
in humid air, Trans. ASME 58, 1965, p. 46.
164. Галактионова Н. А., Водород в металлах, «Металлургия», М., 1967.
165. Hancock G. G., Johnson H. H., Hydrogen, oxygen, and subcritical
crack growth in a high-strength steel, Trans. Metal. Soc. A. I. M. E. 236,
1966, p. 513.
166. Smith H. R., Piper D. E., Downey F. K.. A study of stress corro-
corrosion cracking by wedge-force loading, Engng Fracture Mech. 1, № 1,
1968, pp. 123-128.
167. Л ю б о в Б. Я., Ф а с т о в Н. С, Влияние концентрационных напряжений
на процессы диффузии в твердых растворах, ДАН СССР 84, № 5, 1952,
стр. 939.
168. К о р р о з и я, т. 1—IV, «Мир», М., 1972.
169. Nielsen N. A., Observations and thoughts on stress -corrosion mecha-
mechanisms, ASTM 1970 Gillett Memorial Lecture, Corrosion 27, № 5, 1971,
pp. 173—189.
-170. Ростокер Я., Мак-Коги Дж., Марку„с Г., Хрупкость под дей-
действием жидких металлов, ИЛ, 1962.
171. Романов В. В, Коррозионное растрескивание металлов, «Машино-
«Машиностроение», М., 1960.
ЛИТЕРАТУРА 633
172. Logan H. L., The Stress Corrosion of Metals, Wiley, New York, 1967
(русский перев.: Логан X. Л., Коррозия металлов под напряжением,
«Металлургия», М., 1970).
173. Johnson H. H., Wi liner A. M., Moisture and stable crack growth in
a high strength steel, Appl. Mater. Research 4, 1965, p. 34.
174. Stei ger wa 1 d E. A., Delayed failure of high-strength steel in liquid
environments, Proc. ASTM 60, I960, p. 750.
175. Екобори Т., Физика и механика разрушения « прочности твердых тел,
«Металлургия», М., 1971.
176. Антропов Л. И., Теоретическая электрохимия, «Высшая школа», М.,
1969.
177. Carter С. S., Stress corrosion crack branching in high-strength steels,
Engng Fracture Mech., 3, № 1. 1971.
178. Ryder J. Т., Gallagher J. P., Environmentally controlled fatigue
crack-growth, rates in SAE 4340 steel — temperature effects, Trans ASME,
ser. D, 92, № 25, 1970.
179. Корнфельд М., Упругость и прочность жидкостей, ГИТТЛ, М., 1951.
180. П а р т о н В. 3., Черепанов Г. П., Механика разрушения, в ки. «Ме-
«Механика в СССР за 50 лет», т. 3, «Наука», М., 1972.
181. Те t e lrna п A. S., McEvily A. J., Fracture of structural* materials,
Wiley, New York, 1967.
182. Черепанов Г. П., О точечном взрыве в идеально-хрупком теле,
ПМТФ № 4, 1969.
183. С h е г е р а п о v G. P., R z h e v s k у V. V., Y e r s h о v L. V., On explosion
in a brittle body, Engng Fract. Mech. 4, № 2, 1972.
184. Антика ев Ф. Ф., Параметры сейсмических колебаний, возбужденных
взрывом. Экспериментальная сейсмика, Труды Ин-та физики Земли АН
СССР, № 32 A99), 1964,
185. Нифонтов Б. И., Протопопов Д. Д., Ситников И. Е., Кули-
Куликов А. В., Подземные ядерные взрывы, Атомиздат, М, 1965.
186. Действия ядерного взрыва, «Мир», М., 1971-.
187. М о синец В. Н., Деформации горных пород взрывом, Изд-во АН
КиргССР, Фрунзе, 1971.
188. Cherepanov G. P., On the theory of fluidization, part I, General mo-
model, Ind. Engng Chemistry Fundamentals 11, № 1, 1972.
J89. Cherepanov G. P., On the theory of fluidization, part II, Some one-
dimensional problems, Ind. Engng Chemistry Fundamentals, 11, № 1,
1972.
190. Новые методы оценки сопротивления металлов хрупкому разрушению, сб.
переводов, «Мир», М., 1972.
191. Григорян С. С, Некоторые вопросы математической теории деформи-
. рования и разрушения твердых горных пород, ПММ 31, вып. 2, 1967.
192. Григорян С. С, Иоселевич В. А., Механика грунтов, в ки. «Ме-
«Механика в СССР за 50 лет», т. 3, «Наука», М., 1972.
193. Методы неразрушающих испытаний, сб. переводов, «Мир», М., 1972.
194. Черепанов Г. П., О термобурении, ПМТФ № 6, 1966.
195. Hertz H., Gesammelte Werke, Bd. 1, 1895, S. 179—195.
196. Д и н н и к А. Н., Удар и сжатие упругих тел, Киев, 1909.
197 Roesler F. С, Brittle fracture near equilibrium, Proc. Phys. Soc. 69,
1956, p. 981.
198 В e n d о w J. J., Cone cracks in fused silica, Proc. Phys. Soc. 75, 1960,
p. 697.
199. Cherepanov G. P., So kolinsky V. В., On fracturing of brittle
bodies by impact, Engng Fracture Mech. 4, № 2, 1972.
200. Черепанов Г. П., Каплун А. Б., Пучков Ю. И., О влиянии
масштабного фактора на хрупкую прочность, Проблемы прочности, № 7,
1970.
634 ЛИТЕРАТУРА
201. Черепанов Г. П., Каплун А. Б., К а р асе в Л. П., Пучков Ю. И.,
Оценка хрупкой прочности сварных корпусов из высокопрочной стали
и сплавов, Проблемы прочности, № 12, 1971.
202. Бережницкий Л. Т., Панасюк В. В., Черепанов Г. П., О проч-
прочности составных тел, ослабленных трещинами, в сб. «Концентрация на-
напряжений», вып. 3, «Наукова думка», Киев, 1970.
203. S t a v е г m а п A. I., Mechanical properties of polymers, Proc. Roy. Soc
A282, № 1388, 1964.
204. Гольцев В. Ю., Дроздовский Б. А., Проходцева Л. В.,
Влияние толщины металлических материалов на их способность тормо-
тормозить разрушение, Заводская лаборатория, № 10, 1969.
205. Дроздовский Б. А., Фридман Я. Б., Влияние трещин на меха-
механические свойства конструкционных сталей, Металлургиздат, М., 1960.
206. Потак Я. М., Хрупкие разрушения стали и стальных деталей, Оборон-
гиз, М^ 1955.
207. Пашков П. И., Разрыв металлов, Судпромгиз, Л., 1960.
208. Крагельский И. В., Трение и износ, «Машиностроение», М., 1968.
209. Фомин В. В., Гидроэрозия металлов, «Машиностроение», М., 1966.
210. Урванцев Л. А., Газовая эрозия металлов, Машгиз, М., 1962.
211. Шрейбер Л. А., Механические и абразивные свойства горных пород,
Гостоптехиздат, М., 1958.
212. Пер ник А. Д., Проблемы кавитации, «Судостроение», 1966.
213. А ф а н а с ь е в Е. Ф., Гриценко А. И., Требин Ф. А., Черепа-
Черепанов Г. П., Скорость абразивного износа газонефтепромыслового обору-
оборудования, Нефтяное хозяйство, № 3, 1970.
214. Веллингер К., Четц Г., Изнашивание струей абразивного материа-
материала, Машиностроение, сб. переводов и обзоров иностр. периодич. литера-
литературы, № 2, ИЛ, 1956.
215. Антонов А. А., Методика и некоторые результаты испытаний на износ
сталей и чугуна воздушно-абразивной струей, Нефтяное машиностроение,
Труды МИНХ и ГП, вып. 34, 1961.
216. Нейман Ф., Передача момента количества движения и образование
кратеров под действием гигантских лазерных импульсов, в сб. «Действие
лазерного излучения», «Мир», М., 1968.
217. Бломберген Н., Нелинейная оптика, «Мир», М., 1966.
218. Ах м а но в С. А., Хохлов Р. В., Проблемы нелинейной оптики, «Нау-
«Наука», М., 1964.
219. Действие лазерного излучения, сб., статей, «Мир», М., 1968.
220. Чао Р., Г а р м а й р Е., Т а у н с Ч., Самофокусировка луча оптического
мазера, в сб. «Действие лазерного излучения», «Мир», М., 1968.
221. Чао Р., Гармайр Е., Та у не Ч., Рамановские и фононные лазеры,
в сб. «Действие лазерного излучения», «Мир», М., 1968.
222. Brewer R. G., Rieckhoff К. Е., Stimulated Brillouin scattering in
liquids, Phys. Rev. Letters 13, 334a, 1964.
223 H a r p e r D. W., Laser damage in glasses, Brit. J. Appl. Phys. 16, 1965,
p. 751.
224. Акимов А. И., М и р к и н Л. И., П и л и п е ц к и й Н. Ф., Об особен-
особенностях разрушения прозрачных полимеров при воздействии световых им-
импульсов длительностью 10-3 и 10~8 секунд, Механика полимеров 3, 1967,
стр. 493.
225 Кулиев В. Д., Черепанов Г. П., К теории «горячих» трещин,
ПМТФ, № 2, 1974.
226. Б а дин Дж., Рэффи Дж., Динамика разрушения в стеклах, вызван-
вызванного действием лазерного излучения, в сб. «Действие лазерного излуче-
излучения», «Мир», М., 1968.
227. I r w i п Q. R,, Fracture Mechanics в сб. Structural Mechanics, Proc. 1st
Symposium on Naval Structure Mechanics, 1960, pp. 557—591.
ЛИТЕРАТУРА 635
228. I r win Q. R., Structural aspects of brittle fracture, Appl. Mater. Res.,
Int. J. Properties and Testing Engng Mater. 3, № 2, 1964, pp. 65—81.
229. В ей булл В., Усталостные испытания и анализ их результатов, перев.
с англ., «Машиностроение», М., 1964.
230. Paris P. С, Testing for very slow growth of fatigue cracks, DEL
Research Corporation, Closed Loop 2, № 5, 1970, p. 11.
231. Шерман Д. И., Упругая плоскость с прямолинейными разрезами, ДАН
СССР 26, № 7, 1940, стр. 635.
232. Мусхелишвили Н. И., Основные граничные задачи теории упруго-
упругости для плоскости с прямолинейными разрезами, Сообщ. АН ГрузССР
3, №2, 1942, стр. 103—110.
233. Шерман Д. И., Смешанная задача теории потенциала и теории упру-
упругости для плоскости с конечным числом прямолинейных разрезов, ДАН
СССР 27, № 4, 1940, стр. 330.
234. Черепанов Г. П., Решение одной линейной краевой задачи Римана
и ее приложение к некоторым смешанным задачам теории упругости,
ПММ 26, вып. 5, 1962.
235. Черепанов Г. П., Давление твердого тела на пластины и мембраны,
ПММ 29, вып. 1, 1965.
236. Черепанов Г. П., Задача Римана-Гильберта для внешности разрезов,
ДАН СССР 156, № 2, 1964.
237. Парис П., Си Дж., Анализ напряженного состояния около трещин, в
сб. «Прикладные вопросы вязкости разрушения», «Мир», М., 1968.
238. Баренблатт Г. И., Черепанов Г. П., О влиянии границ тела на
развитие трещин хрупкого разрушения, Изв. АН СССР, ОТН, Механика
и машиностроение, № 3, 1960.
239. Paris P. С., A short course in fracture mechanics, Univ. of Washington
Press, 1960.
240. Та da H., Westergaard stress functions for several periodic crack pro-
problems, Engng Fracture Mech. 2, № 2, 1970, p. 177.
241. Wi gg les wort h L. A., Stress distribution in a notched plate, Mathema-
tika 4, 1957, pp. 76—96.
242. Koiter W. Т., Discussion on the paper «Rectangular tensile sheet with
symmetric edge cracks» by O. L. Bowie, Trans. ASME, ser. E, 32, № 1,
1965, p. 237.
243. I r w i n Q. R., The crack-extension force for a crack at & free surface
boundary, Report № 5120, Naval Research Lab., 1958.
244. Bowie O. L., Neal D. M., Single edge cracks in rectangular tensile
sheet, J. Appl. Mech., ser. E, 32, № 3, 1965, p. 708.
245. В u e с k n e r H. F., Some stress singularities and their computation by
means of integral equations, в сб. Boundary Problems in Differential
Equations, Univ. Wisconsin Press, 1960, pp. 215—230.
246. I s i d a M., Stress intensity factors for the tension of an eccentrically
cracked strip, J. Appl. Mech., ser. E, 33, № 3, 1966, p. 674.
247. Irwin G. R., Liebowitz H., Paris P. C, A mystery of fracture
mechanics, Engng Fracture Mech. 1, № 1, 1968.
248. Bowie O. L, Neal D. M., A note on the central crack in a uniformly
stressed strip, Engng Fracture Mech. 2, № 2, 1,970, p. 181.
249. Bowie O. L., Rectangular tensile sheet with symmetric edge cracks,
J. Appl. Mech., ser. E, 31, № 2, 1964, p. 208.
250. С м е т а н и н Б. И., Некоторые задачи о щелях в упругом клине и
слое, МТТ № 2, 1968.
251. England A. H., Green A. E., Some two-dimensional punch and crack
problems in classical elasticity, Proc. Camb. Phil. Soc. 59, 1963,
p. 489.
252. Lowengrub M., A two-dimensional crack problem, Int. J. Engng Sci.
4, 1966, p. 289.
636 ЛИТЕРАТУРА
253. Sneddon I. N., Lowengrub M., Crack problems in the classical
theory of elasticity, The SIAM Series in Applied Math., Wiley, New York,
- 1969.
254. Александров В. М., Сметанин Б. И., О равновесных продольных
трещинах в пластинах, Тр. VI Всесоюзн. конференции по теории оболо-
оболочек и пластинок, «Наука», М., 1966.
255. Алекса н дров В. М„ Сметанин Б. И., Равновесная трещина в
слое малой толщины, ПММ 29, вып. 4, 1965.
256. W i g g 1 е s w о r t h L. A., Stress relief in a cracked plate, Mathematika 5,
№ 1, 1958, pp.-67—81.
257. Bowie O. L., Analysis of an infinite plate containing radial cracks ori-
originating at the boundary of an internal circular hole, J, Math. Phys. 35,
1956, p. 60.
258. Westmann R. A., Pressurized star crack, J. Math. Phys. 43, 1965,
p. 191.
259. Ярема С. Я., Крестин Г. С, Определение модуля сцедления хруп-
хрупких материалов путем испытания дисков с трещиной на сжатие, Физико-
химическая механика материалов 2, № 1, «Наукова думка», Киев, 1966.
260. Савин Г. Н., Панасюк В. В., Развитие исследований по теории
предельного равновесия хрупких тел с трещинами, Прикладная механика
4, вып. 1, 1968.
261. Черепанов Г. П., Об одном классе задач плоской теории упругости,
,Изв. АН СССР, ОТН, Механика и машиностроение, № 4, 1962.
262. 'Wester ga a rdr H. M., Bearing pressures and cracks, J.'Appl. Mech. 6,
№ 2, 1939.
263. Черепанов Г. П., О напряженном состоянии в неоднородной пла-
пластинке с разрезами, Изв. АН СССР, ОТН, Механика и машиностроение,
№ 1, 1962.
264. L о е b e r J. F., S i h G. С, Green's function for cracks in nonhomogeneous
materials, Trans. ASME, ser. E, № 1, 1967.
265. Баренблатт Г. И., Черепанов Г. П., О равновесии и распростра-
распространении трещин в анизотропной среде, ПММ 25, вып. 1, 1961.
266. Sih G. С, Paris P. С, Irwin G. R., On "cracks in rectilinearly ani-
sotropic bodies, Int. J. Fract. Mech. 1, № 3, 1965.
267. Sih G. C, Liebowitz H., Mathematical theories of brittle fracture,
в кн. «Fracture», vol. 2, Academic Press, New York — London, 1969.
268. Dyson F. W., Quart. J. Math., Oxford Ser. 25, 1891, p.p. 259—288.
269. W a 1 p о 1 e L. J., Some elastostatic and potential problems for an elliptic
disk, Proc. Cambr. Soc. 67, pt. 1, 1970, p. 225.
270. Галин Л. А., О давлении штампа эллиптической формы в плане на
упругое полупространство, ПММ 11, вып. 2, 1947.
271. Kassier M. К., Sih G. С, Three-dimensional stress distribution around
an elliptical crack under arbitrary loadings, Trans. ASME, ser. E, J. Appl.
Mech. 33, № 3, 1966, p. 601—611.
272. Smith F. W., К о b а у a s h i A. S., Emery A. F., Stress intensity fac-
factors for penny-shaped cracks, Trans. ASME, ser. E, J. Appl. Mech. 34,
№ 4, 1967.
273. Kassier M. K., Sih G. C, External elliptical crack in elastic solid,
Int. J. Fract. Mech. 4, № 4, 1968, p. 347.
274. Smith F. W., Emery A. F., Kobayashi A. S., Stress intensity
factors for semicircular cracks, Trans. ASME, ser. E, J. Appl. Mech. 34,
№ 4, 1967.
275. M о с с а к о в с к и й В. И., Рыбка М. Т., Обобщение критерия Гриф-
фитса-Снеддона на случай неоднородного тела, ПММ 28, вып. 6,
1964.
276. Kassier М- К., On the distribution of thermal stresses near an elliptical
crack in an infinite elastic body, Int. J. Engng Sci. 7, Ns 8, 1969.
ЛИТЕРАТУРА 687
277. Седов Л. И., Плоские задачи гидродинамики и аэродинамики, изд. 2-е,
«Наука», М., 1965.
278. Лаврентьев М. А., Ш а б а т Б. В., Методы теории функций комплекс-
комплексного переменного, изд. 4-е, «Наука», М., 1973.
279. Баренблатт Г. И., Черепанов Г. П., О хрупких трещинах про-
продольного сдвига, ПММ 25, вып. 6, 1961.
280. М а р к у з о и И. А., О расклинивании хрупкого тела клином конечной
длины, ПММ 25, вып. 2, 1961.
281. Sin G. С, Stress distribution near internal crack tips for longitudinal
shear problems, Trans. ASME, ser. E, J. Appl. Mech. 32, M 1, 1965.
282. Мирсалимов В. М., Влияние разгружающих отверстий иа развитие
трещины, Проблемы прочности, № 4, 1971.
283. Rice J. R., Trans. ASME, ser. E, J. Appl. Mech. 34, 1967, pp. 287—298.
284. Cherepanov G. P., Afanasyev E. F., Some dynamical problems
¦ of the theory of elasticity, Int. J. Engng Sci., 1974 (в печати).
285. F r e u n d L. В., The stress intensity factor due to normal impact loading
of the faces of a crack, Int. J. Engng Sci., 1974 (to be published).
286. Atkinson C, Head A. K., The influence of elastic anisotropy on the
propagation of fracture, Int. J. Fract. Mech. 2, № 2, 1966, pp. 489—505.
287. Афанасьев Е. Ф., Черепанов Г. П., Автомодельная задача дина-
динамической теории упругости для щели с точечным источником, ДАН
СССР 190, № 6, 1970.
288. Баренблатт Г. И., Салганик Р. Л., Черепанов Г. П., О не-
неустановившемся распространении трещин, ПММ 26, вып. 2, 1962.
289. Atkinson С, The propagation of a brittle crack in anisotropic material,
Int. J. Engng Sci. 3, 1969, pp. 77—91.
290. Седов Л. И., Распространение мощных взрывных волн, ПММ 10,
вып. 2, 1946.
291. Афанасьев Е. Ф., Некоторые однородные решения динамической тео-
теории упругости, в сб. «Механика сплошной среды и родственные пробле-
проблемы анализа» (к 80-летию академика Н. И. Мусхёлишвили), «Наука», М.,
1972.
292. Черепанов Г. П., Некоторые задачи теории трещии в гидродинами-
гидродинамической постановке, ПММ 27, вып. 6, 1963.
293. Костров Б. В., Неустановившееся распространение трещины продоль-
продольного сдвига, ПММ 30, вып. 5, 1966.
294. Костров Б. В., Осесимметричная задача о распространении трещины
нормального разрыва, ПММ 28, вып. 4, 1964.
295. Craggs J. W., The growth of a disk-shaped crack, Int. J. Engng Sci.
4, 1966, p. 113.
296. В u r r i d g e R., Willis J. R., The self-similar problem of the expanding
elliptical crack in an anisotropic solid, Proc. Cambr. Phil. Soc. 66, 1969,
p. 443.
297. Webb D., A t k i n s о n C, A note on a penny-shaped crack expanding
under a non-uniform internal pressure, Int. J. Engng Sci. 7, 1969,
pp. 525—530.
298. Atkinson C, A simple model of relaxed expanding crack, Arkiv for
Fysik 35, № 38, 1967, pp. 469—476.
299. Тимошенко С. П., Пластинки и оболочки, Гостехиздат, М., 1948.
300. Williams M. L., Surface stress singularities resulting from various
boundary conditions in angular corners of plates under bending, Proc.
1st U. S., National Congr. Appl. Mech., 1952, p. 325.
301. Wu E. M., Application of fracture mechanics to anisotropic plates, Trans.
ASME, ser. E. J. Appl. Mech. 34, № 4, 1967.
302. Erdogan F., Tune el O., Paris P., An experimental investigation
of the crack tip stress intensity factors in plates under cylindrical bending,
Trans. ASME, ser. D, J. Basic Engng 84, № 4, 1962, pp. 542-553.
638 ЛИТЕРАТУРА
303. Е г d о g а п F., S i h G. С, On the crack extension in plates under plane
loading and transverse shear, Trans. ASME, ser. D, J. Basic Engng 85,
№ 4, 1963, pp. 519—527.
304. F о 1 i a s E. S., On the theory of fracture of curved sheets, Engng Fract.
Mech. 2, № 2, 1970, pp. 151—164.
305 Ярема С. Я., С а в р у к М. П., Напряжения в цилиндрической оболочке
с произвольно ориентированной трещиной, Физико-химическая механика
материалов 5, № 3, «Наукова думка», Киев, 1969.
306. Кудрявцев Б. А., Напряжения в эллипсоидальной оболочке с произ-
произвольно ориентированной трещиной, МТТ № 2, 1971.
307. Черепанов Г. П., О выпучивании мембран с отверстиими при растя-
растяжении, ПММ 27, вып. 2, 1963.
308. Черепанов Г. П., Некоторые задачи теории упругости и пластично-
пластичности с неизвестной границей,, в сб. «Приложения теории функций в меха-
механике сплошной среды», т. 1, «Наука», М., 1965.
309. Черепанов Г. П., О местном выпучивании мембран, МТТ № 1, 1966.
310. Вольмир А. С, Устойчивость упругих систем, Физматгиз, М., 1963.
311 Б р и д ж м е н П., Физика высоких давлений, ОНТИ, М., 1935.
312. Черепанов Г. П., О природе «пинч-эффекта» и некоторых других
вопросах теории разрушения, ПМТФ № 1, 1965.
313. Mindlin R. D., Micro-structure in linear elasticity, Arch. Rational Mech.
and Analysis 16, № 1, 1964, pp. 51—78.
314. Sternberg E., Muki R., The effect of couple stresses on the stress
concentration around a crack, Int. J. Solids and Structures 3, 1967, p. 69.
315. Pagano N. J., Sih G. C, Stress singularities around a crack in
a Cosserat plate, Int. J. Solids and Structures 4, 1968, p. 531.
316. Лурье М. В., Использование вариационного принципа для изучения
распространения поверхностей разрыва в сплошной среде, ПММ 33,
вып. 4, 1969.
317. Romualdi I. P., Sanders P. H., Fracture arrest by riveted stiffeners,
Proc. 4th Midwest. Conf. Solid Mech., Texas Univ. Press, 1959—1960,
pp. 74—90.
318. Greif R., Sanders J. L, The effect of a stringer on the stresses in
a cracked sheet, Trans. ASME, ser. E, J. Appl. Mech. 32, № 1, 1965,
pp. 59—66.
319. Bloom J. M, Sanders J. L., The effect of a riveted stringer on the
stress in a cracked sheet, Trans. ASME, ser. E, J. Appl. Mech. 33, № 3,
1966, pp. 561—570.
320. Морозова Е. А., Пар тон В. 3., О влиянии подкрепляющих ребер
на распространение трещины, ПМТФ № 5, 1961.
321. Черепанов Г. П., Мирсалимов В. М., О воздействии ребер жест-
жесткости на развитие трещины, Изв. АН АзербССР № 1, 1969.
322. И в л е в Д. Д., О теории трещин квазихрулкогб разрушения, ПМТФ
№ 7, 1967.
323. А у res D. J., A numerical procedure for calculating stress and deforma-
deformation near a slit in a three-dimensional elastic-plastic solid, Engng Fract.
Mech, 2, № 2, 1970.
324. Б у бе р чан Г. С, Физика алмазов, «Знание», М., 1968.
32'5. Кузнецов В. Д., Физика твердого тела. Изд-во КУБУЧ, Томск, 1932.
326. Сборник физических констант, ОНТИ, М., 1937.
327. Киттель Ч., Введение в физику твердого тела, Физматгиз, М., 1963.
328. Киреев В. А., Краткий курс физической химии, «Химия», М., 1970.
329. W e s s е 1 Е. Т., State of the art of the WOL specimen for fracture tough-
toughness testing, Engng Fract. Mech. 1, № 1, 1968, p. 77.
330. Кис Д. А., Смит X. Л., Ромайн X. Е., Б е р н с т е й и X., Испытание
сварных швов на разрушение, в сб. «Прикладные вопросы вязкости раз-
разрушения», «Мир», М., 1968,
ЛИТЕРАТУРА 639
331. Пейн В. Ф., Включение данных по испытанию на разрушение в специ-
спецификации, в сб. «Прикладные вопросы вязкости разрушения», «Мир», М.,
1968.
332. Н о i е г К. Е., Equations for iracture mechanics, Machine Design 3, № 1
1968, p. 109. в . - i,
333. Тиффани К. Ф., Мастере Д. Н., Прикладные вопросы механики
разрушения, в сб. «Прикладные вопросы вязкости разрушения» «Мир»
М., 1968. ¦¦ •
334. У эй Р. П., Испытания на вязкость разрушения при разработке сплавов,
в сб. «Прикладные вопросы вязкости разрушения», «Мир», М., 1968.
335. S t e i g е г w a I d E. A., What you should know about fracture toughness
Metal Progress 92, № 5, 1967, p. 96.
336. I r w i П Q. R., Fracture of pressure vessels, в сб. «Materials for Missiles
and Spacecraft», Wiley, New York, 1963.
337. Дроздовский Б. А., Проходцева Л. Д., Фридман Я. Б., Ме-
Методы оценки чувствительности к трещине, Заводская лаборатория 33,
№ 12, 1967.
338. Cottrell С. L. M., Fracture toughness concepts applied to the zones of
welded joints, British Welding Journal 15, № 6, 1968, p. 262.
339. Иванова В. С. и др., Усталость и хрупкость металлических материа-
материалов, «Наука», М., 1968.
340. Браун У., Сроули Дж., Испытания высокопрочных металлических
материалов на вязкость разрушения при плоской деформации, «Мир»
М., 1972.
341. Кауфман Д. Г., Вязкость разрушения листов, плит и многослойных
клееных панелей из алюминиевых сплавов 7075-Т6 и 7075-Т651, Труды
Американского общества инженеров-механиков, серия Д, 89, № 3, 1967.
342. Кауфман Д. Г., Гунзиккер X., Испытание алюминиевых сплавов
на вязкость разрушения, в сб. «Прикладные вопросы вязкости разруше-
разрушения», «Мир», М., 1968.
343. М у л е р и н Дж. Н., Чувствительность высокопрочной стали к коррозии
под напряжением в зависимости от вязкости разрушения, Труды Амери-
Американского общества инженеров-механиков, серия Д, 88, № 4, 1966.
344. Peterson M. H., et al., Stress corrosion cracking of high strength
steels and titanium alloys in chloride solutions at ambient temperature,
Corrosion 23, № 4, 1967, p. 142.
345. Novak S. R., Rolfe.S. Т., Comparison of fracture mechanics and no-
nominal stress analyses in stress corrosion cracking, Corrosion 26, № 4, 1970.
346. Chu H. P., Wacker G. A., Stress corrosion testing of 7079-76 alumi-
aluminium alloy in sea water using smooth and precracked specimens, Trans.
ASME, ser. D, 91, № 4, 1969.
347. Judy R. W., D a h 1 b e r g E. P., Stress corrosion cracking test of sur-
surface-flawed specimens of Ti-7Al-2Co-lTa, Report NRL Progress, May 1968,
p. 30.
348. W a t k i n s о n F. E., S с у 11 у J. С, The effect of atmospheric moisture
upon the S. С. С. of an AL-6Zn-3Mg alloy, Corrosion Scf. 11, № 3, 197"l,
p. 179.
349. Brungs D., Cruhl W., Huppatz W., Studien fiber die Beziehung
zwischen interkristal liner Korrosion und Spannungsrisskorrosion bei
AlZnMg3, Aluminium (BRD) 47, № 3, 1971, S. 189.
350 Герасимов В. В., Коррозия алюминия и его сплавов, «Металлургии»,
М., 1967.
351. Тим о но в а М. А., Коррозия и защита магниевых сплавов, «Машино-
«Машиностроение», М., 1964.
352. Engelhardt R., Kurzmann W., Fichenberg P., Untersuchungen
zum Festigkeits und Korrosionsverhalten von Eisen-Nickel-Chrom- und
Kobalt-Nickel-Eisen-Legierungen, NeUe Hutte 16, № 3, 1971, S. 163.
640 ЛИТЕРАТУРА
353. В е г g s t e d t H. U., Direkte Beobachtung des Einsetzes von Spannungs-
risskorrosion am austenitischen Chrom-Nickel-Stahl Werkstoff Nr 4988 in
siedender Magnesiumchloridlosung, Corrosion Sci. 11, № 2, 1971, p. 89.
354. Погодин В. П., Межкристаллитная коррозия и"коррозионное растре-
растрескивание нержавеющих сталей в водных средах, Атомиздат, М., 1970.
355. Веденеева М. А., Томашов Н. Д., Коррозия стали 1Х18Н9 в сер-
сернокислых растворах C11SO4, в сб. «Коррозия и защита конструкционных
металлических материалов», «Металлургия», М., 1961.
356. А ж о г и н Ф. Ф., Коррозионное растрескивание высокопрочных конструк-
конструкционных сталей, Физико-химическая механика материалов 3, № 3, «Нау-
кова думка», Киев, 1967.
357. Василенко И. И., Болтарович А. В., Каличак Т. Н., Меер-
с о н И. Л., Коррозионное растрескивание нержавеющих сталей Х17Н2 и
Х17Н5МЗ в растворах хлоридов, Физико-химическая механика материа-
материалов 3, № 3, «Наукова думка», Киев, 1967.
358. Atkinson С, Williams M. L., A note on the Cherepanov calculation
of viscoelastic fracture, Int. J. Solids and Structures 9, № 2, 1973,
pp. 237—241.
359. Bennett S. J., Anderson G. P., Williams M. L., The time de-
dependence of surface energy in cohesive fracture, J. Appl. Poly. Sci. 14,
1970, pp. 735—745.
360. Fracture Toughness, ISI Publication 121, The Iron and Steel Institute,
London, 1968.
361 H e a 1 d P. Т., S p i n k G. M., W 0 r t h i n g t о n P. J., Post yield fracture
mechanics, Mater. Sci. Engng 10, 1972, pp. 129—138.