Современная теория систем управления. - Леондес К.Т.

Author: Леондес К.Т.
Tags: математика системы управления теория автоматического управления
Year: 1970
Similar
Теория систем автоматического управления
Теория линейных систем автоматического регулирования и управления.
Теория автоматического управления. Часть 1. Теория линейных систем автоматического управления
Методы современной теории автоматического управления. Том 3
Text
                    MODERN CONTROL
SYSTEMS THEORY
MASANAO AOK1, GEORGE A. BEKEY,
DALE D. DONALSON, H. C. HSIEN,
FRANCIS H. KISHI, JAMES S. MEDITCH,
RICHARD A. NESBIT. PETER R. SCHULTZ,
EDWIN B. STEAR, ALLEN R. STUBBERUD
Edited by
CORNELIUS T. LEONDES
Professor of Engineering
University of California, Los Angeles
McGRAW-HILL BOOK COMPANY, INC.
NEW YORK ST. LOUIS TORONTO LONDON SANFRANCISCO SYDNEY

СОВРЕМЕННАЯ ТЕОРИЯ
СИСТЕМ УПРАВЛЕНИЯ
Под редакцией
К. Т. ЛЕОНДЕСА
Перевод с английского
Я. А. КОГАНА, Ю. Э. САГАЛОВА,
И. В. ТИМЕ
Под редакцией
Я. 3. ЦЫГ1КИНА
ИЗДАТЕЛЬСТВО «НАУКА*
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
МОСКВА 1970

6П2. 15
С 56
УДК 519.95
Современная теория систем управления, под редакцией К. Т. Л е о н-
дес а, Главная редакция физико-математической литературы изд-ва
«Наука», М., 1970, 512 стр.
В книге нашли отражение основные методы теории систем управления,
появившиеся к началу 60-х годов.
Основное содержание книги включает в себя вопросы, ранее не изла¬
гавшиеся в советской литературе (исключение представляют главы 7 и 11,
посвященные принципу максимума и анализу и синтезу дискретных систем,
и отчасти главы 1 и 4, в которых рассматриваются методы синтеза линейных
систем с переменными параметрами и методы построения формирующихся
фильтров для случайных процессов).
Главы 3 и 8 вводят читателя в круг идей функционального анализа.
Приводятся примеры применения методов функционального анализа к реше¬
нию прикладных задач управления. В главе 2 излагается, в частности, вывод
уравнений фильтрации Калмэна — Быоси для случая непрерывного времени.
В главе 5 изложены методы анализа нелинейных систем управления с по¬
мощью прямого метода Ляпунова. В главе 6 рассматриваются различные
методы синтеза аддитивных систем. В главе 9 сравниваются различные анали¬
тические методы синтеза оптических линейных систем управления, в частно¬
сти метод динамического программирования и принцип максимума Л. С. Пон-
трягина. Глава 10 является по существу введением в применение методов
стохастической аппроксимации к задачам автоматического управления.
В главе 12 дается описание человека-оператора в системе управления. В главе
13 современные методы анализа и синтеза применяются к системам управ¬
ления летательными аппаратами.
Илл. 93. Библ. 423 назв.
3-3-13
140-69

ОГЛАВЛЕНИЕ
От редактора русского перевода
Предисловие
Глава 1. Методы синтеза линейных систем автоматического
управления с переменными параметрами	 17
1.	1.	Некоторые характеристики линейных систем	  17
1.	2.	Некоторые свойства уравнения (1.1)	 18
1.	3.	Определение дифференциального уравнения по весовой
функции 	 21
1.	4.	Алгебра линейных дифференциальных уравнений	 23
1.	5.	Необходимые операции	 23
1.	6.	Умножение двух дифференциальных уравнений	 25
1.	7.	Единичный элемент 	 27
1.	8.	Обратный элемент операции умножения 	 28
1.	9.	Сложение двух дифференциальных уравнений 	 29
1.10. Нулевой элемент	 31
1.11. Обратный элемент операции сложения		 31
1.12. Умножение дифференциального уравнения	на	скаляр ...	31
1.13. Синтез методом сокращения оператора	объекта	 32
1.14. Синтез системы регулирования с обратной связью при из¬
меняемом объекте	 34
1.15. Синтез системы регулирования при неизменном объекте 34
1.16. Пример	 35
1.17. Замечания 	 36
1.18. Ограничения, накладываемые на выбор дифференциального
уравнения всей системы 	 36
1.19. Алгебраический метод синтеза	 37
1.20. Пример	 40
1.21. Замечания 	 41
1.22. Задача аппроксимации 	  42
1.23. Метод аппроксимации в случае полиномиальных входных
сигналов 	"	 42
1.24. Метод аппроксимации в случае входных сигналов неполи¬
номиального вида	 45
1.25. Пример	 47
1.26. Аппроксимация разложимых функций	 49
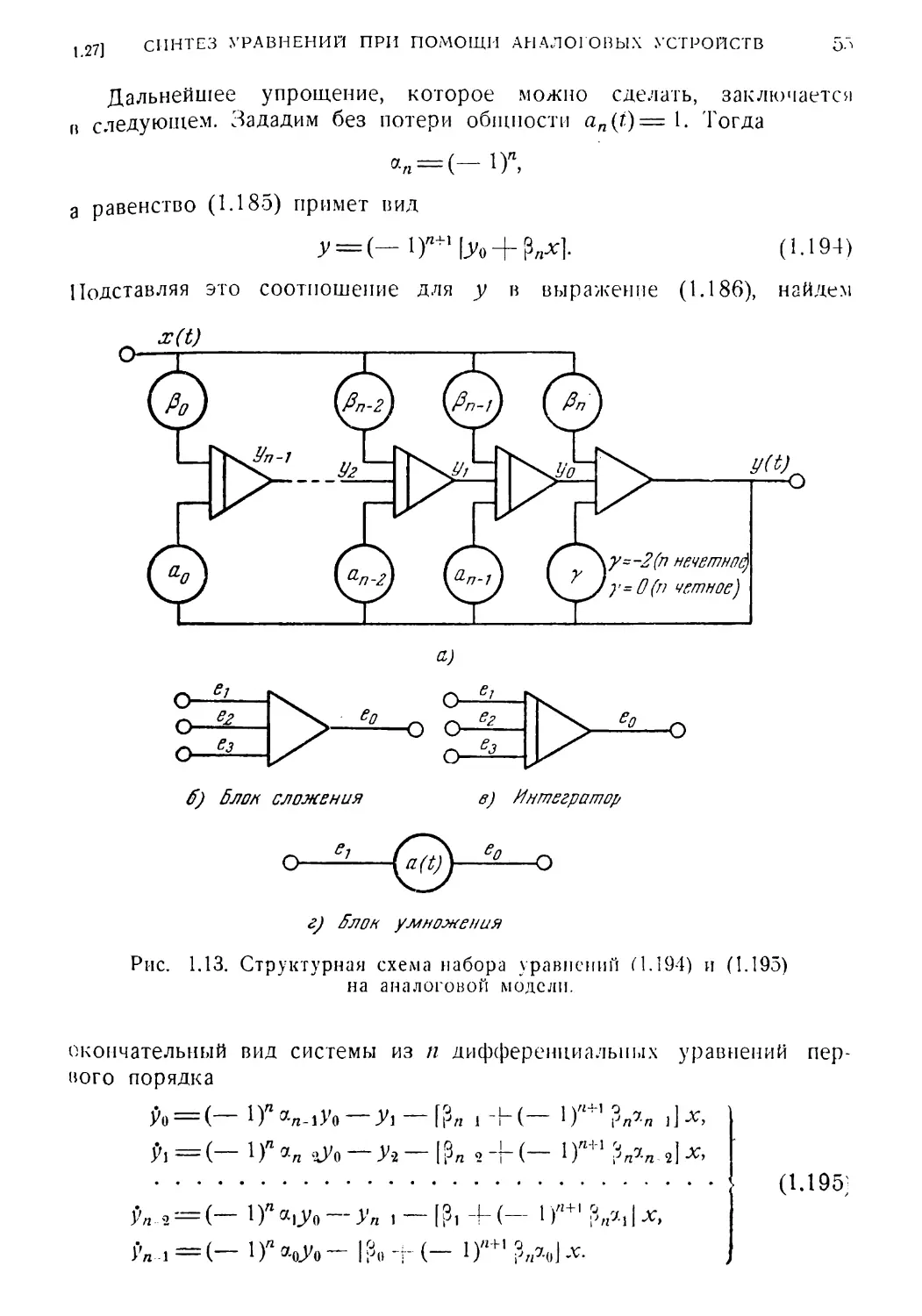
1.27. Синтез дифференциальных уравнений с переменными коэф¬
фициентами при помощи аналоговых моделирующих
устройств	 53
1 ос	^пР0111сние линейных систем	 56
1.29.	Эквивалентные системы	 56

6
ОГЛАВЛЕНИЕ
1.30. Упрощасмость	 60
1.31. Примеры	 65
1.32. Аппроксимация линейных дифференциальных	уравнений	69
1.33. Наилучшая в смысле метода наименьших	квадратов
аппроксимация решений алгебраических уравнений ....	69
1.34. Аппроксимация дифференциального уравнения уравнением
более низкого порядка 	 70
1.35. Пример	 74
1.36. Увеличение порядка интегрального и дифференциального
операторов	 76
1.37. Оценка ошибки аппроксимации  	•	 80
1.38. Пример	 83
1.39. Заключение 	 85
Литература	 85
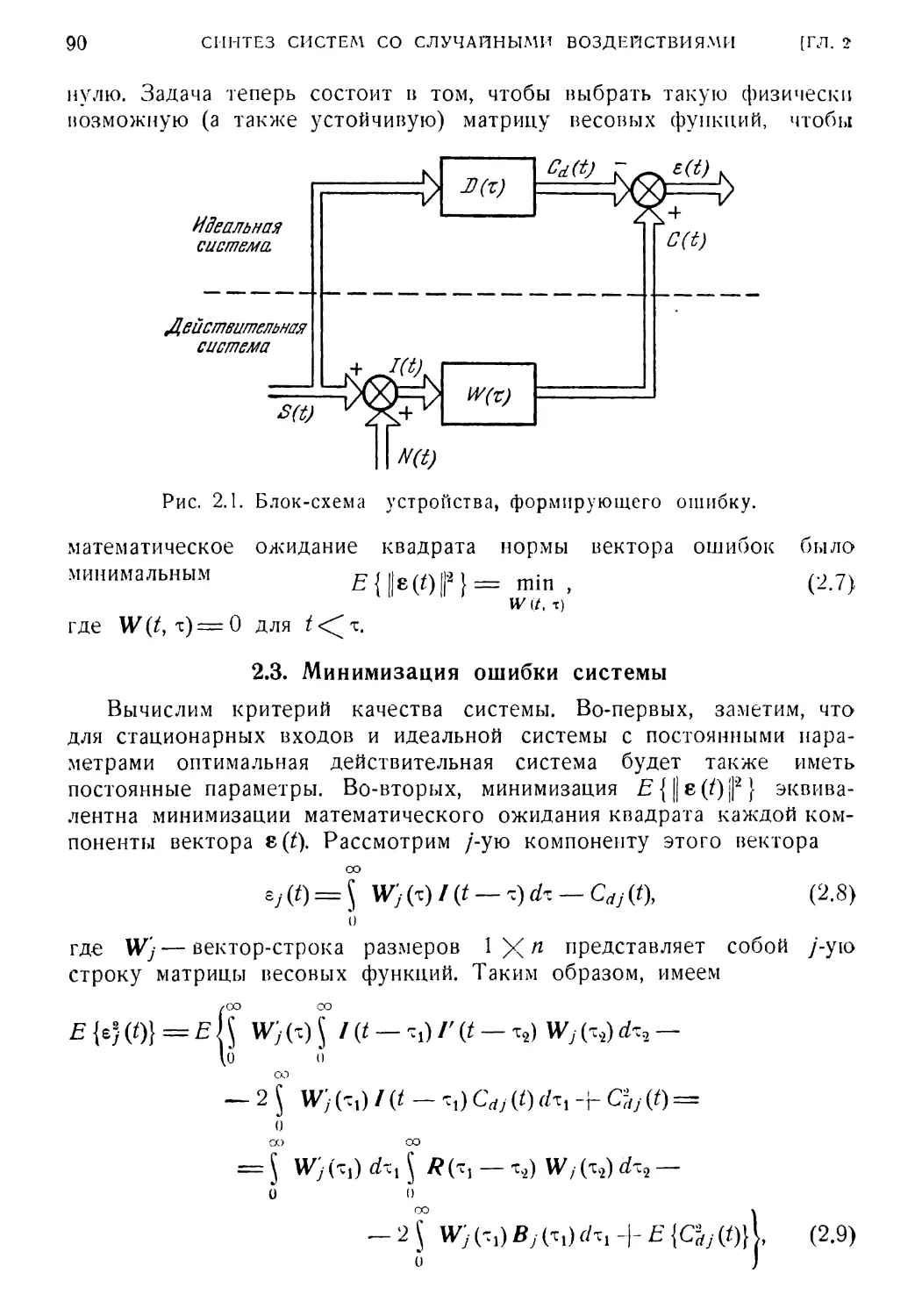
Глава 2. Синтез систем со случайными	воздействиями	 87
Раздел I. Оптимальный синтез многомерных систем со стационарными
случайными воздействиями	 87
2.	1. Введение	  87
2.	2. Постановка задачи многомерной непрерывной фильтрации
в смысле Винера	 88
2.	3. Минимизация ошибки системы	 90
2.	4. Оптимальное уравнение в области изображений	 92
2.	5. Нахождение оптимальной матрицы передаточных функций
методом неопределенных коэффициентов 	 95
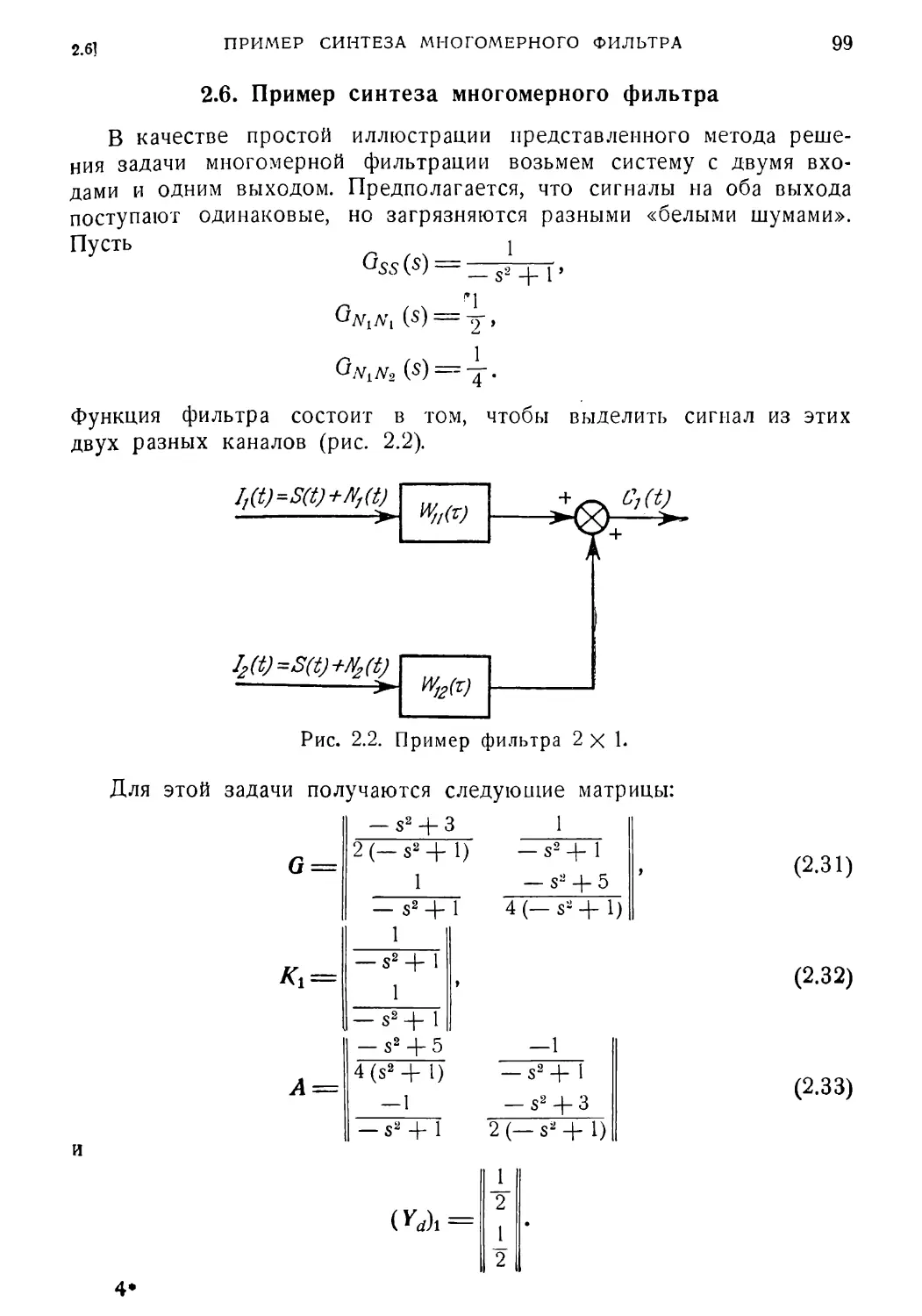
2.	6. Пример синтеза многомерного фильтра	 99	.
2.	7. Нахождение матрицы оптимальных передаточных функций
методом факторизации матрицы спектральных плотностей	101
2.	8. Факторизация рациональной матрицы спектральных плот¬
ностей 	 103
2.	9. Обсуждение методов решения задачи синтеза оптимальных
многомерных фильтров	 111
2.10. Оптимальный синтез многомерных систем управления
с полужесткой структурой	 111
Раздел II. Дополнительные аспекты синтеза систем со случайными
входами 	 114
2.11. Методы описания случайных процессов	 114
2.12. Синтез систем с нестационарными входами	 119
2.13. Метод моделирования сопряженной системы	 125
2.14. Заключительные замечания	 132
Литература 	 132
Глава 3. Функциональный анализ и его применение	к задачам
минимума среднеквадратичной	ошибки	...	137
Раздел I. Некоторые основные понятия	функционального анализа . .	.	137
3.1. Введение	 137
3.2. Типы пространств . . .  		 .	.	138
3.3. Основные неравенства	 141
3.4. Ряды Фурье	  141
3.5. Проекционный оператор 	 142
3.6. Применение теории проекционных операторов	для мини¬
мизации среднеквадратичной ошибки 	 143

ОГЛАВЛЕНИЕ	7
Раздел II. Проблемы среднеквадратичной ошибки	 146
3 7	Неотрицательные операторы в гильбертовом	пространстве
и минимизация квадратичных функционалов		 146
3 8.	Метод наискорейшего спуска в гильбертовом	пространстве	150
3 9	Нелинейная фильтрация случайных процессов	 152
3.10.'	Иллюстративный пример	 154
Литература	 157
Глава 4. Формирующие фильтры для случайных	процессов	...	159
4.1.	Причины, побуждающие заниматься задачей	определения
формирующего фильтра 	  160
4.2.	Исторический очерк 	 161
4.3*.	Предварительные сведения из теории случайных процес¬
сов. Постановка задачи 	  162
4.4.	Классические результаты для скалярных стационарных про¬
цессов 	 164
4.5..	Обобщение метода «факторизации рационального спектра»
на нестационарные процессы	 168
4.6.	Дальнейшее обобщение результатов	 173
4.7.	Некоторые фундаментальные результаты для	нестационар¬
ных процессов	 174
4.8.	Результаты, основанные на разложениях в ряды	 181
4.9.	Представление векторных процессов	 184
Литература 	 193
Глава 5. Анализ нелинейных систем управления с помощью
прямого метода Ляпунова 	 195
5.1.	Введение . . .  	 195
5.2.	Теоремы, определения и обозначения	 204
5.3.	Применение прямого метода Ляпунова и нахождение функ¬
ций Ляпунова	 223
5.4.	Заключение 	 260
Литература	 262
Глава 6. Обзор теории и методов адаптивных систем управ¬
ления 	 264
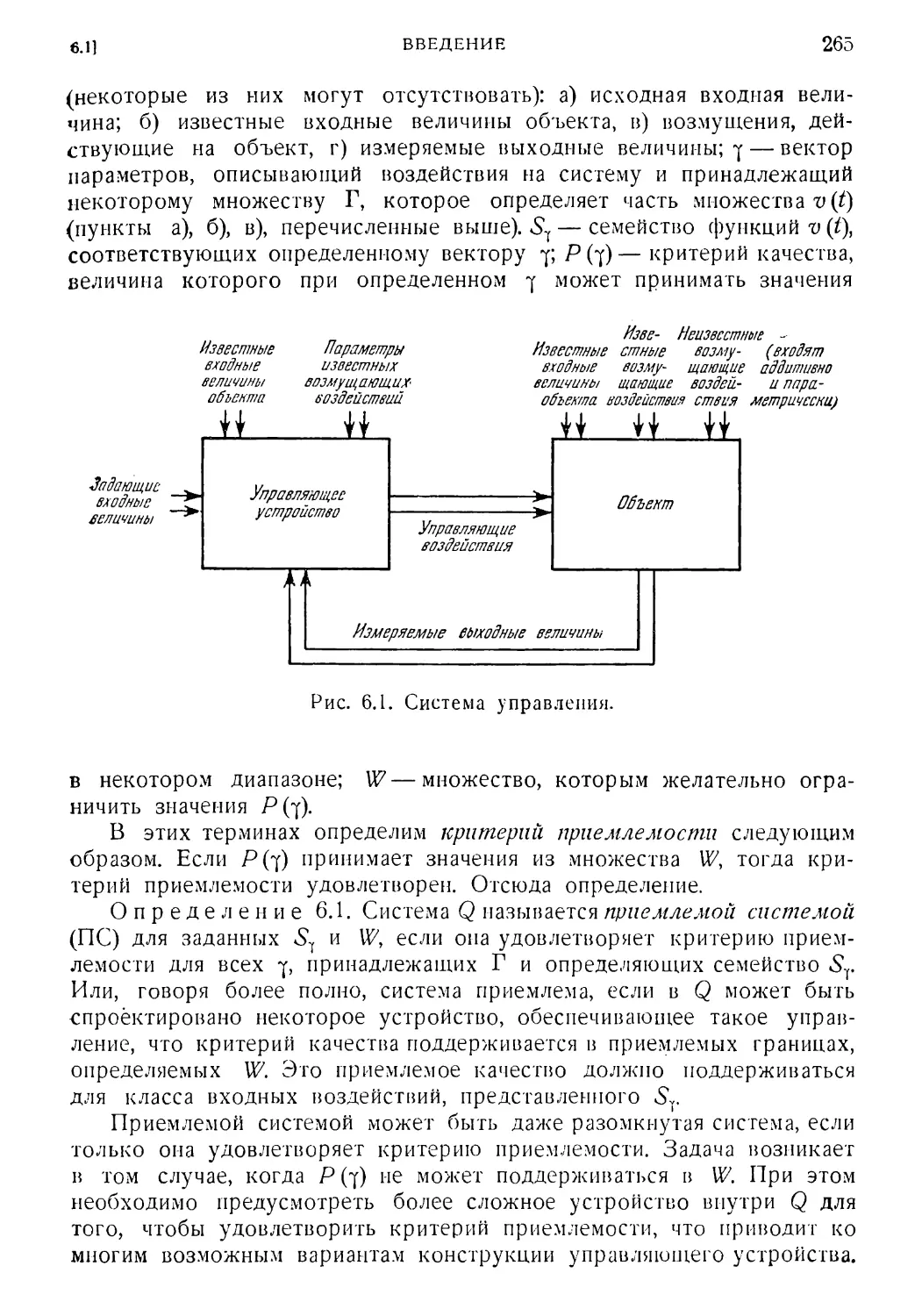
6.1.	Введение	 264
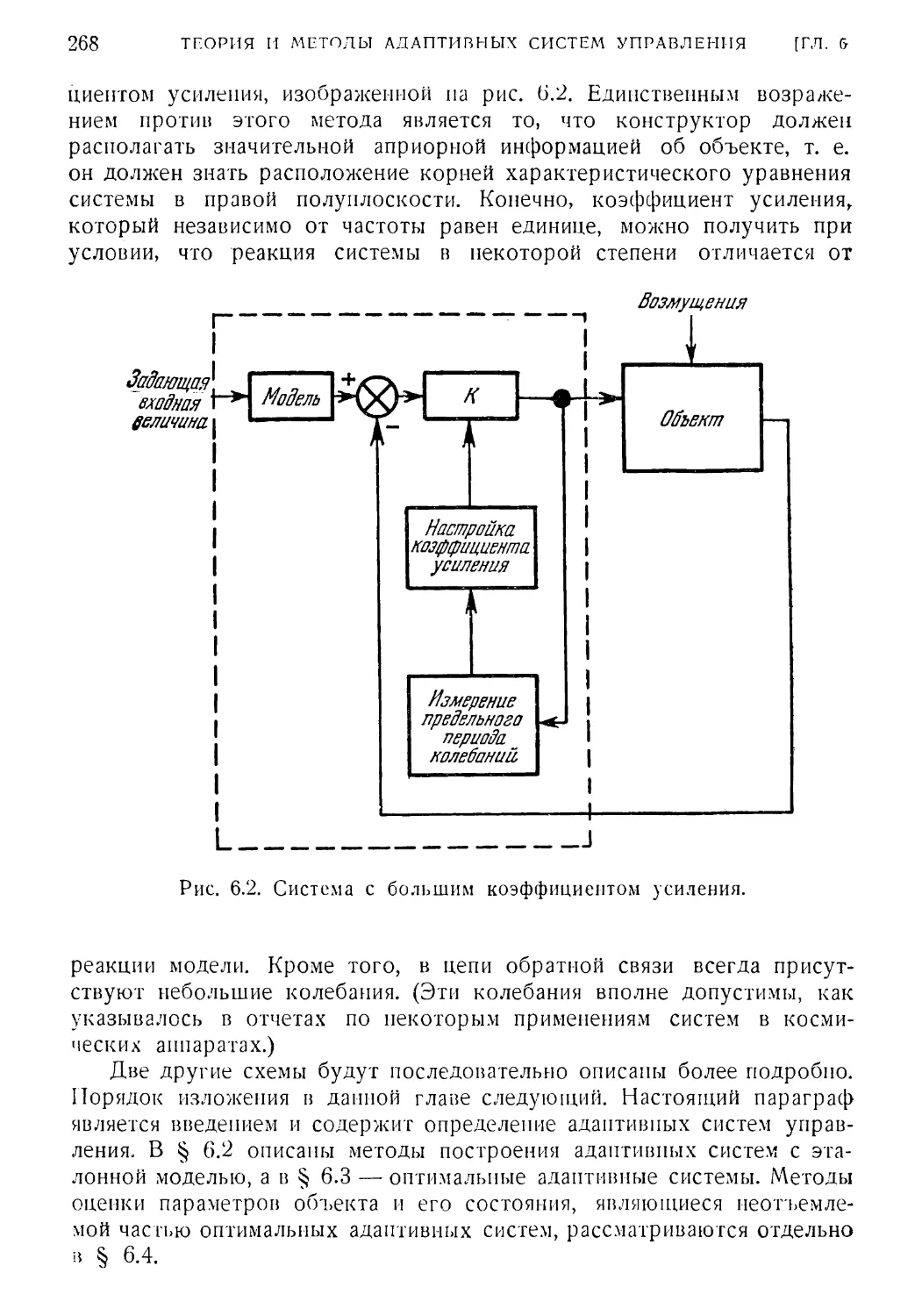
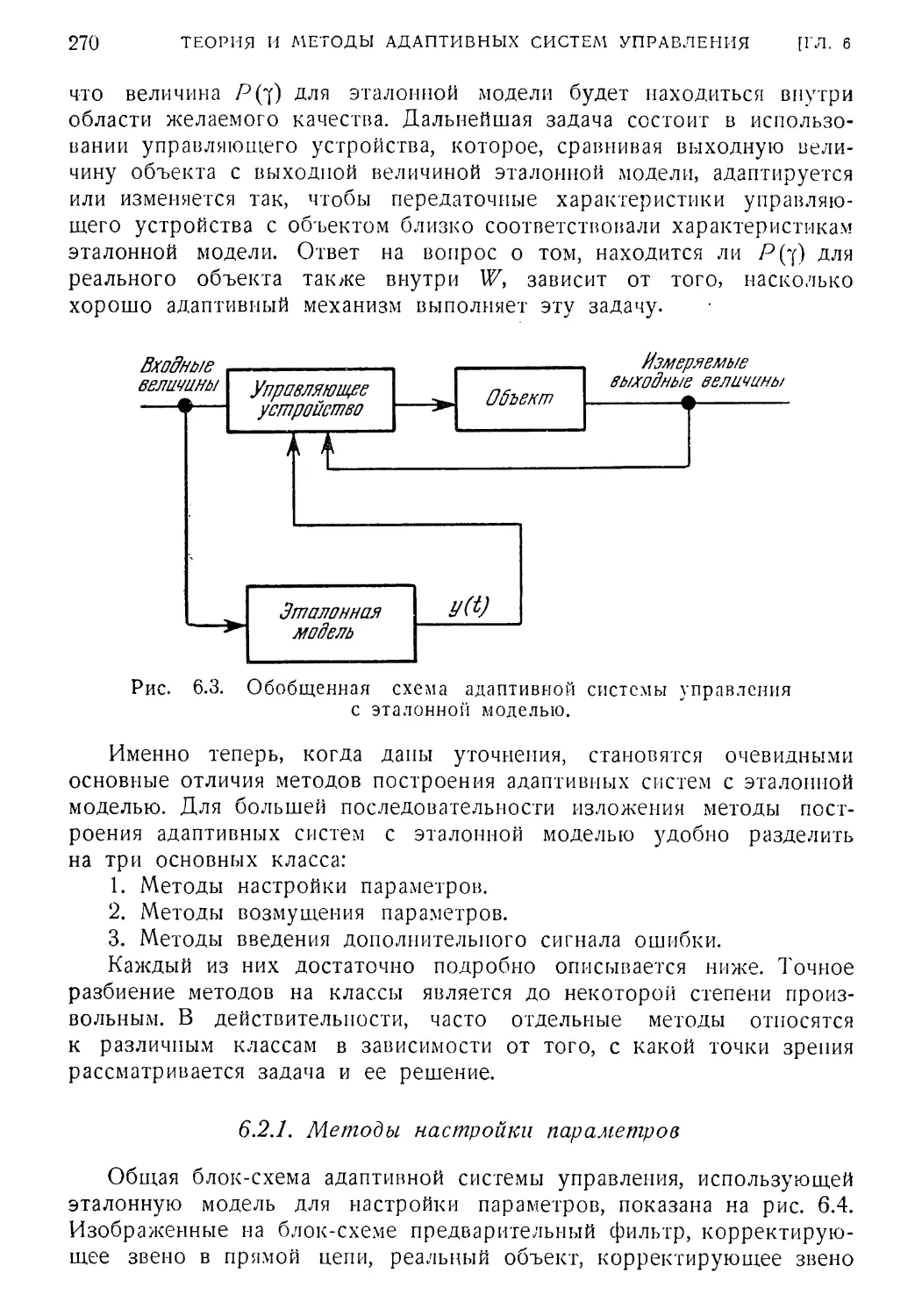
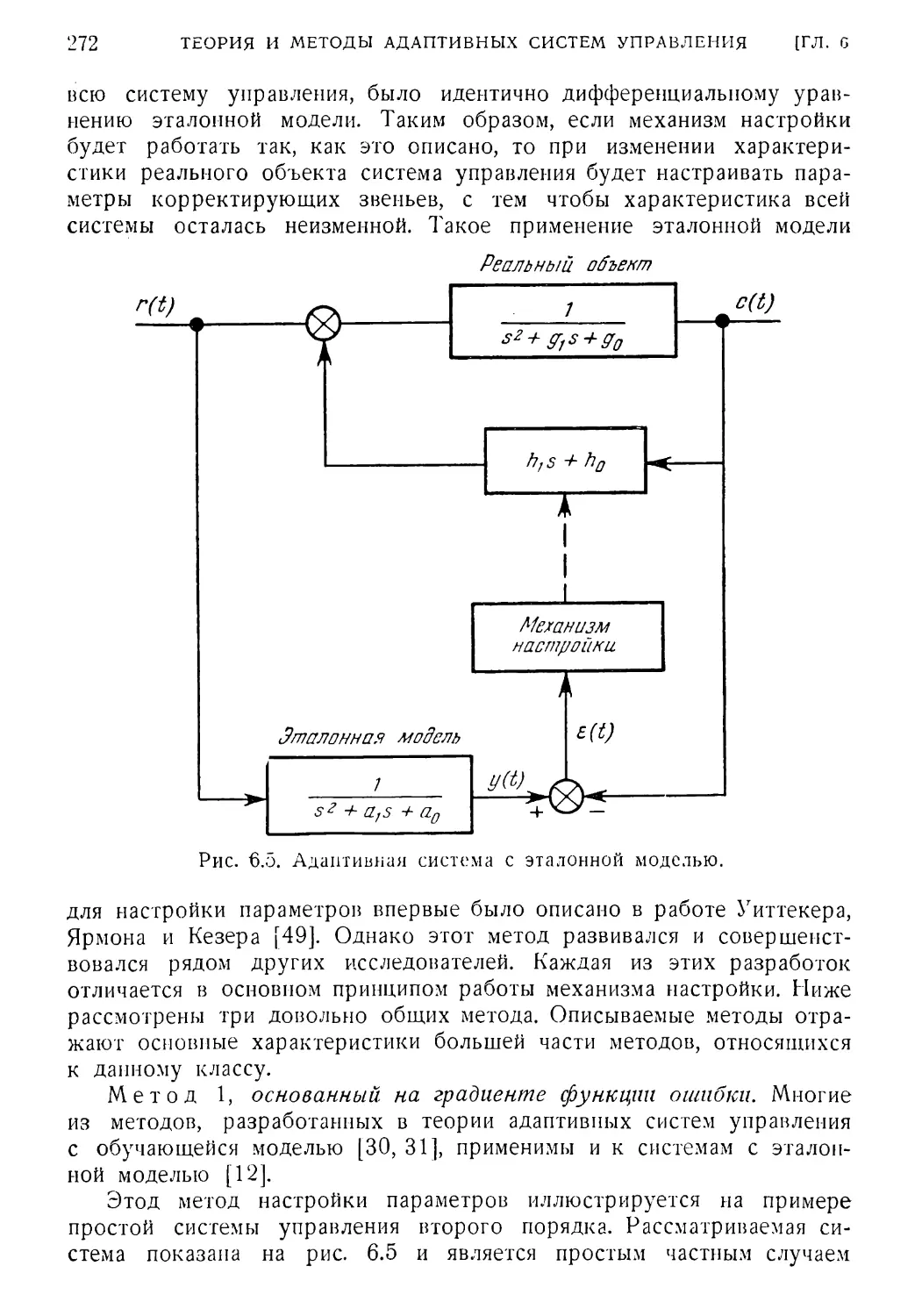
6.2.	Методы построения адаптивных систем с эталонной моделью	269
6.3.	Оптимальные адаптивные методы 	 294
6.4.	Оценка параметров и состояния		 307
Литература 	 316
Глава 7. Введение в принцип максимума Л. С.	Понтрягина	.	.	.	320
7.1.	Постановка задачи 	 320
7.2.	Принцип максимума	 325
7.3.	Вывод принципа "максимума 	 328
04.	Обобщения принципа максимума	 340
7«*	?екот°Рые приложения принципа максимума	 344
'.о. Заключение 	"	 348
Литература  	 349

8
ОГЛАВЛЕНИЕ
Глава 8. Проблема минимума нормы и некоторые другие методы
оптимизации систем управления 	 351
Раздел 1. /.-проблема и задача аппроксимации в линейном нормиро¬
ванном пространстве 	 352
8.1. Введение	 352
8.2. Математическая формулировка	 353
8.3. Приложение к задачам чебышевской аппроксимации	. . .	363
8.4. 1-проблема и задача аппроксимации в линейном нормиро¬
ванном пространстве 	 366
8.5. Аппроксимация в гильбертовом пространстве и определи¬
тель Грама	   367
8.6. Единственность экстремального элемента и наилучшая
аппроксимация 	 369
Раздел II. Приближенное решение функциональных уравнений	.	.	.	371
8. 7. Введение	 371
8. 8. Обратный оператор	 372
8. 9. Сходимость приближенных решений	 374
8.10.	Квазилинеаризация 	 376
Литература	 382
Глава 9. Методы аналитического конструирования в задаче
оптимального управления 	 384
9.1. Введение	 384
9.2. Формулировка задачи	 385
9.3. Метод динамического программирования 	 386
9.4. Решение, получаемое методом динамического программи¬
рования 	 389
9.5. Решение задачи с помощью принципа максимума	 393
9.6. Сравнение методов принципа максимума и динамического
программирования	 396
9.7. Смежные вопросы	 398
Литература 	 398
Глава 10. Некоторые элементы теории стохастической аппрокси¬
мации и ее применение к данной задаче управления	....	400
10.1. Введение	 400
10.2. Пример стохастической аппроксимации	 400
10.3. Пример. Процесс Роббинса — Монро 	 402
10.4. Пример. Процесс Кифера—Вольфовица 	 404
10.5. Одна задача управления 	 405
10.6. Применение методов стохастической аппроксимации	....	407
10.7. Заключение 	 410
Литература 	 411
Глава 11. Анализ и синтез дискретных систем	 413
11.1. Введение	 413
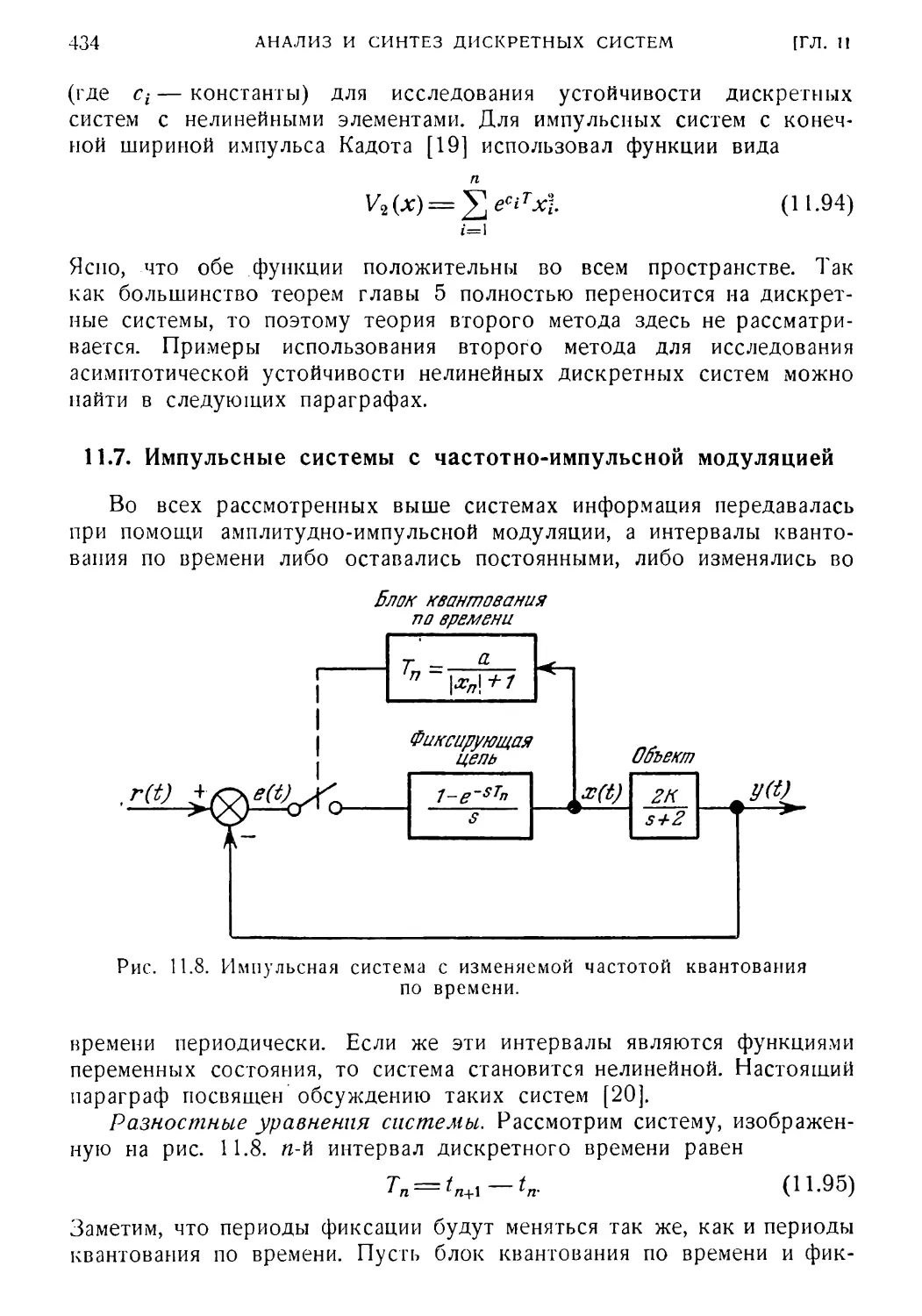
11.2. Процесс квантования по времени 	 414
11.3. Поведение во времени идеализированной импульсной
системы 	 416
11.4. Частотный анализ идеализированных линейных импульсных
систем 	 418

ОГЛАВЛЕНИЕ
9
115 Формулировка дискретных задач с помощью понятия про¬
странства состояний	 421
116 Устойчивость дискретных систем		 430
11*7.' Импульсные системы с частотно-импульсной модуляцией 434
11*8. Широтно-импульсная модуляция.	ШИМ	 438
1L9.' Синтез дискретных систем	 443
Литература	 451
Глава 12. Человек-оператор в системах управления	 454
12. 1.	Введение 	 454
12! 2.	Характеристики человек-оператора в системе управления	455
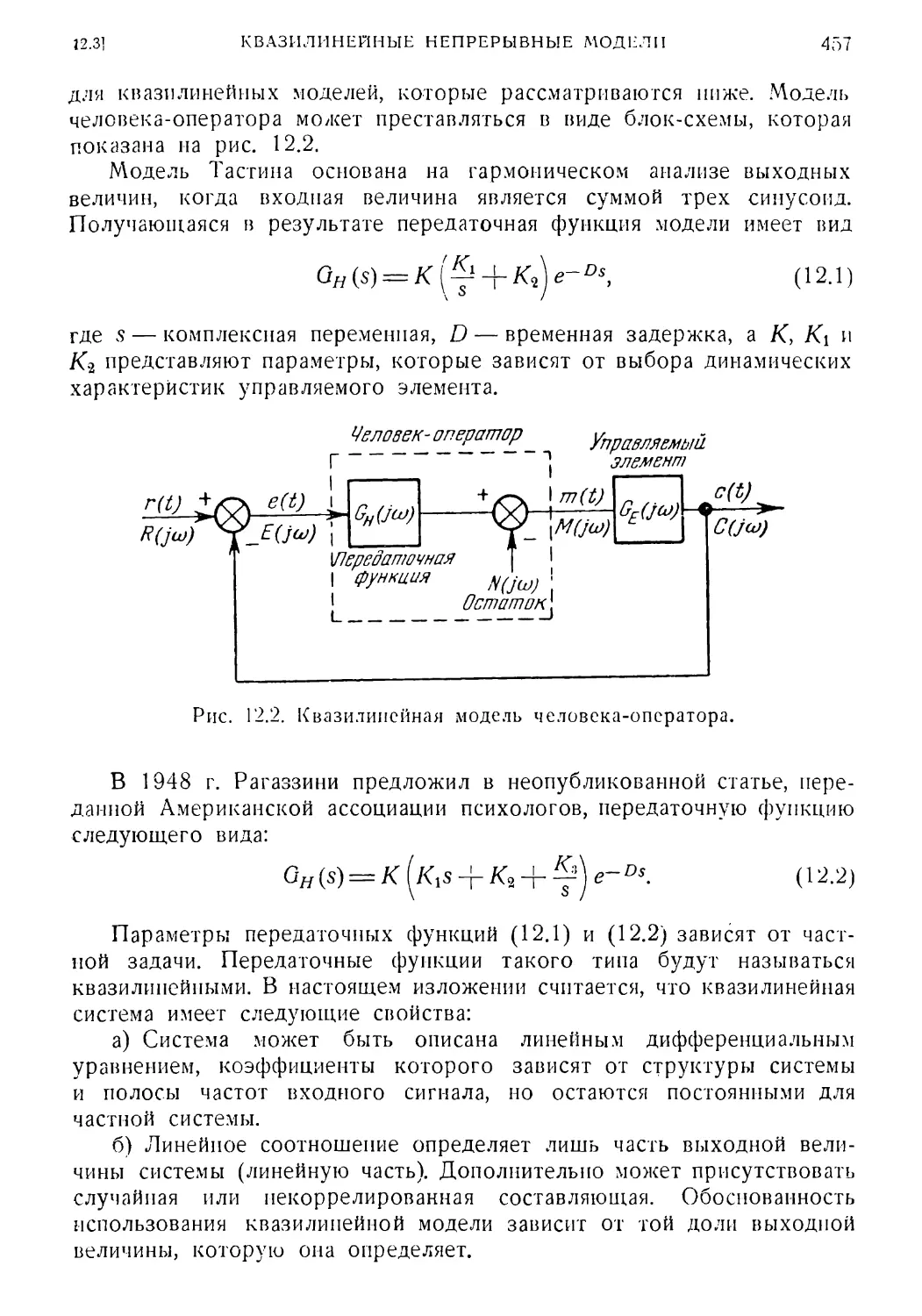
12. 3.	Квазилинейные непрерывные модели	 456
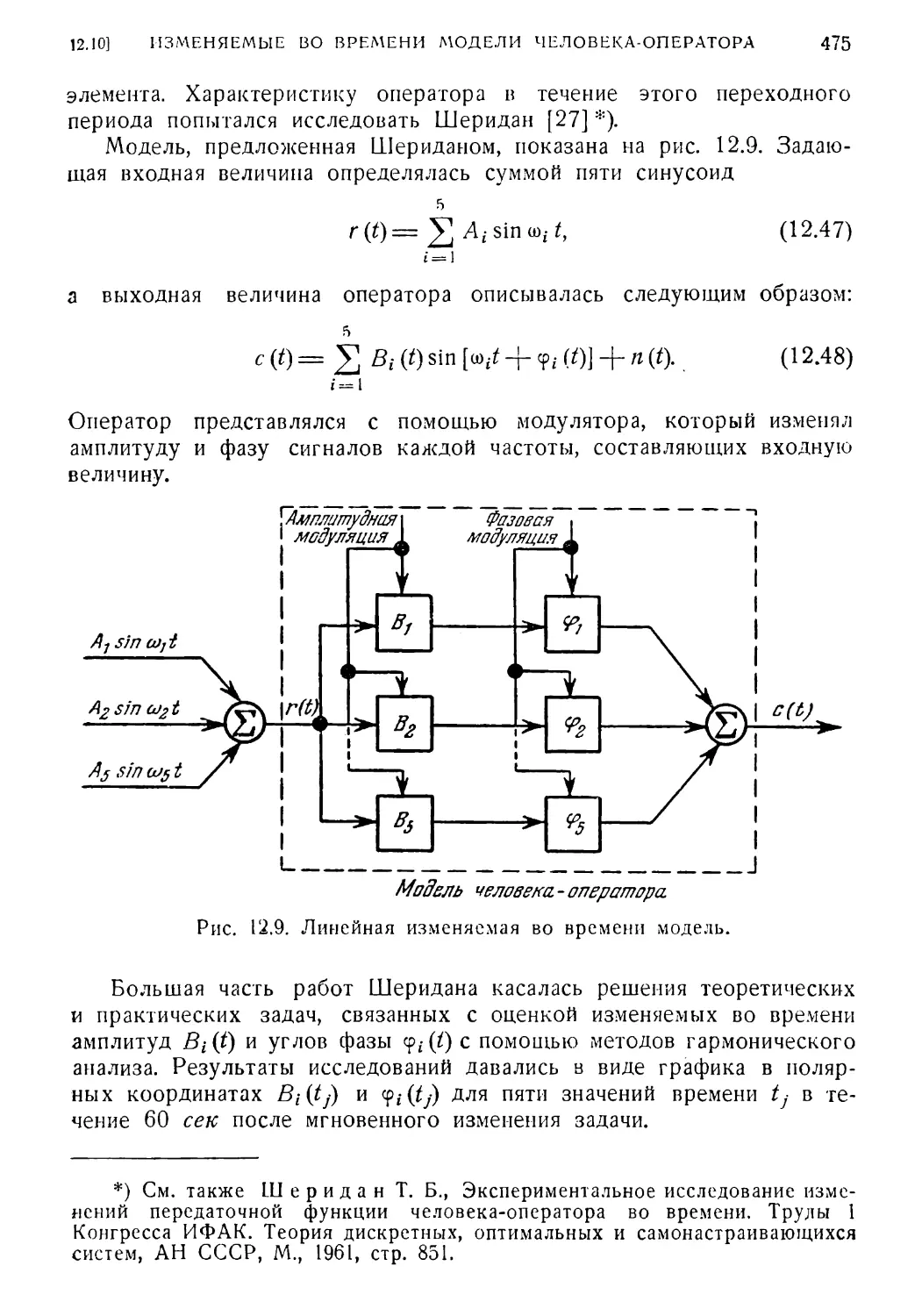
12. 4.	Синтез квазилинейных непрерывных моделей :	 459
12. 5.	Зависимость параметров модели от вынуждающей функ¬
ции 	   462
12. 6.	Недостатки квазилинейной непрерывной модели . . . . >	462
12. 7.	Дискретные или импульсные модели человека-оператора	463
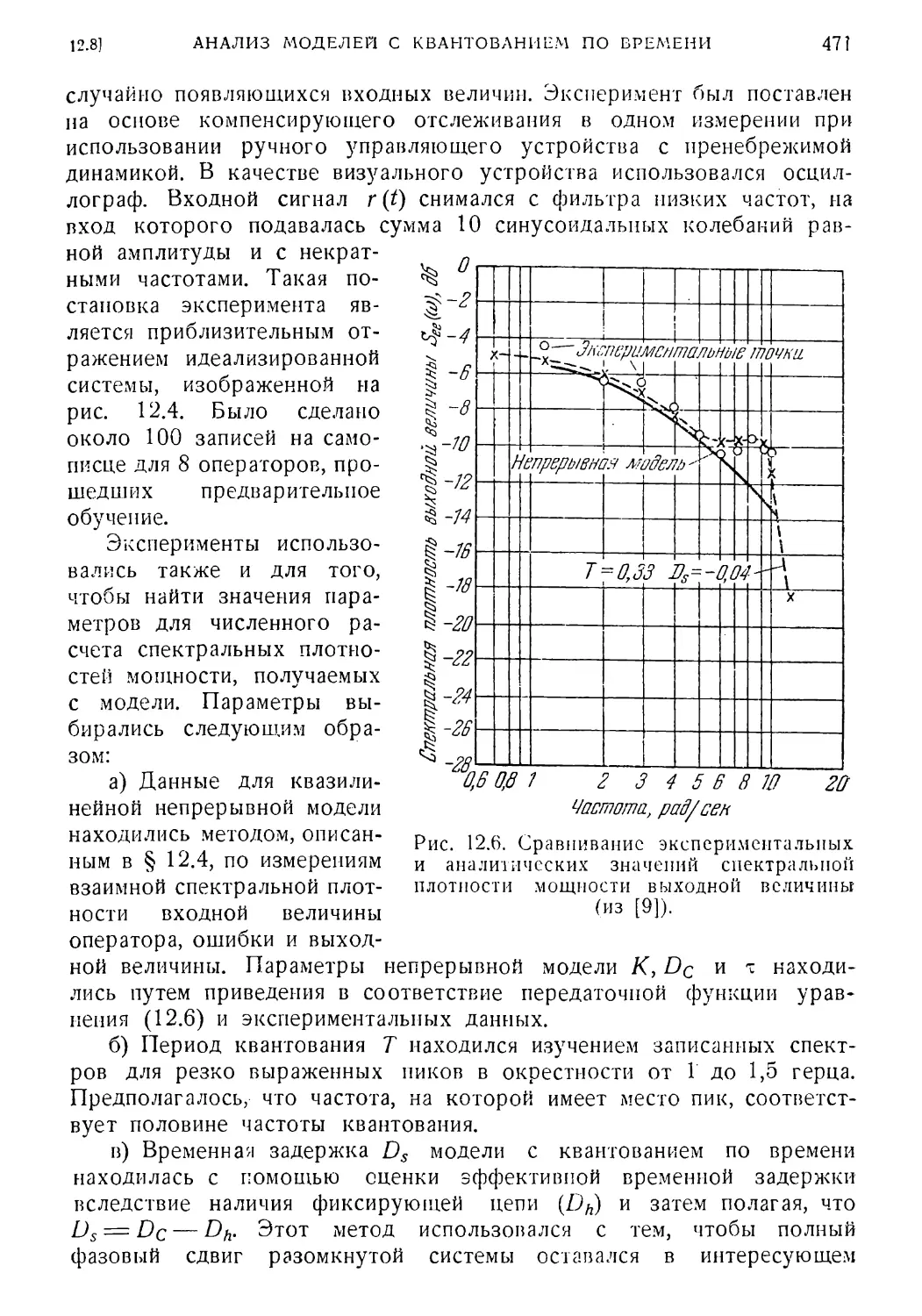
12. 8.	Анализ непрерывных моделей с квантованием по времени
при случайных входных сигналах	 466
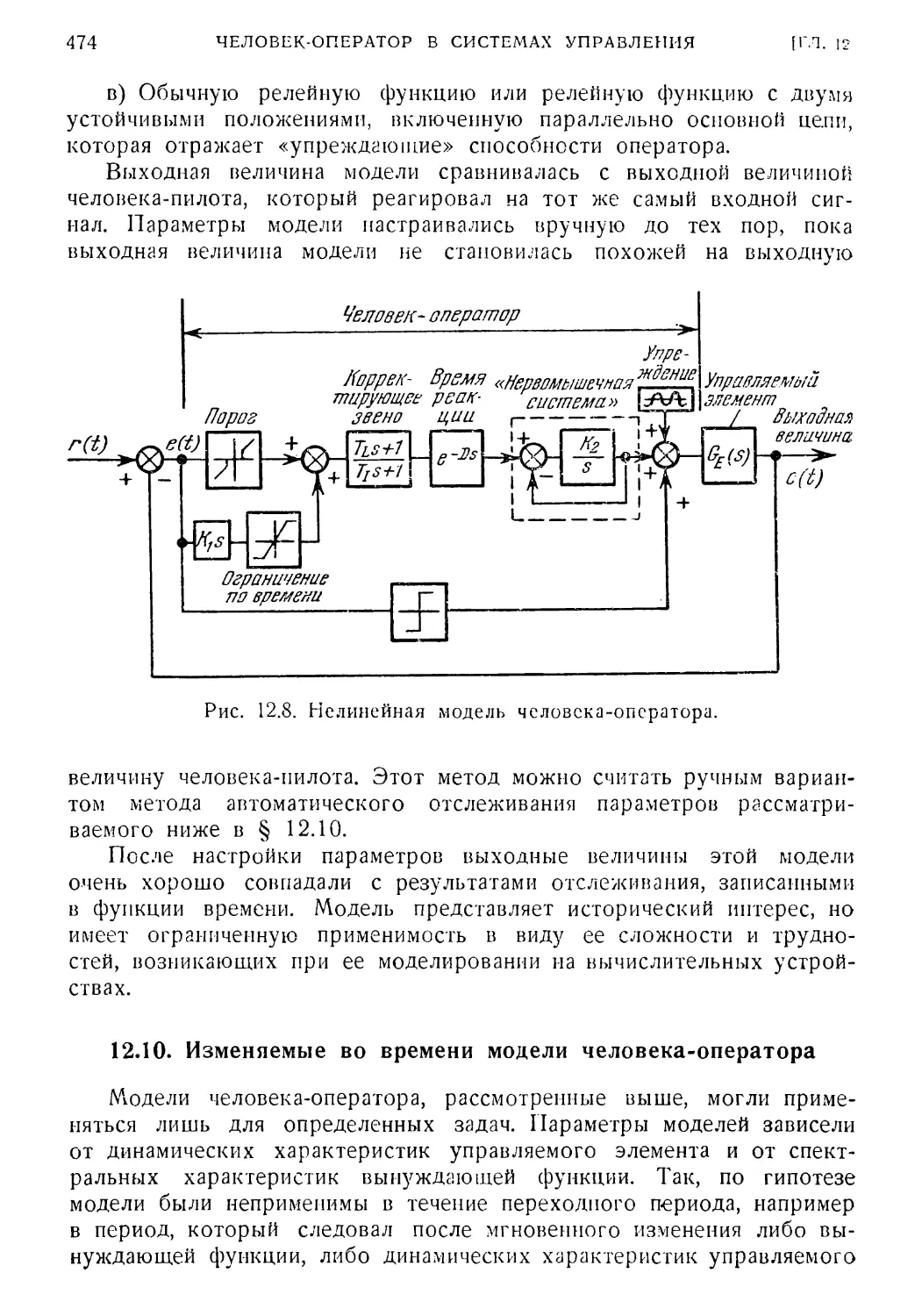
12. 9.	Нелинейные модели человека-оператора	 473
12.10.	Изменяемые во времени модели человека-оператора . . .	474
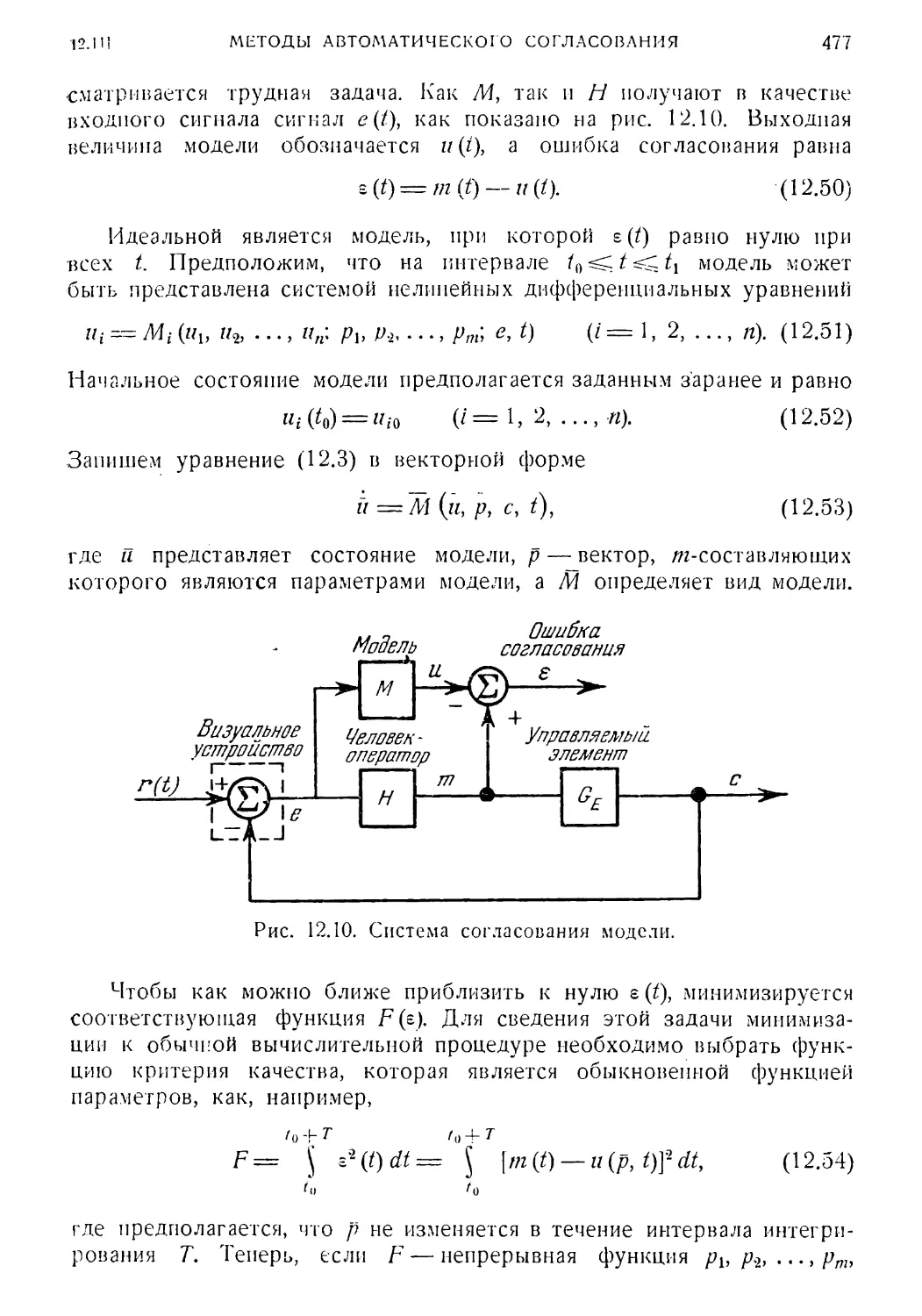
12.11. Методы автоматического согласования (отслеживания па¬
раметров) модели для описания характеристики человека-
оператора [34]	  476
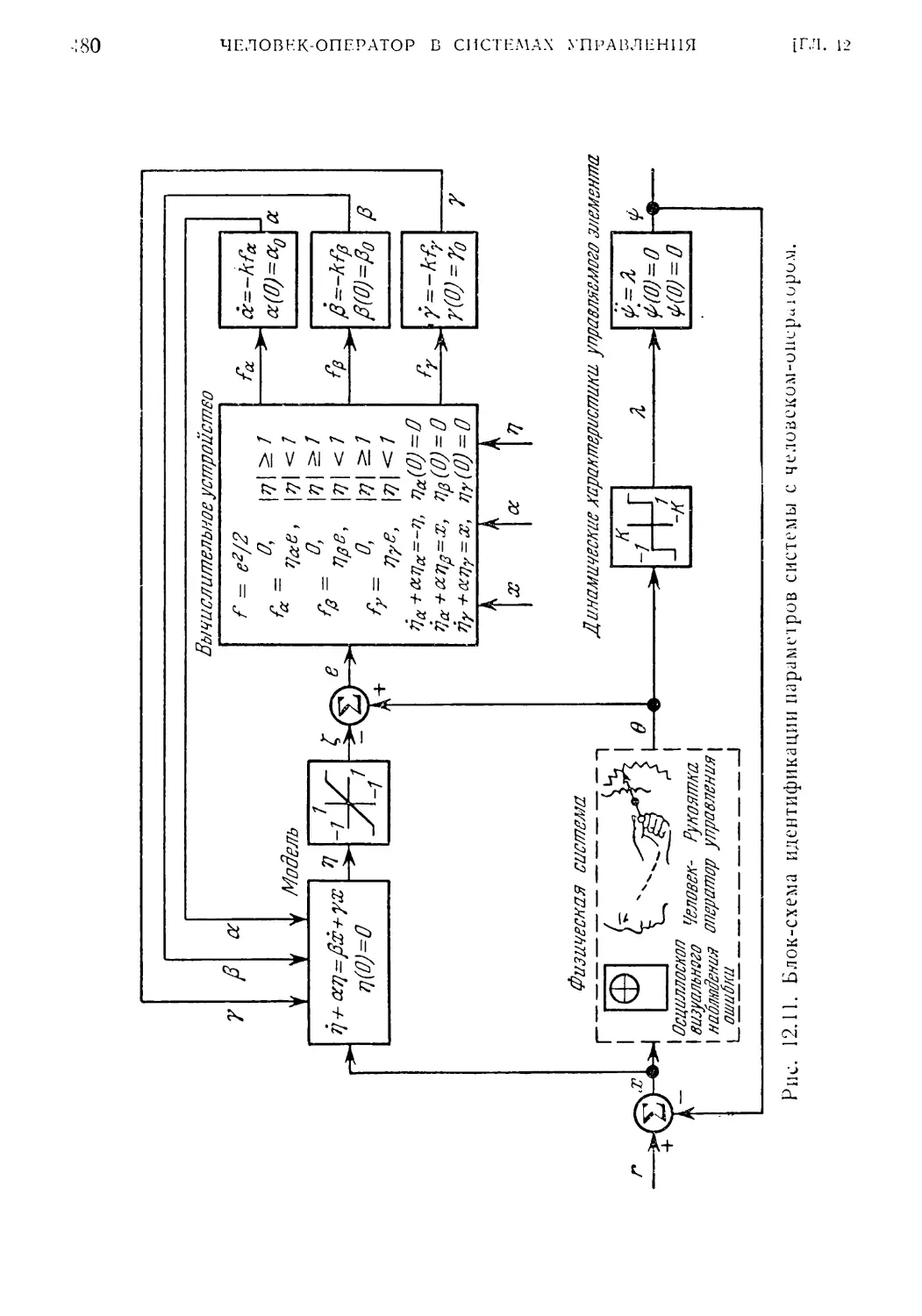
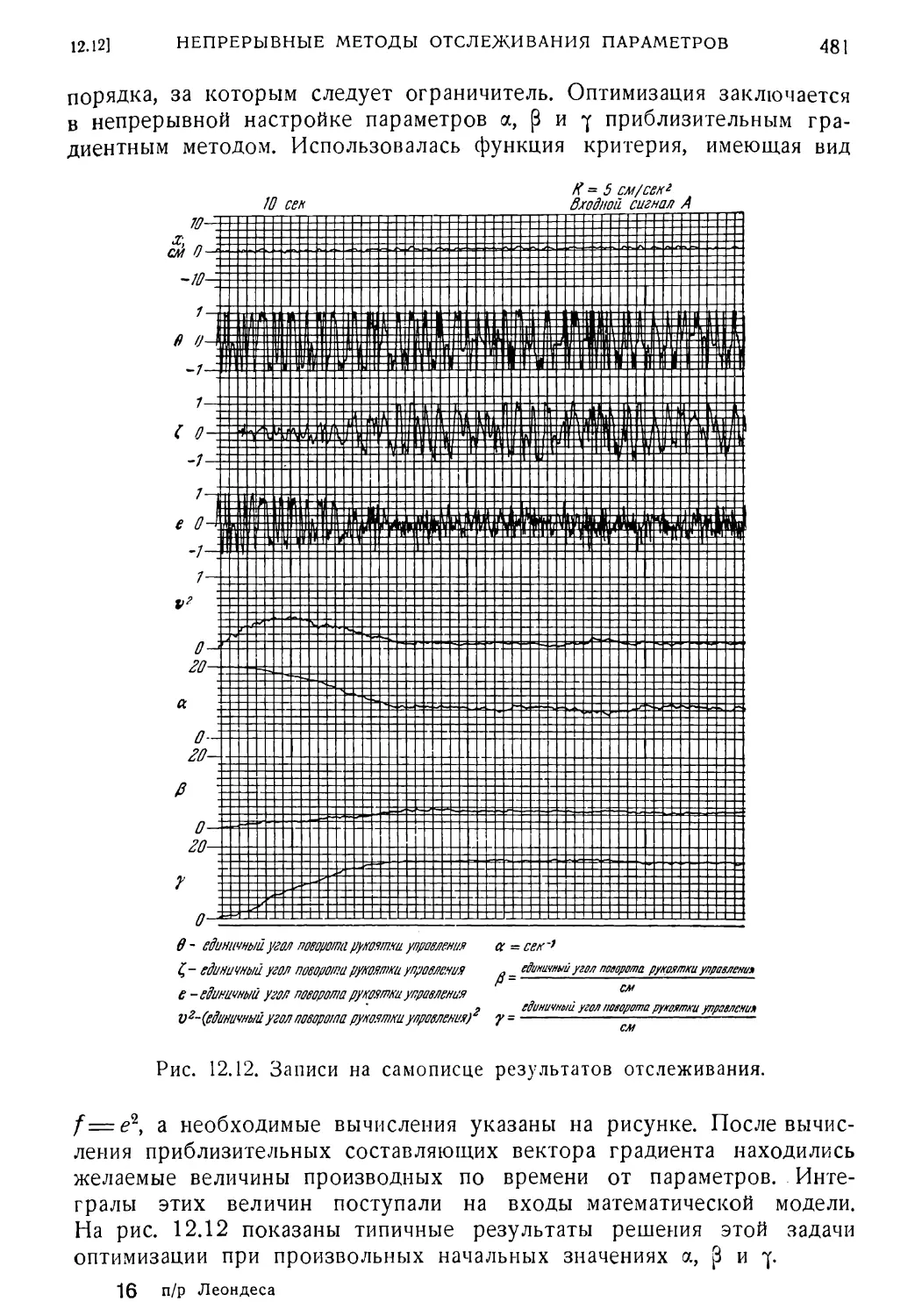
12.12.	Непрерывные методы отслеживания параметров 	 478
12.13.	Согласование модели в случае ортогональных фильтров 482
12.14.	Заключение	 483
Литература	 483
Глава 13. Применение современных методов анализа и синтеза
к системам управления летательными аппаратами	 486
13.1.	Введение	 486
13.2.	Общие свойства уравнений динамики 	 487
13.3.	Общие задачи управления	 492
13.4.	Методы анализа и решения задач управления	 495
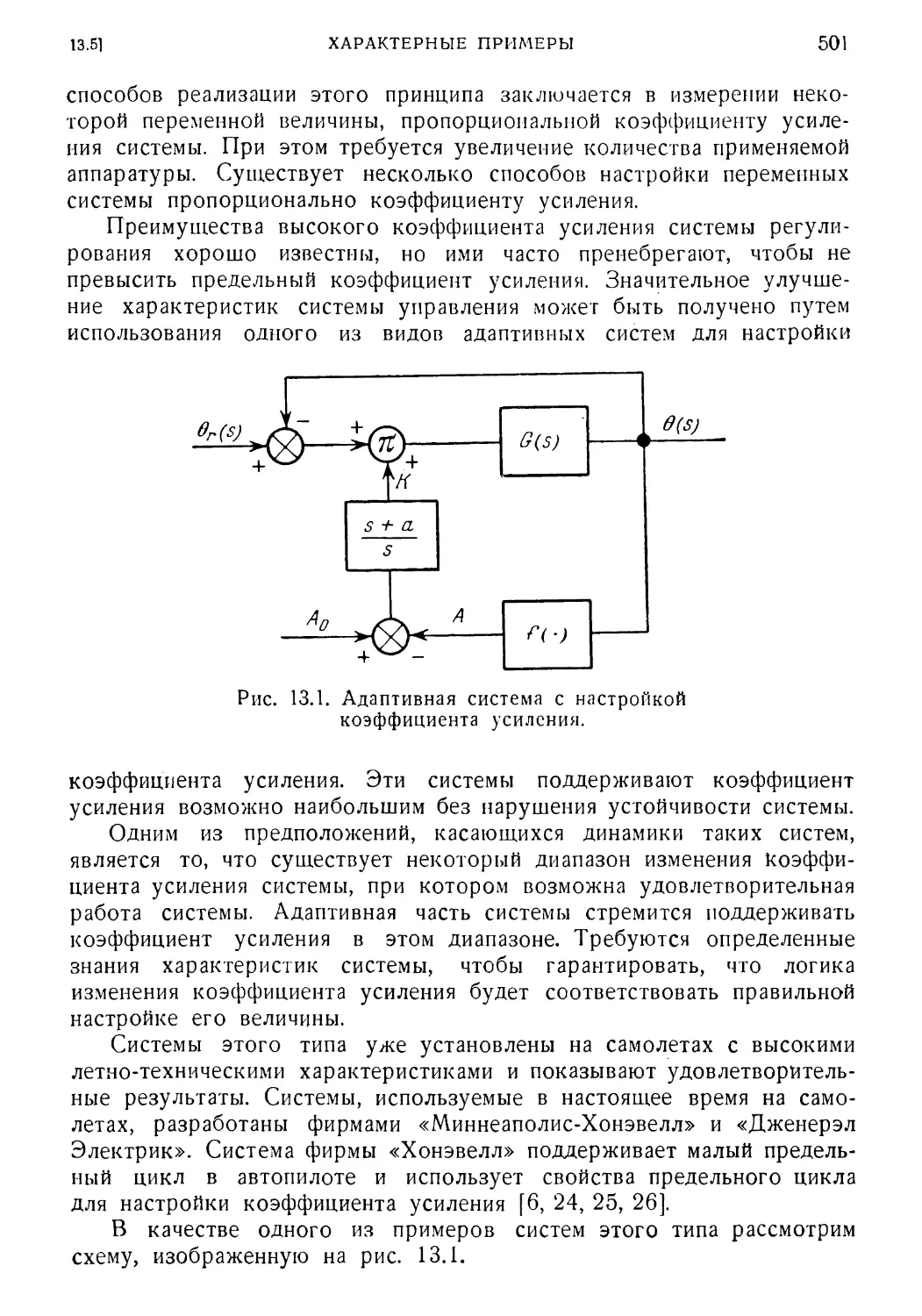
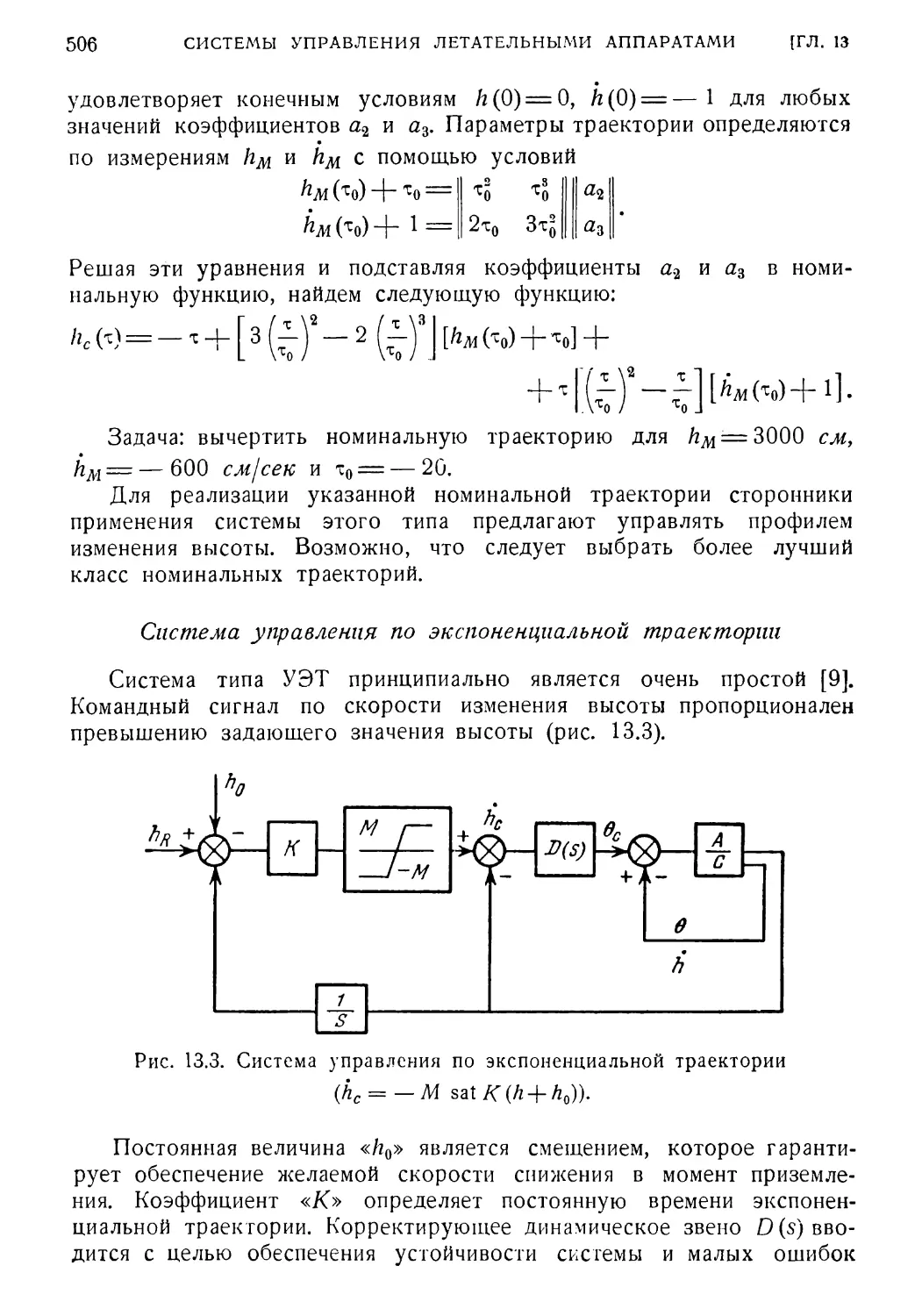
13.5.	Характерные примеры	 500
Литература	 507
Предметный указатель	 509

ОТ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
В настоящее время нет недостатка в книгах по теории и технике
автоматического управления как учебного, так и монографического
характера. В силу быстрого развития теории управления многие из
этих книг устаревают порой до выхода в свет. Поэтому особую
важность приобретают книги, в которых изложены наиболее важные
направления современной теории, созданные в последние годы. Не
перегруженные деталями, эти книги позволяют познакомиться широ¬
кому кругу специалистов с состоянием и перспективами развития этих
новых направлений.
Именно этим требованиям и удовлетворяет предлагаемый совет¬
скому читателю перевод книги «Современная теория систем управле¬
ния», написанной коллективом известных американских специалистов
под редакцией проф. Леондеса.
В книге изложено много новых вопросов, которые до самого по¬
следнего времени обсуждались только на страницах технических жур¬
налов. Это относится к новым методам анализа и синтеза систем
управления (методов функционального анализа, стохастической аппрок¬
симации), теории адаптивных систем и систем с человеком-оператором.
Ряд вопросов, относящихся к сравнительно известным разделам, таким,
как системы с переменными параметрами, поведение систем при слу¬
чайных воздействиях, нелинейные, дискретные и оптимальные системы,
изложены в четкой и ясной форме и представят большой интерес не
только для новичков, но и для специалистов.
Составленная в виде сборника отдельных работ, книга позволит
специалистам с минимальной затратой времени познакомиться с суще¬
ством интересующих его направлений, а также с библиографией ра¬
бот по этому направлению.

ОТ РЕДАКТОРА РУССКОГО ПЕРЕВОДА
1!
Ссылки на литературу, добавленную редактором в библиографию
соответствующих глав, отмечены звездочкой. По сравнению с ориги¬
налом глава 1 дополнена новыми параграфами 1.28—1.38, которые
представляют собой разделы книги [17] автора этой главы.
Книга, безусловно, будет полезна научным работникам, инженерам,
аспирантам, студентам и всем тем, кто пожелает познакомиться с но¬
выми направлениями современной теории автоматического управления.
В переводе книги принимали участие Я. А. Коган, (гл. 2,4,9,10),
Ю. Э. Сагалов (гл. 1, 6, 12, 13) и И. В. Тиме (гл. 3, 5, 7, 8, 11)
Параграфы 1.28—1.38 главы 1 переведены С. К. Арутюновым.
Я. Цыпкин

ПРЕДИСЛОВИЕ
По сравнению с сегодняшним уровнем знаний в начале 40-х го¬
дов этого столетия методов анализа и синтеза систем управления
фактически не было. В то время только начинали развиваться методы
расчета простых опережающих или запаздывающих корректирующих
звеньев с желаемыми временными характеристиками для относительно
простых линейных систем. Метод корневого годографа и связанные
с ним понятия появились всего лишь немногим более десяти лет назад.
Метод гармонического коэффициента усиления, столь полезный при
расчете и исследовании многих нелинейных систем управления, также
появился в 50-х годах. Во многих случаях задачи, возникающие
в приложениях, опережали появление методов, пригодных для их
решения.
Последнее десятилетие характеризуется весьма значительным рос¬
том числа приложений теории систем управления. Благодаря появле¬
нию все более усложняющихся разнообразных прикладных задач
сильно развилась и сама теория. Развитию теории систем управления
способствовало и то, что за это время было поставлено много хоро¬
ших задач, которые привлекли внимание математиков, физиков и инже-
неров-теоретиков. Ярким примером такого интереса к задачам теории
систем управления могут служить работы математиков Р. Велл¬
мана по динамическому программированию и Л. С. Понтрягина по
принципу максимума.
Стоит, вероятно, отметить, что если в начале 40-х годов имевшиеся
теоретические методы во многих случаях были неадекватны много¬
численным прикладным задачам, то в последние годы наблюдается
ситуация, когда многие развитые или развиваемые методы появляются
задолго до возможного их применения, если вообще это когда-либо
можно будет сделать. Однако даже в этих случаях есть примеры, в
которых теоретические результаты приводили в конечном счете к
плодотворным идеям с точки зрения приложений. Развитие теории в
любом случае неизбежно ведет к более глубокому пониманию изуча¬
емых явлений.
Эта книга является хорошим подтверждением некоторых из вы¬
сказанных выше суждений. Большинство из описанных в ней методов

ПРЕДИСЛОВИЕ
13
нпосъ менее пяти лет назад. Возможности применения этих ме-
Подов вполне ясны. Возьмем, например, главу 1 «Методы синтеза ли¬
нейных систем автоматического управления с переменными'парамет¬
рами», написанную Стабберудом. Еще несколько лет назад общие
методы синтеза линейных систем с переменными параметрами нахо¬
дились в относительно неудовлетворительном состоянии. Результаты
исследований Стабберуда за последние годы в значительной степени
способствовали изменению такой ситуации. Эти результаты имеют
многочисленные полезные практические применения, например в не¬
которых задачах управления посадкой самолета, задаче управления
снарядами класса «воздух — воздух» и многих других. К этому мож¬
но добавить, что в ряде случаев при анализе и синтезе нелинейных
систем их можно с достаточной степенью точности аппроксимировать
линейными системами с переменными параметрами. Аналогичные за¬
мечания можно сделать и почти по всему остальному материалу книги.
При выборе содержания этой книги мы исходили из следующих
соображений. Прежде всего отдавалось предпочтение тем методам,
которые, по-видимому, выдержат проверку временем. Кроме того, там,
где это было возможно и уместно, была опущена большая часть из
тех важных методов, которые уже хорошо изложены где-нибудь в
другом месте.
Например, эффективный метод динамического программирования
рассматривается Шульцем в одном из параграфов главы 9 скорее с
целью сравнения, чем с целью вывода, так как уже имеются широко
известные книги и работы, в которых он хорошо изложен. С дру¬
гой стороны, методы, представленные в книге Понтрягина и др.
«Математическая теория оптимальных процессов», довольно под¬
робно рассмотрены в главе 7.
Теперь уместно в нескольких словах обсудить каждую из глав
книги и роль, которую описанные в них методы играют при совре¬
менном состоянии теории управления. Область синтеза линейных авто¬
матических систем с переменными параметрами, рассматриваемая
в главе 1, является предельно важной в прикладной теории систем
управления, и некоторые замечания о характере этой главы были
сделаны выше.
Работы, посвященные синтезу многомерных систем или многопо¬
люсников со случайными воздействиями, появились сравнительно
недавно. Отметим также, что подходящие методы математического
описания случайных процессов, которые могут поступать на вход
систем управления, получили слабое освещение в литературе. Осо¬
бенно это касается более сложных процессов, встречающихся при
проектировании технических систем. Глава 2 поднимает эти важные
вопросы.
Можно с уверенностью сказать, что в следующем десятилетии
Довольно большое число инженеров-практиков будет хорошо знать

14
ПРЕДИСЛОВИЕ
методы функционального анализа и понимать их ценность для реше¬
ния инженерных задач теории управления. Глава 3 вводит читателя
в круг идей функционального анализа. В ней приводятся примеры
применения методов функционального анализа к решению приклад¬
ных задач управления. В последнее время появилось много прекрас¬
ных книг по функциональному анализу, которые предназначены для
инженеров. Особенно здесь стоит отметить очень хорошие учебники,
изданные в СССР.
При использовании методов моделирования, например метода
моделирования сопряженной системы, предложенного более десяти
лет назад Лэнингом и Бэттином для определения среднеквадратичной
ошибки линейной системы с переменными параметрами, на вход ко¬
торой поступает нестационарный случайный процесс, необходимо
уметь получать нестационарный случайный сигнал из стационарного
«белого шума». Кроме того, различные развитые недавно методы
синтеза оптимальных линейных фильтров с переменными параметрами,
на вход которых поступают нестационарные случайные сигналы,
существенно опираются на математическое описание формирующего
фильтра, посредством которого данный нестационарный случайный
сигнал получается из «белого шума». Уже из сказанного можно
усмотреть важность решений задачи определения формирующего
фильтра при рассмотрении довольно широкого класса задач автома¬
тического управления. Поэтому глава 4 посвящена формирующим
фильтрам для случайных процессов.
В последнее время появились достаточно хорошие учебники
по применению прямого метода Ляпунова для анализа нелинейных
систем управления. Среди них книга В. Хана, которая недавно пере¬
ведена на английский язык, и хорошо известная книга Ласаля и Леф-
шеца. Однако в обеих книгах отсутствуют некоторые очень полезные
для практики методы образования функции Ляпунова, например метод
градиента, предложенный недавно Д. Г. Шульцем. Это, конечно,
произошло из-за того, что метод Шульца был опубликован после
выхода упомянутых книг. С момента выхода этих книг появились
и другие новые результаты. Ввиду большой важности прямого метода
Ляпунова для прикладных задач, а также для того, чтобы сделать
ряд полученных недавно интересных результатов более доступными
и возможно более пригодными для инженеров, в книгу включена
глава 5. Среди методов, рассматриваемых в этой главе, отметим
весьма существенный для практики метод Ляпунова для неавтономных
систем.
Учитывая тенденцию все большего усложнения задач управления,
для их решения разрабатываются новые методы. Наиболее интересные
из них с точки зрения приложений дает теория адаптивных систем
управления. Глава б посвящена рассмотрению одного подхода к раз¬
работке различных методов синтеза адаптивных систем управления.

ПРЕДИСЛОВИЕ
15
Не затрагивая здесь вопрос определения адаптивных систем управле¬
ния, оставим дальнейшие замечания до главы 6.
О главе 7 уже говорилось выше.
Глава 8 посвящена развитию подхода к задаче оптимизации
систем, связанного с так называемой L-проблемой моментов
№ Г Крейна. Методы, применяемые здесь, основаны на функциональном
анализе и были рассмотрены ранее в главе 3. В данной главе изла¬
гается Г-проблема Крейна и показывается, как с ее помощью можно
избежать решения двухточечной краевой задачи, возникающей во мно¬
гих оптимальных задачах. Часть из них обсуждается в главе 9; хотя
при этом часто возникают другие вычислительные проблемы подобной
трудности. Указываются и другие важные приложения рассматривае¬
мого подхода.
Глава 9 посвящена рассмотрению и сравнению различных анали¬
тических методов синтеза оптимальных линейных систем управления.
Изучаемые и сравниваемые здесь методы включают динамическое
программирование и принцип максимума Понтрягина. Такое сравнение
должно оказаться весьма полезным для более ясного понимания отно¬
сительной ценности этих методов при решении рассмотренного класса
задач.
Теория стохастической аппроксимации дает один из подходов
к исследованию стохастической устойчивости систем управления.
Несмотря на то, что методы стохастической аппроксимации в настоя¬
щее время мало используются, обзор и исследование задач, которые
можно решать с помощью этих важных методов, вполне уместны,
и эти вопросы рассматриваются в главе 10.
Вычислительные машины дискретного действия играют все боль¬
шую роль в современных устройствах управления. Основой развития
этих устройств являются методы анализа и синтеза дискретных сис¬
тем. Огромная важность этой области ясна из материалов, представ¬
ленных в главе 11.
Человек-оператор присутствует во многих системах управления
либо как неотъемлемая часть, либо как элемент, включающийся в ра¬
боту в случае крайней необходимости, например при выходе из строя
основных узлов системы. В последней ситуации конструкция системы
управления обязательно должна учитывать рабочие характеристики
человека-оператора или его передаточную функцию. Такой аналитиче¬
ский подход можно использовать, например, для установления огра¬
ничений на величины параметров системы управления, чтобы гаранти¬
ровать, что человек-оператор действительно сможет управлять столь
сложной системой, как, например, космический корабль, если вне¬
запно возникнет аварийная ситуация из-за неисправности элементов
системы управления.	»
Глава 12 посвящена общим вопросам математического описания
чел°века-оператора в системах управления.

16-
ПРЕДИСЛОВИЕ
Книга заканчивается главой, в которой содержатся некоторые
замечания о применении теории и методов, изложенных в предыду¬
щих главах, к системам управления летательными аппаратами.
Теперь приятно выразить ряд благодарностей. Прежде всего редак¬
тор хотел бы поблагодарить AFORS (Научно-исследовательское управ¬
ление ВВС США) и особенно тех из этой организации, кто помог
осуществить научные исследования по теории систем управления
в UCLA (Калифорнийский университет, Лос-Анжелос) и других инсти¬
тутах, работающих в этой области. Многие результаты, изложенные
здесь, получены в UCLA и других исследовательских группах, финан¬
сируемых военными организациями. Без такого финансирования эти
результаты, целый ряд из которых имеет большое прикладное значе¬
ние, вряд ли можно было бы получить.
Эта книга создана на основе государственного двухнедельного
летнего курса, читавшегося в UCLA в течение нескольких прошлых
лет. Приятно поблагодарить слушателей, многие из которых были
опытными инженерами-практиками, за их замечания, способствовав¬
шие улучшению курса и книги.
И наконец, очень приятно выразить благодарность коллективу
авторов, которые, несмотря на большую занятость, взяли на себя
ответственность в написании этой книги. Общение с ними в этом
рискованном предприятии доставило мне огромное удовольствие.
А*. 7. Леондес

ГЛАВА Г
МЕТОДЫ СИНТЕЗА ЛИНЕЙНЫХ СИСТЕМ АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
Стабберуд (A. R. Stubberud)
В теории управления хорошо разработаны общие методы анализа
и синтеза линейных систем с постоянными параметрами, но гораздо
меньше уделено внимания анализу и синтезу линейных систем с пере¬
менными параметрами и нелинейных систем. Это объясняется, во-пер¬
вых, тем, что общее решение линейных дифференциальных уравнений
с постоянными коэффициентами находится значительно легче, чем общее
решение линейных уравнений с переменными коэффициентами и тем
более нелинейных дифференциальных уравнений, и, во-вторых, тем,
что во многих случаях эти уравнения достаточно хорошо аппрокси¬
мируются линейными системами с постоянными коэффициентами.
В данной главе рассмотрены методы синтеза линейных систем
автоматического управления с переменными параметрами. Эти методы
являются вполне общими и аналогичны классическим методам синтеза
линейных систем с постоянными параметрами.
1.1.	Некоторые характеристики линейных систем
На рис. 1.1 изображена линейная система общего вида. Входная
величина системы является некоторой функцией времени, обозначае¬
мой x(t), а соответствующая ей выходная величина —у (t). Вообще
говоря, x(t) и y(t) могут быть векторами, однако в данной главе
считается, что они скаляры.
Линейная система определяется следующим образом.
Определение*).
Пусть входной величине системы хх соответствует выходная вели¬
чина уь а х2— выходная величина у2. Система называется линейной,
*) Системы, удовлетворяющие этому определению, иногда называются
линейными системами с нулевыми начальными условиями, но в данной главе
мы будем называть их просто линейными.

18
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
если выходной величине ххсх~\- соответствует выходная величина
\УС\ -{“УчС* для любых постоянных сх и с2.	При этом предполагается,
что	в момент поступления в
y(t)	систему сигнала x(t) сигнал
•	y(t)	и его производные равны
нулю.
Рис. 1.1. Линейная система общего вида W.	Такому	определению	удов¬
летворяют самые- разнообраз¬
ные системы управления, например системы, которые описываются ли¬
нейными алгебраическими уравнениями, линейными обыкновенными
дифференциальными уравнениями и линейными уравнениями в частных
производных. Ниже рассматриваются лишь системы, которые описы¬
ваются линейными обыкновенными дифференциальными уравнениями,
в частности дифференциальными уравнениями вида
%a^W = %b^W’	*«<*<	+	«>.	(1.1)
1=0	i=0
или в операторной форме
L (у) = М (х)у	(1.1)'
где х — входная, а у — выходная величина системы. В дальнейшем
изложении предполагается
1) a,i(t) и bi(t) непрерывны и имеют необходимое число непре¬
рывных производных;
2) без ограничения общности an(t)= 1;
3) начальное значение \y(t^\ равно нулю, т. е. изучается только
передаточная характеристика уравнения (1.1). Такие системы будут
также называться линейными нестационарными системами.
x(t)
W
1.2.	Некоторые свойства уравнения (1.1)
Запишем уравнение (1.1) в следующем виде:
L(y)=r{t\	(1.2)
где r(t) = M(x). Для простоты будем считать, что t изменяется в пре¬
делах	“Не¬
однородным уравнением, соответствующим уравнению (1.2), является
L{u) = 0.	(1.3)
Задавая для уравнения (1.3) п совокупностей (j = 1, 2, ..., п) началь¬
ных условий вида
dt*-1
(	1	при	/ = /,
=	п	'	.	(/=1,	....	«)>	(1.4)
‘ =‘о	(	0	при	/ ф I

1.2]
НЕКОТОРЫЕ СВОЙСТВА УРАВНЕНИЯ (1.1)
19
получим п линейно независимых решений	Так как уравнение
(1 3) линейное, решение n{t) для произвольных начальных условий
£Н = Н1'>	(/	=	0, 1, п— 1)	(1.5)
dt»'
можно записать следующим образом:
П
Н(0= 2 иу-"М/(0.	(1.6)
Функции Uj{t) образуют фундаментальную систему решений уравне¬
ния (1.3). Эта система не является единственной, так как любой дру¬
гой набор п линейно независимых решений v^it) ... vn(t) представляет
также фундаментальную систему, которая может быть выражена через
первую с помощью соотношения
(1.7)
Vi (t)
an .,
Чп
И|(0
МО
аЯ1 •
• • *пп
««(0
или в матричной форме
V = || а I] иу	(1.8)
где [а] — невырожденная матрица констант.
С другой стороны, если п произвольно взятых решений уравне¬
ния (1.3) линейно зависимы, то они не являются фундаментальной
системой. Достаточным условием линейной независимости системы
решений Ui(t) ... un(t) является неравенство нулю определителя
Вронского, или вронскиана
Д =
щ
Щ
un
dat
du2
dun
~dt
~dt
dt
dn-lux
dn~la2
dn~lu,
dtn~l
dtn~l *
• • dtn-l
(1.9)
Остановимся на одном важном решении уравнения (1.3), назы¬
ваемом весовой функцией, которая определяется как решение (1.3)
при начальных условиях
dlu
It1
= о,
/ = х
dn~lu
dtn~1
t = X
(/ = 0, 1, 2, ..., /z-2),	(1.10)
где	f-oo.	С	помощью	произвольной фундаментальной си¬
стемы U\{t) ... un(t) это решение можно переписать как
и (9= 2 h щ (0.
i = 1
(1.11)

20
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
где (3* находятся подстановкой уравнения (1.11) в (1.10) так, что
получаются п уравнений, которые записаны в матричной форме
(1.12)
MO
PiW
0
diii
~dt ,
t = X
dun
dt t = x
MO

0
dn~1ul
dt”'1
t = X
dn~lun
" dt”~l t = k
MO
1
Так как определитель этой системы есть вронскиан, то данная си¬
стема уравнений всегда имеет решение, которое и является весовой
функцией
U(f)=Q(t, z)= 2 МО МО-
i = 1
(1.13)
Общее решение уравнения (1.2) теперь можно выразить через
•весовую функцию при помощи интеграла свертки
y(t)= ^ Q(t, z)r(z)dx.
to
(1.14)
Непосредственной подстановкой легко показать, что y(t) удовлетво¬
ряет уравнению (1.2), если вспомнить, что для
а {х)
z(x)= \ F (х, t) dt
Ь(Х)
справедливо
а {х)
d±— [
dx~ )
ь (Л-)
dF(xy t)
д{х)
db
dt + F(x, a)^-F(x, b)~.
dx'
(1.15)
(1.16)
Определение весовой функции можно обобщить, записывая r(t)
в следующем виде:
40= У bt(f)
i=0
dlx
dt19
(1.17)
Если подставить (1.13) и (1.17) в выражение (1.14), которое затем
проинтегрировать по частям, то найдем
y(t)= $ 2 щЦ){% (- iy d’[bj^ —}*<?)d' + к(0-у(0- (1.18)
/о *=1
0=0

1.3]
ОПРЕДЕЛЕНИЕ УРАВНЕНИЯ ПО ВЕСОВОЙ ФУНКЦИИ
2!
Определим теперь весовую функцию W(t, т) для уравнения (1.1) так,
чтобы при свертке ее с x(t) получалось y(t), т. е.
Из сравнения выражений (1.18) и (1.19) следует, что W(t, х) равна
Выше было показано, что каждому дифференциальному уравнению
вида (1.1) соответствует весовая функция, определяемая формулами
(1.20а) и (1.206). Изложенный метод нахождения W(t, т) для урав¬
нения (1.1) обычно очень труден. В частности, трудно найти фунда¬
ментальную систему решений произвольного линейного дифференци¬
ального уравнения с переменными коэффициентами, и не всегда эти
функции могут быть выражены в замкнутой форме. С другой сто¬
роны, как будет сейчас показано, гораздо легче восстановить диффе¬
ренциальное уравнение, зная его весовую функцию.
Пусть задана весовая функция вида (1.20) и требуется найти соот¬
ветствующее ей дифференциальное уравнение. Значения (т), кото¬
рые определяются выражением (1.21), неизвестны. Порядок дифферен¬
циального уравнения должен быть равен п, так как в W(t, т) входят
п линейно независимых решений Ui(t). Для представления искомого
уравнения в форме (1.1) надо найти аг*(£) и bi(t).
Так как Ui (t) являются решениями однородного уравнения (1.3), то
у (t) = ^ W (ty z) л; (т) dz.
(1.19)
п
W{t, х) = 2 И, (*) а, (х) ~ bn (t) 5 (t — х),
(1.20a)
i = 1
= Writ, T) + MW —т),
(1.206)
где
(1.21)
a — T) — S-функция Дирака.
1.3.	Определение дифференциального уравнения
по весовой функции
п
1 */<о
= 0 (г = 1, 2, ..., п).
(1.22)
Уравнения (1.22) образуют систему п уравнений с п^\-\ неизвест-
ными. Если an(t) положить равной единице, то из этих уравнений
можно найти остальные

22
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
Найдя cij(t\ можно определить Пусть весовая функция Q(t, т),
соответствующая однородному уравнению (1.3), известна. Тогда ре¬
шение уравнения (1.1) выражается в виде (1.19) и в виде
)>(()= \ 0(1,11)
У ьлщИ.
Lk 1 w d№
Ly= О
dQ.
(1.23)
Приравнивая их, найдем
dlx (0)
d(by
dB=^ W(t,B)x(b)dB. (1.24)
to
t\	4= о
Теперь, применяя к обеим частям равенства (1.24) дифференциаль-
п
dP
2,^ dP
ар(ч^£р, получим выражение
р = 0
п	п	V	t
2 b<{t)ifj= 2 мо£» S w&
7=0	р	=	0	L/0
Подставим (1.206) в (1.25) и для простоты записи обозначим
Fo(t) = bn(t),
(1.25)
д‘-‘ W1 (t, х)
dtl~l
д‘-1 W(t, т)
дЖ
(1.26)
Тогда производные в правой части равенства (1.25) определятся
следующим образом:
dP
dtp
t	I
J W(t, B)x(B)dB = J J Wi(t, B)x(B)dB-\-
t0	J	h
P
+ 2 ^[Fp-a(*)*(9] (P = 0, 1, .... П). (1.27)
k= 0
Соответственно можно записать всю правую часть равенства (1.25)
п	t	п	р
2 мо $	2	мо 2	^[Fp'i<{t)	(U8)
р = 0	t	о
Так как
р = о	А>	=	0
ть t
2 5 M9-£p[^iM)]*(e)de=o-
р = 0 to
(1.29)

1.5]
НЕОБХОДИМЫЕ ОПЕРАЦИИ
23
£[/>,(0*(01 = 2	(1.30)
являются биномиальными коэффициентами, то
dk~J
(1.31)
где
2 ь>тё= 2 2 2 (•) “-‘о Si'v.wif.
у=0	p=0A=0/=0u/
Изменяя порядок суммирования в правой части равенства (1.31) сле¬
дующим образом:
п р k	п	р	р	п п р
222 = 222 = 2112.	о-32»
р = 0 k = 0 у = 0 р = 0 у = 0 /г = /	/ = 0 p=jk = j
получим, что
мо= 2 2	'=°- '•2	*	<133>
P=Jk=j
Выражение (1.33) позволяет определить bj(t) по известным ap(t)
и FM
1.4.	Алгебра линейных дифференциальных уравнений
В § 1.5—1.12 вводится применение операторной алгебры линей¬
ных дифференциальных уравнений. Эта алгебра используется в после¬
дующих параграфах для разработки некоторых методов синтеза линей¬
ных автоматических систем с переменными параметрами.
1.5. Необходимые операции
Ввиду того что линейное дифференциальное уравнение вида (1.1)
является линейным преобразованием аг в у, рассматриваемая алгебра
является алгеброй линейных преобразований. В дальнейшем изложе¬
нии заглавными буквами (А, В, С,...) обозначаются дифференциаль¬
ные уравнения вида (1.1).
Алгебра линейных дифференциальных уравнений включает три
операции:
(1) Сложение двух дифференциальных уравнений, т. е.
А-{-В = С.	(1.34)
(2) Умножение дифференциального уравнения на скаляр
Ap(t) = B	(1.35)

24	СИНТЕЗ	СИСТЕМ	С	ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ	[ГЛ.	1
или	р	(t) А = С.	(1.36)
(Если p(t) — const, то В = С.)
(3)	Умножение двух дифференциальных уравнений
В А = С.	(1.37)
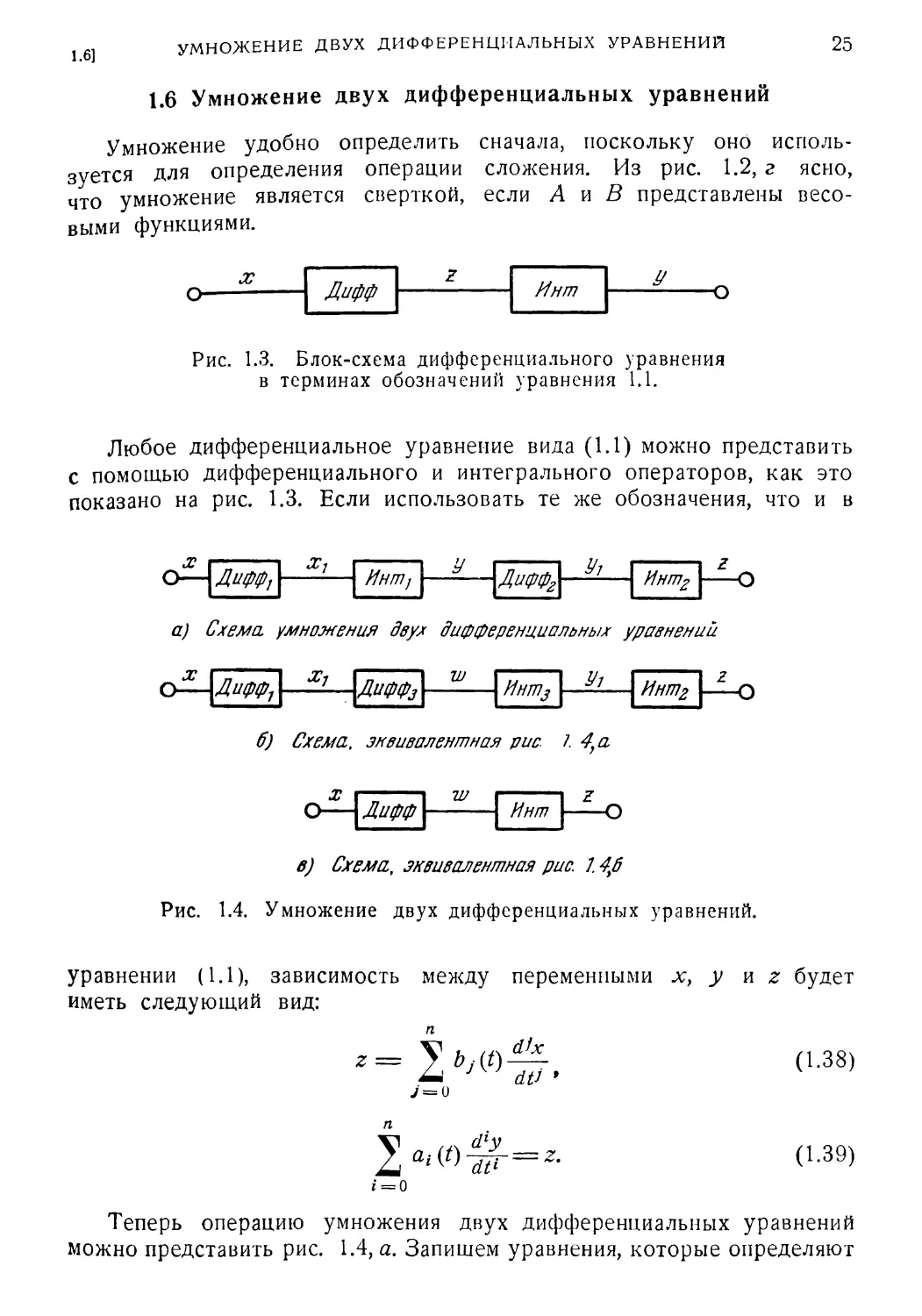
Введенные операции условно показаны с помощью блок-диаграмм
на рис. 1.2. Очевидно, для того чтобы пользоваться этой алгеброй,
а) Сложение двух дифференциальных уравнений
X
т
А
у О —о х
В
б) Умножение дифференциальных уравнений на сксдляр справа
х
А
P(t)
У o — cpL
С
6) Умножение дифференциального уравнения на скаляр слева,
г) Умножение двух дифференциальных уравнений
Рис. 1.2. Операции алгебры преобразований.
следует определить каждую из операций. Кроме того, ниже будут
определены следующие важные элементы этой алгебры:
1. Единичный элемент.
2. Нулевой элемент.
3. Обратный элемент операции сложения.
4. Обратный элемент операции умножения.

1.6]
УМНОЖЕНИЕ ДВУХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
25
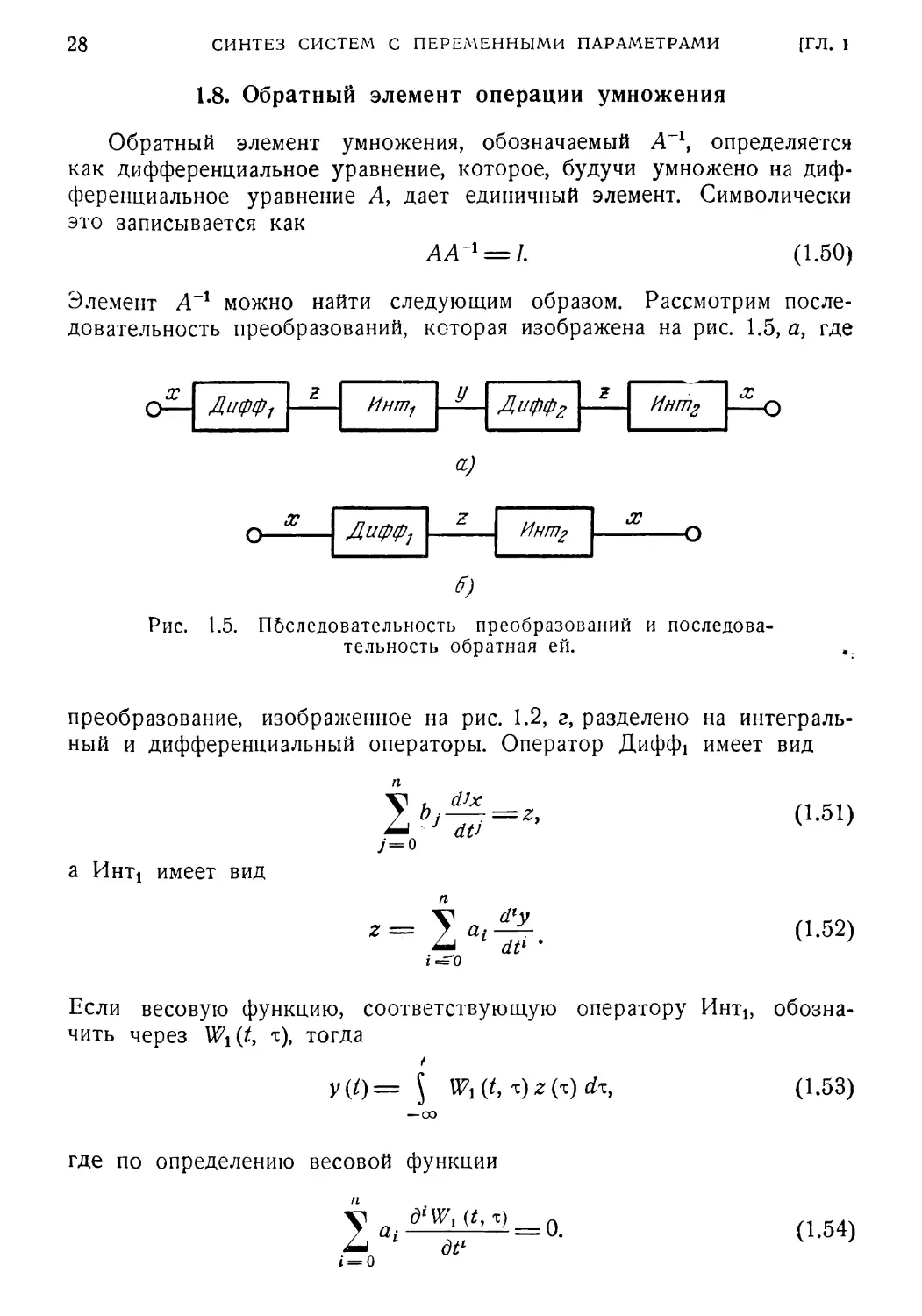
1.6 Умножение двух дифференциальных уравнений
Умножение удобно определить сначала, поскольку оно исполь¬
зуется для определения операции сложения. Из рис. 1.2, г ясно,
что умножение является сверткой, если А и В представлены весо¬
выми функциями.
х
Дифф
Инт
У
Рис. 1.3. Блок-схема дифференциального уравнения
в терминах обозначений уравнения 1.1.
Любое дифференциальное уравнение вида (1.1) можно представить
с помощью дифференциального и интегрального операторов, как это
показано на рис. 1.3. Если использовать те же обозначения, что и в
Дифф,
Х7
Ингл1
У
Диффо
У;
Интр
а) Схема, умножения двух дифференциальных уравнений
х
Дифф1
х,
ДифФз
Интпэ
У?
Инт2
6) Схема, знвивалентная рис. I 4У а
х
Дифф
Инт
в) Схема, эквивалентная рис. 14%б
Рис. 1.4. Умножение двух дифференциальных уравнений.
уравнении (1.1), зависимость между переменными х, у и z будет
иметь следующий вид:
= У мо—
dtJ '
J = o
(1.38)
(1.39)
i = 0
Теперь операцию умножения двух дифференциальных уравнений
можно представить рис. 1.4, а. Запишем уравнения, которые определяют

26
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. t
зависимости между переменными в этой системе:
2ь,т^ =	х,=	2	«,(/>-&	(1.Ю)
у = 0	i	=	0
т	т
2	2	(1-41)
5 = 0	/г	=	0
На рис. 1.4, б два внутренних	оператора	«переставлены». Вообще
говоря, эти операторы не коммутативны, поэтому
Дифф2 ф Диффз,
Hhtj ф Инт3.
Далее необходимо выразить зависимость между хь (о и уг через пара¬
метры уравнений (1.40) и (1.41). Предположим, что эти зависимости
можно записать в виде
т
0-42)
а = 0
И
2А0(*>Ф=®’	(1.43)
(3 = 0
где ga(t) и hp(t) пока неизвестные коэффициенты. Подставляя хх и уь
выраженные через у, в уравнения (1.42) и (1.43), находим следую¬
щее соотношение:
т п а
2 У У I ° U (п rf(tt~c’g«(<)	_
Li Li \cy®a'’ dt'*~C)	dt!+c
a = 0 i = 0 С = 0
n m (3
= 2 2 2{1)кт^Р-^- (..44,
3 = 0 5 = 0 d = 0
Если приравнять коэффициенты при производных одного порядка от
у, то получится система из т-\-пА- 1 совместных уравнений с
т-\-п-\-2 неизвестными. Без потери общности положим hn(t)= 1,
тогда эти уравнения можно решить и найти остальные	1
неизвестные. При таком способе определения ga(t) и h^(t) рис. 1.4, а и
\А,б эквивалентны. Кроме того, объединяя дифференциальные и инте¬
гральные операторы, схему на рис. 1.4, б можно свести к схеме на

1.7]
ЕДИНИЧНЫЙ ЭЛЕМЕНТ
27
рис. 1.4, в. В результате получается следующее уравнение:
V V \ l*\h if\	d*+f'z
£ 2d Li \f) 9 dtm-fi dttk+f'
<3 = 0 k = 0 /=0
r	m	n	a
= 2 2
a = 0 j = 0 r = 0
где x—входная, a z—выходная величина. Таким образом, умножение двух
дифференциальных уравнений, заданных в виде (1.40) и (1.41), может
быть выполнено с помощью последовательности действий, указанных
равенствами (1.42), (1.43), (1.44) и (1.45). Символически операция
умножения обозначается как
АВ = С,	(1.46)
где буква А соответствует уравнению (1.41), буква В—(1.40),
а буква С — (1.45).
1.7.	Единичный элемент
•
Единичным	элементом алгебры называется	такой	элемент,	который,
будучи	примененным	к	функции, оставляет	ее	неизменной.	В ал¬
гебре линейных дифференциальных уравнений единичным элементом
является любое дифференциальное уравнение вида
2 2 <М7)
i = 0	i	=	0
Это можно показать, если выходную величину у записать следующим
образом:
у = х + у1.	(1.48)
Подстановка (1.48) в (1.47) дает
2 M*)j2r=a	(1-49)
<■-=0
Таким образом, ух представляет свободное движение системы (реше¬
ние однородного уравнения, соответствующего (1.47)), а х — вынуж¬
денное движение системы. Если положить начальное условие по у
равным нулю, У\ = 0 и у = х, то уравнение вида (1.47) будет удовле¬
творять определению единичного элемента.

28
СИНТЕЗ СИ СТЕЛА С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. I
1.8.	Обратный элемент операции умножения
Обратный элемент умножения, обозначаемый А-1, определяется
как дифференциальное уравнение, которое, будучи умножено на диф¬
ференциальное уравнение А, дает единичный элемент. Символически
это записывается как
А А-1 = 7.	(1.50)
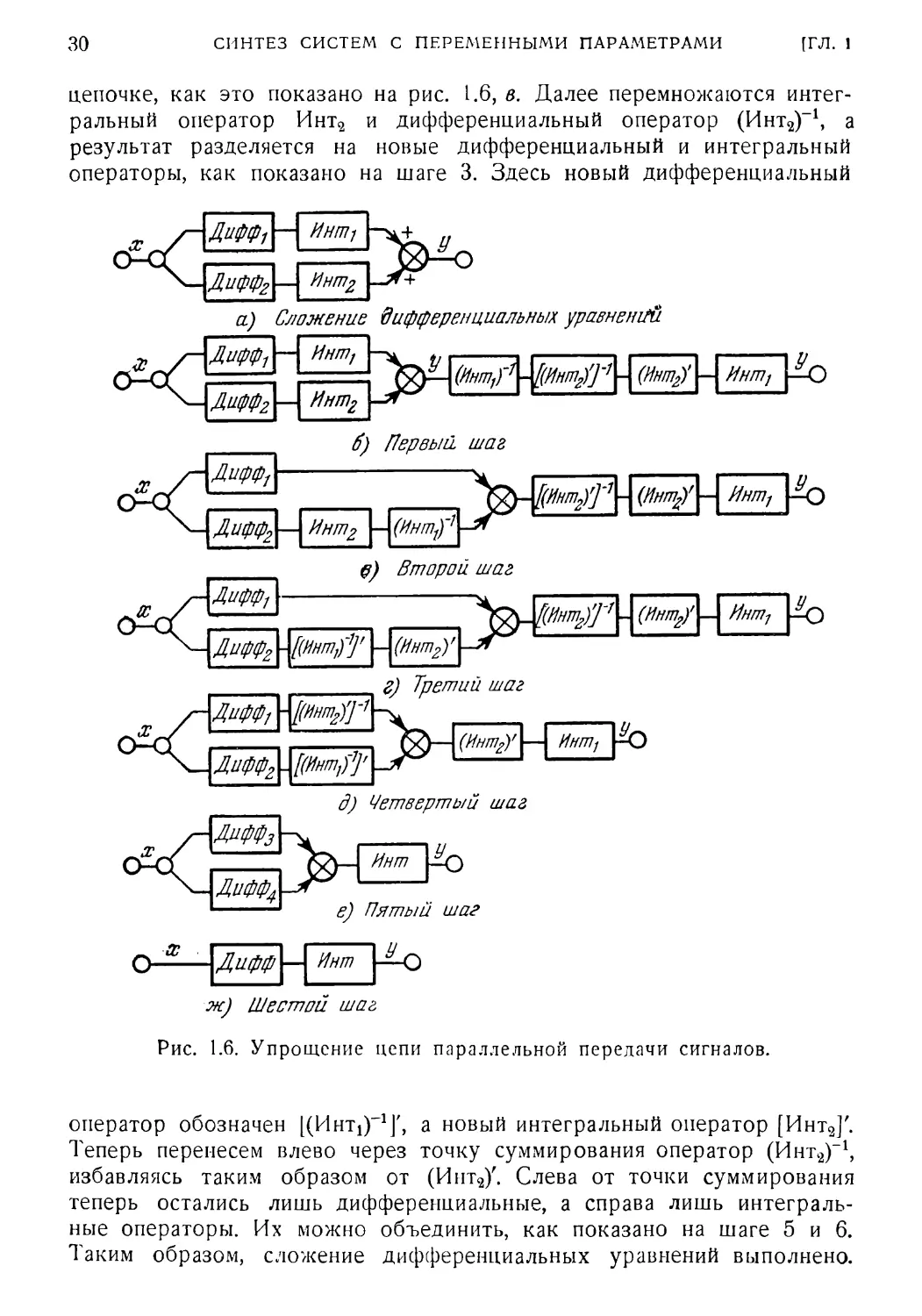
Элемент А-1 можно найти следующим образом. Рассмотрим после¬
довательность преобразований, которая изображена на рис. 1.5, а, где
Дифф1
Инт-f
Диффг
ИнгЛ‘
ги-о
а.)
X
ч
Дифф,
Z
Инт2
X
е
)
V
б)
Рис. 1.5. Пбследовательность преобразований и последова¬
тельность обратная ей.
преобразование, изображенное на рис. 1.2, г, разделено на интеграль¬
ный и дифференциальный операторы. Оператор Дифф! имеет вид
a Hhtj имеет вид
2;U &Х
’~йГз=г'
j = о
X d’y
z= / at ——
dt‘ '
(1.51)
(1.52)
i = 0
Если весовую функцию, соответствующую оператору Инть обозна¬
чить через Wx(ty т), тогда
(1.53)
где по определению весовой функции
2at
i = о
diWl (t, т)
dtl
= 0.
(1.54)

1.9]
СЛОЖЕНИЕ ДВУХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИИ
29
Применяя к y(t) дифференциальный оператор вида
п
(1.55)
получим z(i). Таким образом, дифференциальный оператор (1.55)
является обратным оператору Интп
Если оператор Дифф2 выбрать в этой дифференциальной форме,
то рис. 1.5, & можно свести к рис. 1.5, б.
Если теперь оператор Инт2 имеет вид
то рис. 1.5, б будет изображать единичный элемент, который опреде¬
ляется выражением (1.47) и применение которого необходимо, если
как входная, так и выходная величины должны быть равны аг. Таким
образом, если буква А обозначает дифференциальное уравнение
в котором х — входная, а у — выходная величина, А 1 соответствует
дифференциальное уравнение
где а: — выходная, a у —входная величина.
1.9.	Сложение двух дифференциальных уравнений
Сложение двух дифференциальных уравнений символически изо¬
бражено на рис. 1.6, а. Так же как и в случае умножения, диффе¬
ренциальные уравнения разделены на дифференциальный и интеграль¬
ный операторы. Сложение выполняется шаг за шагом, как указано
с помощью блок-диаграммы рис.	1.6. При первом	шаге исходная
система умножается на последовательную комбинацию из двух диф¬
ференциальных операторов, обозначенных (Интх)-1 и [(Инт^)']-1,
и из соответствующих им обратных элементов операции умножения
Двух интегральных операторов,	Инт, и (Инт2)'.	Следовательно,
эта комбинация представляет единичный элемент. Ввиду того
что система линейна, (Hhtj)-1	можно перенести	влево через
точку суммирования и таким образом избавиться от Инт! в верхней
п
(1.56)
п	#	п
(1.57)
П
п
j
(1.58)

30
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
цепочке, как это показано на рис. 1.6, в. Далее перемножаются интег¬
ральный оператор Инт2 и дифференциальный оператор (Инт2)-1, а
результат разделяется на новые дифференциальный и интегральный
операторы, как показано на шаге 3. Здесь новый дифференциальный
Дифф2 —I Ингл?
а)	Сложение дифференциальных уравнений
'— Дафф2 — Инт2 —
Ингп1 НО
б)	Пврвый. шаг
Дифф2 — Инт2 — (Интг)1
(ИнтУ
—I Инт1 fio
Дифф1
G) Второй шаг
Дифф2 -[(Инт,)'1]' - (Инт2)
>[(Ннт//!\- (Инт/ - Инн?! io
/- Дцфф,Щинтг)']-1
СЬ</ г- ,, m Т&-(#»тгг - ИнгП]
'^Диффг-[(бЩ)]'~*
Z) Третий шаг
ЙЬ
/-\ЛмФФз\-^
C><VJ
3)	Четвертый шаг
Инт Йо
е)	Пятый шаг
X
Дифф —
Инт I-—О
ж)	Шестой шаг
Рис. 1.6. Упрощение цепи параллельной передачи сигналов.
оператор обозначен [(HuTi)"1]', а новый интегральный оператор [Инт2]'.
Теперь перенесем влево через точку суммирования оператор (Инт2)-1,
избавляясь таким образом от (Инт2)'. Слева от точки суммирования
теперь остались лишь дифференциальные, а справа лишь интеграль¬
ные операторы. Их можно объединить, как показано на шаге 5 и 6.
Таким образом, сложение дифференциальных уравнений выполнено.

1 12] УМНОЖЕНИЕ ДИФФЕРЕНЦИАЛЬНОГО УРАВНЕНИЯ НА СКАЛЯР	31
1.10.	Нулевой элемент
Нулевой элемент определяется в алгебре линейных дифференци¬
альных уравнений как дифференциальное уравнение, выходная вели¬
чина которого тождественно равна нулю. Нулевой элемент обозна¬
чается через 0.
1.11.	Обратный элемент операции сложения
Обратный элемент операции сложения для дифференциального
уравнения А определяется как такое дифференциальное уравнение В,
которое при сложении с А дает нулевой элемент, т. е.
А + В = 0.	(1.59)
Совершенно очевидно, что если А является дифференциальным урав¬
нением
с-60»
i =• О	/ = 0
где х — входная, а у— выходная величина, то В имеет вид
dtl	J	dtJ
i = О	7=0
1.12.	Умножение дифференциального уравнения на скаляр
Умножение дифференциального уравнения на скаляр можно рас¬
сматривать как частный случай умножения двух дифференциальных
уравнений, одно из которых является вырожденным уравнением у =
=p(f)x, где л; — вход, а у — выход. Поэтому методы, разработанные
для умножения двух дифференциальных уравнений, можно использо¬
вать и при умножении дифференциального уравнения на скаляр.
В добавление к упомянутым выше свойствам алгебры линейных
дифференциальных уравнений справедливо следующее:
1. Сложение коммутативно, т. е. АфВ = В-\-А.
2. Сложение ассоциативно, т. е. А ~\~(В -f- С) = (А 4- £)-|-С.
3. Умножение не коммутативно, г. е. АВ ф ВА.
(В стационарном случае умножение коммутативно.)
4. Умножение ассоциативно, т. е. А(ВС) = (АВ)С.
5. Выполняется дистрибутивность, т. е. А(В -\-С) —АВ -\- АС.

'62
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
1.13.	Синтез методом сокращения оператора объекта
В этом и последующих параграфах изложены два метода синтеза
линейных систем с обратной связью с переменными параметрами.
Эти методы основаны на изложенной выше алгебре линейных диффе¬
ренциальных уравнений.
Первый метод синтеза является методом сокращения оператора
объекта. При этом последовательность действий такова:
а)	По техническим условиям на характеристики замкнутой системы
определяется либо ее весовая функция, либо описывающее ее дифференци¬
альное уравнение. Желательно, чтобы система задавалась весовой функ¬
цией, так как при этом для любого входа выход определяется интегралом
свертки.
Рис. 1.7. Общая структурная схема системы с обратной
связью.
б) Если задана весовая функция замкнутой системы, то по ней
определяется дифференциальное уравнение, описывающее замкнутую
систему.
в) По дифференциальному уравнению замкнутой системы опреде¬
ляется дифференциальное уравнение разомкнутой системы.
г) Определяется дифференциальное уравнение соответствующих
корректирующих цепочек, и эти цепочки синтезируются с помощью
средств аналоговой вычислительной техники.
Для выполнения таких действий надо уметь (1) определять весовую
функцию или дифференциальное уравнение по заданным техническим
условиям на систему, (2) приводить эту весовую функцию к такому
виду, чтобы можно было спроектировать соответствующие корректи¬
рующие цепочки.
Применение алгебры дифференциальных уравнений к задаче син¬
теза с идейной стороны аналогично применению алгебры преобразо¬
вания Лапласа для синтеза линейных стационарных систем. Преиму¬
ществом такой алгебры является то, что все необходимые операции
можно выполнить символически, и лишь в конце произвести числен¬
ные выкладки.
Для изложения метода воспользуемся схемой системы с обратной
связью, изображенной на рис. 1.7. Здесь г является входной, с — вы-

СИНТЕЗ МЕТОДОМ СОКРАЩЕНИЯ ОПЕРАТОРА ОБЪЕКТА	33
1.13J
ходной величиной, К, G и/У обозначают дифференциальные уравнения,
т	и	е промежуточные переменные	в системе. В дальнейшем
точка	(•)	обозначает операцию, которую	дифференциальное	уравне¬
ние выполняет над переменной и в результате чего получается новая
переменная. Пусть зависимость между входной г (t) и выходной вели¬
чиной c(t) такова, что
с = W- г,	(1.62)
где од?—желаемое дифференциальное уравнение всей системы. Из
рисунка видно, что
у = Н-с	(1.63)
и
е — г—у = г — Н • с.	(1.64)
Так как
т — К • s и c = G-m,	(1.65)
го
r = I-s + HGK-e = V + HQK)-&	(1.66)
в силу того, что
/•£ = 8.	(1.67)
Применяя к обеим сторонам выражения (1.66) обратный оператор
операции умножения для (I-\-HGK\ имеем
е = (/ + ШКГ1-г.	(1.68)
Затем, так как
с = GK • s.	(1.69)
подстановка (1.68) в (1.69) приводит к выражению
с = GK(l + HGK)~l - г.	(1.70)
Сравнение выражений (1.68) и (1.69) показывает, что
U7 = GK (/ + HGKy\	(1.71а)
Выражение (1.71а) можно рассматривать как основное соотношение
для рис. 1.7.
Довольно легко показать, что W можно представить также в виде
W = {I+GHKy' GK.	(1.716)
Таким образом, возможны два способа представления результатов
в следующих параграфах. Все основные соотношения, полученные
далее, выводятся как из выражения (1.71а), так и из (1.716). Будем
называть (а)-результатом и (б)-результатом соотношения, полученные
из выражений (1.71а) и (1.716) соответственно. Теперь рассмотрим
два частных случая блок-схемы 1.7.
2 п/р Леомдеса

34
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
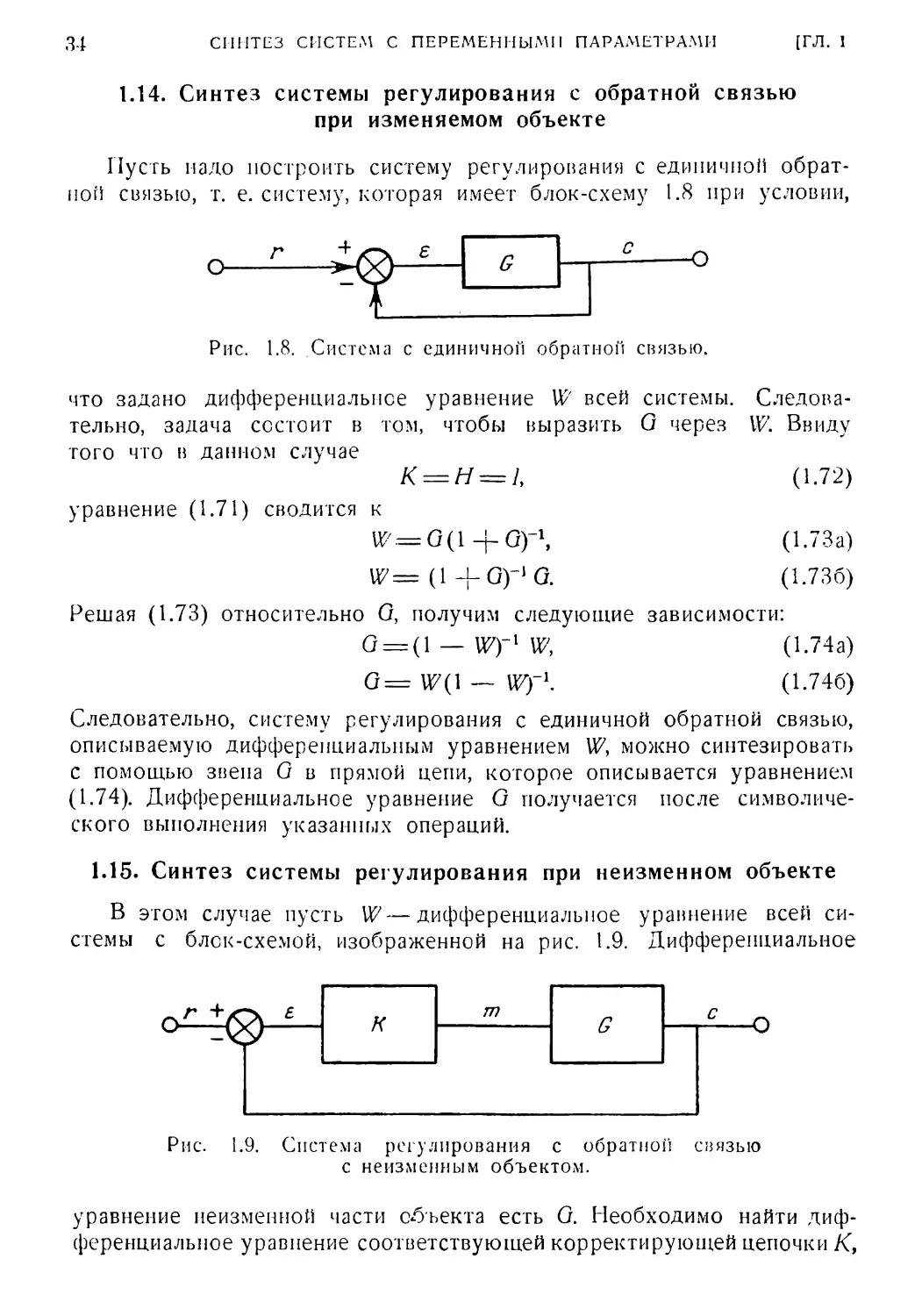
1.14.	Синтез системы регулирования с обратной связью
при изменяемом объекте
Пусть надо построить систему регулирования с единичной обрат¬
ной связью, т. е. систему, которая имеет блок-схему 1.8 при условии,
О
4
->■
-О
Рис. 1.8. Система с единичной обратной связью.
что задано дифференциальное уравнение W всей системы. Следова¬
тельно, задача состоит в том, чтобы выразить G через W. Ввиду
того что в данном случае
К = Н = и	(1.72)
уравнение (1.71) сводится к
W=G(\ +G)-\	(1.73а)
W = (1 +G)"1 G.	(1.736)
Решая (1.73) относительно G, получим следующие зависимости:
G = (l — W)~l W,	(1.74а)
G= W( 1 — Wf\	(1.746)
Следовательно, систему регулирования с единичной обратной связью,
описываемую дифференциальным уравнением U7, можно синтезировать
с помощью звена G в прямой цепи, которое описывается уравнением
(1.74). Дифференциальное уравнение G получается после символиче¬
ского выполнения указанных операций.
1.15.	Синтез системы регулирования при неизменном объекте
В этом случае пусть W—дифференциальное уравнение всей си¬
стемы с блок-схемой, изображенной на рис. 1.9. Дифференциальное
к
т
G
9
Рис. 1.9. Система регулирования с обратной связью
с неизменным объектом.
уравнение неизменной части объекта есть G. Необходимо найти диф¬
ференциальное уравнение соответствующей корректирующей цепочки К,

ПРИМЕР	35
1.161
чем такое, чтобы данная система имела желаемую характеристику,
педеляемую W. Подставляя Н = / в выражения (1.71) и решая их
относительно КУ придем к следующим зависимостям:
К = G-1 (7 — U7)-1 W,	(1.75а)
К = G~' 117(7— Щ~\	(1.756)
Дифференциальное уравнение для К получается после выполнения
действий, символически указанных в выражениях (1.75).
1.16.	Пример
Для	иллюстрации	изложенного метода рассмотрим	следующий
пример.	Предположим,	что объект G на рис.	1.9 задан	дифферен¬
циальным уравнением
Пусть желаемое дифференциальное уравнение всей системы W есть
%Л-2^Л-о = г.	(1.77)
7— U7 получается сложением и определяется
d2z | о dz   d~c | 2 dc I	/1	70
где r — входная, а с — выходная величина. Тогда дифференциальное
уравнение (/— Wfl W будет иметь вид
*£ + 2-*=.(<>	(1.79)
Дифференциальное уравнение К получается из
K = G-1(1 — W)~x Wy	(1.80)
и можно найти, что уравнение для этой корректирующей цепочки
равно
.	2 + Зе-' dt ,	,	_,\
^ + -ТТ^г^^11+е )е =
d2m , 3 + Ae~l dm , 2 4-	,л
= + (Ш)
Таким образом, корректирующая цепочка полностью определяется
Уравнением (1.81). Эту цепочку можно синтезировать с помощью
средств	аналоговой вычислительной техники,	используя	метод, изло¬
женный в параграфе 1.27.
2*

36
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
1.17.	Замечания
Недостатками описанного метода синтеза являются:
1. Коррекция, использующая сокращение оператора объекта, дает
в результате очень сложные корректирующие цепочки.
2. Полное сокращение оператора объекта невозможно, исходя из
практических соображений (это является трудной задачей, если объект
неустойчив).
3. С помощью простого сокращения оператора объекта и приве¬
дения передаточной функции разомкнутой системы к желаемой нельзя
радикально изменить передаточную характеристику системы. Степень
возможных изменений будет определяться физическими соображе¬
ниями.
Даже при этих недостатках данный метод является ценным, так
как дает простое и практически реализуемое решение задачи синтеза.
При выборе дифференциального уравнения W всей системы накла¬
дываются ограничения на соотношения порядков дифференциальных
и интегральных операторов цепи коррекции и всей системы, исходя
из существующих ограничений на структуру объекта, цепь коррек¬
ции и всю систему в целом. Вообще говоря, реальные системы обла¬
дают свойством сглаживания входного сигнала, т. е. система будет
содержать по меиылей мере одно полное интегрирование (порядок
интегрального оператора на единицу выше порядка дифференциаль¬
ного оператора). В крайнем случае их порядки будут равны, но
порядок дифференциального оператора никогда не будет выше, чем
порядок интегрального оператора.
Рассмотрим уравнение (1.71) при Н = 1, т. е. уравнение вида
Исходя из предыдущих рассуждений, на О и К будут наложены
следующие ограничения. Если G имеет вид
1.18.	Ограничения, накладываемые на выбор
дифференциального уравнения всей системы
W= GK (1 -|- ОКУ1.
(1.82)
(1.83)
где с — выходная, а т—входная величина, то	Если	К	имеет
вид

1.19]
АЛГЕБРАИЧЕСКИЙ МЕТОД СИНТЕЗА
37
где //г — выходная, а в — входная величина, тогда R^P. Следова¬
тельно, произведение GK будет иметь вид
т
N-\-R	М	+	Р
2 *<?-= 2	"85)
i = 0	i = О
где с — выходная, в — входная величина и соответственно А/Т-4- R>
В действительности, порядки	операторов в уравнении
(1.85) будут определяться как N -\- R — п и М -|- Р — п, где п — поря¬
док некоторых членов, обших для обоих операторов, однако так
как разница	порядков не изменяется при	уменьшении их	на п, то в
дальнейшем	им	можно пренебречь. Из	выражения (1.85)	запишем
уравнение для (1 ~j- GK)~l
N+R	N+R
У [gt V)+a, (oi -g- =	У gt w ~,	(1.86)
JmU	dt1	dt1 ’
i = 0	i = 0
где у — выходная, a x — входная величина. И, наконец, найдем U?,
подставляя	выражения (1.85)	и (1.86) в	(1.82). Таким образом, W
будет иметь вид
2 {N+R)	CV-f R + M + P)
2 2 к>
1=0 1=0
из ограничений на N, М, R и	Р следует,	что
2 (Д/+ R) —	Я) — (М +	P)^N — М.	(1.88)
Соотношение (1.88) показывает, что при выборе дифференциального
уравнения W всей системы необходимо, чтобы разница порядков
интегрального и дифференциального операторов была равна или
выше разницы порядков интегрального и дифференциального опера¬
торов неизменной части объекта.
1.19.	Алгебраический метод синтеза
Метод, изложенный в данном параграфе, очень напоминает метод,
разработанный в [10], стр. 238. Он позволяет приближенно синтези¬
ровать всю систему, типа изображенной на рис. 1.9, и имеет то пре¬
имущество, что оператор корректирующей цепочки не сокращает
оператор неизменной части объекта. Основным уравнением этого
метода является уравнение (1.75а).
Для удобства изложения данного метода каждое дифференциаль¬
ное уравнение «разложено» на дифференциальный оператор, умно¬
женный слева на интегральный оператор, т. е.
К = litDk, G = IgDg, W= JWDW.	(1.89)

38
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
Теперь, если определить единичный элемент I как
/ = /„/;■,	(1.90)
тогда / — W выразится следующим образом:
(/- W)=lw(Iw'-Dw)	(1.91)
и
(/ _ Wf1 = (/~ 1 _ Dwyl rw\	(1.92)
Подставляя выражения (1.89) и (1.92) в уравнение	(1.75а), найдем К:
К = hDk = D~g4gl (Iw — Dwy4w4wDw	(1.93)
или
lkDk = Dg4g 1 (УУ - Dw)'1 Dw.	(1.94)
Теперь наложим ограничения на К, требуя, чтобы К не сокра¬
щало интегральный оператор объекта. Это предотвращает «сокраще¬
ние» линейно независимых решений дифференциального уравнения
объекта и их замену новой системой динамических уравнений. Огра¬
ничение требует, чтобы (lwl — Dwy1 удовлетворяло соотношению
(Iwl-Dwyl = IgIcy	(1.95)
где /с — все еще неизвестный интегральный оператор. Если в урав¬
нение (1.94) подставить выражение (1.95), оно примет вид
lkDk = DglicDw	(1.96)
После приравнивания интегрального и дифференциального операторов
получатся следующие соотношения:
h = Dg4Ci	(1.97)
Dk = Dw.	(1.98)
Для вывода уравнения коррекции используется уравнение (1.95),
переписанное в виде
Iw1 = Dw + rc4g\	(1.99)
а также равенства (1.97) и (1.98). При рассмотрении этих выраже¬
ний надо помнить, что Ig и Dg известны и фиксированы. Кроме
того, при определении приемлемого дифференциального уравнения
всей системы, при котором система удовлетворяет техническим усло¬
виям, желательно иметь возможность фиксировать как Iw, так и Dw.
Однако при использовании данного метода это невозможно. По тех¬
ническим условиям можно фиксировать лишь Iw, что эквивалентно
возможности фиксировать линейно независимые решения уравнения
всей системы, но невозможности фиксировать постоянные множители
весовой функции. Таким образом, в уравнении (1.99) известны /^ и

i ig]	АЛГЕБРАИЧЕСКИЙ	МЕТОД	СИНТЕЗА	39
/-I в то время как Dw и 1ё1 представляют собой неизвестные, кото
пые следует определить, приравнивая коэффициенты при одинаковых
производных в обеих частях уравнения (1.99). Однако прежде необ¬
ходимо наложить некоторые ограничения на порядки различных
дифференциальных и интегральных операторов. Чтобы легче найти
эти ограничения, определим следующие преобразования. Пусть W
обозначает дифференциальное уравнение
?\v	.
2 h (0 У а, (0	,	bPw	(0=1.	(1 • 100)
i = 0	i	=	0
Пусть К — дифференциальное уравнение
2*.< о£=2*«о-&.	с..».»
i = 0	i	=	0
Пусть G — дифференциальное уравнение
Зр„Д0 = 1.	(1.102)
И, наконец, пусть /с — дифференциальное уравнение
1/г(0~^=*- (1Л03)
г = 0
Как и ранее, теперь подставим в уравнение (1.99) Z^1, известное из
(1.100), /-1, известное из уравнения (1.102), и неизвестные Dw и /с
из (1.100) и (1.103). Приравнивая коэффициенты при производных
одинакового порядка, получим в результате систему совместных
алгебраических уравнений относительно неизвестных at{t) и
Решение	этой	системы дает	Dw и /с.	Для существования	решения
порядки различных операторов должны ограничиваться следующим
образом. На основании физических рассмотрений требуется, чтобы
Pw^Zwy	Pg^Zs,	Pk^Zu.	(1Л04)
Из уравнения (1.99) вытекает, что
Р с “Т~ Р g === Р w или pc = pw-pg.	(1.105)
После приравнивания коэффициентов при производных одинакового
порядка	в	уравнении (1.99)	получим	всего Pw +	1	уравнений с
Z‘WJrPc-\-2 неизвестными. Для существования решения необходимо,
чтобы

40
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
ИЛИ
Pw<zw + Pc+1.	(1.106)
В результате подстановки (1.105) в (1.106) имее!М
Zw^Pg- 1.	(1.107)
Из условий (1.104) и уравнения (1.96) вытекает, что
Zg -)- Р с= Ри ^ Zk = Zw
или
Pc^Zw — Zp	(1.108)
сравнивая выражения (1.105) и (1.108), получим
р Р > 7	  7
1 w	V	^	g
ИЛИ
Pw S* Pg +	— Zg.	(1.109)
Объединяя неравенства 1.107 и 1.109, найдем
pw^2Pg—Zg—\.	(1.110)
Таким образом, условия (1.105), (1.107), (1.110) ограничивают порядки
операторов PWi Zw и Рс. Ограничение для Pw необходимо принимать
во внимание, когда Pw выбирается согласно	техническим	условиям
па систему. Условия для Zw и Рс определяют	приемлемый	вид Dw
и 1С в уравнении (1.99).
Если в выражениях (1.107) и (1.110) выбран знак неравенства,
то число неизвестных будет больше, чем число уравнений. Поэтому
часть неизвестных можно задать произвольным образом, например
так, чтобы оптимизировать некоторый критерий качества.
1.20.	Пример
Пусть объект описывается уравнением
d2c | dc
dt*'Tt
d2c | dc	/1 1 - ч
—	0-Hi)
аким образом,
/	.	Z’	—	,
dt2 ^ dt
Пусть желаемый интегральный оператор всей системы имеет вид
»	d	с	|	_/	d	с | dс §		о/	/ i 1 ■( г, \
JF + Tt + e с’	(1.113)
что удовлетворяет условиям (1.110). Выбирая
Dw = ах (t) — а<х (t\	(1.114)

(1.117)
ЗАМЕЧАНИЯ	41
! .211
удовлетворяющее условию (1.107), найдем, что 1С должно иметь вид
/с = м*)^ + м*>	(1-115)
Подставляя (1.112), (1.113), (1.114) и (1.115)	в	уравнения	(1.99), при¬
дем к соотношению
<14 ,	_(_ Д _1_ е-* . с —
= 5. (<) § + 1^1 (0 + ь« (0] £ + [в, (0 + (01 g	+ «о (0 с.	(1.116)
Приравнивая соответствующие коэффициенты, образуем систему сов¬
местных уравнений
М0=1,
bi (t)-r’o9{t) = e-‘,
«i(0+ 5* (0=1,
а0(0 = *-*.
Решение системы (1.117) будет равно
М0=1,
bQ(t) = e-‘-l,
a1(f) = 2—e~t,
ай (f) — e
Корректирующая цепочка в этом случае определится следующим
образом:
dJL + {e-t _ 1) т = (2 _ е-') | + (*-*) 8.	(1.118)
1.21.	Замечания
Вышеизложенный метод синтеза имеет такие преимущества:
1. Простота решения.
2. Образование корректирующей цепочки, оператор которой не
сокращается с оператором объекта.
Недостатками данного метода являются:
К Характеристика всей системы не может быть определена пол¬
ностью.
2.	Конструктор не может повлиять на вид и устойчивость кор¬
ректирующей цепочки.

42
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. )
1.22.	Задача аппроксимации
Прежде чем синтезировать систему, следует задать ее весовую
функцию, так чтобы система удовлетворяла техническим условиям.
Задание такой весовой функции будет называться задачей аппрокси¬
мации. Фактически независимо от метода синтеза задание весовой
функции соответствует определению дифференциального уравнения
системы, однако более желательно знать именно весовую функцию,
ибо в этом случае для произвольного входного сигнала можно опре¬
делить выходной сигнал, используя интеграл свертки.
Весовая функция или дифференциальное уравнение системы могут
быть получены по-разному, например, непосредственно из технических
условий на систему. В любом случае, если уж то или иное установ¬
лено, то для синтеза системы регулирования можно применить ме¬
тоды, изложенные в предыдущих параграфах.
В настоящем параграфе дается метод определения весовых функ¬
ций для частного класса задач синтеза. Этот класс задач ограничи¬
вается системами, входные сигналы которых выражаются полиномами
времени, а выходные сигналы могут быть аппроксимированы разло¬
жимыми функциями (см. ниже.)
Метод аппроксимации можно сформулировать следующим обра¬
зом. Пусть x(t) (см. рис. 1.1) является полиномом времени и опре¬
деляется выражением
где сп— константа, t — время, а е— время, в течение которого x(t)
действует на линейную систему W. Функция y(t) является выходной
величиной линейной системы на воздействие x(t). Предполагается,
что аналитическое выражение для y{t) можно определить по техни¬
ческим условиям на систему. W является неизвестной линейной си¬
стемой, весовую функцию которой следует определить в таком виде,
чтобы систему можно было синтезировать как систему с обратной
связью. Выход j>(f) запишем в виде (1.19). Подставляя выражение (1.119)
в (1.19), получим
1.23.	Метод аппроксимации в случае
полиномиальных входных сигналов
N
х (t) = X (t — т) = ■
°,

АППРОКСИМАЦИЯ ПРИ ПОЛИНОМИАЛЬНЫХ СИГНАЛАХ	4,4
1.23 J
Теперь задача сводится к решению интегрального уравнения (1.120)
гносительно U7(t, т). К счастью, эго уравнение легко свести к ли¬
нейному стационарному дифференциальному уравнению, которое ре¬
шается достаточно просто. Класс допустимых W(t, т) определяется
выражениями (1.20) и (1.21). В результате подстановки выражения
(1 20) в (1.120) получим соотношение
N	t	N
yx(t, ,) = 2 Д Writ, 0)[0-Tl“dfl + bm(t) 2 cn{t-zf. (1.121)
п=0	"	п	—	0
Процесс решения этого уравнения разбивается на два этапа: (1) опре¬
деление bm(t), (2) определение Wx(t, т).
Сначала дадим метод определения bm(t). Предположим, что
ck(Q ^k^N) является частным значением сп, отличным от нуля,
которое имеет самое меньшее значение индекса, т. е.
N	(	N
Ух#, *)= 2	им*,0)(0—тул+мо 2 cnit-'T- (i.i22)
п = k	"С	п=	k
Далее найдем частную производную /z-го порядка yx(ty ъ) по т
N	t
Wi(t' e)(—lVW(n—i)..-(n — k+l)X
n = k -
N
X (0 _ xy~* M + bm (0 2 cni— 1 f (n)(n - 1)... (Я - k + l)(f - zfk.
n = k
(1.123)
Если теперь в выражении для производной —Ух перейти к пре-
dzh
делу при г—±t, то получим уравнение
д1!Ух {t, -)
dz*
(1.124)
Решая это уравнение относительно bm(t), найдем искомые соотно¬
шения
, &ух (t, z)
(-1)
я :
и (+\
bт()~	(Щ^Г
Зная bm(t)y можно записать
(1.125)
bm{t) Ц	(1.126)
п = 0

44	СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ	[ГЛ.	3
и найти новую функцию yf(7, т) из уравнения (1.122)
N
у* у, т)=ух (t, х) - ьт (о 2 cn(t- xf=
п = О
N t
= 2	W71(<>9)(6-xf	rfO. (1.127)
п= О
Второй вопрос состоит в определении Wi(t,z) из уравнения (1.127).
Сначала возьмем производные от y'x(t, т) по т. Первая производная
равна
лг	/
^(^^(-ОпСЙ-хГЧб-^^^х). (1.128)
/г = 0	т
Производная /г-порядка ^	А/’	—1~	1 равна
t
дкух (*, т)
= 2 Wl{t’ e)(-!)*(»)(«-в-••(«-* + 1)Х
71 = 0
fc—1
X (0 - xrfe db + v	(/!)
>=о х
и N-J- 1 порядка
(А= 1. 2	/V)
(1.129)
(7, х)
**+•'
У<)'
. (—1У+1 (у!) сj -
‘V-^i(7,x)
dx'v-7
(1.130)
7 = 0
Видно, что уравнение (1.130) является линейным стационарным диф¬
ференциальным уравнением, решение которого есть Wi(t, i). Для
решения записанного уравнения необходимо задать N начальных
условий. Эти начальные условия получаются из выражений (1.129)
при т, стремящемся к t, т. е.
к — 1
дкух (t, х)
дхк
= У (—1)/+1 (j\)Cj
j — o
dk~l~JW, (t, x)
д-к-'-i
(1.131)
или
0k 1W, (t, x)
dxk 1
jX)
t'o [ dxk
x	  X)!
►. (— 1У: 1 (/!)О
J —1
0хк '-)
(k = i, 2, ..., /V).	(1.132)
LJ

1241	АППРОКСИМАЦИЯ ПРИ НЕПОЛИНОМИАЛЬНЫХ СИГНАЛАХ	45
И тажение (1.132) определяет систему рекуррентных соотношений,
которые задают N необходимых «начальных условий». В действи¬
тельности,	так	как	производные от (t, т) берутся	по	т,	выражение
(1	132)	определяет	конечные условия. Этого неудобства	легко избе¬
жать, делая подстановку
~. = t — z	(1.133)
в выражениях (1.130) и (1.132). Получающиеся в результате уравне¬
ния легко решаются, после чего, делая обратную замену переменных
z — t — т,	(1.134)
найдем W\(t, т).
Рассмотрим выражения (1.125) и (1.130) в частном случае, когда
полином x(t) вырождается и имеет вид
x(t — z) = cN(t — x)N.	(1.135)
Тогда выражение (1.125) можно записать как
^А'^Ух OVL)
дх
(-'г -
Ьт (*) = Nfc~
а выражение (1.130) — следующим образом
д^+1у'х (t, х)
dxN+l
(1.136)
(_1)ЛГ+1(М)СЛГ Wiit,*)	(1.137)
 ,л .	(Ы38)
N\ cA,
Равенствами (1.137) и (1.138) можно пользоваться в случаях, когда
входной	сигнал	представляется	полиномом	лишь с	одним	ненулевым
коэффициентом.	Ясно, что	рассмотренный	случай	справедлив и для
входных сигналов, описываемых ступенчатыми функциями.
1.24.	Метод аппроксимации в случае входных сигналов
неполиномиального вида
Вернемся опять к рис. 1.1. Предположим теперь, что x(t) не
полином, а некоторая разложимая функция t и т, т. е.
f Л'
*«>=	,з”'
1«;	«,	<1139’

46
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. !
Кроме того, пусть y(t) — также некоторая разложимая функция
(в соответствии с заданными техническими условиями на систему)
м
2 «mC0-Vm(0.
(1.140)
т= 0
о,
*<т.
Предполагая дифференцируемость сп(т), xn(t), zm(z) и ym(t) доста¬
точное число раз, можно считать, что выражения (1.139) и (1.140)
являются весовыми функциями линейной системы. Следовательно,
дифференциальные уравнения, соответствующие каждой из них, можно
определить, пользуясь методом, изложенным в параграфе 1.3.
Рис. 1.1 заменим рис. 1.10. В последнем X является дифференциаль¬
ным уравнением, которое соответствует (1.139), a W — дифферен¬
циальным уравнением, соответствующим неизвестной системе. Если
J(t-z)
Y
W
y(t) ,
Л
\
Рис. 1.10. Система, эквивалентная изображен¬
ной на рис. 1.1.
дифференциальное уравнение Y соответствует весовой функции (1,140),
тогда согласно обозначениям алгебры дифференциальных уравнений
имеем
Y=WX	(1.141)
или
W=YX'K	(1.142)
Равенство (1.142) показывает, что если входная и выходная величины
неизвестной линейной системы являются известными разложимыми
функциями t ит, дифференциальное уравнение всей системы можно
определить, находя произведение Y и Х~л.
Хотя этот метод проще метода аппроксимации для входных сиг¬
налов полиномиального вида, он дает ответ в менее удобной форме,
а именно в форме дифференциального уравнения, а не весовой
функции.
Так как полином (1.119) является разложимой функцией t и 'г,
то очевидно, что данный метод можно использовать также и в слу¬
чаях входных сигналов полиномиального вида. Кроме того, ясно,
что yx(t, т), определяемое выражением (1.120), должно обладать
свойствами весовой функции линейной системы, описываемой обыкно¬
венным дифференциальным уравнением вида 1.1. Однако вследствие
физических ограничений yx(t, т) не будет содержать дельта-функций.

1.25]
ПРИМЕР
41
1.25.	Пример
В качестве примера, иллюстрирующего метод, изложенный в § 1.23,
рассмотрим следующую задачу. Входной сигнал линейной системы
имеет вид
X(t — •z) = 2u{t — т) + 0 — т) — 2{t — т)2.	(1.143)
Из технических условий на систему требуется, чтобы выходной
сигнал имел вид
у ли *)=--<4
+	4-4
о 10
6 1 3 '
о
- --- ТВ 1
3	1
1
[-Д.-3,2
0_12 | 1	3	'	1	^4
1 6 * 1 6 V
(1.144)
При условии, что заданы входной сигнал x(t — т) и желаемый выход
системы, следует определить ее весовую функцию, которую должна
иметь желаемая линейная система. Выходной сигнал yx(t, т) можно
записать, пользуясь выражением (1.122), в котором N = 2, с0 = 2,
С\ = 1, а са = — 2-
Первое, что надо сделать для определения W(ty ?), это найти
bm(t). Переходя к пределу в yx(t, т) при t-+ т+, получим
\imyx(t9 т)=2z=bm(z)cQ.	(1.145)
Следовательно,
(1.146)
2t
Тогда второй член в выражении (1.122) для yx(tf т) будет равен
ьт (0 2 fЛ-(t - *Г = 4- f- - fc - 21* 4- 4Л - 214. (1.147)
п — 0
Подставляя (1.147) в (1.122) и решая последнее относительно yrx (t, т),
получим
у'х (1, т) = 31* —	1:Ч	—	ил	—	2f-z	4-	4IV
о	1	О
Далее найдем производные y'x(t, i) по т
А № _1_	_
3	1	6
гЛ-ъ?- (Ы48)
~у~=—4 i*—б!;ч.
ch	2
L°«
21* Л -f 2lV -f ^ I4 — 21- 4- 4. 14 4
= — 61* 4- 4- 414 — 214-44- 214,
r):y
4 = 4£2 4- * 4У
+	(1.149)
(1.150)
(1.151)

48	СИНТЕЗ	СИСТЕМ	С	ПЕРЕМЕННЫМИ	ПАРАМЕТРАМИ
Пользуясь выражениями (1.130) и (1.132), запишем
д»у'х (*, х)
ах3
:	4-	t	-f	4£т	=	—2с2 И?! (t, т) -j- Cj
(t, X)
dx
[ГЛ. 1
d2U7i (*, x)
w'«’
$X“	’
(1.152)
(1.153)
dWt (f, x)
dx
г>н- <u54)
Желаемая весовая функция определяется из системы уравнений (1.152),
(1.153) и (1.154). Для упрощения алгебраических операций и облег¬
чения решения сделаем следующие подстановки:
/С ■ i v,
ki = 2 t,
*> = 4** + 4.
/(*) = 117,(7, 7 — 0). j
(1.155)
Затем, так как с0 = 2, с\— \ и с2 = —2, выражения (1.152), (1.153)
и (1.154) можно переписать как
dj
dzz
(1.152')
/(0) = 2f2,	(1.153')
r(0) = — t	(1.154')
Решение однородного уравнения, соответствующего (1.152'),
ищется в виде
fc (г) = А е- и* -}-	т^,	(1.156)
где A v\ В зависят от начальных условий, а ^ и ~[2— корни полинома
Т* + 4т —2 = 0.	(1.157)
Частное решение уравнения (1.152') равно
/Р=4-4-|*.	(1.158)
Таким образом, общее решение имеет следующий вид:
f{z) = Ае-ъ* + Be-w + \ — А- — А 0.	(1.159)
Постоянные А и В можно найти, используя начальные условия

t ^	АППРОКСИМАЦИЯ	РАЗЛОЖИМЫХ	ФУНКЦИЙ	49
(1.153') и (1Л54'):
[/ (0) + f - -|] [- 7*] -/' (0) - Ц
А—-	  —	(1.160)
Ъ	1	v
/' (0) + \ л- Ь [/ (0) + у — ^-]
В =	1	=!.	(1.161)
7i —Та	V
После подстановки в эти выражения знамений, определяемых равенст¬
вами (1.153'), (1.154') и (1.155), получим, что
А = 0, В = 0	(1.162)
и, следовательно, /(г) равно частному решению дифференциального
уравнения, т. е.
=	(1.163)
Подставляя (1.155) в (1.163), можно показать, что
Wt(t, z) = t2-\-tx.	(1.164)
Таким образом, искомая весовая функция всей системы равна
W(t, =	—	(1.165)
Можно проверить, что свертка (1.165) и (1.143) даст yx(t> т), равное
заданному выражению (1.144).
1.26.	Аппроксимация разложимых функций
Из рассуждений, приведенных в предыдущих параграфах, следует,
что для большого класса задач синтеза реакция системы на входной
сигнал должна иметь вид разложимой функции. Поэтому для при¬
менения данного метода синтеза необходимо уметь аппроксимировать
функции двух переменных разложимой функцией этих переменных.
По этому вопросу имеются некоторые работы. Например, Круз |8|
предложил аппроксимацию весовых функций последовательностью
импульсов, а Круз и Ван Валькенберг [4| предложили метод аппрок¬
симации весовых функций разложимыми функциями. В данном пара¬
графе описан простой метод аппроксимации функции двух перемен¬
ных разложимой функцией.
Для пояснения этого метода будет рассмотрен пример системы
управления конечным состоянием. Пусть требуется спроектировать
систему, удовлетворяющую следующим техническим условиям. На вход
системы поступает возмущение в виде скачка в некоторый неизвестный
момент времени между t = 0 и t=T. За время 7'S^>T система
должна достичь области, ограниченной отклонением не более п

50
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
процентов от нового положения равновесия (от единицы). С другой
стороны, если система проектируется как нестационарная линейная
система, то сначала следует
определить, исходя из техни¬
ческих условий, реакцию си¬
стемы y(t, х) на ступенчатое
возмущение. По этому y(t, х)
можно найти соответствующую
весовую функцию и довести
до конца проектирование си¬
стемы.
На рис. 1.11 дано изобра¬
жение y(t, х) в двух измере¬
ниях; при этом ось х направле¬
на перпендикулярно плоскости
чертежа. Поверхности у (t, 0)
и У& О ограничивают об¬
ласть допустимого отклика
y(t, х), т. е. такого, который удовлетворяет техническим условиям
на систему. Пусть y(t, 0) и y(t, Т) выбраны в следующем виде:
y(ty 0)= 1 —
y(t, Т)= l—e**"-7),
где а, и а2 выбраны так, что
Рис.
1.11. Представление у (t, г) в
двух измерениях.
(1.166)
У(Т„ T)=y(Ts, Т)= 1
100 •
(1.167)
Видно, что при этом y(t, х) удовлетворяет техническим условиям при
двух значениях х, а именно х = 0 и z—T. Кроме того, величину
при 0 ^ х ^ 7 можно было бы задать еще при нескольких значе¬
ниях х, однако в данном изложении ограничимся лишь двумя значе¬
ниями. Ясно, что если бы y(ty х) могло быть представлено соотно¬
шением, подобным (1.166) при всех 0^х^ 7, то технические условия
были бы удовлетворены полностью. Число значений х, при которых
задается значение y(t, х), например, с помощью выражения (1.166),
будет равно максимальному числу членов получающейся в итоге раз¬
ложимой функции. Таким образом, чем лучше желаемая аппроксима¬
ция, тем выше получается порядок системы.
Заменим рис. 1.11 рис. 1.12 с осью t, нормальной к плоскости
чертежа. Вне области 0<х< 7 y(t, х) произвольно. На границах
области y(t, х) удовлетворяет уравнению (1.166).
Если ограничения на y(t, х) наложены лишь в точках х = 0 и
х=Т, то y(ty х) можно аппроксимировать несколькими способами.
Например, пусть
у (t, -) =у (t, 0) -’г [у (t, Т) -^ (*, 0)] и (i - Т),	(1.168)

1.26]
АППРОКСИМАЦИЯ РАЗЛОЖИМЫХ ФУНКЦИИ
5]
где  Т) — ступенчатая функция, имеющая скачок при т=7.
Тогда y(t, z) соответствует функция, изображенная на рис. 1.12 сплош¬
ной линией. Преобразуя по Лапласу выражение (1.168) относительно т,
получим изображение У (t, s), определяемое равенством
Y(t, S):
s 7
_y{t> 0) , T) — y(t, 0) г
(1.169)
Теперь, если —
Пэйда [1], т. е.
аппроксимировать при помощи аппроксимации
2 (s —3,/Г)
n-sl
(1.170)
s	Т	s	(s2 -f- 4s/Г + 6/7'') ’
тогда
Y(t, s)^ Y*{t, s) =
+ T) y(t, о)]}-»(,.,7.,
Обратное преобразование у* (t, s) обозначается у* (t, т). В уравнении
(1.169) могла быть использована и другая аппроксимация Пэйда.
Очевидно, аппроксимация
получилась бы лучше, если
бы использовался полином
более высокого порядка. Ча¬
стный вид аппроксимации
выбран ввиду ее относитель¬
ной простоты и ввиду того,
что степень числителя ниже
степени знаменателя. Это
последнее условие обеспе¬
чивает равенство нулю вто¬
рого члена в у* (t, z) при : = 0 и, следовательно, у* {t, 0)=^(£, 0).
Находя обратное преобразование от У* (tt s), найдем аппроксимацию
У*(!, z)
y*(t, *)=y(t, 0)
e— 2т/т Sjn
+
-kv (f, T) [l — 3e_2'/rsin +
t:
(1.172)
где = sin 1 (1/3), a y(t, 0) и y(t, T) определяются выражени¬
ем (1Л66).
Из очень грубой оценки точности аппроксимации у* (t, х) видно, что
у*«, о)=y{t, 0),
y*(t, T)=0,398y(t, 0)-f 0,602y(f, 7), }	(1.173)
У* (t, со) =y (t, T).

52
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
Точность аппроксимации данного вида можно повысить двумя спо¬
собами. Во-первых, аппроксимируя y(t} т) несколькими ступеньками
в направлении т (см. рис. 1.11), т. е. записывая
где N—целое, и, во-вторых, используя более высокий порядок
аппроксимации Пэйда для
Другой метод аппроксимации, который мог бы быть использован
заключается в аппроксимации производных более высокого порядка
от y(t, т) последовательностью ступенчатых функций в направлениит
и затем в интегрировании этих функций соответствующее число раз
до получения y (t, т). В качестве примера запишем производную у (/, т),
представленную пунктирной линией на рис. 1.11:
Если это уравнение преобразовать по Лапласу и использовать аппро¬
ксимацию Пэйда в уравнении (1.170) и, наконец, выполнить обратное
преобразование, то найдем аппроксимацию у{0> 0 (t, т), обозначаемую
v*(«. 1) (tt т):
Из сравнения ее с аппроксимацией, которую дает выражение (1.172),
видно, что
Аг
п = 1
(1.174)
У0' ’>(*, т) = -£:И*, У]
v(t, T)—y(t, 0)
т
[«("О — и(у — Т)\. (1.175)
■ Ъе~2r/rsin	j	(1.176)
где ф = sin 1 (1/3). Затем, так как
y*(t, z)=y(t, 0)-h	*>	6)dd,
(1.177)
О
окончательно имеем
y*(t, T) = 0,	<<T.
(1.178)
y*(t, 0)=y(t, 0),
y*(t, T) = 0,U6y(t, 0)-[-0,884_y (<, T),
y*(t, x)=y(i, Г).
(1.179)

I 27] СИНТЕЗ УРАВНЕНИЙ ПРИ ПОМОЩИ АНАЛОГОВЫХ УСТРОЙСТВ	53
Следовательно, этот метод обеспечивает более точную аппроксимацию
для y(t> чем первый метод. И опять-таки аппроксимация будет
лучше, если	т)]	аппроксимируется	большим	числом	членов,
чем использовалось для y(t, т) (см. формулу 1.174).
1.27.	Синтез дифференциальных уравнений
с переменными коэффициентами
при помощи аналоговых моделирующих устройств
Одним из преимуществ представления корректирующих цепей
линейных систем управления в виде дифференциальных уравнений
является то, что такие цепи легко реализуются. В частности, если
характеристики цепи изменяются во времени, ее можно реализовать
при помощи элементов аналоговых вычислительных машин [6].
Дифференциальные уравнения, которые надо синтезировать, имеют
вид уравнения (1.1). Единственную трудность при синтезе таких урав¬
нений представляет моделирование правой части, которая содержит
производные от входного сигнала jc. Эту трудность можно обойти,
если переписать уравнение (1.1) в эквивалентной векторно-матричной
форме:
у = Ay-\-fx,	(1.180)
где у есть я-мерный вектор. Решение уравнения (1.1) тогда равно
y(t) = CTy + ГХу	(1.181)
где с есть я-мерный вектор, а г — скаляр, определяемый соотношением
между (1.1) и (1.180).
Таким образом, задача заключается в отыскании векторного урав¬
нения вида (1.180), эквивалентного уравнению (1.1). Это векторное
уравнение может быть записано в нескольких видах [15], [18], однако
автор считает наиболее удобным единственный вид, который и ис¬
пользован в следующем параграфе. Этот метод выводится так же,
как у Матыаша [6], лишь с небольшими изменениями для удобства
изложения.
Используя обозначения выражения (1.2), запишем
п	п
L=2a‘mi’ л,= 2ь‘т-$-	<1Л821
/-=0 / = 0
Определим два вспомогательных оператора
ц=У ««(о4
_ dt1
i = 0
(1.183)

54
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
(1Л84)
1 = 0
где &i{t) и рг-(£) следует найти.
Теперь предположим, что справедлива следующая система урав¬
нений:
Уъ = — «■пУ — Кх’	(1.185)
— h-л =Ук^г*к.кУ + $п-кх (6=1, 2, в—1),	(1.186)
— $п-\=ЧУЛ-§«х-	(1.187)
Если у0 из уравнения (1.185) подставить в (1.186) при k= \ и найти
из получившегося равенства уъ а затем повторить эту процедуру
при к = 2 и т.д., то все yt исключатся и выражение (1.187) примет
вид дифференциального уравнения /ыюрядка относительно у
у (— 1)' —ia/^J — — У (— I)1' d‘ ^ .	(1.188)
dt'	^	dt{
i = 0	i	=	0
Обозначим через L* и уИ* операторы, сопряженные соответственно
с Lj и
if(y)=S(-	(1-189)
г = 0
Mf(jf)=S(-iy(M(,).	(1.19°)
г=0
тогда уравнение (1.188) можно записать как
L?(y) = -Mnx)>	(1.191)
и если теперь отождествить уравнения (1.1) и (1.188), то
Lf(y)=L(y),
(1.192)
— М?(х) = М(х). 1
Так как для произвольного линейного оператора К справедливо
(К*)* = Ку то уравнения (1.192) можно записать как
L>(y)=L4y),	1
М,(х) = — Л).(4
Другими словами, коэффициенты а и (3 «-линейных дифференциаль¬
ных уравнений первого порядка (1.185), (1.186) и (1.187) опреде¬
ляются из сопряженных операторов L* и уИ*.

СИНТЕЗ УРАВНЕНИЙ ПРИ ПОМОЩИ АНАЛОГОВЫХ УСТРОЙСТВ
Дальнейшее упрощение, которое можно сделать, заключается
п следующем. Зададим без потери общности an(t)= 1. Тогда
ал = (-1)я,
а равенство (1.185) примет вид
y = (-irl[J'o + Ml-	(1-194)
Подставляя это соотношение для у в выражение (1.186), найдем
*7
о
е3
-&-0 о-ег
о
So
б) блок сложения
в) Интегратор
о—^—(V3—^—о
г) блок умножения
Рис. 1.13. Структурная схема набора уравнений П.194) и (1.195)
на аналоговой модели.
окончательный вид системы из п дифференциальных уравнений пер¬
вого порядка
Уо = (—1)Лал-1Уо — У\ — \\Jn 1~Ь(— 1)л,1?лал \\х>
Pi = (— 1Т *л ‘АУо — Уг — I?Л •> -Г (— 1 Г1'1 ?л*л- si -V.
Рпл-—(— 1Т°-\У<\ Ун I — (-Г(— 1 )/1+| ГаI х>
Рн 1 = (- 1 У* ЧУ, - I ?о -1- (- 1 Г' %ч\ х.
(1.195;

56
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
Уравнение (1.194) соответствует уравнению (1.181), а система (1.195) —
векторному уравнению (1.180).
Выражения (1.194) и (1.195) можно реализовать с помощью эле¬
ментов аналоговых вычислительных машин, как это показано на
рис. 1.13, а. Обозначения решающих элементов, которые здесь исполь¬
зуются, даны на рис. 1.13, б, 1.13, в и 1.13, г. Выход eQ сумматора,
изображенного на рис. 1.13, бу равен
= — (<?1 -Г е.2 -f <?■,)•	(1.196)
Выход интегратора е0 на рис. 1.13, в определяется как
t
<?„ = — $(е,+ et-\-et)dt.	(1.197)
И, наконец, выход множительного устройства на рис. 1.13, г равен
е0 =a(t)eh	(1.198)
Преимуществом реализации уравнений (1.194) и (1.195) вместо
уравнения (1.1) является отсутствие дифференцирования.
1.28.	Упрощение линейных систем
При синтезе линейных систем одной из важнейших задач является •
задача получения простейшей формы системы (в смысле количества
используемых элементов). Вообще говоря, невозможно определить,
является ли данная система простейшей, поэтому любая методика
сведения системы к более простой весьма важна.
Хорошо известно, что сложность линейной системы возрастает
с повышением порядка дифференциального уравнения, описывающего
систему, поэтому один из методов упрощения системы есть метод
понижения порядка дифференциального уравнения. Упрощение должно
быть выполнено таким образом, что новое дифференциальное урав¬
нение более низкого порядка либо эквивалентно (определение экви¬
валентности следует ниже) исходному, либо является достаточно хоро¬
шей аппроксимацией исходного.
В § 1.29—1.34 рассматриваются случаи эквивалентной замены
дифференциального уравнения высокого порядка уравнением более
низкого порядка. Системы, для которых такое преобразование воз¬
можно, называются упрощаемыми, а данное свойство называется
упрощаемостью.
1.29. Эквивалентные системы
Дадим определение эквивалентности двух систем.
Определение. Две линейные системы будем называть экви¬
валентными, если при пооизвольном входном сигнале x(t), пода-

1.29]
ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ
57
ваемом на обе системы одновременно, выходные величины обеих
систем будут также идентичны.
Данное определение не зависит от начальных условий.
Эквивалентные дисрференщтлъные уравнения. Рассмотрим диф¬
ференциальное уравнение *)
а'т$=2ь<тт^’
(1.199)
где х — входная, а у — выходная величина.
Любое дифференциальное уравнение, получающееся из данного
при применении к обеим частям уравнения (1.199) дифференциального
оператора
пг
dk
dt*’
Cm®—
(1.200)
li — 0
эквивалентно уравнению (1.199), так как у есть решение нового урав¬
нения, если х является входной величиной.
Такое уравнение может быть записано следующим образом:
Y /А dk
/ ck(t) г
dtk
k = 0
1 = 1
1г = 0
Ум 0—
dd ‘w dt1
i = 0
(1.201)
и если выполнить указанные операции, уравнение (1.201) можно запи¬
сать в виде
т-\-п	т-\-	п
у gdt)**r= У мо—,
Ld 61 dt1	dt1
1=0	i	—	()
(1.202)
где gi (t) и hi (t) определены надлежащим способом.
Уравнения (1.199), (1.201), (1.202) эквивалентны.
Другой эквивалентной формой уравнения (1.201), а следовательно,
и уравнений (1.199), (1.202) является пара уравнений:
2а.«)ё=2».(0^ + -.
t = 0
т
1
/ = 0
(1.203)
(1.204)
k=о
Эквивалентность этой пары уравнений уравнению (1.201) может
быть показана исключением переменной г.
*) Все коэффициенты дифференциального уравнения суть аналитические
функции.

58
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. }
Возможны эквивалентные векторные формы. Уравнения. (1.199)
можно записать в векторно-матричной форме:
_у = (-1ГЧуо + М]>
(1.205)
|А>
а.пЛ —1 0...0
Уо j
Р/г-1
г 1
=
а„_4 0 — 1 ... 0
У\
-Г
Р/г-2
Аг-1
а0 0 0 0
Угпап 1
Ро j
или
(1.206)
У = АУ “Г 0*-
Подобно этому, уравнения (1.203) и (1.204) могут быть записаны
^(-lr'Lvo-bM,
Ml
: I
kv. (1.207)
0
о
0 !!
Уравнение (1.205) может быть записано следующим образом:
х.	(1.208)
'Гак как уравнения (1.199), (1.202) и пара уравнений (1.203) и (1.204)
эквивалентны, уравнения (1.205), (1.207) и (1.208) также эквивалентны.
Исследуем еще одну векторную форму, эквивалентную уравнениям
(1.206)	и (1.208). Покажем, что векторное уравнение типа (1.208)
может быть линейными преобразованиями приведено к виду
З'о
ая-1
— 1
о..
..0
0
0.,
• • о у0
У1
0
—1..
..0
0
0..
..0 у,
Уп-1
*о
0
о.,
..0
(—l)m+1
0..
••о JV I
А)
0
0
о.,
..0
'Чт-г
— 1 .
. . 0 2"o
1
0
0
о.,
..0
т-2
0.,
..0 г,
*т-1
0
0
0
0
Т10
0.
• • 0 гт.,
У
А М
У
+
Р
Z
0 И
Z
о
СО :
со,
А'
ЛГ
COi
р'
(02
0
Н'
щ
0
(1.209)
где
0
Я'п-1
— 1
0.,
,.0
Р' =
0
, А' =
0
— 1
..0
1
Ч
0
0.
..0

1.29]
ЭКВИВАЛЕНТНЫЕ СИСТЕМЫ
59
При эквивалентности (1.208) и (1.209) Мг и Н' могут иметь
любой вид. Преобразование, переводящее (1.208) в (1.209), имеет вид
| Q 0	\щ\\
' " (1.210)
У ■
*1Г
о Р
0)11
Юо I’
где 0 является нулевой матрицей соответствующего размера. Подста¬
вляя в уравнение (1.208) уравнение (1.210), получаем уравнение
||©1
<*).2 !
Q 1 0
0 Р 1
А М
0 Н
Q 0
0 Р
Q~'
0
Q
! о
р
!
о
Q '
0
Р
0
р-х j
0
0)1
0>2
X.
И м|
Q 01
Q
01
| Q 0
А
№
!! о и |
о р|
0
р\
_||о Р
0
Н’
Р
Q 0 II
Р'|
0
1 0 р\
о
(1.211)
Сравнивая уравнения (1.211) и (1.209), можно получить следующие
(1.212)
(1.213)
(1.214)
(1.215)
Используя определение (1.214) матрицы Q и А в (1.209), можно
получить уравнения относительно неизвестных а[,..., ч!п_л матрицы А':
Aqx — Я\= *п л Я\ +	Я* -]-••• + ао Ят	(1.216)
АЯг — Яъ=— Я\	или	Я\ = Яг — Мъ
АЯл — Я,\ = — Яг	или	я г = Яъ~ Aqb
Aqn — Яп= — Япл	или	япЛ = qn— Aqn.
Разбив матрицу Q на столбцы
QH!?i Qi---qn\\
и используя определение |У, получим
Яп = Р.
(1.217)
Таким образом, из уравнений (1.215) и (1.217) может быть получена
вся матрица Q, и тогда уравнение (1.216) запишется так:
Q
= Aq{ — «ft.
(1.218)

60
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
(ГЛ. I
Если матрица Q не вырождена, то из уравнений (1.216) и (1.217)
могут быть получены неизвестные oto, ai,	и т. д., и преобразование,
определяемое уравнениями (1.212), окажется возможным.
Если матрица Q вырождена, будет показано, что система (1.208)
может быть преобразована к структуре, подобной (1.108), по в кото¬
рой матрица А будет иметь порядок меньший, чем п X я*
1.30.	Упрощаемость
Дадим определение упрощаемого уравнения.
Определение. Упрощаемое уравнение
У — Gy fx
которое может быть
(1.219)
преобразовано
(1.220)
(1.221)
— это такое уравнение,
к виду
_\Х Y IIщ
| #2 | 0 ^ || #2
где
у — Ви
и В невырождена.
В уравнении (1.220) только вектор U\ зависит от х.
При определении эквивалентности учитывается выходная величина,
определяемая входным сигналом х, а следовательно, при анализе экви¬
валентности (1.219) и (1.220) вектор щ может не учитываться. Поэтому,
полагая в уравнении
I «1
0
(1.222)
можно говорить об эквивалентности
щ=Хщ-\-^х	(1.223)
уравнению (1.219).
Здесь необходимо найти следующее:
а) условия на G и /, которые показывают, возможно ли упроще¬
ние уравнения (1.219);
б) методику получения матрицы В, которая позволит привести
уравнение (1.219) к эквивалентной форме (1.223). Так как пункты
а) и б) связаны друг с другом, то обе эти задачи будут далее
решаться одновременно.
Пусть в уравнении (1.209)

1.30]
УПРОЩАЕМОСТЬ
61
Если уравнение (1.219) является упрощаемым, то уравнения (1.219)
и (1.209) будут эквивалентны в силу соотношения
у = С • о,	(1.225)
где С невырождепа.
Подставляя (1.225) в (1.219) и сравнивая результат подстановки
с (1.209), получим соотношение
А = С 'GC — С 1 С
g=c-lf.
Построим матрицу Р порядка (т -|- п) X {т~\~ п)
P = [g; Ag; A'q;...; A^-'g].
(1.226)
(1.227)
(1.228)
Учитывая выражения для А и g в уравнении (1/209), матрица Р
будет иметь следующий вид:
Р =
0
0
0 ..
0
(-1Г1
(_!)»-!
ь'п-А
0
0
0 ..
.. (-1)"
2 0
(-1)-1
*п-2
0 -
-1
0
0
0
(-1Г1
а|
1
0
0 .,
0
0
(-If-1
ч
0
0
0
0
0
0
0
0
0
0 .
0
0
0
0
п строк.
.	(1.229)
п столоцов
т столонов
Матрица Р, очевидно, имеет ранг щ ее первые п столбцов линейно
независимы, а (п -|- 1)-столбец есть линейная комбинация первых п
столбцов.
Используя выражения (1.226) и (1.227), матрицу Р можно пред¬
ставить в форме
Р = С 1 {/, 'G — СС •' ] /, \G — СС 1 j’/,..., [G-Се l}n+re-1 /},
так как
(1.230)
Alg= Г С 1 GC — С"1 Cj1' С 1 /= С 1 Го — СС л]* f.	(1.231)
Матрица С—невырожденная матрица порядка (п -\- пг) X (« -Г
матрица Р имеет ранг п} ее первые п столбцов линейно независимы,

62
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
и, следовательно, матрица
p = cp\f,[0 — ССГо — сс
-1 \т-уп-\
/}	(1-232)
должна иметь ранг //; ее первые п столбцов должны быть линейно
независимы.
Представим матрицу С в виде произведения двух матриц:
(т -j- п) X я-матрицы Г и (т -|- п) X /я-матрицы В,
С = [ТВ].
(1.233)
Используя данное представление, уравнения (1.226) и (1.227) могут
быть переписаны следующим образом:
oil гв||—!!гв||=||гв!1
А' ЛГ|
о Н'\
(1.234)
/=||ГВВвг = Гр'	(1.235
по определению g.
Уравнение (1.234) может быть записано двумя уравнениями:
ОГ — Г = ТА\
СВ — В = ТМ' + ВН'.
Записывая матрицу Г в виде п столбцов
r = liYi> Y*•••> Yn|]
(1.236а)
(1.2366)
(1.237)
и учитывая определения А и В’, можно получить уравнения (1.236 а)
и (1.2366) в развернутой форме
f=\n,
G\i — y = *»-i Yx-ra»-2Y«+ ••• +ao'Yn>
<?Y2 — \i = — Yi	или	Yi =\i—G\v
G\z — Y:t = — Yi	или	Y-2	=\з — G\3>
G\n—Yn = — Yn-i	или	Vn-i = Yn — G\n.
(1.238)
(1.239)
(1.240)
Уравнения (1.238) и (1.240) дают возможность сформировать мат¬
рицу Г. Теперь можно, используя выражения (1.238) — (1.240), вер¬
нуться к матрице Р' и вывести условия упрошаемости системы. Пер¬
вый столбец матрицы Р’ определен: эго f. Исследуем второй столбец
этой матрицы:
[G — СС l\f = Gf— СС lf.	(1.241)

1.30]
УПРОЩАЕМОСТЬ
65
Из соотношений (1.227) и (1.225) и определения получим
0
о-7 =
и.
(1.242)
CC'f=yn=f,
поэтому
G/— СС lf— Gf — /= Gy„ - Y„ = — Y/.-1.
Третий столбец матрицы Р' будет иметь вид
(G - СС 11 [- Yn-i] = - IG - СС 11 Yn-, =
= — [Gy„ 1 — СС 1 Yn-iJ-
Теперь исследуем член
CC"]yn_i.
По определению уп_{ очевидно, что
О
С Yn-i =
*/i — l элементов
и, следовательно,
СС 'Yn.^Yn I
(1.243)
(1.244)
(1.245)
(1.246)
(1.247)
(1.248)
Теперь третий столбец матрицы Р' можно представить следую¬
щим образом:
— I Gy л-i — Y«-i]=Y«-2-	(1.249)
Подобным же образом можно показать, что четвертый столбец
есть — Y/i-2 и т- д- поэтому п первых столбцов матрицы Р’ есть
Y'" — Yn-i> \п--> ••• (— If ‘Yi;	(1.250)

64
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
(ГЛ.
(/г —j— 1)-й столбец является линейной комбинацией первых п столбцов:
(_!)«\g - СС1] Yi — (—В" [Gy, - YiJ =
= <** - iYi-T ••• +aoY/z- (1.251)
Заметим, что уравнение (1.251) можно решить относительно вели¬
чин а.
Очевидно, что (1.234) и (1.235), определяющие матрицу
Л =
и вектор
I А М!
О нг
о
о
(1.252)
е=
(1.253)
О
не зависят от подматрицы В матрицы С. Следовательно, подмат¬
рицу В можно выбирать любой, обеспечивающей невырожденность
матрицы С.
Исходя из вышеизложенного, можно сформулировать методику
проверки дифференциального уравнения на упрощаемость.
Пусть имеется дифференциальное уравнение
V = Gy + fx,
(1.254)
где у — вектор N-го порядка. Тогда для упрощения этого уравне¬
ния необходимо выполнить следующее:
1.	Сформировать N X N-матрицу Р'
где
Р — IYa'. — Ya’-ь Yjv-2> • • • (— l^Yil.
\N — f< Yi = Yi+1 — Gy.+i-
(1.255)
2. Проверить ранг матрицы Pf\ если он равен N, то система
неупрошаема.
3. Если ранг матрицы Р' есть n<^N, то система может быть за¬
менена эквивалентной порядка п
где
о) — Л'(о -\- |53v,
у = Г(о,
(1.256)
(1.257)

1.311
ПРИМЕРЫ
65
А' определяется из уравнения
| А Мг
где
О Н
О
о
о
о
=11 C XGC—C 'CL
вектор я-го порядка,
(1.258)
G |! Чм-т> YАг-/П-'ГЬ • • • > YN> Р/г+Ь Рл-’Г2> • • • > Рх]> (1.259)
Ух =/,
Yam = Ух— GyN,
Ya 2 = Yam — Оулм,
УХ-т YN-m+l ayN_m+l,
P — произвольные векторы, выбранные так, чтобы матрица Сбыла
невырожденной.
Таким образом, представлен метод эквивалентного понижения
порядка линейного дифференциального уравнения. Данная методика
является полезной, так как система более низкого порядка может
быть синтезирована меньшим количеством элементов. На практике
это приводит к меньшей стоимости системы.
1.31.	Примеры
Пример 1. Исследуем упрощаемость линейного дифференциаль¬
ного уравнения с постоянными коэффициентами:
у -j- Зф 4-- 2у = х
2х —j— х,
(1.260)
и, если возможно, найдем эквивалентное упрошенное уравнение.
Данное уравнение может быть записано в векторной форме:
То
—3 —1
То
_]_ |
1;
Ti
2 0
Ti
—1
х,
(1.261)
где
3 п/р Леондеса
у 	—	у0	х.

66
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
Следуя изложенной методике, получим матрицу Рг
1 4-2
= l! V-2 — Yi II =
(1.262)
Очевидно, что Yi — —2у2,	следовательно, Р' имеет ранг, равный 1;
поэтому уравнение (1.260) является упрощаемым. Сформируем мат¬
рицу С, используя в качестве первого столбца	произвольный
вектор в качестве второго (учитывая, что этот вектор должен обес¬
печить невырожденность матрицы С:
Тогда
С =
С1 =
1 11
— 1 0|
0 —1
1 1
(1.263)
(1.264)
Уравнение, эквивалентное уравнению (1.261), будет иметь вид
0 —1
1 1
1 1
— 1 0
+
10 -1
И 1
1
—1
или
uv0
1
to
1
to
1 Ко
1
\щ

0 —11
Kl
+
0
дг.
х (1.265)
(1.266)
Из уравнения (1.266) получим эквивалентное уравнение более низ¬
кого порядка:
и0 = —2w0 + jc0.	(1.267)
Пр и н и мая uY = 0, полу ч и м
Уо = Щ	(1.268)
и
у =	—и0 -J- х или щ — —у -\-х.	(1.269)
Подставляя	уравнения	(1.269)	и (1.267), найдем уравнение,	эквива¬
лентное (1.260):
у-^2у = х + х.	(1.270)
В этом	простом примере	гот же самый результат может быть
получен при анализе	корней	полиноминальных операторов	уравне¬
ния (1.260):
(P2-{-3P-f 2)y==(P2 + 2P-l- 1)х	(1.271)
или
(Р + 2) (Р + 1)у = (Р -h 1) (Р + 1) X,

1.311
ПРИМЕРЫ
61
где
Р =
dt *
Сокращая общий корень (Р4- 1), мы сразу найдем уравнение (1.270).
Для уравнений более высокого порядка эта процедура не явля¬
ется очевидной.
В заключении этого примера заметим, что уравнение (1.266) для
их содержит общий корень (Я 4" О в уравнении (1.260), т. е.
(Л+ 1)н, = 0, где Р = А.
Пример 2. Исследуем на упрощаемость и упростим, если это воз¬
можно, уравнение
у -f(1 + е~‘)У + (1 +	+	е~*у = х + е*х.	(1.272)
Используя методику, изложенную в § 1.27, запишем уравнение
(1.272) в векторной форме:
х. (1.273)
Для того чтобы проверить упрощаемо ли уравнение (1.273), соста¬
вим матрицу Р' из векторов у:
У
_(1+^)_1 о
и
0
V —
(1+3<г') 0—1
г1
+
—1
h
о
о
со
1
е~‘
уз -
! о
— 1
— 1
— 1
, Ъ =
<г'
. Y) —
1+е-'
— е-1
— 2е~‘
^' = (Уз — YsYil-
(1.274)
(1.275)
Очевидно, Yi = Y*2 — У:ь поэтому ранг Р' равен 2 и, следовательно,
Уравнение (1.273) упрощаемо.
Матрица С будет иметь вид
0 0
и> следовательно,
С =
С-1 =
1
— е
— 1 0
1
— 1
-<Г' ■
(*-* _ e-t)
0 0
-1 0
<г' 1
(1.276)
(1.277)
3*

(-58
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАЛШ
[ГЛ. 1
С =
ношения
где
0
0
0
— е-*
0
0
(1.278)
е~{ -
■е-'
0
(1.273),
может
быть получено
из со O r-
= Аи-\-
gx>
О.279)
(-(1+0
— 1
0
у = Си, А = С 1
! (i+з^)
0 -
- 1
1 — Зе~1
0
0
С — С^С
g=c-
0
— 1
(1.280)
(1.281)
Подставляя (1.276), (1.277) и (1.278) в (1.280) и (1.281), получим
I — 1 — 1	0
А= 1	0	1	(1.282)
(1.283)
Тогда упрощенное уравнение, эквивалентное уравнению (1.273), будет
иметь вид
! — 1 —
1
0
; 1
0
1
0
0
— е1
0
8 =
1
■ 0
"и ||
— i—ii
щ \
, !° 1
1 0
-р IX,
«1 \
«11
i4
где
Но-
(1.284)
(1.285)
Выделяя и щ из уравнений (1.284) и (1.285), получим дифферен¬
циальное уравнение
У ~тУ У —	(1.286)

1.33]
НАИЛУЧШАЯ АППРОКСИМАЦИЯ РЕШЕНИИ УРАВНЕНИИ
69
которое эквивалентно уравнению (1.272). Эквивалентность становится
очевидной, если к обеим частям уравнения (1.286) применить оператор
1.32.	Аппроксимация линейных дифференциальных уравнений
Выше обсуждалось понятие эквивалентности систем. Было пока¬
зано, что при определенных условиях дифференциальное уравнение
может быть заменено эквивалентным уравнением более низкого порядка.
Понятие эквивалентности двух систем имеет определенную огра¬
ниченность, так как дифференциальное уравнение может и не иметь
эквивалентного уравнения более низкого порядка. В этом случае воз¬
никает задача аппроксимации уравнения высокого порядка уравне¬
нием более низкого порядка.
Необходимость аппроксимации одним дифференциальным уравне¬
нием другого возникает также из-за ограничений, накладываемых на
разность порядков интегрального и дифференциального оператора физи¬
ческой системы. Эти ограничения требуют, чтобы порядок интеграль¬
ного оператора был больше или равен порядку дифференциального
оператора физической системы; разность между порядками интеграль¬
ного и дифференциального операторов замкнутой системы должна
быть больше или равна разности в порядках интегрального и диф¬
ференциального операторов разомкнутого контура. В том случае, когда
эти требования не удовлетворяются, необходимо каким-то образом уве¬
личить разность между порядками интегрального и дифференциального
операторов без значительного изменения выходных характеристик.
1.33.	Каилучшая в смысле метода наименьших квадратов
аппроксимация решений алгебраических уравнений
Рассмотрим задачу нахождения решения следующего уравнения:
где сi — неизвестные скалярные величины, уь у\2, ..., ут — линейно
независимые /г-мерпые векторы-столбцы. Предположим, что п '^> т\
тогда, если у0(у0-.^:0) ,,е принадлежит подпространству G, натяну¬
тому на векторы уь Y* •••> Yто найти точное решение уравнения
(1.288)	невозможно. В этом случае надо искать наилучшее (в опреде¬
ленном смысле) приближенное решение уравнения (1.288). Очевидно,
что наилучшим приближенным решением уравнения (1.288) относи¬
тельно ci будет такое, которое минимизирует квадрат разности векторов
(1.287)
OYl "Г OY-2 "Г ••• -Г СтЧт = Y«>
(1.288)

70	СИНТЕЗ	СИСТЕМ	С	ПЕРЕМЕННЫМИ	ПАРАМЕТРАМИ	[ГЛ.	1
Наилучшим приближением вектора у0 и подпространстве G будет
проекция вектора уо на эт° подпространство. Вектор ошибки дается
выражением
т
e=SciYi —Yo	(1.289)
i= 1
или в матричной форме
8 = Г с — уо,	(1.289а)
где
с= . и THIy, ••• YmI!
Вектор 8 ортогонален к каждому вектору уг, поэтому скалярное
произведение 8 и каждого уг- должно быть равно нулю, т. е.
yJe — 0	(i— 1,	2, ..., т\	(1.290)
где	у7 —транспонированный	вектор	уг*.	Уравнение	(1.290)	может
быть записано в матричной форме:
Г78 = 0,	(1.291)
где	Гг — транспонированная	матрица	Г.	Если (1.289а)	подставить
в (1.291), получим матричное уравнение:
ГТГс— Г7у0 = 0.	(1.292)
Наилучшее приближенное значение с может быть получено из выра¬
жения
с = (ГГ -Т)~1 • Ггу0.
1.34.	Аппроксимация дифференциального уравнения
уравнением более низкого порядка
В § 1.28—1.30 были выведены условия, при удовлетворении ко¬
торых векторное уравнение порядка (яг п)
у = Gy fx	(1.293)
может быть заменено эквивалентным уравнением более низкого по¬
рядка, например порядка п. Эти условия сводятся к тому, что реше¬
ние уравнения
GC — C = CA	(1.294)
должно удовлетворять следующим требованиям:

1.34)
АППРОКСИМАЦИЯ УРАВНЕНИЕМ БОЛЕЕ НИЗКОГО ПОРЯДКА
71
1.	Матрица А должна представляться в следующей форме:
Q М
А =
О Н
(1.295)
где Q — п X «-матрица, 0 — т X л-матрица нулей, М и И—матрицы,
определенные подобным образом.
2. п-м столбцом матрицы С должен являться вектор /.
3. Матрица С должна быть невырожденной.
Естественно, возникает задача: как найти приближенное решение
уравнения (1.294) в том случае, кагда матрица С не удовлетворяет
изложенным	выше условиям. Такое решение позволило	бы	заменить
уравнение	(1.295) порядка (т-\-п) векторным	уравнением	п-rо по¬
рядка. Этому вопросу будет посвящено дальнейшее изложение.
Разделим матрицу С на две подматрицы: (т -j~ п) X л-матрицу Г
и (т -f- л) X яг-матрицу В, т. е.
С = |ГД||.	(1.296)
Если подставим уравнения (1.295) и (1.296) в уравнение (1.294), то
получим два уравнения:
GT — t = TQy	(1.297)
GB — В = ТМ + ВН.	(1.298)
Если найдено наилучшее (в некотором смысле) приближенное ре¬
шение уравнений (1.297) и (1.298), удовлетворяющее условию: л-й
столбец матрицы Г равен. /, то полученное дифференциальное урав¬
нение будет называться аппроксимацией уравнения (1.293).
Для того чтобы получить наилучшие приближенные решения урав¬
нений (1.297) и (1.298), определим матрицы Q и Г следующим
образом:
Q-
а, —1
О
О
ii ;
О
(1.299)
о ... о !
Г = |! Yi> V‘2> • • •. Ynll-	(1.300)
Используя эти определения, а также то, что ун=/. уравнение (1.297)
может быть записано как система уравнений:
GYi — Yi = ®iYi -Г+ ... -rcwV	(1.301)
Yi = У 2 — Gy,,
Ya = Ya — Gy».
1
(1.302)
\ni=yn — Gyn,
У «=/•

72
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. t
Уравнение (1.301) может быть переписано и виде
Га == Gyi — Yi-
(1.303)
где
а =
В § 1.33 показано, что наилучшим аппроксимирующим решением
в смысле метода наименьших квадратов является решение уравнения
Г7Та = Г7'(/у1 — Ггуь	(1.304)
где Г7” — транспонированная матрица. Заметим, что если исходное диф¬
ференциальное уравнение является упрощаемым, то вектор а есть точ¬
ное решение уравнения (1.304). Следующим шагом после получения
приближенного решения уравнения (1.297) будет нахождение решения
уравнения (1.298). Точное (хотя и не единственное) решение уравнения
(1.298) может быть найдено следующим образом. Пусть Ж и Я имеют
форму
М =
Рч
0
0 .
.. 0
Р-2
. о
. о
■ о •
P1 ti
о ..
• • о
• • о
(1.305)
Н-
Т]!
— 1
0 ..
.. 0
ъ
0
— 1
.. 0
Чп
0
0 .
.. 0
(1.306)
Матрица В представляется т столбцами:
в = IIPi, fa Pm И-	(1.307)
Тогда вследствие (1.305), (1.306) и (1.307) уравнение (1.298) можно
записать в следующем виде:
= [J-iYi -[- p^Ya ••• "7“ Р'лУл “Т“ ^lPl ~Т~ ••• “Г	(1.308)
Pi = k-GP* J
Р*=Рз— Gp;t,	(1.309)

1.34]
аппроксимация уравнением более низкого порядка
73
может быть выбран произвольным, однако обеспечивающим не¬
вырожденность матрицы
С = ||ГВ||.	(1.310)
Зная рт и G, можно полностью определить матрицу В из урав¬
нений (1.309). Тогда уравнение (1.308) может быть записано:
1ГВ1
= ОР1 — К.
(1.311)
где
ъ
11 =
и г\ =
'Цт
Уравнения (1.311) могут иметь точные решения \х и rj, так как мат¬
рица || ТВ |! невырождена.
Исходное уравнение (1.293) было аппроксимировано в смысле
минимума среднеквадратичного отклонения уравнением, поддающимся
упрощению.
Аппроксимирующее уравнение имеет вид
и[
Q
М
и[
_L
А
и.г
0
Н
«2
1
0
х,
(1.312)
где
/>=
Уравнение (1.313) может быть записано:
u' = Arur-\-frxг.
(1.313)
Далее аппроксимация уравнения (1.293) может быть записана в сле¬
дующем виде:
У = ОУ+ /JC.	(1.314)
Используя (1.294), можно получить выражение для G':

74	СИНТЕЗ	СИСТЕМ	С	ПЕРЕМЕННЫМИ	ПАРАМЕТРАМИ
Учитывая, что
и
у' = Си'
\ТВ
i I
иЛ
[ГЛ. 1
(1.316)
(1.317)
упрощаемое уравнение, которое аппроксимирует (1.294), будет иметь
вид
Ui =■ Qui —j— f\X	(1.318)
и
y' = Tui	(1.319)
Для того чтобы оценить точность аппроксимации, необходимо полу¬
чить величину вектора ошибки
г=у—у.	(1.320)
В том случае, когда удается получить точное численное решение
уравнений, вопрос оценки не является сложной задачей. Однако,
часто получение точного решения затруднительно, поэтому предла¬
гается методика оценки ошибки аппроксимации. Эта методика изло¬
жена в § 1.40.
1.35.	Пример
В качестве примера получим уравнение первого порядка, кото¬
рое аппроксимирует следующее векторное уравнение:
3	1
-(2 + 0 О
Это уравнение можно записать таким образом:
$ = Gy+fx.
В качестве первого шага положим
II 1
Y=/=|| 2
Затем преобразуем уравнение
G\ — у = aY
в соответствии с (1.301) в уравнение
S> 0
S>\
Уо
+
1
|.хг.
(1
У1
2
(1.321)
— 1
-(2 + 0
= a
(1.322)
(1.323)
(1.324)
(1.325)
Очевидно, это уравнение не имеет решения.

1.351
ПРИМЕР
75
Используя методику, данную в § 1.33, можно найти уравнение,
которое решается относительно а, и полученное решение будет
наилучшим в смысле среднеквадратичного отклонения.
Такое аппроксимирующее уравнение имеет вид
1>2||
а = II 1, 2 |
I— 1
или
откуда
— (24- е)~‘ [
5а = — 5 —
а = — 1 — 4 е~*.
(1.326)
(1.327)
(1.328)
Затем в соответствии с уравнением (1.309) выберем (3 произвольным
образом с единственным требованием, чтобы он обеспечил невырож¬
денность матрицы С:
10
р=
Затем из уравнений (1.323) и (1.329) получим матрицу
111 о
С = \\
С1—
J 2 1
1 о
—2 1
Теперь уравнение (1.311) будет иметь вид
1 0
=
1
2 1
II л
0
Из уравнения (1.332) получим
li= 1, т| = — 2.
(1.329)
(1.330)
(1.331)
(1.332)
(1.333)
Из уравнений (1.328) и (1.333) можно получить уравнение, поддаю¬
щееся упрощению:
2 _,\
-5е j
0 —2
111
и',
~
- 1
Hi
,
1
IU
i
0
или
и = Afuf -р gx.
(1.334)
(1.335)

76
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 5
Из уравнения (1.319)
У'о\
Ill
У\!
= |2
Hi.
(1.336)
Теперь могут быть получены приближенные уравнения первого
порядка относительно у'{) и у\
fi = — (\ -rj-е ‘)У1 ~2х-
(1.337)
(1.338)
Для того чтобы оценить степень аппроксимации, необходимо из
уравнений (1.315), (1.330) и (1.331) получить матрицу
G =
— (з 4-д-1
\	'	о	j
-(2+i-e-1) 0
(1.339)
Наконец, уравнение, аппроксимирующее уравнение (1.322), будет
иметь вид
Г°
К
/	9	,\
-\3+~е- ) 1
-(2+4-е~‘) 0
У»
\y'i
' !|2
X.
(1.340)
Ошибка аппроксимации дается следующим выражением:
|£o
_l
Vo
— vd
Vi
— yl
(1.341)
Величина ошибки может быть оценена при использовании методики,
изложенной в § 1.37.
1.36.	Увеличение порядка интегрального
и дифференциального операторов
Задача аппроксимации, которая обсуждается в этом параграфе,
заключается в следующем.
Пусть Wдифференциальное уравнение вида
V a'v V и t4\ d х
> a.(f)_r__	>	bi (/)—г
_	at*	dti	•
i = 0	i	—	U
(1.342)

1.36]
УВЕЛИЧЕНИЕ ПОРЯДКА ОПЕРАТОРОВ
77
Отпустим, что VI'	обеспечивает желаемые	характеристики	системы
при действии данного входного сигнала x(t), но с точки зрения
реализации данное	дифференциальное уравнение	неприемлемо, так
как разность порядков интегрального и дифференциального операторов
слишком мала, г. е.
п — т A',	(1.343J
где N—требуемая величина разности порядков. Например,
п — т = N — Ь,	(1.344)
где Ь — целое положительное число.
Необходимо найти уравнение
п Ь -f- q	_	т	- \- а
1	(L345)
i = i	i	— 0
решение которого У (t)	будет	достаточно	точно	аппроксимировать
y(t), определяемое уравнением
(1.342). Предлагаемый метод
решения этой задачи иллюст-	о—:—
рируется рис. 1.14.	Дифферен¬
циальное уравнение, у которо¬
го разность порядков	иптег-	Рис-	^	за^ачс	аппроксимации,
рального и дифференциального
операторов равна /;, «включается» последовательно с W, формируя,
таким образом, систему с дифференциальным уравнением W:
IT = WX.	(1.346)
Эта система имеет требуемую разность порядков N.
Свойства	оператора	А'	должны быть	таковы,	чтобы	х' было
близко к х в каждый момент времени.
Иначе говоря, требуется, чтобы ошибка s между х и х' стреми¬
лась асимптотически к нулю
г — х — х\	(1.347)
Очевидно,	что	скорость	стремления ошибки	к	нулю	определяется
надлежащим выбором характеристического уравнения, соответствую¬
щего дифференциальному уравнению, которое описывает ошибку.
Пусть дифференциальное уравнение X будет иметь вид
1=0	i=0
(1.348)

78	СИНТЕЗ	СИСТЕМ	С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ	[ГЛ. !
Предварительно выберем ai(t) постоянным. Выбор их обсуждается
ниже. После того как они выбраны, применим оператор
/ -=0
к обеим частям уравнения (1.347), формируя, таким образом, урав¬
нение
b + q	b + q	b	+	ч
—	о-ад
Ld ‘ dt‘ ^ dt' Ld 1 dt1 '
i = 0	i=()	i	=	0
Подставляя (1.348) в (1.350), получим уравнение для е
Ъ+q	b+q	q
dli	V d'x Y1 / ox
1F= 1 “1F+	—
i = 0	/ = q + 1	i = 0
Вследствие требования асимптотического стремления ошибки к нулю
необходимо, чтобы уравнение (1.351) было не только устойчивым,
но и его правая часть равнялась бы нулю, т. е. необходимо выби¬
рать р таким образом, чтобы выполнялось равенство
2 ‘U52>
г = 7+1	i	=	U
Метод выбора |3z-(f) зависит в общем случае от вида входного
сигнала x(t). Чтобы проиллюстрировать этот метод, рассмотрим три
вида входных сигналов.
Полиноминальные входные сигналы. Допустим
q
x(t)— ^ Cit\	(1.353)
7 = 0
где С( — действительные постоянные. Очевидно, что
—— = 0	(I = q -{- 1, q + 2, ... , q -|- b),	(1.354)
at1
поэтому уравнение (1.352) сводится к
У(«/ — РМ^=0>	(1.355)
ас1
/ = о
и, очевидно, решение для удовлетворяющее этому уравнению,
есть
Р,- = а/.	(1.356)

1 36j	УВЕЛИЧЕНИЕ	ПОРЯДКА ОПЕРАТОРОВ	79
Из анализа уравнения (1.351) ясно, что q выбирается равным
наивысшей степени полииоминального входа, р*— постоянные вели¬
чины, так как постоянны а,-. Результирующее уравнение X является
уравнением с постоянными коэффициентами.
Экспоненциальные входные сигналы. Допустим
я
X(t)= 2 cie"f’	о.357)
У = о
где cj — вещественные постоянные, в общем случае являются
комплексными величинами.
Для того чтобы x(t) было действительной величиной, необходимо
чтобы комплексные величины ^ образовали бы сопряженные пары.
Если (1.357) подставить в (1.352), получается следующее урав¬
нение:
2 *	1	с^=°	с-358»
i = q 1 j = 0	i = 0	i = 0
или
2 2 *iCf{jetjl + 2 2 (“«• — Р/)сЛ>7/'( =°-	(1-359)
i = q -f- 1 у = 0	i = 0 У = 0
Уравнение (1.359) может быть переписано в виде
2 с/Т/<{ 2 ®«-ТУ+ 2 (*«• — Рг)Т/} = °-	(1.360)
у = 0	1	г	=	7	-г	1	i = 0	'
Величины 3; выбираются так, чтобы удовлетворялось уравнение
if	2	— pi)Тт = 0 С/ = 0.	(1.361)
г = q -f 1	i	=	0
Заметим, что, выбирая наивысшее ненулевое значение рг* равным р
получим ровно q -j— 1 уравнение с <7-1-1 неизвестным.
Отметим, что так как at- и — постоянные величины, то р,-
также постоянны; поэтому X представляет собой уравнение с посто¬
янными коэффициентами.
Входной	сигнал	общего вида. Допустим, что	входной	сигнал
является функцией общего вида: cx(t), где с — константа, x(t) — функ¬
ция, имеющая по крайней мере b непрерывных производных. Если
в уравнении	(1.352)	положить q равным нулю, то	это	уравнение
может быть переписано следующим образом:
ь
У. а< + (®° “Г Ро) с* = 0	(1.362)
dt1
i = 1

80
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. I
ИЛИ
откуда
i = \
y.Qx — $Qx}= 0,	(1.363)
b
?•=«.+71	<1'3,i4,
В общем случае [30 является функцией времени, и поэтому урав¬
нение X может быть уравнением с переменными коэффициентами.
Использовать соотношение (1.364) не всегда удобно из-за деле¬
ния на Ху поэтому иногда желательно аппроксимировать входной
сигнал либо полиномиальным, либо экспоненциальным рядом и исполь¬
зовать соответственно уравнения (1.356) или (1.361).
Когда значения выбраны такими, чтобы удовлетворялось урав¬
нение (1.352), уравнение относительно ошибки (1.351) приобретает вид
2«,|f = 0.	(1.365)
i = 0
Уравнение (1.365) является однородным уравнением с постоянными
коэффициентами. Выше было сказано о выборе аг. Теперь выбор
этих коэффициентов становится более очевидным. Они выбираются
так, чтобы ошибка s = a;— х' стремилась к нулю настолько быстро,
что разность между выходными величинами у и у' была мала. В этом
случае очевидно, что выбор аг требует знания решения уравнения W.
1.37.	Оценка ошибки аппроксимации
При аппроксимации данного дифференциального уравнения необ¬
ходимо проанализировать разность между решениями этого диффе¬
ренциального	уравнения и аппроксимирующим	его	уравнением при
определенном	входном	сигнале. Эта разность, или ошибка,	является
некоторой оценкой полученной аппроксимации.
Пусть данное дифференциальное уравнение будет иметь вид
y = Gy-\-fx,	(1.366)
а аппроксимирующее уравнение
yi = GiViJrfiX.	(1.367)
Предположим, что эти уравнения имеют одинаковый порядок и в
общем случае являются уравнениями с переменными коэффициентами.

137]	ОЦЕНКА ОШИБКИ АППРОКСИМАЦИИ	8!
Разность между уравнениями (1.366) и (1.367) может быть записана
в виде
Су —й) — Gy— Gtyi -j- (f—/,) x -f- (Giy — G,y)	(1.368)
или, полагая г=у—уь
k = Glz + (G-Gl)y-\-(f—f1)x.	(1.369)
Теперь положим
В = G — G\	(1.370)
и
b=f—f\.
Тогда уравнение (1.369) запишется
г = G{e -\-By-\- Ъх.	(1.371)
Если можно получить точное решение (1.371), то задача решена.
В общем случае, однако, получить точное решение уравнения бывает
часто затруднительно, поэтому исследуем следующие три возмож¬
ности:
1. Получение точного решения на вычислительной машине.
2. Получение приближенного решения.
3. Получение оценки вектора ошибки.
В этом параграфе рассматривается третий случай. В результате
рассмотрения получается определенная оценка ошибки аппроксимации.
Эта опенка может быть использована для обоснования ценности
аппроксимации.
Для оценки ошибки вводится определение нормы матрицы. Если
дана матрица А, то ее норма определяется следующей формулой:
А =! А	II = (след ААГ)Ш,	(1.372)
т
где	А	—транспонированная	матрица Л. Норма	вектора	ошибки г
в силу	(1.372)	есть	квадратный корень из суммы	квадратов	ее ком¬
понент.
Пусть Wi (ty т) — весовая матрица однородного дифференциального
уравнения
u = GiU.	(1.373)
Тогда решение уравнения (1.371) будет иметь вид
t	t
8(0 = 5	9)в(0).У(0)<*9-{-$	W,(0	0)b(6)Jt-(6)dn. (1.374)

82
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
Используя данное выражение, получим
401=3
\ Wi(t, в)В(в)у(в)М
+
j W, (t, Ь)Ьф)х(Ъ)№
< j.|! W, (t, 6) В (9)у (9) I<79 + j || W, (t, 9) b (9) x (9) || dO ^
•z	T
== (I! W, (7, 9) j| IВ (9) II13» (9) || <79 + {1 W, (7, 9) 11 b (9) || || x (9) || d9.	(1.375)
x	T
Обозначим
I }	(1-376)
yW,, = max||.y(9)|,
Mx = max I x (6) I = max | x (0) |,
тогда
|: e (01 < My \ I! W, (t, 9) IIIВ (9) I df) + Mx $ II W, (t, 9) || || b (9) || <79.	(1.377)
T	T
Положим
(1.378)
где A — постоянная невырожденная матрица и C{t) — матрица с пере¬
менными параметрами. Собственные числа матрицы А имеют отрица¬
тельную действительную часть. Wi(t, 0) есть весовая функция урав¬
нения (1.373), и поэтому она должна удовлетворять уравнению
dt
[ Wx (t, 0)] — AWi (t, 0) + C(O Wt(t, 0),
(1.379)
где Wj(0, b) = I (единичная матрица). Следовательно,
Wi{t, 9)=	—	9)4-	j	W(t	—	a)	С	(a)	W,	(a,	9)	da,	(1.380)
причем W(t — 0) удовлетворяет уравнению
А[щ;-9)] = ли^-9),
(1.381)
где
Щ0 — 0) = 7.
Если собственные числа матрицы А имеют отрицательные ве¬
щественные части, тогда | W(t — 0)|| может быть ограничена экспо¬
нентой, т. е.

1.381
ПРИМЕР	83
где с\ и а — положительные вещественные числа. Тогда из уравне¬
ний (1.380) и (1.381)
II W. (/. в)1<с1в-в‘‘-в> + 5с1е-“‘/-)1С(а)|||| W,(a. 0)|do.	(1.383)
е
Преобразовывая выражение (1.383), получим
 с* IIе w II-II w> (*> e)llg0< ^cj||C(0||.	(1.384)
Ciea0 + ( с, || С (a) |i ||IV, (а, Ще^Ла
О
Интегрируя неравенство (1.384), найдем
i	-|	t
log С,еа0 -J- $ Cl IIС (а) || || W, (а, 0) | еаа da — log ctea0 ^ § с, IJ С (а) | da
t
+Sc,lC(e)l|W1(e, 0) j| еал da	t
  			exp 5 с,! С (а) I da. (1.385)
cle	В
И, наконец, из уравнений (1.383) и (1.385) получим
!№,(*, е)||<с,ехр|—а(^ —0) + jc1||C(a)||flfaj. (1.386)
Тогда из (1.386) и (1.377)
!! * (01| Si j ci exp j_ a (< - 0) + j || С (a) || daj \MV\B (0) fl + Mx |fr(0)|} d0.
(1.387)
Для частного случая, когда (1.371) стационарно, |C(a)|| = 0 и
||£(б)!| и |]£(б)|| — константы, уравнение (1.387) сводится к соотношению
I е (01| :< {Му || В || + Мх || Ъ1} [ 1 - е-*« 'Д.	(1.388)
1.38. Пример
В примере § 1.35 уравнение

84
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
было аппроксимировано уравнением
+
11
X.
(1.390)
У о  II — (3-{-2/5£') 1 у0
у[ — I _ (2+ 4/5^) 0 у\
Используя уравнение (1.387), найдем оценку ошибки аппроксимации для
т = 0.
В соответствии с уравнениями (1.369), (1.370) и (1.378)
А =
— 3	1
— 2 0
С(0 =
I —2/5<г' 0 [j
А/ое'( 01|
Я =
2/5<г* 0
, ь =
01
— 1/бе-' 0
°|
(1.391)
Импульсная переходная функция, определяемая уравнением (1.381),
будет иметь вид
W(t — Q) =
2е~2(*-°)	2е'^~0)	2<гО-°)	^-2(^-0)
(1.392)
Из уравнений (1.391) и (1.392)
II W(t — 6)IP =	—	18е-3^-0>+	Юе-^‘-ь\	(1.393)
4
(1.394)
5 .	.	(1.395)
Полагая в соотношении (1.387) т = 0 и 6i=r0, получим
^ с, А С (a) I ch = Y~\е ° — е~‘ II S
2с1
W
(1.396)
Подставляя уравнение (1.227), (1.395) и (1.396) в (1.220), получим
соотношение
i
С —!— g(o-i)|) dB.
е rg с,Му ехр
1/5/
Оно примет вид
причем
c,Mv exp (-^Д
: —{<?-' - e-at\
/5 (а - 1)	’
W(t — 6)Ц^С1еа^-“).
(1.397)
(1.398)
(1.399)

ЛИТЕРАТУРА
Можно показать, что если а = ~ и сх = У 3, то неравенство (1.398)
удовлетворяется, и уравнение (1.397) может быть записано:
2 УS схр	| Му
|®1! =	у}	°	{e-ti*—е~1\.	(1.400)
Из (1.400) очевидно, что \\г\\ стремится к нулю при	сю,
кроме того, из этого соотношения можно получить неравенство
шах||е|| = Ме^ 1,81Ж>(.	(1.401)
Оценка ошибки аппроксимации, даваемая соотношениями (1.400)
и (1.401), позволяет обосновать необходимость аппроксимации урав¬
нения (1.389).
1.39. Заключение
В этой главе были рассмотрены некоторые методы, которые
можно использовать для синтеза линейных систем автоматического
управления, содержащих заданные элементы, полная характеристика
которых либо меняется во времени, либо должна меняться во вре¬
мени. Изложение является достаточно полным, хотя некоторые вопросы
не исследованы до конца. Изложение этих вопросов можно найти
также в книге [17].
ЛИТЕРАТУРА
1. Truxal J. G., Control Systems Synthesis, McGraw-Hill Book Company,
Inc., New York, 1955. [Русский перевод: T p а к с e л, Синтез систем авто¬
матического регулирования, Машгиз, М., 1959.]
2. Борский В., О свойствах импульсных переходных функций систем
с переменными параметрами. Автоматика и телемеханика, т. 20, июль
1959 г., стр. 848—855.
3. Control Systems Engineering, edited by W. W. Siefert and C. W. Stceg,
Jr., McGraw-Hill Book Company, Inc., New York, I960.
4. С r u z J. B. and Van V a 1 k e n b e r g М. E., The Synthesis of Models for
Time-Varying Linear Systems, Proceedings of the Symposium on Active
Networks and Feedback Systems, Polytechnic Press of the Polytechnic
Institute of Brooklyn, New York, 1960, pp. 527—544.
5. Б а т к о в А. М., К вопросу о синтезе линейных динамических систем
с переменными параметрами. Автоматика и телемеханика, т. 19, январь
1958 г., сгр. 49—54.
6. М а г ы a in И., Методика решения линейных дифференциальных уравне¬
ний с переменными коэффициентами при помощи моделирующих уст¬
ройств. Автоматика и телемеханика, т. 20, июль 1959 г., стр. 839—847.
7. Мальчиков С. В., О синтезе линейных систем автоматического управ¬
ления с переменными параметрами. Автоматика и телемеханика, т. 20,
декабрь 1959 г., стр. 1587—1594.

86
СИНТЕЗ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
[ГЛ. 1
8. Cruz J. В., A Generalization ol the Impulse Train Approximation for
Time-Varying Linear System Synthesis in the Time Domain, IRE Transac¬
tions on Circuit Theory, Vol. CT-6, December, 1959, pp. 393—394.
9. L a n i n g J. H. and Battin R. H., Random Processes in Automatic
Control, McGraw-Hill Book Company, Inc., New York, 1956. [Русский
перевод: J1 э н и н г Дж. и Б э т т и н Р., Случайные процессы в задачах
автоматического управления, ИЛ, М., 1958.]
10.. Computer Control Systems Technology, edited by С. T. Leondes, McGraw-
Hill Book Company, Inc., New York, 1961.
11. Birkhoff G. and MacLaneS., A Survey of Modern Algebra, Mac¬
Millan Inc., New York, 1960.
12. St ear E. B. and Stubber ud A. R., Signal Flow Graph Theory for
Linear Time-Variable Systems, Transactions of the AIEF (Communications
and Electrons), Vol. 58, January, 1962, pp. 695—701.
13. St ubber ud A. R., A Technique for the Synthesis of Linear Nonstatio-
nary Feedback Systems, Part I: The Approximation Problem, accepted for
publication in AIEE Transactions.
14. Stubberud A. R., A Technique for the Synthesis of Linear Nonstatio-
nary Feedback Systems, Part II: The Synthesis Problem, accepted for pub¬
lication in AIEE Transactions.
15. Г л а д к о в Д. И., О синтезе линейных систем автоматического управ¬
ления. Автоматика и телемеханика, т. 22, март 1961 г., стр. 306—313.
16. Miller К. S., Properties of Impulsive Responses and Green’s Functions,
IRE Transactions on Circuit Theory, Vol. CT-2, March, 1955, pp. 26—33.
17. Stubberud A. R., The Analysis and Synthesis of Linear, Time-Variable
Systems, University of California Press, 1964.
18*. Солодов А. В., Линейные системы автоматического управления
с переменными параметрами, Физматгиз, М., 1962.

ГЛАВА 2
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
Хеи (И, С. Hsieh), Леондес (С. Т. Leondes)
Р л 3 Д II Л I
ОПТИМАЛЬНЫЙ СИНТЕЗ МНОГОМЕРНЫХ СИСТЕМ
СО СТАЦИОНАРНЫМИ СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
2.1.	Введение
Современная теория управления вступила в эру, в которой проб¬
лемам многомерных систем уделяется особое внимание. Хотя разви¬
ваясь таким образом, теория управления в значительной степени
отталкивается от предшествующих работ по одномерным системам,
тем не менее возникающие при изучении многомерных систем задачи
часто внутренне отличаются от соответствующих задач в одномерном
случае.
Природу рассматриваемых в первой части настоящей главы задач
можно охарактеризовать просто. Имеется набор стационарных слу¬
чайных процессов, представляющих собой смесь полезных сигналов
и искажающих их шумов. Этот набор входных процессов должен
быть обработан некоторым линейным устройством с тем, чтобы полу¬
чить набор выходных сигналов, оптимальный в смысле минимума сред¬
него квадрата ошибок. Так ставится задача оптимальной линейной
экстраполяции и фильтрации.
Первая работа по оптимальной линейной экстраполяции и фильт¬
рации была написана Н. Винером [1] около двух десятилетий назад.
С тех пор были сделаны различные обобщения основополагающей
теории Винера на другие одномерные задачи. Эти методы синтеза
теперь хорошо известны и могут быть найдены в различных учеб¬
никах [2, 3, 4]. Однако задачи, относящиеся к многомерному случаю,
несмотря на свою чрезвычайную важность для техники, включая управ¬
ление летательными аппаратами и теорию связи, до недавних пор
не исследовались.

88
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
Ранние работы по синтезу многомерных фильтров и систем управ¬
ления со стационарными входами, оптимальных в смысле минимума
квадрата ошибки, принадлежат Хеи и Леондесу [5, 6], а также Амара
[7]. Векторное уравнение Винера — Хопфа было решено методом
преобразования Фурье и методом неопределенных коэффициентов.
Более прямой подход к решению векторного уравнения Винера —
Хопфа получается при факторизации матрицы спектральных плотно¬
стей входа. Однако разработанные к настоящему времени способы
осуществления этой факторизации довольно сложны.- Винер и Масани
j 8, 9] рассмотрели синтез дискретного многомерного фильтра и пред¬
ложили метод факторизации, основывающийся на бесконечных матрич¬
ных рядах. Однако этот метод непригоден для какой-либо практи¬
ческой цели. Юла [10] разработал алгоритм решения задачи факто¬
ризации для рациональных спектральных матриц. К сожалению, его
метод довольно сложен, и факторизация простой рациональной мат¬
рицы требует больших вычислений. Позднее Дэвис [11] дал другой
метод факторизации матрицы спектральных плотностей. Основная
идея его подхода интуитивна, и процедура выполнения факторизации
по сравнению с предлагавшимися ранее несколько проще.
В следующих параграфах формулируется задача среднеквадратич¬
ной фильтрации и выводится в весьма общем виде (с помощью тео¬
рии матриц и операторов) связанное с ней уравнение Винера — Хопфа.
Подробно излагается метод неопределенных коэффициентов, предло¬
женный Хеи и Леондесом, а также Амара. Дается пример, поясняю¬
щий этот метод. Затем показывается, как факторизуется матрица
спектральных плотностей методом Дэвиса. И, наконец, показывается,
как все эти методы применяются для решения общей задачи управ¬
ления системой.
2.2.	Постановка задачи многомерной непрерывной фильтрации
в смысле Винера
Многомерная система определяется как система с я входами и
т выходами. В линейной системе входные и выходные сигналы свя¬
заны посредством матрицы весовых функций. Пусть / {t) — я-мерный
входной вектор, a C(t) — /я-мерный выходной вектор. Для простоты
под вектором всегда понимается вектор-столбец. Обозначим весовую
функцию между k-м входом и у-ым выходом символом Wjk(t, т).
Тогда W(t, т) будет т X я-матрицей весовых функций. И теперь
выходной вектор можно выразить формулой
t
C(t)= 5 W(t,z)i(x)d*.	(2.1)
— ОО
Целью этого параграфа является формулировка задачи теории
виперовской фильтрации в многомерном случае [5]. Для того чтобы

2.2]
ЗАДАЧА МНОГОМЕРНОЙ НЕПРЕРЫВНОЙ ФИЛЬТРАЦИИ
89
облегчить постановку и решение этой задачи, введем некоторые опре¬
деления и обозначения. Пусть X(t), —оо<^<^оо,— я-мерный дей¬
ствительный векторный случайный процесс. Корреляционная матрица
этого процесса определяется формулой
R{s,f) = E{X(s)X'(f)},	(2.2)
где ' — штрих означает транспонирование. Таким образом, R(s,t)
есть т X /^-матрица. Очевидно, что R(sy t) неотрицательно определена
для каждых $ и t и что Rr (5, t) = R(t, s). Обозначим норму матрицы
(квадратной или прямоугольной) символом ||Af|j и определим ее так:
=	(2.3)
В рассматриваемой задаче на каждый вход поступает искаженный
сигнал—сумма ожидаемого сигнала sk(t) и неожидаемого шума nk(t).
Таким образом, входной вектор можно записать как
I{t) = S{t) + N(t\	(2.4)
где S(t) и N(t) — 5-мерные векторы. Предполагается, что и сигнал,
и шум являются действительными стационарными процессами.
Исследуемый фильтр определяется в предположении, что идеаль¬
ный выход может быть результатом любой линейной операции над
входными сигналами. Пусть D (t, т) — матрица идеальных весовых
функций. Тогда идеальный выходной вектор Cd(t) равен
оо
Cd(t)= \ D(t,x)S(x)dx.	(2.5)
— СО
Следует отметить, что идеальная весовая функция может быть
физически невозможной, как, например, происходит в случае экстра¬
поляции. Вектор ошибок системы определяется как разность между
действительным выходным вектором и идеальным выходным вектором
8(0 = с (0-ело.	(2.6)
Формулируемая задача может быть лучше понятна с помощью
рис. 2.1. Часть схемы, расположенная под пунктирной линией, пред¬
ставляет собой действительную систему, в то время как то, что рас¬
положено выше этой линии, представляет гипотетическую идеальную
систему вместе с устройством сравнения, которое выдает сигналы
ошибок.
Без потери общности можно предположить, что как сигнал, так
и шум имеют нулевые средние. Из этого предположения автомати¬
чески вытекает, что математическое ожидание вектора ошибок равно

90
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
нулю. Задача теперь состоит в том, чтобы выбрать такую физически
возможную (а также устойчивую) матрицу весовых функций, чтобы
Идеальная
система
Действительная
система
о
Л(г)
Cd(t)
т
S(t)
т
т
W(Z)
+
'c(t)
Рис. 2.1. Блок-схема устройства, формирующего ошибку.
математическое ожидание квадрата нормы вектора ошибок было
минимальным	£	{j8(0 ,р } _ min ?	(2>7)
w 11, т)
где W (t, т) = 0 для t<^z.
2.3.	Минимизация ошибки системы
Вычислим критерий качества системы. Во-первых, заметим, что
для стационарных входов и идеальной системы с постоянными пара¬
метрами оптимальная действительная система будет также иметь
постоянные параметры. Во-вторых, минимизация £{||е(0|Р} эквива¬
лентна минимизации математического ожидания квадрата каждой ком¬
поненты вектора е(0- Рассмотрим /-ую компоненту этого вектора
e;(0 = S W)(x)/(t-x)dx-C(lj(t),
(2.8)
где W)—вектор-строка размеров 1 X72 представляет собой у-ую
строку матрицы весовых функций. Таким образом, имеем
Е {#5 (0} = Е A W) (х) $ / (* — х,) /'(t - т4) Wj (х4) rfx2 -
о
СО
- 2 ^ W) (х.) I (t - x,) Caj (0 f/x, -f C%j (t) =
0
a)	oo
= 5 Wj (x.) dx, $ *(x, — X,) Wj (x4) dx, -
0	0
OO	4
-2 5 ^(xOBylxOf/x.-l-flQAO} -	(2.9)

23]	МИНИМИЗАЦИЯ ОШИБКИ СИСТЕМЫ	91
где	—	-2) = Е {/(* — т0^(* — т2)} — п X ^-корреляционная мат¬
рица входа,
п X 1-вектор корреляций между входом
и идеальным выходом.
Поскольку последний член в равенстве (2.9) не зависит от Wp
задача сводится к минимизации
со	со
Q ( Wj) = \ W'j Ы dz! $ /? (X! — Хг) Wj ('.2) с/т.2 —
а	о
СО
-2$ И'ДтОВуЫЛ,. (2.10)
О
Определим скалярное произведение двух векторов x(t) и y(t) из
пространства Ц векторных функций, интегрируемых с квадратом,
формулой
ь
х, y = \x'(t)y(t)dt.	(2.11)
а
Введем также обозначение
00
R W, = $ /? (т, — т2) W, Ы dz*	(2.12)
О
Здесь R — очевидно, линейный оператор в я-мерном пространстве Z.2.
Тогда уравнение (2.10) можно записать как
Q(Wf) = RW/9 Wj — 2B„ WJy	(2.13)
где интегрирование при вычислении скалярного произведения произ¬
водится в пределах от 0 до со.
Задача теперь заключается в том, чтобы найти оптимальный век¬
тор весовых функций, который доставит минимум Q. С этой целью
рассмотрим вектор V) такой, что
RVj = Bj для	(2.14)
Подставляя (2.14) в (2.13), а также добавляя и вычитая член RVp
Vp имеем
Q(Wj) = RWp Wj—2RVp Wj + RVp V, — RVp Vp (2.15)
Так как линейный оператор R является самосопряженным, т. е.
Rxy у = Ryy ху
уравнение (2.15) можно записать как
Q(Wj) — RWp Wj-RWp Vj-RVp Wj -j- R Vp Vj —
- R Vj, Vj — R( Wj - Vj), (Wj - Vj) - R V,, Vj. (2.16)

92
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
Далее заметим, что, хотя корреляционная матрица вообще является
неотрицательно определенной, на практике она будет также положи¬
тельно определенной. Поэтому мы будем рассматривать только невы¬
рожденные задачи. Это означает, что для любого Zj
RZj, Zj^O
и
RZp Zj = 0
тогда и только тогда, когда Zj = 0 (всюду, исключая множество
меры нуль*)). Таким образом, Q будет минимальным, если найти
оптимальный W; такой, что
Wj— Vj = О,
или
Wj=V,
Уравнение (2.14) можно теперь переписать как
RWj = Bj для т^О.	(2.17)
14 минимум Q равен
Qmin = -By, Wj.	(2.18)
Следовательно, уравнение (2.17) является уравнением, которому дол¬
жен удовлетворять вектор оптимальных весовых функций. Это обоб¬
щенное уравнение Винера — Хопфа для многомерных систем. Как
было показано, оно дает необходимое и достаточное условие опти¬
мальности.
2.4.	Оптимальное уравнение в области изображений
Из теории фильтрации для одномерных систем хорошо известно,
что для стационарного входного процесса интегральное уравнение
Винера — Хопфа можно решать методом изображений. Если вход¬
ные процессы являются стационарными, то метод изображений
также применим и при рассмотрении многомерных систем, но теперь
соответствующее векторное интегральное уравнение преобразуется
в алгебраическое уравнение относительно передаточных функций
системы [о]. Однако методы определения этих физически возможных
передаточных функций системы совершенно отличны от тех, которые
используются для одномерной системы.
*) Тс, кто не знаком с терминологией теории функций действительного
переменного, могут заменить это предложение в скобках замечанием, что
приводимые рассмотрения справедливы только для функций, имеющих смысл
с физической точки зрения.

2.4]
ОПТИМАЛЬНОЕ УРАВНЕНИЕ В ОБЛАСТИ ИЗОБРАЖЕНИЙ
93
Прежде всего заметим, что вследствие требования физической
возможности матрицы весовых функций системы равенство (2.17)
является необходимым условием оптимальности W только для Tj ^ 0.
'Гак как корреляционная матрица R(z) не равна нулю при отрица¬
тельных значениях аргумента, то для того, чтобы можно было фор¬
мально воспользоваться методом преобразований, уравнение (2.17)
следует видоизменить. Пусть /уСч) определена так, что
fi (т0= 0 для tj.^0.
Тогда уравнение (2.17) можно переписать как
RW, = B, + fj для всех значений	(2.19)
Законность применения преобразования Фурье к уравнению (2.19)
будет прежде всего зависеть от того, имеет ли каждая функция
в этом уравнении преобразование Фурье. Из требований физической
возможности и устойчивости системы вытекает, что матрица переда¬
точных функций может иметь особенности или полюсы только в левой
части 5-плоскости. (Здесь полагается 5 =yw.) Спектральные плотности
стационарных процессов, являющиеся по предположению рациональ¬
ными функциями от 5, будут иметь особенности во всей плоскости
и будут аналитическими в некоторой полосе вдоль мнимой оси.
В частности, спектральные плотности одномерных стационарных про¬
цессов будут иметь полюса и нули, расположенные симметрично
относительно мнимой и действительной осей. Преобразование Фурье
произвольно определенной векторной функции /у, которая обращается
в нуль при Ti ^ 0, может обладать особенностями только в правой
части 5-плоскости. Таким образом, при соответствующем определении
этой функции идеальной системы вектор корреляций между входом
и идеальным выходом системы будет иметь преобразование Фурье.
Установленные выше свойства известных функций в уравнении (2.19),
а также требование физической возможности и устойчивости мат¬
рицы передаточных функций системы безусловно обеспечивают воз¬
можность применения метода изображений. Для нахождения опти¬
мальной матрицы передаточных функций следует наложить еще одно
ограничение на матрицу спектральных плотностей, но это будет
подробно рассматриваться в следующем параграфе.
Применим теперь преобразование Фурье к обеим частям урав¬
нения (2.19). В результате получим
OYj = Kj + Fj9	(2.20)
оо
где 0= ^ R(t)e~st dt— матрица спектральных плотностей вход-
— 00
оо
ных сигналов, = $ Wj{f)e~st dt — вектор передаточных функций
о

94
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
системы, Kj= J Bj(t)e~stdt — вектор взаимных спектральных плот-
— 00
оо
ностей входных и идеальных выходных сигналов, F] = ^ ff{t)e~stdi.
— оо
Здесь, для простоты, аргумент 5 в уравнении (2.20) опушен. Век-
тор Fj, пока еще неизвестный, может иметь особенности только
в правой полуплоскости. Вектор Kj и матрица G будут иметь осо¬
бенности во всей плоскости. Следовательно, вектор GY; будет также
иметь особенности во всей плоскости. Поскольку особенности F]
целиком сосредоточены в правой полуплоскости, должно иметь место
следующее равенство:
{0У/}+ = {*,}+.	(2.21)
Здесь символ { }+ обозначает ту часть функции, которая имеет по¬
люса только в левой полуплоскости. Точнее, применение этой опе¬
рации к произвольной функции Н(s) в 5-области означает, что
оо
{H(s)}+=\h(t)e-s' dt,	(2.22)
и
где
1 700
h(t) = ^p $ H(s)e‘sds.
-ja>
Следует отметить, что в случае, когда H(s) является рациональной
по 5 матрицей, операция { }+ эквивалентна тому, чтобы разложить
каждый элемент этой матрицы в ряд и затем собрать те члены, ко¬
торые имеют полюса только в левой полуплоскости. Однако, когда
H(s) является более общей функцией, для выполнения операции { } ;
следует пользоваться формулой (2.22). Уравнение (2.21) можно рас¬
сматривать как уравнение Винера—Хопфа для задачи многомерной
фильтрации в области изображений. Когда матрица передаточных
функций удовлетворяет этому уравнению, минимум среднеквадратич¬
ной ошибки равен
j СО
£Himin = 2^ $ \^d)10ss{Yd)J-Y)Gls(Ya)j\ds. (2.23)
— }'со
Здесь Gss — матрица спектральной плотности сигнала, Gj$ — матрица
взаимных спектральных плотностей входного воздействия и сигнала,
(Yd)j — вектор идеальных передаточных функций, а звездочка обо¬
значает операцию транспонирования и замену аргумента 5 на — 5.

2.5]
МЕТОЛ НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
95
2.5.	Нахождение оптимальной матрицы передаточных функций
методом неопределенных коэффициентов
Предполагается, что во всех рассматриваемых в этой главе зада¬
чах многомерной фильтрации случайные процессы являются стацио¬
нарными с рациональными спектральными плотностями. В таком
случае рациональная матрица спектральных плотностей будет иметь
следующие свойства:
Cl. G(s) = G(s), т. е. G(s) действительна. Здесь верхняя чер¬
та обозначает число, комплексно-сопряженное к числу, стоящему
под ней.
С2. G' (—s) = G(s), т. е. G(s)— пара-эрмигова матрица. Таким
образом, если положить s=jо), то G (уоо) для действительных ш
будет обычной эрмитовой матрицей.
СЗ. G(yo)) — неотрицательно определенная матрица. Другими сло¬
вами, b'G (j^)b^ 0 для произвольного вектора b и каждого действи¬
тельного конечного со.
Для более подробного ознакомления со свойствами матриц спект¬
ральных плотностей многомерных стационарных случайных процессов
читатель отсылается к статье Крамера [12].
Приступим теперь к решению уравнения (2.20). Умножив обе
его части слева на G-1, получим
У; - Q~l (Kj + FT) - ^(Kj + Fj).	(2.24)
Здесь элементы матрицы Л, являющиеся алгебраическими дополне¬
ниями матрицы спектральных плотностей, не будут иметь полюсов
на мнимой	оси	и, таким	образом, будут аналитическими в	полосе
вдоль этой	оси.	Поэтому	для того, чтобы применение метода изо¬
бражений	было	законно	для решения рассматриваемой	задачи,
матрица спектральных плотностей должна еще обладать свойством
С4. Матрица G 1 (s), обратная к матрице спектральных плотно¬
стей, является аналитической вдоль мнимой оси.
Отсюда можно заключить, что детерминант | G | не должен иметь
на мнимой оси ни одного конечного нуля. Это и есть то добавочное
ограничение, которое нужно наложить на матрицу спектральных
плотностей. Теперь уравнение (2.24) будет вполне определенным.
Каждый член этого уравнения является аналитическим в некоторой
полосе вдоль мнимой оси. Следовательно, мнимую ось можно взять
в качестве пути интегрирования при применении к этому уравнению
обратного преобразования Фурье.
Заметим далее, что детерминант спектральной матрицы | G | будет
всегда рациональной функцией s'2. Если этот детерминант удовлет¬
воряет приведенному выше требованию, т. е. не имеет конечных

96
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
нулей вдоль мнимой оси, то он может быть разложен так, что
где все полюса и нули Gr(s) лежат в левой полуплоскости, а 0~ (s),
равная Gr(— s), может иметь полюса и нули только в правой полу¬
плоскости.
Применять метод изображений и метод неопределенных коэф¬
фициентов для решения рассматриваемого векторного интегрального
уравнения можно только тогда, когда можно факторизовать | G |, как
это сделано в (2.25). Таким образом, уравнение (2.21) можно пере¬
писать как
Исследуем теперь в полученном уравнении каждый член. Из требо¬
вания физической возможности матрицы передаточных функций
фильтра, очевидно, вытекает, что вектор в левой части уравнения (2.26)
может иметь полюса только в левой полуплоскости. Тогда должно
быть справедливо равенство
благодаря матрице А. Несмотря на то, что вектор F] пока еще не
известен, он по своему определению может иметь полюса только
в правой полуплоскости и, следовательно, из-за него количество
полюсов у оптимальных передаточных функций в левой полуплоско¬
сти не увеличится. Поэтому полюса /г-го элемента векторав левой полуплоскости будут состоять из полюсов элементов &-й
\G\ = Q±(s)G-(s),
(2.25)
ИЛИ
(?Yj = ±AKj + ±AFJ.
(2.26)
(2.27)
Вектор	AFj	полностью известен. Следовательно,
оэ
{^ЛАГу} =$*(*) e-«dt,
— У СО
Далее AF] может иметь полюса в левой полуплоскости только

2.5]
МЕТОД НЕОПРЕДЕЛЕННЫХ КОЭФФИЦИЕНТОВ
97
строки матрицы А, и этот элемент может быть выражен как
mk
2 aPsP	p/b(s)
р=о
П(8-"*) П(8-г-Д’
(2.28)
Здесь коэффициенты полинома Py/e(s), по которым можно определить
нули выражения (2.28), неизвестны, так как неизвестен F]. Нашей
основной задачей будет теперь определение порядка и неизвестных
коэффициентов этого полинома. Следует отметить, что для кратных
полюсов rik член (s — rif^ в уравнении (2.28) будет повторяться
столько раз, какова их кратность.
Объединяя уравнения (2.27) и (2.28), получим следующее выра¬
жение для k-Vi компоненты вектора передаточных функций:
Yi* = m
^ > Аь.Ж
к'к^ jk'f
к' = \
S ар$р
Р= 0
(2.29)
Здесь Ak'k — элемент k-vo столбца и &'-й строки матрицы А — яв¬
ляется алгебраическим дополнением соответствующего элемента
в исходной матрице спектральных плотностей. Так как полюса чле¬
нов Ak’k к левой полуплоскости будут в конечном счете аннулиро¬
ваны полюсами G1', оптимальная передаточная функция задается урав¬
нением (2.29), и ее можно записать как
Yjkis)
1	1
-а
05
1
1	i
■ пк
Р = 0 J
1 1
1	Л
1
СО
с*
1	1
-Э
Со
1
а.
1	1
(2.30)
где bv — нули G+, dt — полюса вектора идеальных передаточных
функций (Yd)j в левой полуплоскости, если они отличны от полюсов
спектральных плоскостей и не аннулируются полюсами G+. ak — по¬
люса G', которые не аннулируются полюсами к-го элемента век¬
тора-строки AKj -j- Z7/! , и {Cp} — новый набор неизвестных коэф¬
фициентов,, которые должны быть определены. При данном решении
задачи уравнение (2.30) является более удобной формой записи для
оптимальных передаточных функций.
В предыдущем параграфе было установлено, что оптимальный век¬
тор передаточных функций должен удовлетворять преобразованному
4 п/р Леондеса - •

98
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
уравнению Винера-Хопфа (2.21). Если мы теперь подставим урав«
нение (2.30) в уравнение (2.31) и приравняем вычеты в левой и
правой частях получившегося уравнения, относящиеся к одним и
тем же полюсам в левой полуплоскости, то получим систему линей¬
ных алгебраических уравнений для коэффициентов {Ср}. Число ли¬
нейно независимых уравнений, полученных таким образом, определит
число полностью неизвестных коэффициентов в векторе передаточ¬
ных функций. Как распределяются эти коэффициенты среди компо¬
нент вектора передаточных функций, можно определить из вида
матрицы G, потребовав, чтобы обратное преобразование от {GYj}4
было хорошо ведущей себя векторной функцией времени. Следует
отметить, что определяемый нами оптимальный вектор передаточных
функций должен дать конечную среднеквадратичную ошибку, выра¬
женную уравнением (2.23). Именно этим мы будем руководствоваться
при определении максимального числа неизвестных коэффициентов,
которое можно включить в каждую передаточную функцию. В сле¬
дующем параграфе изложенный метод будет пояснен примером.
Итак, определение оптимального вектора передаточных функций Yj
в задаче многомерной фильтрации методом неопределенных коэф¬
фициентов сс стоит из следующих основных этапов:
1. Факторизуем детерминант матрицы спектральных плотностей
| О | на G+ (s) и G~ (5).
2. Выражаем систему передаточных функций в виде (2.30).
3. Приравниваем вычеты, находящиеся в обеих частях уравнения(2.21),
но относящиеся к одним и тем же полюсам в левой полуплоскости,
и подсчитываем число линейных уравнений, полученных таким обра¬
зом. Отсюда определяем общее число неизвестных коэффициентов
полиномов, стоящих в числителях передаточных функций.
4. Распределяем надлежащим образом среди компонент вектора
передаточных функций вышеупомянутые коэффициенты и затем
решаем получившуюся систему линейных алгебраических уравнений.
Из уравнения (2.30) видно, что полюсы передаточной функции
будут двух видов. Во-первых, все передаточные функции системы
будут иметь полюсы, являющиеся нулями G+(s). Эти полюса, вообще,
совершенно отличны от лежащих в левой полуплоскости полюсов
всех спектральных плотностей. Во-вторых, передаточные функции,
связанные с отдельным выходом, могут иметь в левой полуплоскости
полюсы вектора идеальных передаточных функций (Yd)j.
Следует отметить, что для одномерной задачи фильтрации матрица Л
равна 1. Следовательно, уравнение (2.27) сводится к
Отметим, что

2.6]
ПРИМЕР СИНТЕЗА МНОГОМЕРНОГО ФИЛЬТРА
99
2.6.	Пример синтеза многомерного фильтра
В качестве простой иллюстрации представленного метода реше¬
ния задачи многомерной фильтрации возьмем систему с двумя вхо¬
дами и одним выходом. Предполагается, что сигналы на оба выхода
поступают одинаковые, но загрязняются разными «белыми шумами».
Пусть	1
у\
@лг1&\ (^) == ~2 *
Gnln2 (s) = -j.
Функция фильтра состоит в том, чтобы выделить сигнал из этих
двух разных каналов (рис. 2.2).
W=S(t)+N,(t)
* — >
щ,(V
C,(t)
l2(t)=S(t)+N2(t)
A
W]2(z)
Рис. 2.2. Пример фильтра 2x1.
Для этой задачи получаются следующие матрицы:
— s2 + 3
G =
Кг =
А =
2 (— s2+l)
1
— s2+l 4(— s2+l)
1
-s2+ 1
— s2 + 5
-s2 +
— s2+ 1
— s2 + 5
4 (s2+ О
— s2+ 1
-s2 + 3
— s2 + l	2(—s2+l)
(^)i =
(2.31)
(2.32)
(2.33)
4*

100
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
Таким образом,
G+(S):
G-(S) =
s+j/7
V8 (8+1) ’
s —уТ
Vs (S-1) •
Пусть
Yi(s) =
P t(8)_
s + /7
(8)
S + /7
(2.34)
Здесь P\(s) и P2(s)— два полинома, степени которых нужно
определить. Подставляя уравнения (2.31), (2.32) и (2.34) в уравнение
(2.21), имеем
— s2 + 3 P,(s) , 1 P2(s)
1
2 (— s2 + 1) s + УТ 1 — s2+ls + )/7"
— S2+ 1
1 P,(s) , — s2 + 5 P,(s)
1
— s2+l s+T"7 1 4 (— s2+ 1) s + /7
+
— S2+ 1
Вычисляя и приравнивая вычеты относительно полюсов s — —1 и
s = — V1, имеем из написанного выше векторного уравнения че¬
тыре уравнения для Pi(s) и P2(s):
Pi (-1)	|	1	Р,	(-1)
1
2x2—1+ /7 1 2 —1+1/7
1 Pi (-1)	,	4	Р2	(-1)
2 —1 +/7 1 4 X 2 — 1 +/7	2
4 Pi(-V7)-4-P8(-V7)=0,
2x6
Р2(— V7)=0.
(2.35)
(2.36)
(2.37)
(2.38)
Легко видеть, что уравнения (2.35) и (2.36) и уравнения (2.37) и
(2.38) зависимы. Следовательно, есть только два независимых урав¬
нения, решениями которых Pi(s) и P%(s) будут просто константы.
Таким образом, имеем следующую систему уравнений:
-1 + ут
г т
-1 + /7
1, 2Ci —С2 = 0.

2.7]
МЕТОД ФАКТОРИЗАЦИИ МАТРИЦЫ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
101
Откуда
С\ = -
-1+1/7
+ /7
С= = -
+ 1/7
=Р«(4
Отсюда следует, что две компоненты Кц(5) и ^12 (5) синтезируемого
фильтра имеют одинаковую частоту среза. Однако соответствующие
им коэффициенты усиления обратно пропорциональны мощности шу¬
мов Ni(t) и N%(t). Впрочем, этот результат можно было бы ожидать
заранее. Среднеквадратичную ошибку можно вычислить, используя
уравнение (2.23):
6
1
0+VT)2J
= 0,2743.
Интересно сравнить качество рассмотренного выше многомерного
фильтра с качеством одномерных фильтров, оптимальных по каждому
из двух каналов в отдельности. Для одного первого канала переда¬
точная функция оптимального фильтра есть
O-f/з) s + /3~
и соответствующая ему среднеквадратичная ошибка равна
Е{г2
1
= 0,3660.
Для одного второго канала передаточная функция оптимального
фильтра есть
^)=1+V5s+V5-
и соответствующая ему среднеквадратичная ошибка равна
£{е2} min = -
1
(1+/5)2
= 0,3090.
Итак, очевидно, качество многомерного фильтра, обрабатывающего
входные сигналы двух каналов одновременно, лучше, чем качество
Двух рассмотренных одномерных фильтров.
2.7.	Нахождение матрицы оптимальных передаточных функций
методом факторизации матрицы спектральных плотностей
В одном из предыдущих параграфов показано, что уравнение
Винера — Хопфа в области изображений имеет вид (2.20)
GYf=Kf + F~.
Для нахождения вектора физически возможных передаточных

102
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
функций, удовлетворяющего этому уравнению, можно применить другой
подход. Мы покажем, что этот подход по существу сводится к раз¬
ложению матрицы спектральных плотностей входа на произведение
двух матриц с некоторыми специальными свойствами.
В § 2.4 было установлено, что для того, чтобы некоторая раци¬
ональная матрица была матрицей спектральных плотностей, она должна
обладать тремя основными свойствами: С1, С2 и СЗ. Мы также
показали, что для того, чтобы можно было получить решение инте¬
грального векторного уравнения Винера—Хопфа методом изображе¬
ний, матрица спектральных плотностей должна обладать еще одним
свойством. Это свойство С4 заключается в том, что матрица, обрат¬
ная к матрице спектральных плотностей, является также аналитиче¬
ской вдоль мнимой оси s-плоскости. Предположим теперь, что мат¬
рица спектральных плотностей может быть представлена в виде
G(s) = H*{s)H(s),	(2.39)
где звездочка, как обычно, обозначает операцию транспонирования
и замены аргумента s на —s. Мы требуем, чтобы матрица H(s) об¬
ладала следующими свойствами:
Tl. H(s) вместе с обратной к ней /7-1(s) рациональна и анали-
тична в правой половине s-плсскости.
Т2. H(s) действительна.
Тогда очевидно, что Я* (s), а также обратная к ней (#*)-1(s)
будут аналитичны в левой полуплоскости и могут, таким образом,
иметь полюса только в правой полуплоскости.
Подставим теперь уравнение (2.39) в уравнение (2.20). Имеем
Таким образом,
Н Y, = (+ (Я*)-1/7/.	(2.40)
Поскольку как (Я*)-1, так и F] аналитичны в левой полуплоскости,
{(H*T'Fj}+ = 0.	(2.41)
Поэтому из уравнения (2.40) получим
или
Yj = H-l{{H*ylKj\Jr.	(2.42)
Уравнения (2.41) и (2.42) отчетливо показывают важность требова¬
ния аналитичности Я (s) и Я-1 (s) в правой полуплоскости. Получен¬
ный таким образом фильтр будет физически возможным и устойчи¬
вым. Итак, мы показали, что для применения второго подхода к ре¬

2,8]
ФАКТОРИЗАЦИЯ МАТРИЦЫ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
103
шению многомерной задачи фильтрации достаточно установить
возможность факторизации, т. е. представления в виде (2.39) матрицы
спектральных плотностей G(s). Как только такая факторизация осу¬
ществлена, матрицу передаточных функций оптимального фильтра
можно легко получить, используя уравнение (2.42).
2.8.	Факторизация рациональной матрицы спектральных
плотностей
Задача факторизации рациональной матрицы спектральных плот¬
ностей за последнее время интересовала многих исследователей.
Первый работоспособный алгоритм для осуществления такого раз¬
ложения в замкнутой форме был разработан Юлой [10]. В методе
Юлы используется каноническая форма Смита полиномиальной мат¬
рицы. Было строго доказано, что факторизация таких рациональных
спектральных матриц всегда возможна. Причем процедура фактори¬
зации по своему характеру является алгебраической. К сожалению,
реализовать эту процедуру весьма сложно.
Следует отметить, что разложение матрицы спектральных плот¬
ностей, которое дается уравнением (2.39), можно физически интер¬
претировать как синтез многомерного формирующего фильтра <D(s)
при дополнительном требовании аналитичности <D(s) и Ф-1 (s) в пра¬
вой полуплоскости. Когда этот формирующий фильтр возбуждается
вектором «белых шумов», матрица спектральных плоскостей выход¬
ного сигнала равна
G (S) = Ф (— S) /Ф' (5) = Ф (— 5) Ф'(5).	(2.43)
Здесь единичная / матрица представляет собой спектр «белого шума»,
a G(s)—спектр выходного сигнала. Сравнивая уравнение (2.39) и
(2.43), имеем
//(5) = Ф'(5).
Таким образом, задачу факторизации матрицы спектральных плотно¬
стей можно рассматривать как задачу синтеза «усиленно формирую¬
щего фильтра». Однако следует отметить, что задача синтеза фор¬
мирующего фильтра выделяется среди остальных задач фильтрации
тем, что требует для своего решения определенной изобретатель¬
ности. Поэтому рассмотренный только что нами результат не будет
явно использоваться. Заметив отмеченную выше аналогию, Дэвис [11]
недавно предложил метод факторизации, использующий серию мат¬
ричных преобразований. Этот метод интуитивен по своей природе
и опирается на небольшое число фактов из теории матриц. После¬
дующее изложение весьма близко к вышеупомянутой статье Дэвиса.
Предположим, что устойчивая система Ф(<>) возбуждается векто¬
ром «белых шумов». Если теперь система Ф(5) последовательно

104
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
ГГЛ. 2
соединена с серией последовательно соединенных линейных систем
7\(s),Tn(s) и если результирующая матрица спектральных плот¬
ностей является единичной, то система, полученная в результате по¬
следовательного соединения линейных систем 7\(s),..., Tn(s), должна
быть обратной к искомой системе Ф(5). Эта ситуация изображена
на рис. 2.3, и приведенные рассуждения содержат основную идею
предлагаемого метода факторизации спектральной матрицы. Таким
образом, имеем
Ф-1(5)=Гл(5)7'л_1(5) ... 7\(s)
и
Ф (s) = V(S) ••• Т-а L, (s) Тп 1 (S).	(2.44)
Так как <E>-1(S) — обратный формирующий фильтр, то
... r,(-s)]C(s)[7’i(s) ... T;i_1(s)T'n(s)] = I.
(2.45)
Отсюда имеем
G(s) = [T;'(-s) ... T-l.1(-s)T-\-s)][T^i(s) ...
... Tnii{s)Tn l(s)]' = <b(s)0'(s).
Требование устойчивости Ф(5) и Ф_1(5) заставляет с должной тща¬
тельностью отнестись к выбору каждой компоненты обратного фор¬
мирующего фильтра. Это требование будет очевидно выполнено, если
каждая компонента Tt (5) и обратная к ней ГГ1 (•?) будут по отдель¬
ности устойчивы. Поэтому мы будем считать, что структура каждой
линейной системы имеет один из двух следующих простых типов:
1.	Tt(s) является диагональной матрицей, элементы которой
за исключением одного или нескольких, равны единице. Обратная
к ней матрица будет диагональной с элементами 1 /tjj(s). В этом
случае устойчивость 7\*(s), а также (5) будут заведомо иметь
место, если все элементы tjj(s) будут минимально-фазовыми и устой¬
чивыми.

ФАКТОРИЗАЦИЯ МАТРИЦЫ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
105
2.	Ti(s) является, исключая внедиагональные элементы tnj(s) п-й
строки, единичной матрицей. Обратная к этой матрице совпадает
с ней самой с точностью до возможной перемены знака tn-(s). Для
устойчивости Ti(s) и ГГЧ5) все элементы tnJ(s) должны быть устой¬
чивыми, но не обязательно минимально-фазовыми.
Из рис. 2.3 и уравнения (2.45) сразу видно, что каждая компо¬
нента обратного формирующего фильтра будет преобразовывать
входной спектр в выходной в соответствии со следующим соотно¬
шением:
Gi (5) = Т, (s) Gi_x (.s) Т\ (5)	(/=1,2,..., п\ (2.46)
где
G0(s) = G(s),
Оя (*) = /•
Применяя уравнение (2.46) повторно, получим в результате уравне¬
ние (2.45). Рассмотрим сначала, что получится при преобразовании
(2.46), если использовать компоненты первого типа. При умножении
Ti(—s) на Gi_\(s) у-я строка Gi_i(s) умножается на	а при
умножении матрицы 7\(—s)Gi_1(s) на 7\-(s) ее /-й столбец умно¬
жается на	При применении компонент второго типа произве¬
дение Т i (—s)Gi_i(s) будет отличаться от Gr-_i ($) только п-й строкой,
у-й элемент этой строки получается путем сложения произведений
tnj(— 5) на элементы у-й строки Gi_t (s). Произведение(Тt (— s) Gt_x (s))X
X T'i (5) вычисляется аналогичным образом, только вместо строк мат¬
рицы Tt (s)	(s) рассматриваются ее столбцы, а элементы tnj{—s)
заменяются на tnj-(s). Заметим, что детерминант матрицы преобразо¬
вания второго типа равен единице.
При всех указанных свойствах компонент обратного формирую¬
щего фильтра факторизацию матрицы спектральных плотностей можно
осуществить в три этапа:
1. Этап исключения полюсов: производится преобразование, с тем
чтобы ни один элемент преобразованной матрицы спектральных
плотностей не имел полюсов.
2. Этап редукции детерминанта: полученная после первого этапа
матрица с полиномиальными элементами преобразуется до тех пор,
пока ее детерминант не станет константой.
3. Этап редукции элементов: матрица, получившаяся после вто¬
рого этапа, подвергается дальнейшим преобразованиям, с тем чтобы
получить постоянную матрицу, которая уже может быть факторизо¬
вана.
Эти три этапа осуществления факторизации будут подробно рас¬
смотрены на примере матрицы G(s) второго порядка.
В результате первого этапа описанной процедуры мы исключаем
все полюса каждого элемента матрицы спектральных плотностей

106
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
входа G(s) и получаем матрицу только с полиномиальными элемен¬
тами. Применяя преобразование первого типа, строки и столбцы G(s)
можно умножить на полиномы, которые аннулируют все полюса
в отдельной строке и отдельном столбце. В силу требования устой¬
чивости Ti(s) и 7+ (s) умножение G(s) слева на 7\(—5) должно
исключить полюса в правой полуплоскости, а умножение G(s) справа
на Т\ (5) должно исключить полюса в левой полуплоскости. Поскольку
спектральная матрица является пара-эрмитовой, достаточно рассмат¬
ривать только левые преобразования.
В качестве примера, иллюстрирующего вышеизложенное, факто¬
ризуем матрицу
	—	2s2 + 5	—2s2 — 5s + 13
0(s)= '
(-s + l)(-s + 2)(s+l)(s + 2j (-s+lM-s + 2) (s + 3) (s + 5)
— 2s2 + 5s + 13	—	2s2	-f	34
(— s + 3) (— s + 5) (s + l)(s + 2) (_s + 3)(-s + 5) (s + 3) (s + 5)
(2.47)
Согласно первому этапу нашей процедуры первую строку этой
спектральной матрицы нужно умножить на (—s —|— 1) (—s + 2),
а вторую строку на (—s + 3)(—5 + 5). Это означает, что 7\(—s)
равна
J ,	 v 	 I (	 5	+	(	 5	+	2)	0
II о	(—5	3) (—5	5)
Получающаяся в результате спектральная матрица
Oi (s) = Tl (— s)G(s) T[(s) =
II —2s2+ 5	—2s2	—5s+13
= || — 2s2 + 5s+ 13	—2s2+34
Цель второго этапа состоит в том, чтобы преобразовать эту
матрицу с полиномиальными коэффициентами в другую матрицу с по¬
линомиальными коэффициентами и постоянным независящим от s
детерминантом. Пусть детерминант |Gi(s)| в общем виде представим
как
I о, (5)| = *П (* + «✓)(-« + *>
(2.48)
Здесь +■ — положительные числа или комплексно-сопряженные пары
с положительными действительными частями, и каждое из них может
встречаться в этом произведении неоднократно. Если применить пре¬
образование первого типа 7+s), у которого п-й диагональный эле¬
мент равен l/s + flf, то детерминант преобразованного спектра G2(s)
будет равен
I 0.2 (5) I = ^ Г1 (5 “Г aj) (— 5 "I" +)•

ФАКТОРИЗАЦИЯ МАТРИЦЫ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
107
Таким образом, мы избавились в определителе |Gi(s)| от множителя
(s + fliH—Но получившаяся в результате матрица G2(s) не
является больше полиномиальной матрицей из-за полюсов членов
в п-й строке и 1/—5-f-a,* в п-м столбце. Теперь следую¬
щий шаг состоит в том, чтобы избавиться от этих двух полюсов,
не изменяя детерминанта матрицы. Заметим также, что для того
чтобы это сделать, достаточно рассматривать только левые преобра¬
зования.
Рассмотрим типичный член п-й строки G2(s). Его можно пред¬
ставить в виде
Наша задача заключается в том, чтобы избавиться от членов
Оно имеет детерминант, равный 1. Исследуя элементы л-й строки
матрицы G3(s) = 73(—s) G2 (s) 7'(s), сразу видим, что для того чтобы
не было элементов с полюсами, коэффициенты къ /г2, ..., kn_Y должны
удовлетворять следующим алгебраическим уравнениям:
из этих л совместно рассматриваемых уравнений независимы только
п—* уравнений. Отсюда можно однозначно определить набор коэф¬
фициентов {kr}. Очевидно, описанную процедуру можно повторять до
тех пор, пока результирующая матрица не будет иметь постоянный
tnj (s)
Pnj (s) +
anj
(2.49)
— s + ai
— S + Qi'
где
anj tfij ip-i)'
73(s) будет
1
1
0
ТА- s) =
0
k.
k.
— s —|— Q-i — s —(— CL\ — s —|— &1
n— 1
2 krtrj (a,) + tnj (at) = о (J = 1, 2, ..., n).	(2.50)
r = l
Следует отметить, что, поскольку
I О, (а,) | =0,

108
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
детерминант и полиномиальные коэффициенты. Так, в рассматриваемом
примере
\@i (s) I = (—5 + 0(5 + *)•
Отсюда в качестве 7+—s) выбирается
1 0
T*(-s) =
0
— s +
В результате его применения вторая строка G\(s) умножается на
—*	Вторая строка и первый столбец G3(s) равны
s —р 1
16
— 2s2 -f- 5s -|- 13	^^ ,
— s -f- 1	T"
-s + Г
Тогда преобразованием Г3(—s) будет
T,(~s) =
s+1
Оно должно избавить нас от нежелательных полюсов. Таким образом,
имеем
k[— 2s*+ 5+! +16 = 0
или
16
k= —
3 •
Заметим, что это число k можно также определить из уравнения
[k - 2s2 - 55 + 13+! + [—252 + 34+! = 0.
После этих двух последовательных преобразований будем иметь
G3 (5) = Тз (- 5) Т2 (- 5) Gi (5) Т2 (5) Т'г (5) =
2s2-)-5 ?s +
26	41
3S	3
(26)2
18
(2.51)
10з (s) | = 1.
На последнем этапе нашей процедуры полученная матрица с по¬
линомиальными коэффициентами и детерминантом, не зависящим от 5,
будет подвергнута ряду преобразований, с тем чтобы избавиться от
всех степеней 5 в каждом элементе и получить числовую матрицу.

2.8]
ФАКТОРИЗАЦИЯ МАТРИЦЫ СПЕКТРАЛЬНЫХ ПЛОТНОСТЕЙ
109
Эту постоянную матрицу можно будет затем очень легко факторизо¬
вать. Если детерминант некоторой матрицы равен просто константе,
то в его разложении по степеням 5 коэффициенты при членах с нену¬
левыми степенями 5 должны, очевидно, равняться нулю. Рассмотрим
в каждом элементе исследуемой матрицы члены с наивысшими сте¬
пенями 5. Заменяя оставшиеся члены в каждом элементе нулями, обра¬
зуем новую матрицу. Для примера пусть эти члены с наивысшими
степенями 5 будут
— 2 s6	25s	7s2
— 2s3	2 s4	3 s2
7s*	з5з	_ 2s2
Эта матрица имеет такой вид, поскольку первоначальная матрица
пара-эрмитова. Наивысшая возможная степень s для детерминанта
этой матрицы, а следовательно, и для первоначальной есть s12. Заме¬
няя члены, которые при вычислении детерминанта дадут степени ниже,
чем s12, нулями, получим новую матрицу
— 2s6 2s*	0
— 2s3 2s4	0
0	0—	2s2
Поскольку коэффициент при члене s12 должен быть равен нулю, де¬
терминант написанной выше матрицы будет тоже равен нулю. Это
означает, что по крайней мере две ее строки линейно зависимы.
В данном случае, умножая вторую строку на —s и складывая ее
с первой, можно эту последнюю исключить из рассмотрения. К та¬
кому результату можно прийти, умножая рассматриваемую матрицу
слева на преобразование второго типа
1 -
— S
0
Т (— s) =
0
1
0
0
0
1
Таким образом, после умножения нашей матрицы слева на Т{—s)
и последующего умножения справа на Т'(s) наивысшая возможная
степень s в первоначальной матрице уменьшится на два. Описанная
процедура повторяется до тех пор, пока каждый элемент не станет
константой.
Возвратимся теперь к основному рассматриваемому примеру. Из
уравнения (2.51) видно, что нужное нам преобразование задается
матрицей

110
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
Таким образом, имеем
Oi(s)=Tl(— s)G,(s) T'A(s) =
5
5	3
41 (2б)2
‘ 3
18
= С.
И последним шагом будет факторизация постоянной матрицы. Так
как полученная матрица симметрична и положительно определена, ее
всегда можно разложить на произведение двух невырожденных тре¬
угольных матриц
С = NN\
где N—треугольная матрица с нулями над главной диагональю. Эта
факторизация определяется единственным образом с точностью до
умножения N справа на унитарную постоянную матрицу U. Действи¬
тельно, учитывая, что UU' = /, имеем NU -(NU)' = NN'. Отсюда для
нашего примера
1
ю
Ли
0
Ли Л41
41 (26)2
3 18
л21
л22
0 Я22
Решая это уравнение, получим
N =
V5
41
Поскольку
то
3/5 /5
Gq(s) = f = Т ^G^T'y
T* = N-\
Отсюда окончательная формула для <D(s) находится с помощью урав¬
нения (2.44):
41s + 65	—3s
(s + 1) (s + 2) (s + 1) (s + 2)
41s + 169	—	3s	+	13
(s + 3) (s + 5) (s + 3) (s + 5)
(2.52)
Итак, факторизация данной рациональной матрицы спектральных
плотностей завершена. Следует отметить, что матрица Ф (s), умножен¬
ная справа на произвольную унитарную матрицу, будет также пра¬
вильным ответом для рассматриваемой задачи, так как при этом

2.10]
СИНТЕЗ СИСТЕМ С ПОЛУЖЕСТКОЙ СТРУКТУРОЙ
111
уравнение (2.43) остается неизменным. Можно также легко показать,
что и уравнение (2.42) не изменяется от этого унитарного преобразо¬
вания. Таким образом, полученная оптимальная матрица передаточных
функций является единственной.
2.9.	Обсуждение методов решения задачи синтеза
оптимальных многомерных фильтров
Мы рассмотрели два различных подхода к синтезу оптимальных
многомерных фильтров со стационарными входами. Решение задачи
синтеза методом неопределенных коэффициентов выглядит довольно
просто. Вид оптимальной матрицы передаточных функций предпола¬
гается известным с точностью до коэффициентов полиномов, находя¬
щихся в числителях ее элементов. Эти коэффициенты затем опре¬
деляются путем решения системы линейных алгебраических уравнений.
Однако этот метод отчасти слеп по своей природе. Ответ на вопрос
о том, как распределяются эти коэффициенты среди элементов матрицы
передаточных функций, требует большой наблюдательности.
Решение, получаемое вторым методом, основанным на факториза¬
ции матрицы спектральных плотностей входа, имеет четкую структуру.
Однако шаги, осуществляемые для этой факторизации, несколько за¬
путаны. Следует отметить, что если отказаться от требования устой¬
чивости H-Us) и рассматривать, таким образом, строго задачу о
формирующем фильтре, то факторизацию спектральной матрицы можно
осуществить различными простыми способами. Юла [10] показал, что
матрица H(s) в этом случае будет треугольной матрицей с нулями
под главной диагональю. Матыаш и Шилканек [13] предложили про¬
стой способ осуществления факторизации, основанной на введении
в каждый элемент Ф(5) фазового множителя.
2.10.	Оптимальный синтез многомерных систем управления
с полужесткой структурой
Основное различие между задачей фильтрации и задачей управ¬
ления заключается в степени свободы выбора структуры оптималь¬
ной системы. В задачах фильтрации оптимальная передаточная функ¬
ция, получающаяся в результате минимизационной процедуры, полно¬
стью определяется входным процессом. В задачах же управления
в систему следует включить некоторый заданный объект, выполня¬
ющий определенные задачи. Таким образом, компенсация, вводимая
в систему, соединенную с заданным объектом, должна быть такой,
чтобы система в целом работала в некотором смысле оптимально.
Передаточная функция этой системы будет теперь определяться не
только входным процессом, но и некоторыми свойствами заданного
объекта, например тем, является ли рассматриваемый объект немини¬

112
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
мально-фазовым или нет. В многомерном случае неминимально-фазо¬
вым объектом является система, детерминант матрицы передаточных
функций которой имеет нули в правой половине 5-плоскости. Описан¬
ная задача управления обычно называется задачей с полужесткой
структурой.
Рассматриваемые в этом параграфе объекты являются линейными
устойчивыми системами с постоянными параметрами [6]. На вход
системы будут поступать суммы стационарных случайных сигналов и
шума. Таким образом, в целом эти системы будут также иметь посто¬
янные параметры. Часто необходимо, чтобы система имела обратную
связь между входами и выходами. Но если имеется разомкнутая опти¬
мальная система, то структуру ее обратной связи получить уже легко.
Итак, основной задачей является синтез разомкнутой системы управ¬
ления.
Структура разомкнутой системы управления изображена на
рис. 2.4. Здесь Q(t)—я X я-матрица весовых функций блока
Рис. 2.4. Блок-схема разомкнутой системы
управления.
управления, аР(т) — т X я-матрица весовых функций заданного объек¬
та, 1(f)— я-мерный входной вектор системы, r(t)— /я-мерный век¬
тор управления и C(t)— /я-мерный выходной вектор системы. В боль¬
шинстве практических задач число входов системы обычно больше
или равно числу выходов, т. е. п^пг. Таким образом, имеем
со
г (0 = 5 Qb)I(t — x)dz	(2.53)
О
И
оо
С(0—$ РОО г (t — 0 dz.	(2.54)
О
Комбинация уравнений (2.53) и (2.54) дает
оо	оо
С (9 = $ Р Ы dz2 5 Q („) I{t-zx- т4) dzx.	(2.55)
О	о
Из	рис.	2.4	ясно, что каждый выход системы тесно	связан	со всем
блоком	управления.	Следовательно, мы должны	минимизировать
квадрат нормы вектора ошибок.

2.Ю1
СИНТЕЗ СИСТЕМ С ПОЛУЖЕСТКОЙ СТРУКТУРОЙ
113
Можно легко показать [6J, что и частотной области обобщенное
уравнение Винера—Хопфа для этой задачи управления с полужест-
кой структурой выглядит следующим образом:
Здесь Pjf(s) — передаточная функция объекта, Q/k(s) — передаточная
функция блока управления, Gik,ik(s)— спектральная плотность вход¬
ного воздействия, OikrSk(s) — взаимная спектральная плотность вход¬
ного воздействия и сигнала, (Xrf)y^(s) — передаточная функция идеаль¬
ной системы P*y(s) = Pjf(—s).
Очевидно, что пг X я'2-матрица N, элементы которой имеют вид
является также пара-эрмитовой. Здесь fk используются для нумера¬
ции столбцов матрицы N, a fkr — для нумерации ее строк.
Очевидно, что методы, развитые в предыдущих параграфах, можно
с успехом применить к синтезу управляющих устройств. В большин¬
стве задач управления число входов больше или равно числу выхо¬
дов (п^т). Для превращения разомкнутой системы управления
в замкнутую можно воспользоваться канонической формой слож¬
ных систем, предложенной Фрименом [14]. Синтез устройств управ¬
ления в прямой и обратной связи наилучшим образом можно осу¬
ществить, рассматривая задачу чувствительности для всей системы,
как эго было сделано Горовицем [15].
Для системы с числом входов, равным числу выходов, при усло¬
вии что объект является минимально-фазовым (детерминант era
матрицы передаточных функций не имеет нулей в правой полуплос¬
кости), матрица передаточных функций устройства управления может
быть легко получена как
Здесь Y—матрица передаточных функций оптимальной системы, по¬
лученная при отсутствии объекта, другими словами, Y является ре¬
шением соответствующей задачи фильтрации. Для одномерных систем
аналогичный факт хорошо известен.
(2.56)
(2.57)
Q = P 'Y.

114
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
РАЗДЕЛ II
ДОПОЛНИТЕЛЬНЫЕ АСПЕКТЫ СИНТЕЗА СИСТЕМ
СО СЛУЧАЙНЫМИ ВХОДАМИ
2.11.	Методы описания случайных процессов
Основным при анализе и синтезе любой системы управления со
случайными входами является разработка подходящего математиче¬
ского описания рассматриваемых случайных процессов. Методы, име¬
ющиеся для такого описания, естественно распадаются на две кате¬
гории: экспериментальные методы и методы математического анализа.
Методы, относящиеся к первой категории, применяются для опреде¬
ления спектральных плотностей или корреляционных функций по
реализациям рассматриваемых случайных процессов. Вследствие того
что вообще возможно измерять только выборочные значения случай¬
ных процессов и ограниченных возможностей измерительных устройств,
нужно было разработать методику съема данных, которую бы можно
было вкупе с методами первой категории применить для определения
этих спектральных плотностей и корреляционных функций [4, 17].
Что касается методов второй категории — определение математи¬
ческого описания посредством математического анализа, — то они
заключаются в установлении соответствующей математической модели
данного физического случайного процесса. Эта модель может быть
затем разумно упрощена с тем, чтобы стать более доступной для
анализа. Так, например, по крайней мере в открытой литературе, та¬
кой подход доминирует при анализе весьма важных физических яв¬
лений — теплового, дробового и импульсного шумов. Открытые ра¬
боты, посвященные анализу довольно сложных физических систем,
концентрируются в основном вокруг системы радиолокации [19, 20]
и навигации [21, 22, 23, 24]. Причина этого, конечно, в том, что
указанные системы широко применяются и разработка их анализа
диктуется необходимостью. Работы [25—48] являются дополнительным
источником экспериментальных и теоретических методов описания слу¬
чайных процессов. Кроме того, в книге [38], а также в имеющейся
в ней библиографии представлены аналитические методы определения
влияния весьма сложной системы с обратной связью и нелинейными
элементами на математическое описание входного случайного про¬
цесса.
Возникает естественный вопрос об относительной ценности этих
двух категорий методов описания случайных процессов и о том, ка¬
кая связь существует между ними. Иногда физическая система может
быть столь сложной или неопределенной, что возможность разумного
математического анализа с целью описания соответствующего слу¬
чайного процесса исключается. В качестве одного из примеров ука¬
жем здесь на определение корреляционных функций скорости ветра,

2.11]
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
115
полезных для анализа и синтеза инерциальных систем навигации
с демпфированием скорости [49]. Другим примером является опреде¬
ление спектральной плотности атмосферной турбулентности для ее
последующего использования при построении структуры летательного
аппарата [50]. Еще одним примером, в котором применение матема¬
тического анализа неразумно, является определение спектра океанских
волн для возможного использования его при построении системы
стабилизации корабля [51]. С другой стороны, в некоторых обсто¬
ятельствах было бы непрактично проводить экспериментальные изме¬
рения. Например, экспериментальные данные, необходимые для мате¬
матического описания радиолокационного шума, возникающего при
слежении за целями, получить легко. Однако если желательно изучить
влияние изменения формы цели и ее размеров, то необходимость
разработки математического анализа подходящей математической мо¬
дели рассматриваемой системы диктуется требованиями экономии и
ясности получаемых результатов. Таким образом, понятно, что экс¬
периментальные и математические методы могут либо дополнять друг
друга, либо оказывается возможным применить только один из них.
В этом параграфе из всех существующих экспериментальных ме¬
тодов рассматриваются только экспериментальные методы определе¬
ния корреляционных функций. Такой выбор сделан потому, что кор¬
реляционные функции играют основную роль не только в методах
синтеза, представленных в первой части этой главы, но и излагаемых
ниже. На методах описания случайных процессов посредством анализа
их математических моделей [19, 20] мы здесь останавливаться не
будем. Не будут также затронуты экспериментальные методы опреде¬
ления спектральной плотности отдельного случайного процесса [27]
или взаимных спектральных плотностей пары случайных процессов
[53] и целый ряд других, очень важных для излагаемых ниже мето¬
дов синтеза.
Теперь настало время высказаться по вопросам стационарности
и эргодичности [2]. В предположении эргодичности при обработке
экспериментальных данных для определения параметров рассматри¬
ваемого случайного процесса вместо усреднения по множеству предпо¬
читают использовать усреднение по времени [2]. Нет нужды говорить
что не все случайные процессы являются приближенно стационарными и
эргодическими. Строго говоря, в физическом мире не существует такого
явления, которое можно было бы назвать стационарным и эргодиче-
ским процессом. Такие процессы являются математической абстрак¬
цией. Тем не менее ими достаточно хорошо аппроксимируются многие
физические ситуации. Вопрос о том, когда реальный физический про¬
цесс можно с хорошей степенью точности аппроксимировать стацио¬
нарным и эргодическим процессом, решается на основе эксперимен¬
тальных данных и знания физики рассматриваемой ситуации. Например,
легко видеть без каких-либо предварительных измерений, что шум,

116
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
поступающий на вход радара, следящего за синхронным спутником,
является по существу стационарным и эргодичным. С другой стороны,
легко себе представить, что радиолокационный или инфракрасный шум,
поступающий на вход действующей автономной системы наведения
снарядов класса «воздух — воздух» или «земля — воздух», является
по своему характеру нестационарным [2]. Если мы хотим узнать,
является ли данный случайный процесс эргодичным, то это можно
сделать, проверив выполнимость некоторых математических условий,
фигурирующих в эргодической теореме [2]. Однако ' осуществление
такой проверки может оказаться весьма трудоемким, поскольку для
этого требуется знать явное математическое описание рассматриваемого
случайного процесса. Поэтому, вообще, довольно затруднительно при¬
менить эргодическую теорему к какой-либо сложной физической си¬
стеме. На самом деле ее естественно было бы применить для анализа
математической модели, которая разумно аппроксимирует изучаемую
физическую ситуацию. Экспериментальные методы можно использовать
и для изучения нестационарных случайных процессов. Но хорошо
известно, что пока на практике усреднение по множеству осуществить
значительно труднее, чем усреднение по времени. Так что, когда
можно осуществить усреднение по множеству, при математическом
анализе соответствующей физической модели, видимо, предпочти¬
тельнее рассматривать нестационарные случайные процессы.
Итак, рассмотрим экспериментальные методы определения корре¬
ляционных функций. Согласно основному определению корреляционная
функция двух случайных процессов x(t) и y(t) получается путем
усреднения по множеству и равна [2]
со а
fxyik, к)= \	\ x{h)y{U)f{x,t{,y,t^dxdy. (2.58)
— ОО —оо
Здесь	—совместная плотность вероятности х и y(t2).
Когда рассматриваемые случайные процессы стационарны,
'Уху (к, к) = ?ху (к — к) — Уху (')•	(2.59)
Когда они и стационарны, и эргодичны,
т
§ x{t)y{tkri)dt,	(2.60)
т. е.	в	этом	случае средние по множеству и по времени	совпадают.
При	любом	экспериментальном подходе к определению	корреляцион¬
ных функций усреднение можно осуществить только на конечном
интервале времени и получить таким образом
т
<?ху к, Т)=~ jj* it) У V + -о dt,	(2.61)
0

2.11]
МЕТОДЫ ОПИСАНИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
117
где символ Т введен в качестве аргумента в функцию, стоящую в
левой части этого равенства, для того, чтобы подчеркнуть ее зависи¬
мость от времени, за которое определяется экспериментальная корре¬
ляционная функция. Если усреднить обе части равенства (2.61) по
множеству, то получится, что
сю сю
(?xy{i)= \ S <?Ху(х, T)f{x,y,x)dxdy.	(2.62)
— СО — сю
Это равенство показывает, что в среднем величина	Т)	равна
ср^(т)—истинной корреляционной функции. Нет нужды говорить, что
это очень благоприятный, хотя и неожиданный результат.
Таким образом, если вычислить дисперсию ср (т, Т) и установить
условия, при которых она достаточно мала, то тем самым будут
установлены условия, при которых наша экспериментальная корре¬
ляционная функция, определяемая равенством (2.61), будет в общем
достаточно близка к истинной корреляционной функции. Перейдем
теперь к осуществлению намеченной программы действий. Используя
символ Е[ ] для обозначения усреднения по множеству, дисперсию
экспериментальной корреляционной функции можно записать как
°%у (х, Т) = Е [{®ху (т, 7) — <?ху (т)}2] =	(2.63)
= Е [<р%у (t, 7")] — ср%у (т),	(2.64)
где
т т
Е [<pi„ (Т, 71] = ± ^ Е [х (Му (f, + Т) * Му (*, + ,)] dU dt2. (2.65)
о о
Обозначая
TiV (*, *ь У = Е[х it,)у & + т) х (t2)y (t, 4- Т)],	(2.66)
заметим, что вследствие стационарности
Т*у(х> h, ^) = Т^(Х> °> k — h) = Т*ДХ> v)>	(2.67)
i = t2 — ti.	(2.68)
Таким образом,
т ta
Efolyb Т)]=~ J J Tl-v 0, ^)d->dt2.	(2.69)
о и-т
Меняя порядок интегрирования, имеем
О	Г-f-v	т	т
Е[<?%у^,	т)] =	^	^	^	fxy (х,	v) di2	dy	-f ^	^	^	fXy(x,'>)dUd't.	(2.70)
— То	о	V
Воспользуемся	далее	тождеством	44	(т,	v) =	'][4(T— v)-	Учитывая	его
при вычислении первого интеграла в правой части равенства (2.70)

118
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
и принимая во внимание, что подынтегральные функции в (2.70)
не зависят от t2l сразу получаем
т
E[<?h<b T)] = ji	4)d'<-	(2.71)
о
Но
т
Y> \ (T-v)dv=l.	(2.72)
и
Таким образом, дисперсия вычисляется по формуле
т
(*>	Т) = js J (Т - v) [fxy (т, v) - fxy (,)] dv.	(2.73)
о
Отсюда,	если	мы	хотим, чтобы экспериментально полученное	нами
значение	корреляционной функции с заданной степенью уверенности
отличалось от истинного или среднего не больше чем на некоторую
величину, то можем добиться этого путем соответствующего подбора
параметра Т в равенстве (2.73). Например, если предположить, что
экспериментальные значения корреляционной функции распределены'
нормально (это предположение следует проверить путем соответствую¬
щей обработки экспериментальных данных так же, как это делается
в более простой ситуации), то из элементарной теории вероятностей
вытекает, что для того, чтобы с вероятностью 95% любое полученное
значение экспериментальной функции отличалось от среднего, или
истинного, значения корреляционной функции не более чем на п°/0
необходимо, чтобы
0,01 Щху (т) = 2оху (т, 7)	(2.74)
или, другими словами,
vxv (т)	200
°ху (т> Т)	~
(2.75)
Когда процессы x(t) и y(t) являются стационарными эргодичными
и гауссовскими, равенство (2.75) можно иногда записать так, чтобы п
было явной функцией параметра Т. Бендат [4] сделал это в ряде
случаев и получил весьма обширные численные результаты и графики.
Однако такие расчеты требуют определенных знаний о форме рас¬
сматриваемой корреляционной функции.
В действительности, эти требования не столь уж неразумны.
Например, Блесингэйм [49] установил, что корреляционная функция
скорости ветра имеет вид экспоненциального косинуса. Так что

2.12]
СИНТЕЗ СИСТЕМ С НЕСТАЦИОНАРНЫМИ ВХОДАМИ
119
результаты, содержащиеся в книге Бендата (4J или книге Лэнинга
и Бэттина [2], можно применять при обработке любых эксперимен¬
тальных измерений отдельных стационарных, эргодичных и гауссов¬
ских процессов, если только установлен общий вид их корреляцион¬
ной функции. Кстати, укажем, что Бендат [4] изучает, в частности,
влияние шума на измерения корреляционных функций.
2.12.	Синтез систем с нестационарными входами
В своей основополагающей работе [1] по оптимальному синтезу
систем со случайными воздействиями Винер рассматривал только
стационарные и эргодичные процессы. Однако имеются практические
примеры, когда подлежащие рассмотрению случайные процессы
являются нестационарными [55, 61], и, таким образом, возникает необ¬
ходимость в соответствующем обобщении винеровских методов син¬
теза. Такие обобщения были сделаны Заде. Основные его результаты
опубликованы в короткой заметке [56] в июле 1961 г. После этого
появилось еще несколько статей, посвященных методам синтеза опти¬
мальных систем с нестационарными случайными входами, из которых
мы упомянем лишь [57]. Различные подходы к решению задачи
определения оптимальной, по критерию среднего квадрата ошибки,
весовой функции при нестационарных случайных входах предусмат¬
ривают либо непосредственное решение интегральных уравнений для
этих оптимальных весовых функций, либо использование того обстоя¬
тельства, что рассматриваемый нестационарный случайный процесс
получается в результате прохождения «белого шума» через форми¬
рующий фильтр. Этот последний подход рассматривается в главе 4
настоящей книги, а также у Заде [56]. Здесь мы сделаем обзор двух
довольно важных подходов к решению задачи синтеза системы, опти¬
мальной в смысле минимума среднего крадрата ошибки. Другие под¬
ходы упомянуты в статье Заде [56].
Итак, рассмотрим сначала работу Калмэна и Быоси [57], посвя¬
щенную решению следующей задачи. Определить систему, N выходов
которой	x2(t), ..., ScN(t) будут наилучшими линейными оцен¬
ками, получающимися в результате минимизации среднего квадрата
вектора ошибок [х — х]2 с компонентами, равными квадратам раз¬
ностей между желаемым выходным сигналом системы x^(t\ x*(t\ ...
..., xN(t) и действительным выходным сигналом X\lt\ х* (0> •••
..., xN(t). В качестве входных сигналов оптимального фильтра или
системы Zi(f), z%(t), ..., zm(t) рассматриваются линейные комбинации
компонент вектора полезного сигнала, искаженные «белым шумом».
Явные выражения для них будут написаны ниже. Предполагается,
что рассматриваемый случайный сигнал порождается «белым шу¬
мом», проходящим через линейную, вообще говоря, с переменными

120
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
параметрами систему, а именно
^L = F(t)x(t) + G(t)u(t).	(2.76)
Здесь x(t) — вектор-столбец сигнала, a u(t) — вектор-столбец, ком¬
понентами которого являются «белые шумы» с нулевыми средними.
Корреляционная матрица u(t) равна
cov \и (f), u(z)]=E[u(t), u(z)] = Q(t)b(t — т).	(2.77)
В этих последних двух равенствах прописные буквы обозначают
матрицы, а Е [ ], как и раньше, является символом математического
ожидания.
Действительный входной сигнал системы можно выразить как
* (0 = Hit) х (t) + v (t),	(2.78)
где v(t) — вектор «белых шумов» с нулевыми средними. Компоненты
этого вектора входят в каждую компоненту z(t), а его корреляцион¬
ную матрицу можно записать как
cov [V (0, * (т)] =R(t)b(t — т).	(2.79)
При этих условиях Калмэн и Бьюси показывают, что оптимальная
система определяется уравнением
-g- = IE(t)-k (t) М (f)] X(t) + k (t) z (t).	(2.80)
Таким образом, вид этой оптимальной системы частично определяется
тем, что можно назвать обработкой сигнала, которая задается равенст¬
вом (2.78). Матрица k(t), фигурирующая в уравнении (2.80), опреде¬
ляется как (штрих обозначает операцию транспонирования)
k(t) = P(t)H'(t)R-1(t).	(2.81)
И, наконец, матрица Р(t) является симметричной корреляционной
матрицей вектора x(t) — x(t)\ она получается в результате решения
следующего нелинейного уравнения:
— F(t)P (0 -f Р (0 F (t) - P (t) H' (0 R"1 (t) H(t) P (t) + 0(0 Q{t)G'{t).
(2.82)
В ранней работе Калмэна [58] представлены аналогичные резуль¬
таты для случая дискретных систем. Результаты для этого случая
были получены также Хеи и Леондесом [59]. Рассмотрим далее
второй подход к синтезу системы с нестационарными входами, кото¬
рый был развит Шинбротом [60].
Отклик линейной системы с переменными параметрами, весовую
функцию которой мы хотим оптимизировать в смысле средиеквад-

2.12]	СИНТЕЗ	СИСТЕМ С НЕСТАЦИОНАРНЫМИ ВХОДАМИ	121
ратичной ошибки, определяется как
t
x(t)= 5 W(t, х) i (х) dx.	(2.83)
— СО
Вход i(t) состоит из комбинации сигнал плюс шум, т. е.
i(t) = s(t) + n(t).	(2.84)
Поскольку входное воздействие начинает поступать, начиная с неко¬
торого конечного момента времени, который можно положить рав¬
ным нулю,
t
Jс (0 = 5 Wit, х)j(x)dx.	(2.85)
и
Обозначим желаемый выходной сигнал через (т(0- Таким образом,
среднеквадратичная ошибка, которую мы хотим минимизировать,
задается формулой
t
8 * = Е
11(0 —S W(t, х)г(х)<Ц
о	J
(2.86)
Путем стандартных преобразований получим, что необходимым и
достаточным условием того, чтобы W{t, х) минимизировала в2, является
равенство
t
х)=1 Wit, а)<р ait, a) da для 0 < х < t. (2.87)
Здесь и сра/ является согласно обозначениям предыдущего пара¬
графа корреляционными функциями рассматриваемых нестационарных
процессов. Из определения корреляционной функции имеем
(^> Т)   (Т) 0-
(2.88)
Корреляционные функции нестационарных процессов можно предста¬
вить в виде сумм (см. главу 4)
?«(*> ■')=S ^(t)b9(z),
p = i
а
т)=2 cf{t)bfw
Р = 1
для t^x.
(2.89)
(Такие корреляционные функции называются вырожденными.) Точность
такого представления зависит от а — количества членов суммы. Вос¬
пользовавшись равенством (2.88), заметим, что ®Ss(ft т) можно также

122
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
записать в виде
а
”0= s a?(*)bf(t) для	т>£	(2.90)
р = 1
Обозначая	далее	буквами а, b и с векторы с	элементами	ар, Ь9	и	с9
соответственно,	(2.89)	и (2.90) можно записать	более	коротко:
a! (t) • Ъ (т) для	т ^ ty
х) I а' (х). ъ (t) для T>f,	(2.91)
ср^ (£, т) = с' (0 • Ь (т)	ДЛЯ	т ^ £
Если в качестве входного шума взять «белый шум», то уравне¬
ние (2.87) превратится в
t
<Piw(*> T)=S a)?sj(T> a)^a + ^&(?> т) для	(2.92)
о
При этом мы считали
<Р,*)=<P|i.m& *0,
'0 = <Pmm(*> Т) + Х5(^-
Подставляя (2.91) в (2.92), получим
}
(2.93)
С' (0 • Ь (т) = а' (т) • 5 ь (a) W(t, с) da +
0
t
-|- Ьг (ч) ^ a (a) W(t, a)da-\-Xg(t) т) для 0 ^ т ^ t. (2.94)
-г
Полагая далее
v (*, т) = а! (0 • Ь (т) — а (т). Ь (т)	(2.95)
и записывая в уравнении (2.94) как J ^, в результате
имеем
6(т) =
= ^	W(t, o)t)(i, a)da -\-\g(t, т) для 0	т sg: t.	(2.96)
и
Найдем теперь решение этого уравнения W(t, т), представимое
в виде	суммы	произведений функций, зависящих от	t>	на функции,
зависящие от	т. Такое представление впредь будет	для кратко¬
сти называться разложимым. В частности, мы будем искать
W(t} т) = [Ы (t) • у (0] и (t — т),	(2.97)

2.12)
СИНТЕЗ СИСТЕМ С НЕСТАЦИОНАРНЫМИ ВХОДАМИ
123
где u(t — т) — единичная ступенчатая функция, введенная из соображе¬
ний физической реализуемости. Подставляя (2.97) в (2.96), получим
t
С' (0 — $ а' (о) [h! (t) • yO)] da -b(x) =
для О т	(2.98)
= ft'(0*	a)	da	-f	-	Ху	(т)
_о
Это уравнение, конечно, удовлетворяется, если
т
(а)	b	(т)	=	^	y	(а)v (т> °) do “h (т)>	0	^	т	==с;	t\
(б)
С (0 — 5 а (а)	(0	'	Y	(а)]	da	=	h	(t),
(2.99)
(2.100)
При выводе этого уравнения интегральное уравнение (2.92), в ко¬
тором g(t, т) зависит от двух независимых переменных t и т, было
заменено двумя уравнениями для двух компонент разложимого пред¬
ставления g(t, т). Определим
e'(T)=[fli(T), ...,	аа (т), ^(т), ..., Ьа( т)],
/'(т)=[^(т), ...,	Ьа{т), — аДт), ..., —аа{т)].
Тогда равенство (2.95) превратится в
v(t9	Т) = £?'(Т)./(Т).	(2.101)
И, таким образом, уравнение (2.99(a)) можно записать как
т
^pW = e'(^)-5/(<:')'rp(0)c?0 + xTp(x) для 0 йС^	р=1,	а.
0 (2.102)
Здесь векторы b(t) и у(0 расписаны по координатам. Расписывая
далее покоординатно фигурирующее в (2.102) скалярное произведение,
получим
2а	т
Ьр (х) =	(х) 5 Л (о) Тр (а) л + *Тр W	(2-103)
9 = 1	о
для 0 ^ т ^ ty р = 1, ..., а.
Если	среди компонент £д(т)	вектора е(т) есть линейно независимые,
то уравнение (2.103) можно	преобразовать к виду
Ьр (х) = 2 ея (') $	(°) Тр (°)da + хТр (х)
9 = 1	О
для 0 т	;?=1,	а,
(2.104)

124	СИНТЕЗ	СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ. 2
где функции ед(ъ) уже линейно независимы, а ч)^(т)— функции,
получившиеся из линейных комбинаций соответствующих функций fq (т)
в результате перехода от уравнения (2.103) к уравнению (2.104).
Дифференцируя далее уравнение (2.104) г раз, мы сразу получаем
для функций	систему	дифференциальных	уравнений
Р	т
2 ея (х) 5 ь ^da = Ьч— к'{р ~
<? = 1	0
-202	(2л05)
S=1	q=\
для 0 ^ т ^ ty р = 1, ..., а,
где	обозначает	биномиальный коэффициент
г\  г!
s) s! (г— s)!'
Из уравнения (2.105) при r = 0, 1, ..., t3 — 1 получается (3 систем
уравнений для (3 неизвестных
т
\ ®q (а) 7р (а) ^а>	•••>	?	(/?	фиксировано).	(2.106)
о
В (2.106) необходимо определить именно Переписывая уравне¬
ние (2.105) в матричной форме, имеем
EW = F,	(2.107)
где Егд — элементы r-го столбца и q-й строки матрицы Е — равны ед{х).
Таким образом, определитель матрицы Е является вронскианом ли¬
нейно независимых функций ед(т). Элементами матрицы W являются
функции (2.106). В частности,
т
^«, = К(в)ТР(0)*-	(2Л08>
0
Элементами вектора F являются правые части уравнения (2.105)
Г	Р
Frp = Ьгр СО — А.Гр (О — 2 (Э 2 ея~* (т) к(т) (х)] • (2-109)
5=1	q	=	1
Разрешая уравнение (2.107) относительно матрицы W, получим
W = E~lF.	(2.110)
Дифференцируя уравнение (2.110), получим систему линейных диф¬
ференциальных уравнений для искомых неизвестных -\р. Эти уравне¬

2.13]	МЕТОД	МОДЕЛИРОВАНИЯ	СОПРЯЖЕННОЙ	СИСТЕМЫ
125
ния можно решать на аналоговой или цифровой машине или, если
это возможно, аналитически.
Сделаем здесь одно замечание. Из равенства (2.110) видно, что
элементами матрицы W являются Wcjp. Поскольку q=l, 2, ..., (3,
а р=\, 2, а, это означает, что у нас есть [За уравнений для
определения а неизвестных *[р, т. е. уравнений больше, чем неизвест¬
ных. Может показаться, что система этих [За уравнений несовместна
и не имеет общего решения. Однако такого произойти не может,
так как уравнение (2.99(a)) является интегральным уравнением Воль-
терра [62], которое всегда имеет единственное решение. Существует
много способов выбора а уравнений для определения у. Можно,
например, из матричного дифференциального уравнения, получающе¬
гося в результате дифференцирования уравнения (2.110), выбрать
отдельную строку.
Теперь, когда ”[р(ъ) определены, для того чтобы найти W(t, т)
в уравнении (2.97), остается определить h(t). Это можно легко сде¬
лать с помощью уравнения (2.99(6)). Расписывая уравнение (2.99(6))
покомпонентно, имеем
М9+ S hq(t)\ap(o)-{q(o)do = cp(t) (р = 1,	а). (2.111)
q = 1	0
В уравнениях (2.111) неизвестны только hp(t) или hq(t). Таким обра¬
зом, функции hp(t), а следовательно, и hg(t) могут быть найдены.
Мы изложили метод Шинброта несколько более подробно, чем
метод Калмэна и Бьюси. Причиной этого является несколько более
сложная природа методики Шинброта. Во всяком случае, при прак¬
тической реализации оптимальной системы любым из рассмотренных
методов следует иметь в виду обычные инженерные требования.
В частности, в тех случаях, когда получившаяся оптимальная весовая
функция слишком сложна для практической реализации, следует
исследовать возможность приближения оптимальной системы к неоп¬
тимальной, но зато более просто реализуемой. Отсюда возникает
необходимость развивать методы анализа систем, находящихся под
воздействием нестационарных случайных процессов. Этим вопросом
мы займемся в следующем параграфе.
2.13.	Метод моделирования сопряженной системы
Для простоты рассмотрим сначала линейную систему с перемен¬
ными параметрами с одним входом и одним выходом. Предположим,
что на рассматриваемую систему поступает случайный входной сиг¬
нал x(t), определенный при —oo <^t <^оо, и пусть e(t) обозначает
соответствующую неточность или ошибку, возникающую вследствие x(t).

126	СИНТЕЗ	СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ	[ГЛ. 2
Тогда если W(ty т) — весовая функция, связывающая x(t) и e(t), то
t
е{х) = J w(t, x)x(x)dx.	(2.112)
— ОО
Для того чтобы вычислить корреляционную функцию e(t)y заметим, что
h	12
е(Це(^)= ^ W(tb xi)dxl ^ W(tb i2)x(t,)xWrf-2. (2.113)
— oo	—	oo
Усредняя правую и левую части этого равенства по множеству,
получим
<?ее(*Ь к)= 5 W^> *0*1 5 W{-U-'	4)dx,. (2.114)
Если предположить, что нестационарный случайный процесс x(t)
«Белый
шумъ'
Форми¬
рующий,
фильтр
т
Первонаяаль
иаясистет
Kt)
^	Новая	система	J
Рис. 2.5. Применение формирующего фильтра.
получается в результате прохождения «белого шума» через форми¬
рующий фильтр (рис. 2.5), то (2.114) можно переписать как
  t
?«(<, t) = e\t)= \ W(t, ху) dx, ^ W(t, ^)<р,„(т„ *,)** =
—СО	—	ОС
t	t	t
= $ Wii^xjdxi 5 Wy{t, хг)(х^ — xjdx^ 5 Wx(t,4fdx. (2.115)
—ОС'	—oo	—oo
Задача синтеза, изображенного на рис. 2.5 формирующего фильтра,
рассматривается в главе 4. Здесь мы предположим, что этот форми¬
рующий фильтр уже синтезирован методами, изложенными в главе 4.
Так что задача определения среднеквадратичной ошибки рассматри¬
ваемой системы сводится к нахождению Wi(tyi). Прямой, но чрезвы¬
чайно утомительный способ определения Wi(tyi) состоит в том, что
на вход системы (ty т) подается импульсная функция. С точки

2.13]	МЕТОД	МОДЕЛИРОВАНИЯ	СОПРЯЖЕННОЙ	СИСТЕМЫ
127
зрения применения аналоговой техники удобнее подавать ступенчатую
функцию, которую легко получить на выходе интегратора, если
подать на его вход импульсную функцию. Импульсная функция по¬
дается в момент времени т, а отклик на нее наблюдается в момент
времени i. Для того чтобы определить функцию Wx (t, т) как функ¬
цию т, а это необходимо для последующей ее подстановки в равен¬
ство (2.115), такую процедуру следует повторить для многих значе¬
ний т. К счастью, во многих задачах нет необходимости знать еще
№*(£, т) для многих значений t. Например, при создании системы
управления огнем, ei{t) необходимо определить только во время при¬
ближения снаряда к цели, а не в течение всего времени полета. Однако
даже здесь, когда e2(t) нужно определить только в один или несколько
моментов времени, может потребоваться большая работа.
Поэтому было бы желательно разработать метод моделирования
на аналоговой машине, который позволил бы сразу определить e^(t)
или, говоря другими словами, позволил бы сразу определить W^it, т)
как функцию т. Метод моделирования сопряженной системы, к непо¬
средственному изложению которого мы переходим, как раз и позво¬
ляет это сделать.
Найдем сначала весовую функцию системы, описываемой линейным
дифференциальным уравнением
x(t) = A{t)x(t) + №
(2.116)
где
Xi (t)
/dt)
x(t) =
Xl{t)
’ m=
*n (0
Ш
a A(f)—матрица с элементами	Кроме того, полагаем, что
jt(0) = 0. Пусть М обозначает решение матричного уравнения
dM
— Л[1)М It), |
(2.117)
dt
М (0) = /,
где / — единичная матрица. Для решения уравнения (2.117) восполь¬
зуемся методом вариации постоянной Лагранжа. Полагая х = Ми и
подставляя его в уравнение (2.116), получим
dx л л du(t) , dM(t) ...
ж = мУ)-А1-\	^u(t)	=
= M{t)
dt 1 dt
du (t)
dt
A (t) M (it) u(t) = A (t)M (t) и {t) +/(0. (2.118)

128
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
Отсюда
(2.119)
Таким образом,
н(0= ^ AT' (s)f(s) ds,
(2.120)
о
а
х (0 = $ м (0 АГ1 (s) f (s) ds.
(2.121)
и
Теперь, если из условия физической реализуемости мы определим
матричную функцию k (t, s) как
Функция k(t,s) называется функцией Грина или весовой функцией
системы.
Если вспомнить замечания, сделанные в начале этого параграфа,
то нетрудно понять, что для рассматриваемой нами задачи желательно,
чтобы функция к (t, s) была функцией 5 для некоторого фиксирован¬
ного значения t, то есть для данного Т мы хотим знать k(T, s) как
функцию 5. Далее будет показано, как это можно будет сделать
с помощью сопряженной системы. Введем сначала пару переменных f
и s', связанных с переменными t и 5 соотношениями
где Т — любое фиксированнее действительнее число. Определим
функцию L(t',s') соотношением (штрихи над прописными буквами
обозначают операцию транспонирования соответствующей матрицы,
а штрихи над строчными буквами обозначают различные переменные)
где k'(s,t) — матрица, полученная транспонированием матрицы весо¬
вых функций первоначальной системы. Заметим, что в уравнении
(2.125)	аргументы k' (s, t) — переменные s и t — занимают то же
положение и играют гу же роль, что соответственно t и 5 в урав-
(2.122)
то для ^^0 полученное решение можно записать в виде
оэ
х (t) = ^ k (t, s)f(s) ds.
(2.123)
о
(2.124)
L(f, s’) = k’ (s, t),
(2.125)

2.13]
МЕТОД МОДЕЛИРОВАНИЯ СОПРЯЖЕННОЙ СИСТЕМЫ
129
нении (2.122). Причина такой довольно внезапной перемены обозна¬
чений заключается в том, что мы хотим иметь дело именно с пере¬
менными f и s'. Во всяком случае, исследуем уравнение (2.125)
несколько	более	подробно. Если t'^>s\ то t^c.s	и, следовательно,
k(s,t) = 0.	Таким	образом, L(i',s') = 0 при t'<^s\	как это	и	должно
вытекать из требования физической реализуемости. Если t'^s', то
t^s и отсюда
L (*', s') =	k' (5, t) = [М (s) AT1 (t)\ = [AT1 (t)]'	• AT (5).	(2. i 26)
Определим далее функцию z(tr)
со
гг (f) = J L (f, s') g (s') ds',	(2.12 7)
0
где g(s)— произвольная интегрируемая и непрерывная функция на
действительной прямой. Более подробно равенство (2.123) выражает
отклик системы, описываемой уравнением (2.116), которому соответ¬
ствует матрица весовых функций k(t,s) на входную вынуждающую
функцию f(t). Аналогично z(t') является откликом системы с весовой
функцией L(t\ s') на вынуждающую функцию g(s'). Остается только
получить дифференциальные уравнения, соответствующие системе
уравнений (2.127). Эти дифференциальные уравнения будут похожи
на дифференциальные уравнения (2.116). Приступая к решению наме¬
ченной задачи, перепишем (2.127) как
v
z(f)=\L(f, s')g(s')ds’.	(2.12S)
U
Это можно сделать, так как L(t',s') = 0 для t'<^s'. Дифференцируя
равенство (2.128) и учитывая, что L(t\t)= \ (см. (2.126)), получим
г
Z (О = J w 1 {i’’ s')g(s'} ds' + 1 (f’ Г)ё{Г) =
и
V
д
= j\-~L(t\ S')g(s')ds' + g(t'). (2.129)
0
Вычислим теперь L (tf s') для s' ^ t'.
В этом случае s^ t и L(t'y s') = [АГ1 (t)]F M' (s). Отсюда, no-
dt
скольку df — — 1,
w L s') = w <№ •M (s)> Ж =
d
dt
{M~'(t)}'\-M'(s). (2.130)
5 n/p Леондеса

130	СИНТЕЗ	СИСТЕМ	СО	СЛУЧАЙНЫМИ	ВОЗДЕЙСТВИЯМИ	[ГЛ.	2
Далее
Д- (*)}' = | 4t ’ (0}]'-	(2.131)
Таким образом, нам остается только вычислить Д-{Ж_1(0}- Так как
ftl (t) Ж-1 (0 + Ж (t) Д- {Ж"1 (0} = 0,	(2.132)
то
Д- {Ж-1 (0} = — м-1 (0 (W (0 /И"1 (t).	(2.133)
Но M(t) = A(t)M(t) и поэтому
/И"1 (t) М (/) Ж"1 (0 = Ж-1 (0 Л (t).	(2.134)
Отсюда
-^-{Ж-,(0[= —Ж-"ЧОАф	(2.135)
Таким образом, можно заключить, что
Дг L (f, s') = Л' (0 [М(г)]' Л1' (s) = Л' (0 L (A s').	(2.136)
Тогда i(tf') превращается в
v
г (О = $ Л' (0 L (f, s') ^ (s') <*s' + g(f).	(2.137)
о
Если положить B(f) = A'(t), то z(f) можно переписать как
z (f) = В (f) z (f) -[- g{tr).	(2.138)
Ясно, что матрицей весовых функций этого последнего уравнения
будет L(t\s'). Система, описываемая уравнением (2.138), называется
сопряженной к системе, описываемой уравнением (2.116). На самом
деле, сопряженной системой удобно называть систему, которая опи¬
сывается уравнением, несколько отличным от уравнения (2.138).
Пусть функция y(t) определяется отношением
=	(2.139)
Тогда y{t) = z{t') ^j- = — г(Г)> и уравнение для z (f) превращается в
j(t)=-A'(t)y{t) + h{t).	(2.140)
Система, описываемая этим уравнением, обычно и называется сопря¬
женной к системе, описываемой уравнением (2.116). Итак, если нам

2.13]
МЕТОД МОДЕЛИРОВАНИЯ СОПРЯЖЕННОЙ СИСТЕМЫ
131
нужно найти k (t, s) как функцию 5 для данного значения t (мы те¬
перь вернулись к первоначальным определениям t и 5 в выражении
для k (t, s)), то для этого нужно найти L (s', f) для соответствую¬
щего f. В частности, для того чтобы найти /г (Г, s), достаточно опре¬
делить L'(s', 0), так как
k(Ty s) = V (s', 0).	(2.141)
Таким образом, применение метода моделирования сопряженной
системы для вычисления k(T,t) приводит к следующей процедуре:
(1) Моделируем систему
(2) Полагаем все начальные условия равными нулю.
(3) Запускаем машину и в момент £=0 подаем импульсную (или
ступенчатую) функцию на первый вход системы; результат на выходе
записываем.
(4) Повторяем этот процесс, подавая в момент t = 0 импульсную
(или ступенчатую) функцию на каждый последующий вход; резуль¬
таты на выходе записываем.
(5) Если машина работала в обратном времени, начиная с момента
времени 7, то полученные таким образом п решений образуют
строки k(T,t).
Основная задача, возникающая при осуществлении этой про¬
цедуры, заключается в том, как перейти к моделированию сопряжен¬
ной системы
i(t) = B(f)z(n + g{n
если на машине набрана система,
x(t) = A(t)x(l) + №
Но это сделать легко. Матрица B(f) связана с матрицей A(t) равен¬
ством В (О — A' (t). Используя эту связь, переход от моделирования
первоначальной системы к моделированию сопряженной системы
можно осуществить в два приема:
(1) Функциональные преобразователи, выходами которых являются
компоненты A (t) (или, говоря другими словами, элементы матрицы
A (t)), перебираются — там, где раньше для получения компоненты
аjk(t), производилось умножение на	теперь производится умно¬
жение на
(2) Производится перестройка функциональных преобразователей
Для компонент A (t), с тем чтобы они, начиная с момента 7, работали
в обратном времени.
Читатель, желающий ознакомиться с дальнейшими применениями
сопряженных систем, отсылается к книге [63], в которой также
5*

132
СИНТЕЗ СИСТЕМ СО СЛУЧАЙНЫМИ ВОЗДЕЙСТВИЯМИ
[ГЛ. 2
подробно рассматривается целый ряд превосходных примеров. Методы,
основанные на рассмотрении сопряженных систем, первоначально
развитые Лэнингом и Бэттином [2], применялись со значительной
экономией времени многими исследовательскими группами по всей
стране *).
2.14.	Заключительные замечания
В этой главе были представлены различные методы синтеза
систем, на входы которых поступают случайные процессы. В резуль¬
тате применения рассмотренных методов синтеза получается весовая
или передаточная функция оптимальной системы. По этой весовой
функции надо еще построить замкнутую систему, предназначенную
для решения данной задачи управления. Этот вопрос рассматривается
в разделе I, в котором представлены методы синтеза многомерных
систем. Методы получения оптимальных весовых функций при неста¬
ционарных случайных входных воздействиях изложены в § 2.12.
(Способы реализации соответствующих замкнутых систем изложены
в главе 1.)
Следует отметить, что здесь не рассматривались многие вопросы,
возникающие при попытке применить изложенные выше методы к
практическим задачам [55, 61, 64, 65, 66, 67, 68]. Например, при
синтезе одной системы управления артиллерийским огнем было заме¬
чено, что винеровские методы синтеза приводят к бесконечным откло¬
нениям (в среднеквадратичном) от поверхности управления. В работе
[64] изложены некоторые практические приемы, позволяющие избегать
таких результатов, даже не прибегая к значительному изменению
критерия качества. Это только один пример неизбежно возникающих
практических трудностей. Другие можно найти в приведенной ниже
библиографии.
Наконец, здесь рассматривались только системы, оптимальные
в смысле минимума среднего квадрата ошибки. Бывают, например,
системы, которыми предпочтительнее управлять так, чтобы соответ¬
ствующая ошибка не выходила за заданные пределы. Методы синтеза
систем, оптимальных по такому критерию, представлены в отчете
Бергена [69] и некоторых работах, указанных в обзорной статье
Заде [56].
ЛИТЕРАТУРА
1. Wiener N., The Interpolation, Extrapolation and Smoothing of Stationary
Time Series, John Wiley and Sons, Inc., New York, 1949.
2. Lanin g J. H., Jr., and R. H. В a 11 i n, Random Processes in Automatic
Control, McGraw-Hill Book Co., Inc., New York, 19o6. [Русский перевод:
A) Имеется в виду США (Прим. иерее.)

ЛИТЕРАТУРА
133
Л з и и и г Дж. X. и Бэттин Р. Г., Случайные процессы в задачах авто¬
матического управления, ИЛ, М., 1958.]
3. Davenport W. L., Jr., and W. L. Root, Random Signals and Noise,
McGraw-Hill Book Co., Inc., New York, 1958. [Русский перевод: Давен¬
порт В. Б. и P у т В. Л., Введение в теорию случайных сигналов и шу¬
мов, ИЛ, М., I960.]
4. В е п d a t J. S., Principles and Applications of Random Noise Theory,
John Wiley and Sons, Inc., New York, 1958. [Русский перевод: Бен дат
Дж., Основы теории случайных шумов и се применения, «Наука, М.,
1965.]
5. Hsieh Н. С. and С. Т. Leondcs, On the Optimum Synthesis of Multi¬
pole Control Systems in the Wiener Scnce, IRE Trans, on Automatic Cont¬
rol, Vol. AC-1, No. 2 pp. 16—29, November, 1959.
6. Hsieh H. C. and С. T. L e о n d e s, Techniques for the Optimum Synthe¬
sis of Multipole Control Systems with Random Processes as Inputs, IRE Trans,
on Automatic Control, Vol. AC-4, No. 3, pp. 212—231, December, 1959.
7. Am ar a R. C., The Linear Least Square Synthesis of Multivariable Control
Systems, AIEE Transactions, Part II (Applications and Industry), Vol. 78,
pp. 115—119, 1959.
8. Wiener N. and P. M a s a n i, The Prediction Theory of Multivariate Sto¬
chastic Processes, Part I, Acta Math., Vol. 98, pp. Ill —150, 1957.
9. Wiener N. and P. Masani, The Prediction Theory of Multivariate Sto¬
chastic Processes, Part II, Acta Math., Vol. 99, pp. 93—137, 1958.
10. Y о u 1 a D. C., On the Factorization of Rational Matrices, IRE Trans, on
Information Theory, Vol. IT-7, No. 3, pp. 172—189, July, 1961.
11. Davis М. C., On Factoring the Spectral Matrix, Preprints, 1963 Joint Auto¬
matic Control Conference, pp. 459—467.
12. Cramer H., On the Theory of Stationary Processes, Ann. Math., Vol. 41,
Ser. 2, 1940.
13. Матыаш И., Ш и л к а н с к Я., Генератор случайных процессов с задан¬
ной матрицей спектральных плотностей. Автоматика и телемеханика,
т. 21, № 1, 1960, стр. 29—35.
14. Freeman Н., A Synthesis Method for Multipole Control Systems, AIEE
Transactions, Part II, Vol. 76, pp.	28—31, March, 1957.
15.	Horowitz I. М., Synthesis of	Feedback Systems, Academic	Press, New
York and London, 1963, Chapter 10.
16. Newton G. C., Jr., L. A. Gould and J. F. К a i s e r, Analytical
Design of Linear Feedback Controls, John Wiley and Sons,, Inc., New York,
1957. [Русский перевод: H ь ю т о н Дж. К., Г у л д JI. А., Кайзер Дж. Ф.,
Теория линейных следящих систем. Аналитические методы расчета, Физ-
матгиз, М., 1961.]
17.	Blackman R. and J. Т u к с у,	The Measurement of	Power	Spectra,	Do¬
ver Publications, Inc., New York,	1958.
18. Bennett W. R., Electrical Noise, McGraw-Hill Book Company, Inc., New
York, 1960.
19. M u с h ni о r c, Robert B., Aircraft Scintillation Spectra,- IRE Transactions
on Antennas and Propagation, March, 1960, pp. 201—212 (see Theoretical
Scintillation Spectra НАС TM-271, March 1, 1952).
20. Freeman J. J., Principles of Noise, John Wilcv and Sons, Inc., New
York, 1958.
21. H a m m о n, Robert L., An Application of Random Process Theory to Gyro
Drift Analysis, IRE Transactions on Aeronautical and Navigational Electro¬
nics, September, 1960.
22. Ham m on R. L., Effects on Inertial Guidance Systems of Random Error
Sources, IRE Transactions on Aeronautical and Navigational Electronics,
December, 1962.

134
ЛИТЕРАТУРА
23. Dushman A., On Gyro Drift Models and Their Evaluation, IRE Transa¬
ctions on Aeronautical and Navigational Electronics, December, 1962.
24. N e w t о n, George C., Jr, Inertial Guidance Limitations Imposed by
Fluctuation Phenomena in Gyroscopes, IRE Proceedings, April, 1960.
25. Weaver C. S., Thresholds and Tracking Ranges in Phase-Locked Loops,
IRE Transactions on Space Electronics and Telemetry, Vol. SET-7, No. 3,
September, 1961.
26. Livingston M. L., The Effect of Antenna Characteristics on Antenna
Noise Temperature and System SNR, IRE Transactions on Space Electronics
and Telemetry, Vol. SET-7, No. 3, September, 1961.
27. D e v e 1 e t J. A., Jr., Fundamental Accuracy Limitations in' a Two-Way Co¬
herent Doppler Measurement System, IRE Transactions on Space Electro¬
nics and Telemetry, Vol. SET-7, No. 3, September, 1961.
28. Dworetsky L. FI. and A. Edwards, Principles of Doppler-Inertial Gui¬
dance, ARS Journal, Vol. 29, No. 12, pp. 967—972, December, 1959.
29. Dunn FT H. and D. D. FI о w a r d, The Effects of Automatic Gain Control
Performance on the Tracking Accuracy of Monopulse Radar Systems, Proc.
of the IRE, Vol. 47, No. 3, March, 1959.
30. Dunn J. H., D. D. Howard and A. M. Kin g, Phenomena of Scintilla¬
tion Noise in Radar-Tracking Svstems, Proc. of the IRE, Vol. 47, No. 5,
May, 1959.
31. Delano R. FI., Angular Scintillation of Radar Targets, F1AC TM-233, dated
24 April 1950 (Hughes Aircraft Co.).
32. Much more R. B., Review of Scintillation Measurements, НАС TM-272,
dated December, 1952 (Hughes Aircraft Co.).
33. D e 1 a n o, Richard H., A Theory of Target Glint or Angular Scintil¬
lation in Radar Tracking, Proc. of the IRE, pp. 1778—1784, December,.
1953.
34. Much more R. B., Theoretical Scintillation Spectra, НАС TM-271, dated 1
March 1952 (Hughes Aircraft Co.).
35. Delano R. H., Irwin P f e f f e r, The Effect of AGC on Radar Tracking
Noise, Proc. of the IRE, pp. 801—810, June, 1956.
36. F a v r e a u R. R., H. Low and I. P f e f f e r, Evaluation of Comlex Statis¬
tical Functions by an Analog Computer, Hughes Aircraft Co., presented at
Project Typhoon Symposium III on Simulation and Computing Techniques,
October, 1953, University of Pennsylvania.
37. Angular Scintillation of Radar Targets with Monopulse and Interferometer
Target Seekers, НАС TM-257, dated November, 1950 (Hughes Aircraft
Co.).
38. P о v e ] s i 1 D., R. R a v e n and P. J. Waterman, Airborne Radar, Van
Nostrand Company, Inc., 1958.
39. D e v e 1 e t, Jean A., Thermal-Noise Errors in Stimultaneous-Lobing and
Conical-Scan Angle-Tracking Systems, IRE Transactions on Space Electro¬
nics and Telemetry, Vol. SET-7, No.	2,	June 1961.
40. Meade J. E., A. E. Hastings and	H. L. G e r w i n,	Noise	In Tracking
Radars, Naval Research Lab Report 3759, November 15, 1950.
41. Chittenden R. W., R. J. M a s s a	and J. F. F r a z e r, Evaluation of Satel¬
lite Tracking System Performance	In	the Presence of	Noise	and Interfe¬
rence, Proceedings of the Sxith Conference on Radio Interference Reduc¬
tion, ASTIA No. AD 244, 264.
42. Time Series Analysis Edited by M. Rosenblatt, John Wiley and Sons, Inc.,
1962.
43. S t e с с a A. J. and N. V. O’Neal, Target Noisr Simulator-Closed-Loop
Tracking, NRL Report 4770, July 27, 1956.
44. FI о w a r d D. D. and B. L. Lewis, Tracking Radar External Range Noise
Measurements and Analysis, NRL Report 4602, August 31, 1955.

ЛИТЕРАТУРА
135
45. Lewis В. L., A. J. S t е с с a and D.	D.	Howard,	The	Effect of An
Automatic Gain Control on the Tracking	Performance of	a	Monopulse
Radar, NRL Report 4796, July 31, 1956.
46. S t e с с a A. J., N. V. O’N e a 1 and J. J.	Freeman, A	Target	Simulator,
NRL Report 4694, February 9, 1956.
47. Leshnover S., Prediction of Anisoelastic and Vibropendulous Effects on
Inertial Navigation System Performance in Linear Random Vibration Envi¬
ronments, Proceedings of the National Specialists Meeting on Guidance of
Aerospace Vehicles, May, 1960.
48. S t e w a r t R. М., Some Effects of Vibration and Rotation on the Drift of
Gyroscopic Instruments, ARS Journal, January, 1959.
49. B1 a sin game B. P., Optimum Parameters for Automatic Airborne Navi¬
gation, D. Sc. Thesis, М. I. Т., 1950 (formerly classified secret, now declas¬
sified).
50. Press H. and J. С. H о u b о 11, Some Applications of Generalized Har¬
monic Analysis to Gust Loads on Airplanes, Jour. Aerospace Sciences,
Vol. 22, pp. 17—26, 1955.
51. Marks W. and W. Pierson, The Power Spectrum Analysis of Ocean
Wave Records, Trans. American Geophysical Union, Vol. 33, pp. 834—844,
1952.
52. G о о d m a n N. R., On the Joint Estimation of the Spectra, Cospectrum,
and Quadrature Spectrum of a Two-Dimensional Stationary Gaussian Pro¬
cess, Scientific Paper No. 10, Engineering Statistics Laboratory, New York
University, March, 1957 (Also available as ASTIA Document No. AD 134
919).
53. В a 1 a к r i s h n a n A. V., A Note on the Sampling Principle for Continuous
Signals, IRE Trans. PGIT, June, 1957.
54. Rosenblatt М., Random Processes, Oxford University Press, New York,
1962.
55. Stewart E. C. and G. L. Smith, The Synthesis of Optimum Homing
Missile Guidance Systems with Statistical Inputs, NASA Memo 2-13-59A,
April, 1959.
56. Zadeh L., Progress in Information Theory in the USA, 1957—1960, Part 5:
Prediction and Filtering, Trans. PGIT, July, 1961.
57. К a 1 m a	n R. E. and R.	S. Busy,	New Results in Linear Filtering	and
Predition Theory, Transactions of the ASME, Journal of Basic Engineering,
March, 1961.
58. Kalman R. E., A New Approach to Linear Filtering and Predicition
Problems, Trans. ASME,	Journal of	Basis Engineering March, 1960,	pp.
35—45.
59. H s i e h	H. C. and С. T. L e о n d с	s, On the Optimum Synthesis	of
Sampled	Data Multipole	Filters with	Random and Nonrandom Inputs,	IRE
Trans, on Automatic Control, Vol. AC-5, No. 3, pp. 193—208, August,
1960.
60. Shi nb rot, Marvin, Optimization of Time Varying Linear Systems
with Nonstationary Inputs, Trans. ASME, Vol. 80, 1958, pp. 457—462.
61. Broniwitz L., A New Approach to the Design of Optimal Ho¬
ming Missile Guidance Systems, Raytheon Report BM-2056, August 22,
1961.
62. С о u г a n t R. and D. Hilbert, Methods of Mathematical Physics, Vol. I,
Interscience Publishers, New York, 1953.
63. F i f e г S., Analogue Computation, Vol. IV., McGraw-Hill Book Company,
Inc., New York, 1961.
64. Stewart E. C., Application of Statistical Theory to Beam Rider Guidance
in the Presence of Noise. I—Wiener Filter Theory, NACA, RM A55E11,
1955.

136
ЛИТЕРАТУРА
65. Stewart Е. С., Application of Statistical Theory to Beam Rider Guidance
in the Presence of Noise. II—Modified Wiener Filter Theory, NACA, TN
4278, 1958.
66. IEEE Transactions on Aerospace and Navigational Electronics, Vol. ANE-10,
No. 1, March, 1963.
67. Bat tin R. H., A Statistical Optimizing Navigation Proceedure for Space
Flight, ARS Journal, November, 1962.
68. McLean J. D., S. F. Schmidt and L. A. M с G e e. Optimal Filtering
and Linear Prediction Applied to A Space Navigation System for the Cir-
cumlunar Mission, NASA TN D-1208, March, 1962.
69. Bergen A. R., A Non Mean-Square Error Criterion for the Synthesis of
Optimum Sample Data Filters, Technical Report T-2/133, Electronics Rese¬
arch Labs., Columbia University, 1956 (Also available as ASTIA Document
No. AD 110 180).
*70. Пугачев В. С., Теория случайных функций, Физматгиз, М., 1962.

ГЛАВА 3
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ И ЕГО ПРИМЕНЕНИЕ
К ЗАДАЧАМ МИНИМУМА СРЕДНЕКВАДРАТИЧНОЙ ОШИБКИ
Хеи (Н. С. Hsieh), Несбит (R. A. Nesbit)
РАЗДЕЛ 1
НЕКОТОРЫЕ ОСНОВНЫЕ ПОНЯТИЯ ФУНКЦИОНАЛЬНОГО
АНАЛИЗА
3.1.	Введение
Существует развитая математическая теория функций, и естест¬
венно возникает вопрос, нельзя ли с помощью этой теории решать
задачи управления. В истории теории регулирования вряд ли можно
обойтись без упоминания о тех успехах, которые имели место, когда
удавалось применить в практических задачах строгую математическую
теорию. С появлением вычислительных машин круг практических за¬
дач значительно вырос и нельзя игнорировать проблему их эффек¬
тивного использования.
Последующее изложение имеет целью познакомить с основными
идеями функционального анализа и показать, что они могут быть
использованы для решения некоторых задач управления.
Мы не пытаемся изложить курс основ функционального анализа,
поскольку его можно найти в книге Колмогорова и Фомина «Функ¬
циональный анализ» [10].
Существует много аналогий между векторным и функциональным
анализом. Большинство физических задач может быть сформулировано
без привлечения векторного анализа, совершенно также можно избе¬
жать формализма функционального анализа. Но тот, кто имел дело
с векторными уравнениями физических систем, легко можно понять
ценность изучения векторного анализа, а тот, кто интересуется проб¬
лемами, связанными с функциями, тому, конечно, полезно изучить
функциональный анализ.
Это обсуждение представляет попытку познакомить с предметом
функционального анализа и показать его применение к некоторым

138
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
[ГЛ. 3
задачам. Ниже будет рассмотрен метод наискорейшего спуска реше"
ния некоторых задач минимума среднеквадратичной ошибки и, в ча¬
стности, метод, предложенный А. В. Балакришнаном.
3.2.	Типы пространств
Отправной точкой для многих основных математических построе¬
ний является понятие множества. Элементы абстрактного множества
могут быть самыми произвольными, но в большинстве случаев их
можно мыслить себе как точки, числа или функции. Существуют не¬
которые утверждения или теоремы, имеющие дело со свойствами
множеств, которые могут быть доказаны при довольно слабых пред¬
положениях относительно точной природы элементов этих множеств.
Теоремы, доказанные с минимумом предположений, применимы во
многих частных случаях. В большинстве построений имеется множе¬
ство, элементы которого используются для образования любых мно¬
жеств, участвующих в задаче. Эго множество называется простран¬
ством. Относительно него можно делать дополнительные предполо¬
жения, получая тем самым различные типы пространств.
Метрическое пространство определяется как множество X, в ко¬
тором для каждой пары элементов множества определено расстояние
между ними — метрика р. Эта метрика должна обладать следующими
свойствами для любых jc и у, принадлежащих X (обозначается х,
У G
Р (х> У) О х ф у — положительность,
р(лг, х) = 0
р (х, у) — р (у, х) — симметрия,
Р (х> У) “Ь Р (Уу z)^p(x> z) — неравенство треугольника.
Одним из многих примеров метрического пространства является
множество всех непрерывных функций x(t) на замкнутом интервале
a^t^b с метрикой
г-Ь	-.1/2
?(Х, У)= \(x—yfdt
_а
Другие примеры можно найти в книге Колмогорова и Фомина [10].
Вопросы сходимости последовательности могут трактоваться в тер¬
минах метрического пространства. Метрическое пространство назы¬
вается полным, если любая последовательность Коши [13] сходится
к элементу этого пространства.
Линейное пространство есть множество R элементов х, у, z, ...,
для которых определены следующие операции:

S.2]
ТИПЫ ПРОСТРАНСТВ
139
1. Сложение. Для каждой пары элементов х, у имеется един¬
ственный элемент z = х -\-у, так что выполняются следующие условия:
а) х+у=у-]-х;
в) существует элемент 0 R такой, что х-\-0 = х для всех
х (3 Ry
г) для любых х R существует элемент —х	R такой, что
х -|- (—х) = 0.
2. Умножение на скаляр. Для х R существует ах R
а) а фх) = (аЗ) х;
б) 1 • х = х.
3. Связь между операциями сложения и умножения на скаляр
а) (а -|— Р) х = а.х -{— $х\
б) а (х -\-у) = ах -f- ay.
Линейное пространство называется нормированным, если каж¬
дому х R поставлено в соответствие неотрицательное число ||х||.
Это число называется нормой х и должно обладать свойствами:
1) || х || = 0 тогда и только тогда, когда х = 0;
2) || а* || = | a HI л:||;
3) H+J'IKII-kIIIIj'II-
Полагая р(х, у) = \\х—у ||, видно, что нормированное линейное
пространство является метрическим. Тогда теоремы сходимости, ко¬
торые применимы к любому метрическому пространству, в точности
применимы и к нормированному пространству.
Полное нормированное линейное пространство называется банахо¬
вым пространством, или ^-пространством. Примером нормирован¬
ного линейного пространства является пространство всех непрерывных
функций х:(£), определенных для a^t^b с обычными операциями
сложения и умножения на число и нормой
1*(9И =
J х2 (t) dt
1/2
Оператор А устанавливает правило, по которому элементам одного
банахова пространства R ставятся в соответствие элементы другого
банахова пространства К. Это записывается как
у = Ах.
Примером линейного нормированного пространства, обладающего
многими полезными свойствами, является гильбертово пространство.
Гильбертово пространство есть конечно- или бесконечномерное мно¬
жество Д удовлетворяющее следующим условиям:
1.	Н есть линейное пространство.

140
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
[ГЛ. 3
2. Для каждой пары элементов /, g Н определено скалярное
произведение. Следующие свойства определяют скалярное произведе¬
ние. Каждой паре элементов соответствует число (/, g) и
</. «>=<& />,
<«/. £>=»</> g),
</, «§>=?</. $>,
</,+А *> = </„ g) + (A, s>,
</, />>0, если f ф0.
H есть линейное нормированное пространство, если в качестве
нормы брать величину || /|| = ]//, f *).
3. Пространство Н полно в метрике
Р(х, j/) = j! / — g]\t.
Если пространство Н содержит всюду плотное счетное подмно¬
жество [13], то говорят, что пространство сеперабельно.
Можно показать, что все гильбертовы пространства одной и той же
мощности изоморфны [13]. Пространство Гильберта является тем
естественным пространством, в котором можно изучать функции, и
является также естественным обобщением евклидова пространства
конечной размерности. Одной из реализаций гильбертова пространства
является пространство всех счетных упорядоченных последовательно¬
го
стей х = (хь хь Хз, ..., хп, ...), обладающих свойством ^	00
i = I
со следующими операциями сложения, умножения на число и скаляр¬
ного произведения:
х-\-у = (х1-гУъ Хъ-\-уь хп-\-ую ...),
ах = (ахь ах2, ..., ахп, ...),
со
(х, у)= У) Х<Уг
i^\
Это пространство обозначается /2. Другой также часто используе¬
мой реализацией гильбертова пространства является пространство
функций с интегрируемым квадратом /Г,. Это пространство функций,
для которых ^ | f (t) р cl\x (0<C oo, с обычными определениями сложения
k
*) В качестве упражнения предлагается показать, что V(/> /) обладает
тремя свойствами, предъявляемыми к норме.

3.4]
РЯДЫ ФУРЬЕ
141
и умножения, а скалярное произведение определяется как
</.£>=$/ (О
Я
Хорошо известная операция разложения функций в ряд Фурье
возможна ввиду изоморфизма между L2 и
3.3.	Основные неравенства
В дополнение к неравенству треугольника
11/+*11<Н/11 + Ш.
упоминавшемуся выше, можно вывести другое неравенство, исполь¬
зуя при этом только свойства гильбертова пространства.
Неравенство Бунякопского—Шварца часто применяется в анализе.
Оно выполняется в любом гильбертовом пространстве и имеет форму
К/,	f)(g,	g)
или
!(/> *)XII/llllgll-
Важно знать, когда имеет место знак равенства, так как это дает
решение задачи оптимизации.
Задача. Дано	показать,	что	минимально,
когда
>, = . (A g)
(g. g) '
3.4.	Ряды Фурье
Для того чтобы освоиться с символикой, рассмотрим обычную за¬
дачу разложения функции с интегрируемым квадратом /(t), a^t^b,
ь
в ряд Фурье. В этом случае (/, g) = ^ f (t)g(t)dt, и мы имеем си-
а
стему функций [срь <р2, ..., cpv(^)j, удовлетворяющих соотношениям
/	\ Я ( °> iz£j>
ta. <?/>=«,7=1,, l=h
и, следовательно, ортономированную. Коэффициенты at конечного ряда
N
Фурье ^ ai?i — (в этом равенстве мы подразумеваем, что по
i = 1
дважды повторяющимся индексам в таком выражении, как а*®*, про¬
изводится суммирование по i от 1 до N) могут быть выбраны такими,
N I
минимально.
что
/— 2 а<?;
i = 1

142	ФУНКЦИОНАЛЬНЫЙ	АНАЛИЗ	[ГЛ.	3
Тождество ||/—a^i ||‘2= ji/—crfi + Cf<Pi— ai¥i!! не зависит от
ct и раскрывается следующим образом:
II/— Я;®,- !Р= II /— С,-©,- -f Ctfi — atfi II'2 =
= II /— С/©,- II'2 + </— с,-®,-, Ctfi — a,•©,•> + <c,-cpi — a Ml, /— с,-?г> +
“Ь II (ci — ai) II2-
Здесь коэффициенты Ci выбираются из соображения простоты вычис¬
ления. Так как тождественно верно для всех сь то результат не за¬
висит от этого выбора.
Пусть Ci = (f, сpi). Тогда
</— Ctfi, boj) = b [</, <Pjr>] — Ci (<pi, <py->] = b [</, <pj) — Cj] = 0
И
{b<Dj, f—c^i) = b[{<fj, f) t’i (©_,-, <?,->] = о.
Таким образом,
II /- am ||2 = l| /- d ||2 + S | (a; - c^ |2;
1 = 1
Ci уже фиксированы и правая часть равенства, рассматриваемая как
функция ah имеет, очевидно, минимум при = сг.
Величины at- = (/, ср;) называются коэффициентами Фурье. Функ-
N
ция £=2 а^'1 называется проекцией функции / на линейное под-
I = 1
пространство L. Линейное подпространство может быть образовано
любым подмножеством элементов {fb /2, ..., fm) из Н. Элементами
подпространства будут все функции вида
ТП	ф
*=2 bifi.
i = \
Задача. В конечномерном аналоге приведенных выше рассужде¬
ний я-мерный вектор F может быть аппроксимирован r-мерным век¬
тором G(r^ri), так чтобы величина ошибки \\F — G|| была бы
минимальна. Как следует выбирать компоненты вектора?
3.5.	Проекционный оператор
Для того чтобы кратко изложить приведенный выше результат
без обращения к какому-либо конкретному базису в линейном под¬
пространстве, введем проекционный оператор Р. Пусть L — линейное
подпространство Н. Тогда любой элемент из Н может быть разложен
на две компоненты: одна принадлежит L, а другая ортогональна лю¬
бому элементу из L: f=g-{-hf f Н, g (z L и (/?, ^) = 0 для всех

3.61
ПРИМЕНЕНИЕ ТЕОРИИ ПРОЕКЦИОННЫХ ОПЕРАТОРОВ
143
х L. Проекционный оператор определим как линейный оператор,
обладающий свойствами Pg = g и Ph = 0. (Заметим, что P(Pg) =
= P'2g = Pg, т. е. Р'2 = Р. Последнее свойство иногда принимают за
определение проекционного оператора.) Вышеприведенные рассужде¬
ния относительно проектирования могут быть приведены с помощью
проекционного оператора следующим образом.
Найдем функцию g L, которая минимизирует || /— g||2 для
/6Я:
\\ f—g\? = \\ f — Pf ~т pf — gf =	—	pf \\* -\- (f — pf> Pf>-
f-Pf> g) + (Pf, f-Pf)-(g, f-Pf) + \\pf-g\\\
Так как Pf, g(^L и f—Pf\_L,
II / — g\\2=\\f — Pf II2 + II Pf — g ||2>*
минимум достигается при
g = Pt.
3.6.	Применение теории проекционных операторов
для минимизации среднеквадратичной ошибки
Поскольку математическое ожидание двух случайных величин
обладает свойствами скалярного произведения, то изложенная выше
теория проекционных операторов может быть использована для слу¬
чайных процессов, если положить
</, g) = E(fg).
Случайные процессы с конечной дисперсией образуют линейное
пространство и часто являются разумными моделями некоторых про¬
цессов управления и связи. Для таких задач теория проектирования
позволяет получить уравнения оптимальных в среднеквадратичном
фильтров.
Но эти уравнения, однако, нужно решать, и анализ гильбертова
пространства может быть также использован для решения интеграль¬
ных уравнений. Рассмотрим следующую систему управления:
Требуется минимизировать
II с — г IIs = Е {(с — г) (с — г)} = Е {ее} =Е \е\*

144	ФУНКЦИОНАЛЬНЫЙ	АНАЛИЗ	ГГЛ. 3
для всех i: a^t^b (т. е. t Т). Эта задача эквивалентна сле¬
дующей;
x(t)=r(t) +n(t)
mv
c(t)
и если оптимальное W известно, то для линейной системы по W
и Wq можно найти соответствующее I/*).
Задача фильтрации заключается в том, чтобы оценить сигнал r(t)
по сумме сигнала и помехи x{t) с помощью наилучшей линейной
операции над x(t):
to	А
c(tо)= ^ W (Т0, о) х (сп) do = lim У апх(cr„),
оп->°
Для этого рассмотрим замкнутое линейное подпространство X, об¬
разованное функциями { jc (а); а^о ^t0\. Требуется найти с X так,
чтобы величина
II г —^1Г
была минимальна. Из общих рассуждений, приведенных выше, видно,
что с = Рг и что г — с должно быть ортогонально к любому эле¬
менту из X. Это значит
для всех т:	Учитывая,	что
E[r(t0)x(i)] = Rrx(t0t т),
предыдущее уравнение принимает вид
/о
RrA*о. “0=$	°)Rxx(o, z)da.
а
Это есть основное уравнение Винера—Хопфа и решение его относи¬
тельно W(t0, а) является основной проблемой расчета линейных
фильтров. Другой важной проблемой является определение статистик
различных процессов. Из приведенного выше уравнения видно, что
для расчета оптимального линейного фильтра требуется знать лишь
функции корреляции второго порядка.
*) Не всегда верно. V {ty т) может быть неустойчиво. Смотри книгу
Ньютон Дж. К., Гулд Л. А., Кайзер Дж. Ф., Теория линейных сле¬
дящих систем, Физматгиз, 1961.

3.61
ПРИМЕНЕНИЕ ТЕОРИИ ПРОЕКЦИОННЫХ ОПЕРАТОРОВ
145
Аналогичным способом можно находить и полиномиальные фильтры
Рассмотрим квадратичный фильтр, для которого
to	f0
с (£0) = U7 (t0) а) х (а) do -j- jj ^ К (tQy о, т) х (а) х (т) dz do.
а	а а
Основным вопросом в применении проекционных операторов является
выбор подходящего линейного многообразия [13]. Для указанной выше
задачи подходящим является линейное многообразие X, состоящее из
пар {-хг(a), x(o)x(z) или a^o^.t0,	В	этом	случае	урав¬
нения
RrxVo, У=5 Wo, °) R.v.v (*,	+ $ I К (to, а, t) Rxxx (О, t, dx do,
a	a	a
to
Rrxxif0>	h) = 5 W(t*> a)Rxxx(c> t\> h) do -f-
a
to to
—j- ^ ^ К (t0, О, t) Rxxxx (?>	dsi	do
U 0
должны быть решены совместно относительно К и W. Здесь тре¬
буются статистики не только второго, но также третьего и четвер¬
того порядков.
Иной тип проблемы оптимизации функционалов возникает, если
оптимум искать не в линейном, а в ограниченном, выпуклом под¬
пространстве [13]. Теория проекционных операторов в этом случае
недостаточна.
В качестве другого примера предположим, что мы должны опре¬
делить коэффициент усиления передаточной функции по известной
реакции системы на единичный скачок и наблюдаемой реакции си¬
стемы. Измерение х искажено аддитивным шумом, так что x(t) =
= ks(t)-\- n(t), и если рассматривать только линейные операции над
данными, то
ь	1
k = \х (t) h (t) dU J | h i“ dt oo.
a	0
Если шум имеет нулевое среднее значение, то
ъ
E(k)=k s{t)h(t) dt,
а
b
/.	А
и разумно требовать, чтобы \s(t)h(t)dt = 1. Тогда E(k) есть

146
ФУНКЦИОНАЛЬНЫЙ анализ
[ГЛ. 3
искомая величина /г. Дополнительным требованием к h(t) является мини¬
мум дисперсии оценки Е [(k — kf\
Рассматривая действительное гильбертово пространство Ц на
интервале a^t^b со скалярным произведением
I)
С/. g) = \f{t)g(t)dt,
а
поставленную задачу можно сформулировать следующим образом.
Минимизировать (Rh, Н) при условии (/г, s)=l. (R есть функция
ковариации и поэтому является неотрицательным оператором.)
Свойства гильбертова пространства весьма полезны для форму¬
лировки функциональных задач, когда минимизируется среднеквадра¬
тичная ошибка. Ниже будет дано решение этой задачи методом
наискорейшего спуска в терминах функционального анализа.
Предыдущее изложение имело целью познакомить читателя с не¬
которыми понятиями функционального анализа и его связью с про¬
блемами управления. Дальнейшие выводы используют эти и другие,
не упоминавшиеся здесь результаты. Интересующиеся могут восполь¬
зоваться библиографией [1, 10, 11, 12].
РАЗДЕЛИ
ПРОБЛЕМЫ СРЕДНЕКВАДРАТИЧНОЙ ОШИБКИ
3.7.	Неотрицательные операторы в гильбертовом пространстве
и минимизация квадратичных функционалов
Пусть Н обозначает действительное векторное гильбертово про¬
странство. Линейный ограниченный оператор R, отображающий Н
в НУ называется симметричным или самосопряженным, если для лю¬
бых двух элементов х и у из Н
(Rx, у) = (х, Ry).	(3.1)
Оператор R называется неотрицательно определенным, если в до¬
полнение к свойству симметричности
(Rx, х> ^ 0.	(3.2)
Далее, оператор называется положительно определенным, если
(Rx, х)^>0у х ф 0,	(3.3)
и (Rx, jc) = 0 тогда и только тогда, когда л: = 0 (кроме множества
меры нуль) [13]. Далее мы ограничим наше рассмотрение простран¬
ством вектор-функций с интегрируемым квадратом на конечном
интервале (0, Т), т. е. пространством L2(T). В большинстве рассма¬

3.7]
ОПЕРАТОРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
147
триваемых проблем линейный оператор не только неотрицательно
определен, но и компактен [14]*). Этот оператор характеризуется
тогда счетным множеством собственных значений; все они неотрица¬
тельны. При этом, если их бесконечное число, невозрастающая по¬
следовательность собственных значений, будет сходиться к нулю.
Пусть {XJ — множество невозрастающих собственных чисел и
{ф;} — множество соответствующих собственных функций. Тогда по
теореме Гильберта — Шмидта [1] мы имеем для любого симметрич¬
ного оператора R выражение
оо
Rx= 2 Хг (х, фг> фг	(3.4)
г= I
для каждого х из Z.2. Здесь {X-}—множество ненулевых собственных
чисел. Разложение (3.4) справедливо в смысле сходимости в сред¬
нем [10] для всех операторов вида
Rх = ^ R (s, t) х (f) dty
т
где Т есть область изменения параметра t. Если теперь интеграль¬
ный оператор R неотрицательно определен и имеет непрерывное
ядро, тогда по теореме Мерсера [1] его можно разложить в ряд
оо
R(s, 0= 2 х;ф;О)ф;(t),	(3.5)
i= 1
где штрих означает транспонированную матрицу. Сходимость в сред¬
нем этого ряда является равномерной по обоим переменным s и t.
Абстрактно все проблемы среднеквадратичной ошибки могут трак¬
товаться как проблемы минимизации квадратичного функционала
вида
Q(x) = </?a:, х) — 2 (х, g).	(3.6)
Здесь R есть, вообще говоря, неотрицательно определенный оператор
в L2 и g — данный элемент из Ц. Минимизация производится отно¬
сительно х в L2. Предположим теперь, что в L2 существует элемент
такой, что
Rh = g.	(3.7)
Тогда
Q (х) = (Rx, х) — 2 (х, RH).
*) Оператор А компактен, если он отображает любое ограниченное
множество в компактное.

148	ФУНКЦИОНАЛЬНЫЙ	АНАЛИЗ	[ГЛ.	3
Добавляя и отнимая член -(Rh, h) и используя свойство симметрии Rf
имеем
Q (х) = (Rx, х) — (Rx, ft) — (Rh, х)
-\-(Rh, h) — (Rh, h) = (R(x — h), x — ft)— (Rh, h).	(3.8)
Предположим теперь, что R в действительности положительно опре¬
делен. Точнее, эго значит, что в Z,2 не существует отличного от нуля
элемента такого, что
Rx= 0,	(3.9)
и, следовательно, нуль не является собственным числом оператора R.
Очевидно, что Q будет минимальным, если выбрать
x — h.
Таким образом,
Qmit. (■* =—<§■• h),	(3.10)
и уравнение (3.7) имеет вид
Rx = g.	(3.11)
Это есть интегральное уравнение Винера — Хопфа для данной задачи
минимизации.
Если R компактен, тогда, как известно [1,10], необходимым и
достаточным условием для того, чтобы уравнение (3.11) имело реше¬
ние в 12, является
со
V У:'г<со.	(3.12)
Если ядро интегрального оператора R стационарно (т. е. является
функцией	только	разности двух своих аргументов)	и	его	преобразо¬
вание Фурье	есть	рациональная функция, то общее	решение	уравне¬
ния (3.11) содержит S-функции и их производные различного по¬
рядка на концах интервала Т.
Случай, когда уравнение (3.9) удовлетворяется для х ^ 0, обычно
называется сингулярным случаем, и впервые был рассмотрен в [2,5].
Будем обозначать через И0 подпространство, соответствующее нуле¬
вому собственному значению, т. е.
Rx = 0, х ^ Н0,
и через go — проекцию g на это подпространство. Тогда
g — go~{-gv go £ ^о-	(3.13)
Чтобы минимизировать Q, мы должны взять
x = Kg*.	(3.14)

3.7]
ОПЕРАТОРЫ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
14!)
Так как (g, gn) = (g.J, gn), то
Q(x) = —2K (g» g0).	(3.15)
Очевидно, выбирая К сколь угодно большим, получим
QininC*')2^	(3.1	б)
Рассмотрим	теперь	случай, когда в 12 не	существует	решения
уравнения (3.7).	Покажем, что тогда существует	последовательность
элементов {hn} из 1.2 таких, что
:'i Rhn — g!! -> 0,	(3.17)
и этого будет достаточно, чтобы утверждать, что
Q[nf(*) = lim Q(hn).	(3.18)
/2->-03
Чтобы это показать, образуем последовательность
hn = У	фь	(3.19)
7=1
Очевидно, что (3.17) удовлетворяется.
Прибавим и вычтем теперь величину 2 {Rhtv х) -[- (Rhn> hn).
Получаем
Q (х)= (Rx, х) — 2 (х, g) -j- 2 {Rhn, х) -|-
-j- <Rhn, hn) — 2 (Rhn, x> — (Rhn, h„) =
z== (R (*^ hn)> % hn) (Rhn> hn) ^ \*^’ Rhn g).
Тогда
Q (x) — Q (hn) = {R(x — hn)> x — hn) -j- (Rhn — g, x — hn) >-•
^ 2 {Rhn — gx— hn) = 2 (Rhn — g, x).
Теперь
<Rhn — g,	я->оо.
Следовательно, имеем
Q(x) ^ lim Q(ft„).
Отсюда следует, что
‘ ~~ — 2 ~
»= l
Qi„fW= —lim	h„)	=	—	У	i'll.	(3.20)
n -* oo	И
Результат минимизации квадратичного функционала, как показано
выше, зависит, очевидно, от собственных чисел и собственных функ¬
ций оператора R. Определение этих величин само представляет
трудность. Таким образом, это приближение не является таким уж

150
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
[ГЛ. 3
конструктивным в решении проблемы синтеза. В следующем разделе
мы введем последовательную аппроксимацию решения, основанную
на методе наискорейшего спуска в гильбертовом пространстве. Этот
метод дает самый общий подход для всех проблем минимума средне¬
квадратичной ошибки.
3.8.	Метод наискорейшего спуска в гильбертовом
пространстве
Применение метода наискорейшего спуска для решения проблемы
минимизации квадратичного функционала впервые было введено
Л. В. Канторовичем в СССР [3]. Сравнительно недавно применение
этого метода для решения инженерных задач появилось в литера-
туре [4, 5, б, 7, 8]. В частности, Балакришнану принадлежит боль¬
шое количество оригинальных работ по развитию этого метода и
применению его для решения большого класса инженерных проблем
[5, 6]. Основная идея метода заключается в следующем. Рассматри¬
вается квадратичный функционал Q(jc) в гильбертовом пространстве.
В поисках его минимума возьмем произвольное jc0 в качестве
первого приближения. Попробуем найти «градиент» в точке х0, т. е.
найти элемент z такой, что производная Q (лг0 zz) максимальна
при е = 0. Пусть z0 такой элемент. Так как Q(JCo~h£^o) полином
второй степени от е, он будет достигать минимума для некоторого е0.
Тогда элемент Xi = х0 -j- £о^о принимается за следующее приближе¬
ние и процесс повторяется до тех пор, пока не будет достигнута
требуемая точность.
Рассмотрим теперь квадратичный функционал
Q(x) = (Rx, х)— 2 (х, g).	(3.21)
Здесь R положительно определенный оператор [10]. Пусть
z — произвольный элемент из Ну отличный от нуля. Тогда для лю¬
бого действительного параметра в мы имеем
Q (х —\- 32) = Q (х) —j— 2s (R.x — g, z^(Rz, #).	(3.22)
Предположим, что х0—первое приближение. Для того чтобы
найти градиент, нужно максимизировать выражение
[Q (Xq -j- s2o)]s = o= 2 (Rxq g, Zq).	(3.23)
В силу неравенства Шварца выражение (3.23) будет максимизи¬
ровано для ||г0 Ц = 1, если
г0 = Rx0 — g•	(3.24)

3.8]	МЕТОД НАИСКОРЕЙШЕГО СПУСКА	151
При таком выборе z0 (3.22) будет достигать своего минимума по е,
если
<3'25)
Таким образом, в качестве следующего приближения берем
Х\= Xq-\- е0 (Rx0 — g)
и
Q (-^i) = Q (Хо) - - l!2°'14
(Rz,,, z0) •
Очевидно, что на п-м шаге мы имеем
Хп = Хп_1	гп-\2п-Ь	(3.26)
где
п	(RZfi-u	%п-1)
Q (хп) = Q (xn_t) -	r	.	(3.27)
Zn_i)
Теперь мы покажем, что Q(xn) действительно сходится к истин¬
ной нижней грани [5, 13]
Qinf(*)= lim Q (■*«)•	(3-28)
Из уравнения (3.27) ясно, что
«w=«w- 2 тШл- (3'29)
i = о
Если теперь бесконечный ряд
со
у II гп II*
Li (Rzm zn)
л	г)
п = О
■ ОО,
то Q(xn) будет монотонно стремиться к —со и нижняя грань оче¬
видно достигается. Если же
2<fefc<+«*
п **0
ТО
(Rzw *„><||K|| II zn ||9,

152
Ф У Н К ЦИ О НАЛ ЬН Ы Й АНАЛИЗ
[ГЛ. 3
где
ЦЯ||= sup (Rx, х),
и тогда имеем
(Rzn, zn) — ||/?||
Эго означает, что
оо
2 II !i2<-b оо.
(3.30)
п = 1
Таким образом, получим
И *я II = I!
(3.31)
Однако можно показать [5, 8], что (3.31) достаточно, чтобы утвер¬
ждать
Следует заметить, что сама последовательность {хп} вовсе не
обязана сильно сходиться.
3.9.	Нелинейная фильтрация случайных процессов
Как уже отмечалось, все проблемы среднеквадратичной ошибки
могут рассматриваться как минимизация квадратичного функционала.
При использовании метода наискорейшего спуска не делалось ника¬
ких предположений о стационарности процессов. В этом разделе мы
покажем, что та же самая процедура применима и для нелинейной
фильтрации [5].
Пусть Е— случайная величина. Мы постараемся получить наи¬
лучшую в среднеквадратичном оценку этой случайной величины по
наблюдению случайного процесса x(t) за период O^t^T. Наи¬
лучшей оценкой мы считаем нелинейное выражение вида
с+ 2	(А	А)	*	(А)	*	(А)	•	•	•	X	(A)	dt	1... dtm	(3.32)
где С—постоянная, Wn(th t2, ..., tn) — симметричная относительно
своих аргументов функция, которая принадлежит L%(Tn). Обозначим
через x(t)N-мерный вектор-процесс
Qinf(Jf)= lim Q(x„).
п -у ОО
N Т Т
п = 1 U б
x(f) =
x(ti)
*(А)*(А)
(3.33)

3.91	НЕЛИНЕЙНАЯ	ФИЛЬТРАЦИЯ	СЛУЧАЙНЫХ	ПРОЦЕССОВ
а через К (£) ЛЛмерный вектор весовых функций
153
*(9 =
ти, и)
(3.34)
Wjffr t.b ...,tN)
где t = (th tb tдг) принадлежит прямому произведению про¬
странств TN. Тогда уравнение (3.32) можно записать как
С+ \ Kr(t)x(t)d\t\,	(3.35)
jN
где штрих используется для обозначения транспонированной матрицы.
Задача заключается в таком выборе С и K(t\ чтобы
О
(3.36)
(3.37)
было минимальным. Введем две новые величины
\ = Ь — Е{Ц,	(3.38)
х = х — Е {jc}.	(3.39)
Заменяя в (3.36)	£ и х на ? и л;,	получим С= 0,	так	как £{f} = 0
и £{Jc} = 0. Уравнение же (3.37)	перейдет в
ДА) = £|« — J	ЛГ(*)х(0<ЧЧ}*	(3-4°)
Таким образом,	удобнее рассматривать эти два	новых уравнения.
Правая часть (3.40) может быть раскрыта следующим образом:
/(АГ)=£{|}2_2 ^ tf'(Q£{6*(<)}d|f| +
rfN
+ $	^ K'(s)E{x(s)x'(f)}K(i)d\s\d\t\;
'JiV TN
это, очевидно, можно записать в операторной форме
1{K)—{RK, К) - 2 <*, К) + Е {Г},	(3.41)
где
R(S, 0 = £{i(s)jc'(0}1 WXM
ff(0 = £p(9}
(3.42)

154
ФУНКЦИОНАЛЬНЫЙ АНАЛИЗ
[ГЛ. 3
и R есть компактный и неотрицательный оператор в TV-мерном
пространстве. Очевидно, что выражение, которое должно
быть минимизировано, снова есть квадратичный функционал
Q (К) = <RK, К) = 2 (g, К>.	(3.43)
Уравнение Винера — Хопфа для этой задачи будет
RK = g.
Это уравнение может быть также выведено с помощью проекционной
теоремы. Возможно, что для К из L% (7^) решения не существует.
Однако, используя те же самые рассуждения, что и в § 3.1 и 3.2,
всегда можно найти последовательность {Кп} такую, что
1№-*И-*о
И
Qini(*0= lim Q(Kn).
п -*• оо
Следовательно, для получения аппроксимирующей последовательности
можно воспользоваться методом наискорейшего спуска. Условие
сильной сходимости этой последовательности может быть выражено
в терминах собственных чисел оператора R так же, как и в уравне¬
нии (3.12). Следует заметить, что для нелинейной оценки необходимо
знать более высокие моменты входного процесса.
ЗЛО. Иллюстративный пример
Рассмотрим задачу выделения сигнала из помех. Доступная наблю¬
дению входная величина предполагается заданной в виде
I(t) = S{t)-{-N(t).	(3.44)
Здесь S{t)— известная функция времени, a N(t) — стационарная слу¬
чайная помеха с ковариацией /?лДт). Требуется найти такой линейный
фильтр, управляемый этим входом в течение конечного интервала
времени Г, что отношение выходного сигнала к шуму было бы
максимально в некоторый заданный момент времени t = tx. Это есть
задача о согласованном фильтре.
Для данной простой задачи можно получить аналитическое ре¬
шение [9]. Наша цель — сравнить точное решение и приближенное
решение, получаемое методом наискорейшего спуска.
Обозначим выходные величины сигнала S(t) и шума N(t) через
£0(0 и N0 (0 соответственно. Тогда
т
Sol<i) = $ W(^)S(tl — z)dz = (W, Si),	(3.45а)
U
Л/g («!)=<»', Wi)	(3.456)

3.10]
ИЛЛЮСТРАТИВНЫЙ ПРИМЕР
155
Е {N1 (*,)} = j 5 W{ii) W(т) Rn (и — т) cfa dz = (R W, W).	(3.46)
т т
И
о о
Нужно минимизировать отношение
р — (3'47)
Ясно, что максимизация (3.47) эквивалентна минимизации
Q(W) = E {Nq (0} - Х50 (h)	(3.48)
при соответствующем ограничении на S0(^i)- Здесь X есть множитель
Лагранжа. Уравнение (3.48) удобнее записать следующим образом:
Q(W) = (RW, U7> —2^-Si, wj.	(3.49)
Теперь на основании выше изложенной теории получаем уравне¬
ние Винера — Хопфа
R W= ^S,	0	<	х	sS	Т.	(3.50)
Так как речь идет об отношении сигнала к шуму р, то выбор
числа X несуществен. Следовательно, уравнения (3.49) и (3.50) могут
быть нормализованы
Q(W) = (RW, W) — 2(Sh W)	(3.51)
RW=Si.	(3.52)
Предположим, что в этом примере функция ковариации шума
имеет вид
RN('z) = e-ix\.	(3.53)
Входной сигнал задается формулой
S(0 = cos92irf.	(3.54)
Возьмем 7=1 и = 7. Тогда интегральное уравнение, которое
нужно решить, имеет вид
W(?)dx= sin-2itf.	(3.55)

156
Ф У Н к Ц и О Н АЛ I > И Ы й A11 АЛ 113
[ГЛ. 3
Вообще говоря, решение такого интегрального уравнения будет
содержать 5-функции на обоих концах. Однако при данном конкрет¬
ном S(t) 5-функции учитывать не нужно. Решение принадлежит L.2.
Можно показать, что оптимальная весовая функция фильтра имеет вид
W(t)= ~sm22rJ — 4ti2cos4^.	(3.56)
Минимум Q будет
Qmin = — (Si, Щ=— 10,0572.
Применим теперь к этой задаче метод наискорейшего спуска.
Можно показать, что функция ковариации шума, заданная формулой
(3.53) и рассматриваемая
здесь как оператор R, яв¬
ляется положительно оп¬
ределенной [9]. Восполь¬
зуемся несколько раз
уравнением (3.26). После¬
довательность п р и б л и ж е н -
ных решений изображена
на рис. 3.1. Некоторые'
р е з у л ь т а т ы	вычислений
даны в таблице 1. В
качестве произвольного
начального приближения
выбрано W0 (t) = 0. Инте¬
ресно, что уже после пер¬
вой итерации полностью
выявилась требуемая фор¬
ма решения. Если мы оп¬
ределим ошибку аппрок¬
симации как
щт
Еп= 1
Q(Wn)
(3.57)
Qmin
то из таблицы видно, что
Eio = 5%>
£-0= 1,16%.
Следует заметить, что
существуют и другие ме¬
тоды последовательных приближений, которые могут быть так же
использованы для решения этих задач. Однако метод наискорей¬
шего спуска наиболее фундаментален и прост.
Рис. 3.1. Последовательные приближения
решения в примере при использовании метода
наискорейшего спуска.

ЛИТЕРАТУРА	157
Таблица 1
Некоторые численные решения задачи методом наискорейшего спуска
(Зшш — ю.озтг
Число
итераций
n
иг? = l — Q п)
Число
итераций
n
<>(wn)
И -1-<W
Qm\n
Qill in
1
—0,742040
0,926218
15
—6,822408
0,321639
2
—1,427547
0,858057
20
— 7,826654
0,221786
3
—2,061064
0,795066
25
—8,512110
0,153630
4
—2,646916
0,736814
30
—8,980070
0,107100
5
—3,18820
0,682932
15
—9,299579
0,075331
6
—3,690287
0,633070
40
—9,517746
0,053639
7
—4,154406
0,586922
50
—9,768479
0,028708
8
—4,584077
0,544200
60
—9,885469
0,017075
9 .
—4,981896
0,504644
70
—9,940115
0,011642
10
—5,350292
0,468014
80
—9,965699
0,009098
90
- 9,977733
0,007902
ЛИТЕРАТУРА
1. F. Riesz and В. S z-N a g у, Functional Analysis, Frederick Ungar-
Publishing Co., New York, 1955. [Русский перевод: Рисс Ф. и Секс-
фа л ь в и - Н а д ь Б., Лекции по функциональному анализу, ИЛ, М.,
1954.]
2. А. V. Balakrishnan, Estimation and Detection Theory for Multiple
Stochastic Processes, Journal of Mathematical Analysis and Applications,
December, I960.
3. Канторович Л. В., Функциональный анализ и прикладная математика.
Успехи мат. наук, 3, № б, 1948, стр. 89—185.
4. Е. Р а г z е n, A New Approach to the Synthesis of Optimal Smoothing
and Prediction Systems, Technical Report No. 34, Applied Mathematics and
Statistics Laboratories, Stanford University, July, I960.
5. A. V. Balakrishnan, A General Theory of Nonlinear Estimation Prob¬
lems in Control Systems, presented at the Symposium on Mathematical
Problems in Control Systems, Washington, D. C., November, 1961.
6. A. V. Balakrishna n, An Operator Theoretic Formulation of a Class of
Control Problems and a Steepest Descent Method of Solution, J. Soc. Indust.
Appl. Math. Ser. A: On Control, Vol. 1, No. 2, 1963, pp. 109—127.
7. H.	С. H s i	e h, Synthesis	of	Optimum Multivariable Control Systems by
the Method of Steepest Descent, IEEE Trans, on Application and Industry,
Vol. 82, No. 66, 1963, pp. 125-130.
8. H.	С. H s i	e h, Synthesis	of	Adaptive Control Systems by the Function
Space Methods, Ph. D. Dissertation, Department of Engineering, University
of California, Los Angeles, June, 1963.
9. W.	B. Davenport, Jr., and	W. L. Root, An Introduction to the Theory
of	Random	Signals and	Noise, McGraw-Hill Book Company, Inc.,

158
ЛИТЕРАТУРА
New York, 1958. [Русский перевод: Давенпорт В. Б. и Рут В. Л , Вве¬
дение в теорию случайных сигналов и шумов, ИЛ, М., I960.]
10. К о л м о г о р о в А. Н. и Фомин С. В., Элементы теории функций
и функционального анализа, т. 1 и т. 2. Изд-во Моск. ун-та, 1954,
1960.
11. Р. К. Н a i m о s, Introduction to Hilbert Space, Chelsea Publishing Company,
New York, 1957.
12. J. L. D о о b, Stochastic Processes, John Wiley and Sons, Inc., New York,
1960. [Русский перевод: Дуб Дж., Вероятностные процессы, ИЛ, М.,
1956.]
13. G. J a m е s and R. James, Editors, Mathematics Dictionary, van Nostrand,
Princeton, New Jersey, 1959.
14. Красносельский М. А., Топологические методы в теории нелиней¬
ных интегральных уравнений, Гостехиздат, М., 1956.

ГЛABA 4
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
Стир (Е. В. Stear)
Возможность представления, в некотором подходящем статисти¬
ческом смысле, данного случайного процесса через другой случайный
процесс с более простой вероятностной структурой играла и про¬
должает играть важную роль в развитии общей теории случайных
процессов и в ее приложениях.
В качестве примера здесь можно привести хорошо известную
теорему о спектральном представлении стационарных случайных про¬
цессов. Эта теорема дает гармоническое разложение (т. е. разложе¬
ние Фурье) выборочной функции непрерывного в среднеквадратичном
стационарного случайного процесса. Причем различные компоненты
(Фурье) этого разложения некоррелированы. Если сами компоненты
гармонического разложения рассмотреть как случайный процесс, то
ясно, что оно на самом деле является представлением указанного
выше типа. Гармоническое представление очень полезно тем, что
позволяет применять мощные методы гармонического анализа к изу¬
чению преобразований (например, фильтрации) случайных процессов.
Причем некоррелированность компонент гармонического разложения
имеет здесь решающее значение.
Другое полезное представление указанного выше типа для дан¬
ного случайного процесса получается в результате линейной «фильт¬
рации» «белого шума». Случайные процессы, получающиеся таким
образом, часто называются (особенно в математической литературе)
процессами со скользящим средним. Полезность этого представления
также связана с тем фактом, что компоненты «белого шума», т. е.
его значения, в различные моменты времени некоррелированы. Устрой¬
ство, выполняющее операцию линейной «фильтрации», которая поз¬
воляет получить заданный случайный процесс из «белого шума», часто
называют формирующим фильтром, и мы также будем придерживаться
этого названия. Употребление термина «формирующий фильтр» объяс¬
няется тем, что линейную фильтрацию можно рассматривать как

160
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
операцию формирования спектра, т. е. корреляций между компонентами
гармонического разложения, получаемого в случае стационарных
процессов с помощью «белого шума».
Задачу нахождения формирующего фильтра для данного случай¬
ного процесса естественно просто называть задачей определения
формирующего фильтра. Именно этой задаче и посвяшается настоящая
глава.
В общем случае, когда данный случайный процесс имеет произ¬
вольную непрерывную корреляционную функцию, задача определения
формирующего фильтра не решена. Но при некоторых удовлетвори¬
тельных ограничениях на класс допустимых корреляционных функций
были получены довольно определенные результаты. Эти результаты
излагаются в настоящей главе. Из дальнейшего будет видно, что
теорема о спектральном представлении играет главную роль при
решении задачи определения формирующего фильтра для стационар¬
ных случайных процессов.
4.1.	Причины, побуждающие заниматься задачей
определения формирующего фильтра
С точки	зрения	инженера	по автоматическому регулированию
к решению	задачи	определения формирующего фильтра	главным
образом приводят, во-первых, желание моделировать случайные про¬
цессы с заданными корреляционными функциями, во-вторых, желание
решать задачи линейной среднеквадратичной фильтрации и экстрапо¬
ляции и, в	третьих,	желание	идентифицировать линейные	системы,
используя в	качестве	пробного	сигнала «белый шум».
Для того чтобы промоделировать случайный процесс с заданной
корреляционной функцией, источник «белого шума» соединяется
с устройством, выполняющим функцию формирующего фильтра. Но
чтобы получить процесс с желаемой корреляционной функцией, оче¬
видно, требуется знать решение соответствующей задачи определения
формирующего фильтра.
При решении задач линейной среднеквадратичной фильтрации и
экстраполяции традиционными методами приходится решать интеграль¬
ное уравнение Винера — Хопфа
^i) = 5 ^Ч^1> т)Гхх (V^)
т
где корреляционные функции ГХу(^> t\) и Гхх(г> h) заданы, а весо¬
вая функция W{tb т) наилучшего в смысле минимума среднего квад¬
рата ошибки фильтра или экстраполятора является искомой. Если
наблюдаемый случайный процесс {X (t), t 7j является «белым шу¬
мом», то Гхх (т, £2) = о (т— Е2) и решение уравнения Винера—Хопфа

4.2]
ИСТОРИЧЕСКИЙ ОЧЕРК
161
получается сразу W(th t2) = Гхг(Г2, ^). Отмеченный факт приводит
к мысли о представлении наблюдаемого случайного процесса через
«белый шум» с помощью формирующего фильтра. При этом мы
обращаемся с «белым шумом» так, как если бы он был наблюдаемым
случайным процессом. Решение соответствующего уравнения Винера —
Хопфа теперь получается немедленно, а уже из него нетрудно полу¬
чить W(th т). В этом по существу заключается метод Боде — Шен¬
нона решения таких задач среднеквадратичной фильтрации и экстра¬
поляции. То, что этот метод требует решения соответствующей задачи
определения формирующего фильтра, не вызывает сомнений. Спе¬
циальный вид решения задачи определения формирующего фильтра
требуется также и для более нового метода решения задачи линейной
среднеквадратичной фильтрации и экстраполяции, предложенного
Калмэном и Бьюси. Отсутствие корреляции между компонентами
«белого шума» чрезвычайно важно для обоих упомянутых методов.
Наконец, доминирующая роль задачи определения формирующего
фильтра для идентификации линейных систем (посредством подачи
«белого шума» на их входы и определения корреляционных функций,
получающихся в результате выходных сигналов) очевидна.
4.2.	Исторический очерк
Первый значительный результат, касающийся задачи определения
формирующего фильтра, был, по-видимому, получен Вольдом [1] для
стационарных процессов *), зависящих от дискретного параметра, и
являлся частью его фундаментальной теоремы о разложении.
А. Н. Колмогоров [2, 3, 4] рассмотрел результаты этой теоремы
Вольда с аналитической точки зрения и получил для стационарных
процессов, зависящих от дискретного параметра, некоторые новые
теоремы, часть из которых опять имеет отношение к задаче опреде¬
ления формирующего фильтра. Независимо Винер [5] получил те же
самые результаты, что и Колмогоров, для стационарных процессов,
зависящих от дискретного параметра и имеющих абсолютно непре¬
рывную спектральную функцию, и затем обобщил эти результаты на
стационарные процессы с абсолютно непрерывной спектральной функ¬
цией, зависящие от непрерывного параметра. Таким образом, часть
результатов Винера содержала первое решение задачи определения
формирующего фильтра для стационарных процессов, зависящих от
непрерывного параметра. Затем Ханнер [б] и Карунен [7] получили
различными методами непрерывный аналог теоремы Вольда о разложе¬
нии, которая частично опять имеет отношение к задаче определения
*) «Стационарность» здесь всегда понимается как «стационарность
в широком смысле». Термин «процессы» используется в этой главе вместо
более громоздкой фразы «случайные процессы».
6 п/р Леондеса —

162
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ (ГЛ. 4
формирующего фильтра. Боде и Шеннон [8] при своем упрощен¬
ном эвристическом выводе результатов винеровской теории линейной
среднеквадратичной фильтрации и экстраполяции отметили, что реше¬
ние задачи определения формирующего фильтра является весьма важ¬
ной частью их метода. Следующий значительный результат, касаю¬
щийся задачи определения формирующего фильтра, был получен
Дарлингтоном [9] для нестационарных процессов путем обобщения
метода факторизации рационального спектра, применяемого для ста¬
ционарных процессов. Ранее менее общий результат в этом направ¬
лении был получен Дольфом и Вудбари [10]. Двумя месяцами позд¬
нее Дарлингтона Батков [11] опубликовал статью, в которой были
представлены три метода решения задачи определения формирующего
фильтра, включая один алгебраический. Алгебраический метод Баткова
основан на использовании соотношений между различными частными
производными от корреляционных функций, зависящих от непрерыв¬
ного параметра нестационарных случайных процессов, принадлежа¬
щих некоторому классу. На самом деле этот метод, как указывается
в дальнейшем, пригоден только для довольно специального подкласса
объявленного класса. Леонов [12] предложил довольно хорошее
математическое решение задачи определения формирующего фильтра
для процессов, зависящих от непрерывного параметра (как стацио¬
нарных, так и нестационарных) в терминах разложений по ортого-;
нальным функциям.
Наконец, Калмэн [13] недавно получил хорошую теорему пред¬
ставления для гауссовских марковских процессов, которая имеет
значительную практическую ценность как для стационарных, так и
для нестационарных процессов.
4.3.	Предварительные сведения из теории
случайных процессов. Постановка задачи
В этой главе случайный процесс определяется как семейство
случайных величин {X (t), t 7}, где t — параметр семейства, а Т —
область его изменения. На практике t обычно является «временем»,
а Т «временным интервалом». В тех случаях, когда структура мно¬
жества Т очевидна из контекста, будет использоваться более корот¬
кое обозначение {X (£)}. Без фигурных скобок X (t) будет использо¬
ваться для обозначения выборочной функции случайного процесса
{X (t), t Г}. Предполагается, что все рассматриваемые в этой главе
процессы имеют, если только не указано противное, нулевое среднее
(т. е. EX{t) — 0 для всех t Т). Корреляционная функция YXY{t^ t{)
определяется как Е [-Y(^) У где У (^) комплексно-сопряженное
к У {t\). Далее предполагается, что все процессы, за исключением
«белого шума», непрерывны в среднеквадратичном, т. е. E\X(t) —

4.31
ТЕОРИЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
— ЛД$) |2 -> 0	при ] t — s | —> 0 для	всех ty s	7.	Отсюда вытекает,
что rxxfe^i) непрерывна на 7 X 7. Все пределы случайных вели¬
чин и, в частности, те, которые встречаются при определении произ¬
водной и интеграла от случайного процесса, понимаются как пределы
в среднеквадратичном и равенство X(t)= Z(t), где X(t) и Z(t) —
случайные величины, означает, если	только не указано противное,
что E\X(t)—Z(t)\1 — 0. Для более подробного ознакомления с исчи¬
слением в среднеквадратичном читатель отсылается к книге Лоева [ 14J
(стр. 486 — 506). Процесс {X(t), t 7] называется стационарным
в широком смысле, если ГХх(^> ^i) является для всех tb ^^7
только функцией t2— tv В противном случае он называется нестаци¬
онарным. В дальнейшем для	удобства фраза	«в	широком смысле»
будет опускаться. Процесс {Z(t), t ^ 7} называется процессом с орто¬
гональными приращениями, если 7:([Z(^4)—Z(t^)\ [Z(t%)—Z(^)|) = 0
для всех th tb	^ 7 таких,	что	t3 ^	t{.	Процессы с орто¬
гональными приращениями обладают тем свойством, что их «произ¬
водные» можно формально рассматривать как «белые шумы». Если
E\Z(t2)—Z(^) |2 зависит только t.2 —1\ для всех th £>(^7, то
говорят, что \Z(t)) имеет стационарные приращения, и его «производ¬
ная» может рассматриваться как стационарный «белый шум».
Принимая во внимание вышеизложенное, задачу определения
формирующего фильтра можно сформулировать следующим образом.
Дан действительный непрерывный	в среднеквадратичном процесс
{Z(0>	^1*	Показать, что	{К(0}	может быть представлен в виде
у (0 = $ W(t, x)U(x)dx,
I
где импульсная переходная функция формирующего фильтра W(t, т)
непрерывна, a {U(t\ t 7}—стационарный «белый шум», и дать
конструктивный метод нахождения	W(t, т) (или соответствующего
дифференциального уравнения, если таковое существует). В некоторых
случаях типа тех, в которых существует дифференциальное уравнение
формирующего фильтра, для определенности поставленной задачи
возможно потребуется добавить	случайные начальные условия
п
2 ?*(*) Уь представляющие собой линейную комбинацию действитель-
i ~ 1
пых случайных величин К,-. Функции qt (t) здесь по предположению
непрерывны.
Если определить W(t, i) как характеристику фильтра, обратного
к W(ty т), то посредством прямых вычислений можно формально по¬
казать, что E\Y(t)—jj W(tf т) U (z) d т |2 = 0, если положить U(t) =
г
= \	(t, z) У ('z)d'z, и что W{t, т) удовлетворяет интегральному
г
6*

164
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
уравнению
ГууУъ *0 = 5 W(tb т) W(t{, т)dz.	(4.1)
г
После этого задача определения формирующего фильтра сводится
к решению интегрального уравнения (4.1). Но поскольку (t, т),
как правило, не существует в классе обычных функций и интеграл
^	т)	Y(z)dz	не сходится в среднеквадратичном даже при соот-
т
ветствующей интерпретации W~x (t, т), написанные выше выражения
не имеют строгого математического смысла. Такой смысл им можно
придать, если рассматривать W~l (t, т) как обобщенную функцию [15],
а § W'l(tf т) Y(z)dz как обобщенный случайный процесс [16]. При
т
этом W(t, т) будет опять решением интегрального уравнения (4.1).
В свете сделанных пояснений задачу определения формирующего
фильтра можно свести к решению интегрального уравнения (4.1). Если
для определенности задачи требуется добавить случайные начальные
условия, задаваемые случайными величинами Yt, то (4.1) заменяется
на уравнение
п п
где Tij = Е Yi Yj. Это и есть та формулировка задачи определения
формирующего фильтра, которая будет использоваться в дальней¬
шем. Следует отметить, что такая формулировка требует только зна¬
ния корреляционной функции ГYY{th t2), что является следствием того,
что все рассматриваемые равенства имеют место только в средне¬
квадратичном.
Задачу определения формирующего фильтра можно рассмотреть
и в случае дискретного параметра (Т—счетное множество). Однако
соответствующие результаты приводиться не будут, поскольку они
полностью аналогичны тем, которые получены здесь для случая не¬
прерывного параметра.
4.4.	Классические результаты для скалярных
стационарных процессов
Мы не будем указывать имен авторов, как это было сделано
в историческом очерке, представленных ниже результатов для ска¬
лярных стационарных процессов, поскольку в этом нет какой-либо
необходимости. Подробный вывод приводимых далее результатов,
которые довольно хорошо отражают существо дела, можно прочесть

4.41
КЛАССИЧЕСКИЕ РЕЗУЛЬТАТЫ ДЛЯ СКАЛЯРНЫХ ПРОЦЕССОВ
165
в книгах Дуба [ 171 и Гренандера и Розенблага [18]. Рассматривается
только случай непрерывного времени и естественно Г=(—оо, со).
Если случайный процесс {Р(0}*) является стационарным и непре¬
рывным в среднеквадратичном, он имеет спектральное представление
оо
Y(t)= $ eiiKkdZ (К).	(4.1)
—ОО
Здесь процесс Z(X) имеет ортогональные приращения и E\dZ(k)\2 —
= dFy(ty- Функция Fy(ty называется спектральной функцией про¬
цесса {/(0} и
оо
г,х(.) = £[К(г + т)Тчо]= 5	ЛЮ-	(4.2)
—со
Кроме того, Fy(X) не убывает и, поскольку
оо
S rf/7rM = ryy(0)<oo,	(4.3)
— ОО
ЕУ(Х) имеет также ограниченную вариацию. Следовательно, Fy(X)
может быть представлена в виде суммы трех неубывающих функций:
Fy(X) = FYl (X) + Fy2 (X) + FVi (X),	(4.4)
где Fyl(X) — скачкообразная часть EV(X), Fys(X)—абсолютно непре¬
рывная часть Е>(Х) и Fy?> (У)— непрерывная и сингулярная часть Fy(X).
Этому разложению ЕУ(Х) соответствует разложение {У (t)) на три
взаимно ортогональных процесса {Fi (0}> {^(0} и {^з(0} со спект¬
ральными функциями Fy1(X), F\s(X) и EV;i(X) соответственно.
Если {Y(t)) поступает на вход устойчивой линейной системы,
частотная характеристика которой G(X)**) удовлетворяет условию
оо
$ | О (X) j‘2 dF), (X) < оо,	(4.5)
—со
то выходной сигнал системы {АД^)} будет непрерывным в средне¬
квадратичном стационарным процессом. Его спектральная функция
Fx(X) определяется формулой
х
FxW= $ \G(k)l*dFy(X).	(4.6)
*) По предположению {Y (t)} принимает действительные значения.
**) G(X) соответствует функции С (X) в [17].

166	ФОРМИРУЮЩИЕ	ФИЛЬТРЫ	ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
Следует отметить, что, вообще, не требуется, чтобы О(Х) прйнадле-
оо
жала L2 (т. е. не требуется, чтобы jj | G(k) \2ciX<^ оо. Из (4.6) сле-
— со
дует, что Fx(F) будет абсолютно непрерывной, если таковой является
FyQО- Если FY(k) абсолютно непрерывна и |/K(X) |2 = F'(X), то (4.1)
можно заменить равенством
оо
К(0= S е^‘/у (X)dZ(K),	(4.7)
— ОО
где {Z(X)} имеет ортогональные приращения и Е | dZ(X) \2 — dX.
С другой стороны, предположим, что процесс {Y(t)) порождается
процессом {V(t)\ в соответствии с уравнением
оо
Y(t)= ^ W{i)dV(t — T),	(4.8)
—ОО
где {1/(0} имеет ортогональные приращения, E\dV (f)\2 = dt и
оо
\ I VtZ(т) |2 dx оо. Тогда
— оо
оо
Гуу (tb t2) =5 Wtfi — 0) W(t.2 — 0) <й.	(4.9)
—CO
Из (4.9) следует, что {У (0} стационарен и непрерывен в средне¬
квадратичном. Кроме того, применяя преобразование Фурье к обеим
частям равенства (4.9), легко показать, что
А	оо	оо
Fy(l)= \ |G(X)|*dX< J | G (X) j2 rfX = ^ | Щт)|*<*т.	(4.10)
—оо	—оо	—ОО
Здесь G(k) — преобразование Фурье W(t)*), и, следовательно, FY(ty
абсолютно непрерывна и FY(F) = | G(A) |2. Приращения {V{t)}> рас¬
сматриваемые формально, задаются формулой
V{t2)—V{h) = \U{t)dt,	(4.11)
о
где {U(t)} — «белый шум». Таким образом, (4.8) представляет отклик
линейной системы с весовой функцией U7(t) на «белый шум», а ра¬
венства (4.9) и (4.10) представляют хорошо известные результаты,
обычно получаемые инженерами менее строгим путем **).
*) Здесь применяется 12-теория или теория Планшереля преобразова¬
ний Фурье.
**) Обычный инженерный подход можно также строго обосновать, если
ввести в рассмотрение обобщенные функции и процессы.

4.4)	КЛАССИЧЕСКИЕ	РЕЗУЛЬТАТЫ	ДЛЯ	СКАЛЯРНЫХ	ПРОЦЕССОВ
167
В качестве следствия приведенных выше результатов, при условии
отказа от требования физической возможности формирующего фильт¬
ра, можно сформулировать простое необходимое и достаточное усло¬
вие существования решения задачи определения формирующего фильт¬
ра для непрерывных в среднеквадратичном стационарных процессов.
Если спектральная функция Fy(k) соответствует корреляционной функ¬
ции Ггу(т) процесса {У (()}, то {К(0} может быть представлен
в виде (4.8) тогда и только тогда, когда Fy(l) абсолютно непре¬
рывна. Более того, любую устойчивую систему, частная характери¬
стика которой удовлетворяет равенству | G(X) р2 =	(X), почти всюду
(п. в.) можно использовать в качестве формирующего фильтра для
процесса {У(Щ. Вообще, даже если Fy(^) не абсолютно непрерывна,
то сказанное выше все равно применимо к абсолютно непрерывной
части Fy{k), т. е. к Fy2(k) в разложении (4.4). Если не отказываться
от требования физической возможности, то (4.8) будет иметь место
при несколько более сильных ограничениях. Много лег назад Пэли
и Винер [19] (стр. 32, теорема 12) показали, что если J |G(X)|2£/X<^
<^оо*), где G(X)—частотная характеристика устойчивой линейной
системы, то эта система физически возможна тогда и только тогда,
когда
Если же имеет место равенство \ G (к) \2 = F'y (к), то для физической
возможности рассматриваемой линейной системы (формирующего
фильтра) необходимо дополнительное условие
Таким образом, для того чтобы формирующий фильтр был физи¬
чески возможным, Fy(ty должна быть абсолютно непрерывной и удов¬
летворять условию (4.13). Поскольку приведенные выше ограниче¬
ния на G(X) являются ограничениями только на ее абсолютную вели¬
чину, ясно, что они определяют формирующий фильтр неоднозначно.
Для того чтобы определить формирующий фильтр единственным обра¬
зом (т. е. определить его весовую функцию однозначно всюду, за
исключением множества меры нуль), желательно потребовать, чтобы
*) Предположение непрерывности Ууу (т) гарантирует ограниченность
оо
—со
оо
(4.12)
—ОО
(4.13)
ОО
— оо

168
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
он был минимально-фазовым *), т. е. G(X)=£0 для ImX<^0. Такая G(X)
определяется следующим интегралом (с потерей фазы):
О (X) = ехр
1	£	(1-1- А
2 nl	)	(X-
(1 + Хш) log F'y (w)
со) (1 -|- со2)
da).	(4.14)
Рассмотрим один важный частный случай, когда Fy(F) является
рациональной функцией X2. Тогда G(X) превращается в рациональную
функцию, полюса и нули которой находятся в области ImX^O, и
формирующий фильтр можно описать обыкновенным дифференциаль¬
ным уравнением с постоянными коэффициентами, причем эти коэф¬
фициенты совпадают с коэффициентами полиномов G(X). Хорошо
известно, что в этом случае применения формулы (4.14) для получе¬
ния G(X) можно избежать посредством «простой» факторизации поли¬
номов Fy(k). Именно этот метод рассматривается во всех вводных
инженерных учебниках по теории случайных процессов.
На этом, если исключить некоторые краткие замечания, встре¬
чающиеся в соответствующих местах в оставшейся части главы, мы
заканчиваем рассмотрение стационарных процессов **).
Ясно, что для непрерывных в среднеквадратичном скалярных
стационарных процессов и Т=(—сю, со) задача определения фор¬
мирующего фильтра получила свое окончательное решение до 1950 г.
4.5.	Обобщение метода «факторизации рационального спектра»
на нестационарные процессы
Операцию факторизации рационального спектра в принципе можно
обобщить и применить к некоторому ограниченному классу неста¬
ционарных процессов. Основные результаты здесь принадлежат Дар¬
лингтону, и мы приведем их ниже. Однако сначала изложим некото¬
рые необходимые для этого факты.
Если W(t, т) обозначает весовую функцию линейного фильтра,
на вход которого поступает «белый шум», то корреляционная функ¬
ция VYy{th t2) выходного процесса {Е(0}, когда она существует, выра¬
жается формулой
оо
г Mil, к)= 5	(4.15)
— ОО
*) Фильтр, обратный к физически возможному и минимально-фазовому
фильтру, является физически возможным и устойчивым. Это важно для при¬
менений в линейной среднеквадратичной теории фильтрации и экстрапо¬
ляции.
**) Задача определения формирующего фильтра, по-видимому, все еще
не решена для стационарных процессов, которые не непрерывны в средне¬
квадратичном.

4.5]
МЕТОД «ФАКТОРИЗАЦИИ РАЦИОНАЛЬНОГО СПЕКТРА*
169
Заметим, что, поскольку нижний предел этого интеграла равен —оо,
молчаливо предполагается, что «белый шум» поступал на вход
фильтра непрерывно в течение всего бесконечного прошлого. Если
рассматриваемый фильтр является физически возможным, то W(t, т) = 0
для i^>t, и верхний предел интеграла в равенстве (4.15) можно за¬
менить на min (tht£). Обозначая символом Wa(t,fz) весовую функцию
сопряженного фильтра, имеем Wa (t, т) = W(т, t\ и TYY(tb t%) может
быть теперь эквивалентным образом выражена формулой
оо
Гуy(tu h)= $ W(t„ х) Г (X, *j)dx.	(4.16)
— ОО
Поскольку согласно (4.16) корреляционная функция Гh) является
сверткой двух весовых функций, ее можно интерпретировать как
весовую функцию физически невозможной (самосопряженной) системы,
состоящей из первоначального фильтра и последовательно соединен¬
ного с ним сопряженного фильтра.
Когда рассматриваемый фильтр полностью описывается линейным
дифференциальным уравнением конечного порядка, его реакция V
связана с воздействием Е выражением вида
В (p,t)V (t) = И (f) А (р, t) Е (0,	(4.17)
где B(p,t) и A(p,t) — полиномы по р = ^с коэффициентами, зави¬
сящими от времени:
в (р, о =рп +	{t)pn-'	+	... -f (0, |
A(p, t)—f)mbm_i(t)pm~’1 -)-••• ~bao(0> J
a H(t)—скалярный множитель, также зависящий от времени. Любой
набор п линейно независимых решений, скажем	i—	1,	...,	я,
уравнения
В(р, t) V(t) = 0	(4.19)
образует набор базисных функций (бф) для В(р, t) и для фильтра.
Аналогично любой набор т линейно независимых решений уравнения
А(р, t)E(t) = 0	(4.20)
образуют набор базисных функций для А(р> t). Эти функции назы¬
ваются функциями нулевой реакции (фнр). Если фильтр имеет по¬
стоянные параметры (стационарен), то бф и фнр *) имеют экспонен-
s t
циальный вид е а, где — обычные полюса и нули передаточной
функции фильтра, бф и фнр нестационарных систем также играют
важную роль, даже если их и нельзя представить с помощью про¬
стых коэффициентов, подобных 53.
*) Или их линейная комбинация.

170	ФОРМИРУЮЩИЕ	ФИЛЬТРЫ	ДЛЯ	СЛУЧАЙНЫХ	ПРОЦЕССОВ	[ГЛ.	4
. Когда два фильтра, каждый из которых полностью описывается
дифференциальным уравнением конечного порядка, соединены после¬
довательно, то получающийся в результате фильтр полностью опи¬
сывается дифференциальным уравнением конечного порядка, соответ¬
ствующим «произведению» дифференциальных уравнений этих двух
фильтров. В терминах операторов упомянутые «произведения» можно
представить как *)
где BV — HAE— дифференциальное уравнение общего фильтра. Опе¬
раторы В, А и И можно получить из Въ Въ Аь А2, Н\ и Н2 по¬
средством дифференцирования и алгебраических операций **). Фор¬
мально это соответствует свертке весовых функций этих двух дан¬
ных фильтров. Аналогично сумме весовых функций формально соот¬
ветствует подходящим образом определенная «сумма» соответствую¬
щих им дифференциальных уравнений:
Операторы В и А и скалярный множитель И также можно полу¬
чить из В\, Вь Ах, Аъ Их и посредством дифференцирования и
алгебраических операций ***). Далее, бф В состоят из бф В\ и Я2, но
бф А (фнр «суммы») не связаны каким-либо простым путем с бф
А\ и А2*
Возвращаясь к фильтру, описываемому уравнением (4.17), отме¬
тим, что фильтр, сопряженный к нему, полностью описывается диф¬
ференциальным уравнением
сопряженным к уравнению (4.17). Операторы £*(/?,£) и А7(/>, t) легко
определяются из B(pyt) и A(p,t). Когда рассматриваемый фильтр
физически возможен, его весовая функция, соответствующая уравне¬
нию (4.17), может быть выражена в виде
BxVx=HxAlE) BvV=H2A.1Vx, BV = HAE,	(4.21)
Вх Vx = НхАхЕ,	В2 V* = НъАъЕ,
V=Vi-\-Vif BV — HAE.
(4.22)
(p, t) V(t) = ±H (t) /Г (P, t) E (t),
(2.23)
( n
(4.24)
*) Аргументы опущены для удобства обозначений.
**) Подробности см. в главе 1 этой книги.
***) Подробности см. в главе 1 этой книги.

4.5)	МЕТОД	«ФАКТОРИЗАЦИИ	РАЦИОНАЛЬНОГО	СПЕКТРА»
171
а весовая функция физически невозможного фильтра, соответству¬
ющая уравнению (4.23), — в виде
т) =
'<■
i = 1
(4.25)
О,
t>
«Произведение» уравнений (4.17) и (4.23), соответствующее свертке
(4.16) весовых функций W(t, г) и Wx(t, т), записывается как
(4.26)
Из рассмотрений, следующих за уравнением (4.16), ясно, что весовой
функцией фильтра, описываемого уравнением (4.26), является ГУк(^ь t2),
которая с помощью уравнений (4.16), (4.24) и (4.25) может быть за¬
писана в виде
У —
2twQ'w' '■>'*
i= 1
п
(4.27)
2тт '■<'»
i= 1
Симметрия Гyy{tb t2) выражает тог факт, что уравнение (4.26) явля¬
ется самосопряженным уравнением.
Принимая во внимание вышеизложенные результаты, задачу опре¬
деления формирующего фильтра в том виде, в котором она встреча¬
ется в модели Боде — Шеннона, можно решить, если предположить,
что «сигнал» 5(0 и «шум» N(t) получаются в результате прохож¬
дения «белых шумов», порожденных двумя некоррелированными
источниками через физически возможные фильтры, описываемые линей¬
ными дифференциальными уравнениями конечного порядка. Если бф
и фнр этих фильтров известны, то их весовые функции Ws(t, т) и
W/v(0 т) легко определяются, а Гss(tf т) и IVa4^ т) могут быть
найдены с помощью формулы (4.16). Соответствующие дифферен¬
циальные уравнения и сопряженные к ним также легко определяются,
как это было описано выше (даже если бф и фнр фильтров, порож¬
дающих «сигнал» и «шум», неизвестны). Если F = S-\- N, то
1, t2) = Tss(t\y t^)-{-rNN{th t%), и дифференциальное уравнение
вида (4.26), которому соответствует весовая функция TFF(th t2), можно
найти из самой ГFF(th t2) (или «суммированием» дифференциальных
уравнений, соответствующих Tss(tb t2) и ГдглЧ^ь t2), если TFF(tl} t2)
неизвестна).

172
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
[ГЛ. 4
Таким образом, мы определяем
Bs (р, 0 V(t) = ± Ms (О As (р, t) Е (0,	|
BN(p, t) V(t) = ±H%(t) AN(Pi t)E{t\	(4.28)
BF(P> *) V(£) = ±HHt)AF(p, f)E{t). )
Число бф Вр(р, t), Bs(p, t) и BN(p, t) четно, половина из них — ба¬
зисные функции систем, порождающих S(t) и N(t), а.другая поло¬
вина — бф соответствующих физически невозможных сопряженных
фильтров. С другой стороны, число бф Af(p> t) опять четно, но между
ними и бф As(p, t) и AN(p, t) нет простой связи. Бф AF(p, ~t) следует
искать как решения уравнения
АР(р, t)E{t) = 0.	(4.29)
Решению уравнения (4.29) в стационарном случае соответствует вы¬
числение нулей рациональной спектральной плотности процесса «сиг¬
нал плюс шум». В этом случае спектральная плотность F получается
в результате сложения спектральных плотностей S и N (что соот¬
ветствует	образованию	суммы дифференциальных	уравнений для
^ss(tь U) и rW(^i, У)- При таком сложении полюса сохраняются,
а нули следует вычислять как нули некоторого полинома (что соот¬
ветствует нахождению решения уравнения (4.29)).
Теперь задача определения формирующего фильтра, как она рас¬
смотрена здесь, сводится к нахождению весовой функции WF(t, т)
такой, что фильтры, соответствующие как WF(t, т), так и обратной
к ней, физически возможны и ведут себя подходящим образом (т. е.
устойчивы) при т —>• — оо для всех t, и такой, что
оо
*,)= 5 WF(tb х)	tjdx.	(4.30)
— ОО
Для того	чтобы	сделать	эго, найдем бф Вр(р, t) из	«известных» бф
Bs(P> 0 и	BF(p,	t) и бф	Ар(р, t) путем решения уравнения (4.29).
Далее задача заключается в том, чтобы половину из них отнести
к №>(/, т), а оставшуюся половину — к Wrp{ty т) так, чтобы требова¬
ния, предъявленные выше к Wp(t, т), были по возможности выпол¬
нены. Можно показать, что эта задача имеет решение при условии,
что коэффициенты дифференциальных уравнений фильтров, порож¬
дающих 6* и Л/, регулярны при t = со и являются периодическими
или медленно меняются. Тогда бф либо становятся экспоненциальными
при tz*i оо, либо произведениями экспоненциальных на периоди¬
ческие коэффициенты, либо они ограничены экспоненциальными функ¬
циями при t± оо. Те из бф, которые соответствуют экспонентам
«V с Re vS, 0, относятся к WF(t, т) точно так же, как и в стацио¬

4.6]
ДАЛЬНЕЙШЕЕ ОБОБЩЕНИЕ РЕЗУЛЬТАТОВ
173
нарном случае. Получаемая таким образом WF(ty т) будет иметь тре¬
буемые свойства.
Прежде чем перейти к следующему параграфу, отметим, что в
этом параграфе предполагалось, что Т — (—оо, оо), а относительно
Tpp{tb Ч) было известно, что она равна сумме корреляционных функ¬
ций двух процессов, получающихся в результате прохождения «белых
шумов», порождаемых двумя некоррелированными источниками, через
физически возможные фильтры, описываемые линейными дифференциаль¬
ными уравнениями конечного порядка. Вследствие предположения об
устойчивости формирующих фильтров S и N и выбора интервала Т
ничего не было сказано о начальных условиях для ГFp (th t2) и ГлrN(th t2).
Представляется, что изложенный метод применим более широко, чем
это было показано, хотя точная область его применения, по-видимому,
в настоящее время неизвестна, и в свете работы Калмэна [13] ее
вряд ли стоит определять.
4.6 Дальнейшее обобщение результатов
Выводы предыдущего параграфа можно далее обобщить несколько
другим путем. Соответствующий результат здесь принадлежит Бат-
кову [11] и приводится в основном ради полноты изложения. Если
предположить, что процесс {^(0} имеет корреляционную функцию
^) =
i = 1
п
(4.31)
i = 1
и если qt{f) имеет n непрерывных производных, то qi{t) можно рас¬
сматривать как базисные функции дифференциального оператора
Б(р, t) в уравнении (4.19). Далее bi(t) в (4.18) можно легко найти
из qt{t) путем хорошо известных алгебраических операций [20] (тео¬
рема 6.2). Теперь задача заключается в том, чтобы найти коэффи¬
циенты a,i(t) дифференциального оператора А(ру t). Если предполо¬
жить, что Гуу(^1> U) такова, что ее можно найти с помощью ai(t) из
(4.31), то
В(р, tjTyyitb <в)=о,
в (р, ti)rYY(tu t%) = А (р, ti) W(tb ft),
(4.32)
где
W{t, х) = Ах(р, x)G(t, т),
В(р, t)G(t, —	-	т).
(4.33)
(4.34)

174
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ (ГЛ. 4
Используя равенства (4.33) и (4.34), (4.32) можно переписать как
В (р, ti) Г (*„ к) = А (р, tx) Ла (/?, ^ G (t9, tx\ t9 >	(4.35)
Так как G(f2> можно также найти путем алгебраических операций,
коль скоро известны qi(t\ в уравнении (4.35) остается неизвестным
только произведение операторов А (р, t)Aa(p, t\ которое из него оп¬
ределяется. Теперь остается разложить произведение Л(р, t)Aa(pf t)
на два сопряженных сомножителя. Как указывает Катков, это сделать
очень трудно, за исключением случая скалярного А (р, t), в котором
никаких трудностей не возникает. Конечно, в этом последнем случае
решение было известно уже давно [10]. Было замечено, что задача
факторизации А(р, t)Aa(p, t) в точности является задачей факториза¬
ции Ар(р> t) в работе Дарлингтона.
Вследствие указанной трудности Батков [11] предложил другой
метод определения а*(0*)> основанный на вычислении скачков част¬
ных производных от Гyy(^i, t9) при ti — tz. Батков выводит уравне¬
ние (41), которое согласно его утверждению позволяет получить a^t)
последовательно, начиная с am(t) и кончая a0(t), посредством алгеб¬
раических операций. Однако если тщательно произвести все вычисле¬
ния, предложенные в [11], то оказывается, что каждое последующее
из рекуррентных уравнений сильно зависит от предыдущих, вследст¬
вие чего этот рекуррентный метод несостоятелен. Батков не заметил
указанной зависимости, потому что он не проделал подробно соот¬
ветствующие вычисления, и рассмотрел только простые примеры. Все
попытки модифицировать метод Баткова приводили к системам нели¬
нейных дифференциальных уравнений (типа Рикатти) относительно
di(t), а не к алгебраическим уравнениям, как этого хотелось бы.
4.7.	Некоторые фундаментальные результаты
для нестационарных процессов
Хорошо известно, что для процессов с произвольной корреляцион¬
ной функцией физически возможного фильтра, вообще говоря, не су¬
ществует. Например, как было указано в § 4.4, в стационарном слу¬
чае для физической возможности формирующего фильтра необходимо,
чтобы его частотная характеристика была абсолютно непрерывна и
удовлетворяла критерию Пэли — Винера (4.13). В нестационарном
случае, по-видимому, не существует никакого простого критерия, ана¬
логичного тому, который был получен Пэли и Винером. Учитывая
трудность рассматриваемой задачи, этот факт не слишком удивите¬
лен. В данном параграфе вопрос существования физически возможного
формирующего фильтра рассматривается для класса разложимых
корреляционных функций. Будет показано, что если функция этого
*) Наши a-t{t) — это bi{t) у Баткова, и наоборот.

4.7] НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ДЛЯ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ 175
класса удовлетворяет одному замечательно простому условию, то
физически возможный фильтр существует. Кроме того, мы также
обсудим вопрос о единственности формирующего фильтра. Все эти
результаты рассматриваются в недавнем отчете [21].
Ограничиться рассмотрением разложимых корреляционных функ¬
ций представляется разумным с той точки зрения, что в этом случае
получающийся формирующий фильтр довольно легко реализовать
физически. Эго, конечно, важно для инженерных приложений.
Довольно интересно и поучительно изучить, как обстояло дело
с физической возможностью в двух предыдущих параграфах.
Дарлингтон, по-видимому, вполне осознавал проблему физической
возможности и в действительности дал на нее ответ в двух довольно
ограничительных случаях. Ограничительных в том смысле, что он
предполагал физическую возможность лежащих в основе всех рас¬
смотрений формирующих фильтров сигнала и шума и периодичность
или регулярность на со коэффициентов соответствующих дифферен¬
циальных уравнений. Ясно, что такой ответ довольно далек от желае¬
мого. Батков просто избежал обсуждения вопроса физической воз¬
можности и связанных с этим ограничений, неявно предполагая, что
рассматриваемая им корреляционная функция имеет требуемый вид.
Леонов, работа которого обсуждается ниже, не касался физической
возможности формирующего фильтра, потому что это не требовалось
для рассматриваемых им приложений. Калмэн, работы которого также
обсуждаются ниже, получал только физически возможные фильтры.
Пренебрегая на минуту начальными условиями, покажем, что вопрос
о существовании физически возможного формирующего фильтра сво¬
дится к вопросу о существовании решения нелинейного интегрального
уравнения Вольтерра первого рода
h
Г {th t2) = 5 dx W(th т) W{tb x), ti Зг t-i Ss 0.	(4.36)
0
Когда корреляционная функция разложима, т. е.
п
г (^1, t-г) =	(<,)/>, (*л h к 0,	(4.37)
1=1
в свете формул (4.24) и (4.27) решение уравнения (4.36) целесооб¬
разно искать в виде

176
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
[ГЛ. 4
В таком случае эго интегральное уравнение превращается в
Л	Л	Л	/о
2 41 (<i)Pi (О	= 2 я1к) 2 41 (О \d^i « h (4	(4.39)
1 = 1	t = 1	i = 1	О
А используя линейную	независимость	qi(tx)	и	добавляя начальные
условия, получим
~ t
р«(о=2
j=i
^Мт)8,(т)+Г;,
-О
^0; i=l, п. (4.40)
Таким образом, задача свелась к вопросу о существовании решения
системы (4.40) нелинейных интегральных уравнений Вольтерра пер¬
вого рода. Тем самым мы произвели редукцию уравнения (4.36), ко¬
торое можно рассматривать как бесконечную систему интегральных
уравнений (для каждого значения tx получается одно уравнение).
Обычно при изучении интегральных уравнений Вольтерра первого
рода сначала их преобразуют в интегральные уравнения второго рода,
а затем уже применяют известные стандартные методы исследования
интегральных уравнений Вольтерра второго рода. Для линейных
уравнений такое преобразование легко выполнимо [22]. То, что урав¬
нения (4.40) можно преобразовать в интегральное уравнение второго
рода, возможно, не очевидно, но тем не менее это делается следую¬
щим образом.
Дифференцируя уравнения (4.40), получаем
t	1	п
\ dtfi (х) ру (х) 4- Г,у + р, (0 2 4J (0 h (0- (4.41)
о	J	У=1
Изучение уравнения (4.41) показывает, что множитель при (3,-(0
п
является одним и тем же при всех I и равен ^ *7/(0Ру (0- Пусть
7=1
п
k(t)= ^	Задача	теперь	заключается в том, чтобы опре-
7 = 1
делить неизвестное k(t). Если бы k(t) было известно и не равнялось
нулю для всех ^^>0, то желаемое интегральное уравнение второго
рода можно было бы получить, разделив обе части уравнения (4.41)
на k(t). Хотя на первый взгляд может показаться, что нет никакой
надежды определить функцию k(t), поскольку в нее входят неизвест¬
ные |оказывается эго сделать можно. Решая уравнение (4.41),
находим, что
ргч<)= 2 4П о

4.7] НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ДЛЯ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ 177
Подставляя (4.42) обратно в (4.41), получаем следующее соотно¬
шение:
Таким образом, k{t) можно определить из Г(^, t2).
Очень важно отметить, что если $i(t) действительны, то из урав¬
нений (4.42) и (4.45) вытекает, что J0t	для всех t^O. Итак,
интегральное уравнение первого рода (4.40) преобразовано в инте¬
гральное уравнение второго рода (4.42).
Конечно, остается нерешенным вопрос о том, что делать в слу¬
чае, когда k(t) = 0. В этом случае уравнения (4.41) сводятся к си¬
стеме интегральных уравнений первого рода вида уравнения (4.40),
в котором qi(t) и pi(t) заменяются на Qil) (t) ир\1) (t) соответственно.
Получившееся уравнение можно вновь преобразовать в интегральное
уравнение второго рода так же, как это было сделано ранее с урав¬
нением (4.40). В результате получим
п
pi ’ (0 — 2 Я?' (0 \ dxh СО Р/ (О -г г«7 =
}=1 L«
I j = I	k	=	1	о
из которого, приводя подобные члены, имеем
п
kHt)= 2 q(t)
п
n
г t
- s mo S Я] (0 $Лру(т)р*(т) + 1> . (4.44)
Ho
* = i	j	= i	Lu
:) Ps(T) + Г.-ft =pk if). Следовательно,
k(t) = ±
qjit)p'i (0- q'j" (t)Pj(0 = ± V\ 1 (0. (4.45)

178
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
По гой же причине, что и раньше, требуется, чтобы Л, а (0^0 Для
всех 0. Естественно, если kx(t) = 0, то новое уравнение опять
преобразуется и т. д.
Когда k(t)= 0 (или ki(t) = 0 и т. д.) для некоторых значений t,
но не тождественно, возникает более сложное интегральное уравнение,
Пикара, называемое уравнением третьего рода. Подобные случаи для
линейных уравнений изучались Лалеско [23].
Задача теперь свелась к установлению существования решения
интегрального уравнения второго рода (4.42). Это можно сделать,
используя некоторые результаты, принадлежащие Сато [24], который
исследовал вопрос о существовании решений нелинейных интегральных
уравнений Вольтерра с помощью
теоремы о неподвижной точке. Идею,
лежащую в основе этой теоремы,
можно хорошо продемонстрировать
на следующем простом примере.
Пусть С—множество {х: O^jc^l},
и пусть о(х) — непрерывное одно¬
значное преобразование С в себя
(т. е. о(лг) — непрерывная однознач¬
ная функция, определенная на [0,1],
и значения а(х) принадлежат отрез¬
ку [0,1] для всех лг [0,1]). Тогда
существует некоторая точка х0^-С
такая, что jc0 = a(jt0). Точка х0 называется неподвижной точкой пре¬
образования а (л:). Из рис. 4.1 истинность этого утверждения очевидна.
Также очевидно, что х0 может равняться 1, либо 0 и что она необя¬
зательно единственна (на рис. 4.1 имеется пять неподвижных точек).
Обобщение этого простого результата на более общие множества,
лежащие в более общих топологических пространствах, привело к по¬
лучению довольно мощных теорем (о неподвижной точке), позволяющих
устанавливать существование решений (неподвижных точек) общих
функциональных уравнений и, в частности, интегральных уравнений.
При рассмотрении интегральных уравнений С превращается в некоторый
класс функций, а а является интегральным оператором, например
таким, который стоит в правой части уравнения (4.42). Ясно, что
утверждение о существовании неподвижной точки у а эквивалентно
утверждению о существовании решения соответствующего интеграль¬
ного уравнения. Одна из наиболее общих теорем о неподвижной точке,
используемая Сато, была доказана Шаудером [25] (стр. 260). Эту
теорему можно сформулировать следующим образом:
Теорема Шаудера. Пусть С — непустое компактное выпуклое
множество из локального выпуклого пространства X, и пусть a —
непрерывное однозначное преобразование из С в С. Тогда существует
некоторая точка х0 £ С такая, что а(х0) = х0.
Рис. 4.1. Иллюстрация теоремы
о неподвижной точке.

4.7] НЕКОТОРЫЕ РЕЗУЛЬТАТЫ ДЛЯ НЕСТАЦИОНАРНЫХ ПРОЦЕССОВ 179
При применении теоремы Шаудера основная проблема, конечно,
заключается в том, чтобы найти класс С, подходящий для рассматри¬
ваемой задачи.
Интересно отметить, что фигурирующие в теореме требования
компактности и выпуклости С можно было предвидеть при рассмо¬
трении простого примера, приведенного выше.
Непосредственно, применяя результаты Сато к системе интеграль¬
ных уравнений (4.42), легко получаем следующее важное утверждение.
Предположим, что Гуу(^, t%) имеет вид (4.37), что ф1) (t) и р(" (t)
существуют и непрерывны на [О, 7], что 70, i(0^>0 на [0, 7'] и
что существует неотрицательно определенная матрица такая.
п
что Pi{0)— ^	(0)	= 0 для всех и Тогда физически возмож-
j= 1
ный формирующий фильтр существует и W(t, т) имеет вид (4.38),
где рг(£) непрерывны на [0, Т].
Единственная возможная трудность при применении этого результата
заключается в том, что решение, существование которого утверждается,
может быть, невозможно продолжить на весь [0, Г]. Можно показать,
что из такой невозможности вытекает неограниченность $i(t) и, сле¬
довательно, их разрывность на [0, Т]. В приведенном утверждении
и в тех утверждениях, которые следуют дальше, предполагается,
что рассматриваемое решение можно продолжить на весь отрезок
[0, Г]. Во всяком случае, можно показать, что приведенный результат
имеет место [0, 7'], где 0<^7'<:7. Случаи, в которых $i(t) неогра-
ничены, не очень важны для инженерных приложений, кроме того,
они связаны с вычислительными трудностями.
Когда 701 ,(£) = () на [0, 7|, но	на	[0,	7],	имеет	место
следующая модификация вышеприведенного утверждения.
Предположим, что Гуу(/Ь t^) имеет вид (4.37), что qi(t) и р?] (t)
существуют и непрерывны на [0, 7], что	на [0, 7] и что
существует неотрицательно определенная матрица Г/;- такая, что
п	п
МО)— 2 ^*7^7 (0) = 0 и р\1) (0)— 2 ^ij4T (0) = 0 для всех L Тогда
j =\	;	=	1
физически возможный формирующий фильтр существует на [0, Т\>
его весовая функция имеет вид (4.38), [3t-(£) непрерывны на [0, Т\
и W{t, t) = 0 для t£ [0, 7|.
Дальнейшая модификация первого утверждения, когда о/0(1(0 =
= 71>2(0 = 0 на [0, 7), но Л. з(0^>0 на [0, 7], очевидна. Случай,
когда JQ l(t) = 0 для некоторого f £ [0, 7], но не тождественно, не
рассматривается. Возможно, что удовлетворительные результаты в этом
случае можно получить, следуя работе Лалеско [23].
Наконец, предположим, что в дополнение к условиям, при которых
имеют место вышеприведенные утверждения, qt (t) и pi (t) имеют п

180
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
непрерывных производных на [0, Т\> и определитель Вронского, со¬
ставленный из <7*(0> не обращается в нуль на [0, 7']. Тогда, последо¬
вательно дифференцируя уравнения (4.42), получим, что	имеют
п—1 непрерывную производную на [0, Т]. Отсюда следует, что рас¬
сматриваемый формирующий фильтр может быть описан дифференци¬
альным уравнением вида (4.17), где at{t) и bj(i) непрерывны на
10, Т].
Теперь, после того как мы решили вопрос о существовании физи¬
чески возможного формирующего фильтра, естественно возникает
вопрос о его единственности. Из уравнения (4.40) ясно видно, что
его решение не единственно. В самом деле, если W(tyz) — решение,
то — W(t,~) также является решением. Заметим, что если U7(^, т)
является решением, соответствующим знаку плюс в (4.45), то реше¬
ние— W(t, т) соответствует знаку минус в (4.45). Но остается вопрос,
является ли решение уравнения (4.40) единственным с точностью
до знака. Ответ на этот вопрос отрицателен потому, что может
существовать больше чем одна неотрицательно определенная матрица
удовлетворяющая требованиям приведенных утверждений. А раз¬
личные матрицы Tij приводят к различным решениям уравнения (4.40).
Например, рассмотрим корреляционную функцию
Две матрицы
8	—20/3
Г:.=!| 2 -Щ\ Гг.=
"	|—2/3	1/4	J’	11
Л) (0=1
—20/3	25/41
удовлетворяют требованиям первого утверждения. Далее прямая под¬
становка в уравнение (4.42) показывает, что §i(t) = (2et и р2(^) = —е*
являются на [0, оо) решениями, соответствующими Гг:у, в то время как
3j(f) = —4е* и (32(Т) = Ье** являются решениями на [0, оо), соответ¬
ствующими Г/у. Отсюда Wi(t, т)=2£"(Г~х)—и	т)	=
= —4<г0-”) -j- 5е~2^-т) — весовые функции физически возможных
фильтров, получающихся для матриц Г\j и Гу соответственно. При¬
меняя к Wi(t — т) и W<i(t — ^) преобразование Лапласа, получим
р ( г>\ 	 «S	-f“ 3	Г1 ( Q\ 	 53
Ui(6) — (S+ 1)(5 + 2) И а2(М— (s+ i)(5 + 2)*
Интересно отметить, что передаточная функция системы, соответ¬
ствующей Г,-}, имеет нуль в левой полуплоскости, тогда как переда¬
точная функция системы, соответствующей Г/у, имеет нуль в правой
полуплоскости. Теперь в свете этого примера возникает вопрос, яв¬
ляется ли решение уравнения (4.40) единственным, если в уравнении
(4.45) берется, скажем, знак плюс, а матрица Г,-у, удовлетворяющая

4.8]	РЕЗУЛЬТАТЫ.	ОСНОВАННЫЕ	НА	РАЗЛОЖЕНИЯХ	В	РЯДЫ
181
требованиям приведенных утверждений, фиксируется. Из нижесле¬
дующего утверждения, которое можно доказать методом последова¬
тельных приближений, вытекает, что ответ на этот раз является по¬
ложительным.
Если условия утверждений, сформулированных выше курсивом,
удовлетворяются, то физически возможный фильтр существует на
[О, Т\у а если знак в уравнении (4.45) и матрица Ггу- фиксированы,
то этот формирующий фильтр единственный.
На этом мы заканчиваем рассмотрение вопросов существования и
единственности физически возможных формирующих фильтров для
случайных процессов с разложимыми корреляционными функциями.
Ясно, что уравнение (4.42) можно использовать для вычислительных
целей.
4.8.	Результаты, основанные на разложениях в ряды
Когда процесс {АДО} можно представить в виде бесконечного
ряда, задача определения формирующего фильтра может быть решена
совершенно прямым путем, если только отказаться от требования
физической возможности. Основной результат здесь принадлежит
Леонову [12].
В этом случае задачу определения формирующего фильтра можно
переформулировать следующим образом. Дан «белый шум» {УД £)}*),
где —оо <^t <^оо (т. е. Ту = (—оо, оо)), и нестационарный процесс
{АД£)}, где 0<^t<^T (т. е. Гх=(0, Г)). Требуется показать, что при
некоторых условиях случайная функция процесса {АДО} (выборочная
функция процесса {АД£)}) может быть представлена в виде
где (линейный) оператор Ах определяется по функции АДО **). За¬
дача, обратная к этой, заключается в представлении Y(t) в виде
где Ах — оператор, обратный к Ах- Ниже соответствующие операторы
Ах и Ах будут явно построены и тем самым будет показано, что
поставленные задачи имеют решение. Для этого мы воспользуемся
некоторыми результатами из книги [26].
*) Предполагается, что для всех рассматриваемых здесь «белых шумов»
EY (t) = 0.
**) Пугачев [26, 27] называет равенство (4.48) интегральным каноническим
представлением X (t).
X(t) = AxY(t),
(4.48)
Y(t) = A~xlX{t),
(4.49)

182
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
[ГЛ. 4
Хорошо известно [26], что случайная функция Z(t), где Tz = (a, b),
может быть представлена в виде ряда (каноническое разложение)
Z(t)=	(4.50)
i = i
где Bi — случайные величины, удовлетворяющие условиям
EBiBj = bijDj,	(4.51)
a Zi (it) — некоторые регулярные (неслучайные) функции. Для того чтобы
ряд (4.50) сходился к Z(t) в среднеквадратичном, необходимо и до¬
статочно, чтобы ряд
оо
Tzz (k, k) = Ц DiZi (<,) г, (k)	(4.52)
i = 1
сходился к VZz(U, U) в каждой точке. Определение сходимости в
среднеквадратичном, конечно, имеет смысл только для случайных
функций с конечной дисперсией.
Далее для решения поставленной задачи Y(t) необходимо пред¬
ставить в виде ряда (4.50). Но поскольку У(t) не имеет конечной
дисперсии, сходимостью в среднеквадратичном воспользоваться нельзя,
и	возникает	необходимость введения нового понятия	сходимости.
Леонов	ввел	понятие слабой сходимости в среднеквадратичном **).
Говорят, что последовательность случайных функций Un(t) слабо
сходится в среднеквадратичном к случайной функции U(t\ если
интеграл
т
ап{Т)— J R(t) Un{t)dt	(4.53)
0
при со сходится в среднеквадратичном для любой достаточно
гладкой случайной функции R(t). Под достаточно гладкой случайной
функцией здесь понимается случайная функция с конечной дисперсией,
непрерывная в среднеквадратичном и имеющая необходимое число
непрерывных производных и корреляционную функцию rRR(tht.2),
ос
удовлетворяющую неравенству ^	(£,	t) dt сю. Можно показать,
—оо
что при таком определении сходимости У(t) представимо в виде
оо
т=Есм(Ъ	(4-54)
1 = 1
*) Zi (t) не обязательно ортогональны и —со^а	^оо.
**) Ясно, что это понятие аналогично обычному понятию слабой сходи¬
мости в гильбертовом пространстве [28].

4.8]	РЕЗУЛЬТАТЫ. ОСНОВАННЫЕ НА РАЗЛОЖЕНИЯХ В РЯДЫ	Ш
где ECiCj = bij,	а уi(t)—любая	полная (в L2)	система ортонормиро-
ванных функций	на (—оо, оо).	Ряд в правой части	(4.54) слабо
сходится в среднеквадратичном	к случайной	функции	«белого шу¬
ма» Y(t).
Теперь довольно легко решить нашу основную задачу. Ct- (4.54)
определяются как
С,=71,	(4.50)
где Vi являются коэффициентами разложения в ряд X(t)
со
X (0 =	2 ViX.it),	(4.56)
i = I
a Di = EVl. Линейный оператор Ах в таком случае определяется
как
00
AxY(i)=l Wx(t,z)Y(x)d?,	(4.57)
— ОО
где
оо
wx it, t) = S /D, Xt (t)Уi (X).	(4.58)
1 = 1
Далее из (4.57) и (4.58)
со
AxY(t)= \ Wx (t, x) Y (x) dx —
—OO
CO
= 2 V0(Q = *(9.	(4.59)
i = \
Отметим, что интеграл в (4.59) понимается в среднеквадратичном.
Функции Wx (*, т) и У (t) в уравнении (4.59) можно определить
бесконечно многими способами. Это связано с тем, что согласно
Пугачеву [26] для X(f) можно получить бесконечно много различных
представлений вида (4.56). Однако Леонов показал, что если Y(t)
выбирается так, что имеет место (4.59), то существует одна и только
одна Wx {U т), т. е. представление Wx (t, т) единственно.
Наконец, легко решается и обратная задача. Определим Ах как
со
Ах'Х(1) = \ U7*1 it, х) Л-(х) dx,	(4.60)
где
Ил'	")=	(0	ai	W/	VDit	(4.61)
i= i

184
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
а а,*(т) выбирается так, чтобы
т
\ai{x)Xj{x)dx = bij.	(4.62)
О
Как и раньше, yi{t) — любая полная (в Z>2) система ортонормиро-
ванных функций на (—оо, оо). Тогда из (4.53), (4.60), (4.61) и (4.62)
следует, что
Т	со
Y(t) = \ и?*1 (t, X) X (х) dx = У -^гу, (0.	(4.63)
0	i=\*	1
Как отмечалось выше, ряд в правой части (4.63) слабо сходится
в среднеквадратичном к случайной функции Y(t) «белого шума».
Этим завершается рассмотрение решения задачи определения фор¬
мирующего фильтра и	соответствующей	задачи определения	обрат¬
ного формирующего фильтра с	помощью	разложений в ряды.	Ясно,
что весовую функцию формирующего фильтра в данном случае можно
выписать в виде ряда сразу же, как только будут известны Xi(f)
и Dt для канонического разложения X(t). В своей книге [26] Пуга¬
чев предложил несколько довольно простых методов нахождения
первых п членов разложения вида (4.56). Эти методы позволяют из¬
бежать необходимости определения собственных значений и собствен¬
ных функций интегральных уравнений, фигурирующих в хорошо
известной теореме представления Карунена — Лоева. Вместе с тем
следует отметить, что	решение	Леонова	всегда получается	в виде
бесконечного ряда и, кроме того, нет никаких гарантий физической
возможности получаемого формирующего фильтра или обратного
к нему.
4.9.	Представление векторных процессов
Все случайные процессы, рассматриваемые в этой главе, до на¬
стоящего времени были скалярными, т. е. случайная величина X(t)
принимала скалярные значения при всех t Т. Напротив, в этом
параграфе рассматривается задача определения формирующего фильтра
для векторных процессов. Для одного класса векторных процессов
было получено особенно полезное представление. Калмэн и Бьюси [29]
использовали это представление при выводе своих результатов, ка¬
сающихся линейной среднеквадратичной фильтрации и экстраполя¬
ции *). Выведенное в этом параграфе представление в случае гауссов¬
ских процессов эквивалентно представлению Калмэна [13] для гаус¬
*) Формулировку результатов Калмэна и Бьюси можно прочесть в § 2.12
главы 2 этой книги.

4.9]	ПРЕДСТАВЛЕНИЕ ВЕКТОРНЫХ ПРОЦЕССОВ	185
совских марковских процессов. Однако как методы получения этого
представления, так и его вид не такие, как у Калмэна. Причины,
по которым мы не следуем Калмэну, заключаются в том, что избран¬
ное нами изложение проще и лучше согласуется с предыдущими
параграфами этой главы.
Чтобы лучше понять, как получается приводимое нами представ¬
ление, рассмотрим случай, в котором действительный векторный про¬
цесс {X(t\ t [0, сю)} порождается «белым шумом» {W(t), t ^ [0, сю)}
в соответствии с векторным дифференциальным уравнением первого
порядка
X(t) = F(t)X(t)-\- W(t),	(4.64)
где матрица F(t) непрерывна по t. Тогда
t
X{t) = y (t)X(O) + ® (t) ^ <р-‘ (s) W(s) ds,	(4.65)
6
где (фундаментальная) матрица о (t) является решением матричного
дифференциального уравнения
=	®(0) = /.	(4.66)
Если корреляционная матрица Гxx(t, т) процесса {X{t)\ определяется
как
Txx(t, ^) = E[X{t)XT{*-.)],	(4.67)
где ^(т)— матрица, транспонированная по отношению к A'(t), то
из уравнения (4.65) следует, что *)
т
Гд-д-((> т) = с? (0 [Гд-д- (0, 0) Фт (х) -|- 5 tp-1 (s) Q(s) ср-1 (s)1 ds’0T(X)],
U
о, (4.68)
где
Гот ((, т) = Е [ W (0 Wr(т)] = Q(t)o(t — т).	(4.69)
Здесь предполагается, что Q(t) непрерывно дифференцируемая (т. е.
имеет первую непрерывную производную), симметричная, неотрица¬
тельно определенная матрица. Уравнение (4.68) можно записать в бо¬
лее простом виде
Гхх(*> '0 = <Р(0фС0,	0,	(4.70)
где ф(т) равна члену в квадратных скобках в уравнении (4.68). Эти
результаты наводят на предположение о том, что если (t, т) имеет
вид (4.70), где матрицы ср(£) и ф(т) имеют непрерывные производные
*) Предполагается, что £ [X (0) W1 (£)] = 0 для всех L

186
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [1 Л. 4
и cp(t) невырожденна, то {X(t\ t £ [0, сю)} можно представить в виде
(4.64), где {W(t), t [0, со)}—векторный «белый шум» *). Спра¬
ведливость этого предположения устанавливается в следующем абзаце.
Пусть дан процесс {X(t)\, корреляционная функция которого
имеет вышеперечисленные свойства. Рассмотрим процесс {W(tf),
t £ [0, оо)}, определяемый соотношением
W(t) = X(t) — F(t)X(f),	(4.71)
где F(t)X(f)—наилучшая в среднеквадратичном линейная оценка
X(t) при данном X(t). Строго говоря, предел, используемый для опре¬
деления X(t) в (4.71), обычно не существует как предел в средне¬
квадратичном и, следовательно, нельзя строго говорить о наилучшей
оценке X(t) в среднеквадратичном, потому что X(t) не имеет конеч¬
ной дисперсии. Здесь мы встречаемся с трудностью, аналогичной той,
о которой упоминалось в § 4.3, и эту трудность можно преодолеть
путем рассмотрения обобщенных случайных процессов. Но предпоч¬
тительнее предел, используемый для определения X(t) в (4.71), интер¬
претировать как слабый предел в среднеквадратичном (см. § 4.8).
Также можно интерпретировать и оценку X(t). При таком подходе
проводимое в дальнейшем формальное дифференцирование можег
быть непосредственным образом строго обосновано. Если продолжать
формально, то задача теперь заключается в том, чтобы показать, что'
F (t) можно определить единственным образом из Г^(^, т) и что
{W(0, f£I0> со)} является векторным «белым шумом» (т. е. правая
часть уравнения (4.71) слабо сходится к векторному «белому шуму»).
Поскольку	F(t)X(t) — наилучшая в среднеквадратичном	линейная
оценка X(t)> она удовлетворяет уравнению Винера — Хопфа, которое
в этом случае выглядит как
Е [X(t) X7 (0] — F(t) Е [X (0 Хт (*)] = 0,	(4.72)
Используя (4.70), уравнение (4.72) можно переписать как
Ф(0Ф(0 —/7(0?(0Ф(0 = 0.	(4.73)
Если предположить, что 1^(2, t) невырожденна, то ф(£) также будет
невырожденной,	и	уравнение (4.73) можно разрешить	относительно
F(t)
F(t)=^(t)^(t).	(4.74)
Даже если Txx(t, t) вырожденна для некоторого £^>0, то все равно
как показывает прямая подстановка, F(t) определяемая формулой
*) Здесь предполагается, что <р (0) = ./. Если это ие так, то вместо ср (т)
рассматривается ср (t) ср-1 (0) и (т) переопределяется как <р (0) ф (£). Тогда
указанное предположение выполняется.

4.9]	ПРЕДСТАВЛЕНИЕ ВЕКТОРНЫХ ПРОЦЕССОВ	187
(4.74), является решением уравнения (4.73). Происходит это потому,
что, когда Гxx(iy t) вырождена, уравнение (4.73) будет иметь много
решений, одним из которых будет (4.74) *). Уравнение (4.74) согла¬
суется с уравнением (4.66) и однозначно определяется матрицей ср (t).
Для того чтобы показать, что {W(0} является «белым шумом», рас¬
смотрим Е [ W (t) Хт (т)] для£^>т. Используя уравнения (4.71) и (4.74),
имеем
ВI W(t) Хт(X)] = Е[Х(0 хт (х)] - F (0 Е [*(*) хт (X)] =
= $ (0 ф (х) — т (0 ?-1 (0 ? (0 Ф (х) = °> t >х- (4-75)
Дифференцирование уравнения (4.75) по t дает
=	*>т.	(4.76)
Отсюда, используя уравнения (4.71), (4.75) и (4.76), получим
E\W(t) WTW] =
— E[W (0 X (т)] — E[W (0 WT (т)] FT( т) = 0,	t > т. (4.77)
Наконец, из симметрии Е [ W(t) WT(т)] вытекает, что
E[W(t) WT(z)] = 0,	(4.78)
Равенство (4.78) показывает, что |W(f)} является «белым шумом» и,
следовательно, Tww(t, т) имеет вид (4.69). Для нахождения Q(t) за¬
метим, что из уравнения (4.68) вытекает, что данное ^(^) будет полу¬
чено при
Q (0= ? (0 ^ [ф (0 (?г (0П <рг(А	(4.79)
Это можно доказать прямой подстановкой (4.79) в уравнение (4.68).
(Отметим, что поскольку ср (0) = /, то 1^(0, 0) = ф(0).)
Здесь стоит, вероятно, отметить два основных отличия вывода,
приведенного выше, от того, который был сделан Калмэном [13].
Первое отличие состоит в том, что Калмэн считал процесс {X(t)}
гауссовским и марковским, тогда как выше предполагалось, что кор¬
реляционная матрица {X(t)} имеет вид (4.70). Второе отличие состоит
в том, что Калмэн определяет {W(f)} уравнением
W(t) = X(f) — E[X(t)\X{t)],	(4.71')
*) Калмэн [13] полагает F (t) = о (t) <[/ (t) [о (t) Ф (*)]*, где [«р (0 ф (01* —
■определяемая Пенроузом псевдообратная матрица к [ср (t) ф (0]- Хотя при
этом получается решение F (t)y псевдообратная матрица которого имеет ми¬
нимальную норму (норма — сумма квадратов всех элементов), нет каких-
либо разумных физических причин следовать в определении F (t) Калмэну.

188
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ
[ГЛ. 4
а не уравнением (4.71). Из предположения гауссовости вытекает, что
условное математическое ожидание в уравнении (4.71') является ли¬
нейной функцией X(t) (т. е. F(t)X(t) как раз является наилучшей
в среднеквадратичном оценкой X(t)). А предположение марковости
используется для вывода уравнения (4.75) вместо предположения о том,
что Tx(t, т) имеет вид (4.70). Наконец, стоит также отметить, что из
результата Калмэна вытекает, что Гxx(t, т) имеет вид (4.70).
На этом мы заканчиваем рассмотрение задачи определения фор¬
мирующего фильтра для векторных процессов. В оставшейся части
этого параграфа полученные результаты будут применяться к задаче
линейной среднеквадратичной фильтрации и экстраполяции, которая
рассматривалась Калмэном и Быоси [29].
Одна из формулировок задачи линейной среднеквадратичной
фильтрации и экстраполяции является следующей. Рассмотрим слу¬
чайный процесс {Х(£)}, порожденный «белым шумом» {W(£)} в ре¬
зультате его прохождения через рассмотренный выше формирующий
фильтр:
X(t) = F{t)X(t)-\-W(t\	t2* 0,	(4.80)
и предположим,	что	наблюдается процесс	{Z(t)\, где Z(t) связана
с X (t) соотношением
Z(t) = H(t)X(t)-\~ V(t)=y(t)-\- V{t\ . f0.	(4.81)
Здесь Hit) непрерывна, а {У(0}— «белый шум». Пусть
Tvv (t, z) = E[V(t) VT(z)) = R(t)b(t — т); t, x 2*0,	(4.82)
и пусть R(t) положительно определена. Предположим также, что
В [W(t) VT (т)] = 0; t, х 2*0.	(4.83)
Задача, которую мы хотим рассмотреть, заключается в том, чтобы
найти наилучшую в среднеквадратичном линейную оценку X{ty\t)
величины	X(t{)	при	данных наблюденных	значениях Z(t) на интер¬
вале	где	t\ z. То есть надо найти оценку X(ti\t)f имею¬
щую вид
^	t
А:(<1|0 = 5Л(^ь	(4.84)
6
где A{tb z)— матрица, непрерывно дифференцируемая по обоим ар¬
гументам. Можно показать, что для того чтобы X j t) была наилуч¬
шей в среднеквадратичном линейной оценкой, необходимо и доста¬
точно, чтобы A(th т) удовлетворяла интегральному уравнению

4.9]	ПРЕДСТАВЛЕНИЕ	ВЕКТОРНЫХ ПРОЦЕССОВ	189
Винера — Хопфа *)
t
E\X(tx)ZT{x)} — $ A(tb s)E [Z(s)Zr(x)l ds = 0.	(4.85)
0
Чтобы вывести результаты Калмэна и Бьюси (которые сформули¬
рованы в § 2.12 этой книги), предпримем следующее.
Предположим на минуту, что tx = t. Тогда наша задача превра¬
щается в задачу фильтрации. Дифференцируя уравнение (4.85) по t,
меняя порядок операций d/dt и Е[ ] и используя уравнение (4.80),
имеем
^ E[X(t) ZT (х)] = F(t)E [X(t) ZT(x)] -f E [ W\t) Z‘ (x)],
и	(4.86)
t
^ ( A(t, s)E[Z(s)ZT(x)]ds =
0
t
= [ dA g" s) E [Z (s) Zl (x)] ds + A (t, t)E[Z(t)ZT(x) ], t^x^O.
(4.87)
Но из уравнений (4.80) — (4.83) следует, что W(t) некоррелирована
с V(t) и АДт) для t^> т, a X(t) некоррелирована с У(т) для всех t,
т 0. Отсюда
Е [ W(0 ZT (т)] = 0,	t > т,	(4.88)
и
£[Z(0Zrw] = £lCy(9+ v(9)CvW + ^ (х))7] =
= E\y(t)yT(х)] = Я(0 Е [X(0 ZT (х)] - Е [у (t)VT(х)] =
= H(t)E[X(t)ZT(x)], t^sx.	(4.89)
Объединяя уравнения (4.86) и (4.87) и используя уравнения (4.85),
(4.88) и (4.89), имеем
I
J | F(i)A(t, s) дА£ s) A (t, f)H(f)A(t, s)j X
X £[Z(s)Z7'(x)]ds = 0,	<>x^0.	(4.90)
Далее ясно, что уравнение (4.90) будет удовлетворено, если A{tf т)
будет решением уравнения
F(t)A(t, —	x)	—	A{t,	t) H (t) A (t, x) =
= B(t, x) = 0, t^sxSzQ.	(4.91)
*) Вывод интегрального уравнения Винера — Хопфа для векторных про¬
цессов см. в § 2.3 настоящей книги.

190
ФОРМИРУЮЩИЕ ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
Если R(x) положительно определена для	как предполага¬
лось, то A (t, х) необходимо удовлетворяет также и уравнению (4.91).
В самом деле, из уравнения (4.90) видно, что A(t, z)-\-B(ty х) также
является решением уравнения Винера — Хопфа. Отсюда вытекает,
что
^	t
X(t\ t) -f 5 В (t, x) Z (x) d-z	(4.92)
0
также является оптимальной оценкой для X(t). Теперь с помощью
уравнения Винера — Хопфа можно легко показать, что корреляцион¬
ная матрица разности двух оптимальных оценок обращается в нуль
при t{ = z. Следовательно,
t t
s)E[Z{s)ZT(?)]BT{t, о) ds da = 0.	(4.93)
0 0
Далее из уравнений (4.80) — (4.84) следует, что
Е [ Z (s) ZT (a)} = R(s)Z(s-o) + E\y(s)yr (а)].	(4.94)
Подставляя (4.94) в (4.93), найдем, что если уравнение (4.91) не удов¬
летворяется, то второй член получившегося уравнения неотрицателен,
а его первый член положителен (вследствие положительной опреде¬
ленности R(t)). Отсюда B(ty х) = 0.
Дифференцируя уравнение (4.84) по ty получим
-X(tdt t] = 5 -дА$ Т) z(X)rfx+A (t, t)Z(it).	(4.95)
0
Полагая К(t) = A(t, t) и используя уравнения (4.84) и (4.91), уравне¬
ние (4.95) можно переписать в виде
йХ {tdt 1 0 =F(t)X(t \t) + K(t) Z(t) — H(0X(t | t).	(4.96)
Это — дифференциальное уравнение оптимального фильтра. Для того
чтобы получить решение задачи среднеквадратичной фильтрации,
остается только найти способ вычисления K(t). Это можно сделать
следующим образом.
Пусть X(t | t) определяется соотношением
X (t\t) — X{t) — X(t\ t).	(4.97)
Тогда из уравнений (4.80) и (4.96) вытекает, что X(t, t)—разность

ПРЕДСТАВЛЕНИЕ ВЕКТОРНЫХ ПРОЦЕССОВ
191
между истинным значением и оценкой — удовлетворяет дифференциаль¬
ному уравнению
dX(t\t) =[F{t)_Kit)H{t)]x{t | 0+ W{t)_ K{t) y(0.	(4.98)
Кроме того, воспользовавшись уравнением Винера — Хопфа, можно
легко увидеть, что из уравнения (4.85) вытекает, что
Из равенства (4.99) и того факта, что Z (t) = у (t)-\~ V (t), следует, что
Перейдем далее в правой и левой части уравнения (4.101) к пределу
при т —► t. Такой предельный переход законен, так как обе части
уравнения (4.101) непрерывны по т при любом фиксированном t.
Итак, переходя к пределу в обеих частях уравнения (4.101), учиты¬
вая, что Е [у (Х).УГ(Т)] = Е [Z(i)yT{^)] и (4.100), получим
K{t)R(t) = A(t, t)R(t) = E[X(t | t)yr(t)] =
= E\X(t | t)XT(f)\HT(f) = E\X {t | t)XT(t | f)]tfr(9 =
Поскольку R(t) положительно определена, она невырождена и
Таким образом, мы получили явное выражение для K(t) через Р (t).
Чтобы найти уравнение для вычисления Р (t), рассмотрим
Правую часть уравнения (4.104) можно преобразовать с помощью
уравнения (4.98). Действительно,
А отсюда
E[X(t | 0Zr(t)] = 0,	*>t;>0.
е[х(t | 9л-г(о1 = о.
(4.100)
(4.99)
E [X(f)yT (t)] -\A{t, s)E \y (s)	(t)]	ds	=
о
= A(t, t)/?(x),	(4.101)
(4.103)
dP (t)
(It
е\1^Х^У])хТ(1 I *)] + £[*(* I t)^ XT(t.\ o)"|. (4.104)
= [E(t)-K(t)H(t)E\Xr{t | t)XT(t | 0l-b
-i- E[{ W{t)-K {t) V(t)) X1 {t | <)]. (4.105)

192	ФОРМИРУЮЩИЕ	ФИЛЬТРЫ ДЛЯ СЛУЧАЙНЫХ ПРОЦЕССОВ [ГЛ. 4
Решение X(t\t) уравнения (4.98) можно представить в виде
X(t I ^) = Q (О Q-1 (0) J^(0 I 0)-f
t
+ 2 (0 5 2-1 (О [ W{x) - К (t) V(x)\ dx,	(4.106)
0
где 2 (£) — произвольное невырожденное решение матричного диф¬
ференциального уравнения
2 01) = [F (0 - К (0 Н(0] 2 (0-	(4.107)
Подставляя (4.106) в (4.105) и используя (4.103), получаем
E[{wXQ IkT{t I °] =
= F(t)P (t) - р (0 нт (0 R' (t) Я(0 Р (0 +
+ У Q (0 -!- -J Р (0 нт (0 /Г1 (0 н(0 р (0, (4.108)
где множитель 1/2 возникает вследствие симметрии о-функции, зави¬
сящей от верхнего предела интегрирования. Члены, которые могли
появиться	в	уравнении (4.108),	благодаря начальным	условиям,
отсутствуют потому, что
Х(0 | 0) = АР(0) —	Х(0 |	0) = ЛЧ0),	(4.109)
и	потому,	что	Л^О)	некоррелирована с W{t) и V(^) для	всех t.
А из (4.84) сразу следует, что А"(0 | 0) равняется нулю. Второй член
в	уравнении	(4.104)	получается просто транспонированием	правой
части (4.108). Таким образом, если принять во внимание симметрию
матриц P(t), Q(t) и R(t), уравнение (4.104) превращается в
*£Jp- = F(t)P (<) + Р (f)FT{t) - Р (0 HT(t) R-1 (t)H(t) P (t) + Q (0.
(4.110)
Уравнение (4.110) для вычисления P(t) является нелинейным диффе¬
ренциальным	уравнением Рикагги.	Оно	называется	дисперсионным
уравнением. Начальные условия для P(t) непосредственно получаются
из уравнений (4.102) и (4.109), и
Р(0) = Е [А-(0) Хг	(0)].	(4.П1)
На этом мы заканчиваем вывод результатов, касающихся задачи
фильтрации. Было показано, что оптимальный фильтр полностью
определяется решением дисперсионного уравнения и не зависит от
наблюдаемого процесса {Z(t)}. Это не удивительно, потому что дис¬
персионное уравнение было выведено из уравнения Винера — Хопфа

ЛИТЕРАТУРА
и эквивалентно ему, а оптимальный фильтр, определяемый уравнением
Винера — Хопфа (т. е. A (t, т)), не зависит от	Оптимальный
фильтр определяется уравнением (4.96), где K(t) вычисляется с по¬
мощью уравнений (4.103), (4.110) и (4.111), а начальным условием для
оптимального фильтра является, как отмечалось выше, /^(0 | 0) = 0.
Когда tx ^ t, имеет место задача экстраполяции, и можно легко
показать (см. Калмэн [13]), что
X{tx I =	I 0,	(4.112)
где y(t) связана с Гxx(t, т) уравнением (4.70).
Вопросы существования, единственности и устойчивости решения
уравнения (4.110) здесь не рассматриваются. Читатель, интересующийся
этими вопросами, отсылается к работе Калмэна [13] или Калмэна и
Бьюси [29].
ЛИТЕРАТУРА
1. Wold Н., A Study in the Analysis of Stationary Time Scrvies, Uppsala,
1938.
2. Kolmogorov A., Sur L’Interpolation et Extrapolation des Suites Station-
naires, C. R. Acad. Sci., Paris 208, pp. 2043—2045, 1939.
3. К о л м о г о р о в А. Н., Стационарные последовательности в гильберто¬
вом пространстве, Бюлл. МГУ 2, вып. 6 (1941), I—40.
4. К о л м о г о р о в А. Нм Интерполирование и экстраполирование стацио¬
нарных случайных последовательностей, Изв. АН СССР, сер. мат., т. 5,
№ 1, 1941, стр. 3—14.
5. W i е n е г N., Extrapolation, interpolation, and Smoothing of Stationary
Time Series, John Wiley and Sons, Inc., New York, 1949.
6. H a n n e г O., Deterministic and Nondeterministic Stationary Random Pro¬
cesses, Ark. Mat. l,..pp. 161—177, 1949.
7. Karhunen K., Uber die Struktur Stationarer Zufalliger Funktionen,
Ark. Mat. 1, pp. 141 — 160, i960.
8. В о d e H. and C. Shannon, A Simplified Derivation of Linear Least-
Square Smoothing and Prediction Theory, Proc. IRE 38, pp. 417—426, April,
1950. [Русский перевод: Упрощенный вывод линейной теории сглаживания
и предсказания по методу наименьших квадратов. В кн. Шеннон К.,
Работы по теории инфгрмации и кибернетике, 687—708, ИЛ, М., 1963.]
9. Darlington S., Nonstationary Smoothing and Prediction Using Network
Theory Concepts, Transactions IRE, 1 T-5, May, 1959, pp. 1—11.
10. Dolph C. and M. Woodbury, On the Relation Between Green’s Func¬
tions and Convariances of Certain Stochastic Processes and Its Application
to Unbiased Linear Prediction, Trans. Amer. Math. Soc. 72, May, 1952,
pp. 519—550.
11. Батков А. М., Обобщение метода формирующих фильтров на неста¬
ционарные сл\чайные процессы. Автоматика и телемеханика, т. 20, № 8,
1959, стр. 1081 — 1094.
12. Лео н о в Ю. П., Проблема формирующего фильтра и оптимальные ли¬
нейные системы. Автоматика и телемеханика, т. 21, №6, 1960, стр. 674—
681.
13. Kalman R., New Methods and Results in Linear Prediction and Filtering
Theory, RIAS Technical Report 61 — 1. Also an Appendix to ASD-TR-61-27.
7 п/р Леондеса

194
ЛИТЕРАТУРА
14. Locvc М., Probability Theory, D. Van Nostrand, Princeton, N. J., 1960.
(Русский перевод: Л о э в М., Теория вероятностей, ИЛ, М., 1962.]
15. Г е л ь ф а и д И. М. и Ви ленки н Н. Я., Обобщенные функции,
вып. 4, Некоторые применения гармонического анализа. Оснащенные
гильбертовы пространства, Физматгиз, М., 1961.
16. Гель фан д И. М., Обобщенные случайные процессы, ДАН СССР 100,
№ 5, 1955, стр. 853—856.]
17. Doob J., Stochastic Processes, John Wiley and Sons, Inc., New York, 1953.
[Русский перевод: Дуб Дж. Л., Вероятностные процессы, ИЛ, М.. 1956.]
18. G г е n and с г U. and М. Rosenblatt, Statistical Analysis of Stationary
Time Series, John Wiley and Sons, Inc., New York, 1957. ‘
19. P a I e у R. E. A. and N. W i e n с r, Fourier Transforms, An American Math.
Society Colloquium Publication, 1932. [Русский перевод: Винер H.,
Пэли П., Преобразование Ф\рье в комплексной области, «Наука», М.,
1964.]
20. С о d d i n g t о n E. and N. L e v inso n, Theory of Ordinary Differential
Equations, McGraw-Hill Book Company, Inc., New York, 1955. [Русский
перевод: К о д д и н г т о н Э. А. и Л с в и н с о н Н., Теория обыкновен¬
ных дифференциальных уравнений, ИЛ, М., 1958.]
21. St ear Е., Synthesis of Shaping Filters for Nonstationary Stochastic Pro¬
cesses and Their Uses, AFOSR Report 61-50, August, 1961.
22. Tricomi F., Integral Equations, Intersicencc Publishers, Inc., New York,
1957. [Русский перевод: Трикоми Ф., Интегральные уравнения. ИЛ, М.,
I960.]
23. Lalesco Т., Introduction a la Theorie des Equations Integrales, Gauthicr-
Villars, Paris, 1922.
24. Sato Т., Sur l’Equation Integralc Nonlinear de Voltcrra, Compositio
Mathematica 11, 1953, pp. 271—290.
25. Bcrge C., Espaces Topologiques, Dunod, Paris, 1959.
26. Пугачев В. С., Теория случайных функций и ее применение к зада¬
чам автоматического управления, Гостсхиздат, М., 1957.
27. II у г а ч е в В. С., Интегральные канонические представления случайных
функций и их применение к определению оптимальных линейных систем.
Автоматика и телемеханика т. 18, № 11, 1957, стр. 971—984.
28. Натансон И. П., Теория функций вещественной переменной, Гостех-
издат, М., 1957.
29. К a I m an R. Е. and R. S. Вис у, New Results in Linear Filtering and
Prediction Theory, J. Basic Engr. (ASME Trans.) 83D, March, 1961,
pp. 95—108.

ГЛАВ А 5
АНАЛИЗ НЕЛИНЕЙНЫХ СИСТЕМ УПРАВЛЕНИЯ
С ПОМОЩЬЮ ПРЯМОГО МЕТОДА ЛЯПУНОВА
Дональсон (D. D. Donalson)
5.1. Введение
5.1.1.	Исторический очерк
Прямой метод Ляпунова является общим методом исследования
устойчивости систем обыкновенных дифференциальных уравнении.
Он применим к автономным и неавтономным и к линейным и нели¬
нейным обыкновенным дифференциальным уравнениям. Часто этот
метод называется вторым методом Ляпунова и, так как эти названия
используются в литературе попеременно, это иногда приводит к недо¬
разумениям у неподготовленного читателя.
Впервые эти методы были предложены в самом конце XIX века
русским математиком А. М. Ляпуновым. В 1907 г. работа Ляпунова
была переведена на французский язык. В свсей работе Ляпунов по
существу все методы анализа устойчивости обыкновенных дифферен¬
циальных уравнений относил к одному из двух основных методов.
Первый метод был назван непрямым методом, поскольку он требовал
непосредственного решения исследуемой системы дифференциальных
уравнений. Второй метод был назван прямым методом, гак как в этом
случае рассматриваются критерии устойчивости, которые могут при¬
меняться прямо к системе обыкновенных дифференциальных уравне¬
ний и при этом не требуется решение этих уравнений. Таково исто¬
рическое происхождение двойных названий методов Ляпунова. В этой
главе мы будем называть второй метод Ляпунова прямым, так как
это название точнее отражает суть метода.
До 1940 г. прямой метод Ляпунова почти не применялся. Лишь
в 1940—1950 гг. в СССР впервые обратили внимание на значение
этого метода для анализа нелинейных систем автоматического управ-
7*

196
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
ления. Затем в 1947 г. первый французский перевод работы Ляпу¬
нова был переиздам Принстонским университетом, а около 1955 г.
начали появляться и первые публикации на английском языке. Это
были оригинальные работы и переводы русских и немецких работ.
5.1.2.	Основные идеи прямого метода
Для рассмотрения проблем устойчивости автономных и неавто¬
номных нелинейных систем потребуется предварительно определить
понятие устойчивости более подробно, чем это требуется для линей¬
ных систем. Невозмущенная линейная динамическая система имеет
только одно положение равновесия. Если оно устойчиво, траектории
всех решений при возрастании времени до бесконечности будут
приближаться к этой точке равновесия. Особый случай возникает при
наличии пары чисто мнимых корней характеристического уравнения
системы, так как в этом случае, если система в начальном состоянии
не находилась в точке равновесия, в ней все время будут наблю¬
даться устойчивые колебания. Однако такая ситуация редко встре¬
чается в реальных системах, поскольку корни характеристического
уравнения, по-видимому, не будут чисто мнимыми, даже если этого
специально добиваться. Устойчивость линейной системы не зависит ог
начальных условий, а реакция устойчивой системы на любое непре¬
рывно действующее ограниченное возмущение будет ограниченней.
По существу последнее можно было бы использовать как определе¬
ние устойчивости линейных систем. Гораздо более сложным образом
определяется устойчивость нелинейных систем. Соответствующие опре¬
деления даются в § 5.2, где они рассматриваются с большей мате¬
матической строгостью, чем это требуется сейчас во введении к пря¬
мому методу Ляпунова.
Чтобы получить весьма простую аналогию прямого метода Ляпу¬
нова, рассмотрим систему, показанную на рис. 5.1.
Связь выходной и входной величин описывается уравнением
х -4- ах = г.
Предположим, что г есть равная нулю правая часть, и рассмотрим
реакцию системы при различных начальных возмущениях. В этом
случае уравнение системы может быть записано в следующем виде:
х =—ах.
Самых элементарных сведений из теории дифференциальных уравне¬
ний достаточно, чтобы убедиться, что система будет устойчивой, если а
равно любому вещественному положительному конечному числу. В этом
нет ничего нового для специалиста по системам управления, однако
подход к рассмотрению физических причин, объясняющих поведение
решения этого уравнения, аналогичен прямому методу Ляпунова. За¬

5.1]
ВВЕДЕНИЕ
197
метим, что при любом 0<^а<^оо, независимо от значения, принимае¬
мого ху кроме того случая, когда х = 0, скорость изменения х такова,
что его абсолютная величина |лг| всегда уменьшается. Однако при
х = 0 производная х также равняется нулю. Поэтому л; = 0 есть
точка равновесия для этой системы и система устойчива, так как
при любом конечном по величине начальном условии для х = х{) (как
при положительном, так и при отрицательном) решение уравнения
x(t) будет приближаться при бесконечном возрастании к нулю. Легко
можно показать, что если —оо<^
0, тогда | лег | всегда возра¬
стает при х Ф 0, и поэтому при
таких значениях а эта система не¬
устойчива.
Подобный анализ в системах
второго и более высокого порядка
по отношению к переменной х провести невозможно. Однако в раз¬
личных теоремах, основанных на прямом методе Ляпунова, это делается
для функции Ляпунова, по от¬
ношению к которой применимы
очень похожие рассуждения.
Естественно, что при этом воз¬
никают дополнительные усло¬
вия, которые обеспечивают ма¬
тематическую строгость и га¬
рантируют достоверность по-
Рис. 5.2. Простая система второго лучаемых выводов,
порядка.	J	гт
Применим для иллюстрации
приводимые ниже теоремы, свя¬
занные с прямым методом, к простой линейной системе, изобра¬
женной на рис. 5.2.
Уравнение для этой системы можно записать в виде
х -\-Зх -\-‘2х= г.
Предположим, что г — равная нулю правая часть, т. е.
г = 0.
Тогда система описывается следующим дифференциальным уравнением:
х -f- Ъх -}- 2х — 0 или х = — Ъх — 2jt.
Точка х = 0 будет точкой равновесия системы. Исследование будет
касаться поведения невозмущенной системы при различных началь¬
ных значениях х.
Теоремы прямого метода Ляпунова обычно формулируются приме¬
нительно к системе обыкновенных дифференциальных уравнений
первого порядка, однако уравнения порядка выше первого несложно
2s
*-s+2
г
.7
J;
s+a.
Рис. 5.1. Простая система перво¬
го порядка.

198
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
преобразовать к такому виду. В рассматриваемом примере для этого
вводятся следующие переменные:
Тогда невозмущенная система второго порядка может быть представ¬
лена следующей системой дифференциальных уравнений первого по¬
рядка:
Переменные Х\ и называются обычно переменными «состояния».
В тех случаях, когда они представляют выход системы и его различ¬
ные производные, они могут также называться «фазовыми» коорди¬
натами. Многомерное пространство, в котором вдоль прямоугольных
координатных осей откладываются переменные состояния или фазовые
координаты, называется пространством состояний, или фазовым про¬
странством. В частном случае, который нами рассматривается, этим
пространством является фазовая плоскость, хорошо знакомая каждому,
кто имел дело с фазовыми кривыми простых нелинейных систем вто¬
рого порядка.
Итак, наша система уравнений приведена к виду, позволяющему
применить прямой метод Ляпунова. Теперь можно обратиться к сле¬
дующей теореме.
Теорема. Пусть система дифференциальных уравнений первого
порядка
(2) Функции Xi непрерывны по всем переменным xt во всем про¬
странстве состояний.
Пусть далее существует скалярная функция V(xh хь ..., хп\
принимающая действительные значения, такая, что
(а) V(xh хъ ..., хп) непрерывна и имеет непрерывные частные
производные первого порядка;
(б) V(хь хъ ..., хл)^>0, за исключением точки лгг = 0 при всех
/= 1, 2, ..., п (т. е. V положительно определенная функция);
X = Хь
Х = х1 = JCQ.
(5.1.1)
£i = Xi(x1, ..., хп), г = 1, 2, ..., п,
удовлетворяет условиям:
(1) Л, = *,«). ..., 0)=0,	/=	1,	2,	...,	я.
(в)	1/(0, 0, ..., 0) = 0;
(г) V(х,,	х„)	—	со	при

5.1]
ВВЕДЕНИЕ
199
п	п
(д) 'v==Tt	= lL	(^7	2	х^т'	е- ^ 0ТРИ1«телМ10
i=l	4	1	г=1
ределенная функция). Тогда эта система асимптотически устойчива
в целом *).
Асимптотическая устойчивость в целом означает, что для любых
конечных вещественных начальных условий выход системы будет
стремиться к состоянию равновесия х = 0, х = 0 при £-> оо. Для
линейных систем это определение совпадает с обычным определением
устойчивости.
Рассматриваемая нами система обыкновенных дифференциальных
уравнений первого порядка (5.1.1) удовлетворяет условиям (1) и (2)
приведенной теоремы и имеет соответствующую форму. Задача поэтому
заключается в отыскании скалярной функции V (xh jc2), удовлетво¬
ряющей условиям (а) — (д) теоремы. Существует ряд методов постро¬
ения функции Ляпунова, которые рассматриваются в § 5.3, однако
здесь в этом вводном примере мы не будем останавливаться на этих
методах, так как вопрос о том, как построить функцию Ляпунова,
обычно составляет самую трудную часть анализа устойчивости.
Вообще же, чтобы исследовать устойчивость системы, достаточно
лишь выяснить, существует ли функция, которая удовлетворяет ука¬
занным выше требованиям.
Пусть для рассматриваемой системы
V = ~2 {5х\ -j- 2xiX% -j- x£).	(5.1.2)
Легко проверить непосредственно, что эта функция удовлетворяет
условиям (а), (в) и (г). Так как функция V(хи х.2), задаваемая фор¬
мулой (5.1.2), есть квадратичная форма, то чтобы определить, будет
ли она удовлетворять условию (б) теоремы, необходимо определить,
будет ли эта квадратичная форма положительно определенной. Для
произвольной квадратичной формы от двух переменных
Q (х\, х$) = а*\ + 2ЬхуХ2 -f- сх\	(5.1.3)
необходимыми и достаточными условиями положительной определен¬
ности являются
(а)	а^> 0	(5.1.4)
и
(б)	ас	—	&‘2 > 0.	(5.1.5)
*) О доказательстве теоремы Ляпунова об асимптотической устойчиво¬
сти в целом см. М а л к и н И. Г., Теория устойчивости движения, «Наука»,
1966, стр. 519—520. (Прим. перев.)

200
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Для квадратичной формы (5.1.2)
а = 2,5,
b = 0,5
и
с = 0,5,
поэтому очевидно, что функция (5.1.2) удовлетворяет условию (б)
теоремы. Если теперь производная этой функции по времени удов¬
летворяет также и условию (д), тогда V (хъ х2) есть функция Ляпу¬
нова для нашей системы, а это является достаточным условием асим¬
птотической устойчивости системы в целом.
Чтобы проверить, выполняется ли для V (хъ х2) условие (д), про¬
дифференцируем уравнение (5.1.2) по времени и вместо производ¬
ных по времени от фазовых координат подставим их значения из
уравнения (5.1.1)
V (Xi, Х2) = SXjXj -j- XjX2 -|- X{X2 -f- XoX2 —
= 5xtx2 -j- X\ (— 3x2 — 2x0 Jr xl + хч (— 3x2 — 2x0 =
= — 2 (jq-f *2).	(5.1.6)
Таким образом, V(хь x2) также является квадратичной формой, при¬
чем отрицательно определенной, и условие (д) теоремы выполняется.
Тем самым с помощью прямого метода Ляпунова доказано, что рас¬
смотренная система асимптотически устойчива в целом.
Здесь уместно сделать некоторые замечания, позволяющие эври¬
стически интерпретировать такой анализ. Функция V в пространстве
переменных хь х2 была выбрана таким образом, чтобы она была
положительной во всем пространстве, кроме начала координат, где
все переменные и сама функция V обращаются в нуль.
Полная производная V функции V по времени (в выражение ко¬
торой вместо производных от переменных dxi/dt подставлены их
значения из уравнений системы) принимает отрицательные значения
везде, кроме начала координат, где она также обращается в нуль.
Таким образом, очевидно, что при любом отличном от нуля значении
переменных хг- функция 1/^>0 убывает с ростом времени, так как
V<^0. Прямой метод Ляпунова опирается, таким образом, на иссле¬
дование функции V, которая может зависеть от сколь угодно боль¬
шого числа переменных. Если эта функция обладает нужными свой¬
ствами, к ней можно применить рассуждения, очень похожие на те,
с помощью которых ранее объяснялось поведение простой системы
первого порядка. Однако следует обратить внимание читателя на ряд
дополнительных условий, которые указаны в приведенной выше тео¬
реме, и предостеречь его от попыток проводить анализ, пользуясь
одними лишь интуитивными рассуждениями, хотя эти рассуждения и

5.1]
ВВЕДЕНИЕ
201
полезны для лучшего понимания метода. Строгое доказательство
сформулированной выше теоремы следует в общих чертах приведен¬
ным здесь рассуждениям, однако сами эти рассуждения ни в коем
случае нельзя еще считать доказательством.
Можно рассматривать функцию Ляпунова как аналог потенциаль¬
ной энергии системы. При таком толковании положительная функ¬
ция V и отрицательная V соответствуют системе, рассеивающей энер¬
гию. В этом случае по¬
ведение системы при лю¬
бых начальных условиях
приводит к рассеиванию
энергии до тех пор, пока
она не рассеется полно¬
стью, г. е. все перемен¬
ные Xi не обратятся в
нуль. Последнее условие
есть условие равновесия
для системы, удовлетво¬
ряющей условиям (1) и
(2)	приведенной выше
теоремы. В ряде работ
было показано, что ана¬
логия с потенциальной
энергией иногда помо¬
гает выбрать функцию,
которая может использо¬
ваться как функция Ля¬
пунова. Однако наличие
более формальных мето¬
дов получения функции Ляпунова, по-видимому, ограничивает такое
применение энергетической аналогии.
Приведенная выше теорема допускает геометрическую интерпре¬
тацию. Все рассуждения будут относиться к системе с двумя пере¬
менными, так как это позволит представить геометрические соотно¬
шения на плоскости, однако нетрудно перенести эти же идеи и
в /г-мерное пространство. Рассмотрим функцию Ляпунова, которая
удовлетворяет условиям (а), (б), (в) и (г) теоремы. Постоянным зна¬
чениям V(xh х*) на фазовой плоскости хъ х2 соответствуют замкну¬
тые ограниченные кривые. Если функция V(хъ х%) есть квадратичная
форма, эти кривые будут эллипсами. При возрастающих значениях
константы Ку т. е. при 0 A'i	Кз /С4, кривые V(xh х%) =
= будут иметь вид, показанный на рис. 5.3.
Полная производная по времени функции V (хь х.2) равна
dV __ дУ dxx ■ дУ dx2
dt dA'i dt ‘ dx2 dt *
ф фазовая траек¬
тория отклика
устойчивой,
* с иcmсмь/
t/ормаль к кривой t'=/fy
в точке И, положи тело*
ная в указанном напра¬
влении.
Рис. 5.3. Геометрическая интерпретация кри¬
терия Ляпунова.

202
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Рассматривая точку М, в которой некоторая фазовая траектория
пересекает линию I/ = /С4, можно представить частные производные
функции V как
Геометрически это иллюстрируется на рис. 5.3. Используя эти соот¬
ношения, можно записать dVjdt в виде
Здесь Vn есть проекция тангенциальной составляющей скорости
вдоль траектории движения системы в точке М на нормаль к кривой
V — Кц в точке М. Если теперь dVjdt всюду отрицательна, то и Vn
также должна быть всюду отрицательна. Следовательно, траектория
системы всегда пересекает кривые V = К снаружи. Этого достаточно,
чтобы гарантировать при t—> оо стремление переменных Х\ и х2
к нулю. Это рассуждение можно считать доказательством теоремы
для случая двух переменных и его можно перенести и на многомер¬
ный случай.
В приведенной выше теореме требуется, чтобы V была положи¬
тельно определенной, а V — отрицательно определенной. С тем же
успехом можно потребовать отрицательную определенность функции Г
и положительную определенность V. Существенным здесь является
лишь требование противоположных знаков у функции V и V. Однако
в литературе принято определять V как положительную, и мы будем
придерживаться этой традиции.
Прямой метод Ляпунова может применяться и при доказательстве
неустойчивости системы. Теорема, которая при этом используется,
совпадает с рассмотренной теоремой, за исключением условия (д),
которое заменяется на требование положительной определенности функ¬
ции V (которая, следовательно, должна иметь тот же знак, что
и V). Эта теорема, как и ряд других утверждений, строго формули¬
руется в § 5.2.
Следует заметить, что критерии устойчивости, получаемые прямым
методом Ляпунова, являются только достаточными, но не необходи¬
мыми условиями. Поэтому, если для какой-то системы невозможно
и
где

5.1]
ВВЕДЕНИЕ
203
построить функцию, которая удовлетворяет условиям теоремы об
устойчивости или неустойчивости, это еще не позволяет делать ни¬
каких заключений о ее устойчивости или неустойчивости. Кроме того,
функция Ляпунова, с помощью которой исследуется устойчивость
или неустойчивость системы, определяется неединственным образом.
Можно показать, что если построена функция Ляпунова, определяю¬
щая устойчивость или неустойчивость системы, то существует сколько
угодно функций, с помощью которых также можно судить об устой¬
чивости или неустойчивости этой системы.
5.1.3.	План дальнейшего изложения
Выше мы кратко познакомились с историей прямого метода Ля¬
пунова и рассмотрели одну теорему, поясняющую основную идею
анализа устойчивости. Для иллюстрации эта теорема была применена
к простой линейной системе второго порядка. Изложение в этом
вводном параграфе умышленно проводилось в довольно популярной
форме и сопровождалось рассмотрением некоторых аналогий. Гео¬
метрическая интерпретация для случая двух переменных поясняла
сущность доказательства теоремы.
Ниже все результаты будут приводиться без доказательства. Однако
всюду будут даваться ссылки на соответствующую литературу, в ко¬
торой читатель сможет найти эти доказательства. Теорема, приведен¬
ная выше в настоящем введении, ради простоты содержит ряд огра¬
ничительных условий, от которых, вообще говоря, можно отказаться.
Поэтому эта теорема не встречается в числе теорем, приводимых
ниже. В § 5.2 дается ее более общая формулировка.
В § 5.2 вводятся основные обозначения и определения и приво¬
дятся теоремы, которые могут использоваться при исследовании
устойчивости систем автоматического управления с помощью прямого
метода Ляпунова. Введение специальных обозначений и определений
облегчает понимание и применение этих теорем. В основном эти опре¬
деления приводятся в начале параграфа, однако при необходимости
они будут вводится и далее. Каждая теорема имеет номер, что упро¬
щает ссылки на нее, а также имеет название, которое отражает ее
содержание и помогает выбрать теорему, соответствующую той или
иной задаче. Ссылка на автора дается указанием литературы. В на¬
званиях теорем фамилии авторов не указаны. Теорема 5.1 дает усло¬
вия существования, единственности и непрерывности решения системы
дифференциальных уравнений. В теореме 5.2 рассматривается устой¬
чивость линейных систем, в теоремах 5.3—5.8 — устойчивость нели¬
нейных систем в малой окрестности точки равновесия. Часто удобно
применять эти теоремы сначала для установления локальной устой¬
чивости или неустойчивости положения равновесия, а затем исполь¬
зовать полученные результаты для анализа системы в более широкой

204
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
области или даже во всем пространстве состояний. Ряд теорем, при¬
водимых далее, посвящен расширению и обобщению методов, отно¬
сящихся к прямому методу Ляпунова. В этот параграф включены
также некоторые алгебраические теоремы, которые используются в
теории устойчивости.
В § 5.3 излагается ряд наиболее эффективных методов примене¬
ния теорем устойчивости и методов построения функций Ляпунова.
Приводится ряд примеров. В этом параграфе рассматривается метод
канонических преобразований Лурье, метод Айзермана, .метод Кра-
совского, метод Плисса, а также метод переменного градиента. При¬
водится также пример применения одной из теорем, касающейся
эвентуальной устойчивости, в задаче адаптивного управления. В за¬
ключении параграфа излагается метод оценки верхней границы пере¬
ходного	процесса в системе с помощью прямого	метода	Ляпунова.
В параграфе 5.4 дается краткое резюме изложенного материала и
приводятся некоторые замечания, касающиеся современного состояния
этого метода анализа нелинейных систем управления.
5.2.	Теоремы, определения и обозначения
В дальнейшем для записи систем дифференциальных уравнений,
представляющих анализируемую систему управления, будет удобно
пользоваться	матричными обозначениями. Систему	линейных	диффе¬
ренциальных уравнений первого порядка
Х\ = а\\Х 1 -f"	«1пхп
х% = а^\Х\ ~\~ ашхъ "Ь • • • ~\~ аЧпхп
хп~ ап\х\ апЪх<1 -f- • • • -f" аппхп
можно записать с помощью следующего матричного уравнения:
х=Ах,	(5.2.2)
в котором
Х\
х\
х2
Хъ
, X —
I
хп
хп
Q\ 1 ап ••• а\п
«21 «22 • . • «2л
^п\	•	•	•	&пп
При этом используются обычные операции матричной алгебры.
(0.2.1)

6.2]
ТЕОРНМЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
205
Определение 5.1. Системы, которые можно записать
в виде (5.2.2), называются линейными системами.
Если, кроме линейных членов (5.2.2), в уравнение входят нели¬
нейные члены, такая система может быть представлена в виде
х — Ax~f(x\
в котором
f\ (*)
fn(X)
где fi(x) — некоторые нелинейные функции переменных х,, х.2,..., х„.
Определение 5.2. Нелинейные системы. Системы, которые
можно записать в виде (5.2.3), называются нелинейными системами.
Определение 5.3. Переменные состояния. Переменные хъ
Хъ ..., хп называются переменными состояния, так как в любой мо¬
мент времени они определяют состояние системы.
Определение 5.4. Пространство состояний. /х-мерное
евклидово пространство, по координатным осям которого отклады¬
ваются переменные хь хъ ..., хПУ называется пространством состоя¬
ний. Любая точка в этом пространстве представляет единственный и
определенный набор значений, которые могут принять переменные
xh х<.ъ ..., хп. Таким образом, каждая точка представляет опреде¬
ленное состояние системы.
Если состояние системы задано при £ = 0, тогда при £^>0 пере¬
менные состояния задают траекторию в пространстве состояний. Вид
этой траектории полностью определяется начальной точкой и видом
уравнения (5.2.2) или (5.2.3) *). Очевидно, что эго уравнение (5.2.2)
есть просто частный случай (5.2.3).
Определение 5.5. Стационарные системы. Системы, кото¬
рые описываются уравнениями (5.2.2) или (5.2.3), в которых элементы
матрицы А и элементы функции / не зависят от времени, называются
стационарными системами.
Определение 5.6. Нестационарные системы. Системы, кото¬
рые описываются уравнениями (5.2.2) или (5.2.3), в которых либо
элементы матрицы Л, либо элементы функции / или и те и другие
зависят от времени, называются нестационарными системами.
Определение 5.7. Свободные или не возмущенные системы.
Стационарные или нестационарные системы, которые можно пред¬
*) Требование единственности траекторий накладывает определенные
ограничения на правую часть уравнений (5.2.2) и (5.2.3). См., например,
Петровский И. Г., Лекции по теории обыкновенных дифференциальных
уравнений, «Наука», 1964, стр. 115—118 и 129—130. (Прим. перев.)
(5.2.3)
(5.2.4)

206
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
ставить в виде (5.2.2) или (5.2.3), называются свободными или невоз¬
мущенными системами.
Определение 5.8. Возмущенные системы. Системы, которые
можно представить в виде
где
x = Ax-'rf(x) + R(t),
(5.2.5)
R(t):
Г\ (О
г г (О
гл(0
называются возмущенными системами.
Определение 5.9. Автономные системы. Стационарная не¬
возмущенная система называется автономной системой.
Определение 5.10. Р0 (хувек торные степенные ряды. Вектор
P9(jc) имеет элементами либо нули, либо функции, которые образо¬
ваны из степеней или произведений переменных хь ..., хп по¬
рядка, равного или меньшего 6.
Определение 5.11. Нормы ||л:|| и \х\. Величины \\х\\ и |*|
называются нормами.
Существует два вида норм *). Первая — это евклидова норма
и,?*
А/а
(5.2.6*
Вторая норма называется неевклидовой нормой и задается выраже¬
нием
(5.2.7)
Определение 5.12. ср (f; jc0, t^-решение или траектория
в прпстианстве состояний [11]. Если существует единственная**)
вектор-функция сp(t; л:0, tQ), дифференцируемая по t, такая, что при
*) В качестве норм могут рассматриваться и другие выражения, на¬
пример ||х|| = шах ( | хх I, | д:2 |. ..., | хп |). См. Демидович Б. П.,
i
Марон И. А., Основы вычислительной математики, Физматгиз, 1963,
стр. 238—240. {Прим. перев.)
**) Требование единственности обычно не включается в определение
решения дифференциального уравнения. См. Петровский И. Г., Лекции
по теории обыкновенных дифференциальных уравнений, 1964, стр. 7. (Прим.
перев.)

5.2)
ТЕОРЕМЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
207
любых фиксированных лг0, t0
(а)	Хц,	г'о) = *о>	(5.2.8)
(б) ^ ф (t'< Хо,	t0) = A(f(t; ха, г‘п) + /(ф(г';	xlh t0))	(5.2.9)
в некотором	интервале	11 — t0\^a(t0), то такая	функция	<р	назы¬
вается решением уравнения (5.2.3). Определение решения уравне¬
ния (5.2.2) есть частный случай этого определения.
Теорема 5.1. Существование, единственность и непрерыв¬
ность (см. [6], теоремы 2.3 и 7.1, главу 1; см. также [11]). Пусть
Ax-\-f(x) в некоторой окрестности произвольной точки je0, t0
i |j x - лг01| b (Xq)
R(jc0, <„) = ]	b,	c>0	(5.2.10)
[ К — I ^ c (*o)
непрерывны по x и t и удовлетворяют условию Липшица, т. е. для
любых (х, t) и (у, t) в окрестности R(x0, у0) выполняется условие
II (Ах +/(*)) - (Ау + /(у)) II < л IIJC - у II,	(5.2.11)
где k — положительная константа, зависящая только от b и с.
Тогда
(а) Существует единственное решение ср(£; л;0, t0) уравнения (5.2.3),
определенное для всех t, таких, что 11 — ^0|^а(^0), которое начи¬
нается в точке xQ, t0. Константа a(tQ) определяется как
(5.2.12)
где M(Xq, t0)—максимальное значение, которое принимает непре¬
рывная функция |! Ах -j- f(x) || на замкнутом и ограниченном мно¬
жестве R(xо, t0).
(б) В некоторой окрестности точки дг0, t0 это решение есть не¬
прерывная функция своих аргументов.
Заметим, что условие Липшица требует от функции Ax-\-f(x)
непрерывности только по х. Локальное условие Липшица, написан¬
ное выше, означает, что решение уравнения (5.2.3) существует лишь
в некоторой окрестности х0, ^о- Условие Липшица, которое выпол¬
няется для Ax-{-f(x) всюду, называется условием Липшица в целом.
Если система удовлетворяет условию Липшица в целом, ее решение
или траектория в пространстве состояний не может за конечное
время уйти в бесконечность. Термин «условие Липшица в целом»
эквивалентен термину «глобальное условие Липшица», который
также распространен в литературе.

208
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Определение 5.13. Непрерывные по времени динамические
системы [11]. Если траектория <р такова, что
(а)	ср(£0; *0, ^о) = *о Для всех (дг0, U)\	(5.2.13)
(б) ф (*а; ф(^; х0, Q, ^)=ф(^; х0, U) для всех лг0, t0f th t,
(условие существования и единственности);	(5.2.14)
(в) ср непрерывна по всем аргументам;
(г) ср определена для всех jc0, tQ, t (решение не уходит в беско¬
нечность за конечное время), то система называется непрерывной по
времени динамической системой.
Определение 5.14. Состояние равновесия. Состояние хе не¬
возмущенной динамической системы (уравнение (5.2.3)) есть состояние
равновесия, если
Ахе~]~ f(xe)~ 0 для всех t,	(5.2.15)
или, что то же самое,
ср(£; хе> 0) = хе для всех t	(5.2.16)
Приводимые далее определения касаются различных типов устой¬
чивости и следуют определениям [11].
Определение 5.15. Устойчивость [11]. Состояние равнове¬
сия хе невозмущенной динамической системы называется устойчивым,
если для любого вещественного числа в^>0 найдется вещественное
число 8(е0, *0)>О такое, что из соотношения
il^o — Vsi^8	(5.2.17)
следует
II?С; х0, t0) —	для всех t^t0.	(5.2.18)
Определение 5.16. Асимптотическая устойчивость [ 1.1 ].
Состояние равновесия хе невозмущенной динамической системы на¬
зывается асимптотически устойчивым, если
(а) оно устойчиво,
(б) любое движение, которое начинается достаточно близко от хеУ
стремится	к	хе	при t-> оо. Более	строго,	существует	такое веще¬
ственное	число	г(£0)^>0, что при	любом	вещественном	най¬
дется вещественное число ^({л, дг0, t0) такое, что из || аг0 — хе II (t0)
следует ||<p(<; х0, t0) — jtJjCtJ. для всех
Следует заметить, что асимптотическая устойчивость есть локаль¬
ная характеристика, так как число г (t0) точно не задается и может
быть сколь угодно мало.
Определение 5.17. Равностепенная асимптотическая
устойчивость [11]. Состояние равновесия хе невозмущепной дина*

5.21
ТЕОРЕМЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
209
мической системы называется равностепенно асимптотически устойчи¬
вым, если
(а) оно устойчиво,
(б) любое движение, которое начинается достаточно близко от хе7
стремится к хе при t-*co равномерно по лг0, т. е. число Т в опре¬
делении 5.16 не зависит от х0: T(\i> г(£0)> до¬
определение 5.18. Асимптотическая устойчивость в це¬
лом [11]. Состояние равновесия невозмушенной динамической системы
называется асимптотически устойчивым в целом, если
(а) оно устойчиво,
(б) любое движение стремится к хе при t-+ со.
Определение 5.19. Равностепенная асимптотическая
устойчивость в большом [11]. Состояние равновесия невозмущеи-
ной динамической системы называется равностепенно асимптотически
устойчивым в большом, если
(а) оно устойчиво,
(б) каждое движение при t-> оо стремится к хе равномерно по
jc0 при ЦлГоЦ^г, где г — фиксированное произвольно большое число.
Определение 5.20. Ограниченная траектория [И]. Траекто¬
рия называется ограниченной для любых t0f jc0, если можно указать
такое число B{xQ, tQ), что для всех	||cp(tf; jt0, ^0)||^Z?.
Определение 5.21. Равностепенно ограниченная траекто¬
рия [11]. Траектория называется равностепенно ограниченной, если
В(хо, t0)^B(r, t0) (см. определение 5.20) для всех ||x0||^r-
Заметим, что из асимптотической устойчивости в большом следует
ограниченность траекторий, а из равностепенной асимптотической,
устойчивости в большом следует равностепенная ограниченность.
Определение 5.22. Равномерная устойчивость [11]. Если
в основном определении 5.15 о не зависит от t0, мы имеем равно¬
мерную устойчивость.
Определение 5.23. Равномерная асимптотическая устой¬
чивость [11].	Если	при равностепенной	асимптотической устойчи¬
вости числа о,	г и	7 не зависят	от tQj	говорят, что имеет место
равномерная асимптотическая устойчивость.
Определение 5.24. Равномерная асимптотическая устой¬
чивость в большом [11]. Состояние равновесия хе невозмущенной
динамической системы равномерно асимптотически устойчиво в боль¬
шом, если
(а) оно равномерно устойчиво,
(б) оно равномерно ограничено, т. е. при любом г^> 0 найдется
такое В (г), что при || лс0 — хе\\ ^ г имеет место || ср (t\ х0, t0) — хе || ^ В
Для всех t^t0 и
(в) любое движение стремится при t-+ оо к хе равномерно по
*0 и || х01| ^ г,	где г	— произвольно	большое фиксированное число.
Таким образом, при	любых г^> 0	и	найдется такое число

210	АНАЛИЗ	СИСТЕМ	ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА	ГГЛ. 5
Т (ja, г), что из || Хц —	||	г	следует Ц ср (t; х0) t0) — хе || ^ jx для
всех t ^ tQ -|- Т.
Теперь, пользуясь этими определениями, можно излагать различ¬
ные теоремы об устойчивости. Первая группа теорем приводится
в работе [19] и более подробно в монографиях [6] и [3].
Теорема 5.2. Устойчивость автономных систем. Состояние
равновесия хе = 0 системы
х = Ах	(5.2.19)
равномерно асимптотически устойчиво в целом тогда и только тогда,
когда	вещественные	части	характеристических	чисел матрицы А
отрицательны. Здесь	хв = 0	означает я-мерный	вектор, все	компо¬
ненты которого нули. Подчеркнем, что в данной теореме А — матрица
с постоянными элементами.
Теорема 5.3. Устойчивость нелинейных автономных систем.
Если
(а) каждое решение системы х—Ах равномерно устойчиво
в целом,
(б) f(x) непрерывна в некоторой окрестности jc = 0,
(в) Т*Г при 1*1^°’
тогда для системы
х = Ах -j— f (х), jc(0) = c	(5.2.20)
решение хе — 0 в некоторой достаточно малой его окрестности
является асимптотически устойчивым решением.
Доказательство этой теоремы приводится в работе [6]
(сгр. 343—346) и в работе [3] (стр. 96—102)*).
Теорема 5.4. Неустойчивость решения. Решение хг = 0 си¬
стемы (5.2.20) неустойчиво, если эта система удовлетворяет условиям
(б)	и (в) теоремы 5.3 и если хотя бы один корень характеристиче¬
ского уравнения матрицы А имеет положительную вещественную
часть.
Доказательство этой теоремы приводится в работе [6] (стр. 346—347)
и в работе [3] (сгр. 107—108).
Теорема 5.5. Условная устойчивость нелинейных автоном¬
ных систем. Пусть в системе (5.2.20)
(а)/е характеристических чисел (k^n) матрицы А имеют отри¬
цательную вещественную часть,
0 при ' *' °’
(в)	|/(JCi) — f(Xi) | sg с, | дг,—*s| для I*, | и |*2|^c-2. где ct 0
при 6'2 —► 0.
*) Здесь и в дальнейшем номера страниц указываются по русским изда¬
ниям упоминаемых работ, если таковые имеются. (Прим. перев.)

5.21	ТЕОРЕМЫ.	ОПРЕДЕЛЕНИЯ	И ОБОЗНАЧЕНИЯ	211
Тогда существует ^-параметрическое семейство решений уравне¬
ния (5.2.20), стремящихся к нулю при оо.
В этой теореме утверждается, что, хотя решение, которое начи¬
нается в произвольной окрестности фазового пространства вблизи
точки хе = 0у может оказаться неустойчивым, найдется тем не менее
такая часть этой области, прилегающая к началу координат, что любое
решение, которое начинается там, будет асимптотически устойчивым.
Доказательство теоремы 5.5 приводится в [6] (стр. 360—364) и
в [3] (стр. 108—110).
Теорема 5.6. Устойчивость нелинейных автономных систем.
Частный случай. Пусть
(а)	каждое решение уравнения х = Ах асимптотически устой¬
чиво в целом,
б)	f(x, у) и g(x, у) непрерывны в некоторой окрестности л: = 0,
при 1*1-0,
(г)	| лг (0) j = | с | достаточно мало,
(я)	1 '-*0 ПРИ 1*1 -*0. £■(*- 0) = As(*)•
Тогда нулевое решение хе = 0, уе = 0 системы
х = Ах	f (ху у),	х (0) = с,	(5.2.21 а)
y — g(x,	у\	у (0) = d	(5.2.216)
устойчиво и, кроме того, решение хе = 0 уравнения (5.2.21а) асимп¬
тотически устойчиво.
Некоторые соображения, связанные с доказательством этой
теоремы,	приводятся в [19|.
Теорема	5.7. Устойчивость	нелинейных неавтономных
систем. Пусть
(а) каждое решение х=Ах асимптотически устойчиво в целом,
(б) f(x) непрерывна в некоторой окрестности хе = 0 фазового
пространства,
(в)	при	i*i
и
(Г)	|R(0|<M.
Тогда решение системы
x =	х(0	)	—	с	(5.2.22)
ограничено, если | с | и М достаточно малы.
В работе [19] (стр. 40—43) приводится как строгое доказатель¬
ство этой теоремы, так и ряд эвристических рассуждений, относя¬
щихся к этому доказательству.

212
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Т е о р е м а 5.8. Устойчивость нелинейных неавтономных си¬
стем. Частный случай. Пусть
(а) каждое решение х = Ах асимптотически устойчиво в целом,
(б) f(x, У) и у) непрерывны в некоторой окрестности начала
координат фазового пространства,
(в)	^->0	при	| д; | —»• 0
И
(г)	0	при	I AT j -»■ 0, g(x, 0) = Р., (X).
Тогда решение системы
х = Ах /(х, у)~ М (t\ х (0) — с,
У = ё(х,у),	у	(0)	d
t
ограничено, если |л:| и ^\x(r)\dr ограничены. Доказательство тео-
и
ремы 5.8 приводится в работе [19] (стр. 43—44).
В теоремах 5.3—5.8 рассматривалась устойчивость или неустой¬
чивость в произвольно малой окрестности начала координат фазо¬
вого пространства. Однако эти теоремы не дают никакой информации
о том, каковы размеры этой окрестности. По сути дела, эти теоремы
вообще оказываются мало полезными для определения оптимальных
или субоптимальных параметров при проектировании системы управ¬
ления, поскольку влияние нелинейной части системы дифференциаль¬
ных уравнений учитывается в этих теоремах лишь в малой части
фазового пространства. Тем не менее теоремы 5.3—5.8 могут успешно
применяться для исследования устойчивости состояния равновесия
системы. Это замечание следует иметь в виду при использовании
теорем, относящихся к прямому методу Ляпунова.
Поскольку ориентироваться в приведенных выше теоремах отно¬
сительно просто, знание их, по-видимому, существенно уменьшит
число неудачных применений прямого метода Ляпунова в задачах
анализа устойчивости.
Следующая группа теорем, которая приводится ниже, включает
основные теоремы прямого метода Ляпунова и большинство обоб¬
щений этого метода, которые могут представить интерес для спе¬
циалиста по автоматическому управлению. Эти теоремы в литературе
приводятся в различной форме и по-разному интерпретируются. Для
читателя, желающего более обстоятельно познакомиться с имеющейся
по этому вопросу литературой, ниже приводится соответствующая
библиография.
Относительно теорем, основанных на прямом методе Ляпунова,
следует еще раз специально отметить одно обстоятельство. Оно за¬
ключается в том, что эти теоремы дают не необходимые, а лишь
(5.2.23а)
(5.2.236)

5.2]
ТЕОРЕМЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
21.4
достаточные условия устойчивости и, следовательно, невыполнение
условий теорем, вообще говоря, еще не указывает на то, что иссле¬
дуемая система уравнений неустойчива.
Теорема 5.9. Разномерная асимптотическая устойчивость
в целом для невозмущенных нелинейных неавтономных систем [11].
Пусть для непрерывной по времени невозмущенной динамической
системы
(здесь 0 — /z-мерный нулевой вектор), существует скалярная функ¬
ция V (х, t), имеющая непрерывные по х и t частные производные
первого порядка, такая, что 1/(0, 0 = 0 и
(а)	V (х, t) — положительно определенная функция, т. е. суще¬
ствует непрерывная неубывающая скалярная функция a(||jc||) такая,
что а (0) = 0 и для всех t и всех х ф 0
(б)	существует непрерывная скалярная функция 7(||x|j) такая,,
что 7(0) — 0 и производная V по времени вдоль траектории, начи¬
нающейся в точке t, х, удовлетворяет при всех t и всех х ф 0
следующему соотношению:
(в)	существует непрерывная неубывающая скалярная функция
Р(||аг||) такая, что [3(0)=0 и для всех t
(г)	а (|| х ||) оо при ||jt||->oo. Тогда положение равновесия хв — 0
равномерно асимптотически устойчиво в целом. Функция V (х, t) на¬
зывается функцией Ляпунова для системы дифференциальных урав¬
нений (5.2.24).
Определение 5.25. VI/ — градиент скалярной функции.
х = Ах -}- f (х),
в которой А и / могут зависеть от времени, причем
Л0+/(0) = 0 при всех t
(5.2.24)
(5.2.25)
(5.2.26)
V (Ху 0 = —^jr—^ вдоль траектории, начинающейся в точке t, х>
dV[y{% *о, t0), т]
dz	х	=	t
= Tt +(VV)'[	+	f{x)]	^	-	T	(ll	*	<	0;
(5.2.27)
(5.2.28)

214
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Градиентом VP скалярной функции V(хх, хь ..., xw t) называется
вектор-столбец
dV
VI/=
дх{
дУ
дх2
дУ
(5.2.30)
дхп
Различные комбинации условий теоремы 5.9 позволяют получить до¬
статочные условия для различных более слабых видов устойчивости.
Ниже приводятся соответствующие теоремы.
Теорема 5.10. Равномерная асимптотическая устойчивость [11].
Условия (а), (б) и (в) теоремы 5.9 являются достаточными условиями
равномерной асимптотической устойчивости.
Теорема 5.11. Равностепенная асимптотическая устойчи¬
вость в целом [И]. Условия (а), (б) и (г) теоремы 5.9 являются
достаточными условиями равностепенной асимптотической устойчи¬
вости в целом.
Теорема 5.12. Равностепенная асимптотическая устойчи¬
вость [11]. Условия (а) и (б) теоремы 5.9 являются достаточными'
условиями равностепенной асимптотической устойчивости.
Теорема 5.13. Равномерная устойчивость [11]. Условия (а)
и (в) теоремы 5.9 вместе с условием
V{ху t)^0 для всех Ху t	(5.2.31)
являются достаточными условиями равномерной устойчивости.
Теорема 5.14. Устойчивость [11]. Условие (а) теоремы 5.9
вместе с условием V(ху t)^0 для всех ху t являются достаточными
условиями устойчивости.
Теорема 5.15. Бесконечное время удержания в конечной
области [И]. Условия (а) и (г) теоремы 5.9 вместе с условием
V (Ху t)^c V (Ху t) для всех ху t} где с — положительная постоянная
(5.2.32), являются достаточными условиями бесконечного времени
удержания в конечной области.
Теорема 5.16. Равностепенная асимптотическая устойчи¬
вость в целом для непрерывных по времени нелинейных автоном¬
ных динамических систем [И]. Равностепенная асимптотическая
устойчивость в целом непрерывной по времени нелинейной автоном¬
ной динамической системы
х — Ах —j— / (х), Л0 -j— / (0) — 0
(5.2.33)

5.2}
ТЕОРЕМЫ. ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
215
обеспечивается существованием скалярной функции V(х), которая
[имеет непрерывные частные производные первого порядка по хУ
причем
i (а) V (0) = 0,
(б) \/(jc)^>0 для всех х^О,
(в) V (х)	0 для всех х ф 0,
(г) V(x) -> оо при || JC || —^ оо.
Условие (в) может быть заменено условиями
(в = 1) V(x)^0 для всех х (т.	е.	V(х)	знако-отрицательна),
(в = 2) V [ср (t; х^ £0)] не стремится	к	нулю	при	t^t0	при лю¬
бом и любом Xq ф 0.
Доказательства теорем 5.9—5.16 приводятся в работе [11]*), хотя
в некоторых случаях там используются иные обозначения.
Теорема 5.17. Неустойчивость в целом непрерывных по вре¬
мени нелинейных автономных динамических систем [8, 28]. Если
для непрерывной по времени автономной динамической системы (5.2.33)
найдется скалярная функция V (jc), непрерывная и имеющая непре¬
рывные частные производные первого порядка по х} такая, что
(а) V(0) = 0,
(б) V (jc) ^ 0 для всех х Ф 0,
(в) V (д:)	0 для всех х Ф 0,
(г) V(x)->od при ||л; ||->*00,
тогда эта система неустойчива в целом.
Эта теорема, несколько иначе сформулированная, приводится и
доказывается в работах [8, 28].
Теорема 5.18. Существование функции Ляпунова [11]. Пусть
функция Ax-\-f(x) (уравнение (5.2.3)) удовлетворяет условию Лип¬
шица. Пусть, кроме того, Л0-^-/(0) = 0 и положение равновесия
jce = 0 равномерно устойчиво в целом. Тогда существует функция
Ляпунова V (ху t\ которая бесконечно дифференцируема по х и t и
удовлетворяет всем условиям теоремы 5.9.
Формулировка и доказательство теоремы 5.18 приведены в ра¬
боте [20]. Из нее следует, что существование функции Ляпунова,
удовлетворяющей условиям теоремы 5.9, необходимо и достаточно
для равномерной асимптотической устойчивости в целом.
Теорема 5.19. Линейные системы с вынуждающими силами
[11]. Рассмотрим непрерывную по времени линейную динамическую
систему
х = Ахф DR(t\	(5.2.34)
в которой R(t) есть входное воздействие или вынуждающая сила,
а элементы матриц А и D могут зависеть от времени.
*) См. также М а л к и и И. Г., Теория устойчивости движения, «Наука»,
1966. (Прим. перев.)

216	АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА	[ГЛ.	5
Пусть выполняются следующие ограничения:
(а) ||	ct<^oo	для всех ||jc||=1 и всех t *),
и
(б) 0<^c2^||Z>jc||^c3<^oo для всех ||jc||=1 и всех t
Тогда общее решение уравнения (5.2.35) может быть записано в виде
t
ч (<; Х„ <о)=ф (*. U) *« + 5 ф (t, х) D (х) R (х) rfx **).
h
Относительно этой системы справедливы следующие эквивалентные
предложения:
(1)	при любой равномерно ограниченной вынуждающей силе
!*(0|Хс4<ОО
решение системы равномерно ограничено при всех t^t0
t	I!
1 *(91 =
ф (t, U) ^0 + \ Ф (t, X) D (x) R('.)d X|!^ cs (c4, [| д:0 IIX oo;
I	/0	1
t
(2) при всех t ^ t0 ^ || Ф (^, t)|| d т ^ c6 oo;
to
(3) положение равновесия xe = 0 невозмущенной системы равно¬
мерно асимптотически устойчиво;
(4) существуют положительные константы с7 и с8 такие, что при
любом t^t0
II Ф(*, ^о)||^^_С8(/_/о);
(5) если найдется симметрическая положительно определенная не¬
прерывная по t матрица Q(t) такая, что при всех t^t0
\Q(t)-c„I],
[do/— Q(01
И
(Cl0 — c9)l***)
будут положительно определенными, тогда скалярная функция, кото¬
рая задается выражением
оо
V(x,t)=\ {[ф(х, 0jc]'[QW][®(^0^]}^=^[P(0]jc, (5.2.35)
*) Все ci — конечные положительные постоянные.
**) Ф (t} t0) называется переходной матрицей (матрицей Коши. — Прим.
перев.). Ее элементы могут рассматриваться как импульсные переходные
функции при соответствующим образом подобранных возмущениях и наблю¬
дениях [11].
***) Здесь / означает единичную матрицу. {Прим. перев.)

6.2]
ТЕОРЕМЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
217
является функцией Ляпунова для невозмущенной системы, удовлет¬
воряющей	условиям	теоремы	5.9, причем производная	от	этой функ¬
ции	вдоль	невозмущенного	решения, начинающегося	в	точке х, t,
равна
V(x, t) = — x' [Q (*)] x *).	(5.2.36)
Теорема 5.20. Асимптотическая устойчивость непрерывной
по времени линейной автономной динамической системы [11]. По¬
ложение равновесия хе = 0 непрерывной по времени линейной авто¬
номной динамической системы
х = Ах	(5.2.37)
асимптотически устойчиво тогда и только тогда, когда для любой
симметрической положительно определенной матрицы Q существует
симметрическая положительно определенная матрица Р, которая
п (п -f- 1)	»
является единственным решением системы	у—-	линейных уравне¬
ний
А'Р PA = — Q,	(5.2.38)
причем |]х||2Р есть функция Ляпунова для этой системы.
Теорема 5.21. Обобщение теоремы 5.20 [11]. Вещественные
части характеристических чисел постоянной матрицы А (см. тео¬
рему 5.20) будут меньше а тогда и только тогда, когда для любой
симметрической положительно определенной матрицы Q существует
симметрическая положительно определенная матрица Р, которая яв¬
ляется единственным решением системы п ^ линейных уравнений
— 2аР Л'Р -f РА = — Q.	(5.2.39)
Доказательства теорем 5.19 — 5.21 приведены в работе [11], где
указаны первоисточники, а также проводится обсуждение их значения
и возможностей применения.
Теорема 5.22. Области асимптотической устойчивости для
нелинейных автономных систем [13]. Пусть Q есть содержащая
хе = 0 ограниченная замкнутая область фазового пространства для
системы дифференциальных уравнений
x=Ax+f(x\ Л0-{-/(0) = 0,	(5.3.40)
где Ax-\-f(x) удовлетворяют определению непрерывной по времени
автономной динамической системы. Пусть далее 2 обладает тем
*) Здесь ' означает операцию транспонирования. {Прим. перев.)

218
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
свойством, что каждое решение ср(/; х0, t0), которое начинается в 2,
остается там и при любом t. Пусть, наконец, существует скалярная
функция V{х)у которая непрерывна в 2 и имеет там непрерывные
частные производные первого порядка, и такая, что в области 2
(а) У(0) = 0,
(б) 1/(jc)^>0 для всех х Ф О,
(в) V(je)<^0 для всех х ф 0.
Вместо условия (в) можно рассматривать условия
(в-1) \/(jc)^0 для всех х (т. е. V(х) знако-огрицательна),
(в-2) V[y(t; jc0, tQ)] не обращается в тождественный нуль при
t^t0 для любого t0 и любого х0 Ф 0.
Тогда любое решение, которое начинается в области 2, асимпто¬
тически устойчиво, а точка хе = 0 есть точка равновесия. Доказатель¬
ство теоремы 5.22 приводится в работе [13] (стр. 9—10). Заметим,
что теорема 1 работы [13] и соответствующее доказательство по¬
зволяют получить более общее утверждение, чем теорема 5.22.
Теорема 5.23. Способ нахождения области асимптотичес¬
кой устойчивости для нелинейных автономных систем [3]. Пусть
2 есть замкнутая область, которая определяется неравенством V(x)^Ly
где V(х) есть скалярная непрерывная в 2 функция, имеющая в 2
непрерывные частные производные первого порядка. Пусть для
системы (5.2.40) функция V(х) удовлетворяет в области 2 условиям
(а), (б) и (в) теоремы 5.22 и область 2 ограничена. Тогда любое
решение системы (5.2.40), которое начинается в 2 или попадает туда,
является асимптотически устойчивым и точка хе = 0 есть точка
равновесия.
В теореме 5.23 достаточным условием того, что область 2, опре¬
деляемая неравенством V(x)^Ly ограничена, является 1/(лс)->со
при || х || —> оо. Если
lim mfV(x) = L0
1! X Н — со
область 2 ограничена для всех L<^L0.
В работе [13] (стр. 10 — 14а) дается анализ теоремы 5.23
и приводятся примеры ее применения.
Т е о р ем а 5.24. Исследование ограниченности решений с помощью
прямого метода Ляпунова (теорема Лагранжа) [13]. Пусть для
системы (5.2.40) 2 есть ограниченная окрестность начала координат,
и пусть 2е есть ее дополнение (т. е. совокупность точек, внешних
по отношению к 2). Пусть далее W(x) есть непрерывная в 2е
скалярная функция, имеющая там непрерывные частные производные
первого порядка и удовлетворяющая условиям:
(а) U7(Jt)^>0 для всех х 2е,
(б) U7(jc)^0 для всех х(^2с,
(в) W(x) со при ||л: 1 -* со.

5.2]
ТЕОРЕМЫ, ОПРЕДЕЛЕНИЯ И ОБОЗНАЧЕНИЯ
219
Тогда каждое решение уравнения (5.2.40) ограничено при всех t^O.
Доказательство теоремы 5.24 приводится в работе [13] (стр. 16—19).
Там же рассматривается два простых примера ее применения.
Теорема 5.25. Области эвентуальной асимптотической ус той-
чивости невозмущенных нелинейных неавтономных систем [14].
Рассмотрим непрерывную по времени невозмущенную динамическую
систему
* = А*+/(*),	(5.2.41)
в которой Ли/ могут зависеть от времени и где
Л0+/(0) = 0 для всех t,	(5.2.42)
причем /(jc) имеет непрерывные частные производные первого порядка.
Обозначим ср(£;л;0,£0) решение, удовлетворяющее условию ср (^0; аг0, ^о)=^о-
Пусть 2— ограниченная замкнутая область, содержащая начало
координат. Пусть далее 20— область внутри области 2, обладающая
тем свойством, что решения, которые начинаются в 20 при Г0,
остаются в дальнейшем в 2. Пусть, наконец, существует скалярная
функция V (х, t) такая, что
(а) V(x, t)-+U{x) при t-+oo равномерно по х 2,
(б) V(x, t)->— W(x) при t-+ оо равномерно по х £ 2,
(в) U(x) и W{x) есть положительно определенные функции при
x£Q.
Тогда существует Т0^>0 такое, что ср (t; x0i t0)-> 0 при t-^oo
для всех jc0 ^ L>o и всех	Г0.
Теорема 5.26. Способ определения области эвентуальной
устойчивости для невозмущенных нелинейных неавтономных си¬
стем [14]. Рассмотрим непрерывную по времени невозмущенную ди¬
намическую систему, которая уже встречалась выше в теореме 5.25.
Пусть 2 есть ограниченная замкнутая область, определяемая
неравенством U(x) ^ L (L 0), и пусть выполнены условия (а), (б)
и (в) теоремы 5.25. Пусть далее для любого 8^>0 существует
область, которая определяется неравенством U(x)^L — Ъ. Тогда
найдется	0	такое,	что
ср (t; х0, tQ) -> 0 при t-+ оо
для всех Хо £ 28 и всех	7V
К теореме 5.26 следует добавить, что достаточное условие, при
котором область 2, определяемая неравенством U(x)^L, будет
ограниченной для всех L, состоит в том, что £/(jt)->oo при ||jc||-> оо.
Если же
lim inf U(x) = L0,
II Jf fj - ос
тогда область 2 будет ограниченной для всех L<^L{). Доказательство
теорем 5.25 и 5.26 было получено Лассалем. Оно приведено

220
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
в работе [141. И. Г. Малкиным была доказана весьма важная теорема,
устанавливающая, к какому виду может быть приведена функция
Ляпунова, если уравнение (5.2.40) удовлетворяет некоторым условиям.
Эта теорема изложена в работе [5] (стр. 112). Ниже приводится
формулировка этой теоремы.
Теорема 5.27. Условия записи функции Ляпунова в виде
квадратичной формы [5]. Пусть объект описывается системой диф¬
ференциальных уравнений вида
х = Ах —j- Р (ty Jt),	(5.2.43)
в которых А — матрица порядка п X я, элементы которой есть
непрерывные ограниченные функции времени, а Р — векторная функ¬
ция t и х, координатами которой являются степенные ряды по
хъ ..., хт равномерно относительно t сходящиеся при [|jc||<^£,
с коэффициентами в виде непрерывных ограниченных функций времени.
Пусть далее существует положительно определенная функция V(,х)
такая, что V (х) отрицательно определена. Тогда существует квадра¬
тичная форма в фазовом пространстве хь ..., хП) обладающая теми
же свойствами. При этом квадратичная форма удовлетворяет следую¬
щим неравенствам:
V(x)^a2'^ix!> V (*)«£ — Ь^х!	(5.2.44)
при некоторых а, Ь^> 0.
Этим заканчивается изложение теорем, посвященных разработке
и обобщению прямого метода Ляпунова.
Так как при нахождении и различных преобразованиях функции
Ляпунова часто используются различные теоремы, относящиеся к сим¬
метрическим матрицам и квадратичным формам, ниже для удобства
читателя приводится ряд таких теорем. Большая часть их взята из
работы [4], однако их можно найти также в любом курсе современ¬
ной алгебры *).
Определение 5.26. Матричная запись произвольной квадра¬
тичной (формы. Произвольная квадратичная форма Q от п перемен¬
ных может быть записана в виде
Q (х) = х' Вху	(5.2.45)
где х — /i-мерный вектор-столбец (см. уравнение (5.2.2)), а хТ — век¬
тор-строка, получаемый транспонированием вектора х. В есть матрица
пУ^Пу элементы которой могут быть постоянными либо зависящими
от времени. Эта матрица не обязательно симметрическая, однако,
всегда найдется симметрическая матрица, с помощью которой полу¬
*) См. напр. М и ш и н а А. II., П р о с к у р я к о в И. В., Высшая алгебра,
«Справочная математическая библиотека», Физмаггиз, 1962. (Прим. перев.)

5.2]
ТЕОРЕМЫ. ОПРЕДЕЛЕНИЯ II ОБОЗНАЧЕНИЯ
221
чается та же самая крадратичная форма. Поэтому здесь матрица В
квадратичной формы всегда будет считаться симметрической.
Теорема 5.28. Приведение квадратичной формы к нормальному
виду [4] (стр. 271). Любая квадратичная форма Q над полем вещест¬
венных чисел может быть приведена с помощью невырожденного
линейного преобразования переменных к виду
Q (5) = 21 4-... z-p — 4+1 — ... — 2%	(5.2.46)
Теорема 5.29. Закон инерции квадратичных форм [4] (стр. 272).
Число р положительных *) коэффициентов в нормальном виде данной
квадратичной формы есть инвариант данной формы в том смысле,
что это число зависит лишь от самой формы и не зависит от
способа ее приведения.
Определение 5.27. Положительно определенная матрица В.
Матрица В называется положительно определенной, если квадратич¬
ная форма, соответствующая матрице (5.2.45), положительно определена,
т. е. Q(jc)^>0 для всех	и	всех t.
Теорема 5.30. Положительная определенность квадратичной
формы. 1-й критерий [4] (сгр. 273). Вещественная квадратичная
форма положительно определена тогда и только тогда, когда все
коэффициенты ее нормального вида (5.2.46) положительны.
Теорема 5.31. Положительная определенность симметричес¬
кой матрицы [4] (стр. 273). Вещественная симметрическая матрица В
положительно определена тогда и только тогда, когда существует
вещественная невырожденная матрица Р такая, что В = РР'.
Теорема 5.32. Приведение квадратичной формы к диагональ¬
ному (каноническому) виду. Любая вещественная квадратичная форма
переменных приводится в соответствующем ортонормированием **)
базисе к диагональному виду.
Следствие 1 (из теоремы 5.32). Любую вещественную однород¬
ную квадратичную функцию п переменных можно с помощью орто¬
гонального преобразования привести к диагональному виду.
Следствие 2 (из теоремы 5.32). Для любой вещественной
симметрической матрицы В существует вещественная ортогональная
матрица Р такая, что РВР' = РВР~Х диагональна.
Следствие 3 (из теоремы 5.32). Любая невырожденная вещест¬
венная матрица может быть представлена как произведение B = SR,
где «S есть симметрическая положительно определенная матрица,
a R—ортогональная матрица.
Теорема 5.33. Характеристические числа или собственные
значения матрицы ([21 лемма, сгр. 311). Характеристическими числами
*) И г отрицательных (см. Мишина А. П. и Проскуряков И. В.,
Высшая алгебра, 1962, стр. 149. (Прим. перев.)
**) Эта же теорема справедлива для ортогонального базиса. (Прим. перев.)

222'
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
Г ГЛ. 5
или собственными значениями матрицы В называются числа X такие,
что
| X/—Д | = 0.
Определение 5.28. Характеристической функцией матрицы В
называется функция | X/ — В |.
Определение 5.29. Характеристическим уравнением матрицы
В называется уравнение | X/—/?| = 0.
Теорема 5.34. Корни характеристического уравнения [4]
(стр. 313). Характеристические числа или собственные числа матрицы
В есть корни характеристического уравнения матрицы В.
Теорема 5.35. Приведение квадратичной формы к диаго¬
нальному (iканоническому) виду [4] (стр. 314). Любая квадратичная
форма хгВх может быть приведена с помощью ортогонального пре¬
образования к диагональному (каноническому) виду \z\	-Xnz*,
в котором коэффициенты Xf есть корни характеристического урав¬
нения
|а/-В|=(Х-Х,)(Х-Х2) ... (Х-Х„) = 0
матрицы В.
Следствие (из теоремы 5.35). Все характеристические числа
вещественной симметрической матрицы вещественны.
Теорема 5.36. Положительная определенность квадратичной
формы. 2-й критерий. Произвольная вещественная квадратичная форма
хгВх положительно определена, если собственные значения вещест¬
венной симметрической матрицы В положительны.
Доказательство этого утверждения непосредственно следует из
определения 5.26 и теоремы 5.35.
Теорема 5.37. Положительная определенность квадратичной
формы. 3-й критерий. Произвольная вещественная квадратичная форма
х'Вх положительно определена, если определители всех главных
миноров положительны.
Теорема 5.38. Положительная определенность квадратичной
сформы. 4-й критерий. Произвольная вещественная квадратичная форма
х'Вх положительно определена, если существуют положительно оп¬
ределенные матрицы С и D такие, что bij — Cijdij для всех /, / и t.
Приведенные в данном параграфе теоремы не исчерпывают всех
результатов, относящихся к прямому методу Ляпунова, однако они
охватывают большую часть теорем, применяемых в теории управле¬
ния. Те же самые, а также и некоторые другие теоремы встречаются
в литературе в самых различных формулировках. Выше была сде¬
лана попытка представить их в возможно более одинаковой форме.
Несколько дополнительных результатов будет указано в § 5.3 в связи
с применением прямого метода Ляпунова и построением функций
Ляпунова. Там это более уместно.

5.3]
ПРЯМОЙ МНТОД И ФУНКЦИЯ ЛЯПУНОВА
223
5.3.	Применение прямого метода Ляпунова и нахождение
функций Ляпунова
5.3.1. Введение
Основная трудность при применении прямого метода Ляпунова
заключается в выборе или образовании скалярной функции V(х),
которая удовлетворяла бы условиям теоремы. В большинстве анг¬
лийских публикаций возможность найти функцию Ляпунова представ¬
ляется как искусство, которое зависит от ловкости, опыта и очень
часто от удачи исследователя. Одно время это было действительно
так, однако теперь имеется ряд процедурных и аналитических мето¬
дов нахождения функций Ляпунова. Некоторые из наиболее употре¬
бительных приведены в настоящем параграфе. В отдельных случаях
даны примеры их применения. Ниже будут изложены следующие
приемы: метод канонических преобразований [8, 16, 17, 18, 22], метод
Айзермана [1, 8], метод Красовского [12, 8], метод Плисса [21, 8]
и метод переменного градиента [23, 24]. Перечисленные методы,
по-видимому, охватывают все случаи, в которых применимы методы
Ингверсона [9, 10, 24] и Сегё [24, 25, 26], и поэтому последние
здесь не рассматриваются. Изложение методов ведется в том же
порядке, в каком они перечислялись.
5.3.2.	Канонические преобразования [8, 16, 17, 18, 22]
Преобразование, приводящее систему дифференциальных уравне¬
ний к каноническому виду, называется каноническим. Для систем,
которые могут быть преобразованы к одной из двух канонических
форм, можно построить функцию Ляпунова. Эти канонические формы
называются «первой канонической формой» и «второй канонической
формой». Если система может быть представлена в виде одной из
канонических форм, то можно воспользоваться некоторыми стандарт¬
ными функциями Ляпунова для того, чтобы вывести вторичные кри¬
терии устойчивости. Вторичные критерии устойчивости легко приме¬
няются и не требуют нахождения функции Ляпунова отдельно для
каждой исследуемой системы. Подробно канонические формы рас¬
сматриваются ниже. В работах Лурье [17] и Летова [16] системы
регулирования делятся на системы «прямого и непрямого регулиро¬
вания». В английской литературе нет эквивалентной классификации,
и поэтому эта терминология здесь использоваться не будет.
Системы, к которым применим рассматриваемый метод, обладают
тем свойством, что их можно привести к виду, изображенному на
рис. 5.4. Однако не все системы, приводимые к этому виду, можно
анализировать данным методом. Ниже предполагается, что
г (0 = 0 для всех t'yO.	(5.3.1)

224
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Блок-схема системы может быть представлена в виде рис. 5.5. В каче¬
стве нелинейных элементов ограничимся только такими, у которых
Рис. 5.4. Блок-схема замкнутой системы с одним нелинейным
элементом.
зависимость между входом и выходом может быть представлена
непрерывной функцией
y=f{x\	П 0) = 0,	(5.3.2)
где х — вход элемента, .у — его выход, a f(x)— однозначная и ана¬
литическая функция в достаточно малой окрестности точки л: = 0.
Следует заметить, что нелиней¬
ный элемент не имеет ни одного
интегратора, дифференциатора или
какого-либо накопителя энергии.
Первое каноническое
преобразование [8, 18]
Ниже за основу взята блок-схе¬
ма рис. 5.5. Если G(s) = G1 (s)G2(s)
не имеет кратных полюсов и чи¬
сло полюсов превосходит число
нулей, то система может быть
описана совокупностью дифферен¬
циальных уравнений, называемых
первой канонической формой. В
оощем случае, когда u(sj имеет п полюсов, первая каноническая форма
системы уравнений имеет вид
Yt = X‘z‘ + /(•*)	(*	=	1, 2,..., я)	(5.3.3а)
И
п
х—	(5.3.36)
.1=1
где X; — полюса функции G(s), а — вычеты функции G(s) в точках
X
Нелинейный.
У
элемент
G(s)- Gj(s) G2(s)
Рис. 5.5. Приведенная блок-схема
замкнутой системы с одним нелиней¬
ным элементом.

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
225
А/, взятые с ооратным знаком. Zi называются каноническими пере¬
менными, а а: — по-прежнему входная величина нелинейного элемента.
Нелинейный
X
Г
А
элемент
а.
1
s - Я/
а1
1
s — Яг
1
s — Яп
Рис. 5.6. Блок-схема, соответствующая каноническому
преобразованию.
Дополнительное уравнение получается дифференцированием (5.3.36)
по времени и последующей подстановкой в него (5.3.3а):
%=2 р***—rfw>
i=i
где
и
§i = *ih (г=1, 2,..., я)
П
r=— 2«i.
f = i
(5.3.Зв)
(5.3.4)
(5.3.5)
Из этих уравнений система (5.3.3а) называется главной частью, а
(5.3.36) и (б.З.Зв) — дополнительной. Блок-схема системы, описываемой
8 п/р Леондеса

226
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
первой канонической формой, показана на рис. 5.6. Из этой блок-
схемы видно, что первое каноническое разложение есть просто
главная часть разложения передаточной функции G(s) линейной части
системы
п
0(5) = -2^лу	(5.3.6)
i= 1	1
Вторичный критерий устойчивости
Для систем, приводимых к первой канонической форме, можно
получить вторичный критерий устойчивости, применяя теоремы пря¬
мого метода Ляпунова. К сожалению, вторичный критерий устойчи¬
вости является слишком ограничительным условием, и поэтому мно¬
гие в действительности устойчивые системы отвергаются. Преиму¬
щество его, однако, заключается в том, что он не требует нахождения
в каждом отдельном случае функции Ляпунова.
Для того чтобы вывести вторичный критерий устойчивости, Лурье
[18] использует функцию Ляпунова в виде
v=- 2 2 f+f. + (fwdx•	<5-з-7>
i=\j=\	1	1	d
Эта функция неотрицательна, если
X
а)\f(x)dx = 0,	/	(0)	=	0;	(5.3.8)
о
б) константы аь действительны для соответствующих действитель¬
ных и являются комплексно-сопряженными парами для соответст¬
вующих комплексно-сопряженных пар X,-;
в) Re Х£0 для всех /=1,..., п.
Дифференцируя по времени выражение (5.3.7) и подставляя, как
обычно, (5.3.3а), (5.3.36) и (5.3.Зв), получаем
Выражение (5.3.9) не положительно, если

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
227
Выражение (5.3.9) можно сделать отрицательно определенным,
добавляя к функции (5.3.7) член вида
® = Aiz\ — A%z\-\- ... -j- Asz\ -)- C]ZS +1 zs+2	-j-
"j" 0^ + 3 ZS + 4 “Г ••• 4“ Cs-n- 1 Zn— i zn,	(5.3.1	Г)
в котором А и С—положительные числа. Константы А соответ¬
ствуют действительным каноническим переменным zt (/=1,2,..., s),
а константы Q — комплексным zt (/ = s, s	1,...,	п),
В приведенном выше рассуждении прямой	метод	Ляпунова исполь¬
зовался для вывода вторичного критерия устойчивости. Этот резуль¬
тат можно сформулировать в виде теоремы, называемой теоремой
Лурье.
Теорема 5.39. Вторичный критерий устойчивости 1. {Первая
каноническая форма.) Система, которая может быть приведена к пер¬
вой канонической форме и для которой выполняются указанные
выше условия а) — д), асимптотически устойчива в большом. С по¬
мощью этой теоремы можно найти область устойчивости переменной
л: как область, которая включает точку равновесия х = 0 и на кото¬
рой удовлетворяется условие (а) равенства (5.3.8).
Следует заметить, что с помощью теоремы 5.39 задача нахожде¬
ния функции Ляпунова сводится к решению системы уравнений (5.3.9)
при подходящем наборе at (/=1,..., п). Вообще, этот критерий
слишком ограничителен. Ряд исследователей использовали вместо
функции (5.3.7) функции Ляпунова другого вида и получали другие
вторичные критерии устойчивости, аналогичные условиям а) — д)
[8, 16, 17, 22]. Описание и таблица этих критериев устойчивости
имеются в [8] и [22], где подробно рассмотрено преобразование
к первой канонической форме. Хотя модификации критерия расши¬
ряют область применимости данного метода, однако он слишком
ограничителен в силу своей основной формулировки и отвергает
многие системы, которые в действительности устойчивы. Довольно
легко понять, когда это имеет место. Во всех вариантах данного
подхода ограничения на нелинейный элемент (условие а)) имеет один
из следующих двух видов:
л:
\f(x)dx^ 0,	/(0)	= 0
О
ИЛИ
xf{x)^ 0,	/(0)	=	0.
Второе из этих условий более ограничительно и ему удовлетворя¬
ют лишь нелинейные элементы с характеристикой, лежащей в первом
8*

228
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
и третьем квадранте, как показано на рис. 5.7 (незаштрихован-
ная часть). На этом рисунке изображены три типичные кривые не¬
линейного элемента. Линейный элемент можно рассматривать как
частный случай нелинейного элемента. В случае линейного элемента
у — kx для выполнения ограничений необходимо, чтобы 0 <С^к<^со.
Следовательно, по этим вто¬
ричным критериям устойчиво¬
сти отвергались бы линейные
системы, которые не устойчи¬
вы при всех положительных
значениях коэффициента уси¬
ления разомкнутой системы.
Вследствие слабости ограниче¬
ний на f(x) анализ устойчиво¬
сти одинаков для систем как
с линейной, так и с нелиней¬
ной характеристикой, пока по¬
следняя не выходит из неза-
штрихованной области рис. 5.7.
Следовательно, этот вторичный
Рис. 5.7. ^Ограничения на коэффициент критерий устойчивости будет
усиления нелинейного элемента.	отвергать все системы, для ко¬
торых корневой годограф G(s)
лежит в правой полуплоскости. Поэтому всегда целесообразно, прежде
чем пытаться применить вторичный критерий устойчивости, начертить
корневой годограф для G(s). Причины, по которым система вида
рис. 5.5 может быть отвергнута с помощью данного метода, формули¬
руются следующим образом:
а)	Некоторые полюса G (s) лежат в правой полуплоскости s.
б)	Некоторые нули G(s) лежат в правой полуплоскости пло¬
скости 5.
в)	Корневой годограф G(s) находится не только в левой, но и
в правой полуплоскости.
г) G(s) имеет полюса в начале координат плоскости 5.
д) G(s) имеет кратные полюса.
е) Разница между числом полюсов и нулей G(s) больше или равна
двум (т. е. п —	2).
Константа г (равенство 5.3.5.) не положительна.
Ввиду всего сказанного выше большое число нужных систем
отвергалось бы по вторичному критерию устойчивости, основанному
на первой канонической форме.
Область применимости данного метода может быть расширена,
если ограничиться нелинейными элементами с характеристиками, ле¬
жащими только в первом и третьем квадрантах. Это делается с по¬
мощью метода сдвига нулей и полюсов.

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
229
Метод сдвига полюсов
Область применимости вторичного критерия устойчивости можно
расширить так, чтобы он не отвергал устойчивые системы, коэффи¬
циент усиления которых не ниже некоторой величины. Этой величи¬
ной является нижняя граница коэффициента усиления нелинейного
элемента. Чтобы найти ее, повернем на угол ср против часовой стрелки
ось х. х—входная величина нелинейного элемента. Эго эквивалентно
преобразованию выходной величины у в новую переменную у' по
формуле
У = Г(х)=у — Срх,	(5.3.12)
в которой Ср — действительная константа. Геометрическая интерпре¬
тация дана на рис. 5.8. Угол ср нахо¬
дится из условия
ср = arctg Ср. (5.3.13)
Максимальное значение угла ср, а
следовательно, и максимум Ср опреде¬
ляются как угол, на который можно
повернуть горизонтальную ось плоско¬
сти х—у (рис. 5.8) прежде, чем она
пересечет характеристику нелинейного
элемента.
Вторичный критерий устойчивости
применяется теперь к новой перемен¬
ной У и к функции /'(х), которая долж¬
на удовлетворять вышеприведенным ус¬
ловиям для функции /(х). Если в блок-
схеме рис. 5.5 заменить G(s) на G'(s), то блок, описывающий дина¬
мику системы, будет иметь передаточную функцию G'(s), которая
связана с G(s) следующим образом:
«-<*>-,ЛД,Г	(5'ЗЛ4)
Равенство (5.3.14) показывает, что с помощью корневого годо¬
графа можно легко увидеть, как метод сдвига полюсов устраняет не¬
которые трудности, связанные с преобразованием к первой канони¬
ческой форме. Оно также показывает, почему данный метод назы¬
вается методом сдвига полюсов.
Метод сдвига нулей
Подобным образом можно ограничить максимальное значение
коэффициента усиления нелинейного элемента так, чтобы устойчивая
система не отвергалась по вторичному критерию устойчивости, если
Рис. 5.8. Геометрическая ин¬
терпретация метода сдвига по¬
люсов.

230	АНАЛИЗ	СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА	[ГЛ. 5
ее коэффициент усиления не превосходит установленного максимума.
В этом случае ось у (выходной величины) характеристики нелиней¬
ного элемента поворачивается по часо¬
вой стрелке на угол 0. Геометрически
эго изображено на рис. 5.9. Поворот
оси эквивалентен замене входной вели¬
чины х на х\ где х' = х'—С2у, а
С2 — положительная константа, опреде¬
ляемая по углу 0 как
0 = arctg Cz.	(5.3.15)
Максимальное значение угла 0, а
следовательно, и максимальное значе¬
ние Cz определяются как максимальный
угол, на который можно повернуть
вертикальную ось плоскости jc —у
(рис. 5.9), не пересекая кривую характе¬
рно. 5.9.	Геометрическая	ин-	рисгики нелинейного элемента. Если	пе-
терпретация метода	сдвига	г	х	-
нулей	ременную	х в олок-схеме рис.	о.о	за¬
менить на	новую переменную	х'у	то
блок, описывающий динамику системы, будет иметь передаточную
функцию G" (s), которая связана с G(s) соотношением
О" (5) = G(s) + Cz = N (s) +g«D (s),	(5.3.16)
в котором N(s) и. D(s) — полиномы числителя и знаменателя G(s).
Из равенства (5.3.16) видно, что G" (s) имеет одинаковое число полю¬
сов и нулей. Следовательно, система не может быть приведена к пер¬
вой канонической форме с помощью метода сдвига нулей. Можно,
однако, модифицировать первую каноническую форму так, чтобы
учесть подобную ситуацию. В этом случае выводится вторичный кри¬
терий устойчивости для модифицированной канонической формы. Под¬
робно данный вопрос рассмотрен в работах [9] и [22]. Поскольку
это приводит к дальнейшему ограничению области применимости, мы
не будем подробно останавливаться на этом.
Второе каноническое преобразование
Второй канонической форме в литературе уделяется значительно
меньше внимания, чем первой. По-видимому, она дает мало дополни¬
тельных преимуществ по сравнению с первой канонической формой,
если последняя дополняется методами сдвига полюсов и нулей. Однако
она прямо применима к системам вида, изображенного на рис. 5.5,
в которых G(s) содержит либо кратные полюса, либо полюса в пра¬

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
231
вой полуплоскости s, либо то и другое вместе, и поэтому мы кратко
изложим ее здесь.
Для системы, которая может быть представлена в виде блок-схемы,
изображенной на рис. 5.5, вторая каноническая форма системы диф¬
ференциальных уравнений имеет вид
<^ = a>izi -{-х,	i = 1, 2, т;	(5.3.17)
т
Tt= 2 T**i + 8*-/(*X	(5.3.18)
i = 1
При ЭТОМ
а) (о,- — нули G(s),
б)	8= 2	2	О),-,	(5.3.19)
1=1	1=1
в) X,-— полюса G(s),
т
— п (“<■—
г)	Ъ	=	~^	.	/=1,2,	(5.3.20)
1Д К —«у)
У = 1
]ф1
Если G(s) удовлетворяет некоторым условиям, то система, пред¬
ставимая в виде блок-схемы рис. 5.5, может быть приведена к вто¬
рой канонической форме. Эти условия кратко формулируются в виде
следующей теоремы.
Теорема 5.40. Приведение к второй канонической форме.
Система вида рис. 5.5 может быть описана дифференциальными урав¬
нениями второй канонической формы тогда и только тогда, когда
имеют место следующие условия:
а) все нули со,- функции G(s) простые,
б) число полюсов п функции Q(s) на единицу больше, чем число
нулей т, т. е. п = т -[- 1.
Для второй канонической формы дифференциальных уравнений
получается упрощенный критерий устойчивости, основанный на част¬
ном виде функции Ляпунова (см. [16] и [8]).
Этот вопрос здесь не рассматривается, так как оказывается, что
большинство систем, удовлетворяющих условиям второй канониче¬
ской формы, также легко может быть изучено с помощью преобра¬
зования к первой канонической форме вместе с методом сдвига ну¬
лей и полюсов [8].

232
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
5.S.S.	Метод М. А. Айзермана
Одной из простейших функций V(х\ которая может служить
функцией Ляпунова для нелинейных автономных систем, является
-ч&н
Y
А
1
s +2
Рис. 5. Ю. Блок-схема нелинейной
системы в примере 5.1.
обобщенная квадратичная форма. Для систем частного вида жела¬
тельно иметь процедуру выбора постоянных коэффициентов так,
чтобы квадратичная форма удов¬
летворяла требованиям одной
из теорем устойчивости § 5.2
и тем самым давала ответ на
вопрос об устойчивости или
неустойчивости системы. Один
из таких методов состоит в
следующем:
а) нелинейные элементы ап¬
проксимируются линейными
элементами,
б) находятся коэффициенты
квадратичной формы, так что¬
бы она была функцией Ляпунова
для линеаризованной системы,
в) найденную в б) функ¬
цию V(х) применяют к систе¬
ме с нелинейностями и ис¬
пользуют ограничение, нало¬
женное на dVjdt, для того
чтобы определить границы линейной аппроксимации, которые не
должны превышать нелинейные элементы. Этот метод называется ме¬
тодом М. А. Айзермана [8] и иллюстрируется следующим примером.
Пример 5.1. Пусть нужно исследовать устойчивость системы,
изображенной на рис. 5.10. Если входной сигнал равен нулю, т. е.
г (0 = 0 для t^> 0,
то тогда система может быть представлена уравнениями
х -|— 2л* —{— у = 0,
У =/(*).
Рис. 5.11. Зависимость выхода от входа
нелинейного элемента в примере 5.1.
(5.3.21)

5.3J	ПРЯМОЙ	МЕТОД	И	ФУНКЦИЯ	ЛЯПУНОВА	233
Делая замену переменных
[ = ЛГ, \
1 = Х, )
Хх=.., ,
(5.3.22)
х2 -	'	'
получаем систему дифференциальных уравнений первого порядка от¬
носительно переменных состояния xt и х2
Хх — хъ	\
.	"	.	\	(5.3.23)
х<2 — — 2х.2 f(xi).	J
Зависимость между входом и выходом нелинейного элемента, изо¬
браженная на рис. 5.11, может быть аппроксимирована прямой ли¬
нией вида
y=f(x1)^ 2хх.	(5.3.24)
Тогда
Х\ = хъ	\
\	?	(5.3.25)
х2 = — 2jc.> — 2xv j
Для двух переменных состояния обобщенная квадратичная форма,
которая может служить функцией Ляпунова, имеет вид
V(xh х2) = bnx\ -j- 2Ьпххх2 -]- ЬоЛх\.	(5.3.26)
Дифференцируя по времени (5.3.26) и подставляя (5.3.25), полу¬
чаем
-fit — (— 4£12) х\	-(- (2Ьп — 4Ьп — 4b22) Х\Х2 -j-	— 4Ь22) х\. (5.3.27)
Производная	по	времени dVjdt будет	удовлетворять условиям
теоремы 5.37, если положить
d^t=-x\-x\.	(5.3.28)
При этом постоянные Ь1Ь Ьп и Ь22 можно найти из системы урав¬
нений, которая получается приравниванием коэффициентов при соот¬
ветствующих членах в уравнениях (5.3.27) и (5.3.28). В результате
получим квадратичную форму
V(хь х.2) = -jj- х\	~ XiX.2 +	х\,	(5.3.29)
которая является положительно определенной. Вычислим dV/dt с уче¬
том равенств (5.3.29) и (5.3.23)

234
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
В этом случае условия теоремы 5.37, гарантирующие асимптотиче¬
скую устойчивость в большом, выполняются, если
Эти границы возможного отклонения прямой линии, аппроксимирую¬
щей нелинейность, показаны на рис. 5.11 пунктирными линиями.
Преимуществом метода Айзермана [8] являются:
а) простота,
б) применимость к системам, имеющим более чем один нелиней¬
ный элемент,
в) возможность установить ограничения на нелинейный элемент
слабо нелинейной системы, для того чтобы обосновать использование
линейной аппроксимации при исследовании устойчивости.
К недостаткам относятся [8]:
а) применимость только к системам с нелинейностями, не слиш¬
ком сильно отличающимися от линейной аппроксимации,
б) если система содержит дифференцирование (нули в передаточ¬
ной функции линейной части системы), ограничения на характери¬
стику нелинейного элемента в терминах у, dyjdt и т. д. становятся
достаточно сложными.
Следует заметить, что нелинейная система не обязательно устой¬
чива в большом, даже если ее линеаризованная модель (y = kx)
устойчива для всех значений эквивалентного линейного коэффициента
усиления k.
При применении метода Айзермана ограничения на характери¬
стику нелинейных элементов будут обычно наименее жесткими, если:
а) линейная аппроксимация y = kx выбирается так, что эта линия
делит пополам угол между прямыми, соответствующими верхней и
нижней границе изменения коэффициента усиления нелинейного эле¬
мента f(x)\
б) производная по времени от V(х) приводится к
£1^1	0	или	xtf	(а^)	Ъ>	О
xi
(5.3.31)
0,612 <<" 6,95.
х. ^
1
(5.3.31а)
П
5.3.4.	Применение теоремы Н. И. Красовского [12]
Вторичные критерии устойчивости можно вывести, и не прибегая
к каноническим преобразованиям. Один из таких методов основан
па теореме Н. Н. Красовского и применим к системам, которые

5.31
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
235
могут быть описаны в виде
jb=Ax + f{x) = X =
Хх[хи ..
Х,(хь ..
■>Хп)
Хп (хх,..
• > х^)
(5.3.32)
где Xi — должны быть непрерывными, дифференцируемыми функци¬
ями переменных состояния во всем пространстве, а положение равно¬
весия совпадает с началом координат.
Теорема 5.41 [12]. Вторичный критерий устойчивости (тео¬
рема Н. И. Красовского). Достаточным условием асимптотической
устойчивости в большом системы, описываемой уравнениями (5.3.32),
является существование положительно определенной симметрической
матрицы В такой, что корни характеристического уравнения (собст¬
венные числа) А,- (хъ ..., хп) симметрической матрицы
II В/+{В1У\
удовлетворяют неравенству
Х;<— 8,	/=	1,	2,	...,	п,
где В — положительная постоянная. Матрица I является
системы функций X и равна
/=
дХх
дХ!
dxt
" дхп
дХп
дХп
dxi
'' дхп
(5.3.33)
(5.3.34)
якобианом
(5.3.35)
Практически задача выяснения существования матрицы В> удовлет¬
воряющей условиям данной теоремы, сводится к образованию поло¬
жительной функции с помощью системы функций Xi (заметим, что
это не переменные состояния). Эта функция может быть записана как
V = XBX.
Производная по времени функции V есть
dX=X' IBI + (В Г)' || Х=Х'СХ,
(5.3.36)
(5.3.37)
где С—симметрическая матрица, элементы которой Cij являются функ¬
циями переменных состояния системы xt. Можно показать, что если
выражение (5.3.37) отрицательно определено, то система асимптоти¬
чески устойчива в большом. Следовательно, элементы матрицы В
нужно выбирать так, чтобы они обращали выражение (5.3.37) в отри¬
цательно определенную форму для всех действительных значений
переменных состояния хъ ..., хп.

236
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Описанный выше метод можно считать скорее применением кри¬
терия прямого метода Ляпунова к производным по времени перемен¬
ных состояния, чем применение критерия непосредственно к перемен¬
ным состояния. Эта теорема доказывается в [12]. Данный метод
иллюстрируется применительно к той же системе, которая рассматри¬
валась в примере 5.1.
Пример 5.2 [8]. После замены переменных по формулам (5.3.22)
система приводится к виду
хг = Хх (хъ х2) = хъ
х% — Х% (Х\, х%) —	f	{хi).
(5.3.38)
Для произвольных коэффициентов матрицы В матрица С после под¬
становки якобиана из (5.3.38) имеет вид
с = II в/+ (Я/у || =
— ж
df (хх)\
12 dxx )
bu — 2 bn — b<
df (Xi)
‘ dxx
(2^?12  4^22)
(5.3.39)
Если в (5.3.38) положить
1 df(x О
2 ' dxx
3 df (xy)
C =
dxA
3 # df fo)
8 dx j
— 1
TO
B =
(5.3.39a)
(5.3.40)
Это есть положительно определенная матрица, что можно проверить
с помощью теоремы 5.37, и, следовательно, функция I/, определяемая
выражением (5.3.36), является положительной. Матрица С, а следова¬
тельно, и dVjdt отрицательно определены для функции f(x)y удов¬
летворяющей ограничениям
0,573	(5.3.41)
Ограничения (5.3.41) на функцию f{x) дают достаточное (но не необ¬
ходимое) условие для устойчивости исследуемой системы.
Теорема Красовского имеет приблизительно те же преимущества
и недостатки, что к метод Айзермана. Следует, однако, заметить, что
в тех случаях, когда нельзя определить устойчивость системы этими
методами, результат все же можно получить другим способом.

5.3]	ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА	237
5.3.5.	Метод В. А. Плисса [21]
Другой метод, использующий линейную аппроксимацию нелиней¬
ной системы для определения функции Ляпунова, из которой затем
можно вывести вторичный критерий устойчивости, носит название
метода В. А. Плисса. Этот метод может дать результат для систем,
описываемых дифференциальными уравнениями вида
п
*1= 2 аПх1 + h/(z) С/ = !> 2> • • • > п)>	(0.3.42)
1 = 1
где
гг
2 = 2 kjxj	(5.3.43)
7=1
и а,-у,	hj, kj — константы. На нелинейную	функцию f(z)	наложены
ограничения
а)	/ (0) = 0,	(5.3.44)
б)	ctz2	zf	(z)	Ccfi1.
Используя линейную аппроксимацию в уравнениях (5.3.42), получаем
п
Xj = 2 a-jiXi -j- hjcz (/=1, 2,	,	n).	(5.3.45)
г = 1
Функцию Ляпунова берем в виде
п п
К=42 2 Ьчх1х1 + \*т-	(5-3-46)
£=1j =1
Из этой функции можно вывести вторичный критерий устойчивости,
который формулируется в виде следующей теоремы.
Теорема 5.42. Вторичный критерий устойчивости III. Система,
описываемая уравнениями (5.3.42) и (5.3.43), асимптотически устой¬
чива в большом, если
а) для всех б, = с1-}-в и с = с2 — в, где в — произвольная малая
положительная константа, линейная система (5.3.45) асимптотически
устойчива,
б)	существуют положительные числа	(3 и mij = mji (/, j —
=	1,	2, ... , ri), образующие положительно	определенную	или отри¬
цательно определенную квадратичную форму вида
п п
Q(xь ...,*„)= 2 2 r4xixp	(5.3.47)
;=iy=i

238
АНАЛИЗ СИ СТЕЛА ПРЯМЫЛА ДАЕТОДОЛА ЛЯПУНОВА
[ГЛ. 5
где коэффициенты rt*y вычисляются по формулам
п	п	/	п	п	\
rij— 2	2 mkjbkjJrc[aj 2 mbihk~\~ai 2 mkjhk\-\‘
k = 1	k = 1	\	k	=	1	J
j n	n	\	n
+	2	a,kbkl-\-at ^ а/А;] +2 akhk, (5.3.48)
\ k — 1	/г = 1	/	fe=l
с, < с <
Следует заметить, что для нелинейной системы нельзя установить
асимптотическую устойчивость в большом из того, что линейная
система устойчива для всех значений с из интервала С\<^с <^с».
С точки зрения практического использования недостатком данного
метода является то, что он требует довольно сложных алгебраических
преобразований.
5.3.6.	Построение функций Ляпунова методом градиента
Существует целый ряд способов, позволяющих применять на
практике теоремы прямого метода Ляпунова. Среди них наиболее
гибким, пожалуй, является градиентный метод построения функций
Ляпунова (variable gradient method).
Как уже отмечалось в предисловии к настоящей главе, этот метод,
по-видимому, охватывает все случаи, к которым приложимы методы
Ингверсона [9, 10, 24] и Сегё [25, 26], а также целый ряд других
случаев. В силу этого два последних метода здесь рассматриваться
не будут.
В основе метода градиента лежит предположение о том, что изу¬
чаемая	физическая	система автономна и описывается уравнением вида
х = Ах f(x) = X(jc),	(5.3.49)
где
Л (0) + /(0) = Х(0) = 0.	(5.3.50)
Данное выражение	совпадает по виду с уравнением	(5.2.3).	Однако
здесь для удобства последующих алгебраических преобразований
оказалось целесообразным объединить оба члена — линейный и нели¬
нейный — в один вектор X (л;).
Пусть функция Х(х) удовлетворяет в пространстве состояний
условию Липшица*). Тогда в соответствии с теоремой 5.18 она
непрерывна. Следовательно, все физические системы, асимптотически
*) Функция X (jc) удовлетворяет в области R условию Липшица, если
имеет место следующее неравенство:

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
239
устойчивые в большом, нелинейности которых удовлетворяют усло¬
вию Липшица, отвечают требованиям теоремы 5.18. Этой теореме
можно дать также иную формулировку. Пусть имеется некоторая
физическая система, асимптотически устойчивая в большом. Пусть
непрерывная нелинейность этой системы допускает дифференцирова¬
ние, а ее производная всюду ограничена. Тогда существует некото¬
рая функция V(x)f дифференцируемая бесконечное число раз и по¬
зволяющая доказать устойчивость этой системы прямым методом
Ляпунова.
Для того чтобы функция V (х) удовлетворяла теоремам прямого
метода Ляпунова, она должна быть непрерывной вместе со своими
первыми частными производными. Но из существования у скалярной
функции V (X) первых частных производных по х следует существо¬
вание ее градиента VI7, т. е. я-мерного вектора единичной длины
с составляющими по каждому из направлений xt. Поэтому если
физическая система с непрерывными нелинейностями асимптотически
устойчива в большом, то существует по крайней мере один вектор \v,
который может быть найден по функции V(х) — индикатору этой
устойчивости.
В основе данного метода лежит предположение о том, что из¬
вестна не сама функция V, а ее градиент \7 V7. В обычных пособиях
по векторному исчислению (Ласс [15], стр. 297—301) показывается,
что скалярная функция V представляется единственным образом через
криволинейный интеграл от векторной функции \V, если имеют место
следующие (п—1)я/2 равенства:
w-i.» »•	<**».)
Соотношения (5.3.51) представляют собой необходимое и достаточ¬
ное условие независимости вида скалярной функции V (х) от пути
интегрирования. В трехмерном случае совокупность (5.3.51) эквива¬
лентна равенству нулю ротора вектора. Это составляет основное
содержание теоремы Стокса, известной инженерам-электрикам по
курсу теории поля. Таким образом, уравнения (5.3.51) являются ^-мер¬
ным обобщением теоремы. В дальнейшем изложении они будут назы¬
ваться уравнениями ротора.
Покажем, что градиент yV функции-индикатора устойчивости
в большом V(х) с необходимостью отвечает уравнениям (5.3.51).
Из теоремы 5.18 следует, что из дифференцируемости функции V
бесконечное число раз вытекает существование и непрерывность
производных
*vgL	да.	(5ЛШ)
oxi oxj * dxj дхi	v	J
С другой стороны, если производные (5.3.52) непрерывны во всей
области определения, то в силу теоремы, приведенной в ([27], стр. 220),

240
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
в этой области справедливо равенство
д*У(х) _д2У(х)
d.\'i dxj dxj dxt
(5.3.53)
которое является просто иной записью уравнений (5.3.51).
Таким образом, знание любой из двух функций V(х) либо \V
позволяет единственным образом определить оставшуюся. Из всего
сказанного может быть сделан вывод, который мы представим в виде
теоремы.
Теорема 5.43. Условие существования градиента \У функ¬
ции Ляпунова. Пусть система, описываемая уравнениями (5.3.49) и
(5.3.50), удовлетворяет условию Липшица, а ее состояние равновесия,
jce = 0, асимптотически устойчиво в большом. Тогда существует
некоторая функция \V, криволинейный интеграл от которой равен
V (jc) — функции-индикатору асимптотической устойчивости в большом.
Эта теорема является весьма сильным условием существования.
Если некоторая автономная система обладает нелинейностями, кото¬
рые представимы непрерывными функциями, и сама она асимптоти¬
чески устойчива в большом, то существует некоторый вектор-гра¬
диент, позволяющий установить факт этой устойчивости.
Так как знание любой из функций V или yV позволяет един¬
ственным образом определить оставшуюся, то теоремы Ляпунова
могут быть сформулированы также в терминах функции-градиента.
В частности, теорема 5.16, справедливая для автономных систем, при¬
обретает следующий вид.
Теорема 5.44. Условие асимптотической устойчивости
в большом автономной системы, опирающееся на градиент у У
функции Ляпунова. Пусть для уравнения (5.3.49), удовлетворяющего
условию (5.3.86), определена действительная вектор-функция у У
с элементами VV), отвечающая следующим требованиям:
1 dsVi_dvVj
dxj	dxi
2. у 1ЛАГ(л;) 0, причем тождественный нуль достигается на реше¬
нии уравнения (5.3.49) лишь в начале координат. Скалярная функ¬
ция V(х) определяется как криволинейный интеграл от yV, непре¬
рывна и имеет непрерывные первые частные производные.
3. \/(л:)^>0	при	х ф 0.
4. V(jc)->co при || jc |! —оо.
Если эти условия имеют место, то уравнение (5.3.49) устойчиво
в большом.
Данная теорема является лишь обобщением теоремы существова¬
ния. Однако в отличие от теоремы 5.16 в ее формулировке под¬
черкнута роль вектор-функции градиента.
Если в теореме 5.44 не выполняется условие 4, либо условие 2
справедливо не во всем пространстве, то с ее помощью невозможно

5.3]
ПРЯМОЙ МЕТОД И ФУНКПИЯ ЛЯПУНОВА
241
доказать факт асимптотической устойчивости в большом. В этом
случае приходится привлекать теоремы 5.22 или 5.23 для установле¬
ния устойчивости в более узкой области. При этом особую практи¬
ческую ценность имеет теорема 5.23.
Сравнивая теоремы 5.16 и 5.44, легко заметить смещение акцента.
Задача нахождения функции V, удовлетворяющей теореме Ляпунова,
заменилась проблемой поиска градиента \V, отвечающего уравне¬
нию (5.3.51), с нулевым /z-мерным ротором. Далее, так как обе эти
теоремы эквивалентны, то функции V и clV/clt, найденные по у И,
должны быть таковыми, чтобы с их помощью можно было доказать
устойчивость, используя любую из двух теорем. Поэтому на первый
взгляд может показаться, что задача усложнилась. В действитель¬
ности же она упростилась. Наличие вспомогательных уравнений
ротора позволяет найти некоторое решение проблемы устойчивости,
отталкиваясь от у И.
В соответствии с термином «градиент» в условиях теоремы 5.44
фигурируют вектор у И с п неизвестными координатами. Для того
чтобы этот вектор удовлетворял всем возможным решениям, каждая
из его п координат ищется в форме совокупности п элементов
вида dijXj. Предполагается, что коэффициенты [а] являются функ¬
циями самого общего вида от аргумента ху либо полиномами с зара¬
нее не заданным числом членов, так что
В последнем случае предполагается, что коэффициенты а^ могут
быть представлены в виде суммы некоторого постоянного числа и
слагаемого, зависящего от фазовых координат, т. е.
а\1х1 4“ а12хЪ 4“ • • • 4“ а\пхп
уУ= #21-^1 “4 ^22*^2 4" • • •
ап\х\ 4~	•	•	•	4~	аппхп
V/a .	(5.3.54)
VV'i
j	Clijfc	[	Clijv (x).
(5.3.54)
Поэтому окончательно
[a\\k “f“ a\\v (X)] xl 4“ [aMk 4" anv (X)] x2 “Г • • •
• • • “4 \alnk ~T alnv (-*0] xn
V ^	[a.2i/j	-j-	a%iv	(x)]	Xi	-j-...
Wtlik 4~ ttnlv (-*0] x\ 4“ • • •	4~ Wnnk 4“ annv (*^)] xn
. (5.3.55)
Исследование i-й составляющей вектора градиента
У Vi [dilk J- attv (X)] X1 4“ * * • “1“ [aiik 4- aiiv (X)] xi 4“ • * *
. . . 4~ [aink 4- ainv 0*0] xrr

242
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
позволяет установить ряд интересных факторов. Так, при решении
некоторых задач может потребоваться, чтобы координата содер¬
жала члены, в которые в качестве сомножителей входи г более чем
одна фазовая координата. Очевидно, такие члены могут быть пред¬
ставлены в виде произведения aij(x)Xj. Поэтому вместо коэффи¬
циента aiiv(x) достаточно рассматривать ацъ(х{).
Функция V определяется как криволинейный интеграл от гра¬
диента \V:
=	=	J v(Ть •••> OWTi +
о
ТС2	КП
+ 5	Ъ>	0. •••. °)db-r\ V^C^i. х* •••> ■*«-!> T«)^Tn-
о	и
■ч 5.3.56)
В соответствии с этим в результате интегрирования коэффициен¬
тов ait возникают члены вида
'1
р-,	^	aliv	(-[i)	У;	d~[i.
о
Будем далее предполагать, что aiiv (х) = aiiv(xi). Для положительной
определенности функции V вблизи начала координат необходима
положительность слагаемых аИк. Далее, для того чтобы функция V
была уравнением замкнутой поверхности во всем пространстве и была
к тому же всюду положительно определенной, необходима четность
функции aiiv(Xi) и ее строгая положительность при больших зна¬
чениях х{. И, наконец, при aiik = 0 необходимым условием явля¬
ется четность и строгая положительность aiiv(Xi) при всех значе¬
ниях xt.
Эти свойства коэффициентов ati обусловливаются требованиями,
которым должна отвечать результирующая функция V для того, чтобы
к ней была применима теорема 5.44. В последующих параграфах
этот подход будет развит далее.
По предположению, коэффициенты atjv могут быть функциями фа¬
зовых координат. Поэтому резонно ожидать, что в выражении для V
встретятся весьма высокие степени фазовых координат. Поскольку
это, действительно, имеет место, то вопрос о положительной опре¬
деленности результирующей функции V становится актуальным.
Термин «положительная определенность» обычно используется
в применении к квадратичным формам. Однако, вообще говоря, он
имеет смысл для выражений любого порядка. Геометрический метод
доказательства того, что равенство Г (л;) = const (где V(х) — неко¬
торая скалярная функция) описывает некоторую замкнутую поверх¬

б.З]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
243
ность, приведен в приложении к [24]. В соответствии с этим методом
выражение для функции V строится таким образом, чтобы оно содер¬
жало одну из фазовых координат не выше чем во второй степени.
Это достигается приравниванием одного из коэффициентов йц неко¬
торой постоянной величине и исключением фазовых координат Хх
из оставшихся aijv. Такой выбор коэффициентов носит неоправданно
ограниченный характер. Тем не менее он удовлетворяет геометри¬
ческим соображениям, с помощью которых доказывается замкнутость
поверхностей V(л;) == const.
В задачах автоматического управления член хп зачастую входит
линейно в п уравнений первого порядка, которым- удовлетворяет
движение системы. По этой причине предположения предыдущего
параграфа должны быть отнесены к переменной хп. В частности,
полагают, что апп = 2. Этот произвол в выборе коэффициента апп
в формуле градиента эквивалентен произвольности постоянной (масш¬
табного коэффициента) в формуле для V. При апп= 2 в выражении
для V появляется член х%.
В силу сказанного выше градиент \V может быть представлен
следующим образом:
[a\\k	aUv (Xl)]	-Яд “b [а\Ы	(Xl,	-Я^2> • • • > хп-\)\ X
X	[а\пк “Ь a\nv (ХЬ *Я^2> •••> хп-\)]Хп
[^21 k ~Г ^21т» (Xl> Х<Ь • • • > *Я^/2—l)] Х1 “Ь
+ [аШ X а22т» (ХО] Х2 • • •
[^я1/г	&n\v (х1>	*Я^2> • • • > •Я'n-1)] х\ ! • • • ~\~ ^хп
. (5.3.57)
В ходе анализа требований к функции V наиболее общее выраже¬
ние (5.3.55) для градиента было несколько упрощено и приведено
к виду (5.3.57). При этом без потери общности в качестве коэффи¬
циентов йц были выбраны функции лишь переменной ац. С неболь¬
шой потерей общности один из этих aih в частнссти апп, был выбран
равным произвольной постоянной и, кроме того, было принято, что
a.ijV = aijv{x\1 хь ..., хп_А). Все это было сделано в связи с после¬
дующими требованиями к функции V'. Дальнейшее определение
неизвестных коэффициентов в формуле для \V связано с анализом
обобщенных уравнений ротора (5.3.51).
Рассмотрим расширенную форму уравнений (5.3.51):

244
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
И
dyVj dajLv(xlt ха, ..., х^) х{
dajikXi
dxi
dxi
dajiv (xl9 *2l ... , xn_i) Xi
dfijnv (x 1» '^2» Xn-l)-Xn
dx'i
dxi
равнивая постоянные члены одного знака, стоящие в обеих частях
этих равенств, находим
Таким образом, с помощью уравнений ротора была осуществлена
дальнейшая детализация формулы градиента. Совместный анализ
обобщенных уравнений ротора и dVjdt позволяет найти остальные
неизвестные члены.
Производная dVjdt связана с градиентом соотношением вида
Для того чтобы функция dV/dt удовлетворяла каждой из теорем 5.16
или 5.44, она должна быть по крайней мере отрицательно полуоп-
ределенной.
В общем случае отрицательно полуопределенная форма dVjdt
строится возможно более простым способом. В частности, можно
положить, что
где коэффициент k выбирается первоначально постоянным. Если
производная dVjdt ищется в форме (5.3.60), то остальные члены
в ее выражении должны быть равны нулю. Этого молено достичь,
группируя члены с одинаковыми фазовыми переменными и полагая
коэффициенты atj при них равными нулю. Предполагается, что коэф¬
фициенты dij—постоянные величины, ибо в противном случае для
их сокращения потребовались бы обобщенные уравнения ротора более
сложного вида.
Возможности группирования членов определяются ограничениями,
наложенными выше на коэффициенты агу*. Пусть, например, форма dVfdt
третьего порядка содержит члены вида апхххъ апх\, —ххх\. Неопре¬
деленный член — x^xl не может быть сгруппирован со слагаемым апхгх^
так как коэффициент ап может быть функцией лишь переменной Х\.
Однако если бы член —Х\х\ был сгруппирован с anxl, то его можно
'было бы исключить, полагая ап — х^х^.
&i jk &jiff
^ = vV'x=W'X.
(5.3.59)
^r = -kx! (£>0),
(5.3.60)

5.3]
ПРЯМОЙ МЕТОД И ФУН1ШИЯ ЛЯПУНОВА
245
Значения коэффициентов atj не могут быть выбраны произвольно,
ибо они должны удовлетворять также обобщенным уравнениям ротора.
В действительности, если один из коэффициентов выбирается с целью
сокращения нежелательных членов в dV/dt, то остальные один или
более коэффициентов зачастую могут быть найдены непосредственно
из обобщенных уравнений ротора. Таким образом, форма dVjdt должна
быть по крайней мере отрицательно полуопределенной и, кроме того,
должна удовлетворять требованиям к обобщенным уравнениям ротора
(5.3.51).
Возможно, что функцию dVjdt не удается представить в виде
(5.3.60). Тогда необходимо попытаться представить ее как функцию
двух фазовых переменных, затем трех и т. д. до тех пор, пока dV/dt
не станет отрицательно определенной формой. Если решение на этом
пути все же найти не удается, то, возможно, надо вернуться к функ¬
ции градиента (5.3.55) более общего вида, либо попытаться доказать
неустойчивость системы.
Рис. 5.12. Блок-схема системы управления примера 5.3.
В заключение мы предлагаем следующую схему формального при¬
менения метода градиента:
1. Ищем градиент в виде (5.3.57).
2. Зная выражение для градиента, строим производную	\	Vrx
(см. уравнение 5.3.59).
3. Образуем из dVjdt по крайней мере отрицательно полуопре-
деленную форму и подчиняем ее требованиям, наложенным на обоб¬
щенные уравнения ротора (5.3.51).
4. Зная градиент, определяем функцию V и область замкнуто¬
сти ее.
5. С помощью соответствующей теоремы проверяем условие устой¬
чивости.
Проиллюстрируем эту процедуру примером.
Пример 5.3.
Рассмотрим систему, блок-схема которой изображена на рис. 5.12.
Пусть ее движение в фазовом пространстве задается совокупностью

уравнений
хх = хь
сй = ЧУГХ = Х\ХЪ (аП _ а'2\ — 2х1) ~Ь х\ (fl12 ““ 2) — a'2\XV
III этап.
Если система устойчива, то существует большое или даже бес¬
конечное число функций V и соответствующее число производных
dV/dt. Таким образом, одному-единственному решению исходного не¬
линейного дифференциального уравнения соответствует множество
функций Ляпунова. Именно в этом и состоит преимущество метода
Ляпунова по сравнению с классическими способами определения устой¬
чивости. Соответственно существует и большое число ограничений,
которым должна удовлетворять производная dV/dt, для того чтобы
она могла быть индикатором устойчивости. Однако оказывается, что
если dV/dt по крайней мере отрицательно полуопределенная функция,
то этого уже достаточно для установления псех свойств устойчивости.
В рассматриваемом примере такую функцию можно построить, если
положить коэффициент при ххх.г равным нулю, а коэффициенты при
xl и х\ сделать отрицательными или нулевыми. Последнее имеет место,
если ап равно любому положительному числу между 0 и 2, а коэф¬
фициент а21 — произвольному положительному числу. В силу этого
можно принять, что а21 = а12. Полагая коэффициент при х^х2 равным
нулю, находим
Коэффициент при члене Х\Х^ обращается в нуль, если имеет место
равенство
-ГГ = — -V5 (2 — а,2) — апх\.
<2ц — я12 -j- 2х\.
С учетом всего этого можно записать
JV этап.

6.31
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
247
Вычисляя криволинейный интеграл (5.3.56), находим
V=\yV'dx = \ (owl!-f 2f>) dft -j-1 (a^xi 4- 2Ti!)d-(.2 —
0 0 0
= Y -j-	-j-	а^х{х<2	0 al2 ^ 2.
V этап.
Таким образом, функция V является положительно определенной
формой, причем при ||л;||—>*00 liml/->oo, и, следовательно, уравне¬
ние для V описывает во всем пространстве некоторую замкнутую
поверхность. Так как производная dVjdt также во всем пространстве
является по крайней мере отрицательно полуопределенной функцией,
то в соответствии с любой из теорем 5.16 или 5.44 система, изоб¬
раженная на рис. 5.12, асимптотически устойчива в большом.
Хотя этот иллюстративный пример достаточно прост, однако ис¬
пользованный метод анализа имеет весьма широкое применение. В ра¬
боте [24] приведен целый ряд более сложных примеров, в том числе
анализ системы, обладающей предельным циклом. По-видимому, основ¬
ной сферой приложения этого метола служат автономные системы.
Ими и ограничено настоящее изложение. В работе [24] обсуждаются
вопросы применения метода градиента к неавтономным системам. Од¬
нако полученные здесь результаты выражены не так четко и не имеют
такой общности, как в случае автономных систем.
Результаты приложения метода градиента к автономным системам
могут быть подытожены следующим образом:
1. Метод применим к системам, в которых однозначная, непре¬
рывная нелинейность задается в виде полинома либо иной функции х,
либо в виде экспериментальной кривой.
2. Область приложения метода не зависит от выбора вида системы
координат.
3. Метод позволяет строить функции, доставляющие решение по¬
ставленной задачи. При этом возможен синтез функций, включающих
члены высшего порядка, интегралы и произведения трех фазовых
координат.
Может возникнуть следующий вопрос: какие преимущества имеет
метод обобщенного градиента перед методом поиска функции V.
Смысл ответа состоит в том, что если некоторая функция V имеет
достаточно общий вид, то число членов в произвольной dVjdt ста¬
новится недопустимо большим для целей анализа.
5.S.7.	Некоторые применения теорем устойчивости
Проиллюстрируем теорему 5.26 на примере адаптивной системы [7],
изображенной на рис. 5.13. Предположим, что в момент £ = 0 на
вход системы подается скачок амплитуды R0, причем при t<^0 си¬

248	АНАЛИЗ	СИСТЕМ	ПРЯМЫМ	МЕТОДОМ	ЛЯПУНОВА	ГГЛ.	5
стема находилась в состоянии покоя. Поведение системы при
описывается следующей системой дифференциальных уравнений:
•Р + во.У = Ко,	(5.3.61)
с -j- ачс =	(ao = go-rlh)	(5.3.62)
И
щ-\-а,оЩ = — у у	(5.3.63)
а0 = — q0c + qxc -f- q0u0 -f q{ii0.	(5.3.64)
Выражение (5.3.61) представляет собой дифференциальное уравнение
Физический
процесс
Рис. 5.13. Блок-схема адаптивной системы управления.
с постоянными коэффициентами и правей частью, допускающей пре¬
образование Лапласа. Решая его и подставляя полученное решение
в уравнение (5.3.63), находим также щ. Предполагая, что начальные
условия нулевые, находим следующие выражения для у и п0 и их

6.3]
ПРЯМОЙ МЕТОД II ФУНКЦИЯ ЛЯПУНОВА
производных по времени:
у =	(5.3.65)
ао
у = R0e- <4	(5.3.66)
н0 = -^-[1_(1 -L-a0t)e-°o‘]	(5.3.67)
И
щ = — R{)te~ а<>(.	(5.3.68)
Приведем уравнения (5.3.62) и (5.3.64)	к	виду, удобному для
применения теоремы 5.26. Для этого сделаем следующую замену
переменных:
с = х1-\~у	(5.3.69)
и
a0 = x2Jra0.	(5.3.70)
Подставляя уравнения (5.3.69) и (5.3.70) в (5.3.62) и выражая (5.3.68)
через (5.3.65), находим
х{ = — а0хх — — (1 — е~ а«О х2 — хгх2	(5.3.71)
ап
и
где
Xz = M(qо — qta„) — MqiR° (1 — е-а^)хъ — Mqxxxxb (5.3.72)
М=-Цг {Чй—[%-\-(Яо — Я\ао)аоЩе-а<>‘.	(5.3.73)
ио
Потенциальная функция Ляпунова может быть записана в виде
V (х, t) = x'Bx,	(5.3.74;
где х — вектор-столбец, составленный из фазовых координат хх и х2,
а В — симметрическая матрица второго порядка. Выбор элементов
матрицы В составляет основную тему последующего анализа. Пусть
некоторая квадратичная форма вида (5.3.74) положительно определена,
а ее производная по времени — отрицательно определенная функция.
Тогда эта квадратичная форма удовлетворяет всем требованиям
к функции Ляпунова, и потому изучаемая система асимптотически
устойчива в большом. Эта форма является весьма заманчивой целью,
ради достижения которой стоит затратить усилия, поскольку ее суще¬
ствование гарантирует устойчивость решения рассматриваемой системы
дифференциальных уравнений. Существует, однако, множество систем,
для которых эта цель не достижима. В частности, забегая вперед,
можно отметить, что к этой категории относится и исследуемая сис¬
тема. Однако легко показать, что для весьма широкого множества

250
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
амплитуд скачкообразного входного сигнала и большого числа зна¬
чений <7i и в (5.3.73) данная система устойчива в малом.
Возникает вопрос о том, каковы размеры области устойчивости
вблизи начала координат. Ответ на него может быть получен с по¬
мощью теоремы 5.26. Причина, по которой с помощью прямого метода
Ляпунова нельзя доказать устойчивость этой системы в большом,
станет очевидной из дальнейшего изложения и будет обсуждена.
При выборе элементов матрицы В Ляпунова используются два
критерия. В соответствии с первым из них элементы выбираются
так, чтобы матрица В была положительно определенной. Смысл вто¬
рого критерия сводится к тому, чтобы при выбранных по первому
критерию элементах В область вблизи начала координат, в пределах
которой функция— U^(jc) = lim V(x, t) отрицательна, была как можно
t -*■ со
шире. Для удобства применения теоремы 5.26 также желательно,
чтобы эллипс, задаваемый уравнением [J(x) = Um V(x, t) = L, не имел
t со
значительного эксцентриситета (здесь L — некоторая постоянная).
Перейдем к выбору элементов матрицы В. Для того чтобы мат¬
рица В была положительно определенной, достаточно выполнения
следующих условий:
6И> 0	(5.3.75)
и
ЬпЬш — ЬЪ > 0	(5.3.76)
для всех t ^ Т0. Заметим, что в качестве элементов матрицы В могут
быть выбраны и функции времени, если только этот выбор дает
какой-либо выигрыш. Производная формы V(x) по времени может
быть записана следующим образом:
V(x) = 2 х'Вх + х'Вх.	(5.3.77)
Подставляя правые части уравнений (5.3.70) и (5.3.72)" в (5.3.77) и
производя необходимые вычисления, находим следующее выражение:
V(x) = спх\ -|- 2спххх<2 + сшх\ + стх\хъ — cmXix\, (5.3.78)
где
сп = — 2bna^ -j- 2bl2M (<7о — ^i^o) ~г	(5.3.79)
^ 	 и ^0 Л -a0t\	MqiRo	(	~a0t\
Ca— — bu—[\—e	)	— bl4a9—bn——\\—e
~\- b<^N[ (<7o — <7i^o)	(5.3.80)
= - 2ba	a°‘)	- 2b„	{l-e~ °°') + bn, (5.3.81)
cm — — 2 {bn -)- b^Mqi)
(5.3.82)

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
251
ст = — 2 (bn + b.nMqi).	(5.3.83)
Если положить
=	<5А84>
то коэффициент с]12, стоящий в уравнении (5.3.78) при члене х\х^
обращается в нуль. Далее для удовлетворения условия (5.3.76) необ¬
ходимо выполнение равенства
=	<5-3-85»
где	7i	0	при всех	значениях t. С учетом	этого	коэффициенты
(5.3.79) —(5.3.83) приобретают следующий вид:
си = -2-%-Ьи + Ьи,	(5.3.86)
41
Си = Ь-щ;	- «'“•» + Ь■»	(5'3'87'
= + (5'388)
И
ст = — 2 -д7~ •	(5-3.89)
Выберем далее коэффициенты ^ и Ьп следующим образом:
Ъ = ^МЧ1	(5.3.90)
и
bn = b*nMqv	(5.3.91)
где	сомножители 7	и Ь*г — некоторые положительные	постоянные.
Ограничим отношение <7i/<70 областью значений, при которых величина
М ^ 0 для всех t^O. Тогда условие (5.3.72) имеет место, и для
всех элементов матрицы В и их производных справедливы соотно¬
шения
bu = bu -^-{<70 — [<?о + 07о — qxa^a^\e “Д (5.3.92)
- CLqt
toi + too — ?ia0K] е	,	(5.3.93)
*„= — **,	(5.3.94)
bn= 0,	(5.3.95)
bn =	(1^а“ Wo — [?o + too — ?i*o) *o<] <?" “° V (5.3.96)
= ^11(* ^ a'‘ l?o — [<?o -r (go — <7i«о) Доt] e Д 2X
— ant
X [Q\ 4“ too — #iao) 4 e	•	(5.3.97)

‘252
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
С учетом этого коэффициенты уравнения (5.3.78) могут быть запи¬
саны следующим образом:
Так как величина Ь*^ является общим сомножителем во всех выра¬
жениях, то ее выбор не влияет на дальнейший анализ. Положим ее
равной, например, единице.
сделана отрицательно определенной. Действительно, первые три члена
в уравнении (5.3.78) образуют квадратичную форму. Четвертый член,
равен нулю в силу выбора элементов матрицы В. И, наконец, послед¬
нее слагаемое есть член, зависящий от третьей степени фазовых
координат. Если квадратичная форма, образованная первыми тремя
членами, отрицательно определена, то в некоторой области вблизи
начала координат функция V(x,t) отрицательна. Эго следует из того,
что при малых значениях фазовых координат вторая степень их стре¬
мится к нулю медленнее, чем третья. Далее в силу уравнения (5.3.101)
и выбора значения 7^>0 коэффициент при пятом слагаемом в урав¬
нении (5.3.78) не может быть обращен в нуль. Поэтому, начиная
с некоторых значений фазовых координат, этот член третьего порядка
начнет превалировать над квадратичной формой, причем в зависимо¬
сти от направления движения в фазовом пространстве он может иметь
любой знак. Следовательно, существует некоторая область фазового
пространства вблизи начала координат, в пределах которой функция
V(x,t) положительна. В соответствии с этим последующий анализ
будет связан с применением теоремы 5.26.
Прежде чем продолжать дальнейший анализ, дадим некоторые
конкретные значения параметрам R0, qb q0, а0 системы и остановимся
на выборе коэффициента у. Пусть
■1^°' {ЗД — [2<7о + 9i<*o
— ОоД
T- ао(^Яо Я1ао)(Яь— 9iao)t]e Ь
(5.3.98)
Сп = bti [«о— (1 j~(д<> — <7ia0)]>
41
(5.3.99)
-\-(Яо — Я\а-о)а<>*е ^1} \_Я\ + (<?о — <7i«o)t ] е ^	(5.3.100)
И
(5.3.101)
Теперь можно пояснить, почему функция V(x,t) не может быть
Ко =ю,
я0 = 0,1,
Я\= 1
(5.3.102)
(5.3.103)
(5.3.104)

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
253
<7о=1.	(5.3.105)
Эти значения выбраны не произвольно, однако причина такого выбора
здесь освещена не будет (см. [7]). С учетом этого коэффициенты
(5.3.74) приобретают следующий вид:
си = — 10 {200 —[201 -[- 18,9#]	(5.3.106)
с,* = (0,8 + 0,9т),	(5.3.107)
,e==_[2T+10«(l-rftl<)-(l+T).10-5{l-[l +
4- 0,09#] 4°'T2[l-f 0,9# ] е~°’U]	(5.3.108)
И
с122 = — 2Т.	(5.3.109)
Выбор численного значения коэффициента	у зависит от	поведения
системы при t—►оо. В данном случае для коэффициентов уравнения
(5.3.78) имеем
сп = — 2. 103,	(5.3.110)
с12 = 0,8 + 0,9Т,	(5.3.111)
сп= — 2Т.103,	(5.3.112)
ст = — 2Т.	(5.3.113)
Пусть
Т=Ю8.	(5.3.114)
Тогда при	элементы	матрицы В приобретают следующий вид:
Ьп = Ю3,	(5.3.115)
bn = — 1,	(5.3.116)
&й= Ю'2.	(5.3.117)
Подставляя	эти	коэффициенты в правую	часть уравнения (5.3.74),
видим, что	они	удовлетворяют условию а)	теоремы 5.25,	и поэтому
U(jc) удовлетворяет условию в) той же теоремы для произвольного
Q. Более того, в этом случае эллипсы, описываемые уравнением
U (д;) = const, имеют незначительный эксцентриситет.
Подставляя последовательно уравнение (5.3.114) в (5.3.111) —
(5.3.113) и используя (5.3.78), находим
lim V{x,t) = — W(x)= — [2 • 10:,jq— 1,8- IO^jc2-)-
4-2.1 0”x2 -[-2.1 05ataj4 (5.3.118)

254
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. Г,
Функция W(x) в (5.3.118) и есть та самая функция, которая
фигурирует в условиях б) и в) теоремы 5.25. Если удастся теперь
определить область 2, то W(x) будет отвечать этим условиям. Квад¬
ратичная часть уравнения (5.3.78) отрицательно определена. Поэтому
в некоторой области вблизи начала координат функция— W{x) отри¬
цательна. Геометрическое место точек, разделяющее фазовую плос¬
кость на две области, в одной из которых—W(x) положительна,
а в другой отрицательна, может быть найдено, если положить
— U7(a:) = 0 и построить кривую, отвечающую этому уравнению. Рас¬
четы упрощаются при переходе к полярным координатам. Пусть
Подставляя (5.3.119) и (5.3.120) в уравнение (5.3.118), находим
— Щг, 0) = — 2 • 103r2 [cos2 б — 0,9 • 102 sin б cos б -ф-
-f- Ю4 sin2 б -|- 102r sin2 0 cos б].	(5.3.121)
Приравнивая это выражение нулю и разрешая его относительно г,
Отрицательные значения г смысла не имеют и полагаются равными
бесконечности. Поэтому искомая кривая лежит лишь во втором и
третьем квадрантах фазовой плоскости и не проходит через первый
и четвертый. Рис. 5.14, на котором выделены области положительных
и отрицательных значений функции—W(x;), иллюстрирует эти рас¬
суждения.
Теперь можно применять теорему 5.26. Сначала определяется чис¬
ленное значение величины L. Для этого выражения (5.3.119) и (5.3.120)
подставляются в уравнение (5.3.74), а численные значения коэффици¬
ентов (5.3.115) — (5.3.117) — в элементы матрицы В. Функция U(x)
или U(r,0) приравнивается L, и в результате находится следующее
выражение, связывающее г, 0 и Г:
Это уравнение позволяет провести на фазовой плоскости предвари¬
тельный анализ и определить наибольшее значение Г, которое еще
обеспечивает отрицательность функции — W(x) в пределах области
U(x)—L. В данном случае
xY = r cos б
(5.3.119)
и
х2 = г sin б.
(5.3.120)
получаем
г
cos2 0 — 0,9 • 102 sin 0 cos 0 -j- 104 sin2 О
(5.3.122)
102 sin2 0 cosO
10:5 cos2 G — 2 sin 0 cos G 102 sin2 G
L
(5.3.123)
L = 6,24 • 106.
(5.3.124)

5.3]
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
255
Область Q, определяемая неравенством U(x)^L, отмечена на рис. 5.14
штриховкой. Внутри этой области удовлетворяются условия а), б), в)
теоремы 5.25, а потому здесь справедлива и теорема 5.26. Введем
области Qs, задаваемые неравенством (J(x)=L — 8, и выберем зна¬
чение 7's таким образом, чтобы каждая траектория x(t, t(b х0)
стремилась к нулю при
t—► оо при всех х и
t > Т*
1о^ 1 <>•
Для понимания пре¬
дыдущего анализа необ¬
ходимо дать некоторые
комментарии. Рассматри¬
валась относительно про¬
стая система нелинейных
дифференциальных урав¬
нений, описывающих по¬
ведение адаптивной си¬
стемы управления. Устой¬
чивость этой системы
изучалась с помощью
скачкообразного входно¬
го сигнала амплитуды RQ,
подаваемого в момент
времени t — 0. Преобра¬
зованием переменных бы¬
ла найдена совокупность
уравнений, которая опи¬
сывала реакцию системы
на возмущение, отклоняющее ее от заданной траектории. Эта система
была одновременно нестационарной и нелинейной. Основная цель ана¬
лиза состояла в приведении системы к виду, пригодному для приме¬
нения теоремы 5.26. В ходе анализа были выбраны соответствующие
значения амплитуды входного сигнала и параметры системы. Анализ
был доведен до этапа, на котором теорема 5.26 может быть приме¬
нима. Для моментов времени, больших чем время установления эта¬
лонной модели (при скачкообразном сигнале это составляет примерно
30 сек), величина Ь может быть сделана достаточно малой. Это
в свою очередь означает, что область близка по своим размерам
к Q, и потому время может быть выбрано порядка 30 сек. Пусть
до момента времени 7'8 система не испытывала возмущений, откло¬
няющих ее от заданной траектории. Тогда в соответствии с теоре¬
мой 5.26 при любом будущем возмущении, не выходящем из области
Qe (почти совпадающей с £2), система асимптотически устойчиво стре¬
мится к началу координат. Физически это означает, что даже в том
случае, когда величина g меняется скачком более чем в 200 раз, то
НриваЯ W(X)=0 ддо
150
-W(x) положительна.
135‘
195
-W(x) положительна
210
ш] ж
Кривая W(x) = 0
270°
Рис. 5.14. Фазовая плоскость: область устой¬
чивости адаптивной системы управления.

‘256
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
и тогда управляющее устройство исходной системы устойчиво изме¬
няет характеристику //0 с целью ликвидации этого возмущения. Так
как номинальное значение параметра а0 равно лишь 0,1, то это—
довольно сильное условие устойчивости системы. Все это, конечно,
справедливо лишь спустя 20 или 30 сек после приложения скачкооб¬
разного входного сигнала. Более ранним возмущениям (т. е. меньшим
Т и соответственно меньшим 75) соответствуют большие значения 5
и меньшие по размерам области гарантированной устойчивости. Вид
области устойчивости сохраняется, однако, неизменным. Следует отме¬
тить, что отсюда еще не вытекает обязательная расходимость траек¬
торий, начинающихся за пределами этой области, даже если они
исходят из точек, где функция— W(x) положительна. Это является
следствием того, что теоремы Ляпунова дают только достаточные,
но не необходимые условия устойчивости.
Таким образом, анализ показывает, что при заданном входном
сигнале рассматриваемая система управления асимптотически устойчиво
адаптируется к изменениям ее параметров всегда, за исключением,
может быть, больших возмущений, возникающих спустя короткое время
после приложения скачка на входе. Моделирование этой адаптивной
системы на аналоговой машине дало почти те же самые результаты.
Итак, данная система обладает хорошими способностями адаптации
к изменениям параметра go всюду, за исключением, возможно, боль¬
ших возмущений, возникающих вскоре после подачи входного сигнала.
Обобщение процедуры
Использованный ранее метод нахождения величины L в теореме
5.26 требует графического построения кривой— W(x)= 0. В фазовом
пространстве трех и более изменений такая процедура уже не приме¬
нима. Ниже кратко излагается общая методика применения теоремы
5.26 к системам, поведение которых описывается уравнением (5.2.3)
и которые удовлетворяют уравнению (5.2.43) при квадратичных функ¬
циях Ляпунова. Применение этой методики к теореме 5.23 рассмат¬
ривается в конце раздела. Потенциальная функция Ляпунова может
быть представлена в следующем виде:
V(x,t) = xrBx,	(5.3.125)
где В — некоторая симметрическая матрица, а х—вектор-столбец
фазовых координат. В качестве элементов матрицы В могут быть
выбраны функции времени. Производная функции Ляпунова имеет вид
V (х, t) = — хг С х + хг В f(x\	(5.3.126)
где С—симметричная матрица, определяемая равенством
С = — [ВА + {ВА') + В].
(5.3.127)

5.31
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
257
При исследовании устойчивости необходимо, чтобы матрица А была
невырожденной. В противном случае оказывается чрезвычайно труд¬
ным подобрать элементы В так, чтобы С была положительно опре¬
деленной матрицей.
Следующим шагом является выбор элементов В. В общем случае
этот выбор должен удовлетворять четырем критериям. Первые два
требуют положительной определенности обеих матриц В и С. Осталь¬
ные два критерия подчинены этим требованиям, но тем не менее
также важны. В соответствии с первым из них собственные значения
матрицы В не должны отличаться друг от друга более чем в 10—
20 раз. В соответствии со вторым не должны быть слишком малыми
собственные значения матрицы С. Все эти предложения достаточно
естественны. Тем не менее они могут по крайней мере служить руко¬
водством к выбору элементов матрицы В. Некоторую помощь в опе¬
рациях с собственными значениями матриц В и С как функций
элементов могут оказать характеристические уравнения В и С. Для
этого их надо привести к такому виду, чтобы собственные зна¬
чения лежали на некотором корневом годографе, отвечающем разомк¬
нутой системе, полюса, нули и коэффициент усиления которой
являются функциями элементов матрицы В. Эта процедура описана
достаточно широко и может быть найдена, например, в [7].
После того как элементы В выбраны, возникает вопрос о раз¬
мере области асимптотической устойчивости, которую гарантирует
теорема 5.26. Этот размер в свою очередь зависит от величины наи¬
большего значения Z,, для которого еще справедливо ограничение
U7(jc)^>0 в пределах области U{x)^L. Один из наиболее легких
путей вычисления состоит в преобразовании переменных по формуле
U{x) — x'Dx = zrlz (D = \imB),	(5.3.128)
t -*■ оо
где 1 — единичная матрица. Это преобразование удобно производить
в два этапа. Ыа первом этапе определяется ортогональное преобразо¬
вание, позволяющее представить U (х) в виде
if (х)= U (v) — v'Ay,	(5.3.129)
где А — некоторая диагональная матрица. Элементы А совпадают
с собственными значениями матрицы D, а переменные v и х связаны
соотношением
<v = Px,	(5.3.130)
где Р — матрица ортогонального преобразования. Элементы Р могут
быть найдены в результате решения системы линейно независимых
равенств вида
РР’ = 1	(5.3.131)
и
PD = АР.	(5.3.132)
9 п/р Леондеса

258
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
Зная матрицу Р, нетрудно найти дополнительное преобразование
переменных, позволяющее представить U в виде
U = x'Dx = v'Av = z'lz	(5.3.133)
Зависимость	между	векторами ю и z может быть	представлена в виде
z = Qv,	(5.3.134)
где 0 — диагональная матрица. Элементы матрицы 0-легко находятся
из равенств
02 = А.	(5.3.135)
Зависимость	между	х	и z имеет вид следующего	соотношения:
x = P'0'z.	(5.3.136)
С учетом этого находим выражение для функции — W(x):
— W(x) = — W(z) = —zr [Я'О-1 ] Е [РЪ~1 \ z +
+ 2Г [/>'0-'] D (f(x)!= g w) (5.3.137)
(где Е = lim С).
[ —*■ СО
В терминах ^-переменных граница области, заданной неравенством
U^ L, представляет собой гиперсферу в (т -j- я)-мерном простран¬
стве. Максимально допустимое значение L равно квадрату расстояния
от начала 0-системы координат до ближайшей точки, лежащей на
одном из листов поверхности, заданной уравнением W(z) = 0. Рас¬
стояние задается в евклидовой метрике. Эту точку легко найти, если
перейти к гиперсферической полярной системе координат. Основными
переменными в новой системе служат радиус г и (т-\-п—1) угло¬
вых координат. Подстановка этих переменных в уравнение W= 0
позволяет найти радиус г как функцию (т-\-п—1) угловых коор¬
динат. Эту функцию можно ввести в быстродействующее цифровое
вычислительное устройство, и далее методами спуска или квантова¬
ния пространства (totalspace sampling) найти наименьшее значение г.
Здесь следует сделать оговорку. Каждый лист поверхности, заданной
уравнением W=0, содержит точку минимума. Поэтому в качестве
значения L выбирается наименьший из этих локальных минимумов.
Пусть наименьшее значение г равняется г0. В гиперсферических поляр¬
ных координатах функция U имеет следующий вид:
U=r\	(5.3.138)
Соответственно
L = rl	(5.3.139)
В процессе применения теоремы 5.26 это значение L может быть
использовано вместе с функцией U(x) для построения двумерных

5.31
ПРЯМОЙ МЕТОД И ФУНКЦИЯ ЛЯПУНОВА
259
сечений области 2. Аналогично легко построить двумерные сечения
областей 2S, заданных неравенством LJ(x)^lL — Ъ.
Этот метод может быть использован для определения области 2,
фигурирующей в теореме 5.23. В последнем случае задача упрощается,
ибо для автономных систем при всех 1В = D и С — Е. В противном
случае процедура остается неизменной.
5.3.8.	Определение верхней границы для переходной характеристики
Предположим, что функция Ляпунова — индикатор асимптотиче¬
ской устойчивости системы — найдена. Если производная V(x,t) в этом
случае является отрицательно определенной функцией, то можно
найти верхнюю границу для переходной характеристики системы. Этот
факт легче всего понять, если вспомнить весьма упрощенную аналогию
между прямым методом Ляпунова и реакцией линейной системы пер¬
вого порядка, проведенную в § 5.1. Поведение линейной системы
первого порядка при нулевом входном сигнале (г (0 = 0) может быть
описано уравнением вида
х = —ах,	(5.3.140)
где а — некоторая положительная константа, или, что то же самое,
уравнением
а =	(5.3.141)
При начальном условии х = х0 переходная характеристика системы
при t^>0 имеет следующий вид:
x(t) = xQe~at,	*> 0.	(5.3.142)
В данном случае величина jc есть мера отклонения выходного сигнала
системы от точки равновесия х — 0. Уравнение (5.3.142) описывает
траекторию движения ас к положению равновесия во временной
области. Положительная константа а равна времени, которое необхо¬
димо выходному сигналу для достижения уровня лс0/£, и поэтому она
имеет смысл постоянной времени системы.
Примем, что V(x,t) есть мера расстояния от точки равновесия
до некоторой заданной точки какой-либо траектории решения. Введем
величину
—ЫШ	(53j43)
и	будем	ее	рассматривать в интересующем нас интервале	времени
и	области,	где	гарантируется асимптотическая	устойчивость.	В этом
случае имеет место следующее неравенство:
V(ф (t; Хо, t0)> t)$£V(Jfib (q) e -i	- 4	(5.3.144)
9*

260
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
В случае автономных систем иногда не требуется знания переходной
характеристики во всей области асимптотической устойчивости. В этом
случае уравнение (5.3.143) можно оценить в более узких областях 2,
заданных неравенством
V(X)^L,	(5.3.145)
где L — некоторая положительная константа.
Данная процедура неприменима, если V не является отрицательно
определенной функцией. Это легко усмотреть, например, из следую¬
щего примера. Пусть производная V' отрицательно полуопределена.
Тогда т] равно нулю, и окончательное неравенство (5.3.144) теряет
смысл. Следует также отметить, что величина у\ зависит от выбора
вида функции Ляпунова. В частности, для некоторых систем
значения т], отвечающие двум различным функциям Ляпунова, могут
отличаться по величине на порядок. Тем не менее неравенство
(5.3.144) во всех случаях остается справедливым, хотя одна из систем
имеет переходную характеристику более быструю, нежели другая.
В силу этого данный метод не пригоден для сравнения переходных
характеристик двух систем, но может быть использован для оценки
верхней грани переходной характеристики.
5.4.	Заключение
Предыдущие разделы представляют собой попытку краткого,
хотя и весьма строгого изложения прямого (второго) метода Ляпу¬
нова. Материал излагался применительно к системам автоматического
управления. Некоторые из теорем § 5.2 были изложены в виде,
несколько отличном от того, как они сформулированы в первоисточ¬
никах. Эго сделано с целью унификации обозначений и описания
физических систем на протяжении всего изложения. Был сформули¬
рован ряд теорем устойчивости в произвольной малой области вблизи
положения равновесия, и с их помощью было исследовано значитель¬
ное число нелинейных систем. Эти теоремы зачастую служат пред¬
варительным этапом исследования устойчивости системы, поскольку
в свою очередь они облегчают выбор теорем, необходимых для дока¬
зательства устойчивости в большом, устойчивости в некоторой задан¬
ной области или же вообще неустойчивости системы. Определение
устойчивости нелинейных систем — автономных или неавтономных —
требует гораздо большего труда, чем линейных. Некоторые примеры
уровней устойчивости нелинейных систем приведены в § 5.2. Хотя
эти разбиения области устойчивости и существуют в действитель¬
ности, однако подавляющее число специалистов в области управле¬
ния интересуется, по-видимому, лишь асимптотической, в том или ином
смысле, устойчивостью, и не нуждается в дальнейшей детализации.

5.4]
ЗАКЛЮЧЕНИЕ
261
Наибольшая трудность, которая встречается на пути применения
прямого метода Ляпунова, есть построение некоторой функции 1/,
отвечающей условиям одной из теорем. В § 5.3 приведен целый ряд
прямых и косвенных методов, позволяющих определить эту функцию
для некоторых систем. Ни один из этих методов не является уни¬
версальным, и более того, любой из них может оказаться полезным
там, где отказывают остальные. В применении к нелинейным авто¬
номным системам прямой метод Ляпунова обладает большими потен¬
циальными возможностями. Это наглядно показывает метод градиента.
Однако применение его к неавтономным системам весьма ограниченно.
Так как теоремы Ляпунова дают лишь достаточные, но не необхо¬
димые условия устойчивости системы, то невозможность построения
функции V—индикатора устойчивости или неустойчивости — еще
ни о чем не говорит. Из того, что система не удовлетворяет этим
условиям.устойчивости, не следует ее неустойчивость, и наоборот. Не¬
обходимо также отметить, что функция Ляпунова — индикатор устойчи¬
вости или неустойчивости — определяется не единственным образом.
Более того, можно показать, что из существования одной такой функ¬
ции V следует существование бесконечного числа их. Остановимся
теперь вкратце на вопросе о том, какую информацию несет прямой
метод Ляпунова. Если этот метод применим, то с его помощью можно
определить, устойчива или же неустойчива система. Это — ценная
информация. Однако специалиста в области управления зачастую ин¬
тересует тенденция к перерегулированию и время установления системы
под действием возмущения. Желательно также иметь возможность
использовать критерий устойчивости для выбора коэффициента уси¬
ления системы и параметров компенсирующего устройства. Хотя эти
возможности и обсуждались в литературе [11], однако в настоящее
время они носят весьма ограниченный характер. В частности, в раз¬
деле 5.3.8 отмечалось, что с помощью производной dVjdt можно
оценить время установления системы. Однако любая такая оценка
зависит не только от характеристик рассматриваемой системы, но
также и от вида и параметров выбранной функции \/. Поэтому по¬
добная оценка не может служить истинной характеристикой системы.
В зависимости от вида V эта сценка может сказаться весьма завы¬
шенной. Однако данный метод позволяет сцепить время установления
сверху, и в этом смысле он представляет ценность. Аналогичные
трудности возникают при нахождении параметров системы с помощью
критериев Ляпунова — здесь также оказывают существенное влияние
вид и параметры выбранной функции Ляпунова.
В общем случае критерии Ляпунова не являются таким универ¬
сальным методом анализа и синтеза нелинейных систем, как метод
корневого годографа —для линейных. Эго и не удивительно, поскольку
класс задач, к которым они приложимы, гораздо шире. По-видимому,
эффективность критериев Ляпунова резко повысилась, если бы

262
АНАЛИЗ СИСТЕМ ПРЯМЫМ МЕТОДОМ ЛЯПУНОВА
[ГЛ. 5
был предложен некоторый метод построения функций Ляпунова, не
только удовлетворяющих условиям теорем, но и «адекватных« (в не¬
котором смысле) рассматриваемой системе. Такой метод, вероятно,
был бы настолько сложен, что для его применения потребовались бы
высокоскоростные вычислительные устройства. Однако он мог бы по¬
мочь исследователю найти точную верхнюю грань времени установ¬
ления системы.
ЛИТЕРАТУРА
1. Айзерман М. А., Теория автоматического регулирования двигателей,
Гостехиздат, М., 1952.
2. Beckenbach Е. F., Modern Mathematics lor the Engineer, McGraw-
Hill, N. Y., 1956. [Русский перевод: Бсккенбах Э. Ф., Современная
математика для инженеров, ИЛ, М., 1958.
3. Bellman R., Stability Theory of Differential Equations, McGraw-Hill, N. Y.,
1953. (Русский перевод: Белл м а и Р., Теория устойчивости решений
дифференциальных уравнений, ИЛ, М., 1957.]
4. Birkhoff G. and MacLane S., A Survev of Modern Algebra, Revised
Edition, MacMillan Co., N. Y., 1953.
5. С e s a г i L., Asymptotic and Static Problems in Ordinary Differential
Equations, Ergebnisse der Mathematik und Threr Grenzgcbiete, Neue
Folge—Heft 16, Springer—Verlag, Berlin, 1959. [Русский перевод: Ч e-
з a p и Л., Асимптотическое поведение и устойчивость решений обыкно¬
венных дифференциальных уравнений, «Мир», М., 1964].
6. С о d d i n g t о n E. A. and Levinson N., Theory of Ordinary Differential
Equations, McGraw-Hill, N. Y., 1955. [Русский перевод:	Коддинг-
тон Э. А., Левинсон Н., Теория обыкновенных дифференциальных
уравнений, ИЛ, М., 1958].
7. D о n а 1 s о n D. D., The Theory and Stability Analysis of a Model Refe¬
renced Parameter Tracking Technique for Adaptive Automatic Control
System, Ph. D. Thesis, UCLA, May, 1961.
8. Gibson J. E. et al., Stability of Nonlinear Control Systems by the Second
Method of Lyapunov, Purdue School of Electrical Engineering Report
No. EE 61-5, Lafayette, Indiana, May, 1961.
9. I n g w e r s о n D. R., A Modified Lyapunov Method for Nonlinear Stability
Problems, Ph. D. Thesis, Stanford University, November, I960.
10. Ingwerson D. R., A Modified Lyapunov Method for Nonlinear Stability
Analysis, IRE Trans, on Automatic Control, Vol. AC-6, May 1961.
11. К a 1 m a n R. E. and Bertram J. E., Control System Analysis and Design
via the Second Method of Lyapunov, I, Continuous — Time Systems, Journal
of Basic Engineering (Series D, Trans. ASME), 82:371—393, June, 1960.
12. К p а с о в с к и й Н. Н., Об устойчивости в целом решений нелинейной
системы дифференциальных уравнений. ПММ, т. 18, № 6, 1954.
13. LaSalle J. P., Some Extensions of Lyapunov’s Second Method, RIAS
Technical Report 60-5, AFOSR TN-60-22, Research Institute of Advanced
Study, Baltimore, Md., 1960.
14. L a S a 11 e J. P., Rath R. J., A New Concept of Stability, Paper No.,
415, Research Institute for Advanced Study, 7212 Bellona Ave., Baltimore 12,
Maryland, August 29, 1962.
15. Lass, Harry, Vector and Tensor Analysis, McGraw-Hill Book Co., New
York, 1950.
16. Летов А. М., Устойчивость нелинейных регулируемых систем, Гостех¬
издат, М., 1955.

ЛИТЕРАТУРА
263
17. Лурье А. И., Некоторые нелинейные задачи теории автоматического
регулирования, Гостехиздат,'М., 1951.
18. Лурье А. И., Р о з с н в а с с е р Е. Н., О методах потенциальных функ¬
ций Ляпунова в теории нелинейных регулируемых систем. Труды I Меж¬
дународного конгресса по автоматическому управлению, т. 1, Изд-во
АН СССР, 1961.
19. Margolis М., On the Theory of Process Adaptive Control Systems, the
Learning Model Approach, Doctoral Dissertation, Department of Engineering,
University of California, Lox Angeles, 1959.
20. Massera J. L., Contributions to Stability Theory, Ann. Math., 64: 182—
206, 1956.
21. Плисс В. А., Некоторые проблемы теории устойчивости движения
в целом, Л., Изд-во Леиингр. ун-та, 1958.
22. Rakasius Z. V., Stability Analysis of Nonlinear Control Systems by the
Second Method of Lyapunov, IRE Trans, on Automatic Control, Vol. AC-1,
January, 1962.
23.	Shultz D.	G. and	Gibson	J. E.,	The Variable Gradient Method for
Generating Lyapunov Functions, AIEE Transaction Paper 62—81.
24.	S h u 11 z D.	G. and	Gibson	J. E.,	The Variable Gradient Method of
Generating Lyapunov	Functions	with	Application to Automatic Control
Systems, Purdue University, School of Electrical Engineering, Control
Information Systems Laboratory, Report No. TR-EE 62-3, April, 1962.
25. S z e g о	G.	P.,	A Contribution	to Lyapunov’s Second Method:	Nonlinear
Autonomous Systems, Journal of Basic Engineering, Trans. ASME (D) and
Proceedings of the OSR RIAS International Symposium on Nonlinear Dif¬
ferential Equations and Nonlinear Mechanics.
26. S z e g о	G.	P.,	A Contribution	to Lyapunov’s Second Method:	Nonlinear
Autonomous	Systems,	Paper No. 61-WA-192 presented at ASME Annual
Winter Meeting, November, 1961.
27. Taylor	A.	E\,	Advanced Calculus, Ginn and Company, Boston,	1955.
28. 3 у б о в	В.	Л.,	Математические	методы анализа систем автоматического
управления, Судпромиздат, Л., 1959.

ГЛАВА б
ОБЗОР ТЕОРИИ И МЕТОДОВ АДАПТИВНЫХ СИСТЕМ
УПРАВЛЕНИЯ
Доналъсон (D. D. Donalson), Киши (F. Н. Kishi)
6.1.	Введение
Чтобы хорошо изложить вопросы, касающиеся адаптивных систем
управления, будет полезно определить эту категорию систем управле¬
ния. Понятие «адаптивность» появилось в литературе по управлению
около 1954 г., когда Цянь Сюэ-сэнь [48] в своей книге описал модель
человеческого мозга, предложенную Эшби [2]. Примерно в то же время
Беннер и Дреник [5] сконструировали систему управления, обладаю¬
щую адаптивными свойствами. С тех пор «адаптивными» стали назы¬
ваться самые разнообразные системы управления. Многочисленные
исследователи, таким образом, предложили целый ряд определений
«адаптивных систем управления». Первоначально определения имели
тенденцию ограничиться некоторыми частными случаями. Позднее они
стали более общими, но их число не уменьшилось, и в настоящее
время общепринятого определения не существует.
Прежде чем пояснить, что понимается под адаптивными системами
управления, определим смысл выражения «приемлемая система» *). Эго
выражение является внешней показательной характеристикой работы
исследуемой системы. При проектировании системы управления кон¬
структору в первую очередь необходимо уяснить назначение данной
системы. Четкое описание «приемлемой системы» представляет попытку
выразить количественно достижение конструктора системы.
Сначала объясним некоторые термины. Для этого обратимся
к рис. 6.1. Пусть Q — система, состоящая из управляемого объекта
и управляющего устройства. v{t) — вектор-функция, заданная на ра¬
бочем интервале O^t^T и образованная следующими величинами
*) Заде [53] называл «приемлемые системы» «адаптивными'». Его опреде¬
ление адаптивных систем используется здесь для приемлемых систем.

6.1]
ВВЕДЕНИЕ
265
(некоторые из них могут отсутствовать): а) исходная входная вели¬
чина; б) известные входные величины объекта, в) возмущения, дей¬
ствующие на объект, г) измеряемые выходные величины; у — вектор
параметров, описывающий воздействия на систему и принадлежащий
некоторому множеству Г, которое определяет часть множества v (t)
(пункты а), б), в), перечисленные выше). — семейство функций v (t),
соответствующих определенному вектору	Р(7)—критерий качества,
величина которого при определенном 7 может принимать значения
Известные
входные
величины
объента
Параметры
известных
возмущающих
воздействий
Изве- Неизвестные -
Известные стные возму- (входят
входные возму- щпющие аддитивно
величины щающие воздей- и ппра-
Зпдающие
входные
величины
Л А
Измеряемые еыходныв величины
Рис. 6.1. Система управления.
в некотором диапазоне; W—множество, которым желательно огра¬
ничить значения Р(ф).
В этих терминах определим критерий приемлемости следующим
образом. Если P(j) принимает значения из множества U7, тогда кри¬
терий приемлемости удовлетворен. Отсюда определение.
Определение 6.1. Система Q называется приемлемой системой
(ПС) для заданных ST и Wy если она удовлетворяет критерию прием¬
лемости для всех -у, принадлежащих Г и определяющих семейство Sr
Или, говоря более полно, система приемлема, если в Q может быть
спроектировано некоторое устройство, обеспечивающее такое управ¬
ление, что критерий качества поддерживается в приемлемых границах,
определяемых W. Это приемлемое качество должно поддерживаться
для класса входных воздействий, представленного 5Т.
Приемлемой системой может быть даже разомкнутая система, если
только она удовлетворяет критерию приемлемости. Задача возникает
в том случае, когда Р(ф) не может поддерживаться в W. При этом
необходимо предусмотреть более сложное устройство внутри Q для
того, чтобы удовлетворить критерий приемлемости, что приводит ко
многим возможным вариантам конструкции управляющего устройства.

266	ТЕОРИЯ	и	МЕТОДЫ	АДАПТИВНЫХ	СИСТЕМ	УПРАВЛЕНИЯ	[ГЛ.	б
Для иллюстрации сказанного рассмотрим пример отработки угла
тангажа системой управления самолета. Если на систему поступает
команда или задающая входная величина, то на рули посылаются
сигналы, в результате чего рули, взаимодействуя с воздушным потоком,
создают вращающий момент самолету. Примем в этом примере за
критерий качества процент перерегулирования при действии скачкооб¬
разной команды на высоте у. Для определенной высоты у опытным
путем находятся пределы, в которых колеблется плотность воздуха,
а именно описывается множество, определяющее соответствующую
часть множества v(t). Пусть для этих пределов изменения плотности
воздуха Р(^) изменяется в диапазоне от 0 до 30%. Если этот диапа¬
зон изменения Р (у) лежит внутри допустимого множества W, тогда
система является приемлемой.
В данном примере может оказаться трудным задать Г, W и Р.
Однако их задание определяет точку зрения, исходя из которой можно
характеризовать различные конструкции, предназначенные для поддер¬
жания некоторого критерия качества в заранее заданных пре¬
делах.
Сказанного достаточно, чтобы дать определение различным фор¬
мам Q. В этой связи можно остановиться на том, что понимается под
адаптивной системой управления *). Разомкнутые системы и системы
управления с обратной связью являются хорошо известными формами
систем управления. В противоположность им попытаемся найти отли-'
чительные характеристики адаптивных систем управления. Дадим
определение этим последним. Наряду с определением адаптивных
систем управления определим две другие формы систем и укажем
их особенности.
Определение 6.2. Система называется разомкнутой, если
к объекту приложено управляющее воздействие в виде некоторой
независимой функции времени, получаемой на основе априорных зна¬
ний об объекте.
Определение 6.3. Система управления называется системой
с обратной связью, если управляющее воздействие зависит от зна¬
чения ее переменных (состояние объекта или значения управля¬
емых переменных) и действует так, чтобы получить приемлемую си¬
стему.
Определение 6.4. Система называется адаптивной системой
управления, если управляющее воздействие зависит, кроме пере¬
менных состояний, и от качества или внутренних или внешних ха¬
рактеристик объекта и действует так, чтобы система была при¬
емлемой.
*) Заде [53] использовал термин «адаптивность» для внешней показатель¬
ной характеристики работы системы, в то время как мы предпочитаем исполь¬
зовать этот термин как внутреннюю конструктивную характеристику.

6.1]
ВВЕДЕНИЕ
267
Определение б.З похоже иа другие определения, уже предложен¬
ные ранее, и, возможно, сильнее всего па определение, данное Купе¬
ром и Гибсоном [11]. Однако важно установить достаточно общее
определение, которое охватывает многие адаптивные системы, описанные
в литературе, и все же отличает системы с обратной связью от двух
других форм систем. По сути дела, адаптивные системы управления
отличаются от обычных систем управления с обратной связью нали¬
чием контроля качества, или характеристик объекта, или того и дру¬
гого вместе. Следует заметить, что, хотя адаптивные системы являются
системами с обратной связью, обратное утверждение не обязательно
верно, поэтому есть основания полагать, что с помощью адапти¬
вных систем можно получить лучшее качество. Именно по этим
причинам и изучаются адаптивные системы управления. Заметим,
однако, что и адаптивные системы управления могут не быть при¬
емлемыми.
Из данного определения видно, что обычно описываемые управ¬
ляющие устройства, характеристики которых изменяются в зависи¬
мости от измерений среды (например, измерений состояния воздуха),
относятся к классу адаптивных систем управления.
Существует много форм адаптивных систем. В этой главе не
делается попытки дать обзор всех схем, изобретенных в прошлом,
поскольку по этому вопросу есть несколько хороших обзорных ста¬
тей [1, 11, 37, 44, 47]. Однако, по-видимому, значительную часть
адаптивных систем можно объединить тремя классами схем, которыми
являются (1) схемы с большим коэффициентом усиления, (2) схемы
с эталонной моделью, (3) оптимальные адаптивные схемы. Перечис¬
ление дано в порядке увеличения сложности схем. Поскольку разные
схемы обеспечивают разное качество работы, то на увеличение слож¬
ности следовало бы идти лишь в том случае, если улучшение качества
работы можно и необходимо получить. В настоящее время выбор
частной схемы, по-видимому, зависит от слишком общих качественных
суждений.
Схемы с большим коэффициентом усиления, которые впервые пред¬
ложены Minneapolis — Honewell Company [7, 15, 46], широко обсуж¬
дены и проверены на практике. Коэффициент усиления обратной
связи, охватывающей объект, выбирается столь высоким, как это
только возможно, с целью поддерживать коэффициент усиления всей
системы близким к единице. Поскольку при большом коэффициенте
усиления система может стать неустойчивой, то можно наблюдать
сигнал в цепи обратной связи системы в виде незатухающих коле¬
баний. По этой информации регулируется коэффициент усиления цепи
обратной связи, так чтобы поддерживать систему на границе устой¬
чивости. Характеристика системы, близкая к характеристике модели,
получается независимо от параметров объекта, если данную модель
включить, как показано на блок-схеме системы с большим коэффи-

268
ТЕОРИЯ II МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. Су
циептом усиления, изображенной па рис. 6.2. Единственным возраже¬
нием против этого метода является то, что конструктор должен
располагать значительной априорной информацией об объекте, т. е.
он должен знать расположение корней характеристического уравнения
системы в правой полуплоскости. Конечно, коэффициент усиления,
который независимо от частоты равен единице, можно получить при
условии, что реакция системы в некоторой степени отличается от
Задающий
входная Г
величина |
I
I
Модель
Т"
К
Настройка
козффиииента
усиления
Измерение
предельного
периода
колебаний
Возмущения
Рис. 6.2. Система с большим коэффициентом усиления.
реакции модели. Кроме того, в цепи обратной связи всегда присут¬
ствуют небольшие колебания. (Эти колебания вполне допустимы, как
указывалось в отчетах по некоторым применениям систем в косми¬
ческих аппаратах.)
Две другие схемы будут последовательно описаны более подробно.
Порядок изложения в данной главе следующий. Настоящий параграф
является введением и содержит определение адаптивных систем управ¬
ления. В § 6.2 описаны методы построения адаптивных систем с эта¬
лонной моделью, а в § 6.3 — оптимальные адаптивные системы. Методы
оценки параметров объекта и его состояния, являющиеся неотъемле¬
мой частью оптимальных адаптивных систем, рассматриваются отдельно
is § 6.4.

6.2]
МЕТОДЫ ПОСТРОЕНИЯ СИСТЕМ С ЭТАЛОННОЙ МОДЕЛЬЮ
269
6.2. Методы построения адаптивных систем с эталонной
моделью
Один из общих классов методов, на которые можно разбить
широкий круг методов построения адаптивных систем управления,
называется методом построения адаптивных систем с эталонной
моделью. Предложен целый ряд способов использования эталонной
модели для построения адаптивных систем управления. В этих идеях
имеется много общего, но в то же время большая их часть обладает
значительными различиями. В большинстве случаев исследования или
выкладки, проведенные в связи с определенным методом, показывают
достаточно ясно, насколько себя оправдывает идея этого метода.
Некоторые методы использованы для построения реальных систем
управления. Уиттекер, Ярмон и Кезер [49J описали адаптивную сис¬
тему управления самолета F — 94А по тангажу, рысканью и крену.
Хотя экспериментальные исследования выполнены в этой работе на
самом высоком на сегодняшний день уровне, данные, полученные
в течение реальных полетов самолета, были недостаточно полными
вследствие относительно короткого времени летных испытаний и це¬
лого ряда неисправностей в работе оборудования. Дополнительно
к летным испытаниям проводились довольно широкие исследования
на аналоговой вычислительной машине.
Хотя экспериментальные данные подтверждают правильность идей
метода эталонной модели, их недостаточно, чтобы установить пре¬
восходство некоторого метода над остальными. Поэтому в настоящее
время, по-видимому, невозможно создать общую теорию адаптивных
систем управления с эталонной моделью. Следует отметить, однако, что
если настоящее направление работ сохранится, то вскоре обязательно
появятся несколько достаточно общих методов. По-видимому, нет
необходимости и практической целесообразности попытаться описать
здесь подробно каждый из заслуживающих внимания научных вкладов.
Вместо этого делается попытка выявить главное направление работ,
а затем обсудить, насколько различные методы находятся в стороне
от этого направления. Некоторые методы излагаются гораздо под¬
робнее других, однако из этого не следует, что авторы их считают
более важными.
В методе эталонной модели, как следует из самого названия,
эталонная модель является частью адаптивной схемы. В большинстве
случаев модель действительно является частью реальной системы,
однако иногда она входит в менее явном виде. На рис. 6.3 показана
основная блок-схема, которой соответствует большинство структур
адаптивных систем управления с эталонной моделью, где эталонная
модель является отдельной частью системы. Эталонная модель является
аналоговой моделью желаемой динамической характеристики всей си¬
стемы управления. Используя понятия, определенные в § 6.1, заметим,

270
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. 6
что величина P(j) для эталонной модели будет находиться внутри
области желаемого качества. Дальнейшая задача состоит в использо¬
вании управляющего устройства, которое, сравнивая выходную вели¬
чину объекта с выходной величиной эталонной модели, адаптируется
или изменяется так, чтобы передаточные характеристики управляю¬
щего устройства с объектом близко соответствовали характеристикам
эталонной модели. Ответ на вопрос о том, находится ли Р(ф) для
реального объекта также внутри W, зависит от того, насколько
хорошо адаптивный механизм выполняет эту задачу.
Рис. 6.3. Обобщенная схема адаптивной системы управления
с эталонной моделью.
Именно теперь, когда даны уточнения, становятся очевидными
основные отличия методов построения адаптивных систем с эталонной
моделью. Для большей последовательности изложения методы пост¬
роения адаптивных систем с эталонной моделью удобно разделить
на три основных класса:
1. Методы настройки параметров.
2. Методы возмущения параметров.
3. Методы введения дополнительного сигнала ошибки.
Каждый из них достаточно подробно описывается ниже. Точное
разбиение методов на классы является до некоторой степени произ¬
вольным. В действительности, часто отдельные методы относятся
к различным классам в зависимости от того, с какой точки зрения
рассматривается задача и ее решение.
6.2.1.	Методы настройки параметров
Общая блок-схема адаптивной системы управления, использующей
эталонную модель для настройки параметров, показана на рис. 6.4.
Изображенные на блок-схеме предварительный фильтр, корректирую¬
щее звено в прямой цепи, реальный объект, корректирующее звено

6.2]
МЕТОДЫ ПОСТРОЕНИЯ СИСТЕМ С ЭТАЛОННОЙ МОДЕЛЬЮ
271
в обратной связи образуют замкнутую систему автоматического
управления общего вида.
Свойство адаптивности схемы достигается включением эталон¬
ной модели и механизма настройки параметров. Эталонная модель
является аналоговой или цифровой моделью желаемой динамической
характеристики всей системы управления. В настоящее время этот
метод разработан в таком виде, что структура выбранной модели
должна быть сходна с основной структурой объекта с учетом
доступных корректирующих звеньев. То есть для заданного вида
Предварительный
фильтр
r(t)
>»
Корректирующее Реальный
звено в прямой цепи объект
F(s)
т
L_.
K(s)
G(s)
Д Корректирующее звено
j в обратной связи
-I
Механизм
настройки
т
c(t)
Эталонная модель
Рис. 6.4. Обобщенная схема адаптивной системы управления
с эталонной моделью.
дифференциального уравнения, которым описывается реальный объект,
должна иметься возможность выбрать физически реализуемые ха¬
рактеристики корректирующих звеньев, так чтобы вид характери¬
стики всей системы управления был одинаков с видом характеристики
эталонной модели. Более того, должна иметься возможность так
выбрать параметры корректирующих звеньев, чтобы дифференциаль¬
ное уравнение, которое описывает всю систему управления, было
идентично дифференциальному уравнению эталонной модели для
всех предполагаемых значений параметров реального объекта.
На вход эталонной модели и системы управления поступает один
и тот же сигнал. Выходные величины модели и системы управления
сравниваются, и образуется сигнал ошибки. Сигнал ошибки подается
па вход механизма настройки параметров. Механизм настройки так
изменяет параметры различных корректирующих звеньев, чтобы свести
к нулю сигнал ошибки. Если входной сигнал r(t) отличен от нуля,
то для равенства нулю сигнала ошибки e(t) в течение некоторого
времени необходимо, чтобы дифференциальное уравнение, описывающее

272
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. G
всю систему управления, было идентично дифференциальному урав¬
нению эталонной модели. Таким образом, если механизм настройки
будет работать так, как это описано, то при изменении характери¬
стики реального объекта система управления будет настраивать пара¬
метры корректирующих звеньев, с тем чтобы характеристика всей
системы осталась неизменной. Такое применение эталонной модели
Реальный объект
Рис. 6.5. Адаптивная система с эталонной моделью.
для настройки параметров впервые было описано в работе Уиттекера,
Ярмона и Кезера [49]. Однако этот метод развивался и совершенст¬
вовался рядом других исследователей. Каждая из этих разработок
отличается в основном принципом работы механизма настройки. Ниже
рассмотрены три довольно общих метода. Описываемые методы отра¬
жают основные характеристики большей части методов, относящихся
к данному классу.
Метод 1, основанный на градиенте функции ошибки. Многие
из методов, разработанных в теории адаптивных систем управления
с обучающейся моделью [30, 31], применимы и к системам с эталон¬
ной моделью [12].
Этод метод настройки параметров иллюстрируется на примере
простой системы управления второго порядка. Рассматриваемая си¬
стема показана на рис. 6.5 и является простым частным случаем

6.2]	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ	27,‘Т
адаптивной системы общего вида, изображенной на рис. 6.4. Харак¬
теристика всей системы (определяющей связь между сиг) может
быть записана следующим образом:
с tei 4~ ^i)с 4- teo 4- ^и)с =г (0-	(6.2.1)
Точкой обозначается дифференцирование по времени. Желаемую-
характеристику всей системы, реализуемую эталонной моделью, можно
также записать в виде дифференциального уравнения
У -Г a,j) а»у = г (t).	(6.2.2)
Если удовлетворяются равенства
hi+gi = ax	(6.2.3)
и
h “4 go = ао>	(6.2.4)
тогда вся система управления будет иметь желаемую характеристику.
Адаптивная часть системы состоит из эталонной модели, сумми¬
рующего устройства, служащего для образования сигнала ошибки, и
механизма настройки. Эта цепь определяет информацию о скорости
настройки параметров /гх и /г0, с тем чтобы они «адаптировали» изме¬
нение параметров и ^0. В рассуждения можно также ввести инте¬
грал от этой скорости за время работы системы. Величина введен¬
ного интеграла определяет мгновенные значения hy и h0. Эталонная
модель может рассматриваться как аналоговая модель дифферен¬
циального уравнения, которое имеет желаемые характеристики всей
системы. Если рассматривать адаптивные системы управления с кон¬
структивной точки зрения, то эталонная модель является отдельной
частью конструкции. Механизм настройки представляет часть системы,
которая определяет скорости настройки как 1г{, так и !гь а также
интегралы от этих скоростей. Указанная на блок-схеме входная
информация, поступающая на механизм настройки, представляет собой
ошибку между выходной величиной эталонной модели и выходной
величиной реального объекта. Предполагается, что имеются в распо¬
ряжении первая и вторая производные от сигнала ошибки. Для неко¬
торых реальных объектов такое предположение выполняется с трудом,
но обычно измерить эти производные можно. Задача заключается
в том, чтобы найти уравнения, описывающие работу механизма на¬
стройки. Если на значения, которые принимают параметры /?j и /г0>
не наложено никаких ограничений, тогда независимо от величин ^
и g{) соответствующие коэффициенты в уравнениях (6.2.1) и (6.2.2)
будут одинаковы, если справедливы равенства (6.2.3) и (6.2.4). Отно¬
сительно скорости изменения g{ и g{) делается два предположения.
Предположение 1. g{ и g() меняются медленно по сравне¬
нию с основными постоянными времени реального объекта и эталон¬
ной модели.

274
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
Предположение 2. и go меняются медленно по сравне¬
нию со скоростью настройки параметров hi и /г0, определяемой меха¬
низмом настройки, который необходимо спроектировать.
Последствия нарушений этих двух предположений, равно как и
третьего, которое сформулировано ниже, являются важными вопро¬
сами и	могут	быть	изучены либо с помощью	моделирования	на ана¬
логовой	вычислительной машине, либо посредством	аналитического
исследования устойчивости. Так, например, в работе [12] показано,
что подобная адаптивная система продолжает хорошо'работать, даже
когда эти предположения существенно нарушаются. Предположения
необходимы для вывода уравнений движения, описывающих работу
механизма настройки.
Основным принципом работы механизма настройки является мини¬
мизация квадратичной функции ошибки и ее производных. Можно
использовать функции двух видов
/(£) — ~2 ^°£ Ч~ ^l£ “I-	(6.2.5)
и
/i (£) — y (Яо^ -f- Ч" Я£\	(6.2.6)
где
е = {с—у),	(6.2.7)
а параметры q0j qi и q% представляют константы, которые опреде¬
ляются позже. Функция ошибки, используемая в данном методе, имеет
вид (6.2.5). Хотя выбор функции ошибки является важным с точки
зрения проектирования реальной системы, это не имеет значения для
изложения основных идей метода вывода уравнений, описывающих
работу механизма настройки. Метод одинаково хорошо применим
к функциям ошибки, имеющим вид либо (6.2.5), либо (6.2.6). Допол¬
нительное рассмотрение вопроса выбора вида функции ошибки будет
дано ниже.
Чтобы упростить выкладки, запишем уравнение (6.2.1) в следую¬
щем виде:
с	—j—	—j— ccqC = г (^),	(6.2.8)
ai — gi 4" hi	(6.2.9)
и
ao = go4-fco.	(6.2.10)
Минимальное значение	/(е) равно нулю.	Кроме того, /(г) можно
обратить в нуль на любом интервале времени, когда ошибка и ее
производные равны нулю. Ошибка и ее производные будут нулевыми

6.2]
МЕТОДЫ ПОСТРОЕНИЯ СИСТЕМ С ЭТАЛОННОЙ МОДЕЛЬЮ
275
только тогда, когда ал и а0 равны а{ и а0 соответственно, принимая,
что r{t) не равно нулю. Следовательно, хотя /(в) выражает в явном
виде функцию ошибки между выходной величиной реального объекта
и выходной величиной эталонной модели и значением их производ¬
ных, она в то же время выражает в явном виде функцию ошибки
между и аь а0 и а0. Теперь, введя обозначения
— ах	(6.2.11)
и
80 = а0 — а0,	(6.2.12)
функцию /(в) можно представить как поверхность в евклидовом про¬
странстве /(е), Ьх и 80- Если ог и о0 не равны нулю, то механизм
настройки следует так спроектировать, чтобы ал и а0 настраивались
изменением h{ и /г0. В данном методе относительная скорость на¬
стройки выбирается из условия, чтобы и В0 описывали траекто¬
рию непрерывного наискорейшего спуска здоль поверхности /(в)
в пространстве /(в), Ьх и 80. Смысл понятия непрерывного наиско¬
рейшего спуска сейчас будет объяснен.
Ошибка в и ее производные, кроме того, что они являются функ¬
циями bt и 80, они также функции входной величины г (t\ изменяю¬
щейся во времени. Следовательно, форма поверхности /(в) в про¬
странстве /(в), Sj и 80 будет меняться во времени в соответствии
с изменением входной величины г (t), а также динамических характе¬
ристик системы управления и эталонной модели. Теперь сделаем
третье предположение.
Предположение 3. Механизм . настройки должен быть таким,
чтобы с помощью его параметры ал и а0 в уравнении (6.2.8) под¬
страивались быстрее по сравнению со скоростью, с которой /(в)
изменяется вследствие изменения входной величины г (t).
Предположение 3 позволяет для последующего вывода уравнения
траектории наискорейшего спуска считать /(в) функцией только
и о0. Смысл наискорейшего спуска гораздо легче описать, если по¬
ложить, что и о0 получают конечные приращения в конечные
интервалы времени. Затем эти приращения и интервалы устремим
в пределе к нулю, в то же время оставляя постоянным, их отноше¬
ние. В результате найдем относительные скорости настройки и 8„.
Пусть самые большие приращения, которые могут получать Ьг и oQ
в каждый интервал времени в евклидовом пространстве ^ и 80, огра¬
ничены соотношением
(A8J + A85)1/* = d,	(6.2.13)
где d — заданная константа, а А8Х и Д80 — приращения	и 80 на
данном интервале. По определению, траектория наискорейшего спуска
является траекторией, получаемой при выборе такого соотношения

"276
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
между и Д80, что на каждом интервале происходит максимальное
уменьшение /(г). Это можно сделать, выбирая Д^ и Д80 пропор¬
ционально соответствующим составляющим вектора градиента /(е),
взятым с обратным знаком в данных точках пространства Ъг и 80.
Правильность подобной процедуры доказывается тем, что вектор гра¬
диента в каждой точке перпендикулярен линии равного уровня /(в),
проходящей через эту точку. Так как требуется уменьшать /(в),
приращения имеют знак, противоположный составляющим вектора
градиента. Более полное рассмотрение этого вопроса можно найти
в [30] и [31].
Градиент /(в) в пространстве ох и 80 равен
т/<*>='■'41?+'•%$-■	(6-2Л4>
где i\ — единичный вектор в направлении 8Ь а/0 — единичный вектор
,в направлении 80. Следовательно, будут выбраны следующие прира¬
щения:
Д81 = ._/е^М	(6.2.15)
II
4S-=-*^f	(6-2Л6)
где k — общий коэффициент пропорциональности или константа.
Требуется найти приращения, которые необходимо дать Ъг и 80. Из
выражений (6.2.11) и (6.2.12) видно, что всякое приращение по Ь1 и
о0 должно быть сделано с помощью изменения ах и а0, так как вели¬
чина ах и а0 определена константами, представляющими желаемые
значения параметров. Отсюда приращения, которые следует дать ал
и а0, равны
Аа, = AS4	(6.2.17)
и
Да0 = Д80.	(6.2.18)
Кроме того, так как а{ и а0 — заданные константы, то можно
считать, что уравнения (6.2.11) и (6.2.12) осуществляют просто пере¬
нос исходной системы координат в плоскости ^ и Ь0 или и а0
либо пространства /(г), Ъх и 8П, либо пространства /(в), ол и а0. Учи¬
тывая это, можно записать уравнения, эквивалентные (6.2.15) и (6.2.16),
с помощью ах и а0. Они имеют вид
Д*1 = _А^	(6.2.19)
•И
Доц,= _А-^.	(6.2.20)

6.2]	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ	277
Заглядьшая вперед, заметим, что если исходить из выражений
(6.2.19) и (6.2.20), то искомые уравнения содержали бы в явном виде
ctj и а0 и, следовательно, g{ и gQ. Так как по самой идее метода
адаптации предполагается, что gi и g() в явном виде не известны, то
надо использовать другой подход. Это и будет предметом последую¬
щего изложения.
Предположим на некоторое время, что aj и а0 заданы, а ах и an
следует изменить так, чтобы Ь{ и Ь0 устремились к нулю. Те же
самые рассуждения, которые использовались при получении выраже¬
ний (6.2.19) и (6.2.20) из (6.2.15) и (6.2.16), позволяют найти соот¬
ветствующие приращения значений ах и а0. Они равны.
Да,= —k%^	(6-2.21)
И
Да0 = -А^Д>.	(6.2.22)
Далее пусть на данном интервале времени и Ь0 сколь угодно
малы по сравнению с ах w a0. Тогда и можно было бы изме¬
нять за счет добавления величин Аа{ и Да0 соответственно к а{ и а0.
Однако задача заключается в том, чтобы давать приращения не ах и
а0, а aj и а0. Заметим, что равноценное изменение и о0 получается
при вычитании Аах и Да0 соответственно из а0 и од, а не при сло¬
жении их с ах и а0- Итак, /(г) сводится к нулю, когда Ьх и 80 равны
нулю, а это можно сделать, определяя соответствующие приращения
для ах и а0 и используя их с обратным знаком для изменения од и
а0. Приведенное рассуждение справедливо по крайней мере пока
и &0 считаются сколь угодно малыми. Получающиеся в результате
уравнения для приращений по од и а0 имеют вид
Дя1==А^Йг	(6-2-23)
и
Д,. = /,%М	(6.2.24)
Предшествующее обсуждение и исследование, в результате кото¬
рых выведены	формулы	(6.2.23) и (6.2.24),	является	основным для
понимания рассматриваемого метода синтеза адаптивной системы
управления	с эталонной	моделью, используемой	для	настройки па¬
раметров.
Следует признать, что приращения, определяемые формулами
(6.2.23)	и (6.2.24), не точно соответствуют движению по траектории
наискорейшего спуска. Однако можно показать, что при о, и о0,
сколь угодно близких к нулю, траектория движения сколь угодно

278
ТСОРИЯ и МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. б
близка к траектории наискорейшего спуска. Далее, если движение
не происходит по траектории наискорейшего спуска, то, поскольку
эго все равно спуск, адаптация будет иметь место. Работа системы,
когда Ь1 и S0 не являются сколь угодно малыми, может быть иссле¬
дована с помощью анализа устойчивости и моделированием [12].
Так как желательно установить скорости настройки ол и а0, пред¬
полагается, что интервал времени между моментами, в которые де¬
лаются приращения, и величина приращений стремятся в пределе
к нулю, сохраняя одинаковое отношение. В этом случае мгновенные
скорости настройки оц и а0 равны:
где коэффициент пропорциональности k включен в параметры q2y
qx и q0. Подставляя (6.2.5) в (6.2.25) и (6.2.26) и находя указанные
частные производные, получим
С учетом предположения 2 и формул (6.2.9) и (6.2.10) можно за¬
писать
Производную у по времени можно считать обычной частной про¬
изводной. Изменяя последовательность дифференцирования по вре¬
мени и по аь запишем
(6.2.25)
и
(6.2.26)
и
<*i — — (<7о£ + <7i£ ЯФ) ((<7о ^ + Я\ ^ + Я* - j (6.2.27)
*0 = — (?0в +	+	<}ф)	(?»	+	Ч\	^	+	Чг	•	(6.2.28)
(6.2.29)
И
(6.2.30)
Для удобства введем обозначение
«1 = ХГ
ду
да<
(6.2.31)
и
(6.2.32)
ду  д2у	*9-
дах	davdt	atoa1	at
(6.2.33)

6.21	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ
270
Эта операция является математически строгой, так как предпола¬
гается, что у — величина непрерывная, а ах не изменяется во вре¬
мени. Проделывая подобную операцию для всех членов выражений
(6.2.27)	и	(6.2.28), содержащих частные производные,	и	считая
(6.2.29)	и (6.2.30) точными равенствами, можно записать, что
h\ = — (<7о£ ~г ЯФ Яф) (<7oz/i Я\Щ W4)	(6.2.34)
и
А0 = — (q„e + дф дф) (д0и0 + дщ + ?.ги0).	(6.2.35)
Полученные уравнения определяют скорости, с которыми следует
изменять /?! и /?0. Они являются основными уравнениями, описываю¬
щими работу механизма настройки. Предполагается, что величину
ошибки в и ее производные можно измерить на выходе реального
объекта и эталонной модели. В выражениях (6.2.34) и (6.2.35) не¬
известны лишь иъ щ и их производные. Эти величины можно легко
определить, пользуясь методом Мейсингера [35], который описы¬
вается далее.
Рассмотрим дифференциальное уравнение эталонной модели в том
виде, как оно определено выражением (6.2.2), и найдем частную
производную по параметру ах от обеих частей равенства
^■ + а‘й7+-^ + а°Йг = а	(6'2'36)
Поскольку а{ — константа, производную у по времени можно опять
считать обычной частной производной, и поэтому записать выраже¬
ние (6.2.36) в следующем виде:
d'sy _j_ „ д2у , л ду
даф(2 1 а‘ dajt +а°(?а1 —	(6.2.37)
Меняя порядок дифференцирования в выражении (6.2.37) и исполь¬
зуя обозначения (6.2.31) и (6.2.33), получим
щ -{- ахщ -|- а0щ = —у.	(6.2.38)
Это уравнение является неоднородным дифференциальным уравнением
относительно переменной uh Вынуждающая функция является произ¬
водной по времени от выходной величины эталонной модели, взятой
с обратным знаком. Вид данного уравнения совпадает с видом урав¬
нения эталонной модели. Таким образом, величина щ и ее производ¬
ные по времени, которые входят в выражение (6.2.34), находятся из
относительно простого дифференциального уравнения, имеющего
легко доступную вынуждающую функцию.
Подобное уравнение можно получить для п0> беря частные произ¬
водные в выражении (6.2.2) по параметру а0 и выполняя операции,

280
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
указанные выше. В результате найдем следующее дифференциальное
уравнение:
—р	—У*	(6.2.39)
Это неоднородное дифференциальное уравнение опять имеет
точно такой же вид, как и уравнение эталонной модели, за исклю¬
чением того, что переменной является н0, а вынуждающая функция
совпадает с выходной величиной эталонной модели, взятой с обрат¬
ным знаком. Уравнение (6.2.39) дает возможность определить тре¬
буемые значения	и0	и ее	производные по времени	в выраже¬
нии (6.2.35).
Таким образом, найдены уравнения, которые используются для
построения механизма настройки. Заметим, что эти уравнения не со¬
держат в явном виде gi и g0. По-видимому, уместно сделать не¬
сколько замечаний о найденных уравнениях. Большинство рассужде¬
ний базировалось	на	трех	до некоторой степени ограничивающих
предположениях об относительных скоростях изменения gh g0 выход¬
ных величин эталонной модели и реального объекта, а также пара¬
метров 1ц и /?0. Кроме	того,	предполагалось, что значения	параметров
/?! и /го близки к	тем,	которые обеспечивают правильную	коррекцию
характеристик реального объекта. Работа механизма настройки за¬
ключалась в том, чтобы свести к нулю небольшую, действительно
существующую ошибку. Предположения 1 и 2 выполняются для
многих случаев, возникающих в практике. Предположению 3 можно
удовлетворить, выбирая надлежащие значения qb и q0 в квадра¬
тичной форме функции ошибки. Если сделанные предположения
действительно выполняются и если значения корректирующих пара¬
метров /?! и h0 очень близки к надлежащим в начальный момент
работы системы, то нет оснований считать, что система не будет
адаптироваться к изменению gj и g{). Конечно, представляет интерес
случай, когда исходные значения h{ и /г0 взяты с большой ошибкой
или когда gu или g0 получают довольно большие дискретные прира¬
щения. Ответы па эти вопросы можно найти в работе [12]. Полу¬
ченные в ней результаты показывают, что данная адаптивная система
управления будет достаточно хорошо работать, даже если сделанные
предположения нарушены в значительной степени. Основная идея
настоящего изложения распространена на случай линейных реальных
объектов общего вида с одной входной и выходной величиной, на
случай, когда реальный объект описывается нелинейными дифферен¬
циальными уравнениями некоторых видов, и на случай систем управ¬
ления с несколькими входными и выходными величинами [12]. Далее
приводится пример, где этот метод применяется для системы с нели¬
нейным объектом и линейной эталонной моделью. На рис. 6.6 изо¬
бражена блок-схема такой системы. Уравнение объекта имеет еле-

6.2)
МЕТОДЫ ПОСТРОЕНИЯ СИСТЕМ С ЭТАЛОННОЙ МОДЕЛЬЮ
281
дуюший вид:
~с -Ь tel — gtci) 'с -Г g»c — Р-	(6.2.40)
При достаточно большой выходной величине член g$c2 превысит
и объект может стать неустойчивым. Назначение системы управления
Рис. 6.6. Блок-схема нелинейной системы.
заключается в том, чтобы предотвратить эту возможность. Диффе¬
ренциальное уравнение, описывающее эталонную модель, выбрано
в виде
У -}- а\Р -г а»У — г-	(6.2.41)
Чтобы система управления могла иметь такую характеристику, выби¬
рается следующая обратная связь:
у) = }цс -j- Il,c4' -j- 70с.	(6.2.42)
Запишем дифференциальное уравнение, связывающее входную и вы¬
ходную величины системы управления:
с -j- (сгл — а.2с2) с -J- ol0c =	rt	(6.2.43)
где
(6.2.44)
®i = (£i + h)	(6.2.45)

282
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. 6
ао — (£о ~\~ л0).	(6.2.46)
Как обычно, предполагается, что g2> g\ и gQ медленно меняются
во времени некоторым неизвестным образом. Механизм настройки
должен так изменять /г2, hi и /г0, чтобы независимо от значений,
принимаемых g2, gx и g0, в любой момент времени а2 было равно
нулю, а1	равно аъ а0 равно а0. При выводе уравнения	настройки
используется следующая функция ошибки:
U (е) = \ {Цф1 + qФ* + ftS*).	(6.2.47)
Для того чтобы взять частные производные по аь перепишем урав¬
нение (6.2.41) следующим образом:
lim [у -j— (<2j — а'2У^)У Н~ &ъУ\ == Г'	(6.2.48)
Теперь	найдем уравнения, определяющие скорость	настройки
параметров /г2, hi и h0:
}ц = (Хд =	==Г	(ЧФ11Ъ	“Т"	<7l£^2 ”Т" *7*2® Ид),	(6.2.49)
hi —&i	=	— (<7o£??i Н~ #i£Hi ~j~ <7<2£fri)	(6.2.50).
и
Ло == <*о — “5^ = — 07о£г'о <7i£Ho ~h ЧФ 11о)>	(6.2.51)
где
»'= Z,-	с3-2-52'
», = ^Г	(6.2.53)
И
(6.2.54)
Запишем дифференциальные уравнения, из которых определяются
иь щ и их производные. Для этого продифференцируем уравнение
(6.2.41)	по	соответствующему параметру, выполняя	действия,	описан¬
ные выше,	и	затем,	подставляя	нужное из выражений	(6.2.53) или
(6.2.54), получим в результате
iii a\h\	~Ь аоН\ == —У>	(6.2.55)
Но + HlHo	~f"	== —У»	(6.2.56)
[см. формулу (6.2.48)]

6.2]	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ
283
Для того чтобы записать дифференциальное уравнение, определяю¬
щее иь найдем частные производные (6.2.48) по аь изменяя порядок
действий перехода к пределу и отыскания частной производной.
Произведя дифференцирование, делая предельный переход, выполняя
простые преобразования и, наконец, используя выражение (6.2.52),
придем к уравнению
щ —|— й\Щ —а§щ ==У2У'	(6.2.57)
Теперь есть все уравнения, необходимые для реализации адаптивной
части системы, описываемой в данном примере.
Метод эталонной модели можно также объединить с методом
обучающейся модели, сделав так, чтобы эталонная модель «обуча¬
лась» некоторым параметрам системы и в то же время действовала
как эталонная модель относительно других параметров. Такие си¬
стемы могут оказаться полезными, если необходимо построить систему
управления, имеющую некоторые определенные характеристики демп¬
фирования, но при этом нельзя или нежелательно управлять коэффи¬
циентом усиления или собственной частотой системы, по мере того
как изменяются динамические характеристики объекта. Это обобще¬
ние и развитие основных идей, изложенных выше, содержится в ра¬
боте [12]. Однако в последнем случае еще не проведено достаточных
исследований на аналоговых моделях или аналитического анализа
устойчивости, чтобы надлежащим образом оценить сделанные обоб¬
щения.
Метод 2, основанный на использовании прямого метода
Ляпунова [42, 43]. Были сделаны попытки использовать понятие
устойчивости по прямому методу Ляпунова для вывода уравнений,
описывающих работу механизма настройки как в системе с обучаю¬
щейся моделью [42], так и в системе с эталонной моделью [43].
При выводе уравнений механизма настройки в системе с эталонной
моделью сначала записывается дифференциальное уравнение, описы¬
вающее ошибку между системой управления и эталонной моделью.
Затем следует найти такие уравнения настройки параметров, которые
гарантируют, что дифференциальное уравнение, описывающее ошибку,
будет асимптотически устойчиво. Для этого записываются положи¬
тельно определенные функции Ляпунова для уравнения ошибки и
выбираются уравнения механизма настройки, так чтобы производные
по времени функции Ляпунова были отрицательно определенными.
Эго гарантирует асимптотическую устойчивость функции ошибки,
вследствие чего адаптация будет иметь место. Если рассмотреть
геометрическое доказательство теоремы устойчивости прямого метода
Ляпунова (см. главу 5, § 5.1), можно найти существенное сходство
между описываемым методом и методом 1. Однако в настоящем
случае действительные уравнения механизма настройки несколько

284
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. О
иные. И это отличие в первую очередь является следствием того,
каким образом формализована блок-схема адаптивной системы.
Хотя совершенно очевидно, что изложенная идея является много¬
обещающей, она не рассматривается здесь подробно, так как,
по-видимому, требует проведения дополнительных исследований.
Метод 3, основанный на использовании частных производных
функций ошибки. Этот метод очень похож на метод 1, но в то же
время имеет существенные отличия. Теория этого способа настройки
параметров развивалась в работах, начатых в 1958 г. й описанных
в большом числе публикаций [49, 50, 51, 52]. Самые последние
результаты, которые получили авторы названных работ, отражены
в [38] и [39]. Здесь этот материал излагается в краткой форме.
Читатели, которые интересуются более подробными математическими
выкладками, могут обратиться к [38]. Блок-схема рассматриваемой
системы изображена на рис. 6.4. Механизм настройки работает на
основе использования четной функции ошибки /(г). Работа механизма
настройки подробно рассматривалась при функции ошибки только
одного вида
/(е) = 1е*.	(6.2.58)
После продолжительного обсуждения авторы пришли к заключе¬
нию, что каждый настраиваемый параметр pk должен изменяться не¬
прерывно со скоростью, пропорциональной частной производной
/(в) по pk, взятой с обратным знаком. Уравнение, описывающее ско¬
рость изменения параметра, имеет вид
<6-2-59>
Константа SaK находится в процессе проектирования системы.
В случае, когда /(в) задана формулой (6.2.58), /'(в) = в. Функция
в(t) обычно определяется как разность между реакцией системы
управления и реакцией модели. Главная задача — найти способ вы¬
числения dsjdpk на основе доступных сигналов в системе. Обращаясь
снова к рис. 6.4, находим, что в (t) = c(t)—у (t), и так как y(t) не
зависит от р1о то де/др1{ = дс/др}г Непосредственно dc/dpk определить
нельзя. Однако для нее можно получить достаточно хорошую аппрок¬
симацию следующим образом.
Запишем дифференциальное уравнение системы управления, свя¬
зывающее с (£) и г (t):

«.2]	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ	285
где аь bi и с (t) — функции параметров pk. Произведем дифференци¬
рование уравнения (6.2.60) по параметру pk
хд	д	/ dlc \	^ db;	dfr	да{ cdc
У		(— =	У —	—	— У — —.	(6.2.61)
i = o	дрк	' cW '	j=odpk	dtJ	i = 0 dpk dtl
Если pk изменяется очень	медленно, тогда dpkjdt^ 0, и, изменяя
порядок дифференцирования в левой части уравнения (6.2.61) [38],
найдем уравнение, решение которого даст искомые частные произ¬
водные дс/дрь:
Рассмотрение уравнения (6.2.62) показывает, что в него входят ха-
tl
рактеристический оператор системы управления ^ aidljdtl и коэф-
i=0
фициенты при частных производных дац’дрк и dbj/dpk. Отметим, что
именно отсутствие достаточной информации об этом операторе .и
этих коэффициентах в первую очередь привело к использованию
адаптивных методов. Аппроксимацию значений этих величин можно
найти качественными рассуждениями, рассматривая основную идею
метода эталонной модели. Основные корректирующие звенья должны
быть такими, что если параметры р]г настраиваются надлежащим
образом, то реакция системы управления на входную команду но
существу совпадает с реакцией эталонной модели. Поэтому для до¬
стижения этого в случае, когда вся адаптивная система работает
удовлетворительно, динамические характеристики модели должны
довольно хорошо аппроксимировать характеристики системы управ¬
ления. Следовательно, для того чтобы найти уравнение, по которому
определяется аппроксимация дс!др}о в выражении (6.2.62) можно
использовать известные характеристический оператор и коэффициенты
модели вместо характеристического оператора и коэффициентов
системы управления. Такая аппроксимация обоснована в том случае,
когда отличие между коэффициентами системы и модели не суще¬
ственно. Область, в которой аппроксимация обоснована, является
достаточно большой, чтобы применение этого способа настройки
параметров было целесообразным и эффективным в таких системах,
как адаптивные автопилоты космических аппаратов.
Обсуждение и сравнение методов настройки параметров. Те¬
перь можно сравнить метод 1 и метод 3. Прежде всего в методе 1
представляющие интерес параметры регулируются пропорционально
взятым с обратным знаком соответствующим составляющим вектора
градиента функции ошибки в пространстве параметров. В методе 3
£ ai
dl
dt1
дс
dph
■у dbj dir	yv dai	d‘c
dpk dti	^ dpk	dt‘
(6.2.62)

ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. 6
используются до некоторой степени более эвристические положения,
заключающиеся в том, что данный параметр должен регулироваться
согласно частной производной с обратным знаком от функции
ошибки, умноженной на некоторую положительную константу. Если
в последнем методе эту константу положить равной единице для
всех параметров, тогда эти два метода будут отличаться лишь вы¬
бранными функциями ошибки.
Как в методе 1, так и в методе 3 функция ошибки является
критическим фактором, определяющим работу адаптивной части си¬
стемы. Метод 1 использует функции ошибки и ее производных и для
систем /г-го порядка рассматривает функции следующего вида:
Метод 3 использует функции единственного вида
Це) = 1£*.
Если сравнить результаты, которые даны в [38] и [12], то видно,
что при ступенчатом возмущении параметры настраиваются быстрее
для функций ошибки, используемых в методе 1, чем при функциях
ошибки, используемых в методе 3. Это, очевидно, вызвано влиянием
производных от s(f), включенных в функцию ошибки. Хотя увеличе¬
ние скорости адаптации и кажется желательным, надо помнить, что
добавление в функцию ошибки членов, содержащих производные,
усложняет до некоторой степени механизм настройки параметров.
Если рассмотреть более общие положительно определенные
квадратичные функции ошибки и ее производные, то оказывается,
можно использовать преимущества обоих методов. Например, рассмо¬
трим некоторую функцию
п п
Хотя такая функция ошибки несомненно усложнит конструкцию
адаптивной системы, в некоторых случаях ее применение может ока¬
заться оправданным. По крайней мере этот вопрос является, по-ви¬
димому, предметом дальнейших исследований, равно как и идея
использования понятия устойчивости в качестве основы для вывода
уравнений механизма настройки, которая описана в методе 2.

6.2]	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ	287
При настройке параметров любым из трех методов входной
сигнал системы должен отличаться от нуля. При отсутствии входного
сигнала может иметь место значительная ошибка между действитель¬
ными и желаемыми значениями настраиваемых параметров. Если
после того, как такие ошибки появились, настройка параметров
происходит медленно, то выходная величина системы управления
может сильно отклониться от желаемого значения. Построение про¬
стой системы по методу 1 показало, что настройка параметра может
происходить за время в пределах 10% от основной постоянной вре¬
мени эталонной модели.
Ни метод 1, ни метод 3 не ухудшаются, если на. входной сигнал
системы наложен шум, поскольку такие же шум и сигнал поступают
в контур адаптации. Задача другого рода возникает и может вызвать
затруднения, если шум входит внутрь контура системы управления.
В настоящее время по этому вопросу нет достаточного количества
данных, чтобы сделать какие-либо заключения.
В литературе рассмотрен целый ряд других методов настройки
параметров. Хотя и кажется, что непрерывные системы, описанные
выше, имеют много преимуществ, некоторые случаи требуют приме¬
нения дискретных методов настройки параметров. Некоторые много¬
обещающие результаты упоминались в связи с дискретными методами
настройки параметров, основанными на функциях ошибки, представ¬
ляющих собой интеграл квадрата ошибки, взятый в конечных пре¬
делах [10]. Однако, вообще говоря, оказывается, что функции ошибки,
которые не содержат интегрирования, предпочтительнее, поскольку
они не вводят дополнительного сдвига по фазе в контур настройки
параметров.
6.2.2.	Методы возмущения параметра [32, 33]
Метод, который излагается далее, можно было бы причислить к
уже изложенным методам настройки параметров, однако ввиду его
существенного отличия от описанных выше он рассматривается от¬
дельно. Общая идея метода показана, хотя здесь и не приведены
подробные математические выкладки.
На рис. 6.7 изображена блок-схема адаптивной системы управле¬
ния с эталонной моделью с возмущением основного параметра. Как
и в других методах, выходная величина эталонной модели вычитается
из выходной величины системы, для того чтобы получить сигнал
ошибки е. Образуется функция ошибки. Среди функций ошибки
рассматриваются следующие:
f{e) = e\
Ш=\е\

288
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
Ш = \е\я.
Один из параметров а системы определяется как
а = а0 -j- a.f -j- ах cos u
где а0 — основной параметр системы, — поправка, поступающая
с адаптивной части системы, и o^cosotf — синусоидальный возмущаю¬
щий сигнал, используемый для получения непрерывной ошибки. Сину¬
соидальное возмущение приложено также и к адаптивному механизму.
Поскольку параметр «а» возмущается синусоидальным сигналом,
ошибка будет также содержать составляющую той же частоты.
Величина и знак поправки выбраны так, чтобы уменьшить усред¬
ненную на малом отрезке времени функцию ошибки f (е).
Рис. 6.7. Основная структура адаптивной системы
с возмущением параметра.
Можно синтезировать систему, которая будет настраивать несколько
параметров. Для этого используются возмущающие сигналы, имеющие
различные частоты для каждого регулируемого параметра. При этом
для каждого из них нужен свой адаптивный контур. В работе [33]
утверждается, что если все контуры имеют равный коэффициент
усиления, тогда настройка параметров будет происходить по траекто¬
рии наискорейшего спуска. Для улучшения характеристик можно
было бы включить в адаптивный механизм дополнительные фильтры
и нелинейности.
Основным недостатком данного метода является то, что возму¬
щающий сигнал проходит на выход системы. Этого можно избежать,
используя модель, которая по виду либо одинакова, либо близка к
системе. Тогда возмущающий сигнал прикладывается к параметру

6.2]
МЕТОДЫ ПОСТРОЕНИЯ СИСТЕМ С ЭТАЛОННОЙ МОДЕЛЬЮ
289
модели, соответствующему тому параметру системы, которым следует
управлять. Блок-схема такой системы изображена на рис. 6.8.
Метод возмущения параметра может применяться и в ряде систем,
имеющих другую структуру. Хотя в некоторых случаях адаптивный
Рис. 6.8. Адаптивная система с возмущением параметра.
контур оказывается довольно сложным, однако требуемые вычисле¬
ния могут выполняться при использовании относительно небольшого
числа элементов [32, 33].
6.2.3.	Методы введения дополнительного сигнала ошибки
В обоих методах построения адаптивной системы управления,
описанных выше, адаптация или настройка системы выполнялась
посредством регулировки параметров в системе управления. Далее
описан метод, который рассматривает эту задачу с несколько другой
точки зрения. Обратимся опять к рис. 6.3 и опишем работу адаптив¬
ной системы управления с эталонной моделью следующим образом.
Входной сигнал г (t) поступает как на эталонную модель, так и на
управляющее устройство. На управляющее устройство, кроме того,
10 п/р Леондеса

290
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. 6
подаются в качестве входных величин выходные величины как объекта,
так и эталонной модели. На основании всех этих входных величин
управляющее устройство вырабатывает управляющий сигнал m(t\
который и поступает на объект. Задача адаптивного управляющего
устройства заключается в том, чтобы выработать таксе m(t), при
котором выходная величина объекта будет равна выходной величине
эталонной модели. Этот метод легко попять, если его изложить с той
степенью общности, которая использовалась до сих пор. Сложным
является вопрос конструкции управляющего устройства и выбор
модели. Хотя можно было бы рассмотреть большое число методов
Рис. 6.9. Блок-схема управляющего устройства, скон¬
струированного на основе прямого метода Ляпунова.
построения управляющего устройства, в данном обсуждении мы огра¬
ничимся лишь одним, который, по-видимому, имеет определенные
преимущества.
В излагаемом методе в основу построения управляющего устрой¬
ства кладется условие устойчивости, вытекающее из прямого метода
Ляпунова [18]. При изложении метода будем пользоваться блок-схе¬
мой 6.9. Необходимо заметить, что данную блок-схему легко при¬
вести простой перестановкой элементов к блок-схеме 6.3. Что ка¬
сается нижней части блок-схемы 6.9, то она представляет собой
обычную замкнутую систему регулирования, за исключением допол¬
нительного сумматора в цепи перед элементом с нелинейным коэф¬
фициентом усиления. Этот элемент включен просто для большей
общности рассмотрения. Адаптивность достигается посредством обра¬
зования дополнительного сигнала ошибки еа и введения его в кон¬
тур системы через специальный сумматор. На вид нелинейности
наложены ограничения
(а)	/(0) = 0,	(6.2.63)
(б)	х/ (х)	0, х 0.	(6.2.64)

6.21
МРТОЛЫ ПОСТРОЕНИЯ СИСТЕМ С ЭТАЛОННОЙ МОДЕЛЬЮ
291
Выходная величина объекта определяется следующим уравнением:
п — 1
~ + У а, (/) ^ = /е (t)f(e -f ?„).	(6.2.65)
г“
Предполагается, что коэффициенты в этом уравнении могут быть
выражены как
aiif)  ai ; ai (0» ai (mill)	(0	ai	(max)
(/=1, 2, . . . , П — 1),
k (t) = k -f к (*), Kmin < К (0 < Ktnax,
(6.2.66)
где di и k — константы.
Порядок дифференциального уравнения, которое описывает модель,
может быть равен либо на единицу ниже порядка уравнения замкну¬
того контура системы, включающего объект. Для частного случая,
рассмотренного ниже [18], порядок дифференциального уравнения па
единицу ниже. Его полная характеристика имеет вид
tr- (в-2в7)
i = 0
где L — коэффициент усиления, а являются константами. В иссле¬
дованиях, которые проводились до сих пор [18], делались следую¬
щие ограничения:
а) Входная величина является ступенчатой функцией Ru(t)\
б) Коэффициент усиления в состоянии равновесия равен единице
как для модели, так и для замкнутого контура, включающего объект.
Как следствие этих ограничений в условиях установившегося равно¬
весия c = R, е = 0 и еа — 0. Кроме того, из (б) следует, что
b() = L.	(6.2.68)
Рассогласование между выходными величинами объекта и модели
будет равно
v=cd — с.	(6.2.69)
Далее, если
а) Уравнение (6.2.67) продифференцировать по времени;
б) Уравнение (6.2.65) вычесть из результата действия (а);
С1п~1Си
в)	у	найденное	из уравнения 6.2.67, подставить в выраже¬
ние, получающееся в результате действия (б);
г) Результат действия (в) перегруппировать и в него подставить
выражения (6.2.68), (6.2.69), (6.2.66), при этом замечая, что входная
10*

292
ТЕОРИЯ и МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. в
величина является ступенчатой функцией; то, определяя
tf-'v
Vi (It* 1
(i=t 1, 2,	и),
(6.2.70)
можно записать результат действия (г) в виде векторного дифферен¬
циального уравнения
v= Mv —y(t),
где
М =
V\
V =
V.)
i» v =
V 2
!
i
i
! V !
; Ln \
Vn !
; о 1 оо
0
0 0 10
0
0 0 0 0
0
—т0 —Ш\ —/?ь2 —Мъ
• —тп_
2 —
0
1
.
0
0
•
.
.
.
(6.2.71)
(6.2.72)
0	!!
ii
о	ii
о	о	;
о	о
0 0.0 1
" ^0 (й/1 1 Ь/l з) f^l {йц -L	.	[^Л-2	Ьп _.,)Л~Ьп-:\ 1
(6.2.7В)
°!
о
У(*) =
■ I
о!
л
(6.2.74)
Vo = Мл. i V) v\ - b{an л (t) u2 -\-... -!- bn лап t(i)vn.j —
+ e»-> (0 •»« + K-i (0 —	—	ai (0 4- vu) -'-•••
• • • +	(0	-	bn.,] - a„_8 (t) J- bn -
— \an-i (0 — Md (O e + k (t) f{e — ea). (6.2.75)
Дифференциальное уравнение (6.2.71) описывает ошибку между
выходными величинами модели и объекта. Оно является неавтоном¬
ной возмущенной динамической системой (см. определение в главе 5),

6.2]	МЕТОДЫ	ПОСТРОЕНИЯ	СИСТЕМ	С	ЭТАЛОННОЙ	МОДЕЛЬЮ
293
а по гипотезе [18] Mv—y(t) ограничена для всех v и £^>0 и, кроме
того, для v = 0, в таком случае г> = 0. Если вычислительное устрой¬
ство построено так, что это дифференциальное уравнение асимпто¬
тически устойчиво в большом для всех ступенчатых входных сигна¬
лов, тогда ошибка между выходными величинами модели и объекта
будет стремиться к нулю, т. е. ^->0. Для выполнения этого построе¬
ния используется условие, вытекающее из прямого метода Ляпунова.
Квадратичная функция Ляпунова V(<о) определяется следующим об¬
разом:
V(v) = v’Pv,	(6.2.76)
где Я—положительно определенная симметричная матрица. Поло¬
жительно определенная квадратичная форма, определяемая (6.2.76),
имеет свойства, удовлетворяющие теоремам в главе 5. Если уравне¬
ние 6.2.76 продифференцировать по времени и затем в него подсга-
гить выражение 6.2.71, тогда получим
V (р) = 2 v'PMv — 2v'Py.	(6.2.77)
Если все собственные значения М имеют отрицательные действитель¬
ные части, тогда можно выбрать элементы Р в соответствии с эле¬
ментами положительно определенной диагональной матрицы Q,
чтобы
2 PM = —Q.	(6.2.78)
Подстановка	(6.2.78)	в	(6.2.77) дает
V(v) = — v'Qv — 2 v'Py.	(6.2.79 j
Первый	член	в	правой	части (6.2.79) является отрицательно опреде¬
ленным и будет удовлетворять другим условиям для V, определяемым
соответствующей теоремой в главе 5. Второй член можно записать
следующим образом:
— 2г>'Ру = —2 (p,„v, -f - vinv.i —... -г3V (6.2.80)
Если
З'о = 7 SSn (PlnV 1 -Г*"-2л7-’-2 -Г • • • -Т-Рп,рп)> 0 < Т < со, (6.2.8 1)
где
II при х^>0,
0 при л' = 0,	(6.2.82)
— 1 при -v<^0,
тогда
—2v'Py = —2? < 0	(6.2.83)
и, следовательно, уравнение (6.2.79) будет отрицательно определен¬
ным. Уравнения (6.2.76) и (6.2.79) удовлетворяют условиям теоре¬
мы 5.9 главы 5, если справедливо (6.2.81). Таким образом, если

294
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ (ГЛ. 6
управляющее устройство построено так, что его выходная величина еа
определяет знак у0, который удовлетворяет выражению (6.2.81), тогда
сходимость выходной величины объекта к выходной величине модели
гарантируется.
Системы описанного типа были синтезированы и при моделиро¬
вании показали удовлетворительную работу [18]. Однако число кон¬
кретных применений, которые можно найти для рассмотренного ме¬
тода, вероятно, очень ограниченно вследствие нескольких основных
предположений, которые делаются при проектировании. Действительно,
необходимость иметь ступенчатые входные сигналы, единичный коэф¬
фициент усиления в установившемся состоянии и необходимость по¬
добия модели и объекта, для которого она применяется, являются
сами по себе сильно ограничивающими предположениями. Тем не
менее метод интересен в смысле использования подобных способов
рассуждения в других приложениях. В частности, интересно непосред¬
ственное применение условия устойчивости в процессе проектирова¬
ния системы.
6.2.4.	Замечания по методам построения адаптивных систем
управления с эталонной моделью
В категорию адаптивных систем управления с эталонной моделью
попал целый ряд конкретных схем, предложенных в литературе.
В материале, который изложен выше, сделана попытка провести
дальнейшую классификацию этих методов и выбрать из них наиболее
характерные. Не существует универсальных методов и очень немногие
методы имеют широкое назначение. Выбор надлежащего метода из
существующих весьма сильно зависит от того, где он применяется.
В большинстве случаев необходимо идти на компромисс между слож¬
ностью, надежностью, стоимостью и характеристиками системы. При
этом нет универсальных правил, которыми следует руководствоваться
при выборе относительного веса этих факторов.
6.3.	Оптимальные адаптивные методы
Методы настройки параметров применимы в первую очередь, ког¬
да адаптация происходит при настройке небольшого числа парамет¬
ров. Увеличение числа настраиваемых параметров приводит к увели¬
чению объема вычислений. По мере того как допускается больший
объем вычислений и по мере того как совершенствуются вычислительные
машины, будут искаться все лучшие методы, направленные на увели¬
чение точности системы. В связи с этим исследуются оптимальные
адаптивные методы. Еще одной причиной, заставляющей исследовать
эти методы, является возможность рассмотреть случай, когда на ве¬
личину управляющих переменных наложены ограничения.

6.3]
ОПТИМАЛЬНЫЕ АДАПТИВНЫЕ /МЕТОДЫ
295
По сути дела, оптимальные адаптивные методы решают некото¬
рую задачу оптимизации синтеза сигнала управления при предполо¬
жении, что параметры объекта и его состояние известны. Поскольку
эти величины в задаче адаптации известны не в полной мере, то
неотъемлемой частью всей системы является сценка состояния
и идентификация объекта. Кроме того, для оптимизации необходимо
знать задающую входную
величину. Во многих за¬
дачах задающая входная
величина известна в про¬
цессе управления, как,
например, в системе дви¬
жения по заданной траек¬
тории. В этом случае за¬
дача сводится к регули¬
рованию. Если задающая
входная величина неизве¬
стна априори,необходимо
предусмотреть прогнози¬
рующее устройство. Оп¬
тимальные адаптивные ме¬
тоды схематично пояснены
на рис. 6.10. Одними из
первых исследователей, работавших в области оптимальных адаптив¬
ных методов, были Калмэн [23], Меррием [36], Браун [8], Медич
[34] и Хеи [20]. Отдельные методы, предложенные ими, рассмотрим
в дальнейшем, где попытаемся сравнить эти методы с методами, опи¬
санными в данной главе.
Изложение будет проводиться в следующем порядке. Сначала
излагаются основные принципы построения оптимальных адаптивных
схем. Затем описываются методы решения задачи для линейных объек¬
тов при квадратичных критериях качества и ограничениях на управ¬
ляющую переменную, заданных не в виде неравенств. Величина
отклонения управляемой переменной ограничивается непосредственно
с помощью «штрафных» функций. Эти методы затем распространены
на случай, когда на управляющую переменную наложены ограниче¬
ния в виде неравенств. Даны дна возможных градиентных метода.
Хотя способы идентификации и оценки состояния являются неотъем¬
лемой частью оптимальных адаптивных методов, они изложены от¬
дельно в § 6.4.
Для облегчения изложения рассматривается случай одной вход¬
ной и выходной величины. Результаты можно распространить и на
многомерный случай. Кроме того, обсуждается дискретный случай,
поскольку синтез оптимального сигнала можно выполнять на цифро¬
вой вычислительной машине.
I	1
Рис. 6.10. Схема оптимальной адаптивной
системы.

296
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ (ГЛ. &
6.3.1.	Основные принципы
Оптимальное адаптивное управление предполагается использовать
для поддержания выходной величины объекта, близкой к значениям,
лежащим на некоторой желаемой траектории. Выходная величина
объекта должна так поддерживаться в течение некоторого времен¬
ного интервала, который назовем рабочим интервалом. Другими
словами, необходимо минимизировать критерий качества
где cd(k) — желаемая траектория или задающая входная величина,
с (k)—выходная величина, N\ — число интервалов квантования по
времени, содержащихся в рабочем интервале.
Оптимизация на основе критерия (6.3.1) неудобна по нескольким
причинам'. Во-первых, в результате этого получается разомкнутый
контур управления со всеми нежелательными последствиями. Во-вто¬
рых, объект неопределен в будущем. К тому же, если требуется
применение прогнозирования задающей входной величины, она изве¬
стна только на короткий промежуток времени вперед. В-третьих,
может оказаться, что проведение числовых вычислений в истинном
масштабе времени невозможно. В результате целесообразнее выпол¬
нять оптимизацию периодически. Для этого выберем фиксированный
интервал времени в будущем, который назовем интервалом опти¬
мизации, и выполним минимизацию в этом интервале. Следовательно,
вместо (6.3.1) минимизируем периодически следующий критерий ка¬
чества:
где N — число интервалов квантования по времени, содержащихся
в интервале оптимизации, k — настоящее время.
Взаимное расположение рассматриваемых интервалов во времени
показано на рис. 6.11.
Идея адаптивного управления возникла из желания соперничать
с лучшими способностями человека. Поэтому в качестве общего
принципа берется принцип аналогии с человеком. Подобные сообра¬
жения впервые высказал Меррием [36].
Перед человеком, который столкнулся с задачей управления, на¬
пример при вождении автомобиля, возникает вопрос оптимального
выбора следующего решения в многоэтапном процессе принятия ре¬
шений. Его решение базируется на знаниях настоящего состояния
и знаниях, может быть интуитивных, отклика управляемого объекта
(6.3.1)
k-\-N
J= У 4ТС<*(/) — с (/)]*.
(6.3.2)

ОПТИМАЛЬНЫЕ АДАПТИВНЫЕ МЕТОДЫ
297
(поведения автомобиля). Человек выбирает определенное управление
на основе рассмотрений, захватывающих относительно короткий про¬
межуток времени в будущем. Например, дорожные условия могут
меняться, и человек не будет управлять автомобилем на сухой дороге
так же, как он это делал бы на обледенелой дороге. Если известна
желаемая траектория движения на короткий промежуток времени
вперед (интервал оптимизации) и если известно поведение автомобиля
при управлении им, то человек может приложить надлежащее усилие
к рулевому колесу. Таким образом, критерий, определяемый (6.3.2^
Рабочий интервал
г
Л
Интервал
Интервал
квантования
оптимизации
по времени
и. ■■■—. .
г	А'“—\
О —4W-- t t+NT
1 1	к = О	k-N
Рис. 6.11. Временное соотношение между
рассматриваемыми интервалами.
заменяет собой субъективную оценку обстановки, выполняемую чело¬
веком.
Хотя минимизация выражения (6.3.2) может привести к субопти-
мальной стратегии по сравнению с минимизацией (6.3.1), это единст¬
венно правильный критерий, который можно использовать в данной
ситуации. В проведенных выше рассуждениях присутствовала оценка
состояния и идентификация объекта. Эти функции выполнялись чело¬
веком посредством наблюдения и проверки поведения автомобиля
при управлении им. Точно так же как человек может приспосабли¬
ваться к вождению различных автомобилей (к различному их пове¬
дению при управлении), а также к различным условиям движения
одного автомобиля (дорожные условия, прокол покрышки и т. д.),
адаптивная система управления также должна решать подобные
задачи, если от нее требуется, чтобы она обладала лучшими спо¬
собностями человека.
6.3.2.	Случай линейного объекта и квадратичного
критерия качества
В этом пункте рассматривается алгоритм работы системы в слу¬
чае линейного объекта и критерия качества, определяемого выраже¬
нием (6.3.2). Методы, которые широко обсуждались в прошлом, в
основном касаются этого важного частного случая. В его исследова¬
ние важный вклад внесли в основном Меррием [36] и Калмэн [24].

298
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. Г>
Перед тем как выводить алгоритм работы системы, опишем объект
с помощью вектора состояния.
Предположим, что характеристики объекта мало меняются в те¬
чение интервала оптимизации. Это предположение позволяет исполь¬
зовать дифференциальные уравнения с постоянными коэффициентами,
полняемое обычным способом путем умножения соответствующих со¬
ставляющих векторов и суммирования результатов умножения,
А — // X //-матрица; b, h — //-мерные векторы.
Когда в качестве управляющего устройства применяется цифро¬
вая вычислительная машина, сигнал управления принимает вид сту¬
пенчатого сигнала, показанного на рис. 6.12. При этом
т (О = т (к\ (/г — 1) 7'^	(/г	= 1, 2, ..., N).
В этом случае выходная величина объекта определяется в диск¬
ретные моменты из следующего дифференциального уравнения:
где ср — п X //-матрица, \ — /z-мерный вектор.
В данном параграфе ограничим величину т(к) косвенным путем,
используя штрафную функцию в критерии, определяемом выраже¬
нием (6.112). Поэтому для каждого k минимизируется следующий
критерий:
где а — штраф па применяемое управление.
Будет использоваться вариационный метод или принцип макси¬
мума, а также то и другое вместе (см. главу 7). Чанг [9| и Кац [251 *)
что в свою очередь умень¬
шает объем требуемых вы¬
числений.
О
Опишем линейный объект
с л еду ю щ и м о б р а зо м:
7 21 37 4 7 57
t
х (t) Ах (0 Ьт (0, }
с (*) = ■>, Х{Г) ,	I
(6.3.3)
Рис. 8.12. Ступенчатый сигнал.
где символ { , ) означает
скалярное про и з в еде н не, в ы -
(6.3.4)
J= У, т (('а С) — с (у))'2 -4- -у т (jf,	(6.3.5)
*) Работа Каца 125] оказалась ошибочной. В связи с этими вопросами
см. работу Пропои [551. (Прим. ред.)

6.3]
ОПТИМАЛЬНЫЕ АДАПТИВНЫЕ МЕТОДЫ
299
исследовали принцип максимума для дискретного случая, дающего
только необходимые условия оптимума. Алгоритм, который выводит¬
ся здесь, является по существу алгоритмом Кипиниака [27].
Вариационная задача заключается в минимизации выражения (6.3.2)
при условии (6.3.4). Используя метод множителей Лагранжа, запишем
с учетом ограничений новый функционал, который следует миними¬
зировать:
k '-N
J = 2 "1	^	—	,1*х ^ Т т р {х ^ —
— Фх(/' — 1) — \т (/')).
Согласно необходимым условиям экстремума полный дифферен¬
циал ./ обращается в нуль для независимых дифференциалов x(j)y
tn(J) к p(f). Найдем этот полный дифференциал:
dJ= ^ dx*j \(h*x(j) — cd(j))h + p{J) — Ф*р(/+1)}-г
/=*+1
+ dx* (k + AO {(***(k + N)- сd{k + A/))h-p(k + N)\ +
k~-N
-j- X dm (j) {'J.m (j) — y «p (/)} -f
T- dp* a) {•* (/)—флг с/—в—(/)}—°-
j=k+\
Таким образом,	должны удовлетворяться следующие	соотношения*):
X (j) =	(j),	(6.3.6)
Р (J)=(/	— В+CpVftft** (/ - В — (?*№<,	С/’	-1).	(6.3.7)
m{j) = ~rp(j)	(6.3.8)
и условия трансверсальности
р (k -f- N) = hcd (k + N) — hh*x (k + M).
Подставляя (6.3.8) в (6.3.6), придем к необходимости решить сле¬
дующую двухточечную граничную задачу:
I * С/) I
x(j— 1)
! р (/) !
?
ри-в
*) Заметим, что (ср*) 1 существует, так как ср является фундаментальной
матрицей.

300
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ |( Л. 6
где
tP-r^YY*('fiT1ft/»*
1 YY* (?*)-'
(<?*)lhh*
Of*)'1
ч =
- YY* (г*)“’л I
(?*)-'& Г
При условии, что х{к) задано, и
р (/? —j- N) = he(k —J— N) — hh'x (k —j— /V).
Выразим x(k-{-N) через x(k):
x (k —J— TV)
P(k + N)
= 6'v
x{k) !|
p(k)
l+S 6-v~Vrf(/“ i>
Величину суммы можно подсчитать. Поэтому имеем
= 4>;j
| X {k) ,j
\р(ь) Г
, v !j
гЬ — од = :i
4 ,i ч>*
Таким образом,
х (к + N)+ ftj = упх (к) +	(/,),
hcd (к -j- /V) — hh*x (к -j- TV)	6*2 =	(A)	~п	UV’P (A)-
Исключая jc (& -f TV), найдем
hed (k -f .V) -j- 5,	/г/г-	=	(ife,	-|-	hh*q>.u)	x	(k)	+	(г|),,	-f hh*^H)p {к).
Следовательно, решение, которое определяет сигнал обратной связи,
равно
w (к) = т Y* СФ** -г hh*q>иУ1 (hed {к	N) +
-■!- 6.2 -|- hh*6i — tyn -f- /г/г^г^ц) х (к)).
(6.3.9)
Здесь предполагается, что обратный оператор существует. Должно
быть ясно, что существование этого обратного оператора является
существенным для того, чтобы имелся единственный минимум. На
практике следует проверить и убедиться в том, существует ли обратный
оператор в широком диапазоне изменения параметров.

6.3]
ОПТИМАЛЬНЫЕ АДАПТИВНЫЕ МЕТОДЫ
301
6.3.3. Ограничения на управляемые переменные
в виде неравенств.
Покоординатный градиентный метод *)
В этом пункте рассмотрение, проведенное в пункте 6.3.2, рас¬
пространяется на случай, когда на управляемые переменные наложены
ограничения в виде неравенств. Задача оптимизации становится за¬
дачей нелинейного программирования, для решения которой имеются
многочисленные методы. В задачах управления ограничения имеют
более простой вид, чем в общем случае нелинейного программирова¬
ния. Поэтому можно ожидать, что используемый метод не будет
сложным. В свою очередь простой метод необходим, если следует
осуществить управление в натуральном масштабе времени **). По-ви¬
димому, для управления в натуральном масштабе времени подходят
два метода, а именно, покоординатный метод градиента [17] и упро¬
щенный метод проекций градиента Хо [19]. Первый из двух упомя¬
нутых методов обсуждается в этом пункте, а второй изложен в сле¬
дующем пункте.
Используя уравнение (6.3.4), образуем столбец, который определяет
выходную величину в дискретные моменты как функцию настоящего
состояния и применяемого управления:
(6.3.10)
где
сС0
ft*'
V
0
m{ 1)
ft* Ф
•
ft*0>Y
ft*Y 0
•
Л*Фа
.
.
•
_L_
l
.
с (ДО
i
j ft*<
ф 'V—1 у
	h*y
m(N)
й*фЛ'
с == Gm
fOi
g(>)
0 0!|
g(2)
8( О 0 j
|
•
•
<:
Hi
ll
:
gi ]gi
•
■■■ gN .
1
i
\g(K)
g(l)
*) Этот метод известен как метод Гаусса — Зайделя. (Прим. перев.)
**) Под управлением в натуральном масштабе времени понимается такое
управление, при котором вычисления, необходимые для оптимальной работы
системы, выполняются с помощью вычислительного управляющего устройства
в реальном времени, что обеспечивает непрерывное управление.

302
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
Теперь задача может быть сформулирована иначе, а именно: найти
/д, которое минимизирует *) выражение
J=ik*-cJ	(6-ЗЛ1>
при условии, что
|/и(/)|^М	(6.3.12)
Пусть clr — cd—с0. Тогда выражение (6.3.11) примет вид
J — -I I d' — От ||“.	(6.3.13)
Выражение (6.3.13) определяет в пространстве т гиперпараболи-
ческую поверхность, и задача заключается в том, чтобы найти точку
в выпуклой области, определяемой (6.3.12), которая соответствует
точке минимума на этой гиперпараболической поверхности. При
использовании покоординатного градиентного метода выбирается на¬
чальная точка в пространстве т и определяется градиент 7 в на¬
правлении одной из координат. Затем делается корректирующее дви¬
жение от этой точки в направлении, противоположном направлению
градиента.	Рассматривая	каждую координату	и	повторяя	процесс
геометрически, спускаемся по холму к самой низкой точке из мно¬
жества, которое удовлетворяет ограничениям. Опишем метод более
точно.
Градиент по направлению /гг (у) равен
Vj-l = gjQfn — gjd'.	(б.3.14)
Новое	значение	для	компоненты и (у)	определится	следующим
образом:
=	(6.3.15)
гп находится поиском минимума вдоль направления у-й компоненты.
Развернем выражение для
27 = {G^Gm, т) — 2 ( G*d\ т) ~\dr jf2.
Рассмотрим члены, которые зависят от
Q(ni) = ( G*Gmy т) — 2 ( G*dr, т ).	(6.3.16)
Кроме того,
• еягк>'
,(«)
*) Норма || л || здесь определяется, как |; л:
н -1 S -ч.
г i= I

6.31
ОПТИМАЛЬНЫЕ АДАПТИВНЫЕ МЕТОДЫ
ЗОЯ
где все элементы w[n) равны нулю, за исключением /-го, которой
равен \(*\}. Подставляя mnvx в выражение (6.3.16), получим
Q(m{n) + znw{n))= Q(m{n^) +	{	G*Gm{n)	—
— Q*d\ zv^n) > -j- г% ( Q*Qw'n\ w™ ).
Тогда минимум по частному направлению определится из
Aq( ) = 2 (G*GmSn) —G*d\ w[n)) -f 2e„ < G*Qw<n\ w^>)=0,
т. e.
■ I win' ||2
~л {G*Gw(rl\ win)) *
Все элементы вектора w равны нулю, за исключением /-го эле¬
мента. Следовательно, гп для направления / равно
— 1
EnJ~~WSrr
Поэтому па шаге п мы сделаем /г —1 приближение следующим
образом:
и(л) J
т 0'){пи) = т (jin) — грпр.	(6.3.17)
<1 £/ II
Поскольку	может	выйти	за	границу,	необходимо ограничить
ее величину
/я(у)|л;= sat [т(Цпл'>].	(6.3.18)
-ММ
Величина	в	левой части используется для следующей	итерации.
Таким образом, искомыми уравнениями являются уравнения (6.3.14),
(6.3.17) и (6.3.18). Следует отметить простой вид этих уравнений.
Каждая итерация требует выполнения 4-	 *	операций сложе-
/V2 , oN
ния, ~2 -\-~2 операций умножения и одного деления.
Доказательство сходимости этого метода дал Хилдрет [10]. Схо¬
димость гарантируется только для прямоугольной области в прост¬
ранстве т. Конечно, успех применения любого градиентного метода
зависит от того, насколько начальная точка близка к искомой. Хорошее
первое приближение	находится методом повторного	расчета опти¬
мального управления на основании конечных временных интервалов
в будущем. Хотя оптимизация определяет управляющее воздействие
внутри интервала оптимизации, NT> каждый раз используется лишь

304
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. 6
первая компонента. Однако другие компоненты могут быть исполь¬
зованы в качестве первого приближения для следующих рассматри¬
ваемых интервалов. Если бы изменения, вызванные возмущениями как
объекта, так и входных величин, были малы в течение времени Т,
то оптимальное управление можно было бы рассчитать быстро, по¬
скольку первое приближение было бы очень близким к оптимальной
точке. На рис. 6.13 т(2) в интервале 1 является первым приближе¬
нием /тг(1) в интервале 2. Ошибочным является лишь первое при¬
ближение для последних Т секунд. По этой причине, начиная с по¬
следних Т секунд интервала, процесс итерации повторяется, двигаясь
вперед. Таким образом, первая итерация не портит первое хорошее
приближение в других интервалах.
t t + 7	/
+-		i—1—}
t+{N+1)T
Интервал оптимизации /	Интервал	оптимизации	2
Рис. 6.13. Смещение интервалов оптимизации.
Если нет первого приближения, то можно вычислить решение без
учета ограничений. Первое приближение получаем просто, пропуская
это решение через ограничитель.
Поскольку первоначально определяется лишь одна компонента,
то очевидно, что покоординатный градиентный метод наиболее под¬
ходит для оптимальных адаптивных схем. Результаты экспериментов
приведены в работе [28]. Показано улучшение характеристик по срав¬
нению с обычными дискретными системами.
6.3А. Ограничения на управляемые переменные
в виде неравенств.
Упрощенный метод проекций градиента Хо [19]
Другим возможным методом оптимизации в истинном масштабе
времени является упрощенный метод проекций градиента Хо. В этом
методе делается попытка двигаться в направлении наискорейшего
спуска. Поскольку существуют ограничения, составляющие градиент¬
ного вектора паискорейшего спуска также ограничиваются. Как по¬
казано на рис. 6.14, это осуществляется проектированием градиентного
вектора наискорейшего спуска на гиперкуб. Корректирующее движе¬
ние определяется следующим выражением:
m{nvl)== m^n)-rznw^n\	(6.3.19)
где w^n) — вектор градиента, гп определяется так же, как описано

6.31
ОПТИМАЛЬНЫЕ АДАПТИВНЫЕ МЕТОДЫ
выше:
II win) II2
'~п	(G*Gw(n\ win)) *	(6.3.2	J)
Чтобы не нарушить ограничения, необходимо ограничить применяемое
корректирующее движение. Поэтому
in f1^ = М	при	т^~l)	М,
т{п-\-п	при	М ^	^	М,	(6.3.21)
—М	при	т{/1+])	—М.
Надо подчеркнуть, что этот метод, подобно покоординатному гра¬
диентному методу, применим при ограничениях прямоугольного типа.
Хо рассмотрел сходимость этого метода.
Рис. 6.14. Упрощенный метод проекций
градиента Хо.
Этот метод требует для одной итерации выполнения 2A/2-f- ЗА/ — 4
операций сложения, 2Ar2 -\- 5N операций умножения и одного деления.
Хотя вычисления более громоздки, движение на итерацию может быть
больше, чем в покоординатном градиентном методе. Непосредственного
сравнения изложенных двух методов до сих пор не проводилось.
6,8.5.	История развития оптимальных адаптивных методов
Большой вклад в теорию оптимальных адаптивных методов внесли
Калмэн [23], Меррием [36], Браун [8], Медич [34] и Хеи [20]. Оста¬
новимся коротко на предложенных ими методах.

ЧОГ)
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ
[ГЛ. 6
Один из первых результатов в области оптимальных адаптивных
методов принадлежит Калмэну. Дискретное управляющее устройство,
использованное Калмэном, отрабатывало ошибку на ступенчатое воз¬
мущение за минимальное время. Применение методов теории импульс¬
ных систем дало возможность отработать ошибку за конечное число
дискретных шагов. В более поздней работе Калмэна [24] высказаны
мысли, аналогичные основным принципам, изложенным в пункте 6.3.2.
Он приводит вывод, в котором поочередно используются динамическое
программирование и его собственные алгоритмы решения уравнения
Рикагти. С точки зрения вычислительных трудностей алгоритм ре¬
шения уравнения Рикагти и метод, изложенный в пункте 6.3.2, по-
видимому, эквивалентны.
Меррием также рано начал работать в этой области. Его работа
ограничена рассмотрением случая линейного объекта и квадратичного
критерия и аналогична методам пункта 6.3.2. Он гоже использовал
динамическое программирование. Он описал критерий, с помощью кото¬
рого оптимизация выполняется за конечное время в будущем, однако
не дал экспериментального подтверждения своих основных положений.
Методом Брауна задача оптимизации линейных объектов решается
приближенно; при этом конструкция системы получается проще.
Критерий качества Брауна использует сравнение действительной реак¬
ции системы c(t) и желаемой реакции в периодические моменты,
времени, ограничивая сигнал управления ступенчатой функцией. Эти
моменты выборки с тактом Т секунд представляют моменты времени,
в которые изменяется управляющее воздействие. Хорошее совпадение
с (t) с cd(f) можно получить, уменьшая интервал управления Г, однако
это может сопровождаться увеличением управляющего сигнала m(i).
Таким образом, допустимое управляющее воздействие (с точки зре¬
ния ограничений на величину сигнала управления) определяет интер¬
вал управления, который следует использовать, и точность системы,
которая тем меньше, чем уже эти ограничения сигнала управления.
Следует заметить, что в методе Брауна ничего не говорится о точ¬
ности в течение интервала управления.
Управляющее устройство Медича, работающее в истинном мас¬
штабе времени, также приближенно решает задачу оптимизации.
Вместо «плавающего» интервала оптимизации, описанного в данной
главе, ось времени разделена на равные интервалы. Другими словами,
оптимизация выполняется периодически:
(АЧ;1) Т
Jn= J	+
АГГ
Вместо постоянного сигнала, применяемого Брауном, Медич исполь¬
зует для осуществления оптимизации конечную сумму оргонормаль-
ных функций.

6.4]
ОЦЕНКА ПАРАМЕТРОВ И СОСТОЯНИЯ
307
В методе Хеи, так же как и в пункте 6.3.2, рассматривается
линейный объект и квадратичный критерий. Однако Хеи показал, что
если объект идентифицировать с помощью весовой функции, то
удобнее для оптимизации применять метод наискорейшего спуска
в функциональном пространстве.
6.4.	Оценка параметров и состояния
Задачи оценки параметров (идентификация) и оценки состояния
тесно связаны. А именно, состояние можно оценить,, если параметры
известны, и наоборот. Чтобы выйти из этого затруднительного поло¬
жения, используем следующий основной принцип. Если имеются
в наличии методы идентификации, которые могут работать в условиях
неточных знаний переменных состояния, то идентифицируемый объект
может использоваться для оценки этих переменных состояния. Этот
путь возможен потому, что переменные состояния обычно изменяются
быстрее, чем параметры объекта. Последующее рассмотрение будет
проводиться на основе этих предположений.
6.4.1.	Предварительные замечания
Для решения задачи идентификации предложено много методов.
Здесь рассматриваются лишь те методы, которые имеют следую¬
щие особенности. Во-первых, объект считается линейным и стацио¬
нарным. Стационарность предполагается для интервала времени, начи¬
нающегося с определения данных, необходимых для идентификации.
Во-вторых, идентификация должна выполняться без введения генери¬
руемых извне пробных сигналов. Она должна проводиться лишь на
основании нормальных сигналов, присутствующих в системе. И, нако¬
нец, поскольку в системе неизбежно присутствие шума, должно
обеспечиваться сглаживание.
Для линейных объектов идентифицируется либо весовая функция,
либо коэффициенты разностных уравнений (дискретный случай). Огра¬
ничимся определением коэффициентов. Обсуждение методов опреде¬
ления весовой функции дано в работах Левина [29], Кирра и Сур-
бера [26], Балакришнана [3] и Хеи [21]. Ограничиваясь определением
коэффициентов разностных уравнений, можно воспользоваться по
существу двумя различными подходами: 1) аналитическим методом и
2) методом обучающейся модели. Аналитический метод требует зна¬
ния точного вида разностного уравнения. Эти ограничения отчасти
менее строги в методе обучающейся модели в том смысле, что
моделью более низкого порядка можно аппроксимировать объект
более высокого порядка. В пункте 6.4.2 рассматривается аналитиче¬
ский метод, а в пункте 6.4.3 — метод обучающейся модели.

308
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
Методы, описанные в пунктах 6.3.3 и 6.3.4, требуют дополни¬
тельно к определению коэффициентов разностных уравнений опре¬
деления импульсной реакции в нескольких дискретных моментах
времени. Оба описываемых далее метода могут также применяться
для определения импульсной реакции. Метод обучающейся модели
может оказаться громоздким, если число параметров велико.
6.4.2.	Аналитический метод
Аналитический метод использовался Калмэном [1], но основные
идеи этого метода появились еще в 1951 г., когда Гринберг [14]
рассмотрел способы определения частных производных, входящих
в	уравнения	динамики	и характеризующих устойчивость самолета.
Последующие работы по
этому методу были сделаны
Бигелоу и Руге [6].
Кратко можно сказать,
что метод восстанавливает
уравнение объекта с помо¬
щью измерения входной и
выходной величин п их
предыдущих	значений	(достаточного числа, чтобы определить все
параметры	уравнения).	Фильтрация обеспечивается за счет того, что
делаются избыточные измерения.
Этот метод лучше всего можно пояснить на примере. Определим
коэффициенты следующего разностного уравнения:
с (k) = a jc (& — 1) -j- i^m (fz).	(6.4.1)
Задача состоит в определении и а2. Эти параметры могут быть
неизвестными константами или могут изменяться под действием ок¬
ружающих условий. Обычно с {к) наблюдается не непосредственно,
а с шумом, как показано на рис. 6.15. Таким образом,
г (k) = с (к) -j- v (к).	(6.4.2)
Значения z(k) и т(к) запоминаются для истекшего интервала
времени и предполагается, что по всему этому интервалу параметры
ах и а2 остаются неизменными. Поскольку с (к) нельзя непосред¬
ственно замерять, перепишем уравнение 6.4.1 в функции	z{k)
z(k) — v{k) = *i [z (к — 1) — v(k — l)]-j- wn(k)
или
.г (к) = axz (к — 1) -|- а*т (к) -f- vv (к)3	(6.4.3)
где
(к) —- v (к) — cf.iv (k — 1).
Рис. 6.15. Постановка задачи.

6.41	ОЦЕНКА	ПАРАМЕТРОВ	И	СОСТОЯНИЯ	'309
Имея серию измерений, запишем уравнение 6.4.3 в векторной форме *)
zk = *\4-\ -f--f г>/(>
где
z{k — N+ 1)
и Т. Д.
(6.4.4)
z(k — N + 1)
z(k)
или
zk — Aa -(- yk,
где
A = \?k-\ : mk\
Пусть
zk = Aa,
zk принадлежит многообразию, порожденному векторами zu..\ и д//. [54].
Величина zk не обязательно принадлежит линейному многообразию,
поскольку присутствует член yUt. Так как y\k неизвестен, то целесо¬
образной оценкой параметров могли бы быть величины, которые
получаются проектированием zk на многообразие zk_i и тк. В ре¬
зультате проектирования найдем
(gk — Zk, 2ft-i> = 0,
(gk — gb tnk) = 0
или
«1 (*к-ь гкЛ )-гч(ть, zkS/ = (zk, zk.t),
а, <**_„ тк)-}-о.2(тк, mk) — (zk, тк).
Запишем это с помощью матричного уравнения
А*Аа = A*zk.
(6.4.5)
(6.4.6)
Уравнения (6.2.6) и (6.2.7) известны как нормальная форма урав¬
нений, и если zk_\ и mk линейно независимы, тогда решение опре¬
деляется следующим образом:
а = (А*А)~1 A*zn.	(6.4.7)
Если zn_\ и rfijsj линейно зависимы, то существует много реше¬
ний. Единственное решение можно дать, применяя псевдообращение,
*) Символ k обозначает, что N исходных точек получены в прошлом
от рассматриваемого момента /(.

310
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
которое широко исследовано Пенроузом [40, 41]:
а = A^zky	(6,4.8)
где Av — псевдообращение А.
Рекуррентные методы оценки псевдообращения даны Гревил-
лем [16].
6.4.3.	Метод обучающейся модели
Другим методом, который пригоден для оценки коэффициентов
разностного уравнения, является метод обучающейся модели. Понятно,
что если имеются некоторые априорные оценки неизвестных пара¬
метров, то было бы желательно надлежащим образом использовать
подобную информацию. Это, по всей видимости, служит поводом для
возникновения метода обучающейся модели. Данный метод первона¬
чально изучался Марголисом [31], который использовал функции
чувствительности. Функцию чувствительности использовал также Стеф-
фепсон [45], который зани¬
мался определением парамет¬
ров из результатов летных
испытаний. В методе, связан¬
ном с использованием функ¬
ций чувствительности, имеют¬
ся два сложных момента:
1. Необходимо выбирать
коэффициент усиления в ме¬
тоде наискорейшего спуска;
2. Использовать функции
чувствительности, гообще
говоря, имеет смысл только
для малой области около
пробной точки. Для решения
этих вопросов в данном пункте описан усовершенствованный метод
Ньютона. Основная идея метода обучающейся модели отражена на
рис. 6.16.
Следует упомянуть две другие возможные реализации метода обу¬
чающейся модели. Во-первых, метод квазилинеаризации, описанный
Веллманом и др. [4], для которого найдено, что он очень громоздок
в дискретном случае, и, во-вторых, метод ортогональных функций,
использованный Элкиндом и др. [13]. По-видимому, метод априорной
фиксации постоянных времени модели является грубым.
Изложим рассматриваемый здесь метод на примере. Исследование
устойчивости можег быть, по всей видимости, облегчено, если вместо
проведения операций над ошибкой, как показано на рис. 6.16, ре¬
шить следующую задачу.
Рис. 6.16. Метод обучающейся модели, пред¬
ложенный Марголисом.

6.41
ОЦЕНКА ПАРАМЕТРОВ И СОСТОЯНИЯ
311
Задача 6.1. Найти параметры (aД модели, которые минимизи¬
руют выражение
N
^С/)-^ (/)]*>	(6-4-9:
/= I
где на y(j) наложены динамические ограничения
У (J) = а\У (/ — 1) + а-1т (У).	(в-4-1 °)
Временные индексы пояснены на рис. 6.17 *). В данном случае мо¬
дель (уравнение (6.4.10)) может иметь порядок более низкий, чем
порядок реального объекта (задача сглаживающей модели). Начнем
образовывать начальное пробное значение или оценку параметров а(-
и начальные условия для интервала наблюдения у/(0)(П. При этих
—I
t-T
fr-N
Рис. 6.17. Интервал наблюдения.
начальных пробных значениях решается уравнение (6.4.10) и нахо¬
дится поминальное решение у{)\, j = 0, 1,..., N. Далее записыва¬
ются уравнения, определяющие возмущение уравнения (6.4.10), отно¬
сительно номинальной траектории y(jYl)
by(j) = aТ by (j - 1) +У1) (J - 1) Ъа, (j - 1) -j- /гг (j) ba2(J - 1). (6.4.11)
Добавим к уравнению (6.4.11) другие уравнения, в которых пара¬
метры остаются постоянными. Этот прием использовал Веллман и
др. 14]
bai(J) = bal(i — 1),
8а*(/) = 8а.г(у-1).
(6.4.12)
Пусть
Тогда
*у (у)
I (у) = ba{(j)
оа.2(у)
£(/)=ФС/-1)5(у-1),
(6.4.13)
*) Для простоты обозначений индекс k опущен. Таким образом, при
вычислениях / = 0 —^ / = /е — N и j = N —> j = k.

Л12	ТЕОРИЯ	и	МЕТОДЫ	АДАПТИВНЫХ	СИСТЕМ	УПРАВЛЕНИЯ	(ГЛ.	6
где
а(\
У{Х) (/ — 1)
т (/)
Ф(у-1) =
0
1
0
0
0
1 |
Теперь вместо осуществления оптимизации в задаче 6.1 решим
следующую задачу.
Задача 6.2. Найти начальные условия для уравнения (6.4.10),
при которых минимизируется выражение
N
J='£izw — Уи V)—8/° (/)*>	с6-4-15)
У=!
где на &_у(1)(у) наложено ограничение (6.4.13). Таким образом, не¬
линейная	задача	сведена к линейной. Неоднократно	повторяя реше¬
ние	этой	последней задачи, мы надеемся найти приближенное реше¬
ние первой задачи.
Задача 6.2 решается построением сглаживающей кривой методом
наименьших квадратов. Заметим, что
У1} (/) + 8У1} U) = z (j) -г п(у),	(6.4.16)
где п (у) — расхождение, вызываемое наличием шума и ошибки в на¬
стройке параметров. Пусть
ьу{1) U) = z (у) —_у(1) (у).	(6.4.17)
Правая	часть	в	выражении (6.4.17) известна	и	надо	найти	оу(1)(у)
при	условии	(6.4.13),	которое лучше всего аппроксимирует	2 (у) —
— v(/)(1). Выражение (6.4.17) можно переписать в следующем виде:
й*Б (/)=*(/)—У0 (Л
где h* = || 1 0 01|.
Все уравнения, записанные с помощью (6.4.18), могут быть запи¬
саны через ?(0), используя формулу (6.4.14),
л*Б(0)=г(0)—/»(0)
/1*ф(1, 0)£(0) = z(l)— У4(1),
h*0{N, 0)g(0) = z(N)—y{i){N)
или в матричном виде
Л&(0) = 1,	(6.4.19)

ОЦЕНКА ПАРАМЕТРОВ И СОСТОЯНИЯ
313
где
А =
1 =
h
ЛФ(1, 0)
hO(N, 0)
z(N) — у[1) (0)
г (N) —У1} (N)
(TV-1— 1) X 3-матрица,
— (N-f-l)X 1-вектор.
Для решения уравнения (6.4.19) используется метод псевдооб-
ратения
?(0)(,) = -П(".
По уравнению (6.4.19) можно сделать поправку на исходные
пробные значения параметров и начальные условия
a?' =a'iv	(0),	|
(6.4.20)
Теперь всю последовательность действий можно повторить.
Только что описанная вычислительная процедура вполне может
быть расходящейся. Однако можно использовать методы, которые
применяются при вычислениях на цифровой машине и обеспечивают
монотонную сходимость. Опишем алгоритм, который гарантирует
выполнение этого важного условия.
Исходя из исходных пробных значений и решения, можно вычис¬
лить показатель ошибки
А = 2 (* (У) - У1’ (У))2 — 1 г -У1' |р.
Задача заключается в том, чтобы найти такое оу (/), при котором
значение меньше, чем
^ = Л^и)-у{х)(Л-Ь(Л?-
Разность 7i—Л Должна быть больше нуля:
Jj —J* = \z — V(1) f — [j z —y{l) IP 2 (by, z —y{l) ) — [|oy IP ^ 0
2 < By, г — yW > — j] oy |p 0.	(6.4.21)
«ли
Выражение (6.4.21) является условием сходимости.
Если
<8у,г-У1))^0,

ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. 6
го для достаточно малого оу это условие может удовлетворяться,
поскольку первый член является линейной функцией Ъу, в то время
как второй член является квадратичной функцией. Заметим, что пер¬
вый член в выражении (6.4.21) положителен, гак как это скалярное
произведение ошибки и проекции ошибки на линейное многооб¬
разие.
Условие
< ЧУ, z — y{1\) = 0	(6.4.22)
требует, чтобы у(1) было ближе к г, чем любая соседняя точка, по¬
лучаемая посредством линейного возмущения. Другими словами, гра¬
диент равен нулю, что соответствует локальному минимуму.
Иллюстрация этого метода дана на рис. 6.18. Первой линейной
поправкой является Г.
После решения уравнения (6.4.10) находится точка /, для которой
значение Л может получиться больше чем Jit Если ЛJb тогда
уменьшим поправку Ьу{к) в два
раза, попадая в точку 2. Если J
в точке 2 меньше Jh тогда де¬
лаем поправку,равную Sy(/?)(1) 2.
В противном случае уменьшаем
by(k)^j2	в два раза и пов¬
торяем весь процесс. Исполь¬
зуя такой метод уменьшения
поправки, монотонно прибли¬
жаемся к точке, где условие
(6.4.22) удовлетворяется.
При управлении в нату¬
ральном масштабе времени су¬
ществует ограничение на число
итераций, которое может быть
сделано в течение заданного
времени.	Однако здесь это
ограничение не является та¬
ким сильным, как в задаче синтеза управления, поскольку для мед¬
ленно меняющихся объектов оценка может производиться за более
длинный промежуток времени. Если ограничить число, определяющее,
сколько раз уменьшается поправка в методе, описанном в последнем
параграфе, то может оказаться, что поправка, в результате которой
получается наименьшее J, никогда не будет найдена. В этом случае
поправка	не	будет	сделана,	и	мы	перейдем в	следующий интервал.
Если	поправка	не	будет	делаться	ни	в одном из	интервалов, то метод
теряет смысл. Однако, по-видимому, метод будет применим для класса
задач, где оценки делаются внутри некоторой области около дейст¬
вие. 6.18. Рисунок в двух измерениях,
поясняющий способ внесения поправки.

6.4]
ОЦЕНКА ПАРАМЕТРОВ II СОСТОЯНИЯ
315
вительных значений параметров. Подобный вопрос не кажется сложнее
вопросов устойчивости, возникающих в методе Марголиса.
Экспериментальные результаты применения описанного выше ме¬
тода приведены в работе [12].
6.4.4.	Оценка состояния
Для использования адаптивного управляющего устройства необ¬
ходимо знать переменные состояния в любой момент выборки. В дан¬
ном пункте обсуждается метод оценки этих переменных. Материал,
изложенный в пункте, в значительной степени заимствован из работы
Калмэна [24]. В этом направлении провели исследования также Жозеф
и Toy [22].
Обратимся к объекту, структура которого показана на рис. 6.19.
По известным z(k) и m(k) необходимо оценить состояние x(k) в на¬
стоящий момент. Прошлые значения z(k) и m(k) известны, начиная
*>(к)
«Белый
шум»
т(к)
Упра¬
вление
т
г-1
f(k)
'Состояние
Возмущение
/ нагрузка
v(k)
Шум в изме¬
рениях
**тО
	 /А
Z(k)
ВыхоВ
Ху (к)
Рис. 6.19. Структура объекта.
с некоторого исходного момента. Характеристики объекта G\ и 02
известны в результате предварительной идентификации. Как и при
рассмотрении любой адаптивной задачи, считается, что передаточные
характеристики системы изменяются во времени. По. мере того как
оцениваются новые значения параметров, соответствующие их значе¬
ния, используемые при оценке состояния, будут изменяться. Ковариа¬
ционные матрицы v(k) и w(k) также известны. В качестве источника
шума можно принять «белый шум». Отметим, что спектр возму¬
щения нагрузки может отличаться от «белого шума» из-за нали¬
чия G2.
Заметим, что
x{k) = Xi (k) Xt (/г),

где Х\ (k) известно. Пусть
v(k) = z(k)— h*x{k\
х2 (k) = x(k) — л:, (&).
Теперь требуется определить x2(k) при условии, что заданы услов¬
ные математические ожидания v(/e), /г = 0, 1, ..., к. По x2(k) дела¬
ется оценка состояния
X (k) — Х2 (/г) 4“ Xi (k).
Как видно, здесь можно применить алгоритм калмэновской фильт¬
рации [24] для объектов, изменяющихся во времени.
ЛИТЕРАТУРА
1. Aseltine J. А., М а п с i n i A. R. and S art иге С. W., A Survey of:
Adaptive Control Systems, IRE Transactions on Automatic Control, PGAC-6:
102—108, December, 1958.
2. Ashby W. R., Design for a Brain, John Wiley and Sons, Inc., New York,
1952 (Second Edition, 1960). [Русский перевод: У. Росс Эшби, Кон¬
струкция мозга, М., ИЛ, 1962.]
3. Balakrishnan А. V., Determination of Nonlinear System from input —
Output Data, Presented at the Conference on Identification and Representa¬
tion Problems, Princeton University, March, 1963.
4. Bellman R., К a g i w a d a H. and К a 1 a b a R., A Computational Pro¬
cedure for Optimal System Design and Utilization, Proc. Nat. Acad, of Sci.,
48 : 1524—1528, September, 1962.
5. Benner A. H. and Drenick R., An Adaptive Servo System, IRE 1955-
Convention Record, Pt. 4, pp. 8—14.
6. В i g e 1 о w S. C. and Ruge H., An Adaptive System Using Periodic
Estimation of the Pulse Transfer Function, IRE National Convention Record,
Part 4, pp. 25—38, 1961.
7. В о s k о v i с h B., Cole G. H., M e 11 с n D. L, Advanced Flight Vehicle
Self-Adaptive Flight Control System, Part I Study, Part II Design, WADD
TR-50-651 (Confidential).
8. Braun, Jr., L., On Adaptive Control Systems, Doctoral Dissertation, Poly¬
technic Institute of Brooklyn, 1959.
9. С h a n g S. S. L., Synthesis of Optimal Control Systems, McGraw-Hill Book
Co., New York, 1961. [Русский перевод: Чанг, Шелдон С., Синтез
оптимальных систем автоматического управления, «Машиностроение»,
М., 1964.]
10. Clark R. N. and Wheeler Р. С., A Self-Adjusting Control System with
Large Initial Error, IRE Transactions on Automatic Controls, PGAC, Janu¬
ary, 1962.
11. Cooper G. R. and Gibson J. E., A Survey of Philosophy and State of
the Art of Adaptive Systems, Technical Report No. 1, Contract AF33(616)—
6890, Project 8225, Task 82181, PRE 2358, School of Electrical Engineering*
Purdue University, Lafayette, Indiana, July 1, 1960.

ЛИТЕРАТУРА
317
12. Поп also п П. Г)., The Theory and Stability Analysis of a Model-Refe¬
renced Parameter Tracking Technique for Adaptive Automatic Control Sy¬
stems, Doctoral Dissertation, University of California, Los Angeles, Mav,
1961.
13. Elking J. L., Green D. M. and Starr E. A., Application of Multiple
Regression Analysis to Identification of Time-Varying Linear Dynamic
Systems, Correspondence, IRE Trans, on Automatic Controls, АС-8/ 163—
166, April, 1963.
14. Greenberg H., A Survey of Methods for Dctermining-Stability Para¬
meters of an Airplane from Dynamic Flight Measurements, NACA TN-2340,
April, 1951.
15. Gregory P. C., D a v i s H. М., Future Control Systems for Vehicles
with Large Thermoelastic Effects, ASD TR 61-645, October, 1961.
16. G r e v i 11 e T. N. E., Some Applications of the Pseudo-Inverse of a Mat¬
rix, Si AM Review, 2:15—2, 1960.
17. Hilbreth C., Quadratic Programming Procedure, Naval Research Lo¬
gistics Quarterly, 4:79—85, 1957.
18. Iliza J. C. and Li С. C., On Analytical Synthesis of a Class of Model-
Refcrence Time-Varying Control Systems, IEEE Paper 63—123, presented
at the IEEE 1963 Winter General Meeting, New York, Jan. 27—Feb.
1, 1963.
19. Ho Y. C. and Brcntain P. B., On Computing Optimal Control with
Inequality Constraints, Paper Presented at the Symposium on Multivariable
Control Systems, Boston, Mass., November, 1962.
20. Hsieh H. C., On the Synthesis of Adaptive Controls by the Hilbert Space
Approach, Report No. 62—69, Dept, of Engineering, University of Callifor-
nia, Los Angeles, June, 1962.
21. Hsieh H. C., Synthesis of Adaptive Control Systems bv the Functions Space
Methods Doctoral Dissertation, Dept, of Engineering, University of Califor¬
nia, Los Angeles, Calif., 1963.
22. Joseph H. D. and Tou J. D., On Linear Control Theory, AIEE Trans.,
Part II, Applications and Industry, 80:193—196, September, 1961.
23. Kalman R. E., Design of a Self-Optimizing Control System, ASME
Transactions, 80 : 468—478, February, 1958.
24. К a 1 m a n R. F., E n g 1 a r T. S. and Bucy R. S., Fundamental Study of
Adaptive Control Systems, Tech. Report No. ASD-TR-61-27, Vol. 1, Aero¬
nautical Systems Division, Air Force System Command, Wright-Patterson
Air Force Base, Ohio, April, 1962.
25. Katz S., A Discrete Version of Pontryagin’s Maximum Principle, Journ.
of Electronics and Control, 1962.
26. Kerr R. P. and S u r b e r W. H., Precision of Impulse Response Identifica¬
tion Based on Short Normal Operation Records, IRE Trans. PGAC,
AC-6: 173—182, May, 1961.
27. К i p i n i a к W., Dynamic Optimization and Control, MIT Press and John
Wiley and Sons, Inc., New York, 1961.
28. Kishi F. H., On Line Computer Control Techniques and Their Applica¬
tion to Re-entry Aerospace Vehicle Control, Advances, in Control Systems
Theory and Applications, Volume I, Academic Press, 1964.
29. Levin M. J., Optimum Estimation fo Impulse Response in the Presence of
Noise, IRE Trans.—PGCT, CT-7 : 50—56, March, 1960.
30. Margolis M. and Leondcs С. Т., A Parameter Tracking Servo for
Adaptive Control Svstcms, IRE Transactions on Automatic Control, PGAC-4,
No. 2:100—111, November, 1959.
31. Margolis М., On the Theory of Process Adaptive Control Systems, the
Learning-Model Approach, Doctoral Dissertation, Department of Engineering
University of California, Los Angeles, 1959.

318
ТЕОРИЯ И МЕТОДЫ АДАПТИВНЫХ СИСТЕМ УПРАВЛЕНИЯ [ГЛ. G
32. McGrath R. J., Rideout V. С., A Simulator Study of a Two-Para¬
meter Adaptive System, IRE Transactions on Automatic Control, Vol. AC-6,
No. 1, February, 1961.
33. McGrath R. J., Rajaraman V. and Rideout V. C., A Parameter
Perturbation Adaptive Control System, IRE Transactions on Automatic Cont¬
rol, Vol. AC-6, No. 2, May, 1961.
34. M e d i t с h J. S. and Gibson J. E., On the Real-Time Control of Time-
Varying Linear Systems, IRE Trans, on Automatic Controls, AC-7, No.
4:3—10, July, 1962.
35. M e i s s i n g e r H. R., The Use of Parameter Influence Coefficients in Com¬
puter Analysis of Dynamic Systems, Unpublished Notes, Hughes Aircraft
Company, System Development Laboratories, December, 1957.
36. M с r r i a m C. W., Use of a Mathematical Error Criterion in the Design
of Adaptive Control System, AIEE Transactions, Part II, 79: 506—512, Januarv,
1960.
37. M i s h к i n E. and Braun, Jr., L., Adaptive Control Systems, McGraw-
Hill Book Co., New York, 1961. [Русский перевод: Мишкин Э. и
Б р а у и Л., Приспосабливающиеся автоматические системы, М., ИЛ,
1963.f
38. Osbur n P. V., Investigation of a Method of Adaptive Control, D. s.
Thesis, Massachusetts Institute of Technology, 1961, MIT Instrumentation
Laboratory Report No. T 266.
39. О s b u r n P. V., Whitaker H. P., Kezer A., New Developments in
the Design of Model Reference Adaptive Systems. IAS Report, No. 61—39,
January, 1961.
40. Penrose R., A Generalized Inverse of Matrices, Proc. Cambridge Phil.
Soc., 51 : 406-413, 1955.
41. Penrose R., On Best Approximate Solutions of Linear Matrix Equations,
Proc. Cambridge Phil. Soc., 52:17—19, 1956.
42. Rang E. R. and Johnson C. W., The Learning Model Approach to Self-
Evaluation and the Method of Lyapunov, AIEE Paper No. DP 61 — 603, pre¬
sented at the AIEE Great Lakes District Meeting, Minneapolis, Minnesota,
April 19—21, 1961.
43. Rang E. R. and Stone C. R., Adaptive State Vector Control Adaptive
Controllers Derived by Stability Considerations, Minneapolis-Honey well Re¬
gulator Company, Military Products Group Report 1529-TR 9, Marjch 15,
1962.
44. P у тман P. С., Самонастраивающиеся системы с настройкой по дина¬
мическим характеристикам, Автоматика и телемеханика, т. XXIII, № 5,
май, 1962.
45. Staffanson, Forrest L., Determining Parameter Corrections Accor¬
ding to System Performance-А Method and its Application to Real-Time
Missile Testing, Army Missile Test Center, White Sands Missile Range, Lab.
Res. Rpt. 20, July, 1960.
46. Stear E. B. and Gregory R. C., Capabilities and Limitations of Some
Adaptive Techniques, Report, Flight Control Laboratory, Aeronautical Systems
Division, Wright Air Development Division.
47. S t г о m с r, Peter R., Adaptive or Self-Optimizing Control Systcrns-A
Bibliography, IRE Transactions on Automatic Control, PGAC-4, No. 1:65 —
68, May, 1959.
48. Tsien H. S., Engineering Cybernetics, McGraw-Hill Book Co.,. New York,
1954. [Русский перевод: Цянь Сюэ-сэнь, Техническая кибернетика,
М., ИЛ, 1956.1
49. W h i t a k е г Н. P., Y а г m о п J. and Kezer A., Design of Model Reference
Adaptive Control Systems for Aircraft, MIT Instrumentation Laboratory
Report R-164, September, 1958.

ЛИТЕРАТУРА
319
50. W h i t а к с г Н. Р., Ап Adaptive System Control for of the Dynamic Perfor¬
mance of Aircraft and Spacecraft, iAS Paper No. 59—100, June, 1959.
51. Whitaker H. P., Model Reference Adaptive Control Systems for Large
Flexible Boosters, MIT Instrumentation Laboratory Report E-1036, May, 1960,
presented to SAL-18 Committee on Aerospace Vehicle Flight Control Sy¬
stems on June 16, 1961.
52. Whitaker H. P. and Kezcr A., Use of Model Reference Adaptive
Systems to Improve Reliability, Paper 1936—61, presented to ARS Guidance,
Control, and Navigation Conference, August 7—9, 1961.
53. Zadeh L. A., On the Definition of Adaptivity, Proceedings of the IEEE,
51:469—470, March, 1963. [Русский перевод: Заде JL А., Об опреде¬
лении адаптивности, ТИИЭР, № 3, М., ИЛ, март, 1963, сгр. 499—500.]
54. James G. and James R., Editors, Mathematics Dictionary, van Nost¬
rand, Princeton, New Jersey, 1959.
55 *). Пропой А. И., О принципе максимума для дискретных систем
управления, Автоматика и телемеханика, т. XXVI, № 7, 1965.
*) Добавлено редактором перевода.

ГЛАВА 7
ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА
Медин (7. 5. Meditch)
В настоящей главе излагаются основы принципа максимума
Л. С. Понтрягина [1—4]. Главное внимание уделяется знакомству с
самим методом, его выводом и практической ценностью. Там, где эго
возможно, дается физическая и геометрическая интерпретация резуль¬
татов. Наше изложение будет касаться следующих вопросов. Во-пер¬
вых, мы сформулируем задачу оптимального управления в достаточно
общих терминах и после этого перейдем к формулировке и обсуж1
дению первой теоремы принципа максимума. Во-вторых, дадим вывод
теоремы и некоторые ее обобщения, позволяющие поставить более
общие оптимальные задачи.
7.1.	Постановка задачи
Рассмотрим динамическую систему, состояние которой в любой
момент времени характеризуется п переменными хъ ..., хп. Например,
это могут быть координаты положения и скорости космического
аппарата. Векторное пространство X векторных переменных х =
= (xh ..., хп) называется фазовым пространством системы. Поведение
системы характеризуется изменением во времени векторной перемен¬
ной х, обычно называемой вектором состояния, а х{ (/=1, ..., п)
называются координатами состояния.
Предположим, что система управляема, т. е. имеется возможность
изменять входные величины системы (управления), изменение которых
влияет на состояние системы. Предположим, что имеется г таких
управлений и они характеризуются точкой и, принадлежащей обла¬
сти U r-мерпого евклидова пространства, причем U не зависит от х
и t. Назовем и управляющим, вектором и определим его как и =
= (hi> • • • I nr) £Любую кусочно-непрерывную функцию u=u(t)9

7.1]
ПОСТАНОВКА ЗАДАЧИ
321
определенную на некотором интервале времени	со	значе¬
ниями из U, будем называть управлением *).
Допустимые управления. Управление u{t) будет допустимым,
если каждая его компонента ut (/), /= 1, г, является ограничен¬
ной кусочно-непрерывной функцией такой, что u(t)(^U для всех t,
t0^t^th т. е. на том интервале времени, на котором рассматрива¬
ется работа системы. Начальный момент времени предполагается
фиксированным, а конечный tx может
быть как фиксированным, так и нефикси¬
рованным.
Чтобы проиллюстрировать понятие
допустимого управления, рассмотрим си¬
стему с двумя управляющими входами
щ(1) и щ2(0> на которые наложено огра¬
ничение:
мо]2-[мог2^л1-;
где /Ио — некоторая положительная кон¬
станта. Множество U состоит из внут¬
ренности и границы круга радиуса Л40,
как это показано на рис. 7.1. Таким об¬
разом, в данном примере допустимый
управляющий вектор может иметь любое направление, но его дли¬
на ограничена М0.
Постановка задачи. Предположим, что поведение динамической
системы характеризуется системой дифференциальных уравнений
f i (*^"b • • • > Хп, Hi, * • * > пг) — f i (at, ll) (/ — 1, ..., ti). (7.1)
Пока мы будем рассматривать только те динамические системы, ко¬
торые описываются уравнениями (7.1) с правой частью, не зависящей
явно от времени t. Такие системы называются автономными. Прин¬
цип максимума для неавтономных систем, т. е. тогда, когда правая
часть уравнения (7.1) явно зависит от времени, рассматривается
в § 7.4.
В векторной форме уравнения (7.1) имеют вид
(7.2)
где f(x,u) — вектор-функции от х и и. Функции /*• предполагаются
непрерывными по всем переменным хь...,хп и г/,, ...,иг для
*) Понтрягиным и др. [1—21 были получены более общие результаты
в предположениях, что U есть произвольное хаусдорфово топологическое
пространство, а и (t) — измеримая ограниченная вектор-функция. Однако
для практических применении наиболее интересен случай кусочно-непрерыв¬
ного управления, который и будет рассматриваться здесь.
Рис. 7.1. Множество допу¬
стимых управлений в рас¬
сматриваемом примере.
11 п/р Леондеса

322
ВВЕДЕНИЕ: В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
каждого jc (3 Л и и U. Предположим также, что fi непрерывно
дифференцируемы по хь ..., хп, т. е.
fi (*. и) И dfi^ U> (i,/=1,..., п)
определены и непрерывны для всех х X и и U. Систе1ма, описы¬
ваемая уравнениями (7.1), символически изображена на рис. 7.2.
Если допустимое управление u(t) выбрано и заданы начальные
условия х(/0) = х°у то уравнение (7.2) имеет вид
g = /[*,!»(*)]. хЦа) = л*.	(7.3)
Тогда решение уравнения (7.3) однозначно определяет вектор состоя¬
ния системы (т. е. поведение системы для t^t0, если движение на¬
чинается из начального состояния x(t0) = x°). Хорошо известно, что
это решение является абсолютно
непрерывной вектор-функцией,
удовлетворяющей уравнению (7.3)
всюду в области определения, за
исключением точек разрыва
И (0 [5].
Будем говорить, что допусти¬
мое управление u(f) переводит
точку х° в некоторую точку хх,
если решение x(t) уравнения	(7.3)	проходит через точку xi в неко¬
торый момент времени /ь т.	е.	x(t1) = x1. Предположим теперь, что
качество работы системы может быть количественно оценено некото¬
рым функционалом
J=\fo[x(t), u(t)]dt,	(7.4)
'О
который ниже будет называться функцией стоимости. Величина J
для данного допустимого управления называется стоимостью управ¬
ления. Предположим, что функция f0\x(t),	u(t)\=f0(xli...yxn;
uh ..., иг) определена и непрерывна для всех х X и и U и диффе¬
ренцируема по xiy I = 1, ..., п.
Сформулируем теперь основную задачу, которая будет рассмат¬
риваться ниже: для дайной динамической системы (7.2) с начальными
у слов и я м и х (t о) = х° и для заданной точки х} X найти допустимое
управление, если оно существует, переводящее систему из точки х°
в точку х1 таким образом, что функция стоимости (7.4) принимает
наименьшее возможное значение.
Предположим пока, что /, заранее не фиксировано. Допустимое
управление, дающее решение поставленной задачи, называется опти-
Динамическая
система
.Х1
-Хп
Рис. 7.2. Динамическая система.

7.11
ПОСТАНОВКА ЗАДАЧИ
323
мальным управлением. Соответствующая траектория, соединяющая
точки х° и Xх, называется оптимальной траекторией.
Примеры, (а) Рассмотрим оптимальную задачу, в которой
/0(л', д)=1. Следовательно, уравнение (7.4) будет
J —1\	t§.
В этом случае мннимазация 70 соответствует минимизации времени
перехода из точки х° в х1. Это хорошо известная задача оптималь¬
ности по быстродействию.
(б)	Рассмотрим оптимальную задачу при /0(лг, г/) = |] г/ (^) ||, где ||-||
обозначает евклидову норму. В этом случае (7.4) примет вид
^=5и «(он л.
'о
Минимизация J дает управление, которое переводит систему из
точки х° в точку Xх с минимальным интегральным расходом энергии
на управление.
Эквивалентная	постановка	задачи. Для	облегчения	вывода
принципа	максимума	изменим формулировку поставленной	выше за¬
дачи. Присоединим к фазовым координатам хь хп еще одну
координату х0у определяемую уравнением
^ = /„(л-\ ..., и\ иг).
Функция /о — это та самая функция, которая ранее участвовала в
определении функции стоимости. Если л;0(£0) = 0, то из уравнения (7.4)
видно, что x^{tx) — J. Таким образом, будем теперь рассматривать
систему обыкновенных дифференциальных уравнений
— II)	x0(t0) = Q,
h(x, и)	х, («=*;,	(75)
= tn (X, ll) х„ ((„) = хпп.
Заметим, что правая часть этих уравнений не зависит от хгп.
Введем вектор
л: = (х{), хь ..., хп) = (х0, х)
(/z —|— 1)-мерного пространства X и перепишем уравнения (7.5) в век¬
торной форме
/7 у
“±=Пх,и)>	х(/0)^(О,	х").	(7.6)
11*

324
ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
(Жирный шрифт используется всюду для обозначения (п — 1)-мерных
векторов.)
Далее из уравнений (7.5) следует, что правая часть уравнений (7.6)
не зависит от координаты х0 вектора х.
Пусть u(t) — допустимое управление, которое переводит х° в х\
и x = x(t) — решение уравнения (7.3) при jc(/0) = x°. Обозначим
точку (0, „г0) через х°. То есть х° — это точка, координаты которой
(О, х\, Хп\ причем (л'ь ..., x'h) — координаты вектора л;0 в Л’.
Ясно, что х°—это состояние системы (7.6) в момент t = tQ. Из
этого следует, что решение уравнения (7.6) имеет вид
п
*0 = 5 /о Iх («)> 11 (s)l ds, х — х (t).
to
13 частности, при t = tl получаем
h
ха = \ /о IX (0, и (01 dt = j, х = х\
‘о
Таким образом, решение уравнения (7.6) проходит через точку
xl =(J, х1) в момент i — tv Если обозначить через / прямую линию
в X, проходящую через
точку jc = (0, х1) и пат
раллельную оси x0, то
можно сказать, что реше¬
ние x(t) в момент t = t{
проходит через точку,
лежащую на I с коорди¬
натой Xq = J. И, наобо¬
рот, если u(t) такое до¬
пустимое управление, что
решение системы уравне¬
ний (7.6) проходит через
точку х1 £ I в некоторый
момент времени
с координатой x0 = J, то
Рис. 7.3. Геометрическая интерпретация задачи	тогда u(t)	переводи i х° в
оптимизации для динамической системы вто-	-V . Кроме	того, функцио-
рого порядка.	нал (7.4)	принимает зна¬
чение J. Дадим геометри¬
ческую интерпретацию этих результатов в трехмерном пространстве
для динамической системы второго порядка, принимая х0 за одну ко¬
ординату, ax — (xi, х.2)—за две другие координаты, как показано на
рис. 7.3. Пространство X в этом примере является трехмерным евкли¬
довым пространством, координаты в котором есть (х0, х). Первая ко¬
ордината — это стоимость, вторая — состояние динамической системы.

7.2]
ПРИНЦИП МАКСИМУМА
325
На рисунке изображена также одна из возможных траекторий, соеди¬
няющая (0, хп) с точкой на прямой /. Так как координата х0 яв¬
ляется значением функции стоимости, то требуется найти такое до¬
пустимое управление, чтобы соответствующая ему траектория пере¬
секала линию I в точке с наименьшим возможным значением х0.
Поставим оптимальную задачу в этих новых терминах. Даны
точка jt° = (0, х{]) и линия / в (/2 —!— 1)-мерном фазовом пространстве X.
Линия / проходит через точку (0, х1) и параллельна оси х0. Из мно¬
жества всех допустимых управлений u = u(t), для которых решение
уравнений (7.6) пересекает прямую /, нужно выбрать то, которое
дает точку пересечения с наименьшим значением координаты х0.
7.2.	Принцип максимума
Теперь мы сформулируем и обсудим принцип максимума, про¬
иллюстрировав его применение на частном примере. Начнем с того,
что напишем уравнение (7.6) в виде
/ = 0.1...., л,	(7.7)
и присоединим к этой системе совокупность уравнений
V <*/«[*(*). и (01.	по.
4i — ~ 2d S7i Va ((7'8)
a =0
Целесообразно записать (7.7) и (7.8) в более удобной форме. Для
этого введем функцию Н\
п
Н (1]3, х, и) = ^'f(xy и) = 2	(х,	и),	(7.9)
a = 0
где ф— (я-j- 1)-мерный вектор-столбец ф = (ф0,	<ЬЛ),	а	штрих
означает транспонирование. Мы видим, что Н есть непрерывная функ¬
ция 2я —- 1 — г переменных хь ..., х„; б0, ..., и иь ..., иг. Она
называется гамильтонианом.
Из (7.9) видно, что уравнения (7.7) и (7.8) можно записать в
форме
dxi дН d<l>i дН . А	m
-ж=~шг /=0••••>«•	<7Л°)
Уравнения (7.10) называются системой Гамильтона.
При фиксированных ф и jc Н есть функция только и. Обозна¬
чим точную верхнюю грань Н через М (ф, х)
М (ф, х) = sup Н (ф, Ху и).	(7.11)
и е и

326
ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
Если точная верхняя грань Н достигается на U, то М (я|5, х) яв¬
ляется максимумом Н при фиксированных ф и х. Теперь сформули¬
руем принцип максимума для автономных систем.
Теорема 1. Пусть u(t)— допустимое управление и x(t)—со¬
ответствующая траектория уравнения (7.6), которая в некоторый
момент времени	проходит через какую-либо точку линии /.
Для того чтобы u{t) и x(t) были оптимальны для	необ¬
ходимо, чтобы существовала нетривиальная непрерывная вектор-
функция ф (t) = [ф0 (t), Ф1 (/),..., фя (t)]y удовлетворяющая уравнению (7.8),
такая, что для всех точек непрерывности u(t) гамильтониан /7(ф, х, и)
достигал бы максимума по переменной и £ U на u = u(f), т. е.
Я[ф(0, X(t\ «(01 = Af [ф (0 JC (0].	(7.12)
При этом
фо (0 = const 0 и М [(ф (t), х (t)] = 0.	(7.13)
Принципиальный результат теоремы 1 заключается в равенстве (7.12).
Мы видим, однако, что теорема 1 дает лишь необходимое условие
оптимальности, т. е. оптимальное управление должно удовлетворять
условиям теоремы. С другой стороны, выполнение этих условий для
данного допустимого управления не означает, что оно оптимально*).
Для некоторых задач (например задача максимального быстро-'
действия и задача управления с минимумом затрат для линейных ди¬
намических систем) показано [6-—10], что если существует допусти¬
мое управление, которое переводит х° в х1, то существует и опти¬
мальное управление (не обязательно единственное). Полезность
принципа максимума, а также возникающие при этом трудности ста¬
нут несколько более понятными, если рассмотреть более частный
класс систем. Рассмотрим динамическую систему, описываемую систе¬
мой уравнений
d£ = f{x)+Bu{t),	(7.14)
где х — я-мерный вектор-столбец, и—r-мерный вектор-столбец,
f—я-мерная вектор-функция от х, В — постоянная матрица яХ г.
Предположим, что /—непрерывная функция, имеющая непрерывные
производные по х. На управление наложено ограничение |я;|^1,
/= 1, ..., г. Требуется, чтобы система перешла из данного началь¬
ного состояния x(t0) = x° в определенное конечное состояние х(^) =
= х1 за минимальное время. Заметим, что tx является одним из неиз¬
вестных параметров.
*) О достаточных условиях оптимальности см. Болтянский В. Г.,
Достаточные условия оптимальности и обоснование метода динамического
программирования, Изв. АН СССР, сер. матем., № 3, 1964. (Прим. ред.)

7.21
ПРИНЦИП МАКСИМУМА
327
Как было указано ранее, в задаче, оптимальной по быстродейст¬
вию, /о(х, и)= 1. Следовательно, гамильтониан в этой задаче равен
tf = t0 + f/t*) + <|/£H,	(7.15)
где	обозначения	те	же, что и раньше. Гамильтониан	(7.15)	будет
максимален при
и(t) = sgn [<]/ (t) В}\	th	(7.16)
где	штрих	означает	операцию транспонирования, а функция sgn опре¬
деляется следующим образом:
( +1, У>0.
sgnj;=\-i,y<0
и неопределена для у = 0.
Предполагая, что никакая компонента ф'(^)5 не обращается в нуль
ни при каком подинтервале отрезка	и вспоминая, что
принцип максимума является необходимым условием оптимальности,
можно утверждать, что если в этой задаче оптимальное управление
существует, то оно должно иметь вид (7.16).
Напишем уравнение Гамильтона для данной задачи
£ = f(x) + Bu(f)	(7.17)
И
чг=- 2 Vь(° (/== 1 ■ ■ ■ ’п) (7Л8)
а = 1	' 1
с граничными условиями x(t0) — x° и х(t1) = х1. Так как х° явно
не входит в f(x), индексы / и а пробегают значения от 1 до п,
вместо значений от 0 до п.
Из уравнений (7.12), (7.13), (7.15), (7.16) получаем
М [t (t), х (OJ = фо + <к (*) /[* (01 + Ф' (0 В sgn [<]/ (t) ву.
Так как б0 = const ^ 0, то из этого следует, что
ф' (0 {/ [х (*)] + В sgn [f (0 BY} = - фо = const ^ 0.	(7.19)
Таким образом, уравнения (7.17), (7.18) и (7.19) дают 2лг —]— 1 соот¬
ношение для 2/2-}- 1 переменной х, ф и tv На этом примере мы
наблюдаем два важных аспекта принципа максимума, которые обычно
встречаются в приложениях. Во-первых, видно, что форма оптималь¬
ного управления легко следует из гамильтониана. Это свойство
является очевидным достоинством принципа максимума, так как оно
позволяет найти структуру управляющего устройства. К сожалению,
имеются и недостатки. Заметим, что моменты переключения оптималь-

,328
ВВЕДЕНИЕ в ПРИНЦИП МАКСИМУМА Ji. С. ПОНТРЯГИНА |ГЛ. 7
иого управления определяются функцией Ф(£). Если бы начальные
условия для ty(t) 6i>iли известны, уравнения (7.18) интегрировались
непосредственно, и можно было бы найти моменты переключения
Но в действительности известны только граничные условия для x(i).
В'
№
Решение
■ уравнения
(7.18)
X(t)
Вычисление
начальных
fgT
условии
на Ф
>
К
X1
X
Рис. 7.4. Блок-схема оптимальной системы.
Следовательно, мы имеем дело с нелинейной двухточечной краевой
задачей.
Если предположить, что начальные условия для уравнения (7.18)
известны, то можно получить структурную схему оптимальной системы
по формулам (7.16), (7.17) и (7.18). Эта схема дана на рис. 7.4.
7.3.	Вывод принципа максимума
В этом разделе будет проведен вывод принципиальных резуль¬
татов, содержащихся в формулировке теоремы 1. (Более подробное
математическое изложение этих вопросов имеется в [1, 2].) Наш вы¬
вод принципа максимума будет основан на рассмотрении возмущений
в оптимальном управлении. Рассматривая некоторые свойства этих
возмущений, можно сформулировать необходимые условия, которым
должно удовлетворять оптимальное управление.
Прежде всего введем некоторые новые определения и понятия.
Вариации траекторий и управлений. Пусть x{t)—оптимальная
траектория (начинающаяся в jc°), которая соответствует оптимальному
для данной задачи управлению u(t). Предположим, что варьируется
оптимальное управление. Вследствие этого варьируется и оптималь¬
ная траектория. Обозначим через и* (t) допустимее управление, полу¬
чающееся варьированием управления u(t), а через х* {t)—соответ-

7.3|
ВЫВОД ПРИНЦИПА МАКСИМУМА
329
ствуютую этому управлению траекторию, начинающуюся в точке л;0
Последние п координат вектора х* (t) мы будем обозначать снова
через x*(t).
Рассмотрим варьированные управления следующего частного
вида.
Пусть т, /0^х^£ь—точка непрерывности u{t)y bth 	 %ts —
произвольные неотрицательные числа, a vh	vs	—	произвольные,
u(t)
A	vs
Рис. 7.5. Пример варьированного управления.
не обязательно различные, точки из U. Пусть далее г — малое поло¬
жительное число. Рассмотрим последовательность смежных полуин¬
тервалов
/р х —	^	х
Д>: х — s (8*, + 8*9) < t < х — e8*j
Is: т — в (8^1	^	t	х — £	8^
Частный класс варьированных управлений, который мы будем рас¬
сматривать, задается формулой
( Vi t£- li, I — 1 s,
Предположим, что е и	i=	1,	s,	выбраны	так,	что
5
х — е ^ ^ > *о- Пример варьированного управления изображен на
i = I
рис. 7.5. Величины btt и \ v-t—н(х)| для / = 1, ..., 5 необязательно
должны быть малы, хотя £ является малой величиной.

330	ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА 1ГЛ. 7
Пусть
о t='£ 8 th
i = 1
Обозначим через / полуинтервал (т —	Так	как ва¬
риация и{1) начинается в левой крайней точке /, то имеем
X (т — гЫ) = х* (т — ebt).	(7.20)
Для неварьированной траектории
т
*(т) = л;(х —е8*) +	\ x(t) dt.	(7.21)
t — eS/
Аналогично для варьированной траектории с учетом (7.20)
jc*(t) = jc(t —	(	jc*	(t) dt.	(7.22)
t — eS t
Вычитая (7.21) из (7.22), получим
т
8д:(т) = л:*(х) — jc(x)= $	[х*(0 — x{t)]dt.	(7.23)
т — eS/
Подставляя x* {t) = f[x* {t), «*(£)] и x(t) = f[x(t), м(£)] в уравне¬
ние (7.23), имеем
8* СО = S \f\x* (0, н* (0] — f[x (t), и (01] dt.	(7.24)
т — eS/
Используя определение варьированного управления и* (t), запишем
уравнение (7.24) в виде суммы интегралов
5
8„v(t) = 2 \[f(x*(t), Vi) —f(x (t), u{t))\dt.	(7.25)
*-i /,
Когда	s->0,	длина	интервала / —► 0,	так что
x(t)-+x (т)	на	/.
Е — О
Кроме того, так как влияние вариации управления бесконечно мало,
когда	£ —>	0,	то	x*(t)-+x(f) при е	0,	т.	е.
x*(t)-+x(t)	на	/.
е —► 0
Принимая во внимание два последних выражения, получаем
х* (t) -> х (т).
с —*• 0

7.3]	ВЫВОД	ПРИНЦИПА МАКСИМУМА	331
И так как и непрерывно в точке т, то
и (t) —► и (т)	на /.
Е -► О
Далее из непрерывности / по х и и следует
f[x*(t),	1>,-]=/1*(т),	для t^zlb	(7.26)
где gif)'-?,о0, и
f[x(t), н(<)] = /[.*(х)> и(х)1 + ft(0 для tCz1’	(7-27)
где Л(0,—о0-
Вычитая (7.27) из (7.26) и подставляя результат в (7.25), получим
s
Ьх СО = 2 $	(х).	vi]	—	flx	С0> и (0]} at -{-
+ I	[g{t)~h{t)\dt.	(7.28)
т — Ш
Оценка для последнего члена равенства (7.28) имеет вид
т
\	[g(t)	—	h{t)]dt^max\g(t)	—	h(t)	\3t, t (= ].
т — еб/
Так как	g(t)->0 и	h(t)—>0 при	е	0, этот	член имеет порядок в2
В	первом члене	уравнения (7.28)	каждая	подынтегральная	функ¬
ция постоянна на соответствующем интервале интегрирования /,-.
Поэтому для достаточно малых в (7.28) принимает вид
S*(x) = s|]{/1*(0,	«МИ «<+....	(7.29)
1 = 1
где точками обозначены члены более высокого порядка относи¬
тельно в.
Для дальнейшего удобно записать (7.29) в форме
8л; (т) = jc* (т) — * (т) = вДл; (т) +...,	(7.30)
где
= 2 {/[*«> vt] -f[x(z), «(х)]} Ы,	(7.31)
i= 1
Равенство (7.30) дает вариацию (возмущение) оптимальной траекто¬
рии в момент т при вариации оптимального управления. Вариация
«пробегает» по всей траектории, как это показано на рис. 7.6.
В особенности нас интересует то, как влияет вариация в оптимальном

332
ВВЕДЕНИЕ В ПРИНЦИП МАКСИ Л\УМА Л. С. ПОНТРЯГИИА [ГЛ. 7
управлении па конечное состояние системы. То есть по данному Sat
мы хотим найти	tx т, которое имеет вид
Ьх №) = X* (ti) — X (t{) = г\х (t^).
Отметим, что здесь рассматривается вариация оптимального управле¬
ния только	на интервале	т— so	Следовательно, для
С	Тм т	управление снова	оптимально, т. е. u*(t) = u(t) для t т.
Чтобы	определить	Ах(t{)	по	Дх(т),	нужно решить систему линей¬
ных уравнений
МА-ЧД)1_= У dfi 11	i = 0, 1, п (7.32)
и t	Jmm	UXn>
3 = 0
на интервале	с начальными условиями Ах,- (т), / = 0, 1, ..., п.
В	уравнении	(7.32) AXi(t)	и	Ax,(f)— компоненты вектора Ax(t)>
Gx(tj)	а частыые производные берут¬
ся на оптимальной траекто¬
рии. Решение уравнения (7.32)
в момент дает Дх(^).
Заметим, что системы (7.8)
и (7.32) линейны и однородны,
а матрица
1 dfa\x(t), u(t) 1 1;
dxt ll
уравнения (7.8) отрицательна и
является транспонированной к
матрице уравнения (7.32). Сле¬
довательно, две системы являются сопряженными. Для удобства мы
будем в дальнейшем называть систему (7.8) сопряженной системой
уравнений.
Так как система (7.32) линейна, Дх(^) получается из Ах (т) линей¬
ным преобразованием, которое мы будем обозначать Л/ь - Таким
образом, имеем
Ax(t1) = Atl. Лх&.	(7.33)
До сих пор мы рассматривали множество вариаций оптимального
управления только вблизи одного фиксированного момента т и вы¬
числяли влияние этой вариации на конечное состояние системы. Обоб¬
щим этот результат, взяв конечное число точек вдоль оптимальной
траектории в различные моменты времени ту, /== 1, ..., р. Предпо¬
ложим, что каждая из этих ту- есть точка непрерывности u(t). В каж¬
дой точке ту- введем вариацию оптимального управления, вид которой
показан на рис. 7.5. Предположим, что г достаточно мало и никакие
интервалы / не пересекаются. Тогда для всех ту можно брать одно
и то же s.
(Ср
траектория
Рис. 7.6. Прохождение возмущения оп¬
тимальной траектории.

7.3]
БЫВОД ПРИНЦИПА МАКСИАЛУМА
333
Заметим прежде всего, что вариации независимы и преобразова¬
ние (7.33) линейно. Ввиду этого, применяя те же рассуждения, что
и выше, можно показать, что результирующее влияние всех вариаций
на конечное состояние системы получается суперпозицией влияний
каждого отдельного возмущения. Следовательно,
д*(;,)=У;	7Д*(Т;)’	<7-34)
i~1
где каждое ДлгСу) имеет вид (7.31).
Добавим к вариации оптимального управления вариацию sot ко¬
нечного момента времени tx. оt может быть как положительной, так
и отрицательной (не обязательно малой) величиной, а г то же, что
и выше. Так как теперь рассматривается вариация лишь конечного
момента времени, то и* (t) = и С). Следовательно,
Ц - j- SOt
= \ f[x*(t),u(t)]dt.	(7.35)
вследствие sot t\
Как и прежде, х*	и	для	Ы^О	уравнение (7.35) может
быть записано
Ьх СО | вследствие sot
zf[x(Ul h(*i)] « +	(7.36)
где точками обозначаются члены более высокого порядка малости
относительно s. Для	0,	т.	е.	tx	^	t	t{ -)- sbt, полагаем u(t) —
= u(ti). Тогда (7.36) справедливо как для положительного, так и для
отрицательного bt. Следовательно, учитывая лишь члены первого по¬
рядка по з, имеем
сое СО! вследствие sot 	 еДх(0|	вследствие	sot
s/[*Ci), и Cl)] ot. (7.37)
Из (7.37) получаем
Ал: Cl) (вследствие sot =f[x Ci), w Ci)]	(7.38)
Учитывая (7.34) и (7.38), находим
Дх (*,)=/[.*(#,), f/(/i)] « + 2 Atl. ,Ах(Ъ).	(7.39)
j== 1
Подставляя (7.31) в (7.39), имеем
Д x{ti)=f[x(t1), «(*,)]« +
+ 2 '4^ь V S № O'А ^ -/[■» ('А «/)И Ч (7-4°)
j=1	i	=	\
где верхний индекс используется для того, чтобы показать, что, для
различных точек ^ и о£г различны.

334
ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА (ГЛ. 7
Линейные комбинации вариаций. Если какое-либо ЬЦ обращается
в нуль, то его можно исключить из определения вариации управле¬
ния и* (t) вместе с соответствующим vj. Обратно, добавление нового
vj, для которого существующее ЬЦ равно нулю, не меняет и* (f). В даль¬
нейшем это будет использовано. Действительно, если рассматривается
конечный набор варьированных управлений н'*(£), •••>	т0	можно
предположить, что одни и те же vj входят в разные управления.
Отличие между этими управлениями заключается в том, что ЬЦ и о/
различны.
Вектор Ад:(^) в (7.40) не зависит от s, но зависит от ту-, vi, ЬЦ
и Ы. Обозначим совокупность этих величин через у = {ту, vj, ЬЦ о/}.
Чтобы отметить тот факт, что Ajc(^) зависит от указанных величин,
будем писать Ахг
Рассмотрим конечное число различных у вида
v{> bt{> 8Д
f = vi, Ы{, 8*}
Линейная комбинация у задается формулой
x,y, + ...={v v{> Щ +	ш	+	Х"^+
где X'SsO, A"SsO, ...
Конус достижимости. Будем рассматривать векторы AjcT при
различных у.
Из того факта, что (7.40) линейно по ЬК и bt, следует, что если
у = Х'у' \”у”	X' ^ 0, X" ^ 0, то соответствующие векторы
Ajc связаны соотношением
AjtT = X'Адгг + X"Дх7» +...	(7.41)
Будем рассматривать Дл;т как вектор в (п -j- 1)-мерном простран¬
стве X, исходящий из конечной точки оптимальной траектории
x(tl) = xl. Если рассматривать все возможные у, соответствующие
данному выше определению, то векторы Дл;т образуют в X множе¬
ство К, которое является выпуклым конусом *) в X. Для того чтобы
показать, что к есть выпуклый конус, возьмем две различные точки
bf и Ь" из К. Это значит, что существуют две величины у' и у"
*) Множество К в векторном пространстве X называется выпуклым
конусом, если: (1) имеется вершина О такая, что для любой точки Р множества
К, отличной от О, луч ОР целиком лежит в К, (2) для любых двух точек
множества К отрезок прямой, соединяющий их, целиком лежит в К.

7.3]
ВЫВОД ПРИНЦИПА МАКСИМУМА
335
такие, что Ьг = и Ь" =	Тогда	из уравнения (7.41) имеем
W Н- ГЬ’ = Х'Длу + Г Дду. = Дх(Ху+х"Т">-
Это означает, что точка УЬ'	также	лежит в К. Следовательно,
К есть выпуклый конус в X с вершиной в точке лг(^,) = jcj.
Назовем К конусом достижимости.
Простая геометрическая интерпретация конуса К для системы
второго порядка дана на рис. 7.7. На этом рисунке x(t) есть опти¬
мальная траектория, I — линия, проходящая через точку (0, xi> jc§),
параллельная оси х0, a J—оптимальная (минимальная) стоимость,
соответствующая оптимальному управлению.
х0	I
Рис. 7.7. Геометрическая интерпретация	Рис. 7.8. Модель фазового	про¬
конуса достижимости для системы вто-	странства X.
рого порядка.
Опорная плоскость. Для того чтобы дальнейшие рассуждения
были более ясными, мы будем пользоваться двумерной моделью
(/7 —j— 1)-мерного пространства X, как показано на рис. 7.8. Предпо¬
ложим, что x(t)y	есть	оптимальная траектория, соединяю¬
щая точку jc° = (0, jc°) с точкой (70, Xх), лежащей на линии /, u(t) —
соответствующее оптимальное управление, а К — конус достижимо¬
сти. Так как x(t) является оптимальной траекторией, J0 есть мини¬
мальная стоимость, связанная с переходом динамической системы (7.2)
из начального состояния х° в конечное состояние хК
Ясно, что любой луч, выходящий из вершины конуса К, парал¬
лельный сси х0 и направленный в отрицательную сторону х0, не
может лежать в К. В противном случае нашлось бы допустимое
варьированное управление (t), которое переводило бы систему
(7.2)	из х° в х1 с меньшей стоимостью, чем 70, что противоречит
предположению, что x(t) есть оптимальная траектория. Следовательно,
К не заполняет все пространство Xf и поэтому через вершину К

336
ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
можно провести опорную плоскость, т. е. такую плоскость Г, что К
целиком будет лежать по одну сторону от этой плоскости, как
показано на рис. 7.8. Заметим, что Г неедииственна. Пусть а — нор¬
маль к Г в точке (70, х1), направленная в сторону, противоположную
конусу К, как это показано на рис. 7.8. Эта нормаль является
(и - 1)-мернIлм вектором в ^ с компонентами a{h ah ..., ап. Так как
а направлено в «противоположную сторону» от К, на рис. 7.8 «вниз»,
то а()^;0.	При	таком выборе направления	а	конус	К	лежит	в	отри¬
цательном	полупространстве. Другими словами,	для	любого	Ах К
а' Ддг^О,	(7.42)
где штрих означает транспонирование.
Уравнение (7.42) является основным соотношением, из которого
выводится принцип максимума, сформулированный в теореме 1. Но
прежде чем мы сможем выполнить вывод, необходимо доказать сле¬
дующее вспомогательное утверждение:	если ф (t)= [ф0 (О» Ф1 (0> • • •
•••> 'Ф/iW] есть Решение уравнения (7.8), то тогда
ф' (t)At'.y (т) = const,	(7.43)
гле y(z) — произвольный (п -j- 1)-мерный вектор-столбец.
Чтобы доказать это, покажем, что производная левой части равен¬
ства (7.43) тождественно равна нулю.
Дифференцируя по t, получаем
§1 ft' (0 At.,y е)] =	А1,,У И) +1' (■) Ji fAt,-y (")J-	(7-44)
Уравнение (7.8) в матричной форме записывается как
(t) _ I df[x (0, и (011
dt	дх
tco
и транспонированное к нему
ч) _	.	л	\df[х (*).	« (0]'
dt	т	w I дх
(7.45)
где частные производные берутся на оптимальной траектории и опти¬
мальном управлении.
Подставляя (7.45) в (7.44), правую часть выражения можно запи¬
сать в виде
_ у (0	At	y (т) + у (0 * [А^у (т)]>	(7 46)
Из (7.32) и определения оператора AitT
% wi=I fflwgiiaj Д, ,з (■)•	P.4I)

7.31	ВЫВОД ПРИНЦИПА МАКСИМУМА	337
После подстановки (7.47) в (7.46) последнее обращается в нуль,
и мы получаем
!t'(OPW«] = o;
Следовательно, паше утверждение доказано.
Принцип максимума. Уравнение (7.42) должно удовлетворяться
для каждой вариации оптималь¬
ного управления и вариации ко¬
нечного момента времени.
Рассмотрим сначала одно-един-
ствеиное возмущение оптималь¬
ного управления, как эго пока¬
зано па рис. 7.9. Пусть ^ —
точка непрерывности u(t) и v\—
произвольная точка из U. Так
как рассматривается только одно
возмущение, то в (7.40) полагаем
p = s= 1. Так как конечный мо¬
мент времени также не варьируется,
положим о^ = 0. Таким образом, рассматривается символ *[, для которого
Т = {'с1.	>°. 0}.
Тогда вектор Алг(^), получаемый из уравнения (7.40), для данного ^
имеет вид
\x(t1) = AtrZi {/[лтЫ,®,]—/[лг(т,),иСч)]} 8Д
Подставляя Ajc(^) в (7.42), получаем
а' • Airz	^il — /[-*(ч)> « Oi)]} W,<0.	(7.48)
Для простоты записи мы будем писать (7.48) в виде
а'-Д;1>Т1[А/(^, ti)]Mi<0.	(7.49)
Пусть (0 — [г|?0 (t), op! (t),...,	(0]	—	решение уравнения (7.8) с гра¬
ничными условиями
ty(ti) = a.	(7.50)
Подстановка (7.50) в (7.49) дает
Ф7ОЛьДА/Ч^.)]Ц^0.	(7.5!)
Из уравнения (7.43)
[д/Оь	[Л/0„	т,)].	(7.52)
Так как Л,ьт1 [Д/(г>,, т,)| есть решение уравнения (7.32), для которого
начальным моментом времени является тъ уравнение (7.54) переходит в
ЧЦОЛ,,.,, |Д/(г.„ -1)]==Ч>Ч^1) 1Д/К 4)J-	(7.53)
u.(t)
Рис. 7.9. Единственная вариация в
оптимальном управлении.

338	ВВЕДЕНИЕ	В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ 7
Подставляя (7.53) в (7.51), получим
4>'(ti)A/(w„	(7.54)
Используя определение Дf(vh х,), (7.54) запишем в виде
М’Ч'ч)	«Сч)]}
Ввиду того что Ых положительно,
‘Ф'С'сД {yTJC^i). ®i]— Я*Ы> и(х,)]} <0.	(7.55)
По определению гамильтониана уравнение (7.55) можно записать
в следующей форме:
н ['ф X (Ti)> ^l] < Н (Ti)> X (тД и (тх)].	(7.56)
Так как (7.56) имеет место для любой точки щ ^ U> то имеем
Н [ф (т Д х (т Д и ДД = шах Н [ф (тД х (тД v{] = М [ф (т Д х (tj)].
Vi ей
(7.57)
Более того, выражения (7.56) и (7.57) справедливы для любой точки
tj, являющейся точкой непрерывности u(t), поэтому окончательно
получаем
Н [ф (Д х (0> и (0] = М [ф (Д х (0], U t ^ Д	(7.58)
вдоль оптимальной траектории во всех точках непрерывности u(t).
Таким образом, равенство (7.12) теоремы 1 доказано.
Рассмотрим теперь отдельно вариацию только конечного момента
времени, т. е. символ у, для которого
Т = {0, 0, 0, Ц.
Никаких точек zj нет. Для этого у из (7.40) и (7.42) находим
а^(*(Д,*ДД)]^0.	(7.59)
Подставляя (7.50) в (7.59) и используя определение гамильтониана,
получаем
Н [ф (*Д х СД и (*,)] Ы ^ 0.	(7.60)
Так как Ы может быть как положительным, так и отрицательным,
неравенство (7.60) может удовлетворяться, только если
Н [ф СО, х СД и СД] = 0.	(7.61)
То есть гамильтониан обращается в нуль в конечной точке оптималь¬
ной траектории. Чтобы подчеркнуть, что (7.61) имеет место для
оптимальной траектории, т. е. траектории, вдоль которой гамиль¬
тониан максимален, запишем равенство (7.61) в виде
М 1Ц) (/,), х (/,)J = 0.	(7.62)

7.3]	ВЫВОД	ПРИНЦИПА	МАКСИМУМА	339
Покажем теперь, что (7.62) справедливо для всех t,
Продифференцировав (7.58) по t, получим
dH	 VI (дН	,	д_Н_ dxЛ	,	у ^/i du^
dt	Jii \(^фа dt	'	дха dt J	'	£ dlla dt ’
а = 0	a=l
Подставляя гамильтониан системы (7.10) в (7.63), получаем
dJL= V (ЛзЛ	_ Л СЛЛ	_L Y dJl dJL«
dt	^ \ dt dt	dt dt ]	1	hmi dLla dt
a =0	a	=	1
и после упрощения
dH V dI1 du
= 2 wji-	<7№
0=1
Если U—замкнутое множество в r-мерном евклидовом пространстве
гал1
дН_
ди„
и гамильтониан принимает максимальное значение во внутренних
тт	дН А	1
точках и у то тогда в этих точках ^- = 0,	а=1,	г,	и	уравне¬
ние (7.64) имеет вид — = 0. Если же гамильтониан принимает мак-
тт dH	л
симальное значение на границе с/, то а=1, г, уже не рав¬
няется нулю. Однако в этом случае можно показать, что два вектора
дН dua	1	п
с компонентами и	a = 1, ..., г, ортогональны. Следова¬
тельно, правая часть (7.64) в этом случае также равна нулю. Таким
образом, имеем
М[ф(0, x{t)} = 0,	(7.65)
вдоль всей оптимальной траектории.
Из уравнения (7.50) и того факта, что
фо(*0<0.	(7.66)
Легко видеть,	что	ни одно из /а, а = 0, 1, ..., п,	в уравнениях (7.5)
не зависит от	х0.	Следовательно, при / = 0 в уравнении	(7.8)
§L = °,
Тогда из (7.66) следует, что
<b0(t) = const 0,	t0^t^ U-	(7.67)
Уравнения (7.65)	и (7.67) дают нам уравнение	(7.13)	теоремы 1.
Таким образом, вывод полностью закончен.
Обсуждение результатов. Проблема синтеза. Мы закончим этот
параграф рассмотрением некоторых аспектов задачи реализации, иначе

МО
ВВЕДЕНИЕ В ПРИНЦИП /МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
говоря, синтеза оптимального управления. Как только что было пока¬
зано, граничными условиями для сопряженной системы уравнений (7.8)
является ty(t{) = a, где а есть нормаль к опорной плоскости Г.
Чтобы найти эти граничные условия, нужно знать опорную пло¬
скость Г для конуса допустимых вариаций и вычислить соответствую¬
щий нормальный вектор к этой плоскости. Появляющиеся вычисли¬
тельные трудности очевидны. Но даже если бы можно было вычис¬
лить а, то, прежде чем найти оптимальное управление, нужно еще
проинтегрировать назад, от точки ^ к tQf уравнения ' (7.8). Так как
tA свободно, т. е. заранее не известно, задача еще более усложняется.
Мы видим, что в общем случае проблема синтеза сводится к нели¬
нейной, двухточечной краевой задаче. То же самое было и в частной
оптимальной задаче, рассмотренной в § 7.2.
К проблеме синтеза мы вернемся еще в конце этой главы.
7.4.	Обобщения принципа максимума
В этом параграфе мы рассмотрим две оптимальные задачи, реше¬
ние которых получается обобщением предыдущих результатов.
Принцип максимума для неавтономных систем. Рассмотрим
класс задач, в которых динамические системы задаются уравнениями
^7 =/; (х, и, 0	(/=1,2,...,	п),
и нужно минимизировать функционал
J= \h\x{t), u(t), t]dt.
to
Мы предполагаем, что tx не фиксировано и и £ U. Как и прежде,
введем новую координату
tv
х«— $/о [•*(«)> !Ф)> s]ds;
to
это эквивалентно
d£=fa[x(t),u(t),t],	*0	0.)	= 0.
Сформулируем оптимальную задачу, которую мы хотим решить.
В (п -4- 1)-мерном фазовом пространстве X даны точка (0, х°) и ли¬
ния /, параллельная оси х0 и проходящая через точку (0, х{). Из
множества всех допустимых управлений u = u(i), обладающих тем
свойством, что решение x(t) системы уравнений
^ = /,. (*,	/), х 0.) = (0, *•)	(/ = 0,1,..., п) (7.68)

7.4]	ОБОБЩЕНИЯ ПРИНЦИПА МАКСИМУМА	34:
пересекает /, найти то, у которого точка пересечения с I имеет
наименьшую координату х0.
Мы видим, что задача имеет ту же форму, что и для уравне¬
ния (7.6). Разница заключается лишь в том, что теперь мы допускаем»
чтобы функции /а зависели явно от времени.
Введем еще одну координату хП]Л, определяемую уравнением
ХплЛ (Q — h.
Ясно, что xn^ = t. Следовательно, если мы сделаем эту подстановку
в (7.68), то получим автономную систему
~l = fi{x,u,xn^ (/ = 0. I, ..., я), —1.	(7.69)
Применим принцип максимума к рассматриваемой задаче. Аналогично
сопряженной системе уравнений (7.8) для автономного случая мы
пишем
§=-2;1Л	 ”>
а =0
И
<%+■ _	V ^/а
dt	h dxn+i 7а-
а = 0
Так как xnvX{t) = ty последнее уравнение может быть записано как
а = 0
Рассмотрим теперь функцию
п
2<Ш*. и.	(7-72)
а = 0
Обозначим эту функцию через Н* и положим
п
7/(Т. U, 0= S 'Kfa (х, и, t).	(7.73)
а = 0
Через	М*	и М	обозначим максимум	Н* и Н по	и	при	фиксирован¬
ных Xi	и	ф,*.	Из	уравнений (7.72) и	(7.73) и того	факта,	что
dxn+l  .
dt

ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
получаем соотношение
Н*=Н + Ъп,х и М* = М+%+1.	(7.74)
Так	как	уравнения (7.69) представляют автономную систему,	из тео¬
ремы 1 следует, что
Н* [ф (0, * (0> н (0. *] = М* № (0> * (0> «(0> *]	(7.75)
для	всех	£, являющихся точками непрерывности н(£).	Подставляя
(7.74)	в (7.75), получаем
ЯЖО, *(0, и(0,	= Ж [гр (0, *(*), u(tl t] = — %+l(t).
В [1, 2] показано, что фя.|Л (t{) = 0, так что из (7.71) находим
- W (0 = J 2 dh[x[t)d'tU(t)'t] <|»в (0 at.
Ц а = 0
Из теоремы 1 имеем
ф0 (t) = const 0.
Суммируя эти результаты, получаем принцип максимума для
неавтономных систем.
Теорема 2. Пусть u(t) — допустимое управление, a x(t)—
соответствующая ему траектория уравнения (7.68), проходящая через
некоторую точку линии I в момент tx t0. Для того чтобы и (t) и
x(t) были оптимальными для ^ ^ ^ необходимо, чтобы сущест¬
вовала нетривиальная непрерывная вектор-функция ф (0 = [фо (0, • • •
•••>ФлОО]> удовлетворяющая уравнению (7.70), такая, что для всех
точек непрерывности u(t) гамильтониан достигает максимума по
и £ U при u — u(t), т. е.
Н [я|> (0, х (0, и (0, t] = M[\|> (0, * (0, * (0, *]•	(7.76)
При этом
ф0 (t) = const < 0
и
t п
М №(0, Jf(0. t] = — фл+1 (0=5 2 dfAx[t)tu(t)'t] ф, (0dt.	(7.77)
tl a =0
Принцип максимума для задачи с фиксированным временем.
Будем теперь рассматривать оптимальную задачу для автономного
случая, когда конечный момент tx задан, т. е. когда интервал работы
системы tx —10 является известной константой.
Пусть задана система уравнений
§ — /, (.х, и), х (<о) = (0, х*)	(/	=	0,	1, ... , Я).	(7.78)

7.41
ОБОБЩЕНИЯ ПРИНЦИПА МАКСИМУМА
343
Мы хотим перевести систему в точку, лежащую на линии /, за фикси¬
рованное время tx—tf0, так чтобы координата х0(^) была бы мини¬
мальна. Так как ^ = const, то не нужно варьировать конечный мо¬
мент времени tb т. е. в ^ можно не учитывать bt. Все остальные
результаты, выведенные в § 7.3, остаются в силе. Таким образом,
мы приходим к принципу максимума для задачи с фиксированным
временем.
Теорема 3. Пусть u(t)— допустимое управление и x(t) — соот¬
ветствующая ему траектория уравнения (7.71), проходящая в задан¬
ный момент tx через некоторую точку линии /. Для того чтобы u(t)
и x(t) были оптимальными для t ^th необходимо, чтобы су¬
ществовала нетривиальная непрерывная вектор-функция ф(£) = [ф0(£),
ф! (О, • • • , фл(01» удовлетворяющая уравнению (7.8), такая, что для
всех точек непрерывности u(t) гамильтониан /7(ф, х, и) достигал
максимума по и £ U при n — a(t), т. е.
н [ф (О, X (*), и (01 = м [ф (0, * т	(7.79)
При этом
ф0 (t) = const 0.	(7.80)
Другие обобщения. В заключение этого параграфа упомянем неко¬
торые другие следствия принципа максимума, детали которых изло¬
жены в [1, 2].
Прежде всего обобщение теоремы 3 на неавтономный случай
легко получается путем применения методов и результатов, исполь¬
зованных при выводе теоремы 2. Введением условия трансверсаль¬
ности [1, 2] теоремы 1, 2, 3 могут быть обобщены на тог случай,
когда требуется перевести динамическую систему:	а)	из	фиксирован¬
ного начального состояния в какую-нибудь точку	заданного	подмно¬
жества фазового пространства, б) из произвольного начального со¬
стояния, принадлежащего некоторому фиксированному подмножеству
фазового пространства, в точку другого заданного подмножества
фазового пространства, в) из произвольного начального состояния
в заданном подмножестве фазового пространства в фиксированную
точку этого пространства. При этом возможен случай, когда конеч¬
ная точка движется, т. е. x1 = xl(t).
Основные результаты, полученные выше, могут быть также обоб¬
щены на оптимальные задачи, в которых минимизируемый функционал
имеет вид
сс
о
Наконец, принцип максимума может быть выведен для оптимальных
задач, в которых уравнения динамики системы содержат постоянные

ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. ?
параметры, т. е.
== Д- (X, II, W),	/=	1	п,
где вектор w представляет множество настраиваемых параметров
системы. По существу задача заключается в следующем. До начала
движения выбрать величину w° параметра w и допустимое управле¬
ние u(t) гак, чтобы соответствующая траектория x(t) начиналась
в точке x(t0) = x° и в некоторый момент времени	проходила
через точку x(tl) = x1, а функционал
о
J= 5 /о [х (О, м (0. ®’°] dt
к
был бы минимален.
7.5.	Некоторые приложения принципа максимума
Применим теперь результаты предыдущих параграфов к трем
различным классам задач оптимального управления. Так как реально
для синтеза оптимального управления требуются, вообще говоря,
численные вычисления, рассмотрим лишь свойства оптимального управ¬
ления. В действительности мы найдем, что очень важной особен¬
ностью принципа максимума является то, что он дает соотношение,
из которого легко следуют свойства оптимального управления.
Оптимальное по быстродействию управление при ограничении
на длину вектора управления. В § 7.2 исследовалось оптимальное
по быстродействию управление класса динамических систем с огра¬
ничением на координаты вектора управления | и{ | ^ 1, /= 1, 2,... , г.
Здесь мы рассмотрим ограничение вида Цн(Г)[|^1, t0^t^th где
• || — евклидова норма, определяемая формулой
111 (0 i=V \щ (О]2+••• + [**/■ со]2
Динамическая система описывается системой уравнений
dJi = f(x)+Bu{t).
Все члены этого выражения были определены в § 7.2. Мы хотим
перевести систему из начального состояния jc(70) = jt° в заданное
конечное состояние x(tx) = xx за минимальное время при условии,
что !|н(7)[]^1,	В этой задаче U является единичной
сферой в r-мерном евклидовом пространстве с центром в начале
координат.
Как и прежде, f0(x,a)=\ и гамильтониан для нашей задачи
имеет вид
Н (1]), х, и) —	-\-	<b'/{x)	-j-	уВи,

7.51
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПРИНЦИПА МАКСИМУМА
345
где фо — скалярная функция времени, ф — я-мерный вектор-столбец
ф = (ф1, ф.2) ..., фл) и штрих означает транспонирование.
По теореме 1 фо(0 = сопз1^0,	и	гамильтониан
равен
Н (ф, ху и) = ф'/ (х) + ty'Bu — 1,	(7.81)
где мы положили ф0(£) =—1.
Выражение (7.81) представляет скалярную величину, которую
нужно максимизировать по и при условии + 00|'|^ 1»	При
этом максимизировать в (7.81) нужно только второй член, так как
он один зависит от и. Чтобы сделать этот член как можно больше
при данном ограничении, положим
г'^ = р7щ-’	(7-82)
Из (7.82) видно, что [|z/(f)||=l, tQ^t^tb так что длина век¬
тора управления всегда постоянна, а его направление меняется во
времени в соответствии с уравнением (7.82). Геометрически это озна¬
чает, что конец вектора управления всегда лежит на поверхности
единичной сферы в r-мерном евклидовом пространстве. При мини¬
мизации (7.81) по и мы брали длину вектора и максимально возмож¬
ной, а направление и так, чтобы произведение	было	всегда
положительным.
Гамильтонова система для нашей задачи имеет вид
§ = /(*)+Bu(t),
§ =	(/=1,...,/»)	(7.83)
а = 1
с граничными условиями x(t0) = x° и x(t1) = x1.
Еще одно уравнение, необходимое для определения tu получается
подстановкой (7.82) в (7.81) и последующим использованием урав¬
нения (7.13) теоремы 1.
Тогда
Ф'+ ||ф'(0#||= 1,	^	1	<	tu	(7.84)
Таким образом, имеется 2/2+ 1 соотношение (уравнения (7.83) и (7.84))
и столько же неизвестных x(t), ф(£), tx\ u{f) находится по фор¬
муле (7.82).
Задача минимума энергии при фиксированном времени. Рас¬
смотрим задачу перевода системы
d£ = A(t)x{t)^B(t)u{t)	(7.85)

346	ВВЕДЕНИЕ	В	ПРИНЦИП	МАКСИМУМА	Л.	С. ПОНТРЯГИНА [ГЛ. 7
из начального состояния x(tQ) = x° в конечное состояние x(t{) = xl
за фиксированное время — t0). В уравнении (7.85) х — я-мерный
вектор-столбец, и — r-мерный вектор-столбец, a B{t) w A(t)—непре¬
рывные я X г- и я X я-матрицы.
Мы хотим, чтобы переход произошел с минимальными затратами
энергии на управление. В качестве меры энергии управления возь¬
мем функцию стоимости в виде
о
7=1 ^ u'(t)u(t)dt,	(7.86)
^0
где штрих означает транспонирование. Множество допустимых управ¬
лений U состоит из всех конечных точек r-мерного евклидова про¬
странства.
Наша система имеет вид
§=7«' (0 И (0 = у {[«1 (О]2 + • • • + [И, (О]2}.
Напишем гамильтониан системы, полагая ф0(£) =—1,
Н(ф, х, и) = ф'Ах -j- <1>'Ви — y и'и.	(7.87)
Так как и может быть любой точкой в r-мерном евклидовом про¬
странстве, то значение н, при котором гамильтониан максимален,
можно найти, приравняв нулю производную Н по и. Так как от и
зависят только последние два члена равенства (7.87), определим «новый»
гамильтониан для нашей задачи
Q(\|), х, и) = уВи	^	и'и.
Преобразуем G, обозначив через cj(t) /-тый элемент вектора-строки
произведения tf{t)B(t):
г	г
G(iT х, н)= 2	V	[н/(0]2
/=|
Дифференцируя G по tip /=1,2,..., г, и приравняв полученные
производные нулю, получим
Uj(t) = Cj(t) (/=1,2,..., г),
Напишем эти уравнения в векторной форме
и (0 = [ф' (0 В (*)]',	h.	(7.88)

7.5]
НЕКОТОРЫЕ ПРИЛОЖЕНИЯ ПРИНЦИПА МАКСИМУМА
347
Подставляя (7.88) в (7.86), получаем следующее выражение для мини¬
мальной энергии:
Заметим, кстати, что оптимальное управление (7.88) линейно и не¬
прерывно.
Напишем уравнения Гамильтона для нашей задачи
с граничными условиями x(t{)) = x° и x(t1) = x1. Из уравнений (7.87)
и (7.88) и обобщения теоремы 3 на неавтономные системы получаем
Так как tx фиксировано, уравнения (7.87) представляют 2п соотноше¬
ний с 2п неизвестными и 2п граничными условиями x(t0) = x() и
x(t1) = x1. Ввиду того что оптимальное управление линейно, мы имеем
линейную двухточечную граничную задачу, решение которой дает
оптимальную траекторию и оптимальное управление.
Задача минимума энергии с фиксированным временем при огра¬
ничениях на вектор управления. Рассмотрим ту же самую задачу,
что и выше, но только с ограничениями на координаты вектора и:
I ui (0 |	1, / = 1, 2,..., г; t0 t tx. Гамильтониан для задачи с
данными ограничениями тот же, что и выше:
Однако теперь при минимизации надо учесть ограничения.
Как и в предыдущей задаче, через Cj(t) обозначен у-й элемент
вектора-строки ф' (t) В (t). Тогда часть гамильтониана, зависящая от
управления, имеет вид
Дифференцируя G по ujy j = 1, 2,..., г, и приравнивая полученные
производные к нулю, получаем
Однако вследствие ограничений формула (7.90) справедлива только
для тех t,	для	которых	|с/(0|^	1*	Для	тех	t,	для	которых
(7.89)
М № (0, х СО] =	(0	А	(0	х	(t)	+	ф'	(0	В	(t)	В'	(0	ф	(0	=	const,
/7(ф, х, и) = Ф'Ах -f- ФВи jii'u.
г
г
О (^, гг) = 2 cj (0 Uj (0 — -J 2 \ni (Of-
iij{f) — Cj{t), j— 1, 2,.r; ro=sSt^t]
г-
(7.90)

348	ВВЕДЕНИЕ В ПРИНЦИП МАКСИЛ\УМА Л. С. ПОНТРЯГИНА	|Т.\.	7
| Cj (t) | ^ 1, максимум G будет достигаться при
Uj (0 = sgn Cj (0,	/=1,2,..., г; t{) ^ t ^	(7.91)
Из уравнений (7.90) и (7.91) получаем вид компонент вектора
управления u(t\ изображенной на рис. 7.10. Из рисунка видно, что
управление линейно в некоторой фиксированной области и насыщаете»
при I с, (01 Ss !•
В матричной форме уравнения (7.90) и (7.91) принимают вид
[«к(ОЖОГ, если [>У (0Ж0]sgn[<j/(0Ж0Г=^	1,	(792
sgn [f (0 в (0], если [<1/ (О В (0] Sgn [d/ (О В (01' 2=	1
для	Из	этой	формулы	видно,	что	линейная	часть	(7.92)
Рис. 7.10. Вид управления в задаче
на минимум энергии при ограничении
на координаты вектора управления.
такая же, как и в (7.88) для задачи минимума энергии, но без
ограничений на и.
Уравнения (7.89) с граничными условиями x(t0) = x° и x(t{) = xx
являются уравнениями Гамильтона и для этой задачи.
7.6.	Заключение
Хотя не существует метода решения общей двухточечной гра¬
ничной задачи, которая возникает в приложениях принципа макси¬
мума, однако для некоторого класса задач можно получить числен¬
ные результаты. В большинстве своем эти результаты получены для
задач, в которых динамическая система линейна или управление вхо¬
дит линейно. В заключение мы укажем некоторые частные случаи,
которые рассматривались в литературе.
Задача максимального быстродействия для линейной динамической
системы подробно рассмотрена в [7,11 —14], а задача минимума
энергии управления — в [14—17]. В некоторых из этих работ дается

ЛИТЕРАТУРА
3-19
формальная итеративная процедура получения начальных условий для
сопряженной системы уравнений, и поэтому оптимальное управление
получается как функция времени. Некоторые результаты для задач,
оптимальных по быстродействию и минимуму энергии управления,
•связанные с синтезом замкнутых оптимальных систем, имеются
в 1' 8].
Для отдельных динамических систем в [19] было получено явное
выражение оптимального управления как функции состояния си¬
стемы.
В [20] для решения терминальной задачи для линейной динами¬
ческой системы был применен метод наискорейшего спуска.
В большинстве этих работ авторы сводили решение либо к прямому
применению принципа максимума, либо к использованию отдельных
идей и конструкций, содержащихся в его доказательстве.
Таким образом, хотя принцип максимума не дает прямого метода
синтеза оптимального управления, полезность его в качестве исследо¬
вательского аппарата уже доказана.
ЛИТЕРАТУРА
1. Б о л т я н с к н й В. Г., Г а м к р е л и д з е Р. В., Понтрягин Л. С.,
Теория оптимальных процессов 1. Принцип максимума. Изв. АН СССР,
серия математич. 24, № 1 (I960), стр. 3—42.
2. ПонтрягинЛ. С. и др. Математическая теория оптимальных процессов,
Физматгиз, М., 1961.
3. Б о л т я н с к и й В. Г., Принцип максимума в теории оптимальных про¬
цессов, ДАН СССР 119, № 6, 1958, стр. 1070-1074.
4. Г а м к р с л и д з е Р. В., К теории оптимальных процессов в линейных
системах, ДАН СССР 117, № I, 1957, стр. 9—12.
5. С о d d i n g t о п E. A. and N. Levinson, Theory of Ordinary Differen¬
tial Equations, McGraw-Hill Book Company, Inc., New York, 1955. [Русский
перевод: Коддингтон Э. А. и Левинсон Н., Теория обыкновенных
дифференциальных уравнений, ИЛ, М., 1958.]
6. К р а с о в с к н й Н. Н., К теории оптимального управления. Автоматика
и телемеханика, т. XVIII, № 11, 1957, стр. 960 -971.
7. LaSalle J. P., Time Optimal Control Systems, Proc. Natl. Acad. Sci. U.S.,
Vol. 45, pp. 573—577, 1959.
8. L e с E. B. and L. M a г k u s, Optimal Control for Nonlinear Processes, Arch.
Rational Mech. Anal., Vol. 8, No. 1, pp. 36—58, 1961.
9. R о x i n E., The Existence of Optimal Controls, Mich. Math. J., Vol. 9, pp.
109—119, 1962.
10. Neustadt L. W., The Existence of Optimal Controls in the Absence of
Convexity Conditions, J. Math. Anal, and Appl., Vol. 7, 1963.
11. Neustadt L. W., Synthesizing Time Optimal Controls, J. Math. Anal, and
Appl., Vol. 1, No. 3, pp. 484—493, 1960. [Русский перевод: Нейштадт Л. В.,
Синтез оптимальных по быстродействию систем. Сб. пер. Механика, № 3,
«Мир», М., 1964.]
12. Г и м к р е л и д з е Р. В., Теория оптимальных процессов в линейных си¬
стемах. Изв. АН СССР, серия математич., 22, 1958, стр. 449—474.

350
ВВЕДЕНИЕ В ПРИНЦИП МАКСИМУМА Л. С. ПОНТРЯГИНА [ГЛ. 7
13. Р a i е w о II s к у В. Н., The Synthesis of Optimal Controllers, Proc. of the
Optimum System Synthesis Conf., ASD-TDR-63-119, Wright-Patterson Air
Force Base, Ohio, pp. 76—99, February, 1963.
14. N e u s t a d t L. W., Minimum Effort Control Systems, J. SIAM on Control,
vol. 1, No. 1, pp. 16—31, 1962.
15. Athanassiades М., Optimal Control for Linear Time—Invariant Plants
with Time, Fuel, and Energy Constraints, Trans. A1EE-PT, II. Applications
and Industry, Vol. 81, No. 64, pp. 321—325, January, 1963.
16.	M e d i t с h J. S.	and L.	W. N e u s t a d t, An Application of Optimal	Control
to Midcourse Guidance,	Proc. of Second Congress of the International Fede¬
ration of Automatic Control, Butterworths, London, 1963 (to appear).
17. Med itch J. S., On Minimal Fuel Satellite Attitude Control, Paper No.
XIX-5-IEEE (TOC), 1963 Joint Automatic Control Conference, Minneapolis,
Minn., June, 1963.
18. Neustadt L. W., A Synthesis Method for Optimal Controls, Proc. of the
Optimum System Synthesis Conf., ASD-TDR-63-119, Wright-Patterson Air
Force Base, Ohio, pp. 374—381, February, 1963.
19.	Athans М., P.	L. F a	1 b and R. T. L а с о s s, On Optimal Control	of Self-
Adjoint Systems,	Paper	No. V-5-1EEE (TOC), 1963 Joint Automatic	Control
Conference, Minneapolis, Minn., June, 1963.
20. Balakrishnan A. V., An Operator Theoretic Formulation of a Class of
Control Problems and a Steepest Descent Method of Solution, Jour, of SIAM,
Series A on Control, Vol. 1, No. 2, 1963.

ГЛАВА 8
ПРОБЛЕМА МИНИМУМА НОРМЫ
И НЕКОТОРЫЕ ДРУГИЕ МЕТОДЫ ОПТИМИЗАЦИИ
СИСТЕМ УПРАВЛЕНИЯ
Аоки (М. Aoki)
В последние годы теория управления быстро развивается, и для
оптимизации систем управления используются многие новые математи¬
ческие методы. Цель этой главы — рассмотреть несколько таких ме¬
тодов, которые не используются в других разделах этой книги. На¬
пример, достаточно хорошо известно, что некоторые задачи теории
оптимального управления и оптимизации траектории могут быть
сформулированы как задачи нахождения линейных функционалов с
минимальной нормой, и следовательно, применима теория А-проблемы
моментов М. Г. Крейна [2, 33, 39] *).
A-проблема и родственные с ней вопросы обсуждаются в пер¬
вых пяти параграфах. Математическая формулировка А-проблемы
моментов дана в § 8.2. Развитая в этом параграфе теория приме¬
няется для приближенного решения несовместных систем уравнений
в § 8.3.
В § 8.4 рассматривается вопрос аппроксимации в линейном норми¬
рованном пространстве путем переформулировки A-проблемы в проб¬
лему аппроксимации. Выражение для ошибки выводится в § 8.5 для
случая гильбертова пространства, а вопрос единственности обсуждается
в § 8.6.
В остальных четырех параграфах рассматриваются некоторые
методы последовательных приближений решения функциональных
уравнений.
*) О других подходах см., например, [4].

352
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ
[ГЛ. 8
РАЗДЕЛ I
/.-ПРОБЛЕМА И ЗАДАЧА АППРОКСИМАЦИИ В ЛИНЕЙНОМ
НОРМИРОВАННОМ ПРОСТРАНСТВЕ
8.1.	Введение
Для того чтобы проиллюстрировать связь между проблемой мини*
мума нормы в функциональном анализе и некоторыми проблемами
управления, рассмотрим коротко задачу оптимального быстродействия,
в которой управление u{t) является скалярной величиной.
Более полное изложение этого вопроса читатель может найти
в обширной библиографии, имеющейся в [28].
Задача формулируется обычно следующим образом: для заданных
скалярных функций времени Zi(t) и h{(t) найти такое управление
и (t) из некоторого множества допустимых управлений 2, что
t
(8.1)
о
за минимальное время t=T.
Функции hi {t) удовлетворяют условию
t
^ I hi (т) |д d^<^oo,	1	/	<с	/7,	<7	1,
о
для всех конечных t.
Множество всех точек в л-мерном евклидовом пространстве, в
которые можно попасть с помощью допустимых управлений и за время
[0,2], называется областью достижимости R(t) [28,35]:
^ h (т) и (Ч) dz, и £ 2 J,
где ii = (hb ..., hn).
При соответствующих предположениях относительно h и 2 мно¬
жество R(t) будет ограниченным, замкнутым, выпуклым множеством
в Еп, а минимальное время Т соответствует тому моменту времени 7,
когда z(t) находится на границе R(t). Множество R играет важную
роль во многих современных задачах управления.
Если п принадлежит пространству 7p(0,f)*) и
Q = /и(0:/(|н(01р<*Й 1Р^сЛ, р>1,
I \0	/	J
*) Lp (0, t) = | а: : х — измеримо, \ \ х (s) \р ds < оо
I	и

8.21	МАТЕМАТИЧЕСКАЯ	ФОРМУЛИРОВКА	353
то тогда оптимальное управление н° удовлетворяет условию
it	\1	!Р
Равенство (8.1) можно рассматривать как линейный оператор на
Lq{О, Т\ отображающий Lq в пространство действительных чисел и
удовлетворяющий п ограничениям
т
Ahi = \ht (t) и (0 dt = Z[ (Т),	1	«£/==£	п.	(8.2)
U
Норма оператора (являющаяся линейным функционалом на Lq [26])
определяется как
и лп	I	Ах	I
И =supljTFH
ц*;] !l х II
и равна
/7	V	I	!Р
\!«(0М •
\5	I
Оптимальный оператор Л* имеет норму
И*| = ($\un{t)\pdt\ =Ср.
■ \о
Грубо говоря, норма А — эго затраты или энергия управления,
необходимая для достижения заданной точки за минимальное время.
Если Т фиксировано, а исходная задача формулируется как за¬
дача на минимум энергии [5, 27, 29, 32], т. е. как задача достижения
заданной точки z (Т) за время Т с минимумом затрат на управление
[27, 28], то тогда проблема сводится к минимизации || А || по всем А,
удовлетворяющим условию (8.2).
Это соответствует проблеме минимума нормы [33, 34] в линейном
нормированном пространстве [26].
8.2.	Математическая формулировка
Сформулируем теперь L-проблему. Наше изложение будет следо¬
вать частично работе [2]. Пусть Е — линейное нормированное про¬
странство, а х — произвольный элемент из Е.
Задача А. Даны п линейно независимых элементов хъ..., хп
из Еу не равный нулю вектор с = (съ ..., сп) из Е (евклидового п-
мерного пространства) и положительное число L. Требуется найти
необходимые и достаточные условия существования линейного функ-
12 п/р Леондеса —

354
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕ.М
[ГЛ. 8
ционала из Е* (Е* — пространство всех линейных функционалов над
Е [37]), удовлетворяющего условиям
f(xi)=ci (i= 1, 2,п)
S L.
(8.3)
(8.4)
Пространство Е* называется сопряженным пространству Е. Задачу
А можно сформулировать в несколько другой форме.
Задача А'. Найти функционал с минимальной нормой, удовле¬
творяющий условиям
f () = с ^
где Х\у..хп — линейно независимые элементы из Е, а с = (съ ..сп)—
вектор из Еп. Элемент х, для которого \f(x) | = ||/|| || лег ||, называется
экстремальным элементом /.
Ниже, в § 8.6, мы будем иметь повод обсудить единственность
экстремальных элементов. Здесь же сформулируем другую задачу,
тесно связанную с задачами А и А'.
Задача Б. Дано п линейно независимых элементов хъ...уХп из
Е. Найти X такое, что
-— inf ]| qjCi -j-...-]- \пхп ||,
£.с= 1
(8.5)
где £ =	\п	—	вектор	из	Еп.	Точкой	в	(8.5)	обозначено	обычное
скалярное произведение. Так как
_= inf ||	Д-^11= inf
£.с= 1
|5с|
oil п
1«с| 1
Nr
^Еп
ИЪХ‘\\
i ||
— i
то число X в (8.5) можно определить как
Х = sup
ic|
где
2^
i
Н=\Х-Л£Ет
sup |Sc|,
еея
= 1!
(8.6)
(8.7)
(8.8)
Напишем явное выражение для X как функцию от съ
При этом станет ясно, как связаны задачи А и Б.

8.2]
М АТЕМ АТИ Ч Е С К А Я Ф ОРМУЛ И Р О В КА
355
Если линейный функционал f(x) удовлетворяет уравнениям (8.3)
и (8.4), то тогда
2 to = IP,-/(*«•)
Следовательно,
/2 to,
i
2 to
2^
г*г
2 to*
2 ’,л"1
Найдя точную верхнюю грань правой части (она существует), из
уравнения (8.7) получим
L ^ к	(8.9)
Предположим теперь, что Х(с1? ..., cn)^L и определим на G
функционал ср(дг) следующим образом:
i= 1
i = 1
Тогда норма ср(х) в G, где G—подпространство Е, натянутое на
1 ^ ^ п, будет
 1т(*)1	^5iC'
MPio= sup iiTir = sup
x£Q II
:(СЬ ..., Cn).
По теореме Хана — Банаха [26, 37] ср (л:) может быть продолжен
на Е без увеличения нормы. Пусть f(x) — продолжение ср (аг) на Е,
тогда
11/|| = 1М1о = >'<Ь
f{xi) = <!?(xi)=ch i= 1, 2, ..., п.
Таким образом, X является минимальной нормой функционала,
удовлетворяющего условиям (8.3).
Это основной результат, который показывает связь между зада¬
чами А и Б.
Предложение. Задача А имеет решение тогда и только тогда,
когда L ^ X (сь ..., ся).
Так как конечномерное векторное пространство (22) является
в нашем случае самым простым пространством, мы в первую оче¬
редь рассмотрим задачу А в /я-мерном евклидовом пространстве Ет
12*

356
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ [ГЛ. 8
и укажем множества в Ет, которые могут рассматриваться как до¬
стижимые множества R. Сопряженное (двойственное) пространство Е%,
имеет ту же размерность, что и Ет, и существует единственный ли¬
нейный функционал такой, что /{х{) — сь /— 1, 2, ..., /я, где ct —
данные константы, а {хь ..., хт) — базис в Ет.
Если независимых условий на / будет не т, а п(п<^т), то тогда
существует более чем один линейный функционал, удовлетворяющий
этим условиям.
В терминах сопряженного пространства Е%, это означает, что
в сопряженном базисе могут быть определены только п из т эле¬
ментов. Без потери общности можно предположить, что f(Xi) = ch
1 ^ п.
Эти линейные функционалы образуют (т — я)-мерное подпро¬
странство в Е'т.
В качестве дополнительного условия на / потребуем, чтобы ||/||
была меньше заданного числа L. Это будет также ограничением на
множество линейных функционалов в (т — /г)-мерном подпространстве.
Пусть К — множество таких линейных функционалов, т. е.
Рассмотрим сначала множество К для евклидовой нормы, т. е..
Тогда
где
следовательно,
(8.10)
Возьмем в качестве xt вектор
Xi=fi,
1
тогда
Следовательно, знак равенства в (8.10) достигается
11Л1=(2я)''-.
(8.11)

8.2]
М АТ ЕМ АТ И Ч Е С К АЯ Ф О РМУ Л И РО В К А
351
Рассмотрим теперь множество К, когда норма в Ет задается фор¬
мулой
|| х || = Мах ! Xi j,
где
тогда
!/(*)! =
Следовательно,
| ^ (2 | fi\ ) Max ** = (S I fi I) II
= SUP	<2l/»'l-
хфО IIх II	i
Равенство достигается, так как при
sgn fi, fi ф о,
xt =
имеем
О fl = 0
i/Mi=Si/*i=(Sl/il)il-»i
и, таким образом,
li/ll - 2 т
i= 1
В первом случае, когда норма задавалась равенством (8.11), множество
К будет не пусто тогда и только тогда, когда
' П у 12
2 с? =sSL.
Д = 1	/
Множество К определяется как
K={f:fi = Ci, 1	2	Л<19-(2^|.	(8.12)
П + I	1
Во втором случае К не пусто тогда и только тогда, когда
2
i = 1
и множество К задается как

358
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ
[ГЛ. 8
Если норма ||/|| задана, тогда множество К еще более ограничи¬
вается условием, которому должны удовлетворять функционалы
т	п
Ц Л = 11/II2— 2 с?	(8.14)
* — П -|- 1	I	=	1
ИЛИ
т	п
2	|/Н = 1!/||-1><|.	(8.15)
i= п-\- 1	I	=	1
Условия (8.14) и (8.15) определяют подмножества множеств К и
Сами множества К и К' можно рассматривать как множества
достижимости R, определение которого было дано в предыдущем па¬
раграфе.
Рассмотрим теперь вопрос, достижима ли величина у для неко¬
торого х ^ Еу если
f{xi) — ch 1 ^ ^ пу
и ||/|| задана. Это имеет очевидное приложение к задаче на мини¬
мум энергии. Если .г принадлежит подпространству, натянутому на
векторы {Ху, ..., хп)у то тогда
п	п
х = J] hxt, f(x) = 2 hct,
1	I
и, следовательно, мы решим задачу, выбрав ^ и какое-либо / из К',
так чтобы удовлетворялось условие
t Ьа=У-
i= 1
Если же векторы х и {хь ..., хп) линейно независимы, то будем
обозначать х через хп+{. Возникает вопрос: для каких величин у
выполняется
f(Xn+i) = y>
если / принадлежит К'?
На этот вопрос мы ответим позднее, когда будем рассматривать
линейные функционалы на произвольном линейном нормированном
пространстве (не обязательно конечномерном). Чтобы это сделать,
удобно обсудить сначала задачу Б.
Во-первых, заметим, что в равенстве (8.5) инфинум достигается,
поэтому его можно заменить на минимум, а супремум в (8.7) на мак¬
симум.

8.21
MAT E M AT И Ч E С К АЯ ФОР М У Л И Р О В К А
359
Чтобы доказать это, возьмем последовательность	векторов
из Ew l[i) = (^ \ ... , таких, что
-тг- = lim
i -> оо
2 у*,
(8.16)
№с=1,	/=1,	2,	...
Через {л:(0} обозначим последовательность элементов из Е, где
= ^ +	+	... + ЧЬхп (/ = 1, 2, ...);	(8.17)
jCi, ...> хп заданы. Вследствие линейной независимости xh ...,
любому вектору х из Еп соответствует единственный вектор х, при¬
надлежащий линейному подпространству G пространства Е и наоборот.
Легко видеть, что это взаимно однозначное отображение G на Ет
непрерывное в обе стороны, т. е. G и Е гомеоморфны [37]. Следо¬
вательно, компактность [26, 37) сохраняется. Любое ограниченное
множество в G является компактным. Последовательность {х^}, оче¬
видно, ограничена, следовательно, существует такая подпоследователь¬
ность	которая	сходится	к некоторой точке х°:
lim (?(«') J:, +... +W =	+-	+ ?°Л	(8Л8)
V —► оо
Из (8.16) и (8.18) получаем
1= lim ||^U!| = ||^0jc||.	(8.19)
V —*• оо
Из линейной независимости хъ ..., хп и из равенства (8.18) следует,
что
К= lim Ш ]= 1, 2, п,
^	/'	   пг\	J
Таким образом,
lim с = %° с = 1.
(8.20)
Из (8.7) легко видеть, что функция Х(сь ..., ^удовлетворяет усло¬
виям
а)
Х(с1( ..., с„)>0, если У)с|>0;
1 = 1
б)	i(tch	...,	tcn)	=	\t\\(cu	...,	сп);	(8.21)
в)	•••»	сп	“Ь	сп)	^	X	(сь	...,	Сп)	х	(cv	Сп).

360
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ	[ГЛ.	8
Если вспомнить ход рассуждений в задаче оптимального быстро¬
действия, то станет ясно, что понятие достижимого множества, т. е.
множества функционалов, удовлетворяющих заданным условиям, явля¬
ется основным понятием, используемым для определения оптимального
управления. В связи с этим очень интересно исследовать следующий
вопрос: будет ли выполняться неравенство	..., сп) при
условии ||/||^L, если к {хь ..., хп} добавить erne один линейно
независимый элемент_у из Е? Элементу можно обозначить через xn+i
и рассматривать (п -j- 1)-мерную задачу:
f(Xi) = ch 1= 1, 2, ..., пЛ
f(y) = %	(*-22)
WtW^L.	)
Это возможно тогда и только тогда, когда
X {С\у . . . , Сп, Tj) L.
Таким образом, мы приходим к множеству Кп+v
К'п+\ = {(сь сп, rj :X(clt сп, 1] )*£/.}
или в общем случае
Кт =z {(^1) • • • > ст) • ^ (0> • • • > Cm) 1 }•
Ввиду (8.21) множество с таких, что Х(сь ..., ст)^;£, может быть
получено из Кт растяжением его с помощью параметра t. Таким об¬
разом, в этом параграфе предполагается Х(с1? ..., сп)= 1 и L^> 1.
Из равенств (8.7) и (8.8)
Мах
Ее н
2]
i= I
где
/ п \Ч 2
М = Мах у.
с 6 // \£ = I '
(8.23)
Константа М не зависит от с, поэтому
X (^1, ..., сп)
/ я
Следовательно, X— непрерывная функция аргументов с1у
а содержит евклидову сферу радиуса
Определим константу ji как
jj. = Min
21 bet
i = 1
2 = U
i= 1
(8.24)

82]	МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА	361
Из (8.24)
'"^±Х(С1, сп) = 1.
Таким образом, Кп содержится в евклидовой сфере радиуса
Из (8.21) следует, что Кп выпукло. Следовательно, Кп есть огра¬
ниченное замкнутое выпуклое множество и оно имеет внутренние
точки.
Отождествляя каждую точку (сь ..., сп) £ Еп с точкой (сь ...
сПУ 0, ..., О) (^ Ет (т^>п)у имеем
Х(сь ..., cn)^\(ch ..., ст)у т^>п.
Если (с1у	ст)(^Кт> тогда Х(сь ..., сл)^1, следовательно,
проекция Кт на Еп содержится в Кп. Чтобы показать, что каждая
точка Кп является проекцией некоторой точки Кту обратимся к до¬
казанному выше предложению, что существует функционал, для ко¬
торого
f\Xi) = Ci (i= 1, 2, ..., п),
\\f\\=l{cly О.
Положим с)г
Ck = f(Xk)	(Jz = n-j-1, ...,	m).
Тогда так как X(сь ..., ст с’п+1у ..., с'т) есть минимум нормы, то
1	X (б*1,	Cfj) — JI f || X (^i, ..., сп,	..., ст).
Это доказывает, что проекция Кт на Еп(т^>п) совпадает с Кп.
Следовательно, найдется такая точка Р = {сь ..., сПУ с„+1), что
X(q, с^) = \(сь ..., сПУ с°п + 1)=1.
Это есть точка из К'п+\. Таким образом, прямая линия ru = ciy i =
= 1, 2, ..., п, проходящая через точку Ру дает в пересечении с K'n+i
замкнутый интервал
Ъ = Ch	-	1,	•	•	•	,	Л,	Г{^Г\^ 7]".
Если т] = 'г{ или т| = т", то равенство (8.22) выполняется при ||/|| = А.
Таким образом, неравенство удовлетворяется только для т] из [ч/, tj"J
Х(с1(	,	сп,	TTj)<L.
По основной теореме для каждого т], удовлетворяющего выше
приведенному неравенству, существует / из £* такое, что выпол¬
няются условия (8.22).
С помощью аналогичных рассуждений доказывается следующее
утверждение: если х1у ..., хп, у1у ... у ур — линейно независимые

362
ЛШНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ
[ГЛ. 8
элементы из Е и а(сь ..., cn)<^L, то множество точек (та, т]р),
для которых
и ||/|| образует /7-мерное выпуклое множество в Е*. Из этого
утверждения следует, что если размерность пространства Е больше,
чем п -}- 2, то для любого L^>X(ch ..., сп) задача
имеет континуум различных решений, так как граница /7-мерного
(р^> 2) выпуклого множества решений (п -j-/?)-мер ной задачи имеет
континуум различных точек. Этот вопрос о единственности имеет
важные приложения в теории аппроксимации, которую мы коротко
рассмотрим ниже.
Итак, связь между задачами А и Б кратко можно выразить сле¬
дующим образом: минимизирующий элемент задачи Б является экст¬
ремальным элементом задачи А' (или экстремальным элементом ли¬
нейного функционала минимальной нормы, удовлетворяющего равен¬
ству (8.3) в проблеме А), и наоборот.
Доказательство. Пусть /0 — решение проблемы А с мини¬
мальной нормой, т. е.
Следовательно, х0 является экстремальным элементом функционала /0.
Экстремальным элементом называется такой элемент, который соот¬
ветствует равенству в определении нормы функционала. Обратно, если
Xq — экстремальный элемент для /0, то тогда, читая эти неравенства
в обратную сторону, видно, что х0 есть минимизирующий элемент
задачи Б.
f(xi) = ciJ i= 1, 2, ..., /z,
/\У /г) ==	^	==	•••	у	Pi
f(Xi) = ch i= 1, 2, ..., п,
\\f\\ = L
fo(Xi) = Ci, i= 1, 2, ..., n,
||/oll = 4o> ••• , cn\
и пусть x0 — решение задачи Б, т. е.
п
1
тогда

8.3]
ПРИЛОЖЕНИЕ К ЗАДАЧАМ ЧЕБЫШЕВСКОЙ АППРОКСИМАЦИИ
363
8.3.	Приложение к задачам чебышевской аппроксимации
Рассмотрим приложение L-проблемы для приближенного в смысле
Чебышева решения несовместной системы линейных алгебраических
уравнений. Задача чебышевской аппроксимации хорошо изучена и
имеется большое число работ, посвященных этому вопросу [1, 9, 30, 31].
Потребовалась бы отдельная книга, чтобы рассмотреть проблему
полностью. Поэтому мы остановимся на связи чебышевской аппрок¬
симации с L-проблемой, рассмотренной в предыдущем параграфе. Эта
задача может быть сформулирована следующим образом. Даны
ааЛг -f... 4- а',£п = 1\	/	=	1,2,...,	т\
(8.25)
найти 5 = ;i,
такие, что
Min
1 yfe п
Мах ^ ЯД/ — Л = е.
(8.26)
Величина е является минимумом максимума абсолютной величины
ошибки в уравнениях (8.25). В формулировке этой проблемы без по¬
тери общности векторы (V., а?, ..., аи (/l, Р, ..., 1т) линейно
независимы.
Покажем, как можно применить теорию, развитую в предыдущем
параграфе, в данном случае. Обозначим
i	Л
ап -|-1 —	I.
Уравнение (8.26) можно записать как
Min Мах
7)	1	<	I	<	Г
п 4-1
2 aft
; = 1
при условии
где
п 4- 1
S СМ = !>
< = I
-Ч
Jl
• • • У rln+i)f
i
i= 1, 2, ..
., n,
Чя+1 = 1»
1!
o
1= 1, 2, ..
n>
Oz+l
(8.27)
(8.28)
(8.29)

364	МИНИМУМ	НОРМЫ И МЕТОДЫ ОПТИ/МИЗАЦИИ СИСТЕМ	[ГЛ.	8
Рассмотрим (п-1-	I) линейно независимых векторов из	Ет
л=(а!> 4 •••> аГ)	|
:	}	(8.30)
Лг +I ~ (ая + I’ а/’г + 1’	йп+\) j
Пусть у является	линейной комбинацией уь ..., yn_vX
У = ЪУг -h-. + 'WiJ-Wi.	(8-31)
так что условие (8.28) выполняется. Тогда /г-я координата ук век-
тора у записывается как
п-\- 1
/ = 2 a!l4 (/е = 1, 2,	т).	(8.32)
i = I
Заметим, что равенство (8.32) имеет ту же самую форму, что и ра¬
венство (8.27). Определим норму в Ет как
II .у 11= Мах 1У1-	(8.33)
1 < г < гг
Так как линейные функционалы, заданные на Ет, являются элемен¬
тами сопряженного пространства Е%у которое также является т-мер-
ным пространством [22], то эти функционалы единственным образом
определяются заданием т чисел /\ ..., fm
т
Пу)='£ГУ•	(8-34)
i= 1
Таким образом,
= sup
I/O')!
=2 i^i- (8-35>
v€i? II Tl!
-Г/?1	г'=1
Итак, уравнение (8.26) может рассматриваться как проблема А, т. е.
как задача нахождения функционала / минимальной нормы при уело-
виях f(yi) = ci (/=1, 2,	«4-1):
т.
е=М1п2|/‘|	(8.36)
;= 1
1Д |	2/2 I	I	171	гЩ
а\/ ~г a\f Н“• • • |	1 f =	с\
\	(8.37)
ап+ \f -|- ап + if 4“ • • • ~i~ ап + \ f == Сп + I

5.3] ПРИЛОЖЕНИЕ К ЗАДАЧАМ ЧЕБЫШЕВСКОЙ АППРОКСИМАЦИИ
Таким образом, если ранг матрицы
365
1
flj .
1 z1
• • &п — 1 1
тп
ах .
£
.. ^
1
£ е
сз
есть п(п<^т), тогда из (8.28) и (8.37)
г = Min Max J а[гл -j-... апт1п — /'
7;	1	<	1<	Л
Решение этой задачи сводится к решению задачи
тп
е= Min 2 |/'|
1=1
при условии
тп
2 ^' = 0, /=1,2,
(8.38)
i= 1
2 ilf=-1.
Для того чтобы найти минимизирующее £ в уравнении (8.26), пред¬
положим, что вектор /0=/J, /q, .для которого достигается
|| /о |! = е и /о 9^ 0, z = 1, 2, ..., /я, а г — экстремальный элемент.
Тогда
1/о(А! =
= (21/о1 (Мах|гг|)=||/„!||И|,
следовательно,
2f = AsgIl/‘, /=1,2, от.
Таким образом, для некоторой константы
ТП
ш=к 2 |/ol-
i=i
С другой стороны, так как экстремальный элемент z равеи
я+ I
^=2
(8.39)
(8.40)
i= 1
при
п+ 1
2 <Т»1г = Ь
1=1

366
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ [ГЛ. 8
ТО
/о 0)=/о (2 W) = 2 С л, = 1.	(8.41)
Учитывая (8.40), (8.41) и (8.38), получаем
k  ! =1
т	£	*
2 \Л\
г=1
Из (8.39), (8.41) и предыдущего равенства получаем уравнения для
нахождения rlh ..., т|я+1
п. -}- 1
■7 sgn /о = 2 аЯ> г’ = ь 2> • • • >	(8-42)
/=|
Переходя к исходным обозначениям по формулам (8.29), равенство (8.42)
принимает вид
аП1 Ч" fl2^2	* * • “1“ ал^/г — / = -■-* -----	(8.43)
(/= 1, 2, ..., /и).
Если п = т, то сь ..., определяются из (8.43) единственным об¬
разом.
8.4.	1-проблема и задача аппроксимации в линейном
нормированном пространстве
В этом параграфе мы покажем связь между некоторыми задачами
оптимизации, сформулированными в терминах /.-проблемы, и задачами
аппроксимации в линейном нормированном пространстве [1]. Рассмот¬
рим L-проблему в некоторый момент t из [0, Т]
M£in I 2 ^ (*)	(8-44)
0< г< п 1
при
2^,(Г)=1.	(8.45)
г = 0
где hi(t) — система весовых функций, а с((Т) задано, / = 0, 1, ..., п.
Так как не все ct{T) равны нулю, без потери общности можно счи¬
тать, что с0(Г)^0. Тогда из (8.45)

8.51
АППРОКСИМАЦИЯ В ГИЛЬБЕРТОВОМ ПРОСТРАНСТВЕ
367
Подставляя (8.46) в (8.44), получаем
п
п
2 г(М9=®о(9— £ ^(0.
где
и
Таким образом, задача на условный минимум (8.44) и (8.45) све¬
лась к задаче безусловной минимизации по Si,'..., 1п выражения
Так как все срг в выражении (8.47) известны, то величины St- должны
быть выбраны так, чтобы минимизировать расстояние между точкой ср0
и линейным подпространством, натянутым на элементы срь ..., срл, дру¬
гими словами, Qi, /= 1, 2, ..., п, и есть ближайшая к ср0 точка из ли¬
нейного подпространства, натянутого на векторы срь ..., срл. Это есть
общая формулировка проблемы аппроксимации в линейном нормиро¬
ванном пространстве. Так как в (8.47) ср являются функциями времени,
то S будут также функциями времени.
Если в пространстве введено скалярное произведение и в терми¬
нах этого скалярного произведения определена норма, т. е. если
пространство является гильбертовым, то тогда можно получить точ¬
ное выражение для ошибки аппроксимации.
Пусть ср — наилучшая аппроксимация
п
Min /о — Д] ?г®£ .
(8.47)
8.5.	Аппроксимация в гильбертовом пространстве
и определитель Грама
Р= Min ||?0— С?||,
(8.48)
где
п
(8.49)
i = 1
а ср, срь ..., ср„ заданы.
В этом случае пространство является строго нормированным [1]
(см. § 8.6) и существует единственная наилучшая аппроксимация,

368	МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ [ГЛ. 8
которая является ортогональной проекцией ср0 на линейное подпро¬
странство, натянутое на элементы ср,, срл	из	Н.
Так как ср0 — ср ортогонально к срь /= 1,	2,	я,	то
(?о — Ъ <Рг) = °.	*=1> 2> •••> п•	(8*50)
Из равенств (8.49) и (8.50) получаем систему линейных алгебраи¬
ческих уравнений для определения Xt
п
2 XA?i. <Р/) = (?о> ?/)>	/=1,	2,	...,	п.	(8.51)
i = 1
Пусть
GOPi. •••> ®n) = det[(cs,., сру)].
Определитель G называется определителем Грама [1] и не равен
нулю, так как cpt-, /= 1, 2, п, линейно независимы. Из (8.48)
Р2 = (?о — ®> ?0 —<р) = (?о —<Р> ®о) — (?о — ®> '■?)== (®0. ?о) —(<р, ®о)-
Следовательно,
(<?. <Ро) = (<Ро> <ро) — ра-	(8-52).
Соотношения (8.51) и (8.52) составляют	(n-f	1) уравнение
с (я—|—1) неизвестным Хь ..., Хп и р.
В результате решения
о _£/(?!, ..., Уп, ср0)
G(olf <?п)
Если вместо подпространства, натянутого на п независимых эле¬
ментов из /У, рассматривать множество HnCLH
П	j
2 а-Мь |аг|^аД
для некоторых заданных аь ..., ал, задача становится задачей аппрок¬
симации при ограничениях
Min ||ср0 —ср||,
*6Нп
и уже неверно, что наилучшую аппроксимацию дает ортогональная
проекция ср на /У.
Проблемы аппроксимации в задачах оптимального управления
обычно относятся именно к этому типу [6, 7, 8, 10, 12, 13].

8.6]
ЕДИНСТВЕННОСТЬ ЭКСТРЕМАЛЬНОГО ЭЛЕМЕНТА
369
8.6.	Единственность экстремального элемента
и наилучшая аппроксимация
Ввиду тесной связи L-проблемы с проблемами аппроксимации можно
ожидать, что условия существования и единственности, близкие к ска¬
лярному условию существования экстремальных элементов в L-проб¬
леме, будут подобны условиям единственности наилучшей аппрокси¬
мации в задачах аппроксимации. Необходимым условием единственности
наилучшей аппроксимации является условие строгой нормированное™
пространства. Нормированное пространство Е называется строго нор¬
мированным, если для любых не равных нулю элементов х, у из Е
равенство в условии
1*+уЫЫ+Ы
достигается тогда и только тогда, когда
х=ау или у — ах, а^О.
Чтобы это доказать, допустим, что
/I	п
2 Х*'?г и 2 Х-:?г
1=1	1=1
— две различные наилучшие аппроксимации элемента ср0 в строго
нормированном пространстве Е (ср£ линейно независимы), т. е.
Без ограничения общности можно предположить, что р ф 0 так
как в противном случае из линейной независимости имеем
—- a I,	i — 1, 2, ..., 11.
Рассмотрим ошибку аппроксимации элемента ср0 элементом
71
п
?о— S X«'®^
1=1
=
®о— 2Х‘:,:Рг
i= 1
У h±R9.
/.	9	•**
С одной стороны,
а с другой стороны,
п 4- Е.
То ■
2
• ср.
То
- >
р хг + хг
i = 1
То
_ V>.,J
z_. 1 • ■1
То

370	МИНИМУМ	НОРМЫ	И	МЕТОДЫ	ОПТИМИЗАЦИИ	СИСТЕМ	[ГЛ.	8
Следовательно,
v X« + Xi
р= сро— £—2	’
i
и из строгой нормированности Е следует
Константа а= 1, так как в противном случае ф0 являлось бы линей¬
ной комбинацией срг и р = 0 вопреки сделанному предположению.
Так как а = 1,
S (х« — xi) <Р; = о.
i
Следовательно,
—	/==	1,	2,	, п.
Пусть в L-проблеме и х2 — линейно независимые элементы
такие, что
|| *1 + X* || = ||*1 || + II *2 1-
Пусть /—линейный функционал, для которого (JCi —|— jc2) является
экстремальным элементом. Тогда
| /(* 1 -Г *2) I = II/ IIII *1 + *2 II = II /|| II *1 II + II/IIII *2 11-
Так как
I /(* 1 -г *2) i ^ I /(* 01 +1 /(*2) I ^ Ц/|| || *11| +1|/1| || *21|>
получаем
|/(*i)l =11/111*1 II и |/(*>)! = 1/11*4
Таким образом, если Е строго нормировано для любого линейного
функционала, на Е не существует двух линейно независимых экстре¬
мальных элементов.
Какие пространства являются строго нормированными простран¬
ствами? Из неравенства Гёльдера видно, что Lp(a, b) при (р 1)
все являются строго нормированными.
Однако L(ci,b) и с {а, Ь) не являются строго нормированными,
как показывают следующие примеры [1].
Возьмем x(t) и y(t) из с[а,Ь]*) так что х(£)фу(£), но
шах | х (f)\=x (а) — max \v(t)\=y (а),
t	t
*) с [<2, Ь] = х\ х (t) непрерывна для всех t на [д, Ь\.

8.7]
ВВЕДЕНИЕ
371
тогда
И-к+зМММЖИ-
В L (а, Ь) зададим х и у следующим образом:
1, b^t:
x(t) = <
2
у(<) = 1 — Л'(О,
тогда
I Н~ т II—$ I Н- т I^ ^ — а>
ь—а
и= \
а
Ъ
I.y|l= J \у'
а
b
x\dt = -
dt-.
Следовательно,
но
II *+.v II—IMI + II-H
x(t) Ф ky(f).
Так как пространство не является строго нормированным, задача
аппроксимации в этих пространствах, вообще говоря, не имеет един¬
ственного решения. Рассматривая достаточно ограниченный класс
функций, можно снова восстановить единственность аппроксимации.
Такой пример рассмотрен в [10].
РАЗДЕЛ II
ПРИБЛИЖЕННОЕ РЕШЕНИЕ ФУНКЦИОНАЛЬНЫХ УРАВНЕНИЙ
8.7.	Введение
Часто уравнения, определяющие поведение оптимальной системы
или само оптимальное управление или то и другое вместе, бывают
слишком сложны, чтобы можно было получить готовое аналитическое
решение в замкнутой форме. Методы итерации или методы последо¬
вательных приближений также довольно сложны.

\т
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ
[ГЛ. 8
В таких случаях для нахождения поведения системы, близкой
к оптимальной, или приближенного оптимального управления или
того и другого вместе используют другое уравнение, которое аппро¬
ксимирует в некотором смысле исходное уравнение. Этому типу
аппроксимации и посвящен данный раздел.
8.8.	Обратный оператор
В качестве примера рассмотрим приближенный метод нахожде¬
ния обратных линейных операторов [3].
Пусть А — несингулярный ограниченный линейный оператор с
областью определения и множеством значений из полного линейного
нормированного пространства X.
Рассмотрим процедуру образования последовательных приближе¬
ний оператора Л-1 и вычислим ошибку каждого отдельного прибли¬
жения.
Пусть Rx— первое приближение такое, что
|| 1—АЪ\\ = е<\,	(8.53)
где 1—единичный оператор в X.
Образуем	последовательность {/?„}, элементы	которой	опреде¬
ляются следующим образом:
= Rn (/ -I- тК -'),	(8.54)
где
Тп = {1 — ARn) п= 1, 2, ...,	2;
тогда
I-ARn,y=Ti = {l — ARn)p,	(8.55)
и, итерируя (8.55), получаем
I—ARnt = (/ — ARx)prl.	(8.56)
Таким образом, точность улучшается с ростом степени р.
Определяя	ошибку для каждого Rn как
en = \\A-l — Rn\ | л 35 1,	(8.57)
из (8.56) находим
A-' —Rn.{ = Л"1 (/ — AR^.	(8.58)
Таким образом,
*л+1 = | Л "1 - Rn+l |] < || Л'11|	(8.59)
Так как Л	1	точно неизвестно, то лучше выразить	оценку	ошибки
через /?!. Для	того чтобы это сделать, из (8.58)	и	определения Тх

8.81	ОБРАТНЫЙ ОПЕРАТОР	373
найдем
A '=Ri(I—Ti)-1.	(8.60)
Следовательно,
I! л-1 II < 1R, I!!! / — тх j-' =ss -[	.	(8.61)
Из соотношения (8.59) и (8.61) получаем оценку ошибки
«=1,2,...	(8.62)
В качестве	приложения рассмотрим частный случай.	Пусть X—
гильбертово	пространство И и Д—положительно	определенный
самосопряженный оператор в Н.
Тогда А имеет положительные собственные числа m и М такие,
что
пг (х, х) (Ах, х)^М (лг, х)	(8.63)
для любых х Н. Рассмотрим
Rx = а/,	0	<	а < 2/М,	(8.64)
тогда
е = \\ I — ссД |].	(8.65)
Чтобы показать, что е<^\, введем оператор Та
Та=1— аД.	(8.66)
Тогда
<? = 1ГЛ-	(8.07)
Из (8.63) и (8.66)
1 — у.Л'1	(2'V-	=sS (1	— а/и).
(х, х)	4	>
Следовательно,
Л4 ш  . и	II	1	г\	/	/	2
тгп ^ Та I ^	1	для	0	<С а <" -гг
М + m 11	а 11	^	^	М
2
и минимальная норма достигается при а=-^-^——. Из (8.62)
£
—	л=1,	2,	...
Чтобы ускорить сходимость, начальную величину е возьмем равной
М — m
6 M+mt
что достигается при

374	МИНИМУМ	НОРМЫ	И	МЕТОДЫ	ОПТИМИЗАЦИИ	СИСТЕМ	[ГЛ.	8
8.9.	Сходимость приближенных решений [20, 38]
Пусть 7 — заданный оператор в метрическом пространстве X и
7*—его аппроксимация. Например, 7 может быть обратный опера¬
тор, а 7*—его аппроксимация в виде степенного ряда. Более точно,
предположим, что Т и Т* имеют одну и ту же область определе¬
ния D в Ху и существует положительная константа в такая, что
|]7* —7**[<в	(8.68)
для любого	х	из	D.
Предположим, что задача
Тх — х	(8.69)
может быть приближенно решена, если решена задача
Т*х = х.	(8.70)
Предположим, что 7 есть сжимающее отображение
I TXi — Тх% || ^ к II х{ — х21|,	0	< к < 1,	(8.71)
так что метод итераций может быть использован для решения (8.69)
хп,л=Тхп, п = 0,	1,	...	(8.72)
Для	того	чтобы	делать	вывод о поведении	последовательности \хп)
по поведению {х%}
Хп +1 — 7 * хП)	x^ — Xq,	(8.73)
необходимо исследовать ошибку \\хп—	х%\ на каждом шаге итерации.
Положим
 'J Хп -^/z +1 ||> ^п z— || Хп	+1Ц	((^*74)
И
Еп = \\хп — х%\	Е0 = 0.	(8.75)
Из (8.75) и (8.68)
Еп., 1 = I Тхп — Т*х% J sS\Тхп — Тх% I -f-1 Txt — Т*х% ||	kEn -|- s.
(8.76)
Из (8.76)
Еп+1 ^ кп+ 1Е, + {kn + кп-1 +... + 1) е ^	=	Ь	(8.77)
для всех п. Таким образом, ошибки остаются ограниченными.
Пусть
К = [v :\х- х, I	rf0}.	(8.78)
Тогда, так как
II Хп — Л-, II T^-J d0	(8.79)

8.9]	СХОДИМОСТЬ ПРИБЛИЖЕННЫХ РЕШЕНИЙ [20. 38]	375
для всех п, то х% принадлежит к S-окрестности К для всех п.
Для	любого х К
II х — xf II II х — Xi II + II х, — xf II С j^—k d0 + Eh
do = I x0 — Xi I ^ || x% — xf I + [I xf — ЛГ1 j| = df + Ei
И
Ei —1| xt — Xi j! = |j T*x0 — Tx01| <[ e.
Следовательно,
il x-*4 < bLft ^ + e) + e = 7=* + 8-	(8-80>
Положим
К* = {* : IIX — Xi II < T-^ d* -j- 3}.	(8.81)
Так как К* содержит К9 из (8.80) следует, что если D содержит
S-окрестность /С*, то тогда х% G D для всех п' ^Усть
^я = ||лг* —	(8.82)
где Тх = х. Рассуждая так же, как и при выводе соотношения
(8,76), имеем
C/V+1 ==	~Н || Тх— Тх% |] ke—j— S.	(8.83)
Итерируя (8.83), получим
eN+m^kmeN-\- е(1	.	.-f-Lm	_1),
но
eN = || Х*ы—Х || ^ || X%+ m — X 11 + || Х%+ m — X% IJ =
=== &N-f т ~Г II X'N-\- т	Хм ||,
следовательно,
(1 —ЬШ) ZN+m ^ km \Хм+т — ^)v||~f~ j ^
или
km	?)
eN+m<: f_ km II Х%+т —	+ ] _Zkm -	(8‘84)
Из (8.84)
d*=]	—	*;+11 < || r ** _ t — tx\ _, I +
+ II Tx*- J — 7** II +1 Tx% — T*x* II ^ kd% - x + 2s.	(8.85)
Итерируя (8.85), получим
d%^kNd* + 28.	(8.86)

376
ЛАП НИ МУ А\ НОРЛАЫ И ЛА FiTO IIЫ ОПТИМИЗАЦИИ СИСТЕМ	[Г'Л.	8
Гак как k 1 при всех с у 0, существует такое целое N, что
k"dt 2 с для	nyN.	(8.87)
Следовательно, из (8.86)
Д< 28*	(8.88)
где
8* = 5 -U с.
Применяя (8.88) к (8.84), получим
km	5
eN+m - rZTftm «28* + 1 _F •
Следовательно, для любого с<^0 и достаточно больших п
Сп ^ с 4- 0.
Из (8.82) видно, что последовательность {.*:„} в конечном счете
содержится в 8-окресгности точки х и, следовательно, имеет в ней
предельную точку.
8.10.	Квазилинеаризация
В этом параграфе мы исследуем возможность решения нелинейных
уравнений путем рассмотрения соответствующих линейных уравнений.
Это лишь один пример идеи решения задачи путем трансформации
ее в другую задачу, решение которой затем преобразуется так, чтобы
получить требуемое решение. Эта идея, очевидно, очень важна
и является предметом многих обширных и разнообразных исследо¬
ваний. Так как нельзя рассмотреть даже очень коротко все аспекты
этой темы, мы сконцентрируем наше внимание на квазилинеариза¬
ции [15, 23] и на родственном вопросе положительности операторов [15].
Но и в этом случае в короткой заметке невозможно изложить все
относящиеся сюда факты.
Хорошо известный метод последовательных приближений является
сжимающим отображением [26] и используется, кроме многих других
приложений, для доказательства теорем существования и единствен¬
ности решений для некоторых типов алгебраических, дифференциаль¬
ных, интегральных и других уравнений.
Существует другой вид метода последовательных приближений,
известный как квазилинеаризация.
Рассмотрим аналог ньютоновского метода приближения для диф¬
ференциального уравнения [17]
=	0.	н(0) = с.	(8.89)

8.10]
КВАЗИЛИНЕАРИЗАЦИЯ
377
Предположим, что производная от g(u, t) существует
/ф> 0 = ^ («. о
(8.90)
и непрерывна и монотонно возрастает по и для 0 ^ t tQ. Тогда
схема последовательного приближения дает
=	0	+	(«о	—	^о)	h	(•%	0.	Мо(0)	=	с,
dun +1
:g(«/z> 0 + (ИЛ+1 —	0»	W/i	+	l	(0)=	С,
/2 = 0, 1, 2, ...,
(8.91
где Vo(t)—известная функция времени, непрерывная на [0, £0],
Исследуем один типичный шаг итерации
dw
~dr = s(v> t) + (w — v) h (v, t), w (0) = c.
(8.92)
Пользуясь соотношением
g(v, f) + (w — v)h(v, t)^g(V, t) -]— (w V)h(V, t\ (8.93)
где V—функция, минимизирующая левую часть (8.93), сравним
w — решение уравнения (8.92), и W, определяемое как
d\V
dt
= g(V, t) + (W- V)h(V, t\ W(0) = c.
(8.94)
Чтобы установить соотношение порядка между решениями урав¬
нений (8.93) и (8.94), полезен следующий факт.
Если
d у
— ==a(t)x-Jrb(t),	х{0)	=	с,
-^&za(t)y + b(t), у (0) = с,
то тогда
x(t)^y{t).
Это следует из положительности ядра ехр
^ а (г) dr
(8.95)
(8.96)
(8.97)
, которое появ¬
ляется в выражении для у (t)y если (8.96) переписать в виде
y- = a(t)y-\-b{t)-\-f{t), /(ossO.
(8.98)
Из неравенства (8.93) следует, что решение уравнения (8.92) мажо¬
рируется решением уравнения (8.94), и из (8.97) мы получаем
w(t)^W{t).	(8.99)

378
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ	[ГЛ.	э
Гак как, по предположению, g(u, t) строго выпукла по я, то
g(и, t) — Max [g (г>, t) -j- (U — v)h (v, t)].	(8.100)
V
Если отождествить w из соотношения (8.93) с ип+1 в уравнении
(8.91), то 1/ будет соответствовать ип. Таким образом, W в (8.94)
соответствует в уравнении (8.91). Из (8.99)
W/z+2	^/г	+	1>	Я	=	0,	1, 2,
так же как
и\ ^ Wo-
Таким образом,
щ (0<«! (*)<•••
на общем интервале существования.
Следовательно, сходимость доказана благодаря равномерной огра¬
ниченности {un(t)).
В скалярном случае, который только что рассматривался, при
доказательстве основного соотношения (8.97) мы пользовались тем,
что при любом a(t) ядро всегда положительно. В векторном случае
это уже неверно. Рассмотрим
х(0) = с,
ЧГ^АУ' JT°) = c’
где су х и у — я-мерные векторы и А — постоянная матрица п\п.
Следует ли отсюда, что	Или,	что эквивалентно, следует
ли из
х(0) = 0, что x(t)^ 0?
Так как
t
x(t) = ^eA(t~-s) f(s) dSy
о
где
£jL = Ax + № х (0) = 0,
то неравенство x(t)^ 0,	0,	зависит	от	положительности ем, кото¬
рое уже не всегда положительно, если А — матрица. Достаточным
условием для положительности ем является aLj ^ 0, i ф /, и atj дейст¬
вительны.
Связь между положительностью оператора и методом квазилинеа¬
ризации теперь ясна. Сформулируем задачу в общих терминах.

8.10]
КВАЗИЛИНЕАРИЗАЦИЯ
379
Пусть и — решение нелинейного уравнения, определено на D
I {и) = /(«, х), х £ D,	(8.101)
где L — линейный оператор, определенный на Д a D — замкнутое под¬
множество пространства Еп я-мерного евклидова пространства. Мно¬
жества значений L и / принадлежат метрическому, частично упоря¬
доченному пространству. Пусть /—непрерывная по (к, х\ дважды
дифференцируемая по и и строго выпуклая (т. е. /"^>0) функция
от и для всех конечных значений и и всех х D. Функция f(u, х)у
следовательно, удовлетворяет равенству
f{u, а:) = Max [f(v, x)-\-{ii — v)fu{v, х)]	(8.102)
v
для всех х D.
Предполагается, что граничные условия таковы, что решение
уравнения (8.101) существует и единственно. Без потери общности
граничные условия можно взять в виде
и = 0 для х £ dD,
где через dD обозначена граница D.
Так как максимум в (8.102) достигается при v = u, класс допу¬
стимых функций v может быть ограничен некоторым классом 5,
включающим и. Множество S должно быть выбрано так, чтобы v
было достаточно гладким, чтобы обеспечить существование и единст¬
венность решения для каждого допустимого v в уравнении
I (w) =f\v, x)-\-(w — та) /и (v, х).	(8.103)
Обозначим решение через
w = w[x; v].
Заметим, что для v — u
w[x\ и] = и.	(8.104)
Пусть свойство положительности удовлетворяется для оператора
уравнения (8.103) при всех х из D и при всех v из 5, т. е. если
L(z)— fu(v9 x)z^ 0 для каждого х D и каждого v(^-S и z = 0
для вcexx^dD, то тогда г^О. Сравнивая решения уравнений
(8.101) и (8.103), получаем как следствие свойства положительности,
что
и ^ w \х\ v\, х	Д
и
u = w\x\ г»], х	dD.
Таким образом,
и ^ Max w [х', v],
v £ S

380
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ [ГЛ. 8
из (8.104)
и = Max w [х; тф х ^ D.	(8.105)
v £ S
Как и прежде, уравнение (8.103) может быть использовано для
образования последовательности ип(х), которая монотонно сходится
к и, определяемому равенством (8.105).
Если / вогнуто (т. е. /"	0), а условие L(z)— fa(V> x)z^c0
на D означает, что z^0 на Д тогда операция максимизации в (8.105)
заменяется на минимизацию. Таким образом, итеративная процедура,
основанная на квазилинеаризации, при сформулированных предположе¬
ниях обладает очень важным свойством монотонной сходимости, т. е.
постепенно увеличивающейся точности. При подходящих условиях,
наложенных на функцию / и ее производные, можно показать, что
сходимость квадратичная. Это значит, что существует такая константа /г,
что для достаточно больших п выполняется
I I’n+i — I'n II	/г 1 ип — ип_ 1II2.
Это является определенным преимуществом по сравнению с обычным
итерационным методом Пикара, сходимость которого лишь линейна.
Мы видим, что метод квазилинеаризации может быть использован
для получения нестандартных представлений интересующей нас функ¬
ции, что дает новый подход к решению проблем.
В качестве примера такого необычного представления применим
квазилинеаризацию к стохастическому уравнению, изучавшемуся Велл¬
маном [18]. Он рассматривал
4£- = *(и)+г(Э,	и(0) = с,	(8.106)
где r(t) — случайная функция с заданной функцией распределения.
Пусть g(ii) дважды дифференцируема и строго выпукла по и,
так что имеет место
g (и) = Max [g(и) + (и — v)g/ (v)].	(8.107)
U
Рассматривая пару уравнений
^-=Мах (g (u) + (H — ^g'OOj-r г (9. и (0) = с (8.108)
И
^j- = g(v) + (U-v)g(v) + r<f),	U(0) = c, (8.109)
получаем
U(t; v)^u(t)
для всех V. Следовательно,
Вер [и ^ х] ^ Вер [ U(t; v) ^ х]

8.10]
КВАЗИЛИНЕАРИЗАЦИЯ
381
для всех случайных функций v и —оо а:	-{-	со,	где	u(t)— слу¬
чайная функция, являющаяся решением стохастического дифферен¬
циального уравнения (8.106), которое, по предположению, сущест¬
вует па [0, Т], Тогда для —со<^х<^оо и O^t^T
Вер [и ^ х] = Мах Вер [U(t, v)^x]	(8.110)
где максимизация производится по всем случайным функциям, опре¬
деленным на [0, Г].
Можно опять построить последовательность un(t), распределение
которой монотонно сходится к распределению и.
Напомним, что существует много других методов последователь¬
ных приближений, например метод, основанный на теореме о непо¬
движной точке в псевдометрическом пространстве [20] *) (сжимающее
отображение есть ее частный случай), метод ложного положения
и много других.
Дворецкий в [21] рассматривал метод неподвижной точки при
случайных возмущениях и исследовал сходимость его с вероят¬
ностью 1 и в среднеквадратичном. Подобный тип итеративных схем
известен под названием стохастическая аппроксимация [25] и бывает
полезен при оценке параметров в некоторых нелинейных задачах
управления, а также и в других проблемах оптимизации систем [19,
36]. Эти вопросы более детально рассмотрены в других разделах
книги * *).
Прежде чем закончить параграф, укажем, что применение квази¬
линеаризации вовсе не ограничивается последовательными прибли¬
жениями.
Она может эффектно использоваться для представления неко¬
торых нелинейных функций [16]. Простейшим примером может слу¬
жить
| х | = Мах ху, —1^_у^1.	(8.111)
Здесь нелинейная функция \х\ представлена как огибающая ли¬
нейных функций ху, —l^jy^l. Другим простым примером
является
Min (х, у) = min [срх	(1 — ср)jу].
0 ^ ср 1
Здесь снова нелинейная функция представлена как огибающая линей¬
ных функций.
*) Пространство, для любых двух элементов которого определена
псевдометрика р (.г, у), удовлетворяющая условиям
1)	2) + p(z, У),
2) x=y=z> р (лз у) = 0.
**) См. главу 10. (Прим. ред.)

382
МИНИМУМ НОРМЫ И МЕТОДЫ ОПТИМИЗАЦИИ СИСТЕМ [ГЛ. 8
Усложнения, которые появляются с введением операции максими¬
зации, оправдываются тем, что это может легко привести к решению,
которое другим способом получить довольно трудно, особенно в за¬
дачах, где удается эффективно использовать минимаксную теорему
[7, 11, 24].
Равенство (8.111) несколько более обшей формы [15] записыва¬
ется как
ср (х) = Max L (х, у),	(8.112)
Riy)
где L(x,y)— функция двух переменных, а <р(х)— функция от х,
определяемая равенством (8.112). Все свойства, которыми обладает
L(x,y) как функция от х, при всех у из R(y), являются свойствами
и ср (х). Если эти свойства легче доказать для L (х, у), чем непосред¬
ственно для ср(х), тогда представление (8.112) очень полезно.
ЛИТЕРАТУРА
1. Ахиезср Н. И., Лекции по теории аппроксимации. «Наука», М., 1965.
2. А х и е з е р Н. И. и Крейн М. Г., О некоторых вопросах теории
моментов, Харьков, Гос. научн-техп. изд-во Украины, 1938 (Институт мате¬
матики и механики ХГУ).
3. Altman М., Approximation Methods in Functional Analysis, Lecture Note
given at the California Institute of Technology, 1959.
4. Antosiewicz H. A., Linear Control Systems, Arch. Rat. Mcch. and
Analysis 12, No. 4, pp. 313—324, 1963.
5. Athans М., Minimum Fuel Control of Second — Order Systems with
Real Poles,	Proc. JACC 1964, pp.	232—239, June, 1963.
6. Aoki	М.,	Minimizing Integrals	of Absolute Deviations in Linear Control
Systems, AIEE Trans. Application and Industry, No. 61, 125—128, July, 1962.
7. Aoki М., Synthesis of Optimum Controllers for a Class of Maximization
Problems, Automatica 1, No. 1, 69—80, 1963.
8. Aoki	М.,	On Realization of Given Trajectories in Control	Systems, to
appear in J. Math. Anal, and Application.
9. Aoki М., Successive Generation of Chcbychev Approximation Solution,
to appear in A.S.M.E. Transaction J. of Basic Engineering.
10. Aoki	М.,	P. L. Elliot and L.	A. Lopes, Correction and	Addendum
to Minimize Integrals of Absolute Deviation in Linear Control Systems. To
appear.
11. Arrow J. J., M. J. Beckmann and S. Karlin, The Optimal Expansion
of the Capacity of a Firm, Studies in the Mathematical Theory of Inventory
and Production, Standford University Press, Stanford, Calif., 1958.
12. Барба hi и н E. А., Об оценке среднеквадратичного значения отклоне¬
ния от заданной траектории. Автоматика и телемеханика, т. XXI, № 7,
1960, стр. 941—951.
13. Б ар баш и н Е. А., Об оценке максимума отклонения от заданной тра¬
ектории. Автоматика и телемеханика, т. XXI, № 10, 1960, стр. 1341 —1352.
14. Б ар баш и н Е. А., О приближенном осуществлении движения по за¬
данной траектории. Автоматика и телемеханика, т. XIII. N° 6, 1961,
стр. 681—688.
15. В е с k е n b а с h Е. F. and R. Bellman, Inequalities, Ergebnisse der Mat-
hematik und ihrer Grenzgebiete Neue Folge, Heft 30, Springer — Verlag,
Berlin, 1961. [Русский перевод: Беккенбах Э., Беллман Р., Нера¬
венства, «Мир», М., 1965.]

ЛИТЕРАТУРА
383
16. Bellman R., I. Glicksbcrg and O. Gross, Some Nonclassical Pro¬
blems in the Calculus of Variations, Proc. Amer. Math. Soc. 7, No. 1,
pp. 87—94. February, 1956.
17. Bellman R., On Monotone Convergence to Solutions of a, = g(tii t),
Proc. Am. Math. Soc. 8, pp. 1007—1009, 1957.
18. Bell ma n R., On the Representation of the Solution of a Class of Stochas¬
tic Differential Equations, Proc. Am. Math. Soc. 9, pp. 326—327, 1958.
19. Bertram J. F., Control by Stochastic Adjustment, AIEE Application and
Industry, 1—7, January, 1960.
20. С о 11 a t z L., Application of Functional Analysis to Numerical Analysis,
Tech. Report No. 5, Department of Mathematics, University of California,
Berkeley, Calif., May, 1960.
21. Dv oretzky A., On Stochastic Approximation, Proc. Third Berkeley Sym¬
posium on Math. Stat. and Prob., Vol. 1, 39—55, University of California
Press, 1956.
22. H a 1 m о s P. R., Finite Dimensional Vector Spaces, D. Van Nostrand Com¬
pany, Inc., Princeton, New Jersey, 1958. | Русский перевод: X а л м о ш П. Р.,
Конечномерные векторные пространства, Физматгиз, М., 1963.]
23. К а 1 a b a R., On Nonlinear Differential Equation, the Maximum Operator,
and Monotone Convergence, J. Math, and Mech. 8, No. 4, pp. 519—574,
July, 1959.
24. Karlin S., The Theory of Infinite Games, Ann. Math. 58, 371—401, 1953.
25. Kiefer J. and J. W о 1 f о w i t z, Stochastic Estimation of the Maximum
of a Regression Function, Ann. Math. Stat. 23, pp. 462—466, 1952.
26. Колмогоров A. H. и Ф о м и н С. Б., Элементы теории функций
и функционального анализа, т. 1 и т. 2, Изд-во Моск. ун-та, 1954, 1960.
27. К р а с о в с к и й Н. Н., К теории оптимального регулирования. Автома¬
тика и телемеханика, т. XVIII, № 11, 1957, стр. 960—971.
28. Kreindler Е., Contributions to the Theory of Time Optimal Control,
J. Franklin Inst. 275, No. 4, pp. 314—344, April, 1963.
29. Kulik о wski R., On Optimal Control with Constraints, Bull, de TAcade-
mie Polonaise de Sciences, Serie des sciences Technique 7, No. 4, pp.
285—294, 1959.
30. L a n с z о s D., Applied Analysis, Prentice-Hall, Inc., Englewood Cliffs,
N. J., 1956. [Русский перевод: Л а н ц о ш К., Практические методы при¬
кладного анализа, Физматгиз, М., 1961.]
31. Lang с г R. (Editor), On Numerical Approximation, The University of Wis¬
consin Press,	Madison, Wis., 1959.
32. Neustadt	L.	W., Minimum Effort Control	Systems,	J.	Soc.	Ind. Appl.
Math. Ser. A	on	Control 1, 16—31,	1962.
33. N e u s t a d t	L.	W., Optimization,	a Moment	Problem,	and	Nonlinear Pro¬
gramming, Report No. TDR-169-(3540—10) TN-1, Aerospace Corporation,
El Segundo, Calif., July, 1963.
34. Reid W., Ordinary Linear Differential Operators of Minimum Norm, Duke
Math. J. 29, pp. 591—606, 1962.
35. R о x i n E., A Geometric Interpretation of Pontryagin’s Maximum Principle
RIAS Tech, Report 61 — 15, Baltimore, Md., December 1961.
36. S a k r i s о n D., Application of Stochastic Approximation Methods to
System Optimization, Tech. Report 391, Massachusetts Institute of Technology,
Research Laboratory of Electronics, Cambridge, Mass., July, 1962.
37. Taylor A. E., Introduction to Functional Analysis, John Wiley & Sons,
Inc., New York, 1958.
38. Urabe М., Convergence of Numerical Iteration in Solution of Equations J. of
Science of the Hiroshima Uni. Ser. A, 19, No. 3, pp. 479—489, January, 1956.
39. Z a d e h, Lotfi A., Computer Control Systems Technology, Chapter 14,
McGraw-Hill Book Co., New York, N. Y., 1961.

ГЛАВА 9
МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ
В ЗАДАЧЕ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Шульц (Р. R. Schultz)
9.1. Введение
В этой главе обсуждается задача оптимизации непрерывных линей¬
ных систем, качество которых оценивается по квадратичному крите¬
рию. Используются два метода. Первый из них — метод динамического
программирования, в котором используется принцип оптимальности,
а задача трактуется как оптимизация непрерывного процесса приня¬
тия решений. Этот метод был развит Веллманом и другими авторами.
Второй метод ссноваи на принципе максимума, развитом Поитряги-
ным и его коллегами. Этот метод является обобщением классического
вариационного исчисления.
Подобного рода задача широко обсуждалась в литературе. Неко¬
торые (но далеко не все) из этих работ перечислены в списке лите¬
ратуры в конце главы. Решение задачи хорошо известно. Имеются
три причины того, чтобы рассматривать ее при обсуждении совре¬
менной теории управления. Первая из них заключается в том, что
это одна из немногих задач, для которых аналитические методы дают
вполне удовлетворительные результаты. Вторая причина заключается
в том, что полученное решение можно применить к некоторым прак¬
тическим задачам. Третья — в том, что указанная задача дает методи¬
ческое оружие для иллюстрации и сравнения пользы методов дина¬
мического программирования и принципа максимума при оптимизации
систем управления.
В данной главе ударение делается в первую очередь на первую
и третью особенности этой задачи. Сравниваются решения, получен¬
ные двумя различными способами, и подчеркиваются их отличия и
сходные черты.

9.2]
ФОРМУЛИРОВКА ЗАДАЧИ
385
9.2 Формулировка задачи
Требуется управлять поведением динамической системы так, чтобы
оптимизировать квадратичный критерий качества. Движение системы
в /z-мерном фазовом пространстве описывается следующей системой
дифференциальных уравнений, записанной в векторно-матричной
форме:
x(t) = А (О JC (0 + В (0 и (0 + F (0, * (t0) = х0.	(9.1)
В уравнении (9.1) A(t) — п X /2-мерная матрица, элементы которой
являются кусочно-непрерывными функциями независимой переменной t
(времени); x(t) и В(£) — /2-мерные столбцы; a x(t) — столбец, эле¬
менты которого являются производными соответствующих элементов
столбца x(t). Элементы Bit) также являются кусочно-непрерыв¬
ными функциями. Скалярная функция u(t) представляет входное воз¬
действие, которое должно быть подобрано так, чтобы оптимизиро¬
вать поведение системы. Функция F(t) является /гХ1"меРиой матри¬
цей (вектором), элементы которой представляют собой известные
входные возмущения. Их значения вводятся в регулятор (вычисли¬
тельную машину, в которой формируется u(t)). Однако регулятор не
может изменять элементы F(t).
При заданных начальных условиях х (^0) требуется подобрать u(t)
в интервале t0^t^T так, чтобы минимизировать следующий пока¬
затель качества или платежную функцию:
т
плата = х'(Т) Qx (Г) -f- $ [jc' (5) Р (s) х (s) -j- № ($)] ds =	(9.2a)
to
T
— P (T) + $ (s)P(s)x (s) -f- '‘•h2 (s)] ds.	(9.26)
^0
Здесь P(т) — неотрицательно определенная симметричная n X //-мерная
матрица, элементы которой могут изменяться во времени; Q — неот¬
рицательно определенная симметричная матрица с постоянными эле¬
ментами; а X — положительная скалярная величина. Штрих при мат¬
рицах обозначает транспонирование. Теперь можно записать
р {t) = j-t = х' Qx -}- x'Qx =
= х' [QA + A'Q] х + x'Q [Bn + F\ + [F X нЯ'] Qx, (9.3)
где в правой части опущена независимая переменная t. Таким об¬
разом,
т
Р (0 = Р (?о) ~\~ \ Р (5) ds.	(9.4)
to
13 п/р Леондеса

386
МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ
[ГЛ. 9
Следовательно, подстановка равенства (9.4) в равенство (9.2) дает
т
плата = х' (^о) Qx (tQ) -j- $ [х' (s) Р (s) х (5) -[- hi2 (5)] ds -f-
T
+ $ {xr (s) [A' (s) Q + QA ($)] * (s) +
/'o
-f-x' (s) Q [B (5) и {s) + F (5)] + [F (5) Br (5) и (5)1 Qx (5)} ds. (9.5)
Поскольку первый член в правой части (9.5) фиксирован (потому
что заданы начальные условия х(/0))> плата будет минимизирована,
если добиться минимальных значений второго и третьего членов
в правой части равенства. Поэтому в дальнейшем будем выбирать
такое м(т) в интервале t0^z^:T, при котором минимизируются
второй и третий члены в правой части равенства (9.5).
Переформулировка задачи, когда плата или критерий качества
определяется равенством (9.5), а не (9.2), была выполнена просто для
того, чтобы показать, что это можно сделать. Решение можно легко
получить и непосредственно, не прибегая к переформулировке. Раз¬
личия между этими двумя подходами заключаются в граничных усло¬
виях и форме сопряженных уравнений (уравнения (9.47) и (9.51)) при
решении задачи с помощью принципа максимума, и в граничных
условиях и форме определенных матричных дифференциальных урав¬
нений (уравнения (9.23) и (9.26)) при решении методом динамического
программирования.
9.3.	Метод динамического программирования
Ниже мы увидим, что метод динамического программирования
имеет сходство с вариационным исчислением, заключающееся в том,
что задача отыскания н(т), t0	минимизирующего платежную
функцию (9.2) при условии, что вектор состояния x(t) удовлетворяет
дифференциальному уравнению (9.1), является вариантом проблемы
Больна классического вариационного исчисления. Калмэн показал,
что этот вариант и ему подобные действительно имеют единственные
решения и что оптимальная платежная функция (когда осуществляется
оптимальное управление u{t)\ является дважды дифференцируемой
функцией начальных значений переменных состояния. Читатель, инте¬
ресующийся вопросами существования и связанными с ними, отсы¬
лается к работам Калмэна [1, 2]. В дальнейшем предполагается, что эти
результаты справедливы. При этих условиях возможно использовать
метод динамического программирования для получения аналитическим
путем решения задачи, т. е. оптимальной стратегии и оптимальной
платежной функции. Результаты, полученные методом динамического
программирования, будут приведены в этом и следующих двух раз¬
делах.

9.3]	МЕТОД	ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ	387
Пусть оптимальная платежная функция определяется следующим
образом:
f(x (ф), Т) = min { \ [х'Рх -]- Хгг- -|- х' (A'Q -|- QA) х -f-.
to^s^T v0
+ x'Q (Bu -f F) + (F -f B'u) Qjc] ds [.	(9.6)
Отметим, что при записи подынтегрального выражения в (9.6) опу¬
щена	независимая переменная 5. Отметим также, что	x(t) должно
удовлетворять уравнению (9.1). Для упрощения последующих рас-
суждений определим
А (х, it)	s) = х'Р (5) х —|— ^и * — р х' [ А (s) Q —|— QА (5)] х — |—
+ x'Q [В (s) и + F (s)] + [F (s) + В' (s) и] Qx.	(9.7)
Тогда
f(x(t0), tQi Т)= min |U[a;(5), u(s),	(9.8)
U&rW	J
где
x(t) = A (0 x{t)-\-B (0 u (9 -I- F it),
X(t0) = Xo.
Теперь правую часть равенства (9.8) можно записать в виде суммы
следующих двух интегралов:
ро + °	Т	1
/(лг(ф), ф, Т)= min J J &ds-{- § Adsl. (9.8а)
J
Для малых о можно записать
/(*(Д),	Т)= min |а[лг(Ф), и(*0), ^о]8 +
" (5)
t0<s^ т I
+ { Л rfs -Е О (82)1,	(9.9)
/о + 8	j
где О (о-) — бесконечно малая, стремящаяся к нулю не медленнее,
чем Ь2, т. е. существует число т<^оо такое, что О (о-) не превышает
mb2 при о-> 0. Поскольку A [x(tQ), п(ф), /0] не зависит от г/ (х),
13*

388	МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ	[ГЛ. 9
t0 -|- о	Ту равенство	(9.9) принимает	вид
/[*(*о)>	/0] =	min |д [л; (^0),	и (f0), *0] 8 +
и tfo) |
min \^[х (s), и (s), s] ds -f- О (S2)} =
t0+“<s<Tto	J
= min {А [л;0, мО-о)> ^o] ^ ~\~f(Xo ~j~ ^o>	H—	T')	”f"	О	(^2)}	(9.10)
и (t0)
согласно принципу оптимальности. Величина Bjc0 определяется соот¬
ношением
bx0 = x(tQ)b-\-O(b*) =
— Л (t0) л:05 -j- В (t0) и (t0) 5 -(- F (t0) 5 -j- О (b2).	(9.11)
Пусть \f—матрица-столбец, i-й элемент которой (элемент, составля¬
ющий йо строку) равен частной производной от / по xt. Поскольку
второй	член	в фигурных	скобках в правой	части	уравнения	(9.10)
может	быть	разложен в	ряд Тейлора в	окрестности	точки	jc0,	t0,
можно записать
f(xо, t0, Т)= min (а [лг0, и (t0), *0] 8+/(*<>, t0, 7)+
и (to) V
V/rС*ч)>	Т)%хо-\- ^ (хо> Т)Ь -\- О (S2)j.	(9.12)
Так как f(x0, t0, Т) не зависит от и (to), ее можно вынести из фигур¬
ных скобок и сократить с соответствующим членом в левой части
уравнения. Аналогично четвертый член в фигурных скобках в правой
части уравнения может быть перенесен в левую сторону, так как он
не зависит от n(t0). Поэтому, используя (9.11), получаем
8 = — min {Д [х9, и (i0), t9] о -\-
Oto	и	и	о)
+ V/(*o, to, 7y[i4(<0)^, + e(#0)H(<0) + F(g]8 + O(8*)}.	(9.13)
Разделив обе части уравнения на S и переходя к пределу при 8 -> 0,
получим
zf(x0, t0, Т) = — min {Д (д:0, гг0, *„)-)-
ato	и	(/0)
~\~\f'(x0) to, T)[A(t0)xQ-{-B(t0)ii(tQ)-\-F(t0)]};	(9.14)
f(x0) T; T) = 0 — граничное условие.
Напоминаем, что А [лг0, и (to), ^о] определяется равенством (9.7). Для
получения оптимальной стратегии управления и соответствующей
платежной функции нужно решить уравнение (9.14).

9.4] РЕШЕНИЕ МЕТОДОМ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ
389
Отметим, что значение u(to), полученное при минимизации правой
части уравнения (9.14), есть входное воздействие системы, или управ¬
ление, которое должно использоваться в том случае, если система
в момент времени t0 находится в состоянии х0. Следовательно, реше¬
ние уравнения (9.14) будет давать оптимальную стратегию для всех
состояний x(t0) в момент времени t0. Таким образом, оптимальная
стратегия определяется как функция от x(t) и t, а не как функция
от t для t0^t^T и заданного х0. Эго как раз и требуется в зада¬
чах управления. Итак, оптимальную стратегию и* (t0) нужно предста¬
вить в виде и* (лг0, t0) или п* (xf t). Это будет сделано в следующих
параграфах, касающихся динамического программирования, с той
целью, чтобы подчеркнуть, что оптимальная стратегия определяется
как функция текущих значений переменных состояния.
9.4.	Решение, получаемое методом динамического
программирования
В этом параграфе то обстоятельство, что /(Je0, t0, Т) дважды
дифференцируема, будет использовано для получения решения урав¬
нения (9.14). Из этого решения можно получить оптимальную стра¬
тегию.
Поскольку	A(je0,	н0, *о)—квадратичная функция от и0	и поскольку
Х^>0,	выражение в	фигурных скобках в правой части	(9.14)	будет
иметь минимум, определяемый из условия
^о(х0, Но, O+V/'+o, *0> T)B(t0) = 0.	(9.15)
Подстановка (9.7) в (9.15) дает
и* = — 1 [itQB + B'Qxо + B’sf] =
= -1 [В' ft,) V/(JCо, Ч, Т) + 2В' (Q Ох (<0)1.	(9.16)
Равенство (9.16) определяет оптимальную стратегию и* (:с0, ^о)> когда
система находится в состоянии х0 в момент времени t0. Используя
этот результат в уравнении (9.14) и исключая н0.из правой части
этого уравнения, после некоторых преобразований приходим к соот¬
ношению
= I v/'eB'v/+1 x0QBB'Wf+1 sf’BB’ Qxo +
+ i x-QBB’ Qx0 - У v/' (AX0 + 0 — 4 (++ + F) \f—
— 2FQx0 — x„ [P + Qi4 + A’Q\	Jt0.	(9.17)

390	МЕТОДЫ	АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ	[ГЛ. 9
Предположим теперь, что решение уравнения (9.17) имеет вид
/С^о» Чу Т')== /.’о(^о> T)-J-kl(t0, Т)х0 + хйкгу0Т)х* (9.18)
Другими словами, предполагается, что /(х0, t0, Т) является квадратич¬
ной функцией от переменных состояния. Если предположить, что
члены высших порядков в правой части (9.18) существуют, то после¬
дующие шаги, приводящие к разделению переменных, покажут, что
эти члены тождественно равны нулю.
Теперь
V/(*o, Чу Т)=ЫЧу T) + [k2(t0, T) + k'2(t0, Г)] *о =
= М*о, Т) + К(Чу 7)х0>	(9.19)
где
К (Чу 'Г) = К'(Чу П
Если обозначить dkjdt0 через k (где k может быть любым элементом
из К, ki или /г = /г0), то подстановка (9.19) в (9.17) дает
/г0 Мо ~2 х^хо == 47 (^1 ~Т~ хоЮ ВВ' (&i -р Кх0) -j-
+ 2Х [XoQBB' (ft, -f Кх0) + (*,' + х0К) BB'Qxо] +
у x0QBB' Qx о — лт0 [Р -j- QA -)- >TQ] х^ —
— у (F' -f x'(lA') (kt KXo) — у (ft; + л^К") (Ллг0 + F) — c2F'Qx(l. (9.20)
Приравнивание в обеих частях уравнения (9.20) членов, не зави¬
сящих от х0, членов, линейных по х0, и членов, квадратичных по х0,
дает следующую систему дифференциальных уравнений (поскольку
(9.20) должно быть справедливо при всех х0):
d^=^k’lBB'kl-rkb	(9.21)
~ КВВ% + у QBB’ki —A'ki — KF—2QF =
= — А' — ~К^г\ QBB% -(K-\-‘2Q)F,	(9.22)
= 1 KBB’K + у [QBB'K + KBB'Q] —
— A'I< — К A -
QBPQ _ p _ qA _ A,Qj _	(g_23)
Граничные условия для уравнения (9.14) требуют, чтобы в уравне¬
ниях (9.21), (9.22) и (9.23) выполнялись следующие граничные условия:
k0(T,	Т) = 0,	(9.24)
ki(T,	Т) = о,	(9.25)
К(Т,	Т)= 0.	(9.26)

9,41
РЕШЕНИЕ Л\ЕТОДОЛ\ ДИНАМИЧЕСКОГО ПРОГРАМ.МИРОВАНИЯ
391
Отметим, что если F(t) тождественно равно нулю, то k{ и kQ
также тождественно равны нулю. Тогда оптимальная платежная
функция является квадратичной формой от переменных состояния
(не содержащей ни линейных, ни постоянных членов). Коэффициенты
этой квадратичной формы являются элементами матрицы К. Отметим
также, что матрица К не зависит от F и, следовательно, инвариантна
относительно изменений F.
Когда получено решение уравнений (9.21), (9.22) и (9.23) при
граничных условиях, 'задаваемых равенствами (9.24), (9.25) и (9.26),
оптимальная стратегия, задаваемая (9.16), принимает вид
Таким образом, оптимальная стратегия является линейной функцией
переменных состояния. Этот результат характерен для задач оптими¬
зации, в которых рассматриваются квадратичные критерии качества
и линейные физические системы, поведение которых можно описать
системой уравнений (9.1).
Уравнения (9.21) и (9.22) линейны по /е0 и k\. Следовательно, ре¬
шение их не представляет принципиальных трудностей. Однако в об¬
щем случае, когда элементы матрицы А и вектора В зависят от времени,
вероятно, потребуются того или иного рода вычислительные методы.
Уравнение (9.23) не линейно из-за наличия первого члена в правой
части. Но уравнения такого вида называются матричными уравне¬
ниями Риккати, и их свойства широко изучались математиками. Обсу¬
ждение этих свойств, а также библиография приводятся в работе
Левина [3]. Ниже излагаются некоторые из результатов Левина, пока¬
зывающие, какие действия должны быть выполнены для решения
уравнения (9.23).
Изложение упрощается благодаря следующим обозначениям:
и* (дг0, tn) = - 2},В' (<о) [*1 (to, Т)~гК (to, Т)Хо И- 2Qjc„].	(9.27)
0,=у QBB’ — А',
О, = 2 [Р + QA + A’Q — \ QBB'Q],
(9.28)
(9.29)
(9.30)
Qi = — у BB’Q А.
(9.31)
Тогда уравнение (9.23) можно записать в виде
%(Ь T) = — K(to, r)O»(f0)/C(f„, 7) +
+ Oifo»)K(ffc T)-\-Oo(td — K(to, T)OdU). (9.32)

392
МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ
[ГЛ. 9
Пусть z — 2п X 2я-мерная матрица, определяемая следующей системой
линейных дифференциальных уравнений:
о,(о о9(о»
dz
Ж
Г	С	(9-33>
О8(0	4	()	II
УИ (0 s)=
(9.34)
Пусть	УИ(£, s)— фундаментальное решение	системы	дифференциаль¬
ных уравнений (9.33), т. е. M{t> s) удовлетворяет (9.33) и М (s, s) =
= кт	где	1'in — 2я X 2я-мерная единичная	матрица.	Пусть	s),
M%(t, s),	s)	и Mg(t, s) — n X «-мерные	матрицы,	из которых со¬
ставляется матрица М (t, s) следующим образом:
Ж^, S) M*(t,S) I
M3(t, s) Mi (t, s) I
Тогда граничное условие, задаваемое равенством (9.26), и результат,
формулируемый в теореме 1 работы Левина, означают, что
K(t0< Т)=
= [Ж,(0, Т)К(Т, 7)+Ж2(0, 7)1 [М, (0. Т)К(Т, 7) + Ж4(/0> Г)]-1 =
= м2(0, Т)МТ\и, Т).	(9.35)
Таким образом, решение матричного уравнения Риккати можно полу¬
чить из фундаментальных решений линейных дифференциальных урав¬
нений (9.33).
Кроме того, легко показать, что уравнения (9.18) и (9.19) озна¬
чают, что
х' К%х = \хг (£а + £*) * = у х'Кх = x'k'ix.	(9.36)
Это следует из того факта, что « X «-мерная матрица может быть
разложена на симметричную и кососимметричную составляющие, при¬
чем при образовании квадратичной формы (9.36) слагаемые, образуе¬
мые из элементов кососимметрической матрицы, взаимно уничто¬
жаются. Таким образом, определение К(t0, Т) равносильно решению
задачи оптимизации.
Стоит отметить, что решение этой задачи при бесконечном рабо¬
чем времени (если такое решение существует) можно получить, пола¬
гая tQ—- — оо. Первым условием, при котором решение этой задачи
будет существовать, является случай, когда А — постоянная матрица,
имеющая собственные значения с отрицательными вещественными ча¬
стями, а В постоянна. Калмэн [2] показывает, что решение уравне¬
ний (9.21), (9.22) и (9.23) действительно существует при этих усло¬
виях. Летов [7] также рассматривает эту задачу.
В этом месте стоит упомянуть, что F(t) не обязательно должна
представлять входные воздействия системы. Например, рассмотрим
случай, когда требуется, чтобы система следовала по заданной траек-

9.5]	РЕШЕНИЕ	ЗАДАЧИ	С	ПОМОЩЬЮ	ПРИНЦИПА	МАКСИМУМА
393
тории.	Тогда	в качестве разумного квадратичного	показателя потерь
можно	было	бы выбрать величину
т
потери = $ [pi (5) hi2 (5)] ds,	(9.37)
to
где
pi (s) = [X (s) — xD (s)]' P [JC (s) — xD (s)];	(9.38)
Xd(s) — желаемая траектория, t^s^T.
Если N(t,t0) — фундаментальное решение однородного уравнения,
соответствующего уравнению (9.1), причем N(t0,	t0)	—	единичная
матрица, то полное решение уравнения (9.1) имеет вид
т
X (0 = N(t, t0) {х (t0) + 5 А/-1 (5, t0) [В (S) и (s)^F(s)} ds} =	(9.39)
to
Ч
= N(t, t0) {x (f0) + ^ AM (s, tQ) В (s) a (s) ds} + xD (t).	(9.40)
to
Следовательно, если существует F(t) такая, что желаемую траекторию
можно описать выражением
t
xD (t) = N(t, <0) 5 N-' (s, t0)F(s) ds,
to
to F(t) можно использовать, чтобы описать влияние вида желаемой
траектории на задачу оптимизации. Эта и другие подобные возмож¬
ности следуют из того факта, что дифференциальные уравнения (9.1)
линейны.
9.5.	Решение задачи с помощью принципа максимума
Теперь обсудим решение задачи оптимизации на основе принципа
максимума. При этом будут использованы некоторые видоизменения
понятий, рассмотренных в главе 7, посвященной принципу максимума.
Эти видоизменения заключаются в замене максимизации гамильтони¬
ана минимизацией его. Чтобы подтвердить справедливость принципа
максимума (например, в той форме, как он был развит Розоноэром
[13]), необходимо вектор граничных значений для сопряженных урав¬
нений положить равным градиенту функции потерь, вычисляемому
в конечный момент времени Т. При традиционной формулировке прин¬
ципа максимума [13] гамильтониан максимизируется, а вектор гра¬
ничных значений для сопряженных уравнений полагается равным
минус градиенту оптимального значения функции потерь. Такое видо¬
изменение аналогично замене максимизации функции f(x) на минимиза¬
цию функции —/(^'). При этих изменениях доказательство в [13] по

394
МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ
[ГЛ. 9
существу остается таким же. Следствием же такой модификации яв¬
ляется облегчение сравнения результатов, получаемых здесь, с резуль¬
татами, полученными методом динамического программирования. Это
сравнение можно было бы произвести и без внесения упомянутых
изменений. Выбор той или иной возможности является по существу
делом вкуса.
Уравнения объекта (9.1) воспроизводятся ниже для удобства ссылок
К системе п-го порядка, определяемой (9.1), добавляется следующее
уравнение:
Уравнение (9.42) (определяющее скорость изменения показателя ка¬
чества) добавляется к (9.1) для того, чтобы получить систему (it-1- 1)-го
порядка, записываемую в виде
Здесь х обозначает (п -|- 1)-мерный вектор, часто называемый векто¬
ром состояний увеличенного объекта. Система уравнений, сопряженная
(9.43), имеет вид
Матрица в правой части (9.43) получается транспонированием якоби¬
ана от g по х, т. е. /у-й элемент этой матрицы равен dgifdxj. В на¬
шем случае матрица имеет размеры (п 4- 1) X (п~г *)• Поскольку из
определения g следует, что dgi/dx0 = 0, имеем
z = — A'z — 2z0 [(Р + ArQ -j- QA) x + QBu -f QF\. (9.47)
Принцип максимума Понтрягина (при вышеупомянутых модифика¬
циях) утверждает, что необходимым условием оптимальности системы
х = g (Ху и, f) = A(f)x-\-B (0 и (0 -f F(t).
(9.41)
■*o = go(*. ll> *) = JC'[P + 4'Q + QA]x-!-X?;2-|-
-j- x’Q [Bu -{- F\ -j- [Z7' -}- uBr] Qx — Д (x, u, t). (9.42)
X = g(x, u, t).
(9.43)
(9.44)
z0 = 0,
z0 = const.
(9.45a)
(9.456)
Остальные n уравнений, определяемые (9.44), имеют вид
П
Zi = — 2 aJi (0 zi — z«(x> w> 0,	(9.46)
Уравнения (9.46) можно записать в матричной форме

9.5]
РЕШЕНИЕ ЗАДАЧИ С ПОМОЩЬЮ ПРИНЦИПА МАКСИМУМА
395
управление является минимизация Н (z, х, и, t) по всем допустимым и.
H(z, х, Uy t) определяется в виде
Н (z, Ху Uy t) = z'g {Ху и у t) =
= До [* (р + A'Q + QA) х + hi* +
-j- x'Q (Ви + F) + {F + uBr) Qx] + г'Ах + *Ви + zrF. (9.48)
Минимизация по и (путем взятия частных производных) правой части
(9.48)	дает
и — — ~ (2zaB'Qx -j- B'z) = — а (x, z, t).
(9.49)
Оптимальное управление должно удовлетворять (9.49), так как принцип
максимума Понтрягина (или его модификация, введенная здесь) дает
необходимое условие оптимальности.
В следующем параграфе будет показано, что наибольший интерес
представляет определение поведения объекта и сопряженной системы
вдоль оптимальной траектории. О характере этого поведения можно
узнать, подставляя (9.49) в (9.47) и (9.1). В результате получим
х = [А — у BB'Q х — т^г BB'z
Fy
z = — А'
4 QBBr)z — 2z0 (P + A'Q + QA —
— у QBB'Q ) x — 2z(iQF.
(9.50)
(9.51)
Для разъяснения запишем (9.51) и (9.50) в виде следующей системы
дифференциальных уравнений первого порядка:
2\г(
ВВ'
А — у BB'Q
—2 z0P+ A'Q -T QA — у QBB’Q —А'— у QBB’
+
+!
F II
-2Qf|
x(t0) = x0,
z{T) = 0.
(9.52)
Это — система уравнений, которой должна удовлетворять оптималь¬
ная траектория. Граничное условие z(T) = 0 требуется, чтобы потери
при работе системы в интервале t0^t^T равнялись
т
дг0(^о) = 5 *о (0 dt = потери.
Следовательно, д;0(Г) = 0 для всех х(Т). Надлежащие модификации
изложения, принятого в [13], показывают, что z(T) равно градиенту

396
МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ
[ГЛ. 9
функции потерь в момент времени Т. Поэтому z(T) = 0 и г^{Т)= 1.
Следовательно, при x(t0) = x0 и z(T)= 0 решение задачи оптимизации
требует решения двухточечной краевой задачи. Однако в данном
частном случае дифференциальные уравнения линейны. Следовательно,
решение двухточечной краевой задачи не столь трудно, как в
других случаях (благодаря тому что дифференциальные уравнения
линейны).
Отметим, что сопряженные уравнения соответствуют уравнениям
Эйлера — Лагранжа, возникающим при классической трактовке соот¬
ветствующей проблемы Больца. Применение классического вариацион¬
ного исчисления (в виде проблемы Больца) к решению задачи опти¬
мизации управления обсуждалось Берковицем, Калмэном, Летовым и др.
9.6.	Сравнение методов принципа максимума
и динамического программирования
Для сравнения решения, полученного при применении принципа
максимума, с решением, полученным методом динамического програм¬
мирования, поучительно вывести дифференциальное уравнение, кото¬
рому удовлетворяет градиент оптимального показателя качества, тогда
точка, описывающая состояние системы, движется под влиянием оп¬
тимального управления в фазовом пространстве или пространстве
состояний. Градиент оптимального показателя качества определяется
равенством (9.19). Устранение индекса 0 в (9.19) и дифференцирова¬
ние по t (обозначаемое точкой над символом) дают
I vfix, t,T) = k, (t, Т) + к (t, Т)х-\-К (t, Т) х. (9.53)
Подстановка (9.22), (9.23) и (9.1) в (9.53) после некоторых алгебраи¬
ческих преобразований с использованием (9.19) дает
I v/= — (л' - Y ®вв') V/- 2QF-
— 2(р + A'Q + QA — 1 QBB'^j х. (9.54)
Это дифференциальное уравнение тождественно уравнению (9.51), так
как Zq = 1.
Отметим, что граничные условия для уравнений (9.14), (9.25)
и (9.26) означают, что yf(x, Г, 7') = 0. Но
z(T) = 0.	(9.55)
При таких граничных условиях и z0= 1 сопряженные уравнения
удовлетворяют тем же самым дифференциальным уравнениям и гра¬
ничным условиям, которым должно удовлетворять \/f. Поэтому реше¬
ние сопряженных уравнений в том виде, как они определены урав-

9.61 ПРИНЦИП МАКСИМУМА И ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ 397
пением (9.51) (полученном исключением u{t) из (9.48)), дает у/. Уравне¬
ние (9.51) показывает, как градиент оптимального показателя качества
изменяется вдоль оптимальной траектории. При такой интерпретации
сопряженных уравнений видоизмененный принцип максимума означает,
что для оптимизации качества системы выбирается управление (из
множества допустимых управлений), минимизирующее скалярное про¬
изведение (п-\- 1)-мерных векторов [1, у/(лг, t)\ и (лг0, х). Подобным
же образом уравнение (9.14) можно переписать в виде
О = — min 1д [Хо, и (t), f0] + # + SflAx„ + Ви (t0) + F]}. (9.56)
U (to) 1	Oto
Если минимизирующее значение u(t\ задаваемое равенством (9.16),
подставить в (9.56), то получим как результат, что вдоль оптималь¬
ной траектории должно выполняться следующее соотношение:
I f(x, t,T) = — А [х, и* (О, Ц.	(9.57)
Знак * при u(t) указывает, что оптимальное управление, задаваемое
(9.16), подставляется в А. Ввиду определения А и критерия качества
(см. (9.7) и (9.5)) этот результат не является неожиданным. Он впер¬
вые обсуждался Красовским и Дезоэром в связи с более общей
задачей.
Отметим еще раз, что решение уравнений (9.50) и (9.51), или,
что то же самое, системы уравнений, определяемой (9.52), требует
решения двухточечной краевой задачи. Она возникает потому,
что начальные условия для переменных состояния определены для
начального момента времени tQ, в то время как граничные
условия для сопряженных уравнений заданы в конечный момент вре¬
мени Т.
Граничные условия для дифференциальных уравнений (9.21), (9.22)
и (9.23), определяющих оптимальный показатель качества, также за¬
даны в конечный момент времени (см. условия (9.24), (9.25) и (9.26)).
Однако нет никакой связи между этими условиями и переменными,
описывающими состояние системы, как это имеет место в сопряжен¬
ных уравнениях.
Таким образом, решение этих уравнений значительно проще, чем
решение уравнений (9.52) из-за того, что граничные условия для
переменных состояния определены в начальный момент времени tQl
не имеющий никакого отношения к уравнениям (9.21), (9.22) и (9.23).
Однако нужно задать конечный момент времени Г, для того что¬
бы получить требуемые граничные условия для уравнений (9.21),
(9.22) и (9.23).

398
МЕТОДЫ АНАЛИТИЧЕСКОГО КОНСТРУИРОВАНИЯ
[ГЛ. 9
9.7.	Смежные вопросы
Изложенная задача оптимизации системы управления рассматри¬
валась многими авторами [10, 11, 17, 18, 1, 2, б].
Эту и многие другие задачи оптимизации систем управления
можно изучать с помощью классического вариационного исчисления.
Некоторые математические аспекты этого вопроса обсуждались Бер-
ковицем в [8]. Дрейфус эвристически показал определенную связь
между вариационным исчислением и динамическим программирова¬
нием. Келли обсуждал каноническую структуру оптимальных регу¬
ляторов. Келли и Брекуэлл, Шпейер и Брайсон [22] рассматривали
окрестность оптимальной траектории и использовали вариационные
методы, включая вторую вариацию платежной функции, для получе¬
ния закона управления. Эту работу можно использовать для получе¬
ния законов управления в некоторых нелинейных задачах. Наконец,
Летов показал, как некоторые аналитические результаты для этой
и некоторых других задач можно получить с помощью классиче¬
ского вариационного исчисления. Его результаты в некоторых отно¬
шениях сходны с результатами, представленными здесь. Они не вклю¬
чены в главу, так как надлежащее их изложение потребовало бы
слишком подробных экскурсов в вариационное исчисление.
Наконец, слово в порядке предостережения. Задачи вида, обсуж¬
даемого здесь, — одни из немногих, которые можно изучать в терми¬
нах решений системы линейных дифференциальных уравнений (см. (9.52)
и (9.21), (9.22), (9.23), (9.34) и (9.35)). Если объект содержит нели¬
нейности или показатель качества имеет другой вид, то результаты,
которые можно получить с помощью данных методов, будут менее
законченными и изящными. Обычно для получения численных реше¬
ний необходимо использовать вычислительные методы. Этот тип за¬
дач подробно обсуждается в работе [9].
Балакришнан и Хеи для изучения задач оптимизации, связанных
с данной задачей, помимо вариационных методов, использовали также
функциональный анализ [23, 24]. Для получения оптимального управ¬
ления как функции времени при заданном векторе начальных состоя¬
ний они применяли метод наискорейшего спуска и использовали
понятия теории гильбертова пространства.
ЛИТЕРАТУРА
1. Kalman R. Е., The Theory of Optimal Control and the Calculus of Varia¬
tions, RIAS Technical Report 61-3.
2. Kalman R. E., Contributions to the Theory of Optimal Control Systems,
Boletin de la Sociadad Matematica Mexicana, 1960, pp. 102—119.
3. Levin J. J., On the Matrix Riccati Equation, Proceedings of American
Mathematical Society, Vol. 10 (1959), pp. 519—524.
4. Dreyfus S. E., Dynamic Programming and the Calculus of Variations,
Journal of Mathematical Analysis and Applications, Vol. 1, No. 2 (Sept. 1960).

ЛИТЕРАТУРА
399
5. D с s о е г С. A.,	Pontrvagin’s Maximum Principle and the Principle	of	Op¬
timality, Journal	of the Franklin Institute, Vol. 271, No. 5 (May,	1961).
6. F г i e d 1 a n d B., The Structure of Optimum Control Systems, Transactions
of the ASME, Journal of Basic Engineering, Vol. 84, Series D, No. 1 (March,
1962), pp. 1 — 12.
7. Летов А. М., Аналитическое конструирование регуляторов I—IV. Авто¬
матика и телемеханика, 1960, т. 21, N° 4, стр. 436—441; № 5, стр. 561—568,
№ 6, стр. 661—665, 1961, т. 22, № 5.
8. В е г к о v i t z L. D., Variational Methods in Problems of Control and Pro¬
gramming, Journal of Mathematical Analysis and Applications, Vol. 3, No. 1
(August, 1961), pp. 145—169.
9. К i p i n i a к W., Dynamic Optimization and Control, A Variational Approach
MIT Press — John Wilev and Sons, 1961.
10. Merriam C. W., An Optimization Theory for Feedback Control System
Design, Journal of Information and Control, Vol. 3, No. 1 (March, 1960).
11. Mafriam C. W., A Class of Optimum Control Systems, Journal of the
Franklin Institute,	Vol. 267, No. 4 (April, 1959), pp. 267—281.
12. Brea к well J.	V., The Optimization of Trajectories, Journal	of	Society
for Industrial and Applied Mathematics, Vol. 7, No. 2 (June, 1959),
pp. 215—247.
13. Розоноэр Л. И., Принцип максимума Л. С. Понтрягина в теории
оптимальных систем. Автоматика и телемеханика, 1959, т. 20, № 10,
стр. 1320—1334; № 11, стр. 1441 — 1458; N° 12, стр. 1561—1578.
14. Б о л т я и с к и й В. Г., Г а м к р е л и д з е Р. В., П о н т р я г и н Л. С.,
К теории оптимальных процессов, ДАН СССР, 1956, т. 110, N° 1,
стр. 7— 10.
15. П о н т р я г и н Л. С., Болтянский В. Г., Г а м к р е л и д з е Р. В.,
Мищенко Е. Ф., Математическая теория оптимальных процессов,
Физматгиз, хМ., 1961.
16. К р а с о в с к и й Н. Н., К теории оптимального управления. Приклад¬
ная математика и механика, 1959, т. 23, N° 4, стр. 899—919.
17. Bellman R. Е., Dynamic Programming, Princeton University Press, 1957.
[Русский перевод: Беллман Р., Динамическое программирование, ИЛ,
М.; I960.]
18. Bellman R. Е., Adaptive Control Processes: A Guided Tour, Princeton
University Press, 1961. [Русский перевод: Беллман P., Процессы регу¬
лирования с адаптацией, М., «Наука», 1964.]
19. Bryson А. Е. and W.	F. Denham, Multivariable	Terminal	Control	for
Minimum Mean-Square Deviation from a Nominal Path, Proceedings of the
IAS Symposium on Vehicle Systems Optimization; Garden City, N. Y., Nov.
28—29, 1961.
20. E 11 e r t F. J. and C. W. M e r r i a m III, Synthesis of Feedback Controls
Using Optimization Theory, IEEE Transactions on Automatic Control, Vol.
AC-8,-No. 2 (April, 1963), pp. 89—103.
21. Kelley H. J., Guidance Theory and External Fields, IRE Transactions on
Automatic Control. Vol. AC-7, No. 5 (Oct., 1962), pp. 75—82.
22. В r e a k w e 1 1 J. V., J. L. S p a v e r and A. E. В г у s o n, Optimization of
Nonlinear Systems Using the Second Variation, Journal of Society of In¬
dustrial and Applied Math, on Control, Series A, Vol. 1, No. 2, pp. 193—223.
23. H s i e h H. C., On the Synthesis of Adaptive Controls by the Hilbert Space
Approach, University of California, Los Angeles: Department of Engineering
Report, No. 62—19, June, 1962.
24. Balakrishnan A. V., An Operator Theoretic Formulation of a Class of
Control Problems and a	Stcepest-Descent Method of	Solution,	Journal	of
SIAM on Control, Series	A, Vol. 1, No. 2, pp. 109—127.

ГЛАВА 10
НЕКОТОРЫЕ ЭЛЕМЕНТЫ ТЕОРИИ СТОХАСТИЧЕСКОЙ
АППРОКСИМАЦИИ И ЕЕ ПРИМЕНЕНИЕ К ДАННОЙ ЗАДАЧЕ
УПРАВЛЕНИЯ
Шульц (P. P. Schultz)
10.1.	Введение
В настоящей главе излагаются основы теории стохастической
аппроксимации и показывается, как ее можно применять к решению
задач, возникающих при изучении некоторых типов систем управле¬
ния. Уместно отметить, что теория стохастической аппроксимации
является одним из методов исследования класса задач, связанных с
вероятностной сходимостью, но этим область ее применений не ис¬
черпывается [2, 4, 5, 12]. Рассматриваемые здесь частные случаи
интересны тем, что доказательство среднеквадратичной сходимости
в них выглядит гораздо проще, чем в более общих случаях, и, кроме
того, они представляют интерес с точки зрения методов решения
задач управления. Заметим, что в некоторых довольно общих случаях
можно также получить сходимость и с вероятностью 1. Но этот
аспект теории стохастической аппроксимации не рассматривается в на¬
стоящей главе вследствие его математической сложности.
Качественно и эвристически теорию стохастической аппроксимации
можно понимать как теорию, рассматривающую вопросы сходимости
некоторых последовательностей случайных величин. Этот предмет
привлекал последние годы внимание многих математиков, статисти¬
ков и инженеров. Дело в том, что: а) в теории стохастической аппро¬
ксимации имеется много интересных математических задач, б) ее можно
с успехом применять к задачам управления системами с обратной
связью, фильтрации и статистической оценки.
10.2.	Пример стохастической аппроксимации
В этом параграфе мы докажем, что при некоторых условиях по¬
следовательность скалярных случайных величин сходится в средне¬
квадратичном к действительному числу б. Поскольку эта последова¬

10.2]
ПРИМЕР СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ
401
тельность получается из определяемого ниже уравнения (10.1), по
сходимости этой последовательности в среднеквадратичном или по
отсутствию такой сходимости можно судить об «устойчивости» си¬
стемы, поведение которой можно описать уравнением (10.1).
Пусть {А'л(со)} и {K„((d)} — последовательности действительных
скалярных случайных величин, определенные на точках {со} некото¬
рого выборочного пространства 2. Пусть далее x-t и yt обозначают
значения, принимаемые А"; (со) и Yt (со), и Тп (Аг1 (со), А"2 (со),..., Хп (со)) —
преобразование, измеримое относительно своих аргументов. Опреде¬
лим последовательность случайных величин соотношением
*Л+1 («о) = тя [Xi (ш),	(со), ха (00)] +	(со),	(10.1)
где преобразование Тп удовлетворяет следующему неравенству:
| Тп(хь ..., xn) — Q\^Fn\xn — B\.	(10.2)
Предполагается, что последовательность [Fn} положительных действи¬
тельных чисел удовлетворяет следующим двум условиям:
fU = o,
п = ~
S
<^А для всех 5^>т, А конечно.
п = т
Теперь можно сформулировать и доказать следующую теорему.
Теорема 1. Если условия (10.5а)—(10.5в) выполняются с веро¬
ятностью 1 для всех п, то
lim Е(Хп — 9)2 = 0.	(10.4)
п-+ ОС
Условия, необходимые для выполнения (10.4), имеют следующий вид:
F 04) < оо,	(Ю.5а)
ОО
2 £(Г2)<оо,	(10.56)
п= 1
Е{Уп\хь ..., хп) = 0.	(10.5в)
Теорема 1 доказывается следующим образом. Пусть Y% =
= Е (Хп — б)2 и о% = Е Y%. Из (10.2), (10.5в) и (10.1) имеем
V%+X^FIV% + о*.	(10.6)
Итерируя неравенство (10.6), получаем
Vn+ I === °гё “Г \Fn "j- • • • "Г cmFm+\Fm + 2 • • ■ F% ~Г • • •
... + o\FiFI ...F% + V\F\ ...FI.	(10.7)
(10.3a)
(10.36)

402
ЭЛЕМЕНТЫ ТЕОРИИ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ [ГЛ. 10
Чтобы доказать, что lim 1/£ = 0, заметим, что из (10.7) вытекает сле-
п-юэ
дующее неравенство:
п [	п	\	I	т	—	\	\	п
14+1^2 a} max П	°5	max П П (10*8)
]=т
гкг
п j=k-\-1	/	'	j=	I	/m<k^nj	=	k_i_i
Далее условие (10.36) означает, что частные произведения ILFj огра¬
ничены, а условие (10.56) позволяет выбрать т настолько большим,
чтобы для любого данного е^>0 выполнялось неравенство
оэ
Л2 2 а} < е/2.	(10.9)
j= т
Напомним также, что в (10.56) требуется, чтобы
со
2 < °°-
/= 1
Следовательно,
<*+'<Т + (+ I«?), (п(<?)• <10Л°)
Далее, поскольку т фиксировано, то из неравенства (10.9) и усло¬
вия (10.3а) вытекает, что
п
lim max Y\ F) = 0.	(10.11)
я — со 1	у_/г_|_ 1
Следовательно, существует некоторое N такое, что V2n<^e для всех
л^> N. Но е можно выбрать произвольно малым. Поэтому V2n-+0
при оо и тем самым доказательство теоремы 1 закончено.
Этот и аналогичные ему результаты были получены Дворецким,
который также показал, что ^„(ю) сходятся к 0 с вероятностью
единица при менее ограничительных условиях на Тт чем (10.2).
Интересующийся читатель может ознакомиться с ними в работе
Дворецкого [2]. Отметим также, что, внося в доказательство теоремы 1
небольшие изменения (замена (Xn_vX — 0)2 нормой \\Хп — 0 ||), ее можно
обобщить на случай векторных случайных величин (что соответствует
тому, что состояние системы управления является векторной величи¬
ной). В дальнейшем этот факт будет использован.
10.3.	Пример. Процесс Роббинса — Монро
Процесс Роббинса — Монро будет рассматриваться здесь в терми¬
нах предыдущего параграфа. Этот процесс является классическим
ъ теории стохастической аппроксимации и представляет собой метод
опенки корня 6 функции регрессии по экспериментальным данным.

10.3]
ПРИМЕР. ПРОЦЕСС РОББИНСА — МОНРО
403
Пусть Zx— некоторый случайный процесс, т. е. множество слу¬
чайных величин, зависящих от параметра х. Определим математичес¬
кое ожидание Zx (которое будет функцией х) как
Дх) называется функцией регрессии случайных величин Zx. Предпо¬
лагается, что /(х) существует для всех х.
Рассмотрим последовательность чисел {ап}, где п — целые и
положительные, удовлетворяющую следующим условиям:
Обозначим символом Х% наблюденное значение случайной величины
Zn и определим следующую последовательность случайных величин:
Эта последовательность случайных величин определяет процесс Роб¬
бинса— Монро. Покажем, что при некоторых ограничениях на /(х)
и {Zxj сходимость {Хп} к 0 получается как следствие теоремы 1.
Следствие. Пусть выполнены следующие условия:
1. /(х) является измеримой функцией х,
2. £Z* ^ а2 оо для всех х,
Тогда процесс Роббинса — Монро, т. е. {Хп}, сходится к 0, корню f{x\
Приводимое ниже доказательство принадлежит Дворецкому, кото¬
рый также получил этот результат при менее ограничительных:
условиях.
Доказательство. Определим случайные величины Хп+1 (оо),
Ул(а>) и преобразование Тп(Хп) при помощи рекуррентных соотношений
f{x) = E(Zx).
(10.12>
2“» = оо-
У}а% < оо.
(10.13а)
(10.136)
(10.14)
3.	0<^-£^-<S<oof
ОО	оо
4- 2а„ = со, 2а«<оо.
П = 1	п	=	1
AVm (<*>) = хп- anf{Xn) + Yn(U>),
Yn(w) = -an[ZXn-f(Xn)\,
Tn(Xn)=Xn-a,J(Xn).
(10.15)
(10.16)
(10.17)
Из условия 3 вытекает, что
| Тп (*„) — 0 | =sS | xn — 6 | sup (l — an -—g-)
^ I xn — 0|max(l—Aam Ban—1).	(10.18)

404
ЭЛЕМЕНТЫ ТЕОРИИ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ [ГЛ. 10
Далее, воспользовавшись условием 4, можно определить последова¬
тельность {Fn}, которая будет удовлетворять условиям (10.2) и (10.3а).
В самом деле, учитывая что ап -> 0 при п-> оо, условию (10.2)
можно удовлетворить, полагая Fn = max(l— Аап, Вап—1). А рас-
со
ходимости ряда ^ ап достаточно и для того, чтобы бесконечное
п= 1
произведение	=	0,	как это и требуется в (10.3а). (см., напри-
i = 1
мер, [8], стр. 13—15). Примером последовательности [ап}, удовлет¬
воряющей условию 4, является j-i-j- ^т. е. ал = -^. Выберем далее
Хх((л) так, чтобы ЕХ\<^со. Так как функция регрессии измерима и
удовлетворяет условию 3 для всех х и так как EiZxf^o1 в силу
условия 2,
EYl = а\Е [ZXn -f{Xn)f ^ а%М,	(10.19)
где М конечно. Таким образом, неравенство (10.56) удовлетворяется.
Наконец, из определения функции регрессии (10.12) вытекает, что
условие (10.5в) теоремы 1 также удовлетворяется. Итак, все условия
теоремы 1 удовлетворяются и Е(Хп — 0)2->О при п-> оо. Следова¬
тельно, Хп сходится в среднеквадратичном к 0, корню функции ре¬
грессии. А сравнение (10.14) с (10.15) и (10.16) показывает, что про¬
цесс Роббинса — Монро сходится к корню функции регрессии.
Более общие результаты приведены в работе [2].
10.4.	Пример. Процесс Кифера — Вольфовица
Процессу Кифера — Вольфовица [7] и его обобщениям уделялось
много внимания в литературе. Этот процесс применяется для нахожде¬
ния оценки максимума функции. Сакрисон использовал эти идеи для
получения оптимальных значений параметров фильтра [10]. Более
подробно работа Сакрисона обсуждается в заключении этой главы.
Пусть Zx — случайный процесс с математическим ожиданием
EZx=f{x\ как и раньше. Предполагается, что f(x) является изме¬
римой функцией х. Если z (х) есть наблюденное значение процесса Zx,
то процесс Кифера — Вольфовица определяется следующим рекур¬
рентным образом:
Х„+1 = X„ + bf \Z(xn + сп) - Z(x„ - сп)}.	(10.20)
Ln
Чтобы упростить доказательство, заменим задачу оценки максимума 0
функции регрессии f(x) на задачу оценки минимума 0 функции рег¬
рессии F(x) — — /(.v) случайного процесса —ZX = ZX. Определим

10.5]
ОДНА ЗАДАЧА УПРАВЛЕНИЯ
405
следующую последовательность случайных величин:
^ № сп) F (^п сп)
х%+1 = х* — ьп
+ П, (10.21)
H = -^[Zlrt + Ctt-F№ + ^-ZIrt.Crt + F(^ + g], (10.22)
Тем самым мы видоизменили равенство (10.20). Теперь можно дока¬
зать следующее следствие теоремы 1.
Следствие. Пусть {А^(о))} и {Ул(о>)}—последовательности
случайных величин, определяемые равенствами (10.20) и (10.21).
Кроме того, пусть
оо	оо
а)	У Ьп — со, б) lim сп = 0, в) У (Ч)'<оо,
TI-+CQ	\СП/
п=1	п—\
г)	а2<^оо	для	всех	х,
F(X% + cn)-F(X%-cn)
д)	0 < А •
,В<^ со,
е)	Е {xf) < °i со.
Тогда lim Е{Х% — 6)2 = 0.
п —*■ оо
Доказательство. Определим
тл=п-ья\рЮ + е*-рМ-е*
L	Сп
Тогда
Тп-0 I
: sup
гфЬ
г — 01
 и \F{r-\-cn)—F(r—cn)
4 в„(гя-в)
{max ((1 — Abn), {Bbn — 1))} | г
(10.23)
(10.24)
Отсюда легко показать, что из условий а) — е) вытекают условия
теоремы 1. Это делается почти так же, как и при доказательстве
сходимости процесса Роббинса — Монро. Таким образом, Х% сходится
в среднеквадратичном к 0, минимуму функции регрессии F (х).
Как и в случае процесса Роббинса — Монро, среднеквадратичная
сходимость и сходимость с вероятностью 1 могут быть доказаны
при более общих условиях.
10.5.	Одна задача управления
В этом и следующих параграфах будут рассматриваться некото¬
рые результаты, полученные Бертрамом [1]. Бертрам занимался син¬
тезом регулятора для управления объектом по экспериментальным
данным. Относительно объекта предполагалось, что он линеен, имеет

406	ЭЛЕМЕНТЫ	ТЕОРИИ	СТОХАСТИЧЕСКОЙ	АППРОКСИМАЦИИ	[ГЛ.	10
переменные параметры и один вход и что дифференциальное урав¬
нение, управляющее поведением объекта, имеет вид
п
Xi (0 = 2 а,7 (0 Xj it) -j- di it) m it),	i = 1, ..., n.	(10.25)
7=2
Обратим внимание, что j изменяется от 2 до п, а не от 1 до п.
Требования к коэффициентам	будут сформулированы позднее
в терминах переходной матрицы и шума, сопутствующего измерениям.
Предполагается, что регулятор может измерять все выходные вели¬
чины объекта, однако эти измерения искажаются аддитивным шумом.
Также предполагается, что вследствие квантования измерений по вре¬
мени управление т(1) может изменяться только в дискретные мо¬
менты времени, и, следовательно, m(t) является постоянной на дан¬
ном интервале квантования, т. е.
т (0 = т {к Т), А Г< f < (к -j- 1) Т.	(10.26)
В результате квантования измерений выходных величин объекта по
времени и искажения их шумом или ошибками информация, посту¬
пающая на вход регулятора, на основе которой вычисляется m(t)
(входная величина объекта), имеет следующий вид:
y(kT) = x{kT)-\-n{kT), к = 0, 1,...	(10.27)
Здесь вектор п(к'Г) представляет ошибки в измерениях входного
вектора х(кТ\ а у{кТ) — величину, поступающую на вход регуля¬
тора. Наконец, предполагается, что вектор d(t) может изменяться
лишь в известных пределах. (Эго предположение вводится вследствие
неполных знаний об объекте.)
Задача, которую должен выполнить регулятор, заключается в том,
чтобы возвратить систему из возмущенного состояния х(0) в состоя¬
ние равновесия хг, где
х' =
(10.28)
т. е. хг является вектором, у которого отлична от нуля только пер¬
вая компонента. Кроме того, предполагается, что управление m(t)
имеет вид
m*(t) = al[xr—y(k)\, АГ<*<(Л + 1) Т,	(10.29)
г. е. является кусочно-постоянным и представляет собой линейную
комбинацию компонент разности между вектором состояния равно¬
весия (или желаемым вектором) и вектором измерений выходных

10.6]
прил\енение методов стохастическое! аппроксимации
407
величин объекта. Вектор ак является вектором коэффициентов уси¬
лений регулятора. Индекс к указывает, что эти коэффициенты уси¬
ления меняются во времени.
В следующем параграфе с помощью методов стохастической
аппроксимации будут выведены условия, при которых вектор x(k)
сходится в среднеквадратичном к желаемому вектору хг.
10.6.	Применение методов стохастической аппроксимации
В дальнейшем мы будем рассматривать вектор состояния си¬
стемы (10.25) только в дискретные моменты времени (т. е. t — JzT,
/г = 1, 2, ...). Таким образом, поведение исследуемой системы можно
описать следующим разностным уравнением:
X {к + 1) = Фкх (к) -L dum Ск) =
= ®Л -Г йка\ \х' - х (к) - п (к) 1,	(10.30)
где х(к) обозначает значение вектора x(t) при t = kT. Индекс к
у векторов dk, ак и матрицы Ф/г имеет тот же смысл. Матрица Фк
является переходной матрицей системы (10.25) и определяется с по¬
мощью решения следующего матричного дифференциального урав¬
нения:
^=[аг,.(0]Ф(0.
Ф*=Ф[(Л+1)Л;	|
Ф {{к)Т) = 1 (единичная матрица),	1	(10.31)
[ciij(f)] = матрица коэффициентов уравнения (10.25). J
Поскольку нас интересует сходимость х(к) к хг, целесообразно оп¬
ределить вектор ошибок е(к) = х(к) — хг и исследовать сходи¬
мость е(к) к нулевому вектору по норме. При такой замене пере¬
менных рассматриваемое уравнение движения превратится в
е(k +	1) = (Ф* — dka\) е (k) -f- (Ф,; — /)	— dka]tn (/г).	(10.32)
Но согласно	(10.25) an(t) = 0 для всех L	Отсюда легко	показать,
что (Ф/г)ц = 0 при 1ф 1, а (Ф/г)п=1, т. е. все элементы первого
столбца Фк, за исключением первого (или диагонального элемента),
который равен единице, равны нулю. Отсюда и из того факта, что
только первая компонента вектора хг отлична от нуля (см. 10.28)),
вытекает, что
(Фк — 1)хг = 0.	(10.33)
Следовательно, уравнение (10.32) превращается в
е (А + 1) = (Ф* — dka[) ек —	dhaTkn (/г).	(10.34)

408	ЭЛЕМЕНТЫ	ТЕОРИИ	СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ [ГЛ. 10
Далее будет показано, что при условиях А, В и С (приведен¬
ных ниже)
lim ЕI е (k) || = 0.	(10.35)
k-*-co
Символ ||е(£)|| обозначает норму вектора e(k).
Кроме нормы вектора, необходимо также определить норму мат¬
рицы. Одно из удовлетворительных определений нормы матрицы
получается, если положить
И!1=™хо[т^т]-	(10-36)
Максимум в правой части уравнения (10.36) берется по всем нену¬
левым векторам х. Отметим, что эта норма матрицы зависит от того,
как определяется норма вектора. Следовательно, можно определить
много различных норм для данной матрицы [1, 19]. Кстати, из (10.36)
вытекает, что для любого х
|| Ах I ^ || А || I х ||.	(10.36а)
Условия, из которых вытекает результат (10.35), резюмируются
в следующей теореме.
Теорема 2. Если удовлетворяются условия
A. ||Фл — ^kak\\^^ky где Ри — последовательность положитель¬
ных чисел такая, что
оо
1 гь=°>
г = 0
S
II. pj |тг А °° для всех г, s таких, что s^>r.
i = r
B. Е || п (k) || оо и /г (/г) не зависит от состояния системы
с. ^^(ИХр^сЦл^ИХ00*
k=0
то имеет место (10.35), т. е.
lim £(|И*)||) = 0.
/г со
Теорема 2 доказывается следующим образом. Из (10.36)
\е (k + 1) II ^ IIФА - dhal IIII * (k) II + II dka\ || || п {k) j|.	(10.37)
Определим	Vk = E(\\e(k)\\) и о/; = Е (|| <*/;а*||) Е (|| п (k) ||).	Тогда из
неравенства (10.37) и условия теоремы вытекает, что
Vk+l<\>.kVk + ak.	(10.38)
Положим далее
k
bk,m= П IV	(10-39)

10.61 ПРИМЕНЕНИЕ МЕТОДОВ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ	409
Тогда, «итерируя» неравенство (10.38), получим
/г
<С bk. qVq ~г У] bk. i+\Gh	(10.40)
i = 0
где bkt kJr\ = 1 по определению.
Теперь зафиксируем т. По условию A, bk%m-+ 0 при k-^oo.
Следовательно, Ьк ^У0->0 при k->co. Кроме того,
km	k
2 bk, /+i3i = 2 bk. M3i -f 2	(10.41)
i = 0	i	=	0	t	=	m	-f	1
Далее первый член в правой части (10.41) стремится к нулю при k,
стремящемся к бесконечности, гак как из условия А следует, что
bk, i+1 "■* 0 при k -> оо для всех /, меньших чем т. Поскольку из
условия А вытекает, что br>s ограничены для всех г и 5 таких, что
г ^>5, условие С дает
оо
(10.42)
/г =0
Следовательно, для любого данного е^>0 можно выбрать т на¬
столько большим, чтобы
оо
2&/ы+1°<0	(10.43)
k = 0
Так как произвольно малое в^>0 можно выбрать раньше, чем т>
второй член правой части (10.41) также стремится к нулю при £->оо.
Таким образом,
lim Vk = 0,	(10.44)
k -*• оо
и теорема доказана.
Таким образом, имеются достаточные условия для сходимости
E\e(k -f- 1)|| к нулю или, говоря другими словами, достаточные ус¬
ловия устойчивости рассматриваемой системы управления при наличии
ошибок в измерениях вектора, характеризующего ее состояние.
Заметим, что в условии С требуется, чтобы
E(\dkal||)Е(\пк !|)-> 0 при /г-»-оо.	(10.45)
Это довольно сильное ограничение на характеристики ошибок
измерений. Однако условия теоремы 2 (из которых вытекает
(10.45)) являются достаточными для того, чтобы рассматриваемая
система достигла желаемой точки равновесия (в том смысле, что
lim/:(||e(/e)||) = 0). Отметим также, что предположения о том, что
k-►со

410	ЭЛЕМЕНТЫ	ТЕОРИИ	СТОХАСТИЧЕСКОЙ	АППРОКСИМАЦИИ	[ГЛ.	10
aiy — 0 и хг имеет только одну компоненту, отличную от нуля (см.
(10.25) и (10.28)), могут быть видоизменены при некоторых условиях.
Результаты, полученные в этом параграфе, можно также получить,
если условия (10.38) и предположения, используемые при его выводе,
заменить на условие
со
2 ||(Ф/г-/)лЛ|<оэ.	(10.46)
к =0
Можно показать, что при любом хп удовлетворяющем (10.46), будет
иметь место сходимость аналога (10.37).
Кроме того, для выполнения условия (10.46), с помощью которого
доказывается теорема 2, не обязательно, чтобы (ф/г)г = 0 для 1ф\
и (Ф/г)п=1. Наконец, можно сделать хг функцией времени и тем
не менее найти некоторую последовательность {xr(k)}> удовлетворя¬
ющую (10.47).
10.7.	Заключение
В предыдущем параграфе был рассмотрен один частный случай
стохастической аппроксимации. На основе этого случая были най¬
дены достаточные условия для устойчивости линейного регулятора
с переменными параметрами при ошибках в измерениях регулируе¬
мой величины и возмущении некоторых его параметров. Существует
много других более общих подходов к стохастической аппроксима¬
ции [2, 4, 5, 12], которые могут также оказаться полезными при ре¬
шении задач уравнения.
Методы стохастической аппроксимации применялись и к различ¬
ным другим задачам. Так, Сакрисон [3, 9, 10], обобщая и развивая
результаты работ [2, 7], описал применение методов теории стохас¬
тической аппроксимации к задаче построения оптимального фильтра.
Он предполагал, что критерий качества системы можно оптимизиро¬
вать, регулируя конечное число параметров, и что входные сигналы
являются стационарными и эргодическими случайными процессами.
Критерий качества имел вид математического ожидания от выпуклой
функции, зависящей от разности между действительным и желаемым
выходным сигналом системы. Сакрисон применил в этой ситуации
алгоритм оптимизации, который можно назвать экспериментальным
градиентным алгоритмом. Основная часть указанных работ Сакрисона
посвящена доказательству сходимости этого экспериментального гра¬
диентного алгоритма оптимизации, которое проводится с помощью
методов теории стохастической аппроксимации. В работе Сакрисона
также обсуждаются ограничения на критерий качества, систему и
входные сигналы, которые обеспечивают сходимость предложенного
алгоритма о и т и м и з а ц ии.

ЛИТЕРАТУРА
411
Кушнер [16, 17, 18] описал методы оптимизации систем по экспе¬
риментальным данным и нахождения экстремума неизвестной функции.
Помимо аналитических результатов, в работах Кушнера имеются
результаты моделирования некоторых из предложенных им алгорит¬
мов. Методы Кушнера имеют много общего с методами теории сто¬
хастической аппроксимации.
В библиографии приведены также некоторые другие интересные
статьи. Шметтерер [12] сделал обзор последних результатов в области
стохастической аппроксимации. В работе [12], в частности, рассматри¬
ваются вопросы, касающиеся высших моментов и асимптотических
распределений случайных величин в последовательностях стохасти¬
ческой аппроксимации, правил остановки, скоростей сходимости.
Работы чехословацких ученых по теории стохастической аппроксима¬
ции представлены в [4] и [5]. В большей части их работ рассматри¬
вается теория случайных функций или случайных величин из функ¬
ционального (банахова) пространства *).
ЛИТЕРАТУРА
1. Bertram J. Е., Control by Stochastic Adjustment, AIEE Transactions —
Part II, Applications and Industry, January, I960.
2. Dvoretzky A., On Stochastic Approximation, Proceedings of the Third
Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1, Uni¬
versity of California Press, 1956.
3. Sakrison D. J., Application of Stochastic Approximation Methods to Opti¬
mum Filter Design, IRE 1961 International Convention Record, Part 4.
4. Transactions of the First Prague Conference on Information Theory, Statisti¬
cal Decision Functions and Random Processes, Publishing House of the
Czechoslovak Academy of Sciences, Prague, 1957.
5. Transactions of the Second Prague Conference on Information Theory, Sta¬
tistical Decision Functions, and Random Processes, Publishing House of the
Czechoslovak Academy of Sciences, Prague, 1960.
6. R о b b i n s H. and S. M u n r o, A Stochastic Approximation Method, An¬
nals of Mathematical Statistics, Vol. 22 (1961), pp. 4-00—407.
7. К e i f e r, J. and J. W о И о w i t z, Stochastic Estimation of the Maximum
of a Regression Function, Annals of Mathematical Statistics, Vol. 23 (1952),
pp. 462—466.
8. Ti tch marsh E. C., Theory of Functions, 2nd ed. Oxford University Press,
1939. [Русский перевод: T и т ч м а р ш Е. К., Теория функций, Гостехиз-
дат, М., 1951.]
9. Sakrison D. J., Iterative Design of Optimum Filters for Nonmcan-Square-
Error Performance Criteria, IEEE Transactions on Information Theory, Vol.
IT-9, No. 3, July, 1963, pp. 161 —167.
10. S a k r i s о n D. J., Application of Stochastic Approximation Methods to
System Optimization, MIT Research Laboratory of Electronics Technical Re¬
port No. 391, July 10, 1962.
11. Gardner L. A., Jr., Stochastic Approximation and its Application to Prob¬
lems of Prediction and Control Synthesis, in Proceedings of the International
*) Применение методов стохастической аппроксимации к разнообразным
задачам автоматического управления см. в работе [20].

412
ЭЛЕМЕНТЫ ТЕОРИИ СТОХАСТИЧЕСКОЙ АППРОКСИМАЦИИ [ГЛ. 10
Symposium on Nonlinear Differential Equations and Nonlinear Mecha¬
nics, edited by J. P. LaSalle and S. Lefshetz. Academic Press, NYC., 1963.
12. Schmetterer L., Stochastic Approximation, Proceedings of the Fourth
Berkeley Symposium on Mathematical Statistics and Probability, Vol. 1,
edited by J. Neyman. University of California Press, 1961.
13. Chung K. L., Go a Stochastic Approximation Method, Annals of Mathema¬
tical Statistics, Vol. 25 (1963), pp. 463—483.
14. Kesten H., Accelerated Stochastic Approximation, Annals of Mathemati¬
cal Statistics, Vol. 29 (1958), pp. 41—49.
15. H о Y. C., On the Stochastic Approximation Method and Optimal Filtering
Theory, Journal of Mathematical Analysis and Applications, Vol. 6 (1962),
pp. 152—154.
16. К u s h n e г H. J., A Versatile Stochastic Model of a Function of Unknown
and Time-Varying Form, Journal of Mathematical Analysis and Applications,
Vol. 5 (1962), pp. 150—167.
17. Kushner H. J., Hill—Climbing Methods for the optimization of Multipa¬
rameter Noise Disturbed Systems, Proceedings of the 1962 Joint Automatic
Control Conference, New York City, Paper No. 8—4.
18. Kushner H. J., A New Method of Locating the Maximum Point of an
Arbitrary Multipeak Curve in the Presence of Noise, Proceedings of the 1963
Joint Automatic Control Conference, Minneapolis, Minn., pp. 69—80.
19. Bellman R. E., Introduction to Matrix Analysis, McGraw-Hill, NYC, 1960.
20* Цыпкин Я. 3., Адаптация, обучение и самообучение в автоматических
системах. Автоматика и телемеханика, N° 1, 1966.

ГЛАВА И
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
Бике (G. A. Bekey)
11.1.	Введение
Если сигналы в одной или нескольких точках системы могут
изменяться лишь в дискретные моменты времени, то такие системы
называются дискретными или импульсными. Импульсные системы,
вообще говоря, содержат элементы, работающие от непрерывных
сигналов, элементы, работающие от дискретных сигналов, приборы
для преобразования непрерывной информации в дискретную (они
обычно называются импульсными элементами) и приборы для преоб¬
разования дискретной информации в непрерывную, обычно называемые
фиксирующими цепями. Операции выборки или квантования по вре¬
мени часто бывают периодическими, но могут быть и произвольными.
До настоящего времени анализ импульсных систем с линейными
элементами производился обычно с помощью специальной формы
преобразования Лапласа, называемым ^-преобразованием.
Использование таких преобразований, вообще говоря, ограничи¬
вается линейными системами с периодическим квантованием по вре¬
мени и с малой длительностью импульса, но может быть распростра¬
нено на некоторые другие случаи.
В соответствии с современными тенденциями в теории управления
дискретные системы в настоящее время изучаются с помощью метода
пространства состояний. Как и для непрерывных систем, метод состоя¬
ния и переходов из состояния в состояние дает возможность систе¬
матической формулировки большого класса проблем, включая произ¬
вольные способы квантования по времени и нелинейные операции.
Целью настоящей главы является обзор некоторых свойств линей¬
ных импульсных систем и методов их анализа, формулировка импульс¬
ных проблем с помощью понятия переменных состояний и обсужде¬
ние решения некоторых нелинейных задач. Будет также изложено
применение второго метода Ляпунова для изучения асимптотической
устойчивости дискретных систем.

414
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. И
Настоящая глава не является полным обзором методов анализа
и синтеза. Скорее это есть рассмотрение некоторых избранных проб¬
лем, иллюстрирующих применение метода пространства состояний
к анализу и синтезу импульсных систем.
11.2.	Процесс квантования по времени
Переход от непрерывной информации к дискретной выполняется
посредством выбирающего ключа или «импульсного элемента». Опе¬
рация импульсного элемента (ИЭ) может рассматриваться как моду¬
ляция последовательности импульсов p{t) непрерывным сигналом x(t)>
несущим информацию, как показано на рис. 11.1. Если x(t) исполь¬
зуется для модуляции амплитуды импульсов, процесс называется
амплитудно-импульсной модуляцией (АИМ). Если все импульсы
Импульсный элемент
Входной, сигнал
x(t)
л
Выходной импульс¬
ный сигнал x*(t)
_ ^
\
\
J
Последовательность импульсов
pit)
\
Рис. 11.1. Операция квантования по времени.
имеют одинаковую ширину /?, единичную	амплитуду	и следуют
с периодом Г, то последовательность импульсов может быть запи¬
сана так:
+оо
p(t) = 2 VUt — kT) — u{t — kT — K)\,	(11.1)
k=—co
где u(t) — единичная функция. Тогда выходная последовательность
импульсов (рис. 11.1) описывается формулой
x*(f) = x(t)p(t).	(11.2)
Если ширина импульсов мала, т. е. /г	Г, выход	ИЭ можно
считать просто числовой последовательностью [x(kTv)\. Этот тип
периодической выборки с бесконечно малой шириной импульса мы
будем называть обыкновенным или простейшим квантованием по вре¬
мени. Заметим, что идеализированный ИЭ является усилителем с пере¬
менным коэффициентом усиления, а идеализированный способ кван¬
тования по времени является линейной операцией, т. е.
[а{хi (t) -f- а.2х2 (01* = аух* (t) -j-	аус% (t\	(11.3)

11.2]
ПРОЦЕСС КВАНТОВАНИЯ ПО ВРЕМЕНИ
415
где X\{i) и x%(t) — непрерывные сигналы, а ау и а2 — произвольные
константы. Знак (*) обозначает операцию квантования по времени.
Если способ модуляции зависит от сигнала, ИЭ становится нели¬
нейным прибором. Широтно-импульсная модуляция (ШИМ) и частот¬
но-импульсная модуляция (ЧИМ) являются примерами нелинейной
выборки.
Анализ и устойчивость таких систем рассматриваются в следую¬
щих параграфах этой главы.
Восстановление информации. Восстановление непрерывного сиг¬
нала но дискретному производится с помощью фиксирующих цепей
и экстраполяции. Простейшим прибором восстановления является
фиксирующая цепь нулевого порядка, которая дает на выходе вели¬
чину
xR{t) = x{kT\	(11.4)
т. е. выходной сигнал остается постоянным между моментами кван¬
тования по времени и равен последнему дискретному значению. Более
сложные приборы могут использовать полиномиальную аппроксимацию.
Квантование по уровню. Если импульсный сигнал предназначается
для использования в цифровой машине, его нельзя считать произ¬
вольной величиной. В этом случае амплитуда сигнала выбирается
только из конечной последовательности величин, зависящих от числа
разрядов в регистре машины. Таким образом, импульсный сигнал
должен быть также квантован и по уровню. Квантование по уровню
есть нелинейная операция, которая существенна или несущественна
в зависимости от разрешающей способности вычислительной машины.
В этой главе мы не будем останавливаться на вопросе квантования
по уровню.
Частотные характеристики. Последовательность единичных
импульсов p(t) из (11.1) может быть представлена в виде ряда Фурье
в форме
ЕСО
p(t)= 21	(11.5)
/.■=—or-
где соs—<2izjT есть частота квантования по времени, а коэффициенты
ck находятся по формуле
1 	 —jka>sh
где 1г — ширина импульса.
С помощью (11.5) выходная величина импульсного элемента (11.2)
может быть записана как
=	2	Т> cos ^ № — ?)] j.	(11J)
где y = hws/2.

416
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. 11
Уравнение (11.7) показывает, что амплитудно-импульсная модуляция
приводит к умножению на функцию, которая содержит бесконечное
число гармоник частоты квантования. Следовательно, выходной сигнал
импульсного элемента содержит не только частоты выходного сигнала,
но также бесконечное число боковых частот.
Импульсная модуляция. Математическое представление идеали¬
зированного процесса квантования по времени упрощается, если
импульсный элемент заменить на идеализированный элемент, называемый
импульсный модулятор. Тогда последовательность импульсов кванто¬
вания по времени заменяется на
4-00
p(t)=	2	Ht-kT),	(11.8)
It = — оо
которая является последовательностью импульсов единичной интен¬
сивности. Если на вход идеализированного импульсного элемента по¬
дается непрерывный сигнал x(t), определенный для t^O, тогда вы¬
ходной сигнал ИЭ имеет вид
ос
x*(t)= Yi x(kT)b(t — kT)	(11.9)
k=0
и является последовательностью модулированных импульсов. Равенство-
(11.9) можно рассматривать как предельный случай выражения (11.2),
если предположить, что конечная ширина импульсов ИЭ есть 1//г,
так что выходные импульсы задаются выражением
/Г1 [и (t — kT) — и (t — kT— h)] x(kT)	(11.10)
для h<^T и /г стремится к нулю.
К сожалению, проблемы, возникающие при использовании обоб¬
щенных функций таких, как о (t), в литературе по дискретным си¬
стемам [1—3] решаются лишь эвристически, хотя это можно сделать
вполне строго.
Стационарность. Предположим, что квантуются по времени сиг¬
налы непрерывной, не меняющейся во времени линейной системы.
Так как ИЭ является прибором, зависящим от времени, результирую¬
щие сигналы будут нестационарны. Однако последовательность {x(kT))
будет стационарна.
11.3.	Поведение во времени идеализированной
импульсной системы
Рассмотрим систему, изображенную на рис. 11.2. Сигнал с выхода
идеального ИЭ подается на вход стационарного линейного объекта,
описываемого своей весовой функцией g(t). Так как на вход объекта
подается последовательность импульсов, то выходную величину y(t)

11.3]
ПОВЕДЕНИЕ ИДЕАЛИЗИРОВАННОЙ ИМПУЛЬСНОЙ СИСТЕМЫ
417
можно получить, суммируя отклики на эти импульсы, т. е.
оо
y(t)=	2 g(t-kT)x(kT),	(П.11)
U = О
где x(t) = 0 для f<0. В п-й момент съема
п
у{пТ) —	2 g(nT — kT)x{kT).	(11.12)
/г =0
Сумма	в	(11.12)	называется	сверткой, а последовательность	{^(/гГ)}
по аналогии	с	весовой функцией g(t) называется весовой	последова¬
тельностью, Равенство (11.12) является линейным соотношением между
x(t) / x*(t)
ff(t)
y(t) / y*(t)
Импульсный элемент
Импульсный элемент
Линейная
непрерывная система
Рис. 11.2. Разомкнутая дискретная система.
входной последовательностью \x(kT)) и выходной \у(кТ)} и, следо¬
вательно, характеризует импульсную систему. Заметим, что это соот¬
ношение между дискретными величинами непрерывного сигнала не
требует действительного наличия в схеме ИЭ. Сумма (11.11) дает
отклик, т. е. выходной сигнал системы для любых моментов времени.
Обозначая дискретные моменты времени через tk (O^k^n), равенство
(11.12) можно записать в виде
п
y(<n)='Zlg(tn-ik)x(tk),	(11.13)
к = 0
которое имеет место, даже если процесс квантования по времени не¬
периодический.
Разностные уравнения. Подобно тому как непрерывные динами¬
ческие системы описываются дифференциальными уравнениями, ди¬
скретные динамические системы описываются разностными уравнениями.
В случае периодического процесса квантования по времени разностные
уравнения будут иметь постоянные коэффициенты. Система п-го по¬
рядка описывается уравнением, которое выражает выходную величину
в любой дискретный момент времени через значения входных и вы¬
ходных величин в п предыдущие моменты.
Пример 11.1. Пусть система, изображенная на рис. 11.2, пред¬
ставляет двойное интегрирование. Весовая функция этой системы
(Ц.4)
1^ п/р Леондсса --

418	АНАЛИЗ	И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ	[ГЛ. 11
Из (11.13) получаем
п
y{tn)= Е (Я — k)Tx(tk),	(11.15)
k = 0
где процесс квантования периодический.
Следовательно,
У(<«+»)= S {n-k)Tx{tk)+TE x{tk)	(11.16)
k = 0	k	=	0
и
У(У= Е (п-*)Тх(Ь)+2Т Е x(tk)-\-Tx(tn+l). (11.17)
/г =0	/г	=	0
Объединяя (11.15), (11.16) и (11.17), получаем
У М - Яу (<„+i) + У (У = 7* (<»+0-	(11.18)
Это линейное разностное уравнение второго порядка, которое
связывает входные и выходные величины системы в дискретные мо¬
менты времени съема. Соотношение типа (11.18) можно обобщить,
используя понятие состояния дискретных систем, которое будет введено
ниже в настоящей главе. Заметим, что, так как порядок системы равен
двум, в разностное уравнение (11.18) входят значения величины в два
предыдущих момента времени.
11.4.	Частотный анализ идеализированных линейных
импульсных систем
Рассмотрим снова импульсную систему, изображенную на рис. 11.2.
В соответствии с определением импульсного модулятора квантованный
по времени сигнал записывается как
со
x*(t)= 2 x{kT)b(t— kT).	(11.19)
k = 0
Напишем преобразование Лапласа этого сигнала
оо
**(s)= Е x(kT)e~kTs-	(11.20)
k = 0
Можно показать, что эквивалентным представлением является
-1-00
X*{s) = Y 2 *(s + «MH-i-*--(0),	(11.21)
п= — со

11.4]
ЧАСТОТНЫЙ АНАЛИЗ ЛИНЕЙНЫХ ИМПУЛЬСНЫХ СИСТЕМ
419
где х (0) — начальное значение функции времени, а X (s) — ее пре¬
образование Лапласа. Из уравнений (11.20) и (11.21) видно, что ча¬
стотная характеристика квантованной по времени функции периодична,
т. е.
А'* (» = А* (у о) 4- /i/Ч).	(11.22)
Преобразование	Лапласа выходного сигнала системы	получается из
(11.20):
Y(s) = X* (s) О(s),	(11.23)
где
G(s) = <#[S(0].	(П.24)
Непосредственно применяя соотношения, полученные выше, найдем
преобразование квантованного но времени выходного сигнала системы
Y* (5) = X* (s) G* (5).	(11.25)
Это выражение периодично с периодом ш5. Чтобы	избежать	трудностей,
связанных с вычислением бесконечных рядов гипа (11.25), 5-плоскость
обычно отображается в новую комплексную плоскость, называемую
2-плоскостью с помощью преобразования
z = esT.	(11.26)
При этом преобразовании устраняется периодичность, так как
полосы левой полуплоскости 5 высотой (о5 рад/сек отображаются на
внутренность единичного круга в плоскости 2 [1, 2].
Применяя преобразование (11.26) к (11.20), получаем следующее
определение.
Определение. 2 — преобразованием функции x(t) называется
функция X комплексного переменного 2, вычисляемая по формуле
ос.
X(z) = 2 x(kT)z-k.	(11.27)
k = 0
Если обозначить теперь через G(z) 2-преобразование весовой по¬
следовательности {g{nT)}> то равенство (11.25) примет вид
Y(z) = X(z)G(z).	(11.28)
G(z) называется «импульсной передаточной функцией». Обратное пре¬
образование от (11.28) дает информацию о поведении выходного сиг¬
нала только в моменты съема. Если x(t) разрывно в некоторый из
дискретных моментов времени, то определение (11.27) неоднозначно.
Для того чтобы устранить эту неоднозначность, потребуем, чтобы
в точках разрыва x(t) существовали х(пТ~) и х(пТг), a X(z) опре¬
делим следующим образом:
X {z) = £ .v (А’ /') с 4	(11.27')
k = о
14*

420
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. И
Это соотношение является основным в так называемом «методе
^-преобразования» анализа идеализированных импульсных систем. Этот
метод был введен Гуревичем [6] в США, Баркером [5] в Англии и
Цыпкиным [4] в СССР. Применение ^-преобразования для анализа и
проектирования дискретных систем подробно изложено в нескольких
работах [1—3, 23].
Другие применения z-преобразования. Хотя метод ^-преобразова¬
ния применим главным образом к идеализированным импульсным си¬
стемам, где все ИЭ работают синхронно, его можно распространить
и на некоторые другие задачи. С помощью соответствующих задержек
или упражнений квантуемых по времени функций можно получить
отклик системы между моментами съема. Это изменение называется
модифицированным ^-преобразованием [1—3, 5]. Этим методом могут
быть исследованы системы с несколькими ИЭ, работающими с оди¬
наковым периодом, но с разными фазами, а также, хотя и с трудом,
системы ИЭ, которые работают с разными (но кратными) периодами.
Если период квантования по времени периодически изменяется, то
такие системы также могут быть исследованы методом ^-преобразо-
вания [2, 8, 9]. Однако все эти методы становятся не применимы в не¬
линейном случае.
Связь z-преобразования с разностными уравнениями. Уравнение
(11.28)	является ^-преобразованием соотношения между \х(пТ)) и
{у{пТ)\ и поэтому можно ожидать, что существует очень тесная связь'
между этим уравнением и соответствующим разностным уравнением.
Из определения (11.27) легко видеть, что если
Z{x(nT)} = X(z),
10
Z{x(n-\- 1) T}=zX(z).	(11.29)
Это соотношение сразу дает связь между соответствующими величи¬
нами разностного уравнения и ^-преобразования.
Пример 11.2. Рассмотрим снова систему примера 11.1. Используя
определение (или по таблицам), находим д-преобразование лля g(t) = t
Это выражение можно преобразовать
z-Y{z) — 2zY(z) + Y(z)=TzX{z).	(11.31)
Применяя (11.29) к каждому члену уравнения (11.31), получим
у(п-f-2) Т — 2у (п -f- 1) Т + у(пТ)= Тх{п+ 1) Г, (11.32)
что совпадает с уравнением (11.18).
Таким образом, ^-преобразование является полезным методом
получения разностных уравнений для линейных дискретных систем.

11.51
ФОРЛ\УЛИРОВКА ДИСКРЕТНЫХ ЗАДАЧ
421
11.5.	Формулировка дискретных задач с помощью
понятия пространства состояний
Метод состояния и переходов из состояния в состояние [24],
введенный в предыдущих главах для непрерывных динамических си¬
стем, дает также единую основу и для описания дискретных систем.
Использование метода пространства состояний для дискретных систем
в большой степени обязано работам Калмана, Бертрама [11—14] и
Беллмана [15]. Такой подход дает возможность одним и тем же
способом сжато формулировать как линейные, так и нелинейные
дискретные задачи с любым способом квантования по времени. По¬
лучающиеся уравнения удобны для вычисления на цифровых вычисли¬
тельных машинах. В этой главе мы будем пользоваться понятием
векторного пространства формально. Строгие доказательства читатель
может найти в литературе.
Интуитивное определение состояния динамической системы.
Предположим, что начальные условия, которые описывают динами¬
ческую систему в момент t0, известны. Тогда состояние системы в
момент ty>t0 есть минимальное множество величин, называемых пере¬
менными состояния, достаточных для описания настоящих и будущих
значений выходных величин объекта при условии, что входные вели¬
чины известны. (Более строгое определение смотри в работах Заде
[10]	и Заде и Дезоэра [24].) Ясно, что для непрерывной системы,
описываемой дифференциальным уравнением /2-го порядка, таким
множеством является выходная величина системы у (£) и его (п—1)
производная
Эти величины определяют состояние системы в момент t и могут
рассматриваться как координаты вектора состояния у (t). В § 11.3
было указано, что свободная дискретная система /2-го порядка может
быть представлена с помощью разностного уравнения, которое связывает
выходную величину в /г-й момент дискретного времени со значениями
выходного сигнала в предыдущие п моментов. Таким образом, величины
У Ук)> У ('7<—1)> • • • > У (?к-т) определяют состояние дискретной системы.
Уравнения изменения состояния непрерывной динамической си¬
стемы. Для иллюстрации этого принципа рассмотрим сначала линейную
систему, описываемую векторным дифференциальным уравнением
х— Ах-\- Ви; х(0) = Xq,	(11.33)
где х — //-мерный вектор состояния, и — //2-мерный вектор входных
величин. А и В — матрицы размера п X п и пУ^т. Решение этого
уравнения приведено, например,,в [16,17]
t
X (0 = ф {t —10) X (<0) + 5ф V — ч Ви (т) dx>	о1 -34)
о

422
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. 1Г
где Ф — переходная матрица системы (11.33), определяемая равенством
k =о
ф(*) = е“=2	(1	Ь35)
Решение можно также получить, применяя преобразование Лапласа
к каждому члену уравнения (11.33). В результате получим
X (s) = (si — А)1 х (t0) + (si — A)~lBu (s),	(11.36)
где / — единичная матрица, a X(s) = X[x(t)]. Сравнивая равенства
(11.34) и (11.36), находим выражение для переходной матрицы
системы
ф (t — t0) = [(si — Ay1].	(11.37)
Пример 11.3. Пусть задана линейная система, описываемая
дифференциальным уравнением с постоянными коэффициентами:
У+ 0^ + 0^ = to (О, 1
У(0) = с0, J>(0) = ch I
где константы аъ а0 и b не равны нулю. Обозначим
Х\=У>
(11.39)
х2=у. 1
Тогда уравнение (11.38) можно записать в форме векторного диф¬
ференциального уравнения (11.33) со следующими матрицами коэф¬
фициентов А и В:
II 0	^
А=\\
II —ао —а\
IIО II
В = \\	;	(11.40)
Ь
состояние системы определяется векторами
<Л)|
JC — Г1
И
х(0) =
с 1
(11.41)
Решение можно получить, используя равенство (11.34). Вернемся
теперь к дискретному случаю.
Уравнение изменения состояния линейной дискретной системы.
Рассмотрим линейные импульсные системы с периодическим кванто¬
ванием по времени. Пусть нас интересует поведение системы лишь
в дискретные моменты времени (моменты квантования). В большинстве
систем процесс квантования по времени может быть достаточно
идеализирован, так что приближенно система описывается конечным
набором дискрет, т. е. входных и выходных величин в момент tk и п
прошлых моментов квантования по времени (например, разностное
уравнение (11.27)). Эти дискреты можно рассматривать как перемен-

11.51
ФОРМУЛИРОВКА ДИСКРЕТНЫХ ЗАДАЧ
423
(11.42)
ные состояния системы, а их составляющие — как компоненты вектора
состояния x(tk). Тогда динамика таких систем может быть описана
с помощью векторного разностного уравнения вида
х (tk+\) = Ах (tk)	Ви (tk\
x(t0) = x0
для /г = 0, 1, 2... Как и прежде, х0 — начальное состояние, уравне¬
ние (11.42) соответствует векторному дифференциальному уравнению
(11.33) для линейной непрерывной системы. (Следует заметить, что
описываемая уравнением (11.42) система не обязана быть в действи¬
тельности импульсной: если движение непрерывной системы наблю¬
дается или измеряется каждые Т секунд, то она может рассматри¬
ваться как дискретная.)
Пример 11.4. Пусть линейная дискретная система описывается
разностным уравнением
х {tk+д + а\х (h+i) + аох (tit) = и (tk)y	(11.43)
где u(tk)—входной сигнал, а начальные условия считаются заданными.
То же уравнение после ^-преобразования имеет вид
44 = ■. .	■ j—•	(11.44)
U (z)	2-4-fl^	+ Oo	v '
Если обозначить
Х\ (tk) == Х №k)y
*2 (tk) = X\ (Vl)>
то уравнение (11.43) можно записать как
Х\ {tfi+l) == Xl2 (tk)y
Xzl (*A+l) = — а0*1 Vb) — alX(2 (**) + « (**)•
Эту систему скалярных разностных уравнений первого порядка можно
представить как векторное разностное уравнение
х (tk+\) = Ах (tk) -f- Вы (tk\
x(tQ) = x0,
(11.45)
(11.46)
(11.47)
где
является
констант
x{tk) =
х\ (h)
(11.48)
хч (tk)
вектором состояния, a xQ— начальное состояние. Матрицы
А и В имеют следующий вид:
0
1
10

424
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. II
Решение линейного разностного уравнения получается так же, как
и в непрерывном случае. Применяя ^-преобразование к уравнению
(11.47), получим
zX(z) = АХ (z) -{- ВU(z) -р zx (t0).	(11.50)
Разрешая это уравнение относительно X(z), находим
X (z) = (zl — Л Г1 z* (f0) + (zl — А~1) В U (z).	(11.51)
Так как А — постоянная матрица, то можно вычислить обратное
преобразование уравнения (11.51), чтобы получить x(tk):
к— 1
* (tk) = Ф (У л {to) + 2 Ф &-1 - *»> Ви &»>>	(11 -52)
п = 0
где переходная матрица вычисляется по формуле
Ф {tk)=ZT'{(zl-Arlz},	(11.53)
а второй член в правой части является сверткой, записанной в мат¬
ричной форме. Переходная матрица может быть также получена из
рассмотрения только свободной системы, и это помогает выяснить
смысл понятия перехода из состояния в состояние.
Рассмотрим систему уравнений (11.47) без возмущающего члена, т. е.
x{tk+\)=Ax{tk).	(11.54)
Если начальное состояние системы обозначать через лг(^0), то в пер¬
вый момент дискретного времени (tx = t0 -j- Т) состояние, в которое
переходит система, будет
X(tx)=Ax(t о),	(11.55)
во второй момент
х (t2) = Ах &) = А*х (t0),	(11.56)
в k-Vi момент
x{tk) = Akx{U).	(11.57)
Следовательно, векторное разностное уравнение (11.57) задает после¬
довательность преобразований начального состояния. Из сравнения
(11.57) и (11.52) видно, что переходная матрица идеализированной
линейной импульсной системы может быть записана как
Ф (tk)=Ak.	(11.58)
Векторное разностное уравнение (11.47) можно рассматривать
как рекуррентное соотношение, которое определяет состояние в момент
tk+l по данным значениям состояния и входа в момент th. Такая
форма удобна для решения на цифровой вычислительной машине.

11.51
ФОРМУЛИРОВКА ДИСКРЕТНЫХ ЗАДАЧ
425
Пример 11.5. В качестве подробного примера формулировки
и решения векторного разностного уравнения для линейной дискрет¬
ной системы рассмотрим блок-схему, изображенную на рис. 11.3.
U(t) у'
Фиксирующая
цепь нулевого
порядка
*(th)
;
y(t)
S2
Рис. 11.3. Разомкнутая дискретная система.
Пусть h(t)— выходной сигнал фиксирующей цепи и
xi=y,
=у.
Тогда можно сразу написать
h(tk) = u(tk\
Х2 (tk+l) = Х'2 (tk) ~Г ^ (tk)*
Xi(h+i) = xi(tk)-{- 7^2 (^)4~ Tlj2h{tk).
Вводя соответствующие обозначения, получим
х (^/г+l) = АХ (tk) -j- Bu (tk)y
x(t0) = C,
где x(tk)— вектор состояния в момент tk)
х\ (tk)
х (^к) —
А = 1
О 1
в =
Х2 (tk)
IIГ2/2II
С =
(11.59)
(11.60)
(11.61)
(11.62)
(11.63)
(ct и с\2— константы). Общее решение этого уравнения получается
из (11.52). Используя выражение (11.53), получим сначала переходную
матрицу
1	\	Т
\z—\]	(г—	1)
( 1
!1
о
Ф {tk) = Z-'{[z!-AY'z) =
1 kT
0 1
(11.64)
(11.65)

426
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕЛА
[ГЛ. 11
Из (11.53) легко видеть, что Ф (tk)= Ak. Следовательно, общее
решение можно записать как
k— 1
x(tk) =
kT\\
n = 0
72/ 2 + (k — 1 — n) 72
u(tn). (H.66)
Это выражение описывает состояние системы в момент tk = kT через
начальное состояние x(t0) и управляющий сигнал u(t).
Замкнутые системы. Развитая выше методика полностью при¬
менима и в случае замкнутых систем. Если управляющий сигнал
r(t)
Фиксирующая
цепь нулевого
порядка
Н*к)
S2
Рис. 11.4. Замкнутая дискретная система.
является ошибкой замкнутой системы, как это показано на рис. 11.4,
то ясно, что
u(tk)=r(tk) — x1(tk\	(П.67)
где r(t) — заданный процесс. Дополнив разностные уравнения, полу¬
ченные в предыдущих параграфах для разомкнутой системы, соотно¬
шением (11.67), получим полное описание замкнутой системы.
Дискретные системы с произвольным способом квантования
по времени. Одно из преимуществ понятия пространства состояний
заключается в том, что оно дает единый подход к изучению дискрет¬
ных систем [12], даже если способ квантования по времени произ¬
вольный, а также в случаях, когда
а) требуется знать поведение системы в промежутках между момен¬
тами квантования по времени;
б) период квантования по времени Tk не постоянный, а является
периодической функцией от k\
в) операции квантования по времени асинхронны;
г) квантование многократно;
д) импульсы квантования по времени не мгновенные, а имеют
конечную длительность.
Если объект линейный, то векторное разностное уравнение, полу¬
чающееся в этом случае, также будет линейным, но, вообще говоря,
с зависящими от времени коэффициентами. Если объект нелинейный
или если процесс квантования по времени зависит от состояния

11.51
ФОРМУЛИРОВКА ДИСКРЕТНЫХ ЗАДАЧ
427
системы (как, например, в дискретной системе с широтно-импульсной
модуляцией), то получающиеся нелинейные разностные уравнения
можно записать как
и(Ш	(11.68)
где/—вектор-функция указанных аргументов. Для иллюстрации при¬
менения понятия пространства состояний рассмотрим три примера:
два линейных и один нелинейный.
Пример 11.6. Дискретная система с асинхронным кванто¬
ванием по времени. Рассмотрим систему, изображенную на рис. 11.5,
Рис. 11.5. Дискретная система с асинхронным квантованием по
времени.
где оба ИЭ синхронизированы, но 6*1 отстает от 62 на т секунд.
(Этот пример взят из одной работы Бертрама [14].)
Составление разностного уравнения облегчается, если подходящим
образом выбрать переменные состояния и разделить интервал кванто¬
вания по времени на подынтервалы. Выход системы всегда является
одной из переменных состояния, как эго показано на рис. 11.5. Сле¬
дует заметить, что в этой системе имеют место два типа преобразо¬
вания состояния:
а) операции квантования и восстановления, которые выполняются
в дискретные моменты времени, и
б) операции непрерывного действия, которые происходят в интер¬
валы между моментами квантования.
Разделим интервал Т = tk+l — tk на четыре подынтервала и рас¬
смотрим следующие четыре соотношения:
1.	*(** + ^') = Ф1аг
И. х (tk -j- т+) = D2x (tk -f- 'О,
III. х(tii^l) = Q).2x(tk -|- т+),
IV. x{tt + i) = Dlx(tk + l).
Соотношения I и III соответствуют операциям непрерывных эле¬
ментов, а II и IV — операциям дискретных (квантующих и восстанав¬
ливающих) элементов. Матрицы Dx и D.2 описывают работу ИЭ 6i

428
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. И
и & и имеют вид
D1 =
1
0
0
0
1
0
0
0
0
1
0
0
0
1
0
0
0
у 7^2
0
1
0
0 -
—1
0
0
1
0
0
0
0
0
0
1
(11.70)
(Входной сигнал r(t) предполагается равным нулю.) Поведение системы
в интервале (££, tk-\- т~) определяется матрицей
<DiM =
и можно заметить, что
Фз
1
0
0
0
£-г
0 (1
-о
0
0
1
0
0
0
0
1
(Т —
4
(11.71)
(11.72)
Выражения	(11.69)	можно объединить, чтобы	получить	векторное
разностное уравнение
x(tk+1) = A(y)x(tk)f	(11.73)
где переходная матрица А имеет вид
А (т) = О.Ф, (Т — т) D,Ф, (т).	(11.74)
Как обычно, дискретные моменты времени tk в (11.73) понимаются как tt
Рис. 11.6. Многократная импульсная система.
Пример 11.7. Многократные импульсные системы. Анализ
систем с двумя или более различными ИЭ, работающими с различ¬
ными частотами, может быть проведен методом модифицированного
z-преобразования [1—3], [23]. Формулировка таких задач с помощью
понятия пространства состояний производится так же, как и в пре¬
дыдущем примере, где самый большой интервал квантования по вре¬
мени разбивается на несколько подынтервалов.

11.5]
ФОРМУЛИРОВКА ДИСКРЕТНЫХ ЗАДАЧ
429
Рассмотрим	систему, изображенную на рис.	11.6,	и	предположим
снова, что	r(t) = 0. ИЭ S*— апериодический и	имеет	период	либо 0,5,
либо 1,5 сек. Поэтому последовательность моментов квантования
по времени такова: в момент tk срабатывают оба ИЭ Si и Sb в мо¬
мент tk -f- 0,5 — только S2, в = tk -{- 2, 0 сек — снова оба vS\ и S2.
Таким образом, система описывается следующими уравнениями пере¬
хода из состояния в состояние:
I.	jc -f- 0,5 -) = ф,л:
И. х (tk 0,5+) = Е^х (t,t 4- 0,5),
III. л; +,) = Ф.>х (tk -{- 0,5+),
IV. x(tl+l) — E.2x (tk ,).
Снова уравнения I и III соответствуют непрерывным переходам,
а II и IV дискретным. Дискретные переходы (квантование и восста¬
новление) описываются матрицами
(11.75)
£,=
Поведение системы в интервале (t£, tk-
иошения (11.75—I), где
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
1
0
0
0
0
0
0
1
0
0
, ^2
0
0
1
0
0
0
0
0
1
0
1
0
0
0
0
0
0
0
0
1
0
0
0
0
1
(11.76)
■0,5') определяется из соог-
Ф1 =
1
1 — е ‘
0
0
1 — е
0
(Д
0
0
i~i+2e
0
Л\
4 ) 2
0
1
1 — е
1 — е
0
0
0
Г -1'
\е
,(П.77)
а в интервале (^/г-|-0,5+, tk + i) — из соотношения (11.75—III), где

430
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[Г’Л. 11
Следовательно, векторное разностное уравнение, описывающее
систему в дискретные моменты времени, соответствующее более мед¬
ленному ИЭ, имеет вид
x(tk+1) = Orx(tk\	(11.79)
где полная переходная матрица находится по формуле
(П.80)
Пример 11.8. Дискретная система с нелинейным элементом.
Рассмотрим систему, изображенную на рис. 11.7. Эта система
отличается от той, которая рассматривалась в примере 11.3, допол¬
нительным нелинейным элементом (усилителем с насыщением). Теперь
Рис. 11.7. Нелинейная дискретная система.
уже нельзя применить методы ^-преобразований, однако рекуррентные
формулы можно получить непосредственно. Для этой импульсной
системы они выглядят следующим образом:
р
Х\ (*ft+i) = *1 (<ft) + Тхъ (tk) +	g (и (У), I
X* ih + i) = X* (tk) + Tg (и (tk))	J
или в векторной форме
x(tk+i)=f[x(tk), u(tk)].
11.6.	Устойчивость дискретных систем
(11.81)
(11.82)
Определение устойчивости. В этом разделе мы будем рассмат¬
ривать лишь свободные, или невозмущенные системы (т. е. u(tk) = 0
для всех tk), описываемые уравнением
x(tk + 1)=f{x{tk)}.	(11.83)
Предположим, что система имеет положение равновесия, которое
обозначается хе. Тогда математически система находится в состоянии
равновесия, если
xe = f(xe).	(11.84)
Таким образом, состояние равновесия обладает тем свойством, что
если начальное состояние x(t0) = xe> то повторные итерации по фор¬
муле (11.83) не приводят к изменению состояния. Однако инженера

11.6]
УСТОЙЧИВОСТЬ ДИСКРЕТНЫХ СИСТЕМ
431
интересует вопрос, будет ли система возвращаться к положению рав¬
новесия при возмущениях? Интуитивно система называется устойчи¬
вой, если она остается вблизи точки равновесия. Если система устой¬
чива и стремится к положению равновесия при k-+oo, то она
называется асимптотически устойчивой. Если система асимптотиче¬
ски устойчива при любом отклонении от положения равновесия,
то такая система называется асимптотически устойчивой в большом,
или глобально асимптотически устойчивой.
Сформулируем теперь эти определения более строго [11, 13].
Предположим, точка равновесия находится в начале координат (это
всегда можно сделать с помощью соответствующего преобразования
системы координат), т. е. хе = 0. Пусть jj х|| означает евклидову норму
вектора х:
1*1 = (xf, х)Ч* = (х* + х\ +... + xiyi*	(11.85)
Определение. Состояние равновесия хе устойчиво, если для
любого заданного е]>0 существует &(е)^>0 такое, что для всех
начальных состояний лг0 из сферы радиуса 8
11*0 — хе\\^Ь
решение x(tk) для всех k остается внутри сферы радиуса s:
I! — IIО
Если положение равновесия устойчиво и, кроме того,
lim !*(**) —*е || = 0,
k —*■ ОС
то оно называется асимптотически устойчивым. Если при этом
радиус В начального возмущения может быть сколь угодно большим,
то положение равновесия асимптотически устойчиво в целом.
Важно отметить, что устойчивость определяется здесь в терминах
движения состояния системы в пространстве состояний, а не в тер¬
минах выходных величин системы.
Устойчивость линейных импульсных систем. Свободные линей¬
ные импульсные системы могут быть представлены формулой
*(*ft + i)=	(11.86)
где А — постоянная (независящая от времени) матрица (см. выше
пример 11.5). Решение записывается в виде
x(tk) = Akx(U\	(11.87)
т. е. представляет п последовательных преобразований начального
состояния. Точка нуль хе — 0 асимптотически устойчива в целом
тогда и только тогда, когда элементы матрицы Ak стремятся к нулю
равномерно по k при /г —► оо. Можно показать [12, 17, 24], что это

432
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. И
утверждение эквивалентно следующему:	система асимптотически
устойчива в целом тогда и только тогда, когда корни Хь Х2, ..., \k
характеристического уравнения
det (А — Х/) = 0
(т. е. собственные числа матрицы А) удовлетворяют условию
1Ч<1>	1= 1, 2, k.
Эго утверждение эквивалентно тому, что полюса импульсной пере¬
даточной функции замкнутой системы должны лежать внутри еди¬
ничного круга в плоскости д.
Пример 11.9. Снова рассмотрим импульсную систему рис. 11.4.
Для простоты положим Т— 1. Импульсная передаточная функция
имеет вид
- Tsl
Q(z)-.
У (г)
U (г)
_Г*(г + 1)
2(г-1)«-
(11.6
Знаменатель передаточной функции замкнутой системы (характе¬
ристическое уравнение) при Т = 1 равен
1+0(г) = г*-4
4=°,
(11.89)
и так как корни zt, |	1	1, /=1, 2, система не устойчива.
Запишем разностное уравнение так же, как и в примере 11.5
с дополнительным условием, что система замкнута, и, следовательно,
имеет место равенство (11.67). Для г 0 = 0 векторным разностным
уравнением является уравнение (11.86), где
1/2 1
— 1 1
А =
(11.90)
откуда получаем характеристическое уравнение
(1/2 -X)	1
\ А — X/1 =
1
= 0,
(11.91)
(1-Х)
совпадающее с уравнением (11.89), если X заменить на г.
Устойчивость линейной системы при наличии входного сигнала:
Данное выше определение асимптотической устойчивости относилось
к движению невозмущенных, т. е. свободных, систем.
Если к асимптотически устойчивой системе прикладывается огра¬
ниченный вектор входных величин, то вектор состояния остается
ограниченным. Это утверждение можно сформулировать более точно
в виде теоремы [24], которая дается здесь без доказательства.
Теорема 11.1. Если линейная дискретная система описывается
уравнением
хц-k + i) — Ax(th)~ Bu{tk)	(11.92)

11.6]
УСТОЙЧИВОСТЬ ДИСКРЕТНЫХ СИСТЕМ
и все собственные числа матрицы А лежат в открытом круге | X | <М,
то для всех начальных состояний и любой ограниченной последова¬
тельности векторов \u{tk)) соответствующий вектор состояния x(tk)
будет ограничен.
Другими словами, если Ц «(*,•) II <С М> i = 0, 1, 2, где Ж — неко¬
торое действительное положительное число, то можно найти другое
действительное положительное число с такое, что || х (tk) || с |j х (t0) ||
для всех /г, где x(t0) — начальное состояние.
Применение второго метода Ляпунова к дискретным системам.
Значение так называемого «прямого», или «второго, метода» Ляпу¬
нова для детерминированных асимптотически устойчивых нелинейных
дифференциальных уравнений особенно возросло в последние годы.
Этот метод основан на нахождении некоторой скалярной функции
переменных состояния системы, которая должна удовлетворять опре¬
деленным условиям.
Если такая функция, называемая функцией Ляпунова, существует,
то тогда нулевое решение дифференциального уравнения асимптоти¬
чески устойчиво в большом. Ценность метода заключается в том,
что он позволяет судить об устойчивости системы, не решая диф¬
ференциального уравнения. Подробное обсуждение второго метода
дано в главе 5.
Значительно меньше литературы посвящено применению метода
Ляпунова для исследования асимптотической устойчивости (глобаль¬
ной и локальной) разностных уравнений. Основные работы принад¬
лежат Хану [18], Калману и Бертраму [11, 13].
Дадим формулировку следующей теоремы об устойчивости. (Дока¬
зательство смотри в [11].)
Теорема 2. Если для разностного уравнения
x(tn+l) = f(x(tn))
существует скалярная функция V(х), зависящая от переменных состоя¬
ния системы, такая, что 1/(0) = 0 и
(I)	V(x)^>0,	если х Ф	0,
(II)	\Х[jc(^/г+0]	1/[а:(^*)[	при	k^>K,K конечно,
(III)	V(x) непрерывна по	х,
(IV)	V(x) -> сю.,	если I х	|| —>- сю,
то тогда положение равновесия л; = 0 асимптотически устойчиво
в целом и V(х) является функцией Ляпунова для этой системы.
(Следует заметить, что это условие лишь достаточное.) Как и в непре¬
рывном случае, требуется значительная изобретательность, для того
чтобы находить подходящие функции Ляпунова. Бертрам, например,
в [13] рассматривает применение функций вида
п
V, (X) = 2 С; | Xi |,
£ = 1
(11.93)

434
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. 11
(где Ci—константы) для исследования устойчивости дискретных
систем с нелинейными элементами. Для импульсных систем с конеч¬
ной шириной импульса Кадота [19] использовал функции вида
(л;) = 2 e°iTxl
1=1
(11.94)
Ясно, что обе функции положительны во всем пространстве. Так
как большинство теорем главы 5 полностью переносится на дискрет¬
ные системы, то поэтому теория второго метода здесь не рассматри¬
вается. Примеры использования второго метода для исследования
асимптотической устойчивости нелинейных дискретных систем можно
найти в следующих параграфах.
11.7.	Импульсные системы с частотно-импульсной модуляцией
Во всех рассмотренных выше системах информация передавалась
при помощи амплитудно-импульсной модуляции, а интервалы кванто¬
вания по времени либо оставались постоянными, либо изменялись во
Блок квантования
по времени
Фиксирующая
цепь
1-e~sT”
1
x(t)
2К
S
S -h 2
Объект
y(t)
Рис. 11.8. Импульсная система с изменяемой частотой квантования
по времени.
времени периодически. Если же эти интервалы являются функциями
переменных состояния, то система становится нелинейной. Настоящий
параграф посвящен обсуждению таких систем [20].
Разностные уравнения системы. Рассмотрим систему, изображен¬
ную на рис. 11.8. n-Pi интервал дискретного времени равен
Tn = tn^-tn.	(11.95)
Заметим, что периоды фиксации будут меняться так же, как и периоды
квантования по времени. Пусть блок квантования по времени и фик-

П.7]	СИСТЕМЫ С ЧАСТОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИЕЙ	435
сирующая цепь управляются по закону
Тп~ \e(tn) + 1 I’	(11.96)
т. е. большая ошибка дает увеличение частоты квантования.
Используя те же методы, что и в предыдущем параграфе, полу¬
чаем систему разностных уравнений в дискретные моменты времени
X(tn) =e(tn),	|
y(tn^)=y(.tn)exp(-2Tn)-\-Ke(tn)(l-exp(-2Tn)),	(11.97)
e(t„) =r(tn)—y(tn),	j
где Tn задается выражением (11.96). Уравнения (11.97) можно свести
к одному уравнению
У (*„+i) — — У (tn) {К - (1 + К) ехр [- 2а/(| г (tn)-у (tn) ] + 1)]} +
+ Кг (tn) {1 - ехр [- 2а/( | г (tn)—y(tn) \ + 1)]}.	(11.98)
Это нелинейное разностное уравнение может быть решено последо¬
вательно шаг за шагом, если известно начальное состояние у (to) и
задан входной сигнал r(tn) для tn^>to.
Исследование асимптотической устойчивости. Попробуем теперь
найти функцию Ляпунова для свободной системы, что является доста¬
точным условием асимптотической устойчивости в большом. Если
г(^) = 0, то (11.98) сводится к уравнению
y(tn+i) = -Ky(tn)i-(\-i-K)g[y(tn)},	(11.99)
где
g(tn)=y(tn)exр [- 2а/(\y(tn) | + 1)].	(11.100)
Это — векторное разностное уравнение, где вектор состояния y(tn)
имеет только одну компоненту. Возьмем в качестве предполагаемой
функции Ляпунова квадрат евклидовой нормы
Vi (у О=IIу {tn) IIs (tn?-	(11.101)
Напишем первую разность функции V,
A v, ОО =у (tn+l? - у (tn?.	(11.102)
Так как Vi(yn) положительно определена, непрерывна и стремится
к со при ||.УЯ 1оо, то остается показать, что kVi(y^) отрицательно
определена. Это означает существование в пространстве параметров
а, К области, в которой
Уп^>У'п+1 для всех п.	(11.103)
Из (11.96) и (11.100) получаем g как функцию от 7п и, подставляя

436	АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ	[ГЛ.	II
результат в (11.99), получаем неравенство (11.103) в следующем виде:
У\ [(1 + К? ехр (— 47л) — 2/С (1 -f- К) ехр (- 2 Тп) + К2]	(11.104)
где
Тп = Тп(*,Уп)
согласно уравнению (11.96). Заметим, что из физических соображений
и /С> 0. Следовательно, (11.104) эквивалентно
(1 + Kf ехр (— 4 Тп) — 2/С (1 —J— К) ехр (- 2 Тп) -f К* < 1.	(11.105)
Это неравенство можно использовать для нахождения границ пара¬
метров а и К. Если такие границы можно найти, то 1ДСУп) будет
функцией Ляпунова, а система
асимптотически устойчива в
большом. В качестве примера
пусть для простоты вычисле¬
ний К= 2. Тогда (11.105)
имеет вид
е-*тп(9е-*тп— 12)< — 3
(11.106)
или, ввиду того что е~*тп боль¬
ше нуля для всех Тп^> 0,
имеем
Ъе-'1Тп — 4< — -П • (П-107)
Рассматривая обе части этого
неравенства как две функции
A	и	/2(е~27л)>	можно
получить графически область устойчивости, начертив кривые Д
и Д, как показано на рис. 11.9.
Точки пересечений получаются из решения уравнения /1=/2.
Следовательно, ДР[_у (Д)]	0	при
Jr<>-'«<1.	(11.108)
Ясно, что верхняя граница не может быть превышена, так как для
всех
тп > о, <?-«»< 1.
Нижняя граница означает, что
-27„>li>l,	7'„< у In 3.	(11.109)
Рис. 11.9. Кривая Д и f9 в зависимости
- 2 т “
от с п.

11.71
СИСТЕМЫ С ЧАСТОТНО-ИМПУЛЬСНОЙ модуляцией
Принимая во внимание, что «закон управления» задается выражением
(11.96), получаем
Левая часть неравенства (11.110) достигает максимального значе¬
ния при \у (tn) | = 0, поэтому
а = (1пЗ)/2.	(11.111)
Таким образом, если а ниже границы (11.111), то нулевое решение
нелинейной системы асимптотически устойчиво в большом.
Интегральная частотно-импульсная модуляция. Система, кото¬
рая рассматривалась выше, использовала амплитудно-импульсную
модуляцию с дополнительной степенью свободы — регулируемой
частотой квантования по времени. Чистая частотно-импульсная моду¬
ляция представляла бы последовательность одинаковых импульсов,
частота которых зависит от
входного сигнала модулято¬
ра, как эго показано на
рис. 11.10. Если входную
величину модулятора обоз¬
начить через e{t)y то я-й
интервал между импульсами
Тп = tn+l — tn можно найти
по формуле
fn+ тп
5 e(t)dt = ±K, (11.112)
tп
где К — расчетный пара¬
метр. Уравнение (11.112) по¬
казывает, что если импульс появляется в момент tm то следующий
импульс появится, когда величина интеграла достигает К. При этом
знак импульса совпадает со знаком интеграла в этот момент времени.
Такая модуляция называется «интегральной частотно-импульсной мо¬
дуляцией» и, по-видимому, она подобна той, которая имеет место
в первой системе [25].
Подробный анализ интегральной частотно-импульсной модуляции
(ИЧИМ) применительно к системам управления можно найти в [26].
Этот анализ, проведенный с помощью обобщенного второго метода
Ляпунова, показывает, что предельным состоянием ИЧИМ управляе¬
мой системы второго порядка является предельный цикл, к которому
система сходится асимптотически.
e(t)
Частотно-
импульсный.
модулятор
u(t)
Объект
c(t)
	>—
Рис. 11.10. Интегральная частотно-импульс¬
ная модуляция и графики колебаний.

438
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. 11
11.8.	Широтно-импульсная модуляция. ШИМ
Одним из самых интересных разделов в дискретных системах
является анализ и синтез систем ШИМ. Эти системы существенно
нелинейны. В настоящем параграфе рассматриваются системы ШИМ
по работам Кодота, Борна [21, 27] и Нельсона [22], поскольку они
иллюстрируют полезность тех понятий, которые были введены выше.
Составление разностных уравнений. Система, которую мы рас¬
сматриваем, изображена на рис. 11.11. На управляющие входы линей¬
ного непрерывного объекта с интервалами времени Т поступают
Рис.
Дискретная система с широтно-импульсной
модуляцией.
импульсы с выхода широтно-импульсного модулятора. Прямоуголь¬
ные выходные импульсы модулятора имеют постоянную амплитуду Ж,
переменную длительность и задаются формулой
u(t)=
Msgne(kT) kT^t<^kT-\-h{kT),
(11.113)
kT-\-h(kT)^t<^{k-{-1) T,
a h(kT) (в дальнейшем для сокращения записи просто h (к)) означает
длительность /г-го импульса
h(k)= Т sat	t	(11.114)
где р — положительная	постоянная,	а	функция насыщения опреде¬
ляется как
+ 1	1,
satx = {	х	|аг|^	1,	(11.115)
— 1	—1.
Итак, u(t) — сигнал управляющего входа объекта. Сам объект
описывается векторным дифференциальным уравнением
x{t) = Ax(t)-\-Bu{ 0,	(11.116)
где х (t) — вектор состояния объекта в момент t. Так как объект
предполагается линейным и стационарным, матрица А размерности

11.8]	ШИРОТНО-ИМПУЛЬСНАЯ МОДУЛЯЦИЯ, шим	439
п X п и вектор В размерности п имеют постоянные элементы. Из
(11.113)	видно, что на входе объекта либо 0, либо постоянная вели¬
чина ± М.
| Таким образом, следуя методу § 11.5 для интервала времени
когда входной сигнал объекта равен 7W, получаем реше¬
ние уравнения (11.111) по формуле (11.34)
x(t) = 0(t — t0) х (*0) + Mg (t — Ul	(11.117)
где Ф(0—фундаментальное решение или переходная матрица диф¬
ференциального уравнения (11.116)
оо
ф(0 = ехрЖ= ^ AkU'	(ИЛ18)
к = О
a g(t) — возмущенное решение, определяемое как
t
g{t)=\<i>{u)Bdu.	(11.119)
О
Из (11.117) легко видеть, что
ф(0) = / и	g( 0) = 0,
где / — единичная матрица порядка /г, а 0 — нулевой вектор. Дру¬
гие полезные свойства матриц Ф (t) и g(t) имеются в [17, 22]
Ф (гг -1- v) = Ф (гг) Ф (тг),
(11.120,
Эти тождества следуют из свойств линейных систем.
Применяя полученные выше общие результаты к задаче ШИМ,
когда u(t) задано выражением (11.113), получим уравнение
jc [k Т + h (£)] = Ф[Н (/г)] x(kT)-\- и (k) g [h (АО].	(11.121)
Это выражение соответствует моменту окончания действия импульса
и получается из (11.117), если положить
^ = к 7, t = kT-\-h(k).
Для момента возникновения импульса
*[(£+ 1) T\ = &\T—h(k))x[kT-\-h(k)} + 0.	(11.122)
Уравнения (11.121) и (11.122) можно объединить
х|(А+1)71 = Ф[7'—Л(А)1{Ф[А(А)]ДС(АП + и(А)вг[А(А)]}.	(11.123)
Используя свойства (11.120) переходной матрицы, имеем
Ф [ Т — /г (/г)) Ф [к (/г)] = Ф ( Т)	(11.124)

410
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. И
и, следовательно, для системы получаем одно векторное разностное
уравнение
*[(£+ 1) T] = 0{T)x(kT)-\-u(k)<b[T—h(k)]g[h{k)].	(11.125)
Этим уравнением можно пользоваться при исследовании поведе¬
ния системы.
Устойчивость системы ШИ М. Для того чтобы применить вто¬
рой метод Ляпунова к уравнению (11.125), нужно сначала привести
матрицу А к диагональному виду.
Для простоты рассмотрим класс систем, у которых полюса а,-
передаточной функции Q(s) действительны и различны. В этом слу¬
чае существует действительная иеособая матрица Р такая, что
Р 'АР = J,
(11.126)
где J — диагональная матрица, у которой диагональные элементы
есть полюса т. е.
aj	0	...	0
0	а9	...	0
J= .	*	.	•	(11.127)
0	...	а„
Сделаем теперь преобразование
х = Ру,
отображающее пространство состояний X в пространство Y. Напи¬
шем разностное уравнение (11.125) в новых переменных
3» [(К+ 1) 7] = Е (Т)У (к 7) -{- и (к) Е[Т — h (k)]f[h (/г)],	(11.128)
где
Е{Т) = Р ЛФ (Т)Р —
eaiT 0
. 0
0 еШ ..
. 0
0
0
a Т
. е п
(11.129)
f[k(k)] = P-'g[h{k)} =
!(
1 —/•**)
«1v
/
1 (
1 7 ^ 1 \
Д
1 — е п к)
(11.130)

11.8]
ШИРОТНО-ИМПУЛЬСНАЯ МОДУЛЯЦИЯ, шим
441
Принимая во внимание свойства (11.120), выражение (11.128) можно
упростить
у[(1г-1-1) T] = E(T){y(kT)-u{k)g[-h(k)}}.	(11.131)
Возьмем теперь в качестве функции Ляпунова квадрат обобщенной
евклидовой нормы *) вектора у
V = MP='Zciy'l	(11.132)
i = 1
где Ci — положительные постоянные. Очевидно, что функция V поло¬
жительно определена. Для выполнения достаточного условия асимп¬
тотической устойчивости в большом положения равновесия уе = 0
необходимо показать, что ДрДух^О для всех у. Для этого мы, сле¬
дуя работе Кодата [21J, напишем Д1/[у>(/г)] в явном виде, используя
(11.131)
bV[y(kT))=V[y{k+ 1) T]—V[y(kT)]< 0,	(11.133)
Ci[e2atT(yi+Wi?-y\],	(Н.134)
i= 1
где yi — компоненты вектора состояния, а через Wi обозначено вы¬
ражение
a(k){e —l)	.	10~ч
Wi(k)= ■> а- (11.13a)
Преобразуя (11.134), можно показать, что условие (11.133) сводится
к нахождению постоянных ct таких, что некоторая матрица (эле¬
менты которой определяются через ct и параметры системы) должна
иметь отрицательные собственные значения. Таким образом, можно
найти область параметров, где система с ШИМ (рис. 11.11) асимпто¬
тически устойчива в большом. Этот результат используется для обес¬
печения устойчивости при нестроении компенсирующего блока цепи
обратной связи. Эти идеи лучше всего иллюстрируются на простом
примере из работы Кодога [21, 27].
Пример 11.10. Пусть линейный объект задается передаточной
функцией
(п-13б)
Дифференциальное уравнение для системы в течение интервала дей¬
ствия импульса имеет вид
х = ах-\- и (t),	(11.137)
*) Обсуждение вопроса о выборе в качестве функции Ляпунова раз¬
личных подходящих норм имеется в работе 113].

442	АНАЛИЗ	И	СИНТЕЗ	ДИСКРЕТНЫХ СИСТЕМ	[ГЛ.	и
где u(t) задается уравнением (11.113). Общее решение уравнения
(11.137) записывается как
t
jt(0 = ea<'-4x;(*0)-}-	(x)dx.	(11.138)
to
Обозначим длительность k-vo импульса h(k) через /г*. Тогда для
U — tk и t = tk —\— hk
x(tk-\-hk) = e*hb x(tk)-\-	^	^(<*+л*_,)и(т)а!х,	(11.139)
(k
а для t§ = tk-\-hk> t = (kI) T = tk+\
x (f*+1) = eaC -hh) x{tk-f /U).	(11.140)
Объединяя (11.139) и (11.140), получаем разностное уравнение,
которое описывает данную систему
tkJrhk
:(**)+	^ ea(tk~x)u(t)dt. (11.141)
х (0>+1) = еа
Рассмотрим теперь задачу регулятора r(t) = 0 и предположим, что
в цепи обратной связи (рис. 11.11) стоит только постоянный усили¬
тель afb. Тогда sgne(tk) =— sgn x(tk)y и в интервале (f*, tk-\-hk)
из (11.113) имеем
и (t) = M sgn е (tk) = — М sgn х (tk).	(11.142)
Подставляя в (11.141) и интегрируя, получаем
X (tk+i) = еаГ[х (tk) + (М/а) {е~аЛ* — l) sgn х (<*)]	(11.143)
или, так как sgnx(tk) = x(tk)/\x(tk)\,
— ah.
' (tk+\) = е'
С'-144)
Теперь выберем в качестве функции Ляпунова квадрат евклидовой
нормы, которая в этом тривиальном случае есть просто
V(x) = x*(tk).	(11.145)
Тогда система асимптотически устойчива в большом, если
А V {х) = х1 (tk+\) — x2(tk)<^ 0 для всех x(tk)^z0. (11.146)
Подставим (11.144) в (11.146)
Г М (е~а sat I * (*k) Р J V
— 1<0.	(11.147)

11.9]
СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
443
Это выражение кусочно-монотонно по \x(tk)\ вследствие свойств
функций sat xf и поэтому его максимум и минимум находятся на гра¬
ницах интервалов [0, (3] и [[3, оо]. Следовательно, нужно найти такие
значения а, М, [3 и Г, чтобы в точках |лг| = 0, \х\ = $ и |лг| = оо
выполнялось условие	В результате получаем три неравенства
I. ё
аТ
II.
лТ
1
1
тм
р
тм
в
<1-
„—о-'t
аТ
<1.
(11.148)
111. а < 0.
Заметим, что третье неравенство включает первое, так как
ГвГ-1
аТ
<1
ДЛЯ
а < 0.
Если, например, а = — 1, условие устойчивости сводится к выполне¬
нию неравенства
о-Т
77W /V — 1
1 Р \ — Т
<1-
(11.149)
Итак, для того чтобы система была асимптотически устойчива в боль¬
шом, параметры Т, М и р следует выбирать так, чтобы выполнялось
условие (11.149).
11.9.	Синтез дискретных систем
Предыдущие параграфы этой главы были посвящены анализу ли¬
нейных и нелинейных систем. Целью настоящего параграфа является
изучение проблемы синтеза главным образом линейных систем, спо¬
собных достигать состояния равновесия за минимальное число пери¬
одов квантования по времени. Сначала рассмотрим применение метода
z-преобразования для синтеза дискретной системы управления с ми¬
нимальным временем переходного процесса при специальных типах
входных сигналов. Синтез оптимальных дискретных систем с помощью
понятия пространства состояний будет рассмотрен кратко.
Синтез дискретных систем управления методом г-преобразо¬
вания. Рассмотрим одноконтурные замкнутые системы с квантова¬
нием по времени сигнала ошибки, изображенные на рис. 11.12, и
проиллюстрируем два общих подхода к задаче коррекции в импульс¬
ных системах. Метод частотных характеристик, используемый в ли¬
нейных непрерывных системах, состоит из следующих шагов:
1)	Формулируется критерий качества как цель задачи синтеза.
Таковыми могут быть обычные факторы: время переходного процесса
или величина перерегулирования при ступенчатом входном сигнале,

444
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕА1
[ГЛ. И
минимум среднеквадратичной ошибки или времени, необходимого для
перехода системы из произвольного начального состояния в состоя¬
ние равновесия.
2)	Находится передаточная функция замкнутой системы, исходя
из условия (1) и передаточной функции объекта.
Непрерывное
управляющее
устройстве Объест
r(t) tRyc(tJS
Фиксирую¬
N(s)
fy(s)
Л
щая цепь
1
f ^
-)
а)
Дискретное
управляющее
устройстве
Фиксирую¬
щая цепь
1-е
-sT
Объект
- Gp(s) -
c(t)
Ф- >■
Объект
/
Фиксирую
U(t)
Gp(s)
щая цепь
~ А
Управляющее
устройстве
в цели обрат¬
ной связи
«)
Рис. И.12. Импульсные системы с корректирующими цепями, вклю¬
ченными последовательно в цепь обратной связи.
3) Из (2) вычисляется передаточная функция физически реализуе¬
мого блока управления.
4) Синтезируется точно или приближенно управляющее устрой¬
ство.
Перечисленные выше операции не могут быть выполнены непо¬
средственно для синтеза корректирующего звена N(s), изображенного
на рис. 11.12, а. Передаточная функция этой замкнутой системы

11.9]
СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
44о
имеет вид
GnNGpW
K{Z)— R(z) — \ + GhNGp(z)
(11.150)
где
Ол^Ор(^) = 2{Ол(5)^(5)Ор(5)}
(11.151)
и G/г (5) — передаточная функция фиксирующей цепи. Легко видеть,
что передаточная функция N(s) корректирующего блока не может
быть найдена из уравнения (11.150). Следовательно, для непрерывной
коррекции дискретных систем нужно, вообще говоря, применять при¬
ближенные методы или же метод проб и ошибок [1—3, 23]. Если
же использовать дискретную коррекцию, то импульсная передаточная
функция имеет вид
Следовательно, если требования к системе могут быть выражены
в виде передаточной функции K(z) замкнутой системы, передаточная
функция дискретного корректирующего звена находится по формуле
(11.154). Такие дискретные корректирующие цепи в литературе обычно
называются «цифровыми», поскольку разностное уравнение, соответ¬
ствующее D (д), может быть реализовано на цифровой вычислитель¬
ной машине. (Однако термин «дискретная коррекция» более точен,
поскольку D(z) может быть реализовано также с помощью анало¬
говых элементов и блоков восстановления и квантования по времени
без квантования по уровню, которое имеет место в цифровых маши¬
нах. В действительности, при проектировании строго цифровых кор¬
ректирующих звеньев следовало бы учитывать нелинейный эффект
квантования по уровню.)
Остается показать, как требования к системе могут быть удов¬
летворены соответствующим выбором импульсной передаточной функ¬
ции К (z).
Рассмотрим следующий критерий.
1) Установившееся значение сигнала ошибки в дискретные мо¬
менты времени равняется нулю.
2) Время переходного процесса (т. е. число периодов квантова¬
ния, за которое ошибка в системе станет равной нулю) минимально.
Системы такого типа называются «минимальными». Для того чтобы
(11.152)
где
G(z) = Z{Gh(s)Op(s)}.
(11.153)
Из (11.152) можно сразу написать
D{z)
1 К (г)
(11.154)
G(z) 1 — K(z) •

446
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. и
отразить эти требования в К (z\ запишем сначала передаточнук>
функцию сигнала ошибки
E(z) — R(z)[ 1 —K(z)\,	(11.155)
где R(z) — преобразование входного сигнала.
Так как установившаяся ошибка должна быть равна нулю, то по
теореме о конечном значении из теории ^-преобразования [1—3]
следует
lim е (пТ) = lim (1 —z~l) R (z) [ 1 —K(z)] = 0.	(11.156)
n-i-CO	Z-y\
Рассмотрим теперь полиномиальный вход вида r(t) — tm, для ко¬
торого
я(*)=(т(ил57)
где A(z) — полином от г, не имеющий корней z= 1, а п = т-{-\.
Подставляя (11.157) в (11.156), получаем, что необходимое условие
нулевой установившейся ошибки эквивалентно тому, что 1—К (z)
содержит множитель (1—z~l)n. Следовательно, имеем
1 — K(z) = (\ — z-l)nF(z\	(11.158)
где F (z) — полином от z'1, не имеющий корней z= 1. Требуемая-
импульсная передаточная функция замкнутой системы, гарантирующая
нулевую установившуюся ошибку, имеет вид
K(z)= 1 —(1 — z^)nF(z).	(11.159)
Для того чтобы получить минимальное время переходного процесса,
подставим (11.158) и (11.157) в (11.55) и заметим, что
E(z) = A(z)F(z).	(11.160)
Для того чтобы ошибка обратилась в нуль за минимальное число
периодов квантования, полином F (z) должен иметь минимальную
возможную степень.
Если G(z) не имеет полюсов в начале координат и нулей на или вне
границы единичной окружности, то можно выбрать F(z)= 1, и остается
только удовлетворить условие физической реализуемости. С учетом этого
условия видно, что К (z) для минимальной системы берется в следую¬
щем виде:
На входе скачок K(z) = z'1.
На входе линейная функция K(z) = clz~x—z'\
Квадратичный вход К(z)—3z~l — 3z~2-j-z~3 и т. д. Вообще, если
вход имеет вид r(t) = tmy то минимальная система стабилизируется
за //2-f 1 период квантования.
В этом рассуждении молчаливо предполагалось, что 1) начальные
условия равны нулю, 2) объект не имеет полюсов вне или па гра-

11.91
СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
447
нице единичной окружности, 3) объект содержит достаточно интеграто¬
ров для того, чтобы было возможно сделать установившуюся ошибку
равной нулю для данного входного сигнала.
Обсуждение минимальных систем. К сожалению, изложенный
выше метод синтеза практически не пригоден по следующим сообра¬
жениям:
1) Минимальное время переходного процесса не гарантирует откло¬
нений от нуля в интервалы между дискретными моментами времени.
2) Синтез зависит от нейтрализации полюсов и нулей функции
G(z) для того, чтобы получить передаточную функцию замкнутой
системы К (г) с полюсами только в начале координат. Такая нейтра¬
лизация невозможна, если G(z) имеет полюса вне или на границе
единичной окружности.
3) Кратные полюса К {z) нежелательны с точки зрения чувстви¬
тельности.
4) Минимальные системы оптимальны только для определенного
типа входных сигналов, на которые они проектировались и, вообще
говоря, не являются таковыми для других входов.
Можно показать, что для того, чтобы обойти трудности 1) и 2),
необходимо изменить требования, накладываемые на К(z) следующим
образом:
а) К (z) должно быть ограниченным полиномом от z"1;
б) множество нулей К (z) должно включать все нули функции G(z);
в) множество нулей [1 — К (-г)] должно включать все полюса
функции G(z), расположенные вне или на границе единичного круга.
Эти принципы синтеза лучше всего иллюстрировать на простом
примере.
Пример 11.11. Рассмотрим систему рис. 11.12, в с
и фиксирующей цепью нулевого порядка. Минимальная система для
линейного входа получается синтезом подходящего дискретного кор¬
ректирующего звена. Тогда
(11.161)
Для линейного входа выбираем
[—K(z) = (\ —z'l?F(z)
и сначала положим F(z)= 1. Тогда
K(z)=2z~l — z-*
(11.162)
(11.163)
и получается корректирующее звено
К (г)	_	2(2	—	г-1)

448
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. 11
Из (11.164) видно, что корректирующее звено пытается компен¬
сировать пуль G(z), расположенный на границе единичного круга.
Но хорошо известно, что неполная компенсация ведет к неустойчи¬
вости. Более того, даже полная компенсация дает колебания между
моментами квантования по времени. Рассмотрим ошибку системы
E{z) = R{z)[\ —K(z)\=Tz'\	(11.165)
так что система стабилизируется за два периода квантования. Выход¬
ной сигнал корректирующего звена получается из
Е., (z) --= Е(г) D(z) = у	=
==2г'1 — Зг"2Н-3.г-3 —Зд-4 + ...	(11.166)
Таким	образом,	минимальная система не только требует	идеальной
компенсации	нуля,	но приводит также к колебаниям. Если	изменить
проектирование системы, включив нули G(z) в нули K(z), то получим
1 —K(z) = (l — z~xf Fx (z),	(11.167)
K(z) = (l +z-')F,(z),	(11.168)
где простейшие полиномы, удовлетворяющие этим соотношениям,
имеют вид
F^z) = 1 + 4/5*-1,	(11.169)
F2 (z) = (б/б^-1 — 4/5*-*).	(11.170)
В результате корректирующее звено будет
Р(г) = -“(6/°~4/°г д).	(11171)
и(*> Г- (1 + 4/5г-‘) •	1	■ f
Легко видеть, что	эта усовершенствованная система требует три
периода для стабилизации. Более того, E^{z)— теперь ограниченный
полином и, следовательно, система стабилизируется с нулевой пуль¬
сацией.
Введение в синтез систем, оптимальных по быстродействию.
В последние годы синтез оптимальных импульсных систем с точки
зрения концепции пространства состояний явился объектом интенсив¬
ного исследования [28—37]. Хотя детальное обсуждение этого вопроса
выходит за рамки данной главы, простейшая формулировка задачи
будет приведена здесь. Предположим, что система линейна, от вре¬
мени не зависит и описывается следующим векторным разностным
уравнением:
х (tk+l) = Ax (tk) + hu (у,	(11.172)
где х (tk) — я-мерный вектор состояния, u{tk) — скалярный входной
сигнал, А — матрица п X п и k — я-мерный вектор. Найдем состояние

! 1.9]
СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
4-19
системы в первые два дискретных момента времени
x(t{)=Ax(U) + hu(t о),
x(t.2)= A-x(t{))-\- Ahu(t0)-^-7 ^
Последовательные итерации приводят к
* (tN) = ANx (t0) -г А"-Чш (t{)) +... + Ли (tN_ 0.	(11.174)
Задача оптимального по быстродействию регулятора заключается
в переводе системы из любого начального состояния x(t{)) в начало
координат. Следовательно, требуется, чтобы jc(^v) = 0, и, умножая
предыдущее уравнение на — A~N, получим
* (*0) = _ A xhu (С) — A-*hu (С) —... — A A hu	(11.175)
Если обозначить совокупность u(t0),	через век¬
тор U(tN), где
и^ = и(и_ О,	(11.176)
то формулировка задачи оптимального синтеза сводится к нахожде¬
нию минимального N и соответствующего U(tN), удовлетворяющих
уравнению (11.175), т. е. переводящих систему в начало координат
пространства состояний. Вообще, (J(tN) является ограниченным по
величине,	так	что	рассматриваются только	допустимые	управления,
т.	е.	те	векторы,	которые удовлетворяют	заданным	ограничениям.
Для иллюстрации возможного подхода к задаче рассмотрим сле¬
дующий простой пример [28].
Пример 11.12. Пусть управляемая система задается передаточ¬
ной функцией
°-<s> = ?(JTT>'	(П-'77'
и на вход системы поступает сигнал с выхода фиксирующей цепи,
как это показано на рис. 11.12, в. Векторное разностное уравнение,
описывающее систему, может быть составлено методом, изложенным
в § 11.5. Если обозначить выходной сигнал c(t) = x] (t), с {t) = ат2(/),
то система описывается уравнением (11.172), где
А(Т) =
п-г-ч, _
10 <?-7 н~
Т— 1 +е~
\—е~т
(11.178)
Пусть теперь л;(1)(^0)— начальное состояние, из которого можно
попасть	в	начало	координат точно	за	один	интервал квантования
по	времени. Тогда	из (11.175) получаем
*{1) (U) = — и (<0)	А '	(7) /1(7 ).	(11.179)
Если положить А'1 (Т)h(T) — vb то
*1,,(<о)= —н(*о)«1.	(11.180)
15 п/р Леондеса

450
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. И
Рассмотрим теперь состояния дФ2) (£0), из которых можно попасть
в	начало	координат за два шага. Ясно, что это	эквивалентно тому,
что	состояние,	определяемое равенством (11.180),	может	быть достиг¬
нуто за один шаг. Тогда из (11.180) и (11.175) получаем
(<«) = Л~г (Г)[— и (4) - и (t0) h{T)\ =
= — и(^)А-2(Т)Н(Т) — 11(и)А-г(Т)Н(Т).	(11.181)
Полагая теперь A~‘2h = равенство (11.181) примет вид
x{i) (40 = и (4)щ — и (4>)ф,.	(11.182)
Можно показать [28], что два вектора и линейно независимы
для любых значений Т. Так как любой я-мерный вектор может быть
представлен линейной комбинацией п линейно-независимых векторов,
то отсюда следует, что начало координат достигается за два шага,
поскольку в этом примере x(tk) имеет размерность два. Следова¬
тельно, уравнение (11.181) может быть решено относительно u{t{)
и u(t0):
и (t9) = а„лг, (4,) 4- а,**4 (40, )	(11183)
и (4) = a.,ix, (4) -j- а.пх,г (40. J
Эта последовательность величин зависит только от начального состоя¬
ния jc(^o). Коэффициенты а£/ в (11.183) получаются из решения урав¬
нения (11.182). Но если система находится в момент tx в состоянии,
из которого она может достигнуть начала координат за один шаг,
то ясно, что второе уравнение в (11.183) можно записать в виде
и (4) = 7.ЦХ, (4) + а.пх% (4).	(11.184)
Смысл этого	результата заключается в том, что	оптимальное управ¬
ление может	быть	выполнено в виде линейного	не	зависящего от
времени блока обратной связи. Действительно, корректирующее звено
для этого случая есть просто
F(s) = a„4-a,.2s.	(11.185)
Для того чтобы получить коэффициенты au и а12 в зависимости от
параметров системы, нужно раскрыть уравнение (11.183). Эта проце¬
дура облегчается, если заметить, что
A-i(T)=A(—jT)	(11.186)
и тогда
-е’	-(е^-е1' — Т)	(1Пв71
ап—Т(ет-\ У	а'2_	Т(ег-\?	’	( '	}
Нахождению линейных оптимальных по быстродействию дискрет¬
ных корректирующих звеньев для некоторых типов линейных систем
посвящена работа Мюллина [37].

ЛИТЕРАТУРА
451
Если наложены ограничения на класс допустимых векторов
то можно попытаться разбить пространство состояний на области,
так что оптимальное решение будет известно, если система находится
в одной из таких областей [28—32].
Подобный метод, когда находятся области, из которых система
сходится к началу координат за минимальное число дискретных
моментов времени, может быть распространен и на задачу синтеза
оптимальной дискретной системы с широтно-импульсной модуляцией.
Другой метод основан на нахождении линейных функционалов,
полностью определяющих решение [30, 35, 36]. Можно также показать,
что при некоторых условиях дискретное оптимальное управление стре¬
мится к непрерывному оптимальному управлению, когда период кван¬
тования по времени стремится к нулю.
ЛИТЕРАТУРА
1. Ragazzini J. R. and Franklin G., Sampled-Data Control Systems,
McGraw-Hill, 1958.
2. T о u J. Т., Digital and Sampled-Data Control Systems, McGraw-Hill, 1959.
[Русский перевод: Т у Юлиус Т., Цифровые и импульсные системы
автоматического управления, «Машиностроение», М., 1964.]
3. Jury Е. I., Sampled-Data Gontrol Systems, Wiley, 1958. [Русский перевод:
Джури Э., Импульсные системы автоматического регулирования, Физ-
матгиз, М., 1963.]
4. Цыпкин Я. 3., Теория импульсных систем, Физматгиз, М., 1958.
5. Barker R. Н., The Pulse Transfer Function and its Application to Samp¬
ling Servo Systems, Proc. lnstn. of Elec. Engrs. v. 99, pt. IV, pp. 3021,
1952.
6. H u r e w i с z W., Filters and Servo Systems with Pulsed Data (Chapter 5
of Theory of Servomechanisms, by H. M. James, N. B. Nichols, and
R. S. Phillips), McGraw-Hill, 1947. [Русский перевод: Джеймс X., Ни¬
кол ь с Н., Ф и л л и п с Р., Теория следящих систем, ИЛ, М., 1953.]
7. Ligh thill М. J., Fourier Analysis and Generalized Functions, Gambridge
University Press, 1958.
8. Friedland B., Sampled-Data Systems Containing Periodically Varying
Members, Proc. First 1FAC Congress, Moscow, 1960. [Русский перевод:
Фридланд Б., Импульсные системы регулирования с периодически
меняющимися параметрами, 1 конгресс ИФАК, М., I960.]
9. В eke у G. A., A Survey of Techniques for the Analysis of Sampled-Data
Systems with a Variable Sampling Rate, ASD Technical Report ASD-TDR
62-35, February, 1962.
10. Zadch L. A., An Introduction to State-Spacc Concepts. AIEE Paper 10—1,
presented at the 1962 Joint Automatic Control Conference, June, 1962.
11. Kalman R. E. and Bertram J. E., Control System Analysis and Design
via the Second Method of Lyapunov, II, Discrete-Time Systems, Jour. Basic
Engrg., June 1960, pp. 394—399.
12. К a 1 m a n R. E. and Bertram J. E., A Unified Approach to the Theory
of Sampling Systems, Jour. Franklin Inst. v. 267, pp. 405—436, May, 1959.
13. Bertram J. E., The Direct Method of Lyapunov in the Analysis and De¬
sign of Discrete-Time Control Systems, pp. 79 — 104 Work Session on Lya¬
punov's Second Method, ed. by L. F. Kazda, University of Michigan, Ann
Arbor, September, 1960.
15*

45?
АНАЛИЗ И СИНТЕЗ ДИСКРЕТНЫХ СИСТЕМ
[ГЛ. 11
14. Bertram J. Е., The Concept of State in the Analysis of Discrete-Time
Control Systems, AIEE Paper 11 — 1, Presented at' 1962 Joint Automatic
Control Conference, June 1962.
15. Bellman R., Adaptive Control Processes: A Guided Tour, Princeton Uni¬
versity Press, 1961. [Русский перевод: Беллман P., Процессы регули¬
рования с адаптацией, «Наука», М., 1964.1
16. D е s о с г С. A., An Introduction to State-Spacc Techniques in Linear Sys¬
tems, AIEE Paper 10—2 presented at 1962 Joint Automatic Control Confe¬
rence, June, 1962.
17. Coddington E. A. and Levinson N., Theory of Ordinary Differential
Equations, McGraw-Hill, 1955. [Русский перевод: Кодди.н гтон Э. А. и
Левинсон Н., Теория обыкновенных дифференциальных уравнений,
ИЛ, М., 1955.]
18. Hahn W., On the Application of the Method of Lyapunov to Difference
Equations (in German), Mathcmatische Annalen, v. 136, pp. 402—441 (1958),
Also translated into English by G. A. Bckey and available from Space
Technology	Laboratories, Inc.,	as	STL, Translation TR-61-5110-16, April,
1961.
19. К a dot а Т. Т., Asymptotic Stability of Some Nonlinear Feedback Sys¬
tems, University of California, Berkeley, Department of Electrical Enginee¬
ring Report, Issue no. 264, Series No. 60, January, 1960.
20.	Be	key G.	A.,	Sampled-Data	Models of the Human Operator in a Cont¬
rol	System,	pp.	178— 186, ASD	Technical Report ASD-TDR-62-36, Feb¬
ruary, 1962.
21. К a dot a Т. T. and Bourne H. C., Stability Conditions of Pulse —
Width Modulated Systems through the Second Method of Lyapunov, IRE
Transactions, v. AC-6, pp. 266— 275, September, 1961.
22. Nelson W. L., Pulse—Width Relay Control in Sampling Systems, Trans.-
ASME, series D, v. 83, pp. 65— 76, 1961.
23. Kuo Benjamin C., Analysis and Synthesis of Sampled-Data Control
Systems, Prentice-Hall, 1963.
24.	Z a	d e h L.	A.	and Desoer	C.	A., Linear System Theory: The State
Space Approach, McGraw-Hill, 1963.
25. Li С. C. and Jones R. W., Integral Pulse Frequency Modulated Cont¬
rol Systems, presented at the 2nd Congress of the International Federation
of Automatic Control (IFAC), Basel, 1933. (To be published in the Procee¬
dings of the 2nd IFAC Congress, by Butterworths, 1964.) [Русский перевод:
Ли С. С., Джонс Р. Б., Интегральные системы управления с частотно-
импульсной модуляцией. Международная федерация по автоматическому
управлению; II конгресс ИФАК, Базель, 1964.]
26. F а г г е n к о р f R. L., S а b г о f f А. Е. and Wheeler Р. С., An Integral
Pulse Frequency On-Off Attitude Control System, Space Technology Labo¬
ratories, Inc., Report No. 8637-6117-RJ000. Redondo Beach, CaliL, March.
1963.
27. Kadota Т. Т., Analysis of Nonlinear Sampled-Data Systems with Pulse-
Width Modulators, University of California, Berkeley, Department of Electri¬
cal Engineering Report, Series No. 60, Issue No. 290, June 30, 1960.
28. Kalman R. E. and Bertram J. E., General Synthesis Procedure for
Computer Control of Linear Systems— An Optimal Sampling System, Trans.
AIEE, v. 77. pt. II, pp. 602— 609, 1958.
29. Kalman R. E. and К о e p с к e R. W., Optimal Synthesis of Linear Samp¬
ling control Systems Using Generalized Performance Indexes, Trans. ASME,
v. 80, pp. 1820—1826, November, 1958.
30. N e u s t a d t L. W., Discrete Time-Optimal Control Systems, International
Symposium on Nonlinear Differential Equations and Applied Mechanics, ed.
by J. P. LaSalle and S. Lefsch.ctz. Academic Press, 1963, pp. 267—283.

ЛИТЕРАТУРА
31. Desocr С. A. and Wing J., A Minimal Time Discrete System, IRE
Trans, on Auto. Control, v. AC-6, pp. Ill —125, 1961.
32. D e s о e г С. A., P о 1 а к E. and W i n g J., Theory ol Minimum — Time
Discrete Regulators, presented at 2nd 1FAC Congress, Basel, 1963 (To be
published by Butterworths, 1964). [Русский перевод: Дсзоср С., 11 о -
лак Э., Винг Дж., Теория дискретных регуляторов с наименьшим
временем регулирования. Международная федерация по автоматическому
управлению, 2-й конгресс, Базель, 1964.]
33. Цыпкин Я. 3., Оптимальные процессы в импульсных автоматических
системах. Изв. АН СССР. Энергетика и автоматика, К? 4, 1960, стр. 74—94.
34. Т о u J. Т. and V a d h а п а р h u t i В., Optimum Control of Nonlinear
Discrete—Data Systems, Trans. A1EE, pt. II, pp. 166—171, September, 1961.
35. Красовский IT H., Об одной задаче оптимального регулирования.
Прикладная математика и механика, т. XXI, в. 5, стр. 676 - 677, 1957.
36. Кое peke R. W., A Solution to the Sampled, Minimum Time Problem,
Preprints of 4th Joint Automatic Control Conf., pp. 94—100, 1943.
37. M u 1 1 i n F. J. and deBarbyrac J., Linear Degital Control, Preprints of
4th Joint Automatic Control Conference, pp. 582—588, 1963.
38. П ы ш к и п И. В., Процессы конечной длительности в широтно-импульс¬
ных системах. Автоматика и телемеханика, 21, № 2, 1960, стр. 201— 208.
39. Nelson W. Т., Optimal Control Methods for On-Off Sampling Systems,
Trans. ASME (J. Basic Engr.) v. 84, Ser. D. pp. 91 —101, 1962.
40. Pol a k E., Minimum Time Control of Second-Order Pulse-Width-Modulated
Sampled-Data Systems, Trans. ASME (J. Basic Engr.) v. 84, Ser, D., pp.
101 — 110, 1962.
41. Smith F. Т., A Discussion of Several Concepts used in the Optimization
of Control Systems by Dynamic Programming, RAND Corp. Report P-1665,
April 9, 1959.
42. Monroe A. J., Digital Processes for Sampled-Data Systems, New York
Wiley, 1962.

ГЛАВА 12
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
Бике (G. A. Bekey)
12.1.	Введение
Эта глава касается математического описания характеристики
человека-оператора как элемента замкнутой системы управления.
Рассмотрим упрошенную блок-схему системы, изображенную на
рис. 12.1. Такой схемой может представляться, например, система
Визуальное
устройство
Входная ["Г	!
величина
Выходная
величина
человека-
r(t)
I _
I
	I
\e(t)
Человек-
/ >
Управляемый.
оператор
m(t)
злемент
Выходная величина
системы
-Щ-
Си гнал обратной, связи
G(t)
Рис. 12.1. Простая система управления с человеком-оператором.
ручного управления положением одной из осей космического аппа¬
рата. Задача оператора заключается в том, чтобы зрительно выделить
ошибку системы и уменьшить ее с помощью соответствующих управ¬
ляющих движений. Его реакция должна быть согласована с требова¬
ниями, определяемыми как условием устойчивости, так и динами¬
ческими характеристиками системы.
С точки зрения проектировщика системы управления, весьма
желательно для предсказания свойств системы, чтобы передаточная
характеристика человека-оператора была выражена математически.
Однако построение адекватной математической модели поведения
человека-оператора является чрезвычайно трудным вопросом даже

12.2]
ХА РА КТ Е Р И СТИ К И Ч Е Л О В Е К А- ОП Е РАТО РА
455
для частной задачи *). Некоторые причины этого рассматриваются
в следующем параграфе.
Разработка модели человека-оператора в системе ручного отсле¬
живания содержит ряд попыток применить методы, используемые для
идентификации других физических систем. Можно назвать два основ¬
ных метода, которые здесь применяются. Это «метод спектрального
анализа» и «метод отслеживания параметра». Методы спектрального
анализа применяются для построения как непрерывных, так и дискрет¬
ных моделей. Метод отслеживания параметра основывается на том,
что принимается некоторая модель человека-оператора и параметры
этой модели настраиваются до тех пор, пока не минимизируется
соответствующий критерий, ошибки. Оба метода рассматриваются
в следующих параграфах данной главы, при этом коротко отмечаются
их преимущества и недостатки.
Вследствие того что получение адекватного описания поведения
человека-оператора в сложной системе является трудным вопросом,
почти все работы, сделанные в прошлом, имеют дело с такой же
простой системой управления, как на рис. 12.1. То есть предпола¬
гается, что оператор имеет одну или самое большое две входные
величины. При построении моделей обычно пренебрегают другими
входными величинами и цепями обратной связи. Если визуальное
устройство (рис. 12.1) является устройством, в котором осуществля¬
ется вычитание, и человеку показывается лишь рассогласование между
входной величиной г и управляемой переменной С, то задача известна
под названием «компенсирующее отслеживание». В функции оператора
входит сведение к нулю ошибки е. Если на визуальное устройство
выводятся как задающая входная величина г, так и выходная величина С,
задача называется «преследующим отслеживанием».
12.2.	Характеристики человека-оператора в системе управления
Поведение человека-оператора в системе управления определяется
следующими основными характеристиками [1—4].
а) Время реакции: наличие чистой временной задержки или транс¬
портного запаздывания, что можно ясно наблюдать по ответной
реакции оператора на ступенчатые входные величины.
б) Фильтрация низких частот: тенденция человека, производя¬
щего отслеживание, ослаблять высокие частоты, причем, как показали
непосредственное рассмотрение и гармонический анализ записей кри¬
вых отслеживания, это ослабление увеличивается с увеличением
частоты.
*) Под словом «задача» понимается комбинация частной входной функ¬
ции, управляемого элемента и визуального устройства в системе ручного
управления.

456
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
в) Зависимость от задачи: способность оператора изменять свои
передаточные характеристики для выполнения функций управления
в широком диапазоне динамических свойств управляемого элемента.
г)	Зависимость от времени: зависимость характеристик оператора
от времени, которая проявляется в двух формах: во-первых, его
характеристики изменяются со временем по той причине, что опе¬
ратор обучается; во-вторых, он может чувствовать изменение парамет¬
ров окружающей среды и параметров управляемого объекта и со¬
ответственно изменять свои характеристики.
д) Предвидение: хорошо известная способность человека-операгора
предсказывать курс цели на основе прошлых характеристик [5]. Такая
способность экстраполяции при отслеживании является важной, по¬
скольку это значит, что отслеживание «предсказываемых входных
величии» (например, синусоидальных или прямоугольных колебаний
постоянной частоты) отличается от отслеживания случайных или
случайно появляющихся входных величин. Отслеживание в случае
предсказываемых входных величин названо «прекогнитивпым» («рге-
cognitive») отслеживанием [3, 4].
е) Нелинейность', в некоторых задачах поведение оператора яв¬
ляется, по-видимому, линейным, в то время как в других задачах его
поведение нелинейно.
ж) Детерминированность: человек-оператор является недетерми¬
нистской системой, поскольку его характеристики в одном и том же
эксперименте отличаются от опыта к опыту. Однако его изменчивость
мала в ситуациях, когда время обучения достаточно и когда не ре¬
шается трудная задача. Поэтому детерминистская модель может
использоваться для описания характеристики человека-оператора в ста¬
тистическом смысле.
з) Прерывистость: большое число данных показывает, что чело¬
век-оператор ведет себя при некоторых операциях отслеживания как
дискретная или импульсная система.
Резличные модели человека-оператора, появляющиеся в литературе,
представляют попытки включить в математическое описание основные
характеристики, перечисленные выше.
12.3.	Квазилинейные непрерывные модели
Самыми ранними моделями, которые были построены с точки
зрения техники управления, явились модели Тастина [10] и Рагаз-
зини [И]. Эти модели постулировались как линейные и непрерывные
с дополнительным возмущением неизвестного происхождения. Тастин
назвал «остатком» дополнительный член, который не является резуль¬
татом линейных преобразований входной величины (т. е. составля¬
ющие отклика системы на других частотах, нежели присутствующих
в данном входном сигнале). Название «остаток» все еще используется

12.3]
КВАЗИЛИНЕЙНЫЕ НЕПРЕРЫВНЫЕ МОДЕЛИ
457
для квазилинейных моделей, которые рассматриваются ниже. Модель
человека-оператора может преставлягься в виде блок-схемы, которая
показана на рис. 12.2.
Модель Тастина основана на гармоническом анализе выходных
величин, когда входная величина является суммой трех синусоид.
Получающаяся в результате передаточная функция модели имеет вид
(12.1)
где 5 — комплексная переменная, D — временная задержка, а К, К\ и
/<2 представляют параметры, которые зависят от выбора динамических
характеристик управляемого элемента.
Человек- оператор
Управляемый
элемент
r(t)
Щ
eft) I
_E(joj)
\Лередаточная
I функиия N(Ju)) j
Остатокj
Рис. 12.2. Квазилинейная модель человека-оператора.
В 1948 г. Рагаззини предложил в неопубликованной статье, пере¬
данной Американской ассоциации психологов, передаточную функцию
следующего вида:
Gh(s) = К i^K\S -р -р e~Ds.	(1^-2)
Параметры передаточных функций (12.1) и (12.2) зависят от част¬
ной задачи. Передаточные функции такого типа будут называться
квазилинейными. В настоящем изложении считается, что квазилинейная
система имеет следующие свойства:
а)	Система может быть описана линейным дифференциальным
уравнением, коэффициенты которого зависят от структуры системы
и полосы частот входного сигнала, но остаются постоянными для
частной системы.
б)	Линейное соотношение определяет лишь часть выходной вели¬
чины системы (линейную часть). Дополнительно может присутствовать
случайная или некоррелированная составляющая. Обоснованность
использования квазилинейной модели зависит от той доли выходной
величины, которую она определяет.

458
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
Определение квазилинейности, данное выше, предполагалось Тас-
тииом в его работах, хотя он в явном виде не сформулировал такого
определения. Представляет интерес сделать обзор методов, использо¬
вание которых привело к квазилинейным передаточным соотноше¬
ниям [3, 12].
Филлипс [13] на основе ответной реакции при действии ступенча¬
той функции описал следующую модель:
oH(S)=^m + M£f!.	(12.3)
Мэйн [14] записал кривые ответных реакций при действии сту¬
пенчатых входных величин и получил модели человека-оператора,
проведя гармонический анализ этих процессов. Реакцию на ступеньки
использовали также Хиндман и Бееч [15], которые исследовали ра¬
зомкнутые системы. Их модель имела вид
Gol (s) =	е- Vs.	(12.4)
+ 2£(o„s + ^
Соотношения для разомкнутых систем неприменимы непосред¬
ственно к замкнутой системе с человеком-оператором.
Ответная реакция человека-оператора на чистые синусоиды так¬
же использовалась, но, как уже отмечалось выше, по-видимому, эта
реакция, количественно отличается от той, которая имеет место
при отслеживании более сложных сигналов. Целый ряд интересных
исследований выполнен с синусоидальными входными величинами
[16—18]. Из этих исследований можно сделать два главных вывода:
1) при достаточно низких частотах линейная неизменяемая модель
адекватно представляет основную часть выходной величины опера¬
тора; 2) по мере увеличения частоты, характеристики человека,
производящего отслеживание, постепенно отклоняются от характе¬
ристик, ожидаемых при использовании линейных неизменяемых мо¬
делей.
За последнее время выполнена большая часть важных работ с при¬
менением сложных сигналов, представляющих либо сумму колебаний
синусоидальной формы, либо сумму случайных сигналов, имеющих
соответствующие спектральные характеристики. Тастин использовал
сумму трех синусоидальных колебаний. Расселл [19] использовал
сумму четырех синусоидальных колебаний, а также измерил компо¬
ненты выходной величины, имеющие частоты, одинаковые с теми,
которые присутствовали во входной величине. Элкинд [6] провел
весьма тщательное изучение компенсирующего и преследующего отсле¬
живания, используя входные сигналы, представляющие сумму большого
числа синусоид (до 144), имеющих случайную величину фазового
сдвига. Метод синтеза квазилинейной системы, использованной Элкин-

12.4]	СИНТЕЗ	КВАЗИЛИНЕЙНЫХ	НЕПРЕРЫВНЫХ	МОДЕЛЕЙ	459
дом, будет описан в следующем параграфе. Крэндэл [7] для опреде¬
ления линейных зависимостей применил случайные входные сигналы.
Наиболее сильные на сегодняшний день результаты по исследованию
квазилинейных моделей получены Элкиндом и Крэндэлом.
12.4.	Синтез квазилинейных непрерывных моделей
Модели, описанные Элкиндом, получены методом, который пред¬
ложил Бутон [20] для анализа нелинейных систем при гауссовых
случайных входных сигналах. Теоретические вопросы, связанные
с отысканием передаточных функций при случайных входных сигна¬
лах, рассмотрены подробно Мак-Руэром и Крэндэлом, а также Буто¬
ном и бегло здесь описаны.
По существу метод основан на предположении, что выходная вели¬
чина системы, блок-схема которой показана на рис. 12.2, является
суммой двух сигналов, одного линейно коррелированного, а другого
некоррелированного с входной величиной.
Предполагается, что входная величина r(t) является гауссовым
случайным процессом. Будем стремиться минимизировать ошибку
между выходной величиной т! (t) и действительной выходной вели¬
чиной m(t). Линейный процесс можно описать во времени с помощью
весовой функции h (t) так, что
оо
т' (t) = \ h(z)e(t — x)dx.	(12.5)
О
Ошибка приближения определится следующим образом:
s (т ) — т (t) — тг (0 =
оо
= т (t) — ^ h (т) е (t — z) dz, z 0.	(12.6)
о
Попытаемся выбрать такое h(t), чтобы минимизировать средне¬
квадратичную ошибку, т. е.
е2 (t) — [m (t) — тТ (Г)]2.	(12.7)
Функция h(t), которая минимизирует выражение (12.7), является реше¬
нием интегрального уравнения Винера — Хопфа:
оо
Кт (') = \ h (a) Ree (х — и) du,	(12.8)
б
где Rem(т) — взаимная корреляционная функция ошибки и выходной
величины, a Ree(^)—автокорреляционная функция ошибки.
Чтобы использовать эти зависимости для синтеза квазилинейных
моделей, удобнее выразить их через частотные характеристики. Из
блок-схемы, изображенной на рис. 12.2, преобразование Фурье ошибки

460
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
f Г Л. 12
системы и выходной величины оператора определяется соответст¬
венно следующим образом:
E = R
M = R
1
— N
ge
_1 + GHGF
Ll + ghge\
GH
+ N
1
1 + GHGE_
Ll + °hge_
(12.9)
(12.10)
Выражение частотной характеристики, которая соответствует (12.8),
имеет вид
Sem (/'«>) — Он (/“) See (/“)>
(12.11)
где Sem(jw) — взаимная спектральная плотность мощности ошибки
и выходного сигнала, S(,r(jtо) — спектральная плотность мощности
ошибки, a GH(/<x>)—преобразование Фурье весовой функции h(t).
Используя выражение (12.11), найдем взаимную спектральную плот¬
ность Sre (yw) входной величины и ошибки, а также Srm(j ш) — вход¬
ной величины и выходной величины оператора
SreU*
1
1 + GH (jсо) Gp {jo>)
Srr («)
(12.12)
1 + GH (y’w) GE (ум)
Srr (“)•
(12.13)
В эти соотношения не входит спектральная плотность шум a Snn (со),
поскольку по гипотезе он некоррелирован с входной величиной.
Взаимные спектральные плотности (12.12) и (12.13) могут быть най¬
дены экспериментально. Тогда передаточная функция или квазилиней¬
ная передаточная функция получается как отношение двух найденных
экспериментально величин, т. е.
. Srm (У63)
СЯ(/0)) =
Sre (У‘м) ’
(12.14)
Соотношение (12.14) представляет множество экспериментальных
точек, которые определяют амплитуду и фазу комплексного числа
GH(jw). Если эти точки нанести на график в зависимости от частоты,
то получаемая кривая может хорошо приближаться следующим ли¬
нейным аналитическим соотношением:
0я(/ со):
АГв->°(, + J»TL)
:(T+7“Tv)(i
(12.15)
Если пренебречь динамикой управляемого элемента (т. е. Og(yto)— 1 \
тогда TL и 7/ приблизительно равны нулю и выражение (12.15)

12.41
СИНТЕЗ КВАЗИЛИНЕЙНЫХ НЕПРЕРЫВНЫХ МОДЕЛЕЙ
461
сводится к следующему:
Ке -
°я<М = ТТму	"2Л6>
«Остаточный»	член	представляется с помощью шума, введенного
в выходную	величину	оператора, как показано на	рис.	12.2. Если
определить «передаточную функцию H(jw) замкнутой квазилинейной
системы» следующим образом:
Н('"л=тт-й^ткг	(,2Л7>
а спектральную плотность остатка замкнутой системы
1
S'nnH =
1 + GH(j<*) Gр (уto)
S/w(o>),	(12.18)
тогда спектральная плотность мощности выходной величины опера¬
тора запишется так:
Smm Н = ! И С/со) j2 5ГГ (со) + S'nn (со).	(12.19)
Из уравнения (12.19) видно, что выражение спектральной плот¬
ности выходной величины для тренированного оператора состоит из
двух слагаемых: одного, получающегося в результате линейного пре¬
образования спектра входной величины Srn и другого, являющегося
дополнительным «шумом». Вопрос о том, насколько обоснована ква¬
зилинейная модель, можно теперь связать с той долей полной мощ¬
ности выходной величины оператора, которая предсказывается на
каждой частоте моделью. Это можно сделать, определяя линейную
корреляцию т и г (иногда называемую «когерентной функцией»), сле¬
дующим образом:
g_ 1 _ (12.20)
Элкинд показал в своих исследованиях, что линейная корреляция
равна 0,9 или выше при плоском спектре входной величины с рез¬
ким спадом приблизительно на частоте 0,75 герца или при более
низких частотах. Линейная корреляция быстро падает с увеличением
частотного содержания входного сигнала. При плоском спектре вход¬
ной величины с резким спадом при 1,6 герца р приблизительно
равно 0,75, а при 2,4 герца — около 0,6. Поэтому квазилинейную
модель можно считать обоснованным представлением поведения чело¬
века, осуществляющего отслеживание лишь в ситуациях, когда вход¬
ной сигнал несет незначительную энергию на частотах выше 0,75
герц.

462
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
12.5.	Зависимость параметров модели от вынуждающей функции
Если пренебречь динамикой управляемого элемента, то выраже¬
ние (12.15), описывающее	квазилинейную модель, сводится к сле¬
дую и [ему:
^	Ке ~усоD Ke~j2^D
Ои (/(d) =  	==—	 (12 21)
HV ;	i+j«TN 1 +jfifN-	у l>
Элкиндом показано, что параметры К и fN связаны между собой
в широкой полосе частот входного сигнала. Имеются данные, что
при любых входных сигналах, когда р^>0,9,
К/м= 1,5.	(12.22)
Кроме того, если спектр входного сигнала плоский, то коэффи¬
циент усиления К модели зависит от частоты среза входной функ¬
ции /со следующим образом:
(12.23)
' СО
Равенства (12.22) и (12.23) получены эмпирически, а не из теоре¬
тических соображений. Однако они указывают на зависимость харак¬
теристик оператора от различной трудности задач. Таким образом,-
по мере того как /со увеличивается (и задача становится более труд¬
ной), коэффициент усиления К модели уменьшается, а частота с отри¬
цательным сдвигом по фазе /у увеличивается.
Для всех отслеживаний, в которых соотношения (12.22) и (12.23)
приближенно выполнялись, запаздывание модели было следующим:
D^0,13 сек.	(12.24)
Временная задержка реакции на ступенчатую входную величину
для разомкнутой системы приблизительно равна 0,25 сек. То, что
(12.24) определяет более низкое значение Д является разумным,
поскольку при отслеживании непрерывного сигнала в замкнутой сис¬
теме возможно некоторое предсказание.
Аналогичные работы были сделаны и для преследующего отсле¬
живания. В меньшей степени разработаны квазилинейные модели как
систем компенсирующего, так и преследующего отслеживания при
учете динамики управляемого элемента. Там, где квазилинейные мо¬
дели были уместны, они описывались выражением (12.15).
12.6.	Недостатки квазилинейной непрерывной модели
Квазилинейная модель убедительно доказывает, что при отслежи¬
вании сигналов низкой частоты поведение челсвека-оператора является
приблизительно линейным. Однако дополнительно к тому, что модель

12.7]
МОДЕЛИ ЧЕЛОВЕКА-ОПЕРАТОРА
463
пригодна лишь при ограниченных частотах, она страдает рядом дру¬
гих недостатков. Среди них имеются следующие:
а) Являясь линейной и непрерывной, выходная величина модели
не может содержать частот, отсутствующих во входном сигнале
(которые, как известно, существуют в выходной величине человека-
оператора).
б) Модель не может принять во внимание большое число экспе¬
риментальных данных (обсуждаемых ниже), которые предполагают
дискретное поведение человека, осуществляющего отслеживание.
в) Модель не принимает во внимание предсказывающей способ¬
ности человека-оператора.
12.7.	Дискретные или импульсные модели человека-оператора
Имеется значительное число данных, предполагающих, что ответ¬
ная реакция человека-оператора может быть прерывистой, а не
непрерывной, т. е. он работает на основе дискретных выборок по
времени из входной информации, а не на основе непрерывных вход¬
ных величин [2, 8, 9]. На основе гипотезы, что человек-оператор
ведет себя как дискретная система [9, 3], построено несколько мате¬
матических моделей.
Модель Норса
Первая дискретная математическая модель была предложена Нор¬
сом (22). Норс исследовал поведение типичной модели, описываемой
квазилинейным дифференциальным уравнением, которую предложил
Тастин. Затем он заменил производные в уравнении конечными раз¬
ностями и исследовал получившиеся в результате линейные разност¬
ные уравнения. В окончательном виде его уравнения включают в от¬
ветную реакцию человека, осуществляющего отслеживание, не только
детерминированные компоненты, но также и недетерминированные
компоненты, которые в дискретном случае представляли выборки
из «белого шума».
Подход Норса является очень усложненным и пытается много
учесть. Его недостаток в том, что сосредоточивается внимание на
поведении системы в «моменты выборки», в то время как выходная
величина человека-оператора явно непрерывная. То есть лю¬
бые дискретные процессы, которые могут иметь место, должны
проходить внутри системы, а для того чтобы выходная величина
была непрерывной, в модели следует предусмотреть восстанавли¬
вающий элемент. Норс вычислил спектральную плотность мощности
выходной величины своей модели как в непрерывном, так и в диск¬
ретном случае. Однако, поскольку временные характеристики были

464
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 1?
справедливы только для интервалов квантования по времени в целом»
он не мог сказать ничего более, чем то, что при стремлении этих
интервалов к нулю получающиеся в результате спектральные плот¬
ности приближаются друг к другу.
Исследование, проведенное Уардом с помощью аналогового
вычислительного устюойства
В диссертации, которую Уард представил на рассмотрение в Ав¬
стралии, рассматриваются вопросы исследования импульсной модели,
использующей аналоговое вычислительное устройство [23]. Модель
Уарда показана на рис. 12.3. Результаты исследования, проведенного
Уардом, даны в виде записей на самописце выходных величин вычис¬
лительного устройства, которые сравнивались с записями выходной
Модель человека - оператора
Генератор
колебаний
частоты
2 герца
hV)
—С
'“I
Задер¬
жка
0,3 сек
I
I Фиксирующая I
I цель нуле802о I
I порядка |
Импульсный
элемент 1
Э-\Xf*
Импульсный
элемент 2
Управляемый
элемент
G[(s)
c(tj
Рис. 12.3. Импульсная модель оператора по Уарду.
величины человека-оператора. Параметры модели настраивались вруч¬
ную с целью получить хорошее визуальное совпадение результатов
этих записей. Входные функции образовывались как сумма трех
синусоидальных колебаний, причем самая высокая частота была
равна 0,2 герца, а самая низкая — 0,01 герца. Кажущаяся величина
амплитуды «шума» имела одинаковый порядок как для человека,
так и для модели. Исследование носило ограниченный характер по
следующим причинам: 1) отсутствие аналитической разработки (оче¬
видно, Уард считал, что система является нелинейной просто вслед¬
ствие того, что в системе присутствует импульсный элемент; 2) с точки
зрения моделирования на аналоговых устройствах плохо выбрана
схема квантования и восстанавливающий элемент. Как можно заметить
по рис. 12.3, модель включает в себя импульсный элемент и фикси¬
рующую цепь нулевого порядка, за которыми следуют импульсный
элемент с задержкой (чтобы учесть время реакции) и затем интегра¬
тор. Однако интегратор является фиксирующей цепыо без возврата,

12.71
МОДЕЛИ ЧЕЛОВЕКА-ОПЕРАТОРА
465
и поэтому восстановленный сигнал ошибки ег> не напоминает непре¬
рывный входной сигнал. Тем не менее, хотя исследование Уарда име¬
ет ограниченный характер, оно полезно тем, что еще раз доказывает,
что по крайней мере часть «остаточного» шумового члена, кото¬
рый необходим в непрерывных моделях, можно представить, осу¬
ществляя квантование по времени гармоник.
Передаточные функции F\(s) и Fo(s) модели Уарда также нахо¬
дились эмпирически и записываются следующим образом:
F, М - Л + SS + D	,	(,2.25)
f!<s,= , I c	i~~’	(12,2<’>
sJ -(-2 (4СД to0s -\-	1	-T	0,5s
Квазилинейная импульсная модель
Для синтеза дискретных моделей также использованы методы
спектрального анализа [9]. Такая модель в ее самом простом виде
показана на рис. 12.4 для случая когда динамикой управляемого эле¬
мента можно пренебречь. Человек-оператор представляется с помощью
Визуальное ММемммвек^те^тра^
устройство !~
r(t)
Стационарная	I
случайно	‘
появляющаяся
входная величина
Фиксирую
щаяцснь
Ke'te ! Wt)
1+TNs
I
	I
Рис. 12.4. Дискретная модель человека-оператора.
c(t)
периодического импульсного элемента, фиксирующей цепи и непре¬
рывного звена, описываемого выражением (12.21). С помощью импульс¬
ной модели, изображенной на рис. 12.4, можно решить некоторые
сложные вопросы, возникающие при использовании непрерывной мо¬
дели. Это видно интуитивно из рассмотрения следующих характери¬
стик систем с квантованием по времени:
а) Изменение входного сигнала не оказывает никакого влияния
вплоть до следующего момента выборки.
б) Присутствие импульсного элемента ограничивает частоты, кото¬
рые могут быть восстановлены на выходе системы, величинами, не
превышающими половину частоты квантования.
в) В результате действия импульсного элемента в выходной вели¬
чине генерируются гармоники, распространяющиеся на весь частот¬
ный спектр, даже если полоса частот входного сигнала ограничена.

466
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
г) Фиксирующая цепь, обычно стоящая после импульсного эле¬
мента, является экстраполятором во времени и восстанавливает сиг¬
нал, полученный на основе информации в моменты выборки. Поэтому
фиксирующая цепь первого порядка, которая производит экстраполя¬
цию с постоянной скоростью на основе настоящей и прошлой вы¬
борок из входной величины, сообщает модели характеристики, свой¬
ственные человеку, осуществляющему отслеживание.
д) В пределе, по мере того как частота входного сигнала стре¬
мится к нулю, выходная величина системы с квантованием по времени
стремится к выходной величине непрерывной системы. Это желательно,
поскольку непрерывная модель адекватна при низкочастотных вход¬
ных сигналах. Чтобы изучить влияние квантования на характеристики
системы, модель, изображенная на рис. 12.4, была исследована при
различных фиксирующих цепях и получено выражение функции спект¬
ральной плотности ошибки e(t) и выходной величины c(t) [9].
12.8.	Анализ непрерывных моделей с квантованием
по времени при случайных входных сигналах
Параметры моделей, которые рассматривались выше, могут быть
найдены экспериментально. В этом параграфе описан один из экспе¬
риментов, показано, каким образом найдены параметры и проведено
сравнение характеристик моделей и человека-оператора. В проведен¬
ном эксперименте пренебрегалось динамикой управляемого элемента.
Было найдено выражение спектральной плотности мощности ошибки
и выходной величины модели, которое сравнивалось с измеряемыми
значениями. Эксперименты, которые здесь описываются, являются ил¬
люстрацией того, насколько полезны и правильны квазилинейные модели.
Анализ системы с непрерывной моделью
Рассмотрим	систему отслеживания, изображенную	на	рис. 12.5.
Пусть	входной	сигнал состоит из «белого»	гауссового	шума, про¬
пущенного через фильтр низких частот, и пусть линейная модель
человека-оператора является либо непрерывной, либо дискретной.
Если входная величина линейной неизменной системы является
стационарным процессом x(t), который характеризуется спектральной
плотностью мощности Sxx(w)t то спектральная плотность мощности
выходной величины Syv(o>) равна
Syy^) = \FiJm)fSxxH,	02.27)
где F(j(») — передаточная функция системы. Если источник шума при¬
нимается «белым», тогда
(со) =	= const.	(12.28)

АНАЛИЗ МОДЕЛЕЙ С КВАНТОВАНИЕМ ПО ВРЕМЕНИ
467
Входная велит на системы отслеживания	имеет тогда следующую
спектральную плотность:
Srr(i») = \F(jb>)\*Nb	(12.29)
где передаточная функция фильтра низких частот определяется вы¬
ражением
^(/ш) = Г+7о^д-	(12.оО)
Представляет интерес найти выражение для спектральной плотности
ошибки и спектральной плотности выходной величины, когда пере¬
даточная функция непрерывной модели оператора равна
KHFe~ju>Dc
Q{jw) = Jp—. .	(12.31)
cv	1	+	./rc®	v
где Khe — коэффициент усиления, включающий коэффициент усиле¬
ния К и модели и коэффициент усиления управляемого элемента Кр.
Выходная величина
человека - оператора
Управляемый Вшодна;,
   величина
eft)
«Белый шум»
S>o(co) — Ng
Форми¬
рующий
фильтр
Входной
сигнал
r(t) +
>■
Srr(aj)2
Сигнал
ошибки
e(t)
,(ш)
Модель
человека-
оператора
m(t)
See (&)
Рис. 12.5. Система компенсирующего отслеживания.
Спектральная плотность входной величины определяется следующим
выражением:
N(iodj>
Srr( co) = ^yA.	(12.32)
ГГ	to-
Используя выражения (12.31) и (12.32), найдем спектральную плот¬
ность мощности ошибки
(1 -ф Т“СО“)
= (соз _j_	[(! _i_	+	т2(0з _|_ 2^(cos U>D — то> sin шО)] ’ Ч2-33)
где для удобства опущены индексы при т, К и D. Аналогично спект¬
ральная плотность мощности еы ход ной величины равна
K2<*%N0
See (С0)	^2	_j_ T2W2 _j_ 2ip (cos	о)D   TO) sin (J)/))] ’	2.34)
Выражения	(12.33)	и	(12.34)	представляют	спектральные мощности,
которые можно вычислить по	экспериментальным	данным и сравнить
с теоретическими значениями.

-168
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
Анализ модели с квантованием по времени
Анализ, подобный тому, который был проведен выше, выполнен
для случаев, когда в дискретной модели использованы фиксирующие
цепи нулевого и первого порядка. Однако, поскольку наиболее важ¬
ные результаты получены с фиксирующими цепями первого порядка,
здесь приведены результаты анализа моделей, содержащих только эти
фиксирующие цепи.
Сигналы в импульсных системах, вообще говоря, не являются
стационарными даже при стационарных входных величинах. Поэтому
статистические характеристики, вычисленные на основе усреднений
по множеству, не равны тем, которые вычислены на основе усред¬
нений по времени. В данном исследовании спектральные плотности
находятся по усредненным по времени автокорреляционным функциям.
Теперь рассмотрим форму модели оператора с квантованием по
времени, приведенную на рис. 12.4. Вывод выражения для спектраль¬
ной плотности мощности выходной величины производится способом,
аналогичным для случая непрерывных систем, лишь с теми усложне¬
ниями, которые вводятся квантованными по времени сигналами, имею¬
щими периодический спектр вдоль всей частотной оси. Спектральная
плотность мощности непрерывного сигнала ошибки е (i) не может
быть найдена с помощью единственного соотношения, аналогичного
(12.33), поскольку нет передаточной функции, явно связывающей £(/о>)
и R(Jo)) в системе с квантованной по времени ошибкой. Таким обра¬
зом, необходима более сложная вычислительная процедура. Пусть
C5i(s) представляет передаточную функцию последовательности фик¬
сирующей цепи первого порядка и непрерывного звена, изображен¬
ных на рис. 12.4. Тогда можно показать, что поскольку
C(j^ Gsl (ja)	Л 9 4^
А’* </'••') ~ I + О* (М ’	1	'	’
то спектральная плотность мощности выходной величины опреде¬
ляется следующим выражением:
0Sl (»
Sec И :
5?r(«e),	(12.36)
1 + G*SiU«)
где, как обычно, звездочкой обозначаются квантованные по времени
величины. Спектральная плотность квантованного по времени сигнала
определяется в терминах ^-преобразования 5ГГ(5)
■|- оэ
5?r(s) = yZ[5„(s)lL_ei7-=^ 2	+	(12-37)
П— — СО
Дополнительный коэффициент 1/Г возникает вследствие усредне¬
ния за время периода квантования; Srr(s) является двусторонним пре¬
образованием Лапласа спектральной плотности мощности.

12.8]
АНАЛИЗ МОДЕЛЕЙ С КВАНТОВАНИЕМ ПО ВРЕМЕНИ
Можно показать, что выражение спектральной плотности мощ¬
ности непрерывного сигнала e(t) имеет вид
И = Srr(ш) -1 X, (u>)Re I G*' (/и)
чег; ~ггк , т ~гг\ 1 1 _j_ G*sl(j<a)
(12.38)
где, как и раньше, Srr(jw) является спектральной плотностью непре¬
рывной входной величины, a S?r(jw)—соответствующая спектраль¬
ная плотность квантованной по времени величины. В третьем члене
формулы (12.38) можно узнать выражение (12.36), которое является
спектральной плотностью мощности выходного сигнала c(t). Следова¬
тельно, в формуле (12.38) неизвестен только второй член, который
представляет удвоенную действительную часть взаимной спектральной
плотности г (t) и c(t), обозначаемой Src(ju>).
Для вычисления спектральных плотностей 5гг(оз) по формуле (12.36)
и S„(a>) по (12.38) следует найти ^-преобразование передаточной
функции разомкнутой цепи
0„ (s, = (-r-)	(^).	(12.39)
г-преобразование (12.39) равно
G, (z) =	f	(12.40)
Tz- (z—е )
где
Q,=(27 — D, — t)-f (x— Т)е-^т~°1\	\
Qt= Т — (1 + <?-"г)(27'— О, — т) — 2(t — T)e-^T~D\	(12.41)
Q3 = — Те-аГ-\-(2Т— Di — i)e-aT + (x— 7) я 1 r ~ D>. j
Подставляя (12.40) в (12.36), найдем спектральную плотность мощ¬
ности выходной величины
Хх И ==
= {4Х2(1 + 7"чо2)(1 +<?-2“г — ге-^созшГН! — cosоо7>2} S?r И X
X { Гшг (1 + хчо ;) [(1 + Р; + Р\ + Р|) -j- 2(Р, + P,PS + Р.2Р3) cos u) Т +
-\-2(Pi-{-P1P3)cQs2wT-\-2Pic.os3mT}-i,	(12.42)
где 5^r(w) для входного шума, пропущенного через фильтр, опреде¬
ляется следующим образом:
Nо^о s /z to г, 7
,S*(a) = __-JLB—ь 	(12.43)
v ’	21 (cho)BT—cos w/)	v
Аналогично из (12.38) определим спектральную плотность мощности

470
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
непрерывной ошибки
(Ш) =	(ш)	-f	5££	(Ш)	-	4	Re	,
(12.44)
где
Re С(П
— KFr (Р, со) [(1 + хРсо2) COS соD + СО (Т— т) sin со/)]
- Рсо2(1+т2оо2) (Р10.
А" [со (Г — т) COS со/) -
— Pj j COS соТ —Рi2 COS 2соР —[- Р13 COS Зсо Р)
(1 + ъТ*2) Sin cob] /ч(Р, со)
(12.45)
1 Рсо2(1 +T2cba)(Pi0 + P11COScoP-f P12COs2coP4-P1,COs3coP) ’
а коэффициенты равны
Fr (Р, со) = Р4 -L(P54-P7) cos О) Г+(Р6 + Р8) cos 2со P-f (Р3 -f P9)cos За) Р,
О (Р, ш) = (Р5 — Р7) Sino) 7 -f- (Рс — Р8) sin 2ш 7	(Р3 — Р9) sin 3u> 7,
Pi — (KQi— 7е_аГ)/7,
P.2 = KQJT,
p9=kq3!t,
p4=l_(2-j-e—7)pa —e—rpfc
P8 = Pi-(2 + e-“r)Pa + (l+2e-“7)P3,
Ре — Р-г — (2 ~г а 0 Рз>
р7 = —(2 + e-“r) + (l+2e-ir)Pi —е-а7Р2, [	(12.46)
P8 = (l -j- 2е~а7)— е-аТРь
Р3 = -е—т,
Pi«=l+Pf + PH-Pi
Рп = 2(РН-Р,Ра + Р2Рз),
P« = 2(P,-i-PiP,),
Р13 = 2Р3.
Таким образом, получено выражение для вычисления спектральной
плотности мощности ошибки и выходного сигнала модели с кванто-
ванием по времени через основные параметры непрерывной модели
(К, D и т=1/а) и дополнительные параметры D\ и Р.
Эксперименты и выбор значений параметров
Для проверки возможности построения предлагаемой дискретной
модели была разработана программа экспериментальных исследова¬
ний [9,33]. Измерялись спектральные плотности мощности выходного
сигнала и сигнала ошибки операторов, производящих отслеживание

12.8]
АНАЛИЗ МОДЕЛЕЙ С КВАНТОВАНИЕМ ПО ВРЕМЕНИ
471
случайно появляющихся входных величин. Эксперимент был поставлен
на основе компенсирующего отслеживания в одном измерении при
использовании ручного управляющего устройства с пренебрежимой
динамикой. В качестве визуального устройства использовался осцил¬
лограф. Входной сигнал r(t) снимался с фильтра низких частот, на
вход которого подавалась сумма 10 синусоидальных колебаний рав¬
ной амплитуды и с некрат¬
ными частотами. Такая по¬
становка эксперимента яв¬
ляется приблизительным от¬
ражением идеализированной
системы, изображенной на
рис. 12.4. Было сделано
около 100 записей на само¬
писце для 8 операторов, про¬
шедших предварительное
обучение.
Эксперименты использо¬
вались также и для того,
чтобы найти значения пара¬
метров для численного ра¬
счета спектральных плотно¬
стей мощности, получаемых
с модели. Параметры вы¬
бирались следующим обра¬
зом:
а) Данные для квазили¬
нейной непрерывной модели
находились методом, описан¬
ным в § 12.4, по измерениям
взаимной спектральной плот¬
ности входной величины
оператора, ошибки и выход¬
ной величины. Параметры непрерывной модели К, Dq и т находи¬
лись путем приведения в соответствие передаточной функции урав¬
нения (12.6) и экспериментальных данных.
б) Период квантования Т находился изучением записанных спект¬
ров для резко выраженных пиков в окрестности от 1 до 1,5 герца.
Предполагалось, что частота, на которой имеет место пик, соответст¬
вует половине частоты квантования.
в) Временная задержка Ds модели с квантованием по времени
находилась с помощью сценки эффективной временной задержки
вследствие наличия фиксирующей цепи (Dh) и затем полагая, что
Ds = Dc — Dh. Этот метод использовался с тем, чтобы полный
фазовый сдвиг разомкнутой системы оставался в интересующем
* *
I ~6
Г*
•ч-Ю
1-#
§ -14
~ -16
-18
■20
■22
S
§
и
I
I
>
<- -
_ J/u/LpiMc/ima.
nut
Ш
?т
очна
У
N
s*-:
C-Y
/
кпрврывне
1Я Ml
уде/,
VJ'
рч
К
s
f
s
о
ч
V
i
1
\
Т-
3 Л
Vs~-
:~L
1,0
4"
.А
\
X
0,6 0,8 1	2	3	4	5	6	8	W
Частота, рад/ сен
2Q
Рис. 12.6. Сравнивание экспериментальных
и аналитических значений спектральной
плотности мощности выходной величины
(из [9]).

472
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. |2
диапазоне частот приблизительно равным для дискретной и непрерыв¬
ной моделей.
Вычисление Sce(in) и Scc(o>) по формулам, выведенным выше, про¬
водилось на цифровой вычислительной машине. Типичные результаты
Ошибка человека- оператора
шпшш
Ошибка дискретной модели
:1Ш1 'чтттттФ7 -
FVwUUumm
5
/цшшшннш
iuuw
Выходная величина фиксируюшей иепи дискретной модели
Рис. 12.7. Типичные записи на самописце временных
характеристик дискретных моделей человека-опера¬
тора. Т = 0,33 сек. Все масштабы по вертикали равны.
показаны на рис. 12.6. Нанесенные на график точки представляют
спектральную плотность мощности, измеренную по 10 составляющим
частотам входного сигнала.
Результаты, представленные па рис. 12.6, показывают образование
пика в спектре выходной величины как оператора, так и дискретной
модели. Спектр непрерывной модели, хотя и хорошо совпадает

12.9]
НЕЛИНЕЙНЫЕ МОДЕЛИ ЧЕЛОВЕКА ОПЕРАТОРА
473
с данными на низких частотах, слишком быстро затухает на высоких
частотах. Спектральная плотность мощности дискретных моделей за¬
мечательно согласуется с экспериментальными данными, несмотря па
сделанные идеализирующие предположения.
Следует заметить, что временная задержка Ds модели с квантова¬
нием по времени, показанной на рис. 12.6, является отрицательной,
т. е. модель обладает свойством прогнозирования. Вероятно, что ис¬
пользование фиксирующей цепи с частичным запоминанием скорости,
которая дает в результате меньший фазовый сдвиг, приведет к модели
с положительным значением задержки.
На рис. 12.7 показаны типичные записи на самописце временных
характеристик, получающихся для дискретной модели.
Оценка дискретных моделей
Дискретные модели можно рассматривать как логичное обобщение
предыдущих работ по непрерывным квазилинейным моделям. Непре¬
рывные модели считались адекватным представлением поведения опе¬
ратора, производящего отслеживание, когда полоса частот входных
функций не превышала приблизительно 3/4 герца. В настоящих ис¬
следованиях частота достигает 1,6 герца. Исследования показали, что
для рассматриваемых систем отслеживания частного вида при исполь¬
зовании дискретных моделей спектры выходных величин лучше сов¬
падают с экспериментальными данными. В частности, показано, что
дискретные модели, которые содержат фиксирующие цепи первого
порядка, приводят к результатам, которые согласуются с большим
количеством данных, имеющихся в литературе по вопросу отслежива¬
ния. Необходимо провести дальнейшие исследования, чтобы устано¬
вить, применимы ли дискретные модели в более общих случаях при
различных условиях постановки эксперимента.
12.9.	Нелинейные модели человека-оператора
Квазилинейные модели, рассмотренные выше, могут отражать ряд
характеристик человека-оператора. Нелинейная характеристика вклю¬
чается только в том смысле, что она является возможным объясне¬
нием части «остаточного» члена.
Ряд исследований, проведенных авиационной корпорацией Goodyear
[24—26], был направлен на разработку моделей оператора, которые
бы учитывали ряд других свойств. На рис. 12.8 показана блок-схема
модели Goodyear. Эта модель содержит следующие нелинейности:
а) Зону нечувствительности, которая отражает порог чувствитель¬
ности оператора.
б) Насыщение входной величины по скорости.

474
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
в)	Обычную релейную функцию или релейную функцию с двумя
устойчивыми положениями, включенную параллельно основной цепи,
которая отражает «упреждающие» способности оператора.
Выходная величина модели сравнивалась с выходной величиной
человека-пилота, который реагировал на тот же самый входной сиг¬
нал. Параметры модели настраивались вручную до тех пор, пока
выходная величина модели не становилась похожей на выходную
Управляемый.
элемент
/ Выходная
величина
Рис. 12.8. Нелинейная модель человека-оператора.
величину человека-пилота. Этот метод можно считать ручным вариан¬
том метода автоматического отслеживания параметров рассматри¬
ваемого ниже в § 12.10.
После настройки параметров выходные величины этой модели
очень хорошо совпадали с результатами отслеживания, записанными
в функции времени. Модель представляет исторический интерес, но
имеет ограниченную применимость в виду ее сложности и трудно¬
стей, возникающих при ее моделировании на вычислительных устрой¬
ствах.
12.10.	Изменяемые во времени модели человека-оператора
Модели человека-оператора, рассмотренные выше, могли приме¬
няться лишь для определенных задач. Параметры моделей зависели
от динамических характеристик управляемого элемента и от спект¬
ральных характеристик вынуждающей функции. Так, по гипотезе
модели были неприменимы в течение переходного периода, например
в период, который следовал после мгновенного изменения либо вы¬
нуждающей функции, либо динамических характеристик управляемого

12.10] ИЗМЕНЯЕМЫЕ ВО ВРЕМЕНИ МОДЕЛИ ЧЕЛОВЕКА-ОПЕРАТОРА
475
элемента. Характеристику оператора в течение этого переходного
периода попытался исследовать Шеридан [27] *).
Модель, предложенная Шериданом, показана на рис. 12.9. Задаю¬
щая входная величина определялась суммой пяти синусоид
5
г (0= A* sin ^	(12.47)
i=i
а выходная величина оператора описывалась следующим образом:
5
с (0 = X (*)sin + 'Pi ^)] + п О-.	(12.48)
1 = 1
Оператор представлялся с помощью модулятора, который изменял
амплитуду и фазу сигналов каждой частоты, составляющих входную
величину.
I	J
Модель человека-оператора
Рис. 12.9. Линейная изменяемая во времени модель.
Большая часть работ Шеридана касалась решения теоретических
и практических задач, связанных с оценкой изменяемых во времени
амплитуд Bi(t) и углов фазы ср/ (0 с помощью методов гармонического
анализа. Результаты исследований давались в виде графика в поляр¬
ных координатах Bi(tj) и сдля пяти значений времени tj в те¬
чение 60 сек после мгновенного изменения задачи.
*) См. также Шеридан Т. Б., Экспериментальное исследование изме¬
нений передаточной функции человека-оператора во времени. Труды 1
Конгресса ИФАК. Теория дискретных, оптимальных и самонастраивающихся
систем, АН СССР, М., 1961, стр. 851.

т
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
12.11.	Методы автоматического согласования (отслеживания
параметров) модели для описания характеристик
человека-оператора [34]
В предыдущих параграфах делалось ударение на описание харак¬
теристик человека-оператора с помощью методов спектрального ана¬
лиза. Методы согласования модели основаны на формулировке пред¬
полагаемой математической модели неизвестной системы. На систему
(человек-оператор) и модель поступает одинаковая входная функция,
при этом параметры модели настраиваются до тех пор, пока не будет
достигнуто адекватное согласование свойств модели и системы.
Использование этого метода для отслеживания неизвестных и изме¬
няющихся во времени параметров объекта рассматривалось в главе О
в связи с адаптивными системами управления с эталонной моделью.
В данном и следующих параграфах этой главы делается упор па
применение метода для определения значений параметра, которые
минимизируют соответствующую функцию «ошибки отслеживания»,
т. е. рассогласование выходных величин модели и человека. В иссле¬
дованиях корпорации Goodyear (§ 12.9) и исследованиях, проведенных
Уардом (§ 12.7), согласование определялось визуально. Теперь рас¬
смотрим два метода, с помощью которых согласование между харак¬
теристикой модели достигается путем автоматической (с применением
вычислительного устройства) настройки параметров модели.
Общая формулировка задачи согласования модели
Рассмотрим блок-схему на рис. 12.10. Предполагается, что управляе¬
мый элемент является известной детерминированной системой, имею¬
щей выходную величину c(t), которая однозначно определена для
моментов t^y>t0 с помощью состояния 0Е при t = tQ и m(t) при
t^>tQ. Визуальное устройство, обозначенное символом суммирования,
формирует сигнал ошибки
e(t)=r(t)-c(t).	(12.49)
Человек-оператор Н имеет входную величину e{t) и выходную вели¬
чину m(t). Можно предположить, что, кроме входной величины e(i\
оператор может реагировать и на другие неизвестные нам входные
величины. Поэтому считается, что оператор является недетерминиро¬
ванным элементом.
Основная задача состоит в определении параметров М принятой
математической модели И. Поскольку Н недетерминированный эле¬
мент, детерминированная модель может описать его характеристики
лишь в статистическом смысле. Однако опыт предшествующих исследо¬
ваний гарантирует, что изменчивость человека-оператора мала в слу¬
чаях, когда время обучения оператора достаточно и когда не рас-

12.11!
МЕТОДЫ АВТОМАТИЧЕСКОГО СОГЛАСОВАНИЯ
477
•сматрмвается трудная задача. Как /И, так и Н получают в качестве
входного сигнала сигнал е(/)у как показано на рис. 12.10. Выходная
величина модели обозначается и (г), а ошибка согласования равна
\t) = m (0 — //(0.
(12.50)
Идеальной является модель, при которой e(t) равно нулю при
всех t. Предположим, что на интервале	модель	может
быть представлена системой нелинейных дифференциальных уравнений
щ = (iii, иь н„: рь рл.,рт\ e,t) (/=1,2,..., п). (12.51)
Начальное состояние модели предполагается заданным заранее и равно
(<о) =11 «о	(i — 1. 2. • • •. п).	(12.52)
Запишем уравнение (12.3) в векторной форме
й =М {и, р, с, t),	(12.53)
где а представляет состояние модели, р — вектор, яг-составляющих
которого являются параметрами модели, а М определяет вид модели.
Рис. 12.10. Система согласования модели.
Чтобы как можно ближе приблизить к нулю в (t), минимизируется
соответствующая функция F(s). Для сведения этой задачи минимиза¬
ции к обычной вычислительной процедуре необходимо выбрать функ¬
цию критерия качества, которая является обыкновенной функцией
параметров, как, например,
fo _h Т	Л)	-р	Т
F= г '2(t)dt=	\m(t)	— u(p,t)]-dt,	(12.54)
О,	/о
где предполагается, что р не изменяется в течение интервала интегри¬
рования Т. Теперь, если F — непрерывная функция ръ /л2, ..., рт>

478
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
то необходимым условием минимума F является следующее условие:
vp=(f,f Л-»
\др,’ дрг'	0рт)
Значения параметров, соответствующие минимуму, дают оптимальное
совпадение принятой модели с проводимым экспериментом в смысле
частной функции критерия F.
Настройка параметров, при которой минимизируется F, может
быть выполнена несколькими путями. Если настройк.а такова, что
траектория коллинеарна с вектором VF, тогда она называется траек¬
торией «наискорейшего спуска» [28]. Для произвольной начальной
точки р0 пространства параметров определяется градиент функции
критерия качества F
vF(/?o)-
Затем по соотношению
~ty~0 = -KVF(p0)	(12.56)
определяется вектор приращения параметра. Осуществление итератив¬
ной процедуры по выражению (12.56) дает в результате дискретную
траекторию наискорейшего спуска в пространстве параметров. Этот
метод применялся для определения моделей операторов, выполняющих
одномерное компенсирующее отслеживание.
12.12.	Непрерывные методы отслеживания параметров
Если интервал оптимизации в выражении (12.54) устремить к нулю,
то получается функция критерия качества, зависящая от времени:
/ = 8*(0 = [/я(0 —н(р, t)f.	(12.57)
В противоположность выражению (12.54) функционал / зависит
от всей предыстории вектора параметров р (см. главу 6). Поэтому,
в случае когда модель является динамической системой, значение век¬
тора градиента определить нельзя, если только параметры не фикси¬
рованы. В непрерывном случае можно получить метод «приблизитель¬
ного градиента» и «приблизительного наискорейшего спуска», при
условии что скорость настройки параметров достаточно мала по срав¬
нению с основной постоянной времени модели. Тогда для непрерыв¬
ного случая выражение (12.56) можно переписать следующим образом:
4L = —K4F,	(12.58)
и реализовать его на аналоговом вычислительном устройстве. Этот
метод применили Марголис и Леондес [29] для определения парамет¬
ров и «обучающейся модели» реальной системы. Дональсон [30] пока¬

12.12;
НЕПРЕРЫВНЫЕ МЕТОДЫ ОТСЛЕЖИВАНИЯ ПАРАМЕТРОВ
470
зал для некоторых случаев устойчивость и сходимость непрерывных
методов отслеживания параметров. Попытки увеличить скорость
настройки параметров при реализации алгоритма на аналоговой модели
могут привести к серьезным трудностям, связанным с устойчивостью.
Приближенные градиентные методы, несмотря на их сложность,
были применены Орнстейном [31] и Уертзом [32] для изучения моде¬
лей человека-оператора. Орнстейн реализовал на аналоговом вычисли¬
тельном устройстве уравнения, имеющие вид (12.58), и изменял К
до тех пор, пока система не теряла устойчивость. Он использовал
следующую модель:
Ьи (0 + ей (0 4- du (0 = k [е (t — 0,2) 4- ае (t — 0,2)],	(12.50)
где А?, а, Ь, с и d — параметры, которые следовало определить.
Временная задержка реакции принималась равной 0,2 сек. Использо¬
вался критерий ошибки /=|е|.
Для улучшения сходимости процедуры настройки параметров
Орнстейн применил итеративный метод настройки начальных условий
модели, используя конечные значения параметров pt в качестве началь¬
ных на следующем интервале времени. Хотя его результаты очень
нестабильны и его работа много теряет из-за недостатка аналитиче¬
ских исследований, однако она имеет значение, поскольку представ¬
ляет первую попытку применить для изучения человека-оператора
приблизительный градиентный метод.
Уертз [32] применил наисксрейший спуск при критерии /(s) = s2
и настраивал в уравнении (12.59) лишь параметры k и а. Уертз смог
аналитически доказать сходимость и устойчивость.
Непрерывные методы согласования модели применялись также для
определения параметров нелинейных моделей человека-оператора.
Для иллюстрации метода рассмотрим задачу построения модели чело¬
века-оператора, выполняющего одномерное отслеживание с управляю¬
щим устройством, имеющим два устойчивых состояния [35], которое
показано на блок-схеме рис. 12.11.
Человек-оператор выделяет ошибку между желаемой и действи¬
тельной выходной величиной системы, и посредством регулятора,
имеющего релейную характеристику, прикладывает корректирующий
момент к летательному аппарату. Характеристики летательного ап¬
парата определены просто с помощью его инерции. На летательный
аппарат не действует никакой момент до тех пор, пока рукоятка
регулятора не займет крайнего положения, при котором к аппарату
прикладывается момент определенной величины. Желательно создать
несложную математическую модель, описывающую динамическую связь
входной величины, наблюдаемой человеком, с выходной величиной
регулятора, и в результате включить тот факт, что выходная вели¬
чина регулятора ограничена. На рисунке также показана математи¬
ческая модель как линейное дифференциальное уравнение первого

Вычислительное устройстео
-:so
ЧЕЛОВНК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
■*:
II
1
II
•fc
*1 §
чч
"Л
п S;
?ч
;
к >
\ >
Ч?
^ ^ ^
^ ^ ^ ^ ^ ^ II II II
AI V Al V Л1 V
iE^iEEEEEiE
и **
II
+ +
^ ‘fc.
§
I
fc-A
£
п
+
!
1
I

П II
II
Рис. 12.11. Блок-схема идентификации параметров системы с человеком-операюрим.

12.12]	НЕПРЕРЫВНЫЕ	МЕТОДЫ	ОТСЛЕЖИВАНИЯ	ПАРАМЕТРОВ
порядка, за которым следует ограничитель. Оптимизация заключается
в непрерывной настройке параметров а, р и j приблизительным гра¬
диентным методом. Использовалась функция критерия, имеющая вид
W сен
К = 5 см/сен*
Входной сигнал А
Рис. 12.12. Записи на самописце результатов отслеживания.
f—e2, а необходимые вычисления указаны на рисунке. После вычис¬
ления приблизительных составляющих вектора градиента находились
желаемые величины производных по времени от параметров. Инте¬
гралы этих величин поступали на входы математической модели.
На рис. 12.12 показаны типичные результаты решения этой задачи
оптимизации при произвольных начальных значениях а, р и
16 п/р Леондеса

482	ЧЕЛОВЕК-ОПЕРАТОР	В СИСТЕМАХ УПРАВЛЕНИЯ	[ГЛ.	12
Первый канал записи на этом рисунке представляет входную
величину, которую оператор видит на осциллографе. Вторая запись
является выходной величиной положения рукоятки управления,
а третья — выходной величиной математической модели. Желательно
с помощью непрерывного метода настройки параметров приблизить
третью запись ко второй, насколько эго возможно, при предварительно
выбранном виде математической модели. Ошибка или рассогласование
между желаемой величиной (выходной величиной оператора) и выходной
величиной модели показана на четвертой записи. Пятый канал пред¬
ставляет среднеквадратичную величину ошибки, которая измерялась
с помощью сильно задемпфированного измерительного прибора, имею¬
щего постоянную времени, равную десяти секундам. Каналы б, 7 и 8
показывают записанные значений а, р и у. Обращаясь к этим записям,
можно заметить, что выходные величины модели и оператора сильно
отличаются в течение первых 100 сек и становятся очень похожими
в течение последних 100 сек. Кроме того, видно, что требуется
около 100 сек для того, чтобы параметры приняли приблизительно
устойчивые значения. Присутствие в ошибке гармоник высокой
частоты после первых 100 сек указывает на желательность выбора,
если это возможно, модели более высокого порядка и иллюстрирует
то, что данный способ оптимизации параметров дает возможность
найти оптимальные значения параметров лишь для частного критерия
и частной модели, которые выбраны в эксперименте. Потытки полу¬
чить более быструю сходимость привели к неустойчивости системы.
12.13.	Согласование модели в случае ортогональных фильтров
Элкинд и Грин [36] представили человека-оператора с помощью
линейной модели, образованной набором фильтров с ортонормальными
импульсными характеристиками. Выходная величина модели получалась
как сумма взвешенных выходных величин фильтров. Веса выбирались
из условия, чтобы среднеквадратичная ошибка согласования F (в) = в2
была минимальна (по некоторому определенному интервалу времени).
При обозначениях, указанных на рис. 12.10, ошибка согласования
равна
k
e(t) = m(t) — u(t) = m(t)— ^ bjzj{£),	(12.60)
;=i
если используется k фильтров. Среднеквадратичная ошибка выразится
следующим образом:
7
у jj е (tf dt = V = [т it) — и (Of.	(12.61)
о

ЛИТЕРАТУРА
483
Значения коэффициентов Ьр которые минимизируют (12.61), опреде¬
ляются путем дифференцирования выражения (12.61) по каждому bj
и приравнивания результатов дифференцирования нулю. При этом
получается система из k уравнений, которую можно решить относи¬
тельно Ьр
Когда принимается линейная неизменная модель, тогда для аппрок¬
симации весовой функции используется конечное число фильтров,
выбранных из полной ортогональной системы. При соответствующих
ограничениях метод может быть распространен на линейные системы,
изменяемые во времени. Обычно ограничения требуют, чтобы пара¬
метры системы оставались приблизительно постоянными в течение
интервала измерения Т.
Элкинд и Грин предположили также, что в методах Винера [37]
и Бозе [38] наборы ортогональных фильтров могут использоваться
для представления выходных величин нелинейных систем. Тем не менее
в литературе еще не описывались работы, в которых делается попытка
использовать нелинейную теорию для построения моделей человека-
оператора.
12.14.	Заключение
Характеристика человека-оператора во многих простых задачах
может быть аппроксимирована линейной моделью. Параметры этой
линейной (непрерывной или дискретной) модели будут зависеть
от частной задачи. Параметры квазилинейных моделей определяются
методом взаимной корреляции и методом согласования модели.
В дальнейшем могут потребоваться модели человека-оператора
в задачах, где выполняемые им операции являются нелинейными и,
кроме того, их характер изменяется во времени. Ни один из методов,
описанных выше, не является в настоящее время адекватным для син¬
теза моделей и идентификации их параметров в случае изменяемой
во времени нелинейной задачи. Современные исследования, исполь¬
зующие при согласовании модели приблизительные градиентные методы,
позволяют надеяться, что в течение нескольких следующих лет эта
область будет успешно развиваться.
ЛИТЕРАТУРА
1. Bates J. А. V., Some Characteristics of a Human Operator, Journal of
the I. E. E. (England), v. 94, pt. IIA, pp. 298—304, 1947.
2. С г a i k J., Theory of the Human Operator in Control Systems, British Jour,
of Psych., December, 1947, and March, 1948.
3. M с R u e r D. T. and Krendel E. S., Dynamic Response of Human Ope¬
rators, WADC Technical Report 56—524, October, 1957.
4. M с R u e r D. T. and Krendel E. S., The Human Operator as a Servo
Svstem Element, Jour. Franklin Institute 267:381-403, May, 1959 and
267:511—536, June, 1959.

484
ЧЕЛОВЕК-ОПЕРАТОР В СИСТЕМАХ УПРАВЛЕНИЯ
[ГЛ. 12
5. В о о t о п R. С., The Analysis of Nonlinear Control Systems with Random
Inputs, Proc. Symposium on Nonlinear Circuit Analysis, 2:369-391, April,
1953.
6. E 1 к i n d J. 1., Characteristics of Simple Manual Control Systems, Lincoln
Laboratory Report No. Ill, M. L. T. Lincoln Laboratory, Lexington, Mass.,
April, 1956.
7. К r e n d e 1 E. and Barnes G. H., Interim Report on Human Frequency
Response Studies, WADC Technical Report TR 54-370, June, 1954.
8. Broadbent D. E., Perception and Communication, pp. 268—296, New
York, Pergamon Press, 1958.
9. В e к e у G. A., Sampled Data Models of the Human Operator in a Control
System, Ph. D. Dissertation. Department of Engineering, University of Cali¬
fornia, Los Angeles, January, 1962.
10. Tusti n A., The Nature of the Operator’s Response in Manual Control and
its Implications for Controller Design, Jour. Institution Elec. Engrs. (London)
94 (HA): 190-202, 1947.
11. Ragazzini J. R., Engineering Aspects of the Human Being as a Servo¬
mechanism, unpublished paper presented at the American Psychological
Association Meeting, 1948.
12. Lichlider J. C. R., Quasi-Linear Operator Models in the Study of
Manual Tracking, pp. 171—279 in Developments in Mathematical Psycho¬
logy, ed. by R. D. Luce, Glencoe, Illinois: The Free Press, 1960.
13. Phillips R. S., Manual Tracking, in Theory of Servomechanisms, ed. by
H.	M. James, N. B. Nichols and R. S. Phillips, pp. 360-368, New York,
McGraw-Hill, 1947.
14. Mayne R., Some Engineering Aspects of the Mechanism of Body Control,
Electrical Engineering, 70:207-212, March, 1951.
15. Hyndman R. W. and Beach R. L., The Transient Response of the.
Human Operator, IRE Trans, on Medical Electronics, PGME-12:67-71, De¬
cember, 1959.
16. El Ison D. G., Gray F. et ah, Wavelength and Amplitude Characteristics
of Tracking Error Curves, AAF-AMC Engr. Report TSEAA-694-2D, Wright
Field, Ohio, April, 1947.
17. Walston С. E. and Warren С. E., Analysis of the Human Operator
in a Closed-Loop System, Research Bulletin 53-32, Human Resources Center,
ARDC, Ohio State University, August, 1953.
18. N о b 1 e М., Fitts P. M. and Warren С. E., The Frequency Response
of Skilled Subjects in a Pursuit Tracking Task, Jour. Exp. Psych. 49, 249-56,
1955.
19. Russell L., Characteristics of the Human as a Linear Servo Element,
M. S. Thesis, Massachusetts Institute of Technology, May, 1951.
20. В о о t о n R. C., The Analysis of Nonlinear Control Systems with Random
Inputs Proc. Symposium on Nonlinear Circuit Analysis, 2:369-391, April,
1953.
21. Jackson A. S., Synthesis of a Linear Quasi-Transfer Function for the
Operator in Man-Machine Systems, WESCON Convention Record, pt. 4,
2:263-271, 1958.
22. N о r t h J. D., The Human Transfer Function in Servo Systems, in Auto¬
matic and Manual Control, ed. by A. Tustin, 473—502, London, Butterworths,
1958.
23. W a r d J. R., The Dynamics of a Human Operator in a Control System:
A Study Based on the Hypothesis of Intermittency, Ph. D. Dissertation,
Department of Aeronautical Engineering, University of Sydney, Australia,
May, 1958.
24. D i a m a n t i d e s N. D., Informative Feedback in Jet-Pilot Control Stick
Motion AIEE Applications and Industry, 243-39, November, 1957.

ЛИТЕРАТУРА
485
25. D i a m a n t i d е s N. D., A Pilot Analog lor Airplane Pitch Control, J. Aero.
Sciences, 25:361-71, June, 1958.
26. Goodyear Aircraft Corp., Final Report: Human Dynamics Study, GAC
Report GER-4750, April, 1952.
27. S h e r i d а п Т. B., Time Variable Dynamics of Human Operator Systems,
MIT Dynamic Analysis and Control Lab Report AFCRC-TN-60-169, Camb¬
ridge, Massachusetts, March, 1960.
28. T о m p к i n s С. B., Methods of Steep Descent, pp. 448—79 in Modern
Mathematic for the Engineer, ed. by E. F. Beckenbach, McGraw-Hill Book
Co., 1956. [Русский перевод: Чарльз Б. Томпкинс, Методы быстрого
спуска. В кн. «Современная математика для инженеров», под редакцией
Э.	Ф. Беккенбаха, ИЛ, М., 1959.]
29. М а г g о I i s М. and Leondes С. Т., A Parameter-Tracking Servo for
Automatic Control Systems, IRE Trans, on Automatic Control, AC-4:100,
111, 1959.
30. D о n a 1 s о n D. D., The Theory and Stability Analysis of a Model Refe¬
rence Tracking Technique for Adaptive Automatic Control Systems, Ph.
D. Dissertation, University of California, Los Angeles, May, 1961.
31. О r n s t e i n G. N., Applications of a Technique for the Automatic Analog
Determination of Human Response Equation Parameters, Report NA61H-1,
North American Aviation, Columbus, Ohio, January, 1961 (also available
as Ph. D. Thesis, Ohio State University, Department, of Psychology, 1960).
32. W e r t z H. J., A Learning Model to Evaluate and Aid Human Operator
Adaptation, paper presented at IRE International Congress on Human
Factors in Electronics, Long Beach, California, May, 1962.
33. В ek ey G. A., The Human Operator as a Sampled-Data System, IRE Trans,
on Human Factors in Electronics, HFE-3:43-51, September, 1962.
34. В e k e у G. A. and Humphrey R. E., Review of Model Matching
Techniques for the Determination of Parameters in Human Pilot Models,
Space Technology Laboratories Technical Report 9865-6002-MU000, Redondo
Beach, Calif., Nov. 1962.
35. H u m p h г e у R. E. and В e k e у G. A., A Technique for the Determina¬
tion of Parameters in a Nonlinear Model of a Human Operator, Space
Technology Laboratories Technical Report 9865-6003-MU000, March, 1963.
36. E1 k i n d J. I. and Green D. М., Measurement of Time-Varying and
Nonlinear Dynamic Characteristics of Human Pilots, ASD Technical Report
61-225, December, 1961.
37. Wiener N., Nonlinear Problems in Random Theory, John Wiley and Sons,
New York, 1958. [Русский перевод: Винер H., Нелинейные задачи в
теории случайных процессов, ИЛ, М., 1961.]
38. Bose A. G., A Theory of Nonlinear Systems, Tech. Report No. 309, Res.
Lab. of Electronics, Mass. Inst, of Tech., Cambridge, Massachusetts, 1956.

ГЛАВА 13
ПРИМЕНЕНИЕ СОВРЕМЕННЫХ МЕТОДОВ АНАЛИЗА
И СИНТЕЗА К СИСТЕМАМ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ
АППАРАТАМИ
Несбит (R. А. Nesbit)
13.1.	Введение
Существует много важных задач управления, связанных с проек¬
тированием и эксплуатацией такого класса подвижных объектов, как
летательные аппараты. Эти задачи управления имеют ряд особен¬
ностей, которые могут быть учтены в процессе проектирования
управляющих устройств. Учет «особых факторов», касающихся харак¬
теристик летательных аппаратов, является очень важным при создании
этих управляющих устройств. Разумеется, существуют также другие
задачи, свойственные более общим классам систем управления. Цель
этой главы — перечислить некоторые из задач и указать методы их
решения, которые оказались наиболее приемлемыми. Здесь не де¬
лается попытки рассмотреть полностью особенности характеристик
летательных аппаратов, а скорее описывается их обшее значение
в проектировании управляющих устройств.
При решении новой задачи управления всегда делаются опреде¬
ленные предположения с целью проведения математического или ло¬
гического анализа. Для получения «верных» выводов предположения
должны быть разумными, а логический анализ обоснованным. Это не
означает, что не целесообразно делать упрощающие предположения,
а скорее указывает на необходимость учитывать, к чему могут при¬
вести сделанные упрощения. Существуют определенные представле¬
ния, касающиеся управления летательными аппаратами, которые по
существу могут быть названы теориями. Наиболее важные из них
опираются на использование законов ньютоновской и посленьютонов-
ской механики для описания движения летательного аппарата. Тот
факт, что движение всех объектов данного класса может быть опи¬
сано с помощью законов ньютоновской механики, является главной

13.2]
ОБЩИЕ СВОЙСТВА УРАВНЕНИЙ ДИНАМИКИ
487
объединяющей особенностью подобных задач. В этот класс объектов
входят самолеты, дирижабли, ракеты, планеры, спутники, баллистиче-
ческие управляемые снаряды, ракетопланы, а также другие объекты,
например подводные лодки и суда на подводных крыльях, движение
которых описывается аналогичными уравнениями и характеристики
которых имеют много общего с характеристиками перечисленных
объектов.
Цель дальнейшего изложения состоит в выявлении наиболее важ¬
ных технических задач и указании способов, с помощью которых
они были решены. При проектировании любой системы управления
необходимо сделать некоторые предположения относительно объекта
управления. Первое предположение состоит в том, что объект является
управляемым, при этом систему управления следует построить
таким образом, чтобы она была способной выполнять возложенные
на нее задачи. Очевидное требование, предъявляемое к системе управ¬
ления, часто вытекает из сущности технических условий на систему,
что устанавливает верхнюю границу значений параметров управляю¬
щих устройств, не исключая и значений параметров адаптивных управ¬
ляющих устройств. Кроме того, при создании управляющих устройств
важно учесть характеристики подвижного объекта.
Работоспособность системы управления тесно связана с характе¬
ристиками используемых приборов, устройств обработки данных и
исполнительных механизмов. Другой важной задачей проектирования
управляемого объекта является получение достаточной надежности.
Эта задача, как видно из нижеприведенного примера проектирования
ракетного ускорителя, не является простой. При отсутствии на ракете
аэродинамических вертикальных стабилизаторов отказ автопилота был
бы катастрофическим. Но повысится ли вероятность успешного по¬
лета при установке дополнительных вертикальных стабилизаторов?
Такие вопросы являются типичными для проблемы надежности.
13.2.	Общие свойства уравнений динамики
Одна из общих особенностей задач управления летательными аппа¬
ратами заключается в том, что классические уравнения движения
твердого тела с шестью степенями свободы описывают лишь часть
динамического процесса. Главной задачей управления является пра¬
вильный выбор точек приложения сил и моментов, обеспечивающий
возможность выполнения требуемых маневров [2, 3, 4].
Управляющие силы и моменты создаются или посредством взаимо¬
действия с окружающей средой и потенциальными полями, или
с помощью реактивных устройств. Зависимость этих сил от геометри¬
ческих параметров и положения управляющих поверхностей часто
определяется через сложные динамические характеристики набегаю¬
щего потока, поэтому аналитическое определение полных динамиче¬

488
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
ских зависимостей этих систем является весьма трудной задачей. Для
определения моментов и сил, возникающих при взаимодействии лета¬
тельного аппарата с окружающей средой, часто используются аэро¬
динамические трубы и другие экспериментальные установки. (Интересно,
что братья Райт сконструировали аэродинамическую трубу в своей
велосипедной мастерской.) Другой метод решения задач этого типа
на предварительной стадии проектирования заключается в исследо¬
вании распределения аэродинамического давления с применением уни¬
версальных вычислительных машин, а не специализированных устано¬
вок (т. е. аэродинамической трубы). Этот метод выгоден в том слу¬
чае, когда результаты с требуемой точностью могут быть получены
при меньших затратах по сравнению с экспериментальными исследо¬
ваниями. Эффективное решение уравнения Навье — Стокса на универ¬
сальной вычислительной машине является весьма громоздкой задачей.
Одной из особенностей правильно спрограммированной вычислитель¬
ной процедуры является возможность легкого варьирования геомет¬
рическими параметрами летательного аппарата.
Аэродинамические силы, действующие на аппарат вне атмосферы,
очень малы, а моменты, которыми обычно пренебрегают (как, напри¬
мер, моменты, связанные с градиентом силы тяжести и давлением
солнечного излучения), становятся ощутимыми. Из-за такого измене¬
ния скоростного напора весь класс летательных аппаратов целесо¬
образно подразделить на космические и атмосферные. Конечно, не¬
которые летательные аппараты работают как в космических, так и
в атмосферных условиях, но даже в этих случаях способ управления
обычно изменяется в зависимости от величин скоростного напора.
При аналитическом исследовании уравнений движения, они, как
правило, упрощаются. Первое упрощение обычно состоит в линеари¬
зации уравнений относительно номинальной траектории, а второе
в предположении, что полученные таким образом линейные уравнения
могут быть аппроксимированы уравнениями с постоянными коэффи¬
циентами [2]. Еще одно упрощение можно сделать вследствие раз¬
личных временных характеристик уравнений траектории и уравнений
поворота летательного аппарата относительно траектории. Это раз¬
личие временных характеристик, несомненно, является характерной
особенностью реальной системы, а не только ее линеаризованной
модели, и ясно проявляется в отличии собственной частоты линеари¬
зованной модели. Например, при частоте колебаний твердого тела
относительно поперечной оси порядка 1 рад/сек угловая частота
нормальной силы, искривляющей траекторию движения, могла бы быть
равной около 0,015 рад/сек. Такое разделение частот дает возмож¬
ность отдельного рассмотрения линеаризованных систем управления
движением по траектории и систем управления положением летатель¬
ного аппарата. Отдельно рассматриваемая задача навигации может
включить в себя вопросы динамики разумно упрощенной системы

13.2]
ОБЩИЕ СВОЙСТВА УРАВНЕНИЙ ДИНАМИКИ
489
«автопилот — корпус летательного аппарата». В большинстве случаев
применение различных методов управления основано на результатах
исследования таких упрощенных моделей и затем проверяется по¬
средством моделирования на вычислительной машине и на реальной
системе.
Аэродинамические силы, действующие на летательный аппарат, часто
раскладываются на составляющие вдоль вектора скорости и по нор¬
мали к нему. Составляющая в направлении, противоположном скорости,
называется лобовым сопротивлением, а перпендикулярная к вектору
скорости называется подъемной силой. Аэродинамическое качество
летательного аппарата часто характеризуется максимально возможным
отношением подъемной силы к лобовому сопротивлению. Этот пара¬
метр является одним из характерных показателей конструкции само¬
летов. Существует много других сравнительных показателей кон¬
струкции летательного аппарата и наиболее экономичная конструкция
не всегда имеет максимальное отношение подъемной силы к лобо¬
вому сопротивлению. Для летательных аппаратов, входящих на боль¬
шой скорости в плотные силы атмосферы, существует другой пока¬
затель — удельный вес тепловой защитной системы, а стоимость
системы тепловой защиты зависит также от геометрии летательного
аппарата. Для обеспечения высоких эксплуатационных характеристик
летательного аппарата на дозвуковых и сверхзвуковых режимах могут
потребоваться различные геометрии летательного аппарата. Макси¬
мальное отношение подъемной силы к лобовому сопротивлению LjD
для самолета Л"-15 на дозвуковом режиме равно примерно четырем,
для пассажирского лайнера около 10 и для планера с высокими лет¬
ными характеристиками — около 35. Планирование самолета и по¬
садка с выключенным двигателем возможны при LjD, равном 2 или
несколько меньше. Другим важным динамическим параметром является
нагрузка на крыло. Нагрузка на крыло определяется как вес лета¬
тельного аппарата, поделенный на полезную площадь крыла. Аэро¬
динамическая подъемная сила и сила лобового сопротивления опре¬
деляются через скоростной набор	Диапазон	изменения	ско¬
ростного напора, в котором следует учитывать аэродинамические силы
и моменты, составляет три-четыре порядка. Аэродинамические силы
и моменты приблизительно пропорциональны скоростному напору *).
Для некоторых летательных аппаратов скоростной напор изменяется
очень быстро; в этих случаях постоянный коэффициент не совсем
точно отражает динамику летательного аппарата.
Аэродинамическое явление срыва потока является важным факто¬
ром, который ограничивает эксплуатационные характеристики самолета.
*) Срыв потока и эффект Маха являются причиной отклонения этой
зависимости от линейной.

490
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
Это явление наблюдается, когда угол атаки превышает определен¬
ную величину, и, таким образом, одним из способов предупре¬
ждения срыва потока является ограничение угла атаки. Если на
одном крыле происходит срыв потока, в то время как на другом
нет срыва, то самолет входит в штопор. Штопор и срывы потока
обычно сопровождаются быстрой потерей высоты. Вывод само¬
лета из этих условий полета обычно возможен, если имеется до¬
статочный запас высоты, но для обеспечения удовлетворительного
управления большинством самолетов такие маневры выполнять не
желательно.
Аэродинамические моменты, действующие на летательный аппарат,
зависят также от ориентации летательного аппарата относительно
набегающего потока. Для невращающегося летательного аппарата эти
моменты должны быть уравновешены так, чтобы он находился в со¬
стоянии равновесия, которое определяется углом отклонений рулей.
Если самолет незначительно отклоняется от положения равновесия,
то возникающие при этом моменты могут иметь такое направление,
что летательный аппарат будет возвращаться в положение равновесия.
Такая ситуация соответствует статической устойчивости. Динамическая
устойчивость означает, что линеаризованные уравнения движения имеют
устойчивые корни в окрестности положения равновесия. Одна из
задач аэродинамического расчета состоит в обеспечении достаточной
степени статической и динамической устойчивости летательного ап¬
парата.
В некоторых случаях, как, например, в случае ракеты-носителя,
летательный аппарат является статически неустойчивым и для обе¬
спечения безопасного полета необходим автопилот с соответствующими
характеристиками. Частные производные восстанавливающих моментов
и сил по углам и угловым скоростям называются производными
устойчивости [2].
Производные устойчивости изменяются при изменении числа М.
Другими словами, эти силы и моменты не являются строго пропор¬
циональными скоростному напору. Зависимость сил и моментов от
числа М особенно велика в окрестности М— 1.
Гибкость конструкции летательного аппарата приводит к другому
достаточно общему динамическому свойству систем этого класса
[5, б, 7]. Гибкость корпуса летательного аппарата при конструиро¬
вании автопилотов часто не учитывается, но даже, когда ей пренеб¬
регают, ее присутствие заставляет конструкторов отказаться от не¬
обоснованного выбора высоких коэффициентов усиления автопилота
и всех преимуществ связанных с этим. Форма и частота изгибных
колебаний конструкции аппроксимируются численными решениями
уравнений, описывающих колебания балки. Степень затухания изгибных
колебаний конструкции нелегко предсказать, если в конструкции не
предусмотрено демпфирующее устройство. Во многих случаях колебания

13.2]
ОБЩИЕ СВОЙСТВА УРАВНЕНИЙ ДИНАМИКИ
491
конструкции демпфируются легко. При проектировании автопилотов
для ракет-носителей предусматриваются специальные меры, предотвра¬
щающие неустойчивость конструкции. Расчет конструкции летатель¬
ного аппарата и расчет регулятора в этом случае очень тесно связаны
между собой. Анализ системы управления положением спутника, где
используется пассивная стабилизация, показывает, что в этом случае
требуется демпфирование собственных колебаний.
Другой важной особенностью динамики твердого тела, которая
затрагивает поведение самолета, является тенденция к кабрированию.
Это явление легко представить себе, если рассмотреть вращение
гантели относительно поперечной оси. Термин «кабрирование» исполь¬
зуется применительно к самолету, поскольку кабрирование проявляется
в подъеме носовой части летательного аппарата. Указанное явление
наблюдается при выполнении виража относительно неосновной оси
(обычно при больших углах атаки). Момент кабрирования пропор¬
ционален квадрату скорости виража, и тенденция самолета к кабри¬
рованию должна компенсироваться соответствующим управляющим
моментом. При этом ограничения управляющего момента по тангажу
определяют ограничения скорости виража. С целью координации ма¬
невра возможно использование нелинейной обратной связи.
На самолетах и вертолетах сила тяги используется для увеличе¬
ния аэродинамической подъемной силы и преодоления лобового со¬
противления. Процесс управления этими летательными аппаратами
включает управление силовой установкой. Системы управления сило¬
вой установкой могут осуществлять управление направлением вектора
тяги, его величиной или и тем и другим. Силовая установка может
также иметь систему регулирования напряжения, расхода горючего,
давления, температуры и числа оборотов.
Исполнительные механизмы и датчики систем управления также
обладают динамическими характеристиками, которые должны учиты¬
ваться при анализе и решении задач управления.
Таким образом, общая динамика летательных аппаратов описы¬
вается уравнениями движения твердого тела с шестью степенями сво¬
боды. Аэродинамические силы и моменты зависят от плотности атмо¬
сферы, положения летательного аппарата, скорости полета и поло¬
жения рулей. Кроме обшей динамики, должны учитываться колебания
конструкции летательного аппарата. Силовые установки, датчики
системы управления и исполнительные механизмы сообщают системе
дополнительные динамические свойства, которые зависят от характе¬
ристик конкретных используемых устройств.
Некоторые общие задачи управления могут быть сформулированы
с помощью основных динамических характеристик летательных аппа¬
ратов.
Более полное описание динамических характеристик содержится
в работах [2, 3, 4J.

492
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
13.3.	Общие задачи управления
Задачи динамического управления летательным аппаратом, как
было упомянуто выше, могут быть подразделены на управление по¬
ложением летательного аппарата, управление траекторией, управление
силовой установкой и управление вспомогательными системами. За¬
дачи управления положением аппарата и его траекторией иногда мо¬
гут рассматриваться независимо одна от другой. Независимое рас¬
смотрение этих задач возможно вследствие вышеупомянутого дина¬
мического свойства, заключающегося в том, что временные характе¬
ристики этих систем отличаются по крайней мере на один порядок.
Иногда, например, в спутниках вся задача управления сводится
к управлению положением [8].
В систему управления положением должны входить датчики поло¬
жения и моментные вспомогательные механизмы. Задачу датчиков
может выполнять человек-пилот или соответствующие физические
приборы. В обоих случаях в задачу датчиков входит измерение и
выдача управляющих сигналов.
Следует отметить, что, кроме функций восприятия положения
летательного аппарата и привода в действие силовых исполнительных
органов, пилот может выполнять и другие функции по управлению
аппаратом. В тех случаях, когда он должен полностью полагаться на
показания приборов первичной информации, вопрос о включении его
динамики в замкнутый контур системы управления является спорным.
Одной из важных задач проектирования летательного аппарата
является обеспечение экономически выгодного равновесия между
автоматическим и ручным управлением и объемом индикаторной
информации. Эта задача является лишь одним из примеров более
общей проблемы эффективного использования системы «человек —
машина».
Функция системы управления положением, ручной или автомати¬
ческой, заключается в том, чтобы поддерживать заданное положение
летательного аппарата с удовлетворительной точностью в присутствии
помех. В случае самолета система должна работать в широком диа¬
пазоне изменения скоростного напора и аэродинамических характе¬
ристик самолета. Только благодаря свойствам обратной связи данная
система может быть сделана нечувствительной к этим изменениям.
В системе управления положением ракеты-носителя главной коор¬
динатой управления является направление вектора тяги. Такой тип лета¬
тельного аппарата обычно аэродинамически неустойчив. В качестве
датчика в этом случае используются гироскопы, реагирующие как на
изгибные колебания корпуса ракеты, так и на изменения ее про¬
странственного положения. В задачу управления входит обеспечение
удовлетворительного качества управления положением в широком
диапазоне частот и форм изгибных колебаний без возбуждения не¬

13.3]
ОБЩИЕ ЗАДАЧИ УПРАВЛЕНИЯ
493
устойчивых колебаний конструкции. Динамические характеристики
летательного аппарата меняются вследствие изменения количества
топлива в его баках и изменения скоростного напора. Колебание
жидких масс топлива является также одним из факторов, влияющих
на динамику положения летательного аппарата [7].
Задача управления положением спутника заключается в обеспе¬
чении желаемой точности при возможно меньшем весе и большем
сроке службы системы управления. При исследовании этой пробле¬
мы динамика спутника может быть очень сильно упрощена, так же
как и в случае одного относительно твердого тела. Однако если
к спутнику присоединены длинные провода и штанги, то в этом
случае требуется анализ реальной модели данной орбитальной кон¬
струкции. Эти элементы иногда добавляются к конструкции спутника
для управления его положением так называемым пассивным способом,
когда используются гравитационные моменты.
Процесс управления траекторией включает большое количество
разнообразных маневров: приземление, возвращение, встречу, навига¬
цию, управление входом в плотные слои атмосферы, изменение орбиты,
слежение за станцией, управление орбитальным двигателем. Система,
используемая для управления траекторией, иногда называется системой
наведения. На ракетах-носителях в системе наведения может исполь¬
зоваться инерциальная платформа и специализированная цифровая вычи¬
слительная машина.
Для определения местоположения летательного аппарата датчики
системы управления траекторией могут использовать радиосигналы
радиолокационных систем, радиолучи, световые лучи и карты.
Безопасное и удобное приземление является функцией системы управ¬
ления посадкой летательного аппарата. В процессе посадки воздейст¬
вие ветровых потоков представляет собой возмущающий фактор для
траектории полета. Приземление должно происходить на посадочной
дорожке с малой вертикальной скоростью и при правильном прост¬
ранственном положении летательного аппарата. Существует компромис¬
сное соотношение между ошибками траектории и пространственного
положения, при этом сравнительная важность этих двух ошибок из¬
меняется с изменением расстояния до точки приземления [9, 10, 11, 12].
Траектория входа в плотные слои атмосферы должна удовлетво¬
рять требованиям относительно нагрева поверхности летательного аппа¬
рата и перегрузок [13]. Она должна также учитывать характеристики
летательного аппарата с целью полного использования его потенциаль¬
ных возможностей. Плотность атмосферы является переменной величи¬
ной, и аэродинамические характеристики летательного аппарата
могут зависеть от степени эрозии теплозащитной поверхности. Если
летательный аппарат должен маневрировать, то система управления тра¬
екторией должна обладать способностью выбора и отслеживания
большого количества различных траекторий.

494
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
Управление орбитальным двигателем требует определения траек¬
тории с тем, чтобы обеспечить эффективное использование топлива.
Конечное положение или положение в момент выключения двигателя
и скорость летательного аппарата должны очень тщательно контро¬
лироваться, и этот контроль требует точного измерения. Переход на
другую орбиту имеет много особенностей, аналогичных особенностям
управления орбитальным двигателем, при этом обеспечение эффектив¬
ности использования топлива и точность до сих пор остаются пробле¬
мами [14, 15].
Кроме задач создания управляющего устройства, которое может
осуществлять управление маневром летательного аппарата, существует
множество других задач, общих для всех случаев проектирования
систем управления. В некоторых случаях цена выхода из строя системы
измеряется жизнью человека. Аналитическое решение проблемы надеж¬
ности наталкивается на существенные ограничения, поскольку досто¬
верные выводы должны основываться на достоверных данных. Экспе¬
риментальный подход к решению проблемы надежности ограничива¬
ется тем, что не всегда экономически возможно проводить испытания
образца изделия. Задачу оптимизации надежности сформулировать
достаточно сложно. Одна из трудностей состоит в описании различ¬
ных видов конструкции, другая заключается в оценке видов отказов
и их вероятностей. Существенной трудностью, с которой может встре¬
титься конструктор системы, является также требование обеспечения
частоты отказа, поскольку невозможно проверить или определить
это значение с приемлемой достоверностью. Расчет надежности
отдельных элементов и другие подобные операции иногда дают
удовлетворительные оценки, но они не характеризуют надежности
в целом.
К другим требованиям, предъявляемым к управляющим устройствам,
относятся минимальная стоимость, минимальный вес и минимальная
потеря мощности при наилучших характеристиках, универсальности
и точности.
Такие противоречивые требования являются типичными для ре¬
альных задач, и для их решения необходимы творческий подход к
проектированию, прекрасная организация работ и достаточные капи¬
таловложения.
Новые задачи управления летательным аппаратом возникают при
попытках улучшить характеристики как самого летательного аппарата,
так и его системы управления с целью выполнения таких маневров,
как посадка при отсутствии видимости и посадка на Луну, а также
при попытках повысить точность основных датчиков. Каждое значи¬
тельное усовершенствование в технологии устройства вновь ставит
вопрос усовершенствования системы, а требования, предъявляемые
к системе, стимулируют в свою очередь усовершенствование ее ком¬
понентов.

13.4]	МЕТОДЫ	АНАЛИЗА	И	РЕШЕНИЯ	ЗАДАЧ	УПРАВЛЕНИЯ
495
13.4.	Методы анализа и решения задач управления
Результатом решения задачи управления является создание такой
системы, которая по качеству выполнения функций управления может
успешно конкурировать с другими системами. Основная конкуренция
имеет место на рынке, который суммирует все экономические пока¬
затели системы. Анализ задачи является логической процедурой,
используемой для изучения предполагаемого решения. Различные ме¬
тоды анализа обсуждались в предыдущих главах. Эти и другие методы
могут применяться для анализа принципов построения управляющих
устройств. В данном параграфе будет сделана попытка дать обзор
методов анализа, эффективно используемых для решения задачи управ¬
ления летательными аппаратами.
Как было упомянуто, линеаризация играет важную роль в анализе
управляющих устройств. Линейный анализ очень сложных систем ста¬
новится возможным в результате умелого использования автоматиче¬
ских вычислений. Эти вычисления позволяют осуществить быстрый
и недорогой анализ динамики системы и влияния на нее корректи¬
рующей обратной связи [2, 16].
Один из видов применяемых программ вычисления позволяет
вычислить коэффициенты линейных дифференциальных уравнений по
параметрам летательного аппарата. С помощью этой программы можно
быстро определить характеристики летательного аппарата при различ¬
ных условиях полета и исследовать целый ряд летательных аппаратов.
Другие программы позволяют анализировать системы линейных урав¬
нений с постоянными коэффициентами. Характеристические корни или
полюса уравнений определяются путем разложения на множители
характеристического определителя. Передаточные функции вычисля¬
ются по правилу Крамера по преобразованным уравнениям. Вычисление
частотных характеристик передаточных функций также не вызывает
затруднений. При исследовании используются также правила обратного
преобразования и метод корневого годографа. Эти способы вычислений
успешно конкурируют с другими методами и при решении конкретных
задач являются более выгодными [16].
При решении задачи управления, как правило, используется линей¬
ное приближение. Существует много приемлемых методов расчета
линейных автоматических систем. Понятие чувствительности, введенное
Боде [17] и расширенное Горовицем [16], позволяет объяснить, с при¬
менением количественных оценок, назначение обратной связи. При
нахождении ограничений на соотношения между входными и выходными
сигналами, с целью удовлетворения требований, предъявляемых к ре¬
гулятору, возмущениями, действующими на систему, следует прене¬
бречь. Эти требования к регулятору часто выражаются в значениях
ширины полосы пропускания, коэффициента усиления по мощности,
быстродействия, перерегулирования и максимальных ошибок. Они

496	СИСТЕМЫ	УПРАВЛЕНИЯ	ЛЕТАТЕЛЬНЫМИ	АППАРАТАМИ	[ГЛ.	13
часто определяются положением пары «доминирующих» корней, т. е.
динамические характеристики рассматриваемой системы аппроксими¬
руются решением дифференциального уравнения второго порядка. Этот
метод, называемый методом «доминирующего оператора», часто при¬
меняется для расчета системы.
Требуемая ширина полосы пропускания замкнутого контура всей
системы управления зависит от вида отрабатываемого сигнала. Для
подавления действующих на систему помех требуется некоторая опре¬
деленная комбинация коэффициентов усиления и полосы' пропускания
исполнительных механизмов. Для более подробного ознакомления
с методом линейного расчета, в котором широко используются такие
понятия, как коэффициент передачи и чувствительность, следует обра¬
титься к работе Горовица [16]. Требования к перерегулированию,
предъявляемые к системе в случае линейной модели, становятся более
важными, когда рассматриваются нелинейности. Например, перерегу¬
лирование может стать причиной срыва потока при таких маневрах,
которые в других условиях являются безопасными.
Линейные системы с постоянными коэффициентами можно рассчи¬
тать путем минимизации квадратичной функции стоимости. Этот метод
может потребовать оценки статистических характеристик возмущений
или может изменить коэффициент усиления и точность системы. Вслед¬
ствие высокого порядка уравнений для большинства летательных
аппаратов, метод чувствительности может быть более подходящим.
Однако, при управлении положением спутника или в задаче коррекции
орбиты динамика является достаточно простой и допускает оптими¬
зацию стоимости отклонений ошибки в зависимости от стоимости топ¬
лива. Даже в этих задачах решение обычно налагает ограничения на
вид системы, а оптимальное управление, если не математически, то фи¬
зически является достаточно очевидным [18, 19].
Таким образом, для решения проблемы управления летательным
аппаратом необходимо иметь соответствующий метод расчета сложных
линейных систем, позволяющий удовлетворить техническим требова¬
ниям по ширине полосы пропускания, по быстродействию и чувстви¬
тельности систем. Обеспечение успешного конкурирования с другими
системами должно быть основано на этом принципе.
Изложенные соображения подтверждают целесообразность приме¬
нения автоматических вычислений для осуществления быстрого и эко¬
номичного линейного анализа. Универсальные вычислительные машины
являются необходимым средством для проведения моделирования не¬
линейных управляющих устройств и процессов. Моделирование часто
является наиболее экономичным способом, позволяющим проверить
различные идеи и исследовать отдельные составные части системы.
В некоторых же случаях только с помощью специального экспери¬
мента можно проверить какую-либо гипотезу. Если какая-то идея
сводится на практике к конкретному типу конструкции системы

13.4]	МЕТОДЫ	АНАЛИЗА	И	РЕШЕНИЯ	ЗАДАЧ	УПРАВЛЕНИЯ
497
в металле, то ее окончательная проверка осуществляется посредством
испытания реальной системы. При создании системы важно найти
правильное соотношение между теоретическим анализом, вычислитель¬
ными работами и экспериментальными проверками. При проектирова¬
нии сложных систем теоретический и численный анализ часто является
менее дорогим, чем создание системы и ее испытание. К сожалению,
этот факт иногда используют, чтобы обосновать проведение анализа
без конкретного воплощения идеи.
Часто бывает целесообразно «проверить» расчет посредством срав¬
нительного сложного моделирования. При таком моделировании могут
учитываться зоны нечувствительности, гистерезис, ограничения, сухое
трение или другие нелинейности. Моделирование можно также исполь¬
зовать для определения области управляемости и ограничений характе¬
ристик модели системы. Номинальные траектории также можно найти
посредством полного моделирования уравнений движения. Эти номиналь¬
ные траектории затем можно использовать для дальнейшего проектиро¬
вания, а также для получения линеаризованных уравнений возмущений.
Современные системы управления часто содержат вычислительные
устройства и устройства обработки данных. Обработка данных осу¬
ществляется с целью увеличения отношения «сигнал/шум» на выходе
датчика. Благодаря передаче сигналов в дискретной форме и осуще¬
ствлению соответствующих вычислений чувствительность передающего
тракта к изменению параметров усилителя уменьшается. Усовершен¬
ствование микросхем и использование улучшенных датчиков делают
возможным создание малогабаритных надежных элементов для обра¬
ботки информации. В некоторых случаях в сложных системах управ¬
ления могут использоваться в качестве одного из узлов универсаль¬
ные вычислительные машины. Таким образом, вычислительные машины
используются как для облегчения анализа систем управления, так
и для их реализации. Иногда может быть даже выгодно для анализа
предлагаемых специализированных цифровых регуляторов использо¬
вать универсальные цифровые вычислительные машины, до того как
эти регуляторы будут построены.
Эффективное использование вычислительной машины является частью
общей проблемы «человек — машина». Проблема «человек — машина»
является достаточно старой и всегда актуальной. Желания человека
могут быть рациональными или нерациональными, независимо от этого
назначение машины заключается в том, чтобы служить ему. В неко¬
торых случаях дешевле найти нужного человека, чем изменить машину,
а в других случаях эффективнее простая модификация машины. При¬
мером значения «психологии» в такой ситуации является сохранение
тросов управления в самолетах с очень длинным и гибким фюзеляжем.
Даже если эти тросы неудобны в эксплуатации, тяжелы и дороги,
они являются необходимыми, так как многие пилоты думают, что они
более надежны, чем любые другие устройства.

498
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
Создание моделей человека-оператора является трудной задачей.
В случае простых задач отслеживания цели человек-оператор имеет
некоторое временное запаздывание и обладает определенной способ¬
ностью обработки данных. При выполнении человеком более слож¬
ных задач, как, например, управление и принятие решения, сущест¬
вующие представления поведения человека-оператора являются почти
непригодными. Большинство задач требует от человека большого
опыта, и если он должен принимать участие в работе машины, то
следует рассчитывать на то, что он обладает некоторым минималь¬
ным мастерством. Развитие авиации и ее история стали возможными
только благодаря великолепному умению операторов, перед кото¬
рыми вставали сверхчеловеческие задачи. Однако способности чело¬
века ограничены, и некоторые задачи гораздо лучше могут быть ре¬
шены машиной. Как и во многих других случаях, когда имеется
несколько конкурирующих идей, много времени тратится на превоз¬
ношение достоинств одной или другой идеи вместо того, чтобы попы¬
таться найти их наиболее выгодную комбинацию. Те, кто защищает
мнение о необходимости включения человека в контур системы управ¬
ления, исходят из предположения, что желательно, чтобы определен¬
ные задачи решал человек. Другие, кто придерживается мнения, что
система должна быть полностью автоматической, считают, что пер¬
вый вариант системы может быть более дорогим и менее надежным.
По мере того как совершенствуется оборудование, характер разделе¬
ния функций человека и системы должен пересматриваться. Основным
методом анализа системы «человек — машина» является эксперимен¬
тальное исследование в реальных и искусственно воспроизведенных
условиях. Тщательно разработанное моделирование, в котором исполь¬
зуются вычислительные машины и модели визуальной обстановки,
позволяет воспроизводить реальные ситуации для обучения пилота и
испытания оборудования. Эффективные способы индикации и управ¬
ления упрощают систему «человек — машина», а усовершенствован¬
ные датчики расширяют возможности этой системы.
Вопрос усовершенствования датчиков тесно связан с задачей ана¬
лиза статистических характеристик сигнала и шума. Наиболее рас¬
пространенным методом решения этой задачи стал анализ среднеквад¬
ратичной ошибки. В задачах обработки данных применение согласо¬
ванных фильтров и фильтров Винера расширили возможности отде¬
ления сигнала от шума. Усовершенствованный способ обработки
сигнала может быть достигнут благодаря использованию фильтров
с изменяемыми во времени характеристиками, которые разработаны
Калмэном [19], или их улучшенных вариантов.
Типичный метод обьединения двух датчиков с различными частот¬
ными характеристиками предполагает использование дополнительных
фильтров и объединение выходов. Этот метод был использован для
регулирования скорости изменения высоты путем объединения выхода

13.4]	МЕТОДЫ	АНАЛИЗА	И	РЕШЕНИЯ	ЗАДАЧ	УПРАВЛЕНИЯ
499
пневматического датчика скоростного напора с выходом инерциаль-
ного измерителя скорости.
Если датчики имеют систематические ошибки, то дисперсия траек¬
тории движения вычисляется путем интегрирования отклонений от
номинальной траектории. Эти систематические ошибки в настоящее
время не входят в формулу Калмэна. Анализ ошибок системы наве¬
дения осуществляется обычно путем пересчета дисперсий сигналов
акселерометра, погрешностей гироскопа и отклонения масштабного
коэффициента в дисперсии ошибок положения и скорости летатель¬
ного аппарата. Анализ существенно облегчается применением вычис¬
лительной техники.
Как правило, оптимизация предполагает необходимость некоторых
выборов, предсказание результатов этих выборов и способа упорядо¬
чения результатов в соответствии с их сравнительной предпочтитель¬
ностью. В некоторых задачах динамики летательных аппаратов имеет¬
ся широкая возможность выбора траекторий, существует целесо¬
образный критерий качества и известна связь между этим критерием
и характером траектории. Для решения задач оптимизации может
оказаться полезной математическая теория оптимизации. Одним из
критериев качества является обеспечение минимума топлива. Иногда
выбор параметров траекторий осуществляется таким образом, чтобы
обеспечить возможность простого описания ее вида. Изменение пара¬
метров траектории затем отождествляется с соответствующими изме¬
нениями критерия качества. Если имеются достаточные возможности
выбора в определенном классе траекторий, то критерий качества
может быть сделан близким к оптимальному. Этот способ уменьше¬
ния размерности, называемый иногда методом Рэлея — Ритца, часто
используется для функциональной оптимизации. Используя вариа¬
ционное исчисление, иногда можно решать очень важные задачи [20, 21].
Для решения задач управления полезен принцип максимума, предло¬
женный Понтрягиным и представляющий собой расширение условий
Вейерштрасса [14]. В некоторых случаях оптимальное решение может
быть найдено путем непосредственного решения задачи. Для боль¬
шинства задач управления критерий нельзя непосредственно связать
с возможными выборами параметров. Минимизация расхода топлива
в спутнике может быть не столь важной по сравнению с требова¬
ниями простоты системы, что делает необоснованным анализ или
осуществление оптимальной системы управления расходом топлива.
Может оказаться значительно выгоднее вложить средства в работу
по усовершенствованию конструкции датчика или привода, а не оп¬
тимизировать качество при тех конструкциях, применение которых
допустимо. Еще раз следует подчеркнуть важность рассмотрения
реальной задачи.
Одним из методов оптимизации функционала, который был пред¬
ложен несколькими авторами, является метод наискорейшего спуска

500
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
j 22, 23]. Этот метод для улучшения выбранного управления исполь¬
зует градиент функционала. Получаемая таким образом последователь¬
ность может сходиться к локальному минимуму. Если стоимость
является неотрицательным квадратичным функционалом, то можно
показать, что минимизирующая последовательность сходится и мини¬
мальное значение функционала будет достигнуто. Необходимо заме¬
тить, что не следует недооценивать вычислительные трудности этого
метода. Однако в одной из задач по управлению самолетом при на¬
боре высоты Брайзон и Нейслан получили, что время, требуемое
для набора высоты, уменьшается почти на 45%, если для расчета
траектории использовать метод наискорейшего спуска. Оптимальная
траектория, рассчитанная таким методом, имеет на одном из своих
участков крутую «горку», что является новым элементом по отноше¬
нию к обычной программе изменения траектории.
Во многих задачах управления летательными аппаратами наличие
двух различных состояний системы (рабочий режим и не рабочий
режим) делает аналитическую оптимизацию менее полезной. Если
система тепловой защиты соответствует экстремальным характеристи¬
кам летательного аппарата, то от оптимизации траектории с точки
зрения наименьшего нагрева получается очень малый выигрыш. На¬
много выгоднее попытаться упростить систему управления.
Таким образом, можно сделать вывод, что задачи управления
летательными аппаратами, работающими в атмосферных условиях,
решаются с применением линеаризации, моделирования на вычисли¬
тельных машинах, математического и логического анализа и посред¬
ством эксперимента. Решение этих задач требует наличия определен¬
ного новаторства, капиталовложений и надлежащего руководства.
При анализе системы можно использовать понятие устойчивости,
оптимизацию, теорию случайных процессов и моделирование системы.
Если рассматривается общая задача, использование такого подхода
может стать основой для отыскания новых и эффективных способов
ее решения.
13.5.	Характерные примеры
а)	Управление положением самолета
Как уже было упомянуто, при высоких летно-гехнических харак¬
теристиках современных самолетов условия полета изменяются в широ¬
ких пределах. «Коэффициент усиления» звеньев системы управления
приблизительно пропорционален скоростному напору, а эта величина
может меняться в диапазоне от 5000 кг/м* до 50 кг/м2. Многие
системы не могут удовлетворительно работать в таком диапазоне
изменения коэффициента усиления, и поэтому обычно требуется опре¬
деленная коррекция коэффициента усиления автопилота. Один из

13.51
ХАРАКТЕРНЫЕ ПРИМЕРЫ
501
способов реализации этого принципа заключается в измерении неко¬
торой переменной величины, пропорциональной коэффициенту усиле¬
ния системы. При этом требуется увеличение количества применяемой
аппаратуры. Существует несколько способов настройки переменных
системы пропорционально коэффициенту усиления.
Преимущества высокого коэффициента усиления системы регули¬
рования хорошо известны, но ими часто пренебрегают, чтобы не
превысить предельный коэффициент усиления. Значительное улучше¬
ние характеристик системы управления может быть получено путем
использования одного из видов адаптивных систем для настройки
Рис. 13.1. Адаптивная система с настройкой
коэффициента усиления.
коэффициента усиления. Эти системы поддерживают коэффициент
усиления возможно наибольшим без нарушения устойчивости системы.
Одним из предположений, касающихся динамики таких систем,
является то, что существует некоторый диапазон изменения коэффи¬
циента усиления системы, при котором возможна удовлетворительная
работа системы. Адаптивная часть системы стремится поддерживать
коэффициент усиления в этом диапазоне. Требуются определенные
знания характеристик системы, чтобы гарантировать, что логика
изменения коэффициента усиления будет соответствовать правильной
настройке его величины.
Системы этого типа уже установлены на самолетах с высокими
летно-техническими характеристиками и показывают удовлетворитель¬
ные результаты. Системы, используемые в настоящее время на само¬
летах, разработаны фирмами «Миннеаполис-Хонэвелл» и «Дженерэл
Электрик». Система фирмы «Хонэвелл» поддерживает малый предель¬
ный цикл в автопилоте и использует свойства предельного цикла
для настройки коэффициента усиления [6, ‘24, 25, 26].
В качестве одного из примеров систем этого типа рассмотрим
схему, изображенную на рис. 13.1.

502
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
Функционал А =} (0) является амплитудой или частотой предель¬
ного цикла, а А0 — задающей величиной. Следует обеспечить устой¬
чивость контура настройки коэффициента усиления. Задача проекти¬
рования контура управления коэффициентом усиления совершенно
аналогична задаче расчета устойчивого генератора колебаний. Основ¬
ной контур системы регулирования проектируется так, как если бы
коэффициент усиления К был постоянным, и затем делается прове¬
рочный расчет всей системы.
Ь)	Автоматическая посадка
Проблема автоматической посадки самолета ставит ряд интерес¬
ных задач перед специалистами по системам управления. К настоя¬
щему времени предложено и разработано несколько типов таких
систем. (Система посадки «Аутолэнд» совместной разработки фирм
«Лиевр — Сиглер» и «Сюд—Авиэйшин» установлена на «Каравел¬
лах» итальянских авиалиний.) Существует несколько возможных
способов реализации системы автоматической посадки. Некоторые из
этих способов требуют очень немного или вообще не требуют допол¬
нительного оборудования аэропорта и используют существующие
системы слепой посадки (ССП).
Другой метод предполагает использование дополнительного аэро¬
дромного оборудования, посредством которого создается сканирую¬
щий луч планирования, этот луч берет начало от точки, удаленной
от конца взлетно-посадочной полосы приблизительно на 600 м.
Для посадки на палубу авианосца может потребоваться система
передачи данных. Команды управления, передаваемые на самолет,
могут быть получены на вычислительной машине на борту авианосца,
которая обрабатывает данные радиолокационной станции, данные
инерциалыюй системы корабля и результаты измерения скорости
ветра в районе местоположения корабля. Эти команды в принципе
могут быть переданы в автопилот самолета. Такая система обусловливает
интересное сочетание задач управления и передачи информации. Суще¬
ствует возможность увязать ширину полосы пропускания, требуемой
для передачи данных, со сложностью автопилота.
Другим очевидным требованием к системе посадки является тре¬
бование надежности. Сложность системы посадки на авианосец, о кото¬
рой шла речь выше, приводят к трудностям при обеспечении надеж¬
ности, но тем не менее имеется возможность сделать автоматическое
управление посадкой более надежным, чем управление человеком.
Наряду с обычными шумами в датчиках и изменениями парамет¬
ров самолета система должна бороться с ветровыми возмущениями
и возмущениями, связанными с турбулентностью вдоль траектории
полета. Эти качества системы являются особенно важными в связи
с малой высотой полета самолета. Скорость при заходе на посадку,

13.5]
ХАРАКТЕРНЫЕ ПРИМЕРЫ
503
как правило, превышает критическую скорость в 1,3 раза, и система
управления должна так управлять самолетом, чтобы не допустить
срыва потока или слишком ранней посадки.
Здесь обсуждаются четыре типа систем управления выравнивания
самолета: системы, осуществляющие управления по заданной траекто¬
рии (УЗТ), системы управления по экспоненциальной траектории
(УЭТ), системы управления конечным состоянием (УКС) и системы,
осуществляющие многократное вычисление траектории по конечному
состоянию (У MB). Применение системы типа У КС для посадки само¬
лета обсуждается в тезисах Маттингли [10], где сообщается, что
система успешно прошла летные испытания. В техническом отчете
отделения авиационных систем ВВС США [19] производится сравне¬
ние систем УЭТ и У MB, при этом на динамическую модель четырех
различных самолетов действовали сигналы, соответствующие случай¬
ным ветровым возмущениям, и входные сигналы датчиков [9]. Моде¬
лирование, используемое при таком сравнении, включало воспроизве¬
дение эффекта влияния Земли на поведение самолета в процессе
посадки. Система УЗТ требует измерения продольного положения
самолета, и еще не доказано, что дополнительное усложнение является
необходимым. Кроме того, для предотвращения излишнего маневри¬
рования самолета на этапе выравнивания желательно также осуще¬
ствлять параллельный перенос точки приземления.
с)	Теория управления конечным состоянием
Теория управления конечным состоянием будет изложена в не¬
сколько более простой форме, чем та, в которой она применяется
в вышеупомянутой системе управления посадкой. Изучение системы
управления конечным состоянием позволяет также понять смысл
сопряженных уравнений в задаче оптимизации [12].
Система управления конечным состоянием предназначена для
управления состоянием динамической системы в некоторый момент
времени Т. В качестве этого момента времени берется номинальное
время приземления. Уравнения системы записываются в следующей
форме:
х = A (t) X -f В (0 U, х (*0) = С.
Состояние системы X управляется вектором U'. Уравнение
у = — Агу
является формально сопряженным к однородному уравнению системы.
Решения сопряженного уравнения используются для «условного про¬
гнозирования характеристик» системы. Этим «прогнозированием» явля¬
ется аналитическое решение, характеризующее величину вектора состо¬
яния X(t) в момент времени Т с учетом конкретного управления

504	СИСТЕМЫ	УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
и при отсутствии помех на входе системы. Пусть Y (t) является
матричным решением сопряженного уравнения
У= — АТУ при У{Т) = С.
Тогда это уравнение можно объединить с динамическим уравне¬
нием системы для Х\
(утх) — Утх YTx = YTBu.
Полученное таким образом новое уравнение интегрируется в интер¬
вале от t до 7':
т
Стх (Т) — YTx (t) = 5 YT(х) В (т) и (т) dx.
t
Входящие в это уравнение величины определяются следующим
образом: Стх(Т) — некоторый вектор, описывающий состояние системы
в момент времени Г, величина YT(t)x(t) равна Стх(Т), если вектор
управления и равен нулю. Пусть u = g-\-v, где g—предварительно
заданный программой входной сигнал. Тогда
т	т
Ctx(T)=Yt(0 д: (0-Г S YTBg dx + $ Y'Bv dx.
t	t
Величина
т
Scp= YT(t)x(t) + l YTBgdx
t
T
является условным значением С x(t). То есть если <0 = 0 при
^ Г, то
т
S = С тх (Т) = YT (t) х (t) + 5 YTBgdx.
t
Разность между величиной 5 и условно прогнозируемой 5ср на¬
зывается прогнозируемой ошибкой ер.
На рис. 13.2 показана блок-схема этой системы.
Конструкция управляющего устройства пока еще не определена,
но существует достаточно широкий класс регуляторов, которые обес¬
печивают приемлемые характеристики всей системы. Из соотношения
т
ер = \ YTBv (х) dx
t
можно получить
ер = — Y7Bv.

13.5]
ХАРАКТЕРНЫЕ ПРИМЕРЫ
505
Можно выбрать v=f(ep) и функцию Ляпунова V=eTPe^> 0,
е ф 0, P=const, V=—[fTBT YPe-\-еРУ1 Bf]. (Нижний индекс опу¬
щен.) Из соотношения для V видно, что если erYTBf^> 0 для
и для некоторого Р, то прогнозируемая ошибка будет непре¬
рывно уменьшаться по отношению к норме \\ef = eTPey и если
eTPYTBf>heTPe, то ||е(7)|<бГл(Г“/)||б?(0||.
9
А-
■>ср
YT(t)
Рис. 13.2. Система управления конечным состоянием.
При использовании системы типа УКС для управления посадкой
самолета номинальная функция g выбирается такой, чтобы номиналь¬
ная траектория выравнивания была безопасной и достаточно удоб¬
ной. Регулятор может быть выбран линейным с насыщением. Зона
насыщения позволяет предотвратить выдачу регулятором таких
команд, которые могли бы привести к опасным маневрам самолета.
При осуществлении прогнозирования обязательно учитывается дина¬
мика самолета.
Управляющее устройство с многократным вычислением
траектории по конечному состоянию
Управляющее устройство такого типа использует семейство номи¬
нальных траекторий, каждая из которых удовлетворяет конечным
условиям [9]. В каждый момент времени вычисляется соответствую¬
щая номинальная траектория, проходящая через точку на траектории,
где находится самолет. Команды управления формируются таким
образом, чтобы самолет выдерживал эту номинальную траекторию.
Номинальные траектории иногда описываются полиномами с коэффи¬
циентами, удовлетворяющими требуемым условиям. Например, функция
/г(т) = — т-[-аат2а3т3, i~t — Т

506
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
удовлетворяет конечным условиям /г (0) = 0, h(Q) = —1 для любых
значений коэффициентов а2 и а3. Параметры траектории определяются
по измерениям /г^ и км с помощью условий
км (то) 4“ то —
км Ы + 1 =
2т0
Зт;
Решая эти уравнения и подставляя коэффициенты а2 и аъ в номи¬
нальную функцию, найдем следующую функцию:
\3
hc СО — — т
[hM	-Ь
Задача: вычертить номинальную траекторию для == 3000 сму
hM = — 600 см/сек и т0 = — 20.
Для реализации указанной номинальной траектории сторонники
применения системы этого типа предлагают управлять профилем
изменения высоты. Возможно, что следует выбрать более лучший
класс номинальных траекторий.
Система управления по экспоненциальной траектории
Система типа УЭТ принципиально является очень простой [9].
Командный сигнал по скорости изменения высоты пропорционален
превышению задающего значения высоты (рис. 13.3).
Рис. 13.3. Система управления по экспоненциальной траектории
(hc = -M sat К (h-\-h0)).
Постоянная величина «/?0» является смещением, которое гаранти¬
рует обеспечение желаемой скорости снижения в момент приземле¬
ния. Коэффициент «К» определяет постоянную времени экспонен¬
циальной траектории. Корректирующее динамическое звено D (s) вво¬
дится с целью обеспечения устойчивости системы и малых ошибок

ЛИТЕРАТУРА
507
вертикальной скорости. В отчетах сообщалось, что эта система имеет
хорошие характеристики даже при наличии ветра и при воздействии
на ее вход помех. В системе отсутствует упреждающий элемент для
компенсации эффекта влияния Земли. Эффект влияния Земли на тра¬
екторию полета связан с постоянным изменением высоты в процессе
полета. Для тех самолетов, для которых этот эффект приводит
к значительному смещению точки приземления, командный сигнал
можно изменить посредством соответствующего нелинейного эле¬
мента так, чтобы поддерживать траекторию близкой к экспонен¬
циальной.
Все упомянутые системы управления требуют измерения скорости
и измерения высоты. Эти измерения могут осуществляться различ¬
ными способами, при этом имеет место связь между шириной полосы
пропускания системы связи и объемом бортовой аппаратуры. Слож¬
ная инерциальная измерительная аппаратура может строиться на базе
весьма простых датчиков или при отсутствии бортового высотомера
информация должна передаваться с Земли и с весьма большой ско¬
ростью.
Из этого краткого обсуждения проблемы автоматической посадки
видно, что система управления может строиться на различных прин¬
ципах, каждый из которых может обеспечить работоспособность
системы. Оценка или сравнение различных систем должно произво¬
диться по экономическим показателям, по надежности и эксплуата¬
ционным х ар а ктер и сти к а м.
В заключение автор хочет поблагодарить всех тех, кто помог ему
в понимании вопросов, связанных с управлением самолетами и косми¬
ческими летательными аппаратами, а также своих непосредственных
коллег и особенно Е. Б. Стира,
ЛИТЕРАТУРА
1. Goldstein Н., Glassical Mechanics, Addison-Wesley, Inc., Cambridge,
Mass., 1950. [Русский перевод: Голдстейн Г., Классическая механика,
Гостехиздат, М., 1957.]
2. Etkin В., Dynamics of Flight, John Wiley and Sons, Inc., New York, 1959.
[Русский перевод: Эткин Б., Динамика полета. Устойчивость и управ¬
ляемость, «Машиностроение», М., 1964.]
3. М i е 1 е A., Flight Mechanics, Addison — Wesley, Inc., Palo. Alto, 1962. [Рус¬
ский перевод: M и e л e А., Механика полета. 1., «Наука», М., 1965.]
4. Боднер В. А. и Козлов М. С., Стабилизация самолетов и автопило¬
тов, Гостехиздат, М., 1961.
5. S t е а г Е. В., A Critical Look at Vehicle Control Techniques, Astronautics
and Aerospace Engineering, August, 1963.
6. Prince L. Т., Design, Development, and Flight Research of an Experi¬
mental Adaptive Control Technique for Advanced Booster Systems, ASD-
TDR-62-178, February, 1962, 1—11.
7. Zaborsky J., Luedde W. and W e n d 1 М., New Flight Control Techni¬
ques for a Highly Elastic Booster, ASD-TR-61-231, September, 1961.

508
СИСТЕМЫ УПРАВЛЕНИЯ ЛЕТАТЕЛЬНЫМИ АППАРАТАМИ [ГЛ. 13
8. R о b е г s о n R. Е., Attitude Control of Satellites and Space Vehicles, Advan¬
ces in Space Science, Vol. II, 1960, pp. 351—436, Academic Press, New York.
9. Doniger J. F., Belsky, Reynolds G., HanischB. and Flit A.,
Antomatic Landing System Study, Part I. Results of Airborne Equip¬
ment Studies, Report No. ASD-TR-61-114,	Wright — Patterson	Air Force
Base, Ohio, February, 1962.
10. Mattingly L. K., Application of Terminal Control Techniques for an
Aircraft Landing Flare System, M. S. Thesis, University of California, Los
Angeles, January, 1962.
11. Merriam C. W. Ill, Study of an Automatic Landing System for Aircraft, MIT
OACL Report No. 93, May, 10, 1955.
12. M a 11 h e w s М. V., and Steeg C. W., Terminal Controller Synthesis,
MIT Report No. 55—272, p. 10, November 4, 1955.
13. В г у s о n A. E., Denham W. F., Carroll F. J. and M i к a m i K.,
Determination of Lift or Drag Program to Minimize Reentry Heating,
Journal of Aerospace Sciences, Vol. 29, No. 4, April, 1962.
14. Med itch J. S., Optimal Thrust Programming for Minimal Fuel Mid-
course Guidance, presented at ASD Optimal System Synthesis Conference,
Dayton, Ohio, September 11—13, 1962.
15. Kelley J. H., Falco M. and Ball D. J., Air Vehicle Trajectory
Optimization, presented at SIAM Symposium on Multivariable System
Theory, Cambridge, Mass., Nov. 1—3, 1962.
16. Horowitz, Isaac, Synthesis of Feedback	Systems,	Academic	Press, New
York, 1963.
17. В о d e H. W., Network Analysis and Feedback Amplifier Design, Van
Nostrand, Princeton, New Jersey, 1945. [Русский перевод: Боде Г., Тео¬
рия цепей и проектирование усилителей с обратной связью, ИЛ, М.,
1948.1
18. Eller t F. J. and Merriam C. W. Ill, Synthesis of Feedback Controls
Using Optimization Theory—-An Example, presented at 1962 JACC in
New York.
19. Bryson	A.	E., D e n h a m	W. F,	Guidance	Scheme for Supercircular
Reentry of	a	Lifting Vehicle,	Journal of the	American Rocket	Society,
Vol. 32, No. 6, June, 1962.
20. H e s t e n e s M. R., A General Problem in the Calculus of Variations with
Applications to Paths of Least Time, Rand Report RM-100, March 1, 1949.
21. В r e a k w e 11 J. V., The Optimization of Trajectories, J. Soc. Indust. Appl.
Math. Vol. 7, No. 2, June, 1959.
22. Balakrishnan A. V., A Steepest Descent Method for a Class of Final
Value Control Systems, A-62-1730-211, Aerospace Corporation, April 11,
1962.
23. Bryson A. E. and Denham W. F., A Steepest Ascent Method for Sol¬
ving Optimal Programming Problems, Journal of Applied Mechanics (Trans.
ASME, Series	E), Vol. 29, No.	2, pp.	247—257,	June, 1962.
24. St ear E.	B.	and Gregory	P. E.,	Capabilities and Limitations	of Some
Adaptive Techniques National Conference Proceedings 1962 NAECON,
May, 1962.
25. Ostgaard M. A. and Butsch L. М., Adaptive and Self—Organizing
Flight Control System, Aerospace Engineering, p. 80, September, 1962.
26. О s t g a a r d M. A., S t e a r E. B. and Gregory P. C., The Case for
Adaptive Controls, present to AGARD Flight Mechanics Panel, Paris, July,
1962.

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автономная система 206
Адаптивная система управления 266
Адаптивность 264
Айзермана метод 234
Амплитудно-импульсная модуляция 414
Аппроксимация весовых функций 49
— Пэйда 51
Асимптотическая устойчивость 208, 240
 в целом 20Э, 431
 , исследование 435
— — нелинейных автономных систем 217
  непрерывной по времени линейной авто¬
номной системы 217
  равномерная 20Э
	в большом 209
  равностепенная 203
	в большом 209
Банахово пространство 139
Бесконечное время удержания в конечной
области 214
Больца проблема 386
Брауна метод 306
Буняковского — Шварца неравенство 141
Вариации траектории и управления 328
Вектор состояния 320
— управляющий 320
Весовая последовательность 417
— функция 19, 21, 42, 128
Винера — Хопфа векторное уравнение 88, 92,
94, 101, 141
 интегральное уравнение 144, 148, 160, 189
Возмущенная система 206
Вольтерра уравнение 175, 176
Восстановление информации 415
Вронскиан 19, 20
Вторичный критерий устойчивости 226
Входные сигналы общего вида 79
  полиномиальные 79
  экспоненциальные 79
Выпуклый конус 334
Вырожденная корреляционная функция 121
Гамильтона система 325
Гамильтониан 325
Гаусса — Зайделя метод 301
Гёльдера неравенство 370
Гильберта — Шмидта теорема 147
Гильбертово пространство 139
Глобально асимптотически устойчивая систе¬
ма 431
Глобальное условие Липшица 207
Градиент AV скалярной функции 214
 , условие существования для функции
Ляпунова 240
Грама определитель 368
Грина функция 128
Динамическая система, непрерывная по вре¬
мени 207
Дирака S-функция 21
Дискретная система с асинхронным квантова¬
нием по времени 427
Дисперсионное уравнение 192
Допустимое уравнение 321
Достижимости конус 334
Евклидова норма 206
Задача минимума энергии при фиксированном
времени 345
 — — при ограничениях на вектор
управления 347
— оптимальной линейной фильтрации 87, 144
Закон инерции квадратичных форм 221
Импульсная модуляция 416
Импульсные системы многократные 428
Интегральная частотно-импульсная модуля¬
ция 437
Интервал оптимизации 296
— рабочий 296
Калмэновская фильтрация 316
Каноническая форма 223
  Смита полиномиальной матрицы 104
Каноническое преобразование 223
Квадратичная форма 220
 , закон инерции 221
 , матричная запись 220
 , приведение к диагональному виду 221
 , — к нормальному виду 221
 функции Ляпунова 220
Квазилинейная импульсная модель 465
Квантование по уровню 415
Кифера — Вольфовица процесс 404
Конус выпуклый 334
— достижимости 334
Координаты состояния 320
Корреляционная функция выроженная 121
— — нестационарного процесса 121
Коши матрица 216
Коэффициенты Фурье 142
Красовского теорема 235
Крейна 7,-проблема моментов 15, 351, 363
Критерий приемлемости системы 265
— Пэли — Винера 167, 174
— устойчивости вторичный 226, 235
Лагранжа метод вариации постоянной 127
  множителей 299
— теорема 218
Линейная система 17, 203
    нестационарная 18
 с вынуждающими силами 215

510
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
.Чиненное пространство 138
 : нормированное 139
Липшица условие 207
Ляпунова непрямой метод 195
— прямой метод 14. 195
— теорема 199
— функция 199. 201, 226, 249, 256 и т. д.
Матрица переходная 216
— положительно определенная 221
— спектральных плотностей случайных сиг¬
налов 95
Матричная запись квадратичной формы 220
Мерсера теорема 147
Метод Айзермана 232
— аналитический 308
— Брауна 307
— вариации постоянной Лагранжа 127
— введения дополнительного сигнала ошиб¬
ки 289
— возмущения параметра 287
— Гаусса — Зайделя 301
— градиента 14
— — функции ошибки 272
— квазилипеаризации 310, 376
— Кушнера 411
— Ляпунова непрямой 195
  прямой 14, 195
— многожителей Лагранжа 299
— паискорейшего спуска 138, 150
— настройки параметров 270
— обучающейся модели 283, 310
— ортогональных функций 310
— Плисса 237
— покоординатный градиентный 301
— последовательных приближений 376
— проекции градиента Хо 304
— сдвига нулей 223
— — полюсов 229
_ Хеи 307
— частных производных функции ошибки 289
— эталонной модели 283
Метрическое пространство 138
    полное 138
Многократные импульсные системы 428
Многомерная система 88
Моделирование сопряженной системы 14
Модель Goodyear 473
— квазилинейная импульсная 465
— Норса 463
— Рагаззини 456
— Тастина 456
Модуляция амплитудно-импульсная 414
— импульсная 416
— интегральная частотно-импульсная 437
Невозмущенная система 205
Нелинейная система 205
Непрерывная по времени динамическая систе¬
ма 207
Неравенство Буняковского — Шварца 141
— Гёльдера 370
— Шварца 150
Неустойчивое решение 210
Неустойчивость в целом нелинейных автоном¬
ных систем 215
Норма 139, 206
— евклидова 206
— неевклидова 206
— оператора 353
Нормированное пространство 139
Ограниченная траектория 20)
Оператор компактный 147
— неотрицательно определенный 146
Оператор положительно определенный 146
— проекционный 143
Определитель Вронского 19, 20
— Грама 36S
Оптимальная траектория 323
Оптимальное по быстродействию управле¬
ние 344
Переменные состояния 205
Переходная матрица 216
Планшереля теория 166
Плисса метод 237
z-плоскость 419
Полиномиальные входные сигналы 38
Положительная определенность симметриче¬
ской матрицы 221, 242
Положительно определенная матрица 221
Последовательность весовая 417
Преобразование каноническое 223, 224, 230
— квадратичной формы 222
^-преобразование 413, 419
Приведение квадратичной формы к диагональ¬
ному виду 221
— — — к нормальному виду 221
Приемлемая система 264, 265
Принцип максимума 337, 394
 для задачи с фиксированным време¬
нем 342
 для неавтономных систем 340
Проблема Больца 386
I-проблема моментов Крейна 15, 351, 363
Пространство 138
— банахово 139
— гильбертово 139
—• линейное 138
— метрическое 138
— нормированное 139
— полное 138
— сепарабельное 140
— сопряженное 354
— состояний 198, 205
— фазовое 198
Процесс Кифера — Вольфовица 404
— Роббинса—Монро 402
Пэйда аппроксимация 51
Пэли—Винера критерий 167, 174
Рабочий интервал 296
Равномерная устойчивость 209, 214
 асимптотическая 209, 211
 — в большом 209
Равностепенная асимптотическая устойчивость
208
 — в целом 214
Равностепенно ограниченная траектория 209
Рагаззини модель 456
Рикатти уравнение 192
Сепарабельное пространство 140
Синтез многомерных систем 13
— многополюсников 14
— оптимальных линейных фильтров 14, 88
— — по быстродействию систем 448
Система автономная 206
— адаптивная 206
— асимптотически устойчивая 431
— — — в большом 431
— — — глобально 431
— возмущенная 206
— динамическая непрерывная по времени 207
— дискретная с асинхронным квантованием
но времени 427
— — с произвольным квантованием по вре¬
мени 426

ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
511
Система замкнутая 426
— импульсная многократная 428
— линейная 17, 205
— с вынуждающими силами 215
— многомерная 88
— невозмущепиая 205
— нелинейная 205
— нестационарная 18, 205
— приемлемая 264, 265
 , критерий приемлемости 265
— разомкнутая 266
— свободная 205
— с обратной связью 266
— сопряженная 332
— стационарная 205
— управляемая 320
— упрощаемая 56
— уравнений Гамильтона 325
— устойчивая 431
— функций ортонормированная 141
Системы эквивалентные 56
Слабая сходимость в гильбертовом простран¬
стве 182
  в среднеквадратичном 182
Сложение дифференциальных уравнений 31
Смита каноническая форма матрицы 103
Собственные значения матрицы 221
Состояние равновесия 208
Спектральная функция процесса 165
Стационарный процесс 115
Существование функции Ляпунова 215
Тастина модель 456
Теорема Гильберта— Шмидта 147
— Лагранжа 218
— Ляпунова 199
— Красовского 235
— Мерсера 147
— о неподвижной точке 178
— представления Карунена — Лоэва 184
— Хана — Банаха 355
— Шаудера 178
Теория Планшереля 166
Траектория ограниченная 209
    равностепенно 209
— оптимальная 323
Умножение дифференциальных уравнений 31
Управление 321
— в натуральном масштабе времени 301
— допустимое 321
— оптимальное по быстродействию 344
Управляющий вектор 320
Упрощаемая система 56
Упрощаемое уравнение 60
Упрощаемость 56
Уравнение Винера — Хопфа векторное 88, 92,
94, 101, 144
		интегральное	144,	148,	160,	189
— Вольтерра 175, 176
— изменения состояния линейной дискретной
системы 422
Уравнение изменения состояния непрерывной
динамической системы 421
— Рикатти 192
— Эйлера — Лагранжа 396
Условие Липшица 207
  глобальное 207
Устойчивость 208
— автономных систем 210
— асимптотическая 208
 равномерная 209, 211
	в большом 209
  равностепенная 208
	в большом 209
— неавтономных систем 211, 212
— нелинейных автономных систем 210, 211,
217, 218
	 условная	210
— непрерывных по времени линейных авто¬
номных систем 217
— эвентуальная нелинейных систем 219
		—, область устойчивости 219
Физическая возможность системы 167
Физически возможный фильтр 168
Фильтрация калмэновская 316
Формы канонические 223
Функция весовая 19, 21, 42, 128
  , аппроксимация 49
— Грина 128
— Ляпунова 199, 201, 226, 249, 256
  , квадратичная форма 220
 , построение методом градиента 238
 , существование 215
— матрицы характеристическая 222
— стоимости 322
— «штрафная» 295
5-функция Дирака 21
Фурье-коэффициенты 142
Хана — Банаха теорема 355
Характеристическая функция матрицы 221
Характеристические числа матрицы 221
Характеристическое уравнение матрицы 222
Хо метод проекции градиента 304
Хеи метод 307
Шаудера теорема 178
Шварца неравенство 150
Штрафные функции 295
Эвентуальная устойчивость нелинейных си¬
стем 219
	, область устойчивости 219
Эйлера — Лагранжа уравнения 396
Эквивалентные дифференциальные уравне¬
ния 57
— системы 57
Экспоненциальные входные сигналы 79
Экспериментальное определение корреляцион¬
ной функции 116
Экстремальный элемент 354
Эргодический процесс 115

Современная теория систем управления
под редакцией К. Т. Леондеса
М., 1970 г., 512 стр. с илл.
Редактор Л. Я. Ройтенберг
Техн. редактор В. Н. Крючкова
Корректоры В. П. Горячева, Н. Б. Румянцева
Сдано в набор 28/11 1969 г. Подписано к печати
19/XII 1969 г. Бумага 60X907i6. Физ. печ. л. 32.
Условн. печ. л. 32 Уч.-изд. л. 30,26. Ти¬
раж 11 500 экз. Цена книги 2 р. 38 к. Заказ № 427.
Издательство «Наука»
Главная редакция физико-математической
литературы
Москва, В-71, Ленинский проспект, 15.
Ордена Трудового Красного Знамени Ленинград¬
ская типография № 1 «Печатный Двор» имени
А. М. Горького Главполиграфпрома Комитета
по печати при Совете Министров СССР, г. Ле¬
нинград, Гатчинская ул., 26.
Отпечатано в гос. типогр. «Вайздас», Вильнюс,
ул. Страздялио 1. Заказ № 66.