Author: Никулин Е.А.
Tags: математика автоматика и телемеханика теория автоматического управления
ISBN: 5-94157-440-1
Year: 2004
Text
Е. А. Никулин
Основы ТЕОРИИ
АВТОМАТИЧЕСКОГО
УПРАВЛЕНИЯ
Частотные методы анализа
И СИНТЕЗА СИСТЕМ
Общий курс для студентов, аспирантов
и преподавателей
Анализ и проектирование систем управления
для инженеров-практиков
Методы расчета и компьютерное моделирование
процессов в среде Mathcad
Задания для курсового проектирования, лабораторных
и практических работ
УЧЕБНОЕ ПОСОБ1/1Е
УДК 519.068 (075.8)
ББК 32.96я73
Н65
Никулин Е. А.
Н65 Основы теории автоматического управления. Частотные методы анализа
и синтеза систем / Учеб, пособие для вузов — СПб : БХВ-Петербург,
2004 - 640 с.: ил.
ISBN 5-94157-440-1
ими объектами и конструирование ПКД-
юго проектирования, лобо|ыторных, практических н самостоятельных работ
Для студентов и аспирантов технических вузов, а также преп
и специалистов в области автоматического управления
УДК 519 068 (075 8)
ББК 32.9бя73
Рецензенты:
профессор, дт.н., заведующий кафедрой «Теория испей и тедекоммуяи
Нижегородского тпсуларстнсиного технического унияерс|гтгп>,
действительный 'глеи РАИН, IEEE В В Крылов.
Волго-Вятской академии государственной службы А Т Налсеп
Группа подготовки издания:
Главный редактор
Зам. главного редактора
Зав. редакцией
Редактор
Компькгтсрная верстка
Корректор
Дизайн обложки
Зав. производством
Екатерина Кондукова
Людмила Еремеевская
Григорий Добин
Алексей Семенов
Василисы Сафаровой
Евгений Камский
Игоря Цырулыткова
Николай Тверских
Лицензия ИД N. 02428 от 24 07.00. Подписано в печать 30 07.04.
Формат 70x100'/,, Печать офсетная Усл. печ. л. 51.0.
Тираж 3000 вяз Заказ Ni 3436
'БХВ-Петербург-. 180005. Санкт-Петербург, Измайловский пр . 28
«имеское заялочение на лродухцию. товар Ni 77 98 02 953 Д 001537 03 02
от 13 03 2002 г видено Департаментом ГСЭН Минтдрава России
В ГУП ’Типография •Наука-
199034. Санкт Петербург. 9 линия. 12.
С Никулин 5. А. 1004
С Оформление. нмлтглмттяо 'ВХВ-Птрбпи-. W*
ISBN 5-94157-440-1
Содержание
Предисловие...........................................................б
Введение.............................................................11
B.I Основные понятия теории автоматического управления 1|
В.2. Классификация систем управления.......................... .....14
В.З. Задачи теории автоматического управления 18
Глава I. Математические модели элементов и систем управления.........25
1.1. Классификация элементов систем управления .25
1.2. Статические свойства элементов и систем 26
1.2.1. Соединения статических элементов 2х
1.2.2. Линеаризация статических элементов 31
1.2.3. Статические ошибки в замкнутых системах управления . 36
1.3. Статический анализ и синтез схем на операционных усилителях. 39
1.3.1. Нелинейные статические элементы на операционных усилителях 42
1.3.2. Линейные статические элементы на операционных усилителях .47
1.4. Описание динамики элементов систем управления . 57
1.5. Передаточная функция.......................................... 65
1.6. Соединения элементов и преобразования структурных схем .68
1.7. Чувствительность и стабилизирующие свойства отрицательной
обратной связи........ М
1.8. Динамический анализ и синтез схем на операционных усилителях...81
1.8.1. Динамические элементы на операционных усилителях.............81
1.8.2. Построение схем неминимально-фазовых элементов...............97
1.8.3. Анализ и синтез многокаскадных схем на операционных усилителях 104
Глава 2. Частотные характеристики элементов и систем управления.....119
2.1. Основные частотные характеристики.............................124
2.2. Частотные характеристики типовых звеньев..................... 132
2.3* . Погрешности аппроксимации логарифмических частотных
характерисгик типовых звеньев.................................... 150
2.4. Частотные характеристики сложных систем..................... 157
2.5. Частотные свойства замкнутых систем...........................172
2.5.1 Частотные характерисгоки систем с отрицательной обратной связью 172
Содержание
2.5.2. Расширение полосы пропускания...... 179
15.3. Свойства систем с положительной обратной святые.................... 187
2.6* Анализ полиномов.................................................... 200
16.1 Полиномы низких степеней ........................................... 205
16.1 Структура спектра полинома 208
16 3 Локализация корней полинома........................................ 213
164 Уточнение корней полинома............................................ 219
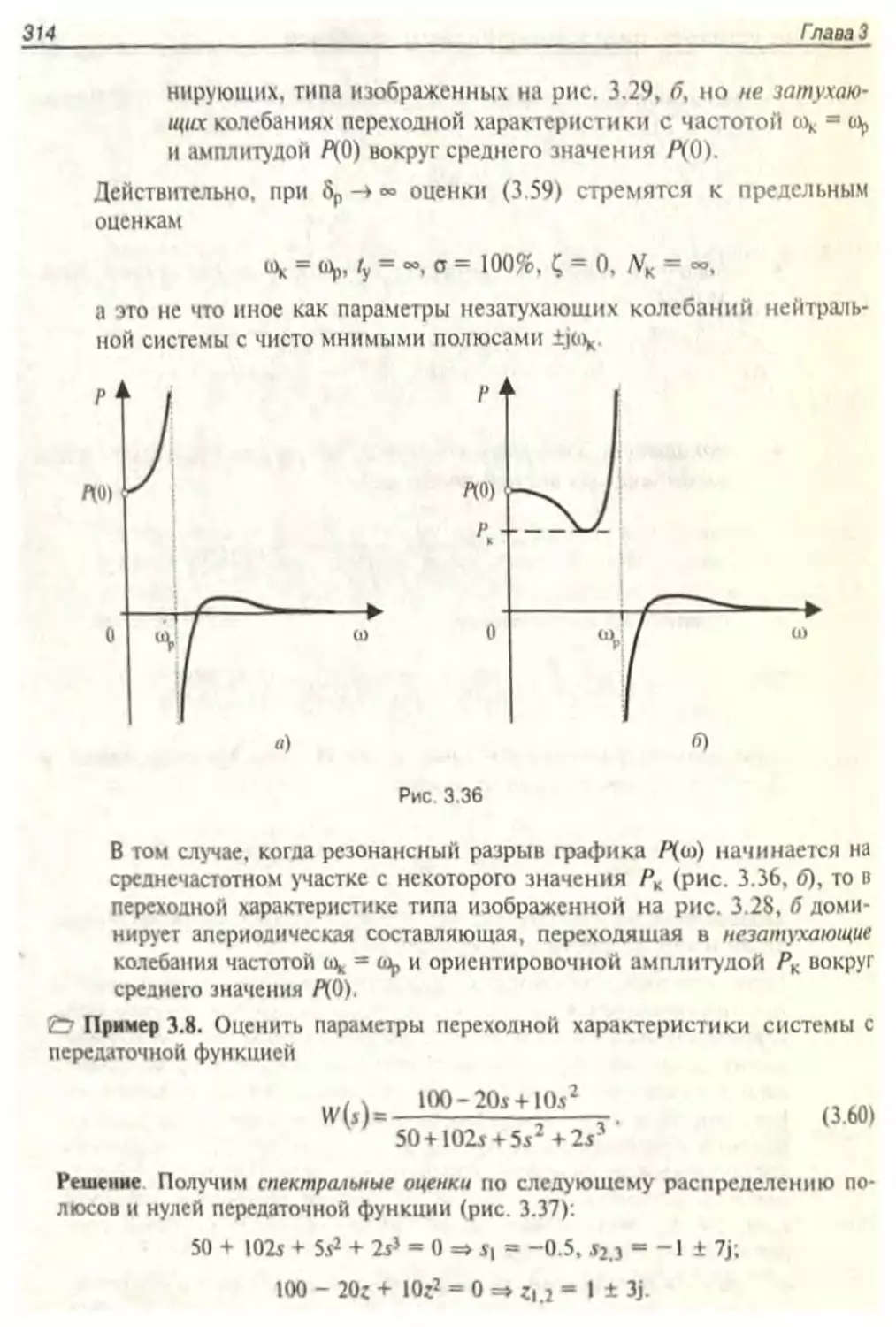
Глава 3. Временные характеристики элементов и систем управления...........242
3.1 Обратное преобразование Лапласа...................................... 243
3.11 Метод разложения Хевисайда ......................................... 244
3.1.2. Табличный метод преобразований Лапласа............................ 250
3.1.3 Программный метод преобразований Лапласа............................255
32. Типовые временные характеристики...................................258
311 Импульсная характеристика.......------.............................................. 258
312 Переходная характеристика —...........................................262
313 Взаимосвязь временных характеристик 264
33. Частотно-временные свойства систем.................................281
3.31 Взаимосвязь частотных и временных характеристик 282
3.3.2 . Трансформации частотных характеристик.......................... 285
3.3 3 Масштабируемые ио времени модели 288
3.4*. Аппроксимационный метод построения временных характеристик............291
3.5. Оценки качества переходных процессов в системах управления.........297
3.5.1 Показатели качества переходной характеристики...................... 299
3 5 2 Спектральные оценки качества........................................301
3.5.3. Частотные оценки качества......................................... 307
Глава 4. Устойчивость систем автоматического управления...................318
4.1 Понятие устойчивости 318
4.2. Условия устойчивости линеаризованных систем........................320
4.3. Алгебраические критерии устойчивости........ . 323
4.3.1. Необходимые условия устойчивости............................... 324
432. Критерий устойчивости Рауса - Гурвица............................... 325
4.4. Построение областей устойчивости параметрических полиномов ........331
4.5. Частотный критерий устойчивости Михайлова .........................342
4.6 Частотный критерии устойчивости Найквиста...........................354
4.6.1. Вывод критерия Найквиста ....................................... .354
46 2 Логарифмический критерий устойчивости Найквиста......................361
4 7 Запасы устойчивости замкнутой системы.......... ......376
4.7.1. Определение запасов устойчивости ................................ 376
Содержание
4.7.2. Алгебраический критерий устойчивости с запасами.............379
4.8*. Устойчивость систем с запаздыванием.......................... 385
Глава 5. Расчет переходных процессов и системах автоматического управления .....397
5.1. Структура переходного процесса.................................. 398
5.2. Метод преобразований Лапласа......................................401
5.3. Метод вариации произвольных постоянных 414
5.4. Метод интеграла Дюамеля.......................................... 418
5.5. Метод пространства состояния..................................... 421
5 5.1. Модель в пространстве состояний.......................... 421
5.5. 2. Расчет параметров моделей в пространстве состояний ........424
5.5.3. Программное моделирование переходных процессов
в пространстве состояний
Глава 6. Методы проектирования систем автоматического управления...........434
6.1. Основные задачи синтеза регуляторов..................................434
6.2. Методы повышения статической точности
(низкочастотный синтез регуляторов)................................ 451
6.2.1. Коэффициенты статтческих ошибок.. ...................... 452
6.2.2. Статические системы управления 454
6.2.3. Астатические системы управления .........................967
6.3. Методы улучшения динамических параметров
(среднечастотный синтез регуляторов)....... 975
6.4. Быстрый синтез систем управления методом
логарифмических частотных характеристик.............................991
6 5 Управление неустойчивыми объектами W2
6 6 Спектральный метод синтеза регуляторов. ......................510
6 6 1 Замкнутая система второго порядка . 516
6 6 2 Замкнутая система третьего порядка 528
6.6 3. Замкнутая система п -го порядка..........................534
6.6.4. Неустойчивая р.тюммтугая система 537
6.7 Системы управления с ПИД-регуляторами 544
6 7 1 Аиштиз ПИД-регуляторов 545
6.7.2. Синтез ПИД-рсгуляторов
6.7.3 Рвали.......ия ПИД-регуляторов 574
Заключение..........................................................579
Приложение 1. Таблицы преобразований Лапласа.....................581
Приложение 2. Задания для курсового проектирования..................612
Список литературы....................................................
Предметный указатель.................................................623
ВВЕДЕНИЕ
все должно быть илюжено так проста, кок
только ооыожно, ко не праще
Альберт Эйнштейн
В.1. Основные понятия теории
автоматического управления
Теория автоматического управления (ТАУ) как одно из основных направле-
ний технической кибернетики изучает свойства различных, в основном тех-
нических устройств с целью заставить их работать с большей эффективно-
стью для человека. Анализ этих свойств дает основания для исследования
возможностей повышения эффективности работы устройств в автоматиче-
ском режиме, т е. без вмешательства человека-оператора. Автоматизация
процессов заключается в проектировании специальных устройств, а в более
широком смысле — систем автоматического управления (САУ), работающих
по принципу «включил и забыл». Назначение системы управления заключа-
ется в том, чтобы заставить управляемый объект выполнять возложенную на
него задачу с желаемым качеством, двигаться по заданной траектории в
пространстве и во времени
Необходимость поддержания постоянного значения или желаемого закона
изменения какой-либо величины возникает в различных отраслях техники:
□ хтектроснабжении — постоянство частоты и напряжения в сети;
□ атомной энергетике — устойчивый и безопасный уровень мощности ре-
актора, определяемый глубиной погружения стержней, поглощающих
нейтроны;
□ авиации и судовождении — движение самолета или судна по заданному
курсу, стабилизация крена и дифферента,
□ космонавтике — выведение летального аппарата на орбиту и его ориен-
тация в космическом пространстве;
□ локации — наведение оси локатора на неподвижную цель или сопрово-
ждение движущейся цели;
12—Д»»Дри**е
□ робототехнике - движение рабочего органа по заданной траектории в
пространстве;
□ химической промышленности — обеспечение требуемых параметров
технмопгческого режима, состава реагентов и готового продукта:
□ металлургической и бумажной промышленности — поддержание толщи-
ны проката в пределах установленного допуска.
Сами по себе объекты, в которых протекают процессы, часто не обеспечи-
вают их желаемого хода, не устраняют отклонений от заданных режимов.
Поэтому такие обьекты упраазения (ОбУ) снабжаются регуляторами, или
устройствами управления (УУ). Управление — это контролируемое воздейст-
вие на объект, предназначенное для достижения цели управления — опре-
деленных критериев качества, которые могут включать в себя следующие
условия:
□ ограничения на максимальное и установившееся отклонения от заданно-
го режима;
□ получение желаемого вида переходных процессов;
□ необходимость компенсации неблагоприятных факторов;
□ уменьшение энергии, затраченной на управление, и т п
Таким образом, система автоматического управления представляет собой
объединение объекта и регулятора В зависимости от субъекта, принимаю-
щего решения о воздействии на объект, управление бывает ручным и авто-
матическим.
Регулирование - это управление с целью обеспечения близости управляемых
координат объекта к их заданным значениям — уставкам. Синонимами по-
нятия уставки являются термины «желаемое» или «эталонное» значение.
Следящее регулирование — это приведение управляемых координат к зна-
чениям заранее неизвестных, но доступных для измерения уставок путем
их сравнения благодаря наличию в системе контура обратной связи (ОС).
Данное понятие включает в себя комплекс технических средств, обеспечи-
вающих:
□ измерение выходной переменной объекта с помощью датчика',
□ измерение или генерирование по определенной программе сигнала ус-
тавки;
□ формирование с помощью сравнивающего устройства сигнала невязки
или ошибки регулирования — разности между уставкой и текущим значе-
нием управляемой переменной;
□ преобразование ошибки регулирования в управляющий сигнал, пода-
ваемый через исполнительное устройство на объект управления.
Введение 13
В правильно спроектированной системе управления сигнал невязки за-
ставляет объект реагировать таким образом, чтобы уменьшить величину
ошибки до допустимого, а в идеале — до нулевого значения. Примером
следящей системы может служить система автоматического наведения ан-
тенны локатора, телескопа, ствола орудия, лазерного луча и т. п. на дви-
жущуюся цель.
Стабилизация — это регулирование управляемых координат к постоянным
уставкам с помошью обратной связи. Являясь частным случаем следящей
системы, система стабилизации нс требует непрерывного измерения уставки
из-за се постоянства в пределах рабочего интервала времени Примером
системы стабилизации может служить кондиционер, поддерживающий в
комнате заданную температуру воздуха.
Программное регулирование — это регулирование координат объекта ио оп-
ределенному закону — заранее известной функции времени Типичными
примерами устройств с программным управлением могут служить
□ робот-манипулятор, переносящий деталь по заданной траектории;
□ программа автопилота яхты, перекладывающая руль в заранее опреде-
ленные моменты времени в процессе ее движения по проложенному
штурманом курсу;
□ система автоматической посадки самолета по специальной траектории —
глиссаде.
При полностью известных условиях работы объекта и в отсутствие факто-
ров, отклоняющих его движение от заданного, программное управление яв-
ляется надежным и дешевым методом регулирования.
Возмущение — это неуправляемое воздействие извне на любой элемент систе-
мы, как правило, затрудняющее достижение цели управления. Примерами
возмущений являются.
□ боковой ветер или течение, сносящие самолет или судно с заданного
курса;
□ утечка тепла через открытые окна, двери, щели в стенах в системе ста-
билизации комнатной температуры;
□ инструментальные погрешности настройки датчиков, из-за чего послед-
ние сообщают регулятору недостоверную информацию о состоянии сис-
темы.
Учет возмущений, возможность их измерить и использовать для корректи-
ровки управления, позволяет противодействовать их вредному влиянию на
объект или, наоборот, использовать (например, попутный ветер при управ-
лении самолетом) для ускорения достижения цели или экономии энергии.
Введение
В.2. Классификация систем управления
Классификация систем автоматического управления производится по сле-
дующим признакам.
□ По принципу регулирования:
• ратикнутые системы с программным управлением (рис. В 1, о);
. разомкнутые системы с управлением по возмущению (рис. В.1, <5);
• замкнутые системы (рис. В.1, а);
• комбинированные системы (рис. В. 1, г)
в)
Рис. В.1
На рис. В.1 обозначено:
• g — уставка, или выходной сигнал генератора уставки;
• е - невязка, или ошибка регулирования;
• х - управление, или выходной сигнал регулятора;
• у- измерение, или выходной сигнал измерительного устройства
(ИУ);
• /о и/, - возмущения объекта и измерительного устройства.
В разомкнутой системе управления информация о текущем состоянии
объекта отсутствует либо не используется, управляющее воздействие вы-
рабатывается по заранее составленной программе, а выходной сигнал об-
разуется как непосредственная реакция на это воздействие. Возможность
измерения возмущений, нарушающих желаемый ход процесса, повышает
эффективность разомкнутого управления благодаря заложенной в регуля-
тор программы компенсации возмущений.
ВввДвНИв 1 5
Обратная связь — важнейшее понятие кибернетики и основной принцип
функционирования сложных систем, позволяющий в реальном времени,
по ходу процесса управления, уменьшать абсолютное значение ошибки
регулирования
е(/) = «(0-ХО (В.1)
на основе измерения текущего состояния объекта у(/) и сравнения его с
уставкой g(f). В отличие от разомкнутых систем, в системах с обратной
связью становится возможной компенсация неизмеряемых возмущений
благодаря их раннему или позднему влиянию на работу системы в виде
увеличения ошибки регулирования.
Если измерение возмущений возможно, то введение в систему автома-
тического управления дополнительного контура управления по возму-
щению позволяет оперативно противодействовать его вредному влия-
нию, не дожидаясь, пока это влияние заметно проявится в выходном
сигнале системы.
Влияние обратной связи на динамику систем всесторонне изучалось в
20 - 30-х годах двадцатого века применительно к задаче конструирования
высококачественных электронных усилителей слабых сигналов, а в 40 -
60-х годах — при разработке систем автоматического управления в энер-
гетике, авиации и космонавтике. Более того, Норберт Винер сделал тео-
рию управления с обратной связью краеугольным камнем целой фило-
софской системы — «кибернетики», охватывающей всевозможные аспек-
ты от автоматики до физиологии, психологии, экономики, политики и
даже этики. Время и развитие альтернативных воззрений несколько
уменьшило великолепие этой картины, однако управление с обратной
связью остается в основе как важнейших идей, так и полезных техниче-
ских приложений.
□ По цели регулирования:
• системы программного управления (цель ип без использования
обратной связи);
• следящие системы (цель r(z) ,сТ>) с пом.МЦЫО обратной связи).
• системы стабилизации (цель: iv) = - const с использованием обрел
ной связи);
• экстремальные системы (цель, лкстремум некоторою показателя каче-
ства управления).
Q По способу формирования сигнала ynpaaiemm регулятором:
• непрерывные, или аналоговые системы (рис. В.2, а);
• дискретные системы, использующие квантование времени А Л/
и/или уровня сигнала X/ = i -Д.г.
Введение
импульсные с квантованием времени, в которых информация об
уровне сигнала кодируется с помощью амплитудной
(рис. В.2. б), широтной (рис. В 2, в) или фазовой (рис. В 2. г)
модуляции;
релейные системы с квантованием уровня сигнала (рис. В.2, д').
Мровые системы с обоими видами квантования (рис В.2. е);
системы с гармонической модуляцией.
Рис. В.2
В непрерывных системах управление вырабатывается аналоговыми уст-
ройствами автоматики, например, схемами на операционных усилителях.
В дискретных системах квантование времени выполняется синхронизи-
рующими устройствами - таймерами, а квантование уровня — аналого-
цифровыми преобразователями. В системах, работающих на переменном
токе, высокочастотные колебания несущей частоты модулируются в соот-
ветствии с величиной и знаком управляющего сигнала низкой частоты.
□ По количеству peey.iupye.uux координат'.
• одномерные системы с одним входом и одним выходом;
• многомерные системы, которые в зависимости от влияния координат
друг на друга делятся на несвязные и многосвязные.
□ По характеру изменения параметров во времени:
• стационарные системы, описываемые уравнениями с параметрами, не
зависящими от времени,
Введение
• нестационарные системы, параметры моделей которых изменяются
во времени. Если эти изменения за рабочий период системы неве-
лики, то по методу замороженных параметров такую систему можно
считать стационарной с параметрами, зафиксированными на теку-
щий период.
□ По распределению параметров в пространстве
• системы с сосредоточенными параметрами, описываемые обыкновен-
ными дифференциальными уравнениями;
• системы с распределенными параметрами, описываемые дифференци-
альными уравнениями в частных производных.
□ По степени идеализации математического описания:
• линейные системы, описываемые линейными алгебраическими и диф-
ференциальными уравнениями;
• нелинейные системы, описываемые НСЛИНСЙНЫМИ уравнениями
□ По соотношению сигнал/шум в передаваемой информации:
• детерминированные системы, в которых отсутствует или не учитывает-
ся влияние шума в параметрах и передаваемых сигналах;
• стохастические системы, работающие при высоких уровнях шумов,
чьи статистические характеристики используются в моделях зашум-
ленных элементов.
□ По характеру переходных процесса*.
• устойчивые системы,
• неустойчивые системы;
• нейтральные системы.
Устойчивость движения как свойство объекта или системы самостоятель-
но возвращаться в состояние равновесия после прекращения действия
отклоняющих сил — вовсе не врожденное свойство всех объектов. Про-
стейшей иллюстрацией этого факта является движение шарика с трением
по различным поверхностям (рис. В.З):
• шарик в яме (а) имеет устойчивое состояние равновесия на дне и ус-
тойчивое движение по склонам ямы;
• состояние равновесия шарика на горе (б) является неустойчивым: ма-
лейшее отклонение приводит к удалению от него. Неустойчивость
также присуща и движению по склонам горы;
• движение шарика по горизонтальной плоскости (в) имеет безразлич-
ное (нейтральное) состояние равновесия там, где он остановится в
результате торможения.
Введение
Рис. В З
В.З. Задачи теории
автоматического управления
Основная задача теории автоматического управления — обеспечение устойчи-
вости системы путем выбора структуры и параметров регулятора или изме-
нения параметров объекта Интуитивно понятие устойчивости означает, что
при любам ограниченном входном сигнале выходной сигнал также является ог-
раниченным.
Устойчивые объекты сами возвращаются в состояние равновесия без всяко-
го управления. Назначение регулятора состоит в улучшении качества пере-
ходного процесса - уменьшении его длительности, максимальных отклоне-
ний от состояния равновесия, демпфировании (сглаживании) колебаний.
Устойчивость многих объектов является условной, зависящей от значений
некоторых параметров, например, коэффициентов усиления или постоян-
ных времени усилителей. Если вмешательство в конструкцию неустойчивого
объекта по тем или иным причинам недопустимо, то на регулятор возлага-
ется решение обеих задач: как обеспечения устойчивости, так и качества пе-
рекатных процессов.
Как пример условной устойчивости рассмотрим акустическую систему, со-
стоящую из микрофона, усилителя и динамика (рис. В.4). При слишком
близком расположении микрофона от динамиков даже в отсутствие голоса
возникает процесс самовозбуждения, слышимый как громкий свист на не-
которой звуковой частоте
Введение
Причина неустойчивости упрощенно объясняется с помощью коэффициен-
тов усиления устройств Им, И'д и воздушного слоя IFB, имеющих, во-
первых, комплексный, а во-вторых, частотно-зависимый характер. Если на
некоторой частоте последовательное соединение блоков в контуре обратной
связи имеет коэффициент усиления амплитуды колебаний
Л = |И'нИ'уН'аИу> I
и фазовый сдвиг
<P-arg(H'MH'yH'aH'1) = O,
то малейший сигнал этой частоты, попав в микрофон из внешней среды,
лавинообразно усиливается в контуре обратной связи до достижения макси-
мальной конструктивной мощности усилителя.
Устранить неустойчивость можно следующими способами:
□ уменьшить | JFy|, т. е. убавить громкость звука регулятором усилителя;
□ уменьшить | IFJ, т. е. отодвинуть микрофон подальше от динамика.
Таким образом, на плоскости параметров |Wy| и существуют области ус-
тойчивости и неустойчивости системы, разделенные границей устойчивости
(рис. В.5). При попадании значений параметров в область неустойчивости
переходные процессы в системе расходятся до насыщения по максимальной
мощности, что ведет к перегреву аппаратуры, аварии, взрыву и другим не-
желательным или катастрофическим последствиям.
Рис. в.5
Системы, устойчивость которых не может быть достигнута никаким изме-
нением параметров, называются структурно неустойчивыми. Устойчивое
управление в этом случае достигается путем перестройки структурной орга-
низации системы управления.
X______________________Введение
Задача програмчного управления — изменение управляемой величины у(/) по
заранее заданному закону (программе) g(i) без учета внешних воздействий.
Примерами могут служить программы автопилота самолета, движения инст-
румента обрабатывающего станка или руки робота по заушиной траектории.
Задача следящего упрощения — изменение управляемой величины yti) по
произвольному и заранее неизвестному закону g(i). Цель слежения е(г) -»О
достигается с помощью отрицательной обратной связи (см. рис. В.1, а). При
е(|) * 0 регулятор отрабатывает ошибку управления в направлении уменьше-
ния ее абсолютного значения |е(4 Примеры следящих систем:
□ сопровождение локатором движущейся цели;
□ повторение роботом, находящимся в агрессивной среде, манипуляций
человека-оператора;
□ выполнение прецизионных операций в микроэлектронике и микрохи-
рургии путем отработки движений инструмента на увеличенном макете
обрабатываемого изделия или органа.
Задача стабилизации — сведение управляемой величины к значению посто-
янной уставки g(0 = const. Стабилизация как частный случай слежения ши-
роко востребована в технических системах со стационарными целями. При
замене по (В.1) переменной >(<)=«(/)- <40 получается модель системы в
отклонениях е(/1. в результате чего задача следящего управления
Яб -»М сводится к задаче стабилизации e(t) -»0 с нулевым состоянием
равновесия.
В качестве вычитателей в системах слежения и стабилизации применяются
устройства самой различной физической природы:
□ механические дифференциалы и рычажные весы;
□ электромеханические гироскопы;
□ электронные дифференциальные усилители.
Задача статического и динамического анализа системы автоматического
управления состоит в исследовании статических (в установившемся режиме)
и динамических (в переходном режиме) свойств системы с учетом взаимно-
го влияния ее элементов друг на друга. Сюда входит определение статиче-
ских ошибок и параметров качества переходных процессов в системе при
различных входных воздействиях
Качество системы определяется параметрами переходного процесса при от-
работке системой возникающих возмущений. К основным показателям каче-
ства относятся:
□ статические ошибки регулирования, или отклонения выходных перемен-
ных от их уставок в установившемся режиме;
Введение 21
□ длительность переходного режима, или время установления;
□ максимальные выбросы (перерегулирования} управляемых переменных за
их установившиеся значения;
□ число колебаний в переходном режиме и степень затухания колебаний
Задача синтеза устройства управления заключается в проектировании техни-
ческого устройства, воздействующего на объект в направлении достижения
желаемой цели управления. Основные функции регулятора-
□ преобразование контролируемых величин в сигналы используемого ре-
гулятором вида энергии — электрической, механической, гидравличе-
ской и т. д.;
□ формирование программных сигналов (уставок),
□ формирование ошибок регулирования;
□ квантование сигналов в дискретных системах;
□ выполнение аналоговых, логических и арифметических операций по
расчету управляющего воздействия;
□ хранение сигналов до момента их использования,
□ распределение сигналов по различным каналам управления;
□ преобразование управляющих сигналов к виду, необходимому для рабо-
ты исполнительных устройств.
Здесь перечислены задачи регулятора в широком смысле, каким фактически
является вся система управления, за исключением объекта Задачей регуля-
тора в узком смысле можно считать пятую из перечисленных функций
Разработка регулятора заключается в выборе его структуры (из чего слагает-
ся управляющее воздействие) и расчете параметров (коэффициентов перед
слагаемыми). Основными компонентами управления могут быть;
□ пропорциональное (П) управление по ошибке регулирования е(Г),
□ дифференциальное (Д) управление по производной ошибки —— .
о/
□ интегральное (И) управление по интегралу ошибки je(r)dT
Рассмотрим принципиальное назначение указанных компонентов на приме-
ре работы автопилота — устройства, обеспечивающего движение судна по
заданному компасному курсу g (рис В.6) Изменение направления движения
Достигается путем отклонения руля на угол х относительно оси судна (пози-
ция А на рис. В.6, а), что при наличии продольного движения создаст вра-
щающий момент и поворачивает судно в сторону отклонения руля.
Введение
□ Пропорциональное управление
лп(0 - М') (В.2)
выполняет главную задачу уменьшения модуля ошибки |?(г)| за мини-
мальное время установления При достижении значения е(г) = 0 (пози-
ция В) руль встает в неотклоненное положение. Поскольку судно имеет
определенный момент инерции, то оно продолжает и дальше вращаться,
отклоняясь от заданного курса в противоположную сторону. Так возни-
кают колебания регулируемой величины у(1) вокруг уставки g. Правиль-
ным выбором параметра регулятора К„ можно несколько сгладить
(демпфировать) эти колебания, но общий характер переходного процесса
на выходе системы остается колебательным.
□ Что делает опытный рулевой в таком случае’ Он начинает заранее пере-
кладывать руль так, чтобы подойти к точке равновесия с минимальной
угловой скоростью /(/) и компенсировать инерцию вращения противо-
положным вращательным моментом, создаваемым рулем, который изо-
бражен пунктиром в позиции В. Дополнительное дифференциальное
управление
Рис. В.6
Введем.
23
□ Наконец, в реальных условиях плавания как на реке, так и на море,
возможны различные неконтролируемые возмущения (ветер, течения),
сносящие судно с курса и создающие установившееся отклонение от
курса еуст (позиция С на рис. В 6, б). Для его устранения в закон управ-
ления добавляется интегральный компонент
хи(Г)жКДе(т)<1т, (В.4)
о
сводящий статическую ошибку е«) с течением времени к нулю за счет
дополнительного отклонения руля в сторону, противоположную сносу
судна (изображено пунктиром в позиции D на рис. В.6, б)
Более детальное изучение компонентов управления и их влияние на свойст-
ва переходных процессов в замкнутых системах будет продолжено в после-
дующих разделах книги. Объединяя пропорциональный, дифференциальный
и интегральный компоненты, получим широко распространенную в практи-
ке автоматического управления структуру регулятора ПИД-типа
x(/)=^e(r)+Kje(T)dT+^^ (В.5)
о «"
Выборочное исключение из (В.5) дифференциального или интегрального
компонента позволяет формировать управляющие воздействия ПИ и ПД
типов (рис В.7). Как правило, пропорциональная составляющая управления
не отключается Возможна и более сложная, чем ПИД. структура корректи-
рующего устройства, например, ПИДД2, включающая компонент управле-
ния по второй производной сигнала невязки е"(г).
Рис. В.7
В общем случае регулятор — это аналоговый или цифровой фильтр, выпол-
няющий преобразование уставок и выходных сигналов системы в управ-
ляющие воздействия.
В заключение перечислим основные требования, которым должна удовле-
творять современная система управления сложным объектом.
Н Введение
□ Система должна предсказуемым образом реагировать на входные воз-
действия и начальные условия, для чего опа должна быть устойчивой.
Неустойчивая система неработоспособна.
□ Поскольку никакая модель не описывает физическую систему полно-
стью, то система автоматического управления должна проектироваться с
определенным запасом устойчивости, предназначенным для компенса-
ции неконтролируемых изменений параметров объекта во времени, а
также их зависимости от условий внешней среды.
□ В системе должна быть обеспечена желаемая точность отработки устав-
ки в установившемся режиме, вплоть до нулевой статической ошибки.
□ Переходные процессы в системе автоматического управления должны
иметь желаемые динамические показатели качества- время установления,
перерегулирование, степень затухания колебаний и другие параметры,
указанные в техническом задании.
□ Система должна быть способной подавлять (компенсировать) влияние
нежелательных внешних возмущений - как статических, так и изме-
няющихся во времени, как детерминированных, гак и стохастических.
ГЛАВА 1
Вначале Баг создал пытпиноаы иконы дви-
жения Этим все и исчерпывается, остальное
Оо1жно получать* в peiy ibmume ри/работки
надлежащих математических методов
Альберт Эйнштейн
Математические модели
элементов и систем управления
Математическое описание системы начинается с разделения ее на элемен-
ты, для которых должны быть составлены уравнения, описывающие их
функционирование. Уравнения составляются на основе анализа физических,
химических, экономических и других процессов, происходящих в системе, с
помощью законов сохранения энергии и вещества, законов электротехники,
гидравлики и т д.
Система уравнений, с достаточной точностью описывающая повеление объ-
екта во времени и пространстве, называется математической моделью. Раз-
работка и уточнение моделей занимает от 80 до 90 процентов времени, за-
трачиваемого на проектирование систем автоматического управления |29|.
Следует отдавать себе отчет, что никакая математическая модель физиче-
ской системы не является точной Можно повышать точность модели, уве-
личивая количество и сложность уравнений, но все равно мы никогда не
достигнем абсолютной точности Нужно стремиться к тому, чтобы модель
адекватно отражала поведение физической системы в области ее работоспо-
собности и в то же время была не слишком сложной, доступной для анали-
тических преобразований и численного расчета
1.1. Классификация элементов
систем управления
Элементы систем управления классифицируются по следующим призна-
кам (16).
□ По функциональному назначению:
• задающие элементы - генераторы уставок;
• ихиеритезьные элементы — датчики;
• суммирующие н вычитающие элементы;
• усиливающие элементы без изменения формы сигналов;
• преобразующие и корректирующие элементы;
• исполнительные элементы.
□ По виду используемой знергии:
• электрические элементы;
• механические элементы;
• еидраашческие элементы;
• пневматические элементы;
• комбинированные элементы.
□ По наличию источника энергии
• активные элементы;
• пассивные элементы.
□ По длительности переходных процессов:
• безынерционные элементы — описываются алгебраическими уравне-
ниями Входные и выходные переменные связаны между собой коэф-
фициентами усиления;
• инерционные элементы - описываются дифференциальными урав-
нениями. У линейных инерционных элементов связи между вход-
ными и выходными переменными устанавливаются передаточными
функциями.
□ По характеру установившегося режима:
• статические элемент, имеющие конечные установившиеся значения
выходных переменных;
• астатические элементы, модели которых нс имеют постоянных уста-
новившихся значений выходных переменных.
1.2. Статические свойства элементов и систем
Статическим называется элемент, у которого при постоянном входном воз-
действии x(f) с течением времени устанавливается постоянная выходная пе-
ременная ЯО Отношение у / х В установившемся режиме называется коэф-
фициентом усиления К.
Математические модели элементов и систем управления 27
Выходная переменная астатического элемента не имеет установившегося
значения, а неограниченно возрастает с постоянными скоростью (напри-
мер, угол поворота электродвигателя при постоянном входном напряже-
нии), ускорением (например, перемещение материальной точки под дей-
ствием постоянной силы) или производной высшего порядка. У такого
элемента, например, при постоянной установившейся скорости изменения
выходной переменной V = dp / dr коэффициент усиления определяется
как отношение V/ х.
Свойства статиэма или астатиэма нс абсолютны, а зависят от выбора выход-
ной переменной Так, если при описании электродвигателя в качестве вы-
ходного сигнала задать не угол поворота <р, а угловую скорость о> = d<₽ / dr,
то получим статический элемент Признак астатизма — наличие хотя бы од-
ного интегратора между входом и выходом элемента или системы
Статической характеристикой (СХ) у = Лх) (рис. I I. о) статического элемен-
та называется зависимость установившегося значения выходной переменной
от значения постоянного входного воздействия Статическая характеристика,
в общем случае нелинейная, может быть гладкой или разрывной (рис. 11.5),
однозначной или многозначной (например, гистерезисной на рис. 1.1, в). Раз-
рывные характеристики присуши релейным элементам и аналого-цифровым
преобразователям. Характеристиками гистерезисного типа обладают, напри-
мер, магнитные элементы и механические соединения с люфтом
Линейный статический элемент имеет гладкую линейную статическую ха-
рактеристику
у(х) » во + О|Х,
где а0 есть смещение в нуле, а коэффициент = Ду / Дт задает коэффици-
ент усиления элемента относительно приращений входного Дх и выходного
Ду сигналов.
Астатический элемент не имеет статической характеристики по причине от-
сутствия установившегося режима при постоянном входном воздействии
Однако может существовать статическая характеристика
для /-ой производной выходного сигнала Д/). Минимальный порядок про-
изводной УЛ(/). имеющей статическую характеристику, называется порядком
астатизма. Он равен числу интеграторов между входом и выходом, не охва-
ченных контуром обратной связи. Статические элементы имеют астатизм
нулевого порядка.
1.2.1. Соединения статических элементов
Статическая характеристика системы, образованной соединением двух эле-
ментов, может быть найдена двумя способами:
□ аналитическим, если заданы формулы статических характеристик исход-
ных элементов;
□ Мафическим, если характеристики элементов заданы графиками.
Рассмотрим основные типы соединений статических элементов и методы ана-
литического и графического расчета их статических характеристик.
□ Параллельное соединение (рис. 1.1 а):
Л*)=/|(х)+Л«-
Графическое построение результирующей характеристики Дх) очень про-
сто (рис 1.2, б): она равна сумме ординат л и уг характеристик парал-
лельно соединенных элементов при одинаковых значениях абсцисс х.
«I Я
□ Последовательное соединение (рис. 1.3, о):
Дх)-Д(Л(Х».
Графическое построение результирующей характеристики Дх) выполняем
следующим образом (рис. 1.3, б):
Математические модели элементов и систем управления
на оси абсцисс характеристики первою элемента выбираем значение
хи по графику/Дх) определяем выходной сигнал ур
рассматривая у\ как входной сигнал второго элемента, по графику
/2(У!) находим значение у;. равное выходному сигналу у последова-
тельного соединения При этом ось у совпадает с осью X,
для каждой пары чисел (х, у} на отдельном графике строим точку ис-
комой характеристики у = /х).
Нелинейные элементы нельзя переставлять местами, т к. в общем случае
Например, для функций Д(х) = I - е_*иД(х) =х2 имеем
1-е ?*(1-е-’У
□ Соединение с обратной связью (рис. 14. о). На рисунке и формулах в
обозначениях ->±» и «Т» верхний знак означает отрицательную обрат-
ную связь (ООС), а нижний - положительную (ПОС»
Запишем уравнения трех блоков системы:
е = хтг.у-/|(е),г-Л(У).
Исключая переменные е и z. получим уравнение связи входа и выхода:
№/|(»ТЛ(У)).
X__________________________________________________________Глава<
Оно имеет решение п виде функции. обратной к статической характери-
стике у JU):
<=r,(y)’/r,<y)±A(.v)
Аналитическое обращение нелинейной функции не всегда возможно.
Так. для функций (х) - 1 - е"1 и Л(*)= П0ЛУчим s - ln(l - у),
откуда следует обратная зависимость
х»-1п(1 -у)±/
Видно, что явной зависимости у =Дх) не существует.
а)
е -» У =/|(е) -> Z тЛ(у) -> X ± I
дает функцию у-Дх) для каждого значения е и показана стрелками для
случаев отрицательной (рис. 1.4,6) и положительной (рис. 1.4. в) обрат-
ных связей.
Математические модели элементов и систем управления
1.2.2. Линеаризация статических элементов
Каждый элемент системы имеет рабочую область изменения входных и вы-
ходных переменных, причем некоторые точки этой области наиболее пред-
почтительны как точки равновесия или как самые удаленные от границ ра-
бочей области. Такие точки называются номииа1Ы1ы.ми. а координаты точки
(хн, Ун) ~ номинальным режимом При слабой нелинейности статической ха-
рактеристики достаточно иметь одну номинальную точку, сильная же нели-
нейность заставляет разбивать область работоспособности на подобласти,
каждую со своим номинальным режимом (рис. 1.5).
В окрестности номинального режима желательно иметь линейное описание
элемента как наиболее удобное для решения задач анализа и синтеза. Ли-
неаризация — это замена реальных нелинейных уравнений, описывающих
функционирование объекта, близкими к ним линейными уравнениями. Ли-
неаризация гладкой функции y=fix) в окрестности номинальной точки
(х„, Ун) выполняется по формуле разложения в ряд Тейлора
Это уравнение касательной к кривой Дх) в точке (.v,„ у„) (рис. 1.6). Приведем
примеры разложения до линейных членов в ряд Тейлора и, где возможно,
при х„ = 0 — в ряд Маклорена некоторых простейших нелинейных функ-
ций одного переменного:
□ е“ + ве“‘" (х - х„ ), е«= I + ах.
□ sin(ax) = sin(«tx„) + a cos(ax„)(x - х„). sin(ax) = ax.
□ cos(ax) » cos(ax„) ~ ° sin(ar„)(x - x„), cos(ar) = I.
Iog/1(ax)= logb(avH)+
Рис. 1.6
Введем тикмиепил от номинального режима
Ьу-у-у^Лх-х-х*
тогда линеаризованное уравнение в отклонениях примет вид
Ду=Г Дх
с коэффициентом наклона касательной
Если стагическая характеристика у = /(х) является функцией вектора пе-
ременных » = (ж, ... л„Г, то линеаризованная характеристика в прираще-
ниях представляет собой гиперплоскость, касающуюся поверхности у = f(x)
в номинальной точке (хи.у,) и описываемую векторным уравнением в
приращениях
Ду £К,Дл( “?/(х)Дх,
— иектор*строка градиента /(ж) в точке х с эле-
ментами
Рассмотрим примеры линеаризации статических характеристик.
Математические модели элементов и снегом управления
33
& Пример 1.1. Устройство умножения двух сигналов г <г *i (рис. I 7, а):
° Л2н 1 <h?| ° Л|" ° У “ *' * Х5"(Х' “ *|н> * ” Х)")’
По этому выражению построена структурная схема умножителя, линеаризо-
ванного в окрестности точки ,г„ - Х|ИХ2„ * 0 (рис 1.7,6). Нелинейная по-
верхность гиперболического параболоида ><лг|. «) изображена на рис 1.7, я.
О
I ' Пример 1.2. Устройство деления двух сигналов у = Х| v (рис. I 8, л)
По этому выражению построена структурная схема делителя, линеаризован-
ного в окрестности точки у„ *• с)м / при х2и • 0 (рис. 1.8. 6) Нелинейная
поверхность гиперболического параболоида H-'i. по иному ориентире
мнного по сравнению с параболоидом в примеря 1.7, изображена на
рис. I 8. в. О
Рис. 1.8
& Пример 1.3. Вольт-амперная характеристика диода, т. е. зависимость
проходящего тока / от приложенного напряжения U и температуры окру-
жающей среды Т. имеет вид (рис. 1.9, а)
( WL ] -SsZk
/(У.Г)=/0(Г e*,r -1 , /0(г)=уТ2е , (1.1)
гае р, = 0.0257 В и Фв = 0.7 В — тепловой и барьерный потенциалы;
л и у — индивидуальные параметры для каждого диода.
Справочные данные номинального режима диода КД512А 110]:
□ /„ = 10 мА при £/, - 1 В;
□ Г, = 25 °C = 298 К.
Предельные параметры диода:
□ обратный* гок /«, = 5 мкА при максимальном обратном напряжении
□ максимальный прямой ток /та = 20 мА;
□ диапазон температур от Гт|п = -25 »С до = 100 °C.
аольт-амп'риуЮ «’’«’'Ристику диода в окрестности точки
(£/и, Г,. /я). Построить рабочую опасть диода в окрестности номинального
Математические модели элементов и систем управления
режима. Оценить изменение тока при изменениях напряжения на
Д{/= 100 мВ и температуры на ДГ= -20 °C.
Решение. Вычислим коэффициенты л и у решением системы уравнений
(1.1) в двух режимах (£/„, Г„, /н) и (-(/оти. 7», 4>о). полагая, что
еХр(-(/отах / = 0:
у = -Ч-е”’ = 37.88 Д.
Тнг К2
Рио. 1.9
Найдем частные производные /((/, 7) по (/и Г.
дЦЦ'Т)\
= 0.0761^
мВ
--(^,,Г)| = ^е ^Ije'"*-1ЬП<рт+Пфв-1/и)-(/,^ = 0.7258^
Таким образом, линеаризованная вольт-амперная характеристика открытого
диода в отклонениях Д(/, Д7и Л/имеет вид
M-Ki&U* КтЬТ
В переменных I'(мВ) и Т(“С) зависимость
/- 10 + 0.076KZ/- 1000) + 0.7258(7- 25) = 0.0761(7+ 0.72587 - 84.2 мА
предстамяет собой уравнение плоскости в пространстве ((/, Г, /}, проходя-
щей через точку ((/,,, 7„, /„) касательно к поверхности /((/, 7) Рабочая об-
ласть диола изображена на рис. 1.9, би ограничена четырьмя прямыми
Г- -25 °C;
7= 100 "С;
0.0761(7 + 0.72587 = 84.2;
0.0761(7+ 0.72587= 104.2.
Левее рабочей области в пределах -25 ”С < 7s 100 “С расположена область
отсечки закрытого диода, а правее — область насыщения открытого диода.
При заданных отклонениях Д(/и Д7получим приращение тока
Д/ = 0.0761 100 - 0.726 • 20 = -6.91 мА
и полный ток 7“ 3.09 мА Истинное значение тока, вычисленное по нели-
нейному уравнению (1.1), равно 4 8 мА. Большая относительная погреш-
ность линеаризации S/ = 35.6% при небольших отклонениях аргументов от
номинального режима объясняется сильной нелинейностью вольт-амперной
характеристики диола. О
1.2.3. Статические ошибки
в замкнутых системах управления
Основа функционирования замкнутой системы автоматического управле-
ния — принцип обратной связи, т е зависимость текущего сигнала, управ-
ляющего объектом, от его состояния, обусловленного предыдущими воздей-
ствиями Обратная связь может быть естественной. присущей объекту, и нс-
куегтвгнно ореониюванной для повышения качества регулирования.
Отрицательная обратная связь действует в сторону уменьшения, а положи-
тельная — в сторону увеличения отклонений выходных координат системы
от их уставок. Деление обратно!, связи на отрицательную и положительную
условно: при определенных частотных свойствах объекта может произойти
инверсия се знака
Математические модели элементов и систем управления 37
Для определения статической ошибки в системе с обратной связью
(см. рис. В I, в) обозначим статические коэффициенты усиления устройства
управления как Лу и объекта вместе с измерительным устройством как Ко.
Тогда в установившемся режиме получим
'уст = ЛуСуст, Ууст ~ Кс'уст
и статическую ошибку регулирования
еуст = S ~ Ууст ° 8 - КуКо'уст =» суст = \ + к к ®
Вывод
В статической замкнутой системе всегда существует ненулевая стати-
ческая ошибка регулирования. Будь она нулевой, то были бы нулевыми
управление хус, и выход у,п. что дало бы ненулевое значение в,-, = g у^.
Полученное противоречие доказывает основное свойство замкнутых стати-
ческих систем
Таким образом, статический регулятор в принципе не может свести невязку к
нулю, а может лишь се уменьшить Для этого нужно увеличивать значение
коэффициента контурного усиления КуК^. Поскольку обычно объект неизме-
няем, то остается единственная возможность — увеличение усиления регу-
лятора Ку до максимально возможного значения Верхний предел этого уве-
личения ограничен мощностью устройства управления и, в большей степе-
ни, требованиями устойчивости замкнутой системы управления, что будет
показано в гл. 4.
На величину статической ошибки влияют также постоянные неконтроли-
руемые внешние воздействия. Так, если на объекте скачком изменится на-
грузка f„, то изменится и выходная координата .ПО В установившемся ре-
жиме замкнутой статической системы благодаря наличию отрицательной
обратной связи автоматически сформируются новые значения у, е и х. зави-
сящие от новой нагрузки.
Для устранения нежелательного свойства статнзма ввелем в состав регулято-
ра дополнительный элемент — интегратор с коэффициентом усиления КЛ
(рис 1,10, о). Докажем от противного, что в установившемся режиме полу-
ченной системы всегда будет достигаться нулевая статическая ошибка Про-
следим развитие процессов НО, х(0 и ></» в пошаговом режиме отсчета вре-
мени (рис. 1.10, б).
Рис. 1.10
Итак, предположим, что к моменту времени Iq в системе установились по-
стоянные значения управления хо. выхода д * go и ошибки «о = go - Л^л0 * 0.
На первом шаге интегратор, отрабатывая постоянную ошибку, дает линейно
изменяющееся управление
x(t) - д + (I - t0).
Оно в свою очередь приводит к линейно изменяющемуся выходу
ХО = (I ~ 4>)>
приближающемуся к уставке д. Тем самым ошибка регулирования
е(/) = ео-КяК0е0 (J-t0),
перестает быть постоянной и при правильно рассчитанном коэффициенте К„
начинает уменьшаться. На последующих шагах процессы e(t), x(i) и ЯО стано-
вятся нелинейными, но общая тенденция развития переходных процессов та-
кова, что с течением времени управление изменяется до тех пор, пока выход
системы не сравняется с уставкой, а ошибка не станет исчезающе малой.
Таким образом, полученное противоречие позволяет сделать вывод: в устой-
чивой астатической системе всегда автоматически устанавливается нулевая
ошибка регулирования При этом выход интегратора равен go / Ко при нуле-
вом входе. Эго справедливо при любой статической нагрузке, действующей
на объект. Скачкообразное изменение нагрузки порождает изменение выхо-
да системы и новый переходный процесс устранения статической ошибки
благодаря наличию интегратора в структуре регулятора и действию отрица-
тельной обратной связи. Управление
называется интегральным, или И-управленнем.
Математические модели элементов и <
Системы с И-управлением являются астатическими (с нулевой статической
ошибкой), но медленными, что объясняется инерционностью процесса ин-
тегрирования ошибки. Системы с пропорциональным управлением
ХО “ V(')
могут быть быстродействующими, но не имеют астатизма. Комбинация
пропорционального и интегрального управления
x(r) = Kne(t)+K„Je(T)dT
'о
с оптимально подобранными коэффициентами Кп и К„ делает двухканальную
замкнутую систему ПИ-управления (рис. 1.11) и астатической, и быстродей-
ствующей [20, 30[. При больших уровнях ошибки работает преимуществен-
но пропорциональная составляющая управления, быстро сводящая ошибку
к значению g / (1 + Кп^о) Окончательное точное сведение ошибки к нулю
возлагается на интегральную составляющую управления.
1.3. Статический анализ и синтез схем
на операционных усилителях
Для практической реализации и моделирования элементов и систем автома-
тики будем использовать широко распространенные средства аналоговой
электроники — операционные усилители (ОУ), позволяющие конструировать
сложные и разнообразные схемы с широким спектром статических и дина-
мических свойств [1,2, 18). Операционный усилитель (рис. 1.12, а) — это
аналоговое устройство усиления разности
ДР =Р-Р
напряжений на его прямом (Р) и инверсном (Р) входах:
Р,ых -
глава I
Усилительные свойства операционного усилителя проявляются в области
линейности его статической характеристики при |ДМ < f/mJM / Л,. иначе он
работает в одной из областей насыщения с выходным напряжением + Г/тм
или -Циы, близким к напряжениям питания +(/,, или -Un. сообразно знаку
величины Д(/(рис. 1.12, б).
<25 о
льные отечественные операционные усилители серий 140, 153, 154, 157,
. 553. 574 имеют следующие параметры |1. 18];
коэффициент усиления разностного (дифференциального) сигнала
Лу» 10* ♦ 10* •= tg(a) (рис. 1.12, б), где а = 90" — угол наклона линейной
части статической характеристики;
□ входное сопротивление R„ от 300 кОм (в операционных усилителях с би
полярным входным каскадом) до 100 ГОм (в операционных усилителях с
входным каскадом на полевых транзисторах);
□ выходное сопротивление R^, = 10 ♦ 300 Ом;
Математические модели элементов и систем управления_______________41
□ напряжение смещения (дрейфа} нуля елр = 0.1 + 10 мВ, равное выходному
Напряжению при нулевой разности Д1/«Он возникающее вследствие
несимметричности параметров элементов принципиальной схемы уси-
лителя из-за погрешностей их изготовления;
□ двухполярное напряжение питания 1/„ - ±(3 + 40) В, определяющее диа-
пазон изменения выходного напряжения е|_Цпах« Unaxl» где
Мппх < Цг
На рис. 1 12, в приведена простейшая схема замещения операционного уси-
лителя, включающая все перечисленные параметры Усилительные свойства
операционного усилителя на линейном участке его статической характери-
стики условно отражены включением в выходную цепь схемы генератора
напряжения — усиленного в Ку раз падения напряжения на входном сопро-
тивлении. Выходная цепь содержит также генератор паразитного напряже-
ния дрейфа нуля епр и выходное сопротивление Япы,
Получим по закону Ома зависимость выходного напряжения от входной раз-
ности напряжений и выходного тока с учетом параметров схемы замещения:
На холостом ходу (/вых = 0) выходное напряжение равно
Цшх “ Ky&U + епр.
При подключении к операционному усилителю сопротивления нагрузки К„
возникает выходной ток
перераспределяющий токи /| и А в верхней и нижней ветвях цепи пита-
ния и создающий зависимость выходного напряжения от сопротивления
нагрузки:
В практических расчетах можно рассматривать опер
идеальным с параметрами
Гпава 1
Л,--./?„ = »./^ = 0,^ = 0,
при которых выходное напряжение ит = становится независимым от
значений /щ*. Л»», %, а также от сопротивления нагрузки. Идеализация
дает следующие ключевые условия анализа и синтеза схем на операционных
усилителях:
□ нулевая разность входных напряжений
№=^* = 0
Ку
при любом выходном напряжении. Потенциальное равенство U -U (но
не физическое соединение входных контактов!) позволяет без изменения
переносить известное напряжение с одного входа на другой;
□ нулевой входной ток
/» = о.
игнорирование которого позволяет оперировать только с токами, проте-
кающими в навесных элементах каскада;
□ независимость выходного напряжения от выходного тока и сопротивления
нагрузки. Это позволяет считать операционный усилитель устройством с
бесконечно большой нагрузочной способностью
niaxj/^J = ”
и использовать его для токовой развязки каскадов друг от друга.
Во всех последующих схемах мы будем изображать операционные усили-
тели без выводов заземления и напряжений питания, имея в виду, конеч-
но, что в реальных схемах они должны быть подсоединены к соответст-
вующим шинам.
1.3.1. Нелинейные статические элементы
на операционных усилителях
Типовыми соединениями с отрицательной обратной связью являются схемы
прямого и инверсного включения операционного усилителя. Допустим, на-
весные элементы простейших схем описываются вольт-амперными характе-
ристиками А */|(М) и 4=Л(Й>). а операционные усилители обладают
В схеме с прямым включением операционного усилителя (рис. 1.13, а) име-
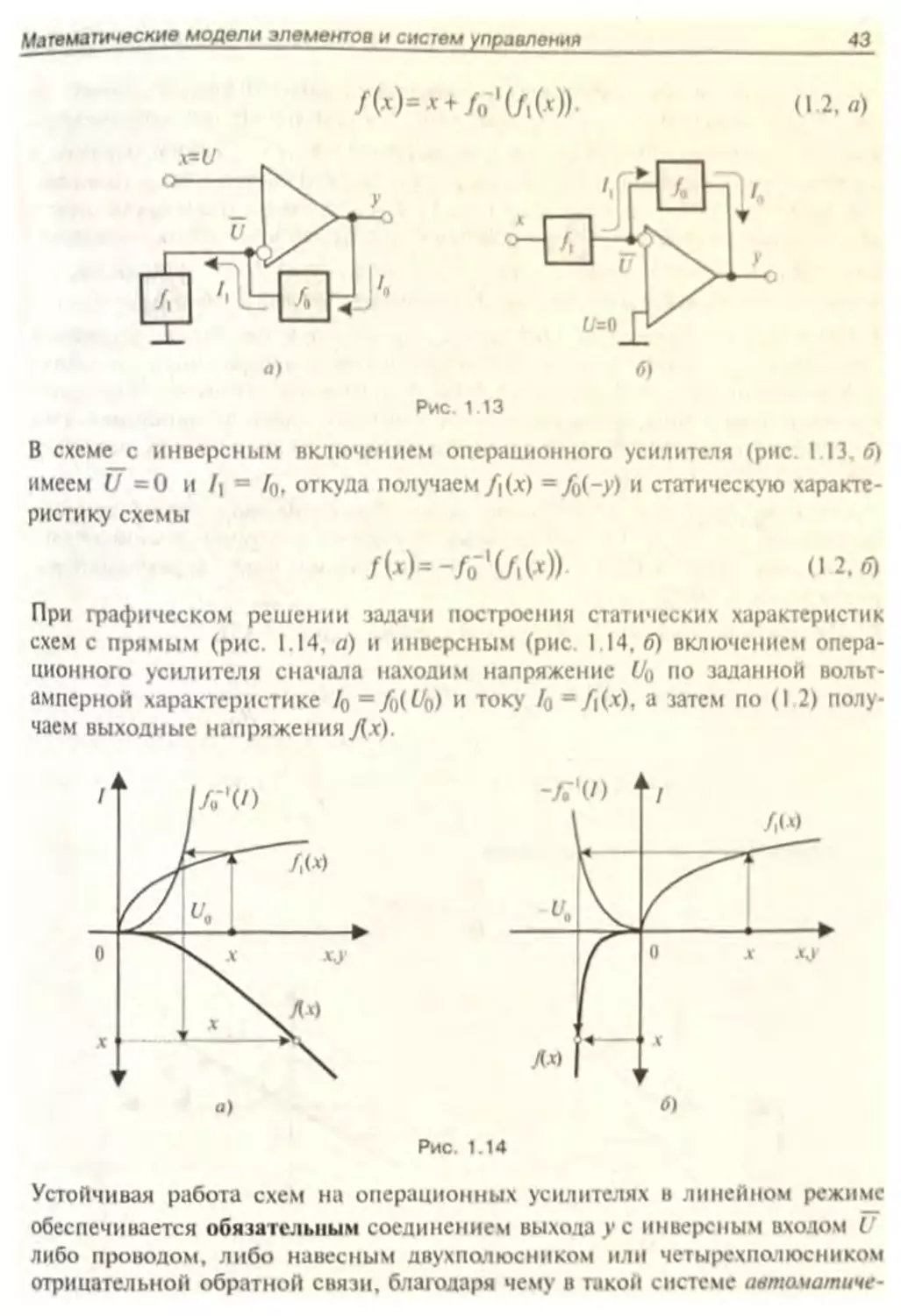
ем U «х и А = /о. откуда получаем/(х) =fa(y -х) и статическую характери-
стику схемы
Математические модели элементов и систем управления
/«»*</о'М))-
Рис. 1 13
В схеме с инверсным включением операционного усилителя (рис. 1 13,5)
имеем U =0 и 1\ = /о, откуда получаем/|(х) =Jo(-y) и статическую характе-
ристику схемы
/W=-/o''(/iW) (12. б)
При графическом решении задачи построения статических характеристик
схем с прямым (рис. 1.14, а) и инверсным (рис I 14, б) включением опера-
ционного усилителя сначала находим напряжение 4/0 по заданной вольт-
амперной характеристике /0 = Л(М>) и току /0 =/|(х), а затем по (1.2) полу-
чаем выходные напряжения Д.г).
Устойчивая работа схем на операционных усилителях в линейном режиме
обеспечивается обязательным соединением выхода у с инверсным входом (/
либо проводом, либо навесным двухполюсником или четырехполюсником
отрицательной обратной связи, благодаря чему в такой системе автачатиче-
Глава 1
ски поддерживается динамическое равновесие. Например, в схеме на
рис 1.13, а изменения г, At/и у синфазны. Часть приращения напряжения с
выхода операционного усилителя передается на вход U . Таким образом, в
системе с отрицательной обратной связью устанавливаются новые равновес-
ные значения 6U и у. В схеме на рис. 1.13, б изменения х и Д(/ происходят в
противофазе с сигналом у. Отрицательное приращение выходного напряже-
ния передается через элемент обратной связи на вход U в пропорции, ус-
танавливающей новые равновесные значения напряжений Д1/ и у
В отсутствие отрицательной обратной связи или при ошибочно созданной
положительной обратной связи усилитель, благодаря огромному значению
Ху и полосе пропускания порядка I МГц, практически мгновенно переходит
в режимы насыщения, расположенные справа или слева от линейного уча-
стка статической характеристики в зависимости от знака разности напряже-
ний Д1/ (см. рис. 1.12, б)
Рассмотрим некоторые простейшие схемы функционального преобразования
хгектрических сигналов на операционных усилителях с отрицательной обрат-
ной связью (рис. 1.15, а- 1.18, я) и их статические характеристики
(рис. 1.15, б- 118. б)
□ Пропорциональный неинвертирующий усилитель (рис. 1.15):
/o'(OW =» y = x+i с коэффициентом усиления схемы "о = tg(a). y=Kv a 0 V 6>
₽ис 1.15
Математические модели элементов и систем управления 45
□ Пропорциональный инвертирующий усилитель (рис. 1.16):
</| - х. /,(</.)=^. U0=-y. f0(U0)=^,
/о'(/)= V => У = -«оу = -у-< = -^
с коэффициентом усиления схемы (не забывайте о знаке минус перед ним!)
K=^ = tg(a).
Рис. 1.17
/о”(/)=Яо/ - У = -^ор
Логарифмический и экспоненциальный усилители могут быть использованы
для построения аналоговых схем точного (в отличие от линеаризованных
схем, структурно изображенных на рис. 1.7 и 1.8) умножения и деления на-
пряжений на основе следующих соотношений:
ln(X|X2) = ln(Xj) + ln(Xj) => XtX2
totuhlnfe) =»
С учетом необходимости компенсации смешений сигналов и их масштаби-
рования на рис. 1.19 построены структурные схемы умножителя (а) и дели-
теля (б) напряжений Х| (В) и Xj (В), использующие нелинейные инверти-
рующие каскады на операционных усилителях и источник напряжения 1 В.
Математические модели элементов и систем управления
Структурная схема делителя напряжений
Рис. 1.19
1.3.2. Линейные статические элементы
на операционных усилителях
Рассмотрим схему каскада на операционном усилителе с отрицательной об-
ратной связью (рис. 1.20), к прямым входам которого зсц * х1я подключены
сопротивления Лц+Я1л. к инверсным входам Хц+зсут — сопротивления
Я21 * Rim, а в цепи обратной связи включено сопротивление Rq. Для того,
чтобы реальный операционный усилитель можно было с достаточной точ-
ностью считать идеальным, нужно выбирать сопротивления всех навесных
резисторов хотя бы на порядок (в 10 раз) меньше паспортного значения Я„ч и
на порядок больше значения /?„мх. Таким образом, с учетом параметров ре-
альных операционных усилителей разных серий рекомендуемый диапазон
номиналов всех сопротивлений схемы составляет [1 кОм. 10 МОм].
Рис 1 20
Напряжения на прямом и инверсном входах операционного усилителя мож-
но найти по законам Кирхгофа и Ома:
£,„=». ^.0.
откуда получим напряжение V, а по аналогии с ним и U
Так как в идеальном операционном усилителе U =U , то на последних вы-
ражений следует
Таким образом, рассматриваемая схема выполняет л операций сложения и т
операций вычитания подаваемых на ее входы напряжений:
Проанализируем последствия добавления в схему заземленных входов Хщ - О
и xjo • 0, соединенных с входами операционного усилителя через сопротив-
ления Як, и Я№ (на рис. 1.20 они изображены пунктиром). Из (1.3) следует,
что это влияет только на коэффициенты Л,,:
□ при введении сопротивления Яц, все они уменьшаются из-за увеличения
знаменателей дробей на Я|, / Яш:
□ при введении сопротивления Ям все числители дробей увеличиваются
на 4, / Я2|,. что ведет к увеличению всех коэффициентов Я"1(;
□ одновременное введение в схему двух заземленных входов xt0 « 0 и
х» 0 позволяет гибко регулировать значения коэффициентов Л'|, как в
сторону увеличения, так и в сторону уменьшения
Задяча синтеза схемы состоит в определении сопротивлений Я,, Я„ и Я, по
заданным значениям коэффициентов усилении Я„ и Я2/ Особенностью этой
Математические модели элементов и систем управления 49
задачи является се недоопредсленность (число неизвестных п + m + 1
меньше числа п + m заданных коэффициентов) и вырожденность Обозна
чим суммы коэффициентов усиления по прямым и инверсным входам:
Si=2>1(. s2 = 5X,
Суммируя в (1.3) коэффициенты Ку, получим ключевую зависимость между
5| и Sy. существующую в любой готовой схеме на операционных усилителях
(рис. 1.20) независимо от числа и сопротивлений навесных резисторов:
и
(1.4)
Для численного расчета (т + 1)-го сопротивления Яу( и ЯЬ по т коэффици-
ентам Кц необходимо доопределить последние уравнения в (1.3) еще одним
условием. Например.
противления инверсных входов будут равны
Ro, тогда со-
Однозначное определение л сопротивлений Яц по и коэффициентам Ktl
также невозможно из-за условия вырожденности, вытекающего из уравне-
ний (1.3) и (1.4):
Если задать произвольно любое сопротивление Яу, то остальные сопротивле-
ния, подключенные к прямым входам, однозначно находятся как
При произвольно заданных коэффициентах К\, и Лу, условие (1.4) скорее
всего не выполнится. Это означает, что схема каскада, изображенная на
рис. 1.20, структурно неполная. В ней не хватает одного из заземленных на-
весных резисторов Я|0 или Я», в зависимости от соотношения сумм 5, и
Sj + I Введение такого резистора эквивалентно добавлению в первое урав-
нение (1.3) нулевого слагаемого = 0 либо Кпы = 0 с положительным
коэффициентом усиления по заземленному входу
К10 ~ + 1 - Si либо К» “ 5i - Si - 1.
Введение заземленных входов изменяет структуру схемы и восстанавливает
баланс (1.4), при этом уравнение (1.3) не изменяется благодаря напряжени-
ям Хю “ 0 либо *» “ 0.
Таким образом, при синтезе схемы нужно свободно выбрать сопротивления
Ry и Д1, а остальные сопротивления вычислять по формулам
(,S)
Замечание
Если в полученной схеме прямой вход хп оказался единственным, то по (1.3)
его коэффициент усиления Кп = & +1 не зависит от Rn Поэтому можно вы-
брать это сопротивление произвольным, в том числе и Rn = 0 — простым про-
водом (рис. 121).
Рис. 121
2* Пример 1.4. Построить схемы на операционном усилителе серии
544УД2Б (Я„ > 1 ГОм, < 200 Ом |18]). реализующие следующие алгеб-
раические соотношения:
□ у = Зхц + 4*12 - бхц (рис. 1.22, в):
5| =^+ 1»7=» Я|| =—у2-, Я2| =-у-.
Сопротивления всех резисторов должны лежать в диапазоне
2 кОм • 100 МОм. Выберем значения Яц = = 300 кОм, тогда
Ян = 400 кОм и /?2Т = 50 кОм.
□ у - 3*ц + 4*12 - 5x21 (рис-122, 4):
5|-7>$+1“6=>*2р“$-.51-1-1,
Ян Rk ж А). Я2| =у-
Выберем Я12 - Яр = 300 кОм, тогда Яп = 400 кОм. Яго = 300 кОм и
«21 = 60 кОм;
Математические модели элементов и систем управления
Рис. 1.22
□ у = Зхц +4хц - 8x21 (рис. 1.22, в):
5| « 7 < 5j + 1 = 9 => /Сю » 5j + I - 5| = 2,
„ _ 2Я|0 2Я|р „ _ Ro
Ли- — . Ли-—. Л21-Т.
Выберем Лю = Л> = 240 кОм, тогда /?ц = 160 кОм, Яц = 120 кОм и
Л2| = 30 кОм.
О
Рассмотрим некоторые принципиальные схемы на операционных усилите-
лях и соответствующие им структурные схемы, выполняющие типовые ал-
гебраические операции.
□ Универсальный одновходовый усилитель (рис. 1.23, а) с коэффициентом
усиления
Рис. 1.23
Подбором сопротивлений схемы можно получить любое желаемое по
знаку и абсолютной величине значение К в интервале
Судя по этой зависимости, границы интервала определяются значениями
Я2 и Я20. Приняв эта сопротивления переменными с общей конструктив-
ной регулировкой
Я2 = ЛЯ.Я2О = (1-МЯ,0$Л5 1.
а остальные сопротивления постоянными и равными R, получим сле-
дующий параметрический коэффициент усиления каскада:
Эта нелинейная регулировочная характеристика построена на рис. 1.23, 6.
Нулевой коэффициент усиления достигается при «золотом сечении»
X 0.382. а интервал ослабления |AJ S 1 составляет X е [0.232. 0.618].
□ Заменяя в схеме универсального усилителя некоторые сопротивления
проводом (Я = 0) или разрывом соединения (Я = ~). получим различные
популярные схемы на операционных усилителях:
• при Я| = Я:,, = “ и Я|0 = 0 - инвертирующий усилитель (рис. 1.24, а):
К=-^2-<0.
Я2
Задав Я3 = получим инвертор:
К=-\,у
• при Я2 = » - неинвертирующий усилитель-делитель (рис. 1.24, б):
• при Я2 = Ям = «• и Яо = 0 - делитель напряжения (рис. 1.24, в)
• при Я2 = Яю - » и Я| - 0 - усилитель напряжения (рис. 1.24, г):
Математические модели элементов и снегом управления
53
• при R-i - Я,,, - Ям = «> и Я| = Яо = 0 — повторитель напряжения
(рис. 1.24, д):
К- 1.
Операционный повторитель аналогичен эмитгерному повторителю
на транзисторе, но в нем обеспечивается точное воспроизведение
входного напряжения увеличенной мощности. Повторитель исполь-
зуется для развязки каскадов схемы друг от друга благодаря его па-
раметрам Я,„ -» и Яаых —> 0.
а)
Рис 1 24
□ Усилитель-вычитатель (рис. 1.25, а), выполняющий операцию
Глава 1
При выборе / Я2 “ Лю / Л| - Кон становится дифференциальные уси-
лителем:
У-ДХ1-Ч).
Задав Я, = Л|0 и Я2 • Ко, получим широко распространенную в автома-
тике схему вычитателя напряжений:
у=Х| -ху.
□ Неинвертирующий усилитель-сумматор (рис. 1.26, а), выполняющий
операцию многовходового сумматора сигналов
(рис. 1.26, б) со всеми положительными коэффициентами усиления
1+А
Рис. 1.26
Синтез схемы по заданным коэффициентам Ку.
Выбором всех одинаковых сопротивлений К можно получить устройство
усреднения входных напряжений (рис. 1.27, а)
Математические модели элементов и систем управления 55
а дополнительным выбором сопротивления /^ = (л - 1)Я в цепи отрица-
тельной обратной связи — устройство суммирования входных напряжений
(рис. 1.27, б):
У = ^Х‘
а) в)
Рис. 1.27
При п = 2 получим = R и широко распространенную в автоматике
схему двухвходового сумматора:
У = Х^Х2.
□ Инвертирующий усилитель-сумматор (рис. 1.28, а), выполняющий опера-
цию вычитания сигналов
(рис. 1.28, б) с коэффициентами усиления (не забывайте об общем знаке
минус перед суммой!)
*)
Рис. 1.28
Глава!
Синтез схемы по заданным коэффициентам К,.
На основе инвертирующих одновходового усилителя и двухвходовопо
сумматора очень просто создается усилитель с переменным коэффициен-
том усиления
ЛЦ) = 2Л-1е |-1,1|УЛе |0, 1|,
который в отличие от схемы на рис. 1.23, а обладает линейной зависимо-
стью уровня усиления от положения движка переменного резистора Бо-
лее того, несложно сделать ступенчатое изменение диапазона усиления
l~rf. d\, где d - степень числа 10 По соотношению
на рис. 1.29, о построена структурная, а на рис 1.29, б — принципиаль-
ная схема мультидиапазонного усилителя с линейной шкалой регулировки ко-
эффициента усиления Щ, </).
Входное напряжение х подается на инвертор с переменным коэффициен-
том усиления, равным -2Л и регулируемым положением движка резисто-
ра л 6 |0, 1|. Выход инвертора суммируется с входным сигналом так, что
в среднем положении движка (X = 03) получим (1 - 2Л)х = 0. Сумма на-
пряжений инвертируется и усиливается в d- I05* раз Показатель поряд-
ка к выбирается путем переключения многопозииионного тумблера. Чис-
ло диапазонов коэффициента усиления легко наращивается в разумных
пределах так. чтобы номиналы всех резисторов схемы укладывались в до-
ер, |1 кОм, 10 МОм].
Математические модели элементов и систем управления_____57
1.4. Описание динамики
элементов систем управления
Статические характеристики определяют лишь установившиеся режимы ра-
боты элементов системы автоматического управления. Переходные процес-
сы описываются уравнениями динамики — дифференциальными уравнениями.
Моделями систем с сосредоточенными параметрами являются уравнения в
полных производных, а с распределенными параметрами — дифференци-
альные уравнения в частных производных Для составления уравнений сис-
тема делится иа элементы.
Пусть W — количество элементов в системе, а у, — выходной сигнал /-го
элемента Э,. Он может быть связан с выходами других элементов Эу непо-
средственно или через сумматоры (вычитатели). Эти элементы не являются
динамическими, т. к. описываются алгебраическими уравнениями.
Для каждого динамического элемента составляются дифференциальные
уравнения на основе законов механики поступательного и вращательного
движений, электротехники и т. п. Порядок каждого дифференциального
уравнения не выше второго. Таким образом, объединяя уравнения элемен-
тов, получим систему из N в общем случае нелинейных дифференциальных
уравнений (16):
ЛЬ’пУр >'••••’= (1.6)
Линеаризация гладкой дифференцируемой функцииД ) заключается в раз-
ложении ее в ряд Тейлора в окрестности номинального режима
(Я....Ж/. *н):
где fiufaj»' У)»' У*л> V/=i.W,xB. х')=0 удовлетворяет уравнению (1.6);
Ду^*1 = у’*’— и Л-т**1 =л<*’-л,1,*’ — отклонения выходных и входных
переменных и их производных k-ro порядка от номинальных значений; сла-
гаемые F, содержат производные f по у**1 и У*1 второго и высших порядков.
После отбрасывания нелинейных функций F„ содержащих производные по-
рядков выше первого, линеаризованная система дифференциальных уравне-
ний примет вил
58____________________________________________________________Глава 1
с коэффициентами — частными производными
Используя оператор дифференцирования р « d / dr, запишем ее в операторной
форме
w«ijv
с полиномиальными коэффициентами
= tyo + ЧфР + lipP1- W = гЛ + гпр.
Полиномы Q/p} и /?,(/>) формируют Ах fl-матрицу Q(p) и fl-вектор Я(р):
Гй|(р) 2|Л'(р)1
е(₽)= ; : . *(₽)=[*1(р) ... Лд,(р)Г
Lgwi(p) - е™Ы]
По правилам матричной алгебры |4, 6| запишем последнюю систему в виде
О(р)а но = адмо
с fl-вектором отклонений выходов элементов ДК = [Ду,(г) ... Д»(т)Р-
Решение этой системы имеет вид
ДЦ/) = е*'(р)Я(р)М/). (1.7,о)
Выходной сигнал линейной системы Ду есть линейная комбинация выход-
ных сигналов элементов Ду, и входного сигнала Дг
M')=f <Wf0+ ОДх(г)=СДГ(г)+ ОДх(г), (1.7, б)
где С = h - cj- I х fl-матрица коэффициентов связи выходов эле-
ментов с выходом системы, а О — коэффициент прямой связи входа систе-
мы с ее выходом. Подставив (1.7, а) в (1.7, б), получим
ДХО = (С(Г‘(Р)ЖР) + 0)ДХО.
Обратная операторная матрица Q~'(p) вычисляется делением присоединен-
ной flx fl-матрицы adj(?(/>) на характеристический полином (ХП) системы —
определитель
Л(Р) = detQ(p).
Математические модели элементов и систем управления 59
Обозначив полином
В(р) = С ad)Q(p) R(p) + D А(р),
в итоге получим операторное уравнение связи отклонений входа и выхода
системы
= адмо
с полиномами Л(р) и В(р). Во временной форме ему эквивалентно диффе-
ренциальное уравнение
дпДу(') + а,Д/(0 + + олД?'’>(0 “ *оМО + Ь^(1) + +
Порядок уравнения п определяет порядок динамической системы Порядок
правой части дифференциального уравнения равен т < л. Так как каждый
из W элементов имеет порядок не выше второго, то обшнй порядок системы
удовлетворяет условию
1 S п 5 2N.
Обычно в системах стабилизации номинальный режим совпадает с состоя-
нием равновесия:
yJ,?(z)=O V* = 02; 4**(»)=0 У*=0Л.
Поэтому операторная форма дифференциального уравнения системы с ну-
левым номинальным режимом имеет вид
*(₽)у(0= B(p)x(f\
A(j>)=a0+aip + ... + a„p" =^atp‘. (1.8)
1=0
в(р)=Ь0+Ь}р + ... + bl„p"‘ ^biP‘.
Операторной передаточной функцией (ОПФ) системы
W{p)=7T\
А(Р)
называется дробно-рациональная функция полиномов операторного уравне-
ния (1.8). Она позволяет компактно записать дифференциальное уравнение
в виде |30|
ХО "
Глава 1
Рассмотрим на практике процесс составления и линеаризации дифференци-
альных уравнений.
2? Пример 1.5. В |13| и немного упрощенно в [22| рассматривается механи-
ческая система, состоящая из тележки и шарнирно установленного на ней в
неустойчивом равновесии перевернутого жесткого маятника (рис. 1.30). Те-
лежка может двигаться в горизонтальном направлении под воздействием
внешней силы/ Параметры системы.
□ 21 — длина маятника;
□ т — масса маятника;
□ Л/ - масса тележки;
□ d - линейное перемещение центра масс тележки;
□ Ф - угол отклонения маятника от вертикали;
□ t, - коэффициент вязкого трения в оси маятника. Момент трения в оси
пропорционален угловой скорости вращения маятника ш = <р';
□ kt - коэффициент вязкого трения тележки о поверхность. Сила трения
о поверхность пропорциональна скорости движения тележки v = if.
Получить нелинейную и линеаризованную модели движения системы в ок-
рестностях неустойчивого (вверху) и устойчивого (внизу) состояний равно-
весия маятника. Входная переменная -Д»), выходные - d(t} и <р(г).
Рис. 1.30
Решение Составим уравнения динамики движения двух элементов системы
(рис. 1.31), используя второй закон Ньютона для поступательного и враща-
тельного движений:
Математические модели элементов и систем управления____________________61
Рис. 1.31
□ горизонтальное движение центра масс маятника описывается диффе-
ренциальным уравнением второго порядка
+ Ain(<p(»)))' = Я(0;
□ вертикальное движение центра масс маятника описывается диф<|»ерсн-
циальным уравнением второго порядка
m/cos(<p(0)" = N(f) - mg-.
□ вращательное движение маятника вокруг своего центра масс описывает-
ся дифференциальным уравнением второго порядка
/ф"(0 = ZNl0sin(<p(0> ~ ///(r)cos(<p(/)) - *«ф'(1),
где J д 2JpA.2dA = ----момснт инерции маятника с погонной
массой р = т / 2/;
□ горизонтальное движение тележки описывается дифференциальным
уравнением второго порядка
=Дг) - - H(t);
□ отсутствующее вертикальное движение тележки описывается алгебраиче-
ским уравнением
О = Я</) - Я(/) - Mg.
Исключив силы N и Н. получим систему двух нелинейных дифференциаль-
ных уравнений:
I/|(rf.<p)=»iM'cos(<p) + (/ +»м/:)р' + А„1ф'-/мл/51п(ф)=а () 9)
[Л(</.ф)=(М +»н)г/*+<:11</' + »|/ф*со5(ф)-п|/(ф')‘ 51п(ф)-/=0.
Линеаризуя эту систему в окрестности номинального режима
a________________________________________________________Глаи1
/„-О. </«=<=<=0. Ф„ =ф'„'Ф*и =0,
падучим линейную модель системы «тележка - перевернутый маятник»
I mid' + (/ + ml1 )₽' + *шф'“ "ЧМ = °-
|(М + m)rf'+kvd'+m/ф' - f » О
или в матричной форме
мпи - адло.
0. ) = [ «4»2 (f+mPp+^p-mg/
[(М+m)p2+fc,,p mlp2
Характеристический папином и две матрицы измерений выходов системы
имеют вид
л(р) = mg«,. р + ((м + ni)ngl - kvka )р 2 -
-((? +т/2У,. +(« +mXo)p3-(m(j +т1г)+пи)р*.
Q=[i О], с,=[о 1].
Таким образом, мы получили операторную модель системы «тележ-
ка - перевернутый маятник» с двумя выходными переменными:
d(t)= CjQ-'(p)R(p)f(t)= ~А-р~ * т12У ДА
2 А(р’ (1.Ю)
ф(г)=С.2,(р)л(р)/(г)=^/(,)
Зададим параметрам системы следующие численные значения: /= 1 м.
m = 6 кт. .W = 11 кг. *. = 8 Н м с. к, = 10 Н с / м Примем для удобства
расчетов ускорение свободного падения равным g=!OM/cJ вычислим
момент инерции маятника / =2кг м> и запишем соответствующие урав-
:ZM- пе^ХыйЫм^:ГРНЫ' "е₽еда— функции системы «те-
8P~y,w(P)=j£l.
А(р) л(р)' (1.П)
[А(р) = 600р + 940р2 -2!6р’ -100р4.
Математические модели элементов и систем управления
Интуитивно понятно, что в данном номинальном режиме перевернутый ма-
ятник неустойчив. Как это можно определить по передаточной функции,
мы узнаем в гл. 4.
Модели перевернутого маятника типичны для объектов, у которых центр
тяжести расположен выше точки или малой плошали опоры, подверженных
воздействию опрокидывающего момента: например, для ракеты на старто-
вом столе или на взлете.
Выполнив линеаризацию уравнений динамики (1.9) в окрестности устойчи-
вого номинальною режима
/„ = 0, d„=j'=< = 0,фи=18<Г. ф'„=ф>0,
получим операторную передаточную функцию системы «тележка - обыч-
ный маятник»:
| „,60*^ )=£.
А\Р> А(р)
[Л(р) = бООр +1100р-’ +21бр’ + 100р4.
Почему этот номинальный режим с положением маятника под тележкой
имеет устойчивое состояние равновесия, также станет понятно после изуче-
ния условий устойчивости элементов и систем в гл. 4. D
Операторный метод представляет дифференциальное уравнение в алгебраи-
ческой форме, благодаря чему он гораздо удобнее для преобразований по
сравнению с преобразованиями в дифференциальной или интегральной
формах. После составления уравнений динамики элементов системы
рекомендуется сразу перейти к их операторной форме путем формальной
замены производных на алгебраические эквиваленты р*у.
Запишем, например, компонентные уравнения радиоэлементов R. С и L в
дифференциальной и операторной формах:
=>lc=CpUr;
UL=A=>UL=LplL.
dt L
& Пример 1.6 На рис. 1.32 приведена электрическая схема моста Вина
Робинсона |2| с входным напряжением г и выходным напряжением
У" (/| - Ui- Составить для этой схемы дифференциальное уравнение и опе-
раторную передаточную функцию.
Решение На основе законов Кирхгофа и формул (1.13) запишем систему
уравнений функционирования элементов схемы:
2RI]=x~U]
RI\=UI
Rl2=x-U3
l2=Cp(U3-U2)
ri3=u2
I^CpU2
y = Ut-U2
Обозначив постоянную времени T= RC и
ценные /| ♦ Ц и У| ♦ (/3 С И последовательно исключая пере-
'* V> М T₽eI=»l/j-x_(| + Tp)Uj
'~ и> w“‘ ® - w‘ I' ’ we. -« -1)« - <1 * Гр>‘и,
=» и 2 Tpx
1 + ЗГр + Г2р2 '
—________- х^Тгргх
'+зтр+т2р2 ' з+дтр+зг^р2'
Математические модели элементов и снегам управления 65
получил* желаемые операторную функцию и дифференциальное уравнение
схемы:
W(р) , ,+Т Р г .у Зу + 97У + ЗГ/ - х + 7V (1.14)
Р 3(1+37> + ТУ)
О
1.5. Передаточная функция
В общем виде линейное неоднородное дифференциальное уравнение систе-
мы с одним входом x(z) и одним выходом у(1) имеет вид
(115)
1=0 1=0
Его решение методом вариации произвольных постоянных достаточно слож-
но. С целью превращения дифференциальной модели динамической системы
с произвольными начальными условиями в алгебраическую модель разработан
метод преобразования Лапласа 15. II, 16, 17. 20, 21, 23, 24. 28, 29, 30]
Временная функция ограниченного роста
Д/): (|A0|s Л/си'У/>0,Д/) = 0У г< 0}
имеет изображение, вычисляемое по следующей форму.» преобразования Лапласа
L{f(r)}= F(i)= J /(r)e-'dr Vr Re(j) > m, (116)
о
где s — оператор Лапласа.
Вычислим, например, с помощью |8| изображение временной функции
Л0 = sin(wr), для которой подходят значения ограничивающих параметров
М = 1 и m = 0:
F(s)= fsin(cor)e"1'df e| —- Y—^sin(tur)-<ocos(uM)j =
о (?+<□-J 10 ?+ш-
иоскольку при j=c + janc>« = 0 имеет место нулевой предел
lim е"“ = lim е^е и = 0
Применяя всем известную формулу интегрирования по частям
Глава 1
получим по индукции изображение (л+1)-ой производной временндй
функции ограниченного роста:
о 0
=a ♦ lim(f W(r>-")-/(")(0)= л{г W(t)}- / <">(о)
о
В частности, изображения первых трех производных имеют вид
ЦГЮ) = " 4rt0) -/'(0),
L{f-(*)» = *W) ~ УДО) - т/'(0) -/'(0)
II ПО ИНДУКЦИИ
Преобразуем по Лапласу левую часть дифференциального уравнения (1.15):
|то-
= Л(зНз)-^§О(з‘уН-»(0)=л(1)г(5)_^? £а/у^-»(0)=
'°* *"® 4-Х) М+1
/=0
JL 0<v +1 a"? полином левой части дифференциального
уравнения. Коэффициенты полинома начальных условий Л.у) могут быть
вычислены по рекуррентной или матричной формулам: ‘
p(3)=po+p1J+...+р^-, л= £e>yCH-0(o)Vf=6r^,
Ро в| а2 ... а„
р, _ аг aj ... 0
A-J [«. 0 ... О
' > (0) '
/(0)
у-"(о)
(1.17, а)
Математические модели элементов и систем управления 67
Возможно, для некоторых читателей более понятными будут прямые зави-
симости коэффициентов полинома As) от начальных условий.
Ре = Л|>(о)+в2/(0)+...+ая.,у<"‘:)(0)+аяу("’,)(0)>
Pi = а, у (0)+ а,у'(0)+... + а„у("’2,(0).
lP,-i = а„у(0)
Аналогично для правой части дифференциального уравнения (1.15) получим
где B(s) = fto + 6|S + . + b^m — полином правой части дифференциального
уравнении. Коэффициенты полинома начальных условий С(т) могут быть
Таким образом, изображение дифференциального уравнения системы имеет вид
адад- ад = адад-ад,
откуда получаем изображение выходного сигнала
Передаточной функцией (ПФ) называется отношение изображения выхода
системы к изображению ее входа
Н'(т)=-Щ| , , (1.19, а)
при нулевых начальных значениях входа, выхода и их производных. Из (1.18)
следует, что в этом случае передаточная функция есть дробно-рациональная
функция полиномов правой и левой частей операторного дифференциаль-
ного уравнения
6в___________________________________________________________Глава I
W(f)=A|j {1J9,<5)
и совпадает с операторной передаточной функцией Wlp) с точностью до
формальной замены оператора дифференцирования р на оператор Лапласа s
Такое совпадение позволяет формировать передаточную функцию непосред-
ственно по коэффициентам дифференциального уравнения. С учетом ска-
занного впредь мы будем использовать символ s и как оператор Лапласа, и
как оператор дифференцирования d / dr.
Если какой-либо объект задан передаточной функцией ИЦ.г) и требуется по-
лучить зависимость (1.18), то нужно действовать следующим образом.
1. Восстановить дифференциальное уравнение (1.15)
2. Преобразовать его по Лапласу при ненулевых начальных условиях.
3. Выразить изображение выходного сигнала Y(s) через изображение вход-
ного Х(т) и начальные значения входного, выходного сигнала и их про-
изводных.
Для примера рассмотрим систему второго порядка с передаточной функцией
Иф)=—=10
3+4з+5г X(j)
Дифференциальное уравнение системы имеет вид
3></) + 4/(/) + 5Г(/) = х(/) + 2х'(/).
Суммируем преобразования по Лапласу слагаемых этого уравнения:
ЗИг) + 4(гДг) - ИО)) + 5(?Пг) - дНО) - У(0)) = №) + 2(лЦд) - х(0)).
Отсюда получаем изображение выходного сигнала динамической системы
при ненулевых начальных условиях:
у(,)= Н2< ,у(х)| (4+54у(0)+5/(0)-2«(0)
3+4j + 5j2 3 + 4д+5т2
1.6. Соединения элементов
и преобразования структурных схем
Для определения передаточной функции системы, заданной структурной
схемой, необходимо уметь получать передаточные функции основных со-
единений элементов (звеньев) 116. 30).
□ Последовательное соединение двух звеньев (рис. 1 33, в)
П-И'|(з)х.у=И'2(з)у|.
69
Математические модели элементов и систем управления
Отсюда получаем передаточную функцию последовательного соединения:
И4т) = «ЗДОД- H'iWH'jW
Передаточная функция произвольного числа последовательно соединен-
ных звеньев равна
И'иве.Ю-ПШ (1.20, а)
□ Параллельное соединение двух звеньев (рис. 1.33, б):
У1 = ИЖ уг = 1F2(j)x, у - у, + yj.
Отсюда получаем передаточную функцию параллельного соединения:
m«) = = »hw + mw-
Передаточная функция произвольного числа параллельно соединенных
звеньев равна
W,up(5)=LW’1(s). (1.20, в)
□ Обратное соединение звеньев (рис. 1.33, в)
е=хт\у0^ъ.у’
где верхний знак «-» соответствует отрицательной обратной связи, а
нижний знак •+• — положительной. Исключая из записанных уравне-
ний вспомогательную переменную е, получаем передаточную функцию
обратного соединения:
—х (120, •)
Здесь снова верхний знак (теперь это «+») соответствует отрицательной
обратной связи, а нижний знак (это «-») — положительной.
Обратная связь широко применяется в автоматике:
• положительная обратная связь — для увеличения коэффициента уси-
ления охваченного ею устройства и генерирования незатухающих ко-
лебаний;
• отрицательная обратная связь — для обеспечения устойчивости сис-
тем, стабилизации движения объектов, уменьшения чувствительности
систем к неконтролируемому изменению параметров элементов и
внешней среды
Структурную схему любой сложности можно путем последовательных пре-
образований привести к простейшему виду с передаточной функцией
(1.19, в). эквивалентному исходной схеме относительно входной и выходной
переменных. Большое число способов эквивалентных преобразований пред-
ставлено в 116, табл. 3.3). Здесь же в табл. 1.1 мы приведем лишь самые не-
обходимые правша структурных преобразований блок-схем.
Таблица 1.1
Преобразование Исходная схема Эквивалентная схема
Перестановка разветвления .4 т ..
I
Перестановка сумматоров
Перенос точки через звено вперед -4Zh L->| t/w|—
Перенос точки через звено назад * т-И w I I
Математические модели элементов и систем управления
Таблица 1.1 (окончание)
Преобразование Исходная схема
Перенос сумматора через звено вперед ——»| w р-> ——►] w | — W | 1
Перенос сумматора через звено назад -— 1/w|—I
Перенос точки через сумматор вперед
Перенос точки через сумматор назад
В процессе структурных преобразований каждое типовое соединение
звеньев (последовательное, параллельное или обратное) заменяется одним
эквивалентным звеном с соответствующей передаточной функцией из
(1.20), а табл. 1.1 помогает перегруппировать элементы структурной схемы
так, чтобы типовые соединения возникали по ходу преобразований. Для
предупреждения ошибок следует обозначать выполняемое преобразование
стрелками и пунктирным выделением, вычерчивать структурную схему по-
сле каждого шага и указывать на ней передаточные функции эквивалент-
ных звеньев.
& Пример 1.7. Разделить сцепленные контуры двухконтурной системы,
изображенной на рис. 1.34, я, и получить ее передаточную функцию
Решение. По методу структурных преобразований после переноса узла ег
вперед через звено получим схему, изображенную на рис 1.34. б. а заме-
на обратного и последовательного соединений упрощают структурную схему
до обратного соединения (рис. 1.34, в). Последняя замена дает один блок
(рис. 1.34, г) с передаточной функцией системы
П_______________________________________________________________Глава 1
Рис. 1.34
Точно такую же передаточную функцию получим аналитическим методом
исключения вспомогательных переменных е, и е2 Запишем уравнения
звеньев системы
«I “ х - Hfo, ej = - Hfy, у = 1Г,е2
в векторно-матричной форме
[-». iwdtHoF' ж,1Ш
и выразим выход системы у через ее вход х
>=[о 4 * Жз ГН- л
2J[-W! l + H^J [of I + W'.Wj+WjH',
Тогда по (1.19. а) получаем передаточную функцию системы:
_____
1 + И'|И',+Н',И'4
Математические модели элементов и систем управления
Теперь покажем, как можно быстро получить этот же результат программным
методом, используя символический процессор программы Mathcad1
□ после (ниже или правее) ключевого слова Given записываем уравнения
звеньев системы с использованием знака условного равенства « = », вво-
димого с клавиатуры клавишами <Ctrl> + <=>:
Given
el = x-W3e2
е2 = Wl cl - W4 у
ye W2c2
□ находим символический результат, возвращаемый функцией Find со зна-
ком символического равенства <•->•>, вводимым клавишами
<Ctrl> + < . >:
W(WI,W2.W3,W4)
Find (у .el ,с2)о
WI
(I + Wl W3+W4 W2)
-> W2
Число аргументов этой функции должно быть равно числу уравнений
системы. Рекомендуется первым в списке аргументов указать выходную
переменную у, а следующими — вспомогательные переменные et, ej и
так далее при большем числе уравнений. В этом случае начальный (нуле-
вой) элемент возвращаемого функцией Find вектора решения имеет вид
произведения входной переменной х на символическое выражение пере-
даточной функции системы через передаточные функции звеньев Для
получения передаточной функции в чистом виде символическому про-
цессору предписано разделить это произведение на х и присвоить резуль-
тат функции пользователя ИЦИ'ь W}, Щ).
Для доведения задачи до логического конца зададимся передаточными
функциями звеньев (см. табл. П.4):
И', = К|, И', = Kjj, W, = Al, W4 = -А1_.
j 1 + T4s
Подставив их как аргументы в функцию W, после упрощения с помощью
символического оператора simplify и приведения подобных членов при
степенях s символическим оператором collect получим следующий ре-
зультат:
I При написании шнноЛ книги исполыю1исшсь версии Mathcad 2000 Из-за громоздкости вы-
ражении о Mathcad некоторые формулы будут приводиться в уменьшенном или "уреинном"
У4 Глава 1
JKI к,. " М ) 1“'"р1“У-*к>..<1С1 _______________(ltT4 >)_______________
Д ’ 1 > |coll«(,l ‘ [(T4.K4 К1) Л(НК1КЗ T4) s. KI Кз]
Таким образом, передаточная функция двухконтурной системы в привычной
записи имеет следующий вид:
________^11
К,К3 4- (1 + к^3г4 > + (К2К4 + Т4 У
□
1.7. Чувствительность и стабилизирующие
свойства отрицательной обратной связи
Функционирование любой реальной системы протекает в условиях отсутст-
вия точной информации о ее параметрах, изменения параметров во време-
ни, влияния на них условий окружающей среды и других объективных фак-
торов, не включенных в математическую модель системы. В разомкнутой
системе все эти факторы приводят к существенному отклонению выходной
переменной от желаемого значения. В замкнутой системе благодаря отри-
цательной обратной связи регулятор чувствует это отклонение e(t) и пытает-
ся скорректировать выходную переменную в сторону уменьшения сигнала
невязки.
Найдем, например, с помощью (1.18) абсолютное и относительное измене-
ния изображения выходного сигнала разомкнутой системы Хр(т), вызванные
изменением ее передаточной функции Л IF|(s) при нулевых начальных усло-
виях:
д ул \
дГрЮ = ДИ-WAW => 8Гр(з)=-у^у=5^(3). (1J1, о)
В разомкнутой системе относительное изменение передаточной функции при-
водит к такому же относительному изменению выходного сигнала.
Абсолютное и относительное изменения изображения выходного сигнала
в замкнутой системе с отрицательной обратной связью (см. рис. 1.33, в)
равны (все зависимое™ от оператора $ для удобства опушены)
ДГ Л1***» X у ДИ,1 X
' Ни'.+ди'.К i+и^ (i+^+a^KXi+w) ’
Математические модели элементов и систем управления
ЗУ* =^= . SW, __5W,
’ г, 1+(W| +aw>0 ЩГГбй^Ж,
При постоянстве передаточной функции элемента прямой цепи И^з) и от-
носительном изменении передаточной функции элемента обратной связи
бИ'о(л) аналогично (1.21, б) получим следующее относительное изменение
выходного сигнала:
8Г*> = —. —М----5% =---
1 + (1+8%Х% 1+5w+_L
° W
(1.21, e)
При малых изменениях передаточных функций |6H^t| << 1 и |8»У « 1 (сим-
вол ««» означает «меньше хотя бы на порядок», г е. в 10 раз) относитель-
ные изменения выходного сигнала оцениваются величинами
зr*.=^u
1+1W 1+_L
Анализ выражений (1.21) позволяет сделать следующие выводы о влиянии
различных дестабилизирующих факторов на относительное изменение изо-
бражения выходного сигнала 8У3(т) в замкнутой системе с отрицательной
обратной связью:
□ относительное изменение передаточной функции элемента прямой цепи
вИ^ уменьшается на выходе в 1 + (1 + раз, а для компенса-
ции влияния этого фактора необходимо твешчивоть произведение
□ относительное изменение передаточной функции элемента обратной
связи 8 % проявляется на выходе системы с противоположным знаком и
с таким эффектом, что для уменьшения влияния этого фактора необхо-
димо уменьшать произведение передаточных функций В') Ч'.,
Во многих замкнутых системах управления регулятор устанавливается в
прямой цепи и его передаточная функция является сомножителем IFifj). а
датчик регулируемой переменной включен в цепь обратной связи с переда-
точной функцией Kz0(x). Компромисс между противоположными требова-
ниями к величине Kzi(.s)Hzo(j) заключается в выборе
□ максимально допустимого с учетом требования устойчивости замкнутой
системы (см. гл. 4) коэффициента усиления регулятора;
□ высокоточного датчика со стабильными характеристиками, не зависящи-
ми от внешних факторов, и близкой к нулю погрешностью 81УО.
Для анализа степени влияния параметра р на некоторую функцию Др) ис-
пользуется понятие чувствительности — отношения относительного изме-
нения функции к относительному изменению влияющего на нее параметра:
<122.®
&Р/Р Ър f(p)
В пределе при Др -т 0 получим важную характеристику системы — функцию
чувствительности зависимости Др) к параметру р:
<122,0
dp /
Если неконтролируемому изменению подвержено несколько параметров
системы pi, pi..р„, то, вычислив чувствительности функции Др(. .... р„) к
параметрам pt
получим следующие формулы расчета относительного и абсолютного изме-
нения функции при одновременном изменении всех параметров р, + р„:
^ = £$'бр, . Л/ = £^Др,=/-6/. (1.22, в)
м <=|
Рассчитаем чувствительность передаточной функции замкнутой системы с
отрицательной обратной связью
'{'Р>
к изменению параметра р. влияющего, в общем случае, на передаточные
функции как прямой цепи H^s.p), так и обратной цепи H^o(s, р):
эи; _ Эр___________I Эр_________dp_j
Эр ' +
л.Wy. ИЦУ р эц _ wiP э%
' др w, H'Ji+H'jH'J Эр 1+^% Эр
Подставляя в (1.23) сначала р = W'i, а затем р = получим чувствительно-
сти передаточной функции IF, к изменению характеристик прямой и обрат-
ной цепей системы управления:
Математические модели элементов и систем управления
71
«.w. _ I „IV, _ JW_
W| l+VW **= l + w,wo'
Забегая немного вперед, где в гл. 2 с помощью подстановки оператора Лап-
ласа х = jco (j — мнимая единица, а ш — частота) передаточная функция ИЫ
преобразуется в комплексную частотную характеристику запишем ус-
ловие глубокой отрицательной обратной связи
|H'|(ja»)%(j(o)|» 1 (1,24)
на всех рабочих частотах системы о>. В (1.24) символ «»• означает «больше
хотя бы на порядок» При выполнении условия глубокой отрицательной об-
ратной связи изучаемые нами чувствительности становятся близкими к зна-
чениям
Продолжая экспансию в частотные методы исследовании систем, сформу-
лируем важное требование к проектируемой системе управления: для
уменьшения влияния на характеристику fip} некоторого параметра р необхо-
димо, чтобы в рабочей полосе частот модуль функции чувствительности
(jio)| был близок к нулю.
Способность отрицательной обратной связи уменьшать влияние параметров
на характеристики системы — одно из ее важнейших положительных ка-
честв Чтобы добиться высокой точности управления в разомкнутых систе-
мах (см. рис. В.1, а), необходимо очень тщательно подходить к выбору эле-
ментов, образующих передаточную функцию !Kt(j). Напротив, системы с
отрицательной обратной связью допускают определенные вариации пара-
метров B'i(s), поскольку их влияние на частоте со ослабляется в
|1 + H/1(jo))Bz0(jco)| раз, а при глубокой отрицательной обратной связи прак-
тически полностью компенсируется
Типичный пример устройств с глубокой отрицательной обратной связью —
схемы на операционных усилителях, имеющих очень большой коэффициент
усиления Ку. Покажем, что при Ку -» «> влияние этого параметра благодаря
отрицательной обратной связи ослабляется до нуля:
□ в инвертирующем усилительном каскаде (см. рис. 1.24, а) находим ток
перетекающий из резистора /6 через точку с напряжением у /(-Ку} в
резистор Ло, откуда получаем коэффициент усиления каскада
При Afy - этот коэффициент становится равным ~Rq / Я2 и не зависит
ни от самого значения Ку, ни от его возможной нестабильности;
□ в неинвертирующем усилительном каскаде (см. рис. 1.24, г) находим ток
перетекающий из резистора Rq через точку с напряжением х — у / Ку в
резистор Л;о. откуда получаем коэффициент усиления каскада
(1.25,6)
В пределе Ку -> ~ этот коэффициент становится равным 1 + Яо / Я2о и не
зависит от изменений значения при условии, что оно остается очень
большим.
Все построенные на качественных операционных усилителях каскады обла-
дают практически нулевой чувствительностью к их параметрам. Благодаря
близости собственных параметров усилителей к идеальным
Лу —э о», Ящ —* °0, Явых —> 0, вдр —> О
передаточные функции каскадов определяются исключительно способом со-
единения навесных элементов и их номиналами.
& Пример 1.8. Рассмотрим схему усилительного каскада на транзисторе с
температурной стабилизацией выходного напряжения (рис. 1.35, а). Из кур-
са электроники известно, что включение сопротивления в эмиттерную цепь
транзисторного каскада повышает стабильность его работы при изменениях
температуры окружающей среды.
Физически стабилизирующее действие отрицательной обратной связи объ-
ясняется так: при повышении температуры токи транзистора возрастают
Эмиттерный ток. протекая по сопротивлению Яэ, уменьшает напряжение
Ufy = х - Л,Л. что уменьшает токи и возвращает выходное напряжение кас-
када почти к его первоначальному значению.
Выберем рабочую точку транзистора (4, tfe,) на линейном участке входной
линеаризованной вольт-амперной характеристики (рис. 1.35,6) с углом на-
клона а и оценим зависимость стабильности коэффициента усиления кас-
Математические модели элементов и систем управления
79
капа от изменения температуры, которое, в свою очередь, приводит к изме-
нениям коэффициента усиления по току Р и входного сопротивления тран-
зистора = ctg(a).
Составим основные уравнения каскада и соответствующую им структурную
схему (рис. 1.35, в):
Затем найдем выходное напряжение и коэффициент усиления каскада:
у~ Un+ ЩУр-х),
w = РД________
’ Я„+Ф+1>,
В отсутствие отрицательной обратной связи при Л, с0 коэффициент усиле-
ния равен
-..а
80 Глава 1
Стабильность коэффициента усиления каскада оценивается частными про-
изводными
Э% _ -pr, Э% -р/?к
dJ?.x (R^+^+W 3RM ' Л,2Х ’
Э% _ dwo RK
ар "(Лю+Ф+1>,)2’ эр ~R.S
и функциями чувствительности (1,22, б) коэффициентов усиления И <, и Ио
к изменению параметров и р:
с*’. "** с*, _ К»с+Я,
R""R,X+(P+1K' 11 " R,x+(p + l)R3’
=4.^=1.
По (1.22. в) получаем относительные изменения коэффициентов усиления
транзисторного каскада с обратной связью и без нее
8% = S^8R„ +S*’8P,
8 Hi = -5RB + 6P.
Оценим температурную нестабильность каскада при следующих исходных
данных:
= 100 Ом, R3 - 1 кОм, Р = 100,
ДЛ„ = -50 Ом => = -0.5,
ДР = 20 => 8Р = 0.2.
□ Чувствительности каскада с обратной связью:
s£ -9.9-Ю4ж0, S*' =0.0109-0.
□ В каскаде с обратной связью 6Ж, = 0.0026 или 0.26%.
□ В каскаде без обратной связи 8 % = 0.7 или 70%.
Таким образом, введение отрицательной обратной связи в виде резистора Rj
уменьшает нестабильность работы транзисторного каскада весьма существен-
но и тем больше, чем больше значение параметра р и отношение Л, / R„
О
Еще одной важной причиной использования отрицательной обратной связи
является ее способность уменьшать влияние внешних возмущений и шумов,
действующих на элементы системы управления. С различными вариантами
точек приложения возмущений и расчетом чувствительности передаточной
Математические модели элементов и систем управления 81
функции замкнутой системы к возмущениям читатель может ознакомиться
в (16, табл. 7.7]. Общие выводы совпадают с полученными выше результата-
ми анализа выражений (1.21):
□ чувствительность к возмущениям, действующим в прямой цепи замкну-
того контура, ослабляется при увеличении коэффициента контурного
усиления;
□ чувствительность к возмущениям, действующим в обратной цепи замк-
нутого контура, отрицательна и ослабляется при уменьшении коэффи-
циента контурного усиления. Для компенсации таких возмущений необ-
ходимо устанавливать в цепи обратной связи элементы со стабильными
характеристиками.
Условия и способы достижения инвариантности (нечувствительности) сис-
темы к возмущениям с помощью специальных корректирующих устройств
будут рассмотрены в гл. 6.
1.8. Динамический анализ и синтез схем
на операционных усилителях
Задача динамического анализа схемы заключается в восстановлении решае-
мого ею дифференциального уравнения или определении ее передаточной
функции. Обратная задача синтеза состоит в разработке схемы по заданным
Дифференциальному уравнению или передаточной функции
1.8.1. Динамические элементы
на операционных усилителях
Пассивными компонентами линейных схем на операционных усилителях
являются резисторы (Л), конденсаторы (С), индуктивности (Z) и их после-
довательные, параллельные и смешанные соединения. Из компонентных
уравнений (1.13) следуют операторные сопротивления (импедансы\ радиоэле-
ментов 2(д):
ZK- Л, Zc(j)-i, 2i.(j) « Li. (1.26)
Последовательное и параллельное соединения элементов Z\ и Z2 имеют, со-
ответственно, сопротивления
Глава 1
В табл. 1.2 приведены импедансы Дх) и схемы простейших двухполюсни-
ков. Смешанное соединение двухполюсников представляется суперпозицией
последовательного и параллельного соединений.
Таблица 1.2
С помощью операторных сопротивлений облегчается определение переда-
точных функций сложных схем Например, схема моста Вина - Робинсона
на рис. 1.32 является параллельным соединением двух делителей напряже-
ния х, поэтому напряжения в средних точках равны (по прежнему использу-
ем обозначение постоянной времени Г= RC):
R
U *HZC 1+7а Tt
2 R + ZC + R\\ZC Л+2_+_Л_ Sl + 3Ts + T2s2 Х'
Сх 1+П
Отсюда получаем выходное напряжение и передаточную функцию схемы:
Эта передаточная функция с точностью до замой..
торной передаточной функцией (1.14), ы з на р совпадает с опера'
Математические модели элементов и систем управления 83
Рассмотрим схему динамического каскада на операционном усилителе с от-
рицательной обратной связью (рис 1.36). Аналогично схеме статического
каскада (см. рис. 1.20) ее выход и передаточные функции входов равны.
у(0=ХИ'1|(/)*и(г)-£И'и(1)х2/(1),
Рис. 1.36
Обозначим суммы передаточных функций входов:
В работающей схеме между этими суммами, как и в (14), устанавливается
баланс
5|($) = Sj(j) + 1. (1.28)
Решение задачи синтеза схемы каскада на операционном усилителе по за-
данным передаточным функциям ее входов и выполняется в
следующем порядке:
□ составляется эскизная принципиальная схема с п прямыми и m инверс-
ными сигнальными входами с неопределенными импедансами Zp и Z^;
□ вычисляются суммы передаточных функций 5|(з), SjU) и проверяется
выполнение условия (1.28). В случае нарушения баланса подбираются
одна или обе передаточные функции И’|0(з) и ИА0(з) с паюжите.1мнни
коэффициентами, удовлетворяющие условию
Глава 1
ад + над - ад +1 + гкад,
а эскизная принципиальная схема дополняется заземленными входами
хю - 0 и (или) х» = 0;
□ выбрав независимые операторные сопротивления Zj/з) и 2о(з), определим
аналогично (1.5) остальные нмпедансы каскада с учетом дополнений
7|0(з) и (или) 23о(з):
При выборе структуры нмпедансов рекомендуется использовать табл. 1.2
основных соединений пассивных радиоэлементов, стремиться к мини-
мальному числу навесных деталей и, желательно, к получению схемы без
индуктивностей.
Разработаем схемы на операционных усилителях, решающие заданные диф-
ференциальные уравнения или имеющие заданные передаточные функции.
& Пример 1.9. Задано дифференциальное уравнение
У+/ = 2х1|+2х[1+Х|2-2х21-Х2|-
После замены операции дифференцирования оператором з оно принимает вид
(1 + з)у = 2(1 + л)х|| + хи - (2 + з)х2|,
откуда следует операторная форма дифференциального уравнения
У = Гц(з)х|| + *12(з)Х|2 - »F2i(3)x21
с передаточными функциями входов
Вычисляем необходимые для проверки баланса (1.28) суммы передаточных
функций по прямому и инверсному входам:
Поскольку условие баланса 5,(г) = 52(s) + 1 оказалось выполненным, то до-
полнительных заземленных входов не требуется, а схема имеет два прямых
входа хп, Х|2 и один инверсный вход х2|. По формулам (1.29) составляем со-
отношения выбора нмпедансов схемы:
Математические модели элементов и систем управления 85
Для того, чтобы операторные сопротивления Z|j(J) и Zn(s) не имели индук-
тивностей, выбираем:
□ Zn(5) = I / Сц$ — конденсатор с произвольной емкостью Си. Тогда
Zi2(s) = 2(1 + 5) / Сц5 — последовательное соединение резистора
Ли = 2 / Си и конденсатора С|2 = Си / 2,
□ Д)(т) = ЛЬ / (1 + 5) — параллельное соединение резистора с произвольным
сопротивлением Ro и конденсатора Q=l//fo (табл. 1.2, п. 5) Тогда
Z21CO = Ло / (2 + j) — параллельное соединение резистора Л2) = / 2 и
конденсатора С2| = 1 / 2R2l = 1 / Ко.
В результате получаем схему, показанную на рис. 1.37.
Рис. 1.37
Задав произвольно номиналы Си = 10 мкФ и Ro = 100 кОм, получим номи-
налы остальных элементов:
Лп = 200 кОм, С12 = 5 мкФ, Со = 10 мкФ, Л2] » 50 кОм, С2| = 10 мкФ.
□
& Пример 1.10. Задано дифференциальное уравнение
У+/ = *п +2jct'| +jti2-2jc2| -х'2|.
В операторной форме оно имеет вид
У" lfn(j)X|| + H'nWxu- И'лМХи
с передаточными функциями входов
^'W=777
Вычисляем суммы передаточных функций по прямому и инверсному входам:
3 + 2з
5,(3) = 2. 5,О)+1 = —
Так как 5,(j) * ЗД) + 1, но у разности сумм
все коэффициенты положительны, то в схему к сигнальным входам хи. *12 "
.гл требуется добавить заземленный вход хщ • 0 с передаточной функцией
w
По формулам (1.29) формируем соотношения импедансов прямых входов Хц
и х,2:
Отсюда видно, что наилучшим будет выбор Z|0(s) в виде резистора Я|0.
Тогда:
□ Zh(j) - Я10 / (1 + 2a) - параллельное соединение резистора Я, , = Л10 и
конденсатора С?ц = 2 / Лю;
□ Z|Xa) = Л|0 - резистор Л|2 = Ящ.
Импеданс единственного инверсного входа х2| равен
Z“W=^-5?Z’«-
"21 vj 2+J
С целью сокращения полинома числителя I + s выбираем
3)(т) = Яо / (I + г) - параллельное соединение резистора и конденсатора
Q - 1 / Яо. Тогда Z2l(s) = Яо / (2 + s) — параллельное соединение резистора
Яд = Яо / 2 и конденсатора С2| = I / Jfy.
В результате получаем схему, построенную на рис 1.38.
Рис. 1.38
Математические модели элементов и систем управления 87
В качестве упражнения читателю рекомендуется самостоятельно произнести
подбор номиналов навесных элементов. С
ЕУ Пример 1.11. Задано операторное уравнение
У - 1Г|1(Л)Х|| + lF|j(j)XI2
с передаточными функциями входов
l + s 1+s
Вычисляем суммы передаточных функций по прямому и инверсному (отсут-
ствующему!) входам:
5,(s) = 2, ад +1 = 1.
Так как обе суммы числовые и $|(з) > ад) + 1, то разность сумм
ад = ад) - ад - 1 = 1
есть передаточная функция по дополнительному заземленному входу
х» = 0.
Записываем условие выбора нмпедансов прямых входов Хц и Х|2:
zu(5)= 1 + 2,)zn(i)
"I2V/
Наилучшим будет выбор элемента 2ц(з) = I / Сцз в виде конденсатора с
произвольной емкостью (Гц. Тогда операторное сопротивление
C||S
есть последовательное соединение резистора Я|2 = 2/Сц и конденсатора
С12=С„.
Сопротивление заземленного инверсного входа хго равно
гм"ч$~гм
и при выборе резистора Zq(s) = Ro также является резистором Rjo = /&>•
В результате проведенного синтеза получаем схему, изображенную на
рис. 1.39. О
Простейшие типовые схемы динамических каскадов на операционных уси-
лителях и их передаточные функции сведены в табл. 1.3, в которой исполь-
зованы следующие условные обозначения для двух безразмерных коэффи-
циентов и трех постоянных времени:
r«=V с« ’q’ Гг ^=L,Cjt =r~ °30)
Дополнительные схемы каскадов можно получить:
□ при гч = 0 выбором Я, = 0 (провод) или Rj = <» (разрыв):
3 при е# = 0 выбором С( = О (разрыв) или Су = «= (провод);
□ при 0, = О выбором Li = 0 (провод) или Яу = »(разрыв).
Такие замены элементов проводом или разрывом следуют из формул опера-
торных сопротивлений (1.26).
Таблица 1.3
nn Элементы схемы Принципиальная схема и ее передаточная функция
z, Z» а) инвертируюншй каскад б) псинаертирующий каскад с входным делителем г, в) исинвертируютий каскад с делителем в ООС
1 Любой Любой -Ш’ МГ ZoW+ZtW , Z0(s) Z|(4)
2 *1 G 1 6oJ 1 1 + Т|0л Ло1
J С| Ь Г0|Д 1 + Г0|Л 1 + Го,1
4 Я, к -во|» 0о,т 1 + 0ор 1 * <ы
$ и> вщ1 i+<W l + fligT 0|0>’
Таблица 1.3 (продолжение)
№ Элементы схемы
« С, *0 -*О1»2 1+toi*2 1 + т?,,г
7 ц Со 1 ^0*’ l+Tj'oJ2 l+t?o*2 <?o*2
8 Л| Ко + Со - LtrW». T|Oj I+vbo +7io)f l + (7bo +7iofc /io*
9 Л| + С, Л> _ Tqi* 1 + TiP Top l+(r01+7h> l+frn+rnV 1+TnJ
10 С| Яо+Q -сю(1 + Гоог) l + r«>s l+cOi +7bos 1 + q0 + Toi-»
11 Я, + С| Q CIO 1 l+qo+Tn* i+r„s
1+7-hJ l+c0| +7’I0s
12 Л| 4;+q> roi 1 l + rOi H-TopS l + Tppj
1 + Toos l + zj0 +T|Oi
Таблица 1 3 (продолжение)
Ns Элементы схемы Принципиальная схема и ее передаточная функция
13 Л, К, -Л)|(1 + 71|Л) l + 7„i 1 + Г|о+7ц5 1 + 'bi + 7b,i
14 с, 1 Q _ 70,5 1 + 7-005 7о,5 1 + (7(ю + 70, )i 1 + (7qq +70| )t l+Too-5
15 Л, К, Q 1 + 7~цД TJo1 1 + 7„5 l + (7|o + 7,i)s l+(7|o+7||)t 7|о5
16 Л| + С| Яо + Q 1+ 7-001 "'"ЧТ (l + ropiXl + r,,!) 710i l+Cio + (7Oi+7ll)t 1 + 7ц1
17 Л| + С| М Q 7qij (1 + 7-001X1 + 7-, ,1) Tqi1 I+(7|>q+70|+Tii)s+7'(107]i5~
1 + (7(х> +7bi +7,,)s +7ооГпТг (ur^xi+Ti.i)
18 Л||С| Ло + Q _ (1+7005X1 + 7-1,1) 7,01 (H-TootXi + Thj) l+(7oo-t-7l))-i-7^l
l + (7oo +701 +7|,)i+Too7|151 7ioJ
Таблица 1.3 (продолжение)
№ Элементы стены Принципиальная схема и ее передаточная функция
19 Я.1С, _ 1 + Tnj “Ч + Го^ 1+rn-> 1 + По + (zio + ^ii)s 1 + rol + (Tbo + 7bi 1 + Too j
20 Я| _ l + 7(X>s + Тро-у2 Tio* 1 + Tops 4~ тоод2 1 + (Too + Гю )s + TqqI2 1 + (Too + Г|0> 4- Tqq-S2 ^io5
21 Л| + С| + £, Н> 7oiv W l-*-(r0l+r,l>4-T?|J2
14-Т1р4-т?152 1 + (Tqi + ^ii )J + 1 + TH4 4-T2?
22 <4 Яо+О, + Le -c1o(1 + 7OO's + tOOa2) 14- TqqS + Tqq J2 1 + coi + 7oos + T^2 cI0 ^Ols ^015
23 Л,ЛС* Q C10 1 14-Ciq4-T,iJ4-T?|? 14-Гп5 4-Т?|52
1 + 7j jS 4" Tj |S 1+Coi +7|0s + 't?0j2
24 Л1 MG IG 9015 i+eoos+T^2 Qpi5 1 + (000 + 001 )s + T00*2 l+fooo+Qoifr + TooJ2 14-0005 4-T^S2
Таблица 13 (окончание)
№ Элементы схемы Принципиальная схема и ее передаточная функция
25 Я,|С, ЛЬ _1 + 0и5 + Т12152 01О5 l + On-y + rfp-2 1 + (0ю+0ц> + Т^2 1 + (0jQ + l)5 + TTli~ 01O$
26 С| 1А> *о.р-2 1 +0QO$ + (T6o +T01)»~ ' + 0QOS + T0O^2
1 + 0OO.V + Тбо-Г 1 + 000$ + (too + Tqi )s2
27 Hi Q 1+еп$+тц$* 1 + 011$ + T21S2 1 + Э1.$+(Чо +ТП>2
*?0‘2
T?OS2 l + eH5 + (Tf0+T?J2
Глава 1
Применения табл. 1.3 вполне достаточно для построения большинства схем
на операционных усилителях. Если задана сложная передаточная функция,
для которой в таблице не находится нужной схемы, то можно:
□ соединять каскады последовательно. При этом их передаточные функции
перемножаются благодаря хорошей развязке каскадов за счет большого
входного и малого выходного сопротивлений операционных усилителей;
□ два последовательных каскада из второго и третьего столбцов с переда-
точными функциями ИЭД и ИЗД можно заменить одним каскадом с
передаточной функцией HAU) (♦з(т), у которого есть как входной дели-
тель напряжения, так и делитель напряжения в цепи обратной связи.
Это вполне допустимо благодаря развязке этих цепей друг от друга внут-
ри операционного усилителя.
В качестве примера использования табл. 1.3 рассмотрим построение эквива-
лента схемы моста Вина - Робинсона (см. рис. 1.32) на одном каскаде опе-
рационного усилителя. Передаточная функция (1.14) комбинируется из пе-
редаточных функций двух каскадов, имеющихся в табл. 1.3:
□ каскад с передаточной функцией B'jU) = 1 / (3 + 97Ъ + 37V) (п. 236),
имеющий коэффициенты
Coi = 2, 71о = 9Г, Тц) =ЗТ2
и номиналы элементов, выбираемые из условий
СЬ»2С1,Л1О) = 9Т,£1СЬ = 3 72;
□ каскад с передаточной функцией IFj(s) = 1 + TV (п. бе), коэффициен-
том То, =Т2 и номиналами элементов, удовлетворяющих условию
£oQ = Г.
В итоге получаем схему на рис. 1.40 с желаемой передаточной функцией
₽ис. 1.40
Математические модели элементов и систем управления 95
Рассмотрим некоторые типовые схемы динамических элементов на операцион-
ных усилителях и их передаточные функции.
□ Универсальный одновходовый усилитель (рис. 1.41) с передаточной
функцией
. . Z0(j) Z0(j)
<U1>
Z,o0)
Рис. 1.41
Решая задачу синтеза схемы, реализующей передаточную функцию
(1.31), представим ее в расщепленном виде:
W(s) = И'Из) - Wfc).
Введем дополнительные передаточные функции IPjoU) и (или) H'joW
минимальной сложности с положительными коэффициентами так, чтобы
выполнилось условие баланса
H'i(j) + H'io(J) = ИЭД + I + Ж»(т).
В крайнем (не самом экономичном!) случае всегда можно перекрестно
задать
И'ю(т) = ^(т) + 1.
- W'i(J).
Тогда, выбрав свободно, например, сопротивления 2io(*) и Z>(t). опреде-
лим по формулам (1.29) остальные сопротивления схемы:
Неинвертирующий сумматор (рис 1.42, о), выполняющий операцию
с передаточными функциями
Синтез схемы по заданным передаточным функциям W'/j):
z2o(*)=
Zp(s)
W)
о) б)
Рис. 1.42
Выбрав резистор Z, = Л„ конденсаторы 7|0(з) = 3>(з) = 1 / Qj и парал-
лельное соединение резисторов = Я, Ц ... || К„. получим неинверти-
рующий интегросумматор (рис. 1.42. б), выполняющий операцию
М о
с коэффициентами усиления К, = | / Rfa
□ Инвертирующий сумматор (рис. 1.43, 0), выполняющий операцию
с передаточными функциями входов
Математические модели элементов и систем управления 97
в том числе инвертирующий интегросуммапюр (рис. 1.43, б), выполняю-
щий операцию
1*1 о
с коэффициентами усиления
Рис 143
1.8.2. Построение схем
неминимально-фазовых элементов
Нетрудно заметить, что в табл. 1.3 нет ни одной схемы так называемого не-
минимально-фазового (термин станет более понятен после изучения частот-
ных характеристик в *1.2) элемента, чья передаточная функция (119, о)
имеет полиномы числителя й(т) и/или знаменателя Л(т) с правыми корнями
и разнозначными коэффициентами (1.30). Тем не менее, накопленных нами
теоретических знаний и практических навыков вполне достаточно ия кон-
струирования таких схем на операционных усилителях.
Обладание умением электронного моделирования неминимально-фазовых
элементов приобретает важное значение при исследовании неустойчивых
систем различной физической природы, с которыми опасно или вообще
невозможно ставить натурные эксперименты для изучения их динамических
свойств. Заменяющая такую систему электронная схема в виде натурального
макета «в железе» или компьютерной модели позволяет безопасно, быстро и
разносторонне исследовать качественные и количественные характеристики
системы, а также возможные последствия ее нестабильного поведения.
Начнем с построения динамических элементов с неминимально-фазовыми
полиномами числителей передаточных функций Я0- Решению задачи син-
теза методом расщепления передаточной функции способствует наличие в
формуле (1.31) двух каналов прохождения входного сигнала через элемент с
разными знаками преобразований
О Пример 1.12. Дано дифференциальное уравнение элемента
у + 7у = .г-«'
с постоянными времени Т> 0 и т = аТ> 0. Исследовав различные вариан-
ты расщепления неминимально-фазовой передаточной функции
на две разнозначные составляющие, автор пришел к следующему наиболее
оптимальному варианту решения этой задачи:
Суммы передаточных функций прямого и инверсного входов составляют
5|^=7+Б’,ад +1 = , + 0L
Для восстановления баланса (1.28) добавляем в схему один заземленный
прямой вход Хю = 0 с передаточной функцией, имеющей все положитель-
ные коэффициенты:
Запишем соотношения
H'iUJZiW = (F1o(3)Z|o(5) => Zt(s) = nZl0(j).
Zfa) - => 4(J) - aZzU).
по которым выберем двухполюсники Z|(j), Z|0(5), Z2(t) и Zq(s):
□ резистор Z|(t) = Л, и конденсатор Zipfa) = 1 / Clo$ такие, что Д(Сю = Г.
□ резисторы Zjb) - Я2 и Zq(s) = /?о = аЯ2.
В схеме каскада, построенной на рис. 1.44, предусмотрены возможности
настройки как постоянной времени Т путем регулировки переменного рези-
стора Я|, так и соотношения параметров т и Г регулировкой переменного
резистора Kq.
Устройство с одинаковыми постоянными времени Т = т и сопротивлениями
Л| = Л2 = Aq. называемое фазовращателем. широко используется в радио-
технике и автоматике для реализации частотно-зависимого фазового сдвига
между входным и выходным гармоническими сигналами без изменения ам-
плитуды последнего. □
Математические модели элементов и систем управления
Типовые динамические элементы с неминимально-фазовыми полиномами
знаменателей передаточных функций Л(л) на одном каскаде, имеющем толь-
ко отрицательную обратную связь, реализованы быть не могут и конструи-
руются как неустойчивые схемы с положительной обратной связью. Получим
передаточные функции двух разных каскадов, изображенных на рис I 45, с
обоими видами обратных связей — как отрицательной через элемент 2о(з),
так и положительной через элемент Z|(j).
Рис. 1 45
□ Вход и выход схемы неинвертирующего типа (а) в соответствии с (1.27)
связаны операционным соотношением
У *Му + H'jUU
с передаточными функциями
Отсюда получаем передаточную функцию каскада
100
Гпава 1
W(,\- - Z,Z,0(Z0+Z20)
l-W'.Cv) z1z,0z2o+z1z1IzM-zllzI0z0 •
(1.32,0)
знаменатель которой при подстановке импедансов двухполюсников
Z||(s), Z|o(s). Z|U). ZjoU) и ZiU) в (1.32, о) может (но не обязательно!)
стать неминимально-фазовым из-за наличия операции вычитания.
Для всех желающих избежать ручных преобразований «многоэтажных»
дробей приводим программный вывод формулы (1.32, о) с помощью
символического оператора simplify процессора Mathcad:
HI* «10
10 ____________(z20 + z0)____________
‘ (z20 zl zlOtzJO zll zl-zll zlO zO)
Уравнение, связывающее входное и выходное напряжения схемы инверти-
рующего типа (б), по (1.27) имеет вид
У = ИМу- НОДх
с передаточными функциями
j,^), Z0(a)
Знаменатель передаточной функции каскада
V0=J^L =------------ZoZ^fZ, -bZjo)------
H'jW-l z0z10z2+z0zI0zM-zlz2z20
при подстановке импедансов двухполюсников Z|(J), Z(o(5), Z2(s), Z20(s) и
ZM в (1.32, 6) также может стать неминимально-фазовым.
Несмотря на отличия передаточных функций в (1.32) друг от друга, они полно-
стью идентичны! В этом легко убедиться, слетав переинлексацию импедансов.
например, в схеме на рис. 1.45. б и формуле (1.32, б) следующим образом:
Z\ -» Z). Zj0 -» ZM,
Zj -»Zu, Z]o -t Zl0, Z> -»Z\.
Поскольку рассматриваемые структуры каскадов наиболее универсальны в
том смысле, что все ранее изученные одиовходовые схемы (см. рис. 1.23.
Математические модели элементов и систем управления 101
1.24, 1.41 - 1.43) являются их частными случаями при некоторых нулевых
или бесконечных импсдансах, хочется задать недоуменный вопрос неужели
безразлично, как подключать к операционному усилителю обратные связи’
Ведь никого не нужно долго убеждать, что при ошибочном замыкании цепи
обратной связи на прямой вход усилителя схема с по.южите.1ыюй связью
становится склонной к самовозбуждению, т с. неустойчивой1
Понять природу динамического процесса самовозбуждения операционного
усилителя невозможно, считая его, что мы до сих пор и делали, статиче-
ским элементом с бесконечным на всех частотах коэффициентом усиления
Кг В следующих главах при анализе частотных и временных свойств каска-
дов с обратными связями будет использована динамическая модель линейно-
го режима операционного усилителя в виде передаточной функции
с конечным большим коэффициентом статического усиления Ку и отличной
от нуля небольшой постоянной времени Ту. А пока нужно помнить, что ох-
ватывание реального операционного усилителя положительной обраткой свя-
зью приводит к его самовозбуждению и неустойчивости всей схемы
& Пример 1.13. Получить передаточные функции двух схем на идеальных
операционных усилителях с положительной и отрицательной обратными
связями, глубина которых регулируется переменными сопротивлениями
(рис. 1.46).
Решение. Обозначим постоянную времени обоих каскадов как Т = КС
□ Подстановка в (1.32, я) импелансов двухполюсников (см. табл. 1.2)
102 Глава 1
дает передаточную функцию схемы неинвертируюшего типа на
рис. 1.46. а:
W(s)=(a+l\ . а 2 0. (1.34, л)
1+(2-а)Тт+Г’т2
Вот как делается подстановка с помощью символического процессора
Mathcad:
Значение переменного сопротивления aR с коэффициентом а > 2 делает
знаменатель передаточной функции 1Цз) неминимально-фазовым, а схе-
му неустойчивой
□ Подставив в (1.32, б) импедансы
- ря. Z.W = Л. zo(*)=^r,
получим передаточную функцию схемы инвертирующего типа на
рис. 146. 6:
(,хя
Значение переменного сопротивления (ЗЯ с коэффициентом Р > 2 делает
знаменатель передаточной функции 1Г(з) неминимально-фазовым, а схе-
му неустойчивой.
& Пример 1.14. Разработать каскад на идеальном операционном усилителе,
моделирующий неминимально-фазовое звено с передаточной функцией
W(e)=—, К>0, Т>0.
l-Ts
Решение Поскольку вовсе не очевидно, какие двухполюсники нужно вы-
брать в схемах на рис. 1.45, чтобы их импедансы. будучи подставленными в
(1.32), дали нужную передаточную функцию, будем проектировать каскад
по обшей методике синтеза схем на операционных усилителях
Запишем дифференциальное уравнение элемента, выраженное относитель-
но старшей производной:
Ему соответствует структурная схема, изображенная на рис. 1.47, а. Вре-
менно разорвав обратную связь у выхода интегратора. запишем операторное
уравнение элемента с двумя входами х и v • у.
। элементов и систем управления
К«) = - »W(s), где W2(i) = ^
Так как условие баланса (1.28) не выполнено, а именно,
то дополним схему заземленными входами *ю и х20 с всегда неминимально-
фазовыми передаточными функциями
^00=^0+» = ^. ^0=5(0=^.
Выбрав произвольно сопротивление Л и емкость С, удовлетворяющие
условию
а также резистор Z|(j) = KR и конденсатор 3)(*) - 1 / Cs, определим по
(1-29) остальные навесные элементы схемы:
Рис. 1.47
104
Глава 1
В результате получаем принципиальную схему каскада (рис. 1.47, (5), выход
которого связан с прямым входом операционного усилителя по петле поло-
жительной обратной связи через резистор Я,.
Проверим правильность построения схемы путем программного вывода ее
передаточной функции с помощью символического процессора Mathcad:
Find (у.el .с2)0
R
substitute. zlO =----——
|+к s
substitute,zl = К-R -К
substitute,z2 = R (-I + T
substitute.z20 = К R
К R
substitute,zO =-----
Ts
simplify
Разработанный элемент имеет правый полюс передаточной функции
5| = Г1 > 0 и расходящуюся составляющую переходного процесса е Ч т. □
Как будет доказано в г«. 3. системы с правыми полюсами неустойчивы В ус-
тойчивых системах с минимально-фазовыми передаточными функциями по-
1.8.3. Анализ и синтез многокаскадных схем
на операционных усилителях
Задача анализа схемы заключается в определении ее передаточной функции
или решаемого ею дифференциального уравнения. При анализе схема де-
лится на каскады четырехполюсников. Так как у операционного усилителя
Я,, >:> то передаточная функция каскада на основе операционного
усилителя практически нс зависит от подключенной к нему нагрузки. При
расчете каскада на пассивном четырехполюснике без операционного усили-
теля необходимо учитывать нагрузку, потребляющую часть входного тока
каскада и изменяющую его передаточную функцию.
Математические модели элементов и систем управления
27 Пример 1.15. Рассмотрим два варианта последовательного соединения
двух четырехполюсников: ЯС-цепочки и СЯ-испочки.
□ В схеме с развязывающим операционным повторителем между цепочка-
ми (рис. 1.48, а) передаточные функции трех каскадов имеют вид
^0=
1 + Тнз'
И^(5) = 1, %(.?)=
с постоянными времени
=Я/С;.
В силу последовательного соединения каскадов получаем передаточную
функцию схемы как произведение трех передаточных функций (1.20, а)
Рис. 1 48
О В схеме с непосредственным соединением цепочек друг за другом
(рис. 1.48, б) происходит отбор части входного тока первой цепочки в
нагрузку — вторую цепочку. Рассчитаем передаточную функцию этой
схемы методом контурных токов:
QI = Рх,у = Cl=»y-CQ-'Px. Ж= CQ-'P.
^ = ЯЬ Z,=^y. Z3~,4-*2
106 Гпава 1
Отсюда получаем передаточную функцию схемы:
- Tns
(• + ?i I1 X1 + 722J)+ 2s
которая, очевидно, отличается от передаточной функции (1.35) дополни-
тельным слагаемым Т| ys в полиноме знаменателя. О
При последовательном соединении каскадов пассивных четырехполюсников
необходимо включать между ними развязывающие операционные повторите-
ли. Тогда передаточные функции каскадов можно перемножать. В отсутствие
повторителей должна учитываться подключенная к каскадам нагрузка.
& Пример 1.16. Рассмотрим схему (рис. 1.49), состоящую из четырех кас-
кадов, первый из которых является пассивным четырехполюсником с на-
грузкой Zj. Запишем уравнения каскадов и определим их передаточные
функции:
У» - ГЛЙ-1^ - И'зи.у» = (РуЛ + «V.
где
_ Z2Z3 z^ ъ z^
Z,+Z2|Z, Z.Zj + Z^+ZjZ, ’ 2 Zj’ 3 z4 ‘ 4 z6"
ментов и систем управления
107
Получим передаточную функцию всей системы в целом методом эквива-
лентных преобразований структурных схем (рис. 1.50):
Рис. 1.50
= __________________ «
(z,Z2 + 7,23+ Z2Z3 ) U4Z6 (Z8 + Z, )Z,, + Z5 (Z6ZQ - Z7Z8 )(zl0 + Z,,
Отметим, что влияние нагрузки первого каскада Z} учтено при записи его
передаточной функции FT,. О
Решение задачи синтеза схемы на операционных усилителях по заданной
передаточной функции не единственно и зависит от сложности последней и
особенно от ее минимально-фазовости Процесс разработки и выбора вари-
анта схемы является многокритериальной задачей оптимизации:
□ следует минимизировать стоимость устройства;
□ желательно использовать типовые схемы каскадов с минимальным чис-
лом индуктивностей;
□ нужно обеспечить возможность желаемой вариации параметров схемы
изменением номиналов минимального числа радиоэлементов.
Рассмотрим некоторые методы синтеза схем иа операционных усилителях со
сложными передаточными функциями
108
Метод последовательных каскадов
Представим передаточную функцию моделируемой системы произведением
простых передаточных функций первого и второго порядков:
Ж0-ПШ (136, а)
Тогда, согласно (1.20, в), моделируюшая схема строится как последователь-
ное соединение каскадов, подобранных с помощью табл. 1.3. Для миними-
зации числа каскадов и навесных элементов рекомендуется объединять в
одну схемы из второго и третьего столбцов.
Пример 1.17. Разработать схему моделирования системы «тележка -
обычный маятник», имеющей передаточные функции (1.12).
Решение Представим эти передаточные функции произведениями функций,
реализуемых каскадами на операционных усилителях из табл. 1.3:
IV (Л- 0.1(1+0.133^0,133?) =
' 1 з(1 +1.681)^+0.1551+ 0.1?)
_ -0.2__________0.5 -(1+0.1331 + 0.133?),
.1 + 1.683 1+0,1551+0.1? __________i__________,
*?!•) ' ад ад)
n.lJe п 236 п 25а
ж , х___________0.01т______ -0.2_______________0.5 , 0
’ (1 + 1.681 )(l + 0.155i+0.1?) 1 + T68j 1 + 0.1551 + 0.1?,
*Ф) ' ' ад)
П lb n 2M П 3o
На рис 1.51 приведена электронная схема моделирования этой механиче-
ской системы с двумя выходными сигналами. Номиналы радиоэлементов
схемы должны выбираться из следующих соотношений:
Рис. 1.51
Математические модели элементов и систем управления
109
RC = 1.68, Я = 0.2Яь С- С|. Я2С=0.31, t|C-0.2;
Ь- = 1, ^. = 0.133, L2C2 = 0.133, ЯС3 = 0 1.
Я Я,
Метод параллельных каскадов
Представим сложную передаточную функцию суммой простых передаточных
функций порядков не выше второго:
Иф)=5Х(з). (1.36, б)
Тогда, согласно (1.20, б), моделирующая схема строится как параллельное
соединение каскадов, реализующих передаточные функции И^з), и вклю-
чает дополнительно алгебраический многовходовый сумматор
& Пример 1.18. Разработать схему ПИД-рсгулятора с передаточной функ-
1У(1)=Яп+-^-+Ялз, (1.37)
параметры которой К„, и КЛ могли бы изменяться произвольно и незави-
симо друг от друга как по величине, так и по знаку'.
Решение. Построим два варианта схемы регулятора, отличающиеся спосо-
бами выбора знаков параметров
□ Первый вариант (рис. I 52) реализован на типовых инвертирующих схе-
мах усилителя, интегратора и дифференциатора с настраиваемыми ко-
эффициентами усиления (см. табл. 1.3, пп. 1в. 2а, За):
«'„о) = -ia
Номиналы сопротивлений Я и емкостей С выбираются свободно. Для
задания желаемых значений модулей коэффициентов К„, Ка и А„ предна-
значены переменные сопротивления, настраиваемые по следующим
формулам:
Выбор знака или отключение любого из компонентов регулятора выпол-
няется соответствующим трехпозиционным тумблером Верхнее положе-
ние тумблера соответствует положительному коэффициенту, нижнее —
отрицательному, а среднее — нулевому.
Рис. 1.52
Управляющее воздействие (В.5) формируется на выходе сумматора с
тремя прямыми и тремя инверсными сигнальными входами, рассчитан-
ного по общей методике синтеза статических схем на операционных
усилителях (см. разд. 1.3.2).
Каждый из компонентов управления, инвертированный своим функцио-
нальным каскадом, в зависимости от положения тумблера, подается на
прямой либо на инверсный вход сумматора, при этом неиспользуемый
вход заземляется. В среднем положении тумблера оба входа заземлены.
□ По второму варианту, изображенному на рис. 1.53, схема строится на
операционных инвертирующих каскадах с постоянными параметрами на-
весных элементов, а регулировка знаков и значений параметров Afn, Кп и
Ка производится с помощью мулыидиапазонных универсальных усили-
телей (см. рис. 1.29. б) С учетом отсутствия инвертирования сигнала в
пропорциональном канале, конечный сумматор выполняет алгебраиче-
скую операцию
х(г>Кп(кпх/пк(1)^-КДХ,4и)Р(тМт^(-Кд(ХлА)^).
Рис. 1.53
□
Если в (1.36) имеются передаточные функции И^з) с неминимально-
фазовыми полиномами знаменателей, то соответствующие каскады конст-
руируются с использованием положительной обратной связи и являются
неустойчивыми.
Недостатком методов последовательного и параллельного соединений явля-
ется возможность появления каскадов с дифференцирующими свойствами,
признаком чего служит наличие оператора s в числителе передаточной
функции. Это весьма нежелательно в многокаскадных схемах, т. к даже са-
мый слабый высокочастотный шум zfcinfw/), пройдя через цепочку из N
дифференцирующих каскадов, многократно увеличит свою амплитуду ЛоЛ
пропорционально Л^-ой степени частоты и заглушит полезную низкочастот-
ную составляющую выходного сигнала.
Другие недостатки рассмотренных методов:
□ необходимость вычисления корней полинома для получения разложе-
ний (1.36);
□ разнотипность каскадов;
□ нерегулярная структура полученной схемы;
□ трудоемкий расчет номиналов радиоэлементов принципиальной схемы
Ill
Метод канонических схем
Метол реализации передаточной функции
H'GMG)
свободный от указанных выше недостатков, основан на построении вспомо-
гательной схемы, имеющей передаточную функцию
и выход Цг), удовлетворяющий дифференциальному уравнению
vW=±x_W-«)_ v (, 38> я)
а, а„ а„ ап
Соединим последовательно п интеграторов, обозначим их выходы справа
налево как v, v,.... а вход самого левого интегратора сформируем по
уравнению (1.38. а) с помощью (л + 1)-входового сумматора. Так как
Wj) = BisjH'M,
то выход системы ></) формируется как линейная комбинация выходов ин-
теграторов (рис. 1.54):
У‘В&у~Ьо1+№ + ... + Ь„^. (1.38,6)
При т < п вводятся фиктивные коэффициенты b„+i = ... = Ь„ = 0. Мето-
дика построения подобных схем унифицирована для любых передаточных
Математические модели элементов и систем управлений
функций, у которых т< п. Структуры схем являются каноническими (тако-
номерными. регулярными, повторяющимися), не имеют дифференциато-
ров, строятся просто, хотя и не всегда гарантируют минимальных затрат
оборудования.
Для практической реализации канонической схемы достаточно п одновходо-
вых интеграторов и не более двух многовходовых сумматоров-вычитателей,
обведенных на структурных схемах (рис. 1.54, 1.55) пунктиром
Интеграторы можно строить как по неинвертирующей (рис. I 56. о), так и пс
инвертирующей (рис. 1.56,6) схемам с постоянной времени ЛС= I Вторая
схема вдвое экономичнее первой по числу навесных элементов В схеме на
инвертирующих интеграторах (рис. 1.55) необходимо учитывать чередованш
справа налево знаков производных ... -з -✓*-» V -»-✓-» v и коэффициентов
суммирования в цепях обратной связи и формирования выходного сигнала.
Рис 1 56
Вынос точки съема г<"> влево за сумматор дает эквивалентные схемные ре-
шения на нсинвертируюших (рис. 1.57) и инвертирующих (рис. 1.58) инте-
граторах с меньшим числом операционных усилителей за счет совмещения
двух функций многовходовыми ннтегросумматорами обратных связей Це-
ной экономии оборудования несколько усложняется расчет схемы
Принципиальная схема интегросумматора строится по типовой методике
синтеза каскада на операционном усилителе на основе операторного диф-
ференциального уравнения
(1.39,0)
Математические модели элементов и систем управления 115
Подставив выражение для ^л> из (1.38, о) в (1.38, б), получим уравнение вы-
ходного сигнала системы:
y= £clv^ + Dx, где D = —, С) = b, - Dat Vi = 0.n-l. (1.39,6)
ЙО °я
& Пример 1.19. Разработать канонические схемы на операционных усили-
телях, моделируюшие систему «тележка - обычный маятник» с одним вхо-
дом, двумя выходами и передаточными функциями (1.12)
W,(,)-------1уф(5)=----------------------------------------
в|Х + a2s + o3s + o4.s + + о?з + о4з
с коэффициентами полиномов
Ьо = 60, Ь\ = 8, 6j| = 8, 622= 6,
о, = 600, о2 = 1100, о3 = 216, о4 = 100.
Решение На рис. 1.59 приведена структурная схема на неинвертирующих ин-
теграторах, моделирующая уравнения (1.39):
Рис 1 59
Начиная построение принципиальной схемы с разработки интегросуммато-
ра, сравниваем суммы
Глава 1
a^s 0^3
и вводим дополнительный прямой заземленный вход л'ю = 0 с передаточной
функцией
а4з s
Составим соотношения для выбора структуры и параметров принципиаль-
ной схемы (рис. 1.60):
Zii(s) = (О| + аг + аз - I + a43)ZI0(s),
<м4(з) = O|Z2i(j) = ojZnU) = fljZijU)
Рис. 1.60
Выбрав свободно значения R и С, удовлетворяющие условию RC = 1, поло-
жим Z|0U) ~ Я10/(1 + ЯюСО — параллельное соединение конденсатора
Сю “ С и резистора
*ю = 7-----------т- = 0.0522Я
(<з,+а2+в3-1)С
Тогда элемент
Zu Ли = (a( + oj + Oj - 1)Л10 = а4Я = 100Я
есть резистор. Выбирая в цепи обратной связи конденсатор = 1/0,
получим сопротивления резисторов
г2|«Я21=^1г = О.167Я, z22 Ru = = 0.0909R .
2п«Яц«-21- = 0.463Я.
а,С
Математические модели элементов и систем управления
Сопротивления выходных каскадов, формирующих выходные сигналы d и
Ф, удовлетворяют соотношениям
R _ *i _i R-h.,.h+h R к .к
-7-5--т—"Г- ’ T~~b°+b'+b''~l = 5- t_ = z’22-* = 5-
*31 °2I *32 ®2I *40 *50
На рис. 1.61 приведена структурная схема системы на инвертирующих инте-
граторах, моделирующая уравнения
Рис. 1.6»
Начиная построение принципиальной схемы с разработки интегросуммато-
ра, сравниваем суммы
и вводим дополнительные заземленные входы xw *0 илц’Ос передаточ-
ными функциями
в43 J
Глава 1
Составим соотношения для выбора структуры и параметров импедансов
принципиальной схемы, построенной на рис. 1.62:
njZnW = a<sZM,
<bsZM » Z2|(j) = fl|Z22(j) = ajZ2j(s).
Рис. 1 62
Задав свободно значения Ли С из условия /?С = 1, выбираем емкостной
тип элементов Zto(j) = ZiU) = 1 / Ст, тогда элементы на входах интегросум-
матора будут резисторами:
Z"3/f|l=7c=009<)9/?' 221в7- = 100Я- Z22 = /?23=y^ = 0.167/?,
ZB Яа = -^ = 0.463/?, Z20 а Л20 = 7--------Т- = 0.353/?.
а3С (а2 - О) - а3 - 1)С
Сопроп1вления выходных каскадов, формирующих выходные сигналы d и
ф, удовлетворяют соотношениям
Т=^15' тН=8’ r^+d2|_z,_,=59- Г’=^-,=5-
«Л Ojt Kj, Кю «50
Еше раз обращаем внимание читателя на то, что все номиналы навесных
элементов рассчитаны в относительных единицах Я. Для получения конкрет-
ных значений номиналов нужно задать этот свободный параметр, например,
равным Я= I МОм. и подставить его во все расчетные формулы. О
ГЛАВА 2
Как много мы знаем, и как маю понимаем
Амйерт Эйнштейн
Частотные характеристики
элементов и систем управления
Эта глава посвящена изучению реакции линейных стационарных элементов
и систем на одно из типовых внешних воздействий — гармоническое казеба
ние. Важность этого воздействия не очевидна, поскольку редко встречаются
системы управления, отслеживающие синусоидальную уставку Однако, ес-
ли известна реакция системы на гармонические колебания всех возможных
частот, то тем самым мы получаем полную информацию об этой системе,
поскольку любой сигнал можно разложить на гармонические составляющие.
Часто удается экспериментально измерить реакцию физической системы на
гармонические колебания, и полученные таким образом характеристики
имеют огромную практическую ценность.
Рассмотрим линейный объект с входным сигналом .x(t) и выходным сигна-
лом y(t), описываемый неоднородным дифференциальным уравнением
(1.15):
аау(г) + ai/(0 + ... + a^(i) - Mrt + ^(0 + ... + Л,,?"’ (/).
К основным задачам исследования сложных объектов относится расчет ие
реходных процессов — зависимостей >(/) при различных воздействиях
Это составляет, пожалуй, главный визуальный результат теории автоматиче
ского управления. Многократное решение линейного неоднородного диф-
ференциального уравнения со сложной правой частью весьма трудоемко и
повторяется каждый раз заново для каждого нового входного сигнала.
IX Глава?
Один из подходов, призванный унифицировать и тем самым облегчить ре-
шение данной задачи и основанный на свойстве линейности объекта, за-
ключается в следующем:
□ входное воздействие представляется взвешенной суммой некоторого
числа типовых сигналов простого вила;
О рассчитывается отклик объекта на типовой сигнал;
□ выходной сигнал формируется как взвешенная сумма откликов на типо-
вые сигналы, составляющие входное воздействие.
К простейшим типовым воздействиям, применяемым в теории автоматиче-
ского управления, относятся колебательные, ступенчатые и импульсные
сигналы. В этой главе изучается прохождение через объекты колебательных
сигналов, а воздействия ступенчатого и импульсного типов булут рассматри-
ваться в гл. 3.
Гармоническое колебание некоторой величины описывается тригонометри-
ческими формулами
И») = А^п((Ш + ф.) или iV) = Л,со5(гш + <ру) (2.1)
и характеризуется следующими тремя параметрами
□ Амплитудой А, — размахом колебания вокруг нулевого среднего значе-
ния. Единица измерения амплитуды совпадает с единицей измерения
самой величины.
□ Частотой ы — скоростью совершения одного цикла колебаний. В автома-
тике принята единица измерения частоты I рад / с — один радиан в се-
кунду, что соответствует длительности цикла 2п = 6.28 с. Во многих техни-
ческих дисциплинах, изучающих колебательные процессы, используется
единица измерения частоты 1 Гц — один герц или один цикл в секунду
Радианная частота ш и циклическая частота /связаны соотношением
ш(рад/с) = 2г/(Гц) (2-2)
и отличаются друг от друга примерно в 6 раз: 1 рад / с соответствует
160 мГц. Колебания частотой/Гц описываются функциями
ИО Asin(2>j/? + <рг) или И/) - H,cos(2r^ + <pj,
не очень удобными для 1-кратного дифференцирования этих сигналов по
времени г из-за множителя (2к)*.
□ Фазой ф, — угловым сдвигом колебательного процесса (2.1) от несме-
щенного (с фазовым углом ц>,= 0) сигнала Л^1п(шг) либо 4«cos(utf). Еди-
ницами измерения фазового угла являются рад (радиан) или градус Фа*
зовый сдвиг ф, и временной сдвиг I, связаны соотношениями
Частотные характеристики элементов и систем управления 121
Ъ-ЫЬ /,=^. (2.3)
ш
Форма описания колебаний функциями (2.1) для решения практических за-
дач неудобна тем, что при каждом дифференцировании функция sin меня-
ется на сов , а сов — на -sin. Такое чередование тригонометрических
функций и их знаков приводит к достаточно громоздкому выражению пра-
вой части дифференциального уравнения (1.15), содержащему обе эти
функции.
Более удобной является общепринятая комплексная форма описания колеба-
ний
v(r)= А,,е^ш'м’^ = A^cos(<or + <pv)+jA,.sin((iM + (pv), (2.4)
где р = -|, как равномерного вращения на комплексной плоскости радиус-
вектора длиной
А-|Ф)|
с угловой скоростью ш и начальным фазовым углом
<P» = atg(i<0))
(рис. 2.1).
Переход от действительных колебаний (2.1) к обобщающему комплексному
“Сражению (2.4) имеет следующие свойства и последствия:
Упрощается дифференцирование комплексной экспоненты:
^)=4j<Ue^- -» = Ло Ч);
производные функции v(z) любого порядка
dr
122__________________________________________________________Глава!
выражаются через эту же функцию, благодаря чему каждая из частей
дифференциального уравнения (1.15) записывается в алгебраической
форме типа
2сЛ(->(,)=р(/)Хс,сшг,
г>4 <*О
а пространство происходящих в системе процессов становится комплекс-
ным, и в нем естественным образом вычисляются как амплитудные, так
и фазовые изменения сигналов в процессе их прохождения через дина-
мические элементы системы;
□ действительные сигналы в (2.1) могут быть получены из комплексной
формы (2.4) как
4^in(<iV + ф>.) = 1т(Ц0}, >4^:os(co/ + <р„) = Re{v(r)},
хотя этот прием в теории автоматического управления остался невостре-
бованным
Частотная характеристика (ЧХ) - это зависимость определенного па-
раметра гармонических колебаний выходной переменной линейного
объекта от частоты колебаний входной переменной в установившемся
режиме функционирования. Широкое применение частотных характери-
стик базируется на том, что входное воздействие произвольного характе-
ра может быть представлено в виде суммы гармоник различной частоты,
каждая из которых передается на выход линейной системы без искаже-
ния формы.
Большинство систем при внезапной подаче на вход периодического воздей-
ствия дают в конечном счете периодический отклик установившейся фор-
мы. За редким исключением, когда в момент приложения входного сигнала
система случайно оказывается точно в состоянии, совпадающем с устано-
вившимся, практически всегда в начале движения будет некоторый интервал
времени, в течение которого затухает начальное отклонение системы от ус-
тановившегося режима.
Таким образом, если на вход невозбужденного линейного устойчивого объекта
подан сигнал в виде гармонического колебания
40 “ ЛдЯп(шг + ф^),
то на его выходе начинает развиваться переходный процесс у(0. который пс
истечении некоторого времени гу становится установившимся процессе»
(рис. 2.2)
УусЛО = Xysintcor + фу).
Частотные характеристики элементов и систем управления
зф)=Дв1п(йХ+<р,)
^('Ь^ип^+Ф,)
А=Л(“)
ф> =<₽>(“)
У всех устойчивых динамических объектов, описываемых дифференци-
альными уравнениями (1.15), амплитуда А, и фазовый сдвиг <₽,. выходно-
го сигнала зависят от частоты входного сигнала о> Иначе говоря, устано-
вившиеся параметры выходных колебаний являются частотно-
зависимыми, и это свойство изменять амплитуду и фазу гармонического
сигнала является свойством самого линейного объекта, а не сигнала, про-
ходящего через него.
Теоретически частотные характеристики определены при изменении угло-
вой частоты ш от 0 до =°. Однако всякое реальное устройство может пропус-
кать гармонические сигналы лишь некоторого ограниченного интервала
частот, поэтому в каждом конкретном случае следует заранее определиться,
в каком интервале частот целесообразно исследование частотных свойств
этого устройства.
Частотные характеристики устойчивого объекта могут быть получены экспе-
риментально с помощью генератора гармонических колебаний и устройства
регистрации временных процессов, например, осциллографа Ввиду отсутст-
вия у неустойчивого объекта установившегося режима ею частотные харак-
теристики не могут быть экспериментально измерены Тем не менее, их
можно формально построить по передаточной функции 1Ит) (она. как из-
вестно, есть иной способ записи дифференциального уравнения объекта и
не зависит от вида входного воздействия), о чем будет рассказано в следую-
щем разделе, и использовать для моделирования системы, включающей не-
устойчивый объект.
С учетом сказанного следует, видимо, разорвать прямую связь данного выше
определения частотных характеристик с параметрами установившихся коле-
баний на входе и выходе объекта, а воспринимать их как еше один способ
описания динамики систем, имеющий в случае устойчивости последних по-
нятный физический смысл.
2.1. Основные частотные характеристики
Для получения коллекции частотных характеристик подставим в дифферен-
циальное уравнение объекта комплексные формы
1х(г)=А,еи“**,), х(')0=А,О<оУе)(“’*,) Vie0, т,
[y(i)=A>ej(“^), у^)=А,^^ Vi=0T7i
входного и установившегося выходного сигналов и их производных:
А>Л*£д10шУ=Ахе^^>У.
i=O 1=0
После сокращения обеих частей уравнения на е,ш', т. е. исключения враща-
тельного движения, получим выражение, описывающее относительное по-
ложение на комплексной плоскости радиус-векторов x(i) и y(z):
А,е*’ =АЛе”- .
Отсюда следует соотношение между амплитудами и фазовыми углами вход-
ного и выходного сигналов:
(2.5)
Введем в рассмотрение следующие основополагающие понятия:
□ - амплитудно-частотная характеристика (АЧХ), или от-
ношение частотно-зависимой амплитуды выходных колебаний к ампли-
туде входных;
□ ф(ш) = ф^ш) - ф, - фазочастотная характеристика (ФЧХ), или разность
между частотно-зависимой фазой выходных колебаний и фазой вход-
ных;
□ (Щсв) - комплексная частотная характеристика (КЧХ), ко-
торая. согласно (2.5). получается из передаточной функции His) путем
формальной замены оператора г мнимой функцией частоты jcn. Как лю-
Частотные характеристики элементов и систем управления
125
бой комплексный объект, комплексная частотная характеристика имеет
вещественную и мнимую составляющие (рис. 2.3):
HXjca) = Л(а>)(«к(ф(ы)) + j • sin(«p(<o))} - Л«) + jQ(“>'
lm{H)
О До» Re|ll|
Рис 2.3
□ Л<о) = Re{ Wj<n)) = y4(to)cos(<p(a>)) — вещественная частотная характери-
стика (ВЧХ).
□ 2(w) = lm{ И^ш)} = ?l(ii>)sin(<p(<a)) — мнимая частотная характеристика
(МЧХ).
Знание вещественной и мнимой характеристик позволяет рассчитать ампли-
тудную и фазовую частотные характеристики по следующим формулам:
Д(со) = . <р(со) = arct^ | (2.6)
Вот самый главный результат описания гармонических колебаний на ком-
плексной плоскости: фактически без решения неоднородного дифференци-
ального уравнения мы можем быстро найти по комплексной частотной ха-
рактеристике И^со). которая просто получается из передаточной функции
H^s}, коэффициент усиления амплитуды сигнала и его фазовый сдвиг на
любой частоте со.
Перечисленные выше частотные характеристики принято строить в равно-
мерном масштабе по осн частот ш> 0. Особое внимание следует уделить по-
строению графика фазочастотной характеристики по ее аналитической за-
висимости (2.6) с помощью ЭВМ, в том числе и калькулятора. Поскольку
Функция arctg возвращает главное значение угла в интервале (-90°. +90°), то
при Дш) < 0 его следует скорректировать:
□ увеличить на 180° или л рад при С(ы) > 0;
□ уменьшить на 180° или я рад при 0(ш) < 0.
Линия на комплексной плоскости, образуемая точками графика B-tyo) при
"вменении частоты ш от 0 до называется годографом или ампптпдно-
Фозовой частотной характеристикой (АФЧХ) Л(<р). Годограф строится как
126
параметрическая функция частоты ш е |0,«) по значениям любой из пар
характеристик: (Я(ш), ф(ш)| или (Лш). 0(ш)(. Заметим, что с математической
точки зрения годограф является отображением на комплексную плоскость
верхней половины мнимой оси плоскости s через функцию 1Щ<о)
На построенном годографе рекомендуется указать стрелкой направление
возрастания частоты и отметить следующие особые точки-
□ начало годографа при <о -> 0;
О конец годографа при ш ->«;
□ пересечения годографа с координатными осями:
• с осью Re| И] на частотах, где = 0;
• с осью lni| И} на частотах, где Ли) = 0;
□ пересечения годо!рафа с окружностью единичного радиуса на частотах,
где Л(ы)» I.
В равномерном масштабе по оси <> графики частотных характеристик
быстро изменяются на низких частотах и медленно — на высоких По-
этому в практических расчетах используются логарифмические частотные
характеристики (ЛЧХ) с соответствующими масштабами по осям частоты
и амплитуды:
□ Д(со) = 20lg(,4(u)) — логарифмическая амплитудно-частотная характери-
стика (ЛАЧХ). строящаяся в логарифмических масштабах как по оси
частот, так и по оси амплитуд;
□ Ф(<а) — логарифмическая фазочастотная характеристика (ЛФЧХ), строя-
щаяся в логарифмическом масштабе по оси частот и в равномерном,
желательно градусном, масштабе по оси фазового угла.
В англоязычной технической литературе логарифмические характеристики
называют диаграммами Боде |11, 22, 291
Обратная зависимость амплитудно-частотной характеристики от логариф-
мической амплитудно-частотной характеристики имеет вид
а(ш)=1Оом^>.
Значение коэффициента усиления А = I соответствует логарифмическому
усилению L = 0. Отрицательная логарифмическая амплитуда L < 0 означает
ослабление сигнала с коэффициентом 0 < А < 1, а значение L > 0 — усиле-
ние с амплитудой А > I.
Единицей измерения логарифмической величины lg(.r) является декада
(дек) — интервал, на концах которого значения к отличаются друг от друга в
10 раз. Примеры декад: |1, 10), (0.2, 2], |о 10я, а 10я*11.
Частотные характеристики элементов и систем управления 127
Для измерения логарифмической амплитуды введена специальная едини-
ца - бел (Б). Названная в честь изобретателя телефона, она первоначально
применялась к мощностям, пропорциональным квадрату амплитуд напря-
жений или токов. Из-за ее слишком большой величины более популярна
десятая часть бела — децибел (дБ). Поэтому при измерении в логарифмиче-
ском масштабе степени усиления амплитуды напряжения либо тока полага-
ют, что декада по оси I. равна 20 дБ
Логарифмическая шкала Igx преобразует равномерную шкалу положительных
величин х > 0 следующим образом:
□ в области х < I происходит растяжение тем большее, чем х ближе к ну-
лю;
□ в области х > 1 происходит сжатие тем большее, чем х ближе к беско-
нечности.
Таким образом, логарифмическая шкала позволяет отобразить на одном
графике больший динамический диапазон изменения величины по сравне-
нию с равномерной шкалой. К тому же человеку присущ именно логариф-
мический масштаб восприятия явлений природы, а именно:
□ музыкальные интервалы между одноименными нотами в разных октавах
слышатся ухом как равные, хотя при этом совпадают не разности, а от-
ношение частот звуков крайних нот;
□ равномерное изменение громкости звука ощущается не при линейном, а
при показательном законе изменения давления воздуха на барабанную
перепонку, благодаря чему человек слышит как шелест травы, гак и рев
ракетных двигателей. При измерении интенсивности звука в логариф-
мической шкале за начало отсчета (ОдБ) принимается звуковое давле-
ние 2 • 10’5 Н / м2, соответствующее среднему нормальному порогу
слышимости уха человека на частоте 1000 Гц [22], а болевой порог гром-
кости составляет 140 дБ;
□ зрительная система человека способна регистрировать количество
световой энергии, начиная от отдельных квантов до ослепляющих
вспышек, чему способствует автоматическая адаптация площади от-
верстия радужной оболочки глаза обратно пропорционально лога-
рифму энергии.
Если равномерная ось частот ые (0, “>) — полубесконечная, то логарифми-
ческая ось lg<o е ~) — бесконечная в обе стороны, поэтому начальные
значения логарифмических частотных характеристик при ш = 0 отсутствуют
Принято ось L проводить через частоту <г> = I рад / с. т. е. в начале коорди-
наты IgCd = 0.
В табл. 2.1 приведены логарифмы Igx и 20lg.< величины х на декаде \\,\0\.
128
Таблица 2 1
1 2 3 4 5 6 7 В 9 10
|дх 0 0.301 0 477 0.602 0.699 0.778 0.845 0 903 0954 1
2О1дх 0 602 9.54 12 04 13 98 15 56 16.9 18 06 19 08 20
На других декадах работают следующие формулы десятичного логарифми-
рования:
lg< 10"х) = и + Igx.
201g(10".v) = 20л + 201gx,
т. е. увелнчение/уменьшение числа в 10 раз увеличивает/уменьшает его ло-
гарифм на I дек или 20 дБ. Полезно также запомнить, что
□ 1 дБ соответствует изменению амплитуды примерно на 12%;
□ 3 дБ эквивалентны изменению амплитуды в Vl раз, т. е. примерно на
40%;
□ 10 дБ соответствуют изменению амплитуды в х/10, т. е. примерно в 3.16
При построении частотных характеристик очень важно уметь точно размес-
тить определенное число (частоту ы или амплитуду Л) на размеченной лога-
рифмической оси. На рис 2.4 изображено расположение различных частот
на нулевой, первой, минус первой и г-ой декадах. Цифры и сетку на частот-
ной оси можно проставлять двумя способами:
□ в логарифмическом масштабе значений ы;
□ в равномерном масштабе значений Igco.
0 0.1 02 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 lgo>
Н—1-----------1-----1----------------i-----1—i1 ~г~ ' H—*
I 2 3 4 5 6789 10 ы
10 20 30 40 SO 60 70 80 90 100
01 0.2 0.3 0.4 O S 0.6 0.7 0 8 0.9 1
10' 210' 310' 4-10' 510' IO*’
Рис 2.4
Если под руками нет ни калькулятора, ни табл. 2.1, ни рис. 2.4, то для быст-
рого логарифмирования в уме можно руководствоваться следующими про-
стыми правилами:
Частотные характеристики элементов и систем управления__________________1_29_
□ запомнить всего два десятичных логарифма: lg2«0.3 и lg3«0,48,
□ умножение/деление числа на 2 увеличивает/уменьшает его логарифм на
0.3 дек, т. е. на 6 дБ;
□ умножение/деление числа на 3 увеличивает/уменьшает его логарифм на
0.48 дек. т. е. на 9.5 дБ;
□ представив число х произведением степеней чисел 2, 3 и 10, получим
формулы приближенного логарифмирования
х - 2‘* 3±я| • 10*" « Igx = ±0.3* ± 0.48m ± п, 20lgx = ±6* ± 9.5m ± 20л. (2.7)
Решим по этим правилам несколько примеров, а для сравнения в конце ка-
ждого из них приведем в скобках округленные до I0'3 точные значения, вы-
численные с помощью калькулятора.
□ lg!5 = lg(3 10 / 2) = 0 48 + 1-0.3» 1.18 (1.176).
□ lg250 = lg(103 / 22) = 3 - 0.3 2 = 2.4 (2.398).
□ lg0.7 - Ig7 - 1 = 0.5 lg50 - 1 = 0.5(2 - 0.3) - 1 = -0.15 (-0.155)
□ £ = -22 = -40 + 18 = 3 6 - 2 20 дБ =M = 23 / I02 = 0.08 (0.0794).
□ A = 120 = 10 • 3 • 22 => L = 20 • (I + 0.48 + 0.6) - 41.6 дБ (41.584).
Как видно, приближенное логарифмирование без привлечения какой бы то
ни было вычислительной техники дает достаточно точные результаты
Амплитудные частотные характеристики дают наглядный ответ на вопрос об
усилительных свойствах элемента или системы на разных частотах входного
сигнала. Поскольку практически все реальные сигналы не являются идеаль-
но гармоническими, а содержат взвешенную смесь гармоник разных частот,
то на выход системы преимущественно проходят те гармоники, на чьих час-
тотах амплитудно-частотная характеристика больше. Например, если на
вход системы, находящейся в состоянии равновесия, подать импульсный
сигнал х(/) = б(г) с изображением Дт) = I (см. табл П.1) и равномерным
спектром X(j<o) = I, то по (1.18) спектр выходного сигнала Mj<o) будет равен
И-Xjco) — комплексной частотной характеристике системы. При произволь-
ном спектре входного сигнала A(ja>) спектр выходного сигнала
Hj<o) = H4j<u).V(j<u)
содержит лишь те гармоники, которые пропускаются системой независимо
от того, какова их доля в спектре входного сигнала.
Таким образом, система, пропускающая с различным усилением одни гар-
моники и поглощающая другие, является фильтром с определенной полосой
пропускания частот. В современной теории автоматического управления
(И, 29] принято включать в полосу пропускания те частоты ш, на которых
коэффициент усиления амплитуды не уменьшается более чем в Л раз
Глава 2
(рис. 2.5, в) или нс опускается более чем на 3 дБ (рис. 2.5, б) ниже уровня
усиления постоянного сигнала-
, Дш) г ДО) - 3.
Иначе говоря, мощность пропускаемых гармоник, пропорциональная квад-
рату амплитуды напряжения или тока, нс меньше половины уровня мощно-
сти постоянного сигнала, имеющего нулевую частоту. Выбор для сравнения
именно нулевой частоты, лежащей в полосе пропускания системы, обуслов-
лен чрезвычайно большой ролью установившегося режима в работе любой
системы управления.
Рис 2.5
Данное определение полосы пропускания условно: оно неприменимо, на-
пример, к астатическим системам, у которых Л(0) = «• (рис. 2.5, в). А у сис-
тем, имеющих на низких частотах дифференцирующие свойства, значение
Л(0) = 0 и полоса пропускания по введенному определению становится ну-
левой (рис. 15, г). В радиотехнике такого рода системы — резонансные уси-
лители — составляют большинство. Поэтому там принято отсчитывать по-
лосу пропускания по уровню, в 41«1.4 раза или на 3 дБ меньшему лтокш-
мума амплитудно-частотной характеристики (22].
С учетом сказанного рассмотрим некоторые типы фильтров и вил их полос
пропускания.
Частотные характеристики элементов и систем управления___________131_
□ Множество отдельных элементов и большинство замкнутых систем
управления представляют собой фильтры низких частот (ФНЧ), усили-
тельные свойства которых максимальны на частотах со е |0, <n,il, где Ц, —
верхняя граница полосы пропускания (см. рис. 2.5, а). Те устройства, кото-
рые называют широкополосными усилителями и полагают их коэффици-
енты усиления постоянными, так или иначе теряют свои усилительные
свойства на высоких частотах, т. е. имеют конечную полосу пропускания
(рис. 2.6, а). Термин «широкополосный» применим к усилителю при ус-
ловии, что его полоса пропускания частот перекрывает полосы пропус-
кания других элементов системы
□ Идеальный фильтр высоких частот (ФВЧ) имеет полубесконечную по-
лосу пропускания |w„,«) (рис. 2.6, б) и применяется для удаления из
сигнала низкочастотных гармоник. Физически реализуемый фильтр вы-
соких частот, как и широкополосный усилитель, имеет конечную верх-
нюю границу полосы пропускания. В качестве примера высокочастотно-
го фильтра можно привести С7?-цепочки с передаточными функциями
Тз / (1+ 7i), устанавливаемые между усилительными каскадами для ис-
ключения распространения постоянной и низкочастотных составляю-
щих сигнала по усилительному тракту.
□ Полосовой фильтр характеризуется двухсторонне ограниченной поло-
сой пропускания . WnJ (рис. 2.6, е) и используется для избира-
132
тельного выделения полезного сигнала нужной частоты из смеси раз-
личных сигналов и шума. Примером полосового фильтра с узкой по-
лосой пропускания может служить колебательный контур радиопри-
емника, настраиваемый на частоту сигнала желаемой радиостанции.
□ Заграждающий (режекторный) фильтр с двумя полосами пропускания
|0, Wnil и (рис. 2.6, г) предназначен для вырезания из сигнала
нежелательных гармоник в полосе частот (ц,|, ц^). Показательными
примерами таких устройств служат фильтры подавления в звуковом сиг-
нале колебаний сетевой частоты 50 Ги или шипа иглы звукоснимателя в
проигрывателе виниловых фампластинок.
2.2. Частотные характеристики
типовых звеньев
Типовые звенья - это элементы, передаточные функции которых имеют в
числителе или знаменателе полином минимальной (от нулевой до второй)
степени с действительными коэффициентами:
□ безынерционный усилитель нулевого порядка с передаточной функцией
□ дифференцирующее звено первого порядка с передаточной функцией
Щх) = Лг.
а форсирующее звено ИТх) = Ml + ТУ); первого порядка с передаточной функцией
а интегрирующее звено первого порядка с передаточной функцией
а апериодическое звено W 1 + ТУ первого порядка с передаточной функцией
функцией
□ форсирующее звено второго порядка с передаточной
IHj) « К( 1 + 2£7У + Г?);
□ колебательное звено второго порядка с передаточной
W(,)------
нащ+тУ
функцией
звено чистого запаздывания с передаточной функцией W(,)= ° .
Частотные характеристики элементов и систем управления
133
Буквенные параметры передаточных функций типовых звеньев должны
удовлетворять следующим условиям.
□ Значения коэффициента усиления К и постоянной времени Т могут быть
любого знака. Типовые звенья с Т< 0 принято называть неминимально-
фазовыми в том смысле, что их фазочастотные характеристики отклоне-
ны от характеристик аналогичных звеньев с положительными постоян-
ными времени Т и левыми корнями полиномов передаточных функций.
□ Коэффициент затухания (демпфирования) звеньев второго порядка
0s£< 1. При 1 полином 1 + 2!j7J + 7V имеет два действительных
корня и две постоянных времени
Следовательно, он может быть разложен на произведение простых мно-
жителей:
1 + 2t,Ts + TV = - j,)(j - д>) “ (1 + Пл)(1 + TiJ), (2.8, 6)
а звено с таким полиномом в числителе или знаменателе передаточной
функции не является типовым: его можно заменить последовательным
соединением двух форсирующих или апериодических звеньев первого
порядка.
□ Время запаздывания т > 0 Далее и впредь до особого упоминания мы бу-
дем рассматривать элементы и системы без запаздываний, т. е со значе-
нием т = 0.
Поскольку любой действительный полином степени л > 2 имеет п корней, а
его комплексные корни всегда попарно сопряжены, то не существует типо-
вых звеньев с полиномами третьей и более высоких степеней: такие пати-
номы всегда можно представить произведением полиномов первой и второй
степеней.
& Пример 2.1, Рассмотрим этапы построения частотных характеристик
типовых звеньев на примере апериодического звена с передаточной
функцией
1 Получим комплексную частотную характеристику, подставив в переда-
точную функцию J = jox
Pb(u)+)Qi№ к
i+j7to
134
Глава 2
2. Получим вещественную и мнимую частотные характеристики, умножив
полиномы B(ju) и на комплексно-сопряженный полином Л(-j<o):
=р(ю)+je((o)= к-»™>
/л(ш)+0л(“) 1+Т2ш2
Построим в равномерном масштабе частот графики вещественной Р(ш)
(рис. 2.7, о) и мнимой 0(ш) (рис. 2.7, б) частотных характеристик:
р(л Рв^л^+Ов^л^) = К
^л(“)+Йл(м) 1+Т2ш2 ’
п(.Л Ов(<о)РЛ(о))-Ра(ш)2л(ш) = -МЪ
/эл(и)+2л(ш) 1+Г2со2
Опорные точки для ручного построения этих графиков:
• при ш - 0 графики начинаются в Я(0) = К и 0(0) = 0;
• на средней частоте ц. = 1 /|7] вещественная частотная характеристи-
ка проходит через точку Р(Шс) = 0.5Z, а мнимая Q(u>c) = -sgn(7) 0.5К
достигает экстремума - минимума при КТ > 0 и максимума при
КТ<Ъ.
• в пределе ш -> ~ оба графика сходятся к нулю.
Годограф Л(<р) как функция параметра ш g |0, ~) удовлетворяет уравнению
Частотные характеристики элементов и ।
135
полуокружности с радиусом 0.5|А| и центром (0.5К, 0), находящейся в со-
ответствующем квадранте, определенном знаками Р(ш) и 0(ш) (рис. 2.8).
Опорные точки годографа:
• при w = 0 он начинается в точке (К, 0);
• на частоте ш = график проходит через точку (0.5К, -sgn( 7) 0.5/0;
• в пределе ш -»•» годограф сходится в начало координат.
4. Построим в равномерном масштабе графики амплитудной Л(<о)
(рис. 2.9, а) и фазовой <р(ш) (рис. 2.9, б) частотных характеристик. Осо-
бое внимание следует обратить на расположение графика фазочастотной
характеристики в зависимости от знаков чисел К и Т:
A(fo) = ^P2(u>)+Q2(w) = . 1*1 ,
Vl + Т ш2
I-arctg(7o>) при К >О,
- arctg(7"(o)+180° при К < О, Т > О,
-arctg(Tw)-180° при К <О, Т <0.
136
Гпава 2
Рис. 2 9
Рекомендуется строить графики амплитудной и фазовой частотных ха-
рактеристик в одном и том же интервале частот и размешать их верти-
кально друг под другом для облеггения совместного использования в за-
дачах исследования устойчивости (см. гл. 4).
Опорные точки для ручного построения амплитудной и фазовой частот-
ных характеристик следующие:
• при ш = 0 графики начинаются в точках Л(0) = |Я|, а <р(0> = 0 при
К> 0 и <р(0) = sgn(7) 180° при АС < 0;
• на средней частоте о = ч амплитудная характеристика проходит че-
рез точку
л(“с)=^= = 0-7|Л'|,
а фазовая - через точку <р(ц) = ф(0) - sgn( 7) • 45°;
• в пределе ш -»« амплитуда сходится к нулю, а фаза — к значению
-sgn(AT) • 90°.
Таким образом, полоса пропускания апериодического звена первого по-
рядка равна |0. Эго значит, что данное звено является фильтром низ-
ких частот.
5. Построим графики логарифмических амплитудной (рис. 2.10, а)
Цш) - 20lg|X| - 10lg( I + TV) ’ (2.9, a)
и фазовой (рис. 2.10,6)
I- arctg(Tw) при К >0.
-arctg(T(0)+ ио» при К < 0, Т > 0. (2.9. 6)
_arctg(Tw)~|80° при К <0, Т<о'
Частотные характеристики элементов и систем управления
137
частотных характеристик в интервале частот ые (O.lov, 10ц.|, где проис-
ходят их основные изменения. Логарифмическая фазочастотная характе-
ристика (2.9, б) строится в равномерном масштабе углов и кососиммет-
рична относительно средней точки
Ф(Ч) - 0.5(Ф(0) + Ф(~))-
Рис. 2.10
Задача построения графиков (2 9) облегчается, если сначала провести
асимптотические логарифмические амплитудную и фазовую частотные
характеристики — АЛАЧХ ДДш) и АЛФЧХ Ф3(ш). состоящие из отрезков
прямых линий — асимптот на низких и высоких частотах Асимптотиче-
ская логарифмическая фазочастотная характеристика имеет еще и со-
пряжение на средних частотах.
Низкочастотная асимптота амплитудной характеристики
. . Г 20 lg | X-1 при <0 < <DC.
Ю ” 1201g | АГ | —201g 17* | со приш>шс
на частотах to S гц. получается отбрасыванием в (2.9, а) слагаемого
7V«1, а высокочастотная при ш > Ч. имеющая наклон
-20 дБ / дек, — отбрасыванием слагаемого I « 7W. Частота
(2.10)
138 Глава 2
на которой пересекаются две асимптоты логарифмической амплитудно-
частотной характеристики, называется частотой сопряжения.
Асимптотическая логарифмическая фазочастотная характеристика состо-
ит из низкочастотной (tosO.lc^) и высокочастотной (шг 10ц) горизон-
тальных прямых, соединенных среднечастотной (0. lot < ш < 10ц.) сопря-
гающей прямой с наклоном ±45°/дек. Например, для коэффициентов
К> 0 и Т> 0 асимптотическая логарифмическая фазочастотная характе-
ристика описывается формулой
(0° приш£0.1шс,
-45°-45°lg(7to) при0.1шс <ш< 10о)с.
-90° приш210шс.
О
Главное удобство логарифмических частотных характеристик, помимо
большого динамического диапазона, — возможность их быстрого построе-
ния по передаточной функции любого типового звена без применения каль-
кулятора или ЭВМ благодаря следующим свойствам:
□ логарифмические частотные характеристики одинаковы по форме для
различных значений и знаков параметров К и Т (можно использовать
шаблоны кривых £(ш) и Ф(ш) из плотного прозрачного материала) и от-
личаются лишь ориентацией:
• изменение величины |А) смещает логарифмическую амплитудно-
частотную характеристику по вертикали вдоль оси £;
• изменение величины |7| смещает обе логарифмические частотные харак-
теристики и частоту сопряжения (2.10) по горизонтали вдоль оси Igw;
• изменение знака коэффициента усиления К смещает логарифмиче-
скую фазочастотную характеристику параллельно по вертикали вдоль
оси Ф на ±180°;
• изменение знака постоянной времени Т зеркально отражает логариф-
мическую фазочастотную характеристику по вертикали вдоль оси Ф.
□ нелинейные логарифмические частотные характеристики можно при-
ближенно аппроксимировать асимптотическими, состоящими из отрез-
ков прямых линий и строящимися непосредственно по передаточной
функции эвена.
Логарифмические характеристики строятся путем проведения гладкого со-
пряжения между асимптотами. Вопросы выбора ширины интервала сопря-
жения и величины отклонений логарифмических характеристик от их асим-
птотических приближений рассматриваются в следующем разделе
В табл. 2.2 приведены годографы и логарифмические частотные характери-
стики всех гиповых звеньев
Таблица 2.2
и его ПФ Ms) АФЧХ А(ф) ЛАЧХ Цш) ЛФЧХ Ф(ш)
Безынерционный усилитель К ej К<0 К>0 Ф- 90° Л>0
0*1 1 10 о>
4*1 0 Я<о) = * 1*1 р соы-о o'l 1 Цо>) = 10 ш 201д|К1 -90° Ф(ш)=1 ° V ' [±1 А’<0 ° при К >0 80° при К <0
Дифференци- рующее звено Ks Q‘ К>0 L4 ОДЯ 90° А~>0
о'| 1 10 <0
0 Яш)-0, гк<о Р ОМ - Кш 1 К<1>) = 20Jg|> П + 201дш -90’ Ф(<о)={_9 К<0 0° при К >0 Ю°приА<0
Таблица 2.2 (продолжение)
и.го’пФИЪ) АФЧХ А(ф) ЛАЧХ Цш) ЛФЧХФЫ
Д<0, Г>0 Q А>0. Т<0 ф
‘£ MlelAI W. А«1.7Х> >- А>0 Г«0
Апериодическое А ,ве"° 1+tr Л<0. /<0 М- *>#. Г>0 i7rV‘ -А7ш [.UIg|A| т ф(т) = 'ам>. ги> ^а>^ Л<0Г«>
£Ы и>, |К|<^ч ш 2 дек = 201д|К1 - 101д(1 + Л, = -ЗдБ Г- лс<^Гш)приК > 0 [- 4TCIj(r«>)t 184Гпри* < 0
звено второго порядна 7*/) 1 fa- г/ \1=, 5- OI дту у %? ~ <zl\zH?3 * 101 wm У7» ' п/'Д! t J •» /.(<•)= 3»|<| с | » -Д».6 + 1д;дБ •(»). мд>- 1 1МГ «ф. < < 0
Таблица 2.2 (продолжение)
Звано и его ПФ Ms) АФЧХ А(ф) ЛАЧХ Цш) ЛФЧХ Ф(ш)
*<0^n Wn А>0 /<0
кф
MigiM/A л,
к>0 к<о?мрт г>0 1 ч t 90° - ! Ь Is’ *' ><
звено К /|.т2«21 1 1 уУ * -90° - -180 — А<0. Т<0 ш Т>0
1 ♦ ЦП ♦ т3,2 4-)- \ 1 ^1-rV^ +(2$Л>)2 / ч -2£Л7ш ’Wp№ -1 4) = 201g 1 К I - Olg^l-rV)2 +(2^<»)2] Лг»-6-1д5дБ Ф((0/ = 2£дех ’ f - arclg [ г при К > 0 -aretg ^^-±180 приК<0 1 1-Та'
Таблица 2 2 (окончание)
Звено и его ПФ Ms) АФЧХА(ф) ЛАЧХ Цш) ЛФЧХ Ф(ш)
. А
~
Q‘ К<0
Д' 20lg|A1
-180“
Звено чистого запаздывания «9- ЧК|\0 Яш) ж J ОЫ» Al Р ^К>0 Ксоз(тш) -Ksin(tu>) 0 1 1 Кш) = 10 ш 2О|д|К1 -ЗбЬ* г по 180“ — при К > 0 Г 801 1 - — при К < 0
Наиболее сложными частотными характеристиками обладают типовые звенья
второго порядка (форсирующее и колебательное) с коэффициентом затухания
О < £ < I Этот коэффициент характеризует безвомратные потери энергии:
• в механическом цементе, например, маятнике, — на трение в точке
подвеса и об окружающую среду;
• в электрическом колебательном контуре — на рассеяние тепла в актив-
ных сопротивлениях резисторов и соединительных проводов;
• в пневматическом или гидравлическом элементе, например, в трубопро-
воде. — на нагревание движущейся субстанции из-за изменения в ней
давления и трения о стенки трубы.
От коэффициента затухания 5 очень сильно зависят все свойства колеба-
тельного элемента:
• величина, обратная удвоенному коэффициенту затухания 2Е, называется
добротностью колебательного элемента Q [15, 18. 22| (не путать доброт-
ность с обозначенной такой же буквой мнимой частотной характеристи-
кой!). При 5 0-5 добротность больше единицы и, как видно из
табл. 2.2. на логарифмической амплитудно-частотной характеристике
появляется пик в окрестности частоты сопряжения wt.
• на частоте сопряжения амплитудная характеристика (рис. 2.11. о)
увеличивается по сравнению с начальным значением /1(0) в Q= 1 / 2£ раз;
• частота, на которой амп.
ется частотой реюнанса
называ-
<1>р = шс^1-2£2 Swc.
(2.12)
При 0<£<1/^2 =0.7 резонанс в недодемпфированнам элементе наступа-
ет на частоте, меньшей частоты сопряжения (рис. 2.11, б), а при с, S 0.7
он вообще отсутствует. Колебательный элемент с таким высоким уров-
нем потерь называется передемпфированнылг,
отношение максимального коэффициента усиления а(о>р )= |К|/2^-J1
к статическому усилению /1(0) = |К называется покамте.кч канюатезьности
Частотные характеристики элементов и систем управления
близким к добротности в интервале существования резонанса
О < £ S 0.7 (рис. 2.11, б). Отметим, что практически во всех учебниках по
автоматическому управлению график Л/(с) ошибочно продолжается и да-
лее в область £ > 0.7, увеличиваясь согласно (2.13) до бесконечности при
£-> 1, что противоречит здравому смыслу ввиду отсутствия резонанса в
передемпфированной системе.
Рассмотрим построение частотных характеристик идеатьшмо колебательного
звена, которое в предельном случае 5 -» 0 имеет бесконечную добротность и
называется автока1ебат&1ьным звеном с передаточной функцией
Для определенности примем К> 0 к Т> 0. После подстановки s = jo> в Ифз)
получим комплексную, вещественную (рис. 2.12, а), мнимую (рис. 2.12, о) и
амплитудную (рис. 2.12, в) частотные характеристики:
*v(jw)=—т-е-, Р(ш)=—т-г, С(ш)’О, А(со)=|---“ч~?!
1-ТЖ 1-rV |1-Г2йг|
Особенностью графиков вещественно)! и амплитудной частотных характе-
ристик является наличие разрывов второго рода на частоте сопряжения
ц. = 1 / Т. которая у колебательного звена совпадает с частотой резонанса
Шр, Явление резонанса проявляется в избирательном усилении колебаний с
частотой Ыр, имеющихся во входном сигнале. В гл. 3, посвященной изуче-
нию временных характеристик элементов и систем управления, будет пока-
зано, что при подаче на вход автоколебательного звена гармонического ко-
лебания с частотой uij, амплитуда выходного колебания неограниченно воз-
растает во времени, что и соответствует значению А(оц>) = <» — отсутствию
установившейся амплитуды.
Нулевая мнимая частотная характеристика С(ш) означает, что график годо-
графа Bjju)) проходит только по действительной оси Р, начинаясь в точке
(К, 0) и заканчиваясь в начале координат (рис 2.12, г). Он также является
разрывным:
• при со —»— 0 годограф удаляется в точку (+<», 0), т. к. Р(и>) > 0;
• при ш -+ + 0 годограф продолжается из точки (-“, 0), т. к. Л“) < 0;
• на частоте ш = щ наблюдается разрыв годографа из-за того, что
1-Г2ш2=0 и функция Лш) имеет разные знаки на интервалах частот
|0, ц.) и (<ц, При использовании годографа для анализа устойчиво-
сти он должен быть непрерывным. Для этого ветви комплексной час-
тотной характеристики Н'Ою) на частоте разрыва Щ соединяются пунк-
тирной дугой бесконечно большого радиуса в отрицательном направлении
(по часовой стрелке).
Частотные характеристики элементов и систем управлений
Логарифмические частотные характеристики автоколебательного звена так-
же являются разрывными:
• амплитудная характеристика
Д(ш) = 201gXf - 20lg|l - 7М
состоит из двух ветвей, устремленных на частоте резонанса в бесконеч-
ность (рис. 2.12, д), в связи с чем в асимптотической характеристике
к двум асимптотам с наклонами 0 дБ / дек и -40 дБ / дек добавляется
третья асимптота — дельта-функция 8(<о - <ц);
• фазовая характеристика
ф J 0°приш<шс.
[-180°прн<о>ц.
на частоте резонанса скачкообразно изменяется на -180’(рис. 2.12. е).
Это явление называется переворотом фазы.
Скачки фазы на +180° и -180°, вообще-то. эквивалентны, поэтому при руч-
ном построении фазовой характеристики будем усювно считать, что у фор-
148 Гпава 2
сируюшего звена второго порядка с передаточной функцией W(s) = 1 + TV
скачок фазы составляет +180°, а у автоколебательного звена с передаточной
функцией Щт) 1 / (I + 7V) он равен -180°.
При машинном построении частотных характеристик соседние точки на
дискретных частотах ш; и мм по умолчанию соединяются отрезками пря-
мых, разрывы исчезают, а характеристики оказываются неверными. Вот по-
чему нельзя всецело полагаться на правильность компьютерных расчетов по
общим формулам в отдельных частных случаях, например, при построении
частотных характеристик звеньев второго порядка при £ -> 0. Понимая
сущность происходящих явлений, нужно в этих случаях предусматривать в
программах специальные способы обработки данных, например, раздельное
построение ветвей разрывных графиков.
Типичный пример бездумного применения теоретически верной форму-
лы — построение фазочастотной характеристики непосредственно по
формуле (2.6), используя имеющуюся в большинстве языков программи-
рования функцию арктангенса atan(x) с одним аргументом
х= 0(ы) / А и) Почему-то многие часто забывают, что эта функция воз-
вращает главное значение угла в интервале <р е (~л / 2, я/ 2). Она не чув-
ствует всех четырех сочетаний знаков вещественного числа Р(ш) и
мнимого числа С(ш), правильно рассчитывая фазу комплексной точки
только в первом и четвертом квадрантах, где Р(ю) > 0. Из-за этого при-
ходится при Лш) < 0 делать коррекцию возвращенного угла путем его
смешения на sgn(Q(o))) 180°. Вообще невозможно с помощью функции
atan вычислить фазовый угол точки И^й) на мнимой оси с нулевой дей-
ствительной частью Р(и>).
Гораздо более эффективным представляется использование другой функ-
ции вычисления арктангенса, работающей с двумя аргументами Р(и>) и
0(ш). В Mathcad |19| и многих языках программирования эта функция
называется atan2(x.y) и возвращает значение угла комплексного числа
х + jy а интервале ф € (-я, я| с учетом обоих знаков аргументов х и у
В Mathcad есть еше одна подходящая функция arg(z) вычисления фазо-
вого угла <р е (-я, я] комплексного числа z = х + jy. Применение функ-
ций atan2 и arg гарантирует правильность построения фазочастотных
характеристик в интервале (-180*. 180*1. кУда умещаются фазочастотные
характеристики всех типовых звеньев до второго порядка включительно.
На рис. 2.13 приведен листинг Mathcad-программы расчета и построения
графиков частотных характеристик колебательного эвена с коэффициен-
том усиления К = 2, постоянной времени Г= 0.05 с, резонансной часто-
той ох, = 20 рад / с (/р = 3.2 Гц) и коэффициентами затухания £ е {0, 0.1.
0.25, 0.5, Ц.
Частотные характеристики элементов и систем управления
Рис. г 13
2.3*. Погрешности аппроксимации
логарифмических частотных характеристик
типовых звеньев
Исследуем абсолютные погрешности
ДДш) = Цш) - £0(ш).
ДФ(<о) = Ф(ш) - Ф„(ы)
аппроксимации нелинейных логарифмических частотных характеристик с
помощью асимптотических характеристик типовых звеньев первого и второ-
го порядков с коэффициентами усиления К > 0 и постоянными времени
Т> 0. Для других знаков чисел К и Г характеристики приведены в табл. 2.2.
В анализе будем использовать нормированную логарифмическую частоту
w=lg(Tw)=lg—,
шс
гае = I / Г— частота сопряжения. Нормировка масштабирует интервал
частот о»е [O.lot, lOod в интервал we [-1, 1) и позволяет глубже понять
свойства погрешностей логарифмических характеристик. Переход от лога-
рифмических частотных характеристик £(<о) и Ф(ш) к нормированным L(w)
и Ф(») осуществляется путем подстановки
7Ъ= 10«.
Апериодическое звено с передаточной функцией vv(5)=]7^
Нормированная логарифмическая амплитудно-частотная характеристика
апериодического звена
Z(w)’201gA'- 101g(l + 10’“)
аппроксимируется двумя прямыми (рис. 2.14, л):
, . [ 201g К Viv S 0 - горизонтальная прямая .
Z_lwl = (
| 201gK’-20w Vw» 0-прямая с наклоном-20 дБ/дек .
Погрешность ее аппроксимации находится следующим образом:
• на низких частотах » < 0 очевидно, что Д£(о>) = - l0lg(I + 102“);
• на высоких частотах w > 0 получим
ДЦ») - -IOIg(l ♦ IO2") + 20w - -lOlgd + 1Q1-) - l0lg(I0-2*) - -I0lg(l0-’* + 1).
Частотные характеристики элементов и систем управления
151
Таким образом, погрешность аппроксимации логарифмической амплитуд-
ной характеристики апериодического звена есть четная функция частоты
Д4(н») = -10lg(l + 10-2М)
и имеет наибольшее отклонение на частоте w = 0, т. е. о> = «ь (рис. 2.14, б):
Л, = ДЦО) =-!0lg2 =-3 дБ. (2.15)
О дБ/дск
2Qt
Рис.2 14
На расстояниях йд = ±1 дек отклонения равны
Д4(Йд) = IOlgl.01 = -0.0432 дБ,
что составляет 1.44% от Л(. Таким образом, логарифмическая амплитудно-
частотная характеристика отличается от асимптотической логарифмической
амплитудно-частотной характеристики в основном на интервале частот
сое |0.lufc, Ютц.) шириной 2 дек вокруг частоты сопряжения ч
Аппроксимируем логарифмическую фазочастотную характеристику
Ф(ю) = -arctg(10*)
тремя прямыми с неизвестным пока параметром £Х» (рис. 2.15, а):
0° Vw S -йф - горизонтальная прямая.
Фа(н,) =
- 45*11 + j V - йф < н- < Йф - наклон - 45/йф град/лек,
- 90° Viv & -йф - горизонтальная прямая.
иг
Гпава 2
Нечетная функция погрешности аппроксимации фазовой характеристики
(рис. 2.15, б)
ДФ(») =
-arctg(lO“)VH’S-fl0,
-arctg(10“j+ 45°fI+^-j V - < w < Пф, (2.16)
-arctg(10“)+90° tf *>$!<„
Рис. 2.15
существенно зависит от О» — полуширины среднечастотной части логариф-
мической фазочастотной характеристики. Оптимальное значение этого па-
раметра находится решением минимаксной задачи
=ar8| min тах|Дф(к] j. (2.17)
Данная запись означает следующий алгоритм определения О*.
I. Задается значение О» и по формуле (2.16) строится график функции
2. Находится максимальная погрешность аппроксимации логарифмиче-
ской фазочастотной характеристики
max ДФ = шах|ДФ( »v)|.
Частотные характеристики элементов и систем управления
3. Пункты / и 2 повторяются для разных и из всех значений шахДФ
выбирается минимальное Соответствующее ему значение О® является
решением минимаксной задачи поиска оптимальной полуширины сред-
нечастотной части асимптотической логарифмической фазочастотной
характеристики.
Так как функция |ДФ(н')| не является гладкой ни по аргументу w, ни по па-
раметру Йф, то решение задачи (2.17) может быть найдено только численны-
ми методами на ЭВМ, что и было сделано с помощью программы на языке
Mathcad. Результаты расчетов приведены на графике тахДФ(О«) (рис. 2.16)
и дают оптимальную полуширину среднечастотной части логарифмической
фазочастотной характеристики О® = 1.013 дек с минимаксной погрешностью
ДФ = 5.534°. Для удобства вполне приемлемо использовать значение
О*» 1 дек, при котором погрешность аппроксимации логарифмической
фазочастотной характеристики нс превышает 5.7Г или 6% от полного ин-
тервала изменения фазы |Ф(“=) - Ф(0)| = 90°
Выводы
• Логарифмические частотные характеристики типовых звеньев первого
порядка с передаточными функциями К (I + Ts) и А' / (1 + ТУ) хорошо
аппроксимируются асимптотическими характеристиками (см. табл. 2.2)
с максимальными погрешностями по амплитуде 3 дБ и фазе 5.7°.
* Ширина среднечастотной части логарифмических характеристик равна
2 дек вокруг частоты сопряжения ut “ 1 /1Т).
Колебательное звено с передаточной функцией
' 1 + 25TS + T1?
Нормированная логарифмическая амплитудно-частотная характеристика
колебательного звена
Д*.« = 201g/T - 10lg((l - Ю2*)2 + 441 102*)
аппроксимируется двумя прямыми (рис. 2.17, о):
{201gК tfw<0-горизонтальная прямая,
201g К - 40w Vie > 0 - прямая с наклоном - 40 дБ/дек.
Четная по частоте функция погрешности аппроксимации амплитудной ха-
рактеристики звена второго порядка
АДч$) = -IOlg((l - 10’W + 442 - IO’2!*!)
зависит как от частоты w, так и от коэффициента затухания 0 < 4 < 1. На
рис. 2.17, 6 изображено по одной из симметричных ветвей AZ.(w, 4) № раз-
ных значений На частоте сопряжения отклонения логарифмической ам-
плитудно-частотной характеристики от ее асимптотической формы вычис-
ляются по формуле
л2(4) = АДО, а = -201g(24) => -6 - 20lg4 дБ. (2.18)
«)
Рис. 2.17
Проанализируем построенные на рис. 2.I8, а зависимости погрешностей
Л2(4) и тахАД4)=тах|ДДн’,4)| от коэффициента затухания 4:
• при 0.25 S 4 < I максимальная погрешность аппроксимации амплитуды
не превышает 6 дБ, а вместо нелинейной амплитудно-частотной харак-
Частотные характеристики элементов и систем управления
теристики достаточно строить асимптотическую логарифмическую ам-
плитудно-частотную характеристику;
при 0 < £ < 0.25 нужно обязательно строить реальную логарифмическую
амплитудно-частотную характеристику с резонансным пикам величиной
Aj(^) для колебательного звена или антирезонансной впадиной глубиной
-Aj(4) для форсирующего звена второго порядка;
при = 0 погрешность аппроксимации на частоте сопряжения стремит-
ся в бесконечность. Это означает разрыв амплитудно-частотной харак-
теристики на две ветви
а) б)
Зависимость Яд(£) полуширины среднечастотной части логарифмической
амплитудно-частотной характеристики от коэффициента затухания ё полу-
чим из следующего соображения. При ъ = I колебательное звено эквива-
лентно последовательному соединению двух апериодических звеньев, даю-
щих на частоте Ql = । дек суммарную погрешность аппроксимации
201g 1.01 =-0.0864 дБ. Поэтому мы будем определять значение QH4) по ми-
нимальной частоте, на которой |д£(и', 5)| - 0.0864 Решение этой задачи с
помощью программы Mathcad приведено на графике построенном на
рис. 2.18, б. Видно, что ширина среднечастотной части логарифмической
амплитудной характеристики ни при каких 5 не превышает двух декад, а
при 5 е [0.6, 0.71 — одной декады.
Аппроксимируем логарифмическую фазочастотную характеристику
’Рвмя прямыми с неизвестным пока параметром О» (рис. 2.19, <»):
156
Глава 2
Фл(») =
0° V»v i -йф - горизонтальная прямая,
-wjl + ^-jv-Йф <»<йф -наклон -90/йф град/дек,
-180° V»v & -Оф - горизонтальная прямая.
Нечетном функция погрешности аппроксимации логарифмической фазоча-
статной характеристики
(Ф(н’)Уи^-йф,
ДФ(и’) = Ф(и’) + 90’(1 + w/йф) V - йф < w < йф,
[фМ + ^О’Уи'^йф
изменяется аналогично графику на рис. 2.15, б. Оптимальное значение по-
луширины среднечастотной части логарифмической фазочастотной характе-
ристики Q* находится решением минимаксной задачи (2.17) для каждого
значения
Результаты вычислений в среде Mathcad приведены на графиках ЙФ(5) и
тахДФ(£) (рис. 2.19, б): сплошные графики — оптимальные, пунктирные —
при линейной зависимости от t Видно, что не увеличивая существенно
погрешности аппроксимации шахДФ, вполне приемлемо принять удобное
значение £!♦ = £, при котором 11° < шахДФ < 23.4°, что составляет от 6 до
13% полного интервала изменения фазы |Ф(«>) - Ф(0)| = 180°.
а) в)
Рис. 2.19
Выводы
• Логарифмические частотные характеристики типовых звеньев второго
порядка с передаточными функциями К • (1 + 2\Ts + TV) и
K/(l + 2VA+ 7V) хорошо аппроксимируются асимптотическими ха-
Частотные характеристики элементов и систем упраоления
157
рактеристиками только при 0.25 < < 1 с максимальными погрешно-
стями 6 дБ по амплитуде и 22° по фазе
При 0 $ £ < 0.25 асимптотическую амплитудную характеристику необхо-
димо дополнить резонансной впадиной или пиком величиной Aj = -6 -
20lg£, дБ (см. табл. 2.2).
Ширина среднечастотной части амплитудной характеристики нс пре-
вышает двух декад, а ширина интервала переворота фазы близка к зна-
чению 2$ декад вокруг частоты сопряжения ц. = I /17*|.
2.4. Частотные характеристики
сложных систем
Передаточную функцию системы И^з) можно представить в виде произве-
дения (1.36, в) передаточных функций типовых звеньев Иф), а комплекс-
ную частотную характеристику W^jco) — произведением типовых комплекс-
ных частотных характеристик ИОДы):
и'6ы)=П^6ш)= П =|пА0“)|е ' = Л0<о)в-1ф^
Таким образом, амплитудная, фазовая и логарифмическая амплитудная час-
тотные характеристики системы, представленной последовательным соеди-
нением типовых звеньев, имеют вил
Л(<о)= П А,(оз). <р(из)= Х<р(Н
L(w)= 201g f] А,(ш)= £201gA,(w)=
Возможность суммирования, в том числе и графического, логарифмических
частотных характеристик типовых звеньев изменяет алгоритм построения час-
тотных характеристик сложных систем, который в сравнении с алгоритмом,
строящим частотные характеристики типовых звеньев (см. пример 2.1), те-
перь выглядит следующим образом.
I Найти нули (корни полинома числителя Я(з)) и полюсы (корни полинома
знаменателя Л(.т)) передаточной функции И)л) и представить последнюю
в виде произведения передаточных функций типовых звеньев И'Дз) Ну-
мерация постоянных времени типовых звеньев Г, сквозная по убыванию
модулей |7}|.
2. На частотных осях lgu> выбрать интервал
158
Глава 2
[max|T,|’ min|7] |
округлить его до целого числа декад и нанести возрастающие частоты
сопряжений звеньев = 1 / | FJ.
3. Построить в общих осях (L, lg<o) асимптотические логарифмические ам-
плитудно-частотные характеристики типовых звеньев Lai(w), а в общих
осях (Ф. Igw) асимптотические логарифмические фазочастотные характе-
ристики Фа1(<о).
4. Согласно (2.19) графически сложить Ц/ш) и Фа,(ы), получив
асимптотические характеристики системы Ц(о>) и Фа(ш).
5. С учетом погрешностей аппроксимации построить реальные характери-
стики системы Цш) и Ф(ш).
6. Построить в равномерном масштабе [рафик амплитудно-частотной ха-
7. По графикам А(ш) и Ф(ш) построить годограф комплексной частотной
характеристики W(jw).
8. Отслеживая проекции точек годографа на беи координат, построить в
равномерном масштабе графики вещественной /\ш) = Re{ и мни-
мой Q(°>) ~ 1пт( частотных характеристик.
Наиболее трудоемким является первый этап, требующий расчета корней
полиномов и разложения их на простые множители. Последний раздел гла-
вы специально посвящен этой теме.
Остальные этапы с помощью табл. 2.2 выполняются за 5 + 10 мин для сис-
тем практически любого порядка. После четвертого этапа нужно проверить
правильность построения асимптотических характеристик по расположению
асимптот на низших (при о> -» 0) и высших (при ш -» ~) частотах. Эта про-
верка легко выполняется непосредственно по коэффициентам передаточной
функции системы.
□ На низших частотах ш « I / max|TJ свойства системы близки к свойст-
вам типового звена с передаточной функцией W(s—0), равной'
• Ло / Oq для статических систем, при этом:
• асимптотическая логарифмическая амплитудно-частотная
характеристика 1>(ш) = 20lg|bo / a<J есть горизонтальная прямая.
• асимптотическая логарифмическая фазочастотная характеристика
Фа(<о) начинается с угла 0" при Д) / > 0 или с ±180° при Ьц / ао < 0;
• / оо. «ели полином числителя передаточной функции
159
Частотные характеристики элементов и систем управления
B(s) = + bk+\S + + Ь^-*)
имеет к нулевых корней, при этом:
• асимптотическая логарифмическая амплитудно-частотная ха-
рактеристика Да(ш) = 201g|At / flol + 20*tgw проходит через
точку La(l) = 20lg|/>* / яо1 с наклоном +20* дБ / дек;
• асимптотическая логарифмическая фазочастотная характери-
стика Фа(ш) начинается с угла 90% при Ьк / а0 > 0 или с угла
90% ± 180° при Ьк/ а0< 0;
• Г*Ьо / в*, если полином знаменателя передаточной функции
A(s) = ?(fl* + + + aZ’*)
имеет к нулевых корней, при этом:
• асимптотическая логарифмическая амплитудно-частотная ха-
рактеристика Z.a(a>) = 2Olg|Ao / fl*] - 20*lgw проходит через
точку Z.j(I) = 2OlgjAo / в*| с наклоном -20* дБ / дек;
• асимптотическая логарифмическая фазочастотная характери-
стика Фа(ы) начинается с угла -90% при Ло / а* > 0 или с уг-
ла -90% ± 180° при Ьо / о* < 0.
□ На высших частотах ш » 1 / min|T,| свойства системы близки к свойст-
вам типового звена с передаточной функцией W(s-»~) = sm*nbm/an, у
которого:
• асимптотическая логарифмическая амплитудно-частотная характери-
стика Д,(ш) = 201g|Z>„ / а„| + 20(от - n)lgw проходит через точку
Д,( 1) = 20lg|Z>„, I а„ | с наклоном 20(л* - л) дБ / дек;
• асимптотическая логарифмическая фазочастогная характеристика
Фа(ш) сходится к углу 90°(л> - л) при bm / а„ > 0 или к углу
90°(/и - л) ± 180° при Ь„/ а„< 0.
Проиллюстрируем на рис. 2.20 аддитивный метод построения логарифмиче-
ских характеристик на примере схемы (см. рис. 1.44) с передаточной функ-
цией
И'(г)=у^,тг°, 7% 0,
представляемой произведением передаточных функций двух звеньев первого
порядка — неминимально-фазового форсирующего и апериодического
И'Нз) - I - V,
1+Гз
Фазочастотные характеристики обоих звеньев Ф|(<о) и Ф*(ш) изменяются от
О" до -90", так что их сумма Ф(<о) = Ф|(ш) + Фз(а>). начинаясь в О', сходится
к -180'. Это означает, что на низких частотах входное и выходное колеба-
ния напряжений совершаются примерно синфазно, а на высоких — почти в
противофазе.
Амплитудная характеристика Цы) = £|(ш) + Lj(<d) в зависимости от соот-
ношения постоянных времени г и Т, определяющих расположение частот
сопряжения ох = 1 / т и (i)p= I / Т, имеет следующие частотные свойства
□ При т < Т (рис. 2.20, а) подъем составляющей L|(w) начинается позже
спада, обусловленного составляющей 1-2(ы). В результате коэффициент
усиления схемы уменьшается с единицы на низких частотах до т / Т < I
на высоких.
□ При т > Т (рис. 2.20, б) спад составляющей Ез(ы) начинается позже
подъема, обусловленного составляющей Li(u). В результате коэффици-
ент усиления схемы увеличивается с единицы на низких частотах до
т/Т > I на высоких
□ При т = Т (рис. 2.20, в) подъем и спад составляющих L|(w) и L2(w) про-
исходят на одних и тех же частотах и компенсируют друг друга. В ре-
зультате коэффициент усиления схемы в установившемся режиме по-
стоянен и равен единице. Поскольку фазовый сдвиг изменяется с
ростом частоты входного сигнала, такая схема называется фазовра-
щателем. Это хорошо видно по графикам входного х(/) и выходного
у(0 колебаний на частотах а)=0.1шг (рис. 2.20, г) и o)=10<i>7-
(рис. 2.20. Л Для правильного ориентирования во времени на гра-
фиках отмечены отсчеты г=ЗГ времени установления постоянных
параметров выходных колебаний
I и систем управления
Рис. 2.20
& Пример 2.2. Построить логарифмические частотные характеристики схе-
мы моста Вина - Робинсона (см. рис. 1 32) с передаточной функцией (114)
wfrh г 1 + Г2*2 X,
з(1 + ЗП+Т2?)
постоянная времени которой Т соответствует частоте сопряжения
/с = 50 Гц.
Решение
1 Прежде всего вычислим значение постоянной времени:
— = —= 3.183 мс.
2nfc 100л
Полином знаменателя передаточной функции A(s) имеет действительные
корни
f|2 = ~-3±^ = {-120. -822.5}
и разложение на простые множители
A(s)=p-~p~p(J+^Xi+^)
с постоянными времени
Г1=2±^Т-8333мс, Т,=^Г = 1.216мс.
1 2 2
причем Г, Т2 - Р. Таким образом, передаточная функция имеет разло-
жение
Глава 2
1 + Г2д
на два апериодических звена и предельный случай форсирующего звена
второго порядка с коэффициентом затухания 5 = 0.
Обозначив частоты сопряжения логарифмических амплитудно-частотных
характеристик типовых звеньев как
<Hi = 120 рад / с, (^ = 314 рад / с, «из = 822.5 рад / с,
построим в частотном интервале ше [1. 10s] асимптотические логарифми-
ческие амплитудно-частотные характеристики Ди, 4о, 412 (рис 2.21, о) и
логарифмические фазочастотные характеристики Ф3ь Ф3о, Ф32 (рис. 2.21, б).
Согласно (2.18) и табл 2.2 асимптота 4о стремится на частоте ц. в
График Фао на этой же частоте претерпевает скачок фазы с 0° до +180°.
Рис. 2.21
Частотные характеристики элементов и систем управления>63
Просуммировав асимптотические характеристики, получим графики Z.u и
Фо, а с учетом погрешностей аппроксимации — графики Цы) и Ф(ю) □
Вместо графического сложения асимптотических характеристик типовых
звеньев можно использовать другой прием ручного построения логарифми-
ческих частотных характеристик сложных систем.
1 Вычислить, пронумеровать по возрастанию частоты сопряжения звеньев
^=1/17,1 и нанести на осях Igw условные обозначения (наклонные
риски) перегибов асимптотических характеристик согласно табл 2.2:
• у амплитудного графика на частотах
• у фазового графика на частотах ± Л*.
2. Построить начальные асимптоты амплитудной и фазовой характеристик
для предельной передаточной функции Щз -» 0).
3. Продвигаясь по осям частот слева направо, изменять наклоны асимптот
логарифмических амплитудно-частотных характеристик на частотах <ц(,
а наклоны асимптот логарифмических фазочастотных характеристик на
частотах ± А».
4. Проверить правильность построения логарифмических характеристик на
высших частотах по предельной передаточной функции -»<»).
& Пример 2.3. Построить все частотные характеристики системы с переда-
точной функцией
z 50з + 99? >4998з3-100/
W -400 - 80005+96Г +1920? +з4 +20з5
I Разложим полиномы передаточной функции на простые множители
JFJU) = Kts, Kt - -0.125 = -2-’, £|(l) = 201sf*i| = -18 дБ. Ф,(0) = -90°;
И'зО)=1 + 2^T3s+T32a\ Ty~ IOc.bh-O.I рад / c, • 0.1;
164
Глава 2
И'40=7Цг-. Д = 0.5 с, 44 = 2 рад / с;
1 + Т4л
И5(j) = I - Zjj, Г7 = 0.02 с, 47 = 50 рал / с.
2. Выберем частотный интервал ше (0.001, 100] и отметим на осях Igw
частоты сопряжения 42 + 47 и риски перегибов асимптотических ха-
рактеристик (рис. 2.22, о, й).
3. Для низкочастотного предела передаточной функции
‘V(w0)=^ = '°125i = W',(j)
построим начальные асимптоты логарифмических характеристик:
Дп1<ш) = 201gw - 18 дБ, Ф0|(<о) = -90’
4. Двигаясь вдоль осей Igw слева направо, изменяем наклоны графиков
4(к>) и Фа(ш) согласно нанесенным рискам.
5. Проверяем правильность построения асимптотических логарифмических
частотных характеристик по высокочастотным асимптотам:
IV(4 -»<»)=— => 4(Ш) = 14 - 201go>aB, Ф,(ш) - 90° » -270°
s
6. Строим реальные логарифмические характеристики, сглаживая переги-
бы асимптотических характеристик с учетом погрешностей аппроксима-
ции (2.15) и (2.18). На частоте 43 амплитудная характеристика имеет
свойства форсирующего звена второго порядка с коэффициентом зату-
хания •= 0.1:
• резонансную впадину величиной ДД = 6 + 201g(0.1) = -14 дБ;
• ширину интервала переворота фазы 2Пф = 0.2 дек.
На частоте 4<, характеристики имеют свойства колебательного звена с
коэффициентом затухания = 0:
• разрыв амплитуды £(а>) на две ветви;
• скачок фазы Ф(ы) на ДФ = -180°.
Частотные характеристики элементов и систем управления
Рис. 2.22
7. График амплитудно-частотной характеристики Л(ш) (рис. 2.23, а), начи-
нающийся и заканчивающийся в нуле, также имеет разрыв второго рола
на частоте <ц.6. На графике отмечены точки с единичной амплитудой.
8. Годограф WO’co) (рис. 2.23, б) начинается и заканчивается в начале
координат, а на частоте шсб разрывается на две ветви Первая ветвь
асимптотически стремится в бесконечность под углом
Ф(и\:б - 0) — -11.14. Вторая ветвь выходит из бесконечности под
ГлаваS
углом Ф((1\:б + 0) = Ф(о^6 - 0) - 180° =-191.14°. Ветви соединены
пунктирной дугой окружности бесконечного радиуса в отрицательном
направлении.
На графике годографа отмечены точки его начала, конца и пересечения с
окружностью единичного радиуса
Рис. 2.23
4. Проходя по годографу, строим графики вещественной Р(ы) (рис. 2.23, в)
и мнимой 0(<о) частотных характеристик (рис. 2.23, г).
□
& Пример 2.4. Построить асимптотические логарифмические характери-
стики и годографы системы «тележка - маятник». Единицы измерения пе-
ременных: И = Н. |</| = см. [<p| = град.
Решение Применим без лишних слов методику, изложенную в примере 2.3.
□ Система с перевернутым маятником имеет следующие разложения пере-
даточных функций (I II) на простые миожители и параметры частотных
характеристик (рис. 2.24):
Частотные характеристики элементов и систем управления
100(б0-8д-8?)
600s+940s2 -216s3-100s4
lO(l-T2sXl + T4j) см
s(i + r,sXi-^Xi+r5s) Н '
ц, (Л______________180-6Г___________
Ф ’ " n(600s + 940s2 - 216s3 - 100s4)~
0.573s град
(l + T,sXl-T,sXl + r5s) H '
(2.20, о)
(2.20, б)
Г| = 1.72 с. Ц;| = 0.58 рад/с;
72 = 0.438 с, сна “ 2.28 рад / с;
Г3 -0.397 с, (^j = 2.52 рад/с;
7i = 0.305 с, Ц;4 = 3.28 рад / с;
7j = 0.244 с, tuts = 4.1 рад / с.
Глава 2
Рис. 2.24
□ Раагожения передаточных функций (1.12) и параметры частотных харак-
теристик (рис. 2.25) системы с обычным маятником следующие:
G) - 100(б0 + 8т + 8?) _
d " 600s+ 1100?+ 216? +100s4 .
/ , й (2.21, а)
_ 1(Д1+ 2^т72$ + TVs у см
^С + Г^ + З^ + Т,2? ) Н '
W9(s) ------------------------------
n|600s+ 1100?+ 216?+100s4 J (221 Q
0.573s________град
(1 + 7-Д + 2$37-}т + Г,2?) Н •
Г, = 1.678 с, <%| = 0.596 рад / с;
Г2 - 0.37 с, (Ц2 = 2.74 рад / с, = 0.18;
Tj - 0.315 с, <цз = 3.17 рад / с, Ь = 0.246.
о
Продолжим обсуждение вычислительных аспектов машинного построения
частотных характеристик, но теперь уже на уровне сложных систем. Глав-
ным образом, это касается правильного построения фазочастотной характе-
ристики ф, = ф(о>,) на всем заданном дискретном множестве частот ш,. Ни
одна из имеющихся в языках программирования стандартных функций ие в
состоянии возвратить результат ф, вне интервала (-я. я|, г к он формирует-
ся не только текущими значениями Лю,) и ®Ч), но и всей предысторией
углов Фу V/ < i. То, что фазовые характеристики могут выходить из интерва-
ла (-я, я|, доказывает график рис. 2.22, б.
Прямое использование в Mathcad-программе функций аеапз или azg при-
водит к тому, что при пересечении графиком фазовой характеристики ф(ы)
(или Ф(ш)) уровней ±180’ наблюдается скачок угла Аф, = <₽,., - ф, при&шзи-
metuHO на +360° (знак скачка противоположен направлению пересечения)
Таким способом на рис. 2.26 построена логарифмическая фазочастотная
характеристика системы с запаздыванием, имеющей передаточную функцию
Глава?
с параметрами Г, = 10 с, Г2 = 1 с, 4 = 0.5 и т = 0.01с. Из трех типовых
звеньев, составляющих данную передаточную функцию, первым «тянет,
фазу вверх на +90° от ее начального нулевого уровня форсирующее звено с
постоянной времени Г|. Далее подключается неминимально-фазовое коле-
бательное звено, дополнительно изменяющее угол на +180°. Наконец, после
частоты ш > 10 рад/с фазовый сдвиг резко уменьшается звеном запаздыва-
ния. На (рафике теоретически гладкой зависимости Ф(ю) хорошо заметно
присутствие скачков.
О Т1:=10 T2s»l 4“0.S г := 0.01
Ликвидировать ошибочные фазовые скачки можно с помощью следующего
алгоритма численного расчета и коррекции фазочастотной характеристики.
I Рассчитать углы ф( V / = 0. л на всех желаемых отсчетах частотного ин-
тервала с помощью стандартных функций acanz или arg, т. с. без кор-
рекции скачков.
2. В цикле I = I, и проверить значение скачка Д<р = ф/ - ч>/— । и при выпол-
нении условия |Дф| > 270° сдвинуть все оставшиеся отсчеты углов
фу V п на величину -эдНДф) • 360“.
Частотные характеристики элементов и систем управления 171
Для обнаружения ложного скачка фазы величиной примерно ±360° выбрано
пороговое значение 270°, благодаря которому остаются в неприкосновенно-
сти имеющие право на существование скачки +180°, свойственные типовым
звеньям второго порядка с параметром £ = 0.
Иллюстрация правильной работы алгоритма приведена на рис. 2.27. Вычис-
ление и коррекцию фазочастотной характеристики выполняет функция
согф(И,ш;, формальными аргументами которой являются имя передаточной
функции W(s) и массив отсчетов частот о». на которых строится фазовая ха-
рактеристика.
TI:» 10 Т2 > I 5 ••= 0 5 т > 0.01
du:-0 001 п—ccilG.Jdu ') l:»0.. n ajj 10
360sign<A)
Рис. 2 27
172
2.5. Частотные свойства замкнутых систем
Принцип обратной связи лежит в основе создания замкнутых систем управ-
ления, обладающих заданными характеристиками. Продолжим, теперь уже в
частотной области, начатое в разд. 1.7 исследование влияния отрицательной
обратной связи на свойства системы, образованной охватыванием элемента
с передаточной функцией ИДО обратным контуром через элемент с переда-
точной функцией H'o(j) (см. рис. 1.33, в).
2.5.1. Частотные характеристики систем
с отрицательной обратной связью
Основное соотношение, связывающее частотные характеристики разомкну-
той и замкнутой систем, получим путем подстановки .? = jo> в формулу
(I.20, в) с верхним знаком «+» в знаменателе:
%G®)=-------(2.22)
’ i+WiGto^Gw)
Мало что в этой обманчиво простой формуле говорит о ее магических воз-
можностях для анализа и конструирования. С целью выявления этих воз-
можностей обозначим контурную передаточную функцию разомкнутой сис-
темы между точками е и z как
ИДО = ИДО ИДО, (2.23)
контурную комплексную частотную характеристику как (ОДю) и контурную
амплитудно-частотную характеристику как Лк(ы) = I В зависимости
от глубины обратной связи, устанавливаемой условием (1.24), рассмотрим
характерные случаи прохождения контурного годографа WK(ju>) по комплекс-
ной плоскости (рис. 2.28).
Частотные характеристики элементов и систем управления___________1_73
□ На частотах, где выполняется условие глубокой отрицательной обратной
связи |» I, контурный годограф отстоит от начала координат
очень далеко, а частотная характеристика замкнутой системы
ЙХ“’
близка к инверсной частотной характеристике элемента обратной связи
%(т) и практически не чувствительна к вариациям параметров элемента
прямой цепи ^(5). Это полезное свойство глубокой отрицательной обрат-
ной связи нами рассмотрено выше, а здесь отметим, что основной вклад
в степень глубины обратной связи в правильно спроектированной систе-
ме должен вносить большой коэффициент усиления элемента ^(5), но
не элемента %($), задаваемого инверсным к желаемой передаточной
функции замкнутой системы H^s).
Если элемент И^т) охвачен отрицательной обратной связью через стати-
ческий элемент Wo(s) = <1 (рис. 2 29, а), то передаточная функция замк-
нутой системы согласно (2.24, а) близка к значению 1 / /Co Уставка #(/) с
полосой частот, на которой усиление элемента прямой цепи такое, что
Л1(в>) » 1 / Ко или £|(ш) > 20 - 20lgA'„ дБ,
отрабатывается следящей системой с масштабированием
y(i)=g(i}/Ko
без искажения формы сигнала (рис. 2.29, б).
Это явление лежит в основе принципа конструирования высококачествен-
ных усилителей с отрицательной обратной связью: для получения стабиль-
ного коэффициента усиления К усилитель с большими, но нестабильны-
ми на разных частотах и во времени коэффициентами усиления
4|(<о) = |H/|(jw)| охватывается цепью отрицательной обратной связи через
174
четырехполюсник со стабильным коэффициентом усиления Ко = 1 / К.
При выполнении в рабочей полосе частот условий
Л|(ш) » Лили £|(о>) > 20 + 201gAfaE
цель конструирования стабильного усилителя будет достигнута.
Применение глубокой единичной обратной связи (Л"о = 1) при условии
соблюдения других важных условий работоспособности, например, ус-
тойчивости, позволяет создать следящую систему с передаточной функ-
цией Wj(s)= I, отрабатывающую на выходе уставку в масштабе один к
одному. Примером такой системы служит операционный повторитель
(см. рис. 1.24, б).
Еще одно важное техническое применение глубокая отрицательная об-
ратная связь находит при создании инверсных систем — устройств, реали-
зующих прохождение сигнала в обратном направлении (рис. 2.30, а). Де-
ло в том, что лишь очень малый класс пассивных четырехполюсников
(симметричные П- и Т-образные схемы) обладает свойством инверсии —
обратимости свойств при изменении направления распространения сиг-
нала на обратное. Большинство четырехполюсников в обратном включе-
нии либо приобретают другие свойства, либо вовсе не работоспособны.
Для реализации этой возможности и необходимы инверсные системы с
обратными передаточными функциями
Согласно (2.24, а) четырехполюсник с инверсной передаточной функци-
ей W?"i(j) конструируется путем включения устройства 1Г(5) в обратную
цепь усилителя с большим усилением А'у (рис 2.30, б). Благодаря стаби-
лизирующим свойствам глубокой отрицательной обратной связи нерав-
номерность частотной характеристики A"y(jb>) >> I практически не влияет
на качество инверсии.
Рис. 2.30
Перечислим несколько прикладных задач, где могут быть полезны ин-
версные системы:
• аналоговое восстановление входного сигнала некоторого устройст-
ва, например, инерционного датчика, качество работы которого не
Частотные характеристики элементов и систем управления 175
удовлетворяет требованиям разработчика системы управления. Ин-
версная система с электронной моделью датчика в тракте обратной
связи, работающая в идентичных внешних условиях, позволяет по
показаниям реального датчика y(i) восстановить состояние объекта
МО;
• синтез устройства, которое легче и дешевле реализовать в виде
инверсного четырехполюсника и установить в цепи обратной связи
операционного усилителя. Ярким примером такого устройства слу-
жит логарифмический усилитель (рис 2.30, в), статическая характе-
ристика которого приведена на рис. 1.17, б. Включение в цепь обрат-
ной связи операционного усилителя биполярного л-р-л-транзистора с
заземленной базой позволяет улучшить многие недостатки [18] про-
тотипа — диодной схемы на рис. 1.17, а.
□ На тех частотах, где влияние отрицательной обратной связи ничтожно,
т. е. |H^(jco)| « 1, контурный годограф проходит в окрестности начала
координат (см. рис. 2.28), а частотные характеристики разомкнутой и
замкнутой систем близки друг к другу:
= H'iGco). (2.24, б)
Если на этих же частотах усиление элемента прямой цепи малб, т. е. вы-
полняются условия
Л|(ш) « 1 или £|(о») < -20 дБ,
то соответствующие гармоники входного сигнала проходят на выход
замкнутой системы с большим ослаблением. Нельзя сказать, что это все-
гда плохо. Например, ослабление высокочастотных шумов является, оче-
видно, полезным свойством.
При близком к нулю усилении Я|(<о) вне полосы пропускания разомк-
нутой системы можно практически безболезненно удалять из нее ста-
рые или добавлять в нее новые звенья, если это ненамного увеличивает
усиление и не приводит к потере устойчивости замкнутой системы На-
пример, в прямой цепи с логарифмической амплитудно-частотной ха-
рактеристикой Z.|(u>) (рис. 2.31, а) ни удаление двух звеньев с одинако-
вой частотой сопряжения и>( (см. результирующую логарифмическую
амплитудно-частотную характеристику £у(ш)), ни добавление нового
форсирующего звена с частотой сопряжения он (см. характеристику
4з(<о)) практически не изменяет полосу пропускания разомкнутой сис-
темы, ее годограф И^ш) (рис 2.31, б, л) и основные свойства замкну-
той системы.
Глава 2
О
Рис 2.31
Данный эффект лежит в основе метода понижения порядка модели слож-
ной системы путем исключения из ее передаточной функции несущест-
венных звеньев, изменяющих амплитудную характеристику Lt((o) лишь
ниже уровня -20 дБ. Тем самым удается упростить модель системы без
существенного ухудшения ее свойств в сравнении со свойствами реаль-
ного прототипа.
На естественный вопрос: а какой выигрыш мы получаем, понижая поря-
док и точность модели’ — есть, по крайней мере, несколько ответов:
• для моделей невысоких, вплоть до третьего, порядков разработано
множество аналитических методов исследования,
Частотные характеристики элементов и систем управления______________177^
• с такими моделями возможно точное аналитическое, и нс прибли-
женное численное решение многих задач анализа и синтеза;
• существенно облегчается подбор параметров чи< lemroro мол -ч....а
ния системы низкого порядка, полученной исключением высокочас-
тотных звеньев ниже уровня усиления -20 дБ, ограничивающих
сверху допустимый период квантования времени,
• при работе инженера < мо (елями невысоких поря псов сушег .......
помощь ему оказывают интуиция и практический опыт общения с
окружающими системами апериодического (первого порядка) и ко-
лебательного (второго порядка) типов, повеление которых он может
предсказать и без сложных расчетов.
□ На частотах, где |1 + (Ик()о>)| = 0, контурный годограф проходит вблизи
точки (-1, j0) (см рис 2.28). Из (2.22) следует, что на стих частотах уси-
ление замкнутой системы очень велико, а при прохождении голографа
точно через эту особую точку стремится в бесконечность:
(2.24,«)
Таким образом, одним из нежелательных последствий введения отрица-
тельной обратной связи может сто/пь появление в замкнутой системе ре-
зонанса и увеличение колебательности переходных процессов вплоть до
потери устойчивости. Особую роль в исследовании устойчивости замкну-
той системы играет точка на плоскости контурного голографа с коорди-
натами (~l,jO).
& Пример 2.5. Разомкнутая система представляет собой некоторое устрой-
ство с передаточной функцией
ж, (•’)= 1--------------------л
() + И).т + 200.т2Д| + 0.1# + з2^
Проанализировать возможность понижения порядка модели разомкнутой
системы и изменение в результате этого понижения свойств системы, ымк-
нутой единичной отрицательной обратной связью
Решение. Построив логарифмическую амплитудно-частотную характеристи-
ку разомкнутой системы (рис. 2.31, я)
£,(ы)» 20lg4 + (Old --------—-------у-ту----—----------
(|-200ti>7 +100ш* I + 0.01Ш2
определяем из условии Z.((ш,,) - Д|(0) - 3 верхнюю границу се полосы про-
пускания ш,, » 0.1 рад / с. Точка сопряжения асимптот логарифмической
амплитудно-частотной характеристики на частоте о>| - I рад / е лежит не
Глава 2
только вне полосы пропускания, но и ниже уровня -20 дБ. Следовательно,
можно попробовать исключить из модели разомкнутой системы два звена с
передаточными функциями (1 -з) и 1 / (I + 0.1з + s2), а затем сравнить
свойства систем с передаточными функциями W'i(a) и
1 + 10з + 200з2
замкнутых единичной отрицательной обратной связью.
□ Сравнение годографов W|(ju>) и Wjflto) обнаруживает их близость почти
на всех частотах и примерно двукратное удаление годографа упрошен-
ной модели от точки (—!. jO) (см. рис. 2.31, в). Видимо, следует ожидать
увеличения колебательности переходных процессов реальной замкнутой
системы в сравнении с процессами в упрощенной модели.
□ Сравнение амплитудно-частотных характеристик замкнутых систем
L,i(w) и L,j(w) (рис. 2.32, а) также дает основания предсказать повы-
шенную колебательность реальной системы в сравнении с упрошенной
моделью из-за немного большей величины ее первого резонансного пи-
ка Измерив частоту резонанса coj, = 0.16 рад / с, можно по формуле (2.2)
оценить циклическую частоту и период колебаний:
Частотные характеристики элементов и систем управления
Рис. 2.32
□ Сравнение реакций замкнутых систем h,j(t) и h,2<t) на стандартное
входное воздействие в виде единичного скачка
хо-|'"р"'га
[ 0 при г < О
при нулевых начальных условиях (в 41. 3 такая реакция названа переход-
ной характеристикой) подтверждает их близость (рис. 2.32. б) и сделан-
ные выше предположения относительно колебательных свойств реальной
замкнутой системы четвертого порядка и ее упрощенной модели второго
порядка. Благодаря чуть меньшей величине резонансного пика ампли-
тудной характеристики упрощенной модели Л,г(ы) ее переходная харак-
теристика A3i(r) затухает немного быстрее, чем характеристика Л,,(О
О
2.5.2. Расширение полосы пропускания
Рассмотрим еще одно замечательное свойство отрицательной обратной связи
расширять полосу пропускаемых частот охватываемой сю системы. При ана-
лизе будем, во-первых, считать элемент обратной связи статическим с пе-
редаточной функцией
и<,(з) - а;,
Гпааа2
Во-вторых, благодаря совпадению п
систем |Щз), аИ5^)} и соотношению
пропорциональных
^0=
K0Wt(s)
1+*Л|0
жесткая обратная связь с коэффициентом Ко * 1 эквивалентна по полосе
пропускания единичной обратной связи, в связи с чем далее будем полагать
/ч,= 1.
Чтобы понять суть явления расширения полосы пропускания, предполо-
жим, что амплитудная характеристика Л|(ю) разомкнутой системы со ста-
тическим коэффициентом усиления ЛГ| = Л|(0) имеет вид, показанный на
рис. 2.33, о. Верхняя граница полосы пропускания удовлетворяет усло-
вию
Л|(о)|,) =0.7Л’|.
Амплитудно-частотная характеристика замкнутой системы находится по
формуле
(2.25)
Качественно оценим ее значения на разных частотных интервалах:
□ на нулевой частоте по (2.25) получим коэффициент статического усиле-
ния замкнутой системы
1 + К|
Ее полоса пропускания отсчитывается по уровню 0.7Ла(0);
О на частотах, где А1(<о) » 1, по (2.24, а) получаем Аз(ш) - 1;
□ на частотах, где Л|(<о)« 1, по (2.24, б) получаем Ла(ш) = Л|(ш).
Таким образом, каких бы больших значений не достигало усиление ра-
зомкнутого контура, в замкнутой системе с единичной отрицательной
обратной связью оно составляет около единицы. В то же время на часто-
тах с большим ослаблением сигналов амплитудно-частотные характери-
стики разомкнутой и замкнутой систем совпадают. Если на всех частотах
Л|(ш) « 1 либо Д|(ш) < -20 дБ, то расширения полосы пропускания не
наблюдается. Далее нас будут интересовать амплитудно-частотные харак-
теристики, пересекающие уровни единичного усиления ЛДщ) = 1 или
Li(w) 0 дБ.
Частотные характеристики элементов и систем управления__________________181_
Очевидно, что полоса пропускания идеального фильтра с вертикальными
фаницами после охватывания обратной связью не изменяется. Благодаря
отрицательному наклону высокочастотного участка амплитудной характери-
стики при замыкании происходит сдвиг верхней границы полосы пропуска-
ния вправо.
Аналогичный эффект сдвига нижней границы полосы пропускания влево
наблюдается при замыкании системы со свойствами фильтра средних или
высоких частот, имеющего положительный наклон низкочастотного участка
амплитудной характеристики (рис. 2.33, б).
Значения границ полосы пропускания замкнутой системы и порождаемые
замыканием эффекты определяются крутизной склонов амплитудной харак-
теристики разомкнутого контура на частотах пересечения ею уровня еди-
ничного усиления А = 1. Поскольку наклон амплитудно-частотной характе-
ристики принято выражать в децибелах на декаду, то рассмотрим воздейст-
вие преобразования (2.25) на отдельные достаточно протяженные (порядка
декады по оси частот) участки логарифмической амплитудно-частотной ха-
рактеристики, пересекающие уровень L = 0 с типовыми наклонами асим-
птот 20/и дБ / дек, где m е{+1. ±2):
□ на участках с наклонами ±20 дБ / дек (рис. 2.34, а) разомкнутая система
аппроксимируется типовыми звеньями JF|(j) » Xts и ИА(з) = Ajj'1, а пе-
редаточные функции замкнутой системы близки к
Их логарифмические амплитудно-частотные характеристики монотонно
изменяют свой наклон от +20 до 0 и от 0 до -20 дБ / дек с частотами со-
Глава 2
пряжения oJhii = I / ^1 и <Ц«2 = ЛГ2 — границами полосы пропускания
замкнутой системы;
□ участки с наклонами ±40 дБ / дек (рис. 2.34, б) аппроксимируют ра-
зомкнутую систему типовыми звеньями W|(s) = К|S2 и W2(s) = K2s2, а
передаточную функцию замкнутой системы — выражениями
Логарифмическая амплитудно-частотная характеристика Л/ы) имеет на
частотах
два острых резонансных пика, приводящих к появлению двух узких по-
лос пропускания и усилению колебательности переходных процессов
замкнутой системы. Особенно опасен этот эффект на частоте <Пр2 с,,ал11
логарифмической амплитудно-частотной характеристики разомкнутого
контура, где коэффициент усиления Л|(и^2) » |, а отрицательный фазо-
Частотные характеристики элементов и систем управления 183
вый сдвиг ф|(о)р2) близок к значению -180". Говорят, что такая замкнутая
система смещается на границу устойчивости.
При еще более отрицательном наклоне амплитудной характеристики ра-
зомкнутого контура £|((о) на некоторой частоте о)к, где выполняются ус-
ловия
£1(шк) > 0, Ф|(Шк) = -180", (2.26)
наступает потеря устойчивости замкнутой системы, аналогичная самовоз-
буждению акустической системы, изображенной на рис. В.4
В заключение анализа получим оценки степени расширения полосы пропуска-
ния при охватывании двух типовых звеньев жесткой отрицательной обратной
связью через элемент с неединичным коэффициентом усиления Л^, # 1.
□ Замыкание апериодического звена первого порядка
Иф)=_2_, к>0, Т>0,
с шириной полосы пропускания
<й„ = у Рал / с, /„ = ~ Гц (2.27)
дает по (1.20, в) передаточную функцию замкнутой системы со свойства-
ми апериодического звена
и следующими коэффициентом статического усиления А„ постоянной
времени 7\ и полосой пропускания ц,/
Гз=7Т77-' “го=^- = (‘ + ^оК (2.28)
1 + лл0 1+лл0 /,
Отсюда следует важное свойство замкнутой системы: произведение коэф-
фициента усиления на полосу пропускания
ЛХ, - Лоз,, (2.29)
есть постоянная величина, независимая от глубины обратной связи. На
рис. 2.35 построены логарифмические амплитудно-частотные характери-
стики разомкнутой и замкнутой систем при К= 100 и трех разных ко-
эффициентах обратной связи Л'о Графики подтверждают полученные
аналитически свойства ширины полосы пропускания <цп: ее линейную
зависимость от коэффициентов К и А;„ но обратную пропоршюзимь-
кость величине К,.
Рис. 2.35
Большинство выпускаемых отечественной и зарубежной электронной
промышленностью операционных усилителей с внутренней коррекцией
(при внешней коррекции к операционному усилителю подключаются на-
весные радиоэлементы, обеспечивающие устойчивость схемы) обладает
передаточными функциями (1.33) и амплитудными характеристиками,
подобными графикам /-(со) на рис. 2.35. В разомкнутом состоянии они
характеризуются (1, 18, 22]:
• усилением в низкочастотной области Ку = 104 + 106;
• полосой пропускания (частотой перегиба логарифмической ампли-
тудно-частотной характеристики) ц, = 6 + 1800 рад / с (1 <- 300 Гц) и,
соответственно, постоянной времени Гу = 0.5 + 160 мс;
• частотой единичного усиления Ш| = К^Оп = 6 + 180 рад / мкс
(1*30 МГц).
При замыкании операционного усилителя цепью отрицательной обрат-
ной связи частота единичного усиления не изменяется, а полоса пропус-
кания расширяется в I + КК0 раз, т. е. примерно пропорционально росту
коэффициента обратной связи /^>. Найдем значение Ко и степень расши-
рения полосы пропускания для простейших и наиболее распространен-
ных в схемотехнике схем каскадов на операционных усилителях:
• коэффициент усиления (1.25, а) инвертирующего каскада
(см. рис. 1.24, о) может быть записан аналогично (2.28) при
"2 + "О “о
Следовательно, степень расширения полосы пропускания в зависи-
мости от номиналов сопротивлений навесных резисторов составляет
Частоты» характеристики элементов и систем управления 1В5
шп В 2 + *0
• коэффициент усиления (1.25, 6) неинвертирующего каскада, изобра-
женного на рис. 1.24, б, записывается в виде (2.28) при
Ко=-Г?Г<1
"О + "20
Степень расширения полосы пропускания в зависимости от номина-
лов сопротивлений резисторов составляет
Win _ J ! Л20 у
“и R20 + R0 '
□ Замыкание колебательного звена второго порядка
W(s)=-------К , Г>0,0<5< 1,
1 + 2^Тз+Т2з2
с резонансной частотой и? = Г"1 и шириной полосы пропускания
(2.30)
определяемой из условия половинной мощности
.2г \ К2 К2
А (“)=/—ТТЙ—=-х-
|l-r2(i)7+4?W 2
дает по (1.20, в) передаточную функцию замкнутой системы, имеющую
свойства колебательного звена
И^) =--------L--------- ------
1 +КК0+2£Ts + T2s‘ l + 2^,T3s + T2s2
со следующими коэффициентом статического усиления Л\. постоянной
времени Т„ коэффициентом затухания резонансной частотой и
полосой пропускания <цп:
®Л)« й»р71 + КК0 -25’ + 7(1 + ^о-257 + (! + /КК,У
186
Глава 2
Отсюда следует аналогичное (2.29) свойство постоянности произведения
коэффициента усиления замкнутой системы на квадрат резонансной
частоты:
/С,(й^ = ^. (2.32)
Ввиду близости частот оу, и оу, свойство (2.32) качественно присуще и
полосам пропускания разомкнутой и замкнутых колебательных систем.
Но самое важное следствие соотношений (2.31) заключается в увеличении
частоты колебаний и степени колебательности таких систем при охваты-
вании их цепью отрицательной обратной связи, т. к. по (2.18) уменьшение
коэффициента затухания приводит к росту резонансного пика Л2(У
Однако длительность переходного процесса, оцениваемая, как будет по-
казано в а. Л числом ЗГ/ 5 с, остается неизменной, что при увеличении
частоты колебаний ведет к росту числа колебаний до затухания
На рис. 2.36, а построены логарифмические амплитудно-частотные ха-
рактеристики разомкнутой и замкнутой колебательных систем при
К= 100 и трех разных коэффициентах обратной связи К„ Семейство
(рафиков на рис 2.36, 6 (обратите внимание на логарифмическую шкалу
по оси ординат!) отображает зависимость оу,(£) / Шп(5) степени расши-
рения полосы пропускания от коэффициента затухания разомкнутой
системы. Графики подтверждают перечисленные выше свойства резо-
нансной частоты «у, и полосы пропускания «у< линейную зависимость
от квадратов коэффициентов усиления К и К, но обратную пропорцио-
нальность квадрату величины Л",.
Рис. 2 36
Частотные характеристики элементов и систем управлений 187
Многообразие способов замыкания системы W\(s) не ограничивается же-
сткой отрицательной связью через статический элемент Ио(г) = Л'о. При
использовании динамического элемента общего вида частотные
свойства замкнутой системы определяются контурной передаточной
функцией (TK(s), вычисляемой по (2.23) Из всего многообразия обрат-
ных связей в практике управления находят применение следующие их
виды:
□ гибкая связь W0(s) = переходящая с ростом частоты ш от нулевой до
бесконечно большой и вносящая в комплексную характеристику WK(j<o)
фазовый сдвиг +90’, постоянный на всех частотах;
□ изодромная связь !To(s) = £0(1 + 7^) / г. переходящая с ростом частоты
о> от бесконечно большой до постоянной с дополнительным фазовым
сдвигом И'цОы) от -90* до 0*.
Достаточно обширный перечень вариантов охватывания различных систем
разными видами обратной связи приведен в [16, табл. 2.4].
2.5.3. Свойства систем
с положительной обратной связью
Настало время разобраться, как положительная обратная связь влияет на
свойства замкнутой системы, имеющей в прямой цепи динамический эле-
мент с ограниченным усилением. Вспомним, что в разд. 1.8.2 нами обнару-
жена эквивалентность двух видов обратной связи — отрицательной и поло-
жительной — в рамках идеальной статической модели усилителя, имеющего
бесконечный коэффициент усиления Ку -> ~ на всем интервале частот
<о е[0,
Почему автор так привязался к операционным усилителям, будто бы в при-
роде не существует других достойных внимания систем? Выбор данных уст-
ройств для исследования влияния обратной связи на свойства замкнутых
систем обусловлен следующими причинами:
□ богатой номенклатурой выпускаемых микросхем операционных усили-
телей с широким спектром параметров;
□ удобством электронного моделирования, в том числе и компьютерного,
разнообразных технических систем с помощью схем на операционных
усилителях;
□ способностью компьютерной электронной модели быстро, дешево и
безопасно работать в самых экстремальных режимах и значениях пара-
метров как операционных усилителей, так и навесных элементов;
188 Глава!
□ возможностью проведения натурного эксперимента с электронной мо-
делью системы для подтверждения результатов компьютерного модели-
рования.
Для более достоверного анализа частотных свойств каскадов с обратными
связями примем динамическую модель линейного режима операционного
усилителя в виде передаточной функции Wy(s) из (1.33) с конечным коэф-
фициентом статического усиления Ку и ненулевой постоянной времени Гу.
Такими параметрами обладают все выпускаемые промышленностью опера-
ционные усилители с внутренней либо с внешней коррекцией, обеспечи-
вающей устойчивость замкнутой схемы благодаря сочетанию на частоте
единичного усиления наклона ЛАЧХ -20 дБ / дек и фазового сдвига при-
мерно равного -90" (см. гл. 4, 6).
Сначала получим передаточные функции И1!*) «правильных» схем усилите-
лей с отрицательной обратной связью путем подстановки в (1.25) функции
Иу(5) вместо коэффициента Ку:
□ у инвертирующего каскада (см. рис. 1.24, а)
где К =----%>-—<*<>, т =-------------->0; (2.33, а)
1+« R1 , яо + /?2 *2 !, к
/?о + R2 *
□ у неинвертирующего каскада (см. рис. 1.24, г)
И<(»)=~,где К--------<1+*°-,
1+TS К0 + /?20 К20
«ю+—£--------
у (2.33, б)
т=-----Ь------->0.
1 + _?м_к
Ro + К20
При всех значениях Ку > 0 вплоть до бесконечного постоянные времени т у
обеих замкнутых систем остаются положительными, а сами системы — ус-
тойчивыми.
Далее переходим к исследованию каскадов, в которых обратные цепи по
ошибке или злонамеренно подключены через сопротивления Ко к прямым
входам операционных усилителей (рис. 2.37). Такой способ соединения дает
передаточные функции (2.33), в которых коэффициент Ку заменен на -Ку. В
результате постоянные времени т при определенных соотношениях номина-
лов сопротивлений и значений Ку могут стать отрицательными, а схемы не-
Частотные характеристики элементов и систем управления
устойчивыми'. В том, что это так, нетрудно убедиться путем непосредствен-
ного вывода передаточных функций и сравнения их постоянных времени с
параметрами т в (2.33):
Рис. 2 37
□ для схемы на рис. 2.37, а:
Я2 /?0 К()Ку
_ Ку У = яо + /г2-Я,*,+(/?() +Яг)7?
У~ 1 + Tys‘
Иф)= - , где К =-----%—, Г =------------£--------: (2.34, о)
1 + ts R «о + Кг j-------------
□ для схемы на рис. 2.37, 6:
Яго Яо
Я) -*-Я20
г Яо + Я
<20-
- (Яо + Яд,
—1---------. (2.М.Ф
—К,
к<>+ к»
Обозначив граничное значение
190
Глава 2
исследуем влияние коэффициента усиления Ку > 0 на параметры К и т пе-
редаточных функций (2.33, б) и (2.34, б). На рис. 2.38 сплошными линиями
построены графики
<13М>
Ку К„
для схемы с положительной обратной связью (рис. 2.37, б), а пунктирными
линиями - (рафики
(2-35Л
1+*Г у 1+^
соответствующие схеме с отрицательной связью (см. рис. 1.24, г). Для опре-
деленности выбрано соотношение номиналов / Луо = I, при котором
я 2. Различия параметров замкнутых систем с разными типами обрат-
ной связи налицо, а качественный анализ их свойств позволяет сделать сле-
дующие выводы
□ При Ку < Krf, что случается при выборе плохого операционного усили-
теля и соотношении номиналов сопротивлений ЛЬ » Лм, происходит
иивс|х:ия знака К < 0, т. е. превращение пеипвертирующего усилителя в
инвертирующий Поскольку постоянная времени т > 0, то замкнутая сис-
тема с положительной обратной связью остается устойчивой При этом
Частотные характеристики элементов и систем управления 191
передаточная функция (2.34, б) имеет левый полюс з, = -1 /т < 0, а пе-
реходный процесс — сходящуюся составляющую е '/т.
□ Пределы Ку -» Кгр ± 0 обладают общими свойствами параметров |Л] -> ~
и М -т о®, но разными знаками их пределов Практически это означает
наличие в выходном сигнале линейной составляющей, пропорциональ-
ной времени t.
□ При Ку > Кф, что практически всегда и бывает, знак К> 0 верный, но
постоянная времени становится отрицательной т < 0. В результате замк-
нутая система с положительной обратной связью становится неустойчи-
вой. ее полюс 5| > 0 — правым, а составляющая переходного процесса
е_,/' расходится. В пределе Ку -> ~, соответствующем «йелнлаиу опера-
ционному усилителю, расходимость становится мгновенной.
Поскольку в конечном итоге исследователя любой системы интересуют ста-
тические и динамические свойства ее переходных процессов, построим на
рис. 2.39, а графики переходной характеристики
апериодического звена первого порядка с передаточной функцией Щз) из
(2.34, б) при различных сочетаниях величин и знаков параметров А' и т Вы-
числив по (2.35) параметры К(КУ) и х(Ку) для ряда значений коэффициента
статического усиления
построим на рис. 2.39, б (обратите внимание на разметку осей координат!)
переходные характеристики каскадов с отрицательной (см рис. 1.24, г) и
положительной (см. рис. 2.37, б) обратными связями.
192
Глава 2
Анализ графиков и всего материала данного раздела позволяет сделать сле-
дующие выводы
□ только отрицательная обратная связь и бесконечно большой коэффици-
ент Ку статического усиления элемента прямой цепи обеспечивают ус-
тойчивое и правильное воспроизведение выходного сигнала замкнутой
системы в соответствии с ее передаточной функцией;
□ уменьшение значения Ку в системе с отрицательной обратной связью
приводит к ухудшению качества отработки входного сигнала:
• увеличивается статическая ошибка — разность выходных сигналов
замкнутых систем с конечным и бесконечным коэффициенгами Ку;
• возрастает инерционность замкнутой системы, характеризуемая по-
стоянной времени т(АГу);
□ система с положительной обратной связью инвертирует знак выходного
сигнала и предрасположена к неустойчивости. Существует некоторое
граничное усиление прямой цепи К,?, определяющее свойства замкну-
той системы:
• при Ку < К^ она устойчива с большой инерционностью т(ЛГу) > Ту,
• с ростом усиления Ку > Кц, система становится все более неустойчи-
вой с малой инерционностью т(Л'у). стремящейся к нулю в пределе
Любая реальная система имеет ограниченную область достоверности линей-
ной (линеаризованной) модели (см. рис. 1.9). Например, линейный режим
работы операционного усилителя действителен при изменении входного
напряжения ДУ в интервале [-(/№ / Ку, / /Су| (см. статическую харак-
теристику на рис. 1.12, б) Если модуль выходного напряжения |У1(ЫХ| пре-
вышает уровень (/„wo то усилитель входит в режим насыщения, имеюший
совсем иную математическую модель.
Ранее в at. I нами были построены схемы каскадов на идеальных операци-
онных усилителях с положительной обратной связью (см. рис. 1.45 - 1.47).
Как теперь стало ясно, она действует на замкнутую систему дестабилизи-
руюше, особенно при большом статическом усилении элемента прямой це-
пи. В то же время, отрицательная обратная связь имеет, как правило, стаби-
лизирующие свойства (см. разд. /7).
Изучим, наконец, одновременное влияние двух типов обратной связи на
свойства замкнутой системы. Согласно (1.32), знаменатель ее передаточной
функции может быть как минимально-фазовым (устойчивым), так и неми-
нимально-фазовым (неустойчивым) полиномом, в зависимости от сочета-
ния типов и номиналов навесных элементов. Таким образом, устойчивость
замкнутой системы является результатом борьбы двух противоположных
тенденций.
Частотные характеристики элементов и систем управления
Например, динамика замкнутого каскада на рис 1.45, а, построенного на
неидеальном операционном усилителе И^Ст) = Л"у / (I 4-Tyj), описывается
достаточно громоздкой передаточной функцией, полученной не без помощи
символического процессора Mathcad:
W,(*)=
=________________________+ ______________________________________
(Zo + Z2OXZ1Z|| + ZUZ1O +zizio)+^y(5Xz|Z|oZjO + Z|Z||Z20 - ZuZ|0Z0)
Ее можно представить в аналогичном (1.20, в) виде
i+w(^w^)-w„(s)y
соответствующем структурной схеме комбинированного обратного соедине-
ния (рис. 2.40, а) со следующими блоками прямой цепи W(s), отрицатель-
ной И'(.г) и положительной обратных связей
--------------------И\(з).
Z|Z|| +Z||Z|0 +Z|ZIO
В частности, если все навесные элементы каскада — резисторы, то
И-(з) =
Л|О (*о + ^10 )
М»_________д-
Л,Я|,+Л|Я|0+ЛцЛ|()
?>»•
(2.36, а)
194
а замкнутая система имеет передаточную функцию апериодического звена с
параметрами (2.28):
№-(,)=— к--------
’ \4-К{К0-Kn)+TyS l + T.ts
(2.36, б)
к - к т -
1+к(к0-к„У >~1+к(к0-к„У
Свойство устойчивости каскада определяется знаком постоянной времени
Г3, которая в зависимости от баланса коэффициентов Ко и К„ может стать
как положительной, так и отрицательной. Обозначив граничное усиление
прямой цепи как
, I Mio(*o + *2о)
41 Кп~Ко Я||Л|(|/?о-Я|Л||/?20 ~ ^1^10^20
(2.36, в)
запишем с учетом положительности коэффициента К условие минимально-
фазовости замкнутой системы I + К(Ка ~ Кп) > 0 в виде неравенств
( 0<К< ПрнК„>Ка.
| К >0при К„ < Ко.
(2.36, г)
В соответствии с ними на рис. 2.40, б (сравните с рис. В.5) построены об-
ласти устойчивости и неустойчивости замкнутой системы в пространстве
параметров {К, Кп}- Видно, что при доминировании положительной обрат-
ной связи над отрицательной устойчивые значения коэффициента К, а, со-
гласно (2.36, о), - и Ку, ограничены сверху тем сильнее, чем больше ука-
занное доминирование.
Численно оценим свойства каскада, построенного на реальном операцион-
ном усилителе 544УД2Б с параметрами |18|
Ку = 10*. f - 15 МГц, Ту = Ку / 2т/| = 10'< с (2.37)
при различных сочетаниях сопротивлений навесных резисторов:
□ если все сопротивления одного номинала Я. то по (2.36, о) получим
К‘ Ку / 3 - 3 333, К„ » I > К„ - 0.5, - -2,
тогда из (2.36, г) следует, что доминирующая отрицательная обратная
связь делает схему устойчивой;
□ при Яо = 2R и остальных сопротивлениях, равных Я, получим
К- 3 333.^-Кп-2/3,
Частотные характеристики элементов и систем управления
195
г. е. положительная и отрицательная обратные связи взаимно компенси-
руют друг друга. Согласно (2.36, й), замкнутая система имеет передаточ-
ную функцию “ 1F(j) с таким же свойством устойчивости, что и
разомкнутая система;
□ при Ro = 3R и остальных сопротивлениях, равных R. совместно с
(2.36, в) получим
К = 3 333, к, = 0.5 < К„ = 0.75, = 4
Неравенство К » K,v означает, что в схеме сильно доминирует положи-
тельная обратная связь, делаюшая ее неустойчивой,
□ для того, чтобы схема с преобладающей положительной обратной связью
была устойчивой, значение Яа должно удовлетворять условию (2.36, г).
Например, при Ку = 10 000 интервал устойчивых значений сопротивле-
ния Rq очень узок и весьма труден для удовлетворения:
С другой стороны, при выборе значения Ro = ЗЯ должен быть малым ко-
эффициент Ку < 12. Понятно, что ни один, даже самый плохой операци-
онный усилитель до такого низкого уровня качества не опускается, по-
этому схема является неустойчивой.
На рис. 2.41 построены годографы И 'к0’а>) контурной передаточной функции
лля перечисленных выше значений Ro Эти графики будут нами использо-
ваны для определения устойчивости замкнутой системы по критерию Найк-
виста, о котором пойдет речь в гг 4.
Одновременное использование положительной и отрицательной обратных
связей на грани их баланса может служить основой конструирования гене-
раторов гармонических колебаний Как сказано в разд. 2.2. незатухающие ко-
лебания в принципе могут возникать на выходе автоколебательного типово-
го звена с передаточной функцией )Цх) * Л'/(1 + 7s?). В действительно-
сти колебательных элементов без обратной связи, обладающих нулевым
коэффициентом затухания 5. не существует. Каким бы добротным ни был
/.С-конгур, все равно неизбежны потерн энергии колебаний на сопротивле-
ниях проводов и материалов радиоэлементов. Следовательно, нужна «под-
качка. энергии, компенсирующая эти потери. Эту задачу и решает правиль-
но подобранная положительная обратная связь.
Пример 2.6. Построить логарифмические частотные характеристики
схем, приведенных на рис 1.46, определить их свойства, условия возникно-
вения колебаний и их частоту
Решение На рис. 2.42 построены искомые характеристики схем неинверти-
рующего (я) и инвертирующего (Л каскадов по их передаточным функциям
(1.34). Анализ графиков дает основания сделать следующие выводы о свой-
ствах схем:
' злементое и систем управления
197
□ первая схема является фильтром высоких частот, что подтверждается
предельными свойствами >И(0) = 0 и ИН = а + I * 0 ее передаточной
функции
ж(.)-(«<.|)-7П(1у-) ;
1 + (2-а)Гт + Т-.Г
□ вторая схема является полосовым фильтром, что подтверждается предель-
ными свойствами ЩО) = 0 и = 0 ее передаточной функции
-(Р + 0—-----$-----r-г;
l + (2-P)Ts + T2?
□ частотные характеристики обеих схем £(ш) и Ф(<в) проявляют колеба-
тельные свойства с частотой резонанса = 1 / Т в интервале измене-
ния параметров а е (0, 4) и р е (0, 4), где модули коэффициентов загу-
хания ( = 1 - 0.5а и £ = I - 0.50 становятся меньшими единицы;
□ при а = 2 и р = 2 знаменатели передаточных функций становятся рав-
ными I + А2, а на частотных характеристиках наблюдаются все при-
знаки автоколсбательности:
• частота колебаний = сор = I / Г,
• бесконечные амплитуды /.(Иц) -» =;
• скачки фаз ДФ(а»к) “ ‘180'-
□ дальнейшее увеличение параметров а > 2 и Р > 2 делает знаменатели и
передаточные функции неминимально-фазовыми, что подтверждается
соответствующими фазовыми характеристиками Ф(ш)
Таким образом, схемы обоих каскадов на операционных усилителях при
выполнении условий автоколебателыюсти
а - 2, р = 2 (2.39)
Могут быть положены в основу конструкций генераторов незатухающих ко-
лебаний частотой о\ = I / RC. регулируемой выбором номиналов резисто-
ров R и конденсаторов С. Баланс обратных связей устанавливается точной
Настройкой переменных резисторов на значения 2Я.
Исследуем, как влияет на условия автоколсбательности (2.39) неидеальность
операционного усилителя. Возьмем, например, схему на рис. 1.46. а и при-
мем использованную ранее модель усилителя Иу(з) = Ау / (I + Гул) как
фильтра низких частот с параметрами (2.37).
Способности символического процессора Mathcaii позволили выполнить
этот нетривиальный анализ и получить следующие результаты.
198
Глава 2
□ Передаточная функция каскада с реальным операционным усилителем
описывает систему третьего порядка:
IV(5.a)=
(g+lXn-Tt)
(2.40, о)
Легко заметить, что при Ау « и конечном значении Ту эта передаточ-
ная функция совпадает с (1.34. а)
Подставив в (2.40, а) параметры операционного усилителя
Ту = 10’* с, получим при a = 2 численно-параметрическое
передаточной функции каскада от постоянной времени Т
Ts(l + Ts)
Ky = 104 и
выражение
W(x,2)=------------------------------------
0.33343 + (ЗООООГ + 1)-10*8з +
+ (р.33343Т + 3 • 10’8 )rs2 + КГ8 Г2?
(2.40, 6)
□ Из трех корней полинома знаменателя два являются комплексно-
сопряженными, а третий — действительным. Например, при постоян-
ной времени Т = 10'3 с, соответствующей частоте колебаний
А = 1 / 2лГ = 160 Гц, получим следующие полюсы передаточной функ-
ции (2.40, б):
= -0.449826 ± 999.955), з3 » -33 346 332.
Левое расположение комплексных корней означает, что колебания, вы-
рабатываемые генератором, будут затухающими, ограниченными экспо-
нентами ^е"044”26' и -е^"044*834'. Время двадцати кратного уменьшения
амплитуды колебаний составляет 3 / 0.449826 = 2.2 с.
Вторым следствием переката от идеальной модели операционного усили-
теля к реальной является небольшое (на 0.0045%) уменьшение частоты
колебаний с 1000 рад / с до 999.955 рад / с.
Третий действительный и далеко отрицательный полюс jj не создает ка-
ких-либо проблем с устойчивостью и быстродействием генератора, т. к-
порождаемая им составляющая переходного процесса cje'33 346 332' затуха-
ет примерно за 0.1 мкс.
□ Условие автоколебательное™ системы третьего порядка с полиномом
знаменателя г
Частотные характеристики элементов и систем управления 199
/1(5) = (1 + tVXl + 05) = 1 + 0|J + fljJ2 + OjS3,
в котором П| = 0, й2 ~ & 11 °] = О*2' имеет вид «|вг = °у Подставляя сю-
да полученные из (2.40, а) коэффициенты
(2-а)кт + (а + 0(зг + Т,) Г + (а + 1)(т + ЗГ)
---------<77й-----------' °г------------------т-
можно вычислить оптимальный параметр а, обеспечивающий как неза-
тухающие, так и нерасходяшиеся колебания. Например, при А'> = I04 * * * *.
Гу = Ю'4 с и Т= 10~3 с получим оптимальное значение а = 2.0009 > 2
Сложная и без кропотливого анализа непредсказуемая зависимость пара-
метра а. регулирующего сопротивление /?(| = aR резистора цепи отрица-
тельной обратной связи, как от свойств установленного в схеме операцион-
ного усилителя, так и от частоты колебаний, делает конструирование гене-
ратора стабильных по амплитуде колебаний весьма непростой задачей.
Важно понимать то, что даже заранее тщательно рассчитанное и жестко за-
фиксированное значение а все равно не гарантирует устойчивой генерации
из-за временного дрейфа параметров операционного усилителя и пере-
стройки частоты колебаний
Выходом из создавшейся коллизии является использование в цепи отри-
цательной обратной связи, задающей значение а, нелинейного резистора
Яо, сопротивление которого зависит от действующего значения падающе-
го на нем напряжения, т. е. от рассеиваемой им мощности. Такой рези-
стор, осуществляющий автоматическую регулировку усиления (АРУ), на-
зывается термистором и должен иметь отрицательный температурный
коэффициент сопротивления (ТКС). Существуют и другие полупровод-
никовые устройства — варисторы, сопротивление которых зависит от те-
кущего падения напряжения Из-за практически нулевой инерционности
использование варисторов при низких частотах генерируемых колебаний
нецелесообразно.
Автоматическая подстройка глубины отрицательной обратной связи проис-
ходит следующим образом:
3 при неконтролируемом возрастании параметра а и начавшейся расходи-
мости выходных колебаний происходит нагревание резистора и
уменьшение его сопротивления благодаря отрицательному температурно-
му коэффициенту сопротивления. Вместе с этим уменьшаются отноше-
ние а = Ло / R и амплитуда колебаний, а схема возвращается в режим
автоколебаний;
200
Глава2
□ при неконтролируемом уменьшении параметра а и начавшемся затуха-
нии выходных колебаний происходит охлаждение резистора и
увеличение его сопротивления. Благодаря этому эффекту значение а и
амплитуда колебаний увеличиваются, возвращая схему на границу ус-
тойчивости.
Для уменьшения колебательности самого процесса автоматической регу-
лировки усиления, зависящей от значения температурного коэффициента
сопротивления и инерционности тепловых процессов, можно вместо од-
ного термистора Я(1 использовать два резистора — постоянный ЛП1 и тем-
пературозависимый Яо; << Ли. так чтобы сумма их сопротивленизт была
равна 2R. С учетом этого дополнения схема генератора гармонических
колебаний выглядит так, как показано на рис. 2.43, в. Колебания возбу-
ждаются в момент замыкании ключа и подачи на вход схемы постоянного
напряжения 6'0. Почему выбран именно такой входной сигнал и как най-
ти амплитуду возникающих автоколебаний станет понятно в гл. 3, по-
священной изучению временных характеристик элементов и систем
управления.
На рис. 2.43, б изображена схема генератора гармонических колебаний, по-
строенная на основе рис. 1.46, б. В отличие от схемы предыдущего генера-
тора здесь источник входного напряжения подключен в обратной поляр-
ности для компенсации инвертирования, присущего передаточной функции
(134, б), хотя это и не принципиально для работы генератора. □
2.6*. Анализ полиномов
В заключительном разделе данной главы, носящем вспомогательное значе-
ние. рассматриваются вопросы разложения сложной системы на типовые
звенья Решение этой задачи состоит в нахождении корней и множителей
Частотные характеристики элементов и систем управления 201
полиномов Л(з) и B(s) передаточной функции системы (1.19, (5). Рассмотрим
полином общего вида
A(s) = an + + ... +
степени п с действительными коэффициентами а, (а„ # 0) и методы расчета
корней уравнения Л(з) = 0.
Основные задачи численного анализа полиномов следующие
□ определение структуры спектра полинома; типа корней (действительно-
го и комплексного) и числа корней каждого типа;
□ локализация корней (определение интервала расположения) и выбор их
начальных приближений;
□ итерационное уточнение корней;
□ факторизация — разложение полинома на простые множители.
& Теорема 2.1 (Гаусса). Полином степени п имеет ровно п действительных
или комплексных корней (каждый кратный корень считается кратное число
раз).
Следствие. Две формы разложения на множители полинома, имеющего
корни 5| ♦ s„:
А(*)=«оП|'"~] = а"П('’-5<)- <24,-в)
□
& Теорема 2.2 Комплексные корни действительного полинома всегда по-
парно сопряжены: каждый корень s,= п, + имеет сопряженный ему ко-
рень sltt = = т]( - jo),.
Доказательство Поскольку s, — корень Л(з), то Л(з,) = 0. Используя аксио-
мы комплексной арифметики
Zl +Z2 =Z| +г2 . Zl -Z2 =Z|Z2
и свойство действительного числа а=а, определим
“Ev/’Lv/ =о = о
j
Следовательно, х, также начнется корнем полинома Л(х).
Следствие Г. если полином имеет комплексно-сопряженные корни
« И/ ± м, то в (2.41, о) произведения комплексно-сопряженных мно-
*ителей дают действительные множители второй степени:
Гпава 2
(i “ “»(♦! )=^"2П? + П?+И?,
НН)-,+г№+гЛ!
с параметрами
Т 1 Е „т
Т< = ;, - -- • = -V, = , ---.
+ц
Следствие 2. степень полинома и число его действительных корней одно-
временно либо четны, либо нечетны. В частности, любой полином нечетной
степени имеет хотя бы один действительный корень.
Обозначим числа действительных положительных, отрицательных и нулевых
корней полинома, соответственно, как л+, л. и «о, а как лк — число пар
комплексно-сопряженных корней, тогда число действительных и общее
число корней полинома равны
лл = л> + л. + л0, л = лд + 2лк,
а разложения полинома на действительные множители имеют вид
*(*)= "ЙО+7»П(1+ W+7}2з2 )
М ы
*(»)*аяз"° П(т -», )fl (i2 - 2пл + ПГ + »?)
м i»l
(2.41,6)
Для расчета корней и множителей полинома необходим определенный
инструмент: компьютер, калькулятор или, в крайнем случае, бумага с ка-
рандашом вместе с хорошо обученной головой, понимающей сущность
методов вычислений и критически осмысливающей полученные резуль-
таты. Лучшим помощником студента, инженера, исследователя и разра-
ботчика является профессиональный программный продукт Mathcad с
богатыми функциональными и интеллектуальными возможностями, раз-
витыми графическими средствами, удобным и дружественным интерфей-
сом (19). На рис. 2.44 приведен листинг Mathcad-программы расчета
корней с помощью функции polyroots, множителей с помощью симво-
лического оператора tector и построения графики полинома пятой сте-
Л(з) = -400 - 200083 - 304? + 4802? + 101? + 50?
(2 42)
Частотные характеристики элементов и систем управления_________________203
График полинома
Корни полинома
polyroots(a)
Рис. 2 44
Переходим к изучению методов исследования действительных полиномов
без использования компьютера |4, 6, 12, 14]. К сожалению, такое положение
вещей еще типично для среднестатистического инженера или студента,
имеющего в нужный момент на вооружении лишь калькулятор, который
желательно должен быть программируемым.
Что касается расчета значения полинома Л(т)|1=< . то следует выполнять его
последовательным умножением
А(с) = ( (а„с + я„-|)с + ... + Л|к + ао.
а не суммированием слагаемых а,<4, которые могут быть настолько разных
порядков, что при округлении произойдет потеря самых малых из них
В процессе расчета корней рекомендуется периодически понижать степень
полинома >4(зг) путем деления его на полином
«з) = «в + *|J + ... +
образованный произведением найденных простых множителей типа (г - st)
или (1 + Тр) для действительных корней s, и (т2 - 2т)(.« + п(г +ш(‘) или
(1 + 25|Т(з + т/д2) для комплексно-сопряженных корней >)/*<*• При деле-
нии образуются полиномы частного
СМ • ср>
C|j+ <Ъ
204
Глава 2
степени / = п - т £ 0 и остатка
D(s) = rfm-li"-1 + ... + + d0.
Деление полиномов можно выполнить вручную «углом» как деление обыч-
ных чисел:
V" +W'H+• • -+fli5+ав bmsm "и +.. .+^+*6
-------------------------c(j'+cHsw+...+C|j+c0 (2‘43, °)
dW4s"4+...+d1j+d0
В соответствии с этим методом деления последовательно рассчитываем ко-
эффициенты со + С/ и do ♦ :
с(=^-, С,_| = а"-|~Ь>»-1С'.....r0-f».~Vici- --fcm-<c;
fc" Ь"> bm
=a«-l ~ •••• dt =Д| -Z>|Cq ~bQCt,
do^ao-btfo.
(2.43, 6)
при этом b, = О V t < 0. Отсюда получаем рекуррентные
и матричные формулы
(2.43, г)
Частотные характеристики элементов и систем управления 205
для вычисления коэффициентов полиномов с определителем обращаемой
матрицы, равным //***(».
Признак делимости Л(з) на B(s) нулевой остаток ZXvi При п>убом расчете
корней будет получен остаточный полином с ненулевыми коэффициентами
rfo + rfm-i- сравнимыми по величине с коэффициентами /1(з) и /?(«). В этом
случае требуется уточнить корни и построить новый полином Bis).
2.6.1. Полиномы низких степеней
Рассмотрим методы нахождения корней и разложения на множители поли-
номов низких степеней п, для которых эти задачи решены аналитически,
т. е. точно.
□ При п = I полином до + Ф* имеет единственный действительный корень
j = -^-.
1 «I
При заданном действительном корне 3| и одном из желаемых коэффици-
ентов а0 или в| полином первой степени имеет разложения
Л(д)-а1(д-дО**ао(1 + Тз),
где
т.-±.±.
а0
□ При л = 2 полином «о + aj3 + ajs1 имеет дискриминант d = af - 4аоа2
и корни
, _ ~а1
,|J ~ 2аг
* Если d > 0, то j| и з2 — два различных простых действительных кор-
ня. При заданных простых действительных корнях 3| * 3J и одном из
желаемых коэффициентов ад или а; полином второй степени имеет
разложения
Я(з) - а2(з - j|)(j - з2) - «о(1 + Т|3)(1 + Туз),
где
Т, =-—Vi=172. Г,Г2 = ^-
»/ «о
Глава 2
Если </=0, то 3|=зу — один действительный корень кратности 2.
При заданном двукратном действительном корне з, и одном из ко-
эффициентов а0 или о, полином имеет рахчожения
Л(з) = в2(з-31)2 = а0(1 + ft)2,
*1 «о
• Если rf<0. то j|2 = 4±j«— два простых комплексно-сопряженных
корня с действительной и мнимой частями
При заданных корнях зц и одном из коэффициентов «о или ау по-
лином второй степени имеет разложения
><(j) = я2(? - 2т]з + т)2 + ю2) = о0(1 + 2£Гз + 7V),
□ При л = 3 полином оо + а|3 + Ojs2 + озз3 имеет корни, вычисляемые по
методу Кардано следующим образом.
& Шаг 1. Заменой аргумента
з = г-^
Зя3
полином Л(з) преобразуется к специальному виду
B(z) = *о + + «з?
с коэффициентами
. at(h 2а? , а?
»0=«0--~2' Ь\ = «| ~~-
Зв3 27дз За,
Шаг 2. Вычисляется модуль 0 и аргумент <р из комплексного вы-
ражения
Шаг 3. Находятся значения
Частотные характеристики элементов и систем управления 207
и корни полинома B(z)
удовлетворяющие условию г, + ;2 + гз = 0.
Шаг 4 Вычисляются корни полинома Л(з):
О
При заданных корнях З], з2, 33 и одном из коэффициентов aQ или аз по-
лином третьей степени может иметь следующие разложения:
• если все три корня действительны, то
A(s) = ai(s - 3|)(з - 3j)(3 - *з) = a0(l + Ги)(1 + Г2з)(1 + 7jS),
где
• если один корень 3j — действительный, а два s2.3 = Л ± jw — комплекс-
но-сопряженные. то
А(д)= а3(з - д,/з2 - 2Пз + П2 + и2 )= «оС + Т|4 + 2&Г,з + Т^г).
где
г1=-—, т2 = — . §=-лг=—=L—r, Г|Г22=—
51 7л2+СО2 yJx\2+lO2 a0
& Пример 2.7. Вычислить корни полиномов знаменателей передаточных
функций (2.20) и (2.21) обеих систем «тележка - маятник»
<4|(з) = 600 + 940з - 216? - 100?,
A,(s) = 600+1100з + 216? + 100?.
Решение. Выполнив по методу Кардано замену аргумента з = г - 0 72 в по-
линоме Л|(з), получим полином
Л|(?) = -151.45 + 1095.52г - 100?,
тогда
V? =-0.757 + J6.937 = 6.978с•'68 =» И = 1.911, «р, - 0.56.
Гпава 2
208
По (2.44) вычисляем корни полинома В|(с), а затем ненулевые корни поли-
нома Л|(з) и его разложение:
2; = -3,377 =» з, - -4.097;
22 = 0.139 =>3з =-0.5815;
23-3.238 =>33 = 2.518;
Л,(j) = -100(з + 4.097)(з + 0.5815)(з - 2.518) =
= 600(1 + 0.244з)( 1 + 1.72з)(1 - 0.397з).
Заменив в полиноме И2(з) аргумент з = г - 0.72, получим полином
5г(г) = -117.35 + 944.48г + 100г3.
тогда
v2= 6.204 =» Г2 = 1.837,ср2 = 0;
2| =0.124 =>3| =-0.596;
22 = -0.062 + 3.075J => з2 = -0.782 + 3.075j;
2з = -0.062 - 3.075j =» 33 = -0.782 - 3.075J;
Л2(з) = 100(з + 0.596)(? + 1.564з + 10.067) =
= 600(1 + 1.678з)( 1 + 0.15543 + 0.0993?).
Вот так были получены разложения полиномов знаменателей передаточных
функций (2.20) и (2.21) в примерах 1.17 и 2.4. О
Достаточно трудоемкие методы (Декарта - Эйлера, Феррари) расчета кор-
ней полинома четвертой степени, связанные с дополнительным решением
полиномиальных уравнений третьей степени, приведены в |6, 14]. Корни
полиномов степеней выше четвертой не имеют аналитических методов рас-
чета и находятся в общем случае численными приближенными методами.
2.6.2. Структура спектра полинома
Определить состав корней каждого типа можно по графику полинома
или по его коэффициентам. Графический метод сопряжен с многократ-
ными вычислениями Л(з) для различных значений аргумента. Он позво-
ляет визуально оценить число действительных корней по числу пересе-
чений или касаний графика с осью абсцисс и локализовать области раз-
мещения этих корней.
График полинома Л(з) степени л, его коэффициенты во. "л и корни 3/ имеют
следующие свойства, иллюстрируемые на рис. 2.45:
□ при четном л противоположные пределы /t(s -» ±<») одного знака:
• Л(±«“) -> +- при а„ > 0 (график /);
Частотные характеристики элементов и систем управления___________209
• Л(±»о) -* -ов при а„ < 0 (график 2).
Следствия:
• при б?()О„ < О график хотя бы дважды пересекает ось s по разные сто-
роны от оси ординат, а полином четной степени имеет хотя бы два
действительных корня разных знаков;
• при аоа„ > 0 график может не пересекать ось г, а полином не иметь
действительных корней;
□ при нечетном п противоположные пределы графика разных знаков:
• Л(+~) -э ±-> при а„ > 0 (график J);
• /1(±о°)->}°° при а„ < 0 (график 4).
Следствие-, график Л($) всегда пересекает ось з хотя бы один раз, а поли-
ном нечетной степени всегда имеет хотя бы один действительный корень:
Sj > 0 при апа„ < 0 либо st < 0 при аца„ > 0;
□ знакопостоянное касание кривой Л(з) оси абсцисс (график 2) означав!
наличие действительного корня четной, а знакопеременное касание (гра-
фик 5) — нечетной кратности;
□ локальные минимум при Я(з) > 0 (графики I, J, 4) и максимум при
A(s) < 0 (график 4) означают наличие комплексно-сопряженных корней
П ±jw с действительной частью т] в окрестности экстремума. Обратное
утверждение неверно: не каждая пара комплексных корней дает на гра-
фике локальный экстремум
Если построение графика полинома вручную затруднительно, то можно
использовать следующие теоремы, устанавливающие структуру спектра
полинома только по его коэффициентам Знание возможного числа каж-
дого типа корней позволяет нс искать тс корни, которых в принципе не
существует.
& Теорема 2.3 (Декарта). У действительного полинома A(s):
□ «о = тах(/}- ад = = ам = 0 - кратность нулевого корня равна числу
подряд следующих нулевых коэффициентов;
□ л+ равно или на четное число меньше числа инверсий знака в последо-
вательности ненулевых коэффициентов полинома Л(з);
□ п- равно или на четное число меньше числа инверсий знака в последо-
вательности ненулевых коэффициентов полинома Я(-з).
□
В связи с чрезвычайной простотой отделения нулевого корня любой крат-
ности далее будем исследовать полином с ненулевыми корнями, структуру
спектра которого можно уточнить с помощью следующих теорем.
& Теорема 2.4 (Фурье - Бюдана). Число действительных корней полинома
Л(т) на интервале з е [о, />| равно или на четное число меньше значения
N(a) - N(b), где N(s) — число инверсий знака в последовательности
(М = (Л(з), /(J),.... Ля)(д)|
значений полинома и его производных в точке s. При расчете значения N(a)
нулевые члены в Q(a) не учитываются. Если при расчете числа N(b) окажет-
ся, что
АЩЬ) в О, Л<">(6) в О, АМ(Ь) = О V i е |* + 1, т - 1 ],
то все АЩЬ) заменяются на (-l)”“/sgn(/l(")(Z')) О
Благодаря возможности интервальной оценки структуры спектра эта теорема
более мощная, чем теорема Декарта. Подставив в Q(s) предельное значение
з = +<», получим число инверсий знака последовательности
0(<») (дя, па„, п(п - 1)а„,. «41.
равное М°») = 0. Учитывая, что числа инверсий знаков последовательностей
0(0) • (д0, О|, 2aj,, л’дя)
и коэффициентов Л(.т) равны, получаем верхнюю оценку N(0) - М“) = МО)
числа л*., соответствующую теореме 2.3.
Плата за простату теорем Декарта и Фурье - Бюдана — возможная неопре-
деленность их оценок с точностью до четного числа.
& Теорема 2.5 (Рауса - Гурвица). У действительного полинома Л(д):
Частотные характеристики элементов и систем управления 211
□ число правых (с вещественной частью Re(5,} > 0) корней равно числу
инверсий знака в последовательности из (л + 1)-го элементов
Л/= {«„, Mh MiM2, М2М}.....M„-iM„}, (2.45)
где Л//есть Лый главный минор лхл-матрицы Гурвица /
Следствие: если все элементы последовательности (2.4S) ненулевые и од-
ного знака, то все корни полинома — левые. Для этого, по крайней мере,
необходимо, чтобы коэффициенты «у, a„-t и а„ были одного знака;
□ число левых (с RefjJ < 0) корней равно числу инверсий знака в последо-
вательности (2.45), построенной для полинома <4(-з).
Следствие-, если все элементы этой последовательности ненулевые и од-
ного знака, то все корни полинома — правые Для этого, по крайней
мере, необходимо, чтобы коэффициенты ад, (-1)’_|л,г.| и были
одного знака.
□
Анализ миноров (2.46) матрицы /' и элементов последовательности (2.45)
показывает, что при переходе от полинома Я(з) к полиному .-l(-s) меняют
знаки:
□ при четном п миноры М2, Mj, Л/6, Мт. и элементы последовательно-
сти (Л/ь М2М3. М<М5. ...};
□ при нечетном л миноры Л/|, М2. М}, М<>,... и элементы последователь-
ности {«„, MiM2, A/jA/i, ...).
В дополнение к теореме Рауса - Гурвица приведем формулу Орландо |Ь|
nU-мД («л
/•I
выражающую предпоследний минор матрицы Гурвица через произведение
всех попарных сумм различных корней полинома Очевидная польза от
формулы (2.47) состоит в том. что если при ап * 0 получен минор Мп-\ = О,
то мы имеем право утверждать, что полином имеет по меньшей мере два
корня с нулевой суммой. Это могут быть либо действительные корни
Т| = -52, либо мнимые корни 5|,2 = ±j<o.
Для соответствия теореме нужно нулевым элементам последовательности М
приписать знаки •+• или «-» так, чтобы в случае действительных корней
5| = -5, числа инверсий знаков в последовательностях, построенных для по-
линомов Л(5) и Л(-5). увеличивались на единицу.
Теорема Рауса - Гурвица дает более определенный результат по сравнению
с теоремами Декарта и Фурье - Бюдана за счет дополнительного формиро-
вания матрицы Гурвица и расчета ее миноров. А если все миноры М, * 0, то
числа правых и левых корней определяются точно.
& Пример 2.8. Оценить структуру корней полинома (2.42)
Решение. Анализируя только степень полинома п = 5 и знаки коэффициен-
тов Oq = -400 и os = 50. получим очень грубые оценки структуры спектра
полинома.
«о = 0, л* е (1, 2, 3, 4,5), я. е (О, I, 2, 3, 4), як 6 {0, 1, 2}.
Используя теорему Декарта, построим диаграммы изменения знаков коэф-
фициентов полиномов Л(з) и Л(-5):
Л(5): -400 -20008 -304 4802 101 50
Л(-5): -400 20008 -304 -4802 101 -50
* | |_________| L => и .6 {0. 2.4);
<0,1,2).
Применим метод Рауса - Гурвица к полиному Л(5):
101 -304 - 400 0 О ‘
50 4802 - 20008 О О
Г- 0 101 -304 - 400 О ,
0 50 4802 - 20008 О
.0 0 101 -304 - 400
а, = 50. М| = 101. Мг = 500 202, М, - 50 020 200, Л/ч = 0, М5 - 0.
Частотные характеристики элементов и систем управления 213
Так как = 0, ад < О и а$ > О, то полином имеет действительные
противоположные корни и последовательность знаков (+, +, +. +, +0, -0} с
одной инверсией Таким образом, число правых корней л+= 1, а число
левых «- = 5-1=4. Это равно числу инверсий знака в
последовательности +, +, -0, -0), построенной для полинома
Л(-т) = -400 + 20008т - 304? - 4802? + 101? - 50?
с минорами
Л/, = 101, М2 = -500 202. М3 = -50 020 200, Л/4 = О, Л/$ = 0.
Из четырех левых корней заведомо один — действительный s2 = ~.f|, а из
оставшихся трех наберется не более одной пары комплексно-сопряженных
корней. Следовательно, л. € (2, 4| и лк е {0, 1).
В действительности полином (2.42) имеет следующие типы корней:
ло = 0, л+ = 1, л, = 2, як = 1.
□
2.6.3. Локализация корней полинома
Локализация корней — это приближенная оценка областей их размещения на
действительной оси или на комплексной плоскости. Наиболее быстрый
способ локализации действительных корней нечетной кратности заключает-
ся в построении графика Л(з) и поиске таких интервалов |.тЛп!п, з/пык| его пе-
ресечения с осью у, что
В точках действительных корней четной кратности (рафик Л(з) лишь каса-
ется оси s, поэтому локализовать их данным методом нельзя из-за одно-
значности функции Л(з) на концах тестируемого интервала. Некоторую яс-
ность в вопрос о существовании действительных корней на интервале |о, Л|
с произведением А(а)А(Ь) > 0 может внести теорема Фурье - Бюдана. Ее
результат N(a) - N(b) = 0 означает отсутствие таких корней
К сожалению, достоверная локализация комплексно-сопряженных корней
полинома высокой степени по его графику затруднительна. На рис. 2.44 в
среде Mathcad построен график функции (2.42), пересекающий ось s в окре-
стности действительных значений 0 и ±2. Оставшаяся пара комплексно-
сопряженных корней -1 ± >/10 j никаких визуальных признаков своего су-
шествования не обнаруживает
Далее рассмотрим некоторые вычислительные методы локализации корней без
построения графика функции Л(з).
214 Глава?
Метод обособленных корней [12]
Метод основан на предположении, что полином с предварительно отделен-
ными нулевыми корнями имеет близкие или удаленные от начала коорди-
наг корни, обособленные, т. е. далеко отстоящие, от остальных корней.
В случае возможного существования близкого к нулю действительного корня
|Л|« W V г е [2, л|
пренебрежем в уравнении Л(Т|) = 0 слагаемыми a2S\ +a„s", тогда из урав-
нения во + Д|Л| = 0 следует оценка такого корня
л, гг~а°
' «1
Если существует удаленный от остальных действительный корень
|Л|| » W V i е [2, л],
то, пренебрегая в уравнении Л($|) = 0 слагаемыми а0 + a„_2s" "2. получим
оценку
Аналогично находятся оценки расположения обособленных от других ком-
плексно-сопряженных корней 5) и «2 = ii путем решения квадратных урав-
нений оо + O|J + ojJ2 = 0 и Ои-2 + Дя-i J + OnS1 » 0 при условии, что отрица-
тельны их дискриминанты, т. е.
а2 < 4аоа2, а£_| < 4ала„_2.
Полученные оценки можно использовать как начальные приближения в
алгоритмах итерационного уточнения корней.
Метод Маклорена [12, 14]
Эффективный метод интервальной локализации действительных корней
предложен Маклерском. Из коэффициентов полинома Л(д) формируются
два вспомогательных полинома A\(s) и Л2(д) с единичными старшими коэф-
фициентами:
+...+(- !)"-• а,, + (_ J)" ао,
д:(,)в*0в4Г" +ал.|зл-1 +... + а1д + аи,
215
Частотные характеристики элементов и систем управления
где а,в о//ап. Тогда все действительные корни локализованы в интер-
вале
-1-""^м7<1(<1+я'"^м7, (2.48.0)
где mt и Mi — максимальные индекс и модуль отрицательных коэффициен-
тов полинома A/(s).
Вместо неравенства (2.48, а) можно использовать неравенство
для полиномов Л|(л) = Л(—у) и Aiis) = Л(т). приведенных к виду с положи-
тельными старшими коэффициентами а„
Если |Л/| / аД » 1 или |A/j / oj » 1, то формула (2.48, б) дает сильно за-
вышенные Гранины интервала локализации Для его сужения рекомендуется
представить полиномы Л|(у) и суммами полиномов с положительными
старшими коэффициентами и приблизительно равными отношениями мак-
симальных модулей к старшим коэффициентам Для каждого слагаемого
Л|,(у) и /Ь,(у) по (2 48) находится интервал локализации его действительных
корней. Тогда интервал локализации действительных корней полинома Л(з)
есть объединение интервалов локализации корней слагаемых полиномов При
удачном разбиении полиномов границы локализации определяются значи-
тельно точнее, чем без такого разбиения.
Метод кругов Гершгорина [4. 6]
Любому действительному полиному
А(у)=а0 + а15 + ...+ая_|у"*|+у"
с приведенными коэффициентами а, = л,/а„ можно поставить в соогвего
вие п х «-матрицу fl, собственные числа которой (корни уравнения
|у/„ - fl = 0) равны корням полинома, который в этом случае называется
характеристическим. Из бесконечного множества подобных матриц с оди-
наковым характеристическим полиномом А(у) выделяются особые канони-
ческие формы Фробениуса
216
Гпава 2
элементы которой есть числа 0, 1 и коэффициенты ~at V i 6 [0, п - 11. В
теории матриц известны методы кругов Гершгорииа, применяемые для лока-
лизации собственных чисел л х л -матрицы F= \fq\.
Круг Гершгорииа G, для /-го диагонального элемента f, описывается нера-
венством
и имеет центр в точке ft на оси Re{y) и радиус
*.-£|4
В частности, в (2.49) матрица F\ имеет л - 1 совпадающих кругов единич-
ного радиуса с центрами в начале координат и один круг радиуса
1=0
с центром в точке -<4-1 (рис. 2.46, а).
Матрица Л имеет п - 1 круг Гершгорииа с центрами в начале координат и
радиусами
Л|=|<ю|, Л,»|а/-||+ 1 V/е 12, л- I]
и круг G„ единичного радиуса с центром в точке -а„_| (рис. 2.46, б).
<)
Размещение корней полинома Л(з) и собственных чисел матрицы F, соглас-
но методу кругов Гершгорииа, удовлетворяет следующим условиям:
□ любой корень лежит, по крайней мере, в одном из кругов и ни один из
корней не лежит вне кругов:
Частотные характеристики элементов и систем управления 217
□ если m кругов образуют область, изолированную от остальных кругов, то
в этой области размешено ровно гп корней,
□ если какой-либо один круг Гершгорина изолирован, т. е.
Э - Jj)[>
то он имеет ровно один действительный корень в интервале
J/Е
Если все круги изолированы, то каждый из них имеет по одному дейст-
вительному корню.
Во многих случаях анализ совместного расположения кругов Гершгорина,
построенных для обеих матриц F\ и F2, позволяет сузить области локализа-
ции корней характеристического полинома этих матриц.
В заключение приведем дополнительные оценки модулей корней полинома, в
том числе и комплексных 112, 16), при следующих соотношениях между ко-
эффициентами:
□ если 0 < аО < al < ... < ап, то |si| < 1 v i е |1, nJ; (2.50, в)
□ если 0 < ап < ... < al < аО, то |si| > I V i е [1, nJ; (2.50, б)
□ если 0 < т < —L- <М V j = 0, л -1. то
aj*}
/Л<Ы< МУ is |1, л|; (2.50,в)
□ если для действительных неотрицательных чисел
выполняются условия 7| > > ... > q„, то модули всех корней полинома
Удовлетворяют неравенствам
| «5 g, + 0.618g, + 0.2213g, + 0.0883g4 + 0.0375g, + (2.50. г)
+ 0.0!85g6 + 0.0074g, +0.008 lg,.
Каждую полученную оценку обособленного корня полинома желательно
Проверить на принадлежность областям локализации корней, найденным
методами кругов Гершгорина или Маклорена.
С? Пример 2.9. Локализовать расположение действительных корней поли-
нома (2.42) подходящими для него методами.
218
Глава 2
Решение. Предполагая у полинома
Л(а) = -400 - 20008s - 304? + 4802? + 101? + 50?
наличие обособленных действительных корней, получим
s, - — = -2.02, s2 = = -0.019992.
1 50 2 20008
Судя по тому, что отношение модулей этих чисел составляет два порядка,
можно считать эти приближения соответственно большим и малым.
Из двух оценочных полиномов второй степени -400 - 20008s - 304? и
4802 + 101s + 50? лишь второй имеет отрицательный дискриминант и
оценки комплексно-сопряженных корней
$«,$ -1.01 ± 9.7478J
с большим модулем |s» s| = 9.8.
Крути Гершгорнна. рассчитанные по матрицам (2.49) для полинома
Л(з) = 50(? + 2.02? + 96.04? - 6 08? - 400.16s - 8),
образуют односвязные области и отсекают на действительной оси s интер-
валы 1-512.24. 508 2| для матрицы f\ и (-401.16. 401.16| для матрицы А
Пересечение этих интервалов дает область локализации действительных
корней (-401.16,401 16].
По методу Маклорена для полинома Л(з) получим и = 5 и
40) = ? - 2.02? + 96.04? + 6.08? - 400.16s + 8 => тх = 4, Л/, = 400.16;
4(s) = ? + 2.02? + 96 04? - 6.08? - 400.16s - 8 => = 2, ЛЛ = 400.16.
Таким образом, получили интервал локализации действительных корней
(-1-1/40046.1 + V400.1б)= (-401.16,7.37) (2.51)
Для сужения левой границы представим 4|(s) = ?n(s) + 4гО) + ?u(s):
4i0) - ? - 2.02? - 2.02s + 8 =» ли = 5, /Иц - 4, - 2.02, -1 - = -3.02;
4t(s) = 96.04? - 388.01s => л)2 - 3, m,2 = I. -I->/388.01/96.04 =-3.01;
4j(s) » 6.08? - !0.13s=» «и - 2, mu - 1, - I - 10.13 / 6.08 = -2.67.
Для сужения правой границы представим 4(s) = 4i(s) + Л22О) + Л2з(т):
4i(s) - ? - 6.08? - 6.08s - 6 => л2| « 5. «21 3 2, 1 + УбХЙ = 2.83;
4jW = 2.02? - 15.68s - 2 => »J2 - 4. «22 = 1. 1 * V1S.68/2.02 = 2.98;
4j(s) = 96.04sJ - 378.4s =» л2з 3 3, ma • 1, 1 + 7-378.4/96.04 = 2.98
Частотные характеристики элементов и систем управления 219
Таким образом, интервал (2.51) сузился до (-3.02, 2.98) = (-3, 3), т. е. в 68
раз. Полученные выше оценки корней з, и sj лежат в действительном ин-
тервале (-3.02, 0), а положительный действительный корень локализован в
интервале (0, 2.98). О
2.6.4. Уточнение корней полинома
После локализации корней следует завершающий этап их уточнения с же-
лаемой точностью. Выбирается начальное приближение корня з*01. принад-
лежащее области локализации. Итерационный процесс уточнения порожда-
ет последовательность приближений д<2), .... /*) к некоторому корню s, и
заканчивается на Л-ой итерации по достижении абсолютной % и/или отно-
сительной е0 погрешностей:
Л(/*>) = 0, Д<« = р) - Щ < е», 8(*> = < е0. (2.52)
Вычисление относительной погрешности следует пропускать при У*1 = 0.
Для исключения «зацикливания» алгоритма при осциллирующей сходимо-
сти рекомендуется ограничить максимальное число итераций числом A’nm
Не представляется возможным рассмотреть здесь огромное число алгорит-
мов, отличающихся:
□ объектом настройки интервалом, корнем или множителем полинома;
□ характером сходимости: глобальным или локальным;
□ скоростью сходимости: геометрической, квадратичной, осциллирующей
и другими свойствами. Остановимся лишь на некоторых методах, которые
можно реализовать без использования компьютера Но для выполнения
расчетов желателен все-таки калькулятор — и лучше, если он будет про-
граммируемым
Метод дихотомии (дробления интервалов)
Поиск действительного корня полинома
s,: = 0
состоит из двух этапов.
□ Нахождение на широком интервале локализации более узкого интервала
Л<°> = |Л«>, /«»].
удовлетворяющего условию разнозначности
А^Л^<0 (2.53)
Глава!
значений полинома А^ = А^0^) на левой Л0) и А^ = а(г^) на правой
И01 границах интервала, и задание на нем начального приближения кор-
ня з*0) (рис. 2.47)
Возможно, что условию (2.53) удовлетворяет исходный интервал локали-
зации В противном случае для нахождения интервала Л(0* длиной Л
можно воспользоваться методом шагов, заключающимся в прогонке ар-
гумента з по интервалу локализации с шагом Л до обнаружения отрезка с
разнозначными концами А0) и + й. Кстати, можно построить ал-
горитм так, что после уточнения корня s, он запомнит его и продолжит
прогонку с целью обнаружения следующего интервала, содержащего ко-
□ Запуск итерационной процедуры дихотомического сужения й-го при-
ближения интервала
Л«»-|Л«, Х*’|Д-0, 1,2,...
путем дробления его на две части внутренней точкой — й-ым приближе-
нием корня полинома
/*) = (!+ (2.54)
где 0 <</*>< 1 — некоторым образом выбранный коэффициент дробле-
ния t-го интервала
При к * 0 проверяются условия (2.52) остановки итерационного процес-
са. и если они выполняются, то процедура уточнения корня s( = ?*> за-
вершена.
Частотные характеристики элементов и систем управления
221
На следующей итерации интервалом Л'1*1* назначается тот из двух по-
дынтервалов |М>, 5<*>] или |л<‘>, И*1], на концах которого значения поли-
нома и опять разнозначны:
дия)д(*.|)<0
Простейшими методами дробления интервала Л**1 в (2.54) являются:
□ половинное (рис. 2.48, в) с фиксированным коэффициентом дробления
rf=0.5,
гарантирующее монотонную сходимость длины интервала
Х(*> = |И*> - /*)| (2.55)
к нулю со скоростью геометрической прогрессии = г/А’*1. знамена-
тель которой <? = 0.5 дает примерно три новые значащие цифры корня
за каждые десять итераций уточнения;
□ пропорциональное (рис. 2.48, б) с коэффициентом дробления
,(4)
= А^'-А^ Р56)
Длина интервала (2.55) монотонно сужается как прогрессия
Х<*'и> = с переменным знаменателем 0 < fl*1* < 1:
(*) при Л^а(т(1,)<0.
" =||-^прц 4(‘>Й‘><0.
Часто бывает, что на начальных итерациях </Л) << I и интервал быстро су-
жается, а на последних итерациях fl**1 -» 1 и интервал практически перестает
сужаться, при этом один из его концов сходится к корню пати нома.
«>
Рис. 2,48
Глава 2
Следует предостеречь от использования отличных от (2.52) критериев
останова итераций Например, выход по длине интервала А’*’ < е„ в ме-
тоде пропорционального дробления может стать невозможен при слиш-
ком малом значении еа. При половинном делении никогда не выполнит-
ся условие
-M=i<Eo
относительного сужения длины интервала
Пример 2.10 Сравнить методы половинного и пропорционального
дробления в задаче расчета действительного корня полинома (2.42) с по-
грешностями £, = «(,= 10~6 при начальном интервале Л’0’ = |-3, 3|.
Решение Проверим корректность выбора начального интервала Л,о>:
Д-З) “ -76 735. Л(3) = 86 825.
Условие (2.53) выполнено, следовательно, на интервале есть хотя бы одни
действительный корень полинома Я(з) Приведем Mathcad-протраммы рас-
чета процесса сужения интервала локализации корня и построения графи-
ков д<*>. М>, а для пропорционального дробления еще и график из-
менения </*’:
□ метод половинного дробления (рис. 2 49) с коэффициентами </*> = 0.5
сходится за 21 итерацию к корню з3 = 1.9999995. При этом изменяются
поочередно обе границы интервалов Л'**;
□ метод пропорционального дробления (рис. 2.50) сходится за 24 итерации
к корню J| = -I 9999989. При этом изменяются только верхние границы
И11 интервалов Л'11, нижняя же граница остается неподвижной: А*’ = -3.
Это значит, что на каждой итерации выбирается левый подынтервал
(Л*>. Начальное и конечное значении коэффициента дробления
равны - 0.469 и = 0.9999989.
Отметим, что при выборе начального интервала Л,о> = (-3.02, 2.98|, по-
лученного в примере 2 9, оба метода сходятся к одному и тому же корню
si -2 А вот при задании интервала локализации согласно (2.51) в виде
Л'1” (-401.16. 7.37] половинное дробление дало сходимость к корню
si=2 за 28 итераций, а пропорциональное и за 10 000 итераций сдвину-
ло точку ?*• от правой границы = 7.37 всего на -0.025. Это объясня-
ется слишком большой разницей порядков значений полинома на концах
интервала:
Л-401 16) - -5 17 10м, Л7.37) - 3.143 106.
Частотные характеристики элементов и систем управления
а : ( -400 -20008 -304 4802 101 S0 )Т
аа :• 10‘* ео > IO-6 ктах .= 1000
Л0 ( -3.0 3.0 ) А(Л0) - ( -76735 86825 »
"Половинное дробление"
Л*-АО
Гог ке 0 кта.х
X«-(rk«-Ao,t)-(l)j»-Ao)
С-А[ч-1к + Х(ак«-0 5)]
break If -<
If к
Л*-|«к-Ч-||
break if Л < ta v \ л -j—j- < to
Л*-1Г[А(|к)с<0.(|к h).(4 rifl
( I * r d к )
PMC.2 49
Рис. 2 50
Частотные характеристики элементов и систем управления_________225
Поэтому в (2.56) получаются коэффициенты дробления I, а в (2.54)
приближения корня з**1 = И0’.
Но бывает, что пропорциональный метод демонстрирует очень быструю
сходимость. Например, при Л<0) = [-1.5,0| он сходится к корню sj = —0.02
всего за три итерации с коэффициентами сужения интервалов
= 0.03. 9<'> = 0.442, 9<2> = 0.9992, = 0 9999996,
тогда как половинный метод сходится к этому же корню за 20 итераций.
На основе проведенного сравнения можно заключить, что более надежным
и устойчивым в работе является метод половинного дробления интервала ло-
кализации корня полинома. Другой метод — пропорционального дробле-
ния — более сложный, капризный и непредсказуемый и потому не гаранти-
рует эффективной сходимости О
Метод итерации
Исходное полиномиальное уравнение ао + °i* + + ans" = ° преобразуется
к виду
т= VW-
Задается начальное приближение корня з<0>, после чего строится последова-
тельность приближений
У*+|> = k = о. 1,2,...
Достаточные условия сходимости этой последовательности к некоторому
действительному корню т, — существование вокруг него окрестности, во
всех точках которой, во-первых,
ат
а во-вторых, попадание приближения ?** в эту окрестность Хорошо, если
это сразу будет начальное приближение /°1.
Скорость сходимости метода итерации к корню г, оценивается скоростью
сходимости геометрической прогрессии
со знаменателем
Я ~ гю.
При У > I последовательность з<*> к корню s, не сходится.
Успешность применения метода итерации весьма чувствительна к выбору
Функции v(j) и значения ?0). Приведем возможные варианты v(J> 11 ее
производной v'(J):
Глава 2
Vt(j)-j + hA(s), V;(j)=1 + M'(j);
В функции V|(s) параметр Л выбирается так, чтобы в возможно более широ-
ком интервале выполнялось условие сходимости
|1 + ЛЛ-О)| < I =» -2 < ЛЛ'(т) < О,
.,/ > dA(s) хп . /-|
A\s)=-^l=2jla's
Если задать начальное приближение корня з<01 из условия Л'(5<01) > 0, то
‘'7рт)<0’ *lW"’^)’
а в точке начального приближения производная
*^(O))=1-^ojj = °
удовлетворяет условию сходимости (2.57).
При выборе дробно-рациональных функций типа 412(5) или 4/3(5) их полюсы
(корни полиномов знаменателей) не должны совпадать с корнями A(s). До-
пустим, это условие не выполняется для простого действительного корня
s, = т}, тогда
*(*)= т \ • «п) * °-
(»-т1)О(з)
Поскольку Л(г)) ~ В(п) = 0. то
ад - (5 - п)ад. Ап) * О, vG)=
Таким образом, при совпадении корня ад с полюсом 4/(5) метод итерации ни-
когда не сойдется к этому корню, т. к. он фактически работает с полиномом
Частотные характеристики элементы и систем управления_________ 227
А(з)=зО(г)-Е(г),
для которого п не является корнем
А(п)*О.
Если корень Л(г) очень близок к полюсу у(г), то окрестность, в которой
выполнено условие сходимости, скорее всего, будет отсутствовать. Это объ-
ясняет невозможность нахождения всех действительных корней полинома
при неудачном выборе разрывной функции у(з).
Для того чтобы исключить действительные полюсы ч»(г). ее знаменатель
подбирается так, чтобы он нигде не обращался в нуль на интервале локали-
зации корней. Но т. к. никакая непрерывная функция у(г) не может в двух
соседних точках пересекать прямую г, имея в них обеих производные
|i|»'(s)| < 1, то такой выбор у(г) в принципе не может дать всех действитель-
ных корней полинома.
2? Пример 2.11. Вычислить действительные корни полинома (2.42)
Л(г) = -400 - 20008г - 304г2 + 4802? + 101? + 50?
методом итерации с погрешностями Еа = ео = 10"6 при начальных прибли-
жениях У°» = -1.5, ?°> = 0.8 и ?°> = 3.
Решение. Исследуем возможности различных функций у(г). Пусть вначале
(у,(г) = г+й(?°)М(г),
где
ТЦГ) =----------------------;------;------Г
- 20008 - 608г + 14406г1 + 404? + 250г4
На рис. 2.51, в, б, в приведены функции Vi(r), vj(г) и итеративные про-
цессы уточнения корней полинома. Графики / соответствуют начальному
значению ?°> = -1.5 и коэффициенту Л(-1.5) = -7.56 10_J. Так как облас-
ти сходимости очень узкие и не включают ни одного корня полинома, то
последовательность имеющая периодический характер, никогда не
сходится.
Графики 2 построены для начального значения = 0.8 и коэффициента
6(0.8) = 9.12- 10-5. Достаточно широкая область сходимости, включающая
корень rj = -0.02, обеспечивает его получение с заданными погрешностями
ь, и t„ за 70 итераций.
Хорошими свойствами сходимости к корню jj = 2 обладает начальное при-
ближение = 3 с коэффициентом 6(3) = -7.2 10** (графики 3). Приме-
няя функцию Vi(r) с этим коэффициентом аз я начального значения
•г*01 = -1.5, получим последовательность приближений сходящуюся к
корню Г| = -2 за 21 итерацию ((рафик -Л. Более того, исследование с по-
Глава 2
мощью Mathcad-программы показало, что при h = Л(3) любые начальные
приближения з*°> е |-3, -0.02) сходятся к корню S| = -2, а любые
/°> е (-0.02, 3) - к корню sj - 2.
10^1 | I | 1 -и» 1 -г
1 1 ? t- t - r~i—Н~т т"г"гг.
Рассмотрим теперь функцию
W, (.1) ------------------z------Z------Т
- 20008 - ЗО4т + 4802? +101? + 50s4
с разрывами второго рода. Графики 5 функций Vj(s), v'j(s) *’ последова-
тельностей /*> для разных начальных приближений У0’ изображены на
рис 2.52, о, б, в Все три значения сходятся к одному и тому же корню
jj “ -0.02 за 3 итерации. Нет ни одного значения з<°>, сходящегося к корням
»1 и SJ. Это объясняется близостью корней к полюсам Vj(s). равным
Частотные характеристики элементов и систем управления
-2.01 =$| и 1.99 = т3. в окрестностях которых не выполняется условие схо-
димости (2.57).
Составим гладкую функцию
, ' 400 + 400163+304?-101/
4 20008 + 4802?+50.?
не имеющую действительных полюсов. На рис. 2.52, а, б, в изображены
графики б функций V4<s), V4O) ” последовательностей s<*>. Начальное при-
ближение з<°> = -1.5 сходится к 3’1 за 4 итерации, а з<°> 0.8 и ?°> = 3 — к
корню 53 = 2 за 6 и 5 итераций соответственно. Нет ни одного значения ?°>,
сходящегося к корню jj, соседнему с j| и Sy Это объясняется отсутствием
около него окрестности, в которой выполняется условие сходимости (2.57).
230Глава?
Метод Ньютона
Этот метод уточнения простых корней известен еше как метод касательных
и описывается итерационной формулой
Налицо сходство (2.58) с методом итерации, использующим функцию
с фиксированным знаменателем Можно ожидать сравнительного
ускорения и расширения области сходимости алгоритма Ньютона благодаря
вычислению на каждой итерации производной полинома Л'(д), которая в
точке корня должна быть ненулевой, а, следовательно, корень — некрат-
ным.
Задав начальное приближение в области локального притяжения какого-
нибудь корня полинома, рекуррентно вычисляем приращения
и новые приближения
/*+|) = jttl + о<*»
до выполнения условий остановки (2.52).
Метол Ньютона имеет квадратичную скорость сходимости к корню s,
более высокую, чем скорость сходимости геометрической прогрессии: за
одну итерацию число верных знаков корня примерно удваивается. При вы-
боре начального приближения з<0) вне областей локального притяжения ал-
горитм расходится или зацикливается.
& Пример 2.12. Вычислить все корни полинома (2.42)
Л(з) “ -400 - 20008т - 304? + 4802? + 101? + 50?
методом Ньютона с погрешностями €, = «„= I0-6 при начальных прибли-
жениях /°> - 0.8, /°» - 1.1 и 1"»> • 3.
Решение. На рис. 2.53 показаны процессы уточнения корней методом Нью-
тона:
□ при начальном приближении = 0.8 последовательность знакопере-
менно сходится к корню 3j« -0.02 за 4 итерации;
Частотные характеристики элементов и систем управления
□ при ?°> = II последовательность с большим выбросом сходится к кор-
ню 5| = -2 за 8 итераций;
□ при ?°) = 3 наблюдается монотонная сходимость к корню 3j = 2 за 5
итераций.
Для получения оставшихся корней разделим по алгоритму (2.43) исходный
полином Л(з) на произведение трех полученных множителей
Д(з) = (г - j,)(j - jj)(j - rj) = ? + 0.02? - 4з - 0.08:
_ 50?+101 ?+4802?-304з!-20008з-400 I ?+0.02зг-4 г-0.08
50?+ s4 200?- 4г | 50?+100з+5000
_ Ю0?+5002?-300?-20008г
~ 100?+ 2?-400?- 8г
_ 5000?+100.г-200005-400
5000?+100?-200003-400
0
Полином частного имеет комплексно-сопряженные корни г 4.5 = -1 ± 755 j.
Таким образом, найдены все корни полинома, имеющего следующие фор-
мы разложения на множители (си разд. 2.6.1):
Л(з) - -400(1 + 50з)( I + 0.5з)(1 - 0.5з)(1 + 0.02г + 0.01?) -
- 50(з + 0.02)(з + 2)(з - 2)(? + 2з + 100).
232
Мы рассмотрели основные численные методы расчега действительных кор-
ней полиномов. Что касается комплексных корней, то (рафик функции Л(з)
не дает оценок их действительных и мнимых частей. Локализация, часто
очень грубая, возможна методом кругов Гершгорииа или по (2.50).
Задав комплексное начальное приближение з<0) = т|<°> + , используем
для уточнения корня метод Ньютона с учетом следующих замечаний:
□ все вычисления в (2.58) производятся в комплексных числах и без при-
менения ЭВМ достаточно сложны;
□ скорость сходимости алгоритма Ньютона на комплексной плоскости
значительно меньше, чем на действительной оси;
□ не любое комплексное приближение сходится к комплексному корню, а
области сходимости алгоритма Ньютона могут иметь самые разнообраз-
ные формы, быть невыпуклыми и неодносвязными, что затрудняет вы-
бор начальных приближений и нахождение всех комплексных корней.
На рис 254. а изображены корневые траектории ньютоновского итераци-
онного процесса (2.58) для начальных приближений
з»0' = 0 + 7j, з«» = 0 + 8j, j«» = 0 + 9j,
сходящиеся к корням з1 = -2, jj = -0.02 и з4 = -1 + >/99 j, соответственно,
за 12,10 и 6 итераций с погрешностями еа = е0 = Ю"6.
Сложность структуры областей сходимости к пяти корням полинома (2.42),
найденным в примере 2.12, проиллюстрирована на рис. 2.54, б. Вблизи гра-
ниц области si расположены мелкие «острова» сходимости к другим корням,
не связанные со своими «материками». При увеличении масштаба изобра-
жение обнаруживает типичные фрактальные свойства: отсутствие гладких
границ и бесконечную степень их дробимости.
Частотные характеристики элементов и систем управления
Рис. 2.54
Эти особенности могут затруднить выбор начальных приближений корней:
очень близкие значения s*0* сходятся к разным корням s,. Примеры сходи-
мости с различных начальных приближений:
□ з<°> = -0.8 + 7.62j сходится к комплексному корню ij за 20 итераций.
□ з<°> = -0.8 + 7.63j сходится к действительному корню tj за 26 итераций;
□ з<°> = -0.8 + 7.64j сходится к действительному корню J| за 27 итераций;
□ 5<0) = -0.8 + 7.65j сходится к комплексному корню Х| за 25 итераций;
□ 5<0) = -0.82 + 7.63j сходится к действительному корню jj за 28 итераций
Для этих итерационных процессов характерны скачки приближений с одно-
го «острова» на другой до попадания в «материковую» область с быстрой
сходимост ью к соответствующему корню
Существует группа итерационных методов нахождения множителей ЯДз) за-
данного полинома вместо его корней. Их рекомендуется применять, если
конечной целью является не вычисление спектра полинома, а разложение
его на простые множители
Ж)=Па(з).
в ряде случаев (полином четной степени с комплексными корнями или с
кратными действительными корнями) данные методы, работающие с дейст-
вительными числами, эффективнее комплексных вариантов корневых мето-
дов. Если полином разложен до простых множителей первой и второй сте-
пеней, то расчет его корней прост.
234________________________________________________________Глава 2
Таким образом, объектом настройки являются коэффициенты приведенных
полиномов B(s) - s + bo первой или В(з) = г3 +6|Г + Ьд второй степени. На-
чальные приближения полиномов
в‘0)(т)»т+^0) или В(0)(тН2+^0)т+^0)
вообще-то произвольны, но для ускорения сходимости лучше выбирать их
по старшим коэффициентам полинома А(з):
□ для множителя первой степени
+ (2.59,0)
«л
□ для множителя второй степени
В{%)-з2+^-з + ^-. (2.59,6)
a« “в
В ходе процесса рассчитывается последовательность приближений В^Чз).
Условия остановки итерационного процесса на £-ой итерации аналогичны
(2.52) для каждого настраиваемого коэффициента и Ь^.
Если найденный множитель В(з) имеет вторую степень, то далее определя-
ется тип его корней по знаку дискриминанта d - b2 - 4Ь0. При d > 0 поли-
ном имеет два действительных корня и разлагается на два множителя пер-
вой степени В противном случае В(з) является простым множителем второй
степени с комплексными корнями.
Далее по алгоритму (2.43) выполняется деление полиномов
с(л)’7^
и ищется множитель полинома частного С(г), являющийся также множите-
лем Л(г). Процесс разложения заканчивается, когда полином-остаток первой
или второй степени является простым. Это последний множитель полинома
Л(г) высокой степени.
Если имеет место сходимость для начальных полиномов &°4s) и первой, и
второй степеней, можно использовать несовпадающие делители обоих полу-
ченных множителей для понижения степени Л(з).
МетодЛина [12,16]
Вычисления на каждой итерации уточнения полинома B(s) = s + bv первой
или B(J) = j2 + b\s + bg второй степени очень просты:
Частотные характеристики элементов и систем управления 235^
□ по алгоритму (2.43) полином Л(л) делится на полином sB^(s) второй или
третьей степени с получением полиномов частного C(s) и остатка D(s).
□ полином D(s) = d\s + d0 первой или D(s) = rfji2 + d^ + d0 второй степе-
ни делится на d\ или d2, образуя следующее приближение полинома
множителя
В^'\л)=л + Ь^ или
Условия сходимости последовательности полиномов й***(з) имеют следую-
щий вид:
□ сходимость к полиному 5(5) = (j - 5,) первой степени при
Г‘ ~ |^5J ' *|< 1 ’ где R^= ~~: (2 60, fl)
□ сходимость к полиному B(s) = (s - st)(s - Sj) второй степени (корни 5, и s,
могут быть как действительными, так и комплексно-сопряженными)
при
r'"=fe4<l
Скорость сходимости оценивается знаменателями геометрической прогрес-
сии
Ч,ВГ)'
При qj^ 1 или qtj> I итерационный процесс расходится. Таким образом,
алгоритм Лина, как и все локальные методы, не гарантирует получения ре-
зультата наверняка. В случае расходимости или зацикливания последова-
тельности полиномов первой степени следует повторить алгоритм для
множителя второй степени.
& Пример 2.13. Разложить полином (2.42)
/1(5) = 505s + 10I54 + 48025s - 304т2 - 200085 - 400
на множители методом Лина с погрешностями расчета коэффициентов
Ч = to “ 10~6.
Решение. Проанализируем выполнение условий сходимости (2.60, о) к трем
множителям первой степени (5- тД. /е(1, 2. 3).
□ Для корня 5| - -2 находим полином частного R(s) = Л(т) / (5 - 5|):
ГЛАВА 3
Законы математики. имеющие какое-либо
отношение к реальному миру, ненадежны, а
надежные математические законы не имеют
отношении к реальному миру.
Альберт Эйнштейн
Временные характеристики
элементов и систем управления
Динамические свойства элементов и систем оцениваются их временными ха-
рактеристиками (ВХ) — реакциями на типовые входные воздействия: гар-
моническое, импульсное и ступенчатое. При гармоническом воздействии
определенной частоты w динамика системы характеризуется изменением
амплитуды И(ы) и фазовым сдвигом <р(ы) установившегося выходного сигна-
ла, т е передаточной функцией и частотными характеристиками системы.
Изучению этих вопросов была посвяшена гл. 2.
Теперь сосредоточим внимание на задаче расчета реакций типовых
звеньев и системы в целом на входные воздействия импульсного и сту-
пенчатого типов. Среди множества различных методов расчета переход-
ных процессов в инженерной практике наиболее распространен опера-
торный метод преобразования Лапласа. Основные моменты этого метода
заключены в следующем:
□ по формуле (1.16) выполняется прямое преобразование Лапласа
X(s) = Цх(')>
входного сигнала x(t) — оригинала, в результате чего получается изобра-
жение сигнала X(s\,
□ с помощью алгебраического преобразования (1.18) находится изображе-
ние Из) выходного сигнала;
□ обратным преобразованием Лапласа
X0 = L-'(Kj))
Временные характеристики элементов и систем управления 243
восстанавливается оригинал у(0 — временная функция выходного
сигнала.
К текущему моменту мы не касались лишь последней задачи — обратного
преобразования Лапласа, к чему немедленно приступаем.
3.1. Обратное преобразование Лапласа
Изображения большого числа экспоненциально ограниченных временных
сигналов
ЛО: |/W| s Meml v t г О
(степенных, экспоненциальных, гармонических) имеют вид дробно-
рациональных функций оператора г
*0=2^**» A(I)=2}a',Z
Л\*> 1=0 i=o
с действительными полиномами B(s) и Л(т) степеней т и п соответственно
В теории функций комплексного переменного известна формула обратного
преобразования Лапласа [16, 20, 21, 23, 30J:
jF0s*<b. (3.1)
2я) Д
Условием сходимости несобственного интеграла с абсциссой сходимости
с > т является прохождение линии интегрирования с + jio V we (-~. ~) по
комплексной плоскости т правее полюсов изображения Дз).
Правильность расчета оригинала проверяется по предельным формулам дтя
начального и конечного значений:
/(О) = lim /(г) = lim jF(t), (3.2. а)
lim f(t)= lim jF(j). (3.2. 6)
Истинное установившееся значение Л00) совпадает с оценкой (3.2, б) только
при условии, что оно существует, а это налагает на изображение Дз) сле-
дующее ограничение: все его полюсы — корни полинома знаменателя —
должны быть левыми
Доказательство формул (3.2) базируется на сравнении двух пределов при
з -> 0 и з ~ конечного выражения преобразования Лапласа производной
функции/'(г) с ненулевым начальным значением
L(T(')I * - ДО)
244
Глава 3
с соответствующими пределами определения (1.16) этого же преобразования:
lim L(f'(r)}= lim [e'''^^df = 0 =» lim jF(s)= /(o);
'-*“o d'
toLHr)}=ltaJe-Mr = /^ = /(-)-/(0) => lim,F(4)=/(~).
о
Формула обратного преобразования Лапласа (3.1) математически сложна и
потому имеет ограниченное применение. Рассмотрим более практичные ме-
тоды получения оригинала по изображению как вручную, так и с помощью
программ.
3.1.1. Метод разложения Хевисайда
Для вычисления несобственного интеграла дробно-рациональной функции
Дз) разложим полином ее знаменателя Л(т), имеющий v различных корней st
(действительных и комплексных) кратностей Л/2 I, на множители первой
степени:
(3.3)
Оригинал//) изображения Дз) может быть вычислен по формуле разложения
Хевисайда'.
Эта «страшная» на первый взгляд формула имеет простую структуру:
/(')=£с.С|(0="Ёс<‘/‘ =c/o+Qi' + - + c/.nl-i'','’l«
'> *-о (3,5)
Оригинал есть сумма v экспонент е’1'. умноженных на полиномы времени
сХО Вычисление полинома сХО степени - I проходит через следующие
этапы:
□ сначала находится вычет
Временные характеристики элементов и систем управления 245
функции F(s) в л,-кратном полюсе J/ путем исключения множителя
(.5-5, )"' из полинома знаменателя A(s)\
□ вычет дифференцируется л, - 1 раз по s и в полученные производные к-
го порядка подставляется s = sf,
□ числа делятся на произведение факториалов к'(п, - 1 + кУ В
результате получаются в обратном порядке числовые коэффициенты
<Ч.п(-1 > •••» сл> с<о-
Более простой метод, не требующий дифференцирования вычетов в кратных
полюсах, заключается в расщеплении F[s) на сумму изображений Ft(s) по
числу различных полюсов — корней полинома Л(з) в (3.3):
(3.6)
Рассмотрим возможные типы слагаемых Ffa).
□ Если степени полиномов 5(з) и Л(з) таковы, что т > п, то в (3.6) есть
изображение
= сЛ + спз + ... + с,1Я _ -", (3.7, а)
порождающее оригинал
/</) = СЛ8(1) + caS'(t) + . - ">(/). (3.7. б)
Возможно, что изображение представляет собой передаточную функцию
некоторого объекта. Тогда при т > п в этом объекте между входом л(г) и
выходом у(1) существует прямая связь — такая, что входной сигнал пере-
дается на выход с коэффициентом усиления сд. его производная х'(/) — с
усилением сц и т. д. При т < п прямая связь отсутствует.
□ Если в изображении полюс з, — действительный и простой (п, = 1),
то в (3.6) существует следующее изображение АДз), порождающее
оригинал /(/):
fl(0= — «* /<(')= сле‘’ (3.8. а)
s-st
Подставив 3 = 5/8 вычет (з - 3/)Дз). получим коэффициент
<х,-я
где производная от полинома знаменателя вычисляется как
Глава 3
A'(s)=at +2a2s +... +na„s"~l . (3.8, «)
□ Если в изображении полюс х( - действительный и кратный (п, > 1),
то в (3.6) существует следующее изображение порождающее
оригинал /(г):
Fiх^х" + ( 8 2 Y +' ’'+ (s-sY' = (х-х У ’
х-х( (х-х,Г (х xj *в1(х xj (з9 в)
/, (0=U +««» + ••• + ^.п, -Н"* “'к’ = 2^*'* •
Коэффициенты glk и cik вычисляются в обратном порядке:
«*"^['<>-1^]] ^.<3.9.0
Сначала находятся коэффициенты
У'^(*) |(в>/ =» с/*-1 =
Напоминаем, что — вычет Дх) в л,-кратном полюсе х/. Сократив
разность
7W-fW-(^r
на х-Х/, получим изображение с п,- 1-кратным полюсом х,. Теперь
можно вычислить коэффициенты
в'А-'У =* ^.«,-2=^^
Повторяя этот прием, последними определяем коэффициенты gn = с»-
□ Если в изображении KOMibiexcm-солрнжениые полюсы х, - П/ + М н
x/ = n(-jw, - простые, то в (3.6) есть следующее изображение /Хх)-
порождающее оригинал /X/):
Временные характеристики элементов и систем управления
где
Ft(.,)= О1.+ М1 + Р, -№ _ 8,о + gns
j-j/ ,»2 -2n,j + n; + w,2'
(3.10, о)
Л(')=(л +)ч,Р'' + (р,
= 2еП(' (р/ cos(io,/) - q, si n(co,/)) = ср'1' cos(w,r + <p,)
8/о=-2(’1,Л+Ю|Ч|>«,)=2л-
p = «Ф, q =Hlo + n,g,i
' 2 ' 2(0,
c, = 2-Jfl2 + <7/2. tg(<P, )= —
Pi
(3.10,6)
Коэффициенты p, и q, можно также получить аналогично (3.8, 6)
(зю.
как комплексный вычет изображения Rs) а простом комплексном полю-
се 3,.
Из-за неудобства сокращения действительного полинома Л(з) на ком-
плексный полином s - з, = з - П, “Ж сократим Л(з) на действительный
полином
(з-з,)(з-^)=з2-2т)Л + П? + Ч2
Тогда
(з -з^з- si)г(з| -( = 8,о + 8,1« = -2», (<?, + )•
откуда
lm{ (з2 - 2ПЛ + И,2 +‘0’к<4.1,}
Л--------------'
Re| (з2 -2V + 1,2 |
Глава 3
□ Наконец, если комплексные полюсы j, = ii( + j<D( и з, =T|,-j<i), имеют
кратность л, > I, то в (3.6) есть следующее изображение F/s), порож-
дающее оригинал/X')'-
Hj-I
=» /,0=e’1,'£f1/cos((Oir + q)lt). (3.11,а)
*•0
Параметры од од Сц и <₽,* находятся аналогично (3.9. б) и (3.10, б):
(З.п, Ф
Обобщая сказанное, проиллюстрируем на рис 3.1 связь расположения по-
люса изображения s, на комплексной плоскости с характером (устойчивым,
неустойчивым или нейтральным), типом (апериодическим или колебатель-
ным) и параметрами (быстродействием, перерегулированием, колебательно-
стью) составляющей оригинала с'1', порождаемой этим полюсом. Опытный
проектировщик всегда держит в голове это наглядное графическое представ-
ление. понимая, как повлияют на свойства оригинала удаление, добавление
или перемещение полюсов изображения на 5-плоскости.
Временные характеристики элементов и систем управления 249
Опытный проектировщик также всегда представляет, как влияют на ориги-
нал нули изображения — корни полинома числителя. Если полюсы Дз) оп-
ределяют отдельные составляющие оригинала е ' то нули — относитель-
ный вес этих составляющих сД/). Чем ближе нуль расположен к какому-то
полюсу, тем меньше вклад соответствующей составляющей в общую сумму
оригинала (3.4).
ЕУ Пример 3.1. Найти оригинал изображения, разложенного на простые
множители:
rt.)
.‘(I..
Решение Полюсы изображения и их кратности равны
3] ш О, Л| = 2;
3i= -l,itj»I;
33= 1. лз = 3;
Д.5 = -1 ± 2j (T14 - -1, = 2). «4 = «5 = 1
С учетом кратностей полюсов дробно-рациональное изображение имеет
следующее разложение на сумму простых дробей:
F (s) = g|1 + -£11 + Сзд + -£iL + 8п + Kii + *40*841*
з ? з + 1 з-l (5-1/ (,-|)? з2 + 2з+5
Вычислим его неизвестные коэффициенты В первую очередь найдем чис-
лители дробей старших кратностей:
Й12=з2Р(з)| =о=8, см=(з + 1>(з)|1ж_|=1. г„=(з-1Уг(з)[_(=-3.
Вычитая найденные дроби из Дз), получим изображение с кратностями по-
люсов, на единицу меньшими:
г/3 г/ г 8 1 3 з7+7з°-з5-Из4-72з3+4з*+72з
w—?(„|)(|.4Ч21.5)—
_ ~з4-7з3+4з + 72 _gyi Sao+Sjl*
" з(1-з)2(з2 +23 + 5)" 3 3-1 (з-lf з2 + 2з + 5
Теперь можно вычислить коэффициенты
Si I = *Г(з) Ц -14.4, вм = (з - ^(з) = 8.5
250 Глава 3
Снова находим разность
гМ 14.4 8.5 -15.4?-15.5?-45.8?+76.7.Т
f(,)- F(i)- V-О =-----------7(a-l/C?+2i+5T-------=
. -15.4?-30.9л-76.7 _ g„ + X40 + g4|J
(л-1Д?+2s + s) л-1 ?+2j + 5
и последние неизвестные коэффициенты
вэ1=0-1Я) [и=-15.375,
*40*841* = 7(Л+15-375 = -0.025л-0.175
?+2s+5 U J-1 ?+2а + 5
Теперь вычислим по (3.8, б) - (3.10, б) коэффициенты оригинала:
/(')= (сю + А Д'1' +С20'12' + U + С31' + ^зг? к'3' + ‘Ч6’’4' +
Сю - 14.4, С|| *12 = 8, см = 1, Cjo = ftt = -15.375, с3| - gn = 8.5,
с . «21 = _j,5, р = «11 = -0.0125, <?4 = S4o + T14^- = -0.0375,
21 2 2w4
С1 = 2^р}+д^ =0.079, ф4 =arctg^ — j-n =-1.893рад=-108.4°.
Таким образом, мы получили решение задачи - временную функцию
Л Л “ 14.4 + 8/ + е-' - (15.375 - 8.5/ + !.5Я)е/ + 0.079е~'с<к(2/ - 1.893).
3.1.2. Табличный метод преобразований Лапласа
Вычисления изображения Дг) по (I.16) и оригинала ДО по (3.4) -(З.П)
достаточно сложны Популярность операторного метода основана на том.
что изображения большого числа временных функций давно вычислены "
протобу.трованы Если бы в докомпьютерную эпоху этого нс было сделано,
то высокая трудоемкость выполнения интегральных преобразований в ка*'
дой отдельной задаче не позволила бы операционному исчислению стап>
мощным инструментом решения самых разнообразных математических "
технических задач.
Временные характеристики элементов и систем управления
Приведенные в Прол. 1 таблицы преобразований Лапласа заимствованы (с
исправлением нескольких ошибок) из учебника-справочника (16. табл. П1 2,
4.1]. Необходимость дублирования таблиц в данной книге объясняется же-
ланием автора сделать их более доступными, г. к. справочная литература по
автоматическому управлению стала в наше прагматическое время библио-
графической редкостью. Подробные таблицы преобразований Лапласа мож-
но найти также в (14, табл. 8.4-1, 8 4-2]
Изображения наиболее часто встречающихся временных функций приведе-
ны в табл. П.1, а по табл. П.2 удобнее совершать обратное преобразование
Лапласа дробно-рациональных функций. Возможности этих таблиц расши-
ряются благодаря использованию свойств оригиналов и изображений, пере-
численных в табл. П.З
Согласно устоявшейся в теории автоматического управления терминологии,
в табл. П.1 и П.2 использованы следующие обозначения параметров (с ин-
дексами и без них) оригиналов, изображений и формулы их связи:
□ а и В — показатели затухания экспоненциальных функций;
□ Гит — постоянные времени типовых звеньев;
□ ш — частота колебаний типового звена второго порядка;
□ О S £ < I — коэффициент затухания типового звена второго порядка;
□ соотношения между параметрами:
аГ= 1,₽Т=5, шГ = 7ьЧ7.(₽1 + а>2)71= I-
В табл. П.2, начиная с п. 72, встречаются выражения типа
в которых знаменатель р может быть нулевым или отрицательным Во избе-
жание сингулярности (при р = 0) или ошибки (при р < 0) вычисления фазо-
вого сдвига тригонометрических функций <р нужна ручная коррекция глав-
ного значения angle, возвращаемого функцией arctg, с учетом знаков чисел р
»<Г-
прирз0и9 = ().
прнр = 0и<7>0.
прн/> = 0и<7<0,
angle + Я при р < 0 и q > 0.
angle - я при р < 0 и q < ft
252
Глава 3
При машинном вычислении фазового угла нужно использовать функции,
возврашаюшие результат в интервале (-л, п|:
<р = atan2(p, q) или <р = arg(/> + j<?).
& Пример 3.2. В качестве иллюстрации применения таблиц прямого и
обратного преобразований Лапласа и выполняя обещание, данное в гл. 2,
рассмотрим поведение автоколебательного звена с передаточной функ-
цией
И,(')=й??’/Г>0’Г₽>0’
на вход которого подано гармоническое колебание х(/) = sin(tOpr) с резонанс-
ной частотой собственных колебаний звена <0р = 1 / Гр.
По табл. П.1, п. 9, находим изображение входного воздействия:
Находим по (1.18) при нулевых начальных условиях изображение выходного
сигнала:
КТ.
Непосредственно такого изображения в табл. П.1 нет, но его можно найти в
более удобной для обратного преобразования Лапласа табл. П.2, п. 78, при
Р = 0 и ШрГр = I:
у(т)=0.5к(мл(шрг)-Шр««»(шр»))=0.51
(3.12, л)
На рис. 3.2 построены графики сигналов 4» и у(Г), которые проясняют сущ-
ность явления резонанса в автоколебательном звене: благодаря отсутствию 8
нем потери энергии (коэффициент затухания £ = 0) происходит
звена входным сигналом с частотой iuj, до бесконечной амплитуды, в чем по-
винно слагаемое WpfcosUy) При этом чем больше частота резонанса, тем быст-
рее нарастает амплитуда выходного сигнала во времени.
Интересно исследовать реакцию автоколебательного звена на входное гар-
моническое колебание х(г) = sin(<n/) с частотой ш # ц,. отличной от резо-
нансной. Теперь изображения входного и выходного сигналов принимают
ВИД
Х0=
ш
Из табл. П.2, п. 84, при рр = 0 и Р = 0 следует оригинал y(t) в виде биений.
т- *. суммы двух незатухающих колебаний — собственных с частотой с^, и
вынужденных с частотой со:
X/) = -q>sin(v + ’р) “ Gin(“f + ф)’
где
Фр = aun2(o, <Ор(тр: - Т2))+ ашп2(о. % )= (1 + sgn(rp - т))-90°,
Ф = аип2(о, <о(т2-Tp2))+atan2(O, <o)=(l + sgn(r-Tp)) 90°.
Гпава 3
После упрощений получим более простое окончательное выражение ориги-
нала при любых соотношениях между постоянными времени Тр и Т или
частотами ц, и ох
(3.12.6)
На рис. 3.3 построены графики входного лс(/) = sin(ow) и выходного (3.12. 6)
сигналов при частотах (в) ш = O.Sojj, и (6) ы = 1.25шр.
Рис. 3.3
Физически биения объясняются следующим образом. Поскольку частоты
резонанса и входного воздействия не равны, но близки друг к npyiy, система
поначалу ведет себя как на рис. 3.2 — раскачивается в такт с внешней си-
лой.
Но с течением времени между собственным и вынужденным движениями
набегает разность фаз в 180е. Они начинают друг дуга компенсировать, что в
результате уменьшает суммарный сигнал.
Нетрудно показать, что в пределе <о-> Шр формула (3.12, 6) путем разреше-
ния неопределенности 0 / 0 по правилу Лопиталя преобразуется в выраже-
ние (3.12, а):
Временные характеристики элементов и систем управления 255
lim y(a).r)=-^-(sin(copr)-co/cos(w/)) =0.5K(sin(w.»)-w rcos(oy)).
2W L<Dp
о
3.1.3. Программный метод преобразований Лапласа
В настоящее время появились компьютерные программы типа Mathcad,
имеющие в своем арсенале высокоразвитое интеллектуальное средство —
символический процессор, способный выполнять множество сложных сим-
вольных операций, в том числе и преобразования Лапласа — как прямое,
так и обратное. Теперь пользователю (студенту, инженеру, академику) не
обязательно иметь под рукой справочник с таблицами для решения задач
операторным методом. Достаточно овладеть несложными навыками работы
с программой и потом испытывать бесконечное удовольствие от быстро по-
лученного результата.
Символические преобразования Лапласа с помощью Mathcad можно выпол-
нить, по крайней мере, двумя способами.
□ Вводим преобразуемое выражение (оригинал Д/) или изображение
устанавливаем курсор на переменной / либо s, затем в меню Symbolics
находим пуню* Transform и выбираем Laplace, либо Inverse Laplace
Результат преобразования появляется строкой ниже Далее его можно
скопировать в буфер и присвоить функции Дз) илиДг).
Недостаток данного способа символического преобразования в том, что
при любом изменении исходной функции или данных, от которых она
зависит, приходится удалять с экрана результат предыдущего преобразо-
вания и повторять все действия заново
□ Набираем в нужном месте Mathcad-документа присвоение
f(t) либо F(s) =
и вводим в пустое поле преобразуемую функцию. Затем правее или ниже
этой строки печатаем выражение
F(s)f(t) либо f(t) : F(s)
и выделяем его правую часть. Нажав в меню панелей на значок _*j. вы-
бираем в раскрывшейся панели символических вычислений оператор
laplace либо inviaplace. В пустое поле (после запятой) полученного
шаблона
F(s) = Г(1) laplacc .а —♦ либо f(l) - F(s) invlaplace . -»
256 Гпава 3
вводим параметр преобразования «I» либо «s». Нажав клавишу <F9> или
установив курсор вне формулы, справа от знака символического равенст-
ва «-»» увидим результат, который будет одновременно присвоен функции
Ял) либо Д г).
Последнее действие выгодно отличает данный способ преобразования от
первого: любое изменение формулы преобразуемого выражения или ис-
пользуемых им данных автоматически обновляет результат.
Если символический процессор не может выполнить необходимое преобра-
зование (это, к сожалению, бывает не так уж и редко), то результат преобра-
зования повторяет исходное выражение. В этом случае придется решать за-
дачу преобразования другими методами.
На рис. 3.4 приведен листинг Mathcad-программы обратного преобразова-
ния Лапласа изображения
с параметрами т= 3, 7= 10 и £ = 0.2. Для сравнения оригинал вычисляется
тремя способами:
□ функция /|(г) получена в символической форме оператором inviaplace.
С помощью оператора float, з оригинал выводится на экран с разреше-
нием три цифры без переноса строки, поэтому на бумаге он отображен в
усеченном виде С большим разрешением в шесть значащих цифр ори-
гинал имеет вид
/|(/) = 1 - e'a02'cos(0.09798/) + 0.10206e'®02'sin(0.09798r);
□ второй вариант оригинала
/1(0 = I - l.005e-«02%in(0.09798r- 84.172*)
получен по табл. П.2, п. 74, без коррекции фазового сдвига, вычисляемо-
го с помощью функции atan. В итоге получен угол ф = -84.172° и невер-
ный результат;
□ третий, верный вариант оригинала
/з(0 « 1 - l.OO5e-o®2'sin(O.O9798/+ 95.828*)
получен также таблично, но с коррекцией фазового угла
V - Ф + 180° = 95.828°,
находящегося во втором квадранте, т. к. [371 -f-1 <0. Правильное
вычисление угла возложено на функцию atg(p,q>, составленную в чисто
учебных целях, поскольку Mathcad имеет идентичную встроенную функ-
цию atan2(p,q).
Временные характеристики элементов к систем управления
257
т := 3 Т := 10 $ := 0.2 F(s) = ->-------------—х
И|ч-2ЛТ» + Г?)
I invlaplace ,s , / ,\ I / „ \
fl(t) :=» F(s) I -> I - I.expL-U.OO I0*jtjcos(9.80 IO" tJ+.IO2ex
f2(t) := 1 - C-e"₽ ‘-sinlw t + Ф) F3(t)I -C e~P 1 sin(cu t + V)
P - 0.02
Ш - 0 098
C • 1.005
Ф = -84.l72deg
v = 95.828 deg
P T2-t=-I
Отметим, что при задании постоянной времени т = 2 получим ₽/• - г = 0 и
сообщение об ошибке: «Found a singularity. You may be dividing by zero», оз-
начающее деление на нуль при вычислении угла по формуле
258 Глава 3
3.2. Типовые временные характеристики
В этом разделе наше внимание будет сосредоточено на изучении реакций
динамических элементов и систем на типовые воздействия импульсного и
ступенчатого видов Поскольку в реальных условиях заранее неизвестно, ка-
кой формы сигнал поступает на вход системы, то для анализа ее качества
выбираются тестовые сигналы. Выбор таких сигналов из всего многообразия
воздействий обусловлен, во-первых, их широким распространением в при-
роде; во-вторых, возможностью аппроксимации произвольных сигналов
комбинацией тестовых; в-третьих, несложностью выполнения с ними ана-
литических и численных операций. Именно таким требованиям, помимо
рассмотренного в гт. 2 гармонического колебания, удовлетворяют воздейст-
вия импульсного и ступенчатого типов.
3.2.1. Импульсная характеристика
Импульсное или ударное воздействие в момент времени т бесконечно малой
длительности и бесконечно большой амплитуды описывается абстрактной
дельта-функцией Дирака, являющейся пределом функции x(t, е) с конечны-
ми длительностью и амплитудой (рис. 3.5. о):
8(,-T)=limxV.E)=|“np,,':T;
t-я) (0 при t # т.
Воздействия импульсного типа в электронных схемах вырабатываются уст-
ройствами синхронизации, возникают при разрядах конденсаторов, при
дребезге контактов переключателей, в результате электромагнитных наводок
и т. п. Сигнал можно считать импульсным, если его конечная длительность
существенно, т. е. на несколько порядков, меньше минимальной постоян-
ной времени элементов системы.
Дельта-функция 6(/) принадлежит классу обобщенных функций [7, 14] и явля-
ется недифферениируемым пределом при т. О непрерывных импульсных
функций МТ, е), имеющих следующие свойства
□ четность относительно аргумента г. x(t, е) ж х(~1, е);
□ начальное и конечное значения Д-°°. е) в х(“. е) = 0;
□ площадь под функцией х(Л е) равна единице при любых значениях е;
□ предел 40. е -» 0) а ширина интервала изменения функции при
е -» 0 стремится к нулю.
Примерами приближающих импульсных функций единичной плошали мо-
гут служить функции плотности вероятности:
□
(рис. 3.5, б);
□ Коши г(т,е)=-- 1 (рис. 3.5, в);
exf
□ Лапласа х(г,е)=—
«Л» делыпа-функцию нужно смотреть как на удобное обозначение, которое всегда
может быть записано в равносильном. но более громоздком виде. (П. Дирак).
Процедура предельного перехода не в состоянии точно определить значение
60) в самой интересной части области ее существования, а именно, в окре-
стности точки 1 = 0. Наиболее успешный путь обхода этого затруднения со-
стоит в отказе от попыток определения значений дельта-функции в каждый
момент времени и в сосредоточении внимания на результатах ее воздейст-
вия или свойствах Иначе говоря, обобщенные функции определяются тем.
что они «делают», а не тем, как они «выглядят*
Свойства смещенной дельта-функции 6(/ - т):
□ четность относительно аргумента / - г 6(/ - г) = 6(т - /);
О нулевая производная
260
Глава 3
Это неочевидное свойство иллюстрируется на примере предела при е ~>0
производной функции плотности Гаусса:
.r,'(tt) = -,-/-=e2f' => limx,'(f.E)= lim , ?Е е2*1 =0.
е’72п ‘-о /372л
Производная или дуплет (22] состоит из двух 6-подобных функ-
ций, действующих в момент времени г с разными знаками и дающих в
сумме 0 (рис. 3.6). Но нельзя игнорировать производную 5((/-т), если
она интегрируется в произведении с некоторой гладкой функцией х(/)
(см. ниже свойство фильтрации). И вообще, нужно рассматривать л-ую
производную 8,(л)(/-т) тоже как обобщенную функцию;
□ несобственный интеграл
J8(r -t)dr = l,
т с. площадь под 6-фуикцией равна единице В конечных пределах интег-
рирования получим
при а*х*ь-
' (0 при Т<а или т>Ь;
□ фиксация сомножители х(т) в произведении функции *(/), непрерывной в
точке т, и б-функшти:
40«(г ~ Т) - Мт)6(/ - т);
□ фильтрации» энменияi Мт) Функции х(0 в несобственном интеграле про-
изведения функции х(о И б-функции. интеграл
Временные характеристики элементов и систем управления_____________261
"jxWt - t)df = JxfrM - = х(т)/5(/ - т)й/ = л(т).
В конечных пределах интегрирования
' рт |0 при т<а нлн T>fc
Интеграл произведения х(1) и в;0-т) берется по частям:
JМ - t)d/ = л(г)5(/ -1)- J/(.)5(r -= х(т)5(т - т)- л'(т)/8(, - г)ф
По индукции получаем формулу интегрирования произведения функции
x(t), неразрывной в точке т, и л-ой производной по t дельта-функции
8«(»-т):
fXr)eW(/-T)d/ = S(-iyxW-1
□ изображение смешенной 8-функции
Ц8(г-г)} = /е-"8(/-т)ф=е-'т.
о
Изображение несмещенной 8-функции равно
Ц60) - е° = 1.
Импульсная характеристика (ИХ) *(/) — это реакция системы на входное воз-
действие в виде несмещенного дельта-импульса 8(т) при нулевых начальных ус-
ловиях.
Согласно (1.18) и свойству изображения функции 8(/). при нулевых начальных
Условиях изображение импульсной характеристики системы есть ее переда-
точная функция И^з). И наоборот. н</) есть оригинал изображения И(з)
L(w</)} = ИО <=> *V) - L-4»W). (З В)
В формулах (3.13) заключена потенциальная возможность решения задачи
идентификации — определения передаточной функции системы по ее реак-
ции на импульсный сигнал единичной площади при нулевых начальных усло-
виях. Для этого нужно как можно точнее описать выходной сигнал
«рсменнбй зависимостью н(Г). а затем по (1.16) либо таблице преобразова-
ния Лапласа получить (Цз).
262
3.2.2. Переходная характеристика
Единичное (ступенчатое) воздействие в момент времени т с бесконечно ма-
лой длительностью фронта описывается единичной функцией Хевисайда -
пределом функции x(t, е) с конечным временем перехода из нуля в единицу
(рис. 3.7, о):
1(/-т)= lim.v(r.E)=P ПрИ ,-Т'
t->o ' [О при кт.
Ступенчатые воздействия в электронных схемах возникают при переключе-
нии напряжения питания, скачкообразном изменении нагрузки, характерны
для выходных напряжений реле, триггеров и других дискретных элементов.
Сигнал можно считать ступенчатым, если конечная длительность его фронта
существенно, т. е. хотя бы на порядок, меньше минимальной постоянной
времени элементов системы.
Единичная функция !(/), как и дельта-функция, принадлежит классу обоб-
щенных функций и является недифференцируемым пределом при е -> 0 не-
прерывных функций Хг. Е), имеющих следующие свойства:
□ х(-~, €) = 0, Х0, е) = 0.5, х(~, в) = 1;
□ кососимметричность относительно среднего значения х(0, е);
□ интервал изменения X».от 0.05 до 0.95 сужается до 0 при е 0.
Примерами приближающих функций могут служить функции распределе-
ния вероятности:
О Гаусса Хг.е)= 0.5+Ф^ j (рис 3,7,6);
□ Коши х(»,е) = О.5 +
(рис. 3.7, в);
Временные характеристики элементов и систем управления_____________263
□ Лапласа >(f.f)^(i.sjl + sgn(r|i-eе | (рис 3 7,?).
Свойства смешенной единичной функции !(/ - т) и ее связь с б-функнией:
□ инвертирование относительно уровня 0.5 при изменении знака аргумента:
!(/-?) = 1 -l(t-i);
□ производные единичных функций являются 5-функциями
□ неопределенные интегралы единичных функций .
□ связь интегралов 5-функций с единичными функциями:
J8(v -t)dv=l(r-т), Js(v-r)dv = 1(т—г);
□ дифференцирование разрывных функций'.
£(4>(г-т))=Л>(/-г)+х(г)5(г-т).
1(ж(г>(т-г))=л'(/>(т-/)-х(т)5(г-т);
а/
а интегрирование разрывных функций:
/л(г)1(г-т)Иг = 1(*-т) /л£>1г.
J мфл)
° изображение смешенной единичной функции
Глава 3
L|i(r-t)| = je'1 l(t-t)dl = Je“”dl =
Несмещенная единичная функция имеет изображение
Переходная характеристика (ПХ) Л(г) — это реакция системы на входное воз-
действие в виде несмещенной единичной функции 1(г) при нулевых начальных
условиях.
Согласно (1.18) и свойству изображения функции 1(1), при нулевых началь-
ных условиях изображение Н(з) переходной характеристики Л(1) и переда-
точная функция системы Щз) связаны следующими операторными соотно-
шениями:
ЦЛ(1)| = «(з)=^ « Л(,)=Е-'^|. (3.14)
Формулы (3.14) тоже можно использовать для идентификации системы по
ее реакции на ступенчатый сигнал единичной амплитуды при нулевых на-
чальных условиях Для этого нужно как можно точнее описать выходной
сигнал временнбй зависимостью h(t), а затем по (1.16) либо таблице преоб-
разования Лапласа получить изображение Я(з), по которому определить
передаточную функцию Щз) = зЯ(з).
3.2.3. Взаимосвязь временных характеристик
Из (3.13) и (3.14) следуют важнейшие соотношения между импульсной и пере-
ходной характеристиками
w(r)=^^ й(»)= Jи(т)3т, (3.15, fl)
Ф о
позволяющие по одной характеристике найти другую, причем удобнее вы-
числять импульсную характеристику путем дифференцирования переходной
Полученные зависимости таят в себе один тонкий момент. Дело в том.
что если переходная характеристика совершает в начальный момент вре-
мени скачок из нуля в состояние Л(0) * 0, то импульсная характеристика
по свойству дифференцирования разрывных функций должна включать
дельтаобразную составляющую Л(0)8(/). При /ЦО) = 0 эта составляющая
отсутствует. Отразим данный факт явным образом в виде следующих за-
Временные характеристики элементов и .
н{/)=Л(о)5(г)+^ « й(/)=Л(о)+(н<т>1т, (3.15. б)
d/ о
где начальное значение Л(0) равно плошади дельта-импульса, входящего в
состав импульсной характеристики в начальный момент времени I = 0.
По формулам (3.13) - (3.15) вычислены и сведены в табл 3.1 импульсные и
переходные характеристики всех типовых звеньев с параметрами К > 0 и
Г> 0. Следует отчетливо понимать, что графики временных характеристик,
содержащих дельта-функцию и ее производные, имеют условный характер
из-за невозможности точно изобразить импульсы бесконечно большой ам-
плитуды и бесконечно малой длительности, какими являются эти абстракт-
ные функции.
Таблица 3 1
Звено и его пе- редаточная функция VKs) Импульсная характеристика w<0 Переходная характери- стика МО
Безынерционный усилитель К h
0 К 8(1) 0 к ко
Дифференци- рующее звено Ks 1 [ „ L .
Г ' К 641
01 " К 6(0
Форсирующее звено первого порядка + Те) 1
0 KWt ♦ 78(0)
°| f Mi(0*78(0)
266 Глава 3
Таблица 3.1 (продолжение)
Звено и его пе- редаточная функция Wts) Импульсная характеристика МЛ Переходная характери- стика МО
Интегрирующее эеено £ $ К h‘ К
0 к 1(й 0 Kt ко
Апериодическое К 1+П К 0.05К к 0Я5К
0 ЗТ t 0 | ' ЗТ 1
Форсирующее звено второго порядка ♦ ЦТж* Tf)
° ««I Н2^7б'(1)*Г5-(|))
01 г «1(0 * 2£73(в * 7*5X6)
Колебательное К •F 0 ‘ Мш Л ‘ 2К К ' 1 i
1 + 2$Гх+Т2*2 ш = — — т
к шТ‘ уУ 37^ -X—1—1— j-e't'/rjjn(u
u)l(r) 0 ф ’ 3775 ' ' Г ^e4,/rsii<(>»+4i)|l(/)
Временные характеристики элементов и систем управления
Таблица 3.1 (окончание)
Звано и его пе- редаточная функция Ms) Импульсная характеристика w(t) Переходная характери- стика мв
Звено чистого запаздывания
Ке~1' От Г К 80-т) От Г К Kt-т)
Наибольший практический интерес представляют инерционные типовые зве-
нья с конечным и ненулевым временем установления временных характери-
стик — апериодическое и колебательное звенья Полюсы передаточных
функций таких звеньев должны быть левыми. Из (3.8) и (3.10) видно, что со-
ставляющие временных характеристик имеют форму экспонент е'' аперио-
дического (при действительном полюсе s,) или колебательного (при ком-
плексно-сопряженных полюсах Si и Ih-i) типов.
Определимся с термином «время установления» Длительность процесса
полной сходимости экспоненты с отрицательной действительной частью
полюса S/ теоретически бесконечна, поэтому на практике применяется поро-
говый метод определения временных интервалов Под временем установле-
ния характеристики y(t) понимается максимальное значение ty, после кото-
рого она вошла и далее не покидает определенной зоны, прилегающей к ус-
тановившемуся значению Ууст Интервал времени те |0. д| называется
переходным режимом, а при / > /у процесс входит в установившийся режим
Принято задавать порог зоны установившегося режима Д равным некоторой
малой части от модуля разности [y>VT - у(0)|. В случае цет = >40) пороговое
значение отсчитывается как Д-ая часть от максимального модуля отклоне-
ния тах[уО) ~ >уст|. Таким образом, зона установившегося режима функции
ИО, сходящейся к уровню у^т, заключена между пороговыми уровнями
Лет “Ди Ууст + Д- Нанеся эти уровни на график у(г), легко визуально опре-
делить время его установления
У Ь-0) - ЛУей s a
На рис. 3.8 приведена Mathcad-программа, в которой строится график
временной функции Д/> (см рис. 3 4) и вычистится время ее установления с
Помощью функции tusctt. f. fuse,Л), аргументами которой являются массивы
*-ых отсчетов времени г* и функции /, уровень и пороговое значение Д.
Функция возвращает отсчет времени, начиная с которого все последующие от-
счеты функции заключены в «трубке», ограниченной уровнями i Д.
268
Clf f(0 - I + I 005 exp(-0.02 t)-sin(0.098-t -95.828-deg)
T > 300 dt:=0.l к :«0.. round (т-dt"') Д := 0.05
tk := k-dt fk:=f(tfc)
tust(t,f,fust.A)for keO.. last(f)
hv«-submatrix(f,k,lasi(f),0,0) - fust
return tk if max(tnax(hv),-min(hv)) < Д
"Нет сходимости”
fma - fust „ , ,
sigma(f,fl).fust) := return — if fl) < fust < fma <- max(f)
fmi-fust
return --------- if fl) > fust > fmi«- min(f)
fust - fl)
ty - tust(t,f, I ,Д) tycrn .- T on error min(T,ty)
о :=sigma(f,0,l)
ty = 136.5 a = 52.928%
Рис. 3.B
Если значениеаприорно неизвестно, то время сходимости процесса ДО »
трубку шириной 2Д можно подсчитать с помощью модифицированной
функции
Временные характеристики элементов и систем управления
tcx(t,f ,Д) =
for кеО. last(f)
Ihv <— submatrixff .k.last(f) ,0,0)
return tk if max(hv) - min(hv) s 2Д
"Нет сходимости"
Оно может отличаться от времени, вычисленного функцией tust Напри-
мер, время сходимости графика на рис. 3.8 равно 134.6 с. тогда как
4= 136.5 с.
В случае отсутствия сходимости обе функции вычисления длительности пе-
реходного процесса возврашают текстовое сообщение нет сходима ти.
Для экспоненциального сигнала y(f)=e"'/T с постоянной времени т>0
значение гу как функция параметра Д является решением уравнения
И'у) - А:
/У(Д) = -т 1п(Д). (3.16)
На рис. 3.9 построены графики y(t) и /у(Д), по которым можно найти время
затухания экспоненциального сигнала при любых значениях Д. Для типовых
уровней сходимости, общепринято равных 5%, 2% и 1%, получим следую-
щие длительности:
□ Гу(0.05) = 2.9957т < Зт;
□ ^(0.02) = 3.912т < 4г,
□ /у(0.01) = 4.605т < 5т.
О т 2т Зт 4т St
0 02 0.05 01 Л
Таким образом, значение времени установления динамического цемента не
абсолютно, а зависит от выбора ширины зоны установившегося режима,
равной 2Д. Далее мы будем использовать значение Л = 0.05. при котором
Гпава 3
время установления экспоненциальной функции оценивается тремя ее посто-
янными времени Применительно к инерционным типовым звеньям такой
выбор порога Д означает, что (см. табл. 3.1):
□ временные характеристики апериодического звена первого порядка с пе-
редаточной функцией
W(s)=-±-
W 1+7$
сходятся с 5%-ой погрешностью за время
ty = 37; (3.17.0)
□ у колебательного звена второго порядка с передаточной функцией
W(s)=-------——
l + 2£7s + 72s2
временные характеристики совершают затухающие колебания с частотой
ш=7ь¥/т
Они заключены внутри экспоненциально сужающейся «трубки» с посто-
янной времени 7/ сходящейся с 5%-ой погрешностью за время
ry = 37/t (3.17,6)
Для более детального представления о колебательном звене в дополнение
к табл. 3.1 на рис. 3.10 построены семейства его нормированных им-
пульсных w(i, с) и переходных h(t, £) характеристик при единичных зна-
чениях коэффициента усиления К, постоянной времени 7 и коэффици-
ентах затухания е (0,0.1,0.2. .0.9, 1).
Рис. 3.10
Временные характеристики элементов и снегом управления
Кроме времени установления, колебательные процессы характеризуются
еще рядом важных параметров (рис. 3.11, о):
• временем разгона отсчитываемым от начата движения до первого
момента достижения уровня установившегося значения переходной
характеристики Луст;
• временем максимума отсчитываемым 01 начала движения до мо-
мента достижения максимального значения переходной характери-
стики Л(/тах);
• перерегулированием а — отношением максимального выброса переход-
ной характеристики Л(/пих)-Луст к разности между установившимся
значением Луст и начальным значением йо- Дчя вычисления перерегу-
лирования можно использовать функцию signa, приведенную на
рис. 3.8.
Графики зависимостей Гу(^), /р(^), /пмх(§) и о(£) построены на рис. 3.11, б.
Обращаем внимание читателя на ступенчатый график гу(£), построенный
с помощью функции tust. Он отличается от изображенной пунктиром
зависимости (3.17, б) времени установления экспоненциальной огибаю-
щей колебательного процесса е
Рис. 3.11
Ввиду важности места, занимаемого колебательными элементами в сис-
темах управления, проанализируем влияние коэффициента затухания §
на временные и частотные показатели (см. рис. 2.11) и сделаем следую-
щие важные выводы:
• при бесконечно малом затухании (£ -»0) колебательный элемент с
постоянной времени Т преврашаегся в автоколебательный с мини-
мальными временами разгона tv = O.SnT и максимума » пТ. но
максимальными временем установления гу -* перерегулированием
272
о= 1, частотой колебаний ш= 1 / Т, а также добротностью £)->«,
резонансной частотой (2.12) <^ = I / Ги показателем колебательности
(2.13) Частотные характеристики автоколебательною элемен-
та приведены на рис. 2.12, а реакции на гармонические колебания с
резонансной и отличными от нее частотами — на рис. 3.2 и 3.3;
• при увеличении коэффициента затухания до 4 - 0.7 происходит рез-
кое уменьшение параметров Гу, a, Q и М наряду с медленным увели-
чением /р и rmax- Частота собственных колебаний ю при этом умень-
шается в два раза, а резонансная <ар — до нуля;
• оптимальным по совокупности показателей качества является уровень
затухания £=l/V2, при котором время установления достигает мини-
мума гу = 2.9Г, перерегулирование а = 0.046 не превышает порога
Д = 0.05, времена разгона и максимума равны, соответственно, 3.297
и 4.47, а резонансная частота и показатель колебательности становят-
ся нулевыми Передаточная функция и комплексно-сопряженные по-
люсы оптимального колебательного элемента имеют вид
<3">
• предельное увеличение коэффициента затухания 4 -» 1 превращает
колебательный элемент в последовательное соединение двух аперио-
дических звеньев с равными постоянными времени Г, которому при-
сущи некоторое увеличение времени затухания до Г, = 4.757, резкий
рост параметров /р -> ~ и tm;ix -> «», уменьшение до нуля собственной
частоты ш и перерегулирования о.
Выполненный анализ быстродействия простейших инерционных элементов
первого и второго порядков имеет большое значение при исследовании
сложных систем, которые часто можно аппроксимировать моделями невы-
соких порядков с хорошо изученными частотными и временными свойства-
ми.
Вычисление временных характеристик сложных систем выполняется любым
методом обратного преобразования Лапласа. Если при расчете импульсной
характеристики *0) можно напрямую использовать формулу Хевисайда (3.4)
для передаточной функции Щз). то переходная характеристика й(г) нахо-
дится обратным преобразованием изображения
я(,)з*ы.41 »и_. „ ,„tl. 0В)
355 ..it-.,г м
В (3.19) числа уил( отличаются от тех же чисел в Щз) из-за дополнительно-
го нулевого полюса изображения I / г единичной функции. По аналогии с
Временные характеристики элементов и систем управления_________273
(3.4) получим формулу разложения Хевисайда для вычисления переходной ха-
рактеристики:
4W.vс.л'. ”»
"*‘L "WIL,
В передаточной функции статической системы нет нулевых полюсов, а изо-
бражение H(s) имеет простой полюс изображения входного сигнала г, = 0.
Согласно (3.8, я), он порождает составляющую переходной характеристики
которая является установившимся значением h(t) при t -» ~
Правильность расчета временных характеристик проверяется по предельным
формулам, вытекающим из (3.2):
|и,(о)= limsW(s)lw(<»)=lini.sWr(.j),
|л(0) = И'(оо),Л(~) = И,(0).
Истинные установившиеся значения временных характеристик совпадают с
оценками (3.21) только при условии, что в передаточной функции все полюсы
левые
Е? Пример 3.3. Рассчитать методом разложения Хевисайда временные ха-
рактеристики схемы моста Вина - Робинсона (см. рис. 1.32), имеющего пе-
редаточную функцию
с постоянными времени (см. пример 2.2)
Т = -^ = 3.183мс, ?! =1±Дт-= 8.333мс, Т2 = 1.216мс
Решение. Вычислив полюсы передаточной функции
»!=--•=-120, s, =- = -822.5,
найдем сначала переходную характеристику (рис. 3.12, я), представив ее
изображение в виде
мТХ- ^(»)_ 1 Т
U х Зт (1 + гЛ1 + Г2т)
Глава 3
Рис. 3.12
Импульсную характеристику (рис. 3.12, (5) получим по (3.15) с учетом на-
чального скачка переходной характеристики с Л(-0) = 0 до Л(+0) =1/3:
• 0.33380+ 53.67е’120' -367.8е‘8225'.
Благодаря отсутствию в передаточной функции правых полюсов граничные
значения »(0) = ~ и и<~) = 0 совпадают с оценками (3.21). О
& Пример 3.4. Рассчитать табличным методом временные характеристики
системы «тележка - маятник» и объяснить их физический смысл.
Решение. Используя результаты примера 2.4, запишем обе передаточные
функции системы с перевернутым маятником в виде
с параметрами
Ь» ~ 10. »| - b2 - -1.333. by - 0.573;
йю - (I + 7н)(1 - Ло(| + Тя);
Временные характеристики элементов и систем управлении 275
Г| = 1.72 с, Тз = 0.397 с, Г5 = 0.244 с.
Проиллюстрируем методику табличного обращения Лапласа при вычисле-
нии импульсной характеристики
В табл. П.2, ПП. 57, 56, 59, находим необходимые составляющие изображе-
ния JKXs) и их оригиналы:
L-i[ fr) l-л Vi2 7 Уз2 е7 _ Уз г, _
W)) (Тз+71ХТ3+Т5) (Ti-^XT-j+Tj)
= 10-9.468еч)5Н' -1.162с252' + О.бЗе’4 12;
r-l f Ь. 1 =, У, Т № F, . № % _
да) (т, +Тз\Т, -Ts) (Т^Т^Тз+Тз) (^-Г.Х^+Г,)
= -О.734е’о58/ +0.39е252' +0.344еч
. , ( У ) h: \ 1>: bi л _
да)= (Т’.+ТДТ.-'ЛГ '_(7-,+7]Хт,+Г,)С ~(Т,-Т,\Т^Т/
=0.427е °”' + 0.982е2 № -1 409е ** ”.
Суммируя составляющие, получим импульсную w/t), а по аналогии и ос-
тальные временные характеристики, построенные на рис. 3.13:
ii’j(/)=IO-9.775e"°58' +0.211е152' -0.436еч
Л^(г)=1О/-17+16.8|е'о}8' +0.0846е2 +0.106еч
н-ч,(О=-О.183е'0Я'-0.422е152' +0.606е*4
Лч,0)=0.315е 058' -0.1б8ег52/ -0.148е 4
Нулевые начальные значения всех полученных характеристик совпадают с
оценками (3.21), а оценки их установившихся значений неверны, т. к. обе
передаточные функции в (3.22) имеют правый полюс з3 = +2.54.
Физическое объяснение возникающих движений следующее В исходном
(номинальном) положении тележка стоит на отметке d = 0 см. а маятник
находится в состоянии неустойчивого равновесия вертикально вверх при
<р - 0°. Под действием импульсной силы единичной энергии (например.
100 Н в течение 0.01 с) тележка скачком приобретает начальную скорость
<(0)=8см/с, а далее катится с торможением и через 3 / 0.58 - 5 2 с оста
276
Глава 3
новилась бы в точке d = 10 см. Маятник после удара, сохраняя по инерции
свое положение, отклоняется влево (ф < 0). теряет равновесие и падает (от-
клонение <р = -90° достигается за 2.12 с), толкая при этом тележку вперед и
разгоняя ее все сильнее Похожие процессы Л,/Г) и Л,(Г) происходят и при
действии ступенчатой единичной силы.
Таким образом, в окрестности номинального состояния неустойчивого рав-
новесия система с перевернутым маятником имеет расходящиеся временные
характеристики (3.23). Причина неустойчивости — правый полюс > 0.
Пунктиром на рис. 3.13, а изображена характеристика w/i) без неустойчи-
вой составляющей 0.211е252' и соответствующая системе с жестко закреп-
ленным вертикальным маятником.
В системе с обычным маятником передаточные функции имеют вид, анало-
гичный (3.22), но с другими параметрами:
Ьо = 10, bt = 62 = 1.333, Ьз = 0.573;
^О+Т^+ада+Тз2»2);
7\ - 1.678 с, Тз = 0315 с, = 0.246.
Используя табл. П.2, пп. 99, 101, 94, получим временные характеристики
для выходов d (рис. 3.14, о) и Ф (рис. 3.14, б):
*,,(/)= 10-10.267e4)i%' +О.73еЧ)782' sin(3.O75i +0.375);
М»)= f «Юг -17 + 17.23е-°+ О.23е"°782' »1п(З.О75г -1.445).
о (3.24)
-О.216е й”6/ -i.iSle'47*2* sin(3 .075г -2.953)
\(г)= О.ЗбТе’05’4' тО.ЗбЗе °782' мп(З.О75г -1.631)
Временные характеристики элементов и систем управления
Поскольку в нижнем номинальном положении маятника все полюсы пере-
даточных функций — левые, то предельные значения устойчивых характери-
стик (3.24) совпадают с оценками (3.21).
Рис. 3.14
Физическое объяснение возникающих движений следующее. В исходном
устойчивом положении равновесия маятника под действием импульсной
силы тележка начинает катиться с торможением и примерно через
3 / 0.596 = 5 с останавливается в точке I0 см. Маятник совершает затухаю-
щие колебания с частотой
или с периодом 7'к =• 2 с, максимальным отклонением от вертикали на 0.66"
и временем установления 3 / 0.782=3.84 с. Эти очень малые колебания ма-
278
Глава 3
ятника слабо воздействуют на тележку ввиду близости комплексных полю-
сов -0.782 ± 3.075j и нулей -0.5 ± 2.69j передаточной функции
Под действием единичной ступенчатой силы тележка разгоняется и далее
катится с постоянной скоростью. Маятник в это время совершает слабые
несимметричные затухающие колебания. Графики временных характеристик
на рис. 3.14 свидетельствуют, что в окрестности состояния устойчивого рав-
новесия система с обычным маятником нейтральна по выходу d и устойчива
по выходу <р. □
£? Пример 3.5. Обосновать выбор источников входных сигналов, возбуж-
дающих гармонические колебания в генераторах, построенных на рис. 2.43.
Решение. Критериями выбора такого источника являются:
□ независимость амплитуды генерируемых колебаний от их частоты;
□ стабильность параметров вырабатываемого источником сигнала;
□ простота технической реализации источника.
Проверим, не подойдут ли в качестве запускающих сигналов типовые воз-
действия — дельта-функция и ступенчатая функция? Для выяснения этого
вопроса вычислим по (3.14) и (3.15, б) временные характеристики генерато-
ров:
□ у схемы неинвертируюшего типа с передаточной функцией (1.34, о) при
Ч)-НЯ
Таким образом, лучшим возбудителем незатухающих колебаний обоих гене-
раторов является единичная функция Хевисайда 1(1), а простейшим техни-
Временные характеристики элементов к систем управления 279
ческим устройством, реализующим этот сигнал, служит механический ключ,
при замыкании которого на вход генератора подается постоянное напряже-
ние UQ (рис. 2.43, а) или -U» (рис. 2.43, б) от батарейки или другого более
стабильного во времени источника напряжения. Для устранения так назы-
ваемого «дребезга» контактов можно заменить механический ключ элек-
тронным триггером. Желательно также момент замыкания ключа совместить
с подачей напряжений питания на операционный усилитель.
Амплитуды колебаний, генерируемых разработанными схемами, равны, со-
ответственно, Зх/2(/0 и 3t/(l. Полноценный генератор должен кроме регули-
ровки частоты колебаний иметь еще и возможность изменения их амплиту-
ды. Простейшими устройствами, реализующими эту возможность, являются
универсальный усилитель (рис. 1.23, я), его частные случаи — инвертирую-
щий усилитель (рис. 1.24, а) или неинвертирующий усилитель-делитель
(рис. 1.24, б), а также мультидиапазонный усилитель с линейной шкалой
(рис. 1.29, б). □
& Пример 3.6. Исследовать влияние величины и знака постоянной времени
форсирующего звена т на временные характеристики системы с передаточ
ной функцией
^)=7Т?- (3.25, я)
1 + 7л
Решение После выделения из передаточной функции коэффициента пря-
мой связи
W Т Т2 s + 1/Г
временные характеристики быстро и просто находятся по формулам (3.7)
и (3.8):
*4)«у80+^-Г«',fl, А(г)= It—e ^ (3.25, б)
Их графики в относительном масштабе времени r/|7J и при различных со-
отношениях постоянных времени т и Г построены на рис. 3.15. Там же с
помощью символов « •• ». • —• и « ° » показано взаимное расположение на-
чала координат, полюса = -1 / Ги нуля Ji » -I / т.
При внимательном изучении графиков и соответствующих им формул
(3.25, б) обнаруживаются следующие юкыюмерности влияния соотноше-
ния знаков и величин постоянных времени на свойства временных харак-
теристик:
Глава 3
Рис. 3.15
Т<0
□ при положительных значениях постоянной времени Т система (3.25, а)
имеет отрицательный полюс i| < 0 , а ее временные характеристики
экспоненциально сходятся к уровням »(") “ 0 и Л(~) = 1;
□ правое положение полюса л > 0 при постоянной времени Т< 0 порождает
неустойчивые экспоненциально расходящиеся временные характеристики;
□ в отсутствие форсирующего эвена (т - 0) система описывается переда-
точной функцией апериодического звена первого порядка с временными
характеристиками из табл. 3 Г,
□ система с равными постоянными времени т и Т обладает временными
характеристиками статического звена МО “ 6(0 и МО “ 1(0 Инерциои-
Временные характеристики элементов и систем управления 281
ность, порождаемая полюсом J|, полностью компенсируется форсирую-
щими свойствами равного ему нуля л Компенсирующие свойства про
являются как в устойчивой, так и в неустойчивой системе;
□ форсирующее звено с постоянной времени т, заключенной в интервалах
О < т < Г или Т< т < 0, улучшает качество временных характеристик в
сравнении с системой, у которой т = 0: уменьшается инерционность ус-
тойчивых и увеличивается инерционность неустойчивых переходных
процессов;
□ форсирующее звено с ПОСТОЯННОЙ времени Л !/' vwtHuiic"
временных характеристик: увеличиваются положительное (при т > 7) и
отрицательное (при т< -7) перерегулирования в устойчивой системе и
скорость расходимости в неустойчивой
□
Теоретический анализ и практическое построение временных характеристик
позволяют сделать следующие выводы относительно влияния на них взаим-
ного положения полюсов и нулей передаточной функции
□ Свойство сходимости характеристик к установившимся значениям оп
рсделястся положением полюсов Наличие в списке полюсов системы
хотя бы одного правого делает ее временные характеристики расходя-
щимися.
□ Начальные и установившиеся значения временных характеристик сис-
тем без правых полюсов удовлетворяют предельным формулам (3.21) и
могут быть найдены по передаточной функции без расчета самих харак-
теристик.
□ При равенстве полюса 5/ и нуля ф можно сокращать полиномы переда-
точной функции на одинаковые множители (з - з,) и (s - ф благодаря
полной компенсации временной составляющей < е ”. при которой вычет
в полюсе st и коэффициент г, обращаются точно е нуль.
□ Нуль Zj, близко расположенный к полюсу з„ частично компенсирует со-
ставляющую с, с'1' за счет почти нулевых значений з, - - 0 и с, = 0
3.3. Частотно-временные свойства систем
К данному моменту читателю должно быть очевидным прямое влияние по-
люсов и нулей передаточной функции системы на динамические свойства ее
временных характеристик. Вспоминая, что абсолютные значения полюсов и
нулей являются частотами сопряжения типовых звеньев (см. табл. 2.2). мы
вправе далее протянуть нить, связывающую временные свойства системы с
282 Глава 3
ее частотными характеристиками. Как видно из рис. 3.1, удаление домини-
рующего (самого правого на плоскости s) полюса от мнимой оси ускоряет
протекание переходного процесса:
□ если этот полюс левый, то самая медленная составляющая переходного
процесса сходится к нулю быстрее, а система, оставаясь устойчивой, ста-
новится более быстродействующей и по этому показателю лучшей;
□ движение доминирующего полюса вправо от мнимой оси увеличивает
скорость удаления переходного процесса от состояния равновесия. Та-
кое повышение быстродействия неустойчивой системы лишь ухудшает ее
свойства и сильно затрудняет управление ею.
Установление связи между частотными и временными характеристиками,
позволяющей прогнозировать поведение системы во времени без построе-
ния ее переходных процессов, составляет предмет изучения данного раздела.
3.3.1. Взаимосвязь частотных
и временных характеристик
Функция времени у(') и ее комплексная частотная характеристика Цк°)> на-
зываемая расхожим термином «спектр», т. е. «разложение на составляю-
щие». связаны прямым и обратным преобразованиями Фурье:
Гб<о)=]у(г> ^Ф; (3.26, а)
О
у(г)=^ IrGtoJe^dw. (3.26,6)
Условия сходимости несобственных интегралов в (3.26):
□ » v I i 0 — ограниченность оригинала у(0 при г г 0;
□ у(0 = 0 V г < 0 — нулевой оригинал при t < 0;
□ все полюсы изображения Из) — левые;
□ | Ц)о>)| -» 0 при ы ~ — абсолютная интегрируемость спектра.
Подставив в (3.26, 6) комплексную функцию
И» - Р/ш) + jQ/ш)
и комплексную экспоненту
s’01' =cos(w»)+ jsin(w/),
Временные характеристики элементов и систем управления 283
получим для I й 0 интегральную зависимость временного сигнала от вещест-
венной и мнимой частотных характеристик его спектра:
У^=2п I ^>^(u)cos(w)~^*(tJ)sin((0f^t0't'
*“ чета» функция ш
+ “ f К (w)sin((0/)+Qy(w)cos(wr)}iw = (3.27)
нечетная функция ш
= - J {л (w)cos(tur)- Q у (to)sin (ow )]йоу
ли
Эта формула вполне пригодна для численного интегрирования, естественно,
в ограниченном частотном диапазоне н> е (О, П| — полосе спектра сигнала.
Значения Ру(ш) и Qy(w) могут быть получены по любой паре амплитудной и
фазовой частотных характеристик сигнала (/l}(w), фу(<о)| или (Z^w), Ф/ш)):
f Py(w)= Л/ш)соа(<ру(ш))= 10OMZ’(*u,cos(®v(w))
| Qy (ш) = А у (to)si п (ф у (<>))= 10° 05t> sin (ф, (и))
Благодаря второму условию сходимости y(t) = 0 V / < 0 возможно |30| упро-
щение формулы (3.27). Заменив в ней / на —Г, получим взаимосвязь частот-
ных характеристик сигнала Ру(е>) и Qy(wY
у(- г) = - J{/». (<d)cos(w/)+ Qy (<o)sin(<iv)]da> = 0 V г > 0.
"о
Складывая и вычитая это выражение с (3.27), получим две зависимости сиг-
нала у(!) отдельно от его вещественной ?/<о) и от мнимой Qy(w) частотных
характеристик
y(r)=-J/’v(io)c°s(iw)iw= --j£v((i>)sin((iv)tta), (3.29)
ло ло
что удобнее для численного интегрирования по сравнению с (3.27).
Установим связь между частотными и временными характеристиками сис-
темы. При нулевых начальных условиях
Ц)о>) = JRjo»A(jto) “ 1Л<») + ЗСЫНЛМ + j(M<»)} “
- (Лш)Л(<а) ~ ОИСМ»)) + + «w)?^)),
284
Гпава 3
откуда получаем зависимости вещественной и мнимой частотных характери-
стик выходного сигнала
= Жш)^ш) - MQ/ш).
(2/ы) = Лш)Ш“) + <?(<d)/\(w),
которые будут подставляться в (3.29):
□ если входной сигнал представляет собой несмещенный дельта-импульс
х(/) = 8(/), у которого
X(jo>) = 1 => Р/ш) = 1, Q/ы) = О,
то Р/ш) = Р(ш), 2х(ш) = С(<1>), а выходной сигнал есть импульсная харак-
теристика, связанная с вещественной и мнимой частотными характери-
стиками системы соотношениями
--J C((i))sin(iiM)dw;
яо
м(г)=-Jp(<o)cos((iv)dto=
яо
(3.30)
О если входной сигнал является несмещенной единичной ступенчатой
функцией х(г) = 1(c), у которой
Х0<о) = 1 / jw =» Р/ы) = 0, 0Х<о) =-!/<□,
то P/w) = 0(ы) / ш, С/ш) = -Р(ш) / и, а выходной сигнал есть переходная
характеристика, связанная с вещественной и мнимой частотными харак-
теристиками системы соотношениями
(3.31)
nJ со nJ со
о о
По формулам (3.30) и (3.31) можно методом численного интегрирования на
ЭВМ рассчитать временные характеристики системы по ее вещественной
или мнимой частотным характеристикам. Последние могут быть получены
по амплитудным и фазовым частотным характеристикам аналогично (3.28):
[р(ш)= a(oj)cos(<p(w))= 10ооп^сов(ф(ш)>
|е(ш)= A(<o)sin(<p(to))= lOOO5/(tu)sin(0(<o))
Подставив в (3.26, 6) вместо Ц)ы) комплексные выражения
wG<o)=a(<»H4
jco ш
получим интегральные зависимости временных характеристик от амплитуд-
ной и фазовой частотных характеристик:
г элементов и систем управления
w(t) = - 7 A(oj)cos((i)Z + ф(о))>),
ло
/,(,)^j4j)sin(wW)d(l).
о
(3.32, о)
(3.32, б)
Таким образом, нами выведен целый «букет» формул (3.30) - (3.32), пригод-
ных как для аналитического, так и для численного расчета импульсной и
переходной характеристик системы путем интегрирования имеющихся час-
тотных характеристик.
3.3.2. Трансформации частотных характеристик
Исследуем теперь, как изменяются временные характеристики системы при
трансформации ее частотных характеристик по амплитуде и частоте. Для
сравнения обозначим эталонную комплексную частотную характерисгику
как (Kitjw), а соответствующие ей эталонные временные характеристики как
»|(г) и Л|(/). Системы с трансформированными характеристиками являются
подобными.
□ Пусть %()0)) = afK|(jto) — комплексная частотная характеристика, полу-
ченная умножением И7,(j<o) на константу а, что эквивалентно последова-
тельному соединению системы с широкополосным усилителем, транс-
формирующим ее амплитудно-частотные характеристики по ординате —
масштабированием амплитудной /1(ы) (рис. 3 16, а) или сдвигом лога-
рифмической амплитудной характеристики Д(ш) (рис. 3.16, <5).
Рис. з. 16
Соответствующие коэффициенту а временные характеристики надобной
системы
Глава 3
Wa(f)=-L ]wa(j^d^ JlV,Garden = aiv,(4
Ла(/)=f = a J Wi (T)dT = ah, (t)
О о
построены на рис. 3.17.
«) б)
Рис. 3.17
Вывод
Умножение комплексной частотной характеристики на константу приводит к
пропорциональной трансформации временных характеристик по амплитуде
□ Пусть Wp(ja))=W^ j — комплексная частотная характеристика, полу-
ценная трансформацией эталонной характеристики (jw) по частоте в Р
раз. При р > 1 это эквивалентно расширению полосы частот подобно!
системы, а при р < 1 - ее сужению (рис. 3.18).
«)
Рис. 3.18
Временные характеристики элементов и систем управления
Соответствующие коэффициенту 0 временные характеристики подобной
системы
н-р (г)= ± Jje-do,=£ j\v, j“P'd<o = (0/}
Лр (0 = J Wp (t)tiT = f н>! (0т>фт) = f w, (t)dt = Л, (0/)
oo о
изображены на рис. 3.19
Рис 3.19
Вывод
Трансформация комплексной частотной характеристики ло оси частот приводит
к пропорциональной трансформации импульсной характеристики по амплитуде
и обратно пропорциональной трансформации обеих временных характеристик
по оси времени
□ При трансформации комплексной частотной характеристики
%₽Gw)=aW'1[j^j (3.33, в)
одновременно по амплитуде в а и частоте в 0 раз на временные характе-
ристики подобной системы действуют сразу оба фактора
»v<1P(r) - ари-|(р/>. = аЛ|(рЛ (3.33. б)
Важнейшим методологическим результатом проведенного анализа влияния
трансформаций частотной характеристики системы на се временные ха-
рактеристики является установление фундаментального свойства подобных
Аномических систем, заключающегося в том. что произведение полосы
288
Глава 3
пропускания на длительность переходного процесса есть некоторая постоян-
ная величина
ц, /у = const. (3.34)
Значение константы в (3.34) индивидуально для каждого класса систем. На-
пример:
□ апериодическое звено с постоянной времени Т обладает по (2.27) поло-
сой пропускания ц, = 1 / Т и по (3.17, а) временем установления
/у = 3 Г, так что произведение этих показателей равно трем,
□ колебательное звено с постоянной времени Т и коэффициентом затуха-
ния обладает по (2.30) полосой пропускания
1/1-252+а/2-4§2 + 4§4
“п(и=-----------7-----------.
а по (3.17, б) временем установления /у = ЗГ/ £, так что их произведение
*^"4 +41^>Зх/72-1^1.931 Vije (0, 1]
зависит от значения £, обратно пропорционального добротности.
3.3.3. Масштабируемые по времени модели
Взаимосвязь частотных и временных характеристик лежит в основе по-
строения масштабируемой модели системы, отличающейся от эталонной мо-
дели разметкой временной и частотной шкал. Допустим, имеется переда-
точная функция некоторого химического процесса, длительность которого
измеряется десятками минут или часов. Понятно, что ожидание результатов
моделирования такой системы в реальном времени чрезвычайно утомитель-
но. Желательно «сжать» время так, чтобы переходный процесс протекал
единицы секунд. Обратное желание замедлить ход течения времени возни-
кает при изучении очень быстро протекающих процессов — взрыва, движе-
ния артиллерийского снаряда, ядерной реакции и т п.
Еше одним стимулом применения масштабируемых по времени моделей яв-
ляется широкое распространение метода компьютерного исследования
сложных систем с помощью программ электронного моделирования — та-
ких, например, как MicroCAP и Electronic Workbench. Поскольку подобные
системы |29| описываются схожими дифференциальными уравнениями И
передаточными функциями, можно исследовать их поведение с помощью
электронных моделей на операционных усилителях. Вот почему автор улс'
лил в своей книге такое большое внимание методам синтеза и анализа схем
на основе этих устройств!
Временные характеристики элементов и систем управления 289
Типичные номиналы используемых в схемах сопротивлений Л, и емкостей
Cj составляют килоомы и микрофарады, постоянные времени R,Cj измеря-
ются в миллисекундах, а рабочие частоты — в килогерцах. Длительности ре-
альных процессов, моделируемых электронными схемами, чаше всего отли-
чаются от модельных длительностей на несколько порядков в обе стороны.
Так что изменение временного масштаба при электронно-программном мо-
делировании подобных систем неизбежно
Средством исполнения желаний может служить временное масштабирование
'м ~ f>
в котором коэффициент т, трансформирует шкалу времени из реальной /
в модельную /м. Например, масштаб т, = 0.001 < 1 заменяет единицу
времени, равную одной секунде, новой единицей — одной миллисекун-
дой, что означает ускорение темпа течения времени и сжатие переходно-
го процесса по оси /. При выборе m, > 1 происходит замедление хода изу-
чаемых процессов.
Согласно (3.33) изменение временного масштаба сопровождается обратно
пропорциональным изменением частотного масштаба:
ш 1
шм = — = тшш, где тш= —
т, т.
Например, ускорение хода процесса при выборе значения т, = 0.001 означа-
ет замену единицы частоты в один герц новой единицей в один килогерц и
приводит к сдвигу всех логарифмических частотных характеристик по оси
частот вправо на три декады.
Как изменится эталонная передаточная функция системы
W(s)* bo+bvt + ...+bms"'
a0+als + ... + a„sn
при масштабировании времени коэффициентом т,? Так как символ г ис-
пользуется и как оператор Лапласа, и как символ дифференцирования
d / dr, и как комплексная функция jeo, то между ним и модельным символом
Ai существует взаимосвязь
d
1 ~т' dt„ *т'3"'
Подставив эту зависимость в Ифг), получим масштабируемую по времени
передаточную функцию
I ГЛе =в,тЛ
м\м/ \ I м/ ao+ct|jM +,.. + аяли
290
Глава 3
Соотношения между масштабируемыми оригиналами и изображениями от-
ражены в первых двух пунктах табл. П.З. Например, в системе «тележка -
перевернутый маятник» из примера 3.4 с передаточной функцией угла от-
клонения из (3.22)
w / ч ____________» ____________
1 (1 +1.72 4» -0.397i)(l + 0.244f)
длительности временных характеристик составляют единицы секунд
(см. рис. 3.13, б). Для замедления этих процессов, например, в 10 раз зада-
дим коэффициент временнбго масштабирования т, = 10, тогда масштаби-
руемая передаточная функция станет равной
5.73зм
а импульсная и переходная характеристики из (3.23) превращаются в сле-
дующие временные функции:
и<РмО«)=Ь-,Кмк)}=-Ь83е'<,058'“ -4.22еоаг,“ + 6.06е-°4,'«,
^(»м)=Ь~1|И/ф>1^мН = 0.315е’оо58'“ -О.168е0252'- -0.148еч)4|'«.
На рис. 3.20 построены (о) логарифмическая амплитудно-частотная характе-
ристика LwMJ и (б) временные характеристики н’,м(гм) и A,M(zM) масштаби-
руемой модели системы «тележка - перевернутый маятник». Для выяснения
отличий модельных характеристик от реальных читатель может сравнить их
с графиками на рис. 2.24, а и рис. 3.13, б.
Рис 3.20
Временные характеристики элементов и систем управления_291
3.4*. Аппроксимационный метод
построения временных характеристик
При численном интегрировании по формулам (3.30) - (3.32) неизбежны ме-
тодические погрешности из-за усечения бесконечного частотного интервала
(0. °°) конечным [О, Я| и трудности подбора оптимального шага интегриро-
вания функций, изменяющихся с переменной частотой. Рассмотрим числен-
но-аналитический метод расчета временных характеристик по кусочно-
линейной аппроксимации вещественной частотной характеристики Жш) и
формулам (3.30), (3.31). Для сходимости несобственных интегралов необхо-
димо, чтобы функция Лы) была интегрируемой, т. е абсолютно ограничен-
ной и стремящейся к нулю при w -»°°.
Допустим, некоторая гипотетическая система имеет треугольную [5| вещест-
венную частотную характеристику (рис. 3.21):
. . fl-ейVO<co< 1.
Р»= OVM>1.
Рассчитаем по (3.30) и (3.31) нормированные временные характеристики этой
системы и оценим их свойства.
□ Импульсная характеристика нд(т) (рис. 3.22, о)
(/)= — / (1 - w)cos((im )dw:
2fsin((iw) cos((iM)+ciMsin(an)~p [ (sin(//2))
4 » r Lo = «l '/2 J
(3.35, o)
имеет начальное и установившееся значения
н-4(0) • «"*, *4(~) = О
292
Глава 3
и время сходимости к уровню 0.05ivd(0) = 0.016 не более Зле. В первом
приближении wM можно аппроксимировать функцией е~'/я/л.
□ Переходная характеристика hM (рис. 3.22, б)
*a(r)=|j^sin(<ot)dco=
0 (3-35, й)
имеет начальное и установившееся значения
Лд(0) = 0, йд(-) = 1
и время монотонной сходимости к уровню 0.95Лд(0) = 0.95 не более Зл с.
в)
Рис. 3.22
В первом приближении Лд(0 можно аппроксимировать функцией
1-е Интегральный синус в (3.35, б) вычисляется с помощью разло-
жения в степенной ряд
и медленно сходится к уровню л / 2. В |16, табл. 4.6| приведены значения
МО-
Пусть имеются расчетные или снятые экспериментально логарифмические
частотные характеристики Цш) и <Мш) По известной формуле
Р(ш)= 10ом/^и)со»(ф(о>))
Временные характеристики элементов и систем управления
рассчитаем вещественную частотную характеристику в конечном множестве
из (л + 1)-ой точки (<о/, Pi) и аппроксимируем ее непрерывной кусочно-
линейной функцией (рис. 3.23) из л отрезков
[(<оь1, Р^), (ш„ Л)| Vi=l^
так, чтобы было <ир = О, Рп = 0.
Представим эту характеристику суммой треугольных вещественных характери-
с коэффициентами трансформации по амплитуде и частоте
Для вычисления высоты /-го треугольника а, нужно найти производную
Как тангенс угла наклона /-го отрезка Р, ^Р, к частотной оси. Понятно, что
На аппроксимации вещественной частотной характеристики не должно быть
вертикальных участков. Для единообразия расчета коэффициента
а„=-Р'ш„ дополним аппроксимацию точкой />гц“0 на свободно вы-
бранной частоте о>и+1 > ы„.
294 Глава 3
В соответствии с закономерностями (3.33) изменения временных характери-
стик при трансформации частотных запишем суммарное действие всех п от-
резков вещественной частотной характеристики как
Ч)= (₽<')= Еи>д(<оД
л' л (3.36)
с весовыми коэффициентами
И* = (/^| - Р/Х, W, = - Pfa.
Таким образом, временные характеристики системы есть взвешенные суммы
нормированных характеристик (3.35), сжатых пропорционально частотам ш/
сопряжения отрезков, аппроксимирующих вещественную частотную харак-
теристику. Весовые коэффициенты и И, пропорциональны изменениям
наклона отрезков, квадратам частот (для №/) или самим частотам сопряже-
ния (для Н,).
При невыполнении условий интегрируемости интегралы (3.30) - (3.32)
расходятся. Это бывает в тех случаях, когда передаточная функция имеет не
все строго левые полюсы или степень полинома числителя передаточной
функции не меньше степени полинома ее знаменателя. В таком случае
необходимо расщепить передаточную функцию
= %0) + B'h(j)
на интегрируемую И'/т) и неинтегрируемую JFh(t) части, порождающие ус-
тойчивые, нейтральные и расходящиеся (неустойчивые) слагаемые времен-
ных характеристик:
|нМ = И',(Г) + *„(г) + н>(0.
Устойчивые слагаемые временных характеристик рассчитываются по изло-
женной выше методике для интетрируемой части передаточной функции
И^и(з). Нейтральные и расходящиеся слагаемые, порождаемые неинтегри-
руемой частью И'н(з). описываются следующими выражениями, дополняю-
щими в отдельных случаях табл. 3.1:
W'h(j) = К =»»„(/)» К • 8(0, Л„(1) - К 1(0: (3.38, а)
Wu(p)~— ~ 1(0, *и(0 = Kt 1(0; (3.38, 6)
W"(*)*H-T2ia ** (3.38, в)
Временные характеристики элементов и систем управления
w-(,)=dK VV₽(/)="Fe’ М')=к '-е' >(»); (3.38. г)
£7 Пример 3.7. Рассчитать аппроксимационным методом временные харак
теристики системы «тележка - обычный маятник» с передаточными функ-
циями
10 + 1.333*+ 1.333?
5 + 1.833?+0.36?+0.167? ’
__________0.573*_________
l + 1.833*+0.36s2 + 0.167*3 ’
Решение Учитывая, что передаточная функция H'/s) является неинтегри-
руемой, представим ее суммой
17 + 2.2675 + I.667*2
1 + 1.8335 + 0.36?+0.167*3
Wrf(*)= у + ^з), где %(*)=-
Построим вещественные частотные характеристики /’..(со) и Р,(ы) (рис. 3.24).
Они хорошо аппроксимируются восемью отрезками В табл 3.2 приведены
Параметры отрезков и расчет весовых коэффициентов и для характе-
ристик /’„(<!>) и Рф(ш).
Рис. 3 24
Таблица 3.2
/ 0 1 2 3 4 5 6 7 e
<д 0 1 2.4 3 3.5 4 7 11 16
p.. -17 -4264 12736 -0.623 2.6 -0 386 0397 -0 482 -0 194 -0 468 003 -O 166 -0 067 0.025 0 0.013
w. H. -10136 -10.136 -12 694 -5 289 -6.313 -1 771 2 736 0 782 1 134 0284 -3 704 -0 529 -1 398 -0.127 -3.412 -0.213
p„ 0 03 0.3 052 0157 0 286 -0 39 -0.12 -0812 -0 226 -0212 -0079 0 049 -0.03 0.012 0.006
wv H, -0142 -0.142 -3.153 -1.314 -3 795 -1 265 7348 2099 4.175 1 044 -1 795 -0 256 -0.77 -0.07 -1532 -0 096
Используя табличные данные, на основе (3.36), (3.37) и (3.38, б) построим
требуемые графики временных характеристик системы:
w/l) - 10 - 10.136^(0 - 12.694^(2.4/) - 5.313wA(3f) + 2.736и»4(3.5/) +
+ 1.134жд(40 - 3.704w4(7/) - I 398н>4( 11г) - 3.412и-4(16/).
h/i) - Юг - 17 - 10.136Л4(/) - 5.289Л4(2.4/) - 1.771й4(3т) + 0.782Л4(3.5/) +
+ 0.284Л4(4») - 0.529Лд(7/> - 0.127Л4(11/) - 0.21 ЗЛ4( 16/).
»Д/) - -0.142^(7) - 3.153м-4(2.4т) - 3.795w4(3t) + 7.348w4(3.5f) +
+ 4.175w4(40 - 1.79Sw4(7/) - 0.77w4(l 1Z) - 1.532н»д(1б/),
Временные характеристики элементов и систем управления
Они очень близки к истинным графикам характеристик (см. рис. 3.14,6),
построенным для сравнения на рис. 3.25 пунктиром. □
3.5. Оценки качества переходных процессов
в системах управления
Что понимается под качеством системы управления? Прежде всего, естест-
венно, система должна быть устойчивой. Не зная передаточной функции и
расположения ее полюсов, мы. тем не менее, можем оценить устойчивость
по сходимости или расходимости переходного процесса на выходе системы,
развивающегося на наших глазах или зафиксированного в виде графика Х6-
298
Глава 3
Для того, чтобы дать системе проявить свои свойства, ее надо вывести из
состояния равновесия (если она в нем была) путем подачи на вход некото-
рого воздействия x(t).
Убедившись в устойчивости системы, мы начинаем интересоваться ее пере-
ходным процессом, его качественными и количественными параметрами,
как то:
□ длительностью переходного режима, которую почти всегда хочется
уменьшить для скорейшего входа в установившийся режим со стабиль-
ными параметрами движения;
□ динамикой движения в переходном режиме, который при высоком бы-
стродействии скорее всего имеет участки с большими выбросами, высо-
кой колебательностью, резкими разгонами и торможениями, приводя-
щими к перегрузке оборудования системы;
□ близостью выходного сигнала к желаемому значению в установившемся
режиме, что характеризует статическую точность регулирования.
Если мы хотим, чтобы сравнение качественных показателей разных систем
было объективным, надо поставить системы в равные условия, выбрав оди-
наковый входной сигнал. Этот сигнал должен быть простой формы, про-
стым в технической реализации и, главное, способным возбудить в системе
все присущие ей собственные движения. Наилучшим тестовым сигналом для
исследования динамики систем является дельта-функция х(/) = 5(/) с равно-
мерной спектральной плотностью X(jw) = 1 на всех частотах в интервале
ше[0, «о). Однако реализация идеальной 8-функции невозможна, да и не
всякая система в состоянии выдержать большую амплитуду аппроксими-
рующего единичного импульса х(/, е) при малом значении е. Наконец, им-
пульсное воздействие с х(<») = 0 не дает возможности оценить статическую
точность системы при ууст = 0.
Указанных недостатков лишена простая в реализации и ограниченная по
амплитуде единичная ступенчатая функция x(t) = 1(/) со спектральной плот-
ностью /(j<o) = -j / ш. Она возбуждает на выходе системы сигнал, называе-
мый переходной характеристикой h(f) (см. разд. 3.2.2), по которой и оцени-
вается способность системы отрабатывать с необходимым качеством произ-
вольные входные воздействия.
По характеру протекания устойчивые переходные характеристики бывают
(рис. 3.26):
□ апериодические (/) и колебательные (2);
□ без перерегулирования (рис. 3.26, а) и с перерегулированием (рис. 3.26, б),
в том числе отрицательным (3).
Временные характеристики элементов и систем управления
3.5.1. Показатели качества
переходной характеристики
В практической деятельности квалифицированного инженера очень важно
не только интуитивно представлять, хорошую систему управления ой спро-
ектировал или нет, но и уметь численно охарактеризовать понятие качества,
владеть различными методами оценивания его показателей. Последние вы-
бираются так, чтобы подчеркнуть наиболее важные требования, предъяв-
ляемые к системе.
Основными показателями качества переходной характеристики являются:
□ начальное и установившееся значения
Ло = lim h(f). Ли = lim Л(г);
□ точность регулирования в установившемся режиме
Др = 0.05|Л. - Ло|;
□ время установления переходной характеристики
/у : |А(г) - Л_| S Д , V I i Гу (3.39)
как время, за которое она окончательно входит н трубку Л. ± Др шириной
2Др вокруг установившегося значения Л_. Функция tustlt. f. fust,а),
предназначенная для вычисления времени сходимости временного про-
цесса Дг) в трубку fy„ t Д, приведена на рис. 3.8:
□ перерегулирование
Р'т» ~fr-|
100%
(3.40, о)
300
Глава 3
как относительная мера максимального выброса переходной характери-
стики за установившееся значение й_. Функция sigma(f, fo, fust), пред-
назначенная для вычисления перерегулирования временного процесса
/г), изменяющегося с начального значения f0 до установившегося значе-
ния^, приведена на рис. 3.8;
□ отрицательное перерегулирование
как относительная мера максимального выброса переходной характери-
стики за начальное значение в противоположную сторону от установив-
шегося состояния (пунктирный график 3 на рис. 3.26, б);
□ параметры колебаний (рис. 3.27):
• частота fK =^Гц;
• период Т. =4-=—с ;
А «>«
• число колебаний в переходном процессе
NK=^-; (3.41)
• степень затухания колебаний за период
Рис. 3.27
пов и систем управления
Совокупность статических (Ао, Л_) и динамических (Гу, о. а_, /к, Тк, NK, О
показателей качества формирует допустимую область протекания переход-
ных процессов, ограниченную сверху мажорантой Лд/G). а снизу — мино-
рантой hm(fy.
hm(i) <. h(l) S ЛлД/).
Расчет переходной характеристики дает точные значения ее показателей ка-
чества, но он, как известно (см. разд. 3.1), очень трудоемок Существуют
косвенные и более простые методы проведения оценок показателей качества,
позволяющие быстро получить информацию о статических и динамических
свойствах системы без сложного вычисления ее временных характеристик.
Некоторое представление о возможности делать такие оценки мы уже полу-
чили в разд. 3.3 при изучении влияния трансформаций частотных характе-
ристик на временные.
Важно понимать, что оценка некоторого параметра несет информацию не о
точном, а, скорее, о наиболее вероятном его значении, и вовсе не обязана с
ним совпадать. Поясним сказанное на следующем примере. В разд. 3.2.3 бы-
ла получена оценка (3.17, б) времени установления импульсной и переход-
ной характеристик типового колебательного звена, а на рис. 3.11, б по опре-
делению (3.39) построен график /у(£) путем трудоемкого компьютерного мо-
делирования с помощью функции eust (см. рис 3.8). Его значения вполне
могли быть получены и в каком-нибудь еще более трудоемком эксперименте
с реальной колебательной системой. Ступенчатый вид графика наглядно
свидетельствует об отличии истинного времени затухания колебаний от его
оценки, сделанной по мажоранте или миноранте
3.5.2. Спектральные оценки качества
Спектральные оценки качества основаны на анализе расположения на ком-
плексной плоскости полюсов 5, и нулей Zj передаточной функции системы
"'«ад-
AI
Согласно (3.20) переходная характеристика Л(г) есть сумма экспоненциаль-
ных составляющих с, (г)еЛ'' и по (3.21) схолнтся к конечному значению
Л(«>) к только при условии, что все полюсы передаточной функции ле-
302
Глава 3
вые. Графики на рис. 3.1 убеждают, что чем дальше левый полюс st отстоит
от мнимой оси, тем быстрее сходится порождаемая им составляющая qe’1'.
Если не все полюсы передаточной функции левые, то переходная характе-
ристика не сходится к конечному значению: она расходится или совершает
незатухающие колебания. Чем дальше правый полюс s, расположен от мни-
мой оси, тем быстрее расходится экспонента е’*'.
Вид переходной характеристики — апериодический или колебательный -
определяется типом полюса — действительный он или комплексный
К основным спектральным параметрам относятся:
□ степень устойчивости
i)=-max{Re(j,)}
(3.43)
как расстояние от мнимой оси до ближайшего левого полюса передаточ-
ной функции при условии отсутствия не левых полюсов В переходной ха-
рактеристике доминирует самая медленная составляющая, соответствую-
щая полюсу с Re(j() = -тр
• при доминирующем действительном полюсе s, = -и (рис. 3.28, а) —
апериодическая составляющая qe*’1' (рис. 3.28, б);
при доминирующей паре комплексно-сопряженных полюсов
“ ~П ± шк (рис. 3.29, а) — составляющая колебательной формы
qc"*1' sin(<o,r ♦ <р,) (рис. 3.29, б);
Временные характеристики элементов и систем управления
а) в)
Рис. 3.29
□ степень быстродействия
y = -min{Re(s|)} (3.44)
как расстояние от мнимой оси ло наиболее удаленного левого полюса пе-
редаточной функции. В переходной характеристике составляющая c,e'v'
изменяется быстрее других и характеризует максимальную скорость ре-
акции системы на входные воздействия, а также определяет выбор шага
квантования времени при машинном моделировании переходных процессов;
□ степень жесткости г = у / и — отношение показателей затухания самой
быстрой к самой медленной составляющей переходной характеристики.
Система с параметром г > 10 называется жесткой. Численное моделиро-
вание переходных процессов жестких систем на ЭВМ сталкивается с
проблемой выбора периода квантования времени ДГ, удовлетворяющего
двум противоречивым требованиям:
• быть достаточно малой величиной ДТ< к / у для того, чтобы согласно
теореме Котельникова [ 15|, известной еще как теорема отсчетов (к ее
обоснованию причастны Коши, Карсон, Найквист, Хартли, Габор,
Блэк и Шэннон [22|>, программа «заметила» бы самые быстрые дви-
жения с постоянной времени, равной 1 / у,
• не быть слишком малой величиной для того, чтобы чисто шагов мо-
делирования ЛГМ = гы / ДГна временном интервале t е(0, гм| с конеч-
ным значением гм > я / л, не превышало разумных пределов
С учетом критических неравенств, наложенных на величины ДГ и Гн,
получим следующую простую оценку необходимого чиста шагов мо-
делирования:
304
□ степень колебательности
как тангенс угла раствора для ближайших к мнимой оси левых комплекс-
ных полюсов -т) ± Шк (рис. 3.29, а). Из (2.8, а) вытекает взаимосвязь ко-
эффициента затухания колебательного звена £ - cos(v) и степени колеба-
тельности:
Основные спектральные оценки качества устойчивой переходной характери-
стики следующие.
□ Верхняя оценка времени установления /у, определенного в (3.39), обратно
пропорциональна степени устойчивости т], а нижняя — степени быстро-
действия у.
-<ту2-(с). (3.48)
у у 11
Действительно, при выбранной точности регулирования Др = 0.05 по
(3.16) получим утроение постоянных времени экспонент ±е~у' и ±е'*)',
ограничивающих самую быструю и самую медленную составляющие пе-
реходной характеристики. То, что эти постоянные времени тп1|п = 1 / у и
Тпш = 1 / П определяются не постоянными времени знаменателя переда-
точной функции Th а действительными частями полюсов Re(s,}, убежда-
ют формулы времени установления процессов в апериодическом (3.17, а)
и колебательном (3.17, б) типовых звеньях.
□ Верхняя оценка перерегулирования определяется степенью колебательности:
aSe1* 100%. (3.49)
Действительно, если ближайшими к мнимой оси являются комплексно-
сопряженные полюсы -т) ± jo\ с углом раствора у/ = arctg(av / и), то в
переходной характеристике доминирует колебательная составляющая
Из условия Лф) = 0 получим значения йД/() в точках максимумов функ-
ции Л(0. чередующихся с точками минимумов (см. рис. 3.27):
Временные характеристики элементов и систем управления
h’i ve~n'(tisin((i)Kt + v)-a)K005(10,,/ + у))= 0,
sin (у)
откуда следует соотношение
tg(oV + V) • tg(v),
из которого находим моменты ьых максимумов функции Л(/):
Значение первого максимума в момент времени /t равно
откуда по определению (3.40, а) находим перерегулирование
-1 j-100%=^1 + е •* -lj-10()%=eM 100%.
□ Оценка степени затухания также зависит от степени колебательности:
-2п
С = 1-е •* 100%. (3.51)
Подставив (3.50) в зависимость Л(/), находим значения /-го максимума
переходной характеристики в момент времени /, и выброса at в /-ом
периоде:
Измерив по графику колебательной переходной характеристики отноше-
ние соседних выбросов о, / Он-i > •• можно по обратной к (3.51) формуле
оценить степень колебательности:
-2л 2л
□ Оценка числа колебаний в переходном процессе определяется как
(3.52)
Действительно, ближайшие к мнимой оси комплексно-сопряженные по-
люсы ~п ± Як лают колебания с периодом Тк = 2л / ov С учетом верхней
оценки в (3.48) по определению (3.41) получим
к 27СТ| 2
Соотношение (3.52) — самый простой способ определения степени коле-
бательности ц = 2NK по визуально наблюдаемому числу колебаний в
затухающем переходном процессе.
□ Оценки влияния нулей передаточной функции (корней полинома числи-
теля) на качество переходных процессов:
нуль ф близкий к полюсу sh компенсирует составляющую с,е*'', по-
рождаемую этим полюсом. Условие близости чисел Zj и s, имеет вид
«шах{|^|, « (3.53)
Действительно, т. к. B(zj) = 0, то при выполнении этого условия в
(3.20) получим В($й = 0, благодаря чему коэффициент с, = 0 Оценки
качества (3.48) - (3.52), выполненные по скомпенсированному полюсу,
являются недостоверными;
нули передаточной функции, не компенсирующие близкие полю-
сы. как правило, ухудшают показатели качества переходного про-
цесса. Действительно, при невыполнении условия близости (3.53)
значение |в(з()| в (3.20) тем больше, чем дальше полюс з, удален от
нулей Zj,
правый нуль с Re(Zy) > 0 может дать отрицательное перерегулирова-
ние (3.40, б) из-за инверсии знаков B(s, - г/) в некоторых вычетах
(3.20) по сравнению с системой, в которой правые нули отсутствуют.
Отрицательное перерегулирование часто приводит к появлению в пере-
ходном процессе системы попятного движения, что, естественно, затя-
гивает его длительность
Временные характеристики элементов и систем управления
3.5.3. Частотные оценки качества
Частотные оценки качества переходной характеристики Л(/) могут быть по-
лучены по передаточной функции М($), вещественной частотной характери-
стике Дсо) и зависимости (3.31) свойств h(t) от Р(ш\.
□ Оценки начального значения ha:
• в соответствии с (3.21) по коэффициентам передаточной функции оп-
ределяем
Ло = НтИ'(^)=
— при т = п,
О при т < и,
sgn^—j о» при т>п;
(3.55, а)
• подставив в (3.54) значение 1= 0, получаем оценку Лд по веществен-
ной частотной характеристике:
о о
(3.55, б)
т. к. интегральный синус сходится к значению я / 2.
О Оценки установившегося значения й_:
• в соответствии с (3.21) по коэффициентам передаточной функции оп-
ределяем
I— при а0 #0, ,, .. ,
а0 (3.56, в)
sgn(Z>j)) o» при а0 =0;
• подставив в (3.54) значение / = »>, получаем оценку показателя Л_ по
вещественной частотной характеристике:
= 2 f/>(0)sin(v)dv = 2ф)7 sin0dv = (3 5Ь
nJ V п j V
ЗОВ______________________________________________________________Глава 3
Следующие оценки динамических показателей качества выполняются на ос-
нове вещественных частотных характеристик, построенных для интегрируе-
мой части передаточной функции И^(5). Соответственно это будут оценки
устойчивой части переходной характеристики Лу(/).
□ Оценки времени установления /у (рис. 3.30):
• по первой частоте
ш,: j/^w) - Я(0)| < 0.05|Р(0)| V ш 5 W|
выхода вещественной частотной характеристики из 5%-ой трубки,
построенной вокруг начального значения Р(0). По (3.36) определяем
самую медленную составляющую переходной характеристики
«|ЛЛ((О|/)= (Р2' -
которая согласно (3.33) и (3.34) сходится за время Зл / Ш| с. Таким
образом, получаем верхнюю границу быстродействия системы:
/v < — с; (3.57, а)
“1
Рис. 3.30
по максимальной частоте однозначности вещественной частотной ха-
рактеристики
OV sgn(P(<o)) = const V 0 < <о < шь
оценивается нижняя граница быстродействия системы (16]:
(3.57. б)
• по частоте установления вещественной частотной характеристики в
5%-ой трубке
tly |«ш>| $ о.О5| А0)| v ш г «у
Временные характеристики элементов и систем управления
309
находится вторая оценка нижней границы быстродействия. Так как
нормированная характеристика hM сходится за время Зл с, то вре-
мя установления графика Л(/) не превышает значения
с. (3.57, в)
“у
Если передаточная функция имеет дифференцирующие свойства и
ДО) = 0, то порог Др = 0.05 берется от максимального модуля веще-
ственной характеристики |Ртах|-
Полученные оценки быстродействия (3.57) согласуются с выводом (3.34)
о том, что чем шире полоса пропускания системы, тем более она быстро-
действующая
□ Оценки перерегулирования а:
• если Дсо) — монотонно убывающая (|F(<o)| < 0) и выпуклая вниз
(Р'(ы) > 0) функция частоты (рис. 3.31). то переходная характеристи-
ка не имеет перерегулирования, т. е. а = 0. Действительно, поскольку
нормированная характеристика Лд(г) монотонна, то немонотонность
графика Л(г) возникает в том случае, когда в (3.36) коэффициенты Н,
разных знаков. При выполнении условий монотонности и выпукло-
сти, наложенных на ры), получим
/»'< , Hi = (^ - Pfai > О V/,
Рис. 3.31
что дает монотонную переходную характеристику Л(г) с нулевым пе-
ререгулированием;
если вещественная частотная характеристика максимальна по модулю
в начальной точке, т. е. |Д0)| = тах|Я(и>)| (рис. 3.32), то перерегулиро-
вание удовлетворяет условию
a S 18Ж. (3.58. а)
Гпава 3
Рис. 3.32
Действительно, если |Лш)| < |Л0)| V <в > 0, то из (3.54) и (3.55, б) следует
Mo>Hsqa2^H»s.,,8P(())_, 1М_.
я л
если — однозначная функция частоты, имеющая пик Ртм
(рис. 3.33), то переходная характеристика имеет перерегулирование
a S 1-18Рпих-/>(°) .1Оо%. (3.58, б)
Р(0)
Рис. 3.33
Для доказательства представим вещественную частотную Р(ы) и пере-
ходную Л(0 характеристики в виде сумм (рис. 3.34)
Лы) - Л(“>) + Р2(ш),
Л(0 - Л1(0 + Л2(/).
Так как слагаемое Л2(т) порождается низкочастотной составляющей
P2(u>), то перерегулирование суммарной характеристики Л(/) создается
только функцией At(0. а из (3.58, а) и (3.56, б) следует
шах(Л(г)| » шах(Л|(/)) S 1.18Рп,ач,
Л.-Л|»+Л2.-ЛО).
Временные характеристики элементов и систем управления
311
Тогда по определению (3.40, а) получаем опенку
ioo% |оо%;
если вещественная частотная характеристика Р(ш) имеет экстремумы
Лих и Pmin разных знаков (рис. 3 35), то переходная характеристика
имеет перерегулирование
[ОТ (ЗЯ <)
□ Оценки параметров колебаний переходной характеристики:
Глава 3
острый пик частотной характеристики на резонансной частоте
Ыр > 0 (рис. 3.35) с коэффициентом резонанса
8.=-^-
свидетельствует о затухающих колебаниях переходной характеристики
со следующими оценками параметров качества:
Получение этих оценок основано на аппроксимации системы в окре-
стности резонансной частоты ыр типовым колебательным звеном со
следующими передаточной функцией и вещественной частотной ха-
рактеристикой:
Ш,
l+2£7b+T:s2
р(о).
»К')=
р (ш)=7 rTv 7~г ^7
(l-rWf +(2^Т<о)2
Из условия /"(ыр) = 0 определяем частоту Шр и максимум веществен-
ной характеристики:
7^4 ₽ р(°)
=~г~' яих" 4(1-4) 4(1 -4)8Р
Удовлетворяющий условию t, < 1 корень квадратного уравнения
4(1 - £)5р *= 1
дает коэффициент затухания колебаний
Эта оценка, кстати, подтверждает, что вещественная частотная харак-
теристика колебательного звена с коэффициентом затухания £ -
не имеет резонансного пика (см. рис. 2.13).
Найдем показатели, описывающие колебательные свойства системы
как функции параметров 6р и ср, которые можно измерить по ее ве-
щественной частотной характеристике с резонансным пиком величи-
ной 8р > 1:
Временные характеристики элементов и систем управления
313
постоянная времени характеристического
1 + 2^7* + 7V
полинома
частота колебаний (мнимая часть комплексных корней поли-
нома)
(4+0
4Л(8р-1)
показатель затухания колебаний (модуль действительной части
комплексных корней полинома)
с у
n r'2Q8;+/8p-i>p(5p-i):
степень колебательности
=(^>T^V2V1+2M-0-
При остром резонансном пике (5Р » 1), пренебрегая единицей в
6р - 1, получим следующие оценки:
Подставляя их в (3.48) - (3.52), получим оценки параметров пере-
ходной характеристики, сформулированные в (3.59).
Если комплексные полюсы передаточной функции не являются
доминирующими в ее спектре, то резонансный пик вещественной
характеристики располагается в среднечастотной части и коэффи-
циент резонанса 8р показывает усиление на частоте по сравне-
нию с близкими частотами, где пик вещественной частотной ха-
рактеристики отсутствует. Быстрые колебания переходной характе-
ристики совершаются вокруг медленно изменяющейся во времени
апериодической функции, определяемой доминирующим действи-
тельным полюсом (см. рис. 3.28, б). Оценки параметров колебаний
$, о, 5 и NK, выполненные по соотношениям (3.59), являются, ско-
рее всего, слишком грубыми;
• разрыв непрерывности вещественной частотной характеристи-
ки на низкой частоте (рис. 3.36, а) свидетельствует о ломи-
Гпава 3
нируюших, типа изображенных на рис. 3.29, б, но не затухаю-
щих колебаниях переходной характеристики с частотой соц =
и амплитудой Р(0) вокруг среднего значения ДО).
Действительно, при 8р -»~ оценки (3.59) стремятся к предельным
оценкам
ОК = Шр, ty = а = 100%, 5 = 0, NK =
а это не что иное как параметры незатухающих колебаний нейтраль-
ной системы с чисто мнимыми полюсами ±)С0ц.
В том случае, когда резонансный разрыв графика Р(и>) начинается на
среднечастотном участке с некоторого значения Рк (рис. 3.36, (5), то в
переходной характеристике типа изображенной на рис. 3.2S, б доми-
нирует апериодическая составляющая, переходящая в незатухающие
колебания частотой <i\ = шр и ориентировочной амплитудой Рк вокруг
среднего значения ДО).
& Пример 3.8. Оценить параметры переходной характеристики системы с
передаточной функцией
W(f)= + (3.60)
50+102з +5s2+2?
Решение Получим спектральные оценки по следующему распределению по-
люсов и нулей передаточной функции (рис. 3.37):
50 + Ю2з + 5а2 + 2? = 0 => 3| = -0.5, Jjj - -1 ± 7j;
loo - 20г + Юг2 = о =» - I ± 3j.
1 элементов и систем управления
315
Рис. 3.37
По (3.43), (3.44) и (3.46) определяем параметры спектра:
П = 0.5, у= 1,л-2, р= 7.
Спектральные оценки качества переходной характеристики, выполненные
по (3.48) - (3.52), следующие.
3 S гу < 6 с, a S 63.8%. С = 0.59,
ш* = 7 рад / с,/, = 1.11 Гц, Тк = 0.9 с, NK = 3.5.
Поскольку комплексные полюсы не являются доминирующими, то оценка
перерегулирования о может оказаться слишком завышенной. Правые нули zi.j
могут ухудшить качество переходной характеристики, в частности, дать отри-
цательное перерегулирование о- из-за переворота фазы колебаний.
Для получения частотных оценок подставим j = jw в передаточную функ-
цию (3.60)
5(tO-(oJ+2j<o(51-(o2J
и построим вещественную частотную характеристику (рис. 3.38)
25(10-<o2)‘+4w2(51-(oJ/
Рис. з.зв
316 Глава 3
Проведя пунктиром характеристик)’, какой бы она примерно была без резо-
нансного пика, выпишем данные, необходимые для оценки параметров ка-
чества переходной характеристики:
ЛО) ° 2, Л«) - 0. Л™ - 2.06, Pmtn - 0.256, Л - 0.57, 8р = 3.6,
uh = 0.1 рад / с, ц, 1.32 рад / с, Wj, - 7.3 рад / с, = 16.9 рад / с.
Частотные оценки качества переходной характеристики, сделанные по
(3.55, б), (3.56, б), (3.57) и (3.58, в), следующие:
Ло = 0. Л_ = 2, тах(2.38, 0.56} S S 94.25 (с), о S 25%.
Частотные оценки качества переходной характеристики, сделанные по (3.59)
Л = 1.2 Гц, Тк = 0.83 с, ty < 5.92 с, a < 80.4%, С > 0.35, NK < 7.2,
могут быть недостоверными, т. к. пик Л“) находится в среднечастотной об-
ласти, а его величина сравнивается с условным значением Рк.
Истинные показатели качества переходной характеристики определим, по-
строив оригинал Л(г) по изображению H^s) /sc помощью табл П.2, п. 99
(рис. 339):
h(t) = 2 - 2.284е"05' + 0.656e-'sin(7/ + 25.66*).
Рис. 3.39
Сделав по графику необходимые измерения, получаем
Ло - 0, Л_ - 2, - 6.25 с, о - 0%.
Т, - 0.92 с, Л - 1.08 Гц. С - 0.62, NK • 4.
Оценки и истинные значения показателей качества переходной характери-
стики Л(0 сведены в табл. 3.3. Сравнение этих данных свидетельствует о хо-
рошем совпадении оценок с истинными показателями, за исключением
времени установления. Небольшая затяжка длительности переходного про-
цесса объясняется наличием у передаточной функции правых нулей. С
Временные характеристики элементов и снегам управления
Таблица 33
Показатели качества Спектральные оценки Частотные оценки Истинные значения
Начальное значение Ло = О Ло»0
Установившееся значение Л_ = 2 Л.«2
Время установления 3Sl,S6c 2.38 51, < 5.92 с Г, =6.25 с
Перерегулирование а 5 63 8% 0 5 25% о = 0%
Период колебаний Г, = 0.9 с 7, =0.83 С Г, = 0.92 с
Степень затухания колебаний {«0 59 С >0.35 5 = 062
Число колебаний N. а 3.5 N,<72 У, = 4
Сопоставляя истинные показатели качества переходной характеристики с их
опенками, делаем следующие выводы
□ спектральные оценки ty и о соогласуются с истинными значениями
лишь при доминирующих полюсах и в отсутствие правых нулей переда-
точной функции;
□ спектральные оценки Д, Тк и 5 близки к истинным значениям. Знание
спектра передаточной функции помогает точно определить частоты гар-
монических колебаний переходного процесса системы по мнимым час-
тям комплексных полюсов;
□ спектральные методы не дают оценок амплитуд составляющих переход-
ной характеристики, поэтому оценки параметров и о, сделанные не по
доминирующим полюсам, могут быть грубыми;
Q спектральные методы не лают оценок статических параметрон - на-
чального ho и установившегося А_ значений.
□ частотные методы дают точные оценки параметров Ло и Л_ только для
устойчивых систем:
□ частотные оценки параметров колебаний близки к истинным значениям
лишь при низкочастотном расположении пика вещественной частотной
характеристики относительно ее других изменений В других случаях
оценки могут стать недостоверными
ГЛАВА 4
Нет ни одного понятия, в устойчивости ко-
торого я был бы убежден
Альберт Эйнштейн
Устойчивость систем
автоматического управления
В результате изучения методов расчета временных характеристик стало по-
нятно, что характер их изменения определяется, главным образом, переда-
точной функцией системы, а именно расположением ее полюсов — корней
полинома знаменателя. Продолжим более глубокое исследование качествен-
ных свойств элементов и систем автоматического управления, определяю-
щих их работоспособность во времени и пространстве.
4.1. Понятие устойчивости
Устойчивость является важнейшим и самым необходимым условием работо-
способности автоматических систем, т. к. включает в себя требование зату-
хания переходных процессов во времени. Система управления с расходя-
щимся переходным процессом неработоспособна. Устойчивость системы оз-
начает, что ее реакция на любое ограниченное воздействие также является
озраииченной Понятие устойчивости нелинейной динамической системы И
условия устойчивости установлены А. М. Ляпуновым.
Как показано в разд. 1.4, модель объекта в виде системы нелинейных диф"
ферснииальных уравнений (1.6) может быть линеаризована в операторной
форме
Л(р)М0 ’ адмо
с отклонениями Лу(0 “ ХО “ У,М и МО “ 40 “ *н(0 от номинальных Рс'
жимов ун(г) и х,|(/). Номинальное движение является невозмущенным.
гласно (118) и (1.19), изображение отклонения выхода объекта равно
Устойчивость систем автоматического управления
дх(5)=И/(з)ДХ(5)+^Ь^.
(4.1)
Устойчивость — это свойство, присущее сугубо объекту и не зависящее от
внешних воздействий. Подставляя в (4.1) нулевое отклонение входного воз-
действия ДАЪ) = 0 и Q(s) = 0, получим уравнение
(«)
с полиномами
Л(«)=£а/, Pi~ ХвудУ(‘'''’',(0)у,=0-',-,4
.=0 1=0 , :
описываюшее свободное движение объекта из ненулевых начальных отклоне-
ний Ду(0), .... ДУ^’^О) от невозмущенного движения
Математическое определение понятия устойчивости по Ляпунову (рис. 4.1, а):
невозмущенное движение y„(t) называется устойчивым по Ляпунову, eciu
V е > 0 3 8Де) > 0: |ду0(0)| < 6/е) => |Дусв(/)| < е V г > 0.
Проще говоря, в устойчивой системе при любых ограниченных отклонениях
начального состояния и его производных от их номинальных значений
дальнейшее свободное движение также является ограниченно отклоненным
от номинальной траектории.
4,f Ч?
«) О)
В неустойчивой системе малейшее отклонение движения от номинального
Режима приводит к его неограниченному отклонению апериодического или
колебательного характера. В действительности неустойчивое движение раз-
вивается не до бесконечности: в лучшем случае - до насыщения элементов
системы по мощности, а в худшем приводит к более катастрофическим по-
следствиям — разрушению объекта, взрыву реактора, падению ракеты и т. п
Если сходимость Л>-са(/) -»0 имеет место при /-><», то такое движение на-
зывается асимптотически устойчивым. Асимптотически устойчивое движе-
ние называется экспоненциально устойчивым, если его траектория не выходит
из сужающейся трубки, ограниченной сверху и снизу экспоненциальными
функциями с отрицательным показателем (рис. 4.1, б):
3 М < «>, т > 0: |Дусв(г)| < Ме~т.
В соответствии с (3.5) если линейный объект устойчив, то он устойчив не
только асимптотически, но и экспоненциально.
Движение, асимптотически устойчивое при любых начальных отклонениях
от номинального режима, называется устойчивым в целом. Устойчивые ли-
нейные объекты всегда устойчивы в целом.
Если существуют определенные границы начальных отклонений, в пределах
которых движение устойчиво, а вне этих границ — нет, то такое движение
называется устойчивы» в малом. Свойство устойчивости в малом присуще
только нелинейным системам. Оно в большой мере ограничивает область
работоспособности таких систем и достоверность их описания линеаризо-
ванными моделями.
4.2. Условия устойчивости
линеаризованных систем
Оценка устойчивости есть оценка возможности осуществлять управление,
поэтому с нее начинается исследование любой системы автоматического
управления. Для определения условий устойчивости линеаризованной сис-
темы (4.1) в силу принципа суперпозиции рассмотрим отдельно движения,
вызванные начальными отклонениями и входным воздействием. Без потери
общности примем невозмушенное движение нулевым:
Ун(0 = 0, хМ = 0.
Из (4.2) вытекает, что свободное движение полностью определяется полино-
мом >4(5) знаменателя передаточной функции, а формула разложения Хеви-
сайда (3.4) раскрывает его характер:
Уя(»)= •
Отсюда следует спектральное необходимое и достаточное условие устойчиво-
сти линеаризованных систем:
Устойчивость систем автоматического управления 321
Re(.v,| < 0 Vi =i?v. (4.3)
Для устойчивости линеаризованной системы пеобходнмо и достаточно, чтобы
все полюсы ее передаточной функции были левыми
Мнимая ось 1т(з) является границей устойчивости движения (см. рис 3.1).
Если в процессе функционирования устойчивой системы из-за дрейфа ее
параметрон хотя бы один полюс перейдет в правую полуплоскость з, то сис-
тема станет неустойчивой. Точка v = 0 мнимой осн называется апериодиче-
ской границей устойчивости, т к. полюс з( = О кратности п, порождает в сво-
бодном движении согласно (3.9, я) составляющую
неколебательного характера. Остальные точки мнимой оси составляют коле-
бательную границу устойчивости, т. к. пара мнимых полюсов кратности
п, порождает согласно (3.11. а) колебательную составляющую
Укл(<) = c,(')cos(bv + Фк)*
Системы, имеющие полюсы слева и на границе устойчивости, называются
нейтральными Строго говоря, переходные процессы в нейтральных системах
не расходятся только если граничные полюсы — простые. Поэтому понятие
границы устойчивости весьма условное и при проектировании системы
управления необходимо добиваться безусловной устойчивости с определен-
ным запасом, задаваемым степенью устойчивости ц — расстоянием (3.43) от
мнимой оси до ближайшего левого полюса. Если условие устойчивости вы-
полнено с запасом
Re(3j S -n V /,
то согласно (3.48) свободное движение затухает за время не большее, чем
3/пс.
Аналогично свободному ведет себя возмущенное движение, порожденное
ненулевыми начальными отклонениями Дх(0).......A.?m-l,(0).
Рассмотрим вынужденное движение, вызванное входным воздействием ф).
Его изображение в (4.1) равно
ПынО) = «Ш)
По теореме свертывания [16, 30| произведению изображений Щз)Л(з) соот-
ветствуют оригиналы — интегралы Дюамеля
| и-(т)х(/ - т)1т. J »v(r - т)х(т)1т (4.4)
о о
Действительно, по определению преобразования Лапласа (1.16), имеем
W(.t)x(j)=je-'MT)jT /е-‘фл(ф>1ф = |/е’1(х4ф)ЦтХ(ф)£1таф = °
О О О О
=||е‘"н(т)4 - T)drdT = Je^'f н(т)г(г - tjdrdr = l|J и{т>(т -1> j.
Ввиду симметричности переменных t и т справедлив и второй оригинал в
(4.4). Пусть входное воздействие абсолютно ограничено:
|х(/)| S V / > 0.
Тогда выходной сигнал должен удовлетворять условию ограниченности
|У.И11 (0=JИ) |4 - T^dr < М Дw(rJ|dT < о».
о о
Отсюда следуют временные условия устойчивости линеаризованной системы.
Необходимое и достаточное условие — абсолютная интегрируемость ее им-
пульсной характеристики Mfl Необходимое, но не достаточное условие ус-
тойчивости — сходимость импульсной характеристики к нулю:
lim 4)=0. (4.5, а)
В соответствии с предельными формулами (3.21) это необходимое условие
равносильно условию
lim{iW'(j)}=0 (4.5,6)
отсутствия астатизма передаточной функции. Достаточное условие устойчи-
вости заключается в том. что все полюсы передаточной функции должны
быть левыми. На примере системы «тележка - перевернутый маятник* с пе-
редаточными функциями (3.22) можно убедиться, что выполнение второго
предельного условия (3.21) для и<<») не гарантирует устойчивости, если не
все полюсы системы левые.
Прямые условия устойчивости системы (4.3) требуют знания полюсов пере-
даточной функции, что для систем высокого порядка представляет сложную
задачу нахождения корней полиномов (см. разд. 26). В действительности
достаточно располагать информацией о качественной ориентации полюсов
на комплексной плоскости относительно мнимой оси. Правила, позволяющие
исследовать устойчивость системы без вычисления полюсов ее передаточной
функции, называются критериями устойчивости, которые делятся на две
группы:
О алгебраические - Рауса. Гурвица и Льенара - Шипара-
□ частотные - Михайлова и Найквиста.
Устойчивость систем автоматического управления
323
Математически все критерии устойчивости эквивалентны, т к. устанавливают
условия принадлежности всех полюсов левой полуплоскости s. С их помо-
щью оценивают влияние параметрических или структурных изменений на
устойчивость, определяют границы допустимых изменений параметров, при
которых в системе управления сохраняется устойчивость и желаемые пока-
затели качества
4.3. Алгебраические критерии устойчивости
Алгебраические критерии устойчивости работают с характеристическим по-
линомом (ХП)
C(x)=co+c1^... + eZ=tc1?’ (46>
(=0
т. с. полиномом знаменателя передаточной функции той системы, устойчи-
вость которой исследуется. Получим передаточную функцию и харак-
теристические полиномы Ц>(т) и C,(s) разомкнутой и замкнутой систем,
изображенных на рис. 4.2:
□ в разомкнутой системе (а)
□ в замкнутой системе с единичной обратной связью (о)
иф)=-^, %(s)=iZw$) ~ ’ А,) 1 Д5):
□ в замкнутой системе с неединичной обратной связью (в)
324 Глава 4
На схемах и в формулах в обозначениях « + » и «±» верхние знаки соответст-
вуют отрицательной обратной связи, а нижние — положительной.
Полином, все корни которого — левые, называется устойчивым. Если все
его коэффициенты — числа, то алгебраические критерии устойчивости ус-
танавливают факт устойчивости либо неустойчивости системы с данным ха-
рактеристическим полиномом. Если некоторые коэффициенты характери-
стического полинома зависят от одного или нескольких параметров, то кри-
терии устойчивости дают соотношения типа неравенств, которые
используются для построения областей устойчивости системы в пространст-
ве параметров.
4.3.1. Необходимые условия устойчивости
Необходимые условия устойчивости полинома состоят в том, что все его ко-
эффициенты должны быть одного знака: либо положительные, либо отрица-
тельные:
>0Vi = 0.n}uk <0 V/ = 0, л}. (4.7)
2? Доказательство Используем систему формул Виста
jls2+jls3+-- + sn-lsn
(4.8, о)
М2...зя =(-!}*
связывающих коэффициенты полинома с его корнями. Общее выражение
для А-ой формулы Виета имеет вил
£Пч =(->)* — V4-U. (4.8,6)
I /-1 ' с«
Суммирование в (4.8. 6) ведется по всем С* сочетаниям произведений к из
п корней полинома, причем кратные корни считаются разными.
Для доказательства необходимости условий (4.7) допустим противное: в ус-
тойчивом полиноме со всеми левыми корнями существует хотя бы один ко-
эффициент <•„-*, знак которого противоположен коэффициенту <•„. Тогда:
Устойчивость систем автоматического управления 325
□ если к — четно, то в (4.8. б) слева сумма произведений четного количе-
ства левых корней положительна, а правая часть с„-* / с„ < 0;
□ если к — нечетно, то слева сумма произведений нечетного количества
левых корней отрицательна, а справа -с,-* / с„ > 0.
Полученные противоречия доказывают необходимость однозначности ко-
эффициентов полинома для его устойчивости, О
Например, система «тележка - перевернутый маятник» с передаточной
функцией (1.11) имеет характеристический полином
C(s) = 600s + 940s2 - 216? - 100?
с коэффициентами q + с4 разных знаков, и к тому же со = 0. Условия (4.7)
не выполнены, что подтверждается наличием у полинома нелевых корней
S| = 0 и s4 = 2.52 > 0. В результате временные характеристики системы рас-
ходятся (см. рис. 3.13), а по их формулам (3.23) видно, что за это ответст-
венны экспоненциальные составляющие е2 52'.
Приведем пример неустойчивого полинома со всеми коэффициентами од-
ного знака:
C(s) = 68 + 9s + 2? + ? = (4 + s)(!7 - 2s + ?). (4.9)
У него есть два правых комитексно-сопряженных корня sy.j = +1 14j Правое
расположение именно комплексных, а не действительных корней неустой-
чивого полинома с коэффициентами одного знака является не частным слу-
чаем, а правилом-, если выполняются необходимые условия (4.7), то все дейст-
вительные корни полинома — обязательно левые Комплексные корни могут
и не быть левыми.
Достаточные условия устойчивости полинома устанавливают дополни-
тельные ограничения на его коэффициенты, которые совместно (по пра-
вилу «И») с необходимыми условиями составляют полный набор ограни-
чений.
4.3.2. Критерий устойчивости Рауса - Гурвица
Исследуя вопрос о расположении корней полинома (4.6) с действительными
коэффициентами (см. разд 2.6.2}, Раус и независимо от него Гурвиц доказа-
ли теорему 2.5, гласящую; число правых корней действительного полинома
C(s) равно числу инверсий знака в последовательности
М - {<„, ЛГ|. Л/, Мъ Л/уЛ/з.Мк-М,}, «Н»
где Л//есть /-ый главный минор лхл-матрицы Гурвица Г
326
Глава 4
(4.11)
М^с^. М2=|^' М3=|с„ с„_, с„.4|. Л/„ = |/'|. (4 121
Как частный случай, из теоремы следует критерий Рауса — Гурвица, дающий
условия устойчивости действительного полинома, при которых число его
правых корней равно нулю: для устойчивости действительного полинома необ-
ходимо и достаточно, чтобы все элементы последовательности (4.10) были
одного знака:
(sgn(c„))% > 0 Vi = 1. п .
В частности:
□ если ся > 0, то все главные миноры должны быть положительны:
Mi > 0, ЛЛ > 0, М3 > 0....М„ > 0;
□ при с„ < 0 знаки миноров должны чередоваться, начиная с М\ < 0:
Ml < 0, > 0. Мз < о,.... (-1)"Л/„ > о.
Можно инвертировать знаки всех коэффициентов с/ (от этого спектр по-
линома не изменяется) и к полученному полиному применить лучше за-
поминающийся критерий устойчивости полинома с положительным ко-
эффициентом с„.
Граница устойчивости системы — это такая конфигурация спектра ее ха-
рактеристического полинома, при которой часть простых корней находит-
ся точно на мнимой оси 1ш{з). а все остальные корни — слева от нее. На-
личие корней на мнимой оси — лишь необходимый, но не достаточный
признак границы устойчивости, т. к. даже единственный правый корень с
Re{J() > 0 делает систему неустойчивой независимо <п расположения ос-
Устойчивость систем автоматического управления 327
Нахождению системы на границе устойчивости соответствует преврашение
некоторых неравенств в (4.7) и (4.13) в равенства. Выделяют два типа грани-
цы устойчивости, соответствующих нулевому последнему минору
Мп = coMn-i = 0:
□ при с() = 0 и С| * 0 характеристический полином имеет простой корень
j| = 0, а система обладает астатизмом первого порядка и находится на
апериодической границе устойчивости;
□ если при со * 0 У полинома есть комплексно-сопряженные корни
J|,2 ~ то по формуле Орландо (2.47) получим значение предпослед-
него минора Л/„_| = 0 и колебательную границу устойчивости. Поскольку
по той же формуле обнуление Мп-\ возможно еще и при наличии у не-
устойчивой системы характеристического полинома с ненулевыми дейст-
вительными корнями s, = ~Sj, то признаком колебательной границы явля-
ется не одно лишь равенство М„-\ = 0, но еще и отсутствие в (4.13) не-
равенств со знаком «<».
На рис. 4.3 приведен листинг с функциями на языке Mathcad. которые мо-
гут быть полезны для программного определения устойчивости полинома
ОД, чьи коэффициенты составляют вектор с = (с0 с, ... сл)г:
□ функцией тас(с), возвращающей матрицу Гурвица (4.11);
□ функцией miG(c), возвращающей вектор миноров матрицы Гурвица
(4.12);
□ функцией RaGu(c), возвращающей в текстовой форме результат иссле-
дования устойчивости полинома С(з) по критерию (4.13). При желании
читатель может модифицировать функцию так, чтобы результат возвра-
щался в цифровой форме, например:
• 1 вместо текста полином устойчив;
• — 1 вместо текста полином неустойчив;
• 0 вместо текстов Алериод. граница устойчивости и КолеОат. граница
устойчивости.
Рассмотрим теперь, какой конкретный вид принимают необходимые и дос-
таточные условия (4.13) устойчивости систем с характеристическими поли-
номами малых степеней. При анализе учтем, что для нечетных степеней
(sgn(c„))2*+l = sgn(c„). а для четных степеней (sgn(c„))24 = I.
□ Устойчивость полинома первой степени
Qj) » га + c(j
определяется единственным условием
sgn(C|)cB>0, (4.14, в)
из которого следует, что коэффициенты <•„ и е, должны быть ненулевыми
и одного знака
Глава £
"Матрица Гурвица"
for ie O..n«- last(c) - I
for je O..n
Г| ^ «-iffo s (it «-n + i-2-j) " n+
miGfc) .= "Миноры матрицы Гурвица"
n <- rows(r <- maG(c)) -1
Мо*-Го,о
for ie I.. n if n
Mj«- |submatrix(r,O,i.O,i)|
M
RaGu(c) .-= 'Критерий Рауса-Гурвица*
M «- miGfc)
5’-»'8п(<ти-1ая(с))
for ieO-n-l
return 'Полином неустойчив* if s"1M, < 0
return ‘Koflcfei. граница устойчивости* if 1 = п- 2лМ, = 0
return "Аисриод. граница устойчивости” if i = n - I л М, = О
‘Полином устойчив*
Рио. 4.3
□ К требованию однозначности коэффициентов с0, с. и с, характеристиче-
ского полинома второй степени
ОД - Св + ср + cj?
приводят условия (4.13) при л = 2:
МчУ,>0)п|£ (4.14.4
□ Характеристический полином третьей степени
Q*) - + ср + с2? + с,,»
устойчив при условиях
Устойчивость систем автоматического управления 329
{sgn(c3)c2 > 0} П {М2 = с(С2 - С0С3 > 0} П (sgn(q)cflM2 > 0|. (4.14. в)
Это предполагает однозначность коэффициентов cq, cj, г3 и положитель-
ность второго минора Л/2. Отметим, что требование однозначности всех
коэффициентов характеристического полинома в необходимых условиях
устойчивости (4.7) излишне: знак коэффициента q автоматически учиты-
вается в требовании М2 > 0, а именно: если знак q противоположен зна-
кам СО, С2 И Сз, то получим М2 < 0.
О Пример 4.1. Проверим по критерию (4.13) устойчивость полинома (4.9) с
положительными коэффициентами со = 68, q = 9. с2 = 2 и q = I:
sgn(q) > 0, М\ = С2 > О,
М2 = С|С2 “ Otto = -50 < 0,
Му = СоМ2 = -3400 < 0.
Двойная инверсия знаков элементов последовательности (4.10)
М={+. +, +}
означает, что полином (4.9) имеет два правых корня. Невыполнение условия
положительности минора Л/2 подтверждает неустойчивость системы с таким
характеристическим полиномом.
Программный анализ устойчивости полинома (4.9) с помощью функций,
определенных на рис. 4.3, приведен ниже:
с := ( 68 9 2 I )Т
( 2 68 0 Л
19 0 miG(c)T = ( 2 -50 -3400 )
0 2 68 J
RaGu(c) = "Полином неустойчив"
□
£7 Пример 4.2. Необходимые условия (4.7) устойчивости полинома
C(s) = 4 + 4j + jJ + j}
выполнены. Составив матрицу Гурвица
По ее минорам Л/, = 1 > 0, Л/2 “ I • 4 - 4 I • 0 и коэффициенту = 4 я 0
«елаем вывод о нахождении полинома на колебательной границе устойчиво-
сти. Действительно, разложение анализируемого полинома на множители
330
ОД) = (1 + J)(4 + ?)
доказывает, что его спектр состоит из одного левого корня j| = — I и двух
чисто мнимых корней sjj = ±2j.
Программный анализ устойчивости анализируемого полинома с помощью
функций, определенных на рис. 4.3, приведен ниже:
с :<= (4 4 I I )Т
miG(c)T = ( I 0 0 )
RaGu(c) = "Колебат. граница устойчивости"
В альтернативной форме критерия устойчивости, предложенной Раусом,
строится таблица из (л + 1)-ой строки в виде перевернутого ступенчатого
треугольника
Pl2 - Pin,
Р22 - Pzn,
Рп2
Рл+1,2
с элементами
Р21 = <«-!. Р22 = сп~3. Р2„г =Ся+|.2у2 ,
зано, что элементы первого столбца
— целая часть числа х. В |6| пока-
таблицы Рауса составляют послед0'
Рн “°n.P2l - рз, =^й_,
м\
М..
Устойчивость систем автоматического управления ЗЗГ
с таким же числом инверсий знака, как у последовательности (4.10). В
формулировке Рауса число инверсий знака у элементов первого столбца таб-
лицы Р равно числу правых корней характеристического полинома, а критери-
ем устойчивости является постоянство знаков всех элементов первого столб-
ца таблицы Р
Очевидно, что в условиях устойчивости Рауса - Гурвица (4.13) почти нс ис-
пользуются более простые необходимые условия (4 7) и в то же время требу-
ется вычислять п - 2 главных минора матрицы Гурвица М2 ♦ М„.\ (миноры
М\ - Сп-\ и М„ = соЛ/,,-| элементарны), что затруднительно для полиномов
высоких степеней.
Необходимые и достаточные условия устойчивости характеристического по-
линома, полученные Льенаром и Шипаром, используют все необходимые ус-
ловия (4.7) и часть главных миноров: либо Му, с четными, либо My,tl с не-
четными индексами |6|. Критерий Льенара - Шипира устойчивости действи-
тельного полинома C(s) формулируется в альтернативной форме.
□ при всех положительных коэффициентах г, > 0 должны быть положи-
тельны либо Му, > 0, либо Л/2А+1 > 0;
□ при всех отрицательных коэффициентах с, < 0 должны быть либо поло-
жительны четные миноры Му, > 0, либо отрицательны нечетные мино-
ры Л/и+1 < 0.
Критерий Льенара — Шипара дает свободу выбора анализируемых миноров
Из двух вариантов нужно так выбрать один, чтобы уменьшить количество и
степени вычисляемых миноров. Например, при п = 8 достаточно найти либо
{Му М4. М6. Л/8), либо (ЛЛ„ Л/5, М2}. Очевидно, что второй набор миноров
предпочтительнее как по количеству, так и по максимальной степени.
4.4. Построение областей устойчивости
параметрических полиномов
Особый интерес представляет исследование устойчивости характеристиче-
ского полинома, коэффициенты которого зависят от одного или нескольких
параметров:
C(s.p)=co(p)+ci(p)s+ +с.(Д>" = £<•,(?)»' (4.15)
•о
При вариациях элементов вектора параметров /5 изменяются зависящие от
Него коэффициенты с,(р), в результате чего могут произойти инверсии зна-
ков в условиях устойчивости (4.13), имеющих в параметрическом варианте
следующий вид:
(sgn(c„(p))yM,(p)>OV/ = l, n. (4.16)
Системы, в которых это возможно, называются условно устойчивыми. Режи-
мы их работы должны выбираться и поддерживаться в некоторой области
устойчивости — множестве точек в пространстве параметров полинома, в
которых выполняются условия устойчивости (4.16). Область устойчивости
отделена от области неустойчивости некоторой границей устойчивости (см.
рис. В5, рис. 2.40, б).
Системы, в которых условия устойчивости выполняются при любых физи-
чески допустимых значениях параметров, называются безусловно устойчивы-
ми. Системы, устойчивость которых недостижима ни при каких физически
допустимых параметрах, называются структурно неустойчивыми.
Сложность исследования устойчивости параметрических систем заключается
в необходимости решения «мынеыиых, в общем случае, неравенств (4.16) в
многомерном пространстве. Результатом решения должна быть область ус-
тойчивости, описанная уравнениями своих границ в пространстве парамет-
ров. При чрезмерной сложности или невозможности аналитического реше-
ния неравенств на помощь приходят численные методы, основанные, напри-
мер. на переборе и тестировании по (4.16) конечного числа точек р в
некотором ограниченном объеме пространства. Многомерность и малые ин-
тервалы дискретизации делают эту задачу разрешимой только с привлечени-
ем высокоскоростных компьютеров и специальных программных средств
(см. рис. 4.3).
& Пример 4.3. Исследовать устойчивость разомкнутой и замкнутой еди-
ничной отрицательной обратной связью систем в зависимости от скалярно-
го параметра р передаточной функции разомкнутой системы
и, (д)- 3p-10 + 2ps__________
р (р-б)+(р + б)$ + (р-2)г2 + 2ps3
Решение. Характеристический полином разомкнутой системы
Cp(x.p)=p-6 + (p + 6)s + (p-2).v2 + 2р?
\i<p) *|>з(р)
имеет область устойчивости Ор, удовлетворяющую следующим условиям
(рис. 4.4):
«СрХр) > 0 V / = 0, 2, 3) U (СрХр) < 0 V / = 0, 2, 3)) П {Мр2(р) > 0}.
где
Wp2<p) = Ср|(Р)Ср2(Р) - СрО<Р)СрЗ(Р) =
- (р + 6)(р - 2) - 2р(р - 6) - -(р - о.8)(р - 15.2).
Устойчивость систем автоматического управления 333
Здесь же на рис. 4.4 приведено программное решение задачи параметриче-
ской устойчивости с помощью функций, определенных на рис. 4 3.
6 г
41 41
0.8 15.2
Ор
а
с(р) := ( р-6 р + 6 р-2 2р )
usi(p) := RaGu(c(p)) = "Полином устойчив"
р :=-10,-9.99.. 20
2--------------------------------------------------
6 15.2
ust(p) I ------------
U-|« -з О 5 10 15 20
Таким образом, разомкнутая система устойчива при 6 < р < 15.2.
У характеристического полинома замкнутой системы
С,(s,р)= 4(р-4)+ 3(р +2> + (р-2)»2 + 2р ?
Г,М гч(р) <•.»(₽)
область устойчивости Оа удовлетворяет следующим условиям (рис. 4.5):
<(МР) > 0 V / = 0, 2, 3) U (сМ < 0 V । = 0. 2, 3» Л (42(р) > 0).
где
л/з2(р) = cjt(p)c,2(p> - с^(р)сл3(р) =
= 3(Р + 2)(р - 2) - »Р(Р - •») = -5(Р - о 4)0» - 6).
334
\\Ч* 'Г
" »*4 Ч>
______---------------------------------1
5 " 0. ‘ '
Рис. 4.5
Таким образом, замкнутая система устойчива при 4 < р < 6. Обшей области
устойчивости разомкнутой и замкнутой систем нет, т. к. Ор П О, = 0. □
& Пример 4.4. Исследовать по критерию Рауса - Гурвица параметрическую
(от коэффициента Р) устойчивость схемы на рис. 1.46, б, построенной как
на идеальном, так и на реальном операционном усилителе.
Решение. Характеристический полином схемы на идеальном операционном
усилителе (А'у = •», Гу = 0)
CU)= 1 + (2-р)7з + 7V
устойчив по критерию (4.14, 6} при значении параметра Р < 2, что, впрочем,
нам уже давно известно из условий минимально-фазовости передаточной
функции (1.34. б)
W(,)= _ф+1)—-----£----
1 + (2-Р)Гз + Т2з2
(см. пример 1.13) и автоколебательное™ (2.39). В дополнение к сказанному
построим корневые годографы — траектории движения корней характеристи-
ческого полинома
,,,.1»-»^ (4.17)
по комплексной плоскости при увеличении параметра р от 0 до ~ (рис. 4.6).
Устойчивость систем автоматического управления____________________335
Рис. 4.6
На разных интервалах изменения параметра схема отличается свойствами
устойчивости и видом переходной характеристики h(i). Последняя, как по-
казано в примере 3.5, повторяет в противофазе выходной сигнал схемы на
рис. 2.43, б
у(1) = -М)Л(0
при подаче на ее вход ступенчатой функции г(/) = -Uo •!(/)•
□ При Р < 2 схема устойчива, оба ее полюса левые с Re(3|.2( < 0, благодаря
чему выходной сигнал сходится:
• при р = 0 апериодически и рассчитывается методом (3 9) как
у(')=</оуехр(-уУ
благодаря действительному двукратному полюсу .Г| = -1;
• при 0 < р < 2 колебательно и находится как
для случая (3.10) простых комплексно-сопряженных полюсов (4 17).
□ При Р = 2 схема становится нейтральной с чисто мнимыми полюсами
X|.2»±yj-
Выходной сигнал совершает незатухающие гармонические колебания
у(0 3 C^iiUav)
с частотой Шц = I / Град / с или/к = I / 2кГГц.
□ При Р > 2 схема неустойчива благодаря правым полюсам с Re|.V| >) > 0. а
ее выходной сигнал расходится:
• при 2 < р < 4 колебательно и рассчитывается методом (3 НО км
.....
для случая простых комплексно-сопряженных полюсов (4.17);
• при р = 4 апериодически и определяется методом (3.9)
y(r)=5i/0yexp^j.
336_____________________________________________________________Главам
применяемым при действительном двукратном полюсе = +1;
• при р > 4 апериодически и рассчитывается методом (3.8) как
**>
для случая действительных простых полюсов 0 < jj < Sj.
На рис. 4.7 построено несколько графиков выходного сигнала при разных
значениях параметра р. Характер переходных процессов подтверждает вы-
полненный анализ свойств схемы, построенной на идеальном операцион-
ном усилителе.
Установка в схему неидеального операционного усилителя с параметрами
~ и Гу > 0 приводит к изменению ее передаточной функции аналогич-
но (2.40, о). Характеристический полином устройства принимает вил
С(т) = со + С|3 + qt2 + cj? с коэффициентами
0) = Ку + Р + 1, d - (2 - МУТ+ (Р + 1)(ЗГ+ Ту).
С2 - (КуГ+ (₽ + 1)(Т + ЗТУ))Г, с3 « (р + 1)ТуП
Применив к нему критерий колебательной границы устойчивости
(4.14, в) в виде C|Q = cocj и разрешив полученное квадратное уравнение от-
носительно р, получим зависимость Р(ЛСУ. Гу, 7) граничного коэффициента
Устойчивость систем автоматического управления 337
от параметров операционного усилителя Ку, Ту и постоянной времени схемы
Т= RC. На рис. 4.8 с помощью Mathcad построены каркасные поверхности
p(/fy, Ту, Т) - 2 с узлами в дискретном множестве параметров
для двух значений постоянной времени Т= I0'3 (а) и Т- 10~5 (б), обратно
пропорциональной частоте генерируемых колебаний/к = I / 2лГ
При использовании в схеме генератора операционного усилителя 544УД2Б с
параметрами Ку = 104 и Гу = КГ4 с получим граничное значение 0 = 2.0009
как при Т= 10'3 с, так и при Т= I0'5 с. Нелинейность поверхности, отде-
ляющей нижнюю область устойчивости схемы от верхней области неустой-
чивости, убеждает в сложном влиянии неидеальности параметров операци-
онного усилителя на отклонение граничного коэффициента 0 от идеального
значения 0 = 2:
□ на низких частотах колебаний до fK = I кГц проявляется лишь обратно
пропорциональное влияние коэффициента усиления Ку,
□ на частотах выше 1 кГц приращение 0 дополнительно увеличивается
квадратично от роста постоянной времени усилителя Ту, обратной его
полосе пропускания.
Таким образом, применение аналитического критерия устойчивости Рау-
са - Гурвица совместно с численным моделированием позволяет получить
оптимальное значение регулировочного параметра 0 для любого реального
операционного усилителя в схеме генератора, приведенной на рис. 2.43, б.
Зависимость сопротивления резистора 0Я от параметров используемого уси-
лителя и от частоты генерируемых колебаний убеждают в необходимости
обязательной антомагической регулировки усиления, поддерживающей схему
^нератора на границе устойчивости (см. пример 2 6). О
а Пример 4.5. Определить структуру и параметры последовательного регу-
лятора, делающего устойчивой замкнутую систему «тележка - перевернутый
маятник» с передаточной функцией из (1.11) и единичной отрица-
тельной обратной связью по углу отклонения <р (рис. 4.9). Степени полино-
мов передаточной функции регулятора R(s) должны быть не выше второй, а
ее полюсы должны быть левыми.
Рис. 4.9
Решение. Запишем передаточные функции объекта управления и регулятора:
w М=__________________________________________= Bv(s)
* ' 600 + 940s-216?-100? D(s)’
_ l>o+6|S+l>2s~ _
a0 + ais+p2s2 Ap(s)
Замкнутая система имеет характеристический полином
C,(s) = D(sMp(s) + Bv(s)Bp(s) = о + cjs + с2? + с3? + + с5? (4.18. а)
с коэффициентами
со = бООоо, С| = 940о() + 600о| + 6/м. Q = ~216д0 + 940^ + 600о2 + 6/>,,
С3 » -IOOoq - 216flj + 940й2 + 6^, q = - 100в| - 216д2, cj = -100а2.
Согласно требованиям к передаточной функции регулятора полином се зна-
менателя /1р(5) должен иметь коэффициенты а, одного знака. Но тогда при
степенях Лр(з), равных 1 и 2. коэффициенты с, не будут удовлетворять необ-
ходимым условиям устойчивости (4.7). Единственно возможная структур3
передаточной функции регулятора допускает полином нулевой степени
Hp(s) = а0.
После нормировки о« = I, устраняющей параметрическую неоднозначность,
получим передаточную функцию регулятора в виде
R(s) - bo + b\s + brf (4.18, 6}
и характеристический полином замкнутой системы C,(s) = m + с,т + Ст? +
+ с>г с коэффициентами и 1
Устойчивость систем автоматического управления___________ 339
со = 600, с( = 940 + 6*о, с2 = -216 + 6дь с3 = -100 + 662.
Так как со > 0 — константа, то необходимые и достаточные условия
устойчивости
(cj > 0) П (с3 > 0) п (ЛА = С|С2 - соСз > 0)
принимают вид неравенств, налагаемых на параметры передаточной функ-
ции регулятора
bt > 36, 3Z>2 > 50. (3*о + 470)(*i - 36) - 100(3*2 - 50) > 0. (4.18, в)
В частности, при *о = 0 два оставшихся параметра должны удовлетворять
условиям
*! > 36, 3*2 > 50, 47*! - 30*2 > 1192. (4.18, г)
Задавшись целью графического изображения области устойчивости в про-
странстве трех параметров регулятора (*о, *ь *2). сделаем перенос осей ко-
ординат:
Ро = *о + 156.7, Р| = *| - 36. р2 = *2 - 16.7.
В новых осях прежняя область устойчивости (4.18. в) удовлетворяет нера-
венствам
Р1 > 0. р2 > 0. РоР| > lOOpj.
Уравнение р0Р| = 100р2 описывает поверхность гиперболического парабо-
лоида, а неравенства в (4.18, в) — область первого октанта пространства
(Ро, Рь Рг). заключенную между плоскостью Р2 = 0 и поверхностью парабо-
лоида (рис. 4.10).
Рис. 4.10
Глава 4
340
Согласно ПДД2-структуре регулятора (4.18, о) и ограничениям на его коэф-
фициенты (4.18. г) в замкнутой системе управления требуется необязательное
измерение угла отклонения маятника от вертикали <р и обязательное измере-
ние либо вычисление в реальном времени угловой скорости ср' и углового
ускорения ф". □
Алгебраические критерии позволяют определить, имеет ли система же-
лаемую степень устойчивости т) — расстояние от самого правого из всех
левых корней характеристического полинома до мнимой оси
(см. рис. 3.28). Для этого сдвинем ось 1ш(з) влево на расстояние г) путем
замены переменной в (4.15):
J = р - П-
В результате сдвига получим условия устойчивости полинома с(р,р), при
которых все его корни лежат левее оси 1т(р), а корни полинома C(s,p) —
левее прямой з = -г, на плоскости з.
Для достижения предельного быстродействия tmm необходимо найти макси-
мальное значение л™> 0, при котором область устойчивости полинома
С(р-Лип»-Р) стягивается в точку. Тогда согласно (3.48) оценка предельно-
го быстродействия системы составляет
& Пример 4.6. Построить допустимую область изменения коэффициентов
передаточной функции регулятора минимальной сложности
Жз) = />|1 + Ajr2
из примера 4.5. в которой замкнутая система устойчива и имеет время уста-
новления < 3 с. Найти параметры регулятора, доставляющие системе пре*
дельное быстродействие.
Решение Подставив j = (4 18, о), получим характеристический по-
лином замкнутой системы со смешенным оператором
С,(р-П)=600 + 940(р-п)+(б61 -21бХр-п)2 +(«>2 -1ООХр-ПУ =
= ho + htp + h2p2 +/^р3
и коэффициентами
*0 - - 6М3 * 600 - 940п - 216П2 Ц. 100лз.
341
Устойчивость систем автоматического управления
Л, = -I2M + 18М2 + 940 + 432q - ЗОО^2.
hi = 6i| - )8^q - 216 + 300q.
h3 = 6й2 - 100.
По (3.48) определяем необходимую степень устойчивости q = I. Подставив
это значение в условия устойчивости полинома третьей степени
{(Йо > 0) П (й2 > 0) П (й3 > 0)} U {(йо < 0) П (й2 < 0) Л (й3 < 0)) Л (А,й2 > й0й3),
получим заштрихованную на рис. 4.11 область О. Значению п = 0 соответст-
вует область устойчивости, ограниченная пунктиром и целиком включаю-
щая область со степенью устойчивости q = 1.
Рис. 4.11
Для определения предельного быстродействия на рис. 4.12 построена по-
верхность границы устойчивости полинома (4.18, а> в пространстве пара-
метров (й|, bi, q). Поверхность имеет ступенчатый характер только из-за то-
го, что изменение параметра q задавалось дискретным с шагом дп = 0.1
Основанию полученной «пирамиды» соответствует область устойчивости
системы с нулевым запасом q = 0. Десятая ступенька ограничивает область
степени устойчивости q = I.
.Глава 4
Рис. 4.12
Вершина пирамиды в точке (6, = 117 24. />2 = 31.24), удовлетворяющей усло-
виям (4.18, г), соответствует максимальной степени устойчивости Птах = 19
и предельному быстродействию, равному zmin = 3 / 1.9 = 1.58 с. СЗ
4.5. Частотный критерий
устойчивости Михайлова
Частотные критерии устойчивости работают с частотными характеристика-
ми, построенными по характеристическому полиному системы С(т) или ее
передаточной функции И4т) Подставив в (4.6) т = jw, получим комплексно-
частотный полином
Qjw) = Яш) + )0(Ш)
с четной вещественной До» и нечетной мнимой ««) частотными характе-
Устойчивость систем автоматического управления
343
Р((й) = с0- с2Ф2 + с40)4 -...
С(ш)=С1(0-С3(1)3 +с5Ш5
(4.19)
График C(jw), построенный u интервале частот <о от 0 до «, называется годо-
графом Михайлова. Он имеет следующие предельные свойства:
□ начальное значение равно C(jO) = ЛО) + j<?(0) в с0 + jO = г„ 1 одограф
Михайлова начинается в точке со на действительной оси Re(Q;
□ на малых частотах ы ~ О начальное направление линии C(jo>) = cu 1 C|<u
из точки со определяется коэффициентом q:
• при С| > 0 график направлен вверх;
• при С| < 0 график направлен вниз;
□ конечное значение в пределе стремится к — годограф уда-
ляется в бесконечность под предельным углом sgn(c„) • 90“/i к действи-
тельной оси.
Примерные виды годографов Михайлова для различных полиномов показа-
ны на рис 4.13. В скобках (л, ±, ±) около графиков перечислены степени
полиномов п и знаки коэффициентов с0 и с(.
Рис. 4 13
гпава 4
Чтобы изучить влияние поведения годографа Михайлова на устойчивость
системы, разложим характеристический полином и его комплексную час-
тотную характеристику на множители первой степени:
М /=1
Согласно (2.19) изменение фазового угла функции C(jco) складывается из
приращений аргументов Д| комплексных функций
4(jw) =j0)-3/
при изменении частоты ш от 0 до Найдем значения А, для корней st раз-
личных типов:
□ действительный левый корень s, дает годографу положительное
приращение угла
а действительный правый корень — отрицательное приращение (рис. 4.14, а)
□ комплексно-сопряженные корни St и ?, дают суммарное приращение
угла, равное положительному значению А| + Аз = л = 2Д_ для левой пары,
и отрицательное значение Aj + А» = -я = 2Д+ для правой пары
(рис. 4.14. 6}.
Таким образом, независимо от типа корней каждый левый корень «закруч"'
нает. годограф Михайлова в среднем на угол 90‘ или один квадрант против
Устойчивость систем автоматического управления
345
часовой стрелки, а каждый правый — на угол, равный -90’ или одному
квадранту по часовой стрелке.
Теперь допустим, что полином Qj) степени л имеет лч правых корней, л
левых корней и ни одного корня на мнимой оси Тогда суммарные измене-
ния аргумента комплексной функции C(jw) в радианах Дф и квадрантах Ьк
равны следующим значениям:
Дф = н+ Д+ + п_ Д _ = (л л+ )" = (2п л)£ = (л - 2л. )у . (4 2())
ДА = л_—л+ =2л_-л =л-2л..
По этим формулам можно найти число правых и левых корней полинома
С(з), построив годограф C(jto) и определив изменения его фазового угла Дф
или Мс
п Дф л-ДА
”+ = 2" я =—2~'
_ л Дф _ л + ДА
”_=2 я 2
(4.21)
Остановимся на ключевом вопросе правильного вычисления изменения ар-
гумента комплексной функции Aarg|C(je)| на интервале частот иге [0,«)
Очень распространена ошибка считать, что ДА равно разности квадрантов
конечного СО00) и начального С(0) положений годографа либо числу квад-
рантов, по которым этот годограф проходит. При этом никак не учитывает-
ся среднечастотное прохождение годографа в окрестности начата координат,
от чего, собственно говоря, и зависит изменение фазового угла Методика
правильных действий такова.
1. Представить себя находящимся в начале координат комплексной плос-
кости с построенным на ней графиком годографа Qjw).
2. Направить взгляд в начальную точку С(0) = Q) на действительной оси.
3. Отслеживая движение точки годографа Aw) + j0w) при изменении час-
тоты и от 0 до », подсчитать угол Дф либо число квадрантов ДА своего
вращения вокруг начала координат.
Вычислим в целях тренировки значения ДА и число правых л. и левых п-
Корней характеристического полинома по графикам годографов, изобра-
женных на рис. 4.13:
Q для всех годографов на рис. 4.13, а получаем ДА = п. Тогда по (4.21) оп-
ределяем, что все эти годографы представляют устойчивые характеристи-
ческие полиномы е числом правых корней л* = 0.
346_______________________________________________________________Глава 4
□ для годографа, обозначенного как (1,определяем ДА = -1 =>
л+ = 1, п~ = 0;
□ у годографа (2, +) находим ДА = 0 => л+ = 1, л_ = |;
□ годограф (3, 0) имеет ДА = +1 =» л+ = 1, л_ = 2;
□ у годографа (5. +) определяем ДА = -1 => л+ = 3, л_ = 2;
□ начальный угол годографа (3, 0, +) не определен из-за того, что со = 0,
поэтому вычисление ДА и и* пока невозможно без дополнительного
анализа условий нейтральности характеристического полинома.
□ из-за прохождения годографа (3, +, +) на средних частотах через начало
координат значение ДА не определено без дополнительного анализа ус-
ловий нейтральности характеристического полинома.
Как мы убедились на двух последних примерах, годограф Михайлова может
оказаться в начале координат в двух случаях:
□ корень = 0 характеристического полинома С(х) означает наличие у не-
го множителя з, благодаря которому C(jO) = со = 0, а годограф на частоте
ш-0 начинается в начале координат;
□ комплексно-сопряженная пара мнимых корней создает у по-
линома С(з) множитель (s2+coj), благодаря которому Oja^) = 0, а годо-
граф на частоте ш = о\ проходит через начало координат.
Для устойчивости характеристического полинома необходимо, чтобы все
его корни были левыми: л. = л. Тогда в соответствии с (4.20) изменение
фазового угла ДА должно быть равно максимальному значению п квад-
рантов, а годограф C(jo>) нигде не должен проходить через начало коор-
динат. Отсюда получаем критерий устойчивости Михайлова: для устойчи-
вости линейной системы необходимо и достаточно, чтобы изменение аргу-
мента годографа ее характеристического полинома степени л было
определенным и составляло ля / 2 рад или л квадрантов при изменении
частоты от 0 до ~
Визуально оценить устойчивость характеристического полинома по годо-
графу Михайлова очень просто: начинаясь на действительной оси, он дол-
жен проходить последовательно п квадрантов против часовой стрелки, пооче-
редно пересекая оси координат и нигде не обращаясь в нуль. В соответствии
с этим правилом все голографы на рис. 4.13, а соответствуют устойчивым
системам, что подтверждено выше получением нулевых значений числа пра-
вых корней их полиномов л+ = 0.
Программное определение изменения аргумента комплексной функций
C(jw) выполняется в следующем порядке.
Устойчивость систем автоматического управления___________________347
1. Формируется массив частот О S Ш/ < ~ Vi = 0. in, на которых должны
строиться точки годографа C(jm/)
2. С помощью функции corp (С, и) (см. рис. 2.27) вычисляются и коррек-
тируются фазовые углы Ф, = arg( C(j<o()).
3. Вычисляется сумма приращений углов ф, - <р,_| для всех ie |1, да|. Бла-
годаря выполненной коррекции фазовой характеристики эта сумма рав-
на разности конечного и начального значений углов.
Дф=Е(ф(-ф,.|) = <₽т-фо
4. Величина Дф округляется до ближайшего целого числа квадрантов.
На рис. 4.15 приведена простая программа, в которой вычислена фазоча-
стотная характеристика <р(ш) годографа C(jw) полинома С(з) из (4.9) в час-
тотном диапазоне оз е |0, 100) и по описанному алгоритму определено, что
изменение фазового угла составляет ДА-= -1 квадрант Ниже построены
графики фазовой характеристики и годографа, по которым визуально опре-
деляется, что полное изменение фазового угла составляет -90’, то же что и
-I квадрант.
Прохождение годографа через начало координат является необходимым (у
полинома есть корни на мнимой оси), но не достаточным (могут быть и
правые корни) условием нейтральности системы. Для разрешения гранич-
ной неопределенности используем метод вариации коэффициентов харак-
теристического полинома, разрешив им изменяться в малой е-окрестности
как с/ ± Е/, Е/ = 0. При этом граничные корни полинома сдвинутся влево
или вправо от мнимой оси, а годограф Михайлова сместится от начала ко-
ординат.
На рис. 4.16 приведены годографы нейтрального характеристического поли-
нома третьей степени (/) и неустойчивого полинома четвертой степени (2).
Исходный годограф соответствует нейтральной системе при условии, что хотя
бы один из двух Е-смещенных годографов, изображенных пунктиром и не про-
ходящих через начало координат, удовлетворяет критерию устойчивости Ми-
хайлова.
График I на рис 4.16, а соответствует апериодической, а на
РИс. 4.16, 6 — колебательной нейтральности. В то же время ни один из
годографов (2) не удовлетворяет условию положительного направления
“ращения и не может быть нейтральным, несмотря на прохождение че-
рез начало координат.
34в
.Глава 4
Рис. 4.16
Устойчивость систем автоматического управления
349
Построим годографы характеристического полинома третьей степени из
примера 4.3
Ср($, р) = Р “ 6 + (р + 6)з + (р - 2)^ + 2р?
для фиксированных значений параметра ре (-6,0.8. 6, 10, 15 2, 20) (рис. 4.17).
3 В соответствии с областью устойчивости, построенной на рис 4.4, лишь
полином Cp(j, 10) устойчив, что подтверждается его годографом, имею-
щим изменение аргумента ДА = 3 и дающим нулевое число правых кор-
ней /»«. = 0.
При р = — 6 и р = 20 изменения аргумента годографов составляют
4Л = — |, что по (4.21) дает л+ = 2 правых корней полиномов Q(j, _6) и
ср(т, 20), а представляемые ими системы делает неустойчивыми
При р = 0.8 годограф проходит через начало координат, а небольшие ва-
риации параметра р = 0.8 ± 0.2 порождают
• при р = о.б гашмраф иоюяойвиой сие гемы с ДЛ в +1 и ”. - I.
* при р = I годограф неустойчивой системы с АЛ « -3 и я, - 3.
350 Глава 4
Следовательно, при /> = 0.8 система является не нейтральной, а неустой-
чивой, несмотря на прохождение годографа через начало координат.
□ При р = 6 годограф выходит из начала координат. Вариации параметра
р = 6 ± 1 смешают годограф:
• при р = 5 влево, делая его неустойчивым с Ьк = +1 и л+ = I;
• при р = 7 вправо, делая его устойчивым с ДА' = +3 и п+ = 0.
Следовательно, при р = 6 система нейтрально.
□ При р = 15.2 годограф также претендует на нейтральность. Вариации
параметра р = 15.2 + 2 дают:
• при р = 13.2 устойчивый годограф с ДА = +3 и п+ = 0;
• при р - 17.2 неустойчивый годограф с ДА = -1 и »+ = 2.
Следовательно, значение параметра />= 15.2 доставляет системе с ха-
рактеристическим полиномом Ср(з, 15.2) нейтральные свойства устой-
чивости.
Переходим к математической формулировке критерия Михайлова, позво-
ляющей исследовать устойчивость как числовых С(з), так и параметриче-
ских C(s.p) характеристических полиномов. Пронумеруем корни вещест-
венной и мнимой частотных функций (4.19) в порядке чередования
/>(ш,р)=0 при ш = а)|(р)<О)3(р)<...<со2„г_,(р);
С(о),р)=О при а) = (о0=0<ш2(р)<...<со2я (р).
При нахождении значений ц(р) решаются алгебраические уравнения от-
носительно квадрата частоты со2 и из полученных корней выбираются только
допустимые значения:
0ДЗ: ш?(р)>0 V/ = l, п-1. <4.22)
Переложим на язык формул словесные формулировки требований к годогра-
фу устойчивой системы:
□ требование начинаться на действительной оси удовлетворяется автома-
тически благодаря действительности коэффициентов полинома С(з): го*
лограф начинается в точке со;
□ требование поочередно пересекать оси координат при возрастании час-
тоты ш от 0 до «• налагает на параметры полинома л - 1 ограничен»'
типа неравенств, полностью поглощавших условия (4.22):
° = (4,23)
Устойчивость систем автоматического управления 351
□ требование вращаться против часовой стрелки в сторону увеличения фа-
зового угла
^Ш)=агс,(тё]
означает <p'(o>) > О V <о > 0 с производной фазочастотной характеристики
р2(ц) g^toXop-Q^Ho») = 6'(ь)И<д)-б(о>Х(<о)
Р2(<о)+О2(ш) P2(w) |cG(o)|2
Подставив сюда наиболее простые выражения производных частотных
функций (4.19) при ш = 0, получим условие однозначности ненулевых ко-
эффициентов характеристического полинома Со и q:
ф'(0)= = >о =» c0(ph(р)> о (4.24)
Со\Р) со(Р)
Таким образом, критерий Михайлова формулируется в следующей математи-
ческой форме: для устойчивости линейной системы необходимо и достаточно,
чтобы коэффициенты Со и С| ее характеристического полинома С(г) были не-
нулевыми и одного знака, а корни to, уравнений Re(C(j<o)) = 0 и lm| C(jto)| = О
чередовались по возрастанию в соответствии с неравенствами (4.23)
Рассмотрим, какой конкретный вид принимают условия устойчивости по
Михайлову (4.23) и (4.24) для систем с характеристическими полиномами
малых степеней.
□ Устойчивость полинома первой степени
Qj) = ср + qs
определяется единственным условием
QKi >0.
из которого следует, что коэффициенты и q должны быть ненулевыми и
однозначными
□ К требованию однозначности коэффициентов <0, q и q характеристиче-
ского полинома второй степени
C(s) = ро + qj + cjji
приводят условия
>0Ь
□ Характеристический полином третьей степени
Qj) = ср + С|4 + «У3 + <У*
гпава 4
устойчив при условиях
Это означает, что пары коэффициентов (с0, cj, {с0, с2}, {с2, cj} должны
быть одного знака и C|Cj > cocj. Таким образом, условия устойчивости
Михайлова совпадают с необходимыми условиями (4.7) и достаточным
условием Рауса ~ Гурвица ненулевые однозначные коэффициенты н по-
ложительный минор Л/2 = С|С2 > сосз-
© Пример 4.7. Исследовать устойчивость числовых полиномов:
□ Qj) = 5+ 14j+ !4?+6? + Л
Дш) = 5 - 143O2 + ы4 = О при со? =0.37 и co| =13.6 ;
(Дш) = 14ы - бы3 = 0 при «о =0 и со2 = 2.33
Так как корни Дш) и Q(u) чередуются, а также о = 5 > 0 и с, = 14 > О,
то годограф C(jco) (кривая / на рис. 4.18) обходит последовательно
ДА = л = 4 квадранта против часовой стрелки, а полином устойчив'.
Рис. 4.18
□ Пз) = 68 + 9з + 2з* + А
Дш) = 68 - 2о? = 0 при со? = 34;
Q((u) = 9ш - и5 0 при (Оц = 0 и ш2 = 9 .
Так как корни Яо» и Q(u» не чередуются, хотя cfl = 68 > 0 и Cj = 9 > 0.т0
годограф не обходит последовательно нужное для устойчивости « =
число квадрантов йсривая 2 на рис. 4.18). Следовательно, данный поли-
ном неустойчив Фактическое изменение аргумента годографа ра»"°
&* - -1. По (4.21) определяем, что из трех корней полинома л+ = 2 Пра-
Устойчивость систем автоматического управления 353
Е5 Пример 4.8. Исследовать, при каких значениях параметров Л', 7, и 72 ра-
зомкнутая и замкнутая единичной отрицательной обратной связью системы
будут устойчивыми. Передаточная функция разомкнутой системы имеет
следующий вид:
И/₽^= л(1+ 7,1X1 + ^)’
Решение. Характеристический полином разомкнутой системы равен
Cp(j) = X1 + 7,s)( 1 + Tis) = j + (Tx + 72)? + Г| 72?
Так как ср0 = 0, то один полюс %(.v) — нулевой, поэтому разомкнутая сис-
тема устойчивой быть не может. Она может быть нейтральной при условии,
что полином частного
С (у)
С„ (*)= = 1 + (Г| + т2 > + 7,72?
я
устойчив. Определим корни его вещественной и мнимой частотных
функций:
(?(ш) = (7, + 72)ш = 0 при ар = 0;
/Хш) = I - Т\ Т2и? = 0 при ш2 = —5—.
Т|Т2
Критерий Михайлова (4.23), (4.24) дает условия
{7|72>0}П(7, + 72>0),
означающие, что при 7, > 0 и 72 > 0 полином Cp(s) устойчив, а разомкну-
тая система нейтральна. При остальных значениях 7, и 72 она неустойчива.
Замкнутая система с единичной отрицательной обратной связью имеет
следующий характеристический полином с частотными функциями и их
корнями
GU) = *+j+(7,+ 72)?+ 7,7^;
0(ш) = (О - 7, Г2(1Р “ 0 при (Ц) = 0 и со2 = ;
'1'2
Лш) = К- (7, + 72)<iP - 0 при со,2
критерий Михайлова дает условия устойчивости замкнутой системы:
(7|>0)П(Г2>0)П(0<ЛГ<Л'ф).
354
Гпава 4
Превышение коэффициентом К граничного значения
^•14-
Г| 12
или его отрицательность ведут к неустойчивости замкнутой системы.
Из всех годографов C3(j(o), построенных на рис. 4.19 для различных значе-
ний К, только тот удовлетворяет правилу огибания начала координат на три
квадранта против часовой стрелки, у которого 0 < К < К^. При К = 0 годо-
граф выходит из начала координат и находится на апериодической границе
устойчивости, а при К = Klv пересекает начало координат в положительном
направлении, что является признаком колебательной границы устойчивости.
Рис. 4.19
4.6. Частотный критерий
устойчивости Найквиста
Метод проверки устойчивости, разработанный Г Найквистом, определяет
устойчивость замкнутой системы по частотным характеристикам разомкну-
той. Метод широко применяется в радиоавтоматикс благодаря его простоте
и возможности использовать экспериментально полученные частотные ха-
рактеристики фактически без знания передаточной функции Критерий
имеет простой физический смысл и исследует условия, при которых отри-
цательная обратная связь становится положительной и делает замкнутую
систему неустойчивой (см. разд. 2.5).
4.6.1. Вывод критерия Найквиста
Рассмотрим систему, образованную замыканием объекта с передаточной
Устойчивость систем автоматического управления
355
контуром отрицательной обратной связи, имеющим передаточную функцию
(рис. 4.20). Замкнутая система имеет передаточную функцию от входа х до
выхода у
w / х _ W(p) _ B(s)A0(s)___= в(в)А„(х)
1 l + W(s>0(T) Л(хМ)+B(s)B0(s) C,(j)
с характеристическим полиномом
Q(j) = Л(.с)Л0(^) + B(s)B0(s).
Рис. 4.20
Временно разорвем обратную связь в точке v перед вычитающим входом
сумматора и определим контурную передаточную функцию (2.23) и характе-
ристический полином разомкнутой системы от точки сигнала ошибки е до
точки и
W'K(5) = U'(5)W'O(J)
. Д(.т)В0(з)
Ск(з) ’
ед - Л(з)4,(з).
Сконструируем операторную функцию Найквиста
W(s) = 1 + IVK(*)= (4.25, в)
специально так, чтобы она стала равна отношению характеристических по-
линомов замкнутого и разомкнутого контуров. Вектор Найквиста
- 1 + И'кбш) (4.25, <5)
соединяет на комплексной плоскости (>К) точку Найквиста X = (-1J0) с
точкой годографа >Fk(jw) (рис. 4.21). Такой способ проведения вектора A'(ju>)
Удобнее, чем параллельный сдвиг графика )HK(j<o) на одну единицу вправо и
Глава 4
слежение за ним из начала координат. Визуально изменение аргумента час-
тотной функции Найквиста (4.25, (5) оценивается углом вращения годо-
графа И^Ош) вокруг точки X.
Рис. 4.21
Допустим, контурная передаточная функция И^з) имеет п+, а передаточная
функция замкнутой системы И^з) — лз+ правых полюсов. Анализируя
(4.25, а), по (4.20) получим следующее изменение фазового угла вектора
Найквиста в квадрантах при увеличении частоты ш от 0 до
ДЛд' = ДЛ3 - Ьк = (и - 2л1+) - (л - 2л+) = 2(л+ - Лз+). (4.26)
Построив контурный годограф Михайлова CK(jw), определим изменение его
аргумента Ьк, а по (4.21) - число Л+ правых корней полинома Ск(з). Далее
потребуем, чтобы характеристический полином замкнутой системы С,(з)
был устойчивым, т. е. не имел правых корней: л|+ = 0. Тогда из (4.26) следу-
ет критерий устойчивости Найквиста, для устойчивости замкнутой системы с
контурной передаточной функцией JF^s), имеющей п+ правых полюсов, необ-
ходимо и достаточно, чтобы вектор Найквиста A'Cjco) при увеличении частоты
w от 0 до «о имел изменение аргумента в квадрантах, равное
Д^=2л+, (4.27)
или 180л+ градусов, или пл* рад
Программное вычисление квадрантного угла Ькц выполняется аналогично
рис. 4.15. Например, для контурной передаточной функции (2.38) с пара-
метрами (2.37), Ло = ЗЯ и соответствующим годографом на рис. 2.41 сле-
дующая программа, использующая функцию сог<р (см. рис. 2.27), правильно
определила, что ААлг = -2 квадранта:
«л./ и» IO4-<2R-RO>
Ws .R0)------------7------—г N (s) := I + Wk (s, 3R)
3<R ♦ R0)\l ♦ I0"4 • j)
m :• 100 i:» 0.. m 1ш, > 0.1 • i ш |0,ш
Устойчивость систем автоматического управления 357
f'Pm-Vo'l
Ф := cor<p(N ,Ш) AkN := roundl ——— AkN = -2
Руководствуясь критерием (4.27) при л+ = 0, делаем вывод, что схема неус-
тойчива. И это действительно так, поскольку при Я(| = ЗЯ нс выполняются
условия минимально-фазовости знаменателя передаточной функции замк-
нутой системы (2.36, г).
По сравнению с рис. 4 15, где частоты ш, задаются в равномерной шкале,
здесь использована логарифмическая, более удобная шкала частот Igtu,, бла-
годаря которой удается меньшим числом отсчетов перекрыть больший час-
тотный диапазон и, самое главное, получить гладкое изображение графика
^(jeo) с более равномерным распределением точек по длине кривой, чем
при выборе равномерной шкалы
При Яо = Я и 2Я</^)=ЯГр как визуальный, так и программный анализ
прохождения соответствующих годографов на рис. 2.41 дают значения
Ak,v = 0 квадрантов, что говорит об устойчивости схем с данными сопротив-
лениями.
Если критерий (4.27) не выполняется, то замкнутая система неустойчива
или нейтральна. В первом случае число правых полюсов ее передаточной
функции можно определить по (4.26) и (4.21):
bkN n-bk-M,
"+ 2 2
Прохождение годографа через точку К является необходимым (передаточная
функция имеет полюсы на мнимой оси), но не достаточный (могут быть
и правые полюсы) условием нейтральности замкнутой системы. Для разреше-
ния граничной неопределенности используем метод вариации коэффициентов
передаточной функции, разрешив им изменяться в малых г-окрестностях. При
этом граничные полюсы замкнутой системы отойдут от мнимой оси, а кон-
турный годограф сместится от точки Найквиста. Исходный годограф If^Ow)
соответствует нейтральной системе, если хотя бы один из двух t-смешенных го-
дографов, изображенных на рис. 4.22 пунктиром, не проходит через точку К и
удовлетворяет критерию устойчивости Найквиста (4.27)
Рис. 4.22
Главам
Так. годограф ^(jto) на рис. 2.41, построенный для сопротивления Ло = Л^,
является нейтральным, т. к. вариации значения Ло в большую и меньшую сто-
роны приводят, соответственно, к неустойчивому и устойчивому годографам.
Назовем охватыванием точки изменение угла поворота вектора, проведенно-
го из этой точки, на четыре квадранта (360° или 2п рад) против часовой
стрелки Тогда условие вращения вектора N(yo) на 2п+ квадрантов можно
заменить вторым, альтернативным, условием охватывания годографом ра-
зомкнутого контура lFK(jw) точки Найквиста ровно и+ / 2 раз
Определим значения переходов годографа И^О'со) через действительную ось
левее точки К в соответствии с рис. 4.23, из которого следует, что переходы
могут быть как «ежи«, так и половинными, а знак перехода равен знаку из-
менения фазового угла. Очевидно, что число охватов годографом точки
Найквиста равно сумме переходов им через действительную ось левее этой
точки. Таким образом, мы получили третью формулировку частотного кри-
терия устойчивости Найквиста, не требующую подсчета изменения аргу-
мента вектора N(ja); для устойчивости замкнутой системы с контурной пере-
даточной функцией имеющей л+ правых полюсов, необходимо и доста-
точно, чтобы контурный годограф HzK(ja)) пересекал действительную ось левее
точки Найквиста в сумме л+ / 2 раз.
0 Rc( И')
Рис. 4.23
На что надо обратить внимание, применяя критерий устойчивости
Найквиста?
□ Число правых полюсов контурной передаточной функции WK(s} можно
вычислить по (4.21), построив годограф контурного характеристического
полинома CK(jw), ш е (0, “), и определив приращение его аргумента ДА:
м-ДА
л. =------.
2
□ Особенно аккуратно годограф ^(ja») должен строиться в окрестности
точки Найквиста. Если он проходит точно через эту точку и при одной
из ±е-вариаций формы удовлетворяет критериям устойчивости Найкви-
ста. а при другой - не удовлетворяет, то замкнутая система находится
на границе устойчивости.
□ Пересечения годографом JFK(jw) действительной оси правее точки Найк-
виста в сумме переходов нс учитываются.
устойчивость систем автоматического управления _______________359
□ Если передаточная функция ({''„(л) = BK(s) / Ск(л) имеет порядок аста-
тизма v, то
Q<(s) = svD(s), где О(л)= cv + cV4.p +... + c„s"’v,
и при ш -» О голограф И^ю) выходит из бесконечности под углом
v(0)=^gn^-v-l|>0°
Такие начальные параметры осложняют определение охвата годографом
точки Найквиста. Для преодоления этого затруднения заменим прямую
линию j = j<o на начальном участке мнимой оси при 0 < to S е дугой ок-
ружности радиуса е (рис. 4.24, в):
V, „ „ _ от
s = ее>*, где е -> 0, 0 < 4/ = — 5 —.
При этом полюс j| = 0 должен оставаться левее направления обхода. Те-
перь годограф при 0 < со < е принимает вид
, х -jvam , -jvwn
И'.6»)=-^= “ -У= 21
e D(jw) е cv
На малых частотах он представляет собой дугу окружности радиуса
начинающуюся на положительной (при Ло / cv > 0) либо отрицательной (при
Ао / ц, < 0) действительной полуоси Re{ и описывающую по часовой
стрелке угол, равный -vn/2 (рис. 4.24, б). В пределе при е -»0 радиус А,
становится бесконечным, но начальное направление и угол поворота сохра-
няются. Принято такую дугу бесконечного радиуса изображать пунктиром и
называть пунктирным дополнением годографа астатической системы.
<0
Рис. 4.24
360____________________________________________________________Глава 4
□ Если у передаточной функции IFJs) мнимые полюсы $|д = ijt^, то
Ck(s)=(j2+(O*)3(s),
и при ш-»о\ годограф разрывается на две ветви, асимптотически
сходящиеся в бесконечности к прямой, наклоненной к действительной
оси под углом
Как и в случае астатической передаточной функции, заменим j = jcoe
малой Е-окрестности частоты о\ дугой полуокружности радиуса е->0
(рис. 4.25, о):
j=j<DK + ее<’. где е->0, -”<цг<".
При этом полюс 5| = jov, как и левые полюсы, должен оставаться слева
от направления обхода против часовой стрелки.
Годорраф ^(jw) на частотах п>к-Е<ш<ык+е представляет собой дугу
полуокружности радиуса /?т, описывающую угол 180" по часовой стрелке
от одного конца асимптоты до противоположного (рис. 4.25, о) В преде-
ле при е -»0 радиус колебательного пунктирного дополнения Я? -»«.
Рис. 4.25
Два последних замечания позволяют сделать следующий вывод.
Если пунктирное дополнение годографа астатической или автоколсбательН®
передаточной функции начинается на действительной оси левее точки < 1 J J
или пересекает ее, то такие отрицательные переходы должны быть вкли>ч‘'||Ы
в общую сумму переходов годографа
Устойчивость систем автоматического управления_____________________361
Во многих учебниках по автоматике истинными критериями устойчивости
Найквиста объявляются формулировки, которые являются лишь частными
случаями рассмотренных выше альтернативных форм этого критерия:
□ при единичной отрицательной обратной связи И'(з) = I контурная пе-
редаточная функция fKK(s) равна передаточной функции разомкнутой
системы Wfs). С ней и работает критерий Найквиста;
□ если контурная передаточная функция не имеет правых полюсов, т. е
п+ = 0, то годограф должен иметь нулевую сумму переходов через
действительную ось левее точки Найквиста (-1, jO), т. е не охватывать
эту точку.
4.6.2. Логарифмический критерий
устойчивости Найквиста
Логарифмическая форма критерия Найквиста основана на однозначном со-
ответствии амплитудно-фазовой и логарифмических частотных характери-
стик. Участок действительной оси Re(левее точки (-I.J0) характеризу-
ется амплитудой Ак > 1 и фазовым углом <рк = д ± Ink рад. Переходам годо-
графа IKK(j(o) на этом участке соответствует пересечение логарифмической
фазочастотной характеристикой Фк(<о) уровней п t 2nk только при уровнях
усиления Ак(ш) > 0. Знаки перехода и изменения фазы совпадают. Если
контурная передаточная функция W'Js) имеет нулевые или мнимые полюсы,
то в разрывах фазочастотной характеристики проводятся пунктирные допол-
нения сверху вниз — в сторону уменьшения фаюного угла. После построения
логарифмических частотных характеристик нужно подсчитать на тех интер-
валах, где Z.K(<o) > 0, сумму переходов графика Фк(и>) через граничные уров-
ни <Ргр = 180' + 3604’, руководствуясь рис. 4.26.
Рис. 4.26
362
Глава 4
Логарифмический критерий устойчивости Найквиста формулируется сле-
дующим образом: для устойчивости замкнутой системы с контурной переда-
точной функцией имеющей правых полюсов, необходимо и доста-
точно, чтобы на интервалах частот, где 2к(ш) > 0, число пересечений характе-
ристикой Фк(ш) граничных уровней фазы Ф^, = 180* ± 360% составляло в
сумме л+ / 2. При устойчивом разомкнутом контуре логарифмический кри-
терий Найквиста требует, чтобы сумма фазовых переходов через уровень «рц,
на частотах, где Lx(w) > 0, была нулевой либо этих переходов не было совсем
Частота последнего перехода характеристики 2-к(ш) вниз через уровень 0 дБ
называется частотой среза ц.р. Она определяет полосу частот усиления ра-
зомкнутой системы. Высокочастотные гармоники уставки на частотах
со^ > сц-р отрабатываются системой тем хуже, чем меньше значение
< 0. Как и полоса пропускания в (3.34). частота среза определяет пре-
дельное быстродействие замкнутой системы, а именно |16|. время установле-
ния /у ограничено снизу аналогичным (3.57, б) неравенством
(4.28)
Wcp
Следует, однако, сказать, что оценка (4.28) является сильно заниженной Ре-
зультаты моделирования переходных процессов в замкнутых системах
управления в ат. 6 свидетельствуют, что действительное время установления
больше указанной оценки в 2 + 3 раза. Тем не менее, мы будем ею пользо-
ваться как гарантированной оценкой быстродействия замкнутой системы по
частоте среза логарифмической амплитудно-частотной характеристики ра-
зомкнутого контура без большого риска ошибиться в предсказании этого
важнейшего свойства.
Устойчивость замкнутой системы определяется поведением частотных харак-
теристик вблизи критических переходов через уровни Z^(w) = 0 и Фк(ы) = фф
Частоту последнего перехода фазочастотной характеристики через граничный
фазовый уровень назовем граничной частотой устойчивости Шф. Если переда-
точная функция И^х) состоит только из минимально-фазовых типовых
звеньев и имеет порядок п < 5, то уровень ф,р = -180" единственен.
При совпадении частот avp = оур замкнутая система находится на границе
устойчивости при условии, что небольшое смещение амплитудной характе-
ристики Д|с((о) вверх или вниз дает необходимую для устойчивости сумму
переходов фазовой характеристики Фк(ш) через уровень Фф.
Сформулируем логарифмический критерий Найквиста для устойчивых разам*'
нутых систем в виде следующих математических условий
к₽<“гр}Л^(Фп,)<0} (4 29 (|)
«ч,:Ь,«о€р) = О. tOq,: Фи(0>,р) = ф|р.
Устойчивость систем автоматического управления 363
Аналогичные зависимости для определения устойчивости замкнутой систе-
мы по частотным характеристикам устойчивого разомкнутого контура
|к<“ф)пк«»Ф><>} (4ВЯ
[шср: Ак((0ср) = 1, (Оф : фк(а)Гр) = фгр
можно использовать как в критерии, оперирующем с годографом ^(j'co), так
и в точных аналитических расчетах при проверке устойчивости сконструи-
рованной системы управления.
Рассмотрев несколько вариантов критерия устойчивости Найквиста, мы
всюду видим неоднозначности формулировок, а именно:
□ в условии (4.27) используется лишь общее изменение ДА> аргумента
вектора Найквиста без требования монотонного увеличения фазо-
вого угла Фд<(о);
□ в формулировке критерия, подсчитывающего число пересечений годо-
графом И^ш) действительной оси левее точки Найквиста, требуется,
чтобы сумма переходов составила п+ / 2. а как она формируется из ал-
гебраических значений переходов (см рис 4.23) не регламентируется
Например, при устойчивой разомкнутой системе нулевая сумма может
быть составлена разнозначными переходами, каждый из которых нару-
шает условие устойчивости (рис. 4.27, а);
□ то же самое можно сказать и о логарифмическом критерии устойчивости
Найквиста, анализирующем сумму переходов фазочастотнон характери-
стики Фк(со) через уровень <р,р (см. рис. 4.26) без ограничений на знаки
отдельных переходов (рис. 4.27, б):
Рис 4.27
в определениях частот ц.р и оу,,. используемых в условиях (4.29). сказа-
но, что это частоты последних переходов амплитудной и фазовой харак-
теристик через соответствующие уровни Но если такие переходы не
единственны, т. е. существуют и на .меньших частотах, то проверка нера-
венств (4.29) сильно затрудняется необходимостью визуального или про-
граммного определения всех критических пересечений.
364
Глава 4
Назовем частотные характеристики с единственным критериальным факто-
ром (знаком угла фу, переходом годографа левее точки Найквиста,
пересечением фазочастотной характеристикой граничного уровня Фгр) безус-
ловно устойчивыми (графики 1 на рис. 4.27), а с множеством значений этого
фактора — условно устойчивыми (графики 2 на рис. 4.27). Таким образом, все
варианты критерия устойчивости Найквиста определяют условную устойчи-
вость. а для проверки безусловной устойчивости требуется проводить до-
полнительный трудоемкий анализ частотных характеристик.
© Пример 4.9. Определить устойчивость замкнутой системы с единичной
отрицательной обратной связью и передаточной функцией разомкнутого
контура
Решение Получим число правых полюсов передаточной функции «^(з) по
критерию устойчивости Михайлова:
q>(j) = 1 + 2з+2? + 40?;
Р(ш) = 1 - 2(1? = 0 при ш? =0.5 ;
2(ш) = 2ш - 40(1? = 0 при (i)q = 0, (»2 = 0.05.
Так как коэффициенты = 1 и С| = 2 — ненулевые и одного знака, но не
выполняются условия (4.23) чередования частот 0 < W| < о>2, то разомкнутая
система неустойчива. Построив годограф Михайлова Cp(j(o) (рис. 4.28), опре-
делим изменение его аргумента ДЛ = -1 н по (4.21) число правых полюсов
разомкнутой системы л+ = (3 + 1) / = 2. Тот же результат получим по кри-
терию Рауса - Гурвица, подсчитав число л* = 2 инверсий знака в последо-
вательности (4.10)
(с3, А/i, = (40, 2, -72, 1296).
1т(с/ ‘
Устойчивость систем автоматического управлений
Для определения устойчивости замкнутой системы по критерию Найквиста
разложим контурную передаточную функцию
на типовые звенья с параметрами
К = 100, 71 = 4,(01 = 0.25,.
Т2 = 3.16, 0)2 = 0.316, $2 = 0.316,
Ту = 0.01, Шз = 100.
Построив на рис. 4.29 логарифмические частотные характеристики разомк-
нутого контура, убеждаемся, что единственный переход графика Ф„(а>) через
уровень ф,р = +180* на частотном интервале ше (0.01, Щр = 1.6), где ампли-
туда /^(ш) > 0, равен 1
Аналогично по годографу И^Ош), изображенному на рис. 4.30, фиксируем
наличие полного пересечения им действительной оси левее точки (-1, jO) в
положительном направлении.
По критерию Найквиста значения этих переходов должны быть равны
я+ / 2 = I. Следовательно, замкнутая система устойчива. О
© Пример 4.10. Определить устойчивость замкнутой системы с передаточ-
ными функциями в прямой и обратной цепях
Решение. Представим контурную передаточную функцию
произведением четырех типовых звеньев с параметрами
Т|= 1,Ш1= I.
7j - 0.5, шз = 2, = 0.
Звенья второго порядка с коэффициентами 51 “ 0 и = 0 разрывают лога-
рифмические характеристики на частотах wj и <oj (рис. 4.31). Значение пере-
хода графика Фк(<») через уровень <р,р = -180’ на частоте wj = «Цр равно I
Устойчивость систем автоматического управления
Звено с автоколебательной передаточной функцией 1/(1 + 7\2j2) разрывает
годограф, построенный на рис. 4.32, на частоте он на две ветви Пунктир-
ное дополнение разрыва создает переход левее точки Найквиста, также
равный -1.
Таким образом, контурная передаточная функция нс имеет правых полюсов,
а сумма переходов ненулевая Следовательно, замкнутая система неустойчи-
ва Если строить годограф без пунктирного дополнения, то сумма переходов
будет нулевой, что даст ложное заключение об устойчивости.
гпава 4
Рис. 4.32
Для подтверждения критерия Найквиста исследуем устойчивость характери-
стического полинома замкнутой системы по точному алгебраическому кри-
терию Льенара - Шипара:
С,(5) = I + 0.25? + з(1 + з)(1 + ?)=•! + * + 1.25? + ? + ?;
Все коэффициенты характеристического полинома положительны, но тре-
тий минор Му < 0. Следовательно, и по алгебраическому критерию замкну
тая система неустойчива. □
Пример 4.11. Исследовать по критериям Найквиста параметрическую ус-
тойчивость замкнутой системы с передаточной функцией в прямой цепи
^)в_!£-
1 + 6з + 5л2
в зависимости от коэффициента отрицательной обратной связи ~ А'
Устойчивость систем автоматического управления
369
Решение. Разомкнутая система устойчива (л+ = 0), т к контурная переда-
точная функция
^0=
10К(1 -T3s)
(1+rjsXl+Tji)
с постоянными времени 7'j = 5 с, 7;“ 1с и 7j = 0.1 с имеет левые полюсы
5| » -0.2 и sj = -1
Влияние модуля параметра К на логарифмические частотные характеристики
заключается в подъеме или спуске амплитудной характеристики Ак(а>) без
изменения фазовой характеристики Фк(со). Инверсия знака К смешает фазо-
вую характеристику по вертикали на 180° без изменения амплитудной. Это
подтверждают асимптотические характеристики, построенные на рис. 4.33
для К = 1 и ЛГ=-|.
Рис 4 33
370
Глава 4
При К = 1 значение фазового угла <ргр = -180* достигается на логариф-
мической частоте lgci>rp “ 0.5 с запасом по амплитуде = 14 дБ, а на
частотах, меньших lgWcP = 0.15, где £к(ш) > 0, переходов фазы через уро-
вень ф,р нет. Следовательно, замкнутая система устойчива. Подняв ам-
плитудную характеристику на 14 дБ, т. е. увеличив коэффициент усиле-
ния А'до 1007 «=5, получим верхнюю границу устойчивости замкнутой
системы. Дальнейшее увеличение параметра К> 5 приводит к ее неус-
тойчивости.
При £=-1 фазовая характеристика начинается с уровня <рГ|) = 180* при
1^(0) = 20 > 0, что дает -1/2 перехода и делает замкнутую систему неус-
тойчивой. Опустив амплитудную характеристику на 20 дБ, т. е. уменьшив К
в 10 раз, получим нижнюю границу устойчивости замкнутой системы Даль-
нейшее опускание характеристики восстанавливает устойчивость системы в
области параметра -0.1 < К S 0.
Таким образом, методом логарифмических частотных характеристик быст-
ро получен интервал устойчивых значений параметра -0.1 < К < 5. В связи
с приближенностью асимптотических характеристик результат также
является неточным.
Точное решение задачи устойчивости методом Найквиста может быть полу-
чено описанным выше способом на основе нелинейных логарифмических ха-
рактеристик
| L, (ш) = 20 + 20lg|+101g 71+Т>- -101g Jl + T'a)2 -101g ф + Т'ш2,
|Ф,(ш)= (1 - sgn(tf ))-90°- arctg(^w)- arctg(r,w)- arctgfcta)
либо путем построения и анализа амплитудно-фазовой частотной характе-
ристики
j А, (<>)= ю|К|
' 1 'Vi + TtWJi + TjW)
|<р,(ш)= (l - sgn(K ))• 90° - arctg( fu))- arctg(T2w)- arctgfaw)
Влияние модуля параметра /Л? иа точно строящийся контурный годограф
заключается в изменении удаления его точек от начала координат с
сохранением их направлений, как при надувании воздушного шара. При
инверсии знака К годограф поворачивается на 180°. То, что это так, можно
убедиться на рис. 4.34, где построены годо1рафы разомкнутого контура с ко-
эффициентами усиления К= I и К « I
Устойчивость систем автоматического управления
371
Рис. 4.34
При К= 1 годограф не охватывает точку Найквиста и не должен ее охва-
тывать, поэтому замкнутая система устойчива При фазовом угле
Фк = -180' модуль годографа равен 0.167 = I / 6 < I. Увеличив значение К
в 6 раз, получим граничный годограф, проходящий точно через точку 8.
Дальнейшее увеличение К> 6 дает неустойчивый годограф, охватывающий
точку Найквиста.
При £=-1 годограф, начинаясь в точке (-10, j0) левее точки 8. дает
-1/2 перехода, следовательно, замкнутая система неустойчива. Чтобы по-
лучить годограф, проходящий точно через точку Найквиста, нужно
уменьшить параметр Л- в 10 раз, а при -0.1 < К< 0 замкнутая система ста-
новится устойчивой.
Вывод. По логарифмическому критерию Найквиста мы приближенно опре-
делили, что замкнутая система устойчива при -0.1 < К< 5. Точный ответ -
0.1 < К < 6 дает частотный критерий Найквиста, основанный на построении
и параметрическом анализе контурного годографа
Для подтверждения полученного результата применим алгебраический кри-
терий Рауса - Гурвица для характеристического полинома второго порядка
ОД) = М10 - j) + (1 + з)(1 + ЭД-1 + 10АГ + (6 - Kls + 5?:
(I + 10ЛГ>0|П(6- АГ>0|,
откуда получаем область устойчивости -0.1 < А' < 6. С
Логарифмический критерий, пожалуй, единственный, пригодный дтя иссле-
дования устойчивости систем, передаточные функции которых неизвестны,
но при этом могут быть экспериментально получены частотные характери-
стики, например, с помощью анализатора спектра или различных программ
Моделирования электронных схем. Если нельзя экспериментально снять ло-
гарифмическую фазочастотную характеристику Фк(«>), то ее можно восста-
новить по логарифмической амплитудно-частотной характеристике /„(ы)
при условии, что передаточная функция И'Дз) не имеет правых нулей и по-
люсов, г. с. является мипимальио-фазовой
372
Методика восстановления минимально-фазовой частотной характеристики
Ф(о>) и передаточной функции 1Цг) по амплитудно-частотной характеристи-
ке /.(го) имеет следующий вид.
□ Логарифмическая амплитудно-частотная характеристика аппроксимиру-
ется кусочно-линейной асимптотической характеристикой £а(<«), участ-
ки которой горизонтальны или имеют наклоны, кратные ±20 дБ / дек.
□ По начальному участку характеристики Д,(ы) и изменениям наклонов ее
участков воссганаатнваются передаточные функции И^т) типовых
звеньев.
□ Произведение функций дает передаточную функцию системы (Цз)
□ С помощью табл. 2.2 строятся логарифмические фазочастотные характе-
ристики типовых звеньев Ф^ы), сумма которых составляет фазовую ха-
рактеристику системы Ф(о>).
& Пример 4.12. Дана экспериментальная амплшудная характеристика £(/)
некоего усилителя звуковой частоты (рис. 4.35, а). Восстановить его переда-
точную функцию и построить логарифмическую фазочастотную характери-
стику и годограф.
Решение Так как размерность частоты/— герц, то постоянные времени ти-
повых звеньев передаточной функции усилителя определяются по частотам
сопряжения /как Г, = 1 / 2п/ с. Обозначим некоторые характерные точки
амплитудно-частотной характеристики буквами А + G. Начальный участок
/.(/). асимптота которого проходит через точку А(/> = 10 Гц, £0 = 0 дБ) с
наклоном +20 дБ / дек, дает передаточную функцию начального звена диф-
ференцирующего типа:
ИМ) = Ks.
Ес коэффициент усиления А' найдем из условия
201g К = £(ш=1)= =^= Au-2Olg(2nfo)= -201g(20n),
откуда получаем А = 1 / 20л = 0.016.
В точке В(/| • 50 Га. Z| = -6 дБ) имеется глубокая впадина, предназна-
ченная для подавления низкочастотных паразитных колебаний, прони-
кающих в усиливаемый сигнал по цепи питания Значит, в передаточной
функции усилителя есть форсирующее звено второго порядка с переда-
точной функцией
W'|(x)=1 + 2^|Tij + T|1j2 ,
постоянной времени Ту - 1 / 2i/i ” 3.18 мс и коэффициентом затухания £|.
определяемым по формуле (2.18):
Устойчивость систем автоматического управления
2018[ 2^ ] = )= 20 ДБ ~ = ° 05’
Вправо от точки
7-a(/i) = Л>(/о) + 201g(/i //0) = 14 дБ
проводим вторую асимптоту £„(/) с наклоном 20 + 40 = 60 дБ / дек
В точке C(f2 = 100 Гц, L2 = 40 дБ) амплитудная характеристика имеет резо-
нансный пик высотой L(f2) - = 8 дБ. Это означает, в передаточной
функции усилителя имеется колебательное звено
с параметрами Т2 = 1 / 2nf2 = 1.6 мс и = 0.5 10"°05 8 = 0.2. Вправо от
точки £а(/г) = 32 дБ проводим асимптоту с наклоном 60 - 40 = 20 дБ / дек.
В точке D характеристика £(/) сходится к горизонтальной асимптоте на
уровне 40 дБ, которая между точками С и D сопрягается с уже построенной
асимптотической характеристикой на частоте f2 = 250 Гц Типовое звено,
уменьшающее наклон на 20 дБ / дек, имеет передаточную функцию
с постоянной времени Т} = I / 2д7з = 0-64 мс.
В точке Е(Д = 3.16 кГц, Д» = 45 дБ) экспериментальная логарифмическая
амплитудная характеристика имеет небольшой резонансный пик высотой
примерно 5 дБ. Значит, в передаточной функции усилителя есть колеба-
тельное звено
с параметрами = I / Infc = 50 мкс и = 0.5 10 °05 5 = 0.28. Вправо от
точки £□(/») = 40 дБ проводим асимптоту с наклоном -40 дБ / дек.
Конечный участок логарифмической амплитудно-частотной характеристики
принимает в точке G(4 = 20 кГц, Ц, = 0 дБ) установившийся наклон
-60 дБ / дек. Эта асимптота пересекается с уже построенной асимптотиче-
ской характеристикой на частоте /5 = 10 кГи. В результате последнее типовое
звено имеет передаточную функцию
с постоянной времени Т$ “ 1 7 Ws “ 16 мкс
Перемножая полученные передаточные функции типовых звеньев ИЗД. по-
лучаем передаточную функцию усилителя:
Рис. 4.35
Х^>7?юмо1ж>пВ<:^ЛТ'',!>О?ЫС ,ВСНЬЯ ЯЮ1ЯЮТСЯ минимально-фазовыми, по-
* усилителя как
Устойчивость систем автоматического управления
375
Путем параллельного отслеживания изменений амплитуды и фазы по гра-
фикам £(/) и Ф(/) на рис. 4.36 построены годографы усилителя >К)ю) в об-
щем виде (в), а для представления о его поведении в близкой окрестности
начала координат — в крупном масштабе (б). О
Рис. 4.36
Для того, чтобы при исследовании радиоэлектронных схем не оперировать с
числами, имеющими большие отрицательные степени порядков, можно вы-
полнить аременнде масштабирование (см. разд. 3.3.3)
= т1 Ъ
преобразующее шкалу времени из реальной / в модельную /м. Удачно подоб-
ранный масштаб т, позволяет получить описание высокочастотных систем в
более удобной для восприятия временной шкале и с примерно одного по-
рядка коэффициентами передаточной функции. Например, при выборе мас-
штабного коэффициента /и, = 1000 передаточная фхнкция усилителя из
примера 4.12 преобразуется в модельную передаточную функцию
w L ) =-----------------------+16|5м-------------------------------
1 + 1.3Ц, + 3j* + !.75j’ +8.02 -КГ2jjJ + 4.94-10Л’ + 6.55 10 5з£
На всех временных характеристиках и переходных процессах, построенных
такой масштабируемой модели, единица времени равна одной миллисе-
кунде, а на частотных характеристиках, построенных на рис. 4.35, единице
частоты соответствует один килогерц
376 Глава 4
4.7. Запасы устойчивости замкнутой системы
До сих пор мы полагали главным условием работоспособности системы ее
устойчивость. Но на практике простой устойчивости замкнутой системы
может оказаться недостаточно, и этому есть по меньшей мере две причины
□ кроме всех остальных качеств, система должна иметь приемлемые вре-
менные характеристики, которые, возможно, не обеспечиваются в
имеющемся устойчивом состоянии;
□ работа вблизи границы устойчивости модели, всегда в той или иной сте-
пени отличной от реальной системы, может привести к неустойчивости
последней из-за неточного знания или дрейфа ее параметров.
Поэтому надежно функционирующая система должна держаться от границы
устойчивости на определенном расстоянии, т. е. обладать некоторым запа-
сом устойчивости. необходимым для гарантированного обеспечения устой-
чивой работы системы управления при возможных отклонениях модели
объекта от реального прототипа. Степень близости замкнутой системы к
границе устойчивости измеряется:
□ в критерии Рауса - Гурвица применительно к характеристическому по-
линому GU) — отличием левых частей неравенств (4.13) от нуля;
□ в критерии Михайлова — минимальным расстоянием от годографа по-
линома C,(jw) до начала координат (0, jO);
□ в критерии Найквиста — минимальным расстоянием между контурным
годографом И^Оы) и точкой Найквиста (-1, jO).
Последним критерием, в основном, и пользуются на практике для оценки
запаса устойчивости замкнутой системы не только по годографу разомкну-
того контура IFt(j<o). но и по его логарифмическим частотным характери-
стикам £Jw) и Фк(ш). Для определенности далее будем считать контурную
передаточную функцию системы устойчивой, а случай неустойчивого разомк-
нутого контура будет рассмотрен в гл. 6.
4.7.1. Определение запасов устойчивости
Запас устойчивости по амплитуде Ц гарантирует, на сколько децибел может
быть поднята амплитудная характеристика £к(ш) до границы устойчиво-
сти — совпадения частоты среза <ц.р и граничной частоты ы,р (рис. 4.37. в).
Польем характеристики на £>дБ означает увеличение коэффициента усиле-
ния разомкнутого контура в раз. Условие запаса устойчивости по
амплитуде, не меньшего, чем £>, имеет вид
Устойчивость систем автоматического управления
Запас устойчивости по фазе <р3 гарантирует минимальное угловое расстояние
от фазовой характеристики Фк((о) до граничных уровней устойчивости <ргр на
частотах, где £к(со) > 0 (рис. 4.37, б):
|Фк(со) “ Фгр1 2 Фэ * ш: £к(ю) > 0.
Рис 4.37
Для того, чтобы система управления имела одновременно оба запаса устойчи-
вости Ly и <р3, логарифмические частотные характеристики разомкнутого
Контура должны удовлетворять неравенствам
[^(о))<-Л, 7ш:|фк.(ю)-ф|р1<ф,,
। , . . ' (4.30. в)
[|фк(и>)-Фгр|>Ф,
При проектировании систем управления приняты следующие типовые зна-
чения запасов устойчивости
□ запас по амплитуде L, = 6 + 20 дБ;
□ запас по фазе <р3 = 30 ♦ 60"
Ненулевые запасы устойчивости, естественно, сужают область устойчивости
замкнутой системы. Может случиться гак, что техническое задание на раз-
работку системы автоматического управления содержит завышенные требо-
вания к запасам устойчивости, одновременное обеспечение которых невоз
Можно. Тогда разработчик системы должен аргументировано объяснить за-
йчику суть противоречий и согласовать с ним новые, более лояльные
Фебования к запасам устойчивости
378 Глава 4
Следует обратить внимание читателя на то, что кусочно-линейная аппрокси-
мация логарифмических частотных характеристик лает слишком грубые оцен-
ки запасов и может использоваться для общего представления о свойствах
системы При проектировании высококачественной системы управления с за-
данными запасами устойчивости все частотные характеристики должны стро-
иться по точным формулам с помощью компьютерной программы
Области логарифмических частотных характеристик, не удовлетворяющие
условиям (4.30, а), называются запретными зонами. Графики характеристик
не должны заходить в запретные зоны (рис. 4.38. а), иначе не будут обеспе-
чиваться требуемые запасы устойчивости или сама устойчивость.
Рис. 4.38
Запретная зона есть и на комплексной плоскости годографа И'Цы)
(рис. 4.38, б). Она имеет вид внешнего сектора, ограниченного углами
Ф,Р±Ф, и дугой окружности радиуса 1/Л, slO’005L’< 1. Аналогичная
(4.30, в) разрешенная область годографа удовлетворяет условиям запасов ус-
тойчивости
|<р,(ш)- фгр| S ф, V <о: (ш)> Л .
(4.30, б)
Частоту <о>, на которой замкнутая система обладает одновременно точными
запасами устойчивости L, и ф„ а неравенства (4.30) обращаются в равенства
Устойчивость систем автоматического управления 379
ДХйЪ) = А<(“э) = ^-> Фк(О1) = Фгр ±Фп (4.31)
назовем частотой запаса В (4.31) знаки «+» и «-» означают прохождение
частотных характеристик, изображенных пунктиром на рис. 4.38, через угло-
вые точки запретных зон U и D с уровнями фаз ± и амплитудами
L* = -1^, Ак = 1 / Xj. Замена условий устойчивости с заданными запасами,
выполняющихся в интервале частот, на условия прохождения частотных
характеристик через угловые точки на одной частоте запаса он может при-
вести к локальному заходу характеристик в запретные области без потери
устойчивости Это означает, что использование соотношений (4 31) для рас-
чета параметров устройства управления может дать (и даст, как будет пока-
зано в гл. 6) не безусловную, а условную устойчивость замкнутой системы с
желаемыми запасами.
4.7.2. Алгебраический критерий устойчивости
с запасами
Несмотря на то, что понятия запасов устойчивости определены в частотной
области, большой интерес представляет получение алгебраического критерия
устойчивости с заданными запасами, аналогичного критерию Рауса -
Гурвица, определяющему устойчивость характеристического полинома
замкнутой системы С3(т) = Лк(г) + BK(s) при нулевых запасах. Облхтание та-
ким мощным инструментом исследования позволяет оценить наличие в
замкнутой системе желаемых запасов устойчивости L, и <₽> непосредственно
по коэффициентам полиномов Лк($) и 5к(з) без построения и просмотра
(визуального или программного) частотных характеристик желаемой ра-
зомкнутой системы.
Поскольку алгебраические критерии работают с характеристическим поли-
номом системы, устойчивость (левое расположение всех корней) которой
определяется, наша задача состоит в конструировании такого полинома для
замкнутой системы, имеющей по одному из запасов устойчивости L, и ф,
либо одновременно оба эти запаса.
□ Обладание замкнутой системой запасом устойчивости по амплитуде в
Ц дБ равносильно простой устойчивости модифицированной системы, у
которой передаточная функция разомкнутого контура равна
а логарифмическая амплитудная характеристика получена подъемом гра-
фика £к(ю) на L, дБ (см. рис. 4,37, а):
380______________________________________________________________Главам
£д(ш) = 4с(“) + 4и
В результате получаем приведенный по амплитуде характеристический
полином
устойчивость которого означает наличие в исходной замкнутой системе
запаса устойчивости по амплитуде не меньшею, чем Д дБ.
□ Допустим, замкнутая система имеет запас устойчивости по фазе, равный
+<рг Сдвинем фазовую характеристику Фк(ш) на угол -<р3, не изменяя
при этом амплитуды LJw) (см. рис. 4.37, б). Полученными частотными
характеристиками (ДДш), Ф,(со)1 обладает физически не реализуемый ра-
зомкнутый контур с комплексной частотной характеристикой
Ж* Д>М>1)-JgF0°>>nfgJ.
Комплексная характеристика модифицированного замкнутого контура
равна
iv /=-?_ BK6m)cos(q>,)-jflK(jto)sin(<p3)
” Д. 6“)+ Вк G<o)cos(<p3)- jBK Gio)si n (<p3)
Характер порождаемой ею комплексной импульсной характеристики оп-
ределяется расположением корней комплексного характеристического
полинома
P(s) = Лк(т) + ВкМс°5(Фз) “ jAU)sin(<p3).
В отличие от действительных полиномов комплексные корни полиномов с
комплексными коэффициентами не являются комплексно-сопряженными.
Тем не менее, для устойчивости модифицированной замкнутой системы не-
обходимо, чтобы они располагались в левой полуплоскости, как, впрочем, и
действительные корни полинома Яз).
Поскольку алгебраические критерии устойчивости работают с действи-
тельными полиномами и операции в (4.10) - (4.13) выполняются с дейст-
вительным числами, целесообразно сконструировать действительный при-
веденный по фазе полипом в виде произведения комплексно-сопряженных
полиномов:
С<п(*)= А%(з)+ 2А,(з)В,G)cos(<p,)+ В2 (з).
Алгебраическая устойчивость этого полинома означает наличие в исход-
ной замкнутой системе запаса устойчивости по фазе не меньшего, чем ЧЬ
Устойчивость систем автоматического управления
381
□ Алгебраический анализ возможности иметь одновременно оба запаса ус-
тойчивости L3 и <р, сводится к проверке простой устойчивости действи-
тельного приведенного по амплитуде и фазе полинома
С^)= A^s)+ 2XsAK(i)BKC0cos(<p,)+ Х2В2(з), we К, = 10........•. (4 32)
В отсутствие требований к любому из запасов /, или <р, его нужно при-
равнять к нулю. Тогда устойчивость полинома Q„(.t) равносильна устой-
чивости полиномов Gn(j) (при L, = 0), Q,(J) (при <р, “ 0) либо С,(з) (при
L, = 0 и <рэ = 0).
При запасе по фазе <р, * 0 корни характеристического полинома (4.32)
имеют следующие свойства:
• общее число корней равно 2пих(л /»1 удвоенной максимальной
степени полиномов Ик(з) и йк(з);
• каждый действительный корень имеет четную кратность и является
общим корнем полиномов AK(s) и йк(т);
• комплексные корни являются попарно сопряженными.
Еще раз напоминаем читателю, что устойчивость приведенного по амплитуде
и фазе полинома С'дф1(з) означает лишь условную устойчивость замкнутой сис-
темы с заданными запасами /., и <р3. К сожалению, разработанный здесь ал-
гебраический критерий не может обнаружить локальные заходы частотных
характеристик £к(о>) и Фк(ю) в запретные зоны и однозначно ответить на во-
прос о безусловной устойчивости замкнутой системы с запасами без допол-
нительных исследований.
& Пример 4.13. Дана контурная передаточная функция разомкнутой
системы:
0= *1-6* 4-100?
₽ +
Определить значения параметра К, при которых замкнутая система будет,
во-первых, устойчива, а во-вторых, иметь запасы устойчивости /, г 6 дБ и
ФзйбО".
Решение. Обозначим полиномы и параметры типовых звеньев передаточной
функции IP'p(s):
Д(д)=Л-6АГз + 100К? = А((1-2§Г|л+Г|гт2), Г, - 10с,§»0.3;
/1(5) - 41 4- jp - XI + ЭД2. Гу - I с.
Точные решения поставленных задач дают алгебраические критерии
1- Характеристический полином замкнутой системы
C3(s) - 4(f) + B(s) = К+ (I “ 6Л>’+ <2 + |00А>’ * **
ЗЮ________________________________________________________________Глава^
устойчив по Гурвицу при 0 < К < 0.1652 = Ац,.
2. Определяем значения Л, = Ю6/20 = 2 и cos(<p3) = 0.5. Приведенный ха-
рактеристический полином (4.32)
С^)=А2(^2А(а)В^4В2(^^с,(кУ
с параметрическими коэффициентами
0>(А) = 4А2. с,(А) = 2ЛК 1 - 24А). cj(A) - 944 А2 - 8А + I.
cj(А) - -4800А2 + 178А + 4. q(A) = 40000А3 + 388А' + 6.
cs(A) = 200А+4, с6(А) = I
устойчив по Льенару - Шипару при выполнении необходимых
едК) >0 Vi =0.6 (отсюда получаем 0 < К< 0.04167) и достаточных ус-
ловий
CS с, q О О
1с, Cj ql сь с4 с2 с0 О
М3(а)=1с6 с4 с2 >0 А М5(А)= 0 Cj с3 q 0 >0
|0 с, с3| 0 с6 с4 с2 с0
0 0 Cj с3 С|
с решением 0 < К < 0.03389 = Ау. Степени полиномов Л/3( А) и A/j(A)
равны соответственно 6 и 9. поэтому аналитическое решение неравенств
весьма затруднительно. Практически целесообразнее с помощью Math-
cad-программы построить графики Л/3(А) и ЛА(А) в интервале допусти-
мых значений Ке (0. 0.04167) и найти удовлетворяющий обоим услови-
ям интервал 0 < К < 0.03389 (рис. 4.39).
Рис 4 39
Устойчивость систем автоматического управления
383
Для сравнения трудоемкости алгебраических и частотных методов нахож-
дения областей устойчивости рассмотрим приближенный и точный вари-
анты решений поставленных выше задач с помощью частотного критерия
Найквиста.
Быстрые приближенные решения получим по асимптотическим логарифмиче-
ским характеристикам (рис.4.40). Построим их для а затем путем
анализа установим Гранины устойчивости замкнутой системы с нулевыми и
с заданными запасами.
Рис. 4 40
ЗВ4
Гпава 4
1. При Д=1 асимптотическая фазовая характеристика Фа(ш) пересекает
граничный уровень фазы фф = 180" на частоте to,p = O.l, |Дс
Z.a(<Orp) = 20 дБ > 0. Для обеспечения устойчивости замкнутой системы
амплитудную характеристику нужно опустить вниз не менее, чем на
20 дБ, а значение Л'уменьшить в 10 и более раз. Таким образом, верхняя
граница устойчивости замкнутой системы проходит на уровне = 0.1.
При Д=-1 и вообще при всех К< 0 пунктирное дополнение характе-
ристики Фа(ш) всегда имеет -1/2 пересечений уровня Фф = 180", т. к.
Д,(ш -»0) -»“ > 0, поэтому' нижняя граница устойчивости замкнутой
системы равна нулю.
Таким образом, в отсутствие запасов замкнутая система устойчива в ин-
тервале параметра 0 < К< 0.1 = К^.
2. Наклон характеристики Ф„(ш) слева от частоты оз,р = 0.1 определяется
коэффициентом затухания = 0.3 и составляет -90" на 0.3 дек. Опреде-
лим логарифмическую частоту' запаса Igor, из условия (4.31):
= Фф + Фз = 240" => Ig ш, =-1-0.3^ = -1.2.
При К= 1 логарифмическая амплитуда составляет величину
£,(<.>,) = 20 - 20 (-0.2) = 24 дБ.
Для обеспечения заданных запасов устойчивости L, и Ф, нужно опустить
асимптотическую логарифмическую амплитудно-частотную характери-
стику вниз на 24 + 6 = 30 дБ, т. е уменьшить коэффициент усиления Д
в 31.6 раза Таким образом, заданные запасы устойчивости замкнутой
системы обеспечиваются в интервале параметра 0 < К < 0.0316 = Ду.
Приблизительность результатов, полученных по асимптотическим частот-
ным характеристикам, связана с неизбежными погрешностями аппроксима-
ции логарифмической частотной характеристики.
Точное решение задачи по критерию Найквиста получим на основе нелиней-
ных амплитудной и фазовой частотных характеристик, описывающих пове-
дение годографа разомкнутой системы И^Оы) (рис. 4.41):
, , |Дк/1-164ш2 +10000Ш4
*)ви-ад—
180* + sgn(K)-90е -arci^ —j-2arc(g(oM.
Устойчивость систем автоматического управления 385
Рис 4 41
1. Решая при К>0 уравнение <р(Шф) = 180*. получим граничную частоту
Шф = 0.0944, откуда находим
Л(Шф) = 6.054 => АГф = 1 / 6.054 = 0.1652
и интервал устойчивости замкнутой системы с нулевыми запасами
0 < К< 0.1652.
2. Решая уравнение <p(o>j) = 240', получим частоту запаса ю, = 0.0531, на
которой
^(Ш)) = 14.755 => К3 = 0.5 / 14.755 = 0.03389.
В результате параметрический интервал устойчивости замкнутой систе-
мы с заданными запасами принимает вид 0 < К < 0.03389.
4.8*. Устойчивость систем с запаздыванием
Практически в любой системе точки приложения управляющих воздействий
пространственно разделены с точками измерения сигналов, необходимых
Для формирования управления Из-за конечной скорости распространения
сигналов любой участок системы имеет транспортное запаздывание, которое
обычно не учитывается либо в силу идеальности ньютоновской физики, ли-
бо для упрощения математической модели объекта. Примерами систем
Управления с транспортными запаздываниями могут служить
Глава 4
□ управление движением удаленного от Земли космического аппарата, от
которого и до которого радиосигналы доходят за время, сравнимое с по-
стоянными времени динамики объекта;
□ управление прокатным станом в металлургии и бумажной промышлен-
ности. где участки воздействия валков на движущуюся ленту проката
пространственно разнесены с участками измерения ее толщины;
□ установки химического и нефтехимического синтеза с длинными трубо-
проводами и малыми скоростями движения по ним реагентов.
Звено чистого запаздывания на время т секунд (рис. 4.42) имеет временные
характеристики (см. табл. 3.1)
w(t) = 8(/ - т), Л(0 = 1(/ - т),
Рис. 4.42
передаточную функцию
M<(s)=L{5(»-T)}=e-“
и частотные характеристики (см. табл. 2.2)
W'(j(o)= е“ ,и” = cosfrto)- jsinfao),
Лю) = cos(tw), 0(«>) = -sin(tw).
Л(<о) = 1, £(<о) » 0, <р(ш) = arcig(-tg(tw)) = —по.
Разделяя выполняемую объектом функцию от задержки ее проявления на
выходе, запишем его передаточную функцию в виде W(.s)c~T', где
I Л(з) — линейная часть передаточной функции без учета чистого
запаздывания на время т. Аналогично отделим линейную часть
Ио(»)“ Во(з)/Ло(з) передаточной функции цепи обратной связи
от ее чистого запаздывания (рис. 4.43).
Устойчивость систем автоматического управления
387
Тогда характеристический полином замкнутой системы с неединичной от-
рицательной обратной связью равен
С,(,)= а(уХ,(»)+ В(5)Я0(л)е-’«’, (4.33)
где тх = т + то — суммарное контурное запаздывание системы Эта транс-
цендентная функция раскладывается в бесконечный ряд Тейлора по степеням
т, поэтому спектральные необходимые и достаточные условия устойчивости
(4.3) и алгебраические условия устойчивости (4 13) неприменимы Благодаря
существованию частотных характеристик звена с чистым запаздыванием,
исследование устойчивости таких систем успешно выполняется по критери-
ям Михайлова и Найквиста [16. 30|. Следует только помнить, что дополни-
тельный фазовый сдвиг -тксо, вносимый звеньями запаздываний, требует обя-
зательной коррекции фазочастотных характеристик с помощью функции
сог<р, как показано на рис. 2.27
Подставив в (4.33) J=jw, получим комплексную частотную функцию замк-
нутой системы с запаздыванием
С30<о) = /((jroMoGto) + 5(jw)BnO)(cos(rK<i>) - jsin(TKo>)) =
= АДсо, cos(tk<d), sin(TKoi)) + jft(“, со$(тхш), sin(tKw))
Для устойчивости замкнутой системы ее годограф C,(jo>) с колебательными
действительной Р/ш, cos(tkm), sin(TKw)) и мнимой 2э(ы, cos(tk<o). sin(rKio)) со-
ставляющими должен по критерию Михайлова огибать начало координат
против часовой стрелки, нигде не обращаясь в нуль. На границах устойчи-
вости при определенных критических значениях частоты (Цф и запаздыва-
ния ткр выполняются условия
f А,(ш,р.cos^to.p) sinfr^J^O.
( Q, (“кр • cos(Tkpa)Kp ) sin^u^ ))= 0.
определяющие границы областей устойчивости замкнутой системы в про-
странстве ее параметров.
По критерию устойчивости Найквиста строится годограф ^(jeo) для ли-
нейной части K^koI-s) = контурной передаточной функции
Влияние запаздывания тк на контурный годограф
проявляется в его спиральном «закручивании» по часовой стрелке (в сторо-
ну уменьшения аргумента) на угол ткы, пропорциональный частоте <и. без
изменения амплитуды Ао(ю) (рис. 4.44,«), Эффект «закручивания» не на-
рушает условий устойчивости замкнутой системы — неохватывание точки
Найквиста годографом И^Ош), — только при условии Лко(со) < I V со 2 0, т е
когда весь годограф Hzt(jw) лежит внутри единичной окружности. В осталь-
ных случаях вносимый запаздыванием отрицательный фазовый сдвиг может
привести к неустойчивости замкнутой системы, в том числе и для мини-
мально-фазовых систем первого и второго порядков, которые без запазды-
вания безусловно устойчивы.
Вывод: астатические системы с запаздыванием всегда условно устойчивы, по-
скольку все они на низких частотах имеют амплитуду /1ко(<о) > 1.
Рассчитаем критическое запаздывание ткр для системы с устойчивым годо-
графом так, чтобы при тк < т^ замкнутая система оставалась устой-
чивой. При тк = 0 годограф совпадает с IKK0(j(o) и тоже устойчив, г. е
не охватывает точку Найквиста (рис. 4.44, 6). При увеличении запаздывания
Тц точка пересечения годографа B'fjco) с единичной окружностью прибли-
жается к точке Найквиста, а при достижении критического запаздывания ткр
совпадает с ней. достигая границы устойчивости на частоте среза
- I.
где Лп(<^р) = 1 и Фко(Шср) - TLpWcp = Фгр. Отсюда находим искомую вели-
чину ткр:
где = Ф«о(<1^р - Ф,р - запас устойчивости по фазе системы без запаз-
дывании.
Для обеспечения в замкнутой системе желаемых запасов устойчивости и
Ф> найдем частоту запаса
Устойчивость систем автоматического управления
389
О»,: Лк0(й)3)= Ю'005^
и из условия
Фко(<»1) - ткр«ъ - <₽J “ Фф
получим критическое запаздывание
т _ фЖ)-Ф.Р ~Ф,
(4.35, 6}
При анализе устойчивости замкнутой системы с запаздываниями по лога-
рифмическому критерию Найквиста строятся частотные характеристики
системы без запаздывания Лко(а>) и Фко(ы) (рис. 4.45) Из условия
Д<о(®>) ~ вычисляется частота запаса и», и на ней — допустимое умень-
шение фазы Фко(аЪ) - Фгр ~ Ф1 Критическое запаздывание определяется по
формуле (4.35, 6). При тк > ткр фазовая характеристика контура с запаздыва-
нием Фк(ш) = Фк0(<“) “ ткш быстрее пересечет уровень ф,р + ч>з, чем ампли-
тудная характеристика Z.K(w) окажется ниже уровня -Ц, и замкнутая систе-
ма станет неустойчивой
£7 Пример 4.14. Методами Михайлова и Найквиста построить области па-
раметрической устойчивости замкнутой системы с запаздыванием, имеющей
контурную передаточную функцию
(1 + аГ
Решение. По методу Михайлова составим характеристический полином
(4.33) в операторной и комплексной формах:
390 ______________._______________________________________Глава 4
С,(з)=1 + 2(1 + ЛГе‘п)г + $2 =» С,0ш) = Р,((о) + )Оэ(со),
где
ЛМ = 1 - со2 + 2Ашк1п(тш). е,(ш) = 2<о( 1 + Acos(tco)).
На границе устойчивости система уравнений (4.34) принимает вид
| /’1(“ч>)=1-«кР +2*lvwKpSin(TKp(0((p)=0,
) Q, ((«)„ )= 2(0^ (1 + ^cos^w^ ))= О
и имеет параметрическое от о\р > 0 и периодическое от / = 0, 1, 2.... решения
(получите их самостоятельно):
>0.
’ 2ш,р 41 2(0^
Ji+4,>-4^tg((oJ
’ 2^ 41 2шкр
Исключая критические частоты
ШЧ> = |^крI*'
получим следующие зависимости критического запаздывания ткр от пара-
метра и целочисленного индекса 12 0:
{2+sgnta,,)<-4i b-4arct/p^|±7*2p^)
t -____________________— v --------------z e (4.301
Величина и знак коэффициента статического усиления разомкнутого конту-
ра К следующим образом влияют на существование и величину критическо-
го запаздывания:
□ при |К| < 1 критические частоты отсутствуют, а замкнутая система ус-
тойчива при любом запаздывании т,
□ при |К | = 1 существует единственное значение <a„ = 1 при котором на-
бор критических запаздываний равен р 1
(2га = 2л, 4п. 6п.... при К = -J;
Устойчивость систем автоматического управления
□ при |К| > 1 существуют две критические частоты
шкр, =|K| + V?"^,
и соответствующие им по (4.36) два критических запаздывания
ткр| < ткр2, формирующие на плоскости {Л'. т) границы заштрихованных
областей устойчивости замкнутой системы (рис. 4 46).
Рис 4 46
На рис. 4.47 построены годографы характеристического полинома замкну-
той системы С,0'о>) для шести пар параметров (Д’, т|, отмеченных на
рис. 4.46 точками:
{АГ— —1.1, те {0,2,3.76», {* = 1.4, те (0, 1,3.64»
Очевиден циклический характер годографа при ненулевом запаздывании.
Сплошные графики, проходящие через начало координат и при малой ва-
риации имеющие положительное изменение аргумента, соответствуют ней-
тральной системе; пунктирные, огибающие начало координат в положи-
тельном направлении, — устойчивой, а штрих-пунктирные — неустойчивой
замкнутой системе.
Годограф, соответствующий паре (АГ» I 4. т = 3.64). на втором цикле прохо-
аит через начало координат, но, тем не менее, является не граничным, а не-
устойчивым. т. к. на первом цикле имеет отрицательное направление изме-
нения аргумента.
Рис. 4.47
Для оценки влияния параметра К на устойчивость по методу Найквиста по-
строим на рис. 4.48 годографы линейной части передаточной функции
по амплитудно-частотной и фазочастотной характеристикам
4<<o)=sgn(K)^-2arclg((o),
откуда видно, что при |ЛГ| < 1 никакое запаздывание не может закрутить го-
°" °ХВаТИЛ ТОЧКУ Найквиста Поэтому замкнутая система
тоте среза* Г°а0Г₽а* касастся единичной окружности на единственной час-
4.,)-^-! А,)- йп(»)-|(=.
По «да фи„„ро„нпих ч,„„,еск„, ип,„ыаа„вй;
тч> = Ф Р = + 2nj = I л + 2га' = я, Зя. 5я,... при № I •
с₽ 2 (2га' = 0,2я,4я, ...при К =-!
Устойчивость.
Рис.4 48
При |Л] > 1 годограф дважды пересекает единичную окружность на
частотах Щр! и сц.р2:
/ ч 2К|шсп , , г—,— . Г"5—
МЧР)= -!y- = J => Чр1=|*МК2-1. а)ср2=|К|-<№-1.
1 + С1)Ср
Им соответствуют критические запаздывания (4.36), формирующие на плос-
кости {К, т} границы областей устойчивости замкнутой системы, выделен-
ных штриховкой на рис. 4.46.
Построенные на рис. 4.49 годографы разомкнутого контура имеют спираль-
ный характер при наличии запаздывания т > 0. Выводы об устойчивости
замкнутой системы совпадают с результатами анализа устойчивости методом
Михайлова для соответствующих параметров {Л', т) 22
& Пример 4.15. Вернемся к изучению акустической системы, состав ко-
торой показан на рис. В.4. Пусть для чистоты эффекта последовательное
соединение микрофона, усилителя и динамика представляет собой иде-
альный полосовой фильтр, имеющий амплитудно-частотную характери-
стику
при/,, </£/.;
(0 при05/</„ или />/,
с регулируемым усилением Л> в полосе частот/е lAi.ZJ 11 нулевую фа-
зочастотную характеристику ф(/) = 0.
Глава 4
Рис. 4.49
Исследовать устойчивость системы, образованной акустическим замыкани-
ем обратной связи через слой воздуха между динамиком и микрофоном. 8
зависимости от толщины этого слоя.
Решение Примем следующую модель ослабления амплитуды звуковых коле-
баний в воздухе в зависимости от пройденного звуком расстояния d:
ЛМ'^-
Согласно этой зависимости вблизи динамика затухание звука практически
отсутствует (4, 1), а при значительном удалении микрофона от динамика
Устойчивость систем автоматического управления
затухание пропорционально квадрату расстояния между этими элементами
системы. Для каждой акустической среды коэффициент /. = 1/</о5 может
быть определен экспериментально путем измерения расстояния 5, на ко-
тором амплитуда звуковых колебаний уменьшается в два раза
Будем, опять-таки ради чистоты эффекта, считать, что фазовые искажения
при прохождении звука через слой воздуха связаны исключительно с транс-
портным запаздыванием на величину t(d) = <// К где V— скорость распро-
странения звука в воздухе Таким образом, фазочастотная характеристика
воздушного промежутка толщиной d с учетом инвертирования знака обрат-
ной связи на рис. В.4 с положительного на отрицательный равна
/ . ?.Тч1 .
<ft(f,d)=n——f рал
По критерию Найквиста неустойчивость изучаемой замкнутой системы воз-
никает на тех частотах, где усиление разомкнутого контура
А(Л d) = Л(/)ЛВ(</) превышает единицу и происходят переходы фазовой ха-
рактеристики Фк(Л d) = Ф(/) + Ф»(/. d) через граничные уровни
Фф/=п(1-20, /е (0, 1, 2,...}. Построим на рис. 4 50, а в равномерном
масштабе частот семейство фазочастотных характеристик <pjf, d) для раз-
личных запаздываний t(rf). Анализ пересечений этими линейными графика-
ми уровней фгр( в пределах полосы пропускания разомкнутого контура
/е 1/н.Ун1 позволяет записать систему неравенств, описывающих области
неустойчивости замкнутой системы в пространстве параметров {Ку, d}
Ку>1 + М2;
(4,38)
de|j4. dti<d,<d„i.
1=0
где rfB = V/и dH = И//, — расстояния, на которых фазовый сдвиг дости-
гает значений q>K(/B, </в) = -п и фк(4<, d„) = -п. Объединение частных облас-
тей, соответствующих отдельным значениям /. состаатяет область неустой-
чивости системы.
На рис. 4.50, б область неустойчивости построена для следующих реальных
данных:
/„ = 100 Гц, /в = 10 кГц, К- 330 м / с, А. = 0.01 м"<
Видно, что частные полосы неустойчивых расстояний d, 6 (dti, dMi), распо-
ложенные выше параболы 1 + k<fi, перекрываются благодаря отношению
частот = 100 > 2. Минимальное ненулевое расстояние, начиная с ко-
торого возможно самовозбуждение акустической системы, составляет всего
<4 = 3.3 см, при этом уровень усиления Ку должен превышать значение
1.00033. С увеличением расстояния «/между динамиком и микрофоном уси-
ление самовозбуждения возрастает как I + М.
396
Глава 4
Рио. 4.50
ношениемЯкмйии?И системЬ| Установить узкополосный фильтр (4.37) с соот-
= пТлЙосИХт°иТ ~ "Р0ПУСКаН,,Я 1 < 2' ТО ,,еСК0ЛЬК0
образуя обособленные мныТзб^ИВ0СТИ о""™** МО1уТ Не пеРекРь,ТЬСИ'
рис 4 50. в построена такая ,1OOTBCP^"‘'c' сказанного на
/н“ 100 Гни/, = ио Гц нсодносвязная область неустойчивости при
ГЛАВА 5
Наши математические затруднения бога не
беспокоят Он интегрирует митрически
Airfepm Эйнштейн
Расчет переходных процессов
в системах автоматического
управления
Моделирование является последней и одной из важнейших задач анализа
систем автоматического управления, позволяющей имитировать поведение
реальной системы в различных условиях эксплуатации, предусмотреть ава-
рийные ситуации или повышенные нагрузки на элементы системы без рис-
ка их разрушения. Моделирование переходных процессов является обяза-
тельным этапом исследования условно устойчивых и неустойчивых систем,
какими являются объекты аэрокосмического, энергетического, химического
и других назначений. Оно заменяет экспериментирование с реальными до-
рогостоящими и часто уникальными объектами, которые в рабочих условиях
всегда должны функционировать устойчиво, надежно и безопасно
Первоначально исследование поведения объектов проводилось вручную пу-
тем аналитического или численного решения уравнений, составляющих мо-
дель системы. Переложение вычислительной нагрузки на компьютер осво-
бодило мозги разработчика системы управления для осмысления результатов
моделирования, совершенствования моделей элементов и методов синтеза.
Следует отметить основные преимущества моделирования, особенно компью-
терного, по сравнению с натурным экспериментом
Q можно исследовать поведение системы при самых разных условиях,
в том числе в гипотетических и запредельных режимах;
О по данным модельных испытаний можно оценить поведение проекти-
руемых, но еше не существующих систем, для принятия решения о це-
лесообразности их изготовления;
О всесторонние испытания системы можно выполнить за сравнительно
короткий промежуток времени;
39В
□ только моделирование способно предсказать поведение в реальных ус-
ловиях объектов одноразового назначения — космических аппаратов, ар-
тиллерийских снарядов и т. п.;
□ моделирование часто является единственным экологически безопасным
и экономически приемлемым методом анализа поведения систем.
До того, как получили широкое распространение быстродействующие циф-
ровые компьютеры, основным методом моделирования было аналоговое
(ом. разд. 1.8). В последнее время этот метод утратил свое былое значение,
однако в некоторых случаях без него обойтись невозможно.
□ В системах имитационного моделирования с оборудованием в контуре
управления |29| зависимость скорости цифрового моделирования от бы-
стродействия компьютера создает дополнительные проблемы с согласо-
ванием машинного и реального времени. Аналоговая модель, работаю-
щая в реальном масштабе времени, находится в состоянии постоянной
готовности, отслеживает процессы по ходу их развития и не тормозит
оборудование, встроенное в контур управления.
□ Если моделируемая система является очень жесткой (г» 10), то отноше-
ние постоянных времени экспонент, составляющих ее переходную харак-
теристику, может составлять несколько порядков. При цифровом модели-
ровании такой системы шаг интегрирования А.Тдолжен задаваться доста-
точно малым, а интервал моделирования /ы — очень большим. По (3.45)
число шагов Nu и время расчета увеличиваются настолько, что модельный
процесс перестает успевать за реальным. Желание ускорить моделирова-
ние путем увеличения шага приведет к потере быстрых движений и сдела-
ет модельный процесс недостоверным. Аналоговое моделирование по сво-
ей природе непрерывно и отслеживает все составляющие переходного
процесса, чьи частоты лежат в полосе пропускания моделирующей схемы.
□ Цифровое моделирование по определению дискретно, так что если воз-
никает необходимость в промежуточных значениях некоторого сигнала
между имеющимися отсчетами, то приходится повторять моделирование
с новым, меньшим шагом интегрирования. Аналоговый сигнал опреде-
лен во всех точках интервала моделирования, а при необходимости
иметь, например, осциллограмму начального участка процесса в иной
временнбй шкале можно построить отдельную схему масштабированной
по времени модели (см. разд. 3.3.3).
5.1. Структура переходного процесса
Изменение состояния системы во времени осуществляется в форме движе
кия Внешне выглядящее как единое целое, движение в действительности
складывается из ряда составляющих, порождаемых различными причинами
Классификация основных видов движений приведена на рис. 5.1
399
Движение уоын(0, вызванное влиянием на объект внешнего воздействия,
называется вынужденным или возмущенным движением. При длительном,
большем времени установления /у, постоянном характере внешних воздей-
ствий объект функционирует в установившемся режиме вынужденного
движения .VycrW. при котором параметры его состояния — значения коор-
динат, скорости их изменения, амплитуды и фазы колебаний — постоян-
ны во времени.
Установившийся режим включает в себя состояние равновесия или покоя —
это движение по номинальной траектории у„(/) в отсутствие внешних воз-
мущений. Тривиальное состояние равновесия — нулевое
у = / = ...= У«-1> »= О,
удовлетворяющее при x(j) = 0 дифференциальному уравнению
A(s)y(t) = B(Mj), где А(з)= Jo,з'. в(з)= . (5.1)
1=0 1=0
описывающему движение объекта. Характер состояния покоя определяется
составом и расположением полюсов передаточной функции объекта
НО = B(s) / Л(х), являющихся корнями характеристического полинома сис-
темы Л(т):
Q если все полюсы левые, то нулевое состояние покоя — устойчивое;
Q нулевой полюс при остальных левых полюсах дает нейтральное (неопре-
деленное) состояние покоя;
J пара мнимых корней характеристического полинома при остальных ле-
вых дает колебательное равновесие;
а достаточно одного правого полюса, чтобы равновесие стало неустой-
чивым.
400
Глава 5
Переходным режимом называется движение объекта между двумя устано-
вившимися режимами. В устойчивых системах переходный режим заканчи-
вается за время /у после окончания внешнего воздействия или установления
его постоянных параметров.
Свободным yn(t) называется движение объекта из ненулевого состояния в со-
стояние равновесия без учета внешнего воздействия, т. с. при х(г) = 0.
Собственным усо6(6 называется движение, совершаемое во время перехода
из одного установившегося режима в другой без учета свободного движения.
На графиках и таблице, изображенных на рис. 5.2, показано соотношение дви-
жений системы на примере колебаний маятника в вязкой движущейся среде.
При расчете переходного процесса определенный момент времени to выби-
рается начальным Состояние объекта при t= t0 называется начальным со-
стоянием или начальными условиями. Начальное состояние с нулевыми зна-
чениями координат объекта и их производных называется нулевыми началь-
ными условиями
В некоторые моменты времени t0, f|, Zj,... входное воздействие х(г) может
изменять свое описание, иметь разрывы, изломы и т. д. При определен-
Расчет переходных процессов в системах автоматического управления 40j
ных свойствах системы это даст разрывы в функции y(f) и ее производных
/')(/). Например, если полиномы передаточной функции Л(.$) и В(х) имеют
равные степени п ~ т, то коэффициент прямой связи входа с выходом ра-
вен D = bn / а„ * 0, а скачки входного сигнала &х(/А) порождают выходные
скачки
М'*) “ DMik).
В связи с этим начальные условия
y(')(/0)=!imy(')(/0 + e)
г-Л
могут отличаться от предначальных условий
у(')(го-О)=Нту(')(го-е)
е-Ю
на величины скачков начальных условий
ДУ/»(/о)в#(1Ь)->')Оо-0).
Переходный процесс на выходе системы развивается как последователь-
ность процессов на интервалах постоянства описания сигнала х(/). В конце
t-ro интервала моделирования р*_), /*] формируются предначальные усло-
вия ~ 0) для следующего к + 1-го интервала |/«. /*-г! По достижении
конечного времени т = /м моделирование заканчивается
Аналитические методы расчета переходных процессов в системах управле-
ния делятся на частотные и временные Частотные методы заключаются в
обратном преобразовании Лапласа изображения выходного сигнала М.г) с
помощью таблиц ПЛ - П.З или по формуле разложения Хевисайда (3.4). К
основным временным методам относятся методы вариации произвольных по-
стоянных, интеграла Дюамеля и пространства состояний
5.2. Метод преобразований Лапласа
Изображение выходного сигнала формируется в соответствии со структур-
ной схемой на рис. 5.3, построенной по формуле (1.18):
К(з)=И/(з)Х(х) + ^1-^1 (5.2)
Изображение X(s) входного сигнала х(/) вычисляется по (1.16) либо находит-
ся по таблице прямого преобразования Лапласа П.1 Сигнал >V) возникает
на выходе блока с передаточной функцией системы Щз), на который по-
ступает входной сигнал xV).
Глава 5
Рис. 5.3
Полиномы P(s) и Q(s) формируются по (1.17) на основе предначальных ус-
ловий входного и выходного сигналов:
На блоки с передаточными функциями Pts) / ли) и Qts) / Л(т) поступает
сигнал, изображение которого согласно (5.2) равно единице. Следовательно,
это несмещенный дельта-импульс 5(f)- Обозначим сигналы на выходах эти*
блоков соответственно как р(Г) и q(i).
Таким образом, налицо три источника и три составные части переходного
процесса. Рассмотрим подробнее структуру движения и свойства составляю-
щих его сигналов.
Свободное движение
₽(»)-Г1 (5.3. о)
П^^^шЛеНуЛевЫМи предначальными условиями уЮ(-О), /е |0.л-Н.
возбуждающими систему только в начальный момент времени, что отражено
403
Расчет переходных процессов в системах автоматического управления
на структурной схеме рис. 5.3 входным сигналом б(/). Свободное движение
непрерывно, оно без скачков продолжает предначальнос движение, что сле-
дует из предельной формулы (3.2, о):
ус(°)==~У^~°^
В устойчивой системе, чья передаточная функция удовлетворяет условию
(3.2, б), свободное движение затухает:
**8^?*'
Вынужденное движение системы
.V.utl(O=L-'^(5)x(5)-50| = '%спш№ (5.3. б)
порождается входным воздействием х(Г), имеющим изображение
у/Л_ Вх(3)
и его ненулевыми предначальными условиями .^(-0)./е (0, т- 1|. возбуж-
даемыми входным сигналом 8(1). Структура вынужденного движения опре-
деляется кратностью и расположением v^,, корней ъ полинома
4ыи(*) = Л(5)ЯХ(5). Начальное значение вынужденного движения также най-
дем по предельной формуле (3.2, а):
У.ын(0)= lim WMO)—~~ [ = —Д.г(о)' limj"*'1 =
’"П a„s т J «л
—Дх(0) принят;
«л
= 0 при п > т;
sgn — I- оо при л cm.
с Учетом непрерывности свободного движения полное движение системы
Х*)=Л»0+Лыи(О • IW М
коРректно вычисляет начальное у(0) и предначальное у(-0> значения вы-
х°ДНого сигнала. Его скачок равен скачку вынужденного движения ЛуВы>Л0)
Ду(0) " Л»(°) +
404
Если входной сигнал имеет в начальный момент времени скачок Д.х(0), то:
□ при л = т, т. е. равных степенях полиномов числителя и знаменателя
передаточной функции, система имеет прямую связь от входа до выхода
с коэффициентом усиления D- Ь„ / а„, а скачок входного сигнала Дх(0)
порождает на выходе скачок Д(<0), равный /)Дх(0);
□ при п > т выходной скачок отсутствует;
□ при п < т передаточная функция имеет прямую связь дифференцирующе-
го типа, а входной скачок Дх(0) порождает на выходе кроме скачка />Лх(0)
еше и дельта-функцию 3(Г), а также, при т > п + 1. ее производные.
В процессе вычисления оригиналов в (5.3) допускается сокращать полино-
мы числителей и знаменателей дробно-рациональных функций на общие
множители, т. к. вычеты в полюсах, совпадающих с нулями, равны нулю. В
то же время не рекомендуется делать поспешное сокращение полиномов пере-
даточной функции на общие множители, г к. в (5.3, в) будет потеряна состав-
ляющая свободного движения с^,соответствующая сокращенному
полюсу 3/.
Рассмотрим особенности расчета переходного процесса при различных спо-
собах описания входного воздействия х(/)
При интервальном описании (рис. 5.4) сигнал x(t) задается кусочно-
определенными функциями х*(/) на каждом из к е 11, W| интервалов време-
ни г 6 |г*_|, /*):
При неравных разносторонних пределах х(М ± 0) на стыках интервалов воз-
никают скачки Ах* = x*(U - Ч |('О. на которые система реагирует скачками
выходного сигнала ДИ4) "° описанному выше механизму возникновения
начального скачка МО).
Расчет переходных процессов в системах автоматического управления
405
Алгоритм расчета переходного процесса методом преобразовании Лапласа при
интервальном описании входного сигнала в виде (5 5) включает следующие
операции, выполняемые в цикле к =0, N -1,
I. По предначальным условиям уЩк ~ 0) и xW(4 - 0) вычисляются поли-
номы Р*(5) и 0*(5)
2. С помощью табл. П 1 прямого преобразования Лапласа находится изобра-
жение оригинала х*(т), записанного в смещенном времени т = / - г*.
3. По формуле (5.2) вычисляется изображение К*(з)
4. По формуле разложения Хевисайда (3 4) или табл. П.2 обратного преоб-
разования Лапласа находятся оригиналы »(т) в смешенном и в ре-
альном времени.
5. Рассчитываются конечные условия текущего интервала У°(г*+|-О) и
х<Л(г*+1 - 0) как предначальные условия для следующего временного ин-
тервала.
Существенный недостаток данного алгоритма заключается в необходимости
вычислять на каждом интервале производные функции и предначальные ус-
ловия для следующего интервала. Можно избежать этих трудоемких опера-
ций, представив входной сигнал суммой полубесконечных смещенных со-
ставляющих:
4)= ) ) (5-6)
Изображения входного и выходного сигналов с учетом запаздываний it равны
406
Глава 5
r(,)= =S'К* (*>”'*+
*=о Aw *=0
гае:
□ X*(s) и )*(s) = H^X^s) — изображения несмещенных входного xk(f) и
выходного »>(/) сигналов;
□ U(s) — изображение реакции системы на ненулевые предначальные ус-
ловия ><0(-0) и xW(-fl).
В результате получаем формулу расчета выходного сигнала
Х»)= tyk(t-tk)i(t-tk)+u(t), (5.7)
4=0
в которой слагаемое
ЖО" L’WW}
представляет собой несмещенную реакцию системы на несмещенную к-у«>
составляющую входного сигнала, а реакция на ненулевые предначальные
условия
есть импульсная характеристика блока с передаточной функцией
(As) * QU)) / A(s). В отличие от интервального алгоритма в (5.7) не требует-
ся вычислять производные, а предначальные условия используются только
один раз для получения сигнала и(г).
Еще более простой, но приближенный метод построения переходного про-
цесса основан на кусочно-постоянной аппроксимации входного сигнала
(рис. 5.6):
х(г) = Ло • 1(»-Г0)+ К'~<к )• = Хк - •»*-!• <5 8)
ы
Обозначив для единообразия начальный скачок как Дх<) = хо и подставив в
(5.7) реакции системы на ступенчатые составляющие входного воздействия
Ук№ = Дх*Л(/ ~ /*),
где й(/) — переходная характеристика системы, равная нулю при / < 0, полу-
чим расчетную формулу
у(/)= )+«(»). (59>
к-О
особенно простую при нулевых предначальных условиях, когда «(/) = О-
Расчет переходных процессов в системах автоматического управления
Рис. 5.6
Для выполнения численного расчета переходного процесса нужно дискрети-
зировать входной сигнал по времени и уровню, Тогда выходной сигнал (5.9)
есть взвешенная сумма смещенных во времени переходных характеристик
А(/ - /*) и реакции на ненулевые предначальные условия «(/).
Получим алгоритм численного расчета переходного процесса при равномер-
ной дискретизации всех сигналов системы в моменты времени
tk = к ДГ, к - О, I, 2.К,
кратные периоду дискретности ДГ. Зададим необходимые исходные данные.
□ интервал моделирования /е |0, К Д7]. состоящий из А равных шагов
длительностью ДГс;
О формулу входного сигнала х(г), по которой вычислим отсчеты входного
сигнала = х(4) VA = О, К;
О предначальные условия ,И°(-0). .^(-О), по которым сформируем с по-
мощью (117) полиномы ЯО и 0(г).
Далее найдем по (3.13) формулу оригинала «(г) с изображением
0(5)) /Л(л) и вычислим отсчеты «* = «(/«). Затем получим по (3.14)
Формулу переходной характеристики системы А(г) и вычислим ее отсчеты
408 Глава 5
Отсчеты выходного сигнала »=></*) находятся по алгоритму (5.9), модифи-
цированному с учетом равномерности дискретизации времени и свойства
причинности переходной характеристики Л(() = О V / < 0:
У/= +и, У/=6ГК. (5.10, в)
t=o
Хотя этот алгоритм вполне самодостаточен для программного построения
графика переходного процесса системы при произвольном входном воздейст-
вии, его можно усовершенствовать так, чтобы каждый отсчет л* использо-
вался только один раз. Подставив в (5.10, а) разности Дх* = х* - x*-i и пере-
группировав слагаемые, получим
У( = Ёх*ЛЛ(-*+«с
При выборе шага дискретизации ST, много меньшего минимальной посто-
янной времени системы 7), из (3.15, а) следует связь между приращением
переходной характеристики и импульсной характеристикой системы:
Shk = wk • ST.
В результате получаем альтернативный алгоритм численного моделирования
переходного процесса системы при произвольном входном воздействии
У/V« = 0?7, (5.10,6)
*=о
используюший отсчеты импульсной характеристики системы wk = w(ik).
Существенным недостатком более простой формулы (5.10, 6) по сравнению
с (5.10, а) является сложность учета возможного присутствия дельта-
функиии 8(f) в непрерывной импульсной характеристике н<г), в то время
как в переходной характеристике Л(г) ее может и не быть.
Выражения (5.10) при нулевых начальных условиях (и, = 0) называются дис-
кретной сверткой благодаря встречным направлениям изменения индексов
сомножителей В пределе при ДГ-» 0 суммы плавно переходят в интегралы
свертки (4.4):
=/^ ~T^Tdr = М « JrfrM' -r>ir.
Таким образом, формулу (5.10,6) можно использовать для численного
расчета интегралов свертки. Трудоемкость вычисления свертки на К вре-
менных отсчетах составляет UK + If арифметических операций умноже-
ния и сложения
Расчет переходных процессов в системах автоматического управления 409
& Пример 5.1. Зададим в учебных целях несложный объект, описываемый
дифференциальным уравнением
/ + 3/+ 2у=У + зг (5.11, в)
с полиномами передаточной функции
A(s) = 2 -г- 3j + 5г = (I + д)(2 + 5), «з) = I + д
и предначальными значениями выходного сигнала
Я-0)-1,/(“0)-0. (5.11,6)
Входное воздействие, график которого изображен на рис. 5 7. задается мето-
дом (5.6) и в кусочно-определенной форме (5.5) как
fO V г <0,
Jt(z)=(r + l) l(0-(' + l) «(»-2)= Ь + 1 V0</<2. (5.11, в)
[о Vf>2.
Рис. 5.7
Решение В спектре передаточной функции
с несокращенными множителями (I +s) полюс j| =-I совпадает с нулем
?i = —1. Рассчитаем методом вычетов составляющие движения, зависящие
от произвольных предначальных условий.
/V) = aiy(-O) + агУ(-О) + <ьу(-0)т = Зу(-О) + /(-0) + у(-0)з,
Q(s) = М-0) = Х-0),
, х . -I J Зу(- 0)+ у'(- 0)+ у(— 0> 1
1 (Г^Т)---------Г
Зу(-О)+ v'(-0)~ v(-°) -I 3y(-O)->-y'(-O)-2>'(-ok -2i _
------------ГЛ 1-2 ~ (5.12)
= (2у(- 0)+ v'(- 0)> - (у(- 0)+ у'(- 0)> .
410
Глава 5
Отметим, что если бы мы сократили полиномы передаточной функции на
общий множитель (I + j), то с новой передаточной функцией первого порядка
2 + s
получили бы вместо (S. I2) неверные составляющие переходного процесса
Л.(0 - Х-0)е’Ч q(t) = 0.
Рассчитаем переходный процесс на двух временных интервалах.
□ На первом временном интервале 0 < / < 2:
MD-/+1=X(S)=-1Д = 1±£;
MW).
s2(l + s\2 + s) s2 -s 2 + j
Подставив в (5.12) предначальные условия (5.11, б) и х(-0) = 0, получим
ус„(0 - 2е' - с Л = 0
и с учетом (5.4) полное движение объекта
ЯО = 2е'' - е-2/ + (0.5/ + 0.25 - 0.25e’29 1(f), (5-U)
в котором 0.5/ + 0.25 есть установившаяся, а -0.25е'2' — собственная со-
ставляющая вынужденного движения. Вычислив производную
/(/) = -2с' + Зе'2* + (0.5 + 0.5е'2/) 1(/) + (0.5/ + 0.25 - 0.25е-2/) • 8(/) =
= -2е’> + 2е'2' + (0.5 + 0.5е'2') • 1(f),
найдем предначальные условия для второго интервала времени:
Я2 - 0) = 1.498, /(2 - 0) - 0.275, х(2 - 0) = 3. (5.М)
Проверим правильность полученного решения (5.13) подстановкой его в
дифференциальное уравнение (5.11, о) при х(/) = (/+1) • 1(1) 11
/(/) - 1</) + 8(0.
/*(/) - 2с' - 4с 21 - с* 1(f) + 6(f),
У+3/ + 2>--(/+2) 1(f) + 5</) ° У + л,
как и должно быть. Если же в (5.4) и (5.13) опустить функции !(/)> т°
получим
ХО - 0.5/ + 0.25 + 2е'' - |.25е’2',
У(0"0.5-2е-'-ь 2.5е'2',
Г(0 - 2е-' - 5е'2'
и несовпадение левой и правой частей дифференциального уравнения:
Расчет переходных процессов в системах автоматического управления
У + .г=(г+2) 1(/) + 8(/).
□ На втором временном интервале I > 2 или в смещенном времени т = / - 2:
х(х) - 0 => X(s) = 0.
Подставив в (5.12) предначальные условия (5.14) во времени т
у(-0) = 1.498,/(-0) = 0.275, х(-0) = 3,
получим составляющие переходного процесса
усв(т)= 3.271е-т - 1.773e-2t, </(т)=з(е'т -e'2t)
и полное движение объекта
у(т)= 3.271е-т - 1.773е'2т +(зе*2’ -Зе*т)- 1(т). (5.15)
сходящееся примерно за 3 с к нулевой установившейся составляющей.
Проверим правильность решения (5.15) подстановкой его в дифферен-
циальное уравнение объекта при .т(т) = 0 и У(т) = —38(т):
у'(т) = -3.271е-1 + 2 -1.773е'2’ + (- 6е2т + Зет )• 1(т).
у'(т)= 3.271е“т -4 1.773е'2т + (12е'й - Зе‘т ) 1(т)- 35(т),
У'(т) + 3/(т) + 2Хт) = -38(т),
У(т) + х(т) =-38(т).
Составим из уравнений (5.13) и (5.15) формулу переходного процесса в еди-
ном времени г по интервалам функционального описания х(/) (рис. 5.8, о):
,, -1-23. VOS, <2. (5 )6 а)
[ 0.27 кН''2) +1.227е'2(,‘2) Vr 2 2
рис. 5.8
412
Глава 5
Для расчета по формуле (5.7) представим входное воздействие (5.11, в) в ви-
де (5.6) с составляющими X|(z) = !(/) и х2(/) = t 1(f):
х0 - х,(7) + х2(/) - Зх,(Л - 2) - x2(f - 2).
Вычислим реакции объекта на эти составляющие
}, L-'j-J-j}-0.5(1 -е ) 1Й;
Переходный процесс на выходе объекта, график которого построен на
рис. 5.8, б, с учетом свободного движения описывается единой формулой
М = Л.0 + УМ + Л0 ~ 3j»i(r - 2) - уг{1 - 2) =
= 2е-' - е’2* + 0.25(2/ + 1 - e^O 1(/) - 0.25(2/ + 1 -
_е-2(/-2>). 1(/-2),
которая в двухинтервальной записи совпадает с (5.16, а). □
На рис. 5.9 представлена Mathcad-программа численного моделирования
переходного процесса системы (5.11) по алгоритму (5.10, б). Необходимые
для работы алгоритма импульсные характеристики объекта и предначальных
условий
w(/) = е 2', «(/) = 2е~' - е"2'
получены с помощью символического процессора Mathcad. Программа по-
зволяет гибко изменять коэффициенты полиномов передаточной функции,
формулу входного воздействия, предначальные условия по входу и выходу,
длительность интервала и число шагов моделирования.
Метод преобразований Лапласа, несомненно, наиболее быстр и удобен для
расчета переходного процесса динамической системы вручную при нали-
чии соответствующих таблиц или с помощью интеллектуальных способно-
стей используемой для численного моделирования программы В отсутст-
вие таковых использование формул прямого и обратного преобразований
Лапласа весьма трудоемко. Рассмотрим некоторые альтернативные методы
моделирования движения сложных систем при произвольных входных воз-
действиях.
Расчет переходных процессов в системах автоматического управления
413
а := ( 2 3 I )Т b := ( 1 I )Т Y0 := ( 1 О )Т
afl + a(s + a2s‘
x(t) :=(t+ 1) Ф(1)-(1+ I) Ф(1 -2) XO := О
w(t) := W(s) inviaplace ,s -+exp(-2 t)
f al a2 1
p := YO q:=brXO
I a2 0 /
a0 + a(s + a2s'
u(t) := U(s) invlaplace ,s -> -exp(-2 t) + 2exp(-t)
tk
tk := 6 К := 600 ДТ := -
k:=O..K tk:=ATk
xk := x(tk) wk := w(lk) uk “(*k)
к
ук:=ДТ ^ XjWk4 + uk
Рис 5.9
414
Глава 5
5.3. Метод вариации
произвольных постоянных
Классический временной метод вариации произвольных постоянных, приме-
няемый для расчета переходного процесса в системе, описываемой диффе-
ренциальным уравнением (5.1) с вектором предначальных условий
>’(-о)
у'(-0)
Г_о= . (5.17)
У«-0(-о)
включает следующие этапы.
1 Находятся корни s,- характеристического полинома
Л(«)=внП(*-.Г(У' ,
где v — количество различных корней, a п< — кратность корня slt причем
£п,=п.
однородного дифференциального уравнения A(s)y(f) = 0 со следующим11
элементами:
• простому действительному корню соответствует решение е**1;
• Hi-кратному действительному корню S, соответствуют п, линейно неза-
висимых решений с1'', те*1',..., t"'
• паре простых комплексно-сопряженных корней Л'/д-ц = г, A с00Т
ветствуют два линейно независимых решения en,'cos(<i)J) 11
ev itn(wj);
• некратной паре простых комплексно-сопряженных кор'1с(|
«/./♦I = Hft jtQr соответствуют щ пар линейно независимых решений
Расчет переходных процессов в системах автоматического управления 4/5
[ еп'' ссй(соД /еп'' со$(шД/',''|еп'' cos(ny),
[en''sin(n>/)l /еп,'$1п((оД.., f''’,cn''sin(u)j)
Решение однородного дифференциального уравнения с точностью до
произвольных постоянных с„ составляющих вектор-строку
С = [с| ... сп], имеет следующий вил:
Уо(д=^.У<(')=СУ(/). (5.18)
3. Составляется невырожденная п х п-мотрица Вронского
v(<)=».
у,(О у'М ... >!-"(<)
У,(>) уМ ... уН>)
=«.Й) г-(>) г*-”й]
,у.« >М ... уМО.
с всегда ненулевым определителем
det{HO} *0,
т. к. функции уМ и их производные линейно независимы.
4- Для получения решения неоднородного дифференциального уравнения
(5.1) произвольные константы с, заменяются переменными функциями
сДт), производные которых находятся путем решения системы л линей-
ных алгебраических уравнений
<(')>’i(0+- +Сл(0уп(') = °-
qWyf-'Wt .♦«ОуК')-^’
или в матричной форме
€'(/>(/)= [О ... О
откуда получаем вектор производных
с'(/)=[о 0 l]v ,0MOv(O=V'B('M4v(O
с КМ - последней строкой обратной матрицы Вронского
(5.19)
416
Глава 5
ГЦ(01 rv„(r) ...
v”(0= - = -
Ы M)...
Интегрированием системы (5.19) с точностью до постоянного вектора А'
находим вектор переменных коэффициентов
C(t)=K+ JV„(T)B(4v(T)dT.
5. Подстановка C(t) в (5.18) вместо вектора С дает решение неоднородного
дифференциального уравнения (5.1):
6. Из этого выражения и его (я - 1)-ой производной при / = —0 находится
вектор К на основе предначальных условий (5.17):
ап
7. Решение неоднородного дифференциального уравнения (5.1) с предна-
чальными условиями (5.17) имеет вид
у(0= «,П>У~'(-ОХ(о4 j Уп М >(т>т V (/)=
М) ‘ ' (5.20)
=“S у,(г)£‘л(-о)у1л,,(-о)+ XИ')/'’и.
Th >i /=1 -о J‘0
Свободная составляющая усв(0 переходного процесса (5.20) порождается не-
нулевыми предначальными условиями (5.17). Как вектор Y(i) фундаменталь-
ных решений однородного дифференциального уравнения и матрица Врон-
ского И/), гак и структура свободного движения системы и его устойчивость
зависят только от спектра характеристического полинома А(з).
Вынужденная составляющая увынО) переходного процесса порождается нену-
левым входным воздействием х(/) и его производными Зависимость от
производных обусловлена степенью полинома B(s), равной т. Из-за лиффс'
реннирования скачков входного сигнала х(1) или его производных выну*'
денное движение может включать скачки и дельта-функции. Н связи с этим
полное движение системы обязательно должно записываться в виде (5^1-
т. е. с использованием единичной функции I(/).
Расчет переходных процессов в системах автоматического управления 417
Как и и частотном методе, расчет переходного процесса можно выполнять
отдельно по интервалам функционального описания входного воздействия
либо целиком на всем интервале моделирования. В последнем случае пред-
начальные условия учитываются только один раз, и нс требуется сопряжения
интервалов друг с другом по конечным и начальным условиям
О Пример 5.2. Решить пример 5.1 методом вариации произвольных
постоянных.
Решение Во избежание подои составляющих свободного инжен^я нельзя
сокращать полиномы /1(5) и В($) на общий множитель (I +з). Система вто-
рого порядка (5.11, а) имеет следующие полюсы передаточной функции
5| =-1,52 = -2,
фундаментальную систему решений
У|(0 = ей(/) » е'Ч
прямую и обратную матрицы Вронского:
X]-v '»[/::»]
По формуле (5.20) получаем:
□ свободное движение, совпадающее с (5.12):
^w-м-о) л-»)[| :[К]=
= (2у(-0)+ у'(-0)>*' -(у(-0)+/(-0)>'2' = 2е*< -е^.
□ вынужденное движение при
л(/)в(/+ I) l(r) - (z+ 1) 1(/-2),
У(0 = 1(0 + 5(0 - 1(/ - 2) - 35(/ - 2)
и правой части дифференциального уравнения (5.11. а)
B(s)x(t) = х(0 + /(О = (/ + 2) 1 (Z) + 5(0 - (/ + 2) 1(т - 2) - 38(/ - 2):
= 0.25(2/ + l-е'2')- 1(/)-О.25(2/ +l-5e1(”2))- <(» -2);
О полное движение (5.4), совпадающее с (5.16):
41В__________ ________________________________________р»М5
y(t) = 2е-' - е‘2' + 0.25(2/ +1 - е'2* )• 1(/)- 0.25(2/ +1 - 5е’2(,“2))-1(/ - 2)=
0.5/ + 0.25 +2е’'-1.25е’2' V0</<2.
О.271е^ + 1.227е‘2('-2) V t £ 2 .
□
5.4. Метод интеграла Дюамеля
Второй альтернативный метод расчета переходного процесса без примене-
ния преобразования Лапласа использует априорно известную импульсную ха-
рактеристику »(/) блока, через который проходит входной сигнал x(t) 115, 16,
20, 22, 30]. Выходной сигнал этого блока при нулевых начальных условиях
Х')= J *»{т)х(/ -т)йт = f х(т)и(' - (5.21)
о о
называется интегралом Дюамеля (4.4) с ядрам w(t). В технической литературе
импульсную характеристику еще называют весовой функцией. Благодаря
встречным направлениям интегрирования ядра и входного сигнала, выраже-
ния (5.21) называют также интегралами свертки. В соответствии с выводом,
следуемым после (4.4), временная функция »(/) является оригиналом изо-
бражения
Из) =
где »Из) — передаточная функция блока, через который проходит сигнал
*(/)
Согласно (5.4) и структурной схеме, приведенной на рис. 5.3, выходной сиг-
нал системы формируется как
И0 = Ус»(0 + (И0 - 4(0) • 1(0
из следующих интегралов Дюамеля.
□ Свободного движения
.vo.(«)=i₽w-^t=p(/)
о
с ядром p(f) — импульсной характеристикой блока с передаточной функ-
цией Дд)/4(т), возбуждающего систему ненулевыми предначальными
условиями выходного сигнала Уп(~0), /е |0. п - |]. функция p(t) являет-
ся решением дифференциального уравнения
А(з)р(П « Я(08(0
при нулевых начальных условиях.
Расчет переходных процессов в системах автоматического управления_419_
□ Части вынужденного движения
j9(T>(r-t)dT = 9(O
о
с ядром q(t) — импульсной характеристикой блока с передаточной
функцией 0(л) / Л(5), возбуждающего систему ненулевыми предначаль-
ными условиями входного воздействия xW(-0),/e 10,/я - 1). Функция
q(t) является решением дифференциального уравнения
Л(5)?(Г) = 0(5)6(0
при нулевых начальных условиях.
□ Части вынужденного движения
v(0=f^H-T)dT
о
с ядром и<0. являющимся решением дифференциального уравнения
Л(5)И</) = 5(5)8(/)
при нулевых начальных условиях.
Для выделения в вынужденном движении собственной усоб(1) и установив-
шейся УустО) составляющих запишем выражение
Увын (')= J “ Wf ~ -?(»)= J Ml" 01т - 4) (5.22)
о о
относительно момента начала внешнего воздействия 10:
У.мИ(')= pfcM-*>-«(')•
'о
Установившийся процесс в устойчивой системе в момент времени / равен |30|
Ууст(') = Нт уВЬ1|,(0= р(тИ-т>1т- От 4) = /н{0)ф-О)10. (5.23)
о
т. к. вследствие необходимого условия устойчивости (4.5, а) имеют место
предельные свойства
lim <?(')= I'm
Вычитая (5.23) из (5.22), получим собственное движение
<524>
420 Глава 5
Отсюда видно, что в устойчивой системе собственное движение (5.24) затуха-
ет, а вынужденное движение сходится к установившемуся
НтУсов(0=0 =» l'm Лин (*)=>>(')•
<0-+-“
Если входной сигнал х(0 не имеет единого функционального описания на
всем интервале моделирования, то. например, представив его способом
(5.6). получим выходную переменную (5.7) в виде
4)=J и<4 - т) £ rt (т - /*) 1(т - tt ) dr + и (/) =
о *=о
= Х J4-th('r-,x)dT+M(/)=
4=0 /(
=х М-'*-’г>*(т)<,т+и(')=
4=0 О
= ЕуЛ'-'Л-К'“'I )+“(')’
4=0
где интегралы Дюамеля
л0»М-'кЮ4т
о
есть реакции системы на несмещенные входные сигналы х*(0 при нулевых
начальных условиях В частности, кусочно-постоянная аппроксимация
функции х(4) методом (5.8) дает расчетную формулу (5.9).
& Пример 5.3. Решить пример 5.1 методом интеграла Дюамеля.
Решение Предварительно по формуле интегрирования по частям получим
выражение
//(М> = /(О)5(г)-/'(о),
являющееся частным случаем (при т = 0) свойства фильтрации производной
дельта-функции, рассмотренного в разд. 3.2.1.
Определим необходимые импульсные характеристики решением по (5.20)
соответствующих дифференциальных уравнений с нулевыми начальными
условиями.
□ *✓*(/) + ЗнГ(0 + 2М0 = б'(/) + 6(4):
4)4 к’ -‘И (*М'(г))<И [се.^[5(т)
Расчет переходных процессов в системах автоматического управления 421
□ р“(1) + 3pV) + 2р</> = у(-0)5'(/) + (Зу(-О) + У(~0»о(0 = о'(/| + 36(/):
p(O=f к -e»](»(rh«-(t))<lT р,j=
-МЮ
□ <f(/) + 3<г(/) + 2q(t) = х(“0)5(/) => 9(0 = 0.
Рассчитаем интегралы Дюамеля для входных воздействий Х|(0 = 1(0 и
х2(0 = I КО:
л (0=Ш К' - =R2’dT=05 (’)•»(').
о о
Уг (')=f - т) • 1(г - т>т = J е-*(| - т>1т= 0.25 (2/ -1 + е’2* )• l(r).
О о
Переходный процесс на выходе объекта описывается формулой
Я/) = Л»(0 + У|(0 + Л(0 _ Зя(/ - 2) - у>(/ - 2) =
= 2е-' - е‘2' + 0.25(2/ + 1 - е’2/) 1(0 - 0.25(2/ + I - • 1(/- 2),
в точности совпадающей с (5.16, б). О
5.5. Метод пространства состояний
Современные методы анализа и синтеза систем автоматического управления
предполагают использование компьютеров для решения трудоемких в вы-
числительном плане задач. К таким задачам относится моделирование пере-
ходных процессов при произвольных входных воздействиях. Разработано
множество алгоритмов решения разнообразных дифференциальных уравне-
ний. Каждый алгоритм требует определенной формы задания исходных па-
раметров системы для моделирования ее движения.
5.5.1. Модель в пространстве состояний
Метод моделей е пространстве состояний (МПС) основан на представлении
Дифференциального уравнения л-го порядка
Глава 5
в котором степень т пашнома B(s) не превышает степени п полинома Л(з), в
виде системы п линейных дифференциальных уравнений первого порядка
vl'(0=ffuvi(0+-+ain‘',(0+Md
.............................................. (5.25,0)
. < (r)= e,tv, (;)+...+a„,v„ (t)+ b„x(t)
и алгебраического уравнения выходной переменной
Я/) - qv|(i) + ... + + Dx(t). (5.25. б)
Эти уравнения имеют эквивалентную векторную форму
4)= Av(r)+ Bx(t\ y(l)= Cv(t)+ Dx(t),
(5.26)
в которой v//) Vi = l, n — переменные состояния модели, однозначно и дос-
таточно определяющие поведение ее выхода y(t) при t > 0 в зависимости
от изменения входа х(/) и вектора предначального состояния v(-0). Мат-
рицы Ле R"'", Be R’*1, Се И*1'" и коэффициент D связывают перемен-
ные состояния и их производные с входной переменной х(/) и выходной
переменной y(t).
Смысл модели в переменных состояния заключается в том, что она сохраня-
ет соотношение между входом и выходом системы, т. е. передаточную
функцию, но в то же время позволяет перейти от одного дифференциально-
го уравнения высокого порядка п к системе п дифференциальных уравнений
первого порядка. Преимущество такого представления в том, что кроме двух
внешних переменных (входной и выходной) в пространстве состояний ста-
новится возможным одновременно исследовать поведение внутренних пе-
ременных системы.
Взаимосвязь между описаниями динамики системы передаточной функцией и
моделью в пространстве состояний можно установить, преобразуя по Лапласу
уравнения системы (5.26) с ненулевыми предначальными условиями И~0):
зЦз) - К-0) - ЛИз) + BX(s) => Цз) = (з/„ - Л)-М-0) + (з/„ - Л)-'5Х(з).
Из) = СИз) + DX(s) = Clsl„ - Л)-'И-0) + С(з/„ - Л)~'ВХ(з) + DX(s),
где 1„ — единичная матрица размерности п х п. Отсюда при нулевом векторе
К~0) получаем выражение передаточной функции системы через матрицы
модели (5.26):
(5.27)
(Из) - С(з/„-АГ'В+ D.
Расчет переходных процессов в системах автоматического управления 423
Обратное преобразование Лапласа л х «-матрицы (з/„ - Л)"1 называется
фундаментальной матрицей системы
Ф(0 = Ь-'{(5/я-Л)-1), (5.28)
с помошью которой можно записать изменение выходной переменной мо-
дели во времени как
И0=СФ(/>(-О)+с[ф(, -т)Вл(т)йт + Ол(/) (5.29)
><•(') . -° _____________________
>.„,(/)
Первое слагаемое в (5.29) представляет собой свободное движение модели,
зависящее только от вектора предначальных условий И_0) Второе и третье
слагаемые составляют вынужденное движение, определяемое входным сигна-
лом х(/).
Вычисление фундаментальной матрицы Ф(г) по (5.28) очень трудоемко даже
для невысоких значений порядка л В то же время можно записать прямое
решение векторного дифференциального уравнения
✓(/) = ЛИО + Вх(1)
по аналогии с таким же скалярным:
v(/)=eA'v(-O)+ |еА^’)Вх(т)0т1
-о
откуда получаем решение задачи моделирования
y(r)=CeA'v(-0)+C |eA(''T)fix(x)dT + Dx(t). (5.30)
Матричная экспонента
е* = /я+Л/ + "1+"1+... = У"1
2! 3! £ й
представляет собой абсолютно сходящийся ряд. вычисляемый за конечное
число шагов с любой наперед заданной точностью для всех п1 элементов
матрицы М
Сравнение двух форм решений (5.29) н (5.30) позволяет записать выражение
фундаментальной матрицы системы в более удобной для компьютерного
вычисления форме:
424
________________________________Глаадд
В (5.26) и (5.30) требуется знать вектор предначального состояния v(~0).
Для его получения составим систему п векторных уравнений предначаль-
ных состояний
y(-0)=Cv(-0)+Dx(-0)
y'(-0)=Cv'(-0)+Dx(-0)=CAv(-Q)+CBx(-0)+ D.r'(-0)
имеющую решение
с блочными матрицами
v(-0)=H-‘ у(-0) ' у'(-0) -// '/ Г х(-о) - л'(-0) (5.31)
У" ’’(-о) 0)
Н = СА , L= О 0 СВ D .. 0 .. 0 О' 0 (5.32)
_САп-' СЛп~2В САа~3В . . СВ D
Матрица Н называется матрицей наблюдаемости Ее невырожденность по-
зволяет оценить вектор состояния модели по измерениям входного и вы-
ходного сигналов системы. Совокупность формул (5.27) - (5.32) дает анали-
тическое решение задачи построения переходного процесса методом про-
странства состояний с известными параметрами {А, В, С, D} и заданными
предначальными условиями входной и выходной переменных.
5.5.2. Расчет параметров моделей
в пространстве состояний
Основная трудность применения модели (5.26) и ее решения (5.30) заключа-
ется в выборе переменных состояния V/(0- Согласно (5.25), они должны
представлять процессы, в которых скорости изменения некоторых величин
зависят от значений этих же величин и входного воздействия. Очень часто
переменные состояния системы имеют отвлеченный характер и не пред-
ставляют собой какие-либо физические процессы в конкретных точках сис-
темы управления.
Количество различных моделей в пространстве состояний бесконечно из-за
свободы выбора переменных состояния. Из множества возможных иарамет-
расчет переходных процессов в <
некого управления
425
ров {Л, В, С, D}, имеющих в сумме n1 + 2n + 1 коэффициент, можно выде-
лить некоторые особенные канонические (закономерные, регулярные) формы.
Число независимых коэффициентов канонической формы должно быть
равно л + m + 1 — числу коэффициентов приведенной передаточной функ-
ции системы
(5.33)
полученной делением полиномов B(s) и Л(з) на старший коэффициент
а„ * 0 и дополнением полинома B(s) фиктивными слагаемыми
= = V = 0.
Остальные п2 + п - m параметров канонической формы - числа 0 и I
Ъ разд. 1.8.3 нами рассмотрена последовательность получения канонической
структурной схемы динамического объекта. Применительно к передаточной
функции (5.33) она изображена на рис 5.10. Ес уравнения состояния (5.25)
принимают вид
(5.34)
Рис. 5.10
426
/лава 5
а параметры модели (5.26) равны
’ 0 1 ... О
(5.35)
-по -а( ... -ля_|
D = b„, ct = bi-\ - Dat-t V i = 1, и.
Заметим, что прямая связь от входа к выходу существует лишь в случае рав-
ных степеней полиномов B(s) и Л(з): при т = п в (5.34) и (5.35) получим
D * 0. Если т < п, то прямая связь отсутствует (D = 0), а при т < и - 1 мат-
рица С имеет нулевые коэффициенты ст+2 + с„. Таким образом, канониче-
ская форма (5.34) имеет п + т + 1 независимый параметр.
Полученная модель в пространстве состояний не очень удобна для расчета
переходного процесса по формуле (5.30) с начального состояния (5.31), т. к.
ее матрица наблюдаемости И относится к матрицам общего вила. Целесооб-
разно строить модель с единичной матрицей Н. Для этого нужна матрица
С=[1 0 ... 0] и структурная схема модели, показанная на рис. 5.11. Уравне-
ния состояния такой модели имеют следующий вид:
rv;=v2 + p,x.
v«-l =v„ +
*>-eoV|---en-ivn+p„x
y = v1+Dx
(5.36)
Рис. 5.11
Расчет переходных процессов в системах автоматического управления___427
рассчитаем параметры модели, выразив переменные состояния в (5.36) че-
рез входную и выходную переменные:
V/ V» = 1.h.
J=0
Подставив эти зависимости в формулу
SV„ « -fl0Vl - - ~ «/T-l
и сгруппировав подобные члены, получим уравнение
£а,?у + *"у = £1 Рч.( + Ьл + ОЛт
1=0 i=0^ >=HI J
Сравнивая его с операторным уравнением
1=0 i=0
получим параметры модели (5.26)
‘ 0 1 ... 0
А~ 0 0 ... 1
-яо — al — Л„-|
с коэффициентами р| + вычисляемыми рекуррентным или матричным
способом:
ГМ
... . с = [1 0 ... о]. D=bn (5.37,в)
[Рл]
Р< = V. - ~«,,-,ьп vi=i,n.
(5.37, б)
в последнем выражении решение всегда существует, т к здесь обращается
Феугольная матрица с единичной диагональю. Коэффициент прямой связи
0*0 лишь при m = я. Если m < л, то прямая связь отсутствует, а при
*"< л - I матрица В имеет нулевые коэффициенты р| + Рл-ж-i Таким обра-
зом, число независимых параметров канонической формы (5.36) равно
л + л - (л - m - 1) л + m + I.
428
ГлаваS
5.5.3. Программное моделирование
переходных процессов в пространстве состояний
Модель (5.36), (5.37) удобно использовать для расчета переходных процес-
сов программным методом, например, в среде Mathcad, имеющей широ-
кий набор встроенных функций решения обыкновенных дифференциаль-
ных уравнений и развитые графические средства отображения результатов
вычислений.
Несмотря на различные методы решения, каждая функция требует задания
следующих величин:
□ дифференциального уравнения в форме Коши
/(/) = F(v, t,...)
путем определения векторной функции Дг, /, ...) е R" векторного аргу-
мента v е Rn, времени I и, возможно, других ранее определенных аргу-
ментов, например, входного воздействия х(/). Вместо ручного определе-
ния единичной функции 1(0 можно использовать встроенную функцию
Mathcad «(t);
□ границ временнбго диапазона моделирования / е |ф, Od и числа К ин-
тервалов между точками вывода решения
□ начального значения вектора состояния Цф);
□ при необходимости — матрицы Якоби / размерности п х (л + 1):
В результате расчета функции возвращают (К + 1) х (л + 1)-матринУ
(рис. 5.12), левый столбец которой содержит отсчеты времени от /0 до /Д. а
строки оставшейся части заполнены векторами решений v(4).
Рис. 5 12
Расчет переходных процессов в системах автоматического управления 429
Перечислим функции Mathcad, предназначенные для численного решения
обыкновенных дифференциальных уравнений |19|:
□ rkf ixed(v, to. tK, к, F) — использует хорошо зарекомендовавший себя в
полувековой вычислительной практике метод Рунге - Кутта четвертого
порядка с постоянным шагом интегрирования, равным (/* - /о) / К’,
□ Rkadept (v, to, tK, к,F) - функции аналогична вышеописанной функции
rkfixed, но выполняет адоптацию (настройку) шага интегрирования к
скорости изменения решения, что повышает точность на быстрых и ус-
коряет расчет на медленных участках переходного процесса;
□ Buistoer (V, to, tK, к, F) - даст повышенную ТОЧНОСТЬ ДЛЯ гладких ре-
шений;
□ Stiffb(V,tO,tK,K.F.J) — использует метол функции Buistoer ДЛЯ ре-
шения жестких дифференциальных уравнений;
□ stiffr(v,to,tK,K,F.j) — использует метод Розенброка для решения
жестких дифференциальных уравнений
При построении графика переходного процесса по оси абсцисс откладыва-
ются значения первого столбца матрицы решений (рис. 5 12). а по оси ор-
динат — значения
Я'*) = ИО*) + Dxitid,
формируемые из элементов второго столбца и отсчетов входного воздействия.
& Пример 5.4. Решить пример 5.1 программным методом пространства со-
стояний в Mathcad.
Решение. На рис. 5.13 приведен листинг программы с решением задачи мо-
делирования переходного процесса в пространстве состояний
Результат моделирования полностью совпадает с графиками y(i), получен-
ными другими ранее изученными методами. О
& Пример 5.5. Рассчитать переходный процесс на выходе схемы моста Ви-
на - Робинсона (см. пример 1.6), описываемой дифференциальным уравне-
нием (1.14)
Зу+97У + 372Г-т+ 7V.
Входное напряжение представляет собой линейно частотно-модулированное
колебание единичной амплитуды:
x(t) = sin(w(/) • /), «ХО = Ц> + О/,
где Ц) — начальное значение частоты при / = 0;
й = ——— — скорость изменения частоты с шо до <о* за время /<.
1К
Построить графики изменения частоты ю(/), сигналов лг(/) и y(t) для следую-
щих исходных данных:
430
.ГлаваS
____ I co
Д = 710 = 3.16, to =- = 100лрад/с, a)0 = —, о>д= (Ц.Д, /л = 0.5 с.
' т Д
Проанализировать полученные результаты совместно с частотными характе-
ристиками схемы (см. пример 2.2).
Решение. Данный пример отличается от всех предыдущих тем, что весьма
затруднительно, если вообще возможно, найти изображение линейно час
тотно-молулированного сигнала для построения переходного процесса ме-
тодом преобразования Лапласа.
На рис. 5.14 приведен листинг Mathcad-программы с решением задачи мо-
делирования схемы моста Вина - Робинсона с линейно частотно-
модулированным сигналом на входе методом переменных состояния. Пара-
метр девиации частоты Д задан так, чтобы диапазон частот сигнала
<И) S ш(/) < ш* составлял 1 дек, а частота на которой согласно амплитуд-
но-частотной характеристике (см. рис. 2.21) происходит полное подавление
колебаний, располагалась в его середине (в логарифмическом масштабе).
Си а:=(2 3 ,,т ь=<' 1 0)Т
Y0 := ( I 0 )Т ХО := ( 0 0 )Т
tk 6 К := 600 x(t)(t+ 1) Ф(0-Ф(2 -1)
В := submatrix(p. 1,2.0.0)
D 0 1 С := ( I 0 ) D := ро
:-B)n D F(!.v)*A.v+Bx(t) vO:=YO-LXO
М := Rkadapt(vO.O.tk.K,F) k := 0 К «к - Mk,o
4“«(<к) Ук:=мк.1 + Охк
Рис. 5.13
Рио. 5.14
432_____________________________________________________________Глава 5
В результате моделирования наглядно проявляются свойства схемы моста
как режекторного фильтра, согласующиеся с его частотными характеристи-
ками. Увеличение частоты входного сигнала приводит сначала к постепен-
ному уменьшению амплитуды выходных колебаний от 0.333 вплоть до их
полного исчезновения. Далее амплитуда выходных колебаний вновь увели-
чивается до 0.333, что равно коэффициенту усиления схемы на высоких час-
тотах. Что касается фазового сдвига, то сначала он отрицательный (выход-
ной сигнал отстает от входного), а затем — положительный (пики графика
у(г) опережают пики х(/)), что также соответствует построенной на рис. 2.21
фазочастотной характеристике Ф(ш).
Отметим, что поскольку частота входного сигнала переменна, то амплитуды
и фазовые сдвиги выходных колебаний нигде точно не соответствуют час-
тотным характеристикам схемы, т. к. по определению они измеряются в ус-
тановившемся режиме, который наступает через ЗГ, = 25 мс. Но этой воз-
можности у схемы нет. Читателю предлагается самостоятельно изменить
форму сигнала, например, так, чтобы при достижении частоты а\. она оста-
валась постоянной. Вот тогда будет видно, что через 25 мс после фиксации
частоты амплитуда выходных колебаний затухнет до нуля. О
Перечислим весьма достойные, по мнению автора, аргументы в пользу мето-
да моделирования сложных систем в пространстве состояний
□ Переменные состояния несут больше информации об объекте по срав-
нению с его передаточной функцией. При надлежащем выборе они мо-
гут описывать физические величины (скорости, ускорения), представ-
ляющие интерес для исследователя.
□ Возможность алгоритмического восстановления неизмеряемых перемен-
ных векторной модели по измерениям входа и выхода превращает метод
пространства состояний в ценный инструмент изучения процессов в
точках системы, труднодоступных или вовсе недоступных для установки
датчиков.
□ Модели в пространстве состояний и схемы их реализации на интеграто-
рах с присущей им легкостью программного добавления в нужные точки
системы внешних воздействий как детерминированного, так и стохасти-
ческого характера, являются наилучшим инструментом для имитацион-
ного моделирования поведения сложных систем в условиях, близким к ре-
альным.
□ Метод пространства состояний одинаково просто моделирует переход-
ные процессы как при произвольных входных воздействиях, так и в не-
стационарных системах, для которых в рамках операторного метода на-
хождение изображений и оригиналов может оказаться проблематичным
или невозможным.
□ Векторная модель системы высокого порядка позволяет легко решать за-
дачи анализа и синтеза с помощью компьютера, тогда как использова-
Расчет переходных процессов в системах автоматического управления 433
ние для этих же целей передаточной функции наталкивается на сложно-
сти вычислительного и интеллектуального характера.
□ Описание в пространстве состояний системы с одним входом и одним
выходом естественно обобщается на случай многомерной и многосвяшой
системы с векторными входом и выходом, исследование которой други-
ми методами чрезвычайно громоздко.
□ Простота перехода от непрерывной модели системы в пространстве со-
стояний к се дискретной модели |25| дала мощный толчок развитию со-
временных методов анализа, компьютерного моделирования и алгорит-
мов цифрового управления самыми сложными техническими объектами
в реальном масштабе времени.
Завершая главу и окидывая взглядом рассмотренные методы расчета пере-
ходных процессов, приходим к окончательному выводу поведение систем во
времени предпочтительнее изучать методом компьютерного моделирования в
пространстве состояний, а не путем решения дифференциальных уравнений,
исчисления интегралов Дюамеля или применения преобразования Лапласа.
Данные конкурирующие методы применимы фактически к системам невы-
соких (первого и второго) порядков Однако для моделей высокого порядка,
какими описываются практически все современные технические объекты,
моделирование в пространстве состояний является необходимым, а часто и
единственным инструментом исследования
ГЛАВА 6
Одно я познал м свою долгую жизнь: вся ма-
ша наука наивна и проста по сравнению с ре-
альностью - и вес же это санов драгоцен-
ное, что у нас есть
Методы проектирования систем
автоматического управления
6.1. Основные задачи синтеза регуляторов
Сложная проблема создания системы автоматического управления с хоро-
шими статическими и динамическими свойствами включает следующие ос-
новные задачи:
□ обеспечение устойчивости (стабилизация) системы и повышение запаса
ее устойчивости;
□ повышение точности регулирования в статическом режиме и обеспечение
нужной степени астатизма;
□ улучшение показателей качества переходных процессов — уменьшение
времени установления /у, перерегулирования а и числа колебаний NK.
Исходя из требований к статическим и динамическим свойствам системы
автоматического регулирования, необходимо выбрать оптимальную с точки
зрения выбранных критериев структуру — состав элементов системы — и
определить параметры элементов. Эти данные позволяют сформировать се
желаемые характеристики на основе компромисса между качеством и точно-
стью, с одной стороны, и простотой технической реализации — с другой.
Обеспечение устойчивости и желаемого качества регулирования в системе
□ целенаправленным выбором имеюшнлея элементов системы. К функцио-
нально необходимым элементам систем управления относятся датчики
Методы проектирования систем автоматического управления_____________435
сигналов, измерительные устройства, усилители мощности, преобразова-
тели сигналов, исполнительные устройства, Они подбираются по специа-
лизированным каталогам и справочникам на основе требований к разви-
ваемой мощности, быстродействию, предельным скоростям и ускорениям,
допустимым статическим погрешностям, помехоустойчивости и т. д. Про-
ектировщик системы управления должен ясно понимать, что улучшение
качества системы в первую очередь связано с оптимизацией свойств самого
объекта управления, чтобы они соответствовали требованиям техническою
задания и делали решение задачи синтеза принципиально возможным;
□ если объект либо вообще невозможно изменить, либо он уже был изме-
нен настолько, насколько возможно, но качество системы все сше не-
удовлетворительно, то остается единственная возможность наделения
системы желаемыми свойствами путем введения дополнительного эле-
мента, который исправляет (корректирует) их в нужном направлении.
Корректирующее устройство — это функциональный элемент системы авто-
матического управления, доставляющий ей необходимые свойства: устойчи-
вость и желаемые показатели качества переходных процессов
Как отмечалось во введении, регулятором в широком смысле является вся
система управления за вычетом объекта. Задача регулятора в узком смысле
состоит в выполнении аналоговых, логических и арифметических операций
по расчету управления, т. е. в чистом виде исполнение функций корректи-
рующего устройства.
Рассмотрим основные типы регуляторов и их свойства.
□ Последовательный регулятор с передаточной функцией Лц(т) (рис. 6.1)
включается в прямую цепь системы непосредственно после сравниваю-
щего элемента или после предварительного усилителя. Передаточная
функция замкнутой системы с последовательным регулятором равна
Рио. 6.1
Простейшим корректирующим устройством данного типа является про-
порциональный усилитель Л„(л) Л'„. формирующий П-управдение
(В.2). Регулятор может дополнительно использовать производи) ю ошиб-
436
ки регулирования е'(6, что, как будет показано ниже, увеличивает запас
устойчивости и улучшает качество переходною процесса. При включе-
нии в закон управления интеграла ошибки обеспечивается астдтизм
замкнутой системы и нулевая установившаяся ошибка о н
практике автоматическою управлении широко распространены про-
мышленные ПИД-ре|уляторы с передаточной функцией (1.37) и на-
страиваемыми параметрами А,,. Д’, и А",, Применяются и более сложные
последовательные корректирующие устройства
□ Прямой параллельный регулятор с передаточной функцией Alin(j)
(рис. 6 2) включается параллельно подлежащей коррекции подсистеме
Й'|(,г) в прямой цепи системы, имеющей передаточную функцию
И1т) - ИШ )Fj(s).
Рис. 6.2
Сравнивая (6.1) с передаточной функцией замкнутой системы с данным
типом регулятора
-« .ЯШ-
получим условия эквивалентности регуляторов
R.W-1+ « R„,M - UW ~ (6.2, в)
позволяющие перейти от одного его типа к другому, возможно, более
простому в технической реализации
Прямой параллельный регулятор в виде широкополосною усилителя е
передаточной функцией А„„(з) “ К„„ может быть полезным, например,»
следующих случаях:
• для устранения в подсистеме с нсминималыго-фазовой передаточной
функцией
>управления
npaaoeo нуля ?i " I / Т| > 0. лающего н переходном процессе отрица-
тельное перерегулирование, путем выбора коэффициента усиления
регулятора
такого, что скорректированная передаточная функция полсистемы
1+ гр
приобретает отрицательный нуль
. для придания по «очной функцией
форсирующих свойств без использования дифференцирующих уст-
ройств. усиливающих высокочастотные помехи:
□ Обратный локальный регулятор с передаточной функцией ЯаДз) (рис. 6.3)
охватывает местной обратной связью - отрицательной (верхний знак)
либо положительной (нижний знак) — подлежашнй коррекции элемент
системы, чаще всего оконечный каскад усилителя или исполнительное
устройство. Последствия охватывания динамических элементов конту-
ром обратной связи подробно рассмотрены в разд. / 7 и разд 2 5.
Рио. 6.3
Сравнивая с (6.1) передаточную функцию замкнутой системы с данным
типом регулятора
получим условия эквивалентности регуляторов:
Яп(*)=----\—Г\ ~ *<v.0 = ± (6.2, 6)
nV/ 1±Й^О)
Локальная положительная обратная связь, кроме целей генерирования
автоколебаний (см. разд. 2.5.3), используется для увеличения статиче-
ского коэффициента усиления охватываемого элемента в существенно
большем диапазоне, чем при подключении последовательного усилите-
ля. Например, охватив устойчивую статическую подсистему с переда-
точной функцией
контуром положительной обратной связи через усилитель ЯолСО =
с коэффициентом усиления
0<*< —,
Кг
получим скорректированную подсистему со следующими передаточной
функцией, статическим коэффициентом усиления и характеристическим
полиномом:
W =1-К2К0Л + зЩз).
Неумеренно большая положительная связь является дестабилизирующим
фактором: сети по недосмотру задано значение Я^, > 1 / К2, то охвачен-
ная ею подсистема становится неустойчивой.
Локальная отрицательная обратная связь широко применяется в автома-
тике для стабилизации и улучшения качества работы элементов системы,
склонных к неустойчивости или слишком инерционных, имеющих
большую постоянную времени При этом неустойчивые или близкие к
границе устойчивости полюсы передаточной функции подсистемы, охва-
ченной локальной отрицательной обратной связью, сдвигаются влево,
что либо делает ее устойчивой, либо повышает степень устойчивости,
быстродействие и уменьшает колебательность:
• неустойчивая подсистема первого порядка с передаточной функцией
Методы проектирования систем автоматического управления_____________________439
охваченная гибкой отрицательной обратной связью дифференцирую-
щего типа /^(s) = TMs при Топ > Т2 / Л'2, превращается в устойчивое
звено
W2 _ К
l+Ts
с постоянной времени Т= К2Т0П - Т2 > 0;
• инерционная подсистема первого порядка с передаточной функцией
и большой постоянной времени Т2 с помощью локальной отрица-
тельной обратной связи через широкополосный усилитель
Лол(5) = КОЛ становится более быстродействующей: ее передаточная
функция
К
1+ЖЛ, "1+Ь
имеет постоянную времени Т =-------< Т2:
1+
• колебательная подсистема второго порядка
с малым коэффициентом затухания << 1 при охватывании гибкой
отрицательной обратной связью /^,(5) = T01s превращается в колеба-
тельную полсистему с увеличенным коэффициентом затухания
Выбрав постоянную времени регулятора из условия
можно превратить колебательное звено в два апериодических устой-
чивых звена с постоянными времени, равными
440
Глава 6
В подсистеме Wjfj), охваченной глубокой отрицательной обратной свя-
зыо. в рабочем диапазоне частот выполняется условие (1.24)
l*2(j“)^(i“)l » I =» А2(ш) + £ол(ш) > 20 дБ,
а ее передаточная функция становится близкой к
И^) . 1
IWjGJVs) RM(Sy
Вывод
Свойства замкнутой системы слабо чувствительны к изменениям параметров
подсистемы IVj(s), охваченной цепью глубокой отрицательной обратной связи
Рассмотрим еще раз (см. рис. 2,30, б) схему усилителя с конечным коэф-
фициентом усиления А’у < », охваченного контуром глубокой отрица-
тельной обратной связи через четырехполюсник с передаточной функ-
цией lF0(s) (рис. 6.4, в). По структурной схеме, построенной на
рис. 6.4, б, определяем передаточную функцию замкнутой системы
Рис. 6.4
Чем идеальнее усилитель в прямой цепи (Ку -л о»), тем ближе эта пере-
даточная функция к идеальному значению, не зависящему от малых
относительных изменений Ку.
Это свойство лежит в основе конструирования схем на операционных
усилителях путем установки навесных элементов в соответствии с тре-
буемой передаточной функцией схемы без учета внутренних свойств
операционного усилителя. Показательный пример такого конструирова-
ния — использование табл. 1.3.
Методы проектирования систем автоматического управления
441
Применение глубокой отрицательной обратной связи — основной способ
навязывания замкнутой системе желаемых свойств и подавления нежела-
тельных свойств
□ Регулятор в цепи отрицательной обратной связи системы с передаточной
функцией /<>(У> (рис. 6.5) является обобщением локальной отрицатель-
ной обратной связи и выполняет аналогичные функции применительно
ко всей системе. Сравнивая с (6 1) передаточную функцию замкнутой
системы
И,',). «'W
Рис. 6.5
получим условия эквивалентности регулятора в цепи отрицательной об-
ратной связи и последовательного регулятора Rn(sY
i+*„QXM*)-i)
М’М*)
(6.2. в)
По сравнению с другими типами корректирующих устройств регулятор в
отрицательной обратной связи незаменим при проектировании следящих
систем с масштабированием уставки (роботов, манипуляторов, тренаже-
ров, прецизионных устройств микроэлектроники и микрохирургии), где
требуется воспроизведение выходным сигналом y(t) формы задающего
воздействия g(t) с увеличением либо уменьшением масштаба в М раз:
.Иг) = Л/Н').
Записав условие инвариантности воспроизведения уставки как равенство
передаточной функции замкнутой системы значению масштаба на всех
частотах уставки
----- = М V5=jo). (6.3)
l+W'fcXO)
Получим передаточную функцию регулятора, решающего задачу мас-
штабного слежения:
R°^~ M ’ Иф)'
(6.4, а)
Отсюда при М = I получаем регулятор для точного воспроизведения устав-
ки на выходе замкнутой системы:
(6ЛЙ)
По формулам эквивалентности (6.2, в) получим передаточную функцию
соответствующего последовательного регулятора
откуда видно, что при I/ = 1 с помощью последовательного регулятора в
принципе невозможно точное слежение за изменяющейся во времени устав-
кой. Регулятор, установленный в контуре отрицательной обратной связи,
такой уникальной способностью обладает.
Как правило, условия инвариантности (6.3) выполнимы лишь в опреде-
ленном диапазоне частот. Если этот диапазон накрывает полосу пропус-
кания системы и полосу частот уставки #0). то на выходе системы будет
наблюдаться масштабная копия уставки у<т) = A/g(T).
Удовлетворив условие статической инвариантности в установившемся ре-
жиме (ш = 0) выбором регулятора-усилителя
<w’’1
получим астатическую систему масштабного слежения без введения в пря-
мую цепь контура управления интегратора, обычно замедляющего пере-
ходные процессы.
Для иллюстрации сказанного построим по алгоритму (5.10, а) и сравним
переходные процессы в следящих системах с объектом из примера 5.1,
имеющим передаточную функцию
цф)=- It*
2 + За + з2
при нулевых иредначальиых условиях и уставкой сложной формы:
«(0=(' + ‘Х1(')-1(г-15))-151((-25)+1^1 + еХр^^^ 1(/-35). (6.5)
На рис. 6.6, а построены процессы слежения за уставкой g(t) с масштаб-
ным коэффициентом М “ 2:
Методы проектирования систем автоматического управления
график / — совпадающие выходные сигналы у(г) = 2g(t) двух следя-
щих систем: с вычисленным по (6.4, о) оптимальным обратным
ПД-регулятором Яо(т) = -1.5 - s и эквивалентным ему по (6.2. е) по-
следовательным ПД-регулятором R„(s) = -4 - 2$;
график 2 — выходной сигнал у(/) следящей системы с вычисленным
по (6.4, в) статическим обратным регулятором Rv = -1.5. передаточ-
ной функцией H^(j) = 2 / (1 + 2s) и временем установления /у = 6 с.
Рис. 6.6
На рис. 6.6, б построены переходные процессы в следящих системах с
коэффициентом масштабирования А/= I:
• график / — совпадающий с уставкой выходной сигнал следящей сис-
темы с оптимальным обратным ПД-регулятором Яо(т) = -I — я
• график 2 - выходной сигнал следящей системы со статическим об-
ратным регулятором Ro = -I, передаточной функцией
W,(s) = 1 / (1 + s) и временем установления гу = 3 с.
Главам
График переходного процесса в системе с последовательным регулято-
ром не показан нз-за принципиальной нереализуемое™ такого типа ре-
гулятора при М= I.
О Комбинированный регулятор по уставке и ошибке (рис. 6.7) формирует
управляющее воздействие
*(/) = хМ + xtf
с изображением
X(s) == Rr(s)E(s) + R^Gts).
Первая составляющая управляющего воздействия xe(t) = /?,.(л)е(/) есть
управление по ошибке и решает главную задачу стабилизации системы и
обеспечения желаемых показателей качества движения в отсутствие регу-
лятора R^s).
Второе слагаемое x/t) - R^s)g(t) в виде прямого, а не косвенного через
контур обратной связи, воздействия уставки на вход объекта есть управ-
ление по уставке. Оно придает системе форсирующие свойства и улучша-
ет динамическое качество слежения за уставкой, увеличивая быстродей-
ствие в ее отработке.
С помощью регулятора по уставке также можно решить задачу масштаб-
ного слежения за уставкой. Приравняв по условию инвариантности вос-
произведения уставки передаточную функцию замкнутой системы
*’w” +«,<.>(.>
(6.6)
к желаемому значению М, получим регулятор масштабного воспроизведе-
ния уставки.
+ -l)/?f(s). (6.7,fl)
Отсюда при М = I вытекает регулятор точного воспроизведения уставки на
выходе замкнутой системы:
jfenww проектирования систем автомагического управления
Л*(,)=^ (6'7,б)
По условию статической инвариантности И^(0) = М. действительному
только в установившемся режиме, получим регулятор-усилитель
Л»=^) + (М-1К(0) (6.7, в)
и астатическую следящую систему бет использования интегратора.
Сравнивая передаточные функции (6.6) и (6.1), получим формулу экви-
валентного перехода от комбинированной системы с регуляторами /Ц.т)
и Rg(s) к системе с последовательным регулятором R„(sY
Высокая эффективность регулятора по уставке иллюстрируется на
рис. 6.8, где построены переходные процессы слежения за уставкой (6.5)
в двух замкнутых системах, нс использующих для чистоты эксперимента
регулятор по ошибке, т. е. при /?,,(т) = 1:
• график / изображает выход замкнутой системы с единичной отрица-
тельной обратной связью без регулятора по уставке, г. е при
R/s) = 0;
• график - точно совпадающий с уставкой, соответствует вычисленно-
му по (6.7, б) оптимальному ПД-регулятору R£s) = 2 + г.
• трафик - выход следящей системы с вычисленным по (6.7, •) ста-
тическим регулятором по уставке Rt(s) = 2, передаточной функцией
(6.6) (K3(j) = 3 / (3 + j) и временем установления /у = 1 с.
Рис. 6.8
Глам£
Очевидно, что введение в систему управления регулятора по уставке
Я/т) существенно улучшает статическое качество слежения благодаря
создаваемому им астатизму. Динамическое качество (высокое быстро-
действие, отсутствие перерегулирования) определяется, в основном, ре-
гулятором по ошибке ЯДз).
О Комбинированный регулятор по возмущению и ошибке с передаточными
функциями Я/з) и ЯДз) предназначен для компенсации действующих на
объект внешних (не управляющих) воздействий Пусть точка приложе-
ния возмущения ДО, проходящего через фильтр Ufa), делит систему на
две подсистемы с передаточными функциями JF|(5) и Ufa) (рис. 6.9).
Система управления может включать ранее спроектированный регулятор
по ошибке Re(s), например, последовательного типа.
Комбинированный регулятор формирует управляющее воздействие
х(1) - х//) + х//)
с изображением
Х(з) • КАз)Е(з) + Я/з)/Ь).
Первая составляющая х,(0 = ЯДт)е(0 есть управление по ошибке и решает
главную задачу стабилизации системы и обеспечения желаемых показа-
телей качества движения в отсутствие регулятора Я/.т)
Второе слагаемое х/Г) • Я/.г)Д/) в виде прямой, а не косвенной через
контур обратной связи, компенсации воздействия возмущения на объект
сеть управление по возмущению, противодействующее его влиянию. По-
нятно. что для компенсации возмущения Д/) необходимо его априорно
знать или иметь возможность измерить.
Записав по принципу суперпозиции операторное уравнение выходного
сигнала
Из) - W^WGU) + ^.т)Жт)
замкнутой системы с передаточными функциями
Методы проектирования систем автоматического управления
447
м=2Я - Ш)
,и 1+яД^О)
получим из условия инвариантности по возмущению H^/s) - 0 передаточ-
ную функцию регулятора
wr(*)
Л/0-
(6.9. a)
полностью компенсирующего произвольное возмущение Д0. Удовлетво-
рив условие статической инвариантности И'^/О) = 0, получим статический
регулятор
И7(о)
иф)’
(6.9, б)
компенсирующий постоянное возмущение Д1) = Jo в установившемся
режиме.
Проектирование главного регулятора по ошибке /?,(.т) может проводиться
независимо от регулятора по возмущению ЯДз). т. к. последний даже при
неполной инвариантности слабо влияет на характеристический полином
замкнутой системы, а значит, и на показатели ее качества.
Высокая эффективность применения регулятора по возмущению показа-
на на рис. 6.10. Для чистоты эксперимента приняты нулевая уставка
gU) = 0 и регулятор по ошибке RJs) = 1 Объект управления взят из при-
мера 5.1 и разделен на две последовательно соединенные подсистемы с
передаточными функциями
И',(,)3Й7* и'-’^=гЬ
Без внешних возмущений замкнутая система пребывает в состоянии ус-
тойчивого равновесия с выходным сигналом y(t) » 0.
Подвергнем вторую подсистему влиянию возмущения Д/). изменяющего-
ся по формуле уставки (6.5) и проходящего через фильтр низких частот с
передаточной функцией
448
„Глава 6
В замкнутой системе с единичной отрицательной обратной связью без
регулятора по возмущению, т. е. при Я/з) = 0, выходной сигнал претер-
певает значительные отклонения от состояния равновесия в сторону те-
кущего возмущения (график Г).
возмущению Я/ = -2 получим передаточную функцию из (6.8)
tv < > ~(7 + 2з)з
V (l + s)(3 + s)(5 +j)
с дифференцирующим и форсирующим свойствами, благодаря которым
статическое отклонение выходного сигнала при постоянном возмущении
равно нулю (|рафик 2).
Оптимальный регулятор по возмущению, рассчитанный по (6.9, а), опи-
сывается передаточной функцией
а выход использующей его системы управления остается невозмушен-
ным ИО = 0. т. е. влияние помехи fil) оказывается полностью скомпен-
сированным.
При проектировании систем автоматического управления применяются
также сочетании различных типов регуляторов. Далее мы будем рассматри-
вать системы с единичной отрицательной обратной связью и последователь-
ным регулятором Я(з), имея в виду, что другие типы регуляторов могут
быть пересчитаны к последовательному типу по формулам эквивалентно-
сти (6.2). Используемое во всех замкнутых системах управления сравни-
вающее устройство, жтясляюшее ошибку регулирования е = g - у, имеет
Методы проектирования систем автомагического управления_____________449
простейшую схемную реализацию в виде каскада на одном операционном
усилителе (рис. 6.11).
РИС. 6.11
В данной главе предпринимаются два fiodxoda к решению задачи симе»
последовательного регулятора:
□ частотный подход, оперирующий частотными характеристиками объ-
екта, желаемого разомкнутого контура и регулятора. По логарифмиче-
ским характеристикам последнего восстанавливается передаточная
функция /?(з);
□ спектральный подход, оперирующий распределением полюсов s, и нулей
Zj объекта, желаемого разомкнутого контура и регулятора. По спектру
последнего строится передаточная функция Я(з).
Переходим к рассмотрению задачи синтеза регулятора частотными метода-
ми. Исходными данными для проектирования являются
□ передаточная функция И^.г) и частотные характеристики Л(ш),
ф(ш), Z(w) и Ф(ы) объекта в прямой цепи системы управления;
□ желаемые показатели качеств;! функционирования замкнутой системы
• статические ошибки регулирования по положению, скорости и про-
изводным высших порядков;
• время установления
• перерегулирование о;
• запасы устойчивости ио амп штуде / и фазе ф.
Методика синтеза последовательного регулятора основана на соотношениях
%.(*)= И'МД
Аж (w) = а(ш)ар (си). <рж (ш)=<р(<о)+ фр М (6. Ю)
£ж(ш)=/.(ш)+£р(ш). Ф„(ш)=Ф(ш)+Фр(ш)1
в которых индекс «ж» обозначает желаемые передаточную функцию и час-
тотные характеристики разомкнутого контура, и на зависимости свойств
450 ,_____________________________________________________________ Глаааб
замкнутой системы (главное из них — устойчивость) от частотных характе-
ристик разомкнутой
Отдельные части частотных характеристик избирательно влияют на показа-
тели качества переходной характеристики замкнутой системы й(г):
□ низкочастотная (НЧ) часть определяет погрешности регулирования в ус-
тановившемся режиме e^t), de,CT(z) / dr и т. д.;
□ от среднечастотной (СЧ) части зависят устойчивость, запасы устойчиво-
сти L, и фа, динамические показатели качества /у и о;
□ высокочастотная (ВЧ) часть должна максимально ослаблять влияние
шумов на работу системы управления.
Каждая из задач обеспечения отдельного показателя качества решается со-
ответствующим методом. Иногда несколько требований могут быть удовле-
творены совместно, в других случаях они оказываются противоречивыми. В
зависимости от приоритетов разработчик принимает компромиссное реше-
ние выбора варианта, облегчая второстепенные, на его взгляд, требования к
системе управления либо ужесточая первостепенные требования
Частотный синтез регулятора с заданной структурой может быть выполнен
следующими методами:
□ аналитический метод использует точные нелинейные частотные характе-
ристики элементов системы для формирования системы уравнений, ре-
шение которой дает параметры регулятора. Важнейшее значение в реа-
лизации метода имеют условия (4.31), при которых приведенная по ам-
плитуде и фазе замкнутая система находится на границе устойчивости, а
сама система обладает одновременно обоими запасами устойчивости L,
(он определяет значение AJ=)0M5t’) и <р3.
Обозначим комплексную частотную характеристику регулятора как
Л(|оэ) = Рр((й) +
где /’р(ы) и 0р(о>) — ее вещественная и мнимая части. Тогда уравнения
(4.31) применительно к желаемому разомкнутому контуру принимают
вид системы
)J/’p2(w,)+ep(w3) = jp
<p(o),)+arctg-^-j = <Prl,±W1.
имеющей решение
Ч- :,М е,м.
р ’ MW
Методы проектирования систем автоматического управления________451
При заданной структуре передаточной функции регулятора R(s) соотно-
шения (6.11) позволяют найти его параметры для каждой частоты запаса
на которой существует решение системы уравнений (4.31). Напомина-
ем (см. разд. 4.7). что это решение гарантирует лишь условную устойчи-
вость с запасами, при которой частотные характеристики желаемой сис-
темы £ж(ш) и Фж(ш) могут заходить в запретные области;
□ графический приближенный метод синтеза регулятора, соединяющий
знания, логику и интуицию разработчика в выборе частотных характери-
стик желаемой системы, часто использует быстро строящиеся асимпто-
тические логарифмические характеристики элементов системы для:
• ориентировочною анализа свойств исходных графиков Цв>) и Ф(<о);
• построения желаемых характеристик /.<«.» и Фх(<о)
• получения на основе (6 10) характеристик регулятора путем графиче-
ского вычитания
£р(со) = £ж(ш) - Цш), Фр(ш) = Фж(ш) - Ф(ш); (6.12)
• восстановления передаточной функции р его частот-
ным характеристикам;
□ графоаналитический метод, использующий графики частотных характе-
ристик для предварительной оценки расположения граничного уровня
Фф = 180° ± 360% (чаше всего используется значение фф = -180‘), зна-
ка «+» или «-» фазового запаса ±<р3 (чаще встречается запас +ф,) и ин-
тервала выбора частоты запаса оз, — всего того, что используется в
уравнениях (6.11) для точного расчета параметров регулятора аналити-
ческим методом
6.2. Методы повышения статической точности
(низкочастотный синтез регуляторов)
Установившийся режим любой устойчивой системы определяется в силу со-
отношений (3.21) предельными свойствами ее передаточной функции
>0), а после подстановки s = jo> — начальными при ш —> 0 свойствами
частотных характеристик: комплексной Hljia) и логарифмических L(w) и
Ф(ш). Начиная с разд. 1.2.3, мы постепенно изучали статические свойства
временных характеристик, их взаимосвязь с частотными характеристиками
(см. разд. 3.3), методы предсказания установившихся значений по переда-
точной функции и частотным характеристикам (см. разд. 3.5.3), условия су-
ществования установившегося режима, т. е. устойчивости (см. гл 4), место
установившегося режима в общей структуре движения (см. гл 5).
4»__________________________________________________Главаб
6.2.1. Коэффициенты статических ошибок
Обозначив передаточную функцию желаемой разомкнутой системы как
)УЖ (Х) = =^+Ь^ + ...+Ьтз"1
a0+ais + ... + ansn
получим передаточную функцию замкнутой системы И$(5) от уставки g(t) до
ошибки регулирования e(t):
1 /*(»)
«+%<(*)
Кб = g(i)" КО = И^И') =» %(а)= 1 - W, (s)=
Разложим передаточную функцию ошибки в ряд Маклорена по степеням г
40» 2 V*.
>=о
(6.13)
“ d. [do + +(а, + (о, +b;)s + -Л1=0
Тогда изображение и оригинал ошибки регулирования, а также выход сис-
темы при нулевых начальных условиях имеют вил
£(1)=We(3)G(5)=c0G(3)+c|iG(3)+c2?G(^)+ • •
e(r)=L’4E(r)}=coH0+qs'(')+‘’2g'(r)+... .
v(<)=«(f)-f(')=(1-co)«(')-clS'(0-C2X'(f)---
(6.14)
Коэффициенты с, называются коэффициентами статических ошибок и харак-
теризуют относительное содержание уставки git) и ее производных в функции
ошибки НО- Для уяснения смысла термина «статическая» в названии коэф-
фициента ошибки запишем с помошью предельной формулы (3.2, й) уста-
новившиеся значения ошибки регулирования и нескольких ее производных:
е>с, = lim(r0 + с(з + c2s2 + .. .)sG(4
= limfco +ср+с2а2 + ...pG(4 (J)
=бтк+С|Х + е2э2 + ...^'gG)
Методы проектирования систем.
453
При действии на входе следящей системы сигналов уставки полиномиаль-
ной формы установившиеся ошибки положения скорости . ускоре-
ния е,^ 11 высших порядков производной находятся следующим образом:
□ при постоянной уставке g(0 = й) с изображением б(з) = я, / т и sG(s) - go
в (6.15) получим
еуст = сь8о, «уст = =(): (6.1б,о)
□ при действии линейной уставки g(t) = &) + g\t с изображением
G(s) = go/ s + g, / S2 пределы в (6.15) принимают вид
суст = «o£o+ci«i 'coSi-«)Гг-eya -... 0; (6.16.6)
□ при равноускоренной (квадратичной) уставке g(z) + g\' + Ri1' с изо-
бражением (7(.v) = .?(J / s . имеем статические ошибки
«усг = «oSi +2С1ЙЗ + •
«уст =2сО«2-
(6.16, в)
Оставшиеся не вычисленными в (6.16) пределы равны нулю при нулевых
коэффициентах ошибок со и С|, в противном случае соответствующие уста-
новившиеся ошибки становятся неопределенными, т. е отсутствующими
В системе с полиномиальной уставкой v-ой степени g(r) = + g]i+ ... + g,f
первые v - 1 статических ошибок могут быть как ненулевыми, так и неоп-
ределенными, ошибка = v!cngv обнуляется при с„ = 0, а ошибки более
высоких порядков всегда равны нулю. При произвольной уставке g(rt.
имеющей бесконечное число коэффициентов разложения g„ установившие-
ся ошибки при со * 0 теоретически отсутствуют. На практике же вводится
некий малый порог А, при вхождении в который считается, что наступил
Установившийся режим, а оставшимися ошибками можно пренебречь.
Таким образом, на основе проведенного анализа мы приходим к выводу, что
возникающие в следящей системе статические ошибки по положению, ско-
рости, ускорению и более высоким порядкам производной определяются не
столько формой сигнала уставки, сколько свойствами самой системы, а
именно присущими ей по (6.13) коэффициентами статических ошибок
Приведем два способа вычисления этих коэффициентов:
□ очень трудоемок способ непосредственного дифференцирования переда-
точной функции ошибки H^s) в (6.13). Вручную с его помощью по си-
лам найти лишь два коэффициента:
Сп =__Л*(5) I =_______“о
Ak Cv)+ (')!,=0 «о +
С = ( —-АД*) 11 = I 4к)ЙЖ0- Ак G)бж(д) 1 _ в|&0 -Др&|
( М)»вМУ L («o*V
□ ббльшую методическую ценность имеет процедура получения нужного
числа коэффициентов C| + cjy одного за другим методом деления «углом»
полинома AK(s) на полином Аж(з) + 5ж(т) аналогично (2.43):
д0 + a,j + a2s2 +.., I «0+Z>04-(fl| + bi)s + (а2 + b2)s2 +...
C0+CiS+C2S2 +...
= до C| = fli ~(qi +z>iko
flo+^o «о+^о
Я2~(Д1+/>1)С|-(Д2+»2)СО
До +b0
(6.17, д)
По индукции получаем алгоритм вычисления коэффициентов ошибок в
рекуррентной и матричной формах:
с( = —— | в/ - X(д • + b, I V/ = 0,1, 2....: (6.17, б)
ao + i,ol >1 J
V а0+Ь0 0 ... 0 1 «о '
С1 = Д] +Ц До+Ьо 0 Я1 (6.17, в)
.CN. aN+bN ... Д|+/»| а0+Ь0 -aN .
Недостающие в (6.17) коэффициенты о, или 6, следует принять равными нулю.
6.2.2. Статические системы управлен ия
Система управления, в которой коэффициент ошибки со * 0, называется
статической. Из (6.17) следует признак статизма — ненулевой свободный
член до * 0 характеристического полинома разомкнутою контура. Допустим.
магического управления
455
на входе статической системы действует постоянная уставка gti) = go
(рис. 6.12). Тогда ошибка регулирования (6.16, в), выходной сигнал системы
в установившемся режиме и относительная погрешность регулирования
равны
В статических системах управления в принципе недостижимы нулевая стати-
ческая ошибка и точное слежение выхода даже за постоянной уставкой Это
свойство наглядно иллюстрируется графиками / на рис. 6.8 и 6 10. Если ус-
тавка не постоянная, а, допустим, линейная, то, согласно (6.16, 6), в замкну-
том контуре устанавливается постоянная скоростная ошибка е'>ст *0, а вы-
ходной сигнал равномерно отстает от уставки.
В зависимости от значения коэффициента статической ошибки ср * 0 или
относительной погрешности 6о статические системы автоматического управ-
ления делятся на следующие группы:
□ грубые, в которых |cq| > 0-05 или 8о > 5%;
□ обычные, в которых 0.02 < |с0| < 0.05 или 2% < Зп < 5%;
□ точные, в которых 0.01 < |с0| S 0.02 или 1% < So s 2%;
□ прецизионные, в которых |с0| S 001 или So S 1%.
Несмотря на то, что в статических системах управления никогда не достигается
точное слежение даже за самой простой — постоянной — уставкой, такие сис-
темы имеют право на существование при условии, что относительная погреш-
ность не превышает допустимого значения Если принято решение проектиро-
вать статическую систему при большой исходной ошибке регулирования, то не-
обходимо принять специальные меры по ее уменьшению.
456 Глава 6
Пусть К = И^О) и Кж = H^fO) = Ао / оо — коэффициенты статического уси-
ления объекта и желаемого разомкнутого контура, связанные по (6.17, а) с
соответствующими коэффициентами статических ошибок формулами
о 1 1
c°si7F,Co=i777
Для уменьшения статической ошибки е>ст нужно увеличивать статическое уси-
ление разомкнутого контура АЛ = К А(0). Поскольку передаточная функция
WV), как правило, неизменяема, то увеличение коэффициента К* возлагается
на регулятор R(s). Это может быть реализовано включением в контур управ-
ления последовательных регуляторов различных типов.
I. Простейшее решение состоит в выборе широкополосного усилителя
(рис. 6.13, а) с передаточной функцией
R(s) = К„ > 1,
реализующего закон пропорционального (П) управления
x(t) = Kne(t).
Усиление регулятора К„, гарантирующее коэффициент ошибки c0Sco,
удовлетворяет условию
(6.18. о)
1/cS-l *
Рис. 6.13
Методы проектирования систем автоматического управления 457
Увеличение коэффициента К„ приводит к подъему желаемой логариф-
мической амплитудно-частотной характеристики /.ж(о>) на
Ln(w) = 201g/Г,, > 0 дБ по сравнению с характеристикой Цы) при неиз-
менности логарифмической фазочастотной характеристики Фд(ш) = Ф(ш)
(рис. 6.13, б). При этом частота среза wtp, смещаясь вправо, может пре-
высить граничную частоту <0гр, нарушив тем самым условия устойчиво-
сти Найквиста (4.29, я). Следовательно, существует верхняя граница уси-
ления Kjirp, определяемая требованием устойчивости замкнутой системы. С
учетом желаемых запасов устойчивости по амплитуде Ц и фазе <р3 допус-
тимый максимум коэффициента усиления Кп вычисляется следующим
образом:
• определяется частота запаса ш,, на которой Ф(ю,) = + <р3.
• вычисляется амплитуда Цс^) и се максимально юпустимое прираще-
ние Д£ = -L, - Цы,) > 0 до уровня
• допустимые значения К„ удовлетворяют неравенству
Кп$10005Л£. (6.18,6)
В случае несовместности неравенств (6.18) задача не имеет решения и
следует либо увеличить коэффициент статической ошибки, исходя из
условия
с0 2^ + 100054tJfp,
либо попытаться решить задачу с последовательным регулятором другого
типа.
& Пример 6.1. Дан объект с передаточной функцией
w^= (l+T.fXl+^Xl+T’ji)' (6.19)
К = 2, Т| =50с, Г2 =10с,Т3 =lc.
Определить алгебраическими и частотными методами:
□ устойчивость, раздельные запасы устойчивости <р® и коэффициент
статической ошибки ср в замкнутой системе без регулятора:
□ условия устойчивости замкнутой системы в зависимости от значений А„
коэффициента усиления последовательного П-регулятора;
□ значения К„ > I. при которых обеспечиваются совместные запасы устой-
чивости
Ц > 6 дБ, ф, г 30’;
(6.20)
458_________________________________________________________Гпава 6
□ минимум коэффициента статической ошибки со при запасах устойчи-
вости (6.20)
Решение. Рассмотрим последовательно решение поставленных задач.
□ Согласно алгебраическому критерию Рауса - Гурвица характеристический
полином замкнутой системы без регулятора
C°(s)= К + (1 + Т|«Х1 + + T3s)= 3 + 61s + 560s2 + 500s3
устойчив, т к. все его коэффициенты одного знака (положительны) и
М2 = 61 560 - 3 500 = 32660 > 0.
Аналитическое решение задачи устойчивости системы без регулятора по
нелинейным логарифмическим частотным характеристикам
L(ta}= 201gK- 10У lg(l + 7}2w2), ф(<о)= -£arctg(7>) (6.21)
Zi* i=i
получим в следующем порядке:
4°^)=0 =» ш°р = 0.0324 рад/с => ф(ш°р )= -78°, <р° =102° >30°;
«ИМф) = -180' => Игр = 0.349 рад / с => A((%) = -30.5 дБ,
1?= 30.5 дБ >6 дБ
Так как ш“р < , то замкнутая система без регулятора устойчива и оба
запаса устойчивости (6.20) в раздельности обеспечиваются.
Приближенное графическое решение по асимптотическим логарифмическим
характеристикам получим с помошыо подобных треугольников (три из
них заштрихованы на рис. 6.14) с наклонами гипотенуз — асимптот ло-
гарифмических характеристик, — кратными соответственно -20 дБ / дек
и -45 град / дек, и вычислив
201gK= 6 дБ, lg(l / 7j) - -1.7, lg( 1 / Т2) = -1,18(| / 7з) = 0:
L^)=0 => lg<-lg(l/T|)+lgK—1.4 =» <о"р-0.04рад/с,
Ф^)э0°-45о-0.7-90’0.6 = -85.5° => ф” =94.5’>30’;
«Коур) - -180' =» lgu>rp • -45 / 90 -0.5 => <п,р - 0.316 рад / с,
£Х<Цр) - 6 - 20 0.7 - 40 0.5 » -28 дБ =* L” = 28дБ > 6лБ
Методы проектирования систем автоматического управления
близки к их точным величинам; во-вторых, подтверждают, что замкнутая
система без регулятора устойчива и оба запаса (6.20) в раздельности
обеспечиваются
Значение коэффициента статической ошибки
с“ =Т+х=0'33
показывает, что без регулятора замкнутая система является очень грубой с
относительной погрешностью воспроизведения постоянной уставки
8g = 33%.
□ Характеристический полином замкнутой системы с П-регулятором
С,(з) - К„К+ (1 + Л.0(1 + Гр)(1 + 7V) “
- К* + I + (7| + Г2+ 7j)i + (Л П + П Гз+ 7} Г,)? + Г, ПГ05
460
Глава 6
устойчив по Гурвицу при
где Кж = К„К= 2ЛГГ1. Учитывая требование Кп> 1, получим алгебраиче-
ские условия устойчивости замкнутой системы:
2 < Кж < 67.32, 1 < К„ < 33.66.
Аналитическое решение получим на основе (6.21) по логарифмическим
частотным характеристикам разомкнутого контура с П-регулятором
~ 201g К„ + £(ш), Фж((о) = Ф(<о)
из условий обеспечения границы устойчивости по Найквисту
(ьър = = 0.349 рад / с} П {£ж(шьР) = 0} Г) {Фж(<оп,) = -180’Г.
20lg= 101gП(1+7)4) => ^ = ^П(1 + Г/Ч) = 6732-
^ = 33.66.
Продолжая графическое решение по асимптотическим частотным характе-
ристикам (см. рис. 6.14), поднимем график Цы) вверх на
£$ = 28 = 40-6-6дБ
до выполнения условия ш^р = ш^р. Это эквивалентно введению в контур
управления последовательного усилителя с коэффициентом усиления
Кшр = 100 / 2 / 2 = 25, что недалеко от истинного значения ХПгр ~ 33.66.
□ Подставив частотные характеристики объекта
, <p(a))=-j}arctg(7;<i)) (6.22)
с параметрами, заданными в (6.19), и значения
X, = 1Ооли- = 2, Фп, - -180", Ф1 = 30’
в условия (4.31), определим частоту запаса со, и верхнюю границу допус-
тимых значений коэффициента Кжз:
Фж(ш,) -150’ =» ш, » 0.16 рад / с;
4ж(ш>) - 0.5 => Кю “O.5^[](| + t/g).J)= 7.734 о» Кт = 3.867,
1 < К„ < 3.867.
Методы проектирования систем автоматического управления__________461_
При этом частота среза <ц.р = 0.104 < о)ф = 0.349.
Графическое решение показано на рис. 6.14:
4>(<1>з) = -150*, Ф(0.1) = -45" 0.7 - 90" = -121.5’ =>
=> lg(05=-H~ =-0.789,
£(<«*,) = 6 - 20 0.7 - 40 0.211 - -16.44 дБ.
Условия наличия в замкнутой системе совместных запасов устойчивости
Лж(ш,) = 0.5, = -150’
достигаются подъемом амплитудной характеристики /.(со) вверх на
Д/=-L, - £(ш>) = 10.44 дБ,
т. е. введением в контур управления широкополосного усилителя с ко-
эффициентом усиления Кт = 3.328.
Таким образом, для совместного обеспечения запасов устойчивости П-
регулятор должен иметь коэффициент усиления I < Кп 3.328, что близ-
ко к истинному интервалу I < Кп S 3.867
□ Минимуму коэффициента статической ошибки cfl соответствуют наи-
высшее допустимое положение характеристики Аж(ш) = £жэ(ш) и макси-
мум коэффициента А'„ = К,п. Отсюда получаем значение
“йТЙ4‘°1М'
т. е. минимальная относительная погрешность в системе управления обьек-
том (6.19) с пропорциональным регулятором составляет 114%. что больше
стандартной погрешности 5%. Полученная система является грубой.
2. По второму методу уменьшения статической ошибки, сохраняющему ус-
ловия устойчивости, используется последовательный регулятор со сле-
дующими передаточной функцией и логарифмическими характеристи-
ками (рис. 6.15, а):
(ш)= 2Olg|A'„| + Ю lg(l + TBW)-10 lg(l + T„W). (6.23)
Фр(со)= arclg(7'll<o)-arc»g(7'H<1’)
/лава в
Рис. 6.15
При Кн > 0 он имеет схему реализации на рис. 6.15, б и отличается от
П-регулятора дополнительным подъемом низкочастотной части ампли-
тудной характеристики на частотах, меньших со,,. и спадом фазовой ха-
рактеристики в интервале частот [ОЛШн, 1 Осо,,]. Наибольший спад на угол
приходится на частоту сои = ^<оишп — среднее геометрическое частот
сопряжений ц, и ш,,. Кстати, в [И] ошибочно утверждается, что этот угол
не превышает 70'.
Четыре параметра К„, Кп, Гн и Тп передаточной функции (6.23) связаны
соотношением
£н. = 2к-^ц
по которому при знании любых трех параметров всегда можно вычислить
четвертый. Коэффициент статического усиления Кц находится по форму-
ле (6.18, а) обеспечения желаемой статической точности со:
(6.24,
И1 Трех остав,ии*‘;я параметров должен обязательно обесле-
/ и ф н,ость 1амкну,ой системы с желаемыми запасами устойчивое’*
ве,иеС1Венную И мнимую части комплексной частот-
ной характеристики регулятора
Методы проектирования систем автоматического управления
463
РТ>^=К»~!Г1' бр(Щ)= Кн |\~2Г,2 Ы
1 + Ти2(О2 р 1+7>2
в (6.11), получим систему двух нелинейных уравнений с тремя неизвест-
ными (рз, Тн и Тп:
1+ТпТ„ со5(фгр±ф3 -<р(со,))
-нт.Ч MW • (6И{)
АГ (Гп-Ш sin(y,p±<p
" 1+ТнМ мк)
Определив по предполагаемым желаемым характеристикам (6.10) гра-
ничный уровень Фгр, знак запаса по фазе ф3 и задав частоту «в, в воз-
можном интервале частот, нужно численно разрешить эту систему отно-
сительно параметров Г,, и Т„, после чего в случае необходимости полу-
чить коэффициент
" Тн н
Недоопределенность системы уравнений (6.24, б) позволяет оптимизиро-
вать замкнутую систему по дополнительному критерию
• можно, например, попытаться найти решение с наименьшим отно-
шением
Т = —
Тп ’
что дает минимальное отклонение желаемой фазовой характеристики
Фж(ш) от исходной Ф(ш);
• по другому критерию максимального быстродейстни.ч, основанному на
соотношении (4.28). минимизируется оценка длительности переходно-
го процесса
/у2 —.
У «<р
где частота среза чр. зависящая от выбора о»„ есть корень нелиней-
ного уравнения Лж(чр) = I:
Л2 ((% К; (l + Г„Хр )= (l + Гкга£);
• по третьему критерию минимума скоростной ошибки cj выбирается па-
раметр <»)• при котором значение этого коэффициента ошибки, вы-
числяемое по (6.17. л), становится минимальным.
464 Глава 6
Подводя итог сказанному, нужно признать, что параметрический синтез
передаточной функции регулятора (6.23) является весьма сложной зада-
чей, требующей многократного решения системы нелинейных уравне-
ний (6.24, б) для разных частот запаса со, и оптимизации полученных
решений по дополнительному критерию, который необходимо заранее
выбрать. При многокритериальной оптимизации ищется определенный
компромисс между решениями, оптимизирующими отдельные критерии
Метод приближенного расчета параметров регулятора (6.23) заключается
в выборе.
• коэффициента общего усиления К„ из условия (6.18, б) обеспечения
запасов устойчивости на частоте
«V Ф(ш,) = Фф + Фз;
• постоянной времени Тп = 1 / uy, из свойства совпадения характери-
стик Ф(ю) и Фж(ш) на частотах со > ср, > Юсц,:
Тп> —; (6.24, в)
(03
• постоянной времени
7-..=-^-Гп. (6.24, г)
Конечно, из-за погрешностей аппроксимации логарифмических частот-
ных характеристик такое быстрое решение не гарантирует точно задан-
ных запасов устойчивости. В частности, запас ф, может уменьшиться на
величину до 5.7Г из-за погрешности аппроксимации (2.16).
& Пример 6.2. Для объекта (6.19) разработать последовательный регулятор,
доставляющий замкнутой системе устойчивость с запасами (6.20) и относи-
тельной статической погрешностью 6Q S 1%-
Решение Для уменьшения коэффициента cj = 0.33 до желаемого значения
cq = 0.01 коэффициент статического усиления, согласно (6.18, а), должен
быть равен
Остальные параметры регулятора найдем двумя частотными методами -
аналитическим и приближенным.
□ Аналитическое решение.
Построим с помощью Mathcad зависимости критериев т(со,), <у(Ф|) и
с.Ч)-*?,.(<>,)+ ККнТ,М)с0
Методы проектирования систем автоматического управления
465
от параметра ш, е |0.02, 0.16] (рис. 6.16). По графику C|(w,) выбираем оп-
тимальную частоту запаса ы, = 0.11 рад / с со значениями критериев
т = 24.69,/у= 44.92 с, с1п)|П = 7.58 с.
Рис. 6.16
В результате численного решения системы уравнений (6.24, б) получены
следующие параметры регулятора и передаточная функция в (6.23):
К„ = 49.5, Т„ = 734.16 с, Т„ = 29.72 с, Кп = 2.01,
□ В приближенном решении (рис. 6.17) используем результаты решения
третьей задачи в примере 6.1
В начале найдем уровень подъема статического участка логарифмиче-
ской амплитудно-частотной характеристики желаемой системы:
£х(0) = 201вЛ-ж = 39.91 дБ.
Далее определяем, что для обеспечения обоих запасов устойчивости на
частоте
(1Ъ= 10-о?» = 0.1626 рад/с
нужен общий подъем логарифмической амплитудно-частотной характе-
ристики на величину Д£ = = 10.44 дБ. откуда получаем значение
коэффициента усиления регулятора
Kn=10oosdt= 3.328.
Глава в
Рис. 6.17
Выберем по (6.24, в) постоянную времени Т„ = 61.5 с, соответствующую
частоте
Ц1 = 0.!<i>, = 0.01626 рад / с.
Правее отметки ш,, проводим характеристику £ж(о)) параллельно характе-
ристике Цо>) и выше ее на 10.44 дБ.
Левее частоты ц, проводим участок желаемой амплитудной характери-
стики с наклоном -20 дБ/дек до пересечения с ее горизонталь-
ным участком на уровне 39.91 дБ в точке
Igw,. = -1.789 -Л91~16 44 = >2.963
20
Отсюда находим частоту ц. - 0.00109 рад / с и по (6.24. г) постоянную
Методы проектирования систем автоматического управления
Таким образом, передаточная функция последовательного регулятора
(6.23) приблизительно равна
Истинные значения запасов устойчивости на частоте а>, = 0.1626 рад/с
составляют 7.49 > 6 дБ по амплитуде и 24.04 < 30° по фазе. □
6.2.3. Астатические системы управления
С помощью последовательного регулятора можно в принципе свести к нулю
коэффициенты ошибок со. .... с,-,. навязав системе остатизм v-го порядка
Из (6.17) следует, что признака.» астатизма v-го порядка является наличие в
передаточной функции разомкнутой системы первых v-нулевых коэффици-
ентов полинома знаменателя:
«# = ...« в<-1 = 0.
Изучим свойства систем с астатизмом низших порядков Допустим, на входе
системы управления с астатизмом первого порядка (v = 1, св = 0.
ci = в| / Ьо * 0) действует постоянная уставка g(t) = gn (рис. 6 18, в). Тогда из
(6.16, в) следуют нулевые абсолютная и относительная ошибки регулирова-
ния, а по (6.14) получаем точную сходимость выхода системы к уставке:
еуст = Сой) = 0. 8о = 046, уу„ = (I - ((,)&> = Д).
Если уставка является линейной временной функцией (например, угол по-
ворота локатора или вала двигателя) ^0 = Д» + д/, как показано на
рис. 6.18, б, то по (6.16, б) и (6.14) получаем, что в установившемся режиме
выходной сигнал замкнутой системы отстает от уставки на постоянное вре-
мя, равное С| секунд:
е)тт = <М1 * °- *усг = °’ -Ууст а 8W “ с1«1 “ А) + Л<' “ fi>
Рис. 6.18
466
Глава(
В системе управления с астатизмом первого порядка коэффициент скоростной
ошибки (। имеет физический смысл отставания установившегося линейного
вы чадного сигнала от линейной уставки. Примерами такого поведения аста-
тических систем служат график 2 на рис. 6.6, б и график 3 на рис. 6.8.
В системе с астатизмом второго порядка (v = 2, <ъ “ С| = 0, о п> /р * 0)
постоянная и линейная уставки отслеживаются точно, а равноускоренная ус-
тавка = go + 81* * 8^ отслеживается, согласно (6.16. в), с постоянной
статической ошибкой es« = icjgy * 0. Системы с астатизмом второго поряд-
ка проектируются, например, для сопровождения и целеуказания объектов,
двигающихся с нулевым или постоянным ускорением (конкретные названия
таких объектов читатель, надо полагать, знает сам).
При астатизме v-ro порядка полиномиальные уставки (V - 1)-ой степени
8(«)=8o+S»»+ - +
отслеживаются точно, а уставки v-ой степени — с постоянной установив-
шейся ошибкой
«уст ° v!c«g, # О,
где с, * о, / bo. В статических же системах полиномиальные уставки отсле-
живаются с полиномиально нарастающей ошибкой. Понятно, что статиче-
ские системы непригодны для слежения за быстрыми целями, итя прецизион-
ного управления технологическим оборудованием в микроэлектронике,
микрохирургии, т. е. там, где недопустимы любые ошибки, в том числе и
статические
Из уравнения (6 17. в) следует, что условием реализации в замкнутой системе
статической инвариантности v-ro порядка
оо - ... “ С-i “ 0, с, * О
является астатизм разомкнутого контура v-ro порядка
Од = ... = flv-1 ’0, <1, # 0.
Такая система имеет контурную передаточную функцию
а се структурная схема содержит v последовательно соединенных интеграто-
ров. Замыкание астатической системы единичной отрицательной обратной
связью должно дать устойчивую систему управления с характеристическим
полиномом
£,(«)’ Ьп ♦ N» ♦ - - ♦ ♦ (<«» ♦ ь» )»* ♦ • • • + («„ * )»", (6.26)
имеющим желаемый спектр Из необходимых условий устойчивости (4.7)
следует, что псе коэффициенты 6». 6,-| и о, + 6,.... , а„ + Ь„ характер)!-
Методы проектирования систем автоматического управления 469
этического полинома (6.26) должны быть ненулевыми и одного знака. Алгеб-
раические необходимые и достаточные условия устойчивости длим » (4.13)
Объект может сам иметь интегрирующие звенья Тогда замкнутая система и
без регулятора будет астатической. В отсутствие у объекта лета таима он дол-
жен быть создан регулятором, вносящим в спектр передаточной функции
И^Дт) Л(.т) Щт) нужное количество нулевых полюсов.
Рассмотрим два метода выбора последовательного регулятора, создающего в
замкнутой системе астатнзм первого порядка, и исследуем свойства полу-
чаемых при этом замкнутых систем. Исходную разомкнутую систему поли-
гаем статической с конечным коэффициентом усиления А - <Ц0) > 0.
I. Простейшее решение состоит в установке в контур управления интегра-
тора (рис. 6.19, в) с передаточной функцией и логарифмическими ха-
рактеристиками
реализующего закон интегральном управления (В 4)
Далее будем налагать коэффициент интегрального усиления А'„ положи-
тельным Для достижения желаемой скоростной ошибки q нижняя гра-
ница допустимых значений А'и выбирается из условия
Рмс. 6 Г9
470
Влияние интегратора на частотные характеристики желаемой системы
проявляется в сдвиге фазовой характеристики вниз на 90° и изменении
наклонов асимптот амплитудной характеристики на -20 дБ/дек
(рис. 6.19, б). В результате граничная частота Ш|Р смешается далеко вле-
во, что создает условия для неустойчивости замкнутой системы даже при
структурно устойчивом объекте. Следовательно, существует верхняя гра-
ница Аи, определяемая требованием устойчивости замкнутой системы. С
учетом желаемых запасов устойчивости L, и <р5 наибольшее допустимое
значение Ки находится следующим образом:
• строится фазочастотная характеристика Фж(<о) = Ф((о) - 90’;
• определяется частота запаса ю, из условия Фж(<о,) = Фгр + Фэ1
• строится желаемая амплитудно-частотная характеристика £.ж(ш), про-
ходящая через точку (w,, -L>) и имеющая наклоны участков на
20 дБ/дек меньшие, чем у характеристики £(<о). Низкочастотный
участок i*(w) или его продолжение с наклоном -20 дБ / дек пересе-
каются с осью L в точке 201g/TM;
• вычисляется разность амплитуд ЛЛ = 201gX'x - Z,(0);
• максимум коэффициента усиления К„ задается условием
К„ <Ю0 05Л£. (6.27,6)
Неравенства (6.27) могут оказаться несовместными из-за конфликта тре-
бований статической точности (поднимает £ж(ы)) и устойчивости (опус-
кает В этом случае следует изменить требования к системе либо
использовать другой метод обеспечения астатизма.
Серьезным недостатком И-управления является значительное снижение
быстродействия замкнутой системы в связи с уменьшением частоты сре-
за <ц.р в силу обратной зависимости (4.28) оценки времени установления
переходного процесса от частоты среза как (у 2 п/ <ц.р.
& Пример 6.3. Для объекта (6.19) разработать последовательный И-
регулятор, обеспечивающий в замкнутой системе устойчивость с запасами
(6.20) и минимальное значение коэффициента скоростной ошибки q. Оце-
нить изменение быстродействия системы с И-регулятором по сравнению с
системой, управляемой П-регулятором.
Решение. Разомкнутый контур с И-рсгулятором имеет следующие переда-
точную функцию и логарифмические частотные характеристики
“ Ы“>) + 2°>В*н ~ 20lgo>. Фж(ш) = Ф(ш) ~ 90’.
Из условий Фж(<1»>) = -150’ и /-*(%) = -6 дБ с учетом выражений (6.21) ПО*
лучим частоту запаса ы, » 0.0213 рад /си допустимый максимум
Методы проектирования систем автоматического управления
471
Kto = iq0^--Jfl(>^iM)=00O8
коэффициента усиления И-регулягора 0 < Кн < JfM„ при котором астатиче-
ская замкнутая система имеет запасы устойчивости L, и <рэ
При максимуме К„ = Кт достигается минимум коэффициента скоростной
ошибки
Такое запаздывание в отслеживании линейно возрастающей уставки, оче-
видно, слишком велико из-за малого значения К„
Для оценки быстродействия системы управления с И-регулятором
из условия Аж(шер) = 0 определим частоту среза = 0.0132 рад/с По (4.28)
получим оценку быстродействия гу > 238.4 с, тогда как в статической систе-
ме без регулятора /у£97с при 0)"р =0.0324рад/с, а в системе с П-
регулятором /у > 30.2 с при <ц.р = 0.104 рад/с. □
На основе проведенного теоретического анализа и полученных результа-
тов решения примера сделаем следующие выводы
• введение в контур управления интегратора делает замкнутую систему
астатической, но резко уменьшает ее быстродействие;
• большая инерционность системы с И-управлением обусловлена ма-
лым значением коэффициента усиления регулятора К„, необходимым
для обеспечения устойчивости.
2- Для сохранения устойчивости, быстродействия и создания астатизма в
качестве последовательного корректирующего устройства используется
изодромный регулятор со следующими передаточной функцией и лога-
рифмическими характеристиками (рис. 6.20, а):
. Lp(u)=20lg|A-11| + 101g(i + 7MV)-20lgco. (6.28)
Фр (ю) = arctg(r„w)- 90°
472_____________________________________________________________________Глава 6
Регулятор строится по схеме, изображенной на рис. 6.20, б, и реализует
закон пропорционально-интегрального управления
о
Л,
_/?о(Со+С|) ,, _ I
"’(Яо+Л.Ко “ (*о^)С,
б)
^*,т.
Рис. 6.20
На низких частотах ш<0.1ы„, в том числе и в установившемся режиме,
ПИ-регулятор эквивалентен интегратору, повышая порядок астатизма на
единицу. На высоких частотах ш > Ютц, он имеет свойства пропорцио-
нального усилителя.
Передаточная функция в (6.28) имеет три параметра К„, К„ и Т„, два из
которых могут быть выбраны независимо, а третий связан с ними соот-
ношением
АГП = АГИТИ. (6.29)
Можно поставить задачу синтеза ПИ-регулятора по двум желаемым тре-
бованиям к замкнутой системе, а именно по ее запасам устойчивости L,
и ф,. Подставив вещественную и мнимую части комплексной характери-
стики регулятора
(?₽(«) - -Ки / ш
в (6.11), получим прямые зависимости коэффициентов усиления ПИ-
регулятора от параметра ш.,:
Методы проектирования систем автоматического управления
473
COS^rp ±Ф, - <p(tO,))
Mfa)
(0,5ш(фф ±ф, -<p(tu,))
Х,а(ы, )
(6.30)
Определив по предполагаемым желаемым характеристикам Lx(<d) и Фж(ш)
граничный уровень фф, знак запаса по фазе ф, и задав множество значе-
ний o>j в возможном интервале частот, по (6.30) строятся зависимости
tfn((i»j) и Л'нС0*»). а в случае необходимости по (6.29) - зависимость от
частоты запаса оз, постоянной времени ПИ-регулятора Т„ = Кп /
Как и в (6.24, б), недоопрсделенность системы (6.30) с тремя неизвест-
ными позволяет оптимизировать замкнутую систему управления по не-
которому дополнительному условию:
• по критерию минимума скоростной ошибки находятся частота ( *, и со-
ответствующий ей ПИ-регулятор, минимизирующий коэффициент
• по критерию максимального быстродействия минимизируется опенка
времени установления переходного процесса (4.28), в которой частота
среза желаемой системы является корнем нелинейного уравнения
/•ж(Чр) = 1:
Ч.р: А2(шДк2+К2а£)=о£.
Быстрый приближенный расчет ПИ-регулятора с минимальным коэффици-
ентом скоростной ошибки q выполним с помощью логарифмических
частотных характеристик следующим образом (рис. 6.21):
Рис. 6.21
474________________________________________________________/ламе
• определим частоту запаса w, из условия Ф(м3) = Фф + фа;
• разность амплитуд Д/ = -L, - Дер,) дает коэффициент усиления ре-
гулятора
АГП <Л0°05ЛГ,
а частота ц, = 0.1 оз, — постоянную времени Ги = 1 / ц,. Тогда полу-
чаем третий параметр регулятора
Для проверки расчетов можно построить характеристику Лж(о>), прохо-
дящую через точку (<д>. -13): правее частоты (р, параллельно £(ш), а ле-
вее — с наклонами на 20 дБ / дек меньшими, чем у £(<о). Отрезок, отсе-
каемый на оси L низкочастотными асимптотами Дж(<о) и £(ш), должен
быть равен 201gК„.
& Пример 6.4. Для объекта (6.19) разработать ПИ-регулятор, даюший
замкнутой системе астатизм первого порядка с запасами устойчивости (6.20)
и минимум коэффициента скоростной ошибки q. Оценить быстродействие
замкнутой системы с ПИ-регулятором.
Решение. Подставив в (6.30) частотные характеристики объекта (6.22) и зна-
чения к, = 2, фф = -180’, ф, = 30’, получим зависимости С|(«р,) и /у(о>з), ана-
логичные построенным на рис. 6 16. По этим графикам выбраны оптималь-
ная частота запаса и, = 0.107 рад /си минимальный коэффициент скорост-
ной ошибки с)тш = 7.717 с.
В результате параметры ПИ-регулятора составили значения
= 1.933, = 0.0648, Ти = 29.83 с,
его передаточная функция в (6.28) равна
частота среза ш, = 0.068 рад / с, а оценка быстродействия /у & 46.1 с.
Приближенное решение по асимптотическим логарифмическим характеристи-
кам представлено ниже:
Ф(и>,) = -150’ => <о, = 0.1626 рад / с => ох, = 0.01626 рал / с, Ги = 61.5 с;
£(w>) = -16.44 дБ => Д£ = 10.44 дБ => К„ = Ю005Л/- = 3.328 , Км = 0.0541.
Полученный изодромный регулятор с передаточной функцией
18.48.1
475
Методы проектирования систем автоматического управления
обеспечивает коэффициент скоростной ошибки q = 9.24 с, частоту среза
= 0.104 рал /си оценку времени установления /у = 30.2 с, что равно бы-
стродействию системы с П-регулятором. О
Вывод
Для практических приложений приближенное графическое решение задачи
синтеза регуляторов с помощью асимптотических логарифмических характери-
стик дает быстрый и вполне приемлемый результат.
Сравнение передаточных функций (6.23) с (6.28) и (6.25) с (6 31) пока-
зывает, что ПИ-регулятор может быть получен из регулятора (6.23) пре-
дельным переходом ш,, -> 0, т. е. при Klt ->« и Тн -> «. При этом коэф-
фициент статической ошибки оо -> 0, а система становится астатиче-
ской, сохраняя все свойства устойчивости и быстродействия статической
системы
6.3. Методы улучшения
динамических параметров
(среднечастотный синтез регуляторов)
Основная задача проектирования эффективной системы автоматического
управления заключается в обеспечении ее устойчивого функционирования с
учетом возможных изменений параметров объекта. Устойчивость замкнутой
системы по Найквисту определяется очередностью пересечения логарифми-
ческими частотными характеристиками разомкнутого контура уровней ам-
плитуды Цшср) = 0 и фазы Ф(Шгр) = Фф. В частности, если разомкнутая сис-
тема устойчива, то для устойчивое™ замкнутой системы должно выполнять-
ся условие соотношения частот
Если нужной для устойчивости последовательности чередования частот нет
либо недостаточны запасы устойчивости, то в контур управления необходи-
мо включить последовательный регулятор, корректирующий желаемые час-
тотные характеристики в направлении перестановки либо раздвигания час-
тот (Цф и Шф друг от друга. В случае, когда запасы устойчивости без регуля-
тора обеспечиваются с избытком, назначение регулятора состоит в
улучшении показателей качества переходных процессов за счет допустимом
уменьшения запасов.
Рассмотрим некоторые возможные способы стабилизации замкнутых систем
управления, устойчивых в разомкнутом состоянии.
I. Простейшее решение (рис. 6.22. г») состоит в выборе последовательного
П-регулятора
Глава 6
lUs) = Кп < I,
опускающего амплитудную характеристику на £n(w) = 201gК„ < 0 дБ при
неизменности фазовой характеристики (рис. 6.22, б). При этом частота
среза о^р, смещаясь влево, должна встать левее граничной частоты Цр,
тем самым восстанавливая условие устойчивости Найквиста <ц.-р < Цр.
Рис. 6.22
С учетом желаемых запасов устойчивости по амплитуде L, и фазе ЧЬ
верхняя граница коэффициента Кп вычисляется в следующей последова-
тельности:
• из условия Ф(ю>) = Фгр + <р, определяется частота запаса сю.,;
• находится необходимое уменьшение амплитуды ДА = £(cpi) + 110
уровня
• максимум коэффициента усиления Кп задается условием
Kn S ю*0-05^ (6.32)
Недостатки стабилизации с помощью П-регулятора:
• увеличение коэффициентов статических ошибок в 1 / К» Р33 "З'за
уменьшения статического усиления разомкнутого контура;
• уменьшение полосы пропускания и быстродействия замкнутой сис-
темы из-за сдвига влево частоты среза <ц.р, определяющей время ус-
тановления /у.
Методы проектирования систем автоматического управления 477
Если позволяет амплитудная частотная характеристика разомкнутого
контура, то П-регулятор можно использовать для повышения быстродей-
ствия и уменьшения статических ошибок системы управления примерно в
Кп раз путем поднятия логарифмической амплитудно-частотной характе-
ристики на величину
AL = - L, - Z.((oJ > 0 дБ
При этом вычисленное по (6.18, б) значение А'п станет больше единицы,
а схехга реализации регулятора такой, что изображена на рис 6 13, a
& Пример 6.5. Для объекта (6.19) с коэффициентом К= 200 определить.
□ устойчивость замкнутой системы без регулятора,
□ условия устойчивости замкнутой системы от коэффициента усиления
П-регулятора Кп > 0;
□ значения Кп > 0. обеспечивающие запасы устойчивости (6 20) £,>6 дБ.
Фз * 30*;
□ минимальный коэффициент статической ошибки Со при заданных запа-
сах устойчивости.
Решение. Рассмотрим последовательно решение поставленных задач
□ Характеристический полином замкнутой системы без регулятора
С“(з)= 201 + 61з +560з2 +500?
неустойчив по Гурвицу из-за отрицательности второго минора:
ЛА = 61 560 - 201 500 = -66340 < 0.
По критерию устойчивости Найквиста, использующему логарифмиче-
ские частотные характеристики (6.21), замкнутая система также неус-
тойчива из-за неверного соотношения частот:
<о°р =0.583 >шф =0.349.
3 В замкнутой системе с П-регулятором характеристический полином
С,(з) - 200Х„ + 1 + 61з + 560? + 500?
устойчив по Гурвицу при условии
о<лг"<^=(^’,У2оо=о-337
Аналитическое решение задачи синтеза П-реплятора по логарифмиче-
ским частотным характеристикам пахучим из следующего соображения,
для устойчивости замкнутой системы нужно опустить £(w) бохсе чем на
6(шц>) = 9.46 дБ с помощью П-регулятора с коэффициентом усиления
*П < 4п> " ,0'®®5 ’*-0.337.
478
Глава 6
□ Для обеспечения обоих запасов устойчивости (6.20) на частоте
со, =• 0.16 рад / с нужно опустить амплитудную характеристику Цы) бо-
лее чем на
+ Ц = 28.25 дБ.
Тогда по (6.32) получим допустимые значения
Ап< А,„ = 10^ 05 2825 = 0.0387.
□ Минимально возможные коэффициент статической ошибки и относи-
тельная погрешность в замкнутой системе с П-регулятором
Соты = =0-114. Somin « 11-4%
совпадают с результатами примера 6.1.
Полученная передаточная функция регулятора Я(.т) = 0.0387 для управле-
ния объектом (6.19) с коэффициентом А' = 200 дает замкнутую систему,
полностью эквивалентную системе с А" = 2 и регулятором /?(л) = 3.87, по-
скольку контурная передаточная функция И'ж(з) = К R(s) в обоих случаях
одна и та же. □
2. Широко распространен способ стабилизации с помощью фильтра низких
частот (схема реализации на операционном усилителе приведена на
рис. 6.23, о) с передаточной функцией и логарифмическими частотными
характеристиками апериодического звена первого порядка:
Я(з)= * • Lp(co)= -101g(l + 7"„2со2), Фр(со) = -arctg( Г„<1>).
т,«*с
Л
Рис. 6.23
Методы проектирования систем автоматического управлении 4/9
Фильтр демпфирует (сглаживает) высокочастотные колебания за счет
уменьшения наклонов логарифмической амплитудной характеристики
на 20 дБ / дек на частотах о» > со» = 1 / 7Н. Выбором постоянной вре-
мени Г„ можно добиться того, чтобы частота сц^ стала меньше частоты
(Оф, восстановив условие устойчивости Найквиста (рис. 6.23, б). При
достаточно малой частоте ц, можно обеспечить и желаемые тапасы ус-
тойчивости L, и ф3 С другой стороны, эту частоту нужно выбирать как
можно большей, чтобы неизбежное снижение быстродействия замкну-
той системы, определяемого сдвигающейся влево частотой среза, было
минимальным.
Важнейшим условием использования фильтра низких частот как средст-
ва стабилизации является обеспечение наклона желаемой амплитудной
характеристики £ж(ш) на частоте среза около -20 дБ / дек, при котором
фазовая характеристика не заходит в запретную зону ф,р ± <р, При более
крутом наклоне амплитудной характеристики возможно пересечение
графиком Фж(и>) уровня фф и в результате — потеря замкнутой системой
устойчивости
Аналитический расчет постоянной времени фильтра низких частот вы-
полняется путем подстановки вещественной и мнимой частей ком-
плексной частотной характеристики регулятора
в (6.11) и формирования системы двух нелинейных уравнений с двумя
неизвестными со, и Т„:
I cosfcprp ±<р,
I + гн2о>,
7,(0, sin(<p,p ±<р, -<р(<о,))
1+гн2«? М(ч)
(6 33)
Определившись по предполагаемым желаемым характеристикам £ж(<о) и
Фж(ш) с граничным уровнем ф|р и знаком запаса по фазе ф„ получим
сначала из (6.33) нелинейное уравнение
MGaJcos^rp ± фэ - ф(а*»)) - I.
(6.34. л)
Решив его относительно частоты запаса о*,. получим искомую постоян-
ную времени фильтра низких частот
480 ГламД
(6Мй)
w,
При использовании фильтра низких частот сохраняется коэффициент
статической ошибки flo, но увеличиваются, т. с. ухудшаются, остальные
коэффициенты ошибок с< и инерционность замкнутой системы, характе-
ризуемая временем установления ее переходных процессов /у.
Графический приближенный расчет постоянной времени фильтра низких
частот Т„ может быть выполнен методом последовательных приближений.
D Шаг 1 Примем фазовую характеристику желаемой системы рапной
Фж(ш) Ф(ш) - 90’.
Шаг 2 Определим частоту мпвеа оз, из условия Фж(<») • Ч>,,, + <р,
ШагЗ Через точку (из,, -£,) проведем асимптотическую амплитудную
частотную характеристику желаемой системы
£ж(и>) = L(w) - 20lg(o
с наклонами асимптот на 20 дБ / дек меньшими, чем у Ци>).
Шаг 4. Определим частоту ози < (и, в точке пересечения асимптот
£,(<о) и /.(то). новые приближения параметра 7,, = I / tt>„ и фазовой
характеристики
Фж(ш) ж Ф(оз) - arctg(TH(i>).
Шаг 5. Если ц, > 0.1оз„ го идти на шаг 2, иначе конец
С
& Пример 6.6. Для объекта (6.19) с коэффициентом К - 200 определить
О условия устойчивости замкнутой системы от постоянной времени
фильтра низких частот Т„;
□ значения Т„. обеспечивающие запасы устойчивости (6.20) / ,-»6 дБ,
т. • J0*
Q максимальное быстродействие замкнутой системы с регулято-
ром-фильтром низких частот при заданных запасах устойчивости.
Решение Рассмотрим последовательно решение поставленных задач.
Q Характеристический полином замкнутой системы с фильтром низких
частот
C/D - К+ (1 ♦ Т||)(1 ♦ 7*ая)(1 + 7р)(1 + 7„х) -
- 20) + (Т„ ♦ 61)з ♦ (61 Г„ + 560)»' + (5607,, + 500)? + 500/',,?
Ml
устойчив по алгебраическому критерию Льенири Шинарп при условиях
{Т„ > <>}П {й, 3366ОТ,,’ - ()()б6674()/,‘ - 93150400Г„ 33170000 > о).
откуда следует область устойчивости твикнутой системы с корректи-
рующим фильтром низких частот:
Тп > Т„„ - I 803.87 с
Аналитичеек / р tune, сошиишкицсе с ал1ебраичсским реше-
нием. получим по уравнениям (6.34) при /, о. ф, - О'. к, - I.
Ф,р -180’. о», - ц.р и частотным характеристикам (6.22) при К- 200
/l((iKp)cos(<(i(oVp)) • -I « Чр ~ 0.043 рад / с.
Г.,,рР^-^
□ IIpiiMi'iii'i ini' / <чтOt "III нс IНИНО ИI
высоком (восьмой) степени приведенного по амплитуде и фате характе-
ристического полинома (4.32) с элементами
A(s) -! + (?;, + 61).f + (61 Гн + 560)? + (56ОГ„ + 500)? ♦ 500 V.
й(т) - 200. А,-2. со»(ф,)«у.
Аналитическое частотное решение гак как фд(ю) - <p(<u> arctg( 7'„ш>
монотонно убывающая функиим частоты, то тапасы устойчивости (6 20)
обеспечиваются при постоянных времени фильтра низких частот
7» * Г,,», а значение 7"|(, находится по (6.34) при а, 2:
<4(<01)со»(ф(ы,) -30*) - -0.5 »» пт, - 0 0214 рал / с.
□ Решая уравнение
определяем частоту ау,, 0.01 33 рал / с и опенку времени уептноыении
/у г 2.36.9 с. что равно быстродействию системы с И-управлением и в 7.8
раза больше, чем в системе с Л-регулятором.
Приближенное графическое решение покатано на рис 6 24.
Глава 6
• опустим фазовую характеристику Ф(ы) вниз на 90°. Из условия
Ф(и>ф)-90' =-до-
определим логарифмическую частоту Iguifp = —1.35. Через точку
(«lip, 0) проведем граничную амплитудно-частотную характеристику
Lxrp(«>) с наклонами на 20 дБ / дек меньше, чем у характеристики
М<о). до пересечения с последней на частоте
>8Ц1ф “ -3 3 < Igwrp “ 1
Таким образом, за одну итерацию мы получили частоту
Шигр - 0.0005 рад / с и постоянную времени Гип, = 2 000 с. что близко
к истинному значению ТН1р = I 803.87 с;
• из условия достижения запаса по фазе
Ф(ш>) - 90' - -150'
Методы проектирования систем автоматического управления
найдем логарифмическую частоту запаса Igor,- -1.68. Через точку
(©,. -6 дБ) проведем желаемую амплитудную характеристику Z.,(w) с
наклонами на 20 дБ/дек меньшими, чем у характеристики Д(а), до
пересечения с последней на частоте
1вЦп = “4.28 < lgw> “ I.
Таким образом, за одну итерацию мы получили частоту сопряжения
«из = O.OOOO52 рад/с и постоянную времени 7JO = 19 200 с одного по-
рядка с истинным значением 7,,, = 12 460 с;
• определяем логарифмическую частоту среза
IgdVp - -198 =» ц.р = 0.0105 рад/с
и по (4.28) оценку быстродействия замкнутой системы:
г 300 с.
Низкочастотная коррекция широко применяется для стабилизации опе-
рационных усилителей путем подключения к специальным выводам
микросхемы конденсатора большой емкости С„. которую, во-первых,
трудно изготовить в микроэлектронном исполнении, а во-вторых, мож-
но оптимальным образом настроить в каждой конкретной схеме. При
больших значениях См, Г„ и, соответственно, малой частоте и\, логариф-
мическая амплитудно-частотная характеристика усилителя пересекает
ось частот с наклоном -20 дБ / дек при фазовом сдвиге -90’, что создает
большой запас устойчивости этой схемы
3. Наилучшим средством стабилизации систем автоматического управле-
ния является устройство, увеличивающее наклон амплитудно-частотной
и подъем фазочастотной характеристик желаемой системы на средних и
высоких частотах. В качестве такою устройства можно принять регуля-
тор (6.23) с обратным соотношением частот сопряжений ц, < <ц( и по-
стоянных времени Гп > Т,„ который, в отличие от рис 6.15, о. увеличи-
вает наклон амплитудной характеристики на 20 дБ / дек в интервале
частот сц, < ш < ц, и локально поднимает фазовую характеристику в ин-
тервале |0.1ы,„ 10wJ.
Рассмотрим предельный случай такого регулятора в виде форсирующего
устройства со следующими передаточной функцией и логарифмически-
ми характеристиками (рис. 6.25, л):
1Л(а)»Гш + Кдд-Ки(Н7>).
М®)“ 20lg|*n|+i0^+rX). (6.35)
[ф^)-arctgfaw).
Данное корректирующее устройство строится по схеме на рис. 6.25, б ।
реализует закон пропорционально-дифференциального управления'
at
“) 6}
Рис. 6.25
Форсирующий ПД-регулятор поднимает всю логарифмическую ампли-
тудную частотную характеристику на 20lgA;, дБ и увеличивает ее наклон
на +20 дБ/дек правее частоты шд. На частотах ю > 0.1 о>л фазовая харак-
теристика желаемой системы поднимается на угол от 0 до 90°. Благодаря
этим изменениям:
• повышается быстродействие замкнутой системы из-за сдвига вправо
частоты среза о^р .
• улучшаются условия устойчивости за счет еще большего сдвига вправо
частоты ш,р при правильном выборе параметров ПД-регулятора;
• ПД-регулятор может сделать замкнутую систему абсолютно устойчивой
благодаря отсутствию пересечения скорректированной фазовой ха-
рактеристики Фж(о>) с граничным уровнем <р1р и самой граничной час-
тоты <1>гр.
Передаточная функция в (6.35) имеет три параметра К„. Кл и Тя, два из
которых могут быть выбраны независимыми, а третий связан с ними
условием
Л-д-ад.
Соответственно можно поставить задачу синтеза ПД-регулятора по двум
желаемым требованиям к замкнутой системе, которыми являются зава-
годы проектирования систем автоматического управления__________485
сы устойчивости L, и <р3. Подставив вещественную и мнимую части ком-
плексной частотной характеристики регулятора
Pf(u>) = К,„ (?р(ш) = КЛо>
в (6.11). получим прямые зависимости коэффициентов усиления ПД-
регулятора от параметра щ,
cos(<p,p ±<р, -<р(ш,))
п = ®
к ып^Фф^ф,))
л WjXjAta)
Определив по предполагаемым желаемым характеристикам LJw) и Фж(ь>)
граничный уровень ф,р, знак запаса по фазе ч>, и задав множество значений
оз, в возможном интервале частот, по (6.36) строятся зависимости и
^(ш,), а в случае необходимости — зависимость Тн{и^) = ^(ш,) /
Как и в (6.30). недоопределенность системы (6.36) позволяет оптимизм
ровать замкнутую систему по некоторому дополнительному критерию.
Например, по критерию максимального быстродействия минимизируется
оценка времени установления переходного процесса (4.28), в которой
частота среза амплитудной характеристики желаемой системы, зависи-
мая от частоты запаса оз,, является корнем нелинейного уравнения
^ж(Чр) = 1:
с^: A2((oq,fe + AfX)=1 (6'37)
Если разомкнутый контур системы устойчив, то ПД-регулятор улучшает
показатели качества переходного процесса повышает быстродействие и
'запасы устойчивости при выборе частоты сопряжения вблизи и немного
левее частоты среза логарифмической амплитудно-частотной характери-
стики объекта о)”р.
Для значительного увеличения быстродействия можно включать после-
довательно несколько форсирующих устройств. Первый каскад предна-
значен для стабилизации системы, а остальные — для повышения каче-
ства ее переходных процессов.
Недостаток ПД-регулятора заключается в обострении дифференцирую-
щих свойств системы на высоких частотах, что приводит к снижению
помехоустойчивости системы и соотношения сигнал / шум.
Выполним быстрый графический синтез стабилизирующего ПД-
регулягора с максимальным быстродействием, стремясь сделать частоту
“л как можно большей и, в то же время, обеспечить запасы устойчиво-
сти L, и <р, (рис. 6.26):
Глава 6
• определим частоту запаса ш, из условия достижения запаса <р3 с уче-
том подъема фазы форсирующим звеном на 90”:
и,: Ф(ш,) + 90" = <рф + ф3.
Такую же частоту получим в точке пересечения фазочастотной харак-
теристики объекта Ф(<в) с уровнем фф + ф3 - 90";
• вычислим частоту сопряжения и постоянную времени форсирующего
звена:
соц = ОЛш, => Тя = I / сол;
• поскольку на частоте форсирующее звено увеличивает ам-
плитуду /-(<Oj) на 20 дБ, то разность \L = -Ц - Цш>) соответствует
удесятеренному коэффициенту широкополосного усиления регулято-
ра, откуда следует
KnS1000SAt-';
• теперь можно найти и третий параметр регулятора Кп = К„ТЛ.
Для проверки расчетов нужно построить желаемую амплитудную харак-
теристику £ж(ш), проходящую через точку (го,, -L*): левее частоты шд па-
раллельно характеристике Цы), а правее — с наклонами на 20 дБ / дек
большими, чем у нее. Отрезок, отсекаемый на оси L низкочастотными
асимптотами графиков ЬЛ(ы) и Цы), должен быть равен 201gK’ll.
2Э Пример 6.7. Для объекта (6.19) с коэффициентом К = 200:
□ определить область устойчивости замкнутой системы с ПД-регулятором
в пространстве его параметров К„ > 0 и Кп > 0;
Методы проектирования систем автоматического управления
487
□ рассчитать первый каскад регулятора, дающий запасы устойчивости
(6.20) и минимально возможное значение коэффициента статической
ошибки с0;
□ с помощью второго форсирующего каскада увеличить быстродействие
замкнутой ПДД2-регулятором системы в 10 раз, восстановив исходное
значение с0.
Решение. Рассмотрим последовательно решение поставленных задач
□ Характеристический полином замкнутой системы с ПД-регулятором
ад = магп + ад + (1 + Г|з)<1 + ада + ад =
= 200К„ + 1 + (200Ка + 61)3 + 560? + 500?
устойчив по Гурвицу при
Ип > -0.005) П > -0.305) П {1-12ЛГл ~ + 0.3366 > 0).
С учетом требований Кп > 0 и Ка > 0 получим в плоскости (КП, Ка} об-
ласть устойчивости системы автоматического управления с ПД-
регулятором (рис. 6.27):
{0 < < 1.12Ai + 0.3366) П( КЛ >0).
Рис. 6.27
Анализ устойчивости частотным методом Найквиста в пространстве двух
параметров затруднителен и потому здесь не привадится.
□ Аналитическое решение по (6.36) и (6.37) с частотными характеристиками
(6.22) при А'= 200 даст в интервале частот ш, е (0.17. 1.95) зависимости
Со(<*Ъ) и Ту (от,), подобные графикам на рис. 6.16. Оптимальные значения
параметров следующие:
• частота запаса », = 1.325 рад/с;
• минкмя №ный ко «ффицнент статической ошибки > <>пчп = 0 00641;
• частота среза tutpi = 0.858 рад / с;
Глава 6
• оценка максимального быстродействия ty > 3.66 с;
• параметры первого каскада регулятора
Лп| = 0.775, КЛ] = 2.701. ГД1 = 3.483 с;
• частота сопряжения cOji — 0.287 рад / с;
• передаточная функция первого каскада регулятора
/?i(5) = 0.775(1 + 3.4835).
На рис. 6.28 построены логарифмические характеристики объекта /.(со).
Ф(со) и желаемого разомкнутого контура Z^i(<»), Фж|(<о) системы с первым
форсирующим каскадом регулятора.
Рис 628
Методы проектирования систем aerot
489
□ Для расчета параметров передаточной функции второго форсирующего
каскада
Ш =* +
используем два условия:
. желаемая частота среза должна быть равна = 10сц,р| = 8.58 рад/с;
• 01Я восстаноазения исходного коэффициента с., передаточная функ-
ция должна иметь коэффициент усиления второго форсирующего
каскада
Постоянную времени второго каскада регулятора Тд определим из усло-
вия ^(с^р) = I __________________
L2 =— | 77- / -3-П~1=6-2с •
На рис. 6.28 построены частотные характеристики и же-
лаемой системы с двумя форсирующими корректирующими каскадами
Таким образом, мы получили полную передаточную функцию двухкас-
кадного ПДдР-регу.тятора
Аз) = Я|(з)Я>(з) = 1 + 9.683 ♦ 21.593-'
и управляемую им замкнутую систему со следующими свойствами:
• оценка быстродействия составила
Ку >0366 с,
что в S2.S и 650.3 (!) раз лучше, чем. соответственно, в системах с
П-регулятором и фильтром низких частот. Реальное быстродействие,
полученное по переходной характеристике замкнутой системы
составило А, » 1.38 с при нулевом перерегулировании Отличие этого
показателя от оценки »у > я / о^,, примерно в 4 раза объясняется тем.
что оценка (4.28) является практически гарантированной. полученной
с большим запасом для большинства реальных систем.
• относительная Погрешность регулирования Л М98Я в 23 рвя
меньше, чем в системе с П-рсгу.тятором, и совпадает с погрешностью
в системе с фильтром низких частот;
• абсолютная устойчивость и запасы устойчивости Z-, = ~ и ♦, > W.
недостижимые другими регуляторами
490
Глава 6
О
Рассмотренные методы синтеза позволяют получить передаточную функцию
последовательного регулятора, решая частные задачи регулирования в низ-
кочастотном и среднечастотном диапазонах. Точное решение этих задач
требует нахождения корней нелинейных уравнений. Кроме того, что этот
процесс сам по себе достаточно сложен, он еще нуждается в задании на-
чальных условий в достаточно узкой области сходимости
Приближенное графическое решение, кроме наглядности, даст приемлемый
результат и рекомендуется для качественных, быстрых расчетов. Его можно
использовать как начальное приближение, уточняемое затем точными ана-
литическими методами
Резюмируя сказанное, выбираем наилучшие типы регуляторов
□ в низкочастотном диапазоне — это ПИ-регулятор с передаточной функ-
цией типа (6.28):
S
□ в среднечастотном диапазоне — это ПД-регулятор с передаточной функ-
цией типа (6.35):
Ш = Я^(1 + Г<л).
Полная передаточная функция последовательного регулятора имеет ПИД-
свойства:
Вклад пропорциональной, интегральной и дифференциальной составляю-
щих в суммарное управление (В.5) регулируется коэффициентами усиления
Кп - К,Л(Г„ + П), ЛГЯ = = АГн^ГиГе.
Для уменьшения уровня шумов в высокочастотном диапазоне желательно
включать последовательно с корректирующим устройством фильтр низких
частот с передаточной функцией
«•w-nfe-
частотой завала амплитуды и, г IOuvp и постоянной времени
Г, - — S ——.
щ. 10шс|)
(6.38)
Методы проектирования систем автоматического управления 491
6.4. Быстрый синтез систем управления
методом логарифмических частотных
характеристик
Свойства системы автоматического управления полностью определяются
частотными характеристиками ее разомкнутого контура Из всех характери-
стик наиболее просто строятся асимптотические логарифмические частот-
ные характеристики, благодаря чему метод синтеза систем управления по
асимптотическим логарифмическим частотным характеристикам приобрел
широкое распространение в научной и инженерной практике. В совокупно
сти с возможностью восстановления передаточной функции объекта по его
частотным характеристикам (см. разд. 4.6.2) описываемая ниже процедура
позволяет инженеру работать с устройствами, передаточные функции кото-
рых он не знает, но может определить по экспериментально построенным
частотным характеристикам.
Методика быстрого синтеза последовательного регулятора по логарифмиче-
ским частотным характеристикам |27| включает в себя следующие этапы
(рис. 6.29).
□ На первом этапе строятся асимптотические логарифмические частотные
характеристики Z.(w) и Ф(ш). соответствующие передаточной функции
разомкнутой системы Щ.О
□ Наиболее сложным является второй этап формализации желаемых
свойств замкнутой системы в виде желаемых логарифмических частотных
характеристик LK(u>) и Ф*(ю). Их формирование выполняете* индивиду-
ально на разных частотных диапазонах (рис. 6.30):
Глава 6
Рис. 6.30
• низкочастотная часть желаемой амплитудной характеристики в ин-
тервале частот 0 < ш< должна иметь наклон 0 или -20 дБ / дек и
отсекать на оси L желаемое значение £»(!);
• среднечастотная часть желаемой амплитудной характеристики в ин-
тервале частот Ц; <ш< Шц должна иметь наклон -20 или -40 дБ / дек
и пересекать ось ы на желаемой частоте среза <^р;
• низко- и среднечастотная части амплитудно-частотной характеристи-
ки соединяются в интервале частот ц, < ы < <ц. сопрягающей частью с
наклоном -40 или -60 дБ / дек;
• высокочастотная часть желаемой амплитудной характеристики при
ш > ц, должна иметь отрицательный наклон от -40 дБ / дек и более,
т. к. она предназначена для максимального ослабления влияния вы-
сокочастотных шумов на работу системы управления.
При формировании желаемой амплитудно-частотной характеристики
необходимо стремиться максимально совмещать частоты сопряжения и
изменения наклонов асимптот графиков £(со) и £ж(ш) с целью упрощения
структуры регулятора за счет исключения лишних типовых звеньев из
его передаточной функции Я(т) = Жж(5) / И^т).
□ На третьем этапе графическим вычитанием
£p(w) = £ж(ш) - Цш), Фр(ш) » Фж(ш) - Ф(ы) (6.39)
находятся логарифмические характеристики последовательного регу-
лятора.
□ По этим характеристикам на четвертом этапе восстанавливаются ти-
повые звенья и передаточная функция регулятора Л(5) по следующей
методике
• начальному низкочастотному участку характеристики £р(ш) с накло-
ном асимптоты t20v0 дБ/ лек соответствует начальное типовое звено
с передаточной функцией
Методы проектирования систем автоматического управления 493
Ес коэффициент усиления
к0=юою'’(,)
определяем по координате Lp(l), отсекаемой на оси L низкочастотной
асимптотой графика Lp(to) или ее продолжением;
• двигаясь слева направо по оси <>. фиксируем частоты сопряжения <11,
асимптотической амплитудной характеристики 1^(<о) Каждому изме-
нению ее наклона на ±20v, дБ / дек соответствует типовое звено регу-
лятора с передаточной функцией (символ ® означает знак «+» для
минимально-фазовых звеньев и «-• — для немннимально-фазовых)
= Jell, Я, (6.40, a)
• составляем из типовых звеньев Я<.ч передаточную функцию pay опора
г=о
□ Назначение пятого этапа проектирования регулятора состоит в получе-
нии фактических показателей качества замкнутой системы путем вычис-
ления по (6.1) ее передаточной функции и построения переходной
характеристики
□ На шестом этапе статические и динамические свойства переходной ха-
рактеристики сравниваются с желаемыми.
□ Если в процессе проектирования желаемые свойства замкнутой системы
достигнуты, то на седьмом этапе выполняется техническая реализация
полученной передаточной функции регулятора:
• последовательный регулятор преобразуется к желаемому типу из тех.
что описаны в разд 6.1, или их комбинации;
• разрабатывается техническое устройство, реализующее регулятор в
требуемой элементной базе.
При недостижении требуемых свойств замкнутой системы желаемые ло-
гарифмические частотные характеристики корректируются, а цикл про-
ектирования повторяется со второго этапа.
На рис. 6.29 пунктиром обозначена модификация алгоритма синтеза регулятора:
0 на третьем этапе по желаемым логарифмическим характеристикам вос-
станавливаетсзг передаточная функция желаемой системы H'ijj);
494------------------------------------------------------------folMg
□ на четвертом этапе вычисляется передаточная функция последователь-
ного регулятора
По сравнению с описанными ранее аналитическими методами ускорение
расчета регулятора методом логарифмических частотных характеристик дос-
тигается за счет:
□ использования кусочно-линейных асимптотических характеристик, ко-
торые быстро строятся по передаточной функции и так же быстро по-
зволяют восстановить передаточную функцию по логарифмическим ха-
рактеристикам;
□ применения основанных на большом опыте проектирования номограмм,
заменяющих с достаточной точностью решение нелинейных уравнений
Рассмотрим подробнее правша построения участков желаемой логарифмиче-
ской амплитудно-частотной характеристики разомкнутого контура £*(«)) в
соответствии с требованиями, предъявляемыми к свойствам замкнутой сис-
темы.
□ Низкочастотный участок определяет статическую точность системы
управления в установившемся режиме и характеризуется верхней часто-
той ц, пропускания сигналов без ослабления (для статических систем),
коэффициентом усиления К и коэффициентом астатизма v„ (рис. 6.31).
Начальный участок низкочастотного участка должен иметь
Рис. б.зг
наклон 0 дБ / дек. если проектируется статическая система управле-
ния. По допустимой относительной погрешности 6о% определяются
коэффициент статической ошибки
60
С° " 100%
гады проектирования систем автоматического управления______________495
и коэффициент К= И^ж<0) статического усиления разомкнутого кон-
тура, удовлетворяющий условию
Кй —-1; (6.42. в)
Со
. наклон ' 1Г> /дек, если проектируемая система управления
должна быть астатической. Порядок астатизма v„ выбирается из усло-
вия точного воспроизведения в установившемся режиме уставки g(6 в
виде полинома (vh - 1)-ой степени. Коэффициент усиления статиче-
ской части передаточной функции К= >КЖ(1) выбирается из условия
обеспечения в замкнутой системе желаемого коэффициента статиче-
ской ошибки cV(|:
К> —. (6.42,6)
Существуют следящие системы, работающие при гармонически изме-
няющихся уставках
g(r) = Xtsin(<>M + фг).
В установившемся режиме ошибка регулирования и выходной сигнал
такой системы также будут гармоническими колебаниями с частотой
e(t) = ^in(<Or/ + фг), y(r) = X^inttOr/ + Ф>).
Определим, каким условиям должны удовлетворять амплитудные харак-
теристики Лж(щ) и £ж(со), чтобы гарантировать жемемый коэффициент
гармонической ошибки сг = А,/ /1г:
4 =|w.(iM4 =|1+1уж10ц)|А> * с’ =|й^=^
Следовательно, при заданном минимальном коэффициенте гармониче-
ской ошибки с, амплитудно-частотная характеристика Лж(ш) разомкнуто-
го контура должна удовлетворять условию
4 (“г )й^-.
а желаемая логарифмическая амплитудно-частотная характеристика
£ж(ш) проходить не ниже точки (wy, -20Igcr) (рис. 6.3 В. Если проектиру-
ется система управления с порядком астатизма vM, го коэффициент Л
выбирается из угловая
496
Глава 6
□ Среднечастотный участок логарифмической амплитудно-частотной ха-
рактеристики с наклоном -20vc дБ / дек (рис. 6.32) определяет устойчи-
вость и динамическое качество замкнутой системы. Для обеспечения ус-
ловия устойчивости Найквиста ц.р < Ыф разомкнутый контур в окрест-
ности частоты среза должен иметь свойства абсолютно устойчивого
минимально-фазового звена первого (vc = 1) или, в крайнем случае,
второго (vc = 2) порядков.
Рис. 6.32
Частота <цр выбирается по заданным показателям качества переходного
процесса и о с помощью изображенных на рис. 6.33 номограмм
rjXOfcpI/’nm / Ро) и о(?пШ1 / Я))- гае Рты 11 Ро — максимальное и начальное
значения вещественной частотной характеристики замкнутой системы
Р3М, задающие аргумент Рщ^ / Ро. имеющий вспомогательный характер.
Из первой номограммы, кстати, видно, что соотношение (4.28) /уЦ.р2х
между временем установления гу и частотой среза <1Ц.р гарантированно
удовлетворяется практически всегда.
Рис. 6.33
। систем автоматического управления
497
Последовательность применения номограмм показана на рис. 6.33
стрелками:
по желаемому перерегулированию a (%) находим аргумент / Ро и
соответствующее ему произведение 1^ времени установления на
частоту среза;
деля это произведение на желаемое время установления /у (с), полу-
чим частоту среза ц,р (рад / с);
по дополнительным номограммам <₽>(/%« / flj) и Рщп/ ft)
оцениваются запас устойчивости по фазе <р, (запас по амплитуде L,
полагается равным 6 дБ) и минимальные значения краевых амплитуд
Ц = £«(iut) и L, = /«(Юц) (дБ), по которым можно определить грани-
цы среднечастотного диапазона:
шс < 10 20v‘ <ocp, ы, > fo20*' wcp.
(6.43. о)
Для обеспечения достаточного запаса устойчивости ширина средне-
частотного диапазона должна быть не менее декады, а частота среза
должна располагаться примерно в его середине:
^>10. 2<^
Юс Шс
(6.43. б)
Впрочем, если наклон среднечастотной части логарифмической ам-
плитудно-частотной характеристики равен -40 дБ /дек (в этом слу-
чае система на средних частотах имеет свойства колебательного
звена), то частоту среза желательно выбирать ближе к меньшей час-
тоте Wfc.
□ Низкочастотный и среднечастотный участки амплитудной характеристи-
ки в интервале ш е mJ соединяются сопрягающей частью, имеющей
наклон -40 или -60 дБ/дек. Сопряжение горизонтальным участком
Длиной более половины декады (рис 6 34, а) неже.тате.и>но, г к оно за-
тягивает переходный процесс на промежуточном уровне с большой ста-
тической ошибкой (рис 6.34. б).
Этот недостаток устраняется дополнительным сдвигом вверх низкочас-
тотного участка амплитудной характеристики, как показано пунктиром
на рис. 6.34, благодаря чему сше и уменьшается коэффициент скорост-
ной ошибки С|.
Глава 6
Рис. 6.34
□ Высокочастотный участок желаемой амплитудной характеристики стро-
ится вправо от частоты Иц, повторяя изменения наклонов характеристи-
ки Цы) разомкнутой системы без регулятора Создание необходимого
для фильтрации шумов наклона не менее -40 дБ / дек достигается вве-
дением фильтра низких частот с постоянной времени
ТЛ$—.
со,
С целью упрощения структуры регулятора рекомендуется по мере возмож-
ности совмещать частоты сопряжения асимптот характеристик Лж(о>) и
Цы). В этом случае логарифмические характеристики регулятора в (6.39)
будут иметь минимальное число перегибов, его передаточная функция
(6.40, в) после сокращения одинаковых множителей будет содержать ми-
нимум типовых звеньев, а схема реализации приобретет простейшую
структуру и стоимость.
& Пример 6.8. Для объекта (6.19) с коэффициентом К= 200 рассчитать и
реализовать на операционных усилителях последовательный регулятор,
дающий замкнутой системе астатизм первого порядка с коэффициентом
скоростной ошибки С| = 0.1 с. показателями качества < 2 с, а < 20% и за-
пасами устойчивости (6.20) > 6 дБ и <pj > 30*.
Решение Построив на рис. 6.35 асимптотические логарифмические характе-
ристики объекта Цы} и Ф(ш), из условия (6.42, б) определим коэффициент
усиления статической части желаемой системы:
= — =,10.
С1
Влево от точки (I. 20) проводим пунктиром низкочастотную асимптоту ам-
плитудной характеристики с наклоном -20 дБ / дек.
Методы проектирования систем автоматического управления
По номограммам (см. рис. 6.33) для a = 20% определяем произведение
'y^tp = 2.5л = 8 и частоту среза амплитудной логарифмической характери-
стики
<цр = 2.5п / 1у = 4 рад/с.
Через точку (и\р, 0) проводим ереднечасто/пную асимптоту также с наклоном
-20 дБ / лек. По номограмме определяем минимальные значения амплитуд
Д, = Z, = 18 дБ, а по (6.43, о) — границы среднечастотного диапазона
0.504 рад/с.
<ов 231.8рад/с.
Так как низкочастотная и среднечастотная части /ж(<а) не пересекаются, то
нужна сопрягающая часть с наклоном -40 дБ / дек Совместим ес левую гра-
ницу их, с частотой сопрнжсння асимптот амплитудной характеристики объ-
SOO Глава 6
сета a>j m 0.1 рад/с, тогда сопрягающая и среднечастотная асимптоты пере-
секутся на логарифмической частоте lg<i\. = -0.6, откуда получаем
<ц “ 0.25 рал / с =» Тс = 4 с,
что удовлетворяет условию (6.44).
Также по (6.44) выберем частоту о>„ = 40 рад / с сопряжения среднечастот-
ной и высокочастотной асимптот желаемой амплитудной характеристики
£#(</>), откуда находим постоянную времени фильтра низких частот
Г, = 0.025 с.
На рис. 6.35 построены асимптотические характеристики /.ж(со) и Фж(ш),
по которым восстановим передаточную функцию желаемого разомкнутого
контура:
*ж(1+7>) 10(1+4д)
* .т(1+Г2^Х1+T,s) j(I+10.tX1+0.025.t)
Рассчитаем реальные показатели качества полученной замкнутой системы:
□ переходная характеристика (6.41)
л, (0=1/4 -I-------1+45 2----------Д -
Ц+4.1Д+1.0025? +0025? )]
= L ' {,(| + 3.84.»Х1 + 0.028тХ1 + 0.231.»)} =
»1+0.044е’°“' + О.145е’”5' -1.189е’433f.
построенная на рис. 6.36, а, имеет апериодический характер, перерегу-
лирование о = 2.8 < 20 (%), быстродействие 1у = 0.6 < 2 (с) и нулевую
статическую ошибку еу„ ж 0;
□ по логарифмическим частотным характеристикам желаемого разомкну-
того контура
К (<о)= 20 lg(K„) +10 lg(l + Т2ш2)-10 |g(l + T2W)-10 lg(l + Т,2Ш2)- 20 lg W.
I Фж (w)= arclg(7>)- arclg(T2w)- arctg(T,ci))- 90“
определяем существование частотного интервала До», £ |o»,j. о>,2|. на гра-
ницах которого один из фактических запасов устойчивости обеспечив®*
ется точно*.
1>ж(“>»|) “ ~6 дБ =» <й,| “ 7.84 рад / с;
ф»(ы12) « -150” =» (Qj2.68.9 рал / с
Методы проектирования систем автоматического управления
Так как выполняется совместное условие
< «Ъ2> П (Фж(<0>|) = -102* > -ISO*) п Ш - -30.7 < -6 дБ).
то желаемые запасы устойчивости обеспечиваются не на одной частоте а
во всех точках интервала частот Лоз..
Желаемые свойства замкнутой системы достигнуты за одну итерацию. Вы-
числив коэффициент статического усиления
г eS. = 0.05
р Л'
и передаточную функцию последовательного регулятора
£pO+Tc«Xi+^Xi+^) 0.05(1 +4^1*Ml* О
"w"W-------------------------------
конструируем с помощью табл. 1.3 принципиальную схему корректирующе-
го устройства на операционных усилителях (рис. 636, б). О
502 Глава 6
6.5. Управление неустойчивыми объектами
До сих пор мы изучали частотные методы управления объектами, устойчи-
выми в разомкнутом состоянии. В соответствии с логарифмическим крите-
рием Найквиста для устойчивости замкнутой системы последовательный ре-
гулятор Я(з) должен обеспечивать нулевую сумму переходов фазочастотной
характеристики через граничный уровень фазы в интервале частот с поло-
жительной логарифмической амплитудной характеристикой.
Неустойчивость разомкнутого контура порождается наличием хотя бы одно-
го правого полюса в спектре его передаточной функции. Рассмотрим воз-
можные способы принудительной стабилизации замкнутой системы.
□ В числитель передаточной функции регулятора Л(з) включаются зве-
нья, совпадающие с неустойчивыми звеньями знаменателя передаточ-
ной функции объекта IK(j). Тем самым в контурной передаточной
функции
^ж(т) - Л(з)НТт)
все правые полюсы теоретически компенсируются равными им правыми
нулями. Оставшаяся часть регулятора должна обеспечить устойчивость
замкнутой системы при устойчивой разомкнутой, т. е. нулевую сумму пе-
реходов по критерию Найквиста.
Недостаток данного способа стабилизации — в возможном фактическом
количественном несовпадении компенсируемых полюсов и нулей из-за
временнбго дрейфа параметров объекта или неточного их расчета Это
качественно изменяет задачу регулятора в смысле обеспечения уже нену-
левой суммы переходов. Ясно, что одно и то же устройство не может ре-
шать противоположные задачи.
□ Регулятор изначально конструируется под неустойчивый объект с л.
правыми полюсами, обеспечивая л+ / 2 переходов характеристики Фж(ш)
через граничный уровень фазы при ЬЛ(и>) > 0 с учетом пунктирного до-
полнения (см. разд. 4.6). Для получения дробного числа переходов, воз-
можно. придется включить в состав регулятора инвертор, изменяющий
сумму переходов на 1 / 2. Предусмотрев желаемые запасы устойчивости,
можно избежать качественной перестройки регулятора при количест-
венном изменении параметров объекта.
В отличие от (4.30, а) условия одновременного обеспечения запасов ус-
тойчивости L, и <г>, в системе управления с неустойчивым объектом при-
нимают вид
(6.45)
L, У<о:|ф(ш)-ф|р|<ф,,
Методы проектирования систем автоматического управления 503
На рис. 6,37 заштрихованы запретные области, куда не должны заходить же-
лаемые контурные логарифмические характеристики £.ж(о)), Фж(<») и голо-
граф И'хОш) при условии, что достигается необходимая сумма переходов п. / 2
вне запретных областей В противном случае ввиду изменения значения л , в
результате дрейфа параметров возможна потеря устойчивости замкнутой
системы.
& Пример 6.9. Для описанного в примере 1.5 объекта «тележ-
ка - перевернутый маятник» разработать астатическую систему слежения
угла отклонения маятника <р(г) за уставкой,«(/) со следующими показателями
качества:
□ быстродействием /у S 0.5 с;
□ перерегулированием а < 30%;
□ коэффициентом скоростной ошибки q S 0.01 с:
□ запасами устойчивости Д, г 6 дБ и <р3 а 30’
Построить графики ДО (Н), </(/) (см) и «₽(/) (град) движения замкнутой сис-
темы с нулевых начальных условий при импульсной уставке
«(/)- 10(1(/)- 1(г-2)).
Решение. Будем строить систему управления на основе критерия Найквиста
для неустойчивых разомкнутых систем. Основная задача проектирования
обеспечение устойчивости системы «тележка - перевернутый маятник», не-
устойчивой в разомкнутом состоянии из-за наличия правого полюса
jj = 1 / Тз = +2,52 в передаточных функциях (2.20)
ГлаваS
WH>'
(K7„X.XW) <,P“/")
с параметрами Kd= 10, Л", “ 0.573, T\ = 1.72 c, fj = 0.438 c, 7j = 0.397 c,
Tt = 0.305 c, 7s = 0.244 с. На рис. 2.24 и рис. 6.38 построены логарифмиче-
ские частотные характеристики объекта L,(u>) и Ф,(ш). Структура передаточ-
ной функции последовательного регулятора формируется из следующих со-
ображений:
Рис. 6.38
□ для обеспечения астатизма первого порядка нужно изменить наклон
низкочастотного участка амплитудно-частотной характеристики с
Методы проектирования систем автоматического управления
+20 дБ / дек на -20 дБ / дек путем введения в регулятор двух изодромных
каскадов с обшей передаточной функцией
При этом низкочастотная часть фазовой характеристики опустится вниз
на угол от -180° до 0°;
□ для устойчивости по Найквисту необходимо, чтобы на частотах, где
> 0, сумма переходов графика Фх(ю) через уровень <ргр = 180* была
равна -1 / 2 е учетом пунктирного дополнения низкочастотной части ло-
гарифмической фазочастотной характеристики. Для этого введем в регу-
лятор следующие элементы:
• инвертор, сдвигающий всю фазовую характеристику вверх на 180° без
изменения амплитудной Теперь пунктирное дополнение будет начи-
наться с уровня <р,р вниз, что дает -1/2 перехода.
• форсирующее звено с передаточной функцией
Л,(5) = Л(1 + TJS),
поднимающее высокочастотную часть фазовой характеристики на
угол от 0 до 90° и изменяющее наклон высокочастотной части ампли-
тудной характеристики на +20 дБ / дек. При надлежащем выборе па-
раметров К, Т|, Т2 и Tj это даст пересечение характеристикой Фж(ы)
уровня фф при Лж(ы) > 0. Тогда сумма переходов составит нужное
значение, равное -1 / 2 + 1 = 1/2;
□ для подавления высокочастотных шумов желательно ввести в регулятор
низкочастотный фильтр с передаточной функцией
Таким образом, мы получили необходимую структуру передаточной функ-
ции последовательного регулятора
«(.).-«,(б.«.а
параметры которой определим следующим образом (рис 6.38):
□ построим низкочастотную асимптоту Аж(ш) с наклоном -20 дБ / дек,
проходящую через точку (I, 40) для удовлетворения требования скорост-
ной ошибки
= 0.01,
506 Глава 6
откуда получаем значение коэффициента усиления регулятора
К= 100/А; = 174.533;
□ по номограммам на рис. 6.33 для заданного перерегулирования о = 30%
определяем
г/ц-р = 3.72л 11.7 =» Wtp = 23.4 рал/с
и Igi^p = 1.37. Через точку (чр, 0) проводим среднечастотную асимптоту
с наклоном -20 дБ / дек;
□ сопряжение низкочастотного и среднечастотного участков желаемой ам-
плитудной характеристики должно иметь наклон -40 дБ / дек. По номо-
грамме. приведенной на рис. 6.33, определяем минимальные амплитуды
4 = £, = 13.4 дБ, а по (6.43, о) — границы среднечастотного диапазона
гое К, ы,|:
ц. S 5 рад/с, го, > 109.5 рад/с.
Проведем сопрягающую асимптоту амплитудной характеристики так. что-
бы она пересекалась со среднечастотной асимптотой на частоте
<о,= 1 / Т|, меньшей 5 рад/с. Для упрощения структуры регулятора со-
вместим частоту ь>| первых перегибов характеристик Z(<o) и Дж(о>). Гра-
фически определяем логарифмическую частоту пересечения lgox = 0.38,
откуда следует
т.= —= 0.416 с-Т3.
го.
Выбираем постоянную времени Т| = 7j = 0.397 с;
□ назначим частоту последнего перегиба амплитудной характеристики
ыь = 125 рад/с и постоянную времени фильтра низких частот
т. = — = 0.008 с.
со.
Правее частоты строим высокочастотную часть амплитудной характе-
ристики с наклоном -40 дБ / дек;
□ с учетом (6.46, о) запишем передаточную функцию желаемой разомкну-
той системы
Сравнив ее с восстановленной по желаемым логарифмическим частот-
ным характеристикам (рис. 6.38) передаточной функцией
-100(14-Л-т)2
aO + T.aXl-Ml + T.a)’
получим остальные постоянные времени регулятора:
Т2 = = 0.397 с, т3 « Т5 = 0.244 с.
Таким образом, передаточная функция последовательного корректирующего
устройства принимает следующий вид
, }_-K(l + T3Sy(l+TiS) = -174,533(И-О.397л)2(1 >0.244.0 46
е2/|>Т t2fi+nnoR0
В полученной замкнутой астатической системе коэффициент скоростной
ошибки равен q =0.01 и удовлетворяются запасы устойчивости, т к же-
лаемые частотные характеристики на рис. 6.38 не заходят в запретные об-
ласти, аналогичные областям на рис. 6.37, а.
Построим на рис. 6.39 графики переходных процессов в системе управления
углом отклонения перевернутого маятника с регулятором (6.46, о) при нуле-
вых предначальных условиях (маятник вертикален и неподвижен, тележка
неподвижна в начале координаты и заданной выше уставке g(t)
Рис 6.39
Глава 6
По принципу суперпозиции переходные процессы в системе имеют вид
Дг) = ЮЛ/z) - ЮЛ/г- 2),
d(t) = 1ОА<Я/) - 10*rf(z - 2),
<р(/) = 10A.(z) - 10й,(/ - 2),
где й//). hjit) и й,(г) — переходные характеристики замкнутой системы в
точках / d и ф. Вычислим их методом разложения Хевисайда соответствую-
щих изображений.
Н М- - К(\+Т^+Т3^(1-Т3^1+Т5з)
' 41+%.(4 ?(KK,(i+rJs)2-s(i+rlsXi-^Xi+TB3))
_ 1.745+4.124+1.818? -0.359? -0.33? -0.0459з5
?(l + 0.784s + 0.144s2 +0.00672? + 0.0000546.x4) ’
Л//) = (1.745/ + 2.752 - 1034.9е ^«' + 196.2e'i8 2,« - 3.439е"5 56' -
- 0.232е-1 «9 !(/);
н (Л - Ш'Ы) kMi-t^Xi + t^O+t^)
'М-М ?(лх,(1 + 73s)2 -з(1 + 7,3X1 - ^1 + *.*))
17.453+11.533з-1.423?-2.215?-0.367?
х3 (1 + 0.7843 + 0.144 s2 + 0.00672? + 0.0000546 s4)’
йхг) «(8.727Р - 2.153/- 2.255 - 0.883е-”«' + 5.1 Не"1821' - 1.5е“5 »'-
- 0.473е-> »5г) 1(1);
н (Д _________Х^С + Тзз)2____________
’ 41+W«(*))’ з(хк,(1 + 73з):-з(1 + Г,зХ1-7-3зХ1 + ^0)
_ __________1 +0.794а + 0.158s2__________
з(1 + 0.784s + 0.144 s2 + 0.00672 s3 + O.OOOO564 s 4 ) ’
*UO = (1 + 0.3837e^«'-2.381e'"l2,' + 1.115e'5 S6'- 0.118с1 8Sr) !(/).
Показатели качества переходной характеристики замкнутой системы й,(г)
ty - 0.425 < 0.5 с, а - 24.1% < 30%
и удовлетворяют требованиям технического задания.
Обсудим характер переходных процессов в устойчивой замкнутой системе с
последовательным регулятором (6.46. б). Формула уставки означает
(|0при0£/< 2с;
'W-|«np«<»U
Методы проектирования <
т. е. устройству управления дано задание в течение двух секунд удерживать
угол отклонения неустойчивого маятника (см рис I 30) на уровне 10°, а за-
тем вернуть маятник в вертикальное положение
Какой должна быть сила Д/), воздействующая на маятник массой т = 6 кг
косвенно через тележку массой М= 11 кг, чтобы обеспечить заданный закон
движения этой системы из двух взаимодействующих тел? Из физических
соображений ясно, что для вывода маятника из нулевого состояния равно-
весия в положительном направлении необходимо краткое воздействие на
тележку в направлении d < 0, а затем резкое изменение направления дейст-
вия силы для стабилизации начавшегося паления маятника Действительно,
как видно из рис. 6.39, начальное значение силы равно ДО) - 8396 Н. а уже
менее чем через 50 мс имеем Д0.0455) = +733.3 Н
Дальнейшее изменение силы, генерируемой регулятором, стабилизирует
угол <р(г) в интервале 10 ± 0.5’ за время /у = 0.425 с, и до момента времени
1=2 с тележка движется равноускоренно под действием линейно нарас-
тающей силы
/^(1) = 17.45/+ 27.52(H)
На втором временном интервале /> 2 с при нулевой уставке g(t) =0 пере-
ходные процессы развиваются в противоположных направлениях и к мо-
менту времени / = 2.425 с маятник возвращается в вертикальное положение,
тогда как тележка движется равномерно вперед со скоростью 21.53 см / с.
На рис. 6.40 построена схема реализации передаточной функции регулятора
(6.46, б) и сравнивающего устройства на операционных усилителях Номи-
налы радиоэлементов удовлетворяют следующим соотношениям:
ЛС"Ч.ЛС,.
Рис 6.40
397> Л| С2 = Ts = 0.244, Л2С = т, = 0.008,
Х'” К = 174.53.3.
510
Глава 6
6.6. Спектральный метод синтеза регуляторов
Ранее, в разд 3.5.2, нами получены зависимости (3.48) - (3.52) оценок пока-
зателей качества переходной характеристики (/у, а, С, Л'к) от параметров (л,
у, р) спектра передаточной функции системы. Высокая достоверность этих
оценок позволяет синтезировать регулятор, доставляющий замкнутой систе-
ме желаемое качество, спектральным методом навязывания передаточной
функции И^з) желаемого спектра — распределения полюсов s, и нулей
Расчет последовательного регулятора спектральным методом выполняется
поэтапно (рис. 6.41).
□ На первом этапе формируется спектр замкнутой системы (з„ Z/) на осно-
ве требований к желаемому качеству ее переходных процессов.
□ На втором этапе с учетом требований статической точности из переда-
точных функций типовых звеньев
составляется передаточная функция замкнутой системы
□ На третьем этапе определяются фактические показатели качества замк-
нутой системы путем моделирования ее переходной характеристики
Методы проектирования систем автоматического управления
□ На четвертом этапе показатели качества переходной характеристики
h2(t) сравниваются с желаемыми значениями. Если в ходе проектирова-
ния не достигнуты желаемые свойства замкнутой системы, то следует
перейти на первый этап для изменения спектра или пересмотра техниче-
ского задания.
□ На пятом этапе формируется передаточная функция желаемого разомк-
нутого контура:
„М-ВЛЬ. -Ж,. Ш <ыт>
□ На шестом этапе находится передаточная функция последовательного
регулятора:
у %(*) _
W(S) (1-W,(t))v(t) (Л,(з)-В,(ф(з)
□ На седьмом этапе выполняется техническая реализация полученной пе-
редаточной функции:
• последовательный регулятор преобраз; I >му типу из тех,
что описаны в разд. 6.1, или их комбинации;
• разрабатывается техническое устройство, реализующее регулятор в
требуемой элементной базе
В случае неудачи в достижении требуемых свойств замкнутой системы
корректируются желаемый спектр или требования технического задания,
после чего цикл проектирования повторяется со второго этапа
Наиболее сложными яатяются первый и второй этапы формализации тре-
буемых показателей качества замкнутой системы в виде ее спектра и переда-
точной функции. Они включают выбор структуры передаточной функции
(степеней полиномов Л3(з) и в,(т)) и ее параметров (коэффициентов поли-
номов а, и bj). Синтез замкнутой системы подразделяется на статический.
Дающий коэффициенты статических ошибок (6.17), не превышающие за-
данных значений со- А. . су, и динамический, гарантирующий желаемые
Показатели качества переходного процесса о и т. п
Для выполнения дальнейших выкладок обозначим передаточные функции
желаемого разомкнутого и замкнутого контуров следующим образом:
(j)= %(i)= .4^ , + (649)
a0+a15 + ... + <ins'1 ao+ot|X + ... + a„3"
□ При статическом синтезе в первую очередь задастся порядок астатизма
желаемой разомкнутой системы v. на единицу больший степени поли-
нома уставки
ГлаваS
g(t)=go + sit+-+s^-ifv~l.
отслеживаемой с нулевой установившейся ошибкой.
Для проектирования статической системы управления с порядком аста-
тизма v = 0 задается максимальный модуль со коэффициента статиче-
ской ошибки:
Отсюда получаем связь коэффициентов «о с Ьо и допустимый интервал
изменения коэффициента статического усиления замкнутой системы
К, = *0 / W
оо - оой> < Z>o < ао + aoQ) => 1 - со s К3 s 1 + ср. (6.50, в)
Дополнительно может быть задан максимальный модуль q коэффици-
ента скоростной ошибки:
k-(ai+6i)co[ = |a|-ot|CO-fr|| < ₽
| во+*о I I о-о
Решая это неравенство, получим дополнительное условие связи пара-
метров передаточной функции И<,(л):
«1 ” «iQi ~ “оП S bi < at - се,со + aoCj. (6.50, tf)
В общем случае, если задан N + 1 максимальный модуль коэффициентов
ошибок «и * сх, то по (6.17, в) степени полиномов ВДд) и Ла(5) должны быть
не менее N, а коэффициенты удовлетворять векторным неравенствам
“ в,-| - 0, Яж(з)=з'’(а,+ +a„3"'v),
Методы проектирования систем авто*
a v младших коэффициентов ошибок равны q>= ... = cy-i = 0. Исключив
их из системы неравенств (6.50, и), получим условия связи параметров
передаточной функции И'(з) для заданных максимальных модулей ко-
эффициентов су + су.
В частности, при v = N = 1 проектируется система управления с аста-
тизмом первого порядка и ограничением С| на модуль коэффициента
скоростной ошибки. Тогда ее передаточная функция должна иметь
параметры, удовлетворяющие условиям
К, = 1, ао = bf), eq - <хоС| S b{ S <Х| + ОоС| (6.51, б)
При v = I и Л( = 2 задаются ограничения q и q на коэффициенты оши-
бок по скорости и ускорению Тогда передаточная функция замкнутой
системы должна иметь параметры, совместно удовлетворяющие услови-
ям (6.51, б) и
<Xj ~ О|С| - OoCj S 6j 5 «2 ~ °lcl «оС2- (651.
Таким образом, статический синтез дает минимальные степени полиномов
Я>(з), /Цз) и соотношения между их коэффициентами, обеспечивающие
заданную точность
□ Динамический синтез передаточной функции замкнутой системы
ГлаваS
заключается в назначении ее спектра — полюсов si и нулей г/ — тах,
чтобы спектральные оценки (3.48) - (3.52) качества переходной характе-
ристики й3(г) не превышали заданных значений:
• времени установления /у (с);
• перерегулирования о (%);
• степени затухания колебаний
• числа колебаний в переходном режиме NK.
Дополнительно могут быть ограничены:
• жесткость системы г,
• полоса пропускания f„ (Гц), связанная с максимальной постоянной
времени знаменателя передаточной функции Т соотношением (2.27)
1;
• другие динамические показатели.
Полюсы г, нужно размешать в области S левой полуплоскости, ограни-
ченной степенью устойчивости т), степенью быстродействия у и углами
= +агсц>(ц), определяемыми степенью колебательности М (рис. 6.42):
-<П<2яГп.
(6.52)
Размещение полюсов в области дает полином знаменателя передаточ-
ной функции
Методы проектирования систем автоматического управления_____________515
Прямой алгебраический метод выбора Л,(з) состоит в анализе устойчиво-
сти .характеристического полинома со смещенным аргументом р. Соответ-
ствующие (6.52) условия
-у < Re(j,) < -п
эквивалентны устойчивости полиномов Л,(р - п) и Л,(-р - у), что нала-
гает определенные ограничения-неравенства на коэффициенты полино-
ма Лз(т).
Дополнительные ограничения дают условия
при которых степени колебательности ц( = комплексных полюсов
J/./+1 = -П/ - М не превосходят заданного значения ц. На основе формул
Виета (4.8), связывающих корни полинома с его коэффициентами, со-
ставляются условия связи коэффициентов друг с другом и со значением
ц. В пересечении с областями устойчивости полиномов Л3(р - ту) и
Л,(-р - у) получим допустимые области определения коэффициентов
полинома Л3(з).
При выборе передаточной функции И,(з) желательно выполнять следующие ре-
комендации.
□ На случай возможного разрыва цепи обратной связи рекомендуется
обеспечить устойчивость характеристического полинома желаемого ра-
зомкнутого контура
Лж(з) = Л,(т) - Д(з).
□ Характеристический полином замкнутой системы Л3(з) должен иметь не-
высокую степень п = 2 * 4 для того, чтобы:
• облегчить задачу размещения л полюсов в допустимой области Si
• упростить структуру переходного процесса, снизить сложность и по-
высить точность его расчета как ручными, так и программными ме-
тодами;
• повысить грубость системы, т. е. ослабить влияние изменений ее па-
раметров на устойчивость.
□ Для упрощения структуры передаточной функции регулятора (6.48) по-
линомы Д,(з)Л(з) и (Л1(з) - fi^(j))fi(j) должны иметь совпадающие корни.
Желательно сохранить в передаточной функции В^з) полюсы s° S -Г).
а в IPi(s) сохранить нули z" передаточной функции Щз). т. е. выбрать
полиномы Bi(s) и В(.ч) кратными, если это не противоречит условиям
(6.50) и (6.51).
516
Глава 6
□ Для уменьшения амплитуд составляющих ошибки регулирования и по-
вышения быстродействия желательно компенсировать близкие к мнимой
оси полосы путем размещения рядом с ними нулей.
□ В передаточной функции ИЦз) нежелательны правые нули, порождающие
в переходной характеристике отрицательное перерегулирование.
□ Во избежание явления резонанса необходимо удалять полюсы передаточ-
ной функции от комплексных полюсов изображения уставки G(s).
Рассмотрим некоторые типовые передаточные функции замкнутой системы
И^з) и методы расчета их параметров.
6.6.1. Замкнутая система второго порядка
Допустим, выбрана передаточная функция замкнутой системы второго
порядка
%(*)=*,------+-* (6.53)
l+a|j + a,.r
устойчивая при (й| > 0} П (аг > 0). Степень числителя т = 1 позволяет вы-
полнить статический синтез по (6.50) при N < I:
I 1-ео*К,*1+со.
lal(l-e0)-c,SKJb|Sa1(l-c0)+A.
Переходя к динамическому синтезу, получим прямые ограничения на допусти-
мые значения коэффициентов aj и аг, эквивалентные размещению полюсов
в области (6.52).
□ Правая граница области определяется заданной степенью устойчивости
(рис. 6.43, в):
Reto) S —т] =» Л,(р - п) = (1 - па, + П^г) + (<»i “ 2na2)p + ajp2,
па, - n2a2 S 1, а| — 2па2 г 0, а2 > 0. (6.55, в)
□ Левая граница области размещения полюсов определяется заданной сте-
пенью быстродействия (рис. 6.43, б):
Reto) г -у =» А(~Р ~ Y) ж (I ~ №i + Y2“j) - (a, - 2ya2)p + a2p2.
ya, - y2o^ S I, 0Ц - 2ya2 S 0, a2 > 0. (6.55. Л
□ Угол раствора области (6.52) размещения комплексных полюсов
31.2 =-П« i РЧ определяется заданной степенью колебательности И Из
формул Виста (4.8) для полинома второй степени следуют соотношения
между полюсами з(, ,т2 и коэффициентами полинома:
Методы проектирования систем автоматического управления
517
= -2П«=-^.
«2
iJ(,+k)=-7
Отсюла получим допустимое соотношение коэффициентов полинома,
при котором выполняется условие Рк S ц (рис 6 43, в):
Я
Рис. 6.43
Заштрихованная область выбора коэффициентов характеристического
полинома из условия 2а2 Serf соответствует максимальной степени ко-
лебательности g = 1 и коэффициенту затухания . при котором в
соответствии с рис. 3.11, 6 достигается наилучшее качество переходной
характеристики. При выборе коэффициентов из условия 4сь <а(: будет
получена степень колебательности ц = 0 и апериодическая замкнутая
система с действительными полюсами Однако, эта система обладает
худшим быстродействием, чем колебательная система с оптимальным
коэффициентом затухания 4от = 1/з/2 .
Пересечение трех областей, изображенных на рис 6.43. дает область распо-
ложения коэффициентов характеристического полинома 4,(з). соответст-
вующую желаемому спектру замкнутой системы
Размещение двух полюсов системы (6.53) в области 5 согласно условиям
(6.55) еще не определяет полностью всех ее динамических свойств, посколь-
ку на них влияют значения коэффициента и нуля 2| •-! / 6,. Рассмот-
рим возможные варианты совместного выбора коэффициентов полиномов
4(*). в>(з) И ИХ корней 3|. 41 И Z|
£12_______________________________________________________________Глава 6
□ Простые полюсы j| * на отрезке действительной оси |—у, —г)| е5 дают
характеристический полином
с постоянными времени апериодических звеньев 7} = -1 / s, и коэффи-
циентами
a -_1_± = г+г a =_L = 7’1T2. (6.56)
S, S2 ‘ J|Jj
Переходная характеристика замкнутой системы с действительными ле-
выми простыми полюсами имеет апериодический характер
(см. табл. П.2, п. 31):
Исследуем зависимость ее свойств от выбора постоянной времени фор-
сирующего звена Л|, считая для определенности, что Г| > Т2. Анализ
монотонности и экстремумов переходной характеристики показывает
(рис. 6.44):
при 0 s 6| S Г| она изменяется монотонно без перерегулирования, а
увеличение коэффициента Ь, форсирует (ускоряет) переходный процесс'.
при 6| > Г| уменьшается время разгона /р, а на графике W) появля-
ется положительное перерегулирование
Методы проектирования систем автоматического управления
518
Значение biom, при котором перерегулирование равно порогу сходи-
мости Др, является оптимальным, доставляющим замкнутой системе с
апериодической передаточной функцией (6.53) максимальное быстро-
действие Дальнейшее увеличение > Л|0(П увеличивает как перере-
гулирование о, так и время установления гу;
• при Ь\ < 0 переходная характеристика имеет, по определению
(3,40, б), нежелательное отрицательное перерегулирование
замедляющее переходный процесс из-за попятного начального дви-
жения.
Для примера построим графики зависимостей о(6|), о-(А|) и /у(6|)
(рис. 6.45) основных динамических показателей качества замкнутой сис-
темы с передаточной функцией второго порядка
' ’(1+дХ1+0.5д)
полюсами 5| = - I, sj = -2 и постоянными времени Г, = I с, 7j = 0.5 с.
Время установления гу вычисляется по определению (3.39) - моменту
вхождения графика h/i) в +5%-ую трубку вокруг установившегося зна-
чения Луст = К3.
Рис 6.45
520
Глава 6
(6.57)
(6.58)
Изучение влияния постоянной времени форсирующего звена системы
(6.53) на показатели качества ее переходной характеристики позволяет
понять общие принципы размещения действительных нулей передаточной
функции л-го порядка с действительными полюсами в области 5. опре-
деленной в (6.52):
• для повышения быстродействия без увеличения перерегулирования
рекомендуется размешать нули между крайними полюсами ближе к
правому полюсу, а постоянные времени числителя bj выбирать между
крайними постоянными времени знаменателя 7} ближе к максималь-
ной:
Г-yS min{j,}Szy 2 maxfo/S-T).
। 0< min{r,}<b, < max{7j}.
• нули и постоянные времени полинома числителя
тах{з,}< Zj <0.
bj > max {Г,}
создают положительное перерегулирование а, но до определенных
оптимальных значений гд>|п и Ь^,П. найти которые можно из условия
о = Ар только путем трудоемкого моделирования, еще больше увели-
чивают быстродействие и являются наиболее рекомендуемыми.
• допустимы также нули Zj< niin{3,} и постоянные времени
О < bj< min{7}|: они не увеличивают перерегулирование, хотя и не
форсируют переходный процесс;
• нежелательны правые нули $ > 0 и отрицательные постоянные времени
bj< 0: они лают отрицательное перерегулирование и существенно за-
тягивают переходный процесс во времени.
□ Разместив два действительных полюса в одной точке
-у S Л - ду S -П,
т. е. делая их кратными, получим коэффициенты характеристического
полинома
а, =-1 = 2Т, а, =-у = Т2 (6.59)
Переходная характеристика замкнутой системы с действительным дву-
кратным левым полюсом равна
Методы проектирования систем автоматического управления__________521
Влияние постоянной времени Ь\ на динамические показатели качества
переходной характеристики аналогично случаю простых полюсов. На
рис. 6.45 пунктиром изображены следующие зависимости от 6| у замк-
нутой системы с передаточной функцией
• перерегулирования при b\ > Т
• отрицательного перерегулирования при Л| < 0:
• времени установления t/b\)
Наилучшие показатели /у, о и нулевое значение а_ достигаются при вы-
полнении следующей рекомендации: желательно размешать нуль ct слева
и вблизи от кратного полюса ,«|. Такой выбор позволяет практически
скомпенсировать кратность полюса, ухудшающую динамические показа-
тели.
□ Разместив в области 5 пару качплексно-сопряженных полюсов
*1,2 = ~Пк ± М с углами раствора ±vk = ±arctg(ov / tjk), получим характе-
ристический полином колебательного звена второго порядка
l+O|j+a2Ji=l+2^l(7'l(j+7’ll2J2
со следующими постоянной времени и коэффициентом затухания
, 1 , . 4, = ПкГк = cos(vJ.
Vni+w;
Коэффициенты полинома зависят от его корней и параметров колеба-
тельного звена следующим образом:
a =_1_1 = ^!!^ = 25Л.
Д| ‘2 (6.60)
522
Глава 6
При выборе значений Пк, ov и полезно помнить, что согласно (3.49)
перерегулирование не превышает 5%, если степень колебательное™ удов-
летворяет условию
а по (3.47) коэффициент затухания Е, > 0.7. Отсюда следуют простые пра-
вила выбора частоты колебаний ш* и угла раствора \|/к без учета располо-
жения нуля, т. е. при Л| = 0:
(ifc < =» < 45". (6.61)
Переходная характеристика замкнутой системы второго порядка с пере-
даточной функцией
1 + 2^1,7^ j + Tk д
и комплексно-сопряженными левыми полюсами имеет затухающий ко-
лебательный характер (см. табл. П.2, п. 74)
Л, (»)= *з {* - Скс'П'' sin(°V + Фк )}
с параметрами
с _ №-21;кр+1
цЛ2 V
где 0 » 6| / ТЛ — отношение постоянных времени форсирующего и ко-
лебательного звеньев передаточной функции замкнутой системы.
Изобразим на рис. 6.46 влияние параметров 0 и 6 |0, 0 на динамиче-
ские свойства переходной характеристики. Анализ ее экстремумов с по-
мощью символического процессора Mathcad показывает, что в колеба-
тельной системе с форсирующим звеном перерегулирование
существует при всех значениях р. а при Р = 0, т. с. при нуле Z| -»
достигает минимума (3.49):
Методы проектирования систем автоматического управления
Эго значит, что никакой действительный конечный пуль в принципе не
может полностью компенсировать колебательное перерегулирование, по-
рождаемое комплексными полюсами
Отрицательное перерегулирование
о_ = 7₽2-25«3+«е “• -I
появляется только при выборе Р < 0, т. е правого пум Ji = - I / 0| > 0, и
резко возрастает при приближении этого нуля к мнимой оси.
Зависимости времени установления переходной характеристики замкну-
той системы Л3(/) от параметров Р и Ек, изображенные на рис. 6.46, б, по-
лучены с помощью функции tust (см. рис. 3.8) при моделировании сис-
темы с передаточной функцией
1 + fc
l + 2V + r '
Максимальное быстродействие при р - О достигается, как и следовало
ожидать с учетом рис. 3.11,0, в колебательной системе с коэффициен-
том затухания 4 = 0 7 Однако, и наличие форсирующего эвена с поста-
524 Глава 6
янной времени Ь\ равных знаков, как свидетельствует выделенный гра-
фик на рис. 6.46, 6, не отменяет вывода о том, что при выборе желаемой
системы колебательного типа нужно стремиться к оптимальному коэффи-
циенту затухания = 1Д/2 =0.7 путем задания по (6.61) полюсов
Л| 2 = -»)» ±Ж с примерно равными значениями т)к и соц н степенью ко-
лебательности р» = I, при которой согласно (3.49) и рис. 6.46, а положи-
тельное перерегулирование не превышает порога Д = 0.05.
Наибольший размах колебаний переходной характеристики минимален
(Q = 1) при выборе постоянной времени форсирующего звена из условия
₽2-2^Р+1 = (РЧ,)2
р
откуда получаем оптимальные по минимуму колебательности параметры
форсирующего звена:
Р-ЬЛ-йЛ. 1|=-г7-
Ьк'к
С учетом резкого роста перерегулирования при р > (рис. 6.46, а) по-
лучаем желаемые области выбора постоянной времени форсирующего
звена и его корня:
Учитывая соотношения = cos(vK) и Г» = I / |.гк|, положение нуля
минимизирующее колебания переходной характеристики системы второго
порядка, легко найти графически (рис. 6.47): из подобия треугольников
<0, fit Zi> и <0. -т)к, 5|> следует, что оптимальный нуль лежит в точке пе-
ресечения перпендикуляра к лучу <0, jt> с действительной осью.
Рис. в.47
Методы проектирования систем автоматического управления
На основании проведенного анализа сделаем следующие рекомендации по
размещению комплексных полюсов зц • -r)k ± и нуля Zi передаточной функ-
ции второго порядка с форсирующим звеном
□ Для уменьшения колебательности переходной характеристики и повы-
шения быстродействия замкнутой системы желательно мл
• полюсы с действительной и мнимой частями удовлетворяющими к*
ловиям оптимального демпфирования.
П < П, S у, <Ц( « п»; (6.62,в)
• нуль не правее точки пересечения три,
вительной осью
(6.62, б)
Л«
□ Неравенству (6.62, б) соответствует следующее условие выбора постоянной
времени форсирующего звена Л,.
(6.62,в)
ni+w; 2
□ Выбор правого нуля ц > 0 приводит к нежелательному отрицательному пе-
ререгулированию и является недопустимым.
□ Если передаточная функция высокого порядка содержит несколько пар
комплексно-сопряженных полюсов -nK ± jtifc, то частичная компенсация
действительным левым нулем (6.62, б) производится для пары с максималь-
ным углом раствора ук, дающей наименьшее затухание колебаний пере-
ходной характеристики.
Таким образом, параметры передаточной функции замкнутой системы вто-
рого порядка вычисляются в следующей очередности:
□ по (6.52) строится область спектра £
□ по (6.54) определяется коэффициент статического усиления Л„
□ выбирается тип и размещение полюсов г, и ъ в области 51
□ по (6.55) либо по (6.56). (6.59) iviii (6.60) находятся коэффициенты ot| и
«г:
□ по (6.54), (6.57), (6.58) и (6.62) размещается нуль ;i и находится коэф-
фициент Л|
526 Глаюб
& Пример 6.10. Для объекта (6.19) с коэффициентом усиления К = 200 и
спектром
{*’=-0.02, *?=-0.1, *’ = -!)
рассчитать последовательный регулятор, создающий в замкнутой системе
второго порядка астатизм первого порядка с коэффициентом скоростной
ошибки CjiO.lc, показателями качества /у < 2 с, а <20% и жесткостью
rs 10.
Решение. Для создания астатизма первого порядка по (6.54) при Со = 0 опре-
деляем значение коэффициента = 1. Из условий (6.52) получим парамет-
ры допустимой области размещения полюсов замкнутой системы
(см. рис. 6.42):
Л И г 1.5, у £ 15, р £ 1.952, V £ 63’. (6.63)
Выберем действительный тип полюсов
-15SJJ < *2 5-1.5,
дающих апериодический характер переходной характеристики Л,(т) Запи-
шем с помощью (6.47) и (6.56) передаточные функции замкнутой и желае-
мой разомкнутой систем как функции параметра Ь\ и постоянных времени
%(*)= -----т,
l+fT.+T^+T.r,^
ш ЛД________- Г 1 + М
^^-*(Т|+Т2-М7-,Г2з)"Кж *(1 + Тжх)'
где
к 1 г т'Тг
Ж'Т|+Т2-*,’ “"Ti+Tj-h,
Перечислим условия, которым должны удовлетворять параметры Ь\. Т\ и Г2.
К обязательным условиям относятся:
□ принадлежность полюсов Т| и т2 области (6.63), а постоянных времени
7| и Т2 — области внутри и на границе треугольника на рис. 6.48:
(>1. Л2> с S ъ 0.0667 < Т2 < Г| £ 0.667; (6.64, о)
527
Рис 6 48
□ условие (6.51, б) обеспечения желаемой статической точности:
С| S0.1 =» 7| + Тг - 0.1 <S М 7| + 7i + 0.1. (6.64, б)
К желательным условиям относятся:
□ условия (6.57) предпочтительного размещения нуля Z| ближе к полюсу
72S6jST|; (6.64, •)
□ сохранение в передаточной функции (♦''„(j) наиболее удаленного поноса
объекта з, =-1 с целью повышения быстродействия замкнутой системы
и упрощения структуры передаточной функции регулятора'
тж =Т’ =1 =» bt = 7| + Тг - Г, Tj. (6.64, г)
Подстановка (6.64, г) в (6.64, б) и (6.64, «) дополнительно к (6 64. а) ограни-
чивает выбор параметров Г| и Ь следующими желательными неравенства-
ми, отраженными на рис. 6.48 областями с пунктирными границами:
-0.1 S Г) 7j S 0.1, r^l.OsZjSl. (6.64, д)
Видно, что неравенство Т\ > 1 несовместно с обязательным условием
(6.64, а) и должно быть заменено неравенствами 0 < 7) < 1, что эквивалент-
но выбору нуля по условию (6.58):
зу S 3| S ?| < 0 =» 6| 2 Г|. (6.64, е)
В результате в замкнутой системе произойдет увеличение перерегулирования и.
возможно, уменьшение быстродействия.
528
Глава 6
Итак, выбираем постоянные времени Г| = 0.4 с и ?2 = 0.2 с в точке, нахо-
дящейся в заштрихованной области на рис. 6.4S, тогда
(Х| = Г| + 7j = 0,6. aj = Г| Т2 = 0.08,
*1 = г, + Т2 - Т]Т2 - 0.52, К* = I / 7\ Т2 = 12.5.
1+0525 2. и^>12^°?4
l+0.6s + 0.08s2 j(l + s)
а передаточная функция последовательного регулятора принимает ПИДД2-
характер:
. S!»»„3.7825 7 33.2, .16.25,J
И'(д) 16s s
Замкнутая система имеет коэффициент скоростной ошибки
Ci = 0.08 < 0.1 с. полюсы S) =-2.5 и S| =-5 внутри интервала
И. -’ll = l~15, “I S|, жесткость г = 2 < 10 и переходную характеристику
A,(t)=l+hzlLe-4T> +^.С-'Л =1 + 0.6е-25' -1.6е-5'
V Т|-Г2 T2-Tt
с показателями качества ту = 0.83 < 2 (с) и а = 5.6 < 20% (рис. 6.49).
* ° - — ------t
I I
0 05 /, I 15 2 т
Рис 6.49
Все требования к качеству переходной характеристики замкнутой системы
выполнены с большим запасом. 2]
6.6.2. Замкнутая система третьего порядка
Рассмотрим теперь порядок конструирования желаемой замкнутой системы
третьего порядка
*,(#)- к, —\±к,+ьу2 , (6 65)
1 + ар + а2д4 + a3s
Методы проектирования систем автоматического управления 529
устойчивой по алгебраическому критерию (4.13) при
(«2 > 0) П {<X|Ct2 > aj > 0) Выбор степени числителя m = 2 позволяет выпол-
нить статический синтез по (6.50. в) при N S 2, т. е. по трем условиям:
p-c0£Af,Sl+q>.
1 a((l -с0)-q * КД £ a,(l -c0)+ q. (6.66)
|a2(l-c0)-a|C| -c2 Sa2(l-c0)-a|C| +c2.
По прямому методу динамического синтеза получим ограничения на допус-
тимые коэффициенты полинома знаменателя aj, а2 и а3, эквивалентные
размещению полюсов в допустимой области спектра (6.52) . При этом будем
использовать критерий устойчивости Рауса - Гурвица (4.13) для полинома
третьей степени с учетом положительности коэффициента а3.
□ Правая граница области коэффициентов определяется «данной степе-
нью устойчивости Re{j/| < -т>:
Л(Р - п) = (I - П“| + П2«2 ' П3аз) + («I ~ 2pa2 + 3n2a3)p +
+ (a2 - Зца3)р2 + ajpJ = Ло + Л|Р + Ajp2 + Ajp3
Этот характеристический полином устойчив либо нейтрален при
/«о 2 0=» п«| - П2“2 + П3<Ъ 51 •
Л2>0=»а2-Зт)а3^0,
/i3>0=^a3>0, (6.67.0)
Л|Л2 > /iq/ij => (а, - 2ца2 + Зп2а3 )(а2 - Зт)<х3)+
+ (па! - п2а2 + п’“з - 1)х3 0.
□ Левая граница области коэффициентов определяется заданной степенью
быстродействия Re{s() 2 -у:
ЛЛ-Р ~ Y) = (I - У<»| + Y2a2 - y3aj) - (a, - 2ya2 + Зу^ф +
+ (a2 - 3ya3)p2 - a3pJ - -go - Sip - ftp2 - &₽’
Этот характеристический полином устойчив либо нейтрален при
So*0=>Ya|-Y2a2+Y3a3ii,
)>2 20=>Зуа3-a2 20,
2f, >0=>а3 >0. (6.67,15)
«14’2 2«0вэ=»(а| -2уа, +Зу2а3|зуа3-а2)-
-(уа|-у2а2+у’а3-1)х3*0
Глава 6
□ Угол раствора области (6.52) размещения комплексных полюсов
*14 = “Лк определяется заданной степенью колебательности ц. Из
формул Виета (4.8) для полинома третьей степени следуют соотношения
между комплексными полюсами 5| и sj со степенью колебательности
Мк = о\ / т)к, действительным полюсом 53 = -т]д и коэффициентами ха-
рактеристического полинома:
*i *2 + *1*3 + *2*з = 2пд»7« + К (1+Д ’ )= ^«
Поверхности постоянного уровня р в пространстве (аь а2, а3) можно
представить как семейство параметрических функций — границ области
размещения полюсов q S t]K 5 у и р* < р:
а2=2Пк<х3+-2Т---Я-
(6.67, в)
По методу размещения в области 5 трех полюсов возможны следующие
варианты.
□ Действительные (в том числе и кратные) полюсы S|, Sj и дают полином
А1(1)=^1 _±-^1 = (‘ + Г,,Х1 + Т2аХ>+Т'з*)
с коэффициентами
(6.68, а)
Методы проектирования систем автоматического управления
531
□ Один действительный полюс 3| - ~п4 и пара комплексных полюсов
jj з = -г)к ± Ж дают характеристический полином
А,(з)=(|+тд1)(|+ад^^2)
с коэффициентами
a2=-y2\=(24,TJ,^J<-
Пя(г)к+“«/
(6.68, 6)
где
П2+Ч ’
5, = ПЛ = cos(vK )= -=-= И, = 7s-
М п.
Для быстрого затухания колебаний комплексные полюсы желательно раз-
мешать у левой границы спектра.
Пк* If-
Переходная характеристика замкнутой системы третьего порядка с до-
минирующими комплексными полюсами будет иметь малое перерегу-
лирование и высокое быстродействие, если полюсы разместить соглас-
но условию оптимального демпфирования (6.62. о) В случае, если до-
минирующим выбран действительный полюс, то угол раствора
комплексных полюсов можно и увеличить, поскольку вес не домини-
рующей колебательной составляющей в переходной характеристике бу-
дет небольшим.
Степень полинома B,(s) ограничена снизу числом заданных коэффици-
ентов ошибок со ♦ сЛ< 11 * N- Коэффициенты bt + 6„ и нули ?| ♦ 5» вы-
бираются из желательных условий (6 57), (6.62), сохранения левых нулей
передаточной функции объекта и подавления ее полюсов, близких к
мнимой оси.
& Пример 6.11. Решить пример 6 10 для желаемой замкнутой системы
третьего порядка.
Решение. Выберем следующие типы и размещение полюсов ц ♦ 5) в области
спектра 5, определенной п (6.63) (рис. 6.50):
Глава 6
Рис. 6.50
□ действительный полюс =-1.5 (ему соответствует постоянная времени
Tt = 0.667 с) разместим на правой границе области 5 с дальнейшим рас-
четом частично или полностью скомпенсировать его нулем z\ = JjJ
□ разместим комплексно-сопряженные полюсы $2.3 =-15 ± 15j с пара-
метрами
= ц, = 15, Тк = 0.0471 с, цк = 1, ljK = 0.707
на левой границе области S согласно рекомендациям (6.62, в).
Вычислив по (6.50, а) при со = 0 значение К, = 1, а по (6.68, <5) коэффици-
енты передаточной функции замкнутой системы
а, = 0.733, а2 = 0.0467, a3 = 0.00148,
составим по (6 49) передаточную функцию желаемого разомкнутого контура:
W (j)~ l+bis+l^s1 +
4«i-6, +(a,-6,> + а352) *(1+Тж1аХ1+W)’ ,
Получим параметры полинома й,(т)
ti г 0, т2 г 0.6| -1| + т, г 0, 6j = t|T2 г 0
из обяютельного условия (6.51, 6) обеспечения желаемой статической
точности
Методы проектирования систем автоматического управления 533
q £0.1 => eq - 0.1 £ 6, £ а( + 0.1 => 0.633 Sq + t2s 0.833 (6.70. а)
и следующих желательных условий, перечисленных в приоритетном порядке:
□ уменьшения перерегулирования и колебательности (6 62, б):
Z2 S - = -30 =» 0 £ т2 < 0.0333 с; (6.70. б)
Пк
□ сохранения в передаточной функции «^(з) полюса разомкнутой систе-
мы =-1:
а, -Ь|+(а2-Ь2)т®+а3(г“)2 =0 =>
=> q + т2 - Т|Т2 = eq - а2 + aj = 0.688; (6.70, в)
□ повышения быстродействия путем компенсации полюса з, нулем
г, = Тя - 0.667 с. (6 70. г)
Построив допустимую область значений т( и т2 (рис. 6.51). отметим несо-
вместность условий (6.70, б) решению системы уравнений (6.70, в) и
(6.70, г). Примем компромиссное решение
т2 = 0.0333 с, Т, = °'^8т?— = 0.677 с.
(6.70, г). Тогда замкнутая система приобретает передаточную функцию
534
Глава 6
iv м_ 1+^+»^
со следующими параметрами и коэффициентом скоростной ошибки
*1 = 0.711,^ = 0.0226, С|= —=О|-*| =0.0226 <0.1,
кж
а ее переходная характеристика (см. табл. П.2, и. 99)
Л1(т)=Е-'{^| = 1+0.0169е’151 -1.0169е'15' cos(15r +0.05°)
сходится эа время ту = 0.219 < 2 (с) с перерегулированием о = 8 .16 <20%
(рис. 6.52).
Рис. 6.52
Желаемая разомкнутая система имеет передаточную функцию (6.69) с пара-
метрами
КЛ = 44.237, ТЖ1 = 7, “ 1 с, ТЖ2 = 0.0655 с.
а передаточная функция последовательного регулятора принимает вид
(i+T.*Xi+^Xi+7?Xi+r*J)
о
6.6.3. Замкнутая система n-го порядка
Существует интересный метод построения системы управления, по которо-
му желаемая замкнутая система имеет характеристический полином
Методы проектирования систем автоматического управления
3/ = Моеж = Wo cos(<p,)+ jWq sin (ф,}
(6.71)
Его корни s„ равномерно распределенные по левой полуокружности радиуса
Ц) (рис. 6.53, а), образуют распределение Баттерворта (13. 22]:
□ при нечетном п один корень действителен и равен -<ц>. а остальные п - I
корней образуют комплексно-сопряженные пары с одинаковыми посто-
янными времени фильтра Баттерворта То - 1 / <Чо;
□ при четном значении п все корни являются комплексно-сопряженными
парами с постоянными времени 7g.
Благодаря равенству в (6.71) постоянных времени все* типовых звеньев сис-
тема, имеющая передаточную функцию фильтра Баттерворта 1 / ЛДз), явля-
ется при больших степенях л наилучшим приближением к идеальному фильтру
низких частот с полосой пропускания [О, (ц>|:
I 1 | 1 JIVOSwSWq.
I А>0<о)| ^1 + (ГоШ)2« =|ovw>wo.
Глава 6
Рис 6.53
Асимптоты ее логарифмической амплитудно-частотной характеристики
имеют наклоны 0 дБ / дек при 0 5 ш 5 шр и -20л дБ / дек при со >
(рис. 6.53, б). Частота ыо называется частотой срыва фильтра Баттерворта.
Максимальная погрешность аппроксимации амплитудной характеристики
фильтра Баттерворта на частоте срыва не превышает 3 дБ по сравнению с
Зл дБ при последовательном соединении л фильтров низких частот с пе-
редаточной функцией 1 / (1 + Tbs)" и похожими частотными характери-
стиками.
На рис. 6.53, в построены переходные характеристики фильтров Баттерворта
при степенях л от 1 до 5 Все графики имеют перерегулирование не более
12.896 и быстродействие от 37"о л° 7.657b.
При выборе подходящей степени л и частоты срыва Щ) необходимо размес-
тить корни полинома Баттерворта в области спектра 5, определенной усло-
виями (6.52). Рекомендуется использовать табл. 6.1, в которой а, обозначают
коэффициенты характеристических полиномов
AU) » I + ар + ... + ans"
степеней л е |1, 5|.
Коэффициенты полинома числителя B,(s) находятся из обязательных усло-
вий статического синтеза (6.50), (6.51) и желательных условий повышения
быстродействия, уменьшения перерегулирования и упрощения структуры
передаточной функции регулятора.
ккого управления
537
Спектральный метод синтеза регуляторов весьма удобен при решении зада-
чи стабилизации объектов, неустойчивых в разомкнутом состоянии, ввиду
определенной независимости размещения желаемого спектра замкнутой
системы от спектра объекта.
Особенностью спектра неустойчивой системы является наличие в ее переда-
точной функции хотя бы одного правого полюса. Задача стабилизации тако-
го объекта состоит в компенсации всех правых полюсов з, > 0 равными им
правыми нулями Zj компенсирующего каскада регулятора с передаточной
функцией RK(s) (рис. 6.54V
Собственно регулирующий каскад с передаточной функцией решает за-
дачу регулирования с желаемым качеством системы, устойчивой после ком-
пенсации. Построим по методике, множенной в разд. I S. электронные мо-
дели некоторых компенсирующих каскадов в виде схем на операционных
Усилителях:
Глава 6
□ схема на рис. 6.55, о имеет передаточную функцию
Як($) = 1-71
с действительным правым нулем С| = I / Т| > 0;
□ схема на рис. 6.55, б описывается передаточной функцией с комплексно-
сопряженными правыми нулями:
Лк(т) - 1 - 2£71 + 7V. г1>2 -|±;
□ схема на рис. 6.55, в с передаточной функцией, имеющей равные по мо-
дулю правый нуль и левый полюс:
□
схема на рис. 6.55, г, передаточная функция которой
Я,(т)=
l-2tJs+T2s2
1+ДТт+Г2?
имеет комплексно-сопряженные правые нули и симметричные им левые
полюсы:
п
V.’V.T
V..T я,.*
Рис 6 55
Методы проектирования систем авто*
Физический смысл введения компенсирующего каскада заключается в по-
давлении им неустойчивых составляющих переходного процесса, порожден-
ных правыми полюсами объекта. Две последние схемы фазовращателей по-
мимо компенсации создают симметричные правым полюсам левые полюсы
разомкнутого контура. Тем самым сохраняется порядок системы, а неустой-
чивость устраняется.
Главным недостатком компенсационного метода управления неустойчивы-
ми объектами является необходимость тонной настройки правых нулей ком-
пенсирующего регулятора на правые полюсы регулируемого объекта В ре-
альности такая настройка неосуществима, да и временнбй дрейф параметров
регулятора или объекта рано или поздно нарушит условия компенсации, в
результате чего система управления станет неустойчивой
Поясним эффект компенсации и влияние дрейфа параметров на примере
коррекции неустойчивого объекта первого порядка Щз) =!/(!- Ts) с по-
мощью компенсирующего регулятора
при равенстве всех постоянных времени Т = Т\ = Л Переходная характе-
ристика объекта является неустойчивой (см. табл. П.2, п. 3):
Л(г) = I -е'/г=>Л(/
Единичный скачок ф) = 1(0, поданный на вход компенсирующего каскада,
создает на его выходе сигнал (см. табл. П.2, п. 4)
равный 1 - 2е-'/ т при Т\ = Тг = Т. Расщепим .<(/) на две составляющие
х|(0 и xi(t) с изображениями
будучи поданными на вход объекта по отдельности, эти составляющие по-
рождают на его выходе неустойниеые сигналы
гй’ "Л" »>
540
Глава 6
Суммарный выходной сигнал
будет устойчивым лишь теоретически при равенстве постоянных времени
Г1 = Г, когда две противоположно расходящиеся экспоненты с одинако-
выми показателями роста в сумме точно скомпенсируют друг друга. По-
скольку параметры Т и 7\ характеризуют разные элементы системы, то их
точное равенство практически невозможно, из-за чего в действительности
переходная характеристика соединения неустойчивого объекта и регулято-
ра будет неустойчивой.
& Пример 6.12. Для системы «тележка - перевернутый маятник» с выходом
<₽(/) разработать последовательный регулятор, обеспечивающий в замкнутой
системе:
□ астатизм первого порядка;
□ коэффициент скоростной ошибки q S 0.1 с;
□ быстродействие /у S 1 с;
□ перерегулирование a S 5%;
□ жесткость г <3.
Решение Передаточная функция %(з) неустойчивого объекта
(см. пример 6 9) имеет третий порядок с простыми действительными полю-
сами - двумя левыми и одним правым:
,“=--1 =-0.582, »?=- — = -4.097, з? = —= 2.518.
1 Т, * Т, ' Т3
Выберем замкнутую систему также третьего порядка с устойчивой переда-
точной функцией (6.65) и прямой метод синтеза ее коэффициентов К*
щ > 0, oj > 0, oj > 0, 6| и Ьг. Из условия астатизма первого порядка со = О
по (6.66) получим
К, - 1.
Определим по (6.52) параметры области спектра £
П-Э.у-9, ц“ 1.048 - 1.
Перечислим условия, которым должны удовлетворять передаточные функ-
ции замкнутой системы (6.65) и желаемой разомкнутой системы (6.69). К
обязательным условиям ошосятся:
□ второе условие (6.66) обеспечения желаемой скоростной точности:
qSO.I =>—0.1 Sa, - 6( £0.1; (6.72,я)
541
□ условия (6.67) размещения полюсов г, jj в желаемой области .5:
ReUj S -3 =>
Ao =1-За, +9а2 -27а3 20.
Л) =<Х| -6а2 + 27а3.
Л2 = а2-9а3 20,
Л3 = А|Л2 -йоа3 >0;
(6 72.15)
Refo} 2 -9 =»
Но =9ot| -81а2 + 729а3 -120,
#1 =(х, -18а2 +243а3
g2 =-а2+27а3 20,
8з =8|«2-8о“з^°;
(6.72. в)
а2=2п,а,+ —
2п;
(6.72. г)
Уравнения (6.72, г) определяют параметрическую кривую «(nJ. ограничи-
вающую в пространстве (ct|. а2} область со степенями колебательности
К желательным условиям относятся.
□ сохранение в передаточной функции 1Иж(з) левого полюса s? и инвер-
тирование правого полюса з° неустойчивого объекта.
/ж2=-1з | а,-bi -(а2-63)3° +aJ^3)J =tt
□ предпочтительное размещение нулей в соответствии с (6.57):
[р, = П1>| - n2M * 1 п |3э = У*»! - Г!*2 S > I
1₽2 =bi-2п/>: 20 J Ip^-lyAjSOl
-у< Zj<, -и < о =>
(6.72. е)
Система уравнений (6.72, д) имеет решение
ct| -bi =-Л?а3. а2 -62 (6.73)
В соответствии с (6.72, в) выберем
«I - 4, = с, = 0.1 => а3 =--44- = 0.0097.
S2Jj
Подставив найденное значение коэффициента а3 в (6.72, б) - (6.72, б), по-
строим на рис. 6.56, а область допустимых значений коэффициентов а, и а2
Выбрав в ней точку
(а, = 0.6, а2 = 0.13),
получим характеристический полином замкнутой системы
4,(1) = 1 + 0.6s + 0.13s2 + 0.0097s3,
корни которого S|,j =-3.79 ± 1.89j и s3 =-5.83 имеют спектральные пара-
метры
Л = 3.79 > 3, у= 5.83 < 9, г= 1.54 < 3, ц = 0.5 < 1.
Вычислив по (6.73) коэффициенты полинома JS,(s)
= а, - 0.1 = 0.5, 62 = а2 - (s3 - s2 }х3 = 0.066,
убедимся (рис. 6.56, 6), что они удовлетворяют желаемым условиям (6.72, е)
с фактическими значениями п и у:
₽1 = П*1 - = 0.949 < 1;
32 = *1 - 2л&2 = 0;
₽3 = 7*1 “ = 0.675 < 1;
Щ = *1 - 2уЬг = -0.268 < 0.
Методы проектирования систем автоматического управления
543
Замкнутая система с полученной передаточной функцией
... / \ 1+0.5а+0.066а2
W, (а)=----------;-------г
1+0.6а+0.13а2 + 0.0097а3
имеет переходную характеристику Л,(г), аналогичную изображенной на
рис. 6.52, с показателями качества
rz = 0.317 < 1с, о = 3.8 < 5%,
удовлетворяющими желаемым значениям. Последовательный регулятор
ч = ВМ) = (1^+^а2Ьг,лХ1-МнМ=
U (A,(s)-fl, (а))вф(а) С1^а2(1+Т3аХ1+Г^)
Рио. 6 57
544
0.5Л|С| - RoCi - Fj, ЯгО, - q, AjQ = Tb A«Gj = A,, AjQ - bt, LCn^bj
CJ
Завершая раздел, мы можем сделать следующие выводы
О спектральные методы синтеза регуляторов весьма эффективны в «ис-
правлении» нежелательных свойств устойчивого объекта путем навязы-
вания ему требуемых динамических свойств;
□ аналитический синтез регулятора спектральным метолом практически
возможен лишь для объектов невысоких (до третьего) порядков. Систему
управления сложным объектом целесообразнее проектировать с исполь-
зованием критерия устойчивости Найквиста;
□ компенсационный метод управления неустойчивым объектом, основан-
ный на целенаправленном введении в спектр разомкнутого контура пра-
вых нулей, компенсирующих правые полюсы объекта, не является гру-
бым в том смысле, что малые отклонения параметров объекта и регуля-
тора от расчетных значений приводят к нарушению условий
компенсации и к неустойчивости замкнутой системы. Следовательно,
проектирование регуляторов для систем управления неустойчивыми объ-
ектами необходимо выполнять на основе критерия Найквиста.
6.7. Системы управления
с ПИД-регуляторами
В промышленных системах управления широко используется трехканаль-
иый ПИД-регулятор, структурная схема которого изображена на рис. В ?
Регулятор имеет передаточную функцию (1.37)
и будучи установленным в прямой цепи контура управления перед объектом
(см. рис. 6.1). формирует управляющее воздействие (В.5)
Л)» K„e(t)+ Киртл1т+ Кл
о
с пропорциональной (В.2), интегральной (В.4) и дифференциальной (В3>
составляющими функциями ошибки регулирования ИО Вклад каждой со-
ставляющей в суммарный управляющий сигнал ИО задастся коэффициента-
ми усиления пропорционального Кп, интегральною К„ и дифференциально-
го Я, каналов
Методы проектироаанкя актам агтомаптчвст’огр управления 545
6.7.1. Анализ ПИД-регуляторов
Начиная инодт свойств ПИД-регулятора. приведем его передаточную функ-
цию (1.37) к обшему яшмеиателю
Отсюда видно, что включение в последовательный регулятор все» трех со-
ставляющих вносит в контурную передаточную функцию B'Jr,» Лз)И1з)
два нуля zi. Z2 и полюс j| = 0. расположенный в начале координат и увели-
чивающий степень астатизма контура на единицу
В зависимости от знаков и модулей параметров Kv. К„ и Кя возможны раз-
личные типы ПИД-регулятора, его передаточной функции 1674), полинома
его корней г и постоянных времени Г= -1 / г. а также свойства лога-
рифмических частотных характеристик и Фр*ш> Спя ясности будем
строить асимптотические логарифмические характеристики)
□ при (Л"и * 0| Л (АГ, ж 0| получим называемый еше изодромным ПИ-
ретулятор (6.28) с полиномом числителя
Вр(т) = Щ? - Z.) = А^( I + Г»т) (6.75. в)
типа форсирующего звена первого порядка со следующими действи-
тельным корнем и постоянной времени:
На рис. 6.58, а построены логарифмические частотные характеристики
регулятора: амплитудная
4р(о>)= 20tg^- — = 20lg|r,| + 10»g(l + Г;а>:20!gш
с частотой сопряжения асимптот щ, = lij “ / ATJ и семейство фазо-
вых характеристик
Фр(ы) = arctg(7» - sgn(AJ 90*
для разных знаков коэффициентов К„ и АГ„;
546
Гламб
Рис, 6 58
□ при (Ки = 0) П (АГд * 0) получим ПД-регулятор (6.35) с передаточной
функцией
й(т) = К„ + Лдт = Afa(j - = /С„( 1 + ад (6.76. в)
типа форсирующего звена первого порядка со следующими действитель-
ным нулем и постоянной времени:
2. Т.= (6.16,6}
Кл
На рис. 6.58, б построены логарифмические частотные характеристики
регулятора: амплитудная
Ц,(ш)= 20lg^K2 + K2w2 = 20lg|Kn| + IOIg(l +Тд2со2)
с частотой сопряжения асимптот ц, - = |Л„ / Кп\ и семейство фазовых
характеристик
Фр(ш) - arag(7>; + (] - sgrKA'n)) • 90’
для разных знаков коэффициентов К„ и Ка,
□ при {К„ *0}Г){л'л *о}п{/С,7 полином ПИД-регулятори (6.74)
4,(3) - Л-Ж(з - гн)(з - <.) - AfM(i + ад(| + ад (6.77. в)
547
представляет собой два форсирующих звена первого порядка со следую-
щими действительными корнями и постоянными времени:
" К„ ±,1К2„-4К,,К3 т К„ ±^К2-4КМК3 „ „ л
Z-=----------2^----------------------2^-------- (б77,Й)
На рис. 6.59 построены логарифмические частотные характеристики ре-
гулятора: амплитудная
Ч(<п>201е^И
= 201g|K„|+ 10lg(l + Т2а>2)+ lOlg^ + Т2(О2 )- 20lg<o
с частотами сопряжения асимптот ц, = Ш < Ц, = fal и семейство фазо-
вых характеристик
Фр(ш) = arctg( 7» + arctg( ТЛш) - sg,n(K„) 90’
при разных знаках коэффициента Л'н и постоянных времени Т„ и Та. Для
наглядности изображения наклонов участков фазочастотной характери-
стики частоты сопряжения выбраны из условия lOOw,, < ох4, при котором
среднечастотные интервалы [0.1ц„ 10ц,| и [0.1ц,, 10ц,| фазовых характе-
ристик форсирующих звеньев не пересекаются.
Рис 6 59
548
На фазочастотных характеристиках особо выделен хрестоматийный гра-
фик, соответствующий соотношению параметров ПИД-регулятора
Л„ > 0, Кд > 0, Кп > 2^К„КЛ , (6 78)
при котором действительны нули < 0 и <„ < 0. положительны посто-
янные времени Гм > 0 и Т3 > 0, а вносимый в разомкнутый контур фа-
зовый сдвиг изменяется от -90" на низких до +90' на высоких частотах
Однако нельзя забывать, что спроектированный ПИД-рсгулятор может
иметь параметры, не удовлетворяющие условиям (6.78). в результате чего
знаки нулей, постоянных времени и вид фазочастотной характеристики
могут быть иными;
□ при {*н*оЖ*4+п <4КМКЛ} полином ПИД-рсгулятора (6.74)
Вр(з)= К, (т2 - 2Т)„4 + ш2 )= К„ (1 + ВДл + Гр2т2) (6.79. а)
есть типовое форсирующее звено второго порядка (см. табл. 2.2) с пара-
метрами
Гр= —= J^>0.-1<Ер = Д" <1 (6.79.6)
(Ор Ин р
и комплексно-сопряженными корнями Z\,2 = Пк ± М с действительной и
мнимой частями
(i>t =
(6.79, а)
На рис. 6.60 построены асимптотические логарифмические характери-
стики ПИД-регулятора с комплексно-сопряженными нулями: амплитуд-
ная
(,(<!))= 20lg|K„| + 101g( (1 -Tfa1 У +(2;рГро>)2201g со
с частотой сопряжения асимптот ц, = 1 / Тр и семейство фазовых харак-
теристик
»,(w)-MC,e - SS.(^,.) *90°
для разных знаков коэффициентов К„ и 4р- Учитывая, что согласно
(2.18) реальная логарифмическая амплитудная характеристика имеет
уровень усиления на -6 - ZOIgf^J дБ меньше, чем асимптотическая, то
ПИД-регулятор с комплексными нулями при малых значениях |у « I
Методы проектирования систем автоматического управления
способен активно подавлять колебания с частотой = ыр, на которой,
возможно, нарушаются условия устойчивости Найквиста
С позиций частотного анализа можно так охарактеризовать влияние со-
ставляющих ПИД-регулятора на амплитудную характеристику
(пунктирные графики на рис 6.58 - 6.60) и на свойства замкнутой систе-
мы управления:
□ пропорциональная составляющая Ап задает минимально возможный
уровень усиления сигнала ошибки eV). что доказывает следуемая из
(6.74) амлитудно-частотная характеристика ПИД-регулятора
Ее минимум достигается на частоте
и составляет
• |Л'Н|, если коэффициенты Аи и Кл одного знака;
• Ап , если коэффициенты А’и и Ад разных знаков.
Увеличение модуля коэффициента пропорционального усиления Кп под-
нимает среднечастотную часть амплитудной характеристики Z-P(w), '«о
мечет аналогичный подъем в этом же частотном диапазоне контурной
амплитудной характеристики и сдвиг вправо се частоты ерем
Если не нарушаются запасы устойчивости, то такой прием позволяет
повысить быстродействие замкнутой системы, получив и побочные эф-
фекты в виде некоторого роста перерегулирования и колебательности
из-за приближения к границе устойчивости;
□ включение в состав регулятора интегральной составляющей К„ / з уве-
личивает порядок астатизма разомкнутого контура на единицу. Если
объект управления статический, т. е. |М[0)| = К < «>, то в устойчивой
замкнутой системе ошибка стабилизации с течением времени сойдется к
нулю. Канал интегрального управления объектом с порядком астатизма
v £ I обеспечивает нулевую установившуюся невязку слежения за поли-
номиальной уставкой v-ой степени. Увеличение модуля коэффициента
интегрального усиления К„ поднимает низкочастотную часть амплитуд-
ной характеристики £p(w) и сдвигает вправо частоту сопряжения оц>;
□ дифференциальная составляющая регулятора А.,г предназначена для
подъема фазовой характеристики разомкнутого контура в средне- и вы-
сокочастотном диапазонах с целью устранения неустойчивости замкну-
той системы либо увеличения запаса устойчивости по фазе. Увеличение
модуля коэффициента Кл поднимает высокочастотную часть амплитуд-
ной характеристики £р(о>) и сдвигает влево частоту се минимума ц,.
Удаление контурного годографа fFK(ju») от точки Найквиста — границы
устойчивости — совместно с уменьшением отрицательного наклона ам-
плитудно-частотной характеристики на частоте среза и сдвига этой час-
тоты вправо приводят к уменьшению колебательности и форсированию
переходного процесса замкнутой системы
С позиций спектрального анализа влияние ПИД-регулятора на свойства
замкнутой системы управления объясняется изменением состава и перерас-
пределением полюсов и нулей контурной передаточной функции
□ дополнительный полюс 5| = 0 в начале координат, внесенный инте-
гральной составляющей, создаст астатизм в бывшей статической ра-
зомкнутой системе или увеличивает на единицу порядок астатизма v ас-
татической системы. Благодаря этому согласно (6.17) становится нуле-
выми I + v коэффициентов статических ошибок с0 = = с, = 0;
□ один или два дополнительных нуля 4, и га. внесенных интегральной и
дифференциальной составляющими, предназначены для компенсации
нежелательных полюсов передаточной функции объекта
• слишком близких к мнимой оси с малой степенью устойчивости п.
определенной в (3.43);
Методы проектирования систем автоматического управлении_____________ДДГ
• I
ности ц, определенной в (3.46);
. правых полюем, порождающих ту* тойч
мы Следует, однако, нс забывать о малой эффективности компенса-
ционного метода устранения неустойчивости реальных систем из-за
временного дрейфа их свойств и сложности точной настройки нулей
регулятора на полюсы объекта.
6.7.2. Синтез ПИД-регуляторов
Рассмотрим некоторые методы расчета коэффициентов усиления пропор-
ционального К„, интегрального К„ и дифференциального Ка каналов ПИД-
регулятора.
Аналитический синтез
Основы аналитического метода синтеза последовательного регулятора с по-
мощью формул (6.11) изложены в конце рам) 6 /, а в paid 6 2и 6.1 он при-
менен к расчету параметров ПИ-регулятора (6.28) и ПД-регулятора (6.35),
управляющих устойчивым объектом с желаемыми показателями качества:
□ коэффициентом статической ошибки с0,
□ коэффициентом скоростной ошибки С|,
□ временем установления /у;
□ запасами устойчивости по амплитуде Л, и фазе ф,.
Применим здесь эту методику к решению задачи синтеза последовательного
ПИД-регулятора, предназначенного для управления объектом с передаточ-
ной функцией 8^s) и частотными характеристиками Я(ы) и ф(о>).
Допустим, что объект является статическим, т. с, имеет конечный коэффи-
циент статического усиления К - ИЮ) > 0 Тогда согласно (6.17) для го «Да-
ния в разомкнутом контуре астатизма первого порядка принчипиа.1ыю необхо-
дима интегральная составляющая ПИД-регулятора с коэффициентом • О
Из пяти параметров К„. К„. К„, Т„ и Г, в двух вариантах описания переда-
точной функции
/?(.,)- Ла!*»***^1 „ (6 Ж), а)
s I
лишь три параметра являются независимыми, а лва оставшихся могут быть
найдены с помощью уравнений связи параметров
Ля - К,( Т, + ГД, К,- К, Г„Т, (6.80, б)
552
Глава 6
Коэффициент интегрального усиления К„, ответственный, кроме создания
астатизма. еще и за обеспечение минимальной либо заданной скоростной
ошибки С|, выбирается из условия (6.27, а):
к„>±- (6.81)
Поставим задачу синтеза ПИД-регулятора по двум желаемым запасам устой-
чивости замкнутой системы L, и <р3. Подставив в (6.11) вещественную и
мнимую части комплексной частотной характеристики регулятора
Рр(ш) = А'п. бп(ш)= А.о- — •
' оз
получим систему двух нелинейных уравнений с тремя неизвестными to,, Кп
и
cos^i tp3-q>(w,))
мК) ’
Кк sin^p,, ±ф,
----------мИ—
Определив по предполагаемым желаемым характеристикам Аж(ш) и Фж(ш)
граничный уровень фазы Фгр, знак запаса по фазе <р, и задав множество зна-
чений ш, в возможном интервале частот, по (6.82) строятся зависимости
и Ад((о,). При необходимости по (6.77, б) рассчитываются зависимо-
сти T„(Wj) и 7^(<jlXj). Комплексно-сопряженные значения постоянных време-
ни на некоторых частотах запаса означают, что регулятор включает форси-
рующее звено второго порядка с параметрами (6.79).
Недоопределенность решаемой системы уравнений позволяет оптимизи-
ровать замкнутую систему по критерию максимального быстродействия пу-
тем отбора значения оз,, минимизирующего оценку времени установления
переходного процесса. Ранее для решения этой задачи мы использовали
весьма грубую оценку (4.28), по которой время установления /у обратно
пропорционально частоте среза ШсР и близкой к ней частоте запаса to,
(см. рис. 6.16). Применим теперь более точный и достоверный спектраль-
ный метод (см. разд. 3.5.2) предсказания динамических свойств замкнутой
системы по значениям корней ее характеристического полинома
C,(s) - В(з)(К» + + Кяз2) + зЛ(з): (6.83)
□ верхней Гут,, и нижней границ времени установления (3.48) по сте-
пеням устойчивости п и быстродействия у, определенным в (3.43) и
(3.44);
Методы проектирования систем автоматического управлений
553
□ максимального перерегулирования (3.49) по степени колебательности и,
определенной в (3.46).
Сложности, встающие на этом пути, связаны с разрешением трех задач:
□ разложения полинома (6.83) в конечный ряд по степеням з. что для каж-
дого объекта легко выполняется либо вручную, либо программным спосо-
бом. например, в Mathcad с помощью символического оператора coeffs;
□ нахождения корней полинома C,(s). что, несомненно, должно выпол-
няться только программным методом, например, с помощью встроенной
в Mathcad функции polyroots;
□ обязательной проверки устойчивости полученной замкнутой системы по
признаку отсутствия нелевых корней характеристического полинома
(6.83) и отбрасывания тех частот запаса а»,, на которых система оказалась
неустойчивой.
Многопараметрическая оптимизация, несомненно, сложнее однопараметри-
ческой, но три зависимости ^утМ(ш>), ^щт(ш,) и сгСаь) несут гораздо больше
информации и позволяют разработчику принять наилучшее компромиссное
решение по выбору параметров ПИД-регулятора.
Вывод
Аналитический параметрический синтез ПИД-регулятора (6 74) представляет
собой довольно сложную задачу, требующую многократного решения системы
нелинейных параметрических уравнений (682) и оптимизации полученных за-
висимостей параметров от частоты запаса по дополнительным критериям
Обсудим условия применимости и возможные модификации разработанного
алгоритма аналитического синтеза ПИД-регулятора.
О Ранее многократно отмечалось, что его интегральный компонент К„ / з
повышает порядок астатизма желаемого разомкнутого контура v на еди-
ницу. Следовательно, если передаточная функция объекта И'(з) уже об-
ладает требуемым порядком астатизма, то структура регулятора может
быть упрошена до пропорционально-дифференциального типа (6.76):
Жз) = *„ + Л^.
Например, при первом порядке астатизма передаточной функции объекта
и заданном минимальном коэффициенте скоростной ошибки е> вместо
(6.81) получим следующее условие выбора коэффициента пропорциональ-
ного усиления регулятора:
554 Глава 6
где К = S(0) / D(0). Тогда, решая первое нелинейное уравнение в
(6.82), получим частоту запаса со,, подставив которую во второе урав-
нение, находим коэффициент усиления дифференциального канала
ПД-регулятора:
sin(<prp±<P,-<lfa))
□ Дифференциальный компонент ПИД-регулятора КдЗ необходим для по-
вышения запаса устойчивости замкнутой системы, быстродействия и
гладкости ее переходной характеристики за счет подъема высокочастот-
ной части желаемой фазовой характеристики Фх(<о) на 90", уменьшения
наклона высокочастотной части амплитудной характеристики Zx(o>) и
сдвига вправо частоты среза ц.р, влияющей на быстродействие. Нужно,
однако, иметь в виду, что для фильтрации высокочастотных шумов на-
клон последней асимптоты графика должен быть отрицательным.
желательно равным -40 дБ / дек. Если в передаточной функции устой-
чивого объекта
+ = .gfc) (6.84.Л
а0+в|»+ - + олз" Л(з)
степени полиномов числителя B(s) и знаменателя Л(г) соотносятся как
т > п - 2, то введение в регулятор форсирующего канала с постоянной
времени ТЛ > 0 уничтожит желаемый наклон высокочастотной части
Z««o).
Следовательно, проектируемый регулятор должен не иметь дифферен-
цирующих свойств, т. е. быть ПЙ-регулятором. В таком случае коэффи-
циент усиления интегрального канала К„ определяется по условию
(6.81), после чего находится частота запаса со, как корень второго урав-
нения (6.82) при КЛ = 0:
K„Mi(Wi) = -»1Ъ5<п(Фп. ± <р3 ~ Ф(<91))-
Наконец, по первому уравнению (6.82) вычисляется коэффициент уси-
ления пропорционального канала ПИ-регулятора
□ Если передаточная функция управляемого объекта ИЦз) обладает требуе-
мым порядком астатизма. например, v = I. а степени ее полиномов ВД
и A(s) в (6.84, б) соотносятся как т 2 п - 2, то может быть выбрана про-
стейшая структура ПИД-регулятора, а именно, пропорционального типа
«з) - К„.
Уровень усиления пропорционального канала рассчитывается по перво-
му уравнению (6.82)
Методы проектирования систем автоматического управления 555
соа(ф гр±ф,-<р(<0,))
Кп°—’
з которое подставлена частота запаса от,, являющаяся решением второго
уравнения (6.82) при Кп = К3 = 0:
Ф,: Ф(Ф1) ’ Фф t Фэ
Если полученный коэффициент не удовлетворяет условиям достижения
желаемых показателей скоростной точности q и быстродействия 1уЛ
‘Hi- 4g}-
то можно попытаться задать другое значение Кп, исходя из этих усло-
вий Затем, построив частотные характеристики желаемого разомкну-
того контура
Ах(ш) = £(ш) + 20lgAn, Фж(о>) = Ф(ш).
следует проверить по (4.30, о) наличие запасов устойчивости, которые
должны быть не меньшими заданных значений Ц и ф,. В случае неудачи
придется ослабить требования технического задания по невыполненному
показателю качества.
Графический синтез
Быстрый приближенный расчет параметров ПИД-регулятора, нацеленный
на достижение минимальной скоростной ошибки и максимального быстро-
действия, наиболее эффективно выполняется в интерактивном режиме об-
щения разработчика системы управления со специальной компьютерной
программой, строящей все необходимые для принятия решений частотные
характеристики по мере ввода пользователем исходных данных и анализа
полученных графических и цифровых результатов.
Опишем более развернуто, чем при наложении графического синтеза ПИ- и
ПД-регуляторов (см. рис. 6 21. 6.26). методику программно-графического вы-
числения коэффициентов усиления ПИД-регулятора К„, А„ и А, с помощью
Maihcad. Построение логарифмических частотных характеристик выполня-
ется аналогично тому, как это сделано на рнс 2.13 и 2.27 Особое внимание
читателя обращается на необходимость обязательного использования функ-
шш согф. устраняющей вычислительные разрывы гладких фазочастотных ха-
рактеристик.
Для простоты и определенности ниже рассматривается процедура конструи-
рования регулятора с неотрицательными параметрами - коэффициентами
Усиления каналов и постоянными времени форсирующих звеньев Это не
556 Глава 6
является критичным моментом: методика работоспособна и при разных зна-
ках параметров, нужно только с пониманием руководствоваться (рафиками
на рис. 6.58 и 6.59, выбирая нужные знаки параметров сообразно поведению
кон!фетных фазочастотных характеристик Ф(и>) и Фж(ы).
Итак, алгоритм синтеза ПИД-регулятора имеет следующий вид
I Строятся логарифмические частотные характеристики объекта Д(ш) и
Ф(ы), а на осях ординат отмечаются уровни запасов по амплитуде -L, и
фазе Фгр ± Фз Конкретные значения граничного уровня Фгр = 180* ± 3604
и знака <р3 определяются визуально по виду графика Ф(ш) и предпола-
гаемому прохождению желаемой характеристики Фж(со).
2. Для получения в замкнутой системе максимального быстродействия с со-
хранением запасов устойчивости следует выбирать как можно правее час-
тоту запаса желаемого разомкнутого контура ш,, определенную в (4.31):
£ж(ш,) = -Д>. Фж(Ф>) “ <Pip ± Фэ
С учетом подъема фазы дифференциальной составляющей регулятора на
частотах со > lOcoj практически на 90* будем искать нужную частоту а
точке пересечения графика Ф(ш) с уровнем ф,р + ф, - 90" (рис. 6.61, в):
ш,: Ф(оЗ}) = Фф ± Фэ ~ 90". (6.86, а)
3. В зависимости от существования этого решения выбираем частоту со-
пряжения ы, и постоянную времени Гд дифференциального канала:
• если частота запаса со, существует, то принимаем
Шд-0.1Ш» =» Гд» 10/ох,; (6.86,6)
• если фазочастотная характеристика объекта Ф(со) не достигает уровня
Фф ± Ф, - 90*. то дифференциальный канал регулятора не обязателен.
В случае принятия решения строить регулятор без дифференциально-
го канала задаем постоянную времени Гд = 0, иначе рассчитываем ее
по (6.86, б), взяв частоту запаса по оценке (4.28) частоты среза желае-
мой системы, обратно пропорциональной желаемому времени уста-
новления 1^:
4. Строим частотные характеристики
Д.д(ш)= L(o>)+ IOIg(l + Г/со2), Фд(о>) = Ф(ы) + arctg( Гдсо) (6.86, «)
последовательного соединения обьскта И^з) с форсирующим звеном
(1+7^з) и визуально контролируем, чтобы фазовая характеристика
Фа((о) не входила в запретную зону ф,р ± <р, левее частоты о»,. Если запас
по фазе потерян, то следует интерактивно подбирать параметры оэл и Гд
в окрестности значений (6.86, 6) до его восстановления.
557
5. Вычислив разность уровня запаса и амплитуды получим ко-
эффициент усиления пропорционального канала регулятора:
- -L, - LaM => К„ < io005At. (6.86. г)
Ь. Для достижения минимальной скоростной ошибки ct частота сопряжения
изодромного звена ы,, должна располагаться как можно правее, не пре-
вышая, однако, частоты (рис. 6.61, а) Отсюда получаем условие вы-
бора постоянной времени интегрального канала:
а>и £ Шц =» Ги ТЛ. (6.86. d)
Используя соотношения (6.80, б), вычисляем коэффициенты усиления
интегрального и дифференциального каналов ПИД-регулятора:
Если передаточная функция объекта (6.84, а) уже обладает первым по-
рядком астатизма, то интегральный канал регулятора не обязателен, че-
му соответствуют предельное значение постоянной времени - и
следующий выбор коэффициентов регулятора вместо (6.86, е):
Кн = 0, КВ=К„ТЛ. (6.86, ж)
О
Рис 6.61
7. В результате выполненных расчетов получены все коэффициенты усиле-
ния каналов ПИД-регулятора Жт) из (6.74). На заключительной стадии
Глава 6
синтеза необходимо провести тестирование частотных и временных
свойств замкнутой системы управления:
• построив частотные характеристики желаемого разомкнутого контура
| ^(<o)=L»+2OlgKn + I0lg^ + TllW)-201gw, (6g6 з)
[ Фж(ш)=Фд(ш)+агс(8(Ти<о)-90°,
визуально контролируем, чтобы фазовая характеристика не входила в
запретную эону <рф ± <р, на частотах, где £ж(ш) > — L3 (рис. 6.61,6)
Если запас по фазе не обеспечивается, то следует интерактивно по-
добрать по (6.86, б, д) частбты сопряжений шд и Шц, нс забывая прове-
рять, чтобы амплитуда Лж(й>1) не превышала уровня запаса -L3;
• продолжив низкочастотную асимптоту желаемой логарифмической
амплитудно-частотной характеристики £ж(ш) до пересечения с осью
L, получим отсчет -20lgq, по которому находим оценку коэффици-
ента скоростной ошибки С|. Если оценка нс удовлетворяет желаемой
скоростной точности, то можно поднять низкочастотную ветвь ам-
плитудной характеристики путем сдвига вправо частоты сопряжения
шц, что равносильно увеличению коэффициента К„ и уменьшению
постоянной времени Ги (см. рис. 6.59) при условии постоянства про-
изведения АГНТИ,
• построив график переходной характеристики замкнутой системы
*,(»)= f1! У'яЩ I = L'11 H'frW |. (6.86, и)
S + Ь(1 + Иг(з)Л(з))/
необходимо убедиться в его устойчивости, сходимости к установив-
шемуся значению Л,. = 1, определить время установления и пере-
регулирование о. Полученные показатели переходной характеристики
сравниваются с желаемыми значениями и в случае неудовлетворен-
ности разработчика качеством движения интерактивный процесс
подбора параметров ПИД-регулятора повторяется.
Спектральный синтез
Смысл спектрального метода синтеза последовательного регулятора Жз).
имеющего собственный состав полюсов и нулей |л/, Ту), заключается в ком-
пенсации нулями нежелательных полюсов объекта s° и навязывании же-
лаемых динамических свойств путем размещения полюсов т, в нужных уча-
стках комплексной плоскости
В отличие от регуляторов, имеющих передаточную функцию общего вида с
несколькими полюсами и нулями, спектр ПИД-регулятора включает макси-
мум два нуля С|. 1} и один полюс 3)t к тому же нулевой. Таким образом, его
Методы проектирования систем автоматического управления 559
возможности ограничены компенсацией не более двух полюсов объекта и
увеличением на единицу порядка астатизма разомкнутого контура.
В зависимости от выбора структуры спектра (ад получим пять типов регу-
лятора, перечисленных в табл. 6.2:
Таблица 6.2
^^^Число нулей ЧИСЛО ПОЛЮСОЬ^ 0 1 2
0 П-регулятор К, ПД-регулятор —
1 И-регулятор К„ S ПИ-регулятор ПИД-регулятор
□ ни одного полюса и нуля соответствуют П-регулятору K(s) = Кп. Замкну-
тая единичной отрицательной обратной связью система управления со-
ответствует выбору коэффициента К„ = I;
□ один полюс 3| = 0 означает И-регулятор Я(з) = / г,
□ один нуль ?| = -1 / ТЛ создается ПД-регулятором
с постоянной времени Тя= КЛ/ К„. В частном случае К„ = 0 получим Д-
регулятор Я(з) = Kas с нулем Zi = 0;
□ полюс = 0 и один нуль ?| = -1 / Т„ характеризуют ПИ-регулятор
□ один полюс 1| =0 II два нуля 1| и л создаются ПИД-регулятором с пе-
редаточной функцией (6.74)
Я(з)»Кп+^+Кд1,
t
числитель которой Др(з) в зависимости от знака разности А',;-4КИКД
имеет действительные (6.77. б) или комплексно-сопряженные (6.79, »)
корни.
Необходимая структура спектра pciyaaropa (а, г| определяется в процессе
анализа полюсов (а°| передаточной функции объекта Щл) - в(л) / Д(т) Как
560 Глава 6
показано в разд. 2.5, в замкнутой системе с отрицательной обратной связью
происходит:
□ расширение полосы пропускания системы, т. е удаление полюсов от
мнимой оси;
□ обострение резонансных пиков, т. е. увеличение степеней колебательно-
сти комплексно-сопряженных полюсов ц и углов раствора v
Доступный ресурс спектра регулятора из одного полюса и двух нулей расхо-
дуется в следующем приоритетном порядке:
□ на создание астатизма желаемой разомкнутой системы с помощью по-
люса регулятора ,Т| = 0, если такой полюс у передаточной функции объ-
екта отсутствует;
□ на компенсацию правых полюсов объекта з° равными им нулями регу-
лятора;
□ на увеличение запаса устойчивости по фазе <р3 с помощью форсирующих
звеньев регулятора (1 - д / ^), модули нулей которых задаются в окре-
стности частоты среза <иьр. определенной с помощью номограмм
(см. рис. 6.33) по желаемым показателям качества замкнутой системы -
времени установления гу и перерегулированию а. Подъем фазовой харак-
теристики разомкнутой системы с помощью форсирующих звеньев регу-
лятора с учетом ее уменьшения интегратором на 90‘ настоятельно реко-
мендуется при разности степеней полиномов объекта п - т> 2;
□ на компенсацию левых полюсов объекта з° с высокой степенью колеба-
тельности ц или с малой степенью устойчивости л, исключая нулевой
полюс, создающий астатизм. Компенсации подлежат те полюсы, кото-
рые, изменив свое положение после замыкания цепи обратной связи,
не попадают в желаемую область спектра замкнутой системы 5, опре-
деленную в (6.52).
Весьма приблизительную оценку расположения полюсов замкнутой сис-
темы с единичной обратной связью Ко = 1 можно сделать по результа-
там исследований разд. 2.5.2 о влиянии обратной связи на свойства ти-
повых звеньев:
• согласно (2.28) у апериодического звена частота сопряжения <о( =-j’
увеличивается в 1 + Л) раз, где К, = Таким образом, при замы-
кании объекта единичной отрицательной обратной связью его действи-
тельный полюс смещается влево тем дальше, чем больше усиление
объекта на частоте сопряжения ш, (рис. 6.62, о);
• согласно (2.31) у колебательного звена с комплексно-сопряженными
полюсами з“(.| ““Лю ±<о,и частота сопряжения ш( увелнчива-
Методы проектирования систем автоматического управления
561
ется, а постоянная времени Т, = 1 / ш, и коэффициент затухания Ъ
уменьшаются в + Kt раз, гае по (2.11) Kt = | H5jo>()| / 2&. При этом
действительная часть г)к/ = / 7', не изменяется, а мнимая часть уве-
личивается с <0, До + Таким образом, при замы-
кании колебательного объекта единичной обратной связью его ком-
плексные полюсы удаляются от действительной осн по вертикали тем
дальше, чем больше усиление объекта на частоте сопряжения ц
(рис. 6.62, б).
Рис 6.62
При оценивании положения полюсов замкнутой системы рекомендуется
рассчитывать значения А, с учетом известной части регулятора, т к. она
существенно влияет на устойчивость характеристического полинома
(6.83). Не стоит, однако, обольщаться насчет высокой надежности и дос-
товерности данного метода оценивания хотя бы потому, что действи-
тельные полюсы объекта s° не всегда превращаются в действительные
же полюсы замкнутой системы s', как это следует из метода Метод не
отвечает также на вопрос, почему устойчивая разомкнутая система после
замыкания может стать неустойчивой, а левые полюсы переместиться в
правую полуплоскость.
После принятия решения о выборе структуры регулятора передаточные
Функции желаемого разомкнутого контура и замкнутой системы примут
формы
со следующими элементами:
562 mans
□ неизвестным коэффициентом Ар — одним из коэффициентов усиления
каналов:
• пропорционального Л'п при выборе П- или ПД-регулятора;
• дифференциального Ка при выборе Д-регулятора;
• интегрального К,, при выборе И-, ПИ- или ПИД-регулятора;
□ полиномом числителя передаточной функции объекта
B(s) - bo + bts + ... + b"!"1;
□ полиномом GpCs), равным:
• l, если выбран П-регулятор;
• 1 + giS с коэффициентом ft = -l/Zi, если выбран ПИ- или ПД-
регулятор,
• 1 + ft* + ft*3 с коэффициентами j?i = -1 / li -1 I ti и g2 = 1 / Zift, ес-
ли выбран ПИД-регулятор;
□ полиномом О(з)=0у+«у+|3 + .. +a„s"’v. равным:
• полиному /Цз) = оо + А|л + ... + a„s” знаменателя передаточной функ-
ции статического объекта;
• статической части A(s) /s= сц + ... + характеристического по-
линома объекта с порядком астатизма v = 1.
Для обеспечения скоростной ошибки, не превышающей значения С|, необ-
ходимо выполнение условий (6.51, б), в которые с учетом принятых обозна-
чений нужно подставить:
□ К^Ьо вместо схо и Ац;
□ AJAft + 61) + Оу вместо <Х|;
□ AJJAoft + 6|) вместо 6|.
В результате получим неравенства
а, — КрЬоС\ < О S а, + КрЬоС],
из которых следует условие выбора модуля коэффициента К„. аналогичное
(6.27, в):
<бет'’
Знак коэффициента А',, выбирается по критерию Рауса - Гурвица (4.13) У®'
юйчивости характеристического полинома замкнутой системы:
sgn(Kp). /^в(т)(^(з) + iD(s) — усюйчивый полином (6М й
Методы проектирования систем автоматического управления 553
Не стоит забывать, что отсутствие правых полюсов разомкнутого контура не
гарантирует устойчивости замкнутой системы, а спектральный метод подав-
ления неустойчивости путем компенсации правых полюсов объекта нулями
регулятора не является грубым в отличие от частотного метода синтеза, ос-
нованного на критерии устойчивости Найквиста.
В целом следует иметь в виду, что спектральный метод сам по себе, т е. без
построения частотных характеристик и расчета корней полиномов, наиме-
нее предсказуем в получении желаемых свойств замкнутой системы из-за
сложной зависимости значений ее полюсов от коэффициентов передаточ-
ных функций объекта и регулятора. Поэтому процесс подбора параметров
ПИД-регулятора часто реализуется так называемым методом «научного ты-
ка», одна из реализаций которого приведена в конце следующего примера.
& Пример 6.13. Для объекта с передаточной функцией
^^(l + T.sXl + ^Xl + rp)’ (6.89)
К = 200. Т, = 50с, Т2 = 10с. Г3 = 1с,
рассчитать тремя рассмотренными методами ПИД-регулятор. создающий в
замкнутой системе астатизм первого порядка с минимальными значениями
коэффициента скоростной ошибки q, времени установления гу и запасами
устойчивости по амплитуде L, > 6 дБ и фазе <р, > 30'.
Решение В первую очередь испытаем приближенный графический метод
синтеза, в котором создается общее представление о частотных характери-
стиках объекта и возможном расположении частотных характеристик же-
лаемой разомкнутой системы.
Следуя изложенному выше алгоритму синтеза ПИД-регулятора, выполняем
следующие действия.
1. Строим на рис 6.63 логарифмические частотные характеристики объекта
Z-(w)= 201g К - 101g(l + Ti2to2)-10lg(l + тЛй2)-10lg(l ♦ TjW)
ф(ш) = -arctg(T|W)- arcig(r2w)- arctgfao)}
а на осях ординат отмечаем уровни запасов по амплитуде -L, и фазе ф,
Судя по интервалу монотонного уменьшения фазовой характеристики с
О' до -270* и с учетом ее будущего подъема регулятором на высоких час-
тотах на 90', следует выбрать граничный уровень фазы ф,р = -180’ и уро-
вень запаса фазы <рп> + ф, = -150’
Проводим уровень фазы ф,р + ф, - 90’ = -240’ и по (6.86, а) определяем
частоту запаса желаемою разомкнутого контура - 2 рад / с.
3. Выбираем по (6.86,6) параметры дифференциального канала ПИД-
регулятора: частоту сопряжения шл = 0.2 рад /си постоянную времени
7» • 5 с.
4. Строим по (6.86, <?) частотные характеристики £д(со) и Фи(о>) последова-
тельного соединения объекта Hz(s) с форсирующим звеном регулятора
(I + М.
5. Определяем отклонение амплитуды Ln(toJ от уровня запаса -L, и по
(6.86, г) вычисляем коэффициент усиления пропорционального канала
регулятора
= 0.96 дБ => Кц = 1.12.
6. С учетом фазового сдвига от -90" до 0", вносимого изодромным звеном
а диапазоне частот ш< 10ы„, с небольшим запасом выбираем по (6.86,
параметры интегрального канала регулятора: частоту сопряжения
ц, = 0.1 рал /си постоянную времени Т„ = 10 с. Тогда по (6.86, е) полу-
чаем коэффициенты усиления интегрального и дифференциального ка-
налов ПИД-регулятора. К„ - 0.074, Ка = 3.72.
Рис 6.63
565
Методы проектирования систем автоматического управления
1. В результате проведенных графических расчетов получена передаточная
функция ПИД-регулятора
яЫ.и2^.172..И2<1М!±51)
в т
Построив частотные характеристики желаемой разомкнутой системы
(6.86, з), убеждаемся в наличии желаемых запасов устойчивости L, и ф,
на всем интервале частот со S ш» где £-д(ш) > -6 дБ
Продолжение низкочастотной части характеристики L*(u>) отсекает на
оси ординат значение -201gC| » 23 5 дБ, из чего заключаем, что коэффи-
циент скоростной ошибки составляет С| - 0.067 с.
Сформировав передаточную функцию желаемой разомкнутой системы
построим по (6.86, и) переходную характеристику замкнутой системы
(рис. 6.64) и определим ее показатели качества /у = 9.06 с и о» 42.5%.
Рис 6 64
Приступая к аналитическому синтезу ПИД-регулятора для управления объек-
том (6.89) с частотными характеристиками
I V^+7iIw’J(l + 7г2“2^+7j’<i>j)’ (6.90)
I ф(о)) = -arctg(T|O))- arctg(r2<i>)- arcig(7jci))l
будем руководствоваться примерным расположением желаемых логарифми-
ческих частотных характеристик разомкнутого контура Фж(ш) и часто-
той запаса оз, = 2 рад / с (см. рис 6 63) Выберем коэффициент скоростной
ошибки равным q = 0.1 и по (6.81) сразу получаем коэффициент усиления
интегрального канала К„ = 0.05.
Гпава 6
Зададим достаточно широкий интервал изменения частоты запаса
«>, е |0.03, 3| и с помощью Mathcad рассчитаем по (6 82) зависимости ^(ш,)
и вычислим корни характеристических полиномов (6.83)
Qj.mJ = 200К„ + (I + 200К,,(<•>,))' + (61 + 200Л'л(<о1»^3 + 560? + 500?, (6.91)
их спектральные параметры П(ы,), Y(<a>), р(аз,) (рис. 6.65, о) и построим на
рис. 6.6S, 6 графики оценок времени установления /упих(оз,), гуп,и верх-
ней границы перерегулирования o(<i>,). Отметим, что оценки (3.48) и (3.49)
строились только на тех частотах из,. где степень устойчивости ц(аз,). вычис-
ляемая по (3.43), была плюжитыыюй, все корни полинома (6.91) были ле-
выми. а замкнутая система устойчивой
<0 fl
Рис. 6.65
Анализируя (рафики, мы видим, что нет единой частоты запаса, на которой
бы оценки параметров /упих и а достигали своих минимумов одновременно
Поэтому выберем два значения частоты оз, и сравним соответствующие *»'
рианты систем управления по фактическим показателям качества их пере-
ходных характеристик йя(/) и h^t) (рис. 6.66, а).
□ На оптимальной по быстродействию частоте запаса оз, = 0.743 рад / с дос-
тигаются минимум верхней оценки времени установления zymax = 18 ° \
и почти минимум нижней оценки /ут|п = 4.7 с, получены оценка перере-
гулирования о = 29.8% и следующие параметры ПИД-регулятора
К„ - 0.468. К„ = 0.05, = 1.076. Ги - 5.32 с, Гя = 4.04 с.
Методы проектирования систем автоматического управления 567
Фактические показатели качества переходной характеристики h^t)
(сплошной график) составили /у = 17.4 с и о = 52.7%
□ На оптимальной по перерегулированию частоте запаса <л, • I 052 рал / с
достигается минимум оценки перерегулирования п = 21.9%. а также по-
лучены двухсторонняя оценка быстродействия 7.5 S (у 5 30.8 (с) И сле-
дующие параметры ПИД-регулятора:
ХП - 0.694, КИ “ 0.05, Кл - 1.85, Г„ - 10.27 с. Та - 3.6 с.
Фактические показатели качества переходной характеристики h,,(n
(пунктирный график) составили /у “ 10.5 с И о = 43 4%.
На рис. 6.66, б построены частотные характеристики обеих желаемых ра-
зомкнутых систем, из которых видно, что, несмотря на точное прохождение
характеристик через точки запасов Щы,) = -L, и Фж(<о,) = 4>гр * ЧЬ. устой-
чивость с запасами является условной, поскольку фазовые характеристики
локально находятся в запретной зоне фц, t в окрестности частоты
ш= 0.1 рад/с. В результате опасного приближения Фж(ш) к граничному
Уровню фазы Фф = -180’ переходные характеристики приобретают повы-
шенную колебательность и перерегулирование, особенно в первой системе,
чья фазочастотная характеристика ФЖ|(ш) подходит к этому уровню ближе,
чем во второй.
Переходим к испытанию спектрального метода синтеза ПИД-регулятора. С
Учетом рис. 6.65 зададим выполнимые требования к замкнутой системе
□ астатизм первого порядка с коэффициентом скоростной ошибки
С| S0.1 с;
□ быстродействие /у S 30 с;
Э перерегулирование a S 20%.
568__________ _______________________________________Гпамд
Заданным динамическим показателям качества соответствует незамкнут^
спектральная область, описываемая по (6.52) граничными неравенствами
Л и 2 0.1, Ц S 1.952, v 63*.
Проанализировав спектр передаточной функции объекта (6.89)
(зГ = -Ю.О2, з2°=-0.1, 4=-1),
убеждаемся в отсутствии у него нулевого полюса и необходимости включе-
ния в состав регулятора интегрального канала, вносящего в спектр разомк-
нутого контура полюс 5| = 0. Задавшись коэффициентом скоростной ошиб-
ки с, = 0.1, по (6.81) выбираем коэффициент интегрального усиления
Ки = 0.05.
Сформируем три варианта компенсирующих нулей (гм, постоянных вре-
мени (Ги, Гя), передаточных функций ПИД-регулятора (6.80, в), замкнутых
систем (6.1) и сравним их спектры (s’) (рис. 6.67, а) и графики переходных
характеристик Л3(/) (рис. 6.67, б), рассчитанных по (6.86, и):
Рио. 6.67
□ еи = з° =-0.02, гя = з2 =-0.1 =» Ги и 50, Тл = 10 =»
-» Л12(з)=3 + ^ + 25з, ^,2(з)= =»
=» з’д = ~0.5±3.12j е 5 . /у “ 5.32 с, о - 60.5 > 20%;
Методы проектирования систем автоматического управления_____569
□ гн =sl° =-0 02, гд =Sj = -1 => Т„ = 50, Л, 1 =»
» яиИ« 2.55+2^+15.. «',„Ы-Й77^7 -
= . -0.05 ± j « 5 . - «О > 3° - 8! s * »*
□ i„=s? = -0.1, 2Л =«"=-> => = 10. = 1 =>
- M')"0.55+v+a5*’ ”
=» sff = -0.01 ± 0.447j е S , /у = 296 > 30 с, а = 93.2 > 20%
Отчетливо проявляется очевидная закономерность: чем ближе к мнимой осн
расположен компенсируемый левый полюс разомкнутого контура, тем более
быстрым и затухающим получается переходный провесе в замкнутой системе
Тем не менее, ни один из грех вариантов компенсации двух полюсов объек-
та нулями регулятора не доставляет замкнутой системе желаемого спектра и
показателей качества переходной характеристики. Читатель может самостоя-
тельно убедиться в том, что все три варианта компенсации одного полюса
объекта дают неустойчивые замкнутые системы.
Таким образом, компенсационный подход к выбору нулей ПИД-регулятора не
гарантирует получения желаемых свойств системы управления В случае же
выбора нулей регулятора, не совпадающих с полюсами объекта, решение за-
дачи синтеза спектральным методом вообще немыслимо без дополнительно-
го исследования частотных характеристик и построения переходных процес-
сов, что в итоге приводит к интерактивной процедуре подбора параметров
регулятора по результатам моделирования (см рис. 6 41)
Некоторое представление о форме области S спектра замкнутой системы
(рис. 6.67, а) в пространстве параметров (А,,. А'.,) при фиксированном коэф-
фициенте Кн = 0.05 дают рис. 6.6S, а, б. Там же построены линии, ограни-
чивающие области с другими оценками времени установления 1У и перерегу-
лирования <т.
Методом моделирования С использованием ФУНКЦИЙ tust И sigma
(см. рис. 3.8) на рис. 6.68, в, г построены области, в которых фактические
показатели качества {/у, о) устойчивой переходной характеристики Л,(г) не
превышают значений соответствующих линий уровня Путем наложения
графиков друг на друга можно очертить области, где замкнутая система об-
ладает обоими свойствами одновременно. Например, при выборе коэффи-
циентов усиления каналов ПИД-регулятора К„ = 0.275, А„ = 0 05 и
= 3.75, находящихся в областях ц S 5 с и о < 30%. получим систему
управления с фактическими показателями качества = 4.25 с и я = 21.3%
Гламб
В заключение примера приведем Mathcad-программу, позволяющую рассчи-
тать ПИД-регулятор путем интерактивного подбора его постоянных времени
или коэффициентов усилении каналов с возможностью визуального контро-
ля устойчивости и запасов устойчивости замкнутой системы по логарифми-
ческим частотным характеристикам /.*(<«) и Фж(со), а статических и липами
Методы проектирования систем автомагического управления
571
ческих свойств — но переходной характеристике Л,(/>. В листинг нс включе-
ны определенные ранее функции согф (см. рис. 2.27). tust и oigma
(см. рис. 3.8).
К .= 200 Т ( 50 10 I )Т
W(” ’* (l+T0.»).()+T,»)(lfTr»)
j?=0.. 500 Ц== -3 + 0.01 । ш(>10Ц
L :в 20log(|W(j ш)|) F =cor<p(W,w)
cl:=0.l Ки:= —— Ки =005
Подбор постоянных времени ре)улятора
(Ти Тд):- ( 10 5 ) R(j) = Ки * ТМ<‘* Тд *1
( Кп Кл ) := ( Ти + Тд Ти Тд ) Ки ( Кп Кд ) = ( 0.75 2.5 )
U :« L +20log(|l+J-Тл <и|) Ед F + agd+J Тд ш) deg''
1ид > U + 20log^ [~* jTJ”([|W| j Рид =FA+arg(l + ) Тиш) deg ’-W
<риД|-.= -240 un:=2 I0<ib'=5 шд:» Гл 1
W»d) * W(s) R<*> L* 20log(|w*(j .J) Rk • ccr»( W*.»»
572
Рис. 6.70
Подбор коэффициентов усиления регулятора
KPl
R(i) := К₽о +------- Кр2$ w*(s) := W(s) R(s)
W1(t). lunyltfy (1I.-S+2.+150-s»)
l*Wx(») I collect ,s (56.-s 8II. S1 + 560.-sJ 500. s4+10.)
. Wj(t) linvlipbce .»
h(t) — I 9666-exp(-J28l-t)-cos( 1.124-1) - .4627 exp
Методы проектирования систем автоматического управлений
hust := Wj(O) Др : 0.05 |husl - h(O)| h(0) - -4>e IO’ 5
He > 500 dt :0.05 k:=0 — hust I
dl
t|,>k dt Ук h(«k)
ty := tusltl.y,hust ,Др) a := sigmafy,h(O),hu>t)
tmod := Tk on error minCTk.l5ly)
ty = 4.25 e = 21.304' . h(ty) -- 1.046
Рис. 6 72
6.7.3. Реализация ПИД-регуляторов
Завершая изучение методов конструирования ПИД-регуляторов, обсудим
некоторые проблемы, возникающие при их реализации. В общем виде
структурная схема трехканального устройства управления по сигналу ошиб-
ки е(г) приведена на рис В.7, а на рис. 1.52 и 1.53 построены два варианта
принципиальных схем ПИД-регулятора с произвольно задаваемыми коэф-
фициентами усиления пропорционального /С,„ интегрального К„ и диффе
ренииального Кл каналов. Вторая схема выгодно отличается от первой ис-
пользованием мультидиапазонного усилителя с линейной шкалой
(см. рис. 1.29), позволяющего устанавливать коэффициенты усиления кана-
лов с высокой точностью в широком динамическом диапазоне
Одна из главных проблем конструирования ПИД-регулятора связана с реа-
лизацией канала производной сигнала ошибки e'(t'). Усиление этого канала
|Адш| линейно возрастает с ростом частоты, в связи с чем на выходе регуля-
тора возможны следующие нежелательные эффекты
□ повышенное усиление высокочастотных составляющих сигнала ошибки, но-
сящих, в основном, шумовой характер. Из-за этого уменьшается отно-
шение полезной составляющей управляющего сигнала х(г) к шумовой,
что дестабилизируюше влияет на объект управления;
□ возникновение импульсов большой амплитуды в моменты скачкообразного
изменения ошибки е(г) =g(t) -y(t). Даже если выходной сигнал системы
у(0 изменяется достаточно медленно, то сигнал уставки g(t) вполне мо-
жет претерпевать скачкообразные изменения, проникающие на вход
дифференциатора. Последствия попадания дельта-подобных импульсов
на входы некоторых технических, в том числе и электронных, устройств
могут быть весьма плачевны: от тихого пробоя какого-нибудь р-п-
перехода до громкого взрыва регулируемой установки от превышения
мощности или случайно проскочившей где-то искры.
Существуют некоторые конструктивные методы частичного устранения
вредных эффектов присутствия дифференциального канала ПИД-
регулятора, из которых назовем следующие:
□ использование дополнительных устройств осла&гения высокочастотных шу-
мов, например, фильтра низкой частоты с передаточной функцией
1 /(1 + Дв). Постоянная времени фильтра Гв, обратная частоте сопря-
жения ш,, должна:
• быть много меньшей минимальной постоянной времени регулятора
Та, чтобы не компенсировать влияние на объект дифференциального
канала;
• удовлетворять условию (6.38), чтобы подавлять высокочастотный шум
на малых уровнях усиления полезного сигнала.
Методы проектирования систем автоматического управления
575
Рассмотрим два способа включения фильтра низких частот в контур
управления:
• установка фильтра последовательно с ПИД-реГуЛятором дает сле-
дующую передаточную функцию устройства управления:
<6,92>fl)
. установка фильтра в дифференциальный канал делает передаточную
функцию регулятора равной
(6 92, 6)
Анализ влияния коэффициентов усиления каналов на логарифмическую
амплитудно-частотную характеристику регулятора Lp(u>) (см. рис. 6.59)
позволяет качественно сравнить две характеристики — £пид(“) с
£д(ш) — и сделать по рис. 6.73 следующие выводы
• последовательное соединение ПИД-регулятора с фильтром низких
частот не изменяет частот сопряжения, постоянных времени, коэф-
фициентов усиления каналов и поведения частотных характеристик
на низких и средних частотах, что позволяет рассчитывать эти со-
ставные части устройства управления (6.92, о) независимо друг от
Друга;
• установка низкочастотного фильтра в дифференциальный ЮШОЛ «ЗШГ-
няет эффективные значения коэффициентов усиления пропорцио-
нального и дифференциального каналов ПИД-регулятора
K'a=Kn + K„Tt, кя = кя +кпт,.
а также зависимые от них частоты сопряжений и постоянные време-
ни звеньев устройства (6.92, й), что, естественно, затрудняет его рас-
чет. Так что данный способ фильтрации высокочастотных шумов во
всем проигрывает первому
Рассмотрим два способа включения фильтра низких частот н контур
управления:
. установка фильтра посгаыпелыю < ши орт
дующую передаточную функцию устройства управления
Япил (J)я "* (6.92, а)
• установи фильтра а дифференциальный канал передаточную
функцию регулятора равной
A',s _ К, + (К, + KJ, > + (*,+ К,Г, Ь:
+ ! + r.j“ л(1 + Г.л)
Яд(.т)=-£«-+*„
(6 92.(Л
Анализ влияния коэффициенте усиления каналов на логарифмическую
амплитудно-частотную характеристику регулятора /.р(и>) (см. рис ь 59)
позволяет качественно сравнить две характеристики /цнд(<о) с
£д(о>) — и сделать по рис 6.73 следующие выводы
• последовательное сое пшенке ПИД-регулятора с фильтром низких
частот не изменяет частот сопряжения, постоянных времени, коэф-
фициентов усиления каналов и поведения частотных характеристик
на низких и средних частотах, что позволяет рассчитывать эти со-
ставные части устройства управления (6 92. а) независимо друг от
Друга;
• установка ни мсочастотного фи тира в шфференцна тьный как 11 том
няет эффективные значения коэффициентов усиления пропорцио-
нального и дифференциального каналов ПИД-регулятора
Г. = *п + V. •*>*** •
а также зависимые от них частоты сопряжений и постоянные време-
ни звеньев устройства (6 92. (5). что. естественно, затрудняет его рас-
чет. Так что данный способ фильтрации высокочастотных шумов во
всем проигрывает первому
Так или иначе. объединение ПИД-регулятора с низкочастотным фи ,.
ром дает структуру устройства управления, точно совпадающую с реи>
мендованной в вывода* paid 6.3 структурой регулятора. аналиги чесю
рассчитанного по критериям максимального быстродействия и мини
мальных ошибок регулирования;
□ при небольших скоростях изменения сигнала уставки ц(Г) и редкю
моментах его скачкообразного изменения в силу почти точного еоот-
ношения
de(t) = d£(t) _ dy(r) dy(r)
dr dr dr dr
можно перенести точку входа дифференцирующего канала с сигмам
ошибки е(Г) на выходной сигнал И0 и строить систему ПИД-управлени*
согласно структурной схеме, приведенной на рис. 6 74, а В этой струк-
туре дифференцируется только сигнал обратной связи, который обычно
изменяется медленно и не создает импульсных сигналов на выходе Д-
канаяа;
□ если имеется техническая возможность измерить производную выходно-
го сигнала Иб=/(г) (например, существуют тахометры — устройств
измерения угловой скорости вращения какой-либо оси), то можно во-
обще отказаться от ее вычисления с помощью дифференциального каиа-тг
и строить предыдущую систему управления по структурной схеме, при-
веденной на рис, 6.74, 6. При использовании скоростной обратной связи
от тахометра — устройства с низким уровнем шумов, сравнимым с ДР)"
гими элементами автоматики,— не происходит дифференцирования сигна-
ла ХО. благодаря чему в системе управления успешно решается пробле-
ма помехоустойчивости.
Рис в 74
сис^вах управления |1|, 29) вместо непреры^
>1иД утграмеиия (В.5). вырабатываемого с^мой. реляи^
т
^горшпм вычисления упражляюших tnagfknKtt . /4 г*) . дискретные от-
счеты времени /4 с помощью г1ри
бамжеиии. т е без тки.шок какой-либо
рования и дифференцирования, игм, шсгрсн
ся в следующем виде
управления
£о г АГ
Изучение дискретных систем управления ие вымят в план данной книги
хотя и представляет огромный практический интерес в <лвреыеин,ю цифро-
вую эпоху Повсеместная компьютеризация кип отраслей промышленности
привела к тому, что сейчас трудно иайти чис • «> управ-
ления более-менее сложными процессами и устройствами Количество пуб-
ликаций по синтезу цифровых регуляторов многократно превышает т/лем
библиографии классической теории автоматического упражнения, осиоюн
ной на методах исследования систем в непрерывной времени Это. однако,
не является причиной отказа от постижения /тих методов точно так же как
овладение клавиатурой компьютера ие избавляет от иесйходимости уметь
писать собственной рукой
Методы теории непрерывного управления, прямого и сйрагтного пресйраю-
ваиий Лапласа, частотные и спектральные полком к хиалиту свойствсмс-
тем и конструированию аналоговых устройств управления сложными о<пек
ими служат тем незыблемым идейным фундаментом, на котором прочно
стоит вся современная теория и практика управления с использованием
микропроцессорных устройств и сложнейших алгоритмов сЮржютки
формации
В заключение не лишним будет еше раз
иедуры анализа и синтеза, рассматриваемые в дан •
ittUK! рПШШХ систем, а ие с самИМ^^грнстики реальной систе-
а точнее, никогда не может точно опи<ят\^‘ „ ппаииинарнои *>-
иы Еше более сужена область применим .^,^.,-„1^ лиалазояе сиг-
Дели, адекватной реальной системе только в о ана-тизэ и синтеза
•«•юв и интервале времени Стедомте-^ ( этой м МИОГХ1
-истем автоматического управления. 5’**nf4rtbM и не г:ере/л|енивать «
ДРУгих книгах, всегда надо относится ср*т
ГМОЖНОС1И ^зработчика системы уттраде-
^нейшей составной частью **’е'1Ы*^10Овиия а конкретной фммче-
кия является применение результатов )и?1*ии Лишь испытания мо-
С*>Й системе путем проведения ^.^й и действенность avo-
“одтвердить адекватность L привлечением »ы <ис.ти:е.1ыиой
Р-’мо». синтезированных в тиши клб*^ Х(Пиро«иия может потребо-
современного компьютер. Про^«
St.-------------------------------------------------------/лама
пять много итераций, связанных с уточнением широкого спектра ланных
от требований технического задания, целей проектировании, струмуры и
параметров элементов системы, допустимых погрешностей аппроы нм.щии
элементов линейными моделями — и методов проектировании плгебран.
ческих. частотных, спектральных и других, которые в данной книге не |Mf
смотрены, но освещены в других источниках.
ЗАКЛЮЧЕНИЕ
ЗчгммЯ л» гмнн чти jmhmom, «олМ huwvo
ет (<тм> П№М№>', н рычлщнЛ лм ммЛ> «Л
HofwututhtMi чучкую
<«mV/wh ЧвнштеЛн
Пришла пора подвести итог нашего долгого путешествии встряну автомати-
ческого управления Теперь читатель может составить собственное пред-
ставленис как о книге в целом, так и о се отдельных находках и упущениях
Понимая, что рассматриваемая гема стала классикой жанра chic полвека на
ад и в нее трудно что добавить, и хотел бы остановиться на тех моментах
научной новизны, которыми данная книга отличается от других паданий,
В главе 1 разработана методика анализа и синтеза схем на операционных
усилителях, позволяющая создать электронную модель любой сложной сис-
темы и исследовать ее свойства методом моделирования, я том числе и про-
граммного.
В главе 2
□ исследованы погрешносги кусочно-линейной аппроксимации логариф-
мических частотных характеристик типовых шеньев и получены опти-
мальные по минимаксному критерию параметры асимптотических ха-
рактеристик;
□ Проанализированы свойства систем с положительной обратной снятью и
получены условия их самовозбуждения Проведено исследование схем
на идеальных и реальных операционных усилителях с испсиыованнем
отрицательной, положительной и одновременно обоих видов обратных
CttR icii
В ги>ве 4 введено понятие одновременного запаса устойчивости замкнутой
системы по амплитуде в фазе и на згой основе получен алгебраический
•фитерий устойчивости с совместными запасами.
8 ^оае &
Q Разработан аналитический метод синтеза регуляторов, достюгошмх
‘•'мкнутой системе одновременно оба запаса устойчивости но амплитуде
и фазе;
Q проведен максимально потный анализ свойств ПИД-регулятора и рцм-
ботаны аналитический. графический. спектральный и программный ме-
тоды расчета его параметров
К отмеченным моментам новизны в отдельных главах можно добавить еще
н насыщенность многих разделов книги примерами решения аналитических
и сложных вычислительных задач в программной среде Mathcad Автор счи-
тает эту уникальную. но простую в освоении программу, работа в которой
ведется на языке привычных в написании формул, идеальным ннсфуиск-
том и помощникам инженера и студента. В современных учебниках по ав-
томатическому управлению, например, в (II. 29), применяется более мощ-
ная математическая программа MatLab со своим специфическим языком
программирования высокого уровня. Конечно, в руках опытного пользой-
теля она способна творить чудеса, но для массового освоения лучше, по
мнению автора, подходит именно Mathcad.
В заключение я не могу не поблагодарить главного редактора надательсты
•БХВ-Петербург» Екатерину Владимировну Кондукову и ее заместителя
Людмилу Юрьевну Еремеевскую за принятие ответственного решения об
издании моей книги, за терпение, благожелательность и требовательность,
проявленные ими при ее подготовке к печати.
Будь рад получить от читателей критические замечания по материалу книги,
сообщения об ошибках ням опечатках, .любые пожелания об улучшении со-
держания и оформления ее будущих изданий. Заранее благодарю каждого за
информацию о цитировании и ссылках на мою книгу в своих научных гра-
дах. Контактный адрес e-mail: nea@mail.nnov.ru, почтовый адрес: Ы)ЗЫХ>.
Нижний Новгород, ул. Минина, 24, Нижегородский государственный тех-
нический университет, кафедра «Вычислительная техника». Никулину Евге-
нию Александровичу
Всегда готов к взаимовыгодному сотрудничеству
С уважением ко всем читателям
£всгюш Никулин
ПРИЛОЖЕНИЕ 1
Таблицы преобразований Лапласа
В приведенных таблицах преобраюмний Лапласа переменные снчшны ме
жду собой следующими соотношения!!
аГ- l.pF-t wr»Jl-V' .(₽’* «ЛР- ।
Тлалччл Л 1 Лрми* Ллаплсл
№ Оригинал <6 Изображай** Нз)
1 6(П 1
2 К») X
3 Г 4
4 и и!
3 »• j*a
1 -О* a l i(s + a) ’(• ♦
Приложение t
Таблица П. 1. Прямое преобразование Лапласа (продолжение)
№ Оригинал ХО Изображение Яз)
7 1 Т2 (s + a)2 (l + Tj)2
8 1"е'ш л! и!ГяИ (з+а)"+1 (1+Тз)”+1
9 sin(W) ш Т з2+со2 ” 1 + Т2з2
10 Ktn(wr) 2 cos ^-7
11 ?sin(cix) 2со(зз2 - со2)
12 c'₽,sin«ur) (о 7~У1-^2 (з + р)2+со2 1 + 2^Тл+Т2.Л2
13 e*rsin((iif) 2(0(5 + Р) ((5 + р)2 +Ш2)2
14 e'*rJsin(<Dr) 2<о(з(5 + р)2-со2) fc+p)2+“2У
15 sin(<Dr ♦ <p) sin (ф)? + Cl) COS (ф) з2 + со2
16 Л1П<ШГ * ф) (д2 ~(02)sin^)+2<осо5(ф)5 (s2+<o2)2
17 (s + p)sin (ф)+сосоз^ф) (з + Р)2 + ш2
Таблицы преобразований Лапласа
Таблица П. 1. Прямое преобразование Лапласа (продолжение)
№ Оригинал 40 Изображение Hs)
18 cos(w) s T2s з2+ю2 l+T’f1
19 zcos(oir) s2 -a>* t2+®2Z
20 Hcos(ax) 2з(г2 -3<о2) (г2 +со2У
21 e‘B'cos(ax) з+Р _ Tfe + Гз) (з+РУ+О)2 l + 2^Ts+T2s2
22 e'l>'rcos(<Qt) ((з+РУ+ш2)2
23 e’^cosfo») 2(з+Р)((з + Р)2-3<о2) ((з+Р)2 +(02)’
24 cos(<ix + <p) cos (ф)з - ш sin (ф) з2 +ш2
25 rcos(cor + <p) (з2 ~(1Г )со$(ф)- 2Ш51п(ф)г (з2+Ш2)2
26 e'p'cos«ur + ф) (з + Р)сО5(ф)-(1КП1(ф) (з + РУ+ш2
27 sin(O)|r)sin(iOi/) 2<0|0>гз (г2 +(о>| ♦(ОзУр +(о>, - ш2 У)
S94 Приложена 1
Таблица П. 1 Прямое преобразование Лапласа (продолжен")
N* Оригинал 80 Изображении Я а)
28 «П(Ш|Г)СОЙШ10 Ы| (л2 + ш2 - t»^) (i2 +((i)f +(Oj)l)t2 +(о>| -w2)2)
29 coMumXxmKuW) j(j2 + (О2 + ш2) (|2 +(Ш| +а)г)2Х»2 +(<1)| -<и2)2)
30 ih(u) <0 52 - or
31 rth((i») 2(05 t2-^2)2
32 (1) (.♦J)»-»’
33 сЫш) S S1 -со2
34 кЬ(ш) з1 +<1}2
3S е"*сЫ<и) _2±₽_ (1+р)2-ш2
Таблица преобразований Лапласа
Таблица П.2. Обратное преобразование Лапласа
Nt Изображение Fit) Оригинал КО
1 1 ОП)!
2 1 at9
3 1 4(1+П) I-с-
4 *6 + п) l-d-atje-"
5 1 ?(1 + П) Ле'"-!)*/
6 l + tt ?(1 + 7>) (t-7Xl-e^*r
7 l + TS + gJ2 л2(1+П) т-Т*( + (Г-т + о«)е"л
8 1 ?(1 + Tj) T!t-e^)-r<Z
9 1 (l + n)2 a2re‘“
10 1 з(1 + П)2 l-d+aOe""
II 1 з2(1 + П)2 2Ле^-!)*/(е-"*!)
12 1 Р(1 + П)2 37-2(-e'“)-n(2*e-‘u)*^
586
Приложение i
Таблица П.2. Обратное преобразование Лапласа (продолжение)
Nt Изображение F(s) Оригинал f (t)
13 (1 + Ъ)2 а’(1
14 (1+п)2 а’Ст+а-атДОе-"
15 1+с 41 + Т5)2 1-(1+а(1-сфОе""
16 41+п)2 1 -(А + Вг)е'®: А = 1 - а2#, В = а - агт + a?g
17 1 (1 + П)3 а3*2 с-а/ 2
18 1-^ + а/ + а2/2/2)е-ш
19 7^? /-ЗГ+|зГ+2г+^у-
20 (i+nf
21 (1+ь/ а3р-2а/ + ^-^-<"
22 1 (1 + П)4 а4г3е-"/б
23 1 /0+п)4 н
Таблицы преобразований Лапласа 587
Таблица П.2. Обратное преобразование Лапласа (продолжение)
N. Изображение F(s) Оригинал fit)
24 (1+Tj)4
25
26 (l + 7s)*
27 1 (1+TpXi+^j
28 (l + MO + M
29 1 + 13 (l + TiS\l+T2s)
30 1 5(l + T,sXl+T,s) l-C.e^+C^C,»^
31 5(1 +Ml+7^) Tl~T2
32 1 + TS + gS2 5(1+M1+M
33 1 52(1+M1+M ‘ - Г, - т2 + C.e^ - C2e“-J: C, =
34 1 S3(1 + T,5X1+M Л _Bt + £_Qe^' + c2e^: C, = • 4 = T* +Т|Г2 +T2,8= Tt * Tj
Приложен^ f
Таблица П.2. Обратное преобразование Лапласа (продолжение)
№ Изображаниа На) Оригинал f(t)
35 1 (l+T.^+Tji)2 Ceaf-(C + Bt)e.~a* : c = r* , . (t\-t2Y B=—r± \ r2(r,-T2)
36 1+0 (l + F.x^ + T^)2 B Т}(1\-Тг)
37 (l+T.iXl^:^2 Ce'“t' + (a - Sr)e “-': C = T' ~T'x+s . гДТ.-Тг)2 (T-TjXMTi-lTjg T22-72t+g т22(Ъ-т2У ’ (г,-т2)г23
38 1 Xi+t.jXi+W 1-Се’в,'+(А + вг)е‘а2': c_ T? (27j-r2)T2 1 (Л-ТгУ (Т,-Т2У ' T|-T2
39 1 + 0 Xi+TifXnW i-Ce-ai'+(A + fl/)e-a2': С=^2^. л_(2Г!-Т2)Г2-Т,т T2-t (t>-t2Y ’ T2(J\-T2)
40 l + o + p2 Ki+Tii»*^)2 1 -Се-Ч + (A + Bt)e-atl: С = • ..(ZT.-Tz^-TtT + g (T2-t)r2+8 (Ъ-т2у ’ (т]-г2у2г
Таблицы преобразований Лапласа
Таблица П.2. Обратное преобразование Лапласа {продолжение)
№ Изображение F(s) Оригинал f(t)
41 1 ^(l+TjsXl+r^)2 t - 7, - 2T2 + Ce‘a'' - (A + B/)e"“2': tiTi-lTjr} T2 c_ 7,3 (7, -T2y ' Ti-T2' (Ti-T2y
42 O+T.^+^s)2 -Ce~a'f+(C+Bt)e~a-•. c=—!—, s = —!— (7,-72/ (7,-7,^
43 s2 (i+t^Xi+^j)2 Ce~a>‘ +(A-Bi)e^!'. C- 1 Л- T>-2T2 ^-т.ут/ (Tt-T2fTl' b = —! (7,-72)723
44 i (l + T.xXl + r^)3 Ae*a|'-(A + Bz + a2)c’a’': 7/ 7, _ 1 A ~ (Г,-T2y -T^T2 ' C ’ 2(7, -T2tf
45 1 + Ts (i+T.^Xi+r^)3 Ae-<v-(A + Br + C/2)e'“1' в- 2.~t Ь-т (7,-7гУ (T'-TjT, ’ 2(7,-7,)r?
46 l + TS + gS2 (1+7,5X1 + 721)’ Ае-^-(А + Вг + Сг)е-02': A = ~Г|^/• (T| -T2y (Ъ-Т.ут} 2(7,-T2 ft
Приложение I
Таблица П.2. Обратное преобразование Лапласа (продолжение)
N» Изображение F(s) Оригинал f(t)
47 1 1 - A<a'' + (a2 + Bt + Ct2 )e~ai' T,3 2T,-T-> Л'\т.-т2ГАг=А,'1'В = (ту-тгГ C 2(Т(-Т2)Г2
48 1 + TS Xi+r^Xi+^y l-A)e'0|f+(a2 + в/+ C/2)e‘“2': A1 = ’ fa -rj (Т|-Г2Ут2 2(T|-T2)T22
49 (i+t^Xi+^F - Ae~a<f +(a+ Bt + Ct2) e'a3‘ д, Ъ B_ 1 C-—1 (r.-Tj/’ Ol-Tj)2^’ 2(T,-T2)r23
50 Mi)W (- A + erje"01' + (A + Bt)e~ai'; Л_ 2Г,Г2 1 (Ъ-т^' (Tt-T2y
51 l+tr (i+7-^(1+r2>y (- A + + (A + в2/)е'“’': ьгг,г,-(г,1ГаХ (Ti-Fj)3 (7i -Т2УТ,
52 i+tt+g? О+^УО+т^У 2Г,ГНУТ>)»2,
Таблицы преобразований Лапласа
591
Таблица П.2. Обратное преобразование Лапласа (продолжение)
N? Изображение F(s) Оригинал Kt)
53 1 ^i+r^yo+^j2 1+(А, - Я|/)е'сцг + (А2 - ta-Tjfc2 _(зт.-г2)г22 ' (Г.-ТгУ (T2-ltf ' В‘~(т}-т2У
54 (i+r^a+T^)2 (А-В1г)с-°*'-(А+в2г)е^: л_ Т\+Т2 _ 1 fa-Tj' 1 (т}-т2^
55 (1+Г,з)2(1+Т2.)2 -(А-/?1г)е-в1'+(А + В,/)е-а’': 2 _ 1 (T-I-Tj)5' ’ (Ti-TifT,2
56 1 ПО+т?) Сг ’ (Т2 -Tt\T2-тзу с> (Гз-Т^Гз-Т2)
57 1 1 |С,е С,-(г.-г2Хт1-Гз)’ Сг (т2-т^т2-т3ус' (Тз-^Хь-г,)
58 1 ,2П(1+7?) c'*(r.-rVr.) C1 (т2-тх\т2-тзус' (Тз-Г.ХЬ-Ь)
592
Приложение 1
Таблица П.2. Обратное преобразование Лапласа (продолжение)
№ Изображение F(s) Оригинал f(t)
59 пм*) Г=1 §С<е С’ (Г.-ТгХ^-Тз)' с2 к2-тДт2-т3У Сз (т3-т,Хл-т2)
60 м ,?С,е с* (г.-лХл-л^ Сг (T2-T^T2-T3y2’Ci (Тз-Т.ХТз-ГзХз
61 П(!+М £с<е-°":С,.= /Я~2 -
62 1 41(1+7}4) 1-EQe-': Q .-ПЙ"7*’
63 ы nfr-г,) *=i. **<
64 ,л22 П(«+М м -JC/e-a'': С, =— П(7}-71) *=1. **г
65 .лгз П(1Т,з) ic^'-.c,— П(7/-П) Ы. ket
Таблицы преобразований Лапласа
593
Таблица П.2. Обратное преобразование Лапласа (продолжение)
Nt Изображение F(s) Оригинал f(t)
66 1 (1 + П)2П(1+7?) (-А+Дг)Гв'+£с<а' В = ~'2 . П(г-т<) Л-ВТ^.С,- T-L 1 (т-ту nfr-т;) Ы, «Л
67 1 41+7*)2П(1+7>) НА] ;с,е-« в. г" . ПСг-т,) к.-=—т4— 1 (т-тУ h(T,-Tt)
68 1 з2(1 + Т5)2П(1 + Т(з) / - 2Т + (А + вОс4" + £ (с,е^ - Г,): -jfeH-W 1=1 T’ft+2 с,= 11 (т-т(^ Шт; -т4)
69 5 (i+n)2na+r,s) (А-В^-^С,^ В = --Т-У . П(г-Г,) Ф Mr-rJC' (r-r.^njr.-r)
Приложение t
Таблица П 2. Обратное преобразование Лапласа (продолжение)
Nt Изображение Не) Оригинал f(t)
70 (1+п)2п(1+гл) (-Л + вг)е-" +1 С,е^': В = J"-- пег-?;) С, = 1 м' т‘) (т-т}У п(т,-т4)
71 । 1+2£Тг+Т2»2 Ce^sindur): С = —Ц- (оТ2
72 ки 1+2&Г»+Т2? Ce'#,sin((Ot + ф): (ОТ3 V~₽TJ
73 1 |(1 + 2^Тз+Т2»2) 1 - Ce^'sintWf + Ф): С = ——. ф = aretgf — 1 (ОТ
74 1 + TJ »(| + 2^Т»>Т2з2) 1 - Cc^'sinlojf + ф): cj0-2P»W r^72_| шТ2 \PT2-rJ
75 Imp2 4+24Т*+Т2?) 1 -Се*ып(шг + ф):
с ыТг
1 - 20Т1 ♦ Cc**'»in(ajr + ф): С = — . ф = 2arclg^ j
Таблицы преобразований Лапласа
Таблица П.2. Обратное преобразование Лапласа (продолжение)
№ Изображение Не) Оригинал f(t)
77 1 + 2^П + Т2? -CeAiwo» - ф): С = —Ц-. ф = arctgl 1 wTJ । P J
78 1 (l + Z^Ts + I2?/ Ce^sinldM) - urcostw»: C = —- 2(ir7
79 1 + тз (i+^n+r2?)2 e*(Asin((DO - Bfcos«nr + ф)): 1-fo J(l-2fr)T2+r ’ 2wV4 ' Id)2?5
80 l + TS + g? J + l^ + T2?)2 e^Asinlccr) - Brcos(ur + ф)): A = , 2(O3T* e= 2ш2Т5
81 1 1 + Ce*(a>7cos(ciir + 2<p) - sin(ux + ф) + urcos«iv ♦ ф)У c'Jf-*••(?)
82 (h^Tj + tVJ CeA-flTlsinlair) + iu»cos(cur - <₽)): c'drs'' ?)
596
Приложение 1
Таблица П.2. Обратное преобразование Лапласа (продолжение)
№ Изображение F(s) Оригинал f(t)
83 CeAsin(uy) - bycos(civ - <р)): C = —<p = 2arctg(1 2<o3T6 Д P J
84 надз+т/з2 Х1+^2Т,5 + Л;5-' - Qe"^' sin(o),r + <p,)- C2e~^' sin(to2/ + Ф;);
«UF '-г/У+^.-р,^2 -Рг^2)?,^2 Wa]
V, - a№<| {20^-0№+т,:)
85 з^ + ^з+Т/з2)* 1 Х1 + ВДз + Т/з2 1 + C,e~* <p, = arctgf sin(u,r + q>,)+ C2e'^' sin(io2z + <p2):
i"-T}( »4(0, -0, -РЛ2)?,1!," Xa4&]
86 з2(1 + 24|Т,з + Т|2з2)Х Х1 + 242Тгз4Т/з2 - A +1 - C|e s‘' sin((O|/ + <p|)- C2e sin(w2f + <p2) A = +p2T22). г TL
“><Л2-Т22)г+4(р1-р2)(з,Т12 <p, -arctgf J
Таблицы преобразований Лапласа
597
Таблица П.2. Обратное преобразование Лапласа /продолжение)
Nt Изображение F(s) Оригинал f(t)
87 7“ГХ С|е'&' sin(to| t + ф|)+ С2е'^' sin(w2»+ф2):
l + Z^s + r/r X ' l + 2£2r2j + T22j2 -Г2 У +4(р, -Рз^Т,2 -PjT-fkrTf
88 l+^s+T2? х 1 1 + 2^ + T/r -Cie'01' sin(a>,r +ф1)-С2е’Вз' sin(co2r Ф2) шД2/(г,2-Т22У+ 4(р, - р, - р;К \-Ti
89 1 П(над+7Л2) fsl ХС,е"^'' sin(<fl,f + ф,): С, = ‘ . /?, = М M,jRi к =(т,2 -Т?У +4(0, -р* ^Т(2 -pt7i2) v—/ 2w,(p,-P1) ] =1. ы г/т/.
(P.-Pj^-^-Wj2)]
90 5П(1 + ^+Т,2?) 1 - £С,е*Л' sin(w,r + ф,): т2л-3 . С'=^7ГЛ'= Л*,, ц Jr, ы я« -к -П:У +4(0, -р*^,Г/ -р^гУ,2?,2.
Приложеие ?
Таблица П.2. Обратное преобразование Лапласа (продолкечк)
№ Изображение F<s) Оригинал f(t)
91 1 м -X+f+£Cte“^ sin(wj+<p4) А=2^Т,2.С,=^=. Rt= ПЯЛ. ,=t 4=1. =fr2 -г*2/ *4(3, -34 for,2 -^T-y,2Tz. г
92 Пб<-2у>+тЛ2) -£C,e~ft'sin(ov+<p,) T2n-S „ с,=-Ц=.я, = fl** TOi-jR, *x|.*»4 R* =fe2 -r2)f *4(3, -34 fo? -3*г?)т;’гЛ -HsWsiH?
93 •22 yc,e’ftz sin(<D,z + 4>,); C, = "-r= • *. = =(Г?-rj +4(3, -34 far2 ~^Т2У2Т-. •НкЖН
(sh-p^h--* ^□-(A-koJuis^-i I 46
MFHSh jUro *!i+i X 1 z^l+U^Z+l X -rf + u + I 96
!isrh”-pFh"“ >;J(!lft-l) -l-‘i = J *U+1 X I ,*rj+*rtz+T X— Я.+1 S6
г\1+ А>.ЭЬ *(* - xn)u’s r!i+i X I ^г1+*1Ъг+1 i f6
(ЦЛИ.Ж1О (s)d aMHixedgocyi «N
(aninaxuotroAj) ежляц аимстогефомь -gу ervwpej
"ё-тйёц^Hre^rd^oaduнПиидц
600
Приложение 1
Таблица П.2. Обратное преобразование Лапласа (продолжение)
№ Изображение F(s) Оригинал f(t)
98 1+Ц j(1 + 2$7j + T2s2) 1 HT,J 1 - Се"₽'sin(wf-<p)- (оГ^О-ТРТ^+Т/ с _ ta-On 1 (1-2РГ1)Г2+Г|2’
99 imp- .Ц| + 2£П + Г2?) Xl + T|j 1 - Ce"₽' sin (со/ - <p)- C|e"“‘':
c 1
wry (1-2РТ1)Г2 +г/ c (Г,-тХ+8 ‘ (1-2PTiX2+T12'
100 ?&+2tfi+TV)X 1 t - Т| - 2РТ3 + Се’р' sin (со/ - <р)+ С|в'а'': с- , т С.- т' ' а - 2рг, У2 + Г,2 ’"n8(7^)-2ire,s(i)
101 1 + 24Тз + Т2?Х Х_!_ 1+7> -Се’^ «п(со/-ф)-С1е’а',: с=——2= ШГ27(1-2РТ|)Г2+Г|2 с, = ! (1-гр/Jr2+г,2
Таблицы преобразований Лапласа
601
Таблица П.2 Обратное преобразование Лапласа (продолжение)
№ Изображение F(s) Оригинал f(t)
102 l + 2^7s+7 .V 1 Се~& sin(w/ - ф)+ Cte'“'' : с=—г 1 , " ; • ШТ3 7(1-237, У‘+Т2 С''Т\(1-2^)Г2+Т‘У
103 1 1+2§П+Г2?Х X(l + T1sXl + T-2s) Се‘А* sin(o)/ + <р)+ С|е’“‘' - С2е'а1': с= * с= -г/— /?,=(1-2РТ,)Г2+Т(2. ( (о7, 1 ( iaT, 'I Ф = агс(й -—— + arcta — ^pr2-ij
104 1+2£7з + 72лг 1 х(1+гЛ»+^) Ce-*1' sin(w +ф)+С|е'“'' -C2e'“y: c = J_ /р-зртУЧт2 _ Tifr-т) U)T] R,R, ' ‘ * Л, =0-2₽7}У2+Т/. ( 0)7, ) ( <i>7> ( ел 'l Ф = arcld । + arctd — + arctd — ДРГ;-1) *Vl-pr)
Приложение I
Таблица П2 Обратное преобразование Лапласа (продолжение!
Nt Иаображаим Я») Оригинал f(t)
105 »♦*+<«* 1{ 1+2$П+т¥ 1 (i+t.iXi+M Ct* sin(uw + ф)+ - CfT** :
e. w7J /?|Я2
106 (•♦Mi+Tji) 1 - Ce"*' sfa(<or + <р)- С,с"“‘' + C2e*“J': С- т с- т? ' (г,-т2Х’ л^С-гр^Х^т/.
107 1+tr fr+fyXi+ij*) 1 - Се'^ нп(ш + ф)- Cte'“'' + C2e'a‘' Сж1 1^~^)Гг+г2 _ т/^-т) WV Л|/?2 ’ ' (Т| -Т2Х ' J
Таблиц* преобразований Лапласа
603
Таблица П.2 Обратное преобразование Лапласа !прмолже**е>
№ Изображение F(s) Оригиналы)
108 l + tl + gf2 4+2^+tv) x(i+r„»+M 1-Се'^яп(<ш*ф)-С|С"в/ ч-Сзс"^: j
с, ш| R,R2
109 l+Zyi+T1*1* X(l+Tl3Xl + T2sj - Се* sin(wr+<₽)- Cf* + Сгс^ aTjRiR: (Г,-Г2И, Я,=(1-23Г,)Г2+ГЛ ( ыТ, 1 ( шГ,
110 Се ^ sin (со/ + ф)+ - С2е а- г- 1 с - 1 ч
1+2^Tj + T2jjX 1 Х(1 + ТД1 + Т25) шт27м?’ ' (й-ъл й(»(1-2₽Т,)Г2+Т2.
Приложение!
Таблица П.2, Обратное преобразование Лапласа (продолжение)
№ Изображение F(s) Оригинал f(t)
111 !—х 1+24П+72? П(н^) м Сс'^ sin(cof+ ф)+£с,е’а'': С=Ж.С, Л . <о.П*. R‘ h(Ts-Tk) li-l *-1. **' Я, =(1-2рг,)Г2 + 7}2, ф = £arct/p^j
112 4*2tfi+r-r)x X—1— П(ьт4«) м l-Ce^' sin(nw + <₽)-£C,e~a’' г-(-тГ' C)_ тГ' ' R‘ n^-7;) У(=1 *=!.**' Я,=(1-2Р7)Г2+72,
ИЗ 1 ?t+2^n+rV)X х—1 по+м - A +t + Се-& sin(aw + ф)+ £С,^1 A = 2PT2 + ir/.C = -tlL. w ®Jn,Ri Q p— . =(l-2PT,)r2+T(2. К. fl^-Ta) *-и*Л ’£Н^Нге,|(й
Таблицы преобразований Лапласа
605
Таблица П. 2 Обратное преобразование Лапласа (продолжение)
Nt Изображение F(s) Оригинал f(t)
114 5 X l + 2^Ts+T2r 1 П(1+^) <=| -Ce-p'Sin(w/ + <p)-ic,e4<-' i*i с_(-тГ’ с - т"' /г(=(1-2₽т,)г2+7;2,
115 l + 2^Ts+T2rX 1 по+т>) Се'^ sin(o)Z+<₽)+ Xcie'V ы с_(-тГ с<_ тг2 /?(=(1-2₽Т,)Г2+гЛ
116 1 1+7Э П(1+2^т;.5+7;2?) W Се’1* -^С,е'д' sin(wj+<p,): С = ^. С, =-£^=. о =(1-2р,т)гЛг2. п,, ы *. = П [ ~т^+< -Р*Vjv ) t«A
606__________________________________________________________Приложение 1
Таблица П.2. Обратное преобразование Лапласа (продолжение)
№ Изображение F(s) Оригинал f (t)
117 1 w j(l + rs) 1 n(i+W+7;V) r=l 1 - Се'01 + JС,е'&' sin(o(/ + <р,) Г-1 •р2л 'т’2/1—2 с=—. <?,=-< г; = (1-2р(т)т;3+т2. »= у artJ М&-М 1
*=!.*«< Д (0, - в* Г “ (ы.2 - 0)2 ) j
118 *2(1+Тз)Х 1 П(1+адз+тЛ2) м -A+t + Ce-™ -^^e^sinCcOir + Oi): n , r2"+l Г21"' A=T+2№2.C = -j—. cf=—4==. i=l г^О-гр^+г2. Rt = fl f-r^ +< -p4 ^7]2 -P^/k2^)1 Ы.ьА m = V arct/ 2<Or(0r-0j L
ф'\=L дь,-pty-к-®*)J
Таблицы преобразований Лапласа
607
Таблица П. 2 Обратное преобразование Лапласа (продолжение)
Nt Изображение F(s) Оригинал l(t)
119 —-—X 1 + Tj П(1 + ВД+7}2*2) 1=1 -Се'ш + £С,е sinfor + cpj м v П1~т^+<-₽‘1- к-\.кп
120 -iLx 1 + Ts х- 1 Г|(1+2№+7Л2) Ce"cu - X Cfi~^ sin((i),t +<₽,): 7»2я-3 'г2п~5 С‘^-.' *Г • П, ^г-: -м’клг) , . у М».;Ь) ,1,
608
Приложение 1
Таблица П.2. Обратное преобразование Лапласа (продолжение)
Nt Изображение F(s) Оригинал f(t)
121 l+2^Ts+TJ?X Ce*^ sin((iM - (p)+ (Д + B/Je-®1': CS"7’ B = ~r ’ A = 2(1-2₽7i)7'27’ib2’ r = (1 - 20T| )r2 + T|2, <p = Zarctg^^-j
122 i Ч+w l-Ce-*** sin(wr - <p)+ (Д - Bt )e‘U1': C = £-, B=\ A = (4fiT2Ti-3T2-Tl1)B2. r=(l-20T,X2+T|2.
123 1+2^П+Г2?Х X(^F -Ce’^sin(<or-<p)+(4 - Вг)г'а'': c * Л=^.в = 1, (oTr r2 7\r г = (1-2РТ|)Г2+Т12.
124 I+^Tj+T2? Х(ьг,«)2 Ce^ sin(ti>r -<p)+ (Д + Вг)е“а|': c r „ 1 <oT2r r2 T|2r г = (1-2₽Т1)Г2+Т12,
Таблицы преобразований Лапласа
609
Таблица П. 2. Обратное преобразование Лапласа {продолжение)
Ns Изображение F(s) Оригинал f(t)
125 1 l + 2£,Ts + T2s2 у- 1 (1+T.iXi+W - Се'1” sin(ш/ + ф)+ qe***1' - (а + Вг)е ; wr-,y[i\ 1 (Ti-Tjki г,=(|-2РТ,)Г2+Т(:. ( ЫТ, ) . ( «Т, )
126 1 S(l + 2^Ts + T232)X Х(1 + Т,зХ1+Тгз)2 1 + Ce’fr sin(io/+ <₽)-С|е'в|' + (А + Bz)s'nj' С = ^Г> С| = в = (Г,-Т2>2‘ л_р(1-рг2Х2 г^О-^^+т/.
127 1 + 2^П+Та?Х 1 Х(1+г1зХ1+П«)2 Се’^ sin(ut+<р)~ Cle'tv + (А + В/> С= > ,С|=. Т2 1 “С! A (Tt-T,):r, (Г1-Г2>2 г(=(1-2РТ(Х2*Т(2.
Приложение 1
Таблица П.2. Обратное преобразование Лапласа (окончание)
Ni Изображение F(s) Оригинал f(t)
128 1+24Гл+Т2?Х -Се’₽' sin(tw + <p)+ C|e’ai' - (А + г— 1 с - Г' Д- , 1 П = (1-237})г2 + т/.
Таблицы преобразований Лапласа 611
Таблица П.З Свойства оригиналов и изображений
№ Оригинал 1(1) Изображение F(s)
1 c/iW + c/jW C|Fi(j) ♦ CiFt(s)
2 ЛаО M;)
3 Л1--С)
4 е^ЛО F(.t + a)
5 {ЯП dffr) ds
6 «7W
7 Л) t Jf(o)1g
8 sin(wt)/0) F(j + j(o)~ F(j - j(o). 2 J
9 cos(wzyU) F(j + j(o)+F(j-j<o).
10 d/(<) dz зЯН-ЛО)
П d"/(0 dz"
12 f/(T>T 0 F0 s
13 J/iW/iO-tfr 0 FiWFj(j)
14 lim 3F(t)
15 lim /(») limiF(<)