Курс теоретической механики Т.2. Динамика - Бутенин Н.В., Лунц Я.Л., Меркин Д.Р.

Author: Бутенин Н.В. Лунц Я.Л. Меркин Д.Р.

Tags: общая механика механика твердых и жидких тел динамика аналитическая механика учебник для студентов главная редакция физико-математической литературы

Year: 1979

Similar

Курс теоретической механики. Т.2 Динамика

Курс теоретической механики. Том 1. Статика и кинематика

Введение в аналитическую механику

Курс теоретической механики. Т.1 Статика и кинематика

Text

Н. В. БУТЕНИН, я. Л. ЛУНЦ, Д Р. МЕРКИН
КУРС
ТЕОРЕТИЧЕСКОЙ
МЕХАНИКИ
ТОМ II
ДИНАМИКА
ИЗДАНИЕ ВТОРОЕ ПЕРЕРАБОТАННОЕ И ДОПОЛНЕННОЕ
Допущено Министерством
высшего и среднего специального образования СССР
в качестве учебника
для студентов высших технических учебных заведений
МОСКВА «НАУКА»
ГЛАВНАЯ РЕДАКЦИЯ
ФИЗИКО-МАТЕМАТИЧЕСКОЙ ЛИТЕРАТУРЫ
1979
22.21
Б 93
УДК 531
Бутенин Н. В., Лунц Я. Л, Меркни Д. Р.
Курс теоретической механики: Учебник. В 2-х томах.
Т. II.: Динамика. — 2-е изд., перераб. и доп. — М.:
Наука. Главная редакция физико-математической
литературы, 1979.— 544 стр.
В книге изложены динамика точки, динамика
материальной системы и твердого тела, элементы
аналитической механики и теории линейных и нели-
нейных колебаний. Более подробно, чем в традици-
онных курсах, излагаются вопросы движения мате-
риальной точки в центральном силовом поле, дина-
мика тела переменной массы, теории гироскопов.
Приводится много примеров прикладного значения.
Книга рассчитана на студентов дневных, вечер-
них и заочных отделений технических вузов с полной
и сокращенной программой по механике, а также
может быть полезной для аспирантов и инженерно-
технических работников.
Илл. 298.
20302 017 1703020000
053(02)-79
© Главная редакция
физико-математической литературы
издательства «Наука», 1979,
с изменениями
ОГЛАВЛЕНИЕ
Предисловие........................................................ 8
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
Глава I. Введение в динамику. Дифференциальные уравнения дви-
жения .......................................................... 9
§ 1.1. Предмет и задачи динамики................................ 9
§ 1.2. Инерциальные системы отсчета. Основное уравнение динамики
точки ......................................................... 10
§ 1.3. Дифференциальные уравнения движения материальной точки . 16
§ 1.4. Первая задача динамики.................................. 17
§ 1.5. Вторая задача динамики ......................... 18
§ 1.6. Прямолинейное движение материальной точки....... 24
§ 1.7. Задачи ................................................. 27
Глава II. Прямолинейные колебания материальной точки ............. 35
§ 2.1. Вводные замечания ...................................... 35
§ 2.2. Свободные колебания .................................... 37
§ 2.3. Свободные колебания при линейно-вязком сопротивлении ... 43
§ 2.4. Свободные колебания при трении скольжения .......... 50
§ 2.5. Вынужденные колебания................................... 53
§ 2.6. Вынужденные колебания при наличии вязкого сопротив-
ления ......................................................... 58
§ 2.7. Электродинамические аналогии. Понятие об исследовании коле-
баний материальных систем с помощью электронных аналого-
вых машин.................................................... 64
Глава III. Общие теоремы динамики точки........................ 68
§ 3.1. Теорема об изменении количества движения материальной
точки.......................................................... 68
§ 3.2. Теорема об изменении момента количества движения матери-
альной точки................................................... 71
§ 3.3. Работа силы. Мощность................................... 76
§ 3.4. Теорема об изменении кинетической энергии .............. 84
§ 3.5. Силовое поле. Потенциальная энергия..................... 85
§ 3.6. Интеграл энергии. Понятие о рассеивании полной механичес-
кой энергии ............................................. 96
§ 3.7. Задачи.................................................. 98
Глава IV. Движение материальной точки в центральном силовом
поле.......................................................... 102
§ 4.1. Дифференциальное уравнение траектории точки, движущейся
в центральном поле сил........................................ 102
§ 4.2. Виды траекторий. Круговая и параболическая скорости . . . 104
§ 4.3. Определение параметров околоземной траектории по начальным
условиям .................................................. . 107
§ 4.4. Траектории искусственных спутников Земли............... 109
1*
4
ОГЛАВЛЕНИЕ
§ 4.5. Определение времени полета по эллиптической орбите (урав-
нение Кеплера)................................................ . . 113
§ 4.6. Траектории, пересекающие земную поверхность . . . . .\ 116
§ 4.7. Задачи.................................................\ ' 119
Глава V. Несвободное движение....................................... 123
§ 5.1. Определение несвободного движения. Связи. Принцип освобож-
даемое™ ........................................................... 123
§ 5.2. Уравнения связей; классификация связей................ 125
3 5.3. Движение точки по гладкой неподвижной поверхности .... 127
§ 5.4. Движение точки по гладкой неподвижной кривой....... 130
§ 5.5. Естественные уравнения движения. Математический маятник . 133
§ 5.6. Теорема об изменении кинетической энергии для несвободного
движения .......................................................... 141
§ 5.7. Метод кинетостатики для точки (принцип Даламбера)......... 142
§ 5.8. Задачи на применение метода кинетостатики................. 143
§ 5.9. Явление невесомости....................................... 145
Глава VI. Динамика относительного движения материальной точки . 151
§ 6.1. Переносная и кориолисова силы инерции...................... 151
§ 6.2. Условия относительного покоя .............................. 158
§ 6.3. Применение уравнений относительного движения и покоя . . . 159
§ 6.4. Теорема об изменении кинетической энергии в относительном
движении .......................................................... 168
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ МАТЕРИАЛЬНОЙ СИСТЕМЫ
Глава VII. Материальная система................................... 171
§ 7.1. Центр масс............................................... 171
§ 7.2. Внешние и внутренние силы..........................’. . . 172
§ 7.3. Свойства внутренних сил.................................. 174
§ 7.4. Дифференциальные уравнения движения системы материаль-
ных точек...................................................... 175
§ 7.5. Задача двух тел ......................................... 176
§ 7.6. Общие замечания ......................................... 179
Глава VIII. Теорема об изменении количества движения- материальной
системы .......................................................... 180
8.1. Количество движения материальной системы...............- 180
8.2. Теорема об изменении количества движения материальной
системы...................................................... 182
§ 8.3. Теорема о движении центра масс .......................... 184
§ 8.4. Теорема Эйлера.......................................... 187
$ 8.5. Задачи................................................... 189
Глава IX. Теорема об изменении момента количеств движения матери-
альной системы ................................................... 200
§9 1. Момент количеств движения материальной системы ...... 200
§ 9 2 Краткие сведения о моментах инерции...................... 202
§ 9.3. Теорема об изменении момента количеств движения м^д-ериаль-
§ 9 4. Примеры и задачи........................................ -105
§ 9.5. Дифференциальное уравнение вращения твердого тела вокруг
§ 9.6. Момент количеств движения системы, участвующей в сложном
движении ................................... • ............. » 211
ОГЛАВЛЕНИЕ
5
§ 9.7. Теорема об изменении момента количеств относительного дви-
жения материальной системы..................................... 216
§ 9.8. Примеры и задачи......................................... 219
Глава X. Теорема об изменении кинетической энергии материальной
системы.......................................................... 225
§ 10.1. Кинетическая энергия материальной системы и способы ее
вычисления..................................................... 225
§ 10.2. Кинетическая энергия твердого тела....................... 227
§ 10.3. Работа сил, приложенных к материальной системе.......... 233
§ 10.4. Теорема сб изменении кинетической энергии материальной
системы ....................................................... 238
§ 10.5. Задачи.................................................. 240
§ 10.6. Закон сохранения полной механической энергии материаль-
ной системы.................................................... 245
§ 10.7. Теорема об изменении кинетической энергии относительного
движения ...................................................... 248
Глава XI. Динамика тела переменной массы...................... 252
§ 11.1. Понятие тела переменной массы............................ 252
§ 11.2. Уравнение движения точки переменной массы................ 253
§ 11.3. Количество движения тела переменной массы................ 254
§ 11.4. Теорема об изменении количества движения тела переменной
массы.......................................................... 256
§ 11.5. Уравнение Мещерского..................................... 258
§ 11.6. Задача Циолковского...................................... 259
§ 11.7. Формула Циолковского для многоступенчатой ракеты .... 262
§ 11.8 Задачи................................................... 264
ДИНАМИКА ТВЕРДОГО ТЕЛА
Гл а в XII. Геометрия масс ........................................ 268
§ 12.1. Введение................................................. 268
§ 12.2. Основные определения..................................... 268
§ 12.3. Примеры вычисления моментов инерции..................... 273
§ 12.4. Моменты инерции относительно параллельных осей (теорема
Гюйгенса—Штейнера) ........................................'. . 277
§ 12.5. Момент инерции относительно произвольной сси, проходящей
через данную точку ............................................ 279
§ 12.6. Эллипсоид инерции........................................ 281
§ 12.7. Свойства главных осей инерции............................ 283
§ 12.8. Вычисление моментов инерции относительно произвольных осей 285
§ 12.9. Вычисление тензора инерции .............................. 286
§ 12.10. Задачи на вычисление моментов инерции ................. 288
Глава XIII. Динамика простейших движений твердого тела............ 293
§ 13.1. Основные задачи динамики твердого тела.................. 293
§ 13.2. Количество движения, момент количеств движения и кинети-
ческая энергия твердого тела ................................... 294
§ 13.3. Поступательное движение твердого тела.................. 298
§ 13.4. Дифференциальное уравнение вращения твердого тела вокруг
неподвижной оси и уравнения для определения реакций под-
шипников ....................................................... 299
5 13.5. Добавочные динамические реакции. Статическая и динамиче-
ская уравновешенность тела ..................................... 302
6
ОГЛАВЛЕНИЕ
§ 13.6. Задачи .......................................... 305
§ 13.7. Физический маятник........................................ 309
§ 13.8. Экспериментальное определение моментов инерции ............ 311
§ 13.9. Плоское движение абсолютно твердого тела.................. 313
§ 13.10. Задачи............................................................... 315
Глава XIV. Динамика твердого тела, имеющего одну неподвижную
точку. Движение искусственного спутника относительно центра масс 329
§ 14.1. Дифференциальные уравнения движения твердого тела, имею-
щего одну неподвижную точку ................................................. 320
§ 14 2. Движение твердого симметричного тела, имеющего одну непод-
вижную точку, по инерции (случай Эйлера).......................... 322
§ 14.3. Геометрическая интерпретация Пуансо......................................... 326
§ 14.4. Устойчивость вращения твердого тела вокруг главных осей
инерции .......................................................... 328
§ 14.5. Движение твердого тела, имеющего неподвижную точку, под
действием силы тяжести (случай Лагранжа).......................... 330
§ 14.6. Главный вектор и главный момент сил тяготения............................... 333
§ 14.7. Дифференциальные уравнения движения ИСЗ относительно
центра масс....................................................... 337
§ 14.8. Относительное равновесие ИСЗ............................................... 339
§ 14.9. Плоское движение ИСЗ по круговой орбите..................................... 341
Глава XV. Теория гироскопов............................................................ 343
§ 15.1. Введение................................................................... 343
§ 15.2. Основное допущение элементарной (прецессионной) теории
гироскопов.................................................. 344
§ 15.3. Теорема Резаля...................................... 346
§ 15.4. Основное свойство свободного (астатического) гироскопа . . . 347
§ 15.5. Закон прецессии оси гироскопа....................... 349
§ 15.6. Момент гироскопической реакции...................... 354
§ 15.7. Уравнения движения гироскопа в кардановом подвесе .... 358
§ 15.8. Частные случаи движения гироскопа в кардановом подвесе . 362
Глава XVI. Метод кинетостатики ........................................................ 366
§ 16.1. Метод кинетостатики......................................................... 366
§ 16.2. Главный вектор и главный момент сил инерции твердого
тела.............................................................. 369
§ 16.3. Определение добавочных динамических реакций опор движу-
щегося тела....................................................... 370
§ 16 4. Задачи на определение добавочных динамических реакций . . 371
Глава XVII. Теория удара............................................................... 377
§ 17.1. Основные определения....................................................... 377
§ 17.2. Коэффициент восстановления................................................. 380
§ 17.3. Удар материальной точки об идеально гладкую поверхность 382
§ 17.4. Потеря кинетической энергии при ударе материальной точки
о неподвижную поверхность......................................... 384
§ 17.5. Теорема об изменении количества движения и теорема об
изменении момента количеств движения материальной системы
при ударе......................................................... 385
§ 17.6. Удар, действующий на тело, закрепленное в двух точках . . 387
§ 17.7. Условия отсутствия ударных реакций. Центр удара. 388
§ 17.8. Удар двух тел........................................ 390
6 17.9. Частные случаи удара двух тел.................. 392
§ 17.10. Задачи ......................................... 393
ОГЛАВЛЕНИЕ
7
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
Глава XVIII. Аналитическая статика................................ 400
§ 18.1. Введение............................................... 400
18.2. Связи.................................................. 401
§ 18.3. Виртуальные перемещения голономных систем.............. 405
§ 18.4. Идеальные связи ....................................... 411
§ 18.5. Принцип виртуальных перемещений ....................... 413
§ 18.6. Обобщенные координаты и обобщенные силы ............... 420
§ 18.7. Условия равновесия в обобщенных координатах............ 429
Глава XIX. Аналитическая динамика................................. 431
§ 19.1. Общее уравнение динамики .............................. 431
§ 19.2. Уравнения Лагранжа второго рода........................ 433
§ 19.3. Задачи на составление уравнений Лагранжа второго рода . . 435
§ 19.4. Особенности применения уравнений Лагранжа второго рода
к системам с неидеальными и неудерживающими связями . . 443
§ 19.5. Выражение кинетической энергии через обобщенные скорости
и координаты................................................... 447
§ 19.6. Обобщенный интеграл энергии............................ 449
Гл-ава XX. Малые колебания механических систем с одной и двумя
степенями свободы около положения устойчивого равновесия .... 453
§ 20.1. Определение положений равновесия...................... 453
§ 20.2. Устойчивость положения равновесия. Теорема Лагранжа —
Дирихле. Критерий Сильвестра .......................... 456
§ 20.3. Малые колебания консервативной системы с одной степенью
свободы около положения устойчивого равновесия................. 464
§ 20.4. Случай произвольной возмущающей силы.................. 468
§ 20.5. Определение периодических решений .................... 474
§ 20.6. Малые колебания консервативной системы с двумя степе-
нями свободы около положения устойчивого равновесия . . 478
§ 20.7. Задачи ............................................... 483
§ 20.8. Нормальные координаты ................................ 493
§ 20.9. Функция рассеивания Релея............................. 494
§ 20.10. Влияние сил сопротивления на колебания системы около
положения устойчивого равновесия .............................. 497
§ 20.11. Приближенный метод вычисления корней характеристиче-
ского уравнения................................................ 499
§ 20.12. Вынужденные колебания ................................ 504
Глава XXI. Автономные нелинейные колебания систем с одной сте-
пенью свободы.............................................. 507
§ 21.1. Введение............................................. 507
§ 21.2. Фазовая плоскость ............................ 508
§ 21.3. Методы построения фазовых траекторий .................. 517
§ 21.4. Метод припасовывания. Понятие об автоколебаниях ....... 526
§ 21.5. Метод медленно меняющихся коэффициентов (метод ван-дер-
Пол я) ................................................. 533
Предметный указатель ............................................. 541
ПРЕДИСЛОВИЕ
Второй том настоящего курса рассчитан на студентов тех-
нических вузов с полной программой по теоретической механике.
По сравнению с традиционными курсами в книге более подробно
рассматриваются общие теоремы динамики системы, движение
материальной точки в центральном силовом поле, динамика тела
переменной массы, теория гироскопов, некоторые вопросы ана-
литической механики, а также теории колебаний.
В 1972 г. авторский коллектив понес тяжелую утрату —после
непродолжительной болезни скончался Яков Львович Лунц.
При подготовке второго издания, выполненной Н. В. Бутениным
и Д. Р. Меркиным, частично или полностью переработаны и
заново изложены некоторые разделы курса, написаны новая XXI
глава, посвященная элементам теории нелинейных колебаний, и
§§ 14.6—14.9, в которых изложены основы теории движения искус-
ственного спутника Земли относительно центра масс, добавлено мно-
го новых задач, пересмотрен весь текст, исправлены замеченные
опечатки.
Учитывая, что учащиеся многих втузов нуждаются в более
углубленном изучении ряда важнейших разделов механики, Глав-
ная редакция физико-математической литературы издательства
«Наука» предприняла издание ряда книг, дополняющих настоящее
руководство. К настоящему времени изданы следующие прило-
жения: Н. В. Бутенин «Введение в аналитическую меха-
нику», Я. Л. Лунц «Введение в теорию гироскопов», Д. Р. Me р-
кин «Введение в теорию устойчивости движения» (два издания),
Я. Г. Пановко «Введение в теорию механических колебаний»,
Н. В. Бутенин, Ю. И. Неймарк и Н. А. Фуфаев «Вве-
дение в теорию нелинейных колебаний», Я. Г. Пановко «Вве-
дение в теорию механического удара».
Авторы выражают глубокую благодарность профессорам
В. Г. Демину, Я. Г. Пановко, В. К. Прокопову, С. М. Тарту,
а также Л. М. Гриншпуну, А. Г. Мамиконову, Г. Д. Мошкову и
Г. С. Шпаку, замечания которых позволили существенно улучшить
содержание книги.
ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ
ГЛАВА I
ВВЕДЕНИЕ В ДИНАМИКУ.
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
§ 1.1. Предмет и задачи динамики
Два предыдущих раздела курса механики— статика и кинема-
тика—в сущности, мало связаны между собой. Каждому из них
•соответствует свой особый круг понятий, задач и методов их
решения. В статике рассматриваются задачи о равновесии, а также
задачи об эквивалентных преобразованиях систем сил; при таких
преобразованиях даже не ставится вопрос о том, какое движение
тела вызывают приложенные силы. В кинематике изучается дви-
жение «само по себе», вне связи с теми силами, под действием
которых оно происходит.
Изолированное рассмотрение двух указанных проблем вызы-
вается чисто методическими соображениями построения курса
механики и, строго говоря, не вытекает из существа задач меха-
ники. Дело в том, что между действующими силами и движением
существует глубокая внутренняя связь, которая отмечается уже
в самом определении понятия силы. Эта связь принимается во
внимание в динамике, предметом которой является изучение дви-
жения с учетом действующих сил.
Среди практических задач механики лишь небольшое число
допускает чисто статическое или чисто кинематическое исследова-
ние: в большинстве случаев необходимо полное, т. е. динамическое
изучение тех или иных механических явлений. При этом исполь-
зуются установленные в статике способы приведения сил, а также
разработанные в кинематике методы описания и изучения движе-
ния; поэтому статику и кинематику можно рассматривать как
введение в динамику, хотя они имеют и самостоятельное значение.
При всем разнообразии динамических задач выделяют две их
категории. К первой категории относятся задачи, в которых дви-
жение тела (или механической системы) является заданным, и
требуется найти силы, под действием которых это движение про-
исходит {первая задача). В другую категорию входят задачи про-'
тивоположного характера: в них силы являются заданными, а
10
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ Г
движение — искомым (вторая задача). Эти задачи называются основ-
ными задачами динамики.
При формулировании основных законов динамики пользуются
понятием материальной точки. Под материальной точкой понимают
тело конечной массы, размерами и различием в движении отдель-
ных точек которого по условиям задачи можно пренебречь.
В дальнейшем будет показано, что поступательно движущееся тело
можно рассматривать как материальную точку с массой, равной
массе всего тела.
§ 1.2. Инерциальные системы отсчета.
Основное уравнение динамики точки
В основании динамики лежат законы, впервые в наиболее
полном и законченном виде сформулированные Исааком Ньютоном
в книге «Математические начала натуральной философии» (1687 г.).
В качестве первого закона Ньютон принял принцип инерции,
открытый Галилеем, который можно сформулировать следующим
образом: изолированная материальная точка находится в состоя-
нии покоя или равномерного и прямолинейного движения.
Под изолированной материальной точкой понимается материаль-
ная точка, которая не взаимодействует с другими телами или
когда силы, действующие на точку, взаимно уравновешиваются.
Важнейшим обстоятельством при изучении движения тел отно-
сительно друг друга является выбор системы отсчета, что в свою
очередь связано с принятым представлением о пространстве и
времени. Естественно поставить вопрос: по отношению к какой
же системе отсчета справедлив принцип инерции?
Ньютон, формулируя законы динамики, ввел в рассмотрение
модель пространства и времени, которая предполагает наличие
абсолютного неподвижного евклидова трехмерного пространства
и абсолютного времени, т. е. времени, одинаково текущего для
всех наблюдателей, где бы они ни находились и каково бы ни
было их движение.
Исходя из этого представления о пространстве и времени,.
Ньютон и предполагал возможность существования абсолютной,
неподвижной системы отсчета (системы координат), не связанной
с материальными телами; для такой системы отсчета он и считал
справедливым принцип инерции.
Последующее развитие представлений о пространстве привело
к полному отрицанию понятия абсолютного пространства. Поэтому
понятия «покой», «постоянная скорость» и т. п. лишены объектив-
ного смысла: пользуясь этим термином, необходимо указать,
в какой системе отсчета рассматривается движение. Но движение,
происходящее с постоянной скоростью в одной системе отсчета,
может представляться ускоренным в другой системе отсчета; по-
§ 121 ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧЕТА И
этому принцип инерции не обладает универсальностью, хотя, как
показывают наблюдения, в некоторых системах отсчета принцип
инерции оказывается справедливым.
Введем определение: системы отсчета, в которых справедлив
принцип инерции, называются инерциальными системами отсчета
(инерциальными системами координат). Подчеркнем, что об инер-
циальности или неинерциальности той или иной системы отсчета
можно судить только на основе опыта. В частности, установлено,
что гелиоцентрическая система координат (т. е. система координат
с началом в центре Солнца и осями, направленными на «непод-
вижные» звезды) весьма близка к инерциальной системе.
Следует, однако, иметь в виду, что гелиоцентрическая система
отсчета может считаться инерциальной только для движений
внутри Солнечной системы, ибо центр масс Солнечной системы
движется по криволинейной траектории относительно центра
нашей Галактики с относительной скоростью, примерно равной
3-105 м/сек, и ускорением порядка 3- 10-13 м/сек2.
Легко видеть, что система отсчета Alt которая движется отно-
сительно инерциальной системы отсчета Ао поступательно и начало
которой имеет постоянную по модулю и направлению скорость,
также является инерциальной. Это вытекает из того, что ускоре-
ние точки в системе Аг не отличается от ускорения точки в си-
стеме До. В этом утверждении состоит принцип относительности
Галилея.
Наоборот, в системах отсчета, движущихся относительно инер-
циальной системы отсчета не поступательно или не равномерно,
принцип инерции не имеет места; такие системы называются
неинерциальными. Если движение некоторой системы отсчета про-
исходит с относительно малыми ускорениями относительно инер-
циальной системы отсчета, то при решении практических задач
иногда можно пренебречь малой неинерциальностью (например,
непнерциальностью геоцентрической системы, связанной с Землей);
при этом приближенно принимают, что принцип инерции выпол-
няется и в такой системе отсчета.
Развитие физики привело к концу XIX и началу XX века
к необходимости создания других моделей пространства и вре-
мени. Так, например, в специальной теории относительности,
в которой рассматриваются только инерциальные системы отсчета,
моделью пространства и времени является четырехмерное прост-
ранство-время, т. е. пространство и время уже не считаются
независимыми друг от друга.
Еще более сложная модель пространства и .времени исполь-
зуется в общей теории относительности (теории тяготения), в кото-
рой рассматриваются неинерциальные системы отсчета. Эта модель
уже предполагает зависимость пространства и времени от тяготею-
щих масс и полей.
12
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ I
Выводы как специальной, так и общей теории относительности
при скоростях тел, значительно меньших скорости света, совпа-
дают с выводами классической механики, а это значит, что клас-
сическая механика (механика Ньютона) является предельным
случаем механики, основанной на принципах теории относитель-
ности.
Фундаментальное значение для всей динамики имеет следующий
основной закон динамики (второй закон Ньютона^. сила, действую-
щая на материальную точку, сообщает ей ускорение, которое
в инерциальной системе отсчета пропорционально величине силы
и имеет направление силы. В аналитической форме этот закон
представляется в виде основного уравнения динамики
mw = F, (1.1)
где F —сила, действующая на материальную точку, w —ее уско-
рение, т — масса материальной точки, являющаяся мерой ее инерт-
ных свойств.
Из формулировки основного закона динамики вовсе не вытекает,
что в динамике исследуются движения, происходящие только в инер-
циальных системах. В главе VI мы будем рассматривать движение
в неинерциальных системах, однако таких, движение которых
относительно инерциальной системы задано; на языке кинематики
задача сведется к выражению относительных ускорений через
абсолютные ускорения.
Отметим, что равенство действия и противодействия двух мате-
риальных точек (третий закон Ньютона), о котором уже говорилось
в начале курса статики, является общим законом всей механики
и справедливо не только в задачах статики, но и в ’задачах
динамики.
Приведем еще одно фундаментальное положение механики —
закон независимости действия сил: если на материальную точку
действует несколько сил, то ускорение точки складывается из тех
ускорений, которые имела бы точка под действием каждой из этих
сил в отдельности.
Зто значит, что при действии на материальную точку сил
Fb F2, ..., F„, каждая из которых сообщает точке соответственно
ускорения Wj, w2, ..., w„, ускорение материальной точки будет
w = w1 + w2 + ... + w„.
На основании (1.1) можно записать
mw1 = F1, mw2 = F2.......mw„ = F„.
Складывая между собой эти равенства, получим
m (wx + w2 +,.. + w„) = Fx + F2 +... + Fn,
§ 12]
ИНЕРЦИАЛЬНЫЕ СИСТЕМЫ ОТСЧГТА
13
или, на основании закона независимости сил,
mw = Fx + F2 + ... + Fn = 2 Fft,
k=t
n
где 2 Ffe — равнодействующая всех сил, приложенных к мате-
t = i
риальной точке.
Таким образом, движение материальной точки под действием
сил Fb F2, ..., F„ будет таким же, как и при действии одной
силы, равной их геометрической сумме (равнодействующей).
В принципе основные законы динамики играют роль постулатов,
из которых как следствие вытекают все результаты, полученные
ранее в статике, и даже некоторые из аксиом статики.
В сжатом виде законы динамики можно сформулировать следую-
щим образом:
1. Существует такая система отсчета, в которой материальная
точка находится в покое или движется равномерно и прямолинейно,
если на нее не действуют силы. Такая система отсчета называете}
инерциальной (иногда ее условно называют неподвижной).
2. В<Инерциальной системе отсчета вектор ускорения материаль-
ной точки пропорционален вектору силы, действующей на эту
точку.
3. Две материальные точки взаимодействуют друг с другом
так, что силы их взаимодействия равны по величине, противоположны
по направлению и имеют общую линию действия.
4. При действии на материальную точку нескольких сил ее
ускорение равно сумме ускорений, которые имела бы точка при
действии каждой силы в отдельности.
Отсюда следует, что систему сил, действующих на точку,
можно заменить их равнодействующей.
Из основного уравнения динамики следует линейная зависимость
между модулем силы и модулем ускорения
F = mw. (1.2)
Эта зависимость дает возможность опытного определения массы
материальной точки. Здесь имеются два подхода.
Массу некоторой материальной точки можно принять за еди-
ничную массу т0. Тогда, измеряя ускорения, приобретаемые под
действием одной и той же силы двумя различными материальными
точками (одна из них единичной массы), получим из (1.2)
F = mw, F = m0w0. (1.3)
Следовательно, т = mowo/w. Масса т0 установлена. Величина отно-
шения ускорений w0/w определяет количество эталонных единиц
массы, содержащихся в т.
14
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ I
При таком способе измерения массы сила выражается через
единицы массы и единицы ускорения по формуле (1.2).
В международной системе единиц СИ эталоном массы служит
1 кг. Единицы длины и времени — 1 м и 1 сек.
Единица силы называется ньютоном. Из (1.2) следует
1 н = 1 кгм/сек1'.
Заметим, что часто применяется и более мелкая единица силы —
динт,
1 дина =10-5 н = 0,001 кг-0,01 м/сек? =\ г-см/сек2.
Аналогично вводится один килоньютон (кн), который равен
1000 ньютонов.
Рассмотрим теперь другую возможность использования основ-
ного закона динамики. Можно, как и в статике, назначить эталон
силы. Для измерения сил могут, например, служить пружинные весы.
За эталон силы часто принимают силу тяжести на поверхности
Земли одного килограмма массы. Такую единицу называют кило-
граммом, но, в отличие от килограмма —массы, записывают при
помощи символа кГ. Здесь масса измеряется в производных еди-
ницах, имеющих размерность
[т] = [Е][^Г.
Если оставить без изменения масштабы длин и времени, то
получим техническую систему единиц. Единица массы называется
в ней т. е. м. (техническая единица массы),
1 т. е. м. — 1 кГ -сек?/м.
Ниже при решении задач мы будем пользоваться как между-
народной (СИ), так и технической системой единиц. Разумеется,
масштабы всех единиц в пределах той или другой системы будут
выбираться, исходя из соображений удобства решения той или
иной задачи.
Масса, определяемая из основного уравнения динамики (1.2),
называется инертной массой.
Однако существует и другой путь измерения массы.
Из закона всемирного тяготения следует, что между двумя
материальными точками массы т± и т2, отстоящими друг от друга
на расстоянии г, возникают силы взаимодействия, определяемые
формулой
F = f^, (1.4)
где / — гравитационная постоянная.
Закон всемирного тяготения открывает новую возможность
измерения массы. Пусть, например, т2 = М — масса Земли,
§ 1 2]
ИНЕРЦИАЛЬНЫЕ системы отсчета
15
mi = то— эталонная единичная масса, т — измеряемая масса,
из (1.4) можно получить два соотношения:
Г? С ttloAd р tn/\A
r0=l I г1 = /
Предполагается, что обе массы т() и т помещены в одной
же точке пространства.
Поделив одно из уравнений (1.5) на другое, получим
Тогда
(1-5)
и той
(1.6)
Если г —радиус Земли, то очевидно, что Fx и Fo — силы при-
тяжения на поверхности Земли. Как будет выяснено в главе VI,
эти силы мало отличаются от сил тяжести. Масса, вычисляемая
по формуле (1.6), называется «тяжелой» массой.
Таким образом, отношение масс равно отношению сил притя-
жения.
Итак, масса одной и той же материальной точки может быть
вычислена из двух совершенно различных опытов по формулам
т _ w0 т Ft
т0 ~ w ’ т0 ~ Fo'
Точные эксперименты, проведенные для проверки равенства
инертной и тяжелой масс, показали совпадение этих величин.
Они послужили отправной точкой для создания Эйнштейном тео-
рии тяготения.
В специальной теории относительности показывается, что масса т тела
зависит от его скорости:
где т0 — так называемая масса покоя, v — скорость тела, с—скорость света.
В классической механике рассматриваются движения тел, скорости которых
значительно меньше скорости света. Поэтому, пренебрегая отношением v2/c2
по сравнению с единицей *), считают массу тела постоянной.
Заметим, что если записать в обозначениях дифференциального исчисле-
ния второй закон Ньютона в том виде, как он его сформулировал, то основ-
ное уравнение динамики (1.1) примет вид
d (mv)
_dT“=F-
Эта форма основного уравнения динамики точки, в отличие от уравнения
(1.1), применима не только для тела постоянной массы, но и тел, масса кото-
рых зависит от скорости.
*) Так, например, для второй космической скорости (см. § 4.2) v =
= 11,2 км/сек и у2/с2«=: 1,4- 10-10.
16
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ I
§ 1.3. Дифференциальные уравнения движения
материальной точки
Положение материальной точки М в инерциальной системе
отсчета будем определять ее радиусом-вектором г. Сила F, дей-
ствующая на точку, может зависеть от положения точки, т. е.
от радиуса-вектора г (например, сила тяготения), скорости v =
= — точки (например, сила сопротивления)
довательно, в общем случае F = F^r,
ние динамики точки (1.1) можно записать
d2r у, / dr Л
т = F г, -ту-, t\.
dt2 \ at j
и времени t *). Сле-
и основное уравне-
в следующей форме:
Это равенство, представляющее физический закон, устанав-
ливающий связь между массой точки, ее ускорением и действую-
щей на точку силой, можно рассматривать одновременно как
дифференциальное уравнение, в котором радиус-вектор г явля-
ется функцией, а время t— аргументом. Это уравнение называ-
ется дифференциальным уравнением движения материальной точки
в векторной форме.
Дифференциальное уравнение в векторной форме, естественно,
эквивалентно трем скалярным уравнениям. В зависимости от
выбора осей координат, на которые проектируется основное урав-
нение динамики (1.1), можно получить различные формы скаляр-
ных дифференциальных уравнений движения материальной точки.
Так, например, если спроектировать обе части уравнения (1.1)
на неподвижные оси декартовых координат, то будем иметь
mx = F\, mj = Fy, mz = Fz, (1.7)
где х, у, z — проекции ускорения точки на координатные оси,
FK, Fy, Тг —проекции силы, действующей на точку, на те же оси.
Если пользоваться описанием движения в естественной форме,
то нужно спроектировать основное уравнение динамики (1.1) на
оси естественного трехгранника; в результате получим соотно-
шения
mwx = Fx, mwn = F„, mwb = Fb, (1.8)
где Fx, Fn и Fb — проекции силы на касательную, главную нор-
маль и бинормаль. Вспоминая известные из кинематики выраже-
ния для проекций ускорения ®T, wn и wb на те же направления,
получим
”•5-^ ° = F»- <L9»
*) Подробнее см. в § 1.5.
§ I 41
ПЕРВАЯ ЗАДАЧА ДИНАМИКИ
17
где р —радиус кривизны в текущей точке траектории. Из послед-
него уравнения следует, что сила F, под действием которой дви-
жется материальная точка, лежит в соприкасающейся к траекто-
рии точки плоскости.
В случае плоского движения точки, рассматриваемого в поляр-
ных координатах г, <р, имеем
m(r-r<p2) =Fr, (г2Ф) = /?ф, О-10)
где Fr и Fv — проекции силы на направление радиуса-вектора и
перпендикулярное к нему направление (в сторону увеличения
полярного угла гр).
Мы ограничились наиболее употребительными случаями; ана-
логично можно получить записи дифференциальных уравнений
движения материальной точки в других системах криволинейных
координат (цилиндрической, сферической и т. д.).
§ 1.4. Первая задача динамики
Как было сказано в § 1.1, в практике возникают различные
постановки динамических задач. Прежде всего остановимся на
первой задаче, когда движение задано и необходимо найти силу,
под действием которой происходит это движение.
‘Эта задача решается следующим образом: закон движения
подставляется в дифференциальные уравнения (1.7), (1.9) или
(1.10) (в зависимости от способа задания движения) и с помощью
дифференцирования соответствующих функций определяются
проекции силы. Проследим за ходом решения на примерах.
Задача 1.1. Материальная точка массы т движется в плоскости ху, при-
чем закон движения задан в виде
х = а sin (kt-^-e), У = Ь sin (kt-}-8)-\-c,
где а, b, е, 6, с — любые постоянные параметры. Найти силу, под действием
которой происходит это движение.
В данном случае движение задано в декартовых координатах. Поэтому
выражение координат из закона движения н^жно подставить в дифференциаль-
ное уравненце (1.7). При этом находим
Fx = — mk2a sin (kf + e), Fy — — mk-b sin (kt -)- 6)
или, приняв во внимание закон движения, получим
Fx =—mk2x, Fy = —mk2y-\-mk2c.
Таким образом, сила, действуюдая на материальную точку, будет
F = — mk2r -|- mk2c\,
где r = xi-|-i/j, i и j—единичные векторы осей х и у. Следовательно, мате-
риальная точка движется под действием силы притяжения к началу коорди-
нат, пропорциональной расстоянию от начала координат до материальной
точки, и постоянной силы, параллельной оси у.
ГУ
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ Г
Задача 1.2. Материальная точка массы т движется по окружности
радиуса г с постоянной скоростью v. Найти силу, под действием которой
происходит такое движение.
Здесь движение задано естественным способом; поэтому согласно (1.9)
находим
т. е. заданное движение материальной точки происходит под действием силы,
постоянной по модулю и направленной по радиусу к ее центру.
Задача 1.3. Материальная точка массы т движется по гладкой плоскости.
Ее полярные координаты г и гр изменяются по закону (рис. 1.1)
r = at-\-b, (f = ct-\-d,
где а, Ь, г, и d — положительные постоянные. Определить силу, под дейст-
вием которой происходит это движение.
р Так как
"ХУ г = а, г = 0, ф = с, ф = 0,
р то согласно первому уравнению (1.10) получаем
Ег =—т(а/-|-6)с2 =—тс2г,
т. е. составляющая силы, действующая на ма-
/\ Ф . тернальную точку вдоль радиуса, направлена
0 2 *7 к полюсу н ее модуль растет пропорционально г.
х Согласно второму уравнению (1.10) имеем
Рис- Еф==2тас,
т. е. составляющая силы, действующая на материальную точку по перпенди-
куляру к радиусу, постоянна. Модуль силы, действующей на точку, опреде-
ляется равенством
F = = тс /с2г2 + 4а2.
§ 1.5. Вторая задача динамики
Для определенности изложения будем рассматривать движе-
ние в декартовой системе координат, опираясь на уравнения (1.7).
Как уже отмечалось ранее, сила (и ее проекции), действующая
на материальную точку, в общем случае может зависеть от поло-
жения точки, ее скоррсти и времени.
Приведем несколько примеров переменных сил. На упругой бал-
ке установлен (рис. 1.2, а) не вполне уравновешенный двигатель.
При заданном режиме работы двигателя сила давления на кон-
струкцию, обусловленная неуравновешенностью, является функ-
цией времени; заметим, что эта сила принимается нами не зави-
сящей от того, как под ее воздействием колеблется конструкция.
В этих условиях на кострукцию действует сила P(t), заданная
как явная функция времени t (здесь мы не касаемся вопроса о том,
каким образом указанная конструкция схематизируется в виде
материальной точки). Обратимся к другому примеру.
С Земли произведен пуск космического корабля. После некото-
рого, сравнительно короткого промежутка времени двигатели
4 15]
ВТОРАЯ ЗАДАЧА ДИНАМИКИ
19
?(t)
М
на
выключаются и корабль продолжает движение под действием
практически единственной силы — силы притяжения Земли
(рис. 1.2, б); притяжение других небесных тел в начале движе-
ния пренебрежимо мало. Согласно закону всемирного тяготения
эта сила не постоянна и постепенно убывает с увеличением рас-
стояния г корабля от Земли. Здесь сила Р(г) притяжения зави-
сит от положения корабля, т. е. определяется его координатами.
В качестве третьего примера рассмотрим силы, под действием
которых происходит падение материальной точки в вязкой жид-
кости (рис. 1.2, в). На материальную
точку действуют сила тяжести G и
сила сопротивления жидкости R.
Как показывает опыт, сила R зави-
сит только от скорости падения,
т. е. R = R(t/). В начале процесса,
когда скоро ть мала, эта сила также
невелика, но с возрастанием скорости
растет и сила сопротивления.
Таким образом, зависимости, опре-
деляющие изменение переменных сил,
весьма разнообразны по своей при-
роде; можно указать три простейших
типа переменных сил:
а) силы, заданные как явные
функции времени и не зависящие от
движения материальной точки;
б) силы, зависящие от координат
материальной точки;
в) силы, зависящие от скорости
материальной точки.
Но возможны случаи, когда сила,
действующая на точку, может быть
одновременно функцией от несколь-
ких аргументов. Например, действующая
сила аэродинамического сопротивления при
мосфере (при взлете или снижении) зависит
рабля, и от его скорости, так как плотность атмосферы убывает
с высотой над поверхностью Земли.
Чаще всего на материальную точку одновременно действует
несколько сил .различных типов.
На рис. 1.3, а представлен пример, иллюстрирующий одновре-
менное действие сил различной природы. Неуравновешенный дви-
гатель А установлен на массивном фундаменте В, который в свою
очередь установлен на амортизаторах (на рисунке они схематично
изображены одной пружиной С и гидравлическими амортизато-
рами D).
космический корабль
его движении в ат-
и от положения ко-
20
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ Г
В такой конструкции фундамент может иметь малые верти-
кальные поступательные перемещения (за счет деформации пру-
жин), а при работе двигателя возникают колебания системы.
На фундамент действуют силы четырех типов. Во-первых, сила
тяжести самого фундамента, обозначенная на рис. 1.3, б через G:
G = const. (1-П)
Во-вторых, сила действия двигателя на фундамент, обозначен-
ная на рисунке через Р. Эта сила, меняющаяся во времени задан-
ным образом, представляет переменное динамическое давление на
б)
фундамент, зависящее от величины неуравновешенных масс дви-
гателя и угловой скорости вращения его ротора:
Р = Р(/). (1.12)
В-третьих, на фундамент действует реакция пружины, кото-
рая в любой момент времени определяется деформацией пружины
(т. е. перемещением фундамента):
F = F(y) (1.13).
((/ — вертикальное перемещение фундамента в данный момент).
Наконец, в-четвертых, на фундамент действуют реакции гид-
равлических амортизаторов D. Опыт показывает, что их реакции
полностью определяются скоростью движения поршня в цилиндре
амортизатора, т. е. скоростью самого фундамента:
R==R(y). (1.14)
При поступательном движении фундамента его можно рас-
сматривать как материальную точку; дифференциальное уравне-
ние движения этой точки (в проекции на ось у, которую будем
считать направленной вниз) имеет вид
m^Gy-VPy^ + Fy^ + Ry^. (1.15)
Для того чтобы найти движение фундамента, необходимо решить
это дифференциальное уравнение.
§ 15]
ВТОРАЯ ЗАДАЧА ДИНАМИКИ
21
Подобным же образом дело обстоит и в других задачах.. Сле-
довательно, в общем случае вторая задача динамики приводит
к необходимости решения системы трех дифференциальных урав-
нений:
тх = Fx (х, у, z, х, у, z, f),
mj = Fy(x, у, г, х, у, z, t),
mz =Fz(x, у, z, х, у, z, f),
(1-16)
в которые искомые функции х, у, г входят вместе со своими
первыми и вторыми производными по времени. Уравнения (1.16}
представляют собой систему трех дифференциальных уравнений
второго порядка относительно неизвестных функций х, у и z и,
как уже отмечалось, называются дифференциальными уравнениями
движения материальной точки.
Предположим, что нам удалось проинтегрировать систему
уравнений (1.16) и получить общее решение
х = х (t, Clt ..., Св),
У~ У (A ^i> • > С6),
z = z(t, ..., С6),
(1-17)
где Ср ..., Св — произвольные постоянные интегрирования. В каж-
дую из функций (1.17) могут входить все шесть постоянных, так
как в общем случае уравнения (1.16) не являются независимыми
друг от друга.
Если теперь в соотношениях (1.17) постоянным интегрирова-
ния давать различные числовые значения, то можно получить
совокупность различных решений. Это значит, что под действием
одних и тех же сил, действующих на материальную точку, она
может совершать различные движения.
Например, тело, отпущенное без начальной скорости, будет
падать под действием силы тяжести вертикально вниз по прямой
линии. Это же тело, брошенное под углом к горизонту, будет
двигаться под действием той же силы тяжести (сопротивлением
воздуха пренебрегаем) по некоторой кривой.
Таким образом, задания одних сил, действующих на мате-
риальную точку, еще недостаточно для определения конкретного
закона ее движения. Для того чтобы выбрать из многообразия
решений (1.17) то, которое соответствует решаемой нами конк-
ретной задаче, нужно задать еще начальные условия движения.
Начальное состояние движения точки определяется ее положе-
нием и ее скоростью в начальный момент времени, т. е. радиу-
сом-вектором го = г(О) и скоростью vo = v(O) при / = 0.
В декартовой системе координат нужно задать соответствую-
щие проекции:
22
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ. I
при t = 0
х = х0, у = у0, г = г0, 1
Х = хо, у = у0, z = z0. ] v
Совокупность этих данных называется начальными условиями дви-
жения.
Для выбора значений шести постоянных интегрирования,
входящих в общее решение (1.17) и соответствующих решаемой
конкретной задаче, используются начальные условия движения
(1.18). Это делается следующим образом: во-первых, требуем,
чтобы при / = 0 значения х, у и г, определяемые выражениями
(1.17), равнялись соответственно х0, у0 и г0; во-вторых, продиф-
ференцировав по времени выражения (1.17):
х = х (t, Ct, , Сс),
У = УЦ, Ср ..., С6),
z=z(/> С1( ..., С6),
требуем, чтобы при t = Q эти х, у, z равнялись соответственно
Уо> ^о-
Таким образом, мы получим шесть уравнений для определе-
ния постоянных интегрирования:
х0— х (0, Ср С6),
Уп=у (о, Ср ..., С6),
го = г(О, Ср ..., С6),
хо = х(О, Ср ..., С6),
Уо = У (0, Ср ..., С6),
zo = z(O, Сх> ..., С6).
(1-19)
Решая эти уравнения относительно постоянных Ci, найдем
С; = А(х0, у0, г0, х0, у0, г0) (( = 1, 2, ..., 6). (1.20)
Подставляя найденные значения постоянных в общее решение
(1.17), получим решение задачи, соответствующее данным началь-
ным условиям:
х = Ф1(/, х0, у0,
y = х0, у0,
? = Фз(С х0, г/0,
г0> Х0> У О’ ^о)>
?о> Хо, у о, Zo),
г0> А), Уо> ^о). .
(1.21)
В курсах математики доказывается, что при определенных
условиях, накладываемых на правые части уравнений (1.16) (если
задача механики поставлена правильно, то эти условия обычно
выполняются), решение (1.21) единственное. Это значит, что при
данных начальных условиях и данных силах движение точки
полностью и единственным образом определено.
Следует заметить, что наибольшие затруднения обычно пред-
ставляет первый этап — получение общего решения (1.17); после
§ 15]
ВТОРАЯ ЗАДАЧА ДИНАМИКИ
23
этого постоянные интегрирования определяются без особых труд-
ностей.
Покажем на примере решение второй задачи динамики, при-
чем ограничимся тем случаем, когда на материальную точку
действует постоянная сила.
Задача 1.4. Исследовать движение
материальной точки М массы т под
действием силы тяжести; сопротивле-
нием атмосферы пренебречь (рис. 1.4).
Выберем систему координатных
осей так, чтобы ее начало О совпа-
дало с начальным положением точ-
ки М, ось у направим вертикально
вверх, а оси х и г— горизонтально.
Ось х направим так, чтобы началь-
ная скорость v0 была расположена
в плоскости ху. Из рассмотрения рис. 1.4 следует, что проекции действующей
на точку силы тяжести на оси координат равны Fx = 0, Ру= —mg> Fz = 0.
Следовательно, дифференциальные уравнения движения (1.16) в данном слу-
чае будут иметь вид
mx = 0, mij =—mg, т2==0,
(1.22)
или, после сокращения на т,
х = 0, у — — g, 2 = 0.
Интегрируя эти уравнения, получим общее решение
Х = С1/-|-С4,
У = — + С5,
z = C3t~FCg. '
(1.23)
Для определения постоянных интегрирования С/ необходимо указать
начальное состояние движения точки, т. е. ввести соответствующие начальные
условия. Пусть начальная скорость v0 составляет с осью х угол а. Тогда
в силу выбора координатной системы будем иметь следующие начальные
условия:
при 1 = 0
*о = Уо = 2о == О, x = v0cosa, ;/0 = o0sina, zo = O.
В соответствии с (1.23) имеем
x = Ci, у =— gt -|- С2, z = C3. (1-24)
Используя теперь начальные условия, найдем постоянные интегрирования
С4 = 0, CS=O, Ce = 0, C1 = o0cosa, C2 = v0sina, С3 = 0.
Подставляя эти значения С; в общее решение (1.23), получим уравнения дви-
жения материальной точки, брошенной под углом к горизонту:
at2
x = v0tcosa, y = vot sin a — z = 0. (1-25)
Из этих уравнений следует, что движение точки под действием силы тяжести
происходит в вертикальной плоскости хОу (z = 0). Траекторией точки будет
парабола:
y = xtga — x2^. 8 . (1.26).
2yjcos2a v '
-24
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ I
Таким образом, задача решена Дальнейшее исследование траектории (1 26)
позволит определить дальность бросания и наибольшую высоту подъема
После этого можно поставить задачу об оптимальных условиях бросания,
например, выяснить, при каком угле а достигается максимальная дальность
(если считать значение г0 заданным).
§ 1.6. Прямолинейное движение материальной точки
Выясним, при каких условиях материальная точка совершает
прямолинейное движение.
Пусть материальная точка движется по прямой линии, которую
мы примем за ось х, тогда во все время движения будет у = г =
= 0. Следовательно, на основании уравнений (1.16) должны
тождественно выполняться равенства
/д = 0, Гг = 0, (1.27)
т. е. если точка совершает прямолинейное движение, то сила,
под действием которой происходит это движение, должна иметь
линию действия, совпадающую с прямой, вдоль которой движется
точка.
Однако необходимое условие (1.27) прямолинейного движения
не является достаточным. Например, при движении точки под
действием силы тяжести проекции силы на координатные оси,
лежащие в горизонтальной плоскости, равны нулю, а точка дви-
жется не по прямой, а по параболе.
Для того чтобы материальная точка двигалась по прямой
линии, необходимо и достаточно, чтобы действующая на нее сила
быта все время параллельна начальной скорости точки. Если же
начальная скорость равна нулю, то движение будет происходить
по прямой, параллельной направлению силы.
В самом деле, если направить координатные оси так, чтобы
ось х была направлена по начальной скорости точки, а начало
координат было совмещено с начальным положением точки, то
условия (1 27) будут соблюдены и, следователю,
my = 0, mz =0,
откуда
у ~Сг, z = С2
y = C1t-\~C3, z = C2tJrCi.
Имеем начальные условия- при
тогда
z/ = 0,
( = 0 z/ = 0, z = 0, у = 0, z = 0;
z = 0, (1 28)
т. е. траектория движения точки —прямая линия —ось х. Таким
образом, показана и достаточность условий прямолинейности
движения.
§ 1 6] ПРЯМОЛИНЕЙНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ 2!у
Ниже рассматриваются некоторые задачи о прямолинейном
движении материальной точки, причем во всех случаях коорди-
натную ось х мы будем совмещать с прямой, вдоль которой про-
исходит движение. В таких задачах вектор действующей на точку
силы полностью определяется его единственной проекцией Fx.
Рассмотрим несколько случаев прямолинейного движения
материальной точки, в которых можно заранее указать методы
интегрирования дифференциальных уравнений движения, каждый
из случаев относится к определенному характеру действующей
силы.
1. Прямолинейное движение материальной точки под действием
силы, зависящей только от времени. Дифференциальное уравнение
движения в этом случае имеет вид
mx = Fx(t), (1-29)
откуда
Интегрируя, получим
х = ~ JFa (0 dt + Clt
где под $ Fx (7) dt понимается первообразная функция. Интегри-
руя далее, будем иметь
Х = + (1.30)
2. Прямолинейное движение материальной точки под действием
силы, зависящей только от положения точки. В этом случае
дифференциальное уравнение движения будет
mx = Fx(x). (1.31)
Вводя v — x, получим
.. dv dv dx dv
dt dx dt dx
и, следовательно, дифференциальное уравнение примет вид
v dv = — Fx (х) dx.
После интегрирования найдем
9 Г*
v^^F^dx + C,,
откуда
^Fxdx + Ci,
26
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ. I
или, переходя к проекции скорости,
dx
Интегрируя это уравнение, будем иметь
, (* dx
'2'
Вводя обозначение
dx
Fx(x) dx+Q
получим
/ = Ф(х, Ct, С2).
Решая это уравнение относительно х, найдем зависимость х
от времени и постоянных интегрирования:
x = q>(t, Clt С2). (1.32)
Таким образом, задача решается при помощи двух квадратур.
3. Прямолинейное движение точки под действием силы, зави-
сящей только от скорости точки. Дифференциальное уравнение
движения
тх = Fx (х)
с помощью замены v = x преобразуется к виду
= - dt’
гх (у) т
Интегрируя это уравнение, получим
? F^h + Ci = -^
i Fx(v) ' 1 tn
Если ввести обозначение
(1.33)
dv
то последнее равенство примет вид
t = Ф (v, Cj),
*) Здесь и в дальнейшем знак перед корнем выбирается в зависимости от
направления движения точки в рассматриваемом промежутке времени. Если
х0 > 0, то берется знак «плюс», при противоположном неравенстве — «минус».
Знак может изменяться на противоположный в моменты, когда х = 0.
§ 1.7]
ЗАДАЧИ
27"
ИЛИ
< = Ф(х, Ct).
Решая это уравнение относительно х, будем иметь
с,),
откуда
Если уравнение t = <$(x, нельзя
то поступим следующим образом: вводя
.. dv dv
X = -ут = у- V,
dt dx
перепишем дифференциальное уравнение
mv dv ,
x = \f(t, Cjdt + Cf
решить относительно х,
преобразование
(1.33) в виде
(1.34)-
откуда
(* v dv ,
X=m}FTW)+Ci-
Из этого уравнения находим v = x:
= Сй
и после интегрирования будем иметь
откуда и определим х как функцию времени t.
§ 1.7. Задачи
Задача 1.5. На покоящуюся материальную точку массы пг в момент вре-
мени / = 0 начинает действовать сила, проекция которой на ось х выражается
зависимостью РХ=Р sin оД. Найти закон движения и сравнить решение со слу-
чаем, когда указанная проекция изменяется по закону Рх = Р cos bit.
Совмещая начало оси х с начальным положением точки, получим диф-
ференциальное уравнение движения в виде (1.29):
mx = P sin u>t.
Согласно (1.30) записываем
х = Р sin a>t d/j dt + Ctt + C2,
t. e.
p
X==------5 sin (x)t -4- Cyt -4— Cq*
mco2 1 1 £
28
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ. I
Подчиняя решение начальным условиям:
х(0) = 0, х(0) = 0 при £ = 0,
находим
Ci = ~
та
С2 = 0.
Следовательно, материальная точка движется вдоль оси х по закону
Р
х = —г (ь>1 — sin о>Л.
ты2 ' '
Из графика функции x(t), изображенного на рис. 1.5, а, видно, что точка
постепенно удаляется от начального положения, совершая колебания около
режима постоянной скорости.
Если на материальную
точку действует косинусои-
дальная сила, то дифферен-
циальное уравнение движе-
ния (1-29) будет
тх = Р cos bit
и в соответствии с (1.30)
общее решение имеет вид
— ты2 Cos + С'/ -|-С2.
Из предыдущих начальных
условий находим
поэтому закон движения вы-
ражается при помощи соот-
ношения
р
х =----Г (1 —COS bit).
ты2 ' '
На рис. 1.5, б изображен график этой функции; движение носит колебатель-
ный характер, причем точка не удаляется от начального положения дальше
чем на
2Р
Хтах — т(02
Мы получили на первый взгляд неожиданный результат. В обоих случаях
на точку действовала периодическая сила, изменяющаяся по гармоническому
закону; начальные условия также совпадали, однако отклонения точки от на-
чального положения имеют различный характер. В первом случае наблюдается
систематическое удаление точки от ее начального положения, во втором —
удаления нет, движение имеет периодический характер.
С формально математической точки зрения ничего удивительного здесь нет.
Периодичность изменения ускорения (второй производной от координаты) вовсе
не влечет за собой периодичности изменения скорости (первой производной) и
тем более самой координаты. Применительно к разобранному примеру можно
привести следующие физические соображения. В первом случае сила, а зна-
чит, и ускорение меняются по синусоидальному закону f = Psino>Z. Это зна-
чит, что в течение полупериода (0 sg Z sg л/щ) ускорение было положительно
§ 1-7]
ЗАДАЧИ
29
и точка набирала скорость. Затем направление силы и, следовательно, уско-
рение изменялись и скорость начинала убывать, так что к концу периода
/ = 2л/о) она достигла нуля. Таким образом, проекция скорости х была все
время одного знака (х:&0). Отсюда ясно, что координата х за это время
могла только возрастать и к началу следующего цикла изменения силы она
получила конечное приращение. Такое же приращение отклонения произойдет
за второй и последующие периоды.
Во втором же случае к концу первого полуперивда проекция скорости
окажется равной нулю, в течение последующего полупериода она окажется
отрицательной и, изменяясь по синусоидальному закену, в конце периода
станет равной нулю. Такая знакопеременность скорости приводит к периодич-
ности отклонения х.
Задача 1.6. На материальною точку массы т действует сила отталкивания
Fx, пропорциональная координате х и равная
Fx = сх,
где с — коэффициент пропорциональности. Найти движение точки, если в на-
чальный момент / = 0 х = 0 и х = ц0.
Дифференциальное уравнение имеет вид
тх == сх.
Уравнение движения имеет ту же форму, что и (1.31), однако здесь целе-
сообразнее воспользоваться не общим приемом, а учесть то обстоятельство,
что дифференциальное уравнение является линейным. Перенесем все члены
этого уравнения в левую часть и разделим его на массу т~.
X—— х = 0.
т
Согласно 'общей теории лийейных однородных дифференциальных уравнений
будем искать решение в форме
х = Се“(.
Отсюда
х = Са2са/.
Внесем эти значения для х и х в дифференциальное уравнение и сократим
его на Ceat, в результате чего получим характеристическое уравнение
а2_. fe2 = 0,
где _
6 = 1/" —.
у т
Решая характеристическое уравнение, найдем
«1= —/>, a,2 = k.
Так как оба корня оказались*вещественными, то общее решение дифференци-
ального уравнения будет
x = C1e_ft/-|-C2eftt,
Где Ci и С2 — произвольные постоянные интегрирования, которые определяются
из начальных условий движения.
Имеем
х = — Cike4^ + C2keki.
Подставив в эти выражения для х (/) и х (/) значения / = 0, х = 0 и х==ц0(
получим
0 = С!-|-С2> ц0= — Cjfe+С2/г,
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ. 1
Отсюда
Г Vo
С1=~2Й-
С2 =
Ур
2k'
Подставим эти значения для и С2 в выражение для х:
R I k
где гиперболический синус sh kt определен равенством
pkt — р~kt
sh kt =---g----.
Полученное решение удовлетворяет выбранным начальным условиям (при
t — 0 х = 0, x = Vt)). Если начальные условия будут при / = 0 х = х0, х = 0>
то точка будет двигаться по закону
gfcf g—kt
х ~ х0-----------= х0 ch kt
gkt _l g~kt \
ch W =------------гиперболический косинус). График этой функции изобра-
жен на рис. 1.6 сплошной линией.
При относительно больших значениях времени второй член
новится пренебрежимо малым и можно принять
ста-

(см. штриховую линию на рис. 1.6).
Заметим, что это приближенное решение не удовлетворяет начальным
условиям.
Задача 1.7. Считая, что при прямолинейном движении корабля возникает
сила сопротивления, пропорционал
чая квадрату его скорости, определить
путь, который пройдет корабль после
остановки двигателей за время, в тече-
ние которого скорость корабля умень-
шится в два раза.
Обозначим через т массу корабля и через fo его скорость в момент
остановки двигателей. На корабль действуют три силы: сила тяжести mg,
архимедова сила G и сила сопротивления F, причем F = ao2, где а —постоян-
ный коэффициент жидкостного сопротивления. Первые две силы вертикальны,
а сила сопротивления горизонтальна и направлена в сторону, противоположную
скорости корабля (рис, 1,7).
§ 1.7]
ЗАДАЧИ
31
Напишем основное уравнение динамики (1,1) для рассматриваемого
примера:
т ^ = mg+G4-F.
В проекции на горизонтальную ось х получим
dvx , /?г = — anL at х
Перепишем это уравнение в виде
т dvx ,, —= -adt. vi
После интегрирования получим
-^-=-at + Ci. (1.35) их
Условимся отсчитывать время с момента остановки двигателей корабля, Тогда
при t — 0 vx = v0 и, следовательно,
СХ=--. По
Выражение (1.35) теперь может быть записано в виде vx = (1.36)
rr. dx Так как vx = ~ t то at dx _ mv0 dt m-j-avet
И, следовательно, In (m + av0/) + C2. (1.37)
Постоянную с2 найдем из условия: х = 0 при t — 0, т. е.
Отсюда C2 = — ~ In m и a 0 = — In m-4-C2. a равенство (1.37) принимает вид m , m 4- aiU X = — In ! a m
Подставив сюда соотношение
tn 4- 0W(/ _ v0 tn vx ’ Л *
получаемое из формулы (1.36), окончательно имеем
x=—In—. a vx
Полагая иЛ = п0/2, найдем путь, который пройдет корабль за время, в те-
чение которого его скорость уменьшится вдвое:
c m 1 о S = — In 2, a
32
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ 1
Задача 1.8. Точка массы т падает на Землю из состояния покоя под дейст-
вием постоянной силы тяжести. Найти скорость и закон движения точки,
если сила сопротивления пропорциональна квадрату скорости (R = k2mv2, где
k — постоянная).
Дифференциальное уравнение движения имеет вид
mx = mg — mk2x2,
т. е. соответствует форме (1.33).
Последуем указанному выше пути решения и обозначим ii — v. Это позво-
лит привести уравнение движения к уравнению первого порядка
^ = g-^2.
или
g—k2V2
После интегрирования получим
1___
2/e|/g
Vg + hv
У g—kv

Так как движение начинается из состояния покоя, то v = 0 при t = 0 и ^ = 0.
Следовательно, имеем
1 1пГ|+^ = <,
2Hzg У g—kv
откуда
V~"k e2ktV&+l.
что ц -> gjk при t -> со, т. е. скорость падения
пределу.
Из этой формулы следует,
стремится к определенному
dx
Перейдем теперь к нахождению закона движения, Так как v == —, то
dx — -------—----dt,
k e2ktVg_^x
или
i_ d(^L±£2!J2)
~k2 ^e-ktVg ;
отсюда
X 1 ln(^-H-wrg‘)+Ca.
kl
При / = 0 x=0, следовательно, C2 = — In 2. Таким образом, имеем
1 , ^tVg+e-ktVg
x~~k2 n 2
§ 1.7]
ЗАДАЧИ
33
Даже при сравнительно небольших значениях времени ktVgi
поэтому, пренебрегая слагаемым е~к*^, получим приближенно
• 1 , ektVi ^g, In 2
X~k* П 2 “ k 1 k* '
т. e. движение по истечении некоторого промежутка времени становится прак-
тически равномерным.
Как н в предыдущем примере,
иости не удовлетворяет начальным
это решение вследствие своей приближен-
условиям; это можно понять, рассматривая
рис. 1.8, где графически представлены
точное и приближенное решения.
Задача 1.9. Материальная точка начинает движение в вязкой жидкости
с горизонтальной скоростью, равной по модулю ц0. Движение начинается
из точки с координатами х = 0, y=h, z=0 (рис. 1.9). На точку действуют
сила тяжести и сила сопротивления жидкости, пропорциональная скорости
(R — kmv, где k — коэффициент пропорциональности). Найти закон движения
точки.
В качестве координатной плоскости ху примем вертикальную плоскость,
проходящую через направление начальной скорости точки; ось у направим
вертикально вверх.
Силы, действующие на точку, равны
P = mg, R = — kmv.
Дифференциальные уравнения движения имеют вид
mx=.—kmx, my——kmy — mg, m2=—kmi,
или
х + &х = 0, y-\-ky=—g, 2-{-k2 = G.
Система уравнений движения распадается на три линейных уравнения, общие
решения которых будут
x = C±-^-C,ie~kt, у — С3-]-С^~к1—2=С^-\-С^~к^,
К
Так как
х= — Cake~kt, у=~С^ке~к1 — ^-, 2= — Ceke~kt,
то при начальных условиях:
2 Н, В. Бутенин и др.
04
ВВЕДЕНИЕ В ДИНАМИКУ
[ГЛ I
при t = 0
*о = О. y»=h, zo=0, х0 = п0> г/о = °. А> = 0
получим
C* = -JT’ С^+¥’ С^~12’ С* = °- С« = °
и тогда
1 —e~kl
х=Оо-т--
y = h+g
\—e~ht — kt
№
z = 0.
Отсюда следует, что движение точки будет происходить в вертикальной плос-
кости.
Для получения закона движения при отсутствии сопротивления среды
следует k устремить к нулю; тогда получим
0^2
x = vot y=h~-^-, z = 0.
ГЛАВА II
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
§2.1. Вводные замечания
Среди различных сил, которые могут действовать на мате-
риальную точку, особое место занимают восстанавливающие силы,
т. е. силы, стремящиеся вернуть
точку в положение равновесия.
Такие силы зависят от отклоне-
ния точки от положения равно-
весия и направлены к положе-
нию равновесия.
Как мы увидим ниже, вос-
станавливающие силы придают
движению материальной точки
колебательный характер. При-
рода этих сил весьма разнооб-
разна. Три случая показаны на
рис. 2.1.
В первом случае (рис. 2.1, а)
восстанавливающая сила обу-
словлена упругими свойствами
пружины и возникает вследствие
деформации пружины. Во вто-
ром случае (рис. 2.1, б) при вер-
тикальных отклонениях плаваю-
щего понтона от положения
равновесия возникает допол-
нительная (архимедова) сила,
также направленная против от-
клонения и играющая роль вос-
станавливающей силы. В третьем
случае (рис. 2.1, в) имеется в
виду материальная точка, нахо-
дящаяся в прямолинейном сквоз-
ном канале, который проходит внутри Земли. Если тело отклонено
от положения равновесия, возникает составляющая силы притя-
жения, направленная к положению равновесия.
2*
36 прямолинейные колебания материальной ТОЧКИ [ГЛ. II
Однако, кроме восстанавливающих сил, в подобных случаях
одновременно действуют, как правило, также силы сопротивления
R(x), зависящие от скорости движения; таково в схеме рис. 2.1, а
трение между телом и горизонтальной поверхностью, в схеме
рис. 2.1, б —зависящее от скорости сопротивление воды, в схеме
рис. 2.1, в —сопротивление воздуха и трение скольжения. Наконец,
возможно, что к материальной точке приложена возмущающая
сила, т. е. сила, являющаяся заданной функцией времени.
Настоящая глава посвящена систематическому исследованию
всех вариантов сочетания указанных сил в случае прямолинейного
движения материальной точки. Хотя эта задача представляет
практический интерес и сама по себе, но еще более важно, что
ее решение можно почти без всяких изменений использовать для
многих других случаев колебаний.
Дело в том, что различные по своему физическому содержанию
колебательные явления описываются одинаковыми дифференциаль-
ными уравнениями, поэтому выводы, полученные при изучении
колебательного движения в какой-либо одной области, могут быть
использованы и в других областях.
Наиболее просты для исследования те случаи колебательных
движений, когда восстанавливающая сила пропорциональна откло-
нению точки от положения равновесия, а сила сопротивления
пропорциональна скорости точки. Соответственно проекции вос-
станавливающей силы и силы сопротивления на ось х имеют вид
Fx —— сх, Rx =— bx.
В этих случаях дифференциальные уравнения движения линейны;
соответственно такие колебания также называются линейными *).
В зависимости от того, какая комбинация сил действует на
материальную точку, колебательное движение приобретает те или
иные типичные особенности. В следующей таблице дана сводка
различных изучаемых в дальнейшем типов линейных колебаний:
Действующие силы Дифференциальное уравнение Наименование вида колебаний
Восстанавливающая сила F(x): Fx= -сх тх + сх = 0 Свободные колебания
Восстанавливающая сила F (х) + сила сопротив- ления R (х): Fx= — сх, Rx= — bx тх Ьх + сх = 0 Свободные колебания при наличии вязкого трения
*) Термин «линейные колебания» никак не связан с прямолинейностью
траектории точки и определяется исключительно линейностью дифференциаль-
ных уравнений.
§ 2.2]
СВОБОДНЫЕ КОЛЕБАНИЯ
37
Действующие силы Дифференциальное уравнение Наименование вида колебаний
Восстанавливающая сила F (х) + возмущающая сила Q (/): Fх — — сх, Qx = Qx (t) тХ + сх = Qx (t) Вынужденные колебания
Восстанавливающая сила F (х) -|- сила сопротив- ления R (х) + возму- щающая сила Q (/): Fx= — сх, Rx (х) = = — bx, Qx = Qx(t) тХ + bx + сх = Qx (t) Вынужденные колебания при наличии вязкого тре- ния
Возможны и более сложные случаи, когда сила зависит одно-
временно от координаты х и времени t и не может быть пред-
ставлена в виде суммы Fx (х) и Qx (t), а также когда сила зависит
от координаты х и скорости х, причем силу нельзя представить
как сумму F (х) и R (х). Эти случаи здесь не рассматриваются.
§ 2.2. Свободные колебания
Рассматриваемая задача характеризуется тем, что на мате-
риальную точку действует только восстанавливающая сила', в линей-
ных задачах ее модуль пропорционален отклонению точки от
положения равновесия. Проекция восстанавливающей силы на
ось х равна
Fx =— сх, (2.1)
где с — коэффициент пропорциональности, а дифференциальное урав-
нение движения точки имеет вид
тх = — сх.
Положив с/т — k2, получим
Jc + fe2x = 0. (2.2)
Таким образом, движение материальной точки под действием вос-
станавливающей силы описывается линейным однородным диффе-
ренциальным уравнением второго порядка с постоянными коэф-
фициентами.
Характеристическое уравнение этого дифференциального урав-
нения имеет вид
а2-Н2 = 0.
38
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ. П
Так как его корни —чисто мнимые числа:
= ki, «2 = — ki,
то общим решением дифференциального уравнения (2.2) будет
х = Сх sin kt-\-C2 cos kt, (2.3)
где Cj и C2 — постоянные ийтегрирования.
Для большего удобства анализа этого решения введем новые
постоянные интегрирования а и е, положив
C1 = acose, C2 = asine,
Это можно сделать, так как из этих соотношений постоянные
а и е определяются через С\ и С2 с помощью формул
а=УС| + С|, tge = -g-.
Тогда
х = a cos е sin kt ф- a sin е cos kt,
или
х = а sin (kt ф-е). (2.4)
Постоянные а и е (или постоянные CL и С2) определяются
заданными начальными условиями — начальным положением и
начальной скоростью движущейся точки.
Таким образом, под действием восстанавливающей силы мате-
риальная точка совершает движение по синусоидальному закону,
т. е. гармоническое колебательное движение. Такие колебания
называются свободными колебаниями.
Из уравнения (2.4) видно, что наибольшее отклонение мате-
риальной точки от положения равновесия (амплитуда колебаний)
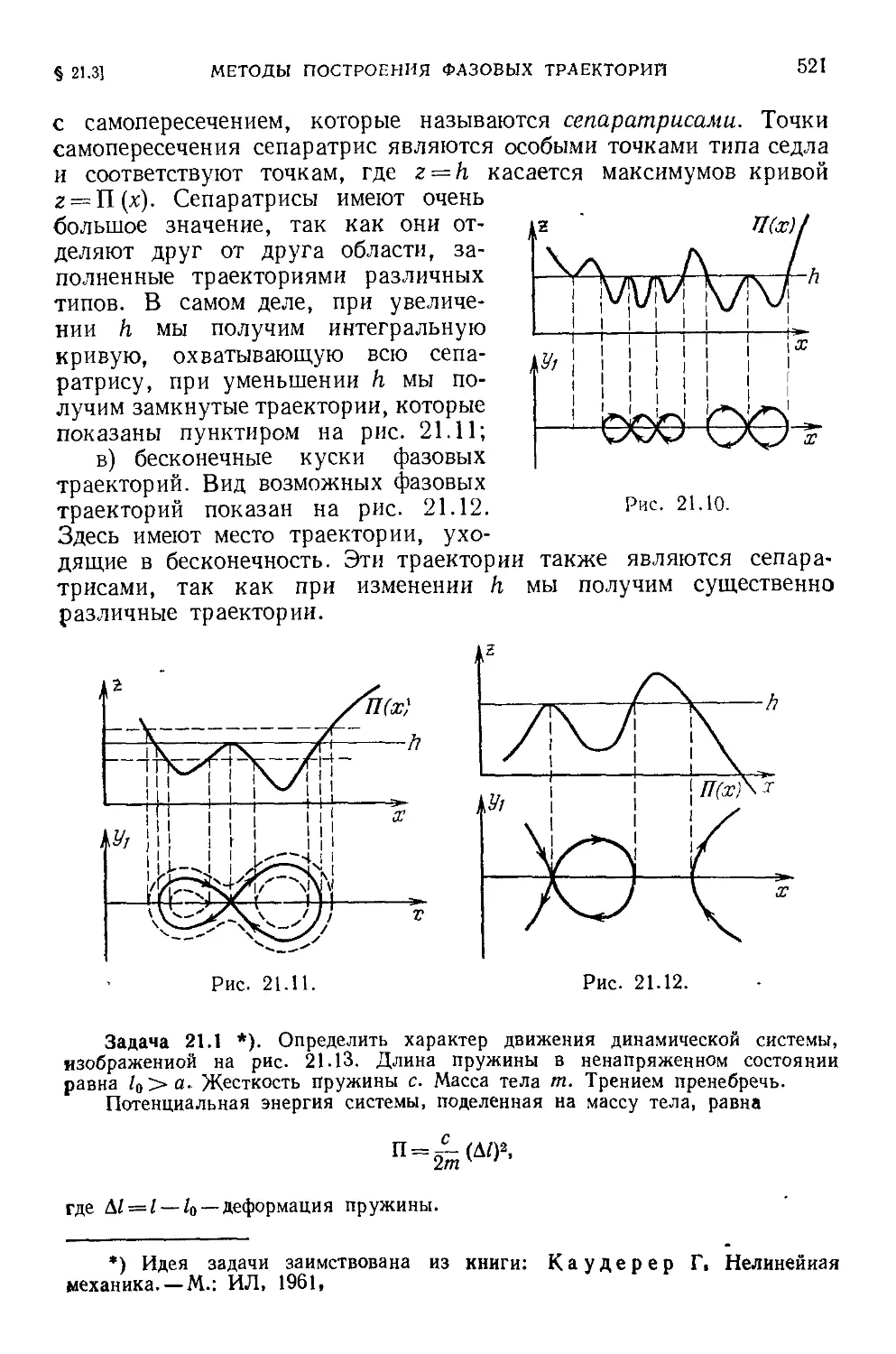
равно а.
Аргумент (/г^ф-е) называется фазой колебаний, а величина
е — начальной фазой.
Величина k называется угловой частотой колебаний и опреде-
ляет число колебаний, совершаемых точкой за 2л секунд. В даль-
нейшем величину k для краткости будем называть просто часто-
той. Частота колебаний k не зависит от начальных условий и
определяется только параметрами системы (величинами с и т).
По этому признаку частоту свободных колебаний называют также
собственной частотой.
Для определения амплитуды и начальной фазы колебаний вос-
пользуемся начальными условиями, которые должны быть заданы
(в противном случае колебательный процесс не полностью опре-
делен). Пусть в начальный момент i = 0 известны начальное поло-
жение материальной точки х = х0 и начальная скорость х = х0.
“S 2.2]
СВОБОДНЫЕ КОЛЕБАНИЯ
39
Тогда, подставив в уравнение движения (2.4) и в выражение для
скорости
х = ak cos (kt + е) (2.5)
t — Q, х = х0 и х = х0, получим для определения а и е два урав-
нения:
x0 = asine, x0 = afecos8.
Отсюда находим
а=Ух1 + ^-, tge = -^* *) (2.6)
и поэтому закон движения точки определяется следующим урав-
нением:
х= j/"xg + ^"-sin^Z + arctg^. (2.7)
График свободных колебаний материальной точки представлен
на рис. 2.2; здесь отмечены начальное отклонение х0, амплитуда
колебаний а, а также промежуток времени Т, в течение которого
происходит одно полное колебание. Этот наименьший промежуток
времени, по истечении которого движение точки полностью повто-
ряется, называется периодом колебаний. Зависимость между перио-
дом колебаний и частотой определится из условия периодичности
движения:
k (t 4-Т) 4- 8 = kt 4- 8 + 2л,
Т = 2л]/-^. (2.8) Рис. 2.2.
Таким образом, период колебаний, так же как и частота, не
зависит от начальных условий. Это свойство колебаний называется
изохронностью. Как видно из (2.8), период и частота колебаний
определяются величиной колеблющейся массы т и коэффициентом
пропорциональности с, причем с увеличением массы и уменьшением
Коэффициента с период колебаний увеличивается.
*
•^0 л л - «ГС Х0 л «П
> о 0 е -X-, а при -А < 0
хи 2 ’ н х0 2
£сли х0<0, то при -£->0 я е -Д а при — <0
*о 2 г х0 2
40
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ. 1Г
Задача 2.1. Груз массы т подвешен на пружине, массой которой можно-
пренебречь (рис. 2.3). На колеблющийся груз действуют две силы: сила
тяжести mg и сила упругости F, создаваемая пружиной. Составить дифферен-
циальное уравнение движения.
Отметим на рис. 2.3 три положения: Ot— положение нижнего конца пру-
жины в ее недеформированном состоянии (/0 — длина пружины в недеформиро-
ванном состоянии), О —положение равновесия груза, висящего на пружине,
М — текущее положение груза при его движении. Обозначим расстояние ОгО
через 6СТ (статическая деформация пружины) и направим ось х вертикально
вниз, выбрав начало отсчета в положении равновесия груза (точка О).
По закону Гука при относительно небольших перемещениях модуль силы
упругости пропорционален деформации пружины. В нашем случае деформация
пружины равна |6ст4-х|, поэтому F = с | ост + х |, где с—коэффициент пропор-
циональности, называемый коэффициентом жесткости пружины. Очевидно, что
коэффициент жесткости численно равен силе, которую нужно приложить к концу
пружины, чтобы
деформировать ее на единицу длины. Проекция силы F на
ось х равна — с (бст + %). Дифференциальное уравнение дви-
жения груза имеет вид
mx = mg —с (6СТ х).
Если груз находится в равновесии, то сила тяжести mg
уравновешивается силой упругости, которая в положении
равновесия равна сбст (так как в этом случае х=0). Следо-
вательно,
mg = cb„. (2.9).
Принимая это во внимание, приведем дифференциальное
уравнение движения груза к виду
или
тх = — сх,
"х где
Рис. 2.3.
Полученное дифференциальное уравнение совпадает с уравнением (2.2).
Поэтому груз, подвешенный к пружине, совершает гармонические колебания
с частотой k-
Если начало координат взять в точке или в верхнем неподвижном
конце А пружины, то дифференциальное уравнение движения усложнится. Так,
если начало координат выбрано в точке (Д, то Fx =—сх и уравнение движения
груза примет вид
mX = mg—cx,
или
xA-k'2X = g.
Если начало координат выбрать в неподвижном конце А пружины, то
Fx = c(x—10), где 10 — длина пружины в недеформированном состоянии, Диф-
ференциальное уравнение движения груза
mx = mg—с (х —10)
после упрощения приводится к форме
x + k4=g+k40.
Таким образом, рациональным выбором начала отсчета можно упростить форму
дифференциального уравнения движения и, следовательно, его решение,
$ 2.2]
СВОБОДНЫЕ КОЛЕБАНИЯ
41
Задача 2.2. На понтон (рис. 2.1, б) действует его вес G и архимедова
выталкивающая сила F. Исследовать вертикальную качку понтона.
В состоянии равновесия вес понтона О уравновешивается архимедовой
силой F. Если это состояние по какой-либо причине нарушается и понтон
дополнительно погрузится в воду, то согласно закону Архимеда выталкива-
ющая сила возрастет, т. е. получит приращение, направленное вверх. Понятно,
что при любых отклонениях понтона от положения равновесия приращение
силы F будет направлено против отклонения. Если понтон прямостенный (в пер-
вом приближении это можно принять), то приращение архимедовой силы про-
порционально отклонению х и определяется соотношением
AF = — ySxi,
где у — удельный вес воды, S — площадь, ограниченная ватерлинией (площадь
сечения понтона горизонтальной плоскостью на уровне поверхности воды).
Действительно, произведение Sx определяет дополнительно вытесненный объем
воды, так что произведение ySx равно «потере веса» по закону Архимеда, т. е.
приращению модуля силы F.
Допустим, что после нарушения состояния равновесия понтон будет предо-
ставлен самому себе. В любой момент последующего движения на понтон дей-
ствуют две силы: сила тяжести G = /ng (направленная вниз) и архимедова сила
F + AF (направленная вверх). Дифференциальное уравнение движения в проек-
ции на ось х имеет вид
тХ= mg—F—ySx.
Учитывая, что tng — F, найдем
mx-|-ySx=0,
т. е.
Полученное дифференциальное уравнение совпадает с подробно исследо-
ванным уравнением (2.2). Поэтому, независимо от начальных условий, можно
сразу найти период (2.8) вертикальной качки понтона:
Пусть, например, площадь ватерлинии понтона равна 20 л2 и его вес
/ 30 \
составляет 30 Т. Тогда находим fy=l T/xfi, m=g~g -сек2/*) Т = 2-3,14Х
п / 30 000 о л_
Х У 9,8 • 1000 • 20 ~ 2,45 сек"
Приведенное решение грубо приближенное, так как выталкивающая сила
определялась по закону Архимеда, справедливому лишь для условий покоя.
В данном случае следовало бы рассмотреть более сложные явления гидродина-
мического характера, связанные с движением воды при качке. Как показывают
более подробные исследования, эти дополнительные обстоятельства можно учесть,
условно добавляя некоторую массу воды («присоединенную массу») к массе
понтона.
В заключение рассмотрим еще одну задачу.
Задача 2.3. Для определения коэффициента сухого трения может быть
использована установка, изображенная на рис. 2.4. Она состоит из двух валов,
вращающихся с одинаковыми угловыми скоростями в разные стороны, на кото-
рые кладется пластина. При совпадении центра тяжести пластины С с середи-
ной расстояния между осями (точкой О) пластина находится в равновесии под
42
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ. 1Г
действием равных и противоположно направленных сил трения FA и Ffl,
Исследовать движение пластины, если в начальный момент ее равновесие было
нарушено.
Если каким-либо способом нарушить состояние равновесия пластины, то
она придет в движение в горизонтальной плоскости. Вследствие смещения
центра тяжести С давления на диски окажутся неодинаковыми. Соответственно
нарушится равенство сил трения, причем
Рис. 2.4.
равнодействующая сил трения ока-
жется направленной к точке О,
т. е. в сторону положения равнове-
сия, и будет восстанавливающей
силой. Благодаря действию этой
силы возникает процесс свободных
колебаний, период которых зарисит
от свойств трения между пласти-
ной и валами. Это позволяет по
опытным значениям периода коле-
баний определить коэффициент тре-
ния f.
Для вывода соответствующей
формулы составим дифференциаль-
ное уравнение горизонтальных ко-
лебаний пластины. Вдоль оси х действуют сила трения, приложенная в точ-
ке А, равная fNA и направленная вправо, и сила трения, приложенная
в точке В, равная fNB и направленная влево. Если центр тяжести пластины
смещен от положения равновесия на величину х, то
Na = L2T^ NB = iirQ’
где Q — вес пластины, 21— расстояние между осями валов *).
Дифференциальное уравнение движения пластины имеет вид
.. 1 — х _ , 1-\-х _
Положив fgll — k2, получим
£'+&гх = 0;
отсюда сразу следует, что период колебаний равен
Т = 2л ~\f
Г fg
Разрешая последнее уравнение относительно /, получим окончательную формулу
4л^
gT*
Определив из опыта период колебаний Т и зная расстояние между осями колес
2/, найдем отсюда коэффициент трения скольжения.
*) Здесь мы, в сущности, использовали уравнение статики. Уравновешен-
ность сил, направленных перпендикулярно к оси Ох, следует из того, что
ускорение пластины в этом направлении равно нулю.
§ 2 3]
СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ
43
§ 2.3. Свободные колебания при линейно-вязком сопротивлении
Рассмотрим прямолинейное движение материальной точки под
действием линейной восстанавливающей силы и линейной силы
сопротивления. Совместим начало координат с положением равно-
весия точки. Проекция восстанавливаю-
щей силы F на ось х равна — сх. Так О R F и
как сила сопротивления R всегда на- *
правлена в сторону, противоположную
направлению скорости точки, то проек- Рис. 2.5.
ция силы сопротивления на ось х рав-
на — Ьх, где b — коэффициент пропорциональности, характеризую-
щий сопротивление среды (рис. 2.5).
Таким образом, дифференциальное уравнение движения точки
запишется следующим образом:
тх = — сх — Ьх. (2.10)
Вводя обозначения c/m = k2, blm=2h, получим
х 2hx + k2x = 0. (2.11)
Это—линейное однородное дифференциальное уравнение второго
порядка с постоянными коэффициентами. Характеристическое
уравнение имеет вид a2 -j-2/их + й2 = 0, и его корни равны
«! = — й + ]/й2 —й2, а2 =— h~yh2 — k2.
Характер движения точки существенно зависит от соотношения
величин h и k.
Если h<k (случай малого сопротивления), то корни харак-
теристического уравнения комплексно сопряженные. Если h^-k
{случай большого сопротивления), то корни вещественные. Рас-
смотрим подробно каждый из этих случаев.
1. Случай малого сопротивления Корни характеристи-
ческого уравнения будут
= — h + i У k2 — /г2, <х2 = — h — г У k2 — h2.
Общее решение дифференциального уравнения имеет вид
х = е~ы (Сх sin k*t^ С2 cos k*t), (2.12)
где k* — Ук2 — h2, Cj и C2 — постоянные интегрирования.
Для большей наглядности введем новые постоянные а, е при
помощи формул
У —a cose, C2 = asine.
Тогда получим
x = ae’wsin (2.13)
44
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ 1Г
Из этого уравнения видно, что х->0 при /->оо (так как е~ы->0)^
т. е. движение является затухающим. Это затухающее движение
носит колебательный характер, так как, приближаясь (при /->оо)
к состоянию равновесия, система будет проходить через это
состояние бесконечное число раз в моменты времени, равные
4 _ пл —е
Г" — k* ’
где п = 1, 2, ... (рис. 2.6).
Движение, описываемое формулой (2.13), не является периоди-
ческим, так как с течением времени последовательные максималь-
ные отклонения точки от положения равновесия уменьшаются.
Важно, что максимальные отклонения точки от положения равно-
весия хотя и уменьшаются с течением времени, но промежуток
времени между двумя любыми последующими отклонениями
(например, в сторону положительного направления оси х) есть
постоянная величина, равная 2n/k*. Эту величину условно назы-
вают периодом затухающих колебаний.
Рассмотрим подробнее график движения (см. рис. 2.6). На
этом рисунке кривые х = аегы и х= — ае~ы являются границами
области, внутри которой располагается график движения.
Вычислим моменты времени, соответствующие максимальным
отклонениям точки от положения равновесия. С этой целью най-
дем скорость точки
х = — hae~ht sin -\-ak*e~ht cos (fe^-f-e) (2.14)
и приравняем ее нулю. Будем иметь
А*
tgr/+8)=v
§ 2.3] СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ 45
Отсюда следует, что если t’ (наименьший корень полученного
уравнения) соответствует первому максимальному отклонению
в положительном направлении оси х, то последующие максималь-
ные отклонения в положительном направлении оси х будут дости-
гаться в следующие моменты времени:
где п = 1, 2, .... а
/у, * * 2 л 2л
~k* “ Уд2-д2’
Из этой формулы видно, что при вязком трении период зату-
хающих колебаний больше периода незатухающих колебаний,
равного 2л/6.. Максимальные отклонения а0, alt соответст-
вующие моментам времени
t', t' + T*, t' + 2T*, ..., t' + nT*,
равны
Од =ae~ht' sin (k*f -фе), at = ae-h,-t’+T>'> sin (k*t’ -pe), ...,
an = ae~hV'+nT*'1 sin (k*f -f-e),
при этом учтено, что
sin [ft* (f+ mT*)4-8] =
= sin [k* (t’ + m^ + ej = sin (k*f 4-8 + 2лт) = sin (k*t' 4-e),
где m = 1, 2, 3, ...
Из формул для tz0, alt ... видно, что отношение последующего
максимального отклонения вдоль положительного направления
оси х к предыдущему постоянно и равно
n=-^- = e-ftr. (2.16)
°zn-l
Таким образом, амплитуды затухающих колебаний при вязком
сопротивлении убывают в геометрической прогрессии. Величина
т] (знаменатель геометрической прогрессии) называется декремен-
том колебаний (или фактором затуханий), а модуль натурального
логарифма этой величины
А = йТ (2.17)
называется логарифмическим декрементом колебаний *).
-Hl ут*
*) Иногда вводят г) = е 2 и Л=—g- > т . е. сопоставляют два последова-
тельных наибольших по модулю отклонения в разные стороны.
46 ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. И
Заметим, что если t-=t" является положительным корнем уравнения
sin 1> то моменты времени, в которые график движения касается
кривой ae~ht, будут:
t", t’ + T*, t" + 2Т*, ...
Декремент колебаний можно определить как отношение отклонения при
t—t"^-nT* к отклонению при — 1) Т*.
Для определения постоянных интегрирования используем
начальные условия: х = х0, х = х0 при / = 0.
Подставляя эти условия в уравнения (2.13) и (2.14), получим
уравнения для определения постоянных а и е:
x0 = £sine, хп = — ha sin 8 Д-ak* cos 8,
откуда
„ , l/"v2 I (Xo + ^Xo)2 о _ k*X0
o+ ........’ tg8-17+7«0 •
2. Граничный случай (й = й). Корни характеристического
уравнения в этом случае будут вещественными и кратными:
<хх = а2 = — h,
и, следовательно, общее решение уравнения движения (2.11) имеет
вид
х = е-«(С1 + С20, (2.18)
где Сх и С2 — постоянные интегрирования. Принимая во внима-
ние, что
х = — he~ht (Сх 4- C2Z) + C2erht,
получим при начальных условиях: х = х0, х = х0 при / = 0 сле-
дующие уравнения для определения постоянных интегрирования
Сх и С2:
%0 — Cj, х0 = hC2-\-C2.
Отсюда
Сх = х0, С3 = х0+hx0.
Таким образом, для заданных начальных условий уравнение
движения точки запишется в виде
х = е ы [х0 + (х0 + /гх0) /]. (2.19)
Из этой зависимости следует, что в рассматриваемом случае
движение точки уже не носит колебательного характера, но оста-
ется затухающим движением, так как х—>• 0 при /~>оо*).
*) При t -> оэ множитель стремится к нулю, а множитель, стоящий
в квадратных скобках, стремится к бесконечности. Раскрывая неопределенность
(например, по правилу Лопиталя), найдем, что х -» 0 при t -> оэ.
§ 2.3]
СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ
47
Такое движение называется апериодическим.
Для построения графиков этого движения найдем момент вре-
мени, соответствующий максимальному отклонению точки от поло-
жения равновесия, и момент времени прохождения точки через
положение равновесия. ггч
Приравнивая производную по времени
от х нулю:
-h[xQ + (xo + hxo)t] + xo + hxo = 0, ° I
О
имеем -Н ЭН , t
f
э h (%о И-
Из условия х = 0 получим
1 *0 ~)- >1Хо
Для х0>0, *о>О имеем t3>0,
/]<0 и график движения имеет вид, по- °
казанный на рис. 2.7, а.
Если х0 > 0, то при х0 -С 0 и | х01 < hx0
будет /э<0, ^<0, т. е. экстремальных Рис. 2.7.
точек нет и график движения имеет вид,
показанный на рис. 2.7, б; при хо<0 и | .r0 | > hx0 получаем, что
;э>0, t1>0- Это значит, что точка, получив начальную скорость,
пройдет в дальнейшем движении положение равновесия (при t-t^
и при t — t3 достигнет положения, соответствующего максималь-
ному отклонению точки от положения равновесия. Далее точка
будет асимптотически приближаться к положению равновесия.
График движения для этого случая показан на рис. 2.7, в.
Отметим, что при х0<0 характер графиков не изменится.
3. Случай большого сопротивления (h > k). В этом случае корни характе-
ристического уравнения
^ = — ^ + //12 — ^2, а2 = — h — / /С-/О
являются действительными и отрицательными. Общее решение уравнения дви-
жения (2.11) имеет вид
х=С1е^‘+ Сгеа^. (2.20)
Так как
х = afije0,11 + а2С2еа2‘,
то при начальных условиях: х = х0, Л = х0 при t = 0 уравнения для определения
постоянных интегрирования будут
Xq = Ci 4~ cciCi 4~ ocgCg.
Найдя отсюда
„ а2Хо— х0 х0 — ajXo
С1 =-------- И G о =-----------
«2 — «1 а2 —«1
48 ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. II
и годставив эти Cj и С2 в выражение (2.20), получим
у_а2Хо—catt . *о—ai*o eatt (2.21)
а2 —он ~ а2 —ccj ' ' ’
Это уравнение описывает апериодическое затухающее движение (х->0при
t -> со, так как и а2 отрицательны).
Продифференцировав выражение (2.21) по времени и приравняв получен-
ный результат нулю, получим значение t = t3, соответствующее максимальному
отклонению точки от положения равновесия:
t 1 1п “з (А> —«рсо)
9 «! — а2 (хо —ОЗД,) ‘
Принимая во внимание, что о^а^й2 и а2 — а2 = —2 Уh2 — k2, это выражение
можно переписать в виде
t = 1 in Г1 + 2K'^fe2|a2|x0-
3 ЧУ h2-k2 L ^(xo+|a2|x0)
Счевидно, что t3 будет больше нуля для тех значений х0 и ха, для которых
_________>0.
^0 + I a2 I х0
Момент времени flt в который координата х, определяемая формулой (2.21),
обращается в нуль, найдем по формуле
= —!----in xo~aix°. = *------In Г1 - _
dj — a2 х0 — a2xo 2 Уh2 — k2 [_ *o +1 a2 I xo J
Отсюда следует, что будет больше нуля при
. , । <0.
+ I a2 I х0
Виды графиков 'движения для рассматриваемого случая (h>k) представ-
лены соответственно
для х0 > 0, х0 > 0 на рис. 2.7, а;
для ха > 0, х0 sg 0, но I х0 I 0, х0 < 0, но | х0 j > | a21 хо на рис. 2.7, в.
Задача 2.4. При наблюдении колебаний груза весом 3 кГ по виброграмме *)
было установлено, что «огибающая» графика затухающих колебаний имеет вид
графика показательной функции (экспоненты), причем за один период ампли-
туда колебаний уменьшается вдвое. По той же виброграмме определено, что
период колебаний равен 0,3 сек. Определить коэффициент жесткости пружины
я коэффициент h силы вязкого сопротивления.
Для решения задачи используем следующие соотношения:
Т* = am-i _chT* k —
s yk^h2' am ’ V « '
Подставив в эти формулы числовые данные, получим
= 0.3. =
yk2~h2 V 3
*) Виброграммой (или осциллограммой) называется полученный в экспе-
рименте график колебаний.
§ 2.3] СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ 49
Решая эти уравнения относительно с, h и k, находим
/1 = 2,31 сек-1, & = 21,1 сек-1, с =1,36 к.Г!см.
Задача 2.5. Пользуясь данными предыдущей задачи, определить, во сколько
раз следует уменьшить массу груза, чтобы свободное движение системы стало
апериодическим,
г-, , . т ,
Пусть — новая масса, тогда, вводя обозначение л=— , будем иметь
__________________________ _ т1
, b Ьк -и Г с ~i ск
hi — л— = я— и *1 = I/ — =1/ — •
1 2nti 2т У mi Ут
Условия задачи будут удовлетворены, если hi = ki< т. е.
^- = 1/'— или hk = kyrk.
2т Ут’
Используя данные предыдущей задачи, получим, что массу следует умень-
шить в
. /й\2 /21,1\2
раза'
Задача 2.6. Материальная точка совершает затухающие колебания под
действием линейной восстанавливающей силы и силы сопротивления, пропор-
. „ , b
циональнои первой степени скорости, причем постоянная /г = ^— составляет
одну десятую от частоты k незатухающих колебаний (/г/Jfc = 0,1). Определить
разность между периодами затухающих Т* и незатухающих Т колебаний, а
также во сколько раз уменьшится амплитуда затухающих колебаний через во-
семь полных колебаний.
Составим отношение периодов колебаний
2л !
Т* Vk2 — h2 _ ! hi\~'2
Т~ 2л ~V к2)
k,
Так как по условию задачи число h/k мало, то, пользуясь хорошо извест-
ной приближенной формулой (1 -|-х)а як 1 -|-ах, справедливой при малых зна-
чениях | х | и любых а, получим с достаточно хорошей точностью
Т ~ 1 + 2 k2 ’
Отсюда
Т*-Т _ 1 /г2
Т ~ 2 k2'
Следовательно, период затухающих колебаний Т* превышает период неза-
тухающих колебаний Т всего на 0,005 = 0,5% (по условию задача Л/£ = 0,1).
Рассмотрим теперь ряд последовательных амплитуд затухающих колебаний:
По, Qi, ... , ап. Так как эти амплитуды убывают по закону геометрической про-
грессии, то
а„ = аог]л,
где г] —декремент колебаний, определяемый формулой (2.16). Отсюда
°о =ghT’n
ап
50
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ И
Заменив период затухающих колебаний Т* на его приближенное значение
Т = 2я/й, получим
2лЛл
а°
— = е R ,
«а
Внеся сюда /1 = 8 и йД = 0,1, найдем
Таким образом, при относительно небольшом значении сил сопротивления
(Л/fe = 0,1) период затухающих колебаний мало отличается от периода незату-
хающих колебаний, но колебания гасятся весьма интенсивно — через восемь
колебаний амплитуда уменьшается в 152 раза, т. е. колебания практически
прекращаются.
§ 2.4. Свободные колебания при трении скольжения
Для простоты рассуждений рассмотрим движение прикрепленного к пру-
жине тела весом mg по шероховатой горизонтальной плоскости. Совместим
начало координат с точкой, соответствую-
щей положению тела при недеформиро-
ванном состоянии пружины (рис. 2.8).
, Дифференциальное уравнение движе-
X ния тела имеет вид
tnx = Fx + Тх>
рис 2 8 где = — сх— проекция на ось х силы,
действующей на точку со стороны пру-
жины (с — коэффициент жесткости пру-
жины), 7\-— Проекция на ось х силы сухого трения. Сила сухого трения
направлена в сторону, противоположную направлению скорости тела, и по
модулю равна fN — fmg, где / — коэффициент трения.
Таким образом, окончательно дифференциальное уравнение движения тела
распадается на два знакомых нам линейных уравнения:
тх =— cx-\-fmg (х<0),
тх = — сх—fmg (х > 0),
или
(х<0),
i' + ^x = — fg
(х > 0),
(2.22)
(2.23)

где по-прежнему к2 = с!т.
Допустим, что груз смещен от исходного положения вправо на расстояние
Хо — ао и затем свободно, без начальной скорости, отпущен. Тогда движение
начнется при следующих условиях:
х = п0>0, х = 0 при Z = 0.
Предполагается, что в указанном смещенном положении восстанавливающая
сила больше силы трения, т. е. ca0>fmg, или a0>fg/k'i. При нарушении
этого условия 'движение не начнется. Для интегрирования уравнения (2.22)
введем новую переменную
Тогда
Ё+^ = 0.
§2 4]
СВОБОДНЫЕ КОЛЕБАНИЯ ПРИ ТРЕНИИ СКОЛЬЖЕНИЯ
51
Общее решение этого уравнения имеет вид
£ = а sin (ki -f- е),
т. е.
х = а sin (« + 0 + ^-,
(2.24)
где а и 8 — постоянные интегрирования. Для их определения воспользуемся
приведенными начальными условиями, тогда получим
fg л
« = е=т.
Следовательно, груз будет двигаться по закону:
х—(ао—^-^cos£Z + ^|. (2.25)
Однако это справедливо лишь до тех пор, пока скорость
х = — (а0——\ksmkt (2.26)
остается отрицательной, т. е. до момента ti = n/k.
При этом значение х, соответствующее крайнему левому положению, равно
_fg (a'_fg\_ (а 2fg\
Амплитуда Oi = —Xx первого отклонения влево определяется равенством
Я1 — а0 —
Vg
№ ‘
В рассмотренном интервале времени тело совершит половину колебательного
цикла относительно среднего положения fg/k^-
Дальнейшее (обратное) движение возможно, если
Допустим, что это условие соблюдается; тогда начнется движение вправо при
новых начальных условиях
x = xt = —at, х = 0 при / = 0.
Дифференциальное уравнение движения на этом участке имеет вид
х+*2х=-&. (2.27)
Решение дифференциального уравнения (2.27) при указанных начальных
условиях запишется следующим образом:
х = COsW-||,
* = fai — sin kt (x>0).
\ /
(2.28)
В конце второго участка движения х = 0, откуда следует, что промежуток
времени, в течение которого происходит движение во втором этапе, равен
t2—n!k, т. е. =
52 ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. 1Г
Подставляя значение t = t2 в уравнение (2.28), получим наибольшее откло-
нение в конце второго этапа:
а- а -У^-
аг—аг—^-.
Если при этом а2>^-, то вновь начнется движение влево. Здесь нужно снова
обратиться к дифференциальному уравнению (2.22) и решать его при следую-
щих начальных условиях:
х=а2, х = 0 при / = 0.
Понятно, что при этом вновь приходим R уравнениям (2.24) — (2.26),
в которых а0 следует заменить на а2. Легко заметить, что на каждый полу-
период максимальное отклонение тела от начала координат уменьшается на
величину, равную причем длительность каждого полупериода равна л/й.
Имея в виду сказанное, можно записать следующую последовательность
максимальных отклонений через каждый полупериод:
2fe 2fg
ai=a0--^, a2 = ai—^,
„ _n 2fs n 2fe
a3—°2—^2 , ••• > an — an-l ^2 •
Складывая почленно все равенства, найдем
2fgn
ап = аа—
Таким образом, при сухом трении последовательные амплитуды колебаний
убывают по закону арифметической прогрессии, разность которой равна 2/g/ft2;
период затухающих колебаний при сухом трении равен периоду незатухающих
колебаний 2л/й. Напомним, что при вязком трении амплитуды колебаний
убывают по геометрической прогрессии,
а период затухающих колебаний
больше периода незатухающих ко-
лебаний.
Колебания будут происходить
до тех пор, пока сила упругости сап
в одном из крайних положений не
сделается меньше силы трения fmg:
сап <fmg,
или
a <fS-
Пользуясь выражением для ап,
получим
аа = хо < (2л + 1) .
Это неравенство может служить . для определения числа полуколебаний до
остановки груза, или начального отклонения х0 по известному числу полуко-
лебаний п.
На рис. 2.9 построен график колебаний. Параллельно оси времени про-
ведены две прямые: x—fgjk2 = b и х = — fg!№ = —Ь. Около верхней прямой
располагаются косинусоиды, соответствующие движению влево (нечетные полу-
периоды), а около нижней прямой— косинусоиды, соответствующие движению
§ 2.5]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
53
вправо (четные полупериоды). Если какой-либо полупериод заканчивается
в полосе, расположенной между двумя прямыми, то движение прекращается;
эта полоса называется зоной застоя. «Огибающие» графика движения имеют
вид наклонных прямых.
Задача 2.7. В системе, изображенной на рис. 2.8, коэффициент жесткости
пружины с = 2 кГ!см, вес груза 3 кГ и коэффициент сухого трения /=0,1.
Какому условию должно удовлетворять начальное отклонение х0 груза, чтобы
до полной остановки он совершил не более 10 полных колебаний?
По условию задачи должно выполняться неравенство
х0< (2л+ 1)
где п—число полупериодов. Подставляя сюда п = 20,
с 9
*2 = 981 = 654 сек~2,
т 3
получаем
41/g 41.0,1-981 £
=------654----= 6’15 СМ-
§ 2.5. Вынужденные колебания
Рассмотрим прямолинейное движение материальной точки под
действием восстанавливающей силы и внешней возмущающей силы.
Возмущающая сила может быть произвольной функцией времени,
однако мы ограничимся простейшим, но практически весьма важ-
ным случаем, когда сила изменяется по гармоническому закону.
Пусть проекция возмущающей силы на'ось х равна /fsin(p/ + 6),
где Я —амплитуда и р — частота возмущающей силы, б —началь-
ная фаза. Тогда дифференциальное уравнение движения матери-
альной точки вдоль оси х имеет вид
тх — — сх-\-Н sin (р/4-б),
или
x-)-£2x = /70sin (р(ф-б), (2.29)
где
Решив дифференциальное уравнение (2.29), мы определим закол
движения материальной точки. Общее решение неоднородного
линейного дифференциального уравнения (2.29) равно сумме реше-
ний: частного решения уравнения (2.29) и общего решения одно-
родного уравнения
х + k2x — 0.
Общее решение последнего уравнения мы уже знаем!
Xl — a sin (kt + e),
54 ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. II
где а и е — постоянные интегрирования. Если p=£k, то частное
решение уравнения (2.29) будем искать в виде
ха = Л* sin (р/ + б),
где А* — неизвестная постоянная. Для ее определения подставим
выражения х2 и х2 =— А*р2 sin (pt-\-ty в уравнение (2.29):
— А*р2 sin (р(-)-б) + А*£2 sin (pt + б) = Но sin (pt 4-6),
или
А * (k2 — р2) sin (pt + б) = Но sin (pt + б).
Для тождественного выполнения этого равенства должно быть
д *
№ — рг’
Частное решение имеет вид
x2 = ^-2sin(^ + 6). (2.30)
Следовательно, общее решение уравнения (2.29) запишется
в форме
x = asin (fe^ + e)+fe2^°^sin (p/-j-6). (2.31)
Постоянные а и е зависят от начальных условий. Таким обра-
зом, искомое движение материальной точки является суммой гар-
монических колебаний, происходящих с собственной частотой k,
и гармонических колебаний, происходящих с частотой возмущаю-
щей силы р. Подробно исследуем второе слагаемое в (2.31), опи-
сывающее чисто вынужденные колебания и не зависящее от началь-
ных условий.
Амплитуда чисто вынужденных колебаний равна
А - |,Д°- г (2.32)
I — рг I '
Перепишем решение (2.30), используя формулу (2.32):
х2 — A sin (п^Ц-б) (k>p),
х2 = — A sin (pt + б) = A sin (pt + б — л) (k < р).
Из полученных соотношений следует, что при р</г фаза
вынужденных колебаний совпадает с фазой возмущающей силы;
при р>& вынужденные колебания сдвинуты по фазе от возму-
щающей силы на л.
Проследим зависимость амплитуды вынужденных колебаний
от отношения частот p/k. Для этого преобразуем выражение
. амплитуды вынужденных колебаний
§ 2.5]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
55
где хСт = Н/с — величина статического отклонения точки от поло-
жения равновесия при действии силы,
значению возмущающей силы. Обозна-
чим
Величина ц представляет собой коэф-
фициент динамичности', он показывает,
во сколько раз амплитуда колебаний
превосходит статическое отклонение.
Из графика (рис. 2.10) видно, что при
р/£->1 коэффициент динамичности рез-
равной максимальному
ко возрастет.
Вернемся теперь к общему решению (2.31). Записав его в виде
х = Сг cos kt-(-C2 sin kt+ sin (pt + 6), (2.34)
определим постоянные интегрирования, если х = х0, х = х0 при
t = 0.
Подставив начальные условия в уравнение (2.34) и в выра-
жение для скорости движения
х = — kCx sin kt + kC2 cos kt + cos (pt + 6),
К Рй
получим
С1 = *о-Д^пб, C2 = ^-f^cos6.
Подставляя Сх и С2 в соотношение (2.34), будем иметь
х = х0 cos kt ф-у sin kt —
~ sin ftcos kt+ cos 8 sin kt) + ^-5sin (pi4-6). (2.35)
К -p \ rC ] К p
Такая запись решения позволяет установить, что даже при
нулевых начальных условиях (.го = О, Д, = 0) точка будет совер-
шать колебания, происходящие с собственной частотой; они опре-
деляются членом —Нп (k2 — р2)1 [sin б cos kt Ц-у cos б sin kt'j, при-
чем амплитуда этих колебаний не зависит от начальных условий.
При частоте р, близкой к собственной частоте k, благодаря
сложению двух колебаний близкой частоты, одинаковой ампли-
туды и противоположных по фазе, наступает своеобразное явле-
ние, называемое биением.
56 прямолинейные колебания МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ и
Пусть p/kt^X, тогда выражение (2.35) при хо = О и хо = 0
примет вид (приближенно полагаем р/6=1, но ft2 — р2#=0)
х = tsin (pt + б> - sin + б)ь
ИЛИ '
х = 2^5 sin ^-t cos (р/ + 6). (2.36)
График этого движения представлен на рис. 2.11.
Показанные здесь биения представляют собой колебания, про-
исходящие с частотой р возмущающей силы, причем амплитуда
этих колебаний медленно меняется, следуя также периодическому
закону.
Рис. 2.11.
Рассмотрим теперь случай, когда собственная частота совпа-
дает с частотой возмущающей силы, т. е. p = k. Частное реше-
ние уравнения (2.29) в этом случае нужно искать в виде
x2 — At sin (pt + y). (2.37)
Подставив выражение (2.37) в дифференциальное уравнение
(2.29), получим
2Ар cos (pt + у) — Но sin (pt + 6).
Введя обозначение ф = р^ + у, перепишем это соотношение
в виде
2Ар cos q> = Но sin q> cos (б — у) + 7/0 cos ф sin (б —у).
Это равенство будет тождественно удовлетворено, если
Но cos (б — у) = 0, Hosin (б — у) — 2Ар.
Отсюда
Л ~ 2р ’ Y 0 2
и, следовательно,
х2 sin (pf + 6~y) =- cos (р/ + б).
§ 25]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
5Г
Общее решение имеет вид
х = a sin (pt + е) — ~ cos (pt + б).
При начальных условиях х = х0, х = х0 имеем*)
х = х0 cos pt-\-~- sin pt +Да[cos 6 sin pt — pt cos (pt + 6)]. (2.38)
На рис. 2.12 показан график функции х2. Как видно, при
k = p происходит неограниченное возрастание амплитуды колеба-
ний, причем рост амплитуды линеен q __
во времени. Это явление носит назва- 1*
ние резонанса.
Задача 2.8. Груз М веса Р прикреплен к нижнему концу В вертикально-
расположенной пружины, жесткость которой равна с, а длина в ненапряжен-
ном состоянии 10. Верхний конец пружины А перемещают по закону a sin pt
в вертикальном направлении (рис. 2.13).
Определить вынужденные колебания груза М, приняв /* = 0,4 кГ, с —
= 0,04 кГ/см, /о=30 см, р — 7 сек-1, а = 2 см. Выберем начало координат
в точке О и проведем ось х вертикально вниз. Если 10 — длина пружины
в ненапряженном состоянии, то удлинение пружины равно х — a sin pt—10 и,
следовательно, сила, действующая на груз со стороны пружины, равна
Fx = —с (х — a sin pt — /0).
Дифференциальное уравнение движения имеет вид
или
£4-£2x=g4-/70 sin Р^ + ^,
где
Я Р » ло р •
Введем новую переменную z согласно равенству
_________________ г = х-(Р/с + 10У,
*) Это решение можно получить из (2 35), раскрывая неопределенность,
которая возникает при p-t-k.
58 ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ II
тогда дифференциальное уравнение движения преобразуется к следующей
форме:
= sin pt.
Введение новой переменной г равносильно переносу начала координат
в положение равновесия груза. Вынужденные колебания груза определяются
формулой (2.30):
Подставляя сюда числовые значения параметров, получим
г==4 sin It см.
Так как x=z-j-Р/с-[-1, то
х==(4 sin 7/4-40) см.
В этом случае амплитуда колебаний груза (4 см) вдвое больше амплитуды
колебаний точки подвеса пружины. Заметим, что груз колеблется около сред-
него положения, удаленного от верхнего конца пружины на 40 см; этому по-
ложению соответствует состояние равновесия груза.
§ 2.6. Вынужденные колебания
при наличии вязкого сопротивления
Рассмотрим движение материальной точки вдоль оси х под
действием линейной восстанавливающей силы, вязкой силы сопро-
тивления и возмущающей силы, проекция которой на ось х равна
/7 sin (р/-(-б).
Дифференциальное уравнение движения имеет вид
тх =— cx — bx + H sin (pt-]- б).
Положив c/m = k2, bltn = 2h, = получим
x-|-2/ix + fe2x = /yosin (р( + б). (2.39)
Решение дифференциального уравнения (2.39) складывается из
двух решений: общего решения соответствующего однородного
уравнения и частного решения х2 уравнения (2.39).
Как показано в § 2.3, при k>h решение однородного урав-
нения записывается в виде
х1 = е ht (Сх sin k*t + С2 cos k*t),
где Clt С2 — постоянные интегрирования, a fe* = prfe2 — h2.
Частное решение уравнения (2.39) будем искать в виде
х2 = А sin (pt + y), (2.40)
где А и у — неопределенные постоянные величины. Таким обра-
зом, мы предполагаем, что частное решение описывает колебания
постоянной амплитуды, происходящие с частотой возмущающей
силы.
§ 2.6] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ
5?
Т‘2 = —рМ sin(p; + y)
х2 в уравнение (2.39), получим;
Находя х2 и х2:
х2 = рА cos (pt + y),
и подставляя значения х2, х2,
— р2А sin (pt + у) + 2hpA cos (pt + у) +
+ k2A sin (pt + y) = Ho sin (pt + 6).
Положив р/4~У = Ф и воспользовавшись соотношением
sin (pt 4-6) = sin (ф + 6 — у) = sin q> cos (6 — у) -)-cos cp sin (6 — y),
для определения Л и у будем иметь следующие уравнения:
A (k2 — р2) = Но cos (6 — у), 2phA — Но sin (6 — у),
откуда
Но
(2.41)-
А —
V (^—p^p+Wp2
tg(6-y) = ^. (2-42).
Подставив найденные значения А и у в частное решение, по-
лучим
х2 = г Я|1"_ sin (pt + 6 + у'),
2 К(^2—p2)2+w2
где
у' = у — 6.
Таким образом, общее решение дифференциального уравнения.
(2.39) имеет следующий вид:
х — е~м (Сг sin k*t-\-C2 cos k*t) -|-
+ sin (^ + 6 + y'). (2.43}
у (k2—p2)2 + 4/i2p2
Для определения закона движения материальной точки нужно-
найти постоянные Сх, С2. Пользуясь начальными условиями: х = х0,
х = х0 при t = 0, получим значения постоянных
ci = ^[x0 + hx0-hA sin (6 +у')-Др cos (6 +у')],
С2 = х0 — A sin (6 +у'),
где А — амплитуда вынужденных колебаний.
Подставив значения Сх и С2 в уравнение (2.43), найдем закон
движения материальной точки в рассматриваемом случае:
х = е sin k*t + %оcos k*t^ —
— e~ht -^7 [h sin (6 + y') + p cos (6 + y')] sin k*t +
+ Л sin (6 + y') cos k*t\ ф-Л sin (pt 4-6 + y')’
60
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ и
Следовательно, движение материальной точки складывается:
из свободных затухающих колебаний (первое слагаемое), обуслов-
ленных начальными условиями; из затухающих колебаний (вто-
рое слагаемое), имеющих собственную частоту, но вызванных
действием вынуждающей силы, и чисто вынужденных колебаний
(третье слагаемое). Так как первые два движения с течением вре-
мени затухают, то основным колебанием, определяющим характер
движения материальной точки, является чисто вынужденное ко-
лебание с амплитудой А и частотой р. Следует заметить, что
при наличии сопротивления вынужденные колебания сдвинуты
по фазе относительно возмущающей силы на у'.
Вводя обозначения z — p/k, $ = h/k, перепишем формулу (2.41)
в виде
А = — , 7==^ = Хет ...= (2.44)
Р- K(1-zT+W '
У \ &J k2 &
где хст = Hjk2 = Н/с представляет собой статическое перемещение,
вызываемое постоянной силой Н.
Введем в рассмотрение коэффициент динамичности
р = — = =, (2.45)
хст К(1-г2)2 + 4^
который характеризует динамический эффект, вызываемый вы-
нуждающей силой.
Исследуем зависимость коэффициента динамичности от г —
отношения частот вынуждающей силы и собственных колебаний
в среде без сопротивления, а также от коэффициента (3, харак-
теризующего сопротивление среды. Очевидно, что, найдя зависи-
мость коэффициента динамичности от г и (3, мы тем самым опре-
делим и зависимость от них амплитуды вынужденных колебаний.
Найдем экстремум функции
^ = (1-г2)2 + 4р2г2. (2.46)
Для этого приравняем нулю производную
^- = 2(1-г2) (—2г) + 8р2г = 0. (2.47)
Корнями этого уравнения будут
г1 = 0, г2 = /Г^2р, г3 = -/Т^2Г2. (2.48)
Так как г 5=0, то корень г3 должен быть отброшен. Найдем вто-
рую производную от у
2 = 12г2-4(1-2р2).
§2 6] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ 61
Для гх = 0 при 1— 2р2<0, т. е. при р>|/'2/2,
g = 4(2P2-l)>0
и, следовательно, функция у имеет минимум, а коэффициент ди-
намичности р —максимум. Других действительных корней при
этих значениях р уравнение (2.47) не имеет.
Если р<^г, то для Zj = 0 ^<0- Это значит, что р при
этом имеет минимум. Для корня же г2 = ]/1 — 2р2
g = 8(l-2Р2) > 0,
т. е. при г=г2 коэффициент динамичности имеет максимум.
Заметим, что всегда г2 1 и, только когда р = 0 (среда без
сопротивления), г2=1. Ранее было показано, что при р = 0 и
г3=1 решение (2.40) не имеет смысла и его нужно искать в виде
(2.37).
Максимальное значение коэффициента динамичности найдем,
подставив г2 = ]/1—2р2 в формулу (2.45):
|imax =--J_____ (2.49)
г 2рК1-Р2
На рис. 2.14 показаны кривые, определяющие зависимость
коэффициента динамичности от z = plk. Каждой из кривых coot-.
ветствует определенное значение fi — h/k. Пунктирная линия про-
ходит через точки максимума.
Из рассмотрения этого рисунка следует, что амплитуда вы-
нужденных колебаний при г, достаточно большом и достаточно
малом по сравнению с г=1, очень мало зависит от сопротивле-
ния среды. При г, близких к г=1, влияние сопротивления на
амплитуду вынужденных колебаний весьма существенно.
При ?->со амплитуда вынужденных колебаний асимптотиче-
ски стремится к нулю. Это значит, что при большой частоте воз-
мущающей силы по сравнению с собственной частотой амплитуда
вынужденных колебаний весьма мала.
На рис. 2.15 представлена зависимость сдвига фазы вынуж-
денных колебаний относительно возмущающей силы в зависимо-
сти от г и р. Отметим, что при г=1 сдвиг фазы равен л/2 при
любом значении р. Резонансом при колебаниях в среде с сопро-
тивлением называют вынужденные колебания при z=l, т. е. при
p = k, что отвечает примерно максимальному значению амплитуды
вынужденных колебаний.
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
(ГЛ. II
$ 2.6] ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ ПРИ ВЯЗКОМ СОПРОТИВЛЕНИИ
63
Задача 2.9. Под двигатель В (рис. 2.16) требуется подвести фундамент.
Необходимо определить такую толщину кладки а, чтобы коэффициент дина-
мичности не превышал единицы для всех частот вынужденных колебаний,
передаваемых от двигателя фундаменту. Сопротивление грунта можно схема-
тизировать как реакцию упругих сил F и вязких сил R, вызванных внутрен-
ними силами сопротивления. Отнесенные к единице площади фундамента,
коэффициенты жесткости и вязкости соответственно равны с=2000 Т/л3 и
6 = 60 Т -сек.)аР. Плотность фундамента р = 0,25 Т сек?!м*.
Введем систему координат хОу, выбрав ее начало О в положении равно-
весия центра тяжести фундамента.
Обозначим через S площадь
основания и представим проекцию
вынуждающей силы Q на ось х в
виде QX = H sin pt. Тогда уравне-
ние движения
mw = F -f- R -f- Q + mg
в проекции на ось х дает
aSpx =— cS (х+Л0) —6Sx-f-
+aSpg+// sin pt.
Здесь мы воспользовались очевид-
ными равенствами
m=aSp, Fx = — cS(x-f-X0),
Rx^ — bSx,
где Xo — статическая осадка фунда-
мента.
Приведем уравнение движения
его на aSp и воспользуемся равенством aSpg = c).„:
, b . с Н . ,
х-4---хН-----х= —5— sin pt.
ар ар aSp
Д7
Рис. 2.16.
к нормальному виду. Для этого разделим
Сравнивая с уравнением (2.39), найдем
2ар ’
й2 = —-
ар
Следовательно, безразмерный коэффициент вязкости равен
в=А = —
k 2 К пре
Коэффициент динамичности р при всех частотах р не будет превосходить еди-
ницы, если потребовать, чтобы кривая р (г) не имела максимума при г2 =
= 1—2f}2. Следовательно, должно выполняться неравенство р >= фл2/2 или
b V2
. 2 арС 2
Отсюда получим толщину кладки а:
Ь2
а 2рс •
Подставляя в это неравенство данные числовые значения параметров, получим
3600
а 2 • 0,25 • 2000 м'
64
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ. II
§ 2.7. Электродинамические аналогии.
Понятие об исследовании колебаний материальных систем
с помощью электронных аналоговых машин
Колебательные процессы, происходящие в различных физи-
ческих системах, описываются часто одинаковыми математиче-
скими уравнениями. Это обстоятельство дает возможность уста-
новить аналогию между системами различной физической при-
роды. Наиболее полно эта аналогия установлена между механи-
ческими и электрическими системами.
Рис. 2.19.
Рассмотрим механическую систему с одной степенью свободы,
движение которой описывается следующим дифференциальным
уравнением:
тх 4- Ьх 4- сх = Q (t). (2.50)
Здесь х —координата, т — масса точки, b — коэффициент сопро-
тивления среды, с — коэффициент жесткости пружины, Q(t)—
возмущающая сила. Символически систему, отвечающую уравне-
нию (2.50), изображают обычно схемой, показанной на рис. 2.17.
Рассмотрим теперь электрический контур, в котором индук-
тивность L, омическое сопротивление R, конденсатор емкостью С
и внешний источник энергии э. д. с. Е (/) соединены последова-
тельно (рис. 2.18). Согласно второму закону Кирхгофа сумма
падений напряжений на отдельных участках цепи равна разно-
сти потенциалов на концах зажимов, т. е. э. д. с. источника
г di
энергии. Падение напряжения от индуктивности равно L-^~, где
i — сила тока, падение напряжения от омического сопротивления
равно Ri, а падение напряжения в конденсаторе определяется
§2 7]
ЭЛЕКТРОДИНАМИЧЕСКИЕ АНАЛОГИИ
65
1 г-
равенством -^-q, где q — заряд конденсатора. Следовательно, по
второму закону Кирхгофа будем иметь
или, учитывая, что
1 dt ’

(2.51)
Сравнивая с уравнением (2.50), видим, что колебания меха-
нической системы с одной степенью свободы и изменение заряда
в электрической цепи описываются с точностью до обозначений
совершенно одинаковыми дифференциальными уравнениями. Сле-
довательно, между этими системами можно провести аналогию,
сопоставив заряд q с координатой х, индуктивность L с массой т,
омическое сопротивление R с коэффициентом сопротивления среды,
величину, обратную емкости , с коэффициентом жесткости с и
электродвижущую силу Е (t) с возмущающей силбй Q(t).
Для электрического контура с параллельно соединенными
элементами (рис. 2.19) на основании первого закона Кирхгофа
будем иметь (складываются токи)
w । 1 (* । /“> du • /у»
-R + г j u = 1(0 >
где « — напряжение.
' Дифференцируя по времени, получим
С , I du . I di
+ Tu ~~dE-
Здесь мы имеем другую систему аналогий, в которой коорди-
нате х соответствует напряжение и, массе т соответствует
емкость С конденсатора, коэффициенту сопротивления среды b
отвечает проводимое ь коэффициенту жесткости пружины с—
величина, обратная индуктивности у, и возмущающей силе
Q (/) — скорость изменения тока
3 Н. В. Бутенин и др.
66
ПРЯМОЛИНЕЙНЫЕ КОЛЕБАНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ
[ГЛ. II
Сведем результаты в таблицу электродинамических аналогий.
Механические величины Электрические величины
1-я аналогия: сила- напряжение 2-я аналогия: сила—ток
1. Координата х Заряд q Напряжение и
2. Масса т Индуктивность L Емкость С
3. Коэффициент жесткос- ти с Обратная величина ем- кости —Q- Обратная величина индук- 1 ТИВНОСТИ -д-
4. Коэффициент сопротив- ления среды b Омическое сопротивле- ние R 1 Приводимость
5. Сила Q (/) Э. д. с. Е (t) di Скорость тока
Для того чтобы электродинамическими аналогиями можно было
пользоваться без употребления переходных коэффициентов, доста-
точно выразить все величины в международной системе единиц СИ.
Пользуясь электродинамической аналогией можно для каждой
механической системы построить соответствующую электрическую
цепь, уравнения которой будут с точностью до обозначений сов-
падать с уравнениями движения механической системы. Электри-
ческая цепь, в отличие от механической системы, компактна;
кроме того, процессы, происходящие в ней, хорошо наблюдаются
на осциллографе. Эти соображения лежат в основе конструкции
электронных аналоговых (моделирующих) машин*).
Аналоговые машины имеют набор смонтированных быстро
настраиваемых элементов индуктивностей, емкостей, сопротивле-
ний или других элементов, создающих аналогичный эффект. Сое-
диняя эти элементы в соответствующие цепи, можно определить
все параметры, характеризующие движение механической системы,
для которой собранная цепь является аналогом. В частности,
весьма просто определяются частоты собственных колебаний
системы. Для этого достаточно включить в цепь э. д. с. Ео sin at
и увеличивать частоту о> до тех пор, пока не наступит резонанс.
*) Электронные аналоговые машины выпускаются промышленностью мно-
гих стран, в том числе промышленностью СССР.
§2 7] ЭЛЕКТРОДИНАМИЧЕСКИЕ АНАЛОГИИ ' 67
Соответствующая частота —собственная частота системы. Эта
работа не требует высокой квалификации (сложность работы на
собранной схеме примерно та же, что и сложность настройки
радиоприемника) и может быть выполнена за сравнительно корот-
кий промежуток времени с относительно большой точностью.
С помощью электронных аналоговых машин можно решать
нелинейные задачи, когда линеаризация дифференциальных урав-
нений движения по каким-либо причинам недопустима, а также
задачи, приводящие к линейным дифференциальным уравнениям
с переменными коэффициентами. В заключение отметим, что
в современных аналоговых машинах устанавливается, как пра-
вило, не электродинамическая, а электроматематическая анало-
гия, когда математическим операциям сложения, умножения,
дифференцирования, интегрирования и т. п. отвечает соответст-
вующий электрический элемент. Такие машины более универ-
сальны.
ГЛАВА III
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
§ 3.1. Теорема об изменении количества движения
материальной точки
При интегрировании дифференциальных уравнений движения
в конкретных задачах эти уравнения подвергаются различным
однотипным преобразованиям, зависящим от характера действую-
щих сил. Поэтому целесообразно проделать такие преобразова-
ния в общем виде. Общие теоремы динамики точки и представ-
ляют собой преобразования дифференциальных уравнений дви-
жения, причем в различных теоремах выделены и связаны между
собой те или иные характеристики движений. В результате по-
лучаются удобные зависимости, широко используемые для реше-
ния конкретных задач динамики.
Заметим, что в основном уравнении динамики
mw = F (3.1)
„ dv
масса материальной точки — величина постоянная и что w = ^.
Это позволяет переписать уравнение (3.1) в виде
d4(mv) = F,
откуда следует, что
d (mv) = F dt. (3.2)
Вектор Q=mv, равный произведению массы точки на ее ско-
рость, называется количеством движения материальной точки.
Произведение силы на элементарный промежуток времени ее
действия, т. е. F dt, называемся элементарным импульсом силы.
Уравнение (3.2) выражает теорему об изменении количества
движения материальной точки в дифференциальной форме:
элементарное изменение количества движения материальной
точки равно элементарному импульсу силы, приложенной к этой
точке.
Рассмотрим теперь движение материальной точки на конеч-
ном промежутке времени. Пусть в момент t = 0 скорость точки
? 3.1]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
69
равна v0, а в момент t равна v. Тогда, интегрируя уравнение
(3.2), можно записать
t
mv — mv0 = ^Fdt. (3.3)
о
Интеграл, входящий в правую часть этого соотношения, назы-
вается импульсом силы за промежуток времени [О, I]. Таким об-
разом,
изменение количества движения материальной точки за конеч-
ный промежуток времени равно импульсу силы, приложенной в точке,
за тот же промежуток времени.
Если воспользоваться декартовой системой координат, то бу-
дем иметь
г = xi + у j + zk, v = xi + yj + zk, F = F J + Fyj + Fzk,
где x, у, г —координаты точки, х, у, z — компоненты ее скорости,
Fx, Fy, Fz — проекции силы, a i, j, к —единичные векторы осей
координат. Тогда, проектируя векторное равенство (3.3) на оси
декартовой системы координат, получим три скалярных соотно-
шения:
/ t t
тх — mx0 — ^Fxdt, my — my0 = \)Fydt, mz — mi0 = ^Fz dt. (3.4)
ooo
Здесь, как и ранее, х, у, z — проекции скорости материальной
точки на оси координат в момент времени t, х0, у0, z0 — те же
проекции в момент / = 0, Fx, Fy, Fz — проекции силы F.
Как отмечалось в § 1.2, в общем случае F может быть функ-
цией координат точки, ее скорости и времени, т. е.
F = F (х, у, z, х, у, z, t)
и, следовательно, проекции силы также являются функциями этих
величин:
Fx = Fx(x, у, г, х, у, z, /),
Fu — Fv{x, у, г, х, у, z, 0,
Ег = Ег(х, у, г, х, у, z, t).
Поэтому для фактического вычисления интегралов, с:оящих
в правых частях уравнений (3.4), нужно знать координаты ма-
териальной точки как функции времени. Но определение х, у
и г как функций времени и ееть то, к чему мы стремимся,
решая вторую задачу динамики. Если эти функции откуда-либо
известны, то отпадает необходимость пользоваться уравнениями
(3.4). Таким образом, в общем случае теорема об изменении
количества движения новых возможностей для решения задачи
не открывает.
70
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ III
Однако, если сила является функцией только времени, инте-
гралы в правых частях уравнений (3.4) могут быть вычислены
и можно получить первые интегралы уравнений движения
тх — тх0 = Фг (t), ту — ту0 = Ф2(/), mz — т?0 = ф3 (/), (3.5)
где
t t
Ф} (t) F( dt, Ф2 (t) = ^Fydt,
о о
Ф3 (0 = $F* dt
о
•—проекции импульса силы на оси координат.
Дальнейшее интегрирование также не представляет принци-
пиальных трудностей:
t t
х-х0 = xot + J Ф1 (0 dt, y-yo=-yot + ^ J ф2 (0 dt,
О о
I
z-zo = zot + ^- у Ф3(() dt.
о
Здесь х0, у0, г0 —начальные значения координат в момент вре-
мени t = 0.
Если сила постоянна, т. е. Fx = ЛП Fy=-A2, FZ = A3 (4lt Л2, A3—посто-
янные величины), то
mx—mx0 = Ait, my — my0 = A3t, tnz — mz3 = A^
и
Д /2 Д /2 До/2
х = х0 + х0/ + -2^-, У^Уа + М + -^-, г = г0 + ^+-^~.
В частном случае при z/o = io = O, Л2 = Л3 = 0 будем иметь
тх —тх0 = Л1< (3.6)
и
х=х0-|~Х(/ -f- > (3.7)
т. е. материальная точка совершает равнопеременное прямолинейное движе-
ние вдоль оси х.
Задача 3.1. Определить промежуток времени Т, необходимый для того,
чтобы материальная точка веса Р, Движущаяся по горизонтальной прямой
под действием постоянной силы F, увеличила свою начальную скорость
в п раз. •
Примем прямую, вдоль которой движется точка, за ось х; тогда на осно-
вании (3.6) имеем
у (nv0—v0)= FT,
откуда
Т = -^-(л-1).
Fg
-§ 3 21
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА
71
§ 3.2. Теорема об изменении момента количества движения
материальной точки
Вновь вернемся к основному уравнению динамики (3.1) и
умножим его векторно слева на радиус-вектор точки г, опреде-
ляющий положение материальной точки относительно какой-либо
точки О, которую будем называть центром:
rxmw = rxF. (3.8)
Принимая во внимание, что w = преобразуем левую часть
этого уравнения следующим образом:
dv d , , dr
rxmw = rxm-^ = j (гх mv) — x mv.
TT dr
Ho — v и векторное произведение параллельных векторов
vxmv равно нулю. Поэтому rxmw = -j (rxmv) и уравнение
(3.8) можно записать в виде
^-(rxmv)=rxF. (3.9).
Вектор Ko = rxmv называется моментом количества движения
материальной точки относительно центра (точки О).
Вектор M0 = rxF нам известен из курса статики и представ-
ляет собой момент силы, приложенной к точке, относительно
центра.
Таким образом,
dKn
-^ = мо. (3.10)
Это уравнение выражает собой теорему об изменении момента
количества движения материальной точки:
производная по времени от момента количества движения
материальной точки относительно какого-либо центра равна
моменту силы, приложенной к точке, относительно того же
центра.
Векторное уравнение (3.10) эквивалентно трем скалярным
равенствам.
Принимая точку О за начало системы координат xyz и запи-
сывая векторные произведения в виде определителей третьего
порядка, вместо (3.10) получаем
i j k
х у г ,
Р X Ру р£
i 1 k
xyz
mx my tnz
d
dt
72
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ III
откуда
т ~ = уРz - zFy,
m^(zx — х2) = zFx — хРг,
m^(xy-yx) = xFy~yFx.
(З.И)
Полученный результат можно сформулировать следующим образом:
производная по времени от момента количества движения
материальной точки относительно какой-либо оси равна моменту
силы, приложенной к точке, относительно той же самой оси.
Как видно из уравнений (3.11), при их интегрировании необ-
ходимо вычисление интегралов от правых частей. Однако вычис-
ление этих интегралов возможно только тогда, когда х, у и z
известны как функции времени, но тогда отпадает вообще надоб-
ность в применении равенств (3.11).
Тем не менее существуют случаи, когда теорема об изменении
момента количества движения дает возможность эффективно
решать задачи динамики.
К ним относится прежде всего случай действия центральной
силы. Этим термином мы будем пользоваться применительно
к любой силе, линия действия которой проходит через некоторую
фиксированную точку пространства *) (полюс). Так, например,
при изучении движения Земли в Солнечной системе на Землю
действует сила притяжения Солнца, все время направленная
к центру Солнца.
Изучим действие центральной силы. Момент силы относительно
точки, через которую проходит линия действия, тождественно
равен нулю. Следовательно, согласно равенству (3.10) момент
количества движения материальной точки относительно полюса
является постоянной величиной:
Ко = г х mv = const.
(3.12)
Таким образом, мы получим сразу три первых интеграла дви-
жения:
m (r/z - zy) = clt
m (zx — xz) = c2,
m {xy - yx) = c3.
(3.13)
На основании этих результатов можно сделать некоторые
общие выводы о характере движения материальной точки.
*) В § 3,5 будет дано несколько более узкое определение центральной
силы.
§3 2]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА
73
Для этой цели введем понятие секторной скорости. Секторная
скорость вводится как вектор, характеризующий быстроту изме-
нения площади поверхности, описываемой радиусом-вектором.
Пусть в момент времени t материальная точка находится
в точке А траектории, а в момент времени t-\-Ы — в точке At
(рис. 3.1). Площадь До треугольника OAAt равна половине мо-
дуля векторного произведения радиуса-вектора г на вектор пере-
мещения Ar = г (i + Д/) — г (0, т. е.
До = у | г х Дг I.
Разделив обе части этого соотношения на Д/ и переходя к пре-
делу при Д/->0, получим
<7 = lim S = lim 4lrxSI = -flrxvl> -(3.14)
д/-»о д/->о z I I z
так как lim д-? = v — скорость точки в момент времени t.
Д/->0
Формула (3.14) определяет модуль секторной скорости. Заме-
тим, что величина секторной скорости может быть вычислена как
площадь треугольника, по-
строенного на векторах г
и V. За направление век-
тора секторной скорости
примем направление век-
торного произведения ра-
диуса-вектора на скорость
точки. Тогда вектор сек-
торной скорости равен
q = y(rxv), (3.15)
т. е. секторная скорость равна половине векторного произведения
радиуса-вектора точки на ее скорость.
Сравнивая (3.15) с основным выражением для Ko = rxniv,
можем написать интеграл (3.12) в следующей форме:
Ко = 2mq = const. (3.16)
Следовательно, в случае действия центральной силы сектор-
ная скорость точки есть постоянная величина, т. е. радиус-вектор
точки описывает равные площади в любые одинаковые промежутки
времени. Этот результат называется законом площадей. Но, кроме
того, из (3.16) следует, что траектория точки является плоской
кривой. В самом деле, вектор q сохраняет постоянное направле-
ние в пространстве, поэтому на основании формулы (3.15) можно
74
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ ИГ
утверждать, что вектор г будет все время расположен в пло-
скости, перпендикулярной к вектору q, т. е. траектория точки
лежит в этой плоскости *).
Предположим, что движение происходит в плоскости и поло-
жение точки определяется полярными координатами г и ф. Тогда
г = гг°, v = гг°-J-r<fр° (том I, § 9.4) и формула (3.15) может быть
записана в виде
q = ~2 г2ф (г°хр°) = у г2фк, (3.17>
где к = г°хр° — единичный вектор, перпендикулярный к плоскости,,
в которой происходит движение.
Если вектор q является постоянной величиной, то его проек-
ция на направление, определяемое направлением вектора к, также
постоянная величина, т. е.
<7* = уГ2Ф = с, (3.18)
где с —постоянная величина.
Соотношение (3.18) называется законом площадей. Это соотно-
шение может быть получено и другим путем. Если плоскость,
в которой расположена траектория, будет плоскостью ху, то
вместо векторного равенства (3.16) можно записать
2т<?г = т (ху — ух) = const,
или
1 . . ..
<7z = у (ху - ух) = с,
где с —постоянная величина.
Так как в полярных координатах
x = rcos<p, r/ = rsin<p,
то, принимая во внимание, что
х = г cos <р — гф sin ф, у = г sin ф 4-гф cos ф,
получим
1 2-
<7г = у Г2ф = С.
*) Возможно и другое доказательство. Умножим обе части каждого и»
уравнений (3.13) на х, у, г и сложим. В результате получим
С1Х + С1У + сз2 = 0.
Это означает, что координаты точки удовлетворяют уравнению плоскости.
Следовательно, траектория есть плоская кривая.
'§ 3.2]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВА
75
Задача 3.2. Траектория наиболее удаленной от Солнца планеты Плутон
имеет вид эллипса, причем расстояние от Солнца до Плутона меняется от
4,46 • 10s км до 7,4 • 109 км (рис. 3.2). Определить отношение между макси-
мальной и минимальной скоростью Плутона.
Секторные скорости точки, движущейся по эллипсу, в моменты прохожде-
ния через положения максимального и минимального удаления одинаковы:
1 1
— и г • = — и . г
2 max min 2 min max •
Следовательно, искомое отношение составляет
^max /^mln = rmax /rminj
т. е.
ymax/%in = 7,4/4,46= 1,66.
Задача 3.3. Шарик, привязанный к нерастяжимой нити, скользит по глад-
кой горизонтальной плоскости; другой конец нити втягивают с постоянной
скоростью и в отверстие, сделанное на плоскости. Определить движение ша-
рика, если известно, что в начальный момент нить расположена по прямой,
расстояние между шариком и отверстием равно /?, а проекция начальной ско-
рости шарика на перпендикуляр к направлению нити равна о0 (рис. 3.3).
На шарик действует сила, направленная вдоль нити. Так как эта сила
центральная, то момент количества движения шарика относительно точки О
является постоянной величиной и справедливо соотношение (3.18).
Постоянную с найдем из начальных условий: при Z = 0 r — R, <f = v0/R,
Подставляя эти выражения в (3.18), находим
/?Фо = ^оЯ-
Таким образом, для всего последующего процесса движения имеем *•
г2ф = Rva,
По условию задачи скорость, с которой втягивается нить, равна и, откуда
следует, что ? = —и. Приняв во внимание начальные условия, после интег-
рирования получим
r = R — ut.
Тогда уравнение для определения ф примет вид
dq __ Rv0
dt ~ (R—uty'
76
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ III
Интегрируя и имея в виду, что ф = 0 при t=0, находим
vet
ф R — иГ
Чтобы построить траекторию шарика, исключим из уравнений для г и <р
время /; тогда получим величину радиуса-вектора г в функции полярного
угла <р:
r=_E^L_
ucp uq
Траектория шарика представляет собой свертывающуюся спираль. С прибли-
жением шарика к началу координат угол ср растет все быстрее и быстрее,
т. е. скорость вращения радиуса-вектора возрастает. При t -> R/u эта скорость
стремится к бесконечности.
§ 3.3. Работа силы. Мощность.
Перейдем к понятию работы, с помощью которой мы получим
еще одну общую теорему динамики материальной точки.
В элементарном курсе физики понятие работы вводится сле-
дующим образом. Пусть материальная точка М движется по пря-
мой линии ВС и F — некоторая
постоянная по модулю и направ-
лению сила, приложенная к точ-
ке М. Будем считать, что точка
М движется в одном направле-
нии от положения ЛК до поло-
жения М2. Обозначим наимень-
ший угол между силой F и
скоростью v точки М через а
(рис. 3.4). Тогда работой постоянной силы F на прямолинейном
отрезке MtM2 называют произведение модуля силы на величину
перемещения з = Л11Л12 и на косинус угла между ними
Alt2 = Fs cos~b. (3.19)
Конечно, это равенство можно записать в форме скалярного
произведения
41>2 = F-s, (3.20)
где s = МгМ2 — вектор перемещения точки.
Напомним, что единицей измерения работы в системе СИ
является джоуль (1 дж= \ нм), а в технической системе — ! кГм
(1 кГм 9,81 дж).
Приведенное определение работы силы применимо только
в том случае, если сила постоянна по модулю и направлению,
а точка приложения силы перемещается прямолинейно.
Перейдем к общему определению работы силы, считая, что
сила может изменяться по модулю и направлению, а точка М
§3 3]
РАБОТА СИЛЫ. МОЩНОСТЬ
77
приложения силы F перемещается по любой криволинейной тра-
ектории ВС от до М2 (рис. 3.5, а). Разобьем отрезок кривой
МгМ2 на п произвольных, но малых участков, обозначив длину
участка с номером k через As*. Не внося больших погрешностей
в вычисление, можно считать каждый участок прямолинейным
отрезком и что при перемещении точки /И вдоль этого участка
сила F остается постоянной по модулю и направлению. Тогда
согласно формуле (3.19), работа силы на k-м участке будет при-
ближенно равна Fk cos ак As*, а на всем пути от ЛД до М2 —
сумме работ на отдельных участках
41,2^ У F* cos a* As*.
k = i
Точное значение работы получим, переходя к пределу, при
условии, что число участков п неограниченно возрастает, а длина
каждого участка As* неограниченно убывает:
п
Л1>2 = lim У, F* cos a* As*.
As ^O й
Такой предел называется криволинейным интегралом первого
рода по дуге МГМ2 и обозначается следующим образом *):
Л112= Feos a ds. (3.21)
Для того чтобы, пользуясь формулой (3.21), вычислить работу
силы, нужно выразить произведение F cos а как функцию длины
дуги s. В подавляющем большинстве случаев это очень трудно
*) Происхождение этого термина очевидно: подынтегральная функция
F cos а вычисляется на кривой, а в качестве переменной интегрирования
берется длина дуги s.
78
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ III
выполнить, поэтому обычно пользуются криволинейным интег-
ралом второго рода. Для того чтобы сделать этот переход, вве-
дем в рассмотрение элементарную работу силы (это понятие имеет
самостоятельное значение, и мы будем неоднократно пользовать-
ся им).
Под элементарной работой d'A силы F понимается выражение,
стоящее под знаком интеграла (3.21):
d'A = F cos a ds. (3.22)
В кинематике было показано, что дифференциал пути ds равен
модулю дифференциала радиуса-вектора г, т. е. ds — \dr\. Сле-
довательно, элементарную работу силы можно представить сле-
дующим образом:
d'A — F | dr | cos a,
или, через скалярное произведение векторов F и dr,
d'A^F-dr. (3.23)
Теперь, сравнивая выражения (3.23) и (3.20), можно опреде-
лить элементарную работу силы как работу ее на прямолиней-
ном перемещении dr при условии, что величина и направление
силы на этом перемещении не меняются. Напомним, что dr =
— vdt. Это означает, что вектор dr совпадает по направлению
с вектором скорости v точки (рис. 3.5, б).
Запишем выражение (3.23) через проекции векторов, входя-
щих в скалярное произведение:
d'A =FX dx-\-Fy dy-\-Fz dz. (3.24)
Даже в тех случаях, когда сила F зависит только от поло-
жения точки М, т. е. от координат х, у, z точки М, правая
часть этого равенства не представляет, как правило, полный
дифференциал некоторой функции координат А (х, у, г). Поэтому
в обозначение элементарной работы d'A после буквы d ставится
наверху знак «штрих» *) (в § 3.5 будет рассмотрен особый класс
сил, для которых правая часть равенства равна полному диффе-
ренциалу функции координат).
Все три выражения (3.22), (3.23) и (3.24) для элементарной
работы силы эквивалентны. Поэтому, пользуясь равенствами (3.21),
(3.22) и (3.24), получим другую формулу для вычисления работы
силы F на отрезке MjM2 дуги ВС
Л112= J FxdxA-FydyA-Fzdz. (3.25)
м ,м2
*) В некоторых книгах элементарная работа обозначается символом 6Д.
В настоящем руководстве символ 6.4 применяется для обозначения работы
силы на виртуальном перемещении 6г (см. § 18.3).
§3 3]
РАБОТА СИЛЫ МОЩНОСТЬ
79
Правая часть этого равенства называется криволинейным ин-
тегралом второго рода (все функции Fx, Fy и Fz вычисляются
на кривой МгМ2, а дифференциалы координат dx, dy, dz связаны
между собой через ее уравнение).
Если сила F зависит только от положения точки, т. е. от
координат х, у, z точки М приложения силы, то работа вычис-
ляется непосредственно по формуле (3.25) и при этом совершенно
не нужно знать закон движения точки М по кривой. Если же
сила F зависит не только от координат точки приложения, но
и от ее скорости и от времени t, то для вычисления работы
силы нужно знать уравнения движения точки
x = x(0. y = z = z(t). (3.26)
Отсюда
dx = xdt, dy = ydt, dz — zdt. (3.27)
Подставив в формулу (3.25) вместо координат точки их зна-
чения из (3.26), вместо проекций скорости производные по вре-
мени от этйх величин и вместо дифференциалов координат их
значения из (3.27), мы сведем криволинейный интеграл (3.25)
к обычному определенному интегралу
Л,2= $ (Fx^ + Fyy + P^)dt, (3.28)
п
где и ^ — моменты времени, в которые точка М проходит
положения и М2 соответственно (см. рис. 3.5, а).
Пусть теперь на материальную точку М действует несколько
сил Fb F2, ..., F„. Легко доказать (читатель без труда сделает
это самостоятельно), что работа равнодействующей сил, приложен-
ных к материальной точке, на некотором перемещении равна сумме
работ составляющих сил на том же перемещении
Д = Д1 + Д2 + - • • +
Прежде чем перейти к примерам, рассмотрим один частный
случай, когда действующая на точку М. сила сохраняет постоян-
ное направление и модуль (F = const). Вычислим работу такой
силы при перемещении точки М по некоторой траектории ВС
от положения /И, до положения /И,2 (рис. 3.6, а). Для этого
воспользуемся формулой (3.21), учтя, что F cos ads = F dr.
Имеем
Alt 2 = J F-dr.
м,мг
Вынесем постоянный множитель F за знак интеграла и при-
мем во внимание, что при движении точки /11 от ЛД до Л1а
80
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ III
радиус-вектор г меняется от гх до г2 (см. рис. 3.6, а). Тогда
последовательно получим
A,2 = f-$ dr = F-(r2-r1),
или, учитывая, что г2 —r1 = M1M2,
2 = F • /И1Л12 = Fs cos а,
где s = M1M2 и а —угол между неизменным направлением силы F
и вектором перемещения М^М2-
Так как последнее равенство совпадает с (3.19), то это озна-
чает, что при постоянной силе формулу (3.19) можно применять
при перемещении точки Л1 по любому криволинейному пути,
если только под s понимать кратчайшее расстояние между началь-
ным и конечным положе-
этой
ниями точки приложения
силы.
Применим полученный
вывод к вычислению ра-
боты силы тяжести P = mg.
Сила тяжести направлена
вертикально вниз; произ-
ведение s cos а равно
модулю вертикальному
ремещению Н точки М
(рис. 3.6, б). Поэтому
Alfi = ±PH, (3.29)
т. е. работа силы тяжести
равна произведению моду-
силы на вертикальное перемещение точки, взятому со
по
пе-
ля
знаком «плюс», если точка М опускается, и со знаком «минус», если
точка М поднимается. Формулой (3.29) для вычисления работы
силы тяжести мы будем неоднократно пользоваться в дальнейшем.
Рассмотрим две задачи на непосредственное применение полученных ранее
формул.
Задача 3.4. Проекции силы определены равенствами
Fx=—py, Fy = px, Fz = 0,
где р — некоторое положительное число, ахи у — координаты точки приложе-
ния силы F. Определить работу силы F при движении точки приложения ее
от начала координат О до точки М с координатами х, у в трех случаях:
1) точка приложения силы перемещается от О к А! по кратчайшему пути;
2) точка приложения силы перемещается сначала по оси х, а затем по прямой,
параллельной оси у; 3) точка приложения силы перемещается сначала по оси у,
а затем по прямой, параллельной оси х (рис. 3.7).
§33]
РАБОТА СИЛЫ. МОЩНОСТЬ
81
Прежде всего заметим, что сила F перпендикулярна к радиусу-вектор у г
точки приложения силы. Для того чтобы доказать это, достаточно составить
скалярное произведение векторов г и F. Имеем
г • f =xFx + yFy + zFz = x(— ру) + У (px)=0.
Так как скалярное произведение равно нулю, то векторы г и F перпенди-
кулярны *). Отсюда следует, что при движении точки по первому пути от О
до М по прямой ОМ работа Ai силы F будет равна нулю. Покажем это ана-
литически, пользуясь формулой (3.25). Для этого напишем прежде всего урав-
нение прямой ОМ
y = kx,
где k — угловой коэффициент. Отсюда
dy = k dx.
Применим теперь формулу (3.25), учтя при
этом заданные проекции сил, уравнение прямой ОМ
и значение dy. Последовательно получим
Д1= ( Fxdx + Pydy-\rPzdz= $ (— py)dx-F
ом ом
Рис. 3.7.
X
-ф (рх) dy — j [(— pkx) + (рх) k] dx = 0.
о
Во втором случае разобьем весь путь интегрирования на два участка:
от О до В и от В до М (см. рис. 3.7). На первом участке от О до В у = 0
и dy = 0, на втором участке от В до М х = const и dx = 0. Имеем
х у у
Д2 = $ = + $ =<\Pxdx+<\Pydy= \pxdy = pxy.
ом о'в вм о о о
В третьем случае разобьем весь путь интегрирования тоже на два участка:
от О до С и от С до А1 (см. рис. 3.7). На учгстке от О до С х=0 и dx — 0,
на втором участке от С до М у = const и dy=0. Имеем
У X X
Аз= $ = $ + $ =\ру dy + \Fx'dx = ^(—py)dx= — pxy.
ом ос см о о о
Итак, работа рассматриваемой силы F на первом пути равна нулю, на
втором пути рху и на третьем пути — рху. Этот пример наглядно показывает,
что в общем случае работа силы зависит не только от начального и конечного
положений точки приложения силы, но также и от пути, по которому эта
точка перемещается. Отметим еще, что во всех трех случаях данного примера
для вычисления работы силы не нужно знать закона движения точки, ее массу
и скорость.
Задача 3.5. Вычислить работу силы сопротивления, действующей на
корабль, за время, в течение которого скорость корабля после остановки дви-
гателей уменьшится вдвое (см. задачу 1.7).
Так как сила сопротивления направлена в сторону, противоположную дви-
жению корабля, то угол а=180°. Пользуясь формулой (3.21) и значением
*) Силы такой структуры встречаются весьма часто (следящие силы, дей-
ствующие на упругие стержни, силы радиальной коррекции в гироскопиче-
ских устройствах и т. п.). См., например, Мерки нД. Р. Введечие в теорию
устойчивости движения, изд. 2-е. —М : Наука, 1976.
82
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ. III
„ / dx'
модуля СИЛЫ F, получим I Vx = 2l
А =— а j vzdx = — a j vl dt,
0
где t — значение времени, при котором скорость корабля уменьшилась вдвое.
Для дальнейших вычислений нужно знать закон движения корабля.
Воспользуемся результатами задачи 1.7 (стр. 31). При решении этой задачи
была установлена следующая зависимость скорости корабля от времени t
(см. равенство (1-36)):
v - mv° .
х т + <хг>(/
Подставив это выражение для скорости в последнее равенство, будем иметь
т3и°;
А = ~а \ —I'1—» dt.
J (m + апоО3
о
После интегрирования получим выражение для работы как функции времени
1________11
2 [(m-|-at>(/)2 maJ’
Пользуясь выражением для скорости, найдем
(3.30)
mA-avot = —
v
Теперь равенство (3 30) приводится к виду
Д==®([,2_1,2). (331)
Для того чтобы найти работу силы за время, в течение которого скорость
уменьшится вдвое, нужно в последнем равенстве положить о = и0/2. Получим
Д = —-|.,ОТ2
О
В отличие от предыдущей задачи, здесь работа силы зависит от массы н
скорости тела.
В § 3.4 будет показано, что формула (3.31), полученная здесь путем ана-
лиза конкретной задачи, является общей для любых сил, действующих на
материальную точку.
Остановимся теперь кратко на понятии мощности силы. В эле-
ментарном курсе физики мощность определяется как количество
работы, производимой в единицу времени. Это определение при-
менимо, конечно, только в том случае, если в равные промежутки
времени сила производит равные работы. Нам остается распро-
странить это определение на общий случай, когда работа произ-
водится не равномерно.
Вычислим работу силы F от некоторой фиксированной точки ML
до точки М (см. рис. 3.5а)
. А ='5 Fxdx-\-Fydy-vFsdz.
§3 3]
РАБОТА СИЛЫ. МОЩНОСТЬ
83
При движении точки М работа А силы F будет с течением
времени t меняться. Для того чтобы получить работу А как
явную функцию времени t, достаточно воспользоваться форму-
лой (3.28), заменив в ней фиксированный верхний предел интег-
рирования /2 на переменный предел t:
t
A (t) = (Fxx + Fyij + Fzt) dt. (3.32)
Теперь мощность N силы F легко определяется как скорость
изменения работы:
lim
м — о
АЛ dA
At dt ’
(3.33)

где А рассматривается как функция времени t.
Легко видеть, что полный дифференциал работы, выраженной
как функция времени t по формуле (3.32), равен элементарной
работе силы d'A. Действительно, если рассматривать работу как
функцию времени t, то, пользуясь формулой (3.32), найдем
dA (/) = (Fxx + Fvij + Fzz) dt ~ Fx dx A- Fу dy A- Fz dz,
что совпадает с выражением (3.24) для элементарной работы.
Таким образом, имеем
dA(f)=d'A, (3.34)
или, пользуясь равенством (3.23),
dA(/) = F-dr. (3.35)
В этих равенствах предполагается, что правые части выражены
с помощью соотношений (3.26) и (3.27) через время t. Теперь
мощность W силы F можно записать следующим образом:
или
дг = F v =FxxA-FyijA-Fzz, (3.36)
т. е. мощность W равна скалярному произведению силы F на
скорость v точки приложения силы.
Теперь под знак интеграла в формулу (3.28) можно внести
мощность:
^2
Alf2 = \N (t)dt. (3.37)
ц
Если изменение работы происходит равномерно, т. е. мощ-
ность постоянна, то A=Nt и тогда
д
N=~. (3.38)
84
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ ИГ
В этом случае, как уже отмечалось, мощность равна количе-
ству работы, производимой в единицу времени.
Единицей измерения мощности в системе СИ является ватт
(1 em=l дж/сек), а в технической системе —1 кГм-сеьг1. В тех-
нике применяются также более крупные единицы мощности:
1 кет = 1000 ет и так называемая лошадиная сила (1 л. с. =
= 75 кГм сек).
§ 3.4. Теорема об изменении кинетической энергии
Найдем связь между работой сил, приложенных к материаль-
ной точке, и изменением скорости точки. Для этого воспользуемся
основным уравнением динамики
dv с
т Щ =
где F — равнодействующая всех сил, приложенных к материаль-
ной точке. Умножим обе части этого равенства скалярно на диф-
ференциал радиуса-вектора dr.
m~J-dr = F-dr. (3.39)
В правой части стоит элементарная работа d'A равнодейст-
вующей всех сил, приложенных к материальной точке; левую
часть можно представить в следующей форме:
dv , dr , , , fmv2\
т ,, • dr = т-п- dv — ту av=d -д- ;
dt dt \ 2 J
при этом учтено, что скалярный квадрат вектора равен квадрату
его модуля (y-v = v2). Теперь равенство (3.39) примет вид
d(^) = dM. (3.40)
Половина произведения массы точки на квадрат ее скорости
называется кинетической энергией материальной точки
Т = т^. (3.41)
Уравнение (3.40) дает дифференциальную связь между кине-
тической энергией и элементарной работой: полный дифференциал
кинетической энергии материальной точки равен элементарной
работе всех действующих на эту точку сил.
Будем рассматривать все члены, входящие в равенство (3.40),
как функции времени t. Тогда, учитывая соотношения (3.33),
(3.34) и деля обе части равенства (3.40) на dt, получим
Ж)”"’ <3-«)
§3 5]
СИЛОВОЕ ПОЛЕ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
85
т. е. полная производная по времени от кинетической энергии'
материальной точки равна суммарной мощности всех действую-
щих на точку сил.
Пусть теперь материальная точка М перемещается по кри-
вой ВС от положения М1 до положения Мг (см. рис. 3.5, а).
Обозначим через vt и v2 скорость точки М в положениях Мг и
М2 соответственно и проинтегрируем обе части равенства (3.40)-
по кривой Л41Л42:
J У d'A.
М,М2 М,М2
Правая часть этого равенства равна работе ЛЬ2 силы F на-
пути МгМ2, при вычислении левой части следует иметь в виду,,
что криволинейный интеграл от полного дифференциала некото-
рой функции равен самой функции. Таким образом, будем иметь
= (3.43)
т. е. изменение кинетической энергии материальной точки при
переходе ее из начального в конечное (текущее) положение равно
сумме работ на этом перемещении всех сил, приложенных к точке.
С помощью только что доказанной теоремы об изменении кине-
тической энергии можно решать следующие две основные задачи.
В первой определяется скорость материальной точки в конце
или начале движения. Решение этой задачи с помощью равен-
ства (3.43) имеет смысл, конечно, только в том случае, если
работу всех сил, приложенных к материальной точке, можно
вычислить, не зная закона движения, т. е. не интегрируя урав-
нения движения. К задачам второго типа относится вычисление
работы силы по заданной скорости. Использование формулы (3.43)
для решения задач такого ,рода особенно полезно в тех случаях,,
когда трудности, связанные с определением закона движения и
вычислением интеграла (3.28), сравнительно велики (см. задачи 3.12
и 3.13) или когда неизвестна аналитическая зависимость силы
(см. задачу 10.4).
§ 3.5. Силовое поле. Потенциальная энергия
В этом параграфе рассматриваются позиционные силы, кото-
рые зависят только от положения материальной точки в прост-
ранстве.
Будем называть силовым полем область (часть пространства),
в каждой точке которой на помещенную в ней материальную
точку действует сила, однозначно определенная по величине
и направлению в любой момент времени. Таким образом, в
86 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ [ГЛ III
силовом поле должна быть известна одна векторная функция F,
зависящая от радиуса-вектора точки г и времени t’.
F = F(r, t)
или три скалярные функции — проекции силы F
Fx = Fx(x, у, г, 0. Fy = Fy(x, у, г, t), F2-=Fz(x, у, z, t),
где х, у, 2 —координаты точки.
Силовое поле называется нестационарным, если сила F зави-
сит явно от времени t, и стационарным, если сила не зависит
от времени / явно. В дальнейшем будем рассматривать только
стационарные силовые поля, когде сила зависит только от поло-
жения точки, т. е. от ее радиуса-вектора
F=F(r),‘
а ее проекции являются функциями координат точки
Fx = Fx(x, у, г), Fy — Fv(x, у, г), Fz = Fz(x, у, г). (3.44)
Отметим два общих свойства таких полей:
1. Работа сил стационарного поля зависит в общем случае
от начального Мг и конечного М2 положений и траектории, но
не зависит от закона движения материальной точки по траекто-
рии.
2. Имеет место равенство
^2.1 ~ ^i,2> (3.45)
где A1j2 —работа сил стационарного поля при движении мате-
риальной точки от Mi к Л42, а А2, х — работа сил поля при дви-
жении точки по той же траектории в обратном направлении от
М2 к
Первое свойство следует непосредственно из формулы (3.25),
а второе — из формулы (3.21) (модуль и направление силы F
в каждой точке траектории не зависят от направления движения
и времени t, а угол а между скоростью v и силой F при изме-
нении направления движения перейдет в л —а). Заметим, что
для нестационарных силовых полей эти свойства не имеют места.
Рассмотрим какое-нибудь стационарное поле и вычислим работу
сил поля при перемещении материальной точки из положения Mt
в положение М., по двум различным траекториям (рис. 3.8).
Работу сил поля при движении по первой траектории обозначим
через А}, г, а работу сил поля при движении по второй траек-
тории обозначим через А]И2. В общем случае эти работы не равны
между собой:
А], 2 7= Ацг
„(см. задачу 3.4).
§3 5] ' СИЛОВОЕ ПОЛЕ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
Среди стационарных силовых полей важное место занимают
поля, работа сил которых не зависит от траектории (пути) дви-
жения материальной точки и определяется только положением
начальной и конечной точек пути. Такие силовые поля называ-
ются потенциальными (консервативными). Согласно определению*
для потенциальных сил работа не зависит от пути и,
следовательно, для них имеет место равенство М}
А>\ 2 = А^2 = А1<2, (3.46)
где I и II — любые пути, по которым материаль- \ \
ная точка может перейти от к М2, а Л12— \ W
общее значение работы. \ \
Пусть точка М с координатами х, у, z яв-
ляется точкой в области заданного потенциаль-
ного силового поля. Выберем в этом же силовом рис gg
поле произвольную точку Мо, зафиксируем ее
положение и назовем нулевой точкой. При движе-
нии материальной точки от положения М до нулевой точки Мо
работа сил потенциального поля будет зависеть только от поло-
жения точки М, т. е. от ее координат х, у, г, так как положе-
ние точки Л40 неизменно, а работа сил потенциального поля не
зависит от пути. Следовательно, работа сил потенциального поля
Амм* при движении материальной точки от точки поля М до
точки Мо является некоторой функцией координат х, у, z точки М.
Эта функция называется потенциальной энергией и обозначается
греческой буквой П. По определению
П (х, у, z)—Amm0', (3.47)
при этом предполагается, что функция П (х, у, г) однозначна и
непрерывна вместе со своими производными до второго порядка
включительно.
Из приведенного определения потенциальной энергии вытекает,
что нулевая точка —это точка, в которой потенциальная энергия
условно принимается равной нулю.
Покажем, что потенциальная энергия определяется с точностью
до аддитивной постоянной.
Действительно, выберем вместо точки Л40 другую нулевую
точку — точку Ми и обозначим соответствующую потенциальную
энергию через ГР. По определению будем иметь
П* = А
1 пммр
Так как работа сил потенциального поля не зависит от пути,
то выберем путь от М до М(- так, чтобы он проходил через точку
88
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ. III
Л40 (рис. 3.9). Разбивая весь путь от М до AfJ на два участка:
от М до Мд и от Л40 до М*, получим
П * ~ I. ./ -4- А.. ..*
ММо 1 AfoAf о •
Первое слагаемое равно потенциальной энергии П при старой
нулевой точке Мд, а второе слагаемое постоянно (не зависит от
координат х, у, z точки М). Обозначая это слагаемое через С,
получим
п* = п + с,
что и доказывает сделанное замечание.
Предположим, что потенциальная энергия силового поля изве-
стна, т. е. известно значение функции П в каждой точке области
существования силового поля. Найдем, чему равна работа сил
Рис. 3.10.
потенциального поля при переходе материальной точки из поло-
жения Мх в положение М2. Для вычисления работы выберем
путь от точки Mi до точки Мо проходящим через точку М2
(рис. 3.10). Разбивая путь МгМ2Мд на два участка МгМ2 и /И2Л10,
получим
AmiM„ = АмгМг + Ам2м0-
По определению Ам,м(, = П1, а АЛ(2Л1о = П2, где Щ —потен-
циальная энергия в точке П2 — потенциальная энергия
в точке /И2, следовательно,
А m,m, -- П1 — П2, (3.48) i
т. е. работа сил потенциального поля при перемещении мате-
риальной точки равна разности потенциальных энергий в началь-
ной и конечной точках пути.
Силовое поле задается обычно проекциями силы на оси коор-
динат, т. е. функциями (3.44).
Для того чтобы решить вопрос о том, является ли это данное
силовое'поле потенциальным, докажем предварительную теорему;
§ 3 5]
СИЛОВОЕ ПОЛЕ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
89-
Для того чтобы силовое поле (3.44) было потенциальным, необ-
ходимо и достаточно, чтобы существовала такая непрерывная-
однозначная функция координат П (х, у, z), называемая потен-
циальной энергией поля, частные производные от которой удовлет-
воряют равенствам
х~ дх ’ ду ’
= (3-49)
Докажем сначала необходи-
мость этих условий. Предполо-
жим, что силовое поле является
потенциальным, т. е. работа от
пути не зависит.
Вычислим работу сил поля
на перемещении точки из поло-
жения М с координатами х, у, z
в положение Мг с координатами
хДДх, у, г (рис. 3.11), выбрав за путь прямолинейный отрезок,,
соединяющий точки М и (он параллелен оси х). Пользуясь
формулами (3.48) и (3.25), получим
П (х, у, г)-П(х + Дх, у, г) = ( Fxdx-\-Fydy-\-Ftdz.
'мм,
Так как при выбранном пути координаты у и г не меняются, то
dy = dz = 0 и полученное выражение примет вид
* +Дх
$ Fxdx = II(x, у, г) —П(х4-Дх, у, z).
X
По теореме о среднем
х4-Ах
Fx (х, у, z) dx = Fx (х + 6 Дх, у, г)Дх,
X
где число 0 удовлетворяет условию 0<6<1. Следовательно,
после деления на Дх будем иметь
Fx(x + t\x, у, г) = — П .
Переходя к пределу при Дх->0, найдем
r t \ дП
Рх(Х, у, 2) = -^.
Аналогично получаются и два других равенства (3.49).
90
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ. III
Перейдем к доказательству достаточности условий (3.49). Пред-
положим, что условия (3.49) выполнены.
Используя условия (3.24) и (3.49), получим
d'A =Fxdx + Fydy + Fz dz=:~^dx + ^dy + ^ dz\
Так как потенциальная энергия П зависит только от коорди-
нат точки, то выражение, стоящее в скобках, равно полному
дифференциалу &П; следовательно,
d'A = —dn. (3.50)
Пусть точка переместилась из положения в положение Л42,
'тогда
п2
^4i,2= $ d'A ~dll = Пг — П2, (3.51)
MMG П‘
что совпадает с формулой (3.48). Это доказывает достаточность
условий (3.49) (работа зависит только от значений потенциальной
энергии в точках и Мг и не зависит от пути).
Условие (3.49) часто берут в качестве определения потенциаль-
ного поля. Тогда из соотношения (3.51) вытекает независимость
работы от пути.
Перейдем теперь к решению поставленной задачи: как, зная
только проекции силы (3.49), определить, является ли силовое
поле потенциальным. Продифференцируем первое равенство (3.49)
частным образом по у, а второе по х. Имеем
dFx дШ dFy <М1
ду дх ду’ дх ду дх *
Так как смешанные частные производные не зависят от порядка
дифференцирования, то из равенства правых частей следует
равенство и левых частей; иначе говоря, если поле потенциально,
то проекции сил должны удовлетворять условию (два других
равенства получены аналогичным методом)
дрх dF.; dFy dF, dF, dF v
= = = (3-52)
Справедливо обратное утверждение (мы не будем останавли-
ваться на доказательстве его): если условие (3.52) выполнено, то
силовое поле потенциально.
При решении задач на исследование силовых полей вначале
по условию (3.52) проверяют, является ли заданное поле потен-
циальным, а затем, если окажется, что условие (3.52) выполнено,
то определяют потенциальную энергию поля, пользуясь опреде-
лением (3.47): потенциальная энергия П в данной точке М (х, у, г)
равна работе сил поля на перемещении от точки М до нулевой
§3 5]
СИЛОВОЕ ПОЛЕ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
9Г
точки, в которой потенциальная энергия условно принимается
равной нулю. Так как путь интегрирования не имеет значения,
то его выбирают обычно так, чтобы все вычисления свести
к минимуму.
Проиллюстрируем сказанное двумя простыми задачами чисто методического-
характера.
Задача 3.6. Проверить является ли силовое поле
Fx = — РУ, Fy — px, Fs = 0
(3.52). Имеем
dFy
дх Р'
(3.52) не выполнено, то заданное поле
потенциальным.
Воспользуемся первым равенством
dFx
ду ~~ Р’
Так как первое равенство условия
не потенциально (в задаче 3.4 непосредственными вычислениями было пока-
зано, что работа такой силы
не потенциальна).
Задача 3.7. Проверить,
силовое поле
Fx = xy2, Fy = x2y,
и если оно потенциально, то
ную энергию
Так как
зависит от пути движения и, следовательно, сила
потенциально ли
найти потенциаль-
поля.
dFx dFu
-ч— = 2ху,
дх а
dF, dFx
= 0,
ду '
дГг
Рис. 3.12.
^=—_=_ = _
дг ду дх дг
то условие (3.52) выполнено и заданное поле
потенциально.
Для определения потенциальной энергии
поля нулевую точку выберем в начале коорди-
нат, а путь интегрирования построим следующим образом: из точки М с ко»
ординатами х, у, г будем двигаться сначала параллельно оси г до точки В,
расположенной в плоскости ху, затем из точки В — параллельно оси у до точ-
ки С, находящейся на оси х, а затем по оси х от точки С до начала коорди-
нат (рис. 3.12). Пользуясь определением (3.47), последовательно получим
МВ ВС со
На первом пути х — const dx = 0, у = const, dy = O, а г меняется от г до 0;
на втором пути z = 0, dz = O, х = const, dx = 0, а у меняется от у до 0; на третьем
участке у — 0, dy = O, г —О, dz — О, а х меняется от х до 0. Имеем
ооооо
П = j Fг dz + j Fу dy + j Fх dx = j г2 dz + j х2у dy
z у х г у
(в третьем интеграле Fx = xy2 = 0, так как у — 0). Интегрируя и учитывая,
что во-втором интеграле х — const, получим
П = -|х2!/2-1гз.
“92 ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ [ГЛ III
Легко проверить, что если вычислить от этой потенциальной энергии част-
ные производные по х, затем по у и г, то получим заданные проекции сил
с обратным знаком, что соответствует равенствам (3 49).
Наряду с потенциальной энергией многие авторы вводят в рас-
смотрение силовую функцию U (х, у, г), которая отличается от
потенциальной энергии только знаком, т. е.
(/ = —П.
Условия потенциальности силового поля (3.49) в этом случае
имеют вид
р —дЛ р —dLL р —д£
х~~ дх ' ду ’ г дг ‘
Потенциальное силовое поле допускает удобную и наглядную
геометрическую интерпретацию.
Геометрическое место точек, в которых потенциальная энергия
сохраняет постоянное значение, т. е. П (х, у, z) = C, образует
поверхность, которая называется эквипотенциальной поверхностью.
Через каждую точку потенциального поля можно провести только
одну такую поверхность (рис. 3.13).
Ясно, что работа сил поля при перемещении материальной
точки из начального положения в конечное, когда оба эти поло-
жения находятся на одной и той же
эквипотенциальной поверхности, равна
нулю, так как
/к = Пх — П2 — С — С = 0.
1 Эквипотенциальные поверхности об-
I ладают еще одним интересным свойст-
вом. Допустим, что материальная точка
перемещается вдоль произвольной кри-
Рис. 3.13 вой на эквипотенциальной поверхности,
и пусть закон движения точки x = x(t),
>y = y(t), z = z(t). Тогда для любого момента времени t должно
,выполняться равенство Г1|х (/), y(t), г(1)] = С.
Продифференцируем обе части этого тождества по t:
ЭП dx . dll dy . йП dz „
дх dt ' ду dt ' дг dt
'Согласно (3.49) будем иметь
+ Fyij + Fzz = 0,
«ли
F-v = 0.
'Следовательно, в любой момент времени действующая на точку
сила перпендикулярна к скорости точки. Но вектор v лежит
5 3 5]
СИЛОВОЕ ПОЛЕ ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
93
в касательной плоскости к эквипотенциальной поверхности,
поэтому сила F нормальна к эквипотенциальной поверхности
(см. рис. 3.13).
Введем понятие силовой линии как кривой, в каждой точке
которой касательная коллинеарна с силой данного силового поля.
Очевидно, что уравнение такой линии может быть записано так:
______Эх_ _____dy_______ __ dz__ ,г~ о.
Fx(x, у, z) “ F^(x, у, z) — Fz (x, у z) '
Уравнения (3.53) выражают условия пропорциональности проекций
двух векторов: силы F и дифференциала радиуса-вектора силовой
линии dr (этот вектор всегда направлен по касательной линии).
Из уравнений (3.53) следует система двух дифференциальных
уравнений с двумя неизвестными функциями у и z\
dz _ Fz (х, у, г) dy _ Fy (х, у, z) *
dx ~~ Fx (х, у, г)' dx ~ Fx(x, у, г) ‘ ( • /
Через каждую точку силового поля проходит одна и только
одна силовая линия, являющаяся решением системы (3.54), кроме
особых точек — состояний равновесия, где Fx = Fy = Fz = Q.
Из определения силовых линий следует, что они пересекают
все эквипотенциальные поверхности ортогонально (см. рис. 3.13).
В заключение остановимся на понятии градиента силового
поля. Если задана какая-либо скалярная функция Ф (х, у, z), то
вектор Е, образуемый по формуле
_ ЭФ . , ЭФ , , ЭФ ,
Е = -ч- 1 + дг j + -s-k,
дх ' ду 3 ' дг
называется градиентом функции Ф. Обычно пользуются таким
обозначением:
grado=-^’ + ^J+эгк-
Выражение для силы
F = Fxi4-FJ4-FJ<
в случае потенциального поля с помощью (3.49) можно преобра-
зовать к виду
с /эп. эп, эп. \ , „
F = — =- 1 + л- J + а- к == — grad П.
\дх ' ду 3 ' dz / °
Таким образом, в потенциальном поле силу можно рассматривать
как взятый с обратным знаком градиент функции П (х, у, г).
Покажем, как вычисляется -потенциальная энергия для неко-
торых часто встречающихся силовых полей.
94
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ. III
1. Потенциальная энергия поля силы тяжести. Совмещая пло-
скость хОу с какой-либо горизонтальной плоскостью (рис. 3.14),
для проекций силы тяжести будем иметь
Fx = 0, Fy = 0, Fz = — mg.
Можно проверить, что условия (3.51) выполняются.
Элементарная работа равна
d' А = Fx dx 4- Fy dy-\- Fz dz = — mg dz.
Следовательно, работа силы тяжести при перемещении матери-
альной точки из точки О в какую-либо точку М равна согласно
(3.25)
г
АОм — — $ mg дг — — tngz.
о
(3.55)
Но так как потенциальная энергия в точке М поля
работе, которую совершает сила при перемещении точки
ложен и я
равна
из по-
М в положение О, то
П = ЛЛ10 = ш^?. (3.56)
Эквипотенциальные поверхно-
сти mgz = C образуют семейство
горизонтальных плоскостей, а си-
ловыми линиями являются пря-
мые, параллельные оси г.
2. Потенциальная энергия поля
центральных сил. Центральной си-
лой будем называть силу, которая
в любой точке пространства на-
через некоторую точку поля
правлена по прямой, проходящей
(центр), причем модуль силы F
зависит только от расстояния г точки до центра.
Если этот центр выбрать за начало координат, то для цент-
ральной силы можно написать
F(r) = Fr (г) у,
(3.57)
где Fr(r) = ±F(r) (знак « + » для силы отталкивания, а знак
« —» для силы притяжения).
Проверим, выполняется ли условие (3.52). Так как
Fx = />(r)y, Fy = Fr(^4’ ^ = ^(r)y
и, кроме того,
г = /х2 4-,/2 4-гг,
$3 5]
СИЛОВОЕ ПОЛЕ. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ
95
то
dFх__ d Г Fг (г)1 дг___ху d rfr (г)1
ду —Х dr [ г J ду г dr [ г J ’
9Fу__ d Г Fг (г) 1 дг _ху d Г Fг (г)~|
дх У dr L г J дх г dr г J'
Следовательно,
dF У = дрх
дх ду ‘
Остальные равенства (3.52) также выполняются.
Для вычисления потенциальной энергии найдем работу цент-
ральной силы при перемещении точки из некоторого произволь-
ного положения М в фиксированное положение Л10.
Элементарная работа имеет вид
d' А = F • dr = Fr (г) ~ = Fr (г) dr.
Тогда потенциальная энергия будет равна
П (г) = Амм0 — $ F, (г) dr. (3.58)
Г
Здесь эквипотенциальные поверхности П (г) = С —сферы с центром
в начале координат, а силовые линии образуют пучок прямых,
выходящих из начала координат.
В частности, центральной силой является гравитационная сила.
Согласно закону всемирного тяготения
F = -/^L Fr(r)^-f^,
где f — постоянная тяготения, и т2 — массы притягивающихся
материальных точек, а г —расстояние между ними.
Примем за точку Мо бесконечно удаленную точку; тогда, при-
меняя (3.58), получим
со
П(г) = —= — . (3.59)
Г
3. Потенциальная энергия восстанавливающей силы пружины.
Примем за фиксированную точку Мо, в которой потенциальная
энергия равна нулю, положение конца недеформированной пру-
жины (положение самой пружины не играет роли). Пусть длина
пружины в недеформировапном состоянии равна г0, а в положе-
нии М равна г (рис. 3.15). Тогда величина Fr(r), входящая
в равенства (3.57) и (3.58), имеет вид Fr(r) = — c(r — ru). При
96
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ IIJ
г <г0 упругая сила пружины является по отношению к центру
(точке крепления) отталкивающей, при г > г0 — притягивающей.
Подставляя Fr (г) в (3.58), получим
II(r) = -C^(r-r0)dr = ^^,
Y ИЛИ
Уо# П (г) = с4. (3.60)
„У Здесь к = | г — г01 — модуль прира-
z щения длины пружины.
Рис. 3.15. Из формул (3.51) и (3.60) сле-
дует, что работа восстанавливаю-
щей силы пружины при перемещении конца пружины из поло-
жения Л^! в Л42 равна
(3.61)
Здесь Xj и Х2 —деформации, соответствующие начальной и конеч-
ной точкам пути.
§ 3.6. Интеграл энергии.
Понятие о рассеивании полной механической энергии
Предположим, что все силы, действующие на материальную
точку, потенциальны. Тогда элементарная работа сил, приложенных
к точке, будет d'A —— сЕП и равенство (3.40) принимает вид
Интегрируя обе части этого равенства, найдем
Т4-П = /1, (3.62)
где /г — постоянная интегрирования (она называется постоянной
энергии).
Равене во (3.62) называется интегралом энергии. Интеграл
энергии показывает, что при движении точки в потенциальном
поле сил сумма кинетической и потенциальной энергий (полная
механическая энергия) есть величина постоянная (закон сохранения
механической энергии).
Равенству (3.62) можно придать и такой вид:
Л+п^л + щ, (3.63)
§ 3 61
ИНТЕГРАЛ ЭНЕРГИИ
97
где 7\ и Т2, rtj и П2 —значения кинетической и потенциальной
энергий в положениях Mt и М2 соответственно.
Интеграл энергии (3.62) справедлив при условии, что все
силы, действующие на материальную точку, потенциальны. Если
хотя бы одна из сил не потенциальна, то равенство (3.62) будет
нарушено. Рассмотрим, какое влияние оказывают силы сопротив-
ления (они, как правило, имеются всегда) на полную механичес-
кую энергию. Итак, будем считать, что
на материальную точку действуют по- У,
тенциальные силы (их потенциальная
энергия равна П) и силы сопротивле-
ния Fc. Относительно последних мы не р уу
будем делать никаких ограничений: €*/
они могут быть постоянны по модулю /
(сухое трение), пропорциональны любой |
степени скорости (вязкое трение) или
любым иным образом зависеть от ско- Рис- 3,16‘
рости точки, ее положения и времени t.
Единственное предположение (оно для сил сопротивления есте-
ственно) состоит в том, что сила сопротивления всегда направ-
лена противоположно скорости v точки (рис. 3.16).
Элементарная работа потенциальной силы F равна —dll, а эле-
ментарная работа силы сопротивления будет Fc-dr. Равенство
(3.40) принимает вид
dT = — dll + Fc • dr.
Перегруппируем члены, разделим обе части равенства на dt и
dr
учтем, что ^- = v:
i(T+n) = Ft.v.
Угол между силой сопротивления Fc и скоростью v равен 180°;
скалярное произведение Fc • v=Fcv cos 180° = — Pcv. Следовательно,
^(Т + П) = -Есц<0. ' (3.64)
Так как производная по времени отрицательна, то полная меха-
ническая энергия под действием сил сопротивления убывает или
рассеивается, переходя, конечно, в другие формы энергии, напри-
мер в тепловую.
Модуль мощности |Fc-v| = Fcv силы сопротивления может
служить мерой убывания полной механической энергии. Если
модуль силы сопротивления равен \Ьх\ (линейно-вязкое сопро-
тивление), то Fcv =— bx2 =—2^-. Величина bv2/2 называется
диссипативной функцией Релея, удвоенная величина которой
в данном случае служит мерой рассеивания (диссипации) энергии.
4 Н. В. Бутении и др.
98
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ. П1
§ 3.7. Задачи
Задача 3.8. Какова длина разбега самолета, вес которого Р=18 000 кГ,
тяга, развиваемая двигателем, Ф = 4000 кГ, общая сила сопротивления R —
= 1000 кГ, взлетная скорость ц = 216 км/час.
Применим теорему об изменении кинетической энергии
mv2 mvl
-------f^_R}S.
вертикальную
Полагая начальную скорость ц0 = О, получим
mv2 1 8 000 - 602 ,,nn
s ~2 (ф-R)- 2-9,81 -3000 00 М'
Задача 3.9. Самолет, вес которого Р=10 Т, совершает посадку, имея
скорость снижения п0=2 м/сек. Подъемная сила при посадке
N = 6 Т, жесткость амортизационной системы с=1 Т/см. Со-
противление в амортизационных стойках шасси при прямом
ходе постоянно и равно Д = 3 Т. Определить наибольшую
осадку самолета, считая, что за время срабатывания стойки
горизонтальная скорость v остается неизменной (рис. 3.17).
Применим теорему об изменении кинетической энергии.
В начальный момент вертикальная составляющая скорости
и6 —2м/сек, в конечный момент —Ui = Q. Работу восстанав-
ливающей силы пружины определим по формуле (3.61). По-
лагая 0М = к, получим для работы всех сил (силы тяжести mg,
силы сопротивления R, подъемной силы N и силы упругости
амортизаторов)
Рис. 3.17.
Л0Л1=тгА,-7?А,-^---NK.
Величина полной начальной скорости равна + величина скорости
в конце процесса сжатия амортизационной системы равна v. Поэтому прира-
щение кинетической энергии составляет
mv2 m(u2-|-u|) mu|
_ ___ .
По теореме об изменении кинетической энергии имеем
mul гм А2 »и
---^ = mgA,—ДА,----g---Nt"
откуда
А, (mg—R—N ± \T[mg^R^Ny+m^l:).
Для крайнего нижнего положения следует перед корнем взять знак «плюс».
Тогда, после подстановки численных значений, найдем
А,=0,01 ^1 + у 1+д~4001 = 21,2 см.
Задача 3.10. На какую высоту Н над поверхностью Земли поднимется
ракета, запущенная в вертикальном направлении с поверхности Земли, если
?е начальная скорость равна и0? Какую начальную скорость надо сообщить
ракете, чтобы она неограниченно удалялась от Земли? Сопротивлением атмос-
феры пренебречь, Радиус Земли Д = 637О км (рис, 3,18),
5 3.7J
ЗАДАЧИ
99
механической энергии, имея в виду, что
а потенциальная энергия силы тяготения
fmM fmM
~~R~ R + lT'
Применим закон сохранения
конечная скорость ракеты и = 0,
определяется по формуле (3.59):
mvj
2
Здесь т — масса ракеты, /И—масса Земли, f — гравитационная постоянная.
От двух последних постоянных можно избавиться, заметив, что при r = R
(т. е. на поверхности Земли) сила притяжения приближенно равна силе тяжести
t тМ
откуда fM=gR2. Тогда
~2—m§R=-R + H-
Разрешая уравнение относительно H, получим
Н Rv‘‘
2gfl-c/
Теперь нетрудно ответить на второй вопрос. Согласно условию задачи должно
быть Н = со и, следовательно,
4gR — V2 = 0, v0 = V 2gR = /2-9,81 10 3 • 6370 =11,2 км/сек.
Задача 3.11. С какой скоростью должна быть запущена с поверхности
Земли ракета, чтобы она могла достигнуть той точки С между Землей и
Рис. 3.18.
Луной (рис. 3.19), где силы притяжения Земли и Луны равны. Расстояние между
центрами Луны и Земли d = 370 000 км, а отношение их масс Мл и А43 равно
1/80. Радиус Земли 7? = 6370 км.
В точке С должно выполняться равенство
mfM3 fmMn
(d-r0)2'
fmM г.
Потенциальная энергия силы притяжения Луны Пл -—При-
меним закон сохранения механической энергии (полагая, что в точке С ско-
рость ракеты равна нулю)
mug fmM3 fmM л
~2 R d—R =
fmM3 fmM л
Го d — ro‘
4*
100
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ ТОЧКИ
[ГЛ. III
^=2
Используя равенство [M3=--gR2, получим
gR2 R2
80(d-R) 8 rQ '
и =11,1 км/сек.
gR2 1
8O(d-r0)J
Задача 3.12. Сани спускаются с горы. Начиная с точки А (рис. 3.20),
их притормаживают силой F таким образом, что до конца спуска (точки В)
скорость саней остается постоянной. Определить работу, совершаемую силой F,
если вес саней Р, а высота горы h.
В отличие от предыдущих задач, здесь наряду с потенциальной силой —
силон тяжести Р — действует непотенциальная сила F. На основании теоремы
об изменении кинетической энергии имеем
mv2 mv/ р F
~2 2~“ /1ЛВ"глАВ-
Так как начальная и конечная скорости
саней одинаковы, то
4лв + /|лв=0-
Для работы силы тяжести имеем
Л₽в=М.
откуда Afab=—Ph. Найдем эту работу путем непосредственного вычисления.
Так как скорость саней постоянна, то сумма проекций сил на направление
скорости равна нулю, т. е. В sin а — F = 0, и, следовательно,
F = Р sin а.
где sin а
можно определить из равенства
dy
sin а = ~
ds
Вычислим мощность силы торможения;
.,F с г dy ds
N F • v= — Fv= — p~r -r..
' ds dt
Здесь мы приняли во внимание, что сила торможения F и скорость v имеют
противоположные направления. Работа силы торможения за время спуска
саней выражается следующим образом:
Т Th
,VF (t)dt=-P §^dt=-P dy——Ph,
О 0 0
Задача 3.13. Материальная точка совершает прямолинейные затухающие
колебания под действием линейной восстанавливающей силы, создаваемой
пружиной жесткости с, и силы сопротивления, пропорциональной первой
степени скорости (R=—bv). Определить работу силы сопротивления за одно
полное колебание материальной точки, а также максимальную работу этой
силы при неограниченной продолжительности колебаний.
В момент времени, когда материальная точка достигает максимального
отклонения, скорость ее равна нулю. Поэтому, применяя теорему об измене-
нии кинетической энергии для перемещения от начального до последующего
максимального отклонения, получим
0 = Дуп-|-Дс,
§ 3.7]
ЗАДАЧИ
101
где Луп —работа упругой силы пружины, а Ас — работа силы сопротивления.
Так как деформация пружины X при максимальных отклонениях материальной
точки равна соответствующей амплитуде, то согласно формуле (3.60) будем
иметь
£
^уп=~2” а$)’
где а0 — начальная, а — последующая амплитуды.
Следовательно, работа силы сопротивления за один период будет равна
Дс= — у («о —а!)-
Если выразить последующую амплитуду аг через предыдущую а0 с по-
мощью фактора затухания г] по формуле (2.16), то последнее равенство при-
мет вид
(1- п2)>
где
—hT*
т) = е
причем й = (т — масса точки), Т* — период затухающих колебаний.
За п полных колебаний работа силы сопротивления будет равна
£
= 2" (ао~ап),
или, учитывая, что а„ = аот]л,
Лс= --|° (1 -П2")-
Так как г)< 1, то при п->-оо будем иметь
л max_
2 ‘
Такова максимальная работа, которую совершат силы сопротивления при
неограниченной продолжительности колебаний.
Работу силы сопротивления можно, конечно, вычислить и путем непос-
редственного применения формулы (3.25). Для этого нужно воспользоваться
решением (2.13) дифференциального уравнения затухающих колебаний матери-
альной точки:
x — ae~hl sin (k*2 = k2 — h2 = ~—h,2
Отсюда нужно найти х, а затем Rx — — bx (Ry — RK = 0). После чего рабо<
та силы сопротивления определится путем вычисления интеграла
т*
Лс=—ba2 § e-2W [—h sin (й*/ + е)+&* cos (й*/+ в)]2 dt.
Этот путь непосредственного вычисления работы по общим формулам
требует, очевидно, значительно большей затраты труда, чем применение тео-
ремы об изменении кинетической энергии,
ГЛАВА IV
ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ ТОЧКИ
В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
§4.1. Дифференциальное уравнение траектории точки,
движущейся в центральном поле сил
В § 3.2 были установлены свойства движения точки в поле
центральной силы. Напомним эти свойства.
Во-первых, траектория движения точки — плоская кривая.
Центр, через который всегда проходит линия действия силы,
лежит в плоскости траектории. Удобно описывать движение
такой материальной точки в полярной системе координат с полю-
сом в центре силового поля. Полярную ось направим пока про-
извольно. Тогда положение точки в плоскости ее движения будет
определяться полярными координатами г и ср. Для центральной,
силы имеем выражение
F = Fr(r)y, . (4.1)
где Fr (г) — проекция силы на радиус-вектор точки.
Во-вторых, имеет место закон площадей (секторная скорость
остается постоянной). В полярных координатах соблюдается
равенство (3.18):
уг2ф = с. (4.2)
Перейдем к составлению дифференциального уравнения движе-
ния материальной точки в центральном поле.
Воспользовавшись найденным в кинематике (том I, глава IX)
выражением для радиального ускорения точки wr = r — гф2, запи-
шем общее уравнение динамики
m\v = Fr (г)
в проекции на радиус-вектор г:
т(г — гф2)= F, (г). (4.3)
4 П ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ТРАЕКТОРИИ ТОЧКИ ЮЗ
В соответствии с интегралом площадей (4.2) уравнение (4.3)
может быть переписано в виде
= (4-4)
Для определения траектории движения в полярных коорди-
натах перейдем в этом уравнении от независимой переменной t
к полярному углу ф.
В силу интеграла площадей (4.2) имеем
dr _ dr dtp _ 2с dr _ _д d / 1 \ . г.
dt ~ dtp dt ~ r2 dtp ~ dtp\r Г >
Продифференцируем это выражение по времени п вновь восполь-
зуемся интегралом площадей (4.2):
d2r d / dr \ dtp 2с d / dr \
dt2 dtp \ dt / dt r2 dtp \ dt )'
Приняв во внимание соотношение (4.5), перепишем этот результат
в виде
d2r = _ 4с2 da / ц
dt2 г2 dtp2 \ г /' ' ' '
Подставляя это выражение в уравнение (4.4), получим
г2 dtp2\r) г3 ~ т
Вводя теперь новую искомую функцию u = i/r, будем иметь
d‘iu 1 у г (“) it о\
Полученное соотношение (4.8) и есть дифференциальное урав-
нение траектории материальной точки, движущейся под действием
центральной силы (уравнение Бинэ).
Наиболее важным случаем центральной силы является грави-
тационная сила планеты или любого другого небесного тела.
Ньютоновская сила притяжения планеты, принимаемой за шар
с радиальным распределением плотности, действующая на мате-
риальную точку, находящуюся вне пределов шара, равна
F —(4-9)
где f — гравитационная постоянная, /и —масса материальной точки,
М — масса планеты, г —расстояние точки от центра планеты.
Можно избавиться от произведения [М, если известна сила
притяжения на поверхности планеты, т. е. при r — R. Для Землй
эта сила притяжения равна mg, где g —ускорение свободного
104
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ IV
падения тела относительно невращающейся Земли. Аналогично
определяется g и для других планет.
Таким образом, при г = R из равенства (4.9) получим
= fM=gR2,
после чего (4.9) принимает вид
F = (4.10)
Следовательно, в данном случае Fr (г) = Fr = — mgR2u2.
При движении точки вне пределов земной атмосферы, но в дос-
таточной близости к ее поверхности, можно пренебречь действием
гравитационных сил со стороны других небесных тел и считать,
что на точку действует только сила (4.10). В этом случае диф-
ференциальное уравнение траектории (4.8) примет вид
4с2 ,
где р = -^5-= const.
§ 4.2. Виды траекторий.
Круговая и параболическая скорости
Исследуем решение основного дифференциального уравнения
(4.11). Общее решение этого уравнения можно представить в сле-
дующей форме:
« = у + a cos (ср —е), (4-12)
где а и е —постоянные интегрирования. Вспоминая, что w = l/r,
перепишем уравнение (4.12) в виде
г = т----(4.13)
1 +е cos (ср —е) ’ ' г
где е = ар — постоянная величина.
Уравнение (4.13) определяет траекторию материальной точки,
движущейся под действием ньютоновской силы притяжения.
Для упрощения анализа введем новую переменную ф = <р — е.
Очевидно, что теперь угол ф будет отсчитываться не от перво-
начально взятого фиксированного направления, а от некоторого
нового направления Oxlt повернутого относительно первого на
угол е (рис. 4.1). Конечно, вид траектории от такой формальной
замены переменных не может измениться.
§ 4 21
ВИДЫ ТРАЕКТОРИЙ
105
Теперь уравнение (4.13) примет вид
Таким образом, вид траектории определяется единственным
образом через постоянные р и е. Несколько дальше будет пока-
зано, как определить эти по- к
стоянные по начальным уело-
виям. V"/'
Из курса аналитической гео- \ rldtx
метрии известно, что кривые \ /v\x
(4.14) представляет собой кони-
ческие сечения ). 0 Фиксированное
Тип траектории определяет- направление
ся значением величины е, назы-
ваемой эксцентриситетом кони- Рис. 4.1.
ческого сечения.
В дальнейшем примем, что е > 0; это соответствует выбору
положительного направления полярной оси Охг (гр = О) от центра О
на ближайшую к О точку траектории, называемую перицентром
(для земных спутников — перигеем).
Если е<1, то знаменатель в правой части (4.14) никогда не
•обращается в нуль, следовательно, кривая второго порядка не
имеет бесконечно удаленных точек. Это может быть только эллипс.
В часгном случае, когда е = 0, получаем r = p = const, т. е. эллипс
превращается в окружность.
Если е>1, то появляются бесконечно удаленные точки при
двух значениях угла ip, полученных из уравнения
1 -|-е cos ip = 0, ,
т. е. при
1|; == ± arccos ( — у) •
Таким свойством обладает только гипербола.
Наконец, при е = 1 знаменатель обращается в нуль при г]? = л.
Кривой второго порядка, имеющей бесконечно удаленную точку
только при одном значении полярного угла гр, является парабола.
На рис. 4.2 изображены возможные траектории при е:>0 и
одинаковом для всех траекторий расстоянии от центра О до пери-
центра. Это расстояние в соответствии с уравнением (4.14) равно
г -г - р
Гтш- Го— 1+е .
*) В декартовой системе координат, для которой x1 = rcosip, yi — r sin гр,
уравнение (4.14) приводится к виду х? 4-у* = (р — extf, т, е, все траектории
могут быть только кривыми второго порядка.
106
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ IV
Установив, что тип траектории определяется значением эксцен-
триситета е, найдем зависимость эксцентриситета от начальных
условий.
Сначала сделаем это, отнеся начальные условия к тому моменту
времени, когда точка пересекает ось*! (см. рис. 4.1), т. е. при г]? = 0.
В соответствии с формулой:
(4.14) имеем
dr ____ ре sin г|>
dip (1 + е cosip)2 ’
Следовательно, при ф = 0 по-
лярный радиус г достигает экс-
тремума ^— = 0^. Это значит»
что при ф = 0 и любом е скорость
точки перпендикулярна к ра-
диусу-вектору г0, определяю-
щему положение точки.
Имея в виду, что ф = ф и по-
перечная скорость ир = гф, пере-
пишем интеграл площадей в виде
1
~2 пр = с.
Пусть теперь r = r0, v = v0 при ф = 0. Для этих начальных
условий в соответствии с уравнением (4.14) будет
г = р
Г° 1+е •
Отсюда находим
е = -^--1. * (4.15>
Так как для рассматриваемых начальных условий v„~v0, то>
1 4с2
с= 2 rovo и, учитывая, что р = ^, получим
« = ^-1- (4.16>
Это соотношение является основным и позволяет найти интервалы
скоростей, которым соответствуют те или иные виды траекторий-
Эллиптические траектории (е<1) определяются неравенством
В частности, если е = 0, то траекторией будет окружность;
при этом начальная скорость vQ имеет значение
^1 = ^0
>§4 3]
ОПРЕДЕЛЕНИЕ ПАРАМЕТРОВ ОКОЛОЗЕМНОЙ ТРАЕКТОРИИ
107
и называется круговой скоростью. Круговая скорость, вычисленная
из условий движения вблизи Земли (r0 = R), называется первой
космической скоростью'.
= 7,9 км!сек.
Параболической траектории соответствует значение е = 1, т. е.
по формуле (4.16) скорость
Найденное значение скорости называется параболической скоростью.
Если начальная скорость задана-вблизи Земдщ то параболическая
скорость
р2 = У 2gK = 11,2 км/сек
называется второй космической скоростью.
При сообщении такой начальной скорости точка неограниченно
удалялась бы от Земли.
Гиперболические траектории характеризуются неравенством
€>1, которому соответствуют начальные скорости

§ 4.3. Определение параметров околоземной траектории
по начальным условиям
Найдем теперь зависимость эксцентриситета от начальных усло-
вий в случае, когда материальная точка в некоторый момент вре-
мени начинает движение из точ- ,
ки Ао вне пределов атмосферы . s'
(рис. 4.3).
Пусть материальная точка в ____''х
некоторый момент времени начи- 'х?
нает движение из точки Ло вне / \ \
пределов атмосферы только под / 1
действием силы притяжения Земли Г 1
(рис. 4.3). \ • /
Определим параметры траекто- У
рии р и е, если известны: г0 —
расстояние от центра Земли до Рис. 4 3.
точки Ло, и0 —величина скорости
материальной точки в положении Ло, 0О —угол наклона вектора
скорости к местному горизонту, т. е. к плоскости, перпендику-
лярной к радиусу-вектору точки До.
Найдя параметры траектории, мы затем легко определим началь-
ный полярный угол i|;0 (см. рис. 4.3) и тем самым узнаем пока
не известное направление оси Oxlt
108
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ IV
Так как в точке Ло скорость ур = ц0со5 90, то согласно фор-
муле (4.2) секторная скорость равна
с = у ПА cos (4.17)
Подставляя это выражение в формулу для р, получим
4с2 f2vs cos2 0 / Uo \2
Р = = = cos2 90 = rov cos2 60, (4.18)
где v1 = ']^gR2/г0 — круговая скорость в точке Ао, a v = (-—) .
\vi J
Из формулы (4.14) следует, что
есозф = у — 1. (4.19)
После дифференцирования этого выражения по времени получим
, dip р dr
— е sin ф -%- =---Ч- -дг.
т dt г2 dt
г-, dr , .
Принимая во внимание равенства -др — Уг (радиальная скорость),
ф = ф и г2ф = 2с, перепишем полученное выражение в виде
esinip = -^-or. (4.20)
Для рассматриваемых начальных условий ф = ф0, г = r0, vr ~
==o0sin90 (рис. 4.4) выражения (4.19) и (4.20) с учетом формул
(4.17) и (4.18) примут вид
/'V'Ur
\ . r0V COS2 6n , , - .
\ е cos Фо = -2—^-—— — 1 = v cos2 90 — 1 ,
0 <4-21)
е sin фо = r°v С-- и0 sin 90 —
Х>р \________ т Г0и0 cos 60 0 0
/\^Фо\ = V sin 90 COS 90. (4.22)
। 1 Отсюда находим
е=]/ (v cos2 90 — 1 )2 + v2 sin2 90 cos290=
Рис. 4.4. =1^1—v (2 — v) cos2 90. (4.23)
Зная параметры траектории р и е, можно найти из формулы (4.19)
начальный полярный угол ф0, т. е. положение полярной оси Охр.
cos фо = Lp_ _ 1 \ 1 = — # (4.24)
\ г0 ] е К1 — v (2 — v) cos2 0О '
Иногда удобно ввести дополнительный угол фо = л — ф0 (см. рис. 4.3),
для которого
С05ф;= г (4.25)
К1— v (2 — v) cos2 0О
§4 41 ТРАЕКТОРИИ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ 109
Таким образом, траектория точки полностью определяется тремя
параметрами ra, v и 0О и формула (4.14) может быть записана
в виде
г___________vr0 cos2 б0____
1 +cos ip К1 — у (2—v) cos2 60
Рассмотрим некоторые частные случаи.
Пусть
е = ]/1 — v (2 —v) cos20o = 0.
Отсюда имеем
v2 — 2v + sec2 0О = 0
и, следовательно,
v = 1 Д- — sec2 0О.
Это значит, что е = 0 может быть только при 0о = О и v = l. При
этом г = г0, т- е- орбита будет окружностью, а необходимая началь-
ная скорость равна
Для параболической траектории
е = ]/1 — v (2 — v) cos2 0О = 1,
что выполняется при
v = 2
и любом угле 0О. Начальная скорость v0, необходимая для дви-
жения по параболической траектории, равна
Уо = У1/2 = |Л®.
§ 4.4. Траектории искусственных спутников Земли
Пусть рассматривается движение материальной точки из положения Ао.
В этом положении точка расположена на высоте h над земной поверхностью и
обладает начальной скоростью ц0, направленной под углом 90 к местному гори-
зонту.
Как установлено, при ц0<и2 траектория материальной точки есть эллипс,
один из фокусов которого находится в центре Земли.
Из уравнения траектории (4.14) видно, что максимальное расстояние мате-
риальной точки от центра Земли достигается при
cosipOT = —1 (4.26)
и равно
'max = TZT. ’ (4-27)
по
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ IV
Соответствующая точка траектории называется апогеем. Минимальное расстоя-
ние точки от центра Земли достигается в перигее и равно
'•т1п=-ГТр7- ' (4-28)
Таким образом, максимальное расстояние точки от поверхности Земли
составляет
йтах=~г^------
ГПаХ J ~ g
а минимальное расстояние равняется —
к Р_________п
"min 1_|_г к-
В зависимости от конкретных значений и0 и 60 траектории могут оказаться
пересекающимися либо не пересекающимися с поверхностью Земли. Найдем,
при каком значении <?0 и фиксированном значении угла 0О траектории не будут
пересекать поверхность Земли, т. е. могут быть траекториями искусственных
спутников Земли.
Для траектории, не пересекающей поверхности Земли, должно выполняться
неравенство
^min
т. е. согласно (4.28)
-Г^>Я. (4.29)
Принимая во внимание (4.22), получаем
rov cos2 So > R (1 + К1 —v (2 —v) cos2 60),
или, так как rQ = R-}-h,
[(R+h) v cos2 0O-R]2 > R2 [1 -v (2-v) cos2 0O].
После небольших преобразований и подстановки v = v%/vl найдем
-^-[(R+A)2cos260-R2]>2/?/i. (4.30)
Для выполнения этого неравенства необходимо, чтобы
cos 60 > cos 6J,
где
D
Из соотношения (4.30) получаем значение и0, при котором траектории
1очки не будут пересекать поверхность Земли:
Ко > vk,
где _____
gR2
R ~\~h
Отметим, что при Й = 0 это условие имеет смысл только при 0о = О и прини-
мает вид ___
Vo > VgR-
Y (R + й)2 cos2 60 —R2 ' (4,31)
§4 4] ТРАЕКТОРИИ ИСКУССТВЕННЫХ СПУТНИКОВ ЗЕМЛИ Ш
Определим величины большой и малой полуосей эллипса (4.14). Величина боль-
шой полуоси
'•тах + ''mln ₽ I 1 1 \ _ ₽
а~ 2 — 2\1— е ф 1+е/ 1— е* ’
или, учитывая соотношение (4.22),
°- v(2 —v)cos2 60 “ 2-v (4,32)
Из формулы (4.32) следует, что величина большой полуоси не зависит от
угла 0О и определяется только величиной начальной скорости р0.
Найдем теперь расстояние между фокусами эллипса 2с:
2с = 2 (0-rmin) = 2ае. (4.33)
Отсюда, кстати, видно, что эксцентриситет е-с/а. Малая полуось эллипса
b связана простым соотношением с величинами а и с:
Ь = = а уТ^=/ар. (4.34)
Изучим характер
v = t'o/t'i При v0>vk.
изменения траекторий спутников в зависимости от
Для простоты положим- что 0О = 0. Из (4.20) тогда
следует
sinipo = O, cos q>o = —~ (—-1V (4.35)
в \ Г Q /
Имея в виду, что прн 0о = О согласно (4-23)
е = ]/1 — v (2—v)== | V— 11 и, кроме того,
p = rov, получим
С05фо= | (4-36)
Прежде всего остановимся на случае, когда
v> 1; из (4.36) имеем
। v— * 1
cos ф0=_—=1.
Следовательно, ф0 = 0 и положительное на-
правление полярной оси совпадает с направ-
лением ОА0 (рис. 4.5). Напомним, что мы ус-
ловились считать е >. 0. Это эквивалентно
выбору положительного направления поляр-
ной оси от притягивающего центра через пе-
ригей.
На рис. 4.5 показаны три траектории
спутников при различных значениях начальной
скорости (цх < г?о < и2) и 6о = О- Это семейство
в точке О и перигеем в Ао.
эллипсов с общим фокусом
Обратимся теперь к случаю v<l. При этом е = 1— v и в соответствии
с (4.36)
' V — 1
со8ф0 = т—_=_],
т. е. фо=л. Следовательно, направление на перигей противоположно ОА0,
Точка Ао становится апогеем, и семейство эллипсов (o*<vo<Vi) имеет вид,
изображенный на рис. 4.6,
112
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ IV
Уравнения эллипсов (4.14) при 6о = О принимают вид
г____________________________трУ
(4.37)
1 + I V — 1 I cos ф ’
Перигейное расстояние находится из (4.37) при ф = 0. Заметив, что при у>1
|v—l|=v— 1, а при v<l |v— 1 | = 1—v,
получим
min 'о
Полагая в
_ Г0У
min 2______v
последней формуле = найдем
Аналогично,
расстояние
ГрУ
'max — 2 —V
2R
4R + h-
при ф = л, определим
апогейное
max 'о
Большая полуось эллипса
(4.34); при этом е2 —(1—v)2,
r0
а~2—у ’
определяется по формуле (4.32), а
b = a]f 1 — e2 = a]/rv (2 — v).
малая из
(4.38)
Найдем теперь период обращения спутника по эллиптической орбите.
Исходя из интеграла площадей, имеем
S=ct,
где S —площадь, описываемая радиусом-вектором точки за время t, с —сектор-
ная скорость.
За время Т полного оборота спутника радиус-вектор опишет полную пло-
щадь эллипса S = nab. Следовательно, должно выполняться равенство
лаЬ = сТ.
Вспомним, что согласно (4.18) и (4.34)
Ь = \'ар, с = у Кpg/?2 •
Теперь получим
Г = яТ = 2л]/^2- (4.39)
Таким образом, для двух спутников, движущихся по различным эллипти-
ческим орбитам с большими полуосями ах н а2 и периодами обращения Тх и
Т2, имеем
Отсюда выводится известное соотношение
TJ
Т1 а* •
§4 51
ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ПОЛЕТА
113
Эга формула справедлива не только для задач о движении спутников Земли,
но и вообще для -случаев движения материальной точки по эллиптической
орбите вокруг любого притягивающего центра. Применительно к Солнечной
системе эту формулу установил путем обработки наблюдений И. Кеплер (тре-
тий закон Кеплера).
§ 4.5. Определение времени полета
по эллиптической орбите (уравнение Кеплера)
Пусть движение спутника происходит по эллипсу с полуосями а ч b
(рис. 4.7). Опишем из центра эллипса окружность радиусом, равным большой
полуоси. Через точку А на эллипсе проведем линию, перпендикулярную
к линии апсид (оси х). Пусть точка пересечения этого перпендикуляра с окруж-
ностью будет Al. Угол Е между отрезком О1Д1 и линией апсид называется
эксцентрической аномалией. Найдем связь между углами Е и if (истинной
аномалией). Из рассмотрения рис. 4.7 следует, что
a cos Е — г cos ф = с,
где с—половина фокусного расстояния. Подставляя в это выражение (см. фор-
мулу (4.14))
Р
1 -j- е cos ф ’
будем иметь
„ р cos ф
a cos Е----------—г
1 + е cos ф
Так как е = с/а и р/а=1—е2, то
„ с , р cos ф е -4- cos ф
cos —_____ - *___. — ___ 1 ♦
а 'а 1 + е cos ф 1 + е cos ф ’
(4.40)
= с.
отсюда следует, что
Рис. 4.7.
, cos Е — е
cos ф = 1(4.41)
т 1 — е cos Е
Если теперь в уравнении траектории (4.14) заменить угол ф с помощью
выражения (4.41) иа угол Е, то получим
г = а(1—ecosE). (4.42)
Для дальнейшего нам необходимо определить еще и sin ф. По свойству эллипса
имеем (см. рис. 4.7)
В соответствии с рис. 4.7 получим
AiB = asmE, ДВ = гзшф
и, следовательно,
a sin Е
Используя выражение (4.42), будем иметь
sin ф
_ К1 — е2 sin Е
1 — е cos Е ‘
(4-43)
114
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ. IV
Перейдем теперь к определению времени полета спутника. Для этого вос-
пользуемся интегралом площадей (4.2):
г2 г2
^~2с^~2с^’
так как -ф = <р—е. В соответствии с формулой (4.42) получим
а2(1— ecosE)2
dt = —i----------->- йф. (4.44)
На основании зависимости (4.41) имеем
. ... sin Е (1 —е2) dE
sin ф dip = ——----4—_.
т (1—ecosE)2
Отсюда, учтя соотношение (4.43), получим
,, КТ-’-ё2 dE
йф = -i-------FT.
1 — е cos Е
Следовательно, выражение (4.44) может быть переписано в виде
Д2 1/[ — е2
d< = (1 — е cos Е) dE,
или
Е
— = \ (1 —е cos Е) dE,
О
где t0 — момент времени прохождения через перигей,
2с 2с(1—е2)3^2
а2 КТ^ё2 “ р2
После интегрирования найдем
Е—е sin Е — п (t^t0). (4.45)
Полученное уравнение носит название уравнения Кеплера.
Уравнение Кеплера устанавливает связь между эксцентрической анома-
лией Е и временем движения точки.
Для того чтобы определить положение точки в данный момент времени,
следует по уравнению Кеплера определить угол Е, соответствующий данному
моменту времени, затем по найденному Е, используя формулы (4.41) и (4.42),
определить фиг.
Решению уравнения Кеплера посвящено много работ. Изложение спосо-
бов его приближенного решения можно найти в курсах небесной механики.
В качестве примера применения уравнения Кеплера определим период
обращения точки по эллиптической орбите.
Так как /0 —момент времени прохождения через перигей, то при / =
где Т — период обращения, Е = 2л. Из уравнения Кеплера получаем
пТ = 2л.
Отсюда
Г = —
п
Так как
_ 2с (1 — е2)3/2
— р2 >
§ 4.5]
ОПРЕДЕЛЕНИЕ ВРЕМЕНИ ПОЛЕТА
115
а р2 = а(1—е2)= — (см. § 4.3), то п=у и
Г = 2Л
Эта формула была уже нами получена в § 4.4.
В заключение этого параграфа найдем выражения для проекций скорости
и ускорения точки на радиальное и поперечное направления при ее движении
по эллиптической траектории через эксцентрическую аномалию.
Так как иг = Л и ур = гф —гф, то в соответствии с формулой (4.42) имеем
. „dE Z1 r^W'dE
vr=aesmE^, Op = a(l-e cos E)-^.
Ранее было найдено
dip ]/1 —e2
dE 1—e cos E ’
а из уравнения (4.45) следует, что
Отсюда
dE _ п ап
dt 1—е cos Е г
Таким образом
a2en sin Е а2п К1 —е2
vr =----------, v„ =-----------------.
г г > р г
Морулъ скорости будет
_ т—- а2п i/~i--------5---гк 1 Г 1 +е cos Е
v = T/ и2 + и2 = —- V 1 — е2 cos2 Е = ап I/ т—!---—,
’ ' р г К 1—ecosE
Косинус угла между вектором скорости и радиусом-вектором материальной
точки равен
, „ vr е sin Е
cos (v, г) = — = - .....-
и ]1—e2cos2E
Для получения проекций ускорения на радиальную и поперечную оси
используем равенства
mwr=Fr, mwp = Fp,
где Fr— — mgR , Ер = 0. Отсюда
wr = -^-, wp — 0
Модуль ускорения равен
gR2 п2а3
w = = —s—.
г2 г2 ’
так как
у а3-
116
движение точки в центральном силовом поле
[ГЛ. IV
§ 4.6. Траектории, пересекающие земную поверхность
В этом параграфе мы ограничимся рассмотрением только тех эллип-
тических траекторий (е < 1), которые
где
все
Рис. 4.8.
пересекают земную поверхность.
Условием пересечения траектории
с земной поверхностью является нера-
венство (см. § 4.4)
и2
-|[(R+/i)2 cos® 0О—Z?2J <
и1
Это условие будет выполнено, если
cos 60 < cos 6*,
cos 6*
_R_
R + h'
Следовательно, если 60 > 0*, то
траектории (эллипсы) пересекут
земную поверхность.
Если же 60 < 6J, то земную по-
ектории, для которых начальная
верхность пересекут только те тра-
скорость удовлетворяет неравенству
2Rh
и° 1 V (Я + /г)2соз20о-Я2 •
(4.46)
Рассмотрим траекторию, которая изображена на рис. 4.8.
Найдем угол ф! (см. рис. 4.8) между прямой ОА0 и большой осью эллипса.
Для апогея созфт =—1, следовательно, фт = л; но фт = ф0-|-ф1, значит,
ф1 = л —ф0. (4.47)
Так как в точке До выполняется равенство
Г° 1 -|- е cos фо ’
то
' , Р — Го , р — Го
cos фо = ог и Фо = arccos —
ег0 его
Таким образом, учитывая, что p = rov cos2 60, имеем
, v cos2 0о—1
фг = л — arccos---------------
или
ф! = arccos
1 — у cos2 0р
е
(4.48)
Выразим длину дуги окружности радиуса г0> проходящей через точки До
и Во, через величину v0 и угол 0О. В силу симметрии эллипса относительно
его большой оси имеем
S« о =2г ф .
Ао&о 0’1
Принимая во внимание формулу (4.48), получим
SAoBo=2/'»arccos
1 — V COS2 00
е
(4.49)
§ 4 6]
ТРАЕКТОРИИ, ПЕРЕСЕКАЮЩИЕ ЗЕМНУЮ ПОВЕРХНОСТЬ
117"
Длина дуги АВ определяется формулой
sab — •
(4.50>
При h R эту величину будем считать дальностью полета на пассивном
участке траектории (см. рис. 4.8).
Исследуем характер зависимости угла ipj от угла 0О при различных фикси-
рованных у, т. е. Vq.
Запишем формулу (4.48) в виде
cosip!
1 — v cos2 So
К1 — v (2 — v) cos2 So
(4.51>
При v = 2 формула (4.51) принимает вид
cos ipt = 1 — 2 cos2 60=— cos 26o
и, следовательно,
ip! = n— 26O.
При v=l имеем _________
cos ipi = К1 — cos2 60 = sin So,
t. e.
ip! = f - So-
Найдем теперь значение угла 0O, при котором грх имеет максимальное зна-
чение при данном фиксированном у. Введя в формуле (4.51) замену z = cos2 60»
получим
, 1 — ZV
cos гр, — ..... .
j/l-v(2-v)z
(4.52)-
Продифференцировав это выражение по г, найдем
— sin ipi ~v (2~v) г] + (1—уг) (2 —у) у
dz
[1—у(2—у) г]3/2
Приравняв нулю числитель правой части этого равенства, получим урав-
нение для определения того значения z, при котором грх имеет максимальное-
значение:
2 [1 — у (2 —v) г] —(1 —vz) (2 —у) = 0.
Отсюда
г = cos2 60 = 2~(;- (4.53)
Следовательно, ipi имеет экстремум только при v< 1. Формулу для опре-
деления максимального значения грх найдем, подставив результат (4.53) в вы-
ражение (4.52): ____
cosip^ax = --|^~V . (4.54)
Определив из выражения (4.53) у и подставив это в формулу (4.54),
получим cos ip™ax = sin 260.
Отсюда 1р7ах=у-2б0. (4.55)
sai8
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ IV
Из этой зависимости вытекает, что угол будет максимальным при за-
данном v, если
ео = Т“¥- (4-56>
На рис. 4.9 построены зависимости ipi от 0О при различных значениях v.
•Пунктиром показана линия максимумов (4.55).
Рис. 4.10.
е. v0) задано, определим угол 0О для получения
Предполагая, что v (т.
необходимого угла фи при условии пересечения траекторией земной по-
верхности.
D
Рассмотрим сначала случай v = Vi < 1. По формуле cos 0*= , находим
R-\-h
угол 0* (заметим, что при h < R угол 0J близок к нулю). Из рассмотрения
рис. 4.10 видно, что при Vi < 1 заданный угол фп < л/2 может быть достиг-
нут при двух значениях угла 0О:
0o = 6oi> 60 = 602 (Ooi < 0о2).
Если 0Q2 < 6*> то обе траектории пересекут земную поверхность только при
(см. условие (4.46))
2Rh
поверхность только
1 (R + /i)1 2cos20ol-R2 ’
то траектория, полученная при 6o = 0oi» пересечет земную
при
2Rh
1 (R + Л)2 cos2 0О1 - R- '
.При 0М > 0* обе траектории пересекут земную поверхность.
S 47]
ЗАДАЧИ
11»
Этот же заданный угол фц -может быть достигнут при
, л Фи
(4.57>-
но уже при v2 < Vi, т. е. при меньшей начальной скорости (см. рис. 4.10),
Значение v = v2, при котором заданное значение фи достигается при 0О —
Л _Ф11
4 2
, найдем, используя формулу (4.53):
1 __ 2 cos 260____2 sin фи
cos2 So ~ l+cos20o 1 + sin фи '
Отсюда следует, что начальная скорость должна быть равна
1/ 2 sin фи
(4.58>-
Формулы (4.57) и (4.58) даю' возможность по заданному углу "Ф11 найт»
угол 0О и минимальную начальную скорость о0, обеспечивающие получение-
этого угла фи-
Пусть v = v3>l. В этом случае заданное ф1 = фп или ф1=ф12 может
быть достигнуто только при одном значении угла 0о = 0$з или 0О = 0’8 (см,
рис. 4.10). При этом, если 0* <0« (0* <0оз)> то траектория пересечет земную
поверхность при любом v < 2. Если же 0J > (0£>0„3), то пересечение
произойдет только при выполнении условия (4.46).
§ 4.7. Задачи
Задача 4.1. Спутник движется по круговой орбите на высоте h от поверх-
ности Земли. Какую дополнительную скорость нужно сообщить спутнику,
чтобы он перешел на параболическую орбиту?
Спутник, двигаясь по окружности вокруг Земли на высоте h, имеет кру-
говую скорость, равную
v .... Л Г sR2
1 V R+h'
Для того чтобы спутник перешел на параболическую орбиту, он должен при-
обрести параболическую скорость, соответствующую высоте h, т. е.
v
2 V R + h-
Следовательно, спутнику нужно сообщить дополнительную скорость, равную-
рд = р2-Н1=1/'(К2-1).
Г К ~Г<1
Пусть Л = 200 к,и = 2-105. м, радиус Земли R = 6,37 • 10е м, g = 9,81 м]сек?,
тогда
Рд = 3219 м]сек.
Задача 4.2. На какой высоте h следует запустить спутник по круговой
орбите, чтобы период обращения его равнялся периоду обращения Земли во»
круг своей оси (24 часам) *).
*) Если орбита спутника лежит в плоскости экватора и направление дви-
жения совпадает с направлением вращения Земли, то спутник будет все время
располагаться над одной и той же точкой земной поверхности; такой спутник ,
называется стационарным,
120
ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ
[ГЛ. IV
Из формулы для периода обращения (4.39) следует, что
аз=т.2
4л2 •
Так как орбита круговая, то a = R-srh,
. Подставляя g-=9,81 м'сек1-, R = 6,37 10е м, Т =8,64- 104 сек, находим
h = 35 630 км.
Задача 4.3. Найти начальную скорость, необходимую для того, чтобы тра-
ектория спутника представляла собой эллипс с заданным отношением между
максимальным и минимальным расе оянием от центра Земли. Принять, что
0о = О, т. е. в начальный момент спутник находится на главной фокальной оси
(линии апсид).
При решении будем различать два случая: 1) начальная скорость больше
круговой скорости, т. е. начальная точка является перигеем орбиты; 2) началь-
ная скорость меньше круговой скорости, т. е. начальная точка является апо-
геем орбиты.
В первом случае, когда v> 1, обозначим
rmax=,<r<)’ rmin = ro>
где х> 1—заданное число. Пользуясь формулой (4.37), имеем
v _
гтах 2____V Г°’ rmin г°’
отсюда
v 2х
X=S----- и v=7-;-----.
2—v 1-|-х
'Так как v = vl/vf, где Oi = Kg/?2/ro > то искомая начальная скорость равна
1 Г 2х
1 + X
Большая и малая полуоси соответственно равняются а==—г0, Ь=Гцух.
На рис. 4.5 возле каждого эллипса указаны соответствующие значения х=
= 1,4, 9.
Во втором случае, когда v < 1, удобно обозначить
rmax=r°’ rmin х1г0'
причем xj является заданным числом, меньшим единицы. Пользуясь формулой
.(4.37), найдем, что
_ _ v
^max r°' rmin 2______v Г°
и Xj выражается формулой
v
^=2=Т-
Отсюда находим
2х! Г 2xi __
v=i+^ и w
§ 4.7]
ЗАДАЧИ
121
При этом, если Xi> RJra, то эллипсы не пересекают поверхность Земли
(см. рис. 4.6); если же HiCR/ro, то эллипсы пересекаются с поверхностью
Земли (такие траектории могут быть использованы для так называемых субор-
битальных полетов). Соответствующие эллипсы изображены на рис. 4.11 при.
Xi = 0,2; 0,4.
Задача 4.4. Спутник, движущийся по круговой орбите А радиуса rAt
переводят на круговую орбиту В радиуса гв (гв> гл).
Для этого сначала переводят спутник с круговой орбиты А на эллипти-
ческую орбиту, апогей которой расположен на расстоянии гв от центра Земли
(рис. 4.12); а затем, сообщив дополнительную скорость, переводят на круговую
орбиту В. Определить величины дополнительных скоростей, которые следует
сообщить спутнику на орбите Айв апогее переходного эллипса, чтобы выпол-
нить предполагаемый переход с орбиты А на орбиту В.
При движении по орбите А спутник имеет скорость
V = 1/^-
1Л У га'
Для перевода спутника на эллиптическую орбиту, расстояние апогея-
которой от центра Земли равно гв, его скорость должна быть увеличена.
Величина необходимой скорости была найдена в задаче 4.3 и равна
-1 Г 2х
где Х = г/
Следовательно, добавочная скорость, которую нужно сообщить спутнику,
будет
Скорость спутника vB в апогее эллипса найдем из интеграла площадей
VArA = vBrB-
Отсюда
rA VA / 2
Vj3~Va^b~^~V1AV
122 ДВИЖЕНИЕ ТОЧКИ В ЦЕНТРАЛЬНОМ СИЛОВОМ ПОЛЕ [ГЛ. IV
Так как иа орбите В круговая скорость спутника должна быть равна
то величина дополнительной скорости, которую следует сообщить спутнику
для перехода на орбиту В, будет равна
^=^-^="14 V ~~V1A У мгЬо)-
Суммарное увеличение скорости спутника при переходе с орбиты А иа
орбиту В определяется соотношением
л , * /х — 1 1 / 2 , 1
Д1о + Дас; = о1д —т— 1/ -j— + —11.
1л\^х г 1+х /х /
ГЛАВА V
НЕСВОБОДНОЕ ДВИЖЕНИЕ
§5.1. Определение несвободного движения. Связи.
Принцип освобождаемое™
В первой главе при формулировке основных задач динамики*
точки мы исходили из предположения, что на движение точки
не наложено никаких ограничений, т. е. все ее три координаты
могут меняться любым образом. Надлежащим выбором закона
изменения силы F и начальных условий можно заставить мате-
риальную точку двигаться по любой траектории. Примером может
служить движение управляемого космиче-
ского корабля. В подобных случаях мате- О__________
риальная точка называется свободной, а ее &
движение — свободным движением. / \i
В других случаях на движение могут \
быть наложены те или иные ограничения. •
Рассмотрим, например, материальную точ-
ку, находящуюся на конце нерастяжимого Рис. 5.1.
стержня длины I, другой конец которого
с помощью шарнира закреплен в неподвижной точке О (рис. 5.1).
При любых силах, приложенных к материальной точке, она совер-
шает движение по поверхности сферы, радиус которой равен длине
стержня. Координаты точки не будут независимыми, так как он»
должны удовлетворять уравнению сферы
х24-г/24-г2 —/2 = 0. (5.1)
Из этого уравнения одна из координат, например координата
х, может быть выражена через остальные две:
х = ± К/2 — У2 — г2. (5.2)
Скорость точки всегда располагается в касательной плоскости,
проведенной к сфере в точке, где находится в данный момент
материальная точка.
Таким образом, в рассматриваемом примере начальные усло-
вия не могут быть выбраны произвольно, так как координаты
начального положения должны удовлетворять уравнению (5.1),
424
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ V
а начальная скорость должна быть расположена в касательной
плоскости, проведенной к сфере в точке начального положения
материальной точки.
Итак, существуют случаи движения материальной точки, когда
некоторые ограничения вынуждают точку совершать движение по
строго фиксированной поверхности (в рассматриваемом примере
таким ограничением является стержень). Можно привести при-
меры, когда ограничения принуждают материальную точку дви-
гаться по строго определенной линии (например, кольцо, наса-
женное на изогнутую проволоку, будет двигаться только вдоль
проволоки). Ограничения также вынуждают материальную точку
двигаться лишь в некоторой части пространства. Во всех этих
случаях независимо от действующих сил координаты точки опре-
деленным образом связаны между собой и выбор начальных
условий не может быть произвольным.
Будем называть материальную точку несвободной, если вслед-
ствие тех или иных ограничений она при действии на нее любых
сил совершает движение по строго фиксированной линии, поверх-
ности или находится все время в строго фиксированной части
пространства. Движение такой точки называется несвободным, дви-
жением.
Ограничения, благодаря которым материальная точка вынуж-
дена совершать несвободное движение, называются связями; это
понятие уже встречалось в курсе статики.
При изучении несвободного движения пользуются также зна-
комым из курса статики принципом освобождаемости, который
заключается в следующем, при рассмотрении несвободного движе-
ния следует действие связей на материальную точку заменить
реакциями этих связей и рассматривать материальную точку
как свободную, но находящуюся под действием как сил активных,
так и реакций связей. Если обозначить через F равнодействую-
щую всех активных сил, приложенных к точке, а через R —рав-
нодействующую всех реакций связей, то основное уравнение
динамики примет вид
mw = F-|-R. (5.3)
Следует иметь в виду, что реакция связи неизвестна и может
возникнуть задача об определении этой силы.
В проекциях на оси системы координат Охуг в соответствии
с уравнением (5.3) получим
mx — Fx-\-Rx, ту = FU + Ry, mz = Fz + Rz.
Эти уравнения позволяют решать задачи, когда заданы дви-
жение и активные силы и требуется определить реакции, а также
когда заданы активные силы и требуется определить закон дви-
жения и реакции.
§ 5 2]
УРАВНЕНИЯ СВЯЗЕЙ. КЛАССИФИКАЦИЯ СВЯЗЕЙ
125
§ 5.2. Уравнения связей; классификация связей
Независимо от фактической реализации тех или иных связей,
наложенных на материальную точку, они могут быть заданы
аналитически. Уравнения линии или поверхности, по которым
совершает движение точка, называются уравнениями связи. Если
точка принуждена оставаться в некоторой области пространства,
то связь аналитически задается в виде неравенств.
Если материальная точка движется по линии, то уравнения
связи имеют вид
fi(x, у, г) = 0, f2(x, у, z) = 0, (5.4)
где /у (х, у, г) = 0 и f2(x, у, г) = 0 —уравнения тех поверхностей
линией пересечения которых является траектория точки. В слу
чае плоского движения по заданной кривой уравнение свя
зи можно записать в форме
f(x, у) = 0. Например, в кри-
вошипно-шатунном механизме
(рис. 5.2) точка А шатуна движет-
ся по окружности радиуса, рав-
ного длине кривошипа. Уравне-
ние связи получает вид
х*а + у*а-г2 = 0.
Рис. 5.2.
Ползун В движется по прямой, и для него уравнение связи имеет •
вид ув = ®- Неизменность расстояния между А и В выражается
уравнением
(хл —хв)2 + г/д =/2.
При движении точки по поверхности уравнением связи является
уравнение этой поверхности
f(x, у, z) = 0. (5.5)
Уравнение сферы (5.1) в рассмотренном выше примере и является
уравнением связи. Заметим, что если в этом примере вместо
стержня взята гибкая нерастяжимая нить, то точка получит воз-
можность совершать движение не только по поверхности, но и
внутри сферы радиуса, равного длине I нити. Вместо уравнения
связь в этом случае аналитически задается неравенством
х2 + у2 + г2-/2^0. (5.6)
Следовательно, если “какая-либо поверхность, определяемая урав-
нением f (х, у, z) = 0, ограничивает область движения точки, то
вместо уравнения связи следует взять одно из неравенств:
f(x, у, z)«sO (5.7)
126
НЕСВОБОДНОЕ ДВИЖЕНИЕ
(ГЛ. V
ИЛИ
fix, у, z)2s0.
Перейдем теперь к классификации связей.
Если связь со временем не меняется, т. е. время t явно1
в уравнение связи не входит, то связь называется стационарной
(склерономной). Таковы, например, связи, удовлетворяющие усло-
виям (5.4), (5.5) и (5.7).
Если же связь изменяется во времени заданным образом, то
уравнение связи содержит явно время t. Такие связи называются
нестационарными (реономными).
Например, если длина стержня I на рис. 5.1 будет изменяться
по какому-либо заданному закону, в частности, пусть / = /оф-
-J- a sin at (10>а), то уравнение связи будет иметь вид
х2 + у2 + г2 — (/0 + a sin at)2 = 0.
Следовательно, в общем случае при изменении связей во вре-
мени они могут быть заданы следующим образом:
при движении точки по поверхности
f(x, у, г, Z) = 0; (5.8)
при движении точки по кривой
0(х, у, г, 0 = 0, f2(x, у, г, 0 = 0; (5.9)
при движении точки в ограниченной области
~f(x, у, г, /)=с0 или f(x, у, г, 0^0. (5.10)
Связь называется удерживающей, если уравнение связи имеет
вид равенства, как, например, уравнения (5.4). Это означает,
что при любых условиях точка движется по заданной поверх-
ности или кривой. Связи, которые задаются с помощью нера-
венств, например, в виде (5.7) или (5.10), называются неудержи-
вающими.
Примером неудерживающей связи служит связь, определяемая
неравенством (5.6). Следовательно, связь является неудерживаю-
щей, если точка может покидать ее в какую-либо одну сторону.
Наконец, введем еще понятие об идеальной связи. При дви-
жении точки по поверхности или по кривой реакция связи может
быть разложена на нормальную и касательную составляющие.
Касательная составляющая реакции представляет собой силу
трения. Очевидно, что чем более гладкой будет поверхность или
кривая, тем меньше будет касательная составляющая реакции.
Если поверхность или кривая абсолютно гладкие, то реакция
будет направлена по нормали.
Для точки идеальными связями будем называть связи без тре-
ния, реакции которых не имеют касательных составляющих *).
*) Более полное определение идеальных связей будет приведено в главе XVIII.
§5 31 ДВИЖЕНИЕ ТОЧКИ ПО ГЛАДКОЙ ПОВЕРХНОСТИ 127
§ 5.3. Движение точки по гладкой неподвижной поверхности
Для изучения движения материальной точки по поверхности
используем уравнение (5.3).
В проекциях на оси системы координат Охуг имеем
mx = Fx-\-Rx, ту =Fy + Ry, mz = Fz-\-R1,. (5.11)
Эти три уравнения содержат шесть неизвестных: три координаты
точки (х, у, г) и три неизвестные проекции Rx, Ry, Rz реакции.
Но, как мы видели, координаты точки должны также удовлетво-
рять уравнению поверхности, по которой движется точка. Это
дает четвертое уравнение
f(x, у, z) = 0. (5.12)
Конечно, четырех уравнений для определения шести неизвестных
недостаточно. Для получения двух недостающих уравнений
используем условие идеальности связи.
Так как поверхность, по которой движется точка, идеально
гладкая, то реакция направлена по нормали к поверхности.
Г радиент
grad/^i+fj + fk
6 ' дх 1 ду ’ 1 дг
представляет собой вектор, который также направлен по нормали
к поверхности.
Условие коллинеарности реакции R и grad/ и дает недостаю-
щие два уравнения:
Rx__Ry__Rz _
дх ду дг
Таким образом, уравнения (5.11) —(5.13) в принципе дают
возможность решить задачу о движении точки по гладкой непод-
вижной поверхности. Из уравнений (5.11) и (5.13) можно исклю-
чить реакции связей. Для этого обозначим равные Отношения
(5.13) через X, т. е.
Rx__Д,/ __Rz_«
5/ ~д£~дГ~^'
дх ду дг
Тогда-
и уравнения (5.11) теперь примут такой вид:
mxx=Fx + ^x, my = Fy + Xdl, mz = Fz + ^. (5,15)
128
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
Присоединяя к этим уравнениям уравнения связи (5.12),
получаем систему четырех уравнений с четырьмя неизвестными
х, у, z и После отыскания этих неизвестных по формулам
(5.14) можно определить проекции реакции. Модуль реакции равен
R = VRi + Rl+Rl = IX11/" (|)2 + Ш + g)2. (5.16)
Реакция определяется выражением
R = + = X grad f.
\dx 1 ду 3 дг / ь '
Уравнения (5.15) называются уравнениями Лагранжа первого рода.
Задача 5.1. Рассмотрим движение тяжелой материальной точки массы tn
но внутренней поверхности цилиндра
радиуса г; ось цилиндра горизонтальна
(рис. 5.3). Совместив начало коор-
динат с какой-либо точкой оси ци-
линдра, направим ось х вертикально
вниз, ось у — горизонтально по ра-
диусу цилиндра, а ось г —по оси ци-
линдра.
Примем, что в начальный момент
положение точки определяется коор-
динатами х=0, у —г, z = 0. Положим
также, что начальная скорость на-
правлена параллельно оси цилиндра
и равна у0. Это значит, что в началь-
ный момент
х = 0, д/ = 0, z~u0.
На материальную точку действуют сила тяжести mg и реакция R, направ-
ленная по радиусу. Уравнение связи (цилиндрической поверхности) имеет вид
f (х, у, г) = х2+$/2 —г2=0.
Подставим Fx=mg, Fy = Fz = Q, ^=2х, -|~ = 2У и -|j-=0 в уравне-
ния (5.15). В результате получим
mx = zng-|-2Xx, ту = 27.у, mS = 0. (5-17)
Из третьего уравнения системы (5.17) после интегрирования и использо-
вания начальных условий получим
т. е. расстояние от начальной плоскости ху растет пропорционально времени.
Умножая первое уравнение системы (5.17) на у, второе уравнение — на х
и вычитая из первого уравнения второе, найдем
т (xy — yx) — mgy.
Умножая теперь первое уравнение системы (5.17) на х и складывая его
о вторым уравнением, умноженным на у, будем иметь
tn(xx+yy) = mgx+2‘k (х2+у2). (5.18)
§5 3] ДВИЖЕНИЕ ТОЧКИ ПО ГЛАДКОЙ ПОВЕРХНОСТИ 129
Перейдем к цилиндрическим координатам
х=гсо8ф, У —г sin ф, 2 = 2.
Так как
Х = —Гф Sin ф, // = гфсСвф,
X — — rq> sin ф — гф2 cos ф, у = гф cos ф — гф2 sin ф,
то уравнения (5.17) и (5.18) примут вид
тгг ф=— mgr sin ф,
или
<р-|-у8Шф=0 (5.19)
и
— /пг2ф2 = mgr cos ф+2V2. (5.20)
Записав уравнение (5.19) в виде
0
ф с!ф =—у- sin ф dtp,
после интегрирования получим
Ф2 £
-77- = — COS ф + С.
2 г т
Так как ф = л/2, ф = 0 при t = 0, то с = 0 и, следовательно,
ф2 = -у^-со8ф. (5.21)
Из этого уравнения видно, что при выбранных начальных условиях дви-
, , л л л
жение будет происходить в области, где со8ф>0, т. е. при —^-СфС-^-.
Подставляя выражение (5.21) в уравнение (5.20), будем иметь
. 3/ng
Л =----н-5 cos <р.
2г
В соответствии с формулами (5.14) получаем
Rx = k 'gr=— 3/ng cos2 ф,
Ry = X = — 3mg sin ф cos ф,
/?г=0.
Модуль реакции равен
R = 3mg cos ф.
Реакция равна нулю при ф = ±л/2. Максимальное значение реакции будет
при ф = 0 и равно R — 3mg.
Для определения закона изменения угла ф нужно проинтегрировать урав-
нение (5.19). Это'будет сделано в § 5.5.
6 Н. В. Бутении в др.
130
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
§ 5.4. Движение точки по гладкой неподвижной кривой
При движении материальной точки по кривой уравнения связей имеют вид
fi (х, У, z)=0, /2 (х, у, г) = 0, (5.22)
где fi(x, у, г) = 0 и f2(x, у, г) = 0 — уравнения поверхностей, линия пересе-
чения которых является траекторией точки (рис. 5.4).
В этом случае в уравнении (5.3) реакцию R следует рассматривать как
сумму реакций, т. е.
R = Ri+R2, (5.23)
где Ri и R2—реакции, заменяющие действие соответственно первой и второй
связи, уравнения которых имеют вид (5.22). Поэтому дифференциальные урав-
нения движения запишутся в виде *
mx = F x4"Rix + ^2x>
тУ—Fy-f- + (5.24)
m2 = Fz -J- /?1г R2z.
Эти уравнения содержат девять неизвестных: три координаты и шесть проекций
реакций.
Присоединяя к уравнениям (5.24) два уравнения связи (5.22) и условия
идеальностей связей
Riy Riz
(5’25)
дх ду дг
и
дх ду дг
получим девять уравнений с девятью неизвестными. Из этих уравнений можно
исключить проекции реакций. Для этого отношения в выражениях (5.25) и
(5.26) соответственно обозначим через и Х2 и получим
р A dfl р б д/1 (5.27)
р 1 р Л ^2 R -1 (5,28)
§ 5.4]
движение точки по гладкой кривой
131
Следовательно, уравнения (5.24) примут следующий вид
mx = Fx + lkl — + A-2 3^ ,
A * dx dx ’
my = Fy + ^ + ^d^,
(5.29)
Система (5.29) совместно с уравнениями связи (5.22) образует систему
пяти уравнений с пятью неизвестными х,
Реакции Rj и R2 определяются формулами
i+4i
dy
i-Ji- j + -^-kj = A.2grad f2.
Модули этих реакций равны
Ri = b,
R2 — Х2
Ri = i Ki |
r2=im

г, Aq и Х2.
А.1 grad fi,
f, (5.30)
О
Рис. 5.5.

Задача 5.2. По проволоке, имеющей форму параболы,
уравнения связи (параболы) имеют вид (рис. 5.5)
Л(х, у, г) = 2у — х2 = 0,
/2(х, у, г) = г = 0.
Найти реакцию связи при нулевых начальных
Подставляя
условиях,
движется
колечко;
(5.32)
*L = - 2x,
dx
ox
в уравнения (5.29), получим
dfi о
ду
> = 0,
dy
^=o,
dz
dfz .1
dz
mx = mg—2А-1 х, 1
mj( = 2A,1, У
/nz = A,2. J
Из второго уравнения связи имеем 2 = 0 и, следовательно, к2 = 0.
Умножая теперь второе уравнение на х и складывая его с первым урав-
нением, получим
(5.33)
x + xy=g.
Так как согласно уравнениям (5.32) у = ^х2, то
у=хх и у = х2-]-хХ.
Подставим полученное выражение у в уравнение (5,34);
X (1 +x2) + xx2=g.
(5,34)
Заменив
dx dx .
* = -^- = т~ x>
dt dx
б»
132
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
найдем
(хх2—g) dx-J-x (1 + х2) dx = 0.
Это уравнение в полных дифференциалах, и его решение имеет вид
x2(l+x2) — 2gx = C,
где С — постоянная интегрирования.
При нулевых начальных условиях (х = у = 0, х=у = 0 при t = 0) полу-
чаем, что С =0 и, следовательно,
х2(1+х2) —2gx=0,
или
2gx
1+х2 '
(5.35)
Продифференцировав выражение (5.35) по времени, найдем
2хх
_ 2g (1+х2) —2gx2x *
(1 + х2)2
откуда
,, g(l-*2)
(1 + Х2)2 •
Учитывая, что у — х2 + хИ, получим
g*(3 + *2)
у (1+х2)2 ‘
Тогда на основании второго уравнения системы (5.33) имеем
. _ /ng х(3 + х2)
1 2 (1+х2)2 •
Конечно, это же выражение можно получить и из первого уравнения системы
(5.33). На основании формул (5.27) можно выразить проекции реакций через
абсциссу колечка:
О дК_________*2(3 + х2)
Rx K1 дх ~~ 8 (1+х2)2 ’
n %т х (3 + х2)
Ry~^ ду 8 (1 + х2)2 •
Найдем скорость колечка в зависимости от его абсциссы. Так как у=х& и
учитывая, что х>0, имеем
v = Ух2 + у2 = х V1 + х2>
или, принимая во внимание равенство (5.35),
o = K2gx-
Этот результат можно было получить и сразу, применяя теорему об изме-
нении кинетической энергии. Действительно, так как работа реакции, направ-
ленной по нормали к кривой, равна нулю, то
ти2
~2~ = mgx
и
v = V 2gx>
§5 5]
ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
133
Рассмотренный пример показывает, что нахождение реакций с помощью
уравнений Лагранжа первого рода (уравнений (5.29)) приводит к громоздким
выкладкам. Поэтому этот метод и не нашел широкого практического приме-
нения. В следующем параграфе будет показано, как эту задачу можно решить
значительно короче.
§ 5.5. Естественные уравнения движения.
Математический маятник
При изучении несвободного движения материальной точки по
неподвижной кривой иногда удобно использовать уравнение (5.3)
в проекциях на оси естественного трехгранника (глава I, § 1.3).
Эти уравнения имеют вид
mwx = Fx + Rx, mwn = Fn + Rn, mwb = Fb + Rb.
Подставляя сюда проекции ускорения
dvx v2 п
получим
= + m^ = Fn + Rn, Q = Fb + Rb. (5.36)
Уравнения (5.36) называются естгственными уравнениями дви-
жения. Из третьего уравнения следует, что бинормальная состав-
ляющая реакции определяется статически через бинормальную
составляющую активной силы и от закона движения точки не
зависит.
При заданных активных силах и известных уравнениях связи
уравнения (5.36) позволяют определить закон движения точки
и реакции связей. Заметим, что между проекциями реакции Rx,
Rn, Rb обычно существует простая связь.
При движении точки по шероховатой кривой проекция Rx
представляет собой силу трения скольжения. Модуль силы тре-
ния скольжения равен
\R,\=fVRn + Rl,
где / — коэффициент трения скольжения.
Сила трения скольжения всегда направлена противоположно
скорости, следовательно,
Rx = -fVRn + Rl>^-.
Если движение происходит по идеально гладкой кривой, то
Rx — 0 и естественные уравнения движения принимают вид
m^- = Fx, m^- = Fn + Rn, 0 = Fb + Rb. (5.37)
134
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
Отметим, что в этом случае первое уравнение служит для
определения закона движения, а второе и третье —для определе-
ния реакции связи.
При движении точки по плоской, неподвижной шероховатой
кривой уравнения (5.36) запишутся в виде
m^-^Fx+Rx = Fx-f^Rl + Rl^t
(5.38)
Для примера, рассмотренного в предыдущем параграфе, второе уравнение
системы (5.38) можно записать следующим образом (см. рис. 5.5):
mv2 п
——- = R — mg sm а,
где а — угол, образуемый касательной к параболе с осью х.
Исходя из уравнения параболы
</ = -*-*2-
имеем
p' = x = tga. (5.39)
Отсюда
X 1
sin ct = . cos ot = (5.40)
/1+%2 К i+*2
Из курса высшей математики известно, что радиус кривизны кривой нахо-
дится по формуле
(1+/2)3/2
у"
Учитывая соотношение (5.39), получим
Р= (1+х2)3'2 •
Так как v = ]/2gx, то
г, mv2 , 2gx х x(3 + %2)
R = ---F mg sin a = m -s ;y- + mg = mg —*——Лг .
p (l+%2)3/2 K* + *2 (l-j-x2)3/2
Следовательно,
„ x2(3 + x2) D x(3 + %2)
R*~ me (i+X2)2 • Ry~mg (i-p^ •
Применим теперь уравнения (5.38) для изучения движения
математического маятника.
Математическим маятником называется материальная точка,
движущаяся под действием силы тяжести по гладкой окружности,
расположенной в вертикальной плоскости. Практически это можно,
§ 5-5]
ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
135
например, осуществить, подвесив материальную точку к невесо-
мой нерастяжимой нити, другой конец которой закреплен. При
этом начальная скорость подвешенной точки должна распола-
гаться в вертикальной плоскости перпендикулярно к радиусу.
Положение точки будем определять углом <р, образованным
нитью с вертикалью (рис. 5.6). Если т — масса точки, то дей-
ствующая на точку сила тяжести равна mg. Пусть длина нити
равна I.
Так как
1Ч = ^Ф> = — mg sincp, Fn — — mg cos g),
то уравнения (5.37) будут иметь вид
mlip = — mg sin<p, т/ф2 =— mg cos g> + Rn‘,
при этом учтено, что реакция направлена вдоль нити и, следо-
вательно, Rx = 0.
Перепишем эти уравнения в следую-
щей форме:
g> + y sing> = 0, (5.41)
= т/ф2 +mg cos д>. (5.42)
Уравнение (5.41) служит для опреде-
ления закона движения маятника, а урав-
нение (5.42) —для определения реакции
нити.
Пусть в начальный момент (t = Q) нить
отклонена от вертикали на угол д> = гр0 и
отпущена с начальной угловой скоростью Ф = ФО. Определим ре-
акцию в зависимости от угла д>, а также и закон движения точ-
ки д> = д> (0-
Согласно уравнению (5.42) для определения Rn в зависимости
от угла д? нужно выразить величину ф2 через этот угол.
Представив ф в уравнении (5.41) в виде '
..___ d dg>.
Вспоминая, что при g> = g>0 Ф = Ф0, можем записать так:
1 Г ?
—-1 \ йф2 = — g I sin<р dg>,
<р*о «’»
136
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ V
откуда
/ф2 = 2g (cos <р — cos <р0)-НФо *)• (5.43)
Подставляя этот результат в уравнение (5.42), получим
Rn = m/фо + mg (3 cos <р — 2 cos <р0).
Пусть ц0 = /ф0 —начальная скорость точки; тогда
Rn = + mg (3 cos ф — 2 cos <p0). (5.44)
В частности, формула (5.44) позволяет найти угол ф = ф],
при котором для заданных начальных условий связь перестает
быть удерживающей (нить сомнется). Это произойдет, если Rn — Q'.
+ mg (3 cos q>x — 2 cos <р0) = 0.
Отсюда следует, что
cos фх = у (2 cos
Если потребовать, чтобы связь была удерживающей вплоть
до значения (р] = л, то начальная скорость должна равняться
Vo = r(3 + 2 cos (p0)gl\
при этом маятник будет совершать круговое движение. В частно-
сти, при фо = О получим
v0 = V5gi-
Если начальная скорость равна нулю, то фо = О и формула
(5.43) примет вид
/ф2 = 2g (cos <р — cos<p0). (5.45)
Следовательно, во все время движения должны выполняться
неравенства cos <р Sa cos ф0 и (рс <р0.
Перейдем к определению закона движения маятника. Вводя
обозначение k2 = gll, перепишем уравнение (5.41) в виде
ф + £2 sin <р = 0.
Рассмотрим сначала случай малых отклонений, когда можно
принять
Sin ф «а ф.
В этом случае дифференциальное уравнение движения
Ф ф- £2ф = 0
*) Этот результат можно получить короче, используя теорему об измене-
нии кинетической энергии (см. § 5.6).
§ 55]
ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
137
совпадает по форме с дифференциальным уравнением свободных
линейных колебаний.
Следовательно, угол <р меняется по гармоническому закону
Ф = Фо cos kt 4--у sin kt.
Период малых колебаний маятника равен
Т = -^-=2л)Л-, (5.46)
т. е. при малых углах отклонения период не зависит от началь-
ного отклонения ф0 (колебания маятника изохронны).
Теперь найдем период колебаний маятника при любых углах отклонения <р.
Рассмотрим случай, когда колебания начинаются вследствие начального откло-
нения <ро, причем начальная скорость ф0 равна нулю.
Из уравнения (5.43) следует
-^- = ± у /2 (cos Ф —cos фо).
При возрастании угла ф здесь должен быть взят знак «плюс», а при обратном
движении — знак «минус».
При указанных начальных условиях движение начинается от значения
ф = ф0 в сторону уменьшения угла ф. В течение первого полупериода скорость
отрицательна и в последнем выражении должен быть взят знак «минус». Если
длительность полупериода обозначить через tlt то из выражения для скорости
следует равенство
«1 __— Vo
С <#=_/L С .
J г g J у 2 (cos (р — cos (ро)
отсюда находим
________________________________фо
~ S У 2 (cos ф —cos фо)
При обратном движении, т. е. при изменении угла ф от значения — фо до
значения ф0, скорость ф>0 и, значит,
to _Фо
С L С .... .
J г g J у 2 (cos (р — cos (ро)
О —(ро
где t2— время движения.
Отсюда
г-------------------------- Фо
^2 = 2 1/ - ( rf(P
2 ' g К 2 (cos ф — cos ф0) *
Период колебаний Т равен
_--- <Ро
1 = ^ = 2f d(f .
Г g J у cos (р — COS (ро
138
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ V
Входящий сюда интеграл не относится к числу элементарных. Преобразуем
его следующим образом. Так как
cos <р = 1 — 2 sin2 -2- f
то
Введем новую перемеииую ip:
• Ф
sm у
sin ib =-----------
• фо
s,n 2
Тогда
d<p =
2 sin cos ip dip
1 — sin2 sin2 ip
и, следовательно,
Интеграл
л/2
(5-47)
dip
sin2 <p
называется полным эллиптическим интегралом первого рода. Значения этого
интеграла зависят только от начального угла <р0 и могут быть найдены в таб-
лицах специальных функций.
Приближенное значение Д' при достаточно малых значениях <р0 можно
найти путем разложения подынтегрального выражения в ряд
1 — sin2 -у-
sin2ipj !/ = 1sin2-^-sin2ip + ...
Ограничиваясь двумя написанными членами, получим
л/2
'< =« j +4sin2 IF sin2 ^==у + уsin2
О
и, следовательно,
Ги«2«1/±(1+±!,пЛ).
§ 5.5]
ЕСТЕСТВЕННЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
139
„ . Фо Фо
Если можно принять sm =« , то
(!+<). (5.48)
Формулы (5.46) и (5.48) для периода колебаний различаются множите-
/ П)2 \
лем (l+~jg )• Значение этой поправки зависит от начального угла <р0 и
приведено в следующей таблице:
10° 20° 40’ 60° 90’
1,0019 1,0076 1,0304 1,0684 1,1539
Рассмотрим задачу о движении точки
Задача 5.3. Лыжник спускается с горы,
принять за окружность радиуса г (рис. 5.7).
Коэффициент трения скольжения равен f-
Определить скорость лыжника в точке В, если
в начальной точке А его скорость равнялась
нулю.
Так как в данном примере нормальная
реакция 7?„>0 и vx=v, то уравнения (5.38)
будут иметь вид
dv СП
т = mg cos tp — fRn,
niifl
mg sin <p+Rn. (5-49)
по шероховатой кривой.
причем его траекторию можно
Рис. 5.7.
Для исключения реакции умножим второе уравнение на f и сложим с пер-
вым уравнением:
dv , .mv2 . , .
т ~dt+ ~Г = ms <COS ф — Sm ф)’
Учитывая, что о = гф, имеем
* '^ + M’2=g(c°s<p — f sin <p),
но так как
йф йф dtp _ 1 d (ф2)
dt dtp dt 2 dtp ’
то
+ 2/Ф2 =~ (cos <p—/ sin <p). (5.50)
Уравнение (5.50) представляет собой неоднородное лннейиое дифферен-
циальное уравнение первого порядка относительно фа.
Общее решение однородного уравнения
У + 2/ф2=0
dtp
140
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
имеет вид
ф?=.Се”“2/'р, (5.51)
где С — постоянная интегрирования.
Частное решение уравнения (5.50) будем разыскивать в виде
ф| = A cos <р + В sin <р, (5.52)
где А и В — неопределенные коэффициенты. Для их определения подставим
выражение (5.52) в дифференциальное уравнение (5.50); тогда получим
(2fA + В) cos ф + (2/В — Л) sin ф=у^ созф —f sin ф.
Для тождественного удовлетворения этого равенства необходимо, чтобы коэф-
фициенты при sin ф и cos ф в обеих частях равенства были соответственно
равны друг другу. Это позволяет получить два уравнения относительно неиз-
вестных А и В:
2Af + B=^, -А + ЩВ = —^-.
Отсюда
6g/ . 2g (1-2Н
г (1+4/2)’ r(i+4f2)-
Таким образом, искомое частное решение имеет вид
ф2 - 6g/ cos ф’ + 2g<1~2^
ф2~г(1+4/2) ф+г(1+4/2) ф>
Складывая решения (5.51) и (5.53), получим общее решение дифференциального
уравнения (5.50):
ф,2_ Се-+- I 6g/ СОЗ ф 1 2g Sin ф (554)
ф °® +г(1+4/2) ф+ г (1+4/2) •
По условию задачи ф = 0 при ф = а, следовательно,
Ce~2fa + cos a I 2g ‘ sin а — 0 г
Le +r(i+4/2) Cosa+ г (1+4/2) sma-0.
Отсюда находим постоянную
С = — r^4f2) e2fa [3/ cos a + (1 2/2) sin a].
Подставляя полученное выражение в формулу (5.54) и учитывая, что г>2=
— г2ф2, окончательно получаем следующую зависимость v2 от угла ф:
V2 = — е2/<a- [3/ cos a + (1 _ 2/2) sin a] +
+ [3/ cos ф+ <* ~2/2) sin фЬ (б-55)
Нормальная составляющая реакции Rn равна
Rn = sin ф = —y-^^-e-2/«p-a> [3/cos a + (l — 2/2) sin a] +
H-[3/cos ф + (1 — 2/2) sin ф1 + т^ sin ф* (5-56)
§ 5 6]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
141
В последний момент рассматриваемого интервала движения, т. е. при
<р = л/2, получим
и2 = -Т+5р е ’ 2 “Wos а 441-2Н sin а]+1^-0-2/3), (5.57)
Rn = — уу%р е cosа4-(1 — 2/2) sinа]4-(1 — 2f2)4-/ng.
(5.58)
Если трением пренебречь и принять /=0, то по формулам (5.57) и (5.58)
ггйдем
v3 = 2gr(l—sin а), Rn = mg(3— 2 sin а).
§ 5.6. Теорема об изменении кинетической энергии
г .-я несвободного движения
Пользуясь принципом освобождаемое™, запишем соотношение
(3.40) для случая несвободного движения в виде
d = F • dr + R dr,
(5.59)
где R —реакция связи.
Результат (5.59) формулируется следующим образом: элемен-
тарное изменение -'".нетической энергии при несвободном движении
равно элементарной работе как активных сил, так и реакции связи.
Но при наличии идеальной стационарной связи работа реак-
ции на перемещении точки равна нулю и теорема об изменении
кинетической энергии для несвободного движения имеет тот же
вид, что и для свободного движения.
Если же связь идеальная, но нестационарная, то вектор пере-
мещения dr может быть не перпендикулярен к реакции R. В зтом
случае реакция направлена перпендику-
лярной вектору относительной скорости.
Поэтому при нестационарных связях
'работу реакции следует учитывать.
Задача 5.4. Тяжелое кольцо М веса Р
может скользить без трения по дуге окруж-
ности радиуса г, расположенной в вертикаль-
ной плоскости. К кольцу привязана упругая
нить МО А, проходящая через гладкое непо-
движное кольцо О и закрепленная в точке А.
Дано, что натяжение нити равно нулю,
когда кольцо М находится в точке О, а коэф-
фициент жесткости нити равен с (рис. 5.8).
В начальный момент кольцо находится в точке В и имеет скорость, рав-
ную нулю. Определить давление N, производимое кольцом на окружность. На
кольцо действуют сила Р, сила натяжения нити F и реакция R. Выразим
модуль силы F через угол ф (см. рис. 5.8). По условию задачи F=c-0M
(ОЛ1 — удлинение упругой нити). Так как ОМ =2r cos ф, то
F = 2cr cos ф.
142
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
Следовательно,
Fn = 2cr cos2 ф,
Рп =— Р cos ------------2<р1 = — Р sin 2<р.
• Второе уравнение системы (5.36) в данном случае имеет вид
^-Р.+Г.+К..
т. е.
----=— Р sin 2q> + 2cr cos2 ф + Д„.
(5.60)
Используем теорему об изменении кинетической энергии для нахождения
скорости о, принимая во внимание, что начальная скорость кольца о0 = 0:
. = + (5.61)
где Ар, Ар, Ар — соответственно работа сил Р, F и R. По условию задачи
связь стационарная и идеальная, следовательно, Д^ = 0. Для определения Ар
заметим, что
h = г sin 2ф.
Значит,
Ap = Ph = Pr sin 2ф. (5.62)
Далее находим
где и Хк— удлинения нити при положении кольца в точках В и М.
По условию задачи длина нити в нерастянутом положении равна О А, сле-
довательно,
Хн = 2г, ХК = ОА4 =2г cos ф.
Поэтому
Ар— 2сг2 (1 — cos2 ф) = 2cr2 sin2 ф. (5.63)
С помощью выражений (5.62) и (5.63) преобразуем соотношение (5.61)
к виду
— = Pr sin 2ф + 2cr2 sin2 ф.
Подставляя найденное значение mv2 в выражение (5.60), найдем нормальную
реакцию Rn:
Rn = 3P sin 2ф +cr (1 —3 cos 2ф)
и, следовательно, так как R =—N,
Nn=— 2Р—cr — 3 (P-f-cr) cos 2ф.
§ 5.7. Метод кинетостатики для точки (принцип Даламбера)
Наряду с рассмотренными методами изучения несвободного
движения точки удобным для решения первой задачи динамики
несвободной точки является метод кинетостатики. Особенно удобен
§ 5 8]
ЗАДАЧИ НА ПРИМЕНЕНИЕ МЕТОДА КИНЕТОСТАТИКИ
143
этот способ, когда требуется определить реакцию связи при задан-
ных законе движения точки и активных силах.
Содержание этого метода заключается в следующем. Перепи-
шем уравнение (5.3) в виде
F + R + (— М = 0. (5.64)
Введя обозначение — mw = J, (5.65)
получим F + R + J = O. (5.66)
Вектор J, равный по модулю произведению массы точки на ее
ускорение и направленный противоположно вектору ускорения,
называется силой инерции.
Равенство (5.66) представляет собой уравнение движения
материальной точки,-записанное в форме условия равновесия сил.
В этом и заключается существо метода кинетостатики.
На основании уравнения (5.66) можно утверждать, что в каж-
дый момент движения сумма активной силы, реакции связей и силы
инерции равна нулю. При этом следует иметь в виду, что к мате-
риальной точке приложены только силы F и R, т. е. активная
сила и реакция. Сила же инерции к точке не приложена.’Поэтому
на уравнение (5.66) нельзя смотреть как на условие равновесия
активной силы, реакции и силы инерции.
Метод кинетостатики является лишь формальным приемом
сведения уравнения динамики к уравнению статики, однако при
решении практических задач
такой прием может обладать
рядом достоинств.
Реакция связи в соответ-
ствии с уравнением (5.66)
равна
R = -(F + J).
§ 5.8. Задачи на применение
метода кинетостатики
Задача 5.5. Самолет, двигаясь
в вертикальной плоскости, выходит
из пикирующего полета на гори-
зонтальный полет по окружности
радиуса г (рис. 5.9). Скорость са-
молета в момент выхода на горизонтальный полет максимальна и равна v.
Определить, каким должен быть радиус г, чтобы реакция связи, действую-
щая на летчика, была в п раз больше нормального веса летчика (число
п называется перегрузкой).
На летчика, находящегося в самолете, действует сила притяжения к Земле
Q и реакция R, Нормальное ускорение самолета (и летчика) равно v2[r и
144
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
направлено к центру окружности. Сила инерции, равная Qv2/(gr), направлена
по радиусу окружности в сторону, противоположную нормальному ускорению.
Запишем уравнение (5.66) в проекции на вертикаль в точке выхода
самолета:
«-<5-^-0.
По условию задачи R — nQ, следовательно,
nQ — Q — ^ = 0.
gr
Отсюда находим
r-g(n-l)
Если, например, ц = 900 км/час = 2Ъ0 м/сек, п = 5, то
2502 ~ 1АОО
9,81 .(5-1)= 600 М’
В этом случае давление тела летчика на сиденье в пять раз больше его
нормального веса и летчик будет чувствовать себя так, как если бы его вес
возрос в пять раз.
Любопытен другой частный случай, относящийся к условиям, имитирующим
ощущение невесомости. Для этого нужно, чтобы реакция сиденья равнялась
нулю; при этом давление летчика на сиденье также равно нулю. Здесь следует
принять п = 0 и тогда по полученной выше фор-
у муле найдем
у г V2
у Г
Знак «минус» означает, что траектория полета
—* —------------------*- должна иметь выпуклость сверху, как это пока-
J 4 <27 зан0 на рис. 5-9, б.
Задача 5.6. Летчик на самолете выполняет
,,р правильный вираж со скоростью v. Угол крена
равен у. Определить радиус виража г.
р iQ Правильным виражом называется полет са-
молета без скольжения по дуге окружности в гори-
зонтальной плоскости с неизменным углом крена.
Будем рассматривать самолет как материальную точку, к которой прило-
жены следующие силы: сила притяжения к Земле Р, подъемная сила F, сила
тяги Ф и сила лобового сопротивления Q (рис. 5.10). Согласно (5.66) будем
иметь
P + F + ®+Q + J = O. (5.67)
Ускорение центра тяжести самолета wn = v2/r, а модуль силы инерции
J = Pv2/(gr).
В проекциях на оси координат уравнение (5.67) дает
pv2
---—+ Fsiny = 0, —P4-Fcosy = 0, Ф — Q = 0. (5.68)
Из последнего уравнения следует, что при выполнении правильного виража
Ф = <2, т. е. сила тяги уравновешивается силой лобового сопротивления. Из
второго уравнения можно найти, что сила притяжения к Земле уравновеши-
вается вертикальной составляющей подъемной силы;
P=Fcos у.
§5 9]
ЯВЛЕНИЕ НЕВЕСОМОСТИ
145
Из первого уравнения определяется радиус виража
Pv2 v2
gF sin у ~ gtgy '
Если будет нарушено какое-нибудь из равенств (5.68), то правильный
вираж станет неосуществимым (возникает скольжение, а также снижение или
подъем самолета). Следует иметь в виду, что данному углу крена у соответ-
ствует определенная скорость полета (она определяет подъемную силу).
Задача 5.7. Шарнирно-стержневая система (рис. 5.11) вращается вокруг
вертикальной оси АВ с угловой скоростью <о. Стержни МА и МВ считать
невесомыми и имеющими длину / каждый. Определить усилия в стержнях,
если в точке М находится сосредоточенная масса т и угол Z АМВ — Ъа..
Ускорение массы т равно <о2/ cos а и направлено по горизонтали к оси
вращения. Соответственно сила инерции равна
7 = m(1)2/cosa и направлена по горизонтали от оси
вращения. Обозначая через 7\ и Т2 усилия в
стержнях, напишем уравнение (5.66):
w J —J— Ti —1~ Т2 —J —0.
В проекциях на оси х и у получим
—1\ cos а —- Т2 cos а + mo2 I cos а = 0,
— mgA-T-i sin а — Т2 sin а = 0.
Решив эту систему, найдем
_ _ muPl mg _ _ ma>2l _ mg
1 2 2 sin а ’ 2 2 2 sin а '
Заметим, что при малых значениях угловой скорости со усилие Т2 отрица-
тельно, т. е. нижний стержень сжат (силой тяжести). При со = ^/~у
усилие Т2 равно нулю, а при больших значениях со оно положительно.
§ 5.9. Явление невесомости
В этом параграфе рассматривается явление, которое по уста-
новившейся традиции, хотя и не вполне точно, называется неве-
сомостью.
Предположим, что платформа А движется по вертикали с задан-
ным ускорением w, причем на платформе установлены пружинные
весы, на которых лежит груз С. Стрелка весов фиксирует силу,
с которой груз давит на весы (рис. 5.12). Когда платформа нахо-
дится в покое (или движется равномерно), стрелка весов устанав-
ливается против деления шкалы, соответствующего весу груза С.
В дальнейшем это показание пружинных весов будем называть
истинным весом. Выясним, какое давление оказывает груз на весы,
если платформа движется вниз с ускорением w.
На груз действуют две силы: сила тяжести mg и реакция R
(рис. 5.13) со стороны чашки весов. Уравнение движения груза
имеет вид
R 4- mg — mw,
(5.69)
145
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ. V
или, в проекции на вертикальную ось х (положительное направ-
ление—вниз),
mw = mg — R.
СледовательнЬ, величина реакции весов равна
R = m{g—w). - (5.70)
Такую же величину имеет направленное вниз давление R',
которое тело оказывает на весы.
Понятно, что деформация пружины под действием силы R'
окажется меньше, чем в состоянии покоя. Стрелка весов остано-
вится против деления шкалы, на котором мы прочтем новый «вес»
груза; он окажется равным mg — mw. Его отношение к истинному
У
R
W []
- mq
весу составляет п — 1 ——
(н — коэффициент перегруз-
ки). Конечно, сила притяже-
ния тела к Земле не изме-
нилась, так как гравитацион-
ное поле Земли не зависит
от того, движется ли груз
или находится в покое. Из-
менились лишь силы взаимо-
действия между грузом и
чашкой весов.
Рис- 5-12. Рис. 5.13. Продолжим опыт далее и
будем увеличивать ускорение
w. При этом реакция, как это видно из (5.70), уменьшается. Нако-
нец, при w = g она станет равной нулю и стрелка весов уста-
новится на нулевом делении шкалы. Взаимодействие между грузом
и чашкой весов исчезает. Говорят, что наступила «невесомость».
Если ускорение w превзойдет значение g, то груз оторвется
от весов и будет свободно падать. Платформа, опускающаяся
с большим ускорением, будет удаляться от падающего груза.
Если же груз связан с весами, то платформа будет увлекать его
вниз, причем перегрузка станет отрицательной и сила действия
груза на весы окажется направленной вверх.
Вернемся к состоянию видимой невесомости, когда перегрузка
равна нулю. Это состояние приводит к непривычным ощущениям
у человека, находящегося в лифте, в космическом корабле или
самолете. Он действительно перестает чувствовать вес своего тела.
Для того чтобы объяснить смысл этого явления, разберемся
в причине ощущения веса (или весомости), к которому привыкает
человек в обычных земных условиях.
В обычных условиях между отдельными частями человеческого
тела существуют силы взаимодействия. Рассмотрим, например,
§ 5.9]
ЯВЛЕНИЕ НЕВЕСОМОСТИ
147
силы, действующие на голень стоящего на полу человека (рис.
5.14).
На голень, кроме силы тяжести Р, действует реакция N,
приложенная в коленном суставе, и реакция пола R (речь идет
о весьма схематичном представлении действительных сил).
Силы Р, N и R уравновешены. Аналогичная картина распре-
деления усилий может быть изображена и для всех других
мысленно выделенных частей тела.
Таким образом, массовые силы (силы тяжести) и поверхностные
силы (реакция пола), приложенные к сложной системе материальных
точек — человеческому телу, вызывают появление многочисленных
внутренних сил.
Именно появление этих внутренних сил (натяжение
мышц, реакции суставов, давление на нервные оконча-
ния вестибулярного аппарата и т. п.) вызывает у чело-
века ощущение весомости. Человек привыкает к ощуще-
нию всей этой совокупности сил.
Предположим теперь, что человек опускается вниз
с ускорением g. Как было установлено выше, при этом
исчезает реакция со стороны опоры, т. е. R = 0.
Следовательно, уравнение движения голени примет
вид
P + N = ^g. (5.71)
Рис. 5.14.
Отсюда получим N = 0. Рассматривая уравнения движения
других мысленно выделенных частей человеческого тела, придем
к аналогичному результату: исчезают внутренние силы взаимодей-
ствия между отдельными частями тела. Исчезает и ощущение
весомости. В этих условиях теряют смысл привычные понятия
«верх» и «низ».
Оттолкнувшись от опоры, человек приобретает дополнительную
скорость и движется до тех пор, пока не натолкнется на преграду.
Конечно, внутренние силы могут возникнуть и в таких усло-
виях. Однако их происхождение на этот раз не связано с тяго-
тением. Человек может, например, взять в руки эспандер и
растягивать его обеими руками. При этом обязательно возникнут
внутренние силы — силы натяжения многочисленных мышц, которые
будут возрастать по мере растяжения пружины эспандера.
На каплю воды (рис. 5.15) продолжают действовать силы
поверхностного молекулярного натяжения, и они не дадут ей разру-
шиться. Эти внутренние силы вызовут появление давления в капле,
т. е. опять возникнут силы взаимодействия между отдельными
материальными точками механической системы.
Перейдем теперь к выяснению более общих условий, при ко-
торых возможно появление невесомости. Для этого определим,
148
НЕСВОБОДНОЕ ДВИЖЕНИЕ
[ГЛ V
пользуясь полученным уже представлением, более точно понятие
невесомости.
Представим себе, что тело Q (рис. 5.16) движется поступательно
с ускорением w относительно инерциальной системы координат
в поле массовых сил, т. е. сил, действующих на все точки тела.
Обозначим через F равнодействующую этих массовых сил, дейст-
вующих на точки тела.
Выделим в теле Q произвольный объем массы т. На этот объем
будет действовать две силы: внешняя сила f и равнодействующая
всех внутренних сил R.
Определим состояние невесомости следующим образом: тело Q
находится в невесомости, если равнодействующая всех внутренних
сил, приложенных к любому элементу, выделенному в теле, равна
нулю.
Найдем, каким условиям должны удовлетворять силы f, чтобы
тело находилось в состоянии невесомости.
Напишем уравнения движения для всего тела и для выделенной
части тела Q массы т; массу всего тела примем равной М:
Mw = F, mw = f+R. (5.72)
Используя условие невесомости R = 0, из (5.72) получим
F f
= /5-73>
Условие (5.73) должно выполняться для любой массы т, выде-
ленной в теле. Это условие является также и достаточным. Исполь-
зуя условие (5.73), получаем из уравнения (5.72)
/ F f \
R = mw — f = m--------| = 0.
\ т т )
Условие (5.73) имеет простой смысл.
Для обеспечения невесомости необходимо и достаточно, чтобы
внешние массовые силы, приложенные к выделенным элементам
тела, были пропорциональны массам этих элементов, а их направ-
ление для всех элементов было одинаковым.
§ 5 9]
ЯВЛЕНИЕ НЕВЕСОМОСТИ
149 '
Этими замечательными качествами как раз и обладают силы
гравитации. Они пропорциональны массам тех тел, на которые
действуют, и если тела достаточно малых размеров, то направления
сил можно считать для всех точек одинаковыми.
Таким образом, тело будет находиться в состоянии невесомости,
если равнодействующая всех внутренних сил, обусловленных нали-
чием сил гравитации, приложенных к любому элементу, выделенному
в теле, равна нулю.
Напомним, что равнодействующая внутренних сил, обуслов-
ленных наличием других причин (не силами гравитации), может
быть при этом и не равна нулю.
При полете стабилизированного космического аппарата с выклю-
ченным двигателем и вне пределов атмосферы его экипаж нахо-
дится в условиях, близких к невесомости. Условие (5.73), если
пренебречь размерами тел, для него выполняется, так как един-
ственные активные силы, действующие на аппарат и его экипаж, —
гравитационные. Разумеется, это условие соблюдается только при
Рис. 5.17.
поступательном движении аппарата (иначе ускорения всех точек
нельзя считать одинаковыми и условие (5.73) оказывается неспра-
ведливым).
Предположим теперь, что включен реактивный двигатель, разви-
вающий силу тяги Ф (рис. 5.17). Тогда к космическому кораблю,
кроме силы тяготения F, приложена еще сила Ф. В то же время
активные силы, действующие на тело Р, не изменились. Нарушено
условие невесомости (5.73).
При включении двигателей все тела, не закрепленные в кабине,
переместятся в сторону, противоположную вектору тяги. Опять
возникнет ощущение «весомости», хотя при этом сила тяготения
может и не действовать.
Такое же явление возникает и при торможении аппарата
в атмосфере. Сила сопротивления S (рис.5.18) действует только
на аппарат и приложена к его поверхности. К человеку, находя-
щемуся в кабине, она не приложена, поэтому нарушается условие
невесомости — космонавта отбрасывает в сторону, противополож-
ную S, т. е. в направлении вектора скорости v (рис. 5.18).
Следует отметить, что на участке торможения реакция R может
достигать значительной величины. Ее можно определить, исходя
из обычного уравнения движения (5.72), если только пренебречь
150 НЕСВОБОДНОЕ ДВИЖЕНИЕ [ГЛ V
силой тяготения f, которая мала по сравнению с R. Из (5.72)
имеем
R = mw.
Отношение 7? к весу mg (перегрузка) здесь окажется равным
tnw W
п =---------------------------= —.
mg g
Перегрузки нередко достигают величин порядка 8 ->-10.
В предыдущей главе было показано, что при маневре самолета
в вертикальной плоскости может быть достигнута нулевая пере-
грузка или невесомость. Для этого должен быть осуществлен
маневр типа «горки» с радиусом кривизны траектории в верхней
точке, определяемым по формуле
у2
Р=у. (5.74)
Например, при v — 720 км < ас = 200 м/сек радиус кривизны должен
быть равен 4,08 км.
В окрестности этой точки условие невесомости строго не будет
соблюдаться, тем не менее состояние человека окажется близким
к невесомости Такой имитацией явления невесомости пользуются
при тренировках летчиков-космонавтов.
Совершенно аналогичное явление может наступить и в земных
условиях —при движении автомобиля по мосту. В средней точке
моста при соответствующей скорости
u = ]/gp,
определяемой в зависимости от кривизны пролета по формуле (5.74),
наступит мгновенное состояние невесомости.
Состояние, довольно близкое к невесомости, испытывает пара-
шютист при свободном падении с большой высоты с нераскрытым
парашютом. Пока сопротивление атмосферы мало (в начальный
период и на большой высоте), ускорение падения близко к g и
поэтому состояние парашютиста мало отличается от невесомости.
Более длительное состояние невесомости можно получить при
помощи так называемого «баллистического броска» самолета. Для
этого самолет должен выдерживать строго скорость и траекторию
полета тела, брошенного под углом к горизонту в пустоте.
ГЛАВА VI
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
МАТЕРИАЛЬНОЙ ТОЧКИ
§ 6.1. Переносная и кориолисова силы инерции
В предыдущих главах мы опирались на основное уравнение
динамики точки (второй закон Ньютона), которое справедливо
только в инерциальных системах отсчета. Напомним, что инер-
циальной называется такая система отсчета, в которой справедлив
принцип инерции (первый закон Ньютона). Во многих случаях
задачи динамики сводятся к исследованию движения в той или
иной неинерциальной системе. В сущности, неинерциальной явля-
ется и привычная для нас система отсчета, связанная с Землей.
Впрочем, только весьма тонкие опыты (например, наблюдения
за отклонением падающих тел к востоку, за вращением плоскости
качания маятника) могут обнаружить неинерциальность геоцент-
рической системы отсчета. В большинстве приложений систему
координат, жестко связанную с Землей, можно считать инерциаль-
ной.
Значительно заметнее проявляется неинерциальность систем
отсчета, связанных с ускоренно движущимися техническими объек-
тами—от ускоренно поднимающегося лифта до искусственного
спутника или космического корабля, совершающего взлет с Земли.
Если связать систему отсчета с кораблем, автомобилем или само-
летом, движущимися по криволинейным путям или тем более с рото-
ром быстроходной турбины, то неинерциальность окажется столь
значительной, что основное уравнение динамики окажется неверным.
Значит, окажутся неверными и многочисленные следствия из этого
уравнения, доказанные в предыдущих главах.
Настоящая глава посвящена изучению движения материальной
точки в неинерциальных, системах отсчета Ниже будет дан метод
составления уравнений движения материальной точки в неинер-
циальной системе отсчета. В этом, собственно, и состоит основная
задача, которую предстоит решить.
Главная идея, которая положена в основу вывода соответст-
вующих динамических уравнений, связана с задачей чисто кине-
матического характера, которую мы рассматривали в кинематике:
152 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ VI
по заданному относительному движению точки и при известном
движении подвижной системы координат определить абсолютную
скорость и абсолютное ускорение точки. Мы воспользуемся этими
результатами для того, чтобы научиться составлять уравнения
движения материальной точки в не-
мики
инерциальных системах отсчета.
Предположим, что известны силы,
которые действуют на материальную
точку, а также задано движение по-
движной системы координат относи-
тельно некоторой инерциальной си-
стемы (в дальнейшем будем называть
ее неподвижной системой).
Поставим своей задачей найти
относительное движение точки, т. е.
движение в неинерциальной системе
отсчета.
Напомним, что задать движение
подвижной системы координат можно
при помощи трех координат ее начала (рис. 6.1): x0(t), y0(t),
z0(f) и трех углов Эйлера: 6, <р.
В неподвижной системе справедливо основное уравнение дина-
mw = F-|-R.
(6-1)
Здесь, как и выше, F — равнодействующая всех активных сил,
R — равнодействующая реакций связей, tn — масса материальной
точки, w —ее ускорение.
Используем теперь теорему Кориолиса (том I, § 13.3) и вы-
разим абсолютное ускорение через относительное, переносное и
кориолисово:
w = wr + we4-wc. (6.2)
Подставляя (6.2) в (6.1), получим
mwr + tnwe + tnwc = F + R.
Перенося часть членов в правую часть, придем к векторному
уравнению
mwr = F + R + (— mv/e) + (—mwc). (6.3)
Отсюда ясно, что произведение массы материальной точки на
ее относительное ускорение не равно сумме равнодействующей
всех активных сил, действующих на нее, и равнодействующей
реакций связей.
Последние два вектора в правой части уравнения (6.3) должен
ввести наблюдатель, находящийся в неинерциальной системе отсче-
§ 61]
ПЕРЕНОСНАЯ И КОРИОЛИСОВА СИЛЫ ИНЕРЦИИ
153
та, для того, чтобы в этой системе отсчета основное уравнение
динамики сохранило форму второго закона Ньютона.
Векторы —mwe и —mwc называются «силами инерции». Первый
называется переносной силой инерции, второй — кориолисовой силой
инерции.
Будем в дальнейшем пользоваться обозначениями
Je = —mwc, Jc = —mwc = —2m(«>xvr), (6.4)
где co — угловая скорость переносного движения.
Таким образом, уравнение (6.3) приобретает привычную форму
основного уравнения динамики (второго закона Ньютона):
mwr=F 4- R + -L + •!<:• (6-5)
Мы получили следующее правило:
Для того чтобы составить дифференциальное уравнение дви-
жения материальной точки в неинерциальной системе координат
в форме второго закона Ньютона, необходимо к действующим на
точку активным силам и реакциям связей присоединить перенос-
ную и кориолисову силы инерции.
В неинерциальной системе координат силы инерции проявляют
себя как обычные силы, с которыми мы имеем дело в инерциаль-
ной системе отсчета. Переносная и кориолисова силы инерции
вызывают относительное ускорение, они могут деформировать тело
и даже разрушать его, они совершают работу и т. п. Вместе с тем
необходимо помнить, что, в отличие от обычных сил, например
силы тяготения, величина и направление которых зависят только
от характера взаимодействия тел и не зависят от выбора неинер-
циальной системы отсчета, переносная и кориолисова силы инерции
определяются выбором неинерциальной системы координат.
Кроме того, мы не можем указать внутри Солнечной системы,
с которой связана гелиоцентрическая инерциальная система, тела,
в результате взаимодействия с которыми возникают силы инерции.
В общей теории относительности согласно принципу эквива-
лентности, выдвинутому А. Эйнштейном, природа сил тяготения
и массовых сил инерции в относительном движении тождественна.
Остановимся на способах определения сил инерции и напомним
правила вычисления соответствующих ускорений.
Для того чтобы найти переносное ускорение, необходимо знать
движение подвижной системы координат. Формула для определения
переносного ускорения имеет вид (том I, § 13.3)
we = w0 + «>x (ыХр) + ехр. (6.6)
Здесь (о, е — угловая скорость и угловое ускорение подвижной
системы координат, w0 — ускорение ее начала и р — радиус-вектор
точки в подвижной системе координат (см. рис. 6.1),
154 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ VI
Во всех случаях вычисления переносного ускорения и пере-
носной силы инерции полезно представлять переносное ускорение
как абсолютное ускорение точки, закреплен-
/ с ной в подвижной системе координат.
/ Для определения кориолисова ускорения
/ каждый раз необходимо перемножать два
вектора ш и vr (рис. 6.2), так как
vic = 2«> X vr.
*6’ При составлении уравнений движения
w материальной точки относительно поступа-
Рис. 6.2. тельно движущихся систем отсчета следует
иметь в виду, что кориолисовы силы инер-
ции отсутствуют (ш=0); а переносные силы инерции не зависят от
положения, занимаемого точкой в подвижной системе отсчета.
Рис. 6.3.
Задача 6.1. Точка М неподвижна в неподвижной системе отсчета х10у1
{рис 6.3) и находится на расстоянии ОМ от ее начала. Система координат хОу
вращается равномерно против хода 4acoi "
лярной к плоскости рисунка, с угловой
движения точки М в подвижной (вра-
щающейся) системе координат хОу.
Так как точка М неподвижна, то
ее абсолютная скорость равна нулю. Пе-
реносная скорость ve = (&xOM. Таким
образом,
v = ve + vr = 0, vr = —ve = —g>xOM.
Следовательно, в относительном дви-
жении точка движется по окружности
с центром в О, но Гв направлении, про-
тивоположном вращению подвижной си-
стемы координат. Для наблюдателя она
будет двигаться по ходу часовой стрел-
ки В соответствии с этим изобразим век-
тор относительной скорости (см. рис.
6 3) vr.
Переносное ускорение найдем, за-
крепив мысленно точку в подвижной
системе координат. Тогда точка будет вынуждена участвовать во вращательном
движении подвижной системы. Поскольку вращение равномерное, то враща-
тельное ускорение равно нулю и остается только осестремительное ускорение,
равное по величине
we = a2R.
Оно направлено к точке О.
Переносная сила инерции Je = —mwr направлена в противоположную сто-
рону (от центра), ее часто называют центробежной силой инерции. Величина
этой силы Je=-imMR.
Перейдем теперь к определению кориолисовой силы инерции. Вектор
•угловой скорости вращения системы хОу направлен перпендикулярно к пло-
скости рисунка на читателя. Следовательно, векторное произведение 2e>xv,
направлено в ту же сторону, что и переносная сила инерции. Однако корио-
лисова сила инерции противоположна по направлению wc и поэтому направлена
стрелки вокруг оси, перпендику-
скоростью и. Составить уравнение
§ 6.1] ПЕРЕНОСНАЯ И КОРИОЛИСОВА СИЛЫ ИНЕРЦИИ
155
к центру О. Величина кориолисовой силы инерции определяется из равенства
Jс = 2т о) X vr \ = 2ma>vr sin ~ = 2тшиг = 2тш2Я.
точка М
составить
оси АВ (рис. 6.4). Внутри
Таким образом, кориолисова сила инерции оказалась противоположной
переносной силе инерции. Равнодействующая этих сил направлена к центру
и равна по величине ma>2R. Уравнение относительного движения принимает вид
mwr ——mco2R, где R — ОМ.
Задача 6.2. Трубка, изогнутая по окружности радиуса R, равномерно вра-
щается с угловой скоростью <о вокруг вертикальной '" ' "
трубки находится материальная
массы т. Пренебрегая трением,
дифференциальное уравнение движения мате-
риальной точки М в трубке и определить ха-
рактер этого движения, если в начальный
момент точка М, находясь на одной горизон-
тали с центром трубки, была отпущена без
начальной скорости.
Свяжем с трубкой координатные оси Охуг,
выбрав начало координат О на оси враще-
ния АВ трубки в ее центре. Ось х проведем
горизонтально так, чтобы она пересекла труб-
ку, ось у построим перпендикулярно к трубке
(на рис. 6.4 ось у не показана — она направ-
лена на читателя),
вращения. Положение точки М будем опреде-
лять углом q> (см. рис. 6.4).
Выбранная система координат Охуг яв-
ляется неинерциальной системой отсчета, по-
этому движение точки М относительно трубки следует написать в виде
нения (6.5). Так как на точку действуют сила тяжести mg и нормальная
ция трубки N, то уравнение движения будет
mwr = mg + N4-Jg + Jc-
При равномерном вращении трубки переносное ускорение we точки М
состоит только из одной осестремителыюй составляющей, модуль которой равен
Rco2 sin ф. Следовательно, переносная сила инерции Je, численно равная
т/?<о251Пф, направлена перпендикулярно к оси вращения от нее (см. рис. 6.4).
Так как относительная скорость vr = RcpT, то кориолисово ускорение
а ось z совместим с осью
урав-
реак-
wc = 2Rcp (со хт)
направлено параллельно оси у. Следовательно, и кориолисова сила инерции
Jc = —2m /?ф (со ХТ)
направлена параллельно оси у в сторону, противоположную направлению wc.
Нормальную реакцию N разложим на две составляющие: одну направим по
главной нормали к относительной траектории от М к О, а вторую N2—перпен-
дикулярно плоскости трубки (на рис. 6.4 силы Jc и N2 не показаны).
Уравнение движения теперь можно записать в виде
mwr= mg + Ni N2 Je Jc.
Запишем это уравнение движения в проекциях на направление т, учитывая,
что проекция относительного ускорения точки М на касательную т равна Rep, а
проекции на т векторов Nt, N2, Jc равны нулю:
mR + <о2 sin ф cos ф.
(6-7)
Это и есть дифференциальное уравнение движения точки М внутри вращаю-
щейся трубки.
Заметив, что
d® dip dtp .dm Id,. m
ф - dF ~ d<p ~df "" ф dip ~ “2 Ity
получим
(ф2) = — 8Шф + «2 sin ф COS ф.
После интегрирования имеем
1 s 1
Ф2 = d cos Ф + тг 0)2 sin2 ф + С.
£ t\ Z
По условию задачи ф = л/2, ф = О/при t = 0. Значит, С = —ы2/2 и
— <о2соз
cos ф.
Значения угла ф, при которых скорость точки М обращается в нуль,
получим из условия
2 f—<о2со5ф ] cos ф = 0. (6,8)
Рассмотрим два случая.
1. Угловая скорость вращения трубки <о мала и удовлетворяет условию
R '
2 ст
В этом случае > 1
в нуль:
и только второй
cos ф = 0.
множитель может обратиться
Отсюда
л л
ф1 — у фз — — у
(индекс «два» временно пропускаем).
Корень ф1 соответствует начальному положению точки М,
Из выражения (6.7) найдем
О- 0
Фф = ф1= R фФ = Фз=#' > °’
2 ст
Это означает, что при точка М будет совершать во вращающейся
г\
трубке колебания от одной до другой горизонтали.
2, Угловая скорость трубки удовлетворяет условию
2g
Я *
§ 6.1]
ПЕРЕНОСНАЯ И КОРИОЛИСОВА СИЛЫ ИНЕРЦИИ
157
В этом случае уравнение (6.8) имеет три корня:
зх 2g эт
ф1=-2> Ф2=атссо8—, ср3 = ——.
Согласно уравнению (6.7) будем иметь
Фф=ф1 = -|, ФФ=ф2=-ртфг>0.
Следовательно, при со2 > точка А4 совершает во вращающейся трубке
л 2g
колебания только в первой четверти от ф1 = -% до ф2 = arccos .
Задача 6.3. Балка ЛС равномерно вращается с- угловой скоростью ш
в горизонтальной плоскости вокруг вертикальной оси АВ. Одновременно по
балке движется с постоянной относи-
тельной скоростью и ползун м массы т
(рис. 6:5). Определить: 1) изгибающий
момент относительно оси вращения,
действующий на балку; 2) закон из-
менения движущей силы F, обеспечиваю-
щей равномерное движение ползуна по
балке, если коэффициент трения между
ними равен f.
Построим систему координат Ахуг,
жестко связанную с балкой: ось х на-
правим по балке, ось у — горизонтально,
перпендикулярно оси х, ось г — по вер-
тикальной оси вращения вниз.
На ползун действуют движущая си-
ла F, сила тяжести mg, сила трения FTp,
нормальная реакция N балки АС. Эту
нормальную реакцию балки разложим
иа вертикальную N, и горизонталь-
ную N2 составляющие.
Основное уравнение динамики отнс
случае имеет вид
mw/. = mg+F+FTp + N1 + N2+J(, + Jc.
По условию задачи ползун движется равномерно по прямолинейной балке;
следовательно, wr = 0,
mg+F + FTp+Nl + N2+Je+Jc = 0.
Действие кориолисовой силы инерции Jc передается на балку, в резуль-
тате чего создается изгибающий момент А4”зг относительно вертикальной оси г,
модуль которого равен Jcx, где х — расстояние от оси вращения до ползуна
(см. рис. 6.5). Модуль кориолисова ускорения равен 2ии, следовательно,
модуль изгибающего момента относительно оси вращения будет
Al“3r = 2mwux = 2mu (хо + «О.
где хв—начальное расстояние ползуна от оси вращения.
Перейдем к определению силы F. Для этого запишем полученное ранее
уравнение в проекциях на оси координат х, у, г. Имеем (см. рис. 6,5)
F—77Тр-|-7е = 0, —7V 2Jc — G, mg — Л\ = 0>
158 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. VI
Из второго и третьего уравнений найдем
Ni=mg, N2 = J с = 2т<£>и.
Найдем полную нормальную реакцию балки и силу трения:
N = + F,p — jN = fm j/g2 + 4w2u2.
Модуль переносной силы инерции при равномерном вращении балки опре-
деляется равенством
Je = mwe = тхьр = т(х0^-и1) <о2.
Учитывая полученные значения для силы трения и переносной силы
инерции, найдем '
F ~ т [/ Kg2 + 4<o2u2 — (x0 + ut) <o2].
По такому закону должна изменяться движущая сила F, чтобы в сделан-
ных предположениях ползун равномерно двигался по вращающейся балке АС,
§ 6.2. Условия относительного покоя
Из основного уравнения (6.5), в частности, вытекают условия
относительного покоя. В этом случае относительная скорость и
относительное ускорение точки равны нулю (vr = 0, wr = 0), сле-
довательно, и кориолисова сила инерции обращается в нуль
(так как vr = 0). Уравнение относительного покоя приобретает вид
F + R + Je = 0. (6.9)
Если выполняется условие равновесия (6.9), то отсюда вовсе
не следует, что после придания материальной точке начальной
скорости точка будет двигаться равномерно и прямолинейно, как
это имеет место в инерциальных системах. Дело в том, что при
сообщении точке относительной скорости, во-первых, появляется
кориолисово ускорение Jc = —2m(&xvr)=£0 и, во-вторых, может
измениться переносное ускорение (оно зависит от положения
точки в подвижной системе отсчета) и, следовательно, изменится
переносная сила инерции.
Из уравнения (6.5) можно вывести еще одно следствие. Най-
дем такие системы координат, в которых выполняется первый
закон Ньютона. Для этого достаточно потребовать, чтобы при
отсутствии сил точка двигалась равномерно и прямолинейно.
Из (6.5) следует, что
J, + JC = O. (6.10)
Отсюда ясно, что условие (6.10) будет выполняться, если
переносная сила инерции в любой точке равна нулю:
Je — — mvie — 0.
Действительно, в этом случае подвижная система отсчета
должна двигаться поступательно равномерно и прямолинейно, но
§ 6.3]
ПРИМЕНЕНИЕ УРАВНЕНИЙ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
159
тогда ее угловая скорость равна нулю и кориолисова сила инер-
ции также обращается в нуль. Уравнение (6.10) выполняется.
Другими словами, для того чтобы подвижная система коорди-
нат была инерциальной, достаточно, чтобы ее начало двигалось
с постоянной скоростью, а угловая скорость системы все время
равнялась нулю:
w0 = 0, (о = 0.
В этом случае всегда равны нулю обе силы инерции и основ-
ное уравнение (6.5) приобретает вид
mwr = F + R.
Следовательно, в этом случае соблюдается и второй закон Нью-
тона.
Таким образом, если существует хотя бы одна система от-
счета, в которой выполняются законы Ньютона, то существует
бесчисленное множество таких систем. Все они движутся друг
относительно друга поступательно равномерно и прямолинейно.
§ 6.3. Применение уравнений относительного движения и покоя
1. Вращающийся космический аппарат. Создание искусствен-
ного поля тяготения. Космонавты недалекого будущего, находясь
в продолжительном межпланетном
вестные трудности физиологиче-
ского характера, в частности, из-
за явления невесомости. Имеются
проекты космических кораблей,
в которых предполагается исполь-
зовать вращение вокруг центра
масс всего аппарата или его
кольцевой кабины для создания
искусственного поля тяготения
(рис. 6.6).
Определим, с какой угловой
скоростью должна вращаться
кольцевая кабина, наружный ра-
диус которой R, чтобы имитиро-
полете, будут испытывать из-
Рис. 6.6.
вать силу земного тяготения.
Предполагаем, что аппарат вращается с угловой скоростью ш от-
носительно оси г некоторой инерциальной системы координат и
летит с выключенными двигателями.
Тогда во вращающейся кабине на человека, находящегося
в относительном покое, действует сила реакции опоры N. Кроме
того, необходимо согласно уравнению (6.9) приложить переносную
160 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ (ГЛ. VI
силу инерции Je. Получим уравнение равновесия
N + Je = O. (6.11)
Здесь Je —центробежная сила инерции. Если пренебречь разме-
рами человека по сравнению с радиусом R, то
Je = mm2R. (6.12)
Реакция опоры должна быть направлена к оси вращения.
Отсюда ясно, что человека будет прижимать к наружной
боковой стенке корабля. Эта стенка станет для него «полом».
Величина реакции на основании выражений (6.11) и (6.12) равна
N = та2 R.
Потребуем, чтобы эта величина была равна весу mg в земных
условиях:
mg = ma2R.
Отсюда найдем угловую скорость вращения

Пусть, например, наружный радиус кольца R = 20 м; тогда
/9,81 л *7 1 6,7 л 11» е:!
^-0,7 сек-1, п = -9--^0,11 аоб/сек.
Таким образом, один полный оборот будет совершаться при-
мерно за девять секунд.
2. Измерение ускорений движущихся тел. Для управления
движением ракеты
Z|Z/
на активном участке, самолета, подводной
лодки ит. п. необходимо знать положение
и скорость какой-либо точки аппарата, а
также угловые координаты аппарата. По
вектору ускорения некоторой точки аппарата
можно путем интегрирования найти скорость,
а затем и координаты этой точки.
Рассмотрим принцип действия простей-
шего измерителя ускорений — акселерометра
(рис. 6.7). Допустим, что аппарат подни-
мается вертикально вверх. Тогда на груз М,
укрепленный на пружине, ось которой (ось
чувствительности) совпадает с направлением
движения аппарата, действуют две силы:
сила тяжести Р и сила упругости пружины F.
Если аппарат поднимается равномерно,
то эти силы взаимно уравновешиваются и
стрелка акселерометра устанавливается на делении mg, ука-
зывая вес груза М.
§6 3] ПРИМЕНЕНИЕ УРАВНЕНИЙ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ 161
При ускоренном движении, когда ускорение направлено вверх,
в уравнение относительного покоя необходимо включить еще пере-
носную силу инерции Je = — mw. Тогда уравнение равновесия
согласно (6.9) примет вид
P+F + Je = 0.
В проекции на вертикаль это дает
— —mw) = 0, F = m(w-}-g).
Стрелка установится против соответствующего деления, изме-
ряя силу F. Величина ® + называется кажущимся ускорением.
Шкалу можно градуировать не в масштабе сил, а в масштабе
ускорений, так как кажущееся ускорение wK пропорционально
силе, действующей на пружину:
w* = w + g = ~. (6.13)
Отсюда ясно, что при непрерывном измерении &ук *) можно опре-
делить из (6.13) ускорение аппарата относительно Земли
w = wK — g. (6.14)
Теперь, чтобы получить текущее значение скорости, нужно
проинтегрировать сигнал w, начиная с момента начала движения:
v(0 = $IA (t)-g] dt.
о
Эта операция может выполняться электронным прибором. С по-
мощью второго такого прибора интегрируется скорость и опреде-
ляется координата г точки крепления акселерометра:
i
z = \v (/) dt.
о
Для получения трех координат аппарата, очевидно, необхо-
димо иметь три акселерометра. Их можно расположить по трем
взаимно перпендикулярным осям. Измеряя кажущееся ускорение
по каждой из осей, определяют затем проекции скорости и коор-
динаты движущегося аппарата.
Следует, однако, заметить, что при повороте тела на ось
чувствительности акселерометра проектируется только часть уско-
рения g. Для определения проекций этого вектора необходимо
знать угловые координаты (например, углы Эйлера) аппарата.
Такую информацию могут дать другие бортовые приборы —гиро-
скопы.
*) Колебаниями массы М пренебрежем,
в Н. В. Бутеннн и др»
162 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. VI
3. Размыв берегов рек. Замечено, что в северном полушарии
правые берега рек обрывистые, а левые пологие. Это явление
может быть объяснено следующим образом (правило Бэра).
На некоторый объем воды, заключенный между двумя сече-
ниями реки, текущей с юга на север (рис. 6.8), действуют три
силы: сила тяжести Р, реакция дна Q, реакция берега F. Для
записи уравнения динамики в неинер-
циальной геоцентрической системе ко-
ординат, которая равномерно вращается
с угловой скоростью со (один оборот в
сутки), необходимо ввести в уравнение
переносную и кориолисову силы инер-
ции. Тогда согласно (6.5) получим урав-
нение движения
,nwr = F + P + Q + J₽ + Je. (6.15)
Переносное ускорение направлено
к оси вращения Земли. Следовательно,
переносная сила инерции направлена
в противоположную сторону. Кориоли-
24z
Рис. 6.8.
сово ускорение находится по правилу векторного произведения
2coxvr и поэтому направлено по параллели на запад. Кориоли-
сова сила инерции направлена в противоположную сторону —на
восток.
Если спроектировать (6.15) на направленную на запад каса-
тельную к параллели, то получим
F — Jc = 0.
(6.16)
Здесь мы воспользовались тем, что относительное ускорение рас-
положено в плоскости меридиана. Оно направлено при равномер-
ном течении к центру Земли.
Из (6.16) получим (см. рис. 6.8)
F — 2mavr sin ср, (6-17)
где ф — геоцентрическая широта места (угол между радиусом ОМ
и экваториальной плоскостью).
Итак, реакция берега направлена налево, если смотреть по
течению реки. Значит, сила давления воды на берег по третьему
закону Ньютона должна быть направлена противоположно, т. е.
она действует на правый берег реки.
Заметим, что это правило справедливо для всех рек, текущих
в северном полушарии. Это объясняется тем, что в северном
полушарии при любом движении точки по поверхности Земли
горизонтальная составляющая кориолисова ускорения всегда
направлена влево от относительной скорости (см. том I, задачу 13.7).
§ 6.3] ПРИМЕНЕНИЕ УРАВНЕНИИ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ 163
В южном полушарии размываются левые берега рек.
Формулу (6.17) можно привести к виду
F 2Pvr® sin <р
Т~ gl ’
где / — расстояние между сечениями реки, Р — вес выделенного
объема воды. Величина q = Pvr/l называется секундным сбросом
реки. Величину FH = f назовем погонным давлением. Тогда
£ _ 2со<? sin <р
' ~ g '
Для реки со сбросом </ = 2000 Т/сек на широте ф = 60°
( 2-2000 Кз 2л nnoI- .zp,
^ = -^8T--2--247W = 0'025 Т’М-
Если правый берег считать отвесным с подводной частью глуби-
ной в 10 м, то на каждый квадратный метр будет действовать
сила
Р = = 2,5 кГ.
В результате длительного воздейст-
вия таких сравнительно небольших сил
берег с .течением времени размывается.
Река «наступает» на правый берег,
оставляя слева по течению низменные
луга, а справа крутые обрывы.
4. Уклонение линии отвеса от на-
правления радиуса Земли. Рассмотрим
силы, действующие на материальную
точку М, подвешенную на нити (рис.
6.9). Будем предполагать, что точка
находится в покое относительно Земли.
Обозначим силу тяготения через F (F = mg0, причем g0 —
гравитационное ускорение), переносную силу инерции, обуслов-
ленную вращением Земли, через Je и силу натяжения нити
через Т. Тогда условием равновесия точки М будет векторное
равенство (6.9). В нашем случае
T+F + Je = 0.
(6.18)
На рис. 6.9 геоцентрическая широта обозначена через ф. Угол ф
между линией отвеса и экваториальной плоскостью называется
географической широтой. Из чертежа ясно, что угол у между
радиусом Земли и линией отвеса связан с ф и ф соотношением
ф = Ф + у-
6*
164 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. VI
Спроектируем (6.18) на направление нити и на перпендикуляр
к этому направлению:
Т — F cos уф-Je cos (ф + у) = 0,
F sin у — Jе sin (ф + у) = 0.
Пренебрегая малой величиной у по сравнению с геоцентри-
ческой широтой -ф, из первого уравнения получим
Т F— Je cos ф = mg0 — ma2R cos2 ip = m (g0 — co2p cos ф), (6.19)
где p —радиус географической параллели.
Силу, равную по модулю и направленную противоположно
натяжению Т, называют силой тяжести и обозначают через mg.
Из этого определения следует, что сила тяжести равна геомет-
рической сумме силы притяжения F и силы инерции переносного
движения, вызванной вращением Земли.
Из равенства (6.19) можно найти ускорение силы тяжести на
поверхности Земли
g = gb(l _5C0SA*’)'
Таким образом, g — переменная величина, зависящая от широты
места.
Наименьшее значение она имеет на экваторе:
=9>82 - (2А00У6370 •105=9’78 ^2-
Из второго уравнения можно найти угол отклонения у отвес-
ной линии от радиуса Земли, т. е. разность между географической
и геоцентрической широтами:
о2/? sin 2ib
Slny^Y№—
Например, на широте Ленинграда (ф = 60°)
_ со2/? КЗ _ |Сз _
4^0 1160
Максимальное отклонение наблюдается на широте ф = 45° (у ^6').
Переносной силой инерции, вызванной вращением Земли,
объясняется также и сжатие Земли. Земля имеет форму геоида,
т. е. тела, ограниченного поверхностью, в каждой точке которой
потенциальная энергия силы тяжести (равнодействующая силы
притяжения и силы инерции переносного движения Земли при
ее вращении вокруг своей оси) имеет постоянную величину.
Такой поверхностью будет поверхность океанов и морей в рав-
§6 3]
ПРИМЕНЕНИЕ УРАВНЕНИИ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ
165
новесном положении. Поверхность геоида заменяют обычно эллип-
соидом вращения, сжатие которого по данным измерений равно
а — Ь 1
а ~ 298,3 ’
Как правило, сжатием Земли пренебрегают и считают, что сила
тяжести mg направлена вдоль радиуса к центру Земли.
5. Маятник Фуко. В 1851 году Фуко продемонстрировал
в Пантеоне опыт с маятником, подвешенным на длинной нити.
Плоскость качания маятника медленно вращалась в направлении,
противоположном вращению Земли.
Для объяснения эффекта Фуко воспользуемся уравнениями
относительного движения в системе координат, связанной с Землей.
Направим ось г по линии отвеса в данной точке Земли вверх,
ось х — перпендикулярно к оси г
Проекции угловой скорости Земли на оси прямоугольной
системы координат выражаются через географическую широту
места ф (рис. 6.10):
сож = 0, = со cos ф, сог = м sin ф.
Уравнение движения маятника имеет вид
mwr= F-J-T-p Je4- Jt. (6.20)
Здесь Т —реакция нити, F —сила притяжения Земли, Jc —кори-
олисова сила инерции, Je— переносная сила инерции.
Выше было показано, что сила притяжения F, складываясь
с переносной силой инерции Je, дает силу тяжести mg, направ-
ленную параллельно линии отвеса, т. е. параллельно оси г.
Введем цилиндрическую систему координат (рис. 6.11) и будем
определять положение маятника при помощи трех координат: р,
биг (см. также т. I, § 9.10). В положении равновесия маятник
находится в начале координат.
166 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ VI
Спроектируем на 'оси ер, е0, к угловую скорость вращения
Земли
сор = со cos <р sin 6, со0 = со cos ф cos 9,
сог = со sin ф.
Проекции линейной скорости будут
vP = p, Ve = p9. vg = z.
Поэтому кориолисова сила инерции принимает вид
Jc = — 2mo)xvr = — 2т
еР
сор
ее
«о
fe
к
“г
«г
(6.21)
Реакция нити Т имеет проекции на оси цилиндрической
системы, определяемые равенствами
Тр=-ТРГ, Т0 = О, TZ = T~. (6.22)
Запишем теперь уравнение (6.20) в проекциях на оси ер, е0, к.
При этом воспользуемся тем, что сумма F4-Je = mg направлена
по оси г и, следовательно, проекции ее на ер и е0 равны нулю.
Используя (6.21), получим
mwp = 2mcop9 sin ф — 2mai cos ф cos 9 — T у,
mw& = 2mcoz cos ф sin 9 — 2mcop sin ф,
• (6.23)
. £__2
mwz = — mg + 2mcop cos ф cos 9 — 2mcop6 s in ф sin 9 ——.
Заметим, что г = / — ф^/2 - p2 = / (1 — у 1 —а проекции
ускорения на оси цилиндрической системы координат будут
шр = р —62р, ®0 = p9 + 2p9, w2 = z.
Уравнения (6.23) содержат три неизвестные функции р, 9, Т
(г выражается через р). Интегрирование этой системы в общем
виде оказывается довольно сложным. Поэтому мы ограничимся
приближенным интегрированием. При отклонениях маятника от
вертикали, малых по сравнению с его длиной (р«С0, можно счи-
тать z = i = z = 0.
Тогда из второго уравнения получим
р9 ф- 2р9 = — 2сор sin ф,
или
(р26ф-®р2 sin ф) = 0.
§6 3] ПРИМЕНЕНИЕ УРАВНЕНИИ ОТНОСИТЕЛЬНОГО ДВИЖЕНИЯ 167
Отсюда следует первый интеграл (интеграл площадей)
р26 сор2 sin <р = с.
Предположим, что в какой-нибудь момент времени маятник
проходил через начало координат; тогда р = 0 и с = 0. Следова-
тельно,
9 + со sin ф = 0, 0 = — со sin ф.
Отсюда видно, что плоскость качания маятника вращается в сто-
рону, противоположную вращению Земли, но с меньшей угловой
сила
к плоскости меридиана
скоростью.
6. Отклонение падающих тел к востоку. При падении мате-
риальной точки вблизи поверхности Земли на нее действует
тяготения F = mg0. Присоединяя к ней
переносную и кориолисову силы инер-
ции, напишем дифференциальное ура-
внение относительного движения для
свободной материальной точки
mwr= F 4- Je+Jc.
Сумму переносной силы
и силы тяготения можно
силой тяжести F -ф Je = mg,
mwr = mg + Jc.
Вектор скорости свободно падаю-
щего тела близок к вертикали места.
Поэтому кориолисова сила инерции
Jc = — 2mo)Xvr почти перпендикулярна
(рис. 6.12) и направлена на восток. Спроектируем последнее урав-
нение на ось г, направленную по вертикали вверх, ось х, направ.
ленную на восток, и ось у, направленную на север:
инерции
заменить
и тогда
тх = — 2та (z cos ф — <лу sin ф),
ту = — 2гшх sin ф,
mz = — mg-\-2mx cos ф.
(6.24)
Здесь ф — географическая широта места, g — ускорение силы
тяжести на широте ф.
Интегрирование системы проведем сначала для <в = 0. Полагая,
что в начальный момент времени х0 (0) = у0 (0) = z0 (0) = 0, получим
хо(0=0, у) = 0, zo(0= — gt.
Найдем теперь поправки к этому приближенному решению, полагая
х = х0 + х1( У = УоЛ-Уи z = z0 + z1.
168 ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ. VI
После подстановки в (6.24) получим
х\ == 2agt cos ср, i/i = 0, z1 = 0.
Отсюда при нулевых начальных условиях имеем
jq = agt2 cos <р, %! cos ф, (/i = 0, г1 = 0. (6.25)
При падении с высоты h время падения связано с t равенством
, , / 2Л\1/2
h = ^~, t={ —
2 \ g J
Полное отклонение на восток получим, подставляя в (6.25) время f:
1 ( 2h \з/2
X = у Mg- COS ф J .
§ 6.4. Теорема об изменении кинетической энергии
в относительном движении
Все общие теоремы динамики точки сохраняют свою форму
и в относительном движении. Не надо только забывать присое-
динять в разряд действующих на точку сил переносную и корио-
лисову силы инерции. Некоторое исключение составляет теорема
об изменении кинетической энергии в относительном движении.
Покажем, что при ее использовании нет необходимости учитывать
кориолисову силу инерции.
Уравнение движения имеет вид
= F-(- R + Je — 2т (wxv,). (6.26)
Умножим левую и правую части (6.26) скалярно на относительную
скорость
mvr • = F vr + R • vr + Je • vr — 2m (w x vr) • vr.
Последнее слагаемое равно нулю, так как вектор vr перпен-
дикулярен к векторному произведению axvr.
Отсюда получим
где N — мощность активных сил, сил реакции и переносной силы
инерции. Знак относительного дифференцирования теперь опущен,
так как дифференцируется скалярная функция времени.
Обозначив кинетическую энергию относительного движения
через Тг, т. е,
т - mv"
ir~ 2 >
§ 6.4]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
169
перепишем (6.27):
dt
(6.28)
Интегрируя по времени (6.28) от некоторого начального момента
времени t0 до текущего t, получим
t
Trl,-V?' = \N dt.
to
Но интеграл, стоящий справа, — работа всех сил при перемещении
точки из начального положения в конечное. Таким образом,
Т(1) _ Т(0) = Ло1 = + ЛЯ + д/.
Изменение кинетической энергии в относительном движении
равно сумме работ всех действующих сил и переносной силы инер-
ции. В некоторых случаях переносные силы инерции могут быть
консервативны (поле однородных сил инерции, поле центробежных
сил).
Доставка груза на стационарный спутник. Спутник, движущийся по кру-
говой экваториальной орбите в направлении вращения Земли с периодом, равным
одним суткам, называется стационарным (рис/
6.13). Такой спутник «висит» над экваториальной
точкой Земли. Он может быть использован для
решения задач глобальной связи, а также удобен
в качестве межпланетной станции.
Ранее в § 4.7 был найден радиус орбиты ста-
ционарного спутника. Оказалось, что г0 = 42 000 км.
Если теперь из г0 вычесть радиус Земли, то полу-
чим высоту орбиты над поверхностью Земли
Я = г0 —Д = 42 000—6371 =35 629 км.
Решим следующую задачу.
Задача 6.4. Какую работу необходимо затра-
тить, чтобы доставить груз с поверхности Земли
на стационарный спутник, полагая, что
исходит в экваториальной плоскости?
Свяжем с Землей и спутником вращающуюся систему координат.
К грузу следует приложить силу тяготения F, силу инерции Je перенос-
ного ускорения и силу тяги Т. Будем считать, что в начальный и конечный
моменты относительная скорость равна нулю. Тогда на основании теоремы об
изменении кинетической энергии в относительном движении можно записать
Дп + Д/а + ДГ3 = О,
где Xf2 — работа силы тяготения, она отрицательна, и Д/3— работа центро-
бежной силы инерции — положительная величина. Отсюда работа силы тяги
дТ дЕ д.1
<*12 л12 ^12’
Для гравитационных сил потенциальная энергия была вычислена ранее
(§ 3.5):
движение
ракеты с
грузом про-
1Ь=-^
170
ДИНАМИКА ОТНОСИТЕЛЬНОГО ДВИЖ. МАТЕРИАЛЬНОЙ ТОЧКИ [ГЛ VI
Найдем потенциальную энергию центробежной силы инерции. В условиях
задачи (спутник «висит» над Землей, ракета движется в экваториальной плос-
кости) имеем
Je = та2г.
Эти силы центральные, поэтому их поле консервативно.
Примем в качестве фиксированной точки для вычисления потенциальной
энергии центр Земли, тогда, по определению потенциальной энергии,
о г
С С
IIj (r) = Амо= I ma2rdr =— i ma2rdr =----------—,
r 0
Отсюда работа силы тяги окажется равной
_ _ f mgR2
Д12 I г
to2r2 \ ! mgR2 , rrus>2rl \
D /, , ®2₽\ 3mgR2 , со2₽
=^(1+-2г)—^r=m^(1+-v

Заметим, что
со2Я 1
2g — 580 ’
~ 0,226,
2г0
следовательно,
Д?2 = 0,776 mgR.
Для подъема одного килограмма груза потребуется затратить работу
4^=6371.109.0,776 = 5,13- 10» кГм,
ОБЩИЕ ТЕОРЕМЫ ДИНАМИКИ
МАТЕРИАЛЬНОЙ СИСТЕМЫ
ГЛАВА VII
МАТЕРИАЛЬНАЯ СИСТЕМА
§7.1. Центр масс
В первой части курса динамики мы изучали законы движения
одной материальной точки, находящейся под действием прило-
женных к ней сил. В практике чаще встречаются более сложные
случаи, когда движение одной материальной точки или одного
тела нельзя изучать изолированно от движения других мате-
риальных точек (тел). Так, например, движение Луны относи-
тельно Земли существенным образом зависит от движения Земли
относительно Солнца, вращение коленчатого вала двигателя внут-
реннего сгорания зависит от движения его поршней и т. п. Эти
и многочисленные другие примеры заставляют нас перейти от
изучения движения одной материальной точки к изучению дви-
жения материальных систем.
В механике под материальной системой понимают совокупность
материальных точек, движения которых взаимосвязаны. Твердое
тело рассматривается как неизменяемая материальная система
с распределенной по объему массой. Эта модель представляет,
конечно, некоторую идеализацию твердого тела, так как при этом
не учитываются расстояния между молекулами или кристаллами
тела. Однако эти расстояния настолько малы по сравнению с раз-
мерами самого тела, что предположение о сплошном распределении
массы не вносит сколько-нибудь заметных погрешностей в вычис-
ления.
Массой М материальной системы называется сумма масс всех
точек, входящих в систему:
- (7.1)
*= I
где mk — масса материальной точки с номером k, ап —число всех
точек системы.
Центром масс или центром инерции материальной систе-
мы называется геометрическая точка, радиус-вектор г которой
172
МАТЕРИАЛЬНАЯ СИСТЕМА
[ГЛ. VII
определяется равенством
п
гс=4’2"гл’ <7-2>
4=1
т. е. точка с декартовыми координатами
п п п
= mkXk, Ус = ~м^ mkyk’ гс= лГ 2 <7’3)
4=’| 4 = 1 4 = 1
В этих формулах rk и xk, £4 — соответственно радиус-вектор
и координаты fe-й материальной точки.
При непрерывном распределении массы суммы, стоящие в пра-
вых частях формул (7.2) и (7.3), переходят в соответствующие
интегралы.
Легко видеть, что центр масс твердого тела, находящегося
в однородном поле силы тяжести, совпадает с его центром тяжести.
Действительно, умножим числитель и знаменатель правой части
формулы (7.2) на модуль ускорения силы тяжести g:
п
4 = 1
Учитывая, что произведение Mg равно весу Р тела, a mkg —
весу pk k-n материальной точки, получим
п
Гс=~р 2рьГь'
4=1
что совпадает с выражением для радиуса-вектора центра тяжести
твердого тела (том I, глава VIII).
В динамике следует говорить о центре масс материальной
системы, а не о центре тяжести. При определении центра масс
материальной системы можно пользоваться методами, установлен-
ными в статике для определения центра тяжести (метод симметрии,
метод расчленения, метод отрицательных масс и т. п.). Необхо-
димо отметить, что положение центра масс твердого тела не
меняется относительно точек тела. Если же система состоит из
перемещающихся друг относительно друга материальных точек,
то положение центра масс системы относительно ее точек может
изменяться.
§ 7.2. Внешние и внутренние силы
В курсе статики мы делили все силы, приложенные к твердому
телу или к системе тел, на активные силы и реакции связей,
понимая под первыми силы, не зависящие от связей. Там же
§ 7.2]
ВНЕШНИЕ И ВНУТРЕННИЕ СИЛЫ
173
было показано, что силы можно разделить и на две другие группы,
а именно на внешние и внутренние.
Напомним еще раз определения внешних и внутренних сил.
Силы, действующие на точки системы, называются внешними, если
они вызваны действием тел, не входящих в систему. Силы, выз-
ванные взаимодействием точек, входящих в систему, называются
внутренними. Обозначаются внешние силы верхним индексом «е»,
а внутренние — верхним индексом «i» (от начальных букв фран-
цузских слов exterieur —внешний и interieur — внутренний):
Fe —внешняя сила, F‘ — внутренняя сила.
Для иллюстрации введенных понятий рассмотрим силы, приложенные
к движущемуся прямолинейно по горизонтальной дороге автомобилю (рис. 7.1).
Прежде всего на автомобиль действует сила тяжестй G. Эта сила внешняя,
так как она вызвана действием Земли — тела,
не входящего в рассматриваемую материальную
систему (автомобиль). Она одновременно яв-
ляется и активной, так как не зависит от свя-
зей. К активным внешним силам относится
также аэродинамическая сила сопротивления
воздуха Fc; эта сила непосредственно не зависит
от связей и вызвана сопротивлением окружаю-
щей среды. Применим теперь принцип осво-
бождаемое™ и заменим действие связи (дороги)
ее реакциями Nx, N2, F1f F2. Первые две силы
Рис. 7.1.
дороги
трения,
представляют равнодействующие нормальных составляющих реакций
к передним и задним колесам, а силы Fj и F2 — равнодействующие сил
вызванных вращением ведомых и ведущих колес (см. раздел Статика, стр. 95).
Силы Nx, N2, Fx и F2 — внешние, так как они обусловлены действием дороги,
которая в систему не входит. Таким образом, к авто-
мобилю приложены шесть внешних сил: G, Fr, N,,
n2, fv f2.
Сила давления газов на поршни двигателя, силы
давления поршней на шатуны и шатунов на криво-
шипы коленчатого вала, силы трения на осях колес
и т. п.—это все внутренние силы системы.
F/
Рис. 7.2.

Отметим, что в некоторых случаях внеш-
ние силы появляются за счет действия внут-
ренних сил. Так, например, внешняя сила
трения скольжения F2 между задними коле-
сами автомобиля и дорогой (см. рис. 7.1) не
может возникнуть без внутренних сил, пере-
дающих вращающий момент на ведущие ко-
леса. Точно так же внешние силы трения F*
и F2 между подошвами ботинок и полом не
могут возникнуть без внутренних мускуль-
ных усилий человека (на рис. 7.2 показаны все внешние силы,
действующие на идущего вправо человека).- Если выключить двига-
тель автомобиля или если человек не будет создавать мускульных
усилий, то соответствующие внешние силы трения обратятся в нуль.
174
МАТЕРИАЛЬНАЯ СИСТЕМА
[ГЛ VII
Рассмотрим еще один пример. Если пренебречь силами притя-
жения звезд, то нашу Солнечную систему можно рассматривать
как изолированную механическую систему, на которую не дей-
ствуют никакие внешние силы. Силы притяжения между отдель-
ными телами всей Солнечной системы являются активными внут-
ренними силами.
§ 7.3. Свойства внутренних сил
Из третьего закона Ньютона следует, что внутренние силы
входят попарно, причем, если точка В действует на точку А
с силой F‘i, а точка А действует на точку В с силой F^, то эти
силы равны по модулю и направлены по одной прямой в проти-
воположные стороны (рис. 7.3):
F^ = -F;. (7.4)
Из этого следуют два свойства внутренних сил системы.
Первое свойство. Геометрическая сумма всех внутренних
сил системы {главный вектор внутренних сил) равна нулю'.
2 F*=°-
k=i
(7.5)
где F* — равнодействующая внутренних сил, приложенных к точке
с номером k.
Второе свойство. Геометрическая сумма моментов всех
внутренних сил относительно произвольной точки пространства
(главный момент внутренних сил) равна нулю'.
2 rfexF^ = °. (7.6)
\ s' k= 1
Г; \ Для системы, состоящей из двух точек А
\< и В с силами взаимодействия FJ и F‘2 (см.
О рис. 7.3), это свойство очевидно. Действи-
Рис. 7.3. тельно, так как F^ = —Fi, а плечи относи-
тельно точки О у обеих сил равны, то мо-
менты этих сил численно равны, но направлены в противополож-
ные стороны. Доказательство первого и второго свойств для лю-
бого количества внутренних сил следует теперь из того, что они
входят в систему попарно.
Равенство нулю главного вектора и главного момента внут-
ренних сил материальной системы не означает, что эти силы урав-
новешены. Это объясняется тем, что внутренние силы приложены
к разным материальным точкам, которые в общем случае могут
перемещаться друг относительно друга. Хорошим примером, иллю-
§ 7.4] ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ 175
стрирующим сделанное замечание, может служить Солнечная
система, планеты которой и их спутники совершают весьма слож-
ные движения под действием одних внутренних сил.
§ 7.4. Дифференциальные уравнения движения
системы материальных точек
Рассмотрим систему, состоящую из п материальных точек.
Применим принцип освобождаемое™ и заменим связи их реак-
циями. Обозначим через F* и F* равнодействующие всех внешних
и внутренних сил, приложенных к fe-й материальной точке. Тогда
каждую точку можно рассматривать как свободную, движущуюся
под действием сил F* и F*. Применим к каждой точке второй
закон Ньютона:
~ Fl + Fl’
^^- = F« + F-
(7.7)
или, в проекциях на неподвижные оси декартовых координат,
mkXk — -Х* +
= (fe = l, 2, .... п).
mkzk = Zek± Zlk
(7-8)
Векторные уравнения (7.7) или эквивалентные им скалярные
уравнения (7.8) представляют дифференциальные уравнения дви-
жения материальных точек всей системы. Число диф-
ференциальных уравнений в векторной форме равно п,
а число дифференциальных уравнений в координатной
форме равноЗп. Следовательно, общее решение зависит
от 6м произвольных скалярных постоянных. Ко-
нечно, если все точки движутся параллельно одной
плоскости или одной прямой, то число дифферен-
циальных уравнений (7.8) в первом случае будет
равно 2м, а во втором п.
Проиллюстрируем методы составления дифферен-
циальных уравнений (7.8) на элементарном примере.
Задача 7.1. Два тела веса Q и G связаны между собой
тросом, перекинутым через блок (рис. 7.4^. Пренебрегая
силами трения, а также массой троса и блока, определить
закон движения грузов и натяжения троса.
Система состоит из двух материальных точек (оба тела
поступательно), движущихся параллельно одной прямой. Следовательно, мы
будем иметь два дифференциальных уравнения движения в проекциях на ось х.
Предположим, что правый груз движется с ускорением xt вниз; тогда левый
Рис. 7.4.
перемещаются
176
МАТЕРИАЛЬНАЯ СИСТЕМА
[ГЛ. VII
груз будет двигаться вверх с ускорением х2 =— хг Мысленно освободимся от
связи (троса) и заменим ее реакциями и Т2. Считая теперь оба тела свобод-
ными, составим дифференциальные уравнения движения в проекции на ось х:
— 7\, iti2x2 = G— Т'з-
Учтем теперь, что Я2= — Х1, rn^Qjg, m2 = G/g и Т1 = Т2 = Т (так как
силами трения, а также массой троса и блока пренебрегаем; строго последнее
равенство будет доказано в примере § 19.1); тогда получим
l-g^Q-T, -2-x^G-T.
g g 1
Решая эти уравнения относительно ускорения хг и натяжения Т троса, найдем
,, Q-G о QG
^-q+gs' t~2q+g-
Из этого решения видно, что правый груз движется равноускоренно вниз,
если Q > G, и вверх, если Q<G. При Q = G оба груза находятся в покое или
движутся равномерно (это зависит от начальных условий). Отметим, что натя-
жение троса при Q G не равно весу соответствующего груза.
§ 7.5. Задача двух тел
В качестве второго примера на составление дифференциальных
уравнений движения материальной системы рассмотрим следующую
задачу. Две свободные материальные точки М± и М2 с массами
т1 и т2 соответственно движутся под
Z1 л/А действием сил ньютоновского притя-
жения. Определить закон движения
1* / системы.
/ В небесной механике и теории
2 Движения искусственных спутников
— —-----------Земли эта задача является одной из
/О & основных (она называется задачей
двух тел). В главе IV решалась ана-
логичная задача в предположении,
Рис- 7-5, что тело, обладающее большей мас-
сой, неподвижно (в теории движения
больших планет —это Солнце, в теории движения искусственных
спутников — небесное тело, вокруг которого движется искусствен-
ный спутник).
Введем инерциальную систему отсчета Охуг и обозначим через
гх и г2 радиусы-векторы соответствующих точек, а через г — радиус-
вектор точки М2 относительно Afx. Из рис. 7.5 видно, что
Г = Г2-Гр
По закону всемирного тяготения имеем
р _р - г mim*
Г1 —Г2~~1 г2
(7.9)
(7.10)
где ^ — гравитационная постоянная.
§7 5]
ЗАДАЧА ДВУХ ТЕЛ
177
Направление силы Fx определяется единичным вектором г/г,
а силы F2 —единичным вектором —г/г (обе силы направлены по
одной прямой в противоположные стороны).
Дифференциальные уравнения движения в векторной форме
(7.7) для рассматриваемой системы будут таковы:
сРг! пцт^ г
“ (7.11)
<йг2 _ , тхтг г
т2 dt2 I Г2 г '
где вектор г определен равенством (7.9), а г = | г |. Умножим пер-
вое уравнение (7.11) на т2, а второе на тА и после этого вычтем
почленно из второго уравнения первое:
miO12 (dt2 dt2) ' г2 г '
или, сокращая на т1 и преобразовывая левую часть,
т d2 r \ f + г
т2 dp И а — Г11-----------------/ г
Учтем теперь равенство (7.9):
ml2!— f т*(т1+тд r 17 1
"*2 dt2 ’ r2 r ' - \•1 z ’
Из этого уравнения видно, что материальная точка /И2 дви-
жется относительно точки как относительно неподвижного
центра, масса которого равна не mlt а М = т1-]-т2. Следова-
тельно, пренебрежение движением точки большей массы вносит
в расчеты погрешность, относительная величина которой опреде-
ляется равенством
е= М-т1 _
т1 тг ’
Если т2 — масса искусственного спутника, а т^ — масса Земли,
то относительную погрешность е можно только вычислить, но не
измерить (так как мы не располагаем столь чувствительными при-
борами). Если же т2 — масса планеты, а т^ — масса Солнца, то
эта ошибка для Земли равна 0,000003, а для Юпитера (самой
большой планеты Солнечной системы) —0,001.
Перейдем теперь к исследованию движения двух тел относи-
тельно их центра масс. Для этого прежде всего покажем, что
центр масс С рассматриваемой системы находится в покое или
движется равномерно и прямолинейно. Действительно, сложив
почленно оба уравнения (7.11), получим
или, интегрируя,
л- + т2ДГ = Л1А’ <7-13)
178
МАТЕРИАЛЬНАЯ СИСТЕМА
[ГЛ. VII
где А —произвольный постоянный вектор (скалярный множитель
М=т1-\-т2 введен для удобства).
Воспользуемся формулой (7.2) и найдем радиус-вектор центра
масс системы
гс = (т1г1+т2г2)-
Дифференцируя по времени, получим скорость vc центра масс С:
drc 1 / dr dr \
Сравнивая с первым интегралом уравнения (7.13), найдем
vc = А.
Пусть при t — 0 vc = voC. Тогда последнее равенство примет вид
Vc = voC,
т. е. центр масс находится в покое (если в начальный момент
vc = 0) или движется равномерно и
прямолинейно (если в начальный мо-
мент vc =/= 0) *).
г Очевидно, что центр масс С рас-
сматриваемых точек и М2 находит-
г/ ся на прямой, соединяющей эти точки
рис 7.6. (рис. 7.6). Будем теперь откладывать
радиусы-векторы гх и г2 точек и М2
от точки С. Тогда дифференциальные уравнения движения (7.11)
примут вид
rf2ri = _ f n
1 dt2 1 (Zl+rs)2 /-! ’
d2r2 ______, mtm.2 r2
2 dt2 I (Г1 + г2)2 r2-
(7.14)
Центр масс делит расстояние между точками Мг и М2 на
части, обратно пропорциональные массам:
1-1 _ тг
Г2 mt
Составим из этой пропорции две производные пропорции!
ri _ т2
4~ г2 mi 4~ т2 ’
/~1+г2 _ mi + m2
r2 mt
Отсюда
_mt + m2r
т2 11
mt+m2
mt 2
'•i + G
*) Установленное здесь свойство центра масс в задаче двух тел является
частным случаем теоремы о движении центрй масс материальной системы
см. § 8.4. следующей главы.
5 7.6]
ОБЩИЕ ЗАМЕЧАНИЯ
179
Внесем эти равенства в дифференциальные уравнения движе-
ния (7.14):
(Ртг _ f ml mpn2гх
id/2 ' ("h + mtf г* Г1’
с!2г2 _ , ml т^2 г2 ' ‘ '
m2-dP~ —1(т1 + т2у ri )
Из этих уравнений видно, что движение каждой точки отно-
сительно их центра масс происходит как движение вокруг непод-
вижного притягивающего центра с мас-
„ ml
сои (mx+m2)2
для первой точки и
-—J——для второй. При соответст-
(mi + m2)2
вующих начальных условиях обе точки
движутся по эллипсам, имеющим общий
фокус С, совпадающий с центром масс
системы (рис. 7.7). В частности, траек-
тория планеты представляет эллипс,
фокус которого совпадает не с центром рис. 7.7.
Солнца, а с центром масс системы
Солнце — планета (влиянием других небесных тел пренебрегаем).
Эта точка отстоит от центра Солнца на небольшом расстоянии,
которым в первом приближении можно пренебречь.
§ 7.6. Общие замечания
На первый взгляд может показаться, что изучение движения
материальной системы можно свести к составлению и анализу
дифференциальных уравнений (7.7) или (7.8). В принципе эта
точка зрения справедлива, но практически реализовать такой путь
исследования удается только для систем, состоящих из небольшого
числа материальных точек (свободных или имеющих сравнительно
простые связи, как это имело место в рассмотренных примерах).
Сложность использования дифференциальных уравнений движения
(7.7) или (7.8) состоит прежде всего в том, что, как правило, мы не
знаем аналитического выражения внутренних сил и реакций связей.
В теоретической механике разработаны методы, которые позво-
ляют обойти основные трудности, возникающие при использовании
дифференциальных уравнений движения материальной системы
в форме (7.7) и (7.8). С этой целью прежде всего вводятся
некоторые векторные и скалярные величины, характеризующие
в какой-то степени движение всей материальной системы (так
называемые меры движения). К ним относятся вектор количества
и вектор момента количеств движения, а также кинетическая
энергия материальной системы. Зная характер изменения этих
величин, можно составить частичное, а иногда и полное пред-
ставление о движении материальной системы.
ГЛАВА VIII
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
МАТЕРИАЛЬНОЙ СИСТЕМЫ
§8.1. Количество движения материальной системы
В конце предыдущей главы было отмечено, что о движении
материальной системы можно составить частичное, а иногда и пол-
ное.представление по характеру изменения некоторых векторных
или скалярных величин, называемых мерами движения. В каче-
стве первой такой меры мы рассмотрим вектор количества дви-
жения материальной системы.
Количеством движения материальной точки называется, как
известно, векторная величина, равная произведению массы точки
т на ее скорость v, т. е. вектор mv. Количеством движения
материальной системы называется вектор Q, равный сумме коли-
честв движения {главный вектор количеств движения) точек, вхо-
дящих в систему.
Q=YimkNk. (8.1)
fe=i
Так как vA = rA, где rfe — радиус-вектор й-й точки, проведенный
из начала инерциальной системы отсчета, то равенство (8.1) можно
преобразовать следующим образом (массы точек постоянны):
Q = 2 5=2 mkTk-
k=i k=i
Пользуясь выражением (7.2), сумму, стоящую под знаком про-
изводной, заменим произведением Мгс, где М — масса всей системы,
а гс — радиус-вектор центра масс:
О Ч
или
drr
Q = M-£.
at
§ 8.11
КОЛИЧЕСТВО ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ системы
181
UI р
Производная есть скорость Vc центра масс системы. Окон-
чательно имеем
Q = Mvc,
(8-2)
т. е. количество движения материальной системы равно массе
всей системы, умноженной на скорость ее центра инерции.
Равенство (8.2) можно прочитать также следующим образом:
количество движения материальной систе- ____
мы равно количеству движения ее центра аЛ^/^ААк
масс, если сосредоточить в нем массу всей АаА<^ААа\
системы. г//А
Задача 8.1. Однородный полый цилиндр мае- хА/Л А/А1
сы т = 20 кг катится без скольжения по гори- \ААА7АА/А/
зонтальной плоскости со скоростью ц = 2 м/сек ^^ААЛ/А'
(конечно, это скорость центра цилиндра; рис.
8.1). Определить количество движения цилиндра.
Количества движения отдельных -точек ци- Рис. 8.1.
линдра имеют различные направления. Их главный
вектор Q (количество движения всего цилиндра) совпадает по направлению
со скоростью центра масс цилиндра, а его модуль определяется равенством
Q = moc = 40 кг • м/сек — 40 н- сек = 4,08 кГ -сек.
Вектор количества движения Q может быть задан своими про-
екциями, выражения
для которых непосредственно следуют из
формул (8.1) и (8.2) и теоремы о проек-
ции суммы векторов:
Рис. 8.2.
п
Qx= У, mkvkx = MvCx,
п
Qy = У "Wky = Ml>Cy,
п
Qz = У rnhVhs =MvCz.
k = l
(8.3)
Кроме инерциальной системы отсчета О&у^, построим посту-
пательно перемещающуюся систему координат Сх2у2г2, начало
которой совпадает с центром масс С (рис. 8.2). Теперь движение
каждой материальной точки можно рассматривать как сложное
движение: переносное вместе с осями Сх^у^г2 и движение относи-
тельно этих осей. Поэтому количество движения можно предста-
вить как сумму количеств переносного и относительного движения
Q = Q'rQ\
182
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. VIII
Так как в относительном движении vCr = 0 (центр масс системы
С совпадает с началом координат подвижной системы отсчета
Сх^гг2), то согласно формуле (8.2) Qr = 0 и, следовательно,
Q = Qe.
Таким образом, количество движения материальной системы
характеризует ее поступательное движение вместе с центром масс.
§ 8.2. Теорема об изменении количества движения
материальной системы
Теорема. Производная по времени вектора количества движения
системы материальных точек равна главному вектору всех внеш-
них сил, действующих на систему.
Для доказательства теоремы перепишем дифференциальные
уравнения движения (7.7) материальной системы в следующей
форме:
mre^ = K + F‘
(8-4)
и сложим почленно все уравнения:
П П Н
2 к+2F>-
= 1 - I ' I
Первая сумма, стоящая в правой части равенства, равна глав-
ному вектору Fe всех внешних сил, а последняя сумма по первому
свойству внутренних сил равна нулю (см. формулу (7.5)). После
преобразований левой части получим
п
d? 2 ^=FF,
k=l
или, учитывая равенство (8.1),
<3T=F*. (8.5)
что доказывает теорему.
В проекциях на неподвижные оси декартовых координат век-
торное равенство (8.5) эквивалентно трем скалярным:
§ 82]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
183
Из этой теоремы вытекает несколько следствий.
1. Внутренние силы непосредственно не влияют на изменение
количества движения материальной системы (они могут оказать
косвенное влияние через внешние силы; см. окончание § 7.2).
2. Если главный вектор всех внешних сил, действующих на
систему, равен нулю, то вектор количества движения материаль-
ной системы остается постоянным по величине и направлению.
Действительно, по условию Fe = 0. Тогда из равенства (8.5)
будем иметь
^ = 0.
dt
Отсюда
Q = Q0 = const, (8.7)
где Qo —начальное значение вектора Q.
3. Если проекция главного вектора всех внешних сил, прило-
женных к системе, на некоторую неподвижную ось равна нулю,
то проекция количества движения материальной системы на эту
ось остается постоянной.
Пусть проекция главного вектора всех внешних сил на ось х
равна нулю: Xе = 0. Тогда из первого равенства (8.6) будем иметь
Отсюда
Qx = Qox = const, (8.8)
где Qo* — начальное значение проекции Qx.
Первые интегралы (8.7) и (8.8), определяющие второе и третье
следствия, называются законами сохранения количества движения
материальной системы.
Пользуясь введенным ранее понятием импульса силы, преоб-
разуем равенство (8.5). Для этого умножим обе части на dt и
проинтегрируем в пределах от t0 до t:
t t
\d§= \ Fe dt,
to to
ИЛИ
Q(0-Q(*o)=i dt.
to
Обозначим количество движения материальной системы в мо-
мент времени t через Q, а в момент t0 — через Qo, и воспользуемся
выражением (3.3) для импульса силы. Тогда окончательно получим
Q —Q0 = Se, (8.9)
где Se = 2 — главный вектор импульсрв всех внешних сил.
184
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ VIII
Таким образом, приходим к теореме об изменении количества
движения материальной системы в интегральной форме (теорема
импульсов)- изменение количества движения мат°риальной системы
за промежуток времени [70, /] равно главному вектору импульсов
всех внешних сил, приложенных к системе, за тот же промежу-
ток времени.
Векторное уравнение (8.9) эквивалентно трем скалярным
равенствам в проекциях на оси инерциальной системы координат:
Qx Qox =
Qy-Qoy=Sey, (8.10)
Qz Qoz =
В этих формулах Sex, Sey и S| — проекции главного вектора
импульсов всех внешних сил на оси координат, a Qx, Qu, Qz и
Qox, Qoy, Qoz —значения проекций количества движения мате-
риальной системы в момент времени t и t0.
Теорема импульсов широко применяется в теории удара.
§ 8.3. Теорема о движении центра масс
Внесем в равенство (8.5) выражение для количества движения
материальной системы (8.2):
или, учитывая, что масса системы постоянна^ получим
dvr
M^=F‘. (8.11)
Это равен тво по виду совпадает со вторым законом Ньютона,
dvc
записанным для точки с массой М и ускорением wc = ~,
к которой приложена сила Fe. Равенство (8.11) представляет
математическую запись теоремы о движении центра масс: центр
масс материальной системы движется как материальная точка,
в которой сосредоточена вся масса системы и к которой прило-
жены все внешние силы, действующие на систему.
Напомним, что Fe — главный вектор всех внешних сил, при-
ложенных к системе.
Векторное равенство (8.11) эквивалентно трем скалярным:
dvr„ r dvr. „
М^=Хг, M~ = Ze. (8 12)
Здесь предполагается, что оси декартовых координат неподвижны.
§ 83]
ТЕОРЕМА О ДВИЖЕНИИ ЦЕНТРА МАСС
185
Необходимо помнить, что центр масс представляет геометри-
ческую точку (см. рис. 8.1). Кроме того, внешние силы фактиче-
ски приложены не к центру масс, а к точкам системы. Вместе
с тем эта геометрическая точка при движении системы перемеща-
ется по закону, определенному приведенной теоремой.
Из этой теоремы вытекает несколько следствий.
1. Одними внутренними силами нельзя изменить характер
движения центра масс системы. Внутренние силы могут оказать
косвенное влияние на движение центра масс только через внеш-
ние силы.
2. Если главный вектор всех внешних сил, действующих на
систему, равен нулю, то центр масс материальной системы нахо-
дится в покое или движется равномерно и прямолинейно.
Действительно, если Fe = 0, то из равенства (8.11) будем иметь
dv,,
М-£ = 0.
at
Сокращая на М и интегрируя, получим
Vc = voc = const, (8.13)
где voC — начальная скорость центра масс.
3. Если проекция главного вектора всех внешних сил системы
на некоторую неподвижную ось равна нулю, то проекция скорости
центра масс системы на эту ось не изменяется
В самом деле, если Xе = 0, то из первого уравнения (8.12)
найдем
, dvr.
М-^ = 0.
at
Отсюда
vCx = const. (8-14)
4. Пара сил, приложенная к твердому телу, не может изме-
нить движение его центра масс (она может вызвать только вра-
щение тела).
Рассмотрим примеры, иллюстрирующие закон движения центра
масс.
Пример 1. Движение с помощью сил трения. На человека,
стоящего на горизонтальном полу, действуют две внешние силы:
сила тяжести G и нормальная реакция пола N. Для движения
в горизонтальном направлении (перемещения центра масс чело-
века) этих сил недостаточно. В начале движения при перемещении
одной ноги вперед за счет мускульных усилий вторая нога стре-
мится переместиться назад, так как центр масс человека должен
остаться в покое. В результате этого между подошвой второй
ноги и ‘полом возникает сила трения, направленная вперед
(см. рис. 7.2). Эта сила трения является движущей для человека.
186
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. VIII
Если пол будет абсолютно гладким, то одними мускульными уси-
лиями человек не сможет перемещаться.
Точно так же движение автомобиля по горизонтальной дороге
осуществляется с помощью внешних сил трения скольжения,
которые возникают между полотном дороги и ведущими колесами
автомобиля (см. рис. 7.1). Эти внешние силы трения возникают
за счет внутренних сил, создающих вращающий момент на оси
ведущих колес, и наличия шероховатой связи (дороги). Если
полотно дороги достаточно гладкое (например, при гололеде), то
даже при большом вращающем моменте, создаваемом внутрен-
ними силами, автомобиль не сможет начать движение.
Спортсмен, опускаясь на парашюте, может управлять движе-
нием центра масс своего тела, в частности, при известном опыте
он может приземлиться вчзаданном круге. Осуществляется это
управление за счет изменения внешних сил сопротивления воз-
духа. Это достигается подтягиванием с помощью мускульных
усилий (внутренних сил) строп парашюта.
Пример 2. Движение тел Солнечной системы в неподвижной
системе координат. Пренебрегая притяжением далеких звезд,
нашу Солнечную систему можно считать изолированной, т. е.
считать, что на тела Солнечной системы действуют только внут-
ренние силы. По второму следствию теоремы о движении центра
масс центр масс Солнечной системы, расположенный вблизи центра
Солнца, находится в покое или двигается прямолинейно и рав-'
номерно. Наблюдения показывают, что он перемещается со ско-
ростью 20 км/сек к некоторой точке небесной сферы, расположен-
ной вблизи звезды Веги и называемой апексом. Таким образом,
движение планет Солнечной системы является сложным: их тра-
ектории относительно системы отсчета, связанной с центром масс
Солнечной системы, — эллипсы (если пренебречь силами взаимного
тяготения планет), а траектории относительно далеких звезд —
пространственнее эллиптические спирали.
Пример 3. Движение искусственного спутника Земли при выходе
из его кабины космонавта. Пусть центр масс С всей системы
(искусственного спутника Земли вместе с находящимися в нем
космонавтами) движется под действием сил тяготения Земли по
некоторой траектории LL' (рис. 8.3, положение /). При выходе
космонавта из кабины спутника их общий центр масс будет пере-
§ 8.4]
ТЕОРЕМА ЭЙЛЕРА
187
мешаться с той же скоростью и по той же траектории (так как
внешние силы не изменились), но спутник и космонавт разойдутся
по разные стороны от нее (см. рис. 8.3, положение II). Когда
космонавт возвратится в кабину спутника, последний перейдет
на прежнюю траекторию (положение III). Конечно, эти явления
будут происходить только в том случае, если космонавт не поль-
зуется микрореактивными двигателями.
§ 8.4. Теорема Эйлера
Дифференциальная форма теоремы об изменении количества
движения материальной системы имеет важные и интересные при-
ложения в механике сплошной среды. Рассмотрим одно, самое
простое, но очень интересное приложе-
ние *).
Пусть некоторая сплошная среда (жид-
кость, газ) движется внутри трубы перемен-
ного сечения. Выделим часть трубы объе-
мом w (рис. 8.4). Будем считать, что этот
объем ограничен боковой поверхностью
трубы и двумя ее поперечными сечениями
ох и сг2, причем Oj и сг2 означают одновре-
менно и площади поперечных сечений (см.
рис. 8.4). Обозначим через vlt v2 и v
средние скорости частиц среды, протекаю-
щих соответственно через сечения <т1, ст2
и некоторое среднее сечение <т. Тогда в
единицу времени через сечение будет
кости, равная p^Vi, а через сечения ст2 и сг —массы р2<т2ц2 и рсгц,
где Pi, р2 и р —плотность среды в соответствующих сечениях.
Будем считать, что движение среды установившееся. Это озна-
чает, что скорости отдельных частиц среды и ее плотность
в каждом сечении не изменяются с течением времени I. В этом
предположении (оно является основным) через каждое сечение
в единицу времени будут протекать равные количества массы
среды, т. е.
Мс = Pi^i = Р2а2у2 = P<w. (8-15)
где через Mz обозначена секундная масса — масса среды, проте-
кающей через любое сечение трубы в единицу времени. Размерность
секундной массы в системе СИ равна кг-сект1, а в технической
системе — кГ м~1 сек.
протекать масса жид-
*) Доказательство будет вестись в упрощающих предположениях (см., на-
пример, Седов Л. И. Механика сплошной среды. — М.: Наука, 1976; Лой-
цянский Л. Г. Механика жидкости и газа,—М.: Наука, 1978,
188
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. V1H
Перейдем теперь к вычислению изменения количества движе-
ния среды, заполняющей объем w. Пусть в момент времени t
рассматриваемая среда занимала объем w, заключенный между
сечениями и <т2, а в момент времени t-\-dt эта же масса среды
занимает объем, ограниченный сечениями crj и <т2 (см. рис. 8.4).
Тогда изменение количества движения рассматриваемой массы
среды произойдет только за счет потери количества движения
в объеме между сечениями и и возрастания количества дви-
жения в объеме между сечениями <т2 if <т2.
Так как при установившемся движении в единицу времени
через сечения и <т2 проходят одинаковые массы, равные Л4С, то
за время dt через эти сечения пройдут массы Л1с dt. Их количе-
ства движения будут Mzdtvr и Mcd/v2, а изменение количества
движения dQ рассматриваемой массы среды за то же время опре-
делится равенством
dQ = Л4С dt v2 — Mz dt vx.
Отсюда
^ = Mcv2-McV1.’ (8.16)
В этом равенстве произведения и Mcv2 называются секунд-
ными количествами движения среды в сечениях <т1 и <т2.
Внешние силы, действующие на среду, можно разбить на две
категории:
1) силы массовые, или объемные, т. е. такие, которые дейст-
вуют на каждую частицу рассматриваемой среды независимо от
того, находятся ли эти частицы внутри выделенного объема или
на его поверхности;
2) силы поверхностные — силы, действующие только на частицы,
лежащие на поверхности объема.
К массовым силам относятся прежде всего силы тяжести.
Поверхностные силы —это силы давления стенок на среду, силы
трения выделенного объема среды о стенки и т. п.
Обозначим через Fo6 главный вектор всех внешних объемных
сил, а через Fn0B —главный вектор всех внешних поверхностных
сил. Тогда, применяя к рассматриваемой массе среды теорему об
изменении количества движения материальной системы в ее диф-
ференциальной форме (8.5), получим
__р । р
1 об Т 1 пов»
или, пользуясь соотношением (8.16) и перенося все члены в одну
сторону,
Роб Рдов 4~ McVi — Л1су2 = 0. (8.17)
§85]
ЗАДАЧИ
189
Это равенство представляет математическую запись теоремы
Эйлера, которую можно прочитать следующим образом: сумма
главных векторов объемных и поверхностных сил, а также секунд-
ных количеств движения среды, протекающей через два поперечных
сечения трубы, равна нулю, если векторы секундных количеств
движения направить внутрь выделенного сечениями объема.
В проекциях на неподвижные оси декартовых координат век-
торное равенство (8.17) дает
^об + Апов + Л4су1л- — = О,
Гоб + ^пов + — Л1СУ2Й = О,
20б + ^пов + Л1с1»1г —Л4сцгг = 0.
(8.18)
§ 8.5. Задачи
Задача 8.2. На корме находящейся в покое баржи установлен автомобиль.
В некоторый момент времени автомобиль начал перемещаться по палубе,
направляясь к носу баржи. Пренёбрегая сопротивлением воды движению баржи,
определить ее скорость v в зависимости
от скорости автомобиля и относительно aq
баржи (учет сил сопротивления будет »- u Т
дан в следующей задаче 8.3). Масса I 7 _
баржи равна mt, а масса автомо-
б иля т2. --------- -—: ~u --------
Рассмотрим систему, состоящую Т777,д
из баржи и автомобиля. В условиях
задачи внешними силами, действую- р g g
щими на систему, будут вертикальные ' ' '
силы тяжести mg, mg и архимедова
сила G (рис. 8.5). Проекция этих сил на горизонтальную ось х равна нулю,
и, следовательно, проекция количества движения всей системы на эту ось
сохраняет постоянное значение, равное начальному:
Qx = Qxo = const.
Количество движения баржи равно mg, а количество движения автомо-
биля m2(u-|-v) (при вычислении нужно иметь в виду, что количество движе-
ния определяется для абсолютных скоростей). Считая, что баржа движется
в сторону, противоположную автомобилю (см. рис. 8.5), найдем проекцию
количества движения всей системы на ось х-
Qx = — mg + m2(u — v). (8.19)
Будем отсчитывать время с начала движения автомобиля. Тогда при / = 0
«=0, и=0. Внося эти значения для и и v в выражение для Qx, получим
Qxo = О-
Учитывая, что проекция на ось х количества движения системы не ме-
няется, будем иметь
— mg т2 (и — п) = О
Отсюда найдем скорость движения баржи v как функцию скорости авто-
мобиля
т,
v= —-—и.
т!-^-тг
(8,20)
190
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. VIII
Так как полученное выражение для скорости v положительно, то сделан-
ное предположение о том, что баржа движется в сторону, противоположную
движению автомобиля, является верным.
Из формулы (8.20) видно, что в условиях задачи (отсутствие сил сопротив-
ления) скорость баржи v прямо пропорциональна относительной скорости авто-
мобиля и. В частности, в момент остановки автомобиля остановится и баржа.
। При отсутствии сил сопротивления эта остановка баржи должна произойти
в результате динамического эффекта, вызванного взаимодействием внутренних
сил между баржей и автомобилем. Заметим, что за все время движения количе-
ство движения системы не изменяется, а происходит перераспределение скоро-
стей тел, входящих в систему.
. В заключение этого примера отметим, что сделанное предположение ^£>6
отсутствии сил сопротивления движению несущего тела (баржи) является,
конечно, идеализированным и на практике, за исключением аналогичной ситуа-
ции в космосе (см. § 9.8), оно не оправдано. Поэтому формула (8.20) спра-
ведлива только при сделанных предположениях и в реальных земных условиях
она дает весьма приближенное решение, которым не всегда можно пользоваться.
В частности, вывод, что баржа остановится одновременно с прекращением дви-
жения автомобиля, не подтверждается наблюдениями — после остановки авто-
мобиля баржа, изменив "предварительно направление движения на противопо-
ложное, будет продолжать движение в сторону перемещения автомобиля. Это
явление, вызываемое взаимодействием внутренних сил системы с внешними
силами сопротивления, будет разобрано в следующей задаче.
Задача 8.3. В условиях предыдущей задачи определить скорость движе-
ния баржи, считая, что при ее движении возникает сила сопротивления, про-
порциональная первой степени скорости, а автомобиль перемещается относи-
тельно баржи по закону, график которого изображен на рис. 8.6, б (в началь-
ном промежутке времени 0 sg t < /] автомобиль движется равноускоренно,
затем в промежутке равномерно и, наконец, на третьем этапе t2
равнозамедленно).
Рис. 8.6.
В отличие от предыдущей 'задачи, теперь, кроме внешних вертикальных
сил тяжести mjg, m2g и архимедовой силы G, приложенных к системе, на
баржу действует еще одна внешняя сила — сила сопротивления F=<xv, где
,а— коэффициент пропорциональности. Эта сила направлена в сторону, про-
тивоположную скорости баржи v (рис. 8.6, а). Проекция количества движе-
ния системы на ось х была определена в предыдущей задаче —см. формулу (8.19):
Чх = — (mi 4- т2) v + т2и.
Внося это выражение для Qx в первое уравнение (8.6) и учитывая значе,
ние силы сопротивления F, получим
, , , dv du
— (nh + mz) м ±т2 - =av,
§ 8.5J
ЗАДАЧИ
191
ИЛИ

(8.21)
В этом уравнении коэффициент k и функция / (() определены равенствами
mi + tn2 mx + тг dt
Учитывая, что автомобиль движется относительно
ускоренно (и =const > О), затем равномерно (и =0) и,
ленно (ii = const <0), получим
баржи сначала равно-
наконец, равнозамед-
а,
f(t) =
О,
— а,
О,
О === t - tit
tr^t^t2,
t2^t^T,
t^T,
(8.22/
где положительное число а пропорционально ускорению автомобиля на первом
интервале Os£(C:(i времени его движения:
а = — = = ——— tg S (8.23)
гп-^ ^2 dt -ф- ti -ф-
(значение иа и угла Р видно на рис. 8.6, б). Для простоты мы считаем, что
время разгона автомобиля равно времени его торможения Т — t2:
tt = T-t2. (8.24)
Поэтому на третьем этапе f(t) =— а.
Для первого промежутка времени O^t^ti уравнение движения (8.21)
согласно (8.22) примет вид
~i-kv = a. (8.25)
Это линейное неоднородное дифференциальное уравнение первого порядка
с постоянными коэффициентами решается очень легко и его общее решение
можно записать в следующей форме:
n = C1e-fc< + |- (O^t^tr) (8.26)
(читателю полезно самостоятельно получить это решение).
Произвольную постоянную интегрирования Cj найдем из начальных усло-
вий: в начале движения при ( = 0 скорость баржи о = 0. Подставим эти зна-
чения для (нов общее решение (8.26):
о=с1+|.
Отсюда Ci = — a/k. Внеся это значение для Ct в (8.26), получим скорость баржи
на первом интервале времени
o = y(l-e-w) (O^isS/j). (8.27)
В конце этого промежутка времени скорость баржи будет
01-(8.28)
192 ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ [ГЛ. VIII
На участке равномерного движения автомобиля дифференциальное уравне-
ние (8.21) на основании равенства (8.22) примет вид
g + te = 0.
Общее решение этого уравнения запишем в следующей форме *):
о = С2с-* (8.29)
Постоянную интегрирования С2 найдем из условия: при t=ti v — t^.
После подстановки получим C3 = v1. Следовательно, на втором интервале вре-
мени скорость баржи изменяется по закону
п = (8.30)
где определено равенством (8.28).
В конце этого периода скорость баржи будет
= (8.31)
На третьем интервале времени (участок торможения автомобиля) дифферен-
циальное уравнение (8.21) принимает вид
dn । .
+ = — a
Его общее решение запишем в следующей форме:
п = Сзв~*(/~м-у (/а«/^Т).
Произвольную постоянную С3 найдем из условия: при /=/8 v = vs- После
подстановки получим
„ । а
С3 = v2 + -у,
Следовательно, на третьем интервале времени скорость баржи изменяется
по закону
(8.32)
Скорость баржи в конце этого периода (при остановке автомобиля) будет
v*+~k)e k(T 2>-у
Внесем в это равенство значение н2 из (8.31), затем учтем значение
из (8.28) и примем во внимание равенство (8.24). После элементарных преобра-
зований получим
V3 = —V1(l (8.33)
Из этого выражения видно, что н3<;0. Это означает, что на участке тор-
можения автомобиля баржа изменяет направление движения на противополож-
ное и начинает двигаться в сторону движения автомобиля, причем в момент
остановки автомобиля баржа не останавливается, а продолжает движение.
*) Эта форма решения совпадает ио существу с решением (8.26) уравне-
ния (8.25) при а=0. Действительно, решение (8.29) можно записать так:
v =C3ekt'e-ki =Ce-kt,
что совпадает с (8.26) при а = 0 (C' = C2ew‘ —новая постоянная).
§ 8.5)
ЗАДАЧИ
193-
Момент времени t3, когда баржа изменяет направление движения, можно иайти.
из равенства (8.32), положив в нем / = /3 и о = 0:
.-*(/,-/,)_ А
k '
0=
е
Отсюда
, , , 1 , kv2-\-a
'з^ + yln-^-.
Перейдем к определению закона изменения
новки автомобиля Уравнение (8.21) при
В общем решении этого уравнения
о = С4г‘('-7'! (t
произвольную постоянную интегрирования С4
п = о3. Следовательно, С4=п3 и скорость
баржи будет изменяться по закону
„=^-*(/-7) (t^T). (8.34)
На рис. 8.7 по равенствам (8.27), (8.30),
(8.32) и (8.34) построен график закона из-
менения скорости баржи v = v(t) (на гра-
фике учтено, что за положительное направ-
ление движения баржи принято направле-
ние, противоположное направлению движе-
ния автомобиля).
Рассмотрим теперь случай, когда про-
межуток времени tt = T —12 очень мал и
его практически можно считать равным нулю
малый промежуток
навливается — рис.
скорости баржи после оста-
t^T принимает вид
условия: при t—T'
найдем из
времени набирает скорость
8.8, а).
(автомобиль за пренебрежимо
ц=«о и так же быстро оста-
Воспользуемся равенством (8.28) и подставим в него значение а из (8.23)г
т2 ив 1— е~ы*
П1=—- , ,----—
т!-\-т2 k ti
При 0 имеется неопределенность вида 0:0. Для раскрытия ее вос-
пользуемся правилом Лопиталя:
Dm п1 = —Игл ~е
7 Н, В, Бутевин в др.
т2
т!-^т2
194
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. VIII
Таким образом, при /j->0 будем иметь
Pi =------;----«о-
(8.35)
После набора автомобилем этой скорости баржа будет двигаться по
закону (8.30), если положить в нем /1 = 0:
v = v1e-ftz (0<t<T). (8.36)
Скорость баржи перед началом торможения автомобиля определяется равен-
ством
п2 = п1е-*7'. (8.37)
Скорость движения баржи в конце торможения автомобиля найдем из
равенства (8.33) при t2 — T:
= — (\—e-kT) = v2~vli
где Vi и v2 определены равенствами (8.35) и (8.37).
График скорости баржи при /1 = Т — Л>->0 показан на рис. 8.8,6.
Явления, описанные в этом примере, читатель может наблюдать самостоя-
тельно; при переходе человека с кормы лодки к ее носовой части (или наобо-
рот) лодка сначала начнет двигаться в сторону кормы, а затем при остановке
человека движение лодки будет происходить в обратном направлении.
В заключение этого примера отметим, что качественная сторона закона
изменения скорости движения не зависит от сделанных предположений (7 —
— F = au). Читатель может убедиться в этом самостоятельно, разобрав
для примера случай, когда сила сопротивления воды пропорциональна не пер-
вой, а второй степени скорости дви-
жения баржи (Г = р.о2, где р, —коэф-
фициент пропорциональности).
Задача 8.4. Груз веса Р = ЗТ
скользит вниз по наклонной эстакаде,
свободно лежащей на земле. Вес эста-
кады G — 2T, коэффициент трения
скольжения между грузом и эстака-
дой / = 0,2, угол наклона а = 30°.
При каких условиях эстакада остается
неподвижной?
Эстакада будет находиться в по-
кое до тех пор, пока сила трения F
между землей и эстакадой не достиг-
нет своего предельного значения,
равного /0Л', где /0 — коэффициент трения покоя, а Л? —сила нормаль-
ного давления. Для определения силы трения F н нормального давления V
рассмотрим систему, состоящую из груза и эстакады. На эту систему дей-
ствуют следующие внешние силы: сила тяжести груза Р, сила тяжести эста-
кады G, нормальная реакция земли N и сила трения между землей и эстака-
дой F (рис. 8.9, а).
Обозначим скорость движения груза через v. Очевидно, что скорость v
направлена параллельно наклонной плоскости и поэтому проекции количества
движения груза, а следовательно, и всей системы (количество движения эста-
кады равно нулю, так как она находится в покое) на координатные оси х и у
будут (рис. 8.9, а)
Qx = — v cos ct, Q.y — — v sin a.
§ 8.5]
ЗАДАЧИ
195
Применим теперь теорему об изменении количества движения системы
в дифференциальной форме и равенства (8.6). Пользуясь выражениями для
и Qy, с помощью рис. 8.9, а получим
Р dv г Р dv . п , ,,
----— cos а = F, т-sin а = —G — P4-N,
g dt g dt
Отсюда найдем силу нормального давления
W = G-J-f) —— — sin а.
g dt
Эстакада будет находиться в покое, если сила трения F не превышает
своего предельного значения f0N, т. е. при F<faN.
Из полученных соотношений найдем
Р dv < Р dv .
----cos а < f0 G 4- Р ,~7 sin а
g dt g dt
или
P dv
f ~gdiC°Sa
G + P-L^sina'
g dt
Для полного решения задачи необходимо определить ускорение dvjdt.
Для этого рассмотрим движение одного груза (рис. 8.9, б). На груз действуют
сила тяжести Р, нормальная составляющая реакции наклонной плоскости
и сила трения Fj, по модулю равная fNv Составим дифференциальные уравне-
ния движения груза в проекциях на оси х' и у’:
— = Р sin а — Т7,, 0 = Л', — Р cos а.
g dt
Из второго уравнения найдем Nr = P cos а, следовательно, F1 = fN1=:
= fPcosa,- Внесем это выражение для F± в первое уравнение и определим
из него ускорение груза:
dv . .
= (sin а — f cos a) g.
После подстановки в неравенство, определяющее f0, получим
, Р (sin a—f cos a) cos а
0 G + Р cos а (cos а Д- f sin а) '
Этому условию должен удовлетворять j0 — коэффициент трения покоя
между землей и эстакадой, чтобы последняя не пришла в движение. В усло-
виях примера (G = 2T, Р = ЗТ, f = 0,2 и а = 30°) найдем
/о >0,19.
В главе XVI мы решим эту задачу другим методом.
Задача 8.5. Электромотор прикреплен с помощью четырех болтов к гори-
зонтальному основанию. В результате затяжки каждый болт создает вертикаль-
ное давление Р1=12,5к/'. Коэффициент трения покоя между мотором и осно-
ванием /о = 0,2. Определить величину бокового давления на болты, если ротор
электромотора, имея небольшой эксцентриситет е = 0,5 мм, равномерно вра-
щается с угловой скоростью со==50л сект1 (п=1500 об/мин). Вес статора
Gj= ЮО кГ, вес ротора G = 50kP (рис. 8.10).
7»
196
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. УНГ
При вращении ротора центр тяжести его (точка С) будет описывать окруж-
ность, радиус которой равен эксцентриситету е. В результате этого корпус
электромотора будет стремиться совершать горизонтальные колебания. Этому
стремлению препятствуют болты и сила
трения между электромотором и основа-
нием (фундаментом).
Обозначим через FTp силу трения
между основанием и статором мотора,
через Fj —суммарную горизонтальную
составляющую силы давления болтов на
статор мотора и через F — равнодействую-
щую сил FTp и Fi- Так как последние на-
правлены всегда в одну сторону, то
F = F Tp-\-F !•
Нужно иметь в виду следующее: если
сила трения FTp по модулю меньше
своего предельного значения /q/V, где
N—величина нормального давления, то
покое только за счет сил трения. В этом
Рис. 8.10.
в
корпус мотора будет удерживаться
случае 771 = 0 и F = FTp. Как только сила трения достигнет своего предельного
значения, в работу вступят болты, причем модуль силы Fx можно будет опре-
делить из последнего равенства
F1 = f-TTp = T-^.
Таким образом, имеем
(8.38)
_ ( 0, если F sg fvN,
1~~(F — f0N, если F^zf0N.
Рассмотрим теперь систему, состоящую из статора и ротора. Количество
движения статора равно нулю (он неподвижен), а количество движения ротора
равно — vc где vc — скорость его центра тяжести С. Модуль скорости точки С
равен еа, а проекции вектора vc на оси х и у будут (рис. 8.10)
t>Cy~— s'n
движения всей системы равны
Q
Qu=------еа sin at.
у g
vCx — ea cos at,
Следовательно, проекции количества
n G
Qx — — ea cos cor,
g
Внешними силами для системы будут: сила тяжести статора Gj, сила
тяжести ротора G, четыре силы Рх затяжки болтов (их равнодействующую
обозначим через Р), нормальная составляющая реакции основания N, сила
трения FTp и боковые составляющие давления болтов Ft (F= FTp+ F]). Вос-
пользуемся теоремой об изменении количества движения системы в дифферен-
циальной форме и применим уравнения (8.6). Пользуясь полученными выра-
жениями для и Qy, с помощью рис. 8.10 получим (рассматриваем первый
полуоборот, в течение которого сила F будет направлена влево)
«О COS at
P-Gi-G,
d / G . :
-3-------ею sin cor
dt \ g
или, выполняя дифференцирование и умножая первое уравнение на — I
— «о2 sin at =F,-------ею2 cos at —N — P — Gi — G,
g g
« 8.5]
ЗАДАЧИ
197
(8,39)
Найдем из второго уравнения силу нормального давления
N = Р 4- Gi -}- G —ею2 cos mt.
Будем считать, что У всегда положительно, и введем в рассмотрение функцию
ф (и/) = F — f0N = — есв2 sin со/ —/0 (р 4- Gi + G-— еар cos со/ j.
ё \ ё /
Отметим, что входящая в это выражение предельная сила трения покоя
f0N является величиной переменной (так как N изменяется).
Учитывая соотношение (8.38), найдем (Osgce/^n)
( 0, если Ф (со/) sg О,
1 I Ф (со, /), если Ф(со/)Э;0.
Преобразуем функцию Ф (со/):
Ф (со/) = есо2 (sin со/ 4- /о cos со/) — fa (Р 4- Gi -|- G),
Воспользуемся равенством
Zo=tgT,
в котором ф — угол трения. Функцию Ф (со/) можно привести теперь к виду
/у
4 Ф (со/) — — sin (со/ 4-ф) — /о (Р 4- G1 -J- G).
Максимальное значение функции Ф (со/) достигается при sin (св/-|-ф) = 1:
G £0)2
Если это выражение неположительно, то при любом значении угла со/
функция Ф (со/) 0. В этом случае сила трения не превосходит своего пре-
дельного значения и болты не оказывают давления на мотор (Е1 = 0). Это имеет
место при условии
(8,40)
ecB2sg-y (P-J-Gx-j-G) sin <p.
(8.41)
Если же неравенство (8.41) будет иметь обратный смысл, то при некото-
ром a>t = со/х функция Ф (со/) обратится в нуль. Угол поворота со/х легко нахо-
дится из уравнения Ф(со/х) = 0, или, после очевидных преобразований,
sin (со/х + ф) = (Р 4- Gi + G) sin ф. (8.42)
С момента времени / = /х функция Ф (со/) начнет возрастать и сделается
положительной (4— наименьший корень уравнения (8.42)). С этого же момента
болты начнут оказывать давление на мотор, равное Ех = Ф(со/).
При угле св/2, определяемом уравнением
со/2-|-ф = л: — (св/х4-ф), (8.43)
функция Ф (св/) опять сделается равной нулю, давление болтов прекратится
и мотор снова будет удерживаться одной силой трения. При св/ > л характер
распределения сил будет повторяться в обратном порядке,
198
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
[ГЛ. VIII
В данном примере
го)2 = 0,0005 (50л)2 = 1,25л2 м/сек2,
-g- (Gx + G+Р) = 39,2 м/сек2, fo = tg ф = 0,2,
sin ф~ 0,196, <р ~ 0,198 (11°).
Условие (8.41) не выполняется и, следовательно, одной силы трения недо-
статочно для удержания в горизонтальном положении мотора. Значение угла a/j
найдем из уравнения (8.42):
sin (ю<х + ф) = • 0,196 0,64,
со/х + ф = 0,695 (40°), otf х ~ 0,497 (29°).
Таким образом, при 0 at g; Oj/ мотор удерживается одной силой тре-
ния. Начиная с момента времени в работу вступают болты, действие кото-
рых прекращается в момент времени t2; угол ш/2 определяется равенством (8.43):
ы/2 = л — иГх — 2ф = 2,247 (129°).
В промежутке u>t1 < <в/ < <а/2 суммарная сила давления болтов найдется
из равенств (8.39) и (8.40):
?х = 63 sin (со/ + ф) — 40.
При со/$= со/2 сила Ft снова обращается в нуль. График проекции силы Fj]
на ось х изображен на рис. 8.11.
М
О
Рис. 8.11.
Максимальное давление, приходящееся на один болт (сила давления мотора
на болты равна по модулю /д и направлена в сторону, противоположную Fx),
равно 5,75 кГ, а при отсутствии трения (/о = О) оно составляет 15,75 кГ. Сле-
довательно, сила трения снимает в данной системе две трети всей нагрузки
на болты и существенно облегчает условия их работы.
При большом эксцентриситете сила давления Fx, меняющая свое направ-
ление с каждом полуоборотом ротора (в нашем примере 3000 раз в минуту),
может достигнуть величины, прн которой болты будут сломаны.
Если увеличить затяжку болтов, т. е. увеличить силу Р, то можно соз-
дать такое нормальное давление N, при котором мотор будет удерживаться
в горизонтальном положении одной силой трения и болты не будут испыты-
вать горизонтальных давлений. Критическое значение для силы Р найдем из
неравенства (8.41):
В рассматриваемом примере будем иметь Р 170 кГ. Следовательно, каж-
дый болт нужно затянуть с силой 42,5 кГ (напомним, что Р — суммарная сила
затяжки всех четырех болтов), т. е. затяжку болтов нужно увеличить в 3,4 раза.
§ 8.5]
ЗАДАЧИ
199
Задача 8.6. Горизонтальный участок
гнутое под углом 90° колено. Определить
изогнутую часть трубопровода,
если его диаметр равен 60 см,
удельный вес пульпы у =
= 1,2 Т/м3 и скорость ее тече-
ния у = 6 м/сек.
Рассмотрим изогнутуючасть
трубопровода и обозначим че-
рез Oj и о2 площади попереч,
ных сечений его в начале и
конце изгиба, а через vi и
v2— векторы соответствующих
скоростей пульпы (рис. 8.12, а).
Ось х направим вдоль оси сим-
метрии изогнутой части трубо-
провода, а ось у — перпендику-
лярно к ней. По условию за-
дачи модули о1 = п2 = п, а век-
торы vj и v2 составляют с осью
х углы, равные 45°. Силы
тяжести направлены вертикаль-
но, и их проекции на оси х
и у равны нулю (на рис. 8.12,
проекции главного вектора сил
и составим первые два уравнения
и Гпов
пульпу
Отсюда находим
трубопровода
динамическое
а.)
показан
земснаряда
давление Р
имеет изо-
пульпы на
6)
Рис. 8.12.
сверху). Обозначим через Хпов
ВИД
давления стенок трубопровода на
(8.18):
Хпов — М.zv cos 45° — Л4со cos 45° = 0,
Гпов — sin 45°-|-Л1со sin 45° = 0.
а
Хпов = Л4^|/2, Гпов = 0.
Таким образом, главный вектор поверхности сил направлен по оси х (это
очевидно из соображений симметрии). Сила добавочного динамического давле-
ния Р на трубопровод равна по модулю Хпов и направлена в противополож-
ную сторону (рис. 8.12, б):
P = l'MU. (8.44)
По определению имеем (см. формулу (8.15))
A4c = ptiti.
Плотность пульпы р связана с ее удельным весом равенством
а площадь поперечного сечения трубопровода a = nd2/4.
Внося выражения для Л4С, р и а в равенство (8.44), получим
4g
После подстановки численных значений у= 1,2 Т/м3, d = 0,6 м, v — б м/сек,
найдем динамическое давление пульпы на трубопровод:
Р= 1,76 Т,
ГЛАВА IX
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ
ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ СИСТЕМЫ
§9.1. Момент количеств движения материальной системы
В предыдущей главе было показано, что, исследуя вектор
количества движения материальной системы, можно составить-
представление о ее поступательном движении. Вращательное дви-
жение материальной системы характеризуется другой векторной
величиной, а именно — моментом количеств движения. В этой
главе мы рассмотрим способы вычисления этой величины и ее-
связи с другими динамическими характеристиками системы,,
с помощью которых можно составить частичное, а иногда
и полное описание вращательных движений материальной си-
стемы.
Момент количества движения Ко одной материальной точки
определяется равенством Ko = rxmv. Моментом количеств дви-
жения Ко материальной системы относительно центра О назы-
вается сумма моментов (главный момент) количеств движения
всех материальных точек, входящих в систему, относительно того-
же центра-,
п п
Ко = У, Кол = У, Г* Xmkvk. (9.1)
Л=1 А=1
В этом равенстве гк — радиус-вектор материальной точки М*
с началом в центре О, тк и v* —масса и скорость этой
точки. Если материальная система представляет непрерывно
распределенную материальную среду, заполняющую некото-
рый объем, то сумма, конечно, переходит в соответствующий
интеграл.
Как всякий вектор, момент количеств движения Ко может
быть задан своими проекциями. В частности, равенство (9.1)
в проекциях на оси системы координат Охуг записывается
S 9.1]
МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ
201
следующим образом:
п
Кх~ У1 WlkfjjkVkz 2kVky)>
k = \
п
S mk{zhVkx—XkVkl),
k = 1
п
Кг= S т* (XkVky— ykVkx),
k = I
(9-2)
где Ху, ук, zk — координаты точки Mk.
По этим формулам можно определить проекции Кх, Ку, Кг
(моменты количеств движения материальной системы относительно
координатных осей), а следовательно, и сам вектор Ко.
Момент количеств движения твердого тела, вращающегося
вокруг неподвижной оси. В этом примере нас интересует не момент
количеств движения Ко твердого тела
как вектор, а только одна его проек-
ция Kz на ось вращения г тела.
Пусть твердое тело вращается с уг-
ловой скоростью со вокруг неподвижной
оси z (рис. 9.1). Выделим в теле эле-
мент объема М с массой dm и будем
рассматривать его как материальную
точку. При вращении тела вокруг не-
подвижной оси элемент объема М будет
двигаться по окружности с центром в
точке О и радиусом, равным расстоя-
нию hz от точки М до оси вращения.
Проекция скорости v элемента объема М
на касательную к окружности равна ®г/1г, а проекция количества
движения на ту же ось будет vx dm = сог/1г dm. Так как плечо век-
тора v dm относительно оси вращения равно hz, то момент ко-
личества движения элемента объема М относительно оси г равен
vT dm hz = azhz dm. Для всего тела будем иметь
Кг — $ oizhl dm,
где интегрирование распространено на массу всего тела.
Проекция угловой скорости сог одинакова для всех точек тела,
и, следовательно, ее можно вынести за знак интеграла:
Kz — az^hldm.
Получившийся интеграл зависит только от характера распределе-
ния массы в теле и не зависит от его кинематического состояния
202
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ. IX
Он называется моментом инерции тела относительно оси г
и обозначается символом Iz (в § 9.5 будет показано, что момент
инерции тела представляет меру его инерции во вращательном
движении):
= (9.3)
В этих обозначениях будем иметь
ZCz = / Z^Z
(9.4)
т. е. момент количеств движения твердого тела, вращающегося
вокруг неподвижной оси, относительно оси вращения равен произ-
ведению момента инерции тела относительно этой оси на проек-
цию угловой скорости тела на ту же ось.
§ 9.2. Краткие сведения о моментах инерции
Теории моментов инерции будет посвящена специальная
глава XII. Здесь же мы весьма кратко остановимся на основных
определениях и сообщим некоторые формулы, не останавливаясь
на их выводах.
Моментом инерции материальной точки относительно неко-
торой оси называется произведение массы т этой точки на квад-
рат ее расстояния h до оси, т. е. величина mh2. Моментом инер-
ции материальной системы относительно оси называется сумма
моментов инерции всех точек системы относительно той же оси.
Так, например, момент инерции материальной системы отно-
сительно оси г равен
п
/г= 2 mkhlz,
k = i
где hkz — расстояние от точки с номером k до оси г.
При непрерывном распределении массы сумма переходит
в интеграл (9.3).
По определению момент инерции представляет существенно
положительную величину. В нуль момент инерции может обра-
титься только в одном частном слу-
чае, когда все точки системы распо-
ложены на оси, относительно кото-
рой вычисляется момент инерции.
Размерность момента инерции в
системе СИ равна кг-м2, а в техни-
ческой системе — кГ м -сек2.
Для примера определим момент
1
dx
hz=x
Рис. 9.2.
инерции однородного тонкого стержня
массы М и длины I относительно оси г, проходящей перпендику-
лярно к стержню через его конец (рис. 9.2).
§ 9.3] ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ 203
Направим ось х вдоль стержня и выделим на нем элемент длины dx. Рас-
стояние fiz от этого элемента до оси z равно х, масса единицы длины стержня равна
м
М/1, а масса выделенного элемента dm — —j~dx. Внесем эти значения для hz
и dm в выражение (9.3) и учтем, что переменная интегрирования X изменяется
от 0 до L Тогда
г L 12 j L 9 м ,
/ = 1 hi dm = I х2 -г- dxt
J J I
о
или, интегрируя,
/г = 4 MP.
Таково значение момента инерции однородного тонкого
стержня относительно оси, проходящей перпендикулярно
к стержню через его конец.
Момент инерции /Сг однородного тонкого стержня
длины / и массы М относительно оси г, проходящей пер-
пендикулярно к стержню через его центр тяжести С,
будет равен
/Сг=4м/2- (9-б)
Не останавливаясь на выводе (см. § 12.3), заметим, что момент инерции
однородного кругового цилиндра массы М и радиуса R относительно оси г
цилиндра (рис. 9.3) определяется формулой
Iz = ~MR*. (9.7)
Это выражение для момента инерции не зависит бт высоты цилиндра Н и
поэтому оно справедливо и для однородного кругового диска.
Оче.нь часто вводят радиус инерции тела относительно оси,
понимая под ним расстояние р от оси до точки, в которой нужно
сосредоточить массу М всего тела, чтобы момент инерции точки
относительно данной оси равнялся моменту инерции тела отно-
сительно той же оси. По определению имеем
/ = Мр2. (9.8)
Здесь М — масса материальной системы, I — ее момент инерции
относительно данной оси, р —радиус инерции системы относи-
тельно этой же оси.
§ 9.3. Теорема об изменении момента количеств движения
материальной системы
Рассмотрим материальную систему, состоящую из п мате-
риальных точек. Мысленно освободимся от связей, заменим их
действие реакциями и разобьем все силы (включая реакции свя-
зей) на внешние F* и внутренние F*. Тогда все точки системы
204
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
можно считать свободными и к каждой из них применима теорема
об изменении момента количества движения (см. (3.10)):
-^- = M0(Fe„) + M0(F‘).
Складывая почленно, получим
П J|Z ” л
2m°(fo+ 2m°(f*)«
fc=l fe=l й = 1
В левой части равенства вынесем знак производной за знак
суммы; в правой части равенства первая сумма равна главному
моменту Mq всех внешних сил относительно центра О, а вторая
сумма, на основании второго свойства внутренних сил, равна
нулю (см. формулу (7.6)). Имеем
* = 1
или, учитывая выражение (9.1),
(9-9>
Это уравнение представляет математическую запись теоремы
об изменении момента количеств движения материальной системы:
полная производная по времени вектора момента количеств движе-
ния материальной системы, вычисленного относительно неподвиж-
ного центра, равна главному моменту всех внешних сил относи-
тельно того же центра.
В проекциях на неподвижные оси декартовых координат,
начало которых совпадает с центром О, векторное равенство (9.9)
эквивалентно трем скалярным:
Т = Т = (9.10)
Из этой теоремы вытекает несколько следствий.
1. Внутренние силы непосредственно не влияют на изменение
момента количеств движения материальной системы (они могут
оказать косвенное влияние через внешние силы; см. § 7.2).
2. Если главный момент всех внешних сил относительно неко-
торого неподвижного центра равен нулю, то момент количеств
§9 4]
ПРИМЕРЫ И ЗАДАЧИ
205
движения материальной системы относительно того же центра
не изменяется по модулю и направлению.
Действительно, если Мо = 0, то равенство (9.9) принимает вид
отсюда
Ко = Ко = const, (9.11>
где Ко —начальное значение вектора Ко-
3. Если главный момент всех внешних сил относительно неко-
торой неподвижной оси (например, оси х) равен нулю, то момент
количеств движения материальной системы относительно этой
оси не изменяется в процессе движения.
Если Mx = 0, то согласно первому равенству (9.10) будем иметь
отсюда
Кх = К.х — const. (9.12)
Первые интегралы (9.11) и (9.12), определяющие второе и
третье следствия, называются законами сохранения момента коли-
честв движения материальной системы.
§ 9.4. Примеры и задачи
Теорема об изменении момента количеств движения материаль-
ной системы имеет очень интересные и практически важные при-
ложения. В этом параграфе мы" рас-
смотрим примеры и задачи, иллюстри-
рующие применение теоремы и ее след-
ствия, причем некоторые из них имеют
самостоятельное значение.
1. Плоскость Лапласа. Солнечная система
является изолированной (если пренебречь вли-
янием других звезд), и ее движение опреде-
ляется только внутренними силами притяже-
ния. Так как внешние силы отсутствуют, то
на основании второго следствия момент коли-
честв движения Ко всей Солнечной системы
сохраняет постоянное направление относительно далеких «неподвижных»
звезд. Поэтому сохраняет неизменное положение и плоскость л, пер-
пендикулярная к вектору Ко (рис. 9.4). Эта плоскость (ее называют плоско-
стью Лапласа) имеет большое значение в астрономии, так как относительно
нее ориентируют орбиты планет.
2. Скамейка Н. Е. Жуковского. Для демонстрации теоремы об изме-
нении момента количеств движения материальной системы и ее следствий
206
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
Н. Е. Жуковский построил прибор, состоящий из горизонтальной платформы,
которая может вращаться вокруг вертикальной оси с пренебрежимо малым
трением. Мы опишем два опыта, хорошо иллюстрирующих теорему.
а) В примере 1 § 8.3 было показано, что при отсутствии внешних сил
человек не может изменить положения своего центра тяжести. Покажем, что,
находясь в аналогичных условиях, человек может повернуться. Предположим,
что человек стоит на скамейке Н. Е. Жуковского и держит над головой колесо
или какой-нибудь другой предмет, который может вращаться вокруг верти-
кальной оси (рис. 9.5).
Будем считать, что вся система, состоящая из человека, платформы и
колеса, сначала находилась в покое; затем внутренними силами колесо рас-
кручивается (это можно сделать, например, второй рукой). Так как моменты
всех внешних сил относительно вертикальной оси вращения равны нулю (силы
тяжести параллельны оси вращения, а линии действия реакций опор плат-
формы пересекают ее), то момент количеств движения Кг всей системы отно-
сительно этой оси должен сохранять постоянное значение, равное начальному:
Кг = К1г + К1 = 0, (9.13)
где Кг и Кг — моменты количеств движения относительно оси z колеса и
человека с платформой.
Равенство (9.13) должно сохраняться все время. Поэтому, если одно из
слагаемых, например Кг> положительно, то второе слагаемое отрицательно.
Это означает, что при вращении колеса в одном направлении человек вместе
с платформой будет вращаться в обратном направлении. Если, повернув
колесо на некоторый угол, затем прекратить его вращение, то платформа
с человеком, повернувшись в обратном направлении на некоторый другой угол,
также прекратит свое вращение.
В § 9.8 будет показано, как используется этот метод космонавтами для
поворота и ориентации при свободном полете в космосе.
б) Второй опыт, хорошо демонстрируемый на скамейке Жуковского, состоит
в следующем. Человек стоит на платформе, держа в руках гантели. Его рас-
кручивают, после чего вращение происходит по инерции. Моменты внешних
сил, действующих на систему «человек — платформа», относительно вертикаль-
ной оси вращения равны нулю. Поэтому момент количеств движения К2 системы
§9 4]
ПРИМЕРЫ И ЗАДАЧИ
207
относительно этой оси сохраняет постоянное значение. Предположим, что
человек, держа руки с гантелями по швам, вращается с угловой скоростью wL
(рис. 9.6, а). Обозначим момент инерции всей системы в этом положении
через It. Тогда согласно формуле (9.4) будем иметь Если человек,
расставив руки с гантелями, будет держать их на уровне плеч (рис. 9.6, б),
то момент инерции всей системы относительно оси вращения z увеличится
(увеличатся расстояния от гантелей до оси г). Обозначим новый момент инер-
ции через /2 и новую угловую скорость через и2. Согласно той же формуле
(9.4) в новом положении Кг = 1^г- Так как момент количеств движения К?
относительно оси вращения не изменяется, то
/2со2 = A.wi-
Из этого равенства следует, что oj2<wl (ибо /2> Д). Таким образом, человек,
поднимая руки до уровня плеч, уменьшает свою угловую скорость, а при
опускании рук увеличивает ее.
Задача 9.1. Тележка D поворотного подъемного крана движется с постоян-
ной по модулю скоростью и относительно стрелы ВС крана. Мотор, вращаю-
щий кран, создает осносительно оси вращения АВ крана постоянный
Л4рр. Определить угловую скорость и вращения
стояния s тележки D до оси АВ, если вес
тележки вместе с грузом равен Р, а момент
инерции крана (без тележки и груза) отно-
сителЗно оси вращения АВ равен /. Враще-
ние крана начинается в момент времени,
когда тележка находилась на расстоянии s0
от оси АВ (рис. 9.7).
Рассмотрим систему, состоящую из вра-
щающейся части крана и тележки с грузом.
Для решения задачи применим теорему об
изменении момента количеств движения си-
стемы относительно неподвижной оси вра-
щения крана (см. третье уравнение (9.10)):
dK.^ =ме
dt *
На рассматриваемую систему действуют
следующие внешние силы и моменты: сила
тяжести тележки с грузом Р, сила тяжести
крана Q, вращающий момент Л1вр и реак-
ции опор А и В крана (на рис. 9.7 показаны их составляющие). Моменты от-
носительно оси z сил тяжести Р и Q и реакций опор А и В равны нулю
(силы Р и Q параллельны оси г, а линии действия реакций пересекают ее).
Поэтому
момент
от рас-
крана в зависимости
(9-14)
*П = ^вр-
(9.15)
Перейдем теперь к определению момента количеств движения системы
относительно оси вращения крана. Система состоит из двух движущихся тел:
вращающегося крана и тележки с грузом (тележка и груз движутся одина-
ково, и их можно рассматривать как одно тело). Следовательно,

(9.16)
где и К*г— моменты количеств движения относительно оси z крана и те-
лежки соответственно.
Кран представляет собой твердое тело, вращающееся вокруг неподвижной
оси. Поэтому согласно формуле (9.4) /С* = ^иг.
208
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
Тележка участвует в сложном движении Ее относительная скорость
равна и, а модуль переносной скорости уе равен swz, где s —расстояние от
тележки до оси вращения (размерами тележки пренебрегаем). Абсолютная
скорость тележки
v = u + ve,
а количество ее движения
mv=mu + mve.
Следовательно,
где KTzr и 1Сге — моменты количеств относительного и переносного движений
тележки относительно оси г.
Так как вектор ти пересекает ось г, то = Вектор количества пере-
нрсного движения mve находится в горизонтальной плоскости и перпендику-
лярен к оси г. Поэтому
или, учитывая, что t>e = wzs,
К} = та/.
Внося найденные значения для К* и в (9.16), найдем
Аг = /сог + тсог52 = (/ + т«2) а,- (9.17)
Подставив выражения (9.15) и (9.17) в равенство (9.14), получим дифферен-
циальное уравнение движения рассматриваемой системы
~ + ms2) шг] = Мвр . (9.18)
В этом уравнении величина s является переменной, причем S = us, где us—
проекция относительной скорости и тележки на ось стрелы ВС (us = u, если
-тележка ’'валяется от оси вращения крана, и us — — и в противном случае).
Так как по условию задачи и — величина постоянная, то
s — s0 = ust.
Интегрируя уравнение (9.18), получим
(/-\-rns2) сог = Л1Вр/Ц-С. (9.19)
В начальный момент (/ = 0) по условию задачи = Поэтому из формулы
(9.19) следует, что С = 0. Заменим в равенстве (9.19) время t через расстоя-
ние s и найдем ы2:
Угловая скорость может быть выражена также как функция времени:
Мвр t '
= у-.----------ТУ, (9-21)
/ + m(s0 + us/)2 v /
В частности, при неподвижной тележке us = 0
_ Л4вр/
Шг ~~ I + ms2 ‘
$ 9 51 ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВРАЩЕНИЯ 209
Из соотношений (9 20) и (9 21) видно, что знак совпадает со знаком Л1вр.
Это означает, что направление вращения крана всегда совпадает с направле-
нием вращающего момента Л4вр— факт физически очевидный.
§ 9.5. Дифференциальное уравнение вращения твердого тела вокруг
неподвижной оси
Рассмотрим твердое тело, вращающееся вокруг неподвижной
оси г.
Вращение твердого тела вокруг неподвижной оси обеспечи-
вается специальными приспособлениями (подшипниками и под-
пятниками). Освободимся мысленно от связей и, заменив их соот-
ветствующими реакциями, будем в дальнейшем счита.ть вращаю-
щееся тело свободным. Обозначим через 1г момент инерции этого
тела относительно оси вращения и через шг —проекцию его угло-
вой скорости на ту же ось. Тогда момент количеств движения
Kz твердого тела относительно оси вращения будет равен (см.
формулу (9.4))
/Сг =
Внося это выражение в третье равенство (9.10), получим диффе-
ренциальное уравнение вращения твердого тела вокруг непод-
вижной оси
= (9.22)
При вычислении главного момента всех внешних сил, прило-
женных к твердому телу, относительно оси вращения нужно
учитывать, что реакции идеальных (без трения) опор в уравнение
(9.22) не войдут, так как линии их действия пересекают ось вра-
щения и, следовательно, их моменты относительно этой оси равны
нулю. Если же опоры создают моменты трения,' то последние
необходимо учитывать.
Сравним дифференциальное уравнение вращения твердого тела
вокруг неподвижной оси с дифференциальным уравнением прямо-
линейного поступательного движения твердого тела
(9.23)
Сравнивая уравнения (9.22) и (9.23), видим, что между ними
можно провести глубокую аналогию: линейной скорости v посту-
пательного движения тела соответствует его угловая скорость оз
при вращении вокруг неподвижной оси (в уравнениях рассматри-
ваются соответствующие проекции скоростей); силам, вызывающим
поступательное движение тела, соответствуют моменты сил, вызы-
вающих его вращение; массе тела в уравнении (9.23) соответ-
ствует момент инерции в уравнении (9.22). Так как масса тела
210
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
представляет меру его инерции в поступательном движении, то
из сделанного сопоставления следует, что момент инерции тела
представляет меру его инерции во вращательном движении.
Дифференциальное уравнение вращения твердого тела вокруг
неподвижной оси (9.22) полезно сопоставить с формулировкой
второго закона Ньютона: произведение массы точки на ее уско-
рение равно сумме всех сил, приложенных к точке. Аналогично
можно прочитать и -уравнение (9.22): произведение момента инер-
ции тела на его угловое ускорение равно сумме моментов всех сил,
приложенных к телу.
Задача 9.2. К ротору электромотора приложен вращающий момент Л1вр,
изменяющийся по закону Л1вр = Л10 — хсо, где Мо и х— некоторые положитель-
ные постоянные, характеризующие двигатель (постоянная х называется кру-
тизной характеристики мотора), а со — угловая скорость ротора. Определить
закон изменения угловой скорости со в период разгона ротора, если его мо-
мент инерции относительно оси вращения равен I.
Совместим положительное направление оси вращения г с направлением
вращающего момента Л4вр. Тогда Л1г = Мвр = Л10 — хсо и сог = со (направление
вектора угловой скорости в период разгона ротора совпадает, конечно, с на-
правлением вращающего момента).
Силы трения учтены постоянными Л40>и х, поэтому сумма моментов всех
внешних сил, приложенных к ротору, будет равна Л1вр = Л40 —хсо. Дифферен-
циальное уравнение вращения твердого тела (9.22) в данном случае прини-
мает вид
= —хсо. (9.24)
Для определения закона изменения угловой скорости со от времени нужно
решить это дифференциальное уравнение. Ддя этого~разделим переменные
I d
т?-----= “‘
Л40 —хсо
и проинтегрируем обе части равенства .
— 1п (Мо—хсо) = ?-|-С.
В начале разгона при ? = 0 со = О. Подставляя это условие в полученный
первый интеграл, найдем постоянную интегрирования
С = — — In Мо.
х
Внесем это значение для С в последнее равенство
— ~ 1п (Л40—хсо) = [—1п Мо,
Группируя члены с логарифмами, получим
|"тг? = -т'- ‘925>
Отсюда
21*
, х ‘
1 —» = е
Мо
§9 6]
СИСТЕМА, УЧАСТВУЮЩАЯ В СЛОЖНОМ ДВИЖЕНИИ
211
и, следовательно,
(9.26)
Это равенство и определяет закон изменения угловой скорости. С ростом
времени t второй член в скобках стремится к нулю. Поэтому угловая ско-
рость ротора, монотонно увеличиваясь, стре-
мится к своему предельному значению, со-
ответствующему установившемуся режиму:
йуст = ^. (9.27)
Процесс разгона двигателя называется
переходным процессом (его график показан
на рис. 9.8). Переходный процесс считается
для большинства электродвигателей закон-
ченным, когда угловая скорость и> достиг-
нет 0,95 своего предельного значения. Про-
определить,
должительность ?|1ер переходного процесса легко
формулой (9.25). Имеем
пользуясь
(9.28)
При со/сОуСТ = 0,95 время rf = Znep. Следовательно,
, / , 3/
^пер — х 1п 20 ~ —
Момент инерции ротора / и крутизну характеристики двигателя х подби-
рают из условия, чтобы время переходного процесса находилось в заданных
пределах (для электроприводов большинства механизмов ^пер не превышает
2 — 3 секунд).
§ 9.6. Момент количеств движения системы,
участвующей в сложном движении
Во многих случаях движение материальной системы относи-
тельно инерциальных осей рационально представить как сложное
и разложить его на простейшие
движение материальной системы
осей так и относительно
движения, при этом очень часто
удается упростить вычисление
момента количеств движения.
Введем подвижные коорди-
натные оси Cx2y2z2, перемещаю-
щиеся поступательно относи-
тельно инерциальных осей
®1%1У121’> начало отсчета подвиж-
ных осей совместим с центром
масс С материальной системы
(рис. 9.9). Будем рассматривать
как относительно неподвижных
поступательно перемещающихся
212
ТЕОРЕМА об изменении момента количеств ДВИЖЕНИЯ (ГЛ IX
осей Cx2y2z2. Пусть Mk— одна из точек материальной системы.
Еведем обозначения: mk — масса точки Mk, rk — ее радиус-вектор,
проведенный из начала Ог неподвижных осей, pfc — радиус-вектор
той же точки, проведенный из начала С подвижных осей, гс —
радиус-вектор начала подвижных осей (т. е. центра масс) в си-
стеме OiXjt/iZi. Очевидно, что
г* = гс + р*. (9.29)
Из кинематики известно, что скорость vk точки Mk относи-
тельно неподвижных осей складывается из переносной vek и
относительной vrk скоростей:
vft~ veft +
Учитывая, что подвижные оси перемещаются поступательно,
будем иметь
dpk
Vek = VC, =
Следовательно,
vft = vc + vrft. (9.30)
Момент количеств абсолютного движения Koi материальной
системы относительно неподвижного центра Oj равен
Кщ = 2 Г* у (9.31)
k = i
Аналогичным образом определяется момент количеств относитель-
ного движения К£ материальной системы относительно начала
С подвижных осей Cx2y2z2 (абсолютная скорость vk заменяется
относительной скоростью v^, абсолютный радиус-вектор г* точки
Мь ее радиусом-вектором pfe в подвижной системе координат):
п
Кс= S p*xmftvrft. (9.32)
k = i
Установим два тождества, которым должны удовлетворять ра-
диусы-векторы р* и относительные скорости vrk. Положение
центра масс системы в осях Cx2y2z2 определяется равенством (см.
формулу (7.2))
п
РС~~М mkPk'
k^i
Так как начало подвижной системы координат совпадает с цент-
ром масс, то рс = 0; следовательно,
п
2 mftpft = 0. (9.33)
к = 1
§9 6]
СИСТЕМА, УЧАСТВУЮЩАЯ В СЛОЖНОМ ДВИЖЕНИИ
21?
Дифференцируя это соотношение по времени и принимая во вни-
мание, что =Vrk, получим
п
У Wv,* = 0. (9.34)»
k= 1
Таким образом, движение любой материальной системы в по-
ступательно перемещающихся осях, начало которых совпадает
с центром масс системы, удовлетворяет тождествам (9.33) и
(9.34).
Преобразуем теперь выражение для момента количеств абсо-
лютного движения Koi- Для этого внесем в формулу (9.31) значе-
ния г* и vft из равенств (9.29) и (9.30):
Koi= У (rc + P*)xm*(vc + vr*).
k = i
Раскроем в правой части скобки и разобьем все выражение на че-
тыре суммы:
Koi= Srcxm*vc+ ypkXmkvc+ У rcX mkvrk+ PkXmkvrk..
k ~1 k = 1 k = 1 k — 1
Учтем следующие обстоятельства; а) множители rc и vc не зави-
сят от индекса суммирования k, и их можно вынести за знак
суммы; б) скалярный множитель тк можно отнести к любому
векторному множителю; в) последняя сумма в правой части в соот-
ветствии с (9.32) равна Ко- На этом основании выражение для Kqj
можно представить в виде
Ко1 = гсх( 2 S m»Pk} Xvc + гсх У mkVrk + V<rc,
'k= i / k ~ i / k = i
Согласно тождествам (9.33) и (9.34) второе и третье слагаемые-
п
равны нулю, а ть = М, где М — масса всей системы. Следова-
А = 1
тельно,
Koi = rcx4fvc+K^ (9.35)-
или
K0i=M01(Mvc) + K/c. (9.36)
Это равенство можно прочитать следующим образом: момент
количеств абсолютного движения Koi относительно неподвижного
центра Ог равен сумме момента относительно того же центра
214 ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
количества движения центра масс системы, в предположении, что
в нем сосредоточена вся ее масса, и момента относительно центра
масс количеств относительного движения системы, причем послед-
нее движение рассматривается по отношению к поступательно
перемещающимся координатным осям, начало которых совпадает
с центром масс системы.
В проекциях на неподвижные оси координат векторное равен-
ство (9.36) эквивалентно трем скалярным:

(9.37)
Задача 9.3. Эпициклический механизм состоит из неподвижной шестерни /,
кривошипа OjC и сателлита II (рис. 9.10). Кривошип СЦС массы пц вращается
с угловой скоростью и
Рис. 9.Ю.
вокруг оси, проходящей через центр О1 ше-
стерни / радиусом R. Считая сателлит //
однородным диском массы т2 и радиуса г,
а кривошип однородным тонким стержнем
длины [ = 7?4-г, определить момент коли-
честв движения механизма относительно не-
подвижной оси вращения кривошипа.
Построим две системы координат: не-
подвижную OiXtt/tZj и поступательно переме-
щающуюся систему Сх2у2г2, начало которой
совпадает с центром тяжести сателлита II;
д координатные оси OjZj и Сг2 направлены на
читателя. Так как шестерня I неподвижна,
то момент количеств движения КЛ эпици-
клического механизма относительно непод-
вижной оси Zj будет

где и К*1 — моменты количеств движения относительно оси OjZj криво
шипа и сателлита соответственно.
Кривошип представляет твердое тело, вращающееся вокруг неподвижной
оси 0^. На основании формулы (9.4) имеем
К*р = /*рсо,
где и = иг —проекция угловой скорости кривошипа на ось гь а 1*р — его
момент инерции относительно той же оси. Для однородного тонкого стержня
согласно формуле (9.5)
/кр = ^т1/2= 1 {R + r}2'
Следовательно,
^Р= ‘-^(Я + ^со.
Подвижная шестерня участвует в сложном движении. Поэтому для вы-
числения момента количеств движения сателлита относительно оси СЦг^
§ 9.6]
СИСТЕМА, УЧАСТВУЮЩАЯ В СЛОЖНОМ ДВИЖЕНИИ
21&
воспользуемся третьей формулой (9.37):
(m2V с) + Ксг,-
Построим в центре тяжести С шестерни II вектор количества движения
т^С (см- Рис- 9.10). Плечо вектора т^с относительно оси O1z1 равно 1 =
= R-]-r. Следовательно,
;W;1(ra2v'c) = fflr'c (Я + О-
Движение шерстени II относительно осей Сх2у2г2 представляет вращение
вокруг оси Сг2. Поэтому согласно формуле (9.4)
^C'z2 = /Z2 Ю1Ь
В этом равенстве~ m2r2 — момент инерции относительно оси Сг^ ше-
стерни II (см. формулу (9.7)) и Ы]|—ее угловая скорость.
Внося Л4г1 (m2vc) и К.гСг в выражение для К”, получим
/<‘;=т2(Я + г)пс+ *
Для полного решения задачи нам осталось вычислить модуль скорости ос
центра тяжести С шестерни II и ее угловую скорость а>1ь
Точка С принадлежит одновременно и кривошипу OZC. Поэтому
vc = a> (R-\-r).
Мгновенный центр скоростей Р шестерни // совпадает с точкой касания обеих
шестерней. Скорость точки С, как точки шестерни II, определяется равен-
ством
пс = гсоп.
Сравнивая оба выражения для скорости точки С, найдем
R + r
«п=—
Подставим значения для vc и а>ц в выражение для R*1 и сгруппируем члены:
R‘J=m2(R + r)^R + y 'ум .
Теперь найдем момент количеств движения Кг всего механизма относи-
тельно оси OiZi.
Г 1 / з \1
К2, = (/?+г) |^-д- mi (R-\-r) т2 f R+^ ю •
Это выражение можно записать в форме (9.4):
Кг, = /*₽«, (9.38)
где величина
^пр = (#+г) £ g- т, (R -j-r) +m2 ^R + tj' (9.39)
называется приведенным к оси OrZi моментом инерции механизма.
Заметим, что приведение момента инерции механизма к одной и той же
оси можно производить различными методами. В данном примере это приве-
дение выполнено при вычислении момента количеств движения системы,
*216
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ. IX
-'§ 9.7. Теорема об изменении момента количеств
«относительного движения материальной системы
Доказанная в § 9.3 теорема относилась к абсолютному движе-
нию, т. е. к движению материальной системы относительно инер-
циальных осей. Кроме того, предполагалось, что точка, относи-
тельно которой вычислялся момент количеств движения, непод-
вижна. Эти ограничения вносят известные неудобства при изучении
вращательных движений тел, не имеющих неподвижных точек
«(самолеты, корабли, ракеты, приборы, установленные на них и
т. п.). В этом параграфе мы рассмотрим, какой вид принимает
теорема об изменении момента количеств движения для относи-
тельного движения.
Будем изучать движение материальной системы относительно
подвижных осей О2х2г/2г2, перемещающихся поступательно относи-
тельно инерциальных осей О&у^. Напомним, что все законы
.динамики, установленные для материальной точки, движущейся
в инерциальной системе отсчета, остаются справедливыми для ее
-относительного движения, если только к силам, действующим
на точку, присоединить переносную и кориолисову силы-инерции
(см. главу VI).
Подвижные оси О2х2у2г2 перемещаются по условию поступа-
тельно. Поэтому ускорения Кориолиса wkc и соответствующие
Кроме того, при поступа-
(2%2l/222 переносные ускорения
всех точек одинаковы и
равны ускорению wo2:
Wfee = Wo2.
Следовательно,перенос-
ная сила инерции k-и точки
определяется равенством
ike = — mkv/ke = — mkwOi,
(9.40)
где mh — масса точки.
На рис. 9.11 показаны
координатные оси О1х1г/1г1
k-я точка материальной си-
стемы, к внешней F* и внутренней F* силам которой присоеди-
силы инерции, mkwkc, равны
'тельном движении подвижных
нулю,
осей О
;нена переносная сила инерции —mkwo2-
Теперь координатные оси O2x2y2z2 можно считать неподвижными.
В применении к теореме об изменении томента количеств дви-
жения это означает, что в равенстве (9.9) момент количеств абсо-
.лютного движения Ко,, вычисленный относительно неподвижной
-.точки, нужно заменить на момент количеств относительного дви-
§ 9,7] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ МАТЕРИАЛЬНОЙ СИСТЕМЫ 217
жения Ко,, вычисленный относительно начала 02 подвижных осей:
О2х^2гг, и к моментам внешних сил нужно присоединить моменты
переносных сил инерции всех точек системы:
п
k=1
Согласно (9.40) имеем (см. рис. 9.11)
5 Mo, (J*<J = 5 Р*х(—/nftwo2).
k= i * — i
Скалярный множитель mk отнесем к вектору р*, а общий'
множитель—wo, вынесем за знак суммы:
У Мо, (Jfte)= 2 W*X(—w0,).
k = 1 ft = 1
В соответствии с формулой (7.2) сумма, стоящая в скобках,
равна Мрс, где М — масса всей системы, а рс — радиус-вектор
центра масс в подвижной системе координат. Следовательно,
У Мо, (J*e) = МРс X (— WOs) = Pc X (—Aiwo,).
k = 1
Произведение — Mwo, назовем переносной силой инерции
центра масс, в предположении, что в нем сосредоточена масса М
всей системы. (При поступательном движении осей О2х2у2г2 пере-
носное ускорение центра масс С равно ускорению полюса wo,-)
Будем считать, что сила инерции —Mwo, приложена в центре
масс. Тогда произведение РсХ(—Mwo2) представляет собой момент
силы —Mwo, относительно подвижного центра О2:
Мо, (—Aiwo,) = Pc X (—A4wo,). (9.42)-
Учитывая введенные обозначения, равенству (9.41) можно при-
дать следующий вид:
^22- = Мо, + МО2(— Afw0,). (9.43}
Это уравнение представляет математическую запись в векторной
форме теоремы об изменении момента количеств относительного
движения. В проекциях на поступательно перемещающиеся оси
218
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ. IX
Д, у2, га оно дает следующие три скалярных уравнения:
^ = Ml2 + MX2(-Mw02),
^ = < + M,2(-MwO2), } (9.44)
^ = ML + M22(-Mw0J.
В частном, но весьма важном случае, когда начало О2 посту-
пательно перемещающихся осей совмещено с центром масс С ма-
териальной системы, уравнение (9.43) существенно упрощается.
Действительно, в этом случае рс = 0,
Mo, (— Mwo2) = рс X (— Mwo2) = О
и уравнение (9.13) принимает вид
dKr
-дГ = Мс- (9-45)
В проекциях на поступательно перемещающиеся оси х2, у2, г2
будем иметь
dKrx „ dKr , dKr,
-dT-^ -dT = ^. (9.46)
Сравним уравнение (9.9) с уравнениями (9.43) и (9.45). В пер-
вом из них при вычислении момента количеств движения Ко,
учитываются абсолютные скорости точек материальной системы
и за центр выбирается неподвижная точка. В уравнениях (9.43)
и (9.45) при вычислении момента количеств движения Ко2 учи-
тываются скорости точек материальной системы относительно
поступательно перемещающихся осей O2x2y2z2 (или Cx2y2z2) и за
центр выбирается начало подвижной системы координат.
В правой части уравнения (9.43) к моментам внешних сил
нужно присоединить момент относительно подвижного центра
переносной силы инерции—Mwo2.
Отметим, что если за полюс выбрать центр масс, то теорема
об изменении момента количеств относительного движения (урав-
нение (9.45)) по своей форме полностью совпадает с аналогич-
ной теоремой об изменении момента количеств абсолютного дви-
жения (уравнение (9.9)).
Остановимся подробнее на уравнении (9.45). Так как оно
по своей форме в точности совпадает с уравнением (9.9), то дви-
жение материальной системы относительно ее центра масс про-
исходит так же, как если бы последний был неподвижен. Все следствия
теоремы моментов количеств движения относительно неподвижной
§ 9.8}
ПРИМЕРЫ И ЗАДАЧИ
219
точки остаются справедливыми и для момента количеств движе-
ния относительно центра масс. В частности, если сумма моментов
всех внешних сил относительно центра масс равна нулю, то момент
количеств движения Кс сохраняет постоянную величину и направ-
ление; если сумма моментов всех внешних сил относительно оси,
проходящей через центр масс и перемещающейся поступательно,
равна нулю, то момент количеств движения относительно этой
оси сохраняет свое первоначальное значение.
§9.8. Примеры и задачи
Рассмотрим несколько примеров, иллюстрирующих доказанные
теоремы.
Пример 1. Псворот космонавта. Предположим, что космонавт
вышел из космического корабля и совершает свободный полет.
Будем считать, что космонавт отделился от корабля без враще-
ния и что силы тяготения небесных тел (например, Земли), дейст-
вующие на космонавта, сводятся к одной равнодействующей F,
проходящей через его центр масс С. Тогда момент сил тяготения
относительно центра масс С будет равен нулю и, следовательно,
момент количеств движения относительно точки С сохраняет по-
стоянную величину и направление. Возникает вопрос: может ли
космонавт без применения реактивных микродвигателей повер-
нуться в нужном направлении?
Чтобы ответить на этот вопрос, вспомним первый опыт на
скамейке Жуковского, в котором поворот человека достигался
поворотом колеса (или руки). Так как движение материальной
системы относительно центра масс происходит по тем же законам,
что и относительно неподвижной точки, то любая прямая, прохо-
дящая через центр масс космонавта и перемещающаяся поступа-
тельно, играет ту же роль, что и ось скамейки Жуковского. По-
этому поворотом руки космонавт может повернуть свое тело
в противоположном направлении.
Пример 2. Изменение угловой скорости спортсмена. Рассмот-
рим вращение спортсмена, совершающего прыжок с вышки в воду.
Во время прыжка на спортсмена действует одна внешняя сила
(сопротивлением воздуха пренебрегаем) — сила тяжести. Эта сила
приложена к центру масс С спортсмена и, следовательно, она не
создает момента относительно точки С. Поэтому момент количеств
движения Kez спортсмена относительно горизонтальной оси г,
проходящей через его центр масс перпендикулярно к плоскости
движения, остается без изменения:
Kcz = const.
Движение спортсмена относительно поступательно перемещаю-
щейся оси г представляет собой вращение вокруг этой оси. Тогда
'220 ТЕОРЕМА ОВ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ (ГЛ. IX
согласно формуле (9.4)
Ксг = 1сг®,
где Icz — момент инерции относительно горизонтальной оси г, а со —
угловая скорость спортсмена (направление оси г выберем так,
чтобы со = сог).
В начале прыжка спортсмен, отталкиваясь от трамплина,
сообщает телу угловую скорость coj, имея момент инерции ICz = Л-
Затем в процессе прыжка он группируется (складывается), умень-
шая тем самым момент инерции Icz — Iz- Учитывая, что Ксг = const,
получим
^2®2 = ^1®1‘
Так как /2</1, то сорх^, т. е. в середине прыжка, когда спорт-
смен группируется, его угловая скорость увеличивается.
Перед входом в воду спортсмен снова выпрямляется, увели-
чивая момент инерции I и уменьшая тем самым свою угловую
скорость.
Весь процесс изменения угловой скорости спортсмена за счет
изменения его момента инерции совпадает со вторым опытом
на скамейке Жуковского (см. § 9.4). Роль оси скамейки играет
горизонтальная ось г, проходящая через центр масс спортсмена.
Пример 3. Методы стабилизации вращения космического аппа-
рата. В силу различных случайных причин космический аппарат при
отделении от последней ступени ракеты получает небольшую уг-
ловую скорость По. Для выполнения различных работ (фотогра-
фирования Земли и небесных тел, изменения орбиты, стыковки
с другим космическим аппаратом, торможения перед посадкой
и т. п.) космический аппарат необходимо надлежащим образом
ориентировать, для чего прежде всего необходимо прекратить его
вращение.
Рассмотрим два метода, с помощью которых можно остановить
вращательное движение аппарата.
а) Первый метод основан на введении реактивного момента Л4р.
Предположим, что космический аппарат вращается вокруг оси Сг2,
проходящей через его центр масс и перемещающейся поступа-
тельно относительно инерциальных осей координат. Два парал-
лельно расположенных сопла реактивного микродвигателя уста-
навливаются на некотором расстоянии друг от друга (на рис. 9.12
ось Сг2 направлена на читателя, а сопла А и В находятся
в плоскости рисунка). При отделении продуктов сгорания созда-
ется момент Мр (см. главу XI), управляя которым можно сначала
остановить вращение космического аппарата, а затем повернуть
его таким образом, чтобы ось Сх, жестко связанная с ним, приняла
нужное направление (например, была бы направлена по вектору
«скорости центра масс или на какое-нибудь небесное тело).
§ 9 8]
ПРИМЕРЫ И ЗАДАЧИ
221
Так как вращение космического аппарата может происходить
вокруг любой оси, то он должен иметь три пары таких реактив-
ных двигателей, расположенных в трех взаимно перпендикулярных
плоскостях.
б) Второй метод основан на применении вращающихся масс.
Пусть по-прежнему космический аппарат вращается с угловой
скоростью Q вокруг поступательно перемещающейся оси Сг2,
проходящей через центр масс аппарата С. Будем считать, что
силы притяжения, действующие на космический аппарат, приво-
дятся к одной равнодействующей F, проходящей через точку С.
Рис. 9.12.
Рис. 9.13.
Тогда момент внешних сил (сил притяжения) относительно центра С
будет равен нулю.
Поместим внутри космического аппарата небольшой маховичок
Г. Для простоты будем считать, что жестко связанная с аппаратом
ось вращения маховичка Г совмещена с осью Cz2 (рис. 9.13).
Рассмотрим систему, состоящую из маховичка Г и космического
аппарата (без маховичка). Так как сумма моментов всех внеш-
них сил, относительно поступательно перемещающейся оси Сг2
равна нулю, то момент количеств движения всей системы относи-
тельно этой оси сохраняет постоянное значение. Поэтому, если
заставить вращаться маховичок Г в ту же сторону, что и косми-
ческий аппарат,- вращение последнего начнет тормозиться.
Остановимся на этом явлении несколько подробнее.
Система состоит из двух тел, вращающихся вокруг поступательно переме-
щающейся оси Сг2. Момент количеств движения всей системы относи-
тельно оси Сг2 будет равен сумме моментов количеств движения относительно
этой же оси космического аппарата и маховичка Г. В соответствии с форму»
Лой (9.4) будем иметь
/<CZ2 = /0Q4-/(Q + со),
где /0 и / — моменты инерции относительно оси Сг2 космического аппарата
(без маховичка Г) и маховичка Г соответственно, Q — угловая скорость косми-
ческого аппарата относительно системы осей Сх2у2г2, перемещающихся посту-
пательно в инерциальной системе отсчета, и со —угловая скорость маховичка Г
222
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
относительно космического аппарата; при этом предполагаем, что оба тела
вращаются в одну сторону, QZa = Q и сог2 = со.
Так как = const, то
(Q-(-со) = /qQq +1 (^о_Ь°Со). (9-47)
Здесь Ро и <оо —начальные значения Q и со.
Будем отсчитывать время с момента запуска маховичка. Тогда ыо = О.
Решим теперь полученное уравнение относительно Q:
Q = Q0— , , со. (9.48)
'о + '
Положив Q=0, найдем
<о = ^±/-й0. (9.49)
Таким образом, для того чтобы остановить вращение космического аппа-
рата (Q=0), маховичку Г необходимо сообщить угловую скорость со, опреде-
ляемую равенством (9.49), причем вращение маховичка должно происходить
в ту же сторону, что и вращение космического аппарата (знаки со и Qo одина-
ковы). Отметим, что торможение космического корабля происходит не за счет
сил трения, а путем использования динамического эффекта, при котором осу-
ществляется перераспределение угловых скоростей тел, входящих в систему.
Конечно, так же как и в первом методе, на космическом аппарате нужно
установить три маховичка, оси вращения которых должны быть взаимно пер-
пендикулярны.
Первый способ стабилизации, в отличие от второго, требует одновремеииой
затраты энергии. В этом состоит основное его преимущество.
Покажем, что с помощью маховичков космический аппарат можно повер-
нуть на заданный угол.
Предположим, что до запуска маховичка Г космический аппарат ие вра-
щался (Qo = 0). Тогда равенство (9.47) примет вид (соо = О)
(/0 -(-/) Q -|- /со = 0,
или
«'•+z>3+'f-0-
Здесь ф— угол поворота космического аппарата, отсчитываемый в поступа-
тельно перемещающейся системе отсчета Схгу2, а ср—угол поворота маховичка
относительно аппарата. '
Интегрируя последнее равенство, получим
(/о+/) (Ф—Фо) + / (ф сро) = О,
где фо и ср0 — начальные значения углов ф и ф. Отсюда
ф — фо = — 1-^- (Ф — Фо)-
т. е. для того, чтобы повернуть космический аппарат на угол ф—ф0, нужно
повернуть маховичок в противоположную сторону на угол (ф —Фо)-
Задача 9.4. Для поворота космического аппарата используется электродви-
гатель-маховик, уравнение вращения которого на движущемся аппарате
имеет вид
^ + 1ш = и, (9.50)
at 1
§ 9.81
ПРИМЕРЫ И ЗАДАЧИ
223
где со — относительная угловая скорость ротора электродвигателя (маховика),
Т — его постоянная времени*), и — управляющее воздействие, принимающее
значения ± «о-
Определить продолжительность разгона tly когда u = u0, и торможения
(и =—По) маховика, если первоначально невращающийся космический аппарат
при неподвижном маховике требуется повернуть иа заданный угол др и оста-
новить. Ось вращения маховика проходит через центр масс космического ап-
парата; движение считать плоским. Моменты инерции маховика и аппарата
относительно общей оси вращения соответственно равны / и /0.
Интегрируя уравнение (9.50) при u = u0 = const (период разгона) и началь-
ных условиях: <о = О при £ = 0, получим (см. решение уравнения (8.25))
<о = 7'к0(1-е-//т) (9.51)
В конце разгона угловая скорость маховика сщ будет равна
<о1 = 7'и0(1—е—(9.52)
Интегрируя уравнение (9.50) при и = —(период торможения) и учиты-
вая, что со=<ох при t = tlt получим (см. решение (8.32))
<о = —• Т и0(сох-|-Те (Zx (9.53)
В конце торможения маховик останавливается. Внося в равенство (9.53) <о = 0,
найдем
В условиях задачи космический аппарат и маховик должны вращаться
в разные стороны, поэтому из уравнения моментов будем иметь
(Й —<о) = 0;
при этом учтено, что в начальный момент Й = <о = 0 (Q — угловая скорость
космического аппарата). Полагая Si — d^/dt, найдем
/ dt
или
(9.55)
--1--Ар = со dt,
о
где др — заданный угол поворота аппарата.
Разобьем промежуток интегрирования (0, /j-}-^) на Два промежутка: (О, 4)
и (^i, G + ^з)- В первом промежутке со определяется равенством (9.51), а во
втором — равенством (9.53). Следовательно, равенство (9.55) принимает вид
с,
^±1аР= J Ги0(1-е-1'т) dt + [ [-Пго + (со1 + 7Ч)е-(/-/',/7' ] Л,
о £
или, после интегрирования,
Ь±1^=Ти0 [t1 + T(e-f^T- 1)]_7-Ио/2_7-(а1 + 7-Ыо) {е~^т - 1).
*) Постоянный параметр Т имеет размерность времени t. В теории автома-
тического регулирования и теории управления такие параметры называются
постоянными времени.
224
ТЕОРЕМА ОБ ИЗМЕНЕНИИ МОМЕНТА КОЛИЧЕСТВ ДВИЖЕНИЯ [ГЛ IX
Пользуясь (9.52) и (9.54), найдем из последнего равенства
/1 = т + <2, (9.56)
где
’-Ш*- - <957)
Внесем значение /х из (9.56) в равенство (9.52) и полученное значение
для <ох подставим в (9.54). Тогда после сокращения иа Тиа получим
e-t,/T = 1 .
2 —е~(<2 + т,/7' ’
отсюда
-цте-^1Т _2g-t.IT + 1=0
Решим это квадратное уравнение относительно e~t2lT. Имеем
е-<!/7'=ет/7' (l-l/l-e—с/г)
(перед радикалом взят знак «минус», так как е~*г/Т < 1).
Последнее равенство преобразуем к следующему виду:
а— Х/Т
et./T = е ___________.
1_]/1-е-г/г ’
или, умножая и деля иа сопряженное выражение,
Логарифмируя это равенство, найдем /2, затем из (9.56) получим fx:
;х = т+ Т In (1 +У1 -е~т/7'), <2= Т In (1 +У"1 -е“т/г). (9.58)
Эти равенства определяют время, в течение которого электродвигатель — махо-
вик должен работать в режиме разгона (и = и0) и режиме торможения (и =—и0)
для того, чтобы повернуть космический аппарат на заданный угол ф.
ГЛАВА X
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
МАТЕРИАЛЬНОЙ СИСТЕМЫ
§ 10.1. Кинетическая энергия материальной
системы и способы ее вычисления
Как известно, кинетической энергией одной материальной
точки называется половина произведения массы т точки на квад-
рат ее скорости. Кинетической энергией материальной системы
называется сумма кинетических энергий всех точек, входящих
в систему. Обозначается кинетическая энергия символом Т. По
определению имеем
п
T = ~^mkvl. (10.1)
л —1
Стоящие в этом выражении скорости vk точек материальной си-
стемы определяются относительно инерциальной системы отсчета.
Во многих случаях движение
материальной системы относитель-
но инерциальных осей целесооб-
разно представить как сложное и
разложить его на простейшие дви-
жения. При этом очень часто
удается упростить вычисление ки-
нетической энергии системы.
Введем подвижные координат-
ные оси Ох2г/2г,2, перемещающиеся
поступательно относительно инер-
циальных осей Будем
рассматривать движение материальной системы как относительно
неподвижных осей О^у^, так и относительно поступательно
перемещающихся осей Ох2//2г2. Пусть Mk — одна из точек мате-
риальной системы массы mk. Введем обозначения: г* — радиус-
вектор точки Mk, проведенный из начала Oj неподвижных осей,
р/г — радиус-вектор той же точки, проведенный из начала О по-
движных осей, г0 — радиус-вектор начала подвижных осей в си-
стеме Ор^у^ (рис. 10.1).
8 Н. В. Бутенин в др.
226
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
В соответствии с формулой (9.30)
v* = v0 + vftr, (10.2)
где vft—скорость точки Mk, v0 —скорость начала О подвижных
осей, vkr — скорость точки Мк относительно поступательно переме-
щающихся осей Ох21/2г2.
Под кинетической энергией относительного движения будем
понимать выражение
п
Тг=^тЛ, (10.3)
4 = 1
получающееся из (10.1) заменой абсолютней скорости vk точки Мк
ее относительной скоростью vAr.
Учтем теперь, что скалярный квадрат любого вектора равен
квадрату его модуля, т. е. а2 = а2. Поэтому выражение (10.1)
для кинетической энергии можно записать следующим образом:
т = 2 m^Vk’
4 = 1
или, пользуясь равенством (10.2),
п
Т = У 2 mh(yo + Vft^2'
4=1
Возведем скобку в квадрат и разобьем сумму на три части:
Т2 m*(vo + 2vo,v*'- + v^)==
Л = 1
п п п
=4 2 2 2
4 = 1 4 = 1 4=1
Последняя сумма равна кинетической энергии Тг относительного
движения; в первой и второй суммах множители Vo и v0 не зави-
сят от индекса суммирования и их можно вынести за знаки сумм:
п п
T = \-vb 2 mft + v0- mkvkr+Tr.
k = 1 й = ]
n n
Выражение У, mk равно массе всей системы М, а У mkvkr =
4=1 4=1
= MvCr, где vCr — скорость центра масс С относительно поступа-
тельно перемещающихся осей Ох2г/2г2. Докажем последнее утвер-
ждение.
§ 10 2|
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА
227
В соответствии с формулой (7.2) имеем
п
Рс=М 2 ш*р*>
4 = 1
где рс — относительный радиус-вектор центра масс.
Дифференцируя по времени, получим
dpc 1 у dpk
dt ~ М Z dt ’
4 = 1
ИЛИ
п
Vc'=i 2 mkNkr'
4 = 1
что и доказывает справедливость сделанного замечания.
На этом основании последнее выражение для кинетической
энергии можно привести к следующему виду:
T = lMt>20 + Mv0-vCr + 7\. (10.4)
Если начало подвижных осей О совпадает с центром масс
С системы, то v0 = vc и оС/. = 0. В этом случае последнее равен-
ство упрощается:
T^^-Mvl + Tcr. (10.5)
Словами его можно прочитать следующим образом (теорема
Кенига): кинетическая энергия материальной системы в ее абсо-
лютном движении складывается из кинетической энергии (1/2Mvc)
центра масс, в предположении, что в нем сосредоточена масса
всей системы, и кинетической энергии ТСг системы в ее движении
относительно поступательно перемещающихся в инерциальном про-
странстве вместе с центром масс осей Сх^у2г2.
В следующем параграфе мы рассмотрим, как используются
полученные формулы для определения кинетической энергии мате-
риальной системы.
§ 10.2. Кинетическая энергия твердого тела
Очень часто материальная система представляет твердое тело
или' совокупность твердых тел. В связи с этим нужно уметь опре-
делять кинетическую энергию твердого тела при различных видах
его движения.
Так как твердое тело рассматривается как непрерывно распре-
деленная масса, то все суммы, входящие в выражения для кине-
8*
228
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
тической энергии материальной системы, переходят в интегралы,
а масса m,t отдельной точки заменяется дифференциалом dm.
Поэтому для твердого тела формула
(10.1) примет вид
T = (10.6)
где интегрирование производится по
массе всего тела.
1. Кинетическая энергия твердого
тела, движущегося поступательно. При
поступательном движении твердого тела
скорости всех его точек одинаковы (рис. 10.2). Вынося о2 в фор-
муле (10.6) за знак интеграла, получим
Т = у v2 j dm,
или, учитывая, что [dm = M, где М — масса всего тела,
Т = уМи2. (10.7)
Таким образом, кинетическая энергия твердого тела, движу-
щегося поступательно, равна половине произведения массы тела
на квадрат его скорости.
Формула (10.7) применима также для
случая, когда скорости всех точек материаль-
ной системы равны между собой по модулю.
Например, по такой формуле можно вы-
числить кинетическую энергию ремня, уча-
ствующего в передаче вращения от одного
шкива к другому.
2. Кинетическая энергия твердого тела,
вращающегося вокруг неподвижной оси.
Модуль скорости любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равен со/1г, где со —модуль угловой скорости
твердого тела, a h, — расстояние от точки
до оси вращения г (рис. 10.3). Подставляя в формулу (10.6) зна-
чение скорости точки v — <ahz, получим
Т = у У M2hi dm,
или, вынося за знак интеграла со2 (угловая скорость одинакова
для всех точек тела и от переменной интегрирования не зависит),
Т = у<в2 у hi dm.
§ 10 2]
КИНЕТИЧЕСКАЯ ЭНЕРГИЯ ТВЕРДОГО ТЕЛА
229
Полученный интеграл согласно формуле (9.3) представляет
момент инерции тела 1г относительно оси вращения. Следова-
тельно,
(10 8)
т. е. кинетическая энергия твердого тела, вращающегося вокруг
неподвижной оси, равна половине произведения момента инерции
тела относительно оси вращения на квад-
рат угловой скоррсти тела.
3. Кинетическая энергия твердого тела,
имеющего одну неподвижную точку. При
сферическом движении твердого тела мо-
дуль скорости любой его точки М опре-
деляется равенством (рис. 10.4)
v =
где © — угловая скорость тела, a ha — Р«с- 10-4-
расстояние от точки М тела до его мгно-
венной оси вращения. Сравнивая с предыдущим случаем, когда
v = a>h2, получим выражение для кинетической энергии твердого
тела при его сферическом движении

(10.9)
где /и —момент инерции тела относительно мгновенной оси
вращения.
Заметим, что, несмотря на внешнее сходство формул (10.8)
и (10.9), между ними имеется и существенное различие. Положение
оси вращения z неизменно отно-
сительно тела, поэтому момент
инерции 12 в формуле (10.8) с те-
чением времени не меняется. По-
ложение мгновенной оси вращения
в общем случае меняется относи-
тельно тела, вследствие чего момент
инерции в формуле (10.9) есть ве-
личина переменная.
4. Кинетическая энергия твер-
дого тела, движущегося произ-
вольным образом. Пусть твердое
тело движется произвольным образом относительно инерциальных
осей. Введем поступательно перемещающуюся систему координат
Сх,г/2г,, начало которой совместим с центром масс С тела, и вос-
пользуемся теоремой Кенига (формула (10.5)):
Т =4л1иЬ + Гг.
230
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
Движение тела относительно поступательно перемещающихся
осей Сх2у2г2 представляет собой вращение с угловой скоростью со
(рис. 10.5). Поэтому кинетическая энергия относительного дви-
жения определится формулой (10.9):
Т,/- = -2/са><°2,
где —момент инерции тела относительно оси, проходящей
через его центр масс С и совпадающей с вектором угловой ско-
рости (О.
Подставляя значение Тг в выражение для Т, получим
Т =1л1^ + |/Сисо2.
(10.10)
Это равенство представляет математическую запись теоремы Ке-
нига для свободного твердого тела, которую можно прочитать
следующим образом: кинетическая энер-
гия твердого тела складывается из ки-
нетической энергии поступательного
движения вместе с центром масс и ки-
нетической энергии в его движении
относительно центра масс.
В общем случае момент инерции /Со
представляет переменную величину.
5. Кинетическая энергия твердого
тела при плоском движении. При плос-
ком движении твердого тела вектор уг-
ловой скорости го всегда перпендикулярен к плоскости движения,
совпадая с поступательно перемещающейся координатной осью Сг2
(на рис. 10.6 оси О& и Сг2 не показаны).
Заменив в моменте инерции 1Сю формулы (10.10) нижний
индекс Сео на Сг2, получим выражение для кинетической энергии
твердого тела в случае плоского движения:
Т Mvc + ^ /сгга2. (10.11)
Ось Сг2 ще меняет своего положения относительно тела, и,
следовательно, момент инерции 1сгг не меняется с течением вре-
мени. Это обстоятельство существенно упрощает все вычисления.
Прежде чем перейти к примерам,'сделаем два замечания.
а) При вычислении кинетической энергии твердого тела, дви-
жущегося произвольным образом или участвующего в плоском
движении, формулы (10.10) и (10.11) не всегда являются самыми
простыми. Иногда удобнее пользоваться более общей формулой (10.4)
(см. пример в конце параграфа).
§ 10.2]
кинетическая энергия твердого тела
231
б) Если материальная система состоит из нескольких тел, то
ее кинетическая энергия Т будет равна сумме кинетических
энергий Т] всех тел, входящих в систему (это непосредственно
вытекает из определения):
Т = 7\ + Т2 + ... + 7\. (10.12)
Рассмотрим примеры на вычисление кинетической энергии мате-
риальной системы.
Задача 10.1. Каток К массы mi лежит на горизонтальной плоскости.
Каток обмотан тросом, перекинутым через блок Б радиуса г. К свободному
концу троса прикреплен груз Г массы т3. При опускании груза со скоростью о
трос, разматываясь, приводит в качение
без скольжения каток К (рис. 10.7).
Определить кинетическую энергию си-
стемы, если момент инерции блока Б
относительно оси вращения равен /2;
каток считать однородным круглым ци-
линдром, массой троса пренебречь*
Система состоит из трех тел: кат-
ка К, блока Б и груза Г. Поэтому ее
кинетическая энергия Т будет равна
7' = 7'к + 7'б+7'г,
где ТБ и Тг —кинетические энергии катка, блока и груза соответственно.
Груз Г движется поступательно. Его кинетическая энергия Ту согласно
формуле (10.7) будет равна
Tr = ~mav2.
Блок Б вращается вокруг неподвижной оси. Согласно формуле (10.8) его
кинетическая энергия
= ~2. ^2ШБ,
где <оБ—угловая скорость блока.
Скорость точки касания блока с тросом равна скорости v груза Г. Следо-
вательно, ц = Отсюда соБ=ц/г и
1 '
Каток К участвует в плоском движении. Кинетическую энергию Тк катка
найдем по теореме Кеиига (см. формулу (10.11)):
ТК ^~2 т^с + Т lCz^K,
где vc—скорость центра С катка, сок—угловая скорость катка, 1Сг —его
момент инерции относительно оси Сг2 (на рис. 10.7 ось Сг2 направлена на
читателя).
Скорость верхней точки Е катка К равна v- Точка Р касания катка
с горизонтальной плоскостью является мгновенным центром скоростей. Поэтому
v
VC~2'
232
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
Угловую скорость <ок найдем из равенства
vc = 7?(0k,
где R — радиус катка. Отсюда
vc v
Момент инерции катка относительно его оси Сг2 определяется формулой
(9-7):
/Сг =4^2-
Внося значения vc, сок и /Сг,2 в выражение для Тк, после очевидных
преобразований получим
3
ГК=~16 т^~'
Теперь находим кинетическую энергию Т всей системы:
7- = AmiU2 + l/2^ +-1тзц2,
или
Л4про2,
(10.13)
где величина
3 /
М п р = у т1 + + т3
(10.14)
называется приведенной массой системы.
Рассмотрим задачу на применение формулы (10.4).
Задача 10.2. Твердое тело массы М вращается вокруг горизонтальной
оси О?г (ось 02j перпендикулярна к плоскости рис. 10.8); момент инерции тела
относительно оси вращения Ог равен /. Определить кинетическую энергию тела,
если ось подвеса Ог перемещается гори-
зонтально со скоростью v0 (эта скорость
может быть переменной).
Построим неподвижные оси О±х1у1 и
подвижные оси Ох2р2. Движение тела
относительно осей Ох2у2 представляет
вращение вокруг оси- Ог^. Обозначив
через ср угол между осью х2 и прямой
ОС, где С —центр тяжести тела, найдем
кинетическую энергию в относительном
движении
7\ = у/ф2-
Модуль скорости точки С относительно осей Ох%у2 равен Лф (считаем ф > 0);
направление скорости vCr показано иа рис. 10.8. Скалярное произведение
векторов vQ и vc будет vQ • vCr~ voh<f cos <p. Пользуясь формулой (10.4), най-
дем кинетическую энергию тела
Т = Mvl±Mvoh<fcos(p+ g /ф2, (10,15)
§ 10.31 РАБОТА СИЛ, ПРИЛОЖЕННЫХ К МАТЕРИАЛЬНОЙ СИСТЕМЕ 233
Применение теоремы Кенига потребовало бы больших выкладок, так как
нужно было бы определить абсолютную скорость точки С и перейти от момента
инерции относительно оси Сг к заданному моменту инерции относительно оси Ога.
§ 10.3. Работа сил, приложенных к материальной системе
В дальнейшем нам нужно будет вычислять суммарную работу
внешних и внутренних сил, приложенных к материальной системе.
При этом возникает ряд особенностей, на которых полезно оста-
новиться подробнее.
Предположим, что при своем движении материальная система
перешла из одного положения, которое она занимала в мойент
времени t0, в другое положение, соответствующее моменту времени
t. Обозначим Через А полную работу, которую совершают при
этом перемещении системы все приложенные к ней силы, причем
работы внешних И' внутренних сил будем обозначать соответст-
венно через Ае и А‘, так что
А = Ае + А‘. (10.16)
Если через А* и А* обозначить работу, которую совершают
внешние и внутренние силы, приложенные к k-и точке системы,
при переходе ее из первого положения во второе, то по опреде-
лению будем иметь
A'=-£Aek, А‘=2Х
k=i k=i
1. Работа сил тяжести. Если материальная система находится
в однородном поле тяжести, то на каждую ее точку Мк массой mk
действует внешняя сила F®=mZ;g, элементарная работа d'Aek ко-
торой равна mkg-drh. Направим ось z вертикально вверх.
Тогда проекции силы F* будут равны 0, 0, — mkg и
d'Aek = mkg drk = —mhg dzk.
Найдем теперь сумму элементарных работ всех сил тяжести,
приложенных к системе:
У, d'Aeh = — У mkg dzk = — gd^ mkzk
*=1 4=1 * = I
или, учитывая третье равенство (7.3), будем иметь
У d'Aek == — gM dzc,
k=\
где M — масса всей системы, а гс — аппликата ее центра тяжести.
234
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
Полная работа сил тяжести при переходе системы из первого
положения во второе определится равенством
гс
Ae = — Mg $ dzc = — Mg(zc — Zqc),
гос
или
A^Mg(z,c-zc)=P(zoC-zc). (10.17)
В этом равенстве гс и гоС — значения аппликаты центра тяже-
сти системы в ее конечном и начальном положениях, а Р — вес
всей системы.
Таким образом, полная работа сил тяжести системы
равна весу всей системы, умноженному на вертикальное пере-
_________________ мещение ее центра тяжести.
~~i х 2. Работа внутренних сил твер-
\ дого тела. Докажем, что сумма ра-
[ I б°т всех внутренних, сил абсолютно
у В*—/ твердого тела на любом его переме-
щении равна нулю.
-----.—-— Пусть Fj и Fj — внутренние силы
Рис. 10.9. взаимодействия точек В и D твердого
тела (рис. 10.9). По третьему закону
Ньютона они равны по модулю и направлены по одной прямой
в противоположные стороны:
F.j = — Fj. (10.18)
Составим сумму мощностей этих сил:
Nl = f; • vB + Fa • VD = F; • vB — Fj • vD = Fj • (vB — VD),
где vB и vD — скорости точек В и D соответственно.
Примем точку D за полюс. Тогда согласно известной формуле
кинематики __
vb = Vd + &XDB,
где со —угловая скорость тела. Внося это значение для скорости
точки В в последнее равенство, получим
№<=Fj-(w/DB).
Скалярное произведение двух взаимно перпендикулярных век-
торов Fj и eaxDB равно нулю (так как вектор etxDB перпен-
дикулярен к вектору DB, коллинеарному с силой Fj). Поэтому
№‘ = ^j = 0,
/=1
§ 10.31
РАБОТА СИЛ, ПРИЛОЖЕННЫХ К МАТЕРИАЛЬНОЙ СИСТЕМЕ
235
причем полную мощность можно распространить, конечно, на все
внутренние силы твердого тела (они входят попарно).
Так как сумма мощностей внутренних сил твердого тела равна
нулю, то будет равна нулю и сумма работ этих сил:
А‘=^А- = 0, (10.19)
/=1
что доказывает сделанное утверждение.
Аналогично можно доказать (мы не будем останавливаться на
этом), что сумма работ внутренних сил абсолютно гибкой и нера-
стяжимой нити равна нулю.
3. Работа силы, приложенной к твердому телу, вращающемуся
вокруг неподвижной оси. Пусть сила Fe приложена к некоторой
точке тела, отстоящей от неподвижной
оси вращения г на расстоянии h. Точка
приложения силы описывает при движе-
нии тела окружность радиуса h. Разло-
жим силу Fe по осям естественного трех-
гранника и обозначим ее составляющие
через Ft, F)j и F* (рис. 10.10). Работа
составляющих сил Fn и F* равна нулю,
так как эти силы перпендикулярны к пе-
ремещению точки их приложения. Следо-
вательно, работа силы Fe равна работе ее
касательной составляющей F£. Для эле-
ментарной работы будем иметь
d'Ae = Fxds = Fxhdq,
где ds = h dq> — дифференциал дуговой координаты точки прило-
жения силы, a dip — дифференциал угла поворота тела.
Учитывая, что произведение Fxh равно моменту силы Fe отно-
сительно оси вращения тела, получим
d' Ае = Mez dip,
(10.20)
т. е. элементарная работа силы, приложенной к твердому телу,
вращающемуся вокруг неподвижной оси, равна моменту этой силы
относительно оси •вращения, умноженному на дифференциал угла
поворота тела.
Работа силы Fe на конечном угле поворота определится
равенством
ф
Ae=\Mzd(p, (10.21)
Фо
236
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
где ф0 и ф — начальное и конечное значения угла ф, определяю-
щего положение тела (если момент Мег зависит не только от угла
поворота ф, но также от угловой скорости со и времени t, то
нужно перейти к новой переменной интегрирования).
Если момент внешней силы не изменяется во время движения
тела, т. е. = const, то
Ле = Мг(ф-ф0). (10.22)
Деля обе части равенства (10.20) на dt, получим выражение
для мощности силы, приложенной к твердому телу, вращающе-
муся вокруг неподвижной оси:
Ne = Nzaz. (10.23)
4. Работа потенциальных сил. Понятие потенциальных, или
консервативных, сил, действующих на систему материальных точек,
вводится как естественное обобщение понятия потенциальной
силы для одной материальной точки.
Позиционные силы, зависящие только от положения системы,
называются потенциальными, если работа их на перемещении
системы из начального положения в конечное положение не за-
висит от пути, по которому происходит это перемещение.
Потенциальная энергия определяется как работа всех сил при
переходе системы из данного положения в положение, условно
принимаемое за нулевое (положение, при котором П = 0):
П-Лм,Мо, (10.24)
где М и Л40 символически обозначают положения системы в дан-
ном и нулевом положениях.
Так же как и для одной точки, легко показать, что работа
потенциальных сил при перемещении системы из одного положе-
ния в другое определяется равенством
4,2^-Щ, (10.25)
где Щ и П2 — значения потенциальной энергии системы в ее
начальном и конечном положениях.
Потенциальная энергия зависит от координат материальных
точек, составляющих систему, т. е.
П = П (xlt уг, zt, ..., хп, уп, zn).
Предполагается, что функция П однозначна и непрерывна
вместе со своими производными до второго порядка включительно.
Легко показывается, что частные производные от потенциаль-
ной энергии, взятые с обратным знаком, равны соответствующим
проекциям сил:
—f‘» = ~I? = (10.26)
§ 10.31
РАБОТА СИЛ, ПРИЛОЖЕННЫХ К МАТЕРИАЛЬНОЙ СИСТЕМЕ
237
Часто можно найти потенциальную энергию отдельных сил,
входящих в систему. В этом случае потенциальная энергия систе-
мы будет равна сумме потенциальных энергий:
П=2П/. (10.27)
/=1
Наконец, во многих случаях полезно разделить потенциальную
энергию на энергию внутренних и внешних сил. Общая потен-
циальная энергия будет равна их сумме:
П = ГВ + Пг. (10.28)
Так же как и для одной точки, рационально иногда пользо-
ваться силовой функцией U, которая отличается от потенциальной
энергии только знаком:
U = — П.
5. Работа внутренних сил трения скольжения сочлененных тел.
В различных устройствах между движущимися телами возникают
силы трения скольжения. Эти
силы приложены к обоим трущимся
телам. Вычислим полную работу
внутренних сил трения сочленен-
ных тел.
Предположим, что тело В
движется поступательно со ско-
ростью v, а тело С скользит по Рис- 1011-
нему с относительной скоростью и
(рис. 10.11). Между этими телами возникают силы трения F^p
и Ftp, работу которых нужно определить.
При указанном на рис. 10.11 направлении относительной ско-
рости и сила трения FtP будет приложена к телу С, а сила тре-
ния FtP —к телу В. Конечно,
F'i __ ____
Тр ------г тр*
(10.29)
Мощность Mi-р этих сил будет равна
N‘p = N4 + N* = FtP • (u + v) + Fip • v(
при этом учтено, что абсолютная скорость тела С равна u + v
(направление скорости v тела В не имеет значения).
Принимая во внимание равенство (10.29), получим
Мтр = Fip (u + v) — Ftp • v = Fip и.
238
ТЕОРЕМА ОБ ИЗМЕНЕНИИ .КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
Сила трения FjP, приложенная к телу С, направлена всегда
в сторону, противоположную относительной скорости и. Следова-
тельно, угол между векторами FtP и и равен 180° и их скалярное
произведение будет равно —F‘Tpu. Таким образом,
А4р = — KpU, (10.30)
т. е. полная мощность внутренних сил трения скольжения двух
сочлененных тел равна взятому со знаком минус произведению модуля
силы трения на модуль относительной ско-
рости.
Из равенства (10.30) найдем сумму эле-
ментарных работ d'Ayp внутренних сил тре-
ния (d'A — Ndt и и=-^-\:
d'ArP = —Ftp dxr, (10.31)
где dx,. —элементарное относительное пере-
мещение.
Рис. 10.12. Аналогично доказывается, что для вра-
щающихся сочлененных тел (рис. 10.12)
полная мощность и элементарная работа всех внутренних сил
трения определяются равенствами
Л^тр-----ЛДрй),,
d'A‘p = —МТр dcpr,
(10.32)
(10.33)
где Л4тр —модуль момента сил трения относительно оси вращения,
со,. —модуль относительной угловой скорости и dq>r — элементарное
относительное угловое перемещение тела С.
§ 10.4. Теорема об изменении кинетической энергии
материальной системы
Рассмотрев методы вычисления работы сил, приложенных
к материальной системе, и ее кинетической энергии, перейдем
к установлению зависимостей, связывающих эти величины. Для
этого освободимся мысленно от связей, заменив их соответствую-
щими реакциями. Обозначим через F* и F), равнодействующие
всех внешних и внутренних сил, приложенных к материальной
точке Mk системы. Рассмотрим два момента времени: начальный tQ
и текущий (или конечный) t. Пусть модуль скорости точки Mk
в момент времени t0 равняется vok, а в момент времени t — vk.
Тогда для каждой точки материальной системы будет справедлива
§ 10 4]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
239
теорема об изменении кинетической энергии:
mnvn mnV0n
2 2
Аеп + Ап,
где Aek и А* —работа сил F* и F* на действительном перемещении
точки Mk.
Складывая почленно все равенства, получим
п п п п,
12 -у 2 = 2+ 2
fe=i k=i k=i k=i
или, учитывая выражение для кинетической энергии (10.1),
Т - То = Ае + А1', (10.34)
где Тп — начальное значение кинетической энергии, а Ае и А‘ —
работа всех внешних и внутренних сил системы.
Равенство (10.34) представляет математическую запись теоремы
об изменении кинетической энергии материальной системы: изме-
нение кинетической энергии материальной системы при переходе
ее из начального в текущее (конечное) положение равно сумме работ
на этом перемещении всех внешних и внутренних сил, приложен-
ных к точкам системы.
Продифференцируем равенство (10.34) по времени:
dT __ dAe dA1
dt dt dt '
Учитывая, что производная от работы по времени равна мощно-
сти У* силы Fft, получим
(Ю.35)
Это уравнение представляет собой аналитическую запись теоремы
об изменении кинетической энергии в дифференциальной форме:
полная производная кинетической энергии по времени равна сумме
мощностей всех внешних и внутренних сил, приложенных к системе.
Необходимо подчеркнуть, что в правую часть равенства (10.34)
входит работа (в равенство (10.35) — мощность) всех внутренних
и внешних сил, приложенных к системе.
Рассмотрим несколько простых примеров.
При движении автомобиля, оснащенного двигателем внутрен-
него сгорания, движущей силой является сила трения F2 между
ведущими колесами и полотном шоссе (см. рис. 7.1). Без этой силы
движение автомобиля осуществить нельзя (см. пример 1 § 8.3).
240
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
(ГЛ. X
Однако сила трения F2 при отсутствии проскальзывания колес
работу не производит (так как эта сила приложена в мгновенном
центре скоростей Р ведущего колеса, элементарное перемещение
dr? которого равно нулю). Полезную работу при перемещении
автомобиля производят внутренние силы давления газов, образо-
вавшиеся при сгорании горючей смеси.
Точно так же при движении человека по горизонтальному полу
или при его подъеме по лестнице движущими силами являются
силы трения между полом и подошвами ног человека или реакции
ступеней лестницы. Однако полезную работу производят не эти
внешние силы, а внутренние мускульные усилия человека.
Прежде чем перейти к задачам, отметим два класса сил, кото-
рые не нужно учитывать при применении теоремы об изменении
кинетической энергии системы (так как их работа равна нулю):
I) реакции связей без трения;
2) внутренние силы абсолютно твердого тела и абсолютно
гибкой и нерастяжимой нити (см. п. 2 § 10.3).
§ 10.5. Задачи
С помощью теоремы об изменении кинетической энергии
в интегральной форме определяют:
скорости точек материальной системы (в тех'случаях, когда,
зная перемещение системы, можно вычислить работу всех прило-
женных к ней сил);
работу одной из сил, приложенных к системе (когда по усло-
вию задачи скорости точек материальной системы известны или их
можно определить другими методами).
Дифференциальная форма теоремы об изменении кинетической
энергии системы применяется для составления дифференциальных
уравнений движения, а также для
определения ускорений (линейных
или угловых).
Мы начнем с задачи, иллю-
стрирующей метод определения
скоростей.
Задача 10.3. В системе, рассмотрен-
ной в § 10.2, груз Г под действием
силы тяжести опускается из состояния
покоя вниз. Определить скорость v
груза Г при опускании его на вы-
и трением на оси блока пренебречь.
Рассмотрим внешние силы, действующие на систему. На груз Г действует
сила тяжести m3g, на блок Б действуют сила тяжести m2g и реакция опоры
(на рис. 10.13 показаны ее составляющие X и Y), на каток К действуют сила
тяжести mjg и реакция горизонтальной плоскости, которая разложена на нор-
мальную составляющую N и силу трения F (без силы треиия F каток не ка-
Рис. 10.13.
соту h. Трением качения катка
§ 10.5]
ЗАДАЧИ
241
тился бы, а скользил). Внутренние силы учитывать не нужно, так как согласно
§ 10.3 сумма их работ равна нулю.
Применим теорему о конечном изменении кинетической энергии материаль-
ной системы:
Т — Та = Ае.
Воспользуемся выражением для кинетической энергии рассматриваемой
системы (10.13):
Г = уЛ4прц®,
где приведенная масса определяется равенством (10.14):
3 /
34 Пр = -g- m1 + + m3-
Движение начинается из состояния покоя, поэтому 7'0 = 0. Перейдем
к вычислению работ сил, приложенных к системе. Работа сил ’m2g, X и Y
равна нулю, так как точка их приложения неподвижна. Работа силы тяжести mtg
катка К равна нулю, так как эта сила перпендикулярна к перемещению точки
ее приложения С. Работа нормальной реакции N и силы трения F равна нулю,
так как эти силы приложены в мгновенном центре скоростей Р катка К>
элементарное перемещение которого <4гр = 0. Таким образом, осталась одна
сила тяжести m3g груза Г, работа которой равна m3gh. Итак,
Ae = m3gh.
Внося выражения для Т и Ае в уравнение энергии и учитывая, что То = О,
получим
Mnpv2 = m3gh.
Отсюда находим скорость груза в зависимости от высоты h:
Простота решения задачи объясняется прежде всего тем, что все элементы,
входящие в уравнение (10.34) (работа сил и кинетическая энергия системы),
вычисляются без интегрирования дифференциальных уравнений. *
Перейдем теперь к рассмотрению случая, когда с помощью
теоремы о конечном изменении кинетической энергии материальной
системы вычисляется работа сил.
' Задача 10.4. Космический аппарат вращается вокруг оси Сг2, проходящей
через его центр масс и перемещающейся поступательно относительно инер-
циальной системы координат. Определить работу, которую необходимо затра-
тить, чтобы с помощью вращающегося маховичка Г прекратить вращение кос-
мического аппарата (см. рис. 9.13). Угловая скорость вращения космического
аппарата до запуска маховичка равнялась Qo, его момент инерции (без махо-
вичка) относительно оси вращения Сг2 равен /0; маховик вращается относи-
тельно оси Сг2, его момент инерции относительно этой оси равен / (см. § 9.8).
Маховичок Г вращается под действием внутренних сил для системы «кос-
мический аппарат —маховичок». Характер этих сил нам неизвестен, поэтому
вычислить их работу непосредственно мы не можем. Так как работа сил входит
в уравнение (10.34), которое при Ае = 0 принимает вид
Т-Тй = А1,
242
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
то будет естественно воспользоваться им для определения искомой величины.
Внутренние силы, под действием которых вращается маховичок Г, не
изменяют движение центра масс С системы, поэтому при вычислении кинети-
ческой энергии достаточно учесть только ее вращательное движение.
Система состоит из двух тел, вращающихся вокруг оси Сг2- Ее кинети-
ческая энергия Т определяется равенством
Г=1/0Й2+у/(Й+®)2.
Здесь первое слагаемое — кинетическая энергия аппарата, второе — кинетическая
энергия маховичка, й —угловая скорость аппарата относительно инерциальной
системы координат, со— угловая скорость маховичка относительно аппарата,
В начальный момент до запуска маховичка й = й0 и со = 0. Поэтому
Ео=4(7о + /)
В момент прекращения вращения космического аппарата Q = 0. Следова-
тельно, для этого момента времени
г=-2-/(л
Внося эти выражения в Т — — получим
(/„ + /) Щ = Д*‘,
где Д’ — искомая работа внутренних сил системы.
Для полного решения задачи необходимо знать величину угловой ско-
рости <о, которую нужно сообщить маховичку, чтобы остановить вращение
космического аппарата. Для этого достаточно воспользоваться теоремой об
изменении момента количеств движения относительно оси Сг2. Такая задача
решалась нами в § 9.8. Воспользуемся полученной там формулой (9.49):
После подстановки значения со и элементарных преобразований найдем
д«‘=У А (/<>+/) й§.
Такую работу должны совершить внутренние силы системы, приводящие во
вращательное движение маховичок, чтобы прекратить вращение космического
аппарата (конечно, здесь учтена только полезная работа).
Отметим, что применение теоремы об изменении кинетической
энергии позволило вычислить работу внутренних сил, несмотря
на то, что нам не известна их аналитическая структура.
В заключение этого параграфа рассмотрим задачу на составле-
ние дифференциального уравнения движения материальной системы
с помощью теоремы об изменении кинетической энергии в диф-
ференциальной форме.
Задача 10.5. Груз Г весом Р поднимается с помощью электрической лебедки
(рис. 10.14). Барабан Б приводится во вращение электромотором, который
§ 10 5]
ЗАДАЧИ
243
создает вращающий момент Л4вр, изменяющийся по закону
' Л/вр = Л/0 —хы,
где Л4о и х — положительные постоянные, характеризующие мотор, а ы— угло-
вая скорость барабана.
Моменты инерции блока В в барабана Б относительно их осей вращения
соответственно равны /2 и [г-, радиус блока равен, г, радиус барабана R.
Определить закон движения груза и на-
тяжение троса. В начальный момент
система находилась в покое; массой троса
пренебречь.
Для того чтобы определить харак-
тер движения груза, нужно прежде всего
составить дифференциальное уравнение
движения всей системы. Конечно, для
этого можно расчленить систему, мыс-
ленно разрезав трос, ввести силы натя-
жения троса и затем составить три диф-
ференциальных уравнения движения:
одно для вращения барабана, второе
для вращения блока и третье для прямо-
линейного движения груза. Все уравне-
ния нужно решать совместно, причем
прежде всего необходимо исключить силы
натяжения троса. Такой метод решения
задачи требует хотя и не сложных, но
утомительных преобразований.
Теорема об изменении кинетической энергии материальной системы в диф-
ференциальной форме

представляет большие удобства, так как в это уравнение не войдут силы натя-
жения троса (сумма работ, а следовательно, и мощностей реакций троса и дру-
гих внутренних сил равна нулю).
Воспользуемся этим уравнением. Кинетическая энергия рассматриваемой
системы
Т = Л + Т2 + Тз,
где Тг, Т2 и Т3 — кинетические энергии барабана, блока и груза соответственно.
Барабан Б и блок В вращаются вокруг неподвижных осей, поэтому согласно
формуле (10.8)
о
где сов — угловая скорость блока. Очевидно, что сов= следовательно,
т 1 , Я2 2
Г2 = у Л -~т® .
Груз Г движется прямолинейно и поступательно со скоростью v = Ra, его
кинетическая энергия
1 Р
Та= g RW,
244
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
(ГЛ. X
Подставляя значения 7\, Т2 и Т3 в выражение для кинетической энергии
системы, получим
г=1/пр®2,
где приведенный к оси вращения барабана момент инерции системы опреде-
ляется равенством
/?2 Р
Л1р=Л+ уг Л+— Я2.
Перейдем к вычислению мощностей. Мощность сил тяжести барабана и
блока, а также реакций их опор равна нулю, так как точки приложения этих
сил неподвижны. Мощность силы тяжести Р груза Г будет
Л\ = Р • v=Pv cos 180° = — Pv = — PRu.
Мощность Л'2 сил, создающих вращающий момент Л4вр, вычислим по фор-
муле (10.23):
N2 = Л4вр® = (Л40 — х<в) <о.
Таким образом,
Ne = (Мо — PR — хы) ы.
Подставляя значения Т и Ne в уравнение = Ne-\-Nl и учитывая, что
в данном примере Л'‘ = 0, получим
/при — = (M0-PR -х<в) и,
или, сокращая на со,
/пр-^- = М0-Р/?-х(о.
Это дифференциальное уравнение движения системы отличается от рас-
смотренного ранее уравнения (9.24) только значением входящих в него постоян-
ных. Поэтому воспользуемся решением (9.26) уравнения (9.24), сделав в нем
соответствующие замены:
(в
к х '
Груз Г будет подниматься со скоростью
о = (в/? = /?
M0 — PR
X
По прошествии
ничтожно малым
ной скоростью
некоторого
промежутка времени член е п₽ сделается
и движение груза будет происходить практически с постоян-
D M0—PR
VytT — R z
Перейдем к вычислению сил натяжения троса на участке груз —блок.
Мысленно разрежем трос и заменим его действие реакцией SP Теперь груз Г
движется под действием силы тяжести Р и натяжения троса St (рис. 10.15, а).
Груз движется вверх с ускорением w=dvjdt. Состарим дифференциальное урав-
§ 10.61
ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
245
нение движения груза в проекции на ось у, направленную вертикально вверх.
Имеем
Отсюда
g dt
Вычислим производную скорости по времени
и
пр
dv M0 — PR
~тг = к----------е
dt /Пр
и подставим ее в выражение для Sf
__—t
е "Р
51=р 1+АЛ!^
' g 'пр
Для вычисления силы натяжения троса на участке барабан — блок мысленно
разрежем трос в двух местах (на участке барабан —блок и на участке блок —
груз), заменив его реакциями S[ и S2 (рис. 10.15, б). Составим дифферен-
циальное уравнение вращения блока вокруг
неподвижной оси
h-^-^S2r-S'r.
Учитывая» что SJ = S1} получим
/ 2 ЛОп
s2=si+7-_dr-
S7
Ц)
Имеем
R
сов =----<0,
а-)
dcoB
~~dT
R da R Mq — PR “T”*
_ — —_______e "P
Рис. 10.15.
/пр
Пользуясь выражением для Sj, найдем натяжение троса
блок
г di
на участке барабан —
S2=P + P

пр

И
С течением времени множитель е ПР станет достаточно малым и в уста но-
вившемся режиме Si = S2 = P.
§ 10.6. Закон сохранения полной механической энергии
материальной системы
Из теоремы об изменении кинетической энергии материальной
системы вытекает закон сохранения полной механической энергии.
Предположим, что все силы (внешние и внутренние), действую-
щие на систему, консервативны. Пусть система под действием.
246
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
этих сил перешла из начального в некоторое текущее положение.
Обозначим значение кинетической энергии системы в начальном
положении через Тп, а в рассматриваемом через Т. Применим
к этой системе теорему о конечном изменении кинетической энергии:
Т-Т0 = Ае + А‘ = А.
Так как по условию силы, действующие на систему, консерва-
тивны, то будет справедливо равенство (10.25):
Л = П0 —П,
где По и П — значения потенциальной энергии в начальном и теку-
щем положениях.
Тогда будем иметь первый интеграл
или
Т — Т0 = П0 —П,
T + n = /[,
(10.36)
где постоянная
h — Л> + По
равна начальному значению полной механической энергии (напом-
ним, что полной механической энергией называется сумма потен-
циальной и кинетической энергий).
Уравнение (10.36) называется интегралом энергии и оно выра-
жает закон сохранения полной механической энергии системы:
если система движется под действием одних консервативных сил,
то сумма кинетической и потенциальной энергии сохраняет постоян-
вую скорость движения стержня, если
ное значение. Интеграл энергии
(10.36) и некоторые его обобще-
ния имеют большое значение в
теории устойчивости движе-
ния *).
Рассмотрим пример на при-
менение интеграла энергии.
Задача 10.6. Однородный тонкий
стержень АВ длиной I движется в вер-
тикальной плоскости, скользя своим
концом А по гладкой горизонтальной
прямой (рис. 10.16). Определить угло-
в начальный момент она равнялась ф0
и стержень составлял с горизонтом угол q>0.
Освободимся мысленно от связи (гладкой горизонтальной плоскости) и
заменим ее реакцией N д. Теперь можно считать стержень Свободным, находящимся
под действием двух вертикально направленных сил: силы тяжести стержня Afg
*) См., например, Мер кин Д. Р. Введение в теорию устойчивости дви-
жения,— 1-е изд. —М.: Наука, 1971,—2-е изд.—М.: Наука, 1976,
§ 10.6]
ЗАКОН СОХРАНЕНИЯ ПОЛНОЙ МЕХАНИЧЕСКОЙ ЭНЕРГИИ
247
и реакции Мд. Работа реакции Мл равна нулю, а сила тяжести Afg— консер-
вативная сила. Поэтому будет справедлив интеграл энергии (10.36):
т+п=л.
Выбрав за нулевое положение горизонтальную плоскость, по которой
движется точка А стержня, найдем потенциальную энергию силы тяжести Afg
n = Mgt/c,
где Ус — ордината центра тяжести стержня.
Имеем (см. рис. 10.16)
I .
</с=уSln Ф’
следовательно,
П = ~ Afg/ sin ф.
Кинетическую энергию стержня найдем, пользуясь теоремой Кенига для
плоского движения твердого тела (см. формулу (10.11)):
Здесь vc — скорость центра масс С стержня, a ICz — его момент инерции отно-
сительно оси, проходящей через точку С перпендикулярно плоскости движения.
Согласно формуле (9.6) /Сг=— Ml2. Кроме того, и2с = х^-1~Ус’ где
„ -г I . I .
хс — абсцисса центра масс стержня. 1ак как ус = --^ sm^>, то ус — -g- cos ф • ф.
Внося эти значения для /Сг, vfc и ус в выражение для кинетической энергии,
получим
1 / п \ 1
Т = "2 М V+ Т Ф2 COS2 Ф ) + ^4 М12Ч2'
ИЛИ
1 Л4/2
г = у Afx^ + -g^-( 14-3 cos2ф) ф2.
Учитывая полученные выражения для Т и П, найдем интеграл энергии
для рассматриваемой системы
1 Ml2 1
У 24“ (Ч-Зсо82ф) ф24- — Mgl япф = й,
где h — постоянная энергии, которую можно найти из начальных условий:
при / = 0 ф = ф0, ф = фо, хс = хоС;
здесь xqC — начальное значение проекции скорости центра масс стержня на
ось х (эта величина по условию задачи не задана).
Внося начальные условия в интеграл энергии, получим
1 Ml2 1
й = у Ш2С +~^~ (* + 3 cos2 ф0) ф2 + -2 Mgl sin ф0.
248
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИКсТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
После подстановки найденного значения h в интеграл энергии, приведем
последний к виду
Z2 Z2
х*с + -|2“ (1 + 3 c°s2 Ф) Ф2+Sl sin ф = х\с + jy (1 + 3 cos2 qj») ф2 + gl sin <p0.
Покажем, что проекция хс скорости vc центра масс С стержня остается
постоянной во время движения. Действительно, сумма проекций всех внешних
сил на неподвижную ось х равна нулю. Поэтому согласно третьему следствию
теоремы о движении центра масс (см. формулу (8.14))
vCx = xc = const,
т. е.
*С = *оС-
Тогда последнее выражение для интеграла энергии упрощается и прини-
мает вид
-^2 (1 + 3 c°s2 ф) Ф2+g sin (р = (1 + 3 cos2 ф0) Фо + g sin фо-
Отсюда найдем угловую скорость стержня
। . । _ -1 /~ (1+3 cos2 фр) Zcpg + 12g (sin <р0 — sin ф)
™ г Z (1 +3 cos2 ф)
В момент падения на горизонтальную плоскость (ф = 0) угловая скорость
стержня будет
ф = у’|/Л (14-3 cos2 фо) ф2 + 12 япфо.
Любопытно отметить, что угловая скорость стержня не зависит от началь-
ной скорости его центра масс (если бы горизонтальная плоскость была не
абсолютно гладкой, то это было бы несправедливо).
В заключение этого параграфа сделаем одно замечание.
Интеграл энергии в форме (10.36) имеет место для систем,
движение которых определяется только консервативными силами.
Если, помимо консервативных сил, система подвержена действию
сил сопротивления, то происходит убывание полной механической
энергии; если же материальная система соединена с источником
энергии (например, двигателем), то полная механическая энергия
возрастает.
§ 10.7. Теорема об изменении кинетической энергии
относительного движения
Если движение материальной системы рассматривается в системе
координат Охуг, перемещающейся по данному закону относительно
инерциальной системы отсчета, то в правую часть уравнения энер-
гии (10.34) необходимо ввести работу переносных и кориолисовых
сил инерции, а в левую часть должна входить кинетическая энер-
§ 10.7] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ 249
гия относительного движения системы. Тогда вместо уравнения
(10.34) получим
п п
тГ — Тг0 = Ае + А1 + У, У Акс,
k=1 4=1
где Аке и Акс — работа переносных и кориолисовых сил инерции.
Но в соответствии с результатами § 6.4 работа кориолисовых сил
инерции равна нулю. Поэтому уравнение- энергии примет вид
п
Тг-Тго = Ае + А‘+ % Аке. (10.37)
• k = i
Если подвижные оси координат перемещаются поступательно
относительно инерциальной системы отсчета, то последнюю сумму
в (10.37) можно упростить. Действительно, в этом случае пере-
носные ускорения всех точек будут одинаковы и равны ускорению
начала подвижных осей О, т. е. wfee = w0. Имеем (для поступа-
тельно движущихся осей dp = dp)
У d'Ake = У Jfce-dpA = — У mkwke • dpk = — У mkw0-dpk.
k= i k=i k = i k=i
Так как ускорение w0 полюса О от индекса суммирования не
зависит, то его можно вынести за знак суммы:
У d Аке = — ( У, tnk dpk}' w0.
k=\ 4 = 1 '
Из формулы (7.2) следует 2 тк dpk = M dpc, где M — масса всей
системы, а рс — радиус-вектор ее центра масс в подвижной системе
координат. Поэтому
У, d'Ake = — Mwodpc-
k = ।
При переходе системы из начального положения в текущее
положение сумма работ переносных сил инерции будет равна
У Аке= У \d'Ake = (—Mwodpc) = X (—A4w0),
k=i A=i
где символом А (— Alwn) обозначена работа переносной силы инер-
ции центра масс, в предположении, что в нем сосредоточена масса
всей системы.
Уравнение (10.37) можно записать теперь в следующей форме:
Тг-Тг1)^Ае + А' + Д(— Mw0). (10.38)
250
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
[ГЛ. X
В этом равенстве кинетическая энергия и работа всех сил,
включая переносную силу инерции центра масс, вычисляются для
движения системы относительно подвижных осей Oxyz, переме-
щающихся поступательно относительно инерциальной системы
отсчета.
В дифференциальной форме уравнение (10.38) принимает вид
^ = № + №-A1w0.vaC, (10.39)
где vrC — относительная скорость центра масс.
Если w0 = const, т. е. ускорение полюса постоянно по модулю
и направлению, то сила инерции переносного ускорения центра
масс будет консервативна с потенциальной энергией
П*=—Mw0-pc. (10.40)
Если, кроме того, силы, приложенные к системе, тоже потен-
циальны, то будем иметь интеграл энергии
7\ + П + П*=/1, (10.41)
где П — потенциальная энергия всех внешних и внутренних сил,
приложенных к системе.
Задача 10.7. К потолку железнодорожного вагона подвешен физический
маятник (твердое тело, имеющее горизонтальную ось вращения, вокруг которой
оно колеблется под действием силы тяжести).
В начальный момент маятник удерживался в
положении, при котором прямая ОС была го-
ризонтальна (см. рис. 10.17; Ог— ось враще-
J7 ния, С—центр масс маятника). Затем маятник
был отпущен без начальной скорости. Опре-
делить угловую скорость маятника в момент
прохождения его центра масс через вертикаль,
если масса маятника равна М, его момент
инерции относительно оси вращения равен /,
а железнодорожный вагон движется прямоли-
нейно с постоянным ускорением w и ОС = 1.
Пусть ось г укреплена на движущемся '
вагоне (на рис. 10.17 вагон не показан). На-
правим подвижную ось у горизонтально в сто-
рону ускорения вагона w, а подвижную ось х
вертикально вниз. Мысленно будем считать вагон
неподвижным, введя одновременно переносную силу инерции центра масс маят-
ника—Mw. Кинетическая энергия Тг относительного движения маятника
вычисляется по формуле (10.8) как кинетическая энергия твердого тела, вра-
щающегося вокруг оси г;
гг=Х/ф2.
В начальный момент прямая ОС была горизонтальна, в конечный момент—,
вертикальна. Работа силы тяжести Mg на заданном перемещении будет равна Mgl,
а работа силы инерции + Mwl (знак «+», если в начальный момент центр
§ 10 7] ОТНОСИТЕЛЬНОЕ ДВИЖЕНИЕ 251
масс С находился на положительной части оси у, и знак «—» в противопо-
ложном случае). Поэтому (7,г0 = 0)
~ = ± Mwl\
отсюда найдем угловую скорость маятника в момент прохождения им вертикали
ф у 2Ml (g
Для рассматриваемой системы имеет место интеграл энергии (10.41). При-
мем положение маятника, при котором прямая ОС горизонтальна и ордината
точки С положительна, за нулевое. Тогда при перемещении маятника из дан-
ного положения в нулевое работа сил Afg и — Afw будет
Ag = Ug = — Mgl coscp, Лда = П* = — Mwl(\ — sin ср).
Следовательно, интеграл энергии (10.41) примет внд
X /ф2—Mgl coscp— Mwl (1 — sin ф)=й1,
или
X iqz—Mi (gcoscp — w sin <p)=/i,
где h^ht+Mwl.
ГЛАВА XI
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
§ 11.1. Понятие тела переменной массы
В теоретической механике, как правило, рассматривается дви-
жение материальных систем и твердых тел, масса которых пред-
полагается постоянной. Однако можно привести большое коли-
чество примеров, когда при движении тела его масса вследствие
присоединения или отделения от него материальных частиц зна-
чительно изменяется. Например, на активном участке движения
ракеты от нее отделяются продукты сгорания топлива, составляю-
щего значительную часть исходной массы заправленной ракеты
на старте. Решение задачи о движении ракеты как о движении
тела постоянной массы в этом случае будет неверным.
В связи с этим возникает проблема разработки методов реше-
ния задач на движение тел с переменной массой, т. е. задач
механики тела переменной массы *).
Перейдем теперь к определению понятия «тела переменной
массы».
Будем считать массу материальных точек, из которых состоит
тело, постоянной. Исходя из этого, под телом переменной массы
будем понимать тело, масса которого изменяется вследствие про-
цесса отделения от него или присоединения к нему материальных
точек.
Это значит, что точки, изменяющие массу тела, не возникают
и не исчезают, а лишь вводятся в рассмотрение или исключаются
из него.
Введенное определение тела переменной массы позволяем рас-
сматривать механику тела переменной массы как один из разде-
лов механики системы материальных точек, так как все исследо-
вания движения такого тела можно выполнить методами класси-
ческой механики.
В дальнейшем рассматривается только тот случай, когда
весьма малы как масса каждой отделяющейся или присоединяю-
*) В настоящее время вместо термина «тело переменной массы» часто поль-
зуются термином «тело переменного состава».
§ 11.2]
УРАВНЕНИЕ ДВИЖЕНИЯ ТОЧКИ ПЕРЕМЕННОЙ МАССЫ
253
щейся точки, так и время между последовательными отделениями
или присоединениями точек. Это предположение делает возмож-
ным такую предельную идеализацию процесса изменения массы, при
которой последняя может быть принята непрерывной и дифферен-
цируемой функцией времени.
Хотя при мгновенном изменении массы тела на величину
массы отделяющейся или присоединяющейся частицы скорость
тела меняется скачкообразно, величина этого изменения также
будет убывать с убыванием массы этой точки и в пределе ско-
рость тела можно считать также непрерывной и дифференциру-
емой функцией времени.
Пусть масса тела в начальный момент времени / = 0 равна т0.
Обозначим через т1 (t) массу отделившихся частиц к моменту
времени t и через т2 (/) — массу присоединившихся к телу час-
тиц к этому же моменту времени t. При непрерывном присоеди-
нении и отделении частиц от тела функции т1 (t) и тг (I) будут
возрастающими положительными и при / = 0 mj(0) = 0, m2(0) = 0.
Таким образом, массу тела в момент времени t можно опре-
делить по формуле
т = т0 — т1 (/)ф-т2(/). (11.1)
Если т1(/) = 0, то происходит только процесс присоединения
частиц; если т2 (0 = 0 — только процесс отделения.
§ 11.2. Уравнение движения точки переменной массы
Рассмотрим простейший случай, когда тело движется посту-
пательно и, следовательно, его можно принять за материальную
точку. Предположим также, что происходит процесс только отде-
ления.
Пусть масса тела в момент времени t равна т, а скорость
равна v. Количество движения тела в этот момент времени
равно
Q = mv. (И.2)
Так как рассматривается случай отделения частиц, то масса
тела будет уменьшаться. Следовательно, изменение массы за про-
межуток времени Д/ определится равенством
Дт = т (i ф- Д/) — т (t) <; 0.
Предположим, что к моменту времени отделившаяся
°т тела частица массы |Дт| приобрела скорость и'. Скорость же
тела переменной массы к моменту времени /ф-Д/ обозначим через
254
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
[ГЛ. XI
Количество движения тела и отделившейся частицы в момент
времени t-{-At будет
Q (/-}- А/) — (т — | Am {) (v±Av) + ! Ат | ц' =
= (т + Am) (v+Av) — Amu'. (11.3)
Согласно теореме об изменении количества движения имеем
]im Q(/ + AQ-Q(Q
ДГ-»0
где Fe — равнодействующая всех сил, приложенных к телу.
Перепишем это выражение, используя формулы (11.2) и (11.3):
1- Г Av Am . , , Am Av]
lim lm-rr—rr(u — v)H—гг- = F
д<_01 Az & Az J
Отсюда получаем
mw — (u — v) — F\
или
mw = Fe4-O, (П-4)
dv _ dm
где w = ^ — ускорение точки, Ф = ^-у1г, vlr = u — v— относитель-
ная скорость отделяющейся частицы, и —скорость отделяющейся
частицы в момент времени t.
Вектор
® = (11.5)
называется реактивной силой.
Уравнение (11.4) получено, независимо друг от друга, раз-
личными авторами. Обычно это уравнение называют уравнением
Мещерского, так как его работа *) оказала наибольшее влияние
на развитие механики тела переменной массы. Более подробно
уравнение Мещерского будет рассмотрено в § 11.5.
§ 11.3. Количество движения тела переменной массы
Рассмотрим общий случай и не будем считать тело перемен-
ной массы материальной точкой. Кроме того, будем считать, что
частицы не только отделяются, но и присоединяются к телу.
Переменная масса тела в момент времени t определяется
равенством (11.1).
*) Мещерский И. В, Динамика тела переменной массы.—С.-Петер-
бург, 1897.
§ 11.3] КОЛИЧЕСТВО ДВИЖЕНИЯ ТЕЛА ПЕРЕМЕННОЙ МАССЫ 255
Согласно формуле (8.2) количество движения любой системы
материальных точек постоянной массы, а следовательно, и твер-
дого тела вычисляется по формуле
Q = myc, (П-6)
где т — масса материальной системы, a vc —скорость центра масс
этой системы.
Рассмотрим теперь тело переменной массы. Благодаря про-
цессу присоединения и отделения частиц в теле происходит пере-
распределение масс и поэтому центр масс тела может не оста-
ваться в какой-либо фиксированной точке тела. Он будет совер-
шать сложное движение: будет двигаться со всем телом (переносное
движение) и будет перемещаться по отношению к телу (относи-
тельное движение). Так* например, по мере выгорания топлива
центр масс ракеты перемещается относительно ее корпуса.
Итак, абсолютную скорость центра масс можно представить
формулой
Vc = VeC + VrC, (11.7)
где veC — переносная скорость центра масс тела, т. е. скорость
той точки тела, с которой в данный момент t совпадает центр
масс, a vrC — скорость центра масс по отношению к телу, т. е.
по отношению к системе координат, жестко связанной с телом.
Рассмотрим наряду с телом переменной массы тело постоянной
массы и предположим, что в момент времени t массы точек, их
расположение и скорости для обоих тел одинаковы. Тогда коли-
чество движения определится равенством
Q = У mkvk,
k=i
где п — число точек, составляющих тело, mk — масса й-й точки,
a vA —ее скорость. Так как, по предположению, массы и скорости
точек обоих тел одинаковы, то количества движения этих тел
также будут равны.
Поэтому количество движения тела переменной массы будет
определяться формулой (8.2), но вместо скорости vc следует
поставить veC, так как для тела переменной массы это и есть
скорость той точки тела, с которой совпадает в данный момент
времени центр масс тела. Следовательно, количество движения
тела переменной массы будет равно
Q = mveC.
Эта формула, конечно, верна и для тела постоянной массы, так
как для этого случая vc = vec-
256
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
[ГЛ. XI
Если тело движется поступательно, то veC = v, где v —ско-
рость тела, и, следовательно, количество движения определится
формулой
Q = mv. (11.8)
§ 11.4. Теорема об изменении количества движения
тела переменной массы
Для системы материальных точек постоянной массы теорема
об изменении количества движения (см. формулу (8.5)) имеет вид
^ = Fe, (11.9)
где Qo — количество движения, Fe —главный вектор всех внешних
сил. Эту формулу можно записать в виде
litn Qo - Qo (О = Р (11.10)
Рассмотрим теперь тело переменной массы. Предположим,
что в процессе движения этого тела к нему присоединяются и
одновременно отделяются от него частицы. Одновременно с этим
телом рассмотрим систему постоянной массы, причем предположим,
что в момент времени t обе эти системы совпадают, т. е. массы
и скорости точек этих систем одинаковы.
Следовательно, количества движения тел переменной и посто-
янной масс в момент времени t будут равны
Q(0 = Qo(0. (П-11)
где Q (t) — количество движения тела переменной массы.
Пусть к моменту времени /-]-Д/ от тела отделятся частицы
с общей массой, равной Дтп и присоединятся частицы с общей
массой, равной Дт2. Тогда в момент времени t 4- Д/ масса тела
будет равна
т (I + Д/) = т (t) — \т14- Дт2- (11.12)
Если обозначить через QT (t 4- Д/) количество движения в момент
времени всех частиц, отделившихся за время Д/, а через
сиа+до — количество движенца в момент времени всех
частиц, присоединившихся за время Д/, то количество движения
системы постоянной массы в момент времени /4-Д^ будет равно
Qo (t 4- М) = Q (t 4- Д/) 4- Qj (/ 4- ДО - Q, (t 4- ДО. (11.13)
где Q (t 4- ДО — количество движения тела переменной массы
в момент времени /4-Д(.
Обозначим через и( скорость в момент времени /ф-Д^ центра
масс отделившихся частиц, а через щ — скорость в тот же момент
§ 114]
ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ
257
времени центра масс присоединившихся частиц; тогда на основа-
нии формулы (11-8), получим
Qj (t-\- &t) = AmjuJ, Q2 (t-\- kt) = Дт2и2.
Используя эти выражения, перепишем равенство (11.13) в виде
Qo (14- Д/) = Q (1 + ДО + Д/^uf — Дт2и'>.
Подставляя теперь это выражение в формулу (11.10) и учитывая
ртвенство (11.11), получим
lim Q (^ + Др ~ Q (0 + AwtU'; — Am2u' р
д/—*о л/
Д/
или
lim
Д/->0
откуда
Q(*+*p-Q(0=Fg_ lira lim
Д/->0 Д/-.0 д‘
dQ __ ре dm-t dm2
dt Г dt U1‘‘ dt °2’
(11.14)
где ut и u2 —скорости центров масс соответственно отделяющихся
и присоединяющихся частиц в момент времени t.
Соотношение (11.14) и представляет собой математическую запись
теоремы об изменении количества движения тела переменной
массы.
Для случая только одного отделения частиц тела
т = т0 — (t)
и, следовательно,
dm ______________________ dm± dm2_______«
IT dF’ ~dF'~'J‘
Тогда уравнение (11-14) примет вид
^ = Fe + fU1. (11.15)
Для случая только присоединения частиц
т = т0 4- т2 (/)
dm2 ___dm
dt dt ’
уравнение (11-14) будет
dQ
dt
। dm
= F + diU*
(11.16)
9 H. В. Бутенин и др.
258
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
[ГЛ. XI
Для случая равенства секундного расхода и секундного при-
роста масс
, ... п dm, dm„
-m1(0 + m2(/) = 0, =
и
t/Q Е1 I / \ /1 1 « -7\
~dt = Fe+“dT(U2~Ul)- (И.17)
В заключение этого параграфа отметим, что вывод теоремы
об изменении количества движения тела переменной массы нами
получен в предположении, что отделившиеся частицы сразу же
после отделения прекращают свое взаимодействие с точками тела
переменной массы,. а влияние присоединившихся частиц начи-
нается только с момента их присоединения к телу.
§ 11.5. Уравнение Мещерского
Пусть тело переменной массы движется поступательно, тогда
согласно формуле (11.8) имеем
(11.18)
Q=mv.
Дифференцируя это соотношение по времени, получим
dQ dm , dv
Ей = ’дт v + m Ш •
dt dt 1 dt
Так как согласно соотношению (11.1)
dm dm± dm2
~di = dt~ ' ~dt~'
a yi = dvldt, to
Подставляя это выражение в уравнение (11.14), будем
dm, . . . dm2 , .
mw = F -дг(и1-у)+тг<и*-у)-
Это уравнение получено И. В. Мещерским и носит его
тор
dm, , . . dm., , .
ф=-дг(и1-у) + дг^-у)
называется реактивной силой.
В дальнейшем будем рассматривать только случай
частиц, имеющий наибольший технический интерес.
иметь
(11.19)
имя. Век-
(11.20)
отделения
Для него
уравнение (11.19) сводится к виду
„е dm1 . .
mw = Fe--^-(u1-v).
§ 11.6]
ЗАДАЧА ЦИОЛКОВСКОГО
259
Так как vlr = u1 —v есть относительная скорость отделяющихся
частиц, а
dm, _ dm
dt dt '
то предыдущее уравнение движения можно записать следующим
образом:
mw = ре + ^У1, = Ре + ф, (Н.21)
где Ф определяется формулой (11.5). Так как при отделении
частиц dm/dt<_0, то реактивная сила Ф направлена в сторону,
противоположную направлению скорости vlr.
§ 11.6. Задача Циолковского
Рассмотрим движение ракеты, запущенной с поверхности Земли
вертикально вверх (рис. 11.1). Будем предполагать, что ракета
движется поступательно. Движение ракеты будем рассматривать
в системе координат с началом в точке пуска, ось х которой
направлена вертикально вверх. х
В проекции на ось х уравнение (11.21) будет
.. dm
mx — Fx — -^ vlr,
(11.22)
так как vlr направлена в сторону, противопо-
ложную положительному направлению оси х.
Здесь Fex представляет собой результирующую
силу земного притяжения и силу аэродинамиче-
ского сопротивления атмосферы. Реактивная сила
будет направлена в сторону положительного направления оси х,
dm , а
так как < 0.
dt
Как уже было сказано, при доказательстве теоремы об изме-
нении количества движения предполагалось, что отделившиеся
частицы между собой и телом не взаимодействуют. Но в действи-
тельности в отбрасываемой газовой струе частицы взаимодействуют
Друг с другом и с ракетой.
Кроме того, -на ракету действует сила атмосферного давления,
зависящая от высоты х над поверхностью Земли. Эта сила не
входит в состав силы аэродинамического сопротивления и не
зависит от скорости ракеты v.
Пусть s —площадь выходного сечения сопла, р — давление
в газовом потоке на срезе сопла, а р (х) — статическое атмосфер-
9*
260
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
[ГЛ. XI
ное давление. Тогда сила, обусловленная давлением газового
потока и статическим давлением атмосферы, будет
s[P~P (*)]•
Прибавляя эту силу к реактивной силе, получим тягу дви-
гателя
Рх = — + S [Р - Р Wk
При движении в пустоте р(х) = 0 и тяга будет
dm
Рх = — ~^ Vlr + sp.
Это соотношение записывают в виде
’ dm
P* = ~liiV‘
где
. sp . dm „
Ve = Vlr + J-, q =— -77 >0.
e Lr'q dt
Величина ve называется эффективной скоростью истечения
(ve>vK).
Таким образом, при решении задачи о движении ракеты нужно
вместо уравнения (11.22) взять следующее:
mx = Fx-d~ iv + s[P-P(x)L
Решение этого уравнения в общем виде представляет значитель-
ные трудности из-за сложности .закона изменения аэродинами-
ческого сопротивления, входящего в Fex, и находится за рамками
курса теоретической механики.
При отсутствии атмосферы это уравнение примет вид
mx = Fex-d-^ve, (11.23)
где Fsx представляет собой силу тяготения.
Если пренебречь сиЛой притяжения Земли и сопротивлением
атмосферы, то уравнение (11.23) упрощается:
dv dm
т-п = — -ту Ve-
dt dt e
Поставленную таким образом задачу впервые решил К. Э. Циол-
ковский.
Предположим, что масса ракеты m = m(t) является непрерыв-
ной функцией времени, а эффективная скорость истечения
постоянна (ve = const). Отметим, что т (0) = ти — стартовая масса
ракеты.
§ 11-6]
ЗАДАЧА ЦИОЛКОВСКОГО
261
Перепишем уравнение движения ракеты в виде
Интегрируя это уравнение, получим
v (/) = — ve In т + С,
где С — произвольная постоянная интегрирования.
По условию, при / = 0 и(0) = 0; тогда
О = — ve In пг0 + С
и, следователвно,
С = ve In т0.
Итак, скорость ракеты в момент времени t равна
= 1п^.
Эта формула называется формулой Циолковского.
Пусть к моменту времени t = tK произошло полное сгорание
топлива в ракете. Скорость ракеты в этот момент времени будет
и (/к) = ve In —,
где mK — т(tK) — масса ракеты без топлива.
Введем в рассмотрение число Циолковского
тк’
тогда формула для скорости ракеты в момент сгорания всего
топлива примет вид
v = ve In z. (11.24)
Эта формула также называется формулой Циолковского.
Из рассмотрения формулы (11.24) следует, что скорость ракеты
в момент, когда весь запас топлива будет израсходован, пропор-
циональна эффективной скорости истечения газов и натуральному
логарифму от числа Циолковского.
Формула Циолковского (11.24) указывает на два возможных
пути увеличения скорости ракеты к моменту сгорания топлива.
Первый путь —это увеличение эффективной скорости истечения
газов, второй путь — увеличение числа Циолковского.
В настоящее время для используемых в ракетах химических
топлив эффективная скорость истечения газов ve 2500 м/сек
и несколько выше. Получение химических топлив, позволяющих
получить более высокую эффективную скорость истечения газов,
связано с большими трудностями. Увеличение числа z также
представляет трудную техническую задачу.
262
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
, [ГЛ XI
Найдем^ каким должно быть г, чтобы ракета к моменту сго-
рания топлива при уе = 2400 м/сек получила первую космическую
скорость («« 8000 м/сек).
При рассмотрении этой задачи, запуская ракету с Земли,
нужно иметь в виду, что вследствие земного тяготения, сопро-
тивления атмосферы, затрат на осуществление программного дви-
жения ракеты фактическая скорость ракеты после сгорания топ-
лива будет меньше скорости, даваемой формулой (11.24). По
некоторым данным потери в скорости составляют 10—15%.
Поэтому определение числа г проведем, исходя из необходимости
получения скорости v = 9000 м/сек.
Согласно формуле (11.24) найдем
V
z~eVe= е3’75 42,5.
Это значит, что m0 = 42,5 тк, т. е. стартовая масса ракеты
должна быть в 42,5 раза больше массы ракеты без топлива. Иначе
говоря, вес топлива должен составлять примерно 98% от старто-
вого веса ракеты. Для современных ракет число Циолковского
значительно меньше 42,5.
Как следует из приведенного расчета, получение космических
скоростей с помощью одноступенчатой ракеты в настоящее время
вряд ли возможно. Для этих це-
лей используются многоступенча-
тые ракеты.
§ 11.7. Формула Циолковского
для многоступенчатой ракеты
На рис. 11.2 приведена при-
мерная схема многоступенчатой
ракеты.
Многоступенчатая ракета со-
стоит из нескольких ступеней и
полезного груза.
После израсходования топлива
в ступени она отделяется от ос-
тальной конструкции.
Введем понятие субракеты.
Под субракетой понимается сово-
купность работающей ступени, всех неработающих ступеней и
полезного груза, причем для данной субракеты все неработающие
ступени и полезный груз являются «полезным грузом», т. е.
каждая субракета рассчитывается как одноступенчатая ракета.
На рис. 11.2 указана нумерация ступеней и субракет.
§ П.7]
ФОРМУЛА ЦИОЛКОВСКОГО
263
Применяя формулу Циолковского (11.24) к каждой субракете,
получим;
после полной отработки первой ступени скорость второй суб-
ракеты
Пх = v'e' In гх,
где v'e’ — эффективная скорость истечения в первой ступени, г± —
число Циолковского для первой субракеты;
после отработки второй ступени скорость третьей субракеты
и2 = И1 + иё21 In г2 = v'e" In гг 4- nJ.21 In га,
где nJ.21 — эффективная скорость истечения во второй ступени,
г2 —число Циолковского для второй субракеты;
наконец, после отработки п-й ступени скорость полезного груза
v = v(el) In гх + v(e‘’ In г2 + .. v(en)\nzn, (11.25)
где v™ — эффективная скорость истечения из п-й ступени, гп—
число Циолковского для п-й субракеты.
Если приближенно считать, что для всех ступеней относи-
тельная скорость истечения одинакова:
п(1) = у(2) = — у(«) — 71
е е ' е е1
то согласно формуле (11.22) будем иметь
v = ve In (гхг2... г„) = ve In Z, (11.26)
где
Z = V2...z„. (11.27)
Для упрощения выкладок положим, что у всех субракет числа
Циолковского также одинаковы:
zx = г2 =... = гп,
тогда формула (11.26) примет вид
v = nvelnz. (11.28)
Отсюда видно, что конечная скорость полезного груза про-
порциональна числу ступеней (конечно, при условии, что и zi
одинаковы).
Найдем число г, которое должна иметь каждая ракета для
достижения полезным грузом скорости v = 9000 м/сек (ve =
= 2400 м/сек).
При п= 1 (одноступенчатая ракета)
9000
г = е2400^42Д
264 ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ [ГЛ. XI
при /1 = 2 (двухступенчатая ракета)
9000
г = е2-2400 ^6,48,
при п = 3 (трехступенчатая ракета)
9000
г = е3'2400 ^ 3,49.
Из этих данных видно, что при реальных числах Циолков-
ского космических скоростей можно достигнуть, применяя только
многоступенчатые ракеты.
§ 11.8. Задачи
Задача 11.1. Ракета движется в однородном поле сил тяжести вертикально
вверх с постоянным ускорением а> (см. рис. 11.1). Сопротивлением атмосферы
пренебрегаем. Эффективную скорость истечения газов ve считаем постоянной.
Определить: 1) закон изменения массы ракеты; 2) время Т, за которое масса
ракеты уменьшится вдвое. Определить также закон изменения массы при от-
сутствии поля тяготения.
В рассматриваемой задаче Fex =—mg (g—ускорение силы тяжести), по-
этому уравнение (11.23) имеет вид
dm
mw==~~dF v^~mS-
Разделяя в этом уравнении переменные, получим
4m = w + g dt
m ve
Интегрируя и принимая во внимание, что стартовая масса ракеты m(0) = m0,
будем иметь
1 1 w+g,
In m — In ma =---— t,
ve
откуда
a>+g }
v
m = m«e e .
Для момента времени T по условию задачи
_ 5L+A т
m0 v
~£=тое е
и, следовательно,
Еслв ракета движется вне поля тяготения, то g = 0 и
- — t
v„
т — т$
§ 11.8]
ЗАДАЧИ
265
Задача 11.2. Ракета движется вертикально вверх в однородном поле тя-
жести. Эффективная скорость истечения газов ve постоянна. Изменение массы
ракеты происходит по закону
т = tnae~al
(а и т0— постоянные величины).
К моменту времени = топливо сгорает. Определить, при каком значе-
нии а ракета достигает максимальной высоты подъема *).
Уравнение движения ракеты (11.23) для рассматриваемого случая имеет вид
тое~а1Х = — moe~atg + am^~atve,
или
*'=— g-\-ave = (k— l)g,
где
g
Интегрируя, получим
х=(й-1)^ + и0, (11.29)
где о0 —начальная скорость ракеты. Считая, что при /=О х=0, найдем
x==(k-\)^- + v(lt. (11.30)
Полученное выражение описывает движение ракеты при работающем двигателе.
Пусть масса ракеты после сгорания топлива равна тк; тогда момент вре-
мени сгорания tK найдется из условия
— аС
тк = тое к>
откуда
/K = lin/ZZ» = A,
а тк а
где |т = 1пг (г — число Циолковского).
Скорость ракеты в момент времени t = tK определится из формулы (11.29):
Xi = (k — \ ) gt & + v0= (k — 0 ~~ + ио-
К этому моменту времени высота подъема ракеты согласно уравнению (11.30)
будет равна
<r = (*-1)g+^-
Начиная с момента времени t = tK, ракета будет двигаться только под
действием силы притяжения Земли. Высота, на которую поднимется ракета
после момента времени / = /к, равна
JC? 1 Г,. 14 Iх , I2
= 2^= + Ч •
Таким образом, полная высота подъема ракеты будет
й = х1+л = (^1)^ + ^ + 1[(4-1)^ + ^.
*) Космодемьянский А. А. Экстремальные задачи для точки пере-
менной массы,—ДАН СССР, 1946, т, 53, № 1, с. 17—19,
266
ДИНАМИКА ТЕЛА ПЕРЕМЕННОЙ МАССЫ
[ГЛ XI
Найдем теперь максимальную высоту подъема, считая И функцией а.
Применяя обычный способ отыскания максимума функции, т. е. находя про-
изводную от И по а и приравнивая ее нулю, мы определим значение а, при
котором достигается максимальная высота подъема. Эта максимальная высота
равна
(УгЦ + ^о)2
Птах —------5----
2g
и достигается при а = оо, т. е. при мгновенном сгорании топлива. Мгновен-
ное сгорание топлива влечет за собой бесконечно большое ускорение ракеты
в начале движения, и, следовательно, полученное условие максимального подъ-
ема ракеты (а = со) практически невыполнимо и недопустимо.
При постепенном сгорании топлива ускорение ракеты будет конечным, но
при этом неизбежен проигрыш в достигаемой высоте. Коэффициент k = avelg
называется коэффициентом перегрузки (давление любого груза в ракете на
свою опору точно в k раз превосходит величину силы притяжения груза
к Земле) *).
Зададимся каким-либо фиксированным значением коэффициента пере-
грузки k. Тогда a = kg!ve. При этом значении а и при vo = O высота подъема
ракеты будет.
|л2и2
При Уо = О
Следовательно,
рМ
Wr . е
max = .
2g
W =//max —-г—~ .
К
Из этой формулы (формулы Космодемьянского) следует, что уменьшение
коэффициента перегрузки влечет за собой уменьшение максимальной высоты
подъема ракеты. При 6 = 4 она будет на 25% меньше, чем Дтах.
Задача 11.3. Ракета движется вертикально вверх с постоянной скоростью
(см. рис. 11.1)г Эффективная скорость истечения газов постоянна. Сила
притяжения к Земле обратно пропорциональна
до центра Земли. Сопротивлением атмосферы
изменения массы
Так как для рассматриваемой задачи
Fe - mSR2
х (R + *)3 ’
то уравнение (11.23) будет иметь вид
dm _ mgR2
1Г Ve ~ (R + x)2
По условию задачи скорость ракеты v0 постоянна, т. е.
dx
~dt
ракеты.
квадрату расстояния от
пренебречь. Определить
и! = 0,
= 0.
== v0~ const,
ракеты
закон
(11.31)
откуда
х — v^t+С •
*) Пусть груз, находящийся в ракете, имеет массу mt; тогда на основа-
нии принципа Даламбера имеем
— niig (k — 1) — nirg+R = 0,
где R — реакция, действующая на груз. Следовательно, R = kmxg.
§ 11.8]
ЗАДАЧИ
267
При / = 0 х=0, следовательно, С — 0 и
x—v^.
Подставляя это выражение в соотношение (11.31), получим
1 dm ______________________________________g/?2
т dt — ve (R + УоО2 ‘
Интегрирование дает
In т =
gR2 . . c.
vove (R + u(/)
Так как при t = 0 m(O) — mo, то
0,= In m0 —
vove
Подставляя это значение в предыдущее равенство, найдем после очевидных
преобразований закон изменения массы ракеты
gHt __
о„(« + ао0
т = тое ' 0 •
Задача 11.4. Ракета движется в поле земного тяготения вертикально вверх
так, что ее масса изменяется по закону m = mrf~at, где а и т0 — постоянные
величины. Эффективная скорость истечения газов постоянна. Начальная ско-
рость равна нулю (ио = О)- Пренебрегая сопротивлением атмосферы, определить
скорость ракеты как функцию х, где х—высота подъема ракеты над поверх-
ностью Земли (см. рис. 11.1).
По условию Ft = ~ уравнение движения ракеты (11.23) имеет вид
dv
т ~di ~ '
Так как m = moe~at, то после
dv
dt (R + x)2
Принимая во внимание, что dx=vdt, и умножая обе части полученного
уравнения на v dt. будем иметь
mgR- dm
" (Я + х)2 ~ ~dt~ Ve'
подстановки получим
ctD2
vdv=- (R+xy dx+ave dx-
Интегрируя уравнение
о
I v dv =
о
о о
получим
1
V2
отсюда найдем закон изменения скорости ракеты от высоты х ее подъема

или
1
,Я + х
2(o»e-g/?2)
V R(R + X) •
ДИНАМИКА ТВЕРДОГО ТЕЛА
глава хп
ГЕОМЕТРИЯ МАСС
§ 12.1. Введение
Динамика твердого тела является важным разделом теорети-
ческой механики, что объясняется прежде всего теми приложе-
ниями, которые она имеет в самых различных вопросах техники.
Так, например, конструирование и расчет станков, железнодорож-
ного и автомобильного транспорта, управление полетом, самолетов
и космических аппаратов, борьба с качкой судна, конструирова-
ние и расчет гироскопических приборов, сохраняющих заданную
ориентацию или автономно определяющих нужное направление
(гироскопические компасы, гировертикали), и т. п. основаны на
динамике твердого тела.
Движение тел существенным образом зависит от характера
распределения масс. В этом мы уже убедились на ряде примеров.
Так, спортсмен при прыжке в воду, группируясь (т. е. меняя
распределение масс), увеличивает свою угловую скорость (см.
пример на стр. 219), время установления угловой скорости ротора
электромотора зависит от момента инерции ротора (см. пример
на стр. 210), скорость вращения маховичка, которую необходимо
сообщить ему для прекращения вращательного движения косми-
ческого аппарата, зависит от соотношения моментов инерции (см.
пример на стр. 221—222) и т. д. Поэтому изучение динамики
твердого тела начинается, как правило, с вводной главы, посвя-
щенной геометрии масс. Из самого названия видно, что в этой
главе изучается не движение твердого тела, а только характер
распределения его массы.
§ 12.2. Основные определения
Как уже отмечалось, в теоретической механике считается, что
масса твердого тела распределена непрерывно (см стр. 171).
Возьмем в теле некоторую точку и выделим небольшой объем
Дц с массой Дт так, чтобы выбранная точка находилась внутри
§ 12 2]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
269
этого объема. Отношение
_ Дт
Vcp—
называется средней плотностью объема Ап тела, а предел этого
отношения
. v Дт
у= lim -т-
Др-»0 Ди
— плотностью тела в данной точке (предполагается, что при
Аи->0 выбранная точка остается все время внутри объема Ди)
Если тело неоднородно, то его плотность меняется от точки
к точке. Отнесем тело к системе координат Охуг. Тогда для не-
однородного тела плотность у будет функцией координат
у = у(х, у, г).
Масса неоднородного тела вычисляется по формуле
М = § у dv = $ jj (j у (х, у, г) dx dy dz.
Плотность однородного тела одинакова во всех его точках,
причем
(12.1)
М .
у = у = const,
где М — масса тела, а V — его объем.
В § 9.2 было дано определение момента инерции относительно
оси- моментом инерции материальной системы относительно оси
называется
точек системы
от точек до
распределении
в интеграл.
Возьмем в
dm = у dv и координатами х, у, г. Квад-
раты расстояний от этого элемента до
координатных осей х, у, г будут соот-
ветственно равны (рис. 12.1)
h2x = y2-\-z2, hl — z2-\-x2, hl = x2-\-y2.
сумма произведений масс
на квадраты расстояний
оси. При непрерывном
массы сумма переходит
теле элемент с массой
(12.2)
Следовательно, моменты инерции тела относительно коорди-
натных осей определяются равенствами
Ix = \(y2 + z2)dm, Iy = ^(z2+ х2) dm, 1г = ^(х2 + у2) dm. (12.3)
В этих формулах * под символом $ F (х, у, г) dm подразумевается
интеграл, распространенный по массе всего тела. Такое условное
обозначение вводится для простоты записи. Конечно, при непо-
270
ГЕОМЕТРИЯ МАСС
[ГЛ ХИ
средственном вычислении интеграла нужно перейти к тройным
интегралам по объему, причем дифференциал массы dm = ydv —
— ydxdydz. В дальнейшем будет показано, что в некоторых слу-
чаях тройной интеграл можно заменить двойным или даже обыч-
ным определенным интегралом.
Одновременно с осевыми моментами инерции введем полярный
момент 10, определив его как сумму произведений масс точек
материальной системы на квадраты их расстояний до данного по-
люса О. Если за полюс взять начало координат О, то квадрат
расстояния от элемента dm до точки О будет равен г2=х2+(/2+?2
и, следовательно, полярный момент инерции твердого тела можно
вычислить по формуле
/0 = $ (*2 + У2 + z2) dm. (12.4)
По самому определению полярный момент инерции зависит только
от выбора полюса и не зависит от направления координат-
ных осей.
Сравнивая равенства (12.3) и (12.4), легко установить формулу
/л + ^ + Л = 2/0. (12.5)
Оть етим два свойства моментов инерции относительно трех взаимно пер-
пендикулярных осей.
1. Момент инерции относительно любой из осей всегда меньше суммы
моментов инерции относительно двух других осей, но больше их разности,
Действительно, например,
1х + 1у~ Iz — 2^ & dm>0,
/х—/у—/2 = —2 j х2 dm < 0;
отсюда
hdx + Iy. Iz>lx-ly. (12.6)
Этому свойству можно дать простое геометрическое толкование: из трех
отрезков, длины которых пропорциональны моментам инерции относительно
трех взаимно перпендикулярных осей, всегда можно построить треугольник.
2. Сумма моментов инерции относительно трех взаимно перпендикулярных
осей не зависит от направления этих осей.
Это свойство вытекает из равенства (12.5).
Из первого свойства следует, что моменты инерции тела относительно трех
взаимно перпендикулярных осей нельзя задать произвольно — они должны
удовлетворять соотноштн1ям (12.6).
Напомним, что радиусом инерции тела относительно данной
оси называется расстояние р от оси до точки, в которой нужно
сосредоточить массу М всего тела, чтобы момент инерции точки
относительно данной оси равнялся моменту инерции / тела отно-
сительно той же оси:
/ = Л4р2.
(12.7)
§ 12 2]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
271
Осевые и полярные моменты инерции всегда положительны,
так как они представляют сумму положительных чисел. В нуль
осевой момент инерции может обратиться только в одном частном
случае, когда все материальные точки системы расположены
на оси, относительно которой вычисляется момент инерции.
Для полной характеристики распределения массы тела отно-
сительно данной системы координат, кроме осевых моментов инер-
ции Ix, Iу и 1г, вводят еще центробежные моменты инерции. Для
одной материальной точки центробежным моментом инерции
1Х1) называется произведение ее координат х и у на массу точки
т, т. е. величина хут (аналогично определяются центробежные
моменты инерции 1уг и Iгх). Центробежными моментами инерции
твердого тела называются величины, определенные равенствами
lxy — ^xy dm, I yz — ^yz dm, IzX = \zxdm. (12.8)
Как видно из (12.8), центробежные моменты инерции симмет-
ричны относительно своих индексов-
Iху ~ Iух> Iyz = Izyi Izx = 1xz-
Центробежные моменты нельзя задавать произвольно. Действительно,
из неравенства
j (*— УУ1, dm^O
следует
j (№ + у2) dm 2 j ху dm,
или, пользуясь формулами (12.3) и (12.8),
Ixy *2“ Iz' Iyz "2" Ц' Гх
(два других неравенства получаются аналогично).
Центробежные моменты инерции зависят не только от направ-
ления координатных осей, но и от выбора начала координат.
В связи с этим часто говорят о центробежных моментах инерции
в данной точке, понимая под этим, что начало координат сов-
падает с данной точкой.
В отличие от осевых, центробежные моменты инерции могут
иметь любой знак и обращаться в нуль. Главной осью инерции
тела называется ось, для которой оба центробежных момента
инерции, содержащие индекс этой оси, равны нулю. Например,
если /хг = I^ = 0, то ось г —главная ось инерции тела. Главной
центральной осью инерции называется главная ось инерции, про-
ходящая через центр масс тела.
Отметим два частных случая, когда можно сразу определить
характер оси.
ЧП
ГЕОМЕТРИЯ МАСС
[ГЛ XII
1. Если тело имеет плоскость материальной симметрии*),
то для всех ее точек ось, перпендикулярная к плоскости сим-
метрии, является главной осью инерции.
2. Если тело имеет ось материальной симметрии, то эта ось
является главной центральной осью инерции и называется осью
динамической симметрии.
Докажем для примера второе свойство (первое доказывается
аналогично). Возьмем на оси материальной симметрии произволь-
ную точку О и построим систему координат с началом в этой
точке, направив ось г по оси симметрии, а оси х и у перпенди-
кулярно к оси г произвольным образом. В силу материальной
симметрии относительно оси z каждой точке А тела с коорди-
натами (хА, уА, гА) и массой dm
будет соответствовать другая точка В
такой же массы и с координатами
(— хА, — уА, гА) (рис. 12.2). При
составлении интегральных сумм для
центробежных моментов инерции Iхг
И /уг будем иметь
xz dm + (— х) z dm - О,
yz dm + (— у) z dm = 0.
Следовательно,
/« = 0, /9г = 0,
т. е. ось г —главная центральная ось инерции (она будет цент-
ральной, так как центр масс тела находится на оси симметрии).
Осевые и центробежные моменты инерции часто обозначаются
первыми буквами латинского алфавита:
/Х = Д, Iy = B, IZ = C,
Iyz = D, IZX = E, lxy = F. (12.9)
Матрица, составленная из осевых Ix, Iy, Iz и взятых с обрат-
ным знаком центробежных моментов инерции — Ixy, — Iyz, — 1гх,
называется тензором инерции в данной точке **):
(О Оу ОЛ
-lyx ly -lyz\ (12.10)
Ох Оу О /
*) Под материальной симметрией понимается не только геометрическая
симметрия, но и симметричное распределение плотности.
**) Для того чтобы матрица была тензором, необходимо, чтобы ее элементы
(в данном случае моменты инерции) удовлетворяли некоторым условиям инва-
риантности относительно преобразования поворота осей координат Рассмот-
рение этого вопроса выходит за рамки данного курса. Заметим только, что
моменты инерции удовлетворяют этим условиям.
§ 12 3]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ МОМЕНТОВ ИНЕРЦИИ
273
В силу симметрии центробежных моментов инерции этрт тен-
зор имеет шесть составляющих. Тензор инерции характеризует
распределение масс тела относительно данной точки.
Размерность всех моментов инерции (осевых, полярных и
центробежных) в международной системе СИ равна кг м2, а в тех-
нической -кГ-м- сек2.
§ 12.3. Примеры вычисления
моментов инерции
Приведем несколько примеров
вычисление моментов инерции.
1. Моменты инерции однородного пря-
моугольного параллелепипеда. Вычислим
моменты инерции относительно осей Сх,
Су, Сг, проведенных через центр масс
параллельно ребрам; масса параллелепипеда
Воспользуемся первой формулой (12.3):
на
Рис 12 3
М, длины ребер 2а, 26, 2с (рис. 12.3).
lx=\ (У2+ г2) dm.
Г, , J . . . ММ
Заменим дифференциал массы dm на у dv = y dx dy dz, где у = р- = , и
перейдем к тройному интегралу
1Х— j j j ?(!/2 + г2) dx dy dz =
а Ъ
Этот интеграл можно представить следующим образом.
М
8abc
или, интегрируя,
М Г 63 с31 М
^ = 8^(2а2с2-з+2а262т] = -3 <62+с2>-
Таким образом, моменты инерции однородного прямоугольного парал-
лелепипеда относительно центральных осей определяются равенствами (Iу и 1г
получены круговой перестановкой букв)
М * М М
G=4-(b2 + c2), = (<? + &), /^-„(а2 + П (12 11)
О О О ete
Из этих формул следует, что момент инерции прямоугольного параллеле-
пипеда относительно оси, проходящей через его центр масс перпендикулярно
к некоторой грани, равен одной трети массы тела, умноженной на квадрат
половины гипотенузы рассматриваемой грани.
Центробежные моменты инерции равны нулю, так как координатные плос-
кости являются плоскостями материальной симметрии.
Очень часТо выбором соответствующего элемента можно сразу свести вычис-
ление момента инерции к обычному интегралу.
Проиллюстрируем это на следующих примерах.
274
ГЕОМЕТРИЯ МАСС
[ГЛ XII
Тело
Момент инерции
Отрезок прямой
1Х=^ГМ^ !Х'=^ГМ1*
Площадь прямоугольника
1Х=~МЬ\ 1у = ~Ма*,
О о
/«=4-м +ь2)
Площадь эллипса.
Прямоугольный
параллелепипед
1Х~±-МЬ*, /у = ~Ма\
/сг = ~М(а* + Ь°)
/х=4гм(Ь2+с2)> 1у = ~М(а^ + с2),
о <5
/г = 4~М (аз -р Ь2}
О
Прямоугольная пирамида
а—*-<«’+»>
§ 12 3]
ПРИМЕРЫ ВЫЧИСЛЕНИЯ МОМЕНТОВ ИНЕРЦИИ
275
Тело
Момент инерции
Прямой, круглый цилинйр

Прямой круглый конус
О / 1 \ о
^=^=20 M(~THi + R2), h = ~^MR*
276
ГЕОМЕТРИЯ МАСС
[ГЛ XIГ
2. Момент инерции однородного цилиндра относительно его оси. Пусть
радиус цилиндра равен /?, а его масса М. Построим цилиндрическую трубку
радиуса р (р < R) и толщиной dp (рис. 12.4). За элемент массы dm возьмем
массу этой трубки. Такой выбор элемента массы объясняется тем, что рас-
стояния от всех его точек до оси цилиндра одина-
ковы и равны р.
Обьем трубки с точностью до членов высшего
порядка равен
dv = 2npH dp,
Рис. 12.4.
а ее масса
dm = V dv = у 2лрН dp.
В этих равенствах Н — высота цилиндра, а у —его
плотность.
Объем всего цилиндра V = nR-H. Следова-
тельно,
М М
V “ nRW

Умножим элемент массы на квадрат его расстоя-
ния до оси цилиндра р2. Тогда
R
f 2М С
/= \ р-dm=-R3 j р3 dp.
О
Вычислив интеграл, найдем момент инерции одно-
родного круглого цилиндра относительно его оси:
(12.12)
3. Момент инерции однородного шара относительно оси, проходящей через
его центр. Построим прямоугольную систему координат, начало которой сов-
падает с центром шара О. В силу симметрии все три осевых момента инерции,
1Х, 1у и 1г, равны между собой:
lx = ly=l^l.
где / — их общее значение.
Из формулы (12.5) найдем
3/ = 2/0;
отсюда
9
/ = у/0. (12.13)
Таким образом, задача свелась к вычислению полярного момента инерции
шара относительно его центра.
За элемент массы возьмем массу шарового слоя радиусом р и толщиной
dp. Выбор такого элемента массы объясняется тем, что расстояния от всех
точек шарового слоя до его центра О равны р.
Объем слоя du = 4np2dp, а его масса dm-—ydv, где
_Л1 _ М
§ 12 4] МОМЕНТЫ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПАРАЛЛЕЛЬНЫХ ОСЕЙ 277
Здесь М—масса шара, у — его плотность, R— радиус. Полярный момент инер-
ции шарового слоя относительно его центра О равен р2 dm, следовательно»
R *
/0= j pMm= J р2 А21з4ЛрМр = 3^ J p4dp,
0 0
или
• Q I
/0 = yAH?2.
Зная полярный момент, найдем "из равенства (12.13) момент инерции I
однородного шара относительно оси, проходящей через его центр:
/=-| МРг.
о
На стр. 274 н 275 приведена таблица моментов инерции простейших одно-
родных тел.
12.4. Моменты инерции относительно параллельных осей
(теорема Гюйгенса — Штейнера)
Существует простая связь между моментами инерции тела
относительно параллельных осей, одна из которых проходит через
центр масс. Эта связь устанавливается теоремой Гюйгенса —Штей-
нера: момент инерции 1 тела отно-
сительно некоторой оси равен сумме
момента инерции 1С тела относи-
тельно оси, проходящей через центр
масс параллельно данной, и произве-
дения массы тела на квадрат рас-
стояния между осями.
Действительно, пусть оси / и II
параллельны, причем ось / проходит
через центр масс С тела. Возьмем
начало координат в точке С, сов-
местим ось г с осью /, а ось у на-
правим так, чтобы она пересекала
ось II (рис. 12.5). Выделим в теле
произвольный элемент массой dm и опустим на него перпенди-
куляры на оси I и //, обозначив их соответственно через р и рх.
Согласно определению моментов инерции будем иметь
1с = $Р2 dm,
I = $ pi dm.
По теореме косинусов найдем
• pi = р2 + d2 — 2pd cos а,
или, учитывая, чго pcosa = z/, где у —ордината элемента/
pi =p2-j-d2 — 2dy.
278
ГЕОМЕТРИЯ МАСС
[ГЛ XII
Рис. 12.6.
Подставим это выражение для pf в формулу, определяющую мо-
мент инерции /:
/ = (р2 + d2 —• 2yd) dm р2 dm -)-d2^ dm— 2d^ у dm.
Первый интеграл равен Ic, второй —массе тела М, а третий—
нулю (согласно формуле (7.3) у dm = Мус = 0, так как начало
координат совпадает с центром масс). Следовательно,
I = Ic + Md2, (12.14)
что доказывает теорему.
Формула (12.14) широко используется в практиче-
ских расчетах при определении моментов инерции тел
относительно осей, не проходящих через центр масс.
Кроме того, применяя метод разбиения, с помощью
этой формулы можно определить осевые моменты инер-
ции тел сложной формы. Поясним это примером.
Задача 12.1. Маятник, изображенный на рис. 12.6, состоит
из тонкого однородного стержня длиной I и массой т1 и круг-
лого однородного диска радиусом R и массой тг. Определить
момент инерции /г маятника относительно оси его вращения Ог (ось Ог на-
правлена перпендикулярно к плоскости рисунка).
Маятник состоит из двух тел: стержня и диска. Поэтому
где и —моменты инерции относительно оси соответствующих тел.
Момент инерции стержня /°т = mtP, а момент инерции диска найдем
по формуле (12.14):
/« = /£+
где /® = m2R2 — момент инерции диска относительно оси, проходящей через
его центр масс параллельно осн Ог, a d = l-\-R — расстояние от центра диска
до оси Ог. Имеем
/?=lm2J? + ffi!((+R)>.
Пользуясь выражениями для моментов инерции стержня и диска, найдем
момент инерции маятника относительно оси Ог:
Д =у тУ2 + т2 [1 Ra-H/4- R)2].
Установим формулы для центробежных моментов инерции,
аналогичные формуле (12.14). Для этого построим две системы
координат со взаимно параллельными сторонами: Ох1у1г1 и Схуг,
где С —центр масс тела (рис. 12.7). Обозначим через а, b и с
§ 12 5] МОМЕНТ ИНЕРЦИИ ОТНОСИТЕЛЬНО ПРОИЗВОЛЬНОЙ ОСИ 279
координаты точки С в системе Ох^^. Тогда формулы перехода
от одной системы координат к другой системе будут
х± = а + г, У1 = Ь-\-у, Z1=c-\-z.
По определению центробежных моментов инерции имеем
/Х1Л = $ х±у± dm = (а ф- х) (Ь ф-у) dm,
илг, раскрывая скобки, группируя
члены и вынося постоянные мно-
жители за знак интеграла,
1Х,У, = ab\dm ф- а у dm +
- b ^х dm ф- ху dm.
Первый интеграл равен массе тела
М, два средних интеграла равны нулю
(так как они соответственно равны Рис. 12.7.
Мус и Мхс), а последний интеграл
равен 1ху. Таким образом, имеем (две другие формулы получены
аналогично)
/Mctb ф- /Ху, /y,z, = Ьс ф- Iуг, I— ас1 хг. (12.15)
§ 12.5. Момент инерции относительно произвольной оси,
проходящей через данную точку
Возьмем в теле точку О и примем ее за начало системы коор-
динат Oxyz. Проведем через точку О произвольную прямую OL,
составляющую с осями х, у, z
/L углы а, Р и у соответственно.
/ Требуется определить момент
р/ инерции / тела относительно оси
/\Р OL, считая, что известны его
1 X осевые \х, Iу, Iz и центробеж-
ные IХу, Iyz и 1гх моменты инер-
------------ции.
У Для решения задачи возьмем
“'х в теле произвольную точку М
Рис- 12-8- массой dm и с координатами х,
у, г и опустим из нее перпенди-
куляр NP на прямую OL (рис. 12.8). Момент инерции тела отно-
сительно оси OL определяется равенством
1 = р2 dm,
где р —длина отрезка NP.
280
ГЕОМЕТРИЯ МАСС
(ГЛ XII
Из треугольника ONP найдем
р = rsin а = 11охг
где 10 —единичный вектор оси L.
Имеем
10 X Г = cos а cos 3
к
cos у
• i
X у Z
= (г cos р — у cos у)
+ (х cos у — г cos а) j 4- (у cos а — х cos Р) к.
Отсюда
р2 = 110 х г |2 = (г cos р — у cos у)2 4-
4- (х cos y — z cos а)2 -ф (у cos а — х cos р)2,
или, раскрывая скобки и группируя члены,
Р2 = (^2 _|_ г2) cos2 а _|_ ^2 _|_ д-2) cqs2 р _|_ (%2 _|_y2j COS2 у _
— 2 ху cos a cos р — 2yz cos р cos у — 2zx cos у cos ct.
Подставим это значение для р2 в выражение для момента
инерции /, разобьем интеграл на сумму интегралов и вынесем
в каждом из них cos a, cos р и cos у за знаки интегралов. Тогда
получим
1 = cos2 а (у2 4- z2) dm 4- cos2 р (г2 4- х2) dm 4-
4- cos2 у (х2 4- У2) dm — 2 cos а cos р \ху dm —
— 2 cos р cos у yz dm — 2 cos у cos a § zx dm.
С помощью соотношений (12.3) и (12.8) найдем
I = lx cos2 а 4-1у cos2p 4- /г cos2 у — 2/ху cos а cos р —
— 21 уг cos р cos у — 21 гх cos у cos а. (12.16)
Формула (12.16) является искомой. Пользуясь ею, можно
найти момент инерции / относительно оси OL, зная осевые и
центробежные моменты инерции.
Если координатные оси являются главными относительно сво-
его начала, то центробежные моменты будут равны нулю и фор-
мула (12.16) примет более простой вид:
/ = Ix cos2 а 4- 1и cos2 Р 4- /г cos2 у. (12.17)
Задача 12.2. Дана однородная прямоугольная пластинка с массой М и
«сторонами 2а и 26. Требуется определить момент инерции / относительно диаго-
нали.
Построим систему координат Схуг с началом в центре масс пластинки.
«Ось х направим параллельно стороне 2а, ось {/ — параллельно стороне 26,
§ 12 6]
ЭЛЛИПСОИД ИНЕРЦИИ
281
а ось г — перпендикулярно к плоскости пластинки (на рис 12 9 ось г не пока-
зана— она направлена на читателя).
Координатные оси являются главными центральными осями инерции, так
как тело симметрично относительно этих
осей Имеем (рис. 12 9)
а „ Ь
cos а = , cos В =
}/a2_|_ft2> |/а2_^2-
у = 90°, cos у = 0.
Пользуясь таблицей моментов инерции,
найдем
/„ = 4-44*2, / * Ма?,
6 * о
Рис. 12 9
/л = у Л1(а2 + *2).
Внося эти значения в формулу (12.17), полу^йм момент инерции одно-
родной пластинки относительно ее диагонали:
1
3
/ = 2-41*2
Ц2
Я2-]- *2
41а2
*2
Я2-]- *2 ’
или, после упрощения,
/ = -| 41
Я2*2
ц2-|-*2-
§ 12.6. Эллипсоид инерции
Возьмем в теле точку О и проведем через нее ось OL. Пусть
момент инерции тела относительно этой оси равен I. При изме-
нении направления оси' OL будет изменяться момент инерции 1.
Простое и вместе с тем очень нагляд-
ное представление об изменении мо-
мента инерции в зависимости от из-
менения положения оси, проходящей
через данную точку О, дает следую-
щее геометрическое построение.
Отложим на прямой OL отрезок
ОМ (рис. 12-. 10), длину которого в
соответствующем масштабе определим
равенством
OM = r=-U. (12.18)
Построим систему координат Ох1у1г1 (на рис. 12.10 оси хъ
уг и г, не показаны). Обозначим координаты точки М в этой
координатной системе через хх, ух и гР Так как точка М при-
надлежит прямой OL, то будем иметь
cos а = у = хх ]Л7, cos р = у = ух ]Л7, cos у = у- = гх У7,
где а, р и у —углы, определяющие направление оси OL.
282
ГЕОМЕТРИЯ МАСС
[ГЛ ХИ
Внесем эти выражения для направляющих косинусов прямой
0L в формулу (12.16) и сократим полученное выражение на Г.
IXlxl + Iyiy'i + /г121 - 2/X1,/1x1z/1 - 21 - 2/21Х,г1х1 = 1. (12.19)
Этому уравнению второго порядка удовлетворяют координаты
точки М на прямой 0L. Следовательно, оно определяет поверх-
ность, которую описывает точка М при изменении направления
прямой 0L.
Расстояние от начала координат О до точки М, принадлежа-
щей поверхности (12.19), определяется равенством (12.18). Так
как момент инерции I тела относительно любой оси всегда поло-
жителен и в нуль не обращается, то все точки поверхности (12.19)
находятся на конечном расстоянии от начала координат (случай
бесконечно тонкого стержня из рассмотрения временно исключа-
ется). Из всех поверхностей второго порядка этому условию удов-
летворяет только эллипсоид. Поэтому построенная указанным обра-
зом поверхность называется эллипсоидом инерции.
Из аналитической геометрии известно, что уравнение эллип-
соида может быть упрощено, если за координатные оси взять три
взаимно перпендикулярных направления главных диаметров по-
верхности. В таких осях уравнение эллипсоида не содержит членов
с произведениями координат и имеет вид
М2 + /# + Л?2=1- . (12.20)
На рис. 12.10 показаны эллипсоид инерции, построенный для
точки О, и координатная система Охуг, в которой уравнение
эллипсоида инерции имеет вид (12.20).
Из формы уравнения видно, что в этих осях все центробеж-
ные моменты равны нулю. Следовательно, для каждой точки
существуют три главные оси инерции.
Сравнивая уравнение эллипсоида в канонической форме
х2
а2
с уравнением эллипсоида
ным осям инерции, найдем
1
а = —_
Vix ’
Из этих равенств следует, что большему главному моменту инер-
ции соответствует меньшая ось эллипсоида инерции.
Если среди моментов инерции тела относительно главных осей
в данной точке нет равных, то эллипсоид инерции называется
с2
инерции (12.20), отнесенного к глав-
b = —L-. с =
§ 12.7] СВОЙСТВА ГЛАВНЫХ ОСЕЙ ИНЕРЦИИ 283
трехосным. При двух равных моментах инерции (например,
7* = /^) эллипсоид инерции превращается в эллипсоид вращения.
Если же 1Х = 1У = 1г, то эллипсоид инерции вырождается в сферу;
соответствующие точки называются шаровыми.
Так как между моментами инерции 7 v, 1У и Iг должны суще-
ствовать соотношения (12.6):
I х~Р 1и^> 1 г. 1 у + 1/л, +
то не всякий эллипсоид может служить эллипсоидом инерции.
Для бесконечного тонкого стержня эллипсоид инерции вырожда-
ется в бесконечный круговой цилиндр.
В заключение этого параграфа отметим, что для эллипсоида
вращения любая ось, лежащая в экваториальной плоскости (плос-
кости равных полуосей эллипсоида) и проходящая через данную
точку, является главной осью инерции. Это следует из того, что
за главный диаметр эллипсоида вращения можно взять любой
диаметр, лежащий в экваториальной плоскости. Этот же резуль-
тат можно получить и из формулы (12.17).
§ 12.7. Свойства главных осей инерции
В предыдущем параграфе было показано, что в каждой точке
можно построить главные оси инерции, т. е. оси, относительно
которых центробежные моменты инерции равны нулю.
Пусть некоторая ось, например ось z, является главной для
точки О. Поставим следующий вопрос. Существуют ли на этой
оси точки, для которых ось Oz также будет главной осью инер-'
ции? Для решения этой задачи построим
в точке О главные оси инерции Oxyz.
По определению главных осей будем
иметь
Ixy = \ху dm = 0, 1уг = \yz dm = 0,
lzx — \^x dm = 0. (12.22)
Покажем прежде всего, что при по-
вороте вокруг оси г осей х и у ось г
останется главной осью инерции. Дей-
ствительно, построим систему коорди-
нат Ox1z/1z1, в которой ось Zj совпадает
с осью z, а оси хх и ух составляют с осями х и у угол а соот-
ветственно (рис. 12.11). Возьмем в теле произвольную точку.
Между ее координатами х, у, z и xlt ух, гх существует очевидная
связь:
%! = х cos а -)-у sin а, уг= — х sin а 4- у cos а, гх — г.
284
ГЕОМЕТРИЯ МАСС
[ГЛ. XII
Вычислим центробежный момент инерции IXtZi. Имеем
JX1Zi = х1г1 dm = J (х cos а + у sin а) z dm —
— cos a^xz dm 4- sin a yz dm.
Так как оси x, у и z—главные оси инерции и для них спра-
ведливы равенства (12.22), то /X1Z1 = 0. Аналогично показывается,
что 7</1Z1=0- Таким образом, при пово-
роте вокруг главной оси инерции z двух
других осей х и у ось г остается главной
осью инерции.
Перейдем теперь к рассмотрению ос-
новного вопроса. Если данная ось, на-
пример ось г, является главной осью
инерции для точки О, то существует ли
на этой оси другая точка, для которой
ось z является главной осью инерции?
Для ответа на этот вопрос выберем на
оси г точку 0г и построим систему ко-
ординат O1x1z/1z1, в которой ось Zj совпа-
дает с осью г, а оси х1 и уг параллельны осям х и у соответ-
ственно (рис. 12-12). Формулы перехода имеют вид
Xi = х, У1 = у, zY = z- h,
где h — 00r.
Имеем
I x,z, = -Vi dm = ^x(z — h) dm = J xz dm — h § x dm,
ly,Zl = § yxZi dm=^ у (z — h.) dm= \ yz dm — у dm.
или, учитывая равенства (12.22) и (7.3),
7x1Z1 = — Mhxc, l4lZl = —Mhyc,
(12.23)
где M — масса тела, a xc и yc — координаты центра инерции тела
в системе Охуг.
Для того чтобы ось z (zj была главной осью инерции для
точки Ог, необходимо и достаточно, чтобы оба центробежных мо-
мента инерции Ix,z, и Iy,z, равнялись нулю. Но согласно форму-
лам (12.23) это возможно только при хс = 0 и ус = ®, т. е. если
центр масс тела находится на оси г и, следовательно, ось г яв-
ляется главной центральной осью инерции. Таким образом, глав-
ная центральная ось инерции является главной центральной
осью инерции для всех своих точек, а нецентральная главная
ось инерции является главной осью инерции только для одной
своей точки.
§ 12 8]
ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
285
§ 12.8. Вычисление моментов инерции
относительно произвольных осей
При вычислении моментов инерции обычно стремятся восполь-
зоваться таблицами моментов инерции и теоремой Гюйгенса —
Штейнера. Однако очень часто ось, относительно которой необ-
ходимо определить момент инерции, не параллельна ни одной из
главных центральных осей инерции и не проходит через центр
масс. В этих случаях наиболее
рационально комбинировать фор-
мулу (12.17) с теоремой Гюйген-
са — Штейнера и данными таблиц.
Пусть для тела известны глав-
ные центральные моменты инер-
ции 1Х, 1у и 1г. Предположим да-
лее, что дана прямая LL', отно-
сительно которой требуется вы-
числить момент инерции I тела.
Проведем через центр масс тела
прямую //', параллельную LL'.
Так как прямая LL' задана, то
Рис. 12.13.
должны быть известны углы а,
Р, у между этой прямой (или, что то же самое, прямой 1Г) и
главными осями инерции х, у и z (рис. 12.13). Вычислим по фор-
муле (12.17) момент инерции Д тела относительно оси //':
= lx cos2 а + 1У cos2 р ф- 1г cos2 у. (12.24)
Тогда по теореме Гюйгенса— Штейнера момент инерции отно-
сительно оси LL' будет равен
I^ + Md*, (12.25)
где М — масса тела, a d — расстояние между осями LL' и W.
Углы а, р и у, а также расстояние d необходимо определить
из условия задания прямой LL'. Конечно, не представляет труда
найти эти величины, если заданы уравнения прямой LL', но
обычно их значительно проще определить из условий задачи.
Задача 12.3. Требуется определить момент инерции / прямого кругового
конуса относительно образующей SB (рис. 12.14); радиус основания конуса
равен R, высота равна Н.
Построим систему координат Cxyz. Центр масс С конуса находится на его
высоте OS, причем ОС = -^-OS = i Н. Ось z направим по оси конуса, ось у —
параллельно основанию так, чтобы она пересекла образующую SB, ось х—пер-
пендикулярно к плоскости yz. Координатные плоскости yz и xz являются
плоскостями симметрии, поэтому оси х, у и z—главные центральные оси инер-
286
ГЕОМЕТРИЯ МАСС
[ГЛ XII
ции конуса. Построим прямую sb, параллельную образующей SB; углы между
Прямой sb и осями х, у, г соответственно равны; а = 90°, р = 90° + (р, у = <р,
Z
Рис. 12.14.
где tp — угол полураствора конуса. Внося эти зна-
чения углов а, р и у в формулу (12.24), получим
/1 = Iу sin2 q> +1z cos- tp.
По таблице моментов инерции найдем
3/1 \ 3
;* = 20M(4-H2 + n- ^ = T0MR2-
Из рис. 12.14 определяем
R Н
Sin (р = -7-— , COS (В = ------ -,
VH2 + R2 ^H2 + R2
Подставляя эти выражения в формулу для /у,
получим
- / Д] R2 (.£. //2 | 02 \
1-20 + \ 4 П +R )
Расстояние d от центра масс С конуса до образующей найдем из тре-
угольника CES:
Я р
d = CS sin ср = —Я-—.
4 ^H2 + R2
Теперь с помощью формулы (12.25) легко находим момент инерции I конуса
относительно его образующей;
•“ 3 R2
§ 12.9. Вычисление тензора инерции
При решении различных задач динамики, в частности, при определении
динамических реакций опор твердого тела, вращающегося вокруг неподвижной
оси, необходимо знать не только осевые,
но и центробежные моменты инерции
относительно вполне определенных ко-
ординатных осей; короче говоря, необ-
ходимо знать тензор инерции / в про-
извольно выбранной координатной си-
стеме (см. формулу (12.10)). Конечно,
при вычислении составляющих тензора
инерции можно пользоваться основны-
ми формулами (12.3) н (12-8). Однако
в тех случаях, когда известны моменты
инерции тела относительно главных цен-
тральных осей, задача может быть суще-
ственна упрощена.
Пусть тензор инерции / тела тре-
буется определить для прямоугольной
системы координат Охуг. Будем считать, что нам известно положение центр;
масс С тела, т. е. известны координаты хс, ус, гс в системе Охуг, направле-
ния главных центральных осей инерции х', у', z' и соответствующие моменты
инерции /х,, 1у,, /2, — см. рис. 12-15 (в отличие от ранее применявшихся обо-
значений, главные центральные оси обозначены штрихами). -
§ 12 9]
ВЫЧИСЛЕНИЕ ТЕНЗОРА ИНЕРЦИИ
287
Построим вспомогательную систему координат Cx"y"z\ оси которой парал-
лельны соответствующим осям системы Oxyz. Тогда направления главных
центральных осей Сх'у'г' будут определяться таблицей направляющих коси-
нусов:
X’ у' 2’
X, х" «11 «12 «13
У’ у” «21 «22 «23
г, z" «31 «32 «33
02.26)
В этой таблице осу—косинусы углов между соответствующими осями; так,
например, oc32=cos(z, z/') = cos(z", у').
Моменты инерции Iх, Iу и Iz относительно осей х, у и г можно вычислить
по формуле (12.25). По формуле (12.24) имеем
/1Л. = ОС^ Ix, -J- ОС^/у, -J- 0С^/г,.
Квадрат расстояния между осями х и х” равен, очевидно, расстоянию от
точки С до оси х, т. е. y£-f-z£. Поэтому согласно формуле (12.25) будем иметь
(две другие формулы получаются аналогично)
!х= М (Ус +гс) + а111х' + + а131г"
'у = М (гС + 4) + ^х' + + 4з7л'>
= м (х2с + у2с) + a.-3iIx, + + a23Iz,.
(12.27)
Перейдем к вычислению центробежных моментов инерции тела относи-
тельно осей х, у, г. Рассмотрим произвольную точку N тела. Пусть ее коор-
динаты в системе Сх'у'г' будут х', у' и г', а в системе Охуг — х, у, г. Этй
координаты связаны формулами преобразования
х = хс + апх' + «12У' + ос18г',
у = ус + а21х'+а22у' + а23г',
г = гс + а31Х'+а32^+а33г‘-
Так как оси х', у', г' являются главными центральными осями инерции
тела, то все центробежные моменты инерции относительно этих осей и все
статические моменты равны нулю:
= ? x'z/'dm = 0, /= f у'г' dm — Q, I_,„, = fz'x' dtn = 0,
^x'dm = Q, ^y'dm = Q, ^z'dtn — G. (12.28)
По определению центробежных моментов инерции имеем
lxy = \xydm.
288
ГЕОМЕТРИЯ МАСС
[ГЛ XII
Подставим сюда значения х и у из формул преобразования, раскроем
скобки и сгруппируем члены:
!ху = хсУс 5 A'!+(Vc + “nM 5 х' dm +
+ (а22хс + а!гУс) 5 У' dm + (Vc + ai3f-'c) dm +
H-OC11<Z21 J Х'* dm + «12^22 j У'2 ^ + ana23 j Z/2 +
4“ (^11^22 “b ^12^21) J X'y' dm 'i“
+ (осцОСгз + ^13^21) J x dm + (^12^23 + ^13^22) J y'z' dm,
или, учитывая равенства (12.28),
/Ху = МХсУс + а11а21 J dm + ai2a22 У’" dm + ai3a23 j Z'2 dm-
Так как оси х и у взаимно перпендикулярны, то
°Ч 1а21 + а12а22 + а13а23 = 0;
отсюда
а13а23 =--- (а11а21 + а12а2г)'
Подставим это выражение в последнее равенство для I ху.
/Ху = Л1хсУс + а1Л1 J dm + ai2a22 5 У'2 dm-(aiia3l + a!2a22) 5 Лт’
или, группируя члены,
,ху = МхсУс + а-ца21 У U'2-z'2) dm + a12a225 (у'2-г'2) dm.
Добавляя н вычитая в первом интеграле у'2, а во втором х'2, будем иметь
1ху = МхсУс + апа21 (Х'г+У'!} dm — ^ (г'2 + У'2) dm] +
+ «12«22 (у'2 + х'2) dm — j (z'2-i-x'2) dm].
Пользуясь выражениями (12.3) для осевых моментов инерции, найдем (две
другие формулы получены аналогичным методом)
1ХУ = МхсУс + аиа21 U2- - М+«12«22 (/г< - 1у,).
'у. = МУсгС + a2ia31 ( ‘г’ - Ч + a22a32 ('г - 1 У') ’
1гх = мгсхс + ana31 (/г, - /х,) + a12«32 (Z2, -
(12.29)
Формулы (12.27) и (12.29) дают решение поставленной задачи об определе-
нии тензора инерции / в произвольной системе координат Охуг.
§ 12,10. Задачи на вычисление моментов инерции
Задача об определении тензора инерции сводится к определению осевых
и центробежных моментов инерции. Если нам известен тензор инерции для
главных центральных осей инерции, то его составляющие для произвольных
осей определяются формулами (12.27) и (12.29). Однако нередко направления
главных центральных осей инерции нам не известны. В этих случаях прихо-
дится прибегать к основным формулам (12.3) и (12.8).
Задача 12.4. Однородный диск D радиусом г и массой М насажен на вал,
установленный в подшипниках А и В (рис. 12.16). При сборке были допущены
§ 12.Ю]
ЗАДАЧИ НА ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
289
погрешности, в результате которых ось вала
в точке О, не совпадающей с центром С диска;
пендикулярна к плоскости диска и составляет с
момент инерции диска относительно оси вра-
щения АВ и его центробежные моменты инер-
ции 1хг и Iуг (положение осей Ох и Оу будет
указано в дальнейшем).
Пусть прямая ОЕ представляет проекцию
оси вращения АВ на плоскость диска. Опустим
из центра С диска на прямую ОЕ перпенди-
куляр и примем его за ось Су'; ось Сх' по-
строим в плоскости диска перпендикулярно
к оси Су'; ось Сг’ перпендикулярна к плос-
кости диска. Очевидно, что оси Сх', Су' и
Сг' — главные центральные оси инерции дис-
ка. Через точку С проведем ось Сг", парал-
лельную оси вращения г, ось Су" совместим
пересекает плоскость диска
кроме того, ось вала ие пер-
ней угол 90° — а. Определить
с осью Су', а ось Сх" проведем перпендику-
лярно к осям Су" и Сг”. При таком построении координатные оси г, г”, х'
и х" будут лежать в одной плоскости, причем уюл между осями х’ и х"
равен а. Оси Ох и Оу параллельны осям Сх" и Су".
Таблица направляющих косинусов имеет вид
х' y’ z'
%* х" cos a 0 —sin a
У’ у" 0 1 0
Z, zff sin a 0 cos a
Обозначим координаты точки О в осях Сх'у'г', связанных с диском, через
е, 6, 0 (см. рис. 12.16). Тогда координаты центра С диска в системе Охуг будут
хс = —ecosa, Ус = —zc = —esina.
Из таблицы моментов инерции найдем (§ 12.3)
/х- = /м- = 4'л1г2> lz. = ^Mr\
л у 4 г 2
Воспользуемся далее третьей формулой (12.27):
1г=М (х2с + Ус) + «з/х' + “за7// + азз7г''
В нашем случае согласно таблице направляющих косинусов a3i= sin а,
«32 = 0, a33 = cosa. Пользуясь соответствующими выражениями, получим
1г — М (е2 cos2 a + б2) +Mr2 sin2a-|—Mr2 cos2 а,
или, группируя члены,
/л = Л1 |^62 + ^е2 + у r2j cos2a4-i г2 sin2aj, (12.30)
10 Н. В. Бугеннн и др.
290
ГЕОМЕТРИЯ МАСС
[ГЛ XII
Теперь с помощью формул (12.29) найдем после очевидных преобразований
центробежные моменты
= Me2 sin 2а4- Mr2 sin 2а, /уг = Л4бе sin а. (12.31)
При правильной сборке будем иметь е = 6 = 0, а = 0. Следовательно,
1г= у Mr2, /хг = 1уг = 0, что очевидно.
Задача 12.5. Вращающаяся часть подъемного крана состоит из стрелы KF
длиной L и весом G, противовеса Г
D весом Q и груза Е весом Р. Стрела состав-
ляет с вертикальной осью вращения угол а.
Определить момент инерции 1г крана отно-
сительно оси вращения z и центробежные
моменты, считая противовес D и груз Е
точечными массами, а стрелу — однородной
тонкой балкой. Оси координат и геометри-
ческие размеры показаны на рис. 12.17;
оси х и х' перпендикулярны к плоскости
рисунка.
Система состоит из трех тел: стрелы KF,
противовеса D и груза Е. Поэтому
Для точечных масс имеем
= — L2 sin2 а.
z g
/? = — d2,
г g
Момент инерции IFF стрелы KF относительно оси вращения крана вычислим
по формуле (12.17):
/^=/^соз2(хСг) + /^соз2([/', z) + /£Fcos2(z', г).
В нашем случае (х^?г) = 90э и cos(x', z) = 0, /£F = 0 (по условию задачи
стрела KF представляет собой тонкую балку), cos(z', z) = sina и I^,F —
= -}-—L2, Следовательно, момент инерции /г всего крана относительно оси
3 g
вращения г будет
/г==^-б12 + у sin2a(j- + Pj. (12.32)
Центробежные моменты инерции 1 ху и 1хг равны нулю, так как вся си-
стема находится в плоскости уг. Учитывая, что система состоит из трех тел,
будем иметь
yz ‘yz i‘yz^‘yz'
Для точечных масс D и Е
= —— d/i
уг g
е __
уг
Р_
g
L sin a (h— I + L cos a).
§ 12.10] ЗАДАЧИ НА ВЫЧИСЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ 29]
Центробежный момент инерции стрелы KF найдем путем непосредст-
Q
венного интегрирования. Для этого выделим элемент dy' с массой dm = —:- dy',
gL
Координаты этого элемента —
y = z/'sina, г = у'cosa-]-/i,
где у' — расстояние вдоль стрелы от точки К до элемента dy'. Имеем
L
iKF С j & С /и ' ' • j ! GL . / h L \
Цг =J Vzdm~gL. \ (h+y cosa) У sma dV — — smaly + ycosa).
о
Для всей системы будем иметь
LsinaTGL | h ! . GL . „,\
Iуг = —-— cos a + P (L cos a — I) j -f- — PL sin a + -g- sin a — Qdj.
Если центр масс лежит на оси вращения, то
PL sin а Ц- sin a — Qd = 0
и выражение для центробежного момента упрощается:
, L sin a TGL , n '
Iуг =--------- cos a + P (L cos a — I)
S о
(12.33)
Задача 12.6. Определить тензор инерции однородной тонкой пластинки,
имеющей форму прямоугольного треугольника, для осей координат, связан-
ных с его катетами; длины катетов равны а и Ь
(рис. 12.18).
Так как плоскость пластинки совпадает с
плоскостью ху, то для всех точек г = 0; формулы''
(12.3) и (12.8) принимают вид
Ix = ^y2 dm, ly = ^x2 dm, —
lXy=^xydm, / jf£ = O, Iyz = ®*
Пусть у — поверхностная плотность пластинки,
Тогда ее масса М будет равна
М =— yab.
В качестве элемента пластинки возьмем прямоугольник со сторонами dx
и dy, его масса dm = y dx dy.
Уравнение гипотенузы можно записать как уравнение прямой линии
в отрезках, отсекаемых на осях:
а Ь
Отсюда найдем
Ь ,
У=^(а-х),
10«
292
ГЕОМЕТРИЯ МАСС
[ГЛ XII
Пусть х будет внешней переменной интегрирования, а у—внутренней.
Тогда пределы интегрирования по х будут 0 и а, а пределы интегрирования
по у суть Ои (а—х). Имеем
а
О
(а — х)3 dx
yb3
За3
yb3 (а — х)4
За» 4
Так как y = 2M/(ab), то
1Х = ~МЬ3,
fy=~Ma2, lg=~M(a*+bZ) (12.34)
1у получено надлежащей заменой букв).
Перейдем к вычислению центробежного момента инерции
b ь
— (а—х) — (а-х)
а а а а ' f
1ху=^ *У dm = y dx § xydy=-¥-$xy2 I dx =
0 0 0 0
a a
==^2 x(a“"x)2^x==2o2 У (a2x — 2ax2 + x3) dx=
о о
a
yb2 / „ x2 2 _ x4\ v
=h(a3 2--з“3 + т =й°262'
(
Подставляя значение у, найдем
М
1ху = -^аЬ, (12,35)
Тензор инерции имеет такой вид:
/ м .. м и
I 6 ь 12 аЬ
/ м а м
\2аЬ Та
о о
о
о
ъ («2+^
ГЛАВА XIII
динамика простейших движений твердого тела
§ 13.1. Основные задачи динамики твердого тела
В статике нами были рассмотрены условия равновесия систем
сил, приложенных к абсолютно твердому телу, и условия, при
которых твердое тело находится в покое. Задание движения твер-
дого тела и определение скоростей и ускорений точек твердого
тела было рассмотрено в кинематике. При изучении динамики
твердого тела встают более сложные задачи. Эти задачи делятся
на две основные группы. К одной группе относятся задачи,
в которых по заданному движению твердого тела требуется опре-
делить систему сил, под действием которых происходит это дви-
жение. К другой группе относятся задачи, в которых по задан-
ным силам, действующим на твердое тело, требуется при опреде-
ленных начальных условиях найти закон движения тела, а для
несвободного тела найти также реакции связей.
Свободное твердое тело имеет шесть степеней свободы, следо-
вательно, для определения положения в пространстве требуется
шесть независимых между собой
параметров. В качестве таких
параметров чаще всего выби-
рают координаты центра масс
твердого тела и углы Эйлера
или какую-либо другую систему
углов, наиболее удобных в рас-
сматриваемой конкретной задаче.
Пусть твердое тело движет-
ся по отношению к неподвиж-
ной (инерциальной) системе ко-
ординат O1x1y1z1 (рис. 13.1).
Предположим, что система ко-
ординат Cx2y2z2, имеющая на-
чало в центре масс тела, движется поступательно, а система
координат Схуг жестко связана с твердым телом.
Очевидно, что координаты центра масс (ххс, Ую 2ic) и углы
Эйлера 9, чр, <р, которые составляет система координатных осей
Рис. 13.1.
294 ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. ХИГ
Схуг с осями системы Сх2у2г2, полностью определяют положение
твердого тела.
Для того чтобы решать сформулированные задачи динамики
твердого тела, следует найти уравнения, связывающие эти пара-
метры с силами, действующими на твердое тело. Этих уравнений
должно быть шесть, так как число независимых параметров равно'
шести.
Для получения этих уравнений воспользуемся теоремой о дви-
жении центра масс (§ 8.3) и теоремой об изменении момента
количеств движения в относительном движении по отношению
к системе координат, движущейся поступательно и имеющей
начало в центре масс твердого тела (§ 9.7).
Согласно теореме о движении центра масс:
Alwc = Fe
имеем
Ш1С = ГХ1,
Wic = ^>
Mz1C = F*„
(13-1)
где хгс, УгС' г1С — координаты центра масс в неподвижной системе
отсчета Ox1y1zl, a Fl,, Feyt, /’tI —проекции главного вектора всех
внешних сил на .те же оси.
Используя теперь теорему об изменении момента количеств
движения в относительном движении (§ 9.7):
dKc
Т = Мс’ (13.2)
аналогично можно получить три соотношения, связывающие углы
Эйлера с моментами сил относительно координатных осей. Вывод
этих соотношений будет приведен в главе XIV.
Эти соотношения и уравнения (13.1) и дают возможность ре-
шать сформулированные выше задачи динамики твердого тела.
§ 13.2, Количество движения, момент количеств
движения и кинетическая энергия твердого тела
Для составления дифференциальных уравнений движения твер-
дого тела при различных случаях его движения нам придется,
как уже говорилось, пользоваться общими теоремами динамики
системы. Поэтому в этом параграфе приводятся выражения для
количества движения, момента количеств движения и кинетиче-
ской энергии твердого тела для различных случаев его движения.
§ 13 2] КОЛИЧЕСТВО ДВИЖЕНИЯ. МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ
295
Количество движения твердого тела выражается в соответствии
с формулой (8.2) следующим равенством:
Q = Mvc, (13.3)
где М — масса тела, vc —скорость центра масс.
Если твердое тело имеет одну неподвижную точку, то ско-
рость его центра масс определяется формулой
vc = о х гс,
где ю — угловая скорость, а гс — радиус-вектор центра масс, про-
веденный из неподвижной точки тела.
Проекции вектора количества движения на оси координат,
имеющих начало в неподвижной точке тела, найдем из соотно-
шения
Q = М (<й X Гс) = М
Ох
ХС
j
Оу
Ус
к
ог
гс
i
где ых, му, —проекции угловой скорости, хс, ус, гс — коорди-
наты центра масс, i, j, к —единичные векторы координатных
осей. Проекции вектора количества движения будут равны
QX = M (шугс — а>гус),
Qy = M (агхс — и>хгс),
QS = M (ахус - <£>ухс).
(13.4)
При вращении твердого тела вокруг неподвижной оси вектор
его угловой скорости направлен по оси вращения. Если теперь
ввести систему координат с началом в какой-либо точке оси вра-
щения, а ось г совместить с осью вращения, то вектор угловой
скорости представится в виде
м = ыгк = фк,
где ср-?угол поворота тела.
Формулы (13.4) в этом случае будут иметь вид
Qx = — Мус®, Q.y = Mxcq, Qz = 0. (13.5)
Момент количеств движения системы относительно начала
координат определяется формулой (9.1):
К= У, г4хтл,
fc = i
где rft —радиус-вектор k-й точки системы, и vh — ее масса и
скорость.
296
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ ХИГ
Проекции момента количеств движения на координатные оси
имеют следующий вид (9.2):
п
Кх = У ^к (Ук^кг 2к®кд)>
k = i
п
Ку = У, mk(zkvkx —xkvks),
k = t
п
Кг “ У^ ttlh (ХуОуу Ук^кх)'
(13.6)
Если твердое тело имеет одну неподвижную точку, то скорость
его любой точки находится по формуле
v = (й X г,
где ю — угловая скорость.
Выражения для проекций скорости v имеют вид
vx — a>yZ— агу,
иу = соре — Сйл2,
= Сйх1/— СЙ^Х, .
(13.7)
где х, у, z —координаты рассматриваемой точки.
Подставляя эти формулы в первое равенство (13.6) и переходя
для твердого тела от суммы к интегралу, получим
Кх = 5 [У (ыхУ — аух) — z (шлх — сйх?)] dm =
= $ [“ж (у2 + г2) — ауху — ыгхг] dm.
Так как сйх, ау и а>г не зависят от переменных интегрирования,
то
Кх = 5 (У2 + ?2) dm — <£>y^ ху dm — az^ хг dm.
В этом равенстве 1Х — $ (у2 ф- z2) dm — момент инерции твердого
тела относительно оси х, Ixy = ^xydm и Ixz = J xz dm — центробеж-
ные моменты инерции. Проделав аналогичные выкладки с выра-
жениями для Ку и Kz, получим
КХ ~ Х^Х Iху^у 1XZ^Zi
Ку = 7 ху®х + 7 у<йу 7 уг(£>г,
Кг — 1хг^х 7уг<йу ф* 7г(йг.
(13.8)
Если оси координат, имеющие начало в неподвижной точке О
тела, будут главными осями инерции тела, то lxy = lxl=x lyg = Q
§ 13 2] КОЛИЧЕСТВО ДВИЖЕНИЯ, МОМЕНТ КОЛИЧЕСТВ ДВИЖЕНИЯ
297
и формулы (13.8) примут вид
Кх—I Ку— I у®У' Кг— К^г‘ (13.9)
Формулы (13.9) определяют проекции момента количеств дви-
жения абсолютно твердого тела, имеющего одну неподвиж-
ную точку, на оси координат, жестко связанные с телом. Из
формул (13.8) и (13.9) видно, что в общем случае проекции вектора
<» и проекции вектора К не пропорциональны между собой, сле-
довательно, направления векторов К и ю не совпадают.
При движении тела вокруг неподвижной оси при условии,
что ось г направлена по оси вращения тела, имеем
Кх= 1 хг®г — ЛггФ,
Ку— 1 уг^г= 1 угФ,
Кг — I г^г = I лФ •
(13.10)
Перейдем теперь к нахождению кинетической энергии абсо-
лютно твердого тела, имеющего одну неподвижную точку. Кине-
тическая энергия твердого тела определяется формулой (10.6):
Т = у J и2 dm,
или (так как v v = и2)
Г = у j* v -v dm.
Подставляя в эту формулу выражение для скорости точки твер-
дого тела v = <oxr, получим
Г = у j v-(<axr)dm.
Вспоминая свойства скалярно-векторного произведения
v • (ю X г) = w (г X v),
будем иметь
Т = f <й • (г х v) dm = ~ ю • Г (г X v) dm,
но так как K = $(rxv)dm есть момент количеств движения, то

(13.11)
298 ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА (ГЛ. ХИГ
Используя формулы (13.8), перепишем выражение (13.11}
в виде *)
Т = -g- (<&ХКХ + <вг/Сг) =
= У ~ — 21 уг<£>у<£>г). (13.12}
Если оси координат х, у и г совпадают с главными осями
инерции, ТО 1ху= 1хг = 1уг = ^ И
7, = y(/xoJ + 7^4-7^). (13.13).
При вращении тела вокруг неподвижной оси,' например оси z,
имеем
®x = ®y = 0
и, следовательно,
Т = ~1г^=^1г^. (13.14}
Примечание. Из формулы (13.12) следует, что
-- I х^х ^хуау Ixz(,)z- Kxt I
Ixy^x + I уыу 1уг(лг — Ку> ( (13.15}
дТ г , . , 1Z
=--- ‘xz^x — 1угыу + 1г<»г = Кг, j
т. е. частная производная от кинетической энергии твердого тела,,
имеющего неподвижную точку, по проекции угловой скорости
на какую-либо ось, равна моменту количеств движения относи-
тельно этой оси.
§ 13.3. Поступательное движение твердого тела
Рассмотрим сначала решение первой задачи динамики. Пусть
тело движется поступательно и координаты центра масс тела
являются известными функциями времени. Это значит, что отно-
сительно поступательно движущейся системы координат Cx2y2zt
тело находится в покое. Следовательно, угловая скорость и мо-
*) Формулу (13.12) можно получить и другим путем. Представив выраже-
ние для кинетической энергии в виде
7’ = 4 j (vx + vl + vl) dm
и подставляя сюда выражения для vx, vy и уг из (13.7), получим формулу
(13.12).
<§ 13.4]
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВРАЩЕНИЯ
299
мент количеств движения тела относительно центра масс равны
нулю и в соответствии с (13.2)
М£ = 0.
Таким образом, для осуществления поступательного движения
необходимо, чтобы главный момент всех внешних сил относительно
центра масс был равен нулю.
Отметим, что условие Мс = 0 не является достаточным для
поступательного движения тела, так как при этом тело может
совершать движение относительно центра масс. Характер этого
движения будет рассмотрен подробно в главе XIV.
Легко показать (мы не будем останавливаться на этом), что
если главный момент всех внешних сил относительно центра
масс и начальная угловая скорость тела равны нулю, то тело
будет двигаться поступательно (необходимое и достаточное усло-
вие поступательного движения).
Так как координаты центра масс (х1С, ylC, г1С) являются
известными функциями времени, то, вычисляя вторые производ-
ные (х1С, у1С, г1С) и используя соотношения (13.1), получим про-
екции главного вектора всех внешних сил (F£,, F^, Fezj).
При решении второй задачи динамики, если заданы FeXl, Feyi
и Fz,, соотношения (13.1) будут представлять собой уже диффе-
ренциальные уравнения движения, и решение их при определен-
ных начальных условиях определит движение центра масс.
Если заранее известно, что тело движется поступательно, то
на уравнения (13.1) можно смотреть как на дифференциальные
уравнения поступательного движения твердого тела.
§ 13.4. Дифференциальное уравнение вращения твердого тела
вокруг неподвижной оси
и уравнения для определения реакций подшипников
Твердое тело, вращающееся вокруг неподвижной оси, является
примером несвободного твердого тела. Следовательно, при изуче-
нии его движения необходимо применить принцип освобожда»
емости, т. е. действие связей (в данном случае подшипников)
следует заменить реакциями этих связей и рассматривать твер-
дое тело как свободное.
Введем две системы координат с началом в какой-либо точке О
оси вращения (рис. 13.2): неподвижную OxjZ/jZj, где ось гх совпа-
дает с осью вращения тела, и подвижную Охуг, жестко связан-
ную с твердым телом (ось z совпадает с осью вращения тела).
Положение тела будем определять углом ср между плоскостями
х10г1 и хОг,
300
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. ХИТ
Отметим, что направления реакций подшипников заранее не
известны. Пусть ХА, УА, ZA — проекции реакции Ra; Хв, У в,
Zb —проекции реакции RB на оси подвижной системы координат
Oxyz\ тогда можно записать
Ra = -Ха* + Ya] + 2дк, Rb — 4--f-Z^k, (13.16)
подшипни-
где i, j, к —единичные векторы осей Oxyz.
Для нахождения закона движения тела и реакций
ков воспользуемся теоремами об изменении количества движения
и момента количеств движения си-
стемы:
(13.17)
^ = Fc+Ra + Rb,
<2К
^ = Mc0 + M0(R4) + M0(Rb).
(13.18)
Чтобы получить уравнения для
определения движения и реакций
подшипников, необходимо векторные
уравнения (13.17) и (13.18) записать
в проекциях на оси координат.
Так как координаты центра масс
хс, ус и центробежные моменты инер-
ции 1хг и 1уг в подвижной системе
координат будут постоянными, то
(13.17) и (13.18) целесообразнее проектиро-
векторные уравнения
вать на оси подвижной системы координат.
Итак, определяем векторы Q и Ко в подвижной системе коор-
динат:
Q — Од 4- Qy] 4~ Qzk,
Ко = Ад + Ху j + Агк.
(13.19)
(13.20)
Из курса кинематики известно, что если какой-либо вектор а
задан в подвижной системе координат, то абсолютная производ-
ная от этого вектора
da___da
dt ~ dt
(13.21)
где <o — угловая скорость подвижной системы координат; ==
•=-^-i-|--^-j+-^-k — относительная производная.
5 13.4] . ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ ВРАЩЕНИЯ 301
Поскольку векторы Q и Ко определены в подвижной системе
координат, то согласно формуле (13.21) имеем
£Q_dQ
dt ~dt
dK0 dK0
dt — dt
<BXK0,
(13.22)
где о —угловая скорость твердого тела (система Охуг с ним
жестко связана), причем
dQ dQx . . dQy , dQz
dK0 dKx . dKy . dKz,
~dT ~ ~dt~ 1 + ~dF J + dt k
(13.23)
Уравнения (13.17) и (13.18) с учетом (13.22) принимают вид
т w '7 Ко = Mo + мо (Ra) + Mq (Rb) •
(13.24)
Пусть координаты подшипников А и В соответственно будут
0, 0, гА и 0, 0, гв (на рис. 13.2 приведен случай, когда гА =—а,
гв — Ь); тогда
Гд = гдк, Гв = г£к.
Моменты реакций подшипников определяются по формулам
M0(Rд) = ГдХ Rд =
1
о
*А
j k i j
0 г* , Mo (Rb) = Гв X Rb = 0 0
Ya ZA XB yB
к
гв
ZB

откуда
Мх (Кд) = — ЗдУд,
Mx№B) = -zBYB,
My(RA) = zAXA, A/HRa) = 0, |
Му (Rb) = zBXB, M2(Rb) = 0. J
(13.25)
Учитывая, что ю==фк, а также соотношения (13.19), (13.20)
и (13.25), запишем уравнения (13.17) и (13.18) в проекциях на оси
302 ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. XIII
подвижной системы координат:
^-ф^ = ^ + Хл + Хй,
+ 4>Qy = + А + УBi
0 = F‘ + Za + Zb,
^-фКу==Мех-гдУА~гР1Ув, '
фМл = Му гдХд 4- ZbXb,
ме
dt lvlz'
В соответствии с (13.5) и (13.10) получим
— мУсФ — Мхсф2 = Fx 4- ХА 4- Хп,
Мхс§ — Мусу2 = F у-\- У д 4* У в,
0 = К4-2д4-2в; (13.26)
— Ixzty + I угф2 = Мх — гАУ а — гвУ в,
— ~ IхгФ? — My-^-ZAXA ~У ?вХв,
7г<р = Мег.
Последнее уравнение системы (13.26) реакций не содержит и
было уже получено раньше (§ 9.5). Оно позволяет по заданному
закону вращения тела <р (t) определить момент главного вектора
внешних сил Мег относительно оси г или по заданному моменту
Мег при заданных начальных условиях определить закон движе-
ния тела.
Первые пять уравнений служат для определения реакций.
Продольные реакции ZA и ZB входят только в третье уравнение
и от характера движения не зависят, т. е. будут такими же, как
и при неподвижном теле. Мы можем определить только их сумму.
Если предположить, что продольная реакция в подшипнике В
равна нулю, то реакция ZA — — Fez.
§ 13.5. Добавочные динамические реакции.
Статическая и динамическая уравновешенность тела
Поперечные составляющие реакций, определяемые из первого,
второго, ^четвертого и пятого уравнений (13.26), обусловливаются
характером приложенных сил, законом движения тела, а также
расположением оси вращения относительно тела.
§ 13.5]
ДОБАВОЧНЫЕ ДИНАМИЧЕСКИЕ РЕАКЦИИ
303
Предположим, что ось вращения тела является главной цент-
ральной осью инерции, т. е. xc = yc = 0, Iхг = I^ = 0. Тогда, урав-
нения для определения поперечных реакций подшипников (13.26)
примут вид
о=К+хелт+х£, .
0 = FH^ + ^T, ^27)
0 = М-глУ?-гвУвт,
0 = М + глУ7 + гвУсвт. J
Реакции, определяемые из этих уравнений, обусловливаются
действующими на тело активными силами. При этом следует
иметь в виду, что силы, действующие на тело, могут зависеть
от закона движения тела (например, силы сопротивления, зави-
сящие от скорости вращения).
Уравнения (13.27) имеют такой же вид, как и уравнения
VCT VCT Х/СТ
статики для неподвижного тела; поэтому реакции Ал, Ав, гд,
Увт условно называют «статическими» реакциями. Употребляя
этот термин, следует помнить, что реакции, определяемые из
уравнений (13.27) при движении тела, могут отличаться от чисто
статических реакций, определяемых по уравнениям (13.27) для
неподвижного тела, так как силы, действующие на вращающееся
тело, как было уже сказано выше, могут зависеть от характера
движения тела.
Возвращаясь к рассмотрению уравнений (13.26), представим
реакции Хл, Хв, Ул, Ув в виде суммы реакций, определяемых
уравнениями (13.27) и реакциями Хд, Х§, Ул, У^, обусловлен-
ными как характером распределения масс в теле, так и харак-
тером движения тела, которые назовем добавочными динамическими
реакциями'.
хл = хдл+хс;, хв=Хв4-хв, 1
ул = удл + услт, Ув = У^ + Ув- / ’ ’
Тогда в соответствии с уравнениями (13.27) и соотношениями
(13.28) получим из (13.26) уравнения для определения добавочных
динамических реакций
-М£/с<р-Мхсф2 = Х^ + Хдв,
? I О «у
— 1хД> + 1уЛ2 = — ZAYaA-ZBYi,
— lyzty ~ Iхгф2 = ^ЛХЛ ф- гвХй.
304
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ, XII!
Выясним теперь, при каких условиях добавочные динамические
реакции равны нулю. В этом случае уравнения (13.29) будут
иметь вид
*сФ2 + УсФ = 0, хсф - г/сф2 = 0,
Ixzi? - W2 = 0, /хгф2 +1yzi? = 0.
(13.30)
Эта система однородных линейных алгебраических уравнений
относительно хс, ус, 1хг, 1уг распадается на две независимые
системы уравнений с одинаковым определителем, не равным нулю:
|Ф
|ф2
ф2| = Ф2 + Ф4¥=0,
так как для вращающегося тела угловая скорость ф и угловое
ускорение ср одновременно в нуль не обращаются.
Следовательно, единственным решением уравнений (13.30)
является
%с = Ус = ®, Ixz = Iyz = Q- (13.31)
Если же теперь принять, что условия (13.31) выполнены, то
уравнения (13.29) примут вид
хяА-\-хяв = о, П + г§=о,
гдХд ф-= 0, zaYa -\-ZbYb = 0,
единственным решением которых является Хд = Хв = У^ — У в =0,
так как гв — гА =ф=0.
Остановимся на условиях (13.31) несколько подробнее. Усло-
вие хс = 0, ус —означает, что центр масс тела находится на оси
вращения. Если оно выполнено, то говорят, что тело стати-
чески уравновешено. Как видно из приведенного анализа, для
уничтожения динамических реакций одной статической уравнове-
шенности тела недостаточно. Необходимо, кроме того, чтобы
центробежные моменты инерции относительно оси вращения рав-
нялись нулю (/хг = 0, /уг = 0). Таким образом, для того чтобы
при вращении тела вокруг неподвижной оси не возникали добавоч-
ные динамические реакции, необходимо и достаточно, чтобы ось
вращения была главной центральной осью инерции.
Как будет показано в следующем параграфе, динамические
реакции иногда во много раз превосходят статические реакции.
Поэтому во всех случаях, когда это возможно, стремятся умень-
шить или полностью уничтожить их. В особо важных случаях
это достигается специальной балансировкой.
? 13 61
ЗАДАЧИ
305
§ 13.6. Задачи
Задача 13.1. Центр тяжести махового колеса, вес которого Р = 300 кГ,
находится на расстоянии 1 мм от горизонтальной оси вала; расстояния под-
шипников от колеса равны между собой.
Найти реакции подшипников, если вал вра-
щается равномерно, делая я = 1200 об/мин.
Маховик имеет плоскость симметрии, перпен-
дикулярную к оси вращения.
Возьмем начало координат в точке О
пересечения оси вращения с маховиком. Ось х
подвижной системы координат направим по
прямой, проходящей через точку С. Оси г
и Zj направим по оси вращения (рис. 13.3).
Очевидно, что при таком выборе подвижной
системы координат хс =—1 мм, ус = 0.
Так как маховик имеет плоскость сим-
метрии, перпендикулярную к оси вращения,
то центробежные моменты инерции равны нулю, т. е, /хг = 0, /уг = 0.
Для рассматриваемой задачи
.. . ЯП л - 1200
<р = °, ср= _ = = 40л сак-».
Поскольку маховик находится в середине между подшипниками, то
I I
гд-----2 > гв ~ 2 >
Где / — расстояние между подшипниками.
Статические реакции равны:
х1Л=4=150 кг> =4=150 кр-
Для определения добавочных динамических реакций воспользуемся урав-
нениями (13.29). Для данной задачи они имеют следующий вид:
-~ХС^^Яа + ^В’
о~у*а+у*в,
о=_|ха+4-хд.
Решая эти уравнения, получим
^ = ^ = -4хсФ2 = -240 ^> УЯа = УЛв = 0-
Таким образом, добавочные динамические реакции в 1,6 раза превосхо-
дят статические; направления их линий действия вращаются вместе с махови-
ком, оставаясь все время параллельными линии ОС.
Задача 13.2. Вычислить добавочные динамические реакции в подшипни-
ках Л и В при вращении вокруг оси АВ однородного тонкого кругового
306
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. XIII
диска CD, предполагая, что ось АВ (рис. 13.4) проходит через центр диска,
но вследствие неправильного рассверливания втулка составляет с перпенди-
куляром к плоскости диска Z. АОЕ = а = 0,02 рад. Дано: вес диска Р =
3,27 кГ, радиус его г = 20 см, число оборотов п = 30 000 об!мин, расстояния
40 = 50 см, ОВ = 30 см. Ось АВ считать
абсолютно твердой и ' положить sin 2а =
=2а.
Начало подвижной системы коорди-
нат Oxyz, жестко связанной с диском, вы-
берем в центре диска О (см. рис. 13.4).
Из условий задачи следует
хс = 0, ус = 0, гд = — «=—50 см,
zB = b = 30 см.
Статические реакции равны 1,23 кГ и
2,04 кГ.
Момент инерции Iг диска и его цен-
тробежные моменты Ixz и lgZ были по-
лучены в задаче 12.4 § 12.10. По формулам (12.30) и (12.31) для нашего
случая (е = 6 — 0) найдем
lz = у 44r2cos2a + у Mr2 sin2a, Mr2 sin 2a, Iyz = 0.
Так как угол a мал, то, ограничиваясь членами первого порядка малости
относительно а, получим
=“2-44 г2, 4д.г = —44г2а, 1 уг = 0,
Имеем далее п = 30 000 об/мин.
ф = "г = ЮООл сек"1.
oU
Уравнения (13.29) примут вид (cp = const и ф —0)
о=х$+х$, 0=гд+уд,
0 = aY^-bY^, -1л4г2аф2 = -аХд+&Хд,
откуда получим
уд_____уд _ Л4г2аф2
ЛА лв 4(а + &)>
ГД=г£=0,
или
Х& ______хд — ^r2grl2 ‘ Ю8
А в 4g (a-j-Ь)
820 кГ,
Реакции опор свелись к паре сил; модуль каждой реакции в 250 раз
превосходит вес самого диска и в 400 раз максимальную статическую реакцию.
Задача 13.3. С какой угловой скоростью должна равномерно вращаться
вокруг катета АВ — 1 однородная пластинка, имеющая форму равнобедренного
прямоугольного треугольника ABD, чтобы полное боковое давление на ниж-
нюю опору равнялось нулю? Расстояние между опорами считать равным длине
катета АВ,
« 13 0)
ЗАДАЧИ
307
Начало подвижной системы координат возьмем в точке В. Ось г напра-
вим по вертикали вверх, а ось у проведем в плоскости пластинки. Следова
тельно, в этом случае гА ——I, гв = 0.
Из рис. 13.5 следует, что хс = 0,
ус = 1/3. Найдем сначала поперечные
статические реакции. Уравнения для их
определения имеют вид
Х"+Х" = 0, У£ + У£=0,
у^-р£=о, -х^=о,
где Р— вес пластинки.
Из этих уравнений следует
р
ХСТ VCT___л VCT___ VCT___
А=лВ—и’ Y A—~Y В— “У"
Так как по условию задачи ф = 0, то уравнения (13.29) запишутся следующим
образом:
о=хд+х£, -^Ф2=П+^,
'И>2='П.
Центробежные моменты инерции были найдены в задаче 12.6 § 12.10. При
ч равных катетах и выбранном направлении осей из формулы (12.35) найдем
12 “ 12g’ 1хг °’
Поскольку /хг = 0, то будем иметь
ХЗ=Х£ = 0.
Реакции Уд и У^ определяются из уравнений
__— гё2—уД-1_уД ____д2 /уд
3gf + yb> ~i%;4-1yA’
•откуда
У5=—— Ф2. У »== — ——Ф2
12g '₽ ’ yb~ 12g4>-
В задаче требуется определить угловую скорость ф, при которой полная
^реакция
гл=>7+У^=о.
©ту угловую скорость найдем из соотношения
откуда
Ф=2]/Ь
308
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. ХИГ
Задача 13.4. Вращающаяся часть подъемного крана состоит из стрелы KF
длины L, противовеса D и груза Е (рис. 13.6). При включении постоянного
Рис. 13.6.
оси вращения вертикально вверх,
а = 0, &=Я.
по модулю тормозящего момента кран,
вращавшийся до этого с угловой ско-
ростью п=1,5 об/мин, останавливается
через две секунды. Считая стрелу KF
крана однородной тонкой балкой, а про-
тивовес D и груз Е точечными массами,
определить динамические реакции опор А
и В крана в конце его торможения. Длина
стрелы /. = 30 м, расстояние между опо-
рами крана // = 3 м, длина свисающей
части троса 1= 18 м, вес стрелы G = 8 Т,
вес груза Р = 10 Т, угол а = 45°; центр
тяжести всей системы находится на оси
вращения крана (предполагается, что
груз Е находится все время в плоскости
крана).
Начало подвижной системы координат
возьмем в опоре А, ось г направим по
ось у проведем в плоскости крана. Тогда
По условию центр тяжести всей системы лежит на оси вращения. Поэтому
хс — 0, Ус~®-
Так как система плоская, то /хг = 0. Кроме того, в конце вращения
крана ф=0.
Добавочные динамические реакции опор вращающегося крана найдем из
уравнений (13.29), которые в нашем случае примут вид
о=х^+х$,
0 = Г^ + Г£, о = -яг«, =
Отсюда находим *
Угловая скорость вращения крана в начале торможения была
При постоянном по модулю тормозящем моменте ф —const. Так как время
торможения t = 2 сек, то
ф л .
ф = __=__ сек 2.
Центробежный момент инерции !уг для рассматриваемой системы был най-
ден в задаче 12.5 § 12.10. Для статически уравновешенного крана имеем (см,
формулу (12.33))
, L sin a [GL , „ .,
1уг ——-— |^-у cos а + Р (L cos а — Z)j.
Подставляя числовое значение величин, входящих в полученные формулы,
найдем
/^=1927’ мсек2, = — Х^ = — 5,ОТ,
§ 13.7]
ФИЗИЧЕСКИЙ МАЯТНИК
309-
Таким образом, в конце торможения добавочные динамические реакции-
опор вращающегося крана образуют пару сил, лежащую в плоскости, перпен-
дикулярной к плоскости крана. В менее благоприятных условиях (например)
при меньшем времени торможения или меньшей длине I свисающего троса,
добавочные динамические давления резко возрастают.
§ 13.7. Физический маятник
Физическим маятником называется твердое тело, вращающееся
вокруг неподвижной оси под действием силы тяжести. Рассмот-
рим случай, когда ось вращения горизонтальна. Проведем через
центр тяжести С тела плоскость, перпендикулярную к оси вра-
щения. Точка пересечения О этой плоскости
называется точкой подвеса. Примем эту точку
нат. Ось г направим по оси вращения,
оси х и у расположим в плоскости, прохо-
дящей через центр тяжести и точку под-
веса, перпендикулярно к оси вращения
(рис. 13.7). Дифференциальное уравнение
вращения тела вокруг оси г согласно § 9.5
запишется следующим образом:
где ср —угол между неподвижной осью хх и
линией ОС (см. рис. 13.7).
Так как в этом случае
с осью вращения
за начало коорди-
Рис. 13.7.
Ме2 = — Mga sin ср,
где М — масса тела, а —расстояние от точки О до центра тяже-
сти (а = ОС), то дифференциальное уравнение движения тела:
примет вид
= — Mga sin ср,
или
.. , Mga . п
cp-t-’-jS-sin ср = 0.
'г
Рассмотрим случай малых колебаний, для которых можно при-
нять sincp^cp. Тогда уравнение движения можно записать в сле-
дующей форме:
<р + ^(р = 0, (13.32)
а его общее решение имеет вид
ср = A sin t + е^.
310
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. XIII
Отсюда следует, что угол ср изменяется по гармоническому за-
кону с периодом колебаний, равным
Г = 2л/яг«- <13'33>
Сравнивая дифференциальное уравнение движения математи-
ческого маятника
cp + y-sincp = O (13.34)
с уравнением движения физического маятника, можно утверждать,
что математический маятник, имеющий длину
'-jfe. (1S.35)
будет двигаться так же, как и физический маятник.
Величина I, определяемая формулой (13.35), называется при-
веденной длиной физического маятника.
Представляя по теореме Гюйгенса— Штейнера (§ 12.4) момент
инерции тела относительно оси z в виде
/г = /с + А4«2,
где 1С — момент инерции тела относительно оси, проходящей через
центр тяжести тела параллельно оси г, получим для приведенной
длины физического маятника выражение
(i3-36)
Откладывая эту величину от точки подвеса в направлении
центра тяжести, получим точку 0г (см. рис. 13.7), которая на-
зывается центром качания. Расстояние от центра тяжести до
центра качания равно
= (13.37)
Покажем, что точка подвеса и центр качания обладают свой-
ством взаимности (теорема Гюйгенса).
Пусть ось вращения проходит через центр качания; тогда для
.новой приведенной длины согласно формуле (13.36) получим
1Г
1 Мб?! 1 1
На основании равенства (13.37) имеем
следовательно,
— а + ai —
§ 13 81
ОПРЕДЕЛЕНИЕ МОМЕНТОВ ИНЕРЦИИ
311
Таким образом, если старый центр качания сделать новой
точкой подвеса, то старая точка подвеса станет новым центром,
качания, что и доказывает свойство взаимности.
§ 13.8. Экспериментальное определение моментов инерции
Рассмотрим два способа экспериментального определения мо-
мента инерции неоднородных твердых тел или тел сложной кон-
фигурации: способ качания с использованием теории физического-
маятника и способ крутиль-
ных колебаний.
Способ качания проиллю-
стрируем на следующем при-
мере. Пусть требуется найти
момент инерции шатуна отно-
сительно оси, проходящей
через центр тяжести С ша-
туна параллельно осям его
проушин. Для определения
момента инерции шатуна от-
носительно оси, проходящей
через точку А параллельно
оси проушины, шатун подве-
шивают на призму А (рис.
13.8, а) и, отклонив его на
сия, измеряют период колебания шатуна. Зная период колеба-
ния, по формуле (13.33) определяют момент инерции шатуна
относительно оси качания:
. QciT-
1а~ 4л2 ’
где а —расстояние центра тяжести шатуна от оси качания, Q —
вес шатуна.
Затем по теореме Гюйгенса — Штейнера вычисляют момент
инерции относительно центральной оси:
1с = 1А-^а2 = (13.38)
g g \4л2 } ' '
Для определения величины а шатун подвешивают на нити
в точке В и определяют реакцию R давления шатуна на штырь
динамометра D (рис. 13.8, б). Затем из формулы
Rl — Q (а — г) = О,
где г — радиус проушины, находят величину
Rl + Qr
а = —Д-*-.
Рис. 13.8.
малый угол от положения равнове-
'312
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. ХИГ
Подставив значения а в формулу (13.38), вычисляют 1С.
В рассмотренной схеме эксперимента наибольшую ошибку дает
определение величины а, поэтому применяют иную схему экспе-
римента.
Если требуется найти момент инерции тела относительно про-
извольной оси (рис. 13.9), то способом качания сначала опреде-
ляют период колебаний тела относительно оси, на которую жестко
насажены два цилиндра, с известными моментами инерции. Затем
определяют период колебаний исследуемого тела относительно
той же оси без цилиндров. Тогда, если период колебания тела
совместно с цилиндрами равен
г Mga ’ '
а период колебаний тела без цилиндров
то, исключив величину а, получим
О J'f2___р2
где Го — момент инерции цилиндра относительно его оси.
Рассмотрим теперь способ крутильных колебаний.
При определении момента инерции тела способом крутильных
колебаний тело подвешивают на упругом стержне или струне так,
чтобы центр масс тела лежал на продолжении оси стержня
(рис. 13.10). Закрутив стержень, жестко связанный с телом, на
малый угол ср, измеряют период колебания системы. Так как при
малом угле закручивания момент упругих сил пропорционален
углу закручивания, то дифференциальное уравнение крутильных
..колебаний системы имеет вид
/сФ = —
§ 13.91
ПЛОСКОЕ ДВИЖЕНИЕ АБСОЛЮТНО ТВЕРДОГО ТЕЛА
313
где /г — постоянный коэффициент, характеризующий упругие свой-
ства стержня (струны).
Период колебаний, очевидно, будет равен
, Т = (13.39)
Затем на тот же стержень подвешивают тело (например, диск),
момент инерции которого относительно оси ОС известен и равен /с,
и измеряют период колебаний Т' в этом случае. Этот период ко-
лебаний определяется формулой, аналогичной формуле (13.39):
Г = 2я/^.
(13.40)
Исключая из равенств (13.39) и (13.40) неизвестный коэффи-
циент k, получим формулу для определения момента инерции
, / Т \2
Ic~lc•
§ 13.9. Плоское движение абсолютно твердого тела
Свободное твердое тело будет совершать плоское движение,
если в нем существует плоское сечение, относительно которого-
масса тела распределена симметрично; силы, действующие на тело.
расположены в плоскости этого сече-
ния, а начальные скорости всех точек
тела расположены в плоскостях, парал-
лельных плоскости сечения. Движение
тела можег быть плоским также и
в силу наложенных на него связей, но
это уже будет несвободное движение.
В кинематике было установлено, что
положение твердого тела, совершающего
плоское движение, определяется тремя
параметрами. За эти параметры выбе-
рем координаты центра масс тела и
угол поворота тела относительно оси,
Рис. 13.11.
перпендикулярной к рас-
сматриваемому плоскому сечению тела.
Пусть система координат Сх2у2, имеющая начало в центре
масс тела, движется поступательно относительно неподвижной си-
стемы координат Орсд/г Положение тела будет полностью опре-
делено, если известны координаты центра масс тела (х1С, г/1С) и
угол ср между осью х2 и осью х системы координат Сху, жестко
связанной с телом и имеющей начало в центре масс тела
(рис. 13.11).
В соответствии с теоремой о движении центра масс из урав-
нений (13.1) получаем зависимости, связывающие координаты
314
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. XIII
центра масс тела и проекции главного вектора всех внешних сил
(Л'х,, Fey^, приложенных к твердому телу:
MxlC = FeXl, 1
Му 1С =Feyt, J
(13.41)
где М — масса тела.
Используя теперь теорему об изменении момента количеств
движения в относительном движении (13.2), получим зависимость
между углом ср поворота тела и силами, действующими на тело.
Так как в системе координат Сх2уг твердое тело совершает
вращательное движение вокруг оси, проходящей через центр масс
перпендикулярно к плоскости движения тела, то момент количеств
движения тела относительно этой оси в соответствии с равенством
(13.10) будет равен Лс = Л?Ф- Следовательно, на основании тео-
ремы (§ 9.7) имеем
1с(р = Мес, (13.42)
где /с —момент инерции тела относительно оси, перпендикуляр-
ной к плоскости движения тела и проходящей через центр масс
тела, а Мс — главный момент всех внешних сил относительно
той же самой оси. Уравнения (13.41) и (13.42) позволяют решать
задачи динамики плоского движения твердого тела.
Если движение твердого тела задано, т. е. координаты центра
масс (хгс, Угс) 11 угол ср являются известными функциями вре-
мени, то в результате подстановки вторых производных от этих
функций (х1С, Ухе» ф) в уравнения (13.41) и (13.42) находятся
силы, под действием которых происходит движение тела.
Если же заданы силы, т. е. известны FXl, Feyi и Мс, то урав-
нения (13.41) и (13.42):
Mx1C = FXt,
Му1С = РеУ„
Icif = Mec
(13.43)
будут представлять уже систему трех обыкновенных дифферен-
циальных уравнений, определяющих плоское движение твердого
тела*). После решения этих уравнений и определения постоянных
интегрирования получим закон плоского движения свободного
твердого тела
XlC — X1C(t), У1С—У1С({), Ф = Ф(О-
*) Если траектория центра масс задана, то вместо первых двух уравнений
системы (13.43) иногда целесообразно взять уравнения в проекциях на каса-
тельную и нормаль к траектории центра масс.
§ 13.10]
ЗАДАЧИ
315
Если тело совершает несвободное движение, то в число дей-
ствующих сил следует включить реакции связей. Уравнения,
движения тела в этом случае будут
М-Чс — FXl
Му 1С — Fexi + Ryt >
(13.44)
где RX1 и Ryt — суммы проекций всех реакций соответственна
на оси и ylt а Мс — сумма моментов всех реакций относи-
тельно центра масс. В этих уравнениях FXl, Fe,,.
к внешним активным силам. К уравне-
ниям (13.44) следует еще добавить урав-
нения связи.
Заметим, что иногда вместо одного из
дифференциальных уравнений (13.44)
бывает целесообразно применить теоре-
му об изменении кинетической энергии.
§ 13.10. Задачи
Задача 13.5. Однородный стержень длины 21
и массы М за один из своих концов подве-
шен на нити длины а, массой которой можно
пренебречь, к неподвижной точке О. Стержень
вместе с нитью отклонили влево от вертикали
на угол а и отпустили без начальной скорости
(рис. 13.12). В момент, когда стержень, пройдя
и Мес относятся
Рис. 13.12.
положение равновесия, составлял с вертикалью
угол Р(Р<а), нить оборвалась. Определить закон движения стержня после-
обрыва нити.
Найдем сначала угловую скорость стержня, координаты и проекции ско-
рости центра масс стержня на неподвикные координатные оси Ояцц в момент
обрыва нити. В соответствии с теоремой об изменении кинетической энергии
имеем
/ош2
— (a-j-l) (cos р — cos а),
где
/0 = /с + Л4(а + /)2 (/С=^г)
— момент инерции стержня относительно точки О, 1С — момент инерции стер-
жня относительно его центра масс.
Следовательно, угловая скорость стержня в момент обрыва нити равна
„ _ ж _ 1 /" 2A?g +О (cos Р —cos «т
ф V /С + Л4(а + /)2
Координаты центра масс стержня в момент обрыва нити будут
x1C = (a-H)cos0, ylC = (а + /) sin 0,
316
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. XIH
а проекции его скорости на оси координат
х1С = — (а + 0 <о sin р, с/1С = (<*-(-/) со cos
Угол между стержнем.и осью хг в момент обрыва равен <р = р.
Дифференциальные уравнения движения стержня после обрыва нити имеют
вид (единственная внешняя сила — сила тяжести Mg — приложена в точке С)
МХ1С = Mg, Mi/1C = 0, lc(f = 0,
и, следовательно, общее решение этих уравнений будет
\С = ^ + С1, ^1С = С2> *₽ = сз.
Х1С = ^2~+С/ + С4, Z/1C = C2/+C5.
<р = С3/ -|- С$.
Произвольные постоянные интегрирования определим из начальных усло-
вий: при / = 0
x1C = (a4-Z) cos р,
х1С = — (а + 0 со sin р,
Ф = Р>
У1с = (а + 1') sin Р>
с/1С = (а-Н) w cos р,
ср = со.
Значения произвольных постоянных будут
(?! = —(a-f-Z) а> sin (3, C2 = (c? + Z) со cos (3,
С4 = (с? + /) cos р, С5 = (а + /) sin р,
Подставив эти значения в общее решение, получим закон движения стержня
после обрыва нити
Сд — со,
св=р.
вижной
st2
х1С = -^2-(«4-Z) (<о/ sin р — cos р),
у1С = (а + 1) (со/cos Р + sin Р), ср = со/ + р.
Задача 13.6. Конец В невесомого стержня АВ соединен шарнирно с непод-
опорой. К другому концу стержня прикреплен тяжелый однородный
диск радиуса г. В начальный момент стержень зани-
мал вертикальное положение. Получив ничтожно ма-
лую скорость, стержень начинает вращаться вокруг
шарнира.
Определить угловую скорость диска и угол ме-
жду вертикалью и стержнем в момент, когда состав-
ляющая реакции шарнира, направленная вдоль
стержня, равна нулю.
Центр масс диска движется по окружности
радиуса I -ф г с центром в точке В, следовательно,
уравнение движения центра масс диска в проекции
на нормаль к его траектории будет иметь вид
(рис. 13.13)
pV2
H7+Ij=pcosq>+^.
v — скорость центра масс, Rn — нормальная реакция,
где Р — вес диска, с л л "...
направленная от точки В вдоль стержня. Из этой формулы следует, что
Pv2
Rn =“ —г-н— Р cos Ф>
§ 13.10]
ЗАДАЧИ
317
Для определения скорости о в любой момент времени воспользуемся тео-
ремой об изменении кинетической энергии.
Так как стержень вращается вокруг горизонтальной оси, проходящей
через точку В, то
1 = Р (/ф-г) (1 — cosqp),
где /д — момент инерции диска относительно точки В, равный
Р/-2 р р г ! г \21
^=2? + 7(г+/)2=^(г+/)2[2+Ы]-
Следовательно,
ф,_ 2 (r-t-Z) Р (1 — cos <р)
1В
Принимая во внимание, что v2 = (l-|-r)2 ф2, имеем
К„ = ^-[4-(44-п)со9ф],
где
/ г \2
"=2+(т+г) •
Пусть в момент, когда Рп=0, угол ф = а, тогда
4 — (4-|-zi) cosa=0.
Отсюда
4
COS « = ,
4-|-n ’
а угловая скорость в момент, когда /?„ = 0, будет
Ф 2УГ (4 + «) (/ + /)’
Задача 13.7. Однородный стержень длины I и веса Р одним концом укреп-
лен при помощи идеального шарнира в точке А, другой конец стержня удер-
живается нитью ВС, образующей со стержнем угол 90э (рис. 13.14). Стержень
составляет с горизонтом угол а. Определить, насколько изменится давление
балки на шарнир А в момент внезапного обрыва нити
Для определения реакции в шарнире А
и натяжения нити составим уравнения ста-
тики (см. рис. 9.14):
— RgSina=0, ^i^ + ^ficosa — Р = 0,
' Pl
--g-cosa-|-PB/ = 0,
откуда
riA = -f-(1 + sin2 “)
VCT Р • о П Р
Х1Л=sm 2a, /?B = -g-cosa.
Если нить оборвется, то стержень начнет
ние вокруг шарнира А,
ВС.
совершать вращательное движе-
318
ДИНАМИКА ПРОСТЕЙШИХ ДВИЖЕНИЙ ТВЕРДОГО ТЕЛА [ГЛ. XIГГ
Дифференциальные уравнения движения можно записать в виде *)
У Х1С — Х1А,
~^У1С'=У1А~Р’
г •• Pl
/дф = —-уСОвф.
Из очевидных зависимостей
I
Х1С= 2 С0Яф’
(13.45)
I
У1С = ~2 sin<₽
найдем
«... « ..
*1С = — <Р Sin <р — ср2 COS ф,
I .. I .
У1С = ~2~ фсозф-----g- ф2 sm ф.
Так как в момент разрыва нити ф = а, ф = 0, то
I .. . .. I ..
х1С =---g-фяпа, y1C = -j ф cos а.
Теперь из уравнений (13.45) с учетом выражений (13 46) для этого момента
времени получим
" ЗР ЗР
X, . =~гг- sin 2а, Г , = Р---т—cos2 а.
1А g 1А 4
(13.46)
Изменение реакций будет равно
Х1А - Х1 а = 4 sin 2а- Г1А-гм=-4С082а-
Рис. 13.15.
Задача 13.8. Однородное тело массы М, имеющее форму полуцилиндра
радиуса R, поставлено на горизонтальную шероховатую плоскость и выведено
из состояния равновесия, после чего предоставлено самому себе. Определить
период малых колебаний, которые
будет совершать тело, если из-
вестно, что проскальзывать по
плоскости оно не может. Трение
качения отсутствует (рис. 13.15).
Составим дифференциальные
уравнения движения тела, учиты-
вая, что на него действуют три
внешние силы: сила тяжести Р,
сила трения скольжения FT и нор-
мальная составляющая реакции в
точке касания N. Выбрав начало
координат в точке О касания тела
й плоскости в тот момент, когда тело находится в равновесном состоянии, и
яаправив оси координат, как показано на рис. 13.15, получим на основании
формул (13.43) следующие три дифференциальных уравнения движения:
Му1С = —
lc<f=^FT (R — a cos ф) — Na sin ф,
*) Здесь используется то обстоятельство, что точка А неподвижна,
§ 13.10]
ЗАДАЧИ
319
где 1С — момент инерции тела относительно оси, проходящей через центр
масс С перпендикулярно к плоскости тела, а — расстояние DC.
Исключая Гт и N из третьего уравнения при помощи первого и второго,
получим
/сф = — (R — a cos ср) — a sin <р (W1C-}-44g), (13.47)
Но так как диск перекатывается без скольжения, то
х^с = Rtf — a sin <р, у1С = R — a cos <р.
Ограничиваясь случаем малых колебаний (sin <pss=<p, cos<p«sl), находим
*1С=(/? —a)<p, y1C = R — a,
x1C = (R — a)(p, г/1С = 0.
Подставляя последние значения в уравнение (13.47), в котором также пола-
гаем cos<p«»l и sinq>Ra<p, получаем
/с<р =—М (R-~a)2q> —Mgaq>,
или
.. , Маа
(₽ + Ic + (R-a)2M ф = °‘
Отсюда находим период малых колебаний диска
' Mga
Вычислим теперь величины а и /с-
Величина а, определяющая положение центра тяжести однородного полу-
диска, была определена ранее (том I, глава VIII). Она равна
Определим момент инерции полукруглого диска относительно оси, прохо-
дящей через точку D. Согласно определению момента инерции относительно
оси он равен половине момента инерции круглого диска с массой 2М относи-
тельно той же оси. Так как последний равен Л41?2, то интересующий нас
момент инерции ID = MR2. Воспользовавшись затем теоремой Гюйгенса —
Штейнера, имеем
= 1 q -|- Мд2.
Следовательно,
lc=ID~ Mcfi = у — Ма2-
Используя найденные значения а и получим окончательное выражение
периода малых колебаний полукруглого диска
Заметим, что период Т не зависит от массы диска и определяется лишь его
радиусом,
ГЛАВА XIV
ДИНАМИКА ТВЕРДОГО ТЕЛА,
ИМЕЮЩЕГО ОДНУ НЕПОДВИЖНУЮ ТОЧКУ.
ДВИЖЕНИЕ ИСКУССТВЕННОГО СПУТНИКА
ОТНОСИТЕЛЬНО ЦЕНТРА МАСС
§ 14.1. Дифференциальные уравнения движения твердого тела,
имеющего одну неподвижную точку
Целью этого параграфа является
установление зависимостей
между параметрами,
определяющими положение тела (например,
углами Эйлера), и силами, приложенными
к телу. Эти зависимости дадут возможность
решать основные задачи динамики для тела,
имеющего одну, неподвижную точку.
Для получения этих зависимостей вос-
пользуемся теоремой об изменении момента
количеств движения (§ 9.3):
= (14.1)
где Ко — момент количеств движения тела
относительно неподвижной точки О тела,
Мо — главный момент всех внешних сил относительно той же точки.
Пусть неподвижная система координат Oxxylz1 имеет начало
в закрепленной точке тела. Свяжем жестко с телом подвижную
систему координат Охуг с началом в той же точке О (рис. 14.1).
При движении тела его моменты инерции и центробежные-
моменты инерции в неподвижной системе координат будут пере-
менными величинами, так как тело при своем движении изменяет
свое положение относительно осей этой системы. В подвижной же
системе координат, жестко связанной с телом, моменты инерции
и центробежные моменты инерции являются величинами постоян-
ными .
Учитывая это обстоятельство, будем считать вектор момента
количеств движения тела Ко определенным в подвижной системе
координат, жестко связанной с телом. Тогда в соответствии с
§ 14.1]
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ
321
зависимостью (13.21) уравнение (14.1) можно записать в виде
dKn
-^ + ®xK0 = MS,
(14.2)
где
rfK0 dKx • dKy . dKs k
dt ~ dt ' dt dt
(14.3)
a Kx, Ky, Кг — проекции вектора Ко на оси системы координат
Oxyz\ i, j, к —единичные векторы осей х, у, г; <в —угловая ско-
рость тела.
Имея в виду формулу (14.3), а также известное равенство
перепишем уравнение (14.2) в проекциях на оси подвижной си-
стемы координат:
^ + (ЯуКг-ЯгКу)^Мех,
^ + {и)гКх-^хКг) = Меу,
-^ + Му~^уКх)^Мег,
(14.5)
где и>у и сог — проекции угловой скорости тела на оси под-
вижной системы координат, Мх, и М? —главные моменты
всех внешних сил относительно тех же осей (см. § 9.3).
Если подвижную систему координат Охуг выбрать таким обра-
зом, чтобы координатные оси х, у и г были главными осями инер-
ции для точки О, то все центробежные моменты инерции будут
равны нулю и согласно (13.9)
Кх = 1х(дх, Ку = 1у(ду, Кг = 1г®г. (14.6)
Уравнения (14.5) примут следующий вид:
1х^~ + (К-1у)^г^Мех,
/у^ + (1х-/г)^х = Меу, (14.7)
Уравнения (14.7) называются динамическими' уравнениями
Эйлера. Присоединяя к ним кинематические уравнения Эйлера
11 И. В, Бутенин и др.
322
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
(том 1, § 14.3)
(Dx = ф sin 0 sin <р + 6 cos <р,
= ф sin Ocos <р — 9 sin <p,
юг = ф cos 0 + Ф,
* (И.8)
получаем полную систему уравнений, необходимую для решения
задач динамики твердого тела, имеющего одну неподвижную точку.
Если задается закон движения тела, т. е. задаются углы
Эйлера как функции времени, то уравнения (14.7) и (14.8) поз-
воляют определить силы, под действием которых происходит за-
данное движение.
Если же задаются действующие на тело силы, т. е. можно
считать известными проекции главного момента всех внешних сил
Мех, Меу, Мег, то уравнения (14.7) и (14.8) представляют собой
систему шести дифференциальных уравнений первого порядка для
определения углов Эйлера как функций времени.
Иногда при решении конкретных задач бывает выгодно вво-
дить подвижную систему координат, не связанную жестко с телом.
Пусть такая система координат Ох2у2г2 имеет также начало в не-
подвижной точке тела. В этой системе координат уравнения (14.5)
запишутся в виде
dt2 + (w^^z2 w22^2) ~ МХг,
dK„
d(2 + (wz2^G2 tt»x2/^z2) = Mya,
+ (o)x2M,2 wi/2Ax2) = Mzt,
(14-9)
где wX2, <Лу2, оэ2г — проекции угловой скорости подвижной системы
координат на собственные оси.
Интегрирование дифференциальных уравнений движения твер-
дого тела, имеющего одну неподвижную точку, представляет зна-
чительные математические трудности. Мы рассмотрим лишь наи-
более простые случаи, а именно случай вращения динамически
симметричного тела вокруг неподвижной точки по инерции (слу-
чай Эйлера) и случай движения под действием силы тяжести,
когда тело имеет относительно неподвижной точки ось динами-
ческой симметрии, а центр тяжести лежит на этой оси (случай
Лагранжа ).
§ 14.2. Движение твердого симметричного тела, имеющего одну
неподвижную точку, по инерции (случай Эйлера)
В этом параграфе будет рассмотрен наиболее простой случай
движения твердого тела, имеющего одну неподвижную точку,
а именно случай движения по инерции.
§ 14 2]
ДВИЖЕНИЕ СИММЕТРИЧНОГО ТЕЛА
323
Если главный момент всех сил, приложенных к твердому телу,
относительно неподвижной точки тела равен нулю, т. е. Мо = 0
то динамические уравнения Эйлера (14.7)
« = <=< = 0),
примут вид
/x^ + (/z-/J^G)2 = 0,
+ (Av ~ Л’) = 0,
h^ + (Iy- Л) (0^ = 0.
(14.10)
Умножая первое из этих уравнений на 1х<ах, второе —на 1ушу,
третье —на 1га>г и складывая затем уравнения между собой,
получим
7>.
аых dti>u dm.
или
|^(П^4-7^^4-7^) = 0;
отсюда
ГХЬЛ% +/у <д2у + Г^г = Ко = const. (14.11)
Это уравнение представляет собой первый интеграл уравнений
движения (14.10) и означает, что модуль момента количеств дви-
жения сохраняет постоянную величину во все время движения.
Конечно, этот интеграл можно получить и непосредственно из тео-
ремы об изменении момента количеств движения. Так как Ме = 0,
то
^=0
dt и
и, следовательно, Ко = const. Учитывая равенства (13.9) Кх =
= 1х(лх, Ку = 1у<Лу, Kz = Iz^z, найдем
Гх + Гу toy 4- Гг<У>1 = Ко = const.
Умножая теперь уравнения (14.10) соответственно на <пх, а>у
и и проделывая аналогичные выкладки, получим еще один
первый интеграл
/ло)л + + Л®г = 2/i = const,
где h — постоянная энергии.
Механический смысл этого интеграла состоит в том, что кине-
тическая энергия тела во все время движения остается постоянной
величиной. Найденный первый интеграл можно также получить
из закона сохранения полной механической энергии T-\-H = h
(П = 0, так как тело движется по инерции).
11*
324
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл XIV
Определение углов Эйлера даже в этом простом случае явля-
ется довольно сложной математической задачей. Поэтому обра-
тимся к частному случаю, когда
IX — I у Ki
т. е. рассмотрим тело, у которого ось z представляет собой ось
динамической симметрии.
Уравнения (14.10) при этом будут
7х^ + (Л-/.)®^=0, '
j г ।
+ = [ (14.12)
dcog_«
/г dt
Из третьего уравнения следует, что
сог = ыго = const. (14.13)
Имея в виду, что момент количеств движения Ко твердого
тела имеет постоянный модуль и направление, неподвижную ось
zt направим по вектору Ко (рис. .14.2). При таком выборе нап-
равления оси гх проекции векто-
ра Ко на оси подвижной системы
координат Охуг будут равны

Рис. 14.2.
Кх = Ко sin 9 sin <р,
Ку = Ко sin 6 cos Ф,
= 7<о cos 9.
У? С другой стороны,
Кх = 1Х^Х,
Ку = 1уШу,
Kz — 1 г^г-
(14.14)
(14.15)
Сравнивая выражения для Кг в формулах (14.14) и (14.15) и
учитывая равенство (14.13), найдем
откуда
Ко cos 9 = 7/ого,
cos 9 = cos 90 == const.
ло
Таким образом, угол нутации 9 является постоянной величиной:
6 = 9в. (14.16)
§ 14 2]
ДВИЖЕНИЕ СИММЕТРИЧНОГО ТЕЛА
325
Кинематические уравнения Эйлера (14.8) теперь принимают
вид
(ол = ф sin 60 sin <р,
и>У = ip sin 60 cos <р,
сого = Ф cos е0+ф.
(14.17)
Из соотношений (14.14) и (14.15) находим (1х — 1у)
Ко sin 6 sin <р = 1хи>х, Ко sin 6 cos <р = Ix^y,
или, учтя формулы (14.16) и (14.17),
Ко sin 0о sin <р = /хф sin 0fl sin <р, Ко sin 0о cos <р = 7хф sin 0О cos <р.
Откуда
Ко = Л4
и
ф = ^ = п = const. (14.18)
* X
Таким образом,
ф == nt + Фо»
где фо —значение угла ф в момент времени t = 0. Из третьей
формулы уравнений (14.17) имеем
ф = <n~fl — п cos 0о = «! = const (14.19)
и, следовательно,
ф —«i^ + фо,
где <р0 —начальное значение угла <р.
Итак, решение дифференциальных уравнений движения твер-
дого тела, имеющего одну неподвижную точку, в рассматриваемом
случае будет
9 = %.
Ф = nt + ф0,
ф = п^ + ф0- .
(14.20)
Произвольные постоянные 60, Фо» Фо» п и п1( входящие в решение
(14.20), связаны между собой соотношением (14.19), т. е.
ыго —ncos 60 = «1.
Это значит, что решение (14.20) содержит в выбранной системе
координат только четыре независимые между собой произвольные
постоянные интегрирования. Однако направление вектора момента
326
ТВЕРДОЕ ТЕЛО. ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл XIV
Рис. 14.3.
количеств движения, с которым мы связали систему координат
Ох1у1г1, постоянно и определяется в произвольной координатной
системе двумя независимыми произвольными
постоянными.
Поэтому решение (14.20) является общим
решением уравнений (14.12). Движение,
описываемое уравнениями (14.20), называет-
ся регулярной прецессией. При этом движе-
нии ось симметрии тела г описывает кру-
говой конус с углом раствора 26О, равно-
мерно вращаясь вокруг постоянного направ-
ления вектора момента количеств движения
Ко с угловой скоростью ф = п; одновременно
само тело равномерно вращается вокруг оси
симметрии г с угловой скоростью ф = лгх.
На рис. 14.3 показаны неподвижная ось гх (с ней совпадает век-
тор Ко), ось симметрии тела и направления вращений.
§ 14.3. Геометрическая интерпретация Пуансо
При отсутствии динамической симметрии решение задачи о движении твер-
дого тела вокруг неподвижной точки по инерции описывается эллиптическими
функциями. Мы проведем лишь качественный " ~
ветствии с формулой (12.20) уравнение эл-
липсоида инерции, построенного для точки О
в подвижных осях Охуг (точка
движная точка тела), жестко
с телом, имеет вид
анализ,
О — непо-
связанных
данный Пуансо. В соот-
враще-
(14.21)
Пусть точка Р с координатами х, у, г
будет точкой пересечения мгновенной оси
вращения тела с эллипсоидом инерции
(рис. 14.4). Обозначая через р радиус-век-
тор точки Р, проводимый из неподвижного
полюса О, будем иметь
p = xi+yj + zk,
где 1, j, к — единичные векторы осей систе-
мы координат Охуг.
Так как вектор угловой скорости св направлен по мгновенной оси
ния, то
р _ СО^_
р ~~ со ’
отсюда
со
со =— р
р
и
(О
(Or =— X,
р
со
со
(0^ — — Zt
Р
(14.22)
§ 14 3] ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ ПУАНСО 327
Рассматриваемое движение тела происходит по инерции, поэтому кинети-
ческая энергия тела является постоянной величиной и на основании формулы
(13.11)
2Т = Ко • <в = Кхах + Куи>у+Кгаг = 2h. (14.23)
Подставляя сюда выражения (14.6) и (14.22), получим
02
^(Ixx^+Iyy^+I^) = 2h.
Так как координаты'*, у, г точки Р должны удовлетворять уравнению эллип-
соида инерции (14.21), то
со = р|/Л2Л, (14-24)
т. е. длина радиуса-вектора р точки Р пропорциональна величине угловой
скорости тела.
Отметим, что из формулы (14.23) вытекает
2й
= (14.25)
ЛО
т. е. проекция угловой скорости тела на направление момента количеств дви-
жения в рассматриваемом случае является постоянной величиной.
Проведем теперь через точку Р касательную плоскость к эллипсоиду инер-
ции. Уравнение этой плоскости имеет вид
IХхх'-\-1 Ууу'Izzz'— (14.26)
где *', у', г'—текущие координаты касательной плоскости, а х, у, г — коорди-
наты точки Р-
Используя формулы (14.6) и (14.22), запишем вектор Kq в виде
Kq= /jc05*! 4* Iy^yi + 7
или
Ko= — (/Xxt -f- /yyj +1 Zzk).
Тогда, вводя радиус-вектор текущей точки касательной плоскости
г ==x'i+y'j-(-г'к,
представим уравнение (14.26) в виде
£к0-г = 1. (14.27)
Уравнение плоскости, перпендикулярной к вектору момента количеств
движения и находящейся на постоянном расстоянии от неподвижной точки
тела, как известно из аналитической геометрии, имеет вид
где г — радиус-вектор текущей точки плоскости, a d — расстояние от начала
координат.
Эта плоскость будет касаться эллипсоида инерции в точке Р, если вы-
полняется равенство
328
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл XIV
вытекающее из соотношений (14.27) и (14.28). Отсюда, принимая во внимание
(14.24), получим
d = ~^ = const (14.29)
"о
Следовательно, касательная плоскость, проведенная в точке Р к эллипсоиду
Рис. 14.5.
инерции, перпендикулярна к вектору момента
количеств движения и находится на постоян-
ном расстоянии d, определяемом форму-
лой (14.29), от неподвижной точки тела. Отсюда
следует, что эта плоскость будет неподвижной
по отношению к неподвижной системе коорди-
нат, так как вектор Ко является постоян-
ным вектором. Эллипсоид инерции касается
этой плоскости в точке Р, находящейся на
мгновенной оси вращения; поэтому скорость
точки касания равна нулю.
Таким образом, движение по инерции
твердого тела, имеющего одну неподвижную
точку можно представить как качение без
скольжения эллипсоида инерции по неподви-
жной плоскости, перпендикулярной к моменту количеств движения и находя-
щейся на постоянном расстоянии от центра эллипсоида (рис. 14.5).
§ 14.4. Устойчивость вращения твердого тела
вокруг главных осей инерции
Предположим, что твердое тело, имеющее одну неподвижную
точку, вращается по инерции с постоянной угловой скоростью Й
вокруг некоторой оси, совпадающей с одной из главных осей
инерции. Не нарушая общности, будем считать, что ось вращения
совпадает с главной осью инерции г. Тогда
сол = 0, (0^ = 0, coz = Q = const.
Эти значения проекций угловых скоростей можно рассматривать
как решение динамических уравнений Эйлера (14.10).
Выясним, будет ли такое вращение тела устойчивым, т. е.
изменится ли оно, если сообщить телу произвольное, но доста-
точно малое изменение вектора угловой скорости (например, неболь-
шим ударом по телу), или это движение в основном сохранится,
вызвав только очень малые колебания оси вращения г.
Итак, пусть вектор угловой скорости Й тела, вращающегося
равномерно вокруг оси г, получил небольшое возмущение, в резуль-
тате которого проекции угловой скорости изменили свои значения
и сделались равными
= (Оу = (О2, (Ог = Й 4“ ®з,
причем в начальный момент возмущения (Оц со2 и “з малы по срав-
нению с Й. Внесем эти значения и>у и озг в уравнения Эйлера
§ 14 41
УСТОЙЧИВОСТЬ ВРАЩЕНИЯ ТВЕРДОГО ТЕЛА
329
(14.10) и сгруппируем члены:
1Х + (7г - 1у) Й«2 + (7г - Iy) G)2®3 = о,
1у^+ (/. - Л) £2<О1 + цх - Л) <0^3 = о,
/^ + (7у-7г)<о1(Й2 = 0.
Предположим, что во все время движения сщ, <п2 и и3 остаются
малыми по сравнению с Q. Пренебрегая тогда их произведениями
(члены второго порядка малости), получим
7^ + (7г-7!/)Йй)2 = О,
7/“2 + (7*-7,)QW1 = 0,
J _ Л
lz dt ~u-
Из третьего уравнения следует, что w3 = w30, а первые два
уравнения легко приводятся к виду
^(2 4” IХ1 х ( У Л) W1 —О,
d^(i>2 , Q2 у > г \ ! г . п 4
~~di^~ + ТхГу х ( у w2 = О'
Если (Jx — 7г) (!у — /г) > 0, то <j)1 = <j).v и w2 = ®!/ выражаются
через тригонометрические функции и во все время движения
остаются малыми величинами (так как их начальные значения
были малы).
Если же (7Л. — 7г) (1У — 7г) < 0, то «4 = сох и со2 = <лу выражаются
через показательные функции и с течением времени принимают
сколь угодно большие значения.
Следовательно, условие устойчивости вращения тела по инер-
ции вокруг главной оси инерции г сводится к неравенству
(7Л-7г)(7,-7г)>0,
т. е.
/х>Л. или 7Л-<7г, 1у<1г. (14.30)
Таким образом, вращение вокруг главной оси инерции устой-
чиво, если момент инерции относительно этой оси является наи-
большим или наименьшим из трех главных моментов инерции. За-
метим, что проведенный анализ математически недостаточно строг,
так как точные уравнения заменялись приближенными, но
можно показать (мы не будем останавливаться на этом), что полу-
ченные результаты остаются верными и при строгом рассмот-
рении.
330
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
§ 14.5. Движение твердого тела, имеющего неподвижную точку,
под действием силы тяжести (случай Лагранжа)
Второй практически важный случай движения твердого тела с одной не-
подвижной точкой (случай Лагранжа) соответствует следующим условиям:
1) эллипсоид инерции для неподвиж-
ной точки тела является эллипсоидом
вращения (/х= /у);
2) центр тяжести тела лежит на
оси г, которая является осью симмет-
рии эллипсоида инерции и называется
осью динамической симметрии тела.
Введем две системы координат с
общим началом в неподвижной точке О
тела. Оси подвижной системы Охуг на-
правим по главным осям инерции тела,
а неподвижную систему координат вы-
берем так, чтобы ось гх была направ-
лена вверх (рис. 14.6).
указать три первых интеграла движения.
Во-первых, имеет место интеграл энергии
7’ + П = /1. (14.31)
Так как кинетическая энергия тела с одной неподвижной точкой равна
то, используя равенства (14.8), можно записать
7' = у Me2 + ip2sin2 0) + y 1г (ф cos 0 + ф)2.
Потенциальная энергия выражается формулой
П = Mgz1C = Mgzc cos 0.
Таким образом, интеграл энергии (14.31) записывается в виде
-i-/х (02 + ф2 sin2 0) 4--i-(ф cos 0 + ф)2 + Л4§гс cos 0 = й. (14.32)
Во-вторых, интеграл момента количеств движения относительно оси гх
(сила TWg параллельна оси гх):
Проекция момента количеств движения иа ось гх равна сумме проекций
на эту ось составляющих момента количеств движения по осям подвижной
системы координат Охуг, т. е.
KZ1 = KX sin 0 sin ср -f- Ку sin 0 cos ср + Кг cos 0.
Так как Кх = ^х^х< Ky = !yy и Кг=/гсог, а w-v> и иг определяются
по формулам (14.8), то будем иметь
KZ1 = /^.ф sin2 0 + 1г (ф COS 0 + ф) cos 0
и, следовательно,
/(ф sin2 0ф- 1г (фсоэ 0ф-ф) cos 0=сх. (14.33)
§ 14 5]
ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ
331
В-третьих, интеграл момента количеств движения относительно оси z
(линия действия силы Mg пересекает ось г):
Кг = ^2>
т. е.
/гог= Iz (фсоз0-|-ф) = с2. (14.34)
Интегралы (14.32) — (14.34) могут быть получены и непосредственно из ди-
намических уравнений Эйлера *).
Используя интегралы (14.33) и (14.34), исключим из интеграла энергии
(14.32) фиф.
Из формулы (14.34) найдем
ф cos 8-(-ф =у-. (14.35)
' Z
Формулу (14.33) перепишем в виде
^=^.(^О8 0 + Ф)со3? (14.36)
г Iх sin2 6 ' .
Подставляя теперь выражения (14.35) и (14.36) в интеграл энергии,
будем иметь
у со9 °=Сз’
% alii V
где
, 1 с!
с3-/г 2
Полученное уравнение перепишем в виде
/х02 sin2 6= —(Cj— сч cos О)2— 2MgzcIx sin2 6 cos 0-1-2^/^ sin2 0.
Оно представляет собой дифференциальное уравнение первого порядка отно-
сительно 0. Для его исследования введем замену
и = cos б; тогда и = — 0 sin 0
и, следовательно,
/% и2 = — (сх — с2и)2 — 2Mgzclx (и — и3) + 2c3Ix (1 — и2).
Вводя обозначение
f (u) = -\S1-c2u)2-2MgzcIx (u-u2) + 2Ixc3 (1 -и2), (14.37)
будем иметь
Ixu2=f(u), (14.38)
откуда
Время t выражается через и эллиптическим интегралом, а следовательно, и
эллиптической функцией t. Зная и как функцию /, мы тем самым опре-
*) Суслов Г, К, Теоретическая механика,—М.: Гостехиздат, 1944.
332
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
деляем угол нутации 8 как функцию времени I. Используя уравнения (14.35)
и (14.36), определяем затем ф и ср как функции времени. Таким образом,
поставленная задача приводится к квадратурам.
, Мы не будем проводить операции интегрирования, а постараемся выяс-
нить характер движения, исходя из свойств функции f (и). Согласно равенству
(14.38) функция f (и)ЭгО. Поэтому в некоторой области значений и, заключен-
ных между —1 и -f- 1 (так как и = соз6), функция [(и) должна быть поло-
жительна. Учитывая также, что
f (— оо) = — оо,
f(+ 1) = -(с!-с2)2<0,
/(-1) = -(п + г2)2<0,
f(+ со) = + оо,
мы заключаем, что кубическое уравнение f (и) = 0 имеет три вещественных
корня, «j, и2, и3 (и1<и2<и3), а график функции f(u) имеет внд, изображен-
ный на рис. 14.7. Таким образом, для
действительного движения и заключено
между Ui и и2.
Так как и = cos 6, то угол нутации 6
при движении тела будет изменяться
в пределах
82<е<81, (14.40)
где 6х = arccos ult 02 = arccos и2.
Для наглядного представления о
характере движения тела построим
сферу единичного радиуса с центром в неподвижной точке тела. Отложим на
оси г единичный вектор, конец которого назовем апексом. Очевидно, что апекс
будет все время находиться на поверхности построенной нами сферы. В силу
условия (14.40) апекс все время будет находиться в полосе между двумя
параллелями, соответствующими углам и 62 (рис. 14.8). Вид траектории
апекса в этой полосе зависит от скорости прецессии ф.
Приведем без доказательства три возможных случая движения апекса.
1. Скорость прецессии ф сохраняет знак и не обращается в нуль. В этом
случае траекторией апекса будет волнистая кривая, касающаяся граничных
параллелей (рис. 14.8, а).
2. Скорость прецессии ф сохраняет знак, но обращается в нуль. Очевидно,
что ф может быть равной нулю лишь при 6 = или 6 = 62 (доказывается, что
только при 6 = 62), иначе ф изменила бы знак во время движения. Траекторией
апекса будет кривая с точками возврата (сферическая циклоида). Вид траек-
тории показан на рис. 14.8, б.
§ 14.6]
ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ТЯГОТЕНИЯ
333
3. Скорость прецессии ip меняет знак во время движения. В этом случае
траекторией апекса будет кривая с петлями (рис. 14.8, в).
Рассмотрим случай, когда движение будет регулярной прецессией (0 = 0О =
= const, ф = const и ф = const). Это будет иметь место при и1 = и2 = “о (т- е>
корни уравнения /(и) = 0 кратны), или
Si = 62 — 0о> . _
и
• Oi — Сп COS 0q . С2 ,
ф = -Ц 7 „ . ’ “ = п = const, ф = — п COS 00 = П1 = const.
Y Ix sm2 0o Ц
Уравнение /(и) = 0 будет иметь кратные корни, если одновременно
/' (ио) = О, или
с2 хМ«гс (1-3“о)-2/Л“о = О- <14 41)
^тому уравнению должны удовлетворять начальные условия, чтобы осущест-
влялось регулярное прецессионное движение.
Условие (14.41) можно упростить. Действительно, при регулярной пре-
цессии 0 = 6o = const, ip=n = const, 
Сз= 2ZHiC-«Sj+Л1^С“°=- ~ M8ZcU°'
Подставляя эти значения для clt с2 и с3 в уравнение (14.41),, получим
‘x'z {пио + п1) П (1 - “о) - ГХМ&С (1 - “о) - /Ж (1 - “о) = °-
После деления на /Л(1— ul) и замены uo = cos0o будем иметь
(1 х— Iп2 cos 0Q— IznnxMgzc = 0. (14.42)
Это уравнение представляет собой условие существования регулярной пре-
цессии в случае Лагранжа.
Отметим, что при движении по инерции при 1х=1у=£ 1г тело всегда
совершает регулярную прецессию, а в случае Лагранжа только при началь-
ных условиях, удовлетворяющих условию (14.42). При движении по инерции
ось прецессии совпадает с неизменным направлением вектора момента коли-
честв движения, а в случае Лагранжа ось прецессии вертикальна.
§ 14.6. Главный вектор и главный момент сил тяготения
С развитием космической техники возникли новые задачи механики,
в частности большое значение приобрело исследование движения искусствен-
ного спутника Земли (ИСЗ) относительно его центра масс. Это движение
может быть вызвано различными силами. Учитывая характер настоящего руко-
водства, мы ограничимся постановкой задачи и исследованием некоторых
частных случаев движения ИСЗ относительно центра масс под действием
334 ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ [Гл XIV
центрального поля сил тяготения, создаваемого Землей, в следующих пред-
положениях *):
1. Размеры ИСЗ конечны, но они малы по сравнению с расстоянием R
от центра Земли О до центра масс спутника. Иначе говоря, если I — макси-
мальный линейный размер спутника, то отношение 1/R значительно меньше
единицы:
^-.<1. (14-43)
2. Предполагается, что равнодействующая сила F, с которой Земля дейст-
вует на материальную точку массы т, находящуюся вне Земли, определяется
законом всемирного тяготения
F = -P^r- О4-44)
где р = /М — гравитационный параметр Земли (М — ее масса, f — гравитацион-
ная постоянная), г — радиус-вектор, проведенный из центра Земли О к мате-
риальной точке. Таким образом, пред-
полагается, что Земля создает обыч-
ное ньютоновское поле сил притяже-
ния.
3. Не учитывается движение Зем-
ли относительно Солнца, т. е. пред-
полагается, что Земля неподвижна.
Построим две системы подвижных
координатных осей: первая система
Ох0у0г0 с началом в центре Земли О
и осью Огд, проходящей через центр
масс С спутника; вторая- система
Cxiy^i с началом в центре масс спут-
ника и осями Хг, yt, z1; параллель-
ными осям х0, Уо> г0 (оси Ог0 и Czi
в ИСЗ точку массы dm, положение
которой относительно координатной системы Cx^Zl будем определять радиу-
сом-вектором р или координатами Хр yi, zt. На основании (14.43) будем счи-
тать отношения Xi/R, yjR и zjR членами первого порядка малости. Проведем
теперь из центра Земли радиусы-векторы г и R (см. рис. 14.9). Имеем
r=R + p. (14.45)
Сила dF, с которой Земля действует на выбранную точку, определяется
формулой (14.44):
dF=— — г dm. (14.46)
Отсюда, пользуясь равенством (14.45), найдем проекции силы dF на оси
Х1, У!,
dFx=—ii~dm, dF =-—y,~dm, dF =—n^~^dm. (14.47)
Возводя обе части равенства (14.45) в скалярный квадрат, получим
r2=«2+2R-p+p2 = ^2+2/?z1+x? + i/f + 2?-
*) Более подробное изложение этого вопроса, свободное от некоторых
сделанных ниже предположений, можно найти, например, в монографии:
Белецкий В. В. Движение искусственного спутника относительно центра
масс. — М.: Наука, 1965. Там же дано исследование влияния других факторов
(аэродинамических сил, магнитного поля Земли, светового давления и т. п.)«
на движение ИСЗ относительно центра масс.
совпадают — см. рис. 14.9). Выделим
§ 14.6]
ГЛАВНЫЙ ВЕКТОР И ГЛАВНЫЙ МОМЕНТ СИЛ ТЯГОТЕНИЯ
335
Следовательно,
1 1 Л , о г1 . +
Т-Щ1+2Я +----------' <14-48)
3
?-г-('+2%+,,!+«-+г!) ’• <14Л9>
Разложим левую часть равенства (14.49) в ряд бинома Ньютона и ограничимся
членами первого порядка малости *). Имеем
Внеся это выражение для 1/г3 в равенства (14.47), получим с принятой точ-
ностью
dFxt=~^^dm’ dF^--^dm + ^^dm. (14.51)
Интегрируя эти равенства по массе всего спутника и учитывая соотношения
x1dm = 0, ^y1dm = 0, ^z1dm=0 (14.52)
(начало координат совпадает с центром масс спутника С), найдем проекции
главного вектора F сил притяжения Земли
Fx, = 0. ^=0, (14.53)
где т— масса спутника.
Из этих выражений видно, что с принятой точностью размеры ИСЗ не
влияют на главный вектор сил притяжения Земли и, следовательно, центр
масс спутника движется по эллипсу, один из фокусов которого совпадает
с центром Земли О (см. главу IV). Заметим, что такая постановка задачи (она
называется ограниченной) применяется не только при изучении движения ИСЗ
относительно центра масс, но и в классических задачах о прецессии оси
Земли и либрации Луны.
В дальнейшем будем считать, что координатная плоскость CxjZt (следо-
вательно, и плоскость Ох0г0) совмещена с плоскостью л орбиты центра масс
спутника. Тогда оси i/х и у0 будут все время перпендикулярны к неподвижной
плоскости орбиты, а ось xt будет совпадать с ее трансверсалью (см. рис. 14.9).
Построенная таким образом координатная система Cx^Zi называется орби-
тальной системой.
Перейдем теперь к вычислению главного момента сил тяготения Земли
относительно центра масс С. Найдем сначала момент dMg силы dF,’приложен-
ной к выбранной точке с массой dm. Имеем
dM£ = pXdF = 1 Х1 dF Xi j У1 dFvl k Z1 d\
*) Ряд бинома Ньютона
(1 +%)“ = 1 4-ах +- (а-1) 2! x2 + ...
сходится абсолютно и равномерно для всех х, удовлетворяющих условию
|х| < 1.
336
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
Отсюда найдем моменты относительно осей ylt гг:
dMex^yldFz-z1dPyi, dMeyi = z1dFXi-x1dFZi,
Mez-\dPy-y^FXt,
или, пользуясь равенствами (14.51),
dMe =3 уЛ drn — ^y! dm,
v> к3 Xй
dMyl = —3^xizidm + ^zxidm< (14.54)
dM‘ =0.
2, J
Интегрируя эти равенства по массе всего спутника и учитывая (14.52),
получим значения моментов сил тяготения относительно орбитальных осей
Х1, У1, Z1-.
(14-55)
где I и /х —соответствующие центробежные моменты инерции.
Так как спутник вращается относительно орбитальных осей, то центро-
бежные моменты инерции !х и I являются переменными величинами.
Для того чтобы перейти к постоянным моментам инерции, введем еще одну
систему координат Схуг, в которой оси, жестко связанные со спутником,
направлены по главным центральным осям инерции спутника (рис. 14.10).
Положение новой координатной системы Cxyz относительно орбитальной системы
Cxji/jZj будем определять таблицей направляющих косинусов:
X У 4» 2
*1 а, а2 а3
У1 Pi З2 Рз
Z1 Yi Y2 Y3
Из девяти величин а*, (3*, у* (А=1, 2, 3) независимых только три, так
как направляющие косинусы удовлетворяют трем условиям единичности и трем
§ 14 71
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ ДВИЖЕНИЯ ИСЗ
337
условиям ортогональности:
а^+а|+аз = *>
Р? + ^+₽! = 1.
Y1 +?2 +Тз= 1>
а1Р1 +а2Рз + а,,Рз— 0>
Yi«i+У2а2 + Тзаз = 0,
Т1а1 + Тза2 + Тз&з = 0.
(14.56)
(14.58)
Таблица косинусов представляет ортогональную матрицу А, равную обрат-
ной матрице А*1. Поэтому каждый элемент этой матрицы равен своему алгеб-
раическому дополнению, в частности,
Т1 = а2Рз —«зРз- Y2 = a3Pi —«1Рз, Тз = а1Р2—«2₽1- (14.57)
Обозначим моменты инерции спутника относительно осей х, у, г через 1Х,
1у, 1г соответственно. Тогда, пользуясь формулами (12.29) и учитывая приня-
тые здесь обозначения, получим при xc = yc = zc = 0
Ixtzt = ®1Y1 (Iz— I^)+а2?2 (Iz Iy)<
= P1Y1 Oz—Ci-) + fCY2 (lz~ ly)-
Момент относительно оси x вычислим по формуле
Щ=м'а1+м^1+м'гЛ.
Внесем в это равенство значения Л4^, Л4® и Л4^ из (14.55), а затем вос-
пользуемся формулами (14.58). Тогда после очевидных преобразований получим
Мх=3]^(!г-1у)Ъ («хРа-а2Р1).
или, пользуясь последней формулой (14.57),
(14.59)
(1у-1х) Т1у2
(две другие формулы получены аналогичным методом).
Формулы (14.59), определяющие проекции главного момента сил тяготения,
действующих на ИСЗ, содержат не переменные, а постоянные моменты инерции;
кроме того, они симметричны. Этим они выгодно отличаются от формул (14.55).
§ 14.7. Дифференциальные уравнения движения ИСЗ
относительно центра масс
Обозначим через £2 абсолютную угловую скорость ИСЗ (скорость относи-
тельно осей С£т]£, имеющих начало в центре масс спутника и перемещающихся
поступательно относительно инерциальной системы отсчета,—эти оси на
рис. 14.9 не показаны). Пусть Qx, Qy, Qz— проекции этого вектора на оси х,
у, г соответственно. Воспользуемся динамическими уравнениями Эйлера (14.7),
внеся в них значения моментов Мех, Му и Мег из равенств (14.59) и заменив
338
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
одновременно вектор <в на £2. Тогда получим *)
Iх + (4г /у) £2(/£2г = 3 j-- (4г “ 1 у) ТгТз ,
dQu ц
fy ~df h(^x Iг) йгйл = 3 (Iх fg) ТзТ1 >
Iz + (lу ~ Л) QxQy = 3 i (Iy~Ix) V1V2).
(14.60)
Эти три уравнения содержат шесть неизвестных функций: Qv, Q&, Q-, у1(
у2, Тз- Поэтому их нужно дополнить уравнениями, определяющими закон из-
менения направляющих косинусов. Для этого обозначим через <в угловую
скорость вращения орбитальной системы координат и через ix, jj, кг —орты
ее осей. Так как плоскости Ох0г0 и Cxlzl неподвижны, то орбитальная система
вращается вокруг неподвижной оси Оу0. Поэтому
Воспользуемся формулами (том I, глава XIII)
dkt
dF = “xki-
(14.61)
dit ,
-5r = -<ok1,
kiXii = h.
dkj
IT-05'1’
dii . dji
d7 = “x^ dF=“xb
или, пользуясь (14.61) и формулами
hX ji = k], jiXk1 = i1,
^- = 0,
dt
Для того чтобы спроектировать эти равенства на подвижные координатные
оси Схуг, скрепленные с ИСЗ, нужно выразить абсолютные производные, стоя-
щие в левых частях равенств (14.62), через локальные производные. Имеем
dix dii , ~ ,
1Г=л+йх,1 = -“к1-
Проектируя обе части этого равенства на оси х, у, г и учитывая, что про-
екции координатных ортов равны соответствующим направляющим косинусам,
найдем (две вторые группы уравнений получены из (14.62) аналогичным ме-
получены из (14.62)
найдем (две вторые группы уравнений
тодом)
dai Л
= а2Йг — азйу — соу!,
da2 г. г.
= а3й х — а!Йг — иу2,
d«3 ъ
__ ' ’ — ai£2j/ И2ОЛ й>Уз>
dyx • ~
~df — Тг£2г — Тз£2 у + ЫЛ1,
dy»
~d(~~ Тз^х — wa2>
dyo
~df = У1П у — Уг£2 х + <°аз-
(14.62)
(14.63)
^ = р2Йг-₽3Й,,
^=fW~|W
-^- = Pi£2^

*) Уравнения Эйлера (14.7) выведены для случая, когда тело имеет одну
неподвижную точку. Так как теоремы об изменении момента количеств движе-
ния относительно центра масс и неподвижной точки имеют одну и ту же
форму, то динамические уравнения Эйлера (14.7) применимы и в данном случае
(см. формулы (9.9) и (9,45)),
§ 14 8]
ОТНОСИТЕЛЬНОЕ РАВНОВЕСИЕ ИСЗ
339
Эти девять кинематических уравнений (они называются обобщенными урав-
нениями Пуассона) вместе с тремя динамическими уравнениями Эйлера (14.60)
составляют полную систему дифференциальных уравнений движения ИСЗ от-
носительно центра масс. В этих уравнениях 1Х, /у, /г и ц— известные посто-
янные величины, R и со — в общем случае известные функции времени, опреде-
ляемые из кеплерова движения центра масс спутника, Qv, Qyt Qz, aft,
(&=1, 2, 3) —искомые функции времени. He останавливаясь на методах реше-
ния этих уравнений (в общем виде они решаются только для частных случаев),
заметим, что шесть первых интегралов нам известны — это равенства (14.56).
§ 14.8. Относительное равновесие ИСЗ
Большое практическое и теоретическое значение имеют условия относитель-
ного равновесия ИСЗ, т. е. условия, при выполнении которых спутник не будет
перемещаться относительно орбитальной системы координат Cxxj/iZj. Мы будем
решать эту задачу в предположении, что центр масс ИСЗ движется по окруж-
ности радиуса R. Как известно, в этом случае угловая скорость ы вращения
орбитальной системы CxiyiZi определяется равенством
ц>2 = ^ = const. (14.64)
При равновесии ИСЗ относительно осей xlt ylt Zi все направляющие коси-
нусы a*, ft* и уь будут постоянными числами; при этом девять обобщенных
уравнений Пуассона обращаются в тождества (читатель без труда может про-
верить это самостоятельно). Кроме того, при относительном покое абсолютная
угловая скорость спутника О будет равна угловой скорости <в вращения орби-
тальной системы Cxxj/xZj, т. е. Й =<в, или, учитывая равенство (14.61),
O = coj1 = coj. (14.65)
В проекциях на оси х, у, г, жестко связанные с ИСЗ, будем иметь
йу===С0р2> ^2 — ирз,
причем все эти величины в силу сделанных предположений постоянны и,
следовательно, их производные по времени равны нулю.
Внесем эти значения проекций угловой скорости и значение р,/7?3 из ра-
венства (14.64) в уравнения (14.60) и сократим их на со2. Тогда получим
Uz Iу) РгРз = 3 Uz 1у)УгУз’ 1
Ux—Iг) РзРх = 3 (1Х—/г)Уз?1> г (14.66)
Uy — Iх) PiP2 = 3 (1у — Лс) YlYa- '
Будем считать, что среди моментов инерции /х, I у, 1г иет равных. Для
определенности положим
1у>1х>1г. (14.67)
Тогда, сокращая уравнения (14.66) на не равные нулю множители, получим
РзРз = ЗТ2Тз, РзР1 —ЗузТх, • Р1р2 = ЗУ1У2. (14.68)
Покажем, что среди корней этих уравнений имеются нулевые корни.
Действительно, предположим, что все корни уравнений (14.68) отличны от
нуля. Тогда, перемножая почленно эти уравнения, найдем
P?PiPi = 27V2Y2Y2,
или
РтРгРз = — 3 3 У1У2У3'
340
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
Деля почленно это равенство на уравнения (14.68), получим
Р1 = ±КЗур р2=±К Зу21 Рэ=±КЗу3.
Умножив первое уравнение иа второе иа р2 и третье на р3, а затем
почленно сложив, будем иметь
Pi + Pi + = ± V 3 (PiYi + РгТа + РзТз)-
Это равенство невозможно, так как согласно (14.56) его левая часть равна
единице, а правая —нулю. Это доказывает, что среди корней уравнений (14.68)
имеются нулевые. Пусть р3 = у2 = О. Тогда первое уравнение (14.68) превра-
тится в тождество, а второе и третье примут вид
YsYi = 0, ₽1р2 = 0-
Отсюда Yi = 0, Pi = 0, Тз=р2=1 (так как сумма квадратов одноименных коси-
нусов равна единице). Из полученного решения и равенств (14.56) следует, что
a2 = a3 = 0, at=l.
Таким образом, таблица направляющих косинусов в относительном равно-
весии ИСЗ имеет вид *)
Эта таблица йоказывает, что в сделанных предположениях относительное
равновесие ИСЗ возможно только в том случае, если его главные центральные
оси инерции х, у, г совпадают с координатными осями орбитальной системы
CxiPiZi- Иначе говоря, в относительном равновесном положении одна ось
эллипсоида инерции ИСЗ будет все время направлена к центру Земли, вторая
ось будет перпендикулярна плоскости орбиты и третья ось будет лежать
в плоскости орбиты, перпендикулярно прямой ОС.
Остановимся очень кратко на вопросе устойчивости положения относитель-
ного равновесия. В конце § 20.2 будет показано, что если к центру Земли
будет направлена большая ось эллипсоида инерции ИСЗ (ей соответствует
наименьший момент инерции), то это положение ИСЗ будет устойчиво **). (Здесь
мы пользуемся интуитивным представлением об устойчивости движения, кото-
рое было изложено в § 14.4. Строгое определение устойчивости равновесия
будет дано в главе XX, § 20.2.) В следующем параграфе мы дадим аналити-
ческое доказательство этого утверждения для плоскопараллельного движения
ИСЗ, а сейчас ограничимся рассмотрением одного примера.
*) Заметим, что другие решения уравнений (14.68) не дают принци-
пиально новых результатов и они будут совпадать с данным решением при
соответствующей замене обозначений осей yi, г±.
**) См. также цитированную на стр. 334 книгу В. В. Белецкого или
книгу: Румянцев В. В. Об устойчивости стационарных движений спутни-
ков,— М.: Изд-во ВЦ АН СССР, 1967,
§ 14.9] ПЛОСКОЕ ДВИЖЕНИЕ ИСЗ ПО КРУГОВОЙ ОРБИТЕ 341
Пусть спутник состоит из дНух точечных масс, соединенных невесомым
стержнем длины 2/ (спутник типа гантели). Согласно формулам (14.51) на каж-
дую точку будет действовать сила, проекции которой определяются равенствами
Fz,=-^m + 2^m’
где т — масса каждой точки.
В выражении для F первое слагаемое не влияет на вращательное дви-
жение спутника (при вычислении моментов оно выпадает —см. формулы (14.54)
и (14.55)). Поэтому в дальнейшем будем учитывать только второе слагаемое
в Fz . Составим дифференциальные уравнения силовых линий (см. 3.51))
dxi dy2 dgj
xi !У1 „ г1 ’
или, упрощая,
Отсюда
dxr _ dy-t _ dZj
*i ~ У1 ~~ 2zT‘
Ci
21 х? ’
г
1 </?
где Ci и С2 — произвольные постоянные интегрирования.
На плоскости х^ силовые линии и их направления имеют вид, показан-
ный на рис. 14.11 (аналогичная картина имеет место на плоскости у^). Из
рисунка видно, что если спутник-гантель находится в плоскости орбиты (пло-
скости ха), то каждая точечная масса
будет стремиться к оси zlt т. е. к ра-
диусу-вектору центра масс спутника.
Легко видеть, что если в начальный
момент ось тела (стержень спутника-
гантели) близка к направлению оси Zi,
то при малом возмущении движение
будет иметь колебательный характер
(то же явление будет происходить в
плоскости t/А). Таким образом, если
в начальный момент времени ось спут-
ника-гантели будет направлена к Зем-
ле, то это равновесное положение
будет устойчиво.
Обратим внимание теперь на то,
что для гантели Ix — Iy = ml2, = Ч
(ось г направлена по оси спутника-
гантели), т. е. момент инерции относительно оси наименьший. Это
для данного спутника устойчивостью относительного равновесного
при котором ось спутника с наименьшим моментом инерции
к центру Земли.
объясняется
положения,
направлена
§ 14.9. Плоское. движение ИСЗ по круговой орбите
Рассмотрим плоское движение ИСЗ относительно центра масс, предполагая,
что ось Су все время перпендикулярна плоскости орбиты. В этом случае рт =
= р3 = а2 = у2 = 0. Введем угол 8 между осями гх иг (рис. 14.12). Тогда будем
иметь
Vi = cos (zi, х) = — sin 8, уз = cos (гц г) = cos 0,
342
ТВЕРДОЕ ТЕЛО, ИМЕЮЩЕЕ НЕПОДВИЖНУЮ ТОЧКУ
[Гл. XIV
Обозначим через Йг угловую скорость ИСЗ относительно орбитальной
системы координат Cx^^zf, очевидно, что в плоском движении йг=0]р Абсо-
лютная угловая скорость й спутника опреде-
ляется равенством
й == 0) “I- Й f
или, учитывая значения йг и со (см. формулу
(14.65)), получим
й = (и + 'б) jj.
Следовательно, в рассматриваемом случае
плоского движения спутника проекции его уг-
ловой скорости на оси х, у, г, жестко связан-
ные с ним, будут равны
йд- = 0, йу = (£> + в, Йг = 0.
Внесем полученные значения для (й = 1, 2, 3) н йх, йу, йг в уравне-
ния (14.60), считая, что центр масс спутника движется по круговой орбите
(в этом случае величина и, определяемая формулой (14.64), является постоян-
ной). Из трех уравнении (14.60) первое и третье уравнения обратятся в тож-
дества, а второе уравнение примет вид
/у 'б +3ю2 (1Х — /г) sin 9 соз 0 =0. (14.69)
Будем считать, что 1х~>1г- Тогда это уравнение приводится к дифферен-
циальному уравнению движения математического маятника для угла 20. Дейст-
вительно, положив
ф = 20,
преобразуем уравнение (14.69) к виду
ф+й28шф = 0, (14.70)
где
fe2 = 3W2^~sA. (14.71)
‘у
Дифференциальное уравнение (14.70) совпадает по форме с дифференциаль-
ным уравнением движения математического маятника. Поэтому все выводы,
относящиеся к математическому маятнику, справедливы и для ИСЗ, совер-
шающего плоскопараллельное движение. В частности, отсюда следует, что рав-
новесное положение ИСЗ, при котором большая ось эллипсоида инерции
направлена к центру Земли, является устойчивым положением относительного
равновесия. Точно так же, как и математический маятник, ИСЗ может при
определенных условиях совершать круговые движения. Наконец, период малых
колебаний ИСЗ около устойчивого положения относительного равновесия опре-
деляется формулой
или, если принять во внимание равенство (14.71),
т*
где Г* =2л/ю —период обращения спутника вокруг Земли,
ГЛАВА XV
ТЕОРИЯ ГИРОСКОПОВ
§ 15.1. Введение
В современной технике под гироскопом *) понимают твердое
симметричное тело, которое может вращаться вокруг оси симметрии
с угловой скоростью, значительно превышающей скорость вращения
самой оси симметрии.
Примером гироскопа может служить волчок, имеющий непод-
вижную точку О (рис. 15.1).
Наиболее простым гироскопическим прибором является гиро-
скоп в кардановом подвесе (рис. 15.2). Ротор вращается вокруг
своей оси симметрии АА', причем ось вращения установлена
в подшипниках, укрепленных во внутреннем кольце, которое может
вращаться вокруг оси ВВ'. Вращение внутреннего кольца проис-
ходит в подшипниках, укрепленных в наружном кольце. Наконец,
наружное кольцо может вращаться вокруг оси СС в неподвижно
укрепленных подшипниках. Таким образом, ротор может совер-
*) Слово «гироскоп», буквально означающее «указатель вращения», обра-
зовано французским физиком Фуко из двух греческих слов: -уороп (гирос) —
вращение и mon&v (скопейн) — смотреть, наблюдать. Этими словами Фуко
назвал построенный им в 1852 г, прибор для демонстрации суточного враще-
ния Земли (см. § 15.4),
344
ТЕОРИЯ ГИРОСКОПОВ
[Гл. XV
шать три независимых друг от друга вращения вокруг осей,
пересекающихся в одной точке —центре ротора, которая при дви-
жении гироскопа остается неподвижной. Заметим, что точка пере-
сечения осей карданова подвеса или неподвижная точка называ-
ется точкой подвеса гироскопа.
Приведенные примеры гироскопов — волчок и гироскоп в кар-
дановом подвесе — представляют примеры гироскопов с тремя сте-
пенями свободы, так как для описания их движения необходимо
иметь три независимых между собой параметра. Если же, напри-
мер, у гироскопа в кардановом подвесе закрепить наружное
кольцо, то ротор гироскопа будет иметь возможность вращаться
только вокруг своей оси симметрии и оси внутреннего кольца,
т. е. будет иметь две степени свободы. Такой гироскоп называется
гироскопом с двумя степенями свободы.
Гироскоп обладает рядом замечательных свойств, позволя-
ющих широко использовать его в технике. Так, на всех морских
и океанских судах установлены гироскопические компасы, рабо-
тающие значительно точнее и устойчивее магнитных компасов;
широко применяются гироскопы для получения на движущемся
объекте (корабле, самолете, ракете) вертикали места, знание ко-
торой необходимо, в частности, для определения текущих коор-
динат объекта; с помощью гироскопов стабилизируются орудий-
ные платформы на корабле; гироскопы используются для измере-
ния с высокой степенью точности угловых и линейных скоростей
и ускорений; они применяются при прокладке туннелей, бурении
скважин и т. п. Подробное описание гироскопических устройств
и их теории читатель может найти в специальных руководствах *),
здесь же мы дадим только краткое изложение основных свойств
гироскопа, являющихся теоретической базой современного гироско-
пического приборостроения.
§ 15.2. Основное допущение элементарной (прецессионной)
теории гироскопов
Пусть гироскоп совершает быстрое вращение вокруг своей оси
материальной симметрии с угловой скоростью ©х, а эта ось в свою
очередь вращается с угловой скоростью ©2. На основании тео-
ремы о сложении вращений тела абсолютная угловая скорость
гироскопа св равна геометрической сумме угловых скоростей ©х
и со2, т. е.
0) — -J- ©2*
*) См., например, Лунц Я- Л. Введение в теорию гироскопов.—М.:
Наука, 1972; Ишлинский А. Ю. Механика гироскопических систем. — М.:
Изд-во ' АН СССР, 1963; Ройтенберг Я- Л. Гироскопы.—2-е изд. — М.:
Наука, 1975; Магнус К. Гироскоп; теория и применение. Перевод с немец-
кого,— М.; Мир, 1974,
§ 15.2] ОСНОВНОЕ ДОПУЩЕНИЕ ТЕОРИИ ГИРОСКОПОВ
345
Рис. 15.3.
собственного вращения ю,, направление
Построим систему координат Охуг, совместив ось г с осью
симметрии гироскопа (рис. 15.3, а). Тогда оси этой системы ко-
ординат будут главными осями инерции; следовательно, проекции
момента количеств движе-
ния на оси х, у, г опреде-
ляются равенствами
/Сх = I х®2х> Ку — I увд%у,
Кг = Iz (®] + 4>2г),
где 1Х, 1У и /г —соответ-
ствующие моменты инер-
ции гироскопа, причем
— 1у (так как ось г —
ось симметрии).
Таким образом, мы мо-
жем назвать три непарал-
лельных направления: на-
правление угловой скорости
абсолютной угловой скорости ю и направление вектора момента
количеств движения К (кинетического момента) тела *).
Для современных гироскопов угловая скорость пц собствен-
ного вращения достигает 6000 сек-1 (порядка 60 000 об/мин)
и даже более, в то время как угловая скорость со2 оси гироскопа
не превышает обычно 0,01 сек-1.
Найдем угол между кинетическим моментом К и осью сим-
метрии г. Для этого рассмотрим наиболее неблагоприятный слу-
чай, когда вектор угловой скорости вращения оси гироскопа ю2
перпендикулярен оси г, т. е. лежит в плоскости Оху, и, следова-
тельно, югг = 0. Найдем составляющую К* вектора К, располо-
женную в плоскости Оху. Имеем
К* = Кх + Кй = /ж®гг +
или, учитывая, что для гироскопа 1Х — 1У,
К * = /х (Ю2Х + ®ад) = Л ®2,
т. е. составляющая К* вектора К совпадает по направлению
с вектором (i)2 (рис. 15.3, б).
Согласно последнему равенству и рис. 15.3, б угол б между
вектором К и осью г определится из равенства
tg9 =
К* = Да2
К 2 / гС’Ч
*) Если нет специальной оговорки, го предполагается, что кинетический
мокент К вычисляется относительно точки подвеса гироскопа.
346
ТЕОРИЯ ГИРОСКОПОВ
[Гл. XV
Обычно для гироскопов /Д7г~0,6. Если, кроме того, при-
нять, что од Д:; 3000 сек1, a w2sc0,01 сект1, то получим следую-
щую оценку:
tg 9 ^0,6 ^- = 0,000002.
OUUU
Отсюда
8 0,4".
Очевидно, что эта величина пренебрежимо мала. Поэтому, не
внося большой погрешности, можно считать, что вектор кинети-
ческого момента К совпадает с осью динамической симметрии
гироскопа, т. е. можно положить
К = Дод =/годк, (15.1)
где к —орт оси симметрии гироскопа.
Теория, построенная на этом основном допущении', называется
элементарной или прецессионной теорией гироскопов*).
§ 15.3. Теорема Резаля
Для изучения движения гироскопа удобно пользоваться теоре-
мой Резаля, которая представляет по существу кинематическую
интерпретацию теоремы об изменении момента количеств движе-
ния материальной системы. Согласно последней имеем
= (15.2)
где Ме —главный момент всех внешних сил, приложенных к си-
стеме, относительно неподвижной точки.
Производная от К по времени представляет собой «скорость»
и конца этого вектора **), т. е.
и, следовательно, равенство (15.2) можно записать в следующей
форме:
и = Ме. (15.3)
*) Более строгое обоснование прецессионной теории гироскопов и рас-
смотрение условий, при выполнении которых она дает приемлемые для прак-
тики результаты, приводятся в книге: - Мер кин Д. Р. Гироскопические
системы.—2-е изд. — М.: Наука, 1974.
**) Слово «скорость» взято нами в кавычки, так как размерность вектора и
не совпадает с размерностью обычной скорости (размерность вектора К не
равна размерности длины). В дальнейшем, помня условность этого слова, мы
опускаем кавычки.
§ 15.4]
ОСНОВНОЕ СВОЙСТВО СВОБОДНОГО ГИРОСКОПА
347
Полученная формула представляет собой теорему Резаля: ско-
рость конца вектора момента количеств движения (кинетического
момента) равна главному моменту всех внешних сил.
Теорема Резаля имеет общий характер, но особенно удобно
пользоваться ею в теории гироскопов. Это объясняется тем, что
согласно равенству (15.1) величина и направление вектора кине-
тического момента нам известна — модуль вектора К равен 1ги>1у
а направлен он по оси динамической симметрии гироскопа. Поэтому
с помощью зависимости (15.3) мы можем получить закон движе-
ния оси симметрии гироскопа по заданному моменту внешних сил
или, зная закон движения оси гироскопа, определить момент сил,
под действием которых происходит это движение.
§ 15.4. Основное свойство свободного
(астатического) гироскопа
Рассмотрим гироскоп с тремя степенями свободы. Если сумма
моментов всех внешних сил, приложенных к гироскопу, относи-
тельно неподвижной точки равна нулю, то гироскоп называется
свободным (иногда его называют астатическим или уравновешенным).
Из этого определения видно, что центр тяжести свободного гироско-
па должен совпадать с точкой подвеса его. Если пренебречь массой
рамок и трением в осях, то уравновешенный гироскоп, установлен-
ный в кардановом подвесе, будет свободным.
Предположим вначале, что гироскоп не вращается, т. е. нахо-
дится в покое. Если ударом (толчком) сообщить оси такого невра-
щающегося гироскопа небольшую угловую скорость, то очевидно,
что в дальнейшем ось гироскопа будет равномерно вращаться
с той угловой скоростью, которую сообщили ей при ударе. Совер-
шенно иначе будет вести себя ось гироскопа, если до удара
гироскоп вращался с большой угловой скоростью вокруг оси
симметрии. В этом случае ось свободного быстро вращающегося
гироскопа останется практически неподвижной. Действительно,
для свободного гироскопа М1? = 0 и, следовательно, согласно фор-
муле (15.2)
К = const,
или, учитывая, что в рамках элементарной теории гироскопа
справедливо соотношение (15.1),
Дсщк = const.
Из этого равенства следует, что вектор к, определяющий направ-
ление оси гироскопа, сохраняет в инерциальной системе отсчета
неизменное направление.
Подействуем теперь на свободный гироскоп кратковременной
силой, возникающей при ударе. Так как скорость и согласно
348
ТЕОРИЯ ГИРОСКОПОВ
[Гл. XV
формуле Резаля (15.3) не будет равна нулю только в промежутке
времени действия этой кратковременной силы, то ось гироскопа
практически (в рамках прецессионной теории) не изменит своего
направления. Более полный анализ (см. § 14.2) показывает, что
удар вызывает в свободном гироскопе колебания его оси очень малой
амплитуды, но большой частоты *). Эти колебания (они назы-
ваются нутационными') не учитываются в прецессионной теории
гироскопов.
Доказанное свойство, являющееся основным для свободного
гироскопа, формулируется следующим образом: ось быстро вра-
щающегося свободного гироскопа устойчиво сохраняет свое направ-
ление в инерциальной системе отсчета’, удары или толчки могут
вызвать вибрацию оси гироскопа очень малой амплитуды, но не
отклонение ее от первоначального положения.
Из этого свойства следует, что при установке на Земле сво-
бодного гироскопа ось последнего будет сохранять неизменное
направление относительно далеких звезд. Следовательно, относи-
тельно Земли ось свободного гироскопа будет поворачиваться
в сторону, противоположную вращению Земли. В 1952 г. этот
опыт показал Л. Фуко (вслед за маятником, носящим теперь его
имя), дав тем самым второе экспери-
ментальное доказательство вращения
Земли. Этот же опыт дал основание
Л. Фуко назвать построенный им при-
бор гироскопом (см. примечание на
стр. 343).
Свойство свободного гироскопа ис-
пользуется и в технике. Так, если уста-
новить быстро вращающийся свободный
гироскоп на движущемся объекте (са-
молете, ракете, торпеде) и придать его
оси требуемое направление, например,
на звезду или цель, то ось такого гиро-
скопа будет устойчиво сохранять задан-
ное направление при любом движении
объекта. Это неизменное направление оси гироскопа может быть
использовано для управления и коррекции движения объекта,
ориентации его и т. п.
Проиллюстрируем сказанное. Пусть на ракете установлен свобод-
ный гироскоп, ось которого совпадала в начальный моменте осью
ракеты и была направлена на звезду (рис. 15.4, а). Предположим
далее, что ось ракеты должна сохранять заданное ей в начальный
момент направление, но в силу случайных причин отклонилась
*) См., например, книгу (стр, 131 — 135), ссылка на которую приведена
в примечании на стр. 346,
§ 15 5]
ЗАКОН ПРЕЦЕССИИ ОСИ ГИРОСКОПА
349
от него на некоторый угол а. Так как ось установленного на ракете
свободного гироскопа сохраняет первоначальное направление, то
возникновение угла рассогласования между осями ракеты и гиро-
скопа (рис. 15.4, б) немедленно зафиксируют чувствительные
элементы, которые подадут полученный сигнал на устройство, управ-
ляющее вращательным движением ракеты (см. стр. 221). В резуль-
тате ракета повернется в обратную сторону и ось ее займет перво-
начальное направление. Очевидно, что вся эта система может
быть использована не только для стабилизации заданного направ-
ления оси ракеты, но и для поворота ее*).
§ 15.5. Закон прецессии оси гироскопа
До сих пор мы рассматривали свободный гироскоп, т. е.
гироскоп, на который не действуют никакие внешние силы или,
точнее, для которого сумма моментов всех внешних сил относи-
тельно точки подвеса равна нулю. Рассмотрим
теперь гироскоп, к которому приложена внеш-
няя сила, создающая момент относительно точки
подвеса.
Пусть к гироскопу приложена сила Р, как
это показано на рис. 15.5. Если гироскоп не
вращается, то под действием силы Р ось гиро-
скопа будет перемещаться в сторону действия
силы. Если же скорость собственного вращения
гироскопа достаточно велика, то действие силы Р
вызовет совершенно другое движение оси ги-
роскопа. Действительно, момент Ме силы Р от-
носительно неподвижной точки будет направлен
перпендикулярно плоскости, проходящей через
линию действия силы и точку О, т. е. перпендикулярно плоско-
сти рисунка, на читателя. Согласно теореме Резаля конец векто
ра К приобретает скорость
ц = Ме.
Это означает, что ось гироскопа начнет движение в направлений
момента Ме перпендикулярно к линии действия силы.
Такая же картина будет наблюдаться и у гироскопа в карда-
новом подвесе, если к внутреннему кольцу приложить силу F
(рис. 15.6). Момент этой силы F направлен по оси внутреннего
*) Описанная схема использования свободного гироскопа носит принципи-
альный характер и в практических условиях она может быть реализована для
сравнительно короткого промежутка времени. Это связано с тем, что построить
свободный гироскоп очень трудно, так как полностью не устранимые силы
сопротивления создают моменты, уводящие с течением времени ось гироскопа
от первоначального направления.
350
ТЕОРИЯ ГИРОСКОПОВ
[Гл XV
Рис. 15.6.
кольца, и, следовательно, ось гироскопа начнет совершать враще-
ние вокруг оси наружного кольца. *
Движение оси гироскопа под действием приложенной силы
называют прецессией, а угловую скорость вращательного движения
оси — угловой скоростью'прецессии оси гироскопа.
Найдем модуль угловой скорости прецессии (о2. Согласно фор-
муле v = o) хг для скорости точки твердого тела в его вращательном
движении скорость и конца вектора К
определяется равенством
и = (в2х К.
Учитывая, что и = Ме и К = /гЮ1, найдем
Ме = (в2 х(15.4)
Отсюда
Ме /, к
®2==7^цДпТ’ <15-5)
где 9 — угол между осью гироскопа г и век-
тором угловой скорости прецессии (в2 (на
рис. 15.5 угол 6 = л/2, но в общем случае он отличен от прямого).
Из всего сказанного следует, что под действием внешних сил
ось быстро вращающегося трехстепенного гироскопа начинает пре-
цессировать. Скорость и конца вектора кинетического момента К,
направленного по оси симметрии гироскопа, равна по модулю и
совпадает по направлению с главным моментом относительно
точки подвеса внешних сил. Угловая скорость прецессии, опреде-
ляемая равенствами (15.4) и (15.5), пропорциональна главному
моменту внешних сил Ме и обратно пропорциональна кинетическому
моменту /.«ц гироскопа и синусу угла между осью гироскопа г
и вектором угловой скорости прецессии (в2. Это свойство гироскопа
называют законом прецессии оси гироскопа.
Закон прецессии лежит в основе устройства различных приборов;
этим же законом объясняются некоторые явления, на первый
взгляд кажущиеся парадоксальными. Приводимые ниже примеры
дают представление о применимости закона прецессии.
Пример 1. Гироскопический измеритель скорости подъема ра-
кеты. Для определения скорости подъема ракеты применяется
прибор, состоящий из гироскопа, помещенного в кожух (на рис. 15.7
гироскоп *) показан пунктиром); кожух вместе с гироскопом может
вращаться вокруг горизонтальной оси О, укрепленной на валике ОА,
который в свою очередь может вращаться вокруг вертикальной
оси Таким образом, гироскоп имеет три степени свободы: собствен-
*) В технических устройствах гироскопом служит обычно ротор электро-
мотора, помещенный в закрытый кожух, в котором укреплен статор,
§ 15 5]
ЗАКОН ПРЕЦЕССИИ ОСИ ГИРОСКОПА
351
ное вращение вокруг горизонтальной оси симметрии гироскопа г,
вращение вместе с кожухом вокруг оси, проходящей через точку О
перпендикулярно плоскости чертежа, и вращение всей системы
вокруг вертикальной оси £. Кинетический момент К гироскопа
направлен, как всегда, по оси г.
Предположим, что ракета под-
нимается вертикально вверх с уско-
рением w. Тогда, применяя прин-
цип Даламбера, можно считать
ракету неподвижной, если к силе
тяжести гироскопа mg присоеди-
нить силу инерции J = — mw. Обе
силы mg и J направлены в одну
сторону и они создают относи-
тельно точки О момент Ме, перпен-
дикулярный плоскости Ог£; мо-
дуль его определяется равенством
Ме = ma(g-j-u>),
где а — расстояние от центра масс
гироскопа С до точки О (см.
рис. 15.7). По теореме Резаля
Рис. 15.7.
скорость и крнца кинетического
момента гироскопа К будет равна Ме, а по закону прецессии
угловая скорость вращения оси гироскопа со2 равна Ме/К, или
та , . ,
где 1г — момент инерции гироскопа, а (щ —его угловая скорость
собственного вращения.
Обозначим через гр угол поворота оси гироскопа г относи-
тельно оси тогда = Внося это значение для со2 в по-
следнее равенство и учитывая, что w = dvfdt, где v — искомая
скорость подъема ракеты, получим
dip та / . dv \
dt \ dt J ’
Интегрируя и принимая во внимание, что при t = 0 v = 0 (на
старте ракеты ее скорость равна нулю), найдем
та / 1 \
Отсюда
v = -£-iib — at.
та 1 »
Из этого равенства видно, что, зная
скопа и время подъема ракеты, можно
угол поворота оси гиро-
определить ее скорость.
352
ТЕОРИЯ ГИРОСКОПОВ
[Гл XV
Наличие члена —gt создает некоторые неудобства. Поэтому
для непосредственного измерения скорости v подъема ракеты уста-
навливается дифференциальный механизм (см. рис. 15.7), нижней
шестеренке которого сообщается с помощью специального часо-
вого механизма угловая скорость = mga/I^, где — угловая
скорость прецессии оси гироскопа г при неподвижной ракете.
Очевидно, что угловая скорость Й вращения корпуса дифферен-
циала определится равенством
Q = 4 (®2 - ®з) •
или, если учесть значения со2 и со2,
,, difij та dv
dt 21^ dt ’
где ф>! —угол поворота корпуса дифференциала.
Интегрируя это равенство при прежних начальных условиях,
найдем

Отсюда
та
2T^V’
2/г(О!
та
Ф1.
V
ружено, что во время полета
Рис. 15.8.
Таким образом, вертикальная скорость подъема ракеты опре-
деляется по углу поворота корпуса дифференциала.
Пример 2. Прецессия артиллерийского снаряда. При стрельбе
из гладкоствольных орудий продолговатыми снарядами было обна-
ряды кувыркаются и при паде-
нии ударяются, как правило, не
головкой, где расположен взры-
ватель, а каким-либо другим
местом. Для того чтобы снаряд
в полете не кувыркался и при
падении ударялся головкой,
внутреннюю часть ствола орудия
начали делать нарезной, в ре-
зультате чего снаряд, вылетая
из ствола орудия, стал приоб-
ретать большую скорость соб-
ственного вращения вокруг оси симметрии. Это обеспечило устой-
чивость оси снаряда, кувыркание его прекратилось, и при па-
дении он начал ударяться головкой. Рассмотрим это на первый
взгляд далеко не очевидное явление более подробно.
Предположим, что быстро вращающийся вокруг своей оси
симметрии снаряд занимает в некоторый момент времени положе-
ние, изображенное на рис, 15.8. Так как теорема об изменении
§ 15 5]
ЗАКОН ПРЕЦЕССИИ ОСИ ГИРОСКОПА
353
момента количеств движения материальной системы относительно
центра масс С имеет ту же форму, что и относительно неподвиж-
ной точки (см. формулы (9.9) и (9.45)), то при изучении враща-
тельного движения ’снаряда его можно рассматривать как трех-
степенной гироскоп с неподвижной точкой С. На снаряд действуют
сила тяжести mg и силы сопротивления воздуха. В простейшем
случае можно считать, что последние приводятся к одной силе F,
направленной в сторону, противоположную скорости vc центра
масс снаряда С, причем точка А приложения силы F находится
на оси снаряда на расстоянии а от С (см. рис. 15.8). Сила тя-
жести mg не создает, очевидно, момента относительно точки С,
а момент силы сопротивления F относительно этой точки опреде-
ляется равенством
Ме = Fa sin у,
где у —угол между осью симметрии снаряда г и силой F, или,
что то же самое, вектором т, направленным по касательной
к траектории центра масс снаряда. В сделанных предположениях
момент Ме направлен всегда перпендикулярно плоскости стрельбы
(в условиях рисунка —на читателя).
По теореме Резаля скорость и конца вектора кинетического
момента снаряда К будет всегда равна Ме, а по закону прецессии
численное значение угловой скорости вращения оси снаряда со2,
направленной все время по т, определяется равенством
0)2 — К sin у ’
где К =/^ — кинетический момент снаряда (/г —момент инерции
снаряда относительно оси симметрии г, a coj —угловая скорость
собственного вращения его).
Пользуясь выражением для Ме и К, окончательно найдем
Так как вектор угловой скорости ®2 всегда направлен по т,
то ось снаряда г будет описывать в естественном трехграннике
траектории точки С конус с небольшим углом раствора, равным 2у
(см. рис. 15.8). Ось этого конуса совпадает все время с касатель-
ной к траектории центра масс, и, следовательно, снаряд, летя
без кувыркания, ударяется о цель своей головкой.
Пример 3. Прецессия оси волчка. Рассмотрим быстро вращаю-
щийся волчок, ось которого отклонилась от вертикали на угол у
(рис. 15.9). Сила тяжести mg, приложенная к центру тяжести
волчка С, направлена вертикально вниз. Эта сила создает момент
относительно точки опоры волчка, перпендикулярный плоскости,
проходящей через ось волчка г и вертикаль О£. Реакция опоры N
12 Н. В. Бутеиин и др.
354
ТЕОРИЯ ГИРОСКОПОВ
[Гл. XV
проходит через точку О, и, следовательно, ее момент относительно
этой точки равен нулю. Сравнивая волчок с артиллерийским сна-
Рис. 15.9.
рядом, мы видим, что между ними
имеется полная аналогия. Действи-
тельно, точка С, вектор т, сила F и
сила mg снаряда (см. рис. 15.8) соот-
ветствуют точке О, вертикали ОС, силе
mg и реакции N (см. рис. 15.9). По-
этому ось волчка будет описывать во-
круг вертикали ОС круговой конус с
углом раствора 2у, причем угловая ско-
рость прецессии определится равенством
ю2
_ mSa
I
где а — расстояние от точки опоры О до центра тяжести волчка,
1г — его момент инерции относительно оси симметрии г, coj — уг-
ловая скорость собственного вращения волчка.
§ 15.6. Момент гироскопической реакции
Рассмотрим теперь случай, когда движение оси гироскопа
задано и требуется определить возникающие при этом силы.
Будем считать, что гироскоп вращается с постоянной по величине
угловой скоростью (Dj вокруг своей оси
симметрии, а эта ось в свою очередь
вращается (прецессирует) с угловой ско-
ростью (й2. Так, например, ротор, по-
казанный на рис. 15.10, вращается
с постоянной угловой скоростью вокруг
своей оси симметрии, подшипники ко-
торой закреплены в рамке, вращаю-
щейся с угловой скоростью (в2 вокруг
вертикальной оси.
Момент внешних сил Мс, под дейст-
вием которых ось гироскопа прецесси-
рует с угловой скоростью (й2, опреде-
ляется равенством (15.4). Этот момент создается силами Q и Q',
приложенными к валу гироскопа со стороны подшипников А и В.
На основании третьего закона Ньютона можно утверждать,
что на подшипники Л и В со стороны гироскопа будут действо-
вать силы F и F', равные по модулю и противоположно направ-
ленные силам Q и Q'.
Главный момент этих
сил относительно неподвижной точки
равен по величине и противоположен по направлёнию моменту Ме.
§ 15.6]
МОМЕНТ ГИРОСКОПИЧЕСКОЙ РЕАКЦИИ
353
Такой момент называется моментом гироскопической реакции или
просто гироскопическим моментом.
Гироскопический момент Мг равен
Мг = -Ме = /г (®!Х®г).
Отсюда найдем модуль момента гироскопической реакции
= /zo)jO)2 sin 9, (15.6)
где 6 — угол между осью симметрии гироскопа и осью прецессии.
Пара сил F, F', момент которых относительно точки О равен
гироскопическому моменту, стремится совместить ось гироскопа
с осью прецессии.
Отметим, что тело, на которое действует
гироскопический момент, может под действием
этого момента совершать движение. Например,
пусть наружная ремка гироскопа в карда-
новом подвесе жестко укреплена на каком-
либо основании (рис. 15.11). Пусть угловая
скорость ротора равна (щ и направлена так,
как указано на рис. 15.11. Сообщим теперь
основанию угловую скорость <о>. Пара сил F,
F', момент которых относительно неподвиж-
ной точки равен возникшему гироскопиче-
скому моменту Мг, будет поворачивать внутреннее кольцо в на-
правлении, указанном на рис. 15.11 стрелкой, т. е. в направлении
кратчайшего пути совмещения вектора (оси гироскопа) с векто-
ром (в2 (угловой ci оростью вынужденной прецессии).
Это дает возможность сформулирогать следующее правило
(правило Г рюэ — Жуковского): при сообщении оси гироскопа при-
нудительной прецессии ось гироскопа стре-
7777777777777777
Рис. 15.12.
мится кратчайшим путем установиться па-
раллельно оси принудительной прецессии
таким образом, чтобы направления векторов
и <й2 совпали.
Изложенное свойство гироскопа широко
используется в технике. Приводимое ниже
описание одного прибора дает об этом ясное
представление.
Пример 4. Гироскопический измеритель
угловой скорости (гиротахометр). Рассмотрим
простейшую схему гиротахометра с двумя
степенями свободы (рис. 15.12). Гироскоп
вместе с кожухом может вращаться вокруг оси у, ось симметрии
гироскопа г удерживается в положении равновесия пружиной (на
рис. 15.12 показанр спиральная пружина). Предположим, что
корпус прибора вместе с основанием, на котором он установлен,
12*
356
ТЕОРИЯ ГИРОСКОПОВ
[Гл XV
вращается с постоянной угловой скоростью w2 вокруг оси
В результате возникает гироскопический момент, стремящийся
совместить ось гироскопа г с осью вынужденной прецессии
Величина этого момента определится равенством (см. формулу
(15.6) и рис. 15.12)
Мс = /г®!®2 sin fy — а\ = cos а,
или, для малых углов,
Л1Г =
При повороте оси гироскопа г на угол а пружина создает
момент, равный еа (с —коэффициент жесткости пружины), уравно-
вешивающий момент гироскопической реакции. Таким образом,
будем иметь
еа = /га>1со2;
отсюда
с
— а
2
Шкалу прибора размечают в единицах угловой скорости, и
стрелка указывает сразу искомую величину.
Вернемся к рассмотрению сил, возникающих при вынужденной
прецессии оси гироскопа.
При сообщении оси собственного вращения гироскопа или оси
какой-либо быстро вращающейся части машины принудительной
прецессии возникают гироскопиче-
ские давления на подшипники, в ко-
а а
к.----2---
Рис. 15.13
теперь сообщить
тикальной оси с
ческий момент
) торых укреплена ось.
|Q' Пусть ротор (маховик) вращается
X с угловой скоростью (Щ вокруг оси АВ,
и—закрепленной в подшипниках А и В
В7^ (рис. 15.13).
Если вес ротора Р, то статиче-
ские давления на подшипники будут
равны Р/2 для случая, когда ротор
находится на равных расстояниях от
подшипников (см. рис. 15.13). Если
ротору принудительную прецессию вокруг вер-
угловой скоростью (й2, то появится гироскопи-
Мг = /г ((Dj X(D2),
где 1г — момент инерции ротора относительно собственной оси
вращения.
Гироскопический момент, приложенный к оси, согласно пра-
вилу Грюэ— Жуковского будет стремиться повернуть ось так,
§ 15.6]
МОМЕНТ ГИРОСКОПИЧЕСКОЙ РЕАКЦИИ
357
чтобы векторы ©j и ю2 стали параллельными. Но этому препят-
ствуют подшипники А и В. Сила Q, приложенная к подшипнику А,
и Q', приложенная к подшипнику В, образуют пару сил, момент
которой равен гироскопическому моменту.
Так как векторы и ю2 в рассматриваемом случае взаимно
перпендикулярны, то величина гироскопического момента равна
Л4Г = ЛсохЮа.
Направлен гироскопический момент перпендикулярно к плоскости
рисунка, на нас. Момент пары сил (Q, Q') по величине равен Qa,
следовательно,
Qa =
откуда
О = О' = /гЮ1--2-
(15.7)
Силы Q и Q' и представляют собой гироскопические давления
на подшипники.
В рассматриваемом случае в подшипнике В статическое давле-
ние и гироскопическое давление имеют различные направления,
а в подшипнике А — одинаковое
направление. _____________________________
Задача 15.1. Определить макси- t-----
мальные гироскопические давления на ___
подшипники быстроходной турбины, I i |
находящейся на корабле, подвергаю- I * *1
щемся гармонической килевой качке _ . - .,
с амплитудой 9° и периодом 15 сек, и '
считая, что ось ротора турбины па-
раллельна продольной оси корабля. Ротор, имея вес 200 кГ и радиус инер-
ции 0,8 м, делает 18 000 об/мин; расстояние между подшипниками равно 1 м.
Рассмотрим рис. 15.14. При килевой качке изменяется угол дифферента
корабля. Закон этого изменения имеет вид
0 = 0 sin 1,
где по условию задачи
£) = 9° = ^_, 7=15 сек.
Принудительная прецессия ротора происходит вокруг оси, перпендикуляр-
ной к диаметральной плоскости корабля, т. е. к плоскости симметрии корабля,
проходящей через его киль.
Угловая скорость принудительной прецессии равна
• _ 2лО 2 л; ,
6 ~ -у— cos у- г.
Максимальная величина этой угловой скорости
• 2л£)
м2 “щах р •
358
ТЕОРИЯ ГИРОСКОПОВ
[Гл, XV
Так как ось вращения ротора и ось принудительной прецессии взаимно
перпендикулярны, то максимальное значение гироскопического момента будет
Л4Г= /(Ог(О2,
где / = — 0,64^13,06 кГ -м-сек2— момент инерции ротора, а
S
2л .18 000 ___ 2п2 1
“1 =----60----=6ООЯ СвК ’ “2 = 20Й5 ~ 15 •
Согласно формуле (15.7) максимальные давления на подшипники равны:
/ыгм, 13,06-600л
<? = <? =—р- ~-----[j----~ 16Ю кГ.
Гироскопический момент направлен по вертикали вверх или вниз в зави-
симости от знака 6. Силы Q и Q', приложенные к подшипникам, расположены
в горизонтальной плоскости перпендикулярно диаметральной плоскости корабля.
Эти силы, превосходящие в данном примере статические давления в 16 раз,
периодически (каждые 7,5 сек) меняют свое направление на противоположное,
способствуя тем самым преждевременному износу подшипников.
§ 15.7. Уравнения движения гироскопа в кардановом подвесе
Изложенная в предыдущих параграфах элементарная теория гироскопов
основана на пренебрежении нутационными колебаниями оси гироскопа. Рас-
смотрим теперь более общую теорию.
Сначала выведем дифференциальные уравнения движения гироскопа в кар-
дановом подвесе (см. рис. 15.2) с учетом массы наружной и внутренней рамок,
Пусть неподвижная система координат Оху)^ имеет начало в неподвижной
точке О. Ось Zj направим по оси вращения наружного кольца (рис. 15.15).
Начало подвижной системы коо’рдинат Охуг возьмем также в точке О и свяжем
эту систему координат с внутренним кольцом. Ось х направим по оси враще-
ния ротора, ось у — по оси вращения внутреннего кольца, а ось г— перпенди-
кулярно осям х и у, таким образом, чтобы система Охуг образовала правую
систему координат. Отметим, что линией пересечения подвижной плоскости Оху
и неподвижной Оху/х является ось у,
§ 15 7]
УРАВНЕНИЯ ДВИЖЕНИЯ ГИРОСКОПА
359
Положение ротора можно определить следующими тремя углами: углом <р
поворота ротора вокруг оси х, углом О', т. е. углом меЖду неподвижной осью Zf
и осью z (углом поворота внутреннего кольца вокруг оси у) и, наконец, углом
ф —углом поворота наружного кольца вокруг оси Zj. Угловая скорость <pi
направлена по оси х, угловая скорость ftj — по оси у, и угловая скорость фк£ —
по оси zT (рис. 15.16).
Векторы i, j, k—единичные векторы осей Охуг, а векторы i1( jj, kj—.
единичные векторы осей O^i/jZj.
Найдем теперь проекции угловой скорости внутреннего кольца и ротора
на оси подвижной системы координат. Для внутреннего кольца, которое совер-
шает вращение вокруг осей zT и у, имеем
<оЛ. = ф cos f-’^ + ft j =— ф sin ft, (£>y = b, n>z=ipcosft. (15.8)
Обозначая через p, q и г проекции угловой скорости ротора на оси х, у и г,
получим
р = ф—ipsinft, <7 = ft, г — зр cos ft. (15.9)
Проекция скорости наружного кольца на ось zT равна
* :
(Ог, =ф-
Мы не будем вводить систему координат, жестко связанную с ротором,
так как ротор представляет собой симметричное тело относительно оси х и
поэтому любая ось в плоскости уг для ротора будет главной осью инерции.
Однако для вывода уравнений движения ротора можно воспользоваться фор-
мулами (14.9). Будем только помнить, что введенная при выводе формул
(14.9) система координат Ох^у.^ в рассматриваемом случае является системой
координат Охуг. Проекции момента количеств движения ротора на оси х, у и
z согласно формулам (13.9) и (15.9) будут
= /х (ф — Ф sin ft),
Ку = 1уЯ = 1уЬ,
Kg = IZr = Iу Ф COS ft,
(15.10)
где 1Х— момент инерции ротора относительно его оси вращения, 1у = 1г=£ 1Х —
экваториальные моменты инерции ротора.
Для внутреннего кольца проекции момента количеств движения имеют
такой вид:
Kx = l'xti>x = — /хф Sin ft, Ky = It№y = Iy$, 7<г = /г(Ог = /гф COS ft, (15. 11)
где l'x, Iу, /г —моменты инерции внутреннего кольца соответственно относи-
тельно осей х, у и г. Наружное кольцо вращается только вокруг оси гх, и
для него имеем
= (15.12)
где 1'г,—момент инерции наружного кольца относительно ее оси вращения.
Перейдем к составлению уравнений движения ротора вокруг оси х *). На
основании первой формулы (14.9) имеем
at У z z у х
*) Николаи Е. Н. Теория гироскопов.—М.: Гостехиздат, 1948.
360 ТЕОРИЯ ГИРОСКОПОВ [Гл. XV
Используя соотношения (15.8) и (15.10), получим
(ф-фвшО)+<>фсозФ(/г—Iy) = Mext
где Мех — момент всех внешних сил, приложенных к ротору, относительно оси х.
Так как 1г = 1у, то
1Х (ф — ф sin О') = Л1®. (15.13)
Вокруг оси у вращаются как ротор, так и внутреннее кольцо. Для ротора
согласно второму уравнению (14.9)
_А+й)Л_юЛ=Л4-, (15.14)
где М'у —момент всех сил, действующих на ротор, относительно оси у.
Для внутреннего кольца
= (15.15)
где М"у — момент всех сил, действующих на кольцо, относительно оси у,
Складывая почленно уравнения (15.14) и (15.15), получаем
(Ку + Ку) + <Ог (Кх + Кх) - Ы.Г (К, + Кг) = Меу,
где мСу = Му -\-М'у —момент всех внешних сил, действующих на ротор и
внутреннее кольцо, относительно оси у.
Используя соотношения (15.8), (15.10) и (15.11), имеем
(1у-\-Гх) 0+ ф cos Ф (/хр —Лф sin О) 4-ф2 sin О cos О (l у + 1у) = Меи,
или
(ly + l'u) $ + ^хРф cos (jx—1у — /г) ф2 sin Ocos О = Л4®. (15.16)-
Перейдем теперь к составлению уравнения движения относительно оси zx.
Во вращении вокруг оси гг участвуют ротор, внутреннее и наружное кольца.
Так как ось zt неподвижна, то для ротора будем иметь
где
KZi = Кг cos О — Кх sin О
— проекция момента количеств движения ротора на ось гг; — сумма мо< .
ментов всех сил, действующих на ротор, относительно оси Zf.
Таким образом,
-^-(Xicos6'-KJ.sin6') = MP . (15.17)
Для внутреннего кольца уравнение движения относительно осн гх имеет вид
(15.18)
§ 157]
УРАВНЕНИЯ ДВИЖЕНИЯ ГИРОСКОПА
361
где
Кг, = К^ cos ft- Кх sin ft (15.19)
>— проекция момента количеств движения внутреннего кольца на ось гг;
Мъх к — момент всех сил, действующих па внутреннее кольцо, относительно
ОСИ 21-
Для наружного кольца имеем
-^-=Л^1К, (15:20)
где “ — момент всех сил, действующих на наружное кольцо, относительно
оси zv
Складывая почленно уравнения (15.17), (15.18) и (15.20) и учитывая ра-
венства (15.12) и (15.19), получим,
~^[(Кг + Кг) COS ft — (Кх+Кх) Sin '0'4-/г,'ф]=Л1*1,
где Mez —момент всех внешних сил, действующих на рассматриваемую систему
(ротор, внутреннее и наружное кольца), относительно оси гх; /^ — момент
инерции наружного кольца.
Принимая во внимание равенства (15.10) и (15.11), перепишем полученное
уравнение в виде
-^[(Jy~r Г) $ cos2 ft — (ixP—/x’i’sin ft) sin =
или
[(/у + Гг) COS2 ft + Гх Sin2 & + /г,] Ф — IxP sin ft — Ixpb COS ft—
—2 (ly + l'z — l'x) ’(’ft sin ft cos ft=MeZi,
Учитывая уравнение (15.13), найдем
[(/(, + 1г) cos2 ft4-/x sin2 ft + Zz’J ф —/xpft cos ft —
—2 (ly + l’z — Ix) ifft sin ft cos ft = Ai^ sin ft. (15.21)
Таким образом, дифференциальные уравнения движения гироскопа, в кардано-
вом подвесе имеют вид
1хР = Мех,
(ly + Iy) ft+/xPii’cosft — {Гх— 1у — Гг)ф sinft cosft = Al*, (15.22)
[(/41+ I'z) cos2 ft 4- Ix sin2 ft 4- /г,] ij> —/xpft cos ft—
— 2 {Iу 4- l'z — Гх) 4ft sin ft cos ft = MZt 4- Mx sin ft.
Решение этих уравнений представляет собой большие математические труд-
ности.
Предположим, что Мх = 0-, это значит, что полезный момент, вращающий
ротор вокруг его оси, уравновешивается моментом сил трения. Тогда
р = ф—ф sin ft = <o = const.
Для современных гироскопов угловая скорость ф собственного вращения
ротора значительно больше угловых скоростей рамок, следовательно, можно
принять и я» ф. Кроме того, предположим, что угол ft во все время движения
остается малым, и примем sinft = ft, cosft=l. Также пренебрегаем всеми чле-
362
ТЕОРИЯ ГИРОСКОПОВ
[Гл XV
нами, содержащими произведения угловых скоростей ф и и их квадраты.
Уравнения (15.22) при этом примут вид
+//оф = Л4*,
Вф—/А.<о4 = Л1®!>
(15.23)
где A = ly+ly, B=ly+Iz+ht-
Уравнения (15.23) называют техническими уравнениями гироскопа. Введем
величину Н = 1,ы, часто называемую кинетическим моментом гироскопа. Тогда
уравнения (15.23) примут вид
ЛФ-1-Яф=Л1*,
В^-НЬ^М^.
(15.24)
§ 15.8. Частные случаи движения гироскопа
в кардановом подвесе
Рассмотрим сначала случай, когда Л4^ = 0, Л4^=0. Уравнения (15.24)
при этом будут
Л+Н*-"' I (15.25)
Исключая из этих уравнений яр и ip, получим
Н2 •
Характеристическое уравнение этого линейного дифференциального уравнения
с постоянными коэффициентами имеет вид
Я2
а3+ два==0’
откуда находим корни характеристического уравнения
а1 = °, а2 = (у —, a3 = -iy
Общее решение уравнения запишется следующим образом;
^С1 + С2со5^ + Сз51п^,
где С1( С2 и С3— постоянные интегрирования.
Так как согласно уравнениям (15.25)
*i Д к
Ф= — О
и
л „ Н . Ht , „ Н Ш
$ = — С2 Г--^ Sin + С3 г___________ COS ,
V АВ у АВ у АВ К АВ
•Л я2 Ht Я2 . ш
-О* = — С2--cos -------С3-----sin' г - .
АВ К АВ АВ У АВ
§ 15 8]
ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ГИРОСКОПА
363
ТО
. Н Ht Ht \
Ф =—- С2 cos —yr—4-С3 sin - —- ,
В \ К АВ К АВ)
откуда, интегрируя, получим
, , /'Л' / _ . Ht Ht \ , _
ф = I/ — С2 sin -у—- — С3 cos у^.- +с4,
Г В \ К АВ V АВ)
где С4 —постоянная интегрирования. Пусть при / = 0 (начальный момент) 0’=0,
ф = 0, Ь — Ьо, ф = фо- Тогда уравнения для определения постоянных интегри-
рования будут иметь вид
С1+С2 = 0, с3-^=К
у АВ
-/4сз+с4=°,
следовательно,
= = Сз='Т’^<” С4=4^о-
С4 в общее решение, получим частное
Внося эти значения для С4, С2, С3 и
решение
„ В . Ht \ , V АВ а . Ht
0 =-----% 1 — cos—т=-1 ------О о sm -- - ,
Н У АВ) # У АВ
, КАВ , . Ht А . /. _ Ht \
Ф =-----Фо sm г__4---п<1 1 ~ cos л— .
V Н VАВ Н ° \ VАВ)
Из этого решения следует, что ось гироскопа будет совершать
В . А •
ное движение около положения '6 =----ф0, ф=—fy>. Частота
Н Н
называется* частотой нутации. Период нутацион-
ных колебаний
колебатель-
k=
V АВ
Если фо = О, то
„ Илв а . Ht
О’ sm г___,
Н уАВ’
, А г, /< Ht \
Ф =--Фо 1—COS—7=- .
Н \ УАВ)
Рис. 15.17.
Таким образом, сообщение кольцам гироскопа угловых скоростей приво-
дит их, а следовательно, и ось гироскопа в колебательное движение.
Рассмотрим еще случай, когда к внутреннему кольцу гироскопа приложена
постоянная сила Р (рис. 15.17). В этом случае Меу — аР, Мег =0 и уравнения
движения принимают вид
Л&+ Н^> = аР,
Вф-/М = 0,
(15.26)
364
ТЕОРИЯ ГИРОСКОПОВ
[Гл. XV
Общее решение этих уравнений складывается из общего решения однород-
ных уравнений (15.25) и какого-либо частного решения уравнений (15.26).
Частное решение будем искать в виде
Подставляя эти решения в уравнения (15.26), получим
НМ2 = аР, —НМ^О,
откуда
М1 = 0, Л12 = ^
Таким образом,
О’ — Ci 4- С2
Ht . Ht
cos 4- С3 sin —-—-,
V АВ VАВ
(С2 sin
\ Клв
С3 cos
+С«4-— А
Н
ф
Пусть начальные условия будут: при
/ = 0
Так как
О’=О, лр = О,
0,= '0'о>
л п Н . Ht „ Н
Ъ = —С2 ——=? sin — 4- С3 г_ cos _,
клв Клв Илв V ав
п Н HI , „ Н . Ht \ ар
С2 ——= cos 4- Сх ——sin г ) 4-
У АВ V АВ АВ VAB) Н
Ht
то уравнения для определения постоянных интегрирования имеют внд
^0=CsW’
, Н , аР
2 Клв + н ’
4'о=
откуда
В . , ВаР
Н ^»+ Н2 >
Г -
Сз Н Фо-
С,
г, В : ВаР
Cg-^ifo---
и, следовательно,
. В /, аР\/, Ht \
V =------тЬп------1 — cos г____
н \ н удв)
В аРВ\ . Ht
.Я Н* К АВ
, Уав 4 . • Ht
1------О0 sin Л,
Н у АВ
i|> =

4 =
О = С1-|- Cg>
0 =
С4 = ^-^о
— (1 — cos
Я Л
— А
н
§ 15 8]
ЧАСТНЫЕ СЛУЧАИ ДВИЖЕНИЯ ГИРОСКОПА
365
Пусть 6о = О, *j>o —0; тогда
„ аРВ /, Ht \
V =---- I — cos — — ,
ЯЧ У АВ )
. У АВ _ . Ht , аР ,
ф = —1--аР sm г Ч t.
Н* К АВ Н
(15.27)
Из уравнений (15.27) следует, что внутреннее кольцо будет совершать
нутационные колебания около положения
д*___аРВ
Н2 ’
а на равномерное вращение наружного кольца с угловой скоростью аР/H на-
кладываются нутационные колебания.
Очевидно, что чем больше Н — кинетический момент гироскопа, тем будут
меньше амплитуды нутационных колебаний. При больших Н нутационные коле-
бания являются колебаниями очень высокой частоты с пренебрежимо малой
амплитудой. В связи с этим во многих случаях нутационными колебаниями
пренебрегают и считают, что
аР
0, = 0, ф = -^-<.
Поэтому говорят, что ось гироскопа совершает чисто прецессионное дви-
жение с угловой скоростью i( = aPIH (§ 15.5).
ГЛАВА XVI
МЕТОД КИНЕТОСТАТИКИ
§ 16.1. Метод кинетостатики
Так же как и для одной материальной точки (см. § 5.7), диф-
ференциальным уравнениям движения материальной системы
можно придать форму уравнений статики. Этот метод часто при-
меняется в инженерных расчетах, особенно при определении дина-
мических реакций опор твердого тела.
Рассмотрим материальную точку Мк системы. Обозначим массу
этой точки через mk, ее ускорение — через wft и равнодействую-
щие всех активных сил, приложенных к точке, и реакций связей
соответственно — через Fft и RA. Тогда основному уравнению дина-
мики (второму закону Ньютона), написанному для каждой точки
системы:
miw/j = F* + Rft (£ = 1, 2, .... л),
можно придать вид уравнения статики
Fft + R* + Jft = 0 (&=1, 2....п), (16.1)
где сила инерции Jfe определена равенством (см. § 5.7)
Jft = — tnkwk. (16.2)
Складывая почленно все уравнения (16.1), получим
t F*+ X **+ X J* = °-
fe = l fe = l fe = l
n
Первая сумма У Fft равна главному вектору F всех актив-
t = i
п
дых сил, приложенных к системе, вторая сумма У R* — глав-
k = \
п
ному вектору R реакций связей и последняя сумма У Jft — глав-
fe=i
ному вектору J сил инерции. Таким образом, можем написать
F + R + J = 0, (16.3)
§ 16 1]
МЕТОД КИНЕТОСТАТИКИ
367
т. е. в каждый момент времени сумма главных векторов активных
сил, реакций связей и сил инерции движущейся материальной
системы равна нулю.
Выберем произвольный полюс О и проведем из него к точке
Мк радиус-вектор rft. Умножая каждое из уравнений (16.1) век-
торно на соответствующий rk слева и складывая все произведе-
ния, получим
п п п
У, rftxFft+ у rfexRft+ У r*xJft = 0.
fe=i ft=i fe=i
Первая сумма равна главному моменту Мо всех активных сил,
приложенных к системе, вторая сумма — главному моменту Мо
всех реакций связей системы, а последняя — главному моменту Мо
сил инерпии, причем все моменты должны быть вычислены отно-
сительно выбранного полюса О.
Следовательно, будем иметь
МоЦ-Мо + Мо = 0, (16.4)
т. е. в каждый момент времени сумма главных моментов актив-
ных сил, реакций связей и сил инерции движущейся материаль-
ной системы равна нулю.
При вычислении главных векторов F и R и главных момен-
тов Мо и Мо активных сил и реакций связей нужно учитывать
только внешние силы, так как главный вектор и главный момент
внутренних сил равны нулю.
Двум векторным уравнениям (16.3) и (16.4) соответствуют
шесть уравнений в проекциях на оси декартовых координат:
Fx-\-Rx-[- Jх — ^,
Fy-YFy-Y J £/ = 0,
Fx + Rz + J г — О,
Mx + Mf + м/ = 0,
М, + Л4?+< = 0,
М, + М?+М/ = 0.
(16.5)
За оси координат можно выбрать любую систему декартовых
осей, как неподвижных, так и перемещающихся произвольным
образом в пространстве, следует только каждый раз определять
соответствующие проекции главного вектора J и главного момента
Мо сил инерции.
Движение твердого тела вполне определяется этими шес-
тью уравнениями кинетостатики, точно так же как равновесие
твердого тела вполне определяется соответствующими шестью
368
МЕТОД КИНЕТОСТАТИКИ
[Гл. XVI
уравнениями (тремя уравнениями проекций и тремя уравнениями
моментов). Если рассматривается система, состоящая из несколь-
ких тел, то можно составить соответствующие уравнения кине-
тостатики для каждого тела в отдельности.
Из всего сказанного следует, что применение метода кинето-
статики для твердого тела требует прежде всего умения вычис-
лить главный вектор и главный момент его сил инерции. Зная
их проекции на выбранные оси координат, следует составить
уравнения кинетостатики (они отличаются от уравнений равно-
весия твердого тела только тем, что к активным силам и реакциям
связей присоединены силы инерции) и затем определить неизве-
стные величины.
Покажем теперь, что уравнения (16.3) и (16.4) представляют
математическую запись теоремы об изменении количества движе-
ния и' теоремы об изменении момента количеств движения мате-
риальной системы соответственно.
В самом деле, главный вектор всех сил инерции равен
п п п
j=2 jfe=— 2 2
k = \ k^\ A = 1
n
так как = Но сумма 2 mfcv/; = A4vc есть количество дви-
й = 1
жения Q материальной системы. Следовательно,
J=-4r = -Alwc. (16.6)
т. е. главный вектор всех сил инерции точек материальной си-
стемы равен производной по времени от количества движения
материальной системы, умноженной на —1.
Главный момент всех сил инерции равен
Mo = S r*xJft = — ^rkxmkwk.
, k=i t=i
dvb dvb d . .
Так как = a rtxmt-^- = y(r,.xmtvt), to
= (16.7)
и
где Ко = У, х mkvk — момент количеств движения материальной
Й = 1
системы.
Таким образом, главный момент всех сил инерции равен произ-
водной по времени от момента количеств движения материальной
системы, умноженной на —1.
§ 16.2]
ГЛАВНЫЙ вектор и главный момент
369
Заменяя в уравнении (16.3) главный вектор сил инерции выра-
жением (16.6), а в уравнении (16.4) главный момент сил инер-
ции выражением (16.7), получим соответственно теоремы об изме-
нении количества движения и момента количеств движения
материальной системы.
§ 16.2. Главный вектор
и главный момент сил инерции твердого тела
На основании выражения (16.6) главный вектор сил инерции
твердого тела может быть найден по формуле
J = — Mwc, (16.8)
т. е. главный вектор сил инерции твердого тела равен силе инер-
ции его центра масс, в предположении, что в нем сосредоточена
масса всего тела (этот вывод справедлив для любой материальной
системы).
Перейдем к вычислению главного момента сил инерции твер-
дого тела.
Рассмотрим сначала случай, когда тело движется произволь-
ным образом. Выбирая за полюс центр масс С тела, на основа-
нии формулы (16.7), имеем
Пусть система координат Схуг жестко связана с телом. Тогда
в соответствии с формулой (14.2) можно записать
NlJc = — dKr dt “xKc (16.9)
и, следовательно, MJCX = dKCx dt (®Дсг (йгКсу),
М£у-- dKCy dt (в>гКсх <£>xKcz), (16.10)
^Cz dt (fi>xKcy ЫуК-Сх)-
Подставляя в эти выражения значения проекций момента
количеств движения, вычисленных для неподвижной точки (13.8):
Ксх 7=1Iх^х Iху®у — 7лгС0г,
Key = — Ixy^x + I у<йу — I уг(£>г,
Kez — Ixz^x Iyz^y 4" I i г,
370
МЕТОД КИНЕТОСТАТИКИ
[Гл. XVI
получим
Мех = — 1хгх + 1ху (Ну - <0х<0г) + Ixz (ег + а>ха>у) -
- lyz (®1 — Wy) - Uz — /у) <Лу<Лг,
Мсу= IyZy-V Iyz (fiz <'>/'’х) + 1 ух (ex + ыуаг) (16 11)
“ Ixz («х - W|) - (/x - lz) <'V'’x,
Л^Сг = Iz&z “I” I xz (Ex ^y^z) "4" Iyz (&y T" ^x^z)
- Ixy (Wy - ®£) — (1 у - 7x) .
Эти формулы определяют главный момент сил инерции твердого
тела в общем случае его движения. Если тело имеет неподвиж-
ную точку, то за полюс следует выбрать эту точку.
Из формул (16.11) легко получаются все частные случаи.
Случай плоского движения твердого тела, имеющего плоскость
материальной симметрии. Если ось г перпендикулярна к плоско-
сти материальной симметрии, совпадающей с плоскостью движе-
ния, то
XZ 7yz 0, &Х &у 0, 0)д- СОу 0.
Теперь из формул (16.11) найдем, что
Мсх~ Мсу — 0, Мсг — —Icz^z-
(16.12)
Случай вращения твердого тела вокруг неподвижной оси. Выбе-
рем в качестве полюса произвольную точку на оси вращения,
ось г совместим с осью вращения, а оси х и у скрепим с вра-
щающимся гелом. Векторы е и со направлены по оси вращения г,
и, следовательно, их проекции на оси х и у равны нулю:
со* = = 0, ех = е4, = 0.
Подставив эти значения в формулы (16-11) и принимая во вни-
мание, что а>г = ±а>, получим проекции главного момента сил
инерции твердого тела, вращающегося вокруг неподвижной оси:
Mx=Ixztz-Iyz<*\ MJy = Iyztz + Ixz\ Ml^—lz&z- (16.13)
§ 16.3. Определение добавочных динамических реакций
опор движущегося тела
При движении несвободного твердого тела реакции связей Rft
складываются из статических R” и добавочных динамических R*
составляющих:
ra = rcat+r£.
§ 16 4]
ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ДОБАВОЧНЫХ РЕАКЦИЙ
371
Аналогичным равенствам удовлетворяют главные векторы и
главные моменты реакций связей
R = RCT + R«, м£ = М§ст + М§д. (16.14)
Как уже отмечалось (см. § 13.5), статические реакции удов-
летворяют следующим шести уравнениям:
FX + R7 = Q, Fu + R^ = 0, Fz + R? = 0, 1
Мх + М?ст = 0, Му + Л4*ст = 0, Мг + Л4?ст = 0. |
Подставим в уравнения кинетостатики (16.5) значения проек-
ций главного вектора R и главного момента М§ реакций связей,
определенных равенствами (16.14):
Fx + /?7 + ^ + A = 0,
Fy + ^T + ^+^ = 0.
Fz+/?r+«5 + A = 0,
м,+м^т+М?я+лъ7 = о,
МУ + Л4^СТ + Л4^ + Л4/=О,
Л4г + Л4?ст + Л4?д + Л4/ = О.
Учитывая равенства (16.15), которым удовлетворяют статиче-
ские реакции, получим уравнения для определения добавочных
динамических реакций опор движущегося твердого тела:
^ + Л = 0, 7?Н^ = 0, /?5+Л = 0, )
Л4*д+Л47 = 0, М^д+Л47 = 0, М^д + М/ = 0. |
Отметим, что при составлении этих уравнений не нужно учи-
тывать активные силы. Наконец, заметим также, что в частных
случаях число уравнений может уменьшиться; например, при плос-
копараллельном движении твердого тела их число будет равно
трем.
§ 16.4. Задачи на определение
добавочных динамических реакций
Добавочные динамические реакции можно определить различ-
ными методами, в частности, можно для этих целей использовать
общие теоремы динамики (см. § 13.4). Одним из наиболее про-
стых методов определения добавочных динамических реакций
является метод кинетостатики. Мы проиллюстрируем его на не-
скольких задачах.
372
МЕТОД КИНЕТОСТАТИКИ
[Гл. XVI
Рис. 16.1.
Задача 16.1. Две материальные точки Мг и М2, массы т каждая, при-
креплены с помощью горизонтальных стержней к вертикальной оси АВ
(рис. 16.1). Пренебрегая массой стержней и оси АВ, определить дополнитель-
ные динамические реакции опор А и В вала, если вся система вращается
с постоянной угловой скоростью и. Длина
стержней равна а, расстояние между ними
равно h, расстояние между опорами И.
При равномерном вращении всей системы
ускорения точек Л-lj и Л12 будут- направлены
к оси вращения и численно равны ato2. Силы
инерции Jx и J2 направлены в противоположные
стороны (см. рис. 16.1); модули этих сил равны
между собою:
Д == /2 = таен2.
Из рисунка видно, что силы инерции Jx
и J2 составляют пару сил с моментом, численно
равным maafih. Так как пара сил может быть
уравновешена только другой парой сил, то добавочные динамические реак-
ции R^ и R^ опор А и В составляют пару сил, момент которой равен
R^H. Из равенства модулей моментов пар
R^H = mau>2h
найдем добавочные динамические реакции
ra = rb
Задача 16.2. Груз веса Р скользит вниз по наклонной эстакаде, свободно
лежащей на земле. Вес эстакады G, коэффициент трения скольжения между
грузом и эстакадой f, угол наклона
равен а (рис. 16.2, а). При каких
условиях эстакада не начнет движе-
ние?
В главе VIII эта задача была
решена с помощью теоремы об изме-
нении количества движения матери-
альной системы. Решим теперь эту
же задачу, используя метод кинето-
статики. Для этого рассмотрим сна-
чала отдельно движение груза (рис.
16.2, б). Так как груз скользит вниз
по наклонной плоскости, то сила
Рис. 16.2.
Р
инерции —w, где w — ускорение
груза, направлена вверх. Применяя
к грузу уравнения статики, найдем
Psina—Л——t»=0, Vx — Pcosa = 0.
g
Из второго уравнения найдем нормальное давление Vx, а затем из первого
уравнения найдем силу инерции груза (напомним, что Fx = fVx)
р
Vx = Pcosa, — w = P (sina—f cosa).
Рассмотрим теперь систему, состоящую из груза и эстакады (см. рис. 16.2, а).
Внешними силами для этой системы будут: сила тяжести Р груза, сила тяжести G
§ 16.4]
ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ДОБАВОЧНЫХ РЕАКЦИИ
373
эстакады, сила нормального давления земли N и сила трения F между землей
и эстакадой. Присоединим к этим силам силу инерции —w груза и составим
два уравнения статики:
„ Р п
F-----w cos а=О,
g
N — G — PA----w sin а = 0.
g
Отсюда найдем силу треиия F и нормальное давление У:
F = — uicosa, N — G+P------------tasina,
g g
P
или, учитывая найденное ранее значение силы инерции — ш,
F = Р (sin a —f cos a) cos a,
N = G-{-P — P (sina—/cosa) sina = G + P (cosa-f-f sin a) cos a.
Эстакада будет находиться в покое, если сила трения F меньше своего
предельного значения, равного f0N:
Р (sin a—f cos a) cos a < f0 [G4-P cos a (cos a-)-/ sin a)].
Отсюда найдем условие', которому должен удовлетворять коэффициент трения
покоя /о, чтобы при движущемся грузе эстакада оставалась в покое:
Р (sin a—/ cos a) cos a
'° > G P (cos a + f sin a) cos a ‘
в кото-
Сравнивая решение этой задачи методом кинетостатики с решением,
ром использовалась теорема об изменении количества движения материальной
системы (стр. 194), мы видим, что оба
метода приводят практически к оди-
наковым уравнениям.
Задача 16.3. Электромотор, уста-
новленный на горизонтальной балке,
поднимает с помощью троса груз веса
Р. Радиус барабана, укрепленного на
оси мотора, равен г, а момент инерции
барабана вместе с ротором равен /.
Пренебрегая весом троса, определить
динамические реакции опор А и В
балки, если груз*поднимается с уско-
рением w. Линейные размеры указаны
на рис. 16.3. Предполагается, что
плоскость рисунка является плос-
костью материальной симметрии дви-
жущихся частей.
Груз поднимается с ускорением w. Его сила инерции, равная по модулю
р
— w, направлена вниз. Угловое ускорение вращающихся частей направлено
по ходу часовой стрелки, следовательно, главный момент сил инерции направлен
согласно формуле (16.12) против хода часовой стрелки и равен по модулю /е
(на рис. 16.3 знак минус у силы инерции груза и у момента сил инерции
барабана не показан, так как их направления указаны на рисунке). Главный
374
МЕТОД КИНЕТОСТАТИКИ
[Гл. XVI
вектор сил инерции барабана равен нулю, ибо его центр масс неподвижен.
Вводим динамические реакции опор. Активные силы не учитываем и, считая
условно барабан и груз неподвижными, составляем уравнения равновесия для
сил инерции и добавочных динамических реакций. Мы составим два уравнения
моментов (главный момент сил инерции можно рассматривать как момент
некоторой пары) и одно уравнение для проекций сил. Имеем
£Л1м=0, I&A-R^b—~ wa = 0, /е — w (b — а) = 0, (16.17)
2^=°- х«=о.
Учитывая, что е==и>/г, легко теперь найдем
4’1 + (16.18)
Задача 16.4. В одной из конструкций лесовалочной машины конец А
дерева АВ перемещается с помощью захвата Е с постоянной скоростью по
горизонтальной направляющей, причем ствол дерева, поперечными размерами
которого пренебрегаем, все время
опирается на каток /< Вес дере-
ва G, его момент инерции относи-
тельно оси, проходящей через
центр масс С перпендикулярно к
стволу, равен /, расстояние
АС — 1, превышение катка К над
горизонтальной направляющей
равно Н (рис. 16 4). Определить
добавочные динамические состав-
ляющие реакции катка К и за-
хвата Е в зависимости от угла ф.
Воспользуемся методом кинето-
статики. Отбросим активные силы
(вес дерева) и введем добавочные
16.4). Так как движение является
сил инерции будет определяться ра-
динамические реакции опор (см. рис.
плоскопараллельным, то главный момент
венством (16.12):
Alc2 = -Zczez.
Главный вектор сил инерции согласно формуле (16,8) равен J =—A4wc =
G
=----w
g
С
его проекции на оси х и у будут
, _ G . , G ..
«/ v — X r J — у f-,
g с’ у g с
Предположим, что е хс и ус известны (мы найдем их несколько позднее).
Примем центр масс С за центр приведения сил инерции и изобразим на рисунке
составляющие их главного вектора и главный момент M.JCz (предпола-
гается, что J х, Jy и MJC2 положительны). Считая в соответствии с методом
кинетостатики, что силы инерции и добавочные динамические реакции уравно-
§ IS 4]
ЗАДАЧИ НА ОПРЕДЕЛЕНИЕ ДОБАВОЧНЫХ РЕАКЦИИ
375
ьешены, составим три уравнения равновесия этих сил:
Jх + Хд — Nд sin ф = О,
^+Гд+^со5ф = 0, (1619)
М]с, 4- J, I cos ф — / sin ф + А,д —Д— = 0.
' У г х т sin ф
Из этих уравнений найдем динамические составляющие реакций
N* = -^~(Jxl sin(p_jy совф —М^г), j
ХД = ^8Шф-/х, f (16'20>
Кд = — (Nx cos ф + •/(/) ' J
Для полного решения задачи нам осталось найти 1>с> ус и е = ф, после
чего сразу определяются Jх, Jу и М^г. По условию задачи точка А пере-
мещается равномерно по оси х со скоростью v0. Совместим начало координат О
с начальным положением точки А. Тогда
ОД = ц0/, А/(' = b — vat,
где 6 = ОК'= const.
Имеем
, н
tg‘P=-b=V
Дифференцируя по времени, получим
Ф = Hvq
cos2 ф (Ь — *
Отсюда найдем углсГвую скорость (Ь — iict = Я ctg ф)
ф=-^-51П-ф. (16.21)
Дифференцируя по времени еще один раз, найдем угловое ускорение
е -- sm 2фф,
или, пользуясь равенством (16.21),
e = -j^ sin 2ф ып2ф. (16.22)
Координаты центра масс определяются формулами (см. рис. 16.4)
хс = v(t4-1 cos ф, Ус = 1 sin ф.
Дифференцируя два раза по времени, получим
хс =— 1ф sin ф — /ф2 cos ф, ус = /ф cos ф —/ф2 sin ф.
Подставляя сюда значения ф и ф = в из равенств (16.21) и (16.22), цосле
элементарных преобразований будем иметь
л:с = —3-^- I зт^фсовф, Ус = — Зсоз2ф) зт3ф.
376 МЕТОД КИНЕТОСТАТИКИ [Гл. XVI
Теперь находим
Л = -~*с = 3у я2Ьт <pC0S<p’
=----— ус = — I (1 — 3cos2<p)sin*<p,
ё s
г V*
MJCz = — /е = — I sin 2ф sin2 ф.
Подставляя эти выражения для Jх, Jу и M.qz в равенства (16.20), опре-
делим добавочные динамические реакции Мд, Хд и Уд:
№ = 2 (— sin4 фcoscp,
VI Vl 19 , Л ЯПФ о G Л • 1
лд = -Е^- 21 —с2+/ —п2- — 3 — / sm4 ф созф,
#2 L \ g / Н g J *
Гд = - [2 Z2 + /j Z(1 -Зсоз2ф)] sin3ф.
ГЛАВА XVII
ТЕОРИЯ УДАРА
§ 17.1. Основные определения
Во многих случаях можно наблюдать явление, называемое
ударом, когда за очень малый промежуток времени т скорости
точек тел изменяются на конечную величину. Так, например, если
мяч падает на горизонтальный пол, имея в начале соприкоснове-
ния с полом скорость v, и отскакивает от пола со скоростью V,
то изменение скорости V — v представляет конечную величину,
а весь процесс удара происходит за ничтожно малое время т.
Чтобы за очень малый промежуток времени т скорости точек
тела изменились на конечную величину, силы, действующие на
тело, должны быть очень велики. Действительно, пусть под дей-
ствием силы F материальная точка массы т за очень короткий
промежуток времени т изменила скорость на конечную величину
V —v, где v и V — скорости точки до и после удара соответственно.
Применим к материальной точке второй закон Ньютона
m^ = F, (17.1)
или
mdv= F dt.
Интегрируя это равенство от нуля до т, получим
mty -v) = $F dt. (17.2)
О
Пользуясь теоремой о среднем, найдем
т (V - v) = Fcpx,
где Fcp —среднее значение силы F за -время ее действия. Отсюда
р _m|V-v|
Гер— т
Так как числитель правой части этого равенства представляет
конечную величину, а знаменатель очень мал, то даже среднее
378
ТЕОРИЯ УДАРА
[Гл XVII
значение силы F очень велико. В дальнейшем силу, действующую
в течение очень короткого промежутка времени, модуль которой
достигает большой величины, будем называть ударной силой.
Как правило, мы не знаем закона изменения ударной силы F,
но примерный график
ее модуля можно построить. До удара и
после него сила F равна нулю, а в про-
межутке (0, т) ее модуль достигает очень
большой величины. Очевидно, что график
модуля силы F должен иметь вид, изо-
браженный на рис. 17.1; на этом же ри-
сунке показано среднее значение Fcp.
Для того чтобы примерно оценить
модуль силы F, рассмотрим простейший
пример. Предположим, что камень весом
Р = 1 кГ падает вертикально вниз с вы-
соты Д=10 м на панель, причем после
падения он не отскакивает. Считая, что
продолжительность удара т = 0,001 сек, найдем среднее значение
силы Fcp.
В условиях задачи скорость камня в начале удара v = V 2gН ~
~ 14,1 м/сек (сопротивлением воздуха пренебрегаем), а скорость
после удара V равна нулю. Пользуясь последней формулой, получим
„ Р V 1 14,1 г—
^с₽ “ ~g Т ~ ’ ДДоГ — 1410 кГ'
Это только среднее значение силы F; если считать, что мак-
симальное значение силы F вдвое больше среднего значения
(см. рис. 17.1), то получим Fmax = 2,8 Т. Эти числа наглядно
показывают, почему иногда при ударе происходит разрушение тел. _
Вернемся к равенству (17.2), правая часть которого равна
импульсу S силы F:
S = $Fdt (17.3)
о
Теперь равенство (17.2) принимает вид
m(V-v)=S. (17.4)
Вектор S называется ударным импульсом (или импульсом уда-
ра). Очевидно, что численно ударный импульс равен площади зашт-
рихованной фигуры рис. 17.1.
В теории удара материальной точки вместо уравнения (17.1)
пользуются уравнением (17.4), в котором импульс удара S пред-
ставляет конечный вектор.
Так как продолжительность удара т очень мала, то в теоре-
тической механике пренебрегают всеми величинами, имеющими
§ 17.1]
ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ
379
порядок т. Иначе говоря, в теоретической механике принята сле-
дующая идеализация удара: при конечном ударном импульсе удар
происходит мгновенно.
Найдем перемещение точки за время удара. Для этого рас-
смотрим ударный импульс в момент времени t, где 0<Д<т.
Имеем
t
S (0 = $ F (0 dt.
о
Обозначив скорость точки в момент времени t через V (t),
получим из равенства (17.4)
v(0 = v+4-s(0-
Так как V(/)=-^-, то, интегрируя последнее равенство от О
до т, получим
r2-ri = (v + ~SCp) т,
где и г2 — радиусы-векторы точки в начале и конце удара,
a Scp —среднее значение импульса S (/) в промежутке [0, т].
Правая часть этого равенства имеет порядок т, и ею можно
пренебречь, положив г2 —гг = 0. Таким образом, в рамках сде-
ланной идеализации перемещение точки за время удара равно нулю.
Если на точку действуют ударная сила F (/) и обычная медленно
меняющаяся во времени сила Р (/), то их общий импульс Si за
время т будет равен
Si = $ F (/) dt + $ Р (0 dt.
о о
Первое слагаемое равно ударному импульсу S; применяя ко
второму слагаемому теорему о среднем, получим
Si = S + PcpT.
Так как второе слагаемое имеет порядок т, то им можно
пренебречь. На этом основании при исследовании процессов,
происходящих при ударе, медленно меняющиеся, ограниченные
по модулю силы не учитываются.
Все сказанное можно отнести не только к ударным силам,
возникающим при контакте тел, но и к любым другим силам,
характер изменения которых во времени изображен на рис. 17.1.
Такие силы возникают при взрыве в полости, при распространении
упругих волн в сплошной среде и при так называемых разрывах
в газе.
380
ТЕОРИЯ УДАРА
[Гл. XVII
§ 17.2. Коэффициент восстановления
При соударении двух тел в точке контакта возникают ударные
силы, приложенные к каждому из тел. Они имеют одинаковые
модули и противоположно направлены. Пренебрегая трением, будем
считать, что ударные силы и их импульсы и S2 направлены
по общей нормали к поверхности соударяющихся тел (рис. 17.2).
Как показывают наблюдения, гипотеза
g ,\ об абсолютной твердости тел является
n I недостаточной для объяснения процесса
удара и необходимо учитывать физиче-
/ п \ ские св°йства тел. Сам процесс удара
I можно разбить на две фазы. В течение
I у' \ д \ первой фазы происходит сближение тел
\ г ) по линии общей нормали, в результате
* \. ) чего проекция на нормаль относителен
ной скорости точки контакта тел умень-
Рис. 17.2. шается до нуля. Вслед за этим начи-
нается вторая фаза удара: тела, восста-
навливая свою форму, начинают удаляться друг от друга, нор-
мальная составляющая относительной скорости точки соприкосно-
вения, переменив знак, возрастает по абсолютной величине, но не
достигает, как правило, своего значения в начале удара.
Полное исследование процесса удара требует подробного рас-
смотрения физических свойств тел, что выходит за рамки теоре-
тической механики. Однако, как показывают опыты, в первом
приближении можно принять следующую гипотезу (гипотеза Нью-
тона): отношение модуля нормальной составляющей относительной
скорости точки контакта тел после удара к ее величине до удара
есть некоторая физическая постоянная, характеризующая физи-
ческие свойства соударяющихся тел, но не зависящая от их мас-
сы и относительной скорости. Эта физическая постоянная называ-
ется коэффициентом восстановления. Обозначая коэффициент восста-
новления через е и учитывая, что полного восстановления скоро-
сти, как правило, не происходит, будем иметь
0s£8=cl. (17.5)
В предельном случае, когда е = 1, удар называется абсолютно
упругим-, во втором предельном случае, когда е = 0, удар назы-
вается абсолютно неупругим. В остальных случаях (0<е<; 1)
удар называется не вполне упругим или просто упругим. Заметим,
что при абсолютно неупругом ударе двух тел нормальная состав-
ляющая относительной скорости точки соприкосновения после удара
равна нулю. Для таких тел весь процесс удара заключается только
в первой фазе; после максимального сближения тел восстановления
их формы в точке контакта не происходит и оба тела движутся
§ 17.2]
КОЭФФИЦИЕНТ ВОССТАНОВЛЕНИЯ
381
в дальнейшем совместно (в частности» оба тела могут остановиться)
или одно тело скользит по поверхности другого.
Перед тем как перейти к дальнейшему, напомним еще раз, что
гипотезу Ньютона об ударе и все выводы, которые из нее полу-
чаются, можно применять только в качестве первого приближения
к реальным процессам, происходящим в телах при ударе. Это
приближение оказывается достаточно хорошим, если при ударе
наблюдается только местная деформация тел вблизи точки контакта.
Если же при ударе происходит деформация всего тела, то гипотезу
Ньютона применять нельзя *).
Обозначим через п единичный вектор общей нормали к поверх-
ностям тел в точке контакта, направленный внутрь второго тела.
Пусть Uj и и2 — скорости точек контакта первого и второго тел
в начале удара, a Uj и U2— соответствующие величины в конце
удара. Тогда, по определению коэффициента восстановления, будем
иметь
I (u2-.Ui).-n I (17.6)
I (u2 —Ui) n I
или, учитывая, что относительная скорость при ударе изменяет
направление,
(П2 — П») п = — е (и2 — щ) • п. (17.7)
Наконец, если ввести два единичных вектора п» и n2 (п = п2 =
= — rij), направленные внутрь первого и второго тел соответственно,
то последней формуле можно придать следующую
симметричную форму: "-
U2 • п2 + U1 • П1— —8 (и2 п2 и» • п»), (17.8)
Этими формулами мы воспользуемся в даль-
нейшем.
Коэффициент восстановления может быть из-
мерен следующим образом (рис. 17.3). Представим
себе, что одно из соударяемых тел выполнено
в виде плиты и неподвижно закреплено в горизон-
777777777777777777777
Рис. 17.3.
тальном положении, другое тело —шарик. Шарик
поднят на высоту А» над плитой и отпущен без начальной скорости.
Скорость его в момент соприкосновения с плитой вычисляется
по известной формуле ____
p = T/2g/z1.
Измерив высоту /12, на которую поднимается шарик после отска-
кивания, можно найти его скорость в конце удара
К = ]/2^2.
*) Подробное рассмотрение процессов, происходящих в твердых телах при
ударе, и анализ различных гипотез даны в книге: Пановко Я. Г, Введение
в теорию механического удара. —М.: Наука, 1976.
382
ТЕОРИЯ УДАРА
[Гл XVII
Таким образом, коэффициент восстановления оказывается равным
v Г К
Значения коэффициентов восстановления для различных пар
соударяемых материалов приводятся в справочниках. Так, например,
при соударении стекла со стеклом е = 15/16, стали со сталью е = 5/9,
дерева с деревом е = 1/2.
§ 17.3. Удар материальной точки
об идеально гладкую поверхность
Материальная точка после удара о неподвижную поверхность
(рис. 17.4) изменяет свою скорость. Со стороны поверхности на
точку во время контакта действует ударная реакция. Полагаем,
что поверхность идеально гладкая, так что реакция и ударный
импульс S направлены по нормали к поверхности.
Воспользуемся теперь теоремой об изменении количества дви-
жения при ударе (формулой (17.4)):
mN — mv — Sn. (17.9)
Проектируя это уравнение на оси тип, получим (см. рис. 17.4)
Ут — ft = 0, |
Таким образом, касательная составляющая скорости сохра-
няет свою величину и направление. Нормальная составляющая
Заметим, что
всегда изменяет направление, модуль же ее
меняется в зависимости от величины удар-
ного импульса S.
Пусть известны коэффициент восстановле-
ния е, модуль скорости точки до удара v и
угол а, составленный вектором скорости v
с нормалью к поверхности (см. рис. 17.4).
Требуется определить угол отражения (3, ско-
рость точки после удара V и ударный
импульс S.
Исходя из определения коэффициента вос-
становления, найдем Уп = е|и„|, или Vn =
= —evn. Из уравнений (17.10), как мы уже отмечали, следует
сохранение касательной составляющей скорости после удара,
т. е. Vt = vt.
| | = и cos a, ut = usina,
V„ = Vcosp, Vt=I/sinp.
(17.П)
§ 17 3]
УДАР ТОЧКИ О ГЛАДКУЮ ПОВЕРХНОСТЬ
383
Поэтому
V sin В = v sin а, V = v sin ” . (17.12)
r ’ sin р ' '
Подставим теперь значение V в формулу для Vn и используем
связь нормальных проекций скорости после удара и до удара
с коэффициентом восстановления е.
_ I Vn |_ V cos fl _ sin a cos fl __ ctg fl
I vn I ~ у cos a cosasinfl — ctg a
Теперь без труда определяется угол (3:
ctgfl = ectga, fl = arcctg (e ctga). (17.13)
Для вычисления модуля скорости после удара воспользуемся
тригонометрическим тождеством
sin fl — г
/1+Ctg2fl
Из равенства (17.12) получим
V = usina]/l+ctg2fl =wsina|<i+e2ctg2a. (17.14)
Из формул (17.13) и (17.14) следует: а) для абсолютно упругого
удара (е = 1) fl = a, V = v; б) для абсолютно неупругого удара
(е =0) fl = л/2, V = ut = usina. Таким образом, при абсолютно
неупругом ударе материальная точка «рикошетирует» от непод-
вижной поверхности, сохраняя лишь касательную составляющую
скорости.
При любом не вполне упругом ударе (е<1) модуль скорости
отражения всегда меньше модуля скорости падения и угол отра-
жения больше угла падения. В самом деле,
tgfl = ytg«, tg fl > tg a, fl>a,
V = v ]/ sin2 a-T 82 cos3 a, V < v.
Определим ударный импульс. Для этого подставим в равенство
(17.10) Vn = —svn, vn~ — и cos а и найдем S.-
'S = m(Vn — vn) = m(l +e)ucos a. (17.15)
Из этого соотношения видно, что максимальное значение удар-
ного импульса при заданных коэффициенте восстановления и модуле
начальной скорости v достигается при прямом ударе (а = 0). При
абсолютно упругом ударе (е=1) импульс удваивается по сравне-
нию с импульсом при абсолютно неупругом ударе (е = 0).
384
ТЕОРИЯ УДАРА
[Гл. XVII
§ 17.4. Потеря кинетической энергии при ударе материальной точки
о неподвижную поверхность
Изменение кинетической энергии при ударе определяется как
разность значений кинетической энергии в конце и в начале удара:
(У2—и2).
Но из равенств Vx = vx и Уя = е|v„| следует, что
У2 = У£+У| = 8го’+г4, =
Подставляя значения квадратов скоростей в разность значений
кинетической энергии, получим
Л-Л = -у(1-е2)иД. (17.16)
Таким образом, при абсолютно упругом ударе (е = 1) кинетическая
энергия материальной точки не изменяется, а при е<1 проис-
ходит потеря кинетической энергии. Наибольшая потеря будет при
абсолютно неупругом ударе, когда е = 0. Уменьшение кинетической
энергии при е < 1 обусловлено переходом механической энергии
в другие формы энергии, в частности в тепловую.
Формулу (17.16) можно преобразовать к другому виду. Для
этого заметим, что из равенства касательных составляющих ско-
ростей Vx = vx следует
| V - v | = Vn +1 v„ | = е | v„ | +1 Nn | = (1 + e) | v„
Отсюда
и, следовательно,
T2-7\ = -^^(V-v)2. (17.17)
Разность V —v называется «потерянной скоростью».
При абсолютно неупругом ударе (е = 0) из (17.17) получим
Т2 —(V — v)2,
т. е. потеря кинетической энергии равна кинетической энергии
потерянной скорости. В общем случае потеря кинетической энер-
гии составляет j-^-ю долю кинетической энергии потерянной ско-
рости (теорема Карно).
§ 17.5) ТЕОРЕМА ОБ ИЗМЕНЕНИИ КОЛИЧЕСТВА ДВИЖЕНИЯ 385
§ 17.5. Теорема об изменении количества движения
и теорема об изменении момента количеств движения
материальной системы при ударе
Воспользуемся интегральной формой теоремы об изменении
количества движения материальной системы (§ 8.2) и перепишем
равенство (8.9) в форме
Q2-Qx = Se. (17.18)
Здесь Qj и Q2 — количество движения системы в начальный и
конечный моменты времени, Se —главный вектор импульсов всех
внешних сил.
Применим равенство (17.18) к ударным силам и выразим коли-
чество движения через скорость центра масс. Получим
M(Vc-vc) = Se, (17.19)
где vc и Vc —скорости центра масс в начале и в конце удара,
Se —главный вектор импульсов всех внешних ударных сил (им-
пульсы неударных сил при ударе, как уже отмечалось ранее,
не учитываются).
Так как при ударе перемещения всех точек, к которым были
приложены ударные силы, равны нулю (см. § 17.1), то центр
масс системы при ударе не меняет своего положения, скорость же
центра масс меняется мгновенно.
Перейдем к определению изменения момента количеств дви-
жения системы при ударе. Сначала в качестве полюса выберем
неподвижную точку О.
Для одной материальной точки теорема импульсов (17.3) дает
mkVk-mkvk^Sek + Sik. (17.20)
Здесь Sfe —импульс внешних ударных сил, S* —импульс внутрен-
них ударных сил, действующих на точку.
Умножая каждое из равенств (17.20) векторно на rfe и скла-
дывая все равенства, получим
п
К02-К01= 2 rftxS£. (17.21)
k = i
Сумма моментов импульсов внутренних сил в правую часть
(17.21) не вошла, так как она равна нулю.
Доказательство этого свойства проводится совершенно анало-
гично тому, как это было сделано для главного момента внутрен-
них сил в § 7.3. Если обозначить сумму моментов импульсов
всех ударных сил через Lq, то будем иметь
К02 ~ Кщ =
13 Н. В. Бутении ц др.)
386
ТЕОРИЯ УДАРА
[Гл. XVII
Изменение момента количеств движения системы относительно
неподвижного полюса при ударе равно сумме моментов импульсов
всех внешних ударных сил относительно того же полюса.
Если в качестве полюса выбрать центр масс С системы, то фор-
мула (17.21) примет вид
Кс2—Kci= У, r*XS*,
k = i
(17.22)
где Кеа и Kci — моменты количеств относительного движения
материальной системы в конце и начале удара (см. § 9.7), а ц—
радиус-вектор точки приложения ударного импульса, проведенный
из центра масс С системы. Уравнение (17.22) следует из того,
что теоремы об изменении момента количеств движения относи-
тельно неподвижного полюса и центра масс имеют одинаковую
математическую форму.
Запишем уравнения (17.21) и (17.22) в проекциях на оси коор-
динат. Для твердого тела в качестве осей координат удобнее
выбрать оси, жестко связанные с телом; начало координатной
системы следует выбрать либо в неподвижной точке О тела (если
такая точка существует), либо в его центре масс С. Следует отме-
тить, что при ударе все точки системы, в частности твердого тела,
не перемещаются. Поэтому можно выбрать любую систему коор-
динатных осей, жестко связанных с телом, и заменить векторные
уравнения (17.21) или (17.22) тремя скалярными уравнениями
(см. § 13.2):
IX (^Ж ®ж) Iху (^(/ IXZ (^Z ®z) = LX)
— I ух (^* ®лг) “И I у (^ у Iуг (^z ®z) = Ly>
— Iгх (Q« ®лг) гу (^у ®у) “И Аг (й2 ®z) = Lz-
(17.23)
В этих уравнениях сох, &у, a>z и йх, йу, й2 —проекции вектора
угловой скорости тела в начале и конце удара, 1Х, 1У, 1г, 1ху,
Ixz, 1Уг — соответствующие моменты инерции тела, Lx, Ly, Lz —
проекции главного момента импульсов внешних ударных сил.
Если за оси координат приняты главные оси инерции тела,
то уравнения (17.23) примут такой вид:
1х — ®л) — Lxt
1у (®У ®») = Ау,
/г (й2 сог) = Ь2.
(17.24)
Для плоского движения твердого тела, когда ось г проходит
через центр масс С перпендикулярно к плоскости движения, и
для тела, вращающегося вокруг неподвижной оси, уравнения
§ 17-6]
ТЕЛО, ЗАКРЕПЛЕННОЕ В ДВУХ ТОЧКАХ
387
(17.23) упрощаются (сол = соу = 0):
I xz (^z ®z) =
— I yz (^z ®z) =
7z(^z ®z) — Лг-
(17.25)
Наконец, если тело имеет плоскость материальной симметрии,
параллельно которой происходит движение, и все ударные силы
лежат в этой плоскости, то из трех уравнений остается только
одно:
/z(Sz-co.) = U. (17.26)
§ 17.6. Удар, действующий на тело,
закрепленное в двух точках
На тело, закрепленное в точке В шарнирно (рис. 17.5) и
в точке А при помощи подпятника, действует ударный импульс
S. Во время удара в точках А и В возникают реакции, имеющие
также характер ударных сил. При зна-
чительных ударных воздействиях реак-
ции могут достигать значений, опас-
ных с точки зрения прочности подшип-
ников и оси.
Возникает задача определения удар-
ных импульсов реакций при заданных
динамических характеристиках тела
(масса, моменты инерции) и при из-
вестном ударном импульсе, действую-
щем на тело.
Пусть S — ударный импульс, дей-
ствующий в точке М на тело. Сов-
местим плоскость уАг с плоскостью,
проходящей через центр масс С тела.
Теорема об изменении количества движения при ударе и теорема
об изменении момента количеств движения примут для нашего
случая следующий вид:
М (VC2~ vci) — S + Sz Sb,
Кд2 — Кд1 — r K X S г в X Sb,
(17.27)
(17.28)
где SA и Sb —импульсы реакций, г.^ —радиус-вектор точки М.
Заметим, что скорость центра масс параллельна оси х:
vc = ю х гс = - сог«/с1
13*
388
ТЕОРИЯ УДАРА
[Гл. XVII
и, следовательно, векторное уравнение (17.27) в проекциях на оси
координат приводит к трем скалярным уравнениям:
5* + SАх + SBx = Мус (coz — йг),
By + S Ay + = О,
>5дг4-5г = 0.
(17.29)
'Здесь 5дл:, SAy, SAz, SBx, SBy — проекции ударных импульсов
на соответствующие оси координат.
Теперь перейдем к составлению второй группы уравнений,
вытекающей из векторного равенства (17.28). В проекциях на оси
координат эти уравнения в общем виде совпадают с уравнениями
(17.25). Для того чтобы воспользоваться этими уравнениями, вы-
числим прежде всего момент ударного импульса (импульсы реак-
ций вычисляются непосредственно). Имеем
j к
гжх8 =
хм
Ум гм —
Sg Sz
= (Ум8г — гмЗу) i + (zmSx — xMSz) j 4- (xMSy — Ум$х) к,
где хм, ум и zM — координаты точки М приложения импульса S.
Уравнения (17.25) принимают следующий вид:
7лг (£2г <вг) = Ум^г zMSy zBS Ву,
~ 7yZ (Пг ®г) = ZaiSx XmSz -j- ^вВ Bxt
z) x^Sу y^Sx,
(17.30)
Из последнего уравнения определяется приращение угловой
скорости вращения за время удара:
сог — -г- (xMSy yMSx). (17.31)
1 Z
Для определения неизвестных импульсов ударных сил остается
подставить йг — в уравнения (17.29) и (17.30) и решить систему
пяти уравнений с пятью неизвестными: 5Лг, SAg, SAx, SBx, SBy.
§ 17.7. Условия отсутствия ударных реакций. Центр удара
Сначала найдем условия, которые необходимы для того, чтобы
при ударе не возникали ударные импульсы реакции. Примем,
что ударные импульсы в точках А и В равны нулю, и найдем
те ограничения, которые эти условия накладывают на остальные
величины, входящие в уравнения (17.29) и (17.30). При этом будем
§ 17.7]
УСЛОВИЯ ОТСУТСТВИЯ УДАРНЫХ РЕАКЦИИ
389
считать, что —®г#=0. Из уравнений (17.29) и (17.30) получим
5Л = — Мус&г-®:), ч
5, = 0,
Sz = 0,
е е _ z /о а I (17.32)
Ум$г 2м$у — Ixz (“г мг),
%М^х = Iуг (^г ®г)>
XMSy Ум^х~^г(^г мг).
Из второго и третьего уравнений следует, что внешний удар-
ный импульс должен иметь направление, параллельное оси х,
т. е. он должен быть перпендикулярен к плоскости, проведенной
через ось вращения и центр масс
тела.
Для удобства дальнейших рас-
суждений введем новую систему ко-
ординат Олу^г, с осями, параллель-
ными исходным осям, и с началом в
точке О (рис. 17.6), находящейся на
оси вращения тела г, причем- АО =
= гЛ1к. В новой системе координат
г1Л1 = 0. Импульс S, по доказанному,
должен лежать в координатной плос-
кости х1Оу1 и быть параллельным
оси %! (см. рис. 17.6).
В новой системе координат урав-
нения (17.32) сохраняют свой вид.
Рис. 17.6.
Полагая в них Sy = Sz = 0, а также г1Ж = 0, используем сначала
четвертое и пятое уравнения. Имея в виду условие Q»— игу=0,
получим
7^,2, — 0, 7^,-0,
т. е. ось вращения должна быть главной осью инерции для точки О.
Из первого и последнего уравнений находим
(17.33)
Здесь мы воспользовались тем, что у1М — ум, у1С — ус, 1Z1 — 1г.
Значит, линия действия импульса S должна отстоять от оси вра-
щения на расстояш и, равном приведенной длине физического
маятника (см. § 13.7).
Таким образом, если удар не передается на опоры, то должны
выполняться следующие условия: 1) линия действия ударного им-
пульса должна быть перпендикулярна к плоскости, содержащей центр
масс тела и ось вращения; 2) плоскость, содержащая ударный
390
ТЕОРИЯ УДАРА
[Гл. ХУ1Г
импульс и перпендикулярная к оси вращения, должна пересекаться
с этой осью в точке, для которой ось вращения является главной
осью инерции-, 3) линия действия ударного импульса должна от-
стоять от оси вращения на расстоянии, определяемом равенством
(17.33).
Легко видеть, что перечисленные условия являются также
достаточными. При их выполнении система (17.32) удовлетворяется
при любых Sx, а тогда из системы уравнений (17.29) и (17.30)
вытекает, что ударные импульсы реакций опор и SB обра-
щаются в нуль.
Точка М в плоскости уАг (см. рис. 17.6), в которой прило-
жен ударный импульс S, удовлетворяющий всем указанным усло-
виям, называется центром удара.
Следует отметить, что центр удара может и не существовать.
Такая ситуация возникает, например, тогда, когда ни для одной
из точек на оси вращения сама ось вращения не является глав-
ной осью инерции.
§ 17.8. Удар двух тел
Пусть два тела с идеально гладкими поверхностями соударяются в точке*
Е (рис. 17.7). Будем считать, что нам известны угловые скорости <о1 и ш2 тел,
а также скорости v, и v2 их центров масс С) и С2 в начале удара. Считая
известными коэффициент восстановления е и динамические характеристики
тел (их массы и моменты инерции), требуется определить угловые скорости Qi,
й2 тел и скорости Vx и V2 их центров масс в конце удара.
Построим в точках £) и £2 (при ударе они совпадают) единичные векторы
th и п2 внутренних нормалей к поверхностям тел. Применяя к каждому телу
теорему о движении центра масс, получим
\С_____х Mi (Vi — Vi)= Stij, )
Л 1' 1 ' 1 I (17.34)
j' ------х. ^2 (V2— v2) = Sn2, J
/ \ ГДе S = S1 = S2*
I I Применим теперь к каждому телу теорему
к \ \ /об изменении момента количеств движения
\. у (формула (17.22)):
ЛКс,== ОТХЩ) 5,
Р"«- ,7'7- (17'35’
Построим в каждом теле системы координат н С2х2у2г2, направив оси
по главным осям инерции (на рис. 17.7 оси не показаны). Тогда два векторных
уравнения (17.35) будут эквивалентны следующим шести скалярным уравнениям:
Д1Д(О|д; = S/.ix, = S).ly, бйДощ — (17.36)
Д2Д<1)2Л = SXzxr £аД^2у “ S/'2y, S^z- (17.37)
В этих уравнениях А(, В[, С/ —моменты инерции соответствующих тел,
Х,„, — проекции векторов г(хп;, а Дсо,х, До),-у, До),г — проекции векторов
Д<»( = 11( — <В/ (г=1, 2). Для каждого тела проекции берутся на оси системы
CpcmiZt, связанные с соответствующим телом (индексы осей в равенствах (17.36).
и (17.37) опущены).
3 17.81
УДАР ДВУХ ТЕЛ
391
Уравнениям (17.34) также соответствуют шесть скалярных уравнений. Таким
образом, мы имеем двенадцать скалярных уравнений, содержащих тринадцать
неизвестных величин: проекции векторов Avj —Vi, Av2 = V2 — v2, Awj, Д<в2
и модуль импульса S. Еще одно уравнение дает гипотеза Ньютона (17.8):
Ua • n2+ Ui • ni=— е (и2 • п2*Е Ui • П1). (17.38)
Здесь ulr u2 —скорости точек контакта до удара, Up U2—скорости соответ-
ствующих точек после удара.
Пользуясь известной формулой кинематики, найдем скорость точки Ej,
принадлежащей первому телу, в конце и начале удара
U, = Vi Г£, ut=Vj гр
Отсюда следует, что
1>1 —“1=(V —У1) + Д®1ХГ£.
Умножим обе части этого равенства скалярно на nj и учтем, что (ДвуХн) П£=
= (rjXn^-Awi,
(Ui — ui) • nt = (Vi — vt) • nt + (Г] x nt) Awp
Умножая теперь первое уравнение (17.34) скалярно на П£ и учитывая, что
) Щ |= 1, получим
с
(У£-Ъ).П1 = ^.
Теперь предыдущее равенство можно записать так:
(Ui — Uj) • nt = -j- kiy &iy -{- Xiz A<0iz,
или, пользуясь уравнениями (17.36),
t 1 Ma Мг\
м-Ц^+^+^+^s.
Аналогично для второго тела
/ 1 XL X* X* \
Складывая почленно оба равенства, получим
U2 • п2-|- Uj • tij — (u2 • n2+ Ui • nt) = GS,
где
M, + M9 X’ X’ Х|, X® XL
G= Ь дН- + ^ + -^ + 7<-+ ^ + -Д- + 7^- (17'39)
/И1/И2 Ai &i Ci Hg #2 Cj
Массы тел и их моменты инерции заданы, а числа Х/г, Х^, X/z представ-
ляют собой кратчайшие расстояния между линией действия импульсов Snp Sn2
и соответствующими осями координат. Эти расстояния вычисляются подобно
тому, как в статике определяются плечи сил относительно осей.
Для того чтобы, например, вычислить | Х1л |, необходимо линию действия
импульса спроектировать на координатную плоскость j/iCjZi и найти плечо
проекции импульса относительно точки С±.
В случае плоского удара, когда все линии, изображенные на рис. 17.7,
лежат в одной плоскости, а ось ?i направлена перпендикулярно к плоскости
чертежа, | Х1г | представляет собой отрезок перпендикуляра, опущенного из
точки Ci на линию действия импульса S.
392
ТЕОРИЯ УДАРА
[Гл XVIF
Таким образом, О можно считать величиной известной. Пользуясь равен-
ствами (17.38) и (17.39), найдем импульс
S= i— (uj • пх -J- u2 • n2). (17.40).
Величину, стоящую в скобке, можно выразить через угловые скорости тел
и скорости их центров масс до удара:
U1 • П!-|-и2 n2=(v1 + <»iXr1) • П! + (У2-|-<В2ХГ2) • п2 =
= Vi • ni + v2 • п24-<а1Л-?.1Х + ш1у^-1у + к>1гЛ1г4_ш2л'^2х + к>2у(.2у + <а2гЛ2г-
Заметим, что — (uj • г^-фиг • п2) = и1г представляет собой положительную величи-
ну, равную проекции относительной скорости точки контакта первого тела отно-
сительно точки контакта второго тела на нормаль п2 (см. рис. 17.7).
Отсюда следует, что
о 1 + С
— известная величина и можно, воспользовавшись формулами (17.34)—(17.37),
найти искомые величины после удара:
S S
V1=vi+xni’ V2=V2+M?n2’
Кх Ку Кг (17'41)
й/л- — Ofv + S-д- , Q= <0^4-5 -g— , Qiz = 4- S -g—.
§ 17.9, Частные случаи удара двух тел
1. Центральный удар. Удар называется центральным, если центры масс
соударяющихся тел находятся на общей нормали, проведенной в точке контакта
(или на линии действия импульсов). Примером
такого удара можег служить удар двух однород-
ных гладких шаров.
По определению центральною удара Г;Хп,- = 0,.
Следовательно, все А, равны нулю и формула (17.39)
принимает вид
Л41-h Л1а
Л^ЛТ, ’
(17.42)
Из уравнений (17.35)
находим, что
ДКГГ =0,
Тогда Дсо,- = 0, т. е. при центральном ударе уг-
ловые скорости тел не изменяются. Скорости же центров масс изменяются со-
гласно уравнениям (17.41). Найдем величину ударного импульса S. Для этого
определим сначала щ/.
а1г — — (uj • П14-Uj • п3) — —»(vi • п14- va • п2).
Введем углы а и [1 (рие. 17.8), составляемые векторами скоростей v2 и v2
центров масс до удара с линией центров. Тогда
ulr ~ vicos а 4- v2 cos р.
Отсюда
$ = (1 + 8) (Vi COS а + о2 cos Р).
§ 17 10]
ЗАДАЧИ
393
Подставляя это выражение в равенства (17.41), найдем скорости центров масс
тел после удара
Vi = vi + (fi cos a + v2 cos P) th,
V2 = v2 + ("1 C0S “ + f2 COS p) П2.
2. Плоский удар двух тел. Будем считать, что оба тела имеют плоскости
материальной симметрии, которые йеремещаются в общей неподвижной плос-
кости. Пусть, кроме того, ударные импульсы расположены в той же плоскости
(это всегда выполняется при цилиндрической структуре тел). При выполнении
этих условий удар называется плоским.
В сделанных предположениях векторы Г/ХП/, <в; и 12 f перпендикулярны
к плоскости движения. Имеем
== Аы/у ~ 9, х== ^ly9, ) __л
^ = |rlxnJ2 = ftl2.
где hi — расстояния от центров масс С/ тел до линии действия импульсов (плечи
импульсов).
Формула для вычисления параметра G принимает вид
(j =--------
(17.43)

Остальные величины определяются
нений (17.36) и (17.37) остаются
только два-
Ci (Qu-o)i2) = SA1.
С2 (Q22 —(022) = S/i2,'lz’40'
причем Й1 и /г2 нужно вычис-
лять, учитывая знак моментов.
С1 "Г С2 •
общим формулам,
(17.44)
из шести урав-
§ 17.10. Задачи
по
но
Рис. 17.9.
Задача 17.1. Два шара с
массами и /я2 движутся
поступательно по взаимно пер-
пендикулярным направлениям
со скоростями V! и v2 (рис. 17.9).
В момент удара линия центров
составляет угол л/4 с направле-
ниями движения шаров до уда-
ра. Считая шары идеально глад-
кими и коэффициент восстанов-
ления равным е, найти скорости
шаров после удара.
Направим координатные оси параллельно прямым, по которым движутся
центры шаров до удара (см. рис. 17.9). Пусть скорость первого шара на-
правлена по оси х- В соответствии с теоремой о сохранении количества дви-
жения системы при ударе имеем
/n1v1-|-m2v2 = m1u1-| m2u2,
Здесь Uj и u2 —скорости шаров после удара,
394
ТЕОРИЯ УДАРА
[Гл. XVIГ
В проекциях на оси координат это векторное равенство дает первые двэ
уравнения для определения скоростей тела после удара:
mjPj = /Wiu1A. + трщ, m2v2 = т^у + т2и2у.
Для получения третьего уравнения воспользуемся формулой (17.8), пере-
писав ее в виде
_ ' П2+ U1 ‘ П1 _ _ И2Лг+ "1Л,
8 = ~ Уг-Пг + у^П! +
Так как
КЙ . /2 /2 /2
win, ~ uix 2 Uiy 2 ’ U<ix 2 и^у 2 ’
Кй И2
c’vi. vi 2 ’ Г2Л< v2 2 ’
то
и2х и2у Щх + Uiy
в =---------;-------.
Pl +v2
Отсюда получаем третье уравнение
1/+ и2х—м2Д = 8 (V1 + p2)‘
Наконец, четвертое уравнение можно составить, используя условие идеаль-
ной гладкости шаров. Так как ударный импульс в этом случае направлен по
общей нормали к поверхностям шаров, то проекция количества движения иа
касательную для каждого шара при ударе не изменяется. Таким образом,
И2 И2 , И2
t>i — uix —g ~2 •
или
Vt +«!//•
Это—четвертое уравнение. Присоединяя к нему предыдущие три уравнения,
получим систему четырех уравнений относительно четырех неизвестных:
tiiy, и2х, и2у. Решение системы имеет такой вид:
ш (1+2Л —е) vi-(1 +е) v2 1+s . , ,
ix 2(1+/г), '* 1у 2(1+/г) ( l + ^2)’
и *<1+8) и - —^(l+e)t;i + [2+A (1-е)]п2
Uix W+kj + и*У~ 2(1+й) •
Здесь через k обозначено отношение масс шаров m1lm2=k. Применим эти фор-
мулы к частному случаю абсолютно упругого соударения шаров одинаковой
массы. Примем также равными и скорости шаров.
Подставляя в формулы A = s=l, Vi = v2 = v, получим
1 1а 1 , 1
Uix"-^ v~ 2-у = 0’ Uiy~~2 v-\--^-v = v,
1 , I 1 1 А
«2l=2-t’+yO = f> и2у= 2 V — у V = °.
•§ 17.10]
ЗАДАЧИ
395
ОА2 и ОА3 соответ-
Таким образом, при ударе происходит обмен скоростями. Первый шар после
удара приобретает скорость, которую имел второй шар до удара, а второй шар
приобретает скорость первого.
Задача 17.2. Элементарная частица М мас-
сы т сталкивается с ядром элемента в точке О
(рис. 17.10). Начальная скорость частицы v0.
После столкновения частица и два осколка ядра
движутся в среде С, где оставляют следы OAlt
ОА2, OAs- По длине свободного пробега ча-
стицы Л4 в среде (отрезку ОА^ определяют
скорость Vi частицы после столкновения.
Масса ядра т3 также известна. Определить
отношение масс осколков ядра, зная углы от-
клонения а, р, у от начального направле-
ния Оу следов всех трех частиц после удара.
Кроме того, известно, что v2 > v3. Удар считать
абсолютно упругим.
Обозначим через т2 и т3 массы частиц со следами
ственно:
m2 + m3 = m0.
Из теоремы о сохранении количества движения системы за время удара
следует, что
miVj + m2v2 + m3v3 = mv0.
«Спроектируем на оси х и у это векторное уравнение:
— m2v2 sin р m3v3 sin у -J- mvt sin a = 0,
m2v2 cos P + m3v3 cos у + m v± cos a = mv3.
Кроме того, так как удар абсолютно упругий, то кинетическая энергия
системы за время удара сохраняется (теорема Карио):
rnyf m2vl m3vl __ ту*
2 2 2 ~ 2 ’ I*'-*')
Из (17.46) найдем v2 и у3.
_ т [c0 sin у — Vi sin (у — a)]
V2~ m2sin(P + y) ’
Г - О • , (17.48)
_ т [о0 sin Р — Qi sin (a -|- Р)] '
Va т3 sin (Р + у) •
Поделив первое уравнение на второе и используя условие ti2 7> t»3, получим
v2 т3 a
v3 = т2 Ь
(17.49)
где введены обозначения
a = o0 sin у —г1! sin (у —а), 6 = о0 sin Р — vi sin (а + Р).
Подставив значения v2 и v3 из равенств (17.48) в уравнение (17.47),
а* Ь* ца — v? .
+ ^7- = -т- sin2 (Р+у).
*»*2 *77д <77
получим
(17.50)
Нам необходимо найти отношение k = m3im2. Помножим обе части (17.30)
ла m2+m3 = m0:
a2(1 + ^) + 62(1+"^ ) = sin2(P+y),
\ *7*2 / \ 777g / т
396
ТЕОРИЯ УДАРА
[Гл. XVI®
ИЛИ
а2 (1 + k) + (1 + (р. _ D$ sin2 (Р+у),
откуда получим квадратное уравнение для определения k
a2k2 — ck + b2 = 0,
где использовано обозначение
С = ~ (о| - f?) Sin2 (р + у) - а2 - Ь2.
Решим уравнение (17.51):
с±Кс2 — 4а2Ь2
(17.51>
(17.52)-
Из двух корней следует выбрать тот, который удовлетворяет неравенству (17.49):
Ъ_
а
Используя соотношение (17.52), получим
Q ± К с2— 4a2b2 Ь „ о,
----- —--------> — с ± у с2 — 4а2Ь2 > 26а,
2а2 а ’
откуда
с — 2аЬ ± Кс + 2аЪ > О,
Следовательно, пригоден только знак «плюс».
Теперь окончательно имеем
т2 2с
Аналогично можно показать, чт
Рис. 17.11.
при v2'v3 < 1 в (17.49) нужно взять знак
«минус».
Задача 17.3. При стыковке дву х кос-
мических кораблей, схематично изобра-
женных на рис. 17.11, возникает удар-
До стыковки движение кораблей было-
плоским и поступательным, а их ско-
рости vj и v2, направленные вдоль осей
симметрии, образовывали между собой
угол р. Линия действия ударного им-
пульса составляет с осью первого ко-
рабля угол а. Расстояния от центров
масс до точки контакта равны /j и /2.
Массы кораблей Mj и М2, а моменты
инерции относительно центральных осей-
перпендикулярных к плоскости движений
и проходящих через центры масс, Ct и С2. Коэффициент восстановления равен е.
Определить ударный импульс, скорости центров масс и угловые скорости-
кораблей после у,-;ара.
Пользуясь формулой (17.44), найдем параметр G:
М, + М2 , Ц , h2
‘ С/‘ С2'
§ 17 Ю]
ЗАДАЧИ
397
Здесь Aj и й2 — плечи импульсов, т. е. расстояния от точек Ох и О2 до линии
действия St и S2. Из рис. 17.11 находим
A1 = /1sina, Л2 = /2 sin (a + P).
Следовательно,
+ Z?sin2a /isin2(a + P)
°- +-------c,------• (17'53>
Найдем проекции скоростей точек контакта на соответствующие нормали;
йри этом учтем, что корабли до стыковки двигались поступательно и, следова-
тельно, u1 = vl, u2 = v2,
u1-n1 = —t»xcosa, u2 • п2 = ц2 cos (a + P).
Внося найденные величины в формулу (17.40), найдем ударный импульс
1 I 6
S =—[их cos a — f2 cos (a + p)]. (17.54)
Отсюда видим, что для стыковки необходимо выполнение условия цх cos а
3so2 cos (a + p).
Перейдем к определению скоростей центров масс после удара. Проектируя
векторные уравнения (17.41) на оси х и у, получим
S S
V 1х = 01 cos Р — cos (a + Р), V2x = v2 + cos (a + Р),
s s
Viy = — OiSinP+-^sin(a + P), 1^ = —_ sin (a + p).
Из второй группы уравнений, учитывая, что до удара корабли двигались посту-
пательно (соХг = «2г = 0), найдем угловые скорости после удара. При этом сле-
дует принять во внимание, что моменты импульсов относительно осей гх и г2
положительны:
о — о —
“1.г — j j
или
S S
Й1г = т<- It sin a, Q2z= l2 sin (a + P).
Cl c2
Если после сближения кораблей стыковка состоялась, то относительная скорость
точки контакта после удара равна нулю. Следовательно, удар можно Считать
абсолютно неупругим и коэффициент восстановления е = 0.
Полагая в равенстве (17.54) е = 0, найдем ударный импульс
S= [ух cos a — v2 cos (a + P)].
Если a = P = 0, то удар будет центральным и в соответствии с общей теорией
Й1г = Й2.г = 0. Корабли после стыковки будут двигаться без вращения. При a
и Р, отличных от нуля (в реальных условиях небольшие отклонения от прямого
центрального удара всегда возможны), корабли начнут вращаться вокруг точки
контакта. Так как ПХг#=П2г, то замок, скрепляющий оба корабля, будет
испытывать при этом дополнительный удар.
Задача 17.4. Храповик, изображенный на рис. 17.12, подвергается в точке А
действию ударного импульса S, Плечи рычага 0B = ix и ВА—12 можно считать
398
ТЕОРИЯ УДАРА
[Гл XVII
однородными стержнями с массами и Л12 соответственно. Угол между пле-
чами рычага ОВА равен — р. Требуется определить, при каком отношении
плеч Zi/Zj и каком направлении линии действия импульса S ударная нагрузка
не будет передаваться иа ось храповика.
Введем оси координат Оху, как указано на чертеже. Координаты центра
масс С храповика определяем, пользуясь тем, что точки и С2 лежат в сере-
динах стержней:
Рис. 17.12.
_ ZH2Z2 cos Р
2М ’
Ус = д]' sin p^j .
Здесь М — масса всего храповика.
Проведем прямую ОС. Она составляет
со стержнем ОВ угол а. Очевидно, что
ус (М1А-2М2) — M2l2 sin Р
ctga — cos р
Если ввести обозначения
Zj Mi + 2M2
Z2 = "’ ’ M2
(A^2),
то последнее равенство примет вид
ctga =
ku — sin P
cos P
Величина и пока не известна. Ее надо найти, пользуясь основным соотно.
шением, определяющим положение центра удара. Прежде всего заметим, что
линия действия ударного импульса S согласно доказанному ранее должна быть
перпендикулярна к линии ОС. Следовательно, она образует с плечом ОВ угол
— а, Опустим из точки А перпендикуляр на ОС и найдем точку С^ —центр
удара.
Длины отрезков гс = ОС и г0 —ОО1 должны удовлетворять условию
МгСгО, = {Ог,
где IОг — момент инерции храповика относительно оси вращения. Найдем эти
величины:
хс M2l2 cos р
Гс — sin а 2/И sin a ’
r0 = OD cos a = (Zi — Z2 sin P + Z2 cos p tg a) cos a.
Для осевого момента инерции получим выражение
Ог~ 3
ЛЛ /2 Г/ 1 \2 72 1
^A + M2[(z1-yZ2sinpj +-^-cos2pj =
= + ЗМ2) If + M2lf - sin Р].
§ 17 10]
ЗАДАЧИ
399
Подставим в основное равенство найденные величины:
М,/2 cos р cos а .
" 9~---------Gi - Sln Р + /2 cos Р tg а) =
£ Э111 СЛ
= 4- [(Ml + ЗМ2) l\ + MJl - 3M2ltl2 sin Р].
О
Разделим обе части уравнения на М2/| и воспользуемся введенными ранее
обозначениями:
3 [(u —sin Р) (feu —sin P)+cos2P]=2 [(fe+ 1) и2 —3u sin Р + 1].
Задача свелась к решению квадратного уравнения
(fe —2) u2 —3u (fe — 1) sin Р + 1 —О,
Отсюда найдем отношение плеч
= 2(?-2Тt3 ~sin ₽ ± К9 (fe-1)2 sin2 р —4 (fe —2)].
Оба корня пригодны, если дискриминант уравнения неотрицателен, т. е.
9(fe—I)2 sin2p —4(fe —2)SsO,
Отсюда следует, что
«1, 2
. „ _ 2/fe-2
sin₽ & Mfe=TT-
Заметим, что всегда k — 2+ М^М2 и поэтому правая часть неравенства—действие
тельное число. Убедимся теперь в том, что это число не может быть больше
единицы. Для этого найдем экстремум функции
М ’ 3 (fe — 1) ’
г (fe) = - ( - /г=2^ —?—=о,
3 \2/fe-2 / (fe-1)2
Отсюда получим
fe—1 —2 (fe —2) = 0, fe = 3.
Нетрудно проверить, что при fe = 3 имеет место максимум, следовательно,
max (fe)= _L
k>2 3
Таким образом, при любом соотношении масс можно подобрать такой угол
у—Р между плечами храповика, что при £ОВА — ~ — р обеспечивается
безударная работа оси храповика.
Интересно, что при отрицательных углах Р (угол между плечами тупой)
невозможно обеспечить безударную работу храповика. Это видно из формулы
для и. Величина 1^12 становится отрицательной, что невозможно.
Линия действия ударной силы определяется углом а. Теперь мы его можем
ВЫЧИСЛИТЬ'
ctga=73Fp ~tgP =
fe
2~(fe—TjcosP [3 {k~ Sin Р ± К9 (fe- I)2 srn2 Р-4 (fe-2)]-tg ₽,
ЭЛЕМЕНТЫ АНАЛИТИЧЕСКОЙ МЕХАНИКИ
ГЛАВА XVIII
АНАЛИТИЧЕСКАЯ СТАТИКА
§ 18.1. Введение
Общие теоремы динамики и полученные из них следствия дают
наглядные и вместе с тем мощные средства исследования движения
материальной системы. Умело пользуясь ими, можно сразу по-
лучить ответ на поставленные вопросы либо составить дифференци-
альные уравнения, решение которых определяет движение си-
стемы.
Однако применение общих теорем связано с известными труд-
ностями. Прежде всего, практически невозможно строго класси-
фицировать задачи и указать, в каком случае какая теорема
приведет быстрее всего к цели.
Кроме того, при составлении дифференциальных уравнений дви-
жения материальной системы с помощью общих теорем динамики
приходится часто расчленять систему, увеличивать число уравне-
ний, наконец, вводить неизвестные величины (реакции связей), опре-
деление которых не всегда требуется по условию задачи. Поясним
сказанное примером.
Предположим, что требуется определить закон движения двух
грузов, связанных между собой нерастяжимой гибкой нитью, пере-
кинутой через блок. При решении этой задачи в § 7.4 мы расчле-
няли систему, вводили две реакции связей (натяжения нитей),
которые затем исключали из полученных уравнений движения.
Конечно, эту задачу можно было решить, не вводя реакции связей,
например, с помощью теоремы об изменении кинетической энергии,
однако в более сложных случаях найти простейший путь к реше-
нию задачи не всегда бывает достаточно легко.
Аналитическая механика дает общие методы, с помощью которых
можно составить дифференциальные уравнения движения, не вводя
реакции идеальных связей. Методы аналитической механики оказа-
лись плодотворными не только в теоретических исследованиях,
йо и в практических инженерных расчетах.
§ 18 2]
связи
401
§ 18.2. Связи
Изложение аналитической механики мы начнем с более под-
робного рассмотрения связей. В главе V уже рассматривались
связи применительно к динамике несвободного движения одной
материальной точки. Обобщим эти понятия на систему материаль-
ных точек.
Система материальных точек называется свободной, если поло-
жения отдельных ее точек и их скорости могут принимать про-
извольные значения. В противном случае система называется несво-
бодной. Значит, для несвободной системы должны быть указаны
ограничения, накладываемые на координаты или скорости (или и
на координаты и скорости) отдельных точек. Эти ограничения
называются связями. Они могут быть записаны в виде уравнений
или неравенств. Конструктивно связи реализуются в виде шарниров,
поверхностей, направляющих, стержней, нитей и т. п.
Рассмотрим несколько примеров.
Пример 1. Две материальные точки соединены жестким, невесомым н нерас-
тяжимым стержнем длины I. Уравнение связи будет
(Х2 — *1)2+ (t/a—!/1)2 + (г2—Z1)2 = P,
где %!, (ц, Zj, !/2> z2— координаты точек.
Пример 2. Две материальные точки соединены абсолютно гибкой, нерастя-
жимой н невесомой нитью длины I. В этом случае связь запишется в форме
неравенства:
(х2 —x;l2 + (t/2 — !/i)2 + (г2 — Zj)2 sS I2.
Если нить натянута, то имеет место знак равенства, в против-
ном случае —знак «меньше».
Прежде чем перейти к рассмотрению других примеров остано-
вимся на связях твердого тела. Твердое тело, как система мате-
риальных точек, представляет несвободную систему. Уравнения
связей между отдельными точками твердого тела выражают неиз-
менность расстояний между ними. Число таких связей и, следо-
вательно, уравнений связей бесконечно велико. Однако было пока-
зано (том I, глава X, § 10.1), что в самом общем случае положение
твердого тела вполне определяется шестью независимыми пара-
метрами, в качестве которых можно выбрать, например, три коор-
динаты полюса и три угла Эйлера (том I, глава XII, § 12.4).
Поэтому, рассматривая связи несвободного твердого тела, целе-
сообразно говорить не о связях между отдельными его точками,
а о связях, ограничивающих движение тела как одного целого
объекта. Соответственно этому для несвободного твердого тела
следует составлять уравнения или неравенства для параметров,
определяющих положение тела.
Пример 3. Однородный стержень АВ длины 21 движется так, что его конец А,
шарнирно укрепленный в ползуне, перемещается по горизонтальной направ-
402
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII
ляющей, а конец В опирается на вертикальную направляющую (рис. 18.1).
Найдем связи, ограничивающие движение стержня.
Горизонтальную составляющую примем за ось х, а вертикальную — за
ось у. Плоское движение тела определяется тремя параметрами: двумя коорди-
натами центра масс хс и ус и углом <р.
Направляющие ограничивают это движение.
Очевидно, что при любом положении стерж-
ня справедливы соотношения
t/c = /sin<p, x^ + y^=aZ2.
Если стержень опирается концом В на
вертикальную направляющую, то во втором
соотношении имеет место знак равенства,
если же конец В отошел от направляющей,
то будет знак «больше».
Связи, которые описываются урав-
нениями, называются удерживающи-
ми; связи, описание которых осуще-
ствляется с помощью неравенств, называются неудерживающими.
В первом примере связь удерживающая, во втором — неудержи-
вающая, в третьем примере одна связь удерживающая и одна —
неудерживающа я.
До сих пор мы рассматривали связи, уравнения (неравенства)
которых не содержат время t явно. Такие связи называются ста-
ционарными. Если же связь зависит от времени явно, то она
называется нестационарной связью.
Пример 4. Трос, наматываясь на барабан, поднимает груз, вследствие чего*
свисающая часть троса укорачивается по заданному закону
Z = Z(Z).
Примем точку схода троса с барабана за начало координат, ось z направим
вертикально вниз, осн х и у — горизонтально. При подъеме груз может раска-
чиваться. Очевидно, что его координаты должны удовлетворять условию
«2t/2-pz2 sgZ2 (Z).
В этом примере мы имеем дело с неудерживающен нестационарной связью-
(так как время входит явно в условие связи).
Остановимся несколько подробнее на неудерживающих связях.
До тех пор пока связь удерживает тело (нить или трос натянуты,
стержень опирается на направляющую и т. п.), в условии связи
стоит знак равенства и мы можем применять к системам с такими
связями все выводы и уравнения, которые будут установлены для
систем с удерживающими связями. Но, в отличие от последних,
неудерживающие связи могут не удержать тело (момент отделения
тела определяется по обращению в нуль соответствующей реакции
связи). Это следует всегда иметь в виду при исследовании систем
с неудерживающими связями (см. § 19.4).
Перейдем к рассмотрению связей, зависящих от скоростей точек
системы.
$ 18.2]
СВЯЗИ
403
Пример 5. Конек АВ движется по поверхности льда. Будем считать, что
конек имеет выпуклое лезвие, которое касается льда в одной точке (рис. 18.2).
В плоскости ху конек может занимать произвольное положение, но ско-
рость v точки касания С конька со льдом должна быть направлена вдоль конька.
Иначе говоря, конек не может соскальзывать в направлении, перпендикулярном
к его лезвию. Зададим положение конька тремя координатами: хс, у'с и <р.
Условие отсутствия соскальзывания принимает тогда вид
Ус ,
= tg Ф>
хс
или
хс sin <р — ус cos <р = 0.
Умножив это уравнение на dt, получим
dxc sin <р — dyc cos ф = 0. (18.1)
Так как это уравнение (так же как и предыдущее) нельзя проинтегриро-
вать, то связь (невозможность конька перемещаться в направлении, перпенди-
кулярном к его лезвию) математически выражается 'уравнением, содержащим
неинтегрируемым образом дифференциалы координат или их производные.
Пример 6. Шар движется по шероховатой
Запишем все условия, налагаемые на движение
шара О удовлетворяет условию (рис. 18.3)
плоскости без скольжения,
шара. Прежде всего, центр
21=3 Я,
(18.2)
где /? —радиус шара, а гх — аппликата его центра О в неподвижной системе
координат ОххУ^. Это обычная неудерживающая стационарная связь.
Учтем: теперь, что шар катится без скольжения. Скорость любой точки
шара определяется равенством
v = vo + <oxp,
где v0 — скорость центра шара, <в —его угловая скорость и р— относительный
радиус-вектор точки. Для точки касания шара Р скорость vp=0 и, следова-
тельно
vo+®xpP = 0.
404
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII
Спроектируем обе части этого равенства на поступательно перемещающиеся
оси х, у, г:
uOx + Vp-w^p = 0’ '
«Oy + oVp-bVp = 0’
1'ог + ыхУр-ыухр=°-
(18.3}
Имеем (см. рис. 18.3)
ао.< = *1’ % = аог = 0-
Хр = 0, Ур==^>
где Xj и У!~координаты центра шара О в неподвижной системе координат хццг!.
Воспользуемся кинематическими уравнениями Эйлера (том I, глава XIV,
формулы (14.6)):
<ол = ф sin 0 sin <р 4-0 cos ф,
(0й = ф sin 0 cos ф — 0 sin ф,
и2 = ф cos 04~ф,
где ф, 0 и ф —углы Эйлера.
После подстановки в уравнения (18.3) получим (третье уравнение обра-
щается в тождество)
%! — R (ф sin 0 cos ф — 0 sin ф) = О,
#1 + Я (ф sin 0 sin ф 4- 0’ cos ф) = О,
или, умножая на dt,
dx1 — R (с!ф sin 0 cos ф — dfj sin ф) = 0, У
4-R (^ф sin 0 sin ф-f-d0 cos ф) = 0. / ('8-4)
Так как эти уравнения нельзя проинтегрировать, то связь шара с плос-
костью (отсутствие проскальзывания) математически выражается двумя уравне-
ниями, содержащими нринтегрируемым образом дифференциалы или скорости
параметров, определяющих положение шара.
Связи называются голономными, если их уравнения могут, быть
записаны в виде, не содержащем производных от координат по
времени или дифференциалов координат.
Связи называются неголономными, если их уравнения содержат
неинтегрируемым образом производные от координат по времени
или дифференциалы координат.
Все связи примеров 1—4 голономные, в примере 5 имеется
одна неголономная связь (18.1), а в примере 6 одна связь (18.2)—•
голономная и две связи (18.4) — неголономные.
Голономная нестационарная и удерживающая связь в общем
случае имеет следующий вид:
f(^-1, У1> ..., хп, уп, гп, /) 0, (18.5)
а голономная стационарная и» удерживающая связь
/(ХЬ У1, ZX, .... хп, уп, г„) = 0. (18.6)
$18 3] ВИРТУАЛЬНЫЕ ПЕРЕМЕЩЕНИЯ ГОЛОНОМНЫХ СИСТЕМ 405
В настоящем курсе мы будем изучать только системы с голо-
номными связями. Системы с неголономными связями излагаются*
в специальных руководствах *).
§ 18.3. Виртуальные перемещения голономных систем
Понятие виртуальных перемещений лучше всего проиллюстри-
ровать на примере одной удерживающей, нестационарной, голо-
номной связи, наложенной на одну материальную точку. Другими
словами, речь будет идти пока об одной материальной точке, дви-
жение которой ограничено связью
f (х, у, z, /) = 0. (18.7)
Пусть в момент времени t точка занимает положение
М0(х0, уп, г0), определяемое радиусом-вектором г0. Зафиксируем
время t и из данного положения /Ио мысленно дадим точке малое
перемещение 6г. Обратим внимание на то, что это малое переме-
щение 6г происходит не под действием приложенных к точке сил
и вообще точка может не реализовать перемещение 6г — это просто
малое перемещение, которое мы мысленно даем точке из данного
положения Мо при фиксированном времени t.
Очевидно, что не всякое даже малое перемещение 6г можно
осуществить, не нарушив связь. Для того чтобы выяснить, какое
и в каком смысле малое перемещение 6г не нарушает связь,
учтем, что после перемещения на 6г точка займет новое положе-
ние, определяемое радиусом-вектором г04-6г. Координаты х', у', г'
нового положения точки будут
х' =А-0 + 6х, У =У0 + Ъу, z'=zo + 6z,
(18.8).
где bx, by, bz — проекции вектора 6г.
Внесем эти координаты точки в уравнение связи (18.7) и
разложим полученное выражение в ряд по степеням bx, by и 6г.
Имеем
f(x0 + 6x, уй + by, z0-\-bz, t) — f (х0, y0, г0, /)ф-
+ (Й) + Ьу + ff) bz + ...„
\dxjq 'dyjo y 1 \dz/0 1 ’
где точками обозначены члены высшего порядка.
Так как первое слагаемое правой части равно нулю (коор-
динаты х0, у0, г0 точки /Ио должны удовлетворять уравнению.
*) См., например, Бутенин Н. В. Введение в аналитическую меха-
нику.—М.: Наука, 1971; Лурье А. И. Аналитическая механика. —М.: Физ-
матгнз, 1961; Н е й м а р к Ю. И., Фу фа ев Н. А. Динамика неголономных
систем. — М.: Наука, 1967,
-406
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII
связи (18.7)), то последнее равенство примет вид
f(xa + dx, у0 + ду, г0 + дг, t) =
(18.9)
Виртуальным перемещением точки называется такое малое
перемещение 6г, мысленно осуществляемое из данного положения
при фиксированном времени t, которое с точностью до членов
первого порядка малости включительно не нарушает связи. Из
этого определения следует, что виртуальное перемещение 6г’(6х,
ду, 6г) должно удовлетворять уравнению, которое получается из
(18.9), если приравнять правую часть нулю, отбросив одновре-
менно все члены высшего порядка. Таким образом, проекции дх,
ду, дг виртуального перемещения 6г должны удовлетворять урав-
нению
(¥} ^>У + Ш 6z = 0. (18.10)
\dxjo 1 \ду /0 у 1 \дг/0 ' >
Иначе говоря, проекции дх, ду, дг виртуального перемещения дг
обращают в нуль первую вариацию уравнения связи при условии,
что время не варьируется-.
6IU, И. г. 0^4f)Qto + (f)/S + (|)ote-0.
Если ввести градиент функции (18.7) при фиксированном
времени t в данной точке Л40
(gradf)o = (|0 i + ®Oj + (J) k.
то левую часть уравнения (18.10) можно представить как скаляр-
ное произведение векторов (grad/% и 6г
(grad f)0 • 6г = 0. (18.11)
Теперь легко выяснить геометрический смысл виртуального
перемещения 6г. При фиксированном времени t уравнение связи
(18.7) определяет в пространстве некоторую поверхность. Как
известно, градиент функции представляет собой вектор, направ-
ленный по нормали к поверхности в данной точке Л40. Из урав-
нения (18.11) следует, что любой вектор виртуального перемеще-
ния 6г перпендикулярен нормали к поверхности, т. е. лежит
в касательной плоскости, проведенной к поверхности (18.7) при
фиксированном времени t в данной точке Л40 (рис. 18.4, а).
Рассмотрим теперь действительное перемещение dr точки.
Прежде всего отметим, что действительное перемещение dr, в от-
личие от виртуального перемещения 6г, происходит под действием
приложенных к точке сил за время dt. Это перемещение направ-
§18 3] ВИРТУАЛЬНЫЕ ПЕРЕМЕЩЕНИЯ ГОЛОНОМНЫХ СИСТЕМ 407*
лено всегда по касательной, проведенной к траектории точки
(так как dr = vdt). Рассмотрим два случая.
1. Связь стационарная. При стационарной связи по-
верхность уравнения связи
f(x, у, г) = 0
не изменяется с течением времени и траектория у точки М цели-
ком лежит на этой поверхности. Касательная плоскость содер-
жит в этом случае скорость v точки М (см. рис. 18.4, а), и,
следовательно, мы можем всегда построить одно виртуальное
перемещение 6г, которое будет совпадать с действительным пере-
мещением dr.
grad Г
Рис. 18.4.
Этот вывод можно получить и из аналитических соображений.
Проекции dx, dy, dz действительного перемещения dr должны
удовлетворять условию
df(x, у, г)м„ = (^)/х + (|)/г/ + (‘|^г = 0.
Это условие будет совпадать с (18.10), если в последнем поло-
жить Sx = dx, dy — dy и &z = dz.
Таким образом, при стационарных связях действительное
перемещение dr совпадает с одним из виртуальных перемещений 6г.
2. Связь нестационарная. При нестационарной связи
поверхность
f(x, у, г, 0 = 0,
построенная при фиксированном времени t, не будет содержать
траекторию у точки М. Это следует хотя бы из того, что при
действительном перемещении за время dt точка М перейдет на
новую поверхность f(x, у, г, t-i-dt)^=O. Поэтому действительное
перемещение dr не совпадает ни с одним из виртуальных пере-
мещений 6г (рис. 18.4, б).
Дадим аналитическое доказательство этого утверждения.
Проекции dx, dy, dz действительного перемещения dr при
408
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл. XVIII
нестационарной связи должны удовлетворять условию
df(x, у, г, t)M, = ^^dx + ^^dy+(^dz + ^^dt = O.
~ fdf\
Так как производная 1^1 не равна нулю, то это условие не
'может совпадать с (18.10) при bx — dx, by^dy и 6z = dz.
Все сказанное хорошо иллюстрируется простейшим примером.
Пример 1. Рассмотрим математический маятник постоянной длины I, дви-
жение которого происходит в плоскости ху (рис. 18.5, а). Уравнение связи
(предполагается, что нить все время натянута) будет
Х2-р.!/2 = /2)
где 1 = const.
Эта обычная стационарная голономная связь. При плоском движении
поверхность, определяемая уравнением связи, вырождается в линию — траекто-
рию движения точки. В нашем случае точка М движется по окружности
Рис. 18.5.
радиуса I. Из положения Af0, которое занимает точка в данный момент вре-
мени, мысленно дадим малое перемещение бг, направленное по касательной
к окружности. Это и будет виртуальное перемещение бг математического маят-
ника. Очевидно, что, меняя модуль и направление вдоль касательной, мы
можем осуществить бесчисленное множество виртуальных перемещений бг.
Действительное перемещение dr будет направлено по касательной к траектории
и оно будет совпадать с одним из виртуальных перемещений (см. рнс. 18.5, а).
Рассмотрим теперь случай, когда длина маятника изменяется по заданному
закону (для определенности будем считать, что она увеличивается). Тогда урав-
нение связи примет вид
х2 + !/2 = /2 у).
Это нестационарная голономная связь. Зафиксируем время t и через дан-
ное положение Мо построим окружность, определяемую уравнением связи при
t — const (на рис. 18.5,6 она показана пунктиром). Виртуальные перемещения бг
направлены по касательной к этой окружности. Однако, в отличие от преды-
дущего случая, когда длина маятника не изменялась, при действительном дви-
жении за время dt изменится не только угол ср, но изменится и длина маят-
ника I. В результате действительное перемещение dr маятника не будет совпа-
дать ни с одним из виртуальных перемещений бг (па рис. 18.5, б сплошной
линией показан участок действительной траектории у маятника при увеличи-
вающейся его длине и возрастании угла q).
$ 18.3] ВИРТУАЛЬНЫЕ ПЕРЕМЕЩЕНИЯ ГОЛОНОМНЫХ СИСТЕМ 40!>
Вернемся к общему случаю. Предположим, что на систему
материальных точек наложено h голономных нестационарных
удерживающих связей
ylt Zj....хп, уп, гп, /) = 0 (i=l, .... Л). (18.12)
Виртуальным перемещением материальной системы называется
такое мысленное малое перемещение бту, .... отдельных ее-
точек из данного положения при фиксированном времени t, при-
котором справедливы равенства
п
У Г® ^+(£) М=° •••><18-13>
AJ L\c'xA/O \ОУ*/0 \O2h/0 J
k = 1
где dxk, 8ук, дгк — проекции вектора 6rfc.
Эти равенства можно интерпретировать на языке многомерной
геометрии. Для этого введем в рассмотрение Зп-мерное простран-
ство и изображающую точку М, положение которой определяется
радиусом-вектором г с проекциями хг, уг, zlf ..., хп, уп, гп. Тогда
левые части уравнений (18.13) можно записать в форме скаляр-
ных произведений
(gradf,)o-6r = 0 (t = 1, .... h).
Здесь (grad ^)0 —вектор, направленный по нормали к поверх-
ности fi — 0 в данной точке Мо при фиксированном времени L
Из этих равенств следует, что виртуальное перемещение 6г изо-
бражающей точки М в Зп-мерном пространстве должно находиться
в касательных плоскостях, проведенных к каждой поверхности
(18.12) в данной точке Мо при фиксированном времени I.
Пример 2. На материальную точку М наложены две связи:
fi(x> У, ?) = 0, /2(х, у, 2)=0.
Найдем направления виртуальных перемещений 6г.
Вектор 6г должен удовлетворять двум условиям:
grad/у • 6г = 0, grad f2 • 6r = 0.
Из этих равенств следует, что вектор 6г лежит одновременно в двух каса-
тельных плоскостях, проведенных к данной точке заданных поверхностей
fi = 0 и /2 — 0. Следовательно, все виртуальные перемещения 6г лежат на пере-
сечении касательных плоскостей, т. е. на касательной, проведенной к линии
пересечения данных поверхностей (рис. 18.6).
Пример 3. Рассмотрим плоский рычаг, шарнирно укрепленный в точке О
(рис. 18.7). Любая точка рычага, например точка М, будет двигаться по ок-
ружности радиуса ОМ. Следовательно, виртуальное перемещение 6r(J точки М
будет направлено по касательной к этой окружности, т. е. перпендикулярно
вектору г^ = 0.1'1. Таким образом, виртуальные перемещения точек рычага
перпендикулярны к рычагу. Модули этих векторов не могут быть выбраны
произвольно, Если в качестве независимого виртуального перемещения взять
410
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл. XVIII
вектор бгдр то виртуальное перемещение, например, точки W (см, рис, 18,7)
можно выразить через бг^.
Действительно, для точки N имеем
ON
т*— ОМ Гм'
•Отсюда
х °-v х
бГл**
Другими словами, модули виртуальных перемещений пропорциональны
расстояниям от точек до оси вращения. Распределение векторов виртуальных
перемещений точек рычага показано на рис 18.7,
В заключение этого параграфа введем понятие виртуальной
работы сил, приложенных к системе.
Пусть система материальных точек занимает в некоторый
момент времени t какое-то положение. Обозначим через F1( ..., F„
силы, приложенные к точкам системы. Из данного положения
при фиксированном времени t сообщим системе виртуальное пере-
мещение 6гь ..., 6rrt. Будем считать, что на этом перемещении
силы Fn F2, ..., F„, приложенные к системе, не изменяются.
Составим сумму работ этих сил на виртуальном перемещении
6г^, 61*2» • • • > 61*л
М= 2 Ffe-6r*.
Эта сумма называется виртуальной работой заданных сил.
Наконец отметим, что очень часто вместо термина «виртуаль-
ное перемещение» употребляют термин «возможное перемещение».
По существу это одно и то же, так как латинское слово virtualis
означает возможный. Однако, если пользоваться словами «возмож-
ные перемещения», то для нестационарных связей мы должны
будем сказать: «действительное перемещение невозможно» (ибо
действительное перемещение dr не совпадает ни с одним из воз-
можных перемещений 6г). Так как на русском языке такая фраза
§ 18.4]
ИДЕАЛЬНЫЕ СВЯЗИ
41Г
звучит неестественно, то в отечественной научной и учебной лите-
ратуре чаще пользуются латинским термином «виртуальное пере-
мещение» вместо однозначного русского — «возможное перемещение».-
§ 18.4. Идеальные связи
Введем еще одну классификацию связей.
Связи называются идеальными, если сумма работ всех реакций
связей на любом виртуальном перемещении системы равна нулю.
Обозначим через R* равнодействующую всех реакций связей,
приложенных к точке с номером k. Тогда условие идеальности
связей будет иметь вид
п
2 R*-6rA = 0. (18.14)
*=1
Для одной материальной точки и одной связи f (х, у, г) = О
условие (18.14) упрощается:
R-6r = 0,
т. е. реакция R идеальной связи перпендикулярна к любому
виртуальному перемещению 6г точки и, следовательно, она направ-
лена по нормали к поверхности связи f (х, у, z) = 0. Это означает,
что при идеальной связи точка движется по поверхности без тре-
ния. Конечно, этот вывод остается справедливым и при движении
точки по линии. Условие (18.14) является естественным обобще-
нием понятия идеальности связи для
одной точки на случай п материальных
точек, подчиненных h связям.
Ввиду фундаментального значения
понятия идеальности связей мы укажем
на три, часто встречающиеся на прак-
тике, идеальные связи.
1. С в я з ь — ж естк а я неизме-
няемая система. Такая связь реа-
лизуется в абсолютно твердом теле,
жестких, недеформируемых стержнях и
т. п. Для примера рас-
смотрим две материальные точки, связанные жестким невесомым
и нерастяжимым стержнем. Покажем, что такая связь идеальная.
Реакции стержня на материальные точки направлены по
стержню, и RB =—Rд (рис. 18.8).
' Из условия нерастяжимости стержня имеем
(гл — Гв)2 = И В)2 (Л В = const).
Варьируя это уравнение связи, получим
(гд-Гв)'(6гл-6гй) = 0,
т. е. векторы (гд — гв) и (6гл — 6гв) взаимно перпендикулярны.
412
АНАЛИТИЧЕСКАЯ СТАТИКА
(Гл. XVIII
Найдем сумму работ реакций связей на виртуальном переме-
щении точек. По определению имеем
Иа • 6гА + RB • 6гв = 6гА - Ид • 6гв = Ид (6г л - 6гв) = 0.
Последнее произведение равно нулю, так как вектор Ид,
совпадающий по направлению с вектором (гд — гв), перпендику-
лярен вектору (бгд — 6г в).
Таким образом, стержень, а следовательно, и внутренние
связи абсолютно твердого тела представляют идеальные связи.
Заметим, что в данном примере работа отдельных реакций на
виртуальном перемещении не равна нулю, но их сумма равна
нулю.
В заключение этого случая отметим одно свойство виртуаль-
ных перемещений точек твердого тела: проекции виртуальных
перемещений точек твердого тела на прямую, соединяющую эти
точки, равны между собой, т. е.
прдВ бгд = прАВ 6гв. (18.15)
Действительно, из ортогональности векторов ВД = Гд —гв и
(бгд —6гв) следует, что прАВ(6гА —6гв) = 0; это равносильно (18.15).
Рис. 18.9.
2. Связь —шарнир без трения. Пусть рычаг укреплен
шарнирно в неподвижной точке (рис. 18.9). При отсутствии тре-
ния виртуальная работа реакции шарнира О будет
6Д = Ио • бГд.
Но точка О неподвижна, следовательно, ее виртуальное пере-
мещение 6г0 равно нулю и 6Д=0. Поэтому шарнир без трения
представляет собой идеальную связь.
3. Связь при качении без скольжения. Пусть по
абсолютно твердой поверхности катится без скольжения другое
абсолютно твердое тело (рис. 18.10). Покажем, что такая связь
идеальная. Действительно, так как оба тела абсолютно твердые,
то трение качения отсутствует (см. том I, § 6.2) и виртуальное
-§ 18.5]
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИИ
413
перемещение 6гР точки Р приложения реакции шероховатой
поверхности равно нулю:
6гр = 0.
Отсюда следует, что работа 6Д = R • 6гР реакции связи R на
виртуальном перемещении тела равна нулю.
§ 18.5. Принцип виртуальных перемещений
В этом параграфе мы будем изучать условия равновесия системы
материальных точек. Прежде всего следует отметить, что слово
«равновесие» приложимо скорее к силам, чем к материальным
телам, и, строго говоря, оно не равнозначно слову «покой». Действи-
тельно, если мы говорим, что все силы, приложенные к свобод-
ной материальной точке, уравновешены, то это означает только то,
что сумма сил равна нулю. Но из этого, конечно, не следует еще,
что точка находится в покое —она может также двигаться рав-
номерно и прямолинейно.
Для того чтобы материальная точка находилась в покое, усло-
вия, налагаемые на силы, необходимо дополнить, очевидно, тре-
бованием равенства нулю начальной скорости точки, причем сово-
купность этих условий на основании закона инерции будет и доста-
точна.
Однако по сложившейся многовековой традиции в динамике
слово «равновесие» применяется не только к силам, но и к си-
стеме материальных точек; при этом под словами «равновесие си-
стемы материальных точек» понимается состояние покоя системы.
При такой трактовке этих слов, учитывая сказанное ранее, можно
сформулировать самые общие условия равновесия системы мате-
риальных точек, а именно: для равновесия системы материальных
точек необходимо и достаточно, чтобы суммы всех сил, действую-
щих на каждую точку системы, и скорости всех точек в началь-
ный момент времени равнялись нулю. Если обозначить через Ffe
и R* равнодействующие всех активных сил и реакций связей со-
ответственно, приложенных к точке с номером k, то математически
условие равновесия запишется следующим образом:
F*+Rft = 0. vA(0) = 0 (£ = 1, ..., п). (18.16)
Эти условия имеют один существенный недостаток — они тре-
буют учета всех сил, включая, разумеется, и реакции связей,
действующих на каждую точку системы. При такой общности эти
условия, за редкими исключениями, не могут быть практически
применены к исследованию равновесия материальной системы, но
их можно использовать для доказательства других, более простых
условий равновесия системы материальных точек.
414
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл. XVIII
В 1788 г. Лагранж, обобщая работы своих предшественников,,
сформулировал весьма удобный в приложениях принцип виртуаль-
ных перемещений, устанавливающий условия равновесия системы
материальных точек с идеальными и стационарными связями. Мно-
гие годы это был именно принцип, т. е. положение, принимаемое
без доказательства. В настоящее время предпочитают, пользуясь
законами Ньютона и их следствиями, все условия этого принципа
строго доказывать, иначе говоря, принцип стали рассматривать
как теорему. Помня об анахронизме названия, мы сформулируем
и приведем доказательство принципа виртуальных перемещений
для частного случая, когда связи не только идеальные и стаци-
онарные, но и удерживающие *).
Теорема (принцип виртуальных перемещений). Для того чтобы
система материальных точек, подчиненная идеальным стационар-
ным и удерживающим связям, находилась в равновесии, необходимо
и достаточно, чтобы работа всех активных сил на любом вирту-
альном перемещении системы и скорости всех точек в начальный
момент времени равнялись нулю. Таким образом, нужно доказать,
что для равновесия системы материальных точек необходимо и до-
статочно, чтобы выполнялись условия
Fft-6rft = 0, v*(0) = 0 (й=1......п). (18.17)
*= 1
Необходимость. Предположим, что система находится в
равновесии. Следовательно, должны выполняться условия
Ffe+R* = 0, vA(0) = 0 (6 = 1, .... п).
Из данного положения дадим системе виртуальное переме-
щение бг1; .... 6г„. Умножим каждое из уравнений равновесия
на бг* и сложим их почленно:
п
У (F* + R*) бгА = О,
* = 1
или
2 Ffe'6r*-|- У, R*-6rA = 0.
k=i k=l
Так как связи идеальны, то последняя сумма равна нулю
(см. (18.14)). Следовательно, при равновесии системы должно
*) Формулировку и доказательство принципа возможных перемещений для
неудерживающих связей можно найти, например, в книге: Суслов Г, К, Тео-
ретическая механика, — М,: Гоиехиздат, 1946.
§ 18.5]
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
415
выполняться равенство
5 Ffe.6rft = 0,
k = i
доказывающее необходимость условий (18.17),
Достаточность. Для доказательства достаточности нужно
показать, что при выполнении условий (18.17) система будет нахо-
диться в равновесии. Мы дадим два доказательства достаточности
условий (18.17).
Первое доказательство основано на применении теоремы об из-
менении кинетической энергии. Предположим, что условия (18.17)
выполнены, но, несмотря на это, система под действием приложен-
ных к ней сил начала двигаться из состояния покоя. По условию
теоремы все связи стационарны, поэтому действительное перемеще-
ние системы за время dt будет совпадать с одним из виртуальных
перемещений 6гь ..., 6гп.
На основании теоремы об изменении кинетической энергии сумма
работ всех активных сил и реакций связей на этом перемещении
будет положительна, так как при переходе из состояния покоя в
движение система получит положительное приращение кинетической
энергии. Итак,
£ (Fft + R*) • 6rft > О,
А= 1
ИЛИ
5 Fft-6rft+ 2 Rfe-6r*>0.
А = 1 А = 1
По условию теоремы связи идеальны, поэтому вторая сумма
равна нулю. Следовательно,
2 Fft-6rfe>0.
А = 1
Несовместимость этого неравенства с принятым предположением
(18.17) доказывает достаточность условий принципа виртуальных
перемещений.
Второе доказательство основано на использовании условий (18.16). Устано-
вим предварительно, что если скорости всех точек равны нулю, то перемеще-
ния, пропорциональные ускорениям точек, являются виртуальными перемеще-
ниями системы. В самом деле, для действительного движения системы уравнения
стационарных, голономных связей должны удовлетворяться тождественно по t;
fl ki (0. У1 (0. Z! (t).Xn (0, yn (t), Zn (01=o (i=i.ft).
416 АНАЛИТИЧЕСКАЯ СТАТИКА [Гл. XVIH
Продифференцировав это равенство по времени, получим
п
У ** + £-+ (i = 1......................Л)- (18Л8)
\ охк оук огк ]
л = 1
Дифференцируя второй раз, найдем
V _i_^L,7 дЛИ-)- V (t 1L dlL ± *,.1 n
2Ддхк k + дук ^k "I” dzk Sk) + 2^ \ k dt dxk Ук dt дук + h dt dzk /
k = 1 k= 1
Так как скорости всех точек в данный момент времени равны нулю, то
последняя сумма исчезает (хй = ^ = ^-0) и проекции ускорений удовлетво-
ряют уравнениям
п
2(1?’+1л+яИ"0 "-1.......................<|819>
*=1
Сравнивая эти уравнения с (18.13) убеждаемся в том, что если положить
8xk = koxk, Syh — koy'h, 6zk = ko^k, илн 6rA = /eow/,, то уравнения (18.13) будут
удовлетворены, так как после сокращения на ko они просто перейдут в ра-
венства (18.19).
Заметим, что доказанное утверждение имеет простой смысл: ускорения точек
при равенстве нулю скоростей направлены по касательным к траекториям дви-
жения (это очевидно, так как при vk = 0 нормальные ускорения шк,г —
= а*/Р* = 0)-
Теперь легко доказать достаточность условий (18.17). Запишем первое
условие (18.17) вместе с условием идеальности связей (18.14):
S Fft.6rA = 0, 2R*-6r* = °-
i=l fe=l
После сложения получим
2 (F* + RA).6rA = 0.
* = 1
Предположим, что при выполнении условий (18.17) движение началось и
точки приобрели ускорения wk- Возьмем в качестве виртуального перемещения
систему векторов, пропорциональных ускорениям точек 8тк — kowk (это можно
сделать, так как по условию связи стационарны и голономны и v* (0)=0).
Тогда последнее равенство примет вид
k0 S (F* + Rft)-w* = О,
*=1
или, учитывая, что для каждой точки справедлив второй закон Ньютона
m*wft = F*-|-RA,
ko S mkwk = Q-
k = i
Это равенство может иметь место только в том случае, если все w* = 0,
Следовательно,
/nAwA = F/i-|-R/j = O (k — 1, ...i n),
§ 18 5]
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
417
характера,
(например,
Рис. 18.11.
Значит, условия равновесия (18.16) выполняются, что дает второе доказа-
тельство достаточности принципа виртуальных перемещений.
Принцип виртуальных перемещений широко применяется при
различных технических расчетах. Прежде чем проиллюстрировать
его на примерах, сделаем несколько замечаний общего
1. Если есть неидеальные связи, то их реакции
силы трения) следует отнести к активным силам.
2. В тех случаях, когда требуется определить
реакцию идеальной связи, нужно мысленно отбро-
сить эту связь, а соответствующую реакцию рассмат-
ривать как активную силу.
3. В некоторых случаях вместо виртуальных пе-
ремещений fir., рассматривают виртуальные скорости
v*, пропорциональные бг*. Действительно, если по-
ложить fir*=-/jov*, то в уравнениях (18.13) проекции
fix*, б//*, бг* вектора бг* заменятся просто на про-
екции х*, у*, вектора v*. При движении системы
со стационарными связями действительные скоро-
сти v* будут совпадать с одной из систем виртуаль-
ных скоростей v*.
Задача 18.1. Кривошипно-шатунный механизм (рис. 18.11)
состоит нз кривошипа ОА, шатуна АВ и поршня, на который
действует сила Р. Известны длина кривошипа I, длина ша-
туна L, угол а между осью цилиндра и кривошипом ОА. Пренебрегая тре-
нием и силами тяжести поршня, шатуна и кривошипа, определить момент
пары сил М, приложенной к кривошипу ОА, при котором механизм нахо-
дится в равновесии.
Введем вспомогательный угол P=Z. ОВА; тогда расстояние ОВ = г можно
вычислить по формуле
r = l cos а 4- L cos 0.
По теореме синусов имеем
sin 0 _ sin а
~Т~ Г~>
или
а 1
sin р =-£- sm а.
Следовательно,
г = I cos а + L |/1—р2 sin2 а,
где р = //В.
Варьируя полученное соотношение, найдем
с /, . , . ц2 sin a cos а ' с
or = — Z sin a + L >— -----] 6a .
\ J' I - p2 sin2 a /
Знак «минус» показывает, что при увеличении угла а расстояние г умень-
шается.
14 Н, В. Бутенин и др.
418
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII
В соответствии с принципом виртуальных перемещений имеем
бЛр + 6Лд[ = 0,
где бЛр и бЛд, — работа на виртуальном перемещении системы силы Р и пары
сил с моментом М соответственно.
Работа пары сил равна произведению момента пары М на угол поворота
кривошипа 6а. Следовательно,
6ЛЛ1 = — Мба.
Учитывая, что вектор бг при положительном ба направлен вниз и сила Р
также направлена вниз, получим
6Л р = Р | бг j = Pl sin а ! 1 + р у —=SK——\ ба.
р \ Kl-psin^a/
Применим теперь принцип виртуальных перемещений:
Гр/ sin а ( 1 + а —C0S —---\ — М1 ба = 0 ,
[ \ VI — p2sm2a/ J
Так как ба можно выбрать произвольно, то квадратная скобка должна
равняться нулю. Отсюда получаем значение искомого момента
.. п, . /, . cos a \
М = Pl sin a 1 + ц —. .
\ V 1 —Ц2 sin2 а/
Задача 18.2. Консольная балка АЕ состоит из двух сочлененных шарни-
ром D балок (рис. 18.12, а). На балку действуют вертикальная сила Р = 16 Т,
равномерно распределенная нагрузка q — \ Т/м и пара сил с моментом М —
= 6 Тм. Размеры показаны на чертеже. Определить реакции опор А, В и С.
Заменим действие равномерно распределенной нагрузки силами Q1 = 2<7 =
= 8 Т и Q2=l'<? = 4 Т (рис. 18.12,6). Для определения реакции Дс освобо-
дим консоль DE от опоры С п заменим ее реакцией Rc, как указано на
рнс. 18.12,8. Сообщим теперь виртуальное перемещение точкам консоли DE.
Так как консоль DE получила возможность поворачиваться вокруг шарнира D,
то все виртуальные перемещения будут перпендикулярны к DC в исходном
положении (см. пример 3 § 18.2 и рис. 18.7).
Используем теперь принцип виртуальных перемещений:
Qi • бгс -|- Rc • бгс = О,
или
Qi-1 Src I-Rc-1 бгс 1=0.
Отсюда
/?C = Q1 = 8 Т.
Теперь освободим балку от опоры В (рис. 18.12, г), заменим ее реакцией
RB, дадим виртуальные перемещения точкам балки и подсчитаем работу на
этом перемещении:
Р • бгг + R/; • бг в + Q2 • бг2 + М б<р = 0,
или
Р | бГ1 \~РВ I SrB I + <4 I Sr2 1 + ^ бФ = °*
§ 18 5]
ПРИНЦИП ВИРТУАЛЬНЫХ ПЕРЕМЕЩЕНИЙ
419
Здесь б<р —угол поворота балки AD вокруг оси А. Из рис. 18.12, г видно,
что модули виртуальных перемещений пропорциональны расстояниям до оси
вращения:
| Srx | = 1 6<р, |бгв|=26ф, | 6г2 | =2,5 б<р.
Следовательно,
(Р — %RB2,5 Q2 -f- М~) 6<р = 0;
отсюда
Р -р 2,5 Q2-р/И
Кд— 2
21 Т.
Освободим теперь все опоры,
'виртуальные перемещения вверх
заменим их реакциями и сообщим одинаковые
всем точкам балки (рис. 18.12, д). Тогда,
Рис 18.12.
пользуясь принципом виртуаль-
ных перемещений, получим
(Яд + Яс + Яс——
~I 6гА| = °
и, следовательно,
^д = С1 + С2 + ^> —
~RB-Rc = ~l Г.
Задача 18.3. К шарнирам В
и С четырехзвенника ABCD
приложены две силы Р и Q,
перпендикулярные звеньям АВ
и CD соответственно. Считая
силу Р известной, определить
силу Q при равновесии системы,
если Z, АВС — 90°, а Д BCD =
= 120° (рис. 18.13). Массами
стержней пренебречь.
Рис. 18.13.
Дадим системе виртуальное перемещение. Так как стержень АВ может
вращаться вокруг оси А, а стержень CD — вокруг оси D, то виртуальное пере-
мещение бгв точки В перпендикулярно АВ, а виртуальное перемещение бгс
точки С перпендикулярно CD (см. рис. 18.13). Применяя принцип виртуаль-
ных перемещений, получим
Р-j бГд|-(?.| 6rCj=0,
14*
420
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII
Учтем теперь, что проекции виртуальных перемещений двух точек inep-
дого тела на прямую, соединяющую эти точки, равны между собой (см. равен-
ство (18.15)). Для точек В и С будем иметь
|бгд ] = | 6гс | cos 30°.
Подставляя это в предыдущее равенство, получим
Р | бгс I cos 30° — Q | бгс j = 0.
Отсюда
Читателю полезно решить последние три задачи с помощью
сбычных уравнений статики твердого тела и сравнить оба метода.
§ 18.6. Обобщенные координаты и обобщенные силы
При решении многих задач механики можно добиться сущест-
венного упрощения, если ввести в рассмотрение так называемые
обобщенные координаты и соответствующие им обобщенные силы.
Определению этих величин и посвящен этот параграф.
Рассмотрим материальную систему, состоящую из п материаль-
ных точек. В инерциальной системе отсчета Oxyz положение каж-
дой точки Mk определяется тремя координатами xk, yk, zk, а поло-
жение всех точек — З/г декартовыми координатами.
Будем считать, что движение системы ограничено h голоном-
ными, идеальными и удерживающими связями
ft (xlt ylt zlt .... xn, yn, z„, t) = 0 (i = l, ..., h). (18.20)
Так как Зп координат xk, yk, zk удовлетворяют h уравнениям
связей, то они не являются независимыми. Очевидно, что число
независимых координат, определяющих положение системы, будет
s = 3n — h. (18.21)
В качестве независимых координат, определяющих положение
системы, можно выбрать s из Зп декартовых координат, выразив
остальные координаты с помощью уравнений связей. Однако та-
кой способ выбора независимых координат не будет лучшим, так
как он часто приводит к сложным зависимостям. Значительно
удобнее ввести s каких-либо независимых параметров qv, ..., qs
(они называются обобщенными координатами), однозначно опре-
деляющих положение системы. По существу, не употребляя этого
термина, мы уже неоднократно пользовались обобщенными коор-
динатами. Так, например, положение математического маятника
определялось углом отклонения его от вертикали (? = ср), поло-
жение твердого тела, имеющего одну неподвижную точку, опре-
делялось тремя углами Эйлера (<7i = T, <?2 = 6> 7з==(Р)> а положе-
§ 18.6]
обобщенные координаты и обобщенные силы
421
ние твердого тела, совершающего плоское движение, определялось
двумя декартовыми координатами полюса и одним углом поворота
тела (<h = xc, <?2 = г/с, <7з==(Р)-
В общем случае обобщенные координаты могут иметь различ-
ный геометрический и механический смысл. Ими могут быть ли-
нейные и угловые величины, а также параметры, имеющие раз-
мерность площади, объема; обобщенные координаты иногда содер-
жат элементы силовых и иных физических характеристик системы.
Итак, пусть положение материальной системы определяется s
независимыми обобщенными координатами *)
<71, Яг, , Яз-
Так как положение системы однозначно определяется обобщен-
ными координатами, а каждая точка системы определяется ее
радиусом-вектором г*, то постедние можно выразить через обоб-
щенные координаты и время:
г* = М<71> •••> Яз, О (А: = 1, ..., п). (18.22)
Эти п векторных равенств эквивалентны Зп скалярным равен-
ствам
Xk = xk (qlt ..., qs, t),
Ук = Ук (Яъ • • •, Яз, 0, (k = l, ..., n).
zk = zk(qlt , qs, t)
Конечно, при подстановке этих выражений для yk, zk в урав-
нения связей (18.20) последние должны обратиться в тождества.
Заметим, что если связи стационарны, то всегда можно вы-
брать такие обобщенные координаты, при которых равенства (18.22)
не будут содержать время I явно.
Обобщенные координаты удобны тем, что они, во-первых,
независимы и, во-вторых, их введение освобождает нас от необ-
ходимости учитывать уравнения голономных связей. Последние
удовлетворяются теперь автоматически по самому смыслу выбора
обобщенных координат.
Если система голономна и число независимых координат,
определяющих ее положение, равно s, то столько же будет и
независимых вариаций координат, характеризующих виртуальное
перемещение системы. Число независимых вариаций координат,
определяющих положение системы, называется числом степеней
свободы системы. Для голономной системы, на которую наложено
*) Иногда вводят так называемые избыточные координаты. В этом случае
число обобщенных координат будет больше числа Зп -h. В настоящем курсе
избыточные координаты не рассматриваются (см., например, Лойцян-
ский Л. Г., Лурье А. И. Курс теоретической механики, ч. II.—М: Гос-
техиздат, 1955; Лурье А. И. Аналитическая механика.— М.; Физматгиз, 1961,
$ 1.4, 7,11, 7,12),
422
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII’
h связей (18.20), число степеней свободы равно числу независи-
мых координат, определяющих ее положение. Очевидно, что для
голономной системы в качестве независимых вариаций координат
лучше всего выбрать вариации независимых обобщенных коорди-
нат bqlt 8qs.
Для неголономной системы число степеней свободы не будет
равно числу независимых координат, определяющих положение
системы. Действительно, пусть, кроме h голономных связей, дви-
жение системы подчинено еще т неголономным или кинемати-
ческим связям, уравнения которых содержат неинтегрируемым
образом производные координат по времени (или их дифферен-
циалы и дифференциал времени dt). В большинстве случаев, встре-
чающихся в практике, неголономные связи содержат производные
координат или их дифференциалы линейно. В этом случае дви-
жение системы будет подчинено т линейным зависимостям вида
dqr Д-.. • + ar3 dq, Ц-ос,. dt — 0 (г = 1, .., т), (18.23)
где ark и аг — некоторые функции qlt ..., q, и t. Заметим, что
при стационарных неголономных связях аг —0 и ни одна из
функций ark не будет зависеть от времени t явно.
Условие неинтегрируемости уравнений неголономных связей
(18.23) является существенным, так как в противном случае после
интегрирования соответствующего уравнения получилась бы конеч-
ная зависимость между qlt ..., qs н t, т. е. голономная, не кине-
матическая связь. В этом случае координаты qlt ..., q< не были
бы независимыми и их число можно было бы уменьшить. Таким
образом, неголономные связи налагают ограничения на свободу
движения системы и одновременно не позволяют уменьшить числа
параметров, определяющих положение системы.
В силу неголономных связей вариации обобщенных координат
bqlt ..., bqs, определяющих виртуальное перемещение системы,
будут подчинены т условиям
«г16<71 + ...4-сс„б7^ = 0 (г=1,
которые получаются из (18.23) заменой dqk на bqk при dt = O
(виртуальные перемещения осуществляются при фиксированном
времени).
Из последних равенств следует, что число независимых вариа-
ций координат (?!,.. , qs будет меньше числа координат и равно
8 — т. Таким образом, число степеней свободы неголономной
системы равно v = s — т, где s — число независимых координат,
определяющих положение системы, а т —число неголономных свя-
зей. Заметим, что число неголономных связей называется сте-
пенью неголономности.
Для конька, движущегося по поверхности льда (пример 5
§ 18.2, рис. 18.2), число независимых координат, определяющих
$ 18 6]
ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СИЛЫ
423
его положение, равно трем (s —3), степень неголономности равна
•единице (т=1—одна неголономная связь (18.1)), число степеней
свободы равно двум (v —3—1—2).
Для шара, катящегося без скольжения по плоскости (при-
мер 6, рис. 18.3), число независимых координат, определяющих
его положение, равно пяти (з — 5), степень неголономности равна
двум (т = 2 —две неголономные связи (18.4)), число степеней сво-
боды равно трем (v=s —т=-3).
Перейдем теперь к определению обобщенных сил. Вычислим
работу 8А всех активных сил па виртуальном перемещении
системы (если имеются силы трения, то они присоединяются
к активным силам):
п
М = 2 F" бг*- оз-24)
fe.=i
Пользуясь равенством (18.22), выразим вариацию 6гй радиуса-
вектора гк через вариации &qlt bq2, .... &qs обобщенных коорди-
нат:
S
^=2^/ (*=1’ 2....................п)- <18-25>
При вычислении 6rft необходимо иметь в виду, что виртуальное
перемещение системы определяется при фиксированном времени t.
Проекции вектора на оси неподвижных декартовых коор-
динат равны, конечно, производным от соответствующих коорди-
нат точки:
(дтк\
\dqj }х
дхк
dq, ’
(дгк\ _ дуь
\dq/y dq/
= (18.26)
\dqjjz dq, ' '
Подставим 6rft из равенства (18.25) в формулу (18.24):
64 = 2 F.-2&4
fe = l fe = I 1=1 ’
или, меняя порядок суммирования, получим
I - 1 \fe = 1 I
Введем обозначения
п
и-‘>2..................»)•
и = 1
(18.27)
424
АНАЛИТИЧЕСКАЯ СТАТИКА
[Гл XVIII
Тогда последнее равенство примет вид
S
М = 2 Ql8q,=Q1bql + Q,bq2 + ... + Qs8qs. (18.28)
/ = 1
Множитель Qy при вариации обобщенной координаты 8qf
в выражении для виртуальной работы активных сил системы
называется обобщенной силой, соответствующей обобщенной коор-
динате qr
Обобщенная сила Qj в общем случае не является силой
в обычном понимании этого слова. Ее размерность зависит от
размерности соответствующей ей обобщенной координаты qj и
определяется равенством
где [Л] —размерность работы.
Если обобщенная координата измеряется линейными величи-
нами, то размерность обобщенной силы совпадает с размерностью
силы; если же обобщенная координата представляет угол, то
размерность обобщенной силы совпадает с размерностью момента,
и т д.
Рассмотрим способы вычисления обобщенных сил.
1. Обобщенные силы можно вычислить по формуле (18.27),
которую удобнее представить в следующем виде (использовано
равенство, выражающее скалярное произведение двух векторов
через их проекции):
<г, = 1 (f‘-< +Fu ' 8-29>
Здесь Fky, —проекции силы Fft на оси декартовой
системы координат.
2. Для вычисления обобщенной силы, например Q1( дадим
такое виртуальное перемещение, при котором все вариации обоб-
щенных координат, кроме bqlt равны нулю:
6<7i#=O, 8q2 = 6q3 = ... = 8qs = 0.
Вычислим на этом перемещении виртуальную работу 8АГ всех
активных сил, приложенных к системе. На основании формулы
(18.28) будем иметь
Mi = Qi8qlt
Множитель при вариации bqt равен первой обобщенной силе.
Аналогичным образом вычисляются остальные обобщенные
силы.
§ 18.61 ОБОБЩЕННЫЕ КООРДИНАТЫ И ОБОБЩЕННЫЕ СИЛЫ 425
3. Третий способ применим только для консервативных сил.
Если силы консервативны, то будут справедливы равенства
Р _ _ дП р __ р
кх дх/, ’ ky dyk ’ kz dzk ’
где П — потенциальная энергия системы.
Внося эти выражения для Fkx, Fky и Fkz в формулу (18.29),
получим
п______VI дхь дП ду_к дП
— \дхк dq, -i" dyk ду, dzk dq,j '
k = 1
или, учитывая, что потенциальная энергия П зависит от обобщен-
ных координат сложным образом через декартовы координаты хк,
Уь и zk,
(/=1, 2, ..., s). (18.30)
Таким образом, обобщенная сила консервативной системы равна
частной производной потенциальной энергии по соответствующей
обобщенной координате, взятой с обратным знаком.
Прежде чем перейти к примерам, еще раз напомним, что при
вычислении обобщенных сил учитываются только активные силы,
приложенные к системе. Реакции идеальных связей не учиты-
ваются (их работа равна нулю); если имеются силы трения, то
они присоединяются к активным силам.
Задача 18.4. В эпициклическом механизме кривошип ОС вращается во.
шестерни I радиуса R, и
круг оси, проходящей через центр О неподвижной
приводит в движение сателлит // радиуса г
(рис. 18.14). К кривошипу приложен вращаю-
щий момент Л4вр. Силы трения создают на
оси С сателлита момент Л4тр. Ввести обоб-
щенную координату и определить соответствую-
щую обобщенную силу, считая, что механизм
расположен в горизонтальной плоскости.
Положение движущихся частей механизма
вполне определяется углом ср поворота криво-
шипа вокруг оси О. Поэтому эпициклический
механизм имеет одну степень свободы. За обоб-
щенную координату q примем угол ср.
На механизм действуют следующие силы:
сила тяжести Р и силы, создающие вращающий
момент Л4вр; к ним нужно присоединить силы
трения на оси вращения С сателлита, момент
которых равен Л4тр. Приложенные к системе
силы (за исключением силы тяжести) не консервативны, поэтому обобщенную
силу, соответствующую обобщенной координате tp, определим вторым способом.
Дадим кривошипу виртуальное перемещение б<р и вычислим работу всех
перечисленных сил на этом перемещении-
6Д = 6Д (Р) + 5Д (Мвр) + 6Д (Мтр).
426 АНАЛИТИЧЕСКАЯ СТАТИКА [Гл XV11T
Виртуальная работа 6Д (Р) силы тяжести равна нулю (так как по усло-
вию механизм расположен в горизонтальной плоскости и, следовательно, пере-
мещение точки приложения силы тяжести перпендикулярно самой силе).
Виртуальная 1абота вращающего момента Л4вр при повороте кривошипа
на угол 6<р будет
ел (ллвр)=м врбф.
Работа силы трения на оси вращения сателлита определяется равенством
еЛ (Л4тр) = — Л4тр 6фг,
где бфг— относительное угловое перемещение сателлита.
Очевидно, что между относительным ‘угловым перемещением бфг сателлита
и угловым перемещением бф кривошипа имеется простая связь:
бфг = убф.
Подставляя это выражение для бфг в предыдущее равенство, получим
ел (Л7тр)=- Л1трбф.
Собирая все члены, найдем виртуальную работу 6Л сил, приложенных
к эпициклическому механизму:
6Л =4л1вр-у AlTpj бф.
Коэффициент при вариации бср обобщенной координаты ср равен обобщенной
силе
X
<2Ф=Мвр-у Л1тр. (18.31>
Таково значение обобщенной силы, если за обобщенную координату при-
нять угол поворота кривошипа Заметим, что полученное выражение для обоб-
щенной силы Q(( справедливо как для постоянных,
так и для переменных моментов А4вр и Л4ТО.
Задача 18.5. Двойной математический маятник
(рис. 18.15) состоит из двух невесомых стержней дли-
ны Zx и Z2, на концах которых укреплены материаль-
ные точки Mt и М2 веса Р^ — т^ и P2 — m2g соот-
ветственно. Первый стержень может вращаться вокруг
неподвижной горизонтальной оси О, а второй — во-
круг горизонтальной оси, связанной с первой точ-
кой. Ввести обобщенные координаты и вычислить
обобщенные силы.
При такой конструкции вся система движется
в вертикальной плоскости, которую мы примем за
плоскость ху (ось z направим перпендикулярно к
плоскости чертежа). Положение двойного математи-
ческого маятника вполне определяется двумя угла-
ми ф! и ф2 отклонения стержней от вертикали, Следовательно, система имеет
две степени свободы. За обобщенные координаты qr и q2 примем углы фг и фа.
Обобщенные силы вычислим тремя способами.
<§ 18 6]
обобщенные координаты и обобщенные силы
427
Первый способ. Найдем
наты точек их приложения
Pix = mig-
Р2Х = m2g
xt = Zj cos ф1,
У1 — 11 sin ф[,
Zl=.Q.
проекции
сил Pj — mxg, Р2 — m2g и коорди-
^=0,
Рг;/ = 0>
х2 = cos ф1 1г cos ф2,
У г == 8Ш ф14~ ^2 sin ф2,
z2 = 0.
Р2г-0;
Обобщенные силы найдем по формуле (18.29), написав ее в развернутом
виде для каждой из величин Qi и <j2 (qt и q2 заменены на дд и ф2):
<2г— ?ix
Да-i dyi
<Эф2 ' 1у дфг
+ Р
дг1 , р дх2 , р ду2 dz2
1г dfp2 '
Подставляя значения проекций сил и координат точек их приложения, полу-
чим
Qi = — ’ntglY sin q)i — m2gli sin (pi = — (mi + m2) g/i sin epi,
Q2^— m2gl2 sin qp2.
Второй способ. Вычислим сначала обобщенную силу Q2. Сообщим
•системе так(е виртуальное перемещение, при котором угол ф1 останется без
изменения, а угол ф2 получит приращение бф2 (рис. 18.16). При таком пере-
мещении системы работу будет производить только одна сила Р2 (точка при-
ложения силы Pi осталась в прежнем положении).
Работу 6Л2 силы Р2 на виртуальном перемещении бф1 = 0, бф2 0 вычис-
лим как работу силы, приложенной к твердому телу, вращающемуся вокруг
неподвижной оси Mt, Момент силы Р2 относительно оси вращения второго
•стержня равен —Р2/2вщф2==—т2§/2зтф2. Поэтому
6Л2 = — m2gl2 sin ф2бф2.
Коэффициент при вариации бф2 равен обобщенной силе
Qa = — m2gl2 sin ф2.
Перейдем к вычислению обобщенной силы QP Для этого дадим системе
виртуальное перемещение бф^О, бф2 = 0 (рис. 18.17). Работу силы Рх вычис-
428
аналитическая статика
[Гл XVIIT
лим по тому же правилу: момент силы Pi относительно оси вращения первого
стержня равен — sin фр Следовательно, работа этой силы на виртуаль-
ном перемещении 6ф1 О, 6ф2 = 0 равна —mi2.lt sin rpi&pt.
Перемещения точек М: и М2 одинаковы (так как при неизменном угле ф2
второй стержень перемещается поступательно). Поэтому виртуальная работа
силы Р2 получится из предыдущего выражения заменой mt и т2, т. е. равна
— m2gli sin ф16ф1-
Сумма работ сил Pj и Р2 на этом виртуальном перемещении будет иметь
вид
6Л1 = —• rn[g/1 sin ф16ф1 — m-zgli sin ф16ф1,
или
6Ai = — ('Щ + ,n2) sin срхбфр
Коэффициент при вариации &pt равен обобщенной силе, соответствующей
обобщенной координате фр
Qi = — («1 + т2) gli sin ф!.
Третий способ. Активные силы Pj и Р2 консервативны. Найдем потен-
циальную энергию П, вычислив ее как работу сил Pt и Р2 при перемещении
системы из данного положения в горизонтальное:
П = — mjg/i cos ф1 — m2g (/j cos ф1ф-1% cos ф2),
или
П — — g/jcos ф! — m2gl2 cos ф2. (18.32}
Обобщенные силы Q, и Q2 найдем теперь по формуле
(18.30):
_ ап _ ап
Q1~ дф, ’ Qi~ дф2-
Выполняя дифференцирование, получим
<21 = — («1 + т2) glt sin ф!, Q2 = — m2gl2 sin ф2.
Из самого определения видно, что обобщен-
ные силы зависят не только от структуры си-
стемы и приложенных к ней активных сил, но также и от выбора
обобщенных координат. Покажем это на примере двойного мате-
матического маятника.
Выберем в качестве обобщенных координат углы ф1 и ф2, как это пока-
зано на рис. 18.18. Тогда потенциальная энергия системы определится равен-
ством
П = — (mi + m2) git cos ф, — m2gl2 cos (ф\ + ф2).
Обобщенные силы вычислим по формуле (18.30):
п - дП
дфИ дф2’
В результате дифференцирования получим
<2ф, =•= — («1 + «г) gh sin ф! — m2g/2 sin (ф\ ф- ф2),
<2ф2 =- — «2^2 sin (ф!+ф2).
Как и следовало ожидать, эти выражения для обобщенных сил отличаются
от Qi и Q2.
§18 7] УСЛОВИЯ РАВНОВЕСИЯ В ОБОБЩЕННЫХ КООРДИНАТАХ 429
Из рассмотренных примеров видно, что наиболее универсаль-
ным методом определения обобщенных сил является второй метод,
основанный на вычислении элементарной работы, но он не всегда
наиболее прост.
§ 18.7. Условия равновесия в обобщенных координатах
Согласно принципу виртуальных перемещений для равновесия
материальной системы с идеальными, стационарными, голоном-
ными и удерживающими связями необходимо и достаточно, чтобы
при vA (0) = 0 суммарная работа всех активных сил, приложенных
к системе, на любом виртуальном перемещении равнялась нулю:
6А = 0.
Будем определять положение системы обобщенными координа-
тами ..., qs. Тогда последнее уравнение согласно формуле
(18.28) примет вид
Qi8ql + Q2672 + • • = . (18.33)
Так как обобщенные координаты qlt ..., qs независимы и,
следовательно, их вариации ..., 8qs при голономных связях
произвольны, то из последнего уравнения следует, что все обоб-
щенные силы ..., Qs равны нулю:
Qi-0, .... Qs = 0. (18.34)
Действительно, докажем, например, что из равенства (18.33)
следует Qs = 0. Для этого возьмем такое виртуальное перемеще-
ние, при котором
6g1 = ... = 6gs_1 = 0, 8qs^0.
Подставляя эти значения для вариаций обобщенных коорди-
нат в равенство (18.33), получим
(?Л^ = 0.
По условию 8qs^= 0, следовательно, Qs = 0. Аналогично уста-
навливаются остальные уравнения (18.34).
Уравнения (18.34) являются искомыми: для равновесия меха-
нической системы с идеальными, стационарными и голономными
связями необходимо и достаточно, чтобы все обобщенные силы
системы равнялись нулю (начальные скорости всех точек считаем
равными нулю).
Если силы, действующие на систему, консервативны, то сог-
ласно равенствам (18.30) уравнения (18.34) примут вид
= 0 -- = 0 — — 0 П 8 351
&71 ’ dq2 и’ •••’ dqs-"-
Рассмотрим пример.
430
АНАЛИТИЧЕСКАЯ СТАТИКА
(Гл XVIII
Задача 18.6. Два груза А и В, находящиеся на гладких наклонных пло-
скостях, удерживают в равновесии груз веса Р при помощи троса, перекину-
того через два соосных блока / и II и свободный блок III (рис. 18.19).
Найти веса грузов Pi
с горизонтом углы а и
И
Р2, если наклонные плоскости составляют
Трением и массой блоков и троса пренебречь.
' Нерастяжимый трос представляет собой
голономную и стационарную связь, уравне-
ние которой можно записать в виде
Xi + x2-}-2x3 = a. (18.36)
Следовательно, система имеет две сте-
пени свободы. Примем xt и х2 за обобщен-
ные координаты. Варьируя уравнение связи
(18.36), получим
6%1 6х2 26%з = 0;
ГП
III
С
Р/
Рис. 18.19.
отсюда
6*3 = — у (6X1 + 6х2).
Сообщим грузам А и В виртуальные перемещения, указанные на чертеже,
вычислим работу сил тяжести Рх, Р2 и Р на этом перемещении и в соответ-
ствии с принципом виртуальных перемещений приравняем ее нулю:
Р1-6гд + Р2-6гв + Р-5гс = 0,
или
Pj j 6rА j sin a + P21 6rB | sin p — P | 6rc | = 0.
Имеем
бгд^бхх, 6rB --.-6x2, | 8rc | = | бх3 I =y (8xi + 8x2).
Подставляя в предыдущее равенство и группируя члены, получим
/ Р\ [ Р\
(Pi sin a —g-1 Sxj + ( Р2 sin Р —% I 6x2 — 0.
Так как 8xt и 6x2 независимы, то остается приравнять нулю коэффициенты
(обобщенные силы) при них:
р
Qi = Pi sin а—у = 0,
Q2 = P2 sin р — y = 0,
(18.37)
Pi = 9~^—>
2 sin a
p - p
2 2 sin p ‘
Эту задачу можно решить, воспользовавшись консервативностью действующих
на систему сил (сил тяжести).
Составим выражение для потенциальной энергии системы. Для этого вычис-
лим работу, производимую силами тяжести при перемещении системы из дан-
ного положения в положение, когда Xj = 0, х2 = 0:
П = — PjXj sin a — Р2х2 sin р + ^ — х3j Р.
Заменяя х3 из формулы (18.36), получим
П = — PjXi sin a — Р2х2 sin р + Р .
Условия равновесия имеют вид (18.35):
t^- = — Pi sin a + ~ = 0, ^- = —Р2 sin р + -^- = 0,
dxi 2 дх2 1 2
Эти уравнения совпадают с уравнениями (18.37).
ГЛАВА XIX
АНАЛИТИЧЕСКАЯ ДИНАМИКА
§ 19.1. Общее уравнение динамики
Рассмотрим систему п материальных точек, движение которой
ограничено h удерживающими идеальными и голономными связями.
Воспользуемся принципом освобождаемоеги и заменим все связи
их реакциями. Обозначим через F* и Rft соответственно равно-
действующие всех активных сил и реакций связей, приложенных
к точке Мк. Рассматривая точку как свободную, движущуюся
под действием сил Fte и Rfe, применим к ней второй закон Ньютона:
= Fft-p Rs,
или
Ffe —mfewfc + Rft = 0 (£ = 1, 2, ..., n). (19.1)
Мысленно зафиксируем время t и дадим системе виртуальное
перемещение 6rft (й = 1, ..., и). Умножим каждое уравнение (19.1)
скалярно на 6г* и сложим их:
У (F* - • 6rfe + У • 6rft = 0.
А = I ft — 1
По определению идеальных связей последняя сумма равна
нулю. Следовательно,
У (Fk-mkwk)-8rk = Q. (19.2)
й = 1
Это уравнение, называемое общим уравнением динамики, может
быть прочитано следующим образом: при движении материальной
системы с идеальными и удерживающими связями работа всех
активных сил FZ( и сил инерции —m,,vjk на любом виртуальном
перемещении системы равна нулю.
Если связи стационарны, то общее уравнение динамики пред-
ставляет собой следствие принципа виртуальных перемещений и
принципа Даламбера.
432
АНАЛИТИЧЕСКАЯ ДИНАМИКА
[Гл XIX
Аналогично принципу виртуальных перемещений, общее урав-
нение динамики (19.2) может быть непосредственно использовано
для решения различных конкретных задач. Рассмотрим пример.
Задаче 19.1 Два тела Л1, и М2 с массами mt и т2 связаны между собой
абсолютно гибкой н нерастяжимой нитью, перекинутой через блок К
(рис. 19.1, а). Пренебрегая массой нити и блока, а также трением, определить
закон движения 1 вузов.
Для решения этой задачи с помощью общего уравнения динамики изобра-
зим на рисунке
все активные силы
fj
-Л
Т,
-годи.
-w?g
а)
сторону,
вниз (см.
«'/Я
Рис. 19.1.
(силы тяжести mAg и m2g) и силы инерции.
Предположим, что тело имеет
ускорение Wj, направленное вниз.
Тогда сила инерции — первого
груза будет направлена вверх. Так
как нить нерастяжима, то уравнение
связи имеет вид (см. рис. 19.1, а)
х, + х2 = const.
ИЛ
Цд
в)
сила
т. е. вверх. Тогда
рис. 19.1, а), а ее модуль
Дифференцируя два раза по вре-
мени, получим
или Х2 =— Xt- Это означает, что ус-
корение w2 второго груза равно по
модулю ускорению первого
но направлено в
инерции второго груза
равен
груза,
противоположную
будет направлена

Я
, *

6)
/П2С02 = = m2W’
где to —общее значение модуля ускорений грузов.
Дадим системе виртуальное перемещение. Варьируя уравнение связей,
получим
6х, —6х2 == 0;
отсюда
6х2 =—
Вычислим работу всех активных сил и сил инерции на этом виртуальном
перемещении и приравняем ее нулю:
(mig — т^) 6xi + (m2g + m2w2) &x2 = 0.
Принимая во внимание, что 6х2 = —&хг и w2 = w1 = w, получим
mi (.8 — to) — «2 (g + ш) = 0.
Сокращая это уравнение на бх, и решая полученное уравнение относительно со,
найдем ускорение системы
/тг, — т,
со =—5------- е.
m-i + т.
Применяя к каждому телу принцип Даламбера (рис. 19.1, б и в) и учиты-
вая последнее равенство, легко получим, что натяжения нити в обеих вет-
вях одинаковы (7’1 = 7'2). Это доказывает сделанное без доказательства со-
ответствующее утверждение в задаче 7.1 (сгр. 176).
§ 19 2|
УРАВНЕНИЕ ЛАГРАНЖА ВТОРОГО РОДА
433
§ 19.2. Уравнения Лагранжа второго рода
Общее уравнение динамики (19.2) дает возможность составлять
дифференциальные уравнения движения, не содержащие реакции
идеальных связей. Для сравнительно простых систем непосред-
ственное применение этого уравнения вполне оправдано, однако
в более сложных случаях использование общего уравнения дина-
мики (Триводит, как правило, к относительно сложным преобразо-
ваниям. Поэтому значительно удобнее пользоваться не общим
уравнением динамики (19.2), а вытекающими из него уравнениями
Лагранжа второго рода, в которых основные трудности преобра-
зования преодолены в общем виде.
Для вывода этих уравнений воспользуемся общим уравнением
динамики (19.2):
2 (Fft-m/^)-6rfe = 0.
4=1
Подставим в это уравнение значение вариации бг* радиуса-вектора
из равенства (18.25):
4 = 1 / = 1
Умножим это уравнение на —1, изменим порядок суммирова-
ния и разобьем сумму- на две части:
2 h тг- РФ 1 12 h тг- РФ
4 = 1 /=1 /=14=1
/=tL*=l 4 = 1
Пользуясь выражением для обобщенных сил (18.27), будем иметь
2 2
/=1 4=I
(19.3)
Первый член, стоящий под знаком суммы, можно, очевидно,
записать в следующем виде:
= (19.4)
в чем легко убедиться простой проверкой, применив правило
дифференцирования произведения.
434
аналитическая динамика
[Гл XIX
Найдем скорость v* как производную радиуса-вектора rft по-
времени, учтя при этом, что время t входит в выражение (18.22)
не только явным образом, но и через обобщенные координаты
•••, qs-
V —dTk Л -1- Л-дТк л Л- _LдТк A J_'drfe /10
Производная обобщенной координаты по времени q = ~ назы-
вается обобщенной скоростью.
Дифференцируя обе части равенства (19.5) частным образом,
по обобщенной скорости, получим тождество
drfe _ dvk
dq/ dq/'
Составим теперь частную производную скорости vft по обоб-
щенной координате qy, учитывая, что обобщенные координаты
входят в правую часть равенства (19.5) через коэффициенты при
обобщенных
(19.6}
скоростях:
dvj; d2rk . , , d-nt . , d2rfe
dqj ~ dqt dqj dqs dqj dt dqt '
дгь .
производная зависит от времени t явно и через:
координаты qlt ..., qs. Поэтому ее полная производ-
Частная
обобщенные
ная по времени равна
d drk d2rfe . d2rfc . , &rk
dt dqf dqj dqt Hi T • • • T gq. gQs 4s "T gq. gt
Сравнивая оба выражения и учитывая, что смешанные частные
производные не зависят от порядка дифференцирования, получим
d__dr, dVk
' dt dqj dqf ‘
Заменим в правой части равенства (19.4) частную производную-
ее выражением (19.6), а производную по времени
выражением (19.7)
dvb
d drk
ее
di dqj
<ЗгА
dvk drd ( dv,.\ dvk
mk-dt-lTqj=dt\ nlkVk -d^)- • dfj
. Замечая, что
dvf, d I 1 „\ dVb
nlkVk'd^
приведем последнее равенство к виду
dv-, dri, d Г д / 1 ,
K di dqj dt {dqj \ 2 "
; mkvlj.
§19 3) ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА ' 435
Теперь уравнение (19.3) можно записать следующим образом:
у ( V Гd д /1 •>) д /1 о 1 < п
2 2 Iт^)-ттН\~Q^q’=°’
,=1 (fe = I )
или, разбивая сумму по k на две части и вынося знак производ-
ной за знак суммы,
у Р д \т,Л д \mkvk_rt\._n
2 jdtdq.- 2 2 dqj 2 2 Р/ °’
/ = 1( k=l k=\ J
По определению
п
k=]
где Т — кинетическая энергия системы. Поэтому общему уравне-
нию динамики можно придать вид
У ~-Q,}f>qf = O.
^i\dt dqj dq; J
Так как обобщенные координаты qlt ..., qs независимы и,
следовательно, их вариации 8qlt .... 67,- при голономных связях
произвольны, то из этого уравнения следует, что все скобки равны
нулю (для доказательства достаточно повторить рассуждения,
с помощью которых из равенства (18.33) были получены уравне-
ния (18.34)):
£w,-£rQi (i=1-2...........sb (19-8)
Это и есть дифференциальные уравнения движения в обобщен-
ных координатах, или, как принято их называть, уравнения
Лагранжа второго рода-, число уравнений равно числу степеней
свободы *).
§ 19.3. Задачи на составление уравнений Лагранжа второго рода
Прежде чем рассмотреть примеры на составление уравнений
Лагранжа, сделаем несколько рекомендаций, вытекающих непо-
средственно из самой формы уравнений (19.8) и способа введения
обобщенных координат.
*) Уравнения (19.8) составлены для случая, когда число обобщенных коор-
динат равно числу степеней свободы. В тех случаях, когда имеются избыточ-
ные обобщенные координаты, форма уравнений Лагранжа усложняется (см,
литературу, приведенную в примечании на стр. 421).
436
аналитическая динамика
[Гл. XIX
Для составления уравнений Лагранжа второго рода нужно:
1) изобразить на чертеже все активные силы, действующие-
на систему; реакции идеальных связей изображать не следует;
если имеются силы трения, то их следует присоединить к актив-
ным силам;
2) определить число степеней свободы и ввести обобщенные
координаты;
3) вычислить кинетическую энергию системы, выразив ее через-
обобщенные координаты и скорости;
4) найти обобщенные силы системы;
5) выполнить указанные в уравнениях Лагранжа (19.8) дей-
ствия.
Задача 19.2. Тонкий однородный стержень длиной I имеет на концах пол-
зуны А и В, которые скользят под действием силы тяжести стержня по направ-
ляющим OD и ОЕ. Направляющие образуют прямой угол DOE, расположенный
у в вертикальной плоскости (рис. 19.2). Пренебрегая мас-
j, ( сой ползунов и силами трения, составить дифференци-
1 альное уравнение движения стержня и найти его угловую
скорость, если направляющая ОЕ горизонтальна.
\ Стержень имеет одну степень свободы, его поло-
жение будем определять одной обобщенной координа-
той — углом ф. На рис. 19.2 изображена только актив-
К ная сила —сила тяжести mg; реакции опор Мд и 1ЧЙ
$ 1 \ изображать не следует, так как они не войдут в урав-
\ некие Лагранжа.
ww//----™Кинетическую энергию Т стержня вычислим по.
О в Е х теореме Кёнига:
Рис. 19.2. 7’ = ^тс,2с + 1./сф2)
где т — масса стержня, vr — скорость его центра масс С, lr = -r=ml2 — момент
ч 12
инерции стержня относительно осн, проходящей через точку С перпендикулярно
к плоскости движения.
Для вычисления скорости центра масс С найдем его координаты (см. рис. 19.2)
1 , . 1 ,
Хс = — I Sin ф, Ус = ^-/СО8ф.
Дифференцируя по времени, получим
хс=2-(фсозф, #с =---------------------g-/ф sin ф.
Отсюда
цс = *с+^с = 4 /2Ф2-
Внося значения для vsc и Iс в выражение для кинетической энергии стер-
жня, найдем
1 /2 11
Т=2 т4 ф2 + ~2 \2т1^’
§ 19 3J
ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА
437'
или
Т = -|-т/2ф2.
Перейдем к вычислению обобщенной силы. Для этого найдем выражение
потенциальной энергии системы, считая, что при горизонтальном положении
стержня она принимает нулевое значение:
„ 1
11 = -g- mgl cos ср.
Пользуясь формулой (18.30). определим обобщенную силу, соответствую-
щую обобщенной координате ср:
л ап 1 , .
Q=-fV=^mg sintp-
Уравнение Лагранжа имеет вид
dt Эф dtp ~
Имеем
дТ 1 d дТ d!{ 1
5ф = 3 ,п/2ф, __ _ = _ от;2ф j = __ ш/2ф.
Так как кинетическая энергия Т от угла ф не зависит, то
Внося полученные выражения в уравнение Лагранжа, получим
~ т/2ф = -i- mgl sin ср,
О Z
или, после упрощения,
Зп
$ = 2^sincp. (19.9>
Это дифференциальное уравнение движения стержня, полученное вторым мето-
дом Лагранжа.
Найдем обобщенную скорость ф. Для этого умножим обе части уравнения:
(19.9) на dtp:
.. , 3g .
ф dtp = ~ sin ф dtp.
Имеем
фйф=Цфйф=б/ф^=фАр=б/^).
Теперь дифференциальное уравнение принимает вид
dW = ~2rdC0S(p-
Интегрируя и умножая обе части уравнения на 2, найдем
ф2 = — 3 cos tp + С.
438
АНАЛИТИЧЕСКАЯ ДИНАМИКА
[Гл. XIX
С = 3 -j-coscpo- Подставляя
Рис. 19.3.
момент трения Мтр на оси
положен в горизонтальной
Пусть стержень начинает движение из состояния покоя, составляя с вер-
тикалью в начальный момент угол ср0. Тогда при <р = <р0 ф = 0 и, следовательно,
это значение для С в последнее равенство, найдем
угловую скорость стержня в функции угла <р:
ф2 = 3-у (cos <р0 — cos гр). (19.10)
Это соотношение можно получить более простым
методом из закона сохранения полной механиче-
ской энергии.
Задача 19.3. Определить закон изменения уг-
ловой скорости со кривошипа ОС эпициклического
механизма, изображенного на рис. 19.3, если масса
кривошипа равна т1, а масса сателлита т2. Кри-
вошип считать однородным тонким стержнем,
сателлит — однородным диском; вращающий момент
Л4В., = М0 — хсо, где Мо и х— положительные по-
стоянные и со —угловая скорость кривошипа;
сателлита считать постоянным; весь механизм рас-
плоскости.
Система имеет одну степень свободы; за обобщенную координату возьмем
угол ср поворота кривошипа. Система состоит из двух движущихся тел, поэтому
ее кинетическая энергия
7’ = 7’1 + 7’2,
где 7\ — кинетическая энергия кривошипа и Т2 — кинетическая энергия са-
теллита.
Так как кривошип ОС вращается вокруг неподвижной оси О, то
т 1 , >
Ti= 2 71“ ’
В этом равенстве (г 4-/?)2 — момент инерции кривошипа относительно
оси вращения, со = ф — угловая скорость кривошипа. Подставляя значение If
в выражение для 7\, получим
(r + R)2 ф2.
Сателлит // движется плоскопараллельно, поэтому его кинетическую энер-
гию Т2 найдем с помощью теоремы Кёнига:
7’2 = 1т2гГ&+ /Ссо2,
тде vc — скорость центра С масс сателлита, /с — его момент инерции относи-
тельно оси, проходящей через точку С перпендикулярно к плоскости движения,
»(о2 — угловая скорость сателлита.
Имеем
С'с = (г + ^)ф. = m2f2’ “2 = ^~й> = -^у-^Ф-
< Следовательно,
Т2 = у m2 (г + R)2 ф2 + у m2r2 у-- ф2,
§ 19 3]
ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА
439 >
или
^2 = 4 «2 (Я + Г)2Ф2-
Складывая полученные значения для 7\ и Т2, найдем кинетическую энер-
гию Т эпициклического механизма:
7,=4/"рф2’ (19и>-
где приведенный момент инерции /пр системы равен *)
/1 3 \
^пр — mi + 2 m2 j + ^)2- (19. 12)1
Обобщенная сила была определена в задаче 18.4 § 18.5 (см. формулу (18.31))
Q = Л4Вр — Л4Тр == Л4о хсо -- Л4тр>
ЕЛИ
Q = Д10 — у Мтр—хф.
Воспользуемся теперь уравнением Лагранжа второго рода
dt дф дф —
Имеем
дТ , . d дТ , .. дТ п
дф — прФ' dt дф — прФ’ дф ~~
После подстановки получим дифференциальное уравнение движения эпицикли-
ческого механизма
I прФ “ Мо — А4Тр хф.
При постоянном моменте трения A4Tp это уравнение легко интегрируется-
(см. задачу 3-2)- Считая, что движение началось из состояния покоя, получим
1 / R .. \[ _ Л. А
Ф = со = — А40--------Л1ТП , / „ ‘ .
т х \ г тр/ \1 —е пр /
С течением времени при /->оо второй член в скобках стремится к нулю и,
следовательно, угловая скорость со кривошипа стремится к предельному зна-
чению
1 / .. R
“пр — X \ 0 г
Мтр
*) В понятие «приведенная масса» или «приведенный момент инерции»
можно вкладывать различный смысл. В данном примере приведенный момент
инерции /пр эпициклического механизма получен при вычислении кинетической
энергии. В примере § 9.6 приведенный момент инерции Z* получен в резуль-
тате вычисления момента количеств движения системы. Сравнивая выражения
(9.39) и (9.12), мы видим, что величина приведенного момента инерции зависит
от метода его введения.
440
АНАЛИТИЧЕСКАЯ ДИНАМИКА
[Гл. XIX
Задача 19.4. Рассмотрим эллиптический маятник, который состоит из тела /,
-перемещающегося без трения по горизонтальной прямой, и маятника II, под-
вешенного к телу I (рис. 19.4). Масса тела / равна Mlt масса маятника А42,
момент инерции маятника относительно оси подвеса /, расстояние от центра
тяжести О2 маятника до оси подвеса h. Составить дифференциальные уравнения
движения эллиптического маятника и, счи-
Z *
Рис. 19.4.
тая угол отклонения маятника от вертикали
малым, определить закон движения, если
начальные скорости равны нулю
Система имеет, очевидно, две степени
свободы. За обобщенные координаты выбе-
рем абсциссу х тела / и угол ф отклонения
маятника от вертикали. Кинетическая энер-
гия Т системы состоит из суммы кинетиче-
ской энергии Т[ и Т;; тел / и II:
Т^Т^Т,,.
Тело / движется поступательно, поэтому
= 1 М^.
Скорость точки подвеса маятника равна х. Кинетическая энергия такого
маятника была вычислена в § 10.2 (см. формулу (10.15)). В обозначениях
данной задачи будем иметь
— А42х2 ф- М2/гхф cos ф + -у /ф2-
Таким образом,
Т =у (Л41ф-Л42) х2ф-Л42/шрсо8фф- — /ф2.
Потенциальная энергия системы
П = — Л12 gh cos ф.
Уравнения Лагранжа для данной системы имеют такой вид:
dt дх дх ^х’ dt бф бф —
Вычислим соответствующие величины:
^ = (Л41ф-Л42) хф-Л42/гф cos ф, ^=0, Qx = — ъ~ = 0,
С/л С/Л С/Л
= /ф ф- M.2hx cos ф, = /ф — Л42/гфх sin ф ф- M2hX cos ф,
дт «л . • п ап . .
ду=~~ ф, Q(p = —-^- = —M2/ig sin ф.
‘После подстановки и очевидных упрощений получим дифференциальные урав-
нения движения сис емы
[(Л41 + Л12) х ф- Л42/гф cos ф] = 0,
/q. -| M2hx cos ф ф- MJig sin ф = 0.
5 19 3]
ЗАДАЧИ НА СОСТАВЛЕНИЕ УРАВНЕНИЙ ЛАГРАНЖА
44 Г
Интегрируя первое уравнение, найдем
(М1Ц-М2) х Ц-М2/гф cos<p = C\.
По предположению х = 0, ф = 0 при / = 0. Следовательно, Сг=0 и последнее-
равенство принимает вид
(Мг + М2) хЦ-/И2/1ф cos <р = 0,
или
J* [(Mi4-М2) x-\-M2h sin <f] = 0.
Отсюда
(Mt -1“ Л42) х Н- sin ф s= С2.
Пусть при / = 0 маятник отклонен на угол <р0- Воспользуемся произволь-
'Ностью выбора начала координат О и подберем его так, чтобы при / = 0
(Mi -|- М2) “I- M2h sin фо = 0.
Тогда С2 = 0 и из последнего равенства найдем
(Mi4-M2) x-[-M2h sin ф = 0,
или
М2 к
X =--т-:--ту- h sm ф.
Mi + M2 ‘
Эти равенства имеют простой механический смысл: центр тяжести С системы
ввиду отсутствия горизонтальных внешних сил движется по вертикали (при
данном выборе начала координат эта вертикаль совпадает с осью г).
Перейдем ко второму дифференциальному уравнению, считая угол ф малым.
Так как для малых углов sin.
Mi4-M2 v
Дифференцируя его два раза получим
М2 ...
Mi + M2 т
После подстановки во второе дифференциальное уравнение значений х, sinq>
и cos ф, найдем
/ М2 \
('-мн^Ф+М2^0-
Легко показать, что коэффициент при ф всегда положителен. Действительно»
согласно (12.14)
/=/О2+м2^,
где 10^—момент инерции маятника относительно оси, проходящей через его
центр тяжести параллельно оси подвеса. Имеем
/____________h2—!,, -I-М /12 — V — ! I МгМз ,9
М,+ М2 Mi + M2ft " °2 + м1 + м2л >0
(для математического маятника h=l и /о* = 0, где I — длина маятника).
-442
АНАЛИТИЧЕСКАЯ ДИНАМИКА
[Гл XIX
Поэтому угол <р изменяется по гармоническому закону (учтены начальные
условия: ф = 0, <р = фо при / = 0)
ф = ф0 cos kt,

где круговая частота k определяется равенством
M2hg
м,+м2
Центр тяжести маятника 02 перемещается по эллипсу (читатель докажет
без труда это самостоятельно), чем и объясняется название маятника.
Задача 19.5. Составить дифференциальные уравнения движения двойного
математического маятника.
Двойной математический маятник (см. рис. 18.15) имеет две степени сво-
боды. За обобщенные координаты возьмем углы фц и ф2. Система состоит из
двух материальных точек, поэтому ее кинетическая энергия равна
7’ = ymit'? + -2 m2vl,
где тх и т2— массы точек, a Vj и v2 — их скорости.
Координаты т/, и х2, у2 точек и М2 найдем, пользуясь рис, 18.15:
х1 = ^1сО5ф1, COS ф1+ l2 cos ф2,
i/i = Zi sin ф1, yt — li sin ф1+/2 sin ф2.
Дифференцируя по времени, получим
Xi = — /1ф1 sin ф1, х2 = — /1 ф] sin ф1 — 12ф2 sin ф2,
1/1 = >'1Ф1 COS ф1, Т/2=11ф1С03 ф, +/1ф2 cos ф2.
Тогда
Ч1=Х?+1/? = /?Ф1,
ч| = х|+1/2 = 1?ф? + 2/112со5 (ф2 —Ф1) Ф1Фг + ^Ф!
и кинетическая энергия системы примет вид
т = у (/П1 + /П2) ‘’1Ф? + «2^2 cos (ф2 —Ф1) Ф1Фг + у «гВД- (19.13)
Обобщенные силы были найдены в задаче 18.5 § 18.5:
<21==— (ffli4-/n2)gli sin фр (?2 = —щ2§/2 sin Фг- •
(19.14)
Перейдем к составлению уравнений Лагоанжа, которые для данной задачи
имеют вид
dt дф1 дф1 dt Эф2 дф2 — ^2’
Составим сначала уравнение для фр Имеем
= («! 4- т2) 1?ф1 + т^г12 cos (ф2 — ф1) ф2,
+ ^Фг + ^Л cos (ф2 — ф1) ф2 —m2l,/2 sin (ф2 —ф1) (Фа —Ф1) фг>
ЭТ . . .
— m2/iZ2 sin (ф2 — ф1) ф1ф2.
§ 19 4] ОСОБЕННОСТИ ПРИМЕНЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА 443'
Подставим полученные выражения в уравнение Лагранжа для координаты
(mi + m2) G2$i + ”}2^2 cos (<Ps — Ф1) Ф2 — mthlz sin (<p2 — <Pi) (ФО — Ф1Ф2) —
~-m2Z,Z2 sin (<p2 — <pj) Ф1ф2 = — (mi + m2)gl1 sin cpx. (19.15)
Деля обе части уравнения на Zj и приводя подобные члены, окончательно полу-
чим (мы выписали сразу второе уравнение, которое получается аналогичным
методом)
(mt + m2) + cos (ср,— <pi) ф2 — m2l2 sin (<p2 — <Pi) Ф1 +
+ (mi + m2) g sin <pi = 0, (19.16)'
/2Ф2 + Й cos (<p2 — cpi) cp> -Hi sin (cpj — cpi) Ф’?+§ sin <p2 = 0.
Интегрирование этих дифференциальных уравнений движения двойного'
математического маятника связано с большими трудностями, однако, если счи-
тать углы отклонения <pi и <р2 малыми, то решение упрощается и может быть
доведено до конца. Задачи такого рода мы б у доч рассматривать в главе XX.
§ 19.4. Особенности применения уравнений Лагранжа второго рода
к системам с неидеальными и неудерживающими связями
Рассмотренные примеры хорошо иллюстрируют достоинства
метода Лагранжа, состоящие в следующем.
Этот метод применим для широкого класса материальных
систем; он экономичен в том смысле, что не требует введения
дополнительных координат и реакций идеальных связей. Наконец,
процедура применения метода Лагранжа одинакова во всех зада-
чах, что имеет большое значение, так как не требует от исследо-
вателя подчас тонких рассуждений, в которых допустить ошибку
значительно легче, чем в математических операциях.
Полезно отметить еще одно достоинство метода Лагранжа. По
существу этот метод энергетический. Это обстоятельство дает воз-
можность использовать метод Лагранжа в теоретической физике
для анализа не только механических, но и других физических
систем.
Необходимо остановиться и на некоторых особенностях метода
Лагранжа, создающих подчас дополнительные трудности. Уравне-
ния Лагранжа получены для систем с идеальными, удерживающими
и голономными связями. Это не означает, что уравнения Лагранжа
нельзя использовать для систем с неудерживающими или неидеаль-
ными связями. Но если для системы с удерживающими и идеаль-
ными связями уравнения Лагранжа полностью решают задачу об
определении закона движения, то для системы с неудерживающими
или неидеальными связями одних уравнений Лагранжа, составлен-
ных для независимых обобщенных координат, может оказаться
недостаточно. Поясним сказанное на задаче 19.2 § 19.3, рассмот-
рев три случая.
1. Связи идеальные и удерживающие. На концах
стержня шарнирно укреплены перемещающиеся без трения пол-
444
аналитическая динамика
[Гл. XIX
зуны, удерживающие стержень на направляющих (см. рис. 19.2).
Этот случай разобран на стр. 436. Так как связи идеальные, то
их реакции учитывать не нужно (поэтому они не изображены на
рис. 19.2). Кинетическая энергия Т и обобщенная сила опре-
делены равенствами
Т =-|-т/2ф2, = sin <р. (19.17)
Уравнение Лагранжа для этой задачи приводится к виду
<p = ~sin<p. (19.18)
Это уравнение, справедливое для всех <р, полностью решает
задачу, так как для его интегрирования не нужно знать ничего,
кроме начальных условий.
2. Связи идеальные и неудерживающие. Стержень
скользит без трения по сторонам прямого угла (рис. 19.5). До тех
пор пока стержень опирается на обе стороны,
связь не нарушена и движение стержня опи-
сывается тем же уравнением Лагранжа (19.18).
Однако сразу пользоваться этим уравнением
практически нельзя, так как неизвестно,
произойдет или нет отрыв стержня от стен-
ки. Поэтому прежде всего нужно определить
возможность отрыва, затем, если отрыв дей-
ствительно происходит, то нужно определить,
при каком угле это произойдет.
Возможность отрыва определяется по
обращению в нуль соответствующей нормаль-
ной реакции. Одного уравнения Лагранжа
(19.18) для этих целей недостаточно, так
как оно не содержит нормальных реакций *).
дополнительно к этому уравнению нужно со-
Естественно, что
ставить еще уравнение, которое содержало бы реакцию NА (отрыв
может произойти, конечно, от вертикальной стенки). Это можно
сделать различными методами, но в данном случае проще всего
приводит к цели теорема о движении центра масс:
mwc = Fc.
Проектируя это равенство на ось х и учитывая рис. 19.5,
получим
hiXc^Na- (19.19)
*) Существуют методы, позволяющие определять реакции идеальных свя-
зей с помощью видоизмененных уравнений Лагранжа второго рода (см.
Лурье А. И. Аналитическая механика.—М.: Физматгиз, 1961, §§ 7,12, 7.13).
Эти методы сложны и в настоящем руководстве не изучаются,
§19 4] ОСОБЕННОСТИ ПРИМЕНЕНИЯ УРАВНЕНИЙ ЛАГРАНЖА 445
Воспользуемся очевидным равенством, устанавливающим связь
между координатами хс и ц> (см. рис. 19.5):
I .
хс = у sin ср.
Отсюда найдем
х’с = уфСО5ф, хс = j (ср cos ср — ф2 sin <р).
Пользуясь теперь уравнением Лагранжа (19.18) и вытекающим
из него первым интегралом (19.10)
ф2 = 3 у (cos q>g — cos <р),
выразим хс, а затем NA через угол <р (предполагается, что ф = 0
при / = 0):
з
%с = ygsin <р (3 cos ср — 2 cos ср0),
з
Мд = -- mg sin ср (3 cos ср — 2 cos <р0).
Отсюда видно, что при угле определяемом равенством
2
COS <Р1 =у cos <р0.
нормальная реакция обращается в нуль, т. е. происходит отрыв
стержня от вертикальной стенки.
Таким образом, уравнение Лагранжа (19.18) определяет закон
движения стержня не для всех ср, как это было в первом случае,
а только для углов, удовлетворяющих не-
равенству
Фо^Ф^Фг
С момента отрыва от вертикальной стен-
ки стержень будет иметь не одну, а две сте-
пени свободы (по предположению движение
происходит в вертикальной плоскости), для
определения движения его в новых условиях
нужно составить уже два дифференциальных
уравнения. В качестве упражнения предла-'
гаем читателю определить угловую скорость
и положение конца А стержня в момент его
падения на горизонтальную плоскость.
3. Связи удерживающие и не-
Рис. 19.6.
идеальные. Учтем силу трения FA в вертикальном ползуне А
(для простоты выкладок трением в ползуне В пренебрегаем)
(рис. 19.6). Будем считать, что сила трения пропорциональна
446
АНАЛИТИЧЕСКАЯ ДИНАМИКА
[Гл. XIX
нормальному давлению:
^А = ^А,
где — коэффициент трения (предполагается, что ползун А дви-
жется вниз, поэтому сила трения F4 направлена вверх).
Положение стержня по-прежнему определяется одной обобщен-
ной координатой — углом ср, поэтому выражение для кинетической
энергии стержня не изменится. Для составления уравнения Лаг-
ранжа нужно определить обобщенную силу Q, соответствующую
углу <р, с учетом силы трения FA. Дадим стержню АВ виртуаль-
ное перемещение бср и вычислим суммарную работу 6Л силы
тяжести mg и силы трения Бл на этом перемещении (работа нор-
мальных реакций Мл и NB равна нулю):
6Л = бАг A-FvA бу а,
где бАг = бср = ~ tngl sin ср • 6<р — работа силы тяжести mg (ис-
пользовано значение для Qlt полученное в первом случае).
Имеем (см. рис. 19.6)
у а = I cos <р.
Следовательно,
бу а — — I sin <р • <5<р.
Подставим в 6А значения 6ЛП буА, FyA и сгруппируем члены;
6Л = I mg — fNа^ sin <р • 6<р.
Обобщенная сила равна коэффициенту при <5<р:
Q = l tng — fNA^si-nW-
Составим теперь уравнение Лагранжа
dt дф 3<р ~
учитывая, что 7' = -|-т/2ф2. После подстановки и выполнения
необходимых действий найдем
4 m/2ip = I ( ^mg— fNл^| sin <р.
Это дифференциальное уравнение движения стержня содержит
неизвестную величину N А. Поэтому необходимо составить еще
одно уравнение для определения нормальной реакции Nл. Для
этого, так же как, и в предыдущем случае, применим теорему
о движении центра масс относительно оси х (см. равенство (19.19)):
mxc = NA.
§ 19.51
ВЫРАЖЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ
447
Воспользуемся полученным ранее результатом
%с = у № cos <р — ф2 sin <р).
Отсюда
Л^а = Y (Ф c0S Ф ~ Ф2 sin ф)-
Внесем это выражение для NA в найденное уравнение Лагранжа:
-1 т/2ф = у mg sin <р — ~ ml2f (ip cos <р — ф2 sin ф) sin <p.
После очевидных преобразований получим
-ф-|- f sin 2<pj ip = -|- + /Ф2 sin <p^ sin <p.
Это уравнение может быть проинтегрировано приближенными
методами.
В заключение отметим, что общность способа составления
уравнений Лагранжа, доведенная до математического алгоритма,
приводит иногда к формальному анализу без ясного понимания
взаимодействия сил. Поэтому в тех случаях, когда необходимо
провести анализ сил, возникающих в системе при ее движении,
целесообразно пользоваться общими теоремами динамики либо
комбинировать эти теоремы с уравнениями Лагранжа, как это
было сделано нами в этом параграфе при рассмотрении второго
случая.
§ 19.5. Выражение кинетической энергии
через обобщенные скорости и координаты
Для дальнейшего нам понадобится значение кинетической энер-
гии Т материальной системы, выраженной через обобщенные ско-
рости и координаты.
Кинетическая энергия Т материальной системы определяется
равенством
п
7’=у 2 т,л-
k=i
Воспользуемся тождеством vf = vk • vft и заменим вектор скоро-
рости vft точки Mk его значением по формуле (19.5). Тогда выра-
жение для кинетической энергии примет вид
k = 1
448
АНАЛИТИЧЕСКАЯ ДИНАМИКА
[Гл. XIX
Возведем скобку в квадрат и сгруппируем отдельно члены второй
степени относительно обобщенных скоростей q, члены первой сте-
пени относительно тех же величин и члены, не содержащие обоб-
щенные скорости. Обозначив первую группу членов через Т2,
вторую через 7\, а третью через То, получим
Т = Та + Т1 + Т0, ' (19-20)
где
т' I ™ Г/дг^ \2 ,2 /drk\2 -а 1
л - ¥ mk 91+---+ж;qs+
/г = I
, 9 drk drk . . , „ drk dtk I
+ 2dq\-d^qiqi + ---+2d^-Wsqs-1Qs\'
T _ V m (drk drk , dr* drk \ (19.21)
fc=l ' .
Введем обозначения
aa = 2 mk дф' Эф ’ &/= 2 дф ‘ Л“- (19-22)
— I •*? = 1
Тогда функции T2 и 7\ можно будет записать в следующей форме:
л=42 2а^. (19-23)
<=1 /=1
л=2ад--’ (19-24>
Г = 1
причем из самого определения коэффициентов а^ (они называются
коэффициентами инерции) видно, что они симметричны относи-
тельно своих индексов:
йу = п/;. (19.25)
В этих выражениях коэффициенты ai; и ф зависят от обоб-
щенных координат qlt q2, ... , qs и времени t, но не зависят от
обобщенных скоростей t)j, q2, ... , qs.
Равенства (19.20), (19.23) и (19.24) показывают, что в общем
случае кинетическую энергию материальной системы можно пред-
ставить суммой квадратичной Т2, линейной 7\ и нулевой То форм
относительно обобщенных скоростей.
§ 19.6]
ОБОБЩЕННЫЙ интеграл энергии
449
При стационарных связях для движения в инерциальных осях
время t явно не входит в выражение радиуса-вектора г,. Все
частные производные ~ будут равны нулю, и вместе с ними об-
ратятся в нуль слагаемые 1\ и То. Поэтому для этого случая
кинетическая энергия системы представляет квадратичную фор-
му обобщенных скоростей
' S S
Jw (19.26)
i=i /=1
коэффициенты которой явным образом не зависят от времени.
Напомним, что кинетическая энергия системы всегда положи-
тельна (как сумма произведений положительных величин т;ц;/2)
и в нуль она может обратиться только при условии, что система
находится в покое. Поэтому квадратичная форма (19.26) всегда
определенно положительна.
§ 19.6. Обобщенный интеграл энергии
Как известно, если силы, действующие на материальную си-
стему, консервативны, то имеет место интеграл энергии — сумм а
кинетической и потенциальной энергий есть величина постоянная
(см. § 10.6):
Т + П = А.
При выводе этого интеграла предполагалось, что движение
изучается относительно инерциальной системы отсчета, а связи
стационарны. Если же в потенциальной системе связи зависят
явным образом от времени t или движение изучается в неинер-
циальной системе отсчета, то в общем случае интеграла энергии
не существует. Это объясняется тем, что при нестационарных свя-
зях движение материальной системы частично осуществляется за
счет сил, изменяющих связи, которые при анализе движения не
учитываются.
Мы покажем, что если кинетическая энергия Т системы, опре-
деленная равенством (19.20), не зависит явным образом от времени
t, то дифференциальные уравнения движения допускают обобщен-
ный интеграл энергии.
Пусть силы, действующие на систему, потенциальны. Тогда
обобщенные силы Q;- будут равны — и уравнения Лагранжа
примут вид
dt дф dq; dq, (/ ~ 1» А • • • , SK
15 Н. В. Бутенин и др.
450
аналитическая динамика
[Гл XIX
Умножим каждое уравнение на (]/ и сложим все уравнения:
2. d дТ VI . дТ VI дП . ,1П о_.
ql dt dqj 2 q/ dq, ~ 2 dq, q^ (19.27)
7 = 1 7 = 1 7=1
Потенциальная энергия П зависит от времени t только через
обобщенные координаты qu .... qs. Поэтому
dll _ ЗП .
dt dqt q^'
7 = 1
Воспользуемся очевидным тождеством (его легко проверить
непосредственно)
2. d дТ _ d -у. дТ . дТ
q^ dt dqj dt dqt q< dq~j q^'
i=i i=i i=i
Кинетическая энергия T равна сумме трех однородных функций
относительно обобщенных скоростей q (см. формулу (19.20)):
7' = 7'2 + Л + 7'о-
Следовательно,
2 ОТ А _ V дТ2 А 1 V дг’ А , V дт<> •
dqt dq; + 2 dq: q< + 2 dq, q>'
/--1 7=1 7 = 1 7=1
По теореме Эйлера об однородных функциях будем иметь *)
^^«, = 2Л + Т,.
С учетом полученных выражений равенство (19.27) принимает
следующий вид-
о dT2 , dTx V dT VI dT . dll
7=1 7=1
Кинетическая энергия T зависит от времени через обобщенные
координаты qlf q2, ..., qs и обобщенные скорости qlt q2, .... ф,
(по условию от времени t она явно не зависит). Поэтому
dr _ vi dT VI ЗГ .
dt dqj qi>2i dqt q^’
Z=1 7=1
*) Напомним эту теорему: сумма произведений частных производных одно-
родной функции на соответствующие переменные равна произведению самой
функции на степень ее однородности,
§ 19 6]
ОБОБЩЕННЫЙ интеграл энергии
451
Таким образом, последнее равенство приводится к виду
„ dT2 сп\ ат _ ап
2 at at at ~ dt ’
или, снова пользуясь равенством (19.20),
d7,0_____________________________________________®
dt "Г” dt dt dt dt — dt '
Приводя подобные члены, получим
| (Та - То + П) = 0, (19.28)
откуда
Т2-Т0 + П = й, (19.29)
Рис. 19.7.
где h — постоянная интегрирования. ,
Равенство (19.20) и представляет обобщенный интеграл энергии
Якоби.
Если связи стационарны и движение изучается относительно
инерциальных осей, то 7'0 = 0 и обобщенный интеграл энергии
вырождается в обычный интеграл Т
4-П = /г.
Проиллюстрируем общую теорию
простым примером.
Задача 19.6. На рис. 19.7 изображена
схема центробежного регулятора. Два одинако-
вых тела и М2, массой пг каждое, могут
перемещаться в пазу АВ. Одинаковые пру-
жины жесткости с неподвижно укреплены на
вертикальной оси вращения О регулятора, а
вторыми концами прикреплены к телам М2 и
М2 Составить дифференциальные уравнения
движения и показать, что при равномерном
вращении регулятора они допускают обобщен-
ный интеграл энергии.
Прежде всего заметим, что движения
Поэтому достаточно рассмотреть движение
Положение тела М2 определяется координатой х1 = (7Л41. Тело участвует
в сложном движении, его относительная скорость равна xlt а переносная XjW.
Поэтому абсолютная скорость будет определяться равенством
тел Мг и М2 независимы,
одного из них, напримеп М,.
D? = x= + w2xf,
а кинетическая энергия
Т =у/ПХ2+-^ /П(02Х?.
В рассматриваемом случае Т2 = ^-тх~, Т2 = 0 и Та=-^- таАх\. При по-
стоянной угловой скорости и кинетическая энергия не зависит явным образом
от времени.
На тело Мг действуют две активные консервативные силы сила тяже-
сти mg и сила упругости пружины Fv Первую силу учитывать не нужно, так
16*
452
аналитическая динамика
[Гл. XIX
как по условию центробежный регулятор вращается в горизонтальной плоско-
сти (ось вращения вертикальна). Потенциальная энергия силы упруюсти равна
I’ = yC(x1-Z)2,
где I — длина пружины в недеформированном состоянии.
Следовательно, рассматриваемая система удовлетворяет всем условиям су-
ществования обобщенного интеграла энергии (19.29), который в данном случае
принимает вид (множитель 1/2 включен в постоянную интегрирования h)
тх2— тсо'2х(-j-с (xt —Z)2=/i.
Было бы грубой ошибкой считать, что здесь имеет; место равенство
Г + П= у mx2 + -g- яй2х’ + ^с(х1 — l)- = h. Физически несправедливость этого
равенства объясняется весьма просто — переносное движение тела Л11 осущест-
вляется за счет неучитываемых нами сил, приводящих в равномерное враще-
ние регулятор.
Составим теперь уравнение Лагранжа
d ______________________________________aiL
dt дх, дх, ~ дх, ‘
Имеем
дТ . d дТ .. дТ , дП‘
= тх,, ~п^~ = тх,, — = та2х1, д— — с(х, — 1).
дх, 1 dt дх, дх, дх, '
Внося найденное в уравнение Лагранжа, получим
тх,— таРх, — — с (х, — I),
или
тх, = — с (хх — Z) 4-н1со2х1.
Это дифференциальное уравнение движения тела Л4 j во вращающемся пазу
АВ, справедливое ка'к для постоянных, так и для переменных значений угло-
вой скорости со, можно получить, пользуясь обычным дифференциальным урав-
нением относительного движения, причем слагаемое та>2х, играет в этом слу-
чае роль переносной силы инерции (кориолисова сила инерции перпендику-
лярна к оси х, и ее проекция на эту ось равна нулю). Обобщенный интеграл
энергии при со = const получается из этою уравнения непосредственным ин-
тегрированием (обе части уравнения нужно умножить на dx, и воспользоваться
тождеством x,dx, = x,dx,).
ГЛАВА XX
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
С ОДНОЙ И ДВУМЯ СТЕПЕНЯМИ СВОБОДЫ ОКОЛО
ПОЛОЖЕНИЯ УСТОЙЧИВОГО РАВНОВЕСИЯ
§ 20.1. Определение положений равновесия
Теория колебаний, начав свое развитие с исследования дви-
жения математического маятника, превратилась в широко раз-
ветвленную самостоятельную дисциплину с весьма сложным мате-
матическим аппаратом. Теория колебаний быстро развивается, что
объясняется значением ее в современной технике.
В настоящей главе мы рассмотрим простейшие вопросы коле-
баний механических систем, а именно — малые колебания систем
с одной и двумя степенями свободы около положения устойчивого
равновесия.
Рассмотрим вначале материальную систему с идеальными, ста-
ционарными и голономными связями, положение которой опреде-
ляется s независимыми обобщенными координатами qlt q2, ..., qs.
Для изучения колебаний около положения равновесия необхо-
димо, очевидно, прежде всего найти те положения, в которых
система может находиться в равновесии.
В § 18.7 было показано, что в положении равновесия все
обобщенные силы системы равны нулю:
Qi = 0, Q2 = 0, ..., Qi = 0. (20.1)
Для консервативной системы эти равенства принимают вид
= 0, д-= 0, ..., = 0. (20.2)
dqi ’ dq2 ’ ’ dqs v 1
Будем считать, что обобщенные силы зависят только от обоб-
щенных координат. Тогда равенства (20.1) или (20.2) можно рас-
сматривать как уравнения относительно qlt q2, ..., qs. Решая
эти уравнения, найдем те положения, в которых система может
находиться в равновесии. Если обобщенные силы зависят не
только от обобщенных координат, но и от обобщенных скоростей
qlt Q?, , <js, то при решении уравнений (20.1) все обобщенные
скорости нужно' приравнять к нулю.
454
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
(Гл XX
Во многих случаях положения равновесия можно определить
из элементарных соображений или с помощью обычных уравне-
ний статики.
Задача 20.1. Определить возможные положения равновесия маятника со
спиральной пружиной жесткости с (рис. 20.1), вес маятника Р, расстояние от
оси подвеса О До центра тяжести С равно /. При верх-
Рис. 20.1.
нем вертикальном положении маятника спиральная пру-
жина находится в недеформированном состоянии. Мас-
сой пружины и трением горизонтально расположенного
цилиндрического подшипника пренебречь.
Система имеет одну степень свободы; в качестве
обобщенной координаты удобно принять угол ср.
Потенциальная энергия системы П складывается из
потенциальной энергии Щ силы тяжести и потенциаль-
ной энергии П2 спиральной пружины. За нулевое примем
верхнее вертикальное положение маятника. Тогда при
переходе маятника из данного положения в нулевое ра-
бота At силы тяжести будет равна потенциальной энер-
гии Пр Имеем
П1 = Л1 = — Р -DE =— Pl (1 —cos ср).
Опыт показывает, что для закручивания спиральной пружины на не очень
большой угол ф требуется приложить момент М, пропорциональный углу
закручивания:
М =с<р.
Коэффициент с называется коэффициентом жесткости на кручение, его раз-
мерность равна размерности момента силы (угол ф измеряется, конечно, в ра-
дианах).
Момент создаваемый пружиной, равен — Сф, и, следовательно, работа А2
(потенциальная энергия П2) сил упругости такой пружины при переходе из-
данного положения в нулевое определится равенством
о
П2= Л2 =— с ф с/ср,
ф
или
П2= у Сф2,
(20,3)
т. е. потенциальная энергия спиральной пружины, работающей на закручива-
ние, равна половине коэффициента ее жесткости, умноженной на квадрат
угловой деформации.
Потенциальная энергия системы равна
П = Щ + П2 = Pl cos ф + у сер3 —Р/, :
Составим уравнение равновесия (20.2):
или, подставляя значение потенциальной энергии П, будем иметь
— Pl sin ср ф- сер = 0 (20,4)
§ 20 I]
ОПРЕДЕЛЕНИЕ ПОЛОЖЕНИИ РАВНОВЕСИЯ
455
(это уравнение легко получить из условия равновесия рычага). Корни уравне-
ния (20.4) определяют возможные положения равновесия маятника.
После того как составлено уравнение равновесия, задачу можно поставить
двумя различными способами.
I. Как выбрать параметры системы, чтобы маятник мог находиться в за-
данном положении равновесия’ Эта задача решается элементарно. Действи-
тельно, пусть требуется, чтобы в одном из возможных положений равновесия
маятник составлял с вертикалью угол <р0. Подставляя это значение угла <р
в уравнение (20.4), получим
’ с<р0 — Pl sin <р0 = 0,
откуда
Р1 = <ро
с sin <р0 ’
В частности, если требуется, чтобы пружина удерживала маятник в гори-
зонтальном положении (<р0 = л/2), будем иметь
При таком соотношении параметров (Р, I, с) маятник может находиться в рав-
новесии, занимая горизонтальное положение.
2. Задача может быть обращена, а именно: все параметры (Р, I и с) за-
даны; требуется определить возможные положения равновесия маятника
Как уже отмечалось, возможные положения равновесия определяются
корнями уравнения равновесия (20.4). Представим это уравнение в виде
sin <Р = <Р>
или
sin <р = х<р,
(20.6)
где новый параметр х определен равенством
с
(20.7)
Один корень уравнения (20.6) очевиден:
Ф1 = 0.
Этому корню отвечает верхнее вертикальное положение равновесия маятника.
Дл!Г определения других возможных положений равновесия нужно найти
остальные корни трансцендентного
уравнения (20.6). Это можно осуще-
ствить различными методами, напри-
мер табличным или графическим. По-
ясним второй способ. Составим два
уравнения:
y=sing>, у--- х<р
и построим их графики (рис. 20.2).
Очевидно, что второй корень ф2
определяется абсциссой точки пересе-
чения обоих графиков, причем каж-
дому положительному корню ф2 отвечает равный по модулю, но отрицательный
корень —ф2. Физически это означает, что положения равновесия маятника
.могут быть как слева, так и справа от вертикали. Кроме того, видно, что
456
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
при х > 1 (с> PI) прямая (/ = Хф не пересекается с синусоидой i/=sin<p.
В этом случае уравнение (20.6) имеет один тривиальный корень <р1 = 0.
Легко показать (мы не будем останавливаться на подробностях), что при
sin сро и т-ч
x = cosm0=—— прямая г/ = Хф коснется второй волны синусоиды. В этом
<Ро
случае х с-0,129 и уравнение будет иметь три корня: <р1 = 0, <р22,286
(130°59') и ф3 = <р0~ 7,725 (442°37')> причем третий корень двойной. При х<
<0,129 прямая t/ = x 0,129*).
Таким образом, если х> 1, то маятник имеет одно верхнее вертикальное
положение равновесия (<pi = 0), при 0,129 <х<1 маятник имеет два положе-
ния равновесия.
§ 20.2. Устойчивость положения равновесия.
Теорема Лагранжа — Дирихле. Критерий Сильвестра
Найдя положения, в которых система может, вообще говоря,
находиться в равновесии, нужно определить затем, какие из этих
положений практически реализуемы или, иначе говоря, какие из
этих положений являются устойчивыми, а какие неустойчивыми.
Поясним сказанное простым примером. Обычный физический ма-
ятник с горизонтальной осью вращения имеет два возможных
положения равновесия — верхнее и нижнее. Очевидно, что верхнее
положение равновесия маятника практически нельзя осуществить,
так как оно неустойчиво, а нижнее положение устойчиво и оно
легко реализуемо.
Вопрос об устойчивости положения равновесия является частным случаем
общей задачи об устойчивости движения. Эта задача имеет в современной тех-
нике большое значение (двигатель должен устойчиво удерживать заданный
режим работы, самолет, ракета, корабль должны устойчиво сохранять задан-
ное направление движения и т. п.). Эти вопросы выходят за рамки настоя-
щего курса, поэтому желающим ознакомиться с общей задачей устойчивости
движения мы рекомендуем обратиться к специальным руководствам **). Здесь
же мы ограничимся только основными определениями и изложением теоремы
Лагранжа — Дирихле.
Не нарушая общности, будем считать, что в рассматриваемом
положении равновесия все обобщенные координаты равны нулю
(для этого достаточно отсчет их вести от положения равновесия).
Выведем систему из равновесного состояния, сообщив в начальный
*) При малых значениях параметра х корни будут велики. Им соответст-
вуют положения равновесия при угле закручивания, большем одного полного
поворота маятника. При таких углах формула (20.3) может оказаться неспра-
ведливой.
**) Ляпунов А. М. Общая задача об устойчивости движения. —М.: Гос-
техиздат, 1950; Чета ев Н. Г. Устойчивость движения. — М.: Физматгиз,
1955; Малкин И. Г. Теория устойчивости движения. —М.: Наука, 1966;
Мер к ин Д. Р, Введение в теорию устойчивости движения.-2-е изд. —М.:
Наука, 1976,
§ 20 2] УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ РАВНОВЕСИЯ 457
момент времени t = t0 небольшие по модулю значения обобщен-
ным координатам и их скоростям
7oi> • • > Qosi 4oi. * • •» 7os
(эти величины называются возмущениями).
Обозначим значения обобщенных координат и их скоростей
при дальнейшем движении системы через
71(0, qs (0; 41(0» •••. 4s (0-
Выберем теперь 2s произвольных сколь угодно малых поло-
жительных чисел
®1, • • • , ®1, • • • > 8s-
Если по этим числам можно найти другие 2s положительных
чисел
61, .... 65; 6'1...6s
таких, что для всех возмущений, удовлетворяющих условиям
I Qoi \ бь • • •. ! 4os । *== 6s, 14oi! • • • > I 4os I 6S,
и для всех t5-t0 будут выполняться неравенства
1 Q1 (0 I < ®1> • • • > I 7s (0 I I 41 (0 I 8|> • • . I 4 s (01 8S,
то рассматриваемое положение равновесия называется устойчи-
вым, в противном случае — неустойчивым.
ЕСли при устойчивом равновесии все обобщенные координаты
и скорости с течением времени стремятся к нулю:
lim qk (0 — 0, lim qk (0 = 0 (£-=1, 2, ..., s),
то рассматриваемое положение равновесия называется асимпто-
тически устойчивым. (Эти определения устойчивости равновесия
представляют следствия из общих определений устойчивости дви-
жения, принадлежащих А. М. Ляпунову.)
Достаточные условия устойчивости равновесия консервативной
системы определяются следующей теоремой Лагранжа — Дирихле:
если в положении изолированного равновесия консервативной си-
стемы с идеальными и стационарными связями потенциальная
энергия имеет минимум, то это положение равновесия устойчиво.
Доказательство этой' теоремы может быть получено как про-
стое следствие теоремы Ляпунова об устойчивости движения (см.
литературу, цитируемую на стр. 456).
Согласно теореме Лагранжа — Дирихле для доказательства
устойчивости равновесия консервативной системы достаточно убе-
диться в том, что потенциальная энергия имеет в рассматриваемом
положении минимум. Для системы с одной степенью свободы опре-
деление минимума решается элементарно. Действительно, в этом
458
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
случае производная второго порядка от потенциальной энергии
по обобщенной координате, вычисленная в положении равновесия,
должна быть положительна (предполагается, что она существует):
О>0- (20-8>
Для консервативной системы, имеющей s степеней свободы,
устойчивость рассматриваемого положения равновесия также опре-
деляется из условия минимума потенциальной энергии. В этом
случае критерий минимума имеет более сложный вид. Установить
его можно следующим образом.
Рассмотрим одно из положений равновесия системы. Не нару-
шая общности, будем считать, что в этом положении потенциаль-
ная энергия равна нулю’
П(0, 0, ..., 0) = 0 (20.9)
(это можно сделать, так как потенциальная энергия определяется
с точностью до аддитивной постоянной).
Разложим потенциальную энергию в ряд Маклорена по степе-
ням qlt q2, ..., qs\
П^, ?2, ..., ?5) = П(0, о, .... 0) + (^-)Л1 + ... + (^)л.+
+4 [(Ш ^+• • •+(|^)о +2 (4ж)о4/14/2+• • •
+ dqs \qs 1^] + ”'
Здесь точками после квадратной скобки обозначены члены выс-
шего порядка относйтельно q2, ..., qs.
Первое слагаемое равно нулю по условию (20.9). Все коэффи-
циенты при qlt q2, ..., qs в первой степени также равны нулю,
так как в положении равновесия должны выполняться равенства
(20.2). Коэффициенты при членах второй степени обозначим сле-
дующим образом:
<20Л0>
Эти коэффициенты, называемые обобщенными коэффициентами
жесткости, вычисляются в положении равновесия при qi — q2 —
.. . = <7, —0, и, следовательно, все с^ — постоянные числа, причем
они симметричны:
с,7 = су1. (20.11)
Учитывая сделанные замечания, получим следующее разложе-
ние потенциальной энергии в ряд по степеням qx, ..., qs:
— “2 (cn<7i + • • + cssQ:> + 2с12(/172 +.. • + 2cs lr sqs i<7.v) -f-..., (20.12)
§ 20 2]
УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
459
или, сокращенно,
' S
п=4 2 2 W/+--M
<=1i=i
(20.13)
где точками обозначены члены высшего порядка.
Предположим, что квадратичная форма в (20.13) определенно
положительна. В этом случае вблизи положения равновесия
<7i = <72 = .. =7s = 0 квадратичная часть потенциальной энергии и
полная потенциальная энергия будут положительны. Так как
П (0) = 0, то это означает, что потенциальная энергия будет иметь
в этом положении минимум и, следовательно, положение равно-
весия устойчиво.
Вопрос о знаке любой квадратичной формы определяется сле-
дующей теоремой Сильвестра: д 1Я того чтобы квадратичная форма
быш определенно положительной, необходимо и достаточно, чтобы
есе главные диагональные миноры матрицы квадратичной формы
были положительны. Доказательство этой теоремы можно найти
в курсах линейной алгебры.
Матрица квадратичной формы (20.13) и ее главные диагональ-
ные миноры имеют вид
— Сц>
А3 —
Си с12 с13 • C1S
С21 с22 с23 • • C2S
С31 с32 с33 • • c3s - (20.14)
^S2 CS3 • • • CSS
сп
С21
С31
С12 С13
с22 f23
С32 с33
CS1 • • • CSS
(20.15)
Таким образом, критерий определенной положительности квад-
ратичной формы (20.13) будет
Д!>0, Да>0, ..., Д5>0. (20.16)
Теперь виден порядок применения теоремы Лагранжа —Ди-
рихле- нужно разложить потенциальную энергию в ряд по степеням
<71, • , Qs, ограничиваясь членами второго порядка малости, опре-
делить обобщенные коэффициенты жесткости и составить опре-
делители (20.15). Если все Д, > 0, то положение равновесия
устойчиво.
Теорема Лагранжа — Дирихле дает только достаточные условия
устойчивости равновесия консервативной системы, но она не дает
никаких оснований судить о том, будет ли равновесие устойчиво
или неустойчиво, если в этом положении потенциальная энергия
не имеет минимума. Для одного частного случая ответ на этот
460
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Рис. 20.3.
вопрос дает следующая теорема Ляпунова: равновесие консерватив-
ной системы неустойчиво, если отсутствие минимума потенциаль-
ной энергии определяется членами второго порядка в ее разложе-
нии в ряд по степеням q.
Ляпунову принадлежит еще одна теорема о неустойчивости
положения равновесия. Обобщение этих теорем дал Н. Г. Четаев
(эти теоремы, а также доказательство сформу-
лированной теоремы Ляпунова можно найти
в курсах по устойчивости движения).
Задача 20.2. Дан двойной маятник со спиральными
пружинами, веса маятников и Р2, их длины Zx и 12
(рис. 20.3). При верхнем вертикальном положении ма-
ятников спиральные пружины находятся в недеформиро-
ванном состоянии. Требуется определить жесткости пру-
жин сг и с2 так, чтобы верхнее вертикальное положение
маятников было устойчивым (силами сопротивления
пренебречь).
Система имеет две степени свободы. За обобщенные
координаты примем углы <рх и <р2 отклонения маятников
от верхнего вертикального положения. Потенциальная
энергия системы П складывается из потенциальной энер-
гии П; сил тяжести маятников и потенциальной энергии П2 спиральных пру-
жин. Приняв вертикальное положение маятников за нулевое, вычислим Щ
как работу сил тяжести при переходе системы из данного положения в нулевое:
Щ = РУ1 cos <pi + Р2 (Zi cos <pi + Z2 cos <p2) — PjZj — P2 (Zi + Z2).
Потенциальная энергия П2 спиральных пружин определится по фор-
муле (20.3):
Пг = ~2 С1Ф1 + ~2 с2 (<Рг ~ <Р1)2>
где (ф2— <pt) — угол закручивания второй пружины.
Потенциальная энергия системы будет равна
П = (Pr + Р2) Zt cos <pi + P2Z2 cos <p2 + y Ci<pi +y c2 (<p2 — q?i)2 — (Pi + P2) It — P2l2.
Обобщенные коэффициенты жесткости су можно определить по формуле
(20.10), но еще проще они определяются при непосредственном разложении
потенциальной энергии в ряд по степеням ф! и <р2. Имеем
, Ф? , । Ф» ।
COS ф1 — 1 — ... , С03ф2=1— J-+ ...
Тогда выражение для потенциальной энергии принимает вид
П = (Л + Р2) ~ + ^2 + ~2 С1<Р1 +
+ с2 (фг — <Р1)2 — (Pi + Рг) ^1 — Рг^г + • • • »
или, группируя члены,
П = -g- [ci4-c2 — (Pi + Рг) ^1] <Р1 —С2<Р1<Р2 +~<у (с2 PJ-г) <Ps + • ••
§ 20.2]
УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ РАВНОВЕСИЯ
461
Сравнивая с общим выражением для потенциальной энергии (20.12), полу-
чим обобщенные коэффициенты жесткости
Сц = С1-}-С2— С12 —с21“ с2» с22 = с2 ^2^2*
Критерий Сильвестра (20.16) для s = 2 сводится к неравенствам
Ai — си > 0,
Аг —
сп
С21
С12
с22
>0,
или, раскрывая определитель,
Сц Z> 0, СцС22 С] 2 0.
Так как сп > 0, то из второго неравенства следует, что с22>0. Поэтому
эти условия можно заменить на следующие:
С22 0, ГцС22 — ^12 0.
После подстановки соответствующих значений получим
с2 — P2Z2 >0, [Ci -j-c2 — (Pi 4" Р2) 5] (с2 Рг^г) (— сг)2 > 0>
или
С2 > Р2^2> С1 + С2— (Р1 + Р2)^1>7 "р , •
<*2 — r 2l2
Решая второе неравенство относительно с1г найдем
с2 2> РД2> Cj > (Pi + Р2) li + - 2 р . .
С-2 — г 2(2
Таким образом, для устойчивости верхнего вертикального положения двой-
ного маятника достаточно, чтобы жесткости пружин сх и с2 удовлетворяли этим
неравенствам. Если хотя бы у одного из неравенств изменить знак на противо-
положный, то верхнее вертикальное положение равновесия будет неустойчивым.
Это следует из сформулированной теоремы Ляпунова (при невыполнении этих
условий отсутствие минимума потенциальной энергии П определяется членами
второго порядка).
В, заключение этого параграфа рассмотрим вопрос об устойчи-
вости относительного равновесия ИСЗ, центр масс которого дви-
жется по круговой орбите (см. § 14.8). Так как устойчивость
рассматривается относительно вращающейся орбитальной системы
координат Cx1y1z1 (см. рис. 14.9 и 14.10), то необходимо учесть
не только потенциальную энергию сил тяготения Пф, но и потен-
циальную энергию центробежных сил инерции П2. Таким образом,
общая потенциальная энергия II будет равна
П = ПГ + П2.
Согласно формуле (3.59) потенциальная энергия силы тяготе-
ния Земли для одного элемента массы dm равна —[idm/r, где
|1 — гравитационный параметр Земли, а г —расстояние от центра
Земли до элемента dm (см. (14.44)). Для всего ИСЗ потенциаль-
ная энергия гравитационного поля Земли определяется равенством
.. С dm
П1 = — н J — -,
где интегрирование распространено на массу всего ИСЗ.
462
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Воспользуемся равенством (14.48) и разложим правую часть
его в ряд по степеням малых отношений x^R, yjR и z^/R. Огра-
ничиваясь членами не выше второго порядка малости, получим
после очевидных преобразований (см. стр. 334)
У = ~R — ~R + 2^2 ~ — yi) I =
= -1+i -2 w+(г«+•
Подставим это выражение для 1/r в Пт и проинтегрируем по
массе всего тела. Учитывая равенства (14.52) и (12.3), найдем
Здесь т — масса ИСЗ,' 1Х„ 1У,, 7г, —его моменты инерции относи-
тельно орбитальных осей xlt и zr соответственно.
Для того чтобы перейти к постоянным моментам инерции, вос-
пользуемся формулами (12.27), учтя при этом принятые в §§ 14.6 —
14.8 обозначения и то, что в нашем случае Хс=Ус = 2с = 0. Имеем
7%, = Iха\ 77га|,
/У. = /й₽!4-^4-Л₽1,
7z, = 7/yi + I уУ г + 7/|>з.
Внесем эти значения для переменных моментов инерции 7Х„
1У, и 7г, в последнее выражение для П. Тогда, используя формулы
a| + ^4-Yl = l (А = 1, 2, 3),
получим
Щ 4- (7x71 + 7,714- 7z7l) - (7х 4- 7, + 7Д.
Отметим, что для круговой орбиты первое и последнее слагаемые
постоянны и, следовательно, их можно отбросить.
Перейдем к вычислению потенциальной энергии центробежных
сил инерции. При движении центра масс ИСЗ по круговой орбите
центробежная сила, действующая на элемент массы dm, опреде-
ляется равенством <o2dmr*, где со — угловая скорость вращения
радиуса-вектора R центра инерции ИСЗ, а г* —вектор, проведен-
ный от оси Оуо до элемента dm параллельно плоскости орбиты
(на рис. 14.9 вектор г* не показан). Очевидно, что проекции
вектора г* на орбитальные оси координат хь ylt zt равны xlt О,
R -ф Zj соответственно. Поэтому потенциальная энергия центробеж-
ной силы элемента dm будет равна (см. формулы (3.50) и (3.25))
— со2 dm jj [%! dxx 4- (7? 4- 2i) dz^ = — 0)2 [у (xi 4- ZD 4- Rzi ] dm,
§ 20.2] УСТОЙЧИВОСТЬ ПОЛОЖЕНИЯ РАВНОВЕСИЯ 463
а для всего ИСЗ
П2 = — <о2 Цу (х\ + г?) 4- Rz^ dm.
Учитывая равенства (14.52) и (12.3), получим
П — — 1
Х12 — 2 Iyi'
или, снова переходя к осям х, у, г,
п2 = -^м + /й₽|+Ш).
При круговой орбите ц/R3 = <о2 = const (см. формулу (14.64)).
Поэтому с точностью до несущественных для нас постоянных
членов в ITj общая потенциальная энергия ИСЗ в относительном
движении будет равна
П = у [3 (Jxyl + lyyl + 1гу1) - (/^ + 1УМ + «]• -
Учитывая соотношения
₽|=1-₽1-₽|, yi = l-tf-Yl,
представим потенциальную энергию в следующей форме:
П = у{3[(/х-Л)?1 + (/й-Л)?|]-
- [(/х - Гу) Р1 + (Л - 1У) РШ + const.
Положение ИСЗ относительно орбитальной системы координат
Сх1у1г1 определяется тремя независимыми параметрами. Пусть это
будут рь Yi> у2. В соответствии с результатами § 14.8 мы будем
рассматривать устойчивость относительного равновесия ИСЗ, когда
большая ось эллипсоида инерции направлена к центру Земли.
В этом положении относительного равновесия а1 = р2 = у3 = 1,
а остальные направляющие косинусы равны нулю (см. § 14.8).
Поэтому при небольших отклонениях от рассматриваемого поло-
жения равновесия направляющие косинусы pit Ря, Yi и Y2 будут
малыми по модулю величинами. На этом основании из соотноше-
ния ортогональности
P1Y1 + ₽2Ya + РзУз = P1Y1 + Y2 - Pi - Р§ + Рз V1 -- Y1 - у! = 0
с точностью до величин высшего порядка найдем, что рз = — у.,.
Внесем это значение для рз в потенциальную энергию, сгруппи-
руем члены и снова отбросим несущественную постоянную. Тогда
получим
П = ~ [3 (lx - 1г) у| + 4 (Iy - Iz) yi + (/, - /Л.) Pi].
464 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ- [Гл XX
Отсюда видно, что при 1 у> Ix> Iz (условие (14.67)) в поло-
жении относительного равновесия (?1 = = ₽i = 0) потенциальная
энергия имеет минимум. На основании теоремы Лагранжа —Ди-
рихле заключаем, что положение относительного равновесия ИСЗ,
при котором большая ось эллипсоида инерции направлена к центру
Земли, устойчиво.
Отметим, что Луна имеет указанное выше распределение масс
(/у> Iд. > /г) и ее большая ось эллипсоида инерции с точностью
до устойчивых колебаний (либраций) направлена все время к цен-
тру Земли. Этим объясняется причина, по которой мы видим
только одну сторону Луны.
§ 20.3. Малые колебания консервативной системы
с одной степенью свободы
около положения устойчивого равновесия
Рассмотрим произвольную консервативную систему с голоном-
ными и стационарными связями, имеющую одну степень свободы.
Положение системы будем определять обобщенной координатой q,
отсчитываемой от положения устойчивого равновесия. Предполо-
жим, что система отклонена на небольшую величину от положе-
ния равновесия и ей сообщена небольшая начальная скорость.
Тогда вследствие устойчивости положения равновесия система
будет совершать движение вблизи этого положения равновесия,
т. е. обобщенная координата q и ее скорость q будут все время
малы по модулю. Это обстоятельство дает возможность применить
приближенный метод исследования движения, основанный на том,
что нелинейные в общем случае дифференциальные уравнения
движения упрощаются и заменяются на приближенные. линейные
уравнения. Для этого, очевидно, достаточно выражения для кине-
тической и потенциальной энергий разложить в ряды по степе-
ням q и q, сохранив в них члены не выше второго порядка ма-
лости.
Для системы со стационарными связями, имеющей одну степень
свободы, кинетическая энергия согласно формуле (19.26) имеет вид
Т = уа(?) q2,
(20.17)
где обобщенный коэффициент инерции a (q) является в общем
случае функцией обобщенной координаты q.
Так как кинетическая энергия Т при q^=0 всегда положи-
тельна, то коэффициент а(<?Дтакже положителен и не обращается
в нуль ни при каких значениях q, в частности,
а (0) -а > 0.
§ 20.3] МАЛЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ 465
Разложим a(q) в ряд Маклорена по степеням q:
и подставим это выражение в равенство (20.17):
£ L \ аЧ /о ' J
Для того чтобы сохранить члены не выше второго порядка
малости относительно q и </, отбросим все слагаемые в квадрат-
ной скобке, начиная со второго:
Г = |<и;г. (20.18)
Это приближенное выражение для кинетической энергии отли-
чается от точного значения (20.17) тем, чти обобщенный коэффи-
циент инерции a (q) заменяется на его значение а в положении
равновесия.
Разложение потенциальной энергии было уже получено (см.
формулу (20.13)). Для системы с одной степенью свободы с при-
нятой точностью будем иметь
П = (20.19)
Приближенные выражения для кинетической и потенциальной
энергий представляют квадратичные формы с постоянными поло-
жительными коэффициентами. Для кинетической энергии это сле-
дует из того, что она всегда положительна и в нуль обращается
только при <) = 0, а положительность коэффициента с в выражении
для потенциальной энергии следует из того, что рассматриваемое
положение равновесия устойчиво (см. примечание к формуле
(20.13)).
Составим уравнение движения, учитывая, что для консерватив-
<Ш
нои системы и =-----=-,
dq
_дТ _ _ <?П
dt dq dq ~~ dq '
Пользуясь выражениями (20.18) и (20.19) и принимая во вни-
мание, что а = const, получим
дТ . d дТ дТ п <9П
д— = aq, .г = <т<7, -<- = 0, -ч- = cq.
dq dt dq 7 ’ dq ’ dq 7
Тогда уравнение Лагранжа принимает вид
aq = — cq,
или
q + k2q=0,
(20.20)
466
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
где
£2 = -
а
(20.21)
Заметим, что число k вещественно, так как коэффициенты а
и с положительны.
Уравнение (20.20) называется дифференциальным уравнением
малых колебаний системы около положения устойчивого равновесия.
Для получения этого уравнения не обязательно прибегать к урав-
нениям Лагранжа второго рода — можно пользоваться любыми
другими методами, например, общими теоремами динамики. Важно,
чтобы в результате получилось линейное дифференциальное урав-
нение второго порядка с постоянными коэффициентами. Однако
изложенный здесь метод является общим, одинаково пригодным
как для простых, так и для сложных систем с несколькими сте-
пенями свободы.
С уравнением (20.20) мы уже встречались при изучении прямо-
линейных колебаний материальной точки под действием линейной
восстанавливающей силы. Его общее решение можно представить
в следующих двух эквивалентных формах:
q — Cj cos kt 4- C2 sin kt,
или
q = A sin (kt 4-e). (20.22)
Произвольные постоянные Сг и С2 или Л и 8 определяются
из начальных условий. Круговая частота k вычисляется по фор-
муле (20.21), а период незатухающих колебаний
Т = 2^ -.= 2л ]/~ (20.23)
Из изложенного видно, что вблизи положения устойчивого
равновесия консервативная система с одной степенью свободы
совершает незатухающие гармонические
колебания.
Задача 20.3. Чувствительный элемент при-
бора для регистраций^вертикальных колебаний
фундаментов состоит из ломаного рычага с
грузом Е и осью вращения О. Рычаг удержи-
вается в равновесном положении, при котором
плечо ЕО горизонтально, вертикально располо-
женной пружиной жесткости с2. При этом две
одинаковые горизонтально расположенные пру-
р . жины жесткости находятся в недеформиро-
нис‘ ' ’ ванном состоянии. ' Момент инерции рычага
вместе с грузом относительно оси вращения О
равен 1. Составить дифференциальное уравнение малых колебаний и определить
гериод колебаний системы; геометрические размеры указаны на рис. 20.4.
§ 20 3]
МАЛЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ
467
За обобщенную координату примем угол поворота рычага <р. Кинетическая
энергия определяется равенством
Г = у/Ф2.
Пусть вес рычага вместе с грузом равен Q, а центр тяжести находится
в точке С. Потенциальная энергия системы складывается из потенциальной
энергии Пх силы тяжести и потенциальной энергии П2 трех пружин.
За нулевое положение системы примем ее равновесное положение. Тогда
Потенциальная энергия Пх будет равна работе силы тяжести Q при переходе
системы из данного положения в равновесное:
Пх = — Qd3 sin <р,
где d3 = OC.
Для малых углов
П1 = — Qd3tp.
Перейдем к вычислению потенциальной энергии пружин П2. Обозначим
через f.~T статическую деформацию вертикальной пружины, ее полная деформа-
ция при малом угле ф будет /ст + ^зф- Деформации горизонтальных пружин
равны d,r[> и —diq>. Теперь найдем
П2= у Ci (П1ф)2 + -2~ С1 (— П1ф)2 + -2 с2 (/ст + ^зф)2-2 еа/ст>
или
n2 = c1dj<p3 + -2- с2 (/ст + ^зф)2—2 c'jCT‘
Потенциальная энергия системы П равна
П = nt + П2 = — Qd3q> + ftp2+ у с, (Д.т + d2<p)2 — ~ c2flt.
Раскрывая скобки и группируя члены, получим
П = (—Qrfs + ф + “2~ (2ci^i+c2d|) ф2.
В положении равновесия должно выполняться равенство (20.2):
рп\ „
э~ =0-
\<?ф/о
Для данного примера
( бф*)о = С2^стб^ + + С2^а) Фк-о~ + c2fZid2 = 0.
Теперь выражение для потенциальной энергии принимает вид
П = у (2cidf + c2d|) <р2.
Пользуясь выражениями для Т и П, составим с помощью схемы Лагранжа
дифференциальное уравнение малых колебаний чувствительного элемента
прибора
/ф (2с,а-( +c2d|) ф = 0,
или
ф=0.
468
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Круговая частота k и период колебаний Т определяются равенствами
k —
2c1d‘2l-\-c2dl ’
применить к системам, в которых,
имеются и силы другой природы,
Рис. 20.5.
Изложенный метод можно
кроме консервативных сил,
например силы сопротивления, или возмущающие силы. Мы не
будем сейчас рассматривать этот вопрос
в общей постановке и поясним его на
разобранном только что примере.
Как известно, собственные колебания чув-
ствительного элемента прибора нужно погасить.
Это может быть осуществлено как за счет есте-
ственных сил сопротивления, так и с помощью
специального приспособления, называемого дем-
пфером.
Рассмотрим ту же схему вибрографа, но
присоединим к нему демпфер D, создающий
силу сопротивления, пропорциональную ско-
рости поршня (рис. 20.5). Обозначим расстоя-
ние от оси вращения до штока поршня через е.
Тогда при малых углах <р скорость поршня
будет равна еф, сила сопротивления —реф (р— коэффициент пропорциональ-
ности), а соответствующая обобщенная сила — ре2ф. Полная обобщенная сила
системы равна
п 511 2*
После подстан вки соответствующих величин в уравнение Лагранжа полу-
чим дифференциальнсе уравнение малых колебаний
/ф = — (2cid2 + c2d2) ср — ре2ф,
(20.24)
или
ф -ф- 2/гф -ф- й2<р = 0,
где k имеет прежнее значение, а
21 •
Обычно h<Zk. Поэтому общее решение будет
(p = <4e"ftz sin Д,]=|/Д2—h2,
что определяет затухающие колебания.
§ 20.4. Случай произвольной возмущающей с иль.
До сих пор мы рассматривали свободные колебания консерва-
тивной системы с одной степенью свободы около положения устой-
чивого равновесия. При отсутствии сил сопротивления дифферен-
циальное уравнение малых колебаний имеет вид
q ф- k2q = 0.
(20.25)
§ 20 4]
СЛУЧАЙ ПРОИЗВОЛЬНОЙ ВОЗМУЩАЮЩЕЙ силы
469
Если же, помимо потенциальных сил, действуют еще силы сопро-
тивления, пропорциональные первой степени скорости, то диффе-
ренциальное уравнение приводится к следующей форме:
q -\-2hq + k2q = 0. (20.26)
Предположим теперь, что, помимо потенциальных сил и сил
сопротивления, на материальную систему действует возмущаю-
щая сила, явным образом зависящая от времени. Обозначим со-
ответствующую обобщенную силу через Q(t). Тогда, после деле-
ния на коэффициент инерции а, получим вместо уравнения
(20.26) следующее дифференциальное уравнение:
q + 2hqk2q = F (t), (20.27)
где F (/) — обобщенная сила, отнесенная к коэффициенту инерции:
(не делая в дальнейшем этой оговорки, будем называть функцию-
F (/) обобщенной' силой).
В §§ 2.5 и 2.6 мы подробно исследовали решение этого урав-
нения в предположении, что возмущающая сила F (t) изменяется
по гармоническому закону. Поэтому в тех случаях, когда функ-
ция F (t) имеет вид
F(/) = Fosin(/?/ + 6),
можно использовать полученные в §§ 2.5, 2.6 результаты. В этом
параграфе мы рассмотрим случай, когда возмущающая сила F (t)
изменяется произврльным образом.
Предположим сначала, что силы сопротивления отсутствуют.
Тогда уравнение (20.27) примет вид
q + &q = F(t). (20.28)
Общее решение этого линейного неоднородного дифференциального
уравнения с постоянными коэффициентами складывается из об-
щего решения соответствующего однородного уравнения и част-
ного решения данного уравнения (20.28). Соответствующее одно-
родное уравнение будет
q+k2q = 0.
Его общее решение имеет вид
q = Dr cos kt-F-Dz sin Л/, (20.29)
где и D2 — произвольные постоянные интегрирования.
470
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Частное решение уравнения (20.28) будем искать в форме
(20.29), предположив, что Dr и являются функциями времени *):
q — D1(t') cos kt + (/) sin kt. (20.30)
Дифференцируя по времени, получим
q = cos kt 4- sin kt — D. k sin kt -j- D„ k cos kt.
dt dt 1 1 i
Нам нужно найти одно частное решение, а мы ввели две неиз-
вестные функции и D2. Поэтому их можно подчинить некото-
рому условию. Потребуем, чтобы сумма первых двух слагаемых
в правой части последнего равенства равнялась нулю:
^icos£/4-~5r'sin^ = 0- (20.31)
dt 1 at ' '
Тогда
q = — Dtk sin kt + DJZ cos kt.
Дифференцируя еще раз по времени, получим
q = — — k sin kt k cos kt — Dxk2 cos kt — D2k2 sin kt.
CI.L Ш
Подставим это выражение для q и выражение (20.30) для q
в уравнение (20.28). Тогда, после приведения подобных членов,
получим
-^ksinkt + ^-knoskt = F(t). (20.32)
Решая совместно уравнения (20.31) и (20.32) относительно
производных dD^dt и dDjdt, найдем
— = —(0 s>n = 4 Р (0 cos kt.
dt k ' ’ ’ dt k v ’
Интегрируя, будем иметь
t t
Dt = — j- f F(g)sin^dg, = j F(£)cosfe|d£,
о d
где через | обозначена переменная интегрирования.
Подставив найденные значения для Dr и Dt в равенство (20.30),
получим частное решение уравнения (20.28):
t t
q = — у cos sin&£ + y sin kt j* F (|) cos k% d%.
о о
*’ Этот метод определения частного решения, предложенный впервые Лагран-
жем, называется методом вариации произвольных постоянных.
§ 20 4] СЛУЧАЙ ПРОИЗВОЛЬНОЙ ВОЗМУЩАЮЩЕЙ СИЛЫ 4/Г
Так как функции cos kt и sin kt не зависят от переменной интег-
рирования то их можно внести под знаки интегралов:
t t
q — — у j* F cos kt Jin kc d% + ~ j F (£) sin kt cos k% d%.
о 0
Объединяя оба интеграла, получим
t
q = у J F (£) [sin kt cos Ag — cos kt sin k%\ d%,
о
или
t
q = ^ F sink (t-^)d^. ~ (20.33)
о
Таково частное решение дифференциального уравнения (20.28)
при произвольной возмущающей силе F (/).
Для того чтобы найти частное решение уравнения (20.27),.
сделаем в нем замену переменных, положив
q = e~htz,
где z —новая неизвестная функция.
Имеем
q = — he~hiz + e~hti, q = h2e~hlz — 2he^h‘z + e~htz.
После подстановки значений для q, q и q в уравнение (20.27) и
приведения подобных членов получим
e~htz + (А2 —/г2) e~htz = F (/),
или, разделив на е~ы,
z(k2 — h?) z = F (t) eh‘.
Будем предполагать, что h<z_k (силы сопротивления не очень
велики). Тогда, положив
/г( = /г2 -/12, (20.34)
мы придем к уравнению (20.28), где функция F (/) заменена на
функцию F(t)er‘, а коэффициент k на kr. Поэтому частное реше-
ние последнего уравнения согласно равенству (20.33) будет
I
г = J e^F (£) sin kx (t - £) dg.
11
*472 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ [Гл. XX
Переходя к старой переменной q = e~h‘z, найдем
I
q = -^- e~h‘ f №F © sin (t — E) de,
J
0
или, внося множитель е~^ под знак интеграла,
t
77 = ~§F©^4)sinM*-^- ' (20.35)
о
Таково частное решение, дифференциального уравнения (20.27)
при произвольной возмущающей силе F(t). Непосредственной про-
веркой легко установить, что частные решения (20.33) и (20.35)
удовлетворяют нулевым начальным условиям, т. е.
q = 0, q = 0 при 7 = 0. (20.36)
Общее решение дифференциального уравнения (20.27) имеет вид
(/г < k)
t
q = e~h‘ (Q cos ktt + C2 sin ktt) + ~ J F © e~hsin (7 - £) 7©
о *
(20.37)
где Cj и C2 — произвольные постоянные интегрирования.
Интегральная форма частного решения (20 35) дифференциального уравне-
ния (20 27) позволяет определять движение системы и после того, как сила F (7)
прекратила свое действие. Поясним это подробнее Пусть сила F (7) до момента
времени 7 = 0 равнялась нулю, а затем в промежутке времени (0, 7|) она при-
няла значение F (7) и, начиная с момента 7 = 7If она прекращает свое действие.
Математически это можно записать следующим образом:
г 0 при 7 < 0,
f(7)=J F (7) при 0 ^7^7!, (20.38)
I 0 при 7 > 7Х.
Будем считать, что до начала действия силы F (7) система находилась
в покое Тогда движение системы определится решением, удовлетворяющим
нулевым начальным условиям, т. е. решением (20.35). Если 7 > 7,, то разобьем
.промежуток интегрирования (0, 7) на два промежутка (0, 7,) и (7Х, 7):
71 7
9 = -^ J e-ft(^'E(5)sinfe1(7-5)dg + J е-^-Ър (g) sin kl (Z_g)
1 о 1 7,
Второй интеграл равен нулю (так как при 7 > функция Е(7) = 0). По-
этому движение системы после окончания действия силы F (7) определяется
равенством
7.
q = £ е-Л|,-&>Е(Е) sin^-g) ф (20.39)
о
§ 20 4]
СЛУЧАЙ ПРОИЗВОЛЬНОЙ ВОЗМУЩАЮЩЕЙ СИЛЫ
473
Если силы сопротивления отсутствуют (й = 0, k^—k), то
ti
q5F г&) sin k(t~® (20-40>
о
Задача 20:4. Прибор, описанный в § 20 (см. рис. 20.4 и 20.5), установлен
в лифте. Сначала лифт находился в покое, а затем начал подниматься вверх
с постоянным ускорением шв. По прошествии секунд стал двигаться равно-
мерно. Определить колебания прибора при равномерном движении лифта.
Будем изучать колебания рычага относительно корпуса прибора, т. е. отно-
сительно движущегося лифта. Для того чтобы можно было рассматривать коле-
бания рычага с помощью тех же уравнений, что и в абсолютном движении,
нужно ввести переносную силу инер-
ции (лифт движется поступательно, и,
следовательно, кориолисова сила инер- f0
ции равна нулю). При движении лифта
вверх с ускорением и'о сила инерции,
приложенная к точке С и равная по
Q
модулю —- ш0, будет направлена вер- ---------------------——J . >
g О t
тикально вниз. Ей соответствует обоб- _ _
q " Рис. 20.6.
щенная сила — - w0d3 (см. рис. 20.4).
Учитывая упругие силы, создаваемые пружинами, и силу сопротивления^
возникающую за счет действия демпфера, вместо уравнения (20.24) получим
/ф= (2cidf -j-c2d2) tp — р,е2ф-|- zuods,
или
ф + 2йф 4- Й2ф = Eq,
где
^ = ~(2с^+с^), h = Fo = -^f-Wo.
Возмущающая сила F (t) удовлетворяет условиям (ее график изображен на
рис. 20.6):
г 0 при t <z 0,
Е(/) = < Fg — const при 0
I 0 при
Нас интересует поведение прибора при равномерном движении лифта, т. е.
при t > ti. Воспользуемся формулой (20.39):
О
<₽ = 17 J F°e~h sin - £ W
0
или, учитывая, что в промежутке (0, функция E = /:'0 = constJ
ti
Ф = -^- ( (/-£) dg.
«1 J
о
474 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ [Гл XX
Вычисляя'этот интеграл, найдем*)
<Р = — 1/г sin ki (z — 5) + ki cos (t - £)1 ’ = д' •
Подставим верхний и нижний пределы и учтем равенство (20 34):
<р = — sinftj(/—G)+cos*i (t~/j)j —
— e~ht sin &i/ + cos fej/U. (20.41)
\ «1 ;)
Это решение справедливо при t > tr. Им можно пользоваться и при t < ti,
•если только положить в нем ti = t. Таким образом, при ускоренном подъеме
лифта стрелка прибора колеблется по закону
ф = {г e~hl sin + cos ~ £
и после окончания ускорения при t закон колебания стрелки прибора
определяется равенством (20.41).
Если применить обычные методы, то нужно сначала решить уравнение
ф + 2йф + й2<р — Fo,
затем найти постоянные интегрирования по нулевым начальным условиям,
после чего определить значения угла <р и угловой скорости ф в момент / =
Полученные значения для <р и ф служат начальными условиями для движения,
описываемого уравнением
ф -|- 2йф ф- &2ф — 0
(первое уравнение справедливо для промежутка 0 <t <_ti, второе для t^zti).
Несмотря на кажущуюся простоту этого метода (он называется методом
припасовывания, или методом поэтапного интегрирования), он требует больших
преобразований, чем определение решения в интегральной форме. Однако глав-
ный его недостаток состоит в том, что он, в отличие от интегральной формы,
не может быть применен при произвольной возмущающей силе F (/).
§ 20.5. Определение периодических решений
Вопрос об определении периодических решений является одним
из важнейших в теории колебаний. Мы рассмотрим случай, когда
движение системы описывается дифференциальным уравнением
(20.28), правая часть которого (возмущающая сила) представляет
некоторую периодическую функцию периода т
F(( + t>F(/).
. Существует несколько методов определения периодического
решения периода т. Мы рассмотрим два из них.
1. Определение периодического движения с помощью ряда
Фурье, Пусть периодическая функция р (() удовлетворяет усло-
*) Интеграл еах sin bx dx легко вычисляется по частям (см. также
Градштейн И С., Рыжик И. М. Таблицы интегралов, сумм, рядов и
произведений. —М.: Наука, 1971).
§ 20 5] ОПРЕДЕЛЕНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ 475-
виям Дирихле и может быть разложена в ряд Фурье
F (t) = ^- + a1sin(pt + s1) + a2sin(2pt + e2) + ...,
где коэффициенты а0, alt а2, ... и сдвиги фаз каждой гармоники-
определяются по известным формулам, а р = 2л/т.
Уравнение (20.28) примет теперь вид
q + k*q = 4-Gj sin {pt + ег) + ц2sin (2pt + e2) +...
Для каждого слагаемого правой части легко определяется
частное решение (см. § 2.5). Поэтому частное решение, отвечаю*
щее всей правой части, будет иметь вид
sin (pt + £1) + fe--(2p)^~sin ^2pt + g2) + • • (20.42)
Это решение справедливо, если р =£ k/п при любом целом п (пред-
полагается, что это условие выполнено). Решение (20.42) опреде-
ляет периодическое движение системы периода т.
Применение ряда Фурье целесообразно использовать для опре-
деления периодического движения системы в том случае, когда
ряд быстро сходится и можно ограничиться первыми несколь-
кими членами.
2. Определение периодического решения в замкнутой форме.
Даже в тех сравнительно редких случаях, когда ряд Фурье
быстро сходится, практически можно получить только приближен-
ное решение. Применение интегральной формы частного решения
(20.33) дает возможность построить точное периодическое решение
(решение в замкнутой форме).
Формула (20.33) определяет частное решение уравнения (20.28),
удовлетворяющее нулевым начальным условиям. Поэтому решение,
удовлетворяющее произвольным начальным условиям (</= и
= при / = 0), имеет вид
г
<7 = <?0 cos « +sin kt j* F (g) sin k {t — %) d%. (20.43)
о
Если возмущающая сила F (/) имеет период т, то вынужденным
колебаниям того же периода должно отвечать периодическое реше-
ние, удовлетворяющее условиям
q (0) = q (т) = q0, q (0) = q (т) = q0. (20.44)
Так как дифференциальное уравнение (20.28) не изменяет
своей формы от замены t на t^-r, то условия (20.44) будут не
только необходимыми, но и достаточными, т. е. решение, удов-
летворяющее этим условиям, будет периодическим с периодом т..
-476
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл. XX
Решение (20.43) уравнения (20.28) является общим. Для того
чтобы оно содержало частное периодическое решение с периодом т,
подчиним его условиям (20.44). Это даст нам два уравнения, из
которых можно будет найти неизвестные для периодического дви-
жения начальные значения обобщенной координаты q0 и обобщен-
ной скорости q0.
Представим формулу (20.43) в следующем виде:
q = q0 cos kt + -у- sin kt 4-
t t
sin kt F (g) cos kE, dt- — cos kt F (^)sin kz dg
о 0
Вычислим производную по времени и разделим ее на k:
qosinkt + ^ cosA7 4-
~ cos kt F (^) cos kt, d£-|- sin kt
L о
t
p©sinAg^
b
Подчиним решение условиям (20.44). Для этого положим t — x и
заменим q на q0, a q на ф,:
q0 = <70 cos kx + sin kx + [Л sin kx — В cos Ат],
4— = — q0 sin kx + cos kx -j- [Л cos kx -\-B sin At],
R к к
(20.45)
где числа А и В определены равенствами
А = § F (£) cos Ag d%,
о
В = F (^) sin А5. d%.
о
(20.46)
Решая уравнения (20.45) относительно q0 и ф,/А, найдем
q0 =----г—[Л sin Атф-(1 — cos Ат) В],
4fesin2-S
=---------г— [— (1 — cos Ат) А 4- В sin Ат].
4k sin-
(20.47)
Внося эти выражения для q0 и qjk в равенство (20.43), полу-
чим после элементарных преобразований искомое периодическое
решение
A cos k + + В sin k (t -ir j . ,
<7=------k \ F®™k(t-l)dl. (20.48)
2A sin -y- b
§ 20.
ОПРЕДЕЛЕНИЕ ПЕРИОДИЧЕСКИХ РЕШЕНИЙ
477
Это решение определяет движение на отрезке [0, т]. На после-
дующих отрезках [т, 2т], [2т, Зт] и т. п. значение обобщенной
координаты и ее график (если он построен) нужно просто пов-
торить.
Множитель sin -%- в знаменателе указывает на возможность
резонанса при £т/2 = пл, или
2тг
— (п—1, 2, 3, ...), т. е.
резонанс может наступить, если
период т возмущающей силы бу-
дет кратен периоду Т = 2n/k
собственных колебаний.
Рассмотрим пример. Пусть пе-
риодическая возмущающая сила изме-
няется по закону, изображенному на рис. 20.7. На отрезке [0, т] будем иметь
( Го при 0 - У t - с ~,
т
( 0 при g- < t si т.
Вычислим коэффициенты А и В по формулам (20.46). Для этого разобьем от-
[j з Гт 1
0, -g- И g- , т , учтя, что во вто-
ром из них Г(/) = 0. Имеем
т/2 х х/2
А = + j j f0cos6gdg = -^-sin4^,
О т/2 0
Т/2
S= j r0sin^dg = A^l-cos^-
0
- (20.49)
(20.50)
Интеграл, стоящий в формуле (20.48), вычислим сначала для момента времени t,
лежащего в промежутке ^0, , когда F = F0:
i
~ Jf (g) Sin *(< — £) dg = -^-cos* (Z — g) (1 —cos *0-
о
Для момента времени t, удовлетворяющего условию -% <_t <С т, получим
t
~ С
k '
о
т/2
F (^)sin k (t — g) f0 sin k (t — g) = Jcosfcf/— — cos kt
о
478
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Таким образом,
р
cos kt) при
2
1С
k '
О
2 ’
Подставляя полученные выражения для чисел А и В, а
интеграла в равенство (20.48), после очевидных упрощений
уравнения (20.28) при заданной возмущающей силе:
/ т \ ( F
р cos k (t + -у ] -г,- (1 — cos kt) при
q = —-------------12. _|_ k
4 2k* /гт Fo Г ./, т\ .Л
cos “ cos k /-----— cos kt \ при
4 fe2 L \ 2 / I
2jt
Положим £т/4 = л, т. e. т==2 - =2T. Тогда на отрезке
т
Os=Z s=
< / SS T.
kt}>
также значения
найдем решение
2
(20.51)
а на отрезке
Fa ,
q=^co&kt.
(20.52)
Примерный график вынужденных колебаний показан на рис. 20.8 (на
отрезке [0, т] он построен обычным путем по точкам, а затем Периодически
продолжен) Отметим, что, несмотря
на кратность периодов (т = 2Т), в
данном примере резонанс не наступил
(он имел бы место при т=7’, т = 37’,
т=5Т и т. п.).
Мы рассмотрели построение
периодических решений в пред-
положении, что отсутствуют
силы сопротивления. Учет их
не представляет труда, нужно
только при выводе воспользоваться формулой (20.37), а не фор-
мулой (20.43) *).
§ 20.6. Малые колебания консервативной системы
с двумя степенями свободы около положения
устойчивого равновесия
Рассмотрим произвольную консервативную систему с голоном-
ными 'и стационарными связями, имеющую две степени свободы.
Положение системы будем определять обобщенными координатами
*) См., например, Л ой ця некий Л. Г., Л у р ь е А. И. Курс теорети-
ческой механики, том II, — М.: Гостехиздат, 1955.
§ 20 6]
МАЛЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ
479
q} и q2, отсчитываемыми от положения устойчивого равновесия.
Вблизи этого положения обобщенные координаты qr и q2 и обоб-
щенные скорости qx и (?2 будут все время малы по модулю, так
как равновесие устойчивое.
Кинетическая энергия системы для s = 2 согласно формуле
(19.26) имеет вид
Т =4[аИ(?ь + 2ai2 (<7i. 9г) 919г + «22 (91. 9г) 9Й- (20.53)
Коэффициенты инерции в общем случае зависят от координат
qx и q2. Разложим их в ряд Маклорена по степеням qv и q2 и
ограничимся малыми нулевого порядка (для того, чтобы кинетиче-
ская энергия содержала члены не выше второго порядка малости
относительно q2, 9i.
«н(91, q2)^au(0, 0)=au, '
«12 (9ь 9г) — «12 (°, °) = «12.
«22 (9i> 9a) —«22 (0, 0) = a22. .
(20.54)
Теперь выражение для кинетической энергии примет вид
Т = у («и91 + 2«129192 + a22ql), (20.55)
где все обобщенные коэффициенты инерции — постоянные числа.
Так как при скоростях, отличных от нуля, кинетическая энер-
гия положительна, то квадратичная форма (20.55) удовлетворяет
критерию Сильвестра (20.16), который для данного случая имеет
вид
а11>0, аг1а22 — а\г > 0. (20.56)
Разложение потенциальной энергии в ряд по степеням qr и q2
дается формулой (20.13). Для системы с двумя степенями сво-
боды получим
П = (Д191 + 2c129i92 + c22q2). (20.57)
Для положения устойчивого равновесия квадратичная форма
(20.57) определенно положительна и она удовлетворяет критерию
Сильвестра (20.16):
си > о,
ciic22 7> 0.
(20.58)
Пользуясь уравнениями Лагранжа
d дТ дТ _ ЗП
dt dq dq ~~ dq
480
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл. XX
и равенствами (20.55) и (20.57), составим дифференциальные урав-
нения малых колебаний. Имеем (ajk = const)
дТ ... d дТ .....
— «п<714-01272, ~аГ~д4Т ~~ «n7i 4- о1272,
дТ „ ОТ
1^”°' -^~~«n7i + «i272-
Следовательно, уравнение для координаты qx будет
Оц714- о1272 = — cuqt - Ci272.
Второе уравнение может быть получено аналогичным способом.
Принимая во внимание, что о12 = а21 и с12 = с21, окончательно
будем иметь
«1171 + «127г 4- «11714- «1272 = 0,1
.. . .. , , л 7 (20.59)
«2171 4- О2272 4- «2171 + «2272 = 0. )
Таким образом, малые колебания консервативной системы
с двумя степенями свободы около положения устойчивого равно-
весия описываются двумя линейными однородными дифферен-
циальными уравнениями второго порядка с постоянными коэффи-
циентами. Решение этих уравнений будем искать в форме
= A sin (kt 4-е), <?2 = .В sin (&/4“е), (20.60)
где А, В, k и е — неизвестные постоянные.
Продифференцируем выражения для qx и q2 дважды повремени t;
qx =— Ak2 sin (kt 4-е), 74 = — S/г2 sin (kt 4- e)
и подставим полученные выражения в уравнения (20.59):
— airAk2 sin (kt 4- е) — a12Bk2 sin (kt 4- 8) 4-
4-СцД sin (kt-\-z) 4- c12B sin (kt 4- e) = 0,
— o2iXA2 sin (kt 4- 8) — a22Bk2 sin (kt 4- s) 4-
4-«2iX sin (kt 4- e) 4-c22 В sin (kt 4-e) = 0.
Для того чтобы эти равенства удовлетворялись тождественно
при любых t, вычислим коэффициенты при sin (kt4-е) и прирав-
няем их к нулю:
(«и - «и^2) А 4- (с12 - a12k2) В = 0, 1
(«21 — «21^2) А 4- (с22 - a22k2) В = 0. J
Эти алгебраические линейные однородные уравнения относительно
А и В должны иметь решение, отличное от нуля (в противном
случае согласно (20.60) ^ = ^ = 0, что соответствует покою, а не
§ 20.6] МАЛЫЕ КОЛЕБАНИЯ КОНСЕРВАТИВНОЙ СИСТЕМЫ 481
движению). Поэтому определитель этой системы должен равняться
нулю:
I Сц — auk2 С12 — a12^2|_Q (20 62)
I c2i — й2х&2 с22 — <з22/с2 I
Раскрывая определитель, получим
(Сц — dnk2) (С22 — Й22^2) — (С12 fl12^2)2 ~ 0» (20.63)
или
(«11^22 - Ян) & - (а^с^ + я22сп - 2clac12) k2 + (cuc22 - с?2) = 0. (20.64)
Уравнение (20.62), или эквивалентные ему уравнения (20.63)
и (20.64), называется уравнением частот, или вековым уравнением.
Докажем, что оба корня этого уравнения относительно k2
вещественны и положительны. Для доказательства обозначим
левую часть уравнения (20.64) или, что то же самое, уравнения
(20.63) через А(&2). Тогда, пользуясь соотношениями (20.56) и
(20.58), будем иметь
А
fe2 = ——в левую часть экви-
°22
А (0) = спс2а — >0, А (оо) > 0,
(°11с12 — а12С11)3 Q д / с22 ) _ (а22с12‘—а12С2з)2 Q
а11 * \ а22 / а22
(значения k2 = 0 и k2 = оо подставлялись в левую часть уравне-
ния (20.64), а значения k2 = ^^- и
валентного ему уравнения
(20.63)).
Это означает, что между
k2 = 0 и k2 = оо график функ-
ции А = А (&2) пересекает ось
абсцисс в двух точках (рис.
20.9), определяющих два по-
ложительных корня k2 и k*
уравнения частот (при по-
строении графика предполагалось для определенности, что
ДА-сЗ2- и
ЙЦ й22 j
Прежде чем перейти к дальнейшему, заметим, что в том слу-
чае, когда уравнения (20.61) распадаются на два независимых
уравнения (это будет при а12 = я21 = 0 и с12 = с21 = 0),
щие частоты колебаний будут (они называются ,
частотами)
, соответствую-
парциальными
Из полученных выражений и рис. 20.9 видно, что парциаль-
ные частоты больше меньшей частоты системы и меньше боль-
шей частоты системы k2.
16 Н. В. Бутеввн и др.
482 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ [Гл. XX
Извлечем теперь из k2 и k2 квадратные корни и воспользуемся
только положительными значениями kv и k2. Каждому корню
и k2 будет отвечать одно частное решение (20.60), причем каждой
частоте kx и k2 отвечают свои значения А, В и е. Частные реше-
ния линейно независимы, поэтому общее решение будет равно их
линейной комбинации:
= А1 sin (kJ gj) + А2 sin (k2t + e2),
q2 = Bi sin (k^ -j- ej + B2 sin (k2t + 82).
Между числами и Въ А2 и В2 имеется связь, которая уста-
навливается уравнениями (20.61). Если подставить в эти уравне-
ния ki или k2, то определитель системы (20.61) обратится в нуль.
Следовательно, из двух уравнений этой системы независимых
только одно. Возьмем одно из этих уравнений, например первое
(при решении практических задач нужно выбирать наиболее про-
стое уравнение), и найдем из него отношение
-у- = = И.- (i = 1, 2). (20.65)
AI С12 —
Каждому значению частоты k± и k2 отвечают соответствующие
значения и ц2. Вычислив их по формуле (20.65), найдем
= НМ1, В2 = р2А2. (20.66)
Теперь общее решение примет вид
q± = A j sin (k^ + 8j) + А2 sin (k2t + 82),
72 = Р-Ml sin +ei) + M2A sin (k2t + 82).
В этом решении частоты kx и kt и коэффициенты h и R2~
известные числа, характеризующие данную систему, Аъ А2, Sj и
б2 — произвольные постоянные, определяемые из начальных усло-
вий движения.
Из формы общего решения видно, что движение системы с двумя
степенями свободы около положения устойчивого равновесия скла-
дывается из двух независимых колебаний:
qi = q'i' + qi\ q2 = q'i' + qT,
где
q'i" = Ai sin (k^ + 8^), q’i2’ = A2 sin (k2t + e2),
q%’ = pjAi sin (kit + ej, ф/1 = u2A2 sin (k2t + 82).
Первое колебание в обеих координатах происходит с частотой
а второе с частотой k2. Эти колебания называются главными.
Коэффициенты Pj и ц2 определяют формы колебаний’, согласно
(20.67)
§ 20.7]
ЗАДАЧИ
483
равенствам (20.65) они имеют простой физический .смысл, пока-
зывая, во сколько раз амплитуда соответствующего главного коле-
бания в одной из координат больше (или меньше) амплитуды
другой координаты.
, Из определения видно, что все координаты в каждом главном
колебании изменяются по гармоническому закону, имея одинако-
вые частоты и фазы. Это означает, что они (т. е. координаты)
одновременно обращаются в нуль, одновременно достигают макси-
мальных значений и т. п., причем координаты в каждом главном
колебании находятся в постоянном отношении щ, не зависящем
от начальных условий.
Частоты колебаний (точнее, круговые частоты) kv и k2, а также
коэффициенты ж и ц2 являются основными характеристиками
малых колебаний системы с двумя степенями свободы.
В заключение отметим, чю методы составления и интегриро-
вания дифференциальных уравнений малых колебаний системы
с двумя степенями свободы около положения устойчивого равно-
весия без всяких изменений могут быть распространены на системы
с большим числом степеней свободы.
§ 20.7. Задачи
При решении задач на исследование малых колебаний системы
с несколькими степенями свободы около положения устойчивого
равновесия можно, конечно, пользоваться получен-
ными формулами. Однако значительно полезнее
для каждого примера производить все преобразо-
вания с самого начала. Это объясняется тем, что
метод запомнить значительно проще, чем формулы.
Задача 20.5. Определить малые колебания двойного ма-
тематического маятника (рис. 20.10).
Выражения для кинетической и потенциальной энергий
двойного математического маятника были получены ранее
(см. формулы (18.32) и (19.13)):
т = у [(mj + m2) 1Ф? + 2m26G cos (cp2 — фх) фхф2 + тг/|ф|],
П = — (mi + m2) gh cos фх — m2gl2 cos <р2.
Среди коэффициентов инерции только один коэффициент, а именно а12 =
= cos (ф2 —фх), зависит от обобщенных координат фх и ф2. Согласно общей
теории заменим этот коэффициент на его значение в положении равновесия при
ф1==ф2 = 0, т. е. положим приближенно
m2/xZ2 cos (ф2 — фх) «= т2/х/а.
Кинетическая энергия двойного математического маятника для малых колеба-
ний принимает вид
7 = 4 [(mi + m2) + 2т2/1/2фхф2 + т21'1ф1].
I W
। ^/9 \
1 г
।
1 I
Рис. 20.10.
16*
484 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ [Гл. XX
Потенциальную энергию разложим в ряд по степеням фх и ф2, ограничи-
ваясь членами не выше второго порядка малости. Имеем
coscp1 = l—coscp2=l—у-.
Следовательно, для малых колебаний (постоянные слагаемые отброшены)
П= ~ (mi + m2) gZicpf+ у и2^2ф|-
Пользуясь этими выражениями для кинетической и потенциальной энер-
гий, составим дифференциальные уравнения Лагранжа, определяющие малые
колебания двойного математического маятника:
для координаты фр
ОТ „. , , . дТ
—=(m1+m2) НФг + яШгФа, -^- = 0,
а'Г 'афГ=+ tCpt+^2^1^зфа, =(mi+1щ) giispi,
для координаты ф2:
^Um^h-W^, ~=о,
d дт .. ап
~dF "аф7 ~ /”2‘1‘2Ф1 + т24фз , -0^- = т2^2ф2 .
Следовательно, уравнения малых колебаний имеют вид (первое уравнение
сокращено на lv а второе на' m2l2; кроме того, все члены перенесены в левые
части уравнений)
(mi 4~ т2) ?1ф1 + m2l2if2 + (mi т2) gq>t = 0, ]
г, г (20.68)
'1Ф1+ W+ № = 0- )
Общее решение будем искать в форме (20.60):
ф! = A sin (ZeZ + e), ф2=В sin (/eZ-[-e).
Отсюда следует
ф1 = —ЛА2 sin (/rf-f-e), ф2 =—Bk2 sin (AZ-|-e).
Подставим значения фр ф2> ф>1 и ф2 в уравнения (20.68) и приравняем
к нулю коэффициенты при sin(AZ-|-e). После группировки членов получим
алгебраические уравнения (20.61):
(mi + m2) (g—ltk2) A — m2l2k"-B = 0, )
— ZiAM + (g - l2k2) В = 0. | (20,69)
Так как Л и В не равны нулю одновременно, то определитель этой системы
равен нулю:
| (^i + ^s) (g—djk2) — m2l2k2 I_
| -hk2 g-l2k2 I-”’
Раскрывая определитель, приведем частотное уравнение к виду
mililfk* — (т1 m2) (Zi -|-Z2) gk2 + (mi 4- т2) g2 = 0.
§ 20.7]
ЗАДАЧИ
485
Дальнейшие вычисления в общем виде производить не рационально. Нужно
задать числовые значения параметров двойного математического маятника либо
соотношения между ними. Будем считать, что оба маятника одинаковы:
/1 = /2 = Z, m1 = zn2 = zn.
Тогда частотное уравнение примет вид
• fc4 —4 -£^4-2 — = 0.
Отсюда найдем две круговые частоты собственных колебаний:
= ^=]/(2 + К2) f. (20.70)
Пользуясь вторым уравнением (20.69), найдем отношения амплитуд
В 1^
А ~ g-Z3A3 •
Подставляя сюда найденные значения для kj и kf, получим / = /2=/)
Si 2-/2
R =
Ai
Следовательно,
-----/2,
/2-1
В2
Н2 = —
а2
2±И = _/2.
1+/2
Теперь можно
{20.68):
S1 = K2 Дъ
составить общее
В2 = -/2Л2.
решение дифференциальных уравнений
Ф1== A sin (kit “I- 6i) 4~ 42 sin (^2^ 4“ е2),
ф2 = 2 Ai sin (&iZ4" Si) — V2 Л2 sin (^2^ 4“ 62),
где ki и k2 определены равенствами (20.70).
Произвольные постоянные At, А2,
Пусть, например,
при Z = 0
(20.71)
ej и е2 находятся из начальных условий.
ф1=0,
Ф1 = О,
ф2 = ф0-
ф2 = 0,
(20.72)
г. е. в начальный момент первый маятник занимал крайнее нижнее положение,
второй маятник был отклонен на угол ф0 и система была отпущена без началь-
ной скорости.
Продифференцируем ф1 и ф2 по времени:
Ф1 = X]fei cos (kit 4- 6i) 4- A2k2 cos (k2t 4- e2),
ф2 = /2X1^1cos + ei)~ ]^2A2k2 cos (k2t 4- e2).
Подставим в эти выражения для ф1 и ф2 и в равенства (20.71) начальные
условия
0 = АА cos ei 4- A2k2 cos e2,
” 0 = /2 Atki COS 81 — /2 42£2COS62,
0 = Ai sin 814- A2 sin e2,
фо = /2 Ai sin 81 — /2 A2 sin e2.
486
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл. XX
Из первых двух уравнений найдем
cos 6i = cos в2=0,
Лх 4“ Д2 — 6,
откуда 6i = Ji/2, е2 = л/2. Теперь вторая пара уравнений принимает вид
л л 1^2
Л1 — Л2 = —g— ф0.
г л /2 л П ч
Следовательно, Л1 = —j-ф0, Л2 =----4“ Фо- Частное решение, соответ-
ствующее начальным условиям (20.72), будет
j/'g' 1
ф!=—ф0 (COSZii^—COS&20, ф2=^фо (COS kit 4-COS k2t).
Главные колебания согласно (20.71) определяются следующими равенствами!
первое главное колебание:
Ф'11, = Л1 sin (kit-\-Zi), ф^’ = |Л2' Aj sin 4-eJ;
второе главное колебание:
Ф12)==Л2 sin (^ + е2), ф?’ = —К2 Л2 sin (&2^ + е2).
Формы главных колебаний изображены на рис. 20.11. Если в первом глав-
ном колебании первый маятник отклонится от вертикали на угол ф”1, то вто-
рой отклонится в ту же сторону на угол ф21) = К2 ф,1’. Во втором главном
колебании при отклонении первого маятника на угол ф'^’ второй маятник откло-
нится в противоположную сторону на угол ф22'= —К 2 ф^1.
Задача 20.6. Определить колебания автомобиля в его средней вертикальной'
плоскости при следующих условиях: вес подрессоренной части автомобиля
равен Q, расстояния от центра тяжести С до вертикальных плоскостей, про-
веденных через оси колес, равны /х и 12, радиус инерции подрессоренной части
относительно центральной - оси, параллельной осям автомобиля, р, жесткости
рессор q и с2.
Так как колебания автомобиля происходят в его средней вертикальной
плоскости, то система имеет две степени свободы. За обобщенные координаты
примем вертикальное перемещение г центра тяжести С автомобиля и угол ф
поворота его вокруг оси, проходящей через точку С параллельно осям
(рис. 20.12).
§ 20.7]
ЗАДАЧИ
487
Кинетическая энергия на основании теоремы Кёнига будет равна
Q
тде /с = —р2 — момент инерции автомобиля.
Потенциальная энергия П системы складывается из потенциальной энергии
П1 — — Qz силы тяжести и потенциальной энергии П2 = ПЛ4-ПД рессор А
и В. Из рис. 20.12 видно, что деформация пружины А от положения равнове-
сия для малых углов равна г— ?i = z — Zicp, а с учетом статической деформации
/л она будет ^л4-г— Zjtp. Поэтому потенциальная энергия пружины А
Пд“у ci ((д + г \ф)2 2‘cj/a'
Аналогично для пружины В
nB = |C2(^ + Z + W~T^b-
Потенциальная энергия всей системы равна
п = - Qz + 1 (/л + 2 - \ф)2 + Сг (fB + Z + /2ф)2 -1 СурА -± с^в.
В положении равновесия при z = 0 и ф=0 должны выполняться равен’
ства (20.2):
^1 ^1 =°-
дг |z=o оср |z=o
ф=0 ф = 0
Имеем
^1 = 0 =[—<2 + С1 (^ + г — /1(Р)+С2(^ + г+/2Ф)]г = 0=— Q + ci/a + C2^B’
ф=о Ч)=О
|г=0 =[— С111 (^ + г-/1СР)+С2/2 (1в + г + Z2(P)]z = 0 = — C1Va + Wb-
Т ф=0 ф=0
Следовательно, параметры системы удовлетворяют условиям
-<2 + сЛ + ^в = 0, -о?Л + с2Ув = °- (20.73)
Раскроем в выражении для потенциальной энергии скобки и сгруппируем
П = (— Q + cJA + <?2/в) z + (c2Z2/B—CjlJл) ф +
+ у (с! + сг) Z2 + (с2^2 — С1У 2Ф + у (Ci/f + Сг1%) ф2,
или, принимая во внимание равенства (20.73),
п = у (<] + С2) Z3 + (С212 — С1?1) 2ф + у (CfZ? + C2Z|) ф2.
Уравнения Лагранжа второго рода
— _______________________5П
di di дг “ дг ’ dt дф дф Ity
488
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл, XX
после очевидных операций приводясся к такому виду:
— 24-(С14-Сг) г + (Сг^2—Ci?i) ср = 0,
g
1сЧ + (C2Z2 - СА) 2 + (ciZi + c2li) Ф = °’
Запишем полученные дифференциальные уравнения малых колебаний авто-
мобиля следующим образом (напомним, что 1С = ~ р2);
Ь €
2 + az + bq = 0, ф + —г+—ф=0,
(20.74)-
где
С14~С2 _ С2^2 — clh __ Clt2L 4-
Л в’ п ё*
(20.75>
“ Q s’ “ Q
Ищем решение уравнений в форме (20.60):
г = A sin (И-|-е), q> = B sin (kt 4-е).
Подставляя г, S, ф и ф в дифференциальные уравнения движения и при-
равнивая нулю коэффициенты при sin (W-f-е), получим систему двух линейных
однородных алгебраических уравнений относительно А и В:
(a—k2) А+ЬВ=0, '
~A + (~-k2\B^0.
(20.76)
Так как при колебаниях А и В не равны нулю одновременно, то опреде-
литель системы должен равняться нулю:
Ь
Р2
a — k*
b
Р2
=0.
Это уравнение частот после раскрытия определителя и группировки членов
примет вид
^-(4+а)^2 +^г~=0’
\р2 / р2
откуда
Q
или
Из первого уравнения системы (20.76) найдем отношения амплитуд
b b
H1 = S7S= k*—a ' М2~ В2== kl—a •
Теперь составим общее решение дифференциальных уравнений малых коле-
баний (20.74):
z = piBt sin (ktt 4- ei) 4- ц2В2 sin (ty 4- e2),
Ф = Bi sin (kit 4- ex) -f- B2 sin 4- ег)-
§ 20.7]
ЗАДАЧИ
489
Здесь и k2, [Xj и ц2 вычисляются по установленным формулам, а произволь-
ные постоянные Blt В2, Bj и е2 определяются из начальных условий.
Рассмотрим численный пример:
Q = 4T, р=1,2 м, /1=1,5 м, /2=1,3л, ci = 0,3 Т/см, с2 = 0,2 Т/см.
После подстановки этих значений получим
#1= 10,06 сек-1, #2=13,9 сей'1,
что соответствует 95,6 колгб/мин и 133 колебании. Найдем теперь отношения
амплитуд
п1 = ^1-==218 см/раЭ = 3,8 см/град,
р2 = ^ =—дбсм/рад ——1,15 см/град.
в2
Таким образом, если в первом главном колебании центр тяжести опустится
на 3,8 см, то автомобиль повернется одновременно по ходу часовой стрелки на
•один градус. Во втором главном колебании прн опускании центра тяжести
на 1,15 см автомобиль повернется против хода часовой стрелки на один градус.
Формы главных колебаний показаны на рис. 20.13.
Первое главное
колебание
Второе главное
колебание
г<г)
Рис. 20.13.
Если ci = c2 = c, /1 = /2 = / (соответствует железнодорожным вагонам), то по
формулам (20.75) будем иметь
с cl*
« = 6 = °- e = 2EQ^
Дифференциальные уравнения малых колебаний (20.74) в этом случае разде-
ляются:
Q
5-]-аг = 0, ф+^2ф = 0,
и, следовательно, колебания в каждой координате будут независимыми друг
от друга
Задача 20.7. Электромотор весом GL = 100 кГ установлен на фундаменте
с помощью амортизаторов, суммарная жесткость которых равна су = 50 кГ/см.
Учитывая упругость фундамента, определить вертикальные колебания системы,
если приведенный вес фундамента G2=1000 кГ, а его упругие свойства харак-
теризуются коэффициентом жесткости с2 = 250 кГ/см (рис 20.14, а).
Схематично представим фундамент в виде тела II приведенной массы G2/g,
установленного на пружине жесткости с2 (рис. 20.14, б). Тело I (мотор) свя-
зано с телом II с помощью пружины жесткости сх.
490
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Обозначим через и 02 положения равновесия соответствующих тел. Ha-
систему, состоящую из двух тел, действуют активные силы тяжести Gj и С2 и
упругие силы пружин. Положение системы будем определять двумя обобщен-
ными координатами Zi и z2 (г/ — вертикальное перемещение центра тяжести.
Положение
равновесия
мотора.
Положение
равновесия
фундамента,
Рис. 20.14.
тела i от соответствующего положения равновесии). Кинетическая энергия?
системы равна
Потенциальная энергия складывается из потенциальной энергии сил тя-
жести и потенциальной энергии двух пружин:
П — — GjZj — G2z2 + Ci (fi + г2 — г1)2 + ~2 с2 (/г + гг)2 —гр Ci/2 —% с^- ’
где fi н /2 — статические деформации пружин. Раскрывая скобки и группируя
члены, получим
П = (— Gj — cji) Zj + (— G2+Ci/i + c2/2) z,2 + '2’ ci (г2 — г1)2+"^ Сгг2
В положении равновесия при г1 = г2 — 0 должны выполняться равенства
(20.2):
Имеем
=—Gi—^(1=0, j =—02+^171+^2 = 0.
\OZi/z1 = Z2 = 0 \OZ2/Zi=Z2 = 0
В силу этих равенств выражение для потенциальной энергии системы примет
вид
П—Т-Г С1 (г2 — г1)2 + ~2 С2г2>
Воспользуемся уравнениями Лагранжа:
dt di dz ~ dz *
§ 20 7]
ЗАДАЧИ
491
Для координаты Zi имеем
дТ G, . d дТ С1я дТ п ап
321 g dt dZi g дг! дг! 1' J '
Подставляя соответствующие выражения и перенося все члены в левую часть,
получим дифференциальные уравнения малых колебаний рассматриваемой
системы (уравнение для г2 составлено аналогично)
-- — C3Z2 = 0,
g
Q
~ ^2 — ciZi + (ci + сг) г2=0.
(20.77)
Будем искать решение в форме (20.60):
21 = Д sin (kt-]-z), z2 — B sin (fe/Д-е).
"Продифференцируем эти выражения для zt и г2 дважды по времени, подставим
в дифференциальные уравнения движения, приравняем к нулю коэффициенты
лри sin (kt ф-e) и сгруппипуем члены:
fci-— k2} Д-с1В = 0,
' g /
— CiA +^!4-с2—^fe2) В = 0.
(20.78)
•"Составим уравнение частот
Ci—— k2 —сг
§
Q
“ С1 С1 + С2 — ~ №
Фли, раскрывая определитель,
k* - [Gi (С1 + с2) 4- G3C1] k2 4- С1с2 _-= 0.
Подставляя численные значения и деля на коэффициент при fe4, получим
fe4 —784fe24-120 000 = 0.
Отсюда найдем fe5 = 209, fe| = 575 и частоты главных колебаний
fe1 = 14,5 сек-1, fe2 = 24,0 сект1.
Из первого уравнения (20.78) определим отношения амплитуд для каж-
дого главного колебания:
д С,— ~tl
492
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл XX
Формы главных колебаний показаны на рис. 20 15. В первом главном
колебании оба тела перемещаются в одну сторону, во втором — в разные сто-
роны (на рисунке по-прежнему точки Oi и 02 — положения равновесия тел).
Первое главное
колебание
Второе главное
колебание
Рис. 20.15.
'г
~pf=-0,17z(f
777777777b
В заключение отметим, что все методы, изложенные для си-
стем с двумя степенями свободы, почти без всяких изменений
переносятся на системы с любым числом степеней свободы.
В частности, уравнение частот малых колебаний консервативной
системы с s степенями свободы имеет вид (см. уравнение (20.62))
С11 —°иЛ2 ^12 — <2д2&2 • £1$
С21 — Я21&2 С22 — ^22^2 •• ^2S

CS1 — aslk2 •• ass&
= 0.
(20.79)
Принципиально можно решить задачу о малых колебаниях
системы с любым числом степеней свободы. Однако в общем слу-
чае при решении задач приходится преодолевать ряд трудностей
чисто вычислительного характера. Наибольшие затруднения воз-
никают при решении уравнения частот (20.79). Уже раскрытие
определителя при s > 2 представляет трудоемкий процесс. Дей-
ствительно, определитель порядка s содержит s! членов, каждый
из которых для уравнения (20.79) состоит из произведения s
биномов вида Сц — atjk2. Таким образом, если раскрыть определи-
тель (20.79), то в общем случае получится 2ss! слагаемых. Так,
для s = 3 число слагаемых равно 23 - 3! = 48, а при s=-4 это число
будет 24 • 4! = 384.
Для того чтобы оценить сложность и значение этой проблемы,
укажем, что над ее решением работали Лагранж, Лаплас, Гаусс,.
Леверье, Якоби, Лобачевский, Крылов и многие другие ученые.
Были разработаны различные точные и приближенные методы,
§ 20 8]
НОРМАЛЬНЫЕ КООРДИНАТЫ
493
позволяющие упростить численное решение уравнения частот и
связанных с этим задач *).
С появлением электронных вычислительных машин многие из
ранее разработанных методов утратили свое значение, некоторые
из них легли в основу программ работы вычислительных машин.
В настоящее время в сложных случаях решение осуществляется
на цифровых электронных вычислительных машинах дискретного
действия. Кроме цифровых вычислительных машин, используются
также аналоговые (моделирующие) электронные машины непре-
рывного действия. Об этом рассказано более подробно в § 2.7.
§ 20.8. Нормальные координаты
Сложность решения дифференциальных уравнений (20.59)
малых колебаний консервативной системы:
«п<71 + «12<72 + cii7i + ci2?2 = 0.1 (20 8().
а21‘71 + а22<?2 + С21?1 + С22?2 = 0 J
объясняется тем, что эти уравнения связаны между собой. Если
бы можно было найти такие координаты 0j и 62 (они называются
нормальными, или главными координатами), в которых дифферен-
циальные уравнения движения имеют вид
XjSj = 0, 62 + /-2^2 — 0, (20.81)
где > 0 и Х2 > 0, то решение определилось бы сразу:
0Х = Aj sin (|/'Х t + ej, 02 = Л2 sin (УХ/ф-е2) (20.82)
(X, A2, Bj и б2 — произвольные постоянные интегрирования).
Покажем, что существует линейное преобразование, с помощью
которого можно перейти от обобщенных координат qY и q2 к нор-
мальным координатам 0Х и 02. Для этого умножим первое урав-
нение (20.80) на /1( а второе на /2 и сложим почленно оба урав-
нения (/г и Z2 —пока не известные множители). Имеем
+ «21U 71 + (й12г1 + а2212) ?2] +
+ [(cnG + сгА) 7i + (ci2^i + с22^г) 7г] = 0- (20.83)
Возьмем еще одно число X и подчиним числа llt 12 и л двум
условиям:
С11^1 4* С21^2 = (flll^l 4*
+ С22^2 = (fl12^1 + fl22^)-
*) Изложение некоторых из этих методов можно найти, например, в сле-
дующих работах: Демидович Б. П, Марон И. А. Основы вычислитель-
ной математики.— М • Физматгиз, 1963, Фадеев Д. К. Фадеева В. Н.
Вычислительные методы линейной алгебры -2-е изд — М • Физматгиз, 1963;
Бабаков И. М. Теория колебаний, —М.: Гостехиздат, 1958.
(20.84)
494
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[ГЛ. XX
Введем теперь новую переменную 0 по формуле
9 = («J1+«21^71+(«12^1+«22^) 72- (20.85)
Тогда дифференциальное уравнение (20.83) примет вид
J! + M = 0. (20.86)
Уравнения (20.84) можно переписать в следующей форме:
(сп - Ади) Zt + (с21 - Хд21) /2 = 0,
(с12 — Azz12) (с22 — ^22) h = 0-
(20.87)
Для существования ненулевого решения этой системы однородных
линейных алгебраических уравнений относительно 1г и 12 необхо-
димо и достаточно, чтобы определитель системы равнялся нулю:
Сц — Хяц
С12 — 7<2|2 С22 — Z<222
(20.88)
Это уравнение совпадает с уравнением частот (20.62), и, сле-
довательно, два корня этого уравнения, и Х2, совпадают с k\
и kl, где k± и 62 —частоты главных колебаний. Так как каждому
корню Xj и Х.2 соответствует своя система значений чисел 1г и Z2
(они определяются из уравнений (20.87)), то согласно равенству
(20.85) мы получим две координаты, 0j и 02, удовлетворяющие
двум уравнениям вида (20.86). Таким образом, преобразование
(20.85) приводит нас к нормальным координатам.
Из приведенного доказательства следует, что переход к нор-
мальным координатам не сокращает вычисления по сравнению
с решением исходных дифференциальных уравнений (уравнение
для определения X совпадает с уравнением частот, а уравнения
(20.87) совпадают с уравнениями (20.61), служащими для опре-
деления форм главных колебаний). Поэтому нормальные коорди-
наты имеют главным образом теоретическое значение для доказа-
тельства различных положений.
В заключение заметим, что кинетическая и потенциальная
энергии в нормальных координатах имеют вид
Т=4(0?-М|), П = 1(М1 + М2). (20.89)
где Ai = 6i и Х2 = 6|.
§ 20.9. Функция рассеивания Релея
Исследуем, какое влияние оказывают силы сопротивления на
движение потенциальной системы. Будем считать, что сила сопро-
тивления FA) приложенная к точке Мк, направлена в сторону,
§ 20 9]
ФУНКЦИЯ РАССЕИВАНИЯ РЕДЕЯ
495
противоположную скорости vfe точки Mk:
где Fk — модуль силы Fft.
Пусть, далее, Fk зависит только от модуля скорости vk. Раз-
лагая Fk = Fk(vk) в ряд по степеням vk и ограничиваясь членами
первого порядка, получим
Fk = Fk (0) + Е*(0)
Если при покое сила сопротивления не равна нулю (Fk (0) =/= 0),
то говорят, что имеется сухое трение. Такой случай встречается
при наличии трения скольжения и трения качения. Если же
Fft(0) = 0, т. е. при покое сила сопротивления равна нулю, то
говорят, что имеет место вязкое трение. Этот случай встречается
при движении в сопротивляющейся среде.
В случае вязкого трения имеем
F* = — bkvk, (20.90)
где все постоянные коэффициенты bk --= Fk (0) неотрицательны (так
как Fk и vk — модули соответствующих величин).
Положение системы будем определять обобщенными координа-
тами qlt q2, ..., qs. Тогда согласно формуле (18.27) обобщенные
силы сопротивления Q) будут равны
п.
k = l
Воспользуемся тождеством (19.6) и выражением (20.90) для
силы Fft:
= 2 bkVk ’ Wj ’
или
при этом учтено, что Nk = v2k.
Введем обозначение
п
<20-91)
Функция Ф называется функцией рассеивания Релея, или дисси-
пативной функцией (происхождение этого термина будет объяс-
нено в дальнейшем). В этих обозначениях обобщенные силы
496
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
(Гл XX
сопротивления примут вид (для общности мы считаем, что число
степеней свободы равно s)
= О‘ = 1>2..............s)' (20-92)
Выразим функцию рассеивания Ф через обобщенные скорости q.
Для этого заметим, что выражение (20.91) по своей форме пол-
ностью совпадает с выражением для кинетической энергии (10.1)
(массы точек тк заменены неотрицательными коэффициентами frfe).
Поэтому при стационарных связях выражение функции Релея Ф
через обобщенные скорости q будет совпадать по форме с анало-
гичным выражением (19.26) для кинетической энергии. Изменятся
только коэффициенты квадратичной формы. Обозначив эти коэф-
фициенты через btj, получим
S S
ф=4 2 2bii^'
(20.93)
причем Ьц = Ь]1.
Будем считать, что на рассматриваемую материальную систему
действуют потенциальные силы и силы сопротивления. Тогда
обобщенные силы
или, учитывая равенства (20.92),
(/ = >. 2....................................»). (20.94)
Дифференциальные уравнения Лагранжа второго рода примут
такой вид:
d дТ дТ ап а®
Л a?/ a?/- dq, dq, (/-1- 2> •••> s)- (20.95)
Покажем, что при наличии сил сопротивления полная механи-
ческая энергия убывает. Действительно, умножим каждое урав-
нение на qq и сложим почленно все уравнения:
2. d ат v дт . v ап . v а® .
qt dt dq, 2 dq, q> 2 dq, qi 2 dq, q>' (20-96)
; = I ( = 1 7=1 / —1
Члены, стоящие в левой части этого равенства, и первая сумма
правой части преобразуются к виду (см. формулы (19.27) и (19.28))
ау^+п),
так как при стационарных связях 7'0 = 0 и Т\ = Т,
§ 20 10] ВЛИЯНИЕ СИЛ СОПРОТИВЛЕНИЯ 497
Функция Релея согласно равенству (20.93) представляет одно-
родную квадратичную форму относительно обобщенных скоростей
Qi, <h, , Qs- Поэтому на основании теоремы Эйлера об одно-
родных функциях (см. примечание на стр. 450) будем иметь
Теперь равенство (20.96) может быть записано в следующей форме:
А(7' + П) = —2Ф. (20.97)
Так как функция Релея Ф согласно (20.91) неотрицательна, то
^(Г+П)«>
и, следовательно, полная механическая энергия под действием
сил сопротивления убывает или рассеивается, переходя, конечно,
в другие формы энергии (например, тепловую). Из равенства
(20.97) следует, что функция Релея может служить мерой рас-
сеивания энергии, чем оправдывается ее название. На этом же
основании силы сопротивления называются часто диссипативными
силами.
Если функция рассеивания Релея (20.93) определенно поло-
жительна относительно обобщенных скоростей, то диссипация
называется полной. Если же функция Релея может, кроме поло-
жительных значений, принимать значения, равные нулю, когда
не все <7 = 0, то диссипация называется неполной, или частичной.
Все выводы этого раздела были получены нами в предполо-
жении, что действуют силы F* вязкого трения, причем их модули
пропорциональны модулям соответствующих скоростей а по
направлению силы Fft противоположны скоростям v* (предполо-
жение о линейности самой системы для вывода формулы (20.97)
не требуется). Полученные результаты можно обобщить на силы
сопротивления более общей природы*).
§ 20.10. Влияние сил сопротивления на колебания системы
около положения устойчивого равновесия
Пусть на потенциальную систему с двумя степенями свободы,
движущуюся около положения устойчивого равновесия, действуют,
помимо потенциальных сил, еще силы вязкого трения. Обобщен-
ные силы сопротивления вычислим по формуле (20.92):
_______________ (/=’-2).
*) См. Лурье А. И. Аналитическая механика. — М.: Физматгиз, 1961,
гл. 5, § 5.11; Меркин Д Р. Введение в теорию устойчивости движения._
М..' Наука, 1976, § 6.2.
498 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ [Гл. XX
где диссипатцрная функция Релея определена равенством (20.93).
Выполняя дифференцирование, найдем
Q'i = — (*/i9i + W (/ = 1, 2).
Присоединяя обобщенные силы сопротивления Q; к уравне-
ниям (20.59) и перенося все члены в левую часть, получим диф-
ференциальные уравнения малых колебаний под действием потен-
циальных и диссипативных сил:
«1191 + «129*2 4* *1191 4* *12*?2 + «1191 + «1292 = 0, )
«2191 + «229г + *2191 + *229г + «2191 + «2г9з = О’ I
Будем искать решение этих уравнений в следующей форме:
^ — А^, q2= А2еи, (20.99)
где Aj, А2 и X —некоторые постоянные числа, которые требуется
определить. Продифференцируем эти выражения для qlt q2 дважды
по времени:
9;=A/ew, 9/ = A;Aew, 9у = A;X2ew.
Подставим значения координат и их производных в уравне-
ния (20.98), сократим полученные равенства на общий множитель
еи и сгруппируем члены. В результате получим два алгебраи-
ческих уравнения:
(«1Л2 + *1А + «11)^1 + («12^2 + *12^ + «12)^2=0, )
(й21^2 4" *21^ 4" «21) 414* (&22№ -ф Ь22к -ф с22) А2 = 0. /
Так как эти линейные однородные уравнения относительно
Аъ А2 должны иметь решение, отличное от нулевого, то опреде-
литель системы должен равняться нулю:
I Яи^фбцХфСц + + _ а
| #2iX2-f-Ь21Х ф c2i ф Ь22к ф с22 I '
Можно доказать (мы не будем на этом останавливаться), что
вещественные части корней этого характеристического уравнения
отрицательны либо равны нулю. Таким образом, корни этого
уравнения могут иметь вид
Х = — h±ni, Х =— т, ’k — Azki,
где h, п, т и k — вещественные положительные числа.
Вещественным отрицательным корням (они бывают при боль-
ших силах сопротивления; см. § 2.3) соответствует апериодическое
движение
q = Ае "lt.
-§ 20.11]
ПРИБЛИЖЕННЫЙ МЕТОД ВЫЧИСЛЕНИЯ КОРНЕЙ
499
Чисто мнимым корням (они могут появиться при частичной
диссипации) отвечают главные колебания вида
q = A sin (kt 4-е).
Комплексно сопряженным корням отвечают затухающие глав-
ные колебания
q = Ae~ht sin (nt 4- e).
Обычно силы сопротивления невелики. В этом случае при
полной (а иногда и при частичной) диссипации все корни харак-
теристического уравнения (20.101) будут комплексно сопряжен-
ными с отрицательными вещественными частями:
— ± П]1, — h2± n2i.
Каждой паре комплексно сопряженных корней отвечает свое
главное затухающее колебание. Поэтому общее решение уравне-
ний (20.98) имеет при этих условиях такой вид:
<71 = sin («4-4644-sin (лг2/-Не2), 1
72 = А^'е-Ы sin («44-61) 4-sin (n2t-\-e2). J
В этом решении из четырех чисел A(,k) произвольных только
два, остальные определяются из уравнений (20.100) подобно тому,
как это было сделано в § 20.6 при определении форм главных
колебаний.
§ 20.11. Приближенный метод вычисления
корней характеристического уравнения
Покажем, что при небольших по модулю силах сопротивления
(случай, чаще всего встречающийся на практике) вычисление
корней характеристического уравнения значительно упрощается,
так как их мнимые и вещественные части приближенно могут
быть вычислены независимо друг от друга. Действительно, при
небольших силах сопротивления можно считать, что они зависят
от малого параметра е:
bjk = ^Jk,
где Ру* — некоторые, вообще говоря, конечные числа.
Характеристическое уравнение (20.101) в развернутой форме
будет иметь вид (с точностью до членов первого порядка относи-
тельно е)
c0V 4- ecjX3 4- а2№ 4- еа3Х ф- сц — 0. (20.103)
Положим е = 0 и Х = ±йг; тогда характеристическое уравнение
(20.103) переходит в уравнение частот незатухающих колебаний
(20.64):
aJA — ajA 4- at = 0. (20.104)
500
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл. XX
Разложим вещественную и мнимую части корня А уравнения
(20.103) в ряды по степеням е, ограничиваясь членами первого
порядка относительно е:
А — ив *4“ Ф 4*
где а, р и у — вещественные числа.
Заметим, что вещественная часть А не имеет свободного от 6
члена, так как все корни уравнения (20.104) относительно k2
вещественны и положительны (см. § 20.7), а следовательно, при
е = 0 корни уравнения (20.103) — чисто мнимые числа.
Вычислим А2, А3, А4, придерживаясь все время принятой точ-
ности. Имеем
А2 = — р2 — 2ер? + 2еар!, А3 =•• - Зесф2 - ф3 + Зф2у) i,
А4 = р4 4* 4ер3у — 4есф3й
Внесем выражения для А, А2, А3, А4 в уравнение (20.103), отде-
лим вещественную и мнимые части и сгруппируем члены по сте-
пеням е, сохраняя члены не выше первого порядка:
[ф0й4 - а.ф2 + а4) + 2Ру (2сфа - а2) е] -
- ₽ei [(4а0р2 - 2д2) а + (яф2 - д3)] = 0.
Это равенство может выполняться при всех е только в том слу-
чае, если
аф4 — яф2 4-я4 = 0, у = 0, (4пф2 — 2я2) а 4-(пф2 — п3) = 0.
Так как у — 0, то мнимая часть корня характеристического
уравнения с точностью выше первого порядка относительно 8
равна корню уравнения (20.104). Иначе говоря, частоты затуха-
ющих колебаний с указанной точностью совпадают с частотами
незатухающих колебаний.
Пусть P7 = fy —одна из частот незатухающих колебаний. Тогда
из последнего равенства будем иметь (мы перешли к старым обо-
значениям А = — h±ni, в которых h = — ае)
1 a,k2, — ая
Формула (20.105) справедлива при условии, что kj не является
кратным корнем уравнения частот (20.104), так как в противном
случае знаменатель правой части этого равенства обращается
в нуль.
Обозначим точные значения корней характеристического урав-
нения (20.103) через А* = — h*±tiji, а приближенные значения
через А/ = — hj±kji, где h, вычислены по формулам (20.105),
a kj — корни частотного уравнения (20.104). Покажем, что сумма
точных значений корней характеристического уравнения равна
§ 20.11]
приближенный МЕТОД ВЫЧИСЛЕНИЯ КОРНЕИ
501
сумме их приближенных значений. Действительно, пусть k\ и k\—•
корни уравнения частот (20.104); тогда по формулам Виета будем
иметь
k\ + kl = a-^, № =
Вычислим по формуле (20.105) соответствующие значения
и h2:
. _ 1 atkl-аз . 1 atkl-аз
1 2 2aokl — а2 ’ 2 2 2а£1-аъ
Найдем затем сумму этих коэффициентов
h -i-h — _L Г aikl — a3 I —a3~|
2 |_2а0^-аа "r 2a0kl~a2\ ’
ИЛИ
, , _ 1 Aatfltklkl — (гаоЯз + аЩг) (^i + 6|) + 2a2a3
i-1- 2 2 4alk[kl-2^ (k^ + kl) +al
Пользуясь выражениями для k\-\-k2 и k\k2t после очевидных пре-
образований получим
л а0
Составим сумму приближенных значений корней характеристи-
ческого уравнения. Имеем (^ = ‘—h±ki)
^1 + ^2~Ь^з + ^4—--2 (/Zi + /l2)-
Учитывая последнее равенство, найдем
+ ^2 + ^3 + \ =--~е-
«о
Воспользуемся теперь первой формулой Виета для точных значе-
ний корней характеристического уравнения (20.103):
^ + ^+Хз* + %4* = -^е.
Сравнивая оба выражения, видим, что суммы приближенных
и точных значений корней характеристического уравнения одина-
ковы. Это может служить дополнительным оправданием введения
приближенных формул (20.105).
На основании доказанного при малом сопротивлении можно-
рекомендовать следующий порядок вычисления корней характери-
стического уравнения:
1. Выделить малый параметр е и привести характеристическое
уравнение (20.101) к виду (20.103).
502
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
[Гл. XX
2. Положить е = 0 и составить уравнение частот (20.104).
3. Определить частоты колебаний, положив tij ~ kj.
4. Вычислить вещественные части корней уравнения (20.103)
по формуле (20.105).
Заметим также, что при малом сопротивлении формы главных
колебаний мало отличаются от соответствующих форм незатухаю-
щих колебаний.
Задача 20.8. Электромотор установлен с помощью амортизаторов на упру-
гом фундаменте (см. задачу 20.7 § 20.7). Гашение возникающих собственных
колебаний осуществляется двумя демпферами А
и В (рис. 20.16), создающими силу сопротивле-
ния, пропорциональную относительной ско-
рости; коэффициент суммарной силы сопротив-
ления 6 = 0,5 кГ • сек/см. Определить параметры
затухающих колебаний.
Скорость электромотора относительно фун-
дамента равна z2— ^i- Будем для определен-
ности считать, что г2>Л>0. Тогда относи-
тельная скорость электромотора будет направ-
лена вверх, а сила сопротивления Flc, прило-
женная к электромотору, вниз; очевидно, что
сила сопротивления F2c, приложенная к фун-
даменту, направлена вверх (силы сопротивле-
ния Flc и F2c для рассматриваемой системы
являются внутренними силами). Из этого следует, что обобщенные силы сопро-
тивления, соответствующие обобщенным координатам гх и г2, будут
& (z2 — 21), <?2 = — b (22 — Zi).
Функция рассеивания Релея (20.93) определяется равенством
Ф = 4&(42-^1)2-
Легко проверить справедливость равенств (20.92):
dii ’ dz2 •
Отметим, что функция рассеивания не является определенно положительной,
так как при ё1 = 22^0 она обращается в нуль.
Присоединяя к правым частям уравнений незатухающих колебаний (20.77)
обобщенные силы сопротивления, получим дифференциальные уравнения зату-
хающих колебаний
St — b (z2 — ^О + пг! — с1г2=0,
S2 + b (z2 — ii) — CiZx + (ct + с2) г2 = 0.
В соответствии с общей теорией будем искать решение в форме
z1=Ae'-t, г2 = Ве'-')
откуда
= = г2 = ВХе«, ^2 = BX2ew.
§ 20.1Ц
приближенный МЕТОД ВЫЧИСЛЕНИЯ КОРНЕИ
503
Подставим эти выражения для г, z и S в дифференциальные уравнения дви-
жения, сократим их на и сгруппируем члены:
+ + —(ЬХ + С1)В=0,
— {ЬК -j- Ci) А * X2 -р +^) В — 0*
Приравнивая к нулю определитель
уравнение
— (М' + н)
этой системы, получим характеристическое
— (67 fi)
X2 + bf'. + Ci + с2
= 0.
Раскрывая определитель, будем иметь
v + b Gi + Gg.Хз+ pci+C2)Gi+ciG2. Х2 4-*^4-^=0.
При заданных значениях (С1=100кГ, G2=1000 кГ, ct = 50 кГ/см, с2=*
= 250 кГ1см, 6 = 0,5 кГ • сек/см) коэффициент Ь можно принять за малый
параметр е = Ь. В принятых для уравнения (20.103) обозначениях имеем
О1О2 „ Gi + Сг (С1 + С2) Gi + ciG2
= °2 = g ’
Яз = С2» ^4 = С1С2^
Причем в а2 отброшен малый член Ь2.
Если в характеристическом уравнении положим 6 = 0 и f. = ki, то получим
уравнение частот
G^2 ki _ (ci+c2)Gi + ciG2 k2 + = Q_
g
Корни этого уравнения были найдены при решении задачи 20.7 § 20.7: k2t =
= 209 сек-2, ki = 14,5 сек'1, /?| = 575 сек'2, k2 = 24,0 сек'1. Внося в формулу
(20.105) соответствующие значения параметров, найдем 61 = 0,105 сек'1, h2 =
— 2,60 сек'1.
Положив приближенно nj = kj, получим корни характеристического урав-
нения
71.2 = —0,105 ± 14,5i, л2, з = —2,6 ±241.
Как уже отмечалось, при малом сопротивлении формы главных колебаний
затухающих колебаний практически совпадают с соответствующими формами
незатухающих колебаний. Поэтому, пользуясь значениями для pj и ц2, вычис-
ленными в задаче 20.7 § 20.7, найдем главные колебания затухающих коле-
баний
г^, = Д1е-0,10^ sin (14,5/4-61), г)2’ = Д2е~2,6' sin (24/4- е2)>
г^,==0,57Д1е-»,1°5' sjn (14,5/4-gj), г!,2’= — 0,17Д2е"М' sin (24/4-е2).
Первое главное колебание затухает значительно медленнее, чем второе. Это
объясняется тем, что в первом главном колебании оба тела движутся в одном
направлении, скорости вычитаются и сила сопротивления Fc = 6(z2—Zi) будет
меньше, чем во втором главном колебании, когда движение тел происходит
в разные стороны.
'504
МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ
(Гл. XX
§ 20.12. Вынужденные колебания
Предположим, что к потенциальной системе, движущейся вблизи
положения устойчивого равновесия, приложены также возмущаю-
щие силы. Обозначим обобщенную возмущающую силу, соответ-
ствующую обобщенной координате q)t через Qj(t). Тогда диффе-
ренциальные уравнения движения можно получить, присоединяя
к уравнениям (20.59) обобщенные силы Qj (0 (для простоты силами
сопротивления пренебрегаем):
1 + «127-2 + Cll^l + С12<?2 — Qi (0, 1 (20 юб)
«21<71 + «22<72 + с2171 + «227г = Сг(0- J
Общее решение системы линейных неоднородных дифферен-
циальных уравнений складывается из общего решения соответ-
ствующей однородной системы и какого-нибудь частного решения
данной неоднородной системы. Соответствующая однородная система
дифференциальных уравнений совпадает с системой (20.59), ее
общее решение определяется равенствами (20.67). Поэтому, если
q( (t), ql(/) — какое-нибудь частное решение системы (20.106), то ее
общее решение будет иметь вид
<71 = А± sin 4- ех) 4- Д2 sin (k2t 4- е2) 4- q*t (0,
q2 = liiAi sin (V4-ex)4-M2sin (k2t 4-e2) 4- ql (t).
Совокупность главных колебаний называется собственными коле-
баниями-, движение, определяемое частным решением q* (t), ql(t) —
вынужденным движением (эти термины иногда нуждаются в уточ-
нении). В тех случаях, когда возмущающие силы изменяются по
.гармоническому закону (HJt р и 6 —заданные числа)
Qy(0 = Hzsin (р^4-6),
частное решение ищется в той же форме:
q* (t) = Mj sin (pt-\-f>),
где My —неопределенные коэффициенты, подлежащие определению.
При этом предполагается, что частота р возмущающей силы не
совпадает ни с одной из частот kr, k2 собственных колебаний.
С помощью линейного преобразования перейдем в уравнениях
(20.106) к нормальным координатам (см. § 20.8)
4-^е1 = Н* sin (pt 4- 6),
§24-^62 = Я| sin (р/4-6),
где Н* — новые амплитудные значения возмущающих сил, a kj—
частоты собственных незатухающих колебаний исходной системы.
(20.107)
S 20.12]
ВЫНУЖДЕННЫЕ КОЛЕБАНИЯ
505'
Из этих уравнений видно, что резонанс в системе наступает
при совпадении Частоты р возмущающей силы с одной из частот-
собственных колебаний.
В качестве примера рассмотрим динамический поглотитель колебаний. На
рис. 20.17, а приведена схема машины, установленной на упругой опоре. Если
частота со возмущающей силы Н sin со/, создаваемой движущимися внутри машины
неуравновешенными массами, близка к собственной частоте ) машины, то
система будет работать в зоне резонанса и на фундамент будет передаваться
чрезмерно большая нагрузка.
Подвесим к машине дополнительный груз массой /и3 (рис. 20.17, б; на.
рис. 20.17,в изображена эквивалентная система).
Рис. 20.17.
(20.108>
Сравнивая системы, изображенные на рисунках 20.14 и 20 17, в, видим»
что они идентичны, поменялись местами только индексы у масс и у жесткостей
пружин. Поэтому дифференциальные уравнения движения системы, изображен-
ной на рис. 20.17. бив, можно получить из уравнений (20.77), поменяв в них
индексы и добавив в уравнение, отвечающее координате zlt обобщенную силу
Н sin а>/:
+ (Ci + с2) — ciZ2 = Н sin е>/,
/Л222 — Н- C2Z2 “ 0.
Частное решение будем искать в форме
?! — Mi sin е>/, г2=Л12 sin о>/.
Подставим значения для гх и г3 в дифференциальные уравнения, сократим их
на sin at и сгруппируем члены:
(ci+c2—MiCO2) Mt — с2М2 = Н,
— с2М i -|- (с2 — /п2е>2) М2 — 0.
Решая эти уравнения относительно Mi и М2, получим
м =________________________________(са-от2ы2)77_________
1 (ci + с2 — niiti)2) (с2 — т2со2) — сI ’
М2 =--------------_________________-
(<Ч + с2 — «iW2) (с2 — т2о>2) — •
506 МАЛЫЕ КОЛЕБАНИЯ МЕХАНИЧЕСКИХ СИСТЕМ [Гл. XX
Теперь находим вынужденные колебания
С2 —М2Ы2 ,, .
г1 =~1--i-------оГТ------57---Г О 81П
(С1 + с2 — /Лхй2) (с3 — т2ы2)—cl
г2 =-.—:----------------------г Н Sln
(ci + с2 — mi«2) (с2 — т2ы2) — с|
Если параметры подвешенного груза подобрать так. что
с2 — т2а2 = 0, (20 109)
то машина не будет участвовать в вынужденных колебаниях. Действительно,
в этом случае
п н • t
21 — 0, 23 -----SHI W
С2
Таким образом, добавочный груз «поглотил» колебания машины. Из равен-
ства (20.109) видно, что для «поглощения» колебаний машины параметры допол-
нительного груза должны удовлетворять условию
У -^-=(0,
Г w2
т. е. динамический поглотитель колебаний нужно настроить на резонанс с часто-
той возбуждающей силы. Заметим, что частота Кс2/ш2 не является одной из
частот системы «машина-|-поглотитель колебаний». Это — парциальная частота;
она соответствует динамическому поглотителю, подвешенному к неподвижной
Опоре.
ГЛАВА XXI
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ СИСТЕМ
С ОДНОЙ СТЕПЕНЬЮ СВОБОДЫ *)
§ 21.1. Введение
В предыдущей главе были рассмотрены колебания динамических
систем, описываемые линейными дифференциальными уравнениями
с постоянными коэффициентами. Эти колебания называются также
малыми колебаниями, так как линеаризация уравнений обосновы-
вается предположением, что отклонения системы от положения
равновесия малы.
Достоинства метода линеаризации состоят в основном в сле-
дующем:
1) во многих случаях этот метод дает вполне удовлетвори-
тельные результаты, описывая достаточно точно процесс колебаний
не только с качественной, но и с количественной стороны;
2) интегрирование линейных дифференциальных уравнений
с постоянными коэффициентами не содержит принципиальных
трудностей и сводится к чисто алгебраическим вычислениям;
3) метод линеаризации применим не только к анализу коле-
баний механических систем около положения устойчивого равно-
весия, но он также может быть использован для исследования
колебаний около любого устойчивого движения механических,
электромеханических, электрических и других систем.
Отмечая достоинства метода линеаризации, следует все же
иметь в виду, что при упрощении дифференциальных уравнений
движения можно упустить ряд явлений, специфичных для систем,
описываемых нелинейными дифференциальными уравнениями.
К таким явлениям, например, можно отнести явление «авто-
колебаний» — периодических колебаний, амплитуда и частота кото-
рых в широких пределах не зависят от начальных условий и опре-
деляются параметрами системы.
*) Андронов А. А., Витт А. А., Хайкин С. Э. Теория коле-
баний,—М.: Физматгиз, 1959.
Бутенин Н. В. Элементы теории нелинейных колебаний.—М.: Суд-
промгиз, 1962
Бутенин Н. В., Неймарк Ю. И., Фуфаев Н. А. Введение
в теорию нелинейных колебаний, —М.: Наука, 1976.
'508
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
Имеются и другие интересные с теоретической стороны и очень
важные по своим приложениям примеры, которые не могут быть
объяснены линейной теорией колебаний. Кроме того, существует
ряд нелинейных зависимостей, которые принципиально не могут
быть линеаризованы (например, характеристика кулонова трения
скольжения).
В связи с этим примерно с конца двадцатых годов нашего
столетия начала интенсивно развиваться теория нелинейных коле-
баний, т. е. колебаний, описываемых нелинейными дифференциаль-
ными уравнениями. Материальные системы, которые описываются
нелинейными дифференциальными уравнениями, называются нели-
нейными системами.
В теории нелинейных колебаний получает более глубокое раз-
витие рассмотрение колебаний динамических систем, позволяющее
изучить явления, недоступные линейной теории колебаний.
Безусловно, что нелинейные задачи значительно многообразнее,
чем линейные, а изучение их представляет значительные трудности.
В настоящей главе, посвященной рассмотрению колебаний авто-
номных нелинейных систем с одной степенью свободы, излагаются
лишь некоторые методы исследования таких систем. Материалы
этой главы следует рассматривать лишь как начальное введение
в обширную и многообразную науку о колебаниях нелинейных
систем.
§ 21.2. Фазовая плоскость
Одним из распространенных методов исследования нелинейных
систем является метод фазовой плоскости (фазового пространства).
Изложению этого метода на примере системы с одной степенью
свободы и посвящен этот параграф *).
Многие задачи теории колебаний материальных систем с одной
степенью свободы приводят к необходимости исследования диффе-
ренциального уравнения вида
x + f(x, х) = 0, (21.1)
где f(x, ^ — нелинейная функция х и х.
Вводя переменную у = х, перепишем уравнения (21.1) в виде
двух уравнений первого порядка:
*) Этот метод, разработанный и примененный к решению некоторых нели-
нейных задач радиотехники, механики, автоматического регулирования
Л- И. Мандельштамом, Н. Д. Папалекси, А. А. Андроновым и другими уче-
ными, позволил решить многие нелинейные задачи и выявить специфические
особенности нелинейных систем,
§ 21 2] ФАЗОВАЯ ПЛОСКОСТЬ 509
Полученная система уравнений представляет собой частный
случай системы более общего вида
i = 0,1
y = Q(x, у, t). f
Если нелинейные функции Р и Q не содержат явно времени,
то система (21.3) называется автономной системой, а колебания,
которые эта система описывает, называются автономными.
Если же функции Р и Q содержат явно время, то система (21.3)
называется неавтономной.
В этой главе будут рассматриваться только автономные системы.
Вводя плоскость переменных х и у — х, будем рассматривать
х и у как прямоугольные координаты.
Для простоты примем, что функции Р (х, у) и Q (х, у) опреде-
лены на всей плоскости переменных х и у. Тогда каждому состоя-
нию нелинейной системы, определяемому координатой х и ско-
ростью у = х, на плоскости ху будет соответствовать точка и,
наоборот, каждая точка плоскости будет соответствовать только
одному состоянию системы.
В связи с этим плоскость ху называют плоскостью состояний,
или фазовой плоскостью. Каждому состоянию системы на фазовой
плоскости соответствует одна точка, которую называют изображаю-
щей точкой.
При изменении состояния системы, т. е. при изменении коор-
динат х и у — х, изображающая точка перемещается по фазовой
плоскости. Траектория изображающей точки называется фазовой
траекторией. Уравнение фазовой траектории представляет собой
зависимость между координатой и скоростью движения рассматри-
ваемой системы.
Целой фазовой траекторией называется кривая, которая описы-
вается изображающей точкой за все время ее движения.
Положение изображающей точки на фазовой плоскости может
быть определено радиусом-вектором
r = xi + ^j
(i и j —единичные векторы осей х и у). Следовательно, скорость
изображающей точки (фазовая скорость) будет равна
v = -^- = xi + yj. (21.4)
Для исходной механической материальной системы производ-
ная х является скоростью изменения координаты х, а производ-
ная у = х — проекцией ускорения. Значит, точки фазовой плоскости,
в которых фазовая скорость равна нулю, для исходной материаль-
ной системы будут соответствовать состояниям равновесия (ско-
рость и ускорение системы одновременно равны нулю).
510
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
Деля второе уравнение системы (21.3) на первое, получим
dy = Q(x, у)
dx = Р(х, у) ’
(21.5)
Решение этого уравнения устанавливает связь между х и у, т. е.
дает интегральные кривые.
Следует иметь в виду, что интегральные кривые лишь в про-
стейших случаях являются фазовыми траекториями. Как это будет
установлено ниже, интегральная кривая может состоять из несколь-
ких фазовых траекторий.
В точках фазовой плоскости, где функции Р и Q одновременно
обращаются в нуль, т. е.
Р(х, у) = 0, Q(x, t/) = 0, (21.6)
скорость изображающей точки равна нулю и, следовательно, для
исходной материальной системы эти точки являются состояниями
равновесия.
Точки фазовой плоскости, координаты которых удовлетворяют
уравнениям (21.6), для дифференциального уравнения (21.5)
являются особыми точками; в этих точках не выполняются усло-
вия теоремы Коши о единственности решения дифференциального
уравнения.
Таким образом, особые точки уравнения (21.5) имеют физиче-
ский смысл как состояния равновесия исходной материальной
системы.
Поведение фазовых траекторий на всей плоскости ху, а также
вблизи особых точек позволяет судить как о характере движения
исходной системы, так и о характере ее состояний равновесия.
В качестве примера рассмотрим простейшую линейную систему.
Уравнение колебаний математического маятника имеет вид
(стр. 135)
Ф 4-у sin ф = 0. (21-7)
Введя обозначения № = g/l и х = <р и считая колебания малыми,
получим х 4- k2x = 0. (21.8)
После замены у = х имеем
у = — k2x, 1 * = £ J (21.9)
и, следовательно, dy k~x dx у ' (21.10)
Единственной особой точкой этого уравнения является точка х = 0,
у = о.
§ 21 2]
ФАЗОВАЯ ПЛОСКОСТЬ
511
Интегрирование уравнения (21.10) дает
у2 + k2x2 —с= const.
Полученная зависимость представляет собой семейство эллип-
сов. Каждый такой эллипс при конкретном значении постоянной с
представляет собой фазовую траекторию, т. е. в этом случае интег-
ральные кривые будут фазовыми траекториями. Полученное семей-
ство эллипсов заполняет всю фазовую плоскость, за исключением
начала координат. В этой точке эллипс, соответствующий с = 0,
вырождается в точку (рис. 21.1).
Особая точка, через которую не
проходит ни одна фазовая траектория и -----
которую окружают замкнутые фазовые f
траектории, называется центром. I ] г
Поскольку модуль скорости изобра- Г vZZ' J х
жающей точки равен \ У
V = /х2 4- у2 = ]/t/2 + k4X2,
то фазовая скорость равна нулю только Вис. 21.1.
в особой точке (х = 0, t/ = 0).
Рассмотрение фазовой плоскости с нанесенными на ней фазо-
выми траекториями позволяет судить о характере движения системы.
Направление движения изображающей точки можно определить
по одному из уравнений (21.9), например, при х>0 у<0, сле-
довательно, у убывает (см. рис. 21.1).
Изображающая точка, начав движение из какой-либо точки
фазовой траектории, по истечение конечного промежутка времени,
возвратится опять в ту же точку, так как фазовая скорость равна
нулю только при х = 0, г/ = 0. Следовательно, система вернется
в свое исходное положение, а это значит, что замкнутая фазовая
траектория соответствует периодическому движению.
Итак, нами установлено, что малые колебания маятника около
устойчивого положения равновесия при любых начальных усло-
виях совершаются по периодическому закону.
Рассмотрим теперь поведение маятника вблизи верхнего поло-
жения равновесия (<р = л).
Введя замену ф = ф + л, перепишем уравнение (29.7) в виде
ф — ~ sin ф = 0.
Для малых ф, после замены ф на х и g/l на k2, будем иметь
х — k2x = 0.
Отсюда
У = k2x,
х~у
(21.Н)
512
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл. XXI
И
dy ___ k2x
dx ~ у
Интегрируя это уравнение, получим уравнения интегральных
кривых —семейство гипербол
у2-^х = с, (21.Г2>
заполняющих фазовую плоскость.
При с = 0 интегральная кривая вырождается в две пря-
мые y^=kx, у =— kx, проходящие через особую точку си-
стемы уравнений (21.11) х = 0, t/ = 0.
При с=#0 интегральные кривые че-
рез особую точку не проходят. Прямые
у = kx и у = — kx являются асимпто-
тами для интегральных кривых, для ко-
торых с=И=0. Расположение интеграль-
ных кривых и направление движения
по ним изображающей точки показано
на рис. 21.2.
Отметим, что прямая y = kx состоит
из трех фазовых траекторий: прямой
у = kx при х > 0, особой точки х - О,
у=0, прямой у = kx при х<0. Это же
относится и к прямой у = — kx.
Таким образом, в рассматриваемом
примере при любых начальных усло-
виях, кроме соответствующих прямой у = — kx, изображающая
точка или удаляется от особой точки или, вначале приближаясь
к ней, затем удаляется от нее, причем движение исходной си-
стемы не является периодическим. Такая особая точка называ-
ется седлом.
Скорость изображающей точки равна нулю только в особой
точке (х = 0, у = 0).
Из этого следует, что состояние равновесия, соответствующее
этой особой точке, является неустойчивым.
Движение по прямой у — — kx соответствует такому случаю,
когда изображающая точка, перемещаясь к особой точке со стре-
мящейся к нулю скоростью, в конечный промежуток времени ее
не достигает. Очевидно, что движение по этой прямой соответствует
такой специально подобранной скорости, когда кинетическая энер-
гия в начальный момент равна работе, которую должны совер-
шить действующие силы, чтобы система попала в положение рав-
новесия.
Такое движение практически получить нельзя, так как нельзя
точно реализовать такие начальные условия. Поэтому для всякого
реального движения особая точка типа седла является неустойчивой.
§ 21 2]
ФАЗОВАЯ ПЛОСКОСТЬ
513
На стр. 43 приведено уравнение движения материальной
точки под действием восстанавливающей силы в среде с линей-
ным сопротивлением
х + 2/гх-j-/г2х = 0.
Заменяя х на у, имеем
у —— 2hy — k2x, х — у
и
(21.13)
dx у '
Единственной особой точкой этого уравнения является начало
координат (х —0, t/ = 0).
Уравнение интегральных кривых при h<zk имеет вид
Q/24-2/ixz/ + &2x2)l/2 = сек*arct? к*х • (21.14)
где k* = ]/ k2 — h2.
Семейство интегральных кривых (21.14) заполняет всю фазовую
плоскость. Фазовая скорость, равная v = y\2hy-\-k2x)2 + y2, нигде
не равна нулю, кроме особой точки,
и стремится к нулю при приближении
к этой точке.
Интегральные кривые являются в
этом случае фазовыми траекториями и
представляют собой спирали, навиваю-
щиеся на начало координат (рис. 21.3).
Движение изображающей точки по' фа-
зовым траекториям происходит к началу
координат (это видно из рассмотрения
уравнений движения). Такая особая
точка называется устойчивым фокусом.
Рассмотрение поведения фазовых
траекторий позволяет сделать вывод, что
при любых начальных условиях материальная точка совершает
затухающие колебания, асимптотически приближаясь к состоя-
нию равновесия.
При h>k уравнение интегральных кривых будет
у2 4- 2hxy + k2x2 = с
JL+h-V№-k2
^+h + yrh^—k2
h
/ /г2 —/г 2
На рис. 21.4 показано примерное расположение интегральных
кривых на плоскости ху. В этом случае фазовые траектории
17 Н« В. Бутенин и др.
514
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
не совпадают с интегральными кривыми, так как каждая инте-
гральная кривая состоит из трех фазовых траекторий: две из них
соответствуют асимптотическим движениям изображающей точки
к началу координат, а третья является особой точкой.
Особая точка, через которую проходят все интегральные кри-
вые, называется узлом. В рассматриваемом случае изображающая
точка по всем фазовым траекториям движется к особой точке,
которая будет устойчивым
узлом.
Для исходной системы ус-
тойчивый узел соответствует
устойчивому состоянию рав-
новесия. Представленные на
рис. 21.4 фазовые траектории
соответствуют апериодическо-
му движению.
На основании фазовых
представлений о простейшей
линейной системе можно сде-
лать следующие выводы:
1. Характер и расположе-
ние фазовых траекторий, на-
правление движения по ним
изображающей точки дают возможность судить о характере дви-
жения исходной материальной системы.
2. Особые точки и их характер определяют характер состоя-
ний равновесия материальной системы.
Эти обстоятельства требуют найти способы и приемы опреде-
ления характера особых точек нелинейных уравнений, а также
найти методы построения фазовых траекторий для нелинейных
уравнений, особенно тогда, когда дифференциальные уравнения
интегральных кривых не удается проинтегрировать.
Рассмотрим предварительно вопрос о типах и характере осо-
бых точек линейной однородной системы общего вида
х = ах + by,
у = сх + dy,
(21.15)
где а, Ь, с, d — постоянные числа.
Характеристическое уравнение этой системы уравнений имеет
вид
а2 — (а ф- (/)« + «(/ — cb = 0. (21.16)
В дальнейшем ограничимся случаями, когда а-|-(/=И=0 и ad —
— Ьс=^=О, т. е. случаями, когда отсутствуют чисто мнимые корни
и нулевые корни.
§ 21 2]
ФАЗОВАЯ ПЛОСКОСТЬ
515
Можно показать* *), что для системы уравнений (21.15) могут
быть следующие типы состояний равновесия:
1. Для корней уравнения (21.16) и а2 действительных и
отрицательных — устойчивый узел; изображающая точка движется
по фазовым траекториям к состоянию равновесия.
2. Для и а2 действительных и положительных — неустой-
чивый узел; изображающая точка движется по фазовым траекто-
риям от состояния равновесия.
3. Для а1 и а2 действительных и разных знаков — седло.
4. Для и а2 комплексно сопряженных при отрицательной
действительной части — устойчивый фокус. Изображающая точка
по фазовым траекториям (спиралям) приближается к состоянию
равновесия.
5. Для аг и а2 комплексно сопряженных при положительной
действительной части — неустойчивый фокус. Изображающая точка
по фазовым траекториям (спиралям) удаляется от состояния рав-
новесия.
Перейдем теперь к рассмотрению нелинейной системы уравнений
х = Р (х, у), )
t) = Q(x, у), J
(21.17)
где Р(х, у) и Q(x, ^ — аналитические нелинейные функции х и
у. Предположим, что система уравнений (21.17) описывает поведение
некоторой динамической системы, а координаты х и у являются
координатами изображающей точки на фазовой плоскости.
Состояния равновесия исходной динамической системы являются
особыми точками уравнения интегральных кривых
и находятся из уравнений
dy = Q (х, у)
dx Р(х, у)
Р (х, у) = 0, )
Q(x, у) = 0. )
(21.18)
(21.19)
Пусть координаты особой точки будут х0 и у0. Поставим воп-
рос об определении характера и устойчивости этой точки, т. е.
об определении устойчивости состояния равновесия исходной дина-
мической системы.
Для ответа на вопрос об устойчивости особой точки с коорди-
натами х0, у0 выясним характер движения изображающей точки
в окрестности особой точки. Для этого введем новые переменные
Н и т], характеризующие отклонения изображающей точки от точки
с координатами х0, у0:
х = х0 + ^, у = у0 + ц.
*) Андронов А. А., ВиттА. А. X а й к и н С, Э. Теория колеба-
ний,—М.: Физматгиз, 1959.
17*
516
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ-
[Гл. XXI
Разложим функции Р (х, у) и Q (х, у) в ряды по степеням §
и т]. Эти разложения имеют вид
р (X, у) = Р (х0, t/0) + Р'х (х0, у0) I + Ру (х0, у0) л + Pl (1, n). 1 2 J 2 .
Q(x, y) = Q{x0, y0) + Qx(x0, y0)l + Qy(x0, y0)i\-\-Qi&, n). J
где Pj (£, л) и Qi (В» л) — функции, в которые g и л входят в сте-
пени не ниже второй.
Так как х0, у0 — координаты особой точки, то
Р(х0, t/o) = O, Q(x0, %) = 0.
Вводя обозначения
а = Рх(х0, у0), Ь — Ру^х^, у0),
с — Qx (^о, Уъ), d = Qy (х0, у0)
и учитывая соотношения (21.20), перепишем уравнения (21.17)
в виде
^ = ^ + И + Л(1 Л),
5 = -Мл+ 01 (В, л)-
(21.21)
Если отбросить в этих уравнениях функции PY (S, л) и Q, л),
то получим линейные уравнения с постоянными коэффициентами
§=аВ + ^Л. '
5 = сВ + ^Л- .
(21.22)
Характеристическое уравнение системы уравнений (21.22) будет
cj? — (а + d) а + ad — cb = 0.
А. М. Ляпуновым было доказано, что в случае, когда оба
корня этого уравнения имеют отличную от нуля действительную
часть, состояние равновесия (особая точка) системы (21.21) асим-
птотически устойчиво, если действительные части корней отрица-
тельны; если хотя бы одна действительная часть положительна,
то состояние равновесия неустойчиво.
В случае, если действительные части корней характеристичес-
кого уравнения равны нулю или если один из корней равен
нулю, а другой отрицателен, то уравнения первого прйближения
(21.22) не дают ответа на вопрос об устойчивости состояния рав-
новесия.
Характер поведения фазовых траекторий вблизи простых осо-
бых точек, т. е. точек, для которых оба корня характеристического
§ 21.3]
МЕТОДЫ ПОСТРОЕНИЯ ФАЗОВЫХ ТРАЕКТОРИИ
517
уравнения имеют отличную от нуля действительную часть, также
определяется уравнениями первого приближения (21.22)*).
Изложенное выше позволяет при определении характера и
устойчивости особой точки нелинейной системы (21.17) пользо-
ваться уравнениями первого приближения (21.22).
§ 21.3. Методы построения фазовых траекторий
Рассмотрим некоторые методы, позволяющие в ряде случаев
точно или приближенно построить интегральные кривые на фазо-
вой плоскости для динамической системы, имеющей одну степень
свободы.
Консервативные системы. Пусть исходная система является
консервативной. Дифференциальное уравнение движения такой
системы можно привести к виду
mx — f (х)
(предполагаем, что f (х) — аналитическая функция).
Это уравнение можно заменить двумя уравнениями первого
порядка:
(21.23)
х = ^. J
Уравнение интегральных кривых в этом случае может быть
проинтегрировано. Так как
1 = ^7 и ydy=if^d^>
то
f=/l+ip(x)dx’ (21.24)
где /i — постоянная интегрирования.
Уравнение (21.24), представляющее собой уравнение интег-
ральных кривых, выражает закон сохранения энергии, так как
тх2 ту2 г. 1 р , . . ,
-у = -j— кинетическая энергия, а П = — — I f (х) dx — потенци-
альная энергия исходной системы, поделенная на массу т.
После замены г/1 = г/фЛ2 соотношение (21.24) примет вид
r/i=/t —П(х). (21.25)
Постоянная h определяется из начальных условий, причем
каждому значению начальных условий соответствует одно значе-
*) См., например, Меркни Д. Р. Введение в теорию устойчивости дви-
жения,—2-е изд. —М.: Наука, 1976,
518 АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ (Гп XXI
ние h, каждому же значению h соответствует бесчисленное мно-
жество значений х и у, удовлетворяющих уравнению (21.25).
Построенная на фазовой плоскости в соответствии с уравне-
нием (21.25) кривая называется кривой равной энергии. Ветви
этой кривой являются фазовыми траекториями.
Из уравнений (21.23) следует, что интегральные кривые пере-
секают ось х, имея вертикальные касательные (х = 0). Кроме
того, согласно (21.25) интегральные кривые симметричны относи-
тельно оси х.
Интегральные кривые будут иметь горизонтальные касательные
в точках, расположенных на прямых, параллельных оси у, для
всех х, являющихся корнями уравне-
ния/ (х)=0.
Так как
Z
а)
П(х)
---z = flt
— z=h
Ущ
yi=Vh- II (х), (21.26)
то для х, удовлетворяющих неравенству
h - П (х) < О,
б)
У^й-П(х)
х
yf^h-II(x)
Рис. 21.5
интегральные кривые действительных
ветвей не имеют.
Особые точки, соответствующие со-
стояниям равновесия исходной динами-
ческой системы, будут в точках фа-
зовой плоскости, где f (х) = 0 и у = 0.
Для удобства введем в рассмотрение
вспомогательную плоскостьхг и построим
на ней кривую г = П(х) (рис. 21.5, «).
Проведя прямую z — h, замечаем, что действительные движения
будут только для х, расположенных левее точки пересечения
кривой г = П(х) и прямой z = h. На рис. 21.5, б показан вид
интегральной кривой на плоскости хух (для z-hi>h интеграль-
ная кривая показана пунктиром).
Рассмотрим случай, когда функция г = П(х) имеет минимум.
Из рассмотрения рис. 21.6 следует, что при h = h0 интегральная
кривая вырождается в особую точку, где /(х) = 0 и у — 0- Для
всех /г>й0 интегральные кривые будут замкнутыми кривыми,
окружающими особую точку (центр).
Замкнутые интегральные кривые соответствуют периодическим
движениям. Период этих движений определяется из уравнения
(21.26).
Так как
У1==№
§ 21 3]
МЕТОДЫ ПОСТРОЕНИЯ ФАЗОВЫХ ТРАЕКТОРИИ
519
то
,, dx _________________________ dx
= 2 ~ Г2[Л-П(х)]’
откуда следует, что искомый период равен
Т = 2 f dx (21.27)
J /2 [Л-П (х)] ’
где хх и х2 —абсциссы точек пересечения интегральной кривой
с осью х.
Пусть потенциальная энергия имеет максимум (рис. 21.7).
При h = h0 интегральная кривая распадается на четыре фазовые
траектории, сходящиеся в особой точке. Эти фазовые траектории
называются усами. При h> h0 все фазовые траектории располо-
жены выше и ниже особой точки, а при h<zha слева и справа
от нее. Характер фазовых траекторий около особой точки подобен
характеру фазовых траекторий у особой точки типа седла.
Рассмотренные случаи являются элементарным доказательством
теоремы Лагранжа —Дирихле и теоремы Ляпунова, приведенных
в § 20.2.
Перейдем теперь к рассмотрению возможных движений на всей
фазовой плоскости.
Будем по-прежнему предполагать, что г = П(х) является ана-
литической функцией для всех значений х.
Построим на плоскости xz эту функцию и выясним возможный
характер фазовых траекторий для какого-либо определенного
значения г.
520
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл. XXI
Возможны следующие случаи:
1. Кривая г = П(х) нигде не пересекается прямой z = h.
Если прямая z = h лежит ниже кривой г = П(х), то на всей
фазовой плоскости не будет движений, так как при этом у будет
мнимым, т. е. движений с такой полной энергией у исходной
системы не будет.
Если прямая z = h лежит выше кривой г = П(х), то на фазо-
вой плоскости будут две симметрично расположенные ветви инте-
гральной кривой (рис. 21.8).
Для любых начальных условий, соответствующих точкам этой
кривой, изображающая точка будет двигаться в одном направлении
и уйдет в бесконечность.
Такие траектории называются убегающими траекториями.
2. Прямая z = h пересекает кривую г = П (х), нигде ее не касаясь
(рис. 21.9).
Для тех значений х, для которых П(х)>/г, фазовых траек-
торий не существует. Для х, для которых П(х)</г, фазовые
траектории могут быть двух видов: замкнутые ветви и ветви,
уходящие в бесконечность. Замкнутые ветви соответствуют пери-
одическим движениям, ветви, уходящие в бесконечность, соот-
ветствуют убегающим движениям.
3. Прямая z = h имеет несколько точек касания с кривой
г = П(х). В этом случае фазовые траектории возможны следующих
видов:
а) изолированные точки, вблизи которых при данном /г нет
фазовых кривых. При изменении h мы будем иметь или замкну-
тую траекторию (при увеличении h) или не будем иметь дейст-
вительных траекторий (при уменьшении h)\
б) изолированные конечные куски фазовых траекторий
(рис. 21.10). Это будут или просто замкнутые траектории, соот-
ветствующие периодическим движениям, или фазовые кривые
§ 21.3]
МЕТОДЫ ПОСТРОЕНИЯ ФАЗОВЫХ ТРАЕКТОРИЙ
521
с самопересечением, которые называются сепаратрисами. Точки
самопересечения сепаратрис являются особыми точками типа седла
и соответствуют точкам, где z = h касается максимумов кривой
г = П(х). Сепаратрисы имеют очень
большое значение, так как они от-
деляют друг от друга области, за-
полненные траекториями различных
типов. В самом деле, при увеличе-
нии h мы получим интегральную
кривую, охватывающую всю сепа-
ратрису, при уменьшении h мы по-
лучим замкнутые траектории, которые
показаны пунктиром на рис. 21.11;
в) бесконечные куски фазовых
траекторий. Вид возможных фазовых
траекторий показан на рис. 21.12.
Здесь имеют место траектории, ухо-
дящие в бесконечность. Эти траектории
также являются сепара-
трисами, так как при изменении h мы получим существенно
различные траектории.
Задача 21.1 *). Определить характер движения динамической системы,
изображенной на рис. 21.13. Длина пружины в ненапряженном состоянии
равна /0 > а. Жесткость пружины с. Масса тела т. Трением пренебречь.
Потенциальная энергия системы, поделенная на массу тела, равна
П = ^-(Д02.
2т' '
где Д/ = / — /о —Деформация пружины.
’) Идея задачи заимствована из книги: Каудерер Г. Нелинейная
механика. — М.: ИЛ, 1961,
522
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
Так как I = }^а2^-х2, 10 = }/'а2-^-х^, то
" -2S (Ег+^-Е^)!- /1+(т)Т-
Рассмотрим малые колебания системы и, ограничиваясь при разложении
в ряд первыми членами одного порядка, отличными от нуля, получим
<2128>
Так как
йП с Г /*о\2 , х3]
dx 2m I \ a J Х a2 J ’
то значения х, где П (х) имеет экстремальные значения, определятся из урав-
нения
Корнями этого уравнения будут
Х!=0, х2 = х0, х3=—х0.
Найдя
d2II _ с Г fx0 \2 Зх2 1
dx2 2т L \ а ) a2 J ’
убеждаемся, что при х = Хх = 0
d2II _ сх2
dx2 2та2 ’
т. е. при х = 0 функция П (х) имеет максимум, равный П (0) —
При х = ± х0
d2II _ сх2 q
dx2 ma2
Примерный вид функции П (х) показан на рис. 21.14, а. На рис. 21.14, (5
показаны фазовые траектории динамической системы. Жирными линиями пока*
заны сепаратрисы.
§ 21.3)
МЕТОДЫ ПОСТРОЕНИЯ ФАЗОВЫХ ТРАЕКТОРИИ
523
Из рассмотрения рис. 21.14, б видно, что для начальных условий в обла-
стях внутри сепаратрис система совершает периодические движения около
устойчивых положений равновесия (х = х0 или х= —хв). В начале координат —
неустойчивая особая точка —седло (неустойчивое состояние равновесия).
Для начальных условий вне сепаратрис система совершает периодическое
движение, симметричное относительно начала координат.
Метод изоклин. Общим методом построения интегральных кри-
вых является графический метод изоклин.
Пусть уравнения движения динамической системы будут
х = у),
y = Q(x, У)-
(21.29)
Уравнение интегральных кривых на фазовой плоскости имеет
вид у), (21.30)
где у)-
Кривая ф(х, у)=с (21.31)
при фиксированном с представляет собой геометрическое место
точек, в которых интегральные кривые имеют одинаковый угол
наклона касательных, и называет-
ся изоклиной.
Метод изоклин заключается в
следующем: на фазовой плоскости
строится семейство изоклин, т. е.
кривые (21.31) при различных зна-
чениях с. Пусть эти значения с
будут q, с2, с3, ...
Отметим, что точки пересечения
изокпин будут особыми точками
уравнения (21.30) и, следователь-
но, состояниями равновесия для
исходной динамической системы.
Возьмем теперь какую-либо
точку А на изоклине, для кото-
рой с — с1г и проведем через нее прз
ую с угловым коэффициентом,
равным с1( затем проведем через эту же точку прямую с угловым
коэффициентом, равным са (рис. 21.15). Разделим теперь расстоя-
ние между точками пересечения этих прямых с изоклиной, для
которой с = с2, на две равные части и обозначим точку деления
буквой Б. Отрезок А Б и примем за отрезок интегральной кри-
524
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
вой между рассматриваемыми изоклинами. Отметим, что для более
точного построения этого участка интегральной кривой значения сг
и с2 нужно выбирать как можно более близкими друг к другу.
Дальнейшее построение проводится аналогичным образом, только
за исходную точку выбирается уже точка Б.
Перейдем теперь к рассмотрению других приемов построения
интегральных кривых, пригодных для некоторых частных случаев.
Метод Льенара*). Метод Льенара является графическим спо-
собом построения интегральных кривых для нелинейных уравне-
ний вида
x-|-<Pi(^) + ^2x = 0. (21.32)
Введем замену x = kt, тогда
. dx dx dx , .. d2x
X — ~г = -т- k И X = -г,й2
dx dt dx dx2
и, следовательно, уравнение (21.32) примет вид
£+ч>(к)+^ = °. (21-33)
где
fdx\ 1 f,dx\
45 \dx/ — k2^1 Vdxj'
dx '
Обозначив = у, получим
dx dy . ,
= Tx — ^~X-
Уравнение интегральных кривых будет
Tv _ — ф (Д —* /21 34)
dx у ' \ • 1
Построим теперь на фазовой плоскости ху кривую
х = — <p(t/).
Возьмем на фазовой плоскости некоторую точку Р с коорди-
натами х и у (рис. 21.16). Проведем из этой точки прямую,
параллельную оси х, до пересечения с кривой х = — <р(у). Обо-
значим точку пересечения буквой М. Из точки М опустим пер-
пендикуляр MN на ось х.
Так как МР = х — [-- <р (у)] = х + q> (у), то тангенс угла наклона
отрезка NP к оси х равен
, PL _ У
18а~МР ~ х+ф(у)‘
*) Стокер Дж. Нелинейные колебания в механических и электрических
системах. —М.: ИЛ, 1952.
§ 21,3]
МЕТОДЫ ПОСТРОЕНИЯ ФАЗОВЫХ ТРАЕКТОРИИ
525
Следовательно, согласно (21.34) направление касательной к интег-
ральной кривой, проходящей через точку Р, будет перпендику-
лярно отрезку NP. 1ц
Таким образом,' построение фазо- м
вой траектории можно провести сле-
дующим образом: через точку Р про-
водим отрезок, перпендикулярный от-
резку NP, на этом отрезке берем
новую точку Рг и определяем на-
правление касательной к интеграль-
ной кривой указанным способом и
т. д. В результате получим ломаную
линию, которая будет тем ближе к
интегральной кривой, чем меньше
будут отрезки ломаной линии.
В приведенной ниже задаче по- Рис. 21.16.
казывается, когда построение Льенара
сразу дает возможность точно построить интегральную кривую.
Задача 21.2. Влияние сухого трения на гармонический осциллятор.
Уравнение движения гармонического осциллятора при наличии сухого
трения имеет вид
x + k-x==Tx,
где Тх = —Т при х>0 и ТХ = Т при х<0 (Т>,0),
Вводя x = kt, получим
d2x [dx\
^ + фШ+ ’
где
(dx\ Т dx
при d?>0
И
(dx \ _ T dx л
*[dtr-T^-k? при d?<0-
Построим на фазовой плоскости кривую
х = — <р(у),
dx
где у = ^.
Очевидно, что при у > 0 функция х = — q> (р) будет иметь вид х = —То,
а при р<0—вид х — Тй (рис. 21.17).
Проводя для любой точки фазовой плоскости, где у > 0, построение Лье-
нара, убеждаемся, что интегральная кривая, проходящая через эту точку,
будет окружность с центром в точке Ох.
526
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
(Гл XXI
Для у < 0 интегральные кривые будут окружностями с центром в точке О2.
Вид фазовых траекторий показан на рис. 21.17. Заметим, что отрезок OtO2
является отрезком стыка фазовых траекто-
рий— зоной «застоя» В точках этого отрезка
величина упругой силы пружины, меньше мак-
симальной силы трения покоя.
§ 21.4. Метод припасовывания^
Понятие об автоколебаниях
Метод припасовывания является
одним из точных методов изучения дви-
жения нелинейных систем и применяет-
ся в том случае, когда нелинейная
функция, входящая в дифференциальное
уравнение движения, может быть заменена ломаной линией, каж-
дое звено которой является прямолинейным отрезком. В этом
случае движение системы будет описываться линейными уравне-
ниями, сменяющими друг друга. Каждому звену ломаной линии
будет соответствовать участок, на котором система описывается
линейным дифференциальным уравнением.
Метод припасовывания заключается в следующем. Задавшись
начальными условиями внутри какого-либо участка и решая соот-
ветствующее линейное дифферен-
циальное уравнение, получим реше-
ние, справедливое на этом участке;
затем определяем состояние системы
(координату и скорость) на границе
с соседним участком, на котором
движение описывается уже другим
линейным дифференциальным урав-
нением; для решения, соответствую-
щего второму участку, за начальные
условия выбираем конечное состоя-
ние па предыдущем участке и т. д.
Особенно наглядно метод припа-
совывания иллюстрируется на фазо-
вой плоскости.
Пусть, например, кривая у = <р(х) (рис. 21.18) делит фазовую
плоскость на две области, в каждой из которых фазовые траекто-
рии определяются соответствующими линейными дифференциаль-
ными уравнениями. Пусть начальные условия задачи соответствуют
точке Ро с координатами х0, у0 на фазовой плоскости в области А.
Точка пересечения Pi(xlt уг) фазовой траектории с кривой
у = ср (%) будет начальной точкой для фдзовой траектории в об-
ласти В. Точка Р2(х2, у2) будет начальной точкой фазовой траек-
тории в области А.
§ 21 4]
МЕТОД ПРИПАСОВЫВАНИЯ
527
Производя такое последовательное припасовывание начальных
условий, мы можем следить за движением изображающей точки
и тем самым судить о поведении динамической системы.
В качестве примера рассмотрим маятник, находящийся в среде
с вязким линейным сопротивлением. Предположим, что на маят-
ник действует постоянный момент, направленный всегда в сторону
движения:
( М при ф>0,
М(ф) = лл 1 ' (21.35)
( — М при ф <0.
Уравнение движения маятника имеет вид
ф + 2йф + й2ср = ± Л10, (21.36)
, „ g п, ь ,. м. , ,
где /г2 = ~г, 2д = —, Л!о = -t (m —масса маятника, г —его длина,
b — коэффициент вязкого трения).
Вводя замену ф = и, перепишем уравнение (21.36) в виде двух
уравнений первого порядка:
dtp
It =
dw_____________________
dt
со,
(21.37)
2йсо —
Расссмотрим часть фазовой плоскости срсо, для которой ф =
= со < 0. Уравнения (21.37) в этом случае будут
dt
= —2йсо-й2ср-/И0.
Дифференциальное уравнение фазовых траекторий имеет вид
dco _ —2/ко —fe2tp—Мо О1 оо
dT----------й-------• (21 -38)
Особая точка ср = со = 0 здесь одна, и при h < k это —
устойчивый фокус.
Если предположить, что уравнение (21.38) справедливо для
всех о), то картина фазовой плоскости будет такой, как показано
на рис. 21.19, а.
Для со>О уравнение (21.37) будет
dco — 2ha>—k2q Мо
dtp co
Особая точка ср = , co = 0 — устойчивый фокус (Л<й).
528
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
Если бы это уравнение было справедливо на всей плоскости
<рсо, то картина фазовой плоскости была бы такой, как
на рис. 21.19, б.
Разрезая теперь обе фазовые плоскости, изображенные
на рис. 21.19, по линии ® = 0, произведем «сшивание» верхней
полуплоскости, изображенной на рис. 21.19, б, и нижней, изобра-
женной на рис. 21.19, а.
Рис. 21.20
На рис. 21.20 изображен характер фазовых траекторий для
рассматриваемой задачи.
Из рассмотрения рис. 21.20 следует, что при достаточно боль-
ших начальных отклонениях движение системы будет колебатель-
ным затухающим и, наоборот, при достаточно малых начальных
отклонениях движение точки будет колеба-
тельным нарастающим.
Это происходит потому, что при малых
значениях угловой скорости момент сил вяз-
»- кого трения меньше возмущающего момента,
а при больших значениях угловой скорости
момент сил вязкого трения больше возму-
щающего момента.
Исходя из этого, естественно сделать вы-
вод о существовании замкнутой фазовой
траектории, на которую наматываются все
остальные фазовые траектории. Эта замкнутая фазовая траектория
соответствует периодическому движению системы, причем параметры
этого периодического движения не зависят от начальных усло-
вий и определяются параметрами динамической системы.
Докажем, применяя метод припасовывания, что эта замкнутая
фазовая траектория будет единственной и движение маятника,
соответствующее этой фазовой траектории, будет устойчивым.
Движению маятника влево (со = ф <; 0) соответствует уравнение
ф + 2/гф /г2<р = — М„.
Интегрируя это уравнение, получим
Ф = е ft'(сх cos£*Z-|-c2 sin fe*Z) —
§ 21 41
МЕТОД ПРИПАСОВЫВАНИЯ
529
где fe*=yrfe2 —7? (предполагается, что k>h). Отсюда
ф = егы[— h (бф cos k*t-\-c2 sin (— ct sinft*/ -\-c2 cos й*7)].
Подставляя начальные условия, найдем
0 = — h^ + k*^.
Следовательно,
. Mq h / , Л4о \
С1 = <Ро + -р> с2 = р. (Фо +-feij-
ф = е-л^(ро 4-^£^cosk*t + Д sink*t^ -
Первая остановка маятника в крайнем левом положении про-
изойдет в момент времени 7 = л/й*. Соответствующий угол обо-
значим через — <рх, т. е. при / = л/й* ф =— <рх, ф = 0. Внося
соответствующие значения в последнее равенство, получим
Ля .
АЛ / I Мл \ , Л4л
— <рх = е fc^q)0+-_J(_ 1)
Ля
Отсюда находим (f = e fc*<l)
<P! = f<Po + (l+f)^-
Легко сообразить, что следующее крайнее отклонение вправо
определится равенством (<р0 заменяем на <рх, а <рх на ср,)
ф2 = /ф1 + (1+П^-.
Таким образом, амплитуды колебаний маятника последовательно
могут быть определены из следующей цепочки равенств:
Фа = 4>if + (1 +f) .
Фл = фл-1/ + (1
Умножим первое равенство на f"-1, второе на Л1-8, ..., послед-
нее на 1 и сложим почленно все равенства. Тогда получим
Фл=Г'-Фо ч- (1 + f) (f-1+in--2 + .. . +1) .
530
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
(Гл. XXI
или, суммируя геометрическую прогрессию,
Перейдем к пределу при и->оо. Учитывая, что /<1 и, следова-
тельно, lim fn = 0, получим
п —*со
Фя = 1±/^. (21.39)
Формулу (21.39) можно получить и несколько другим путем.
Так как
Тл-1 = фл-г^ + (1 + /)
и
фя = фя-1/ + (1 +f)^,
то, исключая отсюда получим
фя = Фи2 + (1+Л2^. (21.40)
Для периодического движения имеем
фя = фя-2 = Ф*.
т. е.
<р*=(рТ+(1+/)2^;
отсюда имеем
т* -- Мо
Т ~ 1-/ Й2 •
Эта величина ср* и есть искомая амплитуда периодического дви-
жения. Таким образом, мы убедились, что в рассматриваемой
задаче могут быть периодические движения, амплитуда которых
не зависит от начальных условий, а зависит от свойств самой
системы.
Однако одного факта определения амплитуды <р* еще недоста-
точно, чтобы утверждать, что такое движение физически может
быть реализовано. Нужно показать, при каких начальных усло-
виях установится это решение и будет ли оно устойчиво. На эти
вопросы можно ответить, построив соответствующую диаграмму,
которая называется диаграммой Кенмгса —Лемерея.
На этой диаграмме рассматривается графически связь между
двумя последовательными максимальными отклонениями одного
знака, т. е. <рл и <р„_2. Согласно формуле (21.40) <р„ можно счи-
тать функцией <р„ 2.
$ 21 4]
МЕТОД ПРИПАСОВЫВАНИЯ
531
На плоскости <рл_2фл эта зависимость между фл 2 и фп изобра-
жается прямой линией (рис. 21.21). Тангенс угла наклона этой
_ 2Лл
прямой с осью ф„ 2 равен е fc* < 1. Проведем еще вспомогатель-
ную прямую ф„ = ф,-2. Пересечение этих прямых и определяет
амплитуду Ф„ = фл-2 = Ф*.
Пусть 2 “ начальное отклонение, меньшее ф*; тогда этому
отклонению будет соответствовать ф^, которому будет соответ-
ствовать максимальное отклонение ф^+2- Продолжая эти построе-
ния, видим, что, как бы мало начальное отклонение ни было,
колебания происходят с возрастающей амплитудой, пока макси-
мальное отклонение не достигнет постоянного значения ф*.
Если теперь взять максимальное отклонение фп_2>ф*, то
по графику найдем следующее ф„, по которому найдем следующее
Ф« + 2 и т. д. Из этого построения видно, что колебания затухают
до тех пор, пока отклонение не достигает постоянного значения ф*.
Итак, в рассмотренном нами примере, несмотря на наличие
вязкого трения, существует устойчивое периодическое движение.
Амплитуда этих незатухающих колебаний не зависит, как
было уже показано, от начальных условий, а определяется свой-
ствами системы. Такне колебания называются автоколебаниями,
а системы, в которых возможны автоколебания, называются авто-
колебательными системами *).
Изолированная замкнутая траектория на фазовой плоскости,
соответствующая автоколебаниям системы, называется предельным
циклом.
*) Термин «автоколебания» введен в теорию колебаний А. А. Андроновым.
532
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл ХХГ
Предельные циклы могут быть устойчивые, неустойчивые и
полуустойчивые.
Если фазовые траектории, близкие к предельному циклу, как
внутри, так и вне его «наматываются» на него, т. е. изобража-
ющая точка приближается к предельному циклу, то такой пре-
фазовые траектории
дельный цикл называется устойчивым и
соответствует автоколебаниям.
Если же траектории разматываются как
снаружи, так и внутри с предельного
цикла, т. е. изображающая точка уда-
ляется от предельного цикла, то такой
предельный цикл называется неустойчи-
вым и физически реализован быть не
может.
Наконец, может быть полуустойчивый
предельный цикл, когда, с одной стороны,
на него наматываются, а с другой —
разматываются.
Картины, показывающие устойчивый, неустойчивый и полу-
устойчивый предельные циклы соответственно, представлены
на рис. 21.22, 21.23 и 21.24.
Таким образом, с математической точки зрения автономные
автоколебательные системы с одной степенью свободы можно опре-
делить как такие системы, уравнения движения которых харак-
теризуются наличием на фазовой плоскости одного или несколь-
ких устойчивых предельных циклов.
С физической точки зрения автономные автоколебательные
системы, грубо говоря, можно охарактеризовать как системы,
способные совершать незатухающие колебания за счет постоянных
источников энергии, причем поступление энергии, расходуемой
системой на преодоление сопротивлений, регулируется самой
системой.
Характерным свойством автоколебательных систем является
то обстоятельство, что «амплитуда» колебаний в широких преде-
§ 215]
МЕТОД МЕДЛЕННО МЕНЯЮЩИХСЯ КОЭФФИЦИЕНТОВ
533
лах не зависит от начальных условий. Это является основным
отличием периодического движения в автоколебательной системе
от периодического движения в консервативной системе.
Хотя в рассматриваемом нами примере период автоколебаний
оказался равным периоду затухающих колебаний в линейной
системе, в общем случае этот период определяется свойствами
самой системы, а не навязывается извне. Это является основным
отличием автоколебаний от вынужденных колебаний.
§ 21.5. Метод медленно меняющихся коэффициентов
(метод ван-дер-Поля)
Существует несколько приближенных методов количественного
исследования нелинейных систем*).
В этом параграфе рассмотрен лишь один из методов, а именно
метод медленно меняющихся коэффициентов.
Пусть уравнение движения динамической системы имеет вид
X + k2X = (х, х),
(21.41)
где (х, х) — нелинейная функция х и х, ц>0.
Мы будем предполагать, что рассматриваемая динамическая
система близка к линейной консервативной. Коэффициент ц
(обычно безразмерный) и будет тем малым параметром, который
будет характеризовать близость исходной системы к линейной
консервативной.
Введем «безразмерное время» x — kt, тогда в силу х = -^-£и
x=—-k2 уравнение (21.41) примет вид
(21.42)
где
*) Изложение этих методов читатель найдет, например, в книгах: Андро-
нов А. А., ВиттА. А., X а й к и н С. Э. Теория колебаний. — М.: Физмат-
гиз, 1959; Боголюбов Н. Н., Митропольский Ю. А. Асимптотичес-
кие методы в теории нелинейных колебаний.—М.: Физматгиз, 1958; Бул-
гаков Б. В- Колебания.—М.: Гостехиздат, 1954; Лурье А. И. Некоторые-
нелинейные задачи теории автоматического регулирования.—М. Гостехиздат,
1956; Малкин И. Г. Некоторые задачи нелинейных колебаний.—М.: Гос-
техиздат, 1956; Н е й м а р к Ю. И. Метод точечных отображений в теории
нелинейных колебаний.—М.' Наука, 1972; Попов Е. П, Пальто в И. П.
Приближенные методы исследования нелинейных автоматических систем.—M.i
Физматгиз, 1960.
534 АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ [Гл. XXI
Вводя У — ^> получим
du . , ч dx
= У), ~^ = У-
Уравнение интегральных кривых будет
dy = — % + ц/(х. У) j 4оч
dx у ' \ )
При р == О рассматриваемая система будет линейной консерва-
'тивной. Фазовые траектории будут представлять собой вложен-
ные друг в друга окружности, окружающие состояние равновесия
х = 0, у — 0.
Решение уравнения (21.42) в этом случае будет
х = a cos тsin т, (21.44)
где а и b — постоянные числа (произвольные постоянные интегри-
рования).
Нашей задачей является выяснение вопроса о том, как изме-
нится картина распределения фазовых траекторий на плоскости ху,
если р будет достаточно мало, но отлично от нуля.
Будем искать решение уравнения (21.42) при р#=0 в виде
(21.44), но а и 6 будем уже считать функциями времени. Оче-
видно, что при заданном х функции а и b недостаточно опреде-
лены, поэтому наложим на них условие, заключающееся в том,
что производная от х по т должна иметь такой же вид, как при
постоянных а и Ь.
Таким образом, имеем
х = a cos т-f & sin т,
dx ... , da , db
-г~ = — a sin т-Р& COS Т-р-;, - COS T + -Г- sinr.
dx dx ' dx
Но в силу условия, наложенного на а и Ь,
~= — п sin т-р & cos т (21.46)
и, следовательно,
cos т-р ~ sin т == 0. (21.47)
dx 1 dx ' '
Вторая производная от х по т будет
d2x , . da . , db
-rv = — a cosт — о sinт —j-sniT-p-^— cos т. (21.48)
dx2 dx dx ' '
Подставляя выражения (21.45), (21.46) и (21.48) в уравнение
<-(21.42), получим
da , db
— — Sin T -p -J- COS T =
dx dx
~yf (a cos т-р & sin t, — n sin т-p & cos r). (21.49)
(21.45)
§ 215]
МЕТОД МЕДЛЕННО МЕНЯЮЩИХСЯ КОЭФФИЦИЕНТОВ
535
Присоединяя к этому уравнению условие (21.47), получим систему
„ da db
уравнении для определения угг и
ci if a v
da . db . n
-7- COS t + -j- S1HT =0,
dx ' dx
— ~ sin т + cos т = pf (a cos т + b sin t, — a sin т + b cos t).
„ da db ,
Решая эту систему относительно -г- и -г-, будем иметь
СП. и с
4^ = — pf (a cos т + & sin т, — a sin т + & cos т) sin т,
dx
db
(21.50)
= р/ (a cos т + b sin т, — a sin т + b cos т) cos т.
Отметим, что уравнения (21.50) —это уравнение (21.42), пре-
образованное к новым переменным. Как видно из (21.50), эта
система уже неавтономная, хотя исходное уравнение было авто-
номным.
Предположим теперь, что при достаточно малом р функции а (т)
и b (т) будут медленно меняющимися функциями т, т. е. такими,
изменениями которых в течение одного периода колебаний исход-
ной системы можно пренебречь.
Это предположение равносильно тому, что производные и
в течение одного периода (2л) считаются постоянными, имею-
щими порядок р.
Тогда, умножая обе части уравнений на dx и интегрируя,
в пределах от 0 до 2л, получим
j f(a cos r-|-&sinT, — a sin t + & cost) sin xdx,
о
(21.51)-
-r- = ~ i f (a cos т -I-b sin x, — a sin т 4- b cos r) cos т dx.
dx 2л J ' v ’
о
В сущности, эти уравнения отличаются от уравнений (21.50) тем,
что в правых частях у них стоят средние интегральные значения
за период 2л от правых частей уравнений (21.50).
Перепишем уравнения (21.51) в виде
= 6)>
=|iQ («, ь\
(21.52)
>536
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
ГГл ХХГ
где
2 л
Р (а, Ь) = — J f(a c0S т + b sin т, — a sin т + b cos т) sin т dr,
о
2л
Q(a, ^) = 2jF Наcos т+ ^s*n т> ~ as'nT +cost) cosrdr.
b
Уравнения (21.52) называются «укороченными» уравнениями
или уравнениями ван-дер-Поля.
Рассмотрим теперь плоскость ab. Очевидно, что согласно (21.45)
состояние равновесия а = О, b = О на плоскости ab будет соответ-
ствовать для исходной системы состоянию равновесия х — 0, у = 0.
Состояния равновесия на плоскости ab, для которых а=£0,
Ь 0, для исходной системы будут соответствовать периодическим
движениям.
Таким образом, изучая состояния равновесия, а также распо-
ложение фазовых траекторий на плоскости ab, мы сможем судить
о возможных движениях исходной системы. Этот прием был впер-
вые применен А. А. Андроновым.
Покажем, что в системе (21.52) при переходе к полярным
координатам переменные разделяются. Пусть
а = р cos ft, & = psinft, (21.53)
тогда
da dp а . dft db dp . t, , „ a. dft
-J— = — COS ft — p Sin ft-j—, -j- = ~ sin ft 4-p COS V -T-,
dx dx r dx ’ dx dx 1 ' dx ’
a cos r + & sin r = p cos (t — ft),
— a sin т 4-b cos т = — p sin (r — ft).
Подставляя эти выражения в уравнения (21.52) получим
2л
cos ft — psinft-^= ~2л j' HP cos (т — ft),’—p sin (т — ft)] sin т dx,
0
2л
sin ft+ p cos ft = st; f Ир cos(t —ft), — psin(x — a)] cost dr,
дТ ЛТ ZJl .I
откуда будем иметь
^• = рф(р),
S = ^(P)-
(21.54)
§ 21.5]
МЕТОД МЕДЛЕННО МЕНЯЮЩИХСЯ КОЭФФИЦИЕНТОВ
537'
Здесь
2л
Ф (р) = — J / (р cos g, — р sin g) sin g d%,
0
4f (p) = 2^- p (P cos I, - p sin ю cos I d%,
где S = t — ft *).
Рассмотрим первое уравнение
^ = рФ (р).
(21.55)
(21.56)
Это уравнение первого порядка и фазовая плоскость для него
вырождается в прямую.
Качественная картина уравнения такого типа полностью опре-
деляется характером и расположением состояний равновесия, кото-
рые располагаются на фазовой прямой. Координаты этих состоя-
ний равновесия являются корнями уравнения
Ф(р) = 0. (21.57)
Пусть один из корней этого уравнения будет р=р0. Рассмот-
рим поведение изображающей точки вблизи этого состояния рав-
новесия. Введем новую переменную и, определяющую положение
изображающей точки вблизи состояния равновесия, т. е. положим
р = р0 + «- Тогда уравнение (21.56) будет
5“=Фф (ро + «)-
Разложим функцию Ф(рофп) в ряд по степеням и:
Ф (р0 + «) = Ф' (р0) и члены высших порядков.
Ограничиваясь членами с первой степенью и, получим урав-
нение первого приближения
^ = рФ' (ро)и-
А. М. Ляпунов доказал**), что при Ф'(р0) 0 состояние рав-
новесия будет устойчивым, если Ф' (р0) < 0, и неустойчивым, если
Ф' (Ро)>0-
Качественно это можно объяснить следующим образом.
Так как при достаточно малом и членами высших порядков
можно пренебречь, т. е. определяющим знак du/dx будет знак
*) Эту замену можно произвести, так как подынтегральные функции пе-
риодические.
•*) См., например, Андронов А. А., ВиттА. А., X а п к и п С, Э,
Теория колебаний.—М.: Физматгиз, 1959,
538
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл XXI
Ф' (ро), то при Ф'(Ро)<О изображающая точка будет стремиться
к состоянию равновесия, а при Ф'(р0)>0 будет уходить от со-
стояния равновесия.
Итак, состояние равновесия р = р0 уравнения (21.56) будет
устойчивым, если
Ф'(р0)<0, (21.58)
и неустойчивым, если
' Ф'(Ро)>О. (21.59)
Закон движения изображающей точки по фазовой прямой
аюжно найти, интегрируя уравнение (21.56):
р
/ \ С dp
р'
/ \ /\ где Р' = Рт=т»
'V'' Рассмотрим теперь уравнение
—V В практике очень часто бывают
' \ TPs' случаи, когда
T(P)SO,
tZ'O*
Рис. 21.25. тогда ^ = 0 и О = О0 — постоянное
число.
Следовательно, на плоскости ab все интегральные кривые
представляют собой прямые, проходящие через начало координат
и имеющие различные углы наклона О = const. Движение по каж-
дой из таких прямых происходит одинаково и определяется урав-
нением (21.56). Состояния равновесия, определяемые уравнением
Ф (р) = 0, будут целиком заполнять окружности (на плоскости ab),
радиусы которых равны корням уравнения (21.57). На рис. 21.25
показан вид плоскости ab в случае, когда уравнение (21.57)
имеет три корня: Pi = 0, р2<р8.
Перейдем к плоскости ху; согласно формулам (21.45), (21.46)
и (21.53) получим
х = р cos $ cos т-{- р sin О sin т = р cos (т — О),
у — — р cos О sin тф-р sin О cos т — — р sin (г — О).
Для какого-либо корня р = р< уравнения (21.57) будем иметь
x — yi cos (т — О0), у — — pi sin (т — Оо), (21.60)
т. е. на плоскости ху будем иметь круговой предельный цикл.
§ 215]
МЕТОД МЕДЛЕННО МЕНЯЮЩИХСЯ КОЭФФИЦИЕНТОВ
539-
Величина О'о в формулах (21.60) произвольна, это соответ-
ствует тому, что на плоскости ab состояния равновесия состав-
ляют целые окружности.
Если рг соответствует устойчивому
состоянию равновесия, то на плос- ---
кости ху будет устойчивый предель- / /х
ный цикл. Все соседние интеграль- / /Y
ные кривые будут спиралями, накру- / // I
чивающимися на этот цикл. Если —' Il I К и _/~77 J Т1—
же pi соответствует неустойчивому \ \ // /
состоянию равновесия, то на плос- -77//
кости ху будет неустойчивый пре-
дельный цикл (рис. 21.26). ---
Рассмотрим теперь случай, когда
Чг(р)у=0. Тогда для какого-либо кор- Рис. 21.26.
ня р = рг уравнения Ф(р) = 0 (мы
будем предполагать, что корни уравнения Ф(р) = 0 не совпадают
с корнями уравнения Y (р) = 0, так как в противном случае
придем к рассмотренному уже случаю) будем иметь dft/dx — p'F (pj
и, следовательно,
& = рЧг (р/)т + #0.
Движение изображающей точки на плоскости ab будет проис-
ходить по закону
а = р; cos [цТ (рО т ф 0О], b = р, sin [рЧ' (Pi) т + Фо],
т. е. по предельному циклу радиуса р = рг.
Устойчивость или неустойчивость этого предельного цикла
определяется характером состояния равновесия р = р/. Направле-
ние движения определяется знаком Т (р;). Остальные интеграль-
ные кривые будут спиралями, накручивающимися на предельный
цикл или раскручивающимися с него.
Переходя к плоскости ху, получим
x = p/cos {[1 — р'Т (р;)]т — >%}, г/ = —р£ sin {[1 — рЧг (рг)] г — 0-о},
т. е. будем иметь круговые предельные циклы, соответствующие
корням уравнения Ф (р) = 0.
Отличием от случая Чт (р) = 0 здесь является то, что мы полу-
чаем поправку на частоту Доз = — р’Г (рг). Картина на фазовой
плоскости останется прежней.
Задача 21.3. Применить рассмотренный метод к уравнению (21,36). Ввод»
в рассмотрение безразмерное время т = И, получим
х U v «V U, l>
540
АВТОНОМНЫЕ НЕЛИНЕЙНЫЕ КОЛЕБАНИЯ
[Гл. XXI
•где
Л4о й2 при dtp dx
/Ио dtp
й2 при dx
Сделаем предположение о близости рассматриваемой системы к линейной
'консервативной. Примем, что 4h/k 1, Л40/й2 «С 1; тогда, введя р.=2й/й, будем
«иметь
‘где
d2tp -^+m2 dx \ dx / J
\ dx ) Mik dq> ~2Г ПРИ IT>0’ Mik dtp _ нт- при -7х- < 0. 2й F dx
(21.62)
(21.63)
Уравнение (21.62) имеет вид уравнения (21.42).
Если искать решение уравнения (21.62) в виде
<p = pcos(r— ft), р sin(r — ft),
то уравнения (22.54) будут
dp _ _ р. / _ 4М2 \ dft _ q
dx 2 л / ’ dx
Так как в рассматриваемом случае
ф(р)=-4-(р-^г). т° Ф'(р)=-4<о.
Следовательно, на плоскости tptp имеется устойчивый круговой предельный
«цикл, радиус которого равен
4М2 2М0
" л nhk
(21.64)
Рассмотрим формулу (21.39). Если предположить, что h/k ^1, ив разло-
..женин е k* пренебречь членами, начиная с члена, содержащего й2, то получим
» 2Л40 / п / й2 \ ’
Ф = (принято, ЧТО k* =k у 1—7,=«Й|-
Следовательно, результат (21.64) можно считать достоверным с точностью
до членов й2 (р2).
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Автоколебания 507, 531
Акселерометр 160
Амплитуда колебаний 38
— — вынужденных 54, 59
Аналогии электродинамические 64—67
Аномалия истинная ИЗ
— эксцентрическая 113
Апекс 186, 332
Апогей 110
Биение 55
Вектор главный сил ииерцйи 368, 369
Виброграмма 48
Возмущение 457
Законы динамики 13 ,
— сохранения количества движения си-
стемы 183
— — момента количеств движения си-
стемы 204, 205
Зона застоя 53
Изоклина 523
Изохронность 39
Импульс силы 69
— — элементарный 68
— ударный 378
Интеграл пчощадей 102
— энергии 96, 246
— — обобщенный 451
Гипотеза Ньютона (при ударе) 380
Гироскоп 343
— астатический 347
— с двумя степенями свободы 344
— с тремя степенями свободы 344
— свободный 347
— , точка подвеса 344
— уравновешенный 347
Гиротахометр 355
Градиент функции 93
Движение апериодическое 47
— вынужденное 504
— несвободное 124
— свободное 123
Декремент колебаний 45
— — логарифмический 45
Демпфер 468
Диаграмма Кеннгса—Лемерея 530
Диссипация неполная (частичная) 497
— полная 497
Единицы измерения массы 14
— — мощности 84
— — силы 14
Колебания автономные 509
— гироскопа нутационные 348, 363—366
— главные 482
— затухающие 44
— изохронные 137
— линейные 36
— — вынужденные 53
— — — прн вязком сопротивлении 58
— — свободные 38
— — — при вязком сопротивлении 43
— — — при тренин скольжения 50
— собственные 504
Количество движения системы 180
— — среды секундное 188
— — твердого тела 295
— — тела переменной массы 225
— — точки 68
Координаты нормальные (главные) 493
— обобщенные 420
Коэффициент восстановления 380
— динамичности 55, 60
— жесткости на кручение 454
— — обобщенный 458
— — пружины 40
— инерции 448
— перегрузки 266
Кривая равной энергии 518
Кривые интегральные 510
Критерий Сильвестра 459
Задача двух тел 176
— динамики вторая 10, 18
— — первая 9, 17
Заков динамики основной 12, 13, 152, 153
— Кеплера третий 113
— независимости дейс'вия сил 12, 13
— Ньютона второй 12, 13, 152, 153
— — первый 10, 13
— — третий *2, 13
— площадей 73, 74
— - прецессии 350
— сохранения механической энергии си-
стемы 246
— — — точки 96
Линия силовая 93
Масса, единицы измерения 14
— инертная 13, 14
— материальной точки 13
— секундная 187
— системы 171
— — приведенная 232
— тяжелая 14, 15
Маятник математический 134
— — двойной 426 v
— физический 309, 310
— Фуко 165
Б42
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Меры движения 179
Метод ваи-дер-Пол я 533
— вариации произвольных постоянных 470
— изоклин 523
— кинетостатики для системы 366
— — для точки
— Льенара 524
— медленно меняющихся коэффициентов
533
— припасовывания 526
Момент гироскопический 355
— главный сип инерции 369, 370
— инерции конуса 275
— — о)резка прямой 274
— — параллелепипеда 273, 274
— — пирамиды 274
— — полярный 270
— — приведенный 215
— — прямоугольника 274
— — системы относительно оси4 202, 210,
269
— — тела относительно оси 202, 269
— — тора 275
— — точки относительно оси 202
— — центробежный 271
— — цилиндра 275, 276
— — шара 276
— — эллипса 274
— — эллипсоида
— кинетический гироскопа 345, 362
— количеств движения абсолютного 212 —
214
— — — системы 200
— — — точки 71
Мощность внутренних сил трения сколь-
жения 237
— силы 82, 83
— —, единицы измерения 84
Невесомость 145, 148
Осциллограмма 48
Ось динамической симметрии 272
— инерции главная 271, 282, 283
— — — центральная 271
Перемещение виртуальное системы 409
— — точки 406
Перигеи ]05, 110
Период колебаний 39
— — затухающих 44
Перицентр 105
Плоскость Лапласа 205
— фазовая 509
Плотность объема средняя 269
— тела в точке 269
Поверхность эквипотенциальная 92
Поле силовое 85
— — нестационарное 86
— — потенциальное 87—89
— — стационарное 86
Полет суборбитальный 121
Постоянная времени 223
— энергии 96 *
Правило Бэра 162
— Грюэ — Жуковского 355
Прецессия 350
— регулярная 326, 333
— , угловая скорость 350
Принцип виртуальных перемещений 414
— Даламбера 143
— инерции 10, 13
Принцип освобождаемое™ 124
— относительности Галилея 11
Процесс переходный 211
Работа виртуальная 410
— внутренних сил твердого тела 234
— — — треиия скольжения 237
— сил, приложенных к системе 233
— — тяжестн 233, 234
— силы 76 — 78
— — элементарная 78
Равновесие неустойчивое 457
— устойчивое 457
— — асимптотически 457
Раднус инерцнн тела 203, 270
Реакция динамическая добавочная
371, 372
Резонанс 57
Связь 124, 401
— голономная 404
— идеальная 126, 411
— йеголономная 404
— нестационарная 126, 402
— неудерживающая 126, 402
— реономная 126
— склерономная 126
— стационарная 126, 402
— удерживающая 126, 402
Седло 512
Сепаратриса 52]
Сила внешняя 173
— внутренняя ] 73, 174
— возмущающая 36
— восстанавливающая 35, 37
— диссипативная 497
— , единицы измерения 14
— инерции 153
— — кориолисова 153
— — переносная 153
— — центробежная 154
— массовая 188
— обобщенная 424
— объемная 188
— переменная 18, 19
— поверхностная 188
— позиционная 85
— потенциальная 236
— реактивная 254, 258
— сопротивления 36
— тяжести 164
— ударная 378
— центральная 72, 73, 102
Силы гравитации 149
Система автоколебательная 531
— автономная 509
— координат гелиоцентрическая И
— — инерциальная 11, 151
— — неинерциальная 11, 151
— — неподвижная 152
— — орбитальная 335
— материальная 171
— неавтономная 509
— нелинейная 508
— несвязная 401
— отсчета инерциальная 11, 13, 151
— — иеинерциальная 11, 151
— свободная 401
Системы единиц 14
Скамейка Жуковского 205, 206
Скорость вторая космическая 107
— истечения эффективная 260
— круговая 107
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
543
Скорость обобщенная 434
— параболическая 107
— первая космическая 107
— «потерянная» 384
— прецессии угловая 350
— секторная 73
— фазовая 509
Спутник стационарный 119, 179
Степень неголономности 422
Субракета 262
Тело переменной массы 252
— статически уравновешенное 304
Тензор инерции 272, 286
Теорема Гюйгенса-Штейнера 277
— импульсов 184
— Карно 384
— Кенига 227
— Кориолиса 152
— Лагранжа — Дирихле 457
— Ляпунова 460
— о движении центра масс 184
— об изменении кинетической энергии
в относительном движении 169, 249, 250
— _ — — — для несвободного движения
141
— — _ _ _ системы 237
— — — — — точки 85
— — — количества движения системы
182, 184
— — — — — — ПрИ ударе 385
— — — — — тела переменной массы 257,
258
— _ — _ — точки 68, 69
— — — момента количеств движения
системы 204
— — — — — — — при ударе 385, 386
— — — — — — точки 71, 72
— — — — — относительного движения
системы 217, 218
— Резаля 346 •»
— Сильвестра 459
— Эйлера 189
Теория гироскопов прецессионная 346
— — элементарная 346
Точка изображающая 509
— материальная 10
— — изолированная 10
— - — несвободная 124
— — свободная 123
— особая 510—517
Траектория фазовая 509
— — убегающая 520
— — целая 509
Трение вязкое 495
— сухое 495
Удар 377
— неупругий абсолютно 380
— плоский 393
— - упругий 380
— — абсолютно 380
— центральный 392
Узел 514
— неустойчивый 515
— устойчивый 514
Уравнение Бииэ 103
— вековое 481
— вращения тела 209, 210
— движения точки в центральном поле 103
— — — векторное 16
— динамики общее 431
Уравнение динамики основное 153
— Кеплера 114
— малых колебаний системы 466
— Мещерского 254, 258, 259
— относительного покоя 158
— частот 481
Уравнения ван-дер-Поля 536
— гироскопа технические 362
— движения гироскопа в кардановом под-
весе 361 д
— — системы 175
— — точки естественные 16, 17, 133
— — — скалярные 16, 21
— Лагранжа второго рода 434
— — первого рода 128
— Пуассона обобщенные 339
— связи 125
— Эйлера динамические 321
Ус 519
Ускорение кажущееся 161
— кориолисово ] 52, 154
— переносное 152, 153
Условия начальные 22
— относительного покоя 158, 159
Устойчивость равновесия 456
Фаза колебаний 38
— — начальная 38
Фактор затуханий 45
Фокус неустойчивый 515
— устойчивый 513
Формула Космодемьянского 266
— Циолковского 261, 263
Функция диссипативная Релея 97, 495
— силовая 92
Центр 511
— инерции (центр масс) 171, 172
— удара 390
Цикл предельный 531
— — неустойчивый 532
— — полуустойчивый 532
— — устойчивый 532
Частота 38
— иутацни 363
— парциальная 481
— собственная 38
Число степеней свободы системы 421
— Циолковского 261, 263
Эксцентриситет 105
Эллипсоид инерции 282
— — трехосный 283
— — шаровой 283
Энергия кинетическая относительного дви-
жения 226
— — системы 225, 418, 449
— — твердого тела .228, 297, 298
— — — —, вращающегося вокруг не-
подвижной оси 229
— — — —t движущегося поступательно
228
— — — —, — произвольным образом
229, 236
— — — —t имеющего неподвижную точку
229
— — — — при плоском движении 230
— — точки 84
— механическая полная 96
— потенциальная системы 236
— — точки 87, 89
Николай Васильевич Бутенин,
Яков Львович Лунц,
Давид Рахмильееич Меркин
КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ
Том И
Динамика
М.» 1979 г., 544 стр. с нлл.
Редактор А. Г. Мордвинове
Техн, редактор Я. В. Кошелева
Корректоры: Г. В. Подвольская, Г. С. Вайсберг
ИБ № 2187
Сдано в набор 03.07 78. Подписано к печати 03 01.79.
Бумага‘60Х90'/|б. тип №3. Литературная гарнитура. Высокая
печать. Условн печ. л. 34. Уч.-изд л. 33,24. Тираж 45 000 экз.
Заказ № 137. Цена книги 1 р. 30 к.
Издательство «Наука»
Главная редакция физико-математической литературы
117071, Москва, В-71, Ленинский проспект, 15
Набрано и сматрицировано в ордена Октябрьской Революции,
ордена Трудового Красного Знамени Ленинградском произ-
водственно-техническом объединении «Печатный Двор» имени
А М Горького «Союзполиграфпрома» при Государственном
комитете СССР по делам издательств, полиграфии и книж-
ной торговли. 197136, Ленинград, П-136, Гатчинская, 26.
Отпечатано в ордена Трудового Красного Знамени Ленинград-
ской типографии № 2 имени Евгении Соколовой «Союз-
по шграфпрома» при Государственном комитете СССР па
делам издательств, полиграфии и книжной торговли»
198052, Ленин! рад, Л-52, Измайловский проспект, 29