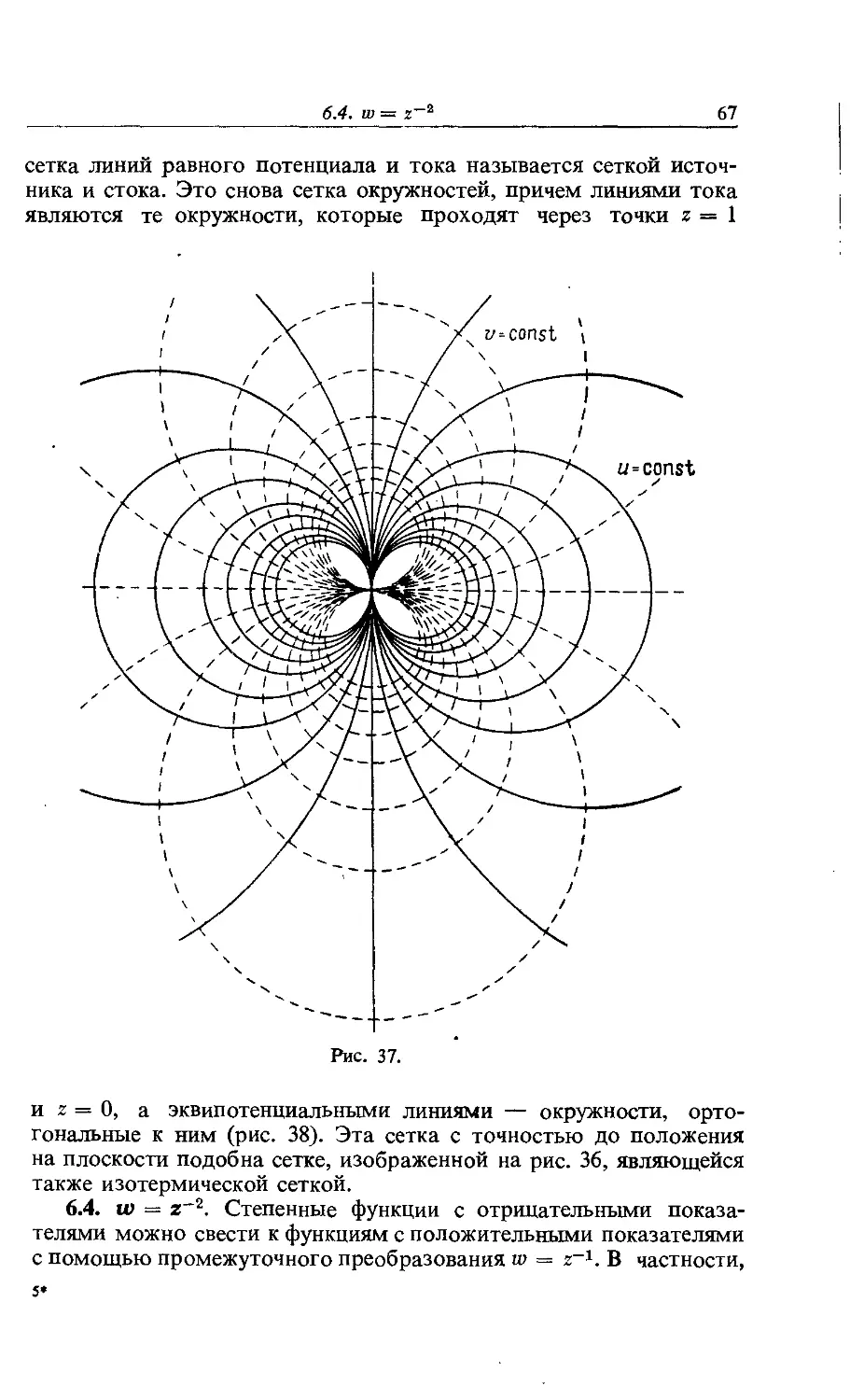
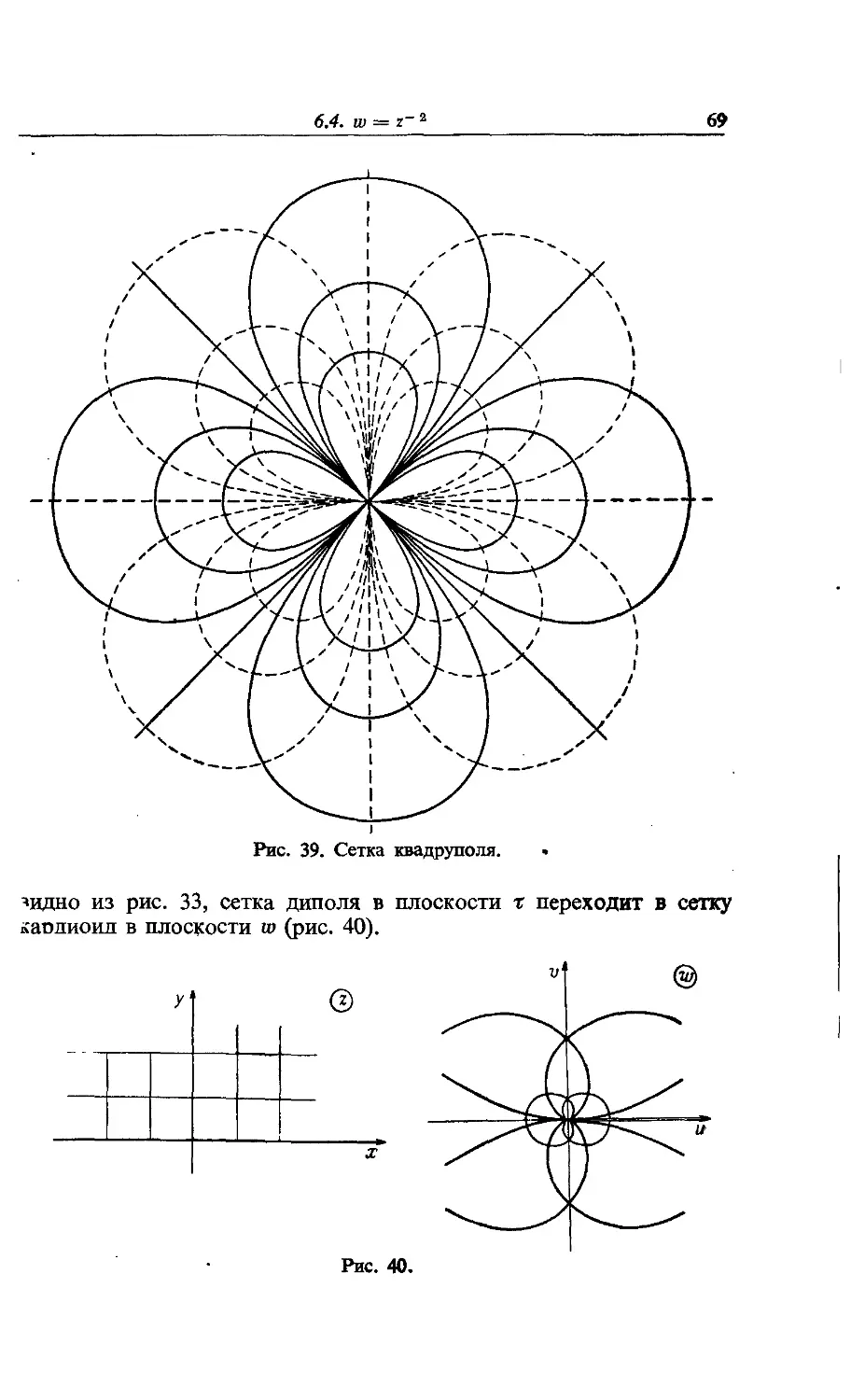
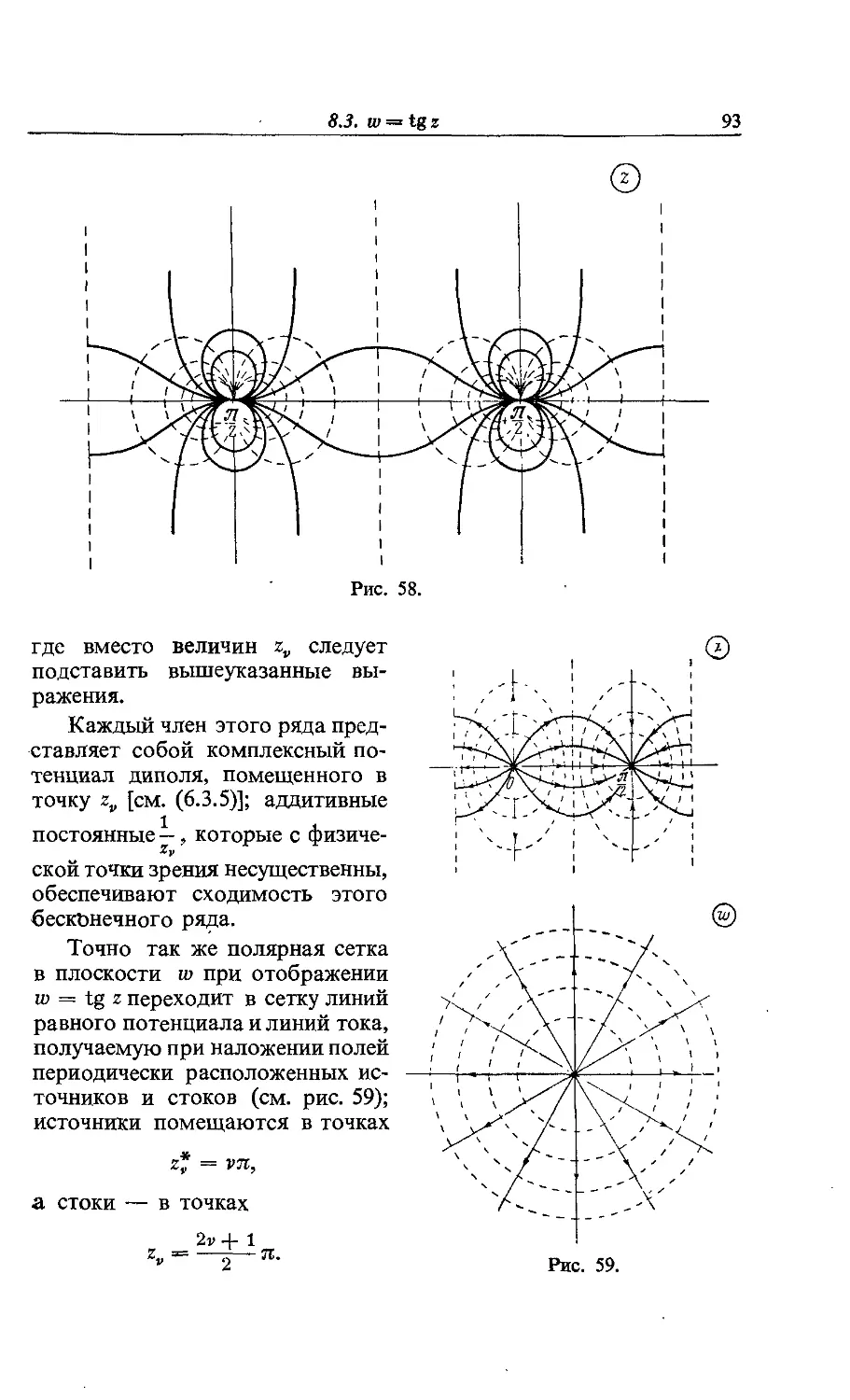
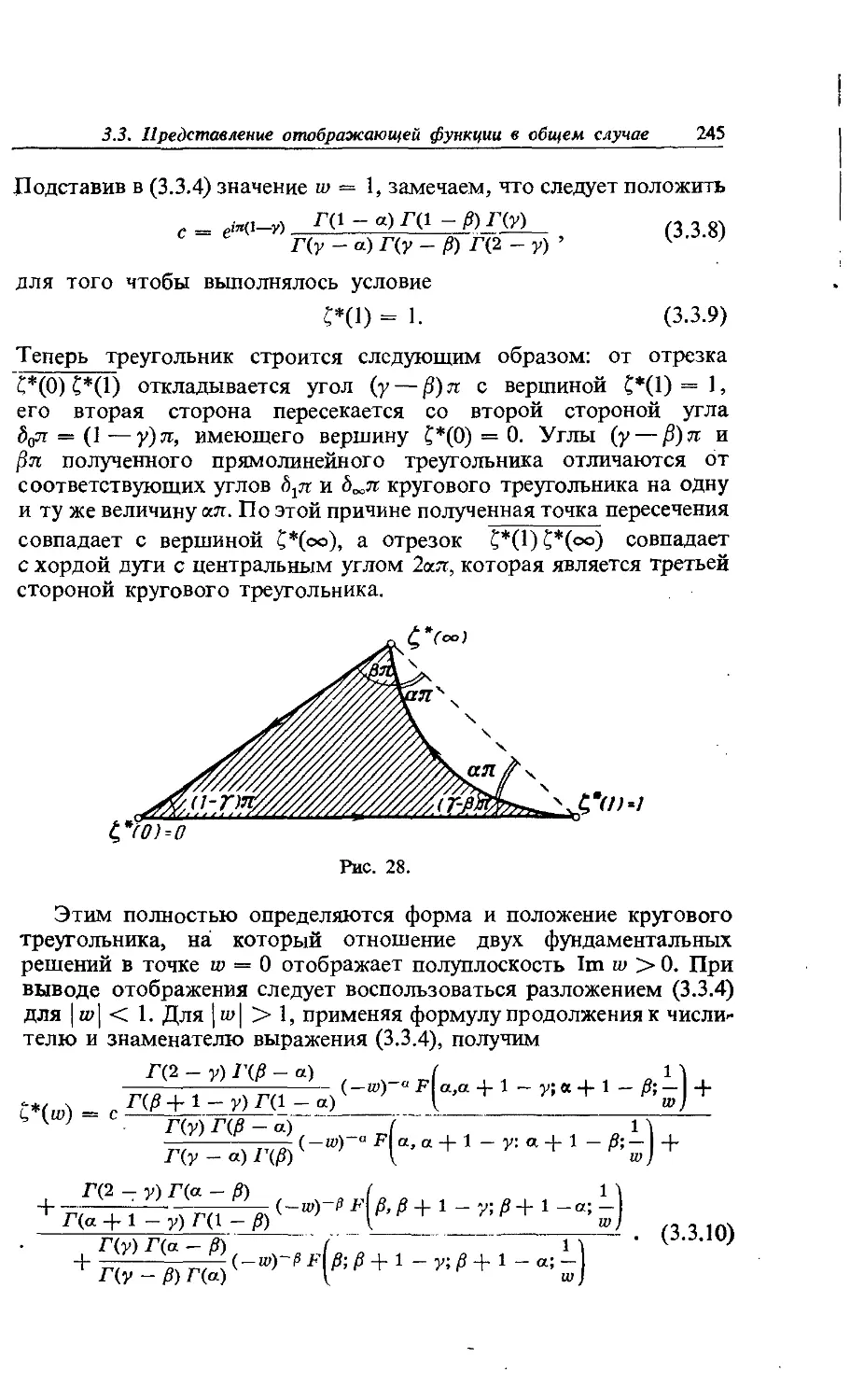
Text
DIE GRUNDl.ElinKN DK1I
MATHKMATIHCllKN
W I 8 8 К N Я С. И А V Т К N
Ilil nil 100
Praxis
der Коп for men
A bbildun.%
v о и
Dr. WERNEH von KOPl'ENFELS.
UIl (I
Dr. FRIEDEMAN.N STALLMANN
SPRINGEH-V ERLAC
Berlin Gottingen Heidelberg.
1959
В. Коппепфельс
и
Ф. Штальман
ПРАКТИКА
КОНФОРМНЫХ
ОТОБРАЖЕНИЙ
Перевод с немецкого
К. М. Фишмана
Под редакцией
Л. И. Волковыского
Издательство
иностранной литературы
Москва 1963
АННОТА ЦИЯ
Книга представляет собой практическое руководство по применению
метода конформных отображений. Содержит краткое изложение основ-
основных понятий теории, описание отображений, осуществляемых элемен-
элементарными и некоторыми специальными функциями, а также методов
отображения областей (односвязных и двусвязных), ограниченных
прямолинейными отрезками или дугами окружностей. Отдельный раздел
посвящен приближенным методам конформных отображений (Теодор-
сена и Гаррика, Гершгорина и др.). Вторая часть книги представляет
собой каталог конформных отображений.
Книга полезна для студентов, инженеров и научных работников
в области гидродинамики и гидротехники, электро- и радиотехники и
других лиц, имеющих дело с применением теории конформных отобра-
отображений.
Редакция литературы по математическим наукам
ПРЕДИСЛОВИЕ РЕДАКТОРА ПЕРЕВОДА
В практике конформных отображений центральное место зани-
занимает, несомненно, отображение прямолинейных и круговых много-
многоугольников, определяемое с помощью формулы Шварца—Кристоф-
феля и дифференциального уравнения Шварца. Наибольшее затруд-
затруднение представляет нахождение неизвестных параметров, входящих
в указанный интеграл и уравнение, особенно так называемых
акцессорных параметров, появляющихся при конформном отобра-
отображении круговых многоугольников. В книге В. Коппенфелъса и
Ф. Штальмана «Практика конформных отображений» основное
внимание уделено теории и практике конформных отображений
многоугольников, прямолинейных и круговых, односвязных и дву-
связвых. Подробно излагаются теория асимптотического интегри-
интегрирования дифференциального уравнения Шварца и проблема опре-
определения параметров, дается полное решение задачи о конформном
отображении четырехугольников (определение неизвестного пара-
параметра сводится к конформному отображению некоторого круго-
кругового треугольника) и р'ассматриваются многочисленные частные
случаи конформного отображения многоугольных и приводящихся
к ним областей, допускающих полное нахождение отображающих
функций.
В начале книги дается краткое изложение элементов теории
функций комплексного, переменного и ее приложений. Изложение
носит полуэвристический характер. Читателю рекомендуется изу-
изучить этот материал по одному из учебников теории функций
комплексного переменного, например, по книге М. А. Лаврентьева и
Б. В. Шабата «Метопы теории функций комплексного переменного»,
М., 1958.
Книга В. Коппенфельса и Ф. Штальмана будет весьма полезна
ессм математикам и инженерам, имеющим дело с конформными
отображениями. В переводе книги исправлены замеченные опе-
опечатки и введен дополнительный список литературы.
Л. И. Волковыский
ИЗ ПРЕДИСЛОВИЯ АВТОРА
История создания этой книги начинается со времен второй миро-
мировой войны, когда группа специалистов по теории функций, среди
которых были Коппенфельс, Крамес, Ульрих и Вегнер, задумала
создать обширную монографию о конформных отображениях.
Первым результатом явилась рукопись «Систематика отображений
многоугольников» (Systematik der Poligonabbildungen), подготовлен-
подготовленная покойным Коппенфельсом. В 1953 г. Э. Ульрих и я продолжили
работу, начатую Коппенфельсом. После смерти Э. Ульриха она
была закончена мною в 1957 г. Ее итогом и является настоящая
книга.
По первоначальному плану предполагалось создать справочник
наподобие книги Камке о дифференциальных уравнениях. Однако
рукопись Коппенфельса и затем мои добавления носили скорее
характер учебника. Это объясняется, главным образом, тем, что
теория конформных отображений (в особенности их «практика»)
значительно у^ке по содержанию, чем теория дифференциальных
уравнений, так что здесь более важной является глубина усвоения,
а не количество теорем и методов. Поэтому книга содержит лишь
небольшое число ссылок на литературу. Я стремился сделать изло-
изложение по возможности независимым от специальной литературы
и цитировал лишь те источники, которые существенно выходят
за рамки этой книги.
У читателя предполагаются знания примерно в объеме универ-
университетского или втузовского курса высшей математики. В связи с
этим изложение общей теории (раздел А, §§1, 2, 4, 9, 10) весьма
сжато; оно имеет целью лишь освежить и углубить уже имеющиеся
сведения. В §§ 11—15 излагаются отображения многоугольников.
Так как они являются основной специальностью автора, то эта
часть, возможно, излишне расширена. Помещение этого круга
вопросов во главу угла казалось мне оправданным благодаря
характеру рукописи Коппенфельса.
Естественно было включить в книгу также основные при-
приближенные методы конформных отображений. К сожалению, у
автора отсутствует практический опыт в этой области, так что он
б ыл лишен возможности критически подходить к изложению этого
Из предисловия автора
вопроса. По этой же причине отсутствуют численные примеры,
которые могли бы возникнуть лишь из приложений, встречаю-
встречающихся на практике. Специальные применения конформных отобра-
отображений почти полностью отсутствуют. Желающих познакомиться
с этим вопросом мы отсылаем к прекрасной книге Бетца.
Названная рукопись Коппенфельса составляет содержание
§ 1—5 раздела Б. Обработке подверглась лишь вводная глава,
изложенная в расширенном виде в §§ 13—14 раздела А. В пункте
F 6.1 также содержатся результаты Коппенфельса. Они не включены
в его рукопись, но опубликованы в Crelles Journal, т. 181, откуда
и заимствованы мной. Остальную часть раздела Б составляют
мои результаты. См. также введение к разделу Б, весьма близкое
к предисловию рукописи Коппенфельса.
Заключая свое предисловие, не могу не назвать с благодар-
благодарностью имя моего уважаемого учителя профессора доктора Эгона
Ульриха.
Я глубоко сожалею о том, что его намерение активно участво-
участвовать в создании этой книги не осуществилось вследствие постоян-
постоянной занятости и скоропостижной смерти. Однако его многочислен-
многочисленные указания учтены в книге, не говоря уже о том, что само возоб-
возобновление работы над ней состоялось по его инициативе.
Ф. Штальман
Гиссен, март 1959 г.
А. ТЕОРИЯ КОНФОРМНЫХ
ОТОБРАЖЕНИЙ
ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ
КОМПЛЕКСНЫХ ЧИСЕЛ И ФУНКЦИЙ
§ 1. Комплексные числа
1.1. Комплексные числа и геометрия на плоскости. Пусть на
плоскости задана декартова система координат (рис. 1). Каждой
точке с координатами х, у мы поставим в соответствие комплексное
число
z = х + iy.
Совокупность точек, представленных таким образом комплекс-
комплексными числами, называется комплексной плоскостью; ось х
называется вещественной осью, ось у — мнимой осью.
Число
z = x—iy у-
называется сопряженным к
числу z, величина
z+1 _
— вещественной частью z,
величина
Z — Z
У =•
= Imz
— мнимой частью z и величина
— модулем z.
Действия сложения, умно-
умножения и деления для комплекс-
комплексных чисел вводятся по обыч-
обычным правилам с учетом равенства г2 = —1; а именно, если
iy2,
то
zi г2 =
A.1.1)
z2 z2
10 § 1. Комплексные числа
Введенное выше соответствие между точками плоскости и
комплексными числами позволяет выражать соотношения между
комплексными числами в геометрической форме и, обратно, пред-
представлять некоторые геометрические соотношения с помощью
комплексных чисел. Например, сложение двух комплексных чисел
zx, z2 геометрически представляет собой сдвиг точки zl на вектор
oz,/, иными словами, если каждое число z изобразить радиусом-
вектором oz, то сложению чисел будет соответствовать сложение
их радиусов-векторов (см. рис. 1).
Модуль числа z означает геометрически расстояние точки z
от начала координат; величина \z1— г2] есть, таким образом, рас-
расстояние между точками z1 и z2. Уравнение окружности с центром в
точке г0 радиуса г запишется следующим образом:
|z—zo|-r, A.1.2)
или, иначе,
(z — z0) (г — Za) = iz - zz0 — zz0 + Zozo = r2. A.1.3)
Неравенства
[z—zoj<r и | г— zo|>r
определяют точки, лежащие соответственно внутри и вне этой
окружности.
Для записи уравнения прямой в комплексной форме восполь-
воспользуемся ее параметрическим представлением. Если вещественный
параметр Я принимает все значения от — оо до + со, то точка
г = Яг0 (го=?0) A.1.4)
описывает прямую, проходящую через начало координат и точку
z0. Уравнение
z = z, + Я ze A.1.5)
представляет прямую, сдвинутую на вектор ozx по сравнению
с предыдущей; уравнение же
г = zy + Я(г2— Zl) A.1.6)
представляет прямую, проходящую через точки zx и z2. Уравнению
прямой можно придать иной вид, если решить его относительно
Я и, учитывая, что Я — произвольное вещественное число, положить
Im Я в. 0. Так, например, для уравнения прямой, проходящей
через точки г, и z,,, получим
Im
1.2. Векторы 11
Вообще уравнение
где а — произвольное вещественное число, есть уравнение пучка
параллельных прямых. Точки, для которых
Im [z ~ н | < 0 (соответственно > 0), A.1.9)
лежат справа (соответственно слева) от прямой A.1.7), если смотреть
из точки zx по направлению z2. Каждое из неравенств A.1.9) опре-
определяет полуплоскость, ограниченную прямой A.1.7). В частности,
неравенства
Im z < 0, Im z > 0, Re z < 0, Re z > 0
определяют соответственно нижнюю, верхнюю, левую и правую
полуплоскости.
Подобным образом можно представить и более сложные геомет-
геометрические фигуры и соотношения в комплексной плоскости; ниже мы
познакомимся с многочисленными примерами.
1.2. Векторы. С помощью комплексных чисел можно изображать
также векторы на плоскости. При этом наряду с радиусами-векто-
радиусами-векторами вида oz мы будем рассматривать свободные векторы с орто-
ортогональными компонентами и, v, ставя в соответствие каждому
такому вектору комплексное число
w = и + iv.
Выше мы показали, что сложению векторов соответствует
сложение комплексных чисел, длина вектора совпадает с модулем
комплексного числа. Скалярное и векторное1 произведения двух
векторов wx и w2 соответственно выражаются в комплексной форме
следующим образом:
(wjio^ = ихи2 + vxv2 = Re (wjWj), A.2.1)
[wxw^[ = UjOj — iijWj = Im (ш1ю2). A.2.2)
Таким образом, скалярное и векторное произведения служат
соответственно вещественной и мнимой частью произведения
wxw2 = (w^) -|- z'fwjwj. A.2.3)
1 Векторное произведение понимается здесь в смысле внешнего произведе-
произведения Грассмана, которое на плоскости является скаляром. Если рассматривать
те же векторы в трехмерном пространстве, то указанная величина есть единствен-
единственная отличная от нуля пространственная компонента векторного произведения.
См., например, S р е г п е г Е., Einftlhrung in die analytische Geometrie, Got-
tingen, 1948, S. 175 if.
12 § 1. Комплексные числа
Это произведение, в отличие от обычного произведения w-^m^,.
инвариантно относительно поворотов системы координат (ср. п. 1.3).
1.3. Преобразования подобия. Рассмотрим линейное преобразо-
преобразование координат
х - aux + а12у, A ЗЛ)
у = а21х + а22у,
или, в матричной записи,
У) \ац а22)\у
Это преобразование можно рассматривать как отображение
плоскости (х, у) на плоскость (х, ~у); при помощи равенств A.3.1)
каждой точке (ж, у) ставится в соответствие точка (х, у), и каж-
каждая фигура на плоскости (х, у) преобразуется в некоторую фигуру
на плоскости (ж, у).
Если матрица (aik) имеет вид
о cos ж — о sin q>\
V V \ = (.е,<Р), Q>0, A.3.3>
q sin ер q cos (p)
то это преобразование называется преобразованием подобия. При
этом каждая фигура отображается в подобную ей фигуру, повер-
повернутую на угол ср, линейные размеры которой отличаются от разме-
размеров исходной на множитель q (коэффициент подобия).
Матрицы вида A.3.3) можно поставить во взаимно однозначное
соответствие с комплексными числами С = I + Щ, отличными от
нуля. А именно, если положить
С = Q (cos ср + i sin cp), A.3.4)
то
P~^ = (O- 0-3.5)
Обратно, каждому отличному от нуля числу С соответствует
пара чисел q, ср, определяемых равенствами
5.1 Re f . Imf ,, ., ,ч
9= С|, соа,ср = -щ-, sin()o = —f-i. A.3.6)
Следует отметить, что при таком соответствии произведению
матриц отвечает произведение комплексных чисел. Умножение
матриц при этом определяется следующим образом: пусть в
обозначениях A.3.2)
х\ _ (П \(х\ (х\ _ (h Л{х\ .
- I — \aik) _ Ь J _ — \.bik) ,
У \У \У Ъ
_ 1.3. Преобразования подобия 13
тогда последовательное применение преобразований (а1к) и (Ь!к)
приводит к линейному же преобразованию
М A.3.7)
с Матрицей (cik), состоящей из элементов
2
Cik = 2ai]bjk. A.3.8)
J-i
Эта матрица называется произведением матриц (aik) и (bik):
Ы-ЫСЬй). A-3-9)
Сравнивая произведение матриц вида A.3.5) с произведением
комплексных чисел A.1.1), получим j | $|йЙ
(СО (С2) = (dC2). A.3.10)
Геометрически это произведение означает последовательное
выполнение двух преобразований подобия. При этом коэффициенты
подобия перемножаются, а углы поворота складываются, т. е.
feb <Pl) (<?2> 4>i) = @192^1 ¦+9J)- A.3.11)
Матричное представление A.3.5) вновь приведет нас к пред-
представлению комплексных чисел точками плоскости, если применить
это преобразование подобия к точке с координатами A,0). Тогда
С=(С)(М, A-3.12)
где С без скобок означает точку С комплексной плоскости. Для
этой точки q равно отношению длин отрезков ОС: 01, т. е. просто
длине ОС, или [С|; угол у равен углу между отрезками 01 и ОС- Этот
угол, определяемый здесь, как и в соотношениях A.3.6), с точностью
до кратного 2jt, называется аргументом С и обозначается
ср = arg С.
Применяя преобразование подобия (С) к произвольной точке z
комплексной плоскости, получим
(О z = @ (Z) f М = (Cz> (Ч = е*. A.3.13)
Таким образом, произведение двух комплексных чисел можно
рассматривать как применение к одному из сомножителей преоб-
14
§ 1. Комплексные числа
разования подобия, определяемого другим сомножителем1. При
этом, в силу A.3.11), модули сомножителей перемножаются, а
аргументы складываются (см. рис. 2).
Свойство комплексных чисел представлять преобразования
подобия при сохранении операции умножения является основой
для широкого и столь удобного
на практике применения их в кон-
конформных преобразованиях. Этим
же можно объяснить и тот факт,
что в пространстве трех и боль-
большего числа измерений нет ничего
аналогичного понятию комплекс-
комплексного числа. Для представления
преобразований числами необхо-
необходимо, чтобы умножение матриц
подчинялось тем же законам, что
и умножение чисел; это имеет
место для специальных матриц
вида A.3.3), но не в общем случае:
свойство коммутативности умно-
умножения, справедливое для чисел
(ab = Ьа), для матриц2, вообще говоря, неверно. Оно не выполня-
выполняется также для поворотов в пространствах трех и большего числа
измерений, что не позволяет представлять их с помощью чисел3.
X
Рис. 2.
1 Следует отметить, что при таком истолковании произведения комплекс-
комплексных чисел оно инвариантно относительно поворотов системы координат:
рассматриваемое же само по себе, оно не обладает этим свойством (ср. конец
п. 1.2).
(Впрочем, абсолютно инвариантным здесь является лишь коэффициент
растяжения. — Прим. ред.)
1 Например, для матриц
имеем
ПН-СКИП-
2 1
1 1
8 И шестую аналогию комплексных чисел представляют собой введенные
Гамильтоном кватернионы. Подобно комплексным числам, они применяются
для построения теории потенциала в пространстве. Однако умножение кватер-
кватернионов не коммутативно, и это настолько усложняет вычисления, что их при-
применение на практике не дает никаких преимуществ.
2.1. Основные понятия
J § 2. Функции комплексного переменного
2.1. Основные понятия. Функция ю(г) называется функцией ком-
комплексного переменного, если независимое переменное z = х + iy
и зависимое w = и + iv являются комплексными числами. Разделе-
Разделение ш на вещественную и мнимую части приводит к двум веществен-
вещественным функциям двух вещественных переменных :
ш(г) = и(х, у) + iv{x, у); B.1.1)
обратно, из каждой пары вещественных функций и(х, у), v(x, у)
можно составить по формуле B.1.1) функцию комплексного пере-
переменного. Однако это разумно лишь в том случае, когда при аналити-
аналитических операциях над такими функциями удобно применять правила
действий над комплексными числами. Как мы увидим дальше, это
относится прежде всего к аналитическим функциям, которыми мы
исключительно и будем заниматься в дальнейшем.
Для более удобного описания свойств функций комплексного
переменного нам понадобятся некоторые основные понятия теории
точечных множеств. Благодаря представлению комплексных
чисел точками комплексной плоскости каждое множество комплекс-
комплексных чисел можно рассматривать как множество точек этой плоско-
плоскости. Если М является таким множеством, то знак z б М означает,
что точка z принадлежит множеству М; соответственно z <J M
означает, что точка z не принадлежит множеству М.
Если все точки, принадлежащие М2, принадлежат также и Мъ
то будем говорить, что множество М„ содержится в множестве Мъ
и писать М„ d My
Множество V называется объединением, или суммой, Мх и
М„ (V = Мх U М„), если V состоит из точек, принадлежащих хотя
бы одному из множеств Мх или М2.
Множество D называется пересечением Мх и М2 (D = Мх Q М2),
если D состоит из тех и только тех точек, которые принадлежат
одновременно Му и М2.
Круг [ср. A.1.2)]
&-2„|<е B-1.2)
образует окрестность точки ?$. При этом е может быть как угодно
малым, но, разумеется, отличным от нуля. Выражение «в некоторой
окрестности точки z0 имеет место .. .» означает: «существует такое
е >0, что в круге B.1.2) имеет место . ..».
Пользуясь понятием окрестности, можно определить внутрен-
внутренние, внешние и граничные точки множества М.
Точка г0 называется внутренней точкой множества М, если
некоторая окрестность z0 целиком содержится в М.
16
§ 2. Функции комплексного переменного
Точка г0 называется граничной точкой множества М, есл
каждая окрестность z0 содержит как точки множества М, так
точки, не принадлежащие М.
Точка z0 называется внешней точкой множества М, если суще
ствует окрестность z0, не содержащая ни одной точки множества Ас
Эти определения соответствуют обычным представлениям;
этом можно убедиться на примере единичного крута (рис. 3): дл
круга
Рис. 3.
: 1 внутренними точками являются все точки, расположи
ные внутри круга. Согласно npi
веденному определению, окруя
ность|г| = 1 состоит из граничны
точек, а внешность круга \z\ >
состоит из внешних точек.
Множество называется открь
тым, если оно состоит только y
внутренних точек; множеств
называется замкнутым, если он
содержит все свои граничнь
точки.
В частности, открытым я]
ляется множество всех внутренне
точек произвольного множесп
М; такое множество мы назове
открытым ядром множества А
Множество внутренних и грани
ных точек множества М являете
замкнутым и называется зам\
канием множества М.
Для дальнейших рассмотрен?
нам понадобится понятие непр
рывной кривой в комплексной плоскости. Исходя из параметр,
ческого представления кривых, мы дадим следующее определени
Пусть на отрезке a=s ;«= 6 заданы две действительные непреры
ные функции х(/) и у@; тогда функция z(t) = x(t) + zy(O предста
ляет непрерывную кривую в комплексной плоскости. Таким обр
зом, каждой точке t отрезка а^(«1) соответствует единственн;
точка z{t), и поэтому кривую z{t) можно рассматривать как непр
рывпый образ отрезка в комплексной плоскости. Точка z(a) назыв
ется началом, z(b) — концом кривой.
Кривая называется гладкой, если функции х@ и y{t) не толы
непрерывны, но и непрерывна дифференцируемы, и производи!
i(/) и ii(l) не обращаются одновременно в нуль. В этом случае крив;
обладает непрерывно вращающейся касательной.
Кривая называется простой, если различным значениям I coo
ветствуют различные значения z, т. е. если отображение z(i) взаим!
Рис. 4. Слева простая кривая,
справа кривая с кратными точками.
2.1. Основные понятия 17
однозначно. Точка кривой, которой соответствуют несколько раз-
разных значений I и в которой, следовательно, кривая имеет самопере-
самопересечение или самокасание, называется кратной точкой кривой.
Точки, не являющиеся кратными, называются простыми.
Кривая называется замкнутой, если ее начало и конец совпадают.
Эта точка считается простой, если она не совпадает ни с какой
другой точкой кривой.
Замкнутая кривая z(t) может быть непрерывно стянута на мно-
множестве М в некоторую точку этого множества, если существует
функция z(t, а), обладающая следующими свойствами:
1. z{t, ос) = z@ при а = 1, z(t, а) = г0 = const при а = 0, где
г0 — произвольная точка множества М.
2. Для каждого а из отрезка [0,1] функция z(l, а) представляет
замкнутую кривую, целиком лежащую в множестве М.
3. Функция z(t, а), как функция двух переменных t и а, непрерывна
при a =s ;=== j,0=s«=s 1. Таким образом, существует непрерывное
семейство замкнутых кривых, лежащих в множестве М, которые
изменяются, начиная от исходной кривой
и кончая кривой, состоящей из одной точки
г0. Если, в частности, исходная кривая —
простая замкнутая, то она может стяги-
ватьея к одной точке тогда и только тогда,
когда все охватываемые ею точки принад-
принадлежат множеству М.
Точечное множество М называется
связным, если любые две точки этого мно-
множества можно соединить кривой, лежащей
целиком в М.
Открытое связное множество называ- Ркс- 5-
ется областью. Замыкание области назовем
замкнутой областью (нем. Bereich). Следует отметить, что, со-
согласно этому определению, каждая замкнутая область «порождается»
некоторой областью, и тем самым не каждое замкнутое связное
множество является одновременно замкнутой областью. В
связи с этим мы под границей замкнутой области будем
понимать границу области, порождающей данную замкнутую об-
область, даже если не все ее точки являются граничными точками
в смысле данного выше определения. Рассмотрим в качестве при-
примера область, полученную из единичного круга |z| < 1 удалением
всех точек радиуса @,1) (рис. 5). Соответствующая замкнутая
область представляет собой замкнутый круг |z|«=l, который
может быть порожден также и кругом |г| < 1. Однако граница
¦)той замкнутой области в указанных случаях различна, ибо в
первом случае радиус @,1) принадлежит границе, во втором
случае — нет.
2 — 6002
18 § 2. Функции комплексного переменного
Строгое различие, которое мы делаем между открытой и замк-
замкнутой областями, целесообразно для того, чтобы выяснить, выпол-
выполняются ли известные свойства функций также и на границе области.
В связи с этим мы будем употреблять выражения «в некоторой
открытой области ...» и «в некоторой замкнутой области ...».
Область называется односвязпой, если каждая замкнутая кривая
в этой области может быть непрерывно стянута в точку. Справед-
Справедливо следующее утверждение: всякая область, граница которой
состоит из одной замкнутой кривой,
односвязна.
1В соответствии с этим область
называется п-связной, если ее граница
состоит из п ^попарно непересекаю^
щихся кривых1. Такую область можно*
превратить в односвязную при помощи
ровно п — 1 простых кривых {разре-
{разрезов), соединяющих друг с другом
граничные кривые (см. рис. 6; трех-
связная область с помощью двух
Рис. 6. разрезов Qi и Q2 превращена в одно-
связную).
Дадим, наконец, некоторые определения, характеризующие
поведение функции в окрестности точки.
1. Число wQ называется пределом функции w(z) в точке z0, если
для каждого еХ) найдется такая окрестность Ue={z, ]z — го| < б},
что для всех z e Ud Z •+• Zo, выполняется неравенство \w(z) — wo\ < e.
2. Число ю0 называется пределом w(z) в точке г0 вдоль кривой
С (z0 ? С), если [ w(z) — w01 < е для всех z e U6 f\ С, z =f= z0.
3. Число w0 называется граничным значением функции ю(г) в
точке г0 границы области G, если | w(z) — wB \ < е для всех z e U6 [) G.
В случае, когда Ua fl G состоит из нескольких областей, доста-
достаточно потребовать выполнения неравенства |w(z)—-юо|<е в
одной из них.2 (Рассмотрим, например, граничную точку z0 = 1/2
области, изображенной на рис. 5. Пересечение G с окрестностью
Ue при достаточно малом 6 распадается на два полукрута, лежащих
выше и ниже вещественной оси. Таким образом, в точке z0 функция
w(z) может принимать два различных граничных значения, смотря
по тому, с какой стороны — снизу или сверху — z стремится к z0.
Граница области G считается здесь дважды, соответственно двум
берегам радиального разреза.)
1 Во ичбежание недоразумений заметим, что граница области не обязательно
состоит п ( кривых, а может иметь и гораздо более сложное строение. Однако
для прак гики интересен лишь случай областей, ограниченных кривыми, поэтому
мы приводим определение n-связной области только для этого случая.
1 Строгое изучение границы см., например, в [6], гл. V. — Прим. ред.
2.2. Векторное поле \9
¦1 Функция называется непрерывной в точке z0, если в этой точке
значение функции совпадает с ее пределом. Функция называется
непрерывной в замкнутой области, если она непрерывна в каждой
внутренней точке этой области и ее значение в каждой точке границы
совпадает с ее граничным значением.
2.2. Векторное поле. Если для функции комплексного перемен-
переменного w(z) рассматривать z как точку плоскости, a w — как вектор,
то данная функция задает плоское векторное поле- Такие поля
встречаются во многих областях физики. Например, при описании
движения жидкости или газа каждой точке движущейся среды сопо-
сопоставляется вектор скорости потока в этой точке. Векторное поле
может также изображать меняющуюся от точки к точке силу
(например, электрического происхождения), действующую на поме-
помещенное в данную точку тело; в этом случае говорят о силовом поле.
В приложениях следует, однако, учитывать, что рассматриваемые
здесь поля; являются плоскими, поскольку функция комплексного
переменного позволяет изображать только такое поле, векторы
которого лежат в одной плоскости и не меняются в перпендикуляр-
перпендикулярном к ней направлении. На практике эти требования не выполняют-
выполняются в точности, однако многие важные задачи можно с достаточной
степенью приближения рассматривать как плоские. Некоторые
примеры будут приведены в § 3.
Для упрощения вычислений целесообразно расположить системы
координат в плоскостях z и w так, чтобы оси х и и были направлены
в одну и ту же сторону, а оси у и v — в противоположные. Таким
образом1, например, вектор w = i направлен в отрицательную
сторону оси у.
Предположим, что функции и(х, у) и v(x, у), определяемые равен-
равенством B.1.1), имеют в некоторой области плоскости z непрерывные
частные производные их, иу, vx, vy. Так как
•т = з" (г + г), у = — (z — z),
мы можем формально считать и и v функциями переменных г и z
(хотя они однозначно определяются значением одного лишь г)
и образовать частные производные по этим переменным. Согласно
1 Принятое авторами непривычное направление осей в плоскости ш, соот-
соответствующее рассмотрению w = и — ia вместо ш = и + io, приводит к расхож-
расхождению с обычной формой записи. Обычно, полагая ш = u + iv равным скорости
течения жидкости, получают формулы для дивергенции и ротора в следующем
виде:
div w = их -\- Vy, rot w = vx — uy.
Обозначая чергз W(r) комплексный потенциал течения (см. дальше), находят,
что ш = W'(z), а не ц; = W'(z), как у автора. — Прим. ред.
2*
20
§ 2. Функции комплексного переменного
обычным правилам дифференцирования, получим
9 _ 1 ( 9 _ / 9 ) 9
2
Пользуясь этими соотношениями, можно записать в комплекс-
комплексной форме дивергенцию и ротор1 вектора w:
или иначе
div ш = иг —
rot w = uv + vx — — (w- — i
Vj = — (div w + i rol w).
B.2.2)
B.2.3)
Далее рассмотрим некоторые криволинейные интегралы в век-
векторном поле io(z). В качестве пути интегрирования возьмем глад-
гладкую кривую С с параметрическим уравнением z(t) = x(t) + iy(t),
a as t =ss ft; интегрирование будем вести от точки г(а) до г(Ь). Так
как, по предположению, существуют производные x(t) и y(t), то
через них можно выразить дифференциалы и элемент дуги2.
= ж dt, dy = у dt, dz = (х + iy) dt,
ds = \dz\ = Yx2 + if dt.
B.2.4)
B.2.5)
x
В каждой точке этой кривой
разложим вектор w(z) на тан-
тангенциальную и нормальную сос-
составляющие wt и шп; пусть при
этом направление касательной
совпадает с направлением пути
интегрирования, а нормаль
направлена вправо от наблю-
наблюдателя, смотрящего в сторону
касательного вектора (рис. 7).
Учитывая выбранное располо-
расположение осей и и v, имеем
Рис. 7.
dx dy
' ds ds
dy dx
" ds ds
B.2.6)
1 Как и векторное произведение A.2.2), ротор является здесь скалярной
величиной. (.1м. сноску 1 на стр. 11.
1 Точки над неременной означает, как обычно, производную по t.
2.2. Векторное поле 21
»¦ Составим следующие криволинейные интегралы:
[wtds= [(udx—v dy) B.2.7)
с с
R
{wn ds = f(u dy + v dx). B.2.8)
с с
Первый из этих интегралов выражает работу, совершае-
совершаемую силой ro(z) при перемещении материальной точки вдоль
кривой С. Эту величину будем называть линейным интегралом.
В поле течения с (комплексной) скоростью w(z) величина wt
представляет собой компоненту скорости, направленную вдоль
кривой С, а ш„ — компоненту, ортогональную к ней. Поэтому
интеграл B.2.8) характеризует количество жидкости, протекающей
через С в единицу времени; этот интеграл называется потоком
через кривую С.
Интегралы B.2.7) и B.2.8) представляют собой вещественную
и мнимую части некоторого комплексного криволинейного интег-
интеграла, а именно, как легко проверить,
[wdz=Uwt + iw^ ds. B.2.9)
с с
Пусть теперь С — простая замкнутая кривая, являющаяся грани-
границей односвязной замкнутой области В, в которой определены и
непрерывны ш(г), div ш и rot ш. Тогда справедливы формулы Гаус-
Гаусса—Остроградского и Стокса:
фюп ds = Г Г div ш dx dy, B.2.10)
с в
( ds = — Г ("rot ш dx dy. B.2.11)
с
Здесь мы предполагаем, что кривая С обходится в положитель-
положительном направлении, т. е. против часовой стрелки. Этому соответ-
соответствует внешнее направление нормали к С.
Объединяя эти два интеграла, как в B.2.9), и принимая во вни-
внимание B.2.3), приходим к следующей простои формуле:
фю dz= 2i Г Гшг dx dg. B.2.12)
с в
Это формальное упрощение приобретает особое практическое
значение в случае, когда ю- = 0 в В, т. е. div w = rot ш = 0. Такое
22 § 2. Функции комплексного переменного
векторное поле называется соленоидальным и потенциальным
(безвихревым). В этом случае
J
ш dz = О
с
вдоль любой замкнутой кривой С, лежащей целиком в В, а такой же
интеграл по незамкнутому пути зависит лишь от начальной и
конечной точки, но не от формы пути1. Интеграл
Z
twdz = W(z) = U(z) + i V(z), B.2.13)
таким образом, определен всюду в В и при фиксированной точке
z0 и переменной точке z представляет собой однозначную комплекс-
комплексную функцию W(z). Вещественная и мнимая части этой функции
представляют собой не зависящие от пути линейный интеграл и
поток между z0 и z. Мы назовем U(z) потенциалом, или потенциаль-
потенциальной функцией, V(z) — функцией тока и W(z) — комплексным потен-
потенциалом.
Практическое значение предыдущих определений состоит не
только в том, что интеграл B.2.13) формально сходен с веществен-
вещественным интегралом, но и в том, что в большинстве случаев с ним
можно оперировать так же, как с вещественным. В частности,
так же как и в вещественном случае, интегрирование является опе-
операцией, обратной дифференцированию. Если определить произ-
производную так же, как в вещественном случае:
Wba) = lim ^!L=_Fi!oI , B.2.14)
то для функции W(z), определяемой интегралом B.2.13), этот предел
существует в смысле определения из п. 2.1, причем
W\z) = ro(z). B.2.15)
Обратно, если комплексная функция W(z) всюду в односвязной
области G имеет производную, равную ш(г), т. е. существует предел
B.2.14), то
г
Г w dz = W(z) — W(z0), B.2.16)
1 Этот факт известен в теории функций под названием интегральной тео-
теоремы Коши. Здесь существенно то, что рассматриваемая область В односвязна,
в противном случае ее следует преобразовать в односвязную с помощью раз-
разрезов, причем путь интегрирования не должен их пересекать.
2.2. Векторное поле 23
причем этот интеграл не зависит от пути (целиком лежащего в G).
Функция W(z), обладающая этим свойством, называется регулярной
аналитической в G1.
Аналитические функции и только они определяют соленоидаль-
ные потенциальные поля. Так как сумма, произведение, частное
и суперпозиция аналитических функций, а также функция, обратная
к аналитической, сами являются аналитическими функциями, то
при помощи перечисленных операций над комплексными функциями
можно получить богатое многообразие различных векторных полей,
чего нельзя сделать так просто никаким другим способом.
Добавим к этому, что все элементарные вещественные функции
легко распространяются на комплексную плоскость и являются
аналитическими (см. конец п. 9.4).
Разделяя интеграл B.2.13) на вещественную и мнимую части,
получаем
Z 2
U(z) = Г» dx — v dy, V(z) = fu dy + v dx. B.2.17)
z, z,
Отсюда следует, что
1 и = Ux = Vy, v = —Uy = Vx. B.2.18)
4' Эти уравнения называются уравнениями Коши—Римана. Обрат-
Обратно, если две непрерывно дифференцируемые функции V{x, у) и
v(x> ll) удовлетворяют уравнениям B.2.18), то функция W(z) =
= и(х, у) + i У (ж,;/) — регулярная аналитическая. Из равенств
div w = rot ш = 0 следует, что
ux=Vyn ~uy=vx; B.2.19)
таким образом, ю(?) является аналитической функцией одновремен-
одновременно с W(z).
Далее, из B.2.18), используя B.2.2), получаем
div w = Uxx + Uyy = 0, rot ш = Vxx + Vyy = 0. B.2.20)
Это так называемое уравнение потенциала; функция F(z, у), удов-
удовлетворяющая уравнению Fxx + Fyy = 0, называется гармонической.
Таким образом, вещественная и мнимая части аналитической
функции являются гармоническими функциями. Однако не из
любой пары гармонических функций' можно составить аналити-
аналитическую: функция У(ж, у) определяется по заданной U(x, у) с точно-
точностью до постоянного слагаемого; а именно, из уравнений Коши—
1 Доказательства этих и дальнейших сформулированных здесь предложе-
предложений читатель найдет в книгах по теории аналитических функций. См. список
литературы в конце книги.
24 § 2. Функции комплексного переменного
Римана и равенств B.2.17) следует, что
Z
V(z) - V(Z()) = | Ux dg - Uy dx. B.2.21)
При выполнении этого условия функция У(ж, if) называется
гармонической сопряженной с функцией U(x, у). В этом случае
функция — U(x, у) является сопряженной с V(x, у).
Можно получить другую форму уравнений Коши—Римана, если
учесть, что нормальная составляющая wn вектора го равна частной
производной функции U по направлению нормали. Обозначая
эту производную через dU/dn, получаем из B.2.8) и B.2.21)
г
П~\ уG \ — Г "_ /7о О Т ООЛ
J О Л
?о
ИЛИ
?- = %. B-2.23)
где 3V/3s обозначает производную функции V(x, у) по направлению
касательной. Легко убедиться, что уравнения B.2.18) представляют
собой частные случаи уравнения B.2.23), если за направление каса-
касательной выбрать соответственно направления оси ;/ и оси х.
Особый интерес представляют линии, вдоль которых потенциал
U(z) или функция тока V(z) постоянны. В силу B.2.18) вдоль этих
линий обращаются в нуль подинтегральные выражения в линейном
интеграле B.2.7), соответственно в выражении потока B.2.8), и,
следовательно, wt = 0, соответственно wn = 0. Рассмотрим сначала
линии V(z) = const. На них обращается в нуль нормальная состав-
составляющая wn, а это означает, что вектор ю всюду направлен по
касательным к этим кривым. Таким образом, в поле скоростей
кривые V = const определяют направление потока и являются как
бы непроницаемыми для него. Эти линии называются линиями
тока.
На кривых U = const обращается в нуль тангенциальная со-
составляющая wt. Поэтому эти линии ортогональны в каждой точке
к вектору го, а стало быть и к линиям V = const1. Поскольку вдоль
них линейный интеграл исчезает, то в силовом поле при пере-
перемещении вдоль линии U = const работа равна нулю. Эти линии на-
называю 1ся эквипотенциальными, или линиями равного потенциала.
1 Это утверждение теряет смысл, если w = 0: в этом случае линии равного
потенциала и тока, вообще говоря, не ортогональны. Это возможно, однако,
лишь в отдельных изолированных точках и не играет существенной роли в
основных рассуждениях.
2.3. Пример. Ньютоновский потенциал
25
Представим себе, что линии равного потенциала и линии тока
изображены на чертеже, причем от линии к линии значения U и V
изменяются на одну и ту же величину. Таким образом, на плоскости
г образуется сетка взаимно ортогональных линий {ортогональная
сетка). Можно показать, что эта сетка «в малом» является квадрат-
квадратной, т. е. ее ячейки приближенно имеют форму квадратов, причем
тем точнее, чем они мельче. Это можно усмотреть следующим
образом. Выберем точку z0 с пересекающимися в ней линиями
U = Uo и V = Vo; спрашивается, как расположены линии U = Uo +
+ d и V = Vo + d. Пусть, например,
расстояние (измеренное по перпендику-
перпендикуляру к U = С70) между линиями U = UQ и
U = Uo + d равно а; тогда приближенно
должно быть
Рис. 8.
причем тем точнее, чем меньше а. С другой
стороны, согласно B.2.23),
9С7 _9V
дп ~ ~ds '
Поэтому при перемещении вдоль линии C7=U0 из точки, где V=V0,
на расстояние а величина V изменится приближенно на d (опять-
таки тем точнее, чем меньше а). Линии
U = Un, U = Un
V =
v =vn
d
Jo> ^ — "-'о
образуют, следовательно, квадратную «в малом» ячейку со стороной
а. Ортогональная сетка, квадратная в указанном смысле, называется
изотермической сеткой (такие сетки находят применение в теории
распространения тепла).
Заметим еще, что на линиях U = const величина -— = -?-
ал да
равна модулю вектора ю. Поскольку вдоль них тангенциальная
составляющая wt равна нулю, то шл с точностью до знака совпадает
с модулем ш и
dU ill,
I Л 1 I 1*
По рассмотренной нами сетке можно определить не только на-
направление вектора поля ш, но и его величину: чем гуще сетка, тем
больше этот вектор, и наоборот.
2.3. Пример. Ньютоновский потенциал. Ньютоновское векторное
поле центральных сил тяготения можно представить на плоскости
функцией _ .
ro(z) = - = ^Рг% . B.3.1)
4 J z х2 + у2
lit § 2. Функции комплексного переменного
Вектор поля ш(г) здесь направлен вдоль радиуса-вектора1;
модуль его обратно пропорционален расстоянию до начала коор-
координат2.
Всюду, за исключением точки z = О, это поле соленоидальное
и потенциальное, так что интеграл B.2.12) равен нулю вдоль любой
простой замкнутой кривой, не охватывающей точку z — 0. Интеграл
B.2.13) можно вычислить, введя полярные координаты. Положим
z = g(cos(p + isin(p); B.3.2)
тогда
dz = (cos <p + i sin ф) dg + q (— sin <p + i cos q>) dq> B.3.3)
и
ю(г) = ccy-fring. B.3.4)
Отсюда получаем (полагая z0 = 1)
г г
W(z) = Г w(z) dz=№ + idq> = log Q + iq> = log z. B.3.5)
i l
Эта функция определяет логарифм комплексного числа, причем
основное функциональное уравнение вещественного логарифма вы-
выполняется также и в комплексной области:
logz1z2 = logz1 + logz2. B.3.6)
Это легко проверить, принимая во внимание геометрический
смысл умножения комплексных чисел [ср. A.3.13)]. Сравнивая
B.3.2) с равенствами
z = e'og г = q g/Vj B.3.7)
приходим к формуле Эйлера
ё* = cos I? Л- i sin q>. B.3.8)
Линиями равного потенциала и линиями тока здесь служат
линии log q = const иq> = const, т. е. окружности с центром в начале
и лучи, выходящие из начала. Так как log q —> — оо при р —¦ 0, то
при постоянном шаге эквипотенциальные линии в окрестно<гги
1 Напомним, что оси и и v направлены, как указано в п. 2.2.
* См. примечание 1 на стр. 19. Сравнение B.3.1) с ньютоновскими силами
тяготения вряд ли удачно. Обычно связанный с B.3.1) комплексный потенциал
B.3.5) рассматривают в виде 2qi log в связи с полем точечного заряда
z — а
(а; 2q) или в виде —+ ш. log (z — а) в связи с вихреисточником (а; Q, Г) обиль-
2л 1
ности Q и интенсивности Г (см. [1], [2]). — Прим. ред.
2.3. Пример. Ньютоновский потенциал
27
начала расположены весьма густо, при удалении же от начала они
удаляются друг от друга, так как log q растет значительно медлен-
медленнее, чем д. Таким образом, получается «квадратная в малом» сетка,
о которой шла речь в 2.2. Такую сетку мы назовем полярной сеткой.
Рис. 9.
Данное поле, рассматриваемое как поле скоростей, представляет
собой поле источника, находящегося в начале координат. Так как
функция тока определяет величину потока через кривую, то в нашем
случае поток через дугу, соответствующую углу <р, равен <р; полный
поток составляет, следовательно, 2я.
Взяв интеграл B.3.5) по окружности, обходящей начало коорди-
координат один раз в положительном направлении, получим значение Ъй.
Таким образом, функция log z не является однозначной в области,
содержащей начало координат: ее значение при каждом обходе
начала увеличивается на 2ти. Поэтому общее значение логарифма
комплексного числа определяется равенством
log z = log q + i<p + Inn i, * B.3.9)
где п — любое целое число (положительное или отрицательное).
Обьино ограничиваются значениями у в некотором определенном
28 § 2. Функции комплексного переменного
интервале длины 2я, скажем — п <ц=ек +п, и называют вели-
величину
logp + i> = log z B.3.10)
главным значением логарифма. Отметим, что потенциальная функ-
функция, будучи вещественной частью функции log z, является однознач- •
ной во всей плоскости переменного z.
2.4. Отображения. При геометрическом истолкований функции
комплексного переменного ш(г) можно также рассматривать из
и z как точки комплексной плоскости. Тогда функция ю(г) определяет
некоторое соответствие между точками плоскости г и плоское! и w,
или, как мы будем говорить, отображение плоскости z в плоскость
ш. При этом каждая геометрическая фигура в плоскости z отобра-
отображается в некоторую, вообще говоря, другую фигуру в плоскости ш.
В этой книге мы займемся изучением связи между геометрическим
характером отображения и аналитической структурой определяю-
определяющей его функции.
Мы ограничимся рассмотрением отображений, определяемых
регулярными аналитическими функциями. Частный случай таких
отображений мы уже изучили в п. 2.2: линии равного потенциала и
линии тока представляют собой не что иное, как прообразы коор-
координатных линий Re W = const и Im W = const плоскости W в
плоскости z, определяемые функцией z = z(W), обратной к функции
W(z). Мы установили, что эти линии образуют изотермическую
сетку; значит квадратная сетка, образованная координатными
линиями плоскости (U, V) (которую мы для краткости будем назы-
называть декартовой сеткой), переходит при отображении z(W) в сетку,
являющуюся «в малом» также квадратной.
Предположим сначала, что декартова сетка преобразуется в
квадратную сетку. Легко видеть, что при таком отображении любая
фигура преобразуется в подобную ей фигуру, длины всех отрезков
умножаются на одно и то же число, а углы между линиями не
изменяются. В общем случае естественно ожидать, что такое отобра-
отображение является «в малом» преобразованием подобия, т. е. прообраз
и образ тем «подобнее друг другу», чем меньше их размеры. Это
отображение тем ближе к преобразованию подобия, чем ближе
изотермическая сетка к точной квадратной сетке. При отображении
подобия «в малом» уже не конечные отрезки, а линейные элементы
приобретают множитель, зависящий от точки, но не зависящий от
направления линейного элемента, углы же между кривыми сохра-
сохраняются и в этом случае.
Этим эвристическим рассуждениям можно легко придать вполне
строгий характер. Для этого рассмотрим отображение, определяе-
определяемое аналитической функцией ш(г) в окрестности некоторой
и воспользуемся тем, что существует производная
2.4. Отображения 29
ro'(z), которую мы будем считать отличной от нуля1 в этой
точке. Формулу B.2.14) можно записать в виде
ш(г) - w(z0) = ш'B0) (z - ze) + оA) (z - zn), B.4.1)
где оA) обозначает величину, стремящуюся к нулю при z -» z0.
Вводя по формулам B.2.4) линейные элементы dz и dro, перепишем
B.4.1) следующим образом:
dro = ro'(z0) dz. B.4.2)
Согласно нашим рассуждениям, относящимся к формуле
A.3.13), равенство B.4.1) показывает, что отображение ш(г) в окрест-
окрестности точки z0 приближенно является преобразованием подобия.
Если пренебречь членом, содержащим оA), то можно считать, что
каждый отрезок zoz переходит в отрезок wow (ш0 = ю(гп)), полу-
получаемый из zQz умножением на число | ю'(г0) | и поворотом на угол
arg w'(z0). Таким образом, все линейные элементы поворачиваются
на один и тот же угол, и, стало быть, угол между каждыми двумя
кривыми остается неизменным. Такое отображение называется
поэтому конформным.
При отображении, осуществляемом аналитической функцией,
сохраняются не только утлы, но и направление обхода. Каждая
достаточно малая окружность с центром z0 преобразуется функ-
функцией ш(г) в кривую, близкую к окружности с центром ш0, причем она
обходится в положительном направлении, если в этом же направле-
направлении совершается обход исходной окружности. Можно показать,
что это свойство сохраняется для произвольных кривых: если
простая замкнутая кривая Cz и ограничиваемая ею область Gz пре-
преобразуются соответственно в такого же вида кривую Cw и ограни-
ограничиваемую ею область Gw, то при обходе вокруг области Gz по
кривой Cz в каком-либо направлении обход вокруг области Gw
по кривой Cw совершается в том же направлении.
Существуют отображения, которые сохраняют углы, но из-
изменяют направление обхода. Простейшим примером служит зер-
зеркальное отражение относительно вещественной оси, определяемое
функцией
ш = z. B.4.3)
Такие отображения мы будем называть антиконформными2. После-
Последовательное применение двух антиконформных отображений дает
1 Особенности, возникающие в точках, где w'{z) = 0, мы рассмотрим на
отдельных примерах (см. § 6). Впрочем, здесь справедливо замечание, сделан-
сделанное в конце сноски 1 на стр. 24.
2 Такие отображения называются также конформными отображениями
второго рода. — Прим. ред.
30
§ 2. Функции комплексного переменного
конформное отображение. Любое антиконформное отображение
можно сделать конформным при помощи суперпозиции с преобра-
преобразованием B.4.3). Стало быть, каждое антиконформное отображе-
отображение может быть представлено в виде шA) или w(z), где w(z) —
конформное отображение.
Рис. 10. Соответствие между углами и направлениями обхода
при конформном (слева) и антикбнформном (справа) отобра-
отображении.
Можно показать, что не только каждая аналитическая функция
определяет конформное отображение, но и, обратно, каждое кон-
конформное отображение, т. е. отображение, сохраняющее углы и
направление обхода, определяется некоторой аналитической функ-
функцией1. Для этого рассмотрим отображение, осуществляемое двумя
непрерывно дифференцируемыми функциями с отличным от нуля
якобианом:
u = и(х, у), v = ф-, у),
B.4.4J
\
При этом дифференциалы преобразуются линейно, что в матричной
записи принимает следующую форму [ср. A.3.2)]:
№(*х*у)(*'\ B.4.5)
\dv) \vx vy)\dij)
(du\ [dx\ _ „
Здесь величины I и I I представляют собой линейные элементы
\dv) \dg)
dw и dz в матричной форме. Для того чтобы отображение было
конформным, необходимо, чтобы преобразование линейных эле-
1 Решоние этого вопроса при весьма общих предположениях содержится в
докторской диссертации Ю. Ю. Трохимчука (МГУ, 1960). Там же имеется под-
подробная библиография. — Прим. ред.
3.1. Электрические поля 31
ментов было преобразованием подобия, т. е. матрица из равенства
B.4.5) должна иметь вид A.3.3). Отсюда следует, что
ux = V "х = — «у» B.4.6)
т. е. выполняются уравнения Коши—Римана. Таким образом,
функция
w(z) = u(x, у) + iv(x, у)
аналитична. Поскольку отображение изотермической сетки в декар-
тову сетку конформно, то каждую изотермическую сетку можно
считать состоящей из линий и = const, v — const, таких, что ю =
= и + iu — аналитическая функция, т. е. из линий равного потен-
потенциала и линий тока. При конформном отображении каждая изо-
изотермическая сетка переходит в изотермическую сетку; таким обра-
образом, сетка линий равного потенциала и линий тока переходит в
такую же сетку. Аналитически это означает следующее: если W(z) =
= U(z) + iV(z) — некоторый комплексный потенциал, то функция
B.4.7)
— такого же типа, если z(?) аналитична. Это сразу следует также
из того, что суперпозиция аналитических функций есть снова
аналитическая функция. Пользуясь этим фактом, можно свести
сложные задачи теории потенциала к более простым с помощью
конформного отображения. В следующем параграфе мы позна-
познакомимся с некоторыми примерами.
§ 3. Примеры решения физических и технических
задач с помощью конформных отображений
3.1. Электрические поля. Рассмотрим плоскую пластинку про-
произвольной формы из электропроводящего материала. Разделим
край пластинки на четыре дуги a, j3, у, Ь (см. рис. 11) и приложим
к дуге а постоянный потенциал 0, а к дуге у — потенциал 1. Тре-
Требуется найти поле тока внутри пластинки.
Поместим пластинку в комплексную плоскость г; пусть поле
тока задается комплексным потенциалом W(z), т. е. линиями рав-
равного потенциала U(z) = const и линиями тока У(г) = const. По
предположению, дуги а и у служат линиями равного потенциала:
U(a)=0, U(y)=l. Дуги^З и Ь должны быть линиями тока, поскольку
ток не пересекает эту часть границы. Если, например, на дуге Ь
положить функцию тока равной нулю V{b) = 0, то на |3 функция
V примет некоторое положительное значение Уф) = У*, пропор-
пропорциональное полному току Г.
V* = cl. C.1.1)
32
§ 3. Примеры решения физических и технических задач
Отдельные линии тока разбивают пластинку между /3 и д на
полосы, которые тянутся от а до у и, разумеется, не пересекают
а
v
IV*
Рис. 11.
друг друга. По каждой такой полосе1 протекает часть dl полного
тока, как если бы эти полосы были изолированы друг от друга;
1 Такие полосы, заключенные между линиями тока, называются иногда
трубками тока.
3.1. Электрические поля
33
поэтому каждую полосу можно рассматривать отдельно от осталь-
остальных. Если такая полоса, ограниченная линиями V(z) = VQ и V(z) =
= Vo + dV, достаточно узка, то ее можно рассматривать как
линейный проводник и применять к ней закон Ома.
Выделим малый участок этой полосы длиной dl при ширине
этого участка db; его сопротивление равно
со =
xdl
s~db
C.1.2)
где у. — удельное сопротивление, as — толщина пластинки. При
величине тока dl разность потенциалов на концах участка равна
dU =*
= — dl.
sdb
C.1.3)
Рис. 12.
С другой стороны, так как отображение плоскости z в плоскость
W конформно, то рассматриваемый участок пластинки, пред-
представляющий собой ограниченный линиями равного потенциала и
линиями тока криволинейный прямоугольник со сторонами dl
и db, отображается в прямоугольник со сторонами dU и dV, причем
отношение сторон сохраняется:
dU
dV
_
db *
Вместе с C.1.3) это дает
C.1.4)
C.1.5)
так что множитель с в C.1.1) должен равняться
с = —.
S
C.1.6)
Таким образом, полный ток I определяется функцией V.
3 — 6002
34
§ 3. Примеры решения физических и технических задач
Переходим от отображения элементарного прямоугольника при
помощи функции W(z) к отображению всей пластинки. Поскольку
вдоль каждой линии тока потенциал растет монотонно от 0 до 1,
а функция тока растет от 0 до V* вдоль каждой линии равного
потенциала, пластинка взаимно однозначно отображается на прямо-
прямоугольник
0=s=ReW=s=l, 0 =s= Im W =s= V*.
Это отображение является конформным всюду, исключая, возмож-
возможно, границу, и сводит сложное поле тока к простому полю в пря-
прямоугольной пластинке. Задача об определении поля электрического
'тока при заданных краевых условиях решается, таким образом, при
помощи конформного отображения пластинки на прямоугольник.
Следует заметить, что отношение сторон этого прямоугольника не
произвольно, а определяется формой пластинки и выбором гра-
граничных дуг. При помощи этого отношения, пользуясь C.1.1) и
C.1.6), можно определить полное сопротивление пластинк:
Рис. 13.
\ Обратно, можно экспериментально измерить электрическое
\ пластинки и тем самым определить конформное отображение пль-
! стинки на прямоугольник. Это позволяет решать и более трудные
\ физические и технические задачи, не поддающиеся эксперименталп-
I * ному решению. Так как потенциал поля легко измерить, то сначалс
V
3.2. Гидродинамические поля скоростей 35
определяют линии равного потенциала. «Пластинкой» служит тон-
тонкий слой слабо проводящей жидкости, дуги а и у делаются из
металла, a j3 и Ь — из диэлектрика. Между ос и у устанавливается
постоянное напряжение. Потенциал в произвольной точке можно
измерить при помощи подвижного штифта.
Для этого лучше всего применить схему мостика, изображенную
на рис. 13. Потенциал UA в точке А определяется из равенства
U A— U а _ *?1 (¦> 1 7Ч
( 7
Vv-Ua Rx+R,' КЗЛ-'>
где Ua и Uy — потенциалы на соответствующих дугах. Сопротивле-
Сопротивления Щ и В2 можно выбрать так, чтобы UA принимало любое за-
заданное значение между Ua и Uy. Штифт передвигают в жидкости
до тех пор, пока гальванометр не покажет отсутствия тока; в этой
точке потенциал равен UA. Таким способом можно легко начертить
линию равного потенциала UA.
Линии тока можно определить тем же методом, поменяв места-
местами проводящие и изолирующие края. При этом линии равного
потенциала и линии тока меняются ролями. Математически это
объясняется тем, что функция W — U + iV заменяется функцией
iW = ¦— V + W, которая также является комплексным потен-
потенциалом.
3.2. Гидродинамические поля скоростей1. Течения жидкостей и
газов в практически важных случаях являются — если не точно,
то с достаточной степенью приближения — соленоидальными и
потенциальными, так что к ним применимы рассуждения § 2. Из
многочисленных приложений мы изложим здесь хорошо изученный
случай обтекания профилей. Рассмотрим, например, профиль
крыла самолета в плоско-параллельном потоке2 (рис. 14). Будем
считать, что картина обтекания остается неизменной при переме-
перемещении в направлении, перпендикулярном плоскости чертежа, так
что поле можно считать плоским. Будем предполагать, что оно
соленоидальное и потенциальное.
Представим поле с помощью комплексного потенциала W =
= U + iV. Так как профиль крыла является линией тока, то V(z)
принимает на нем постоянное значение. К этому краевому условию
присоединяется требование однородности поля при бесконечно
большом удалении от профиля, выражающееся в том, что при
| z] -» оо вектор скорости ro(z) стремится к некоторому пределу ш».
1 По поводу изложенного в п. 3.2 и 3.3 см. [3]. — Прим. ред.
2 Этим охватывается и тот случай, когда профиль движется прямолинейно
с постоянной скоростью в покоящейся жидкости. При этом вводится система
координат, движущаяся вместе с профилем.
з»
36
§ 3. Примеры решения физических и технических задач
Третье условие вытекает из поведения интеграла
ф wdz
с
вдоль замкнутого контура, охватывающего профиль. Этот инте-
интеграл не обязательно обращается в нуль, так как поле внутри контура
не всюду определено. Поток через С равен нулю, так как жидкость
не может втекать внутрь профиля и вытекать из него; однако линей-
линейный интеграл может принимать не равное нулю значение Г, не
зависящее от выбора контура. Эта величина называется циркуля-
циркуляцией. Заданием -Г поле однозначно определяется.
i
1
1
1
1
Рис. 14.
Начнем со случая Г = 0. Тогда функция U(z) однозначна.
Будучи непрерывной на профиле, она принимает в некоторых егс
точках наибольшее и наименьшее значения. Эти точки называются
критическими точками потока; в них w(z) = 0, так как wt — — = I
dV
и (поскольку V = const) wn = — —- = 0. Между критическими точка-
точками U(z) монотонно возрастает на обеих сторонах профиля, так чтс
3.2. Гидродинамические поля скоростей 37
U(z), а с ней и W(z) принимает в противолежащих точках профиля
равные значения. При конформном отображении, осуществляемом
функцией W(z), обе стороны профиля в плоскости z переходят
в один и тот же отрезок в плоскости W, параллельный оси U. Таким
образом, рассматриваемое обтекание произвольного профиля
переходит в простое обтекание отрезка, т. е. в невозмущенное
параллельное течение. Обратно, если известно конформное отобра-
отображение внешности профиля на внешность отрезка, то этим опре-
определяется обтекание профиля.
Расположение критических точек течения при этом тоже одно-
однозначно определяется. Однако из физических соображений необ-
необходимо потребовать, чтобы одна из них лежала на заднем конце
профиля. Чтобы достигнуть этого, приходится рассматривать
течения, циркуляция которых отлична от нуля. Такое течение можно
получить, если к рассмотренному выше течению прибавить неко-
некоторое течение Wr(z) с заданным значением Г, не равным нулю,
удовлетворяющее условию
юр —» 0 при | z\ —* оо.
Для построения такого течения рассмотрим сначала частный
случай, когда профиль представляет собой окружность |?) = г
плоскости С, С = I + Щ- Тогда Wr@ принимает вид
Это поле, в сущности, совпадает с рассмотренным в п. 2.3, если не
считать того, что линии тока и линии равного потенциала поменя-
поменялись ролями. Условие обтекаемости здесь выполнено, ибо профиль
| С | = г является линией тока. Циркуляция также принимает тре-
требуемое значение Г, так как log С при обходе вокруг начала увели-
увеличивается на 2га. Наконец,
»Н0-?,?, C.2.2)
так что вектор скорости обращается в нуль на бесконечности.
Для того чтобы получить Wr(z) в общем случае, нужно с помо-
помощью функции z(C) отобразить взаимно однозначно и конформно
внешность круга | ? | = г на внешность заданного профиля. Это
возможно в силу общих теорем об отображениях (см. п. 10.1).
Комплексный потенциал Wr принимает вид
^r(*)=~log?(z). C.2.3)
Значение Г при таком отображении, очевидно, не меняется-
Выбирая это значение, мы можем поместить одну из критических
38 § 3. Примеры решения физических и технических задач
точек в любое место профиля. Если она расположена на заднем
конце профиля, то Г служит мерой подъемной силы профиля.
Эти рассуждения можно распространить на случай обтекания
нескольких профилей. Приведем здесь результаты, касающиеся
двух профилей; в случае большего числа их соотношения анало-
аналогичны. Задача однозначно разрешается при следующих условиях.
Рис. 15. Обтекание профиля с циркуляцией. Слева вверху — чистая циркуляция
C.2.1) вокруг кругового профиля, внизу — чистый параллельный поток, обте-
обтекающий тот же профиль. Справа вверху — наложение обоих обтеканий кругового
профиля, внизу — конформное отображение этого течения, при котором круго-
круговой профиль переходит в заданный профиль, причем задняя критическая точка
переходит в острие профиля.
1. Профили служат линиями тока, V(z) = Vx и V(z) = V2. '
2. При \z\ —* оо поле становится однородным, т. е. w(z)—» ю„.
3. Циркуляции по контурам, охватывающим профили, равны
соответственно Гг и Г2.
Случай Гг = Г2 = 0 вновь соответствует отображению внеш-
внешности профилей на внешность отрезков, лежащих на прямых
V •» Ух и У = V2, причем их длины и взаимное расположение за-
зависят от формы и расположения профилей и направления потока
(см. рис. 16а).
К этому полю прибавляются поля Wr> и Wrt, для которых Гг,
соответственно Г2, отличны от нуля и векторы скоростей обра-
обращаются в нуль на бесконечности. Такое поле можно получить при
помощи конформного отображения t(z), при котором один из
профилей переходит в окружность, а второй — в концентрическую
3.3. Годограф
39
к ней дугу окружности, так что внешность профилей взаимно одно-
однозначно отображается на внешность окружности и дуги (см. рис.
16Ь). В плоскости ? искомое поле вновь определяется формулой
C.2.1), где Г — циркуляция по контуру, охватывающему тот из
профилей, который переходит в окружность; циркуляция же вокруг
второго остается равной нулю. В плоскости z добавочное поле
определяется формулой C.2.3).
Рис. 16а
Рис. 16Ь.
3.3. Годограф. В некоторых случаях при рассмотрении поля
тока целесообразно применять конформное отображение, даваемое
не комплексным потенциалом W(z), а вектором поля w(z) = W(z).
Исследуем, например, течение по каналу, изображенному на рис. 17.
На большом расстоянии от места изгиба течение можно считать
однородным, причем скорость течения обратно пропорциональна
ширине канала:
wi~fti = hvA* C.3.1)
Стенки канала являются, очевидно, линиями тока, например
V(z) = 0 и V(z) = V*, так что при отображении W(z) изогнутый канал
переходит в прямолинейный с параллельными стенками. Отобра-
Отображающую функцию трудно определить непосредственно; легче
рассмотреть отображение, задаваемое функцией w(z). Для этого
мы отметим на плоскости ю точки, принадлежащие одной и той
же линии тока. Линии тока отобразятся в некоторые линии на
АО
§ 3. Примеры решения физических и технических задач
(г)
плоскости w, семейство которых называется годографом течения,
или многоугольником скоростей.
Определим теперь линии, соответствующие стенкам канала.
Отметим1 сначала точки ю1оо и ю2во, которые считаются известными.
Вдоль каждого прямолинейного участка стенки вектор скорости
сохраняет направление; таким образом, стенки канала переходят
в отрезки от 0 до wlao и до w200. Нужно еще проследить за изменением
величины скорости на стенках.
На внешней стороне изгиба
скорость при приближении к
угловой точке уменьшается от
|н»1оо| до нуля, а затем вновь
растет до |н>2~|; образом этой
стенки служит, следовательно,
ломаная (wleo, 0, ю2~)- На дру-
другой стороне скорость растет
сначала от | ю1оо | (теоретически)
до бесконечности2, а затем
вновь убывает до |ю2~1- Весь
канал, таким образом, отобра-
отображается функцией w(z) на угол,
изображенный на рис. 17, при-
причем линии годографа исходят
из точки ю1те и сходятся в точ-
точке ю2те.
Отображение такого угла на
полосу плоскости W, при кото-
котором ю1ао и wZao переходят в бес-
бесконечно удаленные точки, мож-
можно осуществить с помощью
элементарных функций (это бу-
будет показано в § 5—83). Этим
определяются функции w(W)
и W(w). Учитывая, что
ш,
Рис. 17.
— = w(W),
C.3.2)
1 Напомним, что, согласно п. 2.2, вектор w и точка ш располагаются сим-
симметрично относительно оси и; только в этом случае w{z) есть аналитическая
функция, равная производной W(z).
* Поведение потока в угловых точках можно схематически пояснить сле-
следующим образом. Так как линии равного потенциала ортогональны стенкам,
то ни внутренней стороне изгиба они должны беспредельно сгущаться, а на
внешней - разрежаться; в силу рассуждений п. 2.2, величина скорости при
приближении к угловым точкам стремится соответственно к оо и к 0.
» В § 13 мы изложим метод, позволяющий непосредственно отображать
этот канил на полосу. Математически оба метода, очевидно, эквивалентны.
3.3. Годограф 41
получим функцию
W dW
I w(W) '
<з.з.з)
которая является обратной к искомой функции W(z).
Такое решение задачи не вполне удовлетворительно, так как
бесконечно большие скорости физически немыслимы. На внешней
стороне канала вместо полной остановки тока фактически наблю-
наблюдается завихрение, так что исходное предположение о потенциаль-
потенциальности поля не вполне законно.
Для того чтобы наши методы лучше соответствовали действи-
действительности, будем считать, следуя Гельмгольцу1, что вблизи крити-
критических точек образуется «мертвая зона», т. е. зона стоячей воды,
мимо которой без трения и перемешивания с ней протекает осталь-
остальной поток. Границы этой зоны определяются из условия постоян-
постоянства давления внутри нее, и поэтому, согласно уравнению Бернулли2,
величина скорости вдоль всей границы одинакова. Следовательно,
на годографе границы мертвых зон отображаются в дуги окруж-
окружностей с центром в начале. Поэтому годографы целесообразно
применять при изучении задач, связанных с мертвыми зонами.
В данном случае мы решим задачу, отделив физически «сомни-
«сомнительные» точки годографа w = О и w = оо дугами окружностей.
Годограф займет теперь сектор кругового кольца, который также
можно отобразить на полосу функциями, хотя и довольно слож-
сложными, явное выражение которых известно (ср. п. Б 4.2, пример 1,
а также стр. 330). Интегрируя по формуле C.3.3), получаем комплекс-
комплексный потенциал; при этом границы мертвых зон служат образами
дуг годографа.
Осталось еще подобрать радиусы этих дут, с тем чтобы полу-
получить физически правдоподобную картину течения. Радиусы дуг
определяют давление в мертвых зонах и тем самым точки, в кото-
которых течение отделяется от стенок. На внешней стороне изгиба эта
точка заранее нам не известна; она определяется на основе теорети-
теоретических и экспериментальных исследований поведения граничных сло-
слоев3. На другой стороне канала точка отделения известна: она должна
совпадать с угловой точкой. Так как направление течения изменяется
только между направлениями ю1оо и wioo, то течение, покинув
стенку с этой стороны, больше к ней не возвращается, так что
1 См. Helmholtz H., Ober diskontlnulerllche Fltlsslgkeitsbewegungen,
М. В. Preusslsche Akademie, 1868, 215—228.
2 См., например, Sommerfeld A., Vorlesungen tlber theoretische
Physlk, II, Wiesbaden, 1947, S. 82.
8 См., например, Sommerfeld А., цит. раб. стр. 231 и след.
42
§ 3. Примеры решения физических и технических задач
(Z)
мертвая зона распространяется бесконечно далеко1. Поэтому
ширина течения уменьшается от значения Ь„ до Ъ* и соответственно
скорость ш2оо заменяется скоростью го*»; последнее значение
расположено в правом верхнем углу годографа, и при отображе-
отображении на плоскость W эта точка отображается в правую бесконечно
удаленную точку полосы.
Если внешняя дуга годо-
годографа выбрана правильно,
то точка отделения совпада-
совпадает с угловой точкой; если она
слишком мала (или велика),
то точка отделения смещает-
смещается назад (или вперед). Это
соответствует потокам с
мертвыми зонами в каналах
с большей (или меньшей)
шириной Ь„.
3.4. Задачи о кручении2.
В теории упругости при изу-
изучении кручения цилиндри-
цилиндрического стержня возникает
следующая краевая задача:
в некоторой области Gz плос-
плоскости z — сечении скручен-
скрученного стержня — требуется
найти аналитическую функ-
функцию W(z) = U(z) + iY(z),
мнимая часть которой при
приближении к границе С
стремится к значениям
У(.с) = Ц-.
C.4.1)
Рис. 18.
Как будет показано в § 9,
такие краевые задачи реша-
решаются при помощи конформного отображения области G2 на круг.
Когда область имеет форму многоугольника, эту краевую задачу
Можно непосредственно сформулировать как задачу об отобра-
отображении, если наряду с функцией W(z) ввести ее вторую производную
ТУ"(«) = со(г) = jj(z) + iy)(z), которая также является аналитической
1 На самом деле через некоторое время мертвая зона перемешивается с
потоком, так что указанная картина имеет место лишь вблизи точки отделения.
а См. [1] и указанную там литературу. — Прим. ред.
3.4. Задачи о кручении 43
функцией, так как, согласно B.2.19), первая производная аналити-
аналитической функции, а стало быть, и все дальнейшие являются аналити-
аналитическими.
Рассмотрим какую-нибудь сторону этого многоугольника;
согласно A.1.5), ее можно представить в виде
z = гх + Яег\ C.4.2)
где Я — вещественный параметр, Х1 «s Я =s Я2. Тогда а представляет
собой угол между этой стороной и вещественной осью; мы можем
считать, что он удовлетворяет неравенствам — я/2 < a =з л/2.
Согласно C.4.1), на этой стороне
V(A) = - (zx + Хёа) (zx -J- ?.е~'л) = -г [z^ +
+ Я (zie-'« + \&) + Я2]. C.4.3)
Таким образом,
^ = 1. C.4.4)
Можно показать1, что в случае многоугольника функция W(z),
решение краевой задачи C.4.1), аналитична не только внутри,
но и на сторонах этого многоугольника. Таким образом, функция
U(X) определена на рассматриваемой стороне, причем имеет место
равенство
т.е.
dn^)_ Я№ C46)
С другой стороны, как и для вещественных функций,
dW dH
C.4.7)
l*/l~ U.4. I 14/1 I 14*. 14/1
Учитывая, что
* = е<\ ~ = 0, C.4.8)
получаем
d2W n,-_ daW Oj« / \ м i л\
. = е2' —j- := е2' w(z). C.4.9)
Вместе с C.4.4) и C.4.6) это дает
Im(e2'a«)= 1. C.4.10)
1 Подробнее об этом будет сказано в п. 13.4; см. также н. 11.5.
44
§ 4. Конформное отображение поверхностей
г\
Уравнение C.4.10) задает прямую линию в плоскости со, полу-
полученную поворотом прямой Iraco = 1 на угол — 2а (см. рис. 19).
Эта прямая расположена на
у' расстоянии 1 от начала и об-
образует с вещественной осью
угол, равный — 2а. При кон-
конформном отображении при
помощи функции «(г) сторона
C.4.2) переходит в отрезок пря-
прямой C.4.10). Так как эти рас-
рассуждения применимы к каждой
стороне, многоугольник Gz
преобразуется в область Ga,
ограниченную отрезками пря-
прямых и отличающуюся от обыч-
обычного многоугольника тем, что
отдельные части его площади
могут перекрываться1, а неко-
некоторые стороны могут уходить
в бесконечность. Но поскольку
функция co(z) аналитична, а
потому непрерывна2, Ga цели-
целиком, за исключением вершин,
лежит в конечной части плос-
плоскости. Отысканием функции
co(z) мы займемся в п. 13.5.
Функция W(z) вычисляется пос-
после этого двумя интегрировани-
интегрированиями.
Ч>
Рис. 19.
§ 4. Конформное отображение поверхностей
4.1. Общие соображения. Конформные отображения можно рас-
рассматривать не только на плоскости, но и на других поверхностях.
Они тем более интересны, что допускают применение как в теории
потенциала, так и при изучении отображений поверхностей. Сюда
относится, в частности, конформное отображение поверхности
шара на плоскость, необходимое при составлении географических
и астрономических карт, которое и явилось первым практическим
применением этих отображений.
1 Речь идет о многоугольниках с внутренними вершинами. См. ц. 13.4,
а также 5.1.
а В вершинах многоугольника ш(х), вообще говоря, не аналитична.
4.1. Общие соображения 45
Как и при конформных отображениях на плоскости, основная
задача заключается в построении на поверхности изотермической
сетки. Если установить соответствие между двумя различными
изотермическими сетками так, чтобы линии одной сетки переходили
в линии другой," то~ТсваЩЩ]шЖЗВадалш^
преобразуются ТГячёики другой и отображение, таким образом,
конформноТ" Для~ нналит йчёского выражения этих рассуждений
ЗапишемГ уравнение поверхности в параметрической форме:
х = z(|, rj), у = у(|, rj), z = z(|, rj).
Здесь x,y,z — декартовы координаты в пространстве, ? и rj — пара-
параметры. Это представление можно рассматривать как отображение
плоскости с координатами I, щ на поверхность. Предположим, что
в некоторой области это отображение взаимно однозначно и диффе-
дифференцируемо, т. е. частные производные первого порядка по I и rj
непрерывны. Кроме того, будем считать, что не все миноры второго
порядка функциональной матрицы
fa »« ze\
U, уч v
одновременно равны нулю.
Пусть искомая изотермическая сетка задана уравнениями
и = u(|, rj), v = o(f, rj).
Линиями сетки являются кривые u(|, rj) = const, o(|, rj) — const.
Для аналитической характеристики изометрической сетки будем
исходить из уравнений Коши—Римана в форме B.2.23). Приведен-
Приведенные по поводу этих уравнений рассуждения, выясняющие струк-
структуру таких сеток, целиком переносятся на произвольные поверх-
поверхности. Таким образом, для каждой гладкой кривой на рассматри-
рассматриваемой поверхности выполняется равенство
дп - ds ' (ЦЛЛ)
9 - 9
где д- — производная по направлению кривой, g производная
по нормали, направленной так же, как на рис. 7.
Для явного выражения этих производных представим кривую в
параметрической форме:
I = 1@, и = ч@- D.1.2)
Производная ^— есть производная вдоль другой кривой
I = |(т), г) = ф), D.1.3)
46 § 4. Конформное отображение поверхностей
ортогональной к первой. Обозначим линейные элементы этих
кривых через ds и da, тогда, в обычных обозначениях теории по-
поверхностей ,
Е = ж2. + у| + z§, F = xpv + у#ч + zszn, G = 2* + у2 + z2 f
ds2 = (fi|2 + 2Ff,4, + Gq?) d/2, D.1.4)
здесь индексы при I и щ означают дифференцирование по соответ-
соответствующим параметрам. Из формул D.1.4) делением их на ds2,
соответственно на da2, получим следующие соотношения для
производных | и г) по s и а:
Е|? + 2F|S% + Gr% =1,
El2 + 2F|a4o + Grfc = 1. DЛ-5)
Условие ортогональности этих кривых имеет следующий вид:
В|в|„ + F(|s4o + Чв|„) + G4A = 0. D.1.6)
Записав это условие в форме
|„ (В|, + F4s) + Чо (F|s + G4s) - 0, D.1.7)
получаем
I, = М*Ъ + СИ?,), »?О = -^(В^ + -Р%)- D-1.8)
Для определения /х подставим эти выражения для |а и »jo во второе
уравнение D.1.5); учитывая первое уравнение D.1.5), имеем
(j? (EG — F*) = 1 D.1.9)
или, обозначая, как обычно,
У EG — F2 = W,
находим
/* = ^ • DЛЛ°)
Вернемся к уравнению D.1.1). На рассматриваемой кривой
имеем
g= Ds= 0{|s+ Bf|4e, D.1.11)
!? = "„ = "Л + "A- D-1.12)
Принимая во внимание D.1.8) и D.1.10), получаем из D.1.1)
i [(Fu. - Еищ) |s + (Gu, - Fu4) 4J = D-is + Dli4s. D.1.13)
4.2. Отображения сферы 47
Поскольку отношение |s : rjs может быть выбрано произвольно,
функции и(?, rj), р(.?, щ) должны удовлетворять следующей системе
дифференциальных уравнений, являющейся обобщением уравнений
Коши—Римана B.2.18) на произвольные поверхности:
=
D.1.14)
Таким образом, задача о построении изотермической сетки на
некоторой поверхности равносильна1 решению системы D.1.14).
Если в некоторой области поверхности это решение известно, то-
и и v можно принять за новые параметры поверхности2, они назы-
называются изотермическими параметрами. Считая и и v вещественной
и мнимой частями комплексного параметра
го = и + iv,
мы ставим в соответствие точкам поверхности комплексные числа,
подобно тому как это было сделано в п. 1.1 для плоскости. Рассуж-
Рассуждения, проведенные в п. 2.4, переносятся на произвольные поверх-
поверхности следующим образом: если w = u + iv и со — % + п/> — ком-
комплексные изотермические параметры двух поверхностей3, то отобра-
отображение co(w) конформно тогда и только тогда, когда co(w) —¦ аналити-
аналитическая функция.
В следующих двух пунктах мы подробнее рассмотрим случаи
сферической поверхности и тора.
4.2. Отображения сферы. Пусть на сфере задана географическая
система координат. Обозначим долготу через Я, широту через в;
тогда параметрическое представление сферы в декартовой системе
координат имеет вид
х = R cos X cos в, у =R sin Я cos в,
z = Rsm6, D.2.1)
где R — радиус сферы. Линейный элемент на сфере равен
ds2 = К2 cos2 6dX2 + K2d02; D.2.2)
1 Гаусс показал, что система D.1.14) сводится к обыкновенному дифферен-
дифференциальному уравнению, если поверхность аналитична, т. с. ее параметрическое
представление задается аналитическими функциями. По поводу разрешимости
в случае дифференцируемой поверхности см. Lichtenstein L., Bull. Acad*
Cracooie, 1916, 192—217 [см. также [4] гл. III. — Прим. ред.].
2 Для этого необходимо, чтобы соответствие между точками поверхности
и парами значений и, о было взаимно однозначным. Это всегда осуществимо на
малых кусках поверхности.
8 Речь может идти как о двух различных поверхностях, так и о совпадаю-
совпадающих.
48
§ 4. Конформное отображение поверхностей
таким образом,
Е = R2 cos2 в, F = О, G
W = R2 cos в.
D.2.3)
Дифференциальные уравнения D.1.14) для изотермических пара-
параметров и, v принимают вид
cos0 ve = их,
¦ COS0 ия = V, .
D.2.4)
Одно решение этой системы1 можно получить, положив и = Я.
Тогда, так как рл = 0, v есть функция только от в. Из уравнения
cos в ve — 1 следует, что
D.2.5)
Если при помощи этих функций
отобразить сферу на комплексную
плоскость ш, то меридианы и
параллели преобразуются в пря-
прямые и = const и v = const, парал-
параллельные осям, а вся сфера пере-
переходит в вертикальную полосу,
например
—JI<U=S+JI, —oo<D<+oo.
Это отображение называется
проекцией Меркатора. При этом
области, лежащие вблизи эква-
экватора, почти не испытывают иска-
искажений, с приближением же к по-
полюсам искажение сильно увеличи-
увеличивается; самим полюсам не соот-
соответствуют никакие конечные точки
плоскости w (рис. 20). Это связано
с тем, что линии и = const
Рис. 20. Проекция Меркатора. на сфере сходятся в полюсах, и поэ-
поэтому линии v = const сжимаются
вокруг них, как и на полярной сетке, рассмотренной в п. 2.3. Если
мы хотим отобразить на плоскость хотя бы один из полюсов, то
целесообразно преобразовать изотермическую сетку не в декар-
в(Г
20°
-№
-60°
-80°
-88'
о"-е
7—,—
0—6
о-п
и-Х
1 Достаточно найти хотя бы одно решение и, о. Остальные являются анали-
аналитическими функциями этого частного решения w = u + i".
4.2. Отображения сферы
49
тову, а в полярную сетку на плоскости. Пусть на плоскости С
полярная сетка задана уравнением С = Qe'f; тогда следует поло-
положить1
и =q>, v = — log q,
или, в сферических координатах А и в,
D.2.6)
D.2.7)
Это отображение называется стереографической проекцией.
Его можно получить чисто геометрически проектированием точек
сферы на плоскость. Для простоты будем считать, что радиус
сферы R равен 1. Проведем
плоскость через экватор и
будем проектировать точки
сферы из южного полюса на
эту плоскость (рис. 21). Ясно,
что при таком проектиро-
проектировании А и 9? совпадают.
Далее, угол при вершине S
равен j— _-, так что MQ=
таким
образом, наше построение
полностью согласуется с
уравнениями D.2.7). Кон-
Конформность отображения
также можно усмотреть из
геометрического построе-
построения. Для этого следует
учесть, что треугольник PAQ на рис. 21 — равнобедренный
(AQ — АР), так что проектирующий луч SQP пересекает плоскость
С и сферу под равными углами.
Стереографическая проекция не только конформна, но и обла-
обладает круговым свойством, заключающимся в том, что окружности
и прямые плоскости С отображаются в окружности на сфере, и
обратно. Для того чтобы это показать, запишем уравнения сферы
D.2.1) с помощью комплексного параметра С; получим
Рис. 21. Стереографическая проекция.
х =
1+СС
z = — Ц . D.2.8^
1-КС
1 Заметим, что функция — log о гармонически сопряжена с функцией
4 — 6002
50 § 4. Конформное отображение поверхностей
Окружность на сфере можно получить как пересечение сферы с
плоскостью
ах + by + cz + d = 0; D.2.9)
подставляя сюда величины D.2.8), находим
(d — с) ^ + (а — ib) С + (а + ib) I + (d + с) = 0. D.2.10)
Это, как легко видеть, уравнение окружности A.1.3), вырождающей-
вырождающейся в прямую, когда с = d. Плоскость D.2.9) проходит в этом случае
через южный полюс х = 0, у = 0, z = — 1, что видно и из рис. 21.
В отличие от проекции Меркатора стереографическая проекция
дает взаимно однозначное отображение всей плоскости на поверх-
поверхность сферы. Исключение составляет лишь южный полюс, которому
не соответствует никакая точка плоскости. Это исключение можно
устранить, присоединяя к собственным точкам плоскости так
называемую «несобственную», или бесконечно удаленную, точку1
С = оо и считая, что она соответствует точке S сферы. Эта несоб-
несобственная точка не изображается никаким комплексным числом, так
как невозможно расширить семейство комплексных чисел введе-
введением «несобственного числа», не придя при этом в противоречие
с правилами действий2. Однако на сфере можно рассматривать
преобразования, являющиеся конформными и на южном полюсе,
и, обратно, переводящие произвольную точку сферы в южный
полюс и конформные в этой точке. В таких случаях имеет смысл
приписывать функциям определенное значение в точке оо и, обрат-
обратно, допускать оо в качестве значения функции. Мы будем писать,
например, го(оо) = a, w(a) = оо, го(оо) = оо.
Примером такого конформного отображения окрестности юж-
южного полюса служит следующее преобразование сферы:
/.*=—)., в*= — 0. D.2.11)
Геометрически это отображение представляет собой поворот вокруг
отрезка, соединяющего две противоположные точки экватора
д = 0, Я = 0 и Я = тс, при котором северный и южный полюсы ме-
меняются местами. Ясно, что это преобразование взаимно одно-
однозначно и конформно на всей сфере, так как оно представляет собой
чистый поворот. Соответствующее преобразование плоскости С
задается аналитической функцией
С* = \ . D.2.12)
J Название «бесконечно удаленная» оправдывается тем, что при прибли-
приближении точки Р к южному полюсу точка Q неограниченно удаляется от начала.
2 Например, выражения 0 • сю, — не могут быть однозначно определены.
оо
Для того чтобы полностью описать этой функцией преобразование
сферы, следует пополнить области ее определения и значений соот-
соответственно точками С = о°"и ?* = °°. Положим
С* = оо при ? = О,
у* л г- D.2.13)
С* = 0 При ? = оо.
При этих условиях мы можем исследовать и поведение других
комплексных функций в точке оо, не обращаясь к преобразованиям
сферы. Введем определения.
1. Функция w(z) конформно отображает окрестность конечной
точки z = г0 в окрестность1 точки w = оо, если функция w*(z) =
= —г- конформно отображает окрестность точки z0 в окрестность
нуля.
2. w(z) конформно отображает окрестность точки z = оо в
окрестность конечной точки w = ю0, если функция w(z*) = ю 1 — 1
конформно отображает окрестность точки г* == 0 в окрестность
точки w = и>0.
3. w(z) конформно отображает окрестность точки z = оо в
окрестность точки w = оо, если w*(z*) = конформно отобра-
| I
жает окрестность точки z* = 0 в окрестность точки w* = 0.
Точно так же можно охарактеризовать поведение функции в
особой точке г = оо. Основные понятия, введенные в п. 2.1, пере-
переносятся на точечные множества, содержащие точку оо, если кон-
конформно отобразить эти множества на ограниченные.
Заметим, что рассмотрение преобразований сферы привело нас
к представлению бесконечности на комплексной плоскости в виде
одной точки, в отличие, например, от проективной геометрии на
плоскости, в которой бесконечно удаленные элементы образуют
прямую линию. Такое представление бесконечности содержит
некоторый элемент произвола. Представление, которым мы здесь
пользуемся, имеет то преимущество, что плоскость, как и сфера,
становится замкнутой поверхностью и приобретает весьма простую
топологическую структуру2.
1 Термин «окрестность» понимается здесь в более широком смысле, а именно
окрестностью мы называем любое множество, содержащее окрестность вида
B.1.2).
2 Можно также при помощи D.2.7) поставить во взаимно однозначное
соответствие точкам сферы комплексные числа (включая оо). Мы говорим тогда
о числовой сфере, в отличие от введенной в п. 1.1 числовой плоскости. На этой
сфере многие предложения геометрической теории функций выражаются весьма
просто и наглядно, поскольку точка оо не является исключительной.
4*
52 § 4. Конформное отображение поверхностей
4.3. Отображения тора. Тор есть поверхность, образованная
вращением окружности вокруг оси, лежащей вне ее (рис. 22). Обо-
Обозначая радиус окружности через г, расстояние ее от центра до оси
через R, длину дуги окружности через в и утол поворота через А,
получаем параметрическое представление поверхности тора:
х «= (R + г cos 0) cos А, у = {R + г cos в) sin I, z = г sin 0. D.3.1)
Линейный элемент равен
ds2 = (Л + г cos вJ d№ + г2 dO2, D.3.2)
откуда
JS = (Л + rcos вJ, F = О, G = г2, W = r(R + rcos 0).
Уравнения D.1.14) принимают вид
у + cos
\ve = щ, —[j + cos 0J ив =¦ юд. D.3.3)
Рис. 22.
Как и в п. 4.2, можно положить и = Я; тогда v становится функцией
только от 0. Из первого уравнения D.3.3) следует, что
—r. в
4«
/m r rd6 r ][R—r
^ = J Л+T^os в = у^^ ЯГС tg Г ~RT~r
При изменении 0 от нуля до 2я функция г>@) возрастает на величину
71Г
со = ,,-_— . D.3.5)
4.3. Отображения тора 53
Полная поверхность тора отображается на прямоугольник плоско-
плоскости w
0<и^2л, 0 < v^co.
Соответствие между точками тора и точками плоскости w не
является однозначным, так как и(Х) возрастает на 2л при обходе
вдоль линии v = const, a v(fi) — на со при обходе вдоль линии и =
= const. Каждой точке тора соответствует, таким образом, беско-
бесконечное множество точек w + ncoi + 2тл, где пит — любые целые
числа. Возникает вопрос: существует ли однозначное отображение
тора на комплексную плоскость? Такое отображение всегда можно
осуществить с помощью комплексной функции z(w). Для ее одно-
однозначности на торе необходимо, чтобы она принимала равные зна-
значения во всех точках w, соответствующих одной и той же точке
тора, т. е.
z{w + ncoi + 2пт) = z(w). D.3.6)
Иначе говоря, z(w) есть двоякопериодическая функция с периодами
coi и 2л. Таким образом, задача об однозначном конформном
отображении тора на плоскость решается с помощью двояко-
периодических аналитических функций. Это отображение, однако,
не может быть взаимно однозначным ввиду различия в характере
связности тора и плоскости1. Мы можем сделать его таким, если
равным значениям z, соответствующим различным точкам тора,
поставим в соответствие точки на различных экземплярах комплек-
комплексной плоскости, а затем эти плоскости (листы) соответствующим
образом склеим. С такими образами (которые называются римано-
выми поверхностями) мы встретимся в следующем параграфе.
1 Не каждая замкнутая кривая на торе может быть стянута непрерывным
образом в точку; таковы, например, линии и = const, v = const.
ПРОСТЕЙШИЕ КОНФОРМНЫЕ ОТОБРАЖЕНИЯ
§ 5. Логарифмическая функция
5.1. Римаиова поверхность. Как было установлено в п 2.3, функ-
функция w = log z, точнее, обратная к ней функция z = ew, отображает
декартову сетку плоскос-
плоскости | Гк /¦¦ ^ ти ш в полярную сетку
плоскости z. Обозначая
z = о (cos (р + i sin <р),~„ О
w = и + iv,
получим
и = log р, » =(р. E.1.1)
В частности, при этом
отображении прямо-
прямоугольник
х
E.1.2)
преобразуется в кольцевой
сектор (см. рис. 23)
¦ ® е"^еДе^' EЛ)
Если Uj —» — оо, то пря-
прямоугольник превраща-
превращается в полуполосу,а коль-
кольцевой сектор — в круго-
круговой сектор. Если к тому
же ч2 —* + оо, то получа-
получаемая при этом горизон-
горизонтальная полоса преобра-
и зуется в угловую область.
Картина, возникаю-
возникающая при возрастании v
и v2, не столь наглядна
При этом сначала увеличивается угол, занимаемый кольцевым сек
тором, но лишь до тех пор, пока v2 — vx < 2п. Если же о2 — ^==271
Vj.
Рис. 23.
5.1. Римановаповерхность
55
то в плоскости z мы возвращаемся к исходной точке и отобра-
отображение становится многозначным; как мы видели в B.3.9), точкам w,
отличающимся на кратное 2яг, соответствуют равные значения z.
Можно, однако, получить взаимно однозначное отображение,
если вместо обычной плоскости z ввести более сложную поверх-
поверхность, многократно накрывающую плоскость. В этом случае
каждому комплексному числу соответствует не одна точка, а целое
семейство точек, расположенных над одной и той же точкой
плоскости z, но на различных листах поверхности. Эта поверх-
поверхность отображается на плоскость w таким образом, что различным
точкам семейства w + 2tmi отвечают различные точки поверх-
поверхности, находящиеся над одной и
той же точкой z = ew, но на (г) сш)
различных листах.
Точная структура этой поверх-
поверхности — мы назовем ее римановой
поверхностью, соответствующей
функции log z, — определяется из
требования конформности, а сле-
следовательно, и непрерывности отоб-
отображения. Исходя из этого требова-
требования, мы строим риманову поверх-
поверхность следующим образом. Взяв
прямоугольник E.1.2), располо-
расположим соответствующий ему коль-
кольцевой сектор на одном из листов
поверхности и этот лист обозна-
обозначим номером 0. Продолжим пря-
прямоугольник в сторону возрастания
?>2, присоединяя к нему прямо-
прямоугольники ?>2«= и«= j;35 j73«= j;«= г,4 и т. Д-! причем каждый раз
vv — vv_1 < Ъг. Этим прямоугольникам соответствуют круговые
секторы вида E.1.3); для сохранения непрерывности отображения
мы будем соединять их между собой в том же порядке, что и исход-
исходные прямоугольники. Через несколько шагов первый кольцевой
сектор будет перекрыт с одним из последующих; таким образом,
мы попали на следующий лист римановой поверхности — скажем,
лист № 1. Продолжая этот процесс, мы будем вновь и вновь накры-
накрывать одни и те же секторы, получая тем самым дальнейшие листы
римановой поверхности, расположенные в виде винтовой поверх-
поверхности. Та же картина наблюдается и при движении в обратную
сторону: мы приходим к листам с номерами —1, —2 и т. д.
Расширяя кольцевые секторы до полных угловых областей, как
это описано выше, мы получаем полную риманову поверхность
функции log z, являющуюся образом всей плоскости ю. Она закручи-
Рис. 24.
56
§ 5. Логарифмическая функция
вается вокруг начала координат бесконечно много раз в обе стороны,
напоминая винтовую поверхность.
Описанным приемом можно построить римановы поверхности
для других многозначных функций. К общему принципу построения
таких поверхностей мы вернемся в п. 9.4.
5.2. Преобразование некоторых линий. Рассмотрим сначала
образ произвольной прямой
ю = ю0 +;.»!
при отображении z = ew.
Мы получаем
г = е"°+Лц1
E.2.1)
т. е.
©
Рис. 25.
5.2. Преобразование некоторых линий
57
Это логарифмическая спираль; в частности, при иг = 0 получается
окружность, а при v, = 0 — прямая, проходящая через начало.
Декартова сетка в плоскости w, повернутая по отношению к системе
координат, преобразуется в сетку логарифмических спиралей.
Рассматриваемая в поле скоростей, она представляет собой нало-
наложение источника и вихря; мы говорим тогда о вихреисточнике.
Выделяя из этой сетки две линии тока, мы получаем криволинейную
полосу, ограниченную лога-
логарифмическими спиралями, ко-
торая рассматривается в тех-
нике в связи с ротационными
компрессорами (рис. 25).
Прямую в плоскости z
можно представить в следую-
у|
щем виде:
Im ze-'"» = г. E.2.2)
Здесь г есть расстояние этой
прямой от начала, ср0 — ее угол
с вещественной осью. В поляр-
полярных координатах это урав-
уравнение запишется в форме
q sin (tp — q>a) = г. E.2.3)
В плоскости w это дает
e"sin(y— 9?0) = г E.2.4)
или
и = log г — log sin (v ~ <р0).
E.2.5)
о] 1
Рис. 26.
При изменении г и<р0 эти кривые
переходят друг в друга при
параллельном переносе в плоскости w. Исключение составляют
кривые г = 0; это кривые v = tpa, т. е. прямые, параллельные оси и.
На основании этих рассуждений легко построить образ декартовой
сетки в плоскости z при отображении на плоскость и>. Он изобра-
изображен на рис. 26, где мы ограничили изменение угла q> в пределах от
нуля до ~ . Продолжение этого отображения на риманову поверх-
поверхность логарифмической функции приводит к повторению полу-
полученной сетки в плоскости w.
§ б. Степенная функция
§ 6. Степенная функция
6.1. Общие соображения. Отображение при
степенной функции
Рис. 27.
помощи общей
w = za F.1.1)
с произвольным комплексным а удоб-
удобнее всего рассматривать, предвари-
предварительно прологарифмировав F.1.1):
log гг> = a log z. F.1.2)
Если положить log z = t и log w = т,
то F.1.2) в этих переменных есть
взаимно однозначное отображение
плоскости / на плоскость г, а именно
преобразование подобия. Поэтому
F.1.1) — взаимно однозначное отоб-
отображение римановои поверхности лога-
логарифмической функции над плоскостью z
на такую же поверхность над плос-
плоскостью ю. Точнее, при этом полярная
сетка в плоскости z преобразуется в
декартову сетку в плоскости /; в плос-
плоскости t она поворачивается и растя-
растягивается и отображается в сетку вих-
реисточника в плоскости w (см. п. 5.2.).
Если а вещественное или чисто мнимое,
то эта сетка также полярная.
Для практических применений наи-
наиболее важны степени с вещественными
показателями. Полагая z = де'^, w = ге*°,
переписываем F.1.1) в виде
г = оа, в = аир. F.1.3)
При этом угловая область плоскости
z переходит в угловую область плос-
плоскости и> ¦ с углом, отличающимся от
исходного множителем (а|. Верхняя
полуплоскость z переходит в угловую
область с углом ад, а декартова сетка
(сетка параллельного течения) — в сетку
течения, огибающего угол (см. рис. 28).
Отображение не конформно в точке
z = 0, соответственно w = 0, так как все
углы в этих точках умножаются на а.
6.1. Общие соображения
59
Если показатель — рациональное число а = p/q, то для уста-
установления взаимно однозначного
использовать полную римано-
ву поверхность логарифми-
логарифмической функции. Именно, при
увеличении ц> на 2nq угол 6
увеличивается на 2лр, т. е. q
полным оборотам вокруг точки
z = 0 соответствуют р оборо-
оборотов вокруг точки w = О, так
что мы возвращаемся к исход-
исходным точкам как в плоскости z,
так и в плоскости w. Поэтому,
соединив q-vi лист над плоско-
плоскостью z с первым и р-й над плос-
плоскостью w с первым1, приходим
к взаим но однозначному отоб-
отображению q-листной поверхно-
поверхности над плоскостью z на
р-листную поверхность над
плоскостью w. В частности,
функция w = zn при натураль-
натуральном п отображает обычную
плоскость z на n-листную по-
поверхность указанного типа. В
этом случае w{z) аналитична
также и в точке z = 0. Так как
производная в этой точке равна
нулю, то отображение в ней не
конформно; все углы умно-
умножаются на п. Таким свойством
обладает каждая аналитическая
функция в окрестности точки,
в которой производная поряд-
порядка п отлична от нуля, а все
предыдущие равны нулю. Это
имеет место и для соответ-
соответствующей римановой поверх-
поверхности: если z0 — такая точка,
то полному обходу вокруг
нее соответствует п-кратный
соответствия не обязательно
У
х
Рис. 28.
Рис. 29. Риманова поверхность
функции 22.
1 При этом соединении приходится пересекать остальные листы (см. рис. 29).
(Указанное сседтеше следует понимать как отождествление соответст-
соответствующих краев. Пересечен! е лустсв при построении римановой поверхности
не проводится. — Прим. ред.)
60
§ 6. Степенная функция
©
обход вокруг ее образа ш„; риманова поверхность в окрестности w0
состоит из п листов, ветвящихся вокруг нее. Точка ю0 называ-
называется п-кратной точкой разветвления этой поверхности, или
точкой ветвления (п — 1)-го порядка.
6.2. Функция ш = z2.! В качестве примера степенной функции
мы рассмотрим подробнее функцию ш = г2. В декартовых коорди-
координатах z = х + iy, w = и 4- 'я преобразование имеет вид
и = х2 — у1, v = 2xij. F.2.1)
Кривые и = const и v = const—равнобочные гиперболы. Декартовой
сетке в плоскости w соответствует, таким образом, сетка гипербол
в плоскости z, изображенная на рис. 30. При этом следует учесть,
что риманова поверхность
над плоскостью w двулист-
двулистна; если рассматривать
каждый лист в отдельности,
произведя, например, разрез
по отрицательной вещест-
вещественной полуоси, то функция
w = z2 отображает плоскость
w с разрезом на правую,
соответственно левую, полу-
полуплоскость. Сетка гипербол
изображает два встречных
течения, движущихся в вер-
вертикальном направлении и
разделенных горизонталь-
горизонтальной стенкой. Точка z = 0
является критической точ-
точкой течения, от которой оно
расходится в обе стороны.
Заметим, далее, что пово-
повороту сетки гипербол в плос-
плоскости z соответствует, в силу
F.1.3), удвоенный поворот
декартовой сетки в плоскос-
плоскости w. Поэтому каждая пря-
прямая в плоскости w служит
Рис. 30. образом равнобочной ги-
гиперболы В ПЛОСКОСТИ Z.
Прямым х = const соответствуют в плоскости w параболы с
осями, совпадающими с осью и, и с общим фокусом в начале (софо-
кусные параболы). Уравнения этих кривых получаются из F.2.1),
если считать х постоянным, а у — переменным параметром. По-
Поменяв ролями х и у, приходим к семейству, симметричному с
6.2. Функция w=
61
исходным относительно оси v. Эти два семейства софокусных
парабол образуют параболическую сетку, в которую отображается
декартова сетка плоскости z при помощи функции w = z2. Прямая
у = 0 переходит в вырожденную параболу: проходимую дважды
положительную полуось и; соответственно х = О — в отрицательную
полуось и. Ось х отображается, таким образом, в разрез вдоль
положительной полуоси и; внешности этого разреза соответствует
полуплоскость Im z > 0. При помощи поворотов можно показать,
что каждая прямая плоскости z преобразуется в параболу или в
разрез плоскости и>.
В силу F.1.3) полярная сетка плоскости z переходит в полярную
сетку плоскости ю. Конечно,
предполагается, что полюсы
этих сеток расположены в
начале координат. Рассмот-
Рассмотрим теперь преобразования
полярных сеток с полюсами
в других точках. Если интер-
интерпретировать полярную сетку
как поле источника, то ее
характер сохраняется при
отображении. Конформ-
Конформность отображения сказы-
сказывается в первую очередь
вблизи источника, тогда как
по мере удаления от него
линии равного потенциала
и тока все более и более
искажаются по сравнению с
исходными. Такую сетку
можно рассматривать как
поле источника, искаженное
внешними условиями.
Начнем со случая, когда
полюс сетки в плоскости w
находится в точке w — \.
Этой точке соответствуют
точки 2=1 иг = — 1, так
что можно считать, что образ
этой сетки в плоскости z
представляет собой наложение полей двух источников, располо-
расположенных в точках z = 1 и z == — 1. Это легко проверить. Потенциал
«невозмущенного» поля источника в плоскости ю равен
Рис. 31.
W = log (ю — 1).
F.2.2)
62
§ б. Степенная функция
v'
Отображение w = z2 дает
W = log (z2 — 1) = log (z — 1) + log (z + 1), F.2.3)
т. е. действительно наложение полей двух источников. Эквипотен-
Эквипотенциальные линии этого поля U(z) = const определяются уравне-
уравнением
z — 111 z + 11 = const.
F.2.4)
Как видим, вдоль этих ли-
линий произведение расстоя-
расстояний до точек z = + 1 пос-
постоянно; они называются
кривыми Кассини. В част-
частности, линия
к—1||г+ 1|= 1 F.2.5)
называется лемнискатой
Бернулли; она является об-
образом окружности, прохо-
проходящей через точку ш = 0.
Линии тока^= const, полу-
получаемые как образы прямых
в плоскости w, представля-
представляют собой равнобочные ги-
гиперболы, пересекающиеся в
точках г = 1 и z = — 1
(рис. 32).
Для подобного истолко-
истолкования отображения поля
источника с полюсом z = 1
Рис 32. на плоскость ¦> w следует
учесть, что вся плоскость z
отображается на двулистную риманову поверхность над плоскостыо
w. Таким образом мы получаем поле источника на двулистной
поверхности, причем источник лежит на одном листе, а^жидкость
растекается по обоим листам. Для определения линий равного
потенциала и линий тока заметим, что линии тока, будучи
образами прямых в плоскости z, являются параболами. Линии же
равного потенциала являются образами окружностей
z = 1 + Re'v, F.2.6)
где К — радиус окружности, а у — текущий параметр (угол между
радиусом-векгором и осью х). Тогда
F.2.7)
63. w ¦¦
63-
— параметрическое уравнение эквипотенциальных линий в плоско-
плоскости w. При R = 1 получаем кардиоиду (рис. 33).
6.3. w = г~л. Как показано в п. 4.2, это отображение можно
интерпретировать как поворот сферы. В плоскости оно представляет
собой взаимно однозначное соответствие между плоскостями z и w,
расширенными добавлением
точек z = оо и w = оо;
римановы поверхности сов-
совпадают здесь с обычными
плоскостями. Из всех осталь-
остальных степенных функций
этим свойством обладает
"только функция w = г.
Формулы F.1.3) прини-
принимают вид
r-i, e--9. F.3.1)
Рассматривая каждое из
уравнений F.3.1) в отдель-
отдельности, мы получим два про-
простейших антиконформных
отображения («отражения»
или «симметрии»; ср. п. 2.4):
w = г*
F.3.2)
F.3.3)
суперпозиция которых дает F.3.1). Формулы F.3.2) означают пере-
переход к комплексно сопряженному числу, т. е. зеркальное отражение
относительно вещественной оси. Отображение F.3.3) можно также
понимать как отражение, ноле на плоскости, а на сфере. Из D.2.7)
и второго равенства D.2.11) вытекает, что формулы F.3.3) означают
замену северной широты на южную, т. е. зеркальное отражение
относительно плоскости экватора. Поэтому преобразование F.3.3)
принято называть зеркальным отражением относительно единич-
единичной окружности (т. е. окружности q = 1), а также инверсией.
Инверсию можно охарактеризовать чисто геометрически и в
плоскости. Будем исходить из того, что каждая плоскость, про-
проходящая через две точки, симметричные относительно экваториаль-
нэй плоскости, ортогональна к последней. Эти плоскости пересе-
пересекаются со сферой по окружностям, ортогональным к экватору.
64
§ б. Степенная функция
Поскольку стереографическая проекция конформна и сохраняет
окружности, то и в плоскости все окружности, проходящие
через две точки, симметричные относительно единичной окруж-
окружности, ортогональны к последней. На основании этого свойства
можно следующим образом определить понятие зеркального отра-
отражения (инверсии) относительно произвольной окружности: две
точки симметричны относительно окружности К, если каждая
окружность, проходящая через обе точки, ортогональна-К. Частным
случаем является обычное зеркальное
отражение относительно прямой.
Для того чтобы, согласно этому
определению, построить точку Р*, сим-
симметричную заданной точке Р, нужно'
провести через Р две окружности, ор-
• тогональные к К. Вторая точка пере-
пересечения этих окружностей и есть иско-
искомая точка Р*. Одной из таких «окруж-
«окружностей» является прямая, проходящая
через Р и центр окружности К. Если
Р лежит вне окружности К, то для
построения второй ортогональной
окружности проведем касательные к К
через точку Р; центр искомой окруж-
окружности лежит на середине отрезка,
соединяющего Р и точку касания В
(см. рис. 34). Выполнив это построение, находим, что точка
пересечения ортогональных окружностей лежит на отрезке, со-
соединяющем обе точки касания. Точку Р* можно, таким образом,
определить при помощи этого последнего отрезка. Проводя это
построение в обратном порядке, можно определить точку, сим-
симметричную точке, лежащей внутри К. Из этого построения
вытекает равенство
Мр • Щ>* = ЩР = д2, F.3.4)
где К — радиус окружности К. При R = 1 приходим вновь к F.3.3).
г Для более полной характеристики отображения инверсии уста-
установим прежде всего, что оно антиконформно и сохраняет окружно-
окружности. Оба эти свойства вытекают из связи этого отображения с
симметрией на сфере и из кругового свойства стереографической
проекции. Далее, при инверсии внутренность круга переходит в его
внешность; в частности, центр •— в бесконечно удаленную точку.
Точки самой окружности К остаются неподвижными. Поэтому
каждая окружность, пересекающая К в двух точках, преобразуется
в окружность, проходящую через те же две точки. Поскольку ото-
отображение антиконформно, полученная окружность образует с К
Рис. 34.
6.3. w-
,—1
65
такой же угол, что и исходная, но, как и при отражении относительно
прямой, откладываемый в противоположном направлении (см.
рис. 35). В частности, каждая ортогональная к К окружность преоб-
преобразуется в себя.
Вернемся к преобразованию ш = z-1. Как установлено выше,
оно является результатом последовательного применения зеркаль-
зеркальных отражений относительно единичной окружности и вещественной
М
Рис. 35.
Рис. 36.
оси. Таким образом, оно сохраняет окружности и меняет местами
f' внутренность единичного круга с его внешностью и верхнюю полу-
полуплоскость с нижней. При этом единичная окружность и веществен-
вещественная ось, а также все окружности, ортогональные к той и другой
одновременно, переходят в себя1. Эти окружности образуют пучок2,
разделяющий точки +1 и —1 (рис. 36). Точки + 1 преобразуются
в себя и являются, таким образом, неподвижными точками отобра-
отображения. Каждая окружность, проходящая через них, переходит в
окружность, также проходящую через них. Последовательное отра-
отражение относительно единичной окружности и вещественной оси
означает для малых окрестностей точек + 1 поворот на 180° 3; тем
самым окружности, проходящие через эти точки, преобразуются в
себя. Этот пучок образует вместе с ранее рассмотренным ортого-
1 Если рассматривать их как целое, а не как совокупность отдельных
точек.
2 Пучком окружностей в аналитической геометрии называется совокупность
окружностей, ортогональных к двум различным окружностям (в частности,
прямым). См. Caratheodory С, FuiikUoiirnUicoric I, S. 46 ff, Basel,
1950. (См. также [5]. - Прим. ред.)
3 На сфере, как мы видели, преобразование w = z~x является поворотом
на 180° вокруг оси, проходящей через эти точки.
5 — 6002
66 § б. Степенная функция
нальную сетку1. Каждая окружность одного пучка пересекает каж-
каждую окружность другого пучка в двух точках, соответствующих
друг другу при отображении w = z-1.
Декартова сетка плоскости ш, в силу сохранения семейства
окружностей, переходит в сетку окружностей. Рассмотрим
сначала линии и = const. Соответствующие окружности определя-
определяются следующими условиями.
1. Все они проходят через начало координат, так как прямые в
плоскости w проходят через бесконечно удаленную точку.
2. Все они ортогональны к вещественной оси, в силу конформ-
конформности.
Таким образом, линии и = const переходят в окружности*
касающиеся мнимой оси в начале координат. Их расположение
определяется заданием второй точки пересечения с вещественной
осью; образ прямой и = и0 пересекает вещественную ось в точке
—. Поворачивая этот пучок на 90°, получим образы линий v — const.
Оба пучка образуют изотермическую сетку окружностей, изобра-
изображенную на рис. 37.
Физически такая сетка представляет поле диполя. Пусть источник
с потенциалом W = log (z + s), расположенный в точке z = —s, и
сток с потенциалом W — —log (z — s), расположенный в точке
z = +s, стягиваются к началу координат при одновременном уве-
увеличении их интенсивности на множитель Bs)-1; тогда в пределе
имеем
^диполя = lim I- [log (z+s)- log (z - a)] = I . F.3.5)
s—>0
Таким образом, WflHnoJ1H = w = z~\
Как и в п. 6.2, возникает вопрос об отображении поля источ-
источника, помещенного в точку w = 1. В нашем случае из равенства
W — log (w — 1) получаем
I — 1 ] = bg (z — 1) — log z + in, F.3.6)
т. е. с точностью до аддитивной постоянной2 in, наложение полей
источника в точке z = 1 и стока в точке z = О3. Соответствующая
1 На сфере эта сетка представляет собой сетку географических координат с-
полюсами в точках + 1. Первое семейство — семейство параллелей, второе —
семейство меридианов.
1 Аддитивная постоянная означает для потенциала W(z) лишь изменение
нижнего предела интегрирования z0 в B.2.13).
8 На сфере одно лишь поле источника W = log z уже является сочетанием
полей источника и стока, так как жидкость, растекающаяся в бесконечность,
собирается в южном полюсе. Подобно этому параллельный поток можно рас-
рассматривать на сфере как поток диполя в южном полюсе.
6.4. ш
67
сетка линий равного потенциала и тока называется сеткой источ-
источника и стока. Это снова сетка окружностей, причем линиями тока
являются те окружности, которые проходят через точки z = 1
const
Рис. 37.
и г = 0, а эквипотенциальными линиями — окружности, орто-
ортогональные к ним (рис. 38). Эта сетка с точностью до положения
на плоскости подобна сетке, изображенной на рис. 36, являющейся
также изотермической сеткой.
6.4. w = z~2. Степенные функции с отрицательными показа-
показателями можно свести к функциям с положительными показателями
с помощью промежуточного преобразования ю = zr1. В частности,
5»
68
§ б. Степенная функция
соответствующие римановы поверхности те же, что и для положи-
положительных показателей. Рассмотрим коротко случай w = z~2. В
результате вспомогательного преобразования w = f1 декартова
сетка плоскости w переходит в сетку диполя, изображенную на
Рис. 38.
рис. 37. Напомним, что при отображении t = z2 каждая окруж-
окружность в плоскости t, проходящая через начало, преобразуется в
лемнискату (см. рис. 32). Таким образом, сетка диполя в плоскости t
и тем самым декартова сетка в плоскости ю преобразуются в
сетку лемнискат1 в плоскости г. Физически эта сетка представляет
собой сетку линий равного потенциала и линий тока квадруполя.
Потенциал квадруполя W = z~2 получают путем сближения двух
противоположных диполей при помощи предельного перехода вида
F.3.5) (рис. 39).
Отображение декартовой сетки плоскости г на плоскость w
исследуется при помощи преобразований2 т = ъ~х, w = т2. Как
1 Промежуточные преобразования можно поменять местами: ш =- т2,
т —i г~1. Отсюда можно заключить, что изображенные на рис. 30 равнобочные
гиперболы отображаются при помощи т = z~x в лемнискаты.
" Кнк и в предыдущей сноске, изменение порядка промежуточных преобра-
преобразований показывает, что параболы на рис. 31 отображаются функцией w = t-1
в кардиоиды.
6.4. w — r~
69
Рис. 39. Сетка квадруполя.
^идно из рис. 33, сетка диполя в плоскости % переходит в сетку
каодиоия в плоскости ш (рис. 40).
Рис. 40.
70 § 7. Линейные функции
§ 7. Линейные функции
7.1. Целые линейные функции. Простейшие геометрические пре-
преобразования описываются целыми линейными функциями w =
= az + b и дробно-линейными функциями w = —~—. Начнем
CZ ~^~ и
с исследования отображения
w=z+b. G.1.1)
В силу геометрического смысла сложения комплексных чисел
это преобразование является сдвигом (переносом) числовой плоско-
плоскости на вектор Ь. Все прямые, параллельные вектору Ь, отображаются
при этом в себя; их можно рассматривать как траектории сдвига.
Линии, ортогональные к траекториям и образующие вместе с
ними декартову сетку, мы назовем линиями уровня.
Рассмотрим теперь преобразование
w = sz. G.1.2)
МьГможем считать, что s =j= 0; тогда, логарифмируя, приводим это
преобразование к виду
log w = log z + log s, G.1.3)
аналогичному G.1.1). Таким образом, траектории и линии уровня
преобразования G.1.2) в плоскостях переменных log z и log w обра-
образуют декартову сетку. Возвращаясь к плоскостям z a w, мы должны
различать три случая.
1. log s — вещественное число, т. е. s положительно. Траектория-
Траекториями являются прямые, проходящие через начало координат. Преобра-
Преобразование есть чистое растяжение.
2. log s — чисто мнимое число, т. е. | s\ — 1 (s =?=¦ 1). Траекториями
являются концентрические окружности с центром в начале. Преоб-
Преобразование есть чистый поворот и, следовательно, конгруэнтное
преобразование.
3. log s — произвольное комплексное число. Траекториями явля-
являются логарифмические спирали (см. п. 5.2, ри%_25). Преобразование
есть преобразование подобия (ср.~п. Y3f.
Наконец, рассмотрим общий случай
w = sz+ Ъ. G.1.4)
Случай s = 0 можно исключить; случай s = 1 уже рассмотрен в
G.1.1). Если s =?¦ 1, то преобразование G.1.4) имеет неподвижную
точку, г. е. точку, преобразующуюся в себя. Это точка
7.1. Целые линейные функции
71
Поэтому G.1.4)
писать в виде
можно за-
(ro-C)-e(z-C). G.1.6)
Преобразование приняло фор-
форму G.1.2), причем роль начала
координат играет неподвижная
точка ?. Преобразование явля-
является преобразованием подобия
(возможно, чистым поворотом
или чистым растяжением) с
центром в точке ?.
Целые линейные функции
дают взаимно однозначное и
всюду конформное (даже по-
подобное «в целом») преобразо-
преобразование числовой плоскости на
себя. На сфере и на расширен-
расширенной плоскости это преобразо-
преобразование также взаимно одно-
однозначно и конформно. Полагая
ю* = -.
ш •
= —, имеем1
~ b*
G.1.7)
В соответствии с этим и> = оо
переходит в z = оо и отобра-
отображение в этой точке конформно.
Таким образом, ю = z = С2 =
= 00 — вторая неподвижная
точка отображения G.1.4).
В силу подобия сохраняются
отношения длин отрезков и
углы. Поэтому если три точки
z19 22, z3 переходят в точки wx,
и>2, ю3, то
G.1.8)
— w3
ч — ч
Следовательно, всегда сущест-
существует целая линейная функция,
переводящая две данные точки z
Растяжение
данные
и z
2,
Поворот с
1У растяжением
Рис. 41.
¦ z2, в две заданные
1 См. рассуждения в конце п. 4.2.
72 § 7. Линейные функции
точки wl и т.,, »! + ю2. Этим преобразование однозначно опре-
определяется, и соответствующая функция находится как решение
уравнения
^5 = ^- <7Л'9)
7.2. Дробно-линейные функции. Мы будем предполагать, что
рассматривается дробно-линейная функция
для которой определитель
D = ad—bc G.2.2)
отличен от нуля; в противном случае правая часть G.2.1) обра-
обращается в постоянную. Умножая все коэффициенты а, Ь, с, d на
некоторый множитель, можно добиться равенства D = 1; для
упрощения вычислений мы будем всюду в дальнейшем предпола-
предполагать, что оно выполняется. Формулу G.2.1) можно записать в виде
ю = —1— . G.2.3)
с c(cz-\-d) v '
Каждое дробно-линейное преобразование можно разложить, таким
образом, на более простые1:
w = ± — zlt z, = ~ , z2 = с (cz + d). G.2.4)
с z2
Эти отображения задаются целыми линейными функциями и рас-
рассмотренной в п. 6.3 функцией w = z~l. Все такие функции — а
значит, и дробно-линейные — обладают следующими свойст-
свойствами.
1. Взаимно однозначно и конформно отображают на себя сферу,
соответственно расширенную комплексную плоскость.
2. Сохраняют окружности, т. е. преобразуют прямые и окруж-
окружности в прямые и окружности.
Из 1 и 2 следует, что взаимно ортогональные окружности пре-
преобразуются вновь в ортогональные окружности. На основании
определения симметрии относительно окружности, данного в
п. 6.3 (сохраняющего силу и для симметрии относительно прямой),
точки, симметричные по отношению к некоторой окружности,
переходят в точки, симметричные по отношению к образу этой
окружности. Отсюда следует, что каждая изотермическая сетка
окружностей переходит вновь в изотермическую сетку окружностей.
1 Мы исключаем случай с = 0, при котором преобразование является целым
линейным.
7.2. Дробно-линейные функции 73
Точнее: декартовы сетки и сетки диполей переходят в сетки тех же
типов; то же самое верно для полярных сеток и сеток типа изобра-
изображенной на рис. 38.
Более точные сведения о структуре этого отображения можно
получить, рассматривая его поведение в окрестностях неподвиж-
неподвижных точек. Подставляя в уравнение G.2.1) w = z = ? и учитывая,
что D = 1, получаем
с С2 — (а — d) С — Ь = О, G.2.5)
Ci,a = Yc(а - d ± /(« + dJ~4). G.2.6)
Если а + d -f- 2, то получаем две разные неподвижные точки
d и С2 и уравнение G.2.1) приводится к виду
г
Отсюда1 определяем s:
cC2+d_ , 2
S - Xl^d ~ (°^ + d) =
— о
Вводя обозначения W = w~ } , 7. = г~ г, записываем G.2.7) в
виде
W = sZ, G.2.9)
т. е. уравнение приводится к виду G.1.2). Это позволяет построить
траектории для дробно-линейного преобразования. При этом учи-
учитываем, что полярная сетка в плоскости /?, соответственно в плоско-
плоскости W, переходит в сетку источника и стока в плоскости г, соответ-
соответственно ю, причем источник и сток располагаются в точках d и
С2. Три случая, рассмотренные в связи с G.1.2), приводят к следую-
следующим траекториям в плоскости z (соответственно го).
1. s >0. Траекториями являются окружности, проходящие
: через d и ?2. В этом случае преобразование называется гиперболи-
¦\ иеским2. Если s > 1, то при этом отображении все точки удаляются
! от d (отталкивающая точка) и приближаются к ?2 (притягивающая
V: рючка); если s < 1, то наоборот.
? • 2. |s| = 1. Траектории ортогональны к окружностям, проходя-
проходящим через d и ?а- Преобразование называется эллиптическим.
d щ
1 Например, полагая z = , w= x>.
с
2 Названия «гиперболическое», «эллиптическое», «параболическое» введены
по аналогии с уравнениями второй степени, представляющими гиперболы,
эллипсы или параболы на плоскости.
Гиперболическое
Паpa бол ическое
Рис. 42.
7.2. Дробно-линейные функции 75
3. s — произвольное комплексное число, отличное от s в случае
1 и 2. Траекториями являются кривые, получаемые из логарифми-
логарифмических спиралей при отображении плоскости Z в плоскость г, назы-
называемые локсодромами. Они пересекают все окружности, проходящие
через Ci и ?2, под одинаковыми углами. Преобразование называется
локсодромическим.
Для выяснения, какой из трех случаев имеет место, нет надоб-
надобности вычислять выражение G.2.8); действительно,
а + d^fs +Л=. G.2.10)
Таким образом, отображение является
гиперболическим, если а + d вещественно и \а + d\ > 2;
эллиптическим, если а + d вещественно и [а + d|< 2;
локсодромическим, если а + d — произвольное комплексное.
Если а + d = +2, то отображение имеет лишь одну неподвиж-
неподвижную точку ?. Функцию G.2.1) можно записать в виде
—— = ^— + с. G.2.11)
W— С Z— С V
Это уравнение имеет вид G.1.1). Траектории и линии уровня этого
отображения составляют сетку диполя в плоскости z, соответственно
ю. Такое отображение называется параболическим.
В отличие от целых преобразований дробно-линейные не являют-
являются преобразованиями подобия «в целом», так что соотношение
G.1.8) уже не имеет места. Однако сохраняется двойное отно-
отношение
(«>!, ю2, ю3, ш4) = (zlt z2,zA, zj, G.2.12)
или, в явном виде,
_i ± ; _^ = -b : -5 « G.2.12a)
для четырех пар соответствующих друг другу точек. Это легко
проверить для функции w = z~x; для целых линейных функций это
верно в силу G.1.8), а потому, в силу G.2.4), это верно и для произ-
произвольных дробно-линейных преобразований. Если потребовать,
чтобы три различные заданные точки zt, z2, z3 перешли при дробно-
линейном преобразовании в три различные заданные точки wx, w2,
w3, то это преобразование однозначно определяется. Соответствую-
Соответствующая функция w(z) может быть получена из уравнения
ш-ш, wt-mi = z-z,:Z»-\ _
w — w2 w3 — тг z — z2 z> — z2
С помощью этой формулы можно решить ряд задач на нахожде-
нахождение отображений, о которых будет идти речь в дальнейших пунктах.
76 §7. Линейные функции
7.3. Отображение круга на круг. Пусть в каждой из плоскостей
z и ю задана некоторая окружность; требуется построить функцию,
взаимно однозначно и конформно отображающую друг на друга
круги, ограниченные этими окружностями. Можно при этом
потребовать, чтобы три произвольные точки одной окружи сти
переходили в три заданные точки другой окружности. Если, исходя
из этого требования, составить отображение по формуле G.2.13),
то окружности преобразуются друг в друга, так как окружность
определяется тремя своими точками,
а дробно-линейное преобразование
обладает круговым свойством. Одна-
Однако внутренность окружности перей-
перейдет во внутренность окружности лишь
в том случае, когда обе тройки за-
заданных точек следуют друг за дру-
другом в одинаковом порядке. Это вы-
вытекает из того, что конформные
отображения сохраняют направление
обхода (см. п. 2.4). В противном слу-
случае внутренность одной окружности
переходит во внешность другой, и
наоборот (рис. 43).
На практике часто встречаются случаи, когда заданные точки
находятся внутри круга, а не на границе. Для решения таких задач
воспользуемся предложением, доказанным в п. 7.2, о том, что
при дробно-линейном преобразовании пары симметричных точек
переходят в пары симметричных точек. Поэтому, если потребо-
потребовать, чтобы внутренность одной окружности конформно отобра-
отображалась на внутренность другой и данная внутренняя точка г0 пере-
переходила в данную также внутреннюю точку ю0, то прежде всего мы
должны определить точки z* и w*, симметричные данным относи-
относительно соответствующих окружностей. Каждой паре точек соот-
соответствует пучок окружностей, относительно которых эти точки
симметричны1. Пары zo,z* и ю0, ю* определяют тем самым два
пучка окружностей, к которым принадлежат и данные окружности.
Для того чтобы эти окружности при отображении переходили друг в
друга, можно выбрать на каждой из них еще по одной точке z1
и ш, и потребовать, чтобы эти точки переходили друг в друга.
1 Проще всего это усмотреть для пары 0, оо. Точка, симметричная .: точке
|х>, есть центр окружности. Все окружности, относительно которых 0 и оо сим-
симметричны, имеют центр в начале и, следовательно, концентричны. Дробно-
линейным преобразованием можно перевести 0 и оо в произвольную пару
z0, х*\ пучок концентрических окружностей перейдет при этом в некоторый
другой пучок.
7.3. Отображение круга на круг
77
Точками z0, z*, Zj и ю0, ю*> wi однозначно определяются как окруж-
окружности, так и функция, дающая отображение.
Если потребовать, чтобы пара внутренних точек zt, г2 перешла
в пару внутренних точек ш1, ю2, то эта задача, вообще говоря,
Рис. 44.
неразрешима. Действительно, в этом случае симметричные точки
** ** и поэтому
f
рр
z*, z* и w*, w* также должны переходить друг в друга, у
должны совпадать двойные отношения четырех точек ш15 ю2, wf, ш*
И г15 z2, zf, zf:
J
Zl Z2
— Z?
G-3.1)
Если это условие выполнено, то можно сразу написать искомую
функцию; для этого достаточно в G.3.1) заменить, скажем, zt на z
и »! на ю. Остается выяснить, переходят ли друг в друга заданные
окружности. Для того чтобы это показать, достаточно установить,
что существует только одна окружность К, относительно которой
точки zx и z2 симметричны точкам z* и z*. Заметим сначала, что эти
четыре точки лежат на одной окружности. В самом деле, каждая
окружность, проходящая через две
симметричные точки, ортогональ-
ортогональна -К; с другой стороны, каждая
окружность, ортогональная К, со- /'
держит вместе с каждой точкой ^
симметричную ей. Так, окруж- j
ность, проходящая через г1;:* и |
z2, должна проходить и через г*.
Выберем на окружности К произ-
произвольную точку г0, не лежащую
на построенной выше окружно-
окружности, и проведем окружности через Рис. 45.
\
78 § 7. Линейные функции
точки zt,z*, z0 и z2, z*, z0 (рис. 45). Будучи ортогональными К,
они касаются в точке г0. Если бы существовала вторая окружность,
относительно которой точки zx, z2 были бы симметричны точкам
z*, г*, то она была бы ортогональна двум окружностям, касаю-
касающимся в точке z0, и потому сама проходила бы через точку z0.
В силу произвольности z0, эта окружность совпала бы с окруж-
окружностью К.
Двойное отношение, определенное формулой G.3.1), дает воз-
возможность ввести понятие «расстояния» между двумя точками отно-
относительно окружности. Положим
E(zls z2) = ar th yA(zlt rjj). G.3.2)
Можно показать1, что A(zt, z%) э= 0; для определения E(r1; z^
выбирается положительное значение корня. Тогда выполняются
все аксиомы метрики:
E(z, z) - 0,
E{z1, z^ = E(z2, zj), G.3.3)
причем в последнем неравенстве знак равенства имеет место тогда
и только тогда, когда точки zl, z2, z3 лежат на одной окружности,
ортогональной данной2. Введенное так расстояние служит основой
модели геометрии Лобачевского3, в которой дуги ортогональных
окружностей, соединяющие точки основной окружности, играют
роль прямых линий. Дробно-линейное преобразование, оставляю-
оставляющее неизменной окружность, не изменяет введенного нами рас-
расстояния, и это преобразование можно интерпретировать как дви-
движение в неевклидовой плоскости.
Приведем еще некоторые примеры решения типичных задач на
отображение.
Отображение единичного круга на верхнюю полуплоскость.
1. Пусть при отображении единичного круга на верхнюю полу-
полуплоскость точки zt = е"\ z2 = eitp', z3 = eitp> переходят соответ-
1 Дробно-линейным преобразованием можно отобразить окружность,
проходящую через z1; if, z2, z*, в действительную ось так, чтобы точка z1
перешла в нуль, z2 в 1, zf в ос. Тогда zf переходит в вещественное число,
большее I; двойное отношение полученных точек (не меняюшееся при пре-
обрнчовании) положительно.
2 Последнее неравенство в G.3.3) для обычных расстояний выражает тот
фак г. что сумма двух сторон треугольника всегда не меньше третьей его стороны.
Это соотношение называется неравенством треугольника.
:| См., например, Клейн Ф., Неевклидова геометрия, М.—Л., 1936.
(См. также [6]. — Прим. ред.)
7.3. Отображение круга на круг
ственно в точки w1 = О, ю, =
= 1. Тогда искомая функция
го.
имеет вид
o>(z) = *—±
I р><Рг
G.3.4)
Для того чтобы эта функция дей-
действительно отображала внутрен-
внутренность окружности на верхнюю по-
полуплоскость, ТОЧКИ Zj, Z2, Z3 ДОЛЖ-
ДОЛЖНЫ следовать одна за другой по
часовой стрелке. В противном
случае внутренность круга отобра-
отобразится на нижнюю полуплоскость.
2. Требуется, чтобы центр z = 0
единичного круга переходил в
заданную точку w = w0 верхней
полуплоскости. Точка, симметрич-
симметричная z = 0, есть z = оо, а симме-
симметричная w = ш0, есть w = ю0. Мы
можем еще потребовать, чтобы
точка z = 1, лежащая на единич-
единичной окружности, перешла в точку
w = Wj на вещественной оси. Тогда
искомая функция имеет вид
I— Щ
w — w0 wi wo
Отображение единичного круга
на себя.
В случае единичного круга
расстояние G.3.2) принимает вид
E(zi, "а) = аг Ш
G.3.6)
Оно не должно изменяться при
отображении единичного круга
на себя. Поэтому если zx, z2 и
wi» Ю2 — Две пары соответствую-
соответствующих точек, то
! 1 —
I 1 —
G.3.7)
В частности, если потребовать,
чтобы точка z = z0 перешла в
О 1
Рис. 46.
G.3.5)
Рис. 47.
80
§ 7. Линейные функции
центр w = О единичной окружности, то функция w(z) должна
удовлетворять условию
i „ _ i
G.3.8)
| 1 - zz0 ]
Если приравнять правую часть G.3.8) какой-либо постоянной, то
полученное равенство определит «неевклидову» окружность с цен-
центром z0; оно аналогично уравнению A.1.2) для «евклидовой» окруж-
окружности. Из G.3.8) следует общее
выражение для отображения еди-
единичного круга на себя, при кото-
котором точка г=г0 переходит в ю=0:
с> 48
w(z) =
G.3.9)
где у — произвольное веществен-
вещественное число1.
7.4. Вращения сферы. Как мы
показали в п. 7.2, каждая дробно-
линейная функция отображает
сферу взаимно однозначно и кон-
конформно на себя. Верно и обрат-
обратное: каждое взаимно однозначное
и конформное отображение сферь:
на себя можно выразить дробно-
линейной функцией. В частности
все повороты сферы, т. е. ее кон
груэнтные преобразования на себя
выражаются дробно-линейныш
функциями.
Рассмотрим сначала поворо:
сферы вокруг некоторой оси hi
угол у. Ось пересекает сферу :
двух точках; если ? — одна из них
то вторая есть — j = С, в че*
можно убедиться с помощью сте
реографической проекции. Точки С и С—неподвижные точки преобра
зования; траекториями служат окружности, охватывающие эт
1 у ие может быть аналитической функцией от г, так как ее мнимая част
равна нулю, в силу G.3.8); аналитическая же функция с постоянной мнимс
частью, в силу уравнений Копти— Римана B.2.18) может быть только тожд
ственной константой.
7.4. Вращения сферы 81
две точки, так что преобразование является эллиптическим. Его
можно записать в форме G.2.7):
-Ш-4 = ^^"- G.4.1)
Когда у > 0, при таком отображении поворот от z к ю происходит
против часовой стрелки, если смотреть из точки ?. Вместо задания
оси и угла вращения можно задать пару точек zlt z% и их образы
ю15 ю2. Если эти точки не являются диаметрально противополож-
противоположными — что мы исключаем из рассмотрения, — то поворот сферы
тем самым однозначно определяется. Однако эти пары точек
нельзя выбирать произвольно, так как расстояние между точками
при повороте не изменяется. Для того чтобы выразить этот факт
аналитически, учтем, что при вращении сферы не только точки
1 1
zlt г2 переходят в wlt и?2, но и их противоположные — —, •— — пере-
ходят в — —, — ±7-. Двойное отношение этих четырех точек при
повороте сохраняется. Определим, как и в G.3.1), величину
— Z Z2 ~T~
Полагая z1 = qe^, z2 = 0, получаем отсюда
MQ*, 0) = - Ф = - tg2 [~ - !-) . G.4.3)
Величина ^- — j. составляет половину длины дуги на единичной
сфере, соединяющей точки 0 и Qel<p. Так как величина G.4.2) при
вращении не изменяется, то длина дуги на сфере выражается сле-
следующим образом:
?/<Oi > za) = 2 агс ^ V—4<B1>2г) • G-4.4)
Линейный элемент на сфере будет тогда равен1
EK{z,z+dz)=2I^=dS. G.4.5)
Так же, как и в G.3.9), из правой части G.4.2) можно вывести
1 Это соотношение должно совпадать с определением ds по формуле
D.2.2); в этом можно убедиться непосредственно, применяя формулы D.2.7).
6 — 6002
82
§ 7. Линейные функции
общее выражение для поворота сферы, при котором точка z = z0
переходит в точку ю = 0. Это — дробно-линейная функция
eiy
G.4.6)
7.5. Отображение двух окружностей на две окружности. Для
решения этой задачи примем во внимание тот факт, что две различ-
различные окружности Кг и К2 всегда порождают пучок окружностей,,
т. е. существует в точности одно семейство линий равного потен-
потенциала или линий тока для диполя или источника и стока, содержа-
содержащее обе данные окружности. Следует различать три случая.
1. Заданные окружности пересекаются в двух точках С, и ?2.
Вместе с остальными окружностями, проходящими через обе эти
точки, они образуют пучок, который мы назовем эллиптическим
пучком. При отображении
ш=^ G.5.1)
эти окружности переходят в прямые, проходящие через начало в
плоскости ю.
2. Окружности не имеют общих точек. Тогда они ортогональны
к окружностям некоторого эллиптического пучка и вместе с осталь-
остальными окружностями, обладающими этим же свойством, образуют
так называемый гиперболический пучок. Для нахождения узлов
(т. е. источника и стока соответствующей сетки) следует найти
окружности, ортогональные одновременно к К± и К2. Все ортого-
ортогональные окружности проходят через
точки пересечения каких-либо двух
из них; последние и будут искомыми
узлами Ci и С2 • Если одна из данных
окружностей, например Klt есть пря-
прямая, то на ней лежат центры ортого-
ортогональных окружностей. Для постро-
построения ортогональной окружности,
проходящей через заданную точку Q
на окружности К2, достаточно про-
провести касательную в точке Q до пере-
пересечения с Ку\ этим определяется
центр Мо искомой окружности (см.
рис. 49). Если и Кг, и Кг явля-
являются окружностями, то построение
проводится следующим образом.
Пусть искомая окружность долж-
должна пройти через точку Q на Кг; соединяем Q с центром Мг окруж-
окружности Л'( и откладываем на прямой QMj в любую сторону отрезок
QP, равный радиусу г2 окружности К2. Центр Мо искомой окруж-
Рис. 49.
7.5. Отображение двух окружностей на две окружности
83
ности лежит на пересечении перпендикуляра s к отрезку РМ2,
восставленного из его середины (М2 — центр окружности JQ,
и касательной к Кг в точке Q. Для того чтобы показать это, продол-
продолжим PQ до пересечения1 в точке S с перпендикуляром s. Тогда
M2S = SP и, следовательно, QS = Q'S, где Q' — точка пересечения
МгБ с К2. Таким образом, M0Q = M0Q', причем M0Q' ортогонально
M2S (см. рис. 50). Пересе-
Пересечением полученной орто-
ортогональной окружности с
линией центров2 МХМ2
(которая тоже является
«ортогональной окруж-
окружностью») служат точки
d и С2. Отображение
G.5.1), при котором узлы
переходят в 0 и <х>, преоб-
преобразует Кх и Кг в концент-
концентрические окружности с
центром в начале.
3. Окружности каса-
касаются. Их можно тогда
рассматривать как экви-
эквипотенциальные линии сет-
сетки диполя. Соответству-
Соответствующий пучок окружностей,
касающихся друг друга в
одной и той же точке,
назовем параболическим.
Если при помощи преоб-
преобразования
w = -P~j G.5.2) Рис 50.
перевести точку С в оо, то эти окружности преобразуются в пучок
параллельных прямых.
Рассмотрим сначала те отображения, при которых обе задан-
заданные окружности преобразуются в себя. К ним относятся прежде
всего те преобразования, при которых неподвижными точками
являются узлы, а траекториями — заданные окружности. При
этом можно добиться того, чтобы две любые данные окружности
ортогонального семейства переходили одна в другую.
1 Предполагается, что PQ не параллельно s. Построение, однако, верно и
в этом случае.
2 Если Кг — прямая, то роль линии центров играет перпендикуляр, опу-
опушенный на Кг из точки Мг. См. рис. 49.
84
§ 7. Линейные функции
В общем случае для того чтобы преобразовать две окружности
Kzl и .Кг>2 на плоскости г в окружности Kwl и Kw% на плоскости ю,
можно через каждую из этих пар окружностей провести ортого-
ортогональную окружность и потребовать, чтобы эти последние пере-
переходили одна в другую. При этом точки пересечения z1; z[, z2, z'2
переходят соответственно в
точки ш15 w'1,wi, w2 (см. рис.
51). Наоборот, если при дроб-
дробно-линейном преобразовании
эти четверки точек переходят
друг в друга, то и ортогональ-
ортогональные окружности, и пары данных
окружностей также переходят
друг в друга. Для того чтобы
это было возможно, двойные
отношения этих четверок дол-
должны совпадать. Если положить
TS- \ г1 — Z2 . Zl — Z2
то должно быть
G.5.3)
Рис. 51.
G.5.4)
Подобно G.3.2) и G.4.4), это двойное отношение тесно связано
с некоторой мерой, а именно с угловой мерой. Положим
= 2 arc tgi—A{KlfKJ. G.5.5)
Для двух пересекающихся окружностей величина в(Кг, К^) равна
углу между этими окружностями, точнее, между теми дугами, на
которых лежат точки z1az2. Это легко проверить в частном случае
zx = 1, zi = —1, z2 = e'f, z'2 = —№. Применяя преобразование
G.5.1) с последующим преобразованием подобия, можно при-
привести заданные четыре точки к такому виду, причем окружности
преобразуются в прямые, проходящие через начало координат.
Для концентрических окружностей с радиусами гг и т-2, учитывая,
что arc tg ix = i ar th x, получим1
Z2) = + /logi. G.5.6)
Г
1 Мы предполагаем, что пары zx, z2 и z't, z't лежат по разные стороны от
общего центра окружностей. В противном случае мы получаем «смежный»
угол яг — /log — .
r
7.5. Отображение двух окружностей на две окружности
85
Это выражение представляет собой обобщение понятия величины
угла; при этом непересекающиеся окружности образуют мнимый
угол. Таким образом, две пары окружностей можно отобразить
конформно друг на друга
только тогда, когда они
образуют между собой оди-
одинаковые углы; для пересе-
пересекающихся окружностей это
вытекает из уже известного
свойства сохранения углов
при конформном отобра-
отображении.
Пример. Отображение
двух непересекающихся ок-
окружностей на две концентри-
концентрические.
1. С помощью описан-
описанного выше построения опре-
определяем узлы ?i и С2, соот-
соответствующие этим окруж-
окружностям. Преобразование
™ = s~% G-5.7)
переводит заданные окруж-
окружности на плоскости z в кон-
концентрические окружности на
плоскости ю. В качестве s
мы можем взять любое
комплексное число; напри-
например, можно определить его
так, чтобы одна из концент-
концентрических окружностей имела
заданный радиус и чтобы
заданная точка одной из ис-
исходных окружностей пере-
переходила в заданную точку
соответствующей окружно-
окружности. Если поменять местами
узлы ?i и ?2, то в плоскости
ю внешняя окружность становится внутренней, и наоборот.
2. Для численного решения задачи следует сначала найти двой-
двойное отношение G.5.3). Пусть К21 и К2>2 — данные окружности,
М1 и М2 — их центры, гх и г2 —' радиусы, d — расстояние между
Мх и М2. Проведем через Мг и М2 прямую и обозначим точки ее
Рис. 52а
86
§ 7. Линейные функции
пересечения с окружностями буквами zls z[, г2, z2 (в порядке, ука-
указанном на рис. 52). Вычисляя по этим точкам величину
A(KZ !,Kz2), получаем для непересекающихся окружностей (рис.
52а, I)
Если окружности лежат одна внутри другой, то (рис. 52а, II)
V \ (Г2 rl) " /7 ^ 04
1> кг,г) = /„ I , 42 _ Я • (f.W)
Если одна из окруж-
окружностей, скажем Кг2)
вырождается в пря-
прямую (рис. 52а, III),
то имеем просто
т_ ч а — гл
¦ш,1
Рис. 52Ь
ЮТСЯ В ТОЧКИ Wt = 1, w[ = —1, Ю2 = Д,
G.5.10)
где а — расстояние от
Мх до прямой Kz2.
Предположим, что
прямая М1М2 отобра-
отображена на ось и так,
что Кгл отображается
в единичную окруж-
окружность, а Кг2 — в ок-
окружность j w\ = R > 1.
Пусть при этом точки
zi zi» Z2 > Z2 отобража-
= —К (рис. 52b). Тогда
А
G.5.11)
Поскольку это выражение при отображении не меняется, то должно
быть
Д = .
G.5.12)
причем берется положительное значение корня из соответствующей
величины Л: G.5.8), G.5.9) или G.5.10).
Согласно G.2.13), искомую функцию можно записать в виде
№ — 1 R -j- 1
Z2 — Zl
G.5.13)
8.1. ш = cos г 87
Решая относительно ю, получаем
где
В случаях G.5.8), G.5.9), G.5.10) получим соответственно
A][i, G.5.17)
r- G-5Л8)
Из G.5.14) можно найти узлы эллиптической сетки, определяемой
окружностями Kzl и К2>2. Так как им соответствуют точки w = 0
И Ю = оо, ТО
§ 8. Тригонометрические функции
8.1. id = cos г. Функция косинус для комплексных значений z
определяется через показательную функцию по формуле
cosz = i(e'*+e-<*). (8.1.1)
При помощи переносов и поворотов в плоскости г приходим к
функциям
sin z = cos {%¦ — zI = — (е'г — е~1г), ch z =• cos it •= -(ez + e~2),
sh z = —i sin iz = i (ez — е~г). (8.1.2)
Благодаря этим соотношениям нет надобности исследовать каждое
из отображений, определяемых этими функциями; достаточно иссле-
исследовать функцию ю = cos г.
По формуле для косинуса суммы, справедливой и для комплекс-
комплексных значепий аргумента, с учетом формул (8.1.2) имеем
cos (x + iy) = cos x ch у — i sin x sh y. (8.1.3)
88
§ 8. Тригонометрические функции
Л
Рис. 53.
i
i
гл
й
Ж
ш
0
b
w
щ
я
р
Таким образом,
Re ю = u = cos х ch у,
Im ю = и=— sin x sh у.
(8.1.4)
Рис. 54.
Фиксируя значение у и изменяя
х от 0 до 2зт, получаем в плос-
плоскости и> эллипс с полуосями сЬ у
и (sh j/j и с фокусами в точках
w =-}-\. При этом эллипсы, :
соответствующие положитель-
положительным (отрицательным) у, обхо-
обходятся в отрицательном (поло-
(положительном) направлении. Зна-
Значениям — »/и + у соответст-
соответствуют совпадающие эллипсы.
При у = 0 получается вырож-
вырожденный эллипс, т. е. дважды
пробегаемый отрезок, сое-
соединяющий точки ю = — 1.
При возрастании величины |у|
эллипсы по форме приближа-
приближаются к окружностям.
Закрепляя значение х и
изменяя у от — оо до + оо,
получаем на плоскости ю одну
ветвь гиперболы с фокусами
также в точках ю = +1. Асим-
Асимптотами этих гипербол слу-
служат лучи arg w = +x, что
видно из (8.1.3), если у -* + оо.
При х = ля, где п — целое,
гиперболы вырождаются в
разрезы; а именно при п чет-
четном — в дважды проходимую
полупрямую v = 0, 1 =? " =s оо,
а при п нечетном — в полу-
полупрямую v = 0, — oo«=u«s —1.
Линии х = ^ + п % преобра-
преобразуются в мнимую ось плос-
плоскости ш, проходимую один
раз.
Таким образом, декартова
сетка плоскости z преобразу-
преобразуется в изотермическую сетку,
8.2. ro=(l/2)(f+ 1/0
еостоящую из софокусных эллипсов и гипербол. Соответствующая
система координат (х, у) в плоскости ю, определяемая по формулам
(8.1.4), называется эллиптической системой координат. Введение
этой системы целесообразно в тех случаях, когда точки ю = +1
играют особую роль.
Подобно логарифму, функция, обратная к косинусу, z =
= Are cos w, не является однозначной функцией. Характер много-
многозначности определяется равенствами
cos (z + 2пл) = cos z, cos (— z) = cos z; (8.1.5)
из них следует, что значения функции ю = cos z определены ъо-
всей плоскости z, если они известны, например, на полуполосе
0 «= х =s 2я, — оо < у =s 0.
Из проведенных рассуждений видно, что полуполоса
0 «S Ж =?5 Я, — оо<уя=0
отображается на верхнюю полуплоскость ю, смежная с ней полу-
полуполоса
7Г =?= Ж «= 2я, — оо < у =?= 0
— на нижнюю полуплоскость, следующая — вновь на верхнюю полу-
полуплоскость и т. д.; то же самое наблюдается при движении в сторону
отрицательных х. Переходя от z к —¦ z, мы получаем подобное
разбиение верхней полуплоскости z, так что вся плоскость раз-
разделяется на полуполосы в шахматном порядке, как показано на
рис. 54. Это дает возможность построить риманову поверхность
над плоскостью ш, соответствующую функции ю =• cos z. Она
состоит из бесконечного числа листов, связанных в точках ю =
= ±1; мы не будем подробно рассматривать ее строение.
8.2. ¦w^ol' + f)* Положим в предыдущем преобразовании
е'г =.t; тогда (8.1.1) даст
w=\lt+ \\ \ (8.2.1)
При этом декартова сетка плоскости z переходит в полярную сетку
плоскости t, так что при отображении (8.2.1) полярная сетка пло-
плоскости t преобразуется в эллиптическую сетку плоскости ю. Точнее:
окружности переходят в эллипсы (в частности, единичная окруж-
окружность — в разрез между точками ю — +1), а прямые, проходящие
через начало, — в гиперболы.
1 Эта функция называется функцией Н. Е. Жуковского. — Прим. пере в.
90
§ 8. Тригонометрические функции
Для исследования функции ro(f) в целом учтем, что шахматное
разбиение плоскости z, изображенное на рис. 54, переходит при
отображении t = eiz в разбиение плоскости t на четыре части веще-
вещественной осью и единичной окружностью. Поэтому риманова по-
поверхность, соответствующая функции w(J), состоит только из двух
листов. Это следует также из того, что обратная функция
l(w) - го ± fro2 —1 (8.2.2)
в зависимости от знака корня принимает два различных значения.
Более четкое представление о римановой поверхности мы полу-
получим, подвергнув го и t одина-
одинаковым дробно-линейным преоб-
преобразованиям.
Полагая
w
1-со '
со =
ш - 1
ш + 1 '
(8.2.3)
- 1
1 -т'
получим
со = т2. (8.2.4)
Риманова поверхность над плос-
плоскостью го имеет, таким образом,
ту же структуру, что и для функ-
функции со = т2 (см. п. 6.2), если под-
подвергнуть ее дробно-линейному
Рис 55 преобразованию, переводящему
точки разветвления со = 0, оо в
точки разветвления го = + 1.
Из формулы (8.2.4) вытекает, что полярная сетка плоскости т
переходит в полярную сетку плоскости со, причем, согласно F.1.3),
углы удваиваются, а радиусы возводятся в квадрат. Таким образом,
отображение (8.2.1) переводит сетку источника и стока с узлами
t — +1 в такую же сетку в плоскости го, причем углы между окруж-
окружностями, пересекающимися в точках ю = +1, удваиваются.
В частности, как внутренность, так и внешность каждой окружности,
проходящей через точки t = +1, преобразуется в полную плоскость
н» с рачрезом вдоль дуги окружности между точками го = —1 и
w -» | 1. Отсюда получается и упомянутое уже отображение еди-
единичной окружности на прямолинейный разрез между +1 и — 1.
Другим частным случаем является отображение верхней или нижней
полуплоскости t на всю плоскость и>; разрез здесь простирается от
8.2. u>= A/2)
1/0
91
точки w = +1 вдоль положительной вещественной полуоси до оо,
а затем вдоль отрицательной полуоси до точки1 w — —-1.
Очень важно знать, как отображается декартова сетка плоскости
w на плоскость t. Картину, получаемую при этом вне единичного
круга в плоскости t, можно рассматривать как обтекание круга
параллельным потоком.
Отображение единичной
окружности на разрез,
осуществляемое функ-
функцией ю@> решает в част-
частном случае задачу отоб-
отображения произвольного
профиля на разрез, поста-
поставленную в п. 3.2. Такую
задачу можно решить,
отобразив сначала внеш-
внешность профиля на внеш-
внешность единичного круга
(что значительно проще,
чем непосредственное
отображение на внеш-
внешность отрезка) и приме-
применив затем (8.2.1). При-
Прибавляя к параллельному
течению некоторое вих-
вихревое течение, можно
получить общий вид об-
обтекания окружности (см.
п. 3.2, рис. 15).
77Z7
Рис. 56.
Картину,
шую внутри
возникаю-
единичного
круга при отображении
ю на плоскость
рассмотренного
- . Это течение
плоскости
выше
есть
t, можно получить из
обтекания при помощи отображения t —
течение диполя, при котором единичная окружность служит
непроницаемой перегородкой. Общую картину можно получить
также при наложении параллельного потока, имеющего комплекс-
комплексный потенциал Wx = ~ U на поле диполя W2 ¦= — . Действительно,
ю = Wx + W2 ¦— комплексный потенциал суммы этих полей, и
сетка линий равного потенциала и линий тока представляет собой
не что иное, как образ декартовой сетки плоскости w на плоскости t.
1 Следует учесть, что w = оо представляет собой одну точку. Наглядно
можно представить себе этот разрез на сфере, где он проходит от + 1 к — 1
через южный полюс без разрыва.
92
§ 8. Тригонометрические функции
8.3- w = tg г. Отображение, осуществляемое функцией tg
можно на основании равенства
1
J-
1
~1 —
J
Л
4
1
1
1" ~
I
I
I
I
I
X
Рис. 57.
tgz =
sinz
(8.3.1)
разложить на отображение, опре-
определяемое показательной функцией
I = e2iz, и дробно-линейное пре-
преобразование
(8.3.2)
1
ю = -
1
D-1
Таким образом, декартова сетка1
плоскости z сначала преобра-
преобразуется в полярную сетку плоскости
t, а последняя — в сетку источни-
источника и стока с узлами w = _|г.
В частности, полоса
— оо < у < + оо
преобразуется в правую полуплос-
полуплоскость t, а затем в единичный круг
плоскости w (рис. 57).
Обратно, декартова сетка плос-
плоскости ю переходит в сетку ди-
диполя, расположенного в точке
t = 1. При отображении на плос-
плоскость г получается поле, образо-
образованное бесконечным числом дипо-
диполей, расположенных периодически
на вещественной оси в точках г =
2г>+ 1
' 2
71, V
о,
1, +2,....
В самом деле, функция w = tg г
может быть представлена в виде
суммы бесконечного числа потен-
потенциалов диполей, а именно2
ro=tg2
1), (8.3.3)
1 Кривые я = const и I/ = const можно определить непосредственно из
формулы для тангенса суммы.
г См., например, К п о р р К., Funklionentheorie II (Sammlung Goschen
703), Berlin, 1944, S. 41 f. (См. также [6]. - Прим. ред.)
8.3.
tgz
93
Рис. 58.
где вместо величин г„ следует
подставить вышеуказанные вы-
выражения.
Каждый член этого ряда пред-
представляет собой комплексный по-
потенциал диполя, помещенного в
точку zv [см. F.3.5)]; аддитивные
постоянные —, которые с физиче-
zv
ской точки зрения несущественны,
обеспечивают сходимость этого
бескънечного ряда.
Точно так же полярная сетка
в плоскости ю при отображении
w = tg z переходит в сетку линий
равного потенциала и линий тока,
получаемую при наложении полей
периодически расположенных ис-
источников и стоков (см. рис. 59);
источники помещаются в точках
а стоки
в точках
-71.
Рис. 59.
94
§ 8. Тригонометрические функции
Соответствующее разложение комплексного потенциала в ря;
1
имеет вид1
W = log tg z
[log (z - г?) - log (z - zv) + i] , (8.3.4-
где аддитивная постоянная —- при v = 0 опускается. Эти постоян-
постоянные снова введены для обеспечения сходимости ряда и лишень_
физического смысла.
Рис. 60.
Соответствующее периодическое расположение одних только
источников или только стоков нельзя получить непосредственно ;.
помощью функции тангенса; однако оно может быть найдено npi
помощи отображения полярной сетки плоскости ю посредствоъ
функции ю = cos 2, причем источники лежат в точках zv. Соответ
ствующий ряд сходится здесь только при попарном объединение
источников, а именно, следует составить ряд из пар слагаемы;
вида F.2.3)
W *- log cos z=
— zl)— log(—
(8.3.5
Таким образом мы получим течение, изображенное на рис. 6L
1 Во (пбежание затруднений при установлении сходимости в каждом член::
ряда следует выбирать главное значение логарифма, а затем можно прибавит,
слагаемое вида Ъхта. Этот ряд легко может быть получен из известного раз-
разложения функций sin z и cos z в бесконечные произведения. См. Knopp I-.
цит. раб., S. 2611. (См. также [6]. — Прим. ред.)
НЕКОТОРЫЕ ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ
ПОТЕНЦИАЛА И ТЕОРИИ ФУНКЦИЙ
§ 9. Теорема о среднем
9.1. Теорема о среднем. Рассмотрим вновь интеграл B.2.22),.
взяв в качестве пути интегрирования окружность |z| = g0. Если
функция U{z) гармонична в замкнутом круге [z|=Sg0, то этот
интеграл равен нулю; в полярных координатах это записывается
следующим образом:
2я
I -^— ds = f -=— Qndw = 0. 6.1.1
огт
Отсюда следует, что производная -=— не может быть положитель-
положительной (или отрицательной) всюду на окружности, т. е. должна менять
знак (за исключением случая ^-=0|. Поэтому при переходе к
несколько большей1 или меньшей окружности ] z | = q0 + Ли функция
U(z) не может всюду возрастать (или убывать), а должна сохранять
«в среднем» одни и те же значения.
Чтобы сделать эти рассуждения строгими, умножим (9.1.1) на
— и проинтегрируем от qx до д2; изменяя порядок интегрирования2,.
во
получаем
,.. es 2л 2я 2л
^-'d^e= JU(fe,y)^-Ju(ei,4P)dy-O, (9.1.2)
ел О О О
и, иначе,
2я 2я
(9.1.3)
Это средние значения функции U(z) на окружностях ]2| = рг и
|zj = q2; если U(z) гармонична в большем круге, то эти значения
1 Поскольку V{z) гармонична в замкнутом круге \г\ == Qo, существует и
несколько больший круг, в котором она гармонична.
2 Изменение порядка интегрирования допускается, так как U(z) непрерывна
вместе со своими производными в рассматриваемой области.
96 § 9. Теорема о среднем
совпадают. При qt -> 0 левая часть (9.1.3) стремится к значению
17@); таким образом, окончательно получаем
t7(e,y)dV. (9.1.4)
о
Мы пришли к теореме о среднем в теории потенциала: для любой
функции, гармонической в замкнутом круге, значение этой функции
в центре круга равно ее среднему значению на окружности. Эта
теорема справедлива и для функции V(z), гармонической лишь
внутри круга и непрерывной вплоть до его границы (в смысле
определения непрерывности функции в замкнутой области, данного
в п. 2.1). В этом случае U(o,cp) — граничное значение функции U.
Из теоремы о среднем вытекает важное следствие: функция
U(z), гармоническая в области G и не являющаяся постоянной, не
может иметь внутри этой области та максимума, пи минимума.
Это можно доказать следующим образом. Пусть функция U(z)
имеет максимум М в точке z,, лежащей внутри области G. Поскольку
С7(г) не постоянна, то в области G найдется точка z2, в которой
U(z2) < М. Так как область G связна, можно соединить точки
2j и г2 непрерывной кривой С. Будем двигаться вдоль С от zx к z2;
в силу непрерывности функции U(z) найдется точка z0, в которой
функция впервые примет значение М, а в любой предшествующей ей
точке z*, произвольно близкой к z0, будет U(z*) < М. Найдется
круг \z— zo[ «= e, лежащий целиком в G, граница которого содержит
одну из точек z*. Так как функция U(z) нигде не превосходит М,
ее среднее значение на окружности |z — zo| = г меньше М; в силу
(9.1.4) оно равно величине U(z0), что противоречит предположению.
Аналогично доказывается, что U(z) не может иметь минимума
внутри G.
Отсюда вытекает еще одно следствие: если функция V(z) яв-
является гармонической в открытой области G и непрерывной вплоть
до границы Г, где она принимает постоянное значение, то U(z)
постоянна во всей области. Действительно, мы показали, что u(z)
не может иметь ни максимума, ни минимума внутри G. В замкну-
замкнутой же области G + Г функция U(z), будучи непрерывной, должна
достигать как максимума, так и минимума. Таким образом, и то и
другое является граничным значением функции, поэтому ее значе-
значения внутри G не могут быть ни больше, ни меньше граничных.
А так как эти последние равны между собой, то и во всех внутренних
точках функция принимает то же самое значение.
Так как вещественная и мнимая части аналитической функции
ш(:) «== n(z) + iv(z) являются гармоническими функциями, теорема о
среднем справедлива и для аналитических функций. Ее можно выра-
выразить при помощи комплексного интеграла, заменяя d<p комплексным
9.1. Теорема о среднем 97
дифференциалом dz. Так как z = q ef, а на окружности q = const
имеем dz = iqefdy, то dy = -Д. Из (9.1.4) получим
z- (9Л-5)
Так как подинтегральная функция аналитична в некоторой окрест-
окрестности окружности | г| = q, to путь интегрирования можно изменять
в пределах области аналитичности функции —-. Вместо окруж-
окружности можно взять любую замкнутую кривую, лежащую в области
аналитичности функции ш(г) и обходящую точку г = 0 один раз в
положительном направлении. В такой форме равенство (9.1.5)
превращается в известную интегральную формулу Коши. По сравне-
сравнению с формулой (9.1.4) она имеет то преимущество, что путь
интегрирования в ней произволен; зато она справедлива лишь для
комплексных аналитических функций, но не для вещественных
гармонических.
Применяя конформные отображения, можно существенно обоб-
обобщить теорему о среднем. Пусть z(?) - - аналитическая функция,
взаимно однозначно и конформно отображающая область G пло-
плоскости С на единичный круг | z | < 1 и переводящая точку ? = ?0 в
точку z = 0. Пусть границей G служит непрерывная кривая С, и ее
точки взаимно однозначно и взаимно непрерывно1 отображаются
в точки окружности \z\ = 1. Каждой точке кривой С можно поста-
поставить в соответствие число g?@ = arg z(?).
В силу рассуждений после формулы B.4.7) U*(?) = U(z(C))
является гармонической функцией в области G, если U(z) гармо-
гармонична в круге [ z\ < 1. Таким образом, для каждой гармонической
в G функции U*@, имеющей всюду па С граничные значения,
справедливо равенство
• u*(Co) = 2^Jt/*(OMO, (9.1.6)
с
получающееся из (9.1.4) путем замены переменной2.
1 Ср. с теоремой в конце п. 10.1.
2 Этот интеграл нужно понимать следующим образом. Кривую С, по
предположению, можно выразить в параметрической форме уравнением С =
= С(?0, 0 =s q> < 2я. Тогда граничное значение и(С(ф)) ---= F((p) есть непрерывная
функция от у и интеграл (9.1.6) принимается равным J l'Xtp) dq> (интеграл Стиль-
о
тьеса). Во всех встречающихся на практике случаях С состоит из аналитических
дуг, т. е. допускает параметрическое представление при помощи кусочно аналити-
аналитической функции С@- В этом случае (ср. с п. 11.2) существует производная <р
dm
по t и можно положить ite(O = —- dt.
dt
7 — 6002
98 § 9. Теорема о среднем
Соответствующее обобщение интегральной формулы Коши
(9.1.5) можно получить, учитывая, что на кривой С
j^} ] (9.1.7)
Таким образом, приходим к равенству
"*& = Ш f ю@ d(Iog 2(С))' (9'* -8>
в котором путь интегрирования может быть любой, обходящий
точку Со в положительном направлении и лежащий в области
аналитичности функции ю(?). Если в качестве такого пути выбрать
кривую С, то (9.1.8) распадется на два равенства вида (9.1.6) для
вещественной и мнимой частей.
Функция log z(C) является функцией Грина1 области G с началь-
начальной точкой Со в комплексной записи. Положим
log <С) = Щ, Со). (9.1.9)
Уравнение (9.1.6), если написать ?7@ вместо U*(C), примет вид2
С, Со)- (9.1.Ю)
с
Таким образом, функция Грина позволяет установить связь между
граничными значениями и значениями внутри области СГдляЪроиз-
вольной гармонической функции. Функцию Грина можно опреде-
лйтьГ'независимо от конформных отображений следующими усло-
условиями3.
1. Функция ДС, Со) аналитична по переменной С в области G,
за исключением точки С = Со, в которой она имеет логарифми-
логарифмическую особенность. А именно
ДС, Со) = log (С - Со) + Г(С Со), (9.1.11)
где ^(С, Со) — функция, аналитическая в G.
1 В теории вещественного потенциала функцией Грина называют веще-
вещественную часть введенной ниже функции Г(?, Со). В связи с конформными отоб-
отображениями и ради простоты записи представляется целесообразным определить
функцию Грина как комплексный потенциал. При этом мнимая часть ДС, Со)
определяется с точностью до постоянного слагаемого, так что эта функция
неоднозначна. См., кроме того, Hurvritz A. und С our ant R., Vor-
lesuiiKcn liber allgemeine Funktionentheorie und elliptische Funktionen, 3. Aull.,
Berlin, 1929, S. 405 ff. [В соответствии с общепринятым определением функции
Грини следовало взять — log z(f). См. [1]. — Прим. ред.]
а См. сноску 2 на предыдущей странице.
• См. прим. ред. выше. — Прим. ред.
9.2. Краевые задачи 99
2. ДС, ?q), как функция от С, имеет непрерывные граничные зна-
значения всюду на границе G, причем
ReT(C, С0) = 0 на С. (9.1.12)
Этими условиями функцию Грина можно определить и для тех
областей, которые нельзя отобразить конформно на единичный
круг, например для многосвязных областей.
Если область G можно отобразить конформно на единичный
круг, то зависимость функции Грина от Со легко выразить в явном
виде. В самом деле, если z(C) — некоторая функция, отображающая
конформно G на единичный круг и переводящая точку Со в некото-
некоторую точку г0 = z(?o), то, применяя далее преобразование G.3.9)
единичного круга на себя, мы переведем точку z(Co) в нуль. Таким
образом,
ДС, Со) = log ;ZM^~ ¦ (9-1.13)
1 - z(f) z(C0)
9.2. Краевые задачи. С помощью функции Грина (9.1.9) можно
решить первую краевую задачу теории потенциала: найти функ-
функцию, гармоническую в данной области и принимающую на границе
этой области заданные значения. Действительно, если решение
этой задачи существует1, то оно дается в явном виде формулой
(9.1.10), в которой вместо L7(C) следует подставить заданные гра-
граничные значения. Рассмотрим подробнее случай, когда область G
есть круг радиуса R с центром в начале координат. Отображение
на единичный круг имеет вид
О=|, (9-2.1)
а функция Грина (9.1.13) определяется равенством
ДС,С0)-Ю8ДB;-у ¦ (9.2.2)
Тогда имеем
На границе круга [ С |2 = Cf = Л2 и d? = it, df, и мы можем напи-
написать
[^ 4]. (9.2.4)
1 Вопрос о существовании решения мы оставляем в стороне, так как он не
относится непосредственно к теории конформных отображений. Заметим лишь,
что решение существует при весьма общих предположениях.
7*
100 § 9. Теорема о среднем
Полагая ? = Де", ?0 = Qe'0> получаем
Подставляя последнее выражение в (9.1.10), приходим к интеграль-
интегральной формуле Пуассона:
) = ^/ЦЛ") J ^-+_*Г.Й___ tfjp. (9.2.6)
о
Подобным же образом можно выразить функцию V(C)> гармони-
гармонически сопряженную с U(?), через граничные значения для ?/(?).
Согласно B.2.22), имеем
2
V(z)-V@) = J^-rfs. (9.2.7)
о
Применяя эту операцию к (9.2.6) и меняя порядок дифференцирова-
дифференцирования и интегрирования, получаем
¦2л ее'0
v(^)-v@) = l
о о
(9.2.8)
Здесь внутренний интеграл берется по любому пути, целиком ле-
лежащему внутри круга, а дифференцирование по нормали произ-
производится по переменной Со = Qew. Можно, впрочем, не вычислять
внутреннего интеграла, если учесть, что подинтегральная функция
на основании (9.2.4) может быть представлена в виде вещественной
части некоторой аналитической функции от Со; именно
Ri+q2-2Rq cos (<p — 0) C—Co ' f_|o
Г'^|. (9-2.9)
Значение внутреннего интеграла в (9.2.8) должно поэтому совпадать
с мнимой частью этой же функции
-2Rosin(<p-e) ,Q-1n.
1-е)'
откуда, наконец, получаем
2л
О
9.2. Краевые задачи 101
Объединяя (9.2.6) и (9.2.11), получим формулу Шварца, дающую
выражение комплексного потенциала W(z) = U(z) + iV(z) в круге
через граничные значения U(C) и величину V@):
Wfee») = iV@)
о
При помощи этой формулы можно получить в явном виде реше-
решение второй краевой задачи теории потенциала для круга и тем
самым для всех областей, для которых известен вид их конформных
отображений на круг. Эта задача состоит в отыскании функции
LT(?), гармонической в области G, производная которой -д— по
нормали принимает на границе заданные граничные значения.
Для того чтобы эта задача имела решение, необходимо, чтобы
было, как и в (9.1.1),
V-ds = 0. (9.2.13)
На основании равенства
" V(C2)-V(C1)=J~ds (9.2.14)
вместе с -^— определено также значение V(C) на границе, но с точно-
точностью до постоянного слагаемого. По граничным значениям V(C)
с помощью формулы (9.2.11) можно вычислить значения функции
?7(С) внутри области G (так как 6т@ гармонически сопряжена с
—V(C))- Преобразуя это выражение с помощью интегрирования по
частям, получаем
¦ 2тс
о
j— \v(Reirf) log (R- + р2 — 2Rp cos (<p — 0))l * —
~л L Jo
2л
— ~- f m"*1*) j [R2 + g2 _ 2Rg cos (<p — 0)] dy. (9.2.15)
0
Так как и V(Re''>), и log'(R2 + g2 — 2Лр cos (<p — б)) — периоди-
периодические функции, внеинтегральный член в правой части (9.2.15)
равен нулю. Далее, учитывая, что
102
§ 9. Теорема о среднем
мы получаем искомую интегральную формулу, устанавливающую
связь между гра
U(C) внутри G:
связь между граничными значениями производной-^— и значениями
= tf(o) - A_ jg Я log (JP
cos
- 9) dip.
(9.2.17)
Выражение
log (Л2 + e2 — 2fle cos («p — 0))
log [(С-Co) (С
¦Со)] = лЧССо)
(9.2.18)
называется функцией Неймана для круга. Она играет ту же роль
для второй краевой задачи, что и функция Грина для первой.
Подобно последней, она является аналитической функцией перемен-
переменной С в G с точностью до логарифмической особенности. Так как
С = -т- , то
log [(С-Со) (С-Со)] = log(
(9.2.19)
Эту функцию можно рассматривать как комплексный потенциал
течения, имеющего источник в точке С = Со и сток в точке С = 0, с
окружностью [ С | = R в качестве
непроницаемой перегородки.
Для областей общего вида
функцию Неймана, так же как
и функцию Грина в п. 9.1,
можно определить заданием
следующих условий.
1. Функция iV(C, Со) анали-
тична по С в области G, за
исключением точек1 С = Со и
С = С*, где она имеет логариф-
логарифмические особенности. Точ-
Точнее,
Рис. 61. Функция Неймана.
где л(С, Со) — функция, аналитическая в G.
t(9.2.20)
1 Мы не будем рассматривать характер зависимости Лг(?, ?0) от С*. Как
видно из формулы (9.2.22), значение С* не оказывает существенного влияния на
результат. [Обычное определение функции Неймана см. в [7]. — Прим. ред.
9.3. Разложения в ряды 103
2. Функция N(C, Co) от переменной С имеет всюду на границе
G непрерывные граничные значения с равной нулю мнимой частью
Im ЛЧС, Со) = 0 на С. (9.2.21)
При выполнении этих условий
U(C0) = U(C*) -~ф ЛЧС, Со) fj- ds. (9.2.22)
с
Если область G конформно отображается на единичный круг
функцией г(С), то IV(C, Co) можно записать в явном виде
. Co) = log WO-^o)Hi-*@^o)] t (9.2.23)
где С* — точка, в которой z(C*) = 0.
9.3. Разложения в ряды. Вернемся к формуле Шварца (9.2.12)
и представим интегральное ядро
в виде суммы бесконечной геометрической прогрессии со знамена-
знаменар :
телем
2 ? (?) = 1 + 2 2 (|) е'4^. (9.3.2)
}-, 1 »~1 ч ' r-\
1, т. е.
Этот ряд сходится абсолютно и равномерно при
при |С0| ^= <7-R> где q — произвольное положительное число, меньшее
1, так что (9.2.12) можно интегрировать почленно:
^- Г U(Re{<P) d<p
+
hi fl]v е"в \ и(Ле'") е"''"р d(p- (9-3-3)
о
Разделяя вещественную и мнимую части, положим
ао = i j и(Де1р) ^. Ьо - -ПО),
а„ = — [/(/ге'*) cos vm d<p, bv = — U(JF?e'">) sin
104 § 9. Теорема о среднем
Мы получили не что иное, как коэффициенты Фурье функции U(Re'f).
В этих обозначениях имеем
е'в) = JP [|Y (о, cos vB + bv sin vO),
«) = j? (eX (~bv cos vO + av sin i>0).
v=0 *• '
Так как коэффициенты Фурье (9.3.4) легко вычисляются, а
ряды (9.3.5), как правило, хорошо сходятся внутри круга, это
разложение представляет собой наиболее удобный способ решения
первой краевой задачи для круга. Подобным образом можно
решать и вторую краевую задачу. Имеем
^ = 'до L*= 5 v ^cos v(p + b"sin "рУ, (9-3-6)
коэффициенты Фурье а„ и 6„ вычисляются по формулам
2л 2я
а» = ™ J э^Г cos ^ d<?' 6" = ^ j э^Гsin ^ ^- (9-зл)
о о
Коэффициенты а0, Ьо, естественно, остаются произвольными.
Эти разложения показывают, что каждая гармоническая в
круге функция представима в виде ряда (9.3.5); это же верно и для
любой аналитической функции. Объединяя U(C0) и V(C0) в комплекс-
комплексную функцию W(C0), получаем из (9.3.5) разложение этой функции
в ряд Тейлора:
2сЛ, (9.3.8)
где
cv = ^=Л* . (9.3.9)
Из этого представления сразу следует теорема Лиувилля: каждая
функция, аналитическая и ограниченная во всей плоскости, равна
тождественно постоянной. Действительно, если W(C) — такая
функция, то ее вещественная часть 1/@ также ограничена1, а стало
быть ограничены ее коэффициенты Фурье при произвольно боль-
большом R. С другой стороны, в силу произвольности 11, учитывая
(9.3.9), заключаем, что величины | с„| при каждом v > 0 как угодно
малы и, следовательно, равны нулю. Поэтому W(?) = с0 = const,
что и требовалось доказать.
1 Теорема Лиувилля верна уже в предположении ограниченности веществен-
вещественной части рассматриваемой функции.
9.3. Разложения в ряды 105
Несколько иное интегральное представление коэффициентов
Тейлора cv получается из интегральной формулы Коши (9.1.5).
Положив z = ? — Со> запишем эту формулу сначала в виде
Так как путь интегрирования произволен, его можно зафиксиро-
зафиксировать, считая, что Со изменяется внутри ограничиваемой им области.
Разложим теперь
s- vw (9'ЗЛ1)
с
и почленно проинтегрируем. Сравнивая этот результат с (9.3.8),
придем к равенствам
Путем почленного дифференцирования (9.3.8) можно показать,
что, как и для рядов Тейлора в вещественной области, имеет место
равенство
С„ = -г
-\№\ . (9.3.13)
vl { dZ )g=0
Подставляя в (9.3.8) Со = г — zo> W(z — г„) = ш(г), получаем
общее разложение в ряд
w(z) = 2cv(z-zjr. (9.3.14)
v=0
Коэффициенты этого разложения можно вычислить, пользуясь
(9.3.12) или (9.3.4) вместе с (9.3.9), причем в качестве пути интегри-
интегрирования можно выбрать любую окружность | г — z01 = R, внутри
и на границе которой функция ш(г) аналитична. Таким образом,
каждую функцию ш(г), аналитическую в окрестности точки z = z(),
можно разложить в ряд (9.3.14), сходящийся в каждом круге с
центром z0, внутри которого ro(z) аналитична.
Обратно, каждый степенной ряд вида (9.3.14), сходящийся в
окрестности точки ze, представляет некоторую аналитическую
функцию. При этом два степенных ряда представляют одну и ту же
функцию ш(г)
? с* (z - *„)' = 2 c**(z - ztf = ш(г) (9.3.15)
v=0 i>=0
только тогда, когда с* = с** при всех v. Действительно, вычисляя
коэффициенты разложения ro(z) по формулам (9.3.12) или (9.3.4)
и подставляя их в ряды (9.3.15), получим почленным интегрирова-
интегрированием с„ = с* = с**.
106
§ 9. Теорема о среднем
9.4. Аналитическое продолжение. Пользуясь разложением в ряды
(9.3.14), можно доказать следующую теорему единственности для
аналитических функций: если две функции w^z) и ш.2(г) однозначны
и аналитичны в области G и совпадают в окрестности некоторой
внутренней точки z0, то они совпадают всюду в этой области.
Для доказательства разложим обе функции в окрестности точки
г0 в степенные ряды вида (9.3.14). Так как они совпадают в ок-
окрестности точки z0, то совпадают и коэффициенты разложения cv,
поскольку для их вычис-
вычисления можно использо-
использовать значения функций
на произвольно малой
окружности с центром
z0. Полученный ряд схо-
сходится в наибольшем
круге1 Кг с центром z0,
внутренность которого
лежит целиком в G, и
представляет там обе
функции wt и ю2; следо-
следовательно, они совпадают
в Кг. Для того чтобы
показать, что они сов-
совпадают в произволь-
произвольной точке г* 6 G, со-
соединим г0 и г* кривой
С, целиком лежащей в G. Выбрав на этой кривой точку г15
лежащую в Kt (см. рис. 62), разложим функции wx{z) и ю2(г) в
ряды в ее окрестности. Эти ряды сходятся и совпадают в наиболь-
наибольшем круге К2 с центром z1, внутренность которого лежит в G, так
что данные функции совпадают и в этом круге. Если взять zx доста-
достаточно близко к границе Ки то Кг покроет часть С, не содержащуюся
в Кг. Продолжим этот процесс, выбирая на С внутри К2 точку z2
и разлагая данные функции в ее окрестности в степенные ряды,
сходящиеся в круге К3, покрывающем новый участок кривой С, и
т. д. Таким образом мы строим цепочку кругов. В каждом из этих
кругов функции w^z) и ш2(г) совпадают. Радиусы кругов имеют
положительную нижнюю грань, так как С находится на поло-
положительном расстоянии от границы G. Поскольку С имеет ко-
конечную длину, то точки zv можно выбрать так, чтобы после п
шагов (где п — конечное число) круг Кп покрыл точку z*. В силу
произвольности точки z* совпадение u>1(z) и u>2(z) во всех точках
G доказано.
Рис. 62. Цепочка кругов.
1 См. рассуждения на стр. 104.
9.4. Аналитическое продолжение 107
Из теоремы единственности следует, что аналитическая функция
определена однозначно в своей области аналитичности, если
заданы ее значения в окрестности хотя бы одной точки. Чтобы более
точно выразить это свойство, введем понятие аналитического
продолжения. Пусть функция ш1(г) определена и аналитична в
области Gj. Если существует функция w2(z), определенная и аналити-
аналитическая в более широкой области G2 и совпадающая в Gj с функцией
wx(z), то ш2(г) называется аналитическим продолжением »i(z) в
область G2. Согласно теореме единственности, функция wx имеет
не более одного аналитического продолжения в G2. Совокупность
всевозможных аналитических продолжений данной функции назо-
назовем аналитическим образом или просто аналитической функцией.
В противоположность этому, каждое однозначное задание аналити-
аналитической функции в частной области называется элементом функции.
В частности, степенные ряды в их круге сходимости представляют
элементы аналитических функций.
Если аналитическое продолжение функции существует, то его
можно построить с помощью цепочки кругов, описанной при дока-
доказательстве теоремы единственности. Если можно построить цепочку
кругов, покрывающую данную кривую, то мы говорим об аналити-
аналитическом продолжении вдоль этой кривой. Это всегда возможно,
если существует аналитическое продолжение функции в область,
содержащую эту кривую. В противном случае все круги цепочки
покрывают лишь начальный участок кривой до некоторой точки,
через которую аналитическое продолжение невозможно. Такие
точки называются особыми точками функции.
Рассматривая аналитическое продолжение функции w(z) вдоль
замкнутой кривой, мы можем после обхода кривой прийти к дру-
другому значению функции. Это возможно в тех случаях, когда функ-
функция ш(г) многозначна. Для того чтобы превратить такую функцию в
однозначную, можно различным значениям функции сопоставить
различные листы римановой поверхности (см. п. 5.1), причем теперь
построение этой поверхности осуществляется при помощи цепочек
кругов. В каждом круге функция ro(z) определяется однозначно соот-
соответствующим степенным рядом, так что отдельные круги вместе со
значениями функции на них образуют на римановой поверхности-
функции ю(г) связные круговые области. Два пересекающихся круга
образуют на римановой поверхности единую область, если на их
пересечении значения функции совпадают; в противном случае мы
отнесем их к разным листам поверхности. В частности, два после-
последовательных круга цепочки связаны между собой и на римановой
поверхности. Можно показать1, что этим условием однозначно
1 См., например, "Weyl H., Die Idee der Riemannschen Flache, 3. Aufl.,
Stuttgart, 1955,8. 1—11.
108 § 9. Теорема о среднем
определяется структура римановой поверхности, и мы — по край-
крайней мере теоретически — можем шаг за шагом построить ее, рас-
рассматривая всевозможные аналитические продолжения с помощью
круговых цепочек1.
Из единственности аналитического продолжения следует также,
что вещественную функцию можно продолжить в комплексную
область единственным образом. Это возможно тогда и только
тогда, когда она разлагается в ряд Тейлора, сходящийся на
некотором интервале вещественной оси. Этот ряд сходится тогда
в круге, содержащем данный интервал, и определяет тем самым ком-<
плексную аналитическую функцию, которая на вещественной оси
(по крайней мере на интервале сходимости) совпадает с данной ве-
вещественной функцией. Других аналитических функций с этим свой-
свойством не существует. Полученную функцию мы называем аналити-
аналитическим продолжением вещественной функции в комплексную
область. Для них имеет место следующее важное свойство инвари-
инвариантности функциональных уравнений. Пусть /,(х), /2(х),. .., /п(х) —
вещественные функции, допускающие аналитическое продолжение
в комплексную область, а вещественная функция F(xlt х2,..., хп)
также продолжается в комплексную область по каждой переменной
х„. Тогда, если на вещественной оси выполняется функциональное
уравнение
то оно выполняется и в комплексной области. Действительно, по
предположению, функция F*(x) — Р(/г(х), /2(x),.. ., /„(х)) допускает
продолжение в комплексную область; поскольку она равна нулю
на вещественной оси, а аналитическое продолжение единственно,
то продолжением функции F*(x) может служить только функция
F*(z) == 0. Так, например, в комплексной области сохраняются
теоремы сложения показательной и тригонометрических функций.
9.5. Лемма Шварца. Рассмотрим две односвязные области
Ог и G2, из которых одна (например, G2) содержится в другой, т. е.
О2 С Gj. Пусть Со — общая точка Gx и G2 и Г^С, Со), А(С Со)~
функции Грина, соответствующие этим областям. Тогда
ReriG,Co)-sRer2(C,Co) (9.5.1)
для всех t e G2.
Чтобы это показать, установим сначала, что Re Г„(?> Со) ^ 0.
В силу (9.1.11), Re Г„(?, Со) -¦— °° при С-»С0; следовательно, суще-
существует круг К с центром Со, | С — Со | < ?> на границе которого
Re/'„(С, С„) < 0. В дополнительной области С„ — К функция
Re 1\(C, СA) является гармонической и имеет всюду неположитель-
1 Подробнее о римановых поверхностях см. [8], [9]. — Прим. ред.
9.5. Лемма Шварца
109
ные граничные значения. Согласно принципу максимума для гар-
гармонических функций, доказанному в п. 9.1, Re Г„(С, Со) *= 0 внутри
Gv — К; в силу произвольности выбора е это верно всюду в G,,.
Так как на границе G2, по предположению, Re Г2(С, ?0) = 0
и по доказанному выше Re Г^, Q «? 0, имеем Re[/\(?, Со)—
—,Г2(?, Со)]^ 0- При вычитании логарифмические особенности
функций Грина (9.1.11) взаимно уничтожаются, так что разность
Re A\ ¦- Г2) гармонична в G2. Значит, RelT^, Со) — А(С, ?0I ^ 0
внутри G2, что и требовалось доказать.
Как было показано в п. 9.1, /П„(С, Со) = 1о8 z,.@> где г„(?) -- функ-
функция, конформно отображающая область Gv на единичный круг
и переводящая точку ?0 в нуль. При этом отображении кругу
z\ < q < 1 в плоскости z соответствует область G,,(o) в плоскости
С, определяемая неравенством | zv(?) | < д, или, что то же самое,
Re Г„(С, Со) < !°g p. В силу (9.5.1) для каждого р область G2(g)
целиком содержится в Gj(p), поэтому доказанный факт можно
сформулировать следующим образом: если Gx и G2 — две односвяз-
ные области и G2 с: G1, то для каждого д < 1 имеем G2(g) с Gj(o),
где Gy(p) — прообразы кругов | z\ < g при отображениях Gv(v = 1,2)
на единичный круг плоскости z, переводящих в нуль одну и ту же
точку C0?G2.
Это предложение известно под названием леммы Шварца.
Оно используется для исследования того, как меняется функция,
осуществляющая отображе-
отображение, при изменении отоб-
отображаемой области. Эта лем-
лемма встречается в различных
вариантах1, например в сле-
следующем (если выбрать в
качестве Gx единичный круг):
пусть функция C(z) конформ-
конформно отображает единичный
круг плоскости z на область,
целиком в нем содержащу-
содержащуюся, причем С@) = 0; тогда
| t,(Qe'f) ] «s g для всех q < 1.
Другой частный случай
леммы получается, если об-
области Gx и G2 совпадают. В
этом случае вещественные
части их функций Грина Рис, 63.
1 См., например, Каратеодори К., Конформное отображение, М. —
Л., 1934.
110 § JO. Теоремы об отображении
равны. Следовательно, мнимые части могут различаться лишь
постоянным слагаемым, так что
А(С, Со) = А(С Со) + ia, (9.5.2)
где ос вещественно. Соответствующие функции, дающие отображе-
отображение, отличаются друг от друга множителем, равным по модулю
единице:
*i@ = е* *2@. (9.5.3)
Отсюда, в частности, следует, что единственной функцией, отобра-
отображающей единичный круг на себя и переводящей данную точку
z0 в нуль, является дробно-линейная функция вида G.3.9).
§ 10. Теоремы об отображении
10.1. Теорема Римана. Выше мы оставили открытым вопрос с
том, какие области можно конформно отображать друг на друга.
Поскольку такое отображение непрерывно, оно возможно лишь
для областей, имеющих одинаковый порядок связности. Для
односвязных областей числовой плоскости или римановой сферы
(т. е. комплекЪыой плоскости, расширенной прибавлением точки
z = оо1) имеет место следующая теорема Римана о существовании
конформного отображения: любые две односвязные области
числовой плоскости или римановой сферы, каждая из которых
имеет более одной граничной точки (в частности, области, ограни-
ограниченные одной кривой), можно взаимно однозначно и конформно
отобразить друг на друга. В частности, любую такую область
можно отобразить конформно на единичный круг2.
Эта теорема обобщается на односвязные области на римановых
поверхностях3, т. е. на такие области, которые многолистно покры-
покрывают какую-либо часть плоскости. Именно, имеет место так назы-
называемая большая теорема Римана: каждую односвязную область
произвольной римановой поверхности можно конформно отобра-
отобразить на одну из следующих областей:
1) риманову сферу,
2) комплексную плоскость,
3) единичный круг.
Если, в частности, область ограничена непрерывной кривой,
содержащей более одной точки, то ее можно конформно отобра-
отобразить на единичный круг.
1 О конформности отображений в точке z—oo см. п. 4.2.
' Таким образом, для односвязной области функцию Грина всегда можно
построить при помощи конформного отображения.
8 См. п. 5.1. и 9.4.
10.2. Многосвязные области 111
Эту теорему, как и последующие утверждения этого пункта, мы
приводим без доказательства, отсылая читателя к соответствующей
литературе по теории функций1. Заметим только, что для доказа-
доказательства теорем об отображении можно частично воспользоваться
приближенными методами конформного отображения, излагаемы-
излагаемыми ниже в § 16—18.
Представляет;. интерес поведение такого отображениям граацуе.....
облОСТпй. Об этом теорема Римана ничего не говорит, и нет основа-
основании "ожидать, что отображение конформно вплоть до границы.
Однако для решения краевых задач методом конформных отобра-
отображений существенно, чтобы отображение было непрерывно вплоть до
границы. Это действительно имеет место для областей, ограничен-
ограниченных непрерывными кривыми, а на практике важны именно такие
области. Справедливо следующее утверждение: если односвязная '•
область, ограниченная непрерывной кривой, отображается взаимно
однозначно и конформно на единичный круг при помощи функции
z(C), то последняя непрерывна вплоть до границы2 и отображает
граничную кривую взаимно однозначно на единичную окруж-
окружность.
10.2. Многосвязные области. Для конформных отображений мно-
многосвязных областей нет таких простых предложений, как для одно-
связных областей. Так как характер связности при конформном
отображении сохраняется, то отображать друг в друга можно только
области одинакового порядка связности; однако это условие еще
не гарантирует существования такого отображения. Более того,
каждая многосвязная область характеризуется некоторой совокуп-
совокупностью конформных инвариантов, так что две области отобра-
отображаются друг на друга только тогда, когда их инварианты совпадаю г.
В то время как все односвязные области отображаются в основном
на одну каноническую область — единичный круг, многосвязным
областям соответствует семейство канонических областей, имею-
имеющих одинаковый порядок связности, но различающихся некоторыми
геометрическими параметрами. Такие канонические области встре-
встречаются в связи с определенными краевыми задачами3; доказывая
разрешимость этих задач, мы устанавливаем существование кон-
конформного отображения. На таком пути мы, однако, не получим
практического метода решения задачи об отображении, так как
1 См., например, W с у 1 Н., Die Idee der Riemannschen Flache, 3. Aufl.,
Stuttgart, 1955, S. 82 ft; Behnkc H. und Sommei F., Theorie der analy-
tischen Funktionen einer komplexen Veranderlichen, Berlin—Gottingen-—Heidel-
Berlin—Gottingen-—Heidelberg, 1955, S. 336 ff.
3 Если граница содержит точку с», то непрерывность понимается как
непрерывность на римановой сфере. (О соответствии границ при конформном
отображении см., например, [6]. — Прим. ред.)
8 См., например, задачу о течении в конце п. 3.2.
112 § 10. Теоремы об отображении
для решения краевых задач в свою очередь используются конформ-
конформные отображения. Поэтому мы не будем подробно останавливаться
на этом вопросе.
Другой путь распространения теоремы Римана на многосвязные
области состоит в том, что многосвязную область G превращают в
односвязную, рассматривая ее не на плоскости, а на бесконечно-
листной римановой поверхности FG. Эта поверхность, называемая
универсальной поверхностью наложения области G или универсаль-
универсальной накрывающей, должна обладать следующими свойствами.
Пусть С — замкнутая кривая в G. Проектируя эту кривую на Fc,
получаем там бесконечное множество кривых Сг, С2,. .., по одной
на каждом листе. Эти кривые должны быть замкнутыми на FG
(т. е. начало и конец каждой из них должны лежать на одном листе)
тогда и только тогда, когда С можно стянуть в точку в области G.
Такую поверхность всегда можно построить1; проекция G на эту
поверхность — обозначим ее G — образует связную область на
FG, причем каждой точке G соответствует бесконечное множество
точек на G. Область G односвязна, так как каждая замкнутая кривая
в G может быть стянута в точку, и поэтому (за исключением неко-
некоторых несущественных частных случаев) ее можно, согласно боль-
большой теореме Римана, отобразить конформно на единичный круг.
Преобразуем теперь G с помощью разрезов2 в односвязную
область G*. При этом G распадается на бесконечное множество
конгруэнтных областей G*, G*,..., каждая из которых совпадает
с исходной областью G*. При отображении G на единичный круг
О* переходят в некоторые подобласти Gv, покрывающие единичный
крут наподобие мозаики. Так как отображение G* на G* взаимно
однозначно и тривиальным образом конформно (в силу конгруэнт-
конгруэнтности этих областей), то отображение G* на Gv также взаимно одно-
однозначно и конформно, включая разрезы. Области &„, дополненные
соответствующими разрезами, называются фундаментальными
областями для области G. Они служат каноническими областями
для конформного отображения многосвязных областей. А именно
можно показать, что две области конформно отображаются друг
на друга тогда и только тогда, когда их фундаментальные области
одинаковы; при этом фундаментальные области считаются одина-
одинаковыми, если их можно перевести одна в другую дробно-линейным
преобразованием единичного круга на себя или изменением систе-
системы разрезов.
1 См., например, W е у 1 Н., цит. раб., S. 44 ft.
2 См. п. 2.1, в особенности рис. 6.
10.2. Многосвязные области 113
Рассмотрим подробнее этот метод в случае двусвязных обла-
областей. Пусть область G в плоскости ш ограничена двумя кривыми
С\ и С2, каждая из которых содержит более одной точки. Точки
плоскости, не принадлежащие G, образуют два непересекающихся
замкнутых множества; дробно-линейным преобразованием можно
перевести точку 0 в одно из них, оо — в другое. Тогда в качестве
универсальной поверхности наложения можно использовать опи-
описанную в п. 5.1 риманову поверхность логарифмической функции.
Функция t = log w отображает область G в односвязную, вообще
говоря, криволинейную, полосу S в плоскости t.
При этом отображении сторона ах полосы S соответствует
граничной кривой Cj, проходимой бесконечное число раз, а сторона
а2 — кривой С2. Если соединить Сх и С2 разрезом Q, то полоса S
распадется на конгруэнтные «четырехугольники» Vv, следующие
друг за другом периодически. По теореме Римана полосу S при
помощи функции z(t) можно отобразить на единичный круг; при
этом мы можем потребовать, чтобы ах переходила в дугу — <
< arg z < -к-, а с, — в ДУГУ — тг< arg z < ?г- Четырехугольники У„
переходят в определенные подобласти единичного круга. Эти под-
подобласти, дополненные образами разрезов Q, служат фундаменталь-
фундаментальными областями Gv двусвязной области G.
Значение фундаментальных областей станет яснее, если ото-
отобразить единичный круг на вертикальную полосу при помощи
функции z = tg х (см. п. 8.3). При этом фундаментальные области
bv перейдут1 в конгруэнтные «четырехугольники» Vv. Разрез Q можно
выбрать так, чтобы при отображении на эту полосу он перешел в
отрезок между точками — ^ и ~. Другими образами Q будут отрезки,
соединяющие точки —-г + nia я-т + nia, где п пробегает все целые
числа, а а —• некоторое вещественное число, зависящее от области
G. «Фундаментальные четырехугольники» Vv для G представляют
собой прямоугольники
— ^<Rer<+^, па =s Im t < (п + 1) а, A0.2.1)
причем стороны Re х = — J и Re т= + ~ соответствуют граничным
кривым С\ и С, а стороны Im х = па и Im х = (п + 1) а — разрезу
Q.
Получив, таким образом, нормальную форму фундаменталь-
фундаментальных областей, мы можем ответить на вопрос, когда две данные
1 Это будет подробнее показано в п. 11.1b.
8 —6002
114
§ 10. Теоремы об отображении
двусвязные области допускают конформное отображение друг
на друга. Это возможно тогда, когда фундаментальные прямо-
прямоугольники A0.2.1) равны, т. е. величина а для них одна и та же.
Наоборот, если эти величины различны, конформного отображения
не существует1.
Рис. 64.
В частности, для каждого прямоугольника A0.2.1) существует
круговое кольцо в плоскости С
2a
A0.2.2)
1 В противном случае существовало бы конформное отображение, при
котором прямоугольники равной ширины, но различной высоты переходили бы
друг в друга с сохранением сторон. В том, что это невозможно, проще всего убе-
убедиться при помощи примера из п. 3.1: две прямоугольные пластинки одинаковой
ширины и разных длин имели бы одинаковое сопротивление.
70.5. Краевые задачи в двусвязных областях 115
для которого он служит фундаментальной областью. Отображение
кольца с разрезом на фундаментальную область определяется
— т
функцией С = еа ¦ Таким образом, каждую двусвязную область
можно взаимно однозначно и конформно отобразить на круговое
кольцо, отношение внешнего и внутреннего радиусов которого
зависит от выбора этой области.
10.3. Краевые задачи в двусвязных областях1. При помощи
построенного выше отображения двусвязной области на односвяз-
ную прямолинейную полосу можно решать краевые задачи для
таких областей. Объясним это для первой краевой задачи, пред-
предполагая, что на граничных кривых Сг и С2 области G заданы опре-
определенные граничные значения U1(C1) и U2(C2). При отображении
на прямолинейную полосу граничные кривые преобразуются в
прямые
с вещественными 0,-; граничные значения на этих прямых задаются
функциями Ui@j) и U2(Q^). Так как каждой точке границы G соот-
соответствует бесконечное множество точек
+ j + i(ei + na), п = 0,1,2,...,
то эти функции являются периодическими с периодом а, т. е.
A0.3.1)
При таких граничных значениях мы можем решить краевую
задачу для прямолинейной полосы. Полагая в формуле Шварца
(9-2.12) . , ,
Reh = lg j_ « + f0ij для » |L
для — J
ее'е == tg t,
после несложных преобразований получаем
-I J u^ej [ctg |- J _ r + f©^ + tg a
—oo
4-oo
^ J U2@2) [ctg [ j- ~ т + f02j + tg 2i02] d02. A0.3.2)
1 Необходимые для дальнейшего сведения по теории эллиптических функ-
функций можно найти, например, в [10]. — Прим. ред.
116
§ 10. Теоремы об отображении
Разбивая оба интеграла на сумму интегралов по отрезкам
[па, (п + 1) а], л = О, -_М, -±1,. .., меняя порядок суммирования и
интегрирования и учитывая A0.3.1), находим, что
W(x) = iV@) —
а
- \ J
о
а
+ | J U2@2) J [ctg fe — x + i@2 + na)) + tg 2iF>2 + na)] d02.
A0.3.3)
Ряды, стоящие под знаками интегралов, сходятся абсолютно и
равномерно для всех рассматриваемых значений аргументов и
представляют собой двоякопериодические функции с периодами
Ы и а. В прямоугольнике периодов
0 =s Re 0,- < а, — -3™- «s Im 0,- < j
эти функции обладают простыми полюсами в точках
— !' (т + V-I
соответственно
02 = —мт —^-
Иоследуя поведение этих функций в окрестностях полюсов, прихо-
приходим к их представлению через тэта-функции:
? [ctg (+ - — х + i@t + na)) + tg 2i @,- + na)| =
A0.3.4)
Для нахождения неизвестных пока постоянных с,- рассмотрим два
частных случая поставленной задачи. Если положить L\ == 1,
t72sj0, то, подставляя A0.3.4) в A0.3.3) и интегрируя, получаем
W(t) = iY@) + 1 -^ .
10.3. Краевые задачи в двусвязных областях
117
С другой стороны, решением этой краевой задачи, очевидно,
служит функция
откуда
A0.3.5)
Аналогично, при U1 = О, U2 = 1 получим
A0.3.6)
Таким образом, получаем следующее интегральное представление:
W(t) = zY@) —
A0.3.7)
А
2 »
Заметим, что величины
т
при вещественных 0,- вещественны и не зависят от х. Поэтому
если в выражении A0.3.7) опустить их, то функция W(t) изменится
лишь на постоянную мнимую величину; а так как эта функция
определяется граничными значениями с точностью до мнимого
слагаемого, то решение краевой задачи можно записать в более
простом виде:
118
§ 10. Теоремы об отображении
i.xa
#'l
« Г
x)
2|(т-?
A0.3.8)
причем Vo, вообще говоря, не совпадает со значением мнимой
части W(x) в точке х = 0.
Как и в п. 9.3, решение этой задачи можно представить в виде
ряда. Для этого отобразим прямолинейную полосу на круговое
кольцо, полагая, как в п. 10.2,
Ъг
A0.3.9)
В этих обозначениях, пользуясь известными разложениями лога-
логарифмической производной тэта-функции1, получим для д <
|С|
Лв*-*Ы)
„л@.
?м-1+2.
A0.3.10)
где штрих при знаке суммы означает, что член с п = 0 отсутствует.
Далее, положим, как в (9.3.4),
2 г ®* 1 г • '
-J иК"д е d'i = -J Ufcp,) e '«« qo,- = а„ — i „ ,
0 ° A0.3.11)
i|C7^)^=^JU,.(
1 См., например, Т г i с о m i F. und Kraft M., Elliptische Funktionen,
Leipzig, 1948, S. 170.
10.3. Краевые задачи в двусвязных областях 119
При положительных л это коэффициенты Фурье функций и((ср{),
т. е.
со
иЫ = ао} + 2 an) cos nq>, + Ь<? sin пщ; A0.3.12)
при отрицательных же л
ai!>n = a«, Ь«„= — Ь«). A0.3.13)
Таким образом, интеграл A0.3.8) с учетом A0.3.10) принимает
вид
ib0 g лг log
4- У С" [raa> - fl>Ah =?-"— 4- ГаB) -
A0.3.14)
где Ьо — произвольная постоянная. Легко убедиться в том, что
этот ряд действительно удовлетворяет краевым условиям, положив
? = g-ie'^i соответственно С =
Из разложения A0.3.14) следует, что каждую функцию ?7@'
однозначную и гармоническую в круговом кольце б < I ? I < б'
можно представить в виде ряда
+~
?7@ = у log г + 21 г" (an cos /19s + ,Sn sin л<р), A0.3.15)
где С = гё?. Более того, каждая однозначная аналитическая функция
(? в круговом кольце разлагается в ряд Лорана
2 СПС". (Ю.3.16)
Эти разложения можно получить также из интегральной формулы
Коши, не прибегая к интегральному представлению A0.3.8). Обрат-
Обратно, можно определить из краевых условий коэффициенты an, /9„ и
у, составить на их основании ряд A0.3.14) и прийти вновь к интег-
интегралу A0.3.8). Именно таким путем Вилла и Дини1 впервые (в 1912—
1913 г.) пришли к представлению A0.3.8).
На практике при вычислениях предпочтительнее пользоваться
разложением в ряд A0.3.14), нежели интегралом A0.3.8). Возможно,
1 V i 1 ] а t H., Le probleme de Dirichlet dans une aire annulaire, R. C.
Circolo Mat. Palermo, 33 A912), 134—175; Dini U., II problema di Dirichlet
In un area anulare, e nello spazio compreso fra due sfere concentriche, R. C. Circolo
Mat. Palermo, 36 A913), 1—28. [См. также [10]. - Прим. ред.]
120 § 10. Теоремы об отображении
однако, что при больших а, а также при неподходящем выборе
граничных значений ряд недостаточно быстро сходится. В таких
случаях мы пользуемся формулой A0.3.3), что равносильно не-
некоторому преобразованию тэта-функции.
Кроме того, отметим, что изложенный здесь метод в основных
чертах пригоден и к решению краевых задач для областей более
высокого порядка связности. Вместо двоякопериодических функ-
функций тогда фигурируют автоморфные функции, соответствующие
фундаментальной области G, а вместо тэта-функций Якоби —
функции Пуанкаре. Вычислительная сторона этого метода до сих
пор не подвергалась исследованию.
ТЕОРИЯ И ПРАКТИКА ОТОБРАЖЕНИЙ
МНОГОУГОЛЬНИКОВ
§ 11. Принцип симметрии Шварца
11.1. Автоморфизмы. Во многих встречающихся на практике
задачах об отображении исходные области обладают определенной
симметрией. Следует ожидать, что в этом случае и функции, даю-
дающие отображение, обладают аналогичной симметрией. Для полно-
полного исследования нужно сначала уточнить, что мы понимаем под сим-
симметрией области. Введем с этой, целью следующее определение: каж-
каждое взаимно однозначное конформное или антиконформное отобра-
отображение z* = A(z) области на себя называется ее автоморфизмом. Так,,
например, формула G.3.9) описывает все конформные автоморфизмы
единичного круга. Сочетая их с каким-либо антиконформным
автоморфизмом, например с зеркальным отражением относительно
вещественной оси A(z) = z, мы получаем все антиконформные
автоморфизмы того же круга [см. рассуждения по поводу B.4.3)].
Если область G3 при помощи функции z(C) конформно отобра-
отображается на другую область G2, то автоморфизмы области Gx преоб-
преобразуются при этом в автоморфизмы области G2, т. е. z* =
= z[A(?(z))] есть автоморфизм G2 [C(z) означает функцию, обратную
к z(C)]. В частности, неподвижные точки соответствующих авто-
автоморфизмов преобразуются друг в друга. Симметричные области
характеризуются особенно простыми автоморфизмами. Необходи-
Необходимо поэтому исследовать, какой вид принимают эти автоморфизмы
при конформном отображении на некоторую каноническую область,
скажем на единичный круг. Проведем это исследование для случая
центральной симметрии, периодичности и зеркальной симметрии.
а) Центральная симметрия. Центрально-симметричная область
характеризуется тем, что она переходит в себя при повороте,
например, вокруг нуля: С* = е" С Будем считать рассматривае-
рассматриваемую область односвязной1; отобразим ее на единичный круг та к,
чтобы центр симметрии перешел в начало координат2. Поворот у
1 А-гпэ гичные рассуждения можно провести и для многосвязных областей.
Примеры см. в разд. Б, § 8.
2 Если центр симметрии не принадлежит области, то точка оо — внутренняя.
Ее можно также принять за центр симметрии, так как она неподвижна при
всех поворотах (см. п. 7.1).
122 § 11. Принцип симметрии Шварца
вокруг центра симметрии, переводящему область в себя, будет
соответствовать автоморфизм единичного круга с неподвижной
точкой в нуле. Последний может быть лишь поворотом вокруг
нуля1, причем на тот же угол, что и в исходной области. В самом
деле, каждая кривая, проходящая через центр симметрии, преобра-
преобразуется при этом повороте в некоторую другую кривую. Этой паре
кривых соответствует в единичном круге пара кривых, проходящих
через начало и также преобразующихся одна в другую при соот-
соответствующем повороте. Так как отображение конформно, то углы
между этими кривыми равны;
следовательно, совпадают и уг-
углы поворотов. Таким образом,
г(е " С) = е " 2(С), A1.1.1)
где z(C) — функция, отобража-
отображающая рассматриваемую сим-
Рис. 65. метричную область на единич-
единичный круг так, что центр сим-
симметрии переходит в начало координат. В частности, п конгруэнт-
конгруэнтным частям области соответствуют п конгруэнтных частей еди-
единичного круга (рис. 65).
Ь) Периодичность. Периодическими мы называем области,
преобразующиеся в себя при сдвиге
С* = С + а. A1.1.2)
Пусть G — односвязная периодическая область. В зависимости
от того, имеет ли G одну или две периодические граничные кривые,
мы будем различать периодические области типа полосы и типа
полуплоскости. Если G — типа полуплоскости, то мы отобразим
ее на верхнюю полуплоскость при помощи функции z(?) так, чтобы
точка С = оо перешла в z = оо. Сдвигу A1.1.2) соответствует в
плоскости г дробно-линейное преобразование верхней полупло-
полуплоскости в себя, для которого оо есть единственная неподвижная точка.
Это может быть только сдвиг вдоль вещественной оси, т. е. преоб-
преобразование вида
г(С + а)=г(С) + &, A1.1.3)
где Ъ ¦— вещественное число. Отсюда вытекает также, что периоди-
периодически следующие друг за другом конгруэнтные части G переходят
в конгруэнтные части верхней полуплоскости z.
Если область G типа полосы, то отобразим ее на верхнюю
полуплоскость при помощи функции z(C) так, чтобы одна гранич-
1 См. (9.5.3).
11.1. Автоморфизмы
ная кривая отобразилась в
положительную полуось, а дру-
другая —• в отрицательную. Сдвигу
{11.1.2) соответствует дробно-
линейное преобразование с
(г)
Рис. бба. Периодическая область
типа полуплоскости.
123
(С/
/
/
/
/
1 ",
1 /
1 ',
\ г
— a
il
il
¦¦\
:j
1
,, ,\,.
l
If 1
0
\
\
, ¦ \
\
\
... t
(г)
(Г)
Рис. 66Ь. Периодическая область
типа полосы.
неподвижными точками 0 им, при котором траекториями явля-
являются положительная и отрицательная полуоси, т. е. растяжение.
Преобразование т = log z переводит верхнюю полуплоскость в
прямолинейную полосу 0 < Im т < я, причем растяжение пере-
переходит в сдвиг
т(С+а) = т(О + Ь. A1.1.4)
Здесь также конгруэнтные части G переходят в конгруэнтные
части прямолинейной полосы.
с) Зеркальная симметрия. Пусть G — односвязная зеркально-
симметричная область плоскости С. Можно считать, что осью
симметрии служит вещественная ось, так что преобразование
Z* = l A1.1.5)
переводит G в себя. Выберем какую-нибудь точку Со внутри G,
лежащую на оси симметрии, и, двигаясь от нее в каком-либо напра-
направлении вдоль оси симметрии, фиксируем ближайшую граничную
точку Ci области G. При по-
помощи функции z(C) отобра-
отобразим область G на единичный
круг так, чтобы точка Со
перешла в нуль, d — в 1.
Отражению A1.1.5) тогда
соответствует в плоскости Рис. 67.
124 § П. Принцип симметрии Шварца
z антиконформный автоморфизм единичного круга с неподвижными
точками г = 0 и 2=1. Таким автоморфизмом является зер-
зеркальное отражение относительно вещественной оси. Если бы
существовал другой антиконформный автоморфизм с теми же
неподвижными точками, то вместе с отражением относительно
вещественной оси он образовал бы конформный автоморфизм
с неподвижными точками 0 и 1, который может быть только
тождественным преобразованием. Таким образом, должно быть
г(С) = г(С). (П.1.6)
В частности, участок вещественной оси в плоскости С (оси симмет-
симметрии. G), лежащий внутри G, преобразуется в участок вещественной
оси в плоскости г, лежащий внутри круга, а симметричные части
G — в верхний и нижний полукруги.
11.2. Припцип симметрии Шварца. Рассуждения предыдущего
пункта показывают, что при конформном отображении зеркально-
симметричной области G на единичный круг каждая из ее симмет-
симметричных половин отображается на полукруг. Вид отображения
единичного круга на полукруг известен1, и это дает возможность
отобразить любую из симметричных половин на единичный круг.
Обратно, если известно отображение половины области G на еди-
единичный круг, то можно построить отображение всей области G
на тот же круг.
Каждую односвязную область G, граница которой содержит
прямолинейный отрезок S, можно дополнить до симметричной
области G путем зеркального отражения2 относительно S. Отобра-
Отображая затем G при помощи функции г(С) на единичный полукруг
так, чтобы отрезок S переходил в отрезок вещественной оси z
от — 1 до + 1, мы можем продолжить это отображение до отобра-
отображения всей области G на единичный круг, ставя в соответствие
точкам, симметричным относительно S, точки, симметричные
относительно вещественной оси z. Действительно, если такое
отображение G на единичный круг существует, то, в силу A1.1.6),
должно иметь место такое соответствие; с другой стороны, суще-
существование такого отображения гарантируется теоремой Римана.
Отсюда, в частности, следует, что на отрезке S отображение не
только непрерывно, но и конформно, так что функцию z@ можно
аналитически продолжить из G на G (ср. п. 9.4).
1 См. разд. Б, п. 1.1.
2 При таком отражении может случиться, что некоторые части О перекры-
перекрываются. Тогда поместим G на подходящую риманову поверхность, с тем чтобы
ее перекрывающиеся части лежали на разных листах. Все рассуждения остаются
в силе и в этом случае, так как теорема Римана (п. 10.1) верна и для областей на
римановой поверхности.
11.2. Принцип симметрии Шварца 125
Вообще, пусть Gx и G2 — две области, границы которых содер-
содержат прямолинейные отрезки Sl и S2 соответственно, и пусть z(f) —
функция, конформно отображающая Gx на G2 так, что Sx переходит
в S2; тогда z(C) аналитична на Ях и аналитически продолжается в
область Gx, симметричную с Gx относительно St, причем точки,
симметричные относительно Slt преобразуются в точки, симметрич-
симметричные относительно S2. Короче, если при конформном отображении
один прямолинейный отрезок переходит в другой, то точки, сим-
симметричные относительно первого, переходят в точки, симметрич-
симметричные относительно второго. Это предложение известно под назва-
названием принципа симметрии Шварца1.
Этот принцип можно обобщить, заменяя прямолинейные отрезки
границы дугами произвольных аналитических кривых. Именно,
мы называем кривую аналитической, если ее можно параметри-
параметрически задать функцией z{t) (см. п. 2.1), определенной для a«KS
и аналитически продолжимои в некоторую комплексную область,
содержащую отрезок [а, Ь]. Тогда обратная функция t{z) аналитична
в некоторой окрестности рассматриваемой кривой и конформно
отображает эту окрестность на плоскость t так, что кривая пере-
переходит в отрезок [а, Ь] вещественной оси. Две точки называются
симметричными относительно аналитической кривой, если при
отображении t(z) им соответствуют сопряженные друг другу зна-
значения L Это определение не зависит от выбора параметрического
представления z(t). Действительно, если имеются два различных
аналитических параметрических представления кривой и ^(z),
t2(z) — соответствующие обратные функции, то функция t^Q =
= ?i(z(A)) аналитична и отображает отрезок вещественной оси t2
на отрезок вещественной оси ^. В силу принципа симметрии
Шварца, сопряженные значения t2 перейдут при этом в сопряженные
значения tx.
Таким образом, справедливо следующее утверждение: если две
области Gj и G2 конформно отображаются друг на друга, причем
некоторая аналитическая граничная кривая области Gj переходит в
аналитическую граничную кривую области G2, то отображение
конформно вплоть до этих кривых и точки, симметричные относи-
относительно одной из них, преобразуются в точки, симметричные относи-
относительно другой. Для доказательства следует, обращая параметри-
параметрические представления, отобразить окрестности аналитических гра-
граничных кривых на окрестности отрезков вещественной оси и приме-
применить к последним принцип симметрии Шварца. В отличие от случая
прямолинейных отрезков, в общем случае ничего нельзя утверж-
1 См. Schwarz H. A., t)ber einige Abbildungsaufgaben, J. reine angew.
Math., 70 A869), 105—120, Werke II, 65—83. [Подробности см. в работах 11],
[6]. — Прим. ред.]
126 § 12. Отображения круговых многоугольников
дать о том, насколько далеко можно аналитически продолжать
функцию через граничную кривую. Это зависит не только от раз-
размеров областей Gx и G2, но и от того, в какой части области симмет-
симметрия относительно граничной кривой может рассматриваться как
регулярное антиконформное отображение.
В качестве примера симметрии относительно аналитической
кривой мы рассмотрим симметрию относительно единичной
окружности. Представим для этого окружность в параметрической
форме через тригонометрические функции:
г@ = cos t - ism t = е", 0^t<2n. A1.2.1)
Симметричными относительно окружности будут пары точек
z=e" и z* = eft=~, A1.2.2)
z
т. е. так определенная симметрия совпадает с понятием симметрии,
введенным в п. 6.3 [формула F.3.3)]. То же самое верно для симмет-
симметрии относительно любой окружности.
Симметрия относительно окружности есть антиконформное
отображение всей числовой сферы на себя, причем окружность и
прямая — единственные кривые, обладающие этим свойством.
Поэтому каждую область G, граница которой содержит дугу окруж-
окружности, можно расширить до области G, симметричной относитель-
относительно этой дуги. Тем самым функция, аналитическая на G, аналити-
аналитически продолжается через эту дугу в область G, подобно тому как
это делается в случае прямолинейного отрезка S. Принцип симмет-
симметрии Шварца выполняется, таким образом, для дуг окружностей в
том же виде, что и для прямолинейных отрезков.
§ 12. Отображения круговых многоугольников1
12.1. Дифференциальное уравнение Шварца. Многоугольником,
или, точнее, круговым многоугольником, мы будем называть об-
область, ограниченную конечным числом дуг окружностей или прямо-
прямолинейных отрезков. Эти участки границы называются сторонами,
а точки, в которых сходятся две стороны, — вершинами много-
многоугольника. На практике в основном представляют интерес много-
многоугольники, лежащие на числовой плоскости или сфере, однако дока-
доказываемые ниже факты справедливы при незначительных ограниче-
ограничениях и для многоугольников на произвольной римановой поверх-
1 Относительно изложенного в этом параграфе см. [11]. — Прим. ред.
12.1. Дифференциальное уравнение Шварца 127
ности, т. е. для многоугольников, которые частично перекрываются
на плоскости1.
Рассмотрим сначала конформное отображение односвязного
многоугольника, лежащего целиком в конечной части плоскости z,
на верхнюю полуплоскость ш. По теореме о соответствии границ
(п. 10.1) вершины многоугольника перейдут в некоторые точки
вещественной оси ш, причем отображение можно выбрать так,
чтобы одна из вершин перешла в точку ш = оо. Стороны много-
многоугольника преобразуются в интервалы, заключенные между этими
точками. В силу принципа симметрии Шварца отображающая
функция ш(г) аналитична вплоть до сторон многоугольника и ана-
аналитически продолжается через эти стороны по симметрии.
Выберем какую-нибудь из сторон S и обозначим через s-^z)
преобразование симметрии относительно этой стороны. Много-
Многоугольник Р переходит при этом в многоугольник Р* — 8г(Р), и
аналитическое продолжение функции w(z) из Р в Р*, по принципу
Шварца, дается формулой
ш(в1(г)) = w{?). A2.1.1)
Рис. 68.
При этом продолжении Р* отображается на нижнюю полуплоскость.
ю, причем его сторонам также соответствуют отрезки вещественной
оси ю. Пусть теперь S' — одна из сторон Р*, a s2(z) — преобразова-
преобразование симметрии относительно этой стороны. При этом преобразо-
1 Области, лежащие на числовой плоскости или сфере, назовем однолист-
однолистными. Области же, лежащие на более общих римановых поверхностях, такие,
проекции которых перекрываются, назовем многолистными. Многолистные
многоугольники исследованы в работах Ункельбаха: Unkelbach H., Die
konforme Abbildung echter Polygone, Math. Ann., 125 A952), 82—118; Geo-
metrie und konforme Abbildung verallgemeinerter Kreisbogenpolygone, Math*
Ann., 129 A955), 391—414; 130 A955), 327—336.
128 § 12. Отображения круговых многоугольников
вании многоугольник Р* переходит в р** = s2(P*), и функцию
w{z) можно продолжить в Р** по принципу симметрии:
МФг(*)У) = Ч2) = ">&¦ A2-1.2)
Многоугольник Р** отображается функцией ю(г) в верхнюю полу-
полуплоскость, причем точки геР и s2(si(z)) €^** переходят в одну и
ту же точку ю. Двукратное преобразование симметрии является
конформным преобразованием, а именно дробно-линейным преоб-
преобразованием
Рассмотрим обратную функцию г(ш). Описанному выше анали-
аналитическому продолжению функции w(z) из Р в Р* и далее в Р**
соответствует продолжение функции г(ш) из верхней полуплоскости
в нижнюю и обратно в верхнюю через вещественные интервалы,
¦соответствующие сторонам S и S'. Значения функции г(ш) при этом
az(w) + b „
продолжении переходят в значения -—; :' т . Продолжая этот
CZylVj —у" и.
прием и рассматривая всевозможные аналитические продолжения
функции г(ш), придем к следующему результату. Функция z{w)
неограниченно аналитически продолжается из одной полуплоскости
в другую через интервалы, которые соответствуют сторонам много-
многоугольника. Продолжения через различные интервалы приводят,
вообще говоря, к различным значениям функции, так что z(w)
многозначна (вообще говоря, бесконечнозначна). Различные значе-
значения функции в одних и тех же точках ш связаны дробно-линейной
зависимостью, т. е. если гг(ю) и z2(w) — два разных элемента функ-
функции г(ш) (см. п. 9.4), определенных в одной полуплоскости, то
= az^+b
где коэффициенты а, Ь, с, d зависят от формы многоугольника и от
способа аналитического продолжения.
Построим следующее дифференциальное выражение:
Легко проверить, что это выражение не меняется при замене функ-
функции г(ш) дробно-линейной функцией от нее1. Таким образом,
1 Выражение A2.1.5) составляет «бесконечно малый» аналог двойного отно-
отношения G.2.12) и может быть получено из него некоторым специальным предель-
предельным переходом. В связи с этим кругом вопросов это выражение впервые рас-
рассмотрел Шварц; оно названо производной Шварца.
12.1. Дифференциальное уравнение Шварца
129
тодставляя в это выражение функциональные элементы из A2.1.4),
толучаем равенство
Ы„ = Ww. A2Л.6)
-. е. [z]w принимает одно и то же значение для каждого элемента
пункции z(w) и являете поэтому однозначной функцией от ш.
Если из плоскости ш удалить точки, соответствующие вершинам
лногоугольника, то функция г(ш) конформно отображает осталь-
остальную часть плоскости и является там аналитической вместе со своими
юоизводными, причем z'(w) =h 0. Отсюда видно, что и [г]ш является
лналитической функцией в той же области.
Более точные утверждения относительно функции [z]w можно
•лелать, исследуя ее поведение в окрестностях особых точек. Для
:того рассмотрим какую-нибудь из вершин многоугольника, ска-
кем, в точке z = е. Пусть при отображении многоугольника на
зерхнюю полуплоскость эта вершина переходит в точку w = е.
""ледует различать три случая.
1. Стороны, прилегающие к : = е, при достаточном продолже-
^ии пересекаются в другой точке z = е , отличной от е.
2. Прилегающие стороны представляют собой отрезки прямых;
* этом случае е' = оо. Дробно-линейным преобразованием плоско-
•ти z этот случай сводится к предыдущему.
3. Прилегающие стороны имеют только одну общую точку е,
-. е. они касаются в этой точке.
Рис. 69.
6002
130 § 12. Отображения круговых многоугольников
В случае 1 дробно-линейным преобразованием
мы переведем вершину в начало координат, а прилегающие сторо-
стороны — в прямолинейные отрезки. При этом если пЬ — внутренний
угол многоугольника в рассматриваемой вершине, то пусть точки
многоугольника в окрестности этой вершины переходят в точки
0<argT<Ji6 A2.1.8)
в некоторой окрестности нуля. Последующим преобразованием
Iе = г A2.1.9)
угол A2.1.8) переводится в верхнюю полуплоскость /, так что
часть многоугольника в окрестности вершины е отображается функ-
функцией t(z) в часть окрестности t = 0, лежащую в верхней полуплоско-
полуплоскости. С другой стороны, функция ro(z) также отображает часть мно-
многоугольника, лежащую в окрестности вершины, в часть окрестности
точки w = е, лежащую в верхней полуплоскости. Следовательно,
функция t(w) взаимно однозначно и конформно отображает часть
верхней полуплоскости го на часть верхней полуплоскости t, причем
участок вещественной оси в окрестности точки го = е переходит в
участок вещественной оси в окрестности t = 0. Согласно принципу
симметрии Шварца, отображение конформно и в точке го = е,
так что /(го) аналитичиа в этой точке. В частности, t{e) = 0, а произ-
производная t'(e) отлична от нуля. Согласно (9.3.14), функцию t(w)
можно разложить в степенной ряд вида
Цю) = с3(го—е) + с2(го—сJ + ..., A2.1.10)
где Су =?¦ 0. Поскольку при вещественных го вблизи точки w — е
функция t(w) вещественна, все коэффициенты е„ вещественны.
Из A2.1.10) получается разложение для т(го):
т(го) = (го — е)" [а0 + аг (го — е) + я, (го — еJ + . . .]. A2.1.11)
Отсюда можно вычислить разложение для дифференциального
выражения A2.1.5) в окрестности точки го = е, если учесть, что в силу
A2.1.7) [г]ш = [t]w. Тогда получим
И- ~ 2Г«^ + ^Г-е (»о + Ьх (ш - е) + . . •), A2-1.12)
причем коэффициенты bv также вещественны.
Те же соображения справедливы и в случае 2, т. е. когда обе
стороны прямолинейны. Вместо преобразования A2.1.7) здесь сле-
следует применить преобразование
Т(г)= e?y(z — e), A2.1.13)
переводящее окрестность вершины в угловую область A2.1.8).
12.1 Дифференциальное уравнение Шварца
131
Несколько сложнее обстоит дело в случае 3, когда стороны
касаются в вершине. Здесь целесообразно сначала перевести верши-
вершину в бесконечно удаленную
точку дробно-линечным пре-
преобразованием t(z). Это дости-
достигается при помощи функции
вида
T(Z) = _ "_ + ь.
v J z — е
A2.1.14)
При этом стороны, прилегаю-
прилегающие к вершине, вновь переходят
в прямолиненыей отрезки,
которые, однако, не пересека-
пересекаются в конечной точке, т. е. па-
параллельны. Часть многоуголь-
многоугольника, лежащая в окрестности
данной вершины, преобразу-
преобразуется теперь не в область A2.1.8),
а в прямолинейную полуполо-
полуполосу (см. рис. 70). Если выбрать
а и Ъ в A2.1.14) так, чтобы од-
одна из сторон перешла в поло-
положительную вещественную по-
полуось, а другая — в прямую
Im т = с, то функция /(т),
определяемая равенством
1С
д-о
8*1
1С
/*+|-log/= т,
A2.1.15)
V77777777/
Рис. 70. Вершины многоугольников, в
которых прилегающие стороны каса-
касаются. Изображены три случая: при
5=0 (слева вверху), при 5=1 (справа
вверху) и при 5=2 (внизу).
отображает эту область в верхнюю полуплоскость t в окрестности
точки t = 0. Как и выше, приходим к выводу, что t(w) аналитична
в окрестности точки w — е и разлагается там в ряд A2.1.10). Раз-
Разложение функции т(ю) имеет теперь вид1
т(н>) = (ю — e)~s [а0 + Я1(ш—е) + ...] +^log(u>— e). A2.1.If)
Подставляя это разложение в A2.1.5), получим опять разложение
A2.1.12).
Чтобы изучить поведение функции [z]w в окрестности точки
ш = оо, переведем эту точку в нуль преобразованием со = .
При этом верхняя полуплоскость преобразуется в себя, так что
функция (о( z) тоже переводит многоугольник в верхнюю полупло-
1 Следует учесть, что 5 должно быть целым числом.
9*
132 § 12. Отображения круговых многоугольников
скость, причем вершина, соответствующая точке w = оо, переходит
в точку со = 0. Если соответствующий угол равен «5L, то в силу
A2.1.12) функция [?]ш в окрестности со = 0 разлагается в ряд
[<L = тг + 'Оо + V» + •••)• A2.1.17)
С другой стороны, как легко подсчитать,
4 а. A2.1.18)
так что [г]ш в окрестности точки w = оо разлагается в следующий
1
ряд по степеням — :
Гг1„, = 1 ~ S- -f — -i- -•'¦- + . . . A2.1.19)
На основании разложений A2.1.12) и A2.1.19) можно показать,
что [z]w должна быть рациональной функцией. Пусть е}, е2,..., гп ¦---
вершины многоугольника, ЬХ,Ь2,. . .,Ьп_1,Ьоа — внутренние углы
и с,, с2,.. ., <"„_!, оо — - соответствующие точки вещественной оси
и>. Составим функцию
"—' / 1 A2 h \
A2.1.20)
где 60„ равно коэффициенту 60 в формуле A2.1.12), соответствую-
соответствующему точке w = е„. Функция -F(u') во всей конечной плоскости,
включая точки w = е„, аналитична и стремится к нулю при w —> оо.
Таким образом, она ограничена во всей плоскости и, стало быть,
равна постоянной, в силу теоремы Лиувилля (см. п. 9.3). Учитывая
ее поведение при w —> оо, заключаем, что F(w) == 0, т. е. [z]w —
рациональная функция, равная вычитаемому в правой части A2.1.20).
Обращаясь к разложению A2.1.19), можем записать эту функцию
в следующем виде:
л—1 \ п—4
П-1
2 - п - 6L + 2" «!«»"-* +
V »=1 /
2//(ш-е„)
г=1
Здесь /Зк - некоторые вещественные постоянные, значения которых
не определяются непосредственно формой многоугольника; они
носят названия акцессорных параметров.
Выражение A2.1.21) представляет собой дифференциальное
уравнение относительно искомой функции z(w); оно называется
уравнением Шварца. Его интегрированием мы займемся в следую-
следующем пункте.
12.2. Интегрирование уравнения Шварца 133
Заметим, кроме того, что проведенное рассуждение сохраняет
силу и для односвязных многоугольников на сфере, т. е. для тех,
для которых точка г = оо является внутренне ' или граничной. Для
таких многоугольников функция [z]w ведет себя так же, как и для
ограниченных многоугольников, так как дробно-линейным преоб-
преобразованием точку z — оо можно перевести в конечную точку, а
функция [z]w при этом не меняется. Для функции г(ш), отображаю-
отображающей единичный круг на многоугольник, уравнение A2.J.21) в основ-
основном сохраняется. В этом случае нужно отобразить единичный
круг дробно-линейным преобразованием co(w) на верхнюю полу-
полуплоскость, а затем использовать формулу A2.1.18), где [m]w = 0.
12.?.. Интегрирование дифференциального уравнения Шварца.
Уравнение Шварца есть уравнение третьего порядка, однако оно
легко допускает понижение порядка. А именно, делая замену
±- log р- = ~ = riw) A2.2.1)
dw & dw z' v -* v '
и обозначая через R(w) правую часть A2.1.21), представляющую
собой рациональную функцию, получаем
т. е. дифференциальное уравнение первого порядка относительно
Tj{w). Теперь z(w) выражается через щ(ю) формулой
J n(w)uw
z(w)=j с"' dw. A2.2.3)
Уравнение A2.2.2) есть дифференциальное уравнение Риккати;
его можно свести к линейному уравнению второго порядка. Для
этого положим
-^-A"). A2.2.4)
Тогда A2.2.2) приводится к виду
ЧР"И + \ Щи) ?(») = 0. A2.2.5)
Функция z(w) легко выражается через <p(w). Из A2.2.3) с учетом
A2.2.4) получаем
]ш' A2-2-6)
где С — произвольная постоянная.
134 § 12. Отображения круговых многоугольников
Из теории линейных дифференциальных уравнений известно1,
что между двумя линейно независимыми решениями уравнения
вида A2.2.5) существует следующая связь:
Vl(w) = С%(ш) f-f- ; A2.2.7)
таким образом, z(w) записывается в виде частного двух линейно
независимых решений уравнения A2.2.5)
2(ш) = *№- . A2.2.8)
Очевидно, это остается справедливым при умножении <р(ш) на не-
некоторый множитель. Поэтому если в A2.2.5) сделать замену
<p(w) = r(w)w(w), A2.2.9)
то для ip(w) получается линейное уравнение вида
y>"(w) + p(w)yi\w) + q(w)ip(w) = 0. A2.2.10)
Функция z(w) представляется по-прежнему в виде частного двух
линейно независимых решений этого уравнения. При этом
R(w) = 2q(w) - \ p\w) - p\w). A2.2.11)
В частности, этим преобразованием можно привести дифференци-
дифференциальное уравнение A2.2.5) к виду
1Р"И 2
Г/ п—1 \2 I л—4
4 //"(и, _ е,)
где коэффициенты p(w) и g(w) имеют только простые полюсы.
В дальнейшем мы будем исходить из этого частного вида урав-
уравнения A2.2.5). Так как это уравнение допускает решение в квадрату-
квадратурах лишь в некоторых специальных случаях, мы обратимся к числен-
численному интегрированию, в частности к решению с помощью рядов.
Справедлива теорема о том, что в окрестности особой точки w = е„
пара линейно независимых решений — так называемых канониче-
1 См. Камке Э., Справочник по обыкновенным дифференциальным
уравнениям, М., 1950.
12.2. Интегрирование уравнения Шварца 135
ских решений — может быть следующим образом представлена
в виде степенных рядов:
Kl (Ш — ev) + ос2 (w - е„)
- еJ
= (Ш - е„) 2 [1 + ^ (Ш - е„) + C2 (Ш — О2 +...)•
A2.2.13)
Если 6V — целое число, то вторую из этих формул следует заменить
более общей
<№(»>) = <№(Р) Jlog (и» - О + (ш - О"»~ [1 + & 0" - О + • • О-
A2.2.14)
Коэффициенты разложения « , /?„ и постоянная — легко вычи-
сляются, если подставить эти ряды в A2.2.5), дифференцируя их
почленно и умножая на функцию R(w), тоже разложенную в ряд
[см. A2.1.12)]. Коэффициенты получаемого при этом степенного
ряда определяются коэффициентами выражений A2.2.13), A2.2.14) и
A2.1.12); приравнивая эти коэффициенты нулю, получим систему
уравнений1 для определения неизвестных <zv, j3r.
Более общие разложения в ряды можно получить, применяя
отображение верхней полуплоскости w на себя. Именно, полагая
(о = —лГй' а' > с' вещественны, да— Ъс = I, A2.2.15)
и
y(w) = {cw -\- d).y>(a>),
получаем для у(со) дифференциальное уравнение вида
где [см. A2.1.18)]
+ 1в*(со)гр(а)) = 0, A2.2.16)
R*(co) = (cw + d)* R(w). A2.2.17)
Функция R*(co) как функция со имеет тот же вид, что и R(w) как
функция w. Поэтому если точке w = е„ соответствует точка со = е*,
то функцию ip(u>) можно разложить в ряд по степеням со — е*,
аналогичный A2.2.13) или A2.2.14). С помощью A2.2.15) отсюда
получаются разложения <p(w). В частности, полагая со — — —, полу-
получаем разложение в окрестности точки w = оо, имеющее вид
1 См. ниже, п. 12.5.
136 § 12. Отображения круговых многоугольников
A2.2.18)
причем постоянная с при логарифме отлична от нуля только при
целом 6те.
Кроме того, можно получить канонические разложения в окрест-
окрестностях регулярных точек. Если го = и>0 — такая точка, то имеет
место разложение вида A2.2.13), в котором следует положить
д = I. Таким образом,
ТГ^-^^Т.*'''' A12Л9)
Коэффициенты разложений определяются и в этом случае непосред-
непосредственной подстановкой в дифференциальное уравнение.
Рассмотренные ряды сходятся в каждом круге \w —¦ ev\ < о,
\со — е*| < о, соответственно \w — го(!| < о, не содержащем внутри
никаких особых точек функции Я(го), кроме центра. Можно так
выбрать центры этих кругов и функции со(го), чтобы вся плоскость го
покрывалась конечным числом этих кругов. В этом случае мы полу-
получаем всю совокупность решений уравнения A2.2.5). Любое решение
9?(го) может быть представлено в виде линейной комбинации канони-
канонических решений:
у(ш) = сг<рЫ(ю) + c.2(ff\w). A2.2.20)
Если в точке го = го0 внутри круга сходимости канонического разло-
разложения заданы значения у(и>0) и <р'(го0), то коэффициенты с5 и с2
можно определить из равенства A2.2.20) и равенства, полученного
при его дифференцировании; этим <р(го) определяется во всем круге
сходимости. Тем же способом можно аналитически продолжить
функцию 9 (го) в соседний круг сходимости, который имеет общие
точки с исходным.
Сравнивая разложения A2.2.13) и A2.2.14) с A2.1.11) и A2.1.16),
замечаем, что частное двух канонических решений совпадает с
определенной там функцией т(го), т. е.
го) = -^щ— или т(го) = r(i)— , A2.2.21)
в зависимости от того, содержится в разложении логарифмический
член или нет. Частное решений A2.2.19), которое мы обозначим в
связи с этим через x(w, Год):
т(ю, ид = «т-— , A2.2.22)
12.3. Задача об определении параметров 137
обращается в точке ш = w0 в нуль, а его производная в этой точке
равна 1. Таким образом, функция т(го, и>0) отображает конформно
некоторую окрестность точки w = w() на окрестность начала коор-
координат. Произвольное решение :(«>) уравнения Шварца, в силу
A2.2.20), связано с частным решением т(го, ш„), подобно A2.1.7) и
A2.1.14), дробно-линейным соотношением
4 ct(w, а>0) + rf v J
Так как дробно-линейное преобразование всюду конформно на
числовой сфере, каждое решение г(ш) уравнения Шварца конформно
отображает окрестность каждой регулярной точки функции R(w)
на некоторую область числовой сферы z.
С помощью этих соображений можно не только показать, что
каждая функция z(ro), конформно отображающая верхнюю полупло-
полуплоскость на многоугольник, удовлетворяет уравнению Шварца, но и,
наоборот, что каждое решение этого уравнения отображает верх-
верхнюю полуплоскость на некоторый многоугольник. При этом,
очевидно, можно получить и такие многоугольники, которые частич-
частично перекрываются, так как рассуждения, проведенные при выводе
уравнения Шварца, сохраняют силу и для перекрывающихся много-
многоугольников (см. литературу, указанную в сноске на стр. 127).
12.3. Задача об определении параметров. Интегрированием урав-
уравнения Шварца еще не полностью решается задача об отображении
верхней полуплоскости на заданный многоугольник. Хотя вид диф-
дифференциального уравнения, которому удовлетворяет искомая функ-
функция, полностью определен, однако рациональная функция R(w)
содержит некоторое количество неопределенных параметров, связь
которых с геометрическими характеристиками многоугольника
заранее неизвестна. В этом состоит основная трудность столь
изящного метода Шварца. Так как до сих пор нет никаких общих
методов решения этой проблемы, то остается лишь искать решение
уравнения Шварца «в общем», т. е. определить зависимость
решения от параметров и из совокупности решений выбрать то,
которое дает требуемое отображение. Ясно, что при большом
числе параметров такой способ практически почти безнадежен.
Речь идет о следующих параметрах функции R(w).
1. Расположение особых точек е„. Дробно-линейным преобра-
преобразованием верхней полуплоскости на себя три из них можно всегда
перевести в три заданные точки, например го = 0, 1, оо. Остальные
особые точки этим вполне определяются, так что необходимо опре-'
делить л — 3 существенных величины.
2. л — 3 акцессорных параметра.
Итого следует определить 2л — 6 вещественных параметров;
таким образом, задача о параметрах возникаетуже при рассмотрении
138 ф 12. Отображения круговых многоугольников
кругового четырехугольника (два неопределенных параметра).
С прибавлением каждой новой стороны число параметров увели-
увеличивается на два.
Для выяснения того, насколько эти параметры влияют на форму
многоугольника, заметим прежде всего, что уравнение Шварца
определяет многоугольник с точностью до дробно-линейного
преобразования. Таким образом, параметры могут быть непосред-
непосредственно связаны только с такими геометрическими характеристи-
характеристиками многоугольников, которые не изменяются при дробно-линей-
дробно-линейных преобразованиях. Такими характеристиками являются сле-
следующие.
1. Двойное отношение любых четырех характеристических точек
многоугольника. Такими точками могут служить вершины, а
также все остальные точки пересечения двух сторон. Отметим, в
частности, что две смежные стороны пересекаются как в вершине
e.v, так и в другой точке е'г [см. A2.1.7)], если 6V — не целое; назовем
точки f'v противоположными вершинами.
2. Угол между любыми двумя сторонами в смысле определения
G.5.5). Естественно ожидать, что 2п-— 6 таких постоянных одно-
однозначно определяют многоугольник, однако по этому вопросу, за
исключением случая кругового треугольника1, нет исчерпывающих
результатов.
Для нахождения геометрических характеристик по параметрам
дифференциального уравнения достаточно определить преобразо-
преобразования перехода между парами канонических решений. Пусть,
например,
¦ A2.3.1)
Предполагая, что ни 6V, ни д^ не являются целыми числами,
рассмотрим отношение т„ = -? . Для этого частного решения
вершиной служит е,. = 0, а противоположной вершиной e'v = оо.
То же самое имеем для т^ и соответствующих вершин е^ и е^. Для
отображения, определяемого отношением тг, в силу A2.3.1) имеем
»/« V/1
f,< =--»,т и ?м=-^тг- A2.3.2)
С22 С21
Таким образом, двойное отношение для любого решения z[w)
1 См. Schilling F., lieitrage zur geometrischen Theorie der Schwarz-
schcn s-Funktion, Math. Ann. 44 A894), 161—260. В этой работе чисто гео-
геометрическими методами показано, что круговой треугольник с точностью до
дробно-линейного преобразования однозначно определяется углами при верши-
вершинах. Так как здесь не возникает задачи о параметрах, это следует уже из наших
рассуждений при выводе уравнения Шварца.
12.3. Задача об определении параметров
139
уравнения Шварца выражается через коэффициенты уравнений
A2.3.1) следующим образом:
?v — e,, _ ev
C12 C21
~Vff~vjT
Cll C22
A2.3.3)
Особый интерес представляют еще четыре следующих вырожден-
вырожденных случая:
1. er=V cI§=0, т. е. <> = «>;
2- е, = в'„ сЦ = 0, т. е. <$> ^f)
З.е;=е„, с^=0, т. е. #'
4. si = е;, с^ = 0. т. е. срР
/
Теперь равенство A2.3.3) вместе с A2.3.1) принимает вид крае-
краевых условий в задаче о собственных значениях. Когда возникают
такие условия, задача о пара-
параметрах может быть решена
методами спектральной тео- /
рии1.
Для определения угла между
двумя сторонами следует вмес-
вместо преобразования A2.3.1) при-
привлечь преобразования обхода
для пары решений уравнения
A2.2.5). Пусть, например, двум
рассматриваемым сторонам
соответствуют вещественные
интервалы 1г и 12 плоскости ш.
Продолжим пару линейно независимых решений (например,
каноническую пару) из верхней полуплоскости в нижнюю через
Ii, а затем через 1г обратно в верхнюю полуплоскость. При
этом решения подвергаются линейному преобразованию, которое
соответствует преобразованию A2.1.4) функции z(w):
w1 = aw1 + ftqpo,
Ч>2 = C(Pl + d<p2 ¦
Коэффициенты удовлетворяют условию
ad—hc=> 1,
A2.3.4)
A2.3.5)
'См. Stallmann V., Konforme Abbildung gewisser Kreisbogen-
vierecke als Eigenwertproblem, Math. Z., 59 A953), 211—230.
140 § 12. Отображения круговых многоугольников
поскольку определитель Вронского ср^'2—ЩЦ-'\, составленный из
решений уравнения вида A2.2.5), равен постоянной.
Обратно, найдя дробно-линейное преобразование A2.1.4), даю-
дающее отражение от двух сторон1, образующих угол б, получаем, с
учетом A2.3.5), соотношение
а + d = 4- 2 cos9. A2.3.6)
В частности, для двух смежных сторон и для соответствующих
канонических решений преобразование обхода имеет вид
"О) = emir A)
A2.3.7)
что вытекает непосредственно из разложений
A2.2.13) и A2.2.14). В этом случае в равно внут-
внутреннему углу dv.
Преобразования обхода вычисляются непосред-
непосредственно из преобразований перехода, так как
последние определяют аналитическое продол-
продолжение канонических решений от одной особой
точки к другой2. При продолжении из верхней
полуплоскости в нижнюю и обратно следует учи-
учитывать многозначность канонических решений,
Рис. 72. которая обусловливается наличием показателя
¦~=—" и логарифмического члена [см. A2.3.7)]. В
силу этой многозначности при преобразованиях перехода следует
всегда указывать, к каким функциональным элементам канонических
решений они относятся3.
Двойные отношения A2.3.3) и величины углов A2.3.6) опреде-
определяют вершины многоугольника и окружности, на которых располо-
расположены его стороны, однако сами стороны этим не определяются.
Допуская, что каждая сторона может перекрываться любое конеч-
конечное число раз, мы для данной системы геометрических констант
получаем бесконечное множество круговых многоугольников. Это
1 При этом следует прежде всего учесть, что узлы пучка окружностей,
определяемого этими сторонами (см. п. 7.5), являются неподвижными точками
этого отображения. Переводя эти точки в 0 и ос, получаем нормальную форму
G.2.9), в которой s есть показательная функция угла. Из G.2.10) следует формула
A2.3.6).
2 Очевидно, достаточно знать преобразование перехода от каждой особой
точки к следующей.
а Целесообразно рассматривать здесь функциональные элементы решений
щ и tpi', однозначные в верхней полуплоскости и принимающие веществен-
вещественные значения при стремлении к интервалу е„ < ш < е,,+ 1.
12.4. Асимптотическое интегрирование
141
показано на рис. 73. Поэтому многоугольник определяется не только
геометрическими константами, но и условиями, налагаемыми на
перекрытие.
Связь между условиями, налагаемыми на перекрытие, и пара-
параметрами дифференциального уравнения выражается через нули
канонического решения. А именно tv = 0 при <р^ = 0 и т„ = оо
при ffi = 0, в силу чего любое решение г(го) в нулях функций
(р^(ю) принимает значение tv, а в нулях <pt2)(w) — значение e'v. Таким
образом, если q>^\w) в интер-
интервале <¦„ < w < ev+1 имеет п
нулей, то соответствующая сто-
сторона покрывает вершину е„
п раз; это же верно и для нулей
функции q>^\w) и соответст-
соответствующих противоположных вер-
вершин e'v . В частности, для одно-
однолистности многоугольника на
числовой плоскости канониче-
канонические решения q>^\w) не должны
обращаться в нуль в соответ- Рис- 73.
ствующих интервалах.
12.4. Асимптотическое интегрирование. Для решения уравнения
A2.2.5) мы применим приближенный метод, который позволит
выразить в достаточно обозримой форме зависимость решений от
параметров «в целом», в частности, от акцессорных параметров.
Мы имеем в виду метод асимптотического интегрирования, пред-
предложенный впервые Лиувиллем1.
Для применения этого метода к уравнению A2.2.5) разложим
коэффициент - R(w) в сумму
A2.4.1)
где Q2q(iv) имеет вид
л—4
*w*
х=0
4 //(ю - е„)
. A2.4.2)
Сумма _2" распространяется на «большие» значения bv, т. е. на
1 См. Stallmann F., Koiiforme Abbildung von Kreisbogenpolygonen,
I, II, III, Math. Z., 60 A954), 187—212, 68 A957), 27—76, 245—266.
142 § 12. Отображения круговых многоугольников
те 6„, которые превосходят - . Подобно этому будем считать в
A2.4.2) Ь^ = 0, если §«, «мало», т. е. не больше - .
Положим теперь
4
V <№). A2.4.3)
Благодаря этим заменам уравнение A2.2.5) примет вид1
v = у" + (9Ш — 1 j у, = 0, A2.4.4)
где [!]„, вновь означает производную Шварца A2.1.5). Фиксируя в
этом уравнении г(го) и q(w) и устремляя q к оо, мы можем сделать
i
0(i)
величину ^у- как угодно малой всюду, за исключением точек,
где Q(!) равно оо. Поэтому естественно ожидать, что решения
уравнения A2.4.4), за исключением особых точек, приближенно
совпадают с решениями уравнения
у>"~ гр = О, A2.4.5)
т. е. имеют вид
гр ?« CjC^ 4- с„е~*. A2.4.6)
В точках |0, в которых Q(!) = оо, существует предел
A2A7)
и решения уравнения A2.4.4) вблизи этих точек можно приближенно
заменить решениями уравнения
= 0. A2.4.8)
Эти последние выражаются через цилиндрические функции; пару
линейно независимых решений можно записать, например, в виде
функций Ганкеля:
12) A2.4.9)
1 Коэффициенты уравнения A2.4.4) записаны как функции от ш; ясно, что
их следует считать функциями от |, определяемого формулой A2.4.3).
12.4. Асимптотическое интегрирование 143
Эти частные решения обладают тем свойством, что при больших
значениях [I — |„| они асимптотически приближаются к e±(f—W.
Для установления связи между уравнениями A2.4.4) и A2.2.5)
отметим прежде всего, что функцию |(го) можно представить в
виде интеграла Шварца—Кристоффеля. Как мы покажем в следую-
следующем параграфе, такой интеграл отображает верхнюю полуплоскость
на прямолинейный многоугольник. В нашем случае стороны этого
многоугольника параллельны координатным осям плоскости |;
мы будем называть его ступенчатым многоугольником. Если
q{m) имеет нули в верхней полуплоскости, то отображение верхней
полуплоскости, осуществляемое функцией 1(го), не является одно-
однозначным. Для получения однозначного функционального элемента
следует соединить нули с вещественной осью разрезами. Эти раз-
разрезы можно всегда расположить так, чтобы при отображении ?(го)
их берега переходили в отрезки, параллельные координатным осям.
Тогда функция f (го) отобразит верхнюю полуплоскость с разре-
разрезами на ступенчатый многоугольник. Нулям функции </(«>), содер-
содержащимся в верхней полуплоскости, будут соответствовать вершины
многоугольника с внутренними углами, большими 2тт, так что
он в этих точках не является однолистным, а перекрывается. В
остальных случаях также возможны самоперекрытия ступенчатого
многоугольника; впрочем, для дальнейших рассуждений это несу-
несущественно.
На границе1 полученного таким образом ступенчатого много-
многоугольника лежит конечное число особых точек функции Q(|). Для
исследования характера этих точек определим порядок к функции
q(w) в точке w = wa, как степень младшего члена в разложении
функции q(w) в степенной ряд в этой точке. Пусть мы имеем
<?(го) = (го — Гоо)" [а0 + аг (го — го0) + а2 (го — го^2 + ...], A2.4.10)
где п0 ф 0. Тогда особыми точками Q(l) являются следующие:
1) образы |(е„) тех точек го = е„, которым соответствуют «ма-
«малые» 6„, не входящие в сумму J?' из A2.4.2); если к — порядок функ-
функции q(w) в этой точке, то величина т в формуле A2.4.7) равна
; A2.4.11)
2) образы всех нулей ?(«>),' если го = го0 — такая точка, то q(m)
имеет порядок к > 0 и т принимает вид
i • <12А12)
1 Особые точки Q(?) могут лежать только на границе ступенчатого много-
многоугольника.
144 .<? 12. Отображения круговых многоугольников
В тех точках т = е„, которым соответствуют «большие» ov, порядок
q(w) равен — 2. Полуокрестность (т. е. пересечение окрестности с
верхней полуплоскостью) точки т = е„ отображается функцией
f (и>) на полуполосу ширины ' - , и функция Q(|) стремится в ней
к нулю.
Ступенчатый многоугольник можно разбить на прямоугольники
и полуполосы таким образом, чтобы все особые точки Q(l) лежали в
их вершинах, причем не более чем по одной в каждой из этих
фигур. Тогда можно показать1, что решения A2.4.4) в каждой частич-
частичной области приближенно совпадают с решениями A2.4.8), т. е. с
некоторыми линейными комбинациями функций A2.4.9), причем
для |0 и т следует брать значения, соответствующие особой точке,
принадлежащей данной частичной области.
Для нахождения конформного отображения, которое дает
частное двух решений уравнения A2.4.4). исследуем сначала отобра-
отображение, которое дает частное функций A2.4.9):
Для простоты положим ?с = 0 и рассмотрим преобразование
первого квадранта Re | > 0, Im | > 0. Функция г](|) отображает
положительную вещественную полуось в прямую
v = —icosrtm I- t, sin лгп < [< оо, A2.4.14)
а положительную мнимую полуось — в единичную окружность
ri=p", т — ~</<оо, A2.4.15)
проходимую бесконечное число раз в положительном направлении.
При больших значениях ? функция г)(|) асимптотически прибли-
приближается к показательной функции
т](?)?уе2?, A2.4.16)
так что в рассматриваемом квадранте декартова сетка Re | = съ
Im | = с2 с ростом значений сх и сг все более точно преобразуется
функцией i](|) в полярную сетку \у]\ = e2Ci, argri = 2е2 на римановой
поверхности логарифмической функции. Аналитическое продолже-
продолжение функции i](|) за пределы квадранта осуществляется по прин-
принципу симметрии Шварца зеркальным отражением относительно
прямой A2.4.14), соответственно окружности A2.4.15) (см. рис. 74).
1 См. Stallmann F., Math. Z., 60, 196 ff.
12.4. Асимптотическое интегрирование
145
Благодаря этим свойствам отображения каждая не слишком
малая часть ступенчатого многоугольника отображается соответ-
соответствующей функцией г](?) приближенно на круговой многоугольник.
Точнее: частичный прямоугольник преобразуется в круговой
четырехугольник, причем особой точке функции Q(|) соответствует
вершина с внутренним углом тст, а в остальных трех вершинах
отображение конформно, т. е. три остальных внутренних угла
равны ~. Полуполоса
отоб-
отображается приближенно на кру-
круговой треугольник, причем
особой точке Q(!) опять соот-
соответствует внутренний угол
тст, точке I = оо — угол bjt,
а третьей вершине — угол ^-.
Так как решения w(?) урав-
уравнения A2.4.4) равномерно ап-
аппроксимируются решениями
%(?) уравнения A2.4.8) в каждой
частичной области, то эти час-
частичные области тоже прибли-
приближенно отображаются частным
двух линейно независимых
решений уравнения A2.4.4) на
круговые четырехугольники или
треугольники, которые получа-
получаются из только что рассмотрен-
рассмотренного дробно-линейным преоб-
преобразованием. В силу соотно-
соотношения
a)
0
Рис. 74.
они служат частями кругового многоугольника, получающегося из
верхней полуплоскости при преобразовании, которое дает частное
двух линейно независимых решений уравнения A2.2.5). Искомый
круговой многоугольник состоит, следовательно, из круговых
четырехугольников и треугольников, так же как соответствующий
ступенчатый многоугольник — из прямоугольников и полуполос.
Исходя из этих соображений, легко определить приближение для
кругового многоугольника, соответствующего заданному диффе-
дифференциальному уравнению. Для этого сначала при помощи интеграла
A2.4.3) определяют ступенчатый многоугольник и делят его указан-
указанным способом на прямоугольники и полуполосы. Эти частичные
10 — 6002
146 § 12. Отображения круговых многоугольников
области отображаются соответствующими функциями ?](!) на
круговые четырехугольники и треугольники, которые при по-
помощи дополнительных дробно-линейных преобразований дефор-
деформируются таким образом, чтобы соответствующие стороны
совпали. Для определения этих преобразований1 рассматривается
декартова сетка в плоскости I. В каждой части эта сетка отобра-
отображается соответствующей функцией г](|) в изотермическую сетку,
которую на достаточном расстоянии от особой точки Q(|) можно
приближенно заменить полярной сеткой (см. рис. 74). При некото-
некотором дробно-линейном преобразовании эта сетка переходит в более
общую круговую сетку (сетку источника и стока). При переходе от
одной части к другой эти сетки должны непрерывно переходить
друг в друга, и этим однозначно определяется (чисто геометриче-
геометрически) способ составления искомого кругового многоугольника из
четырехугольников и треугольников. Следует, однако, учитывать,
что изотермические сетки в круговых четырехугольниках и тре-
треугольниках определены лишь приближенно, так что взаимное
расположение частичных многоугольников определяется также
лишь с некоторым приближением. Это приближение тем точнее2,
чем дальше друг от друга лежат особые точки функции Q(|).
Пример. Круговой пятиугольник. Применим изложенный метод
к случаю кругового пятиугольника, у которого все внутренние
углы не превосходят ^ . Тогда величины bv в выражении Q2q(w)
отсутствуют и функция |(ю) принимает вид
dw - Ж
!•=[
l_ dw. A2.4.18)
Если w0 не совпадает ни с одним е„, то ступенчатый многоугольник
с точностью до поворотов и отражений имеет вид, указанный
на рис. 75j причем вершине 10 соответствует точка го= w0. Так как
функция q(w) имеет в ней простой нуль, то этой точке соответствует
значение т, равное - . В точке w = ev имеем к = —1 и, следова-
О
тельно, m = bv.
Разделим ступенчатый многоугольник на 12 прямоугольников3,
1 Эти дробно-линейные преобразования играют ту же роль, что и преобра-
преобразования перехода A2.3.1) для канонических решений.
2 Некоторое улучшение можно получить, применяя вместо функций Ган-
келя более общие конфлюентные гипергеометрические функции. См. Stall-
m а п n I'., Math. Z., 68 A957), 245-266.
8 Это лишь один из возможных способов разбиения. Можно, например,
объединить прямоугольники 1 и 2 или 1 и 5.
12.4. Асимптотическое интегрирование
147
как показано на рис. 75. Для построения круговых пятиугольников
можно исходить из особой точки |0. В этой точке сходятся прямо-
прямоугольники 6, 7 и 10, и функцию z(|), дающую отображение, можно
во всех трех прямоугольниках аппроксимировать отношением
одной и той же пары решений уравнения A2.4.8). Этим обеспечи-
обеспечивается непрерывное продолжение функции, дающей отображение,
из одного прямоугольника в другой. Взяв отношение ?](!) частных
I
/
5
Э
и
г
'#
/2
3
'X'/
it
4
8
9*
Рис. 75.
решений, мы преобразуем эти прямоугольники в круговые четырех-
четырехугольники 6, 7 и 10, указанные на рис. 75. При этом излом границы
ступенчатого многоугольника в точке |0 преобразуется в прямо-
прямолинейный участок (изображении i пунктиром), что естественно,
так как точке ш = го0 не соответствует никакая вершина кругового
пятиугольника.
Рассмотрим теперь прямоугольник 8, прилегающий к 7. Соот-
Соответствующая функция т?A) отображает его на круговой четырех-
четырехугольник, который следует лишь увеличить, чтобы он примкнул к
четырехугольнику 7. При этом необходимо заменить прямолиней-
прямолинейный участок (пунктир) границы четырехугольников 7 и 10 дугой
окружности, с тем чтобы получить угол пд2. Такая замена допусти-
допустима, так как функция я(|) лишь аппроксимирует искомую[функцию
z(|), а не воспроизводит ее в точности. Эта замена тем незначи-
148
§ 12. Отображения круговых многоугольников
тельнее (т. е. тем меньше ее влияние на форму четырехугольников
7 и 10), чем больше размеры соответствующих им прямоугольни-
прямоугольников. Поэтому такой способ непригоден, если особенности функции
<)(!) расположены близко друг к другу.
/
5
г
6
3
7
8
/
3
5
7
г
6
8
пдг
яд-,
Рис. 76.
Аналогичным образом строятся остальные части пятиугольника.
Сначала прямоугольники отображаются при помощи i](|) на кру-
круговые четырехугольники, и остается лишь подогнать их друг к
другу так, чтобы после изменения (как можно меньшего) уже по-
построенных частей прямолинейные участки ступенчатого много-
многоугольника преобразовались в дуги окружностей. Полное постро-
построение показано на рис. 75.
Подобным образом исследуется случай, когда точка гов совпа-
совпадает с одной из точек1 е„. Ступенчатый многоугольник тогда пред-
представляет собой прямоугольник, на одной из сторон которого
находится особая точка, соответствующая wG = е . В этой точке
1 Сюда относится и тот случай, когда /?, = 0, /?0 ф 0. В этом случае ш0 сов-
совпадает с точкой и> = оо.
12.5. Замечания к численному интегрированию 149
к = 0, т = -± . На рис. 76 показано разбиение ступенчатого много-
многоугольника и построение кругового пятиугольника в двух различных
случаях, которые здесь возможны (с точностью до зеркальных
отражений).
Заметим еще, что, непрерывно изменяя параметры, можно пре-
преобразовать ступенчатый многоугольник на рис. 75 в любой из
ступенчатых многоугольников щ рис. 76 (способ преобразования
ясен из нумерации отдельных частей). При построении кругового
пятиугольника такой переход, однако, невозможен (хотя при этом
пятиугольник тоже непрерывно изменяется), так как особые точки
|0 и ?2, соответственно ?а> оказались бы как угодно близко друг
к другу. Этот недостаток в определении параметров следует испра-
исправить с помощью интерполирования.
Рассмотренный пример ясно показывает, что изложенный метод
позволяет легко и почти без вычислений приближенно определить
круговой многоугольник, исходя из соответствующего ступенча-
ступенчатого многоугольника. Легко прежде всего усмотреть, как изменяется
круговой многоугольник в зависимости от изменения ступенчатого.
Обратно, по каждому круговому многоугольнику можно прибли-
приближенно построить соответствующий ему ступенчатый многоуголь-
многоугольник, а затем v етодом, изложенным в следующем параграфе, опре-
определить параметры. Таким образом, без громоздких вычислений
можно получить значения параметров в первом приближении, а
затем улучшить их численными методами1.
12.5. Замечания к численному интегрированию уравнения Шварца.
Для численных исследований целесообразно записать рациональ-
рациональную функцию й(ю) в виде A2.1.20):
Связь между величинами bOv и акцессорными параметрами
выражается следующим уравнением:
Ъ0!=У -?f^ — • 02.5.2)
Для вычисления коэффициентов ая, /Зл канонических разложений
A2.2.13) и A2.2.14) разложим выражение (ш— е,J-—^- в ряд по
1 См. конец п. 12.5.
150 § 12. Отображения круговых многоугольников
степеням ш — е,-:
(ш - e,f *^ = g px(w - etf. A2.5.3)
При этом
(Я
Подставляя разложение A2.2.13) в уравнение, получаем следую-
следующую систему, из которой можно последовательно определить
коэффициенты <хя, рх:
А (А + §,) а; + рЛ_! + р2ссЛ_2 -Ь . . . + p^o^ + Рд = 0,
А (А — 6,) р\ + р^.! + р^Л_2 -г . . . + pA_lP\ + РЛ = 0,
А = 1,2, A2.5.5)
Определить j3ft невозможно, если д, — целое число, 6г = к;
действительно, при А = к коэффициент при р\ обращается в нуль.
Здесь следует различать две возможности.
1. Вычисленные значения р'х.р'г, • • •, pV-i удовлетворяют вто-
второму уравнению A2.5.5) при А = к ~fr 0:
i + РЛ-% + ¦¦¦ + Pk-ift + Pk - 0. ' A2.5.6)
Тогда р\ можно выбрать произвольно, например /3ft == 0. При
таком значении р\ величины /Зк+j, р\+2, • • • определяются из даль-
дальнейших уравнений; таким образом, приходим к разложениям
A2.2.13) или A2.2.14) с с = 0.
Условие A2.5.6) всегда выполняется при д{ = к = 0; однако
в этом случае мы не получаем решений, линейно не зависимых с
<№¦
2. Условие A2.5.6) не выполнено или bt= к = 0. Тогда разло-
разложение A2.2.13) заменяется более общим разложением A2.2.14).
Подставляя его в уравнение, получаем при А з= к уравнение иного
вида, нежели A2.5.5). Для А = к имеем
pA-i "~ ¦ • ¦ + Pft-A + Р* = - ? *, A2.5.7)
откуда определяется величина — ; при к = 0 ее можно выбрать
произвольно. При А > к имеем
A (A- fc)p\, + Pl^_! + ... + рЛ_х Рг + Рх = — JBA— *)аЛ_».
A2.5.8)
12.5. Замечания к численному интегрированию 151
Здесь j3fc также может принимать произвольное значение; положим,
например, j3fe = 0. Дальнейшие коэффициенты j3fc+1, j3fc+2,... вы-
вычисляются из A2.5.8).
Эти уравнения можно применить и при вычислении коэффициен-
коэффициентов разложения A2.2.19). Для этого следует положить 6, = 1,
Pa = Pi = 0. Для остальных р; (а > 1) имеет место формула A2.5.4),
в которой следует е,- всюду заменить на ш0, а суммирование прово-
проводить по всем особым точкам е„. Условие A2.5.6) выполнено, и мы
можем поэтому положить /^ = 0.
Кроме разложений в ряды, можно воспользоваться и другими
методами численного интегрирования. Хорошие результаты дает
здесь метод Рунге—Кутта1, который в данном случае принимает
следующую форму.
Пусть в некоторой точке w = wQ заданы значения функции <р(р)
и ее производной
ф(шо)=9H, <p'{w^=<p'o-
Ищется значение функции и ее производной в точке ш1 = юв + ft.
Введем для этого следующие вспомогательные величины:
л»_ - ,, , 7
Тогда
Ф (ш0 + ft) = n>B + ft ^o + К
hq>' (w0 + ft) = ftQ?o + *',
где
ft'= 1(^ + 4^ +ft,).
При достаточном удалении от особых точек этот метод оказы-
оказывается весьма точным. В качестве «естественного шага» ft в нашем
случае, следуя Коллатцу2, мы выберем величину
ft =
\R(w)
A2.5.9)
1 См., например, Коллатц Л. К., Численные методы решения дифферен-
дифференциальных уравнений, М., 1953.
2 См. С о 11 a t z L., Natilrliche Schrittweite bei numerischer Integration
"von Differentialgleichungssystemen, Z. angew. Math. Mech. 22 A942), 216—225.
152 ff 12. Отображения круговых многоугольников
где постоянной с, в зависимости от требуемой точности, придается
значение между 0,1 и 0,2. Этим определяется число шагов, после
чего можно установить, какой из двух названных методов требует
меньших усилий. В обоих случаях следует предварительно под-
подвергнуть дифференциальное уравнение преобразованию вида
A2.2.15).
Заметим также, что уравнение Шварца можно проинтегри-
проинтегрировать, не выходя за пределы вещественной области. Действительно,
форма кругового многоугольника однозначно определяется фор-
формой границы, т. е. видом функции z(w) при вещественных w. Кроме
того, значения функции z(w) в верхней полуплоскости вычисляются
через ее значения на вещественной оси при помощи интеграла
типа (9.1.10). В нашем случае этот интеграл записывается в виде
* ("о + '"о) = ~ f <") "-Ъ d»> A2.5.10)
71 J (u0 — uJ + vo
где z(u) — значения функции на вещественной оси. В большинстве
случаев, однако, удобнее после соответствующего преобразования1
разлагать решения дифференциального уравнения в окрестности
произвольной точки ю0 верхней полуплоскости в степенной ряд
вида
5Л^)\ A2.5.11)
Эти ряды сходятся во всей верхней полуплоскости обычно доста-
достаточно быстро, так что можно ограничиться такими разложе-
разложениями.
Для определения параметров следует сначала путем асимптоти-
асимптотического интегрирования получить некоторые их первые прибли-
приближения; затем численным интегрированием определяется точная
форма соответствующего многоугольника или его геометрические
инварианты. Исходя из этого, можно путем малого изменения
приближенных значений и линейного интерполирования определить
искомый многоугольник с произвольной точностью. При этом
потребуются, конечно, большие вычисления2, и для решения подоб-
подобного рода задач об отображении придется воспользоваться также
и более общими численными методами, излагаемыми ниже3. Реше-
1 См. также конец п. 12.1.
2 Это существенно зависит, конечно, от имеющихся в нашем распоряжении
вычислительных средств. В первую очередь имеется в виду применение интегра-
интеграторов к решению уравнения Шварца. Для этого наиболее пригодна форма
A2.2.2) в сочетании с A2.2.3).
3 См. § 16—17, в особенности п. 17.3 и 17.4.
13.1. Интеграл Шварца—Кристоффеля 153
ние задачи об отображении при помощи уравнения Шварца выгодно
в тех случаях, когда рассматривается не один, а некоторое множе-
множество подобных многоугольников, поскольку интегрирование так
или иначе проводится для большого числа параметров.
В некоторых частных случаях задача о параметрах решается
прямыми методами, например разложением в ряды по параметрам
с использованием теории возмущений или более общими разложе-
разложениями решений по гипергеометрическим функциям. Мы не будем
подробно рассматривать здесь эти вопросы, а отошлем читателя к
первоисточникам1.
§ 13. Отображения прямолинейных многоугольников
13.1. Интеграл Шварца—Кристоффеля. Рассмотренное выше
отображение многоугольников значительно упрощается в частном
случае прямолинейных многоугольников. Действительно, если все
стороны многоугольника представляют собой отрезки прямых,
то определяемое формулой A2.1.3) двукратное зеркальное отра-
отражение относительно этих сторон представляет собой простое дви-
движение в плоскости и является, таким образом, не дробно-линейным,
а целым линейным преобразованием:
Ф&У) = az + Ъ. A3.1.1)
Относительно таких преобразований инвариантным является уже
выражение
V(W) = ~\og ~- = C A3.1.2)
/v J dw & dw z' ' v '
т. е. функция rj(w) однозначна, если z(w) отображает верхнюю полу-
полуплоскость ш на прямолинейный многоугольник. Следовательно,
мы можем в дальнейшем рассматривать функцию vj(w) вместо
более сложного выражения [z]w.
Несколько изменяя рассуждения п. 12.1, можно показать, что
7](w) — рациональная функция. Если рассматривать только ограни-
ограниченные многоугольники, то r\(w) аналитична во всех точках, в кото-
которых отображение z(w) конформно, так как в этих точках z'{w) ¦+¦ 0.
Поведение rj(w) в окрестностях точек w = е„, соответствующих вер-
1 Rothe H., tjber das Grundtheorem und die Obertheoreme der auto-
morphen Funktionen im Falle der Hermite-Lameschen Gleichung mit vier
singularen Punkten, Mh. Math. Phys., 19 A908), 258—288; Fock V., Ober die
konforme Abbildung eines Kreisvierecks mit verschwindenden Winkeln, J. reine
angeiv. Math., 161 A929), 137—151; Stallmann F., Konforme Abbildung
gewisser Kreisbogenvierecke als Eigenwertproblem, Math. Z., 59 A953), 211—230.
154 § 13. Отображения прямолинейных многоугольников
Для этого следует перенести вершину г = ev отображением вида
A2.1.13)
в точку х — О, после чего можно заключить, как и в A2.1.11), что
функция т(ш) в окрестности точки w = ev разлагается в ряд вида
т(ш) = (ш — е„)«" [а0 + % (ш — е„) -f . . .],
где я:й„ — внутренний угол в соответствующей вершине. Вычисляя
отсюда разложение функции z(w) и подставляя его в выражение
для rj{w), получаем
v(»>) = 6^i+bo + bi(">~o + ---- A3.1.3)
Эти рассуждения легко обобщаются на случай, когда рассматри-
рассматриваемая вершина лежит в бесконечности, е„ = оо. Если вторая точка
пересечения г = е'г прилегающих к ней сторон конечна, то ее можно
перенести преобразованием
ф)=^(г-<) A3.1.4)
в точку г = 0, а затем преобразованием
г = *-Л A3.1.5)
отобразить часть многоугольника вблизи вершины z = ev = <x> на
участок верхней полуплоскости t в окрестности точки t = 0. Отобра-
Отображение A3.1.5) отличается от отображения A2.1.9) для случая конеч-
конечных вершин только знаком при bv. Если мы условимся считать
внутренние углы при бесконечных вершинах отрицательными1,
то разложение A3.1.3) будет справедливо как для конечных, так
и для бесконечных вершин.
Это остается верным и тогда, когда бесконечно удаленная вер-
вершина не имеет конечной противоположной вершины (это имеет
место всегда при целых б„). Такую вершину при помощи сдвига и
поворота
t{z)=e?vz+b A3.1.6)
можно привести к одной из нормальных форм, указанных на рис.
70, так что теперь для т(ю) справедливо разложение A2.1.16):
x(w) = (ю — е„)-Л [а0 + аг (ю — е„) + ...] + ? log (w — ev).
Подставляя его в rj(w), получаем вновь разложение A3.1.3) с отри-
отрицательным 6„.
1 В уравнении Шварца A2.1.21) знак при бг не играет роли, так как <5„
входит в него только во второй степени.
13.1. Интеграл Шварца—Кристоффеля 155
Остается еще исследовать поведение функции 1}(ю) в окрестности
точки w = оо. Применим следующую формулу:
d dz dco d dz d . dm ,,¦> , -,\
-z~ log -j- = — ¦ ••— log -z hj-logj-- A3.1.7)
dw ° dw dm dco & da, dm & dw v '
При со = — имеем
i^-log^ • A3.1.8)
w2 dco dm w v
С другой стороны, так как z(a>) также отображает верхнюю
полуплоскость на многоугольник, то
d , dZ <5o© 1|Т!Т I /1-»1Л\
так что разложение 1}(ш) в окрестности точки w = оо принимает
следующий вид:
фо) = Ч г2 Ч f + ...; A3.1.10)
таким образом, rj(w) —> 0 при w —* оо.
Из тех же соображений, с помощью которых была установлена
рациональность выражения[г]ш, получаем представление для r?(w):
«-1 . ,
«И= 2^^- ¦ A3.1.11)
Принимая во внимание разложение A3.1.10), приходим к выводу,
что величины <5„ связаны соотношением
л—1
2(8,—1)- —й. —1, A3.1.12)
или, иначе,
i;(l-8,) = 2, A3.1.13)
причем последняя сумма распространена на все dv, включая и <!L
(мы обозначаем его здесь через бп). Это хорошо известное выраже-
выражение для суммы углов прямолинейного многоугольника.
Формула A3.1.11) представляет собой дифференциальное урав-
уравнение относительно отображающей функции z(w); именно, это есть
уравнение A2.2.12), в котором все акцессорные параметры равны
нулю, а величины 6„ удовлетворяют соотношению A3.1.13), так
156 § 13. Отображения прямолинейных многоугольников
что член, содержащий y(w), выпадает. Это уравнение можно легко
проинтегрировать. В результате получаем1
фо) = Сх Г //(ш - evy,-> dw+ С2, A3.1.14)
где С, иС2 — произвольные постоянные, C-l =j= 0.
Такое представление отображающей функции известно под назва-
названием интеграла Шварца—Кристоффеля. Из этого интеграла непо-
непосредственно видны свойства отображения. Во-первых, подинтег-
ральная функция всюду, за исключением точек ev и оо, аналитична
и отлична от нуля, так что отображение z(w) вне этих особых
точек конформно. Далее, в каждом интервале ev < w < ev+1 дей-
й\ ствительной оси аргумент подинтегрального выражения
// (ш - eJV-i) = 5 0V - 1) arg (ш - е,)
сохраняет постоянное значение, так что z(w) представляется там
в виде
г(ю) = Cf Г l[\u)—ev^,-1 dw + C^, A3.1.15)
где интеграл принимает только вещественные значения. Отсюда
следует, что каждый указанный интервал отображается функцией
г(ю) на прямолинейный отрезок, С учетом конформности отобра-
отображения это приводит к тому, что каждый интеграл вида A3.1.14)
отображает верхнюю полуплоскость w на некоторый прямолиней-
прямолинейный многоугольник2. Из разложений в ряды в окрестностях особых
точек, которые мы применяли при выводе этого интеграла, можно
заключить, что интеграл обладает требуемыми свойствами также
и в вершинах.
Формально такое же представление можно получить и для
функций, отображающих единичный круг на прямолинейный
многоугольник. В этом можно убедиться, отображая дробно-
линейным преобразованием верхнюю полуплоскость на единичный
круг, а затем производя соответствующую замену переменной под
знаком интеграла A3.1.14). Все особые точки w = ev лежат, разу-
разумеется, на границе единичного круга.
1 Правую часть A3.1.14) можно формально написать в виде отношения
двух линейно независимых решений уравнения A2.2.12), полагая tp-?w) равной
постоянной.
2 Здесь также могут встречаться многолистные многоугольники (когда
I К\ > !)• См., кроме того, соображения в конце п. 12.2, стр. 137.
13.2. Задача нахождения параметров 157
13.2. Задача нахождения параметров. Поскольку акцессорные
параметры равны нулю, задача нахождения параметров в случае
отображения прямолинейного многоугольника сводится к нахож-
нахождению лишь особых точек w = е„, образы которых служат верши-
вершинами многоугольника. Поскольку дробно-линейным преобразо-
преобразованием всегда можно три из них перевести в три заданные точки —
например, в 0, 1, оо, — то остается ровно л — 3 существенных
параметров, т. е. вдвое меньше, чем при отображении кругового
многоугольника общего вида.
Как и выше, задача о параметрах возникает впервые при рас-
рассмотрении четырехугольника; в этом случае она решается без ин-
интегрирования при помощи гипергеометрических функций1. С при-
прибавлением каждой следующей вершины число параметров увели-
увеличивается на единицу; для п > 4 ничего не известно о прямом реше-
решении задачи, за исключением некоторых частных случаев2. Если
интеграл вычисляется в явном виде, то получаются определенные
уравнения для нахождения параметров. В остальных случаях
применимы приближенные методы, описываемые ниже3.
Рассматривая связь между параметрами и геометрическими
постоянными многоугольника, следует учитывать, что дифферен-
дифференциальное уравнение A3.1.11) определяет многоугольник с точностью
до целого линейного преобразования; это выражается наличием
двух произвольных постоянных Сх и С2 в интеграле Шварца—
Кристоффеля. Для параметрического представления, таким обра-
образом, существенны только такие геометрические постоянные, кото-
которые не изменяются при линейных отображениях (т. е. при преобра-
преобразованиях подобия). К ним относятся углы многоугольника и некото-
некоторые отношения длин, которые мы сейчас подробно рассмотрим.
Если многоугольник ограничен, то его можно охарактеризовать
отношениями длин сторон. Обозначая длину стороны s,, соединяю-
соединяющей вершины е,- и е,_х, через /,•, имеем
A3.2.1)
dw
.1 *-4- '
l± = 1 ef-i - e,-1 =
h |efc-i-e*j « „_,
Это приводит к вещественным уравнениям вида
яг От,
1 п—\ ек - •
f fj\w—ev\',-idw = l, f //|u>—eJV»Ai>; A3.2.2)
__ U-i ~ k-i
1 См. разд. Б, п. 4.1 и 5.1.
2 См., например, рассуждения в конце п. 14.1.
3 См. п. 13.5.
158 § 13. Отображения прямолинейных многоугольников
взяв любых п — 3 линейно независимых1 уравнений такого вида,
можно найти п — 3 существенных параметров.
Этот метод непригоден, если несколько вершин2 лежат в беско-
бесконечно удаленной точке, так что прилегающие к ним стороны имеют
бесконечную длину. Для того чтобы свести этот случай к пре-
предыдущему, можно поступить следующим образом. Разложим под-
интегральное выражение в ряд3 в окрестности точки w — et:
- eJV-i = {w~ е(Уг1 [с0 + Cl(w- е,) + . ..] A3.2.3]
и проинтегрируем почленно. Если 6, не является целым отрица-
отрицательным числом или нулем, то этим определяются следующие
функции:
т,-(ш) = (ш - ф [а0 + аг(ш- е,) + ...]. A3.2.4]
Две функции Т;(ю) и tk(w), соответствующие двум особым точкам
е,- и ек, могут различаться только постоянным слагаемым. В частно-
частности, постоянной является разность
*,-i(h>) - Чю) = Я,- A3.2.5)
двух последовательных функций т,(ю) и т,-^»); значение этой
разности легко вычисляется, если в разложения* функций т,(ш) и
t,_i(io) подставить произвольное значение ш0 из интервала (е(_1, е{).
Величина Я,- имеет простой геометрический смысл. Примем во
внимание, что при отображении посредством функции т,(ю) образы
двух смежных интервалов (e,_i, e,) и (eit е,-+1) лежат на прямьк.
1 Независимы, в частности, отношения длин л — 3 различных сторон *
одной из трех остальных.
2 Если только одна вершина лежит в бесконечности, т. е. лишь две сторонь
имеют бесконечную длину, то многоугольник определяется отношениями
п — 2 остальных сторон с точностью до преобразования подобия.
3 Выражения (ш — e^fv~1 определяются здесь, как и всегда в интеграле
Шварца—Кристоффеля, так, чтобы при вещественных w было
(w - г,)*»-1 = [ w - ev f,-1 (w > е„),
(w - e./v = еЫ{-в>~х)\ w - е„ \ бр~г (w < er).
4 Ряды A3.2.3) и A3.2.4) сходятся в каждом круге с центром е,-, не содержа
шем других особых точек. Если круг сходимости не покрывает целиком интервал
e,-_l < w < е,-, то tj(w) следует продолжить вдоль вещественной оси npi
помощи численного интегрирования. Однако подходящими дробно-линейным*
преобразованиями верхней полуплоскости ш на себя [см. A2.2.15)] можно всегдг
добиться того, чтобы по крайней мере один из кругов сходимости покрыва;
весь интервал.
13.2. Задача нахождения параметров
159
пересекающихся в нуле. Если 5,- > 0, то нуль есть вершина соот-
соответствующего многоугольника; если же dt < 0 — не целое число,
то это противоположная верпшна. С помощью т,(ю) общее решение
г(ш) задачи об отображении, определяемое интегралом A3.1.14),
можно представить в виде
-М, 5,<0. <13-2-6>
Таким образом, если всюду в A3.2.1) заменить вершины е,- противо-
противоположными вершинами е, (когда последние не лежат в бесконеч-
бесконечности) и обозначить длины этих
псевдосторон также через lt
то в любом случае
A3.2.8)
Отношения этих псевдосторон
так же определяют многоуголь-
многоугольник, имеющий бесконечно уда-
удаленные вершины, как отно- Рис. 77.
шения истинных сторон опре-
определяют ограниченный много-
многоугольник (см. рис. 77).
Соотношения A3.2.5) игра-
играют для интеграла Шварца—
—Кристоффеля ту же роль,
что и преобразования перехода
для уравнения Шварца. Аналог
преобразования обхода получа-
получается построением контурных
интегралов. Для этого выберем
путь интегрирования, начина-
начинающийся в точке е1+1, проходя-
проходящей по верхнему берегу вещест-
вещественной оси в направлении к е,-,
обходящей в положительном Рис- 78.
направлении точку е{ и возвра-
возвращающийся в точку е,+1 по нижнему берегу той же оси (рис. 78). Если
Si+i > 0> то этот интеграл принимает конечное значение, которое
мы обозначим через ?,¦:
S, = (? Д (ш - e,)\-i dw. A3.2.9)
160
§ 13. Отображения прямолинейных многоугольников
Этот интеграл представляет собой функцию т,+1(ю), аналити
чески продолженную вдоль пути интегрирования, что геометри
чески на основе принципа симметрии Шварца сводится к зеркаль
ному отражению относительно стороны s,-, являющейся образол
интервала (е/—1, е,). Переходя к общему отображению z(w)
которое, согласно A3.2.6), представимо в виде
г(ю) =
и обозначая через ef+1 точку, симметричную с е,+1 относительнс
стороны s(, имеем
<?+!-*+!= ЗД. A3.2.10
Модуль этой величины | C1Si
равен, тем самым, удвоенному рас
стоянию вершины ei+1 от стороны st
Если 6,- не есть целое отрицатель
ное число или нуль, то из рис. 1\
непосредственно усматривается соот-
соотношение
Рис. 79.
S, = |Я,+1|!йпя5,-|, A3.2.1 Г
что подтверждается также прямые
вычислением интеграла при помогщ
разложения A3.2.4). Если Ь( — целое
то подинтегральное выражение од-
однозначно в окрестности et. Тогда при интегрировании A3.2.9) интег-
интегралы по прямолинейным участкам взаимно уничтожаются и оста-
остается только интеграл по кривой вокруг точки1 et. Последний
легко вычисляется с помощью разложения подинтегралъной функ-
функции в ряд. Если 5,- = — А-, то
п
1/> — О** = с_й_! (ш - e,)-*-i + ... + c_1(w— e,.)-i +
+ со + С1(ш~е,.) + .... A3.2.12]
Интегралы всех членов, кроме c_j (ю — ei)~\ обращаются в нуль,
так что
S, = 2rac_!. A3.2.13]
Величина с_г называется вычетом подинтегральной функции i
точке w = е{. При отображении z(w) величина
l A3.2.14;
1 Этот контурный интеграл можно построить здесь и при условии
при этом он также принимает конечное значение.
13.3. Внешние области 161
И
s,-+i, примыкающими к е,. Величину S,- можно явно выразить
через параметры, так что задача о параметрах при появлении цело-
целочисленного угла й;- =s 0 существенно упрощается1. Величину Сх
в формулах A3.2.10) и A3.2.14) можно исключить, разделив основ-
основные геометрические величины друг на друга или на длины некото-
некоторых сторон и введя тем самым, как и в A3.2.1), инвариантные гео-
геометрические постоянные.
13.3. Внешние области. Формула Шварца—Кристоффеля легко
распространяется на тот случай, когда бесконечно удаленная точка
находится внутри рассматриваемого многоугольника2, иными
словами, когда требуется отобразить внешность ограниченного
многоугольника на верхнюю полуплоскость. Пусть при этом
отображении точка z = оо переходит в точку w = ш», лежащую в
верхней полуплоскости. Для того чтобы отображение было там
конформным, необходимо, чтобы функция z~l(w) была в окрестно-
окрестности этой точки аналитична и имела производную, отличную от
нуля, т. е. чтобы имело место разложение
тг-Цю) = (ш — ш.) [а0 + «! (w - wj) + . . .], A3.3.1)
'±яе а0 =h 0, откуда
'¦¦ ¦ г(ш) = (ш — wj-1 [Ьо + b^w—wj) + .. .]. A3.3.2)
Таким образом,
z'(w) = с_2 (ш — ште)-2 + с0 -t- сг (w—w^) + ..., A3.3.3)
т. е. вычет функции z'(w) [ср. A3.2.13)] в этой особой точке равен
нулю. Аналогичное разложение должно иметь место в точке ш =
= ште, так как по принципу симметрии Шварца точка, сопряженная
с Шоо, также должна отображаться в точку z = оо.
Переходя к функции r}(w), можно показать, как ивп 13.1, что
подинтегральное выражение в формуле Шварца —Кристоффеля при
отображении внешней части многоугольника следует умножить на
величину [(ш — ш^) (ш — ш„о)]~2:
A3.3.4)
1 См. примеры в разд. Б.
2 В отличие от общего случая круговых многоугольников (§ 12), при отобра-
отображениях прямолинейных многоугольников точка г = оо играет особую роль,
являясь неподвижной точкой всех целых линейных отображений A3.1.1). Поэто-
Поэтому дифференциальный инвариант A3.1.2) может ие быть аналитическим в точке
z = оо, даже если отображение z(w) конформно в этой точке.
П —6002
162
§ 13. Отображения прямолинейных многоугольников
«Внутренние» углы ndv > 0 следует, естественно, заменить внешними
углами многоугольника, внешность которого отображается.
Для того чтобы вычеты в точках ш = штс и ш =¦ штс равнялись
нулю, должно выполняться условие
"—' 1 Л О
У -™*. + =-* = 0; A3.3.5)
умножая на п?» — ютс и учитывая A3.1.13), можно придать выра-
выражению A3.3.5) следующую форму:
л— 1
1 —
(i - ь.)
е, —
0.
A3.3.6)
В ряде случаев требуется отобразить внешность единичного
круга на внешность многоугольника так, чтобы при этом точка
z = оо переходила в точку ш = оо. Преобразуя соответствующим
образом интеграл Шварца—Кристоффеля A3.3.4), получаем сле-
следующее представление отображающей функции:
п
z(w) = Cl J // (ш _
C2.
A3.3.7)
Здесь все точки е„ лежат на единичной окружности, т. е. ev = ёа"\
они определяются данным многоугольником однозначно с точно-
точностью до поворотов окружности. Условие для вычетов запишется в
следующем виде:
2 (»„ -
= 2 (Ь, - 1) е*" = 0.
A3.3.8)
Рис. 80.
Рассматривая в этом равен-
равенстве величины F„ — 1) eia*
как векторы, мы заключаем,
что они образуют замкну-
замкнутый многоугольник с дли-
длинами сторон bv—1. От-
Отсюда в случае отображения
внешности треугольника
можно тотчас же указать
положение особых точек еь
е2, es, так как треугольник,
соответствующий A3.3.8),
определяется тремя сторо-
сторонами §„ — 1 однозначно
с точностью до поворота.
13.4. Многоугольники с внутренними точками ветвления 163
В случае большего числа сторон получаются некоторые соотноше-
соотношения1 между особыми точками; их также удобно находить из соот-
соответствующего многоугольника (рис. 80).
Задача о параметрах для внешних областей исследуется так
же, как и для внутренних. К определяющим уравнениям A3.2.2)
для точек е„ присоединяется условие для вычетов A3.3.6), соответ-
соответственно A3.3.8). Упомянем еще случай, когда z = оо есть гранич-
граничная точка многоугольника, не являющаяся вершиной. При этом
соответствующую граничную точку можно считать дополнительной
вершиной с углом ¦—п, (т. е. с §„ = —1), причем вычет в этой точке
также должен равняться нулю.
13.4. Многоугольники с внутренними точками ветвления. В связи
с задачей о кручении, рассмотренной в п. 3.4, была поставлена
следующая задача: конформно отобразить область Gz, ограничен-
ограниченную прямолинейным многоугольником, с помощью функции co(z)
на область Gm , также ограниченную прямыми линиями и подробно
описанную в п. 3.4, так, чтобы вершины Gz перешли в вершины Gm.
Эту задачу также можно решить с помощью интеграла Шварца—
Кристоффеля. С этой целью отобразим многоугольник Gz, как и
выше, на верхнюю полуплоскость ш при помощи функции ш(г).
Таким образом,
и> ,
Г .
z(w) = Cj // (ш — erf*-1 dw + С.. A3.4.1)
J v=l
Wo
Покажем, что искомая функция co(w) должна иметь вид
г "Г.
co(w) = P(w) Jl (ш — ev)-2iv dw+y1, A3.4.2)
'где -Р(н>) — многочлен степени 2п — 6
f Р(ю) = а0 + axw + аги? + ... + а2п_„ н>2"-« A3.4.3)
«С вещественными коэффициентами а,,.
¦} Для вывода этой формулы рассмотрим отдельно какую-нибудь
одну вершину е„ многоугольника Gz. Прилегающие стороны sr
I и s,+1 можно записать в виде [см. C.4.2)]
z = ?„ + Aj eiai и z = sv + ?^ cia>, A3.4.4)
1 Например, в случае параллелограмма соответствующий многоугольник
, также является параллелограммом. Следует также напомнить, что E, — Г) и
есть величина смежного угла при соответствующей вершине.
164 § 13. Отображения прямолинейных многоугольников
где <хг— ocj = 7ibv. Легко видеть, что на сторонах sv и sv+l для
функции
_. . . jQ-a^) . ..... . ; .. .
s 2п + 1 , .
или при ov, имеющем вид —~— (л — целое), для функции
+ iev('~ev) +^evev A3.4.6)
выполняются краевые условия C.4.1)
Im w = — .
Эта функция однозначна и аналитична во всем многоугольнике
Gz, за исключением вершины е„. Если положить
W(z) = W0(z) + W*(z), A3.4.7)
то W*{z) аналитична внутри многоугольника, и ее мнимая часть
обращается в пуль на сторонах sv и sv+i, а на остальных сторонах
имеет определенные граничные значения, которые легко находятся
из C.4.1) с учетом известных значений функции W0(z).
При отображении многоугольника на верхнюю полуплоскость
w эти граничные условия преобразуются в следующие условия для
функции Im W*(z(w)) = Im W*(w) = V*(w):
V*(w) = 0 для вещественных w, е„_1 < w < ev+l,
V*{w) = f(w) для остальных вещественных ш,
причем f(w) определяется известными граничными значениями
функции W*(z). В силу принципа симметрии Шварца эта краевая
задача эквивалентна краевой задаче для области, представляющей
собой плоскость w с разрезом вдоль всей вещественной оси, за
исключением интервала (<"„_!, ev+1). . Если определить в этой
области аналитическую функцию, мнимая часть V*(w) которой
на верхнем берегу разреза принимает значение /(ш), а на нижнем —
значение — f(w), то V*(w) обратится в нуль на интервале1 (е„_1> ev+d
1 При зеркальном отражении относительно интервала (ev—1, е,,+1)
область с разрезом преобразуется в себя, а граничные значения изменяют знак.
Решение V*(h>) этой «отраженной» граничной задачи в силу этого изменения
знака равно V*(u») = — V*(w); с другой стороны, в силу симметрии должно
быть V*(w) = V*(w). В интервале (fiv_x, ev+1) имеем поэтому V*(w) =
= - V*(w) = 0.
13.4. Многоугольники с внутренними точками ветвления 165
и совпадет поэтому с введенной выше функцией V*(w). Таким
образом, функция W*(w) аналитична в интервале (<¦„_!, ev+1),
и отсюда вытекает, что W(z) аналитична на каждой стороне
многоугольника Gz.
Поведение искомой функции со(г) в окрестностях вершин можно
определить, разлагая ее в ряд. Прежде всего вторая производная
функции W*(z) в окрестности точки w — ev имеет вид
dW* . dh
_ _
= (a» — evy26"+1 [«o + a, (id — ej + . . .]; A3.4.8)
дифференцируя еще раз по ш, имеем
d?- = (w — e)~2St К + ci (w ~ О + ¦ ¦ •]• A3.4.9)
Далее,
<ao(z) = -—— = const, соответственно oj0(z) = сл + с„ log (z — et,)
A3.4.10)
и тем самым
da>o _ п
dw - U'
соответственно -^ = —~ ^ = (w — ev)~l [b0 + ft, (ш— ev) + .. .],
A3.4.11)
что можно также записать в форме A3.4.9), учитывая, что
8„ = —- — (л - - целое, л э= 0). Таким образом, функция
dm _ dw* , da>0
dw dm dm
в любом случае допускает разложение вида A3.4.9) в окрестности
точки w = ev. Аналогично можно показать, что в окрестности
точки ю = оо имеет место разложение
dm
« + .\ (,3.4.12)
Из Этих разложений представление A3.4.2) для функции со(и>) полу-
получается тем же способом, что и обычный интеграл Шварца—Кри-
стоффеля.
Выражение A3.4.2) отличается от рассмотренного ранее интег-
интеграла Шварца—Кристоффеля полиномиальным множителем. Это
создает дополнительные нули подинтегральной функции, что нару-
нарушает конформность в этих точках. Многоугольник Ош имеет там
точки ветвления того же вида, что и возникающие при отображе-
отображении посредством степенной функции с целочисленным показателем
166 § 13. Отображения прямолинейных многоугольников
(п. 6.1). Многоугольник Ga, таким образом, не однолистен, а покры-
покрывает плоскость со несколько раз. Выбирая соответствующим образом
эти дополнительные точки ветвления, можно достигнуть того,
чтобы все стороны многоугольника касались единичной окруж-
окружности, как это требовалось в п. 3.4.
Решение задачи о параметрах состоит из двух этапов. Первый
заключается в нахождении особых точек е„ отображения A3.4.1).
После определения этих величин следует вычислить коэффициенты
многочлена A3.4.3) и постоянные интегрирования в A3.4.2). Так
как искомые функции зависят от этих величин линейно, задача
сводится в решению системы линейных уравнений. Для этого поло-
положим — при фиксированном го0 —
w
ю<*>(ш) = Г wix) J[ (w — ev)-x>* dw A3.4.13)
J ..lit
2а
WM(z) = w(z1)dz1dz». A3.4.14)
z» г0
Тогда
2л—6 2
W(z) = ^ ах W<-">(z) + (у[ + i y'i) ^ + (Гг + i Уг) z + Уг + ' /з-
A3.4.15)
Выберем на каждой стороне s,- точку z(- и обозначим соответствую-
соответствующие точки вещественной оси ш через ю,-. Если е*а< — направляю-
направляющий вектор стороны s,', то условие C.4.10) приводит к следующей
системе уравнений:
2л—6
2 ах Im [ezta'co{x) (ш,)] + yi sin 2a,- + y'i cos 2а,- = 1, i = 1, 2, . .., л.
A3.4.16)
Следующие л уравнений получаются из условия C.4.1):
2П—6 2 2
2 a* Im WW(z,-) + y[ Im -^- + у^ Re Ц- + у'2 Im z,- +
+ •/%' Re г, + /,' = Zf . A3.4.17)
Этих 2л уравнений достаточно для определения 2л неизвестных,
а именно 2л — 5 коэффициентов многочлена ах и пяти величин
у'и,у"р. В частных случаях возможны некоторые упрощения1.
1 Это имеет место, в частности, для симметричных многоугольников. См.
Франк Ф. и Мизес Р., Дифференциальные и интегральные уравнения
математической физики, М., 1937.
13.5. О приближенном вычислении интеграла Шварца—Кристоффеля 167
13.5. Замечания о приближенном вычислении интеграла Шварца—
Кристоффеля. Существенная трудность при вычислении интеграла
Шварца—Кристоффеля состоит в том, что подинтегральная функ-
функция в особых точках w = ev, вообще говоря, обращается в бесконеч-
бесконечность, и поэтому к нему неприменимы обычные численные методы.
Эту трудность можно преодолеть, разлагая подинтегральную
функцию в ряд. Для определения коэффициентов разложения
целесообразно исходить из дифференциального уравнения A3.1.11),
разлагая правую часть, как в формуле A2.5.3):
п—1 ~
(и- - е,) 2 %=j =2ях(Р- Ф A3.5.1)
Здесь ""', I *
1 во-«1-1, Ях-Хт^ра- A3.5.2)
¦'¦ Отсюда коэффициенты разложения в ряд подинтегральной
фикции
: г'(ш) =СХП{Р— О'*-1 = {w— e,y>ri 2 ся(ш- е& A3.5.3)
v=l Л—О
|южно вычислить следующим образом:
п—1
со=С1//'(е,-е>-1, A3.5.4)
v=]
1с, = д1сл_г + д2ся_2 + . ..
^0)
Интегрируя почленно, получим функцию т,(ш), определенную выра-
выражением A3.2.4):
Т,(ш) = (ш - ф^ j^j (ш - е,)\ A3.5.5)
откуда, согласно A3.2.5) и A3.2.7), определяются стороны, соответ-
соответственно псевдостороны.
Если этот ряд сходится недостаточно быстро, то можно ограни-
ограничиться теми членами разложения A3.5.3), которые обращаются в
бесконечность в точке w = et, а остальные члены численно интегри-
интегрировать обычными способами. Тогда функцию т((ш) можно записать
в следующем виде:
т,(ш) = (ш - eifi 2Q j^rx (ю ~ ei? +
If Г «—1 ' 1
+ С, //(ш- О*' — (н> — ерг* 2ех(р— ер dw;
, J L »-l A-0 J
A3.5.6)
168 § 13. Отображения прямолинейных многоугольников
здесь I выбирается настолько большим, чтобы подинтегральное
выражение осталось конечным. В частности, если Ь} > 0, то можно
взять / = 0, так что сумма сводится к одному слагаемому.
Если 8,- > 0, то с помощью замены переменной можно свести
несобственный интеграл к собственному. Положим
<„ = („,_- ф t w=et + ю*4, dm = 8,- (ш — с,)*,-1 <1ш; A3.5.7)
при этом интеграл Шварца—Кристоффеля принимает вид
*И = ^ J IT Ко)) - е^-Чсо + С2, A3.5.8)
в котором подинтегральное выражение ограничено в окрестности
нижнего предела.
Для численного решения задачи о параметрах можно восполь-
воспользоваться методом Ньютона1. Примем вначале некоторые прибли-
приближенные значения е* для параметров и обозначим через /* длины
сторон, вычисленные на основании этих величин и некоторого соот-
соответствующим образом выбранного значения постоянной Сг.
Тогда
<¦?
'* = icil II\w—e*\Sv~l dw- A3.5.9)
Если стороны данного многоугольника имеют длины /,¦ и
— отклонения приближенных значений от точных, то для вычисле-
вычисления поправок Аек к значениям е* пользуемся следующими равен-
равенствами:
А1, = ]?^-Аек. A3.5.11)
Так как многоугольник с заданными углами однозначно опреде-
определяется л — 2 своими сторонами, то эти выражения представляют
собой п — 2 независимых линейных уравнений для определения
поправок Лек. Одну из поправок можно выбрать произвольно;
например, положим2 Ает = 0, тогда остальные определяются
однозначно из уравнений A3.5.11). Если отображается внешность
1 См. статью П. Ф. Фильчакова в [17] и указанную там литератур. —
Прим. ред.
Это означает, что ет в процессе вычислений остается неизменным.
2
]3.5. О приближенном вычислении интеграла Шварца—Кристоффеля 169
многоугольника, то к уравнениям A3.5.11) следует добавить еще
одно уравнение
2 .Д*—ч1 Аек = 0, A3.5.12)
получаемое дифференцированием условия A3.3.5). Тем самым все
п — 1 поправок однозначно определяются.
На основе вычисленных таким образом поправок получаем
второе приближение
е** = е*+Лек, A3.5.13)
которое, вообще говоря, точнее первоначального, если только
последнее не слишком отличается от истинного решения. Неболь-
Небольшим изменением постоянной Сл это приближение можно еще
улучшить; этот прием можно повторять до достижения требуемой
точности.
Частные производные, фигурирующие в A3.5.11), можно полу-
получить дифференцированием под знаком интеграла. Если е* не сов-
совпадает ни с одним из пределов интегрирования е*__г, е*, то
- О -
где и лежит между е,_, и е,-. Подставляя вместо и такое значение,
получаем без интегрирования вполне удовлетворительное прибли-
приближение для частной производной. Если же е* равно ef_1 или е*, то
путем замены
со = Ч^е^ A3.5.15)
ei — ei-i
следует преобразовать пределы интегрирования в 0 и J. Диффе-
Дифференцирование, по е;, соответственно по ei_l, под знаком получен-
полученного интеграла приводит к следующим равенствам:
г,-
="-' ¦> dw _ V--QL , A3.5.14)
Эти формулы в основном сохраняют силу и в том случае,
когда некоторые вершины бесконечно удалены, причем /,¦ означают
170
§ 13. Отображения прямолинейных многоугольников
здесь длины псевдосторон. Для разложений в ряды следует заменить
подынтегральное выражение частной производной по параметру
К
L=A
A3.5.17)
и вычислить производные ~(k-j=i—l,i) и соответствующие
величины I/. В остальном правые части выражений A3.5.14) и
A3.5.16) сохраняются и в этом случае.
Исключения могут составлять только условия для вычетов
[см. A3.2.14)]. В этом случае следует выбирать уже первое прибли-
приближение так, чтобы оно удовлетворяло этим условиям. Часть урав-
уравнений A3.5.11) заменяется тогда более простыми, получаемыми
дифференцированием условий для вычетов [см. A3.5.12)].
Совершенно иной путь решения задачи о параметрах, состоящий
в сочетании интеграла Шварца—Кристоффеля с излагаемым ниже в
п. 17.1 методом Теодорсена, был предложен Маттье1. Пусть
требуется отобразить многоугольник 6г на единичный круг так,
чтобы заданная точка z0 б Gz перешла в центр круга ш = 0; пусть
задано приближенное отображение u>*(z), определяемое интегралом
Шварца—Кристоффеля:
dw + z
0,
A3.5.18)
где е*
. Функция ro*(z) отображает многоугольник G*, близ-
близй ||
кий к данному, на единичный круг |ю*| < 1. Если ни одна из вер-
вершин Gf не лежит внутри Gz
(этого всегда можно достиг-
достигнуть выбором величины Cj) и
если приближение не слиш-
слишком грубое, то функция w*(z)
отображает многоугольник G2
на область Г плоскости ш, гра-
граница которой близка к единич-
единичной окружности (рис. 81). Пусть
Рис. 81. Ast — расстояние между соот-
соответствующими сторонами st
и sf многоугольников Gj, и G*, которое считается положительным,
если s( лежит внутри G*, и отрицательным в противном случае.
1 См. Matthieu P., Ober die praktische Anwendung der Schwarz —
Christoffclschen Formel. Vorgetragen auf der GAMM-Tagung in Braunschweig, 1952.
Рукопись этого доклада была любезно предоставлена одному из авторов госпо-
господином Маттье.
13.5. О приближенном вычислении инте грала Шварца—Кристоффеля 171
Расстояние Aq* от соответствующих точек области Г до единичной
окружности (отсчитываемое в сторону возрастания р*) при-
приближенно равняется
Ав*ъ~А8(\Щ. A3.5.19)
Если теперь положить ш* = р*е"?>* и выразить границу Г уравне-
уравнением р* = р*(<р*), то приближенно
log Q Fa , <Pi—\ < у < fi- A3.5.20)
Теперь искомое отображение G2 на единичный круг можно полу-
получить, отображая сначала единичный круг плоскости ш на область
Г методом Теодорсена, а затем при помощи г(ю*) область .Г на Gz.
Это приводит к интегральному уравнению
^ у» -у = ^ Jlog o*(qP*(^)) ctg^ dVf A3.5.21)
о
где мы положили ш = ре1'»1 [см. ниже A7.1.4)]. Вычисляя первое
приближение и заменяя log p* выражением A3.5.20), получим
поправку Аук для величины <р* в виде
A3-5.22)
Если 5Л < 1, то все интегралы под знаком суммы сходятся. В про-
противном случае более тщательное исследование границы Г приведет
нас также к сходящимся интегралам1, как будет подробнее показано
в п. 17.1.
1 Приближенная формула A3.5.20) не имеет места в окрестностях особых
точек «*. Однако нетрудно найти лучшее приближение, определяя с помощью
[где с0 находится из A3.5.4)] несколько точек границы Г и соединяя их прямо-
прямолинейными отрезками. Влияние этих точек на результат незначительно, так что
можно обходиться довольно грубыми вычислениями. Если интеграл A3.5.22)
сходится, а 6{ не слишком близки к 1, то более точного приближения границы
не требуется.
172
§ 13. Отображения прямолинейных многоугольников
При вычисленных таким образом поправках система величин
?** =
A3.5.23)
представляет лучшее приближение для искомых параметров. Под-
Подставляя эти значения в A3.5.18) и изменяя соответствующим обра-
образом значение Съ получим более точное приближение w**(z), исходя
из которого можно продолжить этот прием до достижения тре-
требуемой точности.
Рис. 81а.
Этот прием можно также перенести на отображение много-
многоугольников на верхнюю полуплоскость, которое более удобно
для вычислений. Приближенный многоугольник Of накладывается
на G2 так, чтобы вершины е?\ соответствующие точкам w = оо,
соответственно w* = оо, лежали на пересечении соответствующих
сторон s^*> и s{,*> (рис. 81а) и ни одна вершина G* не оказалась
внутри G2. При отображении w*(z) многоугольник Gz преобразуется
в область Г, граница которой близка к вещественной оси id* и
совпадает с ней в окрестности точки w* = оо. Если положить
w* = и* + id*, то эта граница приближенно выразится уравне-
уравнением
/Is,
л—1
<и*
е*,
A3.5.24)
_.? Iе»-1
v=1
аналогичным A3.5.20), с теми же значениями /Ц.
Чтобы перенести метод Теодорсена на полуплоскость, выведем
формулу Шварца для полуплоскости. Полагая
R?J=_
= R
со - i
ш + i
13.5. О приближенном вычислении интеграла Шварца—Кристоффеля 173
(где со вещественно), получаем из (9.2.12)
щ*) - то + i) ад [ш4^ + ^л]*». A3-5.25)
ос
Положим в этой формуле
W(w) = ( (ш — ш*(ш)), A3.5.26)
где w*(w) — функция, отображающая верхнюю полуплоскость на
область Г так, что бесконечно удаленная точка переходит в себя,
а производная -— стремится к 1 при w -> оо. Тогда на вещественной
оси w = и вещественная и*(и) и мнимая i>*(u) части функции ш*(ш)
связаны соотношением
оо
и — u*(u) = 1 - Г D*(co) Г--1 - 4- -~] dco + С, A3.5.27)
оо
где С — произвольная постоянная. Подставляя сюда вместо v*(u)
уравнение границы Г
v*(u) = d*(u*(u)),
получаем, подобно равенству A3.5.21), интегральное уравнение
относительно искомой функции w*(w). Первое приближение приво-
приводит снова к поправкам Аек для значений параметра ejf. Отбрасывая
несущественное1 слагаемое 2°\ч> мы получаем следующее урав-
dm + С. A3.5.28)
i=2 l^ilj el - (О
Постоянную С здесь можно выбрать произвольно, так как
изменение всех параметров на одинаковое слагаемое не меняет
интеграла Шварца— Кристоффеля. Можно, например, считать в
дальнейшем одну из поправок Ает равной нулю или, при отобра-
отображении внешних областей, считать, что выполняется равенство
1 Это слагаемое обеспечивает сходимость интеграла при ш = оо; здесь
же сходимость обеспечивается тем условием, что и*(н*) = 0 в окрестности
точки оо.
2 Относительно сходимости этого интеграла см. рассуждения по поводу
A3.5.20).
174 ' § 14. Многоугольники в изотермических сетках
A3.5.12). Получив уточненные значения параметров
e**=e*k+Aek, A3.5.29)
можно вновь повторять этот прием.
Описанный выше метод имеет по сравнению с методом Ньютона
то преимущество, что он не приводит к решению линейных систем.
Вычисление же интеграла A3.5.28) более затруднительно, чем
A3.5.14), в котором можно воспользоваться уже вычисленными
величинами1. При небольшом числе углов предпочтение отдается
методу Ньютона, при большом — методу Маттье. Быстрота сходи-
сходимости может быть и одинаковой в обоих методах; более точных
данных об этом не имеется.
Оба эти метода предполагают, что система е* достаточно близка
к истинной. Если это не так, то не имеет смысла подставлять в
уравнения A3.5.11), A3.5.22) или A3.5.28) полные значения откло-
отклонений Alt, соответственно /Ц; вместо этого следует с помощью
малых поправок получить после некоторого количества шагов
пригодные начальные приближения. Расчеты для таких началь-
начальных поправок могут вестись довольно грубо и тем значительно
упрощаются.
Для многоугольников, имеющих форму разрезов, один прием
решения задачи о параметрах предложил П. П. Куфарев, бравший
за основу дифференциальное уравнение Лёвнера; по этому поводу
мы отсылаем читателя к первоисточникам2.
§ 14. Многоугольники в изотермических сетках
Применение интеграла Шварца—Кристоффеля распространяется
и на отображения областей, ограниченных не прямыми линиями,
а линиями некоторой изотермической сетки. Если такая сетка соот-
соответствует аналитической функции W(z), т. е. составлена из линий
U(z) = const и V(z) = const, то при отображении на плоскость W
она перейдет в декартову сетку, причем ее линии преобразуются в
прямые, параллельные координатным осям. Рассматриваемая
область перейдет в прямолинейный многоугольник, а именно в
ступенчатый многоугольник (см. п. 12.4). Отсюда вытекает, что
подинтегральная функция в интеграле Шварца—Кристоффеля равна
квадратному корню из рациональной функции, так что этот инте-
интеграл относится к эллиптическому или гиперэллиптическому типу.
1 При вычислении этих интегралов пригодны сравнительно грубые методы
так как точность поправок заранее ограничена.
«Куфарев П. П., ДАН СССР, 57 A947), 535-537; L owner К.
Math. Ann., 89 A923), 103—121.
14.1. Многоугольники в круговых сетках 175
Основные трудности возникают в тех случаях, когда отобра-
отображаемая область содержит внутри или на границе точки, в которых
отображение W(z) не конформно. Такие точки мы назовем крити-
критическими точками сетки; в них сетка имеет сингулярный характер.
Для определенных сеток, соответствующим образом изменяя
интеграл Шварца—Кристоффеля, удается построить отображение,
конформное и в критических точках. Ниже мы рассмотрим это
подробнее.
14.1. Многоугольники в круговых сетках. Так как дробно-линей-
дробно-линейным отображением каждую сетку диполя можно преобразовать в
декартову, а сетку источника и стока — в полярную, то мы ограни-
ограничимся рассмотрением многоугольников в полярных сетках. Функ-
Функция, определяющая сетку, равна
W(z) = log z; A4.1.1)
критическими точками являются г = 0 и i = оо. Область, ограни-
ограниченная линиями полярной сетки (т. е. концентрическими окруж-
окружностями и прямыми, проходящими через начало), представляет
собой круговой многоугольник. Если внутри многоугольника нет
критических точек (но, возможно, они есть на границе), то отобра-
отображением A4.1.1) его можно перевести в обычный прямолинейный
многоугольник, к которому уже применимы методы, описанные в
предыдущем параграфе.
В случае, когда критические точки лежат внутри многоуголь-
многоугольника, мы рассмотрим, как и ранее, конформное отображение мно-
многоугольника на верхнюю полуплоскость при помощи функции
ш(г). Пусть критическим точкам z = 0 и z = оо соответствуют точки
ш = е0 и w = е„о. Так как в них отображение должно быть конформ-
конформным, то функция z(w) имеет следующее разложение:
г(ю) - (го — е0) [а0 + ах (го — е0) + .. .], A4.1.2)
г(ш) = (w — е^)-1 [а0 + ах (ш — ете) + ...], а0 + 0.
Отображая на плоскость W и дифференцируя по ш, имеем
dw w — e.
о
соответственно W'(w) = h .... A4.1.3)
w — eoc K
Так как симметричным точкам w = i0 и ш — i,», также соответ-
соответствуют критические точки (от вида аналитического продолжения
зависит, какая это точка: z = 0 или z = оо), то также
W'(w) = ——— + ..., соответственно W'(w) = — + ....
iv — е0 ш — «в»
A4.1.4)
176
§ 14. Многоугольники в изотермических сетках
Отсюда следует, что при представлении функции W(w) интегралом
Шварца—Кристоффеля последний должен содержать множители
вида
(ш — ек) (ш —
А- = 0,
A4.1.5)
причем следует учитывать, что разложение подинтегральной функ-
функции совпадает1 с A4.1.3).
Отсюда фактически получается искомая отображающая функ-
функция. Для того чтобы в этом убедиться, сделаем отображение
W(z) однозначным, проведя в многоугольнике прямолинейный раз-
разрез от критической точки до границы. Внешность этого разреза
преобразуется посредством логарифма в полуполосу, причем об-
образы берегов удалены друг от друга на 2ni. Стороны многоуголь-
многоугольника при отображении W(z) перейдут в некоторые отрезки прямых.
так что в целом многоуголь-
многоугольник с разрезом в плоскостк
z отобразится на некоторые
прямолинейный многоуголь
ник в плоскости W (см. рис
82).
Аналогичная картинг
возникает при отображенш
верхней полуплоскости и
©посредством W(w). ITpi
„ этом функция W(w) должн;
|| представлять собой интег
|! рал Шварца—Кристоффеля
1^iAic"" ¦чч""ч>чч~ч ic^^x. снабженный мпожитслсл
Рис. 82. вида A4.1.5), а верхня:
полуплоскость w для одно
значности отображения W(w) соответствующим образом разреза
ется между особыми точками w = ek (k = 0, оо) и веществен
ной осью. При обходе вокруг ек интеграл W(w) изменяется н
¦±2 2л(, так что "и здесь образы разрезов отстоят друг от друга н
2л(. Вещественная ось w при отображении W(w) переходит, как
при обычном интеграле Шварца—Кристоффеля, в ломаную линик
поскольку на ней множители A4.1.5) вещественны и отличны о
нуля. Отображение в верхнюю полуплоскость w с разрезами такж
всюду конформно, так как в ней подинтегральное выражение н
имеет ни особых точек, ни нулей.
1 Эти точки можно рассматривать, как дополнительные особенное!
интеграла Шварца—Кристоффеля при б^= 0, причем A4.1.3) и A4.1.4) — некот(
рыс условия на вычеты.
14.1. Многоугольники в круговых сетках
177
Суперпозиция функций z(W) и W(w) дает отображающую
фуНКПр'.Ю
л—1
z(w) = ехр
—— dw
— e<x>)
A4.1.6)
(w — e0) (гс — e0) (w — e
где b* — внутренние углы1 прямолинейного многоугольника,
появляющегося в плоскости W при отображении W(z). Если внутри
многоугольника лежит лишь одна особая точка, то подинтеграль-
ное выражение содержит, разумеется, лишь один множитель
вида A4.1.5). Эта функция отображает верхнюю полуплоскость с
разрезами на многоугольник с разрезами, и поскольку отобра-
отображение однозначно и конформно также в ок-
окрестностях критических точек, она отобра-
отображает всю полуплоскость на весь много-
многоугольник2.
Значительно проще обстоит дело, если все
стороны многоугольника принадлежат одно-
одному пучку сетки, т. е. • — в нашем случае —
когда все стороны лежат на прямых, прохо-
проходящих через начало3. При этом подинтег-
ральное выражение является рациональной
функцией и интеграл может быть вычислен.
Для получения вида отображающей
функции достаточно рассмотреть точки
многоугольника, соответствующие крити-
критическим z = О, оо. Если такая точка является
вершиной многоугольника с внутренним уг-
углом bjt (причем внутренний угол при
бесконечно удаленной вершине отсчитывает-
ся, как и ранее, в отрицательном направлении) и при отобра-
отображении на верхнюю полуплоскость w этой вершине соответствует
точка w — ev, то имеет место следующее разложение в ряд (его
вывод см. в п. 13.1):
(ш — е„)** [а0 + а, (ш — е„) -{ . . .].
Рис. 83, Многоуголь-
Многоугольник, все стороны кото-
которого лежат на прямых,
проходящих через на-
начало координат. См.
Betz A., Konforme Ab-
bildung, S. 246, Berlin —
Gottingen —Heidelberg,
1948 (см. также [2]. —
Прим. ред.).
z(w)
A4.1.7)
1 Если вершины не совпадают с критическими точками, то они являются
внутренними углами и для многоугольника в плоскости z. Образы критических
точек всегда являются особыми точками с й„ = 0 независимо от того, лежат
ли они в вершинах или на сторонах многоугольника в плоскости z. Заметим
также, что в отличие от интеграла Шварца—Кристоффеля, рассмотренного в
§ 13, постоянная С, не произвольна, а определяется из условия A4.1.3).
2 Примеры см. в п. 3.1 и 6.1 разд. Б.
3 Для многосвязных многоугольников возможен случай, когда все стороны
лежат на концентрических окружностях. См. п. 15.3.
12— 6002
178 § 14. Многоугольники в изотермических сетках
Если критическая точка лежит внутри многоугольника, то
справедливо разложение A4.1.2); это же верно, когда она лежит
на одной из сторон, но не в вершине. Этот случай охватывается
также соотношением A4.1.7), если положить в нем д„ = -И. Во
всех остальных (внутренних и граничных) точках многоугольника
функция z(w) аналитична1; это же относится к функции W'(w) =
= — log z, поскольку в этих точках функция z отлична от нуля и
бесконечности. Следовательно, рациональная функция W'(ro) пред-
ставима в форме
w» = 2nH~' A4Л.8)
где сумма берется по образам всех критичес-
критических точек и, возможно, симметричных с
ними, а 6„ — либо значения внутренних
углов, либо величины + 1. Интегрирование
выражения A4.1.8) дает
{) 1TI^-evf,, A4.1.9)
Рис. 84. Многоуголь- г
ник, стороны которого
состоят из дуг лога- где v меняется так же, как и в A4.1.8). Легко
рифмических спиралей, убедиться в том, что эта функция осущест-
осуществляет требуемое отображение.
Приведенные рассуждения легко обобщаются на тот случай,
когда многоугольник в плоскости z ограничен не только окружно-
окружностями и прямыми, но и логарифмическими спиралями с центром
в начале. При отображении W = log z эти спирали также переходят
в прямые, а при отображении посредством интеграла Шварца—
Кристоффеля несущественно, как эти прямые расположены относи-
относительно осей плоскости W. Обращаясь к случаю, когда критические
точки z = 0, оо лежат внутри многоугольника, приходим к выраже-
выражению A4.1.6), которое решает и эту задачу об отображении. Отобра-
Отображения такого рода рассматривались Эфезером2.
14.2. Многоугольники в сетках конических сечений. Пусть теперь
Gz — односвязная область, ограниченная дугами софокусных
эллипсов и гипербол. Эту область можно считать расположенной на
сетке, которая изображена на рис. 53, п. 8.1. Функция, определяю-
определяющая эту сетку:
W(z) = arc cos z; A4.2.1)
1 Но не обязательно конформна; например, в вершинах с внутренними
углами 2л (концы разрезов) отображение z(ro) имеет точки ветвления.
2 К р h с s с г Н., Konforme Abbiidung einfach zusammenhangender Gebiete,
die von Hogen konzentrischer logarithmischer Spiralen berandet sind. J. reine
angew. Math., 187 A949), 131—152.
14.2. Многоугольники в сетках конических сечений 179
критическими точками являются точки z = +1, z = оо. Если ни
одна из них не попадает внутрь Gz, то эта область отображается
функцией W(z) на обычный прямолинейный многоугольник, а
последний можно вновь отобразить на верхнюю полуплоскость
посредством интеграла Шварца—Кристоффеля W(w).
Если же внутри G-. имеются критические точки, то интеграль-
интегральное выражение следует видоизменить. Пусть при отображении обла-
области Gz на верхнюю полуплоскость точки z — + 1,©о переходят в
точки ш = е+1, е_у, ех. Отображение z(w) в этих точках конформно
и в их окрестностях допускает следующие разложения:
z(w) = ± 1 4• (ш — с±]) [а0 + a1(w — a±l) + . . .) A4.2.2)
и
z(uO = (и» — О К 4- «! (ю — *.) 4- .. .]. A4.2.3)
Производные функций z(w) и W(w) по ш связаны соотноше-
соотношением
> Г г г 1 П4 2 4>
*~' \-z\w) 2 [z(w)
Отсюда для подинтегрального выражения W'(w) в интеграле Швар-
Шварца—Кристоффеля получаются разложения в окрестностях точек
ш = е±]:
1
W'(w) = (w — <ч,)~2 [Ьо + Ьг (ю — е±1) 4- . . .] A4.2.5)
и в окрестности точки ш = ех:
\\\w) =-^=}— 4- ft0 4- .... A4.2:6)
Соответствующие разложения имеют место и в сопряженных
точках ё+1,1_г и ёте. Таким образом, для отображающей функции
-т(ю) можно написать следующее выражение:
z(w) =
= eos| Сй | ———w g у ' • -="-' __ du» |.
A4.2.7)
Здесь величины 6*я вновь означают внутренние утлы прямо-
прямолинейного многоугольника в плоскости W. Если не все три крити-
критические точки оказываются внутри G2, то соответствующие множи-
множители под знаком интеграла опускаются.
1U»
180
14. Многоугольники в изотермических сетках
; : Исследуем отображение посредством интеграла W(w) подробней.
Начнем с того случая, когда все три критические точки лежат внутри
Gz. Так как интегрирование ведется от точки е+1, то W(c+l) = О
и z(e+1). = 1 согласно нашим предположениям. Параметры интег-
интеграла следует выбрать так, чтобы при определенном знаке квад-
квадратного корня и интегрировании по пути, лежащему целиком в
верхней полуплоскости, мы имели W(e_1) = л. Кроме того, должно
выполняться условие A4.2.6), налагаемое на вычеты. Для однознач-
однозначного определения значений W(w) соединим точку е+1 с е_х и с е„
и рассмотрим отображение
__а°~ *-~ верхней полуплоскости с
'if-- \w) образовавшимся разрезом1
| (рис. 85). На основании
"' сказанного один берег раз-
/,,///,,г/////'$/////// реза между e+i и е_г пере-
Л ходит в кривую, соединя-
соединяющую T04KHW = 0 и W = п.
777777/
ж
ч
Образом второго берега яв-
является кривая, соединяющая
W=7iuW = 2tivi получен-
ная из первой поворотом
вокруг точки W = л. Обра-
Образами обоих берегов разреза
между е+1 и ете являются
кривые, получаемые друг из
"= друга сдвигом на In. Знак
при вычете в A4.2.6) следует
брать так, чтобы одна из этих
кривых уходила в бесконеч-
бесконечность из точки W=Q, другая
. • — из точки W = 2я. Таким
образом, все четыре берега разреза вместе отображаются в зам-
замкнутую цепь кривых, ограничивающую область Г плоскости W,
имеющую вид полуполосы.
Так как подинтегральное выражение на вещественной оси w
вещественно и отлично от нуля, оно, как и в случае обычного инте-
интеграла Шварца—Кристоффеля, отображается функцией W(w) в
границу прямолинейного многоугольника с внутренними углами
в»я, и зта граница лежит целиком внутри Г. Вместе с границей /'
Рис. 85.
I } Точнее, следовало бы соединить е+1 разрезом также и с вещественной
осью, однако ниже мы увидим, что при исследуемом отображении функция
W(w) однозначна уже в двусвязной области, получаемой из полуплоскости
разрезом вдоль е+1, е_г, е«>.
14.2. Многоугольники в сетках конических сечений 181
она ограничивает двусвязную область, которая как раз и представ-
представляет собой образ верхней полуплоскости с разрезом, проходящим
через е+1, е_ь ете. При последующем отображении z = cos W полу-
полоса Г переходит в плоскость z с разрезом [+ 1, — 1, оо], а
граница многоугольника — в границу G2 (при правильном выборе-
параметра). Таким образом, функция z{w) отображает верхнюю'
полуплоскость w с разрезом на область Gz с разрезом, соединяю-'
щим критические точки. В окрестностях последних отображение!,
однозначно и конформно, так что можно отбросить разрез, полу-!
чая тем самым искомое отображение Gz на верхнюю полуплоскость.
Совершенно аналогично обстоит дело в случае, когда внутри
Ог находятся не все критические точки, а только одна или две.
Чтобы сделать отображение W(w) однозначным, следует вновь
провести на верхней полуплоскости го разрез, соединяющий точки
ek(k = +1> °°) ДРУГ с другом и с вещественной осью. Берега этого
разреза перейдут в некоторые кривые, которые при последующем
отображении z = cos W вновь преобразуются в разрезы. Веществен-
Вещественная ось w преобразуется в ломаную на плоскости W, которой соот-
соответствует граница Gz на плоскости z. На рис. 86а—86d изображены
четыре существенно различных случая.
При наличии особенностей е±1 и ете задача о параметрах весьма
усложняется, тем более что интеграл не берется в вещественной
области. Разобранные полностью примеры приведены в разд.
Б, §7.
Совершенно такие же методы применимы к областям Gz, гра-
границы которых составлены из дуг софокусных парабол. Каждая
парабола с фокусом в нуле преобразуется функцией
W(z) = z2 A4.2.8)
в прямую1 (см. п. 6.2). Критическими точками этого отображения
служат z = 0, оо, и если область Gz не содержит их внутри, то она
посредством A4.2.8) отображается на обычный прямолинейный
многоугольник.
Если критические точки лежат внутри G2, то для отображающей
функции z(w) вновь имеют место разложения A4.1.2), в которых
е0 и ете по-прежнему означают соответствующие точки верхней
полуплоскости w. Учитывая, что
1 Здесь не обязательно ограничиваться ортогональньтй; семействами
софокусных парабол, изображенными на рис. 31, п. 6.2.
¦*.,
Рис. 86а.
I ,
Рис. 86c.
с*,
Рис. 86b.
Рис. 86d.
14.2 Многоугольники в сетках конических сечений
183
получаем для W'{w) разложение
W'(w) = (ш — е0)
соответственно
bL (ш — ср) + ...], A4.2.10)
W'(iv) = (ш — e^,) 2 [bQ + bl{w — ex) + ...]•
Таким образом, находим отображающую функцию г(ш) в
виде
.A4.2.1
е0 И
Исследуем отображение, которое дает интеграл W(w), считая,
что обе критические точки лежат внутри Gz. Если точки
соединить разрезом, то отоб-
отображение становится однозна-
однозначным в верхней полуплоскости "If
w. Два берега разреза преоб- !!
разуются в кривые, соедиия- ео®
ющие точки W = 0hW = ooh
переходящие друг в друга при
умножении на —1. Вещест-
Вещественная ось плоскости w снова
отображается в границу много-
многоугольника. Последняя вместе с
образами берегов разреза огра-
ограничивает двусвязную область
плоскости W, в' которую при
отображении W(w) переходит
верхняя полуплоскость ш с раз-
разрезом (рис. 87). При отображе-
отображении z = W2 образы берегов
этого разреза переходят в раз-
разрез, соединяющий точки z = О
и z = ею, а образ вещественной
оси w (при правильном выборе - -«-_-i.-«««« >
параметров) — в границу мно-
гоугольника Gz. Отбрасывая
разрезы, получаем искомое
отображение верхней полу-
полуплоскости и) на G,. Рис. 87.
0\
184
§ 14. Многоугольники * изотермических сетках
В тех случах, когда
внутри G, лежит только
одна критическая точка, мы
поступаем аналогичным об-
образом, с той лишь разницей,
что разрез проводится в
верхней полуплоскости ш от
точки и>=ек к вещественной
оси. Эти случаи изображены
на рис. 88а—Ь. Примеры
приведены в разд. Б, § 7.
Рис. 88а.
Рис. 88Ь.
15.1. Уравнение Шварца для двусвязных многоугольников
185
Ь.,п
A)
§ 15. Двусвязные многоугольники
15.1. Уравнение Шварца для двусвязных многоугольников. Рас-
Рассуждения § 12—14 можно без затруднений перенести на случай
конформных отображений двусвязных многоугольников. Пусть в
плоскости z задана двусвязная область Gz, обе граничные кривые
С\ и С2 которой состоят из дуг
окружностей и прямолинейных от-
отрезков. Пусть на Сг лежат т вер-
вершин с внутренними углами1 уцп, а
на С2 — п вершин с внутренними
углами Ь^. Пусть этот многоуголь-
многоугольник отображается функцией ш(г) в
том смысле, как изложено в п. 10.2,
на прямолинейную полосу. Для
простоты мы в отличие от п. 10.2
расположим эту полосу так, чтобы
бесконечное число раз пробегаемая
кривая Сх преобразовалась в вещест-
вещественную ось ш, а кривая С2 — в
линию 1ю \и> — -J =0. Если поло-
с\
(vjl
(-1) -'
г *
2 1
7Т777.
жить здесь т =
Ы
2а'
где а
вве-
денная в A0.2.1) положительная вели-
величина, то полоса будет находиться
в верхней полуплоскости ш, а фун-
фундаментальные четырехугольники Vv
будут следовать друг за другом на
расстоянии 1. Функция г(ш), стало
быть, имеет в этой полосе период 1:
<ш)=г(ш+1); A5.1.1)
каждый фундаментальный четырех-
четырехугольник Vv, например следующий:
0 < Re ш < 1, 0<1тш<
A5.1.2)
Рис. 89.
отображается этой функцией на одноевязную область G*, полу-
получающуюся из Gz при соответствующем разрезе (см. рис. 89). Преоб-
Преобразование
С(ю) = е2я™ A5.1.3)
1 Под внутренним углом понимается, естественно, угол, лежащий внутри G2.
186 § 15. Двусвязные многоугольники
отображает фундаментальные области в круговые кольца с разре-
разрезами, так что функция z(?) = г(ш(?)) взаимно однозначно и конформ-
конформно отображает круговое кольцо на Gz.
Пусть вершинам многоугольника G, соответствуют в фунда-
фундаментальном четырехугольнике A5.1.2) т точек w = df. на веще-
вещественной оси и /г точек ш =-*- + е„ на прямой Im (w—^1=0.
Теперь можно показать, что производная Шварца [z]w для
рассмотренной здесь функции г(ш) является однозначной двоя-
копериодической функцией с периодами 1 и т во всей плоскости ш.
Во-первых, функция г(ш) периодична в полосе с периодом 1, поэтому
тем же свойством обладает [г]ш. За пределы полосы ее можно про-
продолжить аналитически с помощью зеркального отражения. Четным
числом зеркальных отражений относительно вещественной оси и
прямой Im I w — — I =0 точка w переводится в w + п%, где п —¦ целое
число. В плоскости z этому соответствует четное число зеркальных
отражений относительно сторон многоугольника, т. е. некоторое
дробно-линейное преобразование. Оба преобразования не изменяют
выражения [z]w, которое, следовательно, периодично с периодом
т. В частности, поскольку, как и в п. 12.1, все ветви функции z(w)
над точкой ю образуются одна из другой дробно-линейным пре-
преобразованием, функция [z]w однозначна в плоскости w.
Как и в п. 12.1, показывается, что поведение функции [г]ш в
окрестностях точек w — d^ и ш = -^ + ev определяется разложе-
разложениями в ряды вида A2.1.12); при этом в силу двоякой периодич-
периодичности функции [z]w ее поведение на бесконечности можно не
исследовать особо. Во всех остальных точках прямоугольника
периодов
0=sRew< I, O=slmu>< |т| A5.1.4)
функция [z]w аналитична. Таким образом [z]w, как двоякопериоди-
ческая функция, определяется однозначно с точностью до постоян-
постоянного слагаемого, и мы можем написать
[*]-= 2" [—А *> (» - *,.; 1, т) ~ ь&> ? (ш - *„!т)] -Ь
2\L^* V (w - |-е„; 1, т) +Ы2>^ (ш _ е |тI+ Ьо. A5.1.5)
Постоянные bft, &i2) и Ьо должны быть вещественными; для того
чтобы выражение A5.1.5) представляло собой двоякопериодиче-
скую функцию, должно выполняться равенство
т п
2Ф + 2№-ь A5.1.6)
15.1. Уравнение Шварца для двусвязных многоугольников 187
Выражение для [z]w содержит следующие неопределенные пара-
параметры.
1. Расположение особых точек d^ и с„. Одну из них можно вы-
выбрать произвольно, так как сдвиг ш* = ш + а переводит парал-
параллельную полосу в себя. Остальные особые точки полностью опре-
определяются многоугольником Gz.
2. Акцессорные параметры tip и bf\ В силу A5.1.6) т + п— 1
из них независимы.
3. Постоянная Ьп.
4. Отношение периодов т.
Итого имеем 2 (яг + п) параметров, т. е. на 6 параметров больше,
чем при отображении односвязного многоугольника с тем же числом
сторон. Однако и двусвязный многоугольник, за некоторыми
исключениями1, определяется заданием 2 (т + п — 3) геометри-
геометрических постоянных. Естественно предполагать, что решения урав-
уравнения A5.1.5) не при каждом выборе параметров отображают
прямоугольник периодов A5.1.2) на двусвязный многоугольник.
Это действительно так. Мы только что установили, что отобра-
отображающая функция г(ш) должна быть периодична в полосе с перио-
периодом I. Из периодичности же функции [z]w следует, что решения z(w)
уравнения A5.1.5) подвергаются дробно-линейному преобразова-
преобразованию, когда аргумент изменяется на величину периода. Вместо
A5.1.1) выполняется, таким образом, более общее равенство
,(UL-l)=-af>±A A5.1.7)
v cz(w) + d ч '
Выражение A5.1.5) определяет тем самым гораздо более общий
класс отображающих функций. Заменив, например, условие A5.1.1)
условием A1.1.3)
г(ш + 1) = г(ш) + Ь,
получим отображение периодических многоугольных областей
типа полосы, рассмотренное в п. ИЛЬ.
Соотношение A5.1.7) содержит три комплексных или шесть
вещественных коэффициентов. Это в точности соответствует шести
дополнительным параметрам уравнения A5.1.5), которые следует
выбрать так, чтобы A5.1.7) приняло форму A5.1.1):
г (ш -Ь 1) = г(ш).
Это соотношение мы назовем условием замкнутости.
1 Исключение составляют следующие случаи. Если одна из граничных
кривых есть двуугольник, то число геометрических постоянных увеличивается
на одну; если полная окружность — на три. В этих случаях соотношение A5.1.7)
подчиняется некоторым ограничениям, независимо от параметров дифферен-
дифференциального уравнения; например, для некоторых решений коэффициенты в
равенстве A5.1.7) должны быть вещественными.
188 § 15. Двусвязные многоугольники
Дальнейшее исследование уравнения A5.1.5) проводится так
же, как и в § 12. Это уравнение следует привести к виду A2.2.5)
и составить канонические решения типа A2.2.13), соответственно
A2.2.14).
С помощью этих решений определяются преобразования пере-
перехода и обхода, к которым присоединяются подстановки вида
<Pi(w + Р) = аФ)(го) + bcp.z(w),
<р2(ш + р) = cy^w) + rf(p,(w), A5.1.8)
где р — период производной Шварца [z]w, р = тх + п (т, п —
целые). В том числе должно выполняться условие замкнутости;
другое условие при р = г устанавливает связь между граниыдми
Cj и С2 области Gz.
Асимптотическое интегрирование, рассмотренное в п. 12.4,
переносится также на этот случай, если заменить рациональное
выражение A2.4.2) соответствующей двоякопериодической функ-
функцией. Интеграл |(ш), определяемый формулой A2.4.3), вновь отобра-
отображает фундаментальный четырехугольник A5.1.2) на ступенчатый
многоугольник. Соответствующий ему круговой многоугольник
определяется теперь методами, изложенными в п. 12.4. Таким
образом, без особых затруднений можно получить представление о
зависимости формы многоугольника1 от параметров уравнения.
К уравнению A5.1.5) применимы также изложенные в п. 12.5
численные методы интегрирования. Однако при большом числе
параметров, которые к тому же входят под знак сложных эллипти-
эллиптических функций, этот способ требует очень больших вычислений.
Поэтому на практике этот метод пригоден лишь для очень простых
многоугольников.
Значительно проще в этом отношении обстоит дело в случае
прямолинейных многоугольников, ибо от общего выражения
A5.1.5) можно перейти к частному случаю интеграла Шварца—
Кристоффеля. Этому посвящен следующий пункт.
15.2. Интеграл Шварца—Кристоффеля для двусвязных много-
многоугольников2. Пусть G2 — прямолинейный многоугольник и г(ш) —
функция, отображающая фундаментальный четырехугольник A5.1.2)
на G2. Тогда, как и в предыдущем пункте, показывается, что
дифференциальное выражение A3.1.2)
ri(w) = т~ l°g:, - = —f
IK } dm ° dw z'
1 Многоугольники понимаются здесь в обобщенном смысле, т. е. как
области, получаемые отображением фундаментального четырехугольника
функциями z(w), для которых выполняются соотношения A5.1.7), более общие,
чем условия замкнутости.
2 См. также [10]. — Прим. ред.
15.2. Интеграл Шварца—Кристоффеля 189
есть двоякопериодическая функция с периодами 1 и т. Из разло-
разложений в ряды, выведенных в п. 13.1, получим выражение
-I)* (го - djr) + 2 (К - 1)|-4 ("> - *„| т) + Ь0.
A5.2.1)
Чтобы эта функция была двоякопериодической, должно быть
2 (У, - О + 2 (К - 1) = 0, A5.2.2)
1
что можно получить и из элементарных геометрических сообра-
соображений.
Покажем, что bQ = 0. Интегрируя A5.2.1), имеем
«» = С, l_[Sfix (w - d\T)Y*-* И [в, (w - е„\х)Г>-1 е^. A5.2.3)
Согласно условию замкнутости A5.1.1), должно быть
г'(ш + 1) = г'(ш). A5.2.4)
Поскольку при замене w на w + 1 ^-функции, входящие в A5.2.3),
не изменяют своего значения, то этим же свойством должен обла-
обладать множитель е6»1", что при вещественном Ьо возможно лишь
тогда, когда />() — 0.
Таким образом, интеграл Шварца—Кристоффеля для отобра-
отображения двусвязных многоугольников имеет вид
z(w) = d f /7 [»x(w ~ d, I r)]^-1 П [*4(ю - e, | r)]",-1 dw + C2.
(J 5.2.5)
Если точка г = oo лежит внутри Gz, то к подинтегральной функ-
функции присоединяется еще множитель вида
[#! (и» — ете | г) *х (ш — е\„ | т)]-2, A5.2.6)
причем вычет в точке w = еж равен нулю. Дополнительные множи-
множители, введенные в § 14, должны быть заменены ^-функциями, если
мы отображаем двусвязный многоугольник в круговой сетке или в
сетке конических сечений.
Без учета дополнительных множителей интеграл Шварца—
Кристоффеля A5.2.5) содержит следующие параметры:
1) m + п особых точек ^ и е„, из которых одну опять можно
выбрать произвольно;
2) отношение периодов т.
190 § 15. Двусвязные многоугольники
Всего имеем т ~ л неопределенных параметров. Им можно
сопоставить m-г л - - 2 геометрических постоянных области Gz,
которые определяют этот многоугольник с точностью до целого
линейного преобразования. Каждая из граничных кривых Съ С2
содержит т — 3, соответственно п — 3, геометрических постоян-
постоянных, так как каждую из них можно рассматривать как границу
одиосвязного многоугольника. К этому присоединяются еще
четыре вещественные постоянные, определяющие взаимное распо-
расположение граничных кривых; они соответствуют двум комплексным
коэффициентам целого линейного преобразования, которое пере-
переводит одну из граничных кривых в заданное положение.
Оставшиеся два параметра служат для выполнения условий
замкнутости. Из периодичности подинтегральной функции в A5.2.5)
следует только условие
z(w + 1) = z(w) + Ь; A5.2.7)
таким образом, при произвольном выборе параметров мы получим
периодический многоугольник1. Два вещественных коэффициента,
содержащихся в комплексном периоде Ь, соответствуют здесь
двум дополнительным параметрам выражения A5.2.5).
Для установления связи между параметрами интеграла Шварца—
Кристоффеля и видом многоугольника G2 нужно сначала вычислить
длины сторон. Эти вычисления, как и в выражении A3.2.1), про-
проводятся целиком в вещественной области. Так, для длин сторон на
С, получим
J
/1, (ю - «yiv-1// ^(ш"~ ^l*' dw> A5-2-8a)
а на2 С2
42) = K-'iI I // 1*4 ("»- "„)l""^1 ПI*, ("»- ОIе' dw. A5.2.8b)
ek-i
Используя эти длины сторон, можно написать условие замкну-
замкнутости в следующем виде:
jr if) fW. = 2" !<?> еы»ь = 0; A5.2.9)
< = 1 А"=1
1 Ср. п. 11.1 Ь. Таким образом, выражение A5.2.5) позволяет также осуще-
осуществлять отображения периодических многоугольников.
2 Здесь использовано равенство A5.2.2). Это равенство не выполняется при
наличии дополнительного множителя A5.2.6). Мы предоставляем читателю
сделать в этом случае соответствующие изменения в формуле A5.2.8b). Случай,
когда какая-либо вершина лежит в бесконечности, мы здесь тоже не рассматри-
рассматриваем. Рассуждения п. 13.2 без труда переносятся на двусвязные много-
многоугольники.
15.2. Интеграл Шварца — Кристоффеля
191
при этом выполнение одного из этих равенств влечет за собой выпол-
выполнение другого. Величины тис,- и zifik означают углы между соответ-
соответствующими сторонами и вещественной осью z; пусть они опреде-
определены так, чтобы было
а;+1 - а, = 1 - у,, 0,t+1 - Ch = 1 - dk. A5.2.10)
Для определения взаимного расположения граничных кривых
вычислим интеграл A5.2.5) по прямолинейному отрезку от особой
точки w = rf,- до точки w = dj -t- т. Путь интегрирования пересечет
Ш = - +
прямую Im I w ¦— ?- j = 0 между точками w = ~
+ ek. Согласно принципу симметрии, при таком продолжении точке
w = dt, + т будет соответствовать в плоскости z точка е?, сим-
метричная
интеграла
с f,- относительно стороны 42) границы С2. Модуль
"Т
I Т m
= I С, f /7 [*i (» - d^-1 // [«4 (ш -
,-1 dw
A5.2.11)
равен, таким образом [ср. с
A3.2.10)], расстоянию между е* и е,-
или удвоенному расстоянию от
вершины f,- до стороны 42) (см-
рис. 90).
Подобным образом вычисля-
вычисляется угол bikn между стороной
на
и стороной
на С2
Угол л{п [ср. A5.2.10)] между sf
вещественной осью z равен аргу-
аргументу подынтегрального выраже-
выражения1 на участке между го = d,_1 и
ю = dt:
a.fi = arg z'(»,;), rf,-_! < ш0 < d,-.
A5.2.12)
Если аналитически продолжить
z'(») из wG в шA 4 т через отрезок
IT Т . 1
2" + <»;(_!, ^—г efc I -> то на основе
принципа симметрии величина
arg z' (roc + т) равна углу между
вещественной осью z и стороной
(то)
1
d, аг
Рис. 90.
1 Здесь, как и в обычном интеграле Шварца—Кристоффеля, arg z'{w) ие
изменяется на отрезках, соответствующих сторонам бг.
192 § 15. Двусвязные многоугольники
sfA), симметричной с sW относительно 42) (см- Рис- 90); поэтому
arg z' (ш0 + т) = arg 2'(Юо) + 2я«Л. A5.2.13)
Для простоты положим ш0 = 0 и продолжим z'{w) из точки 0
в точку т вдоль мнимой оси плоскости w. Этому пу ги принадлежат
стороны 41} и si2) > и мы найдем из A5.2.13) угол л6и. Все остальные
углы л6№ легко вычисляются отсюда при помощи известных внут-
внутренних углов yjrt и <3,д.
Для аналитического продолжения ?9-функций в прямоуголь-
прямоугольник1
— 1 < Re и < 0, 0 «= Im v =s | т j
используется соотношение
[В] (у + т|т)]г = е-'«гB«+1+г) [^(р|т)У (/ = 1,4); A5.2.14)
отсюда, в силу A5.2.2),
arg z'(x) = arg г'@) + я^ d {у -Y)-^n^^ iK - 1). A5.2.15)
Вместе с A5.2.13) это дает
rfn = \ [5 d, (У, - 1) + 2 «„ (^ - 1I • A5-2.16)
Для определения вида многоугольника Gz следует, таким обра-
образом, вычислить
1) т + п — 2 длин сторон A5.2.8а, Ь); остальные две определя-
определяются из соотношения
т
2"* 1{П <*"<* = ^ 42) efa&; A5.2.9а)
1 = 1 к~-А
2) два интеграла вида A5.2.11); вместе с A5.2.16) это даст нам
взаимное расположение кривых Сх и С,.
Тем самым мы получаем т + п + 1 уравнений для определения
величин dh ek, т и С1; причем один из параметров rf,- или ек можно
выбрать произвольно. Численно эти уравнения решаются аппрокси-
аппроксимированием сверху и снизу или с помощью метода Ньютона.
Метод Маттье (см. конец п. 13.5) приводит к затруднениям, свя-
связанным с тем, что здесь уже приближенные многоугольники должны
подчиняться условию замкнутости.
15.3. Частные случаи. Интеграл A5.2.5) выражается в замк-
замкнутой форме, если подинтегральная функция является двоякоперио-
дической. Это имеет место в том случае, когда все стороны соот-
соответствующего многоугольника Gz параллельны. В этом можне
1 По предположению, имеем 0 < d^ < 1, 0 < ev < 1. Таким образом.
для всех д-функций мнимая ось лежит в этом прямоугольнике.
15.3. Частные случаи 193
убедиться следующим образом. Отражение относительно двух
параллельных прямых равносильно сдвигу
Ф&У) - г + Ъ; A5.3.1)
здесь Ъ равно удвоенному расстоянию между этими прямыми.
При таких преобразованиях остается инвариантной уже первая
производная z'(w). Отсюда заключаем, что z\w) двоякопериодична.
Если же это так, то подинтегральная функция z'{w) однозначно
с точностью до аддитивной постоянной определяется заданием
полюсов1 и соответствующих им разложений. Эту постоянную
можно выбрать так, чтобы выполнялось условие замкнутости.
Равенство A3.2.14) устанавливает весьма простую связь вычетов
функции z'(w) в полюсах с формой многоугольника Gz. Подробно
разобранные примеры читатель найдет в разд. Б, п. 8.1.
Вообще отображающая функция z(w) может быть выражена в
явном виде, если все стороны многоугольника Gz принадлежат
одному пучку окружностей. К этому типу относятся также много-
многоугольники, все стороны которых лежат на прямых, проходящих
через начало координат, или на концентрических окружностях.
Двойное зеркальное отражение относительно этих сторон сводится
к преобразованию подобия2
s2(Sj(z)) = az. A5.3.2)
Относительно такого преобразования остается инвариантным
выражение
flog2(w)=z41- A5.3.3)
dm ° v ' z (w) v '
Следовательно, это выражение должно быть двоякопериодическим.
Эта функция определяется в таком случае разложениями в ряды в
окрестностях вершин G?, после чего z{w) вычисляется интегриро-
интегрированием.
Отображающую функцию z(w) можно найти также приемом,
изложенным в п. 14.1, а именно, отображая Gz на прямолинейный
многоугольник с параллельными сторонами с помощью функции
W(z) = log z
и сводя тем самым этот случай к уже рассмотренному. Здесь под-
интегральную функцию W\w) также следует соответствующим
образом дополнить, если критические точки г =» 0, оо лежат внутри
0г. Численные примеры рассмотрены в разд. Б, п. 8.2 и 8.3.
1 Полюсам функции z'(w) соответствуют бесконечно удаленные вершины
многоугольника Gz. Поэтому величины dM, соответственно е„, достаточно опре-
определить только для этих вершин.
2 Точнее, к повороту либо растяжению.
13 — 6002
ПРИБЛИЖЕННЫЕ МЕТОДЫ КОНФОРМНЫХ
ОТОБРАЖЕНИЙ1
Описанные выше методы позволяют в большинстве случаев,
встречающихся на практике, полностью решать задачи об отобра-
отображении. Однако часто приходится рассматривать области с настолько
сложными границами, что отображающую функцию нельзя полу-
получить в явном виде, хотя ее существование обеспечивается теоремой
Римана. Для этих случаев разработан ряд приближенных методов,
важнейшие из которых мы коротко излагаем ниже.
Приближенные методы основываются на весьма различных
принципах, так что любая их классификация содержит большую
долю произвола. С точки зрения практики нам представляется
целесообразным следующее разделение на группы. Одна группа
методов без особой подготовительной работы и больших вычисле-
вычислений дает хотя и не очень точное, но для многих целей пригодное
приближение. Любая же попытка увеличения точности связана с
настолько большой вычислительной работой, что метод теряет
свои преимущества. Такие методы мы будем называть собственно
приближенными методами.
Другую группу составляют методы, для которых зачастую
требуются большие предварительные вычисления. Но коль скоро
метод приведен в действие, то не представляет большого труда
достигнуть любой заданной точности. Поскольку все методы
второй группы в той или иной мере основываются на теории интег-
интегральных уравнений, мы будем их называть методами интеграль-
интегральных уравнений. Эти методы особенно подходят для работы на
вычислительных машинах.
Сначала в § 16 мы рассмотрим исторически раньше возникшие
и более простые по своей структуре собственно приближенные мето-
методы, а затем, в § 17, перейдем к методам интегральных уравнений,
предпочтительным для современной практики. Следует, кроме
того, отметить, что любой приближенный метод требует большого
объема вычислительной работы, так что в любом случае нужно
сначала искать точное решение, даже если весьма вероятно, что
оно окажется очень сложным.
1 К чтому разделу см. [12],[13],[18], [19] и Канторович Л. В. и Крылов
В. И., Приближенные методы высшего анализа, М., 1949. — Прим. ред.
16.1. Метод растяжения 195
§ 16. Собственно приближенные методы
16.1. Метод растяжения1. Пусть односвязная область Go плоско-
плоскости г целиком лежит внутри единичного круга. Покажем сначала,
что любую односвязную и однолистную область G{ на числовой
плоскости или числовой сфере, имеющую более одной граничной
точки, можно отобразить на область вида Go при помощи элемен-
элементарных функций. Действительно, если область G{ имеет хотя бы
одну внешнюю точку С — Са, то существует круг | ? — Са | < е,
не содержащий ни одной точки Gc. Отображая этот круг дробно-
линейной функцией на внешность единичного круга, мы переведем
область Gj целиком внутрь этого последнего. Если же Gc не имеет
внешней точки, т. е. если ее граница представляет собой разрез,
то можно прежде всего перевести линейным отображением две
заданные граничные точки в точки С* = +1. Преобразование
(см. п. 8.2, в особенности рис. 56) переводит внешность любого
разреза между точками С* = +1 и С* = —1 во внешность некото-
некоторой области, так что образ G. в плоскости со уже имеет внешние
точки.
Можно считать, что Go содержит точку 2 = 0, ибо этого всегда
можно достигнуть, отображая единичный круг на себя дробно-
линейным преобразованием. Тогда существует круг \z\ < q, цели-
целиком лежащий в Go; пусть q0 — наибольшее значение q, обладающее
этим свойством. Тогда найдется функция Wj(z) (так называемая
функция растяжения), которая отображает Go в область Gx, также
лежащую внутри единичного круга и содержащую круг |юг| < р„
причем Qi> Qo и m>j@) = 0. Таким образом, область G, заполняет
единичный круг «лучше», чем Go. Этот прием можно повторять,
отображая Gj на G2 и вообще область Gn на Gn+1, причем круг
\wv\ < Qv каждый раз лежит внутри Gv, gn+1 > gn. Если выбирать
функции растяжения подходящим образом, то дп при достаточно
больших п будет как угодно мало отличаться от 1, т. е. граница
Gn будет лежать как угодно близко к единичной окружности.
Согласно лемме Шварца (см. п. 9.5), функция wn(z), отображающая
Go на Gn, как угодно мало отличается от функции w(z), отобража-
отображающей Go на единичный круг. Таким образом, последовательность
/(^(z) сходится к ш(г), и поскольку функции растяжения можно
чадать явным образом, то мы получаем приближенный метод на-
нахождения конформного отображения области Go на единичный круг.
1 В оригинале употреблен термин «Schmiegungsverfahren». — Прим. ред,
13*
196
§ 16. Собственно приближенные методы
Функции растяжения можно задавать различными способам
Одна из них, пригодная во всех случаях и поэтому особенно важнг
для теоретических исследований (доказательство теоремы Рима!
об отображении), строится следующи
образом. Пусть z = а ~ goe'«'« — ближашш
к началу координат точка границы Go. Тогд
сначала при помощи функции
г* =
A6.1.
Круговая
луночка
[ср. G.3.9)] эта точка переводится в точ]
г* = 0. Далее, пусть
и, наконец,
w, == —
1 -
Круг с радиальным
разрезом
A6.1.
Корни определяются здесь так, чтоб
точка z = 0 переходила в w1 = 0. Так к;
точка ветвления z = а лежит на границе G
то отображение конформно всюду внут^
Go. Кроме того, z(wj) — однозначная фун
ция, т. е. каждой точке Gx соответствую
только одна точка Go, так что GY однолис
на на плоскости w1. Более подробное иссл
дование показывает также, что круг \z\ <
отображается функцией A6.1.3) на облает
содержащую внутри себя круг |i»i|<ei
5j > gn. Тем самым доказано растягивающ
свойство функции A6.1.3).
В конкретных случаях функции раст
жения A6.1.3) сходятся слишком медленн
Поэтому был предложен целый ряд функщ
растяжения, сходящихся быстрее, котор]
хотя и не всегда, но в большинстве случа
пригодны для применений. Все эти функщ
обладают одним общим свойством, а име
но они отображают некоторую подобласть G* единичного круг
содержащую Go, на единичный круг, оставляя неподвижным нача.
координат. Область G* должна быть по возможности «ближе» к
и в то же время быть не слишком сложной, чтобы функцию шг1
можно было легко вычислить. В литературе подробнее осталып
изучены следующие области (см. рис. 91):
Круговой
треугольник
Рис. 91.
16.2. Вариационный метод 197
1) круговая луночка;
2) круг с радиальным разрезом;
3) круговой треугольник с двумя прямыми углами.
Соответствующие отображающие функции w^z) даны в разд. Б,
п. 1.1 и 3.1.
При всех его достоинствах этот метод на практике обнаружи-
обнаруживает следующие существенные недостатки.
1. Сходимость довольно медленная, особенно на границе об-
области; в приложениях же наиболее важны именно граничные зна-
значения.
2. Функции растяжения сравнительно сложны, причем для каж-
каждого следующего шага необходимо заново выбирать очередную
функцию. Это затрудняет применение указанного метода при
использовании вычислительных машин. Метод применим только
тогда, когда значения функции можно задать графически.
Ввиду этого он используется лишь при очень небольших требо-
требованиях точности или как подготовительный к методу Теодор-
сена.
Этот метод переносится и на отображения двусвязных областей
на круговое кольцо. Функции растяжения определяются здесь так,
чтобы то одна, то другая граничная кривая как можно точнее отобра-
отображались на концентрические окружности.
Более подробно это изложено в работах
Heinhold J. und Albrecht R., Zur Praxis der konlormen Abbildung,
Rendiconti Circulo Math. Palermo, 3 A954), 130—148.
Albrecht R., Zum Schmiegungsverfahren der konformen Abbildung,
Z. angew. Math. Mech., 32 A952), 316—318.
К о m a t u Y., Ein alternierendes Approximationsverfahren Itlr konforme
Abbildung von einem Ringgebiet au{ einen Kreisring, Proc. Jap. Acad., SI
A949), 146—155.
16.2. Вариационный метод. Предлагаемый метод основывается
на теореме о среднем (9.1.4). Если F(w), w = де?, — аналитическая
функция в единичном круге, непрерывная вплоть до границы, то
имеет место равенство
d<p = 2nF@).
о
Отсюда следует, что
2л
j\F(<J*))d<p^bi\F(O)\, A6.2.1)
о
причем равенство возможно лишь тогда, когда F(w) =» const.
198 § 16. Собственно приближенные методы
Пусть теперь G — однолистная и односвязная область плоскост
z с кусочно гладкой границей С. Пусть, далее, функция w(z) конфорд.
но отображает эту область на единичный крут плоскости ш. та1
что точка z = z0 переходит в точку ш = 0. Если /(z) — произвол!
ная аналитическая в G функция, непрерывная вплоть до границы, т
JV(z
(zI1 dz\ = 11/(г(ш)) j | z'(w) ] rfgs э= 2л
с о
A6.2.;
причем равенство имеет место лишь тогда, когда -Цр- = cons
т. е. когда f(z) = cu/(z).
Поставим следующую вариационную задачу: среди всех аналитг
ческих в G функций f(z), непрерывных вплоть до границы1 и удовлет
воряющих условию /(г0) = 1, найти ту функцию, для которо
интеграл2
A6.2.;
с
принимает наименьшее значение. Решение этой задачи даете
функцией
f*(z) = ^ A6.2.
и определяется однозначно с точностью до множителя, равного п
модулю единице. После этого отображающая функция w(z) опреде
ляется интегрированием. Значение минимума равно
hV*) = г^гп • С16-2-'
1 |"»(z)| V
Эту вариационную задачу обычно решают методом Ритщ
Положим
/(г) = <p%z), т. е. | /(z) | = 9(z) ф), A6.2.(
и примем в качестве n-ro приближения выражение
л
<pn(z) = Vo(z) +
1 В возможно имеющихся угловых точках границы эти условия можв
ослабить.
а Интеграл A6.2.3) допускает следующую геометрическую интерпретация
Пусть область G конформно отображается на область Gm функцией со(г). Есл
положить /(z) =o/(z), то Ii(co') равно длине границы области Gm. Отсюда выт
кает следующее утверждение: если G отображается конформно на область G
с заданным коэффициентом растяжения в точке z= z0, то длина гранично
кривой области Ga принимает наименьшее значение, когда Gm — круг.
16.2. Вариационный метод
199
где y>v(z) — соответствующим образом подобранные линейно неза-
независимые функции. Для того чтобы условие /(%) = 1 выполнялось
при любых а„, должно быть %B„) = 1 и yv(zo) = О при V > °- Опре-
Определим скалярное произведение (y,,»?V) формулой
A6.2.8)
Тогда среди всех функций A6.2.7) наименьшее значение интегралу
MVn) = (Фп'Фп) придает функция <p*{z), которая удовлетворяет
условиям
(9>*,У„) = 0, »- 1,2,..., п. A6.2.9)
Отсюда получаем систему линейных уравнений относительно а„.
Решение <p*(z) записывается в виде
Vo(z) (Vo> Vi) (Vo» Vz) • • • (Vo> Vn)
Vi(z) (Vi. Vi) (Vi> Vz) •••(Vi. Vn)
Vn(z) (Vn> Vi) (Vn> Vz) •••(Vn, Vn) i
Vi) (Vi» Vz)
. Vx) (Vz> Vz)
••(Vi, Vn)
--(Vz. Vn)
(Vn. Vi)(Vn,
A6.2.10)
Наиболее подробно "изучен случай, когда <pn(z) есть многочлен
степени п. Тогда y>v(z) — (г — zo)" и последовательность f*(z) схо-
сходится к функции A6.2.4), если граница С области G — простая
замкнутая кривая; для областей с разрезами это не так.
Что касается вычислений при применении этого метода, то
следует заметить, что число операций при нахождении q>n(z) растет
с ростом л, как п3, так что выражение A6.2.7) становится непри-
непригодным, если для достижения заданной точности требуется большое
число членов. Сами же вычисления несложны и легко программи-
программируются для вычислительных машин.
Описанный метод допускает видоизменение, состоящее в том,
что вместо криволинейного интеграла A6.2.3) берется интеграл
ло площади. По теореме о среднем имеем
1 2я
и, следовательно,
(I
0 0
1 2я
Qd<pdg = ttF@)
A6.2.11)
A6.2.12)
о о
200 § 16. Собственно приближенные методы,
причем знак равенства вновь достигается лишь для функции F(w)
= const. Переходя к плоскости z, получаем, как и в A6.2.2),
/<*.) 2
Лло
">'(*„)
A6.2.13
На основании этого соотношения можно сформулировать вариа-
вариационную задачу: среди всех функций /(z), аналитических в G
для которых /(z0) = 1, найти такую, что интеграл1
= J J
(i)dz^ A6.2.14;
а
принимает наименьшее значение. Решение /*(г) этой задачи также
дается формулой A6.2.4). Численно эту задачу можно решить, ка*
и предыдущую, при помощи выражения
п
Ш=%B)+ 2 «„?>„(*)• A6.2.15)
Объем вычислений здесь примерно такой же, как и в случае криво-
криволинейных интегралов. Теоретическое преимущество второго метода
состоит в том, что не нужно налагать никаких ограничений на глад-
гладкость границы области, хотя на практике это не играет роли.
Дальнейшие сведения по этому вопросу можно найти в работах
Bieberbach L., Zur Theorie und Praxis der konformen Abbildung, Rendi-
conti Circulo Math. Palermo, 38 A914), 98—112.
S z e g 6 G., Uber orthogonale Polynome, die zu einer gegebenen Kurve der
komplexen Ebene gehoren, Math. Z., 9 A921), 218—270.
Новые результаты приведены в работе
N е h a r i Z., The Kernel Function and the Construction of Conlormal Maps,
Nat. Bureau of Standards, Appl. Math. Ser., 18 A952), 215—224.
16.3. Графический метод. Изотермическая сетка характеризуется
следующими свойствами:
1) кривые разных семейств взаимно ортогональны;
2) ячейки являются «в малом» квадратными.
Эти свойства можно использовать для графического постро-
построения изотермических сеток.
На практике обычно задается некоторое граничное условие.
Первое приближение изотермической сетки строится произвольно»
но с учетом граничных условий, а затем исправляется на основе
геометрических свойств. Условие ортогональности проверяется,
например, при помощи зеркальной линейки. Далее, при достаточно
мелком и равномерном разбиении ячейки должны все более и
1 В обозначениях сноски 2, стр. 198, величина /2(со') равна площади области
Gm. Таким образом, из всех областей, на которые отображается G при заданном
коэффициенте растяжения в точке г0, наименьшую площадь имеет круг.
17.1. Метод Теодорсена — Гаррика
201
более приближаться по форме к квадратам. Это свойство лучше
всего проверяется проведением диагональной сетки (см. рис. 92),
которая также должна быть изотермической, в частности ортого-
ортогональной.
При некотором навыке и умении чертить можно быстро строить
требуемые приближения, так что этот метод часто применяется на
практике. Численным аналогом этого метода является разностный
метод Либмана, который также применяется в таких задачах.
Рис. 92.
Более подробные исследования геометрической структуры изо-
изотермических сеток см. в работах1 Ringleb F., Numerische und
graphische Verfahren der konformen Abbildung, Heidelberg, 1944.
О методе Либмана см. КоллатцЛ. К., Численные методы решения
дифференциальных уравнений, М., 1953; см. также Runge С,
Z. Math. Phys., 56 A908), 225—232.
§ 17. Методы интегральных уравнений
17.1. Метод Теодорсена—Гаррика2. В основе этого широко
применяемого ныне метода лежит следующая идея. Пусть функция
w(z) конформно отображает единичный круг плоскости г на конеч-
конечную однолистную область G плоскости ш, причем ю@) = 0 (так
1 См. также [14] и указанную там литературу. — Прим. ред.
2Theodorsen Т. und Garrick I. E., General potential theory
of arbitrary wing sections, NACA Rep. № 452 A933).
202 § 17. Методы интегральных уравнений
что начало координат лежит внутри G) и ш'@) -— вещественное
число. Тогда функция1
«(Z) = log^ A7.1.1)
аналитична в единичном круге. Пусть, далее, границей G является
кусочно гладкая кривая С. Если z = re"", w = де'9, то точки этой
кривой определяются уравнением
ш(е'>) = q(<p) e'eM. A7.1.2)
На границе единичного круга функция co(z) принимает значение
(о(е'-р) = log (?(<?;-) + i [%) — <р],
т. е. log g((p) и 0((р) — у служат вещественной и мнимой частями
некоторой функции, аналитической в единичном круге. Согласно
(9.2.12), при q = Я = 1 и V@) = 0 эти величины связаны соотно-
соотношением
2л
g^*/). A7.1.3)
Если же задана не функция ш(г), а граница С области G своим
уравнением q = оF), то A7.1.3) представляет собой интегральное
уравнение с неизвестной функцией О(ср):
2л
%) = Ч> + il'og (?(%)) ctg^-p dv». A7.1.4)
Определив из этого уравнения функцию Q{<j>), можно легко найти
с помощью формулы Шварца (9.2.12) функцию co{z), а затем и
функцию ш(г), отображающую единичный круг на область G.
Для областей, близких к единичному кругу, т. е. таких, граница
которых мало отличается2 от единичной окружности, интегральное
уравнение A7.1.4) решается методом последовательных приближе-
приближений. С этой целью положим
= <р,
2л A7.1.5)
= ч> +
Эти интегралы, однако, лишены смысла благодаря особенности
подинтегральной функции при tp = (р. Для получения сходящихся
1 Функция a>(w)a=a>(z(w)) равна регулярной части y(w, 0) функции Грина
(9.1.11) для области G при С„ = 0.
а Точнее, для граничных кривых, удовлетворяющих условию A7.1.8).
17.1. Метод Теодорсена — Гаррика 203
интегралов примем во внимание, что мнимая часть аналитической
функции, определенная формулой (9.2.11), не изменяется при добав-
добавлении постоянного слагаемого к граничным значениям веществен-
вещественной части. Поэтому можно провести следующее преобразование:
2я 2л
ctg Z^± dw = J [F{W) -1%)] etg Т^Л. dw =
о
= - J [*(? + 0 - Hf - 0 ctg ^ dt. A7.1.6)
В частности, если F(cp) непрерывно дифференцируема, то при малых
е имеет место приближенное равенство
е
J [F {ср + t) - F {ср — 0] ctgj <*' fb 4еР"(9)), A7.1.7)
о
а интеграл от е до ж вычисляется обычными приближенными мето-
методами.
Соответствующим образом измененная последовательность
A7.1.5) сходится к решению 0(9?) исходной задачи, если
^e<l. A7.1.8)
Геометрически это условие означает, что граница С области G
пересекает окружности q = const под углами, меньшими 45°.
В частности, любой луч, проведенный из начала координат, пере-
пересекает границу лишь один раз1.
При этом погрешность n-го приближения д^п\(р) удовлетворяет
Следующей оценке:
П ¦ 100%)-0@1^ C-SL, A7.1.9)
|де е — величина, определяемая неравенством A7.1.8).
Таким образом, последовательные приближения сходятся со
скоростью геометрической прогрессии. Более точные оценки содер-
содержатся в соответствующей литературе2.
Вычисления особенно упрощаются, если участвующие в них
функции разложить в ряды Фурье и применить метод тригономешри-
1 Области, обладающие этим свойством, называются звездными.
2 Warschawski E., On Theodorsen's method of conformal mapping
of nearly circular regions, Quart, appl. Math., 3 A945), 12—28. Ostrowski
A. M., On the Convergence of Theodorsen's and Garrik's Method of conformal
mapping, Nat. Bureau of Standards, Appl. Math. Ser., 18 A952), 149—164.
204 § 17. Методы интегральных уравнений
ческой интерполяции. С этой целью выделим на единичной окруж-
окружности плоскости г 2N точек с аргументами
и положим
#} = Я'Хмд, 4V) = log е@«Ы). A7.1.10)
Из выражения
(P \ 2 Г cos nyft + Ь<"> sin пчУ A7.1.11)
п=1
найдем приближенные значения коэффициентов Фурье
2JV—1
a(nv) = — ? Fkv) cos п щ, п = 0, 1,. . ., N,
2n-i A7.1.12)
Ь„ = — 2 F%' sin nwk, n = 1, 2, . . ., N — 1.
Согласно (9.3.5), сопряженная с F^> гармоническая функция
определяется равенством
N
&к —<рк = 2(— ^п cos гирк -г «п sin n^fc) A7.1.13)
с точностью до погрешности за счет замены ряда Фурье его частич-
частичной суммой. Подставляя сюда вместо dp и Ь$ их значения A7.1.12),
получим формулу
б?+1> -?>* = -±2 (Fun - И1 „) ctgf, A7.1.14)
в которой следует положить F1±2N = F1. Вместе с A7.1.10) и
начальным значением
в? =
<Рк
это равенство определяет каждое следующее приближение б?г) и
1<}?\ причем следует заметить, что конечная сумма A7.1.14) имеет
вид, в точности соответствующий интегралу A7.1.7). Если этот
метол сходится, то с помощью пределов
вк = lim 0|f>, Fk = lim Ff>
V—>oo V—>oo
и соотношений A7.1.12) вычисляются коэффициенты Фурье ап и
Ь„. В качестве приближения co(z) для функции A7.1.1) получаем
17.2. Интегральное уравнение Гершгорина и Лихтенштейна 305
функцию
N—1
ад -|
а для Отображающей функции w — функцию
ш(г) = геЭД. A7.1.16)
Функция w(z) отображает единичный круг на область G, граница
которой С пересекает кривую С в 2N точках, соответствующих точ-
точкам г = е'«"*. В промежуточных точках легко определить точность
приближения. Если последняя недостаточна, то этот метод следует
повторить с большим числом точек, например 4N, причем в ка-
качестве первого приближения можно принять уже найденные зна-
значения вк и Fk.
Описанный здесь метод приближения с помощью рядов Фурье
особенно выгоден для областей с гладкими и аналитическими
границами. Напротив, отрезки нерегулярности кривой лучше
учитывать прямым вычислением видоизмененного интеграла A7.1.5)
[соответственно A7.1.6)]. Особенно выгоден тот случай, когда
граница частично совпадает с единичной окружностью, так что
log q@) отличен от нуля только на частичном интервале.
Этот прием переносится и на двусвязные области с использо-
использованием интегральной формулы, выведенной в п. 10.3. Подробности
| Можно найти в соответствующей литературе1.
17.2, Интегральное уравнение Гершгорина и Лихтенштейна2.
! Пусть G — односвязная область плоскости z с кусочно гладкой
| драницей С. Требуется определить функцию W(z) = U{z) + i V(z),
* аналитическую в этой области, по заданным граничным значениям
¦ функции V(z) на С. Мы попытаемся решить эту задачу с помощью
интегральной формулы Коши, которую запишем в виде
^. 07.2.1)
" С
I Введем полярные координаты с центром С — г, положив
f С — z = ff2e'w. A7.2.2)
I
» 1GarrickI. E., Potential flow about biplan wing sections, NACA Rep.
'I № 542 A936).
" ! Lichtenstein L., Zur konformen Abbildung einfach zusammen-
| hangender schlichter Gebiete, Arch. Math. Phys., 25 A917), 179—180;
Гершгорин С. А., О конформном отображении односвязной области на
: круг, Матем. сб., 40 A933), 48-58.
206
§ 17. Методы интегральных уравнений
Рассматривая вещественную часть равенства A7.2.1) и прини-
принимая во внимание, что
df daz , . ,
получаем
A7.2.3)
Здесь z — точка внутри G. Если z стремится изнутри к граничной
точке z*, в которой С имеет непрерывно вращающуюся касательную
[с направлением, определяемым, со-
согласно A7.2.2), величиной y>z*(z*)], то
первый интеграл A7.2.3) распадается
на два интеграла. Один из них берется
в пределах от %»(z*) до %.(z*) + л
(т. е. контур С обходится полностью),
а второй — от %*B*) -I- я до %.(z*) + Ъь
с постоянной подинтегральной функ-
функцией U(z*), так что его значение равно
лС(г*). Таким образом, для граничной
точки z* с непрерывно вращающейся касательной имеем
У г-(г9)
= i J [
V(C) ^
A7.2.4)
Если z* — угловая точка С с внутренним углом жд, то соответ-
соответствующие рассуждения дадут
= i J [
A7.2.4а)
Сюда включается при б = 1 и предыдущий случай. Для простоты
мы будем в дальнейшем считать кривую С всюду гладкой.
Так как, по предположению, граничные значения У(г*) известны,
A7.2.4) представляет собой интегральное уравнение относительно
(/(г*). Это уравнение можно решить методом последовательных
приближений. Положим
l f^ A7.2.5)
A7-2.6)
и построим последовательность функций (ряд Неймана)
ио(г*) = у(г*),
U(z*) = lim
17.2. Интегральное уравнение Гершгорина и Лихтенштейна 207
Согласно теории интегральных уравнений Фредгольма1, сходимость
последовательных приближений существенно зависит от собствен-
собственных значений однородного уравнения
i%.. A7.2.7)
В нашем случае это уравнение имеет собственное значение 1,
которому соответствует собственная функция U{z*) = 1. Отсюда
следует, что функция y(z*) не может быть выбрана произвольно,
а должна удовлетворять определенным условиям, сводящимся к
условию однозначности V(z*). Поэтому решение неоднородного
уравнения A7.2.4) определяется с точностью до аддитивной по-
постоянной. Все остальные собственные значения уравнения A7.2.7)
по модулю больше 1. Стало быть, последовательность A7.2.6)
сходится с быстротой геометрической прогрессии. Если А* — наи-
наименьшее по модулю собственное значение уравнения A7.2.4),
большее 1, то погрешность n-го приближения Un(z*), определенного
формулой A7.2.6), удовлетворяет оценке
I и„(г*) - U(**)| ^ С г **~"_х . A7.2.8)
Собственное значение Я* будет тем больше, чем ближе область
G к кругу. Так, для эллипса с полуосями а и Ъ имеем2
Щ A7.2.9)
Я=.
Для установления связи между граничной задачей, сформули-
сформулированной в начале этого пункта, и задачей об отображении можно
вновь воспользоваться функцией, определенной равенством A7.1.1).
Пусть в наших обозначениях w(z) — функция, отображающая об-
область G на единичный круг, причем точка z = 0 (предполагается,
что она является внутренней точкой области G) переходит в
точку ш = 0. Положим тогда3
W(Z)=ilog-z?. A7.2.10)
Таким образом, полагая z = те*, w = qeie, имеем
U(z*) = 0 — 9», V(z*) = log r, A7.2.11)
1 См., например, S с h m ei d 1 с г W., Integralgleichungen, Leipzig, 1950,
S. 270 ff.
2 Roy den H., Pacific J. Math., 2 A952), 385—394; См. также
Ahlfors I.. V., Pacific J. Math., 2A952), 271—280. Подробное исследо-
исследование сходимости приведено в работе Warschawski S. E., On the
solution of the Lichtenstein-Gershgorin integral equation in conformal mapping,
Nat. Bureau of Standards, Appl. Math. Ser.. 42 A955), 7—29.
3 По сравнению с A7.1.1) переменные z и w здесь меняются ролями.
208
§17. Методы интегральных уравнений
и интегральное уравнение A7.2.4) принимает вид
где
%*)- <p(z*) = 7(**) + | J [6@ - 9<0] *%.. A7.2.12)
с
y(z*) = i J log г(С) ^2,* • A7.2.13)
Этот интеграл можно несколько преобразовать. Рассмотрим
выражение
h J [1о
%•] = ~ Re [ J log C^.] . A7.2.14)
Подинтегральная функция аналитична всюду, за исключением
точек С = 0 и С = z*, поэтому путь интегрирования С можно
заменить контуром, указанным на рис. 94, состоящим из дважды
проходимого прямолинейного от-
отрезка между точками С = 0 и С = г*,
малой окружности с центром С = 0
и двух круговых дуг с центром
С = z*. На прямолинейных участках
* величина d?/(C—г*) вещественна, а
г ! вещественная часть функции log С
однозначна, так что интегралы по
этим участкам взаимно уничтожа-
уничтожаются. Точно так же обращается в
нуль интеграл по малой окружности
с центром С = 0. На оставшихся
двух дугах а> = const, так что daz* = 0, и, устремляя их радиус
к нулю, получаем
Рис- 94.
f()
= -1 [ J
= — Ф*)~ 2C(z*), A7.2.15)
где /3(z*) — угол между касательной в точке z* и отрезком [0, z*]
(рис. 94). Таким образом,
Wz* —У\г ) — 2p(z*). A7.2.16)
17.2. Интегральное уравнение Гершгорина и Лихтенштейна 209
При этом нужно особенно следить за правильным выбором
ветви многозначной функции <j?@- При нашем определении пути
интегрирования <р@ меняется от y{z*) до <p(z*) + 2я. Эту трудность
можно обойти, вычитая из <р(С) функцию 2ft.(?) и сделав тем самым
подннтегральную функцию однозначной. Имеем
(
I J 9@ dft. = ^ J fa© - 2ft.(C)] dft. + i ( 2ft. dft. -
+ я A7.2.17)
с
и, учитывая, что t/>**(z*) — j5(z*) = g>(z*), получаем
y(z*) = ф*) + ж +1 J fog) - 2ft<0] "ft* • A7.2.18)
с
Уравнение A7.2.12) можно, таким образом, написать в виде
бB*) = 2<p(z*) + я + i J [6@ - 2ft.@] dft.. A7.2.19)
с
Это с некоторым видоизменением форма интегрального уравнения,
данная Гершгориным. Следует заметить, что как 0(z*), так и 9?B*) —
многозначные функции на С. Чтобы сделать их однозначными,
можно потребовать, чтобы в некоторой точке 2* = г1 обе они имели
скачок, равный 2тт. Тогда функцию ft*@ следует выбрать так,
чтобы подинтегральная функция стала непрерывной, т. е. со скач-
скачком, равным я в той же точке. Оставшуюся постоянную в 0(z*) можно
выбрать так, чтобы было 0(zj) = 0; при этом точка z* = zy пере-
переходит в w = 1. Этим 0(z*) однозначно определяется.
Численное интегрирование при этом методе становится весьма
простым независимо от того, исходим ли мы из уравнения A7.2.12)
или A7.2.19). В качестве переменной интегрирования имеет смысл
выбрать длину дуги; тогда получим
dWz, = im ,. = ^^jf_/,~ ds. A7.2.20)
При помощи N точек деления ?„, п = 1, 2,..., N, разобьем гранич-
граничную кривую на N равных по длине дуг. Если С всюду гладкая и
F@ однозначна и непрерывна на С, т. е. периодична как функция
длины дуги, то простейшая приближенная формула
/ ^t"^ -w-\f У \ /11 Л ^1\
s?& — 2j ^чСп) A7.2.21)
с п=
14 — 6002
210 § 17. Методы интегральных уравнений
(где / — длина кривой С) является наилучшей. Действительно,
если бы мы снабдили отдельные слагаемые суммы в правой части
A7.2.21) различными множителями, как, например, в формуле
Симпсона, то этим мы нарушили бы равноправность1 точек деления
?„. Итак, приближенное решение уравнения A7.2.19) можно найти с
помощью следующих формул:
Ф+1) = Ърк + тг + 2 Лы [6М - 2%п] =
= tf + 2А*п%\ A7-2.22)
где
<Fk = <F&uX У'кп = %*(?„)>
А — J— sin (Vnn — Укп)
Лк* ян' !:„-с»г •
Наибольшую трудность составляет нахождение величин t,ky
Фк > Чкп и ^/fn • Эта подготовительная работа требует гораздо больше
усилий, чем при методе Теодорсена, однако нахождение последова-
последовательных приближений здесь проще и может быть проведено точнее
благодаря непрерывности подинтегральной функции. Нет надоб-
надобности также в стеснительных ограничениях на характер грани-
границы. При медленной сходимости можно вместо вычисления последо-
последовательных приближений решать непосредственно систему урав-
уравнений A7.2.22).
Разумеется, вместо A7.2.10) в качестве W(z) можно выбирать и
другие функции, если, как это часто бывает на практике, требуется
решить граничную задачу, а не задачу об отображении. При под-
подходящем выборе этой функции можно применить описанный метод
и для отображения многосвязных областей2.
17.3. Альтернирующий метод Шварца3. В отличие от предыдущих
этот метод выполняется в вещественной области и является методом
1 Это равноправие нарушается, если граничная кривая или функция /•'(?)
имеют нерегулярности. Такие нерегулярности могут быть учтены путем
распределения точек разбиения и выбора соответствующей квадратурной фор-
формулы.
"Канторович Л. В. и Крылов В. И., Приближенные методы
высшего анализа, 3 изд., М., 1949; R о у d e n H. L., Pacific J. Math., 2 A952),
271—280.
8 S с h \v а г z Н. Л., Ubcr die Integration dcr partiellen Dillerentialgleiclrang
1 «= 0 unter vorgeschriebenen Grenz- und Unstetigkeitsbedingungen,.
8z2 Э(/а
M. B. PrcuCischc Akademie, 1870, 767—795, Werke 2, 144—171.
17.3. Альтернирующий метод Шварца
211
решения первой краевой задачи1 теории потенциала. Он позволяет
найти решение краевой задачи для объединения областей, если из-
известно общее решение для каждой из них в отдельности. Таким
способом можно определить функцию Грина для этого объедине-
объединения и получить, таким образом, его конформное отображение на
единичный круг.
Будем исходить из следующих предположений. Пусть G2 и
G2— две области плоскости z (которые для простоты предполагаются
односвязньши) и G = Gj U G2 — их объединение2. Пусть С19 С2 и
С — соответственно границы этих об-
областей; общую часть границ Сг и С обоз-
обозначим через х1 = С\ П С, а часть С15 не
принадлежащую С, — через &; таким
образом, С2 = <*-[ + /?j. Точно так же С2
разлагается в сумму <*2 + /32. Будем пред-
предполагать, что дуги рг и /32 нигде не каса-
касаются друг друга, а пересекаются под
углами, отличными от нуля.
Предположим теперь, что нам извест-
известно общее решение первой краевой задачи
для каждой из областей Gu G2 и тем самым найдены функции Грина
/\(С, z) и .Г2(С, z), так что для функции U(z), гармонической в Gv,
выполняется равенство (9.1.10)
Рис. 95.
v=\,2.
A7.3.1)
Таким образом, для функции f-'(z), гармонической в G, с заданными
граничными значениями
имеем
1
A7.3.2)
, ft).
Мы получили систему интегральных уравнений относительно
неизвестных функций Ь'(/3„). Решив эту систему, мы на основании
A7.3.1) найдем функцш<\и(г) во всей области G, т. е. решим постав-
поставленную задачу.
1 В отличие от данного метода метод п. 17.2 можно назвать методом
решения второй краевой задачи.
2 Обозначения см. в п. 2.1.
14*
212 § 17. Методы интегральных уравнений
Систему A7.3.2) в наших предположениях можно решить мето-
методом итераций. Выбрав сначала произвольные граничные значения
Uo@i) на Р1г найдем из первого уравнения A7.3.2) соответствующие
значения UO0^. Подставляя последние во второе уравнение, найдем
следующее приближение U^^) и вообще
A7.3.3)
Итерации сходятся со скоростью геометрической прогрессии,
причем тем быстрее, чем меньше влияет Uv{^-d на U?fy и Uv0d
на ^„^(/Jj), т. е. чем больше перекрываются дг и G2.
Этот метод легко переносится на случай большего числа об-
областей. Мы охватываем, таким образом, широкий класс областей,
среди которых многие важны для практики. Форма граничной
кривой, в отличие от рассматриваемых в п. 17.1 и 17.2, далеко не
произвольна, зато отпадает требование, чтобы область G была
близкой к круговой. Поэтому метод особенно удобен для сложных
многоугольных областей.
Основная работа при вычислениях заключается, как и в п. 17.2,
в нахождении функции Грина. Поэтому следует ограничиваться
частичными областями Gv с возможно более простыми функциями
Грина; к ним относятся круг, круговой двуугольник (в частности,
полукруг и угловая область) и круговой сектор. Следует также
разбивать область на части, которые как можно больше перекры-
перекрываются, с тем чтобы ускорить сходимость итераций. От выбора
частичных областей существенно зависит объем вычислений. Стоит
также сначала проверить, какой из методов более выгоден для
вычислений: данный метод или изложенный в следующем пункте.
17.4. Метод Неймана для пересечения областей. Как показал
Нейман1, альтернирующий метод следующим образом переносится
на пересечение областей. Пусть, как и ранее, заданы две области
Gl и G2 с границами Сх и С2 и С — граница области G = Gx U G2.
Граничные кривые разлагаются также на части С„ = <*„ + /5„,
где <*„ = С„ П С. Пусть для каждой из областей Gv известна функция
Грина -Г„(С, z), при помощи которой мы будем решать краевую
задачу для пересечения G* = Gl f\ G2. Пусть С* — граница G*;
требуется определить функцию U(z), гармоническую в G* и прини-
принимающую на С* заданные граничные значения U(C*) = F(C*).
Для этого представим U(z) в виде
Щг) = Ut(z) + ВД. A7.4.1)
» Neumann С, Leipziger, Ber., 22 A870), 264—321.
17.4. Метод Неймана для пересечения областей 213
Функции ?7„(г) гармоничны в соответствующих областях Gv и
принимают на границах <*„ определенные граничные значения
?/„(<*„) = /„(а,). Эти значения /„(<*„) можно выбирать произвольно1,
но так, чтобы на участках <*„, принадлежащих С*, выполнялось
равенство
Л(«„) + UM = -Р(а„). A7.4.2)
Этими условиями функции Uj(z) и U2(z) определяются однознач-
однозначно. Действительно, если бы существовало второе разложение
то в G* было бы
и, согласно теореме единственности анали-
аналитических функций (см. п. 9.4), это равенство
выполнялось бы в Gj и в G2. Тогда функция
t/1(z) — U*(z) аналитически продолжалась
бы из Ga в G2 и представляла собой гармо- Рис 96.
ническую функцию во всей области G. Эта
функция должна тождественно равняться нулю, так как равны нулю
ее граничные значения на С. Таким образом, U^z) = U*(z) и
U2(z) = U*(z), т. е. разложение A7.4.1) единственно.
Неизвестные пока граничные значения Е/Д/у удовлетворяют
системе интегральных уравнений
ft A7.4.3)
(a2, ^ + ^ J U^ dr2(|32, ^.
Вместе с уравнениями
A7.4.4)
которые следуют из A7.4.1), уравнения A7.4.3) определяют функции
С/„(/Г) однозначно. Эта система уравнений решается методом
итераций, как и система A7.3.2). Задавая произвольно нулевые
приближения UfKP-d и ^"Х/У, вычисляем следующие прибли-
1 Граничные значения /_,(<*,,) не влияют на результаты. Их изменение озна-
означает только наложение гармонической в G функции u(z), так что Vx(z) и Ut(z)
заменяются соответственно функциями U,(z) + u(z) и U^z) — u(z). Обычно
выбирают /„(a,.) ^ 0.
214
§ 17. Методы интегральных уравнений
жения по схеме
iJ/iM dPi («1, ft) + ~\ Uftft) drx (ft, ft),
A7.4.5)
Итерации сходятся при следующем предположении: пусть
&x(z) — функция, гармоническая в G1; с граничными значениями
^i(ai) = 0' ^i(ft)=l; тогда должно быть Uj(ft)^M<l; для
соответствующим образом определенной в G2 функции Ua(z) Должно
выполняться то же неравенство U2(ft)^ М < \. В этом случае
итерации вновь сходятся со скоростью геометрической прогрессии
со знаменателем М. Это условие всегда выполняется, если дуги
а„ сущее! цуют, а дуги ft не касаются друг друга. Велячяна М тем
меньше — и, следовательно, тем больше скорость сходимости, —
чем больше перекрываются области G1 и G2. Относительно практи-
практических вычислений остается в силе сказанное в п. 17.3. Метод также
непосредственно переносятся на случай большего чясла областей1.
Условие, состоящее в том, что G* есть пересечение двух областей,
можно несколько ослабить. Рассмотрим для этого область G*,
изображенную на рис. 97, состо-
состоящую из круга и описанного ут-
утла. В качестве Gx возьмем круг, а
в качестве G2 — угол; таким обра-
образом, G* не есть пересечение G, и
G2. Если выбрать на at гранич-
граничное значение /^aj) = 0, то на ос-
основании принципа симметрии
Шварца (см. сноску 1 на стр. 164)
функция Uj(z) аналитически про-
~z должается через дугу а,, причем
Рис. 97. U/ft) = —Е7,(/3?), где /3| — дуга,
симметричная с ft относительно
а,. При помощи этого продолжения можно представить U(z) в виде
A7.4.1) везде в G*, и метод итераций A7.4.5) вновь сходится.
Как метод Шварца, так и метод Неймана вполне пригодны для
конформных отображений двуезязных областей. Связь между,
конформным отображением и краевой задачей легко устанавли-
См.
S I а 11 m а n n F., Z^angew. Math, bitch., 38 A958), 279—280.
17.4. Метод Неймана для пересечения областей
215
С,
вается. А именно если Ct и С2 — граничные кривые двусвязной
области G и заданы граничные значения U(C^) = —^-, U(C2) = ~j,
то функция W(z) — U(z) + i V(z), построенная на основе решения
этой краевой задачи, отображает область G на параллельную
полосу, рассмотренную в п. 10.2.
При применении метода Шварца несущественно, является ли
область G = Gj U G2 односвязной. При применении же метода
Неймана для дву связной области
G* требуются дополнительные рас-
рассуждения. Примером служит об-
область G*, изображенная на рис. 98,
являющаяся пересечением кру-
круга G1 с границей Сг и внешности
G2 полуокружности С2. Функцию,
гармоническую в G*, вообще го-
говоря, нельзя представить в виде
суммы функций Ux(z) и U2(z), гар-
гармонических соответственно в Gt и
G2. Сопряженные им функции
Vj(z) и V2(z) однозначны в G*, тоща
как V(z), вообще говоря, много-
многозначна [см., например, A0.3.14)].
Выход заключается в том, чтобы
сделать одну из областей — скажем G, — двусвязной областью
Ъх с известной функцией Грина. Мы можем этого достигнуть,
отобразив Gj на единичный круг плоскости ш так, чтобы некоторая
внешняя для G* точка z = zQ перешла в точку го = 0. Достаточно
малый круг |ш| = о0 перейдет в плоскости z в кривую Сг, также
лежащую вне G*. В двусвязной области Glt ограниченной кривыми
C1vlC1, краевая .задача решается при помощи функции Грина для
кольца Qa < | w\ < 1 (см. п. 10.3). Рассматривая теперь G* как пере-
пересечение Gj и G2 и полагая ^(Cj) = 0, мы опять добьемся сходимости
метода Неймана и получим решение.
Приводит к цели также более простое разложение
Рис. 98.
U(z) = Uj(z) +
CRei\(z, г„).
A7.4.6)
Здесь C7j.(z) и f/2(z) — гармонические функции в соответствующих
односвязных областях, a I\(z, z0) —функция Грина для G1; причем
z0 — точка, внешняя к G*. Постоянная С определяется (заново при
каждом итерационном шаге) так, чтобы для некоторой точки
zx € С, имело место равенство
С Re 1\{гъ z0) = 0.
A7.4.7)
Б. КАТАЛОГ КОНФОРМНЫХ
ОТОБРАЖЕНИЙ
В этом разделе проводится систематический обзор таких облас-
областей (главным образом, многоугольных), конформное отображение
которых полностью определяется математическими средствами, из-
изложенными в разд. А. Заметим, что под полным решением задачи на
отображение мы понимаем не только аналитическое представление
отображающей функции (например, в виде интеграла Шварца—Крис-
тоффеля), но и установление зависимости решения от параметров,
так чтобы в каждом отдельном случае эти параметры определя-
определялись геометрическими постоянными рассматриваемой области.
Решение, полное в указанном смысле, для общих круговых мно-
многоугольников может быть получено лишь для двуугольника и
треугольника, а для прямолинейных многоугольников — также
для четырехугольника. Эти отображения исследуются здесь в
первую очередь, причем как в общем, так и в каждом конкретном
случае большое внимание уделяется задаче о параметрах. Исследо-
Исследование проводится каждый раз «в целом», т. е. функциональная зави-
зависимость геометрических констант многоугольника от параметров
изучается «в целом» и интерпретируется как отображение. Различным
интервалам изменения параметра соответствуют обычно различные
типы многоугольников (различные последовательности вершин),
соответствующих одной и той же отображающей функции.
Решение ищется для частных случаев только тогда, когда в
общем случае его нахождение затруднительно. При отборе этих
частных случаев мы руководствовались соображениями практики.
При этом выясняется, что большинство этих отображений (а также
многих не приведенных здесь) сводится путем простых видоизме-
видоизменений к ранее рассмотренным отображениям треугольников или
четырехугольников; этим подтверждается фундаментальное значе-
значение последних для практики. В большинстве случаев, когда постав-
поставленная задача не сводится к рассматриваемым здесь отображениям,
мы сможем с помощью известных отображений получать прием-
приемлемые приближения1.
1 См., например, EpheserH., StallmannF., Arch. Math., 3 A952),
276—281.
1.1. Несовпадающие вершины. Общее отображение 217
Все отображающие функции исследуются вплоть до получения
их явных выражений, причем отображения границ выражаются
вещественными функциями вещественных переменных. Мы, однако,
не будем стремиться к численному или графическому решению.
Зачастую такие решения очевидны; в более сложных случаях, когда
общего правила дать нельзя, придется ограничиваться интересую-
интересующими нас численными значениями.
Обозначения. Прямолинейные и круговые многоугольники
характеризуются величинами dv, соответствующими внутренним
углам (угол равен bji). Эти величины нумеруются в том же порядке,
что и соответствующие вершины при положительном обходе мно-
многоугольника. Прямолинейные многоугольники обозначаются звез-
звездочкой, круговые — нулем [например, (^ , ^ > Щ >0> Ь 0)°1- Кроме
того, границу прямолинейного многоугольника мы будем назы-
называть простой или кратной в зависимости от того, является ли
бесконечно удаленная точка граничной точкой кратности не более
1 или более 1.
§ 1. Двуугольники
1.1. Несовпадающие вершины. Общее отображение. Выберем в
эллиптическом пучке окружностей (см. А, п. 7.5) с узлами ? = —я,
X, = +а окружность, образующую угол лв с осью пучка (в — пара-
параметр пучка). Для дальнейшего целесообразно различать верхнюю и
нижнюю дуги. Верхним дугам соответствуют значения параметра
на отрезке 0 =? в «? 1, нижним — на
отрезке 1 «? в «s 2. Радиусы окружностей
равны
> <LU)
а расстояние от центра до оси пучка равно
m=a|ctgjr0]. A.1.2)
Пусть двуугольник образован дугами
окружностей Кг и К2, образующих с
осью пучка углы пв1, соответственно лв2 (в1 < 02). Если
1 — вг и 1 — в2 — величины одного и того же знака, то дву-
двуугольник имеет форму луночки, если же их знаки различны, то
двуугольник имеет форму линзы (рис. 2). Внутренний угол дву-
двуугольника равен пд = п (в2 — 01).
Отображение двуугольника (внутренней области) на верхнюю
полуплоскость состоит из двух этапов.
218
§ 1. Двуугольники
Плоскость ?
-af
лв,
К, i
Рис. 2.
Первый этап. При дробно-линейном отображении [см. А
{7.5.1)]
С-*
z =
A.1.3)
один из узлов (? = —а) переходит в точку z = оо, другой (С = а) —
в начало. Окружности Кх и К2 преобразуются при этом в две прямые
Gx и G.z, проходящие через начало (см. рис. 3). Образом двууголь-
двуугольника, ограниченного двумя дугами окружностей, служит угол
пОу< argz<jt(L. A-1.4)
Плоскость г
Рис. 3.
Второй этап. Согласно формуле Шварца—Кристоффеля, ин-
интеграл
dw
= Cw13
A.1.5)
отоб|Х1жает верхнюю полуплоскость ш на внутренность угла
раствором тгб с вершиной в начале. Если положить С = elVl9i, то
получим угол лОх < arg z < лО2.
1.2. Частные случаи
219
Объединяя оба отображения, находим
г = ; ~ а - емчи°
Решая относительно ш, получаем функцию
' A.1.6)
A.1.7)
отображающую внутренность кругового двуугольника на верхнюю
полуплоскость ш. При этом граничные точки ? = га ctg ^~=- и С =
= ia ctg -—¦, лежащие на оси симметрии, переходят соответственно
в точки г = е'яв1 и г = еыв', так что в плоскости ш их образами
являются точки ш = 1 и ш = —1.
Отображающую функцию для внешней области двуугольника
находим из A.1.7), заменяя 0г на 02 и 0., на ftx + 2 (и тем самым
ft = ft, — 0, на 2 — ft):
-". A.1.8)
При этом меняются ролями точки w = +1, являющиеся образами
симметричных точек границы.
1.2. Частные случаи.
1. Полный круг: ft, = ос, ft2 = а + 1
(ft = 1). Согласно A.1.8), функция
„^-e^-pr-i A.2.1)
отображает внешность полного круга,
в котором хорда [—а, а] видна из точек
окружности под углом пос, на верхнюю
полуплоскость ш.
2. Круговой разрез: (^ = 02 = /3 @ = 0). ~ь
В силу A.1.8), функция
w = e
Рис. 4.
Рис. 5.
A.2.2)
отображает внешность кругового разреза, из которого хорда
[—Ь, Ь] видна под углом лE, на верхнюю полуплоскость и>.
Последовательно осуществляя эти два отображения, получаем
отображение внешности круга на внешность кругового разреза.
В частности, для /3 = 2а имеем
Z -\-Ь '
ь
2а
A.2.4)
220 § 1. Двуугольники
При этом каждый круговой разрез, стягиваемый хордой [—Ь, Ь],
переходите полный круг с хордой [—а, а], видимой под углом,
равным половине соответствующего угла для разреза. Прямолиней-
Прямолинейный разрез вдоль базисного отрезка [—b, b] переходит в полный
круг, имеющий [—а, а] своим диаметром (см. А, п. 8.2).
Приложение (профили Жуковского). При отображении внешности
круга К на внешность кругового разреза окружность К1г касаю-
касающаяся К в одном из узлов и содержащая этот круг внутри, переходит
в замкнутую кривую, охватывающую круговой разрез и имеющую
в одном из его концов (который служит образом точки касания
окружностей К и Кх) точку возврата (профиль Жуковского). Пара-
Параметр пучка с базисной окружностью А' определяет выпуклость про-
профиля. Отношение расстояния между центрами этих окружностей
к длине базисного отрезка определяет толщину профиля1.
1.3. Совпадающие вершины.
Если точки пересечения окружностей, ограничивающих дву-
двуугольник, сближаются, то при их совпадении окружности касаются
и мы получаем двуугольник с двумя нулевыми углами. Точка каса-
касания С = ?0 переходит в точку z = <x> при отображении
С — Ьо
При этом образом этой области в плоскости z является параллельная
полоса (рис. 6).
(Z)
Рис. 6.
Отображение этой полосы на верхнюю полуплоскость норми-
нормируется так, чтобы точки ш = 0 и ш = оо являлись образами дважды
учитываемой «вершины» z = оо и чтобы точка ш = 1 была образом
начала z = 0. Отображающая функция (простейший частный случай
формулы Шварца—Кристоффеля) имеет вид
z=c{^. A.3.2)
1 Другие сведения о практическом осуществлении этого отображения, а
также дальнейшие обобщения содержатся в работе Betz A., Konfoime
Abbildung, Berlin—GSttingen—Heidelberg, 1948. (См. также [3]. - Прим. ред.)
2.1. Простые прямолинейные треугольники 221
Так как путь интегрирования полностью лежит в верхней полу-
полуплоскости, получаем
z = С log ш = С (log | ш| + 1 arg ш), 0 < arg ш < я.
Постоянная С определяет ширину и направление параллельной
полосы. Если С вещественно, то положительная полуось плоскости
w отображается на вещественную ось плоскости z. Для определения
значения постоянной С при заданной ширине а полосы вычис-
вычислим интеграл вдоль полуокружности w = е'«>, 0 < <р < п,
отображающейся на отрезок мнимой оси плоскости z. Получим
[см. А A3.2.14)]
1 z(—1) = Cni, A.3.3)
откуда следует, что Сп = а. Следовательно, отображающая
функция равна
г = - log w, 0 < arg w < л. A.3.4)
л
§ 2. Прямолинейные треугольники
2.1. Простые прямолинейные треугольники
Треугольник F,1 — в, 0)*.
Пусть этот треугольник с внутренними углами пв, л A — в), 0
расположен, как указано на рис. 7; расстояние между параллельны-
(W)
Рис. 7.
ми сторонами равно а. Отображающую функцию получаем из
формулы Шварца—Кристоффеля [ср. А A3.1.14)], если в ней
положить
е, = 0, е9 = 1,
12 B.1.1)
б, = в, Ь2 = 1 — в, дх = 0.
Тогда имеем
1
Определение постоянной С. Интегрируя вдоль полуокруж-
полуокружности
ш = Re1, 0 < <р < л,
1
222 § 2. Прямолинейные треугольники
получим при R —» оо
— ш = Стп, С = —- . B.1.3)
(Вычет подинтсгральной функции в точке ш = оо равен — 1.)
Выражение интеграла через элементарные функции возможно
только тогда, когда 0 рационально. Поэтому положим в — —
(р < д; Р, q — натуральные числа).
Подстановка
l)Vq=t B.1.4)
(вспомогательное отображение, при котором верхняя полуплоскость.
w переходит в угловую область плоскости /; см. рис. 8).
При переходе к переменной t отобража-
отображающая функция принимает вид
—P+Q—1
тст^ BЛ'5)
о
Нулями знаменателя являются корни из
я'
"-' единицы
К = еч (v = 0,1,...,9—1).
Разложение на простые дроби дает
- У "
1 '~' 1 Л
У
—— У -— - У — B 16)
t4 — 1 ^=о qt'v I — h 4 ,.=o r;, t — U
При интегрировании каждого слагаемого в пределах от 0 до t
постоянные следует определять так, чтобы каждый интеграл обра-
обращался в нуль при t = 0:
t
r~rv = logi'~Q + const = Iog(l~t) ' (zlJ)
о
причем здесь, как и всюду в дальнейшем, выбирается главное зна-
значение логарифма1, т. е. —п «= Im (log ...) =s n [ср. А B.3.10)].
В качестве отображающей функции получаем
1 Здесь оказывается целесообразным не определять заранее главного
значения логарифма для отрицательных чисел: для них мнимая часть логарифма
может рипнягься как л, так и — п, в зависимости от характера аналитического
продолжения. *
2.1. Простые прямолинейные треугольники
223
Для проверки исследуем поведение этой функции на границе:
t = S т. Интеграл B.1.5) положителен с точностью до множителя
=*±»*/
- с * = + е
t вещественно:
—Onl
-0 + 2 fr
(q — нечетное). Слагаемые, объединенные в пару, являются ком-
комплексно сопряженными, так что сумма их вещественна. Слагаемое
log A — 0 при 0 < / < 1 вещественно, а при / > 1 имеет постоян-
постоянную мнимую часть ¦— п i, так как при прохождении вдоль оси /
точка ветвления t = 1 обходится по полуокружности в верхней полу-
полуплоскости, т. е. в отрицательном направлении. Если q четно, то
суммирование ведется ro v — -q — 1 и прибавляется веществен-
вещественное слагаемое — log [1 .
A1 ^ *
2 ' 2 ' ° '
При 0=2' Р = h ¦ Я = 2 имеем (см. также А, п. 8.1)
(t)
Дробно-линейное преобра-
преобразование многоугольника. Для
упрощения описания тех тре-
треугольников, конформное
угольников, конформное Рис- 9-
отображение которых за-
задается функцией B.1.2) или B.1.8), на рис. 7а и 9а указаны области,
Рис. 7а.
Рис. 9а.
224
§ 2. Прямолинейные треугольники
в которые переходят прямолинейные многоугольники, изображен-
изображенные на рис. 7 и 9, при дробно-линейном преобразовании
С--.
Части полуполосы в окрестности точки z — оо соответствует вер-
вершина с углом, равным нулю, в точке С = 0.
Треугольник A - 6, 1+ 6, - 1)*.
Пусть треугольник с внутренними углами A — в)п, A + Q)n,
—п расположен так, как указано на рис. 10, причем расстояние
Плоскость г
О 1
Плоскость
Рис. 10.
между параллельными сторонами равно а. Отображающая функция
получается из формулы Шварца—Кристоффеля [см. А A3.1.14)],
если в ней положить
ei =
а именно
BЛЛ0)
B.1.11)
Определение постоянной С. Образом точки ветвления ех (ю = 0)
является, согласно рис. 10, точка
5j = 1 — в, Ь2 = 1 + в, д^ = —1,
dw, 0 < в < 1.
г@) = —a (ctg л в + 0 = —
sin я 8
B.1.12)
- 8)
8)
С другой стороны, из интегрального представления1 получаем
г@) = — Се'"9 f ю-9 A — ю)9 dw = —Се'я9В A — в, 1 + в) =
— Се'*90Г@)ГA— 0) =
= —Се'"9 -^L. B.1.13)
sin л8 v 7
1 При этих заменах используются основные свойства Л-функции. См.
Уиттекер Э. Т. и ВотсонГ. Н., Курс современного анализа, М., 1963.
2.1. Простые прямолинейные треугольники 225
Сравнивая эти формулы, находим
С " Д» • С2.Ы4)
Выразить интеграл в элементарных функциях можно только тогда,
когда в рационально. Положим поэтому в = — (р < q; p, q —
натуральные числа) [ср. B.1.4)].
Подстановка
/in _1MI(
(вспомогательное преобразование, при котором верхняя полупло-
полуплоскость w переходит в угловую область плоскости t; см. рис. 8).
При переходе к переменной t отображающая функция прини-
принимает вид
/
о о
Нулями знаменателя являются корни из единицы
tv=e" („ = 0,1,... ,9-1).
Разложение на простые дроби дает
При интегрировании отдельных слагаемых вновь учитываем сказан-
сказанное на стр. 222; отображающую функцию получаем в виде
Для проверки исследуем поведение этой функции па границе:
1т
t = еч т. Интеграл B.1.25) положителен с точностью до множи-
множителя
— *'
е ч = — е ;
t вещественно:
15 — 6002
226
§ 2. Прямолинейные треугольники
(q — нечетное). Слагаемые, объединенные в пару, являются ком-
комплексно сопряженными, так что сумма их вещественна. Слагаемое
log A — 0 при 0 < t < 1 вещественно, а при t > 1 имеет постоян-
постоянную мнимую часть —т (обоснование то же, что и на стр. 223).
Частный случаи: ^, -, — 1
При 0 = -J, Р= 1, 9 = 2
имеем
2*
B.1.18>
Дробно-линейное преобразование многоугольника. Для упро-
упрощения описания тех треугольников, конформное отображение
которых дается функцией B.1.11) или B.1.17), на рисунках 10а и
На указаны области, в которые переходят прямолинейные много-
многоугольники, изображен-
изображенные на рис. 10 и 11, при
дробно-линейном преоб-
преобразовании
Плоскость 7
Плоскость t
Рис. И.
Рис. 10а.
Рис. Па.
В точке С = 0 прямолинейная сторона направлена по касатель-
касательной к дуге окружности («вершина» с углом л). Граничная кривая
имеет в этой точке непрерывно вращающуюся касательную, но
разрывную кривизну1.
1 При обтекании конечного профиля разрыв кривизны граничной кривой
нежелателен, так как при этом появляются вертикальные касательные в точках
перегиба графика скорости потока как функции длины дуги. Рассмотренный
выше треугольник является простейшей областью, граничная кривая которой
имеет конечный скачок кривизны. В этом случае характер отображающей
2.1. Простые прямолинейные треугольники 227
Треугольник F, 2, —1 — 6)*.
Пусть треугольник с углами вл, 2л, — A + 6) л расположен так,
как указано на рис. 12; при этом расстояние от конца разреза до
третьей стороны равно а. Отображающая функция получается из
формулы Шварца—Кристоффеля, если в ней положить
е2 = 0, е2 = 1,
62 = в, д2 = 2, 6^ = —1 — в, B.1.19)
а именно:
в>
-=CJ^^=C|^^i^^+w^rT,|)O<e<l. B.1.20)
1
о г
Плоскость го
Рис. 12.
Определение постоянной С. Образом точки ш = ех = 0 является,
согласно рис. 12,
<0) = a (ctg я0 - 0 = -%~ е-**. B.1.21)
Сравнивая с формулой B.1.20), получаем
Отображающая функция принимает, таким образом, вид
z = a f(we-*Oe (г<^е—1+ ctg ггв — ll, 0 < в < 1. B.1.23)
Укажем еще образ точки т = —1 (конца линии поля, исходящей из
точки z = 0):
/1\ 1 + 20 — cos лЭ . ,» , ».,
г@ ^ « - т. B.1.24)
функции выясняется полностью, что позволяет судить о ней и в общем случае.
См. по этому поводу Koppenfels W., Ebene Potentialstromung Iangs
einer glatten Warid mit stilckweise stetiger Krilmmung, Lirftfahrt-Forsch., 17
A940), 189 — 195.
15*
228
§ 2. Прямолинейные треугольники
Частный случай: I-^, 2, — ^
При в = — имеем
B.1.25
Рис. 13.
Дробио-линейное преобразование многоугольника
Для упрощения описания тех треугольников, кор-
формное отображение которых дается функцией B.1.23), на рисун-
рисунках 12а и 13а указаны об-
области, в которые переходят
прямолинейные многоуголь-
многоугольники, изображенные на рис.
12 и 13, при дробно-линей-
дробно-линейном преобразовании
2.2. Двукратные прямоли-
прямолинейные треугольники.
Треугольник (—6,1 + 0> 0)*.
Если в отображении Рис. 12а. Рис. Ю..
треугольника @, 1 — в, 0)*
(стр. 221) заменить 6 на —0, то точка ш = 0 также перейдет в точъ?
z = оо; получится многоугольник с двумя вершинами в бесконечш
удаленной точке (двукратный профиль, рис. 14).
О 1
Плоскость w
Плоскость z
Рис. 14.
Вычисление дающего отображение интеграла
z = —
dw
о< е < 1,
B.2.1
построенного с той же постоянной, что и на стр. 222 (С = —— |
2.2. Двукратные прямолинейные треугольники 225)
проводится для рациональных значений 6 10 = — , р < q J так же, как
и выше. Подстановкой ,
(ш - 1\~*
= t
I Ш I
(см. рис. 8) интеграл приводится к виду
о о
Нулями знаменателя являются корни из единицы
tv = eq (v-0,1,..., 9—1).
Разложение на простые дроби дает
t-t, q ?ot-t.'
Таким образом, отображающая функция принимает вид
B23)
Проверка поведения функции на границе проводится так же,
как и на стр. 223.
Частные случаи: (—1, 2, 0)*. ^
Здесь 6=1, р = q = 1; » * °#
отображающая функция имеет '° 0 1
ВИД Плоскость г Плоскость t
2 = " [t + log A — «)]. B.2.5) Рис. 15.
С помощью этого отображения Г. Кирхгоф вычислил поле на гра-
границе плоского конденсатора.
(Л О \ ли
— 2 ' 2' ° I #
Здесь в — - , р = 1, q = 2; отображающая функция имеет вид
+log J^i]. B.2.6)
При отображении на плоскость ш получаем
я = 2Л Г]/«Е1 + юя (f^ - уJF—Г)]. B.2.7)
230
§ 2. Прямолинейные треугольники
Дробно-линейное преобразование многоугольника. Для упрощения
описания тех треугольников, конформное отображение которых
дается функцией B.2.1) или B.2.4), на рисунках 14а, 15а, 16а указаны
области, в которые переходят прямолинейные многоугольники,
изображенные на рис. 14, 15, 16, при дробно-линейном преобразо-
преобразовании
В точке С = 0 две вершины многоугольника совпадают.
л.
*
Плоскость г
Рис. 16.
Плоскость t
Рис. 15о.
Рис. 14а.
Рис. 16а.
Треугольник (-6, 2, 6 — 1)*.
Если в отображении треугольника (в, 2, —1 — в)* (стр. 227)
заменить д на —в, то как точка w = 0, так и точка w = оо перейдут
в точку z = оо; образуется двукратный профиль, состоящий из
прямой и не пересекающей ее дважды проходимой полупрямой.
Пусть расстояние от конца разреза до прямой равно а (рис. 17).
Плоскость г / \а
Рис. 17.
Плоскость ги
7Г" / *
2.2. Двукратные прямолинейные треугольники 2Н
Форма и способ вычисления интеграла, даюшего отображение,
остаются неизменными, поэтому в выражении на стр. 227 можно
заменить в на —в. При этом получаем выражение для отображаю-
отображающей функции
г = а Г(ше-'л)-е ~^~~- — etg яв — il, 0 < в < 1. B.2.8)
Укажем снова образ точки w = —1 (конца линии поля, выходящей
из точки z = 0 и являющейся образом единичной полуокружности в
плоскости ю):
Частный случай: [— =
При 6 = 5 имеем
!)'•
§ 3. Круговые треугольники
Функция, отображающая верхнюю
полуплоскость ImrossO на круговой Рис.18,
треугольник плоскости ? так, что вер-
вершины последнего являются образами точек го = 0, го = 1, го = оо,
может быть получена (ср. А, п. 12.21 в виде частного двух линейно
независимых решений «гипергеометрического дифференциального
уравнения»1:
Я(а, ft у; <р, го) = го (го — 1) цГ{р) + [(ос + ]5 + 1) го — у] /(го) +
+ а/5<р(п>) = 0.
Треугольник имеет
в вершине С@) внутренний угол 50я ¦= | у — 11 я;
в вершине СA) внутренний угол йая = |а + ]3 — у\щ
в вершине С(°°) внутренний угол дал = |а — /}|я.
Если стороны треугольника принадлежат двум ортогональным
пучкам окружностей, то гипергеометрическое уравнение интегри-
интегрируется в замкнутой форме. Это возможно в следующих трех слу-
случаях, в зависимости от значений внутренних углов:
(внутренность сектора) (внешность сектора)
1 См., например, Carathdodory С, Funktionentheorie, II, Basel, 1950.
232
§ 3. Круговые треугольники
Основная формула аналитического продолжения гипергеометри-
ческого ряда во внешность единичного круга (определение преоб-
преобразований перехода см. в п. 12.3) получается при помощи инте-
интегрального представления гипергеометрической функции.
Путем такого продолжения можно получить отображение
произвольного кругового треугольника посредством гипергеометри-
гипергеометрических рядов.
В качестве примера рассмотрим отображение внешности сим-
симметричного кругового треугольника с внутренними углами л, л, 2л9
на полуплоскость.
3.1. Решение в замкнутой форме.
Треугольник L, 9, ^Г-
Гипергеометрическое уравнение
61-
с параметрами х = — - ,
o , у = ъ имеет при 0 < в «= !
следующие два линейно независимых решения:
<р2 = A— yV)e, C.1.1)
частное которых
Плоскость
О 1
Плоскость w
Рис. 19.
отображает верхнюю полуплоскость го на внутренность кругового
треугольника, изображенного на рис. 19 (сектор с центральным
углом втс)К Треугольник имеет
в вершине ?@) = 1 внутренний угол 60ji = \у — 11 л = ^- ,
в вершине ?A) = 0 внутренний угол д±л = ]ос + /3 — у\п =лв,
в вершине ?(°°) = е—'"в внутренний угол д^л = | а — ]31 л = |- .
247.
1 Schwarz H. A., J. reine angew. Math., 75 A873), 324; Werke II,
3.1. Решение в замкнутой форме 233
Отображение на границе.
1. Ш < 0: У^ +iY^ I fi|^
ICI = 1, arg С = —20 arc tg У^ю < О.
2. 0< ш< 1: 1 >? >0.
3. 1< ro: arg I = в arg f1"^) = б arg (l — /ro) -
\1 + У)
— в arg A — го) =
Так как ю лежит в верхней полуплоскости, то — л < arg A —
< 0, так что arg A — го) = —л для 1 < го.
Другой вывод.
Из отображения полуполосы (см. рис. 9)
* а Л 1 - t
при переходе к показательной функции получаем
Полагая — = б и
t = Yw, C.1.4)
получаем указанную выше отображающую функцию. (Соответ-
(Соответствие точек здесь иное, нежели при отображении полуполосы на стр.
223, в котором использована замена / = Уw ~ I .
A *»\ п
2' ®' 2 *
Гипергеометрическое уравнение
с параметрами а = — ^, р — ^—, у = — ^, имеет при 0 ф 1
следующие два линейно независимых решения:
частное которых
I Л 1/л.* 1 1 I Л 1/
C.1.6)
234 § 3. Круговые треугольники
отображает верхнюю полуплоскость го на внутренность кругового
треугольника, указанного на рис. 201.
Треугольник имеет
в вершине С@) = 1 внутренний угол дап = \у— 1[зт=^зт,
в вершине СA) = 0 внутренний угол Ьгп = |а + j3—у\п = 0л,
в вершине С(°°) = е~'"<в+1> внутренний угол Ьхп = la — ]3|зт =^я.
Г\
Рис. 20.
Отображение на границе.
1. го <0: Vro = +iy—го, С= ^=г\——^7== =
= e2i(-9 arc tg Y=i + arc tg 6/=^) . | ? [ = 1,
= 2(— багеtg]A=^ + arctgOf=) j
{ < 0, 0 > 1.
2. 0< ro< 1: 1 >? >0.
3. К го < Ь arg С = б argfi-^l^) = 0 arg(l — f^) = — вп.
b \1 + ]/w)
4. ^ < ro: arg I - б arg ^j + arg (-i^j =
= 0 arg A — ]/V) — arg(l — б fw) = —On: + Jt.
Эти рассуждения показывают, что при переходе от значений
д < 1 к значениям б > 1 (это означает перестановку точек ветвления
w — 1 и го = 0) круговой треугольник принимает форму, указан-
указанную на рис. 21.
1 См. Koppenfels W., J. reine angew. Math., 181 A939), 114. tt.
3.1 Решение в замкнутой форме
235
Частный случай.
При 6 = 2 мы полу-
получаем область, указанную
на рис. 22. Так как все
стороны треугольника
пересекаются в одной
точке (таких точек даже
две: С = —1 и С = +1), то
дробно-линейным преоб-
преобразованием этот круговой треугольник можно превратить в
прямолинейный. Действительно, легко проверить, что отобра-
отображающая функция
Рис. 21.
при замене гона- и при последующем преобразовании
2iaC
z =
1-С
C.1.8)
переходит в функцию B.1.25) (рис. 13).
Рис. 22.
Треугольник f| , 6, |j°.
Гипергеометрическое уравнение
2 ' 2 2 '
6 10
с параметрами a = —1 — ~ , ]3 = ^ — х, у
два линейно независимых решения:
1
—= имеет при в > 0
C.1.9)
236
§ 3. Круговые треугольники
Эти решения тесно связаны с решениями уравнений
„/•61-01
(стр. 232 и 233), которые «смежны» с ним, так как соответствующие
аргументы х, fi, у отличаются в них лишь на целые слагаемые.
Согласно Гауссу (Сочинения, т. III, стр. 113),
F(a-l,i3,r-l; w)-F(x, 0-1, у—1; го) =
Полагая здесь
х «=
имеем
„( ¦, 9 1 9
1 в
1
18
Учитывая C.1.1) и C.1.5), получаем отсюда два линейно неза-
независимых решения:
Ф1,2 = A ± У^)вA + eVw) + w(l± f^)8 =
= (l ±fw)e(\ + в^Ъ + w).
Частное этих двух решений
!±ev«±-
C.1.11)
отображает верхнюю полуплоскость го на внутренность кругового
треугольника, изображенного на рис. 23, т. е. на внешность
сектора.
О 1
Плоскость W
Плоскость С,
.Рис. 23.
3.1 Решение в замкнутой форме 237
Исследование поведения отображения на границе мало отли-
отличается от предыдущих случаев. Следует при этом заметить, что
дробь
V
1 - el/w + w
не изменяет знака при го > О, 0 < 2. Сравнение с предыдущим
отображением C.1.6) указывает на влияние дополнительного сла-
слагаемого го в числителе и знаменателе второго сомножителя.
Другой вывод. При только что рассмотренном отображении
внешности сектора мы впервые встречаем область, содержащую
точку ? = оо внутри (а не на границе, как до сих пор). В связи с
этим представляется важным показать, каким образом найти отоб-
отображающую функцию, минуя гипергеометрическое уравнение (реше-
(решение которого нельзя получить непосредственно), методами п.
14.1, разд. А.
Как там указывалось, треугольник следует разрезать, начиная
от точки ? = °°. При этом мы расположим разрез по биссектрисе
сектора от ? = оо до ? = 0. При отображении
W = log]? C.1.13)
он переходит в границу полосы ширины 2тг, в которую сим-
симметрично вложена полуполоса ширины B — в)л, являющаяся обра-
образом сектора. Учитывая соответствие между вершинами треуголь-
треугольника и точками го = 0, 1, оо, положим, согласно формуле А A4.1.6),
W
уш dw
Г *wdw C.1.14)
J (го — 1) (го — е=с) (го — ёоо)' v
По принципу симметрии оси симметрии сектора в плоскости С,
по которой проходит разрез, соответствует единичная окружность в
плоскости го. Поэтому можно положить
foo = е№, ем = <—<», 0 < V <л. C.1.15)
Кроме того, должны выполняться условия для вычетов; в точке
го = 1 вычет функции W'(w) равен б, а в точке го = с» он равен —1.
Поэтому W( го) можно представить также в следующей форме:
W=J
Сравнивая с C.1.14), получаем
'~2
2
ат C.1.16)
6= е 2 + е 2 =2cos а". C.1.17)
238
§ 3. Круговые треугольники
I
Интеграл C.1.16) вычисляется
подстановкой
*=»УпГ; C.1.18)
учитывая C.1.17), получаем
Таким образом,
г +
C.1.19)
Я
I
J I о J I -I
jrloi + i» <ЗЛ-20>
откуда, учитывая C.1.18), приходим
к отображающей функции C.1.12).
С помощью более детального
исследования соответствия границ
заключаем, что при отображении
W(w) круговой разрез в верхней
полуплоскости w, изображенный на
рис. 24, действительно преобра-
преобразуется в границу прямолинейной
полосы ширины 2л: в плоскости W, а
вещественная ось плоскости го — в
границу полуполосы.
3.2. Аналитическое продолжение
гипергеометрического ряда. За ис-
исключением случаев, рассмотренных
в п. 3.1, для отображений круговых
треугольников используются гипер-
гипергеометрические ряды. Как указы-
указывалось в п. 12.3 разд. А, основная
трудность при работе с разложе-
разложениями в ряды состоит в нахож-
нахождении преобразований перехода,
позволяющих переходить от разло-
разложения в окрестности одной точки
ветвления к разложению в окрестности другой точки ветвления.
Ниже мы приведем весьма простой вывод основной формулы
аналитического продолжения гипергеометрического ряда во внеш-
внешность единичной окружности1.
1 Другой вывод преобразований перехода, основывающийся на интеграль-
интегральном представлении Барнеса, можно найти, например, в книге Bieberbach,
Tlu-orlc <1сг gewohnlichen Differentialgleichungen aul funktionenlheoretischer
Gnnidlagc diirgestelll, Berlin- GolUngen—Heidelberg, 1953. Вывод, данный в
тексте, принадлежит В. Копленфел*>су и публикуется впервые.
3.2. Аналитическое продолжение гипергеометрического ряда
239
Будем исходить из представления гипергеометрической функции
в виде определенного интеграла, найденного еще Эйлером (и
представляющего собой частное решение гипергеометрического
уравнения):
= J И3-1 A — (у-?-1 A —
dt.
C.2.1)
Этому определенному интегралу можно придать геометриче-
геометрический смысл, отображая верхнюю полуплоскость / (при фиксиро-
фиксированном значении го < 0) на прямолинейный четырехугольник
плоскости J при помощи неопределенного интеграла:
J{t) = J f-1 A — ty-P-1 (I — wt)~a dt. C.2.2)
Пусть подинтегралъное выражение J(t) однозначно определяется
неравенствами
0 =s arg t «s л, —л =s arg A — f) =s 0, 0 =s arg A — wt) «s л,
а путь интегрирования целиком лежит в верхней полуплоскости.
При этих предположениях интеграл J(t) отображает верхнюю
полуплоскость на внутренность прямолинейного четырехуголь-
четырехугольника с суммой углов 2ж\ его вершины Р \, Ро, Рг, Рх являются обра-
1 ^
зами точек ветвления t = —, 0, 1, оо, а внутренние углы в них
равны A —а)тг, (in, (у — §)л, (х — у т 1)я (рис. 25).
10 Г
w Плоскость t
Рис. 25.
Для простоты будем считать, что все вершины четырехуголь-
четырехугольника конечны. Это означает, что параметры а, E, у удовлетворяют
условиям
/5 > 0, у - ,3 > 0, а — у + 1 > 0, 1 — а > 0,
обеспечивающим сходимость отображающего интеграла во всех
240 § 3. Круговые треугольники
точках ветвления подинтегральной функции. Ясно, что оконча-
окончательная формула не связана с этими ограничениями1.
Векторы трех сторон четырехугольника всегда связаны линей-
линейным соотношением, вытекающим непосредственно из отображения.
Для векторов
\_ Mi ~ Jo ' -Tomi ~ Jo> ^i1 ~ — Ji
это соотношение, вытекающее из теоремы синусов, имеет вид
где мы положили
с
Jl = Г fi-i A — ty-e-i (i — го()-а dL C.2.4)
д
Для получения искомой формулы аналитического продолжения
гипергеометрического ряда следует распространить интегралы
Jo> Jr и Jj'" на комплексные значения го и разложить их в ряды.
В связи с этим следует учесть, что подинтегральное выражение
как функция параметра го разветвляется в точках го = — и го = оо.
Поэтому нужно произвести разрез плоскости го, с тем чтобы точка
1
г» не могла описать замкнутую кривую, отделяющую го = — от
w = оо. Для однозначности определенных интегралов с постоян-
постоянными пределами интегрирования (случаи 1 и 2) это требование
необходимо отнести к каждой точке кривой го = --', где / описы-
описывает путь интегрирования.
1. Если интеграл J\ берется вдоль отрезка 0 < t < 1, то точка
— описывает полуось w > 1. Согласно сказанному выше, нельзя
допускать, чтобы точка го описала кривую, пересекающую эту
полуось, что достигается разрезом вдоль последней.
Для однозначного определения степени положим вдоль пути
интегрирования
arg; = O, arg A — 0 = 0, C.2.5)
arg(l — ro0 = 0 (го<0).
1 Заметим, что последующие рассуждения применимы и в том случае,
когда параметры не удовлетворяют поставленным ограничениям, т. е. когда не
вес нершины четырехугольника конечны. В этом случае роль сторон играют
«периоды», которые всегда конечны. См. К о р р е и f е 1 s W., Das hyper-
^geomeli-lsdie Integral als Periode der Vierecksabbildung, S. B. Acad. Wiss.
Wien, 146 A937), 11—22.
3.2. Аналитическое продолокение гипергеометрического ряда 241
Этим однозначно определяется интеграл Jj в плоскости из с раз-
разрезом вдоль вещественной оси от из = 1 до из = оо. Для | ш| < 1
разложение функции A — wt)~a по степеням ш дает
д = Г /^-i A — /у-"-1 A — ш/)-в d' = cft^y)^) *"(«. /3; у;
о
C.2.6)
2. Пусть J~ есть интеграл по лучу / > 1. Точки из, которые нельзя
обходить, заполняют интервал 0 < из < 1. Разрез следует провести
по этому интервалу, продолжив его до из = оо, лучше всего по полу-
полуоси из > 0.
Вдоль пути интегрирования однозначность подинтегральной
функции обеспечивается условиями
arg t = 0, arg (I — 0 = —я, „
arg(l — н»0 = 0 (ш < 0). ^ '
Подстановка
C.2.8)
преобразует интеграл Jf к предыдущему. В этих формулах следует
положить
arg (—1) = —п, —я < arg (—из). < л, C.2.9)
чтобы для преобразованного интеграла
1
jf = еИМ-у)* (_„,)-« f та-/ (! _ T)-/-^-i ^ _l|-adT) C.2.10)
о
как и для Jo, имели место соотношения
arg г = 0, arg(l— т) = 0, C.2.11)
arg (!-?)= 0 (ш<0).
Тогда.вне единичного круга, т. е. для [ш| > 1, имеет место раз-
разложение
1 ё ' ' гЪ-p+'i) ( w) a x C.2.12)
XF^«-y+I, a-/3-r 1; i) .
16 — 6002
242 § 3. Круговые треугольники
3. Интеграл J\lw также берется по прямолинейному пути.
Разрез в плоскости w следует провести так, чтобы точка — не обхо-
обходила ни одной из точек 0,1, °°, что достигается проведением его
вдоль полуоси w > 0.
Для однозначности подинтегральнои функции при всех значениях
w, для которых —я < arg (—ш) < я, мы положим вдоль (прямо-
(прямолинейного) пути интегрирования
arg / = arg -^ + 7i, arg(l — /) = 0, arg(l — wt) = 0(ш[<0). C.2.13)
В случае отрицательных w[arg(—т) = 0] это соответствует
условиям, поставленным на стр.
239. Подстановка
1 - t= \ —1 , C.2.14)
w v
Рис. 26.
1 — wt = 1 — T
приводит Jllw к виду
1
jj/"' = e'p71 (—w)-P tp~1A —x)~a 1 —— dr. C.2.15)
о
В силу C.2.13), в формуле
arg t = arg ^ = argr -)- arg— + arg(—I)
следует положить
arg(-l)= -fjr, C.2.16)
с тем чтобы в преобразованном интеграле" получить
argT = 0, arg(l — т) = 0, C.2.17)
~l\ =0 (ш<0)
в соответствии с C.2.5). Таким образом, получаем представление
Jllw - ** Sf^T? (--О"' F^> Д - у + 1. ^ - « + 1; j) •
C.2.18)
Подставляя C.2.6), C.2.12) и C.2.18) в C.2.3), приходим к анали-
аналитическому продолжению гипергеометрического ряда на внешность
3.3. Представление отображающей функции в общем случае
243
единичного круга. Пользуясь формулой дополнения для .Г-функции
sin
получаем два разложения:
- v
C.2.19)
3.3. Представление отображающей функции в общем случае.
Формула C.2.19) для аналитического продолжения гипергеометри-
ч еского ряда во внешность единичного круга имеет важное значение
д ля численного решения задачи о конформном отображении полу-
п лоскости на любой заданный круговой треугольник.
Рис. 27.
Пусть в плоскости С задана однолистная область, ограниченная
тремя дугами окружностей (круговой треугольник) и имеющая в
вершинах eo>ci>e~ внутренние углы йоя, Ьхп, й«л, отсчитываемые
в положительном направлении1. Вначале исключим из рассмотрения
значения углов, равные 0 и эт. Указанная последовательность вер-
вершин соответствует обходу области, при котором ее внутренность
остается слева (рис. 27). Требуется отобразить верхнюю полу*
плоскост ь ш на этот круговой треугольник так, чтобы его вершины
служили образами точек ш = 0, ш = 1 и т = оо:
?0 = С@),
C.3.1)
1 Эта область может содержать бесконечно удаленную точку и является
тогда «внешностью» кругового треугольника.
16*
244 § 3. Круговые треугольники
Это отображение осуществляется частным от деления двух
линейно независимых решений гипергеометрического уравнения
Я(а, # у; <р; ю) == ш (w — \)q>"(w) + [(а + /3 + 1) ш — у] <p'(w) +
= 0, C.3.2)
параметры которых определяются по заданным углам следующим
образом:
х " C.3.3)
Для решения этой задачи найдем сначала расположение круго-
кругового треугольника, на который верхняя полуплоскость ю отобра-
отображается отношением двух простейших решений1, а именно фунда-
фундаментальных решений в точке w = О
r*(w) - с (-n>I"F(a + г " V'P + Х " у: 2 " у'ш) f3 3 *>
—л < arg (—w) < 0.
Остается дробно-линейным преобразованием
(С(ш),г0, Cl, с.) = (С*(ш). С*@), C*(D, С*М) C.3.5)
отобразить этот треугольник плоскости С* на заданный треугольник
плоскости ?•
Расположение кругового треугольника в плоскости С*.
Так как, на основании C.3.3),
то в точке
С*@) = 0 C.3.6)
располагается одна из вершин треугольника в плоскости ?*.
Как показывает разложение C.3.4), обе стороны, выходящие
из этой вершины, прямолинейны и образуют угол A —у)л = йотг.
Далее, из C.3.3) следует, что
у — a — /3-S1>0,
причем на основании этого неравенства гипгргеометрический ряд
сходится и в точке ш = 1. Значение его .суммы равно2
|. Re(y-a-^)>0. C.3.7)
1 Учитывая нижеследующие соотношения, мы выбираем в этой формуле
(— ш) в качестве основания степени. Выбор постоянной с еще не сделан.
: . * Соответствующим образом вычисляется значение F(a-fl— у, /S+1 —
-у, 2 - у; 1), так как B - у) - (а +1 - V) -@ + 1 - У) = У - а - ?=А > 0.
3.3. Представление отображающей функции в общем случае 245
Подставив в C.3.4) значение w = 1, замечаем, что следует положить
с = е*A-У) ГA-а)ГA-Р)Г(у) 3 .
Г(у - а) Г(у - р) ГB - у) ' У • • '
для того чтобы выполнялось условие
С*A)=1. C.3.9)
Теперь треугольник строится следующим образом: от отрезка
С*@) ?*A) откладывается угол (у — |3)я с вершиной ?*A)=1,
его вторая сторона пересекается со второй стороной угла
btfi = A — у) л, имеющего вершину ?*@) = 0. Углы (у— Р)л и
/Зд полученного прямолинейного треугольника отличаются от
соответствующих углов Ьгп и Ь^л кругового треугольника на одну
и ту же величину сип. По этой причине полученная точка пересечения
совпадает с вершиной С*(оо), а отрезок ?*0) С*(°°) совпадает
с хордой дуги с центральным углом 2<хл, которая является третьей
стороной кругового треугольника.
Рис. 28.
Этим полностью определяются форма и положение кругового
треугольника, на который отношение двух фундаментальных
решений в точке w = 0 отображает полуплоскость Im ш > 0. При
выводе отображения следует воспользоваться разложением C.3.4)
для |и?| < 1. Для |ш| > 1, применяя формулу продолжения к числи'-
телю и знаменателю выражения C.3.4), получим
ГB - у) Г(Р - а)
Г(у)Г(Р - а)
ГB-у)Г(а-р) е .._„/„ „ . , „ _ 1
-у)ГA"^ l w-l. C.3.10)
246
§ 3. Круговые треугольники
Подставляя вместо с его значение из C.3.8), получаем
*~Л* (_ал-«р(а а+1 - •* +
- (8) Г((8 - а)
(-w)-aF\a,a+l — у; et + 1
- а) Г(а - (8)
+
'(« + 1 ~ V)
- а) Г(а - (8)
ф,
i-'f (8,(8 + 1 - у; Р + 1 - a; i-
р
-Ц. C.3.11)
Г(а) V «>j
Это разложение отображающей функции в окрестности ш = оо
при | ш| > 1 заменяет разложение C.3.4), имеющее место при \w\ < 1.
Учитывая, что
/J —а = й. >0, C.3.12)
на основе полученного представления легко проверить правильность
значения
С*(оо) = е"
построенного выше.
Легко видеть, что таким же способом можно построить отобра-
отображение в случае кругового треугольника, у которого один или два1
угла равны п. В первом случае следует выбрать соответствие между
вершинами и точками ветвления так, чтобы вершина с углом п,
фундаментальное решение в которой содержит дополнительное
логарифмическое слагаемое, соответствовала точке w = 1 (й1 = 1).
Однако поскольку в вышепроведенном рассуждении мы использо-
использовали только фундаментальные решения в точках w = 0 и ш = оо,
решение задачи без изменений переносится и на этот случай.
При наличии двух развернутых углов можно также избавиться
от логарифмических слагаемых, так как этот случай легко сводится
Рис. 29.
1 Случай, когда все три угла цавны п, тривиален.
3.4. Круговой треугольник с двумя развернутыми углами
247
: предыдущему. Ясно, что такой треугольник всегда симметричен
>тносительно некоторой окружности, делящей третий угол, равный
1в%, пополам1 (рис. 29), так что остается отобразить круговой тре-
тольник с углами A —б)я, я,^-
3.4. Круговой треугольник с двумя раавернутыми углами, содер-
содержащий бесконечно удаленную точку2 (внешность профиля). При-
Применяя симметрию относительно окружности или биссектрисы,
лы отображаем полуплоскость 1тш>0 на круговой треугольник
• углами
внугренний'угол профиля равен 26л) (см. рис. 30).
C.4.1)
Плоскость W
Рис. 30.
Согласно C.3.3), параметры гипергеометрического уравнения,
определяющего 9тображение, равны
26-3
1-26
1
2 '
C.4.2)
1 Симметрия становится очевидной, если дробно-линейной функцией преоб-
преобразовать стороны, образующие угол 20л, в прямые.
2 Эту задачу изучал Вольф: Wolff E., EinfluB der Abrundung scharfer
-Untrittskanten auf den Widerstand von Flilgeln, Ing. Arch., 4 A933), 521.
-le пользуясь симметрией области, а отображая ее целиком, он рассматривал
:руговой треугольник с двумя развернутыми углами, и при построении фунда-
фундаментальных решений был вынужден вместо одного степенного ряда строить
вспомогательное решение с логарифмическими слагаемыми, аналитическое
тродолжение которых рассматривается особо. Расположение вершин полу-
'аемого треугольника можно определить лишь в отдельных частных случаях,
да и то приближенно.
248 § 3. Круговые треугольники
Имея эти значения, можно указать, согласно п. 3.3, форму и распо-
расположение треугольника, на который полуплоскость Im ю> О отобра-
отображается отношением C*(w) двух фундаментальных решений в точке
ш = 0 [см. формулы C.3.4) и C.3.11) и рис. 30].
Вершинами являются следующие точки:
?*@) = 0, С*A) = 1, ;*(оо) = i tg ^ + ij n. C.4.3)
Для отображающей функции, согласно C.3.4) и C.3.11), имеют
место представления:
- 2f
4'4 2 2
Г[Т ~ 2~j Г1Т + 2") F{ 2 ~ 4~' Т ~ 2 ' 2 ' W)
\w < 1, C.4.4)
(l в \
Г\- +- ГA - 0) з е
' 12 4 2 4 »jT
Г
. - , . - , _ci e з е
+ ^6 П • ~ "' "U 2'4 2
1 1
;2-6;-
5 0 ^
\Г(в - 1) e l
4 2 l ' 2~4 fl 6 3 6 14
(-ui) F . ;2-6;-
\w]>]. C.4.5)
Линейное преобразование области. Геометрическими постоян-
постоянными профиля в плоскости С служат радиусы R и q граничных ок-
окружностей. Радиус q окружности, противолежащей углу 20л, назо-
назовем «радиусом закругления» кругового двуугольника, ограниченного
двумя остальными дугами, имеющими радиус R.
3.4. Круговой треугольник с двумя развернутыми углами
249
Из рис. 31 определяются вершины кругового треугольника
С(оо) - О,
?@) = — [R sin вп + (R — е) sin еж + q], C.4.6)
?A) = — [R Sin On + (R — q) sin иг] + i q eiat,
где
R cos л0 . V(R - pJ - R2 cos2 лв ,, . _
совяе = — , sinrre = . C.4.7)
Рис. 31.
Дробно-линейное преобразование, переводящее круговой тре-
треугольник плоскости ?* (рис. 30) в треугольник плоскости ? (рис. 31),
в терминах двойных отношений имеет вид
(СИ, ?@), ?A), ?(оо)) = (С*Н, ?*@), ?*A), ?*(оо)) =
= fC*H,0, I.itgnfj + J)) "C.4.8)
[ср. с формулой А G.2.13)].
Внешность всего профиля отображается полученной функцией
?(ш) на плоскость w с разрезом вдоль положительной вещественной
полуоси, причем часть контура, лежащая в верхней полуплоскости ?,
отображается на верхний берег разреза, а симметричная ей
часть — на нанижний берег.
§ 4. Простые прямолинейные четырехугольники
Еще в п. 12.3 и 13.2 разд. А указывалось, что при отображении
многоугольников с четырьмя и более углами мы встречаемся с
задачей о параметрах. Эта задача возникает уже для прямолиней-
прямолинейного четырехугольника и состоит в определении параметров по
250 § 4. Простые прямолинейные четырехугольники
геометрическим константам четырехугольника. Эта задача решается
сначала в общем, «в целом», причем случаи простого и двукратного
четырехугольников приходится исследовать в отдельности (п. 4.1).
Затем мы находим выражение для отображающих функций в
частных случаях четырехугольников с прямыми углами (п. 4.2. и
4.3).
4.1. Решение аадачи о параметрах. Пусть при отображении
полуплоскости Im ш > 0 на внутренность заданного простого
прямолинейного четырехугольника вершинам четырехугольника
соответствуют точки ветвления 0,1, с», Я плоскости ш. Предпола-
Предполагается, что среди внутренних углов Ьоп, д^я, д^, <5Ля, сумма которых
равна 2я [см. А A3.1.13)], не более чем один неположителен. Это
означает, что в точке г = оо находится не более чем одна вершина
четырехугольника, т. е. четырехугольник действительно простой.
Отображающая функция, записываемая, согласно формуле Швар-
Шварца—Кристоффеля, в виде
»¦
z = С [-._. ^ г-р = CJZ , D.1.1)
щ
аналитически зависит не только от ш, но и от параметра X, определя-
определяющего двойное отношение точек ветвления; мы будем выражать
это равенством
г = z(iv; a).
Нормировка отображающей функции осуществляется заданием
двух вершин четырехугольника; например, условия
2@;А) = 0, гA;А) = 1 D.1.2)
выражают тот факт, что образами точек w — 0 и w = 1 служат
соответственно точки г = 0, г = 1. Аналитически это означает,
что нижний предел wQ интеграла D.1.1) выбирается равным нулю,
а множителю С придается значение
С=Л. D.1.3)
Jo
Таким образом, отображающая функция принимает вид
г = г(ш;А)=^ D.1.4)
и дает нам образы остальных двух точек ветвления в виде отноше-
отношений двух гипергеометрических интегралов:
*~;*) = ^, =(А;А) = 4- DЛ-5)
4.1. Решение задачи о параметрах
251
Наглядное истолкование этих отношений, позволяет геометрически
обозреть зависимость от параметра А. Каждому вещественному
значению А соответствует четырехугольник с внутренними углами
йо.-т, SjTr, бея, dfc, форма и расположение которого задается усло-
условиями нормировки с одной степенью свободы; свободные вершины
этого четырехугольника определяются значениями функций D.1.5).
Рассматривая совокупность четырехугольников, соответствующих
всем вещественным значениям А, мы получим геометрические
места их свободных вершин, что позволит нам находить значения
этих функций при вещественных А.
Плоскость z
Плоскость w
Рис. 32.
1. Значениям А < 0 соответствуют четырехугольники вида,
указанного на рис. 32. Геометрическими местами свободных
вершин служат выделенные на рисунке отрезки неподвижных
прямых д0, дх проходящих через точки г = 0 и г =. 1.
2. Так как А = 0 является точкой ветвления рассматриваемых
интегралов, то при переходе к положительным значениям А следует
обходить начало координат. Если обход осуществляется в верхней
полуплоскости, то граничная кривая в плоскости интегрирования
при значениях А между 0 и 1 принимает вид, указанный на рис. 33,
причем при вторичном подходе к нулевой точке последняя не должна
обходиться. Функция г(ш; А) отображает ограниченную таким кон-
контуром область на шестиугольник, представляющий собой четырех-
четырехугольник с выступом в виде разреза. Проследим за граничной
252
§ 4. Простые прямолинейные четырехугольники
кривой последней области при движении из точки z(oo; Я). Сначала
мы двигаемся прямолинейно по направлению к первому образу
точки ш = О, затем поворачиваем на угол A — до)я и продолжаем
путь до вершины г(Я; Я), где углу 2л: в плоскости ш соответствует
поворот на угол Ъя A — бя). Длина следующего отрезка равна
Плоскость г
Плоскость ш
Рис. 33.
длине предыдущего; его конец, также соответствующий точке
w = 0, обозначен на рисунке символом z@; X). Из этой точки мы
возвращаемся к точке г(Д; Я), так как на этот раз мы не обходили
точку ветвления ш = 0. После этого совершаем поворот вокруг
г(Я; Я) в противоположном направлении на половинный угол и
продолжаем движение до вершины z(l; Я). После поворота на угол
A — й,)я возвращаемся в точку г(оо; /).
Поскольку вершины г@; Я) и гA; Я) закреплены, свободные вер-
вершины описывают дуги окружностей, когда / пробегает указанный
интервал (рис. 33).
4.1. Решение задачи о параметрах 253
3. При переходе на интервал А > 1 следует проводить соответ-
соответствующие рассуждения, учитывая, что точка А = 1 есть точка вет-
ветвления рассматриваемых интегралов. Контур на плоскости w,
изображенный на рис. 34, отображается в границу четырехуголь-
четырехугольника с выступом в виде изломанного разреза. Геометрическими
местами свободных вершин г(оо; "/.) и г(Я; Я) являются указанные на
том же рисунке отрезки прямых д'о и д^д'о симметрична д0 относи-
относительно ЗхI.
На каждом из трех рисунков указаны предельные положения
четырехугольника, вырождающегося в треугольник, когда точка
ш = А совпадает с какой-либо из остальных трех точек ветвления2.
Эти предельные положения попарно симметричны3.
Очевидно, что отрезки и дуги, являющиеся геометрическими
местами свободных вершин г(оо; А) и z(A; А), образуют два круговых
треугольника с внутренними углами
6f тг = A — (бх + 5Д)) лг, D.1.6)
6*я = A-~(Ьл + Ь0))л.
1 Указанный на рис. 34 отрезок д'х симметричен с дх относительно д0. —
Прим. ред.
2 Для сходимости интеграла и тем самым для положения предельных точек
решающую роль играют значения показателей д.. — 1. Так, например, если
^о + &х > 1 > то оба интеграла сходятся в точке го = О при А —» 0; в частности,
jX
lim z (А; А) = lim — = 0 (<50 + 5Л > 1).
a_>o х->0 j\
В противоположном случае <50+ 5;. "= 1, которому соответствуют рис. 32—34,
отношение этих интегралов имеет предел, отличный от нуля:
Jo sin E„ -4- 8?) п х ~
lim г (А; /.) = lim 4 =, — \° \ " е'^ (й0 + <5Я ^ 1),
я>0 я>0 j sin д/п
что видно из рис. 32. Аналогичные факты имеют место для предельных пере-
переходов при Л —> 1 и А —> зо.
3 Имеются в виду две пары треугольников, из которых одна, указанная
тонким пунктиром на рис. 32, 33, получается при /. —> 0, а другая, указанная
тонким пунктиром с точками на рис. 33, 34, получается при ). —> 1. К построению
рис. 33 заметим, что дуга окружности, описываемая точкой z(oo; Я), вмещает
угол <5соЯ-и хорда, стягивающая эту дугу, образует с отрезком z@; А), гA; А)
угол 2E^1. Заметим еще, что необычность рассматриваемых авторами отобра-
отображений на четырехугольники с линейными выступами устраняется, если
эти отображения продолжить по принципу симметрии, а именно через
сторону z(k, A), z(l; А) на рис. 33 и последовательно через стороны z(A; A), z(oo; A),
z\X; A), z(i; А) на рис. 34. Это же замечание полезно для уяснения характера
выбранной нормировки отображения. — Прим. ред.
254
§ 4. Простые прямолинейные четырехугольники
Если точка ветвления Я движется по вещественной оси, то г(оо; /)¦
и г(Я; Я) описывают контуры этих треугольников1. На основе прин-
принципа соответствия границ заключаем, что верхняя полуплоскость
комплексного переменного Я конформно отображается функциями
г(оо; Я) и г(Я; Я) на внутренности круговых треугольников.
Плоскость г
Плоскость
Рис. 34.
Этим полностью решается «в целом» задача о параметрах, т. е.
выясняется зависимость «в целом» формы и положения прямолиней-
прямолинейного четырехугольника от параметра Я. Для определения двойного
отношения Я, соответствующего заданному прямолинейному четы-
четырехугольнику и необходимого для вычисления отображающей
функции, поступим следующим образом. Одна из двух свободных
вершин четырехугольника, например г(Я; Я), определяет точку
на границе кругового треугольника (рис. 35). Обращая «функцию
треугольника»
= 4, С4-'-7)
1 Для z(X; /) см. рис. 35, 36. Стороны треугольника, описываемого *(
указаны длинным жирным пунктиром на рис. 32— 34. — Прим. ред.
©; /.),
4.1. Решение задачи о параметрах
255
находим на вещественной оси 7. точку, образом которой служит
указанная точка на границе треугольника. Поскольку отображаю-
отображающая функция ?(.?.) полностью изучена средствами теории гипер-
гипергеометрических функций («в малом», через гипергеометрические
ряды), обращение функции D.1.7) не представляет существенных
трудностей. Полученное таким обра-
образом числовое значение подставляется
в отображающую функцию D.1.4), что
и дает нам конформное отображение
полуплоскости 1тш>0 на внутрен-
внутренность заданного прямолинейного четы-
четырехугольника.
Представление функции треугольника
ч(Я) в виде отношения двух фундамен-
фундаментальных решений в точке 7. = 0.
Представление функции треуголь-
треугольника ?(А) посредством гипергеометрических рядов можно полу-
получить из формулы D.1.7), разлагая определенные интегралы Jq, J{
в окрестности соответствующей точки ветвления. Этой цели
можно достигнуть быстрее, если учесть, что в п. 3.3 уже уста-
установлены форма и положение кругового треугольника, на который
отношение фундаментальных решений в точке 0 отображает
верхнюю полуплоскость. Остается произвести дробно-линейное
преобразование, переводящее треугольник на рис. 35 в треуголь-
треугольник на рис. 28, чтобы получить искомое представление функции
С(Д) в виде дроби
(_;.)!-/ F(a . |_ 1 _ у, р + 1 _ у- 2 - у; А)
Рис. 35.
?*(/)= с*
F(a, P; у, /.)
< arg (—/) < 0.
D.1.8)
Связь между углами D.1.6) кругового треугольника и параметрами
гипергеометрическ'ой функции выражается, как известно, форму-
формулами
й»= 1 —8, —8я=,у —ос —/J, Dл-9)
%*= 1-4-Л = /*-«•
Вершины треугольника в плоскости С лежат, как указывалось
п. 3.3, в точках
С*@) = 0,
?*0) = 1, D.1.10)
г*(оо) = ето~У) !^(у :;Лц = е-
256
§ 4. Простые прямолинейные четырехугольники
Дробно-линейное преобразование, переводящее треугольник на
рис. 35 в треугольник на рис. 28, представляется в виде
(С(Я), «», а0, а,) = (С*(А), С*(оо), 0, 1),
D.1.11)
причем вершины а0, alt a^ треугольника на рис. 35 заданы по постро-
построению. Из рис. 36 находим значения
=
0
= _
D 1Л2)
принимая во внимание подобие прямолинейных треугольников
А(а^,, а0, о,) и /1(ате, 1, 0), имеем, кроме того,
№+л'). D.1.13)
sin 50я
Рис. 36.
С помощью этих значений из D.1.11) получаем
С*(А) - 1
далее,
(а0 - аг) С*(Д) + at '
; D.1.14)
D.1.15)
4.2. Вычисление отображающей функции 257
Наконец, из рис. 36 получаем разность
^^ D.1.16)
и формула
?U = ^7>г5т\ -1 е-'*6' ~ ""^+ *' + **>« е™>- Г*ф] D.1.17)
С(Л) sin (<50 + <5;.) я [ sin <5,я v 'J v '
дает нам искомое представление функции треугольника D.1.7) в
виде частного D.1.8) двух фундаментальных решений.
4.2. Вычисление отображающей функции в частных случаях.
Эллиптические интегралы1.
Пример 1. Четырехугольник I о » «» а • о) (эллиптический интег-
интеграл первого рода).
Отображение полуплоскости Im ш > 0 на прямоугольник осу-
осуществляется эллиптическим интегралом первого рода
/ш(ш - 1) (ш - X)
о
D.2.1)
l(O;x)--0
Рис. 37.
Сохраняя нормировку, принятую в общем случае для простых четы-
четырехугольников, представляем отображающую функцию в виде
2(ш; Я) = -\ . D.2.2)
Jo
Начиная опять с некоторого значения А < 0 и переходя при помощи
аналитического продолжения к отображающим функция.^ при
О < А < 1 и А > 1, получим фигуры, изображенные на рис. 37 (как
1 О конформном отображении с помощью эллиптических интегралов см.
[2]. — Прим. ред.
17 — 6002
258
§ 4. Простые прямолинейные четырехугольники
показывают рис. 32—34 при специальном выборе 6Л = 60 = dt =
Геометрические места свободных вершин г(Я; Я) и
г(оо; Я) представляют собой круговые треугольники с углами,
равными нулю (рис. 38). Отображением границы такого кругового
треугольника на вещественную ось Я решается
задача о параметрах «в целом».
Этот пример примечателен тем, что при лю-
любом расположении точек ветвления образуется
одна и та же область, именно прямоугольник.
Поэтому можно ограничиться расположением то-
точек ветвле:шя, указанным на первом из рисунков
(Я < 0).
Ниже мы рассмотрим сначала отображающую
функцию на границе при Я < 0, а затем определим
Рис. 38. параметры для этого случая.
Отображение границы. Для исследования отоб-
отображения на границе мы приведем неопределенный
интеграл во всех четырех интервалах изменения независимой
переменной ю = и к нормальной форме Лежандра. Этим одно-
одновременно достигается параметрическое представление определенных
интегралов в зависимости от Я, удобное для определения парамет-
параметров. Чтобы перейти к обычным обозначениям, полагаем
?. = — ¦¦
2 =
D.2.3)
При этом к @ < % < 1) есть модуль эллиптического интеграла.
1. В интервале и < 1 напишем разложение
П = А + JI D-2.4)
и затем в интеграле J\ положим
в результате получим
du
D.2.5)
D.2.6)
Этот интеграл (подинтегральное выражение которого вещественно)
подстановкой
и2 cos2 q>
D.2.7)
4.2. Вычисление отображающей функции
259
приводится к нормальной форме Лежандра
Л—Ш
В частности1, для полного интеграла получается значение
JT = —2
2. В интервале Д < и < 0 положим
УН = i/^^m, Уш— 1 = r-yi — н, /ш — Я = Ун — А.
Интеграл
7» = _ f du
Jy(-u)(l -ц)(ц-.
подстановкой
И = — :
1 - и'2 sin2 <p
приводится к нормальной форме
которая выражается через дополнительный модуль х' ¦
Полный интеграл принимает значение
J^2xf(x',~\ .
3. В интервале 0 < и < 1 положим
Интеграл
подстановкой
7" = — i f da
0 Jyu(i-u)(u-
D.2.8)
D.2.9)
D.2.10)
D.2.11)
D.2.12)
D.2.13)
D.2.14)
D.2.15)
D.2.16)
и'2 sin2 у
1 — и2 sin2
D.2.17)
1 Так как и < А, то D.2.9) следует понимать как JJ*°. — Прим. ред.
17*
260§ 4. Простые прямолинейные четырехугольники
приводится к нормальной форме
Jg = — 2ЫР(я,<р).
Полный интеграл принимает значение
Jj = —2Ы f(x, ^\ = J~.
4. В интервале 1 < « разложим интеграл в сумму
Jao = 4 + J'l
и приведем интеграл
и
1
подстановкой
1
U = г—
COS2Q)
к нормальной форме Лежандра
J\ — 2я F(x', cp).
D.2.18)
D.2.19)
D.2.20)
D.2.22)
D.2.23)
Полный шггеграл принимает значение
= ^. • D.2.24)
Таким образом, для нормированной отображающей функции
Jo
получаем следующие представления во всех четырех интервалах:
T'2-J
2.
5-)
^"(Х. 9»)
fir)
4.2. Вычисление отображающей функции 261
В частности, из этих формул находим значение z(A; А), определяю-
определяющее отношение сторон прямоугольника:
4]
т-«(* A)-/-j-l!, и--^. D.2.25)
Обозначая полные эллиптические интегралы обычным образом
К(х) = F\x, Ц,
К(х') - К'{х) =
получаем представление функции треугольника т(А) в интервале
Д<0:
D.2.26)
Обращение этой функции записывается с помощью так называемых
нулевых значений ^-функций #2(У|ТХ $з(у|г) в виДе
D.2.27)
Для #2@| т) и #3@|т) имеем разложения в ряды
1_ 9^ 25
02(О|т)= 2qi +2qi +2g4 + ...
(g = е*«). D.2.28)
#3@]т) = 1 + 2q + 2ф + 2q9 + . ..
Если умножить отображающую функцию на число а > 0, то
ширина прямоугольника примет значение о. Высоту полученного
прямоугольника обозначим через Ь. Полагая тогда
ах = ib, D.2.29)
придем к следующему представлению для вещественного пара-
параметра А:
4)
А=1- ° ¦ D.2.30)
К
262
§ 4. Простые прямолинейные четырехугольники
Пример 2 (эллиптический интеграл второго рода).
В качестве второго частного случая рассмотрим отображение,
осуществляемое эллиптическим интегралом второго рода:
J0
wdw
- 1) (ш - Я)
D.2.31)
Точке ветвления ю =оо соответствует вершина четырехуголь-
четырехугольника, лежащая в точке z = оо. Внешние углы таковы:
D.2.32)
Х<0
-О
2@;\)--0
Рис. 39.
Трем интервалам изменения параметра А соответствуют три
различных расположения точек ветвления и тем самым три типа
многоугольников, из которых существенно различны только два.
Начнем опять со значений ). < 0 и соответствующего им типа
четырехугольников, а затем путем аналитического продолжения
перейдем к типам, соответствующим ин-
интервалам 0 < А < 1 и Я > 1. На рис. 39
изображены все три типа многоугольни-
многоугольников с той же нормировкой и расположе-
расположением, что и в общем случае. (Граница
рве. 40.
Рис. 41.
4.2. Вычисление отображающей функции 263
полуплоскости Im w > О проходится так же, как на рис. 32 —34.)
Задача о параметрах «в целом» приводит к круговому треугольнику,
изображенному на рис. 40, с углами л, 0, л, представляющему собой
геометрическое место вершин прямолинейных четырехугольников,
соответствующих переменной точке ветвления w = Я.
Четырехугольник L, ^, 2, — -А .
Функция, отображающая полуплоскость Im w > 0 на много-
многоугольник, изображенный на рис 41, представляется в виде отноше-
отношения неопределенного и определенного (полного) эллиптических
интегралов второго рода:
J Yw(w -
wdw
; z(w; Я) = Л = ?.. , D.2.33)
; J° r wdw
J ][w(w - 1) (ш - Я)
о
где А — неопределенный параметр, принимающий отрицательные
значения.
Для исследования отображения на границе мы приведем не-
неопределенный интеграл во всех четырех интервалах изменения неза-
независимой переменной w = и к нормальной форме Лежандра. Этим
одновременно достигается представление определенных интегралов
в зависимости ог Я, удобное для определения параметров «в малом».
Чтобы перейти к обычным обозначениям, полагаем, как и в пре-
предыдущем примере,
v'2 1
Л х2 ' 1 - Я •
При этом к @ < к < 1) есть модуль эллиптического интеграла.
1. В интервале и < Я напишем разложение
J% = 3\ -г J\ D.2.34)
и затем в интервале J\ положим
yw = iy—u, 1/w— 1 == i V1 — u, yw — }.= iyX — u; D.2.35)
в результате получим
и
udu
=r . D.2.36)
л
Этот интеграл, подинтегральное выражение которого вещественно,
подстановкой
« = — ^т-V- D.2.37)
ЧУ а ЛАС» А) Ч '
264
§ 4. Простые прямолинейные четырехугольники
приводится к виду
*' J cos2 <p У1 - x2 sin2 g>
0
(ср. со стр. 258). Принимая во внимание формулу
*'2
D.2.38)
^ (tg <p y"P^*2si
cos2 <р У1 - х2 sin2 g>
приходим к разложению
j« = Н i [tg q> /Г— и2 sin2 у + х'г *\у., <р) ~Е(х, ф)\.
2. В интервале Я < и < 0 следует положить
yV = ,• /^н, у»—Т = i/Г~п, 1/ш —;. = yTi^TA.
Вещественный интеграл
и
uda
7" = — Г
"° Jy(
о
подстановкой
Ц)A - U) (U - к)
х'2 sin2 ж
1-х'2 sin2
приводится к виду
Учитывая равенство
d / sin у cos у»
« = -_2кк'2 Г _^^=-
0 J У1 - х'2 sin2 9>
s'n2
- к'2
получаем
_„ 2
0
2 r /9 sin m cos п>
- к'2 ——y
Полный интеграл ¦/? принимает значение
D.2.39)
D.2.40)
D.2.41)
D.2.42)
D.2.43)
D.2.44)
D.2.45)
D.2.46)
D.2.47)
4.2. Вычисление отображающей функции 265
3. В интервале 0 < и < 1 положим
fw=Yu, ]fw—l = ifl—u, fг^-7. = Yu — Я. D.2.48)
Вещественный интеграл
udu D.2.49)
о
подстановкой
u = *^!_f_ D.2.50)
1 — x2 sin2 у
приводится к виду
» = _2lW2 f^?^i^ . D.2.51)
0 J (Kl-x'sin»»I
Учитывая равенство
d I sin 93 cos <p Л ,2 sin2 <p
d<p lyT^] "" K (yT^"^^K
к У1 — кг sin2 <p и
получаем
! И ВШ} ¦ D-153>
Полный интеграл Jj принимает значение
(|j] D.2.54)
D.2.55)
D.2.56)
D.2.57)
D.2.58)
4. В интервале 1 < и
и приведем интеграл
1
подстановкой
к виду
t/i =
разложим интеграл
Jq = ¦
и
- f-
JyU(U
<р
7j -1- Jl
udu
- 1) (и - А)
1
cos2 q>
sin2 у
266 § 4. Простые прямолинейные четырехугольники
Учитывая равенство
-?-(tg?>VT=v*ri^) =
cos2 дэ у 1 — x 2 sin2 05
— —=^=^=z.- + YT— *'2 sia2 y, D.2.59)
fl - x'2 sin2 93 Г> \ >
приходим к выражению
2
к
J« = ? [ tg cp f\ — к'* sin2 <p + к2 F(x', cp) — E(^', <p) ]. D.2.60)
Для нормированной отображающей функции D.2.33) в рассмот-
рассмотренных четырех интервалах имеют место следующие представле-
представления:
кф: ;.) - :(л; А)
__х'2 _1
X2 COS ffl
sin w cos i
^'2 г
2. А < u < 0: г(и; А) = —г
-¦"D)-'¦("¦?)
1 _ и'2 sin2 95 '
sin ф cos y>
-)/->-' ^ 1 /"ч Vl— X2 sin2 m
3. 0 < и < 1: z(u; /.) = —'- r-
x'2 sin2 ф
" = i - x2 sin2 ,
4. 1 < u: z(u; A)
и =
cos2 q>
В частности, из этих формул находим значение г(А; А), выражаю-
выражающее отношение конечных сторон:
= z&; а) = -1
4.2. Вычисление отображающей функции 267
Обозначая следующим образом полные эллиптические интегралы
К(х) = F (х, |) , K(yJ) = К'(х) = F \я\ JJ ,
Е(х) = Е \х, |) , Л(х') = ?'(х) - Е (*', |) ,
полутаем представление в интервале Я < О
2__
f — 1
ь Е(х) - х'2К(х) { 1 -
Если умножить отображающую функцию на число а > О,
то ширина прямоугольной выемки четверти плоскости (раньше
равнявшаяся единице) примет значение а (см. рис. 41); ее высоту
обозначим через Ь. Тогда вещественный параметр Я можно выразить
через отношение — путем численного решения уравнения
A
- А)Е'\ \-К'\
Четырехугольник Ь » g» а » ~ а *
Для выяснения аналитического продолжения и решения задачи
о параметрах «в целом» мы будем применять одну и ту же отобра-
отображающую функцию z(m\ Я) для всех значений Я. Нормировка этой
функции, очевидно, имеет смысл только для типов многоуголь-
многоугольников, которые соответствуют значениям Я < 0. Если отображение
полуплоскости Im w > 0 на многоугольник иного типа рассматри-
рассматривается само по себе, то следует приспособить нормировку к этому
типу и потребовать, чтобы две из вершин многоугольника находи-
находились в точках 0 и 1. Это достигается, если отображающую функцию,
соответствующую рис. 42, представить, например, в форме
w
г wdw
„. J Yw(w - 1) (ш - А)
г*(ш; Я) = 7Г = ~, " • D-2-64)
J
wdw
Vw{w - 1) (w - A)
х
Подлежащее определению значение Я лежит в интервале @,1).
268 § 4. Простые прямолинейные четырехугольники
Для исследования отображения на границе мы приведем неопр*
деленный интеграл во всех четырех интервалах изменения незави-
независимой переменной w = и к нормальной форме Лежандра. Эти1к
одновременно достигается представление определенных интегралоь
в зависимости от А, удобное для определения параметров «в малом
Чтобы перейти к обычным
обозначениям, полагаем
А = х'2, «а = 1 — Я. D.2.65)
При этом у. (О < у. < 1) Z*fO-A)
есть модуль эллиптического ' '
интеграла. 1
I
1. В интервале и < 0 -
разложим интеграл (КЬ)ЩО
J'i= J\ + Jg. D.2.66) Рис. 42.
Положим
fro = (/~", /й»--"i = i VT^ii, У id — Я= j/A—u D.2.67,
и приведем интеграл Jg подстановкой
ij = — «'2tg2y D.2.68)
к виду
У()( )( )
о о
Учитывая равенство
== = 2.V*f ^^^dy. D.2.69)
A- u) JyiK2sin2
= -.=^^— + /F1^!^, D.2.70)
|/1 — x2 sin2 yi
получим разложение
Jg = 2г [tg cp yV—tf sin^p — E(k, tp)]. D.2.71)
2. В интервале 0 < u < А, положив
У^й='/п', Уш—1 = iV1 — п, уш^Я- ffA—u, D.2.72)
приведем интеграл J'/ подстановкой
^4t D.2.73)
^4t
1 — х 2 sin2 95
к виду
- f _==^__ = 2^2 Г —-i^ dy. D.2.74)
J fu(l - и) (А - u) J(yi-»'2sm2,p)
4.2. Вычисление отобразкающей функции 269
Учитывая равенство
(sin ф cos <р у cos2 <p
и'2 fl - х'2 sin2
получим
= + r ,t ^ , D.2.75)
j. = 2 [«* ^ЩЩ= + F{x', ,р) - ЕМ, vj\ . D.2.76)
L ]/1 — и'2 sin2 ф J
Полный интеграл принимает значение
3. В интервале ). < и < 1, полагая
yiiT = /IT, /Ш~-Т = i УТ^^п, /ш — Л = Уи—Х, D.2.78)
приводим интеграл J" подстановкой
" = 1 т^-t- D.2.79)
1-х2 sin2 у v у
к виду
«7? = -i Г , "d" = -2.V f —=^=—5 . D.2.80)
х J Vu(l -и) (u - A) J (У1 - x2 sin2 ф)"
Vu(l -и) (u - A) J (У1
я о
Учитывая равенство
y ^-^s^^ D.2.81)
1.У1 -x2sin2Pj (У1 -^sin2?.)
получим
р^°^| D.2.82)
Полный интеграл принимает значение
?) D.2.83)
4. В интервале 1 < и разложим интеграл
•П = Ji + Ji D-2.84)
270 § 4. Простые прямолинейные четырехугольники
и приведем интеграл Jf подстановкой
u = l^l^tl D.2.85).
cos2 <р к '
к виду
JI = [-—?*= _ 2 [У1ЕЕ1Ш ъ. D.2.86)
1 J Ун(и1)(м A) J cos29> ^
Ун(и-1)(м- A)
1 о
Учитывая равенство
У1 -
получим
_- -Ь /Г—^2sin29>, D.2.87)
Л = 2 [tg 95 /l— x^rinV + F(^', у) — ?(«', V)]. D.2.88)
Таким образом, для нормированной отображающей функции во
всех четырех интервалах имеют место следующие представления:
1. и < 0: z*(n; /.) = z*@; Я) — -$-?-! ^-^ ¦''-
u = — x'2 tg2 y;
sin ф cos 93
2. 0 <• u < Я: г*(и; А) = iJi"
- Б{х.
? x,-
x'2 cos2 ф
" = Г - x'2 sin2 у '
sin q> cos g>
Е(к, ф) - x
3. A < u < 1: z*(u; Я) =
E x,-
ц =
1 - x2 sin2 ф '
4. 1 < u: z*(u; A) = 1 +i-*-r-'-.-~_. -
1 - x'2 sin2 <p
4.3. Вычисление отображающей функции 271
Ич этих формул находим, в частности, значение z*@; Я), определяю-
определяющее отношение конечных сторон:
Gl\ l Л
D.2.89)
Если умножить отображающую функцию на постоянную а >0,
то ширина прямоугольного выступа четверти плоскости (прежде
равная единице, см. рис. 42) будет равна а. Обозначим его высоту
буквой Ь. Тогда значение вещественного параметра Я определяется
ь
Ш зависимости от частного - путем численного решения уравнения
4.3. Вычисление отображающей функции в частных случаях:
Элементарные функции.
Пример 3. Четырехугольники
J.J. *-
Отображение полуплоскости Im ш > 0 на многоугольник с
внутренними углами
осуществляется интегралом
л dl" D.3.1)
J ушA« - 1)
о
[ср. D.1.1)], равным
2Я) [log (]A^ + /i^T) - |] . D.3.2)
Так как
.7'=-ш^-Я), D.3.3)
ю нормированная отображающая функция D.1.4) принимает вид
.(.; Р.) = f = 1 - А [1од (fH + ySTTi) + V^ZS] , D.3.4)
272
§ 4. Простые прямолинейные четырехугольники
причем аргументы квадратных корней и мнимая часть логарифма-
лежат в интервале @, п). Следует заметить, что нормировка теряет
смысл при Я = g , так как в этом случае расстояние между парал-
параллельными сторонами, выражаемое интегралом Jj, обращается в
нуль1. Отдельным интервалам вещественного параметра Я соот-
соответствуют типы многоугольников, изображенные на рис. 43.
Легко установить соответствие между границами этих много-
многоугольников и вещественной осью ш, определяемое функцией D.3.4).
При ш < 0 во всех случаях имеем
r=-a, V
w
'г
-1 = e * fi—u,
log (lA^T + fw~\) = '* — log(f—п Ь YT^li) ,
D.3.5)
так что вещественная часть отображающей функции равна нулю.
При 0 < ш < 1 логарифм является чисто мнимым, а отображаю-
отображающая функция тем самым вещественна. Наконец, при ш > 1 корни
и логарифм вещественны, поэтому отображающая функция имеет
постоянную вещественную часть, равную 1.
Геометрические места, описываемые вершиной г(Я; Я), образуют
треугольник2, одна сторона которого (соответствующая интервалу
О < Я < 1) «гладко» проходит через бесконечно удаленную точку,
соответствующую значению А = Т< . Функция треугольника прини-
принимает вид
D.3.6)
1 Несмотря на это, подобную область можно считать четырехугольником,
так как бесконечно удаленную точку на стороне прямолинейного многоуголь-
многоугольника всегда можно считать вершиной с углом, равным — ж.
1 Легко убедиться на основе общих отображений (рис. 33, 34), что в этом
случае выступы в виде разрезов можно не учитывать. Это объясняется тем, что
вершина z(A; А) является концом разреза.
4.3. Вычисление отображающей функции
273
1егко видеть, что эта функция отображает вещественную ось /.
та контур треугольника; для этого следует записать ее, как интеграл
Лварца—Кристоффеля, в виде
D.3.7)
)бращение в нуль вычета подинтегральной функции в точке /. = --
аналитически выражает тот факт, что сторона треугольника, соот-
зетствующая интервалу 0 < А < 1, «гладко» проходит через беско-
<ечно удаленную точку плоскости ?¦
Обращение функции треугольника дает решение задачи о пара-
летоах (см. также стр. 257).
?,@)-0
Плоскость С,
О 1
Плоскость Л
Рис. 44.
Пример 4. Четырехугольники
Отображение полуплоскости Im ш > 0 на многоугольник с
внутренними углами
b,7i = 2я, bffi = -л-,
осуществляется интегралом [ср. D.1.1)]
= -я,
D.3.8)
равным
/ -i) log A^7 + 1^=1) + f ^i- A) . D.3.9)
18
6002
274
<? 4. Простые прямвлинейные четырехугольники
Так как
D.3.10)
то нормированная отображающая функция D.1.4) принимает вид
z(w; ;.)=!- ? [log {fvo + У^~ l) - ^fz^
причем аргументы квадратных корней и мнимая часть логарифма
лежат в интервале @, п). Следует заметить, что нормировка теряет
, 1
смысл при /. = -7 , так как в этом случае расстояние между парал-
параллельными сторонами, выражаемое интегралом jj, обращается в
нуль (см. сноску 1 на стр. 272). Отдельным интервалам веществен-
вещественного параметра Я соответствуют типы многоугольников, изобра-
изображенные на рис. 45.
О 1
?*- l
-*—?;
Рис. 45.
Исследование соответствия границ проводится буквально так
же, как и в предыдущем примере.
Два последних многоугольника на рис. 45 не однолистны. Для
простоты представим себе, что область, соответствующая интер-
интервалу -< 7. < 1, образуется склеиванием вдоль пунктирных полу-
полупрямых двух однолистных областей, изображенных на рис. 46:
четверги плоскости и трех четвертей плоскости.
Рис. 46.
4.3. Вычисление отображающей функции
275
Аналогично область, соответствующая интервалу Я > 1, обра-
образуется склеиванием однолистных областей, изображенных на
рис. 47, вдоль пунктирных полупрямых.
В критической точке Я = -, для которой нормировка теряет
смысл, прямоугольник вырождается в плоскость с разрезом вдоль
прямоугольной скобы с од-
одной бесконечно длинной
стороной. Отображающая
функция имеет вид [ср. А
О
(Н.1.9)]
D.3.12)
Геометрические места,
описываемые вершиной
г(Я; Я), образуют треугольник
(см. сноску 2, стр. 272), одна
сторона которого (соот-
(соответствующая интервалу 0 < Я < 1) «гладко» проходит через беско-
бесконечно удаленную точку, соответствующую значению Я = -. Функ-
Функция треугольника принимает вид
:(?.)=z(X;X)= I—i[log(yi +
D.3.13)
Легко видеть, что эта функция отображает вещественную ось Я
на контур треугольника, изображенного на рис. 48, если записать
ее, как интеграл Шварца—Кристоффеля, в виде
А
1вг
~ in)
Разлагая подинтегральную функцию в точке Я = j
D.3.14)
A _ 4 АJ A - 4 АJ
[l - I A - 4Д) + . . .] [l + L A - 4А) - .. .]
/-¦;
A - 4 АJ
D.3.15)
обнаруживаем, что вычет в точке Я = - равен нулю; это выражает
18»
276
§ 5. Двукратные прямолинейные четырехугольники
аналитически тот факт, что сторона треугольника, соответствую-
соответствующая интервалу 0 < Я < 1, «гладко» проходит через бесконечно
удаленную течку плоскости ?.
Эта область, рассматриваемая как круговой треугольник, не
однолистна. Представим себе, что она образована склеиванием
трех четвертей плоскости (рис. 48, слева) с разрезом вдоль полуоси
С > 1 и четверти плоскости (рис. 48, в середине) вдоль пунктирных
Пппскость t.
Рис. 48.
полупрямых. В точке ?@) = 0 внутренний угол равен тл, ав точке
СA) = 1 он равен ^ п' ЧТ0 можно видеть из интегрального пред-
представления.
Обращение функции треугольника решает задачу о параметрах
(ср. стр. 257), т. е. определяет параметр Я по заданному концу
разреза ?(Я) = г(Я; Я) в нормированном четырехугольнике на
рис. 45.
§ 5. Двукратные прямолинейные четырехугольники
5.1. Решение задачи о параметрах. Пусть обе конечные вершины
четырехугольника являются образами точек ветвления w — 1 и
ю = Я, а бесконечно удаленные вершины — образами точек вет-
ветвления го = 0 и w = оо. Так как внутренние углы в бесконечно уда-
удаленных точках отрицательны [А A3.1.5)], то положим
-6О = 0О, -6те = 0те. E.1.1)
Внутренние углы в конечных вершинах положительны, причем
хотя бы один из них должен быть больше л, чтобы выполнялось
условие А A3.1.13). Нижеследующие рассуждения справедливы в
обоих случаях, а чертежи соответствуют случаю, когда оба эти
утла больше л. Если, таким образом, положить
51 = 2 —01? 6Л = 2-0Я, E.1.2)
5.]. Решение задачи о параметрах
277
то все углы 6п будут лежать между 0 и я и, согласно А A3.1.13),
% + 0i + 0А + е~ = 2. E.1.3)
Таким образом, отображающая функция принимает вид
С7?
z(w; Х)= С Г
J
~.
E.1.4).
На рис. 49 изображен четырехугольник для случая Я < 0. В качестве
первого условия нормировки введем требование
гA; Р.) = 0, E.1.5)
Рис. 49.
фиксирующее образ точки ветвления ш = 1. Для определения
постоянного множителя С требуется еще одно геометрическое
условие. Это условие не может, как в случае простого четырех-
четырехугольника, состоять в задании еще одной вершины, так как две
вершины находятся в точке z = оо, а четвертая вершина, как и в
предыдущих рассуждениях, должна быть произвольной. Однако
мы можем потребовать, чтобы расстояние от одной из конечных
вершин до какой-либо из двух не прилегающих к ней сторон при-
приняло заданное значение. Аналитически это условие можно выразить
с помощью контурного интеграла вида А A3.2.9). Интегрирование
будет производиться по контуру S, начинающемуся в точке го = 1
(лежащей на верхнем берегу вещественной оси), огибающему
точки го = 0и го = Аи возвращающемуся снизу к точке го = 1
(рис. 49). Величина этого интеграла, согласно А A3.2.10), равна
расстоянию от вершины гA; /) до точки, симметричной с ней отно-
относительно стороны, являющейся образом отрезка го < Я, т. е. удво-
удвоенному расстоянию до этой стороны. Требование, чтобы это
278
§ 5. Двукратные прямолинейные четырехугольники
расстояние равнялось некоторой постоянной, скажем 1, приводит
нас ко второму условию нормировки
J = С f w-»'-x (w — l)-9^1 (ю — Я)-9д+1 dw = 1 E.1.6)
(S) J
(S)
и определяет значение множителя С. Отображающая функция
принимает, таким образом, вид
z = Z(w; Я) = Ц- ,
(S)
и ее значение при w = Я равно
z(A; Я)
(S)
E.1.7*
E.1.8
Если Я пробегает все вещественные значения, так что аналити
ческое продолжение сохраняется, то представление об облас™
значений этой функции от Я можно получить из элементарных гео-
геометрических соображений, в основном повторяющих рассуждения а
стр. 250—257.
1. Четырехугольник B — 6Я, —60, 2 — blt — 6«>)*.
Значениям Я < 0 соответствуют четырехугольники типов, укс-
занных на рис. 50а—d. В результате нормировки отображающей
функции E.1.7) вершина г(Я; Я) лежит на прямой Re z = ^. При это\.
заметим, что существует вполне определенное значение параметр^
Яв, при котором интеграл по контуру S обращается в нуль. В это\„
Рис. 50а.
Рис. 50Ь. Рис. 50с.
Рис. 50d. Рис. 50е.
случае нормировка отображающей функции указанным способом
невозможна, а вершина z@; Я) лежит на продолжении оси симмет-
симметрии (рис. 50с).
Для всех значений Я < Яо вершина z(l; Я) = 0 четырехугольника
лежит справа от оси симметрии; геометрическим местом вершин
5./. Решение задачи о параметрах
279
г(Я; Я) служит полупрямая
Im ? > - ctg лО„.
E.1.9)
(рис. 50b), причем точка 0 лежит правее точки 1, так что чертеж
перевернут.
Наоборот, для значений Я > Я„ вершина z(I; Я) = 0 лежит слева
о г оси симметрии, а геометрическим местом вершин г(Я; Я) является
прямая
Re r = .у
E.1.10)
(рис. 50d).
Наконец, на рис. 50а и 50е изображены треугольники, соответ-
соответствующие двум предельным значениям параметра Я = оо и / = 0.
В случае в0 + 01 > 1, которому соответствуют рисунки 50а—50е,
при Я -» — оо вершина г(Я; Я) стремится вдоль луча, выходящего
из начала координат, к конечному пределу lim г(Я; Я) = lim г(— оо; Я).
Напротив, если в0 + д1 < 1, то этот предел равен бесконечности
(рис. 51а). Положение же предельной точки lim г(Я; Я) = lim z@; Я)
Я_>+0 Я-»+0
зависит от того, будет ли 00 + Q-, > 1 (рис. 50е) или в0 + вх < 1
(рис. 51Ь).
Рис. 51а.
Рис. 51Ь.
Геометрическое место вершин г(Я; Я) при — оо < Я < 0 для
указанной нормировки состоит из полупрямой E.1.9) и прямой
E.1.10) (рис. 52). Значению Я = Яо, при котором нормировка невоз-
невозможна, соответствует несобственная точка г(Я„, Яп) = оо. Соответ-
Соответствующий четырехугольник может быть получен предельным
переходом из четырехугольника на рис. 50с, но не из четырех-
четырехугольников на рис. 50Ь или 50d. Значение функции
z = С Г иг-®-—1 (ш — !)-».+¦ (ш — Я0)-ел+1 dw, E.1.11)
280
§ 5. Двукратные прямолинейные четырехугольники
определяющее образ точки w — Хо, конечно; однако частно<-
г(^о! Хо) бесконечно, так как контурный интеграл обращается i
нуль.
о
-о
до- -
-о/
Рис. 52.
2. Четырехугольник (—в0, 2 — 6Я, 2 — 619 —в»»)*.
Переходя к положительным значениям Я, нужно следить за
тем, чтобы подинтегральная функция была однозначна в окрестно-
окрестностях точек ветвления X = 0 и X = 1. Поэтому переход точк!
ветвления Я к положительным значениям при обходе начала должо-
осуществляться через верхнюю полуплоскость. Следовательно, nps
значениях Я в интервале @,1) граничная кривая принимает форм*
указанную на рис. 53, причем при вторичном подходе к начал*
не следует обходить его. Функция E.1.7) отображает этл
Рис. 53.
граничную кривую в границу шестиугольника, представляющего
собой четырехугольник с выступом в виде разреза. Обойдем грани-
границу этого шестиугольника, начиная от точки г(оо; Я) = оо. Сначала
проходим параллельно мнимой оси в положительном направлении.
Совершив в бесконечно удаленной точке поворот на угол (&0 + 1)я,
продолжаем путь до вершины г(Я; X), где вновь поворачиваем на
угол 2(в? — 1)я, соответствующий углу 2л в плоскости ш. Затем
еще раз достигаем бесконечно удаленной точки, соответствующей
на этот раз значению z@; Я), после чего тем же путем (так как точка
ш = 0 не обходится) возвращаемся в вершину г(Я; Я). Далее
сделаем поворот на угол, равный половине предыдущего, в обрат-
5./. Решение задачи о параметрах
281
лом направлении и продолжим путь до вершины гA;Я). Повернув
да угол (в1 — \)л, вернемся вновь в бесконечно удаленную точку
" @, л;
ввл
Рис. 54.
Рис. 54а.
При переходе к интервалу 0 < Я < 1 путь интегрирования из-
изменяется внутри контура S (см. рис. 53); нормирующий интеграл
ю S и его значение в плоскости z, равное расстоянию от z(l; Я) до
прямой, соединяющей г(оо; Я) и г@; Я), не изменяются.
Геометрическим местом вершин г(Я; Я) для значений Я в интер-
интерзале @,1) является полупрямая
E.1.12)
Лри Я = 0 получаем треугольник, изображенный на рис. 52, а
фи /. = 1 — треугольник на рис. 54а.
3. Четырехугольник (—в0, 2 — В1, 2 — 6;, —6=»)*.
Рассуждения для интервала Я > 1 аналогичны. Переход к зна-
значениям Я > 1 осуществляется вновь в верхней полуплоскости,
лричем путь интегрирования при наличии точек ветвления w — О
in>=l следует деформировать так, как показано на рис. 55 (на
левом рисунке дано промежуточное положение).
Рис. 55.
Эта граничная кривая отображается функцией г(ш; А) в границу
четырехугольника с выступом в виде разреза с изломом, который
282
5. Двукратные прямолинейные четырехугольники
•обходится следующим образом. Начиная с вершины z(oo; А) = со,
проходим сначала полностью некоторую прямую, затем в беско-
бесконечно удаленной точке поворачиваем на угол (в0 + 1)эт и, пройдя
первый образ точки w = 1 [с поворотом на (Qj — 1)я], попадаем
в вершину "(Я; А). Повернув на угол 2@; — 1) я (что соответствует
Гид;-»
Рис. 56.
повороту на 2гг в плоскости ш), проходим второй образ точки w = 1
[с поворотом на —A — вх) л] и приходим вновь в бесконечно удален-
удаленную точку, имеющую теперь значение z@; А). Затем возвращаемся
по тому же пути в последний образ точки ш = 1, равный теперь
гA; А) = 0 [с поворотом на {61 — 1)я]. Придя вновь в точку z(A; A),
поворачиваем на угол, равный половине предыдущего, в обратном
направлении и продолжаем путь до точки г(оо; А) =» <х>, откуда и
был начат обход.
Указанная на рис. 55 деформация пути интегрирования оказы-
оказывает влияние на контур S (пунктир), играющий роль при норми-
нормировке отображающей функции. Начинаясь в точке ш = 1, этот
контур обходит точки ветвления w = 0 и w = А. Так как путь интег-
интегрирования в комплексной плоскости можно непрерывно деформи-
деформировать, не пересекая при этом то-
точек ветвления, то контур S должен
/ Л отступать, когда точка А прибли-
g>=--^ • * жается к нему, перемещаясь в верх-
~ ней полуплоскости. Наконец, ес-
если А принимает положительное
значение А > 1, то на контуре
образуется выемка, при помощи
которой охватывается выступ пути интегрирования вблизи точки А
{рис. 57). Интеграл по этому разрезообразному выступу контура
дает переход от точки гA; А) = 0 к первому (не обозначенному)
образу точки w = 1. Остальная часть контура симметрична относи-
¦--•-. s
Рис. 57.
5./. Решение задачи о параметрах
283
Рис. 58.
тельно полупрямой w < 0. Интеграл, распространенный на весь
контур S, приводит, таким образом, в точку, симметричную пер-
первому образу точки w = 1 относительно образа полупрямой w < 0.
Вследствие нормировки функции E.1.7) эта точка есть г = 1.
Для получения геометри-
геометрического места вершин z(k; л) при
всех значениях параметра Я >0
учитываем, что в силу выше-
вышеприведенных рассуждений точка
г = 0 переходит в точку г = ]
после двух зеркальных отра-
отражений: сначала относительно
прямой г(Я; Я) г(оо; Я), а затем
относительно прямой, прохо-
проходящей через z(oo; Я) = оо. Эти
два отражения дают в совокуп-
совокупности поворот вокруг точки
А, в которой пересекаются оси
симметрии. Угол этого поворо-
поворота равен удвоенному углу ме-
между ними: 2лО^ (рис. 56, спра-
справа). При изменении Я точки
: = 0, z = 1 и А остаются непо-
неподвижными, так что геометри-
геометрическим местом вершин г(Я; Я)
является дуга окружности с
центральным утлом A —б;)я,
стягиваемая хордой ОА. В
точке А эта дуга образует с
вертикалью Re z = ^ угол @,_+
О
?((>>¦-
Рис. 59.
тс, а в нуле — угол (вх + ^ — 9~ |
71 с горизонталью Im г = 0.
Я > 1. При
Я = 1
Концам дуги соответствуют концы интервала
получаем треугольник, изображенный на рис. 54а. При Я -» оо
вершина г(Я; Я) движется по прямой к точке А и совпадает там с
г(оо; Я), так что область распадается на двуугольник (рис. 58) и тре-
треугольную область, изображенную на рис. 50а (заштриховано).
Прямые E.1.9), E.1.10) и E.1.12), являющиеся геометрическими
местами вершин г(Я; /.) при Я < 0 и 0 < Я < 1, соединяются с дугой
окружности
arg
-е,) я,
E.1.13)
284
§ 5. Двукратные прямолинейные четырехугольники
соответствующей Я > 1, и образуют круговой треугольник, изобра-
изображенный на рис. 59. Его граница является образом вещественной
оси Я при отображении, осуществляемом функцией треугольника
?(Я) = 2(Я; Я) =
Вершины треугольника лежат в точках
Л
J
(S)
E.1.14)
E.1.15)
Из рис. 59 находим значения углов:
Ь*п = @0 + 0Л - \)л = A - Ь0~Ь,)щ
Ь*п = C — 01 — 0,) к = FХ + 6; — 1) л,
E.1.16),
= A — 60—
Этот треугольник не является однолистным, так как прямая Re С —
= 2 проходится полтора раза. Такую область можно представить
себе следующим образом. Проведем разрез полуплоскости Re С < т>
вдоль луча arg С = 12 — ^i — ft» I Д° начала координат и вдоль дуги
до пересечения с этим лучом (рис. 60а); тем самым из плоскости
вырезается круговой двуугольник. На эту область накладываем
однолистный круговой треугольник (рис. 60b) и склеиваем их вдоль
пунктирных линий.
Рис. 60а.
Рис. 60Ь.
Этим полностью решается «в целом» задача о параметрах для
двукратных четырехугольников, т. е. выясняется зависимость «в.
целом» формы и положения прямолинейного четырехугольника or
параметра.
5.2. Вычисление отображающей функции 285
5.2. Вычисление отображающей функции в частных случаях:
элементарные функции.
Пример 1.
а) Форма и расположение области в зависимости от параметра Я.
Отображение полуплоскости Im го > 0 на многоугольник с
внутренними углами
1 Я
6;Л = 2 Л, Й„Я = 0, ЬуЛ = 2п> ^<=я = О
осуществляется интегралом E.1.4), в котором
0; = |, 90 = 0, 0Х = J , 0^=0.
Отображающий интеграл принимает вид
Щ. ?Е . E.2.1)
Для нормировки следует вычислить значение этого интеграла по
контуру S (рис. 49, 53, 57). При любом Я этому контуру можно при-
придать вид большой окружности го = Rc'r (К §> 1), проходимой в
положительном направлении. Вычисляя интеграл вдоль этого пути,
представляющего собой обход в отрицательном направлении вокруг
точки w = оо, получаем значение 2rci, как и при вычислении интег-
интеграла Г—; оба интеграла имеют в точке w = оо вычет, равный —1.
При отображении полуплоскости Im го < 0 в окрестности точки
го = оо ширина полосы для обоих отображающих интегралов
равна п. В результате нормировки отображающей функции
;(W; Я) = Jl = ± I" 1/^=4 - E-2-2)
(S) 1
ширина полосы становится равной ^ ¦ Так как это имеет место
для всех значений параметра Я, то тем самым полностью опреде-
определяется положение многоугольника, на который функция г(ш; Я)
отображает полуплоскость Im m > 0.
N
\
\
\
\
Плоскость ю
Рис. 61.
286
§ 5. Двукратные прямолинейные четырехугольники
Если учесть, что при этом отображении окрестность точки w = (¦
также переходит в полуполосу, ширина которой равна половине
вычета подинтегральной функции в точке w = О, т. е. —-=, то пол< ¦-
2 ул
жсние второй конечной вершины многоугольника г(А; Я) можн<
определить, не вычисляя интеграла (рис. 62). Таким образом немед-
немедленно выясняется геометрический смысл параметра А: модх-л*
величины /А равен отношению ширины одной из полос к другой
я < о
0<А<1
Рис. 62.
В дальнейшем мы будем рассматривать отображение полупло-
полуплоскости Im w < 0, ограниченной вещественной осью w, проходимой
в одном направлении, независимо от способа аналитического продол-
продолжения интеграла как функции А от значений А < 0 к значениям
О < А < 1 и А > 1. Поэтому на рис. 53 и 55 следует опустить части
границ от w = А до w = 0 и обратно и соответствующие им разрезо-
образные выступы многоугольников. В случае А > 1 это означает,
что в качестве нижнего предела (ю = 1) отображающего интеграла
следует выбрать точку (не указанную на рис. 55), в которой гранич-
граничная кривая впервые проходит через точку 1. Отсюда вытекает, что
в плоскости z новое начало координат z(\, А) = 0' расположено
1
вправо от прежнего начала на величину 1 -= и совпадает с конеч-
конечной вершиной многоугольника (рис. 62).
Если выбрать прежнее начало, лежащее вне многоугольника (см.
стр. 280 и след.), то геометрическое место точек z(A; А) образует
«треугольник», граница которого является образом вещественной
оси А при отображении
E.2.3)
5.2. Вычисление отображающей функции
287
Обращение этой функции дает решение задачи о параметрах.
Имеем
A - 20* '
E.2.4)
по этой формуле можно определить параметр отображающей
функции E.2.2) для любого четырехугольника одного из указанных
типов [т. е. при заданной вершине г(/; Я) ™ ?(А)].
Плоскость
Плоскость А
Рис. 63.
Ь) Вычисление отображающего интеграла.
Вычисляя интеграл E.2.2) при помощи замены переменной
w - 1
E.2.5)
делающей подинтегральную функцию рациональной, получаем
E.2.6)
Для однозначного определения этого выражения заметим, что под-
подстановка E.2.5) переводит полуплоскость Im w > 0 в первый или
четвертый квадранты, в зависимости от того, выполнено ли нера-
неравенство Я < 1 или Я > 1 (рис. 64).
О Ж Л
О /
Плоскость t
О Г
Плоскость " t
Рис. 64.
Плоскость t
288 $ 5. Двукратные прямолинейные четырехугольники
Интервалу
О < arg w < л
соответствуют интервалы
0<arg*<2-, A<1, E2?)
Переходя к плоскосги т-^- , получаем соответствующие границы
для arg ?-t? :
О < arg - - < 7i, / < 1,
1 - ' E.2.8)
Таким же образом получаем
О < arg Ь±Щ < я, Я < 1,
E.2.9)
При Я > 0 это очевидно (изменение масштаба в плоскости t); при
I— 1 -4- t 1/Х
А < 0 точка г У Я лежит во втором квадранте, поэтому точка —-—'—
оказывается в верхней полуплоскости.
При этих условиях отображающая функция E.2.5) определяется
однозначно; в частности,
Я< 1,
E.2.10)
;ii--H, я>1
2(А; А) =
(см. рис. 62). Сдвиг начала координат в плоскости z в случае Я > 1
(см. рассуждения на стр. 281 и фиг. 3 рис. 62) влечет за собой изме-
изменение знака при переходе от Я < 1 к Я > 1, поскольку аналитическое
продолжение по А не рассматривается, и полуплоскость Im w > 0
отображается на обычный многоугольник (без разрезообразного
выступа).
После удаления выступов в фиг. 2 и 3 рис. 62 становится ясно,
что функция E.2.5) дает только два существенно различных отобра-
отображения, соответствующих «интервалам А<0и0<А<1. [Много-
5.2. Вычисление отображающей функции
289
угольник, соответствующий А > 1, получается из многоугольника
второго типа @ < А < 1) отражением и преобразованием подобия.]
Ниже изучаются отображающие функции в отдельности для слу-
случаев А<ОиО<А <1.
-/
Плоскость
Рис. 65.
Плоскзсть
После умножения на 2а (я > 0) ширина нормированной полупо-
полуполосы становится равной я (ранее она равнялась ^1; ширину второй
полуполосы (равную —-=| обозначим через Ъ. Таким образом, в
формуле E.2.4) для параметра следует положить
случай I: 2я? = я + ib,
случай II: 2я? = я —¦ Ъ (а < Ь).
Получаем
случай I: А} =— ~ ,
E.2.11)
E.2.12)
Функция, отображающая полуплоскость 1гаш>0 на много-
многоугольник, изображенный на рис. 66, согласно E.2.5) и E.2.12),
имеет вид
а2
случай II: Ап = р- (я < Ь).
Четырехугольник L, 0, ^, 0| .
log
1
1 - I
1/ го
» Ь2м>
1/ **
г Ь2ге
— 1
+ а2
- 1
+ а2
• Ь
а
1/ 1-«
I ~~2~ 2
fl - г»
1+«
E.2.13)
причем аргументы корней, согласно E.2.7), находятся в интервале
10, ^-1, а мнимые части логарифмов, согласно E.2.8), — в интервале
19 — 6002
290
§ 5. Двукратные прямолинейные четырехугольники
@, зт). При вычислении логарифма следует иметь в виду, что для
чисто мнимого значения t = it (т вещественно) следует положить
log l±± = log ii-^ = 2j are tg т.
E.2.14)
a-nb
Рис. 66.
hit
I-IX
Рис. 67.
Отображение границы:
1
an
mi
а*
а log
1-й
2Ь arctg ^
_ а2 - Ь2и
¦ — 1
i-ц
а у : 1
1 - .
1-й
1 - ц
а2 + Ь2ц
5.2 Вычисление отображающей функции
291
a log-
I аг-\-Ьги
]f a- 1
Четырехугольник 10, -, -, 0)
=.- + 2baictg\a
Функция, отображающая верхнюю полуплоскость Im w > 0 на
многоугольник, изображенный на рис. 68, согласно E.2.5) и E.2.12),
имеет вид
a log
b2w — a2
Ь2ге - а2
— blog
гс — 1
62гс - а2
1 -a
, E.2.15)
62w> - a2
причем аргументы квадратных корней, со-
согласно E.2.7), лежат в интервале |0, |-) , а
мнимые части логарифмов, согласно E.2.8),
— в интервале @, л).
Отображение границы:
(а2 "\
а log
а2 - Ь2и
— tlog
1
'Hi
a log
If 1-й
(a2 — b2a Га2 — 62ь
If1-»
С а2 - Ь2
— b log —
ь 1М
а 1М__и_ _
" Г а2 - Ь2ц
19*
292 § 5. Двукратные прямолинейные четырехугольники
К и:
Гц - 1 If и - 1
1 -L- а / —
&2ц - а* , , Г 62и - а2
а log .- — Ъ log
1/ ц-1 ° 1 и-1
1 _ 6 ^ 1 _ а /
Г Ь2и —а2 f 62и-а2
Пример 2.
а) Форма и положение области в зависимости от параметра Я.
Отображение полуплоскости Im w > 0 на многоугольник с
внутренними углами
= 271' ^О71 — —п>
осуществляется интегралом E.1.4) с
0д = 2 » в0 = 1, ^i = г '
Отображающий интеграл принимает вид
E.2.16)
Для нормировки следует опять вычислить интеграл по контуру
S (рис. 49, 53, 57), обходящему точку а»=оо в отрицательном
направлении. Так как этот интеграл равен 2ni (вычет в точке w = оо
равен —1), то нормировка отображающей функции
w
z(w; Л) = Jl = JL J/(цГ^1УХ^-~1) J E.2.17)
(S) 1
приводит к тому, что ширина полосы, соответствующей окрестно-
окрестности точки w = оо при отображении полуплоскости Im ю > О,
равна-. Этим, как и в примере 1, определяется положение много-
многоугольника.
5.2 Вычисление отображающей функции
293
Через точку z@; л) = о° граница многоугольника проходит
гладко», т. е. входящие и выходящие стороны направлены одина-
одинаково. Расстояние между ними определяется вычетом подинтеграль-
лой функции в точке да = 0 и равно ~= (это есть коэффициент
зри да в разложении Тейлора функции /(да—1) (да — /) в окре-
окрестности да = 0).
0<Л
Л<0
Рис. 69.
В дальнейшем мы будем рассматривать отображение полуплос-
:ости Im да > 0, ограниченной вещественной осью да, проходимой
: одном направлении, независимо от способа аналитического продол-
продолжения интеграла как функции от X от значений X < 0 к значениям
)<Я<1иЯ>1. Поэтому на рис. 53 и 54 следует опустить части
тэаниц от точки да = X до да = 0 и обратно и соответствующие им
пазрезообразные выступы многоугольников (обозначенные пунк-
"иром). В случае X > 1 это означает, что в качестве нижнего предела
v = 1 отображающего интеграла следует выбрать точку (не указан-
указанную на рис. 55), в которой граничная кривая впервые проходит через
"очку 1. Отсюда вытекает, что в плоскости г новое начало коорди-
координат гA; Я) = 0' расположено влево от прежнего начала на величину
= -{-^Ж E-2.18)
равную удвоенной разности расстояний между параллельными
:торонами) и совпадает с одной из вершин многоугольника.
Если выбрать прежнее начало, лежащее вне многоугольника
см. стр. 280. и след.), то геометрическое место точек г(Я; Я) образует
треугольник, граница которого есть образ вещественной оси Я
при отображении
- - AА)Ж E.2.19)
294
§ 5. Двукратные прямолинейные четырехугольники
(рис. 70). Обращение этой функции дает решение задачи о парамет-
параметрах. Имеем
;. = (/С^Т — ft)*; E.2.20)
значение этого выражения определяется однозначно в плоскости С
с разрезами вдоль вещественной оси от — оо до 0 и от 1 до г»,
если положить
— л < arg С < я, 0 < arg (С,—1) < 2я. E.2.21)
О ' 1
Плюкость Л
Рис. 70.
На верхнем берегу разреза, указанного на рис. 70, имеем
а на нижнем берегу
E.2.22)
i-
-г
E.2.23)
как и показывает соответствие границ на рис. 70. Из формулы
E.2.20), т. е. задавая вершину z{).; X) = С, можно определить пара-
параметр отображающей функции для любого четырехугольника одного
из трех типов (рис. 69).
Ь) Вычисление отображающего интеграла.
Вычисляя интеграл E.2.17) при помощи замены переменной
(делающей подинтегральную функцию рациональной), получаем
(/да_ х+ Уш-1
У(ц> - 1) (ю - А)
°8
1 + А
2 УГ °8
» — 1)
- Х)
. E.2.25)
5.2. Вычисление отображающей функции 295
Для однозначного определения этого выражения отметим, что
в точках верхней полуплоскости w @ < arg w < л)
О < arg /(да—1) (да —Я) <л, E.2.26)
и поэтому, на основе изложенных выше рассуждений (стр. 288),
следует положить
! —— <л, 0 < arg +<;Д < л (X < 1),
X-W E.2.27)
Ш<0, -„<ergl±i^<0 (Я>1).
Отсюда, в частности, для w = X имеем
?.;Х)= -I ^"' , 4~V* A< ' E.2.28)
(рис. 69). Сдвиг начала координат в плоскости z в случае Я > 1
(см. рассуждения на стр. 293 и фигуру 3 на рис. 69) влечет за собой
изменение знака при переходе от 7. < 1 к Я > 1, поскольку аналити-
аналитическое продолжение по А не рассматривается и полуплоскость
Im ю > 0 отображается на обычный многоугольник (без разрезооб-
разного выступа).
После удаления вцступов на рис. 69 становится ясно, что функ-
функция E.2.25) дает только два существенно различных отображения,
соответствующих интервалам Я<ОиО<Я< 1. (Многоугольник,
соответствующий Я > 1, получается из многоугольника второго
типа @ < Я < 1) отражением и преобразованием подобия.) Ниже
изучаются отображающие функции в отдельности для случаев
Я<0 и 0< Я< 1.
После умножения отображающей функции на 2а (а > 0) ширина
нормированной полуполосы становится равной а (ранее она равня-
равнялась 2 ; ширину второй полуполосы обозначим через Ь. Таким
образом, в формуле E.2.20) для параметра следует положить
случай I: 2а? = а + ib,
случай II: 2а? = а — b (а < Ь).
Имеем
случай I-. Я, -1 (fTt~l -f^
296
§ 5. Двукратные прямолинейные четырехугольники
(а < Ь).
Четырехугольник
E.2.30)
3 nl*
Функция, отображающая по-
полуплоскость Ira w > 0 на много-
многоугольник, изображенный на рис.
71, согласно E.2.25) и E.2.30),
имеет вид
z(w; A,) =
a
.xi
у—т
I w — Х\
-1оа — - •—
го—к\
E.2.31)
причем аргументы корней и мнимые части логарифмов лежат в
интервале @, я).
Отображение границы.
и < А,: z(u; Д,) = a +
Г1 -U
J—-+1
+ a log ' "—— 26 arc tg
= a + zb.
— Ai(l - u)
. Ь . 1 и - fa , ..
31 l/^-Aia - и)
5.2. Вычисление отобразкающей функции
297
О < . < I: Ф; У - -tEiifc-« + |
«-,og
¦m*
1 +
JT U
1 —
и — /i .
Четырехугольник —1, д,5, 0 .
Функция, отображающая полу-
полуплоскость Im w > 0 на многоуголь-
многоугольник, изображенный на рис. 72, со-
согласно E.2.25) и E.2.30), имеет вид
z(w; ;.,,) =
-1)
tc-Яц
причем аргументы корней и мнимые части логарифмов лежат в
интервале @, л).
Отображение границы
и < 0: z(u; Я„) = а +
;.ц - ц
._! ^l/^-Z^
298 § 5. Двукратные прямолинейные четырехугольники
О < и < А„: z(u; Ац) = а — Ъ +
Г АиA - и)
. I/ 1-1 I/
1
згг
З + а Hg ifej— _ ь log ^i
^п; *п) = а —b-
-i ^ ^ 1 /1\ п УA — ц) (ц — Дц) 2а .
Л, < и < 1: 2(ч; Д„) = --ii ^ ^ + -arctg
2A; /„) - 0.
1 < и: г(и; Я,,) =
1
]/"-1 1+l/?»<iL-l)"
^^ Ь lg Д^А
а VSEiEM + а log -Л^^ - Ь log
]fl
н-Я„
5.3. Вычисление отображающей функции в частных случаях.
Эллиптические интегралы.
Пример 3.
а) Форма и положение области в зависимости от параметра X.
Отображение полуплоскости Im ю > 0 на многоугольник с
внутренними углами
3 1 3 1
5д7Г = ^ Я, бдЯ = — - 71, SjJI = - Л, бсоЛ = — 2 л
осуществляется интегралом E.1.4) с
д л д
уд = 2 ' Уо = 2 ' W
Отображающий интеграл имеет вид
л д д
2 ' Уо = 2 ' Wi = 2 ' ~ = 2 -
W W
I
и после интегрирования по частям принимает форму
и»
I •"-
W
E.3.1)
+ 2 [-—^U^ . E.3.2)
J Yw(w - 1) (ш - А)
1
5.3. Вычисление отображающей функции
299
Для нормировки следует вычислить интеграл по контуру S
рис. 49). Этот контур представляет собой замкнутую кривую на
двулистной римановой поверхности квадратного корня1. Таким
>бразом, внсинтегральный член (равный оо при w = 0) исчезает,
Л<0
Рис. 73.
д пути интегрирования обоих эллиптических интегралов (первого
л второго рода) можно соединить в один контур, обходящий прямо-
тинейный разрез [Я, 0] в положительном направлении. Таким обра-
образом, контурный интеграл состоит из двух полных эллиптических
штегралов первого и второго рода.
0<л</
Z(K;K)
Рис. 74.
На рис. 74 указаны области, на которые функция
7*
z{w; a) = -j-
E.3.3)
>тображает полуплоскость Im w > 0, если путем аналитического
продолжения от отрицательных значений Я перейти к типам много-
многоугольников, которые соответствуют значениям 0<Я<1иЯ>1.
Геометрическое место вершин
г(Я; Я) = С(Я)
образует контур, который, как и в общем случае (стр. 283 и след.),
1 Можно считать, что эта поверхность получена зеркальным отражением
верхней полуплоскости относительно полупрямой w > 1, а затем относительно
отрезка А < ю < 0.
300
§ 5. Двукратные прямолинейные четырехугольники
ограничивает многолистный треугольник, так как прямая Re С = 2
проходится полтора раза. Этот треугольник можно получить, раз-
разрезая полуплоскость Re С < о вдоль положительной мнимой полу-
полуоси и склеивая левый берег этого разреза с левой граничной прямой
модулярного треугольника, изображенного на рис. 75 в середине.
Ь) Линейная и центральная симметрия.
Легко усмотреть, что в зависимости от знака параметра А
получаются два существенно
различных отображения. Обра-
Образующиеся области различа-
различаются но типу симметрии, а
именно при А > 0 область об-
обладает линейной симметрией,
а при А < 0 — центральной сим-
симметрией (ср. А, п. 11.1а, с). Это
непосредственно видно из выра-
выражения для отображающего ин-
интеграла, который при подста-
подстановке
I
I
О
п
0
2
Рис. 75. * Я ,,, .,
го* = - E.3.4)
W к
преобразуется в себя с точностью до знака, если в качестве нижнего
предела взять УХ Если А > 0, то величина fJ. вещественна; под-
подстановка E.3.4) точкам верхней полуплоскости ставит в соответ-
соответствие точки нижней полуплоскости1. В частности, на вещественной
оси w индуцируется инволюция2, меняющая направление на проти-
противоположное; соответствие устанавливается при помощи полу-
полуокружностей, ортогональных к окружности симметрии w = /А е'*>
(О < ср < я). Наоборот, если А < 0, то уТ лежит в верхней полупло-
полуплоскости, точки которой, таким образом, попарно соответствуют друг
другу. В частности, на вещественной оси w индуцируется инволюция,
сохраняющая направление; соответствие осуществляется полу-
полуокружностями, ортогональными к вещественной оси ю и пере-
пересекающимися в центре симметрии УХ(рис. 76).
1 Необходимо еще произвести отражение относительно отрезка [А, 1],
для того чтобы найти соответствие между точками полуплоскости Im w > 0,
устанавливаемое функцией E.3.4). При этом области в плоскости z ставится в
соответствие ее зеркальное отражение относительно отрезка гA; X) z(A; Я).
2 Инволюцией называется отображение, совпадающее со своим обратным,
А Я
например w* — — , w = — .
w w* , ¦
5.3. Вычисление отображающей функции
301
В обоих случаях на основе этой симметрии отображающий
интеграл простой подстановкой приводится к эллиптическому
интегралу второго рода в нормальной форме (с вещес*енными или
комплексными точками ветвления). Поскольку характер симметрии
в нашем случае виден особенно ясно, мы покажем далее, каким
образом шаг за шагом можно получить эту подстановку для
обоих случаев одновременно.
Линия симме/п
рии -¦
Линейная симметрия (К
А 0 — I
Центральная симметрия ft<
Рис. 76.
1. В случае Я >0 подстановка
IV =
w +
E.3.5)
отображает верхнюю полуплоскость ш на верхнюю полуплоскость
и/ (соответствие устанавливают концентрические полуокружности
с центром ш' = 0). В случае А < 0 верхняя полуплоскость w отобра-
отображается на внутренность единичного круга (соответствие устанавли-
устанавливают диаметры единичного круга). В обоих случаях образы точек
ветвления w = 1 и ш = Я симметричны относительно начала коор-
координат и равны w
2. Подстановка
= + -^—*— (рис. 77).
/' = ш'2
E.3.6)
Плоскость W
-7 О +7
Линейная симметрия
Центральная симметрия (Л<0)
Рис. 77.
302
§ 5. Двукратные прямолинейные четырехугольники
при ?. > 0 отображает верхнюю полуплоскость и/ в плоскость ?
с разрезом вдоль положительной вещественной полуоси. Точки
верхнего и нижнего берега соответствуют друг другу; это соответст-
соответствие устанавливается концентрическими окружностями с центром в
начале, а осью симметрии служит отрицательная полуось t'. При
X < 0 единичный круг в плоскости ш отображается на двулистный
единичный круг в плоскости t', причем в силу центральной симмет-
симметрии лежащие одна над другой точки единичной окружности соот-
Лиия
симметрии I I „
— г — { (/-с.
Ппоскость t
Линейная симметрия (Л^О) ¦ Центральная Лм.метрия (Л < О)
Рис. 78.
ветствуют друг другу; соответствие устанавливается парами
радиусов, лежащих один над другим. (Начало координат служит
точкой ветвления первого порядка; удвоение углов приводит к
совмещению радиусов, устанавливающих соответствие.) Образами
точек ветвления ш = 1ии>=Ав обоих случаях являются лежащие
«одна над другой» граничные точки t =
3. Дробно-линейное преобразование
E.3.7)
переводит лежащие один над другим образы точек ветвления ш = 1
и ш = Я в начало координат плоскости /, если выбрать цг и fx2
следующим образом:
E.3.8)
= fi - П)
= 9A-
= Q A + ПУ-
При А < 0 имеем /л2 = fii и выбираем q < 0, для того чтобы было
Im Aг > 0.
В случае линейной симметрии (А > 0) образом исходной полу-
полуплоскости Im ш > 0 является плоскость t с разрезами по веществен-
вещественной оси от — оо до ц2 и от ^tj до + оо. Соответствие устанавливают
окружности пучка с узлами t = [лх n t = р2.
В случае центральной симметрии (А < 0) соответствующий
образ есть двулистная верхняя полуплоскость Im (>0 с точкой
5.3. Вычисление отображающей функции 305
ветвления первого порядка t = цг. Каждая линия, устанавливаю-
устанавливающая соответствие между граничными точками, состоит из двух
одинаковых дуг окружностей, ортогональных к вещественной оси,,
лежащих на разных листах и выходящих из точки ветвления. Супер-
Суперпозиция преобразований E.3.5) — E.3.7) дает
откуда
где q — неопределенный отрицательный множитель. Верхняя полу-
полуплоскость ю отображается этим преобразованием на линейно- или
центрально-симметричную область, смотря по тому, будет ли А > О
или Я < 0 (рис. 79).
/J/70C - ~
кость i
Центральная симметрия (А <¦!))
Линейная симметрия (X >0)
Рис. 79.
Если же в плоскости z дана линейно-симметричная область с
попарно соответствующими друг другу точками ветвления w = 0, оо
и го = 1, л, то целесообразно вместо верхней полуплоскости ш
взять в качестве исходной области плоскость t с указанными выше
разрезами, так как отображающая функция, преобразованная к
переменной t [E.3.10) при X >¦ 0], переводит верхнюю полуплоскость.
/ в «половину» области. Осью симметрии служит образ отрезка
Наоборот, если в плоскости z дана центрально-симметричная
область, то в качестве исходной области следует выбрать дву-
двулистную верхнюю полуплоскость t (рис. 79, справа). Граница образа
в плоскости z, соответствующая дважды проходимой вещественной
оси t, состоит из двух частей, точки которых центрально-симметрич-
центрально-симметричны. Центр симметрии есть образ точки ветвления t = q (l — /X) •
Отображающий интеграл в рассматриваемом здесь случае пре-
преобразования многоугольника (стр. 298) с учетом равенств
Y(t-ti1)(t^=±eU^~, dt = -q"^dw E.3.11),
преобразуется подстановкой E.3.10) к эллиптическому интегралу
второго рода в нормальной форме
304
5. Двукратные прямолинейные четырехугольники
(w - 1) (ш -
E.3.12)
Точки ветвления в линейно-симметршшом случае вещественны, в
центрально-симметричном — комплексно сопряжены.
Четырехугольник I ~ g' 2' 2' ~ 2 (линейная симметрия).
Для установления связи с отображением посредством эллипти-
эллиптического интеграла второго рода с вещественными точками ветвле-
ветвления (стр. 262) положим в E.3.10) и E.3.12)
Тогда отображающий интеграл примет вид
n[(w -~l)(w'— A) rfui
J ( Ш Ш
«M^'
0</i =
1.
E.3.14)
При преобразовании отображающей функции E.3.3) к переменной t
следует учесть, что контурный интеграл J можно, стягивая контур
(рис. 73), записать в данном случае (Я > 0) в виде J = 2 J\ или,
что еще удобнее, <S)
E.3.15)
J = 2 J»
2П;к)--0
0 А V*
Плоскость то
Рис. 80.
Плоскость t
Тогда из E.3.3) следует, что
E)
г W< _
J у^Г^1иГ^)
_ f
- 1
2J Уш^'ТпГ^н)
—г*
E.3.16)
5.3. Вычисление отображающей функции
305
(; [)
262 по схеме
Верхняя полуплоскость /, являющаяся образом полукруга ра-
циуса УЯ в плоскости w, преобразуется функцией z*(t; [л) на «поло-
«половину области», что было рассмотрено на стр. 262
гз 1 1 п*
^2 ' 2 ' 2' 2) ¦
Четырехугольник j^, — 5,g, — g] (центральная симметрия).
В этом случае, как было показано, отображающий интеграл
Можно преобразовать к эллиптическому интегралу второго рода с
комплексно сопряженными точками ветвления. Это преобразование
не дает преимуществ при осуществлении отображения, так как с
помощью разложения E.3.2) отображающий интеграл можно
* Zfl;X)-0
za-.лУ}
Рис. 81.
привести к интегралам первого и второго рода в нормальной форме
более простым путем, без замены переменной. Поэтому мы сохра-
сохраним первоначальную форму E.3.3) отображающей функции, кото-
которая в подробной записи выглядит следующим образом:
J
(S)
(ш — 1) (ш — А)
dw
wdw
Уш(ш —
-(! +A) J
dw
wdw
,w(w — 1) (ш — А) ¦> Yw(w — 1) (w — ..,
E.3.17)
где /. — определенное отрицательное число. Эта функция отобра-
отображает верхнюю полуплоскость w на центрально-симметричную об-
область, изображенную на рис. 81. Центром симметрии является
образ точки ш = УХ.
20 — 6002
306 § 5. Двукратные прямолинейные четырехугольники
В результате нормировки отображающей функции вершина
z(/; Я) находится на прямой Re г = ^ . При этом, как указывалось на
стр. 278, следует учесть, что существует вполне определенное зна-
значение параметра Я = Яо, при котором интеграл по контуру S обра-
обращается в нуль. Последнее имеет место, если вершина гA; Я) лежит
на продолжении симметричной стороны.
Ввиду центральной симметрии достаточно исследовать отобра-
отображение границы для двух смежных интервалов, например и < Я и
Я < и < 0, а затем с помощью подстановки »* = — рассмотреть
интервалы 0 < и < 1 и 1 < и. Чтобы перейти к эллиптическим
интегралам в обычных обозначениях, положим
Тогда у. @ < у. < 1) есть модуль эллиптического интеграла.
1. Сначала в интервале и < ?. произведем разложение
Ji=Ji + Jt, E.3.19)
а затем в интеграле Jf положим
u, y=4 = zfl — и,
тем самым
^k = ifX^^u; E.3.20)
f-7=-^=^== . E.3.21)
J V(-u)(i-u)a-u)
С помощью подстановки
х- 1
u = -2- —r- • E.3.22)
X2 COS2 <p v
и учитывая равенство
J COS2 <р ]/1 — X2 Sin2 <р
получаем представление
E.3.23)
J" = — [tg^fl^-^sin2?) + F(x; у) — 2?(л:; <р)\ E.3.24)
где F(«; (р) и ?(х; ^) — эллиптические интегралы первого и второго
рода в нормальной форме.
5.3. Вычисление отображающей функции 307
2. В интервале X < и < 0 снова произведем разложение J'{ =
~ J{ + J'i и положим в интеграле J"
п, f^l = fu -/., E.3.25)
так что
o_(^ + A + A) J -¦г_1''_-_ -
. E.3.26)
У(_и)A_и)(ы-А)
д
С помощью подстановки
и = -?со*<р E.3.27)
получаем представление
J" = - [— tg^yi — *'2sin2<p — F(y.'; <p) -\- 2E(y.'; <р)]. E.3.28)
В частности, в случае контурного интеграла J внеинтегральный
(S)
член обращается в нуль, и мы имеем (см. стр. 299)
От знака этого выражения зависит, получаем ли мы первую или
третью область рис. 81. Для второй области модуль у. определяется
из уравнения
2е(у', || - Fix', %\ = 0. E.3.30)
Для нормированной отображающей функции, согласно предыду-
предыдущему, имеют место следующие представления в четырех интер-
интервалах:
1. и < Я: г(щ Я) = г{1; Я) - \ ^LllI^*^? + *<*. ?>.=?*<*, »>
X2 COS2 <f
2i
F\x'. ~\ -
х2
u = — —г- cos2 w.
20*
308
§ 5. Двукратные прямолинейные четырехугольники
Применяя преобразование E.3.4)
мы переходим от 1-го интервала (и < /.) к 3-му @ < и* < 1) и от
2-го Q. < и < 0) к 4-му A < и*) (центральная симметрия), причех
в обоих случаях
~z(u*; /) = z(u; ).) — z(a; л)
E.3.3П
5.4. Вычисление отображающей функции в частных случая:.
Многоугольники с разрезами.
Пример 4. Четырехугольники
0<Л<!
Рис. 82.
Отображение полуплоскости Im w > 0 на многоугольник
внутренними углами
ЬЯП = In, bfpi = -7Г, Ь
осуществляется интегралом E.1.4) с
g Л,
= О
Отображающий интеграл принимает вид
W
j» = Г.. w -} -= d
J [' Ш3 I/Ш - 1
E.4.
5.4. Вычисление отображающей функции
309
Для нормировки следует вычислить интеграл по контуру S
(рис. 49, 53, 57), обходящему точку ш = оо в отрицательном направ-
направлении. Так как этот интеграл равен 2т (вычет в точке w = оо равен
— 1), то нормировка отображающей функции
, л. Jl 1 С W - I
z(w: л) = = — I
V .7 2jt/J ]/„,(„,_!)
dw
E.4.2)
приводит к тому, что ширина полосы, соответствующей окрестно-
окрестности точки ш = оо при отображении полуплоскости Im w > 0,
l
равна - .
Вычисление отображающего интеграла дает
z(w; ;.) = '1 [log (Уш -j- У^= i) - Я |/~ J -1-] , E.4.3)
причем аргументы квадратных корней и мнимая часть логарифма
лежат в интервале @, л:). Трем интервалам изменения веществен-
вещественного параметра Я соответствуют три области, изображенные на
рис. 82.
О I
Плоскость Л
Плоскость
Рис. 83.
Легко выяснить соответствие между вещественной осью w и
границей многоугольника, даваемое функцией E.4.3). Во всех трех
случаях получаем сначала
ю < 0,
log
w = е 2 У—и,
f Ш — 1 =
—[) = у + log (/=П + УТ^ТЦ)
так что отображающая функция имеет постоянную вещественную
часть, равную ^ . При 0 < ш < 1 логарифм является чисто мнимым
и, стало быть, отображающая функция вещественна; при т > 1
310 § 5. Двукратные прямолинейные четырехугольники
корни и логарифм вещественны, так что отображающая функция
принимает чисто мнимые значения.
Геометрическое место вершин z(x; ?.) образует треугольник1
(рис. 82, 83), граница которого при помощи функции
С(А) = z(/; Я) = ^ [log (V)." + УГ-1) — УЩ "[)] E.4.4)
переводится в вещественную ось /. Это легко установить, записав
функцию треугольника в виде интеграла Шварца—Кристоффеля:
из которого весьма просто можно получить разложения функции
С(Я) в ряды. Обращение этой функции дает решение задачи о пара-
параметрах.
Пример 5. Четырехугольник [2, — '- , ' , 0|*.
Отображение полуплоскости Im ш > 0 на многоугольник с
внутренними углами
О О
Ь}п = 2я, 6рЯ = — - я, Ьхж — ^ п, 5,^ = 0
осуществляется интегралом E.1.4) с
б;. = 0, 0О = §, 01 = 1, 0^ = 0.
Отображающий интеграл принимает вид
^ dw. E.4.5)
Для нормировки следует вычислить интеграл по контуру S (см.
рис. 49), обходящему точку ш = « в отрицательном направлении.
Так как этот интеграл равен 2тп (вычет в точке w = °о равен —1),
то нормировка отображающей функции
z{w; Я) = r = Yn.J [/-- ш- йш E.4.6)
(S) 1
приводит к тому, что ширина полосы, соответствующей окрестности
точки w --= оо при отображении полуплоскости Im ш>0, равна -z .
1 По рис. 56 легко убедиться в том, что разрезообразные выступы в этом
случае следует опустить, и поэтому при Я > 1 начало координат неподвижно.
Это вызвано тем, что вершина гр.; /.) является концом разреза.
5.4. Вычисление отображающей функции
311
Вычисляя отображающий интеграл, получаем
причем аргументы квадратных корней и мнимая часть логарифма
лежат в интервале1 @, тг). Трем интервалам изменения веществен-
вещественного параметра А соответствуют три области, изображенные на рис.
84. Области, соответствующие интервалам 0<А<1 и А > 1,
не однолистны и поэтому не так важны для приложений, как пер-
первая, соответствующая интервалу А < 0. Для полного исследования
задачи о параметрах желательно иметь представление о всех типах
многоугольников, получаемых перестановкой вершин.
Рис. 84.
Геометрическое место вершин г(А; А) образует треугольник*
(рис. 84, 85), граница которого посредством функции
ад - <;.; /) - i. [log (/х + ух=1) - ^ f-^1] E-4.
8)
О I
Плоскость Л
Рис. 85.
1 Исследование соответствия границ проводится совершенно так же, как
в предыдущем примере.
2 Ср. сноску на предыдущей странице.
312 § 5. Двукратные прямолинейные четырехугольники
переводится в вещественную ось л (этот треугольник также является
многолистным). Это соответствие легко установить, записав функ-
функцию треугольника в виде интеграла Шварца—Кристоффеля
EА9)
из которого весьма просто получаются разложения функции С(Я) в
ряды. Обращение этой функции дает решение задачи о параметрах.
Пример 6. Четырехугольник |2, — 1> s' — о •
Отображение полуплоскости Im ш > 0 на многоугольник с
внешними углами
3 1
д,тс = Ъг, d,ft — —л, d]7i = 2 л, Ь^п = — -хЛ
осуществляется интегралом E.1.4) с
0д = 0, б0 = 1, в1 = - , бте=2-
Отображающий интеграл принимает вид
JT - JV1! ^- dw- E-4.Ю)
1
Для нормировки следует вычислить интеграл по контуру S
(рис. 49), который сводится к простому обходу вокруг точки ю = 0.
Следовательно, значение интеграла J равно умноженному на 2тп
(S)
вычету в точке ш = 0, т. е. равно1 i -1— . Таким образом, имеем
2(ш; А) - 4 - -
(S)
вследствие такой нормировки отображающей функции расстояние
от стороны многоугольника, соответствующей интервалу 0 < ю <
< 1, до разреза, являющегося образом полуоси ш < 0, равно 2 -
1 Разложение в ряд подинтегрального выражения дает
}.
w — X
m 1 —_- = i
2
}.
5.4. Вычисление отображающей функции
313
Заметим, что при /. = —2 нормировка теряет смысл, так как рас-
расстояние между параллельными сторонами, измеряемое интегралом
J, равно нулю (ср. рис. 86). Многоугольные области, соответствую-
(S)
щие интервалам 0 < ). < 1 и А > 1, не однолистны и указаны на
рис. 87 лишь ради полноты изложения.
Л<-2
А=-2
Z(K;X)
Рис. 86.
-2<\<0
Вычисляя отображающий интеграл, получаем
1 +
»<uU)=-I[
(А + 2) w
w— 1 —
причем аргументы квадратных
корней и мнимая часть лога-
логарифма лежат в интервале @, я).
Легко установить соответ-
соответствие границ, задаваемое функ-
функцией E.4.12). Для ш < 0 аргу-
аргумент логарифма отрицателен,
так как
уш—1 = с
и, следовательно,
1 п l + i ]/w~- 1
—-: log —-—'-г-=
— и
Si
1 - i
E.4.12)
Рис. 87.
мнимая часть отображающей функции постоянна и равна \ ..
При 0 < ш < 1 аргумент логарифма положителен, и поэтому
314
§ S. Двукратные прямолинейные четырехугольники
отображающая функция чисто мнимая. Наконец, при ш > 1 имеем
—- log - •-^J~^rr = - arc tg УйГ— 1,
и отображающая функция вещественна.
Геометрические места вершин z(A; А), изображенные на рис. 86,
87, образуют треугольник (рис. 88), граница которого отобража-
отображается в вещественную ось А посредством функции
E.4.13)
Плоскость
О 7
Плоскость л
ГО)
Рис. 88.
(Этот треугольник также неоднолистен.) Это соответствие легко
установить, записывая функцию треугольника в виде интеграла
Шварца—Кристоффеля:
E.4.14)
из которого весьма просто получаются разложения в ряды1 для
функции ?(А). В конкретном случае, когда z(A; А) задается численно,
обращение этой функции дает решение задачи о параметрах.
Пример 7. Четырехугольник B, —1 — 6,2, — 1 -\- 6)* (разрез с
изломом).
В качестве предельного случая двукратных однолистных четы-
четырехугольников мы получаем следующую область, важную для
приложений: всю плоскость с двумя разрезами вдоль двух лучей.
1 Обратим внимание на полюс подинтегральной функции в точке /. = — 2,
в которой вычет равен нулю. Это означает, что граница многоугольника в
плоскости г в случае ). = — 2 проходит гладко через бесконечно удаленную точку,
как показывает рис. 86, если объединить геометрические места точек "(/; Д).
5.4. Вычисление отображающей функции
315
Такой многоугольник имеет внешние углы
Ькп
2%, e«* = —A—0)я,
oZfl;A)
2тг, Ьол = — A + в) п,
причем вп есть угол пересе-
пересечения одного разреза с про-
продолжением другого (рис. 89).
Преобразуя бесконечно уда-
удаленную точку пересечения этих
разрезов в конечную точку,
мы получаем «ломаный раз-
разрез», изображенный на рис. 93
(плоскость г*). Однако для вы-
вычисления отображающей функ-
функции первое расположение раз-
разреза (рис. 89) предпочтительнее.
Отображение полуплоскости
Im w >0 на эту область дается интегралом E.1.4) при
0.: = 01 = 0, в0 = 1 + в, 0те = 1 - в.
Получаем
2 sin#?
Рис. 89.
? = Г ш-<в+2> (ш — 1) (ш — /) dm =
A -j- 8) + w A + Я) A - 0'-) - ;.8 A - 0)
в A -
1 4- е + /(.1
в"(Г-~в*)
E.4.15)
Для нормировки следует вычислить интеграл по контуру S,
который начинается в точке w = 1 и обходит один раз точки w = X
и w = 0. Так как функция ш—(в+1) при положительном обходе
вокруг нуля приобретает множитель е~2/я9, то контурный интеграл
равен
(S)
ш_ 1} (ш _ А) dw =
E.4.16)
Рис. 90.
316
§ 5. Двукратные прямолинейные четырехугольники
а нормированная отображающая функция принимает вид
X
-9)
-0)
i]; E.4.17)
здесь Я — неопределенный параметр. Соответствие границ очевид-
очевидно: в зависимости от того, является ли ю отрицательным или
положительным, мы получаем точки вертикального разреза или
наклонного, образующего с горизонталью угол I в + - Ьг (рис. 89).
Концы разрезов лежат в точках гA; Я) = 0 и
Я A -f- 0) Л ,, . .„.
Если область задана, то численное значение г(Я; Я) = ^ + ia известно
и параметр Я < 0 определяется как функция от а решением уравне-
уравнения E.4.18).
о/
Плоскость Л
Рис. 91.
Согласно общим рассуждениям п. 5.1, функция %()¦;)?) есть-
функция треугольника, т. е. отображает верхнюю полуплоскость
Я на внутренность кругового треугольника, изображенного в общем
случае на рис. 59. В данном случае, подставляя значения вели-
величин б;, в0> 01; в^, убеждаемся, что треугольник является прямолиней-
прямолинейным1 (рис. 91). Он состоит из полуплоскости Re Я < 2 и лежащего
на ней сектора с вершиной в точке
г(оо; со) = — j etg лО.
1 Интервалам 0</.<1 и Я>1 соответствуют многолистные области
с разрезами в плоскости г, которых мы подробно не рассматриваем.
5.4. Вычисление отображающей функции
317
Эту область легко получить из рассмотрения треугольника с внут-
1 3
ренними углами ^,0,^ из п. 3.1 (рис. 20), которому соответствует
отображающая функция C.1.6):
+ ут) i-eyt
плоскость t
Рис. 92.
Отражая этот треугольник относительно дуги, служащей образом
отрицательной полуоси, получаем вторую область, изображенную
на рис. 92, которая отображается функцией С@ на верхнюю полу-
полуплоскость т, т = У1, с точками ветвления т = —1, 0, 1. Если пере-
перевести точки ветвления дробно-линейным преобразованием т =
= yj-\ в точки 0, 1, оо, то достаточно сдвига и преобразования
подобия для отображения этой области на область, изображенную
на рис. 91.
В этом состоит геометрическое доказательство того, что функ-
функция г(А; X) выражается через уже известную функцию треугольника
?@ формулой
что также непосредственно проверяется аналитически.
Представление E.4.19) подсказывает нам переход посредством
преобразования
Ismnde
E.4.20)
- *•" ' '•> ' ' z* (w; A)
г*, на которой получаемая область принимает вид
на плоскость
внешности разреза с изломом, целиком лежащего в конечной части
318 § 5. Двукратные прямолинейные четырехугольники
плоскости (рис. 93). Отношение / длин сторон есть естественная
геометрическая постоянная этой области, которая связана с при-
приведенной выше константой а равенством1
- = la sin лв + cos яО.
Теперь один конец разреза лежит в точке
z* = 1, а другой — в точке
г*{Х;Х) = len°l = ?-х -^ ' . E.4.21)
Плоскость z* 1Л -г ) J
Рис 93 Обращая функцию треугольника С, находим Я
как функцию отношения длин /, чем и решается
задача о параметрах.
Трехкратный прямолинейный четырехугольник @, 0, 1, 0)*.
Единственным прямолинейным трехкратным четырехуголь-
четырехугольником является полоса с разрезом вдоль некоторого луча, парал-
параллельного ее краям (см. рис. 94). Отображающий интеграл записы-
записывается в виде
С
[^~^Т dw; E.4.22)
1 Д О '
\ва Плоскость to
1
Плоскость ?
Рис. 94.
постоянный множитель С определяется заданием ширины а полосы,
соответствующей окрестности точки ветвления w = Я. Согласно
А A3.2.14), эта ширина численно равна половине вычета в точке
ш = Я, т. е.
1 В плоскости z величина / есть отношение расстояний концов разреза от
точки их пересечения — A — t ctgnO) (рис. 89).
6.1. Четырехугольники в круговых сетках
31 9-
Параметр л определяется соответственно этому из условия,
что в окрестности точки ш = 0 направленная ширина полосы (т. с,
половина вычета в точке ш = 0) равна
— aOi = ЫС -„- = ia .
E.4.24)
Таким образом,
А = в-^- . E.4.25)
Следовательно, отображающая
функция имеет вид
w - 1
w (ш — Л)
dw =
E.4.26)
А) = " log [w-°(ew + 1 — в)]
Рис. 95.
Переходя к показательной функции
z* = еа = vr-e(Qw + 1 — 0),
E.4.27)
получаем область, представляющую собой полуплоскость с разре-
разрезом вдоль некоторого луча. Это отображение рассматривалось в
п. 2.2; посредством сдвига и преобразования подобия полученная
там отображающая функция B.2.8) (соответственно область, изобра-
изображенная на рис. 17) переходит в E.4.27) (соответственно в область на
рис. 95). (См. также вывод общей формулы А A4.1.9), рассмот-
рассмотренный в п. А, 14.1.)
§ 6. Другие многоугольники, отображающие
функции которых могут быть найдены полностью
6.1. Четырехугольники в круговых сетках. Для общих круговых
четырехугольников задача о параметрах уже не разрешима в явном
виде, как в случае прямолинейных четырехугольников. Кроме двой-
двойного отношения точек ветвления, здесь фигурирует еще один акцес-
акцессорный параметр /30 уравнения Шварца А A2.1.21), определение
которого в случае произвольных круговых четырехугольников
возможно лишь приближенно. Задача полностью решается, однако,
для круговых четырехугольников в полярных сетках. Согласно
320
§ б. Другие многоугольники
п. А, 14.1, такой четырехугольник преобразуется в прямолинейный
функцией W — log г.
Все внутренние углы четырехугольников в полярных сетках
должны быть кратными |-. Наоборот, если все внутренние углы
являются нечетными кратными1 ^, то четырехугольник можно
вложить в полярную сетку. Исследуем подробнее2
/"ill з^о
круговой четырехугольник U , - , - , - .
Круговые четырехугольники, изображенные на рис. 96, с внутрен-
внутренними углами
функцией
(г)
W = log z
F.1.1)
(z)
Рис. 96.
1 Четырехугольники с внутренними углами, четными кратными лг/2>
исследованы в работе: Koppenfels W., Konforme Abbildung aus-
i?ezeicluH'tcr Kreisbogenvierecke, S.—B. bayer. Akatl. Wiss., math, naturwiss.
Kl., 1943, 327—343.
2 Cm. Koppenfels W., Konforme Abbildung besonderer Kreisbogen-
Kreisbogenvierecke, J. reine angew. Math., 1§1 A939), 83—124.
6.1. Четырехугольники в круговых сетках 321
отображаются на изображенные под ними прямолинейные пяти-
пятиугольники
Infill]* (п I - - 1\*
I U' 2 ' 2 ' 2 ' 2J И I U' 2 ' 2 ' 2 ' 2) '
При этом граничной точке z = О соответствует в плоскости W
добавочная вершина на оо с внутренним углом пЬ* = 0. Окрестность
этой вершины имеет форму горизонтальной полуполосы шириной
п, что соответствует полукруговой окрестности точки z = 0 в
плоскости z. Отсюда следует условие для вычетов [ср. А A4.1.4)]
в соответствующей точке1 да = е0 = е, так что функция W(w) имеет
вид
— -. F.1.2)
J Y(w - е,) (ш - е2) (ш _
Исследуем сначала зависимость отображающей функции от
параметра е, закрепив для этого остальные особые точки. Чтобы
подчеркнуть эту зависимость, обозначим интеграл F.1.2) через
W(ro; e), а вершины через
W.(e) = W(et; е). сш>
1. Значениям е < ех соот-
соответствуют пятиугольники
того же вида, что и изо-
изображенный на рис. 97. Гео- ,
метрическим местом вер- i
шин Wr(e) является полу- \
прямая
а вершин Ws(e) — положи- —* •
тельная мнимая полуось '
Re W3 = 0, Im W3 > 0. Рис. 97.
F.1.4)
2. При переходе к значениям ех < е < е2 нужно опять следить за
тем, чтобы подинтегральная функция была однозначной (ср. соот-
соответствующие рассуждения в п. 4.1 и 5.1). Поэтому точку да = е
следует перенести в интервал (е1; е^ обходом точки да = ех через
верхнюю полуплоскость да. Тогда граница в плоскости да выглядит
так, как указано на рис. 98, а соответствующая кривая в плоскости
1 В отличие от принятых ранее обозначений мы обозначим этот параметр
буквой е, для того чтобы отличать его от остальных особых точек е,..
21 — 6002
ill
§ 6. Другие многоугольники
W ограничивает прямолинейный пятиугольник с разрезообразным
выступом. Геометрическим местом вершин W^e) (концов разрезо-
образных выступов) является интервал
F.1.5)
IVJ)
t
n
1
i
w,
L
w,
fw) n
0- 98-
-n
(«настоящая» вершина пя-
пятиугольника обозначена
через W*), а геометри-
геометрическим местом вершин
Wg(e) — дважды прохо-
проходимый интервал
ImW3 =
( ' ' '
3. Аналогичным об-
разом совершается пе-
реход параметра в интер-
вал ег < е < е3. Разрезо-
образный выступ на рис.
98 приобретает излом
(рис. 99). В качестве ге-
геометрического места вер-
вершин Wx(e) получаем два-
дважды проходимый интер-
интервал
О < Re W, < Qlt
а вершин
рвал
2»,
W3(e)
i
инте-
инте= 0,
Д
Ir
tl if/ „ „ 4. Наконец, на основе
-_-*у-_^-_-_-_*. О - 2LTT
' тех же рассуждении рас-
Рис 99. сматриваются значения
е > е3 (рис. 100). Геомет-
Геометрическое место вершин Wa(e) лежит на полупрямой
Re Wi = 0, Im Wx< —2n, F.1.9)
а вершин W3(e) — на полупрямой
Re W3 > 0,
Im
= —п.
F.1.10)
6.1. Четырехугольники в круговых сетках
323
Когда е пробегает вещественную ось, Wj(e) описывает гранич-
ую кривую, изображенную на рис. 101. Таким образом, верхняя
олуплоскость е отображается посредством Wx(e) на прямолиней-
ый пятиугольник 12> g' 2,^, —2|' состоящий из четверти плоскости
яг
Рис. 100.
-at
-Ил
Плоскость е
ег
Рис. 101.
г разрезом. Ввиду этого функцию Wx(e) можно представить в виде
интеграла Шварца—Кристоффеля1
W&) = С» Г-
: — e2) (e — e3)
F.1.11)
~де е0 — образ конца разреза в плоскости Wx. Три постоянные
"i, С2 и е0 определяются заданием вершин пятиугольника на рис.
101:
—in,
= —2m,
—2in. F.1.12)
1 Это соответствует тому известному факту из теории эллиптических
¦штегралов, что полный эллиптический интеграл третьего рода выражается
герез неполные интегралы первого и второго рода.
324
§ 6. Другие многоугольники
Отсюда следует, что
= —in,
С, = —in f
/ J У(в -
ег) (е - e2) (e - e3)
de,
F.1.13)
¦J-
ede
-e3)/ J f (e - et) (e - e2) (e - ,
/(e - ej (e - e2) (e .
При таких значениях постоянных, обращая F.1.11), получим урав-
уравнение для определения величины е в зависимости от е„ и Wv Анало-
Аналогичную формулу можно вывести для W3. Интеграл F.1.11) без
труда выражается через эллиптические интегралы первого и второго
рода в нормальной форме. Мы не будем приводить здесь точной
формулы, а ограничимся формой, более удобной для вычислений.
Вычисление интеграла. Интеграл F.1.2) есть эллиптический
интеграл третьего рода. Для его вычисления удобно перейти к
эллиптическим функциям. Положим
-J=
dw
— eO (ш - es) (ш - e3) / J ]/(ш - «^(ш- е2) (ш - e3)
F.1.14)
Плоскость w
//////////////////AS /////////
Функция и(да) отображает верхнюю полуплоскость » на прямо-
прямоугольник (см. п. 4.2, пример 1), нормированный так, что точкам
ю = оо и w = е^ соответствуют
о вершины v(oo) = 0 и v(e^) = ^ •
Пусть остальные две вершины
расположены в точках г>(ег) =
= —y~ и v(es) = | , так что
прямоугольник покрывает об-
область
/
/.
* ' '/
'<„„„Л Ь,„
т.
0
'/ /
,,,,„,,,,^
/ + т
2
1
/
Re v =s ^ >
F.1.15)
Рис. 102.
Тогда обратная функция к>(г?)
двоякопериодична с периодами
1 и т. Отражения относительно двух параллельных сторон переводят
точку »вв+ 1, соответственно вв + т, тогда как соответствующие
отражения в плоскости w возвращают точку на прежнее место
6.1. Четырехугольники в круговых сетках 325
(ср. с рассуждениями в начале п. А 12.1). Этими отражениями вся
плоскость v разбивается на конгруэнтные прямоугольники, кото-
которые, располагаясь в шахматном порядке, соответствуют то верхней,
то нижней полуплоскости (рис. 102), так что каждой точке плоскости
v соответствует одна и только одна точка плоскости ш. Кроме
того, w(v) — четная функция:
го(— v) = w(v); F.1.16)
это доказывается зеркальным отражением относительно сторон
0,\ и 0,1 .
Подстановкой F.1.14) интеграл F.1.2) приводится к виду
v(w)
W(w) = Г , f(a), ч dv. F.1.17)
4 ' J w(v) — w(a) ч '
0
Здесь а = v(e) есть образ точки w = e в плоскости v. Под-
dW ,
интегральное выражение — можно определить, не зная функции
w(v). Действительно, функция — имеет в точке v = а простой
полюс с вычетом, равным 1, и в силу F.1.16) в точке v — —а полюс
с вычетом, равным — 1. Других полюсов в прямоугольнике пери-
периодов
< Im v =
~ dW
нет. Этим -j- определяется с точностью до аддитивной постоян-
постоянной. Так как ш@) = оо и, стало быть, в точке v = 0 выражение
dW е-
—г- обращается в нуль, то эта постоянная также определяется.
-, -- dW
1аким образом, для —г- получается следующее представление
через fi-футции:
5 = |(,-a|T)-|i(D + a|r) + 2|(aJr)> F.1.18)
откуда
4
Переходя к z = ew, получаем, наконец, отображающую функцию
_
»1(a+v)
где v(w) определяется из F.1.14).
326
§ б. Другие многоугольники
Соответствие границ. Интервалам (—оо, ех), (е15 е^, (е2, е^}
(е3,оо) в плоскости w соответствуют стороны 0, ^, -, --^
—2—, 2 й г» ^ в плоскости и. Перечисленным выше четырем пол妕
жениям точки ш = е соответствуют четыре различных положе'""
точки v = а на сторонах прямоугольника. Рассмотоим снг-
случай, когда а лежит на стороне О, ^ > т. е. е < ех (рис.
Плоскость v
Плоское)
Рис. 103.
1. На отрезке 0, a W отрицательно, так что этот отрезок ото».-
жается на полуось W < 0. Корень v = а обходится по мал*,
полуокружности в отрицательном направлении, в силу чего лои
рифмическое слагаемое в F.1.19) получает приращение —in
Тогда отрезок а, - отображается на полупрямую
Re W < Re
a Wx принимает значение
Im W = —<тг,
+
J- (a).
F.1.21
Это вполне соответствует интегральному представлению F.1.11
для Wlt в чем можно убедиться непосредственно, применяя г
интегралу подстановку F.1.14).
2. На стороне ^, "*"т положим о = к + "*» так что F.1.19
примет вид
F.1.22
Два последних слагаемых в правой части этого равенства чисп
мнимые. Для Wjj получаем
W2
т ^- (a).
F.1.23
6.1. Четырехугольники в круговых сетках 327
3. На стороне "Г т, \ положим v = ~L r + и и получим
откуда
W3 = in Bа — 1) + т J- (а). F.1.25)
4. На стороне ^, 0 положим v = | + ш и получим
l*L> + ftiji-(a). F.1.26)
\« "Г la) "l
Точно так же исследуются остальные три положения точки
ш = е, соответственно точки о = а.
Определение параметров. Отображающая функция в форме
F.1.20) явно зависит от параметров а и т, которые следует опре-
определить по геометрическим постоянным четырехугольника. Начнем
с того случая, когда е < ех, а принадлежит стороне 0, ^; положим
^¦ = оиг, Wi + ад = log R = jfcr; F.1.27)
тогда и и |5зг — углы между противоположными сторонами
четырехугольника, определенные по формуле А G.5.5) (см. рис. 96).
Исключая величину ^-(р) из F.1.22) и F.1.26), получаем
а = 1A +а + itP) F.1.28)
и
ря = ^-- I 2 1 = д~ I о 1 ' ' ' ^
Из этих уравнений следует определить значения а и т. Основное
затруднение при нахождении параметра т состоит в том, что зави-
зависимость этого параметра от геометрических постоянных четырех-
- угольника «в целом» неизвестна. Решение уравнения F.1.29) «в
малом» численными методами всегда возможно и удобно в силу
быстрой сходимости рядов для ^-функции. Хорошее приближение
получается уже в случае, если в разложении ^-функции ограни-
ограничиться лишь первым членом
~(v)=nctgnv + .... F.1.30)
328 § б. Другие многоугольники
Подставляя сюда значение аргумента из F.1.29), получим прибли-
приближение для т
fe^J F.1.31)
Приближение F.1.30), а следовательно, и F.1.31) тем точнее, чем
больше [т(, и поэтому должно быть /S <? а. Если это не так, то сле-
следует перейти к случаю е > е3. Более точные разложения в ряды
содержатся в уже упомянутой работе Коппенфельса (см. сноску
2 на стр. 320).
Для определения параметров при ином положении точки е и
соответственно а мы исходим из значений Wx и Ws, определенных в
F.1.3)—F.1.10). При этих значениях формулы F.1.21) и F.1.25) оста-
остаются справедливыми. Так же, как и в F.1.27), следует связать эти
величины с постоянными четырехугольника1, указанными на рис.
96 (т. е. с углами между противоположными сторонами), а фор-
формулы F.1.28) и F.1.29) преобразовать к новым постоянным.
Второй случай: е± < е < е2.
ост = i (W1 + in), fa = Wz,
a-i(l—i/8 + ат),
Приближенное значение для t, пригодное при a <§ /?, здесь равно
Третий^ случай: е2 < е < е3.
\ [а + A + Щ г],
Ф)
Получить простую приближенную формулу, подобную F.1.31),
в этом случае не удается. Ограничиваясь первым членом разложе-
1 Заметим, что в случаях е2 < е < е3 и е > е3 соответствующие четырех-
четырехугольники зеркально-симметричнм четырехугольникам, изображенным на рис.
96. Эта симметрия не влияет на обозначение геометрических постоянных.
6.1. Четырехугольники в круговых сетках 329
ния ^-функции, получаем трансцендентное уравнение
Р Pbs 4е1ЯТ sin л (а + i/St), F.1.33)
которое служит для нахождения приближенных значений т при
Четвертый случай: г > е3.
Приближенное уравнение принимает здесь вид
пригодный при /3 $> а.
Случаи 1 и 4, соответственно 2 и 3, приводят к одинаковым
типам четырехугольников, с точностью до зеркального отражения,
причем одним и тем же геометрическим постоянным соответствуют
взаимно обратные значения |rj. В теоретических исследованиях
можно ограничиться двумя случаями; на практике же будем выби-
выбирать тот случай, который приводит к большему значению |т|.
Связь с дифференциальным уравнением Шварца. Функция z(w)y
отображающая верхнюю полуплоскость w на круговой четырех-
четырехугольник (о» г' 2» ^1 ' УД°влетв0Ряет уравнению Шварца
[] 5
8 5
Согласно АA2.2.8), z(w) представима в виде отношения двух
линейно независимых решений (рх(ш) и <р2(го) уравнения
±Щи>)<р = 0. F.1.36)
Преобразуем это уравнение к новой независимой переменной
dw
и = f
J
- ei) (ш — е2) (ш - е3)
F.1.37)
Эта величина лишь постоянным множителем отличается от вели-
величины v(w), определенной равенством F.1.14). Если выбрать особые
330 § б. Другие многоугольники
точки ev так, чтобы выполнялось условие ех + е2 + es — 0 (что
всегда возможно), то обратная функция к ю(и) совпадает с jp-функ-
цией Вейерштрасса
а>(и) = №;т1>а?, тг = т. F.1.38)
В качестве новой зависимой переменной вводим функцию
4
у(и) = }/(ш — в1) (ш — е2) (го — е3)<р(ш). F.1.39)
е уравнение при этом преобразуется в уравнение Ляме в
ейерштрасса1:
V" —[п(п + 1) ftu) + А] у = 0 f n = в — i) . F.1.40)
F.1.41)
При 5=2 уравнение принимает вид
•его фундаментальными решениями являются функции
_ е+У2и _ —V~Au
Таким образом, отображающая функция имеет вид
z = е2Па. F.1.42)
Так как функция и{ю) отображает верхнюю полуплоскость на прямо-
прямоугольник
О < Re iz < ^- , 0 < Im iz <
то в качестве наиболее общего четырехугольника вида I« » г » 2' 2)
мы получаем сектор кругового кольца (или область, в которую он
переходит при дробно-линейных преобразованиях). Противополож-
Противоположные стороны образуют углы
«2 = Щ?1 . F.1.44)
Этими двумя величинами однозначно определяются параметры
дифференциального уравнения F.1.41): отношение периодов т и
акцессорный параметр А. Таким образом, в этом случае зависи-
зависимость параметров от геометрических постоянных многоугольника
полностью выясняется.
1 См., например, Halphen, Traite des fonctions elliptiques, II, Paris, 1888.
6.1. Четырехугольники в круговых сетках 331
В случае А = О уравнение F.1.41) имеет решения
Wi = u> % = 1» z = и, F.1.45)
и соответствующий круговой четырехугольник есть прямоугольник
F.1.43).
В случае д =-^, п = 1, который изучен сравнительно подробно,
уравнение F.1.40) записывается в виде
у>" - [2<р(и) + jp(a*)] ip = 0, А = jp(a*). F.1.46)
Решениями этого уравнения служат функции
«,, = а{-а* - ц> e«C(«*> » = а(-а* + ц> е-«С(««) (в 1 47)
и отображающая функция принимает форму
«ка» д) F.1.48)
z
<r(a* + u)
выраженная через ^-функции, она в точности соответствует форме
F.1.21). Таким образом, связь между параметрами уравнения и
геометрическими постоянными многоугольника выяснена и в
этом случае. В частности, при переходе с плоскости и на плоскость
v получаем соотношение
а = —, F.1.49)
так что акцессорный параметр А тесно связан с точкой v = a,
которая соответствует критической точке z = 0 кругового четырех-
четырехугольника.
Если точка а* стремится к одной из точек и = ^-, -1 ^ *"*, ~
j т. е. а стремится к v = ^, —*^—, ||, то решения уравнения F.1.47)
совпадают и принимают вид
V = yjp(u) - e, , i= 1,2,3. F.1.50)
Согласно формуле А A2.2.6), отображающая функция z(ro) прини-
принимает форму
z=cL^-=C*f- _=g==F==. F.1.51)
Соответствующими многоугольниками будут прямолинейные четы-
/• 1 1 1 31» fi l 1 з\» /1 1 1 з\»
рехуГОЛЬНИКИ ТИПОВ — ^ 2, 2'2 ' 2'~~2'2'2 ' 2'2'~'2) '
изученные подробно в примере 2 п. 4.2. Этим заканчивается изу-
изучение предельных случаев.
332
§ б. Другие многоугольники
Следует также заметить, что от этого случая можно перейти
к круговым четырехугольникам1 с углами ^, ^, -?-, -^-(в произволь-
произвольном порядке). Исследования совершенно аналогичны; подроб-
подробности см. в цитированной работе Коппенфельса.
6.2. Звездчатые многоугольники. Прямолинейные многоуголь-
многоугольники, имеющие более четырех вершин, можно полностью изучить
при наличии определенной симметрии. Один класс таких много-
многоугольников — мы назовем их звездчатыми — был изучен Рингле-
бом2, хотя и без решения задачи о параметрах. Речь идет о централь-
центрально-симметричных многоугольниках с 2л вершинами, преобразую-
преобразующихся в себя при повороте на угол — (см. рис. 104). Вершины много-
многоугольника распадаются, таким образом, на две группы по п экви-
эквивалентных вершин. Если угол первой группы равен вл, то в силу
А A3.1.13) угол второй группы должен равняться
\l-\~by. F.2.1)
Плоскость w
Плоскость z
Рис. 104.
Этот многоугольник, согласно сказанному в п. А 11.1а, следует
отобразить функцией w(z) на единичный круг так, чтобы центр
симметрии (т. е. точка z = 0) перешел в начало координат w = 0.
При этом всегда можно добиться того, чтобы вершины с углами
вл отобразились в точки
2я/
0,
F.2.2)
1 Таким же образом двумя зеркальными отражениями можно перейти
3
х круговым четырехугольникам с четырьмя углами величины — л (внешность
сектора кругового кольца).
2 R i n g I e b F., Ober die konforme Abbildung von Polygonen, Diss. Jena,
1926. <
6.2. Звездчатые многоугольники
333
Остальные вершины перейдут в точки
w = be2v+\, Ъ = е'", 0 < /} < ~
и интеграл Шварца—Кристоффеля примет вид
z=cUwn — I)9-1 (wn — bn) "
dm.
F.2.3)
F.2.4)
Если еще потребовать, чтобы особая точка ю = I преобразовалась
в точку z = 1, то получим
" — I)
-1
-6") "
F.2.5)
При этом в обоих интегралах следует выбрать одну и ту же ветвь
подинтегральной функции (однозначную в единичном круге).
Эту задачу об отображении вместе с задачей о параметрах
можно свести к отображению прямолинейных четырехугольников,
исследованному в § 4. Для этого произведем замену
It" = t, W = f,
dw=- t"~\
n
Тогда круговой сектор
. 2л
.F.2.6)
О <argro < — , \w\ < 1
F.2.7)
перейдет в круг, с разрезом
О <arg Kin, \t\<\
(рис. 105). Интеграл F.2.4) принимает вид
Плоскость t Плоскость w
Рис. 105.
F.2.8)
f_i)9-i(; —Я) п dt=CJ'o, А=Ь". F.2.9)
При вещественных значениях Я этот интеграл отображает верхнюю
полуплоскость t на прямолинейный четырехугольник с углами
[ср. D.1.1)]. Мы, однако, не будем рассматривать вещественных
334
§ 6. Другие многоугольники
значений, ибо |/[ = 1, причем мы ограничиваемся значениями
О «= arg Я < щ значения жеж arg \<bi приводят к звездчатым
многоугольникам, которые симметричны первым. Поэтому мы
должны осуществить переход от вещественных значений к значе-
значениям |А| = 1.
Как и в § 4, начинаем со значений А < 0. Им соответствует
четырехугольник 12 — в,—, в, — , изображенный на рис. 106.
При нормировке F.2.5) получаем, подобно D.1.4),
Jo
вершины, соответствующие точкам ? = 0и/= 1, суть
z(O;A) = O, z(l; А) = 1.
Геометрическое место вершин z(A; А) лежиткна луче
arg *(А; Я) = J .
F.2.10)
Плоскость z
Рис. 107.
А * -1 О + /
Плоскость t
При А = —1 четырехугольник имеет ось симметрии, которой в
верхней полуплоскости t соответствует единичная окружность
|f| = 1. Таким образом, верхняя полуокружность в плоскости t
отображается на треугольник, изображенный на рис. 107. Отра-
Отражая этот треугольник поочередно относительно сторон, соответ-
6.2. Звездчатые многоугольники
335
О
ствующих интервалам — I < t <0 и 0 < г < 1, получаем звезд-
звездчатый многоугольник, имеющий не только центральную, но и;
осевую симметрию. ,
Продолжим теперь функцию
z(>>.; А) аналитически на единичную _
окружность, исходя из точки А =
= —1. При этом граничная кривая
в плоскости t деформируется так,
как указано на рис. 108. Путем
дальнейшей деформации этой
кривой получаем единичный круг
F.2.8) с разрезом от t = 0 до
t = 1. В плоскости w ему соот-
соответствует круговой сектор F.2.7),
который при отображении z(ro)
переходит в одну из л конгру-
конгруэнтных частей звездчатого многоугольника. В частности, z(A; A>
есть вершина многоугольника, лежащая между вершинами z = 1
и z = е " . В силу постоянства величины угла эта вершина описы-
описывает дугу окружности, когда А пробегает единичную окружность.
Плоскость t
Рис. 108.
Плоскость z(X;\)
Плоскость А
Рис. 109.
На основании п. 4.1 мы знаем, что функция z(A; А) отображает
верхнюю полуплоскость А на круговой треугольник (рис. 109),
который, согласно D.1.9), имеет углы
. F.2.11)
336 § 7. Многоугольники, ограниченные дугами конических сечений
Так как углы лд0 и л6„о равны1, то этот треугольник симметричен
относительно окружности, являющейся образом единичной окруж-
окружности в плоскости А. Эта окружность симметрии и является гео-
геометрическим местом вершин z(A; А) звездчатого многоугольника.
Наоборот, если задано положение вершины многоугольника на
этой окружности, то соответствующее значение А == Ь" можно
найти, обращая функцию треугольника D.1.17). Таким образом,
задача о параметрах для звездчатых многоугольников полностью
решается.
§ 7. Многоугольники, ограниченные дугами
конических сечений
На основе теории, развитой в п. А 14.2, отображение много-
многоугольников, ограниченных софокусными коническими сечениями,
при помощи вспомогательного отображения W(z), переводящего
сетку конических сечений в декартову сетку, сводится к отображе-
отображению прямолинейных многоугольников. Образы «критических точек»
представляют собой дополнительные особенности отображения,
что приводит к увеличению числа параметров. Благодаря этому
полное решение задач на отображение значительно усложняется;
ниже мы рассмотрим лишь некоторые примеры, где отображающая
•функция выписывается явно.
7.1. Внешность и внутренность эллипса, гиперболы и параболы.
Пример 1. Внешность эллипса. Отображение круга на внешность
эллипса осуществляется функцией 2 |' + 7|> изученной в п. А 8.2.
Здесь мы найдем отображение верхней полуплоскости на внешность
эллипса на основе изложенного в п. А 14.2.
Пусть внешность эллипса лежит в плоскости z, а критическая
точка z = оо при отображении на верхнюю полуплоскость w пере-
переходит в точку w = i. Так как отображаемая область не содержит
ни других критических точек, ни вершин, то промежуточное отобра-
отображение W(w) можно, согласно А A4.2.7), записать в виде
~+С2. G.1.1)
Чтобы выполнялось условие А A4.2.6) для вычетов, следует поло-
положить Сх = +2. Возьмем Сх = +2; вычисляя G.1.1), получим
W(w) = 2 arc tg w + C2. G.1.2)
1 С точностью до знака величин <5Г, который несуществен.
7.1. Внешность"и внутренность эллипса, гиперболы и параболы
337
Функция W(ro) отображает полуплоскость Re w > 0 на прямо-
прямолинейную полосу1 ширины п. Положительная полуось w переходит
при этом в отрезок между точками W = С, и W = С, + п. Верхняя
полуплоскость w с разрезом от ю = i до w = оо отображается
поэтому на полуполосу
Re С2 — л < Re W < Re С2 + л, Im W > Im C2.
Если Im С2 > 0, то эта полуполоса функцией г = eos W отобра-
отображается на внешность эллипса с разрезом по ветви гиперболы от
z — оо до его границы; этот разрез соответствует разрезу в верхней
полуплоскости w (рис. ПО).
(W)
С,*Я
il
г
(w)
сг-я
1
1
1
1
1
(г)
Рис. ПО.
Определение постоянной С2. Поскольку вещественная часть С2
не влияет на форму эллипса, то С. можно считать чисто мнимой:
C2 = iV0, V0>0. G.1.3)
Тогда имеем
z = cos W = Y^~tf К1 ~~ w^ eh V<> ~ 2lW Sh Vo^ GЛ-4)
Здесь величины ch Vo и sh Vo равны длинам полуосей эллипса:
ch Vo -a, sh Vp = Ъ (а2 — b2 = 1). G.1.5)
1 См. п. А 8.3, рис. 57.
22 — 6002
338
§ 7. Многоугольники, ограниченные дугами конических сечений
Если требуется отобразить верхнюю полуплоскость на внешность
эллипса с произвольно заданными полуосями а и Ъ, то функцию
G.1.4) следует умножить на постоянную У а2— Ь2. Отображающая
функция запишется в виде
г =
G.1.6)
Пример 2. Внутренность эллипса. Внутри эллипса критическими
точками являются оба фокуса z = +1. Пусть при отображении на
верхнюю полуплоскость точки z = +1 и г = —1 переходят соот-
соответственно в точки1 ю = i и ю = —, где х' <1. Других критических
точек, как и вершин, в отображаемой области нет, так что можно
положить
Рис. 111.
Этот интеграл отображает правую полуплоскость Re w > 0 на
прямоугольник. Преобразуя его к нормальной форме Лежандра,
легко установить положение и размеры этого прямоугольника.
1 С помощью дробно-линейного отображения верхней полуплоскости и?
на себя можно достигнуть того, чтобы любые две внутренние точки приняли
указанное положение.
7.1. Внешность и внутренность эллипса, гиперболы и параболы 339
А именно для w = iu с вещественным и, применяя при 0 < и < 1
подстановку w = i sin <p, получаем
W(w) = i C,[F(/, ф) — K'(x)], W@) = —i C^»; G.1.8)
для 1 < и < —, применяя подстановку1
|/l - x2 sin2 <p
получим
= С^Щк). G.1.9)
Так как w = \ есть образ критической точки г = —1, то должно
быть WI-M = л:. Таким образом, следует выбрать
ух j
С> = Щ-»У С7Л.1О)
так что правая полуплоскость Re ю > 0 отображается функцией
W(w) на прямоугольник
—2м ~ < Im W < 0, 0 < Re W < л.
К.
Тем самым верхняя полуплоскость с разрезом по отрезку, соеди-
соединяющему точки w = 0 и w = 4-, переходит в прямоугольник
— л ~ < Im W < 0, 0 < Re W < 2л:
XL
(см. рис. 111). Функция z = cos W преобразует этот прямоугольник
в эллипс с прямолинейным разрезом от точки z = —1 через точку
z = +1 до границы эллипса; при этом разрезы в плоскостях ги»
соответствуют друг другу.
Чтобы установить соответствие границ, положим
w= ±
тогда для w > 0 получим
W(w) = —ст J ~ J F(x, 0, G.1.11)
а для ю < 0 получим
ТГ(и>) = —ст-^г- + 2л— -^F(x,<p). G.1.11a)
1 Как обычно, здесь ж2 = 1 — и'2.
22*
340 § 7. Многоугольники, ограниченные дугами конических сечений
Таким образом, имеем
rrf -rrl
z(w) = ch л -jf- cos jf- F(x, f)^z ish^-^- sin ¦=- F(tt, <p). G.1.12)
Нижней границе эллипса соответствуют положительные, а верх-
верхней — отрицательные значения w.
В качестве свободного параметра отображающая функция
содержит еще величину х — модуль интеграла Лежандра. Связь
этой величины с геометрическими постоянными эллипса заклю-
чается в том, что ch л -==- и sh л — являются длинами полуосей
Мл. JX.
а, Ь. Таким образом,
|--tb*fl. G.1.13)
и величина q, необходимая для нахождения нулей ^-функции,
равна
Ш ¦ GЛЛ4)
Отсюда величина к вычисляется по формуле [ср. D.2.27)]
Умножая отображающую функцию на У а2— Ь2, получим отобра-
отображение верхней полуплоскости ш на эллипс с произвольно задан-
заданными полуосями а, Ь; отображающая функция может быть записана
в виде
г(ю) = a cos -^- F(x, м) + ib sin ^- F(x, w). G.1.15)
XL jK.
Формула G.1.14) для нахождения х справедлива при любых полу-
полуосях ни Ь.
Отображение эллипса на единичный круг можно получить дроб-
дробно-линейным преобразованием а>(ю), отображающим верхнюю
полуплоскость на единичный круг. При этом целесообразно норми-
нормировать отображающую функцию так, чтобы центру г — 0 эллипса
соответствовала точка со = 0, а направления в начале координат
сохранились. При отображении G.1.12) мнимой оси z соответствует
круг | w | = —=, а точке г = 0 — точка w = —L=. Образ точки w = О
У«' Ух'
лежит на положительной оси z, так что при отображении на единич-
единичный круг эта точка должна перейти в точку со — 1. Поэтому функ-
функцию о)(ю) можно записать следующим образом [см. АG.3.5)]:
i — w Ух' ,- , , ,N
<°=r--\rf- С7-1-16)
7.1. Внешность и внутренность эллипса, гиперболы и параболы $41
Между точками единичной окружности |о|= 1 и соответствую-
соответствующими им по формуле G.1.12) значениями ср существует следующая
связь: если
а = e±ia, 0 <х <я,
то
GЛ.17)
Представляет также интерес обращение ro(z) функции G.1.12).
На основании равенства го = tg go, обращая интеграл Лежандра и
применяя соответствующие модулю я эллиптические функции
Якоби, получаем
* + iK') " -Гк1 7 • С7.Ы8)
' dn I ¦— arc cos z I
\n )
cos + )
dn
Для отображения эллипса на единичный круг получаем отсюда
dn — arc cos z I — Y^
»(«) - -^
dn I —¦ arc cos z I + У^7
\ )
— arc cos z I r I — &, I — arc cos
r I — &, I —
= _l U11^
/¦ 1 \ A
&31 — arc cos z\ г I + #4 — arc eos z\z
Из последней формулы получаем следующее разложение:
быстро сходящееся при небольших значениях эксцентриситета
эллипса.
Пример 3. Внутренность и внешность гиперболы. Требуется
отобразить область, ограниченную одной ветвью гиперболы и
содержащую внутри критическую точку z = 1, на верхнюю полу-
полуплоскость го так, чтобы точки г = 1 и z = оо перешли соответ-
соответственно в точки го = i и ю = оо. Других критических точек, как и
вершин, в отображаемой области нет, так что можно положить
w
W(ro) = Cl f-=5= . G.1.21)
Так как подинтегральное 'выражение в G.1.21) вещественно при
вещественных ю, а ветвь гиперболы соответствует прямой, парал-
342
§ 7. Многоугольники, ограниченные дугами конических сечений
лельной мнимой оси в плоскости W, то С1 должно быть мнимык.
Положим
Вычисляя интеграл, получаем
W(ro) = —-arccos (—iw).
G.1.22
Эта функция отображает правую полуплоскость Re ш > 0 hl
полуполосу
О < Re го < 2?/0, Im ю > О,
а верхнюю полуплоскость с разрезом между ю = i и ш = <ж> — •*¦
полосу
О < Re ш < Un
(см. рис. 112).
(W)
(W)
-Li
i
I
I
I
I
U
Рис. 112.
Функция z = cos W отображает эту полосу на область, лежащую
справа от ветви гиперболы и имеющую разрез по вещественной оси
от точки z = 1 до z ~ оо.
Отображающую функцию z(ro) можно записать в виде
z = ch [^ Аг sh w) cos Uo — i sh (^ Ar sh w\ sin u0. G.1.23)
Соответствие границ и определение постоянной U й. При веще-
вещественных ш формула G.1.23) представляет собой параметрическое
уравнение гиперболы, ограничивающей данную область. При этом
Uo есть угол между асимптотой и вещественной осью. Значениям
О < Uo < ^ соответствует внутренность, а значениям ^ < Uo <ж —
внешность ветви гиперболы. Таким образом, постоянная Uo опре-
определяется однозначно. <
7.1. Внешность и внутренность эллипса, гиперболы и параболы
343
Функция z(ro) становится алгебраической, когда UJn рацио-
рационально. В частности, при ий = ~,п = 1,2,..., функция ro(z) являет-
является многочленом Чебышева n-го порядка:
го = 1 cos (n arc cos z) = i2"-1Tn(z); G.1.24)
так, например,
при л = 1 ю = iz (отображение верхней полуплос-
полуплоскости на левую);
при п = 2 ю = i Bz2 — 1) (равносторонняя гипербола; см.
отображение на рис. 30 разд. А);
при " = 3 го = i Dz3 — 3z), и т. д.
Пример 4. Внутренность параболы1. Требуется отобразить внут-
внутренность параболы на верхнюю полуплоскость так, чтобы крити-
критические точки z = 1 и z = оо перешли соответственно в точки ю == i
и ю = оо. Согласно А A4.2.11), функцию W(w) мы можем пред-
представить в виде
W(w) = Сх Г—-—2, G.1.25)
т. е. вспомогательное отображение то же, что и в G.1.21). Сохраняя
нормировку G.1.22), записываем функцию г(ш) в виде
z{w) = I—- arc cos (—мсI
G.1.26)
Соответствие границ и определение постоянной Uo. Функция
z = W2 отображает полосу 0 < Re W < Uo на внутренность
параболы с разрезом от фокуса z = 0 до г = оо (см. рис. 113).
(w)
(IV)
Рис. 113.
1 Отображение внешности параболы на шЛуплоскость показано на рис. 31
разд. А.
344 § 7. Многоугольники, ограниченные дугами конических сечений
При вещественных го отображающая функция записывается в виде
G.1.27)
Множитель Vl равен расстоянию между вершиной и фокусом
параболы и определяет тем самым форму параболы.
Двуугольники, образованные коническими сечениями. Все рас-
рассмотренные области, ограниченные коническими сечениями, сим-
симметричны относительно вещественной оси z, на которой лежат их
критические точки. Если такую область путем разреза вдоль веще-
вещественной оси разбить на две симметричные подобласти, то отобра-
отображения % = cos W, соответственно z = W2, внутри этих подобластей
конформны и переводят их в обычные прямолинейные многоуголь-
многоугольники в плоскости W. Интегралом Шварца—Кристоффеля W(t)
можно отобразить верхнюю полуплоскость Im t > 0 на один из
таких прямолинейных многоугольников; в нашем случае такими
многоугольниками являются полуполосы или прямоугольники,
отображающие функции которых описаны в п. 2.1 и 4.2. При
таком отображении части границы, лежащей на вещественной оси
z, соответствует интервал et < t < ek. Тогда при помощи функции
(W)
G.1.28)
Рис. 114.
можно отобразить верхнюю полуплоскость - Im t > 0 на квадрант
Re w > 0, Im ю > 0 так, чтобы этот интервал преобразовался в
положительную мнимую полуось ю. Таким образом, получаем
отображение z(ro) квадранта на половину области, ограниченной
коническим сечением, причем линия раздела, являющаяся одно-
одновременно осью симметрии области, соответствует мнимой оси ю.
Продолжая это отображение при помощи симметрии, получаем
искомое отображение верхней полуплоскости ю на всю область.
Этим же способом можно отображать и другие симметричные
многоугольники, ограниченные коническими сечениями. В качестве
примера рассмотрим двуугольник, ограниченный дугами эллипса и
гиперболы, изображенный на pjic. 114. Вещественная ось z разделяет
7.2. -Разрезы вдоль конических сечений
345
(W)
как внутренность, так и внешность этого двуугольника на две сим-
симметричные части. Посредством функции г= cos W половина внутрен-
внутренней области преобразуется в прямоугольник, а половина внешней
области — в много-
многоугольник, подробно изу-
изученный в п. 6.1. Тем
самым задачи об отобра-
отображении сводятся к зада-
задачам, изученным ранее в
п. 4.2 и 6.1. Интересными
частными случаями явля-
являются отображения внеш-
внешности полуэллипса (рис.
115) и полуплоскости с
эллиптическим выступом
(рис. 116).
Точно так же иссле-
исследуется изображенный на
рис. 117 двуугольник, ог-
ограниченный двумя дуга-
дугами софокусных парабол.
Функция z = W2 отобра-
отображает половину внутрен-
внутренней части на прямоуголь-
прямоугольник, а половину внешней
части — на многоуголь-
многоугольник, подробно изученный
в п. 4.2.
7.2. Разрезы вдоль
Рис. 115.
(z)
|
конических сечений1.
Пример 1. Эллипти-
Эллиптические и гиперболические
разрезы. Пусть плоскость
z с разрезом вдоль дуги
эллипса или гиперболы
отображается на верх-
верхнюю полуплоскость го
так, чтобы фокусы z= +1
и z = —1 перешли соот-
ветственнр в точки ю = /
Рис. 116.
L
(W)
Рис. 117.
1 Решение этой задачи дано Грезером [см. G г а е s e r E., Dtsch. Math., 2
A937), 293—300]; вывод несколько отличается от приведенного здесь. Его решение
не доведено до конца и содержит неточность, которую исправил Коппенфельс
[Dtsch. Math., 6 A942), 558—564], решив задачу полностью. (См. также [16]. —
Прим. ред.)
346 § 7. Многоугольники, ограниченные дугами конических сечений
и ю = —. Тогда точке z = оо соответствует точка го = ете, а
концам разреза — точки ю = et и ю = е2 (вещественные). Согласно
А A4.2.7), вспомогательное отображение W(ro) можно представить
в виде w
W(w) = Сх Г-^ш~е1)(ш~!2) — . G.2.1)
J (го - е=») (го - е-») УA + ш2) A + к'2го2)
Для того чтобы функция г = cos W давала искомое отображе-
отображение, должно, во-первых, выполняться условие для вычетов А A4.2.6)
и, во-вторых, в силу соответствия между точками ю = -V и z = —1
должно быть W1-7-1= я при подходящем выборе пути интегриро-
интегрирования. Это равносильно условию однозначности функции W(ro)
в верхней полуплоскости с разрезом от и = i до и = -, так что, в
частности, функция W(w) должна возвращаться к исходному значе-
значению при аналитическом продолжении вдоль вещественной оси ст
ю = —оо до ю = + оо. Это условие можно рассматривать как
условие замкнутости (см. А § 15, стр. 187, 190).
Для того чтобы эти условия выполнялись, следует выбирать
точки е, и е2 определенным образом; именно, они определяются из
равенств w
W(w) = i f fe(i=-} + ^?} + el -SL, , G.2.2)
J \ro - e» ш - e~ J VP(w)
i
P(w) = A + ro2) A + x'2ro2).
Условие для вычетов здесь выполнено, причем знаки выражений
YpIJZ) и ^Pfe^) можно выбирать произвольно; выбирая знаки, мы
получаем эллиптический или гиперболический разрез. Из условия
замкнутости величина с определяется однозначно по формуле
J го — e= yp(w) J ш — ё= УЩш)
с==_— _j= . G.2.3)
dw
r dip
J VP(w)
Для вычисления эллиптического интеграла третьего рода W(w)
целесообразно перейти к эллиптическим функциям. Положим
v(w) = 4 Г-—=?? G.2.4)
2^ J УA + 2) A + '22)
7.2. Разрезы вдоль конических сечений
347
ср. F.1.14)]; эта функция отображает квадрант Re го > 0, Im ю > О
ча прямоугольник
2 ' 4 ' ~~ 1г '
-ели в вьфажении G.2.4) выбрать положительное значение корня
юи вещественных ю. Образы смежных квадрантов получаются
h
(v)
+z
II
II
и
II
(W)
G)
-I
Рис. 118.
о отражения, как указано на рис. 118. В частности,
jckocth ш с разрезом вдоль мнимой оси от точки
- -т до ю = loo соответствует прямоугольник
О < Im у < ^ .
G.2.5)
звоякопериодична с периодами 1 и т. Если v =
прямоугольника G.2.5), соответствующая точке
.утношениемур(е00) = —~^- однозначно определяется
л мы на основе подстановки G.2.4) получим
G.2.6)
К'
г-ет с обычным обозначением т = I — , что следует учиты-
ислении х по значению т. К
¦1ТОМ нами условии YP(u>) > 0 для вещественных w имеем
, > и для Re с,*, > 0 и Im yPJeZj < 0 для Re e^ < 0, если eM лежит
.» полуплоскости с разрезом. При переходе к сопряженным значениям
положить VР(е=) = уР(е«,).
348 § 7. Многоугольники, ограниченные дугами конических сечений
Подинтегральная функция в правой части G.2.6) двоякопериодична
и имеет в прямоугольнике периодов
полюсы в точках v — е» и v — et, = т2~—е^ (рис. 118) с вычетами,
равными соответственно + 1 и — 1. В точке v = ^ и в эквивалент-
эквивалентных ей точках w(v) = оо, и подинтегральная функция обращается
в нуль. Отсюда следует представление1
ш(е<*
Таким образом,
+ e= I
i log У '¦ ± i log
I
± i logЙ^г{
+' A^ + |^ - ^-> ± |^-) + 2Кс)
Здесь знаки при комплексно сопряженных выражениях имеют
следующий смысл для отображения: если v —> «„ по прямолиней-
прямолинейному пути, то i log^j (p -—Ко»), а с ним и W(t>) стремятся к — i оо;
соответственно при v —> г„ имеем W(p) ->-г/ оо, в зависимости
от знака при ilog#t (в — ё«,). Продолжение от W^) до W^)
соответствует отражению относительно образа вещественной оси
v в плоскости W. Если этот образ параллелен мнимой оси W (чему
в плоскости z соответствует гиперболический разрез), то при
этом отражении точка W = —i оо неподвижна. Если же он парал-
параллелен вещественной оси (чему соответствует эллиптический разрез),
то W — —zoo переходит в W — +i'oo. Поэтому верхние знаки в
G.2.8) соответствуют отображению гиперболических разрезов, а
нижние — отображению эллиптических разрезов.
Для определения постоянной с следует вычислить интеграл
G.2.6) в пределах от v = — ^ до v = ^ при значениях «„ и е^. Пере-
Перенося путь интегрирования вверх и вниз и обходя при этом точку
1 Все участвующие здесь ^функции образованы при т= 2i—. Зависимость
от этой величины явно не указана. < "^
7.2. Разрезы вдоль конических сечений
349
' = 6» в положительном направлении, а точку v = е^ — в отрица-
отрицательном (рис. 119), убеждаемся в том, что log^^p—е^) получает
здоль пути интегрирования приращение +in, log^ (v — с*,) —
<-)
триращение — та, a log дА (v — е^) не изменяется. Таким образом,
= - -4[(#(«-) + Jj(
Jj(«-)
G.2.9)
1
7
~2
f
0
1
J[
1
/
j
^ J
\v
Рис. 119.
Чули elt e2 подинтегральной функции в G.2.1) вычисляются, как.
горни квадратного уравнения
G.2.10)
"ак как справедливо равенство
>гображающая функция z(y
жончательную форму.
= cos W(v) принимает следующую
350 § 7. Многоугольники, ограниченные дугами конических сечений
1. Для гиперболического разреза
Z(V) = -1 [— ^i(g
2 1 &(v
_ ^4(» + *°°) Д-«(» + *°°) ей»(«.-+7.) 1 G 2 1
»!(» - е») »j(» - ё») J *
2. Для эллиптического разреза
G.2 12}
Исследование отображающей функции и определение параметров.
1. Гиперболический разрез. Для вещественных у функцию W(»)-
можно записать в виде
W(») = 2i log
— 2jt j 2—
Таким образом, вещественная ось v отображается функцией W(v)
на прямую, параллельную мнимой оси W:
Re W = UB = —2я [^ — Re еЛ . G.2.13)
Этим однозначно определяется расположение гиперболы, по кото-
которой проходит разрез плоскости г; Uo есть угол между асимптотами
и вещественной осью г. Обратно, заданием величины Uo опреде-
определяется Ree^.
Два других параметра, Ime^ и т, определяют положение кон-
концов разреза на гиперболе. В этом случае нет таких простых соот-
соотношений между соответствующими величинами. Для численного
определения параметров следует сначала найти1 величины
1 Если считать заданными величины ?<*, (что более целесообразно), то соот-
соответствующие значения е^ = ш(?оо) вычисляются по формулам
sn
<»)=_BK0)=.
СП
. -№)
>/ГТ ( т\
I отношение периодов равно — |.
7.2. Разрезы вдоль конических сечений 351
е1 и е2 из G.2.10). Соответствующие величины е1>2 на вещественной
оси v определяются тогда из равенств
*i.2= 4f(k,<Pi>2), «1,2= tg<Pi,2- G.2.14)
Подставляя эти значения в G.2.11), определяем искомые концы
разрезов. Проводя эти вычисления для достаточно большого числа
значений параметров, можно при помощи интерполяции опреде-
определить их значения по расположению концов разреза.
Гиперболический разрез симметричен относительно веществен-
вещественной оси г, если Im ех = —^. Отклонение величины Im ете от этого
значения служит поэтому мерой асимметрии разреза относительно
вещественной оси. С другой стороны, отношение периодов X (или
значение модуля х) в основном определяет длину разреза: разрез
уменьшается при увеличении |т|. А именно, отображая внешность
гиперболического разреза плоскости z в плоскость t функцией
г = 2 11 + - вместо функции г = cos W, получаем двусвязную
область, ограниченную двумя прямолинейными разрезами1, кото-
которая с точностью до поворота совпадает с изображенной на рис. 146,
стр. 383. Исследуемое там отображение двусвязной области на
прямоугольник периодов соответствует отображению внешности
гиперболического разреза на прямоугольник G.2.5); поэтому
соотношение между длиной разреза и модулем т, указанное в сно-
сноске 1 на стр. 362, переносится на случай гиперболического разреза.
Для исследования отображения вне вещественной оси w необ-
необходимо продолжить разрез плоскости w до точки етс, для того
чтобы функция W(w) стала однозначной. При отображении z =
= cos W(w) этот разрез переходит в разрез плоскости г, так что
z(ro) однозначна при Im ю > 0 и осуществляет искомое отображение.
Эта связь схематически показана на рис. 119.
2. Эллиптический разрез. Для вещественных v функция W(v)
принимает форму
W(v) = - 2arg *?=?> + Ъго-Ъп (Ш- 1шг.) .
Таким образом, вещественная ось v отображается на прямолиней-
прямолинейный разрез, параллельный вещественной оси W:
Im W = Vo = ~bi № — Im e J . G.2.15)
1 См. G r a e s e r E., цит. раб.
352
7. Многоугольники, ограниченные дугами конических сечений
Тем самым выражение Ime» определяет эксцентриситет эллипса
по которому проходит разрез. Согласно G.1.14), имеем
Vo = 2 °&^n~h • G.2.16
Два остальных параметра, Re ето и т, задают положен»
концов разреза на эллипсе (который определен величиной Ime,»,
Как и в случае гиперболического разреза, последние вычисляются
лишь приближенно. При увеличении | т| длина разреза вновь умень
шается1.
Эллиптический разрез расположен симметрично относительж
вещественной оси, если Ree.» = 0, и симметрично относительна
мнимой оси, если Ree^ — +j. При изменении Re ето от — ^ До г
эллиптический разрез проходит по всем четырем квадранта\
плоскости г.
Для отображения вне вещественной оси остается в силе сказаь
ное в случае гиперболического разреза. Соответствующие соотно-
соотношения указаны на рис. 120.
IV) || (W)
\
О
(IV)
Рис. 120.
Особый случай. Интересное видоизменение приведенных
рассуждений возникает, если разрез проходит через бесконечно
удаленную точку. В этом случае он состоит из двух неограниченны.-
1 При отображении внешности эллиптическогй разреза функцией z =
==—[/-;— получаем двусвязную область в плоскости t, указанную на ри;.
153 (при а = 1).
7.2. Разрезы вдоль конических сечений
353
частей, проходящих по гиперболам (во-
(вообще говоря, различным) сетки коничес-
конических сечений (рис. 121). Точке z = оо соот-
соответствуют в плоскости W две обычные
вершины (полосы ширины ал и B — а) л,
О < а < 2). Пусть в плоскости w этим
вершинам соответствуют две веществен-
вещественные точки ю — е1сх> и. w = е2те. Это при-
приводит к выражению
Рис. 121.
W(w) = г
B-a)
w — е,,
+ c\-?=, G.2.17)
в котором Р(ш) имеет то же значение, что и в G.2.2). Постоянная
с определяется тем, что W(w) возрастает на 2л при аналитическом
продолжении от ю = —оо до ю = +оо.
Переходя к ^-функциям, с помощью подстановки G.2.4) полу-
получаем для W(v) следующее представление:
W(v) = га log '; \ ' ' + i B — a) log -?—{—%—{ -f
+ алЕ1оо + B — a) Jte2oo + л. G.2.18)
Здесь ?loo и e2=o — точки, соответствующие е1оо и е2оо, причем — -^<
< e1=o < e2=o < + -. Для с получаем значение
Ш
Значения е12, соответствующие концам разрезов, получаются от-
отсюда как решения квадратного уравнения
а /p(ei~) (ei,2 — е2~) +
B - а) /Р(^1) (е1>2 —
0. G.2.20)
Соответствие границ и определение параметров. При веществен-
вещественных v, — g < у < 9' значения W(y) лежат на следующих прямых,
параллельных мнимой оси:
v <; е1=о: Re W = [71 = —л [1 — ае1те — B — а) е2 J,
?i«. < у < ?2~: Re W = t/2 = —л [1 — а — ае1<>о — B — а
» >е2<„: Re W = Ь\ + 2л.
G.2.21)
23 — 6002
354 § 7. Многоугольники, ограниченные дугами конических сечений
(W)
-Я ^-1
1
л о
Рис. 122.
Значениями U1 и и„ определяются~ветви гиперболы, на которы:
лежат разрезы. В частности, .. тт
а = U"-Ul . G.2.22
Если величины е1ао и е2са выбрать так
чтобы вьшолнялись условия G.2.21) npi
заданных иг и U2, то остается свободньа
один из этих параметров, а также отно-
отношение периодов т. Эти последние опреде-
определяют положение концов разрезов. Отоб-
Отображение вне вещественной оси схемати-
схематически показано на рис. 122.
Если разрезы симметричны относи-
относительно мнимой оси z (рис. 123а), Toej<«, =
= — -, е2оо = -; если же они симметричнь
относительно вещественной оси (рис. 123b)
то г1ао = 0, е2оо = о- В последнем случаь
выражению G.2.17) следует придать вид:
Рис. 123а.
Рис. 123Ь.
G.2.23
7.2. Разрезы вдоль конических сечений. 355
и величины е12 вычисляются непосредственно:
Формула G.2.18) остается в этом случае без изменений, если заме-
заменить в ней е1те и е2те соответствующими значениями.
Пример 2. Параболический разрез. Пусть внешность параболи-
параболического разреза отображается на верхнюю полуплоскость w так,
что фокус z — 0 и точка z = ©о переходят соответственно в точки
w — -у и ю = (. Если концам разреза соответствуют точки ю = с12,
то, согласно АA4.2.11), получаем следующее выражение для
вспомогательной функции W(w):
W(w) - С, f^LlflL^.) dw.,,== . G.2.25)
Как и в случае эллиптического и гиперболического разрезов, должно
выполняться условие замкнутости, т. е. W(w) должно возвращаться
к исходному значению при аналитическом продолжении вдоль
вещественной оси отш = —оо до w = +оо.
Для исследования отображения границы положим
+ а-Т=^) r dw _^= . G.2.26)
1 + ">2 ) УA + 2) A + '22)
Пусть /A + ш2) A + н'2ю2) > 0 при вещественных w. Мы приведем
интеграл к нормальной форме Лежандра, если при w > 0 положим
тогда получим
Jo = ^ | я №, <Р) - *'2-F(x, ?>)] - 2ft [ 1 - f ij^1] + *2F(«, 9)J •
G.2.27)
Для w < 0 положим
ш = —и = — tgip
и получим
Ju
G.2.28)
23*
3S6 § 7. Многоугольники, ограниченные дугами конических сечений
Таким образом,
и условие замкнутости выполняется, если
Е(к) - хп
G.2.29)
G.2.30)
Значения е12 вычисляются из соответствующего квадратного урав-
уравнения; имеем
-Е
G.2.31)
' Е - х'*К "
В дальнейшем нам понадобятся значения интеграла при мнимых ю:
1
w = ш,
Здесь следует положить
/A + ю2)A +~
тогда получим
J" =^[а(Е(х',<р)-
0,
q> _
sin у — *
= -V [а (?' — и2К'
— К
к'
и2 К'].
G.2.32)
Функцию W(w) можно записать в виде
W(w) = Cj
в частности, при вещественных ю = + tg^o, учитывая G.2.30) и
формулу Лежандра
ЕК' + Е'К — КК' = ~ ,
получим
W(w) = Ct
х'К -Е
;?)/ 1 +
. G.2.33)
Если Сг вещественно, то функция W(w) отображает веществен-
вещественную ось iv на прямую, параллельную вещественной оси W, а именно
ImW = V0 = ^b__. G_234)
7.2. Разрезы вдоль конических сечений
357
При преобразовании z = W2 эта прямая переходит в параболу, у
которой фокус находится на расстоянии У§ от вершины.
Параметры Ь и х определяют положение концов разреза на
этой параболе. Их можно вычислить лишь приближенно, подстав-
(Ю)
Рис. 124.
(W)
ляя в G.2.33) значения G.2.31). Заметим, что при Ь — О разрез сим-
симметричен относительно оси параболы, так что величина Ь может
служить мерой асимметрии параболического разреза. Модуль х
определяет по существу длину разреза, а именно она растет при
увеличении и.
Отображение вне ве-
вещественной оси схемати-
схематически представлено на
рис. 124.
Особый случай. Ис-
Исследуем случай, указан-
указанный на рис. 125, когда
параболический разрез
проходит через беско- —о t
нечно удаленную точку. е> е
В плоскости W точке
z = оо соответствуют две
обычные вершины с уг-
углами 0 и — тс. Пусть в
плоскости w этим верши-
вершинам соответствуют точки ¦=--*"*"
ш = оо и ю=ете, а фо-
фокусу z = 0 — точка Рис. 125.
3 58 § 7. Многоугольники, ограниченные дугами конических сечений
w = г. Это соответствие приводит к следующему выражению:
W(w) = С, rVnii^.ii?) _*!!_ = ¦
J «>- e~ ]Л + ш2
- (et + e2 - e.) [log (
f
- log (l + е„и> + ][\ + el VT+ w2) ~ Щ\ ¦ G.2.35)
Соответствие границ и определение параметров. Если Сх счи-
считается вещественным, то вещественная ось ю отображается на
прямую, параллельную вещественной оси W, а именно:
w < г.: Im W = \\ = J Сх [еА + в,— ете + К ~^!L^^j ,
G.2.36)
ш > ем: ImW = У2 = |- Cj
/
\
Этим определяются параболы, на которых расположены разрезы.
Положение концоз разреза находим, полагая в формуле G.2.35)
ю = et и w = е2. Вместе с G.2.36) это дает нам
четыре уравнения, из которых при заданном поло-
положении разрезов определяются четыре параметра
е,, е2, е^ и Cv.
Если разрез симметричен относительно ве-
вещественной оси z (рис. 126), то е» = 0 и ej = —ег.
В этом случае остается определить только два па-
параметра; формула G.2.35) принимает следующую
простую форму:
W(w) = Сх [f 1 + w2 — е{ (log w —
Ркс 12б - log A+УТТ^))], G.2.35а)
откуда
У1Я-_У2«—ic,<f. G.2.36а)
8.1. Многоугольники с границами на параллельных прямых 359
§ 8. Двусвязные многоугольники1
Конформное отображение двусвязных многоугольников мето-
методом, изложенным в § 15 разд. А, благодаря большому числу пара-
параметров настолько усложняется, что исследовать полностью уда-
удается только простейшие случаи. В дальнейшем мы ограничимся
лишь областями, границы которых состоят из круговых или прямо-
прямолинейных разрезов. Эти области относятся к специальным случаям,
описанным в п. А 15.3, в которых отображающие функции задаются
явно. Различаются следующие три случая: 1) все граничные кривые
лежат на параллельных прямых; 2) все граничные кривые лежат
на прямых, проходящих через начало; 3) все граничные кривые лежат
на концентрических окружностях.
Такие отображения применяются, например, при описании
обтекания двойных крыльев, причем с двух точек зрения. Во-пер-
Во-первых, разрезы можно рассматривать как простейшие формы про-
профилей, так что при помощи определяемых ниже отображающих
функций внешности этих профилей преобразуются в нормальные
области — прямоугольники периодов. Внешние краевые задачи
для профилей решаются тогда при помощи формул, выведенных
в п. А 10.3. Распространяя отображения на профили типа Жу-
Жуковского (см. п. 1.2), можно охватить более широкий класс про-
профилей2.
С другой стороны, с помощью этих отображений можно сводить
задачи об обтекании более общих профилей к задачам об обтекании
профилей типа разрезов (ср. А 3.2, стр. 39, рис. 16). Для этого
следует сначала отобразить внешность профиля на прямоугольник
периодов, а этот последний — на данную область с разрезом3.
Для практической осуществимости задачи об отображении важна
быстрая сходимость #-рядов. Для этого требуется, чтобы отно-
отношение периодов т было достаточно большим. При малых значениях
т, например в случае разрезных крыльев с узким разрезом, ре-
рекомендуется применять следующие ниже формулы не непосред-
непосредственно, а переходя предварительно к значению при помощи
формул преобразования ^-функции.
8.1. Многоугольники, границы которых лежат на параллельных
прямых.
Пример 1- Полуплоскость с параллельным разрезом. Пусть
область, состоящая из полуплоскости с параллельным разрезом,
1 Об этом см. также [16]. — Прим. ред.
2 Flugge-Lotz J., Ginzel J., Ing.-Arch., 9 A940), 268.
8 L a g a 11 у M., Z. angew. Malh. Meeh., 9 A929), 299—305; Г, a m m e 1 E.,
Z. angew. Math. Mech., Z3 A943), 289—291; Mh. Math., 51 A943), 24—34.
360
§ 8. Двусвязные многоугольники
расположена так, как указано на рис. 127. Требуется отобразить ее
на прямоугольник периодов
способом, изложенным в А § 15. Пусть при этом вещественная ось
z переходит в вещественную ось w и точка z — оо — в точку н> = 0.
(г)
ii ly
(w)
0
o\
Рис. 127.
Тогда разрез отображается на прямую 1шш = Щ, причем в силу
симметрии области точки ю = ^ +епю = ^- + 1 — е соответствуют
концам разреза. Тогда, в силу А A5.2.5), интеграл Шварца—Кри-
стоффеля принимает вид
^1^^+Ф) dw+C. (8.1.1)
z(w) = С, [^1^
Согласно сказанному в п. А15.3, подинтегральная функция
должна быть двоякопериодической; точнее, из ее поведения в
точке w = О можно заключить, что она совпадает с ^-функцией
Вейерштрасса с точностью до постоянного множителя и постоян-
постоянного слагаемого. Таким образом,
w f
z(w) = Cj J [К» (ш; 1, т) - р (f- + ?: Ь т)] dw + С2 =
о
= — Сх (С (»; 1, т) + р fj + г; 1, т| ш) + С2. (8.1.2)
Определение постоянных. Имеем
г (w + 1) = г(ш) — Cj [2ij -f p fj + е; 1, tj] .
Так как, в силу условия замкнутости, z(w) должна быть периоди-
периодической с периодом 1, то
= —2г). (8.1.3)
8.1. Многоугольники с границами на параллельных прямых 361
Учитывая это соотношение и формулу Лежандра
получим
z (ю -г т) = z(w) + С?щ1.
Увеличению го на т соответствует в плоскости z отражение относи-
относительно вещественной оси и относительно разреза; при этом z
переходит в z + 2w, где а — расстояние от разреза до вещественной
оси. Поэтому
(8.1.4)
а
л
Далее, при расположении области, указанном на рис. 127, должно
быть С2 = 0. Поскольку мнимая ось служит осью симметрии
области, точке z = 0 соответствует точка го = -, что проверяется
подстановкой в (8.1.2). Таким образом, приходим к окончательной
формуле отображающей функции:
z{w) = — | [5 (w; 1, т) — 2т,w] = — " р- (w \ т). (8.1.5>
Длина разреза зависит также от параметра т. Для его опре-
определения следует найти сначала нули ю = ^ _!: е + п (п—целое)
подинтегральной функции (8.1.2). Для этого исходим из формулы
(8.1.3), которую можно записать в виде
(е3 - <=i) (бз — е2) ,о,,,
- ССГ~Л = — ез — 2?]. (8.1.6)
Для удобства вычислений переходим с помощью формул
*¦ 5_ -. Сп^
. Oil
«1 = 10 + ^'2) К2, е2 = \ (х2 - и'2) К\ е3 - -1 A + «2) X2,
(8.1.7)
к функциям Якоби, модуль которых, как и ранее, вычисляется из
соотношения
Уравнение (8.1.6) принимает теперь следующий вид:
4к2 К2 sn2 2K е. = 4К(К — Е). (8.1.8)
362 § 8. Двусвязные многоугольники
Обращая функцию sn 2K е, мы находим значение е:
Подставляя это значение в (8.1.5), получаем выражение для длины
i разреза:
/=ЦЧф). (8.1.10)
Из этого уравнения, с учетом (8.1.9), можно1 приближенно вы-
вычислить значение т.
Остается исследовать соответствие границ. Для этого полагаем
w = и и w = 2" + Щ 0 < и < 1:
1. ш = ц, г(и) = -^Нт), Imz-0.
2. ю=|-~и, z(u) = ia-~||(uJT), Im z = a.
Пример 2. Два параллельных раареаа. Пусть двусвязная область
состоит из плоскости с двумя разрезами на расстоянии а друг от
друга, расположенными так, как указано на рис. 128. Если w = е12
и ш = у + ?г>4 — образы концов разрезов, а ю = ia — образ точки2
z = оо, то интеграл Шварца—Кристоффеля принимает вид
W
>Х J «?(ш - iff) #!(
1 С этой целью рекомендуется исходить не из отношения периодов т,
К'
а из модуля к, .а затем вычислить из (8.1.9) величины еиг= i — и подставить их
в (8.1.10). Легко убедиться в том, что при фиксированном расстоянии а и воз-
возрастающей длине / величина |т| убывает. Образы линий Re w = const и Im w =
= const образуют в плоскости г изотермическую сетку, которую можно рас-
рассматривать как сетку линий равного потенциала и тока электрического потока,
текущего от вещественной оси к разрезу. При этом |т[ есть разность потенциалов
между вещественной осью z и разрезом при постоянном суммарном токе (см.
п. А 3.1). При увеличении I электрическое сопротивление этого устройства, а
следовательно, и разность потенциалов |т| убывает. Аналогичные рассуждения
справедливы и для последующих задач об отображении в настоящем пара-
параграфе.
2 Путем сдвига, переводящего полосу 0 < Im w < —: в себя, можно достиг-
«уть того, чтобы образ точки z =<oo лежал на мнимой оси.
8.1. Многоугольники с границами на параллельных прямых
363
Как и в первом примере, подинтегральная функция должна быть
двоякопериодической. Так как вычеты в точках ш = 4^ i а должны
равняться нулю, то ее также можно выразить через ^-функцию
Всйерштрасса. Учитывая условие замкнутости [ср. (8.1.3)], имеем
о
= —С{е'Щю — ir>; 1, т) — 2?j] -(- e-'>LS(u> -f to; 1, т) •
= -C [e'v?i (w -
(w -I"
C2- (8.1.12)
Рис. 128.
Определение постоянных. Имеем
2 (ю + т) = z(ro) + 4?ri С cos у.
Это приращение, как и в примере 1, равно Па; следовательно,
С =s—2— . (8.1.13)
Чтобы установить положение концов разрезов, следует опреде-
определить нули w = е,, ?2, 2" + f3 > о" + f4 подинтегралъной функции в
(8.1.12). Последние отыскиваются алгебраически с помощью тео-
теоремы сложения ^-функции. Прежде всего приходим к уравнению
[4 BЧ — ре — pier) (ре - piaf + р'Ч + Jp'4ff] cos у =
= —2i#'?#'/ff sin у, (8.1.14)
где е — один из указанных выше нулей. Так как
Р'2 = 4J»» - (/^ - flf3 = 4 ф - ег) (р - л,) ф - ?з),
то правая часть (8.1.14) представляет собой квадратный трехчлен
от ps. Возводя в квадрат равенство (8.1.14), получаем уравнение
4-й степени относительно ре., имеющее следующие четыре корня:
364 § 8. Двусвязные многоугольники
Переходя к функциям Якоби по формулам (8.1.7), мы можем выра-
выразить нули через интегралы Лежандра, как в формулах (8.1.9). При
вычислениях следует учитывать неравенства
Заметим, далее, что каждому корню ре в интервале 0 < et < 1,
i = 1, 2, 3, 4, соответствуют два значения f,-, в которых jjJ-функция
принимает значение ре, а именно et и 1—е,-. Подставляя их в
формулу (8.1.14), мы определяем, какое из этих значений является
корнем подинтегральной функции. А именно:
2ip'ia > 0 при 0 < а < ^ ,
< 0 при 0 < е1J < |,
>О при -
j > 0 при 0 < es>4 < I,
V ' { < О При 2<fS,4 < 1-
Знак правой части (8.1.14) после подстановки значения ре определяет
интервал, в котором лежат величины е,-.
Подставляя найденные таким образом нули в отображающую
функцию (8.1.12), определяем положение концов разрезов в плоско-
плоскости z. При этом величину С2 можно выбрать так, чтобы один из
концов находился в заданной точке. Остальные три конца опре-
определяются значениями параметров у, а, т. Выбирая эти значения,
можно получить разрезы любой длины и любого расположения,
причем каждый раз параметры определяются лишь приближенно.
При выборе значений параметров можно опираться на следующие
частные случаи1.
1 Отметим, что рассматриваемое здесь отображение решает задачу, по-
поставленную в п. А 3.2, состоящую в определении поля параллельного тока,
обтекающего два профиля, постольку, поскольку можно найти отображение
внешности профилей (двусвязной) на прямоугольник периодов. Путем супер-
суперпозиции этого отображения и только что изученного получаем отображение
внешности профилей на внешность двух параллельных разрезов, причем экви-
эквипотенциальные линии и линии тока соответствуют линиям Re z= const и Im г =
= const в области с разрезами. Отображая внешность профилей на прямоуголь-
прямоугольник периодов, мы определяем параметры т и а (ш = la есть образ бесконечно
удаленной точки в плоскости профилей); постоянная у определяет направление
потока (Anstrsmrichtung). В этом случае задача о параметрах не возникает; следует
лишь определить критические точки потока через нули производной z\w).
L0k
8.1. Многоугольники с границами на параллельных прямых 365
Частные случаи. Если sin у = 0, то (8.1.14) — квадратное урав-
уравнение относительно ре. Каждому из двух корней соответствуют
два нуля го = е1>2 и ш = j + е34, где f2 = 1 —е,, f4 = 1 —?3. Геомет-
Геометрически в этом случае мы
,w) имеем симметричную об-
,%1 \\ 1+^з f •*•_*¦ ласть с разрезами, причем
' ° i ° « ось симметрии перпендикуля-
перпендикулярна к разрезам (рис. 129I.
Если cos у = 0, то разре-
" ] ' ~Ш~Т, | t^T~ зы в СИЛУ (8.1.13) лежат на
[ одной прямой (рис. 130). Ну-
РИС 129 ли располагаются так, что
Нахождение отображающей функции в этом случае упрощается,
если учесть, что, так как разрезы лежат на вещественной оси г,
функция ro(z) отображает полуплоскость Im z > 0 на прямоуголь-
прямоугольник
0<Rero<5, 0<1тш<ф,
h
** а° а*
%,,А !
Рис. 130.
т. е. на половину прямоугольника периодов. Если концами разрезов
являются точки z = а1; а2, as, а4, —оо < ai < а„ < а„ < а4 < оо, то
функцию w(z) можно записать в виде интеграла Шварца—Кристоф-
феля:
г
г dz
J У(г - аг) (z - a2) (z - osj (* -^«7)
dg- - -
J ]/(« - ах) (z - а2) (г - а3) (« - ad)
Для численного исследования отображения приведем этот интеграл,
как обычно, к нормальной форме Лежандра (см. п. 4.2, пример 1,
стр. 257 и след.).
2 В частности, если С2 = 0, то ось симметрии совпадает с мнимой осью г.
366
§ 8. Двусвязные многоугольники
(г)
tw)
2-'«
*Е,
Рис. 131.
Учитывая равенство
Если разрезы одинако-
одинаковы по длине, то в силу цен-
центральной симметрии об-
области ДОЛЖНО быТЬ Iff = j
(рис. 331). В этом случае
нули подинтегралъной
функции определяются
следующим образом.
можно привести это уравнение относительно е к виду
е|> . _,.. Л,„ iK'\ „ К — Е
тг) = г cosy-
(8.1.16)
Это выражение при помощи преобразования периодов второй
степени
iK> \ Г/-1 , ч 2
u -;xj =sn[(l + х) u; ^
[A +«)«;r^
en
с учетом равенства sn2 -f en2 = 1 при значениях у = 2КA + х)е и
2 Уй
У* = z-~— ПрИВОДИ!СЯ К ВИДУ
1 "Т х
[sn2 (у; х*) — сп2 (у; у.*)] cos у —
J? J?
— 2 сп (у; х*) sn (у; у.*) siny = —-„- cos у. (8.1.17)
На основе этого уравнения значения е12 вычисляются следую-
следующим образом. Определяем сначала решения <р уравнения
тт -р
cos B(р — у) = — —=— cos у,
т. е. значения
<р =
arccoS
кЯ j
лежащие в интервале 0 < ц. < л. Этому условию удовлетворяют
два различных значения др12, из которых по формулам
е, =
при
(8.1.18)
8.1. Многоугольники с границами на параллельных прямых 367
ИЛИ
при
2" <4>i< л
определяются значения е,2. Значения. еъ и е4 в силу симметрии
области равны
ея = 1 — f,, в4 = 1
(8.1.19)
Если sin у = 0, то область в плоскости z вдобавок зеркально-
симметрична. Этот случай сводится к рассмотренному в примере
1, если отразить относительно веществен-
вещественной оси как область плоскости г, изобра- i
женную на рис. 127, так и соответству- ¦ ; »
ющий ей прямоугольник в плоскости к». — 1
Тогда в плоскости z получается область, »¦¦¦ | >
изображенная на рис. 132, а в плоскости !
ю удваивается ширина прямоугольника, а Рис. 132.
с ней и значение т.
Пример 3. Бесконечные разрезы. Рассмотрим тот случай, когда
один из разрезов проходит через бесконечно удаленную точку,
как указано на рис. 133. Точке г = оо соответствуют в плоскости ю
две точки на отрезке 0 -«-: ш =s 2; пусть это будут точки аи 1 —а,
О < а <^. Так как в этих точках вычеты интеграла Шварца—Кри-
стоффеля могут быть отличны от пуля, то для отображающей
функции можно принять следующее выражение:
z(w
) = J [
- <г, 1, т) + Щ) + В
+ в: \, т) + Щ) +
= (8.1.20)
= — А '„^ (w — OJt) — iB '^ (w -\- o\r) 4- С lojj «~W, \ '-\T4 -f- C.
i L
(W!
Рис. 133.
368 § 8. Двусвязные многоугольники
Соответствие границ. Пусть А, В, С и С2 вещественны. Иссле-
Исследуем поведение отображающей функции на прямых го = и и w =
1. w = и, а <и < 1 —а.
Все ^-функции, через которые выражается z(w), а также логариф-
логарифмический член вещественны на этом интервале, так что и г(ю)
вещественна.
2. го = ц, 0<и<(ти1— (т<и<1.
Продолжим аналитически функцию z(w) из интервала <т < и <
< 1 — ев смежные интервалы, обходя . особые точки ш = сг и
ю = 1 —а по малым полуокружностям (см. рис. 133). При обходе
такой полуокружности в заданном направлении функция
увеличивается на i л. Так как остальные члены остаются веществен-
вещественными, имеем
Im г = лС при 0 < и <а и 1 — <т<и<1.
Таким образом, расстояние между двумя бесконечными раз-
разрезами принимает значение
(8.1.21)
Для того чтобы интервал 0 < ш < 1 отобразился требуемым
образом на бесконечные разрезы, числа Ли В должны быть разных
знаков. А именно, если w -» а + 0, то ~(w —а)-* + оо; напротив,
если го —> 1 —а — 0, то ~{w + а) -* — оо. Если требуется, напри-
мер, отобразить интервал а < w < 1 — а на разрез, простираю-
простирающийся до — оо, то должно быть z(w) —» — оо как при w -*о, так
и при ю —> 1 — с. Так как рассмотренные отношения ^-функций
определяют поведение г(ю) в окрестностях особых точек, то должно
быть А > 0 и В < 0. Точно так же заключаем, что А < 0 и В > 0,
если разрез распространяется до + оо. Случай АВ > 0 приводит к
многолистньш областям.
3. ю = |- + и, 0 < и < 1.
Имеем
8.1. Многоугольники с границами на параллельных прямых 369
Отсюда следует, что конечный разрез лежит на прямой
Im z = л (А + В + 2<тС).
Указанное на рис. 133 расстояние а2 равно
а2 = \л (А + В + 2аС)\. (8.1.22)
Пусть вновь нули производной z'(ro) равны ш = е12и ю = ^- -f-
+ е34. Для определения их расположения преобразуем подинтег-
ральное выражение (8.1.20) с помощью теоремы сложения. Получим
таким образом уравнение
[4 BЧ -ре-<ро) фе- И2 + (?'% + jj)'2cr] (A + В) -
- 4С [2 g (tr) (fte - ^гтJ - jp'tr (ре - |(to)] =- 2 {В— А) ф<фе,
(8.1.23)
с которым поступим так же, как и с (8.1.14).
Частные случаи. Если /4 = 0, В =у- 0 (или А =у- 0, Б = 0), то
(8.1.20) отображает прямоугольник периодов на область, состоя-
состоящую из полуплоскости с одним конечным и одним бесконечным
параллельными разрезами (рис. 134). Для соответствия границ
Г 1? V
Рис. 134. Рис. 135.
применимы те же формулы, что и в общем случае, и это же отно-
относится к определению нулей функции z'(w). Следует отметить, что
получаемое из (8.1.23) уравнение 4-й степени имеет корень ре = ро.
Разделив это уравнение на ре — ро, получаем уравнение 3-й
степени для нахождения трех нулей функции z'(ro).
Случай А = В = 0 приводит к прямолинейной полосе с разрезом,
изображенной на рис. 135. При этом прямая w = и отображается в
края полосы, а прямая го = ^- + и — на разрез. Формулы для соот-
соответствия границ справедливы и в этом случае, причем at = | С \ л
есть ширина полосы, а а2 = 2ла\С\ — расстояние от разреза до
одного из краев. Оба нуля ю = — + Рз,4 Функции z'(ro) определяются
из уравнения (8.1.23) равенством
^ + -^-; (8-1.24)
24 — 6002
370
,<? 8. Двусвязные многоугольники
отсюда, переходя к функциям Якоби [см. (8.1.9)], получаем зна-
значения FSii:
2К
1
(8.1.25)
f4 = 1 «з-
B частности, при а — ^ разрез проходит посредине полосы. Из
соображений симметрии должно быть es = j (см. рис. 135а). Длина
/ разреза вычисляется в этом случае из (8.1.20):
= — |C|logj/. (8.1.26)
'//////////////////////У/////////////////////////.
Рис. 135а.
Таким образом, в этом частном случае задача о параметрах пол-
полностью решается1.
Центральная симметрия. Для центрально-симметричной об-
области, изображенной на рис. 136, должно быть а = -г. В этом можно
убедиться следующим образом. В силу рассуждений в п. А 11.1
1 В данном случае отображающую функцию можно вывести также следую-
следующим образом: при помощи функции
J VC(C -
плоскость С с разрезами — оо < f < 0 и \ < С, < I отображается на прямо-
С
угольник периодов в плоскости w [ср. (8.1.15)]. При отображении z = — log С +
+ С2 область с разрезом в плоскости С переходит в область плоскости г, изобра-
изображенную на рис. 135а. ,
8.1. Многоугольники с границами на параллельных прямых
371
повороту на 180° вокруг центра симметрии в плоскости z (при кото-
котором отображаемая область переходит в себя) соответствует кон-
конформное отображение полосы 0 < Im го < -J- в себя, а именно
сдвиг, так как оба края полосы неподвижны. Двукратный поворот
Рис. 136.
вокруг центра симметрии представляет собой тождественное преоб-
преобразование плоскости г, так что в плоскости го ему соответствует
¦двойной сдвиг, переводящий один прямоугольник периодов в
другой, т. е. однократный сдвиг есть сдвиг на величину — , где л —
целое. Образы симметричных точек в прямоугольнике периодов
должны, таким образом, отстоять друг от друга на ^ , что, в частно-
частности, относится и к двум образам точки z = оо. Подставляя в (8.1.22)
1
значение а = -, получаем для указанного расположения разрезов
соотношение А + В = 0. Таким образом, центрально-симметрич-
центрально-симметричные области с разрезами характеризуются равенствами
' о = J , А +В = 0.
Уравнение для определения нулей можно представить следую-
следующим образом:
(8.1.27)
Из этого уравнения определяются интервалы, в которых лежат
значения ег-, г == 1,2,3,4. Из приведенных рассуждений вытекает,
24*
372
§ 8. Двусвязные многоугольники
что
С8.1.28)
При этих условиях имеем
в то время как
а также
-л < ?1 < 9 »
О < es < - ,
Интервалы, в которых лежат г1; соответственно е3, зависят от знака
С
величины -г- .
Для дальнейшего исследования уравнения (8.1.27) целесообразно
произвести преобразование периодов второй степени. Введем
величину
>0
<0
>
<
0
0
при
при
при
при
= $ \7а-\; 1, 2т) = \ [р [е- \, i, т)
Возводя (8.1.27) в квадрат, получаем для х уравнение
(ж — е^ (ж — ё2) = ^^ (х — ё„),
(8.1.29)
где ё, соответствуют периодам 1 и 2т. Корни х12 этого квадратного
уравнения лежат в интервалах
С л <^. vCi "^^ оо Ц С<) "С^ Зл) <--^, .
Этим двум корням соответствуют две пары нулей eli2 и g- + ^3,4 •
8.1. Многоугольники с границами на параллельных прямых 373
Переходя к функциям Якоби, получаем
4 ^ 4К
1 ^ф)
4 ^ 4К '
где
#1@12т) _ 1 - к\ .,_ 2 ]
| ~ 1 + ' ' * ~ "+
Здесь следует выбирать верхний знак при F(k, ф,), если — > 0,
-А.
Q
и нижний, если — < 0.
А
Зеркальная симметрия. В случае зеркально-симметричной об-
области, изображенной на рис. 137, должно быть также а — j. Отра-
Отражению относительно оси сим-
симметрии в плоскости z соот-
соответствует в плоскости ю отра- .
жеиие относительно прямой
Re ш = 0, причем точка ш = =====
= 1 — а переходит в эквива-
эквивалентную точку ш = —а, что Рис 537
возможно лишь тогда, когда
а — ¦-. Кроме того, при указанном расположении разрезов должно
быть С = 0; таким образом, зеркально-симметричный случай
характеризуется условиями
о~\, С=0.
Нули функции г'(ш) определяются здесь так же, как и в случае
центральной симметрии. Определим сначала значение
из квадратного уравнения
Ах + bU + (<Ч ~ f^l ~ йз)] +2г](А+В) = 0. (8.1.31)
Если АВ < 0 (что должно выполняться и в этом случае), корни
Ti,2 этого уравнения лежат в интервалах
374
§ 8. Двусвязные многоугольники
и поэтому
4 ±
(8.1.32)
где целые числа щ, i = 1, 2, 3, 4, следует выбирать так, чтобы
было 0 < et < 1.
Пример 4. Иное расположение бесконечных разрезов. Если беско-
бесконечные разрезы расположены так, как указано на рис. 138, то об-
область имеет две бесконечно удаленные вершины с углами 0 и — 2я.
(г)
(w)
Рис. 138.
Следовательно, подинтегральная функция интеграла Шварца—
Кристоффеля имеет в соответствующих точках полюсы третьего
и первого порядков. Расположим эти полюсы так, чтобы вершине
с углом — 2я соответствовала точка w = 0, а вершине с углом
О — точка w = а. Отображающая функция примет вид
х(ю)
2ч) + С (Jl (ш - а)
^- (ш))]
. (8.1.33)
Соответствие границ. Пусть вновь А, В, С и Са вещественны.
1. w — и, а <и < I. Все функции, входящие в выражение
г(ш), вещественны, так что и г(ш) вещественна.
2. ш = и, 0 < и < ст. Как и в примере 3, приходим к выводу,
что логарифмический член приобретает слагаемое in С при пере-
переходе в этот интервал, так что Im г = я С для 0 < и < а, а расстоя-
расстояние между бесконечными разрезами равно
а1=л\С\. (8.1.34)
3. ш = р-+и, 0<и<1. Как и в примере 3, имеем
8.1. Многоугольники с границами на параллельных прямых 375
log— >
Поэтому конечный разрез лежит на прямой Im z = я (В + о С) на
расстоянии а2=,\В+аС\ (8.1.35)
от первого бесконечного разреза.
Отметим также, что А и С имеют разные знаки, если интервал
О < ш < 1 отображается на бесконечные разрезы требуемым обра-
образом. При w —» 0 имеем tyw —* + оо, чем и определяется поведение
функции г(ю) в окрестности точки w = 0. Наоборот, при ш —* а
поведение z(w) определяется логарифмическим членом, а именно
Jog#j(u>— ег)-»---оо. Как и в примере 3, заключаем, что А < 0
и С > 0, если бесконечные разрезы распространяются до — оо,
и что А>0 и С < 0 в противоположном случае. Если А и С
одного знака, то область с разрезами неоднолистна.
Для определения нулей функции z'(u>) преобразуем подинтег-
ральное выражение в (8.1.33) при помощи теоремы сложения;
получим следующее уравнение:
Умножая на
В (Jjte+ 2rj) - С (j ^-il'- + ^ (о)) = 0. (8.1.36)
\г ус - ye ffi ;
получаем отсюда уравнение, содержащее у"е только в квадрате и
потому рациональное относительно <ре. В знаменателе квадратичное
выражение (<ра — jj>eJ встречается лишь в члене вида
в котором числитель и знаменатель можно сократить на tyo — ^е.
Выражение
(fa - W [лр'е + В № + 2,) - С (i &±^i + I; (.))]
X
является, таким образом, многочленом 4-й степени относительно
j()e, нули которого — искомые величины(ре1>2 и(р(|- + eSA\. Отсюда,
учитывая исходное уравнение (8.1.36), получим значения е1>2 и e3i4.
376 § 8. Двусвязные многоугольники
Частный случай. Если С = О, то соответствующая область
имеет один конечный и один бесконечный разрез (рис. 139). Для
определения трех нулей w=s1aw = ^-+ es4 функции г'(ш) служит
уравнение 3-й степени относительно jj)e, получаемое из равенства
Ще + 2т?) = —А$'е (8.1.37)
при возведении в квадрат. С этим
= уравнением поступаем так же, как и с
Рис ]39 уравнением (8.1.14) примера 1.
Симметричная область. Если раз-
разрезы расположены симметрично (рис.
140), то, так же как и в случае зеркально-симметричной области
примера 3, заключаем, что образы точки z = оо отстоят друг
от друга на т>- Кроме того, из (8.1.35) следует, что при указанном
расположении разрезов В = 0. Таким образом, условия
а = \, В=0
характеризуют области с симметричными разрезами.
(i) Г (W)
i
"
¦^/////////////////////////////у//,
—(Ьа&б&ь—о—гК_
0 е, 1 ег 1
Рис. 140.
Отображающая функция с помощью теоремы сложения пред-
представляется в виде
2(ш) = A$w + ?log ($w— ej) + C2, (8.1.33a)
а уравнение (8.1.36) сводится к следующему:
0- (8-L36a)
Приравнивая нулю множитель jj)'e, получаем корни ш = ^- и w -=
= |- 4- п, соответствующие концам конечного разреза. Подставляя
их в (8.1.33а), получаем длину / этого разреза:
I = \A\4fK* — [C|logx'. (8.1.38)
8.2. Многоугольники со сторонами на прямых ЪП
Остальные два нуля ш = г1>2 находим, приравнивая нулю второй
множитель в (8.1.36а). Решая относительно jj)e, получим
Pf = c'-2A-' (8Л'39>
Подставляя это значение <ре в (8.1.33а), получим положения концов
бесконечных разрезов.
Другой вывод отображающей функции в симметричном случае.
Ось симметрии делит область, изображенную на рис. 140, на два
односвязных прямолинейных треугольника типа (—1,2,0)*. В
плоскости iv этим треугольникам соответствуют две половины пря-
прямоугольника периодов, разделяемые прямой Re ш = ¦?. Таким обра-
образом, отображение двусвязной области на прямоугольник периодов
сводится к отображению односвязного треугольника на прямо-
прямоугольник
0<Reu><i, 0<1тш<Щ. (8.1.40)
Для получения этого отображения следует сначала отобразить
треугольник (—1,2,0)* на полуплоскость Im С > 0 при помощи
функции, выведенной в B.2.5), которая с учетом расстояния между
разрезами приводится к виду
[Ц^] (8.1.41)
При этом вершины в точке z = оо переводятся в ? = 0, оо, а концы
конечного разреза — в С = <Xi и С = *j, щ < 0. Функция
с
Г dt.
~ (8.1.42)
2
\
- *х) (С - а2)
отображает полуплоскость Im С > 0 на прямоугольник (8.1.40), при-
причем нормировка интеграла позволяет достичь требуемого соот-
соответствия между вершинами области с разрезами и вершинами
прямоугольника. Обращая интеграл (8.3.42) с помощью ^-функции
Вейерштрасса и подставляя полученное в (8.1.41), находим отобра-
отображающую функцию в виде (8.1.33а).
8.2. Многоугольники, стороны которых лежат на прямых, про-
проходящих через начало.
Пример I. Полуплоскость с наклонным разрезом. Вспомогатель-
Вспомогательное преобразование W = log z переводит двусвязную область
плоскости z, изображенную на рис. 141, в параллельную полосу с
378
8. Двусвязные многоугольники
разрезом в плоскости W. Отображение этой последней области на
прямоугольник периодов осуществляется способом, описанным на
стр. 369 (рис. 135), с помощью функции (8.1.20) при А = В = 0. Так
как ширина полосы равна п, то должно быть С = 1. Таким об-
образом,
ттг/ N 1 if-AW — СП ^) . s~, /о л i\
W (W) = log— 1— . С*.*, ^o.Z.l/
вследствие чего функция z(w), отображающая прямоугольник пери-
периодов на полуплоскость с наклонным разрезом, имеет вид
— ^-«\:\, (8.2.2)
где у — произвольная постоянная, отличная от нуля.
(г) (W)
О
i-a 1
Рис. 141.
Соответствие границ. Пусть у > 0.
1. w = и, 0 < и < 1. Функция z{u) вещественна и ее значения
покрывают ровно один раз вещественную ось, когда и изменяется
в интервале 0 < и < 1.
2. ш = |- + и, 0 < и < 1. Имеем
#4 (и - а)
(г
¦откуда arg z = 2ясг. Следовательно, угол а между разрезом и краем
полуплоскости равен
а = 2ла. (8.2.3)
Этим определяется параметр а.
Положение концов разреза определяется так же, как и в задаче
из п. 8.1, подстановкой нулей производной г'(ш) в отображающую
функцию (8.2.2). Нули z'(u>) совпадают с нулями функции W'(w) =
= — , а последние можно найти по формуле (8.1.25).
8.2. Многоугольники со сторонами на прямых
379
Тем же способом можно построить отображение угловой обла-
области с разрезом, изображенной на рис. 142. Если вя — величина
угла, то функция W = log z преобразует угловую область в парал-
параллельную полосу ширины Вп. В силу (8.1.20) следует положить
теперь С = в, и отображающая функция z(w) принимает вид
(8.2.4)
Рис. 142а.
В соответствии с этим угол между разрезом и границей области
равен
а = 2жав. (8.2.5)
В частности, при в = 2 мы имеем область, изображенную на рис.
142а и состоящую из плоскости с одним конечным и одним беско-
бесконечным разрезом.
Пример 2. Два непараллельных прямолинейных разреза. Рассмот-
Рассмотрим двусвязную область с разрезами, изображенную на рис. 143;
прямые, на которых расположены разрезы, пересекаются в точке
z = 0. Эти прямые принадлежат тогда полярной сетке и
переходят в прямые, параллельные вещественной оси W, при
отображении W = log z. Рассмотрим сначала случай, когда крити-
критические точки z = 0 и z~oo лежат не на разрезах, а внутри области.
(W)
1
и
X X
-ft»
Рис. 143.
Пусть при отображении области на прямоугольник периодов эти
точки преобразуются в точки ш = eG и ш = е„. Образы концов
разрезов мы, как и выше, обозначим через ш = р12и ш = |-+ ?3,4-
Как и в п. А 14.1, убеждаемся в том, что функцию W(w) можно вы-
380 § 8. Двусвязные многоугольники
разить в виде интеграла Шварца—Кристоффеля в форме А A4.1.6),
если заменить множители ш — ev соответствующими значениями
^-функций #,• (ш — ev). Таким образом, в нашем случае интеграл
Шварца—Кристоффеля имеет следующий вид:
W(w) = С\ Г ^ш - **1Ё>Л^1_Ы°*^.-.eJIJ»±<E^S- dm. (8.2.6)
J &г (ш — е0) &г (ш — е0) #! (ш — с») &х (ш — е=о)
Wo
В п. А 15.3 мы видели, что подинтегральная функция W'(w) =
= — (ш) должна быть двоякопериодической. Как и в формуле
А A4.1.3), вычет в точке ш = eG равен 1, а в точке ш = е„ равен — 1;
то же самое имеет место для точек ё0 и ё«,, так как при отражении
относительно разреза в плоскости z начало координат и бесконечно
удаленная точка неподвижны. Кроме того, производная W'(w)
должна быть вещественной при вещественных до, так как образ
вещественной оси ш параллелен вещественной оси W. Поэтому
W(u>) имеет вид
W'(w) = ^ (ш) = | (w - ес) + || (ш - е0) -
-^(ш—е.)—^(ш-^) + у, (8.2.7)
где у — вещественная постоянная. Решая это дифференциальное
уравнение относительно z(w), получим
z(w) = С1в'- »i<"-«.>»i <"-«.> . (8.2.8)
О-! (гс — е») i9-! (гс — етс)
Из условия замкнутости следует, что г(ш) периодична с периодом,
равным 1. Так как у вещественно, то это условие может выпол-
выполняться только при у = 0. Окончательно имеем
/()^(^) (8.2.9)
(ш — е=о) #! (ш —
Соответствие границ. Пусть Сг > 0.
1. w — и, 0 < и < 1. Тогда
i (" - «о)
т. е. z{u) вещественно.
2. w = |- + и, 0 < и < 1. Тогда
' 0,.(ч - е0)
z{u) = С,
2 Me, + «, — #.•
(и -
I
8.2. Многоугольники со сторонами на прямых 381
Таким образом, arg г = л (еа + е0 — етс — е^), так что угол между
разрезами равен
а = л (еа -(- ёа — ете — е^) = 2л (Re е0 — Re e^). (8.2.10)
Для определения нулей w = е-, .. и и> = -- -¦ е, 4 функции W(w)
исходим из уравнения
-|(е")-§Ьс) + ||(е-) + |(e.) = 0. (8.2.11)
С этим уравнением поступим так же, как с (8.1.36). Снова заме-
замечаем, что в произведении F($f, p'e) F(ty<;, — jj)'?) величина jp'e
встречается только во второй степени, а квадраты линейных множи-
множителей в знаменателе сокращаются. Таким образом, левая часть
уравнения
(К* - &>ес) Of* - И) Оре - J?f-) «>? - Ц»ё-) *%, (?'е) F(j(te, - jj)V) = 0
представляет собой многочлен четвертой степени от ре, так как
члены, содержащие высшие степени, взаимно уничтожаются.
Нулями этого многочлена являются величины jj)f1>2 и jj) J^- + ейЛ ,
в которых значения е,- можно определить, переходя к интегралам
Лежандра с учетом исходного уравнения (8.2.11) [см. рассуждения
в связи с формулой (8.1.14)].
Сказанное здесь переносится почти без изменений на тот случай,
когда одна или обе критические точки z = 0 и z = оо лежат на раз-
разрезах. Каждая из них отображается тогда в точки е01, е02, соответ-
соответственно во»! и е^, на верхней или нижней стороне прямоугольника
периодов, совпадающие, если рассматриваемая критическая точка
служит концом разреза. Различные возможные случаи изображены
на рис. 144.
Все выведенные выше формулы справедливы и в этом случае,
если заменить в них еа, е0 на е01, е02 и сте, е^ на етс1, е^2. Так, напри- _
мер, формула (8.2.10) для определения угла а в случае области,
соответствующей верхнему рисунку 144, имеет вид
я = л (е01 + ем — е^ — ё^). (8.2.10а)
Зеркальная симметрия. Задача существенно упрощается, если
разрезы расположены симметрично относительно некоторой окруж-
окружности, как указано на рис. 145. Окружности симметрии соответ-
соответствует в плоскости w ось симметрии, которую можно считать
расположенной на прямой Re w = = . Точкам, симметричным
382
§ 8. Двусвязные многоугольники
относительно окружности в плоскости z, соответствуют тогда точки
прямоугольника периодов, симметричные относительно прямой
Re w = 2 • В частности, точки z = 0 и z = <x> составляют такую
пару, и поэтому должно быть
етс = 1 — ес, соответственно ех1 = 1 — eci, i = 1, 2, (8.2.12)
¦ а
О
/,
о
О[ е*,,
Рис. 144.
в зависимости от того, лежат ли критические точки внутри или на
границе области. В первом случае (рис. 145, вверху) отображающая
функция z(w) имеет вид
z(w) = Ст
#! (ю - е0) »i (Д) - е0)
(IP + е0) »
Уравнение (8.2.11) приводится к виду
> + e0)
(8.2.13)
(8-2Л4)
8.2. Многоугольники со сторонами на прямых
383
т. е. к квадратному уравнению относительно (ре, которое решается
гак же, как уравнение (8.1.31).
х-
(г)
1
\
\
\
\
ч
0
•
1 4 i
\
1
1
еог
Рис. 145.
Если точка z = 0, а следовательно, и точка z = оо, лежат на
одном из разрезов, то во всех формулах следует заменить ео,ео на
eoi» еог и е~> ^~ на е~ъ е~2- Этот случай исследуется так же, как:
предыдущий.
fw)
Рис. 146.
Центральная симметрия. Другой вид симметрии имеет место*
если область (рис. 146) переходит в себя при дробно-линейном
384 § 8. Двусвязные многоугольники
преобразовании
Аг = 1* (8.2.15)
Z
(автоморфизм; см. также п. А 11.1). Пусть неподвижным точкам
z = а и z = —а этого отображения соответствуют точки w = о + I
и w = ~ в прямоугольнике периодов, так что автоморфизму Аг
соответствует автоморфизм
Aw~l+j—w (8.2.16)
прямоугольника периодов. Так как z = 0 и z = оо симметричны
относительно Az, то точки е0 и ете симметричны относительно Aw,
т. е.
в» = 1 -f J—е0; (8.2.16а)
то же самое верно для образов концов разрезов:
gj. = 1 — е,, е2 = 1 — е4. (8.2.16b)
Уравнение для определения производной W'(w) можно записать
следующим образом:
,
Из этого уравнения вычисляется сначала величина jj) (е — ^-1 , а
затем и значения нулей (возможно, с помощью преобразования
периодов; см. в связи с этим выкладки в примере 2, п. 8.1, стр. 366).
Обобщение: ломаный разрез. Полученные результаты легко
распространяются на тот случай, когда один из разрезов имеет
излом в начале координат (рис. 147). Если вол — угол излома, то
Рис. 147. « Рис. 148.
8.3. Многоугольники со сторонами на окружностях
385
зычет функции W'{w) в точке е01 имеет значение вв, а в точке е02—¦
"начение 2—00, так что выражение (8.2.7), соответственно (8.2.9),
изменяется следующим образом:
:(го) = схр j [fl0* (ш - ем) + B - 00) | (ш -
1
#, (и) — воо
i (ш - е02)]
dj (и) —
,2-в.
(8.2.18)
Все приведенные выше рассуждения непосредственно переносятся
ла этот случай. Снабжая множители Ьг {to — ете]) и ¦&1 (ш — е^2) в
знаменателе выражения z(w) показателями L и 2 — в^, получим
1азрез с изломом в бесконечности. Примеры таких областей даны
ла рис. 148.
8.3. Многоугольники, стороны которых лежат на концентриче-
концентрических окружностях.
Пример 1. Круговое кольцо. Двусвязная область, ограниченная
вумя окоужностями (например, изображенное на рис. 149
Г
1
и
(W)
f
Рис. 149.
дуговое кольцо;, может рассматриваться, как многоугольник без
зершин, и представляет собой простейший двусвязный многоуголь-
многоугольник. Уравнение Шварца А A5.1.5) принимает здесь вид
Mw = Ьо; (8.3.1)
-то общим решением является
2+0е I. ¦ (8.3.2)
-5 — 6002
386 § 8. Двусвязные многоугольники
В силу условия замкнутости, величина I/ — -^ есть целое кратное
in, т. е.
Ьа = 2п2я2, (8.3.3)
где п — целое. При п = 1, а = у=1, /5 = 5 = 0 из (8.3.2) получаем
z^e2*"". (8.3.4)
Эта функция отображает прямоугольник периодов на круговое
кольцо
Таким образом, отображение прямоугольника периодов на круго-
круговое кольцо
осуществляется функцией
7 = г2е2я'в', (8.3.5)
параметр т определяется равенством
Поэтому более общая функция (8.3.2) отображает прямоугольник
периодов при п = 1 на двусвязную область1, ограниченную двумя
непересекающимися окружностями. При этом пх есть угол между
граничными окружностями К1гК2, определяемый формулой А
G.5.5) [см. также А G.5.6)]:
V К2) = пх.
Таким образом, задача о параметрах в этом случае полностью
решена.
Пример 2. Внешность круга с концентрическим разрезом2. Пусть
требуется отобразить область, изображенную на рис. 150, на
прямоугольник периодов таким образом, чтобы граничная окруж-
окружность перешла в прямую w = u, а разрез — в прямую ю — ^ + и,
0 < и < 1. Пусть образ точки г = оо есть w = ia, 0 < а < -^ ,
а концам разреза соответствуют точки w = -^ + е и w = -^ -]- 1 — е.
1 При п > 1 образуются многолистные, точнее n-листные области. См. в
связи с этим замечания в конце п. А 12.2, стр. 137.
2 С помощью этого отображения изучается поток с циркуляцией, обтекаю-
обтекающий двойное крыло (п. А 3.2, рис. 16). Здесь применимы те же рассуждения, что
и в примере 2 п. 8.1; см. примечание 1 на стр. 364.
8.3. Многоугольники со сторонами на окружностях
387
.Как и в примере 2 п. 8.2, убеждаемся в том, что вспомогательное
1тображение W{w) можно представить в виде интеграла Шварца—
ХоистоФФеля
(8.3.7)
(г)
la
Рис. 150.
(W)
-1 од интегральное выражение двоякопериодично; вычет в точке
v = ia равен — 1. Так как при отражении относительно окруж-
юсти с центром в начале координат точка z = оо переходит в
' = 0, то вычет в точке w = —; а равен 1. Это приводит к выра-
выражению
W
'(ш) = — ~ (w — ia) + ¦? (w + ia) + у.
(8.3.8)
Значение постоянной у мы найдем, учитывая, что при отображе-
«и W = log г круговой разрез в плоскости z переходит в конечный
разрез плоскости W. При аналитическом продолжении функции
Т(ш) вдоль прямой w = ~ + и от точки « = 0 до точки и = 1 она
зозвращается к исходному значению. Имеем
i 1
t (т +u ~-ia
du = J [w
о
^ак что для функции W(w), определенной формулой (8.3.8), выпол-
выполняется равенство
следовательно, у = 0.
Учитывая, что у = 0, и интегрируя (8.3.8), получаем отобра-
отображающую функцию в виде
388
l? 8. Двусвязные ¦ многоугольники
Соответствие границ.
1. w = и, 0<и<1. ^-функции в числителе и в знаменателе
выражения z(w) комплексно сопряженны и, стало быть, равны»
по модулю. Поэтому |г| =|С| и радиус гх внутренней граничной
окружности равен
Г! = |С|. (8.3.10)
2. w = ~ + и, 0<и<1. Благодаря тому, что
имеем |г]= \С\е2ясг, так что радиус окружности разреза равен
г2 =\С\<?™. (8.3.11)
Таким образом, заданием радиусов гх и г2 величины | С | и сг опре-
определяются однозначно. Для нахождения концов разреза следует
опять определить корни — + е и ~ + 1
-е из уравнения
(8.3.12)
[см. (8.1.24)].
Пример 3. Два концентрических круговых разреза. Пусть дву-
связная многоугольная область состоит из двух круговых разрезов,
расположенных на концентрических окружностях с центром z = 0.
Пусть при отображении на прямоугольник периодов точки z = 0 и
z = оо переходят соответственно в w = е0 и w = ете. Так же, как и
в примере 2, заключаем, что вспомогательная функция выражается
интегралом Шварца—Кристоффеля вида
. (8.3.13)
Г
Z
и
Z „
z +
е,
г
2"
(VJ)
* tq
0
г
4 Рис. 151.
8.3. Многоугольники со сторонами на окружностях
389
Интегрируя, получаем отображающую функцию z(w) в виде
г(и>) = С^('°-->^(™-Ъ}
О-г («с — воо) 0-1 (м? — е0)
(8.3.14)
Соответствие границ.
1. w — и, О < и < 1. При этом |г] = |С|, так что радиус гх
кругового разреза, соответствующий этой стороне прямоуголь-
прямоугольника, равен
гх = |С|. (8.3.15)
2. w = | + и, 0 < и < 1. Имеем zl = [ СI е'4'0~'"~"'¦ + е"} •
Радиус второго кругового разреза равен, таким образом,
г2 = \С\
(8.3.16)
1 !
2 I
*<?<-
Рис. 152.
Нули w = e1>2 и w = j + e3i функции W'(w) определяются из
уравнения
1 (Г ^_1 1У "™ I
— й" (eo) + ^~ (ё„) ) 0- («"-) — ^ (f-) = 0, (8.3.17)
которое исследуется так же, как (8.2.11).
Симметричные области. Как в примере 2 п. 8.2, определение
параметров существенно упрощается, если область обладает не-
некоторой симметрией. В случае зеркальной симметрии (рис. 152)
390
§ 8. Двусвязные многоугольники
можно так нормировать отображение на прямоугольник периодов,
чтобы часть оси симметрии, лежащая внутри области, преобразо-
преобразовалась в отрезки прямых Re ю = О и Re ю = j. Тогда точки w = с0
и w = е^ лежат на этих отрезках, причем на разных или на одном
и том же, смотря по тому, разделяются ли точки z = 0 и z = оо
на оси симметрии разрезами (рис. 152, вверху) или нет (рис. 152,
внизу).
U/
t
Рис. 153.
Может также случиться, что область преобразованием
Az = a~ (8.2.15)
отображается на себя; это имеет место, если центральные углы
обоих разрезов одинаковы (рис. 153). В этом случае справедливы
все рассуждения, проведенные для центральной симметрии (пример
2 п. 8.2, стр. 383 и след.).
Сводка отображений
Рис.
ш
ж
Стр.
217
219
220
221
223
223
224
226
227
228
228
229
230
Замечания
Двуугольники
Частные случаи (применение — профиль Жуков-
Жуковского)
Двуугольники с совпадающими вершинами (па-
(параллельные полосы)
Прямолинейные треугольники
Частный случай — полуполоса
Дробно-линейное преобразование области
Дробно-линейное преобразование области
Дробно-линейное преобразование области
Частный случай (применение
денсатор)
— плоский кон-
392
Сводка отображений
Рис.
щ
ш
ш
ж
% шш.
ш
Ш, Щ
Стр.
232
233
235
243
247
257
262
271
273
285
292
299
308
Замечания
Круговые треугольники
Отображающая функция представима в замк-
замкнутой форме
Отображающая функция представима в замк-
замкнутой форме
Отображающая функция представима в замк-
замкнутой форме
Общий случай:
Отображающие функции являются частными
от деления двух гипергеометрических рядов
Применение — профиль несущего крыла
Простые прямолинейные четырехугольники
Аналитическое продолжение отображающей
функции при помощи отражения дает отобра-
отображение внешности прямоугольника
Двукратные прямоляаейные четырехугольники
Сводка отображений
393
Рис.
Стр.
Замечания
308
310
312
314
318
320
330
336 |
Разрез с изломом
Круговые четырехугольники
Сектор кругового кольца (в результате дробно-
линейного преобразования — круг с двумя
ортогональными выемками)
Многоугольники, образованные коническими
сечениями
(см. также рис. 114—117)
Внешность эллипса
338
Внутренность эллипса
341 | Граница области состоит из полной ветви гипер-
I болы
343 I Внутренность параболы
345 ' Эллиптические и гиперболические разрезы
352 \ Два бесконечных гиперболических разреза
отооражений
Рис.
шшж
ш
Стр.
Замечания
354
355
357
359
362
365
367
369
369
370
Частный случай — симметричные разрезы
Параболический разрез
I
Два бесконечных параболических разреза
Двусвязные многоугольники: параллельные
разрезы
Частный случай — симметричные разрезы
Параллельные разрезы (конечные и бесконечные)
Полуплоскость с одним конечным и одним
бесконечным разрезом
Полоса с параллельным разрезом
Частный случай — симметричные разрезы
374 Другое расположение бесконечных разрезов
376
376
Частный случай
Частный случай (симметрия)
Сводка отображений
395
Рис.
Стр.
Замечания
377
379
379
381
384
Пересекающиеся прямолинейные разрезы
Частные случаи симметрии — см. рис. 145 и 146
Другие расположения разрезов см. на рис. 148
Концентрические круговые разрезы
385
386
388
Частные случаи симметрии — см. рис. 152 и 155
ЛИТЕРАТУРА
КНИГИ ПО ТЕОРИИ КОНФОРМНЫХ ОТОБРАЖЕНИЙ
Bieberbach L., Einfiihrung in die konforme Abbildung, 5, Aufl., Berlin,
1956.
Каратеодори К., Конформное отображение, М., 1934.
Julia G., Lecons sur la representation conforme des aires simplement connexes,
Paris, 1931.
Julia G., Lecons sur la representation conforme des aires multiplement connexes,
Paris, 1934.
Nehari Z., Conformal Mapping, New York—Toronto—London, 1953.
Разделы, посвященные теории конформных отображений, можно найти
также в большинстве курсов теории функций.
В е h n k e H., S о m m e r F., Theorie der analytischen Fvmktionen einer kom-
plexen Veranderlichen, Berlin—Gotlingen—Heidelberg, 1955.
Bieberbach L., Funktionentheorie, Bd I. 3. Aufl., Leipzig u. Berlin, 1930.
Bieberbach L., Funktionentheorie, Bd II. 2. Aufl., Leipzig 1951.
Bieberbach L., Einfiihrung in die Funktionentheorie, Stuttgart, 1952.
Carat heodory C, Funktionentheorie, I, II, Basel, 1950.
Гурвнц А., Теория аналитических и эллиптических функций, М., 1933.
Курант Р., Геометрическая теория функций комплексной переменной, М.,
1949.
КНИГИ ПО ПРИМЕНЕНИЯМ КОНФОРМНЫХ ОТОБРАЖЕНИЙ.
13etz A., Konforme Abbildung, Berlin—Gottingen—Heidelberg, 1948-
Канторович Л. В. и Крылов В. И., Приближенные методы высшего
анализа, изд. 3, М., 1949.
К о b е г Н., Dictionary of conformal representations, Dover Publications,
1952.
Rot he R., Ollendorf F., Pohlhausen K., Funktionentheorie und
ihre Anwendungen in der Technik, Berlin, 1931.
ИСЧЕРПЫВАЮЩАЯ БИБЛИОГРАФИЯ ПО ПРАКТИКЕ КОНФОРМНЫХ
ОТОБРАЖЕНИЙ ДАЕТСЯ В РАБОТАХ:
S е ГА е 1 W., Bibliography of Numerical Methods in Conformal Mapping, Nat.
i. 'Bureau Standards appl. Math. Ser., 18 A952), 269—280.
Ш1 r i с h E., Praxis der konformen Abbildung, FIAT-Bericht angew. Math.,
Teil I, S. 93—118.
ЛИТЕРАТУРА, ДОБАВЛЕННАЯ РЕДАКТОРОМ
[1] Л а в р е н т ь е в М. А. и Ш а б а т Б. В., Методы теории функций
комплексного переменного, 2е изд., М., 1958.
[2] В о л к о в ы с к и й Л. И., Л у н ц Г. Л., А р а м а н о в и ч И. Г.,
Сборник задач по теории функций комплексного переменного, М., 1960.
[3] К о ч и н Н. Е., К и б е л ь И. А., Розе Н. В., Теоретическая гидро-
гидромеханика, М., 1948.
[4] Веку а И. Н., Обобщенные аналитические функции, М., 1959.
[5] Я г л о м И. М., Геометрические преобразования, II, М., 1956.
[6] МаркушевЕЧ А. И., Теория аналитических функций, М., 1950.
[7] К у р а н т Р., Принцип Дирихле, конформные отображения и минималь-
минимальные поверхности, М., 1953.
[8] Н еван л инна Р., Униформизация, М., 1955.
[9] Спрингер Дж., Введение в теорию римановых поверхностей, М., 1960.
[10] Ахиезер Н. И., Элементы теории эллиптических функций, М., 1948.
[11] Голубев В. В., Лекции по аналитической теории дифференциальных
уравнений, 2е изд., М., 1950.
[12] JTj) л.у.3 и н Г. и др., Конформные отображения односвязных и много-
многосвязных областей, сб. статей, М., 1937.
[13] Фильчаков П. Ф., Теория фильтрации под гидротехническими
сооружениями, 1, 2, Киев, 1959, 1960.
[14] Полубаринов а-К о ч и н а П. Я., Теория движения грунтовых вод,
М., 1960.
115] Стретт М. Д. Л., Функции Ляме, Матье и родственные им в физике
и технике, М., 1937.
[16] Седов Л. И., Плоские задачи гидродинамики и аэродинамики, М.,
1950.
[17] Некоторые проблемы математики и механики, СО АН СССР, 1961.
[18] Construction and applicaticn of conforrr.al maps, Appl. Math, ser., 18 A952),
1—280.
[19] Experiments in the computation of ccnformal map», Appl. Math, ser., 42
A955), 1—61.
АЛФАВИТНЫЙ УКАЗАТЕЛЬ
Автоморфизм 121
Акцессорные параметры 132
Альбрехт Р. 197
Альтернирующий метод
Шварца 210
Альфорс 207
Аналитическая функция 23
Аналитический образ 107
Аналитическое продолжение 107
вещественных функций
в комплексную область 107
гипергеометрических
рядов 238
Антиконформное отображение
29, 63
Аргумент 13
Асимптотическое интегрирование
141
Барнес Е. 238
Безвихревое поле 22
Бенке Г. Ill
Бетц А. 220
Бибербах Л. 200, 238
Вариационный мгтод 197
Варшавский С. 203, 207
Ватсон Г. 224
Вейль Г. 107, 111, 112
Вектор 11
Векторное поле 19
Вещественная часть 9
Вилла Г. 119
Внешняя область 161, 243
Вольф Е. 247
Вращения сферы 80
Вычет 160
Гаррик И. 201, 205
Гаусс К. Ф. 236
Гейнгольд И. 197
Гельмгольц Г. 41
Географические ыкарт 4
Геометрия Лобачевского 78
Гершгорин С. А. 205, 209
Гидродинамические поля 35
Гинцель И. 359
Гипербола 60, 89, 341
Гиперболический пучок
окружностей 82
— разрез 345
Гиперболическое отображение 73
Главное значение логарифма 28
Годограф 39
Граничная точка 16
Граничное значение 18
Грассман Г. 11
Графический метод 200
Грезер Э. 345, 351
Гурвиц А. 98
Двойное отношение 74
Дивергенция 20
Дини У. 119
Диполь 66, 91, 92
Задача о кручении 42, 163
параметрах 137, 149, 15J,
168, 187, 189, 216, 250, 276
Замкнутое множество 16
Алфавитный указатель
399
Замыкание множества 16
Звездная область 203
Звездчатый многоугольник 332
Зоммер Ф. 111
Зоммерфельд А. 41
Изотермическая сетка 25, 45,
174, 200
Инвариантность функциональ-
функциональных уравнений 108
Инверсия 63
Интеграл комплексный 21
— контурный 159, 277
— Шварца—Кристоффеля 156,
188
Интегральная формула Коши 97
Пуассона 100
Шварца 101, 103
Камке Е. 134
"Канторович Л. В. 193, 210
Каратеодори 65, 109, 231
Кардиоида 63
Квадруполь 68
Квартернионы 14
Кирхгоф Г. 229
Клейн Ф. 78
Кнопп К. 92, 94
Коллатц Л. К. 151, 201
Комату И. 197
Конические сечения 88, 178, 336
Конформное отображение 29
Коппенфельс В. 227, 234, 238,
240, 320, 321, 345
Краевая задача 99, 115, 211
Крафт М. 118
Кривая 16
— аналитическая 125
Кривые Кассинн 62
Критическая точка 36, 60
Круг 10
Круговая луночка 217
Круговое кольцо 114, 185, 197
— свойство 49, 64, 72
Круговой двуугольник 217
Круговой многоугольник 126,
185
— пятиугольник 146
— разрез 219, 386
— треугольник 197, 231
— четырехугольник 319
Крылов В. И. 193, 210
Курант Р. 98
Кутта В. 151
Куфарев Р. Р. 174
Лагалли М. 359
Ламмель Э. 359
Лемма Шварца 108
Лемниската 62
Лёвнер К. 174
Линейный интеграл 21
Линии равного потенциала 24
— тока 24
— уровня 70
Лихтенштейн Л. 47, 205
Логарифм 26, 54
Логарифмическая спираль 57, 70
Локсодрома 74
Локсодромическое отображение
74
Максимум и минимум гармони-
гармонической функции 96
Матрица 12, 30
Маттье П. 170
Мертвая зона 41
Метод интегральных уравнений
201
— Либмана 201
— Ньютона 168
— растяжения 195
— Ритца 198
— Рунге—Кутта 151
— Теодорсена—Гаррика 201
Мизес Р. 166
Мнимая часть 9
Многоугольник 126
— в сетке конических сечений 178
— двусвязный 185, 359
400
Алфавитный указатель
Многоугольник, имеющий форму
разреза 174, 177, 314, 345, 358
— круговой 126
— ограниченный логарифми-
логарифмическими спиралями 178
— периодический 190
— прямолинейный 153, 188
— скоростей 40
— с точками ветвления 163
— ступенчатый 143, 174
Многочлены Чебышева 343
Модуль 9
Направление обхода 29, 76
Нейман К. 212
Неподвижная точка 65, 70, 71
Неравенство треугольника 78
Нехари 200
Ньютоновский потенциал 25
Область 17
— двусвязная 113, 185, 359
— замкнутая 17
— звездная 203
— многосвязная 18, 111
— однолистная 127
— односвязная 18, 110
— периодическая 122, 187, 190
Объединение множеств 15
Окрестность 15
— бесконечно удаленной точки
51
Ортогональная окружность 64,
77
— сетка окружностей 65, 66, 175,
319
Особая точка 107
Островский А. М. 203
Ось (вещественная, мнимая) 9
Открытое множество 16
— ядро 16
Отношение длин 71
Отображение границы 111
— двух окружностей на две
окружности 82 *
Отображение круга на круг 76
Отражение 63
Парабола 60, 181, 343
Параболическая сетка 61
Параболические разрезы 355
Параболический пучок
окружностей 83
Параболическое отображение 74
Пересечение множеств 15
Периодические области 122, 187,
190
Подобие 12
— в малом 28
Подъемная сила 38
Поле источника 27, 61, 94
и стока 93
Полуплоскость 11
— отображение на единичный
круг 78
— с параллельными разрезами
359, 362
Полярная сетка 27, 54
Потенциал ньютоновский 25
Потенциальная функция 22
Потенциальное поле 22
Поток через кривую 21
Предел 18
— вдоль кривой 18
Преобразование дробно-линей-
дробно-линейное 72
— конгруэнтное 70
— обхода 139
— перехода 138
— поверхностей 44
— подобия 12, 70
— целое линейное 70
Приближенные методы 194
Принцип симметрии Шварца 124
Проекция Меркатора 48
Производная Шварца 128
Противоположная вершина 138,
159
Профиль 35, 247, 359
— Жуковского 220, 359
Алфавитный указатель
401
Прямая линия 10, 56
Прямолинейный многоугольник
153, 188
Прямоугольник 257
Псевдостороны 159
Пучок окружностей 65, 82, 83
Радиус-вектор 10
Разложения в ряды 103, 119, 135,
149
Расстояние 78, 81
Растяжение 70
Риманова поверхность 54, 59,
107, НО
Ринглеб Ф. 201, 232
Ройден Г. 207, 210
Роте Г. 153
Ротор 20
Рунге 151, 201
Ряд Лорана 119
— Неймана 206
— Тейлора 104
Связное множество 17
Сеге Г. 200
Симметрия 121, 302, 332, 366,
370, 376, 381, 383, 389
Синус 87
— гиперболический 87
Скалярное произведение 11, 199
Стереографическая проекция 49
Ступенчатый многоугольник 143,
174
. Теодорсен 201
Теорема единственности анали-
аналитических функций 106
— Лиувилля 104
— о среднем значении 95
— Римана НО
Теоремы об отображении ПО
Тор 52
Точечные множества 15
Точка ветвления 60
Траектории 70
26 — 6002
Трикоми Ф. 118
Трохимчук Ю. Ю. 30
Угловая мера 84
Уиттекер 224
Универсальная накрывающая
поверхность 112
Ункельбах Г. 127
Уравнение потенциала 23
— Шварца 132
Уравнения Коши—Римана 23, 47
Условие замкнутости 187, 190,
346, 355
Флюгге—Лотц Г. 353
Фок В. 153
Формула Шварца для круга 101
полуплоскости 173
прямолинейной полосы
115
— Эйлера 26
Франк Ф. 166
Фундаментальная область 113
Функции гармонические 23, 95
— двоякопериодические 53, 116,
186
— комплексные 15
— многозначные 27, 55, 56, 107
— растяжения 195
— тригонометрические 87
Функциональный элемент 107
Функция Грина 98
— — для круга 99
— Неймана 102
— тока 22
Центральная сила 25
— симметрия 121, 302, 332, 366,
370, 376, 383
Цепочка кругов 106
Цилиндрические функции 142
Циркуляция 36
Численное интегрирование 149,.
167
Численные методы 194
Числовая сфера 51, ПО
402 Алфавитный указатель
Шварц Г. 125, 210, 232 Эквипотенциальные линии 24
Шиллинг Ф. 138 Электрическое поле 31
Шмейдлер В. 207 Эллипс 88, 336
Шпернер Е. 11 Эллиптические разрезы 345
Штальман Ф. 139, 141, 144, 146, Эллиптический пучок окруж-
153, 214, 216 ностей 82
Эллиптическое отображение 73
Эйлерово интегральное пред- Эфезер Г. 178, 216
ставление гипергеометрических
функций 239
Оглавление
Предисловие редактора перевода 5
Из предисловия автора 7
\. ТЕОРИЯ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 9
ГЕОМЕТРИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ КОМПЛЕКСНЫХ ЧИСЕЛ И
ФУНКЦИЙ 9
§ 1. Комплексные числа 9
1.1. Комплексные числа и геометрия на плоскости 9
1.2. Векторы 11
1.3. Преобразования подобия 12
^ 2. Функции комплексного неременного , 15
2.1. Основные понятия 15
2.2. Векторное поле 19
2.3. Пример. Ньютоновский потенциал 25
2.4. Отображения 28
? 3. Примеры решения физических и технических задач с помощью
конформных отображений 31
3.1. Электрические поля 31
3.2. Гидродинамические поля скоростей 35
3.3. Годограф 39
3.4. Задачи а кручении 42
§ 4. Конформное отображение поверхностей 44
4.1. Общие соображения 44
4.2. Отображения сферы 47
4.3. Отображения тора 52
ПРОСТЕЙШИЕ КОНФОРМНЫЕ ОТОБРАЖЕНИЯ 54
§ 5. Логарифмическая функция 54
5.1. Риманова поверхность 54
5.2. Преобразование некоторых линий » 56
§ 6. Степенная функция 58
6.1. Общие соображения 58
6.2. Функция w = z2 60
6.3. w = z~1 63
6.4. ш = х-2 67
404 Оглавление
§ 7. Линейные функции 70
7.1. Целые линейные функции 70
7.2. Дробно-линейные функции 72
7.3. Отображение круга на круг 76
7.4. Вращения сферы 80
7.5. Отображение двух окружностей на две окружности 82
§ 8. Тригонометрические функции 87
8.1. w=cosz 87
1 ( 1\
8.2. ш --/ + - 89
2 I t)
8.3. w -¦¦- tg z 92
НЕКОТОРЫЕ ОСНОВНЫЕ ПОЛОЖЕНИЯ ТЕОРИИ ПОТЕНЦИАЛА
И ТЕОРИИ ФУНКЦИЙ 95
§ 9. Теорема о среднем 95
9.1. Теорема о среднем 95
9.2. Краевые задачи 99
9.3. Разложения в ряды 103
9.4. Аналитическое продолжение 106
9.5. Лемма Шварца 108
§ 10. Теоремы об отображении 110
10.1. Теорема Римана ПО
10.2. Многосвязные области : 11)
10.3. Краевые задачи в двусвязных областях 115
ТЕОРИЯ И ПРАКТИКА ОТОБРАЖЕНИЙ МНОГОУГОЛЬНИКОВ 121
§ 11. Принцип симметрии Шварца 121
11.1. Автоморфизмы 121
11.2. Принцип симметрии Шварца 124
§ 12. Отображения круговых многоугольников 126
12.1. Дифференциальное уравнение Шварца 126
12.2. Интегрирование дифференциального уравнения Шварца .. 133
12.3. Задача об определении параметров 137?
12.4. Асимптотическое интегрирование 141
12.5. Замечания к численному интегрированию уравнения Шварца 149
§ 13. Отображения прямолинейных многоугольников 153
13.1. Интеграл Шварца—Кристоффеля 153
13.2. Задача нахождения параметров 157
13.3. Внешние области 161
13.4. Многоугольники с внутренними точками ветвления 163-
13.5. Замечания о приближенном вычислении интеграла Шварца—
Кристоффеля 167
§ 14. Многоугольники в изотермических сетках 174
14.1. Многоугольники в круговых сетках 175
14.2. Многоугольники 'в сетках конических сечений 17&
Оглавление 405
§ 15. Двусвязные многоугольники 185
15.1. Уравнение Шварца для двусвязных многоугольников 185
15.2. Интеграл Шварца—Кристоффеля для двусвязных много-
многоугольников 188
15.3. Частные случаи 192
ПРИБЛИЖЕННЫЕ МЕТОДЫ КОНФОРМНЫХ ОТОБРАЖЕНИЙ .... 194
§ 16. Собственно приближенные методы 195
16.1. Метод растяжения 195
16.2. Вариационный метод 197
16.3. Графический метод 200
§ 17. Методы интегральных уравнений 201
17.1. Метод Теодорсена—Гаррика 201
17.2. Интегральное уравнение Гершгорина и Лихтенштейна ... 205
17.3. Альтернирующий метод Шварца 210
17.4. Метод Неймана для пересечения областей 212
Б. КАТАЛОГ КОНФОРМНЫХ ОТОБРАЖЕНИЙ 216
§ 1. Двуугольники 217
1.1. Несовпадающие вершины. Общее отображение 217
1.2. Частные случаи 219
1.3. Совпадающие вершины 220
§ 2. Прямолинейные треугольники 221
2.1. Простые прямолинейные треугольники 221
2.2. Двукратные прямолинейные треугольники 228
§ 3. Круговые треугольники 231
3.1. Решение в замкнутой форме 232
3.2. Аналитическое продолжение гипергеометрического ряда 238
3.3. Представление отображающей функции в общем случае ... 243
3.4. Круговой треугольник с двумя развернутыми углами, содер-
содержащий бесконечно удаленную точку 247
§ 4. Простые прямолинейные четырехугольники 249
4.1. Решение задачи о параметрах 250
4.2. Вычисление отображающей функции в частных случаях.
Эллиптические интегралы 257
4.3. Вычисление отображающей функции в частных случаях:
, элементарные функции 271
§ 5. Двукратные прямолинейные четырехугольники 276
5.1. Решение задачи о параметрах 276
5.2. Вычисление отображающей функции в частных случаях:
элементарные функции 285
5.3. Вычисление отображающей функции в частных случаях.
Эллиптические интегралы 298
5.4. Вычисление отображающей функции в частных случаях.
Многоугольники с разрезами 308
406 Оглавление
§ б. Другие многоугольники, отображающие функции которых могут
быть найдены полностью 319
6.1. Четырехугольники в круговых сетках 319
6.2. Звездчатые многоугольники 332'
§ 7. Многоугольники, ограниченные дугами конических сечений 3:»
7.1. Внешность и внутренность эллипса, гиперболы и параболы 33i
7.2. Разрезы вдоль конических сечений 345
§ 8. Двусвязные многоугольники 359
8.1. Многоугольники, границы которых лежат на параллельных
прямых 359
8.2. Многоугольники, стороны которых лежат на прямых,
проходящих через начало 377
8.3. Многоугольники, стороны которых лежат на концентрических
окружностях 385
Сводка отображений 391
Литература 396
Литература, добавленная редактором 397
Алфавитный указатель 398"-
В. Коппснфслъс и Ф. Шталъман
ПРАКТИКА
КОНФОРМНЫХ ОТОБРАЖЕНИЙ
Редактор Н. И. Пдужникова
Художник И. И. Каледин
Технический редактор А. В, Грушин
Сдано в производство 29/Х 195 г.
Подписано к печати 28/V 195 г.
Бумага 60x90 '/n'-lZ.S бум. л.
25,5 печ. л.,
Уч.-изд. л. 21,6 Изд. № 1/0939
Цена 1 р. 71 к. Зак. № 6002
ИЗДАТЕЛЬСТВО
ИНОСТРАННОЙ ЛИТЕРАТУРЫ
Москва, 1-й Рижский пер., 2
Типография «Эдетэми» Будапешт