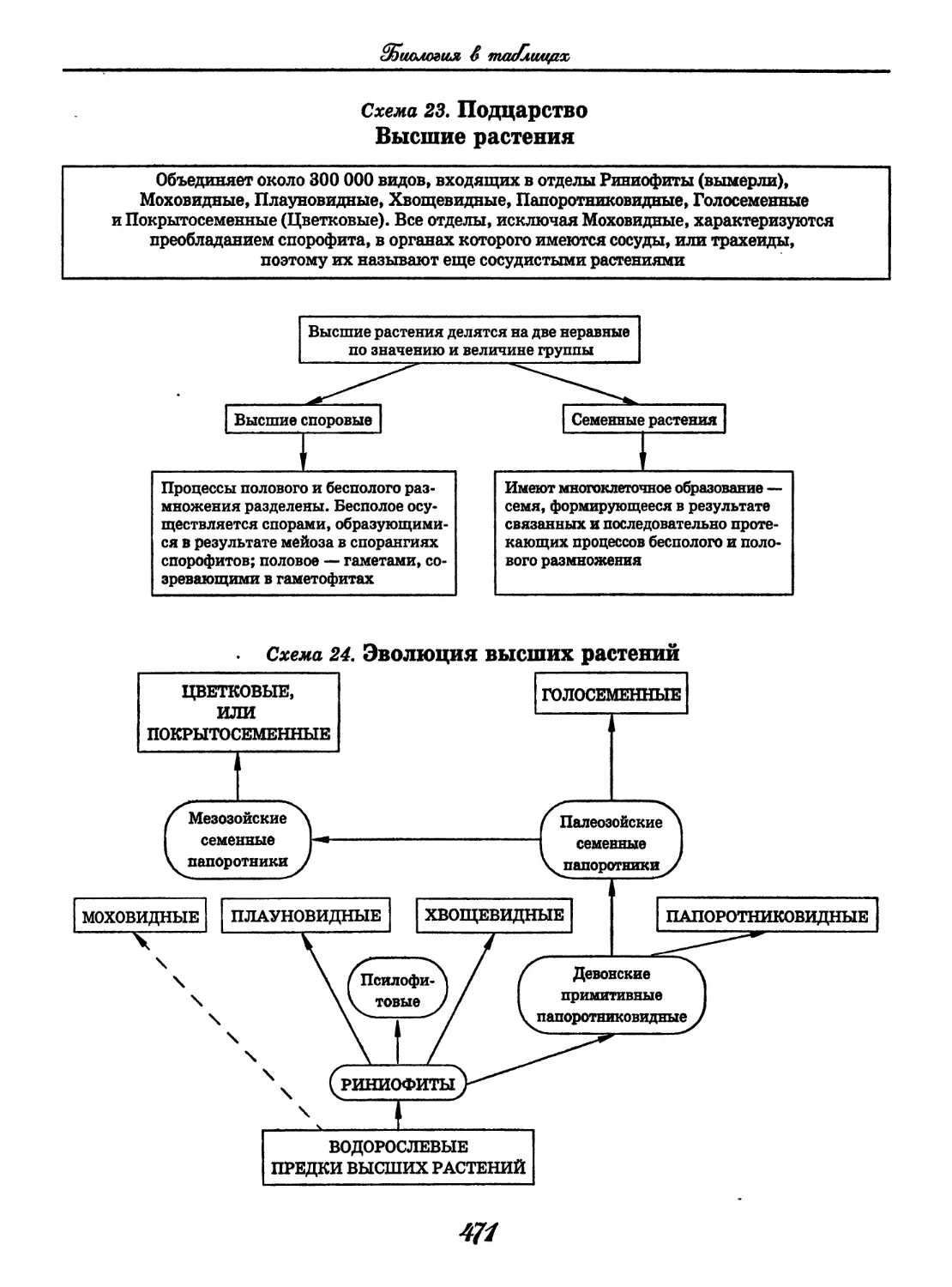
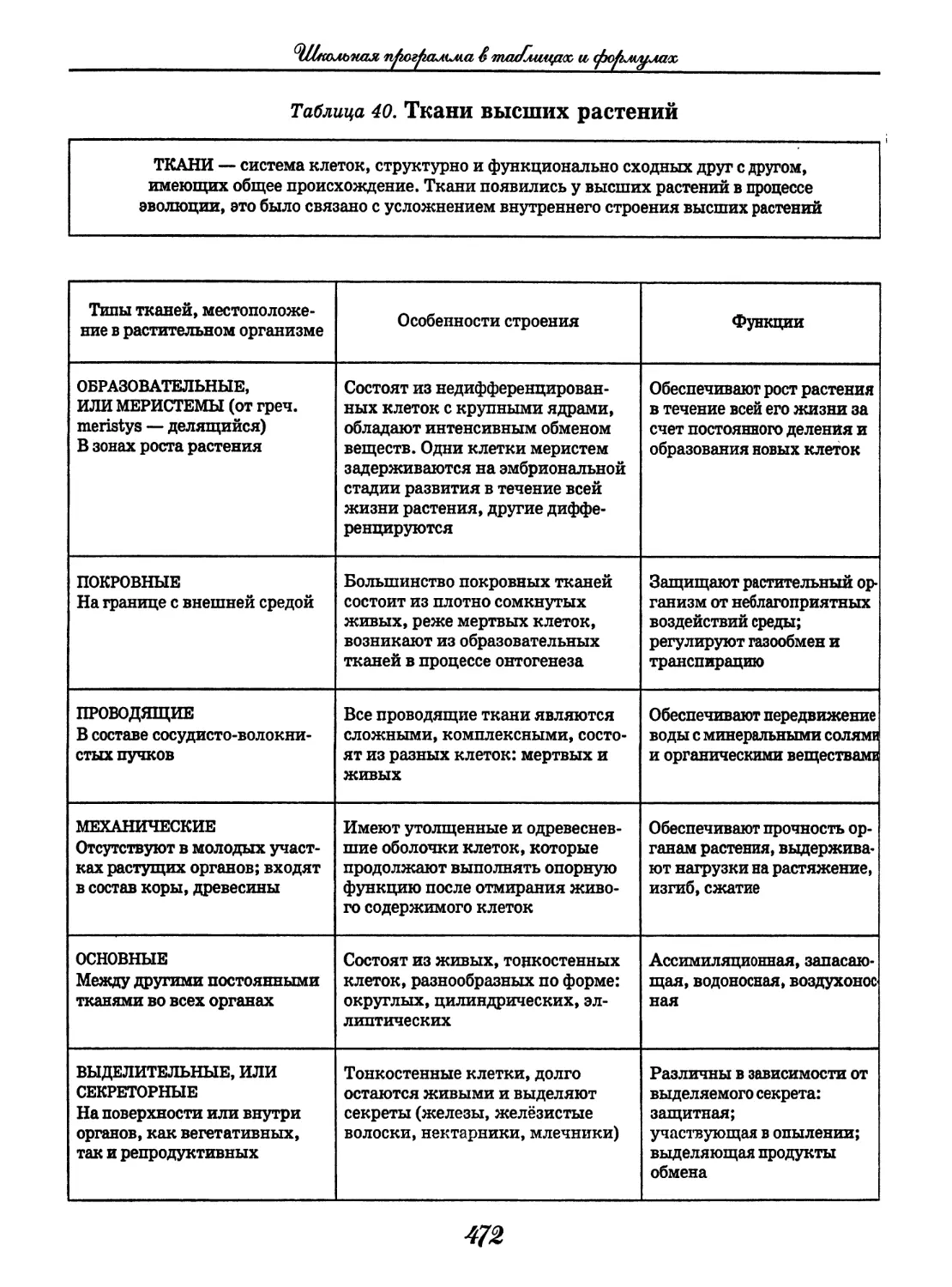
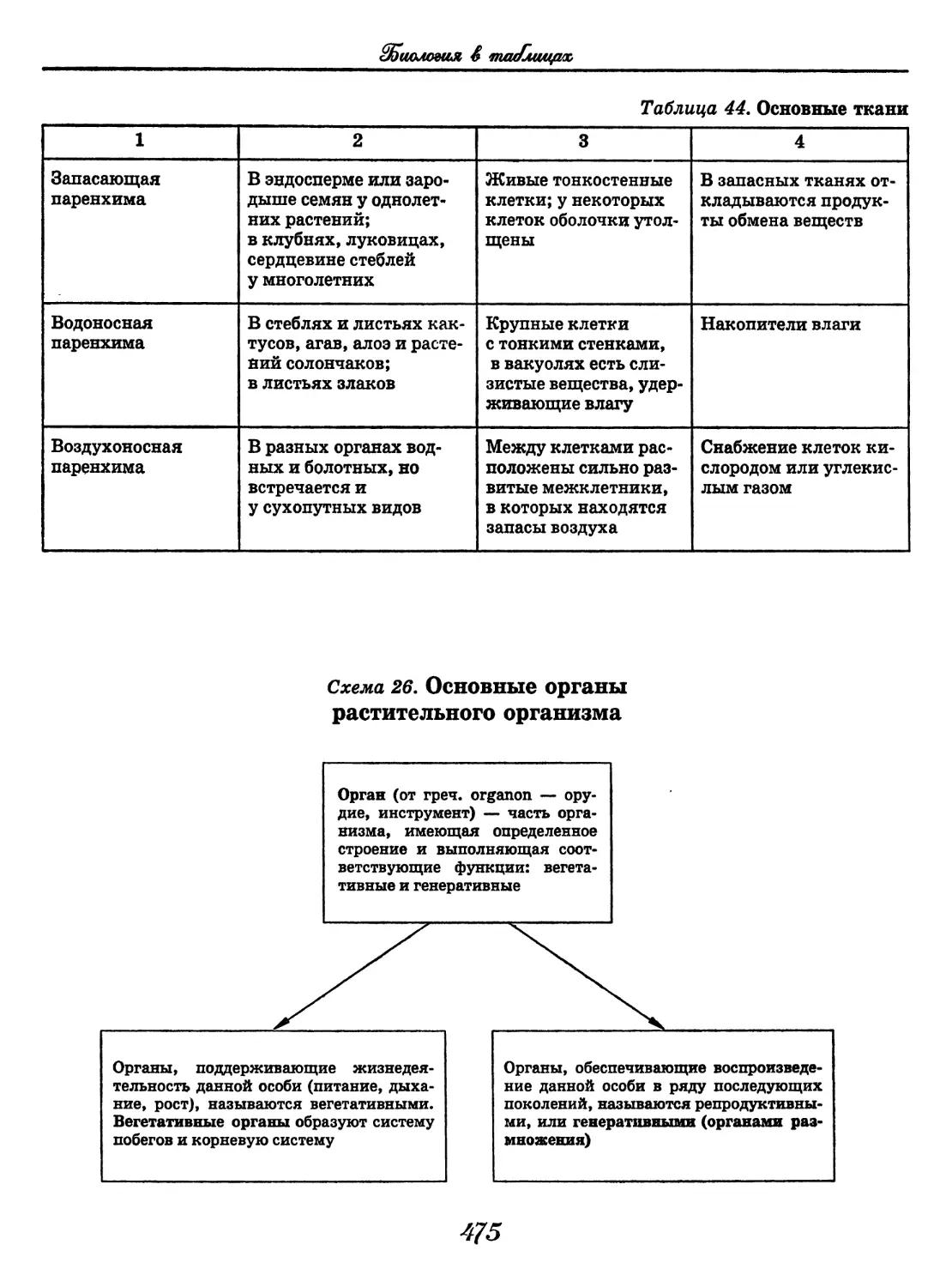
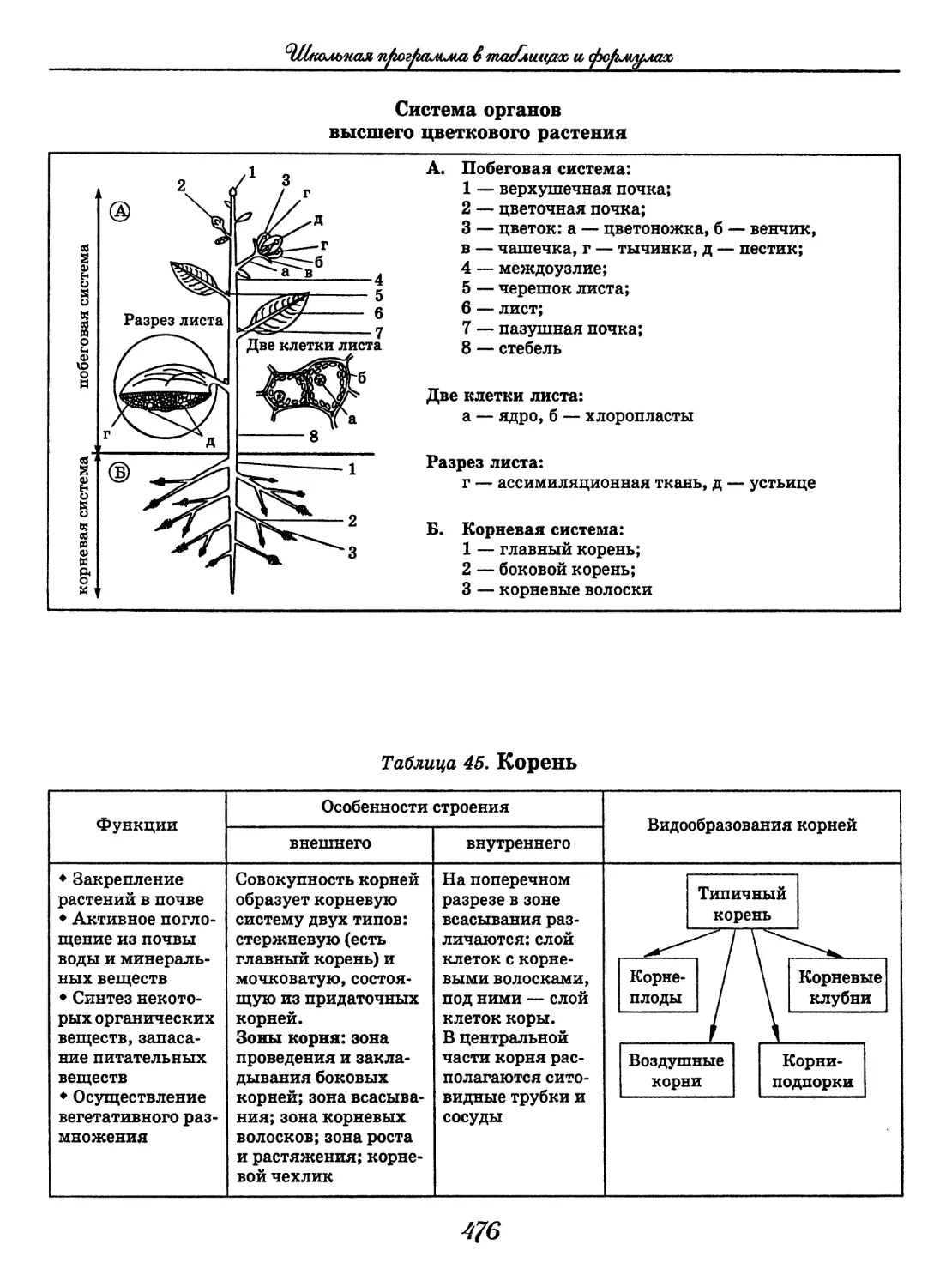
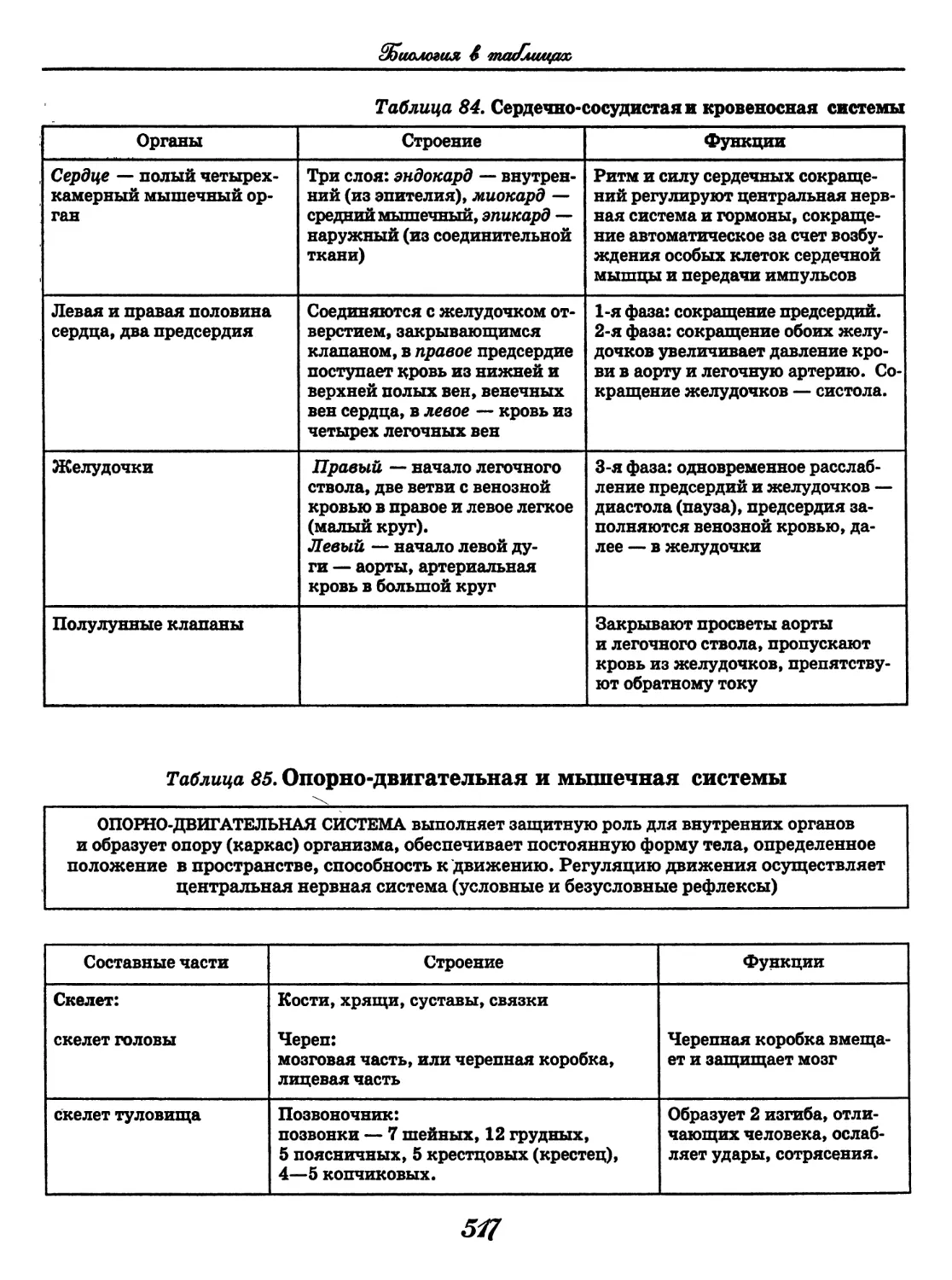
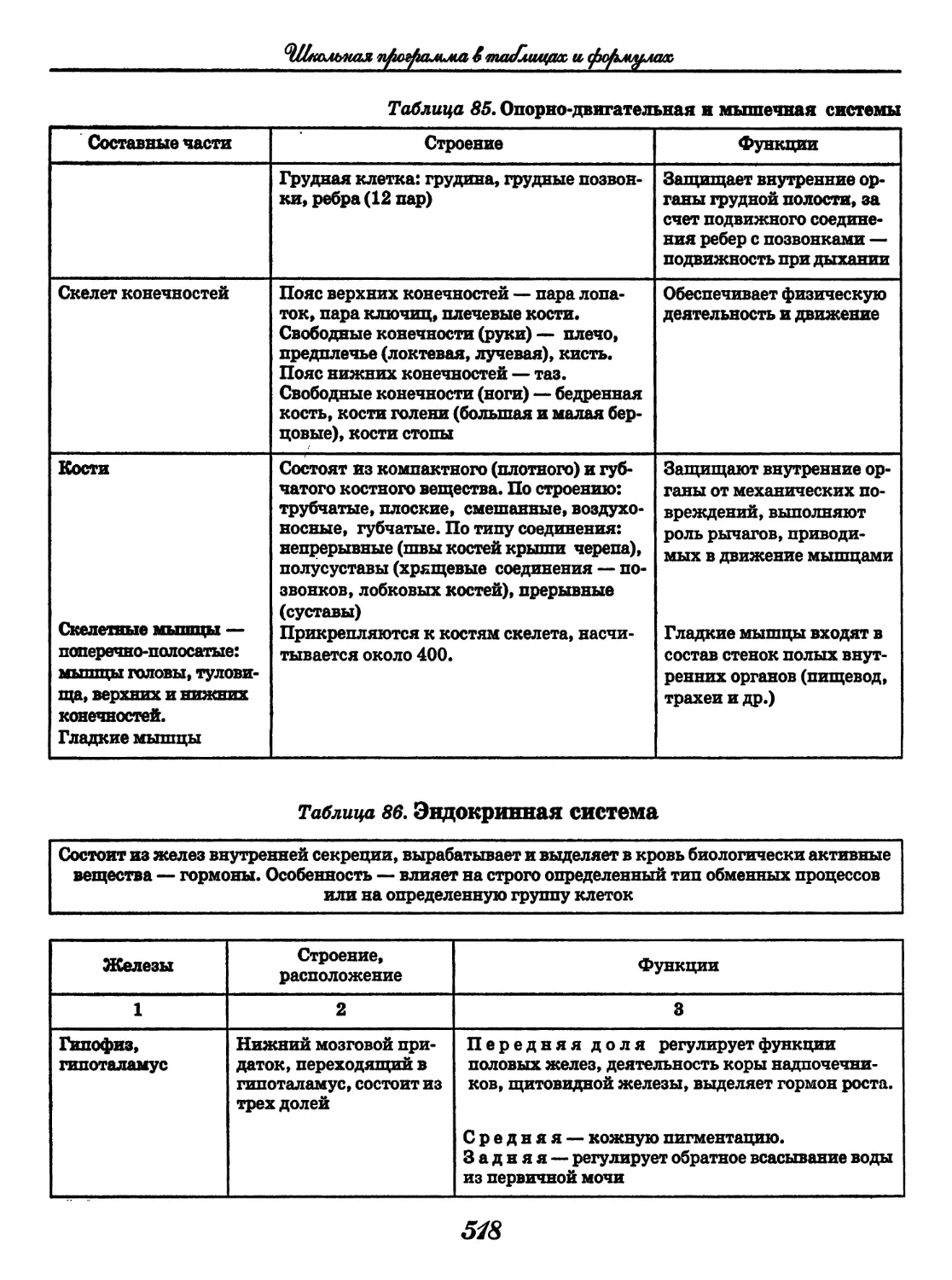
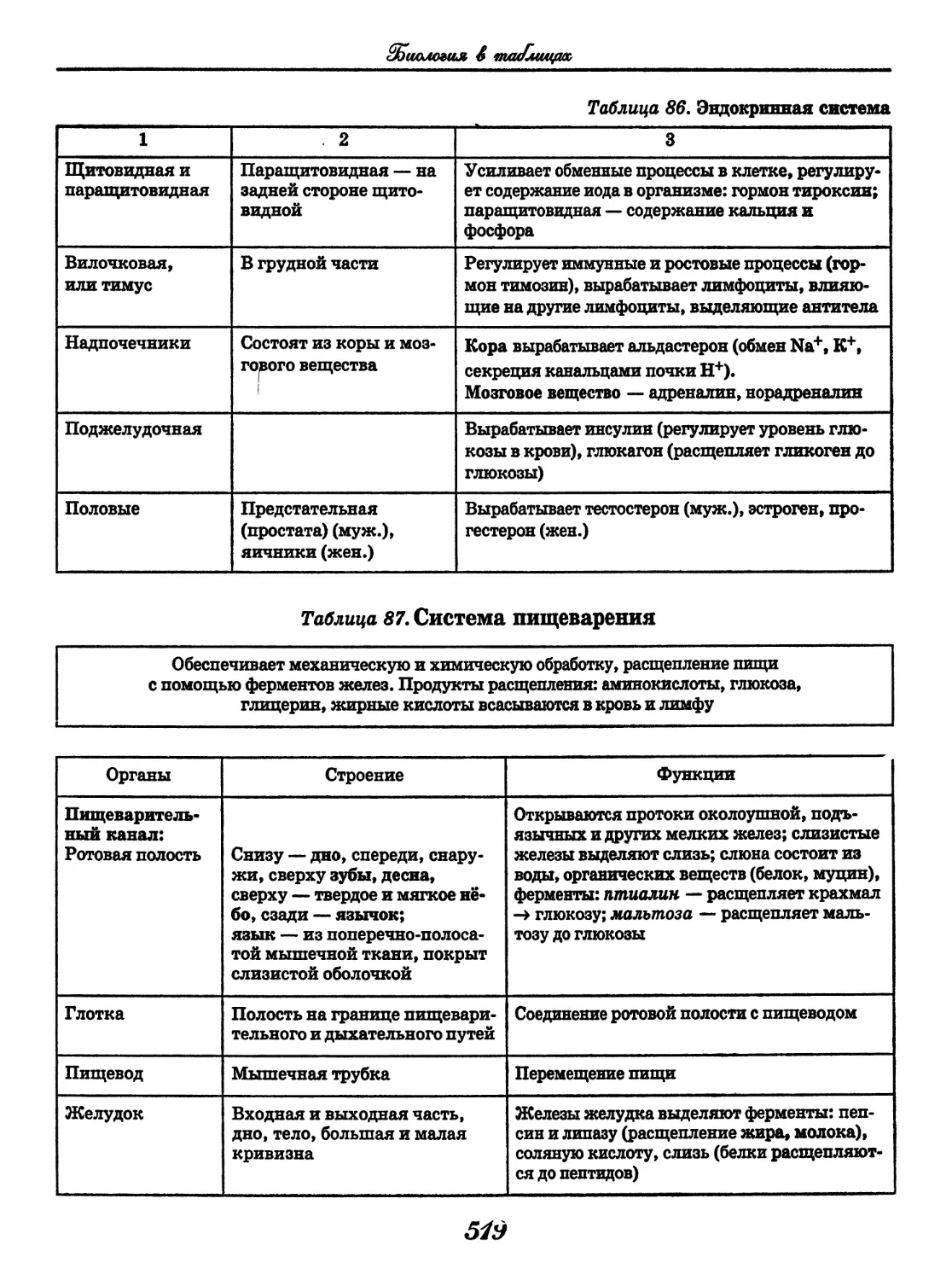
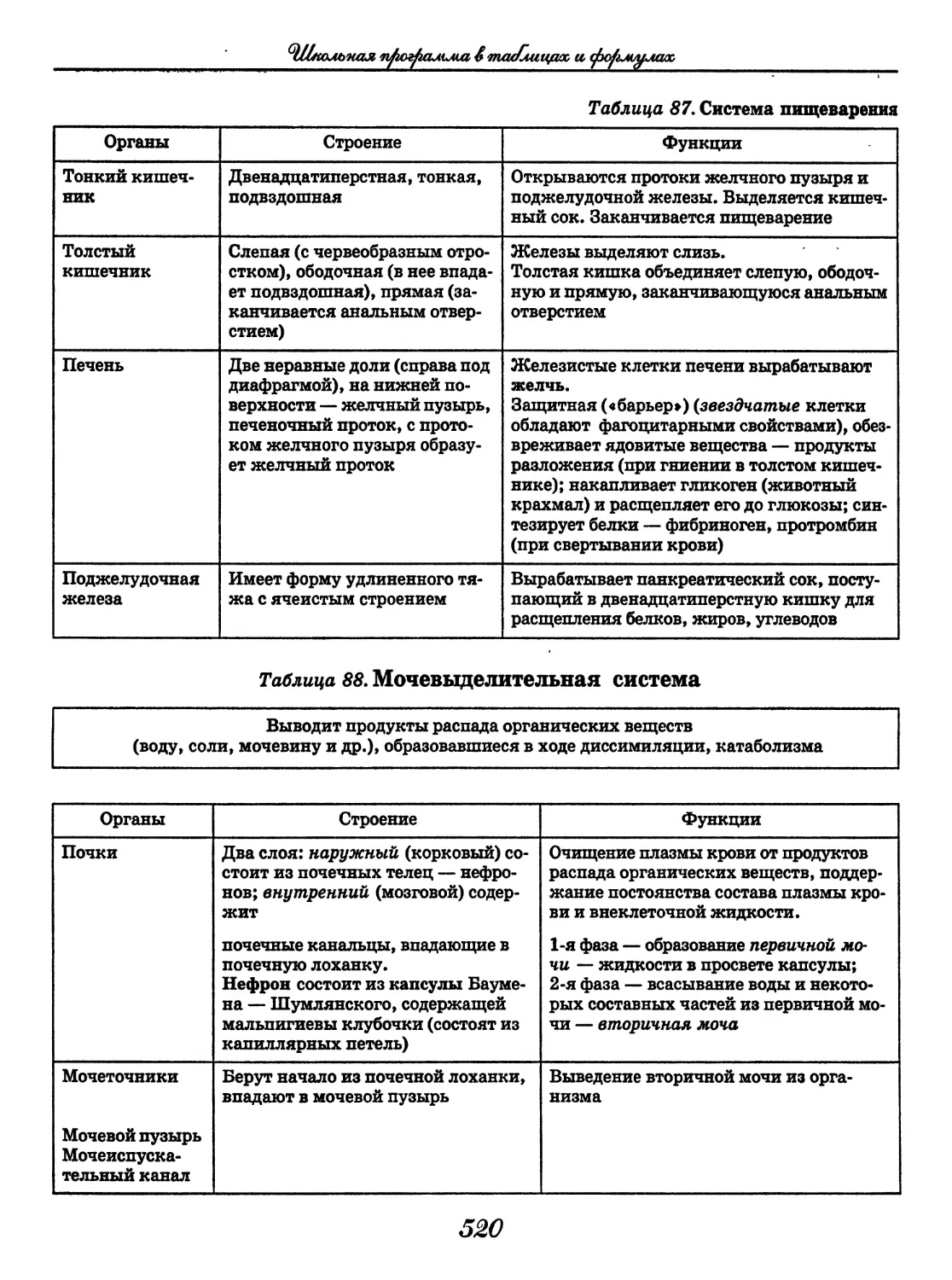
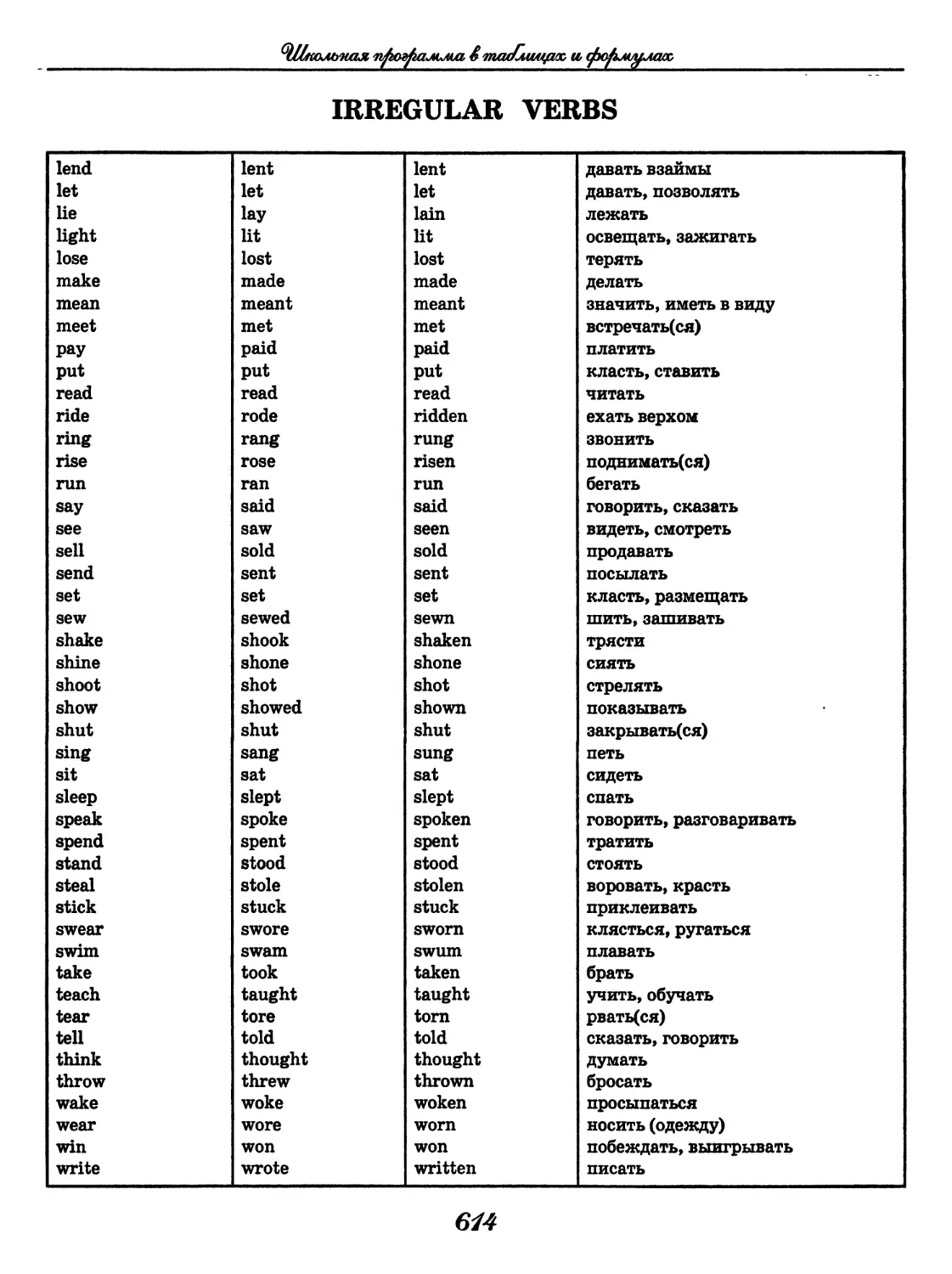
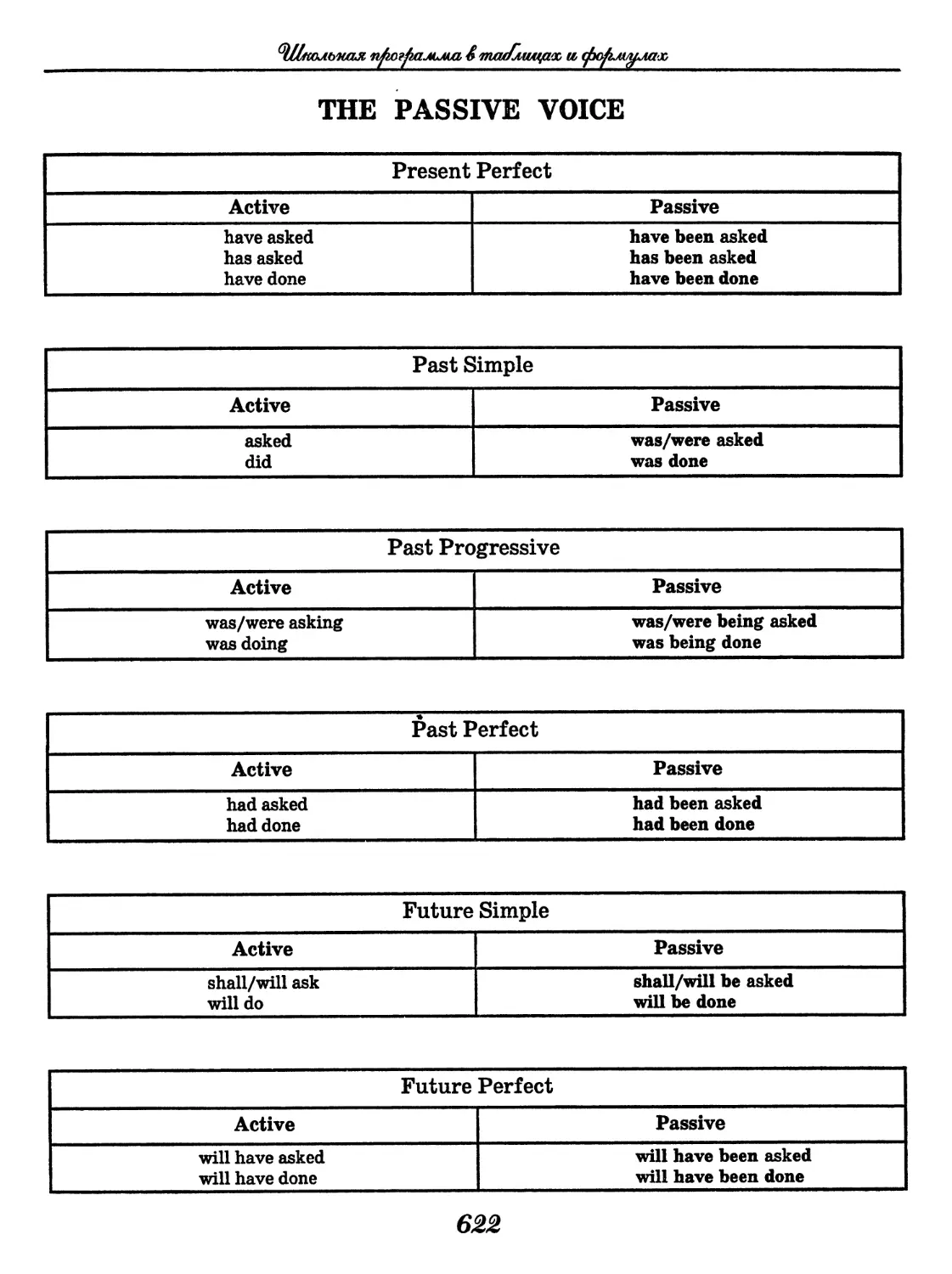
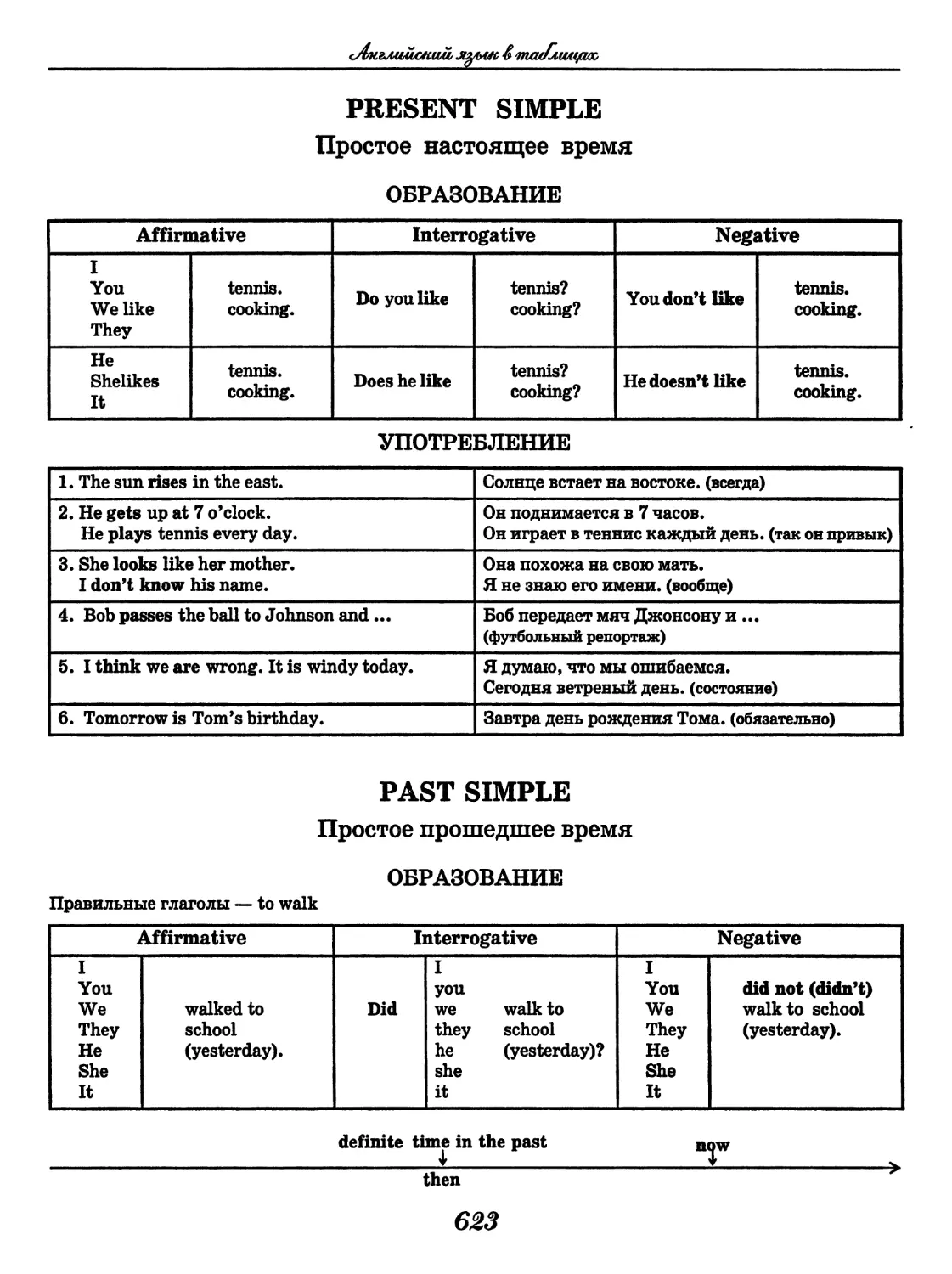
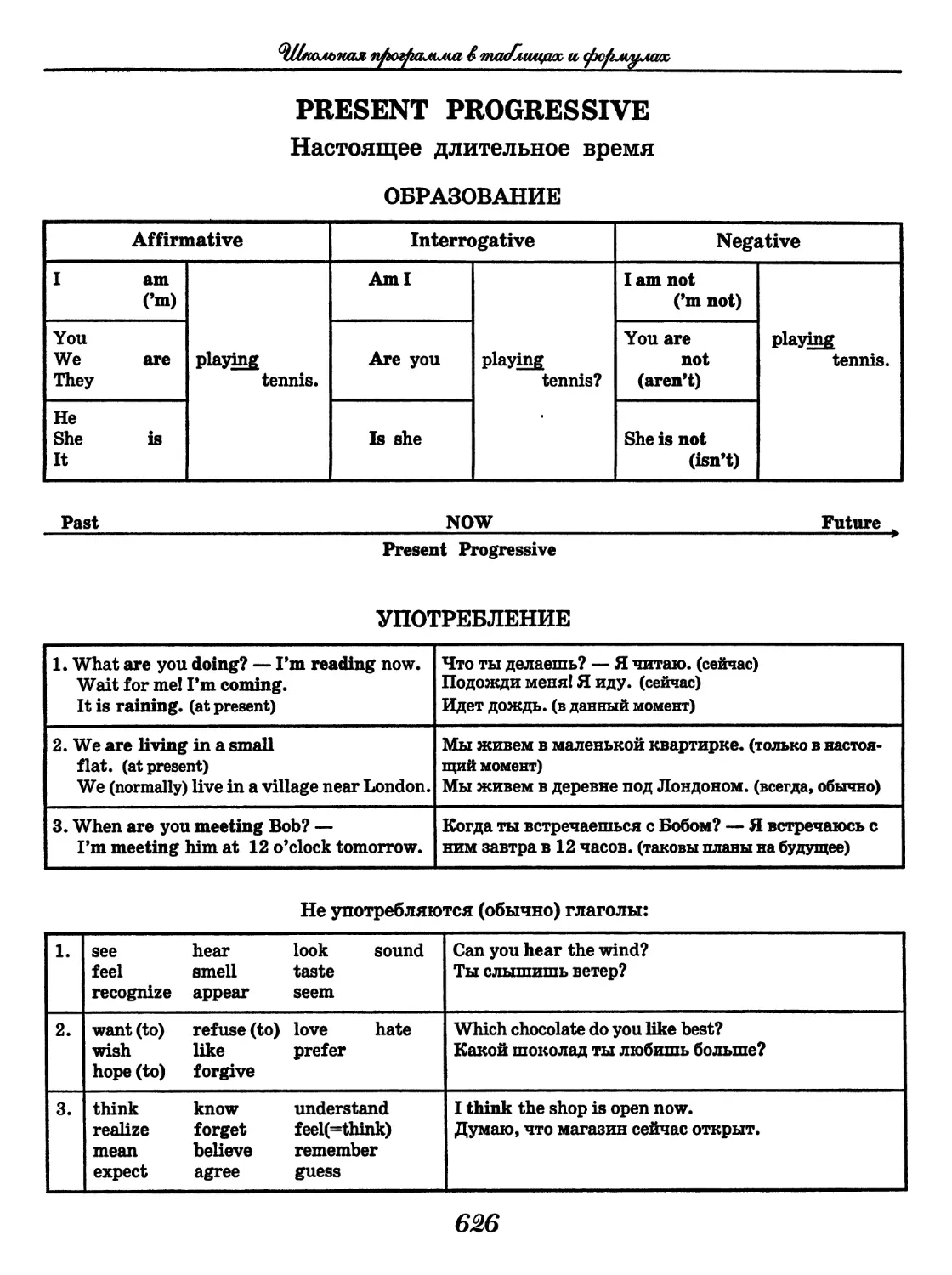
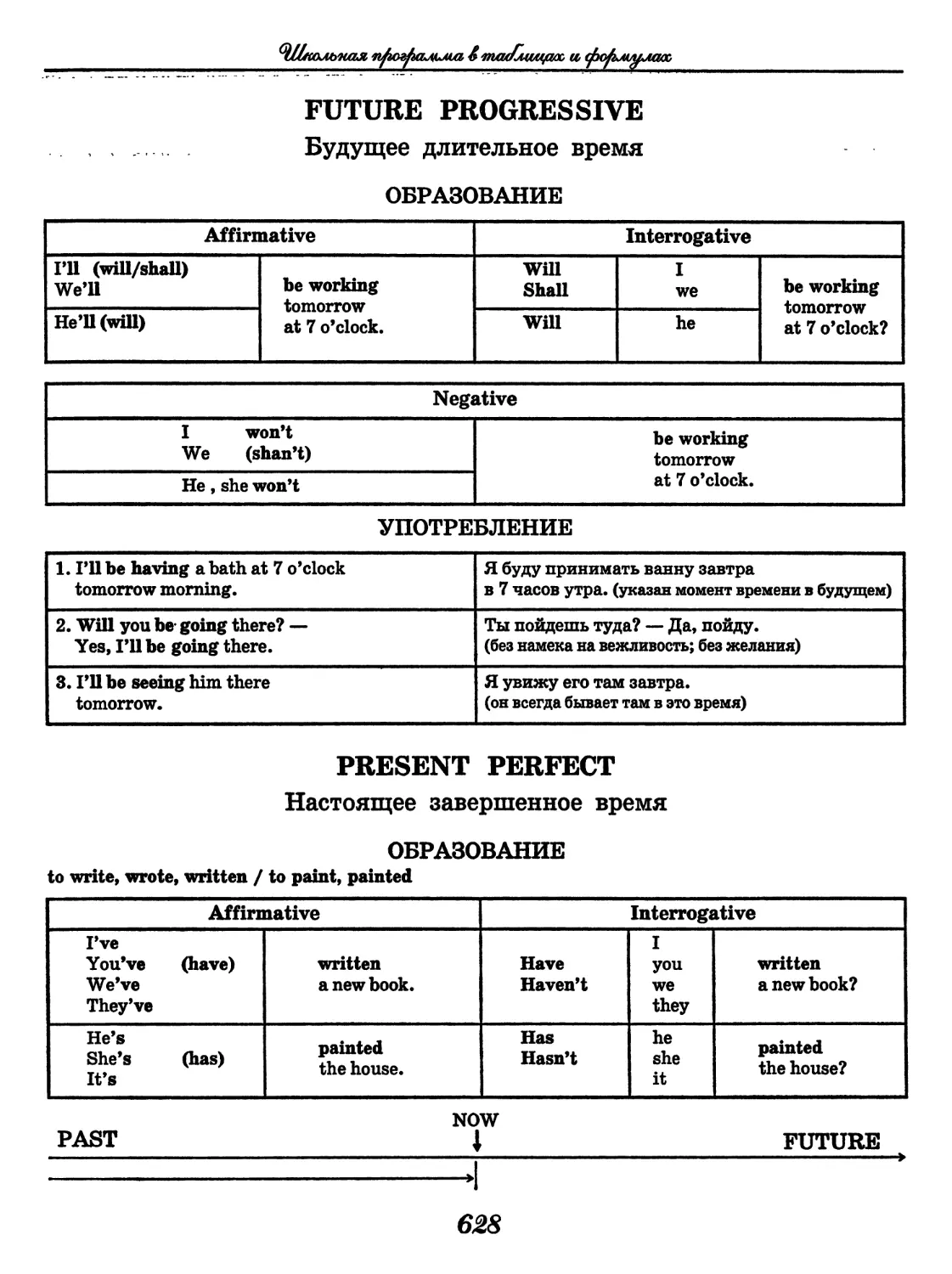
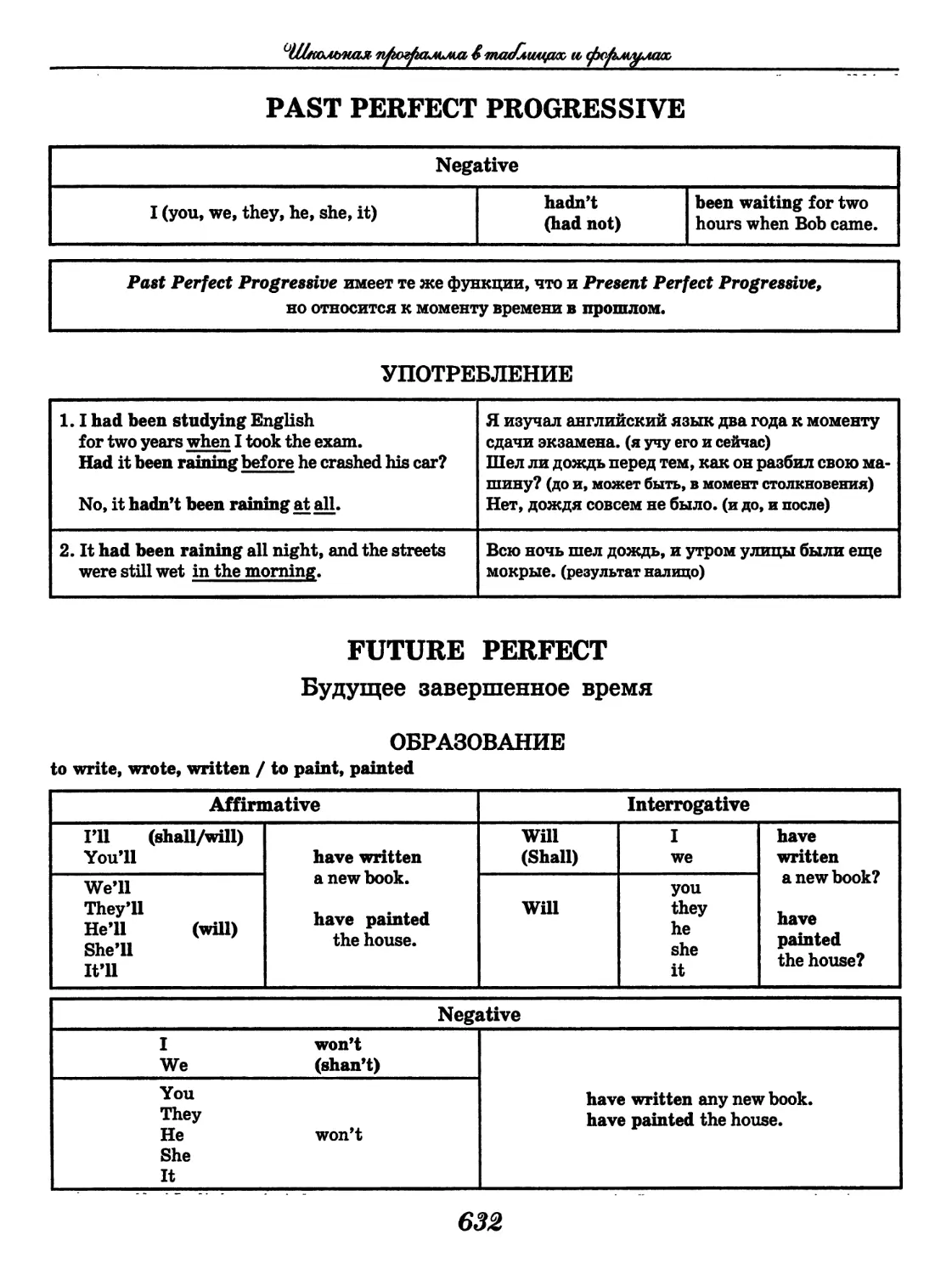
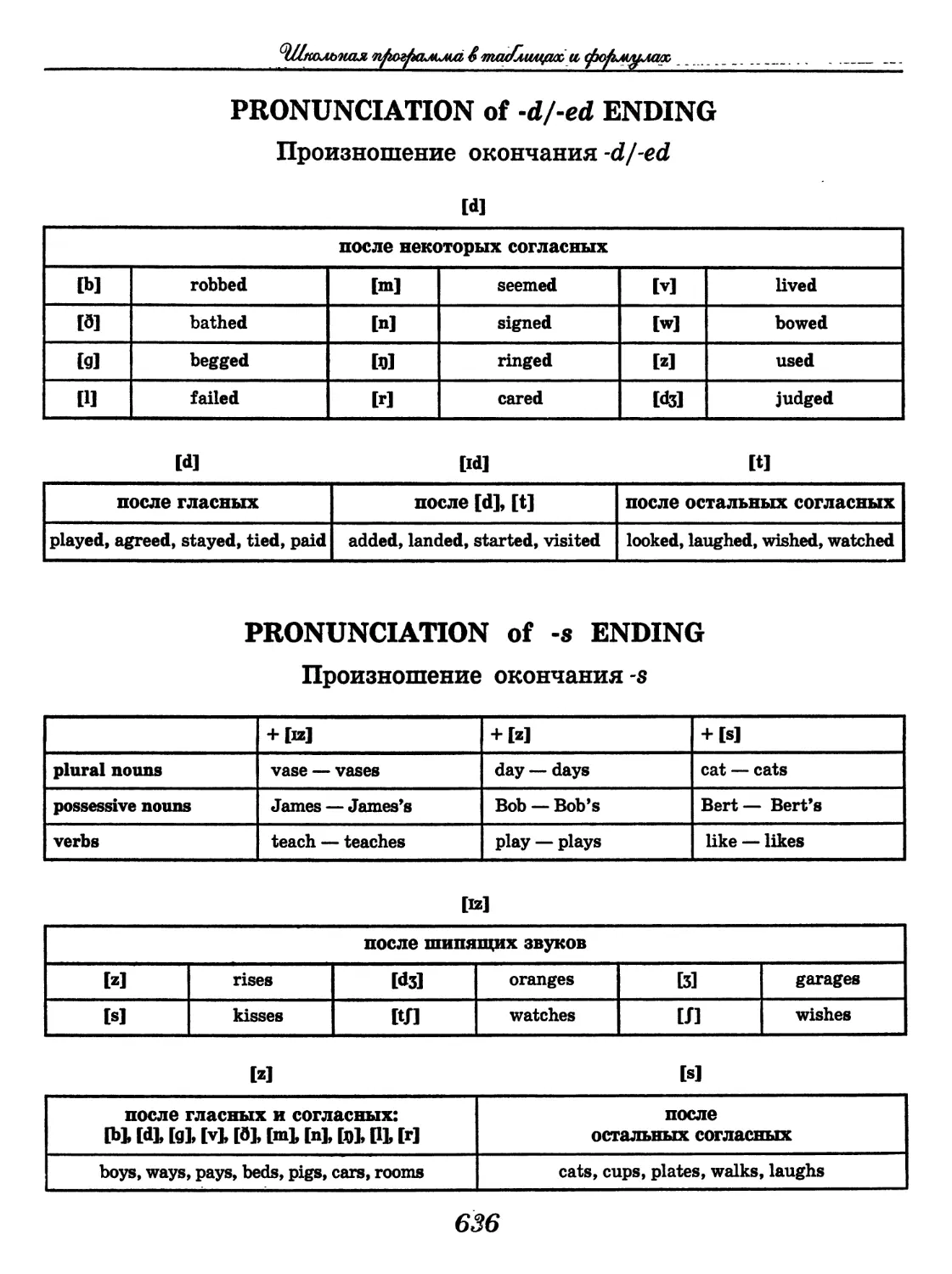
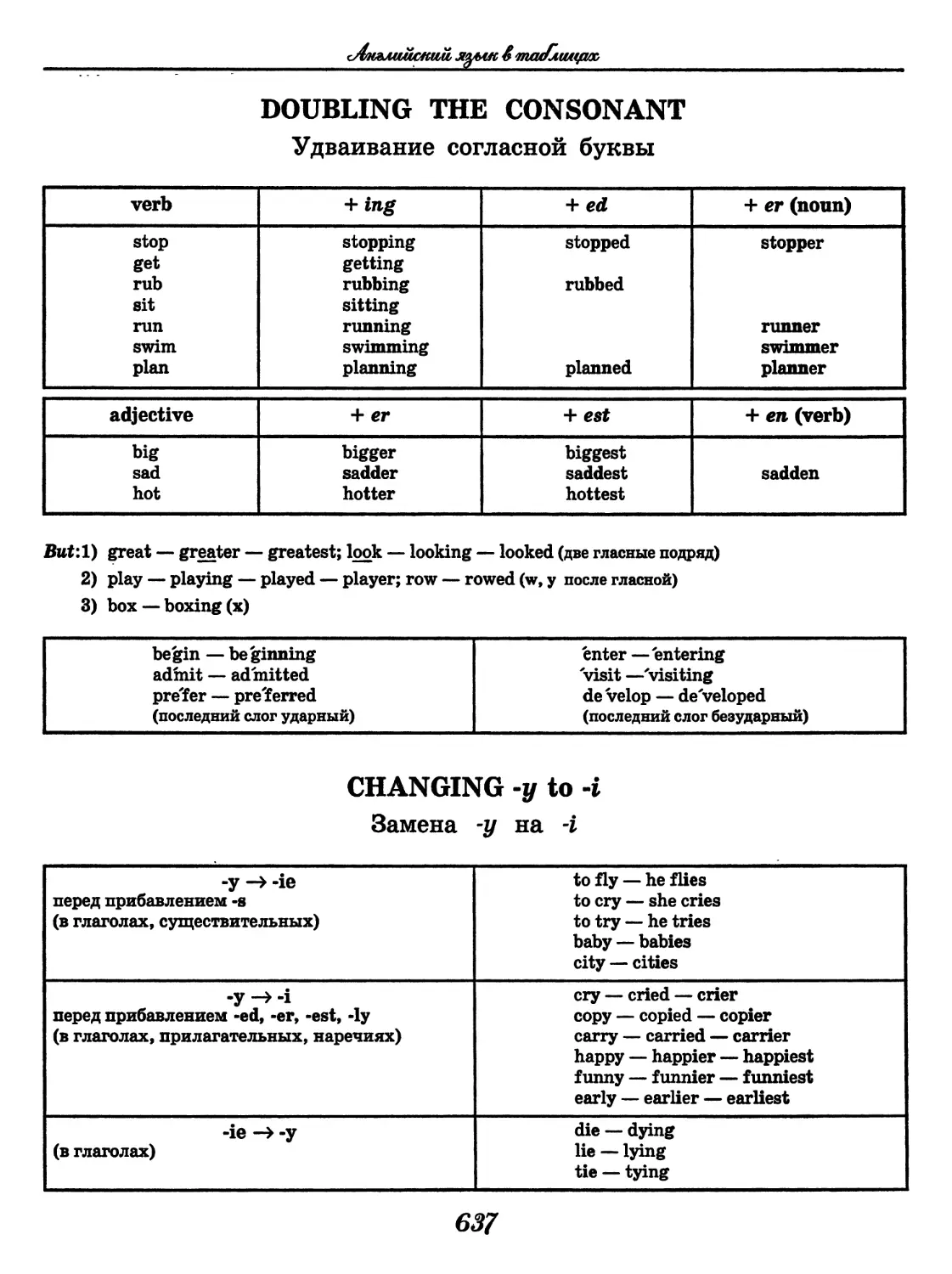
Author: Узлова Е.Е.
Tags: общее школьное образование общеобразовательная школа иллюстративные издания и материалы справочник школьное образование
ISBN: 5—7107—1961—7
Year: 1998
Text
Школьная программа
в таблицах и формулах
Большой универсальный
справочник
Русский язык • История
Математика • Физика • География • Биология
Химия • Английский язык
Москва
Издательский дом «Дрофа»
1998
УДК 373.167.1(08)
ББК 96
Ш67
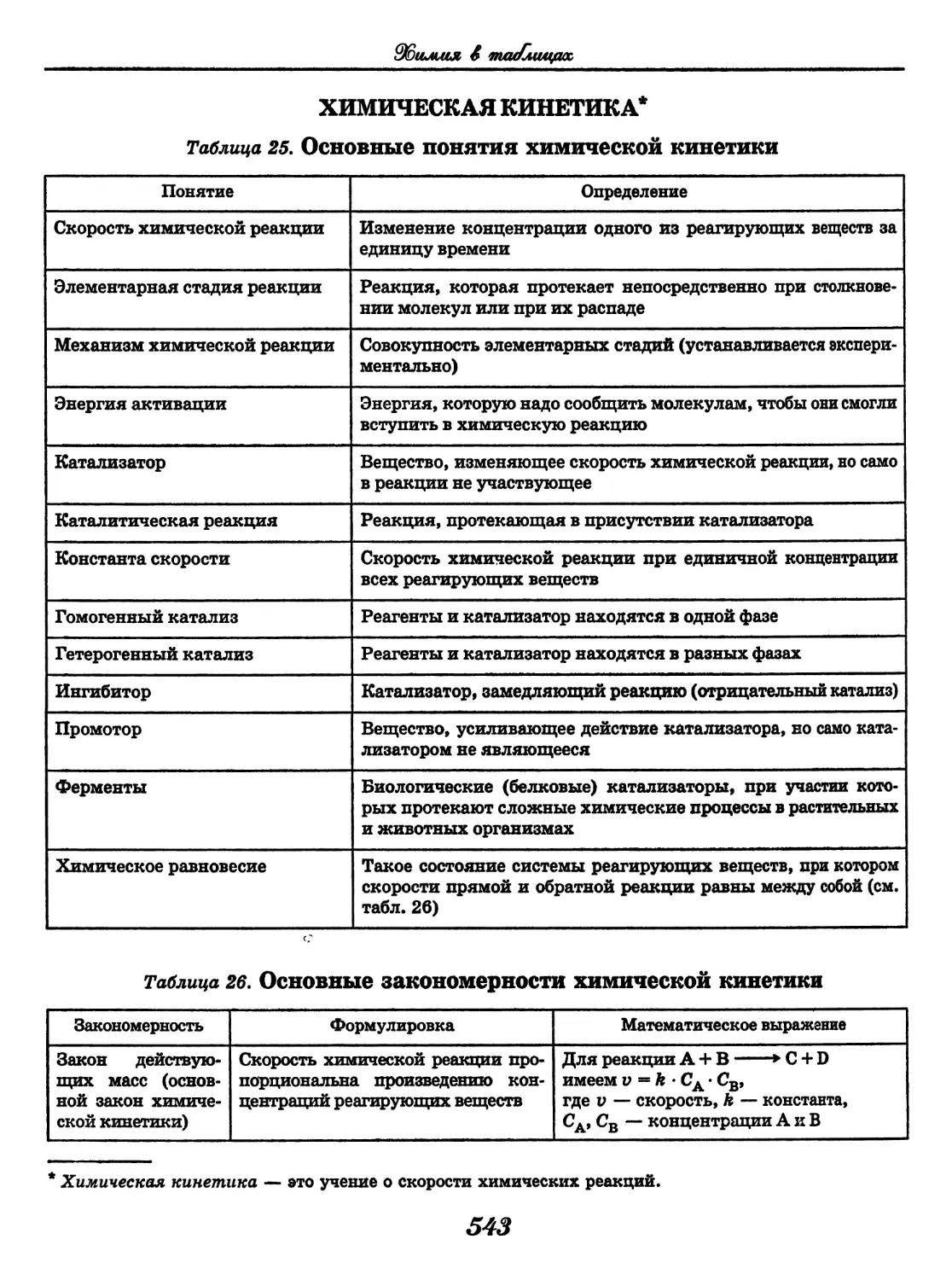
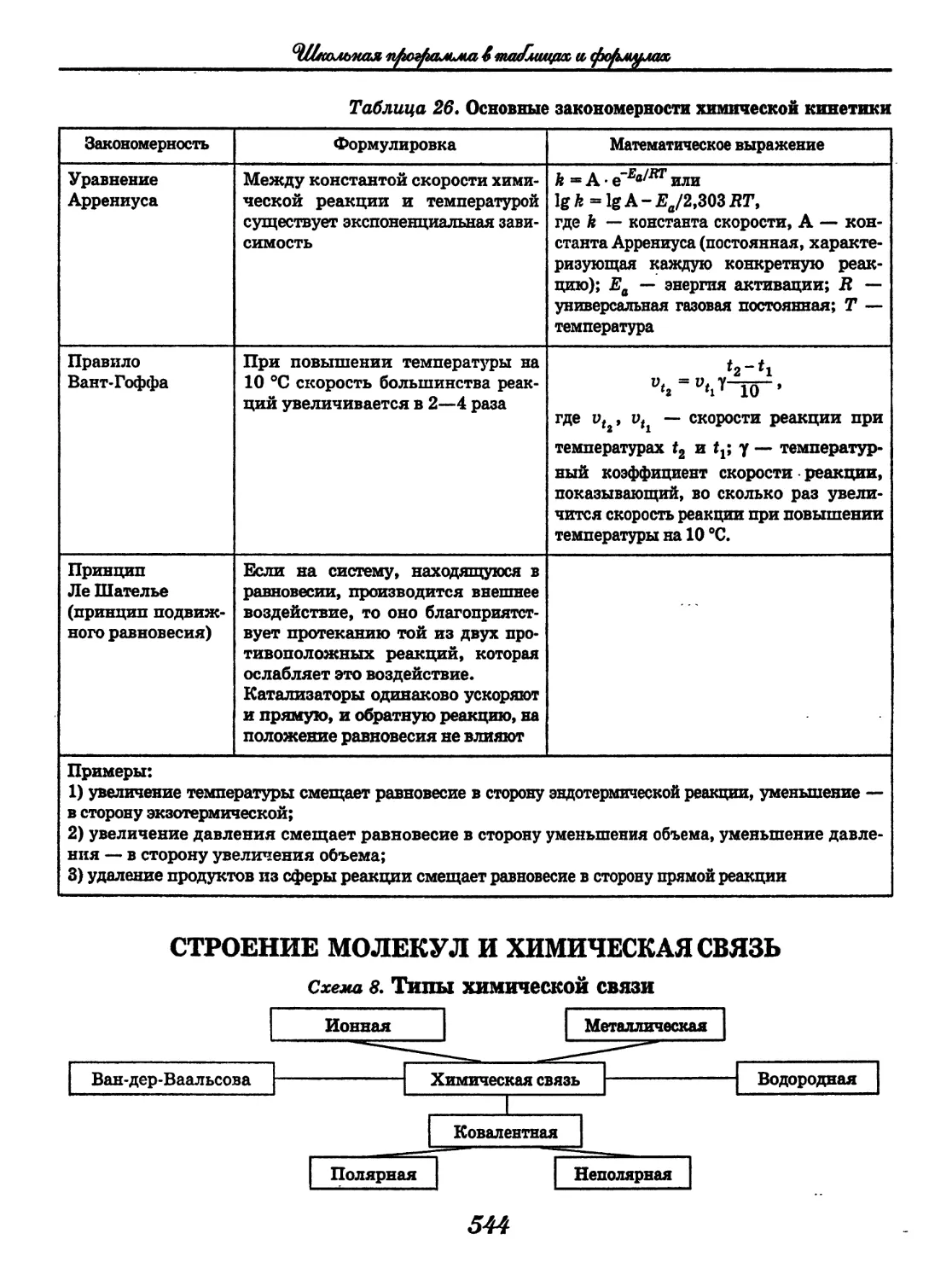
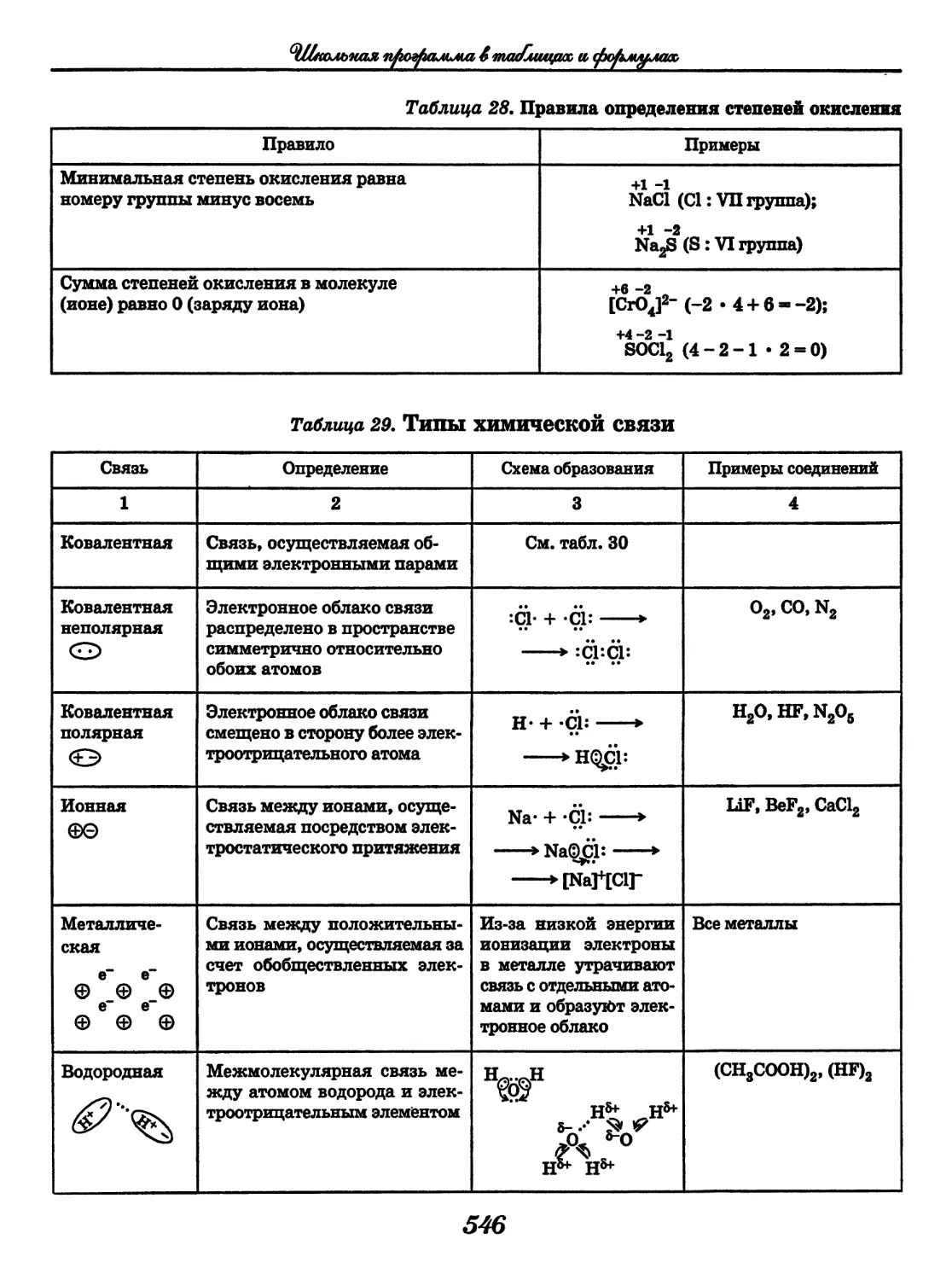
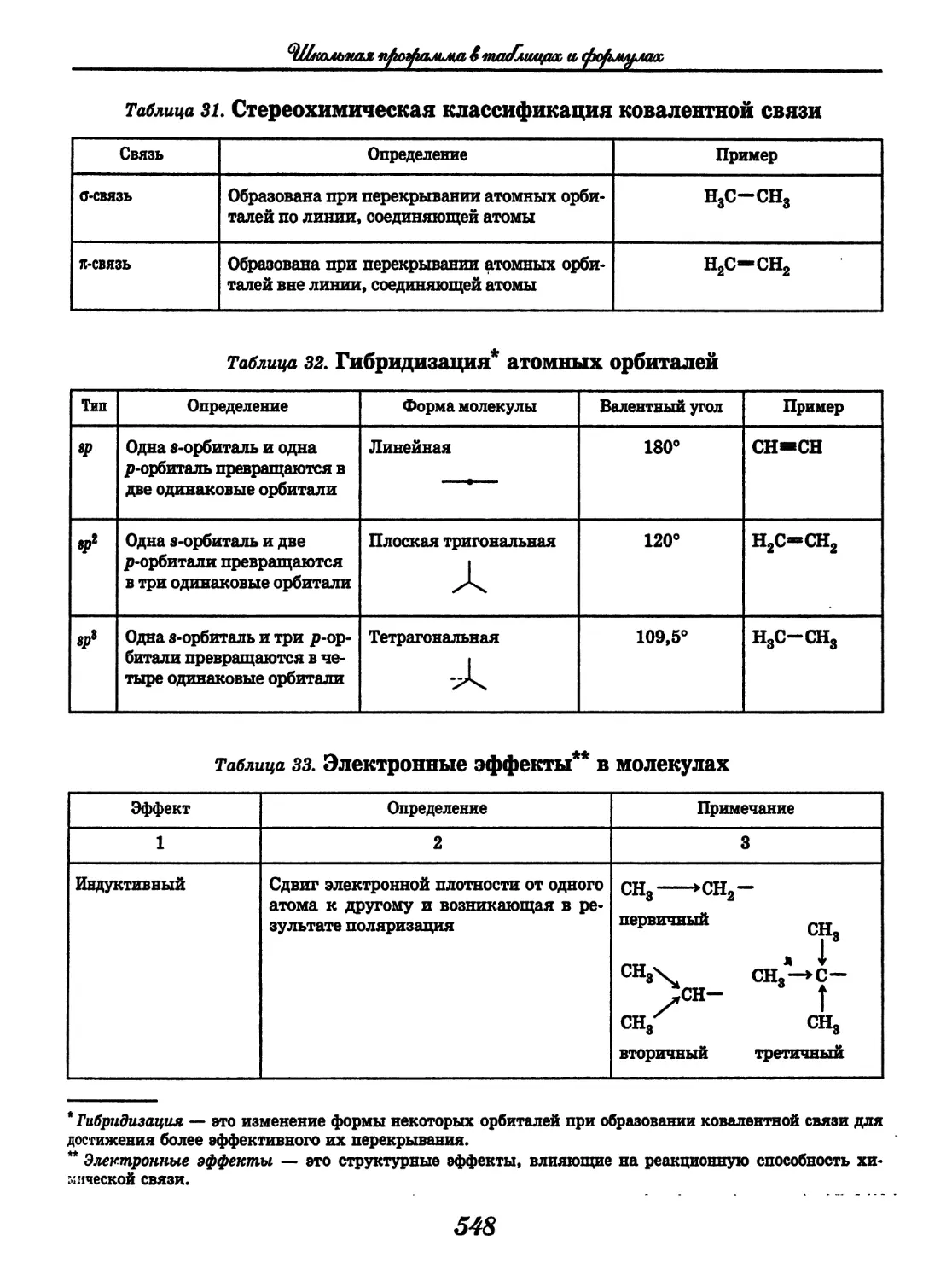
СОДЕРЖАНИЕ
Русский язык
(3. Д. Гольдин, В. Н. Светлышева)........ 4
История
История России XX века в таблицах
{А. А. Данилов)........................ 62
Всемирная история в таблицах
(А. Т. Степанищев и др.)............... 90
Математика
Алгебра в таблицах
(Л. И. Звавич, А. Р. Рязановский)..... 122
Геометрия в таблицах
(Л. И. Звавич, А. Р. Рязановский)..... 184
Математика в формулах................. 267
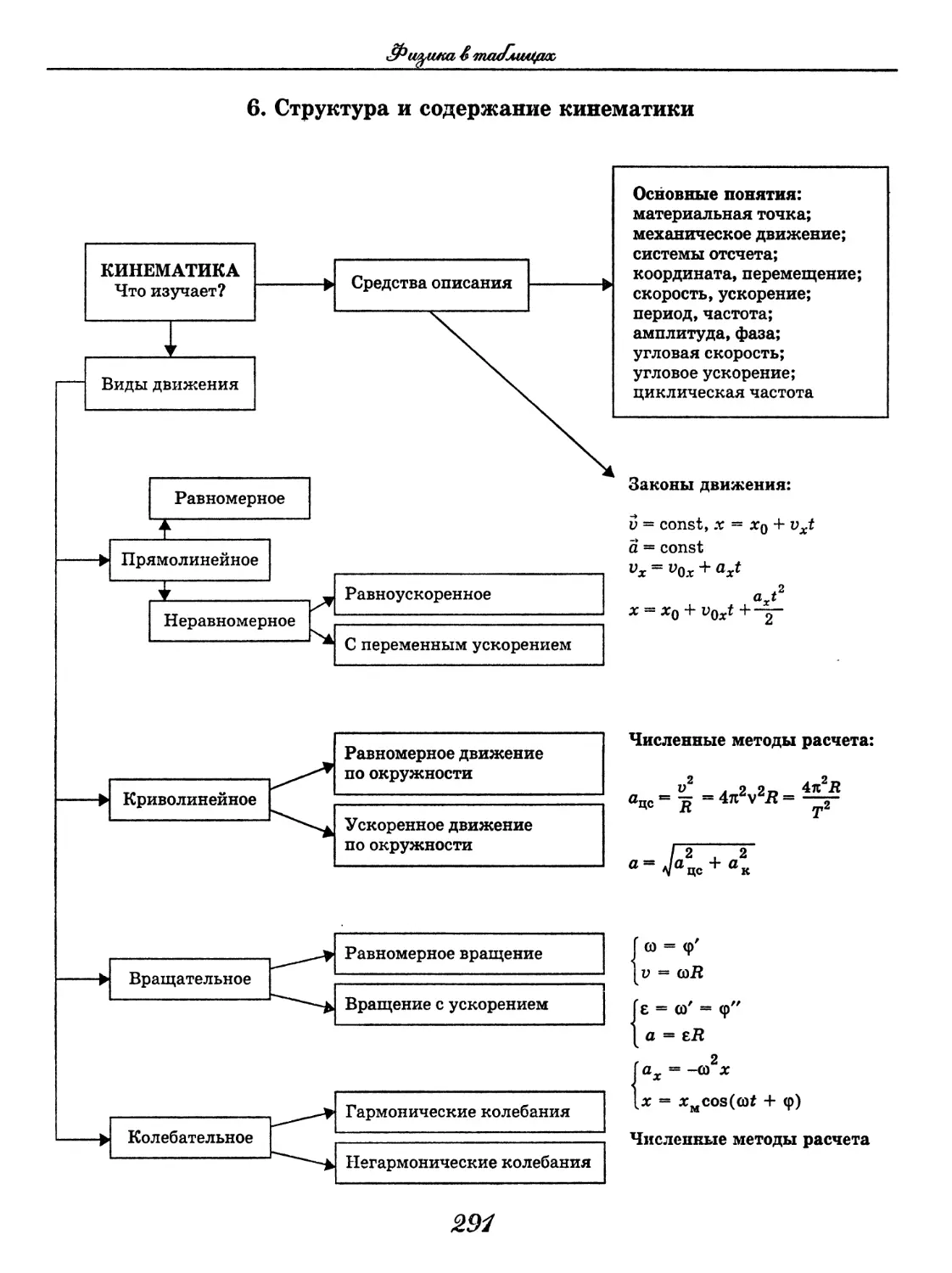
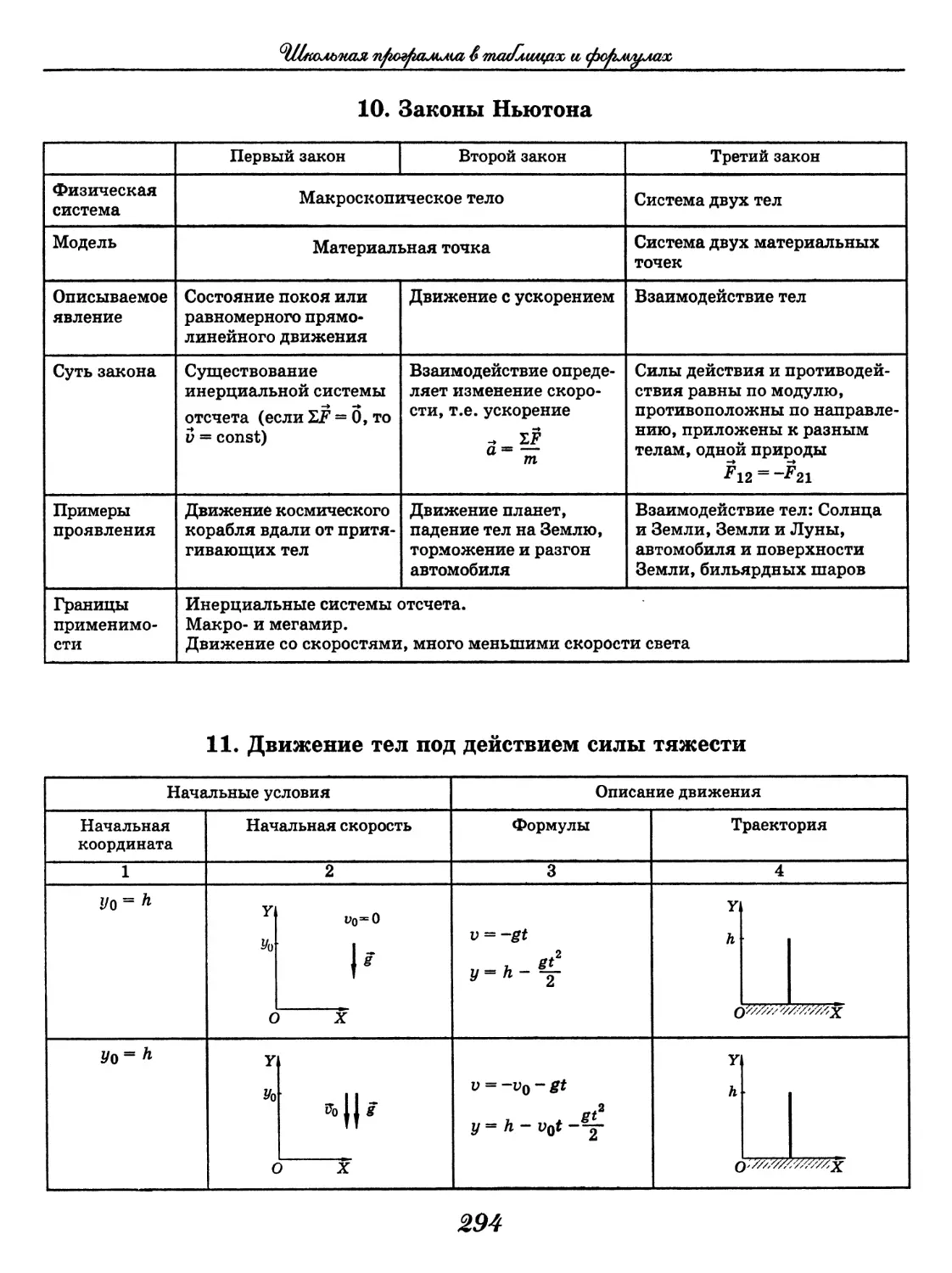
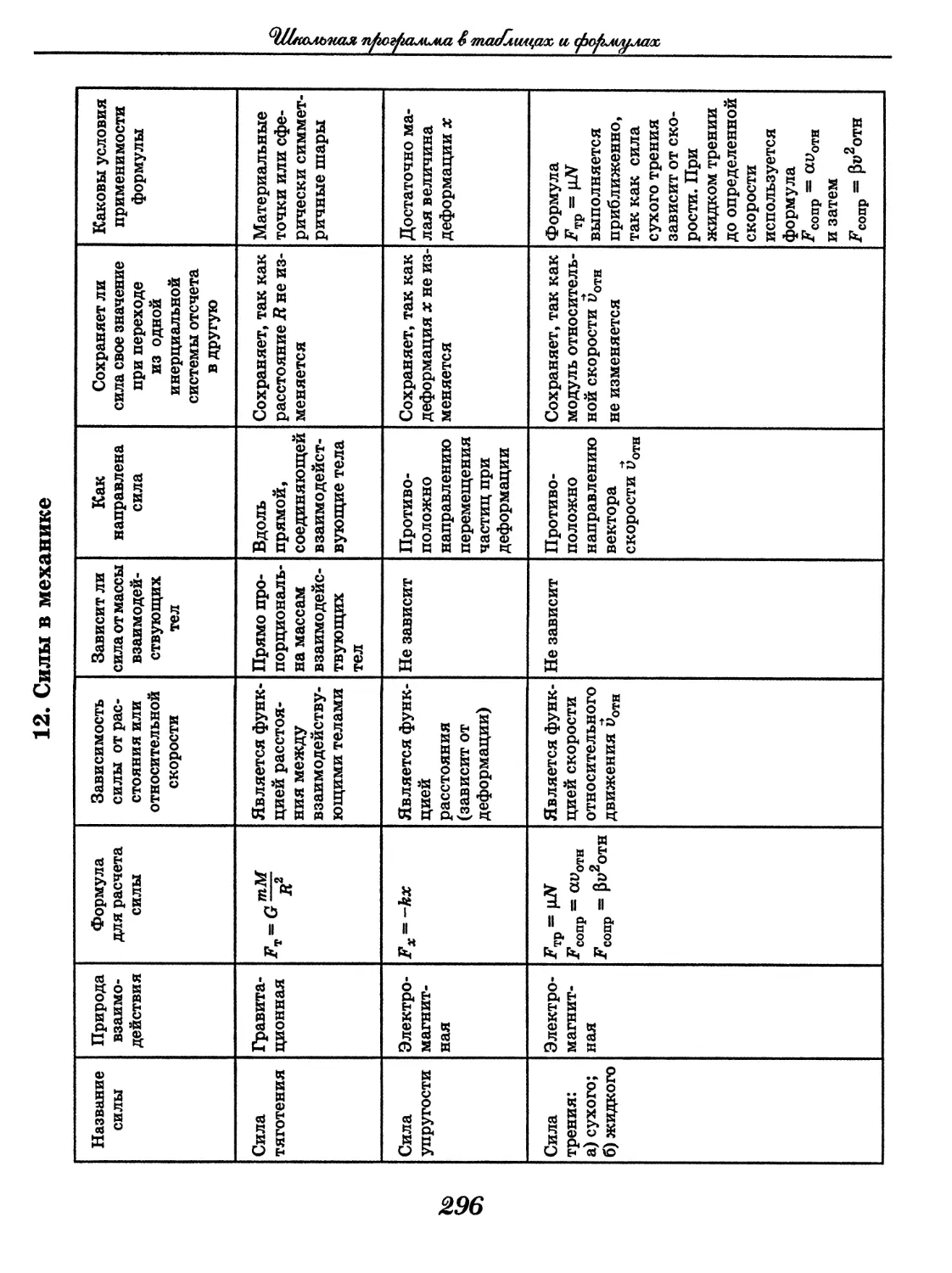
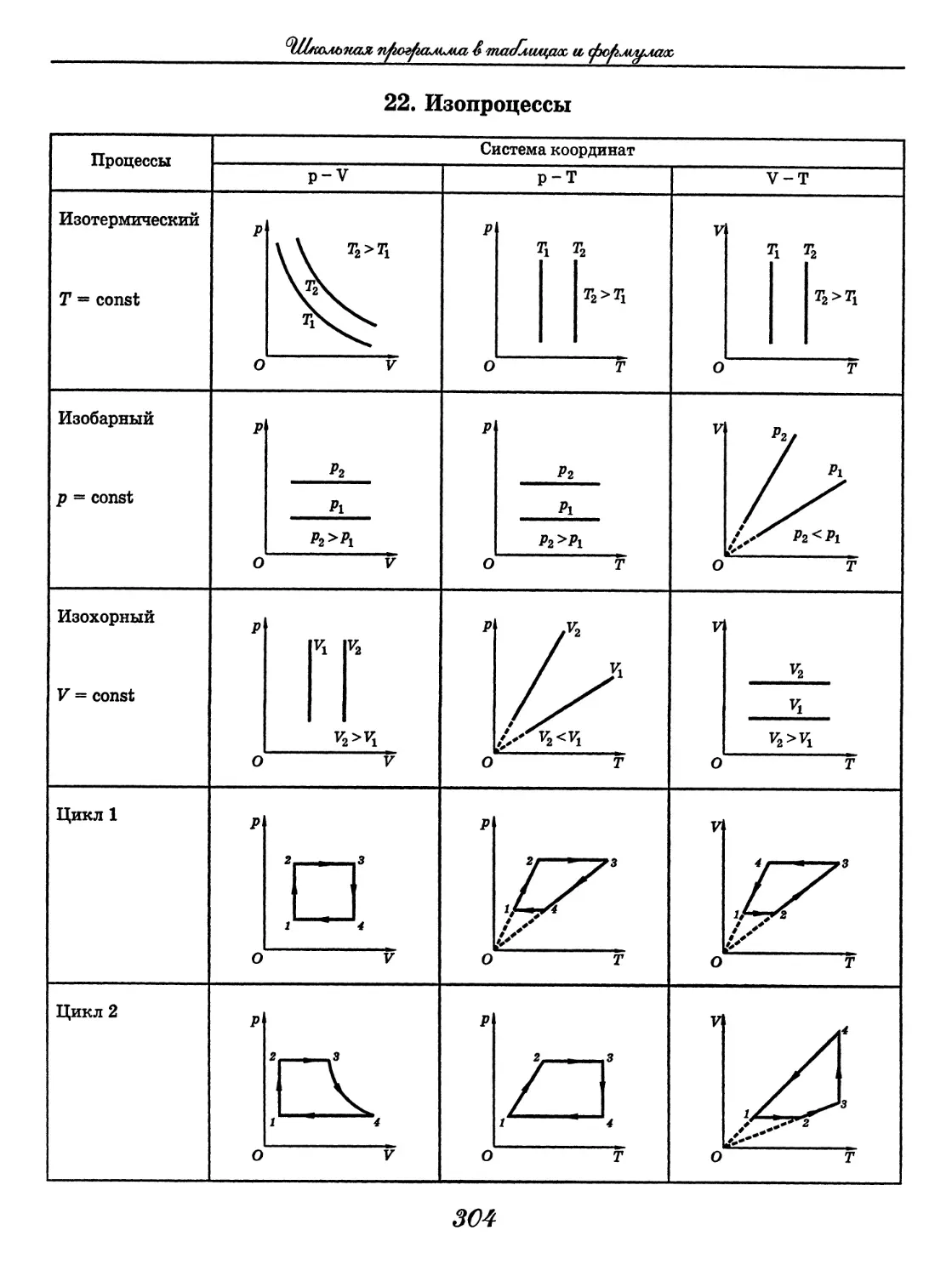
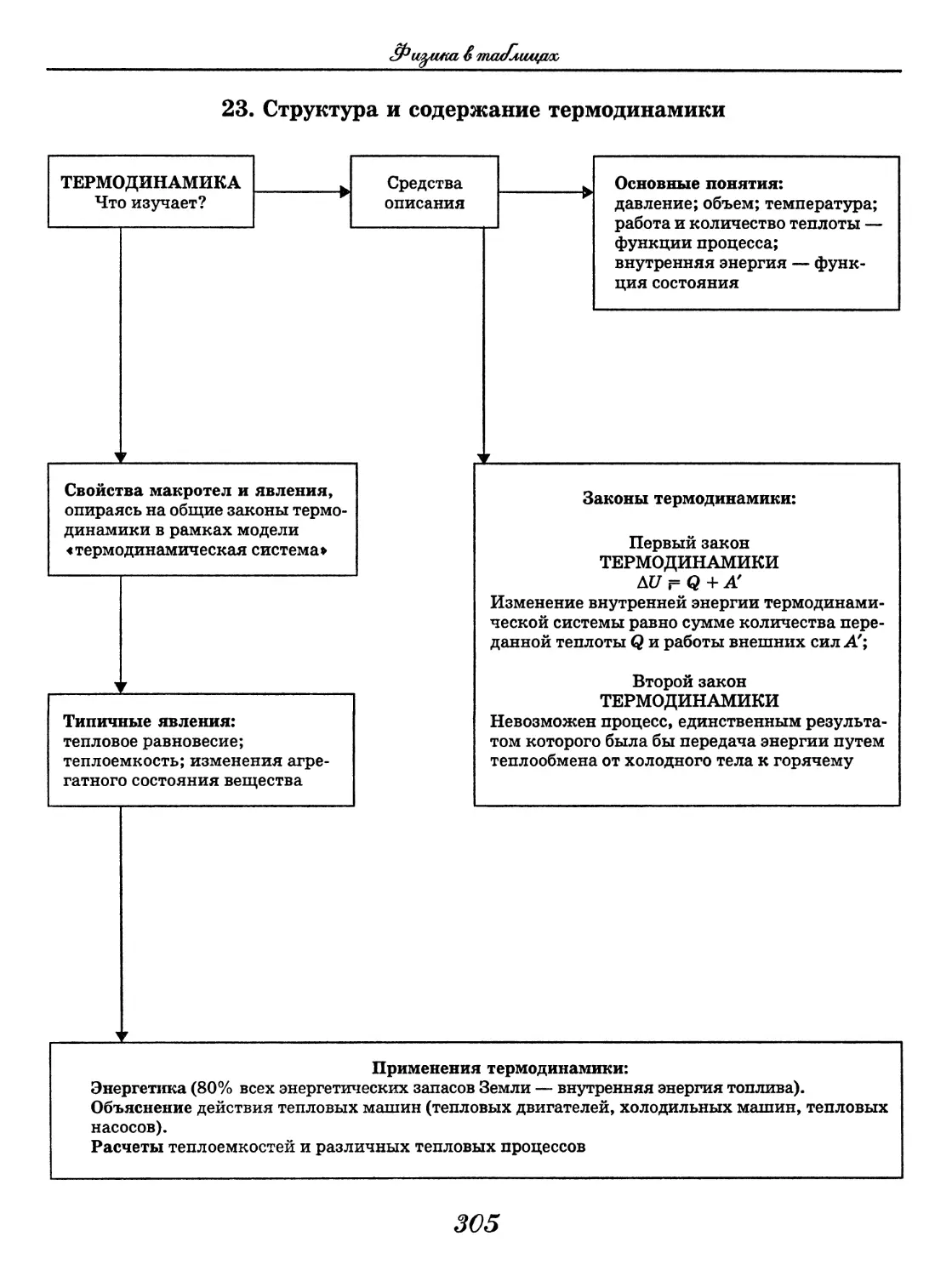
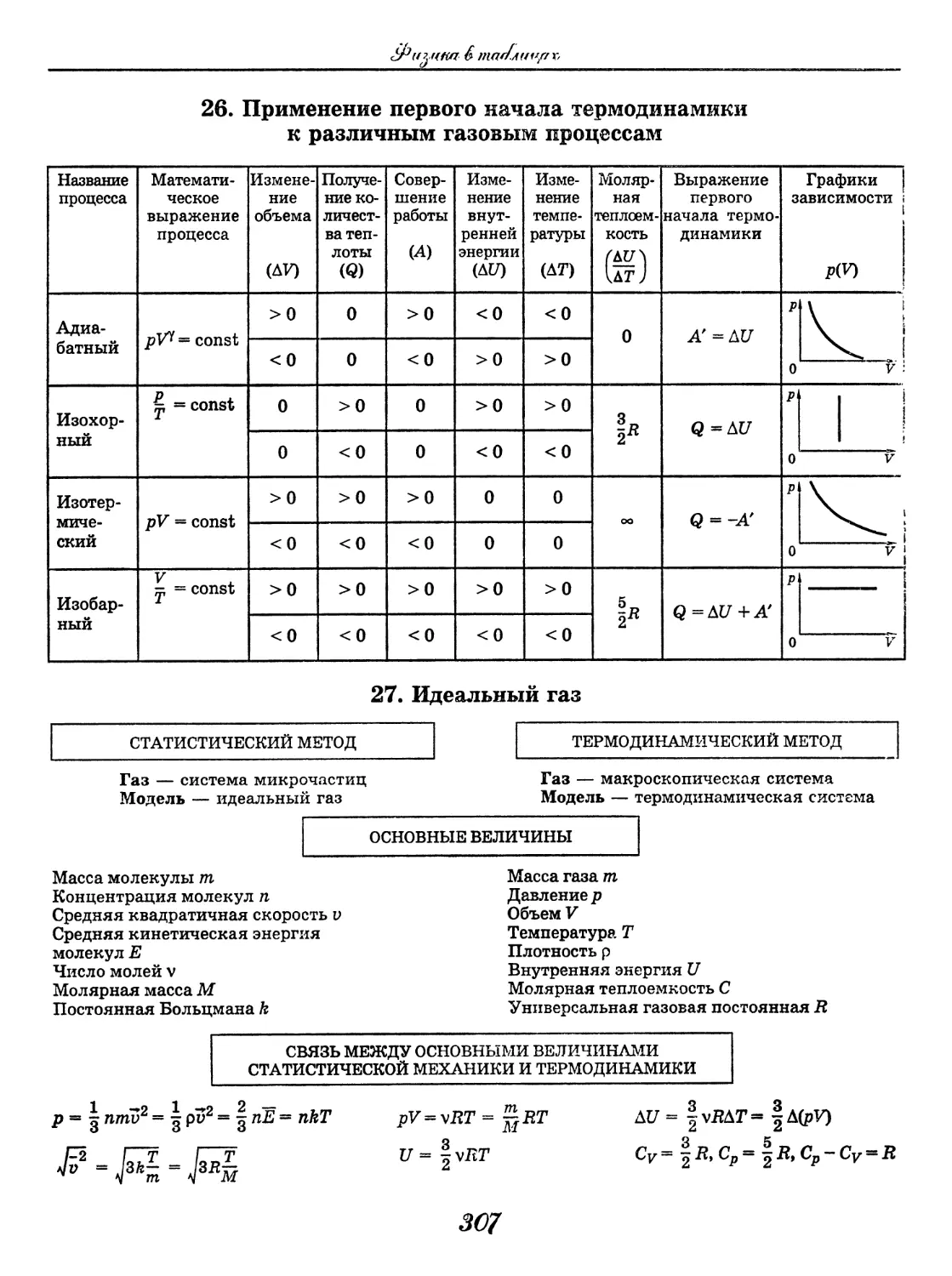
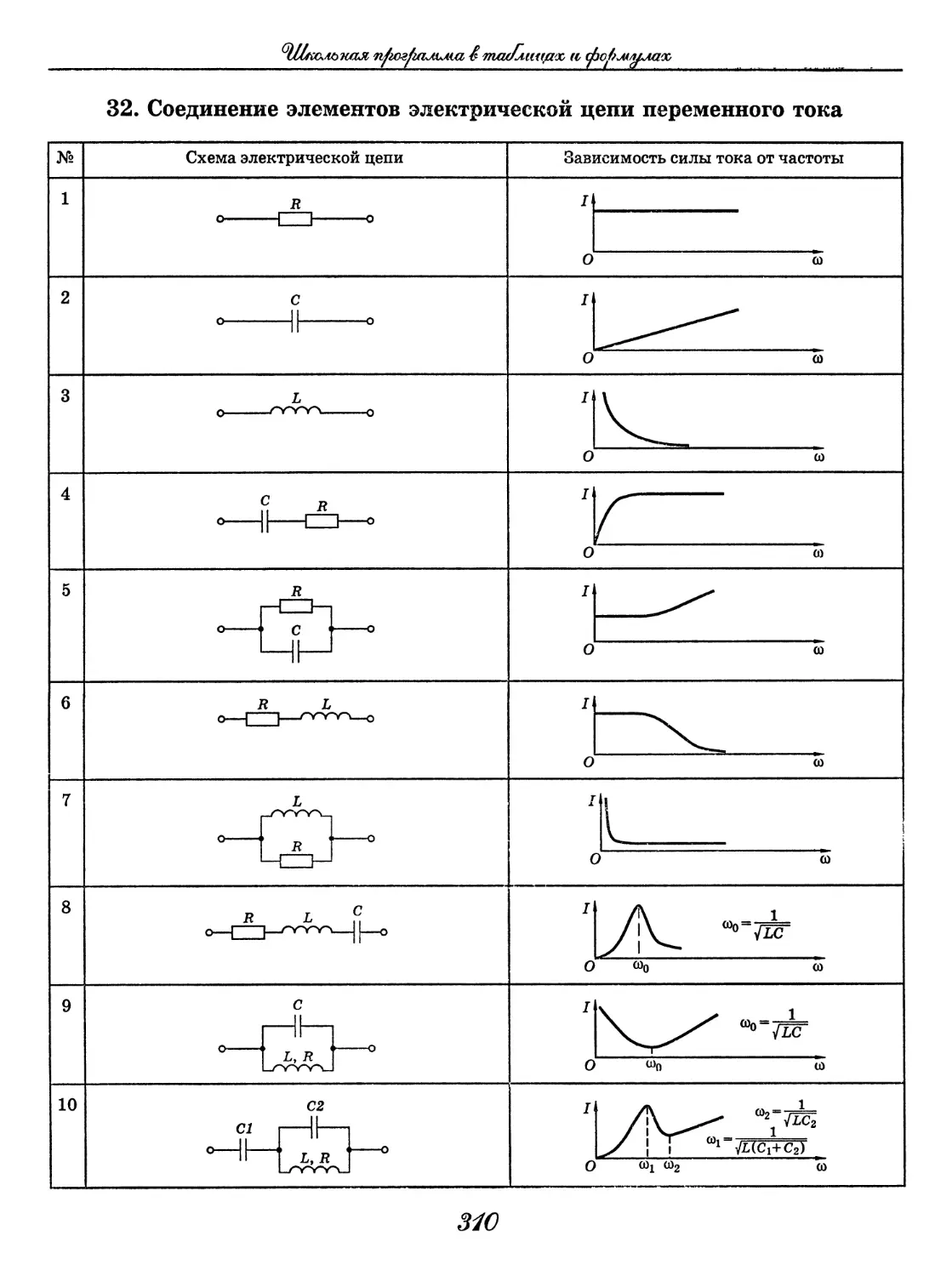
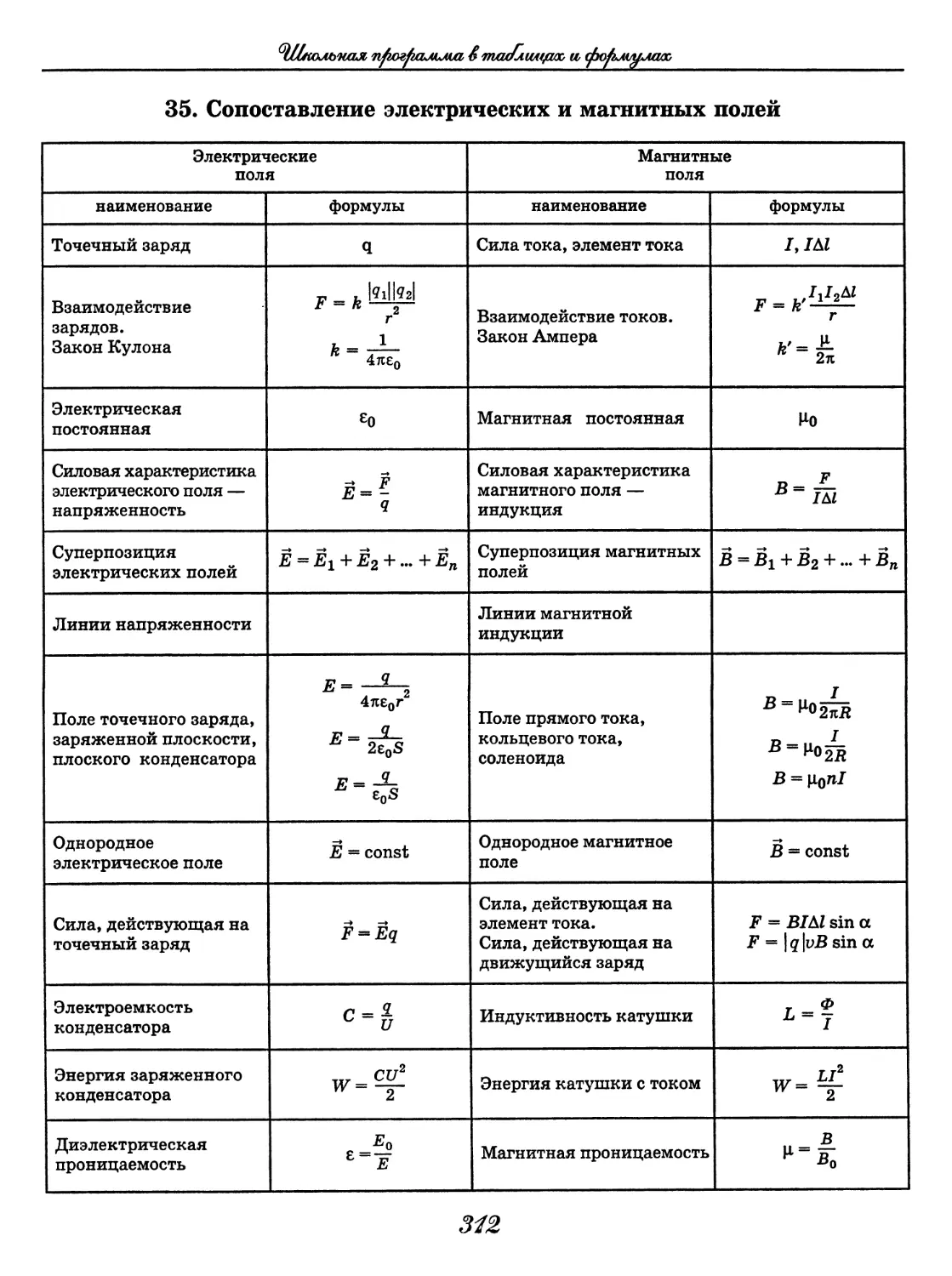
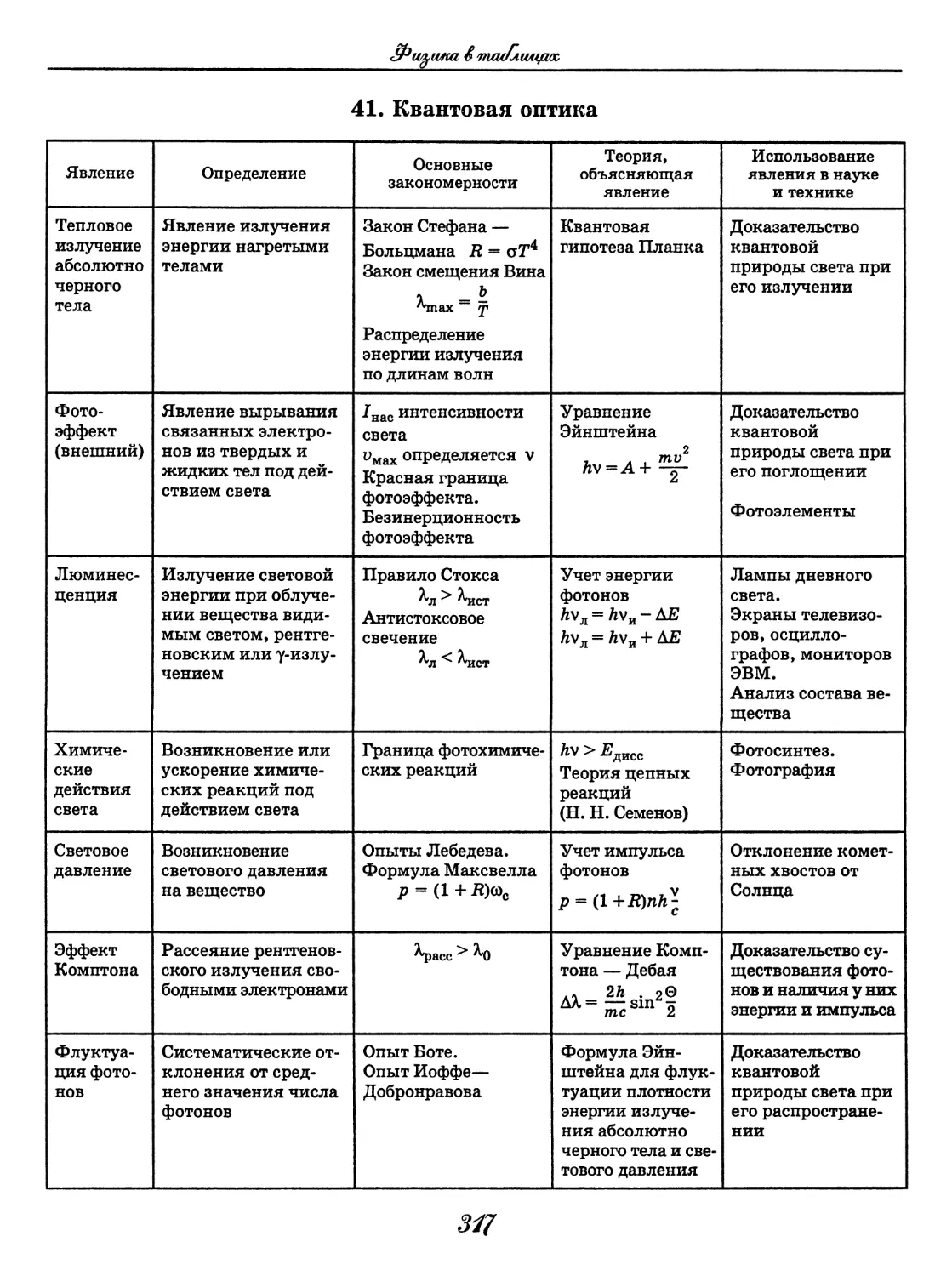
Физика
Физика в таблицах
(В. А. Орлов)......................... 288
Физика в формулах
(В. А. Ильин)..........................330
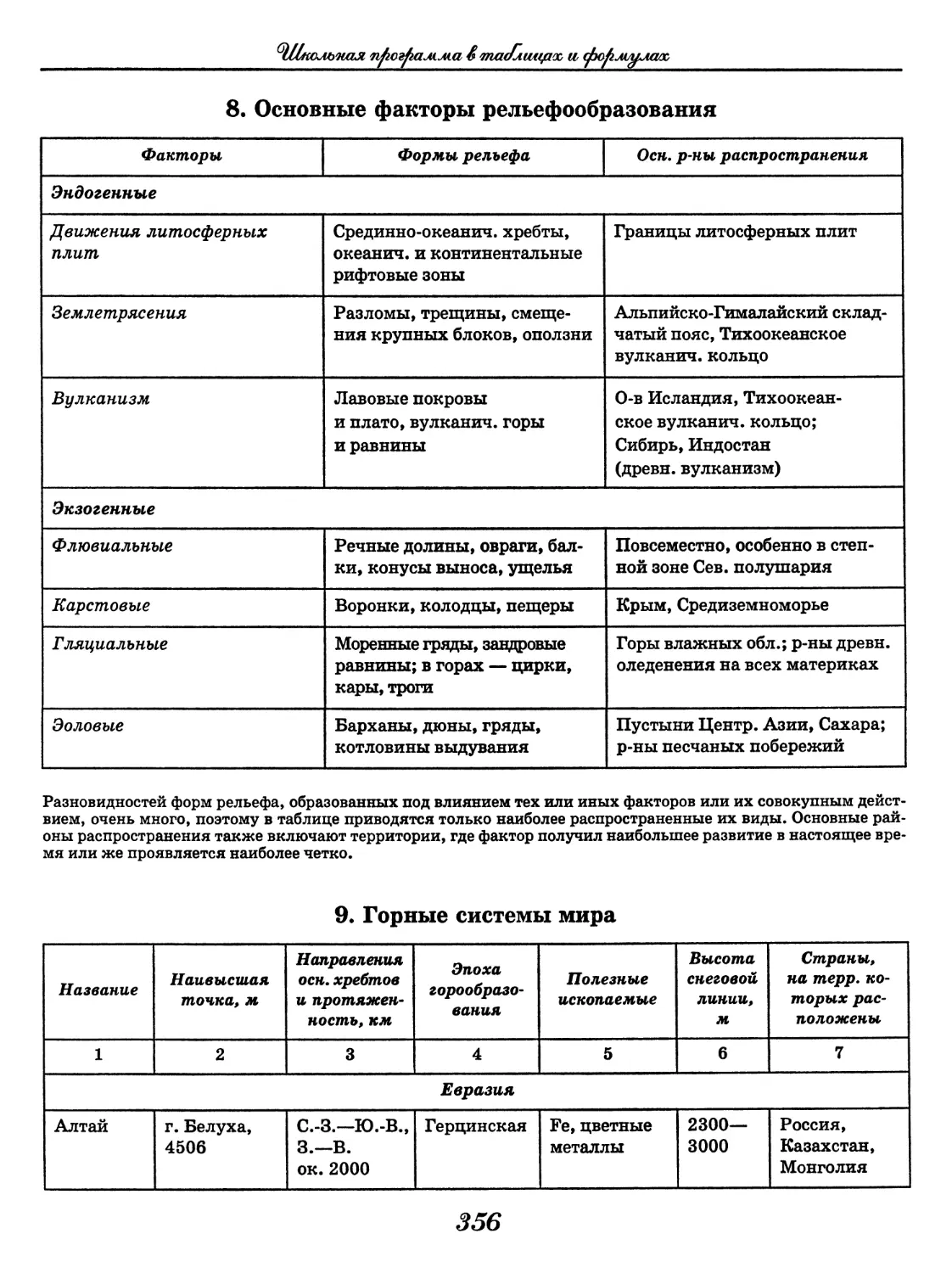
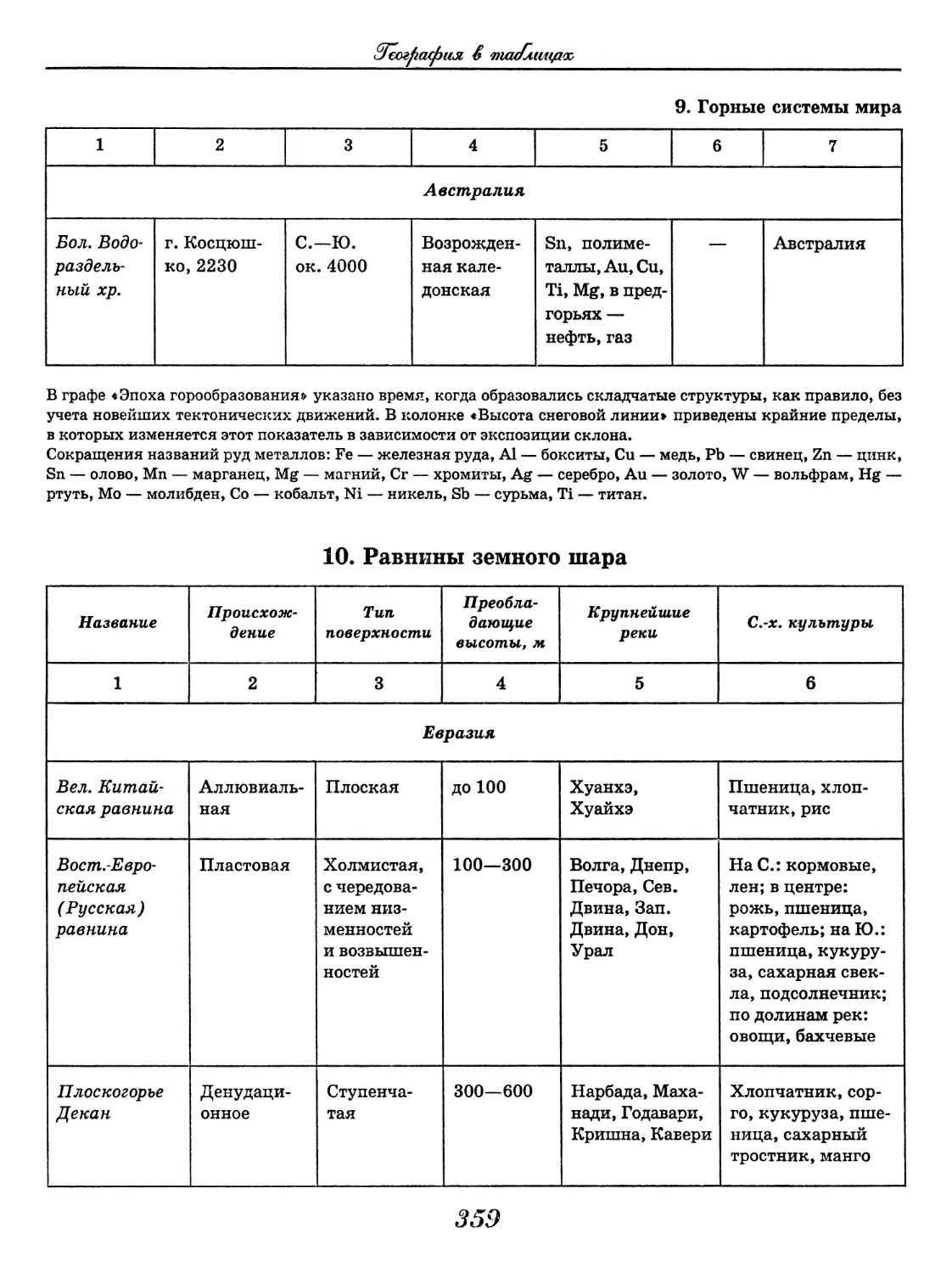
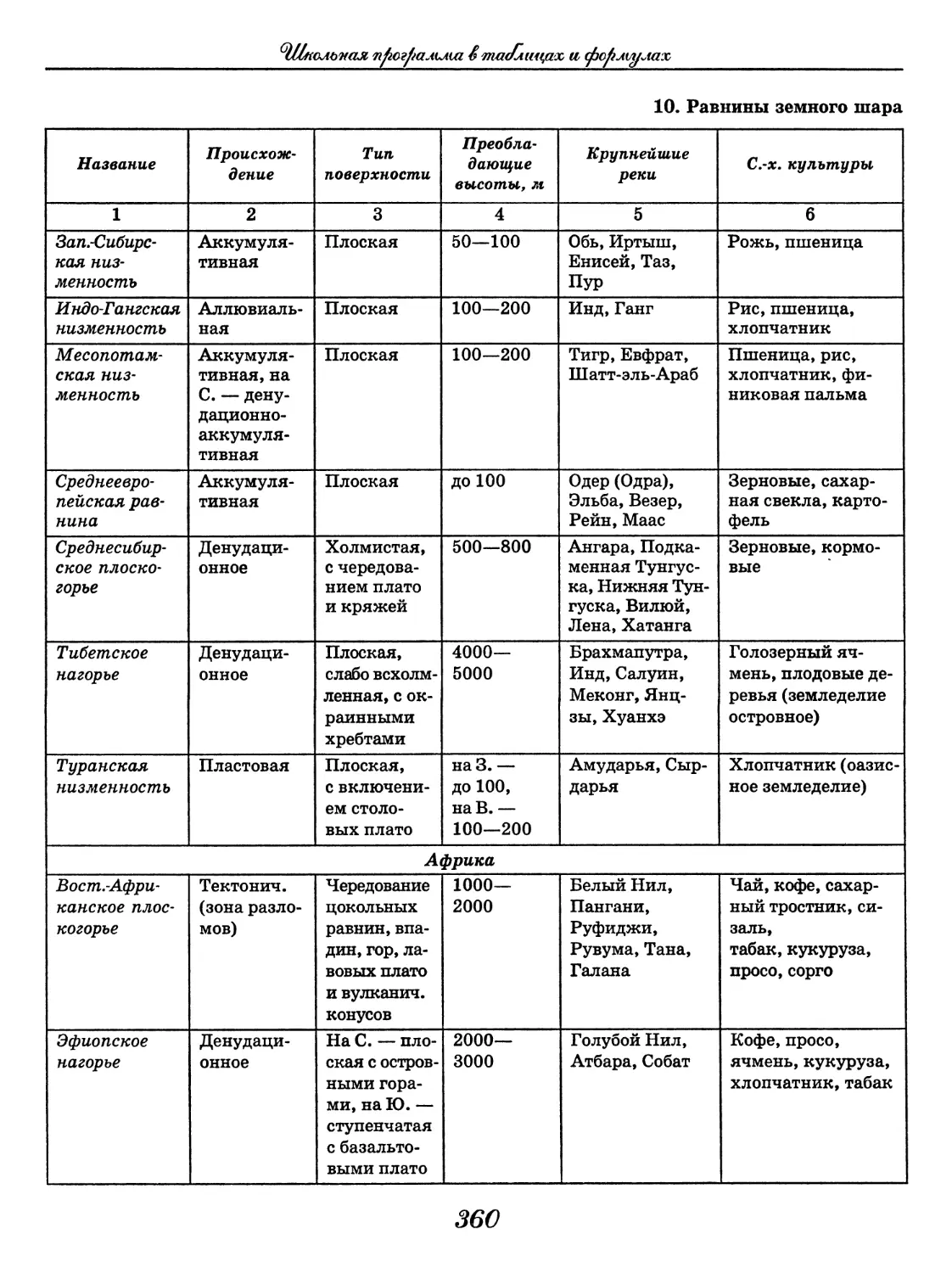
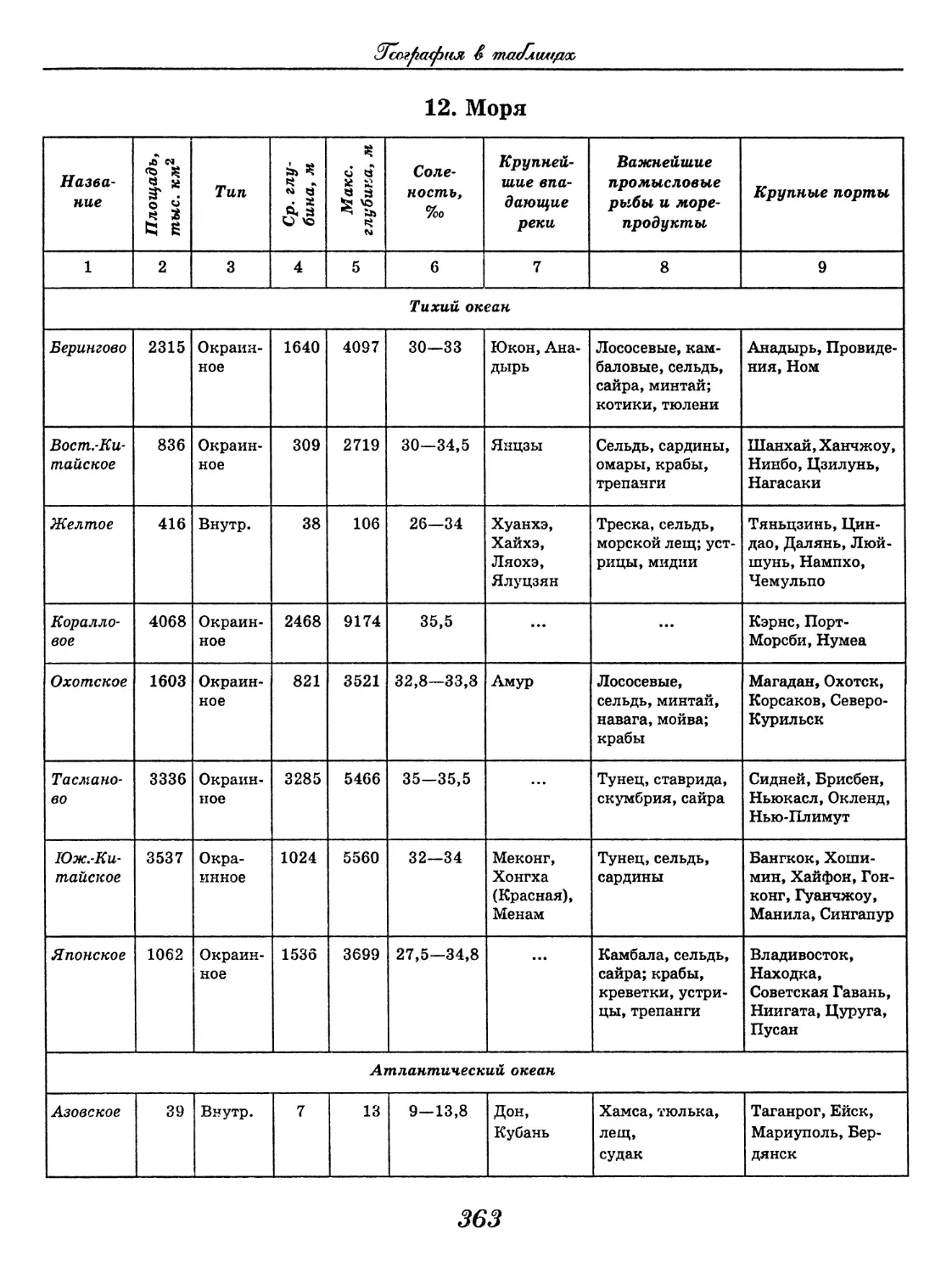
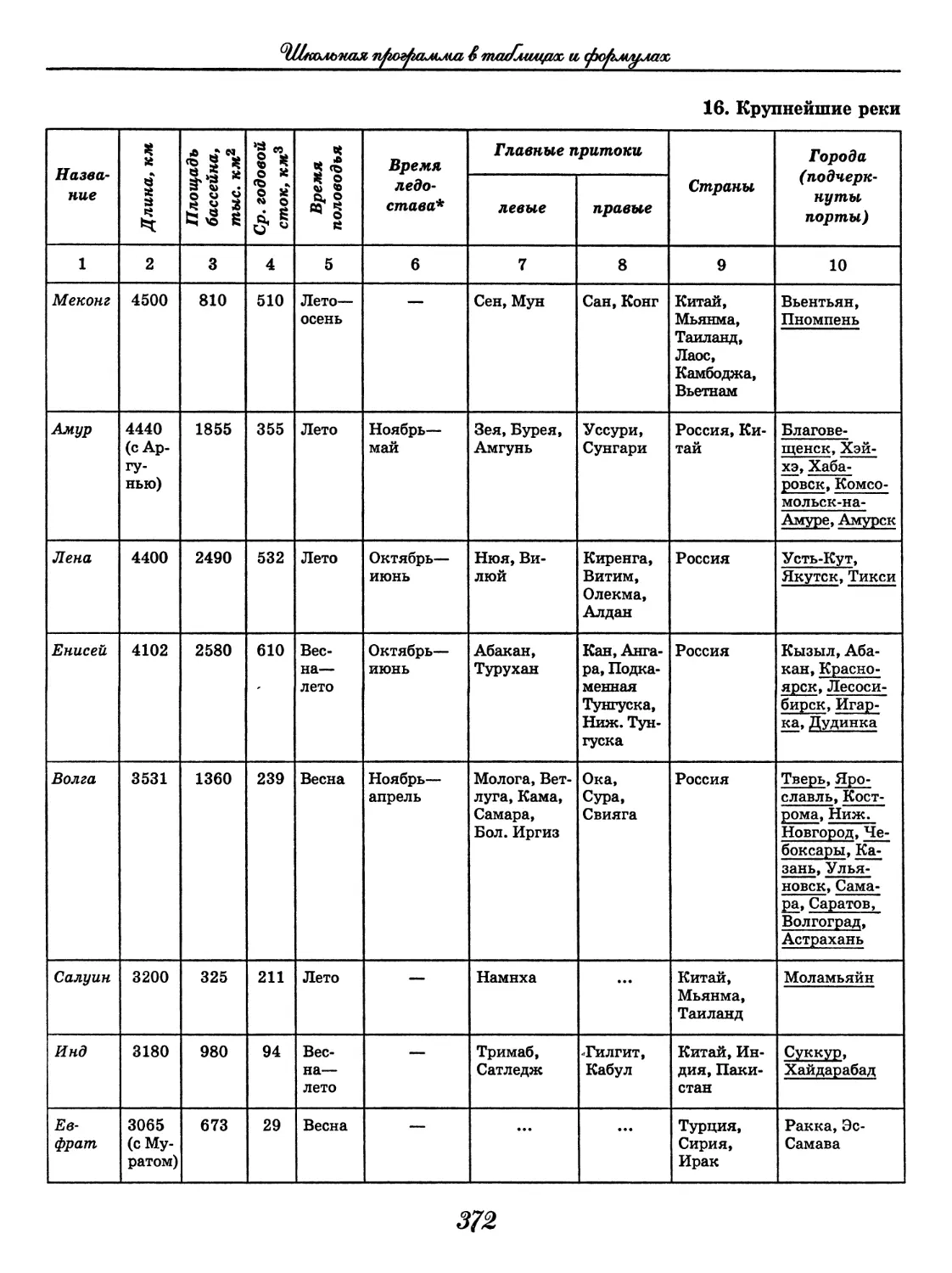
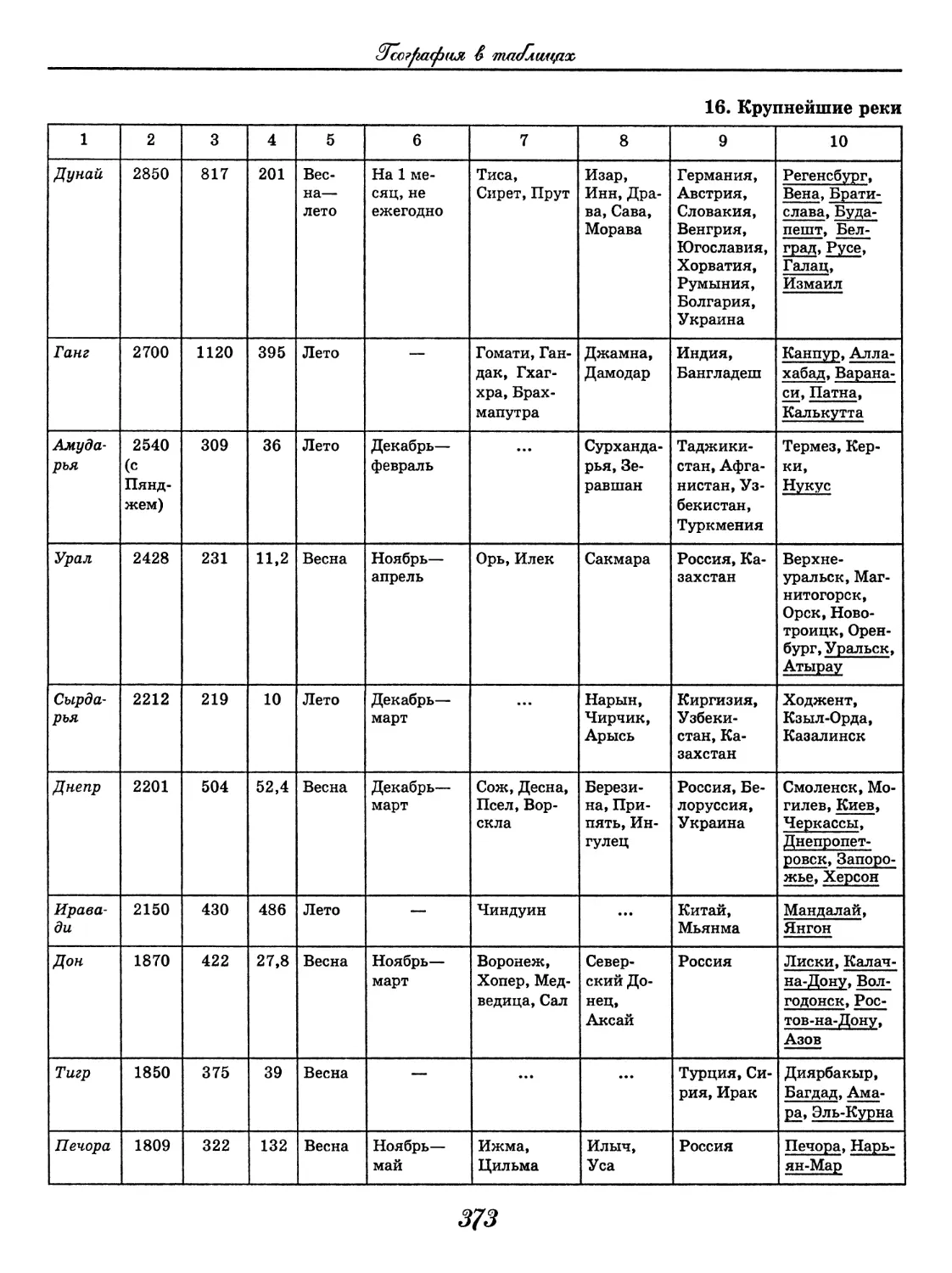
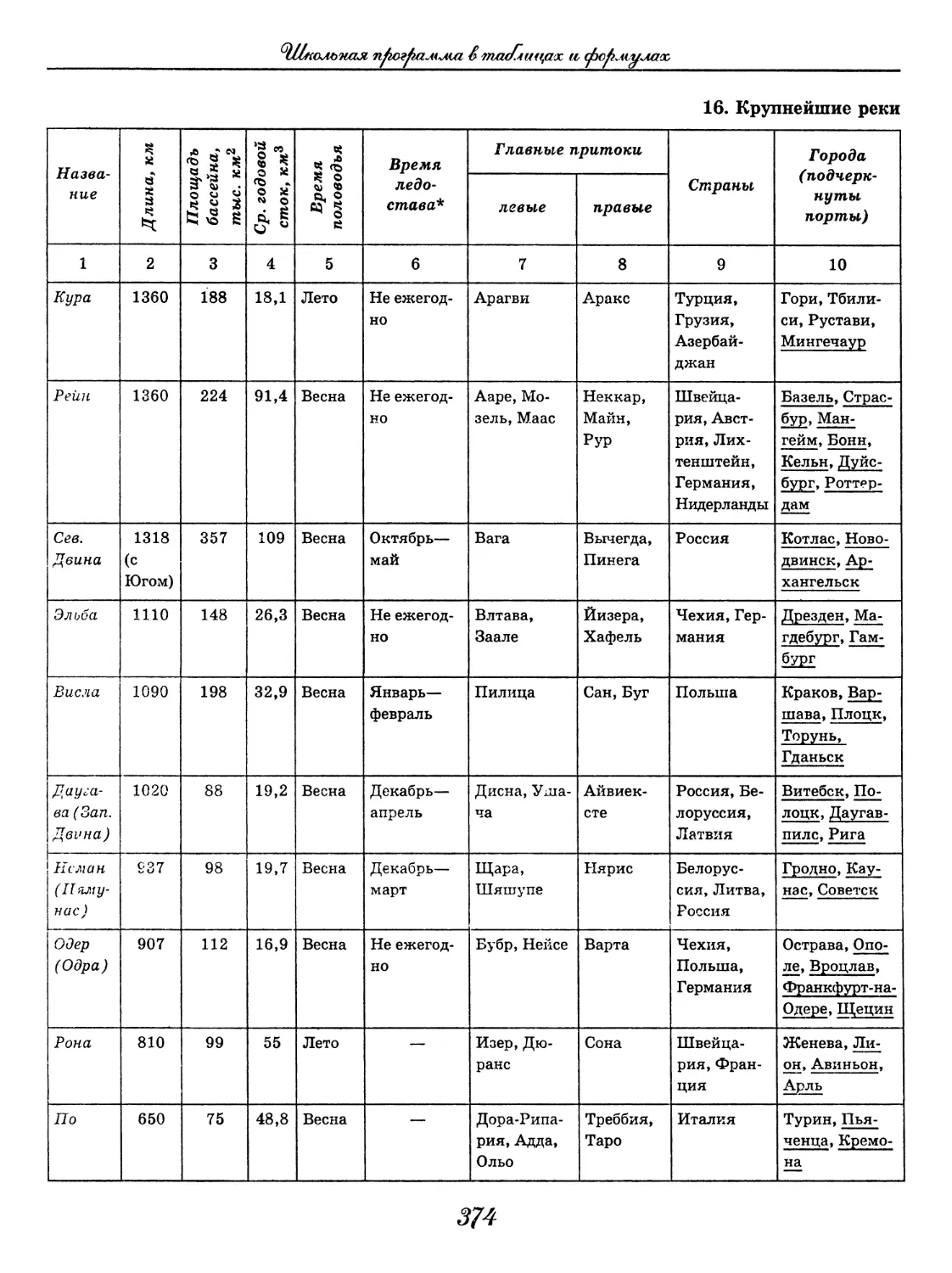
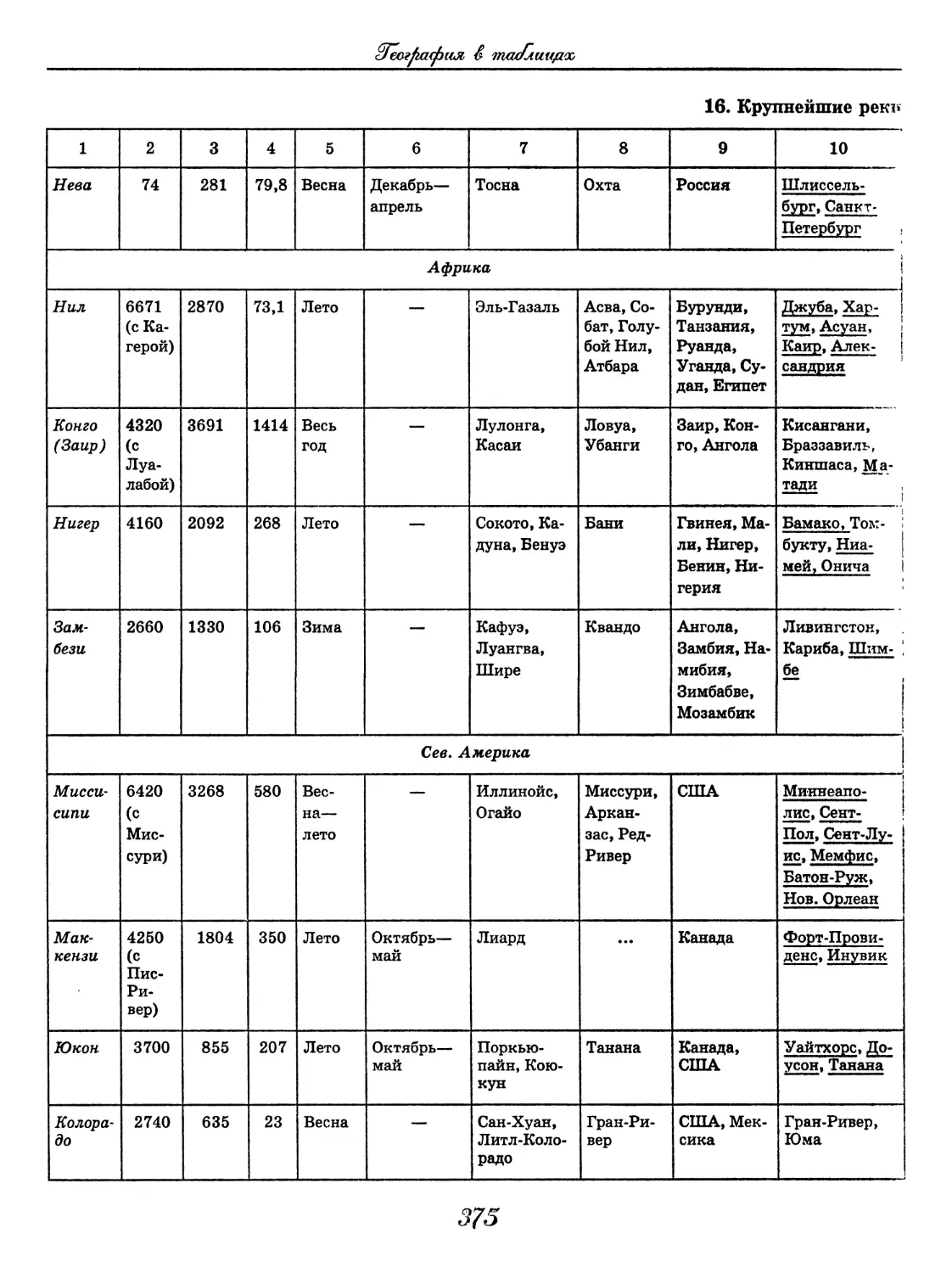
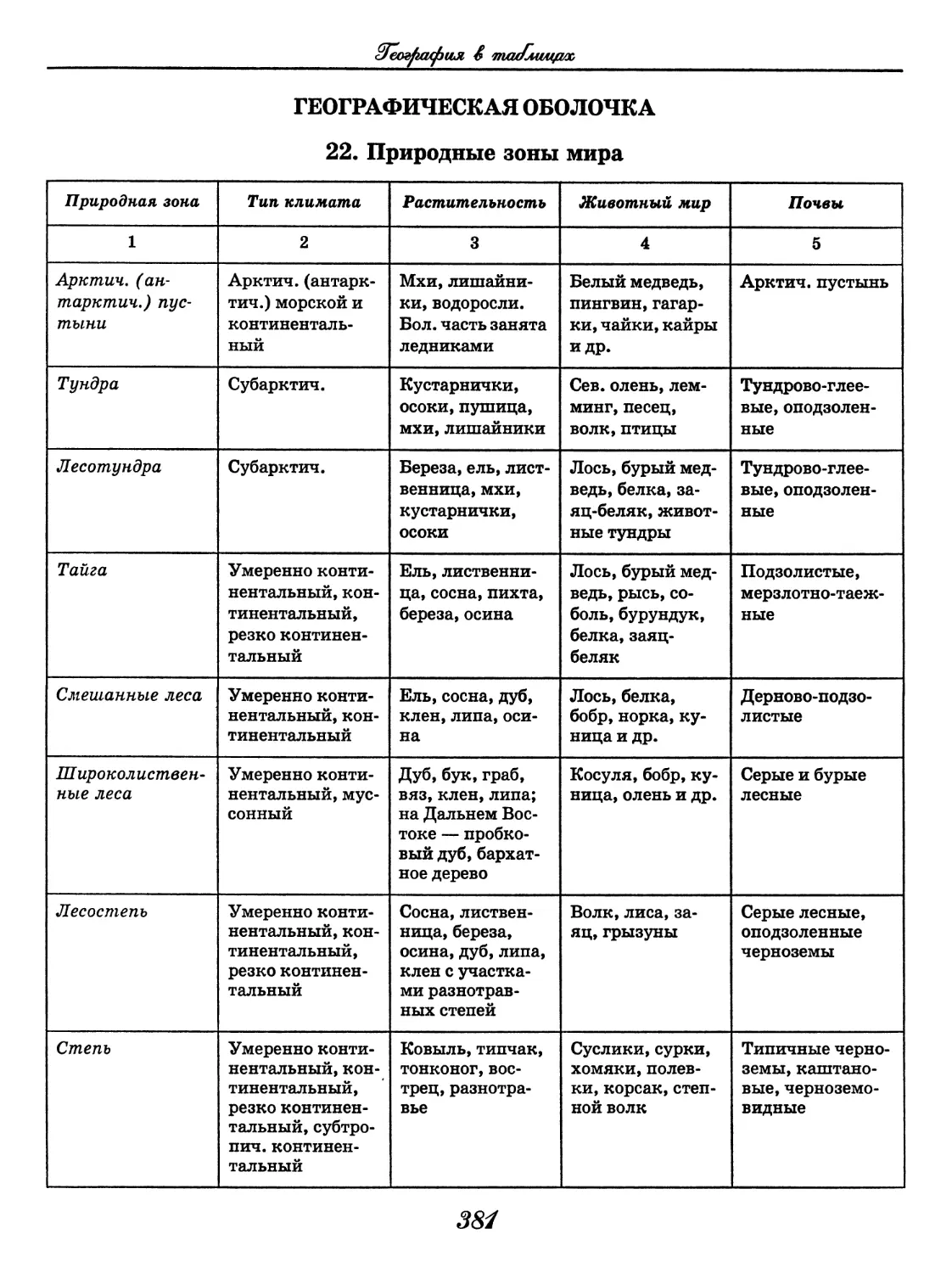
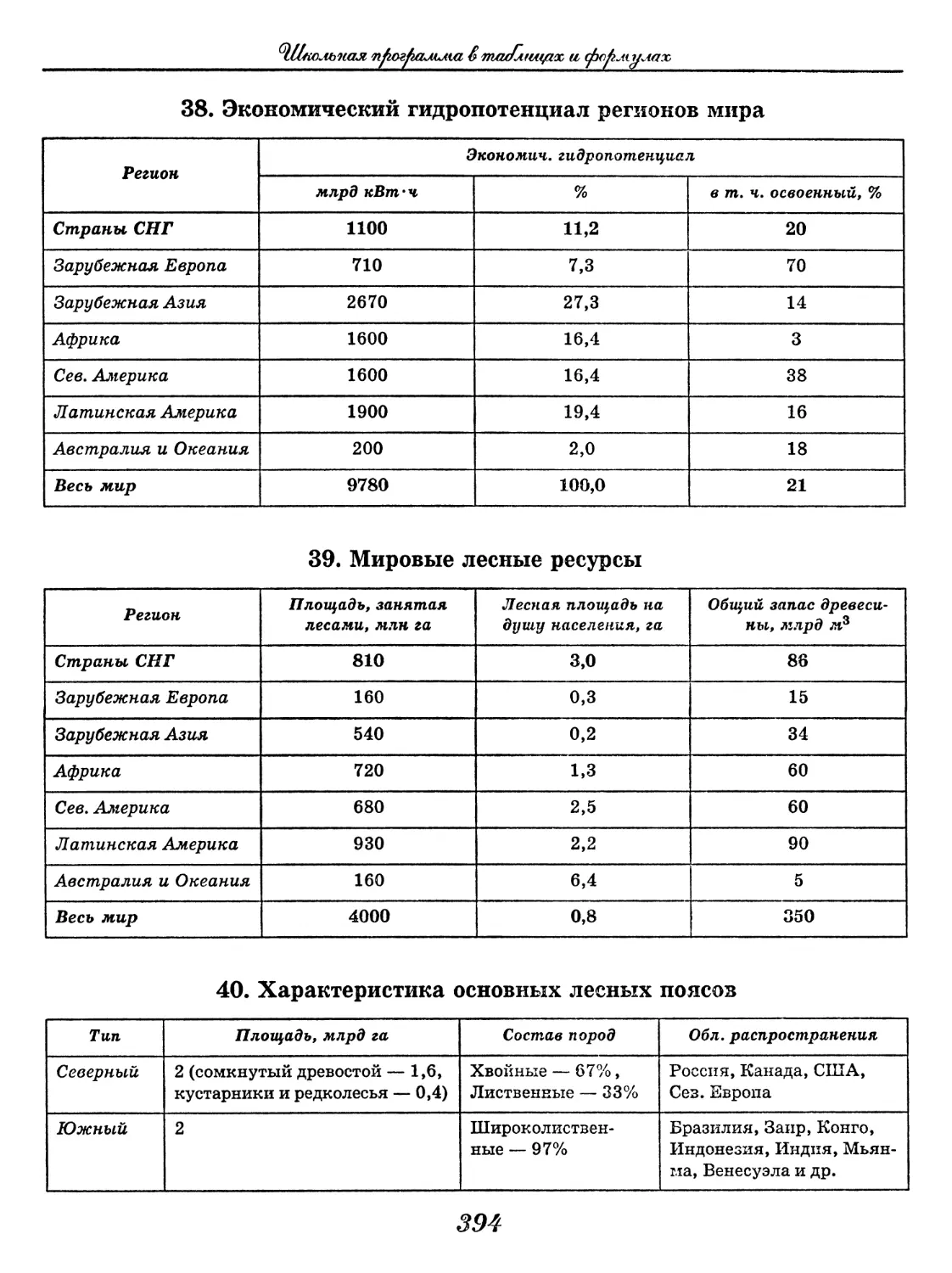
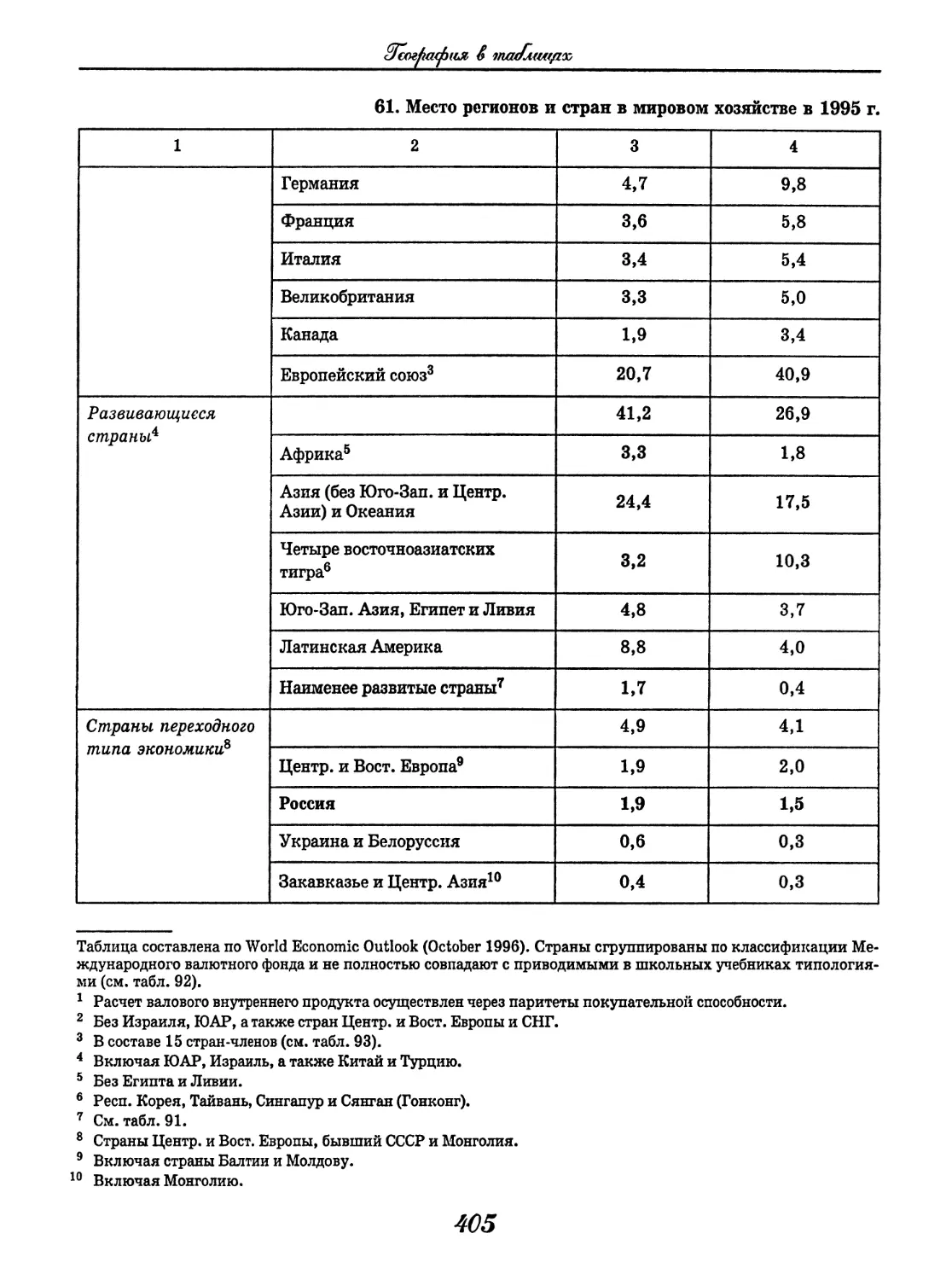
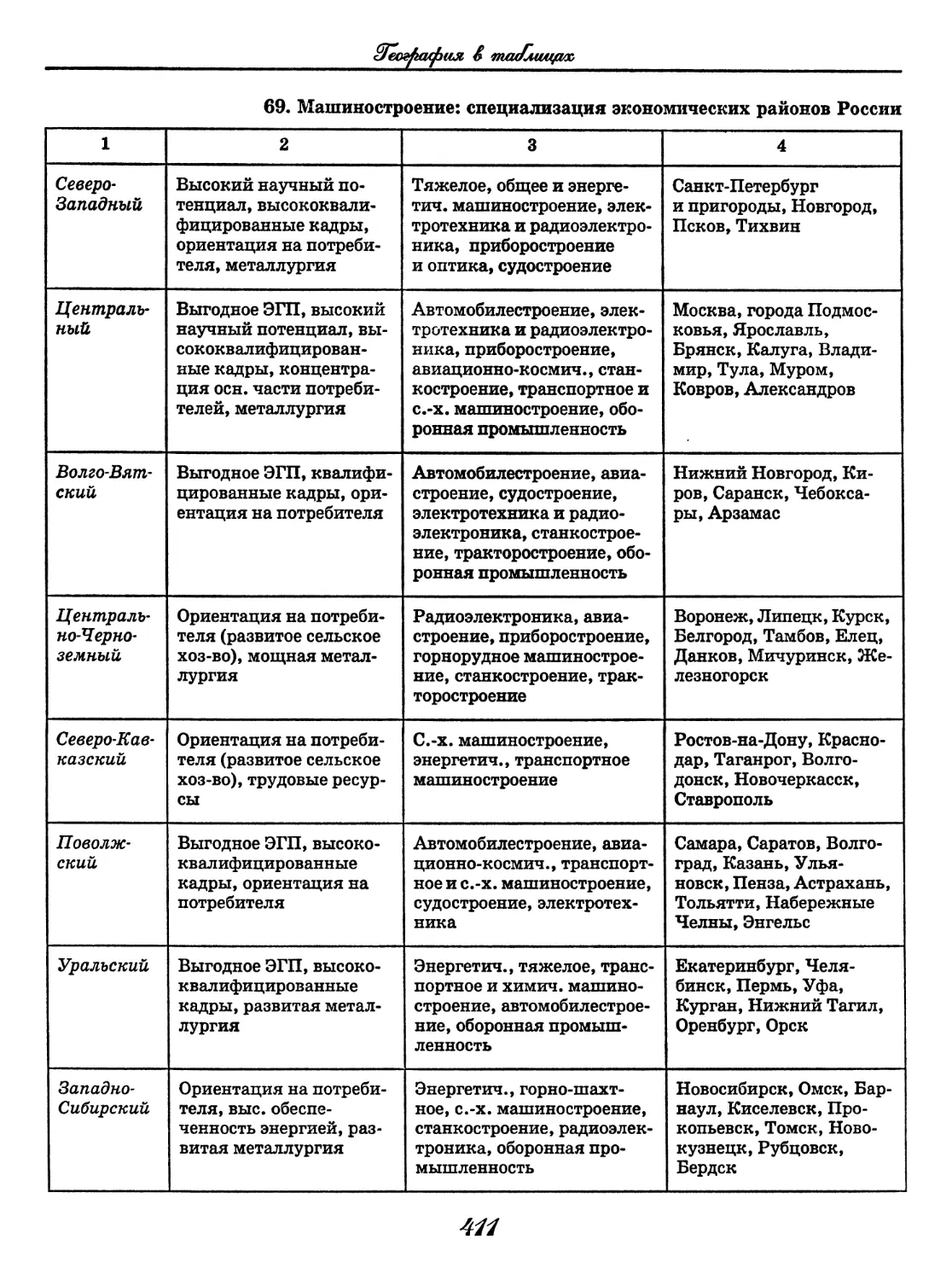
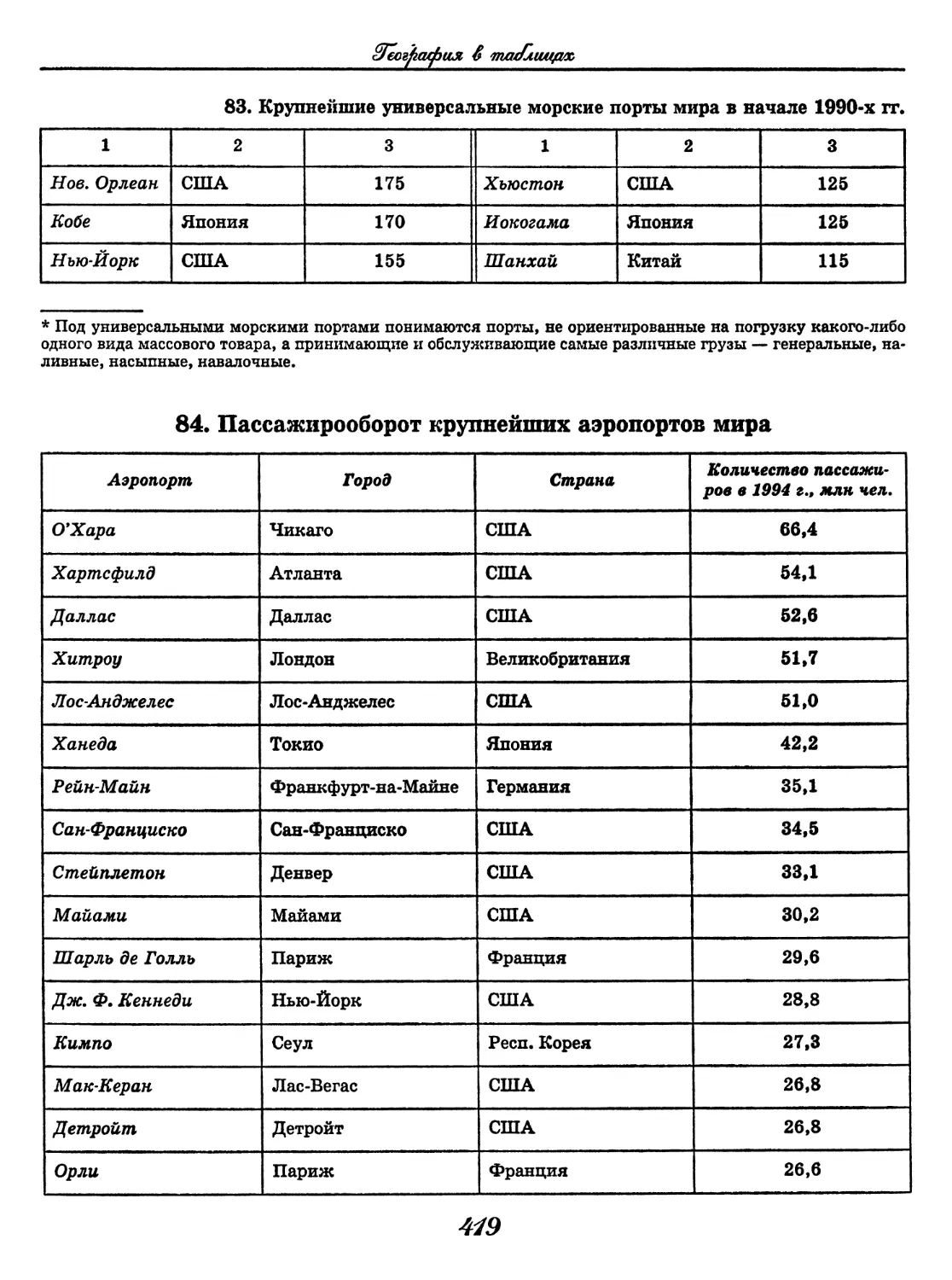
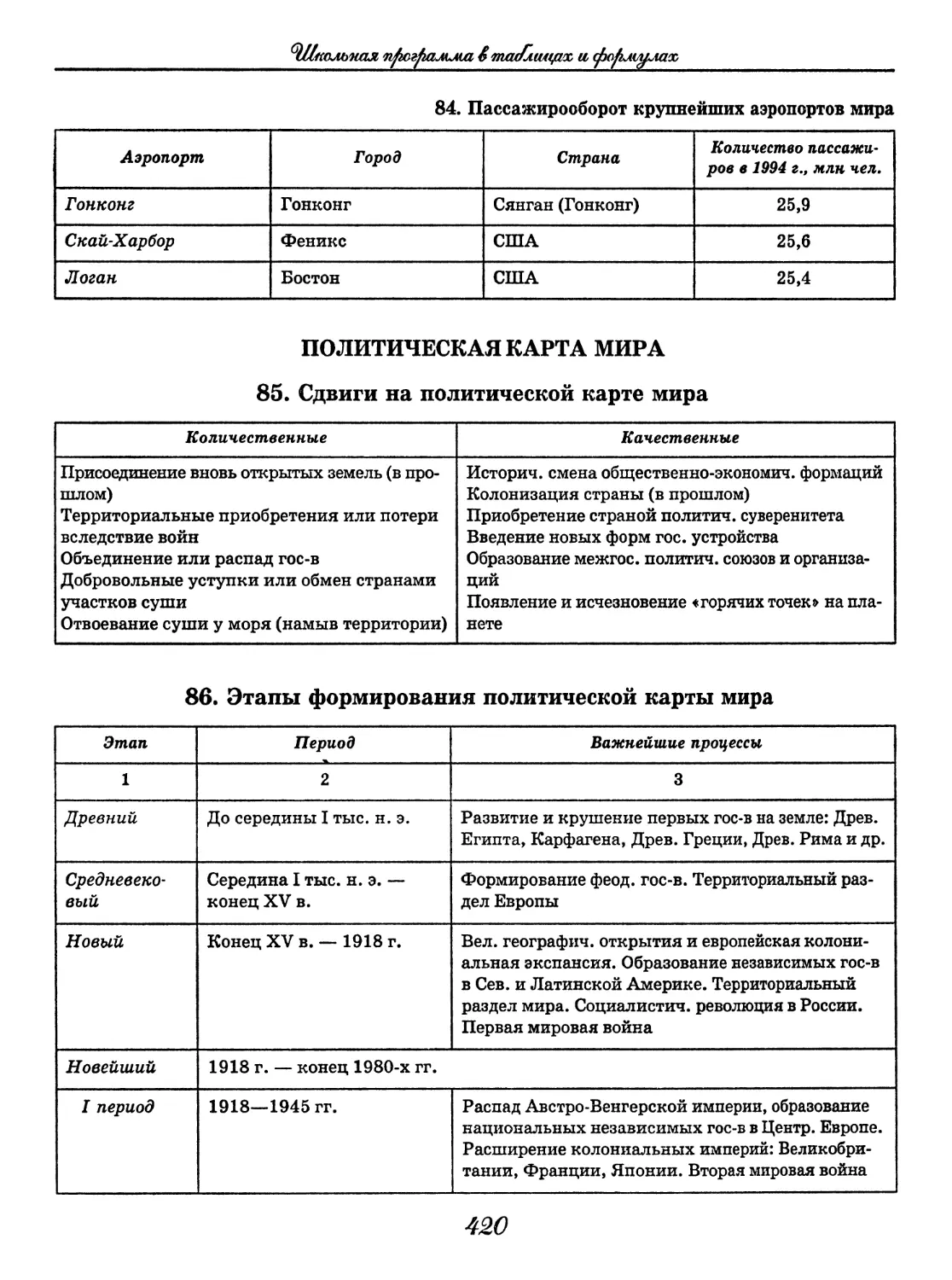
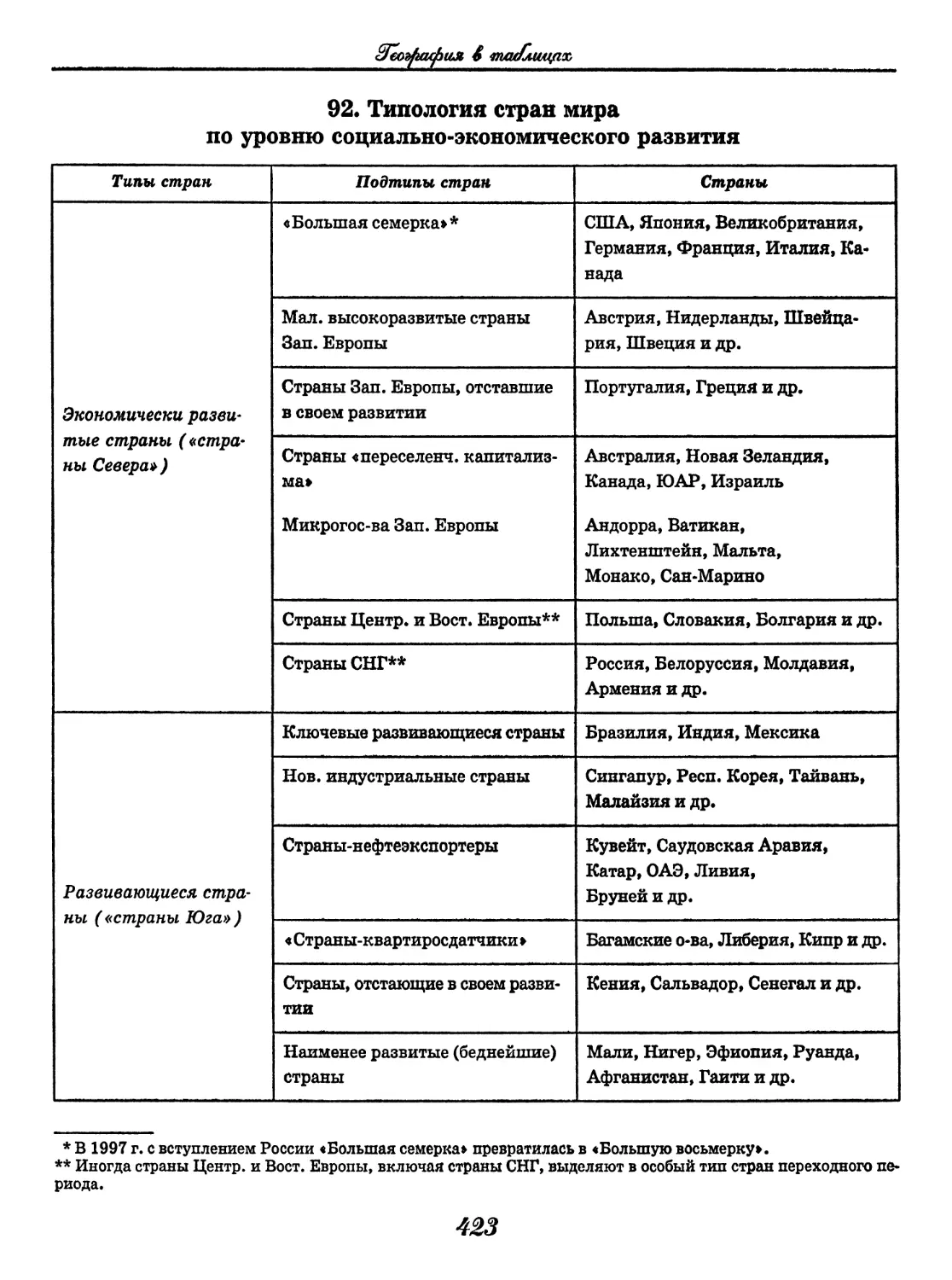
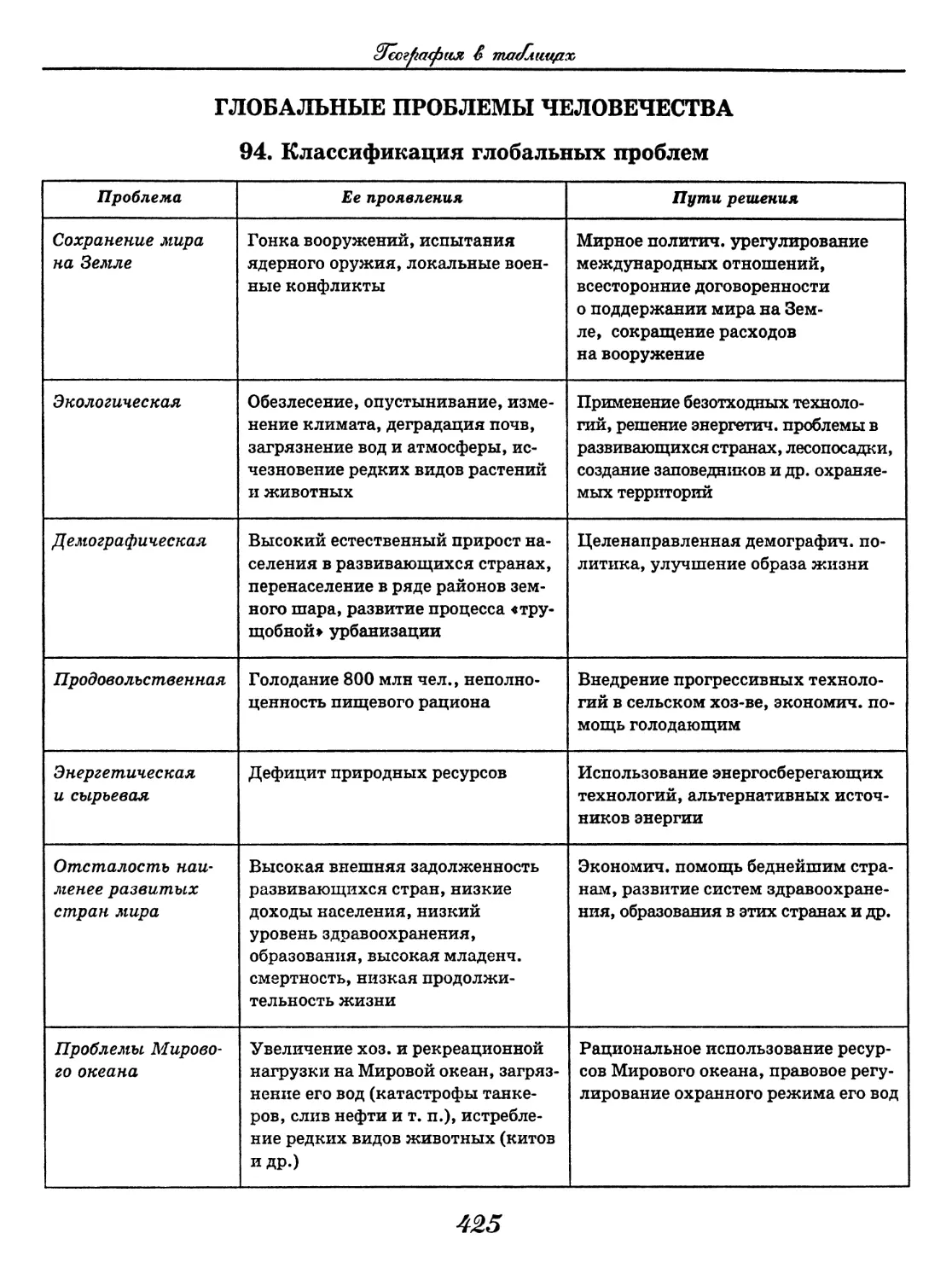
География
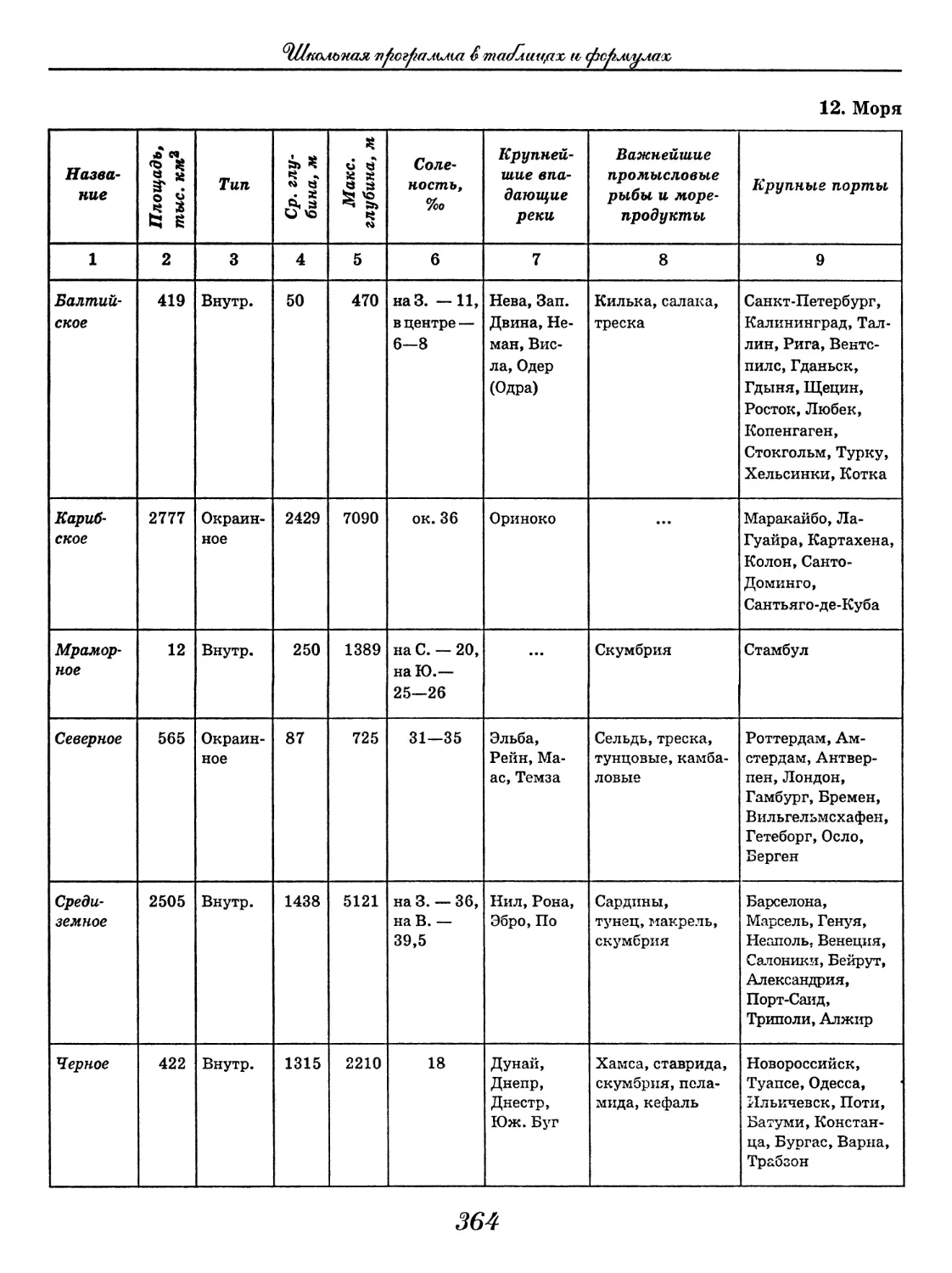
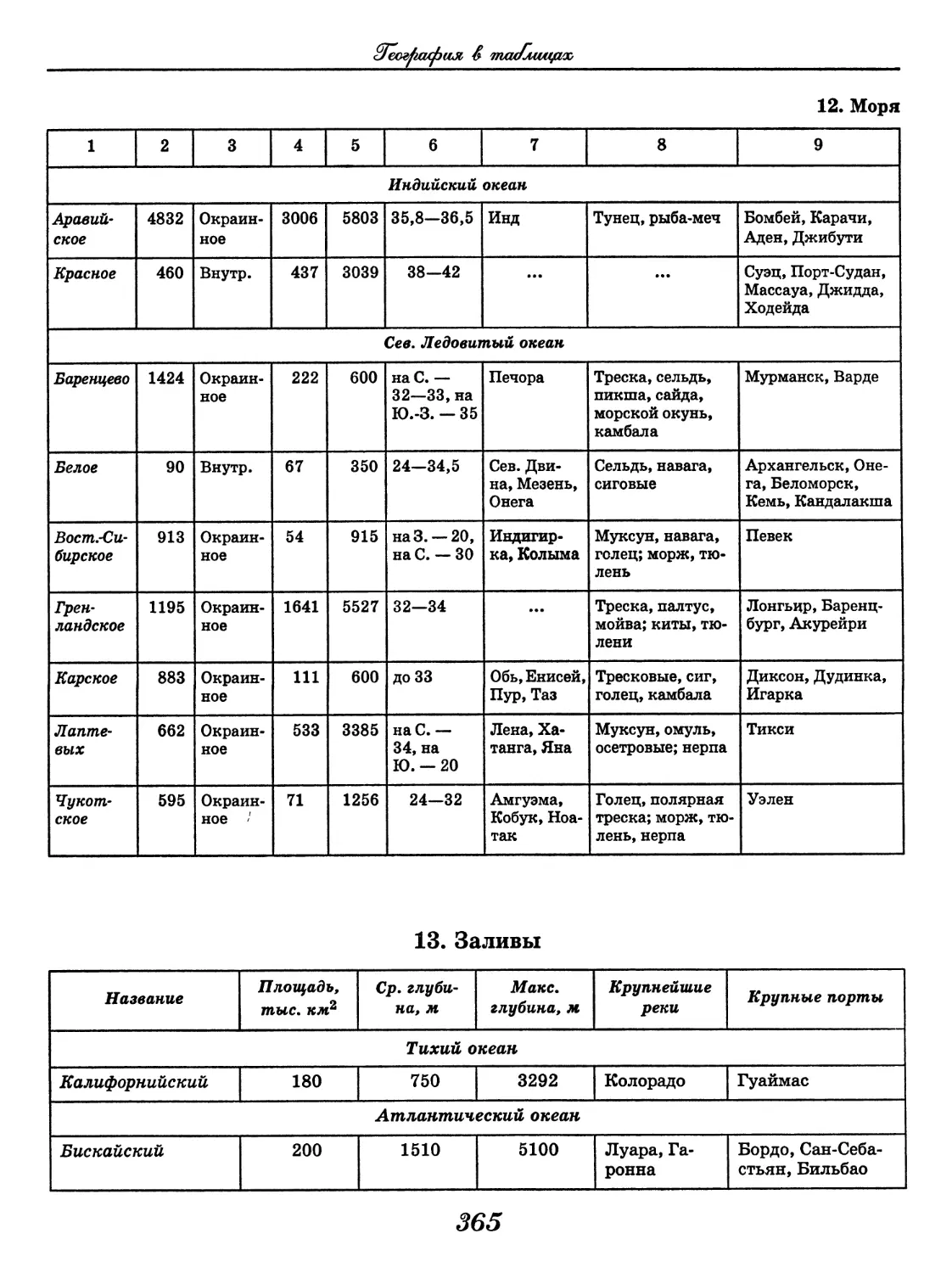
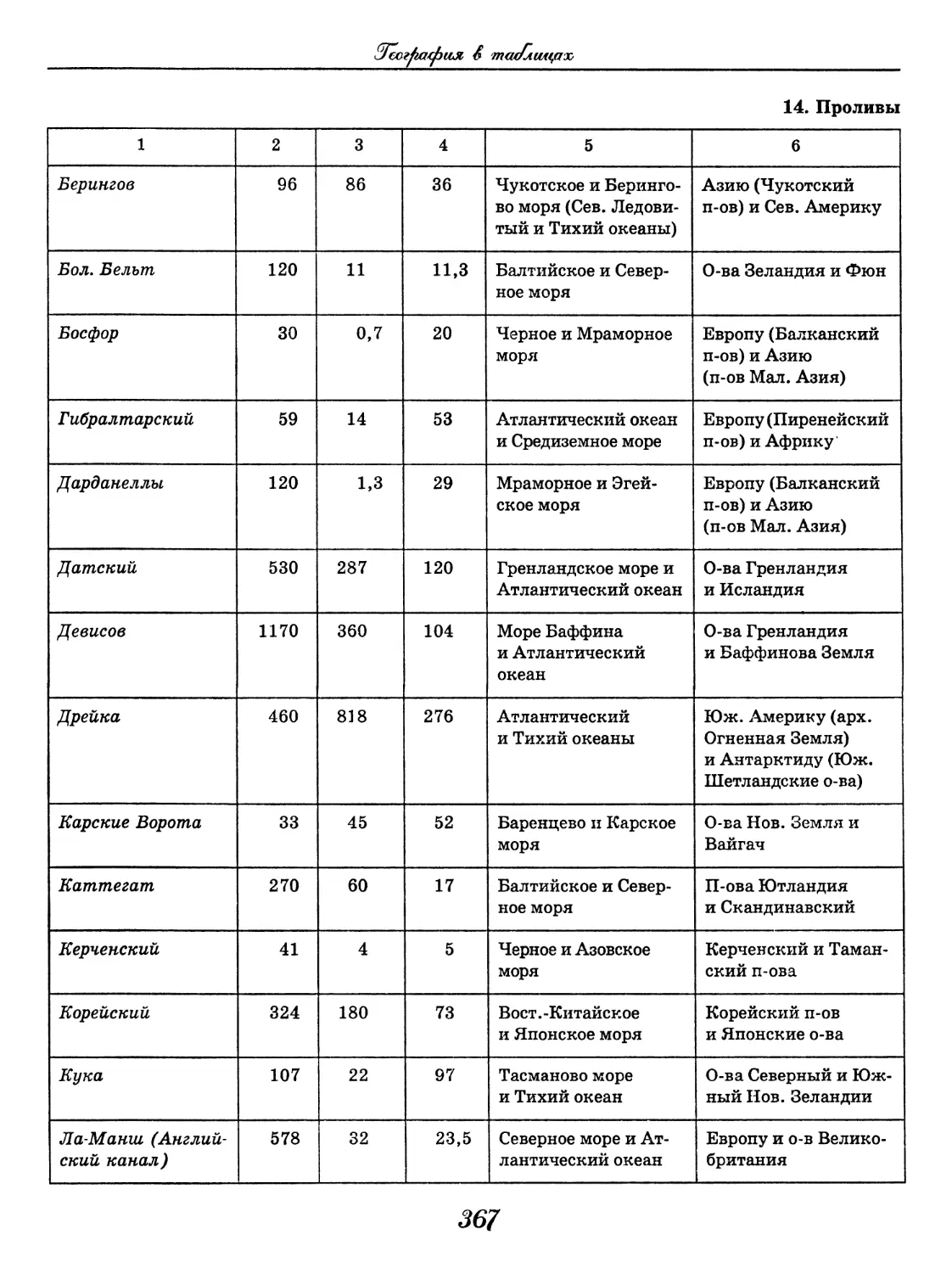
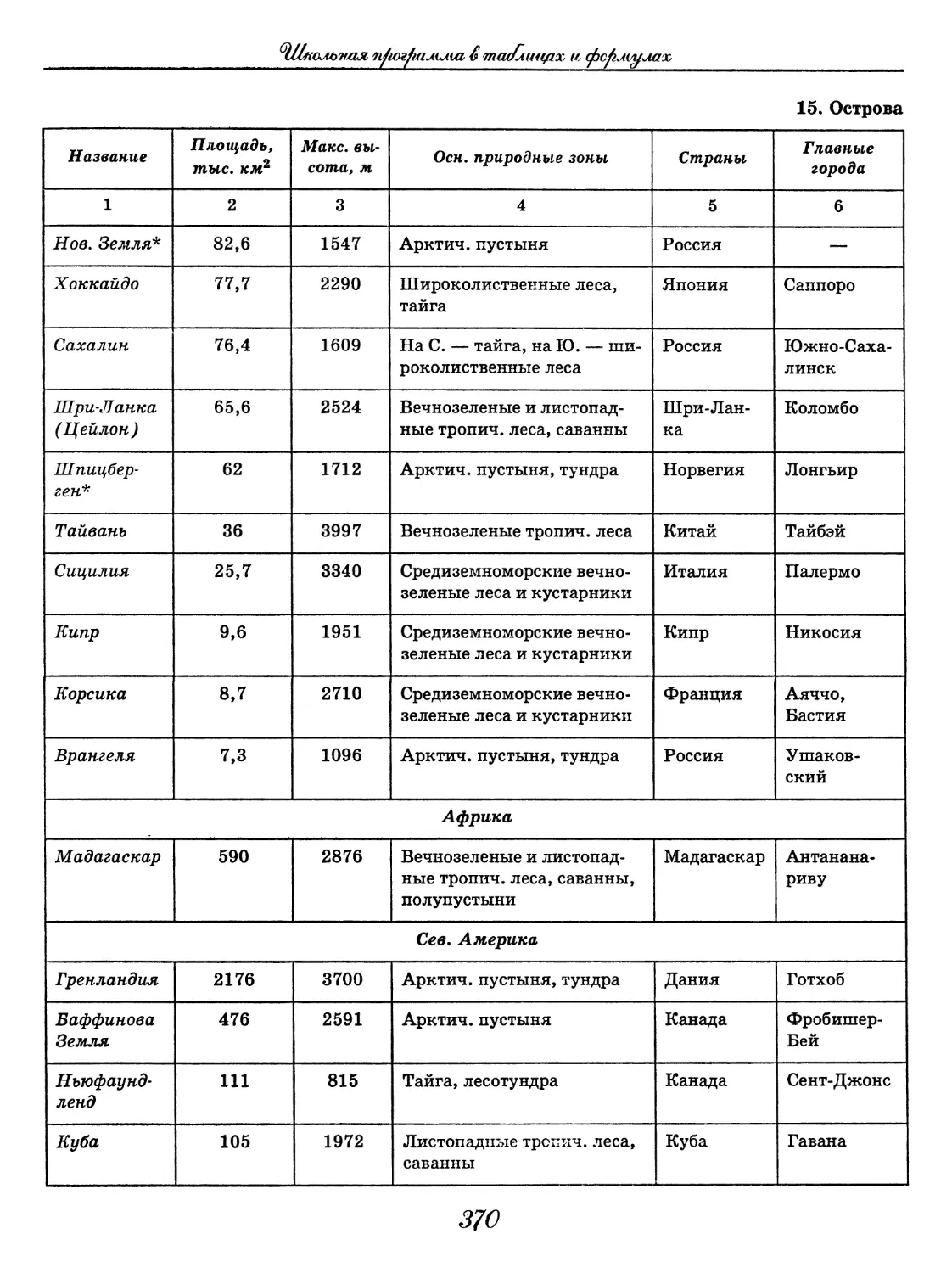
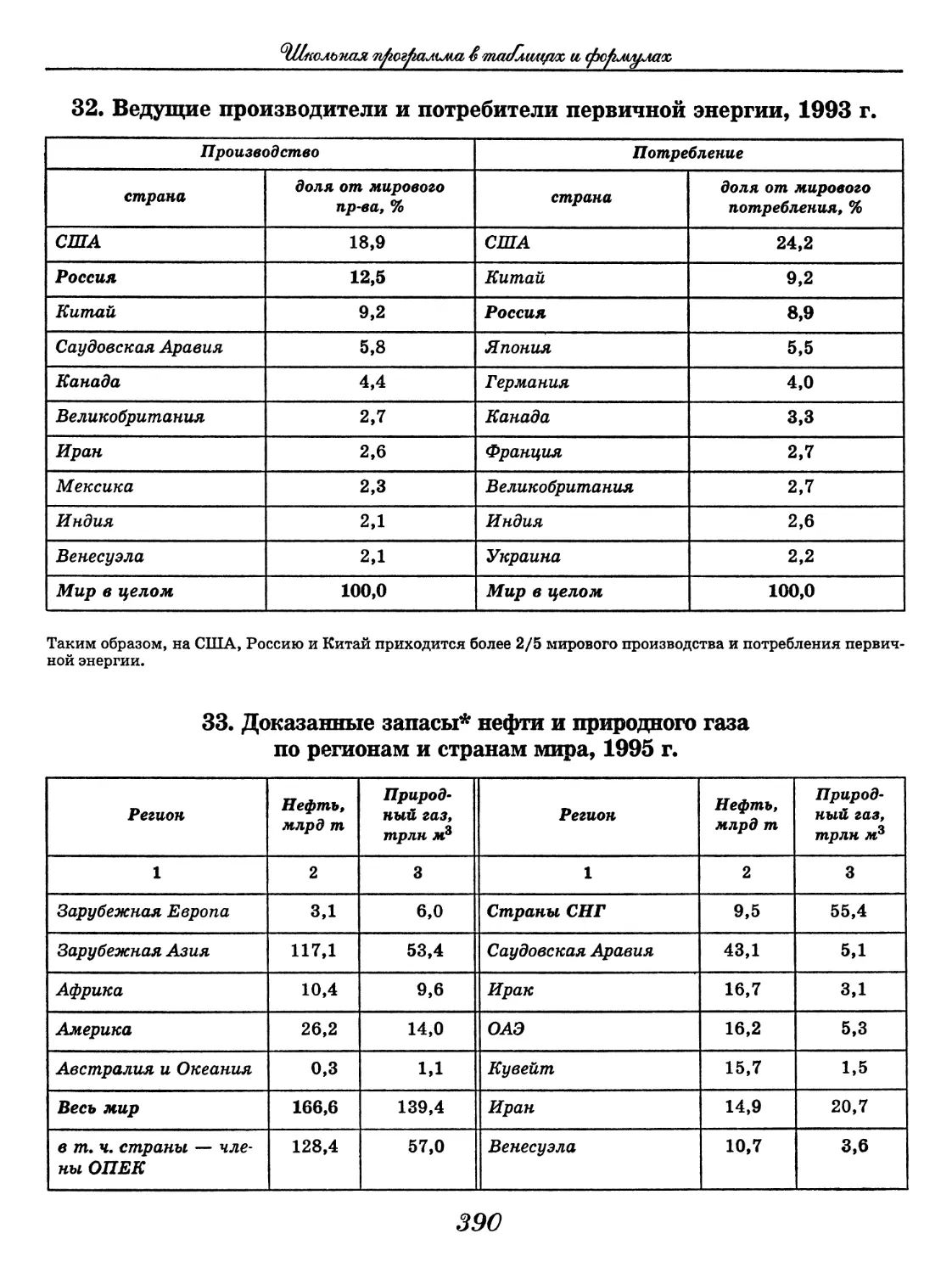
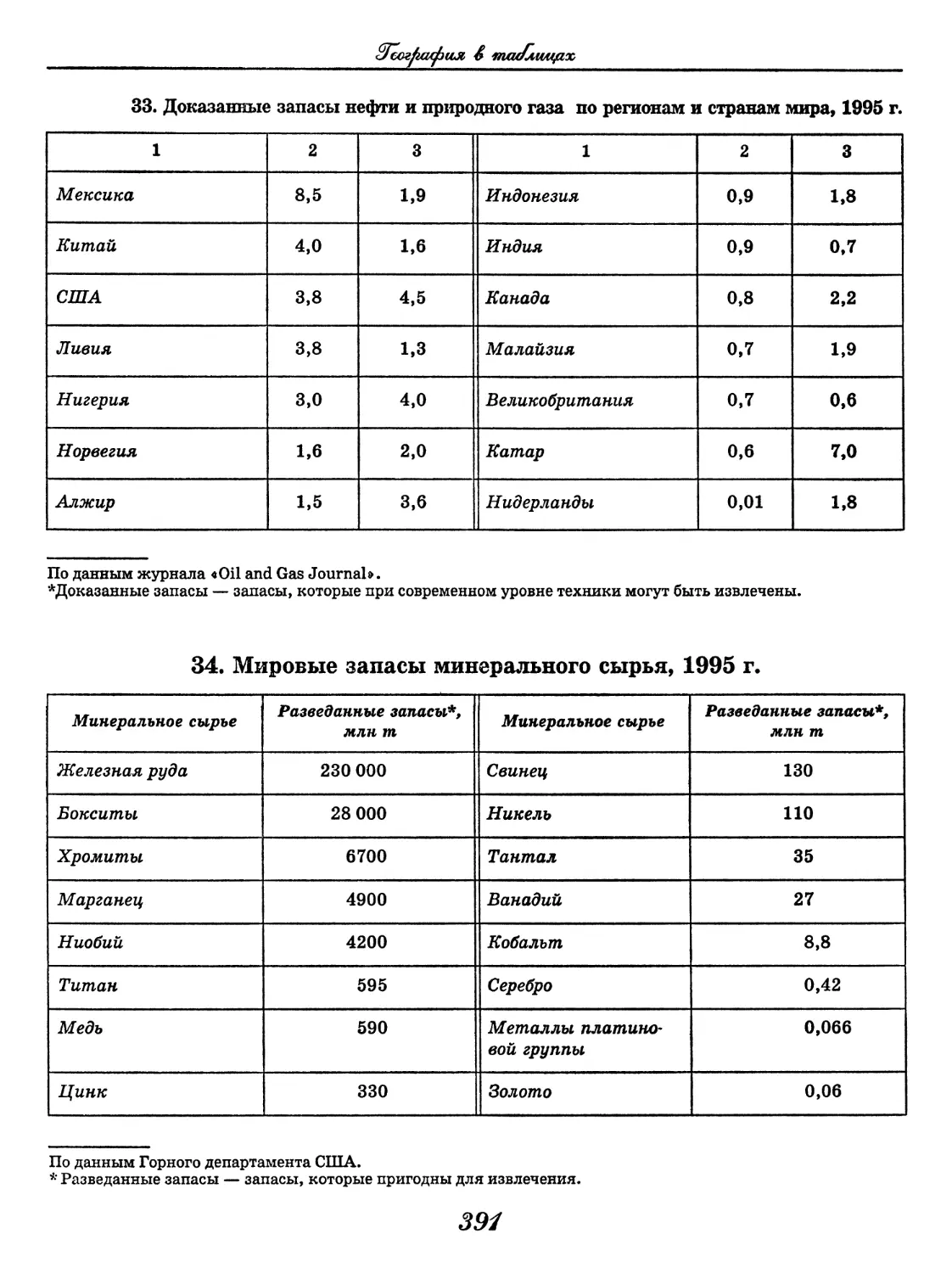
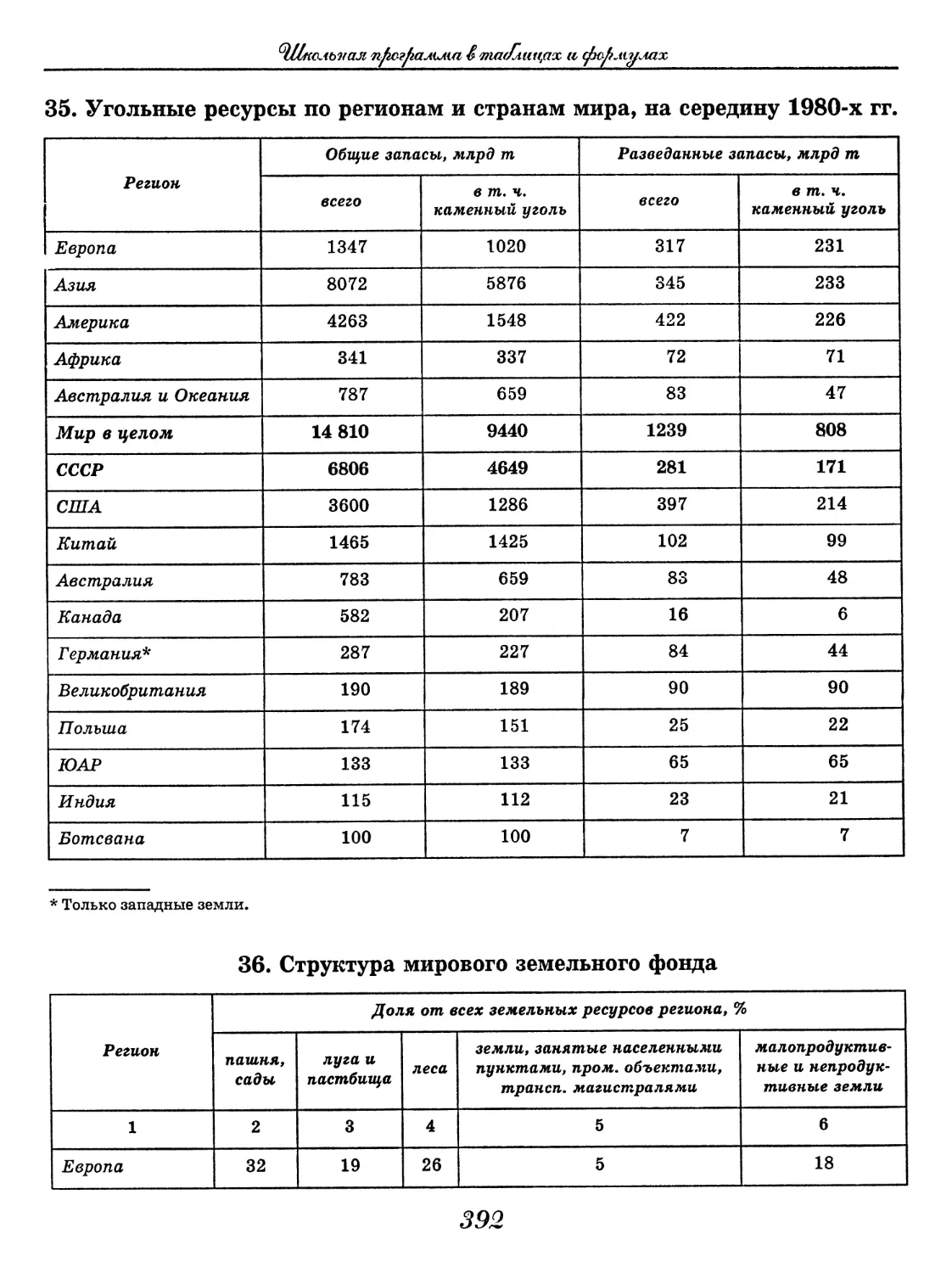
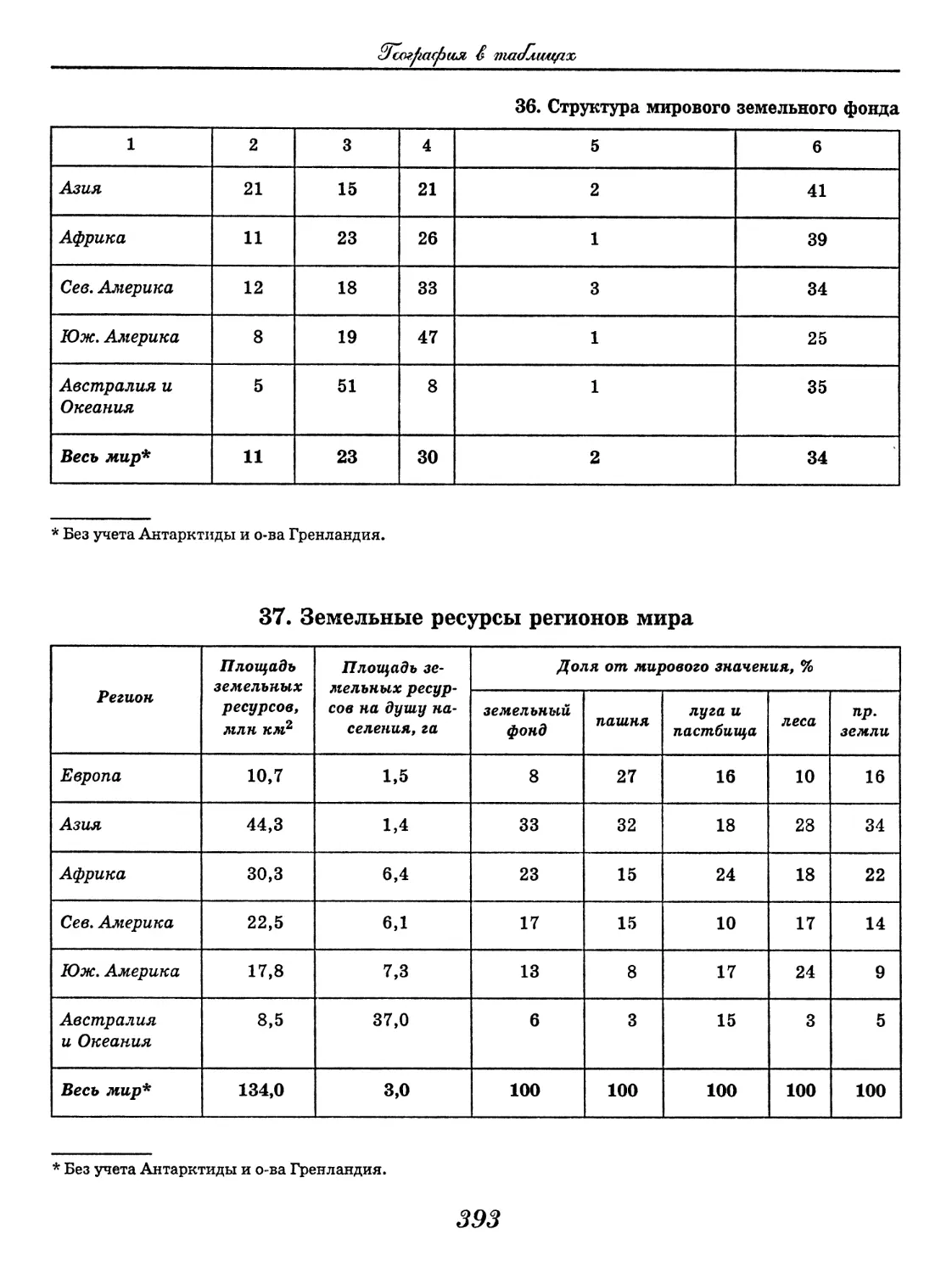
(В. В. Климанов, О. А. Климанова)..... 352
Биология
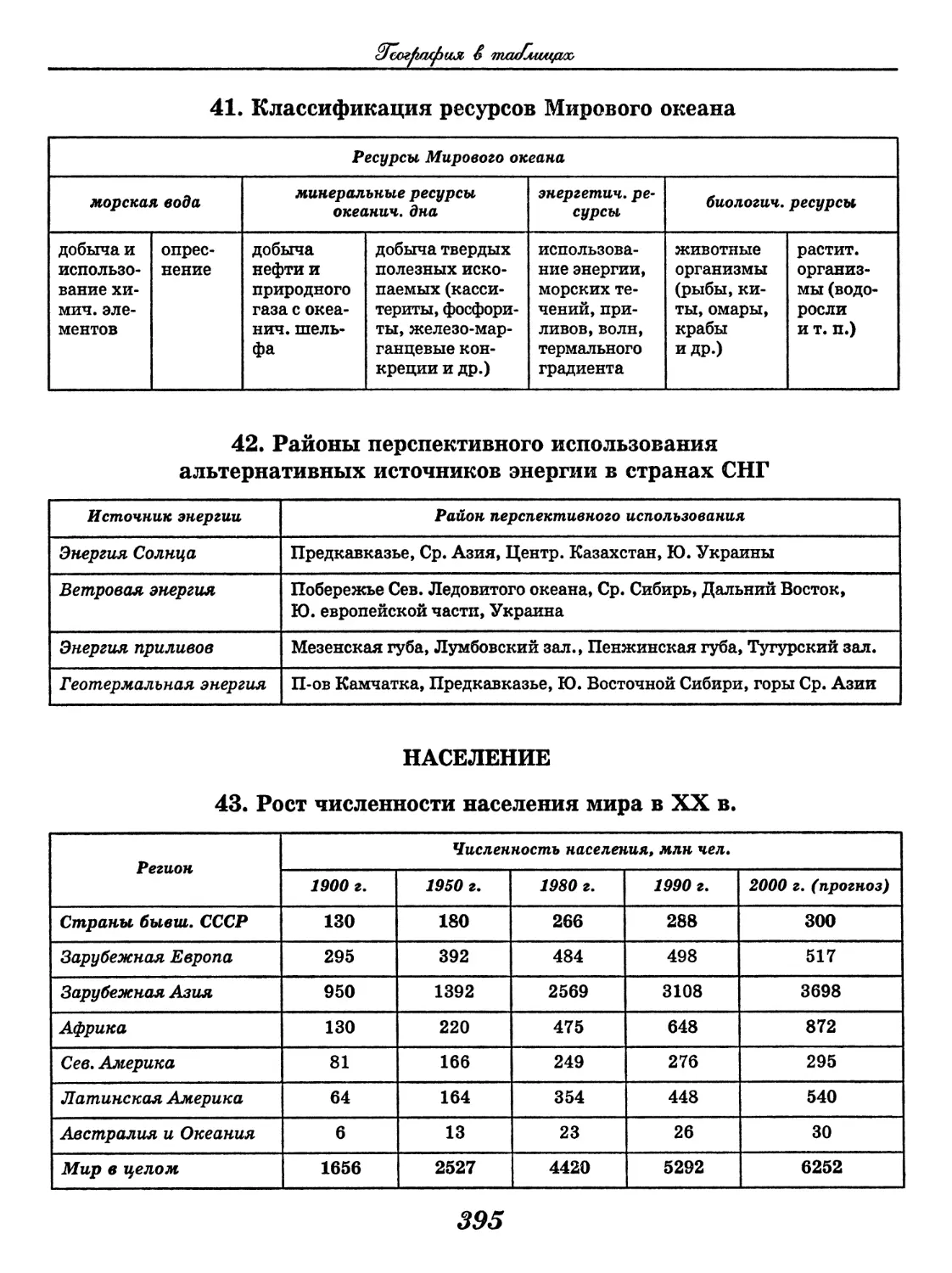
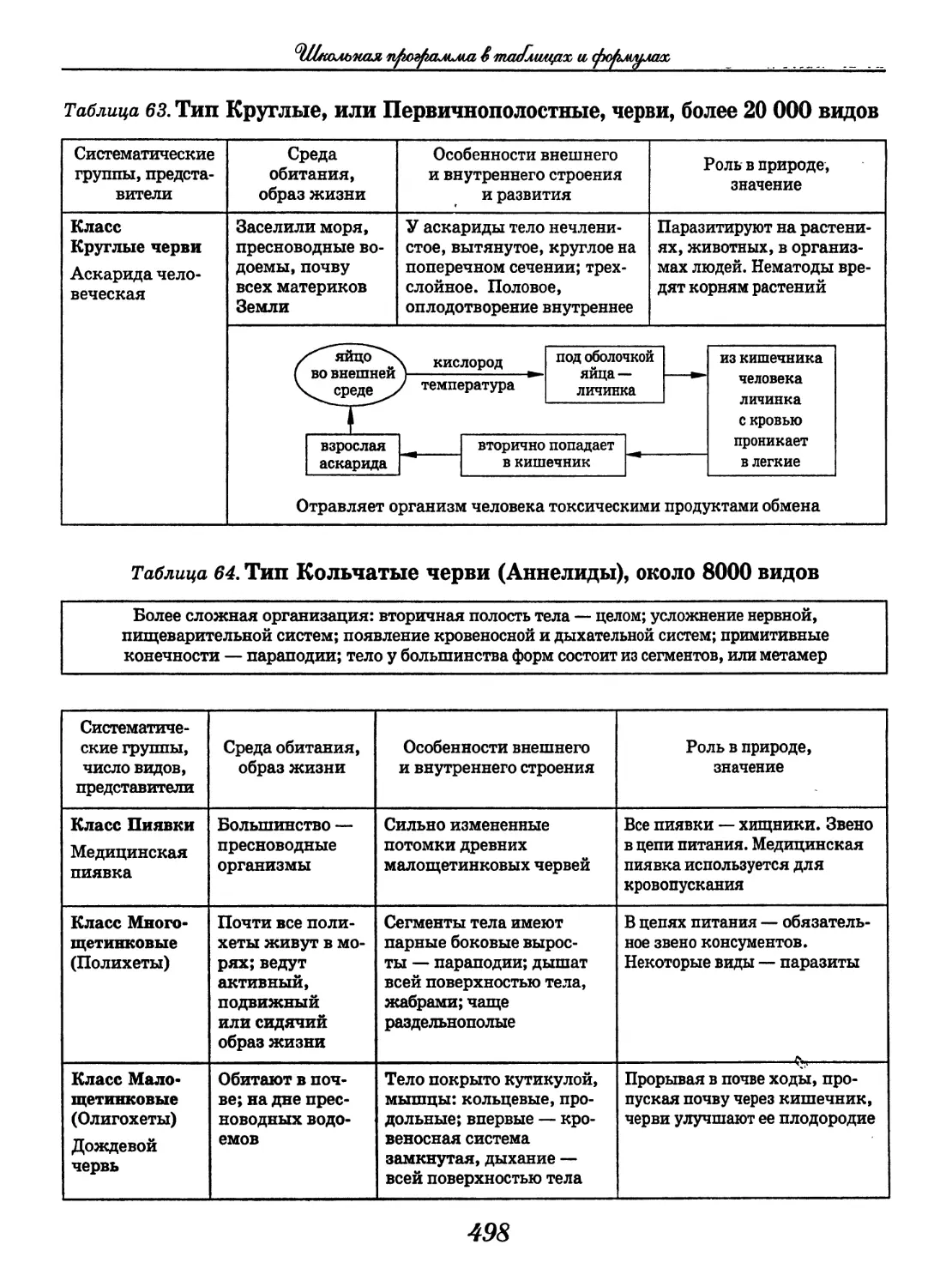
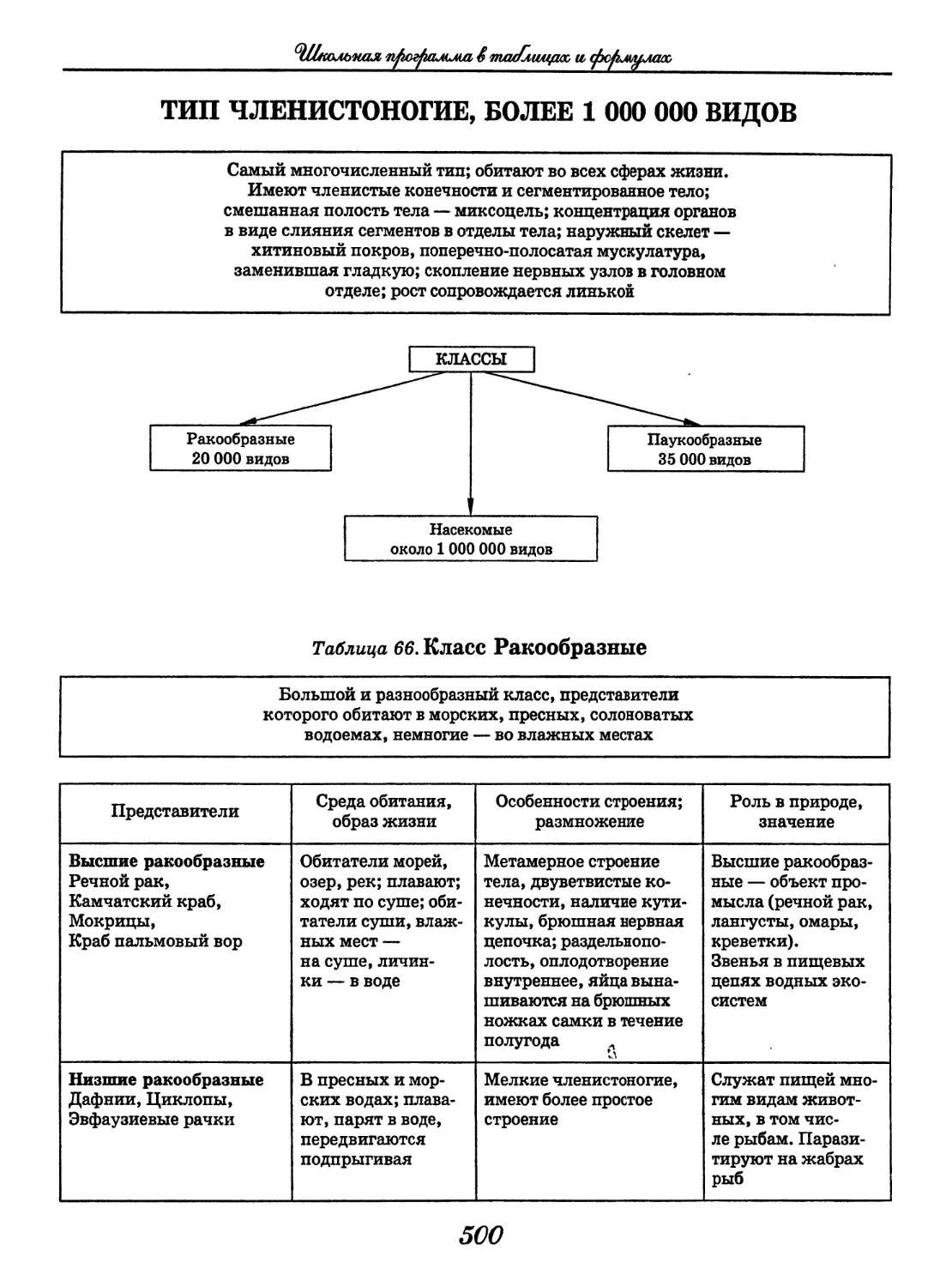
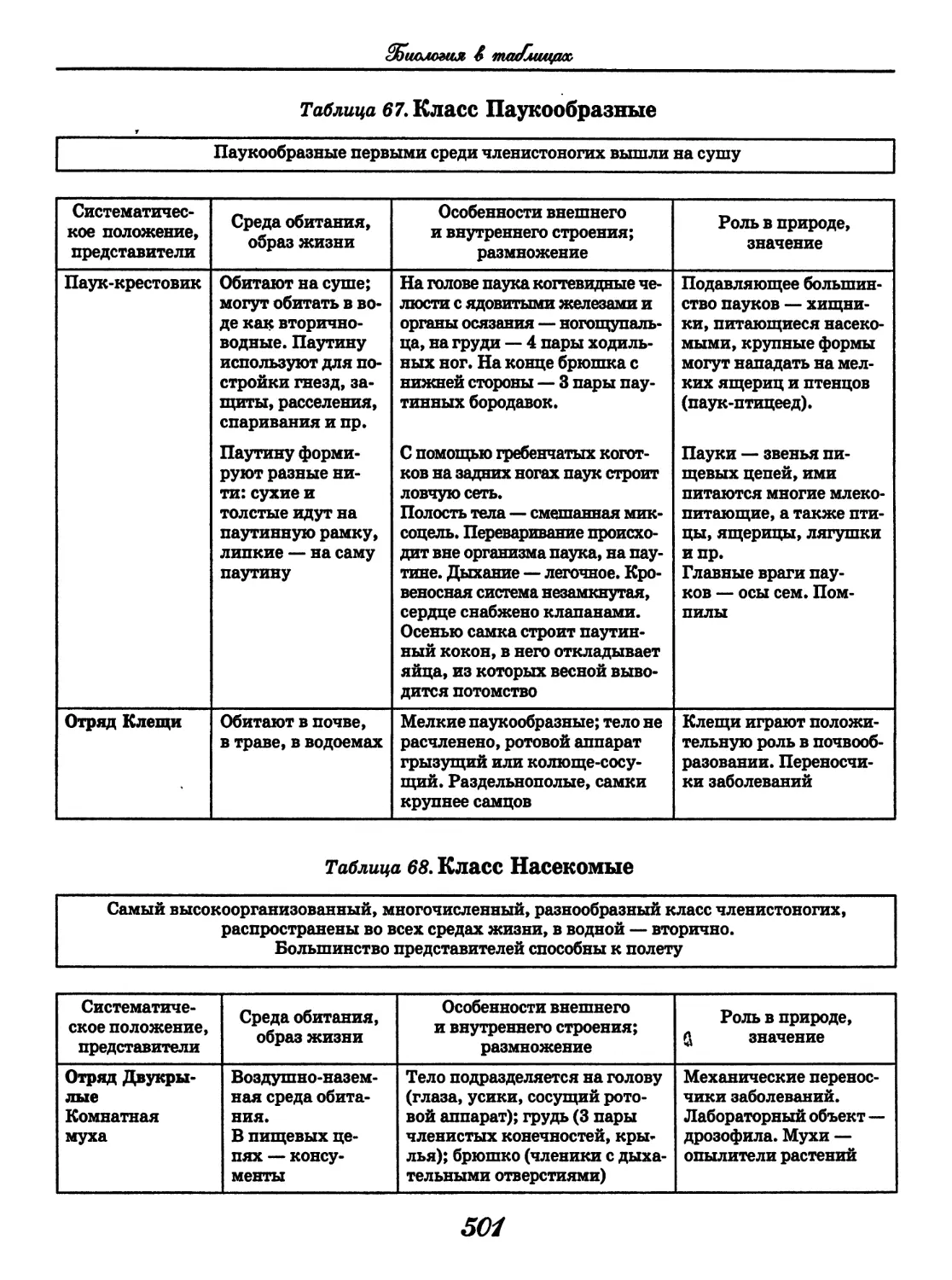
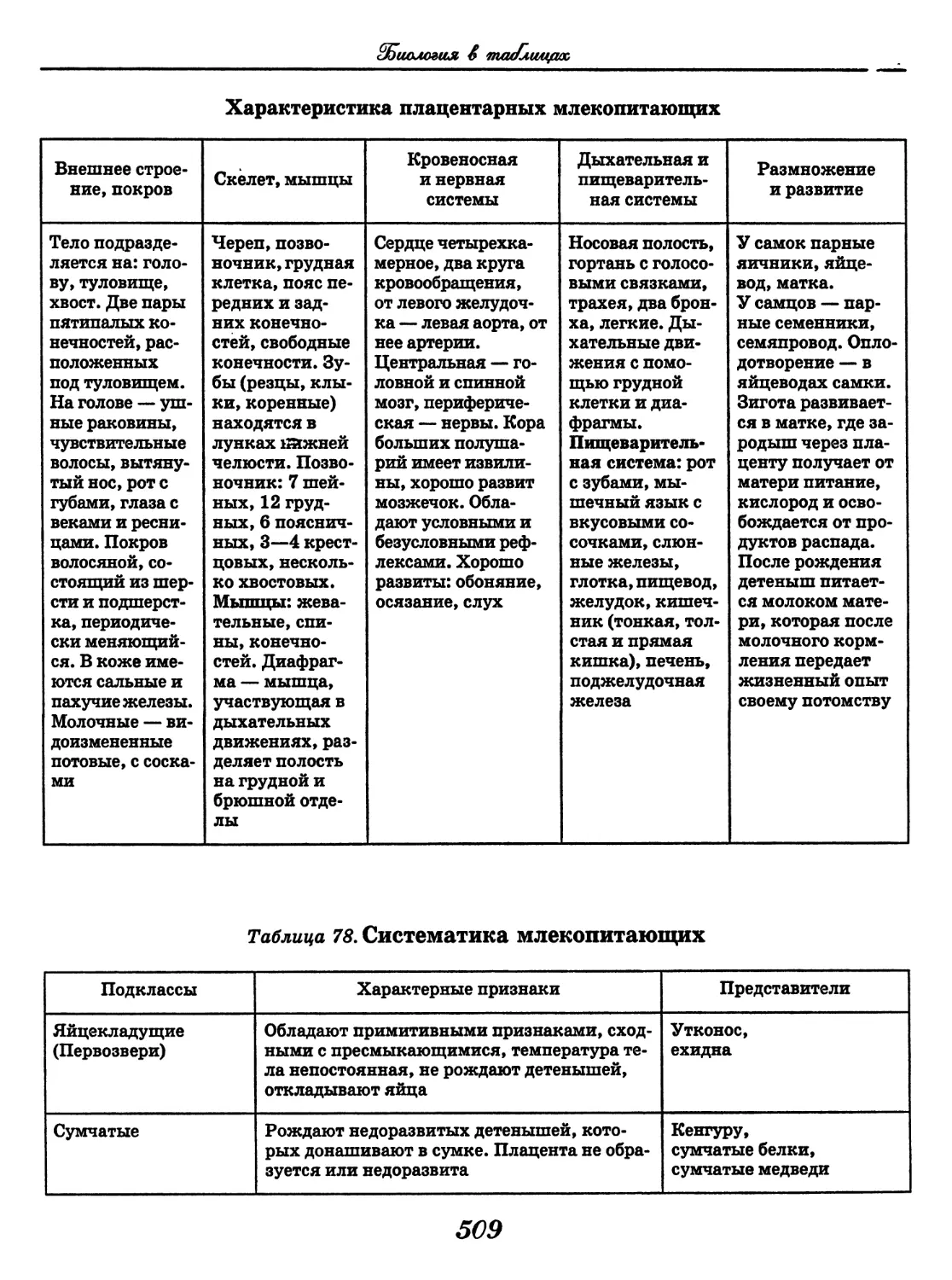
(Т. А. Козлова, В. С. Кучменко)........428
Химия
Химия в таблицах
(А. Е. Насонова)...................... 528
Химия в формулах
(В. В. Еремин)........................ 566
Английский язык
(Ю. Л. Минаев)......................... 590
Школьная программа в таблицах и формулах. Большой универсальный справочник. —
Ш67 М.: Дрофа, 1998. — 640 с.
ISBN 5—7107—1961—7
В справочнике представлен в обобщенном виде теоретический материал по предметам школьного курса.
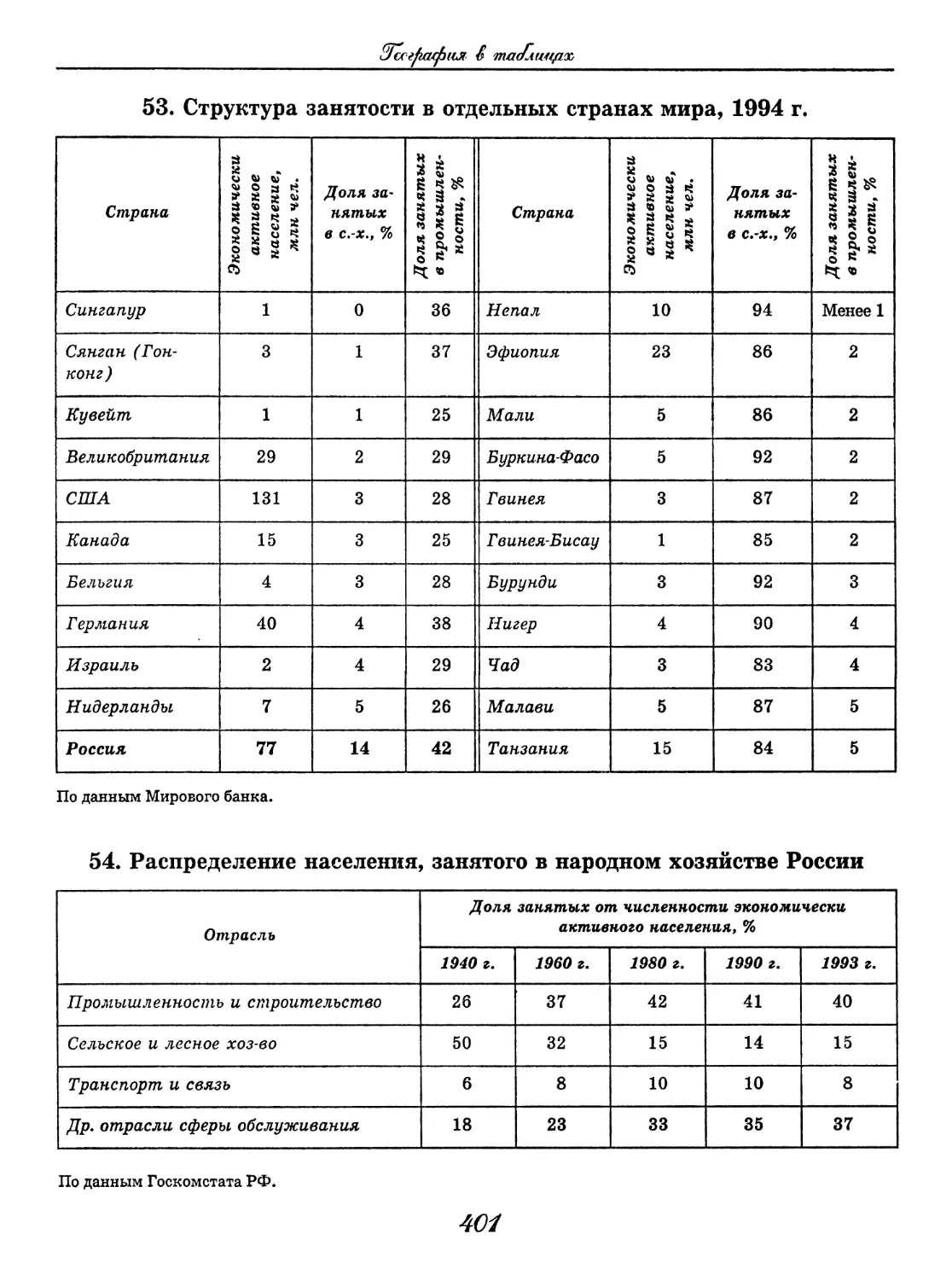
Табличная форма позволяет наглядно представить основные положения школьной программы, способ-
ствует формированию и развитию мыслительных навыков, навыков логического анализа: правила не пре-
подносятся в готовом виде, но выводятся логическим путем из предлагаемой таблицы. Таблицы и схемы
создают зрительный образ и надолго фиксируются в памяти.
Справочник адресован учащимся общеобразовательных учреждений, абитуриентам, учителям и роди-
телям.
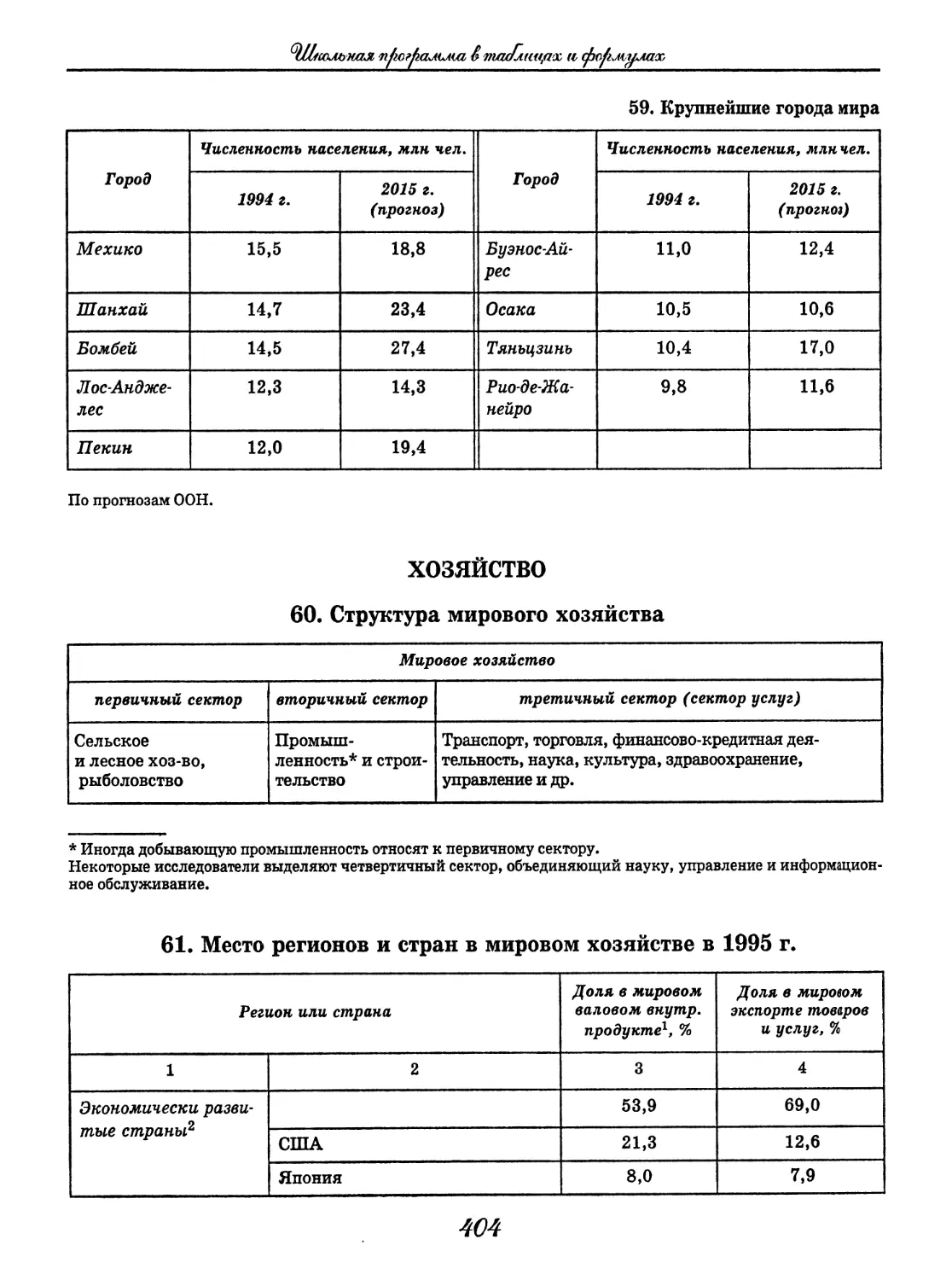
УДК 373.167.1(08)
ББК 96
ISBN 5-7107—1961—7
© «Дрофа», 1998
Русский язык
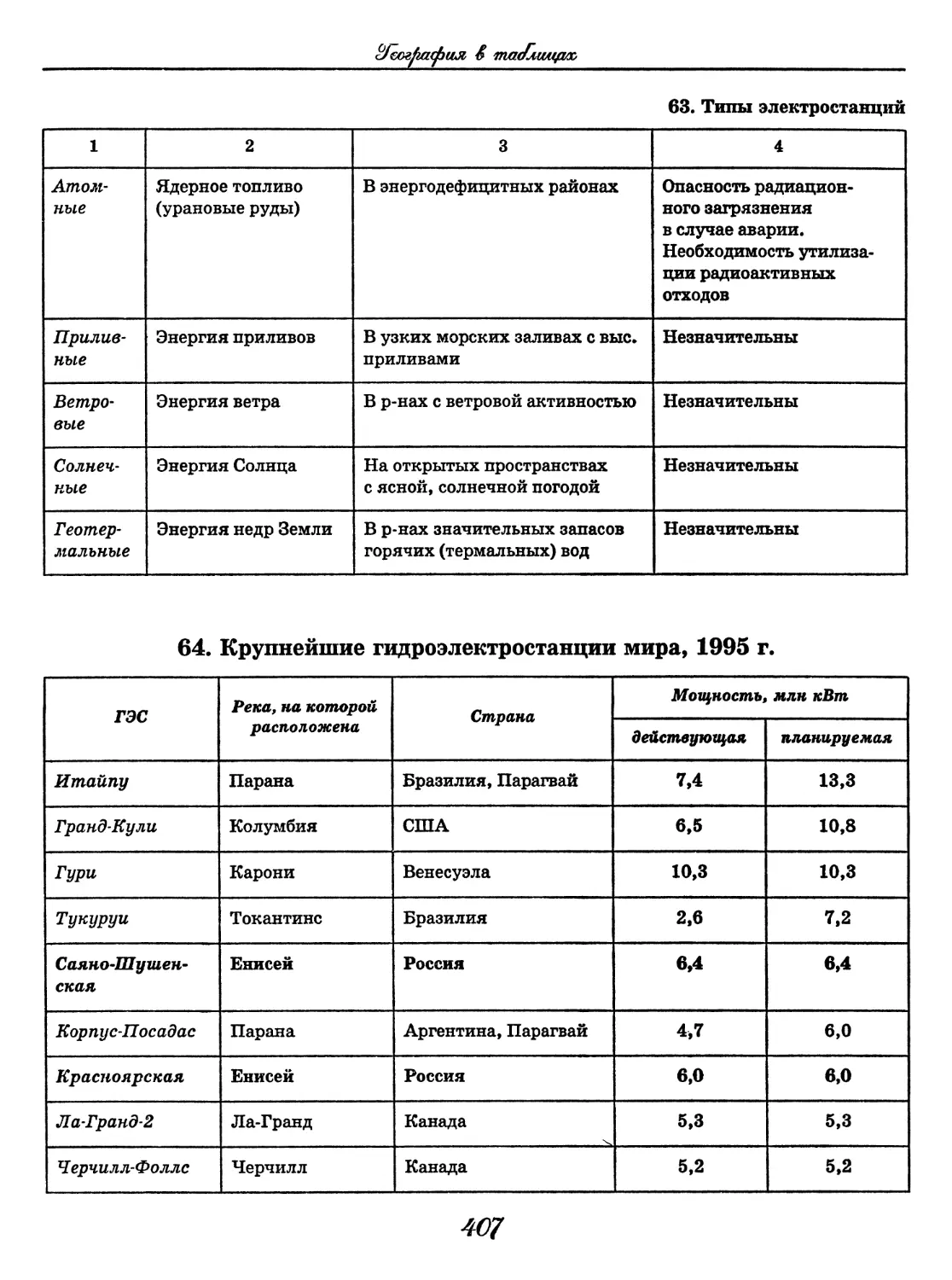
Лексика • Фонетика
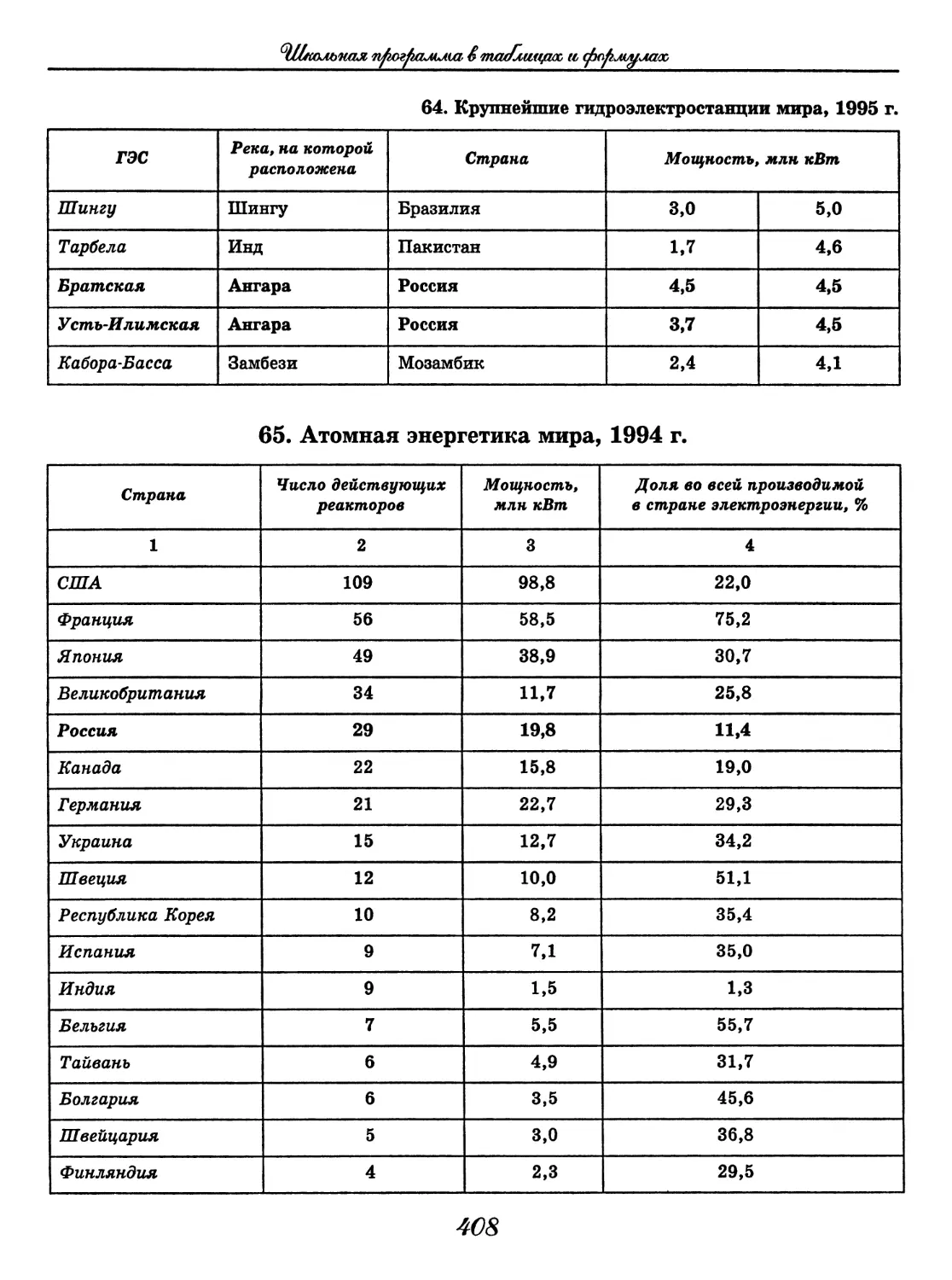
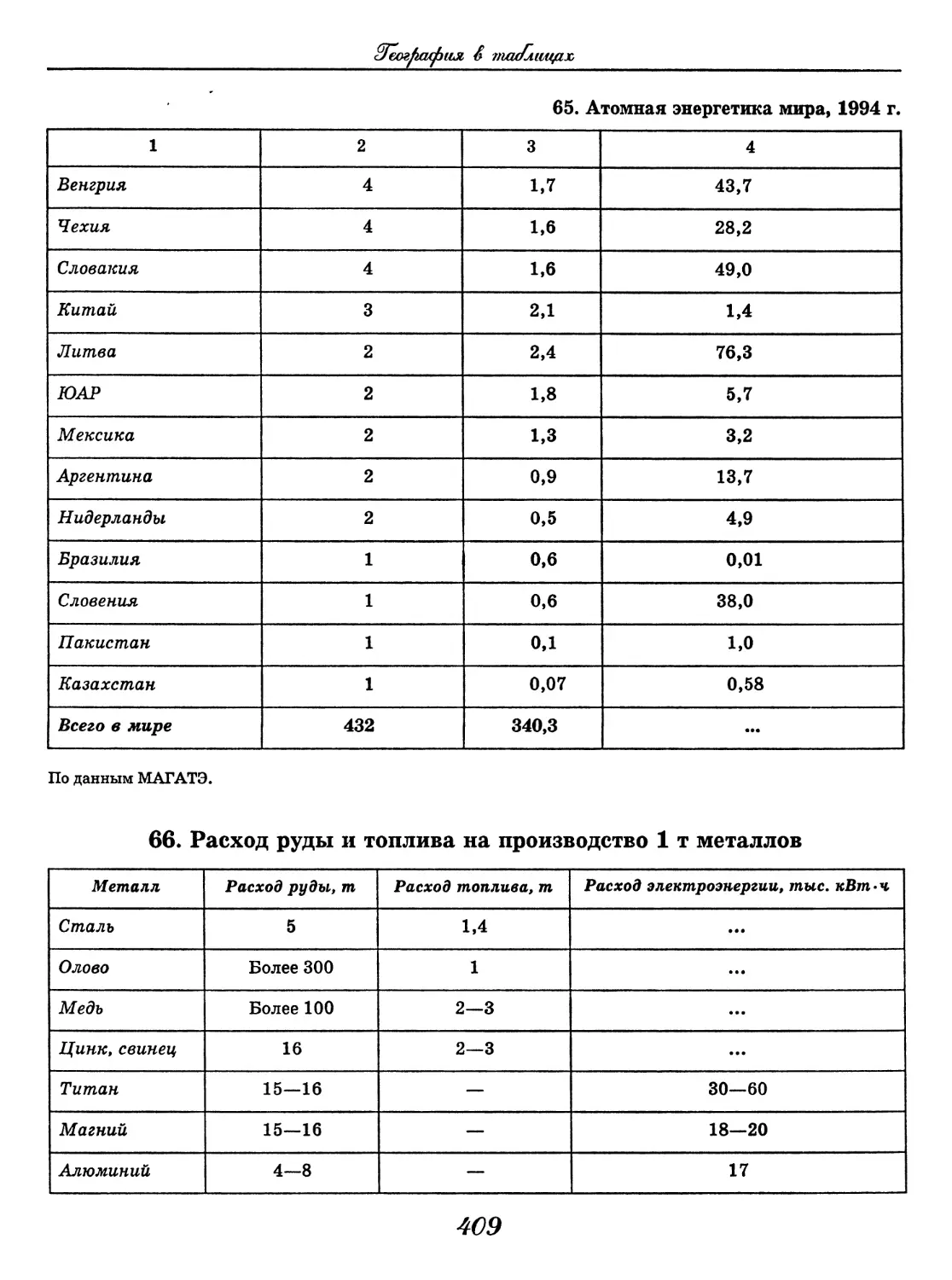
Морфемика • Словообразование • Морфология
Синтаксис
п„ НЕМОТИВИРО- МОТИВИРО- гт?птттт НЕСВОБОД- НОМИНА- ЭКСПРЕС-
ПРЯМОЕ "Г ВАННОЕ (НЕ- ВАННОЕ (ПРО- НОЕ, ФРАЗЕО- ТИВКОЕ СИВНО-
U ПРОИЗВОД- ИЗВОДНОЕ) НОЬ ЛОГИЧЕСКИ (НАЗЫВАЮ- ОБРАЗ-
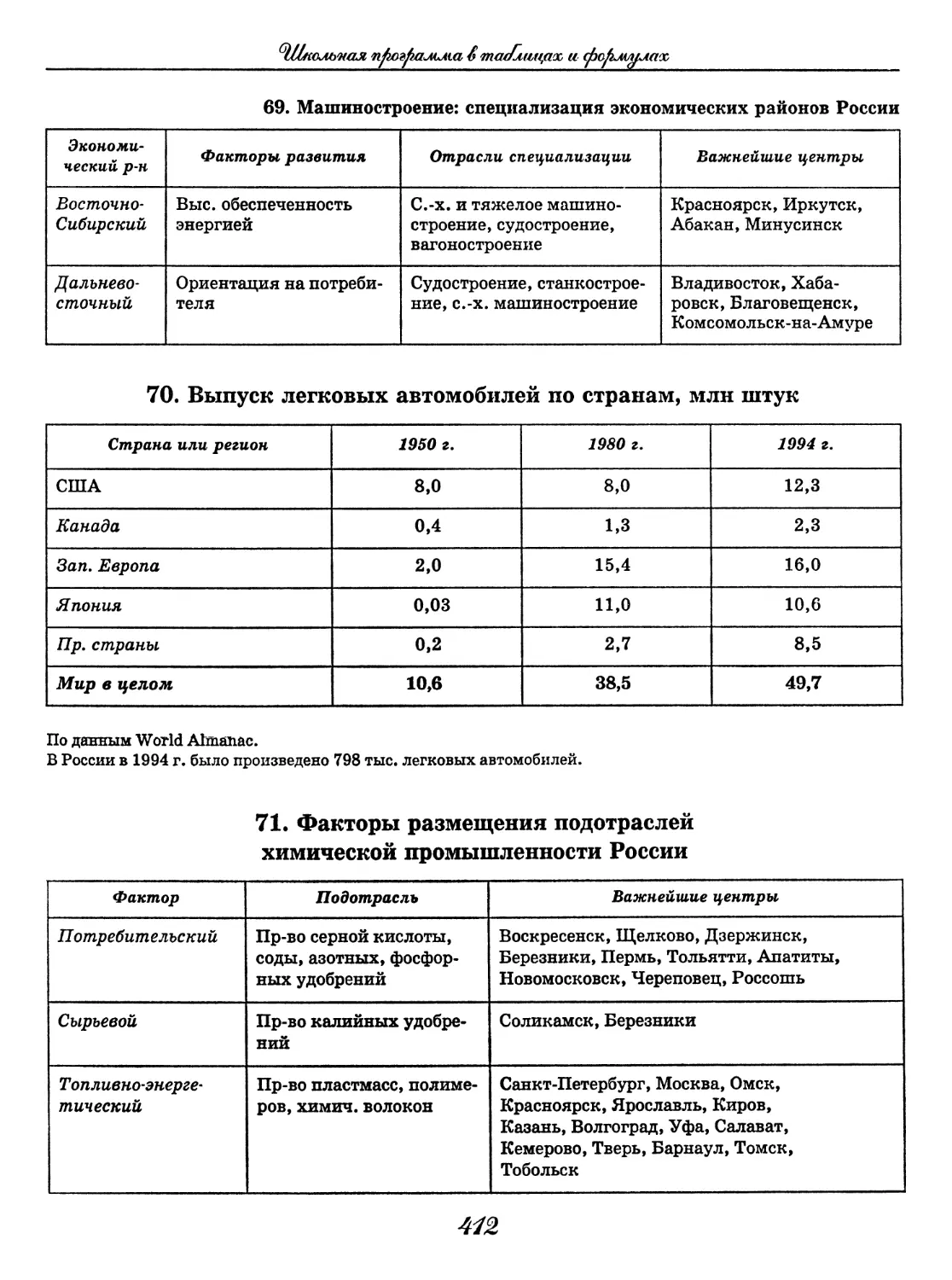
НОЕ) СВЯЗАННОЕ ЩЕЕ) НОЕ
м слово прямо указывает на предмет, его признак, действие и т. д.: атомоход, высо- кая (гора); вылететь (из гнезда), играть (на пианино); спинка (ребенка)
L0 значение обусловлено сравнением, сходст- вом, объединяющим один предмет с дру- гим: высокое (положение), вылететь (из уст), играть (на нервах), спинка (стула)
СО у слова невозможно объяснить происхож- дение значения: земля, трава, новый, иг- - рать, спина
значение можно объяснить либо характер- ным признаком предмета, либо значением производящей основы: ножка (стула), яб- - локо (глазное), теплый (взгляд); земляк, травяной, проигрывать
сл сочетаемость слова с другими словами не ограничивается какими-либо условиями: голова, говорить; синий (очень, в полоску, в клеточку)
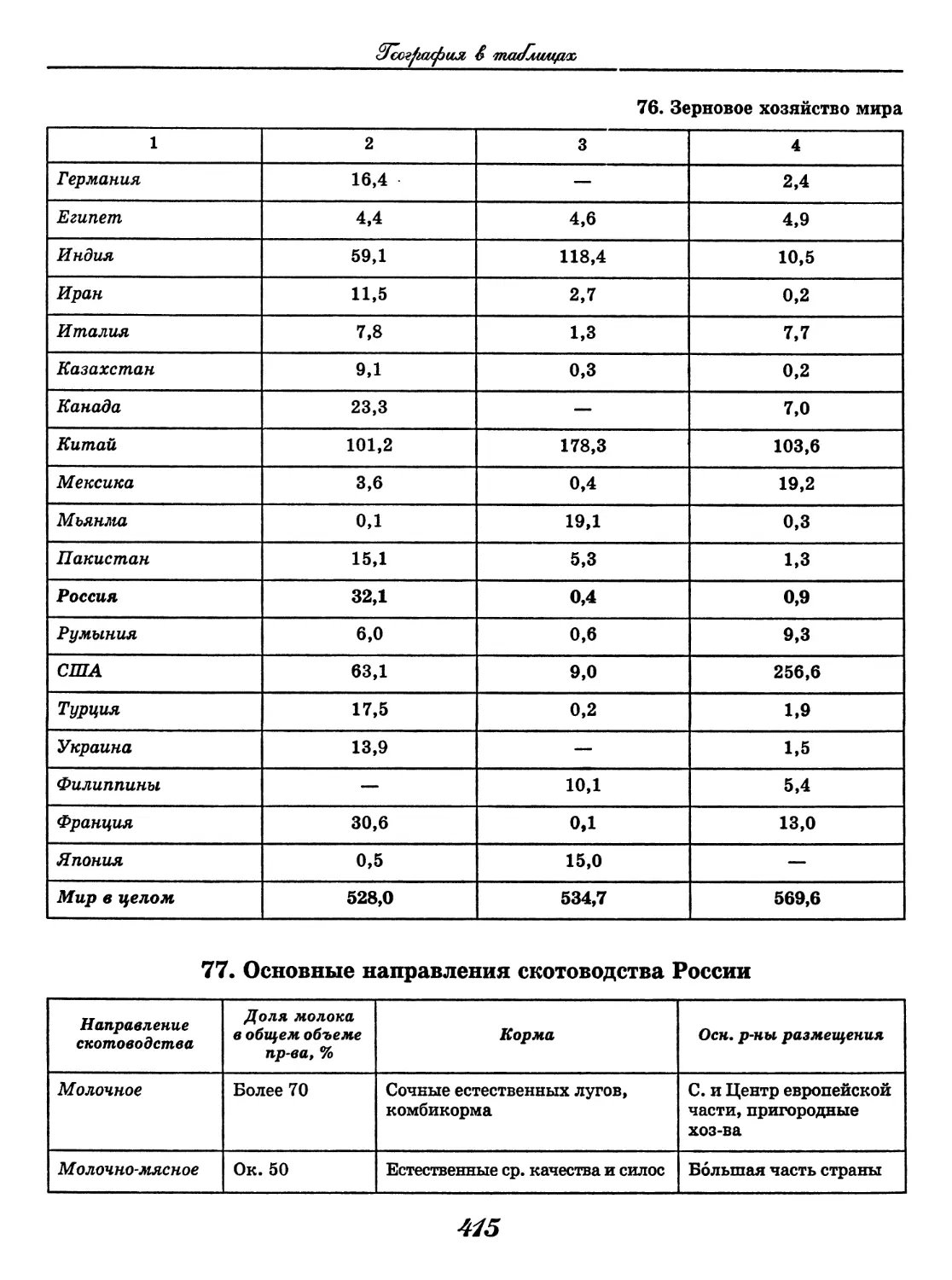
Од значение реализуется только в определен- ных условиях; сочетания возможны г с ограниченным кругом слов: закадычный - (друг), впросак (попасть), кромешная (тьма)
«4 слова используются в речи прежде всего для называния (предметов, явлений и т. д.)
00 слова употребляются для создания образ- ности, оценочности: ахинея, плестись, возмездие
Русский язык в таблицах
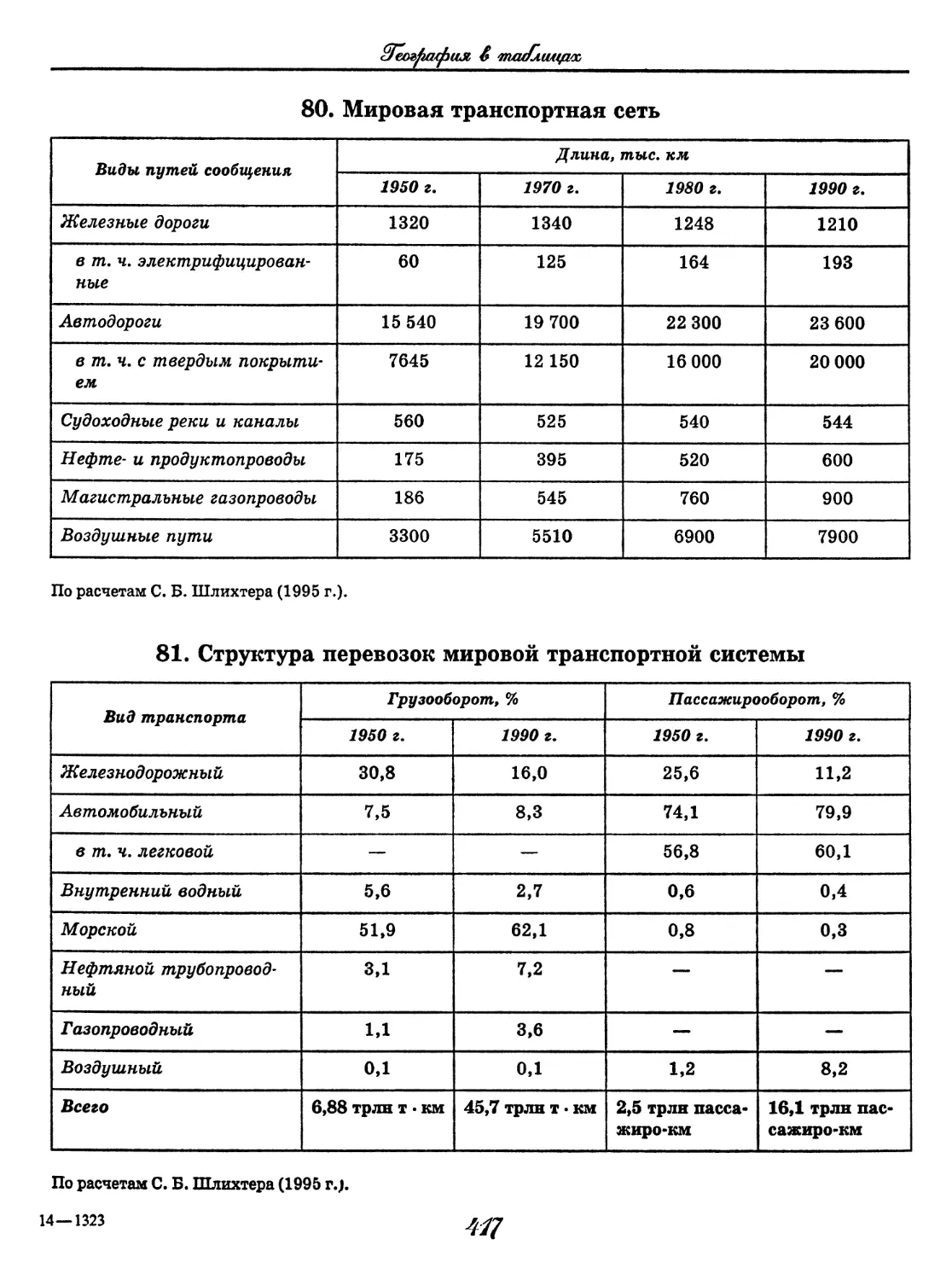
Нисский, л^ы/с £ таблицах
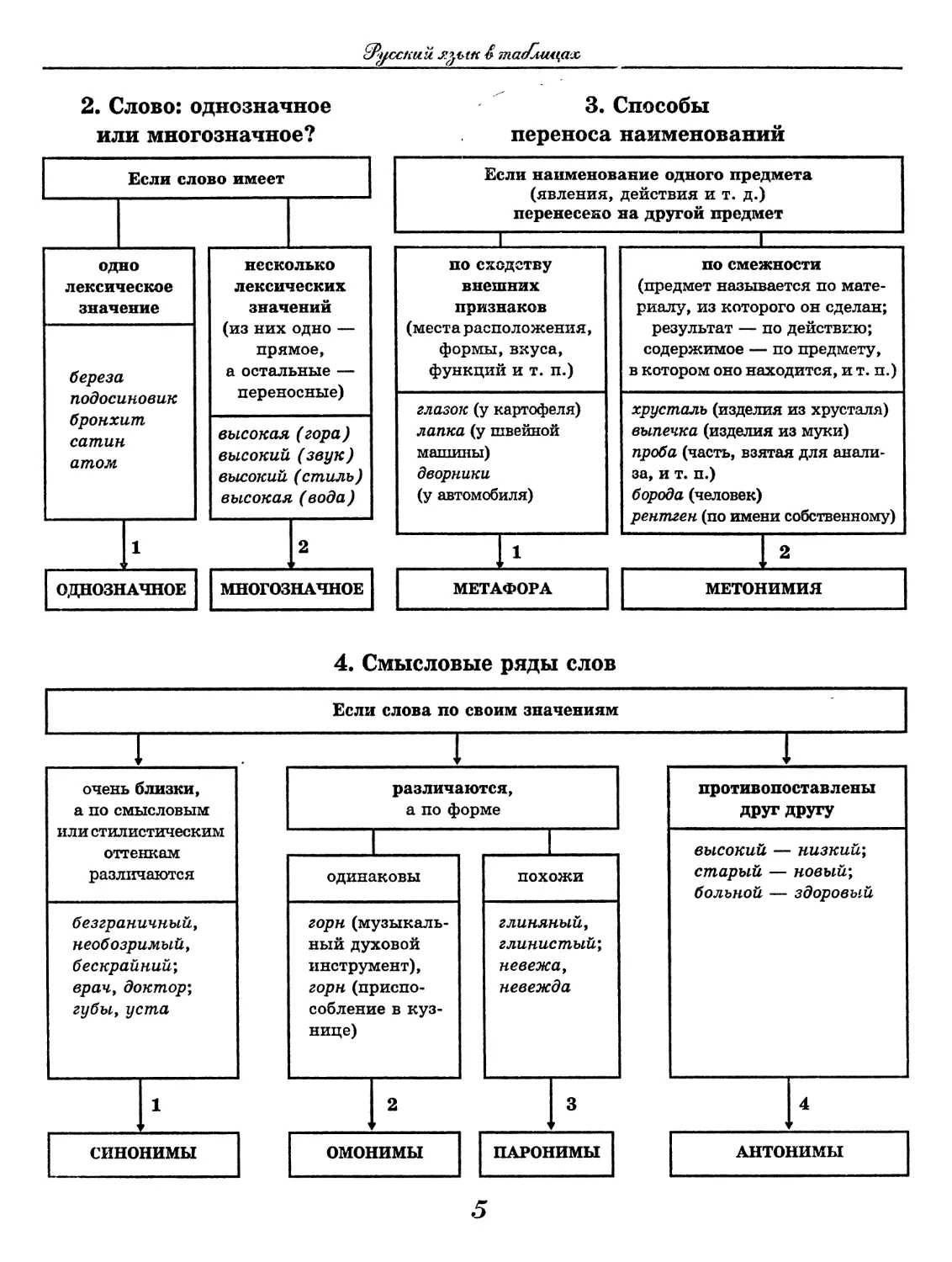
2. Слово: однозначное
или многозначное?
3. Способы
переноса наименований
4. Смысловые ряды слов
5
^Иксмгна.я пф&фммма & таЛлиирх и, фофмл^лах
5. Как отличить многозначное слово от омонима?
6. Место русского языка среди других славянских языков
6
^Русский & maJjwup/x,
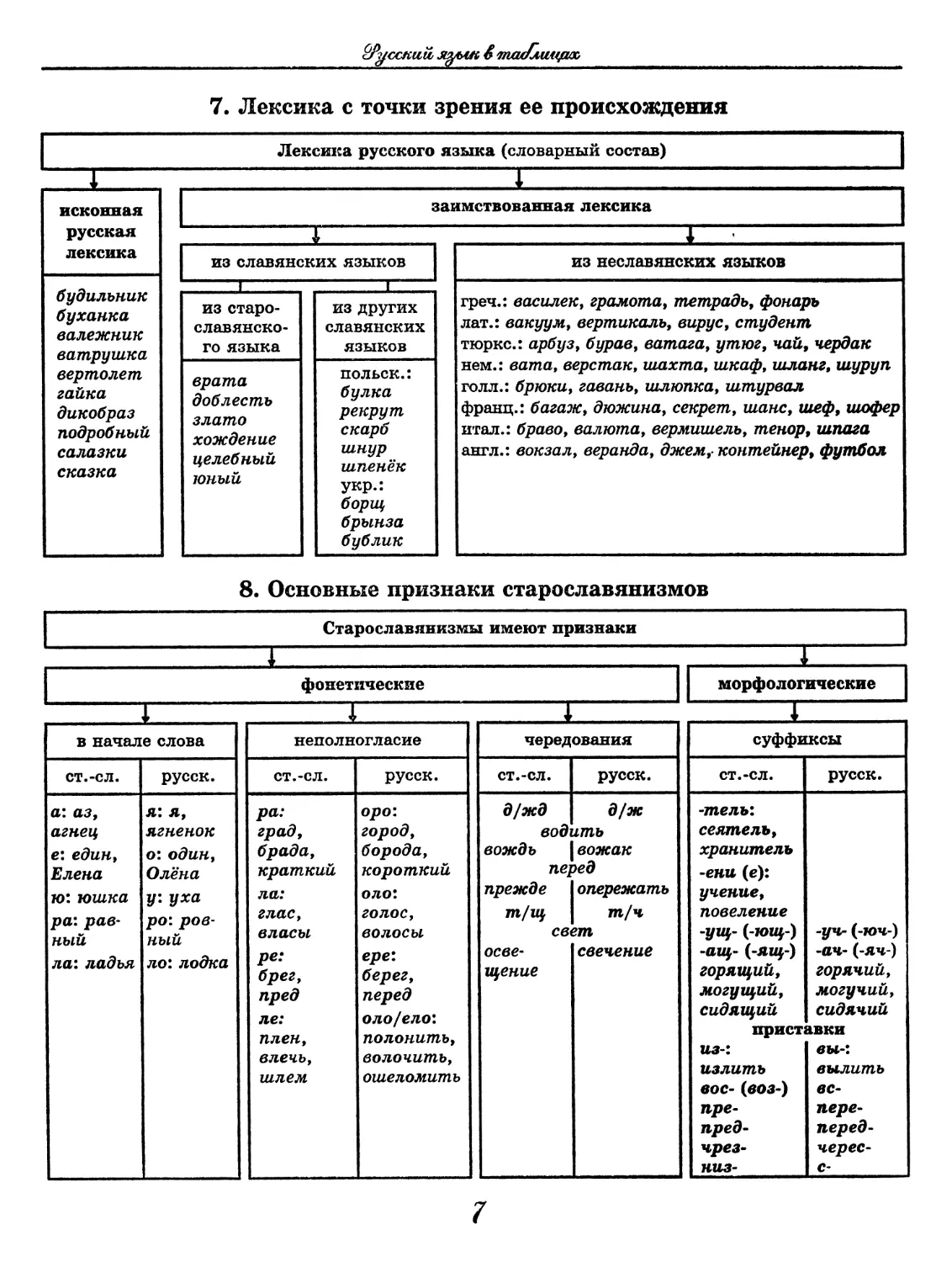
7. Лексика с точки зрения ее происхождения
Лексика русского языка (словарный состав)
..... 1 1
исконная русская лексика заимствованная лексика
1 .. 1 _
из славянских языков из неславянских языков
будильник буханка валежник ватрушка вертолет гайка дикобраз подробный салазки сказка ___ 1 1 греч.: василек, грамота, тетрадь, фонарь лат.: вакуум, вертикаль, вирус, студент тюрке.: арбуз, бурав, ватага, утюг, чай, чердак нем.: вата, верстак, шахта, шкаф, шланг, шуруп голл.: брюки, гавань, шлюпка, штурвал франц.: багаж, дюжина, секрет, шанс, шеф, шофер итал.: браво, валюта, вермишель, тенор, шпага англ.: вокзал, веранда, джем, контейнер, футбол
из старо- славянско- го языка из других славянских языков
врата доблесть злато хождение целебный юный польск.: булка рекрут скарб шнур шпенёк укр.: борщ брынза бублик
8. Основные признаки старославянизмов
Старославянизмы имеют признаки
1 .. 1
фонетические морфологические
1 А 1—_ 1
неполногласие
в начале слова
ст.-сл. русск. ст.-сл. русск.
а: аз, агнец е: един, Елена ю: юшка ра: рав- ный ла: ладья я: я, ягненок о: один, Олёна у: уха ро: ров- ный ло: лодка ра: град, брада, краткий ла: глас, власы ре: брег, пред ле: плен, влечь, шлем оро: город, борода, короткий оло: голос, волосы ере: берег, перед оло/ело: полонить, волочить, ошеломить
чередования суффиксы
ст.-сл. русск. ст.-сл. русск.
д/жд водг вождь | nei прежде 1 т/щ I св< осве- щение д/ж ять 1 вожак зед 1 опережать 1 т/ч ?т свечение -тель: сеятель, хранитель -ени (е): учение, повеление ~УЩ~ (-ЮЩ-) -ащ- (-ящ-) горящий, могущий, сидящий прист; из-: излить вое- (воз-) пре- пред- чрез- низ- -уч- (-ЮЧ-) -ач- (-яч ) горячий, могучий, сидячий авки вы-: вылить вс- пере- перед- черес- с-
бЩкамшал п^офамма, & тас/лиирх и формулах
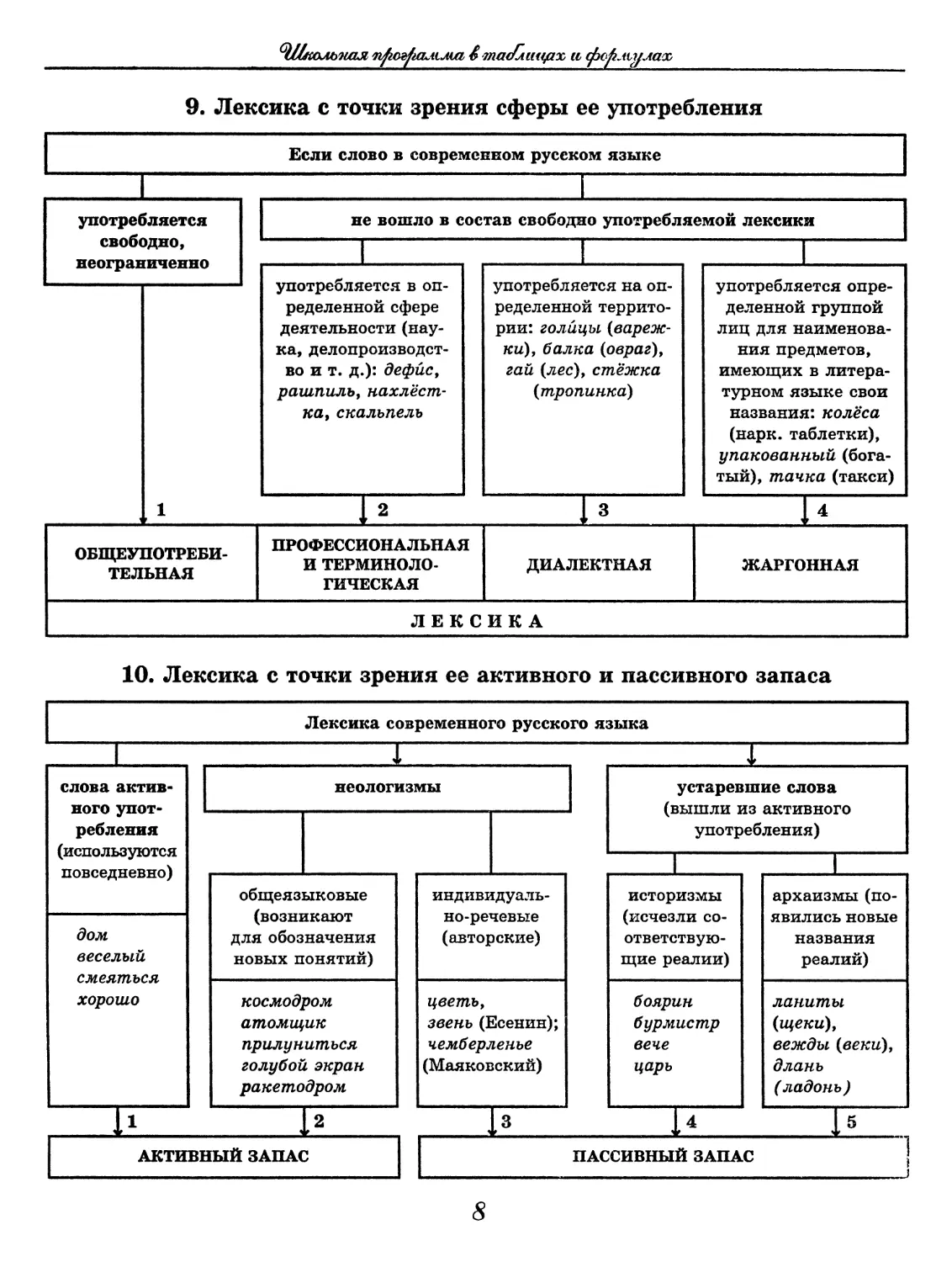
9. Лексика с точки зрения сферы ее употребления
10. Лексика с точки зрения ее активного и пассивного запаса
SPuccftaii л^ык £ma^uaflx
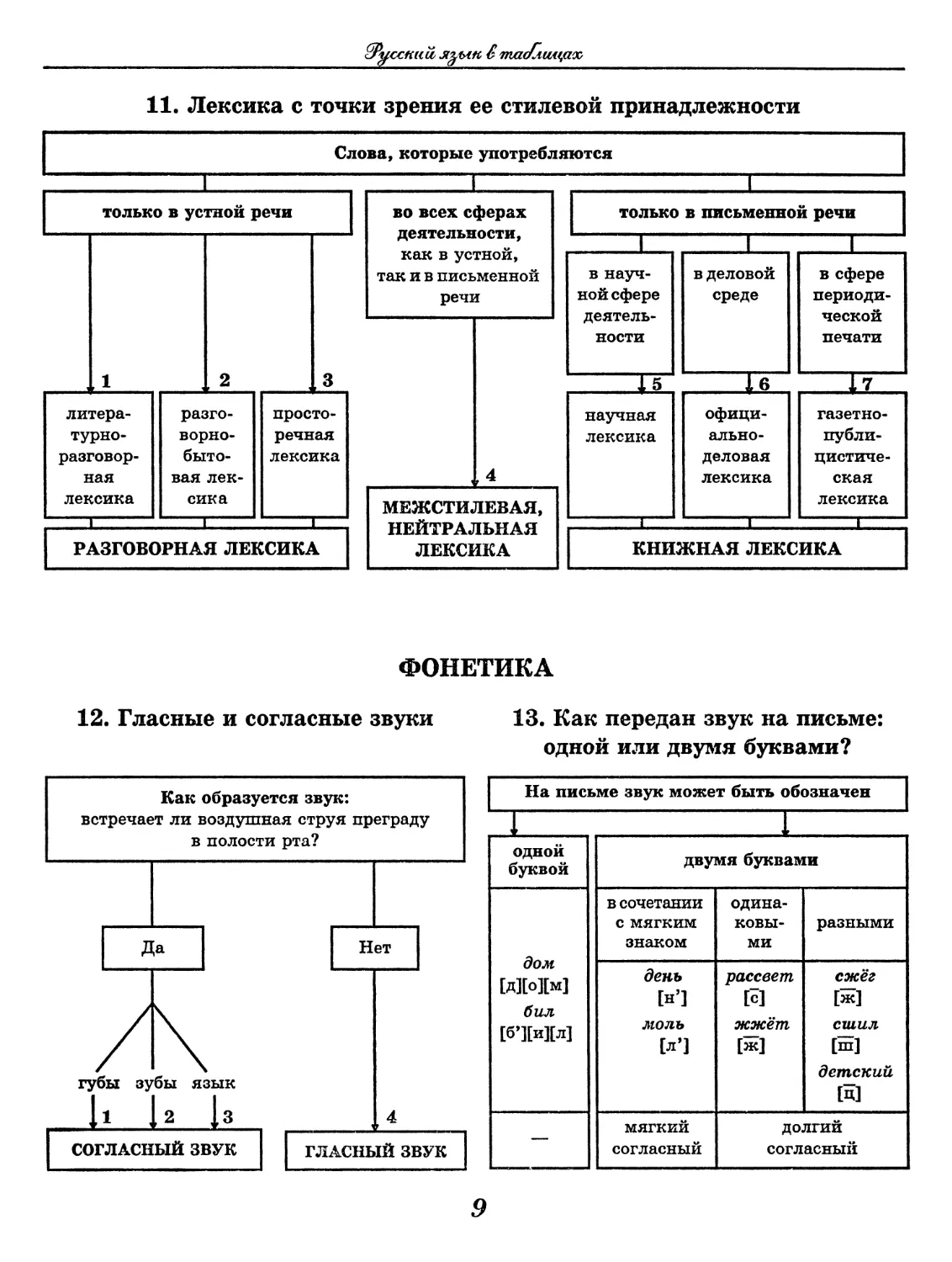
11. Лексика с точки зрения ее стилевой принадлежности
ФОНЕТИКА
12. Гласные и согласные звуки
13. Как передан звук на письме:
одной или двумя буквами?
На письме звук может быть обозначен
ОДНОЙ буквой двумя буквами
дом [Д][о][м] бил [б’][и][л] в сочетании с мягким знаком одина- ковы- ми разными
день [н’1 моль [л’] рассвет [с] жжёт [ж] сжёг [ж] сшил [ш] детский м
— мягкий согласный долгий согласный
9
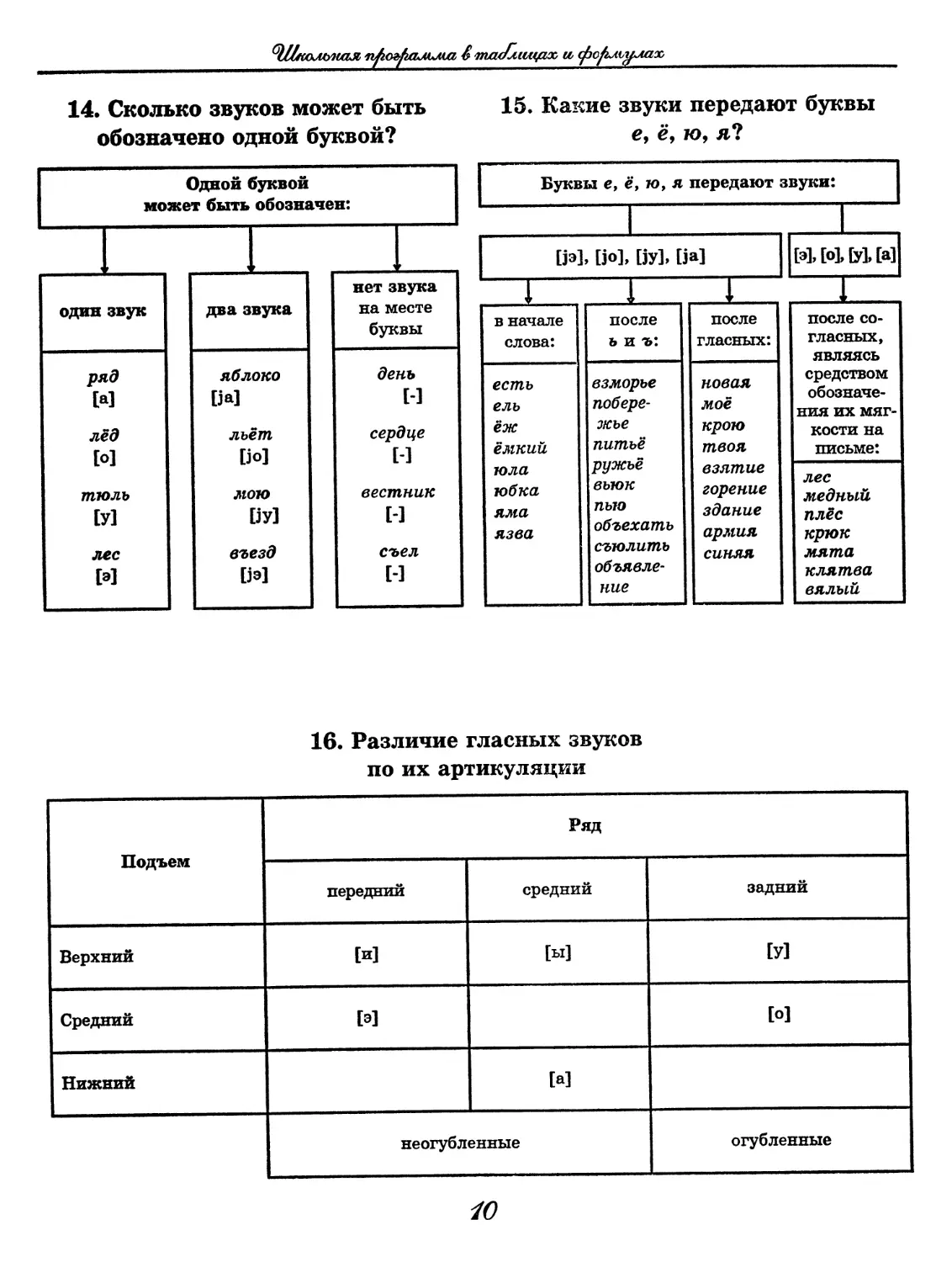
14. Сколько звуков может быть
обозначено одной буквой?
Одной буквой
может быть обозначен:
15. Какие звуки передают буквы
е, ё, ю, я?
Буквы е, ё, ю, я передают звуки:
один звук два звука нет звука на месте буквы
ряд [а] яблоко [ja] день [-]
лёд [О] льёт [jo] сердце [-]
тюль [у] мою [jy] вестник []
лес [а] въезд [ja] съел []
[ja], [jo], [jy], [ja] И, [о], [у], [a]
I 1 :: 1
в начале слова: после ь и ъ: после гласных: после со- гласных, являясь средством обозначе- ния их мяг- кости на письме: лес медный плес крюк мята клятва вялый
есть ель ёж ёмкий юла юбка яма язва взморье побере- жье питьё ружьё вьюк пью объехать съюлить объявле- ние новая моё крою твоя взятие горение здание армия синяя
16. Различие гласных звуков
по их артикуляции
Подъем Ряд
передний средний задний
Верхний [И] [ы] [у]
Средний [а] [о]
Нижний [а]
неогубленные огубленные
/0
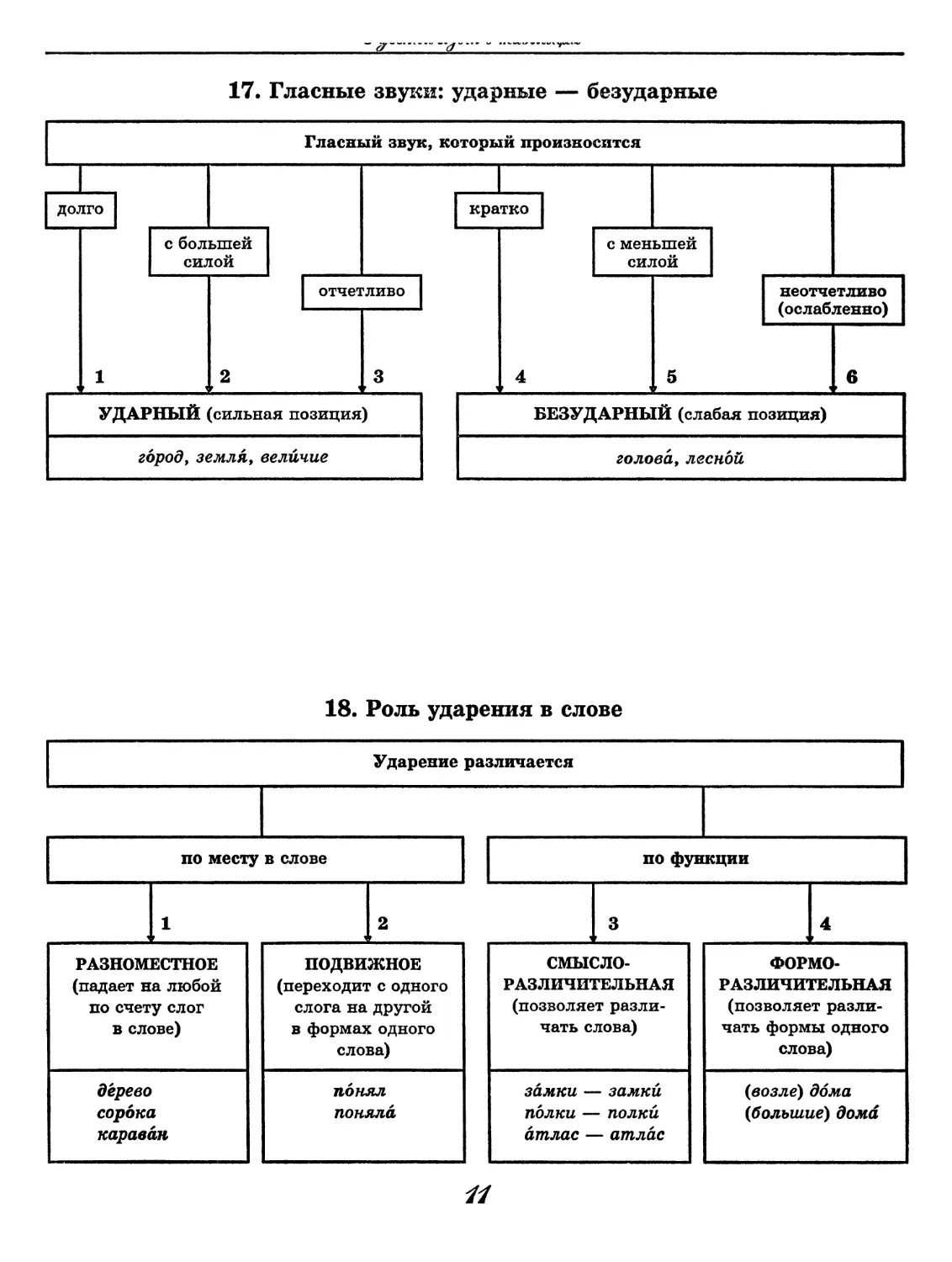
17. Гласные звуки: ударные — безударные
18. Роль ударения в слове
^Штмнал nfiotfn
фс^мшла'зь
19. Как изменяются гласные звуки [а], [о], [э]?
20. Согласные звуки по месту образования
21. Согласные звуки по способу образования
22. Согласные звуки:
сонорные и шумные
Работают ли голосовые связки
при образовании звука?
активно частично
[р], [р’]> [л], [Л>] [м], [м’]( [н], [н’] [j] преобладает голос преобладает шум
[б], [б’] [в], [в’] [г], [г’] [д], [д] [ж], [ж’] [3], [з’] [П], [п’] [ф], [ф’] [к], [к’] [т], [т ] [ш], [ш’] [С], [с’] М, [X’] [ц], [Ч’]
1 2 3
СОНОРНЫЕ звонкие глухие
ШУМНЫЕ
23. Согласные звуки:
твердые и мягкие
При образовании звука поднимается ли средняя
часть языка к среднему (мягкому) нёбу?
1 1
Нет Да
[б] [В] [Г] [д] [ж] [з] [к] [л] [м] и [п] [р] [с] [т] [ф] [х] [ч] [ш] [б’] [в’] [г’] И [ж’] [j] [3’] [к’] [л’] [м’] [И’] [п] [р’1 [с’] [т’] [ф’] [X’] м [ш’]
11 h
твердые согласные мягкие согласные
/3
24. Как изменяются согласные звуки в слове?
(Фонетические законы в области согласных)
Находится ли согласный звук перед гласным, сонорным или перед [в], [в’] (сильная позиция для согласных)?
1 L
Да Нет
1 1 I
звук не изменяется звук изменяется звук не про- износится (выпадает)
1 1 1 1
слабый [сл][б] правда [пр] [д] подыскать [п][д] [к] подвал [п][дв] свить [св’] звонкий перед глухим становится глухим глухой перед звонким становится звонким твердый перед мягким, если одинаковое место образования, становится мягким звонкий в конце слова оглуша- ется
сердце [рц] праздник [з’н’] совестный [сн]
подшить [т] надписать [т] вперед [Ф] просьба [з’] молотьба [д’] власть [с’т’] дневной [Д’н’] смерч [Р’ч’] вместе [в’м’][с’т’] дуб И ряд [т] воз [С]
СИЛЬНАЯ ПОЗИЦИЯ ассимиляция (уподобление одного звука другому, рядом стоящему) закон конца слова упрощение групп согласных
по глухости по звонкости по мягкости
СЛАБАЯ ПОЗИЦИЯ
25. Схема фонетического разбора слова
/4
^Русский £ тсиРлилщх
МОРФЕМИКА. СЛОВООБРАЗОВАНИЕ
26. Последовательность разбора слова по составу
РАЗБОР СЛОВА
I 1 И
Морфемный — из каких значимых частей состоит данное слово? Словообразовательный — как образовалось данное слово?
Указать: 1) окончание и основу; 2) приставку и суффикс; 3) корень (в сложном слове — корни и соеди- нительную гласную) Определить: 1) является ли данное слово производным; 2) если да, указать производящую основу и словообразовательную морфему; 3) способ словообразования
27. Как найти окончание и основу слова?
Слово
неизменяемое
1 2 3 4 5
Все слово представ- ляет собой основу Отбрасывая суф- фикс инфинитива Отбрасывая суф- фикс -л- и родовое окончание 1. Спрягая слово, находим личное окончание. 2. Отбрасывая окон- чание, находим основу настоящего или простого буду- щего времени 1. Склоняя слово, находим падежное окончание. 2. Отбрасывая окончание, нахо- дим основу
находим основу неопределенной формы
Примечание. Одна и та же основа (например, основа привлскательн- прилагательного привлекательный) может быть про-
изводной (по отношению к основе привлеки- глагола привлекать) и в то же время производящей (для основы
существительного привлекательность).
15
^Шпмыигл пфогфамма $ тас/мшрх и, фсфлиумгх,
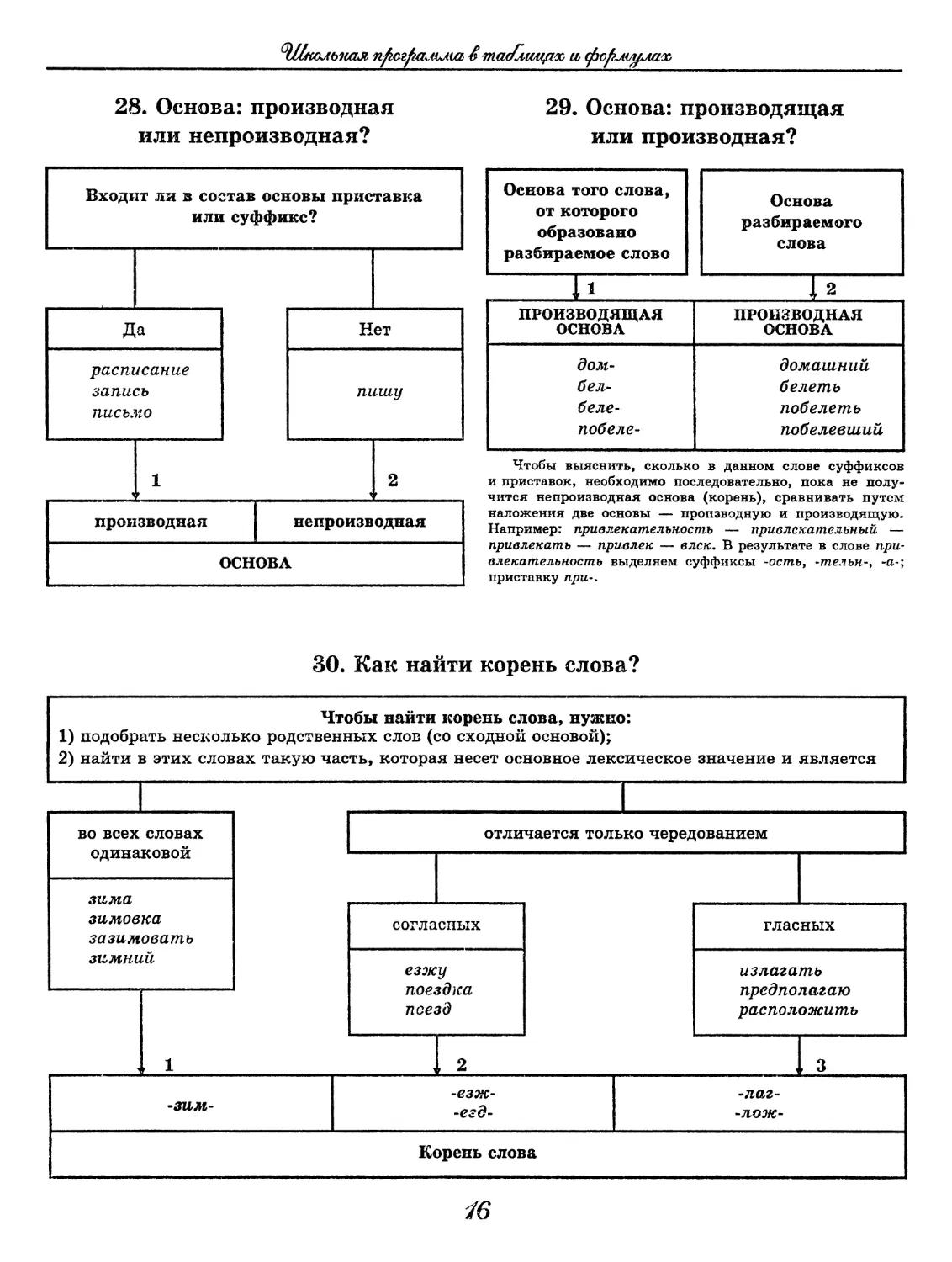
28. Основа: производная
или непроизводная?
29. Основа: производящая
или производная?
Основа того слова, от которого образовано разбираемое слово разбираемого слова
h 12
ПРОИЗВОДЯЩАЯ ОСНОВА ПРОИЗВОДНАЯ ОСНОВА
дом- бел- беле- побеле- домашний белеть побелеть побелевший
Чтобы выяснить, сколько в данном слове суффиксов
и приставок, необходимо последовательно, пока не полу-
чится непроизводная основа (корень), сравнивать путем
наложения две основы — производную и производящую.
Например: привлекательность — привлекательный —
привлекать — привлек — влек, В результате в слове при-
влекательность выделяем суффиксы -ость, -телън-, -а-;
приставку при-.
30. Как найти корень слова?
/6
^Русский я^ык & тскРмшрх,
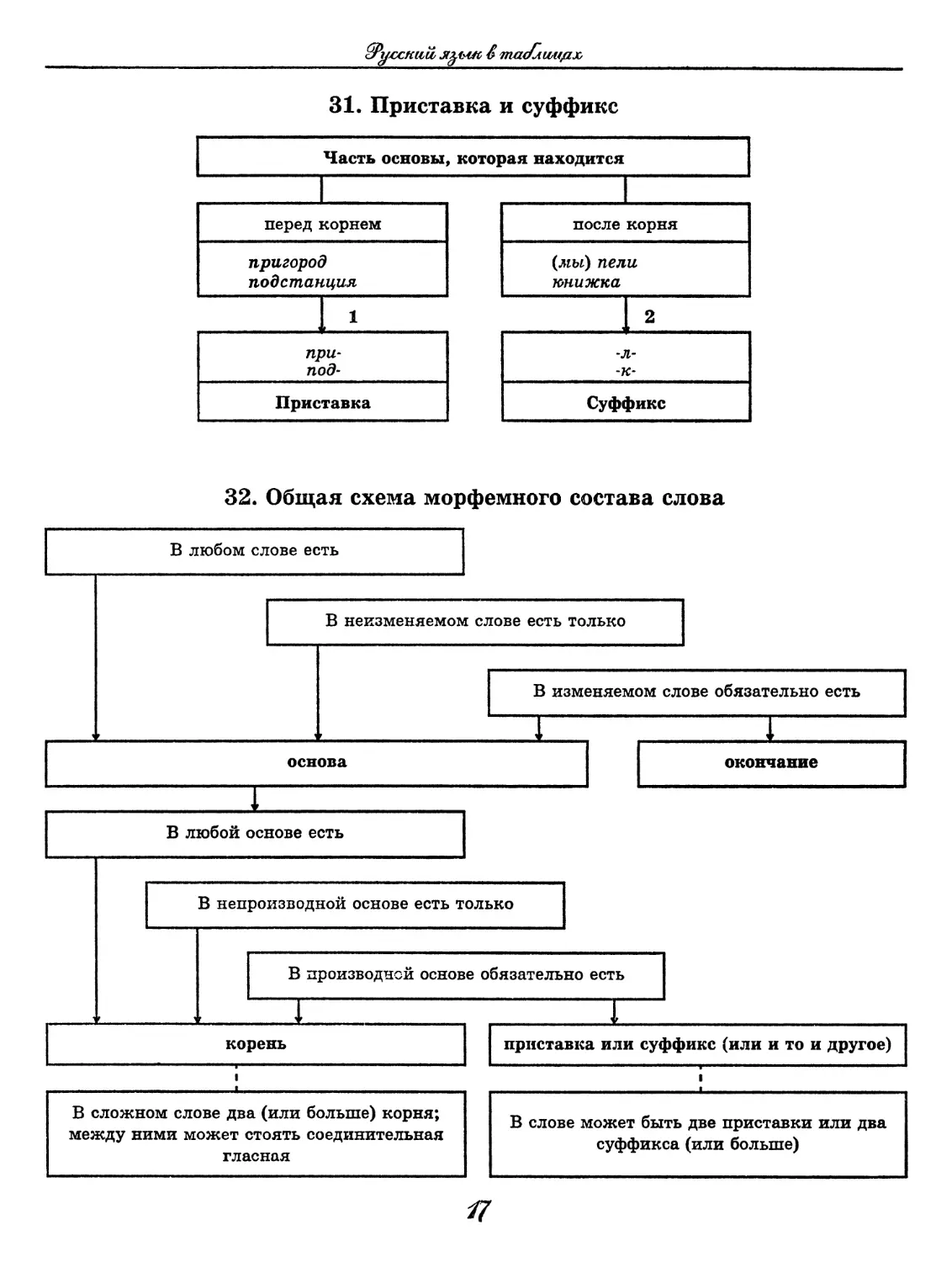
31. Приставка и суффикс
32. Общая схема морфемного состава слова
*7
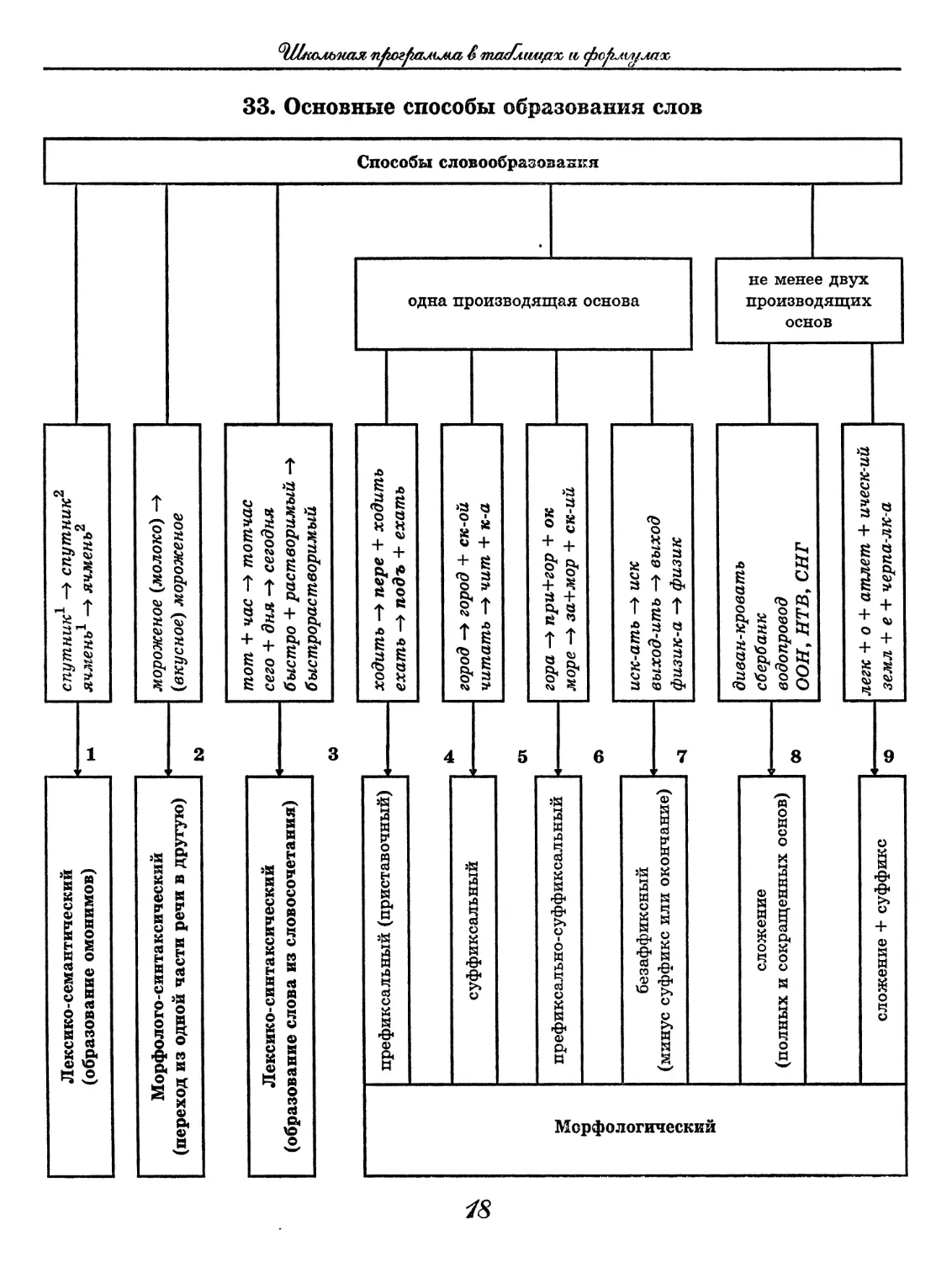
Лексико-семантический (образование омонимов) 1 2 спутник* —> спутник ячмень1 —> ячмень2 Способы словообразования ьшшмшл пфюгфсмълшь & таилиироо и, фофлиулаж, 33. Основные способы образования слов
м
Морфолого-синтаксический (переход из одной части речи в другую) мороженое (молоко) —> (вкусное) мороженое
to
тот 4- час —> тотчас сего + дня -> сегодня быстро + растворимый —> б ыстрорастворимый
Лексико-синтаксический (образование слова из словосочетания)
со
& Морфологический префиксальный (приставочный) ходить —> пере 4- ходить ехать —> подъ 4- ехать одна производящая основа
город —> город 4- ск-ой читать —> чит 4- к-а
суффиксальный
СП
префиксально-суффиксальный гора —> при+гор 4- ок море —> за+мор 4- ск-ий
ф
безаффиксный (минус суффикс или окончание) иск-ать —> иск выход-ить —> выход физик-а —> физик
<1
диван-кровать Сбербанк водопровод ООН, НТВ, СНГ не менее двух производящих основ
сложение (полных и сокращенных основ)
00
легк + о + атлет + ическ-ий земл 4- е 4- черпа-лк-а
сложение 4- суффикс
со
^Русским яуын Р чгим/миукх,
34. Общая схема словообразовательного анализа слова
Является ли слово производным?
Нет Да. В слове есть
производящая основа — это основа того (более простого по своему строе- нию) родственного слова, от которого образовано данное слово словообразовательная морфема — приставка, суффикс
добрый доброта
добр- -от-
производящая основа словообразовательная морфема
МОРФОЛОГИЯ
36. Последовательность морфологической характеристики слова
Части речи (знаменательные и служебные)
изменяемые неизменяемые
1. Наименование части речи 1. Наименование части речи
2. Начальная форма
3. Разряд по значению 2. Разряд по значению
4. Постоянные для данной части речи мор- фологические признаки
б. Признаки формы, употребленной в дан- ном предложении 3. Разряд по структуре
6. Синтаксическая функция (член предло- жения) 4. Роль в предложении (член предложения; средство соединения слов, частей предложения, предложе- ний и т. п.)
7. Особенности правописания (если есть) 5. Особенности правописания (если есть)
/9
0%
омзг4югфоф п xifymrnmti a ъм^тпфгофи
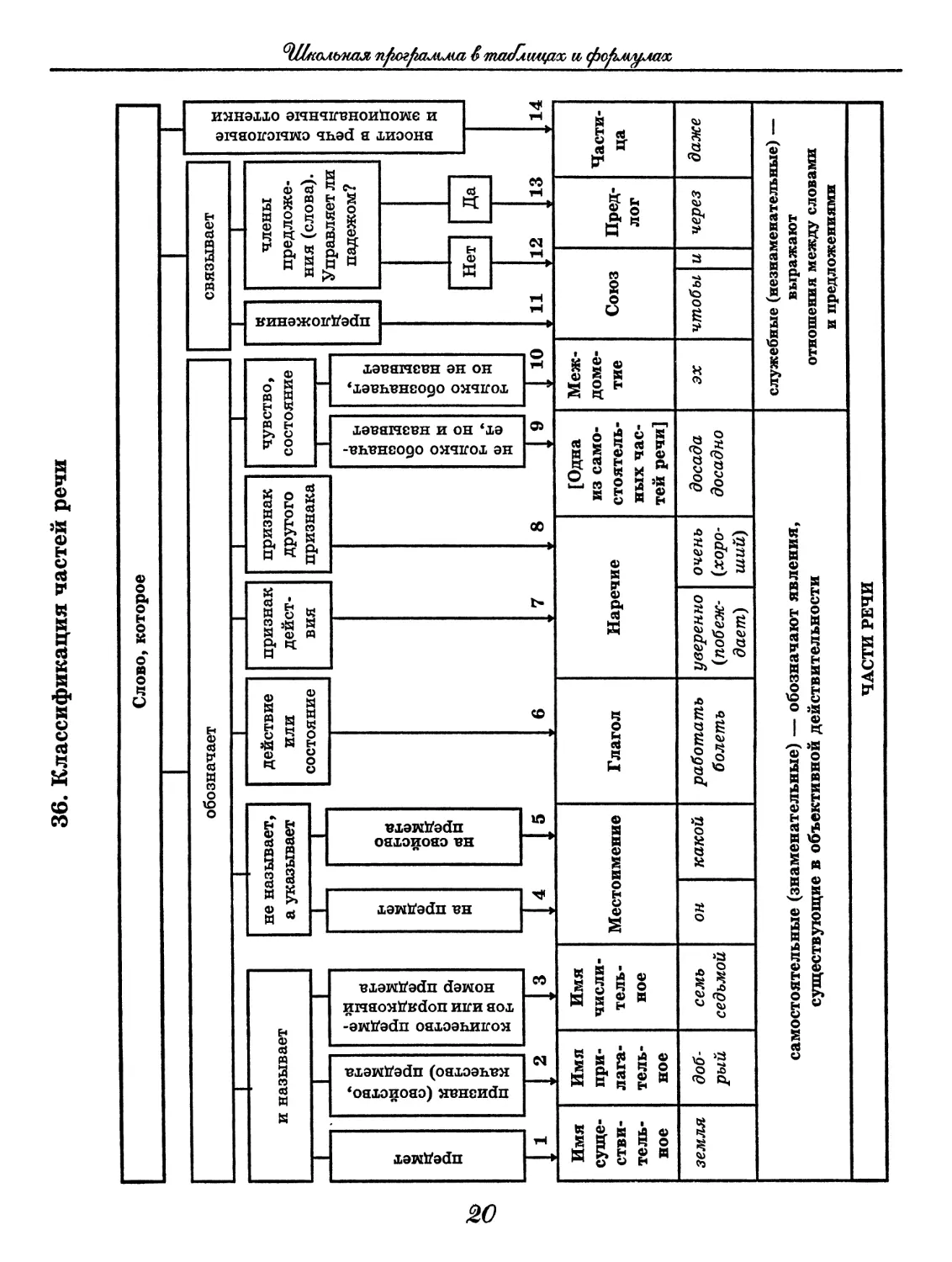
36. Классификация частей речи
CUUJD
ЗНАМЕНАТЕЛЬНЫЕ ЧАСТИ РЕЧИ:
ПОСТОЯННЫЕ ПРИЗНАКИ
37. Существительное:
одушевленное или неодушевленное?
Если форма винительного падежа множественного числа совпадает с формой
родительного падежа множественного числа именительного падежа множественного числа
учеников медведей раков москвичей (жителей Москвы) (взял) королей, валетов (игральные карты) (купил) кукол (нашел) спутников (нам по пути) березы личинки «Москвичи* (автомобили) (запускать) искусственные спутники Земли
1 . 2
ОДУШЕВЛЕННОЕ НЕОДУШЕВЛЕННОЕ
38. Существительное:
собственное или нарицательное?
Если имя существительное является
обобщенным наименованием однородных предметов названием единичного предмета, выделенного из ряда однородных
озеро Байкал
река Ангара
гора Машу к
автомобиль «Волга»
орден (награда) «Знак почета»
человек Юрий
„ 1 2 1 *
НАРИЦАТЕЛЬНОЕ СОБСТВЕННОЕ
21
39. Род склоняемых существительных
40. Род несклоняемых существительных
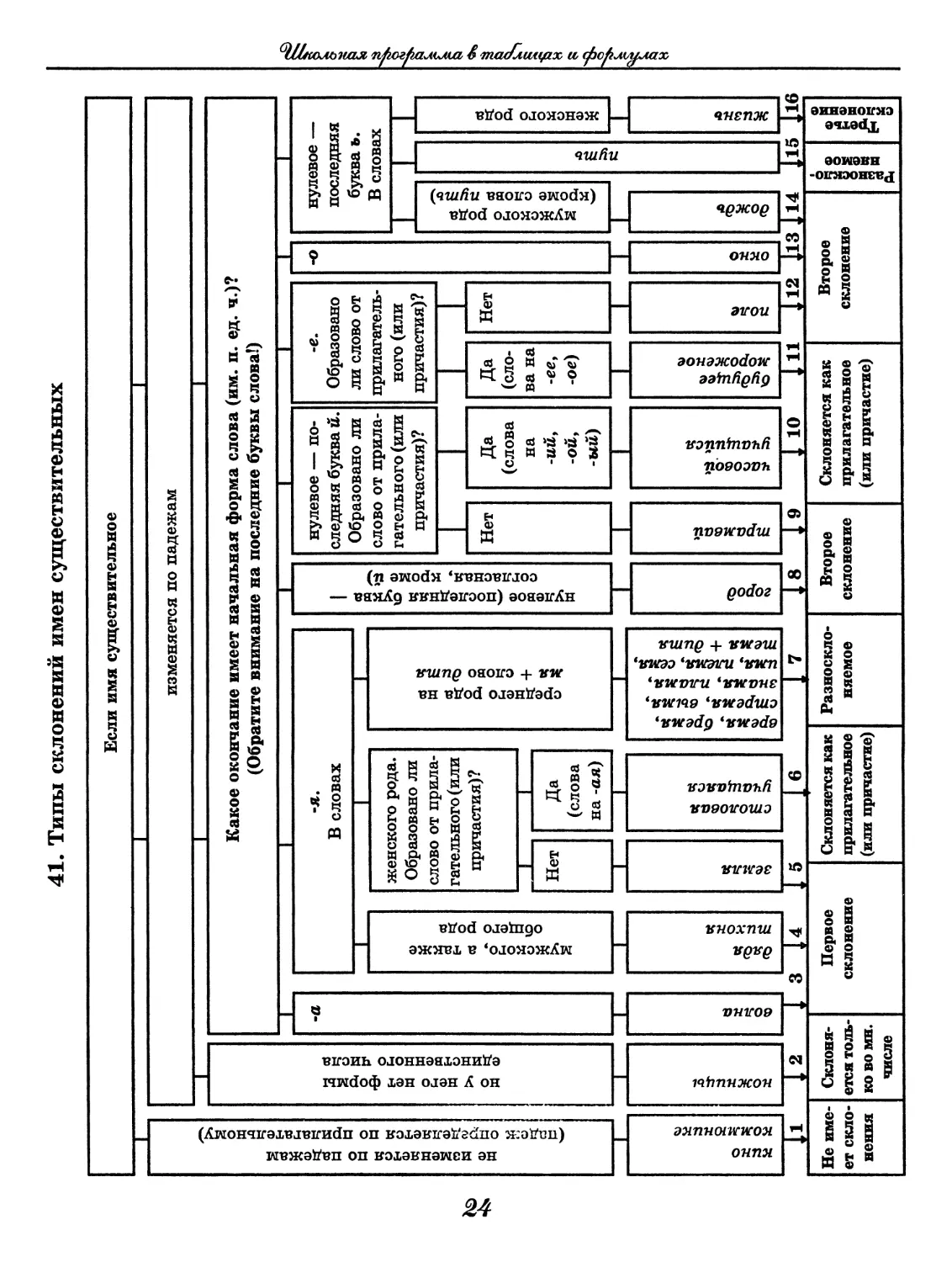
41. Типы склонений имен существительных
42. Разряды имен прилагательных
Такой признак предмета, который
1
выражает его качество и воспринимается сам по себе, независимо от других предметов (основа такого прилагательного, как правило, непроизводная) выражает отношение одного предмета или явления к другому предмету или явлению (основа всегда производная)
1 1 1
одушевленному (лицу или животному) неодушевленному
новый, нов, новее тихий, тих, самый тихий разумный, разумен, разумнейший
отцов (пиджак) заячий (мех) серебряная (чаша) городской (парк) книжный (магазин)
1 2 3
КАЧЕСТВЕННОЕ ПРИТЯЖАТЕЛЬНОЕ ОТНОСИТЕЛЬНОЕ
могут иметь краткую форму, степени сравнения, синонимы, антонимы; образуют отвлечен- ные существительные не имеют степеней сравнения не имеют кратких форм, степеней сравнения, синонимов, антонимов
43. Типы склонения
имен прилагательных
25
^.Uhomtoui п/mfiaMMa & таблицах и,
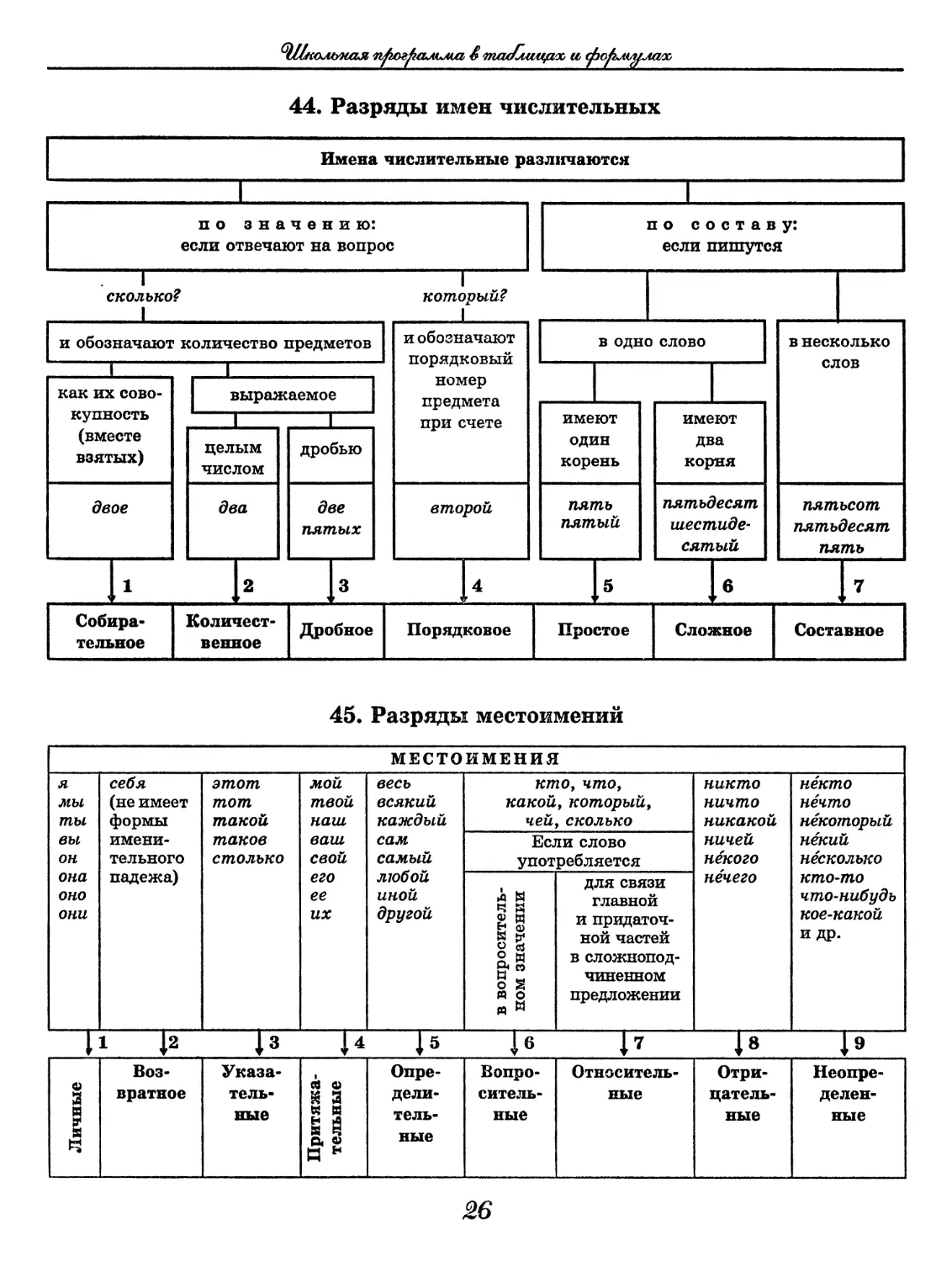
44. Разряды имен числительных
45. Разряды местоимений
МЕСТОИМЕНИЯ
я мы ты вы он она оно они себя (не имеет формы имени- тельного падежа) этот тот такой таков столько мой твой наш ваш свой его ее их весь всякий каждый сам самый любой иной другой кто, что, какой, который, чей, сколько никто ничто никакой ничей некого нечего некто нечто некоторый некий несколько кто-то что-нибудь кое-какой и др.
Если слово употребляется
в вопроситель- ном значении для связи главной и придаточ- ной частей в сложнопод- чиненном предложении
|1 |2 |3 |4 |б |б |7 I8 |9
Личные Воз- вратное Указа- тель- ные Притяжа- тельные Опре- дели- тель- ные Вопро- ситель- ные Относитель- ные Отри- цатель- ные Неопре- делен- ные
26
46. Глагол: возвратный 47. Глагол: совершенного
или невозвратный? или несовершенного вида?
48. Глагол: переходный или непереходный?
27
^Ш^аммал п£юг[гамма & тш/лиирес и формула.
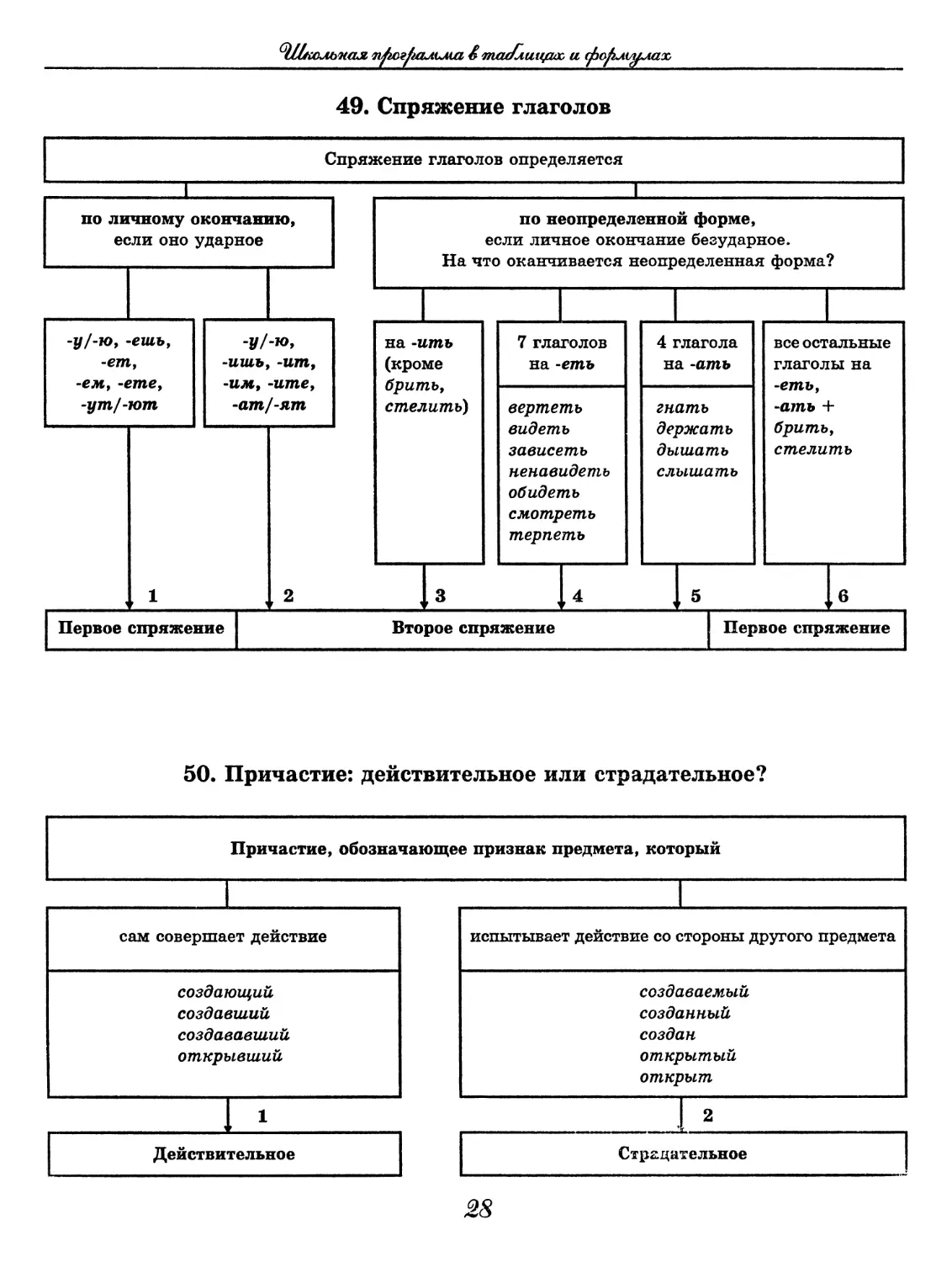
49. Спряжение глаголов
50. Причастие: действительное или страдательное?
28
Нисский ягык & тм</ли,и/1х,
ЗНАМЕНАТЕЛЬНЫЕ ЧАСТИ РЕЧИ: ПЕРЕМЕННЫЕ ПРИЗНАКИ
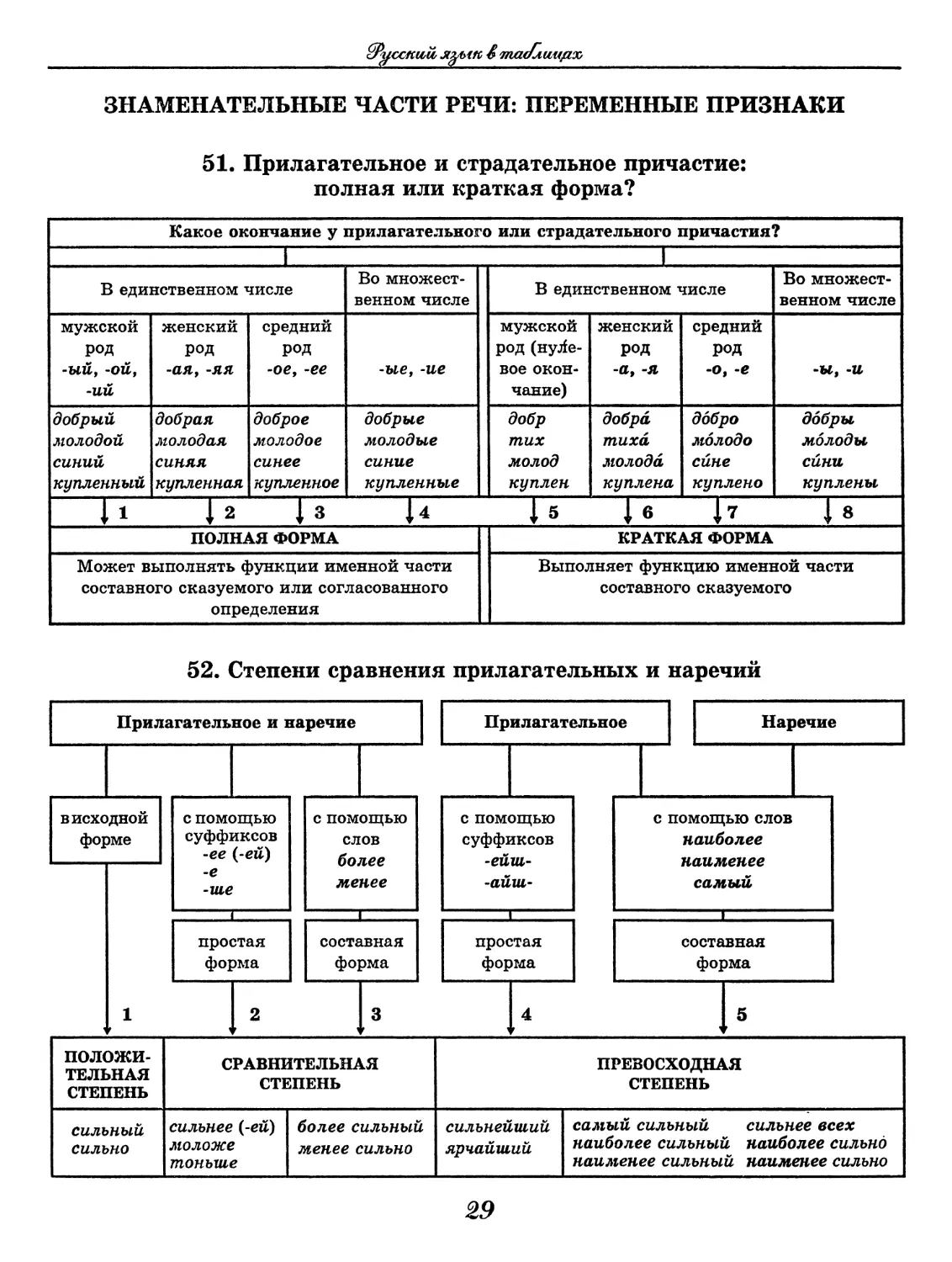
51. Прилагательное и страдательное причастие:
полная или краткая форма?
Какое окончание у прилагательного или страдательного причастия?
I 1
В единственном числе Во множест- венном числе В единственном числе Во множест- венном числе
мужской род -ый, -ой, -ий женский РОД -ИЯ, -ЯЯ средний род -ое, -ее -ые, -ие мужской род (нуле- вое окон- чание) женский род -а, -я средний род -о, -е ~ы, -и
добрый молодой синий купленный добрая молодая синяя купленная доброе молодое синее купленное добрые молодые синие купленные добр тих молод куплен добра тиха молода куплена добро молодо сйне куплено добры молоды сйни куплены
ьо 00 (к СИ ф 00
ПОЛНАЯ ФОРМА КРАТКАЯ ФОРМА
Может выполнять функции именной части составного сказуемого или согласованного определения Выполняет функцию именной части составного сказуемого
52. Степени сравнения прилагательных и наречий
29
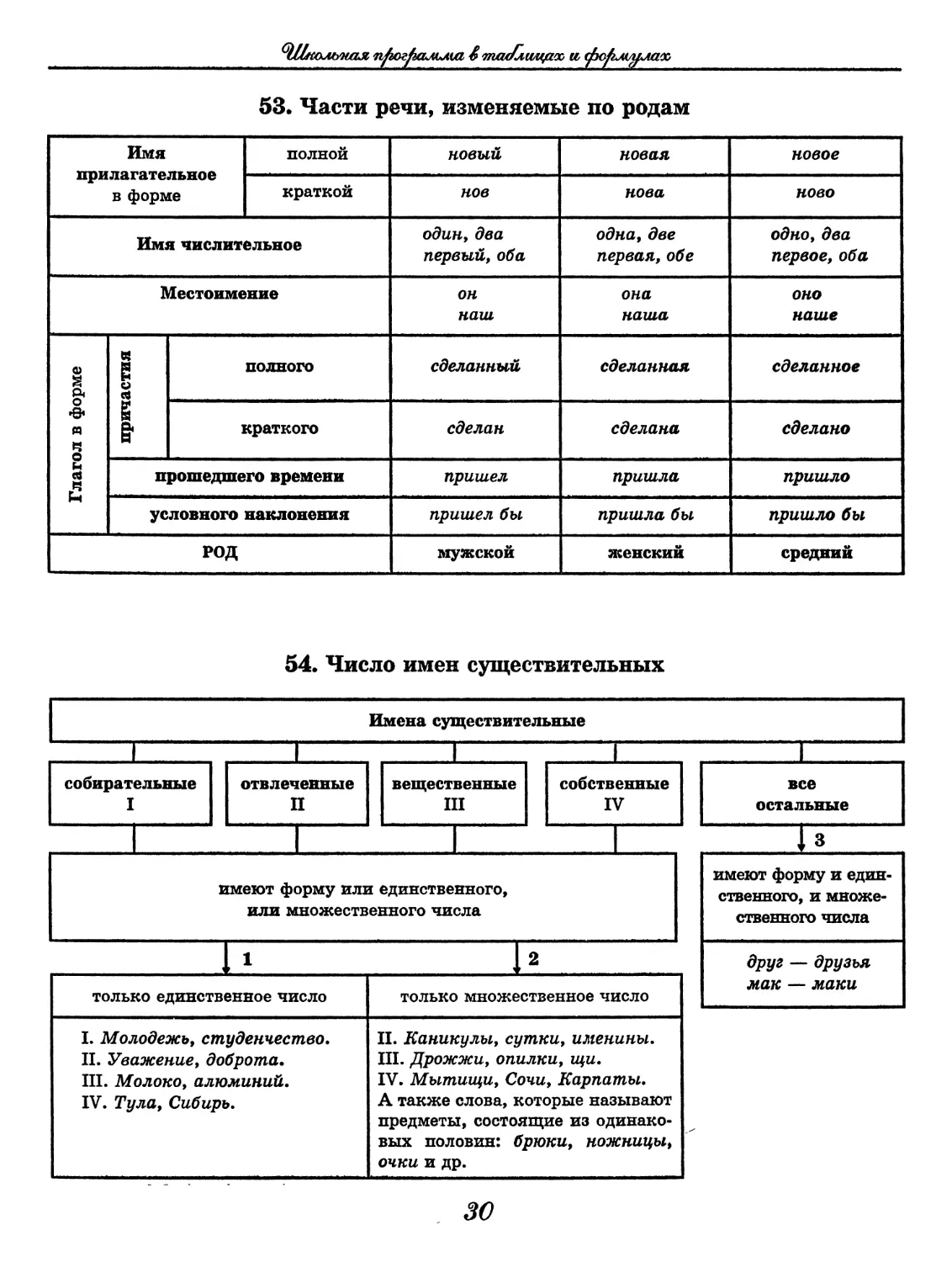
53. Части речи, изменяемые по родам
Имя прилагательное в форме полной новый новая новое
краткой нов нова ново
Имя числительное один, два первый, оба одна, две первая, обе одно, два первое, оба
Местоимение он наш она наша ОНО наше
Глагол в форме причастия полного сделанный сделанная сделанное
краткого сделан сделана сделано
прошедшего времени пришел пришла пришло
условного наклонения пришел бы пришла бы пришло бы
РОД мужской женский
54. Число имен существительных
30
55. Падеж имен существительных
56. Наклонение глаголов
Если глагол обозначает действие,
которое (не) происходит, (не) происходило или (не) будет происходить в действительности к совершению которого говоря- щий побуждает кого-либо (советует, просит, приказывает) которое (не) возможно при каких-либо условиях
(не) помогаю (не) помог (не) помогал (не) буду помогать (не) помогу (не) помогай (не) рисуй (не) смейся (нё) помогал бы (не) рисовал бы (не) смеялся бы
1 ..2 .. 3
ИЗЪЯВИТЕЛЬНОЕ ПОВЕЛИТЕЛЬНОЕ СОСЛАГАТЕЛЬНОЕ (УСЛОВНОЕ)
НАКЛОНЕНИЕ
31
^Шкальная программа & таЛлиарж « формулах,
57. Время глаголов
58. Лицо глаголов
(в форме настоящего и будущего времени)
Если глагол обозначает действие, относящееся к лицу
говорящему: к которому обращаются: которое отсутствует:
я мы ты вы он она ОНО они
читаю смотрю буду читать прочту читаем смотрим будем читать прочтем читаешь смотришь будешь читать прочтешь читаете смотрите будете читать прочтете читает смотрит будет читать прочтет читают смотрят будут читать прочтут
ед. число мн. число ед. число мн. число ед. число мн. число
1 2 3 4 5 6
ПЕРВОЕ ЛИЦО ВТОРОЕ ЛИЦО ТРЕТЬЕ ЛИЦО
32
Нисским я^ык & тш/лиирк
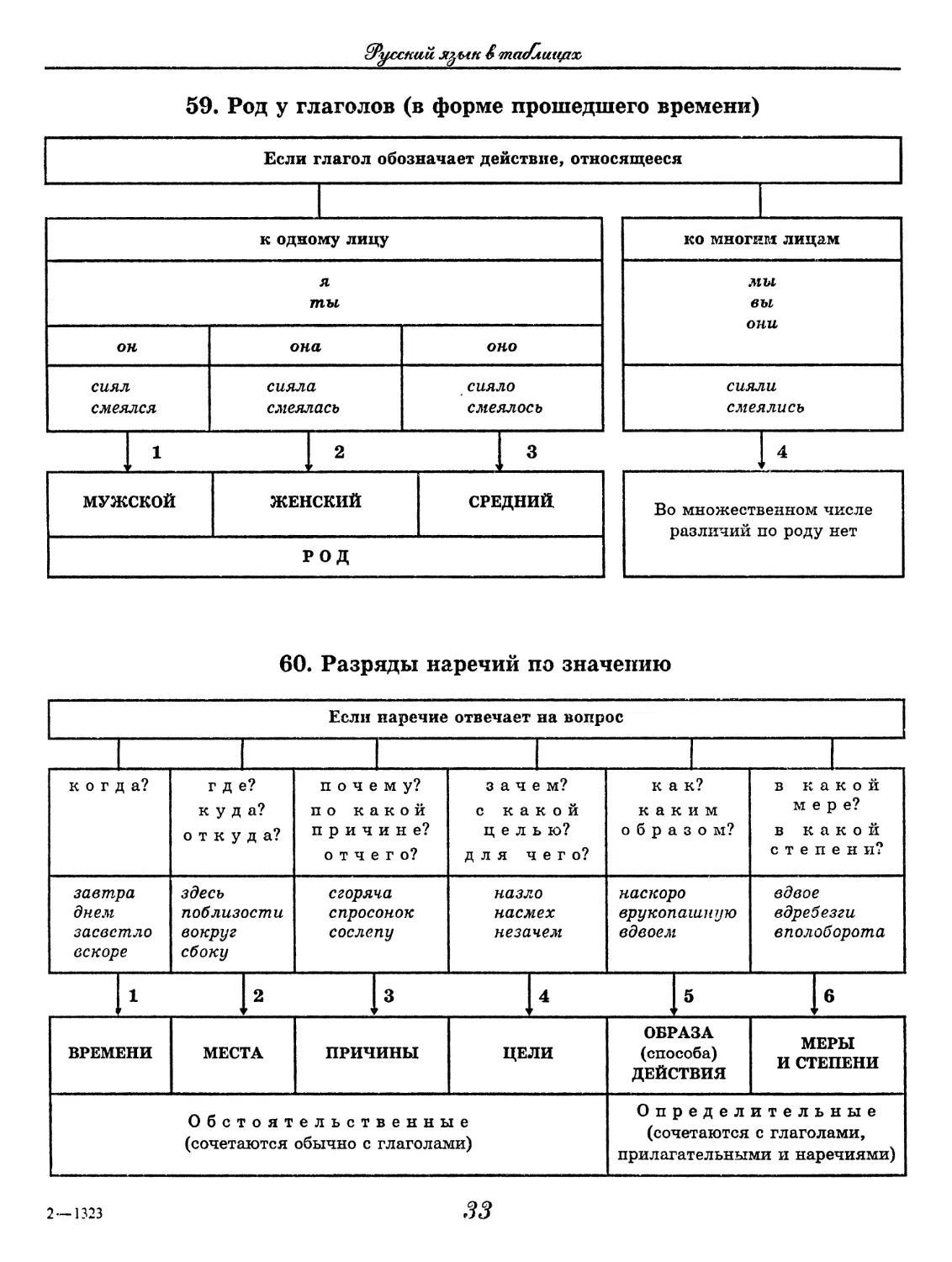
59. Род у глаголов (в форме прошедшего времени)
Если глагол обозначает действие, относящееся
к одному лицу ко многим лицам
я ты мы вы они
он она ОНО
сиял смеялся сияла смеялась сияло смеялось сияли смеялись
12 3 , 4
МУЖСКОЙ ЖЕНСКИЙ СРЕДНИЙ Во множественном числе различий по роду нет
РОД
60. Разряды наречий по значению
Если наречие отвечает на вопрос
когда? где? куда? откуда? почему? по какой причине? отчего? зачем? с какой целью? для чего? как? каким образом? в какой мере? в какой степени?
завтра днем засветло вскоре здесь поблизости вокруг сбоку сгоряча спросонок сослепу назло насмех незачем наскоро врукопашную вдвоем вдвое вдребезги вполоборота
1 2 3 4 5 ,,6
ВРЕМЕНИ МЕСТА ПРИЧИНЫ ЦЕЛИ ОБРАЗА (способа) ДЕЙСТВИЯ МЕРЫ И СТЕПЕНИ
Обстоятельственные (сочетаются обычно с глаголами) Определительные (сочетаются с глаголами, прилагательными и наречиями)
2 — 1323
33
бЩкшыиья п^пг/м.мма & таблицах и, фофмула/ъ
61. Схема морфологического
анализа имен существительных
62. Схема морфологического
анализа имен прилагательных
1. Начальная форма именительный падеж единственное число
2. Разряд по значению конкретное собирательное вещественное отвлеченное
3. Одушевленное — неодушевленное
4. Собственное — нарицательное
5. Род
6. Тип склонения
7. Число
8. Падеж
9. Синтаксиче- ская функция каким членом предложения является
10. Особенности правописания (если есть)
1. Начальная форма (определяется по форме слова, с которым приведено в предложении)
2. Разряд по значению качественное относительное притяжательное
3. Тип склонения твердый мягкий смешанный
4. Род
5. Число
6. Падеж
Для качественных прилагательных*
а) форма полная краткая
б) степени сравне- ния сравнительная превосходная
7. Синтаксиче- ская функция каким членом пред- ложения является
8. Особенности правописания (если есть)
63. Схема морфологического
анализа глаголов
64. Схема морфологического
анализа причастий
1. Начальная форма (инфинитив)
2. Возвратный — невозвратный
3. Переходный — непереходный
4. Вид совершенный несовершенный
5. Спряжение первое второе разноспрягаемый глагол
6. Наклонение изъявительное повелительное сослагательное
7. Время настоящее будущее прошедшее
8. Лицо и число 1 и будущего време Род и число (для с для формы настоящего ши) )ормы прошедшего времени)
9. Синтаксиче- ская функция каким членом предложе- ния является
' 10. Особенности правописания (если есть)
1. Начальная форма (определяется по слову, к которому относится в предложении)
2. От какого глагола образовано (указывается в инфинитиве)
3. Действительное — страдательное
4. Возвратное — невозвратное (для действи- тельных причастий)
5. Время настоящее прошедшее
6. Вид совершенный несовершенный
7. Число
8. Падеж
9. Синтаксическая функция каким членом предло- жения является
10. Особенности правописания (если есть)
34
^Русским, я%ык 6 mjgt£utMfla>
65. Схема морфологического
анализа деепричастий
66. Схема морфологического
анализа наречий
1. От какого глагола образовано (глагол указывается в инфинитиве)
2. Возвратное — невозвратное
3. Вид совершенный несовершенный
4. Синтаксическая функция каким членом пред- ложения является
5. Особенности правописания (если есть)
1. Разряд по значению образа действия меры и степени места времени причины цели
2. Синтаксическая каким членом пред-
функция ложения является
3. Особенности правописания (если есть)
67. Схема морфологического
анализа местоимений
68. Схема морфологического
анализа имен числительных
1. Начальная форма
2. Разряд по значению личное притяжательное указательное возвратное вопросительное относительное отрицательное неопределенное определительное
3. Род (если есть)
4. Лицо, число (если есть)
5. Одушевленное — (если есть) неодушевленное
6. Падеж
7. Синтаксиче- ская функция каким членом предло- жения является
8. Особенности правописания (если есть)
1. Начальная форма
2. Разряд по значению количественное собирательное дробное порядковое
3. Разряд по строению простое сложное составное
4. Род (если есть)
5. Число (если есть)
6. Падеж
7. Синтаксическая функция каким членом пред- ложения является
8. Особенности правописания (если есть)
35
^Школьная программа 4 тщ/лаарх, а фсрлиулах,
СЛУЖЕБНЫЕ ЧАСТИ РЕЧИ
69. Характеристика предлогов
70. Характеристика союзов
36
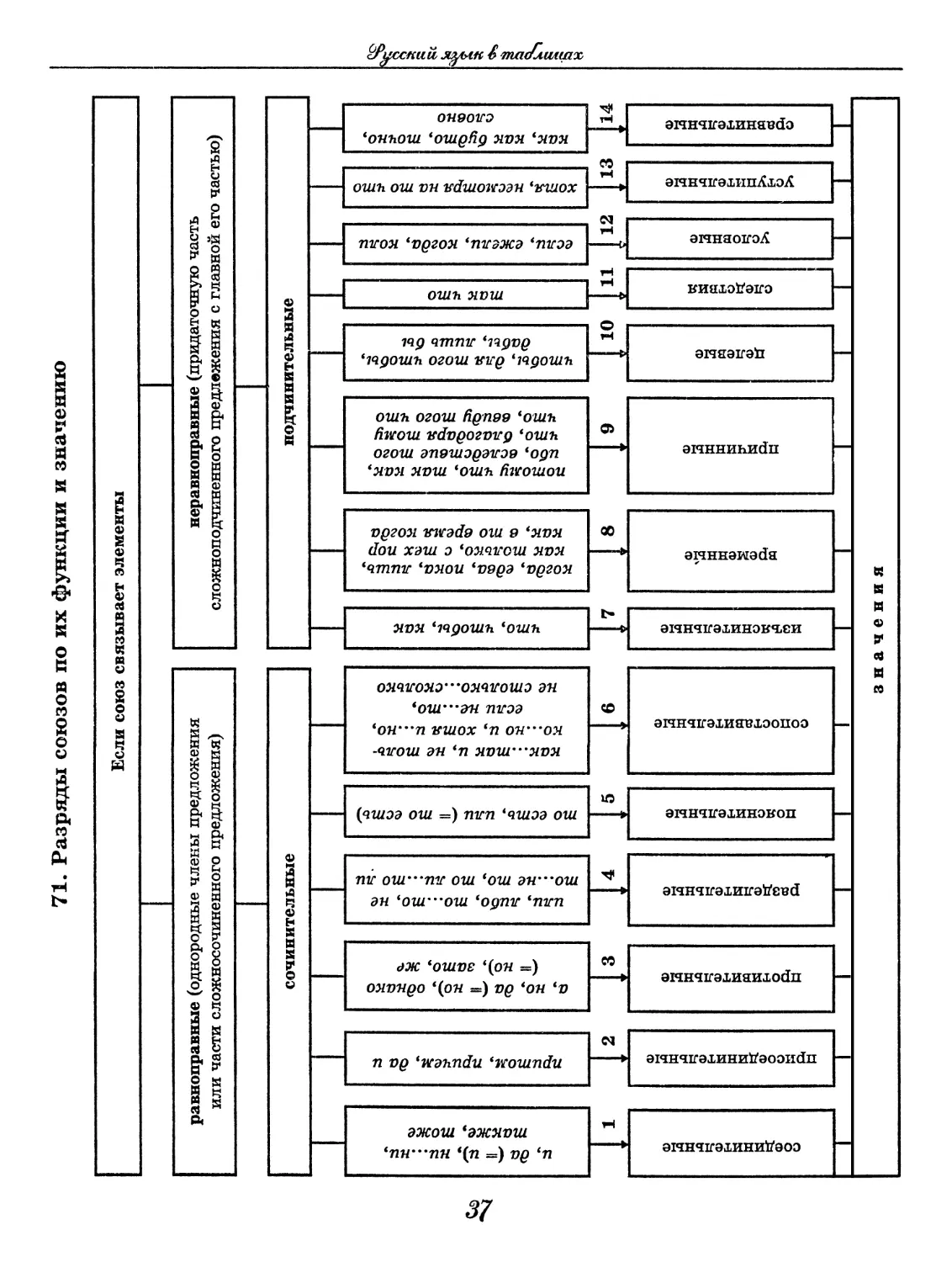
71. Разряды союзов по их функции и значению
8S
Указательные 5 ft ft со ft ft § § ° 3 ° ° х з § 3 g 3 я тС Мм «5 - Частицы (по значению, функции и эмоциональной окраске) 72. Разряды частиц
м
Уточняющие именно, как раз, ровно, точно, в точно- сти
to
Выделительно- ограничительные к ’ И | о ’ о 8 О ,с - з 1
со
Утвердительные 3 3 3 3 §> о е о е ” i Ч * £ ° м° Р
Отрицательные не, нет, вовсе не, отнюдь не, совсем не, далеко не
СЛ
Вопросительные разве, неужели, ли (ль)
Ф
Восклицательные как, что за
М
Усилительные g ’ И R ? ’ 9 • ? • ’ * ’op” <r r - «>
00
Модально- волевые 2 S <> • 5 R< 1 R< - з - - G*
со
Выражающие сомнение O S2 ^2 Й S>^3 g2 a § § » S • §>« Ш 8 § « 9 | h ? ° - R R
О
Обозначающие чужую речь de, дес- кать, мол
м м
Формообра- зующие , a ?: о» o\ o\ h 2 r< <? * ’ 8 - 3 * ft G*
to
Словообра- зующие p,°o‘Ser3o * 2 Q) V R о ft Q) <T 1 м j
й яъын £та/ми!/№
73. Междометия
и звукоподражательные слова
74. Схема морфологического анализа союзов 75. Схема морфологического анализа предлогов
1. Разряд по функции сочинительный подчинительный 1. Разряд по происхож- дению производный непроизводный
2. Разряд по значению 1) для сочинительных: соединительный противительный пояснительный разделительный и др. 2) для подчинительных: изъяснительный временной причинный уступительный целевой условный сравнительный следственный и др.
2. От какой части речи образован (для производных предлогов)
3. Разряд по структуре простой сложный составной
4. С каким падежом употребляется (или может употребляться)
3. Разряд по структуре простой составной
5. Особенности правописания (если есть)
4. Особенности правописания (если есть)
76. Схема морфологического анализа частиц 77. Схема морфологического анализа междометии
1. Разряд по значению усилительная отрицательная выделительно- восклицательная ограничительная указательная вопросительная и др. 1. Разряд по значению побудительное эмоциональное и др.
2. Особенности правописания (если есть)
2. Особенности правописания (если есть)
39
^Окольная &matEitiiiflx, и фо^и.'ула'х,
СИНТАКСИС
ПРОСТОЕ ПРЕДЛОЖЕНИЕ
78. На какие вопросы
отвечают члены предложения?
40
gPyccfuiit л^ы/с £пим/лиирос
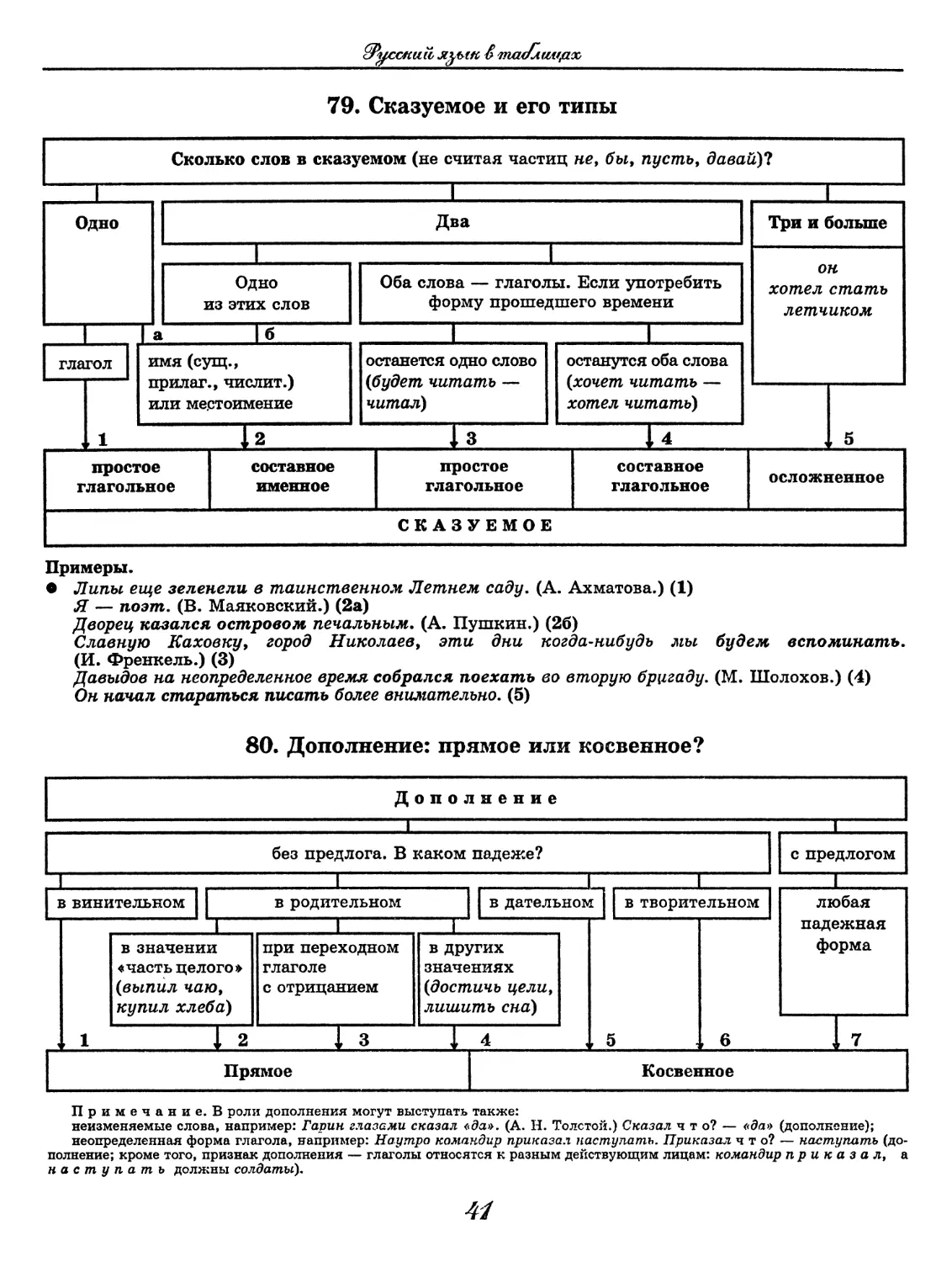
79. Сказуемое и его типы
Примеры.
• Липы еще зеленели в таинственном Летнем саду. (А. Ахматова.) (1)
Я — поэт. (В. Маяковский.) (2а)
Дворец казался островом печальным. (А. Пушкин.) (26)
Славную Каховку, город Николаев, эти дни когда-нибудь мы будем вспоминать.
(И. Френкель.) (3)
Давыдов на неопределенное время собрался поехать во вторую бригаду. (М. Шолохов.) (4)
Он начал стараться писать более внимательно. (5)
80. Дополнение: прямое или косвенное?
Примечание. В роли дополнения могут выступать также:
неизменяемые слова, например: Гарин глазами сказал «да». (А. Н. Толстой.) Сказал что? — «да» (дополнение);
неопределенная форма глагола, например: Наутро командир приказал наступать. Приказал что? — наступать (до-
полнение; кроме того, признак дополнения — глаголы относятся к разным действующим лицам: командир приказал, а
наступать должны солдаты).
4/
бЩлюмная пфоефшлилш & уъас/лкллдой и фофълуулах
Примеры.
• Моя искренность поразила Пугачева. (А. Пушкин.) (1)
— Дед! — позвал он. — Дай воды. (А. Чехов.) (2)
Я не люблю иронии твоей. (Н. Некрасов.) (3)
Больной лишился сна. (4)
Я никому не позволю себя обманывать. (5)
Олово плавим, машинами правим. (В. Маяковский.) (6)
...Уже воображал, как он будет всюду рассказывать об этом своем каламбуре, удачном по
находчивости и смелости. (А. Чехов.) (7)
81. Подлежащее и способы его выражения
Примеры.
• За заставами ленинградскими вновь бушует соловьиная весна. (А. Фатьянов.) (1а)
А самый дерзкий и молодой смотрел на солнце над водой. (Н. Тихонов.) (16)
И опять идут двенадцать... (А. Блок.) (1в)
Она вмешивалась во все, знала все, хлопотала обо всем. (А. Пушкин.) (1г)
Опоздавшие на спектакль не допускаются. (1д)
Грамоте учиться всегда пригодится. (Пословица.) (2)
...Далече грянуло ура... (А. Пушкин.) (3)
Не шутя, Василий Теркин, подружились мы с тобой. (А. Твардовский.) (4)
После этого вечера прошло семь недель. (А. Н. Толстой.) (5)
Пришло несколько новых журналов. (6)
Трое из них приехали недавно; Кто из нас не знает этого? Всякий из нас (каждый из нас,
любой из нас) готов помочь. (7)
«Не стреляйте в белых лебедей» — повесть Бориса Васильева. (8)
42
82. Виды определений
Примеры.
• Переменилась моя родная Сибирь. (В. Астафьев.) (1)
Он родился в городе Воронеже. (2)
Вам нужно доехать до платформы «Жаворонки». (3)
Несколько раз перечел я записку Аси. (И. Тургенев.) (4)
Сильна была в нем привычка спорить; Выстрел слева его насторожил. (5)
83. Распространенное определение
Примеры.
О След, оттиснутый на снегу моей ногой, быстро темнел и наливался водой. (А. Куприн.) (1)
И Россия — мать родная — почесть всем отдаст сполна. (А. Твардовский.) (2)
Очень похожий лицом на мать, характером он был весь в отца. (3)
Старик нащупал возле себя длинную палку с крючком на верхнем конце и поднялся.
(А. Чехов.) (4)
Никто не допускал и мысли покинуть отряд в трудную минуту. (5)
43
QlbtoM'xwi& таЛмшрх и
84. Виды обстоятельств
Примеры.
• Читай не так, как пономарь, а с чувством, с толком, с расстановкой. (А. Грибоедов.) (1)
Его сопровождал молчаливый, не по годам серьезный Яков Сомов. (М. Горький.) (2)
Дня через три потеплело. (А. Куприн.) (3)
Я ночевал в городке у моря. (4)
Сенокос запоздал из-за дождей. (К. Паустовский.) (5)
Пришел мириться к вам, совсем не ради ссоры.
(И. Крылов.) (6)
При каждой неудаче надо анализировать свои ошибки; Несмотря на плохую погоду, экс-
курсия состоялась. (7)
85. Распространенное
обстоятельство
86. Слова, не являющиеся
членами предложения
Примеры.
О Поджав губы, помощник коменданта про-
молчал.
(В. Богомолов.) (1)
Он наводил на нее взгляд, как зажигатель-
ное стекло, и не мог отвести. (И. Гонча-
ров.) (2)
Жди меня, и я вернусь всем смертям на-
зло. (К. Симонов.) (3)
Бой идет святой и правый, смертный бой
не ради славы, ради жизни на земле.
(А. Твардовский.) (4)
Примеры.
• Ах, злые языки страшнее пистолета!
(А. Грибоедов.) (1)
Так разрешите же в честь новогоднего бала
руку на танец, сударыня, вам предложить!
(Ю. Л ев иранский.) (2)
На Алексея все это, видимо, не действова-
ло. (М. Горький.); Гимназия — все ее три
этажа — была насыщена запахом замазки.
(В. Катаев.) (3)
Да у вас дело совсем уже слажено.
(А. Пушкин.) (4)
В тесноте, да не в обиде. (Пословица.) (5)
44
^Русский jqw/c Р пии/лицах
87. Связь между словами в предложении:
независимые и зависимые члены предложения
88. Виды связи между словами в словосочетании
Примеры.
• Это было бледное крошенное создание, напоминавшее цветок, выросший без лучей солнца.
(В. Короленко.) (1а)
Рядом помещалась каморка — хранилище каталогов. (Д. Гранин.) (16)
А враги-дурни думают, что мы смерти боимся. (А. Фадеев.) (2а)
При сторожке находилась огромная черная собака неизвестной породы... (А. Чехов.) (26)
Пехотные полки, застигнутые врасплох, выбегали из леса, и, смешиваясь друг с другом, роты
уходили вразбивку беспорядочными толпами. (Л. Толстой.) (3)
45
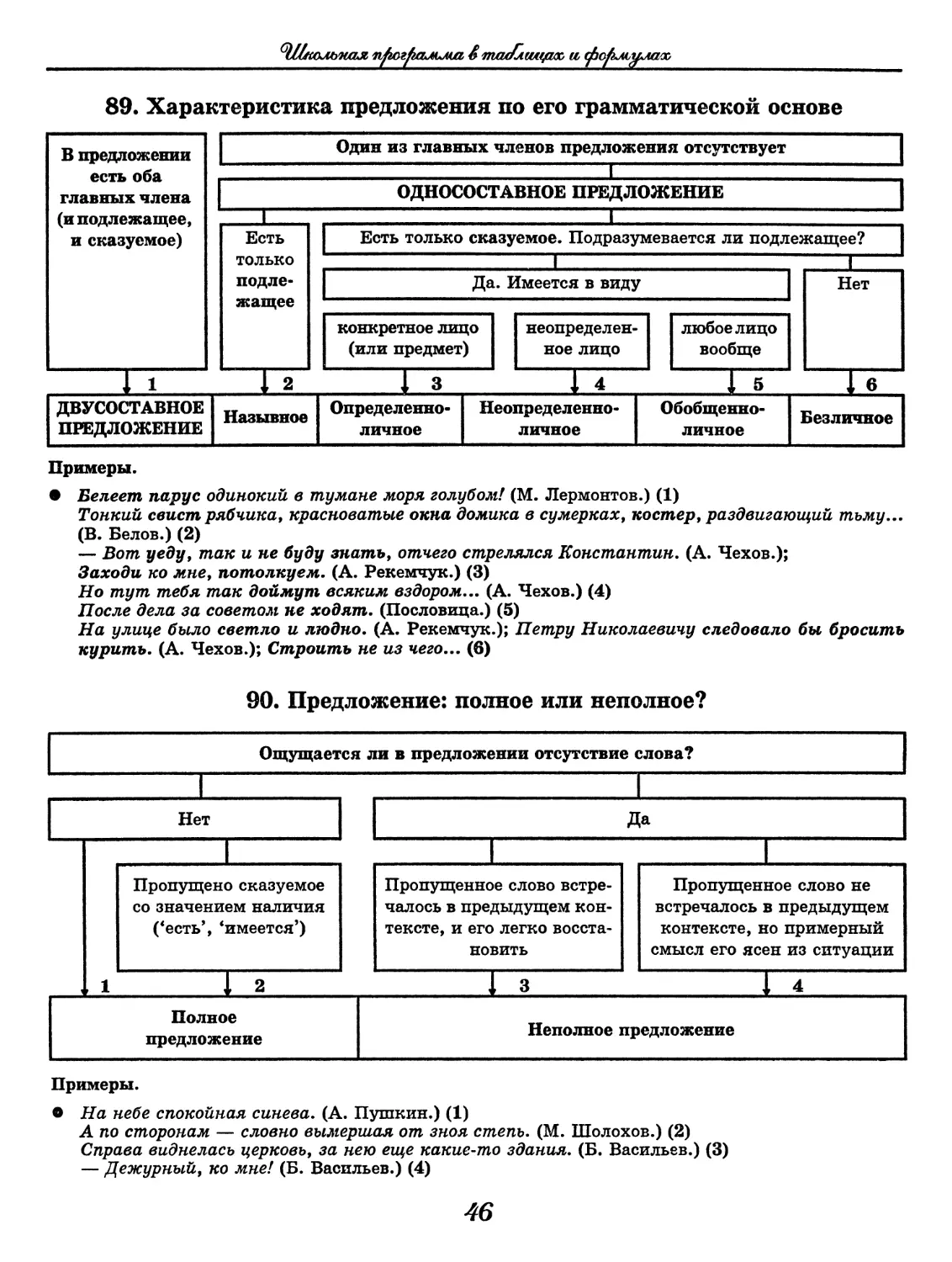
89. Характеристика предложения по его грамматической основе
Примеры.
• Белеет парус одинокий в тумане моря голубом! (М. Лермонтов.) (1)
Тонкий свист рябчика, красноватые окна домика в сумерках, костер, раздвигающий тьму...
(В. Белов.) (2)
— Вот уеду, так и не буду знать, отчего стрелялся Константин. (А. Чехов.);
Заходи ко мне, потолкуем. (А. Рекемчук.) (3)
Но тут тебя так доймут всяким вздором... (А. Чехов.) (4)
После дела за советом не ходят. (Пословица.) (5)
На улице было светло и людно. (А. Рекемчук.); Петру Николаевичу следовало бы бросить
курить. (А. Чехов.); Строить не из чего... (6)
90. Предложение: полное или неполное?
Примеры.
О На небе спокойная синева. (А. Пушкин.) (1)
А по сторонам — словно вымершая от зноя степь. (М. Шолохов.) (2)
Справа виднелась церковь, за нею еще какие-то здания. (Б. Васильев.) (3)
— Дежурный, ко мне! (Б. Васильев.) (4)
46
oT'^catau
& тсииимрх
91. Предложение: распространенное или нераспространенное?
Примеры.
• Поздняя осень. (Н. Некрасов.); Кто-то тронул Боброва сзади за плечо. (А. Куприн.) (1)
Вьюга злится, вьюга плачет. (А. Пушкин.) (2)
92. Распространение и осложнение простого предложения
Примеры.
® Дремлет чуткий камыш. (И. Никитин.) (1)
Права не дают, права берут. (М. Горький.) (2)
В одну скверную осеннюю ночь Андрей Степанович Пересолин ехал из театра. (А. Чехов.);
Из Москвы я выехал последним пароходом. (К. Паустовский.); Кустарник скоро кончился. (3)
Швед, русский — колет, рубит, режет... (А. Пушкин.) (4а)
Постепенно к плеску, стуку, шороху, бульканью, ко всем легкомысленным звукам воды при-
соединились тяжелый гул людских голосов и гортанные выкрики. (К. Паустовский.) (46)
А в лесу, казалось, шел говор тысячи могучих, хотя и глухих голосов, о чем-то грозно пере-
кликавшихся во мраке. (В. Короленко.) (5а)
Потом Леля перевязывала меня, то плача от испуга и стыда, то тут же смеясь сквозь сле-
зы над своей глупостью и моим жалким видом. (К. Паустовский.) (56)
Молодой, нежный месяц, будто забытый жницей серебряный серп, лежал на синем пологе
ночи. (К. Паустовский.) (5в)
— Эге, красавица, у тебя остры зубы! (М. Горький.) (6а, 6)
Тут Дубровский закрыл лицо руками*, он, казалось, задыхался. (А. Пушкин.); ...Они, то есть
секунданты, должно быть, несколько переменили свой прежний план и хотят зарядить пу-
лею один пистолет Грушницкого. (М. Лермонтов.) (5в, 6в)
Да, были люди в наше время! (М. Лермонтов.); Нет, никогда я зависти не знал. (А. Пушкин.)
(6г)
47
^Русский &тд/лии/1х,
93. Структурная схема простого предложения
П
Ш
IV
— связка
— дополнение
— управление
— координация
между
главными
членами
(об^ — обращение
— согласование
---примыкание
— междометие
слова
и предложения
— слова-предло-
жения
Да; Нет
— распространение предложения второстепенными членами
— осложнение предложения однородными членами
— осложнение предложения словами, не являющимися членами предложения
94. Характеристика предложения по отношению к действительности,
по цели высказывания и эмоциональной окраске
Примеры.
© Майскими короткими ночами, отгремев, закончились бои... (А. Фатьянов.) (1а)
Не жалею, не зову, не плачу... (С. Есенин.) (16)
Истоки способностей и дарований детей на кончике пальцев. (В. Сухомлинский.) (2а)
Где начало того конца, которым оканчивается начало? (К. Прутков.) (26)
Родная Земля! Назови мне такую обитель! (Н. Некрасов.) (2в)
Поэзия! Ты служба крови! (И. Сельвинский.) (За)
К обеду приехал лекарь. (А. Чехов.) (36)
48
шхм&ная п[го?пал<.л<а о та&лгщах и (рс>
СЛОЖНОЕ ПРЕДЛОЖЕНИЕ
95. О построении схемы сложного предложения
Для уяснения структуры сложного предложения и взаимоотношений между его частями
нужно уметь построить его схему.
Способы построения такой схемы могут быть различны.
1. Наиболее традиционна структурная схема сложного предложения. Ее элементы можно
обозначить следующим образом:
।----1 — простое предложение, входящее в состав сложного
<1 |> — вводное предложение
— простое предложение, осложненное вводным
С=3:<1 1> — простое предложение с прямой речью
1—Н 1 — бессоюзная связь между частями сложного предложения
— сочинительная связь (между равноправными частями предложения)
— подчинительная связь (между главной и придаточной — неравноправными
частями предложения)
— сопоставительная связь (между взаимообусловленными частями предло-
жения)
Подобную обобщенную схему можно детализировать, вводя в нее дополнительные элемен-
ты, например:
а) в схему сложносочиненного предложения — обозначение сочинительных союзов, одиноч-
ных, повторяющихся и двойных:
или
или [
нс только [
ио и
б) в схему сложноподчиненного предложения — обозначение вопроса к придаточной части,
подчинительного союза или союзного слова и типа придаточной части:
какой? I который
о пр.
почему?" jmaK как
| прич.|
49
русский, яуык & тщ/лицах
95. О построении схемы сложного предложения
в) обозначение последовательности частей сложного предложения, например: Когда весна
придет, не знаю. (А. Фатьянов.)
главная часть
LlJ - -► придаточная часть
2. Однако не во всех случаях структурная схема достаточно удобна. Например, она не отра-
жает расположения частей сложноподчиненного предложения, когда придаточная часть нахо-
дится внутри главной.
Более наглядной здесь может стать построчная схема сложного предложения.
Ее элементы:
— прямая линия — синтаксически равноправные части сложного предложения (бессо-
юзного, сложносочиненного), а также главная часть сложноподчиненного предложения.
— волнистая линия — придаточная часть сложноподчиненного предложения.
Располагая последовательно эти элементы в строке, можно построить схему сложного предложе-
ния и обозначить на ней знаки препинания, а также средства связи и взаимоотношения частей пред-
ложения. Например:
Труд человека кормит — лень портит. (Пословица.)
— ——— . (бессоюзное предложение)
Ум хорошо, а два лучше. (Пословица.)
..-. „и., а —(сложносочиненное
предложение)
Когда в товарищах согласья нет, на лад их дело
не пойдет. (И. Крылов.)
Когда
(сложноподчиненное предложение)
в каком случае?
Человеку, который сам ничего не знает, не о чем
и рассказать людям. (Б. Горбатов.)
(сложноподчиненное предложение с придаточной частью внутри
главной;
П-образная линия соединяет начало и конец главной части; дуга соеди-
няет придаточную часть с той частью главного предложения, в которой
находится опорное слово)
Посмотрю я, где ты достанешь черевички,
которые могла бы я надеть на свою ногу. (Н. Гоголь.)
д (сложноподчиненное предложение с двумя придаточными, одно из
которых является главным по отношению к другому придаточному —
< J последовательное подчинение)
50
бЩноммал nfiotfuiMMa & 'пии/лтщх и, фо^ъмулмь
96. Типы и средства связи
между частями сложного предложения
Примеры.
• Принесли к врачу солдата только что из боя, но уже в груди не бьется сердце молодое. (С. Кир-
санов.) (А)
Он [Пушкин] для русского искусства то же, что Ломоносов для русского просвещения вообще.
(И. Гончаров.) (Б)
Ты потише провожай, парень сероглазый, потому что очень жаль расставаться сразу... (М. Иса-
ковский.) (1)
Он не смотрел на часы и не знал, сколько ждал. (А. Ананьев.) (2)
Хочу оттолкнуть ее от себя — она, как кошка, вцепилась в мою одежду... (М. Лермонтов.) (3)
5/
таалаи/гх,
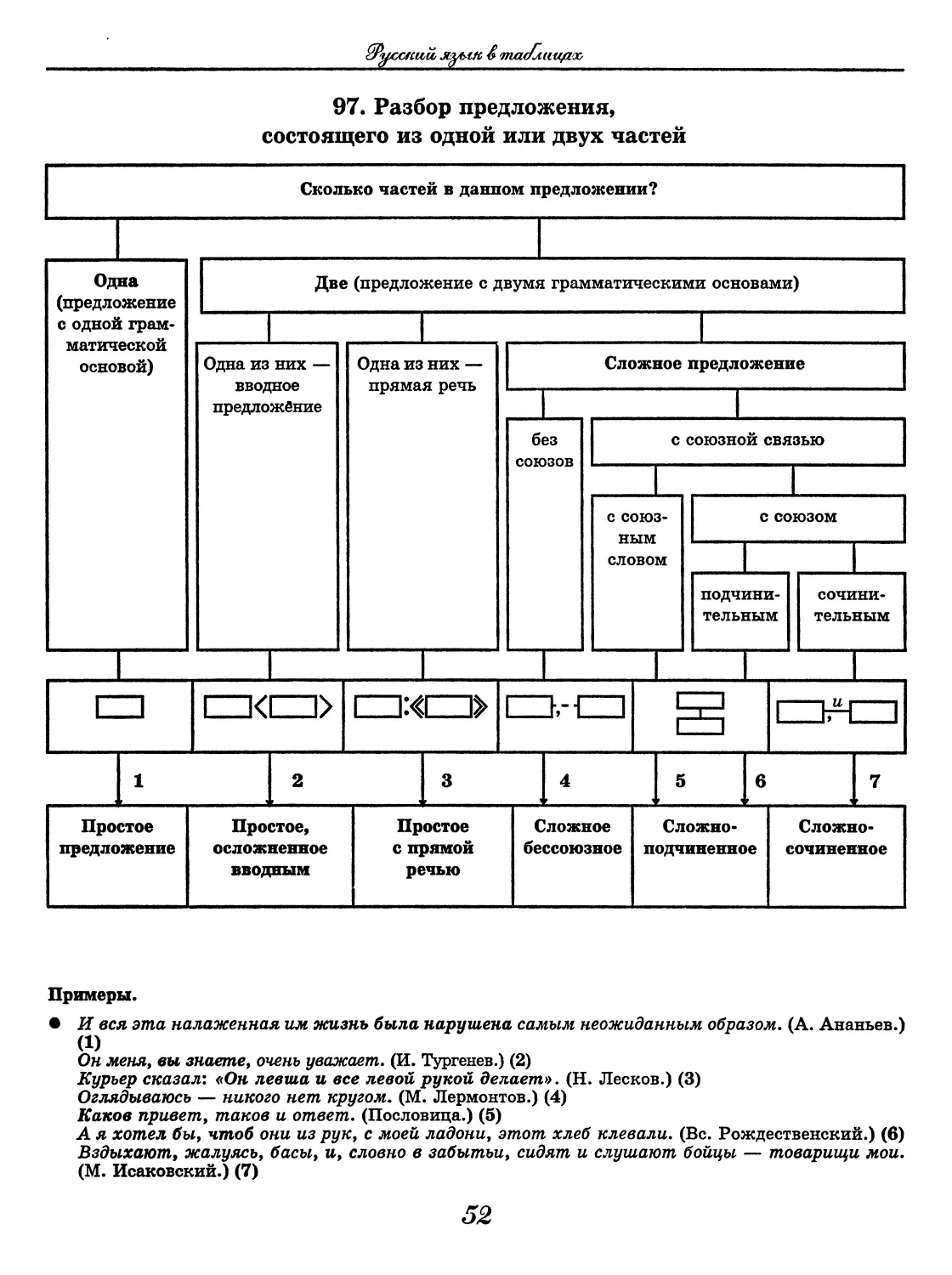
97. Разбор предложения,
состоящего из одной или двух частей
Примеры.
• И вся эта налаженная им жизнь была нарушена самым неожиданным образом. (А. Ананьев.)
(1)
Он меня, вы знаете, очень уважает. (И. Тургенев.) (2)
Курьер сказал: «Он левша и все левой рукой делает». (Н. Лесков.) (3)
Оглядываюсь — никого нет кругом. (М. Лермонтов.) (4)
Каков привет, таков и ответ. (Пословица.) (5)
А я хотел бы, чтоб они из рук, с моей ладони, этот хлеб клевали. (Вс. Рождественский.) (6)
Вздыхают, жалуясь, басы, и, словно в забытьи, сидят и слушают бойцы — товарищи мои.
(М. Исаковский.) (7)
52
tyllftOMMax пф&фсмишъ & тшГмищх ю формулах,
98. Предложение: сложносочиненное или сложноподчиненное?
Примеры.
О Пахнет полынью и мятой, и от соседних болот легкий туман сизоватый низко над степью
плывет. (П. Комаров.) (1)
Не прошло и получаса, как сердце его начало ныть... (А. Пушкин.) (2)
Ему рассказали, в чем дело. (А. Куприн.) (3)
99. Сочинительные союзы — показатели смысловых отношений
между частями сложносочиненного предложения
Примеры.
• Дождик лил сквозь солнце, и под елью мшистой мы стояли точно в клетке золотистой.
(А. Майков.) (1)
В саду горит костер рябины красной, но никого не может он согреть. (С. Есенин.) (2)
То солнце покажется, то снова дождь польет. (3)
53
^Русским, JtfyMtt & тсиРмицаас,
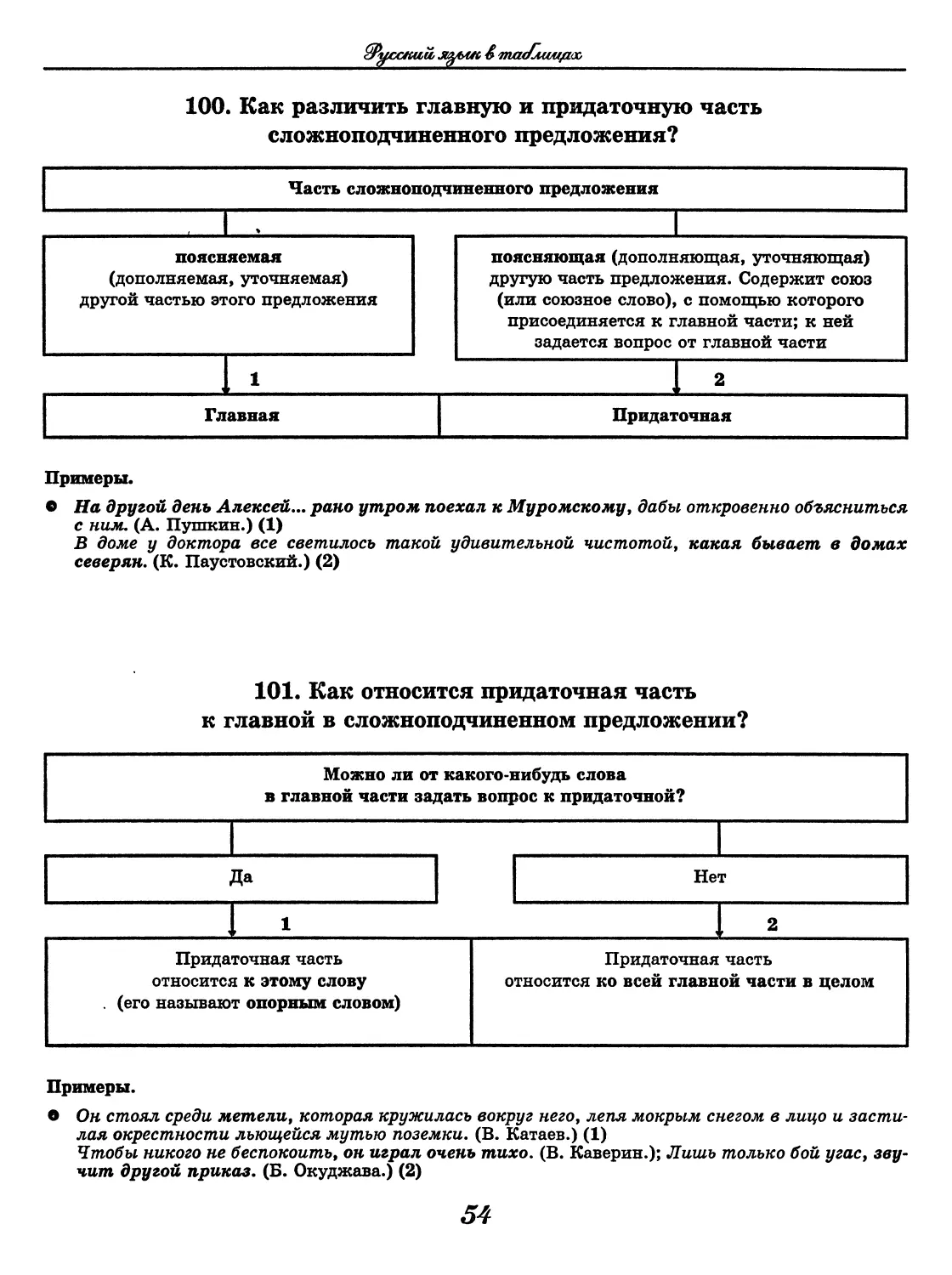
100. Как различить главную и придаточную часть
сложноподчиненного предложения?
Примеры.
О На другой день Алексей... рано утром поехал к Муромскому, дабы откровенно объясниться
с ним. (А. Пушкин.) (1)
В доме у доктора все светилось такой удивительной чистотой, какая бывает в домах
северян. (К. Паустовский.) (2)
101. Как относится придаточная часть
к главной в сложноподчиненном предложении?
Примеры.
• Он стоял среди метели, которая кружилась вокруг него, лепя мокрым снегом в лицо и засти-
лая окрестности льющейся мутью поземки. (В. Катаев.) (1)
Чтобы никого не беспокоить, он играл очень тихо. (В. Каверин.); Лишь только бой угас, зву-
чит другой приказ. (Б. Окуджава.) (2)
54
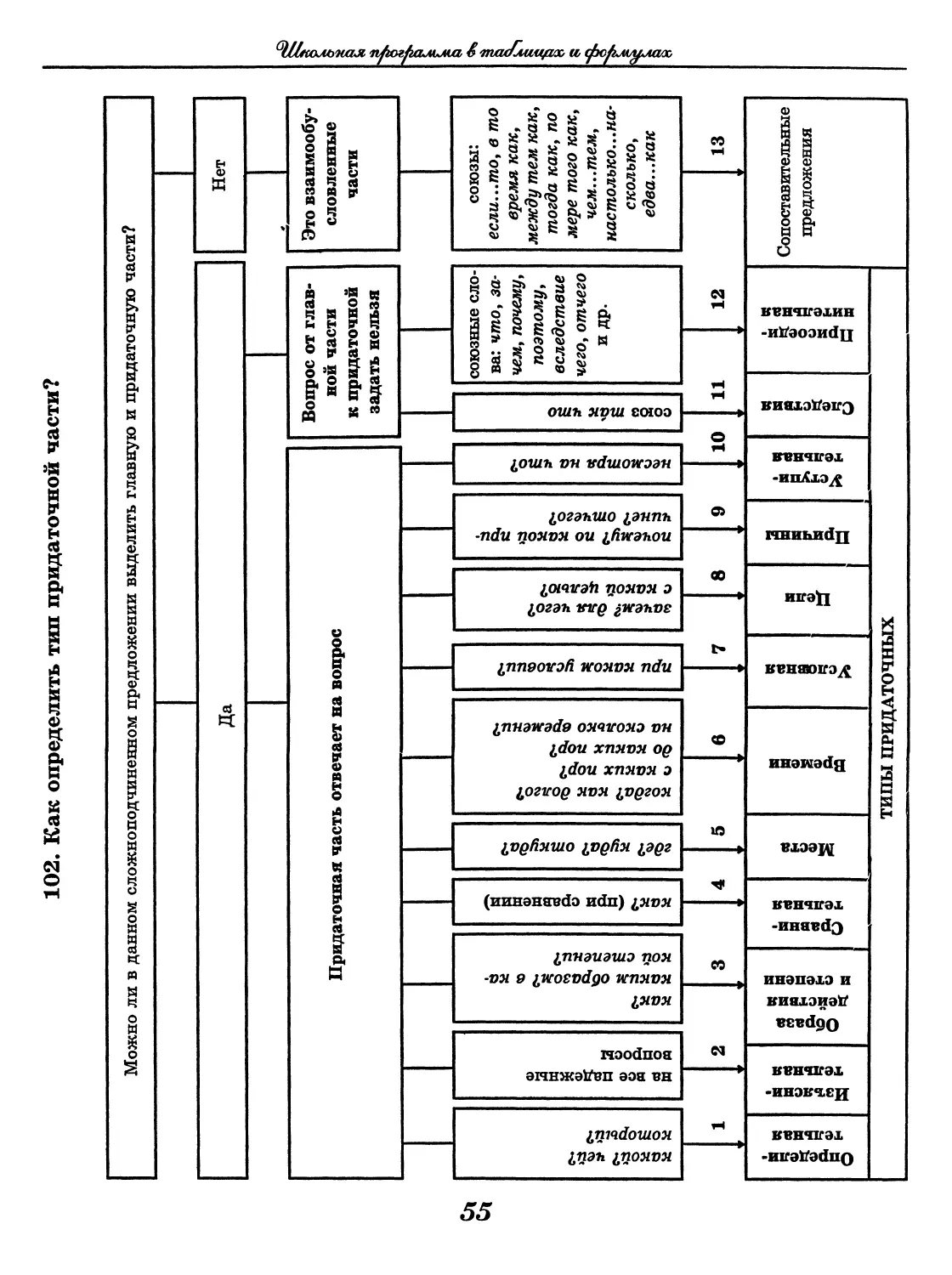
102. Как определить тип придаточной части?
Можно ли в данном сложноподчиненном предложении выделить главную и придаточную части?
Да Нет
Придаточная часть отвечает на вопрос Вопрос от глав- ной части к придаточной задать нельзя Это взаимообу- словленные части
1 2 3 45 6 789 10 11 12
13
Определи- тельная Изъясни- тельная Образа действия и степени Сравни- тельная Места Времени Условная Цели Причины г Уступи- тельная Следствия Присоеди- нительная Сопоставительные предложения
ТИПЫ ПРИДАТОЧНЫХ
§Pyccfcu,ii & тш/лишрх,
Примеры.
• Люблю людей, кому жизнь в радость. (Ф. Абрамов.) (1)
Я хочу, чтоб к штыку приравняли перо. (В. Маяковский.) (2)
Книги он расставил так, что самые нужные были под рукой. (3)
.. .Встретить я хочу мой смертный час так, как встретил смерть товарищ Нетте.
(В. Маяковский.) (4)
Откуда ветер, оттуда и дождь. (Пословица.) (5)
По синим волнам океана, лишь звезды блеснут в небесах, корабль одинокий несется, несется
на всех парусах. (М. Лермонтов.) (6)
Если я заболею, к врачам обращаться не стану. (Я. Смеляков.) (7)
Я встал, чтобы лучше видеть. (8)
Я очень полюбил эту книжку-тетрадку, потому что в ней удивительно гармонично соче-
талось изобразительное с повествовательным. (В. Катаев.) (9)
Сколько я ни напрягал зрение, я не мог увидеть конца этой низины. (В. Арсеньев.) (10)
«Бунт Стеньки Разина» я читал Коновалову часто, так что он уже свободно рассказывал
книгу своими словами. (М. Горький.) (11)
Я остаюсь на даче на всю зиму, что оригинально и ново. (А. Чехов.) (12)
...Она Алексея еще не видала, между тем как все молодые соседки только об нем и говори-
ли. (А. Пушкин.) (13)
103. Структурные особенности сложноподчиненного предложения
с одной придаточной частью
Примеры.
• Мне приходилось ночевать в стогах в октябре, когда трава на рассвете покрывается инеем,
как солью. (К. Паустовский.) (1)
Как появилось зло, так появилось желание бороться с ним. (В. Шукшин.) (2)
С тех пор, как здесь живет профессор со своей супругой, жизнь выбилась из колеи.
(А. Чехов.) (3)
И жизнь, как посмотришь с холодным вниманьем вокруг, такая пустая и глупая шутка.
(М. Лермонтов.) (4)
56
бЩмомная пфогфальма / таЛлищик, и, фофлшмик.
104. Структурные особенности сложноподчиненного предложения
с двумя придаточными частями
1 I3\z\zs>\ &Й однородное подчинение
2 cdb 1 1
3 1 3 1 ш ш
4 Х\хЗ\Х\Х z\z\z\z\z> £ J параллельное подчинение ii
5 xZZZ4 ± ±
6 ZZ^ 1 3 1 di Л
7 i последовательное подчинение
8 i
9 i
10 ZS/4/^^Ч, i
11 X^ 1
12 EHEH3
57
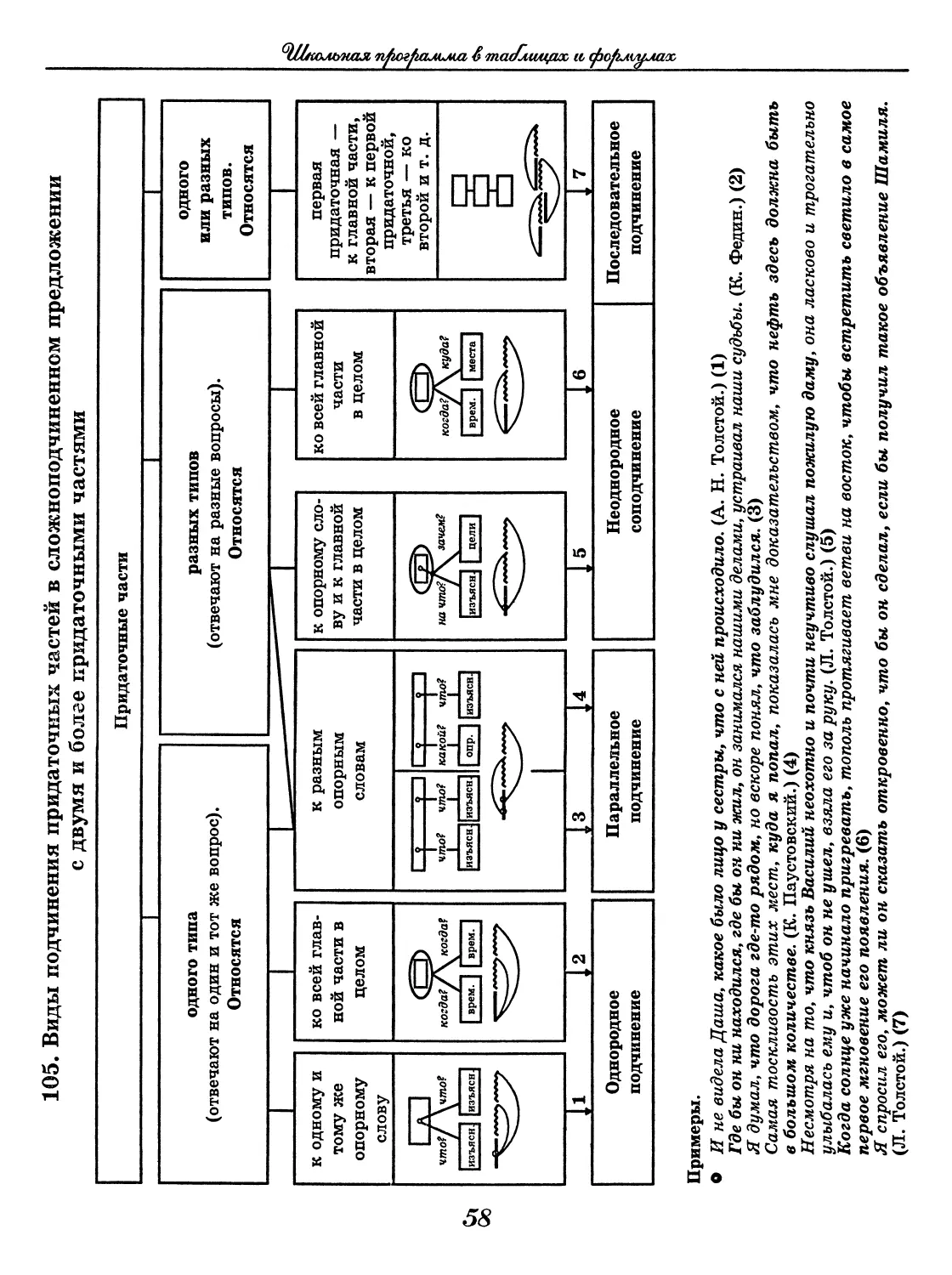
105. Виды подчинения придаточных частей в сложноподчиненном предложении
с двумя и более придаточными частями
Примеры.
О И не видела Даша, какое было лицо у сестры, что с ней происходило. (А. Н. Толстой.) (1)
Где бы он ни находился, где бы он ни жил, он занимался нашими делами, устраивал наши судьбы. (К. Федин.) (2)
Я думал, что дорога где-то рядом, но вскоре понял, что заблудился. (3)
Самая тоскливость этих мест, куда я попал, показалась мне доказательством, что нефть здесь должна быть
в большом количестве. (К. Паустовский.) (4)
Несмотря на то, что князь Василий неохотно и почти неучтиво слушал пожилую даму, она ласково и трогательно
улыбалась ему и, чтоб он не ушел, взяла его за руку. (Л. Толстой.) (5)
Когда солнце уже начинало пригревать, тополь протягивает ветви на восток, чтобы встретить светило в самое
первое мгновение его появления. (6)
Я спросил его, может ли он сказать откровенно, что бы он сделал, если бы получил такое объявление Шамиля.
(Л. Толстой.) (7)
Sfyccftiivi4 пъа^лилщх,
106. Общая схема синтаксического разбора предложения
ПРЕДЛОЖЕНИЕ
Простое Сложное
Бессоюзное Сложносочиненное Сложноподчиненное Сложная синтаксическая конструкция
с одним придаточным с двумя и более придаточными с бессоюзной связью с сочинением и подчинением
подчинение неоднородное соподчинение и сочинением и подчинением сочинением и подчинением
однородное последовательное
1 2 3 4 5 6 7 8 9 10 11
Примеры.
О Ничего не сказала рыбка, лишь хвостом по воде плеснула и ушла в глубокое море. (А. Пушкин.) (1)
...Там на неведомых дорожках следы невиданных зверей; избушка там на курьих ножках сто-
ит без окон, без дверей... (А. Пушкин.) (2)
И Пушкин ласково глядит, и ночь прошла, и гаснут свечи, и нежный вкус родимой речи так
чисто губы холодит. (Б. Ахмадулина.) (3)
Если жизнь тебя обманет, не печалься, не сердись! (А. Пушкин.) (4)
Все бы слушал, как вершина ивы дремлющей шумит, как на темном дне оврага по камням
родник журчит. (А. Плещеев.) (5)
Вот пес без хвоста, который за шиворот треплет кота, который пугает и ловит синицу,
которая часто ворует пшеницу, которая в черном чулане хранится в доме, который построил
Джек. (С. Маршак.) (6)
Дядька не расслышал, как его назвали, только понял, что по имени и отчеству. (Б. Шергин.) (7)
На болоте крячет цапля, четко хлюпает вода, а из туч глядит, как капля, одинокая звезда.
(С. Есенин.) (8)
По лицу Анны Сергеевны трудно было догадаться, какие она испытывала впечатления: оно со-
храняло одно и то же выражение, приветливое, тонкое... (И. Тургенев.) (9)
О Феничке, которой тогда минул уже семнадцатый год, никто не говорил, и редкий ее видел:
она жила тихонько, скромненько... (И. Тургенев.) (10)
Всем известно, что письма бывают веселые или печальные, и поэтому, пока мать читала,
Чук и Гек внимательно следили за ее лицом. (А. Гайдар.) (11)
59
^Школьная nfa&feaMJUi 4 тш/лилщх, и, фо[миулал
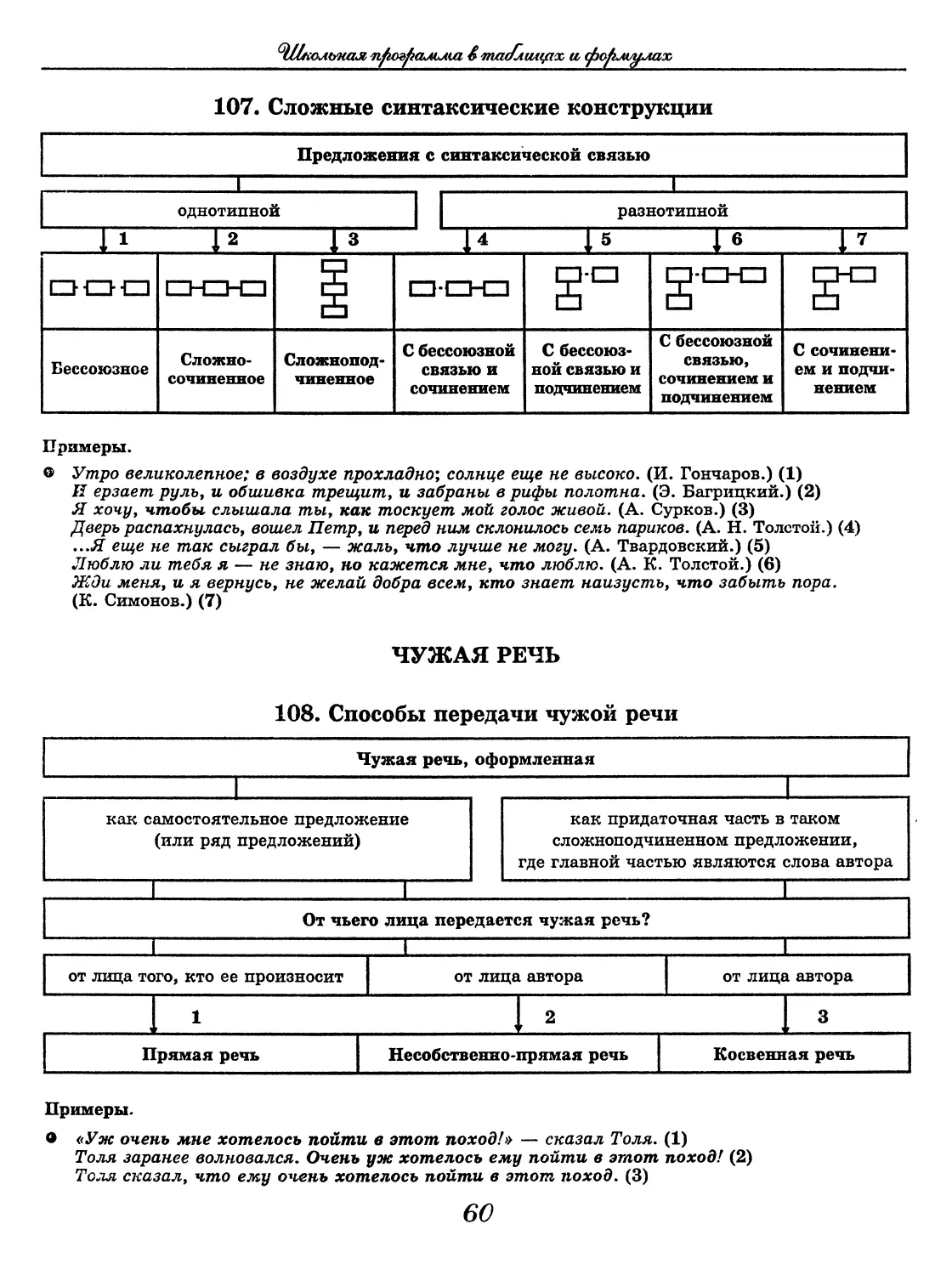
107. Сложные синтаксические конструкции
Предложения с синтаксической связью
|_ 1
однотипной разнотипной
to 00 сл ф <—
00-0 EZHZHZJ [НИ □-EZHZ1 м □ *
Бессоюзное Сложно- сочиненное Сложнопод- чиненное С бессоюзной связью и сочинением С бессоюз- ной связью и подчинением С бессоюзной связью, сочинением и подчинением С сочинени- ем и подчи- нением
Примеры.
о Утро великолепное; в воздухе прохладно; солнце еще не высоко. (И. Гончаров.) (1)
И ерзает руль, и обшивка трещит, и забраны в рифы полотна. (Э. Багрицкий.) (2)
Я хочу, чтобы слышала ты, как тоскует мой голос живой. (А. Сурков.) (3)
Дверь распахнулась, вошел Петр, и перед ним склонилось семь париков. (А. Н. Толстой.) (4)
...Я еще не так сыграл бы, — жаль, что лучше не могу. (А. Твардовский.) (5)
Люблю ли тебя я — не знаю, но кажется мне, что люблю. (А. К. Толстой.) (6)
Жди меня, и я вернусь, не желай добра всем, кто знает наизусть, что забыть пора.
(К. Симонов.) (7)
ЧУЖАЯ РЕЧЬ
108. Способы передачи чужой речи
Примеры.
О «Уж очень мне хотелось пойти в этот поход!» — сказал Толя. (1)
Толя заранее волновался. Очень уж хотелось ему пойти в этот поход! (2)
Толя сказал, что ему очень хотелось пойти в этот поход. (3)
60
История
История России XX века
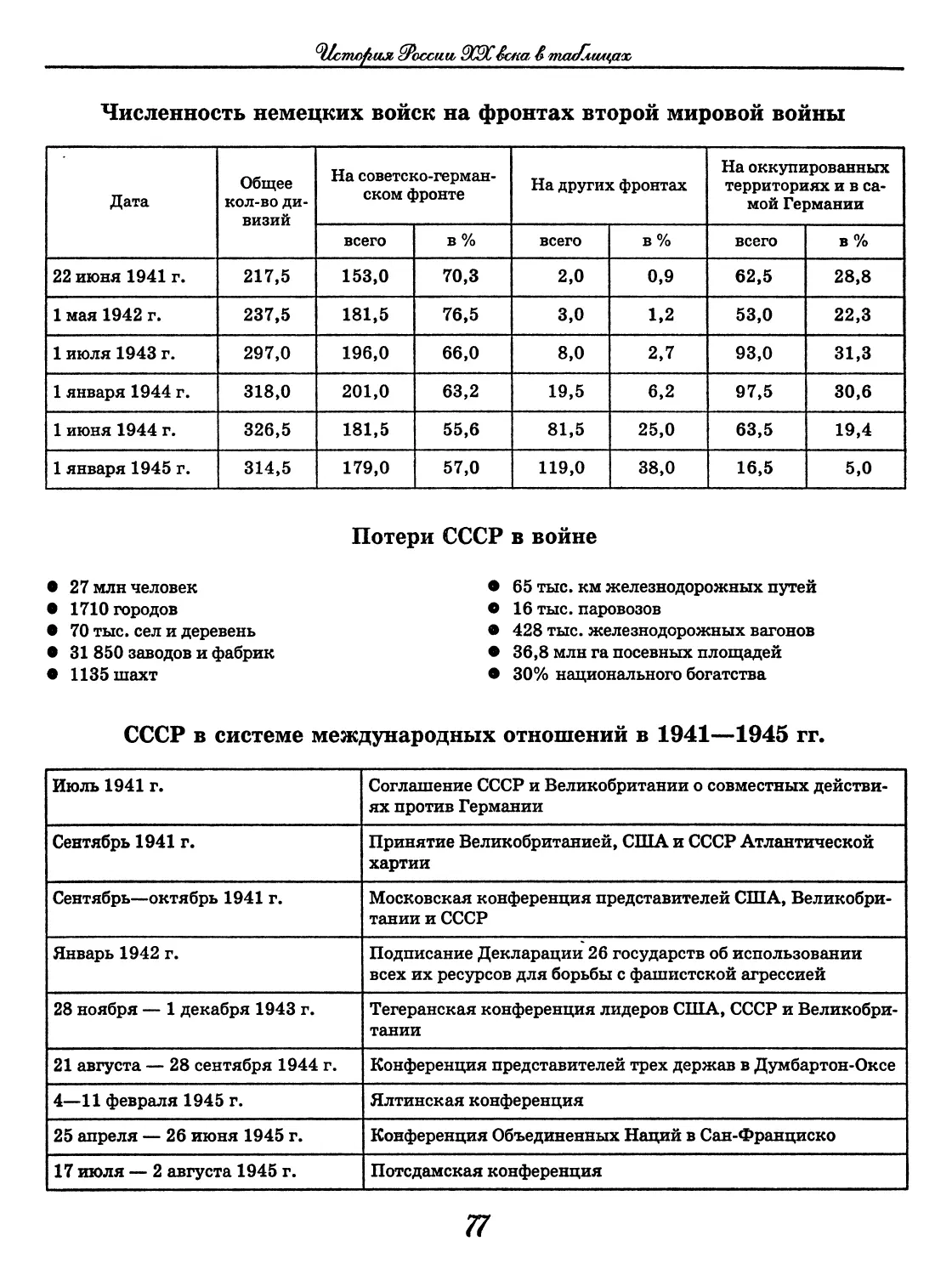
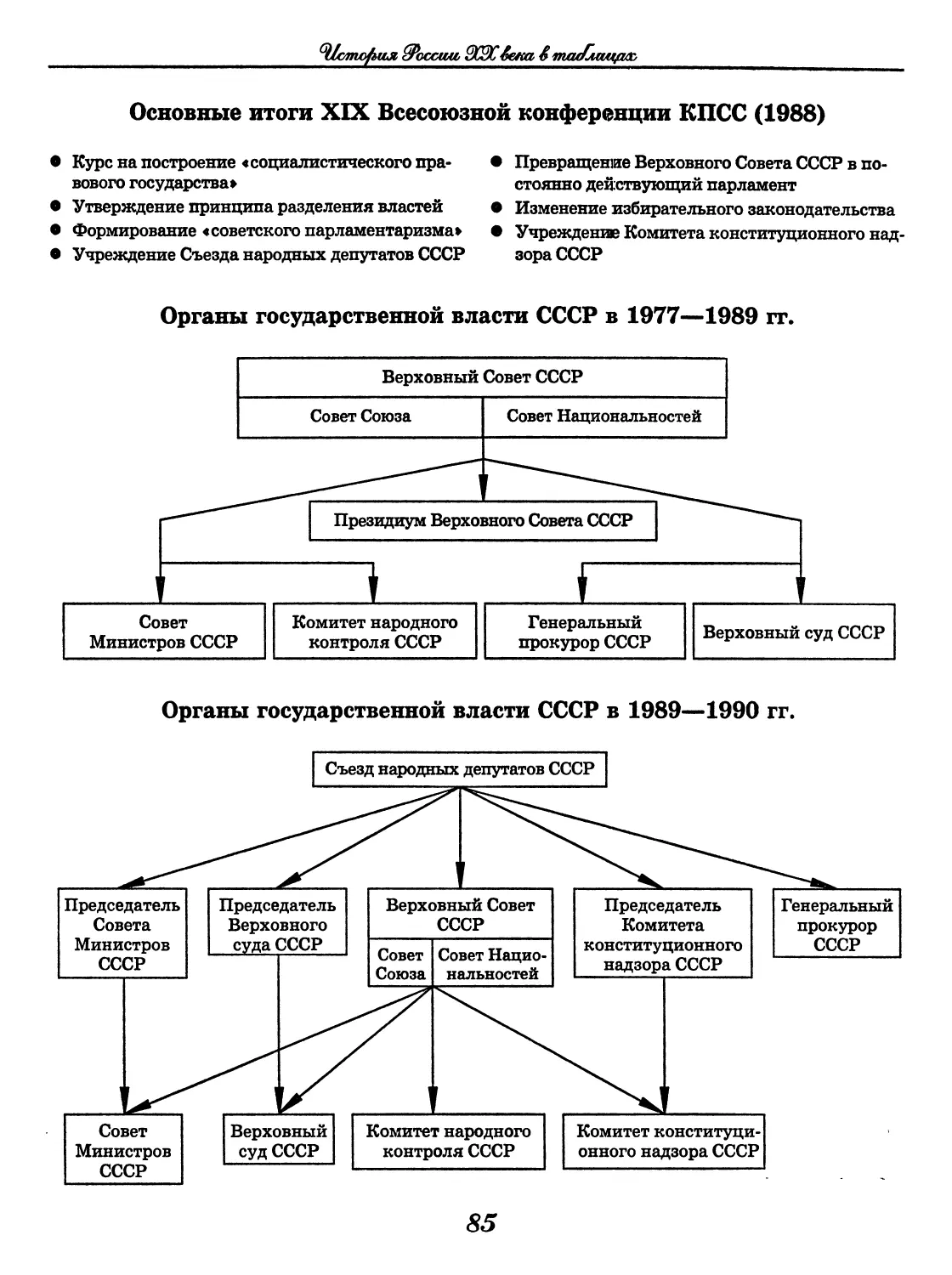
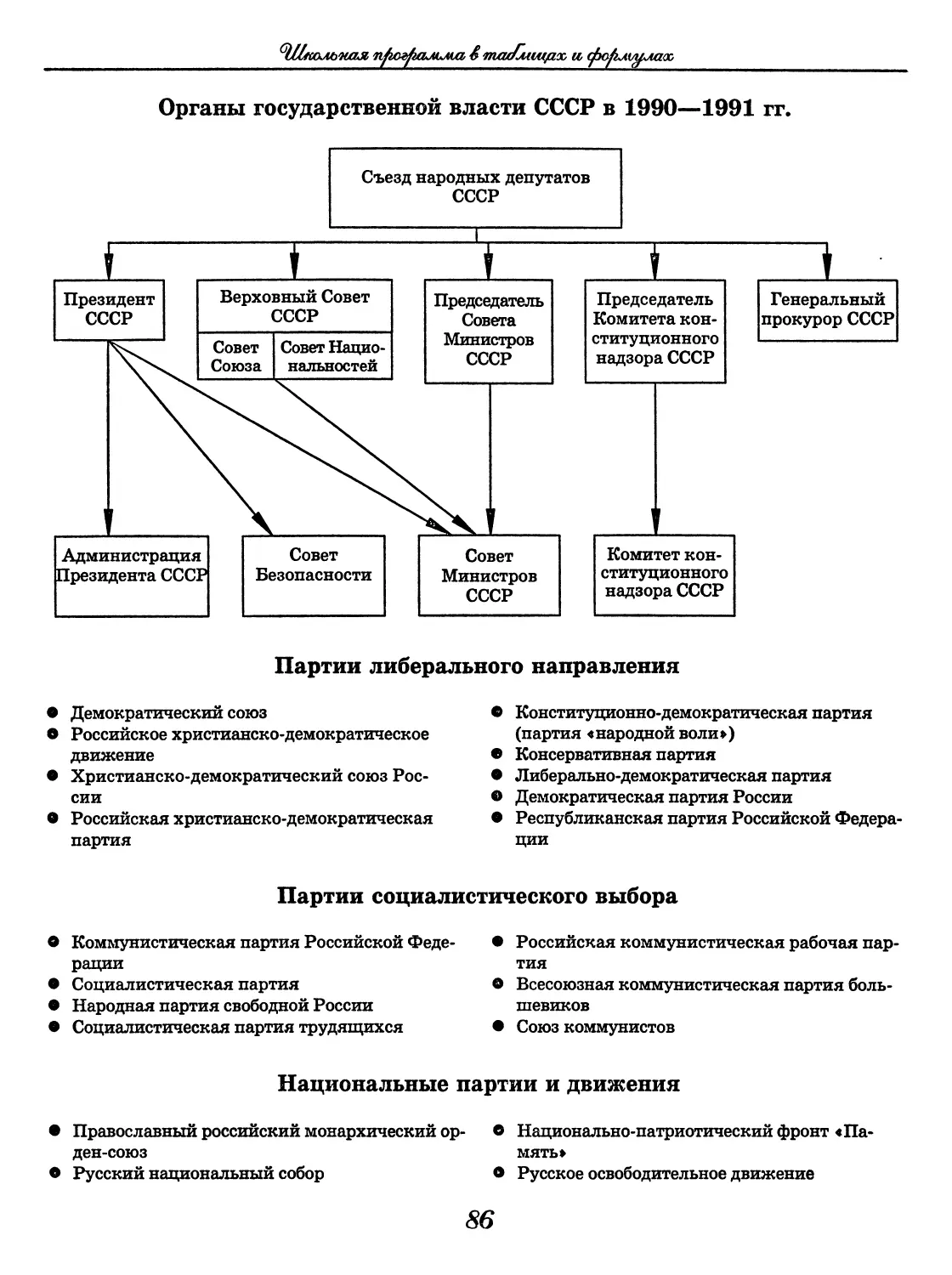
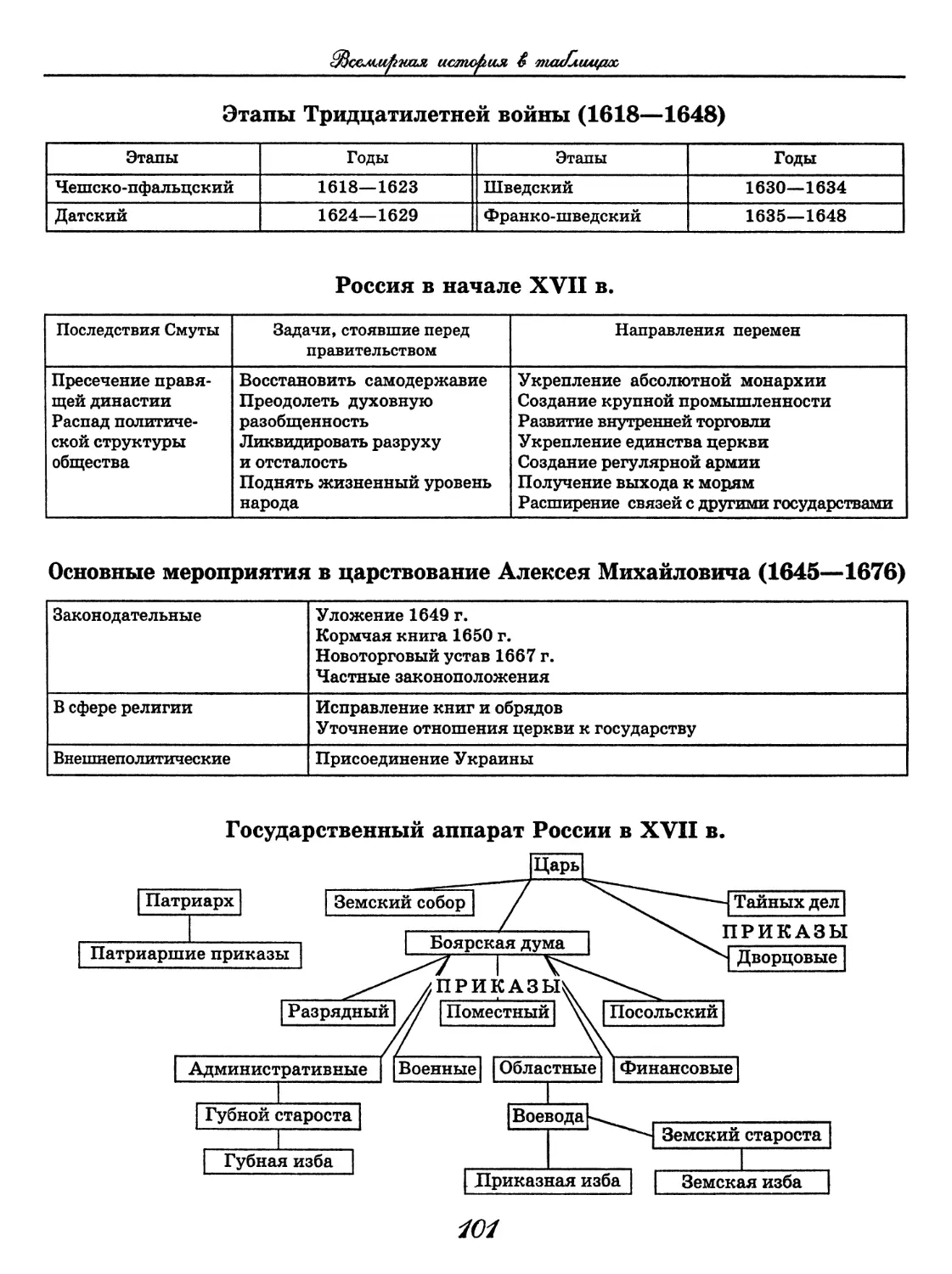
Всемирная история
История России XX века в таблицах
Особенности процесса модернизации на рубеже XIX—XX вв.
Общие проблемы развития Страны «первого эше- лона» модернизации (США, Англия, Франция) Россия и страны «второго эшелона» (Германия, Италия, Япония) Страны «третьего эшелона» (Китай, Латинская Америка)
Начало перехода к модерни- зации экономики Раннее Относительно позд- нее Позднее
Преобладающие факторы развития Внутренние Внутренние и внешние Внешние
Элементы традиционного общества Минимальны Значительны Значительны
Путь перехода к модернизации Революционный Реформаторский Смешанный
Наличие либеральных политических традиций Высокоразвиты Отсутствовали или были минималь- ны Минимальны
Темпы модернизации Средние Высокие Средние
Политическая и социальная стабильность Относительно высокая Низкая Средняя
Характер развития — Догоняющий Догоняющий
Роль государства в экономике Минимальна Высока Значительна
Качественные показатели соц.-эконом. развития Высокие Низкие Низкие
Характер экономики Частнокапиталисти- ческий Многоукладный Многоукладный
Политический строй России в начале XX в.
• Сосредоточение абсолютной законодательной
и исполнительной власти в руках императора
О Высокая степень бюрократизации системы
власти
• Полное отсутствие элементов представитель-
ной демократии и представительных учреж-
дений
• Отсутствие легальных политических партий
62
tylomcfiuji ^России, ЗСЭС^ека 6 та^мицт
Социал-демократические партии России в конце XIX — начале XX в.
О Армянская социал-демократическая партия
«Гнчак»(1887)
© Социал-демократия Королевства Польского
и Литвы (1893)
• Литовская социал-демократическая партия
(1896)
• Всеобщий еврейский рабочий союз в Литве,
Польше и России (1897)
• Российская социал-демократическая рабочая
партия (1898)
О Революционная украинская партия (1900)
О Латышская социал-демократическая рабочая
партия(1904)
• Мусульманская социал-демократическая ор-
ганизация «Гуммет» (1904)
• Украинская социал-демократическая рабо-
чая партия (1905)
О Еврейская социал-демократическая рабочая
партия «Поалей Цион» (1906)
• Белорусская социал-демократическая пар-
тия (1918)
Неонароднические партии России в конце XIX — начале XX в.
О «Дашнакцутюн» (1890)
• Партия социалистов-революционеров (1901)
• Белорусская социалистическая громада (1902)
О Украинская партия социалистов-революцио-
неров (1903)
• Украинская демократическо-радикальная
партия (1904)
• Сионистско-социалистическая рабочая партия
(1904)
• Партия социалистов-федералистов Грузии
(1904)
• Социалистическая еврейская рабочая партия
(1906)
• Трудовая народно-социалистическая партия
(1906)
© Союз социалистов-революционеров (максима-
листов) (1906)
О Мусульманская демократическая партия
«Мусават» (1911)
• Казахская социалистическая партия «Уш-
Жуз» (1917)
О Партия левых социалистов-революционеров
(интернационалистов) (1917)
• Партия революционного коммунизма (1917)
• Украинская партия социалистов-федерали-
стов (1917)
о Украинская партия социалистов-революцио-
неров (коммунистов) (1918)
• Белорусская партия социалистов-революцио-
неров (1918)
© Белорусская партия социалистов-федерали-
стов (1918)
• Партия народников-коммунистов (1918)
Либеральные и консервативные партии России в начале XX в.
• Литовская демократическая партия (1902)
О Конституционно-демократическая партия
(1905)
• Балтийская конституционная партия
(1905)
• «Союз 17 октября» (1905)
• Партия демократических реформ (1905)
• Партия мирного обновления (1906)
• Партия русских националистов («Всероссий-
ский национальный союз») (1908)
• Партия прогрессистов (1912)
О Армянская народная партия «Рамкавар»
(1917)
• Казахская партия «Алаш» (1917)
• Грузинская национально-демократическая
партия(1917)
Монархические партии России в начале XX в.
• «Русское собрание» (1900)
О Русская монархическая партия (1905)
• «Союз русского народа» (1905)
• «Русский народный союз имени Михаила Ар-
хангела» (1908)
63
^Шкальная пфсгфальма 6 таблицах и формулах
Политические организации промышленников
и предпринимателей в начале XX в.
© Всероссийский торгово-промышленный союз
(1905)
© Прогрессивная экономическая партия (1905)
© Торгово-промышленная партия (1905)
© Умеренно-прогрессивная партия (1905)
• Партия правового порядка (1905)
© Конституционно-монархический правовой союз
(1906)
Политические партии России в начале XX в.
Социалистические Либеральные Монархические
Социаль- ный состав Революционная интелли- генция, рабочие, город- ские средние слои, кресть- яне Либеральная интеллиген- ция, городские средние слои, буржуазия, часть по- мещиков Помещики, духовенство, часть крупной буржуазии, часть городских средних слоев, крестьяне
Программ- ные цели Уничтожение частной соб- ственности (в первую оче- редь помещичьего земле- владения) и царского са- модержавия Создание эффективной ры- ночной экономики, по- строение правового госу- дарства, формирование гражданского общества Сохранение традиционных основ экономической и по- литической жизни, отчас- ти — возврат к дорефор- менной ситуации
Политиче- ские требо- вания Установление республи- ки, предоставление граж- данских прав и свобод Ограничение монархии конституционными рамка- ми, предоставление демо- кратических прав и свобод Сохранение и укрепление самодержавия
Тактика Революционная (включая вооруженное восстание) Парламентская борьба Борьба с либералами и ре- волюционерами всеми доступными методами
Реформы П. А. Столыпина
Аграрная реформа ©
Ф Введение свободы вероисповедания 0
© Установление гражданского равноправия ©
Ф Улучшение быта рабочих
Ф Реформа местного самоуправления О
Реформа высшей и средней школы
Введение всеобщего начального обучения
Улучшение материального обеспечения народ-
ного учительства
Полицейская реформа
Цели и направления аграрной реформы П. А. Столыпина
Цели Направления
Снятие социальной напряженности на селе Формирование широкого слоя мелких собствен- ников для обеспечения политической стабиль- ности Отвлечение крестьян от идеи принудительного отчуждения помещичьих земель Сохранение всех форм частной собственности (включая помещичью) Разрушение крестьянской общины Создание хуторов и отрубов Переселенческая политика Развитие крестьянской производственной кооперации Оказание государственной помощи крестьян- ским хозяйствам Обеспечение юридического равноправия кре- стьянства
64
ия cjPoccuu, 9С9С& та/лищш
Результаты аграрной реформы П. А. Столыпина
• Выход из общины 2 млн крестьянских дворов
• К1915 г. количество фермерских хозяйств не
превышало 10% всех крестьянских хозяйств
• Увеличение в среднем на 10% посевных пло-
щадей
• Увеличение на 35% хлебного экспорта
• Увеличение вдвое количества применяемых
минеральных удобрений
• В 3,5 раза возросли закупки крестьянами
сельскохозяйственных машин
• Ежегодные темпы роста промышленного про-
изводства были самыми высокими в мире
(8,8%)
• В Сибирь переселилось 3 млн 40 тыс. чело-
век
• Переселенцы освоили 30 млн десятин целины
• К началу 1917 г. в России насчитывалось
63 тыс. различных кооперативов
• Сельская кооперация обслуживала 94 млн че-
ловек
Военно-политические блоки начала XX в.
Основные направления внешней политики Николая II
Сохранение статус-кво в Европе Усиление присутствия России в Азии
Союз с Францией Обязательство сохранять статус-кво на Балка- нах (договор 1897 г. с Австро-Венгрией) Отказ от раздела Турции (1898) Инициирование созыва международных конфе- ренций в Гааге по разоружению Давление на Японию с целью ограничить ее влияние в Китае (1895) Аренда Порт-Артура и Дальнего Усиление экономической экспансии в Китае, Мон- голии, Корее Строительство КВЖД Получение права транзита войск по КВЖД
Периодизация первой русской революции (1905—1907)
Период восходящего развития революции (январь—сентябрь 1905 г.) Период кульминации революции (октябрь—декабрь 1905 г.) Период спада революции (1906—1907)
Кровавое воскресенье (9 января 1905 г.) Нарастание рабочего, кресть- янского движения Волнения в армии и на флоте Октябрьская политическая стачка Манифест 17 октября 1905 г. Создание либеральных партий Декабрьское вооруженное вос- стание Постепенное затухание волне- ний среди рабочих и крестьян Выборы в I и П Думу Законопроекты П. А. Столыпина Становление новой политиче- ской системы
Предпосылки революционного кризиса 1917 г.
ПРОТИВОРЕЧИЯ ОБЪЕКТИВНОГО ХАРАКТЕРА
• Между городом и деревней • Между русскими и инородцами
• Между центром и окраинами • Между государством и личностью
3—1323
65
ПРОТИВОРЕЧИЯ, СВЯЗАННЫЕ С НЕРЕШЕННОСТЬЮ МОДЕРНИЗАЦИОННЫХ ЗАДАЧ
Сохранение помещичьего землевладения
Незавершенность индустриализации
Формирование национальной элиты
Отсутствие у буржуазии политической власти
• Отсутствие мер по социальной адаптации на-
селения к новым реалиям
О Отсутствие развитых либеральных и парла-
ментских традиций
ПРОТИВОРЕЧИЯ ВРЕМЕННОГО, <КОНЪЮНКТУРНОГО» ХАРАКТЕРА
(СВЯЗАНЫ С ПЕРВОЙ МИРОВОЙ ВОЙНОЙ)
• Неудачи на фронте
• Огромные военные расходы
• Социальные лишения (разруха, голод, гибель
многих солдат)
• Усиление диспропорций в развитии экономики
• Резкое усиление враждебной пропаганды со
стороны Германии
© Нарушение работы транспорта
О Усиление критики либералами царского пра-
вительства
• Прогрессирующий паралич власти
• Активизация революционных сил в армии и
обществе
Альтернативы общественно-политического развития
России после Февраля
Реформаторская (была преобладающей в февра- ле—июле 1917 г.) Радикальная (усилилась с августа 1917 г.)
Леворадикальная (реа- лизована большевика- ми в октябре 1917 г.) Праворадикальная (неудачная попытка ее реализации предпринята генералом Л. Г. Корниловым в августе 1917 г.)
Политические партии России в феврале—октябре 1917 г.
Монар- хические Либеральные Умеренно- социалистические Радикально- социалистические
1 2 3 4 5
О власти Прекра- тили су- щество- ваниев феврале В поддержку Временного правительства и Учреди- тельного собрания, за право- вое государство в форме кон- ституционной монархии или республики В поддержку Вре- менного правитель- ства, за парламен- тарную республику Против власти Временно- го правительства, за Рес- публику Советов как пе- реходную форму к госу- дарству диктатуры проле- тариата
О войне Верность союзническому долгу. Доведение войны до победного конца и присое- динение к России Черно- морских проливов « Революционное оборончество»: от- каз от аннексий и контрибуций, борьба за скорей- шее заключение ми- ра усилиями II Интернационала Немедленное прекраще- ние войны любой це- ной. Превращение вой- ны империалистиче- ской в войну граждан- скую
66
^России ЭСЭС&ма &тш^кшАх
Политические партии России в феврале—октябре 1917 г.
1 2 3 4 5
0 преодо- лении экономи- ческого кризиса Отказ от социально-эконо- мического реформирова- ния до созыва Учредитель- ного собрания За частичные рефор- мы до и радикаль- ные реформы (в ин- тересах трудового народа) после созыва Учредительного соб- рания За немедленное ради- кальное реформирова- ние экономики путем введения «рабочего уче- та и контроля» и т. п.
0 такти- ке и бло- ках «Левый блок» с умеренны- ми социалистами в интере- сах обеспечения социаль- ной стабильности до созыва Учредительного собрания Блок с либералами из-за активизации радикалов и него- товности страны к социалистическим преобразованиям Отказ от любых блоков и соглашений. Противопос- тавление пролетариата и беднейших крестьян всем остальным социальным группам. Уверенность в близости мировой рево- люции
Причины радикализации масс в феврале—октябре 1917 г.
О Крушение традиционных структур власти
и управления сверху донизу
• Реальное многовластие в центре и на местах
О Усиление амбиций лидеров политических
и национальных движений
О Продолжение войны и связанные с ней соци-
альные лишения
• Падение дисциплины в армии
• Военные поражения в июне
О Ухудшение уровня жизни населения (с лета)
• Распад относительной социально-политической
консолидации российского общества
• Популизм политических лидеров радикаль-
ного толка
• Оттягивание социально-экономических ре-
форм до созыва Учредительного собрания
Причины победы леворадикальной альтернативы в октябре 1917 г.
• Нарастание социально-экономических проблем
• Затягивание созыва Учредительного собрания
• Падение авторитета Временного правительст-
ва после корниловщины
• Усиление позиций большевиков после пора-
жения правых радикалов в августе
• Нарастание противоречий между либералами
и правыми социалистами
О Радикализация левого крыла умеренных
социалистов и их организационное оформле-
ние
• Обещания лидеров большевиков решить разом
все проблемы общественного развития
• Осуществление переворота в Петрограде под
флагом ликвидации двоевластия в пользу Со-
ветов
Основные этапы Гражданской войны в России (1917—1922)
25 октября 1917 г. — май 1918 г. Начало вооруженного гражданского противостояния. «Ограни- ченная» война (выступления Краснова под Петроградом, Кале- дина на Дону, Дутова на Урале)
Май—ноябрь 1918 г. Начало полномасштабной гражданской войны: выступление Чехословацкого корпуса, Добровольческой и Донской армий. Десанты Антанты (Англия — в Мурманске, Архангельске, Баку, Мерве; Турция — в Карсе и Батуме; Франция — в Одессе и Се- вастополе)
UL фо/ыииМХ,
Основные этапы Гражданской войны в России (1917—1922)
Ноябрь 1918 г. — весна 1919 г. Усиление военного противостояния красных и белых. Военные операции войск Колчака, Деникина, Краснова, Юденича, Се- менова. Численность армейских частей Антанты в России дос- тигает 200 тыс. человек
Весна — конец 1919 г. Разгром основных сил белых (Колчак, Деникин, Юденич). Эва- куация основных сил иностранных войск
Весна — осень 1920 г. Война с Польшей. Разгром армии Врангеля
1920—1922 гг. Победы красных в Средней Азии, Закавказье, на Дальнем Вос- токе» Завершение Гражданской войны
Белое движение
Идейные основы Важнейшие правительства Главные военные деятели
• Борьба против большевизма • Восстановление единой и не- делимой России • Признание большинством на- селения итогов Февральской революции • Признание необходимости со- зыва Учредительного собра- ния (Земского собора) для оп- ределения будущего страны • Понимание необходимости и попытки решения аграрного, рабочего, национального во- просов • Свобода предпринимательст- ва как главный принцип эко- номической политики • Правительство верховного прави- теля России адмирала А. В. Кол- чака (с ноября 1918 г.) в Омске • «Особое совещание» генерала А. И. Деникина в Екатеринодаре (с августа 1918 г.) • Временное управление Северной области Н. В. Чайковского (позднее — Е. К. Миллера) в Ар- хангельске (с августа 1918 г.) • Северо-Западное правительство генерала Н. Н. Юденича в Талли- не (с августа 1919 г.) • Правительство Юга России гене- рала П. Н. Врангеля в Севастопо- ле (с апреля 1920 г.) Генерал М. В. Алексеев Генерал Л. Г. Корнилов Адмирал А. В. Колчак Генерал П. Н. Краснов Генерал А. М. Каледин Генерал А. И. Дутов Генерал Г. М. Семенов Генерал А. И. Деникин Генерал Н. Н. Юденич Генерал П. Н. Врангель Генерал Е. К. Миллер Генерал Я. А. Слащов- Крымский Генерал В. 3. Май- Маевский Генерал Р. Ф. Унгерн фон Штернберг
Органы государственной власти РСФСР (по Конституции 1918 г.)
Первый состав Совнаркома
Председатель — В. И. Ульянов (Ленин)
Нарком внутренних дел — А. И. Рыков
Нарком земледелия — В. П. Милютин
Нарком труда — А. Г. Шляпников
Наркомы — члены Комитета по военно-морским
делам — В. А. Антонов-Овсеенко, Н. В. Крылен-
ко, П. Е. Дыбенко
Нарком торговли и промышленности —
В. П. Ногин
Нарком просвещения — А. В. Луначарский
Нарком финансов — И. И. Скворцов-Степанов
Нарком иностранных дел — Л. Д. Троцкий
(Бронштейн)
Нарком юстиции — А. Ломов (Г. И. Оппоков)
Нарком продовольствия — И. А. Теодорович
Нарком почт и телеграфов — Н. П. Абилов
(Глебов)
Нарком по делам национальностей —
И. В. Сталин (Джугашвили)
Нарком железнодорожного транспорта —
М. Т. Елизаров
Нарком госпризрения — А. М. Коллонтай
68
^Исто/гия ^России ЗСЭС&ека 6 таблицах,
Состав Революционного Военного Совета Республики (РВСР)
Председатель — Л. Д. Троцкий (1918—1925)
Зам. председателя — Э. М. Склянский
(1918—1924)
Главнокомандующие:
И. И. Вацетис (1918—1919),
С. С. Каменев (1919—1924)
Члены РВСР:
П. А. Кобозев (1918—1919)
К. А. Мехоношин (1918—1919)
Ф. Ф. Раскольников (1918)
К. X. Данишевский (1918—1919)
И. Н. Смирнов (1918—1919)
С. И. Аралов (1918—1919)
В. А. Антонов-Овсеенко (1918—1919)
А. П. Розенгольц (1918—1919)
В. И. Невский (1918—1919)
Н. И. Подвойский (1918—1919)
К. К. Юренев (1918—1919)
И. В. Сталин (1918—1919, 1920—1922)
В. М. Альтфатер (1918—1919)
А. И. Окулов (1919)
И. Г. Смилга (1919—1923)
С. И. Гусев (1919, 1921—1923)
А. И. Рыков (1919)
Д. И. Курский (1919—1921)
Причины победы красных в Гражданской войне
• Социальная и идейная разнородность Белого
движения
• Использование большевиками возможностей
мощного государственного аппарата, способ-
ного проводить массовые мобилизации и ре-
прессии
О Продуманное идеологическое обеспечение во-
енных кампаний
• Поддержка значительной частью населения
лозунгов и политики большевиков
О Отсутствие массовой поддержки населением
белых
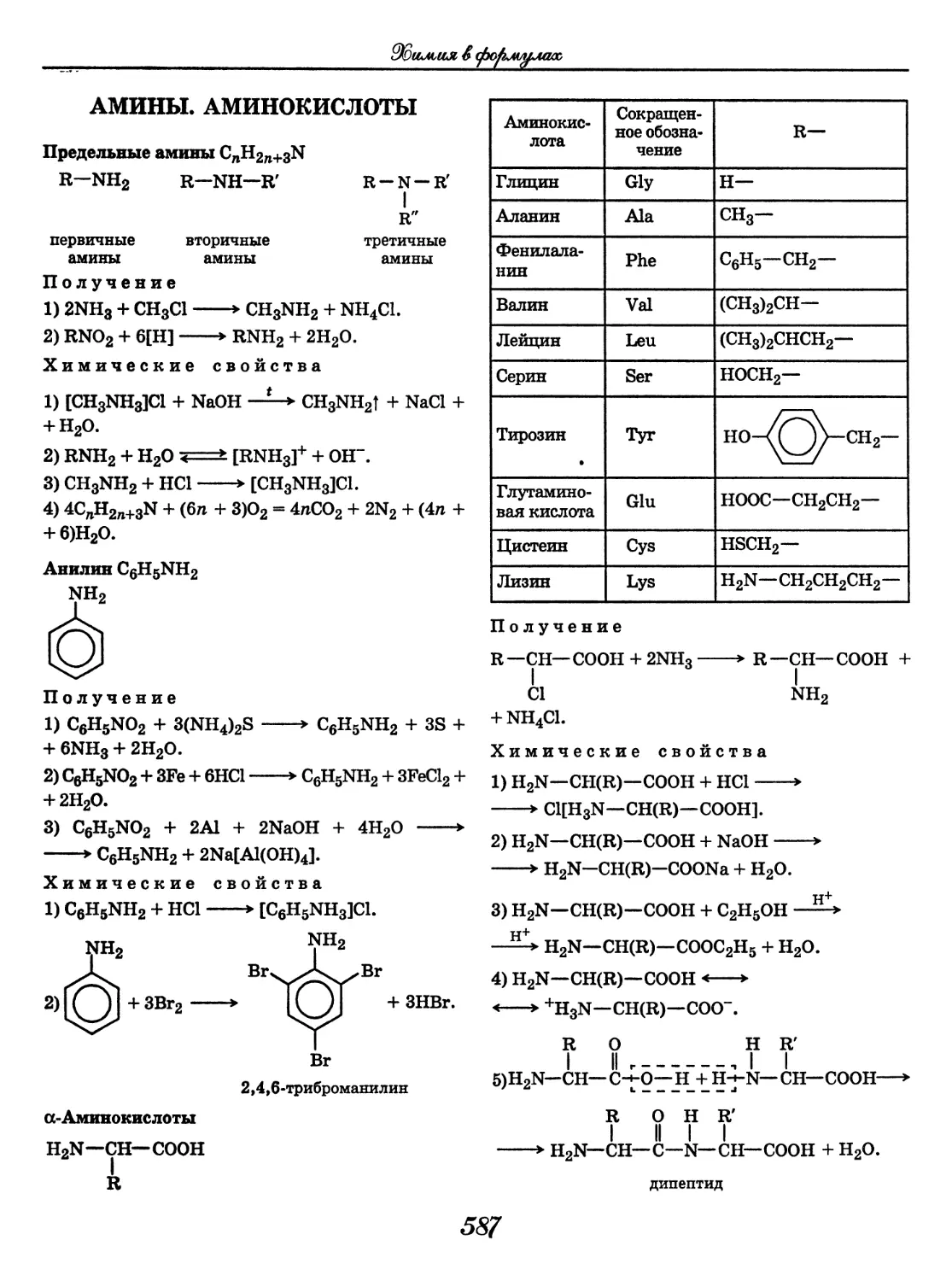
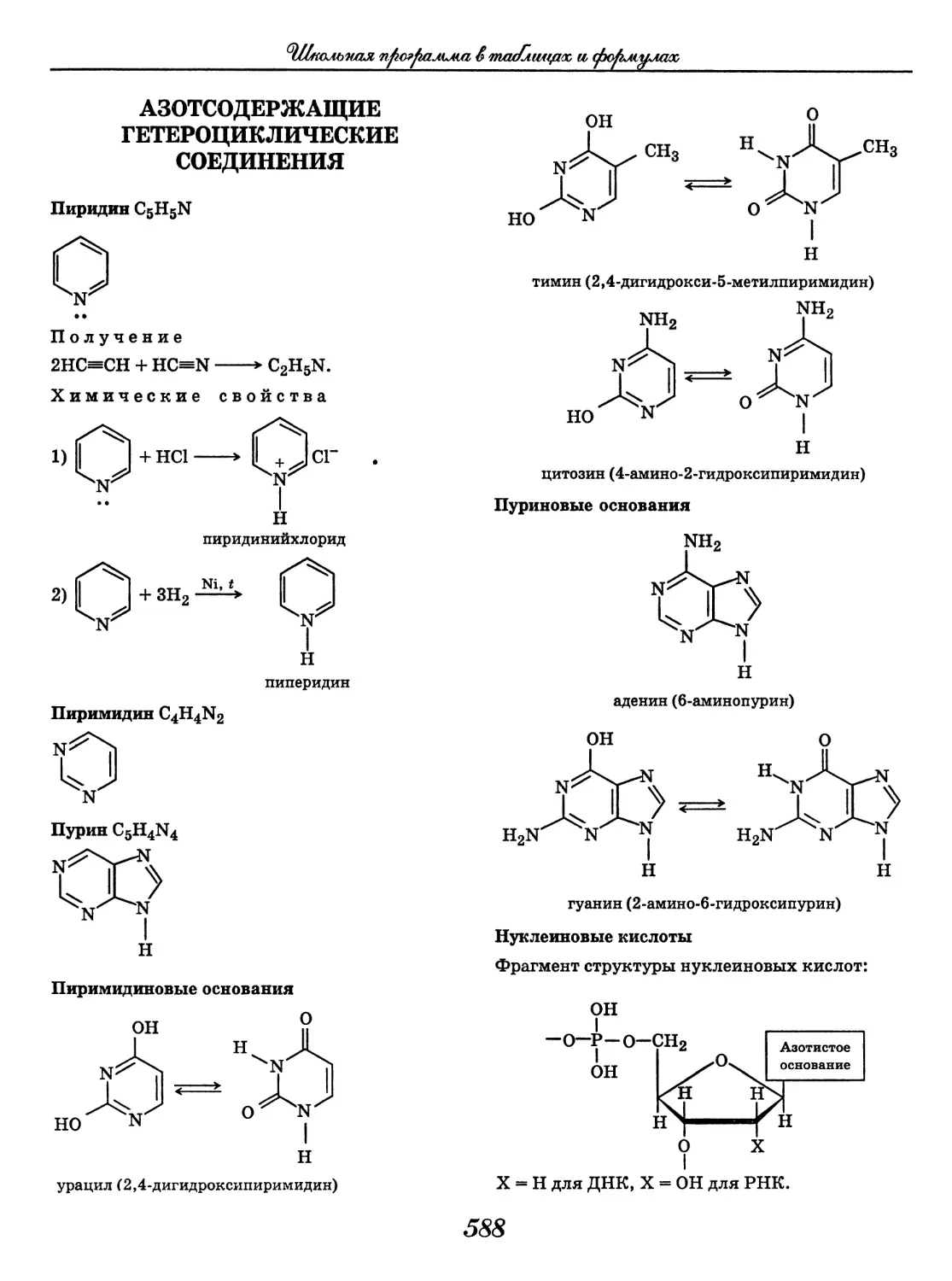
• Центральное положение РСФСР, что позволяло
с успехом использовать промышленную базу
страны и маневрировать резервами
• Нескоординированность действий белых ар-
мий, интервентов
Политика «военного коммунизма»
• Практическое огосударствление промышленно-
сти
• Практическое прекращение товарно-денеж-
ных отношений
• Введение продразверстки
• Милитаризация общества
® Отмена коммунальных платежей, платы за
проезд на транспорте и т. п.
О Введение трудовой повинности
• «Красный террор» против «бывших»
• Бюрократизация государственного аппарата
О Введение уравнительной оплаты труда
Причины перехода к нэпу
• Глубокий социально-экономический и поли-
тический кризис власти
• Массовые восстания в сельской местнос-
ти, выступления в городах, в армии и на фло-
те
• Крушение идеи «введения» социализма
и коммунизма путем ликвидации рыночных
отношений
• Стремление удержать власть любой ценой
• Спад революционной волны на Западе
69
^Шмолъная пфюгфалыиъ & тш/лищмх, и ф^мидла/х,
Нэповская общественная модель
ЭКОНОМИКА
Либерализация экономической жизни при со-
хранении командных высот в руках партии-
государства
Замена продразверстки продналогом
Отход от насаждения коммун на селе
Допущение рыночных отношений
Отмена трудовой повинности
Переход от натуральной оплаты труда к де-
нежной
• Введение элементов хозрасчета на уровне госу-
дарственных трестов и объединений («хозрас-
чет для начальников»)
® Введение тарифной системы оплаты труда
О Относительная стабилизация финансов
О Развитие внешней торговли
• Создание концессий
ПОЛИТИЧЕСКАЯ СИСТЕМА
Сохранение и укрепление авторитарной дик-
татуры
Завершение разгрома оппозиционных полити-
ческих партий
Относительная демилитаризация общества
• Сужение сферы непосредственного государст-
венного вмешательства в общественную
жизнь
• Политические процессы над оппозицией
ДУХОВНАЯ СФЕРА
Насильственное внедрение в сознание маркси-
стской идеологии
Реформирование системы образования
(ограничение доступа к образованию «быв-
шим»)
Ужесточение идеологического контроля
• Введение в Уголовный кодекс статей об ответ-
ственности за убеждения
© Усиление борьбы с неграмотностью
• Активизация антирелигиозной кампании
О Высылка за границу виднейших представите-
лей интеллигенции
Кризисы нэпа и их причины
Изменения в правящей партии в период нэпа
• Запрет фракций в РКП(б)
• Учреждение поста генерального секретаря
РКП(б)
• Усиление контроля партаппарата
• Ограничение внутрипартийной демокра-
тии
• Усиление борьбы в партруководстве во время
болезни Ленина
• Разгром сторонников «мягкого» внутрипар-
тийного режима
• Превращение ОГПУ в инструмент партийной
власти и внутрипартийной борьбы
Ю
GUcnufatji §Россиш ЭСЭС&ла, $ отьаг/лиящх,
Борьба в руководстве большевистской партии
Годы Противоборствующие группировки
1923—1924 И. В. Сталин Г. Е. Зиновьев Л. Б. Каменев Л. Д. Троцкий
1925 И. В. Сталин Н. И. Бухарин А. И. Рыков Г. Е. Зиновьев Л. Б. Каменев (< новая оппозиция »)
1927 И. В. Сталин Н. И. Бухарин А. И. Рыков Г. Е. Зиновьев Л. Б. Каменев Л. Д. Троцкий («объединенная оппозиция»)
1928—1929 И. В. Сталин Н. И. Бухарин А. И. Рыков М. П. Томский («правый уклон»)
Противоречия нэпа
Политическая монополия большевиков Плюрализм форм собственности и хозяйствен- ных укладов
Курс на строительство социализма в одной стране Необходимость активизации внешнеэкономиче- ской деятельности, усиления контактов с внеш- ним миром
Проведение индустриализации, создание мощно- го военно-промышленного комплекса (ВПК) Отсутствие инвестиций в промышленность из оте- чественных и зарубежных источников
Курс на построение общества социального ра- венства и социальной справедливости Усиление социального расслоения. Формирова- ние «новой буржуазии» (нэпманов) и «новой аристократии» (партийно-советской номенкла- туры)
Социально-экономические итоги нэпа
• Быстрое восстановление сельского хозяйства,
промышленности, транспорта
• Возрождение торговли
• Рост численности городского населения
е Повышение производительности труда рабо-
чих
• Повышение уровня жизни
• Ускоренная социальная дифференциация в го-
роде
• Появление «новой буржуазии»
• Ускорение расслоения крестьянства
• Нарастание экономической нестабильности
О Регулярные экономические кризисы
• Рост безработицы
Образование СССР
7/
^Штммая п^мг^гам^м & 'тси/лш/рх и,
Высшие органы государственной власти
и управления СССР в 1924—1936 гг.
Сталинская и бухаринская альтернативы выхода
из кризиса хлебозаготовок
И. В. Сталин Н. И. Бухарин
Оценка причин и сущности кризиса Кризис носит структурный харак- тер: отсутствие прогресса в деле инду- стриализации порождает товарный голод, а мелкое крестьянское хозяйст- во неспособно обеспечить потребности промышленности. Главный виновник кризиса— «кулак-саботажник» Главная причина кризиса — ошибки в выборе и реализации экономического курса (отсутствие резервного фонда промтоваров, разрыв цен на зерновые и технические культуры и др.). Глав- ный виновник — политическое руко- водство страны
Пути преодоле- ния кризиса Принятие чрезвычайных мер: форсирование индустриализации; массовая коллективизация; создание колхозов как формы перека- чивания ресурсов из деревни в город; ликвидация кулачества как «последне- го эксплуататорского класса»; создание социальной базы советской власти в деревне; обеспечение контроля за крестьянством Включение экономических рычагов: увеличение выпуска товаров широкого потребления; достижение сбалансированности цен на зерно и технические культуры; усиление налогообложения кулаков; закупка хлеба за границей; развитие кооперативного движения в деревне
72
^ILynwfjUJt, аРоссии ёКХ&Уса £ тас^лицаас
Советская модель тоталитаризма
ЭКОНОМИКА
• Ликвидация свободы труда и замена ее вне-
экономическим принуждением
• Фактическое присвоение государством средств
производства и рабочей силы
• Государственное регулирование рабочего дня,
заработной платы
• Фактический запрет забастовок
• Экономическая автаркия
• Милитаризация экономики
• Государственное регулирование имуществен-
ных отношений
ПОЛИТИЧЕСКАЯ СИСТЕМА
• Господство однопартийной системы
• Физическое уничтожение политических оп-
понентов
• Сращивание партийного и государственного
аппаратов
• Создание системы официальных (огосударст-
вленных) массовых организаций
© Унификация всей общественной жизни
• Культ харизматического вождя
• Создание мощного репрессивного аппарата
О Мощный аппарат обработки массового сознания
ДУХОВНАЯ СФЕРА
• Огосударствление партийной идеологии
• Изъятие и уничтожение литературы, не ук-
ладывающейся в идеологические рамки ре-
жима
• Государственный контроль над средствами
массовой информации
© Создание единой системы идеологизированно-
го образования
О Идеологическая изоляция страны
О Унификация и стандартизация духовной
жизни
• Деятельность пропартийных творческих союзов
Цели индустриализации в СССР
• Ликвидация технико-экономической отста-
лости
• Достижение экономической независимости
• Подведение технической базы под отсталое
сельское хозяйство
О Развитие новых отраслей промышленности
• Создание мощного военно-промышленного
комплекса
Особенности индустриализации в СССР
• Главный источник накопления — перека-
чивание средств из деревни и трудовой энтузи-
азм советских людей
• Развитие производства средств производства —
главное направление индустриализации
© Милитаризация экономики, создание мощно-
го военно-промышленного комплекса
• Высокие темпы индустриализации
Экономические и социальные последствия индустриализации
Положительные Отрицательные
Достижение экономической независимости Создание автаркической экономики
Превращение СССР в мощную индустриаль- но-аграрную державу Создание возможностей для военно-политической экспансии сталинского руководства
73
Экономические и социальные последствия индустриализации
Положительные Отрицательные
Укрепление обороноспособности страны, созда- ние мощного военно-промышленного ком- плекса Замедление развития производства предметов по- требления
Подведение технической базы под сельсдсое хозяйство Формирование политики сплошной коллективиза- ции
Развитие новых отраслей промышленности, строительство новых заводов и фабрик Стимулирование экстенсивного развития экономи- ки, движение к экологической катастрофе
Цели коллективизации сельского хозяйства
• Обеспечение перекачивания средств из
деревни в город на нужды индустриализа-
ции
• Ликвидация «аграрного перенаселения»
• Ликвидация кулачества как класса
О Распространение влияния государства на ча-
стный сектор сельского хозяйства (полное ого-
сударствление экономики)
О Попытки наладить эффективное сельскохо-
зяйственное производство
Экономические и социальные последствия сплошной коллективизации
Экономические последствия Социальные последствия
Перекачивание средств из села в город Отвлечение огромных средств от развития сельскохо- зяйственного производства и инфраструктуры села
Ликвидация кулачества Укрепление социальной базы сталинской диктатуры
Огосударствление сельскохозяйственного производства Отчуждение крестьян от собственности и результа- тов труда, ликвидация экономических стимулов развития сельскохозяйственного производства
Ликвидация «аграрного перенаселения» Массовый «исход» крестьян из деревень, дефицит рабочей силы на селе
Цели и социальные последствия культурной революции в СССР
Цели Социальные последствия
Утверждение марксистской идеологии в каче* стве государственной («революция в умах») Моноидеологизация духовной жизни, насильст- венное внедрение партийных норм понимания культуры, идеологическая изоляция страны
Создание государственной системы образова- ния, обеспечение всеобщего минимизирован- ного образования Ликвидация неграмотности населения, унифика- ция и примитивизация образования, его идеологи- ческая направленность
Формирование социалистической интелли- генции Наличие к 1941 г. в стране 14 млн представителей интеллигенции
Утверждение метода социалистического реа- лизма в литературе и искусстве Унификация духовной жизни, отсечение всего, что не несет «идеологической нагрузки»
Развитие науки и техники Использование крупнейших достижений фундамен- тальной науки прежде всего в интересах ВПК, идео- логизация научных исследований
%1с/пъо/гш1 ^России ЭСЭС^ека & тш/мил/мь
Основные направления национальной политики в СССР в 30-е гг.
• Укрепление унитарного государства
• Развитие в союзных республиках монокуль-
турного сельского хозяйства и добывающей
промышленности
• Введение славянского алфавита в националь-
ных республиках
• Тенденция к русификации народов СССР
• Использование национальных богатств Рос-
сии в интересах укрепления имперской мощи
Союза
• Национально-государственное строительство:
образование автономных республик, автоном-
ных областей, национальных округов, нацио-
нальных районов
• Сведение к минимуму политических и эконо-
мических прав союзных и автономных респуб-
лик (Конституция 1936 г.)
О Нивелирование национальных культур
и подавление национального самосознания
под видом борьбы с национализмом
Политические репрессии в 30-е гг.
1928 г. <Шахтинское дело» 1933 г. Дело о вредительстве на электростан* циях
1928 г. Дело Вели Ибраимова 1936 г. Дело «троцкистско-зиновьевского террористического центра»
1930 г. Процесс над меньшевиками 1937 г. Дело «антисоветского троцкистского центра»
1930 г. Дело Промпартии 1937 г. «Процесс военных»
1933 г. Дело о некомплектной отгрузке ком- байнов 1938 г. Дело «антисоветского правотроцкист- ского блока»
Политические процессы стали одним из важнейших элементов складывавшегося в стране тотали- тарного режима
Высшие органы государственной власти
и управления СССР в 1936—1977 гг.
Внешняя политика СССР в 20—30-е гг.
1922—1933 гг. Прогерманская ориентация советской внешней политики в целях противодействия «главным потенциальным противникам» — Англии и Франции
1933—1939 гг. Переориентация советской внешней политики на западные демо- кратии. Попытки организации единого антифашистского фронта в Европе
1939—1940 гг. Начало нового сближения с Германией. Подписание пакта о нена- падении и договора о дружбе и границе
75
СССР накануне войны
• Увеличение военных расходов (с 5,4% в годы О Переход к кадровой армии. Увеличение чис-
первой пятилетки до 43,4% в 1941 г.) ленности армии (до 5 млн человек)
• Расширение состава СССР (Прибалтика, За- • Создание новых систем вооружения
ладная Украина и Западная Белоруссия, Бес- • Ужесточение производственной дисциплины
сарабия). Война с Финляндией • Усиление патриотического воспитания
Основные этапы Великой Отечественной войны (1941—1945)
Этапы Основные события
22 июня 1941 г. — 18 ноября 1942 г. Битва за Москву Харьковская и Крымская операции Оборона Сталинграда
19 ноября 1942 г. — 1943 г. Контрнаступление под Сталинградом Курская битва Битва за Днепр
1944 г. — 9 мая 1945 г. Освобождение территории СССР и восточноевропейских стран от фашистской оккупации Разгром гитлеровской Германии
Военное производство СССР и Германии в 1941—1942 гг. (в тыс. шт.)
Виды вооружения СССР Германия Виды вооружения СССР Германия
Орудия 157,3 62,6 Самолеты 29,9 20,0
Минометы 272,3 14,0 Пистолеты-пулеметы 1600 560
Пулеметы 462,3 213,2 Винтовки и карабины 5620 2730
Танки 29,2 10,0
Рост объема военного производства в СССР (в % к уровню 1940 г.)
Отрасли 1940 г. 1941 г. 1942 г. 1943 г.
Авиационная 100 126 178 223
Производство боеприпасов 100 152 218 264
Производство вооружения 100 145 191 200
Танковая 100 112 184 234
Органы государственной власти СССР в 1941—1945 гг.
76
^Истл/гия ^России, SK9CРена, & 'пимРммца'ь
Численность немецких войск на фронтах второй мировой войны
Дата Общее кол-во ди- визий На советско-герман- ском фронте На других фронтах На оккупированных территориях и в са- мой Германии
всего в % всего в % всего в %
22 июня 1941 г. 217,5 153,0 70,3 2,0 0,9 62,5 28,8
1 мая 1942 г. 237,5 181,5 76,5 3,0 1,2 53,0 22,3
1 июля 1943 г. 297,0 196,0 66,0 8,0 2,7 93,0 31,3
1 января 1944 г. 318,0 201,0 63,2 19,5 6,2 97,5 30,6
1 июня 1944 г. 326,5 181,5 55,6 81,5 25,0 63,5 19,4
1 января 1945 г. 314,5 179,0 57,0 119,0 38,0 16,5 5,0
Потери СССР в войне
• 27 млн человек
• 1710 городов
• 70 тыс. сел и деревень
• 31 850 заводов и фабрик
• 1135 шахт
• 65 тыс. км железнодорожных путей
О 16 тыс. паровозов
• 428 тыс. железнодорожных вагонов
• 36,8 млн га посевных площадей
• 30% национального богатства
СССР в системе международных отношений в 1941—1945 гг.
Июль 1941 г. Соглашение СССР и Великобритании о совместных действи- ях против Германии
Сентябрь 1941 г. Принятие Великобританией, США и СССР Атлантической хартии
Сентябрь—октябрь 1941 г. Московская конференция представителей США, Великобри- тании и СССР
Январь 1942 г. Подписание Декларации 26 государств об использовании всех их ресурсов для борьбы с фашистской агрессией
28 ноября — 1 декабря 1943 г. Тегеранская конференция лидеров США, СССР и Великобри- тании
21 августа — 28 сентября 1944 г. Конференция представителей трех держав в Думбартон-Оксе
4—11 февраля 1945 г. Ялтинская конференция
25 апреля — 26 июня 1945 г. Конференция Объединенных Наций в Сан-Франциско
17 июля — 2 августа 1945 г. Потсдамская конференция
бЩнсммая nfazfuiJWUL & тлм/лширдь и, фо[миулсиь
Ужесточение сталинского политического режима после войны
• Укрепление власти Сталина в результате побе-
ды в войне
• Дальнейшая централизация государственного
управления, разбухание государственного ап-
парата
• Дальнейшее сужение демократии на предпри-
ятиях, в колхозах, учреждениях
• Увеличение представительства в Советах пар-
тийно-государственной номенклатуры
• Усиление репрессий: «ленинградское дело»,
«дело врачей», борьба с космополитизмом, ре-
прессии против военных
© Депортация народов (чеченцев, ингушей, кал-
мыков, крымских татар, карачаевцев, черке-
сов, балкарцев)
© Ужесточение идеологического пресса
Распределение капиталовложений
в промышленность СССР в 1945—1950 гг.
Легкая и пищевая промышленность
12%
88%
Тяжелая индустрия
Доходы граждан и цены на отдельные товары в 1945—1952 гг.
Средняя зарплата 500 руб. в месяц 1 кг сливочного масла 62 руб.
1 кг хлеба 3—4 руб. 1 десяток яиц 11 руб.
1 кг мяса 28—32 руб. 1 шерстяной костюм 1500 руб.
Репрессии против народов СССР в 1945—1950 гг.
Народы Численность репрессированных, тыс. человек Народы Численность репрессированных, тыс. человек
Литовцы 400 Эстонцы 50
Украинцы 300 Народы Северного Кав- каза и крымские татары 1500
Латыши 150
Внешнеполитический курс сталинского руководства в 1945—1953 гг.
Установление народно-демократических режи- мов в Восточной Европе Насаждение сталинской модели социализма в восточноевропейских странах
1948 г. — договор СССР с Финляндией Возможность мирного сосуществования
1949 г. — создание в СССР ядерного оружия Первый шаг к будущему военно-стратегическо- му паритету. Начало гонки вооружений
1950—1953 гг. — война в Корее Реальная возможность перерастания «холод- ной войны» в «горячую»
GllcmofiiLX ^России ЭРЭС^ена & таЛлищик,
Страны, вошедшие в Совет Экономической Взаимопомощи в 1949 г.
• Болгария • Польша • СССР
• Венгрия • Румыния • Чехословакия
Альтернативы развития страны после смерти Сталина
«Альтернатива» Л. П. Берия
Курс Н. С. Хрущева
Развенчание культа Сталина Первая волна реабилитаций
Перестройка органов безопасности Передача властных функций ЦК КПСС Совмину СССР
Курс на «коренизацию» руководства национальных республик» подъем на-
ционального самосознания Критика колхозного строя, показ его неэффективности Передача ГУЛАГа Минюсту СССР Начало отхода от экстенсивного раз- вития экономики страны Сокращение военных расходов
Предложение об объединении Герма- нии на демократической основе
Ставка на партийный аппарат Приоритетное развитие сельского хо- зяйства и предприятий группы «А»
Продолжение экстенсивного развития экономики Критика культа личности Усиление внимания к развитию науки и техники, освоению космоса Курс на разрядку международной на-
пряженности
Освоение целины Курс на развернутое коммунистиче-
ское строительство Идея перерастания государства дикта- туры пролетариата в общенародное
Курс Г. М. Маленкова
Линия В. М. Молотова—Л. М. Кагановича
Критика культа личности
Приоритетное развитие предприятий
группы «Б»
Смягчение политического режима
Ставка на госаппарат
Усиление экономического стимулиро-
вания производителей
Идея недопустимости мировой войны
—в»- Сохранение сталинского режима в
неизменном виде
Прекращение репрессий против выс-
шего руководства
—Временный перерыв в «холодной
войне»
в условиях существования ядерного
оружия
Попытки интенсифицировать произ-
водство
Экономические преобразования в 1953—1964 гг.
• Децентрализация управления экономикой
• Создание условий для контроля за деятельно-
стью хозяйственных органов «снизу»
• Образование совнархозов
• Ликвидация отраслевого управления эконо-
микой» сокращение и удешевление аппарата
управления
О Попытки стимулировать внедрение достиже-
ний науки и техники в производство
• Изменения в нормировании и оплате труда
79
GlUtwMHaa п/юг/юмд & тас£лищих, а фофм/ум<х>
Реформирование политической системы в 1953—1964 гг.
• Развитие коллективных принципов руковод-
ства
• Частичное сокращение партийного и государ-
ственного аппарата
• Реабилитация политических заключенных
• Курс на обновление состава партийных орга-
нов
• Развитие общественных начал в деятельности
партийных органов
• Предоставление больших прав местным орга-
нам власти, а также союзным и автономным
республикам
• Исправление нарушений в функционировании
судебно-правовой системы
Страны, подписавшие Варшавский Договор в 1955 г.
• Албания
• Болгария
• Венгрия
• ГДР
• Польша
• Румыния
О СССР
• Чехословакия
Экономические реформы 1965 г.
Темпы экономического роста СССР в 1951—1965 гг.
□ сельское хозяйство
80
ал России 9СЭС Явка 6 тси/лицах.
Итоги реформы 1965 г.
в промышленности
Объем промышленного
производства
150%
100%
Последствия свертыва-
ния реформы 1965 г.
1966 г. 1970 г.
1981—1985 гг.
Построено 1900 крупных
промышленных предприятий.
£3 темпы прироста национального дохода
□ темпы роста производительности труда
Доля физического труда в СССР
к началу 80-х гг.
Удельный вес капиталовложений
в жилищное строительство
в СССР в 1966—1985 гг.
Промышленность Строительство Сельское
хозяйство
1981—1985 гг.
Построено квартир:
в 1960 г. — 2 млн, в 1984 г. — 2 млн.
Увеличение импорта продовольствия в СССР в 1985 г. (по сравнению с 1970 г.)
• Мясо и мясопродукты — в 5,2 раза
• Рыба — в 12,4 раза
• Растительное масло — в 12,8 раза
• Зерно — в 13,8 раза
• Сливочное масло — в 183,2 раза
Изменение структуры экспорта СССР в 1960—1985 гг.
Доля машин и оборудования
Доля нефти и газа
1985 г.
6Ц1ком>наяnfifufiaMia & тш/миц1Х и, формулах,
Прирост доходов на душу населения
в СССР в 1966—1985 гг.
Доля фонда зарплаты
в национальном доходе (на 1985 г.)
5,9%
2,1%
80,0%
36,5% 64,0%
СССР США Швеция,
Швейцария
1966—1970 гг.
1981—1985 гг.
Особенности политического и духовного развития страны в 60—70-е гг.
Особенности Социальные последствия
Разрыв между провозглашенными идеалами развитого социализма и реальной жизнью Все большее закоснение партийно-государствен- ных структур
Нерешенность проблем развития национальных республик Постепенное пробуждение национального само- сознания народов
Уход от анализа реальных противоречий обще- ственного развития Нарастание массового скептицизма, политической апатии, цинизма; догматизм в идейной сфере
Обострение идеологической борьбы Запреты и ограничения в духовной жизни; создание образа «внешнего врага»
Идейная реабилитация сталинизма Возвеличивание нового вождя — Л. И. Брежнева
Противостояние официально-догматической и гуманистической, демократической культуры Формирование духовных предпосылок пере- стройки
Периодизация диссидентского движения в СССР
Период становления (1965—1972) Деятельность А. Синявского, Ю. Даниэля, А. Амальрика, Л. Чуковской, А. Гинзбурга, Ю. Галанскова, В. Буковского, А. Марченко, С. Ковалева, Л. Богораз, П. Григоренко и др. Начало кампании против А. Сахарова и А. Солженицына
Период кризиса (1973—1974) Процесс над П. Якиром и В. Красиным
Период широкого международ- ного признания (1974—1975) Расширение географии диссидентского движения. Высылка А. Солженицына из страны. Образование советского отделения Международной амнистии. Присуждение Нобелевской премии мира А. Сахарову
Хельсинкский период (1976—1981) Деятельность Хельсинкской группы. Процессы Ю. Орлова, А. Щаранского, Г. Якунина, А. Марченко. Ссылка А. Сахарова
Внешняя политика СССР в 1965—1984 гг.
РАЗРЯДКА
1965 г. — эскалация американской агрессии •
во Вьетнаме, начало широкомасштабной по-
мощи СССР — ДРВ; индо-пакистанский воо- ©
руженный конфликт и посредничество СССР в ©
его преодолении
1966—1969 гг. — обострение советско-китай- •
ских отношений, поиски выхода из кризиса
1968 г. — подписание договора о нераспро-
странении ядерного оружия
1971 г. — принятие Программы мира
1972 г. — подписание «Основ взаимоотношений
между СССР и США», ОСВ-1 и договора по ПРО
Начало 70-х гг. — подписание ФРГ договоров
об основах отношений с СССР, Польшей, ГДР,
ёРоссим, 2ШС fata &
О
• 1983 г. — начало размещения американских
ракет средней дальности в Европе и советских
БРПЛ у берегов США
• 1984 г. — дальнейшее усиление напряженно-
сти в советско-американских отношениях
ЧССР; подписание четырехстороннего согла- Совещания по безопасности и сотрудничеству
шения по Западному Берлину в Европе; ликвидация очага военной опасно-
1975 г. — подписание Заключительного акта сти в Юго-Восточной Азии
КОНФРОНТАЦИЯ
1968 г. — вмешательство СССР во внутренние
дела ЧССР; широкомасштабная помощь араб-
ским странам Ближнего Востока
1976 г. — начало развертывания в Восточной
Европе советских ракет средней дальности
1979 г. — введение советских войск в Афгани-
стан; начало широкомасштабной войны
СССР в начале 80-х гг
о
ЭКОНОМИКА
• Кризис жесткого бюрократического управле-
ния сельским хозяйством
• Кризис системы внеэкономического принуж-
дения
Закоснелость партийно-государственных
структур
Ужесточение репрессий против инакомысля-
щих
Резкое падение темпов экономического роста
Упрочение командно-административной сис-
темы управления хозяйством
Попытки дальнейшего усиления централиза-
ции управления в ходе реформы 1979 г.
ПОЛИТИЧЕСКАЯ СИСТЕМА
• Усиление бюрократизации государственной
машины
• Усиление противоречий в социально-классо-
вой структуре общества
• Кризис межнациональных отношений
ДУХОВНАЯ СФЕРА
Усиление разрыва между словом и делом О Идейная реабилитация сталинизма
Уход от объективного анализа положения дел • Нарастание массового скептицизма, полити-
в обществе ческой апатии, цинизма
Ужесточение идеологического диктата
Основные этапы перестройки в СССР
1985—1986 гг. Попытки реализации концепции ускорения социально-экономического разви- тия страны
1987 г. Оформление концепции перестройки. Начало экономического реформирования в рамках «консервативной модернизации»
1988 г. Начало осуществления реформы политической системы
1989 г. Формирование новых органов государственной власти — Съездов народных де- путатов СССР. Нарастание экономического кризиса. Первые забастовки шахте- ров. Начало формирования политической оппозиции
1990 г. Начало ликвидации монополии КПСС на власть. Провозглашение суверенитета союзных республик. Первые попытки сближения М. С. Горбачева с либераль- ной оппозицией. Программа «500 дней». Усиление противостояния центра и республик
1991 г. Резкое обострение экономической ситуации. Нарастание социальной напря- женности. Усиление поляризации в руководстве КПСС. Разработка нового Со- юзного договора. ГКЧП. Конец перестройки
83
tyUftOMMox nfwzfMMMa, & maJj-udtfiix, u, фо^мумюъ
кльчъък&теаы. экономического развития СССР в середине 80-х гг.
Модель экономики «сталинского типа» (тра-
диционный советский вариант полностью ого-
сударствленной экономики)
Умеренно-радикальная, ориентированная на
рынок реформа («венгерский» вариант)
Экономика смешанного типа («китайский» ва-
риант)
• Трансформация планового социалистическо-
го хозяйства в рыночное с помощью «шоковой
терапии» («польский» вариант)
• Модель консервативной модернизации («чехо-
словацкий» вариант)
Этапы реформы экономики в СССР (1985—1991)
1985—1986 гг. Попытки сохранить существующую экономическую систему за счет ускорения научно-технического прогресса
1987—1989 гг. Экономическая реформа 1987 г. Ориентация на переход от административных методов к экономическим при сохранении централизованного управления
1989—1990 гг. Признание необходимости экономического плюрализма. Курс на переход к рын- ку. Борьба вокруг эволюционного и радикального вариантов перехода. Приня- тие правительством Н. И. Рыжкова «радикально-умеренного» варианта
1991 г. Непоследовательность и промедление в осуществлении реформы. Углубление экономического кризиса и обострение социальной напряженности
Экономическая реформа 1987 г.
• Расширение самостоятельности предприятий
на принципах хозрасчета и самофинансирова-
ния
• Постепенное возрождение частного сектора че-
рез кооперацию
• Отказ от монополии внешней торговли
• Более глубокая интеграция в мировой рынок
• Сокращение числа отраслевых министерств
• Признание равноправия новых форм хозяйств
на селе (агрокомбинатов, арендных коопера-
тивов и фермерских хозяйств) с колхозами и
совхозами
Этапы политической реформы в СССР (1988—1991)
1988 г. Провозглашение целью реформы соединения социалистических ценностей с эле- ментами либерализма. Возникновение первых политических партий
1989 г. Выборы и первые Съезды народных депутатов СССР. Политизация и радикализа- ция общественного сознания
1990 г. «Парад суверенитетов». Учреждение поста Президента СССР. Нарастание проти- воречий между законодательной и исполнительной властью. Начало ликвидации монополии КПСС на власть
1991 г. Попытки подписания нового Союзного договора. Ослабление позиций консервато- ров. ГКЧП
S4
Основные итоги XIX Всесоюзной конференции КПСС (1988)
• Курс на построение «социалистического пра-
вового государства»
• Утверждение принципа разделения властей
• Формирование «советского парламентаризма»
• Учреждение Съезда народных депутатов СССР
• Превращение Верховного Совета СССР в по-
стоянно действующий парламент
• Изменение избирательного законодательства
• Учреждение Комитета конституционного над-
зора СССР
Органы государственной власти СССР в 1977—1989 гг.
Органы государственной власти СССР в 1989—1990 гг.
85
бЩгюмная и,
Органы государственной власти СССР в 1990—1991 гг.
Партии либерального направления
• Демократический союз
О Российское христианско-демократическое
движение
• Христианско-демократический союз Рос-
сии
О Российская христианско-демократическая
партия
О Конституционно-демократическая партия
(партия «народной воли»)
• Консервативная партия
• Либерально-демократическая партия
© Демократическая партия России
• Республиканская партия Российской Федера-
ции
Партии социалистического выбора
О Коммунистическая партия Российской Феде-
рации
• Социалистическая партия
• Народная партия свободной России
• Социалистическая партия трудящихся
• Российская коммунистическая рабочая пар-
тия
Ф Всесоюзная коммунистическая партия боль-
шевиков
• Союз коммунистов
Национальные партии и движения
• Православный российский монархический ор-
ден-союз
• Русский национальный собор
О Национально-патриотический фронт «Па-
мять»
О Русское освободительное движение
86
^России ЖУ/ аидюбивсуик
Основные принципы нового политического мышления
О Признание единства противоречивого мира
• Признание невозможности решения полити-
ческих задач с помощью ядерной войны
О Признание невозможности обеспечения безо-
пасности страны военными средствами
О Придание военным доктринам оборонитель-
ного характера
О Признание за каждым народом права на вы-
бор пути развития
• Отказ от переноса идеологических разногла-
сий в сферу межгосударственных отноше-
ний
О Превращение разоружения в фактор общест-
венного развития
Основные направления внешней политики СССР в 1985—1991 гг.
• Отказ от давления и диктата в отношениях со
странами социализма
• Нормализация отношений Восток—Запад
посредством разоружения
О Разблокирование региональных конфликтов
О Установление тесных контактов со всеми
странами, без оказания предпочтения стра-
нам социализма
Предпосылки и последствия распада СССР
Предпосылки Последствия
Глубокий экономический и политический кри- зис в СССР Нарушение экономических связей между быв- шими республиками
Рост национального самосознания Ослабление обороноспособности всех республик
Дискредитация центральной власти Обострение межнациональных конфликтов
Усиление амбиций политических лидеров и ме- стной бюрократии Ухудшение социально-экономического положе- ния населения
Первые итоги экономических реформ 1992—1997 гг.
• Демонтаж плановой экономики
• Переход к преимущественно экономическим
методам регулирования
• Завершение первого этапа приватизации
• Формирование потребительского рынка
• Перемещение деловой активности в негосу-
дарственный сектор
• Обеспечение внутренней конвертируемости
рубля
• Пополнение золотого и валютного запасов
• Постепенная интеграция экономики России
в мировое хозяйство
Социальные потери в ходе реформирования
• Обесценивание денежных сбережений насе-
ления
• Резкий рост цен на товары первой необходи-
мости
• Увеличение уровня безработицы
• Высокий уровень инфляции в 1992—1995 гг.
• Сокращение объемов промышленного и сель-
скохозяйственного производства
• Многократное сокращение расходов на нау-
ку, образование, культуру, здравоохранение
• «Четвертая волна» эмиграции из России.
«утечка мозгов» и талантов из страны
• Рост смертности населения
• Рост коррупции и злоупотреблений служеб-
ным положением
О Ухудшение криминогенной обстановки
• Увеличение налогов на мелкого предприни-
мателя и «среднего» россиянина
87
^Школьная nfuttfioMMa, $ тас/лимрк и, фо^лдаах,
Основные причины трудностей
и неудач реформ 90-х гг. в России
• Неблагоприятная социально-экономическая ситуация
• Половинчатость и непоследовательность реформ
• Ошибки теоретиков и исполнителей реформ
Органы государственной власти
Российской Федерации в 1993—1997 гг.
Президент Российской Федерации
• Является главой государства
• Определяет основные направления внутрен-
ней и внешней политики
• Формирует Правительство РФ
• Представляет Совету Федерации кандидатов
на должности судей Конституционного Суда,
Верховного Суда, Высшего Арбитражного Су-
да, Генерального прокурора РФ
• Формирует и возглавляет Совет Безопасности
О Является Верховным Главнокомандующим
Вооруженными Силами РФ
• Назначает выборы в Государственную Думу
• Распускает Государственную Думу
• Назначает референдум
• Вводит чрезвычайное или военное положение
на территории страны
• Подписывает и обнародует федеральные
законы
Федеральное Собрание
• Утверждает Федеральный бюджет и налоги • Ратифицирует международные соглашения
• Принимает федеральные законы О Объявляет войну и заключает мир
^11стъо/гая ^России 9СЭС&ка & тшРшцах,
Совет Федерации
О Утверждает границы субъектов Федерации
О Утверждает указы Президента РФ о введении
чрезвычайного или военного положения
® Назначает выборы Президента РФ
• Назначает на должность судей Конституци-
онного Суда, Верховного Суда и Высшего Ар-
битражного Суда РФ
• Назначает на должность и освобождает от
должности Генерального прокурора РФ
О Назначает на должность и освобождает от
должности заместителя председателя Счетной
палаты и 1/2 ее членов
Государственная Дума
• Рассматривает вопрос о назначении Председа-
теля Правительства РФ
• Решает вопрос о доверии Правительству РФ
О Назначает на должность и освобождает от
должности председателя Центрального бан-
ка РФ
• Назначает на должность и освобождает от
должности председателя Счетной палаты и 1 /2
ее членов
© Объявляет амнистию
Правительство Российской Федерации
• Разрабатывает и представляет в Госдуму Фе-
деральный бюджет и обеспечивает его выпол-
нение
О Обеспечивает проведение в стране единой фи-
нансовой, кредитной и денежной политики
О Обеспечивает проведение в РФ единой госу-
дарственной политики в области культуры,
науки, образования, здравоохранения, соци-
ального обеспечения, экологии
Конституционный Суд
• Разрешает дела о соответствии Конституции
РФ федеральных законов, нормативных актов
центральной и местной власти, международ-
ных договоров РФ
• Управляет федеральной собственностью
• Осуществляет меры по обеспечению обороны
страны, государственной безопасности, реа-
лизации внешней политики
О Осуществляет меры по обеспечению законно-
сти, прав и свобод граждан, охране собствен-
ности и общественного порядка, борьбе с пре-
ступностью
Верховный Суд
• Является высшей судебной инстанцией по гра-
жданским, административным и иным делам,
подсудным судам общей юрисдикции
Высший Арбитражный Суд
• Является высшим судебным органом по разрешению экономических споров
Всемирная история в таблицах
Этапы эволюции человека
Космическая эволюция, появление жизни на Земле Продолжалась несколько сот млн лет и в ос- новном завершилась в XVII—XII тыс. до н. э.
Биологическая эволюция человека ок. 3 млн лет назад
Культурная эволюция человека ок. 45 тыс. лет до н. э.
Цивилизационное развитие человека в процессе культурной эволюции ок. 8 тыс. лет до н. э.
Периоды эволюции древних цивилизаций
Период первобытной родовой общины (предыстория) 45 000—8000 гг. до н. э.
Период протогосударств 8000—3500 гг. до н. э.
Период древних империй 3500—600 гг. до н. э.
Период античных государств 600 г. до н.э. — 476 г. н. э.
Основные зоны древних цивилизаций
Евро-афро-азиатская Бассейн р. Нил, междуречье Тигра и Евфрата, восточная часть Средизем- номорского побережья
Восточноазиатская Бассейн р. Хуанхэ
Южноазиатская Бассейн р. Инд
Древние государства Востока
Египетская империя 3200—525 гг. до н. э.
Вавилонская империя ок. 3000—538 гг. до н. э.
Ассирийская империя 3000—605 гг. до н. э.
90
Древние государства Востока
Финикийская империя конец Ш тыс. — 322 г. до н. э.
Китайская империя 1765 г. до н. э. — 220 г. н. э. (хронология империи 5 династий до 2000 г. до н. э. науке неизвестна)
Империи древней Индии Х¥Ш в. до н. э. — 415 г. н. э.
Израильское и Иудейское княжества 1400—536 гг. до н. э.
Древнейшие славянские археологические памятники
на территории России (I тыс. до н. э.)
Памятники Городища Памятники Городища
р. Десна Юхновское р. Волга (г. Калязин) у села Городище
р. Ока Старшее Каширское р. Сож (Смоленщина) Лахцеевское
р. Ока Кондраковское г. Москва Дьяковское
Древние цивилизации Востока: политические признаки
• Деспотический характер власти
• Власть сосредоточена в руках правителя
• Возникла харизма вождя
• Утвердился принцип наследования власти
О Начала складываться система силовых власт-
ных структур
• Сформированы многочисленные вооружен-
ные силы
• Появились законодательные основы власти
• Оформилась пирамида власти: органы цен-
тральной власти и местного самоуправления
• Положено начало дипломатической практике
Факторы становления античных цивилизаций
• Ускорение темпов культурной эволюции в ос-
новных цивилизационных зонах
0 Достижения агрокультуры и разнообразных
ремесел
• Развитие товарно-денежных отношений
• Освоение письменности, новый уровень нако-
пления знаний
• Совершенствование законотворчества, его
внедрение в политику и общественную жизнь
Э Возникновение и распространение морально-
этических учений
• Интенсивное развитие международных и меж-
государственных связей
Античные цивилизации: политические признаки
• Заложены основы демократии, республикан-
ской формы правления
• Заложены основы гражданского права и су-
дебной системы
91
• Определены принципы организации коллек-
тивной власти
• Отсутствовала деспотия вождя
• Сформировалась демократическая олигархия
• Дальнейшее развитие получила военная орга-
низация государства
• Усложнились функции государства
• Положено начало межгосударственным союзам
• Появились политические партии и межпар-
тийная борьба за власть
Древнегреческие историки
Имя Годы жизни Главное произведение
Геродот 480—425 гг. до н. э. «История» (в 9 кн.)
Фукидид 460—386 гг. до н. э. «История» (в 8 кн.)
Ксенофонт Афинский 430—380 гг. до н. э. ♦Греческая история»
Полибий 205—125 гг. до н. э. «Всеобщая история» (в 40 кн.)
Диодор Сицилийский 90—21 гг. до н. э. «Историческая библиотека» (в 40 кн.)
Квин Курций Руф I в. до н. э. «История Александра Македонского» (в 10 кн.)
Плутарх 45—127 гг. н. э. «Сравнительные жизнеописания» (50 выдаю- щихся греков и римлян)
Гай Саллюстий Крисп 86—35 гг. до н. э. «История» (в 5 кн.)
Дионисий Галикарнасский I в. до н. э. «Римские древности» (в 20 кн.)
Тит Ливий 59 г. до н. э. — 17 г. н. э. «История от основания Рима» (в 142 кн.)
Корнелий Тацит 55—120 гг. н. э. «Анналы» (в 16 кн.), «История» (в 16 кн.)
Гай Светоний Транквилл 75—180 гг. н. э. «Жизнь двенадцати Цезарей»
Аппиан ?—170-е гг. н. э. «Римская история» (в 24 кн.)
Дион Кассий 155—235 гг. и. э. «Римская история» (в 80 кн.)
Аммиан Марцелин 330—400 гг. н. э. «История» (в 31 кн.)
Факторы влияния античных цивилизаций
на менталитет европейцев
* Накопление знаний
• Отсутствие деспота-правителя
• Неотягощенность хозяйственными заботами
значительной части граждан
• Изменения в характере труда
О Давление идеологии войны
• Углубление социальной дифференциации
• Углубление культурной эволюции
• Обычаи и традиции общины-полиса
• Мифология и отсутствие идеологии харизмы
вождя
• Пережитки тотемизма
92
ил 6 тас/лиирх
Основные стадии цивилизационного
обновления Европы в средние века
Раннее средневековье V — конец XI в. Цивилизационный выбор
Зрелое средневековье XII—XV вв. Становление цивилизации интенсивного типа
Позднее средневековье XVI — середина XVII в. Бурное развитие цивилизации
Варварские королевства в период раннего средневековья
Вестготское 419—511 гг. Одоакра 476—493 гг.
Вандальское 429—545 гг. Франкское 486—843 гг.
Бургундское 457—534 гг. Остготское 493—554 гг.
Система управления Китаем во времена династии Тан (618—907)
Разделение христианской церкви (1054)
93
\ 6 'тлялищнс, и,
Крестовые походы
Первый 1096—1099 гг. Пятый 1217—1221 гг.
Второй 1147—1149 гг. Шестой 1228—1229 гг.
Третий 1189—1192 гг. Седьмой 1248—1254 гг.
Четвертый 1202—1204 гг. Восьмой 1270 г.
Доминанты ментальности древних славян
• Языческое мировоззрение
• Харизматические идеи
• Социокультурная толерантность
• Прямодушие, честность, гостеприимство, не-
притязательность
• Высокая коммуникабельность
Этнические факторы формирования
древнерусской народности
Предпосылки образования
Древнерусского государства
Развитие производительных сил восточнославянских племен Формирование соседской общины Развитие торговли, в т. ч. международной Рост имущественного неравенства Появление системы управления Наличие союзов славянских племен Выделение племенной знати
Аналоги — империя Каролингов, Болгария, Венгрия, Польша
94
^селмАмая tumofiux 6 тм/милдх,
Основные этапы формирования древнерусской государственности
Этапы Временные рамки Правящие князья
Начальный середина IX — конец X в. Олег (882—911), Игорь (912—945), Ольга (945—964), Святослав (964—972)
Расцвет конец X — первая половина XI в. Владимир (980—1015), Ярослав (1015—1054)
Упадок, распад вторая половина XI — середина XII в. Владимир Мономах (1113—1125)
Русская Правда — древнейший свод законов Руси
Особенности южных и северо-восточных земель Древней Руси
Южная Русь Северная и Северо-Восточная Русь
Почва Плодородный чернозем, степи Суглинок, болота, первобытный лес
Реки Полноводные, как правило, притоки Днепра Масса мелких, не имеющих общего центра
Климат Мягкий Суровый
Византийское влияние на Русь после введения христианства
(по С. Ф. Платонову)
Власть Власть митрополита распространялась на всю Русь
Землевладение Церкви и монастыри получали в собственность земли. На церковных землях ус* танавливались византийские обычаи и законы
Просвещение Распространение письменности, создание школ, появление книжников — ученых людей
Законы и суды Духовенство судило подчиненных им людей на основе законов греческой церкви
95
Структура вооруженных сил
Древнерусского государства (X—XII вв.)
Причины раздробленности единого Русского государства
Раздел территории между наследниками Княжеские усобицы Рост крупного землевладения Натуральный характер хозяйства Активное развитие ремесел Рост и усиление городов Усиление местного аппарата управления
Аналог — империя Каролингов
Сословные представительные органы в Европе в средние века
Страна Время образования Название органа
Испания 1188 г. Кортесы
Англия 1365 г. Парламент
Франция 1302 г. Генеральные штаты
Швеция 1435 г. Риксдаг
Германия середина XV в. Рейхстаг
Нидерланды 1463 г. Генеральные штаты
Дания 1468 г. Фолькетинг
Польша конец XV в. Сейм
Основные формы политического устройства удельной Руси
Республика Абсолютная монархия Ограниченная монархия
Новгород, Псков Галич, Волынь Владимир, Суздаль
Западные и восточные аналоги
Генуя, Венеция Золотая Орда Византия
96
SftceMufiHax ticmofi
ал 6 тасЕширх,
Структура новгородской демократии
Аналог — Ганзейский союз
Завоевания монголо-татар в XIII в.
Годы Основные события
1219—1223 Поход в Среднюю Азию, Иран, Закавказье, на Кавказ, в половецкие степи
1223 Битва на Калке. Поражение русских войск
1236 Начало похода на русские земли
1237—1238 Завоевание Владимиро-Суздальской земли
1239—1242 Нашествие на южнорусские земли. Вторжение в Европу
Войны Северо-Восточной Руси 1228—1462 гг. (поН. С. Голицыну)
ВНУТРЕННИЕ ВОЙНЫ
ВНЕШНИЕ ВОЙНЫ
Всего — 90
Битвы — 20 (15 в 1425—1453 гг.)
Взятие городов — 35
Неудачные осады — 5
Всего — 160, в том числе:
со шведами и волжскими болгарами — 44
с литовцами — 41
с ливонцами — 30
с монголо-татарами — 45
Битвы — 50 (в 30 русские одержали победу)
Взятие русских городов — 70
Взятие русскими городов — 15
Неудачные осады — 7
Отражение штурмов противника — 17
Содержание монголо-татарского ига
О Номинальная независимость русских княжеств
О Княжение по ярлыку
• Контроль баскаков за деятельностью князей
• Выплата «выхода» — дани Золотой Орде
• Террор как метод управления
4—1323
97
<^Лм>ль'кая пфлгфал^ма $ таг/лилуасс- и, формулам
Объединение земель вокруг Москвы
Даниил Александрович (1276—1303) Коломна, Переяславль-Залесский
Дмитрий Донской (1359—1389) Углич, Белоозеро, Калуга, Стародуб, Дмитров, Кострома, Галич
Василий 1(1389—1425) Ниж. Новгород, Муром, Вологда, Двинская земля, Малая Пермь
Иван Ш (1462—1505) Ярославль, Ростов, Великая Пермь, Новгород, Тверь, Вятская земля, Чернигов, Новгород-Северский, Стародуб, Брянск, Мценск, Любутск, Гомель, Рыльск
Василий III (1505—1533) Псков, Рязань, Смоленск
Реформы Ивана Грозного в середине XVI в.
1549 г. 1-й Земский собор 1551 г. Стоглавый собор
1550—1556 гг. Военная реформа 1553—1560 гг. Приказная реформа
1550 г. «Избранная тысяча» 1555—1556 гг. «Уложение о службе»
1550 г. Судебник 1556 г. Отмена кормлений
1550 г. «Большая соха»
Территориальное расширение Российского государства в XIV—XIX вв.
Этапы Содержание Результат
I. XIV — середина XVI в. Собирание русских земель вокруг Москвы Образование Русского цен- трализованного государства
II. Середина XVI — конец XVH в. Присоединение других народов (Казань, Сибирь, Украина и т. д.) Россия становится цивили- зационно-неоднородным об- ществом
III. XVIII — начало XIX в. Включение в состав России социумов запад- ного типа (Эстония, Латвия, Литва, Поль- ша, Финляндия и др.)
IV. 20—80-е гг. XIX в. Завоевание Кавказа, Средней Азии. Присое- динение Амурского и Уссурийского краев
Начало книгопечатания на Руси
Дата Событие
1 2
1563 г. Сооружение типографии в Москве
’ 564 г. Издание «Апостола»
98
^семм^.ная uomcfum & пии/лии^их.
Начало книгопечатания на Руси
1 2
1565 г. Издание «Часовника»
Вторая половина XVI в. Издано 20 книг тиражом до 1000 экземпляров каждая
Сущность опричнины в оценках историков
Борьба аристократии с нарождающимся самодержавием Н. П. Павлов-Сильванский, С. Ф. Платонов
Прогресс в утверждении государственных начал над родовыми С. М. Соловьев
Террор — условие сохранения самодержавия Д. Альшиц
Деспотизм и насилие в отношении всех слоев населения С. Б. Веселовский, А. А. Зимин
Борьба удельного и централизованного порядка В. В. Кобрин
Следствие душевной болезни Ивана IV Н. М. Карамзин
Аналог европейского выделения личного домена государя М. В. Довнар-Запольский
Гипертрофированная централизация государственной власти В. О. Ключевский
Итоги опричнины
Разрушена сословная монархия Из 43 членов Боярской думы казнено 19, пострижено в мо- нахи— 3
Разрушена экономика страны Разорено 40% крестьянских дворов. Пашенные земли в центральных районах сократились с 15 до 4 десятин
Огромные жертвы По Синодику Ивана IV уничтожено 22 тыс. человек, в ходе карательной экспедиции в Новгороде — до 15 тыс. человек
Нарушены организация и комплек- тование поместного войска Для испомещения 6 тыс. опричников выселены из своих поместий 9 тыс. дворян
Уничтожен класс собственников
Установлены отношения подданства
Структура «Домостроя» (XVI в.)
Всего около 70 глав
99
Основные черты развития западной цивилизации в XVII—XVIII вв
• Становление капитализма — нового хозяйст-
венного уклада и новой формы собственности
О Рост народонаселения
• Новые технические открытия и развитие ин-
женерной мысли
• Интенсификация труда
• Рост разделения труда и товарного производ-
ства, купеческого капитала и предпринима-
тельства
Ход Нидерландской буржуазной революции
Год Событие
1556 Начало народного восстания против владычества Испании
1572 Восстание нидерландских моряков на севере страны
1577 Захват буржуазией власти в Брюсселе
1579 Заключение соглашения между южными провинциями и Испанией
1579 Подписание северными провинциями Утрехтской унии
1581 Объявление Генеральными штатами о создании Республики Соединенных провинций (Гол- ландии)
Тенденции развития европейской цивилизации в XVII в.
• Утверждение рыночных отношений
• Формирование третьего сословия
• Формирование капитала за счет развития ма-
нуфактур
• Пролетаризация населения и разорение де-
ревни как следствие вступления западного
мира в индустриальную эпоху
Формы колониальной экспансии Запада в XVII в.
Освоение поселенцами-колонистами пустовавших или сла- бозаселенных земель Северная Америка, Австралия, Новая Зеландия, Южная Африка
Миграция новопоселенцев в районы со значительным мест- ным населением и глубокими традициями Южная и Центральная Америка
Колонизация районов с неблагоприятными для европейцев условиями обитания и преобладанием местного населения Африка, Индонезия, Океания, некоторые страны Азии
Колонизация стран с многовековой культурой и сложив- шейся государственностью Индия
Торговые форпосты европейцев в XVII в.
Название компании Задачи
Английская Ост-Индская торговая компания (с 1600 г.) О Осуществление широкой заморской торговли • Борьба с европейскими соперниками О Подавление сопротивления коло- низируемых народов
Голландская Ост-Индская торговая компания (с 1602 г.)
। Голландская Вест-Индская торговая компания (с 1621 г.)
100
нал история 8 пии/лшцгх,
Этапы Тридцатилетней войны (1618—1648)
Этапы Годы Этапы Годы
Чешско-пфальцский 1618—1623 Шведский 1630—1634
Датский 1624—1629 Франко-шведский 1635—1648
Россия в начале XVII в.
Последствия Смуты Задачи, стоявшие перед правительством Направления перемен
Пресечение правя- щей династии Распад политиче- ской структуры общества Восстановить самодержавие Преодолеть духовную разобщенность Ликвидировать разруху и отсталость Поднять жизненный уровень народа Укрепление абсолютной монархии Создание крупной промышленности Развитие внутренней торговли Укрепление единства церкви Создание регулярной армии Получение выхода к морям Расширение связей с другими государствами
Основные мероприятия в царствование Алексея Михайловича (1645—1676)
Законодательные Уложение 1649 г. Кормчая книга 1650 г. Новоторговый устав 1667 г. Частные законоположения
В сфере религии Исправление книг и обрядов Уточнение отношения церкви к государству
Внешнеполитические Присоединение Украины
Государственный аппарат России в XVII в.
101
пАоЖыьма & та</лииАК и, фоЬмммих
Русская армия в XVII в.
Сословное представительство на Земских соборах XVII в.
Противостояние между Османской империей и Россией в XVII в.
Годы Главные события
1637—1642 Овладение Азовом и оставление крепости
1676—1681 Русско-турецкая война
1677—1678 Попытки османов взять крепость Чигирин (Правобережная Украина). Вторая по- пытка была успешной
1681 Бахчисарайский мир: перемирие на 20 лет
Рост территории Российского государства в XVI—XVII вв.
Год Период Площадь, тыс. кв. км
1505 Конец царствования Ивана Ш 2200
1584 Конец царствования Ивана IV 4125
1613 Начало царствования династии Романовых 8580
1654 Конец царствования Михаила Федоровича 2375
1676 Конец царствования Алексея Михайловича 14 520
102
исты
Численность дворянства (мужчины) в России в XVII—XIX вв.
1651 г. 1782 г. 1858 г.
4 464 000 108 000 39 000
По переписи 1897 г., 53% потомственных дворян назвали родным языком русский
Социальные движения в XVII в. и их причины
Соляной бунт 1648 г. Соль облагалась дополнительной пошлиной
Хлебный бунт 1650 г. Резкое повышение цен на хлеб
Медный бунт 1662 г. Выпуск медной монеты, приравненной по стоимости к серебряной
Русское население в Сибири в XVII в. (тыс. человек)
152 788
1622 г. 1662 г. 1709 г.
Внешняя торговля России в XVII в.
Экспорт Импорт Торговые партнеры
Вина, пряности, тонкие сукна, металли- ческие изделия, бумага, золотые и сереб- ряные поделки, аптекарские товары и др. Меха, лес, смола, деготь, лен, пень- ка, кожа, поташ, холст, щетина, са- ло, мясо, икра, хлеб и др. Англия, Голландия, Швеция, Польша, Персия, Бухара и др.
Социальная структура России в первой четверти XVIII в.
Податное население В том числе: крепостные свободное городское население работные люди Дворянство Высшее дворянство 5,6 млн мужских душ, в т. ч. 5,4 млн — на селе 3,2 млн человек 170 тыс. человек 30 тыс. человек 15 тыс. человек, 3 тыс. фамилий, 380 тыс. дворов 500 фамилий, 100 дворов
/03
бЩномтал nfwbfiaMMit6mat/лимрх и,
Органы власти и управления в России в первой четверти XVIII в
Изменения в духовной сфере Российского государства
в первой четверти XVIII в.
Ликвидация независимости церкви от государства Упразднен институт патриаршества Учрежден Святейший Синод — 1721 г.
Создание системы светского об- разования I ступень — 50 «цифирных школ* II ступень — военно-учебные заведения, медицинская, матема- тическая и другие школы Первые учебники: «Арифметика*, «Механика*, «Брюсов ка- лендарь*, «История Свейской войны* Проект основания Академии наук (1724)
Зарождение системы информи- рования населения Газета «Ведомости» (1703) Церковнославянский шрифт заменен гражданским (1708)
104
Основные направления внешней политики России в первой четверти XVIII в.
• Борьба за выход в Балтийское море, развитие • Упрочение позиций России на Каспии и в За-
связей с Европой кавказье
• Борьба за выход в Черное море
Северная война (1700—1721)
1700—1706 гг. Военные успехи Швеции и неудачи России
1707—1709 гг. Единоборство России и Швеции, завершившееся Полтавской битвой
1710—1721 гг. Военные поражения Швеции и успехи России и ее союзников
Реформа государственной власти во второй половине XVIII в.
(проект Н. И. Панина)
Народные восстания во второй половине XVIII в.
1768 г. Крестьянское восстание на Правобережной Украине
1771 г. «Чумной бунт» в Москве
1771 г. Восстание яицких казаков
1773—1775 гг. Крестьянская война под предводительством Е. Пугачева
Политическая структура США: основополагающие принципы
• Система противовесов в осуществлении вла-
стных функций
• Разделение властей
® Независимость ветвей власти друг от друга
© Судебный конституционный надзор
© Федерализм
105
• Постоянное обновление и соблюдение преем-
ственности коллективных органов законода-
тельной власти
о Всеобщее избирательное право
О Многоступенчатые выборы
О Мажоритарная система избрания кандидатов
Особенности американских социумов в XVIII — первой половине XIX в.
Север Юг
Господство свободного труда Широкое применение труда рабов
Фермерский тип землевладения Латифундистский тип землевладения
Развитие капиталистических отношений Консервация рабовладельческих отношений
Стремление к национальной свободе Лояльность по отношению к британской короне
Активная борьба за независимость Пассивное сопротивление колониальным порядкам
После завоевания государственной независимости
Борьба за сильную власть центра Стремление к федерализму
Участие США в войнах (1770-е гг. — конец XIX в.)
Годы Название Участвовало Погибло Ранено
1775—1783 Война за независимость нет данных 4435 6188
1812—1815 Война с Англией 226 730 2260 4405
1846—1848 Мексиканская война 78 705 13 283 4152
1861— 1865 Гражданская война 2 213 363 364 511 281 881
1898 Испано-американская война 306 760 2446 1162
Циклы американской истории от образования США до начала XX в.
1776—1789 гг. Выработка и принятие конституции США
1789—1800 гг. Противодействие консерваторов
1800—1812 гг. Период реформ республиканцев
1812—1829 гг. Период уступок Джефферсона
1829—1841 гг. Эра демократии Джэксона
1841—1861 гг. Господство рабовладельцев в национальном руководстве
1861—1869 гг. Ликвидация рабства
1869—1901 гг. Консервативное правление
106
SfcccMMfiHaz истомил 6 тси/мифк
Партийная принадлежность президентов США (до XX в.)
Политические партии Президенты Годы Политические партии Президенты Годы
Федералисты Дж. Вашингтон Дж. Адамс 1789—1797 1797—1801 Демократичес- кая М. Филмор Ф. Пирс Дж. Бьюкенен Э. Джонсон С. Г. Кливленд 1850—1853 1853—1857 1857—1861 1865—1869 1885—1889, 1893—1897
Республиканско- демократическая Т. Джефферсон Дж. Медисон Дж. Монро Дж. К. Адамс 1801—1809 1809—1817 1817—1825 1825—1829
Демократическая Э. Джэксон М. Ван Бурен У. Г. Гаррисон Дж. Тайлер Дж. Н. Полк 3. Тейлор 1829—1837 1837—1841 1841 1841—1845 1845—1849 1849—1850 Республикан- ская А. Линкольн У. С. Грант Р. Б. Хейс Дж. А. Гарфилд Ч. А. Артур Б. Гаррисон У. Мак-Кинли 1861—1865 1869—1877 1877—1881 1881 1881—1885 1889—1893 1897—1901
Этапы реформирования России в первой четверти XIX в.
(по А. А. Корнилову)
1801—1805 гг. Приступ к реформам 1812—1815 гг. Приостановка реформ
1805—1807 гг. Приостановка реформ 1816—1818 гг. Продолжение реформ
1808—1812 гг. Второй приступ к реформам 1819—1825 гг. Отказ от реформ
Русские национальные начала
(по С. С. Уварову)
* Православие: без любви к вере предков на-
род, как и частный человек, должен погиб-
нуть
• Самодержавие — основное условие политиче-
ского существования России
• Народность: сохранение неприкосновенным
святилища народных понятий
О Цель: «Изгладить противоборство так назы-
ваемого европейского образования с потреб-
ностями нашими; исцелить новейшее поко-
ление от слепого, необдуманного пристрастия
к поверхностному и иноземному, распростра-
няя в оных душах радушное уважение к оте-
чественному.. . >
Порядок обеспечения крестьян земельными наделами
(по Манифесту 19 февраля 1861 г.)
• Устанавливался двухлетний срок составле-
ния уставных грамот
• Крестьяне переводились на положение «вре-
меннообязанных» до их перевода на выкуп
О Крестьяне осуществляли выплату выкупных
платежей
О По окончании выплаты земельные наделы
становились собственностью крестьян
107
п/юг/шм £ таблицам и, фсй^шмс
Принципы организации суда присяжных во второй половине XIX в.
• Бессословность судопроизводства
• Гласность и публичность состязательного про-
цесса
О Независимость судей от администрации
О Решающая роль присяжных заседателей в
определении виновности подсудимого
Экономическая политика С. Ю. Витте (90-е гг. XIX в.)
• Протекционизм в промышленности
• Строительство железных дорог, создание ин-
фраструктуры
• Установление золотого монометаллизма
• Привлечение иностранного капитала
О Изыскание внутренних источников финанси-
рования промышленности
О Одобряя «индустрию», власти опирались на
отношения традиционного общества
• Цель: догнать в индустриальном развитии ве-
дущие страны мира
Мировое производство стали в конце XIX в. (млн тонн)
Страна 1880 г. 1890 г. 1898 г.
Все страны мира 261 738 1469
Россия 19 23 70
Англия 81 222 283
Франция 24 35 88
Германия 43 132 350
США 77 265 552
Доля развитых стран в мировом промышленном производстве (%)
Годы Германия Франция Англия США
1870 13,2 10,3 31,8 23,3
1896—1900 16,6 7,1 19,5 30,1
1913 15,9 6,4 14,0 35,8
Степень милитаризации стран Европы в 80-е гг. XIX — начале XX в.
Страна Рост численности армии, % Число военнослужащих на 1000 мужчин Содержание армии и флота, руб. на 1 жителя
1 2 3 4
Англия 38,8 25,6 15,2
Франция 48,7 52,5 12,5
108
истерия 4 теи/лиироь
Степень милитаризации стран Европы в 80-е гг. XIX — начале XX в.
1 2 3 4
Италия 22,9 27,4 6,3
Германия 44,3 48 9,1
Австро-Венгрия 107 34 4,9
Россия 19,5 33,7 3,9
Военные расходы России в XIX в.
Год Млн руб. Доля в гос. расходах, %
1832 59,3 41,9
1877 218,1 34,5
1897 379,06 29,2
Военные расходы стран Европы в 1897 г. (на душу населения, руб.)
Англия 10,22
Франция 9,12
Германия 6,22
Австро-Венгрия 3,65
Россия 2,99
Расходы Военного министерства России в XIX в. (млн руб.)
Главные статьи расходов 1863 г. 1870 г. 1874 г.
Содержание войск 79,7 87,08 100,8
Административные расходы 10,9 16,5 18,9
Вооружение 4,03 13,8 17,4
Содержание военных заводов 0,3 0,8 —
Всего 94,93 118,18 137,1
Партийная принадлежность президентов США (XX в.)
Республиканская партия Годы Демократическая партия Годы
Т. Рузвельт 1901—1909 Т. В. Вильсон 1913—1921
У. Ф. Тафт 1909—1913 Ф. Д. Рузвельт .. 1933—1945 .
109
СШкмьо<ая £ тас/лилщх, и, <£юклшла(ь
Партийная принадлежность президентов США (XX в.)
Республиканская партия Годы Демократическая партия Годы
У. Г. Гардинг 1921—1923 Г. Трумэн 1945—1953
К. Кулидж 1923—1929 Дж. Ф. Кеннеди 1961—1963
Г. К. Гувер 1929—1933 Л. Джонсон 1963—1969
Д. Д. Эйзенхауэр 1953—1961 Дж. Э. Картер 1977—1981
Р. М. Никсон 1969—1974 Б. Клинтон Избран до 2001 г.
Дж. Р. Форд 1974—1977
Р. У. Рейган 1981—1989
Дж. Г. У. Буш 1989—1993
Политические партии России в революции 1905—1907 гг.
Партии Числен- ность, тыс. чел. Социальный состав
предприниматели, землевладельцы интелли- генция служащие рабочие крестьяне
Монархисты 410 4- 4- 4- 4- +
Эсеры 65 — 11,6 43,2 45,2
РСДРП 170 — 30—31 5 64 —
Кадеты 50 10—20 65 15
Аграрный вопрос в России в начале XX в.
Землевладение Причины кризиса Столыпинская реформа
Казенные удельные, церков- ные земли — 154,6 млн дес. Надельные крестьянские зем- ли — 138,7 млн дес. Частновладельческие земли — 101,7 млн дес. Малоземелье и аграрное пере- население крестьян Низкая механизация и агро- культура Преобладание малоимущих слоев и невозможность интен- сификации производства Передача надела в частную собственность (хутор, отруб) Силовое обеспечение выхода крестьян из общины Кредиты Крестьянского банка Переселение в малообжитые районы
Первая мировая война (1914—1918)
О Продолжительность — 1554 дня
О Число стран-участниц — 38
О Состав коалиций: Англия, Франция, Россия,
США и еще 30 стран; Германия, Австро-
Венгрия, Турция, Болгария
О Число нейтральных государств — 17
О Число государств, на территории которых
проходили боевые действия — 14
О Численность населения стран — участниц
войны — 1050 млн человек (62% населения
земли)
© Численность мобилизованных — 74 млн че-
ловек
© Численность погибших — 10 млн человек
7/6»
нал шуты
Основные причины первой мировой войны
• Стремление развитых стран к экспансии —
территориальному, военно-политическому, фи-
нансово-экономическому, социокультурному
расширению
• Многовековое соперничество:
между Францией и Германией;
между Австро-Венгрией и Россией на Бал-
канах;
между Россией и Германией в польском воп-
росе;
между Германией и Великобританией за гегемо-
нию на морях и в колониях
Противоборствующие коалиции в первой мировой войне
Антанта Четверной союз Нейтральные государства, на территории которых велись боевые действия
Англия, Франция, Россия, США, Япония, Италия, Румы- ния Германия, Австро-Венгрия, Турция, Болгария Люксембург, Албания, Иран
Даты вступления стран в первую мировую войну
Антанта и ее союзники Германия и ее союзники
1914 г. — Сербия, Россия, Франция, Бельгия, Черногория, Великобритания, Япония, Египет 1914 г. — Австро-Венгрия, Германия, Турция
1915 г. — Италия 1915 г. — Болгария
1916 г. — Португалия, Румыния
1917 г. — США, Куба, Греция, Сиам, Либерия, Китай, Бразилия
1918 г. — Гватемала, Никарагуа, Коста-Рика, Гаити, Гондурас
Производство вооружения в годы первой мировой войны
Страна Винтовки Пулеметы Артиллерийские орудия Самолеты
Россия 3 300 000 28 000 11700 3500
Англия 3 854 000 239 000 26 400 47800
США 3 500 000 75 000 4000 13 800
Германия 8 547 000 280 000 64 000 47 300
Австро-Венгрия 3 500 000 40 500 15 900 5400
111
гЛлса- & тш[мшрл и, фокллммкк,
Военные расходы за годы первой мировой войны
Страна Военные расходы, долл. США Расходы на душу населе- ния, долл. США Доля военных расходов в нац. доходе, %
Россия 7 658 000 000 44 13,1
Англия 24 143 000 000 525 34,5
Франция 11208 000 000 280 19,4
США 17 337 000 000 177 8,7
Германия 19 894 000 000 293 24,7
Австро-Венгрия 5 438 000 000 109 18,1
Основные варианты развития стран Запада после первой мировой войны
Революция Реформы Диктатура
Австрия, Германия, Финлян- дия, Венгрия Великобритания, Франция, США, Скандинавские страны, Голландия, Швейцария Италия, Германия, Испания, Португалия
Численность политических партий в России в 1917 г.
Партии Количество членов, тыс. человек
Март Октябрь Октябрь (в армии)
РСДРП(б) 24 350 50
РСДРП(м) 45 (май) 193 23
Эсеры 500 700 250
Эсеры-максималисты 3 50—60
Кадеты 10—12 70 ок. 300 организаций
Участие США в войнах в XX в. (на 1919 г.)
Даты Войны Участвовало Погибло Ранено
6.4.1917—11.11.1918 Первая мировая 4 734 991 110 516 204 002
7.12.1941—31.12.1945 Вторая мировая 16 122 566 405 399 671 846
25.6.1950—27.7.1953 Корейская 5 720 000 33 651 103 284
4.8.1964—27.6.1973 Вьетнамская 8 744 000 58161 153 303
^сммбмая шлпо/гия & тм/лшщ'х, '
Население и территория колоний и полуколоний в XX в. (на 1919 г.)
72%
Основные этапы Гражданской войны в России (по Ю. А. Полякову)
Февраль—март 1917 г. Свержение самодержавия, раскол общества
Март—октябрь 1917 г. Обострение противостояния в обществе, усиление психологии гра- жданской войны
Октябрь 1917 — март 1918 г. Свержение Временного правительства, установление советской власти, распространение вооруженной борьбы
Март—июнь 1918 г. Эскалация насилия, террор с обеих сторон, формирование белых и красных вооруженных сил
Лето 1918 — конец 1920 г. Ожесточенные сражения между регулярными войсками, в том числе иностранными, милитаризация экономики
1921—1922 гг. Затухание боевых действий, их локализация и полное прекращение
Вооружение Белой армии (июнь—октябрь 1919 г.)
Фронт Командующий Количество Всего
штыков сабель
Южный Деникин 107 395 45 687 153 082
Восточный Колчак 95 547 22 581 118128
Северо-Западный Юденич 17 800 700 18 500
Северный Миллер 20 000 — 20 000
Итого 240 742 68 968
Приоритетные направления внешней политики СССР в 20-е гг. XX в.
• Прорыв дипломатической и экономической
блокады страны
• Поиск политических и экономических парт-
неров на Западе и Востоке
• Обеспечение внешнеполитических условий
для социалистического строительства в СССР
• Дальнейшее продвижение вперед «дела ми-
ровой революции»
113
(и1кольная пфвфамллиъ / тр^Фл^щая и, фгф^л^лаор
Нэп в промышленности СССР (1921—1929)
О Поощрение частного и смешанного капитала
О Расширение самостоятельности госпредприя-
тий, хозрасчет
О Ликвидация уравнительной оплаты труда,
замена натуральной оплаты денежной
О Привлечение иностранного капитала
О Образование рынка рабочей силы, отмена
принудительного труда
Нэп в сельском хозяйстве СССР (1921—1929)
О Замена продразверстки натуральным налогом
О Отмена централизованного распределения
продовольствия, возвращение к свободе тор-
говли хлебом и другими продуктами питания
• Ограниченное разрешение аренды земли и
использования наемного труда
О Развитие системы контрактации и сельской
кооперации
Сельскохозяйственное производство в СССР в 20—30>е гг. XX в.
1928 г. Конец 1930-х гг.
Зерно, млн т в год 73 75—80
Мясо, млн т в год 5 4—5
Молоко, млн т в год 30 30
Крупный рогатый скот, млн голов в год 60 50
Потребление продуктов питания в СССР в 20—30-е гг. XX в.
(кг на душу населения)
1928 г. 1940 г.
Мука, крупы 250 196
Картофель 141 143
Молоко и молочные продукты 242 (на 1924 г.) 127 (на 1939 г.)
Мясо, сало и т. п. 35—40 20
Основные черты и итоги индустриализации в СССР (20—30-е гг. XX в.)
Черты Итоги
Напряженные темпы Опора на собственные силы и средства Внеэкономическое принуждение Использование зарубежного опыта Приоритетное развитие тяжелой и оборонной пр эмышл енности Рост числа промышленных предприятий: 1928—1932 гг. — 1500, 1933—1937 гг. — 4500 К 1940 г. по производству важнейших видов промышленной продукции СССР вышел на 2-е место в мире после США
114
\ная астрал 6
Итоги ликвидации неграмотности в СССР
(20—30-е гг. XX в.)
• В 1928 г. расходы на образование составляли
8 руб. в год на одного человека, в 1937 г. —
113 руб.
• За годы двух пятилеток обучено грамоте 40 млн
человек, уровень грамотности в стране достиг
81%
• К концу 2-й пятилетки в стране введено все-
общее начальное образование
• В 1939 г. XVIII съезд партии поставил задачу
ввести всеобщее среднее образование в городе
и семилетнее — в деревне
Причины внутрипартийной борьбы в СССР
(20—30-е гг. XX в.)
О Борьба за политическое лидерство
• Отсутствие легальной оппозиции
• Расхождение во взглядах на пути развития
СССР
О Личные взаимоотношения вождей
Социальный состав советского общества
в 20—30-е гг. XX в.
Год 1928 1939
Общая численность населения, млн человек 152,4 170
Буржуазия, % 4,6 —
Крестьяне, кустари, ремесленники, % 74,9 2,6
Рабочие и служащие, % 17,6 50,2
Колхозники и кооперированные кустари, % 2,9 47,2
ГУЛАГ (30-е гг. XX в.)
На 1 мая 1930 г. На 1 марта 1940 г.
Колоний и лагерей 279 536
Заключенных 171 251 человек 1 668 200 человек
Основные черты советского общества (30-е гг. XX в.)
• Огосударствление всех сфер жизни
© Корпоративный характер общества и общест-
венных отношений
0 Жесткая вертикаль власти с харизматиче-
ским лидером
© Репрессии и внеэкономическое принуж-
дение
© Мифологизация общественного мнения и от-
рицание опыта Запада
© Закрытость страны» тенденции к автаркии
ZZ5
Особенности мирового экономического кризиса 1929—1933 гг.
Масштабность Весь мир (исключая СССР)
Глубина Охватил промышленность, финансы и сельское хозяйство Количество безработных — ок. 30 млн человек Промышленное производство отброшено к уровню начала XX в.
Продолжительность ок. 4 лет
Вторая мировая война
(1939—1945)
Продолжительность, дней 2194
Число стран-участниц 72
Число нейтральных государств 6
Число государств, на территории которых проходили боевые действия 40
Численность населения стран — участниц войны 1700 млн человек (80% населения Земли)
Число мобилизованных 110 млн человек
Число погибших в войне более 60 млн человек
Основные черты цивилизационного кризиса
в 30-е гг. XX в.
• Мировой экономический кризис 1929— • Оформление авторитарно-бюрократического
1933 гг. режима в СССР, ускоренная модернизация
• Внешнеполитическая экспансия стран-агрес- страны «сверху»
соров (нацистской Германии, фашистской В Появление диктаторских фашистских режи-
Италии, милитаристской Японии) мов в ряде европейских стран
Крушение колониальной системы
(40—90-е гг. XX в.)
Годы Количество стран, получивших независимость Годы Количество стран, получивших независимость
1940—1950 8 1961—1970 31
1951—1959 9 1971—1980 25
1960 18 1981 — наст. вр. 7
Z/6
acmoftaji 4 тси/ми/1Х
Численность населения СССР (млн человек)
Итоги боевых действий в Европе СССР
и его союзников в июне—декабре 1944 г.
Восточный фронт Западный фронт
Разгромлено дивизий Германии и ее союзников 96 35
Потери вермахта в живой силе, тыс. чел. 1600 (860 тыс. — безвозвратные) 634 (520 тыс. — безвозвратные)
Освобождено территории, тыс. кв. км 1400 (600 тыс. — территории СССР) 600
Количество населения на освобо- жденных территориях, млн чел. 55 (20 млн — на территории СССР) 76
Потери Красной Армии в оружии и технике
в летне-осенней кампании 1941 г. (%)
Танки 91 Орудия и минометы 90
Самолеты 90 Стрелковое оружие 67
Производство военной продукции в СССР
и Германии (1941—1945) (тыс. шт.)
Виды продукции СССР Германия Виды продукции СССР Германия
Танки и САУ 102,8 46,3 Минометы 351,8 78,8
Боевые самолеты 112,1 89,5 Пулеметы 1515,9 1117,5
Орудия 482,2 319,9 Пистолеты-пулеметы 6173,9 1256,8
7/7
tfahAttyAOX,
Производство промышленной продукции в СССР и США*
СССР, %
1945 г. 1950 г. 1960 г. 1970 г. 1980 г. 1985 г.
Электроэнергия 15 22 33 44 53 58
Нефть, в т. ч. газовый конденсат 8 14 42 80 142 135
Сталь 16 30 71 108 142 190
* Объем промышленного производства в США принят за 100%.
Этапы экономического развития стран Запада во второй половине XX в.
До начала 50-х гг. Восстановление
До начала 70-х гг. Относительная стабилизация
70-е гг. Замедление темпов экономического роста с последующим подъемом экономики
Потребление основных продуктов питания в СССР (на душу населения, кг в год)
Наименование продуктов 1950 г. 1960 г. 1970 г. 1980 г. 1985 г.
Мясо 26 40 48 58 62
Молоко 172 240 307 314 325
Сахар 11,2 28,0 38,8 44,4 42,2
Рыба и рыбопродукты 7,0 9,9 15,4 17,6 18,0
Страны — члены Европейского союза
1957 г. ФРГ, Италия, Франция, Бельгия, Нидерланды, Люксембург
1973 г. Великобритания, Дания, Ирландия
1981 г. Греция
1986 г. Испания, Португалия
Руководящие органы ЕС
Главный политический орган Европейский совет
Исполнительные органы Совет министров, Комиссия европейских сообществ
Консультативный и контролирующий орган Европарламент
//5
^селыфмал истомил & тш/лиир/х,
Основные этапы перестройки в СССР
Весна 1985—1986 г. Курс на ускорение социально-экономического развития страны
1987—1988 гг. Попытки перемен в экономике и внутрипартийной жизни
1989 — весна 1990 г. Кризис политики перестройки и выход социально-политических про- цессов в стране за рамки социалистического обновления
Весна 1990 — лето 1991 г. Переход к президентской форме правления, дальнейшее углубление экономического и политического кризиса в стране, постепенный распад СССР
Численность русских,
проживавших в республиках СССР в 1989 г. (млн человек)
Украина 11,4
Казахстан 6,23
Узбекистан 1,65
Белоруссия 1,34
Киргизия 0,8
Всего 25 млн человек (17,4% общей численности русских)
Национальный доход стран мира в 1991 г.
(на душу населения, долл. США)
Швейцария 33 610 Сингапур 14 210
Япония 26 930 Россия 3220
Швеция 25110 Украина 2340
Российская Федерация в 1994 г.
(в % по отношению к СССР)
Территория 17 млн кв. км 75
Население 149 млн человек 53
Промышленный потенциал 70
Военное производство —— 80
//9
GjUftoMiHax $та/лиици и, фо^ьмулах,
Доля России в мировом производстве сырья и продукции (на 1994 Г.)
Органы государственной власти Российской Федерации (с конца 1993 г.)
ПРЕЗИДЕНТ РФ
глава государства
ФЕДЕРАЛЬНОЕ СОБРАНИЕ парламент, представительный и законодательный орган
СОВЕТ ФЕДЕРАЦИИ по два представителя от каждого субъекта Федерации ГОСУДАРСТВЕННАЯ ДУМА 450 депутатов
ПРАВИТЕЛЬСТВО
высший орган исполнительной власти
СУДЫ
(Конституционный, Верховный, Высший Арбитражный)
Административно-территориальный состав Российской Федерации
Всего субъектов Федерации 89 Автономные округа 10
Республики 21 Автономная область 1
Края 6 Герода федерального значения 2
Области 49
Формы взаимодействия государств — бывших республик СССР (на 1997 г.)
• 12 СТРАН — УЧАСТНИЦ СНГ
• Межгосударственное объединение
• РОССИЯ, БЕЛОРУССИЯ
• Наиболее глубокая форма сотрудничества
• РОССИЯ, БЕЛОРУССИЯ, КАЗАХСТАН, КИРГИЗИЯ
• Углубленная, прежде всего экономическая, интегралу я, б?.? < ующаяся на Таможенном и Пла-
тежном союзах
• СНГ И ГОСУДАРСТВА БАЛТИИ
О Экономические связи
120
Математика
Алгебра • Геометрия
Математика в формулах
Алгебра в таблицах
1. Действительные числа
Множество натуральных чисел
N Натуральные числа 1; 2; 3...
Множество целых чисел
Z N Целые числа состоят из натуральных, нуля и чисел, противоположных нату- ральным. NcZ
0
N_
Множество рациональных чисел
Q Z Рациональные числа представимы как где р —целое, ад — натуральное. NcZaQ
Дроби
Множество действительных чисел
R Q Действительные числа — это бесконечные десятичные дроби. NcZcQcR Рациональные числа — бесконечные периодические дроби. Период не может состоять из одних девяток. Если период состоит из одних нулей, дробь может считаться конечной десятичной дробью. Множество иррациональных чисел. Иррациональные числа — бесконечные непериодические десятичные дроби. Q kJ Q = R
Q
3eN, 3eZ, -6 в N, -6eZ, 0,25£ N, 0,25 й Z, 0,25 e Q, 0,25 ей.
Делимость целых неотрицательных чисел Число а делится на число Ь, если существует с, такое, что а « Ъс. а • Ъ; Ь — делитель а; а — кратное Ь.
Свойства делимости
Нуль делится на любое натуральное число. Любое число делится на единицу. Любое число делится само на себя.
122
i та/мщга
1. Действительные числа
Свойства делимости (продолжение)
Если а > 0 и а • Ь, то а > Ъ. Если а Ь и Ь • с, то а • с. Если а • с и Ь • с, то (а + Ь) • с. Если а • (Ьс), то а • 6, а • с и (а : Ь) • с. Если а-Ьи&’а, тоа = 6. • • Если а • b и k Ф 0, то dk • bh. • • Если а : с и Ъ ’ с, то (ат + Ъп) • с. • • • Если а • с и (а + Ь) • с, то b ’ с. • • •
Деление с остатком Для любых двух натуральных чисел а и Ь найдутся такие целые не- отрицательные g и г, что а-Ъ • q + г, Q^r<b. Если г = 0, то а • Ь. Число г называется остатком от деления а на Ъ.
Признаки делимости
Число делится на два, если его последняя цифра делится на два. на 2
Число делится на пять, если его последняя цифра делится на пять. на 5
Число делится на четыре, если число, составленное из двух его последних цифр, делится на четыре. на 4
Число делится на двадцать пять, если число, составленное из двух его последних цифр, делится на двадцать пять. на 25
Число делится на три, если сумма его цифр делится на три. на 3
Число делится на девять, если сумма его цифр делится на девять. на 9
Число делится на одиннадцать, если алгебраическая сумма его цифр ао " «1 + а2 - а3 + ... + (-1)»~1ап_1 делится на одиннадцать. на 11
Десятичная запись п-значного натурального числах iап-1ап-2“’а2а1а0 °° ®п-1 ’ 10" 1 "* ап-2‘ЮП 2 +... + а2 • 102 + + аг • 101 + а0; at — цифры числа, ап_1 * 0, п € N.
НОК (а; &) Наименьшее положительное из общих кратных чисел а и Ь называется наименьшим общим кратным этих чисел. НОК (15; 10) = 30
НОД (а; 6) Наибольший из общих делителей чисел а и b называется наибольшим общим делителем этих чисел. НОД (15; 10) = 5
НОК (а; Ь) • НОД (а; 6) = а • Ь
Числа а и 6 называются взаимно про- стыми, если НОД (а; b) = 1. Натуральное числор называется простым, если оно имеет ровно два различных делителя (единицу и само это число). 2; 3; 5; 7; 11; 13; 17; 19; 23... — простые числа
123
1. Действительные числа
Свойства простых чисел
Любое натуральное число либо делится на простое, либо взаимно просто с ним. Произведение натуральных чисел де- лится на простое число тогда и только тогда, когда хотя бы одно из них делит- ся на это простое число. Простых чисел бесконечно много (нет самого большого простого числа). Если натуральное число не делится ни на одно простое, квадрат которого не превосходит это натуральное чис- ло, то оно само простое. Любое простое число р (р > 3) представимо в виде p = 6k+l,ke N.
Каноническое разложение натурального числа п(п> 1): п = р”1 • Pz2 • р^3 •, гдеpt — простое, pt <pt + j и 0 < at е N. 120 = 23 • З1 • 51
2. Модуль
|а| = а, а>0 -а, а<0
Основные свойства модуля |а| > 0 |-а| = |а| |а - Ь| = |Ь - а| |а| -1&| < |а ± Ь| < |а| +1&| Геометрическая интерпретация модуля Если точка А на числовой оси имеет коорди- нату а, то расстояние от А до 0 равно |а|.
Расстояние между точками А (а) к В (Ь) на прямой равно |а - Ь\.
Уравнения с модулем
|х| = а |х - Ь| = а \f (*)| = |£ (х)| |/(x)l = £(x)
а < 0 решений нет а < 0 решений нет равносильно объедине- нию уравнений равносильно системе уравнений
© II о а II о а = 0 х = Ь /(х) = g(x) . f(x) = -g(x) f(x) = g(x) ' L Rx) = -g(x) g(x) > 0
а>0 1 1 а а и и । р р х = Ъ- а а > 0 L х = Ь + а
Неравенства с модулем
|х - Ь\ < а |х - &| > а |7(x)|< g(x) 1/ (x)l > g (x)
а<0 решений нет а<0 хе Д равносильно системе: f f(x)<g(x) I f(x)>-g(x) равносильно объединению: Rx)>g(x) . Rx)<-g(x)
а > 0 Ь-а<х <Ь + а а > 0 х<&-аилих>6 + а
Неравенство\f (х)| > |g (х)| равносильно неравенству /2(х) > g2(x) или неравенству (/ (х) - g (х)) (/ (х) + g (х)) > 0.
Z24
2. Модуль
Примеры
Раскрытие модулей
«по промежуткам»
у = |х + 2| + 3 |х| - 2 |х -1|
-201*
х<-2,
у = —(х + 2) - Зх + 2 (х -1) = -2х - 4
-2<х<0,
у = х + 2-Зх + 2(х-1) = 0
0<х<1,
у = х + 2 + Зх + 2 (х - 1) = 6х
х> 1,
у = х + 2 + Зх-2(х-1) = 2х + 4
Решить уравнение
Зх2 - 5|х| -8 = 0.
Заметим, что |х|2 = х2;
введем обозначение |х| = t.
3t2 - 5t - 8 = 0.
tX = -1; t2 = g .
|x| = -1, решений нет.
. , 8 8 8
M з; , x2 з •
8 8
Ответ: х, = -5; х2 = х.
х о Л о
Построить график функции
у = tg х • |cos х|.
Данная функция периодичес-
кая, период Т = 2к.
Построим график на каждом
промежутке знакопостоянства
косинуса.
При cos х > 0
у = sin х;
при cos х < 0
хе
2’ 2 )’
у - -sin х.
3. Действия с многочленами
Сложение многочленов: (а2 + ab - Ь) + (За2 - 2аЬ + Ъ) = 4а2 - аЬ. Вычитание многочленов: (2а -Ь)- (За + Ь) = (2а - &) + (-За - &) = -а - 26. Умножение многочленов: (а + 36)(а -Ь) = а2 - аЬ + ЗаЬ - 362 = а2 + 2а6 - 362.
Формулы сокра] ценного умножения
квадрат суммы (а + Ь)2 = а2 + 2аЬ + Ъ2 разность квадратов а2 - Ъ2 = (а + Ъ) (а - &)
квадрат разности (а - Ь)2 — а2 - 2аЬ + Ь2 разность кубов а3 - Ь3 = (а - Ь) (а2 + ab + Ь2)
куб суммы (а + Ь)3 = а3 + За2Ь + ЗаЬ2 + Ь3 сумма кубов а3 + Ъ3 = (а + b) (a2 -ab + Ъ2)
куб разности (а - Ь)3 = а3 - За2Ь + ЗаЬ2 - Ь3
Z25
бЩмомзнал п^глг^мм^им пии/мшра, a
3. Действия с многочленами
Бином Ньютона: (а + Ъ)п = ап+ С„ ап~г Ь + + С* ап ~ + ... + С\ ая - W + ... + Ъп С1 с2 _ »(» ~ А) сп п' ''п 2 * ск = п' . <& ~пп~ь. п (n - fe)! fe! ’ » » ’ леУ,п>1 (0! = 1; 1! = 1; п!= 1-2 •... • п). Треугольник Паскаля 1 1 1 12 1 13 3 1 1 4 6 4 1 15 10 10 5 1 1 6 15 20 15 6 1 1 7 21 35 35 21 7 1
(а + Ь)4 = а4 + 4а3Ь + 6а2Ь2 + 4аЬ3 + Ь4 (а - Ь)7 = а7 - 7авЬ + 21а5Ь2 - 35а4Ь3 + 35а3Ь4 - 21а2Ь5 + 7аЬ6 - Ь7
Основные приемы разложения многочлена на множители
Вынесение общего множителя за скобку 2аЬ + 14a2 + 2a = 2a (b + 7a + 1); 3a2b3 - 15a3b = 3a2b (b2 - 5a).
Метод группировки ab + ac - b - c = a (b + c) - (b + c) = (b + c) (a - 1).
Использование формул сокращенного умножения a2 + 4ab + 4b2 = (a + 2b)2; a4 + 4 = a4 + 4a2 + 4 - 4a2 = (a2 + 2)2 — (2a)2 = = (a2 - 2a + 2) (a2 + 2a + 2).
Дополнительные формулы (an - 1) = (a- l)(an-1 + an~2 +... + a +1); (a2m +1 + 1) - (a +1) (a2m - a27"'1 +...-a +1).
Многочлены от одной переменной
Общий вид: f (х) = апхп + ап_ гхя~ *+... + а1х1 + а0, п — степень многочлена, at — коэффициенты, ап — старший коэффициент, ап * 0. Если ап — 1, то многочлен называется приведенным. Зх4 - х3 + 2х2 — 5 — многочлен 4-й степени с коэф- фициентами: а4 = 3; а3 = -1; а2 = 2; at = 0; а0 = -5. Квадратный трехчлен — многочлен вто- рой степени ах2 + Ьх + с(а* 0), а — первый коэффициент, Ь — второй ко- эффициент, с — свободный член.
Деление многочленов
Теорема о делении с остатком Р(х) = М(х) • Q(x) + Я(х), где Р(х) — делимое, М(х) — делитель, Q(x) — частное, Я(х) — остаток. Если ос- таток не равен нулю, то его степень меньше степени делителя. Зх3 - х2 - Зх - 2 = Р(х) = (х2 + х - 1) (Зх - 4) + (4х - 6) М(х) Q(x) Л(х) Деление «уголком» _Зх3-х2-Зх-2 1х2 + х-1 Зх3 4- Зх2 - Зх Зх-4 -4Х2 -2 -4х2-4х + 4 4х — 6 Р(х) = Зх3-х2-Зх-2 Л4(х) = х2 + х - 1 Q(x) = Зх - 4 Р(х) = 4х-6
Z26
4 та^лмирк
3. Действия с многочленами
Деление многочлена f(x) на двучлен х — а
Теорема Безу. Остаток от деления многочлена на двучлен х-а равен значению этого многочлена при х = а, т. е. R = /(а). /(г) = (х - а) • Q(x) + /(а) Схема Горнера. Разделить многочлен /(х) = х3 4- 5х2 - 3 на (х - а = 5 ^2 = аз &1 = Ь2 ’ 5 + а2 Ьо * 5 4“ аг R = &q в5 4- Oq й = /(5) = 247 а3 а2 а1 % 5)
5 1 5 0 -3
1 10 50 247
Ь2 \ bQ R
Корнем многочлена называется такое число х0, при котором значение многочлена равно нулю (/ (х0) = 0). Пример. х3 4- 5х2 4- 2х — 8 = 0 Целые корни можно искать только среди чисел -1; 1; 2; -2; 4; -4; 8; -8. Ответ', х = 1; х = -2; х = -4 — корни.
Целые корни многочлена с целыми коэффициента- ми являются делителями его свободного члена.
4. Квадратные корни
Определение арифметического корня Г г. Ь>0, 7а = Ъ <=> ,2 о = а 716 = 4, так как 4 > 0, 42 = 16; 725 * 7, так как 72 * 25; 725 * -5, так как -5 < 0; J^8 не определен. Jo, 36 = 0,6; 74900 = 70; 70,0001 = 0,01; 2< 78 <3; 0,8 < 7oT8 < 0,9.
Тождества Основные свойства
(Ja.'f = а, а > 0 Ja* = |а|, а е R Ja ' Jb = Ja • b Ja la Jb Nb (JZy~Jj Jab - 7R • 7|b| /a _ Ла Nb Jb Ja? = (J\a\)P
Сравнения, связанные с квадратными корнями Если а>Ь> 0, то Та >Vb. Ja + Jb Ja + Ъ. Если a>l,toa> Ja. и Ja >1. Если 0<а<1, to а < Ja п0 < Ja <1.
^Шпальная п/и>г(гамма &таблицах и, &юкмл1лах
4. Квадратные корни
Вынесение из-под корня Ja2 • b = |а| • Л, Ь > 0 Внесение под корень -Ja2b, если а < 0, 6>0 Ja2b, если а > 0
I i? S + it> 4- |оо J со г । Н || — ЦО [Y _5_ 7 ? 7 и + + Id Id Id ICO S -о г> ЦО L_b- L^D [ft 5 • Тз = 7з • 52 = 775 ; -277 =-728; (75 - 2) • 7э + 4л/б = 7(75 - 2)2 • (9 + 475) = 1; (ТЗ -2)- 77 + 473 =-7(ТЗ - 2)2 (7 + 473) =-1.
Иррациональность в знаменателе 2 = 2j3. 5 = 5(73 + 1) = 5(V3 + 1) = 5(73 + 1). 7з 3 ’ Тз -1 (7з - 1)(7з + i) з-1 2
Сравнение среднего геометрического (пропорцио- нального) двух чисел и их среднего арифметиче- ского 2-—* 7йЬ,а>0;&>0. Zj Построение У. 1 > Jn (п ^N) на. числовой прямой 1 1 1
0 1 72 л/з 2 3 J10 х (7п + 1)2 = (7л)2 +12
Примеры
Найти х2 н упростить выражение х = Тз - 272 - 7з + 272. Заметим, что х < 0, т. к. 3 - 2^2 < 3 + 2j2 . х2 = 3 - 272 - 279 - 8 + 3 + 272 = 6 - 2 = 4. Значит, х = -2. , Ответ: х2 = 4; 7з - 272 - 7з + 272 = -2. л/зз — 1 Сравнить числа 72 + 1 и 9 £ Запишем: J2 +1 ? J 2 272 +2 ? ТЗЗ -1 78+3 ? J33 Так как сравниваемые числа положительны, то можно сравнить их квадраты: 17 + 678 ? 33 бТ8 ? 16 7288 > 7256 </зз — 1 Следовательно, J2 + 1 > 9 Zj
128
5. Корни натуральной степени
Определение арифметического корня натуральной степени из неотрицатель- ного числа а nJa = b 1 Ъ > 0 neN, а > 0 J Ьл = а 1/27 = 3; V0, 0000001 = 0,1; 1/1024 = 4; 2 < 1/9 < 3; УЗ = 3; 0,2 < 1/0, 00036 < 0,3. I/O, 008 = 0,2;
Извлечение корня нечетной степени из отрицательного числа Если а < 0, то 2л-Уа = -2га-17^а.
1/^8 = -1/8 = -2; 1/-243 = -1/243 =-3; 1/(7з - 2)3 = -1/(2 - 7з)3 = -(2 - 7з) = 7з - 2.
Корень четной степени из отрицательного числа не определен.
Тождества Основные свойства
Если nJa существует, то (nJa )л = а. 2п1 2n I । Л Va — |а|, а е R 2п - 1/ 2п - 1 _ = а, а е R II II 5:1 st II < ft < йЗ ^1 а-1 '*• о-| И lai а II г? ^.а а71| «^1
Сравнения, связанные с корнями Если а > Ъ > 0, то nJa > nJb . nJa + nJb > nJa + b. Если a > 1, то nJa > 1 и nJa < a. Если 0 < a < 1, то 0 < r\[a < 1 и nJa > a.
Вынесение из-под корня У24 = УЗ“8 = 2 • УЗ ; 47(1 - 72)4-5 =(./2 -1)- У5; 37(1 - T2)3 • 6 = (1 - 72) • 37o.
Внесение под корень 3 • 4T2 = 47з4 • 2 = 1/162 ; -2 • 673 = -6л/26 • 3 = -1/192 ; (1- 73)- 4T2 =-47(1 “ 73)4-2; (1- 75)- 3Т2 = 37(1 “ Т5)3-2.
5—1323
129
бЩяальнал £ mcu£iwtflx и формулах
5. Корки натуральной степени
Тождества (продолжение) Основные свойства (продол.жгппе)
Иррациональность в знаменателе 3 = 3 1/23 = 3-1/8 . 1/2 2 2 + _Vi tl 1/з +1 3-1
Действия с корнями различных показателей ‘Jis : : '7? - л! 3 у 4 • о л/2 • 1/2 • 1/2 = 1/г3 • 22 • 2 = 1/г® = 2.
Сравнить 1/5 и 1/3. 1/5 = 12Т? = 11/125 , 1/з = 12л/з* = 12/81. Так как 125 > 81, то 12л/125 > 12Т81 и 1/5 > 1/3 .
Среднее геометрическое и среднее арифметическое неотрицательных чисел аг + а2 + ... + ап п7а1 • а2 • - • ап < - - Равенство достигается при аг = а2 = ... = ап.
6. Степени. Степенная функция. Функция у — nJx
Степень с натуральным показателем а1 = а ап = а • а - a , п N, а R п раз
Степень с рациональным показателем для неотрицательного числа а 771 П а = ь/а nt Z9 п N Если т < 0, то а > 0. Если т > 0, то а 0. 2 3 З3 = 1/9; О5 = 0; 3 252 = & = 125; 1 (0,04)2 = 70,04 =0,2; 1 (-27)3 не определена.
130
сАлга/^а & тси/лицах
6. Степени. Степенная функция. Функция у = nJx
Степень с целым показателем а° = 1, а # 0 а ел „-«.Л., а Ю| il eq loo 0 cq II r-i CO sb iQicq, тН|О> И II 7 co '
Понятие о степени с иррациональным показателем з3 <3“ <34 (0,3)2 < (0,3)^ <(0,3)1 з3-1 <3* <33-2 (О.З)1-5 < (0,3)^ <(0,3)1>4 З3-14 <3я <33,15 (О.З)1’42 <(0,3)^ < (0,3)1,41 (я = 3,1415...) («/2=1,4142...)
Степень с действитель- ным показателем Г „ f r<0, f г>0, ar, г е R < и 1 (а>0 [ а>0
Свойства степеней аР-аг = а₽ + г (а?)г = аРг аг • br = (ab)r ar'.br =
Свойства степеней, связанные с неравенствами a>b*° UCW Р>г \=>ар>аг г > 0 J а > 1 J , „ 1 1 а>Ъ>0 [ г ,r р> г р г > => a <b \z=^ а <а г < 0 J 0 < а < 1 J
Графики степенной функции У = хг> ге R У Г и , 0 <р < г D(y) = [C Е(у)~[0 возрасте +0°). 1 д- < 1 1; +оо); 1; +оо); 1ет на 1 Z>(i/=[0; + // Ду) = [О; + // возрастает j _ J [0; +00). °o); 00); на у < i p < r < 0 D(z/) = (0;+oo); 1 E(i/) = (0;+00); U убывает на 1 (0;+oo).
0 1 х 0 1 х 0 1 1 1 x
431
4 пии/лиирх а фофлиулах
6ЩшкЛЪ
нал, пфсгфамлш
7. Элементарные функции школьного курса
Линейная функция у = ах 4- Ъ Гпа&ик — пвямая
D(y) = R. У\ у = ах + Ь (а < 0) ч/ - ах + Ъ (а > 0) f у = b (д = 0)
При а = 0 Е(у) = {&} (постоянная), все точки — точки экстремума. При а*0 Е(у) = R.
При а > 0 возрастает на R. При а < 0 убывает на R. Экстремумов нет. /о х
Функция у = kx — прямая пропорциональность (к > 0). Нечетная функция. k1 = tga k2 = tg р {у = М ct х У = М
Квадратичная функция у = ах2 + Ъх + с (а *0)
D(y) = R. Вид графика — парабола. Координаты вершины параболы: & г ч хо = -2^;г/о = у(хо>- Ось симметрии х = х0. При а < 0 yQ — наибольшее значение. При а > 0 yQ — наименьшее значение.
При а > 0 убывает на (-оо; х0] и возрастает на [х0; +оо), Ъ хо~~2а точка минимума, Уо = У(хо> минимум. Е{у) = [у0; +®°)-
При а < 0 возрастает на (-оо; х0] и убывает на [х0; +оо), ь , . х0 = ~ z— — точка максимума, i/0 = i/(x0) — макси- & а мум. Е(у) = (-00; у0]. У , У = ах2 0 1 Четная функция ^Х
D = &2 - 4ас = О
D = Ь2 - 4ас > О
D = Ь2 - 4ас < О
Два корня х1 и х2;
график пересекает ось Ох
в двух точках.
Один корень х0;
график касается оси Ох.
о
Уо
L
У
Уо
о
Нет корней;
график лежит по одну
сторону от оси Ох.
[у /
Уо 1 ж
0 хо X
0 хо
Уо X
132
7. Элементарные функции школьного курса
Дробно-линейная функция ах 4- b , , 9Ьс*о) Вид графика — гипербола jfe о у = - , где k = (be - ad)/c.
Функция у = (k * 0). Вертикальная асимптота х = 0, горизонтальная у = 0.
D(y) = (“°0; 0) и (0; 4-00), Е(у) = (-°°; 0) и (0; 4-ос). Два промежутка монотонности (~оо; 0) и (0; 4-оо); при k < 0 функция \У 1 X k>0 У k
на каждом из них возрастает, при k > 0 на каждом убывает. Экстремумов нет. Нечетная функция. 0 k обратная прого 1 орциональность
Примеры дробно-линейных функций
= 6 - 2х
У 2г - 3
Зх - 2 о , 1
у =-----— = 34------
у х - 1 х - 1
2х - 1 о 3
У = =2-ТТ
3
2х - 3
Q /О
x*3/2;i/*-l;i/ = ^
Функция у = а/х
Функция у = z<Jx
ВД = [0;+оо) = Е(1/).
Возрастает на D(y). Экстремумов нет.
Четностью и нечетностью не обладает.
, 1
У = Г7=-
О(у) = ( -°°; +°°) = Е(у).
Возрастает на D(y). Экстремумов нет.
Нечетная функция.
, 1
у ~ зз7?
nfwefaiJWUL & таблицах и, фофл/улах
7. Элементарные функции школьного курса
Степенная функция у = хп
у' = ПХп 1
п = О; у = 1; D(y) = (-оо; 0) и (0; +оо); Е(у) = {1}.
п > 0, натуральное
п < 0, целое
п — четное
D(y) = R
£(*/) = [0; +оо)
п — нечетное
D(y) = R
E(y) = R
п — четное п — нечетное
D(y) = (-°°; 0) и (0; 4-оо)
Е(у) = (0; 4-00) Е(у) = (-оо; 0) и (0; 4-оо)
Четная функция
Нечетная функция
Четная функция Нечетная функция
п — не целое число
0<п <1
п < О
B(i/) = [O; 4-оо) = ад
P(i/) = (O; 4-оо) = ад
Сравнение графиков
степенных функций
134
7. Элементарные функции школьного курса
Показательная функция у = ах {а > С; а * 1) у' = ах • In а Логарифмическая функция у — logflX (а > 0; а * 1) У'~х.1па
D(y) = R; Е(у) = (0; +°°); один промежуток монотонности; экстремумов нет. Ду) = (0; +оо); Ду) = Я; один промежуток монотонности; экстремумов нет.
а > 1 возраст у а 0 'ает на R \ 1 । *- 1 X а > 1 возр; yi 0 астает на D(y) Г Х
0 < а < 1 убыв 1 у а 0 ает на R 1 0 < а < 1 у( у. 0 эывает на D(y) \i -— х х
е = 2,718281828459045... ~ 2,7 — основание натурального логарифма (logex = In х).
(ех)' = ех (lnxr-1
\ у 1 \dx\ с\ \ 0 d < с < ЬХ1 / / ах1 i 1<а<Ъ log У{ 0 а| 1 logb* logcx^****** \\ Х a<b<l<c<d
Тригонометрические функции
у = sin х у = COS X У =tgx
Ду) R R (-5 +лА; з +nfe)A & Z
Ду) [-1; 1] [-1; 1] R
135
^Школьосая пфогфажлш & пикФлаирх и фофм^лах
7. Элементарные функции школьного курса
Тригонометрические функции (продолжение)
Бесконечное множество промежутков монотонности Убывает на [5 + 2лй; v + 2nk]; возрастает на Н +2nfe?5 +ал]. & Li Убывает на [2nk; л + 2nk]; возрастает на [-л + 2nk; 2nk]. Возрастает на каждом промежутке непрерывно- сти (-5 +nk;l+nk). Сл Li
Точки минимума х = -- + 2nk а х = л + 2nk нет
Точки макси- мума х = | + 2nk х = 2nk нет
Минимумы -1 -1 нет
Максимумы 1 1 нет
Нули X = nk X = 5 + nk X = nk
Промежутки знакопостоян- ства (i/ > 0) (2nk; л + 2nk) (—- +2nk', 5 + 2лй) z z (nk; 5 +nk)
Промежутки знакопостоян- ства (i/ < 0) (-л + 2nk;2nk) (| + 2лй; +2nfe) (| +nk;n + nk)
Период 2k 2k п
Четность Нечетная sin (~x) = -sin x Четная cos (-x) = cos X Нечетная tg(-x) = -tgx
Асимптоты нет нет Вертикальные х = | + nk
Производная cos X -sin x l/cos2x
у = sin x у = cos X У =tgx
Графики 1 । У < "\-я/2 1 У1 n i 5 II // -—- Iй KUN .J*"— * _ • Г* о
-тгЧХ/ -1 °л/2X. х -1 о xl* x
756
гАма/ка & та</лимрх
7. Элементарные функции школьного курса
Обратные тригонометрические функции
у = arcsin х у = arccos х у = arctg х
Жу) [-1; 1] [-1; Л R
Е(у) Г-”] 1 2 2J [0; гс] ' 2’2?
Монотонность Возрастает на D(y) Убывает на D(y) Возрастает на D(y)
Четность Нечетная — Нечетная
Производная 1 /l 2 VI-X (Х*±1) 1 /1 2 */1 -X (х*±1) 1 1 + х2
Графики У i л 2 -1 /\ / 1 У^ X 1 \ 1 1 1 1 1 л л 2 У
л 2
1 Z |/ 0 i л “2 0 *х
л "2
-1 о
8. Основные приемы преобразования графиков
f(x + а) Перенос графика у = f(x) на вектор р (-а; 0). у У =» Jx + 2 г/= Jx Ml I
-2 -1 12 4 х р(-2;0)
f(x) + Ь Перенос графика у = /(х) на вектор р (0; &). У { 1 !/e Jx _
0 -1 <1 X р(0;-1)
~f(x) Симметрия относительно оси абсцисс. У I 1 у = 4х Г • 'Л !
0 1 у = -Jx
Z?7
^ItcMbHax пфсгфшмма & таблицах и, фср-мдлах,
8. Основные приемы преобразования графиков
К~х) Симметрия относительно оси ординат. г- У‘ у- 4-х г у= 4* у. *
0 1
|Г(Х)| Часть графика в верхней полуплоскости и на оси абсцисс без изменения, а вместо час- ти графика в нижней полуплоскости стро- им симметричную ей относительно оси Ох. у = |х2-1| sL
-1 \° -1 у1 х у = X2 - 1
«И) Часть графика в правой полуплоскости и на оси ординат без изменения, а вместо части в левой полуплоскости строим симметричнзпо правой относительно оси Оу. 1 У ~ (0,5)* \ % г ч ч у \ Л |х| У = (0,5)’ 1
D х
f(kx) (Л>0) При k > 1 сжатие к точке (0; 0) вдоль оси абс- цисс в k раз; при 0 < k < 1 растяжение от точ- ки (0; 0) вдоль оси абсцисс в 1/k раз. У> у = sin2x \ 0
Л/ у = sinx Мг \ 2>х
kf(x) (й>0) При k > 1 растяжение от точки (0; 0) вдоль оси ординат в k раз; при 0 < k < 1 сжатие к точке (0; 0) вдоль оси ординат в 1/k раз. У и 2 < 1' 1 у - 2cosx \ У -= сосх
V * / ° \ ** л X <7 х
133
4 тас/лимроь
9. График уравнения с двумя переменными
ах Л-by — с Прямая линия. \у h
0 \
(х - а)2 + (у - Ь)2 = R2 Окружность с центром (а; Ь) радиуса R. У Ь 1
\ а У X
I 2 2 у = а -х Полуокружность с центром (0; 0) радиуса а. У
-а 0 а х
у = ах2 + Ъх + с Парабола вида у = ах2; при а > 0 ветви вверх, при а < 0 ветви вниз; вершина b , ч *о = ~Та ’ У° = у{х0}‘ У(х0) И
0 х0 X
х = ау2 + Ъу + с Парабола вида х = ау2; при а > 0 ветви вправо, при а < 0 ветви влево; вершина b , ч Уо i
0 x(IZo) х
(х - а)(у - Ь) = k fe#O k Гипербола вида у = - ; асимптоты х = а; у = Ь. ’it k<o ! \ _,_ь А»! . [У k>0
1 '/ 0
139
GUlttwbKax п^сг^амма £та/лацрх и фо^ьмдмкх,
9. График уравнения с двумя переменными
|х| + М = 1 Квадрат. 1^4 о л -1
II ТсГ 1 « О -2? Л 4- е "ё- о 1 g Л 21 8 Ромб. । ' b 1 а 0
М-Ы = 1 «Перекресток». И i
Если дан график зависимости F(x; у) = 0, то график зависимости F(x ~а;у -b) = 0 можно получить переносом всех точек на вектор р(а; &); график F (|х|; у) = 0 можно получить, оставив часть графика в правой полуплоскости и на оси ординат без изменения, а вместо части в левой полу- плоскости построить линию, симметричную правой относительно оси Оу; график F(x; |i/|) = 0 можно получить, оставив часть графика в верхней полуплоскости и на оси абсцисс без изменения, а вместо части в нижней полуплоскости построить линию, симметричную верхней части графика относительно оси Ох.
10. Квадратный трехчлен
Квадратный трехчлен ах2 4- Ьх 4- с — это мно- гочлен второй степени; а Ф 0 — первый коэффи- циент; b — второй коэффициент; с — свобод- ный член. График функции F(x) = ах2 + Ъх + с — парабола; Ъ координаты вершины х0 = -^, _т х b2-4ac D у° W 4а 4д •
Выделение полного квадрата: 9 _ ( Ь \2 Ь2-4.ас ах^ 4-OX4-C—ах4-о . 2а) 4а D = Ь2 - 4ас — дискриминант квадратного трехчлена.
ПО
/£лга/[га £ пии/лшцлх,
10. Квадратный трехчлен
Корни квадратного трехчлена
Р <0 Квадратный трехчлен не имеет корней и сохраняет знак первого коэффициента при всех значениях х: a-F(x)>0. а < 0 у *0 а>0 % У, ।
0 ; х XQ 0 х
Р = 0 Квадратный трехчлен имеет один корень / х Ъ (два равных корня) х = х0 = • У функции F(x) два промежутка знакопо- стоянства, на каждом из которых она со- храняет знак первого коэффициента: aF(x) > 0 (х * х0). Парабола касается оси абсцисс в своей вершине. а<0 у { а> 0
0 0
D >0 Квадратный трехчлен имеет два корня: _ -b-JP _ -b + JP х1 2а ’ Л2 ~ 2а У функции F(x) три промежутка знакопо- стоянства. а < 0 у t а> 0 у, jj
~7 г хо \ х Х1>Х2 х\о * хх<х2
Теорема Виета
Если квадратный трехчлен ах2 + Ъх + с (квад- ратное уравнение ах2 4- Ъх 4- с = 0) имеет корни хх и х2 (т.е. D > 0), то Ь с х, 4- х9 = — , хл • Х9 = “ 1 а 1 а Для приведенного (а = 1) квадратного уравне- ния х2 4- рх 4- q = 0 Х1 + Х2 = ХГ Х2 = Обратная теорема: Если числа и 12 таковы, что Ъ с 4- £2 = “““ и ’ *2 = я ’ Т0 0НИ ЯВЛЯЮТСЯ КОР- НЯМИ квадратного трехчлена ах2 4- Ъх 4- с (квадратного уравнения ах2 4- Ъх 4- с = 0).
Пример. Квадратное уравнение х2 - (5 4- )х 4- 57? =0 имеет корни х = 5; х = а/7.
Разложение квадратного трехчлена на линейные множители
Р <0 Квадратный трехчлен на линейные множители не раскладывается.
Р >0 ах2 4- Ьх 4- с = а(х - хх)(х - х2)
D = 0 2 , . , ( Ь\2 ах£ + Ъх + с = а\х - z- \ 2aJ
141
ъльма 4 тас/лищис, и, фсфм^лах
10. Квадратный трехчлен
Составление квадратного трехчлена с корнями и t2
Существует бесконечно много квадратных трех- членов с корнями и t2; они имеют вид “ (£х + tr^x + среди них один приведенный: Х^ — (t^ + t2)x 4" • t2. Пример. Приведенный квадратный трехчлен с корнями 2 и 8. х2 - 10х + 16, так как 2 + 8 = 10, 2 • 8 = 16.
Корни квадратного трехчлена ах2 + Ьх+с
положительны, если *1*2 = 7>° *1+х2 = "7>0 D - Ь2-4ас>0 отрицательны, если Х1 • Х2 = 7 > 0 ъ х1+х2 ~ <0 D = Ь2-4ас>0 одного знака, если . Х1 • х2 ° 7 > 0 D = Ь2-4ас>0 разных знаков, если с Х1 ’ Х2 “ а < 0
11. Прогрессии
Последовательность — функция натурального аргумента.
Задание последовательности формулой общего члена а„=/(п),пеЛ' ап = п2 + п + 41 ах = 43; а2 = 47; а3 = 53;...
Задание последовательности рекуррентным соотношением Дано: а^а^, ...',ап_х ап ~ f(an-V ап-2’ •••’
Числа Фибоначчи: 1; 1; 2; 3; 5; 8; 13; 21; 34; ... . (аг = а2 = 1; ап + 2 = ап 4- ап + х) 1 /yl I /1 /кхЛх Формула общего члена: ап = —^-j J. Свойства: аг + а3 + а5 + ... + а2п + х = а2п + 2; а2 + а4 + а6 + ... + а2п = а2п + 4 - 1.
Арифметической прогрессией называется по- следовательность, заданная рекуррентным со- отношением: аЛ + х = ап 4- d, n е (ах — первый член прогрессии, d — разность прогрессии). Геометрической прогрессией называется после- довательность, заданная рекуррентным соотно- шением: Ъп +1 = Ъп • q (&х 0 — первый член прогрессии; q Ф 0 — зна- менатель прогрессии).
142
Жлга/^м & пии/ли.иА'Х,
11. Прогрессии
Арифметическая (-?) Геометрическая (^)
Допустимые значения аг и d любые и q не равны нулю
Формула общего члена аЛ = аг + (п - 1) • d
Характеристическое свойство an + l+an-l _ 2 а* 5п*0
Формула суммы п первых членов а-. +ап 2аг + (n-l)d sn ~ 2 п~ 2 п . о , 1-дп g*l,Sn - , -Ъ,- 4 п 1-q 1 1-g q = l,Sn=n-b1
Другие формулы ап ат , t ч - d, (n * т) п-т % +1 = + 1 " Sn а1 + an =а2 + an -1 = ••• = ak + ап -k + 1 bn'.bm=qn~m bn , i = Sn > — s n + 1 n + 1 71 ~ ‘ bn -1 = ••• = bk ' - k + 1
Бесконечно убывающая геометрическая прогрессия (0 < |g| < 1) lim q = 0, S = lira. S_ = - . n->oo n-»o° 1 ~q bl Формула суммы: S = 1-9 1
Примеры
0 37 37 0,(37)-0,37+ 0,0037+ - 99 (bj - 0,37; q = 0,01) 1 0,02 0,5(2) = 0,5 + 0,02 + 0,002 +... = 5 + , ’= 1—0,1 1 2 47 Л = 2 + 90 = 90 = °’02’ 9 = 0>1)
Суммирование 1 + 2 + 3 + 4 + ... + n = "(n9+-1); l2 + 22 + 32 + 42 + ... + n2 = ^(ra t. D^n.+JJ 2 o l3 + 23 + З3 + 43 + ... + n3 = n2(n .+ -)2 4
Примеры
Если an арифметическая прогрессия, то -А- + -L_ + _L_ + ... + _±_ = * а2 а2 ' а3 а3 ' +1 п а1 ’ ап + 1 Все натуральные числа, дающие при делении на 7 в остатке 5, имеют вид ап = 7(п - 1) 4- 5 = 7п - 2, n G ЛГ.
143
tyUftMb'Mix nfiotfaawut, &ттьдоСширх, и, (fafiMijAax,
12. Тригонометрическая окружность
Тригонометрической (единичной) окружностью называется ок-
ружность с центром в начале координат, радиуса 1. Точки
единичной окружности можно поставить в соответствие дей-
ствительным числам. Числу 0 ставится в соответствие точка
Ро(1; 0), а каждому числу t ставится в соответствие точка Pt,
полученная поворотом точки PQ (1; 0) на угол t вокруг начала
координат (если t > 0, то поворот осуществляется против часо-
вой стрелки, если t < 0 — по часовой стрелке).
Таким образом, каждому действительному числу t соответ-
ствует единственная точка на единичной окружности Pt,
а каждой точке Pt — бесконечное множество действительных
чисел вида t + 2л&, k ^Z.
Длина дуги P^Pt = t (0 < t < 2я).
I четверть: 0 + 2nk <t<^+ 2nk.
IIчетверть: % + 2nk <t<n + 2nk.
z
III четверть: n + 2nk <t<^ + 2nk .
z
IV четверть: + 2nk <t<2n + 2nk.
z
Связь градусной и радианной мер: а = л •
(радиан); х (радиан) =
Две точки, симметричные относительно
оси абсцисс
оси ординат
начала координат
а = (-!)"£ + ли, п е Z
a = t + itk,k^Z
Вершины правильного п-угольника,
Pt(a;b)
Рк (Р;а)
2 1
144
7га & тш/мыцах
13. Тригонометрические функции
Косинусом числа t называется абсцисса единичной окружности, а синусом — о{ этой точки. Pt(cost; sin0 [ .,Z\ точки Pt эдината Тангенсом числа t называется отношение sin t к cos t (cos t * 0). л sint tg t = 7 & cost Ось тангенсов — прямая x = 1. Котангенсом числа t называется отношение cos t к sin t. cost Ctg t = -T-T (sin t * 0) Olli & Ось котангенсов — прямая у = 1.
-1Д costjl X
I-1 N(ctgt;l) J 1 X = 1
0 = 1
\ 0 L x M(l;tg t)
Основные формулы sin2 t 4- cos21 = 1, t e R. , sint K tg t = ; , t * о + nk, k e z & cost 2 cost ctg t = -г— , t * nl, l e z & sint Дополнительные формулы 1 + tg2t — 2 ’ * 2 + Я7П’771 е cos t 1 4- ctg21 = ' ’*2 , t ф nk, k e z sin t tg t • ctg t = l,/*^,zez
Формулы приведения пре- образуют тригонометриче- , л ские функции чисел л - а, л Зл - 4- а, л - а, л 4- а, —— а, Зя -5- 4- ос в тригонометриче- ские функции числа а R. (Удобно считать а углом первой четверти.) t л- a л4-а Л 2 a Л 2 +a 3л 2 “a Зя , T +a
cos t -cos a -cos a sin a -sin a -sin a sin a
sin t sin a -sin a cos a cos a -cos a -cos a
tgt -tga tga ctg a -ctg a ctg a -ctg a
Периодичность Четность
cos (t + 2л) = cos t Гсоз = 2* tg (t + я) = tg г rtg = Jt cos (-a) = cos a
sin (t 4- 2л) = sin t Tsm = 2n ctg (t + it) = ctg t ^Ctg ~ n sin (-a) = -sin a tg (-a) = -tg a
/45
13. Тригонометрические функции
Значения тригонометрических функций некоторых углов
а, рад 0 л/6 л/4 7С/3 л/2 Я Зл/2
а О’ 30’ 45’ 60’ 90’ 180’ 270’
sin а 0 1 2 л/2 л/3 2 1 0 -1
cos а 1 л/3 2 1 а/2 1 2 0 -1 0
tga 0 1 л/3 1 7з не опр. 0 не опр.
ctg а не опр. 7з 1 1 л 0 не опр. 0
Тригонометрические функции в прямоугольной а Ь sin а = - cos а = - с с а Ь tg а = ctg а - - I треугольнике «К х. с ь J д
Приближение значения тригонометрических функций некоторых углов
а’ 5’ 10’ 20’ 30’ 40’ 50’ 60’ 70’ 80’ 85’
sin а» 0,09 0,17 0,34 0,50 0,64 0,77 0,87 0,94 0,9» 1,00 «cos а
tga = 0,09 0,18 0,36 0,58 0,84 1,19 1,73 2,75 5,67 11,43 = ctga
85’ 80’ 70’ 60’ 50’ 40’ 30’ 20’ 10’ 5’ а
Для малых положительных чисел sin а « а и tg а « а.
Знаки тригонометрических функций по четвертям
sin а cos а tg а и ctg а
У /+ +\ У +\ У ( +\
0 у ЖХ 0 -у к + 0 у
/46
13. Тригонометрические функции
Способы нахождения значений тригонометрических функций числа (угла) a
по формулам по вспомогательному треугольнику
tg а = 3; III четверть
cos а = —0,6; II четверть
|sin а| = 71 - cos2 а = 71-0,36 = 0,8
sin а > 0 => sin а = 0,8
, sina 4
х 1 3
cte°-5S-“4
3
sin a < 0 => sm a = —7=
cos а < 0 => cos а = —Д
ctg а > 0 => ctg а — I
О
1 5 TW
ctg a = ; IV четверть
iz
sin а — 0,1; I четверть
1
4 , 4 2 I69
2 = 1 + ctg2a = yyy
sin а
i • I 12
|sma| = 13
|cos a| = 71-sin2a =
12
sin a < 0 => sin a = -yg
I 144 =
1 169 13
n 5
cos a > 0 => cos a = jg
12
5
799
799
cos а > 0 => cos а = -уд-
tg а > 0 => tg а = -Д=
799
*а-ггй“
Формулы сложения Формулы двойного угла
cos (х 4- у) = cos х cos у - sin х sin у cos (х - у) = cos х cos у 4- sin х sin у sin (x 4- у) = sin x cos у 4- cos x sin у sin (x - y) = sin x cos у - cos x sin у x / . 4 tgx4-tgy я tg (x + у) — , x x > x * 5 + nn> 1-tgxtgy 2 у 5 + яп; x + у * s + яп, n s Z и ы у * | + яп; x - у * | + лп, п s Z cos 2х = cos2x - sin2x cos 2х = 2 cos2x - 1 cos 2х = 1 - 2 sin2x sin 2x = 2 sin x • cos x , o 2tgx tg 2x - , ; 1 -tg2x x * i+ e
/47
13. Тригонометрические функции
Формулы понижения степени Дополнительные формулы
cos2x = | (1 + cos 2х) sin2x = 5 (1 - cos 2х) (sin х 4- cos х)2 = 1 + sin 2х 1 + cos 2х = 2 cos2x 1 - cos 2х = 2 sin2x 1 • „ sm х • cos x = g sin 2x
Формулы половинного угла Универсальная подстановка
I X, /14-cosx lcos2l" V 2 lsm2l" J 2 л х sinx 1-cosx tg z = = : ; 2 1 + cosx sinx x *itk, k^Z z x z x z x N Hicsj Hicq 4 Hieq .T1 ™y *,cq W 1 + N + -g rH ^1 т-H eq II II 4- § д 4 0 *S н
Формулы преобразования
суммы в произведение произведения в сумму
xiy Х—у cos х 4- cos у - 2 cos о ‘ • cos о х + у Х — у cos х - cos у —2 sin % * s^n 2 Л . х+у х-у sm х + sia у - 2 sm % ' cos 2 „ . Х-у х+у sin х - sm у — 2 sm —у • cos , , sin(x + y) . . sin(x-y) tg X 4- tg у — tg X - tg у = — Ё COS X • cos у 6 6 y COS X • cos у , , , sin(y+ x) sin(y-x) ctg x 4- ctg у — . ctg x - ctg у — . . 6 & * sin x • sin у 6 6 * sm X • sm у cos x • cos у = z (cos (x - y) 4- cos (x 4- y)) sin x • sin у = | (cos (x - y) - cos (x 4- y)) sin x • cos у = z (sin (x 4- y) 4- sin (x - y)) л
Формула дополнительного угла ‘
1 q a cos х + b sin х - л/а +Ь • cos (х - а), где cos а - , , sina- , ,а2 + Ъ2*0 / 2 . ,2 / 2 . .2 4-о cl 4-&
/45
таалии/шь
14. Логарифмы
Логарифмом положительного числа а по поло- жительному и не равному единице основанию b называется показатель степени, в который надо возвести число Ь, чтобы получить а. logb a = c (a > 0; b > 0; b 1) тогда и только то- гда, когда Ъс = а Основное логарифмическое тождество: а b = а.
Примеры 5lOes'-T -0.7 logo 3 я l°l»2 3 logo 3 3 8 2 =(23) = (2 2 ) = 33 = 27
Iog2 8 = 3, так как 23 = 8 3 log9 27 = 1,5, так как 92 =27 logn „ 16 = -2, так как 0,25-2 = 16 log25 75 = 0,25, так как 250’25 =
log9 (-7) не определен, так как -7 < 0; log(_2) (-8) не определен, так как -2 < 0, -8 < 0; log1 27 не определен, так как не выполнено условие Ьф1.
Логарифмы по основанию 10 называются десятичными логарифмами'. log10 а = 1g а. Примеры 1g 100 = 2; 1g 0,0001=-4; 1g 100000000 = 8; 3<lg2156<4; -l<lg0,56<0.
a 2 3 4 5 6 7 8 9
Iga » 0,30 0,48 0,60 0,70 0,78 0,85 0,90 0,95
Логарифмы по основанию e называются натуральными логарифмами: loge a = In a. e = 2,718281828459045... иррациональное число; e ~ 2,7.
a 2 3 4 5 6 7 8 9 10 100 1000
In a ~ 0,69 1,10 1,39 1,61 1,79 1,95 2,08 2,20 2,30 4,61 6,91
Свойства логарифмов Основные соотношения Дополнительные соотношения
loga 1=0 hga--—1 Ioga a = 1 , 1 log m a = - a m loga am = m . n n log m a = ~ a m Логарифм произведения: logc (ab) = logc a + logc b. Логарифм частного: logc (a/b) = logc a - logc b. Логарифм степени: logc ak = k logc a. Переход к новому основанию: . logc а Iog» “ - logc Ь loga ь ~ log ьа logn b logm b i — i ~ log/, b log„ c logm c 6c logn b • logm c = logm b • log„ c Io<n b _ ,l°ffn ° a b
149
^Шт-мная пфогральма & ттГлимрм « формулах
14. Логарифмы
Примеры
1 log65 log5 6 □ = 0 = о. Tlog5 49 • log7 25 = Jlogi 49 • log5 25 = = 7П = 2. „ J<*37 J°g3 4 Сравнить: 4 ио logo 4 logo 6 Так как 6 =4 и log3 7 > log3 6, 1°ез7 4 to 4 >6
Сравнение логарифмов
Если 0 < а < 1 и 0 < хх < х2, то loga хх > loga х2. (знак неравенства меняется) Если а > 1 и 0 < < х2, то loga хх < loga х2. (знак неравенства не меняется) Если1<а<5 их>1, to loga x > logft x. Если 0<а<Ь<1пх>1, tologax>log6x. Если 1<а<Ь и0<х<1, то loga x < logft x. Если 0<а<6<1и0<х<1, tologax<log6x.
logb а > 0 тогда и только тогда, когда положитель- ные числа а и b лежат «по одну сторону от едини- цы»: а>О;Ь>Ои(а- 1)(Ь -1) > 0. logb a < 0 тогда и только тогда, когда положи- тельные числа а и & лежат «по разные стороны от единицы»: а>О;Ь>Ои(а- 1)(Ь -1) < 0.
Примеры
log0,7 °’2 < log0,7 °»11 log6 2 < logg 11 log5 7 > logg 7 Сравнить log3 4 и log4 5. I способ. log3 4 ? log4 5 log34-l ? log45-l log3 з ? log4 j ™ 4 5,4,5,5 Так как з > ^ , to Iog3 3 > log3 j > log4 , t. e. log3 4 > log4 5. JI способ. Рассмотрим функцию ч , , In (x + 1) f(x) - logx (x + 1) - lnx при X > 1. In X _ ln(x + 1) f(X}~ n a2 (Inx) _ In * ~ (s + 1) ln (* + 1) <Q x(x + 1) (In x)2 прих> 1. Значит, log3 4 > log4 5, так как функция f(x) убывает..
1о£о,2 7 > log0,8 7 log4 5 < log3 5 < log3 6 => => log4 5 < log3 6
Сравнить log415 и J17. Так как log415 < 4, a J17 > 4, то log415 < 717.
150
15. Уравнения
Корнем уравнения называется значение пере- менной, при подстановке которого в уравнение получается верное равенство. Два уравнения называются равносильными, ес- ’ ли множества их корней совпадают. j
Примеры х3 + х = 0 — один корень: х = 0. (х2 + х - 12) • Jx + 3 = 0 — два корня: х = -3, х = 3. sin (лх) = 0 — бесконечное число корней х s Z. х2 + 2х + 1 = (х + I)2 — верно при всех х R. х2 = х2 + 1 — нет корней (пустое множество корней 0). Примеры х2 = х + 2 и х2 - х - 2 = 0 равносильны. х4 + 2 = -16 и sin3r = 2 равносильны. Vx = 2х - 6 и х = (2х - 6)2 неравносильны.
Неравносильные преобразования могут привести к:
потере корня появлению «посторонних* корней
х(х + 5) = 2х х + 5 = 2 х = -3 Потерян корень х = 0. правильное решение: х2 + 5х - 2х = 0 х2 + Зх = 0 х(х + 3) = 0 х = 0; х = -3 х2 + х -1 _ 4х-3 X ~ 1 X -1 х2 + х - 1 = 4х - 3 х2 - Зх 4 2 = 0 х - 1 и х = 2 «Посторонний» корень х = 1. прав?’Л1 ное решение: |х" + х-1 = 4х-3 [х* 1 [х2-0х + 2 = 0 [ХТ4 1 Ответ: х — 2.
Методы решения уравнений
Разложение на множители Произведение нескольких множителей равно нулю, если хотя бы один из них нуль, а осталь- ные при этом существуют. Г х = 1 г X = 1 (х - 1)(х2 - 4) • а/х = 0 < х = ±2<=> X = 2 х = 0 Л L [_ х = 0 х> 0 Ответ'. 0; 1; 2. Замена переменной (х + 1)4 + х2 = 1 - 2х<=>(х + I)4+ (х2 +2х+1) = 2<=> ft = (х + 1)2>0 * = 1 ] 2 «<| t =-2 f = 1 It +t-2 = 0 t^O ' х = -2 х = 0
Сравнение обеих частей по величине
sin7 х - cos22 х = 1 <=> sin7 х = 1 + cos22 х9
sin7x^ 1 f s^n х ” 1 [sinx = 1 л
=>< о <=> ^ <"-><=> X - - + 2пп, П ^Z
l+cos22x>l J Leos x = 0 [cosx = 0 z
75/
ty.UtifkAb'MaJl nfaxftCLAi'JUl
& тас/лиллАх а,
лщлах
15. Уравнения
Использование монотонности 2х + 5х = 29. Функция /(х) = 2х + 5х возрастает; /(2) = 29 => х = 2 — единственный корень.
3(х + 8)2 - 4(х + 8)(х2 + 2х + Тогда За2 - 4аЬ + Ь2 = 0, а12 х + 8 = х2 + 2х + 2 х2 + х - 6 = 0 хг = -3; х2 = 2 Использование однорс 2) + (х2 + 2х + 2)2 = 0. Пусть 2Ъ±Ъ Ъ g у а и или a g Зх + 24 = х2 + 2х + 2 х2 - х - 22 = 0; _ 1+789 *3,4 2 удности > x + 8 = a; x2 + 2x + 2 = b. r> о a 1-789 1 + 789 Ответ: 3; 2; o ; o
Линейные уравнения (приводимые к виду ах = Ь)
а ^0 b один корень х = - а = Ь = 0 бесконечное множество корней х G Я a — 0, b Ф 0 решений нет
Квадратные уравнения (приводимые к виду ах2 + Ьх + с = 0 (а 0))
_ - ( Ь\2 Ъ2-1ас Равносильными преобразованиями уравнение приводится к виду х + у- = т— . < *а' 4а Наличие корней зависит от знака выражения: D = Ь2 - 4ас (дискриминант квадратного уравнения).
В <0 корней нет D = 0 Ъ один корень х = D > 0 два корня -ъ- Jd -ъ + Jd X 2a ,X" 2a
а > 0 V \У / а> 0 \У a > 0 < i г,/ X1<X2
0 0
Частные формулы для решения квадратных уравнений
Приведенное квадратное уравнение х2 +рх + q = 0 (а = 1) Квадратное уравнение с четным вторым коэффициентом ах2 + 2Ах + с = 0 (b = 2k)
т, тч « -р± 75 Если D > 0, xt, 2 - г 5 р если D = 0, х = -- • & D* = k2-ac (D*=|z>) -k + Jd* k Если D > 0, хЛ 9 — ; если D - 0, x = - • I»2 a a
152
Алгсс/Ьа £ пии/лиирх
15. Уравнения
Неполное квадратное уравнение
ах2 + с = 0 (Ъ = 0) ах2 + Ъх = 0 (с = 0) ах2 = 0
Если ас > 0, решений нет; / с если ас < 0, х = ± I — . . А/ а х(ах 4- Ь) = 0 два корня: х = 0, х = -- . а один корень х = 0
Алгебраические уравнения высших степеней (приводимые к виду /(х) = 0, где f(x) — многочлен степени выше 2)
Разложение на множители х3 - 2х2 - х + 2 = 0 х2(х - 2) - (х - 2) = 0 (х - 2)(х2 - 1) = 0 => х = 2; х = ±1 Подстановка (биквадратное уравнение) х4 - Зх2 + 2 = 0; х2 = t t2 - 3t + 2 = 0 f = 1; f = 2 => x = ±1; x = ±^2
Применение схемы Горнера х3 - 4х2 + х + 6 = 0 Использование монотонности x3 4- x - б^/б = 0 x3 4- x = 6 a/5 Функция F(x) = x3 4- x возрастает на R; Г(л/5) = бТб => х = а/5 — единственный корень.
-1 2 3 1 -4 1 6 => х = -1
1 -5 б 0
1 -3 0 => х = 2
1 0 => X = 6
Возвратное уравнение 2х4 - 5х3 + 6х2 - 5х 4- 2 = 0 Так как х = 0 не является корнем, можно делить на х2. 5 2 2х2 - 5х 4- 6 + “ =0, х х2 2(хг + -У - бГх + + 6 = 0. 1 х2) 1 xj Подстановка: у = х + - ; у2 - 2 = х2 + Л. х X 2(у2 - 2) - 5у + 6 = 0 2у2 - 5у + 2 = 0 Использование однородности Зх2 + 4х(х2 + Зх + 4) + (х2 + Зх + 4)2 = 0 Пусть у = х2 + Зх + 4. Тогда Зх2 + 4ху + у2 = 0. „ 1 Решаем относительно х: х = -у; х = - х у. О Г 2 о Л х = -х --Зх-4 Следовательно, Зх = -х2-Зх-4 Ответ'. -2; -3 ±75 .
Уравнение Jf(x) = g(x) равносильно системе: /(х) = £2(х) ^(х)>0 Неравенства в системах, как правило, проверяю! Уравнение «//(*) = 'Jsi.x) равносильно системе: /(х) = ^(х) /(х) > 0 (или g(x) > 0) а не решают.
153
^Ш/акльная & тас/лилулх и, фор^м^
15. Уравнения
Иррациональные уравнения
Простейшие 73х + 1 = 2 Зх + 1 = 4 х = 1 71-2х = -5 корней нет
Замена переменной
^2-х = Зх + 8
Возведение обеих частей уравнения в степень
5х + 6>0; Зх+4>0
75х + 6 + 73х + 4=2<=> 5х + 6 + Зх + 4 +
,+ 2л/(5х + 6)(Зх + 4) - 4
Пусть у = 7 2 * х > 0.
Тогда х = 2 - у2 и у = 3(2 - у2) + 8 <=>
5х+6>0
7(5х + 6)(Зх + 4) = -4х - 3
3y2 + j/-14 = 0
'5х + 6>0; -4х-3£0
О
1(5х + 6)(Зх + 4) = (-4х-3)
Уравнения, связанные со степенной функцией
С- 2/3 , 1/3 е Л 15х +х -6 = 0 1 х>0 537х* +37х -6 = 0 у = Цх « 2 4 3 3. X X =4
1/3 л у = х >0 5yz + у - 6 = 0 х>0
5у2 + р-6 = 0=>у = 1;у = -| <0 у = 37х = 1, у = 37* = и Ti< II 1 со + CSJ1 СО Н
X1/3 = 1 => X - 1 „ f6? 216 х2 = 4
<5j 125 х = ±2
216 Ответ: х=2.
Ответ: х = 1; х = -7777 • 1ZD
Показательные уравнения
Решение простейших показательных уравнений
основано на монотонности показательной функ-
ции у = ах (а > 0, а 1, D(y) = Я, Е(у) = (0; +°о)).
Простейшее показательное уравнение ах = Ъ
при Ь > 0 имеет единственное решение, записы-
вающееся в общем виде х = loga Ъ.
При Ь < 0 решений нет.
6х = 36 х = log6 36 х =2 2х = - Z 8 х =log2 (1/8) х = -3 100х =10 х = log100 10 х = 0,5 10х = 3 х = 1g 3 ех = 2 х = In 2 625х =-25 решений нет
Уравнения вида = ag^ равносильны уравнению /(х) = g(x).
cAazeJjia £ тгл/лшщх
15. Уравнения
Методы решения показательных уравнений
Приведение к одному основанию X 5х-0,2= 1252 • Тб Зх 1 5х • 5-1 = 5 2 • 52 Зх + 1 5х -1 = 5 2 , Зх + 1 х 1- 2 => х - 3 Логарифмирование обеих частей уравнения 61/X. 2* = 12 Логарифмируем по основанию 2: log2 6 + х = log2 12 <=> « 1 + log2 3 + х2 = (2 + log2 3)x x2 - (2 + log2 3)x + (1 + log2 3) = 0 Ответ-, x = 1; x = 1 + log2 3.
Вынесение за скобку 7х + 7х + 2 = 350 7Х(1 + 72) = 350 350 7х - , - 7 1 + 72 х = 1 Составление отношения 4х + Зх-1 = 4х-1 + Зх + 2 ^х _ 4Х - 1 дх + 2 __ дх - 1 4х-1(4 - 1) = Зх-1(33 - 1) 4х-1•3=3х-1•26 4х-1 26 Му1 26 , 26 , , „х-1 3 зх log| з +1 о 4 z 3 Замена переменной 25х + 5х +1 - 6 = 0 5х = у > 0 у2 + 5у - 6 = 0 У = l;z/ =-6<0 5х = 1 => х = 0
«Завуалированное» обратное число (Тб -2)х +(Тб + 2)х = 18 (Тб -2)(Тб +2) = 5-4 = 1 Пусть (Тб - 2)х = у >0 у +^ = 18=>г/=9±4Тб (Тб - 2)х = 9-4Тб = = (Тб -2)2=>Х = 2 (Тб - 2)х = 9 + 4Тб = = (Тб +2)2 = (Тб — 2)-2 => х = —2 Ответ*. 2; -2. Использование однородности 3-16Х-12Х = 4-9Х Делим на 9х > 0: ’(WP Пусть =у>0=^> Зу2 ~ У ~ 4 = 0 => 4 , л =>у = з;у=-1<о=> Использование монотон- ности 2х + 5х = 29 /(х) = 2х + 5х возрастает наЛ. /(2) = 29 => х 2 — единственный корень.
Логарифмические уравнения Решение простейших логарифмических уравнений основано на моно- тонности логарифмической функции у = loga X (a > 0; а * 1; D(y) = (0; +<=о); Е(у) = R).
155
15. Уравнения
^ИЬю^ЬНОЯ nftOzfuMLAUL & тшм/ллшдх it фоф^л^м.
Типы простейших логарифмических уравнений
1) loga х = Ъ при всех допустимых а имеет единственное решение х = аъ.
2) loga (/(х)) = Ь равносильно уравнению /(х) = аъ.
3) loga (/(х)) = g(x) равносильно уравнению /(х) = а^(х).
4) loga (Дх)) = loga (g(x)) равносильно системе:
/(х) = g(x)
Лх)>0
g(x)>0
Причем любую из двух последних строк можно (и, как правило, нуж-
но) опустить.
В логарифмических урав-
нениях, как правило, со-
вершенно не обязательно
находить области сущест-
вования функций, входя-
щих в уравнение. Доста-
точно проверить,
из полученных корней
уравнения системы удов-
летворяют неравенствам
в системе.
какие
Уравнения, сводящиеся к типу 4
log2 (х2 + х - 2) = 1 + log2 х <=> log2 (х2 + х - 2) = log2 (2х) <=>
х2 + х-2 = 2х [х2-х-2 = 0
<=> <
2х>0 1х>0
х = -1
х = 2
х>0
Замена переменной
lg2^~ ) + lg * х = 7
(1g 10 - lg х)2 + 1g х = 7
У = lg х =>(1 - у)2 + у = 7 =>
Потенцирование уравнений, сводящихся к типу 4
-1) + log3= 2 — 2log 1 (х2) <=> logi (х +1) ~ logi | = logi § “
lg X = 3
У = 3
. у = -2 |_ 1g х = -2
Ответ', х = 1000; х = 0,01.
- logi (х2) <=>
3
11-3
6
х> 0
2(х + 1)
log 1 ~
3
, 1
= logi —2
з 9х
х>0
2(х + 1) _ 1 <=>
х 9х2
3
9
3
3
3
Уравнение с неизвестным в основании логарифма
logx 5 = 3 <=> x>0 <=>- x* 1 <=>x = 3/5 3 E [ x = 5 Ответ'. 3j5. 2 . I X>0 X * 1 X 1 log 2 X = 0,5 <=> X > 0 <=> <=> X Л , ХФ-1 l 2ч0'5 ) X [ |x| = X [ x>0 { X*1 Ответ: x G (0; 1) и (1; +°°). О • ‘ • 5* i a J» f « 4 ° “ * II II II 11 to I 1 СЛ to СЛ1 $ а а н м H A 11 hL ° cnl
/56
сЛлга/ка & таЛлищах
15. Уравнения
sin х = а
Тригонометрические уравнения
cos х = а
решений нет
решений нет
х = (-IJ^arcsin а + лл, п Z
х = ± arccos а + 2лл, л G Z
При |а| 1: л л “ 2 arcsin а % sin(arcsin а) = а arcsin (-а) = -arcsin а а 0 1 2 72 2 Тз 2 1 При |а| < 1: 0 < arccos а < л cos(arccos а) = а arccos (-а) = л - arccos а
arcsin а 0 л 6 Я 4 Л 3 л 2
arccos а л 2 л 3 л 4 я 6 0
arcsin а + arccos а = 5
tg х = а
ctg х = а
у । х = arctg а + ли, л s Z ' /1 ^^tart / X / 1 / 1“ x = arcctg a + ял, n £ Z У t Е 1 а
( 0 :tg a V 4 it arcctg а
I \ / я+arctg ti4**- 1: я+arcctg a\^ У’
При любом а: Л J л ~2 < arctg a < 2 tg (arctg a) = a arctg (-а) = -arctg a a 0 1 Тз 1 /3 При любом а: 0 < arcctg а < л ctg (arcctg а) = а arcctg (-а) = л - arcctg а
arctg a 0 л 6 Л 4 я 3
arcctg a 2 л 3 л 4 я 6
arctg a + arcctg a = 5 A
Частные решения
х = Tin, п Z
л
х = - + 2кп,
n^Z
л
х = - + ли, мл е Z
Ci
COS X = 1
х = 2лл, л £ Z
/57
GlLbtoMmaji программа
йта/лищы и, фофм-улах,
15. Уравнения
sin (Дх)) = а cos (ftx)) = a tg (/(X)) = a
при |а| < 1: /(х) « arcsin а + 2пп L /(х) = я - arcsin а + 2ял n^Z при |a| < 1: f(x) = iarccos а + 2лл n^Z при всех a: /(x) = arctg a + nn n^Z
Методы. решения тригонометрических уравнений
Тригонометрические уравнения, приводимые к уравнениям от одной тригонометрической функции одной переменной, решаются (как пра- вило) подстановкой.
sin2 х + 4cos х = 2,75 1 - cos2 х + 4cos x = 2,75 cos x = t; |t| < 1 t2-4t +1,75 = 0 1 7 t~2i t~2>1 n x = ±5 + 2nn, n&Z О tg x + 3ctg x = 4 3 tgx + tT^ =4 tgx = t t2-4t + 3 = 0 t = 1; t =3 7t X = T +ЛП , — „ x = arctg 3 + Tt7; cos2 x + cos 4x = 0,25 0,5(1 + cos 2x) + 2cos2 2x - 1 = 0,25 cos 2x = u; |u| 1 4u2 + и - 1,5 = 0 1 3 u-2;u- 4 Л z 34 x = arccos(~4) + nn; X = ±2 + ЯП, n G Z D
Однородные тригонометрические уравнения и уравнения, сводящиеся к ним
2sin х • cos х - cos2 х = 0 cos x(2sin x - cos x) = 0 it cos x = 0 => x = ~ + ЛЛ, n Z A 2sin x - cos x = 0 Корни уравнения cos x = 0 не удовлетворяют этому уравнению. ! Делим на cos х i*0: 2tgx-l = 0; х 1 tgx = 2 х = arctg + тсп, n G Z 5sin2 x + sin x • cos x - 2cos2 x = 2 5sin2 x + sin x • cos x - 2cos2 x = 2cos2 x + 2sin2 x 3sin2 x + sin x • cos x - 4cos2 x = 0 cos x Ф 0. Делим на cos2 x: 3tg2 x + tg x - 4 = 0 => tg x = 1; tg x = -~ о я 1 4 x = т + ял; х = -aretgz + ял; 4 о П, k G Z
Разложение на множители
^2 sin x • cos x - 2 = cos x -2 J2 sin x J2 sin x • cos x - cos x-2 + 2A/2sinx = 0 ; cos x(j2 sin x - 1) - 2(1 - J2 sin x) = 0 i J (V2 sin x - l)(cos x + 2) = 0 a/2suix-1 = 0 L cosx + 2 = 0 1 sin X = -= 72 x = (-1)" • + яп; n e Z cos x = -2, корней нет.
158
15. Уравнения
Уравнения, решаемые на основе условия равенства тригонометрических функций
S 7 >in ftx) = sin ф(х) /(х) = ф(х) + 2лА _/(х) = л-ф(х) + 2лп г е Z, k е Z cos /(х) = COS ф(х) /(х) = ф(х) + 2яп f(x) = -ф(х) + 2лЛ п <= Z, k S Z tg f(x) = tg ф(х) /(х) = ф(х)+ЛП л Ф(х)^2+я^ п s Z ,1 е Z
Уравнения с обратными тригонометрическими функциями
arcsin х = а arccos х = а arctg х = а arcctg х = а
I к toia II /Л S. е 3 /Л ° 0 < а < я х = cos а II л о Л 0 < а < л х ctg а
п к а < -g или а > 2 решений нет а < 0 или а > п решений нет Я .Я а < -- или а > & и решений нет а 0 или а > я решений нет
Уравнения с параметрами
I X ( I 2х + 3 ?ешить уравнение х _ а = ® Для каждого зна- тения а. Данное уравнение равносильно системе 2х + 3 = 0 х - а*0 3 х 2 х*а. 3 3 Этвет: при а х = -z , Сл и з три а = -х решении нет. Л Найти все такие значения р, для которых один из корней уравнения х2 - Зрх + 2р2 = 0 равен 1, и для каждого такого значения р найти ос- тальные корни. Для того чтобы один из корней уравнения был равен 1, необходимо и достаточно, чтобы I2 - Зр • 1 + 2рг = 0, т. е. 2рг - Зр + 1 = 0, -1 -1 Pi -1, Р2 2 • Прир = 1 х2 - Зх + 2 = 0, Xj = 1, х2 = 2; 1 , 3 1 Л , 1 прир=2 xJ- gX+ g =0, х1 = 1,х2= 2* Ответ: прир = 1 и прир = . Прир = 1 х2 = 2; 1 1 прир=2 х2=2‘
При каких значениях а уравнение 4х - (а + 2) 2х + 2а = 0 имеет а) хотя бы одно решение; б) ровно одно решение; в) более одного решения? Сделаем замену 2х = t, t2 - (а + 2) • t + 2а = 0, = a, t2 = 2. 2х = 2, х = 1 при любом а. 2х = а, при а < 0 решений нет; при а > 0 х = log2 а. Заметим, что при а = 2 х = 1 совпадает с первым корнем. Ответ: а) при всех значениях а; б) при а 0 и а = 2; в) при 0 <а <2 иа > 2.
159
(Шкомтая пфсгфалма.
& пии/мщах и, формулах
15. Уравнения
При каких значениях Ь уравнения sin2 х - (3 + b) sin х + ЗЬ = 0 и х2 = b равносильны? Если первое уравнение имеет решение х0, то оно имеет и бесконечно много решений вида х0 + 2 nk9 т. е. не может быть равносильно уравнению х2 = Ь9 имеющему не более двух решений. Уравнения равносильны, если они оба не имеют решений. Уравнение х2 = b при b < 0 не имеет решений, второе уравнение равносильно объединению sin х = 3 не имеЮ1ЧемУ Решений при b < -1 или Ъ > 1. Таким образом, оба уравнения не имеют решений, т. е. равносильны при Ь < -1. Ответ: при Ь < -1.
Найти все-значенияр, при которых сумма действительных корней уравнения х2-рх + 3 = 0 мень- ше пяти. (р<5 [Р<5 _ Г ПриР>о хг + х2=р. 12> 0 <=>(-°°;~27з]и[27з;5). Ответ: р е (-оо; -2^3 ] и [2 а/З ; 5).
При каких значениях т уравнения х2 + Зх - т = 0 и тх2 + х + 3 = 0 имеют общий корень? Для каждого такого значения т найти этот корень. Пусть t — общий корень уравнений. Составим систему двух уравнений с двумя неизвестными (t и т): Гt2 + 3t - т = 0 + 3) = т |7(t + 3) = тп Ф + 3) т 12 <=* 2^1 2 <=> S Г/n = 0 [mt+H3 = 0 + 3 = -mt [т = -mt t t =-1 (x2 1 Зх = 0 Притп = 0< общий корень x =-3; npnt = -l т = (—1)(—1 + 3) = -2. [х + 3 = 0 [х2 + Зх + 2 = 0 < общий корень х =-1. 1-2х + х + 3 = 0 Ответ: при т = -2 х = -1; при т = 0 х = -3.
Найти все пары действительных чисел а и Ь, при ко- торых уравнение |х - 1| + |х + 3| = ах + Ъ имеет бес- конечное множество решений. -2х - 2 при х < -3 |х- 1| + |х + 3| = < 4 при-3<х<1 2х + 2 при х > 1 Уравнение имеет бесконечное множество реше- ний, если ах+ Ъ тождественно равно -2х - 2, т. е. а = -2;Ь = -2. Аналогично ах+ Ь тождественно равно 4, т. е. а = 0; 6= 4. Аналогично а = 2; Ь = 2. Ответ: (-2; -2); (0; 4); (2; 2). При каких значениях т уравнение х2 - тх + 1 = 0 имеет два корня, расстояние меж- ду которыми на числовой оси равно 2? Уравнение имеет два различных корня, если D > 0, т. е. т2 - 4 > 0. Расстояние между кор- нями на числовой оси равно . । т - Jb т + Jb пг 1х1"х2|- 2 2 (т2 - 4>0 Г т = 2 72 Имеем систему: <=> Чт2 -4 = 2 = ~2j2 Ответ: т = -2j2, т = 2j2 .
160
оДлга/ка & тк/jutyix
16. Методы решения систем уравнений
Метод подстановки
г _ 6 ~ jx + 5 г/ = 6 У 5 [х2 + Зу = 4 2 , о * х + 3 6 — X У ~ 5 <=>•! 0 <=>• [бх2 - Зх - 2 = 0 / 2 32 Ответ: (-^ ; ), (1; 1). OHIO <М|Ю 1 со Icq ,-н .и II II II II X а> X »> $ X 11 I Ю OHIO * Л ° II II Ч ф й» . * . .* (2х + у = л [cos(3x - 2у) = 0,5 (у — л - 2х (cos(3x - 2л + 4х) = 0,5 Г г л , 2л& *-21 + ~ fcos7x = 0,5 И ~ 21 7 <=> <! <=> n,k^Z 1 у = л - 2х ( л , 2лп Iх 21 7 — 4яп [1У “21 7 (л 2лк 19л 4л&\ Ответ'. ^21 + 7 1 21 “ 7 J’ ( л , 2лп 23л 4лтГ\ , „ 1“й + Т;
Метод алгебраического сложения
сложим [5х + 2у = 9 умножим на 3 (15х + Зу = 27 уравнения [29х = 29 [х = 1 1 <=> 1 <=> S <=> •! [7х - Зу = 1 умножим на 2 [14х - Зу = 2 [7х - Зу = 1 [у — 2 Ответ'. (1; 2).
[cos х cos у = 0,75 с. [sin х sin у — 0,25 в [cos(x - у) = 1 <=> < <=> [cos(x 4- у) = 0,5 Z 1 X Ответ: 4- л(л 4- Jfe); 7 VO 0 иожим уравнения системы 1 ычтем уравнения системы х - у = 2лк я <=> х 4- у = ±д 4- 2лл • \ ( л ; 4- л(л - k) 1; 1-g 4- л(; Г cos xcos у 4- sinx sin у = 1 [cos xcos у - sinx sin у = 0,5 x - у = 2лк л х + У = о + 2лл о х - у = 2лк л х 4- у = -z 4- 2лп о Л \ п 4- A); -g 4- л(п - k) 1, n, k Z.
6—1323
/6/
^Школьная пфагфамма $ тш/мма ч фобму-лах
16. Методы решения систем уравнений
Дополнительные методы
Применение теоремы Виета (х + у = 5 [х- у = 4 х, у — корни уравнения: а2 - 5а + 4 = 0. а = 1; а = 4. Ответ*. (1; 4); (4; 1). Симметрические < Г 2 1 2 О 1 jx + у - Зху = -1 [х + у - ху = 1 f(p2 - 2g) - 3g = -1 lp - g = 1 системы замена X + у == р ху = g
Сведение к объединению более простых систем ГГ х-у = 0 1 2 (1) Гх2 - 5ху + 4у2 = 0 |(х-у)(х-4у) = 0 [Зх -2у = 8 l3x2-2i/ = 8 13х2-2у = 8 Гх-4у = 0 1 9 (2) [Зх“-2у = 8 J* = У (2; 2) (1) [Зх2 - 2х - 8 = 0 (-4/3; -4/3) Jx = 4y <1+7385 1 + V385A <1-7385 1-Т385А “ W-S-4 - 0 ” 1 12 48 И 12 48 J
Использование однородности 1 6Х ХУ^У 0 Умножим первое уравнение на (-3), 1х2 + 2у2 = 3 второе — на 5 и сложим. Г - 9х2 + Зху - Зу2 = -15 Г-4х2+ 3ху + 7у2 = 0 |(у + х)(7у-4х) = 0 l5x2 + 10у2 = 15 tx2 + 2j/2 = 3 (х2 + 2у2 = 3 ГГу + х = О г(1;-1) [х2 + 2у2 = з L(-i; 1) <=> Г<7Тз 4j3 Л (7у-4х = 0 ^9’9/ [х +2у = 3 ( 4л/3 Л L LI 9 ’ 9 J Л и 11 / 1 11 4ТЗ> Г 7j3 4j3\ Ответ: (1; -1); (-1; 1); 1 -g- J; —g-; —g- J.
1G2
тш/лиирх,
17. Неравенства
Строгие неравенства Нестрогие неравенства
Число а > Ъ (а больше &), если разность (а - Ь) положительное число. Если а < Ь, то Ь > а. В этом случае разность (а - Ъ) отрицательное число. а<& с > d
Свойства числовых неравенств
а9Ь — любые числа а9Ъ — положительные числа
Если а > b иЬ > с, то а > с (свойство транзитив- ности). Если а >Ъ, то a+c>b+c (с R). Если а > Ь и с положительное число, то ас > Ъс. Если а > Ъ и с отрицательное число, то ас < Ьс. Если a>bnc>d, тоа+ob+d. тл , Л 1 1 Если а > b > 09 то - < т • а Ъ Если а > b > 0 и с > d > 0, то ас > bd. Если а > b > 0 и т N9 то ат > Ьт. Если а > & > 0 и т <^N9 то т*/а > ™Jb .
Двойное неравенство (а < Ъ < е)
Сложение двойных неравенств a^b^c, р^т <q =>a+p^b+m<c+q Умножение двойных неравенств с положи- тельными членами 0 < а < b < с; 0 < р < т < q => ар < bm < cq
Методы доказательства неравенств
Составление разности (если разность двух чисел положительна, то уменьшаемое больше вычитае- мого). Метод использования известных неравенств. Метод усиления (использование транзитивности). Использование монотонности функции, примене- ние производной. Пример. Доказать неравенство: 6х > 14- х при х > 0. Рассмотрим функцию f(x) = ех - 1 - х. f'(x) = = ех - 1 > 0 при х > 0. Следовательно, f(x) возрас- тает на [0; 4-оо). Но /(0) = 0. Значит, f(x) > 0 при х > 0. При х = 0 неравенство обращается в ра- венство. Итак, ех - 1 - х > 0, то есть ех > 1 4- х при х > 0.
Сравнение средних величин положительных чисел (а > & > 0, at > 0, п ^N)
Среднее арифметическое двух чисел а + Ь 2 п чисел а1+а2 + --*+ап п
Среднее геометрическое двух чисел Jab п чисел ’л/а1 ' а2 ' ’ ал
Среднее гармоническое двух чисел 2аЬ _ 2 а + & 1 1 а b п чисел п а1 а2 ап
163
’'‘Шкальная пфгогфалима & таблицах и, фофлуулах
17. Неравенства
Сравнение средних величин положительных чисел (а > Ъ > 0, at > 0, п е N) (продолжение)
Среднее квадратичное двух чисел 1 2 , ,2 а +Ъ N 2 п чисел /2,2, ,2 а^ 4-^2 4" ••• 4" ап N п
/а2 4- &2 а + Ъ г-? 2 а Ч 2 Jbbt^-^b а^Ъ (верно и для п чисел)
Линейные неравенства (приводимые к виду ах > Ь; ах > Ъ\ ах <Ь; ах Ъ)
3 • х > -6 х > -2 х е (-2; 4-00) -5 • х > 1 X С 0 хе(-оо;-1] 0-х <2 х GR 0-х >8 ХЕ{0}
(Тб -77)х>(л/5 -77) х < 1, так как 75 - 77 < 0 х е (-ОО; 1)
Квадратные неравенства (приводимые к виду ах2 4- Ъх 4- с > 0, ах2 + Ъх 4- с <0, а >0)
Для решения квадратного неравенства вычислим дискриминант D = Ъ2 - 4ас и определим корни квадратного трехчлена.
Неравенство D<0 D = 0 D>0
\Х1 Х2 J
X х
ах2 4- Ъх 4- с > 0 xER X е (-ОО; х0) U и(х0; 4-оо) х е (-ОО; хг) и (х2; 4-оо)
ах2 + Ъх 4- с < 0 решений нет решений нет х е (Хр х2)
Простейшие иррациональные неравенства
Jx <а Jx > а
а < 0 решений нет х>0 « х е[0; 4-оо)
а = 0 решений нет х >0«х е(0; 4-оо)
а > 0 0< х < а2, х е [0; а2) х > а2 <=> х е (а2; 4-оо)
764
& 7пас/лия1д^
17. Неравенства
Простейшие иррациональные неравенства (продолжение)
77(xj <я(х) 4Rx) > g(x) JRx) > Jg(.x)
равносильно системе 1#(х) > 0 • f(x)<g2(x) [f(x) > 0 равносилы io объединению систем fg(x)<0 |f(x) 0 (g(x) > 0 \f(x)>g2(x) равносильно системе I7(x)>g(*) U(x) > о
Простейшие показательные неравенства
ах <т ax >m afM < m > m
тп 0; а > 0, а*1 нет решений x^R нет решений X ^D(f)
т > 0; а > 1 X < loga7n x > logam f(x) < logam /(x)>logam
тп>0;0<а<1 х > logam x < logam f(x) > logam /(x) < logam
afW > ав(х) при а > 1 равносильно неравенству Дх) > g(x) при 0 < а < 1 равносильно неравенству Дх) < g(x)
Простейшие логарифмические неравенства
тпея logax < т logax > m logj(x) < m logafW > m
а > 1 ( т \х<а [х> 0 x>am [fW<am l/(x)>0 f(x) > am
0<а<1 х > ат 1 x<a lx>0 /(x) > am [f(x)<am l/(x)>0
loga/(x) < logag(x) 1ogH(r)^)<logH(l)g(x)
при а > 1 равносильно системе I7(x)<g(x) [ftx)>0 при 0 < а < 1 равносильно системе (7(x)>g(x) |g(x) > 0 равносильно объединению < |Н(х)>1 /(x)<g(x) и • [/(x)>0 систем неравенств: Я(х) > 0 H(x)< 1 /(x)>g(x) g(x) > 0
Примеры простейших тригонометрических неравенств
sin х < —1,3 sin х > -1,3 sin x < 71,3 sin x > 71,3
решений нет, -I sin х 1 X ел x R, так как sin x < 1 < 71,3 решений нет
/65
^Шкальная пфогфамльа & тш/лияцах и, фофлА/улал
17. Неравенства
sin x < -0,5
sin x > -0,5
73
Sinx < "2“
cos x < -30’7
cos x < In 3
к
cos x > - 3
cos x > e0’* 2 *
решений нет
x ед,
так как cos x 1 < In 3
x ед,
. - n
так как cos x > -1 > - 3
решений нет,
так как с0,2 > 1
л
2
J2
cos x < —z-
Li
cos x < 0,5
cos x > 0
cos x > 0,7
tgx 7з
x e (2яп - arccos 0,7;
arccos 0,7 4- 2лп) n Z
ТС 7C “1 _ „
о +7:n , П
Z o J
i66
17. Неравенства
Более сложные примеры решения тригонометрических неравенств
(Л ЗяА
cos 12x--g-1 < О
sin х > cos х
tg2x < 3
(п , л Зл
t £ 12лл + g > 2
7t Tit
2лп + т x < -г + 2лп,
4 4
п <=Z
„ л „ Зл Зл
2лп + o<2x--z-<-z- + 2лп
Z о А
7л 15л
ЯП + Jg < X < -jg- + 1И, П Е 2
Пусть у - cos x. Тогда
бу2-у - 1<0
1у1 < 1
6cos2x - cos x -1 < 0
111 1
"3<У<2 =* "3<C0SX<2
гп ( 1
х 61 2лп - arccos I-д
2лл - arccos 11 и f 2лп + arccos z; 2лп + arccos f-l
Z j \ Z к о
или
x G f 2лп - arccos \ 2лп - g-j и Г| + 2лп; arccos f-| ^ + + 2лп\ n Z
167
tax
17. Неравенства
sin х - sin 2х < 0
sinx (1-2 cosx)< 0 —- Используем метод интервалов на тригонометрической окружности, ( считая х [0; 2л). 1 [ к 5 тс xjrc F(x) = sinx (1 - 2 cosx); F(x) = 0 => x = 0; л; x;-x-. Д О о / \ x s [*2лп + х; л + 2лн] u Г2лп + ^г; 2л + 2лп"|, n \ дл"- L о J L ® J \ - о\/х Jo) у 3
Примеры неравенств с обратными тригонометрическими функциями
arccos х < -5 решений нет, так как 0 arccos х тс arrcos х > -4 х €= [-1; 1] тс arccos х < £ хе (0,5; 1] arccos х > 1 х [-1; cos 1)
arcsin х < л хе[-1;1] arcsin х <-1,7 решений нет, так как я . . Я arcsin х g . п arcsin х -g хе[-1;-0,5] arcsin х > 0 х е (0; 1]
arctg х < 2 х ей, так как л , л ~2 < arctg х < 2 arctg х > 5 решений нет tilt- V/ .2? Н А” ья ° 1 Й ш к arctg х < 0 X е (-ОО; 0]
Метод интервалов (промежутков)
Методом интервалов решают неравенства, при- веденные к виду F(x) > 0 или F(x) < 0, (F(x) > 0 или F(x) 0). Метод основан на том, что непрерывная на про- межутке функция может менять знак только в тех точках, где ее значение равно нулю (но мо- жет и не менять). Алгоритм применения метода Найдем D(F(x)) и промежутки, на которых Дх) непрерывна. Найдем нули функции Дх) — значения х, при которых Дх) = 0. Нанесем на числовую ось найденные промежут- ки и нули. Определим интервалы знакопостоянства и в ка- ждом из них поставим найденный подсчетом или рассуждением знак. Выпишем ответ.
Примеры
х(х - 4)(х + 5)2 > 0 _ ут Рассмотрим функцию Р(х) = х(х - 4)(х + 5)2. -5 о 4 * D(F) = R, функция непрерывна наЯ. Я(х) = 0 в точках х = 0; х = 4; х = -5. Д-6) > 0; Д-1) > 0; Д1) < 0; Д5) > 0. Ответ: (-°о; -5) и (-5; 0) и (4; °°). х(х - 4)(х + 5)2 < 0 при х £ {-5} и [0; 4].
168
17. Неравенства
Примеры (продолжение)
х(х + 2) < х-5 " ' Рассмотрим функцию . х(х + 2) ВД- 'х-5 D (F) = (-°°; 5) и (5; оо). F(x) = 0 в точках х = 0; х = -2. F(-3) < 0; F(-l) > 0; F(l) < 0; F(6) > 0. Ответ: (-°0; -2] о [0; 5). 4- _ -2 0 5 * 73х 4-1 > 2х. Приведем неравенство к виду: *]3х 4-1 - 2х > 0. Г(х) = 73х + 1 -2х. D(F) = [-^ ; +оо). Найдем нули этой функции. fx>0 73х +1 - 2х = 0 « [Зх + 1 = 4хл Р(х) = 0 при х = 1. F(0) > 0; F(5) < 0. Л Г 1 _ Ответ: Q; 1 . • 6 L о j 1 3
18. Неравенства с двумя перемеными
ах + Ьу + с>Оиах + Ьу + с <0 —
полуплоскости (а2 4- Ь2 * 0)
ах2 + Ьх + с>у
и ах2 4- Ъх 4- с < у
ау2 + Ьу + с>х
и ay2 + by + с <х
граница — прямая
ах 4- Ъу 4- с = О
граница — парабола
ах2 4- Ъх 4- с = О
граница — парабола
ау2 + by + с = х
у к
(х - xQ)(y -yQ)>k
и (х - x0)(i/ - yQ) < k (k * 0)
(х-хо)(у-1/о)>О
и (х - x0)(z/- z/0) < 0 (й = 0)
(x-x0)24-(i/-i/0)2>7n
и (х - х0)2 4- (у -1/0)2 < тп; (тп > 0)
граница — гипербола
(х - х0)(у - у0) = k (две ветви)
граница — две прямые
х=хоиу = 1/о
граница — окружность
(х - х0)2 + (у - у0)2 = т
т — радиус окружности
169
19. Дифференцирование
Производной функции f в точке х0 называется предел отношения приращения функции А/ = 7(х0 + А*) ““ 7(х0)к приращению аргумента Дх при стремлении Дх к нулю. ,,, ч г /(х0+Дх)-/(х0) f(x0)~ hm Дх -» 0 АХ Операция нахождения производной функции называется дифференцированием.
Необходимое условие дифференцируемости функции
Для того чтобы функция 7 была дифференци- руема (имела производную) в точке х0, необхо- димо (но недостаточно), чтобы она была непре- рывна в этой точке (т. е. Д7(х) = 7(х) - 7(х0) -> 0).
Примеры нахождения производной функции f по определению
/(X) = X2 х0 = 2 f(2)= lim (2 + У—— = lim 4Ax+Ax = lim (4+Дх) =4 дх->о Дх дх->о Дх дх-»о
/(х) = Vx х0 0 ч 37х0+Дх-з/^ (х0+Дх)-х0 1 f(x0)- lim — hm — — Дх->0 Х Ax^0(3J(x0+Ax)2 + 3/(x0+Ax)x0 + 3,/x^)Ax З-3^
/(х) = sin х о . Дх ( , ДхЛ sin(x0 + Ax)-sinx0 2sin 2 • cos хо+ 2 J f(xn)= hm - = hm =cosxn 0 дх->о Дх дх->о Дх u
Дх) = |х| • X2 х0 = —2 _ч .. |-2 + Дх| • (-2 + Дх)2-8 (2 - Дх)(-2 + Дх)2-8 7(-2) = Ьт 5 = hm =-12 Дх->0 Дх Дх-»0 Дх
Пример непрерывной, не дифференцируемой в точке х0 функции
(М 1 н II 03 s"= .. (2+Дх)-2 -0 Дх .,,оч / (2) = lim 'А / ! = hm 1 предел не существует, 7 (2) не существует. Дх -»о Дх Дх -»о Дх
лх) = 37^i Хо = 1 j т ^/(1+Дх)-1-0 ?/Дх 1- 1 „ „,1Ч 7 (1)= hm = lim — = lim —. - = оо, /(1) не существует. Дх-»0 Дх Дх-»0 Дх Дх-»0 з/д^2
Вторая производная Производные высших порядков
Лх)=(Г(х)Г /(П)(Х) = (/(П-1)(Х)У
(cos х)" = (-sin х)' = -cos х z ( 4 3/2*) 3 — 5/2 3 (7i) ) 8* 8Т/
ЦО
ЛлгаЙга 4 тах/лаидх
19. Дифференцирование
Табличное дифференцирование Производная сложной функции (ftu(x)))' = f (и) • и'(х)
(с)' = 0, с Ей (константа) (х)' = 1, xEJ? (xn)' = пхп ~1, п ЕДГ, х ЕЕ; или -п Е^, х 0; или п & Z, х > Q (cos х)' = -sin х, х е R (sin х)' = cos х, х R 1 тс (tg х)' = 2 , X * 2 + nk, k &= Z COS x z (ctgx)' - - 2 , X nk, k^Z sin x (In x)' = ^ , x e (0; +oo) (logax)'-xlna, xe(0;+oo) (ex)' = ex, x^R (axY = axln a, x (и71)' = пип “1 - и'* (cos и)' = -sin и • и' (sin u)f = cos и • и' V 1 (tg w) - 2 ’ U cos и (ctg и) - 2 ' “ sin и /IV1' (ln и) = - • и (eu)z = eu • и’ (au)' -au • In a -u'
* u = u(x)
Производная обратной функции
Функции у = /(х) и у = ф(х) взаимообратны. f(d) = b <=> а = ср(д) | f(a) • <pz(fe) = 11
(arcsin X)' — , X CZ (-1; 1) 71 ~х2 (arccos х)'- . , хЕ( 1; 1) 71-х2 (arctg х)' - ,, х cz R 1+х (arcctg х)' — „, х £ Я 1+х (arcsin u)' — . • u' Jl-u2 , V 1 . (arccos u) = - • и 7i - и2 (arctg u) - , • и 1+u (arcctg u) — , • и 1+u
Основные формулы Следствия из основных формул
(и 4- и)' = и' 4- v' (и-v)' = и -v + и-v' fuY и' • v - и • v' U " V2 (и - и)' = и' - и' (с • и)' = с • и'
Примеры
/ г\/ . г , sin Jx (cos Jx) --sm л/х • (Jx) -- J ((2х2 - х + I)10)' -= 10 • (2х2 - х + I)9 • (2х2 - х + + 1)' = 10 • (2х2 - х + I)9 • (4х - 1).
жыьмая ппсгпалллла
С (I
иах,
19. Дифференцирование
Физический смысл производной Геометрический смысл производной
Пусть з = s(t) — зависимость пути от времени, то- гда: v = v(t) - s'(t) Скорость — производная пути по времени. а = a(f) = v'(t) = s"(t) Ускорение — производная скорости по времени (вторая производная пути по времени). Касательной к графику функции /(х) в точке х0 называется прямая, задаваемая уравнени- ем: У=/(х0) + /'(х0)-(х-х0) f(x0) = tgaKac = /?Kac Значение производной функции в точке рав- но угловому коэффициенту касательной к графику функции в этой точке.
Касательная к графику функции
Уравнение касательной (не вертикальной) к графику функции у = /(х) в точке графика с абсцис- сой х0: y = f(x0) + f'(x0)-(x-x0)
Если функция /(х) не имеет производной в точке х0, но непрерывна в этой точке, то у графика функции в этой точке либо вообще нет касательной, либо есть вертикальная касательная.
у = |х| не имеет касательной в точке графика с абсциссой х = 0. у = ?/х имеет в точке графика с абсциссой х = 0 вертикальную касательную х = 0.
Примеры, решения задач на составление уравнения касательной
Составить уравнение касательной к кривой у = х3 - х2 в точке графика с абсциссой х0 = 1. Координаты точки касания х0 = 1; yQ = I3 - I2 = 0. у' = Зх2 - 2х => kK&c = у'(1) = 1. Уравнение касательной: i/ = 0 + l-(x-l) => | е/ = х —-1|.
Составить уравнение касательной к кривой ftx) = (х2 4- 6х 4- 3)/2, не пересекающей прямую у = 2х 4- 5. Так как касательная не пересекает прямую у = 2х 4- 5, значит, она параллельна касательной. Следова- тельно, f'(xQ) = 2. Но f'(x) = х 4- 3. Отсюда х0 4- 3 = 2 и х0 = -1. Ордината точки касания yQ равна ((-I)2 4- 6 • (-1) 4- 3)/2 = -1. Координаты точки касания (-1; -1). Уравнение касательной у = -1 4- 2(х 4-1) или |у = 2х 4-1|.
Составить уравнение касательной к кривой у = х3, проходящей через точку Q; -1). Пусть (х0; у0) — точка касания. Тогда у0 = Xq ; kK&c = 3xq . Уравнение касательной у = Xq + 3Xq(x - х0). Точка (5; -11 лежит на касательной. Поэтому -1 = х« + 3xq Г- -х01 => 2xq - Xq - 1 = 0 => х0 = 1 => =>Уо = k Уравнение касательной у = 1 4- 3(х - 1) или | у = Зх - 21.
да
19. Дифференцирование
Исследование функцш при помощи производной
Монотонность функции
Теорема Лагранжа
Если f(x) непрерывна на [а; д] и дифференцируема
на (а; &), то существует с (а; Ъ) такое, что
Да)-Д&)=Г(с)«(а-&).
(Заметим, что таких точек с на (а; Ь) может быть и более одной.)
Для исследования функции f(x) на монотонность можно исследо-
вать ее производную на знакопостоянство.
Если f'(x) > 0 на (а; &), то Дх) возрастает на (а;Ь).
Если Дх) непрерывна на [а; 6], то Дх) возрастает
на [а; Ь].
Если f\x) < 0 на (а; &), то Дх) убывает на (а; Ъ).
Если Дх) непрерывна на [а; &], то Дх) убывает
на [а; &].
Дх) = х2 - 6х + 1; f'(x) = 2х - 6 > О при х > 3 =>
Дх) возрастает на [3; -К»).
/(х) = ; f\x) = —==
2^-х
убывает на (-оо; 0].
< 0 при х < 0 => Дх)
Если Дх) возрастает и дифференцируема на [а;Ь],
то f\x) > 0.
Если Дх) убывает и дифференцируема на [а; 6],
то f\x) 0.
Критические точки функции
Внутренние точки области определения функции, в которых производная равна нулю
или не существует, называются критическими точками функции.
х
/'(хо) = О;
х0 - крит. точка;
Ы ~ fmax’
7'(хо) = О;
х0 - крит. точка;
f min’
xQ - крит. точка;
Дх0) не является экстремумом.
Критические точки (примеры)
f । У^
/ 0 *о * 0 0 ?
f\x^ не существует; /'(х0) не существует; Нет критических точек;
х0 - крит. точка; х0 - крит. точка; х0 = 0 не является внутренней
Дх0) не является экстремумом. Лхо) fmin • точкой области определения.
ЛЗ
19. Дифференцирование
Критические точки (примеры) (продолжение)
4 /1\ У 1 х. 1 yi\ 1U
1 1 4
0 хо X -3 0 4 х 0 х0 х
Нет критических точек; х0 — точка разрыва. f(x) = 0 при всех х е (-3; 4); /'(-3), /'(4) не существуют; все х s [-3; 4] критические точки. /'(^о)не существует; х0 — крит. точка; Яхо) ” min*
Экстремумы
х0 G D(f) — точка максимума Дх), если существует 8 > 0 такое, что при х (х0 - 8, х0 4- 8) Д*0)>Дх) х0 е D(f) — точка минимума Дх), если существует 3 > 0 такое, что при х е(х0-3,х0+8) /(х0)</(х)
Точки максимума и минимума функции называются ее точками экстремума, а Значе- ния в них — экстремумами (максимумами или минимумами).
f'(xQ) = 0 при х <х0 f'(x) > 0; при х > х0 f'(x) < 0 /'(х0) = 0 при х < х0 Д(х) < 0; прих >х0 /'(х) >0 Г /
У. max /Т\
0 хо \ х
0 VJZ х min
Примеры критических точек различных функций
1) у = |х|; х0 = 0; y\Q) не существует; 3) у = х3; х^ = 0; у'(0) = 0; экстремумов нет. z/(0) = 0 — минимум. 4) у = 2х - |х|; х0 = 0; у'(0) — не существует; 2) у = х2; х0 = 0; у'(0) = 0; у(0) = 0 — минимум. экстремумов нет.
Примеры исследования функций на монотонность
Дх) = х3 4- х2 4- х - 5; f\x) = Зх2 4- 2х 4-1 > 0 при х е R\ f(x) возрастает на Я. /(х) © Дх) = х3 - Зх; f(x) = 3(х - 1)(х 4-1) = 0 при х = -1 и х = 1; Дх) возрастает на (-00; -1] и на [1; 4-оо); Дх) убывает на [-1; 1]. /(х) ® -1 0 1 ® м f(x) = 2x+^;/'(x) = 2-4; X X f'(x) = 0 при х = 1; Дх) возрастает на (-оо; 0) и на[1; 4-оо); Дх) убывает на (0; 1]. /(х) ®0 © 1 ®
' /(X) Дх) тпях. mm Г(Х> разрыв min
/(х) = х4 - х3; /'(х) = ,, а Г3 Дх) возрастает на ; • Дх) убывает на ^”°°; 00 JL FT 1 О со *’ ОО д н со © i to ' ° О © * >AIW 00 © < Дх) = х + ;;Д(х) = 1-Ц; х х f(x) возрастаете на (-°°; -1] и на [1; +°о); /(х) убывает на [-1; 0) и на (0; 1]. А»> ©-1 Q о © 1 ® ж х Ах) max раз- mm рыв
Дх) \KP^-T- ~ / min '
Ьа & maJjuutflX’
20. Исследование функций
Область определения функции jD(/) — множество значений х, при которых функция определена.
Н + й? % II II S S 2 D(f) = {x|x*l} Z(x) = 471-x D(7) = {x | x < 1} /(х) — ^2х-х2 -1 £(/) = {!} f(x) = 1g х + 1g (-х) 2>(П = 0
Область значений функции E(f) — множество значений, которые мо- жет принимать /(х) при х е Р(/). (Все значения а, при которых уравнение /(х) = а имеет решения.)
/(х) = х3 - Зх Д/) = й /(х) = 1+ X E(f) = {y\y*l} /(x) = л/2х-х2 E(f) = {у \ у 1} /(х) = 1 + 74х-х2-4 ДП = {1} /(х) = sin х + cos х E(f)~{y\-j2
Четность Нечетность
/(-х) = /(х),хеР(П /(-x) = -/(x),xep(f)
График четной функ! телыю оси ординат. у X1 х /-Х 0 щи симметричен относи- x \ График нечетной функ тельно начала коордиш у । -X у ции симметричен относи- 1T. 0 XX
Примеры, четных функций /(х) = х4-21x2; g(x) = 5x + 5~x ф(х) = ?/1 ~ х + 3/1 + х Примеры нечетных функций й(х) = х3 - 20х; и(х) = 5х - 5-х и(х) = 71 “X - 71 + х
/(х) = sin х - cos х не обладает четностью или нечетностью.
Периодичность
/(X - 0 = /(X + 0 = /(х), X е В(Л, t * 0 Число t называется периодом функции, а наименьшее положитель- ное значение t основным периодом функции (Т).
/(х) = sin 4х т 2п п Г“Т“2 /(x) = cos 2лх 2 л T = — = 1 1 2k 1 II £ Ь-I II oo 1 . II СаЭ a ooi к /(х) = 17 t (0; +оо) основного периода нет
/(х) = х + sin х; /(х) = cos(x2) — непериодические функции.
График периодической функции состоит из повто- у ряющихся фрагментов на отрезке длины Т; на любом таком отрезке периодическая функция Л принимает все свои значения. -Д—2. -72 f (х) = sm х - cos х, Т - 2к ’к '/’Ч 5к /X. yiv; < Зк V/ ш х 4 4
20. Исследование функций
^ИЬсскльная пфюфальма & тлм^лацах, и, формулах
Корень (нуль) функции —
значение аргумента, при котором значение функции равно нулю.
f(x) = 4х - i
корни: х =±-
л
Дх) » X • 71-Х
корни: х = 0;
х = 1
корень: х = 0
Дх) = sin х + cos х
л „
корни: х = -^ + ли, 71 EZ
/(х) = -Д-
v ' sm х
корней нет
Промежуток знакопостоянства —
промежуток, на котором все значения функции положительны
(или отрицательны), а на любом его расширении нет.
Примеры
Дх) = Зх2 + 5х - 8; Дх) < 0 при х
z g
f(x) >0прих е
к о
Дх) =х 2; два промежутка знакопостоянства 0) и (0; +°°), на обоих функция положительна.
Монотонность
Функция Дх) называется возрастающей на промежутке I, если для любых хг и х2 из этого промежутка Xi > х2 Дх^) > Дх2). Промежуток I называется промежутком воз- растания функции Дх), если на этом промежут- ке функция возрастает, а на любом его расшире- нии нет. Функция Дх) называется убывающей на проме- жутке I, если для любых хг и х2 из этого проме- жутка Xi > х2 => ДХ]) < Дх2). Промежуток I называется промежутком убыва- ния функции Дх), если на этом промежутке функция убывает, а на любом его расширении нет.
Промежутки возрастания и убывания называются промежутками монотонности функции.
Критерий монотонности функции
Дх) возрастает на промежутке, если Д(х) > 0. Дх) убывает на промежутке, если Д(х) < 0.
Примеры
f'(x) = 6х + 5;
Дх) = Зх2 + 5х - 8;
ч Л 5
/(х)>0прих >-g;
Дх) возрастает на промежутке
5
Г(х) < О при х < -g;
Дх) убывает на промежутке
—оо
-5-1
6J •
Дх) = ; два промежутка монотонности 0) и (0; 4-оо); на обоих функция возрастает.
Дх) = Зх + 4 возрастает на Я, один промежуток монотонности 4-о°).
176
20. Исследование функций
Критерий монотонности функции (продолжение)
f(x) = Зх2 + 6х - 8;/'(х) = 6(х + 1) = 0 при х = -1; /'(-2) < 0 => /(х) убывает на (-«>; -1]; /'(0) > 0 => Дх) возрастает на [-1; +°о); х0 = -1 — точка минимума; /(-1) = -11 — минимум.
/(х) = х3 — экстремумов нет.
Исследование функции при помощи производной. Построение графика
Найдите D(f). Найдите производную, критические точки, ис- следуйте знаки производной. Найдите промежутки монотонности, точки экстремума, определите вид точек экстремума. Найдите экстремумы функции. Исследуйте функцию на четность, нечетность, периодичность (периодическую функцию луч- ше исследовать на промежутке длины Т). «Набросайте» эскиз графика. Найдите £(/). Найдите несколько значений функции (по крайней мере по одному в каждом промежутке монотонности). По возможности Исследуйте поведение функции на концах облас- ти определения и в точках разрывов. Найдите горизонтальные и вертикальные асим- птоты. Найдите корни и промежутки знакопостоянства функции. Постройте график функции
Пример X У- 2^ • X +1 D(y) = R. , 1 • (х2 + 1)-х • 2х У 2 2 (х2 + 1) у' существует при х у' = 0 при х = ±1. / чх 1 ^min У( 1) £ ’ ^ша: У । -1 0 1-х2 2 2 ’ (1+Х ) /9 1 © -=——-е—е——х у mm max к = ^(1) = 2 ‘ 1 Функция нечетная: у(-х) = ~у(х). ч Г 1 11 [~2; г] • X 1 lim у == lim — = lim = 0. *-»~xZ + l + 1 X у = 0 — горизонтальная асимптота; вертикальных асимптот нет. у = 0 при х = 0 (корень), у > 0 при х > 0; у < 0 при х < 0.
11 - - • _11 х 2
/77
бЩнюмная & таблицах rz фсфьм/умх
21. Нахождение наибольшего и наименьшего
значений функции на промежутке
Наибольшим (наименьшим) значением функции f(x) на I называется
такое число М (т), что существует х0 е I такое, что f(xQ) = М
(/(х0) = тп), М > f(x) (т /(х)) для всех х из I.
I I I I I
Наибольшее и наименьшее значения непрерывная на I функция может принимать либо на кон-
цах промежутка (если это числа), либо в критических точках, лежащих внутри промежутка.
Алгоритм нахождения наибольшего и наименьшего на [а; &] значений функции, непрерывной на [а; Ь].
1) Найдите f(a) и /(&) — значения функции на 3) Найдите значения функции в критических точ-
концах промежутка. к ах.
2) Найдите критические точки функции внут- 4) Из всех найденных значений выберите наиболь-
ри промежутка (т.е. на (а; Ъ)). шее и наименьшее; они и будут наибольшим и
наименьшим значением функции на [а; Ь].
Пример
f(x) = 8х* 2 - х4 S * *, X е [-1; 3]. /(-1) = 7; /(3) = -9;
f'(x) = 16х - 4х3 = 4х(4 - х2) = 0 => х = 0; х = 2; х = -2 £ [-1; 3]. f{0) = 0; /(2) = 16.
max {7; -9; 0; 16} = 16 => max /(х) = 16; min {7; -9; 0; 16} = -9 => min /(x) = -9.
[-1; 3] [-1; 3]
Пример
Если непрерывная функция имеет на промежутке I единственную точку экстремума и этот экс-
тремум максимум (минимум), то в этой точке достигается наибольшее (наименьшее) значение
функции.
/(х) = sin х + 7з • cos х, х е [0; л]. /(0) = 7з; /(л) = -л/З ; f'(x) = cos х - а/З sin х;
г- 1 Л
/'(*) = 0 при cos х = 73 sinx =>tgx = —р =>х = ~ +лй ^[0; л]при& = 0. ,
73 0 / (х) о у и к
(ТС\ Л /— Л г-
max /(х) = /I X ] = sin д + 7з cos ~ = 2; пип /(х) = Дл) = -J3 6
[0; я] \^Оу О О [0; я]
Задача
В полукруг радиуса R вписать прямоугольник наибольшей площади
так, чтобы одна его сторона лежала на диаметре полукруга, а две верши-
ны — на дуге полукруга.
Обозначим стороны прямоугольника АВ = х,
/ 2 2
AD = 2у. Тогда его площадь S = 2ху. Заметив, что у = fjR - х , получим
S = 2х• 7я2 - X2 =2- 7я2х2 - х4,хе(0;Л).
Исследуем на максимум функцию Дх) = R2x2 - х* при х £ (0; R).
f(x) = 2R2x - 4х8 = 2x(R2 - 2х2).
А О У D
/75
& 'пшЛлица/х,
21. Нахождение наибольшего и наименьшего значений функции на промежутке
Задача (продолжение)
R
Г(х) = 0 при х = -у= (так как х (0; R)).
„ R
Следовательно, при х = -у= площадь прямоугольника наибольшая.
а/2
R
Ответ. Прямоугольник имеет наибольшую площадь, если его стороны х = —р, 2у = Rj2.
f (X)
е-
Г(х)
R
J2
©
22. Первообразная и неопределенный интеграл
Функция F(x) называется первообразной функ- ции f(x) на промежутке I, если для всех х из этого промежутка F'(x) - f(x). Множество всех первообразных функции Дх) на- зывается неопределенным интегралом и обозна- чается jf(x)dx.
Если F(x) одна из первообразных функции Дх) на I, то любая первообразная функции f(x) на этом промежутке имеет вид F(x) + С, где С ей. jf(x)dx = F(x) + С, где F(x) — любая первообраз- ная Дх), а С ей.
Свойства первообразных
Первообразная f'(x) равна Дх) + С. Если первообразная Дх) равна F(x), то первооб- разная ДО равна F(t). Если первообразная Дх) равна F(x), то первооб- разная йДх) равна kF(x). Пусть первообразная /г(х) равна Fj(x), перво- образная /2(х) равна F2(x), тогда первообраз- ная /г(х) + /2(х) равна Fx(x) + F2(x). Пусть первообразная Дх) равна F(x), тогда перво- образная f(kx + р) равна tF(Ax + р). К
Для того чтобы доказать, что функция F(x) являет- ся первообразной функции f(x) на промежутке I, нужно показать, что для всех х из этого промежут- ка F'(x) = f(x) (т.е. воспользоваться определением). |
Задачи
Доказать, что функция F(x) = | sin 2х + х является первообразной для функции Дх) = 1 + cos 2х на R. F'(x) — 5 cos 2х • 2 + 1 = 1 + cos 2х = Дх). Полученное равенство верно для всех действительных значений х.
Найти первообразную функции Дх) = Зх2 - 1, график которой проходит через точку М(1; -1). Любая первообразная функции Дх) = Зх2 - 1 имеет вид F(x) = х3 - х + С. График искомой первообразной пройдет через точку М(1; -1), если F(l) = -1, т. е. I3 -1 + С — = -1 => С = —1. Ответ. F(x) — х3 - х - 1.
/£9
ДДольпал nfuxfuiMMa
22. Первообразная и неопределенный интеграл
Задачи (продолжение)
Найти первообразную функции /(х) = cos2 . X 1 11 Преобразуем /(х) = cos2 % = (1 + cos х) = g + g cos x. Первообразная суммы равна сумме первообразных. Следовательно, первообразная F(x) = | х + + 1 sin х + С, где С — произвольная постоянная.
Найти неопределенный интеграл jsin Зх • cos х dx. Jsin Зх • cos х dx = | j (sin 4x + sin 2x) dx = | • • cos 4x + • cos 2x j = -| cos 4x - cos 2x + C.
Найти первообразную для функции /(х) — „ 4х - 1 Преобразуем fix) — „ - Л 1. Следовательно, первообразная _ 1 *\2х-1 2х + 1) F(x) = 5 1п|2х - 1| - J 1п|2х + 1|1 = I In 2х ~ 1 + С. 2 Vs 2 > 4 2х+1
Таблица первообразных
f(x) F(x) Промежуток I
k kx + C R
ха (а*-1) a + 1 - +c a + 1 a e N, x e Я; -a e N, x e (-oo; О) и (0; +°°); aEZ, X E (0; +oo)
1 X In |x| + C (-oo; 0) или (0; +oo)
ех ex + C R
ах X a Г- +c Ina R
cos X sin x + C R
sin х -cos x + C R
1 2 COS X tgx + C f-? +nfr; ? +лл\ k^Z
1 . 2 sm x -ctg x + C (лй;n + nk), k^Z
180
23. Определенный интеграл и его приложения
Если функция Дх) непрерывна на промежутке I числовой оси, содержащем точки х = а и х = &, то разность значений F(b) - F(d) (где F(x) — первообразная f(x) на I) называется определен- ным интегралом от функции Дх) от а до &: b Jf(x)dx =F(b)-F(a). a
Определенный интеграл есть число.
Основные свойства
& & & J/(x)dx = $f(t)dt = j/(z)dz а а а jf(x)dx =0 а b а jf(x)dx = -jf(x)dx а Ъ b c b ^f(x)dx = j/(x)dx + J7(x)dx, если a, b и c — a a c любые точки промежутка I непрерывности Дх) b b ^kf(x)dx = k • jf(x)dx a a b b b l(fi(x) + f2(x))dx = Jfi(x)dx + j/2(x)dx a a a
Дополнительные свойства
Ь pb + q j/(px + g)dx=^ J f(t)dt a pa+q a a Если Дх) четная, то j f(x)dx = 2 • Jf(x)dx. -a 0 a Если Дх) нечетная, то J f(x)dx = 0. -a (x V J/(t)dt =/(x) U J
Примеры
4 4 4 J J~x f * +x dX \3/2 + l/2j 1 i 1 = |(43/2-l) +2(41/2-l) = | -7 + 2-1 = ^ О о о 1 X x+1 1 1 f25* + 5* * гГ25\* л , f/5\* 1 . dx - | 5Л lOdx + |5Л 50dx - J ’'ЦО/ о ±и 0 0 1 1 = 10j2,5xdx + 50j0,5xdx = 0 0 = in. 2>5X 1 X= 15 +-2£ U In 2,5 0 In 0,5 0 In 2,5 + In 2
2 3-2 + 4 f dx 1 f dt 1 1 10 (3x + 4)2 3’H2 3^ -1 3(-l) + 4 1/1 1\ 7 3<10 3j 90 3x + 4 = t
/5/
бЩксммьая пфогфальма & та^лмщах ti фофлиула/х
23. Определенный интеграл и его приложения
Площадь криволинейной трапеции
Фигура, ограниченная прямыми у = 0; х = а; х = Ь и графиком непрерыв-
ной и неотрицательной на [а; &] функции /(х), называется криволинейной
ъ
трапецией. Площадь криволинейной трапеции S = ff(x)dx
а
Вычисление площадей
s = J(/x(x)-g(x))dx +
а
b
+\{f2W~S{x))dx
С
S = J(f(x)-g(x))dx +
а
Ъ
+ \(g(x)-f(xY)dx
Вычисление объемов тел вращения
Криволинейная
трапеция
(вокруг оси Ох)
ь
vox~tff\x)dx
а
Конус
= \nR2H
О
& тхи/млиря,
23. Определенный интеграл и его приложения
Вычисление объемов тел вращения (продолжение)
Шар у, -r( 0 « = 7яа-хг 'х R R Vm = n J (>jR2-x2)2dx = 2nj(R2-x2)dx = -R 0 / з/ A Л f _2 X Л 4 ~ = 2л LR х - -z- = 5ЯЙ3 К о J 0 д
Путь, пройденный материальной точкой за время (t2 > *i) при прямолинейном движении со скоростью v(t)9 равен: *2 S = J v(t)dt. *1
Приложение
Факториалы и степени
п п! 2В Зв 5П
0 1 1 1 1
1 1 2 3 5
2 2 4 9 25
3 6 8 27 125
4 24 16 81 625
5 120 32 243 3125
6 720 64 729 15625
7 5040 132 2187 78125
8 40320 264 6561 390625
9 362880 512 19683 1953125
10 3628800 1024 59049 9765625
Геометрия в таблицах
1. Элементы теории доказательств
«А => В» — данная теорема; «В => А» — об- ратная теорема; «не А => не В» — противоположная теорема; «не В =ф не А» — теорема, обратная противо- положной. «Необходимо и достаточно» заменяется на «тогда и только тогда, когда». Четырехугольник тогда и только тогда яв- ляется параллелограммом, когда его диаго- нали, пересекаясь, делятся пополам. Диагонали четырехугольника, пересекаясь, делятся пополам тогда и только тогда, ко- гда четырехугольник является параллело- граммом.
Если из А следует В, то А достаточно для В, а В необходимо для А. Если из А следует В, а из В следует А, то А не- обходимо и достаточно В. Отношение обладает свойством симметрии, если из того, что А находится в данном отно- шении к В следует, что и В находится в дан- ном отношении к А. Примеры симметричных отношений: параллельность прямых, перпендикуляр- ность прямых, параллельность плоскостей, перпендикулярность плоскостей, равенство чисел, равенство фигур.
Для того чтобы четырехугольник был парал- лелограммом, необходимо, чтобы диагональ делила его на два равных треугольника (но недостаточно). Для того чтобы четырехугольник был парал- лелограммом, достаточно, чтобы все его сто- роны были равны (но не необходимо). Для того чтобы целое число делилось на 3, не- обходимо и достаточно, чтобы сумма его цифр делилась на 3. Для того чтобы треугольник был прямо- угольным, необходимо и достаточно, чтобы квадрат одной из его сторон был равен сумме квадратов двух других. Отношение обладает свойством транзитив- ности, если из того, что А находится в дан- ном отношении с В, а В с С следует, что А и С находятся в данном отношении. Примеры транзитивных отношений: равенство чисел, подобие фигур, отношения «меньше» и «больше» (<;>), параллельность несовпадающих прямых и плоскостей.
ZS4
<Иеолит[шя £ тси/лицах
ПЛАНИМЕТРИЯ
2. Углы и параллельность
Углом называется фигура, образованная двумя лучами, выходящими из одной точ- ки (вершины). Луч, выходящий из вершины угла и деля- щий его пополам, называется биссектри- сой угла. В^ А ^^биссектп^. Z. jdAC с AM — биссектриса => вершина — угла Z ВАМ = Z. САМ
Угол называется развернутым, если его стороны лежат на одной прямой. Градус — величина (градусная мера) угла, 1 равного тол части развернутого угла, lov В с АА ВАС — развернутый Ае(ВС) 21 ВАС = 180°
Радиан — величина угла, градусная мера которого равна 1 — 1. Центральный угол в 1 радиан стягивает ду- гу, длина которой равна радиусу окруж- ности. Центральный угол, стягивающий а дугу длины а, равен ь = а радиан. а с г—5 хА 2&Радиан дЛ.АВ = Д - а \ / дл. CmD , >< R -а радиан
Угол, равный половине развернутого, на- зывается прямым (90°). Угол меньше прямого называется острым. Угол больше прямого, но меньше разверну- того называется тупым. Н\ < А р с .s'' A BAD = 90° — прямой А САВ < 90° — острый • 90’ < А ВАН <180° — тупой В
Смежные углы Два угла, у которых одна сторона общая, а две другие являются дополнительными лу- чами, называются смежными. Сумма смежных углов равна 180°. Угол, смежный с прямым, — прямой. С "'В ВАС и Z- CAD — смежные Z. ВАС 4-Z. CAD = 180°
Вертикальные углы Два угла, стороны одного из которых явля- ются дополнительными лучами сторон дру- гого, называются вертикальными. Вертикальные углы равны. л R А ВАС, A HAD — вертикальные Г Ч-D А ВАН, A DAC — вертикальные \ А ВАС = AHAD
185
мольная п
мслса
и фотмшлах
2. Углы и параллельность
Угол между прямыми
Углсш между двумя пересекающимися пря- мыми называется меньший из вертикаль- ных углов, образовавшихся при пересече- нии. Прямые, образующие прямой угол, называ- ются перпендикулярными. \Ь Z (а, Ь) = Z ARB С Z BFC (Z AFB = Z BFC) => \ => (Z.(a, b) = 90°) => (a 1 b)
Две прямые плоскости, не имеющие общих точек, называются параллельными. b a\\boar\b = 0
При пересечении двух прямых третьей (секущей) образуются пары углов: (1; 2); (3; 4); (5; 6); (7; 8) накрест лежащие, (1; 8); (5; 3); (4; 6); (7; 2) соответственные, (1; 3); (2; 4); (5; 8); (7; 6) односторонние. c c о О Л
Пересечение параллельных прямых секущей
Накрест лежащие углы равны (Z 1 = Z 2; Z 3= Z 4; Z 5 = Z 6; Z 7 = Z 8). Соответственные углы равны (Z3 = Z5;Z1=Z8;Z2 = Z7;Z4 = Z6). Сумма односторонних углов 180° (Z 1 +Z 3 = Z5 + Z 8 = Z 2 + L 4 = = Z 6 + Z 7 = 180°).
Аксиома параллельности Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
Признаки параллельности прямых Если две различные прямые параллельны третьей, то они параллельны между собой (транзитивность параллельности). Если при пересечении двух прямых треть- ей накрест лежащие углы равны, то пря- мые параллельны. Если при пересечении двух прямых треть- ей соответственные углы равны, то пря- мые параллельны. Если при пересечении двух прямых треть- ей сумма односторонних углов равна 180°, прямые параллельны. a / b / c (a || b; b || c) => (a || c) p n *—m
/56
2. Углы и параллельность
Сумма углов треугольника равна 180°.
Теорема Фалеса
Если на одной из двух пря-
мых отложены несколько
равных отрезков и через их
концы проведены параллель-
ные прямые, пересекающие
вторую прямую, то и на ней
отложатся равные отрезки.
Деление отрезка
на равные части
А1В1 \\А2В2 || А3В3 \\А4В4=>
=> В^В2 — В2В3 — В3В4
ные отрезки
вс5 II с4м41| с3м31| с2м21|
II с1м1=> ам1 = м1м2 =
= м2м3 = м Зм 4 = м4в
«Расширенная» теорема Фалеса
Если на одной из двух прямых
отложены несколько отрезков
и через их концы проведены
параллельные прямые, пере-
секающие вторую прямую, то
на ней отложатся отрезки,
пропорциональные данным.
С1 II с2 II С3 II С4 ^Г^2 * ^2^3 ‘
• ^3^.4 = ‘ ^2^3 ‘ ^3^4
3. Множества (геометрические места) точек на плоскости
Множество точек, равноудаленных от двух дан- ных точек, есть серединный перпендикуляр от- резка, соединяющего эти точки (на нем лежат центры окружностей, проходящих через дан- ные две точки). с о, В АО = ОВ;с1.АВ X (Х« с)<=>(АХ = ХВ)
Множество точек, равноудаленных от сторон данного угла (меньшего, чем развернутый), есть биссектриса угла (на ней лежат центры ок- ружностей, касающихся сторон угла). А_ z AQC = /_ ВОС (X е ОС) «• (р(Х, ОА) = в^- =Р(Х,ОВ))*
р(Х, а) и р(Х, ОА) — обозначение расстояния от точки до прямой.
/57
^Цлсаьнал пфсфамма £ тщ/мщх и, фсфм^лах
3. Множества (геометрические места) точек на плоскости
Множество точек, равноудаленных от двух па- раллельных прямых, есть параллельная им прямая, проходящая через середину отрезка их общего перпендикуляра (на ней лежат центры окружностей, касающихся данных прямых). a a || b, c || a (p(X, a) = p(X, fr))»(Xe c)
Множество точек, равноудаленных от двух пере- секающихся прямых, есть две взаимно перпенди- кулярные прямые, на которых лежат биссектри- сы вертикальных углов, образовавшихся при пе- ресечении данных прямых (на них лежат центры окружностей, касающихся данных прямых). n. 6I lx z!\ a/ / 1 m a n b ~ X & m (p(X, a) = p(X, &)) <=> или LX e n
Множество точек, удаленных на данное рас- стояние от точки, есть окружность с центром в данной точке. 1 X \ ° *'a'l p(X, 0) = a
Множество точек, удаленных на данное рас- стояние от прямой, есть две параллельные ей прямые. X b - a c t Y ' m p(X, a) = p(Y, a) = m b || а; с || a
Множество вершин прямоугольных треуголь- ников с данной гипотенузой есть окружность, построенная на гипотенузе как на диаметре (ис- ключая концы гипотенузы). X ^1/ / 1 V /Jl Z.AXB = 90°
Множество точек, из которых данный отрезок виден под данным углом, есть две симметрич- ные, опирающиеся на данный отрезок, дуги (ис- ключая концы этих дуг). ( / x: AAXB^AAYB
Окружность Аполлония Множество точек М, таких что AM = kMB, есть окружность с диаметром N\N2 на прямой АВ такая, что ANr: NrB = k hAN2 : N2B = k(k* 1). A SKA \ о \ J 2
188
^еомятАия 6 таблицах,
4. Треугольник
Неравенство треугольника В любом треугольнике каждая сторона меньше суммы двух других сторон.
а~Ъ <с < а + Ъ, где а, Ь, с — длины сторон тре- угольника, причем а > Ъ. 3 а С Z. ВАМ =АВ+АС
Внешний угол треугольника равен сумме двух внутренних, не смежных с ним углов.
Сулша углов треугольника 180°.
В треугольнике против большей стороны лежит больший угол, против
большего угла — большая сторона.
.2
а2 + Ъ2 = с2
а2 + Ь2 < с2
остроугольный
ь
прямоугольный
ь
тупоугольный
Признаки равенства треугольников
По двум сторонам и углу ме-
жду ними (С У С).
По стороне и двум прилежа-
щим к ней углам (У С У).
По трем сторонам (С С С).
Сходственные (соответствующие) элементы равных треугольников
равны.
Признаки подобия треугольников
По двум сторонам и углу ме-
жду ними (С У С).
По двум углам (У У).
По трем сторонам (С С С).
189
^Шпомная п/гофалсма & тгии/лимра. и фофмумгас,
4. Треугольник
Прямая, параллельная стороне треугольника, от- секает от него треугольник, подобный данному. Сходственные линейные элементы подобных треугольников пропорциональны сходственным сторонам. Периметры подобных треугольников относят- ся как сходственные стороны. Площади подобных треугольников относятся как квадраты сходственных сторон. В pq\\ac^aabc^apbq=> АВ _ АС _ ВС , А’^дР'д/л РВ PQ BQ коэффициент подобия 'j д АА, С 1 АВ + АС + ВС _ ®АВС _ »2 РВ + PQ + BQ &PBQ
Примеры подобных треугольников
в / AABC^ANBM k= АВ АС _ ВС AT bn ~ MN ВМ В /7 ААВС™ AABjB / / _ АВ АС _ ВС А Bj с * АВг “ АВ ввх
Медиана
Медианой треугольника называется отрезок, который соединяет вершину треугольника с се- рединой противолежащей стороны. А :МА1=вм’мв*=
Медианы треугольника пересекаются в одной точке (центре тяжести треугольника) и делят- ся этой точкой в отношении 2:1, считая от вер- шины. ХАТ1 = СМ : МСг =2:1 ..2 2 2Ь2 + 2с2 - а2 ААч = m 7 и 1 а 4
Медиана делит треугольник на два равновели- ких треугольника. Три медианы делят треуголь- ник на шесть равновеликих треугольников.
Биссектриса
Биссектрисой треугольника называется отрезок биссектрисы внутреннего угла треугольника. Все биссектрисы треугольника пересекаются в j одной точке — центре вписанной в треуголь- । ник окружности. Биссектриса делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам треугольника. А^Г***"^ \°/ / ^0)/ ~7\~—4л CAt _АС _ ab / 1 AjB ~ AS => СА1 - jVZ: вХч/АУ а ту лс АО Ь + с ХУ оз;- — АА2г =АВ • АС - АХВ • АгС АЛ 2 АВ АС А - ЛВ~ЛСт2
190
/ 'тш/лищъх,
4. Треугольник
Биссектрисы внутреннего и смежного с ним
внешнего углов треугольника перпендикулярны.
Биссектриса внешнего угла неравнобедренного
треугольника пересекает продолжение противо-
лежащей стороны в точке, отстоящей от концов
этой стороны на расстояния, пропорциональ-
ные длинам двух других сторон.
L в м с
ALAM =90°
LB _АВ
LC АС
Высота
Высотой треугольника называется отрезок пер-
пендикуляра, опущенного из вершины тре-
угольника на прямую, содержащую противоле-
жащую сторону.
Все высоты треугольника пересекаются в одной
точке — ортоцентре треугольника.
AAV BBV СС\ — высоты А АВС
ААХ = Ла; ВВХ = hb; СС± = hc\H — ортоцентр
±+1+±=1
ha hb hc Г
г — радиус вписанной окружности
Средняя линия
Средней линией треугольника называется отре-
зок, соединяющий середины двух сторон тре-
угольника.
Средняя линия параллельна третьей стороне и
равна ее половине.
Серединный перпендикуляр
Серединным перпендикуляром называется пря-
мая, перпендикулярная стороне треугольника
и делящая ее пополам.
Все серединные перпендикуляры сторон тре-
угольника пересекаются в одной точке — цен-
тре описанной около треугольника окружно-
сти. Около каждого треугольника можно опи-
сать окружность и притом только одну.
Точка пересечения серединных перпендикуля-
ров треугольника является точкой пересечения
высот треугольника, образованного средними
линиями данного.
^Шкальная mfuxfuuMMa i тш/мща'х, и, ффмумгх
4. Треугольник
Площадь треугольника
„ 1 L, 1 t 5Д 2 а^а 2 2 С^с SA=^ab sin С — я ас sin В = к Ьс sin А u Z Z л В
SA = 1р(р - а)(р - Ь)(р - с) (формула Герона) 5д = гр _abc ЬД“ 4R р=^(а + Ъ + с) — полупериметр г — радиус вписанной окружности R — радиус описанной окружности А ь С
Теорема косинусов Теорема синусов
а2 = Ь2 4- с2 - 2bc cos А Квадрат стороны треугольника равен сумме квадратов двух других сторон без удвоенного произведения этих сторон на косинус угла меж- ду ними. а _ Ъ _ с _ sin A sin В sin С Стороны треугольника пропорциональны си- нусам противолежащих им углов.
Вписанная окружность В каждый треугольник можно вписать окруж- ность и притом только одну. Ее центр — точка пересечения биссектрис. Радиус (г) вычисляется по формулам: В г = - Р г = (р-а) • tg^ =(p-b) • tg| = (р —с) • tg^ г= !(Р - а)(Р - Ь)(Р - с) _ S N Р Р р — полупериметр уУ// ОТ ±АС; / ov iab,ow ±вс УТХу AV = AT = p-a BV~BW = p-b ТС CW = CT=p-c
Описанная окружность Около каждого треугольника можно описать окружность и притом только одну. Ее центр — точка пересечения серединных перпендикуляров к сторонам треугольника. Радиус (R) вычисляется по формулам: й= ° = ь = с 2 sin A 2sinB 2sin С р- аЬс R~ 4S в ( R 70 44 ABX = ВгС; АСг = CtB; BA1=A1C OAt 1BC; OBt A. AC; (X^ =AB OA = OB = ОС = R
192
ёГсольсгл/тя & таЛлил'/ьх
4. Треугольник
Прямоугольный треугольник
Сторона прямоугольного треугольника, противо- лежащая прямому углу, называется гипотену- зой, две другие стороны называются катетами. a катет □ b катет
Теорема Пифагора Квадрат длины гипотенузы равен сумме квадра- тов длин катетов. с2 = а2 + Ъ2
Свойства прямоугольного треугольника Медиана, проведенная к гипотенузе прямоуголь- ного треугольника, равна половине гипотенузы. Только в прямоугольном треугольнике центр описанной окружности лежит на стороне тре- угольника (совпадает с серединой гипотенузы). В а С c OA = OB = OC = R = Jc ъ A &
Площадь прямоугольного треугольника S = ; S = \ch, h — высота, проведенная к гипотенузе
Тригонометрические функции острых углов прямоугольного треугольника
Синусом острого угла в прямоугольном тре- угольнике называется отношение противолежа- щего катета к гипотенузе. Косинусом острого угла в прямоугольном тре- угольнике называется отношение прилежащего катета к гипотенузе. Тангенсом острого угла в прямоугольном тре- угольнике называется отношение противолежа- щего катета к прилежащему. Котангенсом острого угла в прямоугольном треугольнике называется отношение прилежа- щего катета к противолежащему. а . .a b , a sin a = -; cos a = -; tg a = T c* c b ft = 90° - a b «2^ , b b sin P = sin(90° - a)= - = cos a cos P = cos(90° - a) = = sin a tg P = tg(90° - a) = = ctg a
Пример. sin 54° = cos 36°; tg 89° = ctg 1°
Значения тригонометрических функций некоторых углов
0° 30° 45° 60° 90° 180°
sin 0 1 2 1 J2 1 0
cos 1 2 1 72 1 2 0 -1
tg 0 1 7з 1 7з не опр. 0
7—1323
193
^Шмкльнал программа, 4 пии/лиирл и, фо^им^мхх
4. Треугольник
Признаки прямоугольных треугольников
Если квадрат одной из сторон треугольника равен сумме квадратов двух других сторон, то такой треугольник прямоугольный. Если медиана треугольника равна половине соответствующей ей сто- роны, то треугольник прямоугольный.
Решение прямоугольных треугольников
Дано: гипотенуза и острый угол. х = a cos а у — a sin а р = 90° - а ₽ у с X Дано: катет и острый угол. х = a tg а у = У^''а cos а а □ X
Дано: высота, опущенная на гипотенузу, и ост- рый угол. h h х _ у = X = — * cos a sin а \ h J' У \ z = h ctg а t = h tg a К'z Катет, лежащий против угла ловине гипотенузы. А 1 2 с 30°, равен п0‘ ^41 -1 Тз в 2
Соотношения в прямоугольном треугольнике
а to и Я, Ъ и н и J? £ £ -? £ Г |! " Н с- a Q м н* • • в а С Л ь А
Вычисление радиусов вписанной и описанной окружности
2R = АВ = с = (Ь - г) + {а - г) => а + Ь — с =>2R = a + b-2r^>r = х р-с и 2(R + г) == а + Ь Ь - г г С \ х. Ь - г а-г г
194
mfuix &тт/м«/№
4. Треугольник
Треугольники классифицируют по сторонам: разносторонние, равно- бедренные, равносторонние; а также по углам: остроугольные, тупо- угольные и. прямоугольные.
Треугольники разносторонние равнобедренные равносторонние
остроугольные Л А
тупоугольные —
прямоугольные 1 —
Равнобедренный треугольник
Равнобедренным треугольником называется треугольник с двумя равными сторонами. Общая вершина равных (боковых) сторон назы- вается вершиной равнобедренного треугольника, а третья сторона основанием. вершпна равнобедренного треугольника Л основание
Свойства равнобедренного треугольника Углы при основании равны. Высота, проведенная из вершины равнобедренно- го треугольника, является медианой и биссек- трисой (осью симметрии). Высоты (биссектрисы, медианы), проведенные к боковым сторонам, равны. 01/ в <Г \ ^1 -1- ВС <=> АА, = СС, h СС11.АВ
Все эти свойства равнобедренного треугольника обратимы и могут быть использованы для получения признаков равнобедренного тре- угольника.
Правильный треугольник
Правильным (равносторонним) называется тре- угольник, все стороны которого равны.
195
бЩкомная программ / тш/лищах, и, формулах,
4. Треугольник
Правильный треугольник (продолжение)
Свойства правильного треугольника Все углы равностороннего треугольника равны 60°. Только в правильном треугольнике совпадают точки пересечения медиан, биссектрис, высот, серединных перпендикуляров. Эта точка назы- вается центром правильного треугольника и является центром вписанной и описанной ок- ружностей. Центр правильного треугольника делит его высоты в отношении 2:1, считая от вершины. Только в правильном треугольнике: 2 а Л = 2г=57г = -7=. 3 1 CZo /60 „ 3
А в U АВ = ВС =АС = а AA1=BB1 = CC1 = h _ а/З Л -уа
Площадь равностороннего треугольника а2 л/3 S~ 1
Дополнительные теоремы о треугольнике
Теорема Чевы Отрезки АА19 ВВр ССХ тогда и только тогда пе- ресекаются в одной точке, когда: АВг CAt ВСг В^С ’ А^В * С^А = k в С, —И1 1 вх с
Теорема Менелая Точки А,, Вр Сх тогда и только тогда лежат на одной прямой, когда: АВг ВСг САг В^С ' С^А ’ А^В =1' А А, С
Теорема Стюарта АА± = Z, тогда 2 2 Ъ ах 4- с а2 Z2 = _ а а at + а2 1 z А с / ^14^ / a2^V с
196
gJeoMemfiua &maJjmufl'K,
4. Треугольник
Дополнительные теоремы о треугольнике (продолжение)
Центры вневписанных окружностей лежат в точках пересечения биссектрисы внутреннего и двух биссектрис внешних углов треугольни- ка. АТг = АТ2 = 1 (АВ + ВС + СА) =р г, ВК=р-с;СК=р~Ъ W/^Xi су V* J Г2у_^
5. Параллелограмм
Параллелограммом называется четырехугольник, противополож- ные стороны которого попарно параллельны.
Свойства параллелограмма Диагональ делит параллелограмм на два равных треугольника. Противоположные стороны параллелограмма равны. Сумма соседних углов параллелограмма 180°. Диагонали параллелограмма, пересекаясь, де- лятся пополам. В ц—-С 1 ZA + ZB = 180°
Дополнительные свойства параллелограмма Биссектриса угла параллелограмма отсекает от него равнобедренный треугольник. Биссектрисы соседних углов параллелограмма перпендикулярны, а биссектрисы противопо- ложных углов параллельны или лежат на од- ной прямой. Диагонали параллелограмма делят его на четы- ре равновеликих треугольника. в—£_с \ AB~BF ВМ ± AF У ВМ II DK A D
Высоты параллелограмма обратно пропорцио- нальны соответственным сторонам паралле- лограмма. Высоты параллелограмма, опущенные из одной вершины, образуют угол, равный углу паралле- лограмма при соседней вершине. В д С
А а / а 1 1 /1, а:Ь = т- : т-; /Ъ ha hb L/d A(ha;hb)-AA
Середина любого отрезка с концами на противо- положных сторонах параллелограмма лежит на прямой, проходящей через середины двух дру- гих сторон. В /Е с р 1Г 7~ Гр У JM У А В
197
^Шнслъная 6 таблицах, и ^ю^л/сулах,
5. Параллелограмм
Признаки параллелограмма
Если в четырехугольнике две противоположные стороны равны и
параллельны, то это параллелограмм.
Если в четырехугольнике противоположные стороны попарно рав-
ны, то это параллелограмм.
Если в четырехугольнике диагонали, пересекаясь, делятся пополам,
то это параллелограмм.
Периметр параллелограмма Р = 2а + 2Ъ а / a / Lb' ></
Площадь параллелограмма S = aha = bhb S — ab sin <p S = | djdg sin a
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его четырех сторон. о о о 9 di + do = 2а + 2Ь Ь
Квадрат
Квадратом называется прямоугольник, у которо- го все стороны равны (ромб с прямыми углами). Квадрат обладает всеми свойствами ромба и прямоугольника. Квадрат — правильный четырехугольник. в а А а J ? /d а Ь й о to ч «X II II II Мм мн О о Йм tol II Н-ь
Площадь квадрата S = а2 = I d2
Ромб
Ромбом называется параллелограмм, все стороны которого равны.
Свойства ромба
Диагонали ромба взаимно перпендикулярны.
Диагонали ромба лежат на биссектрисах его уг
лов.
Высоты ромба равны.
В ромб можно вписать окружность
1, * 1 . Л
г = ~ Л = a sin А.
л ci
Ромб обладает всеми свойствами параллело
грамма.
h = a sin А = a sin В = 2г
198
5. Параллелограмм
Ромб (продолжение)
Признаки ромба Если в параллелограмме диагонали взаимно перпендикулярны, то это ромб. Если диагональ параллелограмма лежит на биссектрисе его угла, то это ромб. Если стороны четырехугольника равны, то это ромб.
Площадь ромба s = = ha = a2 sinA = 2 ^1^2
Прямоугольник
Прямоугольником называется параллелограмм, у которого все углы прямые.
Свойства прямоугольника Диагонали прямоугольника равны. Около прямоугольника можно описать окруж- ность D 1 j 1 / 2 , , 2 Я = 2 = 2 Прямоугольник обладает всеми свойствами па- раллелограмма. А D а в AC = BD = d OA = OB = OC = OD = ъ „ 1J ~ R ~ 2 d2 = a2 + b2
Признаки прямоугольника Если в параллелограмме диагонали равны, то это прямоугольник. Если в параллелограмме один угол прямой, то это прямоугольник. Если в четырехугольнике три угла прямые, то это прямоугольник.
Площадь прямоугольника S- = ab S = d2 sin a
6. Трапеция
Трапецией называется четырехугольник, две стороны которого па- раллельны, а две другие не параллельны.
Элементы трапеции ВС T1AD — верхнее и нижнее основания, АВ и CD — боковые стороны, АС п BD — диагонали, MN — средняя линия, MN = l(BC+AD). Высота трапеции ВВг — расстояние между прямыми оснований. 3 Af/_ с В h ₽ -уС ДЛГ
h \
А В, и A D BBX±AD, ВВ1 = Л
Z99
(Щшкльная nftiOtfmjU.AUi & та/мирх и, формулах
6. Трапеция
Площадь трапеции S - h • MN = |л(ВС + AD) = ^AC-BD* х sin Z_(AC, BD)
Неравенство для сторон трапеции AB + CD>AD-BC CD. || BD В__ а ..Г.
2SACD.
Неравенство для диагоналей трапеции АС + BD>AD + BC h AD1
ъ D a Di d1 + d2>b + a
Разбиение трапеции на параллелограмм и треугольник
iC ВВХ || CD; 11/ \2 V2 BCDB1 — параллелограмм; . />-а\ а \ „ = а=ЩР R 2
A k l^\.2 . a \>^-aCC1\\AB;
А Вг D AD = b=> АВг -b-a. АВССг — параллелограмм.
Если известны стороны трапеции, можно вычислить по формуле Герона площадь отсеченного 2£д 2£д треугольника (SA), высоту трапеции (h = -r-g- или h = 77-^) и площадь трапеции. ** АНj с j и
Построение трапеции по основаниям и боковым сторонам
Пусть заданы отрезки а, &, lv Z2, причем + + 12 > Ъ - а (Ъ > а): неравенство для сторон трапеции. 1. Строим AABBj по трем сторонам: b - a, lv 12. 2. Проводим через точку В прямую ВХ || ABV 3. На лучах ВХ и ВХУ строим отрезки ВС = = BXD = а. ^гл&^яАВСВ — искомая. В В ex А' . А Ь- а В1 Л ь-а вг D Y В а С /ч\ А Ь-а Вх а п
Теорема о четырех точках трапеции Середины оснований, точка пересечения диаго- налей и точка пересечения продолжений боко- вых сторон трапеции лежат на одной прямой. Р / !/ BL = LC 1/ „ \ АТ = TD
Свойства треугольников в трапеции. АВОСDOA ВО СО а 8вос (а~\2 OD ОА b’ SD0A 1&J &АОВ = S COD а В — Tr?vc / ///^\\
200
Геометрия &maJdtiuflx
6. Трапеция
Построение трапеции по основаниям и боковым сторонам (продолжение)
Отрезок, параллельный основаниям, проходя- щий через точку пересечения диагоналей. ab 2аЪ OQ = OP=-—-,PQ= а + о а + о Ву. . а * С р/ - \<? / /° X. \ -Ав
Отрезок, параллельный основаниям и деля- щий трапецию на две равновеликие части. рр = а +b. ^2 О 3 -3 • _
В трапецию можно вписать окружность тогда и только тогда, когда сумма оснований равна сумме боковых сторон. BC+AD=AB + CD в \ хXL А — о А А * в
Равнобокая трапеция
Равнобокой (равнобедренной) называется тра- пеция с равными боковыми сторонами. tb- {ь. / '\ata 1 ' !\ ( - - - /Л \ \/ \ to /С//° /\ £ * II to о и 8 и ь о II to
Свойства равнобокой трапеции Диагонали равнобокой трапеции равны (dx = d2). Углы при одном основании равнобокой трапе- ции равны. Только около равнобокой трапеции можно описать окружность; она совпадает с окруж- ностью, описанной около любого треугольни- ка с вершинами в вершинах трапеции. Ее центр лежит на серединном перпендикуляре к основаниям трапеции. Если центр описанной окружности лежит на основании трапеции, то ее диагональ перпен- дикулярна боковой стороне.
В равнобедренную трапецию можно вписать окружность, если боковая сторона равна сред- ней линии. п Zr / \ г А/ _С г ° /\ = 2г = й / X и
201
^Шмхльная nfozfuiMJiui 6 тси/лимАХ, и
7. Окружность
Окружностью называется множестве на одинаковом расстоянии от данной1
Отрезки в окружности Для любой точки М окружности с центром О выполняется равенство: ОМ = R (отрезок ОМ — радиус окружности). Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности (D). D = 2R
Длина окружности С = 2nR.
Дуга окружности Часть окружности, заключенная между ее дву- мя точками, называется дугой.
Две любые точки М nN окружности определя- ют на ней две дуги: MkN п MIN. Любую из этих дуг стягивает хорда MN. Равные дуги стягиваются равными хордами.
Длина дуги АСВ = Ra, где а — величина угла АОВ в радиа- нах; . _ 7С<р . _ _ АСВ = 2?tq7v » гДе Ф — величина угла АОВ в loU градусах.
Крут
Кругом называется часть плоскости, ограниченная ок- ружностью. Для всех точек N круга выпол- няется неравенство: ON R. Часть круга, ог дугой и двумя называется сектл Любые два радт два сектора. Т^секто} у^сектб
о точек плоскости, находящихся точки (центра окружности).
lz
k М I
1 1 1 \ Н
г
граниченная радиусами, юром круга, иуса задают Часть круга, ограниченная ду- гой и стягивающей ее хордой, называется сегментом. Любая хорда делит круг на два сегмента. Сегмент, задаваемый диамет- ром, называется полукругом. /сегмент\
202
IJUUfltX,
7. Окружность
Круг (продолжение)
Диаметр, перпендикулярный хорде, делит эту хорду и стягиваемые ею дуги пополам. Если диаметр делит хорду, не являющуюся диа- метром, пополам, то он ей перпендикулярен. 1 f X V ° Л I MN 1 AB =5 AT = ВТ
Если две хорды АВ и CD имеют общую точку М, то AM • МВ = СМ • MD. Для данной точки М внутри окружности произ- ведение отрезков хорды, на которые делит ее данная точка, есть величина постоянная и равная: (В + ОМ)(В-ОМ). с Аг\) ( \ \/ \ ' / 'ч'— AM 'MB = (R + OM)(R - ОМ) = й2 - ОМ2
Центры всех окружностей, проходящих через две данные точки, лежат на серединном перпен- дикуляре к отрезку с концами в данных точках. 1 \(/^ °2 1 Pi \/
Прямая и окружность
Прямая, имеющая с окружностью одну общую точку, называется касательной к окружности; прямая, имеющая с окружностью две общие точки, — секущей. Прямая касается окружности тогда и только то- гда, когда диаметр, проходящий через общую точку прямой и окружности, перпендикулярен этой прямой. секущая^ \ °/ Ч а \ касательная" ОМ JL а
Если расстояние ОМ от центра окружности до прямой больше радиуса — прямая не имеет с окружно- стью общих точек; равно радиусу — прямая касается окружности; меньше радиуса — окружность высекает на пря- мой хорду длиной 2 • Ул2 — ОМ2. С /)\ > OM>R OM = R OM<R
Если окружность касается сторон данного угла, то: центр окружности лежит на биссектрисе угла, отрезки касательных равны между собой. )биссектриса AM = AN
203
бЩмальнал nfimfiaatMa
7. Окружность
Прямая и окружность (продолжение)
Если из точки вне окружности к ней проведены касательная и секущая, то квадрат длины от- резка касательной равен произведению всего отрезка секущей на его внешнюю часть. Произведения длин отрезков секущих, прове- денных из одной точки, равны. —• АТ2 = АВ-АС = =AX-AY = □ "I =(OA-R)(OA + R) = =OA2-R2
Две окружности
Если расстояние d между центрами двух окружностей больше сум- мы (Вх + R2 < d) или меньше разности (2?х - R2 > d) их радиусов, то окружности не имеют общих точек.
( „ \d \ 7 °2 J R^ + R2 < d / / / \ \ 1 1/7 1 \ 7 X. / / 2?x R2 > d
Если + R2 = d или R1 - R2 = d, то окружности касаются (внешним или внутренним образом).
внешнее касание внутреннее касание
/ ь-° \ 1 Ч ) >°2 ) + R2 = d I °1 1 \ (\2 У Rl-R2 = d
Если R± - R2 < d < Rx + R2, to окружности имеют общую хорду.
А i
1 (°- м\ \n 1 °' ( 1 °2 \ „
\ \ °2' \ м \ T.r • i iviiy =jx-. -m^-a IN j i z / у ^O,AO, 4 0= 1 ?
В MN = R9-R< + d & 1 d
Две окружности, имеющие общий центр, назы- ваются концентрическими. м 1 LN = °-
7 Лf^ = Я1-Я2 d = 0
204
£Гесмеп1[гил &тпа/лшщх,
7. Окружность
Углы в окружности
Центральным углом в окружности называется угол между двумя ее радиусами. Градусная мера центрального угла равна гра- дусной мере дуги, на которую он опирается (из- меряется дугой, на которую он опирается). Р ААОВ=АРВ = а°
Угол, вершина которого лежит на окружности, а стороны содержат хорды, называется вписан- ным углом. Вписанный угол измеряется половиной дуги, на которую он опирается. Вписанный угол, опирающийся на диаметр, прямой. Вписанные углы, опирающиеся на одну и ту же дугу, равны. А z ВАС=А ВРС= I \х\ (\\° । 1 - \ Л J \ \ \ = ъВМС \>Z1 Ум \ \ \7 2 А ВАС = 90° В А
Вписанные углы, опирающиеся на одну и ту же хорду, либо равны, либо их сумма 180°. А \ 1 /X АВРС = АВАС А ВАС + А ВТС = 180°
Угол между хордой и касательной измеряется половиной содержащейся в этом угле дуги ок- ружности. \ ° \/ \ Уо АВАС=\вМА
Угол с вершиной внутри окружности (угол ме- жду двумя хордами). Ь' V АВАС = АСС.В + С1И \ J V \ / + ^^5^ = Ум 1 ~ — = 5 (ВМС + B.LCA В z
Угол с вершиной вне окружности (угол между двумя секущими). „Z. ВАС = L С.ВВ. - \м 1 1 - \ - z. сс,в = а^-А- с\ Iх 1 V 7 ^(В.МС. - BLC)
205
^Шкальная пфсфамлла & тгш^лилщх м фоф.м.^лах
7. Окружность
Общие касательные двух окружностей
Если одна окружность лежит вне другой, то у них четыре общие касательные. Если одна окружность касается другой сна- ружи, то у них три общие касательные.
две внутренние касательные J. — _ (4^— — J—L ZSA 2. 1— — _ — XjnA, d = O1O2 > R± +J?2 ZO1 = Ё^ПГ2 d; M'M* + (Л1 " Л2)2 = d2 Ro 2 no /02 = R~HT2 di + (Й1 + Д2>2 = d2 одна внутренняя касательная V "А 21.1 \ в ^2 d = Rx + 2?2 •^1-^2 = 2 7^1-^2 м,в=ва=вм9 Л 4
Если одна окружность каса- ется другой изнутри, то у них одна общая касательная. Если окружности пересека- ются, то у них две общие касательные (две внешние касательные, внутренних ка- сательных нет). Если одна окружность лежит внутри другой, то общих каса- тельных нет.
( QizY4 \ °* / 2 Если ОХО2 = d, то МгМ2 +(Я1-й2)2 = </2 ( © \ \ °* /
Вписанная окружность
Окружность называется вписанной в много- угольник, если она касается всех его сторон. Ее центр должен принадлежать всем биссектри- сам внутренних углов этого многоугольника. Ее S радиус можно вычислить по формуле г = —, где S — площадь, ар — полупериметр многоуголь- ника. Не во всякий многоугольник можно вписать ок- ружность. в \ ' \ XZ Е D
206
7. Окружность
Вписанная окружность (продолжение)
В любой треугольник можно вписать окруж- ность и притом только одну. Ее центр лежит в точке пересечения биссектрис внутренних углов, а радиус может быть вычислен по формулам: S г= - Р АВС r=(p-a)tgg = (p-b)tg^ =(p-c)tg 2» где S — площадь треугольника, ар — его полу- периметр. \ 4 \ =^i =р~а \f \ ВС1 = ВА1=р-Ь ~ г = =р~с вЛл 1 р=±(а + Ь + с)_ 2 2^ полупериметр V
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. в /\ ° AB + CD = BC + AD с
Описанная окружность
Окружность называется описанной около мно- гоугольника, если она проходит через все его вершины. Ее центр лежит на всех серединных перпендикулярах сторон (и диагоналей) этого многоугольника. Радиус вычисляется как ради- ус окружности, описанной около треугольника, определенного любыми тремя вершинами дан- ного многоугольника. to /\ \ / Л [ \ х 7 /ft' 1 V- +1 to 11 Р О Ь II 11 S о to to II 11 5 to и
Около любого треугольника можно описать окружность и притом только одну. Ее центр ле- жит в точке пересечения серединных перпенди- куляров сторон треугольника, а радиус вычис- ляется по формулам: а _ ь с 2sin А 2sin В 2 sin С п-аЬс R~~ZS а, Ь, с — длины сторон треугольника, S — его площадь. Я в в -/ /РАЛ ( / \хЛ ( 4Яс 1 / 1 1 J № J \ J V-У \ У Z.B<90°=>Z.AOC<2B ZB>90’=> => ЛАОС = 180°- 2В
207
6Щномна& £ тси/лшлк и фо^ьллулах,
7. Окружность
Описанная окружность (продолжение)
Около четырехугольника можно описать ок- ружность тогда и только тогда, когда сумма его противоположных углов равна 180°. 1 \ с Z.A+ АС = АВ + Л2) = 180° D
Теорема Птолемея Во вписанном четырехугольнике произведение диагоналей равно сумме произведений его про- тивоположных сторон. АС • BD=AB • CD + BC • AD —
8. Площади
Площади равных фигур равны.
Если фигура составлена из нескольких фигур, не имеющих общих
внутренних точек, то ее площадь равна сумме площадей этих фигур.
Фигуры, имеющие равные площади, называются равновеликими.
Площадь квадрата
S = a2
Площадь прямоугольника
S = ab
Площадь параллелограмма
S = а • ha = Ъ • hb
S = ab sin а
Площадь треугольника
Основные формулы
S=^aha=^bhb=^chc
S = iab sin С = ~ ас sin В = ~ be sin А
Л Л Л
Формула Герона
S = 7р(р - а)(р ~ Ь)(Р ~ с), гдер = | (а + 6 +
+ с) — полупериметр
208
^Геометрия £ тги/лащгх
8. Площади
Дополнительные формулы S = гр, где г — радиус вписанной окружности „ аЪс п S = , где R — радиус описанной окружности S = 2R2 sin A sin В sin С / Г 7 1 Z / л / ^47 =4^ и
Некоторые соотношения площадей треуголь- ников 1 х Yf XX/ AABC^AMNC X. 7/Х CCx = h-,CX^ х-,АВ = с >4 / SMNC X2 MN2 Q 2 2^ в SABC h С
Площади подобных треугольников (фигур) от- носятся как квадраты сходственных элементов (сторон, медиан, высот и т. п.), их отношение равно квадрату коэффициента подобия.
Площади треугольников, имеющих равные вы- соты (общую высоту), относятся как стороны, соответствующие этим высотам. а/л.— с В &BFG ~ 1,
Площади треугольников, имеющих равные сто- роны, относятся как соответствующие этим сто- ронам высоты. 1 Е 3 &ABC • &AEC = : EE1
Площади треугольников, имеющих равный угол (или общий угол), относятся как произведения сторон, содержащих этот угол. В F ImTiiiSabc = ab ac &AFE AF ’
Медиана делит треугольник на два равновели- ких треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников. J8 SABB± = r Sf T A ^ACCx = SC1CB °ЛАВ = = = SAjGB “ A Bx = ^BGCj * ^CjGA
209
^[шхльная программа, £ та</лацах и, ф<фмумих,
8. Площади
Некоторые соотношения площадей треугольников (продолжение)
Площадь прямоугольного треугольника. „1,1, S = g ab = g ch . аЪ h = — с □ s 1 1 1 s' \ b В а С
Площадь правильного треугольника. a273 5 4 в ,£\ a C
Примеры решения задач на нахождение площадей
Пример 1. Дано: СМ = 2MB; CN = NA; SARr = S. Найти: SMBAN. Решение: SCMN _СМ-CN _ 2 1_1 _ 1 sabc СВСА 3 2 3^CMN зь=> 1 2 &MBAN = &АВС ~ &CMN = ^~3^=3^‘ С \ A Пример 2. Дано: 3CAX = AjB; AO = OAY; = S. Найти: S0BAi. Решение: AABA± и &ABC имеют общую высоту, про- ^АВАг AtB веденную из вершины А => = bABC bts -3 =^s -3s - 4 “ 4Ъ- 3 ВО — медиана ДАВАг => S0BA^ = § / А
210
8. Площади
SfcoMcmfiuji 6 т<и£и«щх
Примеры решения задач на нахождение площадей (продолжение)
Пример 3.
Дано: AU = | BU-, ВТ = ^СТ; АХ = XY YC;
Sabc ~
Pl анти: XUTY*
Решение:
SATB = | &АВС = § ® (общая высота).
2 2
SBTU = з $ авт = g (общая высота).
2
Аналогично, S^c — g S;
1 _4
$axu ~ 9 =* Sxuty “9 5-
Пример 4.
Дано: УХ II AC; XZ || АВ; SBXY = 8г; Scxz = S2.
Найти: SAYXZ.
Решение:
ДХУВ~ДС2Х=>
&AYXZ ~ * SAXZ ~
S2 = 2js^2
//S1
^CXZ~
Площадь трапеции
S = . h = MN • й,
а и & — длины оснований,
й — высота, MN — средняя линия.
Пусть заданы основания а, Ь и боковые сторо-
ны АВ = lv CD = 12. Проведем СЕ || АВ.
Тогда АЕ = a, ED = Ь- а, СЕ = lv
ECD
СС1 = h= j, - а • ^ecd вычисляется по форму-
ле Герона.
Соотношение площадей фигур, связанных с трапецией
^аов ~ $ cod ~ JS1S2
Sdoc ~ а$1 ~ ь$2
211
8. Площади
Соотношение площадей фигур, связанных с трапецией (продолжение)
Площадь произвольного четы-
рехугольника
S = АС • BD • sin а
а
Площадь ромбоида
S=\aC • BD
Площадь произвольного мно-
гоугольника (триангуляция)
&ABCD = ® 1 + ®2 + ® 3 +
где Е — произвольная точка
внутри многоугольника.
в
с
D
Площадь правильного n-угольника
„ 1 „ „ nR2 . 2я
S==2rP S=— Sm^’
2
o па , л
S~—'zlsn
S = nr2 tg
Tl
S = kP, k — апофема.
Площади правильных многоугольников
„ 6R2 . 2п SjSR2
S6=-2-sm-g=-F-
„ 8R2 . 2п „„2 /х
So = —ту- sin-з- = 2R J2
° Z о
12Я2 2л 2
S12 = — sini2 =3R
А^2 = ••• = а
Р = ап — периметр
R — радиус описанной окруж-
ности
г — радиус вписанной окруж-
ности
Площадь круга
S = Jtfl2 = 7D2 =
4 2
C — длина окружности,
D = 2R — диаметр.
Площадь сектора
S = — Д2
° 2 180°
S= Jb2oc
la радиан =
Площадь сегмента
S = |jR2(a - sin a),
a — радианная мера дуги
АтВ или АпВ (соответственно
для сегментов АтВ или АпВ).
^Геомет^ия бтси/лиирл,
8. Площади
Соотношение площадей фигур, связанных с трапецией (продолжение)
Пример 1. Площадь большого полукруга лВ2 _ —н- . Площадь каждого из ма- (R\2 "UJ ЛЫХ полукругов 5 . Л Площадь заштрихованной фи- „ лВ2 лВ2 ЗлВ2 Пример 2. АО = 27?; AC = R*/3 (по т. Пи- фагора). Площадь АСОВ = 2SAC0 = = R2j3. Площадь сектора 2 COBK=±R2?f = ^~. Z и О Площадь заштрихованной Пример 3» S = R2(j3 + /у/у^о/а
2 8 8 1! N I 05 со К 1 1 loo f О СЦ г эд \7 и *|ео эд 1 з . ё °5 -& и
А R О R в А в
СТЕРЕОМЕТРИЯ
9. Основные аксиомы и определения
Через любые три точки, не лежащие на одной прямой, проходит одна и только одна плос- кость. В* "Х /а .
Если две точки прямой лежат в плоскости, то и вся прямая лежит в этой плоскости. \ ^*^£1 ) \ / Afea, Leal_„ х, У г г —a C ci У M g a, L g a 1
Если две плоскости имеют общую точку, то они пересекаются по прямой, проходящей через эту точку. В любой плоскости выполняются аксиомы пла- ниметрии. / /и 5х/ / Afep=> /и is ' / a n P = a /В / => • M e a <—J a3M
Две прямые, имеющие только одну общую точ- ку, называются пересекающимися. 1 fl lb a c\b = M
213
9. Основные аксиомы и определения
Две прямые, лежащие в одной плоскости и не имеющие общих точек, называются параллель- ными. 4 — а || Ъ => (а с а; Ь с а)
Две прямые, не лежащие в одной плоскости, называются скрещивающимися. 1 а/ а / !// & / / v а — Ь
Прямая, все точки которой принадлежат плос- кости, называется прямой, лежащей в этой плоскости. г'а X аса
Прямая пересекает плоскость, если у них есть только одна общая точка. / X^Af / а п а = М
Прямая называется параллельной плоскости, а плоскость — параллельной прямой, если они не имеют общих точек. а а || а, а II а
Две плоскости, не имеющие общих точек, назы- ваются параллельными. а II Р
Два луча называются сонаправленными, если один из них является частью другого, или если они лежат на параллельных прямых в одной полуплоскости относительно прямой, проходя- щей через начала лучей. ,, а \ / NM и NK сонаправ- АХ и BY сонаправлены лены. АХ || BY
Прямая называется перпендикулярной плоско- сти (а плоскость прямой), если прямая перпен- дикулярна любой прямой, лежащей в стой плоскости. а
\ с ' \ г—" а) । / | а ± а => (а 1 с, а 1 Ь)
SeoMcmfiuji 6тш/мярх
10. Теоремы стереометрии
Через прямую и не лежащую на ней точку про- ходит одна и только одна плоскость. 7 а / , / / к* Г аса / / Мёа=><! / аМ* / [Mg а
Через две пересекающиеся прямые проходит одна и только одна плоскость. 7 V. / 7 а / (а с а /ъ / а<~>Ь = М=>\, / ’ / [&са
Через две параллельные прямые проходит одна и только одна плоскость. .. . [аса \ \ а II b => 4 X ъ.а/ [6 с а
Если точки А, В, С, D не лежат в одной плоско- сти, то прямые АВ и CD (АС и ВВ, AD и ВС) скрещиваются. Если прямая АВ лежит в некоторой плоскости, а прямая CD пересекает эту плоскость в точке, не лежащей на АВ, то прямые АВ и CD скрещи- ваются. / \ с J \ А.в.сеа] АВ —CD \ п 1 АС — BD D*a J AD —ВС
Если одна из параллельных прямых пересекает плоскость, то и другая прямая пересекает эту плоскость. а / (а / / J а " b | => b п а / у- •— а п а 1
Признак параллельности прямых Если две прямые параллельны третьей, то они параллельны между собой. с — \ \ а|1с1 II и к II 1 => а " Ь b II с J
Признак параллельности прямой и плоскости Если прямая, не лежащая в плоскости, парал- лельна какой-либо прямой, лежащей в плоско- сти, то она параллельна этой плоскости. а а IIЪ1 / _) , [ => а II а 7ъ —-——/ b с а j Q а/
215
^Школьная nfm/taMM & та/мцлх и, формулах
10. Теоремы стереометрии
Если одна из пересекающихся плоскостей про- ходит через прямую, параллельную другой плоскости, то линия пересечения плоскостей параллельна этой прямой. !у р ] a r> Р = Ъ / аса • => а || Ь а || р
Если каждая из пересекающихся плоскостей проходит через одну из двух параллельных прямых, то прямая пересечения плоскостей па- раллельна этим прямым. f а/ с = а n р I /а ] аса I I а II с Л-S ь с Р | =* I b II с а || Ъ ]
Если две пересекающиеся плоскости пересече- ны третьей плоскостью по параллельным пря- мым, то линия их пересечения параллельна этим прямым. —А \ а п р = с —ту--, у г> а = а I с || а у п р = Ь f 1с || b а II b
Если две пересекающиеся плоскости пересече- ны третьей плоскостью по пересекающимся прямым, то точка их пересечения лежит на линии пересечения плоскостей. А \'\ Г\ к V1 \ »> AVr \
Углы с соответственно сонаправленными сторо- нами равны. s' в . s'} С С Z. BjAjCi = Z. ВАС
Признаки параллельности плоскостей Если две пересекающиеся прямые одной плос- кости соответственно параллельны двум пересе- кающимся прямым другой плоскости, то эти плоскости параллельны. М, а ) a cxb — М ~ а с а; Ъ С а к У а || а.; & || Ь, Ijj аг С Р; Ьг С р ► =>а || р
Если две плоскости параллельны третьей, то они параллельны между собой. х у ———у а II Y / Р II у! =>а|| р
216
1самАтприя & 7па(/л1щал
10. Теоремы стереометрии
Свойства параллельных плоскостей Если плоскость пересекает две параллельные плоскости, то прямые пересечения параллель- ны. ( Та 1 1 Р) к у п а = а /у.—У r> Р = b => а II Ь К а || р
Если прямая пересекает одну из параллельных плоскостей, то она пересекает и другую плос- кость. /а / а г\ а 1 , „ „ о /Р ! / а||рНапР
Если плоскость пересекает одну из параллель- ных плоскостей, то она пересекает и другую плоскость. /а / / у 4 Г /—z а II Р 1 р /у у г> а | ' г
Через точку, не лежащую на плоскости, можно провести одну и только одну плоскость, парал- лельную данной плоскости. м 7. । ь~~~— М Й а 1 а1 II а а С а ► => существует < b± II Ъ => суще- b С а ах п = М ствует единственная плоскость р || а, М е р
Признак перпендикулярности прямой и плос- кости Если прямая перпендикулярна двум пересе- кающимся прямым плоскости, то она перпен- дикулярна самой плоскости. с 1 а X a r> b а) aSa’^('a>=^c-La У с А. а f clb
М7
^Школьная пфофамма
4 пии/лшдмь it фофмулак
10. Теоремы стереометрии
Признак перпендикулярности прямой и плоскости (продолжение)
а) Если прямая перпендикулярна одной из па-
раллельных плоскостей, то она перпендикуляр-
на и другой.
б) Если две плоскости перпендикулярны одной
и той же прямой, то эти плоскости параллель-
ны.
в) Через точку проходит единственная плос-
кость, перпендикулярная данной прямой.
=> существует единственная плос-
Meal
Meal
кость a 1 а <= I М & а
\М е a
а) Если одна из параллельных прямых перпен-
дикулярна плоскости, то и другая прямая пер-
пендикулярна этой плоскости.
б) Если две прямые перпендикулярны одной
плоскости, то эти прямые параллельны.
в) Через точку проходит единственная прямая,
перпендикулярная данной плоскости.
в) М е a => существует единственная прямая
ala,Меа<=Мё а
Теорема о трех перпендикулярах
Если (ортогональная) проекция наклонной пер-
пендикулярна прямой на плоскости, то и сама
наклонная перпендикулярна этой прямой.
Если наклонная перпендикулярна некоторой
прямой плоскости, то и (ортогональная) проек-
ция наклонной на эту плоскость перпендику-
лярна этой прямой.
Если плоскость проходит через перпендикуляр
к другой плоскости, то она перпендикулярна
этой плоскости.
<=> (& 1 т)
a С a
a 1 р
218
10. Теоремы стереометрии
Перпендикуляр к одной из двух перпендику- лярных плоскостей либо лежит в другой плос- кости, либо ей параллелен. а /\ а । । a a
1 ъ/ I 1 / 1 1 p / 1 1
а ± | al | j => а С а или а II а
Если две пересекающиеся плоскости перпенди- кулярны третьей плоскости, то и линия их пе- ресечения перпендикулярна этой плоскости. а V а ) / „ - - у ) а п р — а] а ± у => а 1 у P±Y
Угол, образованный наклонной и плоскостью, не больше угла между этой наклонной и любой прямой плоскости. Углом между наклонной и плоскостью называ- ется угол между наклонной и ее ортогональной проекцией на эту плоскость. а Р ГЧ р±7 any а ±у т Су Z (а, Z / -I. ZQxf / & = пр^а л/ b = пру a у) = a = Z. (a, b) < p = Z. (a, m)
Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны. ль j—+~а J Р [ => АВ - CD II а || & I
Теорема Фалеса Параллельные плоскости, пересекающие пря- мые и отсекающие на одной из них равные от- резки, отсекают равные отрезки и на других прямых. а/ \Ь I \ с / Л Т8! а1 " а2 II а3’ /“Г Аз, = -BfrBs’ / ^1^2 = ^2^3
219
^Школьная nfwzhaMMa
& таблицах, и, ффмуяах,
11. Расстояния в пространстве
Расстояние между точками А и В равно длине отрезка АВ. Расстояние есть неотрицательное число. .4 в р(А,В)=АВ>0
Расстояние между точкой и фигурой (множест- вом точек) равно нулю, если точка принадле- жит фигуре, или длине наименьшего отрезка, одним из концов которого является данная точ- ка, а другим — ближайшая точка фигуры (если такой отрезок существует). м XeF,AeF * F AJ~^ p(MyF) = MA \ хХ p(KyF) = Q V МХ>МА
Расстояние между двумя фигурами (множества- ми точек) равно нулю, если фигуры имеют об- щую точку, и расстоянию между ближайшими точками этих фигур, если такие точки сущест- вуют. > p(FpF2) = 0 (р ’ F2> = АА е А2 g F2
Расстояние от точки до прямой, не содержа- щей эту точку, есть длина отрезка перпендику- ляра, проведенного из этой точки на прямую. м \ \ Mia Р(М, а) = МА 5-—Ае а, МА ± а
Расстояние от точки до плоскости, не содер- жащей эту точку, есть длина отрезка перпенди- куляра, опущенного из этой точки на плос- кость. м\, 7~-\ / ) Mia (а —s' р(М,а) = МА Ае а, МА ± а
Расстояние между двумя пересекающимися прямыми равно нулю. а п Ъ = А, р(а, Ъ) = 0
Расстояние между двумя параллельными пря- мыми равно длине отрезка их общего перпенди- куляра. а II Р(а’ =2М*1 =А2&2 G а^2 G Вхе Ь;В2е Ь А,ВЛ ± а, А2В2 ± а
Расстояние между двумя параллельными пря- мыми равно расстоянию от любой точки одной из этих прямых до другой прямой. ь а II &, А е а => р(а, Ь) = р(А; &)
Расстояние между двумя скрещивающимися прямыми равно длине отрезка их общего пер- пендикуляра (такой отрезок единственный). •'L-— ь а — Ь р(а, Ь) =АВ, Ае at Be Ь, АВ Л. а, АВ Ab
220
4 таблицах
11. Расстояния в пространстве
Расстояние между двумя скрещивающимися прямыми равно расстоянию от любой точки од- ной из этих прямых до плоскости, проходящей через вторую прямую параллельно первой, или расстоянию между двумя параллельными плос- костями, содержащими эти прямые. (а Р(а,₽) ) (a — b => a || b, s aCa)=> p(a, b) - p(b, a) у a — b,aCa, b С P => p(a, b) = p(a, P)
Расстояние от прямой до непараллельной ей плоскости равно нулю. а Я а => р(а; а) = 0 Ч? ЬСа=> р(&; а) = 0
Расстояние между прямой и параллельной ей плоскостью равно длине отрезка их общего перпендикуляра. Расстояние от прямой до параллельной ей плоскости равно расстоянию от любой точки этой прямой до плоскости. \ Г 4^"^ В — a || a, A e a, В e al AB la; AB la [ X p(a, a) = AB j lAf e a, a || a p(a, a) — p(M, a)
Расстояние между двумя параллельными плос- костями равно длине отрезка их общего пер- пендикуляра. (а 1 1 / —a II Р» A e а, В e P, B / AB±a,AB±P У p(a, P) = AB
Расстояние между двумя параллельными плос- костями равно расстоянию между точкой од- ной из этих плоскостей и другой плоскостью. । A .a || p, A e a / p(a, p) = p(A; P)
Расстояние между двумя параллельными плос- костями равно расстоянию между любой парой скрещивающихся прямых, лежащих в этих плоскостях. (а •/ ос || р, а С а; Ь С Р; а — Ъ & / Р(а. Р) = Р(а» Ь)
Расстояние от точки до сферы равно модулю разности расстояния от этой точки до центра сферы и радиуса сферы. S м —/Д p(M,S) = MA — MO-R, Ае S 1 oS j p(Afv S) = МХАХ = R- MjO; AieS р(м, s) = \mo - 4
221
^Школьная nfm/iaMM / тхи/лищьх, и
11. Расстояния в пространстве
Расстояние между двумя шарами, не имеющи- ми общих точек, равно разности расстояния ме- жду их центрами и суммы их радиусов. Г °\М Дх^\\ Qp Q2 не имеют общих точек p(Qx, Q2) » ОгО2 - (Rt + R2)
12. Множества точек пространства, связанные с расстояниями
Множество точек пространства, удаленных от данной точки на данное расстояние R, есть сфе- ра с центром в данной точке радиуса R (R > 0).
Множество точек пространства, удаленных от данной прямой на данное расстояние R, есть ци- линдрическая поверхность (R > 0). /<ЦИ Ц-П \ у
Множество точек пространства, удаленных от данной плоскости на данное расстояние а, есть две параллельные ей плоскости (а > 0). dCi га а* ^7 Ау II ₽1> а II Р2’ =-^М2 = а М2^ МуМ2 ± а, А е а, А е М±М2
Множество точек пространства, равноудален- ных от двух точек, есть плоскость, проходя- щая через середину отрезка с концами в этих точках перпендикулярно прямой, проходящей через эти точки. В этой плоскости лежат центры всех сфер, проходящих через данные точки. Аэ (a AM = МВ;АК = КВ \В АВ La
Множество точек пространства, равноудален- ных от трех точек, не лежащих на одной пря- мой, есть перпендикуляр к плоскости этих то- чек, проходящий через центр окружности, опи- санной около треугольника с вершинами в этих точках. На этом перпендикуляре лежат центры всех сфер, проходящих через данные точки. 1 м ] ОА = ОВ = ОС\. МО 1 а 1 —У => МА = МВ = МС
Множество точек пространства, равноудаленных от четырех точек, не лежащих в одной плоско- сти, есть единственная точка — центр сферы, проходящей через данные четыре точки.
222
& тш^ииах
12. Множества точек пространства, связанные с расстояниями
Множество точек пространства, равноудален-
ных от двух параллельных прямых, есть плос-
кость, проходящая через середину отрезка об-
щего перпендикуляра этих прямых и ему пер-
пендикулярная .
В этой плоскости лежат центры сфер, касаю-
щихся этих прямых.
Множество точек пространства, равноудален-
ных от двух пересекающихся прямых, есть две
плоскости, перпендикулярные плоскости этих
прямых и проходящие через биссектрисы уг-
лов, образованных этими прямыми.
Множество точек пространства, равноудален-
ных от прямых, содержащих стороны тре-
угольника, есть четыре прямые, перпендику-
лярные плоскости треугольника, проходящие
соответственно через центр вписанной и каж-
дый из трех центров вне вписанных для этого
треугольника окружностей.
Множество точек пространства, равноудален-
ных от сторон данного треугольника, есть
перпендикуляр к плоскости треугольника, про-
ходящий через центр вписанной в него окруж-
ности. На этом перпендикуляре лежат центры
всех шаров, касающихся сторон треугольника.
а) Множество точек пространства, равноудален-
ных от двух параллельных плоскостей, есть
параллельная им плоскость, проходящая через
середину отрезка их общего перпендикуляра.
В ней лежат центры всех шаров, касающихся
обеих плоскостей.
б) Множество точек двугранного угла, равно-
удаленных от граней этого угла, есть биссек-
торная полуплоскость этого угла. В ней лежат
центры всех шаров, вписанных в этот угол.
а || Ь, X g a, Y е b, М е а
ХУ ± а, XY± a, XY _L Ъ
XZ = ZY
=>MX = MY
ХО 1 (АВС)
ОСХ = ОАХ - ОВг
ОС± ± АВ, ОАг ± ВС, ОВГ А. АС
а|| р,у || a,AB±a,AC = CB
Хе у=>р(Х,а) = р(Х, р)
Z. (М, АВ, Х) = А (Х,АВ, N)
Хеу=>р(Х,а) = р(Х, р)
223
<'Шш>м>'ная п/гогЬамма, / тас/мщах. и, фсклшлах
12. Множества точек пространства, связанные с расстояниями
Множество точек пространства, равноудаленных от двух пересекающихся плоскостей, есть две биссекторные плоскости, проходящие через прямую пересечения этих плоскостей и деля- щие образованные двугранные углы пополам. В них лежат центры всех шаров, касающихся обеих плоскостей. X1 jT*4 T’z \ / /у
г Z. (а, у) = z. (р, у) Хе Y=>p(X,a) = p(X,P) Z (а, 5) = Z. (р, 5) Ye 5 =>р(У, а) = р(У, Р)
13. Углы в пространстве
Угол между прямыми
Угол между параллельными или совпадающи- ми прямыми считается равным нулю. а а = Ъ ‘'"'"'a i ь (а?Ъ) = Z. (а, &) = 0
Углом между пересекающимися прямыми назы- вается наименьший из углов, образованных при пересечении прямых. \мЛ- X а п Ь = М; A (a, b) = Z РМТ
Углом между скрещивающимися прямыми на- зывается угол между пересекающимися пря- мыми, соответственно параллельными данным скрещивающимся. а~ — а — Ъ; аг || a; bt II b; alnbl-M Z (а, Ь) = А (а,, &Р
Две прямые называются перпендикулярными (ортогональными), если угол между ними прямой.
Угол между двумя прямыми находится в пределах от 0° до 90°. 0° < z. (а, Ь) < 90°
Примеры нахождения углов между двумя прямыми в многогранниках
Пример 1. Дан куб. 1) Z(AB, DiCj) = 0° 2) Z.(AD, ВСр = Z.(BC, ВСг) = 45° з) z.(dc, вер = zKPiCp вер = эо° 4) А^Вр вер = z(.db, вер = во° (Д PBCj — правильный) 5) A(AXD, BCJ = /-(BjC, вер = 90° А 6) A(ABV BCJ = A(DCV ВС J = 60° 7) /.(AjC, ВСр = 90° (теорема о трех перпендикулярах) С1
с
" -X 1 1. 1 * J /
в
224
tJeoMemfum 4 таблицах
13. Углы в пространстве
Примеры нахождения углов между двумя прямыми в многогранниках (продолжение)
Пример 2. Дан правильный тетраэдр
1) A(DO, AB) = 90° (DO 1 (ABC))
2) Z-(AD, BC) = 90° (теорема о трех перпендику-
лярах)
8) A(DO, KZ) - Z-(DO, BD), так как KZ || BD
4) A(AK, BZ) = Z_(AK, KZJ, где KZX « BZ.
Рассмотрим Д AKZX.
AK=^iKZ1^lBZ^l^;AZ21 ~a2 + g)2 -2a-|
AZ2! =AK'2 + A'Zi -ZAK'KZ! cos <p, где <p = Z(Aff, KZp (теорема косинусов в A AKZJ.
Дано:
АВ = ВС = СА - AD = BD =
— CD = a
ВК — КС,Ке ВС
DZ = ZC,Ze DC
cos Z. ACD (теорема косинусов в Д AZ1C).
Следовательно, Z.(AK", KZj) = <р — arccos g.
Угол между прямой и плоскостью
Прямая называется перпендикулярной данной плоскости, а плоскость — перпендикулярной прямой, если прямая перпендикулярна любой прямой, лежащей в этой плоскости. Q перпендикуляр & | к плоскости 1 у т С а => Z_(m, а) = 0’ а ± а =>Z.(a, а) = 90’ А(АВ, а) “ Z. А0ВА = <р; \ • Р(А, а)
Прямая, пересекающая плоскость и не перпен- дикулярная ей, называется наклонной к этой плоскости.
Угол между прямой, параллельной данной плоскости (или лежащей в плоскости), и данной плоскостью считается равным нулю.
Если прямая и плоскость взаимно перпендику- лярны, то угол между ними считается равным 90°. Синус угла между наклонной АВ и плоско- стью, в которой лежит точка В, равен отно- шению расстояния от точки А до этой плос- кости к длине отрезка АВ.
Угол между наклонной и плоскостью равен уг- лу между наклонной и ее проекцией на эту плоскость (ортогональной проекцией). Угол между прямой и плоскостью находится в пределах от 0° до 90°. 0°<д(а, а) <90°
Примеры нахождения углов между прямой и плоскостью
Пример 1.
Дано: ABCDAjBjC^j^ — куб. Найти: <р = Z.(BDV (ВВХСХ)).
Решение:
1. DjC-i ± (BBjCp => BC-l — проекция BDX => ф = Z. DxBCr
D^C, al al
г.ВДВОДаШф.^.-^ --(„ли^ф--^-^
. 1 .1
=>Ф=агсаш-т= = arctg-y=.
8—1323
225
13. Углы в пространстве
Примеры нахождения углов между прямой и плоскостью (продолжение)
Пример 2.
Дано: ABCPA1B1C1Z>1 — куб.
Найти: <рх = Z.(AZ>p (DAjBJ); ф2 = Z.(CZ>V (DA^)).
Решение:
1. ADX LA^D', АгВг 1 (АА^) => А1В1 1 ADV
2. ADi 1 (DA^) => ф! = 90°.
3. ADt ± (DAjBj); ADj n (DA^y) —F=> FC — проекция CDt на (DAjBj) => ф2 = ADjCF.
FDt j
4. В Д D.FC sin ф, = 77-7, - x => Ф2 = 30°.
Пример 3.
Дано: ABCD — правильный тетраэдр, AM = MD, M e AD.
Найти: ф = A(BM, (BDC)).
Решение: К — середина ВС.
1. (DAK) 1 (ВВС), так как ВС 1 (DAK).
2. (DAK) n (ВВС) = DK, МТ 1DK,T 6 DK=* МТ 1 (ВВС) => ВТ — проекция
ВМ на (ВРС) => ф = /-МВТ.
3. МТ — я р (А, (ВРС)) = = 5 а /|, где а — сторона тетраэдра; ВМ = =>
4b у о Z
МТ 72 . 72
=> Sin Ф = = -у => Ф = arcsin -у.
Двугранный угол
Двугранным углом называется пересечение двух
полупространств, образованных непараллельны-
ми плоскостями. (Фигура, образованная двумя
непараллельными полуплоскостями, имеющи-
ми общую границу.)
Общая прямая полуплоскостей называется реб-
ром двугранного угла, а полуплоскости — гра-
нями двугранного угла.
Z(X,(AB),Y)-
двугранный угол
аса а±АВ;
Ьср ЪА_АВ
anb = O; Z.(a, Ь) —
линейный угол
Z(X,(AB),Y) =
e Z_(a, Ь)
Линейным углом двугранного угла называется
пересечение этого двугранного угла и плоско-
сти, перпендикулярной его ребру. (Угол между
двумя перпендикулярами к ребру двугранного
угла, лежащими в гранях двугранного угла и
имеющими на ребре общее начало.)
а ± АВ; а± ± АВ;
b А.АВ;Ь11АВ
A(M9(AB)9N) = £(a9 Ъ) =
= Z.(a1,b1)= ZMCW =
= ZLM1O1^
8Шф =
Р(М; р)
р(ЛГ; АВ)
Величина двугранного угла считается равной
величине его линейного угла.
Все линейные углы данного двугранного утла
равны между собой.
Величина двугранного угла находится в преде-
лах от 0° до 180°. 0° < Z.(M, (АВ), N) < 180°
Синус линейного угла двугранного угла ра-
вен отношению расстояния от любой точки
одной из граней двугранного угла до плоско-
сти другой грани к расстоянию от этой точки
до ребра этого двугранного угла.
ил 6 тшСшцмс,
13. Углы в пространстве
Примеры нахождения двугранных углов в кубе
Пример 1.
Дано: ABCDA-fi^C^D^ — куб.
Найти: а = Z. (Ар (ВС), В).
Решение:
1. АгВ 1 ВС’, АВ ± ВС => а = ААгВА.
2. А АХВА = 45° => а = 45°.
Пример 2.
Дано: ABCDAlBxClD1 — куб.
Найти: <р = Z. (Ар (BD^), Cj).
Решение:
1. BBt 1 (AjCjD); BDX n (AjCtD) - O; A^O - OCt = OD; ОАг 1 BBf,
OCj ± BDX => A AlOC1 - <p.
2. Д AjBCj — равносторонний => A A1OC1 = 120° => <p — 120°.
Угол между плоскостями
Плоскости называются перпендикулярными,
если они образуют прямой двугранный угол.
а ± Р => Z.(a, Р) = 90°
Угол между параллельными или совпадающи-
ми плоскостями считается равным нулю.
a И р => Z(a, Р) = 0°
Угол между пересекающимися плоскостями ра-
вен меньшему из двугранных углов, ими обра-
зованных (т. е. каждый из трех остальных не
меньше данного).
Угол между двумя плоскостями равен углу ме-
жду перпендикулярными им прямыми.
Z(a,p) = <pe (0°,90°)
а ± а, Ъ ± Р
А(а, р) = ^(а,Ь)
Угол между двумя плоскостями находится в пределах от 0° до 90°.
0° < Z.(a, р) < 90°
227
6Щ,1(ом>ная nfuafiOMMa, 4 тш/лимрдь и,
13. Углы в пространстве
Трехгранный угол МАВС М — вершина; МА, МВ, МС — ребра. А АМВ, ААМС, А ВМС — плоские углы трех- гранного угла. — вершина /uioc/cuaZV'4S4^e AMВ — С, угол ААМС — В, / АВМС=А а+в>с,а + с>в, 1 В + ОА А + В + С< 360°
Неравенство трехгранного угла*. сумма двух плоских углов трехгранного угла больше третьего плоского угла.
Теорема синусов трехгранного угла sin А _ sin Ё _ sin С sin A sin В sin С Теорема косинусов трехгранного угла cos С = cos А • cos В + sin А • sin В • cos С, где А, В, С — величины двугранных углов при ребрах МА, МВ, МС соответственно; С, В, А — величины плоских углов, противо- лежащих соответственно АВ, АС, ВС.
Многогранный угол МАХА2..АЛ М — вершина; МАХ, МА2, ..., МАп — ребра; А АгМА2, ..., АЛ_ХМАЛ — плоские углы много- гранного угла. ~ дМ — вершина плоский г у гол A АХЛ4А2 4” А *4* X/ / • + •+АА^МАп < Зб0’ М'ЛХ°
Сумма плоских углов выпуклого многогранного угла меньше 360°.
14. Основные задачи на построение в пространстве
В любой плоскости выполняются все построе- ния планиметрии. Через три точки, не лежащие на одной пря- мой, через прямую и точку вне ее, через две пе- ресекающиеся прямые, через две параллельные прямые ыожао провести плоскость и притом только одну. Через точку, не лежащую на данной прямой, можно провести только одну прямую, парал- лельную данной прямой.
Через точку, не лежащую в данной плоскости, можно провести бесконечное множество пря- мых. параллельных этой плоскости. аз S' ' а2^ а1Хг' М £ а; С а^а^а^М а, II а, а2 II а, а3 II а
228
^Ц»метп^гия 6 тии/лиирх
14. Основные задачи на построение в пространстве
Через точку, не лежащую на данной прямой, можно провести бесконечное множество плос- костей, параллельных этой прямой. /а\< - ' ' Mia, т II а 04 || а, а2 II а, а3 || а п а2 г» а3 = т
Через точку, не лежащую на данной плоскости, можно провести плоскость, параллельную дан- ной, и притом только одну. (^3 л ’ ч М i а \а ) а || а; b II а; a n b = М s' а С Р; Ъ С Р; => Р II а
Через точку можно провести плоскость, пер- пендикулярную данной прямой, и притом толь- ко одну. \М/$ а Т \ М е а, а Са СЗ J X е Р; а С Р; МТ±а;ТХ±а=> =>(МТХ) = у±а
Через точку можно провести прямую, перпен- дикулярную данной плоскости, и притом толь- ко одну. V f а\ J м Mi а, а С а => существует плос- Л кость Р э М, Р ± а => ... ) => р п а = с MKLc^MKVa.
Через точку можно провести бесконечно много плоскостей, перпендикулярных данной плоско- сти. Г > / (а2/ / хД jr2. / 1 Vs / \ ) 4 V а (/1 X? / Af/Ц Л MKLa I а1ла2па3 = МК / аг ± а; а2 ± а; а3 ± а
Через одну из скрещивающихся прямых можно провести единственную плоскость, параллель- ную другой прямой. (XJ — а — b; т II Ъ => а II Ъ
229
вЩшхАъная пл
фофмумя
15» Построение сечения куба
Построить сечение куба, проходящее через точки М, TV, L.
16. Ортогональное проектирование
Ортогональной проекцией (мы будем говорить
просто проекцией) точки на плоскость называ-
ется точка пересечения перпендикуляра, прове-
денного через данную точку к плоскости, и са-
мой плоскости.
Мы будем обозначать: пра А = В
Свойства ортогонального проектирования
Если точка лежит на плоскости, то пр£ К = К.
Проекция прямой есть прямая (или точка).
Проекция отрезка есть отрезок (или точка).
230
16. Ортогональное проектирование
Проекции наклонных Если из одной точки на плоскость проведены несколько наклонных, то: равные наклонные имеют равные проекции, равным проекциям соответствуют равные наклонные, большая на- клонная имеет большую проекцию, большей проекции соответствует большая наклонная. & м К М0 = пр^М — {МА = МВ) о , \Д ^{м^м^у м0 с) (МС>МА)& с^(МпС>МпА)
Длины проекций отрезков, лежащих на парал- лельных прямых (или на одной прямой) про- порциональны длинам самих отрезков. А 1, О я ft ир орц II A ’w Зго чн гч HJ5 а q a И я и а eq О ч ft «Г йГ ьГ \ /jA
1 ~ai \а 1 в 1 с _£i__ 1
Длина проекции отрезка равна произведению длины этого отрезка на косинус угла между плоскостью проектирования и прямой этого от- резка. А /иУ® 5J в Л AjBj = прдАВ = АВ cos q> ф = Z. (АВ, а)
Площадь проекции многоугольника равна про- изведению площади этого многоугольника и ко- синуса угла между плоскостью проектирования и плоскостью многоугольника. << ~пр* (pip2wv ХЛ» S^S’COsq»
Параллельное проектирование Параллельной проекцией точки на плоскость в направлении прямой 1, не параллельной плос- кости, называется пересечение проходящей че- рез точку прямой, параллельной или совпадаю- щей с 1, и плоскости проектирования. Мы будем обозначать: пр„А = В. Ортогональное проектирование есть частный случай параллельного. Параллельное проектирование обладает всеми отмеченными свойствами ортогонального проектирования. 1 / / J АВ || 1, В е а — i / В - прдА
231
^Шламмая пфюфамма, & тш/лимрдс, и, фофмумк.
17. Призма
п-угольной призмой называется многогранник, две грани которого — равные n-угольники с со- ответственно параллельными сторонами (осно- вания) t а остальные п граней — параллелограм- мы (боковые грани). n-угольная призма имеет: п + 2 грани, Зл ребра, 2п вершины. а || Р; А, В, С,De р; f« Вр С„ Р, е а верхнее 1 “Г И основание1J J CD || C^D^\ (rNN ТЪ DA1 X? Y / нижнее' АА^ || ВВ1 || СС1 II DD1 основание . . , - ААг = 1 — боковое ребро ВР1 — диагональ
Высотой призмы называется расстояние между плоскостями ее оснований. (Отрезок перпенди- куляра к плоскостям оснований, заключенный между ними.)
Диагональ призмы — отрезок, соединяющий две вершины, не лежащие в одной грани. У n-угольной призмы п(п - 3) диагонали.
Призматической поверхностью называется по- верхность, состоящая из прямых, содержащих боковые ребра призмы и частей плоскостей бо- ковых граней, заключенных между этими пря- мыми. / / / / а1 II а2 II а3 И а4 ^/•Х/ Четырехгранная призматическая поверхность
Перпендикулярным сечением призмы называется сечение призматической поверхности плоско- стью, перпендикулярной боковому ребру. Угол между плоскостью перпендикулярного се- чения призмы и плоскостью ее основания равен углу между боковым ребром и высотой призмы. —-/& \! l/Шйб \ ^MNP— перпендикулярное _ \с сечение / AG ± АВС А (АЛ,, AG) = A ((MNP), (АВС))
Площади боковой и полной поверхности приз- мы «бок = -Р1 • 1 ®полн = 2^0 + «Р1 • J 1 гДе — периметр перпенди- / ГГ^Ч^1 кулярного сечения, 1 — длина / £н| _ / / бокового ребра, So — площадь основания, Н — высота приз- мы, S± — площадь перпенди- кулярного сечения.
Объем призмы y=s0.H V=sx'l
232
17. Призма
Прямая призма
Прямой называется призма, боковое ребро которой перпендикуляр- но плоскости основания.
Все боковые грани прямой призмы прямоуголь- ники. Все двугранные углы при ребрах основания прямой призмы прямые. Линейные углы двугранных углов при боковых ребрах прямой призмы равны соответствую- щим углам основания. Высота прямой призмы равна ее боковому реб- РУ- А. Н~1 А to/^i /Ъ Г / i Г 1 / <» « / =4 L ° i / О 1 ААг 1 (АВС), L Z.ABC = Z.(A,BBpC) Ро — периметр основания Sn — площадь основания
Объем прямой призмы V = S0*H Площади боковой и полной поверхностей прямой призмы ®полн в ®бок 2 • So
Правильной называется прямая призма, в основании которой лежит правильный многоугольник.
Около призмы можно описать шар тогда и только тогда, когда она прямая и около ее осно- вания можно описать окружность. R2 = г2 + 0,25Я2, R — радиус описанного шара, г — радиус описанной окружности. 1 ’1
А С1 Н=1 ОА = ОВ = ОС - ОАг = в = ОВХ = ОСХ OFt = OF2 = |я; АА, 1 (АВС)
В призму можно вписать шар тогда и только тогда, когда в ее перпендикулярное сечение можно вписать окружность и диаметр этой ок- ружности равен высоте призмы. Л = г = 0,5Я;Л= R — радиус вписанного шара, г — радиус впи- санной окружности. А. — О, I 1 ’X? р / (MNP)LAAi ' -/*- L>*c ^FT - R \ 10 с 1 0.0 в 1
В прямую призму можно вписать цилиндр, ес- ли в ее основание можно вписать окружность. л F Г j / । 1 «я .л- М* ’ * г > cf у ГА - - “ V*'
233
17. Призма
Прямая призма (продолжение)
Около прямой призмы можно описать ци- линдр, если около ее основания можно описать окружность. В i k 1 1 1 i ’ £1!
Пример призмы, одна грань которой перпенди- кулярна основанию <?i
c
A
\ * \ V * \
A J B (ABBj) ± (ABC)
Пример призмы, внутри которой нельзя про- вести перпендикулярного сечения В этом случае при вычислении объема рас- сматривается перпендикулярное сечение приз- матической поверхности (все формулы верны). c 4^-^—TX / / ''У 1 7вх * (WKZ)±AAt
Параллелепипед
Параллелепипедом называется призма, в основании которой лежит параллелограмм. Все грани параллелепипеда — параллелограммы. Противоположные грани параллелепипеда равны и параллельны.
У параллелепипедов и только у них любую пару параллельных граней можно принять за осно- вания. В зависимости от выбора оснований можно рас- смотреть три высоты. C, A, ^7' Sj^7 L /D1 / /S2 t 1 / / /. V^Z.-Jc A D
Объем параллелепипеда
Свойства диагоналей параллелепипед Диагонали параллелепипеда пересекаются в од- ной точке и делятся ею пополам. Сумма квадратов диагоналей параллелепипеда равна сумме квадратов всех его ребер. dj + d* + d| + d* = 4a2 + 4Ь2 + 4c2 чГ n A BQ -if 4" II II И 4. o' ef eq oz \\ V 1 ^4° A \ \ \ Pxye 4 ay
234
17. Призма
сЯевлштЖия 6 тш/лгшрх.
Параллелепипед (продолжение)
В параллелепипед можно вписать тетраэдр.
1
Объем такого тетраэдра равен g части объема
параллелепипеда.
= g ^1^2 Р s*n
Прямым называется параллелепипед, у которо-
го боковое ребро перпендикулярно плоскости
основания.
Диагонали прямого параллелепипеда вычис-
ляются по формулам:
d\ — а2 + Ъ2 + с2 + 2ab cos а
d! = л2 + Ъ2 + с2 - 2аЪ cos а
А
ABCD — параллело-
грамм (а ^90°)
AAj 1 (АВС)
ACt = AjC — dt;
BD} = BfD = d2> * ^2
Прямоугольным называется прямой параллеле-
пипед, в основании которого — прямоугольник.
Все диагонали прямоугольного параллелепипе-
да равны.
d2 = а2 + Ь2 + с2
ABCD — прямоугольник
AA1A.(ABQ,AB 1AD
Куб
Кубом называется прямоуголь-
ный параллелепипед с равными
ребрами.
Диагонали куба пересекаются в
точке, являющейся центром впи-
санной и описанной сфер.
Куб, вписанный в сферу
к = з7з,
R — радиус описанной
сферы, а — ребро куба.
Сфера, вписанная в куб
1
г=2а’
г — радиус вписанной сфе-
ры,
а — ребро куба.
АВ = а
ОА = ОВ = ОС = ОВ = ОА1 = ОВ1 =
= OC,=ODi=R =
* *
АВ = а
Центр сферы — точка О —
равноудаленная от всех гра-
ней куба.
235
18. Пирамида
Пирамидой называется многогранник, одна
грань которого — произвольный многоуголь-
ник, а остальные грани — треугольники, имею-
щие общую вершину.
М — вершина пирамиды, Av А2, ...» Ап — вер-
шины основания. Всего п + 1 вершина.
МАг — боковое ребро, Ар42 — ребро основания.
Всего 2п ребер.
Многоугольник АгА2..Лп — основание пирами-
ды.
Треугольник МАХА2 — боковая грань. У пира-
миды п + 1 грань, из них п боковых.
Сечение, параллельное основанию пирамиды,
представляет собой многоугольник, подобный
основанию.
Плоскость этого сечения разбивает боковые
ребра и высоту пирамиды на пропорциональ-
ные отрезки.
Площади сечения и основания относятся как
квадраты их расстояний до вершины пирами-
ды.
Сечение отсекает от пирамиды пирамиду, по-
добную данной.
Угол АхМА2 — плоский угол при вершине
пирамиды.
Двугранный угол М(АгА£Ак — угол при реб-
ре АхА2 основания (угол наклона боковой
грани к основанию).
Двугранный угол А1(МА2)А3 — угол при бо-
ковом ребре МА2.
Высотой пирамиды называется расстояние
от вершины пирамиды до плоскости ее осно-
вания. МК =* Н — высота пирамиды.
(А^з) II (AJA^A')
рСМ^А^-Я
р(М.(А;А^А') = Я'
А1А2..*Ап А^А2>~Ап
МАг МА2 МАп н
МА\ = МА2 “ = ЛЩ ” Я'
МАуА^.А* ~ МА{А’2..А'п
Площадь боковой поверхно- сти пирамиды sfc.-s1+sa+...+s„, Sx, S2, ...» Sn — площади бо- ковых граней пирамиды. Площадь полной поверхно- сти пирамиды ®полн = ®бок So — площадь основания. Объем пирамиды г- |hs„
236
фия 6 mat£t.u,uflx
18. Пирамида
Тетраэдр
Тетраэдр — это треугольная пирамида. Все четыре грани — треугольники и любая из них мо- жет быть принята за основание этой пирамиды (можно рассмотреть четыре высоты). Площади боковых граней тетраэдра обратно пропорциональны опущенным на них Высотам.
Отрезки, соединяющие середины скрещиваю- щихся ребер тетраэдра (бимедианы тетраэдра), пересекаются в одной точке и делятся ею пополам. D / 4 IrX 1Д1 С! В
Отрезки, соединяющие вершины тетраэдра с точками пересечения медиан противолежащих граней (медианы тетраэдра), пересекаются в од- ной точке и делятся этой точкой в отношении 3:1, считая от вершины. / \ ЛФУь I 1 P / M >\w / V/ to
Если два тетраэдра имеют общий трехгранный угол (два равных трехгранных угла), то их объ- емы относятся как произведения ребер, обра- зующих этот угол. VABCD = АВ АС АР Уав1с1р1 АВ1 ‘ АС1 ’ AD1 D Z. a-Y \ / \z C1C
Правильный тетраэдр
Правильным называется тетраэдр, все грани которого — правильные треугольники. p / ’1 ^4. / ’l /hUyc 1 в AB=AC = BC=AD = BD = CD = a DO = H = aJ^;FO = r=^H; r = p(F, (ABC)) » p(F, (ABD)) - p(F, (ACD)) = = p(F, (BCD)) FD = B=|ff; FA = FB = FC = FD = R S = &ABC + SABD + &ACD + &BCD
Основные формулы R-lH r=±H R+r = H 4 R — радиус описанного шара, г — радиус вписанного шара.
Площадь поверхности правильного тетраэдра Объем правильного тетраэдра a3J2 12
237
^Пкоммал тфагфамма, & пии/мищх и, фор мулах
18. Пирамида
Правильная пирамида
Правильной называется пирамида, основание которой — правильный многоугольник, а вер- шина проектируется в центр основания. М /Д. /7 1 VX Акджт /,*-т ~Х*к\т Л ' ТА MF±(A1A2A3) А1\Г/* Д/ 4 FA1=FA2 = - = FA6
Все ребра равны. Все боковые грани — равные равнобедренные треугольники. Все двугранные углы при ребрах основания равны (боковые грани одинаково наклонены к основанию). Все плоские углы при вершине равны. Все двугранные углы при боковых ребрах равны. Все высоты боковых граней, опущенные на реб- ра основания (апофемы), равны.
^2 ^3 ДЫ
Площадь боковой поверхности правильной пирамиды
S = kp, rjsfi k — апофема, р — полупериметр основания. ~ *^осн ~ S = , где S0CH — площадь основания, COS ОС а — двугранный угол при ребре основания.
Пирамида, все боковые ребра которой равны между собой Около основания можно описать окружность и вершина пирамиды проектируется в центр этой окружности. Все ребра одинаково наклонены к основанию. Около такой пирамиды можно описать шар. Центр описанного шара лежит на прямой, со- держащей высоту пирамиды. //1 <\ //1 1\ / / t \т / < \ Л\ \ / 1 \Az F '•-ГА) ) / / ( F**— ./ МА = МВ = МСс= MD=>FA = FB = FC = FD, MFI (ABC) MT=TC,OT.LMC^>OA = OB = OC = = OD = OM = R, R — радиус описанного шара. (H - R)2 + FC2 = R2
Пирамида, одна из боковых граней которой перпендикулярна основанию Высота лежит в грани, перпендикулярной осно- ванию пирамиды. M / / \ " zC ) ( A / F e a, MF 1 (ABC) B ' MF C (AMD)
238
<мьирл
18. Пирамида
Пирамида, все двугранные углы при ребрах ос-
нования которой равны между собой
В основание можно вписать окружность и вер-
шина пирамиды проектируется в центр этой ок-
ружности.
Площадь боковой поверхности вычисляется по
тем же формулам, что и для правильной пира-
миды.
Высота вычисляется по формуле:
Н = г tg Р, где г — радиус вписанной в основа-
ние окружности, а Р — двугранный угол при
ребре основания.
В такую пирамиду можно вписать шар, центр
которого лежит на высоте.
„ х Р
R = г • tg |, где R — радиус вписанного шара,
г — радиус вписанной в основание окружности.
Fea, MF А(АВС)=ьРАх 1.AD, FBt 1АВ,
FCX 1 ВС, FDt 1 CD,
FAl = FDj = FCX = FBX = r — радиус вписанной
в основание окружности
OF = R — радиус вписанного в пирамиду шара
ВгО — биссектриса Z. MBtF
Пирамида, две соседние боковые
грани которой перпендикулярны ос-
нованию
Высотой служит общее боковое реб-
ро этих граней.
Пирамида, две несоседние грани ко-
торой перпендикулярны основанию
Высота лежит вне пирамиды на пря-
мой пересечения плоскостей, содер-
жащих грани, перпендикулярные
основанию.
м
Fea, MF ± a
(МАВ) 1. a, (MDC) 1. а
(ABM)n(DCM)~ MF
Пирамида, два двугранных угла при
соседних ребрах основания которой
равны
Высота проектируется на биссектри-
су угла между данными ребрами.
А (М, (АВ), С) = А (М, (AD), С)
Fea, MF 1 a
AF — биссектриса A BAD
239
QUttoMmax пАсфалима
18. Пирамида
Пирамида, в основании которой
прямоугольный треугольник и все
боковые ребра равны
м
Fea, MF ± а,
(МАВ) 1 (АВС)
FA = FB = FC
О — центр описан-
ного шара
МТ = ТВ,ОеMF
ОМ = ОА = ОВ = ОС = R
19. Усеченная пирамида
Усеченной пирамидой называется часть полной пирамиды, заключенная между основанием и параллельным ему сече- нием. F 'A* ч ' п ч / А > s Лдхкес верши на / '^'t4r’2r \ 3 / £i г*2 '\ ХЧ / 8» 1 Д 7 1 Д / / 1 \ боковая * - I / / * 1 \ гРанъ / 1 ( Л1 х. / \ 1 нижнее \ //у / \ I основание \у / \ нижнего / \ основания ал 8 / х 2 / X. плоскость нижнего / основания j/
Сечение называют верхним основанием усеченной пирамиды, а основание пол- ной пирамиды — нижним основанием усеченной пирамиды. (Основания по- добны.) Боковые грани усеченной пирамиды — трапеции. В усеченной пирамиде Зп ребер, 2п вер- шин, п + 2 грани, п(п - 3) диагонали. Расстояние между верхним и нижним основаниями — высота усеченной пи- рамиды (отрезок, отсеченный от высо- ты полной пирамиды).
Объем усеченной пирамиды V= Ih(S + JS~s + $), о S и s — площади оснований, Н — высота Площадь полной поверхности усеченной пирамиды равна сумме площадей ее граней.
Правильной усеченной пирамидой на- зывается часть правильной пирамиды.
Часть апофемы правильной пирамиды называется апофемой правильной усе- ченной пирамиды.
240
^Гссмлт^ил пии/лии/гх
19. Усеченная пирамида
Правильная усеченная пирамида (продолжение)
Для правильной усеченной пирамиды (а также для усеченной пирамиды, все двугранные углы при ребрах нижнего основания которой равны) верны фор- мулы: S6OK = *(P+P)’ Р и р — полу периметры оснований, k — апофема; «бок = (-8 - S): cos а, а — двугранный угол при ребре нижне- го основания, S и s — площади основа- ний. F //П'\ . /fit»-1 1 \ ап°Фема / 1 «\ \г\ / п1 ’я\ \ \ А D ABCDA'B'C'D'— правильная усеченная четырехуголь- ная пирамида. ABCD, A'B'C'D'— квадраты
Если в усеченную пирамиду можно вписать шар, то его радиус равен половине высоты пирамиды.
20. Правильные многоугольники и многогранники
Многоугольник называется выпуклым, если он лежит в одной полуплоскости относительно лю- бой прямой, содержащей его сторону. Правильным многоугольником называется выпук- лый многоугольник, у которого все стороны рав- ны между собой и все углы равны между собой. Любой правильный многоугольник являет- ся вписанным и описанным, центры вписан- ной и описанной окружностей совпадают с центром многоугольника (точкой пересече- ния серединных перпендикуляров сторон, биссектрисе углов).
ая — сторона, гп — радиус вписанной окружности, Rn — радиус описанной окружности, kn — апофема, Рп — периметр, Sn — площадь. 4? u А? /Гk-r / А» -1 U о J ‘
Общие формулы 180°(п - 2) а„ = - п п _. _ап . 180° _ _ 180°. _ _ гп _ ап rn kn 2 Ctg п Д»008 л ’ Rn 180° Л 180° сов 2 • sin п п „ П „2 . 360° П 2 х 180° 1 „ S„ = к R- sin = -г а_ ctg я г„Р„ я 2 я п 4 я 6 п 2ЯЯ
241
20. Правильные многоугольники и многогранники
Формулы для многоугольников с числом сторон п ® 3, 4, 6, 8,12
п а Г R S Связь между г и Л
3 60° aj3 Лл/3 3 а2ТЗ —£~ R=2r
4 90° а 2 aj2 ~2~ а2 R-rj2
6 120° а СО © ЬО ьэ col ЯТЗ =2г
8 135° а(1 + 72) 2 aji + 272 2 2а2(1 + 72) г я 72 + 72 B“C0SS" 2
12 150° а(2 + J3) 2 а • 72 + Тз За2(2+ ТЗ) [СО + N II «12 СП о о II
Многогранник называется выпуклым, если он
расположен по одну сторону плоскости каждого
плоского многоугольника на его поверхности.
Выпуклый многогранник называется пра-
вильным, если все его грани — равные пра-
вильные многоугольники и в каждой верши-
не сходится одинаковое количество ребер
(все многогранные углы при вершинах одно-
именны).
Грани — правильные
треугольники
Грани — правильные
четырехугольники
90°
Грани — правильные
пятиугольники
Правильный треугольник
Три ребра в одной вершине
3 • 60° < 360° — тетраэдр.
Четыре ребра в одной вершине
4 • 60° < 360° — октаэдр.
Пять ребер в одной вершине
5 • 60° < 360° — икосаэдр.
Шесть (и более) ребер в одной
вершине сходиться не могут:
6 • 60° = 360°.
Квадрат
Три ребра в одной вершине
3 ♦ 90° < 360° — куб (гекса-
эдр).
Четыре (и более) ребер в одной
вершине сходиться не могут:
4 • 90° = 360°.
Правильный пятиугольник
Три ребра в одной вершине
3 • 108° < 360° — додекаэдр.
Четыре (и более) ребер в одной
вершине сходиться не могут:
4 • 108° > 360°.
Правильные многоугольники, имеющие более пяти сторон, не могут
быть гранями правильного многогранника (уже для шестиугольни-
ка: 3 • 120° > 360°).
242
SeoMemfutxSmaJjmuflx
20. Правильные многоугольники и многогранники
Общий вид
D
в
F
В I
м
о'
с
Икосаэдр
С,
Куб
/с
в
Додекаэдр
Тетраэдр
Октаэдр
Тип многогранника Число Площадь поверхности Объем
ребер граней вершин
Тетраэдр 6 4 4 a2Js а372 12
Октаэдр 12 8 6 2 а2 7з а872 “Г
Икосаэдр 30 20 12 5а2 7§ jg Д8(3 — 75 )
Куб (гексаэдр) 12 6 8 ба2 д а8 8
Додекаэдр 30 12 20 За275(5 + 275) ^-(15 + 775)
Для всех выпуклых многогранников выполня- Р + 2 — В + Г,
ется формула (теорема) Эйлера'. где Р — число ребер, В — вершин, Г — граней.
Примеры разверток
1 1
Тетраэдр
Октаэдр
Икосаэдр
Куб
Додекаэдр
Вписанные и описанные многогранники
Куб и октаэдр
С]
в
Куб и тетраэдр
А]!?! = aj2; АВ = а
С
Додекаэдр и икосаэдр
Я
243
20. Правильные многоугольники и многогранники
Вписанные и описанные многогранники (продолжение)
Октаэдр и шар
Шар и октаэдр
АВ = а
ОА = ОВ = ОВ=ОМ = Я=^
FO + OM = FM=AC=
= BD = aj2
АВ = а
ОТ~г=±
Л
21, Цилиндр
Цилиндром (прямым, круговым) называется
тело, полученное при вращении прямоугольни-
ка вокруг прямой, содержащей его сторону.
Круги с центрами Ог и О2 — основания ци-
линдра, отрезок АВ — образующая (АВ = Z),
отрезок О^А == О*В — радиус основания, отрезок
OjO2 (расстояние между плоскостями основа-
ний) — высота цилиндра (Н — I), прямоуголь-
ник ABCD — осевое сечение, отрезок АС — диа-
гональ осевого сечения, прямая ОХО2 — ось вра-
щения, точка F (середина отрезка О1О2) — центр
симметрии.
Развертка цилиндра — прямоугольник и два
круга.
Площадь боковой поверхности цилиндра
S6oK = 2nRH = 2nRl
Площадь полной поверхности цилиндра
(площадь его развертки)
Вполв = 2яВ2 + 8^ = 2л(В + H)R
Объем цилиндра
F=S0 • H = nR2H
244
21. Цилиндр
Около цилиндра всегда можно описать шар.
Его центр лежит на середине высоты.
R2 = г2 + 0,25Н2,
R — радиус шара, г — радиус основания ци-
линдра.
В цилиндр можно вписать шар, если диаметр
основания цилиндра равен его высоте.
В = г = 0,5Я,
R — радиус шара, г — радиус основания ци-
линдра.
АО = ВО = СО = РО = Л
Призма, вписанная
в цилиндр
Призма, описанная
около цилиндра
Цилиндр, вписанный
в конус
АО2 = О2В = R
CD = GL = H; C^G-r
R - г __ R __ г
Н ~FO~2 “ FO - Н
R_
Г Нк- Н
Нк — высота конуса,
Н — высота цилиндра
Сечения цилиндра плоскостями
Сечение цилиндра плос-
костью , парале л л ьной
оси цилиндра, — пря-
моугольник.
Сечение цилиндра плоскостью, пер-
пендикулярной оси цилиндра, — круг.
течение, проходящее через
середину ОгО2, делит ци-
линдр на два равных тела.
001 — ОО2 => ^вепх ^нижн
245
22. Конус
Конусом (прямым, круговым) называется тело, по- лученное при вращении прямоугольного треуголь- ника вокруг прямой, содержащей катет. Точка М — вершина конуса, круг с центром О — основание конуса, отрезок МА = 1 — образующая, отрезок МО = Н — высота конуса, отрезок ОА = R — радиус основания, отрезок ВС = 2R — диаметр основания, треугольник МВС — осевое сечение, Z. ВМС = р — угол при вершине осевого сечения, Z. МВО — ф — угол наклона образующей к плоско- сти основания. м 1 / \' \\1 / \'а'х / "Г ~'’С\ д Г R 1 *'' \ "г ° У В
Развертка конуса — сектор круга и круг. Z. ВМВ* = а — угол развертки. Длина дуги развертки BCBt« 2nR = la (а радиан) \а \ ]с 1/ . / ( •OJ
Площадь боковой поверхности -8бок = ^ Площадь полной поверхности (площадь развертки) Saom^nR(l + R)
Объем конуса Г=|лВ2Я
Связь между углом а развертки и углом Р при вер- Р шине осевого сечения a = 2л sin g
Сечения конуса плоскостями
(KPL) II МТ
Сечение конуса плоскостью, про-
ходящей через вершину конуса, —
равнобедренный треугольник
Сечение конуса плоскостью, (ABC) II МО
перпендикулярной оси кону- МО — высота конуса,
са, — круг МТ — образующая
246
Зеомгт^тя тш£имща>
22. Конус
В конус всегда можно вписать шар. Его центр ле- жит на оси конуса и совпадает с центром окружно- сти, вписанной в треугольник, являющийся осевым сечением конуса. NI-6 & в в Я I И В + .» я 2. ьо|-е 5 -в
Около конуса всегда можно описать шар. Его центр лежит на оси конуса и совпадает с центром окружности, описанной около треугольника, яв- ляющегося осевым сечением конуса. М ДГ ( ) \ ° / \ J у z2 2
23. Усеченный конус
________________________________I____________
Усеченным конусом называется часть конуса, за-
ключенная между основанием и параллельным ос-
нованию сечением конуса.
Круги с центрами и О2 — верхнее и нижнее осно-
вания усеченного конуса, г и R — радиусы основа-
ний, отрезок АВ = I — образующая, а — угол наклона
образующей к плоскости нижнего основания, отре-
зок ОгО2 — высота (расстояние между плоскостями
оснований), трапеция ABCD — осевое сечение.
H = l sin а
Я2 + (Я-г)2=Ч2
В усеченный конус можно вписать шар тогда и
только тогда, когда образующая равна сумме ра-
диусов оснований.
Яш = 0,5Я
247
23. Усеченный конус
Развертка усеченного конуса — часть кругового кольца и два круга. м /\1 / \р ( \ 2nr X. (у) z MFK = 2-Rl~- - ф ф — угол развертки
Площадь боковой поверхности усеченного конуса 5бок = яг(г + Д) Площадь полной поверхности усеченного конуса «ПОЛИ = S1 + S2 + «бок = (г + Л) + nR2 + ЯГ2
Объем усеченного конуса V=i • яН(Л2 + гЛ + г2) О
Около усеченного конуса всегда можно описать шар. Его центр лежит на прямой ОгО2. / ; CF = FD; OF ± CD => О — центр описанного шара. R — радиус описанного шара, рав- ный радиусу окружности, описанной около ДАСП
24. Сфера и шар
Сферой называется множество точек пространства, удаленных от данной точки (центра сферы) на данное расстояние R > 0 (радиус сферы). (Сферой называют фигуру вращения полуокружности вокруг ее диаметра.)
Шаром называется множество точек простран- ства, находящихся от данной точки (центра ша- ра) на расстоянии, не большем данного (Л > 0 — радиус шара). (Шаром называют часть пространства, ограни- ченную сферой. Шаром называют фигуру вра- щения полукруга вокруг его диаметра.) с / / \ г " * ос R ' J к / \д?— / ww п CD — диаметр сферы; А, В е S AM = MB=>OMLAB
Диаметр, проходящий через середину хорды, не являющейся диаметром, перпендикулярен этой хорде.
Площадь поверхности сферы 5 = 4яЛ2 Объем шара V=S^L v 3
24. Сфера и шар
Шар (сфера) и плоскость
Плоскость, имеющая со сферой (шаром) одну общую точку, называется касательной плоскостью, более одной общей точки — секущей плоскостью. Прямая, имеющая со сферой одну общую точку, называется касательной прямой, две общие точки — секущей прямой.
Пусть р(О; а) — расстояние от центра шара (сфе- ры) с центром О и радиусом R до плоскости а. Если р > Я, то шар (сфера) и плоскость общих то- чек не имеют. р > R \ J OMLw, S ОМ = р (О; а); р > R
Если р < R, то пересечение шара (сферы) и плос- кости есть круг (окружность) радиуса г. /„2 2 г= л/R - р Всякое сечение шара (сферы) плоскостью есть круг (окружность). р<л 1 ZZ р = 0 / (X \ большой круг / 1
Сечение шара плоскостью, проходящей через центр шара (р « 0), называется большим кругом шара. Эта плоскость является плоскостью симметрии шара и делит его на две равные части (два полу- шария).
Признак касательной плоскости Если плоскость проходит через конец диаметра сферы и перпендикулярна ему, то эта плоскость касательная к сфере. Если р = В, плоскость и шар (сфера) имеют одну общую точку. Плоскость касается шара (сферы). <^\/ ОМ ±а
Свойство касательной плоскости Плоскость, касательная к сфере, перпендику- лярна диаметру (радиусу), проходящему через точку касания.
Признак касательной прямой Если прямая проходит через конец диаметра сферы и перпендикулярна ему, то эта прямая касательная к сфере. J( \о ] r/l J OMc\t-M’t OM Lt => t — касательная
249
бЩмоммал nfiozfuL^LAUL & mwfjuuip/x, а
24. Сфера и шар
Шар (сфера) и плоскость (продолжение)
Все касательные прямые, проходящие через одну точку сферы, лежат в одной плоскости, ка- сательной к этой сфере. I О J t1J.OM;t2±OM,t3l.OM=> => t,, t2, с a, al ОМ
Отрезки касательных, проведенных из одной точки (лежащей вне сферы) к сфере, равны. А, В, С — точки касания => / => МА = МВ = МС
Шаровой сегмент
Секущая плоскость разбивает шар на два шаро- вых сегмента. Н — высота сегмента, 0 < Н < 22?, г — радиус основания сегмента, г = 7Н(2Я - Я).
XwEzbc-- \ \R J X Я2
Объем шарового сегмента У = лЯ2Гй - 1я) \ М J
Площадь сферической поверхности шарового сегмента S = 2nRH
Шаровой слой
Шаровым слоем называется часть шара, заклю- ченная между двумя параллельными сечениями. Расстояние (Н) между сечениями называется вы- сотой слоя, а сами сечения — основаниями слоя. Площадь сферической поверхности (объем) ша- рового слоя может быть найдена как разность площадей сферических поверхностей (объемов) шаровых сегментов.
Шаровой сектор
Шаровым сектором называется фигура вращения кругового сектора вокруг не имеющего с ним общих внутренних точек диаметра круга*.
* В школьном курсе обычно рассматривается вращение кругового сектора вокруг прямой, содержащей
радиус, который ограничивает сектор.
250
24. Сфера и шар
Шаровой сектор (продолжение)
Объем шарового сектора О ✓ \ / 9 У\\ ffL 1 1 (Л 4 •*х 1 1 1 1
Площадь сферической поверхности шарового сектора равна площади сферической поверхно- сти соответствующего шарового сегмента./»
Площадь полной поверхности шарового сектора S = Jtfl(2H+ 72ЯЯ - Я2)
Две сферы
Две сферы» имеющие общий центр» называются концентрическими.
Две сферы, имеющие одну общую точку, каса- ются друг друга. ОгО2 « R + г (внешнее касание) ОХО2 = |.R - г| (внутреннее касание) \ »o’ у \ ' / / У^х /оГЛ \у
Если |Я - r| < OtO2 < R + г, то сферы пересека- ются по окружности, радиус которой может быть найден, например, как высота треуголь- ника со сторонами Я, г и OjO2, проведенная к стороне OtO2. / 1 О г pSL * 4 1 Г J \ \ \ \ 1
Через две точки пространства можно провести бесконечное множество сфер. Их центры лежат на плоскости, проходящей через середину от- резка» перпендикулярно прямой, содержащей этот отрезок. R2 = р2 + 0,25а2 \ “1 । а \|/;- У-* ЛГЯ = а р = р (О, МЯ)
251
^Шксм'иаяn/mftajiMi 4 тси/лииаа и формулах
24. Сфера и шар
Две сферы (продолжение)
Через три вершины треугольника можно про- вести бесконечное множестве/сфер. Их центры лежат на прямой, перпендикулярной плоско- сти треугольника и проходящей через центр описанной около треугольника окружности. R2 = р2 + г2 р = р (О, (MLN))
Через четыре не лежащие в одной плоскости точки можно провести сферу и притом только одну.
Описанная сфера
Сфера называется описанной около многогран- ника, если она проходит через все его вершины. Для того чтобы около многогранника можно было описать сферу, необходимо (но недоста- точно), чтобы около любой его грани можно было описать окружность.
Центр описанной сферы (если таковая есть) ле- жит в плоскостях, перпендикулярных ребрам многогранника, проходящих через их середи- ны; а также на прямых, перпендикулярных граням многогранника, проходящих через цен- тры описанных около граней окружностей. Радиус описанной сферы равен радиусу сфе- ры, проходящей через любые четыре, не ле- жащие в одной плоскости вершины много- гранника.
Около любой треугольной пирамиды можно описать сферу. Около n-угольной пирамиды можно описать сферу тогда и только тогда, когда около ее осно- вания можно описать окружность. с । -'/V 1 1 / ? Го % 1
Около призмы можно описать сферу тогда и только тогда, когда призма прямая и около ее основания можно описать окружность. А1 В ТХ* I вх । и ч 1 ч V ч ч L 1 1 1 4 01
Сфера называется описанной около цилиндра, если на ней лежат окружности оснований ци- линдра. Около цилиндра всегда можно описать сферу. R2 - 0,25Я2 + г2 /Г-А\ 1 1 / 1 I п\ - — 4- 4 11 Н| ’/
252
^еомет^ил 6 тш/лшщх
24. Сфера и шар
* Описанная сфера (продолжение)
Сфера называется описанной около конуса, ес- ли на ней лежат вершина и окружность основа- ния конуса. Около конуса всегда можно описать сферу; ее радиус равен радиусу окружности, описанной около осевого сечения конуса. с Л7Г> / ' . \,я \ ( /о<\ 1 V—
Если сфера касается граней двугранного угла, то ее центр лежит на полуплоскости, делящей этот двугранный угол на два равных двугран- ных угла. R = ОМ sin (р = ML • tg ф — т, где 2ф — величи- на двугранного утла, ОМ — расстояние от цен- тра сферы до ребра, т — расстояние от центра сферы до грани. / а JL / /&с / ( \ / J ) ( > МК Ll;MLLl
Вписанная сфера
Сфера называется вписанной в многогранник, если она касается всех плоскостей, содержащих грани многогранника во внутренних точках граней. В треугольную пирамиду всегда можно впи- сать сферу. В n-угольную пирамиду можно вписать сфе- ру тогда и только тогда, когда биссекторные плоскости всех двугранных углов пирамиды имеют общую точку.
В прямую призму можно вписать сферу тогда и только тогда, когда высота призмы равна диа- метру окружности, вписанной в основание. В призму можно вписать сферу тогда и толь- ко тогда, когда ее высота равна диаметру ок- ружности, вписанной в ее перпендикулярное сечение.-
Если в многогранник можно вписать сферу, то: V = lRS„n„„, 3 ПОЛИ’ V — объем многогранника, ^полн — полная поверхность многогранника. А. / р ^^Xj^^**^****0 в
Сфера называется вписанной в цилиндр, если она касается оснований цилиндра и цилиндри- ческой поверхности. В цилиндр можно вписать сферу тогда и только тогда, когда его высота (образующая) равна диаметру основания. 2? = 0,5Н = Л. ’ Сф
253
24. Сфера и шар
Вписанная сфера (продолжение)
Сфера называется вписанной в конус, если она касается основания конуса и конической по- верхности. В конус всегда можно вписать сферу. Л = Г • tg| =S^c:(r + Z) В /|\ /1 \ / 1 \ 1 [ R ! \1 / 4 \ /V*1 \
25. Поверхности и объемы
Площадь полной поверхности многогранника равна сумме площа-
дей его граней.
Площадь боковой поверхности призмы можно вычислить как: сумму площадей боковых гра- ней; произведение периметра перпендикуляр- ного боковому ребру сечения призматической поверхности на длину бокового ребра. ®бок = / С9 / /
Площадь полной поверхности призмы: ^полв = ^бок
Площадь боковой поверхности пирамиды равна сумме площадей ее
боковых граней.
Для правильной пирамиды:
S6ok = 2^
Р — периметр основания
k — апофема
Для пирамиды, все двугранные углы при осно-
вании которой равны между собой (все высоты
боковых граней, проведенные к ребрам основа-
ния, равны):
S -А.
бок cog ф
So в ^ABCD
254
25. Поверхности и объемы
Площадь полной поверхности пирамиды 5П0ЛН = So + S6oK
Площадь боковой поверхности цилиндра S^2nRH • * ** н
Площадь полной поверхности цилиндра «поли = + Н) = 2S0 + S6oK
Площадь боковой поверхности конуса ®бок = 1 * •
Площадь полной поверхности конуса ^полн = + 0 = + &бок
Площадь боковой поверхности усеченного ко- нуса 5бок = Я<Л + г)* /А I 1 | Гу । 1
Площадь полной поверхности усеченного кону- са Sn<wm = ЛГ2 + Лй2 + n(R + r)l
Площадь поверхности сферы S = 4tiR2 й н
Площадь сферической поверхности сферичес- кого сегмента S^ZnRH Площадь полной поверхности сферического сег- мента 5полн • «бок + яг2 = 2яЛН + яг2 1 к 1 \ О / г2=В2-(Я-Я)2 = (2Я-Я) • Я
Поверхность вращения отрезка АВ, не имеюще- го с осью 1 общих внутренних точек, равна про- изведению проекции этого отрезка на ось и дли- ны окружности, радиусом которой служит от- резок серединного перпендикуляра отрезка с концами на оси и на отрезке. 1 А А о з Л л.в / R < S = AXBX . 2пМ0 = 2nRH
Отношение поверхностей подобных тел равно квадрату коэффициента подобия.
Объемы равных тел равны.
Если тело разбито на несколько тел, не имеющих общих внутренних
точек, то его объем равен сумме объемов этих тел.
255
бЩнальнал тае/лица'Х, и фо0ьмумиъ
25. Поверхности м объемы
Объемы тел (продолжение)
Объем призмы равен: произведению площади ее основания на высоту V-S0H; произведению площади ее перпендикулярного сечения на боковое ребро V \ / II 11 11 М Й5 О^5 s- Й5
Объем пирамиды равен одной трети произведе- ния площади ее основания на высоту. y=|s0H С<Г1оГ ICO <-< ICO II II 11 1 1 1 1 s' 1 X ICq7 1 /
Объемы призм (пирамид), имеющих равновеликие основания, отно- сятся как их высоты. Объемы призм (пирамид), имеющих равные высоты, относятся как площади их оснований.
Объемы тетраэдров, имеющих общий трех- гранный угол, относятся как произведения ре- бер, содержащих этот угол. D VABCD AB AC AD VAB.C1D1 AB-^AC^ADy c
Объем тетраэдра может быть найден по фор- муле: Т7 1 . . V = г abc sin ф, о где а и Ь — длины скрещивающихся ребер, с — расстояние между ними, <р — угол между ними. D PXB C
Объем усеченной пирамиды y=|H(S1 + s2+7s1s2) - »\ к * \ \ 1 «A V ,c° \ °y 4 О 1 /
Объем многогранника можно получить, разбив его на не имеющие общих внутренних точек тетраэдры (триангуляция) и суммировав их объемы. Если в многогранник можно вписать шар, то объем многогранника равен: V = Л5„АПИ> R — радиус вписанного шара, <8пола — пло- щадь полной поверхности многогранника.
256
ия1тш/миц1л
25. Поверхности и объемы
Объемы тел (продолжение)
Объем цилиндра V = TtRzH Объем конуса У=|лЯ2Я, О Объем усеченного конуса У = 5 Я(Я2 + Яг + г2) О
Объем шара А У = дЛЯ3 О Объем шарового сегмента V = nH2 • (r - iffl \ & J Объем шарового сектора о У= ^лЯ2Я О
Вычисление объема тела вращения с помощью интегралов. ь Vox~njf2(x)dx а У. </ = /(*) а 0 1
Отношение объемов подобных тел равно кубу коэффициента подобия.
26. Метод координат
Координаты точки на прямой
Координаты середины отрезка: хх + х2 хс 2 Длина отрезка в координатах (расстояние между двумя точками): MN = |хх - х21 М(хх) N(x2) Точка М прямой АВ целят отрезок АВ в от- ношении 1 (считая от А), если AM = \МВ (**-1). Координаты точки, делящей отрезок АВ в отношении 1: _ ха + Ххь Хт 1 + 1 А(ха) Д(хь)
0 С(х£) MW
Координаты точки на плоскости. Прямоугольная система координат
Координаты середины отрезка: izl „„ „ (Ха + Хь Уа + Уъ\ АС = СВ=*С[ ; —-и— у А ЛЛ } Длина отрезка в координатах: АВ " кха - *ь)2 + (Уа “ Уб)2 у i А . РХ 1 1 1 । Уь 1 ха °J » / 1 7 ° /* и — Z * to н
Координаты точки, делящей отрезок АВ в отно- шении 1(1?* -1): —> —> /ха + 1хь уа + AM = ХМВ => М [ ° . ; - ° —з- l \ 1 т А 1 т Л /
9—1323
25/
26. Метод координат
Уравнение прямой
Общее уравнение прямой 1: ах + by + с = 0 (а2 + Ь2 0)
С а = 0 III Ох ь = о 1П Оу с = 0 OeZ
У У У, 0
0 ах + —\^х by + с = 0 "01 by + с = 0 0 аз С + 1 с = 0 ах • + by = 0
Уравнен; (Ь*0): y = kx+j ie прямой с Ха угловым коэф > k - tg а т ——-*х фициентом Уравнение прям т п юй У в отрезках (с л *0):
0 0 -ДР— X
Уравнен) М(х0; у0) ie прямой, проходящей через точку с угловым коэффициентом k. У = Уо + Ь • (х-х0)
Условие: параллельности двух прямых. СМ И г-4
Условие: перпендикулярности двух прямых. м № II 1
Угол мел мыми. еду двумя (неперпендикулярными) пря- tg<p = Зг* 1
1 + k1k2
Расстоян ах + by + не .от точки М (х0; у0) до прямой с = 0. |ох0 + Ьу0 4- с| = Р(М,о
7а! + Ьг
Уравнен] ДЯЩИХ Ч( вектору i ае пучка прямых (всех прямых, прохо- грез точку М (х0; у0) перпендикулярно г(а; Ь)). а(х “ *о) + Ъ(у - у0) = 0
Уравнение окружности
с центро] к в начале координат х2 + у2 = г2, г > 0
с центроз и в точке M(xQ, yQ) (х - х0)2 + (у - у0)2 - г2, г > 0
Любое уравнение вида х2 + у2 + ах + by + с = 0 задает на плоскости либо окружность, либо точку, либо пустое множество. ( 1 V а. ( °2 + &2 г + 2а) +1у + 2Ь) " 4 ~С
258
SfeoMemfuiM 4 muuJm
26. Метод координат
Координаты точки в пространстве. Прямоугольная система координат в пространстве
Координаты точек на кубе:
О (0; 0; 0) А (0; а; 0)
В (а; а; 0) С (а; 0; 0)
О' (0; 0; а) А' (0; а; а)
В' (а; а; а) С' (а; 0; а)
Координаты середины отрезка: АС = СВ =э
„(ха + хЬ Уа + Уь га + гЪ\
=*С 2 5 2 ; 2 )
Длина отрезка в координатах:
АВ = J<xb - ха* 2 + (уь - ye)2 + (Zb - za)2
2 (аппликата)
у (ордината)
Координаты точки М, делящей отрезок АВ в отношении X, X * -1:
--> А --> fxa + ^ХЬ У а + tyb 2 а + ^гЬ\
АМ-Х-МВ И (JL—4-^; W)
Уравнение плоскости
Общее уравнение плоскости:
ax + by + cz + d = O (a2 + b2*0)
Уравнения координатных плоскостей.
х — О — плоскость уОг
у = 0 — плоскость xOz
2 = 0 — плоскость хОу
п (а; Ъ; с)
ах + by + cz + d = 0
у п (a, b, с) ± S (нормальный
вектор)
Частные уравнения плоскости
Уравнение плоскости, проходящей через
точку Мо (х0, у0, z0), перпендикулярно вектору
п (а; Ь; с).
а(х - х0) + Ь(у - у0) + c(z - z0) = 0
259
^Шкальная п^юфамма & тш/лицах и фо^итумх
26. Метод координат
Уравнение плоскости (продолжение)
Уравнение плоскости в отрезках (d 0). Z i Р * 7 N 1 СК, + гы с -Ь | н н |g / / S/ о
Угол между двумя плоскостями °1ж + ^1У + ciz + = 0 и а2х + b2y + c2z + d2 = 0. а1а2 ^1^2 с1с2 COS ф = -z.^^====—========== / 2 , ,2 , 2 /2,-2, 2 + С| • ^а2 + + С2
Условие параллельности двух плоскостей. и- r-Ч I CSJ О 1 О II г-1 1 eq II TH 1 eq
Условие перпендикулярности двух плоскостей.
Расстояние от точки M(xQ9 yQ, z0) до плоскости ах + by + cz + d = 0. |ах0 + byQ + cz0 + d| р 7? + ь2 + <?
Параметрическое уравнение прямой (проходя- щей через точку Мо параллельно вектору $). х * х0 + at • У = Уо + Р* 2 = Zo + yt 2 ] х 1 2 III s — направляющий м° вектор прямой о 7 мо (*<)’ у& zo) е 1 s(a; Р; у) || 1
Уравнение прямой, проходящей через две точки М(Хр yv Zj) и N(x2, у2, z2) х - хг _у ~ ух _ Z - zx хг ~ Х1 Уг~ У1 z2 ~ 21
Угол между двумя прямыми, заданными в пара- метрической форме. Наг + Р1Р2 + Y1Y2I COS ф = Й + Рх + ъЙ + Рг + Ъ
Условие параллельности прямых, заданных па- раметрически. 04: а2 = Pi: Р2 = Yt: Y2
Угол между прямой и плоскостью. |аа + ЬВ + су| / 2 , ,2 , 2 / 2 , q2 , 2 л/а + Ь + с * а/сс + р + у
260
SecMcmfuiM 6 тск/лицах,
26. Метод координат
Уравнение сферы
с центром в начале координат х2 + у2 + г2 = г2; г > 0
с центром в точке М(х0, у0, г0) (х - х0)2 + (у - у0)2 + (г - z0)2 = г2, г > 0
Уравнение х2 + у2 + г2 + ах + by + cz + d = 0 задает в пространстве ли- бо сферу, либо точку, либо пустое множество. Г х1 f хГ х Ч? хГ X 1 f а2 + b2 + с2 , 1X + 2«J + 1У + 2bJ + 1 2 + 2е ] = 4 d
27. Векторы и координаты
Векторйм называется направленный отрезок. Вектор характеризуется направлением и длиной. Направление — множество сонаправленных лучей. Длина вектора |5| — расстояние от начала век- тора до его конца. в а s' А/ АВ = |а| = |АВ|
Коллинеарные векторы. Сонаправленные и противоположно направленные векторы. Яр а2, аз> а4 S а* коллинеарные векторы Л(21 II ^2 II S3 II ^4) s' 51 tt 52 — сонаправлен- ные векторы Xх Дз 53 И 54 — противополож- но направленные векторы
Равенство векторов. Qi II 04 $ sis* II =£ 04^*
Угол между векторами. Z. (ВС, CD ) = Z. (ВС, ВА ) = 108° В. fc.c —> —> —> —> / Г А(АВ, ВС) = А(АВ, AD) = 72° /720 / ~ ВС» АВ CD Ab TD —» —» Z. (АВ ,AD) = A(CB,CD) = 72°
,267
бЩкомная nfozfiajbJML & тщ/мицих, и
27. Векторы и координаты
Ортогональные векторы.
a±&<=>z(a, &) = 90°
а ± Ь — ортогональные векторы
Компланарные векторы — это векторы, лежа-
щие в одной плоскости или в параллельных
плоскостях
*1
' 1 ' 1 1 в! _ _
ci___> ______>
AAV АВ, ВгВ — компланарные
AD, D1A1, С1В1 — компланарные
DDp DC, DA — некомпланарные
Пример 1 (нахождение угла между двумя век-
торами на плоскости)
Пример 2 (нахождение угла между двумя
векторами в пространстве)
Z(AB, CD) = 135°; Л (AD, CD) = 45°
Если |АВ | = 2; |ВС | = 1, то
А (АС, GD) = arctg 2; Z. (BD, DC) = я - Z. BDC.
По теореме косинусов:
ВС2 = BD2 + DC2 - 2BD • DC • cos Z BDC.
1 = 13 + 8-2713 • 272 • cos ZBDC.
Z BDC = arccos =»Z(BD, DC) =
Z. (А,В; DCX) = 90°; Z. (СА; DB1) = 90°
A(Dc[',CA) =/L(Dc[, CjAi ) = 120°, т. к.
Д DCXAX — равносторонний
A(DB^ DC) = A D в ADB^C =>
=> Z. (DBj; DC) — arctg J2
Сложение векторов
Правило ломаной.
a + b + c = OA+AB+BC=OC,
где ОА = а; АВ = Ь; ВС = с
Правило параллелограмма.
a + b^OA + ОВ =OF
262
З'еамет.^шя & тш£шмрх
27. Векторы и координаты
Сложение векторов (продолжение)
Законы сложения. 3 + 4- 3 (3 + Ь) 4- с = 3 + (Ъ 4- с) 3 4-0=3
Противоположные векторы. d / S г S' У => а = Ъ = -а; а 4- Ъ = 0 / 2 tl Ъ Вычитание векторов / а - & = а + (-&) /а// AG --b; OG = ВА / ОА. +AG = OG > > > &В а - Ь = ОА - ОВ = ВА
Умножение вектора на число ОА =а;ОА’ = X • 3 (X > 0) |ОА'| = Х • |а| в =Ь;ОВ' = Ц • М|1 < 0) о \ОВ' 1 - -ц • Й О.а=б
Законы умножения вектора на число (скаляр), а • (Ха) = (аХ) • а 1 • а = а -1 • а = -а (а + Х^а = аа + Ха Ца + Ь) = Ха + Х6
Разложение вектора с на плоскости по двум не- коллинеарным векторам а и Ъ (а || Ъ). । с/ ’) с - ОА + OB =xa + yb — ’ » • разложение вектора с 0 по векторам “1 а и Ь, где а JI Ь
Разложение вектора г пространства по трем не- компланарным векторам 3, Ь и с. с. - —> —» —> —> ‘ r=OR ~ОА +ОВ +ОС = » .Г _ -» _ \ » **ха + уЪ + гс — \ разложение вектора г “ Ц & по векторам а, Ь, с, в где а, Ь, с некомпланарны
Примеры разложения вектора
Пример 1. р G г АВ =а; AD = b;BG:GC = 2; AF = ±АС = |(а + &) = |а + р/\ \ —> —» —> ( iv -> i~* —* —* —> - _ “\ DG = DC + CG = а + -я & = а- BD = AD-АВ =b-a \/ g 4 7 А " D
263
tyUftoMHon nfutofiaMMa &ши/ми/Ах a
27. Векторы и координаты
Примеры разложения вектора (продолжение)
Пример 2. в g р АВ =а; ВС = b;AD = 4BC=>AD = 4b; AF = |(а + Ь) = |а + —> —> —> -> /4^ 4-*\ 4^ 16 -> j /j? \ \ FD = AD - AF =4Ь-(?а + ^Ь =-^а+ а// \\ О/О 5 // \ \ MN = 2FN =2 • (^ = §6 = 0 • a+lb ЛА Ч \0 у 0 0 А
Пример 3. АА^ = а; АВ = &; АО = с; AVG = GDX; C^F = FC У^^ С, > > — —) ~~~) / 1 \ . —» /1 \ Д \ тч GF = GA, + А,А+АС + CF = 1-дс +(-а) + (Ь + с)+ да = УХ* V 2 > V* J А = — — а + Ъ + с + | а = — | а + b + с D с
Пример 4. d АВ =а;АС ^b-rAD-=c;DG=jCD;DF = FB /\ 4 с/ O\\F FC =FA+AC =(-la-lc]+b = -la + b~lc. / a \\ n GF =GD +DF I CD + IDB =^(c-b)+ l(a-c)= la -lb -lc 4 2 4х '2х '2 4 4
Условие коллинеарности двух векторов г -> -* г ха + yb = 0 а II b « { „ 1х2 + у2^ 0 а || b <=> а = М или Ъ = ца, если •> •> а^0;Ъ*0
Условие компланарности трех векторов а, Ь, с — компланарные векторы <=> Г -> _> j ха + yb + 2С = 0 ix2 + у2 + г2#0 а, Ъ, с — ненулевые компланарные векторы, то а — ab + Ре.
Скалярное умножение векторов а • b = |а| • |b| • cos Z. (а, Ь)
Законы скалярного умножения. d'b = b • а а • a>jO; a • Ji = |a|2 -|a| •_* |&|< а • b ^Ja| • |S| a • (b + e) = d’b + d'C a • b = Ooa±b a • & = |a| • npa6 = |&l • npba
264
пии/лимрх
27. Векторы и координаты
Скалярное умножение векторов (продолжение)
Формулы применения скалярного умножения к решению задач. . а 3 • b ab (“’ч~|гП5| п₽4“_ТьГ
Пример 1. у Определить угол между BD и DC. Введем систему координат. Тогда В (0; 2); в - С (1; 2); D (3; 0), BD (3; -2), DC (-2; 2). 2 ДД-55 3(-2) + (-2)-2 -6 1 c 21 X i X 1 45ГЧ x
IbdI • |вС| 7з2 + (-2)2 • 7(-2)2 + 22 ^26 1 С1 2 D 5^26 > 5726 = _~gg— Z(BZ>; DC) = л-arccos-gg-.
Пример 2. t Определить Z(DCi; CA) = а. Введем систему координат. Тогда A (0; 0; 0); А С (a; a; 0); D (a; 0; 0); (a; a; a); (0; a; a); CA (-a; -a; 0). DC^CA 0-(-a) + a-(-a) + a-0 -a2 -1 |5cJ|.|cl| To2 + a2 + a2 • 7(-a)2 + (-a)2 + 02 2a2 2 C Следовательно, a = Z(5cJ; CA) = 120°. B. Cl
» 1
BX---. O1 c
А ТЧ * A D
Координаты вектора на плоскости. Основные формулы
Если вектор а плоскости имеет координаты (хх; yj, sl вектор Ъ имеет координаты (х2; i/2)то: а + Ь - (хг + х2; у2 + у2) а-Ь = (х1-х2',у1-у2) ka = (feXj; ky^), fee R aa + P& = (axj + 0x2; ауг + py2), a, P e R ab = xxx2 + yxy2
Длина вектора в координатах на плоскости. |a| = 7*1 + »где ®(*v У\)
Угол между двумя векторами на плоскости. . £. *1*2 + У1У2 A (a9 b) = arccos ; -гт, /2,2 /2.2 7*1 + У1 ' >JX2 + У2 где alx^, уг), b(x2; y2)
Условие коллинеарности векторов а(хг; уг) и Ь(х2; у2) на плоскости. *1: *2 =° У1: У2 raxi + px2 = 0 fXj = Xx2 или или + Py2 = 0 1У1 = ^2 2 2 la2 + p2*0
265
бЩкомнал пАвгкамма & тси/мшрх, и, фофмилах
27. Векторы и координаты
Координаты вектора на плоскости. Основные формулы (продолжение)
Условие ортогональности векторов 3(хг; уг) и &(х2; у2) на плоскости. *1*2 + У1У2 = 0
Координаты вектора в пространстве. Основные формулы
Если вектор а пространства имеет координаты (х*; ух; zj, а вектор Ь имеет координаты (х2; у2; г2), то: d + $i=(xl +х2; уг + у2; z1 + z2) a-b = (x1-x2;y1-y2; г1-г2) ka - (йхг; куг; kzj, ke R аа + (Jb = (axj + Px2; ayt + Py2; azt + pz2), a, рей ab = хгх2 + yxy2 + 2^2
Длина вектора в координатах в пространстве. |a| = 7xi + У1 + г1»a(*v Vv 2i>
Угол между двумя векторами в пространстве. Mfl, b) = *1*2 + У1У2 + 2122 = arccos ——=——===—======== / 2 , 2. 2 / 2. 2,2 7*1 + У1 + 21 • VX2 + У2 + 22 2(*р УГ, zj, b(x2; y2', z2)
Условие коллинеарности векторов a (хх; уг\ zt) и Ь (х2; у2; z2) в пространстве. м и g ©a ь* •-* ‘ й II II II s ”•* >> J co to bo *» я H fcl S || fl X Й P Q P N IQ , 1- b- H. + + + 4- м м та хо та kj 0 M ~ 0 0 0
Условие ортогональности векторов а(хх; у^; zx) и Ь(х2; у2; z2) в пространстве. *1*2 + У1У2 + 2122 = 0
Математика в формулах
АРИФМЕТИКА
Законы арифметических действий
переместительный:
а + Ъ — Ь + а
а’Ъ = Ь-а
сочетательный:
(а + Ь) + с - а + (Ь + с)
(а • Ь) • с — а • (Ь • с)
распределительный:
(а + Ь),с = а,с + Ь,с
Правила знаков при умножении (делении) чисел
Множители (делимое и делитель) Результат
Ч" — ——
— Ч"
Правила действий с рациональными числами
(дробями)
а с ad + be
Ь+ d~ bd
а с ad - be
b d° bd
a c
b'd~bd
a c _ ad
b'd~ be
Геометрическая прогрессия
формула в-го члена:
сумма п первых членов:
свойство:
bi' = &2 ’ Ьп_ 1 = — = Ьк • Ьп_к
сумма п первых членов бесконечно убывающей
геометрической прогрессии (0 < |g| < 1):
bi
S = -L-
1-5
Некоторые числовые ряды (конечные)
1 + 2 + 3 + ... + (в-1) + п - П(ЛО+
А
1 + 3 + 5 + ...+(2в-3)+ (2в-1) = в3
2 + 4 + 6 + ... + (2п - 2) + 2в = п (п +1)
I* 2 + 22 + З2 + ... + (в -1)2 + в2 =
в(в + 1)(2в + 1)
6
2
I2 + З2 + 52 + ... + (2в -1)2 =
О
Арифметическая прогрессия
формула в-го члена:
ап = ах + (в -1) d
сумма п первых членов:
аг + ап 2аг + d(n - 1)
= 2 n ~ 2 *r
свойство:
а1 + ап = а2 + = ••• = ак + ап-к
I3 + 23 + З3 + ... + (в —1)3 + в3 =
I3 + З3 + 53 + ... + (2в -1)3 = в2 (2в2 -1)
Пропорция
а _ с
Ь~ d
равносильна следующим равенствам:
ad = be;
а _ b. d _ с
с ~ d' b ~ а*
b d
а с
267
бШмалыиыьпЬсг/мЕА1лиа
Среднее арифметическое
Свойства квадратного (арифметического) корня
двух величин:
а + Ъ
2
п величин:
Д1 + д2 + — + ап
п
Ja • Jb = Jab Jab = TH • */[b| nJa • nJb = n-Ja b
/а _
Nb J\b\
№ - (7H>“
nJa _ la
nJb
(nJa)m~nJa™
Среднее квадратичное
двух величин:
/2 , ,2
а + о
Ч 2
пвеличин:
/1,2,2,2?
/- (ах + а2 + ... + а„)
Среднее геометрическое (среднее пропорцио-
нальное )
двух величин:
Jab
Формулы сокращенного умножения
квадрат суммы: (a + b)2 = a2 + 2ab + b2
квадрат разности: (a - b)2 = a2 - 2ab + b2
куб суммы: (a + b)3 = a3 + 3a2b + Sab2 + b3
куб разности: (a - b)3 = a3 - 3a2b + 3ab2 - b3
разность квадратов: a - b = (a - b) (a + b)
сумма кубов: a3 + b3 = (a + b) (o' - ab + b2)
разность кубов: a3 -b3 -(a- b) (a2 + ab + b2)
Бином Ньютона
п величин:
"7а1 • а2 • ••• • ап
(a + o) =a +C„a b +...4-C,a b +
' ' n n n
+ ... + bn
Золотое сечение
Величина а делится на части х и а - х так, чтобы
х = 7«(а ~ х) = ^5—- • а = 0,618 а
Выделение квадрата двучлена из квадратного
трехчлена
2 ( 2 Ь С А
ах +Ьх + с-а х + -х + - =
I в a J
АЛГЕБРА
Свойства степени
а° = 1
(( к к2 А
= а I х2 + 2=-х 4---5 +
и 2« 4а2)
4а\
С
а
Теорема Виета (свойство корней)
квадратного уравнения ах + Ъх + с = 0:
. b с
^1 + ^2^-^ xi'x2“a
приведенного квадратного уравнения
x2+px + q = 0:
Xi + x2 = -p; xi-x2 = g
268
иИмтематима &
Теорема Виета (свойство корней)
приведенного кубического уравнения х3 + рх2 +
+ qx + г = 0:
хх + х2 + х3 = -р
хгх2 + х2х3 + XjXg = q
XiX2X3 = -г
Формула корней квадратного уравнения
ах2 + Ъх + с = 0:
— Ъ ± </&2 — 4ас
Х1-2“ 2а
приведенного квадратного уравнения
х2 + рх + q = 0:
Гг
^i.2 = -f ±а/4- " «
квадратного уравнения с четным вторым коэф-
фициентом ах2 + 2kx + с = 0:
-k ± Jk2 - ас
Х1, 2 “ а
Формула Кардано — формула корней неполного
кубического уравнения у3 + ру + q = 0:
I I 2 3 । / 2 2
„ = з _2 + 22 + Р. + з _2 _ 22 + Р.
у N 2 N4 27 *| 2 */4 27
2
Координаты вершины параболы ах + Ъх + с:
_ Ъ _ 4ас - Ь2
х°~~2а’ Уо~ 4а
Определение логарифма
Логарифмом числа Ь по основанию а называется
показатель степени, в которую нужно возвести а,
чтобы получить Ь.
loga Ь = с <=> ас = Ъ
Свойства логарифма
log», а
Ь ь =а logal = 0
loga а = 1 loga ат = т
Действия с логарифмами
логарифм произведения:
logc (ab) = logc а + logc b
логарифм частного:
logc(f) = logca"logc&
Действия с логарифмами
логарифм степени:
logc ак = k logc а
логарифм корня:
logc nJa « ±logca
переход к новому основанию:
logc а
1о6»а-Ко
Дополнительные формулы
1 logn ъ loem ь
10ga Ъ = . a log6 а lognc
log„ Ъ log„ а
log„b-logmc = logmb-lognc а =Ь
Факториал 1 • 2 • 3 •... • п = п!
Основное свойство факториала л! = п • (л - 1)!
Формула Стирлинга (факториалы больших
чисел)
nl»(‘ -V (9^ (l + 4- _1_ +
ej ^2яп|<1 + 12п + 2 288п2
In (л!) «Гл + 5^1nn-n + ln а/2л
Соединения
Размещения из л по тп элементов — соединения,
отличающиеся самими элементами или их по-
рядком.
= (п- т)\ =П — (п-т + 1)
Перестановки — соединения, отличающиеся
только порядком элементов.
Рп = n! = 1 • 2 • 3 •... • п
РП = А"
Сочетания из п по т элементов — соединения,
отличающиеся только самими элементами.
Ат
~т _ _______
п ml (п - тп)! Рт
- п (п " 1)(п ~ 2)...(п - m + 1)
”” 1 • 2 • 3 •... • т
269
& и фо/мшлах
Соединения
Свойства сочетаний:
гт _ пп - т пт + 1 _ + 1
сп Сп + 1 Сл +
С°+е'„ +С^+...+с:-, + с;-2"
Неравенства
|а + &|<|а| + |&| |а-Ь|>||а|-|Ь|| а2 + Ь2> 2|аЬ|
а , Ь „ а + Ь гг
т+->2 (аЬ>0) —5—> Jab (а>0, b>0)
о а z
Комплексные числа
г = х + iy (i2 = -1)
Re z = х — действительная часть комплексно*
го числа,
Im z = у — мнимая часть комплексного числа.
Комплексно-сопряженные числа
z = а + ib и ~z = a-ib
Действия с комплексными числами
Zj + z2 = (Xi + х2) + i(j/i + у2)
Z1 — z2 = (*1 - *2> + - У2)
гГ z2 = (*1*2 “ У1У2) + *(*1^2 + Х2У1>
Z1 *1*2 + У1У2 . Х2У1 ~ Х1У2 .
Z-------Г7Т- + 1 —2 , 2 <*2*0)
2 X2 + y2 X2 + y2
Тригонометрическая форма записи комплекс-
ных чисел
z = г (cos ф 4- i sin ф)
Модуль комплексного числа
|z| = г = Jx2 + у2
Аргумент комплексного числа
Arg z = arg z 4- 2nk (k « 0,1, 2,...),
где arg z = ф — главное значение аргумента.
Показательная форма записи комплексных
чисел
iq>
z = re v
Формула Эйлера
|ф । •
е = cos <р +1 sm ф
Произведение и частное комплексных чисел
+ Ф2)
= Fir2[cos (<Pi + ф2) + i sin (Ф1 + Ф2)]
Z1 Г1 *(<₽! ~ ф2)
z2 = г2 6 ~
Fj
= - [cos (Ф1 - ф2) + i sin (Ф1 - ф2)] (z2 # 0)
г2
ТРИГОНОМЕТРИЯ
Тригонометрические функции
в прямоугольном треугольнике
а Ь
sm а = - cos а = -
с с
, а х b
tg а = g ctg а = -
Тригонометрические тождества А sin а А cos а tg а - _ ctg а - . cos а 6 sm а
2 2 cos а + sin о 1 = 1 tg a • ctg a = 1
cos а = 71 ~ sin2a sin a - 71 - cos2a
х 1 tga= -г— в ctg а
1 + ctg2a= - S 1 1 4- ГУ — 1
in2a £ । Tg Cl 2 cos a
Формулы сложения тригонометрических функ-
ций
sin (а ± р) = sin а cos Р ± cos а sin Р
cos (а ± Р) = cos а cos р т sin а sin р
Л tg а ± tg В
tg (а + Р)= -f----f-2-
1Т tg а tg Р
. . .оч ctg а ctg р Т 1
ctg (а ± р) = р ----
ctg р ± ctg а
Тригонометрические функции кратных углов
sin 2а —2sin а cos а cos 2а=1-2 sin2а
cos 2а — cos2 а - sin2 а cos 2а = 2cos2a-1
sin За — 3sin а - 4sin3 а
cos За = 4cos8 а - 3cos а
270
jltameMumutta
Тригонометрические функции кратных углов
sin 4а-8 cos’asin а- 4 cosasinа
cos 4а = 8cos4a - 8cos2 а +1
tg2a =
2tg a
1 - tg2a
ctg 2a =
tg 3a =
з
3tg a - tg a
1 - 3tg2a
ctg 3a =
. 2 ,
ctg a - 1
2ctg a
3
ctg a - 3ctg a
3ctg2a - 1
tg 4a =
4tg a - 4tg3a
1 - 6tg2a + tg4a
ctg 4a -
ctg4a - 6ctg2a + 1
4ctg3a - 4ctga
Тригонометрические функции половинного угла
.а 1 - cos а а /1 + cos а
Sin 2 = J-----2----- C0S 2 = 4-------------2-----
х a sin а 1 - cos а
s 2 1 + cos a sin а
а _ sin а 1 + cos а
с g 2 ~ 1 - cos a e sin а
Сумма тригонометрических функций
, . о _ . а±Р аТр
sin а ± sm р = 2sm cos 2
. о n a + P a - P
cos a + cos p = 2 cos —g—cos-
cos а - cos Р = -2 sin —5-*- sin
2
a - P
2
. , . о sin (а ± р)
tg а ± tg р i %
к cos a cos Р
. . . Q , sin (а ± Р)
е sin a sin р
cos а + sin а = J2 cos (45’ - а)
cos а - sin а = 72 sin (45’ - а)
. , . о cos (а - Р)
tg а + ctg Р =------
& и cos a sin Р
. . о cos (а + Р)
tga-ctg₽ — cos „ sto р
tg а - ctg а = -2 ctg 2а
Сумма тригонометрических функций
, , „ 2 <x « Л . 2 a
1 + cos a = 2 cos 5 1 - cos a = 2 sm 5
1 - sin a = 2 sin2 ^45° - g j
Понижение степени тригонометрических функ-
ций
.2 1 - cos 2а 2I + cos 2а
sm а -------z---- cos а » 1 - о---
4 А
з 1
sin а= (3sina-sin За)
з 1
cos а= j (cos3a+3cosa)
sin4 a = I (cos 4a - 4cos 2a + 3)
cos4 a = 3 (cos 4a + 4cos 2a + 3)
Произведение тригонометрических функций
• „.nnc R _ sin (a + P) + sin (a - P)
sm ot cos |5 2
_ cos (a + P) + cos (a - p)
cos a • cos P ---1------------ r
45
. o cos (a - P) - cos (a + P)
sm a • sm P ----- ro----------1“
Формулы приведения тригонометрических
функций
sin (±а + пп) = ±(-1)” sin а
cos (±а + пп) - (-1)” cos а
sin [±а + ? + лп| =(-l)ncosa
cos | ±а + 5 + пп । » +(-l)n sin а
\ Z )
tg [ а + 5 + лп| =-ctga
ctg | а + 5 + пп | « -tg а
Соотношения между обратными
тригонометрическими функциями
arcsin х = -arcsin (-х) = х - arccos х —
- arctg -=^==
2/7
Соотношения между обратными
тригонометрическими функциями
Пределы некоторых последовательностей
arccos х = п - arccos (-х) = g - arcs*n х =
lim (——— +
п —> оо\П 4- 1
—1— + ... + =1п2
л + 2 2п)
г П<Х л
lim — =0
arctg х = -arctg (~х) = ~ arcctg x =
lim \
= arcsin
arcctg x = к - arcctg (-x) ~ ~ arcte x =
= arccos
г 10gbn П
hm =0
П-»оо д
. 1
sm -
-Г=1
п
п
lim
lim
X
Производная
НАЧАЛА АНАЛИЗА
у' = f{x)= lim
Ay
Ах
Предел функции. Свойства
lim с = с
х-+а
lim (Дх) + g(x)) - lim Дх) + lim g(x)
х-+а х-+а х-ьа
lim (Дх) • g(x)) = lim Дх) • lim g(x)
х-ьа х-*а х-*а
f(T\ Iim Z(X)
1; Т\х) _ х-^а
х-Гаё(х) limg(x)
х-+а
lim (k • Дх)) = k • lim Дх)
х-+а х-*а
Пределы некоторых последовательностей
а> 0,Ь> 1, а> 0, р — натуральное число.
( 1Y*
lim 14— = е
П -> *Д. nj
1Р + 2Р + ... + пр 1
lim------------------------ --------7
п ~ пР + 1 р + 1
п
lim —: ==е lim 77 = О
П —> *» П*
,. 1Р + Зр + ... + (2л - 1/ 2Р
hm----------------------_д-------------= ——
р + 1
п
вторая производная:
Г(х) = (/'(х))'
производные высших порядков:
Г(п)(х) = (/п-1)(х))
Производные некоторых функций
(С)' = 0 (С — константа) (х)' = 1 (cos x)' = -sin x (sin x)' = cos x
(х2)' = 2х (tg X)’ = 2
COS X
(xn), = nx'1’1 . . 1 (ctg X) = - 2
sin x
(arccos x) —
х 7i - x2
Г—V - п 1^7 + 1 < • 4' 1 (arcsin X) =
4 7 X 7i - x2
(arctg x) = „ 1 + X
(n,rL\' / 4 V_ 1
(Vx) - — ^arcctg x) n
пл7хп • 1 1 + X
(1g х)' - lg e •V (in X)' - 1
<1о^>' - x l„a
(axy = ax In a
272
cAianve^itaTnufta &
Правила вычисления производных
Интегралы некоторых функций
(и = и(х), V = и(х))
(и + vY = и' + v'
(и • vY = u'v + uv
Ги\' u'v - uv*
UJ - „2
(u - vY = u' — v'
(cuY = cu'
fuY _ uz ,
kc; c
Производная сложной функции
(и (i>(x)))' = u'(v(x)) • v'(x) (unY = n •и1'1- и'
(cos uY = - sin и • u'
(tg uY = —-u
cos u
(аи)' = au • In a • u'
(sin u)' = cos и • и'
(ctg u) --------• и
sin и
л v - 1 '
(ln “) - - • и
/ Ux Z U r
(e ) = e -u
Производная обратной функции
f(x) и g(x) — взаимообратные функции;
если существует f'(xQ) и g'(xQ), то
s'w- rh
Свойства производных высшего порядка
(и + v)(n) = иМ + v(n) (uv)(n} = £ С* uWv(n - к)
k = о
Первообразная F(x) функции /(х)
F'(x) = /(x)
Неопределенный интеграл — это общее выраже-
ние F(x) + С для всех первообразных функций от
данной функции Дх):
F(x) + С = | ftx) dx
Основное свойство
(J f(x) dx)' = f(x)
Интегралы некоторых функций
j k dx = kx + С
п + 1
[ хп- dx - ——— + С
J п + 1
j dx =1п |х| + С
fex dx-ex + C
f ах dx = р— + С
J In а
| cos х dx = sin х + С
j sin x dx = -cos x + C
j —— dx = tg x + C
1 cos x
Г —-g— dx = -ctg x + C
J sin x
J tg x dx = -In I cos x I + C
ctg x dx = In I sin x I + C
Основные правила интегрирования
J k • f(x) dx- k- J /(x) dx
J (ftx) + g(x)) dx = l f(x) dx + j g(x) dx
Формула Ньютона—Лейбница
I
b
/(x) dx = F(b) - F(a) = F(x)
a
Свойства определенного интеграла
a ba
j f(x)dx = O j f(x)dx = -j f(x)dx
a a b
b c b
j /(x)dx=j /(x)dx+j f(x)dx
a a c
b b
j k • f(x) dx = k-1 f(x)dx
a a
b b b
f (f(x) + g(x)) dx= J f(x) dx + j g(x) dx
a a a
b ^pb + q
J f(px + q)dx= - j /(t)dt
a pa + q
a a
Если f(x) четная, то j /(x) dx = 2 j f(x) dx
-a 0
a
Если /(x) нечетная, то j /(x) dx = 0
-a
b
m(b -a)< f(x) dx M(b - a), где Mum — наи-
a
большее и наименьшее значения /(х) на [а; Ь]
273
^Школьная пАог/иъл/ьма / ma^MMipx и, фоклшмгх
Площадь криволинейной трапеции
ъ
8 = J ftx) dx
а
Ъ
S = -f f(x)dx
а
Ь
s = f \f(x)l dx
а
Несобственные интегралы — интегралы с беско-
нечными пределами и интегралы от разрывных
функций.
4-00 Ъ
[ f(x)dx= Вт [ f(x)dx
J ъ -> 4-00 J
a a
b b
[ f{x)dx = lim [ f(x)dx
J a -> J
— OO d
4-00 c b
f f(x)dx — lim f /(x) dx + lim [ /(x) dx
"* a—>—oo*' d—>4-oo*
-oo a c
Значения некоторых несобственных интегралов
Ь
s=f (f(x)-g(x))dx
а
00 j 2
Р х dx п
00 , 2
Р х dx л
г +1" 12
sinx , п
----dx = о
х 2
Длина кривой
ь _________________
I = J 71 + (/'(«)) 2 dx
а
j sin(x2) dx = j cos(x2) dx =
J In x . л2
-------7 dx = «
J x - 1 6
о
Площадь поверхности вращения
ь ________________
S = 2reJ Г(х) 71 + Г(*))2
а
Объем тела вращения
ь
(f(x))2dx
а
ГЕОМЕТРИЯ
МНОГОУГОЛЬНИКИ
Треугольник
Обозначения:
А, В, С — вершины, а также углы
при этих вершинах;
а9Ь9 с — стороны, противолежащие
углам А, В, С соответственно;
Ла, hb9 hc — высоты, опущенные
на стороны а, б, с соответственно;
тпа, тпь, пгс — медианы;
1а91Ъ91С — биссектрисы;
R — радиус описанной окружности;
г — радиус вписанной окружности.
2/4
L формулах
Площадь треугольника
Л 1 . 1.ь 1 ь
S 2 g bhb 2
S=xab sin С = I ас sin В = | be sin А
S= 7р(Р - а)(р - b)(j> - с) (р = |(а + Ъ + с)}
S = rp
S =
Прямоугольный треугольник
S=|ab=»5ftc fZC =90“)
Теорема Пифагора
c2 = a2 + b2 (ZC = 90“)
Я= | = те
abc
4R
Медиана, биссектриса, высота
2 2Ь2 + 2с2 - а2 ,2 Ьс((Ь + с)2 - а2)
—*— 1°= (?;?
,2 4р(р - а)(р - Ь)(р - с)
па “ ----------2----------
а
Высоты и стороны треугольника
, , 111
h. : hh : h. — - : г : -
а ° е а b с
Теорема косинусов
а2 = Ь2 + с2 - 2bc cos А
Ъ2 = а2 + с2 - 2ас cos В
с2 — а + Ь2 - 2ab cos С
Теорема синусов
sm A sin В sm С
ас'.а = а'.с bctb = b: с bc-.h=‘h-.ac
Квадрат
q__ 2_ 1 ,2
cl —-
P = 4a
d = aj2
„ 1 . aj2
R 2d= 2
1
r=2a
Прямоугольник
1 2
S- ab= g d sin <p
n 1 . 1 Г2 ; ?2
B = 2 d = 2 4o. + b
P = 2 (a + b)
Параллелограмм
S = aha — bhb
S = absina
« 1,, •
S - ^d^sm <p
P = 2 (a + b)
dl + d22 = 2 (a2 + 62)
Теорема тангенсов
a + b +e a + P tg 2 _ etg g
a - b +o. « ~ P tg 2 CO. 1 <M а bo -Н»
a + c , a + у te 2 _ CQ.ICM bo Q
a - c tff a - Y tg 2 2 '
b + c ctgl
b - c tw II eb OQ UD to 1
2/5
ОКРУЖНОСТЬ И КРУГ
Ромб
Длина окружности
С = 2пг
длина дуги, соответствующая центральному уг-
лу в п’:
г пг
£-180* п
lfc 1 .
г - 2 « “ 2 asui “
Р — 4а
Трапеция
а + b 1 , , .
S = —— * h = g d^sin <р
средняя линия MN = % (а + Ь)
Свойства хорд, секущих и ка-
сательной
BS'ES = CS‘DS
MB-MC^MD- ME
МА1 2 = MB -МС = MD • ME
Углы в окружности
Произвольный выпуклый четырехугольник
а + Р+ у+8 = 360’
(а, р, у, 8 — внутренние углы че-
тырехугольника)
2 । 12 । 2 । ,2 । । л 2
а + Ь + с + d = dj + d2 +
Площадь круга
(т — отрезок, соединяющий се-
редины диагоналей)
ZBAC = ZBOC ^ВАС = 180’ - 5 ZBOC
* 2
j2
S = пг2 = я -у
4
Cd
4
Сегмент и сектор
S = g d1d2sin ф
Правильный многоугольник (п сторон)
центральный угол а = 360*: п
внешний угол Р = 360’: п
внутренний угол у = 180” - р
_ Г^2 2 „ — . СС
ап — 2 7-R ~ г = 2Bsm %
„ , а
= 2rtg2
а а
2 sin g 2 tg £
1 2 1 2 1 2 ОС
S = 2 Папг ~пг *6 2 = 2 nR sin а = 4 П°п ctg 2
ос а ос
а = 2R sin х h = 5 tg 7
Z Z 4
площадь сектора: S0ABC = |
площадь сегмента:
sabc ~ Sqabc ~ Sqac
МНОГОГРАННИКИ
Обозначения:
V — объем;
Sn<WIH — площадь полной поверхности;
S6oK — площадь боковой поверхности;
So — площадь основания;
Р0 — периметр основания;
Р±—периметр перпендикулярного сечения;
I — длина ребра; h — высота.
276
Призма
^бок PjJ' ®полн
F=S0-ft
прямая призма:
S^-Pol d-h)
Параллелепипед
вполн = 2 (ab + Ьс + ас)
V=abc
л2 - п2 Д. к2 X х.2
а = а + о + с
Формула Эйлера
^~L+F=2
N — число вершин, L — число ребер, F — число
граней выпуклого многогранника.
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
Обозначения:
а — ребро,
V — объем,
S — площадь боковой поверхности,
R — радиус описанной сферы,
г — радиус вписанной сферы,
Н — высота.
Куб
®полн "“6 а
V=a
d2 - За2
Пирамида
^=|s0-a
правильная пирамида:
^бок = 2 ' k
(Ро — периметр основания,
k — апофема)
Куб
правильный тетраэдр:
S = a2V3
R = h (R — радиус описанной сферы)
г = h (г — радиус вписанной сферы)
Дл/б
12
усеченная пирамида:
7=|a(S1+a/S^ +S2),
где Sjl и S2 — площади основа-
ний
S6ok • (si - s2): cos а (« — дву-
гранный угол при ребре ниж-
него основания)
Октаэдр
277
Додекаэдр
g3(15 + 7TB)
V 4
S = 3a275(5 + 2^5)
„ aj3(l + ТВ)
R~ 4
= aT10(25 + 11VB)
r 20
Икосаэдр
5a3(3 + J5)
v 12
S = 5a273
„ a J2(5 + JB)
R~ 4
aj3(3 + J5)
r 12
Шаровой сегмент
а2 = й(2Я-й)
S6oK^2nRh = n(a2 + h2)
Snwa = я (2Rh + а2) - п {h2 + 2а2)
У=яй2(й - тП
ТЕЛА ВРАЩЕНИЯ
Цилиндр
5бок = 2л7?й
Sn0JIH = 2яЛ2 + 2яйй
У=яЯ2й
Конус
«бок ~ пВ1
SmnB~nR(R + l)
1 2
У=
о
усеченный конус:
«6oK'=nZ(-R + г)
4™.-eta+»(B"+^
V- 5Я»(Л2 + Яг+гг),
О
где Виг — радиусы оснований
Шар
«сферы = 4ЛЙ2 = nd2
У=^яй3=^
о о
Шаровой сектор
S = nR (2й + а)
2nR2h
V 3
ДЕКАРТОВЫ КООРДИНАТЫ
НА ПЛОСКОСТИ
Расстояние между точками А(х1, yt) и В(х2, у2)
АВ = 7(Xj - х2)2 + " Уг)2
Деление отрезка в заданном отношении
= хг + Хх2 yi + Хуг
Х~ 1 + X ; У~ 1 + X ’
где А(х1( yt) я В(х2, у2) — концы отрезка, точка
АС
С(х, у) делит АВ в отношении = X
Координаты середины отрезка
«1 + *2 У1 + У2
х= 2 ’ У~ 2 ’
где A(xv уу) я В(х2, у2) — концы отрезка
Уравнение прямой на плоскости
общее уравнение: ах + by + с = 0;
если а — 0, прямая параллельна Ох;
если Ъ = 0, прямая параллельна Оу;
если с = 0, прямая проходит через начало коор-
динат;
2/8
Уравнение прямой на плоскости
с угловым коэффициентом: y = kx + b
k — тангенс угла наклона прямой к оси Ох;
проходящей через заданную точку A(xQ, у0):
У “ Уо ь
------ =fe
х - х0
k — угловой коэффициент;
х , у
уравнение прямой в отрезках: - + g «1
а, Ь — отрезки, отсекаемые прямой на осях;
проходящей через две заданные точки A(xv у^
и В(х2, у2):
У ~ У1 = х - Xj
Уг ~ У1 х2~ Х1
Расстояние от точки (х0; у0) до прямой
ах + by + с — 0:
|ах0 + Ъу0 + с|
/ 2 . . 2
*Ja + Ь
Взаимное расположение прямых
а1х + &1У + С1 = О и а2х + Ь2у + с2 = О
условие параллельности:
а^- a2bi = 0
условие перпендикулярности:
ala2 &1&2 = 0
координаты точки пересечения:
— ^*С2 ~ ^2С1 _ g2cl — glC2
° ~ a2^1 al&2 ” a2^1
угол a между прямыми:
|al&2 ~ a2&l|
sm a = ,.. :
/2 , ,2 /2,-2
fja^ 4- ft* /Ja2 + &2
|aia2 + &1&2I
cos a = . ...-.', . '
/2,-2 /2,-2
Va2 + &2
Взаимное расположение прямых
у = k±x + Ьх и у = Ь2х 4- Ъ2
условие параллельности:
= ^2
условие перпендикулярности:
^1^2 = ""1
Взаимное расположение прямых
у = kxx Л-Ъ1пу = k2x 4- Ь2
координаты точки пересечения:
&2 ” ^1^2 ~~ ^1^2
Уо= k1-h2
угол а между прямыми:
tga =
kj ~ ^2
1 4* ft,fe2
Уравнения кривых на плоскости
парабола: у = ах +Ьх +с
у2 « 2рх
2 2
х У 1
гипербола: = 1
а b
окружность с центром в начале координат:
2.2 о2
X +у ^Вг
окружность с центром в точке (а; &):
(х-а)2 + (у-&)2 = Я2
2 2
X U
эллипс: -2 4- “2 = 1 (а, & — полуоси эллипса)
а Ь
Формулы преобразования декартовых коорди-
нат
при параллельном пере-
носе*.
х^х'^а у-у' + Ь
или
х' = х-а у' = у-Ъ
при повороте вокруг начала координат на угол а:
х = х' cos а - у' sin а
у = х' sin а + у' cos а
или
х' = х cos а 4- у sin а
у' = -х sin а 4- у cos а
279
Полярные координаты
х = р cos <р у = р sin ф
р=7«2 + у2
А (о. сгА
ДЕКАРТОВЫ КООРДИНАТЫ
В ПРОСТРАНСТВЕ
Уравнение плоскости
общее уравнение:
ах + by + cz + d = 0;
а — 0, плоскость параллельна прямой Ох;
Ь = 0, плоскость параллельна прямой Оу;
с = 0, плоскость параллельна прямой Ог;
d = 0, плоскость проходит через начало коор-
динат;
а = Ь = 0, плоскость параллельна плоскости хОу;
а = с — 0, плоскость параллельна плоскости хОг;
b = с = 0, плоскость параллельна плоскости yOz;
уравнение прямой в отрезках (а, Ь,с — отрезки,
отсекаемые плоскостью на осях):
*+|-3=1
а о с
проходящей через точку А(х0, у0, z0) перпенди-
кулярно вектору п (а, Ъ, с):
a(x-xo) + &(y-yo) + c(z-zo) = O
Угол между плоскостями
a1x + &1y + c1z + d1 = 0 и a2x + 62p + c2z + d2 = 0
I ага2 + 6j&2 + CjcJ
COS ф = =========—===========
/ 2 , .2 .2 / 2 , ,2 . 2
^аг 4- &х + сх Ja2 4- 62 + с2
Условие параллельности двух плоскостей
аг Ьг сх
а2 С2
Условие перпендикулярности двух плоскостей
ах&2 &1&2 + С1С2 = О
Расстояние от точки Мо (х0; у0; z0) до плоскости
ах + by + cz 4- d » О
_ I ож° + &у° + с*о + d|
Р” 7a2 + ъ2 + с2
Уравнение прямой в пространстве
канонические уравнения прямой, проходящей
через точку Af0(x0; у0; z0) параллельно вектору
s (Z; тп; и):
х - х<> у ~ yQ z - г0
I т п
Уравнение прямой, проходящей через две точки
Mi (Хр yt; г^пМг (х2; у2; z2):
х ~ хг У - У! = Z - гг
х2 ~ Х1 У2 ~ У\ г2 ~ г1
уравнение прямой — линии пересечения плос-
костей:
(ахх + Ъху + cxz + dx = 0,
(a2x 4- b2y 4- c2z 4- d2 = 0
Угол между прямыми
X - хх _ у - Ух _ Z - 2х
h ~ т1 ~ Л1
X - Х2 у - у2 z - z2
и —1------- — = :
*2 п2
Р1^2 + ^1^2 Л1Л2|
COS ф = =====—==============
Y £2“ 2. 2 /,2 . 2Т 2
^1г + тх + пг + т2 + п2
Условие параллельности двух прямых
1г тг пг
^2 ^2 ^2
Условие перпендикулярности двух прямых
1г12 4- т1тп2 4- nxn2 = 0
жу „ х ” хо У “ У о 2 ~ *о
Угол между прямой —j— = ----------- = ------
4 774 74
и плоскостью ах + by + cz + d = О
I al + Ът + cn|
Y / 2 , , 2 , 2 /,2 . 2~ 2
•la + Ь + c *11 Л-т + n
Условие параллельности прямой и плоскости
al + bm + сп = О
Условие перпендикулярности прямой и плос-
кости
а _ Ь_ _ с
1 ~ т ~ п
280
ЛЪатематика, / ффмумих,
Условие принадлежности прямой плоскости
'al + Ът + сп = О,
ах0 + by0 + сг0 + d = О
УРАВНЕНИЯ ПОВЕРХНОСТЕЙ
ВТОРОГО ПОРЯДКА
Эллипсоид
Сфера
2 . 2 . 2 7*)2д
х + у + г = R
2
Эллиптический параболоид
2
а
ъ2
Гиперболический параболоид
2 2
X у
2 A2 ~^Z
а Ь
Однополостями гиперболоид
Двуполостный гиперболоид
Конус
2
X
а2
2
y__L.
,2 2
Ь С
2 2
£. + У.
2^,2
а b
Гиперболический цилиндр
Эллиптический цилиндр
Параболический цилиндр
у2 = 2рх
+
2.81
ВЕКТОРЫ
Координаты вектора с началом в точке А(Хр ур
zx) и концом в точке В(х2, у2, z2):
АВ (х2 - хх, у2 - yv z2 - zx)
Сумма векторов a (хх, ух, гх) и b (х2, у2, г2):
а + b = с (хх + х2, ух + у2, zx + г2)
Свойства сложения векторов:
а + b — Ь + а (а + Ь) + с = а + (Ь + с)
а + 0 == а а + (-а) = О
Умножение вектора на число
X • а (х, у, z) = с (Хх, Ху, Хг)
Свойства умножения:
(Хц)а = Х(ца) (X + ц) • а = Ха + ра
X (а + Ь) = Ха + ХЬ 0 • а = ХО = О
Свойства проекций вектора на ось
Скалярное произведение векторов
а (xv ур Zj) и b (х2, у2, г2):
a-b = ххх2 + уху2 + zxz2 = |а| • |&| • cos (а, Ъ)
Свойства скалярного произведения
a'b = b'a
а-а>0 а,а = |а|2
а (Ь + с) = а -Ъ + а • с
(ka)b^'k(ab)
Д^янл вектора а (х, у, г):
1-1 I 2 . 2~ 2
|а|= л/х + у +2
Угол между векторами
а(«1» У1> 2Х) и Ь (х2, у2, г2):
а • Ь
OT(e’bW
*1*2 + У1У2 + 2122
7*1 + У1 + 21 • 7*2 + У 2 + 22
Условие коллинеарности векторов
= Хх2
а II Ъ « хг: х2 в : у2 - • z2 или
У1 = ^У2
<= ^^2
Условие ортогональности векторов
а±&<=>а-& = 0 или хгх2 + ух у2 + zxz2 = О
Векторное произведение векторов
с = [а Ь]
|с| = |а| • |Ь| sin (р
Свойства векторного произведения
[а b] = -[b а]
[(а 4-Ь) с] = [ас] 4-[be]
[(Ха)Ь] = 1[аЬ]
[аЬ] = 0 <=> а II Ъ
Смешанное произведение векторов
(векторно-скалярное произведение)*.
а*Ь* с = [а Ь] с
ОПРЕДЕЛИТЕЛИ
Определитель второго порядка
д 1 b 1
= ахЬ2~ ^2^1
а2 Ь2
Определитель третьего порядка
а1 С1
а2 Ь2 С2
аз сз
— а^Ь2с2 4- biC2a2 4- а2Ь2Сх с1Ь2а3
“Ь1а2с3 ~ а1с2^3
282
^(^атгуемлшыша £ фофлуулах
Основные свойства определителей
замена строк на столбцы:
Основные свойства определителей
суммирование строк:
т-4 см со ООО т-4 см со иО гО иО i-t см со сз сз q — CJ сз- © п сз- © ьэ ьэ ьэ сь сз- © w w со т-4 СМ со ООО т-4 СМ СО Л иО нО т-4 СМ СО СЗ СЗ СЗ S5S ^1 а2 ^2 ^2 ^*®2 аз &з сз + ^аз
перестановка двух строк:
°2 &2 С2
а1 &1 С1
°3 *3 с3
вынесение общего множителя элементов строки:
а1 С1 а1 Ьг Cj
Ха2 А#&2 ^*с2 =х СМ О см иО см Q
со о СО «О со е со о со иО со е
нулевая строка (столбец):
сумма произведений элементов строки (столб-
ца) на их алгебраические дополнения:
ai С1
а2 ^2 С2
а3 &3 с3
^2 ^2 » ®2 ^2
&з с3 а3 с3
а2 Ь2
аз Ьз
сумма произведений элементов строки (столб-
ца) определителя на алгебраические дополне-
ния соответствующих элементов другой стро-
ки (столбца):
а1 &1 С1
^2 С2
а3 &3 с3
а1 С1
ООО
°3 *3 сз
О Ьг
0Ь2
0Ь3
С1
С2
сз
= 0
пропорциональные строки:
а1 С1
1а3 Х63 Хс3 = 0
аз &з с3
Решение систем двух линейных уравнений с
двумя неизвестными
(atx + bty = ct
]а2х + b2y = с2
сумма элементов столбца (строки):
а। &i 4" b 1 с 1 а । с °1 С1
®2 ^2 ^"^2 ^2 =к см О см иО см Q + а2 с2
а3 ^3^ ^3 с3 со о со »С со Q СО О < СО СО СЗ
С1 bi «1С1
д = а1 Ь1 *0 Х = СМ иО см о у- а2 с2
а2 ^2 а1 Ъ1 а1
04 иО СМ СЗ СМ гй СМ СЗ
283
ммая nfiotfiaMMa & тси/лищмх и, фо[гмум1'л
СПРАВОЧНЫЕ ТАБЛИЦЫ
Квадраты натуральных чисел от 11 до 99
1 2 3 4 5 6 7 8 9
1 121 144 169 196 225 256 289 324 361
2 441 484 529 576 625 676 729 784 841
3 961 1024 1089 1156 1225 1296 1369 1444 1521
4 1681 1764 1849 1936 2025 2116 2209 2304 2401
5 2601 2704 2809 2916 3025 3136 3249 3364 3481
6 3721 3844 3969 4096 4225 4356 4489 4624 4761
7 5041 5184 5329 5476 5625 5776 5929 6084 6241
8 6561 6724 6889 7056 7225 7396 7569 7744 7921
9 8281 8464 8649 8836 9025 9216 9409 9604 9801
Кубы натуральных чисел от 1 до 10
X 1 2 3 4 5 6 7 8 9 10
3 X 1 8 27 64 125 256 343 512 729 1000
Простые числа от 2 до 997
2 3 5 7 11 13 17 19 23 29 31 37 41 43
47 53 59 61 67 71 73 79 83 89 97 101 103 107
109 113 127 131 137 139 149 151 157 163 167 173 179 181
191 193 197 199 211 223 227 229 233 239 241 251 257 263
269 271 277 281 283 293 307 311 313 317 331 337 347 349
353 359 367 373 379 383 389 397 401 409 419 421 431 433
439 443 449 457 461 463 467 479 487 491 499 503 509 521
523 541 547 557 563 569 571 577 587 593 599 601 607 613
617 619 631 641 643 647 653 659 661 673 677 683 691 701
709 719 727 733 739 743 751 757 761 769 773 787 797 809
811 821 823 827 829 839 853 857 859 863 877 881 883 887
907 911 919 929 937 941 947 953 967 971 977 983 991 997
Степени чисел 2, 3 и б
п 2В 3* 5В п 2В зв 5В
0 1 1 1 6 64 729 15625
1 2 3 5 7 128 2187 78125
2 4 9 25 8 256 6561 390625
3 8 27 125 9 512 19683 1953125
4 16 81 625 10 1024 59049 9765625
5 32 243 3125 6 64 729 15625
284
<Л{ателатлиш, & сМг^илах,
Факториалы чисел от О до 10
п 0 1 2 3 4 5 6 7 8 9 10
п\ 1 1 2 6 24 120 720 5040 40320 362880 362880
Значения функции у = ех
X -3 -2 -1 1 2 3 4 -0,5 0,5 1/3
ех 0,05 0,14 0,37 2,72 7,39 20,09 64,60 0,61 1,65 1,40
Десятичные логарифмы чисел от 1 до 10
п 1 2 3 4 5 6 7 8 9 10
1g п = 0 0,30 0,48 0,60 0,70 0,78 0,85 0,90 0,95 1
Натуральные логарифмы чисел от 1 до 10
п 1 2 3 4 5 6 7 8 9 10
In п « 0 0,69 1,10 1,39 1,61 1,79 1,95 2,08 2,20 2,30
Некоторые значения тригонометрических функций
Аргумент Функция
sin а cos а tga ctg а
0*(0) 0 1 0 не определен
15’ (й) л/З - 1 2^2 7з + 1 272 2- 7з 2 + ТЗ
18’ (я) Тб - 1 4 7б + ТВ 272 75-1 7ю + 275 710 + 275 75-1
1 2 7з 2 1 л 73
36‘© 75-75 272 75 + 1 4 710 - 275 75 + 1 75 + 1 7ю - 275
1 л 1 72 1 1
^ + 1 4 75-75 272 75 + 1 710 - 275 710 - 2«/5 75 + 1
7з 2 1 2 7з 1 7з
75 + 75 272 75-1 4 7ю + 275 75-1 75-1 710 + 275
285
чыпыышл
Некоторые значения тригонометрических функций
Аргумент Функция
sin а cos а tga ctg а
л/з + 1 272 Уз - 1 272 2 + Уз 2- УЗ
о о 1 0 не определен 0
Правильные многоугольники
Число сторон Центральный угод Радиус Площадь Связь между гиВ
вписанной окружности описанной окружности
п а г R S
3 60е аЛ 6 аЛ 3 а Л 4 Я = 2г
4 90е a 2 вУ§ 2 z а2 Я = гЛ
6 8 120е 135* ! О УЗ 2 а 6 2а2(1 + Л) 8а2 Л 2
a(l + Л) 2 аЛ + 2У2 2 Г п Д°С09 8 °
12 150е а(2 + У§) 2 За2 (2 + Л) _ У2 + У2 2
(СО + О II > в ьо! о о to + W “ II
Правильные многогранники
Название Число S V
ребер граней вершин
Тетраэдр 6 4 4 а2 УЗ а9Л
12
Октаэдр 12 8 б 2агЛ с? Л
3
Икосаэдр 30 20 12 5агЛ ^а3(3-Уб)
Куб 12 6 8 6а2 а3
(гексаэдр)
Додекаэдр 30 12 20 За2Уб(б + 2У5) 3 ^(15 + 7У5)
286
Физика
Механика • Молекулярная физика и термодинамика
Электричество и электромагнетизм • Колебания и волны
Оптика • Квантовая физика
Физика в таблицах
1. Материальный мир
-288
Zfoufytuta & ши/лищш
3. Физическая картина мира
V 1 т 1 т
Исходные философские идеи и представления Физические теории Связи между теориями
► материя ► движение ► пространство и время ► взаимодействие —► принцип соответствия — ► принцип симметрии — > принцип сохранения — ► принцип относительности — > принцип дополнительности — ► принцип причинности — > диалектика необходимости и случайности
i ± ± £
Классическая механика Статистическая физика Электро- динамика Квантовая физика
1 1 ; “ "J
Основание Ядро Следствие Интерпретация
Эмпирический базис Идеализирован- ный объект Система величин Процедуры измерения Система законов Законы сохранения Фундамен- тальные постоянные Объяснение фактов Практические применения Предсказания нового Истолкование основных поня- тий и законов Осмысление границ применимости
4. Основные физические теории
Теория Область пространства Типичные объекты Тип взаимодействия Типичные явления (процессы)
Механика 1025+10-8 м (условно) Звезды, пла- неты, тела на Земле Гравитационное. Электро- магнитное Движение в пространстве макротел: звезд, планет, кораблей, самолетов и т. п.
Электро- динамика 1025ч-10“17м (условно) Поле. Волны. Заряды Электро- магнитное Существование электрических полей. Распространение волн. Свет. Электрические токи. Магнитные поля
Квантовая механика КГМО"18 м Атомы, элект- роны в атомах и молекулах Электро- магнитное Квантование энергии атомных систем. Излучение и поглоще- ние света. Взаимодействие атомов
10—1323
289
нал
& 'пгаЛнюрос а фофлсу^
tax
4. Основные физические теории
Теория Область пространства Типичные объекты Тип взаимодействия Типичные явления (процессы)
Квантовая электро- динамика 10~8+10~18м Электроны. Фотоны Электро- магнитное Взаимодействие фотонов и электронов: тепловое излуче- ние тел, тормозное излучение, эффект Комптона и др.
Теория силь- ных и слабых взаимодейст- вий 10~13+10~18м Элементар- ные частицы Сильное. Слабое Взаимные превращения элементарных частиц
Статистиче- ская физика 1025+10~17м От систем электронов до систем звезд Любое Движение молекул в жидкости и газе, радиоактивный распад, плазма и др.
Термоди- намика 1025-*-10~3 м (условно) Любые макро- системы Электро- магнитное Теплопередача. Работа
5. Структура и содержание механики
Понятия: механическое движение; макроскопическое тело; механическое состояние; материальная точка; системы отсчета (инерциальные и неинерциальные); взаимодействие; виды движения; основные механические величины
Принципы: дальнодействия;
суперпозиции; относительности; симметрии; сохранения
Законы Ньютона всемирного
Законы для сил: тяготения; упругости; сухого и жидкого трения
Законы сохранения: энергии;
импульса; момента импульса
Основные — поступательного движения; характеристики: — вращательного движения; — колебательного движения Объяснение явлений равновесия тел, невесомости, подъемной силы природы и техники: крыла самолета, реактивного движения и др. Использование колебательного и вращательного движений в технике
290
6. Структура и содержание кинематики
291
бШяальная
пфофамма, & maJluufix и, формулах,
7. Графики движений
Равномерное движение Равноускоренное движение
Формула График Формула График
a TT vq a Ti uq
Скорость t«o I II та ух v = Vq + at VX1 VQx . g Hc I
0 ~t 0 t 0 t
Ускоре- ние а = б ах 0 t й! II ci г* 1 «Cl ax 0 ax 0
t t
Переме- щение S = vt Зх . at2 s = vot+ -% 3x J Sx
0 t 0 t 0 t
Коорди- ната X = Xq + vxt X XQ x = x0 + axt2 +vof+-i- X XQ X XQ
0 t 0 t 0 t
8. Движение с ускорением
Вид движения
Равноускоренное прямолинейное движение Равномерное движение по окружности
Взаимное направление скорости и ускорения По одной прямой (в одну или противоположные стороны) Под прямым углом друг к другу
Постоянно ли ускорение: а) по модулю б) по направлению а) постоянно б) постоянно а) постоянно б) изменяется
Формула скорости 0 = vq + at - 2nR v=^-
Формула ускорения II Cl 1 2 2 а = R = 4л2 vzR
Формула координаты axt2 х = х0 +vOxt+ — „ . 2п . х = R sm у t _ 2л у = R cos у t
292
ила
$ тгии/лшир/х,
9. Структура и содержание динамики
Законы для сил:
т1т2
тяготения F = G —5—
R2
упругости Fx = -Лх;
трения FTp = ilN
293
10. Законы Ньютона
Первый закон Второй закон Третий закон
Физическая система Макроскопическое тело Система двух тел
Модель Материальная точка Система двух материальных точек
Описываемое явление Состояние покоя или равномерного прямо- линейного движения Движение с ускорением Взаимодействие тел
Суть закона Существование инерциальной системы отсчета (если SF = 0, то v = const) Взаимодействие опреде- ляет изменение скоро- сти, т.е. ускорение Силы действия и противодей- ствия равны по модулю, противоположны по направле- нию, приложены к разным телам, одной природы j?12 = -F 21
Примеры проявления Движение космического корабля вдали от притя- гивающих тел Движение планет, падение тел на Землю, торможение и разгон автомобиля Взаимодействие тел: Солнца и Земли, Земли и Луны, автомобиля и поверхности Земли, бильярдных шаров
Границы применимо- сти Инерциальные системы отсчета. Макро- и мегамир. Движение со скоростями, много меньшими скорости света
11. Движение тел под действием силы тяжести
Начальные условия Описание движения
Начальная координата Начальная скорость Формулы Траектория
1 2 3 4
Уо = h У % С ио=О I* ) X V = -gt У- h 2 У h С )'//////'/. ///////,х
!/0= Л Y % ЗЬ || g v = -v0 - gt , gt2 у= h-vQt —2" У h
( ) X q'///////////////,X
294
&и£и1М £ пии/лищгх,
11. Движение тел под действием силы тяжести
1 2 3 4
Уо= 0 У По j 1 v = v0 - gt y=vot-^ У %nax
с X c
Уо~ 0 Y а Ц) Is' vx = vq cos а vy = v0 sin gt x = v$t cos а gt2 у = vot sin а - у У
С ) X c )'' -,/s
У0= h У 11 _£о 'Vlcq Uol ® ?* "o 1 "h L 11 P> » H S3> Y h Sb
Уь Iе' V --ч/ с Г у l-Лу
С ) X C ) X
У Л vx = u0 cos а , Пп
1/ = Vo s^n а x = (R3 + й) sin y f
+ S со О 00 II II Н ООО Н £ »0 R3 h / / 1 ( Яз C -^z 1 > /7-Л '/ Vx
0 । X у = (R3 + h) cos у t \ \ — —-* *
295
12. Силы в механике
296
Название силы Природа взаимо- действия Формула для расчета силы Зависимость силы от рас- стояния или относительной скорости Зависит ли сила от массы взаимодей- ствующих тел Как направлена сила Сохраняет ли сила свое значение при переходе из одной инерциальной системы отсчета в другую Каковы условия применимости формулы
Сила тяготения Гравита- ционная ТЯ ЛЧ ШМ & -2 Л Является функ- цией расстоя- ния между взаимодейству- ющими телами Прямо про- порциональ- на массам взаимодейс- твующих тел Вдоль прямой, соединяющей взаимодейст- вующие тела Сохраняет, так как расстояние R не из- меняется Материальные точки или сфе- рически симмет- ричные шары
Сила упругости Электро- магнит- ная Fx — -kx Является функ- цией расстояния (зависит от деформации) Не зависит Противо- положно направлению перемещения частиц при деформации Сохраняет, так как деформация х не из- меняется Достаточно ма- лая величина деформации х
Сила трения: а) сухого; б) жидкого Электро- магнит- ная и И £ Б» О О CQ > а со. л и и и g< g- Л д д л о о . f _ о о Ьц Рц Рц Является функ- цией скорости относительного движения v0TH Не зависит Противо- положно направлению вектора скорости v0TH Сохраняет, так как модуль относитель- ной скорости иотн не изменяется Формула FTp = nW выполняется приближенно, так как сила сухого трения зависит от ско- рости. При жидком трении до определенной скорости используется формула -^сопр = С^ОТН и затем ^сопр = pv2OTH
&та/ли1(/1х
13. Статика
Изучает условия равновесия твердых тел
ВИДЫ РАВНОВЕСИЯ
Устойчивое
Безразличное
Неустойчивое
СРЕДСТВА ОПИСАНИЯ
Модель тела в статике — абсолютно твердое тело.
Связь — препятствие движению тела: поверхность, веревка и т. д.
Реакция связи — сила, действующая на тело со стороны связи, по нормали к направлению
возможного перемещения.
Момент силы: М = ±Fd,
где d — плечо силы.
Особый случай:
Fi + F2 + F3 + ... = б — первое условие равновесия тела.
Mi + М2 + М3 + ... = 0 — второе условие равновесия тела.
297
бЩкаль
хая п^ог^гамма
<ах.
14. Сила, работа, энергия
Формула График Формула График
Тело брошено вертикально вверх Сила тяжести FT= mg Л mg С h Тело колеблется под действием силы упругости Сила упругости Гж = -кх F* хх 0
Работа силы тяжести А = FS cos а F = mg; S = h а = 0; А = mgh Л mg С h Работа силы упругости kxx kx2 в ~2" Х1 2~ х2 Fx -12-2^2^ Xj 0
Потенциальная энергия 2?п = mgh L mgl 'п Потенциальная энергия F Ьд 2 Еп К. 1 y\ 1 .
0 Н h Х1 0 *2 X
Кинетическая энергия 2 _ mv _ 2 = mg(H - h) Ек С 1 Н h Кинетическая 2 г, ГПУ энергия Ек = -у- = __ /у2 - \ 2 \Х1 х2 / Ек *1 0 *2X
Полная энергия 2 Е = mgh + —%- = = mgH Е Полная энергия „ _ kx2 ту2 Е-~2~ +~2Г ~ kx2 E
1 1 i j i 1
С 1 Н h *1 0 X2X
15. Законы сохранения в механике
Закон сохранения Какова математическая запись закона В каких системах отсчета вы- полняется закон Какие требования предъявляются к внешним силам, действующим на систему тел Какими должны быть внутренние силы, действующие в системе тел Известны ли случаи нарушения законов сохранения
Закон со- хранения импульса Хтпи = const Ътух = const < "LmVy = const Хтпи2 = const В инерци- альных ZF = 0 Любыми Нет
Закон со- хранения энергии £к + = const тпи2 . . + mgh = const 1 2 .2 ту , hx . -5—1—= const а л В инерци- альных 1А = 0 Консервативными (потенциальными) | силы тяготения 1 силы упругости Нет
Закон со- хранения момента импульса L = const /со = const mvr = const В инерци- альных ZM = 0 Любыми Нет
298
16. Гидро- и аэростатика
Общие свойства жидких и газо- образных тел 1. Способность как угодно изменять свою форму под действием сколь угодно ма- лых сил. 2. Жидкости и газы ведут себя как упругие тела в отношении деформации все- стороннего сжатия и растяжения. 3. Для всякой площадки в жидкостях и газах существует только нормальное dF напряжение р == называемое гидростатическим давлением. 4. Величина гидростатического давления в данной точке жидкости и газа одинакова для всех направлений площадки
Закон Паскаля Давление на поверхности жидкости, произведенное внешними силами, пере-
(1663) дается жидкостью одинаково во всех направлениях
Закон Архимеда На всякое тело, погруженное в жидкость (или газ), действует со стороны этой
(III в. до н. э.) жидкости (или газа) выталкивающая сила, равная весу вытесненной телом
жидкости (или газа), направленная вертикально вверх и приложенная к центру
тяжести вытесненного объема
Принцип отвердения ГА = F^
Pz^Pi + PoSh
F = (p2 -Pi)S = pQghS = p0Vg
Условие равно-
весия Fa = mg
Устойчивое равновесие
Барометрическая формула
для изотермической атмосферы
299
17. Гидро- и аэродинамика
Ъюювюле понятия гидро- и аэродинамики Линии тока — линии, касательная к каждой точке которой указывает направление скорости потока. Стационарный поток — поток, при котором линии тока совпадают с траекториями отдельных частиц. Токовые трубки — поверхность, образованная линиями тока. Скорость жидкости (газа) во всех точках одного и того же сечения одинакова
Модель При стационарных течениях жидкости (и даже газы) можно считать несжимаемыми жидкостями, т. е. мы не пренебрегаем изменениями давлений, обусловленными изменениями степени сжатия, но пренебре- гаем изменениями объема
Уравнение неразрывности струи g Hi} *л» ^2^1 ” bl» V / —р-ч. V2 2 Ат = const S1V1 = S2V2
Уравнение Д. Бернулли (1738) „ГГ~ ,Р2 р1| +•» ' 1 Ч V2 тэ 1 + М" СО ГО м ~ .i НК) 1 II § S-
Реактивное движение У та =t 1 II ft ТЬц
Движение тел в жидкостях и газах
Сопротивление трения F ~ го Сопротивление давления F~rW С Э vk V При v < vK F ~ v При v > ик F ~ и2
Подъемная сила крыла самолета ||5 /IIТ Ry — подъемная сила Rx — сила лобового сопротивления
300
^та/ми/рл
18. Гармонические колебания
№ Формулы Графики
1 X = хм cos cot q = qM cos cot xtq О
А т At т st t 4 \ 2 / 4 4
2 x' = v = -xMco sin cot g' = i = -gMco sin cot x',q' О
\ Г h ЗГ X 5Т i \ 4 /2 4 \ 4
3 x" = a = -xMco2 cos cot q" - -q^fi? cos cot О
1 Еч J «к Еч|е,
4 mco2x2 2 EK = „ snr cot A T2 2 L(0 Ям 9 ^магн 2 ОЙ Ем1 О
Т Г ЗТ т 5Т t 4 2 4 4
5 m<4x2 2 Ea = —2— coszcot zn0)2^M 2 Еэл = 2 cos2<of
Г Т ЗТ Т 5Т t 4 2 4 4
6 2 2 7ПСО Xu E = EK + Ea~ 2M mco2g2 E ~ ^эл. Дмагн “ 2 Е О
Г Т ЗТ 7» 5Т t 4 2 4 4
304
19. Классификация колебаний
Тип колебаний Каковы условия возникновения колебаний Чем определяется период колебаний Чем определяется амплитуда колебаний
Свободные Колебательная система (КС) при наличии первоначаль- ного запаса энергии Собственными парамет- рами КС. Т = 2л Т = 2nJ^;T = 2njLC Начальными условиями
Вынужденные Любая система при нали- чии внешнего, периоди- чески изменяющегося воздействия Частотой внешнего, периодически изменяю- щегося воздействия Амплитудой внешнего воз- действия, соотношением частот ^внешн “ vco6ctb> диссипативными потеря- ми энергии в КС
Автоколеба- ния Автоколебательная система (АКС) при наличии внеш- него источника энергии Собственными параметрами КС Параметрами АКС (ее нелинейностью)
Параметриче- ские Колебательная система (КС) при периодически изме- няющихся параметрах КС Собственными параметрами КС Соотношением частоты изменения параметров КС с ее собственной частотой
20. Классическая и релятивистская механика
Физические идеи, понятия, законы Классическая механика Релятивистская механика
Принцип относительности Во всех инерциальных системах отсчета механические явления протекают одинаково (при одинаковых начальных условиях) Во всех инерциальных системах от- счета все явления протекают одина- ково (при одинаковых начальных условиях)
Закон сложения скоростей V = Vq + v' Уо + V = , 1 + сг
Длина Абсолютна 1 = Iq 1 V2 Относительна 1 » Iq 1 —5 у с
Промежуток времени Абсолютен т = То Относителен т = И
Импульс р = mv -> mv Г г
302
Фиямна & mat/мшрлс,
20. Классическая и релятивистская механика
Физические идеи, понятия, законы Классическая механика Релятивистская механика
Второй закон Ньютона F = та F*ma
Энергия уединенного тела U — внутренняя энергия F- mcZ IS — 1— 2 >--2 N c 2 Приv«c E = me2 +
Кинетическая энергия тела 2 - 2 e E — Eq 2 При v « c EK=
21. Структура и содержание молекулярно-кинетической теории
303
22. Изопроцессы
304
tiztuta & таЛмицмс,
23. Структура и содержание термодинамики
305
бЩномнал программа, & тшГммцга, и,
306
iPuzuwi- & тащишь
____(/ ‘
26. Применение первого начала термодинамики
к различным газовым процессам
Название процесса Математи- ческое выражение процесса Измене- ние объема (ДП Получе- ние ко- личест- ва теп- лоты (Q) Совер- шение работы (А) Изме- нение внут- ренней энергии (АУ) Изме- нение темпе- ратуры (ДТ) Моляр- ная теплоем- кость МУ А UtJ Выражение первого начала термо- динамики Графики | зависимости < I P(V)
Адиа- батный р№ — const >0 0 >0 <0 <0 0 A'=AU pt \ 1 \ I i
<0 0 <0 >0 >0
0 V :
Изохор- ный - const 0 >0 0 >0 >0 СО 1СЧ Q=AU p I i
0 <0 0 < 0 <0 J
0 V
Изотер- миче- ский pV = const >0 >0 >0 0 0 оо Q =-А' p \ I
<0 <0 <0 0 0 i
0 V
Изобар- ный V у = const >0 >0 >0 >0 >0 0$ Ю1(М Q=EU+A' p —
<0 <0 <0 <0 <0
0 V
27. Идеальный газ
СТАТИСТИЧЕСКИЙ МЕТОД ТЕРМОДИНАМИЧЕСКИЙ МЕТОД
Газ — система микрочастиц Модель — идеальный газ Газ — макроскопическая система Модель — термодинамическая система
ОСНОВНЫЕ ВЕЛИЧИНЫ
Масса молекулы т
Концентрация молекул п
Средняя квадратичная скорость и
Средняя кинетическая энергия
молекул Е
Число молей v
Молярная масса М
Постоянная Больцмана k
Масса газа т
Давление р
Объем V
Температура Т
Плотность р
Внутренняя энергия U
Молярная теплоемкость С
Универсальная газовая постоянная R
СВЯЗЬ МЕЖДУ ОСНОВНЫМИ ВЕЛИЧИНАМИ
СТАТИСТИЧЕСКОЙ МЕХАНИКИ И ТЕРМОДИНАМИКИ
1 -*9 1 -*9 2 -= - m
р — q nmv = g pv = g nE - nkT
pV=vRT= ~RT
U= %vRT
Li
AU = |vJ?4T = |д(р7)
c7=|b,cp=|b,cp-cf=b
307
28. Симметрия при типизации кристаллических твердых тел
Тип кристалла Центры симметрии (частицы, образующие решетку) Силы взаимодействия в кристалле Основные свойства Примеры кристаллов
Молекуляр- ный Молекулы Ван-дер-Ваальса, диполь- дипольные, водородные связи Низкая температура плавления. Низкая твердость Нафталин
Металличе- ский Положительные ионы Электромагнитные между электронным газом и поло- жительными ионами) Высокая электро- и теплопроводность Металлы
Ковалент- ный Атомы или группы атомов Ковалентные связи Очень высокая темпера- тура плавления. Очень большая твердость Алмаз, кремний
Ионный Ионы (положитель- ные и отрицатель- ные) Электромагнитные (между ионами) Высокая температура плавления. Хрупкость Поварен- ная соль
29. Структура и содержание классической электродинамики
308
^fou^ufta &maJjuutfi'b
31. Сравнительные свойства гравитационного
и электростатического полей
Основные Виды полей
характеристики гравитационное электростатическое
Объекты взаимодействия Все тела и частицы Заряженные тела и частицы
Формула силы тлт9 R2 г2
Напряженность II Tty Трц I II ты
Разность потенциалов <р2 - <Pi = g(h2 ~ Л1) <р2-ф1=Я(<*2-<*1)
Работа по перемещению тела или заряда А = mg(h± - /г2) А = mgh А = g(<pi - ф2) A = qEd
Работа по замкнутой траектории 4 = 0 4 = 0
309
программа $ таЛмшрх, а фофмл^м'х,
32. Соединение элементов электрической цепи переменного тока
№ Схема эл( эктрической цепи Зависимость силы тока от частоты
1 О R —| | о I
0 со
2 о С —н ° I
0 со
3 о L -/VYY> о I
0 60
4 0 2 R н- I
0
5 R С ’ 11 > I
’ и
п
II
6 J ? L I
О 00
7 О ' L R I ( 11 _
) со
8 R L I /\ “0=7zF J I
0 С00 00
9 С L, R I <0°=7ьс°
। и
0 ' О>0 со
10 С1 о II С2 II j 1 mi = -/L(Ci+C2)
1Г <1 - Q
° II " т тэ
LZYYWJ 0 I COj (02 СО
340
'и^ияа & пик/лищгх,
33. Соединение элементов электрической цепи постоянного тока
№ Схема электрической цепи Закон Ома № Схема электрической цепи Закон Ома
1 Ь Д а и_аь 1 R 5 н-т R г
О I 1 - — -о R + пг
2 & t t г д^ t а , = Ugb 6 Z4 ! |g> г т ё-ца г
Д* + ° 1
3 R1 , Ugb 7 ё, Г
b о R2 а > о R^2 п< Г
Д^ + ^2
к- — — -И » _ г
4 -ч|^ R 1 R + г । н [£ п ? R + - п
34. Электромеханическая аналогия
Поступательное движение Вращательное движение Электромагнитные величины
Смещение х Угловое смещение а Заряд q
Скорость х' Угловая скорость а' Сила тока q'
Ускорение х" Угловое ускорение а" Скорость изменения тока q"
Масса гп Момент инерции I Индуктивность L
Жесткость при растяжении k Жесткость при кручении k Величина, обратная электроемкости х О л
СилаД Момент силы М Напряжение U
Коэффициент жидкого трения г Коэффициент жидкого трения г Сопротивление R
Импульс р = mv Момент импульса 1 со Поток магнитной индукции Li j
Работа dA = Fx'dt Работа dA = Ma'dt Работа dA = Uq'dt
Мощность Р = Fx' Мощность Р = Ма' Мощность Р = Uq'
Кинетическая энергия /2 Ек = ^~2" ,2 т/. та Кинетическая энергия I и п № Энергия магнитного поля L
Потенциальная энергия 2 ГТ ьа2 Потенциальная энергия я-у о Я2 Энергия электрического поля
Период свободных колебаний Т-2к^ Период свободных колебаний Период свободных колебаний T = 2nlLC
Волновое сопротивление р = Jkm Волновое сопротивление р = Jki Волновое сопротивление
311
35. Сопоставление электрических и магнитных полей
Электрические поля Магнитные поля
наименование формулы наименование формулы
Точечный заряд q Сила тока, элемент тока 1,1Ы
Взаимодействие зарядов. Закон Кулона г k = —— 4тсе0 Взаимодействие токов. Закон Ампера F = k г ь'=А К 2я
Электрическая постоянная е0 Магнитная постоянная Но
Силовая характеристика электрического поля — напряженность Ьэх II Силовая характеристика магнитного поля — индукция F В= ГТ,
Суперпозиция электрических полей Е = Ei + Е2 + ••• + Еп Суперпозиция магнитных полей В = Bi + В2 +... + вп
Линии напряженности Линии магнитной индукции
Поле точечного заряда, заряженной плоскости, плоского конденсатора 4ле0г Е= 2^S Е e0S Поле прямого тока, кольцевого тока, соленоида to to 7 и ” 5 0 ° = gh ah
Однородное электрическое поле Е = const Однородное магнитное поле В = const
Сила, действующая на точечный заряд F = Eq Сила, действующая на элемент тока. Сила, действующая на движущийся заряд F = BI&l sin a F = | q |uB sin a
Электроемкость конденсатора ъ II qi^ Индуктивность катушки II
Энергия заряженного конденсатора ™ 2 Энергия катушки с током T Г2 W= — 2
Диэлектрическая проницаемость 00 II Магнитная проницаемость II =L
312
36. Силы электромагнитной природы
Название силы Что описывает сила Математическое выражение силы Направление силы
Фундаментальные силы Сила Кулона (электростатиче- ская) Электростатическое взаимодействие элект- рических зарядов м. ыц 4ле0ег
Электрическая сила Действие электриче- ского поля на точечный электрический заряд F = qE A n Л I о
Сила Лоренца Действие магнитного поля на движущийся электрический заряд Fji = l^lBv sin a • •••••• • •••••• s • • J • •v • • • • • • • • •
Сила Ампера Действие магнитного поля на проводник с током Fa = BIl sin a X X X X X X X Fa X X X XI X X X I 5 X X X X| X X X X X X X X I X X
Молекулярные силы Сила упругости Взаимодействие деформированных тел = -kx j—„о
Сила трения Взаимодействие трущихся тел F^ = ]iN V
Сила поверхност- ного натяжения Взаимодействие молекул на границе среды F = al Направлена по касатель- ной к поверхности, пер- пендикулярно к линиям, ограничивающим поверх- ность
313
^Школьная программа & пии/лиирх и
формулах
37. Электрический ток в средах
Среда Носители зарядов Основные законы Вольт-амперные характеристики Технические применения
Металлы Свободные электроны / = -=;/ = nevS 1b р = р0(1 + аг) I 0 У 1| Z_ и nlz U Электротехника
const p=po(l + af)
Электро- литы i I Положитель- ные и отрица- тельные ионы , т. 1 мт. тп = kit = It NAe п т u~v V 1 = г ,гдеУ — потенциал поляри- зации электрода I 0 V и Гальванопластика, рафи- нирование металлов, электрометаллургия, полировка, травление
! \ I 1азы j ! < Электроны, по- ложительные и отрицательные ионы 2 qEI=^~ >WK 1и зависит от интенсивности ионизатора I 1Н Тлеющий разряд: реклам- ные трубки, люминесцент- ные лампы. Искра: искр, обработка материалов. Дуга: сварка, резка, плавка. Коронный разряд: очистка газов от примесей
0 и
Вакуум i Любые заряжен- ные частицы, индуктируемые в вакуум (чаще электроны) 2 2 х/1вых Г Выпрямители, усилители, генераторы, электронно-лучевые трубки (осциллографы, телевизоры)
0 и
Полупро- водники Свободные элек- троны, свя- занные электро- ны (дырки) 1 = 1э+1я I J Электроника
—6 р — п и и переход
314
SPufyiuca & та/мцах
38. Электроэнергетика
39. Шкала электромагнитных излучений
Частота V, ГЦ Длина волны 1, м Название диапазона Основные методы генерации Методы фиксации и область применения
до 103 более 3 • 104 Низкочастотные колебания Генераторы перемен- ного тока Электротехнические (электротехника)
103 3-105 Радиоволны Генераторы радиочастот Генераторы СВЧ Радиотехнические (радио- техника: телевидение, ра- диосвязь, радиолокация)
1012 3 ♦ 10"3 Инфракрасное излучение Излучение молекул и атомов при тепловых и электрических воздей- ствиях Тепловые и фотографиче- ские (теплицы)
3,8 • 1014 8•10-7 Видимый свет Глаз Фотографические Фотоэлектрические (жизнь на Земле)
7,5 -1014 4•10“7 Ультрафиолето- вое излучение и мягкое рентгенов- ское излучение Излучение атомов при воздействии ускорен- ных электронов Фотографические Фотоэлектрические (меди- цина)
3-1017 10-9
3•1О20 КГ12 Рентгеновское и у-излучение Атомные процессы при воздействии ускоренных заряженных частиц Фотографические Ионизационные (медицина, металлургия)
ю23 3 • 10~15 у-излучение Ядерные процессы Радиоактивный распад Космические процессы Ионизационные (метод меченых атомов)
315
бЩкоммал программа, / таблицах и, формулах
40. Волновая оптика
Явление Определение Теория, объясняющая явление Проявления в природе. Использование в технике
Интерферен- ция света Сложение когерентных световых волн, при котором возникает ус- тойчивая во времени интерферен- ционная картина максимумов и минимумов освещенности. Условия когерентности: (Vi = v2> Д(р = (pi - (р2 = const) Волновая теория Гюйгенса — Френеля. Электромагнитная теория Максвелла Радужные цвета тонких пленок. Просветление оптики. Интерферометры. Метрология. Контроль качества поли- рованных и шлифован- ных поверхностей
Дифракция света Огибание светом препятствий, отклонение от прямолинейного распространения. Условие наблю- дения: d - jVk. В лабораторных условиях: Волновая теория Гюйгенса — Френеля. Электромагнитная теория Максвелла Гало. Дифракционная решет- ка как спектральный прибор. Голография
Дисперсия света Аномальная дисперсия Зависимость скорости света в ве- ществе от частоты волны. Зависимость показателя прелом- ления от частоты световой волны. Резонансное поглощение света Электронная теория Лоренца Радуга. Спектроскоп. Спектральный анализ
Поляриза- ция света Выделение из естественного света свободных колебаний с определен- ным направлением вектора напря- женности электрического поля Е Электромагнитная теория Максвелла. Теория анизотропи- ческих свойств кристаллов Поляроиды. Поляриметры — опре- деление концентрации сахара, органических кислот в растворах
Эффект Доплера Изменение воспринимаемой час- тоты колебаний, обусловленное относительным движением наблю- дателя и источника световых волн Электромагнитная теория Максвелла. Специальная теория относительности Определение величины и направления движения автомобилей и самолетов, а также скорости планет и звезд в астрономии
Эффект Че- ренкова — Вавилова Излучение света электронами, дви- жущимися со скоростью, превы- шающей скорость света в среде Волновая теория Гюйгенса — Френеля. Электромагнитная теория Максвелла Счетчики Черенкова. Определение скорости заряженных частиц в ядерной физике
316
41. Квантовая оптика
Явление Определение Основные закономерности Теория, объясняющая явление Использование явления в науке и технике
Тепловое излучение абсолютно черного тела Явление излучения энергии нагретыми телами Закон Стефана — Больцмана R = оТ4 Закон смещения Вина ^max = j’ Распределение энергии излучения по длинам волн Квантовая гипотеза Планка Доказательство квантовой природы света при его излучении
Фото- эффект (внешний) Явление вырывания связанных электро- нов из твердых и жидких тел под дей- ствием света 1нас интенсивности света vMax определяется v Красная граница фотоэффекта. Безинерционность фотоэффекта Уравнение Эйнштейна , . , mv2 hv=A + л Доказательство квантовой природы света при его поглощении Фотоэлементы
Люминес- ценция Излучение световой энергии при облуче- нии вещества види- мым светом, рентге- новским или у-излу- чением Правило Стокса > ^ист Антистоксовое свечение < ^ист Учет энергии фотонов Avл = AvH - ДЕ Av л = AvH 4- ДЕ Лампы дневного света. Экраны телевизо- ров, осцилло- графов, мониторов ЭВМ. Анализ состава ве- щества
Химиче- ские действия света Возникновение или ускорение химиче- ских реакций под действием света Граница фотохимиче- ских реакций Av > Едисс Теория цепных реакций (Н. Н. Семенов) Фотосинтез. Фотография
Световое давление Возникновение светового давления на вещество Опыты Лебедева. Формула Максвелла Р = (1 + Л)<ос Учет импульса фотонов р = (1 4-Д)пА^ Отклонение комет- ных хвостов от Солнца
Эффект Комптона Рассеяние рентгенов- ского излучения сво- бодными электронами \)асс > Ч Уравнение Комп- тона — Дебая .. 2Й • 2© ДХ= — sm тс z Доказательство су- ществования фото- нов и наличия у них энергии и импульса
Флуктуа- ция фото- нов Систематические от- клонения от сред- него значения числа фотонов Опыт Боте. Опыт Иоффе— Добронравова Формула Эйн- штейна для флук- туации плотности энергии излуче- ния абсолютно черного тела и све- тового давления Доказательство квантовой природы света при его распростране- нии
317
калькам 'nfioifiaM.AUi и формулах
42. Строение атома
Энергетические диаграммы
Спонтанное излучение
Вынужденное излучение
А. Эйнштейн (1916)
~n \rfhvrin ftvwXl
___________________________
Е,-------------------------
Eq...— ©“"Оюе .....
-ЛЛЛ— АЛА—/iv
•АЛТ— ада—Av
Av — Е2~Е\
£1--------------------
Shti' tuta, $ тш/мщах
43. Физика атомного ядра
44. Модели строения ядра
Название Год Автор Состав ядра Что объясняет Трудности модели
Протонно- электрон- ная ДО 1932 М. Кюри Ядро состоит из протонов и электронов (^ = А, Ne = A-Z) Массу и заряд ядра Устойчивость ядра Спиновая азотная катаст- рофа XjN (спин ядра це- лый, а составляющих его 14 протонов и 7 электро- нов — полуцелый)
Протонно- нейтрон- ная 1932 Д. Д. Иваненко В. Гейзенберг Ядро состоит из протонов и нейтронов (Np-Z, Nn=A-Z) Массу и заряд ядра Существование изотопов Нет строгой теории ядерных сил
Капель- ная модель 1936 Я. И. Френкель Н. Бор Ядро представ- ляет собой шаро- образную каплю сверхплотной, заряженной жидкости Насыщение ядер- ных сил Механизм деле- ния ядра Энергию связи Устойчивость ядра Заряженная жидкость подчиняется законам квантовой физики
319
бЩномжая п^гсг!гамма & тхи/лицах и, фо^гмумх,
45. Классификация частиц
Наименование частиц Символ Масса Спин в еди- ницах h Электрический заряд в элементарных зарядах е Время жизни, с
час- тицы анти-час- тицы в массах электрона те в МэВ
Фотон V 0 0 1 0 Стабилен
Лептоны Электронное нейтрино ve ПН пт Ve vt 0 0 0 0 0 0 1/2 1/2 1/2 0 0 0 Стабильно
Мюонное нейтрино Стабильно
Тау-нейтрино Стабильно
Электрон е- Ц- т- е+ Ц+ т+ 1 207 3492 0,511 105,66 1782 1/2 1/2 1/2 -1 1 -1 1 -1 1 Стабилен
Мюон 2,2 • 10~6
Тау-лептон 1,46 • 10-12
Адроны Мезоны Пи-мезоны р° п+ п- 264,1 273,1 134,96 139,57 0 0 0 1 -1 1,83 • 10"16 2,6 • 10~8
Ка-мезоны К+ К° 1 о 966,4 974,1 493,67 437,7 0 0 1 -1 0 1 1 их 00 ь* ьэ о ® • • 00 >-* »-* о о 00 £
Эта-нуль- мезон П Т| 1074 548,8 0 0 2,4 • 10-19
Нуклон Протон Нейтрон р п р п 1836,1 1838,6 933,28 939,57 1/2 1/2 1 -1 0 Стабилен(?) 103
Гипероны Лямбда- гиперон А° А° 2183,1 1115,6 1/2 0 2,63 • Ю-10
Сигма- гипероны МММ 1 о + М« М> 1 О 1 2327,6 2333,6 2343,1 1189,4 1192,5 1197,4 1/2 1/2 1/2 1 -1 0 -1 1 8 • 10-11 5,8 • 10-2° 1,48 • 1О~10
Кси-гипероны О 1 [I] [I] [III [1)1 1 о 2572,8 2585,6 1314,9 1321,3 1/2 1/2 0 -1 1 2,9 • Ю"10 1,64 • Ю"10
Омега-минус- гиперон 3273 1672,2 3/2 -1 1 8,2 • 10-11
320
^Ри^нка 6
ти/ла«,ал
47. Характеристики кварков
Наименование Кварки Антнкварки
Символ Спин в единицах Я Электрический заряд в элементарных зарядах Барионный заряд и с t 1/2 2/3 1/3 d s Ь 1/2 -1/3 1/3 й с t 1/2 -2/3 -1/3 d § b 1/2 1/3 -1/3
48. Построение мезонов и барионов
Мезоны Барионы
частица состав частица состав частица состав
л+ ud p uud L" dds
п~ ud p uud L" dcTs
п° (ий - dd) n udd S° USS
„0 П (ии + dd- 2ss) л/6 n udd
US Л0 [ud]s =0 USS
к~ US Л0 [ucZ]s uu dss
к° ds E+ uus dss
о ds + © О uus [u2]s [u2]s 1 1 sss sss
11 — 1323
321
^Шкальная п^юграл^.им
6 таблицах а формулах,
49. Взаимодействия в природе
Вид взаимо- действия Квант поля Радиус действия Относительная интенсивность Участвуют во взаимо- действии Зависимость Е (В) Проявление
Ядерное (сильное) Пионы и каоны КГ15 м 1 Тяжелые частицы (нуклоны) Экспонента наЖ1(Г15, далее — нуль Устойчивость атомных ядер
Электро- магнитное Фотоны оо 1/137 Заряженные частицы и фотоны _ 1 R Устойчивость атомов, моле- кул, макротел
Слабое Бозоны 10-13 м кг10 Все частицы, кроме фотона (и гравитона) Неизвестна Нестабильность элементарных частиц
Гравитаци- онное Гравитоны (гипотеза) ОО 10“33 Все тела и частицы 1 Устойчивость звезд, планет- ных систем
50. Эволюция взгляда на физическую картину мира
Физическая картина мира (ФКМ) Примерное время существования Ученые, внесшие наибольший вклад в развитие ФКМ Основные законы, теории, принципы
Механическая XVI—XVIII вв. Демокрит, Галилей, Декарт, Ньютон Принцип относительности; законы ди- намики; закон всемирного тяготения; законы сохранения
Электроди- намическая XIX — начало XX в. Фарадей, Максвелл, Эйнштейн Закон Кулона; закон электромагнит- ной индукции; уравнения Максвелла; специальная теория относительности
Квантово- полевая Начало XX — середина XX в. Планк, Эйнштейн, Бор, Резерфорд, де Бройль, Гейзенберг, Шредингер Гипотеза Планка; идеи Эйнштейна; постулаты Бора; корпускулярно- волновой дуализм
322
'иммьа, & тси/лшукх,
51. Расстояния в природе и размеры тел
Расстояния Численное значение, л:
Расстояние от Земли до самого далекого объекта во Вселенной, обнару- женного к настоящему времени ю26
Расстояние до ближайшей соседней звездной системы — галактики в со- звездии Андромеды 2•1022
Диаметр звездной системы — галактики, в которую входит Солнце 1021
Расстояние от Земли до ближайшей соседней звезды в созвездии Центавра 4•1016
Расстояние от Земли до Солнца 1,5 • 1011
Диаметр Солнца 1,4 109
Расстояние от Земли до Луны 3,8 • 108
Диаметр Земли 1,3- 107
Длина Нила — самой протяженной реки в мире 6,7 • 106
Самая глубокая впадина на поверхности Земли 1,1 104
Самая высокая гора на поверхности Земли 8,9 • 103
Высота эвкалиптов — самых высоких деревьев до 150
Длина самого большого животного на Земле — синего кита 33
Мировой рекорд по прыжкам в длину 8,9
Рост самого высокого человека 2,85
Размеры амебы 5 • 10-4
Толщина человеческого волоса 10"4
Диаметр красного кровяного шарика 10'5
Диаметр вируса гриппа 8 • 10"8
Длина молекулы гемоглобина 1,5 • 10"8
Расстояние между атомами в твердом теле 1О“10
Диаметр ядра атома урана 10'14
Диаметр протона 1,6 • 10~15
Минимальные размеры областей внутри элементарных частиц, доступных экспериментальному изучению с помощью современных ускорителей IO"17
323
^Школьная пфогфамям $тш/лища/х, а, формула.
52. Длительность процессов в природе
Длительность процессов Численное значение, с Длительность процессов Численное значение, с
Возраст Солнца и Земли Время существования жизни на Земле 238 Период полураспада 92 U Возраст каменного угля Период обращения Солнца вокруг центра звездной системы — Галактики Время, прошедшее после вымирания динозавров Возраст человека как вида Время, прошедшее после последнего оледенения Земли Средняя продолжительность жизни человека Период обращения Земли вокруг Солнца (год) £ 2!2 2 2 о ь. 1-ЧгНтчО О О О i-ч zi ±4 О О гН гН . . . 00 CD cq CD 03 00 г-н cq Период обращения Земли вокруг своей оси (сутки) Время жизни свободного нейтрона Время, за которое свет проходит расстояние от Солнца до Земли Промежуток времени между двумя ударами сердца человека Минимальный интервал времени между событиями, которые чело- веческий глаз может восприни- мать раздельно Время одного взмаха крыла ко- либри Время одного взмаха крыла комара Время, в течение которого атом излучает свет Время жизни короткоживущих элементарных частиц 8,64 • 104 103 5 • 102 1 10-1 10~2 10-3 10“9 5 • 10"24
53. Скорости в природе и технике
Скорости Численное значение, лс/с Скорости Численное значение, м/с
Скорость света Скорость движения самых далеких галактик Скорость электронов в кине- скопе телевизора Скорость движения Солнца по орбите вокруг центра Галактики Скорость движения Земли по орбите вокруг Солнца Третья космическая скорость Вторая космическая скорость Первая космическая скорость Скорость движения Луны по орбите вокруг Земли Максимальная скорость пасса- жирского реактивного самолета ЗЮ8 1,4 • 108 108 2,3 105 ЗЮ4 1,7 • 104 1,1 • 104 7,9 • 103 103 7 • 102 Средняя скорость движения моле- кулы азота при температуре 0 °C Максимальная скорость автомобиля Максимальная скорость локомотива на железной дороге Максимальная скорость полета сокола Максимальная скорость гепарда Рекорд скорости человека в беге на дистанции 100 м Рекорд скорости человека в марафонском беге Рекорд скорости человека в ходьбе на 50 км Рекорд скорости человека в плавании на 100 м Скорость черепахи Скорость улитки 5 • 102 5 • 102 102 102 3,1 • 101 101 5,5 3,4 2 5 • 10~2 1,4 • ЦТ3
324
Фишю / maJjuutfbx
54. Массы объектов природы и техники
Объекты природы и техники Численное значение, кг Объекты природы и техники Численное значение, кг
Вселенная ю53 Космическая станция 104
Наша Галактика 2,2 • 1041 Автомобиль 103
Солнце 2 • Ю30 Человек 102
Земля 6•1024 Колибри (самая маленькая птица) 10"3
Луна 7,4 • 1022 Капля воды 10'5
Атмосфера Земли 5•1018 Муха 10“6
Плотина Братской ГЭС 1О10 Снежинка 10'7
Пирамида Хеопса 6-109 Бактериальная клетка 5 • 10-12
Главное здание МГУ 5 • 108 Молекула пенициллина 10~17
Останкинская телевизионная башня 5,5 107 Молекула воды 3 • 1О"20
Синхрофазотрон 107 Вирус гриппа 6 • 10-19
Ракета 106 Ядро урана 4 • 1О“20
Самый большой из китов 1,5 • 105 Атом водорода 1,7 • 10-27
Самолет 105 Электрон 9,1 • 10~31
55. Громкость звука в природе и технике
Объекты природы и техники Интенсив- ность звука, Bm/j^ Уровень звукового давления, Дб Объекты природы и техники Интенсив- ность звука, Вт/я? Уровень звукового давления, Дб
Реактивный двигатель 100 130 Машбюро. Громкий разговор 10"6 60
Сильные раскаты грома 10 120 Слабая работа радиоприемника 10“7 50
Пневматический молоток 10"1 110 Разговор вполголоса 10"8 40
Кабина самолета 10“2 100 Читальный зал библиотеки 10"9 30
Вагон метрополитена 10~3 90 Тиканье карманных часов. Шепот 10“10 20
Шумная улица 10"4 80 Шорох листьев в лесу 10"11 10
Салон автомобиля. Вагон трамвая 10"5 70 Порог слышимости ю-12 0
325
ильная птюгпалблш & ?паалицах и
56. Силы в природе и технике
Объекты взаимодействия Численное значение, Н Объекты взаимодействия Численное значение, Н
Сила тяготения между Землей и Солнцем Сила тяготения между Землей и Луной Сила тяги космических ракет Сила давления при изготовлении искусственных алмазов Сила тяги тепловоза 00 а> о ° о о 01 ** © со со Сила удара футболиста по мячу Сила удара боксера Сила сжатия руки, сжимающей динамометр Сила притяжения электрона к ядру в атоме водорода Сила звукового давления у порога слышимости IN3 tso СП СЛ о о 5 о ° <о 00 м “
57. Энергия в природе и технике
Объекты природы и техники Численное значение, Дж Объекты природы и техники Численное значение, Дж
Метагалактика Взрыв сверхновой звезды Излучение Солнца за год Энергия, принимаемая Землей за год Сильное землетрясение Взрыв водородной бомбы Запуск ракеты 1054 1044 Ю-зз 1026 1О20 1018 1012 Удар молнии Потребление энергии человеком за сутки Смертельная доза рентгенов- ского излучения Частицы в ускорителе Фотон видимого света Электрон в атоме водорода Химическая связь __ „ Ю 2 2 0) 00 00 । । гН 2 2 2 ° 2 ® 2
58. Температура в природе и технике
Объекты природы и техники Численное значение, К Объекты п