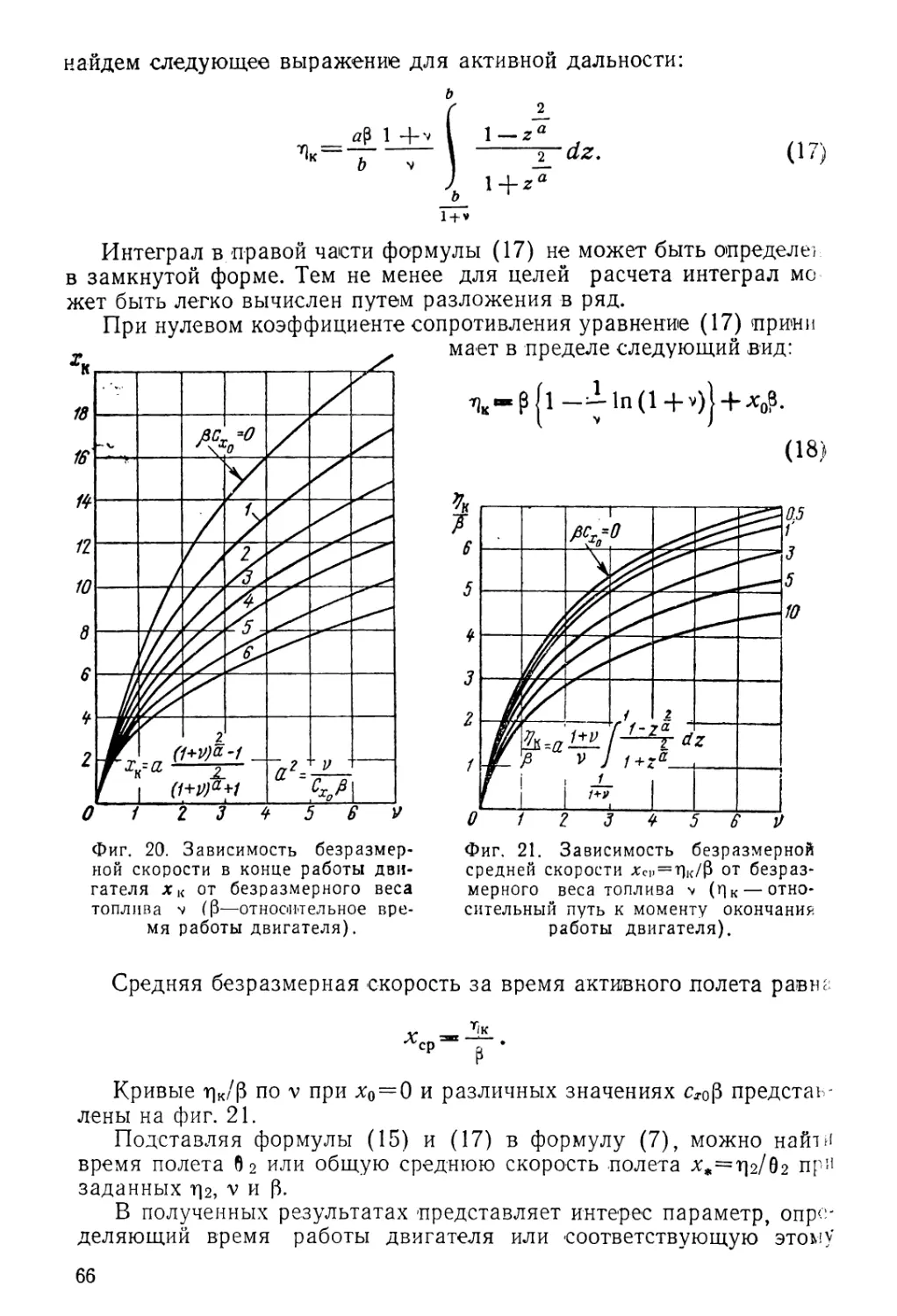
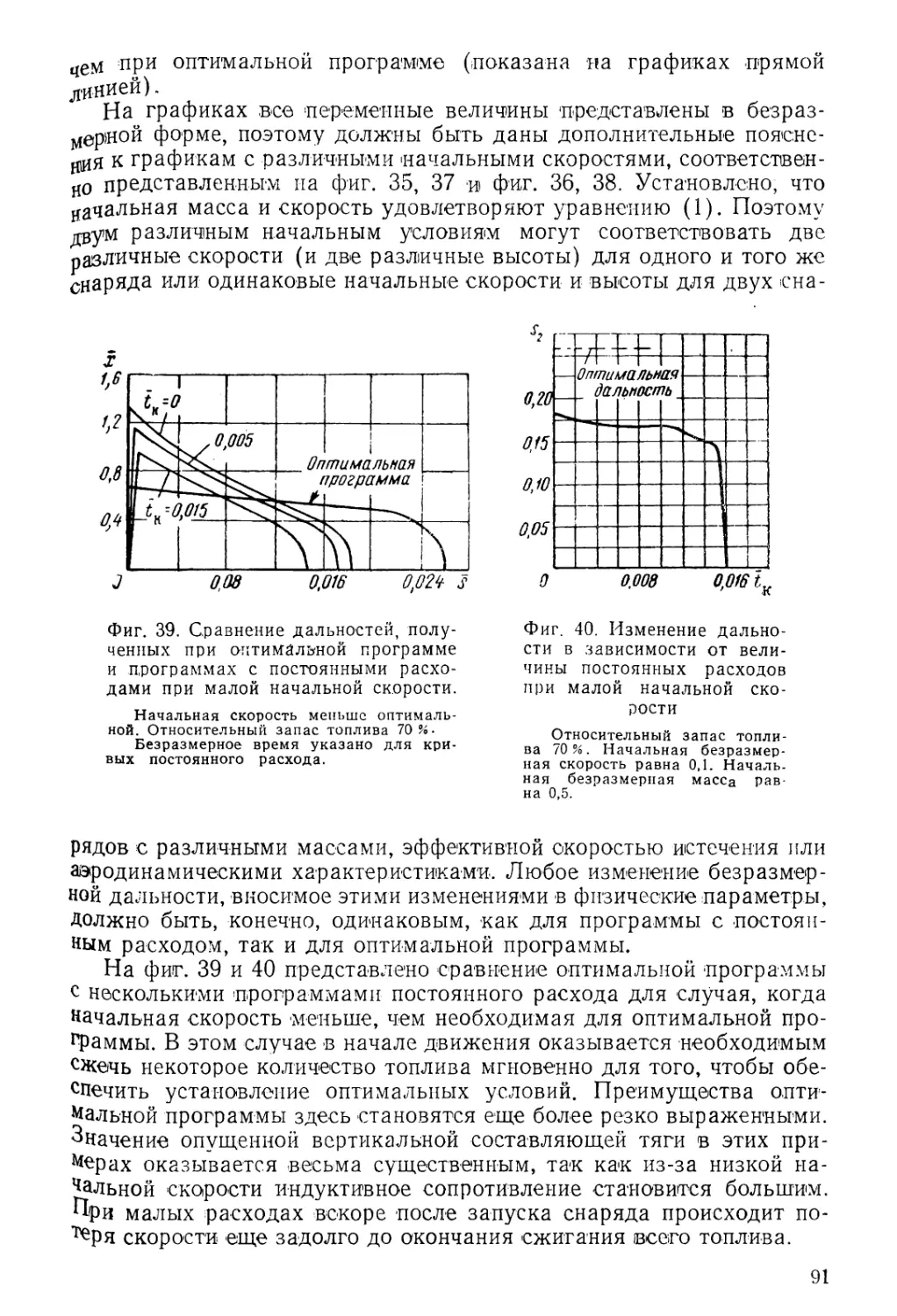
Author: Садовский И.Н.
Tags: ракеты военная техника аэродинамика издательство машиностроение техника полета
Year: 1959
Text
ИССЛЕДОВАНИЕ
ОПТИМАЛЬНЫХ
РЕЖИМОВ
ДВИЖЕНИЯ
РАКЕТ
Ч
ОБО РО НГИЗ • 1959
ИССЛЕДОВАНИЕ
ОПТИМАЛЬНЫХ РЕЖИМОВ
ДВИЖЕНИЯ РАКЕТ
СБОРНИК ПЕРЕВОДОВ
ИНОСТРАННЫХ СТАТЕЙ
Под редакцией
канд. техн. наук И. Н. Садовского
ГОСУДАРСТВЕННОЕ
ИЗДАТЕЛЬСТВО ОБОРОННОЙ ПРОМЫШЛЕННОСТИ
Москва 1959
Книга представляет собой сборник переводов иностранных
статей, посвященных решению задач по определению оптималь¬
ных законов изменения тяги двигателей ракет и ракетных са¬
молетов, оптимальных траекторий набора высоты ракетным
самолетом-перехватчиком, оптимальных соотношений ступеней
составных баллистических ракет и другим вопросам выбора
проектных параметров и соотношений для ракет и ракетных
самолетов.
Книга предназначается для работников научно-исследова¬
тельских институтов и конструкторских бюро, а также препода¬
вателей, аспирантов и студентоз высших учебных заведений,
интересующихся баллистическим проектированием и расчетом
проектных параметров современных ракетных летательных
аппаратов.
Редактор инж. Е. В. Латынин
Зав. редакцией инж. А. И. Соколов
ОТ РЕДАКТОРА
Непрерывное совершенствование авиационной и ракетной техни¬
ки стало возможным в результате беспрерывно ведущихся теорети¬
ческих, экспериментально-исследовательских и конструкторских ра-
Авторские исправления
Стр.
Строка
Напечатано
Должно быть
7
14 снизу
dMx
dt lr
dt
53
8 и 12 сверху
отсасывания
отбрасывания
81
10 сверху
dM/dt ==—7Й
dM!dt= — М
99
102 и
8 и 9 снизу
уравнения (13)
Ф
\\'
103
106
и (15)
15 сверху
[10]
(10)
112
4 сверху
Mimino
Mini ню
189
G снизу
pit)
p(t)
189
5 снизу
т
\ р
232
уравнение (3)
Uy — ■■■ ийу
1
\ «1°
i
Заказ № 394/1655
ся невозможным получить строго экстремальные решения,
поэтому при такого рода исследованиях речь идет об отыскании
некоторых оптимальных характеристик при некоторых идеализиро¬
ванных предпосылках. Изучение таких оптимальных решений по¬
зволяет выделить классы типовых наилучших траекторий, наивы¬
годнейших законов изменения массы, наивыгоднейшего деления со¬
ставной ракеты на ступени и другие характеристики, с которыми и
3
целесообразно сравнивать реально получаемые характеристики
создаваемых промышленностью объектов.
В настоящее время установлено, что 'наиболее адекватным физи¬
ческой сущности этого класса задач является математический аппа¬
рат вариационного исчисления.
За последние 4—5 лет за рубежом были опубликованы интерес¬
ные статьи по исследованию различных оптимальных режимов ме¬
тодами вариационного исчисления.
Наша Родина, давшая миру таких ученых, как И. В. Мещерский
и К. Э. Циолковский, является родиной теоретических основ совре¬
менной ракетной техники и астронавтики и первой в мире страной,
создавшей и осуществившей запуски трех искусственных спутников
Земли большого веса и искусственной, вращающейся вокруг Солн¬
ца планеты.
Достигнутые нашей страной успехи в области ракетной техники
демонстрируют прежде всего превосходство социалистической си¬
стемы над капиталистической, ибо даже такая высокоразвитая в
техническом отношении страна, как США, не смогла первой создать
межконтинентальную баллистическую ракету и первой осуществить
запуск искусственного спутника Земли.
Советские искусственные спутники и искусственная планета —
это часть целой системы технических решений, ставших возможными
благодаря плодотворной деятельности многих замечательных рус¬
ских ученых.
Значительное место в русской науке отведено общетеоретиче¬
ским основам ракетной техники — механике тела переменной массы
и ракетодинамике. Некоторые фундаментальные труды в этих об¬
ластях, написанные русскими учеными еще в конце прошлого сто¬
летия, широко известны во многих странах мира, хотя во многих
работах иностранных авторов и делались попытки замалчивать или
приуменьшать роль русских ученых, основателей теории движения
ракет.
Начало 'механики тел переменной массы можно датировать появ¬
лением замечательной работы профессора Петербургского универ¬
ситета И. В. Мещерского «Динамика точки переменной массы», из¬
данной в Петербурге в 1897 г. 1
И. В. Мещерский впервые вывел общее уравнение движения точ¬
ки переменной массы, считая процесс изменения массы совершаю¬
щимся с течением времени непрерывно.
Уравнение Мещерского в векторной форме имеет вид
я / d*u гл . db/]i / \
М — = F Н (и — v),
dt dt у }
где M(t) —масса движущейся точки в данный момент времени;
v — ее скорость по отношению к некоторой неподвижной си¬
стеме осей координат;
1 И. В. Мещерский, Работы по механике тел переменной массы, Гостех-
издат, 1952.
4
F — равнодействующая всех внешних сил, приложенных к
точке;
и — абсолютная скорость отбрасываемых точкой частиц.
Разность (и—v) представляет собой относительную скорость от¬
брасываемых точкой частиц, а (и—v) dM/dt — реактивную силу,
обусловленную процессом отделения частиц.
Уравнение Мещерского и до настоящего времени является исход¬
ным при решении различного рода задач динамики точки переменной
массы.
В 1903 г. знаменитым русским ученым К. Э. Циолковским в жур¬
нале «Научное обозрение» была опубликована работа «Ракета в ко¬
смическое пространство», в которой в результате решения так на¬
зываемой первой задачи была впервые получена формула, опреде¬
ляющая скорость полета ракеты в безвоздушном пространстве:
*>('+t)-
где V,- — скорость истечения газов из сопла ракетного двигателя;
Мт — масса топлива на борту ракеты перед стартом;
Мк — масса ракеты после окончания работы двигателя. 1
Используя эту формулу, Циолковский исследовал движение в
.пространстве, где нет сопротивляющейся полету среды, и показал,
что ракета может получить космические скорости, если только запас
топлива достаточно велик по сравнению с массой корпуса ракеты.
Выведенная им формула получила мировую известность и сейчас
является фундаментальным основанием для расчета ракет всех
классов.
Так называемая вторая задача Циолковского об определении)
закона изменения скорости и расстояния в функции времени для
точки переменной массы, движущейся вертикально й однородном поле
силы тяжести, без учета силы сопротивления среды, дает отправные
идеи для постановки ряда конкретных экстремальных задач в ра¬
кетной технике. Согласно выводам, следующим из второй задачи
Циолковского, для достижения возможно больших высот подъема
ракеты, при указанных выше условиях и при постоянной скорости
истечения струи газов из ракетного двигателя Vr, выгоднее возмож¬
но быстрее сжигать располагаемый на ракете запас топлива. Легко
установить, что если поставить задачу об отыскании условий, при
которых только активный участок полета был бы наибольшим, то
оказывается, что, .при ^о = 0 и Vr = const необходимо сжигать топливо
таким образом, чтобы ускорение ракеты, сообщаемое ей реактивной
силой, было бы ровно в два раза больше ускорения силы тяжести.
Известно также, что при мгновенном сгорании и отбрасывании
продуктов сгорания всего запасенного количества топлива высота
подъема должна быть в два раза больше, чем при медленном сжи-
1 К- Э. Циолковский, Труды по ракетной технике, Оборонгиз, 1947.
5
га-нии, когда обеспечивается максимальная протяженность активно¬
го участка.
В задачах исследования режимов движения реальных ракет ука¬
занные два случая решения, вытекающие из второй задачи Циолков¬
ского, представляют лишь теоретический интерес в связи с наличием
в реальных условиях атмосферной среды, оказывающей сопротивле¬
ние полету, а также вследствие невозможности осуществить мгновен¬
ное сжигание больших количеств топлива. Очевидно, что при увели¬
чении секундных расходов массы необходимо считаться с увеличе¬
нием размеров и веса двигателя, что в свою очередь при данном весе
ракеты должно снижать запас топлива на борту ракеты и, следо¬
вательно, высоту подъема. С другой стороны, даже практически осу¬
ществимое быстрое сжигание топлива на практике может оказаться
невыгодным, так как может приводить к быстрому нарастанию ско¬
рости ракеты в плотных слоях атмосферы у Земли, в связи с чем
значительная часть энергии расходуемого топлива будет тратиться
не на дальнейшее увеличение скорости полета, а на преодоление со¬
противления среды.
Следовательно, оптимальные режимы движения ракет должны
определяться с учетом сил сопротивления среды и весовых и энерге¬
тических характеристик ракеты и в первую очередь ее двигательной
установки.
В начале двадцатых годов некоторые иностранные авторы
(Р. Годдард, Г. Оберт) пытались решить простейшие экстремаль¬
ные задачи такого рода.
Метод решения задачи Годдарда был мало убедительным, так
как он привел лишь качественные доводы о существовании наивы-
годиейшего режима набора высоты. Обертом приближенно решалась
другая задача об оптимальном режиме набора высоты в предполо¬
жении, что в каждый момент времени масса ракеты и плотность воз¬
духа постоянны. Оберт показал, что наивыгоднейшая скорость по¬
лета при квадратичном законе сопротивлений должна быть такой,
чтобы в любой момент движения имело место равенство силы со¬
противления и силы тяжести.
Решение Оберта позволяет выявить некоторые свойства опти¬
мальных движений точки переменной массы, однако, как показал
профессор Московского государственного университета А. А. Космо¬
демьянский, рассуждения и выводы Оберта имеют только прибли¬
женный характер.1
Попытка решить задачу об оптимальном режиме вертикального
подъема точки переменной массы более точно была сделана немец¬
ким ученым Г. Гамелем при помощи методов вариационного исчи¬
сления при упрощающих допущениях об экспоненциальном законе
изменения плотности воздуха с высотой и постоянстве скорости исте¬
чения газов из сопла двигателя Vr и ускорения силы тяжести g. Хотя
принятые Гамелем допущения не вызывают принципиальных возра¬
жений, по крайней мере при решении задач, связанных с ракетами,
1 А. А. Космодемьянский, Механика тел переменной массы. Изда¬
тельство ВВИА им. Н. Е. Жуковского, 1946.
6
летающими на относительно низких высотах, его решение не полу¬
чило развития и применения. Последовательное изложение теории
механики тела переменной массы дано в работах проф. А. А. Космо¬
демьянского. Им было доказано, что точное решение задачи об
оптимальном режиме движения точки переменной массы, при кото¬
ром она набирает максимальную высоту, имея заданный запас
массы, можно получить строгими методами вариационного исчис¬
ления.1
В его работах по механике тел переменной массы приводятся
последовательные исследования оптимальных режимов движения
ракеты при линейном и показательном законах изменения массы.
Дается систематическое применение методов вариационного исчи¬
сления к определению наивыгоднейших режимов работы ракетного
двигателя, а также ставится и исследуется задача о наивыгоднейшем
режиме набора высоты и о режиме, определяющем минимальное
время полета в заданную точку пространства.
Задача об оптимальном режиме прямолинейного движения точки
переменной массы с одновременным присоединением и отделением
частиц (т. е. при более общих условиях, чем в случае ЖРД) решается
следующим образом.2
Пусть плотность среды постоянна и в начальный момент t — U
точка имеет скорость v0. Движение происходит в однородном поле
силы тяжести под углом 0 к горизонту. Допустим, что
dM 1 q dM2
dt ~Х dt ’
где р — постоянный коэффициент, характеризующий увеличение
массы отбрасываемых частиц cLM\ по сравнению с массой присоеди¬
няющихся частиц dM2.
Уравнение Мещерского для этого случая движения будет иметь
вид
М— = — Mg*sin0 — Qj(^) — vr—— v).
dt * XIV / dt r dt \ 2 /
Здесь Qi(^) —сила лобового сопротивления в данный момент
времени.
Принимая абсолютную скорость присоединяющихся частиц и2
равной нулю и имея в виду принятое выше условие, получаем
Пусть Mi = M0f, где f=f(t) —монотонно убывающая функция
времени, характеризующая закон отделения частиц, обладающая та¬
ким свойством, что / (0) = 1, тогда
М = М0/+±М0(1-/) = М0(а/ + Ь).
1 А. А. Космодемьянский, Механика тел переменной массы, Изда¬
тельство ВВИА им. Н. Е. Жуковского, 1946.
2 А. А. Космодемьянский, Лекции по механике тел переменной
массы. Ученые записки МГУ им. М. В. Ломоносова, «Механика», вып. 154, 1951.
7
Производя подстановку, обозначая
qg-1==g-sine
М0
и деля обе части уравнения на М0, имеем
(«/ + ^7=-(fl/ + %rQW-7(K- bv).
at at
Переходя к новым переменным
dv dv df dv df dv „
— = v—; — =v -~v— /.
dt ds dt ds dv ds
получаем
(af + b)v^-=—(af + b)gl — Q1 (v) — vf(Vr—bv) .
ds ds
Если в начальной точке траектории М = М0, v = v0 и относитель¬
ная масса /=1, а в конечной точке траектории v = vK, а относитель¬
ная масса / = fK, то пройденный путь будет выражаться следующим
интегралом:
__ Г Kaf-Ь Ь) 4-fv (vr — bv)] v dv
J (<*f+b)gi ■+ <?(v)
Исходя из этого соотношения можно сформулировать следующую
вариационную задачу.
Среди класса функций f = f(v) найти такую, которая дает макси¬
мальное значение интегралу 5 и удовлетворяет в концевых точках
следующим граничным условиям: при v = v0 относительная масса
f= 1 и при v = v\ относительная масса /=/к. Разумеется, необходимо
предположить, что функции f=f(v) удовлетворяют всем ограничени¬
ям, формулируемым в курсах вариационного исчисления для про¬
стейших задач на экстремум интегралов.
Сформулированная задача сводится к исследованию экстремума
интеграла 5.
Если обозначить
HI* Г -Л m+b)+/v(Vr-bv))y
(af+b)gx + Q( v)
то условие экстремума интеграла 5 будет записываться в виде
d дН дИ q
dv dfv dv
Производя дифференцирование, подстановки и упрощения, полу¬
чаем
Q [v (а + 26) - Vr] + bgx (2bv -Vr)-\--^- (vVr - bv2)
r ■ &V
“ agi (Vr - 2bv)
Это соотношение определяет ©ид функции f(v), ори которой ре¬
ализуется оптимальный режим движения точки переменной массы.
Оно показывает, что между массой точки, ее положением на траек¬
тории и скоростью движения существует вполне определенная зави¬
симость, если режим движения является оптимальным.
Зная f=f(v)y можно найти скорость v как функцию времени.
В самом деле, можно записать
(я/ + ь) = - (а/ + b)gl — Q(v) — ^~{Vr~bv).
at av at
Разрешая это уравнение относительно dt и беря интеграл, полу¬
чаем
{(af+b)+/v(Vr~-bv)]dv
(я/+ Ь) gi + Q (v)
V\
Так как функции / и f'v нам известны как рациональные функ¬
ции v, то этот интеграл можно свести к известным квадратурам и,
следовательно, получить некоторую зависимость вида
t = cp(u),
из которой можно найти скорость v для любого значения t, лежаще¬
го в интервале времени, соответствующего рассматриваемой задаче.
чпо а
f=f(v) и v=--v(t),
можно найти
/=/(*),
т. е. определить секундные расходы массы, обеспечивающие макси¬
мальный путь s. В частном случае, когда происходит только отделе¬
ние частиц, 6 = 0; а— 1, в результате чего получаем
дО
Q(v-Vr) + -f-vVr
т ^—.
Полученные уравнения экстремали могут быть использованы как
исходные для исследования движения ракеты и в неоднородной ат¬
мосфере, если принять достаточно простой закон убывания плотно¬
сти воздуха с высотой. Если задан показательный закон изменения
плотности и квадратичный закон сопротивления воздуха, вся задача
по отысканию оптимальных характеристик прямолинейного подъема
ракеты, как показал Космодемьянский, может быть сведена к квад¬
ратурам.
Задача о режиме, обеспечивающем минимальное время полета в
заданную точку при прямолинейном полете в однородном поле тяго¬
тения, формулируется как вариационная изопериметрическая задача.
Для тех же условий, что приведены выше, пройденный путь задан
положением начальной точки движения. Необходимо определить вид
9
•функции- f(v), при котором заданный путь s точка проходит в мини¬
мальное время. Математически задача сводится к исследованию
экстремума интеграла 5 при заданном интегральном условии
\(af+ b)+f'v(Vr — bv)]vdv
(af+b)gi + Q(v)
= const.
Для определения вида функции f(v) составляется дифференци¬
альное уравнение Эйлера
d дФ дФ ~
а неопределенный множитель Лагранжа %=const.
После дифференцирования, подстановки и преобразований полу¬
чаем экстремаль рассматриваемой изопериметрической задачи в сле¬
дующем виде:
Зная / как функцию скорости, можно найти закон изменения мас¬
сы как функцию времени, следуя методу, изложенному выше. Пара¬
метр Я -подбирается так, чтобы условия в концевых точках выпол¬
нялись.
И. В. Мещерский первый поставил и решил несколько простых
обратных задач в динамике точки переменной массы.
А. А. Космодемьянский рассмотрел общую обратную задачу пря¬
молинейного движения с учетом всех основных сил, а также обрат¬
ные задачи при естественном методе задания движения и так назы¬
ваемый полуобратный метод. Ему же принадлежат формулировки
основных теорем динамики тела переменной массы, теоремы о кине¬
тическом моменте и кинетической энергии и вывод основных урав¬
нений аналитической динамики тела переменной массы.1
В 1946 г. Д. Е. Охоцимским была также решена вариационная
задача о подъеме ракеты в атмосфере на максимальную высоту. Ре¬
шение было получено как для случая однородной, так и неоднород¬
ной атмосферы при g'=const и применительно к использованию зако¬
на сопротивления воздуха, заданного таблицами Сиаччи. Им же рас¬
сматривалась вариационная задача об оптимальном законе расходо¬
1 А. А. Космодемьянский, Основные теоремы механики тела пере¬
менной массы, Ученые записки МГУ им. М. В. Ломоносова, «Механика»,
вып. 152, 1951, а также работы, указанные выше.
dv dfv df
о,
где
(1 + \v) (Vr -bv)-f- + Q f (a + *)(!+ At>) - A (Vr - bv)]
b
agi sin 0 [A Vr — b (1 + 2Аг/)]
a
10
вания топлива и оптимальном угле бросания баллистической -ракеты
дальнего действия.1
В 1957 г. Д. Е. Охоцимским и Т. М. Энеевым опубликована рабо¬
та, содержащая решение некоторых вариационных задач, связанных
с запуском искусственного спутника Земли. Ими рассмотрены зада¬
чи об одновременном подборе как программы для -направления тяги,
так и режима расходования топлива, задача о подборе оптимальной
программы для многоступенчатого ускорителя с различным числом
ступеней в предположении, что режим расходования топлива яв¬
ляется заданным, а также проведено обобщение задачи о выведении
спутника на орбиту на случай движения в центральном поле тяго¬
тения с учетом вращения Земли.2
Большое число исследований по отдельным вопросам механики
тела переменной массы опубликовано в многочисленных периодиче¬
ских и непериодических изданиях различных научных учреждений и
учебных заведений. Число таких работ настолько велико, что состав¬
ление их достаточно полного перечня представляет большие труд¬
ности.
Несмотря, однако, на богатство отечественной литературы, совет¬
ский читатель заинтересован в ознакомлении о работами зарубежных
ученых в области исследования оптимальных режимов полета ракет
и определения различного рода оптимальных соотношений. Этой це¬
ли и служит настоящий сборник «Исследование оптимальных режи¬
мов движения ракет».
В сборнике собраны наиболее интересные работы, относящиеся к
этой теме и опубликованные в иностранной литературе за последнее
время.
В целях удобства статьи сгруппированы в четырех разделах, по¬
священных следующим четырем общим проблемам:
1. Оптимальные режимы вертикального подъема ракет-зондов.
2. Оптимальные режимы движения ракетных самолетов и само¬
летов-снарядов.
3. Оптимальное направление тяги и методы подбора ступеней
баллистических ракет.
4. Оптимальные режимы полета ракет в межпланетном простран¬
стве.
Выводы и заключения, формулированные авторами статей, вклю¬
ченных в сборник, в большинстве своем известны советскому чита¬
телю, однако сами методы подхода к решению различного рода
задач определения оптимальных режимов движения ракет и ракет¬
ных самолетов представляют несомненный интерес.
Некоторые же результаты, например, оптимальный закон измене¬
ния тяги ракеты при полете с набором высоты, программа быстрей¬
шего набора высоты ракетным самолетом, режим работы двигателя
1 Д. Е. О х о ц и м с к и й, К теории движения ракет, «Прикладная матема¬
тика и механика», т. X, вып. 2, 1946.
2 Д. Е. О х о ц и м с к и й, Т. М. Энеев, Некоторые вариационные задачи,
связанные с запуском искусственного спутника Земли, «Успехи физических наук»,
т. LXIII, вып. 1а, 1957.
11
ракетного самолета при горизонтальном полете на максимальную
дальность, разбивка составной баллистической ракеты на ступени
для случая, когда удельные тяги ступеней и конструктивные харак¬
теристики ступеней различны, и некоторые другие заслуживают вни¬
мательного изучения со стороны специалистов, интересующихся
вопросами выбора оптимальных проектных параметров и полетных
программ.
Сборник предназначается для работников научно-исследователь¬
ских институтов и конструкторских бюро, а также преподавателей,
аспирантов и студентов высших учебных заведений, интересующихся
баллистическим проектированием и расчетом проектных параметров
современных ракетных летательных аппаратов.
В переводах статей принимали участие инженеры Ю. Р. Красон-
тович, И. Ф. Борисов и А. Т. Бойцов.
И. Садовский
РАЗДЕЛ I
ОПТИМАЛЬНЫЕ РЕЖИМЫ
ВЕРТИКАЛЬНОГО ПОДЪЕМА РАКЕТ-ЗОНДОВ
Г. ГАМЕЛЬ
ОБ ОДНОЙ ЗАДАЧЕ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ,
СВЯЗАННОЙ С ДВИЖЕНИЕМ РАКЕТЫ1
Рассмотрим вертикальный -подъем ракеты, т. е. твердого тела
переменной массы М, движущегося под действием силы тяжести, со¬
противления воздуха Q и реактивной силы, обусловленной истечени¬
ем газов. На основании закона Ньютона и закона сохранения мате¬
рии составим дифференциальное уравнение движения
+Vr^+Q(s,v) + Mg = 0, (1)
at at
где 5 — путь ракеты;
t — время,
v = ds/dt — скорость ракеты;
Vr —■ относительная скорость истечения газов.
Сделаем следующие допущения:
1) приняв, что ракета достигает высоты, не превышающей
200ч-300 км, будем считать g постоянным; 2) не будем принимать
во внимание влияние массы, теряющейся с уходящими газами, на
силу сопротивления воздуха; 3) не будем учитывать изменение им¬
пульса внутри ракеты, связанного с перемещением фронта горения
и т. д.; 4) не будем принимать во внимание вращение Земли.
Обозначим через Мк конечную массу ракеты, а через М0 ее на¬
чальную массу и сформулируем задачу следующим образом: заданы
1 G. Hamel, Uber eine mit dem Problem der Rakete zusammenhangende
Aufgabe der Variationsrechnung, «Zeitschrift fur angewandte Mathematik und
Mechanik», Band 7, Heft 6, Dezember 1927, S. 451 -e 452.
Работа Гамеля, написанная более 30 лет тому назад, помещается здесь по¬
тому, что она является по существу первой работой, в которой задача об опти¬
мальном режиме подъема ракеты решалась строгими математическими метода¬
ми. Последующие статьи I раздела настоящего сборника в значительной мере яв¬
ляются развитием этой работы Гамеля.
13
Мк, максимальная высота полета ракеты Н, натальная скорость v0
лтри /о = 0 и 50 = 0 и постоянная скорость истечения газов Vr. Требует¬
ся определить минимальное значение начальной массы М0.
Эта задача была поставлена Годдардом [1], который пытался ре¬
шить ее с использованием недостаточно точного математического ап¬
парата. Ниже эта задача решена методами вариационного исчи¬
сления.
Рассматривая уравнение (1) как линейное дифференциальное
уравнение с переменной М, можно его проинтегрировать и, подставив
в решение значения переменных в конце полета, найти следующее
выражение для М0:
уо_ д» _gt_ v0 [ ик £^к
Mq = * ^ Г _L Q (Sj v) eVr У г dt + Ке Vr Vr Vr ш
J V г
О
Здесь через /Е, vK и sK обозначены значения переменных в момент
окончания работы двигателя, т. е. в начале пассивного участка
полета.
Ограничимся проблемой ракеты как таковой, т. е. примем уо = 0.
Результатом этого будет отсутствие экстремума в строгом смысле
слова и наличие только некоторого нижнего предела, к которому,
однако, можно сколь угодно приблизиться, если предположить, что
в начале полета скорость v очень быстро увеличивается от нуля до
некоторого определенного значения. В дальнейшем изложении тер¬
мин «минимум» употребляется для обозначения именно этого нижне¬
го предела, являющегося действительным минимумом.
Таким образом мы приходим к задаче, которая записывается сле¬
дующим образом:
4
М)=] /е> s> 0 dt + F(vк, £K) = min.
О
При этом мы свободны в выборе значений sK и tR.
Величины vK и sK, напротив, связаны уравнением, вид которого
можно установить на основании следующих соображений: в момент
израсходования топлива ракеты текущее значение массы становится
равным конечному ее значению М = МК и начинается пассивный по¬
лет, при котором ракета продолжает набирать высоту за счет расхо¬
дования накопленной кинетической энергии. При этом уравнение дви¬
жения имеет вид:
MK^ + Q(s,v) + MKg = 0
at
, , dF ъ
или иначе /-| = 0. Это последнее уравнение относится к категории
dt
уравнений вида vdv/ds = f\(v, s), и решение этого уравнения после
подстановки конечных условий £> = 0 при s = H имеет вид
14
При больших значениях Я, соответствующих большому s, это
решение в связи с малостью Q на больших высотах почти точно со¬
впадает с формулой
v=V2g (H—s).
Отсюда получается еще одно граничное условие ^К = ф(.9к), кото¬
рое можно непосредственно подставить в F. После этого дополни¬
тельный член будет иметь вид ЕГф^), 4]. Однако при отыскании
минимума М0 граничное условие не может быть с самого начала
использовано в выражении интеграла в связи с тем, что, как извест¬
но, всегда можно найти другое значение vK в конце экстремалей, при
котором интеграл изменится сколь угодно мало.
Итак, требуется найти минимум интеграла при постоянных sK и 4.
Это типичная вариационная задача, которая сводится к решению
уравнения Эйлера и отысканию регулярных экстремалей без точек
пересечения.
Кроме того, при вполне законном допущении Q>0; dQ/dv>Q;
d2Q/dv2>0, где знаки равенства справедливы только при i> = 0, полу¬
чается также
На основании этих допущений, к которым прибавляется еще
dQ/ds<0, можно получить результат в общем виде.
Таким образом, интеграл сам по себе имеет ясно выражен¬
ный минимум. Трудности начинаются только при варьировании sK
и tK и соответственно sK и vK. При этом можно сделать следующие
выводы:
1. Имеется одна единственная стационарная конечная точка
sK = s0y vk = Vq, в которой dMJdsK = 0 и dMJdtk = 0. Эта точка лежит
на кривой у = Ф(5), и таким образом' это конечное условие является
естественным в смысле Куранта.
2. Если варьировать sx и vK по кривой v = -y\:(s), то в точке (s0, о0)
имеет место действительный минимум.
3. При любых вариациях дискриминант членов второго порядка
равен нулю:
и таким образом точки s0, U достигают возможные пикообразные об¬
ласти, в которых значения М0 будут меньшими, чем в точке (s0, ^о)-
4. Такого рода пикообразная область может достигать кривой
^ = ф(5) только с внешней стороны.
Эти особые точки не могут рассматриваться как конечные значе¬
ния (sK и ик), так как при этом чрезмерно высокая скорость ракеты
d2f;dv2> 0.
дШ д2М
15
в конце активного полета должна мгновенно уменьшаться путем
мгновенного увеличения массы ракеты, что физически неосуществи¬
мо. Математически наличие минимума гарантируется неравенством
dM)dt<0. Таким образом в данном случае имеет место действитель¬
ный минимум.
ЛИТЕРАТУРА
Годдард Р., Метод достижения очень больших высот.
Hoddard R., A Method of Reaching Extreme Altitudes, Washington, 1919,
Smithsonian Institute.
С. ТЗЯН и. P. ЭВАНС
ОПТИМАЛЬНОЕ ПРОГРАММИРОВАНИЕ ТЯГИ
ВЫСОТНОЙ РАКЕТЫ-ЗОНДА1
При вертикальном полете ракеты аэродинамическое сопротивле¬
ние ракеты и сила тяжести имеют одинаковое направление, прямо
противоположное направлению силы тяги, что в значительной мере
облегчает расчет закона изменения тяги двигателя ракеты. Такой
расчет производился Ф. Малина и А. Смитом [1]. Они показали, что
если аэродинамическое сопротивление отсутствует, то наилучший
способ использования топлива заключается в том, чтобы его израсхо¬
довать в наикратчайшее время. Теоретически ракета с заданным от¬
носительным весом топлива может достигнуть наибольшей высоты,
если импульс тяги, развиваемый двигателем ракеты, будет мгновен¬
ным, в результате чего скорость ракеты также мгновенно достигнет
максимально возможного значения. Этот результат может стать бо¬
лее понятным, если рассмотреть другой крайний случай, при котором
тяга двигателя ракеты в каждый данный момент времени будет рав¬
на весу ракеты. Тогда ракета, находясь под действием ускорения,
равного нулю в течение всего времени работы двигателя, не будет в
состоянии оторваться от земли. Поэтому когда аэродинамическое со¬
противление пренебрежимо мало, длительная работа двигателя раке¬
ты определенно невыгодна.
При наличии лобового сопротивления большая скорость, достиг¬
нутая на малых высотах, при импульсном разгоне приведет к очень
большому сопротивлению, которое уменьшит максимально возмож¬
ную высоту подъема ракеты; действительно, расчеты, произведенные
Малина и Смитом, а позднее Айви, Боуэном и Оборном [2] показали,
что при постоянной тяге оптимальное начальное ускорение должно
быть в пределах от 1 до 3g, изменяясь в зависимости от отношения
сопротивления к весу. Однако более общей задачей является опре¬
1 Н. S. Т s i е n and Robert С. Evans, Optimum Thrust Programming for
a Sounding Rocket, «Journal of the American Rocket Society», 1951, vol. 21, No. 5,
September, pp. 99— 107.
16
деление оптимального закона регулирования тяги, т. е. нахождение
оптимального закона изменения тяги по времени, обеспечивающего
достижение максимально возможной высоты. Этот закон выражает
лишь теоретический проектный оптимум. Конструкция реальной ра¬
кеты усложняется и утяжеляется вследствие придания двигательной
установке устройств для регулирования тяги, и поэтому невозможно
достичь точно оптимальных условий. Однако теоретический оптимум
служит как бы эталоном для сравнения и показывает, в какой мере
можно улучшить летные характеристики ракеты при помощи регу¬
лирования тяги.
Одно из ранних исследований проблемы оптимальной программы
изменения тяги было произведено в работе Гамеля [3]. Он принимал
в этой работе упрощающее допущение о том, что плотность воздуха
с высотой уменьшается по экспоненциальному закону и что эффек¬
тивная скорость истечения Vr и ускорение силы тяжести g не ме¬
няются с высотой. Пользуясь методом вариационного исчисления,
он дал решение задачи об оптимальном режиме подъема ракеты.
Однако его статья была очень краткой и трудной для понимания.
В настоящей работе авторы ставят своей целью подробное рассмотре¬
ние задачи об оптимальном регулировании тяги и приводят некото¬
рые численные примеры.
ПОСТАНОВКА ЗАДАЧИ
Обозначим массу ракеты через М и путь, пройденный к моменту
времени t, через s. Подобно Гамелю, примем эффективную скорость
истечения газов из ракетного двигателя Vr постоянной. Тогда ско¬
рость ракеты равна dsjclt или 5. При заданной форме ракеты аэроди¬
намическое сопротивление Q является функцией пути 5 и скорости 5.
Если ускорение силы тяжести g постоянно, то уравнение движения
ракеты на активном участке полета будет Иметь вид
(М_
dt
+Fr(£+*)=
Q (s, s)
Vr
0)
Путь 5 отсчитывается с момента сообщения ракете начального
импульса разгона. Поэтому в момент начала маршевого активного
участка полета / = 0, s = 0, М = М\\ s = su где М{ и бд—масса и ско¬
рость полета ракеты сразу же после окончания действия импульса
разгона. В конце активного участка полета t = tK; М = МК; s = sK, s = sK:
Мк—конечная масса ракеты.
С учетом этих граничных условий уравнение (1) для массы в на¬
чале маршевого участка М\ можно представить в следующем виде:
Мх = е Ут
П ( \ *+£* SK~'rgtK
Vf dt+M Vr
Vr
(2)
2 394
17
Если Мо есть начальная масса ракеты, включающая запас топли¬
ва, необходимый для сообщения начального импульса и придания ра¬
кете начальной скорости s\, то мы имеем
М0=МгеЪ. (3)
Решая совместно уравнения (2) и (3), получаем
. 's+gt sk + ^k
мо= I е Vr dt+MKe Vr . (4)
О
Уравнение (4) не содержит в явном виде скорости после разгона
s±. Если скорость в начале маршевого движения равна нулю, то изме¬
нение ускорения ракеты происходит плавно. Если же эта скорость не
равна нулю, то запуск ракеты должен производиться путем сообще¬
ния ей некоторого импульса и с увеличивающимся в дальнейшем
ускорением. Однако в любом случае уравнение (4) определяет пол¬
ную начальную массу ракеты Л40, включающую запас топлива для
импульсного разгона.
Сформулируем основную задачу отыскания оптимального закона
регулирования тяги следующим образом: при заданных значениях
А*к, Vr, g и функции сопротивления Q(s, s) требуется найти такую
функцию s(t), при которой величина М0 будет минимальной.
Дополнительными граничными условиями являются: 5(0) =0, а
также требование, чтобы sK и sK были такими, чтобы общая высота
подъема ракеты Н была максимальной. Пусть при заданных значе¬
ниях Мк и Q(s, 5) значения sK и sK связаны каким-либо соотношени¬
ем, например:
Sk=<p(sk), (5)
где ф — известная функция. Например, на очень больших высотах,
где аэродинамическое сопротивление вследствие малой плотности
воздуха пренебрежимо мало,
sK^V2g{H-sK). (6)
Чтобы найти условия для решения этой вариационной задачи,
выразим искомую функцию в виде
S = s(t), (7)
где s(0) =0.
Введем теперь произвольную функцию р (() такую, что
Л (0) =0. (8)
Тогда любая функция, близкая к s(t), может быть представлена
в виде
7(/)=s(f)-H(e)T|(f), (9)
18
где k — параметр, не зависящий от времени, По уравнению (8) фун¬
кция s(t) удовлетворяет начальному условию 5(0) =0. Продолжи¬
тельность активного участка полета или время горения топлива при
оптимальном полете равно tK. Для закона, близкого к оптимальному,
время горения составит Таким образом k является функцией в.
При оптимальном режиме при изменении 5 значения k и е обра¬
щаются в нуль.
Поэтому
*(°)-°; | (10)
*(,)s •*'((>). (
Учитывая только члены первого порядка относительно е, по¬
лучаем
SK==;5(^K + e)= 5(^K)"feS(^K)+^ (0) £Y) (tKY> (11)
= (^Ц+е= * Ск + *)=s(tK) + es (tK) + k! (0) Щ (tK), (12)
где Tj = dj\ldt. Так как sK и sK должны удовлетворять уравнению (5),
то, следовательно, образованная новая функция s(t) должна соот¬
ветствовать ракете, достигающей той же заданной максимальной
высоты при новых граничных условиях. Следовательно,
sk = 9(sk)+(^)Sk(sk~sk)+ • • • =
= S(^)+(S,K(S“_Sl()+ • • '
(13)
Значения sK и sK могут быть подставлены в уравнение (13) из
Уравнений (11) и (12).
Произведя некоторые упрощения, получаем
Шч 4 (° - 4 (°] (0)=s 1[t'y- Шч5 <у- <Н)
Из этого уравнения определяется затем значение &'(0), которое
позволяет получить решение для функции s(t)y полностью удовлет¬
воряющее веем граничным условиям.
При заданной функции тДО полная начальная масса М0 будет
зависеть от величины е. Пусть
F (5,5, t)~ Q (5,5) e yr . (15)
2*
19
Тогда, сделав подстановку уравнений (9) и (12) в уравнение (4),
будем иметь
Мо(£)=-^ j* F[s + k(e)y[,s+k(z)4\,t\dt-\-
О
j~ h<KU"<.<K)+k («П<у-1-*ум* j
+ Me
(16)
Условие для s(t)y соответствующее оптимальному решению, т. е.
такому, при котором M0 = M0min, может быть теперь выражено про¬
сто в виде
'дМ0-
, =о.
дг Л=о
Выполнив необходимое дифференцирование, находим
(17)
+
+ -Н^(5к)5к,О+-Нмкк+^Т^(0)л(и]^ ^ .
V Г V г
По согласно принятому ранее для функции г|(/) условию необ¬
ходимо, чтобы г| (0) =0. Следовательно, для того, чтобы предыдущее
выражение равнялось нулю, необходимо положить
dF d /dF \ q
ds dt \ ds )
(18)
5K + ^K
^(о)дд(^)/к+^ск,5Лк)+^кК+й-+^(о)л(У]б ^ =o.
(19)
Уравнение (18) представляет собой известное уравнение Эйлера—
Лагранжа. Уравнение (19) отражает принятые дополнительные ус¬
ловия задачи. Исключая значение /У(0) из уравнений (14) и (19),
имеем
0 =
X
X F (s„ SK, tK) + Мк
[{(S<к 71 (0 ~ 71 (U} (S“ + g) + ri (У Х
20
Но л (0 является произвольной величиной. Поэтому для того,
чтобы удовлетворить полученному уравнению, множители при вели¬
чинах Т|(^к) и л(*к) должны одновременно обращаться в нуль. По¬
этому имеем
V ds / *к
К+в‘к
И^)Ч(Ч
^(SK, «к. С)+Д<
414
е у' =0.
(20)
(21)
Уравнения (18), (20) и (21) дают теперь возможность полностью
решить поставленную вариационную задачу. Закон регулирования
тяги должен быть таким, чтобы в каждый данный момент активного
участка полета он удовлетворял уравнению (18), а в конце актив¬
ного участка полета—уравнениям (20) и (21).
Эти условия могут быть выражены в более простой форме с по¬
мощью уравнения (15). Тогда уравнение (18) примет вид
dQ _ дЩ ■ дЮ » 1
ds ds ds ds2 Vr
+ (& + g) + £- (s + ^)l.(22)
ds Os V r
Если сопротивление задано как функция 5 и 5, то уравнение (22)
представляет собой дифференциальное уравнение для определения
траектории s(/). Уравнения (20) и (21) можно представить в сле¬
дующем виде:
4*4
dQ \ I Q ($ю Sk)
д* Ч ^
+
+Ш^<s■•s■>+MЧ<s•+г,-0 (23>
Q («К. «к) + Мн
(dl)sKS*
+g
= 0,
(24)
где индекс «к» обозначает, что величины в этих уравнениях с таким
индексом относятся к моменту времени t = tK.
Если уравнение (5) представляет условия в начале пассивного
участка полета, то уравнение (24) автоматически удовлетворяется.
В самом деле, за время пассивного участка полета реактивный дви¬
гатель не работает и топливо не расходуется, следовательно,
dMjdt = 0. Тогда уравнение (1) приводится к виду
/
\dt
+ g
MK + Q(sK,sK) = 0.
(25)
21
Полученное уравнение (25) совпадает с уравнением (24). Исклю¬
чив величину (d<p/ds)SK из уравнений (23) и (24), находим оконча¬
тельное выражение для условий в конце активного участка полета в
следующем виде:
(_j_
Л ds Л Vr J
: (^А + QK + MKg) (QK + MKg),
где Qk = Q(5k, sk) —лобовое сопротивление в момент прекращения
работы двигателя. Однако множитель (Mk5k-|-Qk + Mk£) не может
равняться нулю, поэтому
'(JQ\ , Qk
Л ds Л Vr
-QK + MKg.
(26)
Теперь задача оптимального регулирования тяги может быть
рассмотрена более конкретно. Так как сила лобового сопротивления
входит в уравнение (22) только линейно и однородно, то независимо
от формы ракеты это дифференциальное уравнение представляет со¬
бой уравнение второго порядка относительно s(t). Однако только
при одном начальном условии 5(0) =0 начальная скорость s± остает¬
ся неопределенной. Поэтому в качестве второго дополнительного ус¬
ловия берется уравнение (26), относящееся к концу активного
участка полета. Следовательно, для заданной формы ракеты и для
заданной конечной массы МЕ существуют соответствующая опти¬
мальная начальная маршевая скорость 5i и оптимальный закон из¬
менения тяги, при котором достигается заданная высота Я. В общем
случае оптимальное решение включает начальный импульс при
старте.
КВАДРАТИЧНЫЙ ЗАКОН СОПРОТИВЛЕНИЯ
Для расчета принимаем, что плотность воздуха изменяется с вы¬
сотой по экспоненциальному закону. Изменение силы сопротивления
принимается пропорциональным квадрату скорости. Тогда лобовое
сопротивление можно выразить в следующем виде:
Q = Q0s2e~as. (27)
В данном уравнении коэффициент сопротивления — постоянный.
Подставляя это выражение в уравнение (22), получаем
5 х lx<2~{~ (1 — Р)х 2ft] (28)
g Р(*2 + 4* + 2)
где х и р — безразмерные параметры
<29>
22
Интегрируя уравнение (28), находим значение t(x) и s(x)n
sL
Vr
Т i., 2*-|-(l—Р) — Т 2xj -|-(1 —P)~t~T
— = ln —+ —In
х 2 2ж + (1 —р) + 7
Р + 1
In ■
2jci Н- (1 — Р) — Т
■**+(! — Р) х — 2Э
2 -■ лс? Н-<1 —P)JC! — 2р ’
« = * - *, + In 2* + Р - Р) ~ Т ,. 2„ + (1 - Р) + Т_
2 2х + (1-р) + Т 2х1 + (1-р)-1
, р + 3 )п д:2 + (1-р)д;-2р
■*? + (!2?
(30)
(31)
-zp
т = /(1-р)2 + 8р. (32)
Выражение для текущей массы М находим из уравнений (27),
(28), (30) и (31):
[*2 + (i_p)jc 2р] X
мк 1 MKg
где
X
9х + 2
хк 4" 2
8* к
+ ^К+ Кг |
JC2 + (l-P)jf-2P Л2 + (1_Р)ХК-2Р
Подставляя х = хи t = О, находим массу Mi после разгона
(33)
ж.
QoV'r
jWk Л1к^
pXl
(*1 + 2) — (хк 2)
('к—+4г)
ATf + (1 — Р)^1 —'2р
*2 + (1-(3)дгк-2р
+
(34)
Начальная масса ракеты, включая стартовый заряд, определяется
уравнением (3) или через безразмерное выражение скорости х:
MQ = Mxex'.
Поэтому
М0 Mi
(35)
Значение тяги в любой момент можно получить из уравнения (1),
имея в виду, что Р = VrdM/dt:
Q0V2r
xle-*s + _
М
(36)
MKg MKg мк
где коэффициент продольной перегрузки s/g может быть вычислен
по уравнению (28).
Граничные условия даются уравнениями (5) и (26). Подставляя
в уравнение (26) уравнение (27), находим
QqV;
MKg
■ xfe
1 -\-хк
(37)
!) При переводе в формулах (31) и (32) выправлены обнаруженные в ориги¬
нале опечатки. Так, в формуле (31) исправлен множитель (Р+1)/2 на (Р+3)/2
н в формуле (32) исправлен член 4Р на 8Р. (Прим. ред.).
23
После израсходования всего топлива уравнение движения будет
иметь вид
(S+£) Мк + Q0s2e-« = 0 (38)
и может быть легко проинтегрировано. Используя условие, что на
конечной высоте s = Н скорость 5 = 0, получим выражение для отно¬
сительной скорости хк в начале пассивного участка полета:
... ^
M*g dz_^ (39)
где
—as.
(40)
Интеграл в уравнении (39) можно вычислить разложением в ряд
e-bz*L = \n\z\ bJ-+™L- . . . (41)
* 1...1! 2...2I 4 7
При любом заданном значении Н и параметре сопротивления
QoVr2/MKg уравнения (37) и (39) дают возможность определить зна¬
чения хк и asK. Параметр Q.oVr2IMKg является безразмерным отно¬
шением сопротивления к весу ракеты.
Для иллюстрации теории был произведен численный расчет па-,
раметров для двух высот и скоростей истечения. При этом принима¬
лось, что
1 1
a *= .
6680 м
В первом случае высота .принималась равной 152 км, а скорость
истечения 1680 м/сек, во втором случае—высота—915 км, а скорость
истечения—2440 м/сек.
Условия в конце активного участка определялись методом после¬
довательных приближений, а именно: задавался параметр QoVr2/MKg
и в уравнение (37) подставлялось какое-либо значение vK. Опреде¬
ленное при помощи этого уравнения значение asE подставлялось в
уравнение (39), откуда определялось новое значение vK и т. д. Вычи¬
сления могут быть упрощены, если для первого грубого определе¬
ния vK использовать график зависимости QoVr2/MKg от ик, прибли¬
женно представляющий прямую линию в логарифмической сетке (ло¬
гарифмические координаты берутся только для QoV^/M^g). Более
точное значение vK находится последовательными приближениями
по уравнению (31).
При расчетах задавались значения QoV^/Mxg, но конечные ре¬
зультаты для удобства сравнения были выражены через QoVr2/M0g.
Член Q0Vr2 представляет собой силу сопротивления при движении
ракеты со скоростью, равной скорости истечения, на уровне моря.
Таким образом, параметр QoVr2/M0g выражает отношение этой силы
к начальному весу. На фиг. 1—8 представлены результаты этих рас¬
четов. Анализ их 'приведен ниже.
24
Фиг. 1. Зависимость отношения
масс М0/Мк и Mi/Mк от парамет¬
ра сопротивления QoV^ /M0g.
Точки на кривой соответствуют от¬
ношению масс ракеты с постоянной
тягой.
Полная высота подъема #=152 км,
скорость истечения Уг=1680 м/сек.
м0д
Фиг. 2. Зависимость отношения
масс М0/М к и Mi/Mkot параметра
сопротивления Q0V^/M0g.
Точки на кривой соответствуют от¬
ношению масс ракеты с постоянной тя.
гой.
Полная высота подъема #=915 км,
скорость истечения Кг=2440 м/сек.
мвд
Фиг. 3. Зависимость безразмерной
начальной скорости Xi=vi/Vr, без¬
размерной скорости в конце активно¬
го участка полета xK = vK/Vr, безраз¬
мерной высоты в конце активного
Участка полета asK от параметра
сопротивления Q0V^/Mog.
Полная высота подъема #=152 км, ско¬
рость истечения У/.=1680 м/сек.
мо9
Фиг. 4. Зависимость безразмерной
начальной скорости x\ = vjVг, безраз¬
мерной скорости в конце активного
участка полета хк =vK/Vr, безраз¬
мерной высоты в конце активного
участка полета asK от параметра
сопротивления QoV,/M0g.
Полная высота подъема #=915 км,
скорость истечения 1^=2440 м/сек.
25
v м/сек
1824
/520
1216
9/2
608
\ 304
О
у Сопротивление
отсутствует
30400 60800
S, м
Фиг. 5. Зависимость скорости v от
высоты s при различных значениях
параметра сопротивления Q0V~r /M0g.
Полная высота подъема #= 152 км,
скорость истечения Vr=1680 м/сек.
Сопротивление
отсутствует
9/200
30400 60800
S. м
31200
Фиг. 6 Зависимость скорости v от
высоты 5 при различных значениях
параметра сопротивления.
Полная высота подъема #=915 км,
скорость истечения У,. =2450 м/сек.
Фиг. 7. Зависимость отношения тяги Фиг. 8. Зависимость отношения тяги
к начальному весу P/M0g от време- к начальному весу P/M0g от време¬
ни t для различных значений парамет- ни t для различных значений пара-
ра сопротивления QoV^/M0g. метра сопротивления Q^V^/M^g.
Полная высота подъема #=152 км, ско- Полная высота подъема #=915 км. ско¬
рость истечения Кг = 1680 м/сек. рость истечения Уг=2450 м/сек.
26
ЛИНЕЙНАЯ ЗАВИСИМОСТЬ СОПРОТИВЛЕНИЯ ОТ СКОРОСТИ
При сверхзвуковой скорости полета более вероятна линейная за¬
висимость сопротивления от скорости, т. е.
Q = (4s + £)e-
(42)
В этом случае сопротивление вновь соответствует экспоненциаль¬
ному закону изменения плотности воздуха, но с увеличением скоро¬
сти коэффициент сопротивления уменьшается. Подставляя выраже¬
ние (42) в уравнение (22), получаем
лг!+(^-р)дг-[р+Ж<, + в
(43)
где х и р определены уравнением (29). Интегрирование уравнения
(43) дает
-£=J- In¬
i', s
2А
2х+(щ-?)+х- 2*1+(Д-р)“
х2+х(^г-?У
+ж*1+*\
0CS — X — Хл-\-(\ -j ^ ...
p(4 + p+lk) [n2* + (lk~p)~* 2xl + (jvr~?J) + X
2А / В \ / В \
2^+(—-р)+х ^+(^-р)-х
р)
где
ГТв
(44)
+
(45)
(46)
27
Масса М в любой момент может быть найдена из уравнения
И+Ч^-?)-Кр+тк(1+Р)])
с
MKg
х
X
в
х -4- J- 1
' AVг '
'(£-0-
Х‘+Ж + 1
'■ + 4^ “И
+ AVr (1+')
+
+ <?
'к+-уГ
(47)
Начальная масса М0, в которую входит стартовый заряд, может
быть получена из уравнения (47) и (35):
^ ф.+'H'.+.V >) х
ж.
Ч -1-*1
MKg
/ В
X
(ж-*)-
в
+ AVr
(1+Р)
ехк
(48)
Значение тяги может быть получено из уравнения (1):
Р AVr
MKg MKg
(х+жУ‘,+~й;(1+ т)- (49)
Ускорение s/g может быть определено из уравнения (43). Гранич¬
ные условия даются уравнениями1 (26) и (5). Подставляя уравнение
(42) и (43) в уравнение (26), имеем
(xl + хк- —) е -"к -1. (50)
MKg \ к hAVr AVr)
Для получения зависимости, выраженной уравнением (5), необ¬
ходимо определить траекторию на пассивном участке полета. Ис¬
пользуя уравнение (42), уравнение движения для пассивного участ¬
ка полета можно представить в следующем виде:
—+ 1
AVr
MKg
X -
в
AVr
w = 0.
(51)
Проинтегрировать это уравнение непосредственно нельзя. Одна¬
ко, учитывая, что сопротивление воздуха мало, можно в первом при-
28
ближении им пренебречь и решить уравнение (51) приближенно, а
затем внести в него необходимую поправку. Обозначим значение
относительной скорости без учета сопротивления воздуха через х° и
небольшую поправку для х—через х'. Тогда
х = х°-\-х/.
Уравнение для х° имеет простой вид:
^+it=0.
ds V2r
(52)
(53)
Подставляя уравнение (52) в уравнение (51) и пренебрегая чле¬
нами со степенями выше первой, получим
dxr
ds
+ xf + Ё_\е-«e0.
ds MKVr \ AVr)
(54)
Это выражение представляет собой дифференциальное уравнение
относительно поправки хг.
Решение уравнения (53) дается формулой
“=* У 2(1 (*#-«).
(55)
Подставляя уравнение (55) в уравнение (54), имеем
В
dx' , х' AVr
dt
MKg
■Р
1
AV_r_
/ 2ps
где l = aН—as.
Интегрируя, получим решение для хг
х
1 АУГ
'VT
№
-а И
j/z-
В
AVг_
/2?
с2 dz
(56)
Интеграл в уравнении (56) можно вычислить путем разложения
в ряд. Рассмотрим для этого
/(5) = jVze'dz.
Пусть z = l( 1—а), тогда
Путем разложения корня, стоящего под интегралом, в ряд и по¬
членного интегрирования, выражение для /(£) может быть представ¬
лено в виде
т=V* {и-1 ] ■“ [*■- (1 + т —— р - (i+«+-f)] - •• •}
— 1 Нр—я
тогда
1 AVг
VI мк g
Р /(«)■
AVrVW
>}'
(57)
Решая совместно уравнения (50) и (57), определяем скорость
и высоту в конце активного участка полета ракеты для любого дан¬
ного значения параметра AVrjMKg. Если значение В = 0, то величина
*о9
Фиг. 9. Зависимость отношения
масс MQ/MK и М\/Мк от параметра
сопротивления ЛРГ/М0£.
Полная высота подъема Н=915 км,
скорость истечения Гг=2450 м/сек.
Точки на графике соответствуют отно¬
шению масс ракеты с постоянной тягой.
*о8
Фиг. 10. Зависимость безразмер¬
ной начальной скорости xlf безраз¬
мерной скорости в конце активно¬
го участка полета хки безразмер¬
ной высоты а5к в конце активно¬
го участка полета от параметра
сопротивления AVr/MQg.
Полная высота подъема //=915 км,
скорость истечения Гг=2450 м/сек.
AVT представляет собой сопротивление ракеты на уровне моря при
полете ее со скоростью, равной скорости истечения.
Были произведены расчеты для высоты #=915 км, скорости ис¬
течения 1/г = 2440 м/сек при отсутствии сопротивления при нулевой
скорости и 1/6700 (1/ж). Расчеты производились по методу, ана¬
логичному тому, который излагался ранее для первого случая. Ре¬
зультаты расчетов показаны на фиг. 9—12. Параметр AVr!MKg в
данном случае представляет собой отношение сопротивления ракеты
при скорости полета, равной скорости истечения Vr на уровне моря,
к начальному весу.
Для того, чтобы оценить возможный выигрыш, полученный изме¬
нением тяги по оптимальному закону, по сравнению с ракетой обыч¬
ной схемы было проведено несколько расчетов при постоянной тяге
30
для тех же законов сопротивления. При этом предполагалось, что в
случае постоянной тяги ракете не сообщается начальный импульс,
а отношение тяги к начальному весу принималось равным P/M0g =
=2,7. Величина 2,7 была заимствована из работы [2]. Сравнение
полученных результатов подсчета проводилось при одинаковых значе¬
ниях отношения сопротивления при скорости полета, равной скоро-
Фиг. 11. Зависимости скорости v от
высоты s при различных значениях
параметра сопротивления AVr/M0g-
Полная высота подъема #=915 км, ско¬
рость истечения Гг=2450 м/сек.
Фиг. 12. Зависимость отношения тяги
к начальному весу P/M0g от време¬
ни t для различных значений пара¬
метра сопротивления AVrlMQg,
Полная высота подъема #=915 км.
Скорость истечения Vr=2450 м/сек.
сти истечения 1/г, к начальному весу M$g и для одинаковых конеч¬
ных высот Я. При постоянной тяге отношение масс М0/Мк получи¬
лось большим (вследствие меньшей величины Мк)у чем это имело
место при оптимальной тяге. Вычисления отношения начальной мас¬
сы М0 к конечной Мк проводилось методом последовательных при¬
ближений с конечной ошибкой порядка 1 % в сторону уменьшения.
Полученные результаты расчетов для случаев постоянной тяги по¬
казаны точками на фиг. 1, 2 и 9.
ВЫВОДЫ
Получены некоторые общие характеристики для линейного и
квадратичного законов изменения сопротивления. Как видно из
фиг. 3, 4, 7, 8, 10 и 12, при малых значениях параметров сопротив¬
ления средняя тяга и начальная скорость являются высокими.
Вследствие этого ракета будет быстро сжигать топливо и на преодо¬
ление силы тяжести будет расходовать небольшую часть своей энер-
31
гии. По мере возрастания параметра сопротивления все большее ко¬
личество энергии будет расходоваться на преодоление силы сопро¬
тивления. Из этого следует, что на малых высотах более выгодным
будет полет на малой скорости. Поэтому при малых значениях пара¬
метра сопротивления начальная скорость и тяга должны быть мень¬
ше, чем при больших параметрах, и тогда высота в конце активного
участка полета будет большей. Важно отметить, что во всех случаях
оптимального режима полета существует определенная начальная
скорость, которая должна создаваться начальным (разгонным) им¬
пульсом тяги.
Другим выводом для обоих законов изменения сопротивления яв¬
ляется то, что они характеризуются подобными зависимостями отно¬
шения начальной массы к конечной М0/Мк от параметров сопротив¬
ления (см. фиг. 1, 2 и 9). При заданной общей высоте подъема Н
отношение MJMK с увеличением параметра сопротивления возра¬
стает. С уменьшением параметра сопротивления отношение
асимптотически приближается к величине e°llVr (отсутствие сопро¬
тивления), где значение V\ такое, что ракета обладает кинетической
энергией на уровне моря, равной потенциальной энергии в конечной
точке подъема ракеты.
В общем случае при оптимальном законе регулирования тяга
двигателя ракеты после разгона ракеты до скорости V\ должна воз¬
растать с увеличением высоты. Исключениями из этого правила яв¬
ляются случаи, когда значения параметра сопротивления достигают_
очень больших величин или когда ракета обладает очень низким
сопротивлением. В этих случаях на некоторых участках активного
полета тяга должна постепенно уменьшаться. Это явление может
быть следствием или очень медленного возрастания ускорения ра¬
кеты или же очень быстрого уменьшения массы ракеты. Уменьшение
тяги становится понятным, если учесть то, что «ускоряющая» сила
является главной составной частью тяги, равной произведению мас¬
сы в данный момент времени на ускорение. Однако наиболее веро¬
ятен случай, когда тяга непрерывно увеличивается. Для ракеты с
нерегулируемым двигателем это увеличение тяги создается авто¬
матически, до определенного предела, вследствие уменьшения
атмосферного давления с высотой. Но в большинстве случаев
такое увеличение тяги составляет лишь малую часть того потребного
прироста тяги, который был определен в приведенном здесь
расчете.
При линейном законе изменения сопротивления начальная ско¬
рость получается больше, а время активного полета меньше, чем
при квадратичном законе изменения сопротивления (для одинаковых
отношений масс М0/Мк).
Это является следствием того, что с увеличением скорости в слу¬
чае линейного закона сопротивление возрастает медленнее. Следова¬
тельно, при линейном законе изменения сопротивления будут выгод¬
нее большие начальные скорости при меньшем времени активного
полета. При квадратичном законе сопротивление увеличивается про¬
порционально квадрату скоростей; в этом случае выгоднее принять
•32
меньшие начальные скорости и более продолжительные активные
режимы полета.
В качестве примера, дающего представление о порядке величины
параметров сопротивления QoVr2/M0g и AVr/MQgt можно взять дан¬
ные по ракете V-2. При скорости истечения 1830 м/сек сопротивле¬
ние ракеты примерно равно 45 т. Начальный вес ракеты равен 11,3 т.
Таким образом, при скорости истечения 1830 м/сек отношение сопро¬
тивления на уровне моря к начальному весу ракеты равно пример¬
но 4. Следовательно, величина параметра ЛКГ/Л40Я^4. Для случая
квадратичного закона изменения сопротивления величину параметра
QoV^/Mug лучше принять равной 10 в связи с тем, что при квадра¬
тичном законе сопротивления получается заниженная величина со¬
противления (против действительных условий) в течение большей
части активного полета, в особенности на малых высотах. Так как
максимальная высота подъема ракеты V-2 составляет примерно
160 км, то при QoVr2/Mog= \0 из графика на фиг. 3 может быть най¬
дено значение оптимальной начальной скорости, примерно равной
450 м/сек. При меньшем сопротивлении начальная скорость может
быть большей. Следовательно, оптимальный закон регулирования
тяги в этом случае должен включать значительный начальный (раз¬
гонный) импульс.
Для сравнения были произведены расчеты отношений масс для
ракет с постоянной тягой. При этом принималось, что законы сопро¬
тивления те же, что и в случае ракет с регулируемой тягой, началь¬
ная скорость ракеты равна нулю, а начальное ускорение равно 1,7#
(величина начального ускорения выбрана в соответствии с вывода¬
ми, полученными в работе [2] для ракет с высокими характеристи¬
ками). В рассмотренных случаях для постоянной тяги эта величина
ускорения не может быть оптимальной вследствие ее зависимости
от реальных законов сопротивления. Результаты вычислений для
ракеты с постоянной тягой представлены на фиг. 1, 2 и 9. Оказы¬
вается, что преимущества идеальной ракеты уменьшаются, если ра¬
кете с постоянной тягой придать оптимальную начальную скорость
и правильно выбрать начальное ускорение. В действительности, не¬
сомненно, для случая линейного закона сопротивления начальное
ускорение, равное \Jg, является слишком малым (см. фиг. 9). Более
правильное представление о возможном выигрыше в случае приме¬
нения оптимального закона регулирования тяги дает график, приве¬
денный на фиг. 2. Легко заметить, что по отношению к начальной
массе М0 выигрыш от регулирования является небольшой величиной.
С другой стороны, нужно иметь в виду, что полезная нагрузка высот¬
ной ракеты составляет весьма небольшую часть начального веса.
Поэтому, если даже выигрыш в начальном весе, полученный при
оптимальном регулировании, будет незначительным, для увели¬
чения полезной нагрузки этот выигрыш может оказаться сущест¬
венным.
Конечно, численные результаты, полученные в настоящем расче¬
те, дают только качественную картину. При любом практическом
расчете, связанном с определением оптимального режима изменения
3 394
33
тяги, наряду с учетом дополнительного веса ракеты, вызванным
устройством для регулирования тяги, необходимо знать более точную
зависимость функции сопротивления от скорости.
ЛИТЕРАТУРА
1. Малина Ф. и Смит А., Анализ полета ракеты-зонда.
Mali па F. and Smith A., Flight Anal isis of the Sounding Rocket, «Jour¬
nal of the Aeronautical Sciences», 1938, vol. 5, pp. 199—202.
2. А й в и Г., Б о у э и Е. и О б о р н и JL, Введение в проблему характеристик
ракетного самолета.
Jvey Н., Bowen Е. and Oborny L., 'Introduction to the Problem of
Rocket-Powered Aircraft Performance, NACA Technical Note, No. 1401, 1947.
3. Гамель Г., Об одной задаче вариационного исчисления, связанной
с движением ракеты.
Hamel G.f Uber eine mit dem Problem der Rakete zusammenhangende
Aufgabe der Variationsrechnung, «Zeitschrift fur angewandte Mathematik und
Mechanik», Berlin, vol. 1, 1927, pp. 451 —452.
Г. ЛЕИТМАНН
ОПТИМАЛЬНОЕ ПРОГРАММИРОВАНИЕ ТЯГИ
ВЫСОТНЫХ РАКЕТ i
ВВЕДЕНИЕ
Одна из наиболее важных задач внешней баллистики высотных
ракет заключается в определении условий подъема заданной полез¬
ной нагрузки на заданную высоту при минимальном расходе топли¬
ва. Достижению больших высот препятствуют два основных факто¬
ра: сила тяжести и сила лобового сопротивления; обе эти силы
уменьшаются по мере подъема на высоту. К сожалению, способы
уменьшения влияния этих двух факторов противоречивы. Потери
импульса, обусловленные силой тяжести, пропорциональны полет¬
ному времени; потери, обусловленные силой лобового сопротивления,
пропорциональны некоторой степени скорости. В связи с этим для
уменьшения потерь, связанных с силой тяжести, следует уменьшать
полетное время, т. е. стремиться к возможно более высокой скорости
полета; стремление уменьшить потери, связанные с сопротивлением,
требует ограничения скорости полета. Поэтому одной из проблем,
стоящих перед конструктором высотных ракет, является определе¬
ние оптимальной программы изменения тяги, т. е. такой зависимо¬
сти тяги от времени, которая обеспечивала бы оптимальный компро¬
мисс в деле уменьшения потерь как от силы тяжести, так и от силы
сопротивления и таким образом сводила бы к минимуму потребное
для подъема количества топлива.
Первый американский исследователь в области ракет Р. Г. Год¬
дард в своей работе «Метод достижения очень больших высот» [Г[
1 G. A. Leitmann, Optimum Thrust Programming for High-Altitude
Rockets, «Aeronautical Engineering Review», vol. 16, No. 6, 1957, pp. 63 — 66.
34
впервые обратил внимание на проблему программирования тяги.
При математическом исследовании этой проблемы Годдард рассмат¬
ривал идеализированную -ракету в виде прямого кругового конуса,
в верхней части которого размещена полезная нагрузка. Оболочка
ракеты непрерывно отбрасывается (с нулевой скоростью относитель¬
но остающейся части ракеты) по мере продвижения фронта горения
топлива (фиг. 13). Годдард пришел к выводу о существовании реше¬
ния задачи путем следующих рас-
суждений: «Допустим, что на не¬
которой высоте по пути подъема
ракеты скорость подъема будет
очень велика. Тогда сила сопро¬
тивления воздуха (пропорцио¬
нальная квадрату скорости) так¬
же будет очень велика. С другой
стороны, при очень малой скоро¬
сти подъема в течение длительно¬
го периода времени нужна будет
сила для уравновешивания силы
тяжести. В обоих случаях требу¬
емый запас топлива будет очень
велик. Отсюда следует, что ско¬
рость подъема должна иметь
строго определенное значение в
каждой точке пространства».
Годдард указывает далее, что
определение требуемой зависимо¬
сти скорости от времени полета
является новой нерешенной задачей вариационного исчисления.
В связи с этим он отказался от строгого рассмотрения задачи и дал
приближенное решение численным методом.
Почти через 10 лет после опубликования (в 1919 г.) классической
работы Годдарда, Гамель [2] в краткой заметке отметил нестрогость
решения Годдарда и указал на возможность решения задачи метода¬
ми вариационного исчисления. В последнее время другие исследова¬
тели, в том числе Тзян и Эванс [3], Лоуден [4] и Лейтманн [5, 6],
исследовали необходимые условия существования минимальной на¬
чальной массы ракеты, необходимой для полета на заданную высоту
при заданной массе пустой ракеты.
ТЕОРИЯ ВОПРОСА
Обозначим через М массу ракеты и через 5—высоту в некоторый
момент времени t. Обозначим далее точкой над буквой дифферен¬
цирование по времени. Примем, что сила аэродинамического сопро¬
тивления Q является функцией только s и s, и будем считать эффек¬
тивную скорость истечения Vr и ускорение силы тяжести g постоян¬
ными (учет изменения ускорения силы тяжести с высотой несколько
изменяет форму решения [6]). Условия в начальный момент полета
с работающим двигателем (г = 0) обозначим индексом «0», условия
Фиг. 13. Идеализированная ракета
Годдарда.
35
в момент окончания работы двигателя (t = tK)—индексом «к». Сим¬
волы плюс «+» и минус «—» при индексах обозначают условия в
момент времени, непосредственно следующий за моментом t = О, и
момент времени, непосредственно предшествующий !Моменту t = tK.
Будем считать координату s(t) непрерывной на протяжении всем
траектории ракеты; функции s(t) и М(1) будем считать непрерыв¬
ными в интервале времени 0<t<tK. По условиям задачи допускается
нарушение непрерывности 5 и М только до начала движения при
£ — 0, т. е. предполагается импульсный разгон ракеты при старте
(ниже будет показано, что импульсный разгон ракеты является
одним из условий решения).
В начале полета с работающим двигателем £ = 0, s = s0==0,
s = s0 = 0 и М = М0. После начального импульсного разгона
s = s0+ = s1 = 0, но s = s0+—sl и М = М0+ = М1. В момент оконча¬
ния работы двигателя t=tK_, s = sK_ = sK, s=sK^ = sK и М=
= МК_ = МК (так как эти функции считаются непрерывными).
Однако ускорение 5 и секундный расход топлива М не считают¬
ся непрерывными в момент окончания работы двигателя. Так,
при t=tK__ s = sK_ и М=МК_, а в начале пассивного полета
t=tK, s = sK и Ж = ЖК = 0.
Уравнение движения ракеты при вертикальном подъеме, состав¬
ленное без учета вращения Земли и учитывающее только аэродина¬
мическое сопротивление и силу тяжести, имеет вид
VrM+(s+g)M+Q(s, s)= 0. (1)
При интегрировании уравнения (1) в пределах периода началь¬
ного разгона 8, где $-*0, получается
MQ = Mle°'lv‘-. (2)
Уравнение движения при пассивном полете отличается от урав¬
нения (1) только отсутствием члена VrMy равного нулю, в связи с от¬
сутствием тяги двигателя.
Задача сводится к следующему. Заданы MR, Vr, g и функция
Q(s, s); требуется найти функцию s(t), обеспечивающую полет ра¬
кеты на высоту Н при минимальной начальной массе М0. При интег¬
рировании уравнения движения при пассивном полете в пределах от
s = sK до s = Н (s = sK и s=0) получается зависимость между sK и г\.
вида
5к = ф(5к). (3)
Методами вариационного исчисления можно показать, что для
обеспечения минимума М0 необходимо выполнить следующие усло¬
вия. На протяжении всего полета с работающим двигателем О
должно быть
+jLt^QU0. (4)
ds \ ds2 dsds Vr ds Vr ds Vr
36
В момент окончания работы двигателя t = tK_
5“[^+n"T.”4?+Q(s'"s')-
(5)
При выполнении этих условий задача отыскания оптимального
решения, т. е. функции s(t), соответствующей стационарному значе¬
нию Мо, является определенной. Уравнения (3) и (5) могут быть
решены относительно sK и sK. Уравнение (4) представляет собой
дифференциальное уравнение второго порядка относительно s(t),
при интегрировании которого значения sK и sK определяют начальные
условия. При интегрировании уравнения (4) в интервале 0<7<7К
получаются значения tK и s\. После этого можно проинтегрировать
уравнение (1) и определить ЛД:
Мх = е~^~г
Затем из уравнения (2) может быть найдено значение начальной
массы ракеты М0. Из уравнения (4) можно определить ускорение s,
после чего из уравнения (1) получается выражение для тяги дви¬
гателя:
P = -VM = M(s-\-g) +Q. (7)
Нетрудно показать [6], что первый интеграл уравнения (4) имеет
вид:
s+gt
y-K+Q-s('f+l)K'=0' <8)
Из уравнения (8) следует непосредственный вывод о том, что s
не может быть равно нулю в интервале 0<Ct<CtK. Действительно, при
s=0 Q = О, однако Mg^О и, следовательно, Отсюда следует
Sc+=si-^O, что подтверждает необходимость начального импульсно¬
го разгона ракеты.
СПЕЦИАЛЬНЫЙ СЛУЧАЙ
Сила лобового сопротивления обычно определяется по формуле
Q^pFc,*2, (9)
где о — плотность воздуха;
Р — характерная площадь;
сл — коэффициент лобового сопротивления.
Плотность воздуха р является функцией высоты s. Коэффициент
сопротивления сх является функцией числа М и числа Рейнольдса и
таким образом является функцией скорости и высоты. В качестве
простейшего допущения можно принять, что сх является постоян-
к—
И
0+
s+gt SK+gfK
е vr dt+MKe vr
(6)
37
ным. Зависимость р от и достаточной точностью можно считать
экспоненциальной. При этих допущениях получается
Q = Q0sV-«
где
(10)
ро — плотность воздуха на уровне моря;
а — постоянная.
При подстановке выражения силы сопротивления по формуле (1)
в уравнение (4) последнее принимает вид
где
s = ^[^2 + (1 _p)jg_2p]
g $[х*-^4х + 2]
S V п
Х = — = — И В =
vr vr г
(П)
aVi
Уравнение (И) может быть проинтегрировано, в результате чего
определяются s(x) и t(x):
«»*-*+JL ln.2* + (l-P)-T . ^ + q-P) + 7 +
2 2* + (l-p) + 7 2xi + (1 — P)— 7
3 + i
In
^2 + (1_р)д:_2Э
дс*+(1-р)д:1-2р
ML — in £l _l J_ In 2x + (1 ~ ^ ~~ 7 2x! + (! ~ ^) + f .
Vr *2 2je + (1 — P) + T 2xi -f- (1 — (3) — 7
.1+1 In *2 + (l-P)*-2p
^ 2 ^ + (i_p)jfl_2p ’
(12)
(13)
где
Т = П(1~Р)2 + 8р .
После подстановки выражений (12) и (13) в проинтегрированное
уравнение (1) получается
мк
X
х + 2
Хк + 2
S‘K
jr2 + (l-p)jf-2p хк -|- (1— Р) хк — 2р
+ е
хк+ у.
(14)
После этого может быть получено выражение для тяги в виде
р Q0v2r
MKg MKg
+
м
м.
1 + —
g
(15)
38
Уравнение (3) приводится к виду
'К
(16)
где
= ZH=e-a”.
Интеграл уравнения (16) может быть вычислен с помощью сле¬
дующего интеграла, значения которого табулированы [7]:
Решение задачи осуществляется в такой последовательности:
а) решаем уравнения (16) и (17) относительно sK и xR;
б) подставляем значения sK и хк вместо s к х в уравнение (12) и
определяем Х\\
в) используя это значение х± и подставляя х = хк в уравнение (13),
находим tK;
г) находим из уравнения (14) М(х) и используем уравнения (15)
и (И) для определения Р(х).
Так как t(x) известно, то можно определить М и Р как функции
времени t.
Пусть требуется обеспечить полет ракеты до максимальной вы¬
соты
у
или путем разложения интеграла в ряд
Уравнение (5) принимает окончательный вид:
(17)
ЧИСЛОВОЙ ПРИМЕР
Рассмотрим ракету со следующими данными:
Qo/MK = 3,05- 10_6 му Уг=1680 м/сек.
Н= 149 ООО м
‘при минимальном общем расходе топлива.
Примем а = 6720 мг1 и g = 9,81 м/сек2.
39
Используя уравнения, выведенные в предыдущем разделе, на¬
ходим
5Я= 19 100 м;
tK = 18,7 сек.;
MJMU=2,1;
г'к= 1620 м\сек;
г»! = 671 м/сек-,
М01МК=3,14.
На фит. 14—16 показаны кривые изменения относительных вели¬
чин секундного расхода топлива М0тн=М/Мв, скорости x = vjVr и
V
*4
0.8
0,6
0,ч
0,2
/
8 f? 16 20
teen
Фиг. 14. Массовый расход
топлива как функция вре¬
мени.
в 12 16 20
t.ceк
Фиг. 15. Безразмерная ско¬
рость как функция времени.
ускорения s/g как функций времени. Идеальная программа измене¬
ния тяги требует достижения скорости ^ = 671 м!сек под действием
импульса тяги нулевой продолжительности. На практике импульс
нулевой продолжительности может
быть заменен кратковременным разго¬
ном при большой тяге. После этого по¬
лет может быть продолжен при идеаль¬
ной программе изменения тяги. Для
исследования влияния замены идеаль¬
ного начального импульса реальным
разгоном с ускорителем на максим-аль-
ную высоту, достигаемую ракетой, рас¬
смотрим случай, когда разгон осуще¬
ствляется за время 1,2 сек., при котором
расходуется то же количество топлива
М0—М1у что и при идеальной про¬
грамме.
Примем, что дальнейший полет совершается при идеальной про¬
грамме изменения тяги. Учтем также конечное время нарастания тяги
ускорителя и падения тяги в конце работы, приняв продолжитель-
Фиг, 16. Коэффициент
дольной перегрузки
функция времени.
про-
как
40
лость обоих процессов по 0,1 сек. Величина секундного расхода топ¬
лива во время разгона при принятых данных получается вполне
достижимой. Так, например, при массе ракеты после выгорания топ¬
лива Мк=14,9 кгсек2/м тяга ускорителя равна 23 500 кг. Реальная
программа изменения тяги по времени показана на фйг. 17. Для
сравнения рассмотрим также полет ракеты на максимальную вы¬
соту при постоянной тяге (фиг. 18).
Фиг. 17. Реальная программа изме- Фиг. 18. Зависимость максимальной вы-
нения тяги по времени. соты полета ракеты от массового расхо¬
да топлива при постоянной тяге.
Интегрирование уравнений движения для рассмотренных случаев
было выполнено на цифровой (вычислительной машине IBM701; в
результате получились следующие значения максимальной высоты
полета ракеты:
Программа изменения тяги
Максимальная высота
Идеальная программа
149 ООО м
Реальная программа
144 000 м
Программа при наивыгоднейшем значении посто¬
янной тяги двигателя
134 300 м
Из этой таблицы видно, что замена идеальной программы тяги
по времени реальной программой приводит к уменьшению высоты,
Достигаемой ракетой, на 3,5%. При замене реальной программы ре¬
жимом наивыгоднейшей постоянной тяги высота полета ракеты
Уменьшается еще на 6,6%.
ВЫВОДЫ
На основании проведенного исследования следует сделать вывод,
Что идеальная программа изменения тяти по времени может быть
заменена приближенно соответствующей ей реальной программой с
Разгоном при большой конечной тяге вместо импульсного разгона;
41
при этом максимальная высота полета ракеты уменьшается незна¬
чительно. Вопрос о целесообразности программирования тяги и со¬
ответствующего усложнения системы регулирования двигателя для
увеличения максимальной высоты полета ракеты сверх достижимой
при наивыгоднейшей постоянной тяге следует решать отдельно в
каждом конкретном случае.
ЛИТЕРАТУРА
1. Годдард Р., Метод достижения очень больших высот.
Goddard R., A Method of Reaching Extreme Altitudes, Smithsonian Misc.
Coll., 1919, vol. 71, No. 2.
2. Гамель Г., Об одной задаче вариационного исчисления, связанной с
движением ракеты.
Hamel G., Uber eine mit dem Problem der Rakete zusammenhangende
Aufgabe der Variationsrechnung, ZAMM, 1927, vol. 7.
3. T з я н С. и Э в а н с P., Оптимальное программирование тяги высотной
ракеты.
Tsien Н. and Evans R., Optimum Thrust Programming for a Sounding
Rocket, «Journal of American Rocket Society», 1951, vol. 21, No. 5.
4. Лоуден Д., Оптимальные траектории ракеты.
Law den D., Stationary Rocket Trajectories, «Quarterly Journal of Mechanics
and Applied Mathematics», 1951, vol. 7, Part IV.
5. Л e й т м а н h Г., Решение задачи Годдарда методами вариационного
исчисления.
Leitmann G., A Calculus of Variations Solution of Goddard’s Problem,
«Astronautica Acta», 1956, vol. II, Fasc. 2.
6. Л ейтманн Г., Диссертация, Калифорнийский университет.
L е i t m,a n n G., Ph. D. Dissertation, University of California, Berkeley.
7. Я н к e E., Э д м e Ф., Таблицы функций, Нью-Йорк, 1943.
Jahnke E. and Emde F., Tables of Functions. Dover Publications, New
York, 1943.
Г. Л ЕЙТМАНН
РЕШЕНИЕ ЗАДАЧИ ГОДДАРДА
МЕТОДАМИ ВАРИАЦИОННОГО ИСЧИСЛЕНИЯ1
I. СУЩНОСТЬ ЗАДАЧИ
Задача, сформулированная Р. Г. Годдардом, может быть пред¬
ставлена в следующем виде: какова должна быть зависимость скоро¬
сти ракеты от времени, чтобы при данной полезной нагрузке до¬
стигнуть заданных высоты и скорости таким образом, чтобы началь¬
ная масса ракеты была минимальной?
Для решения поставленной задачи Годдард рассмотрел идеали¬
зированную ракету, а также некоторые основные характеристики
реальной ракеты. Схема такой идеализированной ракеты Годдарда
изображена на фиг. 13.
1 G. A. L е i t m a n n, A Calculus of Variations Solution of Goddard’s Pro¬
blem, «Astronautica Acta», 1956, vol. 2, Fasc. 3, pp. 56 — 62.
42
Идеальная ракета представляет собой правильный круговой ко¬
нус с условной полезной нагрузкой Мк, расположенной в его верши¬
не. Годдард предположил, что по мере выгорания топлива частицы
корпуса непрерывно отделяются от ракеты с нулевой скоростью по
отношению к остающейся ракете. Предполагалось также, что ско¬
рость отделения частиц сгоревшего топлива относительно ракеты
постоянна.
Годдард доказал существование минимальной начальной массы
(т. е. минимума топлива), необходимой для того, чтобы поднять за¬
данную полезную нагрузку на установленную высоту путем следую¬
щих рассуждений.
«Если на любой промежуточной высоте скорость подъема будет
очень велика, то сопротивление воздуха (изменяющееся в зависи¬
мости от квадрата скорости) будет также большим. С другой сторо¬
ны, при очень малой скорости подъема в течение длительного перио¬
да времени нужна будет сила, уравновешивающая силу тяжести.
В обоих случаях необходимая масса (топлива), которая должна
расходоваться, будет чрезмерно высока. Отсюда очевидно, что ско¬
рость подъема должна иметь определенное значение в каждой точке
пространства».
Годдард выдвинул положение, что определение зависимости опти¬
мальной скорости от времени представляет новую и еще нерешенную
задачу вариационного исчисления. Поэтому он отказался от строгого
решения и предложил приближенное решение этой задачи [1]. Необ¬
ходимо отметить, что основные допущения Годдарда состояли в тОхМ,
что аэродинамическое сопротивление, сила тяжести и ускорение при¬
нимались постоянными на большом числе участков траектории.
В настоящей статье автором используются более точные методы
вариационного исчисления для исследования соотношений, необхо¬
димых для нахождения минимальной начальной массы ракеты.
II. РЕШЕНИЕ
В статье приняты следующие обозначения:
М — полная масса ракеты в данный момент времени;
s — путь;
5 — скорость полета ракеты;
Q — лобовое сопротивление;
g — ускорение силы тяжести;
к — постоянная доля dM, соответствующая оболочке, отбрасы¬
ваемой с нулевой скоростью относительно ракеты;
VT —скорость отброса массы сгоревшего топлива относительно
ракеты;
"(•) —символ, обозначающий дифференцирование по времени.
Уравнение движения ракеты при вертикальном подъеме (без
учета влияния вращения Земли) может быть записано в виде:
MVr(l—k)+M(s+g) +Q = 0.
(i)
43
После израсходования всего топлива уравнение движения примет
вид
AfK(S + g-) + Q = 0, (2)
где Мк — оставшаяся после выгорания топлива масса (условная по¬
лезная нагрузка).
При заданной высоте Я и скорости Я уравнение (2) имеет сле¬
дующее решение:
s = cp(s). (3)
Если выгорание топлива заканчивается на достаточно большой
высоте, где сопротивлением можно пренебречь, то уравнение (3)
будет иметь вид
S =V2g{H-s) + fP.
При этом налагается дополнительное ограничение: ускорение
силы тяжести g считается постоянно. Для средних высот, порядка
160 км, это допущение вносит погрешность не более 5°/о реальной
величины ускорения. Однако необходимо отметить, что ценой неко¬
торого усложнения решение может быть получено и с переменной
величиной g.
Аэродинамическое сопротивление может быть написано в сле¬
дующем виде:
Q = \?Fcxs\ (4)
где р—плотность воздуха;
Cj> — коэффициент лобового сопротивления; ~ " '
F — характерная площадь ракеты (обычно наибольшая пло¬
щадь поперечного сечения).
В данной задаче плотность воздуха является функцией пути 9.
Коэффициент сопротивления сх зависит от чисел М и Re, и поэтому
с достаточным приближением его можно выразить как функцию вы¬
соты S И скорости 5.
Для тела с формой, подобной форме рассматриваемой здесь иде¬
альной ракеты, изменяющаяся площадь поперечного сечения F
может быть выражена в виде
F= аМ2!3, (5)
где коэффициент пропорциональности а дается выражением
-(y-*P*ctg9) 2/3; (6)
здесь о#—условная плотность ракеты;
О — половина угла при вершине конуса.
Понятно, что при постоянной условной плотности ракеты пр ко¬
эффициент пропорциональности а будет постоянным.
44
Таким образом мы имеем дело с проблемой, которая может рас¬
сматриваться как одна из задач типа Майера [2].
Исходя из принятых выше допущений можно записать
Q=-T oaM^cxs2=M-izq (s, s), (7)
так что уравнение (1) примет вид
MVr(\-k) + M(s + g) + M^q{s, 5) = 0. (8)
Если принять
да=с;, (9)
то уравнения (8) и (9) можно будет написать в следующем виде:
Ф г *= MVr (1 — k) + М (v + g) + МЩ (5,5) = 0; (10)
Ф2 = 5 — ^ = 0. (11)
В целях исследования свойств оптимальной траектории берем
вариации и ЗФ2; эти вариации соответствуют «близлежащим»
траекториям. Если «близлежащие» траектории удовлетворяют урав¬
нению движения, то
8Ф'=0' ) (12)
8Ф,=0. I
Применяем множители Лагранжа М(/) и Я2(0 и образуем сумму
Тогда уравнение (12) может'быть написано в следующем
виде:
ГXjM2/3 - Х21 5s + — (X 8s) -f jM2'3 ^2. - X,Af - Xj/W - xjto +
L ds J dt [ &v J
+ 4 (XtAf 8®) + F \(v + g) + A KqM-Ч* — \Vr{\ — k) I0M +
<** L 3 j
+ 4 [хУД1-0^]=°. (13)
Предполагается, что скорость s=v на активном участке полета
непрерывна, однако необходимо допустить возможность разрыва в
значении скорости s в начале и в конце активного участка полета.
Разрывность в значении 5 эквивалентна мгновенному изменению
величины скорости. Теоретически это изменение может быть вызвано
45
мгновенным приложением импульса. Следовательно, можно написать
условия:
при £ = 0
s = 0,
s = v = 0,
м=м,
о»
= X
70'
при £=0+
s = 0,
S = 'l»=*s1 = '01,
при t=t~
s = s'
перед началом приложения начального
импульса
I
► после окончания действия начального
импульса
S = V = S к = Нк,
М = М к,
== 'k’l к» )
при t=tK (конец горения)
s = s„, }
\ перед началом действия конечного им-
I пульса
S = <V = SK=VK% I
М = МК,
} после окончания действия конечного им-
I пульса
Условия при t = tK соответствуют условиям начала пассивного
участка полета.
Интегрируя уравнение (13) в пределах от до t=t~y т. е. в
пределах времени работы маршевого двигателя, получаем
v,{ 1 - k) [хп ш, - >/ злд = х;к ss; - х21 з5(3 + х;к аг -
— ХцУИ] 8г»1 +
J 1
1 ds
+
) уи2.'3 — \М - Х,уИ - Х2
dv
3S +
dv +
\ (V + g) + нрКяМ-w _uyr(\ - k)
ZM\dt.
(14)
46
Множители Лагранжа являются все еще произвольными. Для
того чтобы выразить Ш0 только как функцию Ss и Sv, налагается
следующее условие:
М^ + £) +-|-xrfM-1,3-W(l-£)=0. (15)
О
Так как Ss и Sv произвольны, то их коэффициенты в отдельности
должны равняться нулю, т. е.
XjM2/3 — — Х2=0,
ds
XjAJ2/3 ii _ X Af _ Х,Ж - X2=о.
dv
(is)
Уравнения (8), (15) и (16) могут рассматриваться как система
четырех дифференциальных уравнений с зависимыми переменными
Хи %2, М и 5. Исключим из уравнений величины %\у и М, для чего
сначала получаем следующее соотношение:
Х2=XjM2'3 [ $2- + q- 1. (17)
2 1 L д» 3 VV (1 — *) J
Окончательно исключив %2 и М, приходим к уравнению Эйле¬
ра—Лагранжа
°l=-WLv + ?4i +
ds ds dv dv2'
1
3 Vr(\-k)
+ + — — C + £)?]. (18)
ds dv 3 К/- (1 — k) j
Уравнение Эйлера—Лагранжа должно удовлетворять условиям
активного участка полета, за исключением моментов, соответствую¬
щих началу и концу работы двигателя.
Если допустить разрывность скорости при значениях t = 0 и t = tK,
то для мгновенных импульсов имеют место следующие выражения:
Af0 = M1evvu-*),
(19)
Мк = Мке
Имея в виду уравнения (15) и (16), уравнение (14) можно пре¬
образовать к виду
Можно записать следующие граничные условия:
6s (0) <= 6s0=0 1 — значения s (0) и М (£K) точно опре- )
bM(tK) = bMK — 0 | деляются;
bv(tK) = bvK = -^-bsK
OSK
— имеется в виду уравнение (3) при
t=tK;
[(21)
6s(^“) = 6s|(=8sK = os(^K) —так как перемещения являются
непрерывными.
)
Необходимым условием существования минимальной начальной
массы М0 является
Шо = 0. (22)
Используя выражения (17), (19), (21) и (22), можем привести
уравнение (20) к следующему виду:
дд | я_
dv 3Vr(\-k) J
*'кК
■
Мке
'='к
К
1/3
. (23)
dsK
Уравнения (3) и (8) позволяют записать уравнение (23) в сле¬
дующем виде:
, Т/з
(g + M-^qK). (24)
Уравнения (24) и (3) должны удовлетворяться при t = tK. Если
функция s~v при t = tK неразрывна, то в конце активного участка
полета нет никакого импульса и уравнение (24) принимает вид
9 {$к) [U + зм1-*)к'к=M*3g+q«‘
(25)
Уравнение Эйлера—Лагранжа (18) является дифференциальным
уравнением второго порядка относительно s(t), подчиненным
начальным условиям s|0+|=0 и s|0+|=Uo.
Начальная скорость v0 точно не устанавливается, но, тем не ме¬
нее, она определяется на основании того, что должны удовлетворять¬
ся уравнения (24) или (25).
III. ЧАСТНЫЙ СЛУЧАЙ
Для того чтобы получить решение оптимальной задачи, необхо¬
димо установить вид функции сопротивления q(s, s). Часто прини¬
мается квадратичный закон изменения сопротивления, т. е. предпо¬
лагается, что коэффициент сопротивления Cj.=const. Это допущение
используется и здесь для решения частной задачи.
48
Из изложенного выше имеем
q (s, s) —paCjS2 [см. формулу (7)].
Приемлемым приближением для функции р = р (s) является
р = Рое-«, (26)
где ро есть плотность воздуха на уровне моря, а а = const.
Следовательно, можно написать
q (s, s) = Re-*ss2, (27)
где
R = -yPoac*- (28)
Интегрирование уравнений Эйлера—Лагранжа (18) произво¬
дится достаточно просто. Введем обозначения:
Я V
X = ■
3V> (1 — зкг(1 — k)
в = Z. *
г 9аК2(1—^)2 *
Т = [(1 —Р)2 + 8р]1/2.
(29)
)
Тогда уравнение (18) может быть выражено в следующем виде:
5 X [Х2 -|- (1 — Р) ЛГ - 2Р]
g ${х* + 4х + 2)
Интегрирование уравнения (30) для s(jc) и t(x) дает
<х$=л; —— Ш ^ + 0 ~ Р) ~ Т.. if + 0-Ё1+1 +
2 2* + (1-р) + т 2xj + (1-P)-7
(30)
3 + р д;2 + (1-р)лг-2р
jf? + Cl — Р) — 2р
1П . 2 , ~ / оГ (31)
g j. jn £j_ , _T_ jn 2x + (\ — fS)— t _ 2xi + (1 — P) Ч~ К .
3V,(l-fe) x 2 2jc + Cl — P> + T ’ 2L*:x + (» — P) —T
, l + sm , (32)
2 jt;+(i-p)*,-»
Из уравнения (32) получаем
s = s(0 (33)
н. следовательно, из уравнений (31) и (33)
s = s(t); (34)
Из Уравнений (30) и (33) имеем
s = s(t). (35)
4 394 49
Для квадратичного закона сопротивления решение уравнения
свободного полета [уравнение (2)] дается в следующем виде:
н
2 2(3 -
RVr
3Vr(\—k)
е M*g
■? ( \
RVг
20 — £
-2ре м«е КХ
(36;
где
и
Ек=е-«к; %н--
Г
bz
э-аН
(bz)2
Ы!
2-2!
(37)
Конечно, если заданная высота подъема s = H является предель¬
ной высотой подъема, то s = H = 0. Если сопротивление в свободном
полете мало, то уравнение (36) может быть заменено следующим вы
ражением:
sK=[H2 + 2g(H-sK)]'l2. (38)
Граничное условие, выраженное уравнением (24), примет вид
R
--
л
1
ге
1
1/3,-
vKvKe~as« =
[муга-v J
-
3Vr(l—k)
Дополнительное граничное условие (25) будет
g+MK Re~*s«vi
R
1 +
3Vr(\-k) J
vie as«=M]!3g.
(39)
(40)
При определении положения высоты 5 и скорости s в конце актив¬
ного участка полета могут быть три случая. Эти случаи иллюстри¬
руются на фиг. 19.
Случай первый. Кривые, определяемые уравнениями (36)
и (40), имеют точку пересечения. В этом случае они могут быть ре¬
шены относительно sK и sK.
Случай второй. Кривые, определяемые уравнениями (36)
и (40), не имеют точки пересечения. Однако уравнения (36) и (40)
могут оба удовлетворять условиям для значений sK = H и sK = H (т. е.
до заданного конца полета свободный полет не имеет места). Этот
случай может быть при условии, если vK'<H. В этом случае можно
подставить sK = H и vR = H в уравнение (39) и решить его относитель¬
но vK'.
Случай третий. Наконец, если уравнения (36) и (40) не
имеют общего решения и vK'^>H [из уравнения (39)], то в этом слу¬
чае требования вариационного исчисления не будут удовлетворены.
50
Следовательно, предполагаемого значения минимума не существует.
Однако можно показать, что при мгновенном приложении импульса,
т. е. при мгновенном сгорании всего запаса топлива с тем, чтобы
достичь значения vK = v0, масса ракеты будет минимальной. Этот слу¬
чай может иметь место при очень малом отношении сопротивления
к весу. Хорошо известно, что в
предельном случае, когда сопро¬
тивление равно нулю, мгновенный
импульс должен обеспечить ма¬
ксимальную высоту подъема ра¬
кеты.
Наша задача состоит в том,
чтобы найти M(t) и потребную ми¬
нимальную массу М0. Для этой
цели интегрируем уравнение (8).
Замена переменной
(41)
позволяет выразить уравнение (8)
в форме линейного уравнения.
ЗК,(1 — £)m + (s + g) m + q = 0.
(42)
Фиг. 19. Три случая взаимного
расположения кривых, определя¬
емых уравнениями (40) (а, б, в)
и (36).
Это уравнение легко можно проинтегрировать:
те
s+gt
,ЗП,(1 — к)
3Vr(i —*)
S+gt
?iv'{x-k)dt.
(43)
Подстановка вновь значения М и использование уравнения (29)
позволяют представить уравнение (43) в виде
8(к
Me
+*И
s2 | х +
е
М;е
[,л. а
3V/-11 — А>J _|_
ЗНГ(1 -*) asl dx.
(44)
Имея в виду уравнения (30), (31) и (32), можно произвести пол¬
ное интегрирование, что дает
9/? 1/2(1 — б)2
X
M{t) =
х + 2
■$хге*> [-Ч + (1 —P)*i —2р]Х
хк +2
8‘к
+ [*+•
+ М?е[ K+3^-«J
Х<?
-4Л' + з1мГ^)
X
(45)
4*
51
Во втором случае (случай «б») значение Мк в уравнении (45)
заменяется величиной М/, а хк—величиной хк\
При этом очевидно, что tK = t~.
Определение величин sK и vK (или sK и i/) позволяет решить урав¬
нение (31) относительно х± и уравнение (32) относительно tK; так
как услозная полезная нагрузка Мк известна, то значение М/ (для
случая «б») находится из уравнения
Окончательно находим из уравнения (45) при ^=0 и х=х\.
Затем определяем начальную массу М0 из уравнения
В третьем случае (случай «в») значение М0 выражается просто:
1. Годдард Р., Метод достижения очень больших высот.
Goddard R., A Method of Reaching Extreme Altitudes, Smithsonian
Inst. Publ., Misc. Collect., 71, No. 2, 1919.
2. M а й e p А., Об общих проблемах вариационного исчисления.
Mayer A., Uber das allgemeinste Problem der Variationsrechnung, Leipzig;
Akademie der Wissenschaften, 1879.
3. T з я н С. и Эванс P., Оптимальное программирование тяги высотной
ракеты.
Tsien Н. S. and Evans R. C„ Optimum Thrust Programming for a soun¬
ding Rocket, «Journal of the American Rocket Society», 1951, vol. 21, No. 5,
pp. 99 — 107.
4. JI о у д e н Д., Оптимальные траектории ракет.
Lawden D., Stationary Rocket Trajectories, Quart J. Mech., 1954, 7, 488.
Г. ЛЕИТМАНН
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ ДЛЯ ВЫСОТНОЙ РАКЕТЫ
С ОТДЕЛЯЮЩИМСЯ УСКОРИТЕЛЕМ1
Задача определения оптимального режима изменений тяги для
высотных ракет, т. е. проблема достижения заданной высоты с задан¬
ной конечной массой и минимальной начальной массой рассматри¬
валась в работах [1—5]. Суть оптимального режима движения ракеты
состоит в придании ракете начальной скорости под действием им¬
1 G. A. Leitmann, Stationary Trajectories for a High-Altitude Rocket with
Drop-Away Booster, «Astronautica Acta», 1956, vol. II, Fasc. 3.
(46)
M0 = M1e3x>.
(47)
где хк определяется из уравнения (36) при sK = 0.
ЛИТЕРАТУРА
52
пульса тяги, т. е. путем мгновенного расходования части топлива.
Это идеальное требование в практическом случае может быть при¬
ближенно осуществлено приданием ракете начальной скорости с по¬
мощью ускорителя большой тяги.
В ранее рассмотренных случаях масса в конце выгорания топли¬
ва, включающая как полезную нагрузку, так и сухую (без топлива)
двигательную установку, принималась известной. Более того, уско¬
ритель рассматривался как часть ракеты, и влияние отсасывания
ускорителя на движение ракеты не учитывалось.
Здесь мы рассмотрим оптимальную задачу, в которой заданной
величиной является действительная полезная нагрузка, а не конеч¬
ная масса ракеты и учитывается факт отсасывания ускорителя.
I. ФОРМУЛИРОВКА ЗАДАЧИ
Обозначим через М массу конструкции ракеты и через 5 высоту,
достигнутую за время t. Будем предполагать, что лобовое сопротив¬
ление Q является функцией только величин 5 и 5 и для заданной схе¬
мы ракеты известно.
Эффективная скорость истечения газа Ут и ускорение силы тяже¬
сти g принимаются постоянными.
В начале активного участка полета /=0, 5 = 0, 5 = 0 и М=М0.
После приложения импульса тяги, но до отбрасывания ускорителя
еще имеем ^=0 и 5 = 0, но s = v°~=vi/ и Af = Af0_=M1/; параметры
движения после отбрасывания ускорителя обозначим: s = v0+=vi и
М = М°+ = М,.
Будем предполагать, что ускоритель отбрасывается мгновенно с
нулевой скоростью относительно основной ракеты. В конце выгорания
топлива t = tKy s = 5K, s=vK и М = МК.
Массу действительной полезной нагрузки обозначим через Ма.а.
Обозначив отношение массы сухого маршевого двигателя ракеты
к массе маршевого топлива ракеты через гДв и отношение массы кор¬
пуса ускорителя к массе топлива ускорителя через гуск, где гДъ и /уск—
заданные величины, а также обозначив массу топлива ракеты через
Мтр, а массу топлива ускорителя через Mryoli, можно записать
^п.н + 0 + Гдв) ^т.р + 0 + Гуск) Мт уск,
Ml = М° - = Мп н + (1 + гдв) Мт р + гускЛ/т>уск, ^
Мх — М° + = Мпи + (1 + ^дв) Мт р,
М =М 4* г М
iriK rJn.H I ' AB^riT.p* J
Задача будет состоять в том, чтобы по заданным значениям Мпн,
Гдв, ^Уск, У г, g и Q(s, s) определить такую функцию 5(^), при которой
М0 будет минимальной. Дополнительными условиями являются:
*(0) =0 и такое соотношение между 5К, vE и Мк, которое обеспечи-
вает достижение заданной высоты 5.
53
И. РЕШЕНИЕ
Уравнение вертикального полета без учета влияния вращения
Земли записываем в виде
(2)
Для свободного полета М = 0. Решение уравнения свободного по¬
лета, соответствующего предельной высоте s, может быть выражено
в виде
s=cp(s, М). (3)
При t = tK имеем
= Л^к)- (4)
Можно получить необходимое условие для минимального значе¬
ния М0 при помощи метода Майера [71.
Пусть sst), тогда уравнение (2) может быть написано в следую¬
щем виде:
ф1== VrM + (v + g)M + Q(s, v) = 0,
Ф2 = 5 — v = 0,
где s—s(t)—искомая оптимальная функция.
Из уравнений (5) имеем
8Ф, = К,3 М + (v + g) Ш + М Ъг> + 8s + 8® =■- 0,
ds dv
8ф2 = о5 — 8^=0.
(5)
(6)
Затем вводим множители Лагранжа Xi(t) и ^(t) и составляем
сумму ИХгЗФг. Допуская законность поочередного дифференцирова¬
ния и имея в виду уравнение (6), получаем следующее выражение:
хД->;2
1 ds 2
8S + JL(X28S)
at
d_Q_
dv
-a2 — —XjAf
bv +
+ ±Q4Mbv)+ [хД + ^-Х^ЗМ+А^^/И^О. (7)
at at
Интегрируем уравнение (7) в пределах между моментом отделе¬
ния ускорителя и моментом полного израсходования топлива ракеты:
\Уг *МК ^^1 — ^21^51 ^ч2к05к "Ь ^11^1^1
t„
-4.Af.4-J
3s +
о v
OV +
[^i + s*) — vА ^ 1 dt,
(8)
54
Выражаем Ш0, а также и Шь как функцию только Ss. Следо¬
вательно, на неопределенные множители к\ и Х2 налагаются условия
К (v + g)—\vr=0,
dQ
dv
•Х2 —Х1УИ-Х1М=0.
(9)
Имея в виду произвольность значения Ss, из уравнения (8) по¬
лучаем
(10)
xi——Ч=о
1 c>s 2
— ^21 ^51 b ^11^1 *jC°\ 0^)
Для мгновенного импульса при ^=0 будем иметь
M0=Mie
(12)
Так как 5 = 0 и ускоритель отбрасывается с нулевой скоростью по
отношению к основной ракете, то
S5i = 0; Vi=vb
Далее, имея в виду уравнения (3 и 4), имеем
ду
8s.
dsK дМк
Для стационарного значения М0
Ш0 = 0.
Используя определения (1), получдем
ЪМ„
УгЪМ, = \гуске
VrbMK = rpi±^М, [гуск (/ - l)- 1
1 “Г rr
— 1
(13)
(14)
(15)
(16)
(17)
Подставим теперь уравнения (14), (16) и (17) в уравнение (11).
Следует иметь в виду, что SsK и ^ являются независимыми вариа¬
циями, так что коэффициенты при них должны каждый в отдельно¬
сти обращаться в нуль. Интегрирование уравнений (9) дает
Из уравнений (2) и (9) найдем при t=tK
dQ , Q
(18)
Таким образом, уравнение (И) окончательно приводится к виду
= MKg+QK (20)
dQ О
dv Vr_
rP(1 + гУск) (* 'm^)e Vr — VkO+rp)K'— (21)
Исключая >wi и X2 из уравнений (2), (9) и (10), получаем уравне¬
ние Эйлера—Лагранжа в виде
g,.+ (2i+i')^ + J-(«+g)Q]-
-*=0. (22)
ds
d*Q , d^Q • , 1
—— —
dv ds dv2 Vr
Начальная масса Мо будет иметь экстремальное значение в том
случае, если линейное дифференциальное уравнение (22), являю¬
щееся уравнением второго порядка относительно s(t), будет удов
летворяться на активном участке полета и будут выполняться усло¬
вия (20) и (21).
III. ПЕРВЫЙ ИНТЕГРАЛ
Уравнение Эйлера—Лагранжа (22) имеет первый интеграл
l=Mg+Q-v(*L+JL)-0. (23)
Это можно проверить путем дифференцирования значения I
-v(J^v+W-i + JLW+±dQ\ (24}
\dsdv dv2 Vrds Vr dv J
Используя уравнения (2) и (22), можно уравнение (24) перепи¬
сать в виде
/=-4*+/i^)- (25)
Если
/ = 0,
то / = —v е=0. (26)
Однако, если I действительно есть первый интеграл е, то
/—/к= - ^mdt=0. (27)
Но из уравнения (20) следует, что /*=0, т. е. / = 0, поэтому соот¬
ношение (26) удовлетворяется.
56
Решение теперь может быть произведено следующим способом.
Уравнение Эйлера—Лагранжа может быть проинтегрировано
[1, 2, 5 и 6], в результате чего получаются следующие выражения:
Sk = SkK. ®к),
(28)
О-
Уравнения (28) могут быть решены относительно Pi(sK, vK) и
ts(sK) 0К), и результаты решения могут быть подставлены затем в
уравнение (21).
Затем могут быть решены уравнения (4), (20) и (21) относитель¬
но sKj vK и MR. Получив значение Мк, сразу же непосредственно опре¬
деляем и величину Л4ТР. Из уравнений (1) и (12) получаем затем
значение МТусЕ, т. е.
Мт.-
уск
Кроме того, на активном участке полета значение М определяет¬
ся из уравнения (23).
IV. ЗАМЕЧАНИЯ
Интегрирование уравнения движения (2) дает
Рк+g'K р v+4t
МхеVr - Мке Vr = \-У- е vr dt. (30)
о т
Уравнение (30) должно удовлетворять решению оптимальной
проблемы (20). Это легко можно показать.
Одной из форм уравнений (28) является
SK
-к ds
, г as
"k + J —
(Ж _|_ _5_у _ q] е Vr - \(*Я. + SL\ v _ Q
\ dv ^ Vr) vJ<=o V dv vr) ^
0
в Vr =
t=t„
(31)
5ds
Подстановка уравнения (24) при £=0, t—tK и t=j—
о ь
Уравнение (31) сразу же приводит к уравнению (30).
Для того, чтобы существовало минимальное значение М0, оно
Должно удовлетворять уравнению (21). Однако это невозможно при
всех значениях гр и rJCK. В частности, если гр=0, то уравнение (21)
Может быть удовлетворено только, когда гуск=0.
57
Однако случай гр=0 представляет собой до некоторой степени
особый случай, так как при этом Мк=Мп.к и решение чрезвычайно
упрощается.
V. СЛУЧАЙ НЕОТДЕЛЯЕМОГО УСКОРИТЕЛЯ
В этом случае рассматривается оптимальная задача, в которой
ускоритель органически связан с основной ракетой с заданной полез¬
ной нагрузкой. Эта задача представляет практический интерес по
следующей причине. Если конечная масса ракеты задана, то тогда
оказывается заданной и масса израсходованного топлива и сухой
двигательной установки.
Однако масса сухой двигательной установки практически бывает
неизвестна до тех пор, пока не станет известным количество топлива,
необходимое для достижения заданной высоты. Но высота в свою
очередь зависит от количества сжигаемого топлива.
Оптимальное решение в случае неотделяемого ускорителя полу¬
чается совершенно аналогично решению, которое было применено
.для задачи с отделяемым ускорителем. В этом случае имеем
М0=( 1 +Гуск) ^т.уск + О +Гр)^т.р + ^п.н5
М0+ = М°~ = М° = М1 = г ускМТ'УСК + (1 + Гр) Мтр + Л4ПН;
Мк = гускМт,уск + rpMTtP + Мпл. (32)
При решении, аналогичном предыдущему, приходим к тому же
уравнению Эйлера—Лагранжа—уравнению г = 0 (22). Однако урав¬
нение (11) преобразуется к виду
*1к
ГР
Таким образом,
гуск — гр м л + =
грТ~1 > дмк vr) (34)
) +
‘к dsK
х1к=мк-^-+х2к =о.
При гускфгр m (34) 'получаем
1+_ау_Мк=0_ (35)
дМк Vr
Так как ду/дМк—непрерывная функция гр и гуск, уравнение (35)
применимо также и для случая, когда tyCK->rv. Тогда уравнение (34)
снова приводит к уравнению (20).
Короче говоря, все уравнения, за исключением уравнения (21),
остаются теми же, что и в случае отбрасываемого ускорителя.
Уравнение же (21) заменяется уравнением (35).
Порядок решения следующий.
S3
Из уравнения (35) значение Мк получается как функция sR. По¬
лученное значение Мк подставляется в уравнения (20) и (4). Затем
эти уравнения решаются относительно sK и vK. После этого уравнение
(7) может быть использовано для определения значений vx и tK, а
уравнение (35)—для определения значения Мк. Затем, как и преж¬
де, определяется значение Afx.p, Мт.уЖ.
Решение последней задачи упрощается и приводится к виду, рас¬
смотренному в работах [1—3, 5], если гр=гу!;к = 0. При этом уравне¬
ние (35) отсутствует и AfK = Afn.;(.
ЛИТЕРАТУРА
1. Тз ян С. и Эванс Р., Оптимальное программирование гяги высотной
ракеты.
Tsien Н. S. and Evans R. С., Optimum Thrust Programming for a Sound¬
ing Rocket, «Journal of the American Rocket Society», 1951, vol. 21, No. 5,
pp. 99 —107.
2. Лоуден Д., Оптимальные траектории ракет.
La w den D., Stationary Rocket Trajectories, «Quarterly Journal of Mecha¬
nics», 1954, No. 7, p. 488.
3. Лейтманн Г., Проблема оптимального программирования тяги.
Leitmann G., The Problem of Optimum Thrust Programming, Nav.-Ordn.
Test Station, Techn. Note 5038—11, 1955.
4. Лейтманн Г., Решение задачи Годдарда методами вариационного
исчисления.
Leitmann G., A Calculus of Variations Solution of Goddard’s Problem,
«Astronautica Acta», 1956, vol. 2, pp. 56—62.
5. В a p д Л., Исследование вариационных задач программирования тяги.
Ward L., A Calculus of variations Problem in Thrust Programming, Nav.-
Ordn. Test Station, Techn. Note 3502—2, 1955.
6. Лейтманн Г., Интегрирование уравнения Эйлера—Лагранжа и числен¬
ные примеры программирования тяги.
Leitmann G., Integration of the Euler—Lagrange Equation and Numeri¬
cal Example for Optimum Thrust Programming, Nav.-Ordn. Test Station, Techn.
Note 5038—10, 1955.
7. Майер А., Об общих проблемах вариационного исчисления.
Ма yer A., Uber das allgemeinste Problem der Variationsrechnung, Leipzig,
Akademie der Wissenschaften, 1878.
РАЗДЕЛ II
ОПТИМАЛЬНЫЕ РЕЖИМЫ ДВИЖЕНИЯ
РАКЕТНЫХ САМОЛЕТОВ И САМОЛЕТОВ-СНАРЯДОВ
А. ПАККЕТТ и Р. ЭДВАРДС
ОПТИМАЛЬНЫЕ ХАРАКТЕРИСТИКИ
РАКЕТНЫХ СНАРЯДОВ МАЛОЙ ДАЛЬНОСТИ 1
I. ВВЕДЕНИЕ
В общем случае дальность ракетного снаряда определяется отно
шением веса топлива к общему весу снаряда, лобовым сопротивле¬
нием, атмосферными условиями и законом изменения расхода топли¬
ва по времени. Следует отметить, что дальность снаряда в извест¬
ной степени является условной характеристикой.
В случае снарядов очень большой дальности в качестве макси¬
мальной дальности следует, по-видимому, считать расстояние до
точки падения снаряда на землю. При определении дальности таких
снарядов играют существенную роль ускорение силы тяжести и
подъемная сила.
В случае снарядов меньшей дальности, совершающих полет в
основном на постоянной высоте, определение максимальной дально¬
сти носит более произвольный характер. Так, например, можно опре¬
делять максимальную дальность как дальность до точки, где ско¬
рость снаряда падает ниже некоторого минимального значения, вы¬
бранного по условиям обеспечения требуемых характеристик снаря¬
да в конце полета. Можно также определять максимальную
дальность как дистанцию, на протяжении которой средняя скорость
не падает ниже некоторого минимального значения.
В случае снарядов малой дальности допустимо значительно упро¬
шенное исследование летных данных без учета влияния подъемной
силы и силы тяжести. В настоящей статье рассмотрены некоторые
стороны-исследования такого рода. Характер принятых допущений
делает количественные результаты исследования весьма приближен¬
ными, однако относительное влияние различных параметров пред-
1 A. Puckett and R. Edwards, The Optimum Performance of Short-
Range Rocket Powered Missiles, Institute of the Aeronautical Sciences, Preprint
No. 279.
60
ставлено правильно. Проблема общего исследования летных данных
снаряда большой дальности требует учета различных форм траекто¬
рий, изменения плотности воздуха с высотой и т. д. и, очевидно, зна¬
чительно сложнее рассматриваемой ниже задачи.
Исследование характеристик снарядов малой дальности может
сводиться к определению различных параметров.
Так, например, при рассмотрении данного снаряда -при данных
атмосферных условиях может быть задан вес топлива и. закон рас¬
ходования топлива. Эти данные полностью определяют закон изме¬
нения скорости снаряда. Если задать то или иное значение дальности
полета, то можно определить среднюю скорость снаряда на этой
дальности и скорость в конечной точке.
Можно исследовать зависимость средней скорости и скорости в
конце полета от секундного расхода топлива и выяснить, сущест¬
вует ли оптимальная программа расходования топлива, обеспечи¬
вающая получение максимального значения средней скорости или
скорости в конце полета. В такой постановке эта задача, естественно,
эквивалентна определению минимального веса топлива, необходимо¬
го для получения заданной средней скорости или скорости в конце
полета на заданную дальность. Эта задача эквивалентна также
определению максимальной дальности при заданном весе топлива и
заданной средней скорости в конце полета.
В первой и простейшей форме задачи можно принять секундный
расход топлива постоянным, и в этом случае единственным перемен¬
ным параметром будет время работы двигателя. При решении задачи
в более общем виде можно рассматривать различные законы изме¬
нения расхода топлива по времени и отыскивать оптимум, поль¬
зуясь методами вариационного исчисления.
II. ОБЩИЕ УРАВНЕНИЯ
Примем, что общее время полета снаряда 'малой дальности состо¬
ит из двух периодов — период полета при работающем двигателе
или активного полета и период полета при неработающем двигателе
или пассивного полета. Введем следующие условные обо¬
значения:
М — текущее значение массы снаряда,
М0 —начальная масса снаряда,
Мк — масса снаряда после выгорания топлива,
Мт — масса топлива,
s — путь снаряда,
t — время,
tK — длительность активного полета (продолжительность работы
двигателя),
Схо — коэффициент сопротивления при нулевой подъемной силе,
F — характерная площадь снаряда,
v —скорость снаряда,
Ут — эффективная скорость истечения газов из сопла двигателя,
р —плотность воздуха.
61
Индекс ( )о относится к величинам в момент старта снаряда
индекс ( )к—к концу активного участка полета и индекс ( )г—и
концу полета.
Уравнение движения ракеты при горизонтальном полете с рабо¬
тающим двигателем имеет вид
Mli+c^'YFv2+v^=0' (li
Уравнение движения при пассивном полете имеет вид
M*^ + c«>TFv2=0' (2)
Плотность воздуха о считается постоянной.
Эти уравнения удобно привести к безразмерному виду, положит
т~^~ (безразмерная масса);
х — -^~ (безразмерная скорость);
1 _ 2мк .
F р
0 = — (безразмерное время);
А
т] = — (безразмерная дальность);
А
B-W ( = 0К);
А
_ МТ
Мк '
Величина К может быть названа «баллистической длиной» снаря¬
да. Эта величина тесно связана с «баллистическим коэффициентом»,
обычно применяемым при баллистических расчетах снарядов, и при¬
близительно равна произведению удвоенной длины снаряда на отно¬
шение плотности снаряда к плотности воздуха. Обычные значения
этой величины близки к 1000. Так как безразмерная дальность сна¬
ряда г\ является функцией только других безразмерных параметров,
то действительная дальность снаряда увеличивается при увеличении
его абсолютных размеров.
Уравнение (1) в новых переменных имеет вид
dx . a dtri л /о\
+ +тг=0: (3)
аналогично уравнение (2) принимает вид
• С,0х2 = 0. (4)
м •
62
Секундный расход топлива dm/d В в общем случае может быть
задан как функция времени. Коэффициент сопротивления сх0 являет¬
ся функцией скорости. Уравнение (3) в общей нелинейной форме мо¬
жет быть проинтегрировано только численным методом. В качестве
первого упрощения можно коэффициент сопротивления принять по¬
стоянным, соответствующим некоторому среднему значению. Урав¬
нение (3) в общем виде и после этого останется нелинейным относи¬
тельно я(0), однако уравнение (4) для пассивного полета может
быть непосредственно проинтегрировано. В результате получается
±~±=сх О(0-Р), (5)
X
где хк—скорость в конце активного участка полета.
Безразмерная скорость определяется формулой
1 ds d'f) /£?v
X— = —. (6)
Vr dt db w
Интегрируя уравнение (5), находим соотношение между общим
временем полета 02 и полной дальностью rj2:
1
2 —
слОхк
Если бы была известна зависимость скорости хк и пути в конце
активного участка полета г\к от относительного количества топлива v,
длительности активного полета р и закона изменения расхода топли¬
ва по времени, то задача была бы полностью решена. Так как срсд-
„няя скорость на полной дальности равна г]2/0 2, то уравнение (7)
связывает среднюю скорость полета с дальностью и данными двига¬
тельной установки.
Скорость в конце полета также может быть выражена через даль¬
ность в виде
х2 = хке-сМъ-Ъ). (8)
Прежде чем переходить к конкретным задачам, установим неко¬
торые общие положения относительно этих уравнений и выясним их
физический смысл.
Возвращаясь к уравнению (3), можно положить
т
где
/(0) = 1» f(f) = 0, когда |>1.
После этого, проинтегрировав уравнение в пределах времени
активного полета, находим
е=Р Р
I {1+v/(f)Hv+^j'x2rf9=v- (9)
о о
63
Эту зависимость -можно представить в схематической форме:
xK=v—p V як—qCxoXK Г)к, (10)
где р и q — некоторые числа, значения которых лежат между нулем
и единицей. Величина в левой части уравнения (10) соответствует
количеству движения снаряда в конце работы двигателя. Первый
член в правой части уравнения соответствует полному импульсу пер¬
воначального запаса топлива. Второй член в правой части соответст¬
вует потерянному импульсу, сообщенному некоторой части топлива
и затем отброшенному с уходящими газами; при малых v и c*o вели¬
чина р близка к 0,5. Последний член соответствует затрате импульса
на преодоление сил аэродинамического сопротивления.
На основании уравнений (8) и (10) можно прийти к очевидным
выводам в отношении зависимости скорости в конце полета х2 от
времени работы двигателя или, что равносильно, от активной даль¬
ности снаряда г\к. При постоянной полной дальности имеем
dJf2 - —
х2 хк
Если поддерживать режим расхода топлива по времени таким,
чтобы величины р'и q не испытывали значительных изменений при
изменении Г1к> то можно написать
_L_rf£2_^—ех о(1-<?) >0 (11)
х2 4'г\к 1 “Ь“Ь ЯсхОг\к
Иньгми словами, скорость в конце полета всегда увеличивается
при увеличении активной дальности (или времени работы двигате¬
ля). Для получения максимальной скорости в конце полета на за¬
данную дальность следует выбирать длительность активного участка
полета равной полной длительности полета, что, впрочем, более или
менее очевидно также и на основании физических соображений.
Естественно, что при этом, как и прежде, не задается закон измене¬
ния тяги двигателя по времени.
Анализ уравнения (7) не позволяет сделать столь же очевидных
выводов в отношении влияния программы работы двигателя на
общее время полета или среднюю скорость снаряда. Увеличение р
непосредственно увеличивает длительность полета, однако одновре¬
менное увеличение ты уменьшает длительность пассивного участка
полета. В связи с этим возможно наличие оптимального режима ра¬
боты двигателя, обеспечивающего минимальное общее время полета.
Дальнейшие исследования показывают, что при определенных
значениях дальности и средней скорости снаряда такой оптимум дей¬
ствительно существует. При других значениях дальности и средней
скорости наивыгоднейшее время работы двигателя может быть рав¬
но нулю или может быть равно общему времени полета—в зависи¬
мости от закона изменения тяги по времени.
64
III. СЛУЧАЙ ПОСТОЯННОЙ ТЯГИ ДВИГАТЕЛЯ
При постоянном секундном расходе топлива и, значит, при посто¬
янной тяге двигателя закон изменения массы снаряда *во время
активного полета имеет вид
т
^+-Ях~ттЛ)- (,2)
После подстановки этого выражения в уравнение (3) переменные
разделяются, что позволяет проинтегрировать уравнение:
\ С* dx 1 Г* db
Сх О I а2 — .*2 1+'
(l—-1-1)
\ 1+vp/
где a2=v/Cro (3, a х0 — скорость снаряда в момент старта.
На основании этого выражения находим скорость снаряда при
активном полете:
х=а Д*° ^(14)
Скорость б конце работы двигателя -при этом будет равна:
2
(1 + *)
1в
*к=а ^(15)
а + xq
При дг0=0 и при очень малой величине коэффициента сопротив¬
ления или очень малом времени работы двигателя (а->-оо) формула
(15) может быть заменена приближенным выражением
ДСК = Х0 + In (1 + V)-■*£££ {I in* (1 4- V) - *0 In (1 + V) - *о2} • (16)
При коэффициенте сопротивления, равном нулю, эта формула
переходит в известное выражение ,vK=ln(l-|-v). Кривые хк по v при
*о=0 и различных значениях Схо |3 показаны на фиг. 20.
Для получения активной дальности снаряда необходимо проин¬
тегрировать уравнение (14) по времени. Приняв
ь = /а-хо_у z=bfx v_i\
\«+*0/ V i+vp/
5 394 65
найдем следующее выражение для активной дальности:
ъ
y1k==
яР 1 -4-''
1-
1 +za
■dz.
(17)
Интеграл в правой части формулы (17) не может быть определен,
в замкнутой форме. Тем не менее для целей расчета интеграл мо¬
жет быть легко вычислен путем разложения в ряд.
При нулевом коэффициенте сопротивления уравнение (17) прини
мает в пределе следующий вид:
Фиг. 20. Зависимость безразмер¬
ной скорости в конце работы дви¬
гателя хк от безразмерного веса
топлива v (|3—относительное вре¬
мя работы двигателя).
;pjl_2-ln(l+v)} + *08.
(18)
Фиг. 21. Зависимость безразмерной
средней скорости лгСи = Лк/Р от безраз¬
мерного веса топлива v (г|к — отно¬
сительный путь к моменту окончания
работы двигателя).
Средняя безразмерная скорость за время активного полета равна
Кривые г|к/(3 по v при *o = 0 и различных значениях предстан-
лены на фиг. 21.
Подстазляя формулы (15) и (17) в формулу (7), можно найти
время полета 0 2 или общую среднюю скорость полета х*=т]2/02 при
заданных yi2, v и р.
В полученных результатах представляет интерес параметр, опре¬
деляющий время работы двигателя или соответствующую этому
66
зремени дальность активного полета г|к. На фиг. 22, 23 и 24 пред¬
ставлены графики л** как функции отношения активной дальности к
полной дальности y\Jr\2 при различных значениях г\2 и v. При этих
расчетах начальная скорость х0 была принята равной нулю, среднее
значение коэффициента сопротивления было принято равным с*о =
= 1/3. Так как x* является функцией произведения сх0 л, то приведен¬
ные кривые могут быть использованы после введения соответствую¬
щих лоправок при любом значении коэффициента сопротивления.
Фиг. 22. Зависимость безразмерной средней скорости полета х +
при постоянной тяге двигателя от отношения г\к/ц2 (Цг — безраз¬
мерный путь к концу движения).
Первым интересным результатом является то, что при малых
дальностях средняя скорость полета монотонно уменьшается при
увеличении г\к. Так, например, при значениях безразмерной дально¬
сти r|2 = 1, 2 и 3 и любой желательной средней скорости максималь¬
ное значение при заданной массе топлива получается при нуле¬
вом времени работы двигателя.
Однако при безразмерной дальности г|2 = 4 средняя скорость по¬
лета незначительно увеличивается при увеличении г\к и достигает
максимума при малых значениях т]к. При значениях г|2 = 5 и 6 наблю¬
дается отчетливо выраженный максимум х* при значениях т]к/т]:ь
близких к 0,5, т. е. при условиях, когда время работы двигателя со¬
ставляет около половины общего времени полета. В качестве наибо¬
лее показательного примера влияния времени работы двигателя ука¬
жем, что при безразмерной дальности 142 = 6 и средней скорости
**=0,5 необходимая масса топлива составляет v = 4 при нулевой про¬
должительности работы двигателя и v = 2,8 при т]к/т]2 = 0,4.
5*
A
Уг
Фиг. 23. Зависимость безразмерной средней скорости полета х*
п,ри постоянной тяге двигателя от отношения Лк/Лг.
0,8
0,7
0,6
I
^v--5
1
t
/ —
г
1-Ъ =
V
с
и
1/з
J
о, г о, у о,б о,в 1,о
Уг
Уг
Фиг. 24. Зависимость безразмерной средней скорости полета х*
при постоянной тяге двигателя от отношения Лк/Л-2.
68
Критические значения т]2 и л*,при которых оптимальное время
работы двигателя больше нуля, могут быть вычислены во формуле
(7) после подстановки d02/dp = O и хл
определения производных dr\Jd$ и
dxjdfi из уравнений (16) и (18). Полу¬
ченные таким образом граничные кри¬
вые для нескольких значений *0 пока¬
заны на фиг. 25. Из этой фигуры, как
й из фиг. 22, 23 и 24, ясно видно, что
при *о = 0 критическая дальность поч¬
ти не зависит от **. Можно считать
приближенно, что оптимальная дли¬
тельность работы двигателя равна ну¬
лю во всех случаях, когда произведе¬
ние схцГ[2 меньше 1,3.
Практически соответствующая это¬
му дальность почти для всех снарядов
слишком велика для того, чтобы мож¬
но было говорить о снарядах «малой
дальности»; исключение могут состав¬
лять только очень малые снаряды
с большим лобовым сопротивле¬
нием.
При конечном *0 дальность, при которой становится выгодным
время работы двигателя, отличное от нуля, оказывается значитель-
Фиг. 25. Критическое значение
безразмерной дальности при
нулевом оптимальном времени
работы двигателя и постоянной
тяге.
Фиг. 26. Зависимость безразмерной средней скорости л'*
от отношения ЧкЛЬ при постоянной тяге двигателя.
но меньшей, но так же, как в предыдущем случае,—почти не зави¬
сящей от *.*. При *о=0,1 критическая дальность уменьшается до
69
значения, определяемого при малых средних скоростях полета при
ближенным соотношением
СгО 112=1,0.
Влияние х0 на изменение х* можно проследить по фиг. 26, гдо
приведен график изменения х* по отношению т]к/т12, при полной
дальности л2=3,0 и v = 0,5 и 1,0.
IV. ПЕРЕМЕННЫЙ РАСХОД ТОПЛИВА
При возможности изменять по желанию расход топлива или тягу
двигателя должна существовать некоторая оптимальная программа
изменения тяги двигателя, обеспечивающая минимальное время по
лета при заданном весе топлива и заданной дальности или минималь¬
ный вес топлива при заданном времени полета. Изменение тяги дви¬
гателя (или массы снаряда) связано с изменением скорости по урав
нению (3). Так как это уравнение является линейным относитель¬
но т, то переменная масса может быть представлена как фvнкция
скорости х. Решение уравнения (3) в форме зависимости т от v
имеет вид
ех° (1 + v) — j* сх0х2ех db I. (19)
о >
В соответствии с этим получаются следующие выражения: для
расхода топлива в конце полета
v=е~~х° |ех* + J сх0х2ех (/9j — 1 (20)
и для полной дальности
■Ц2=]хс1в. (21)
0
При каждом заданном значении скорости в конце -полета х2 ми¬
нимум интеграла (20) обеспечивается очень простым условием:
x==const = —
е2
Это условие соответствует программе изменения тяги, предусмат¬
ривающей импульс тяги в начале полета, достаточный для достиже¬
ния скорости х*, постоянную тягу на протяжении всего полета и вто¬
рой импульс тяги, достаточный для достижения скорости х2 (при¬
нято х2>х*).
Необходимое количество топлива, естественно, уменьшается при
уменьшении х2, по крайней мере, до значения х*. Однако при даль¬
нейшем уменьшении х2, при котором х2 становится меньше х*, физи¬
ческая интерпретация уравнения (20) становится абсурдной, так как
в этом случае в конце полета должен иметь место отрицательный
импульс тяги (с отрицательным расходом топлива). В связи с этим
70
найденный оптимум не имеет физического смысла. Необходимо, од¬
нако, исследовать, нельзя ли все же уменьшить потребное количество
топлива путем уменьшения х2 до значений ниже л*, и в случае, если
это действительно возможно, определить, какова должна быть про¬
грамма изменения тяги.
Ясно, что при х2<С** должен существовать участок полета при
неработающем двигателе или при малой тяге двигателя, при которой
замедление снаряда несколько меньше, чем при неработающем дви¬
гателе.
В связи с этим рассмотрим график изменения скорости по време¬
ни, показанный на фиг. 27.
Этот график характеризуется на¬
чальным импульсом, при котором до¬
стигается скорость xKi работой дви¬
гателя при постоянной тяге на про¬
тяжении времени (3, выбранного та¬
ким образом, чтобы средняя ско¬
рость была равна х*9 а в конце пас¬
сивного участка х2, значение которой
было бы ниже х*.
Рассмотрим теперь малое изме¬
нение Ах описанного закона, пока¬
занное пунктиром на фиг. 27. При
этом заметим, что в предположении
положительной тяги новая кривая
изменения скорости должна прохо¬
дить ниже первоначальной в области Р<Сб<^2. Примем, что средняя
скорость остается по-прежнему равной х*, откуда следует
Р о2
I* ДxdO= —j Ах dO.
о Р
Изменение скорости в интервале времени 0<^б<^(5, при котором
получается минимальное значение потребного запаса топлива, полу¬
чается путем определения условий, обеспечивающих минимальное
значение интеграла в формуле (20) в пределах интервала времени р.
Однако для этого, как и прежде, скорость должна быть постоянной
и соответствующей уравнению
о2
Ахк$= — | Ах do.
Общая вариация v в соответствии с уравнением (20) -равна
ех° Av = — J {(xl + 2xK) ех* — (х2+2х)ех) AxdO. (22)
э
Так как хк всегда больше х и так как Дл: всегда должно быть
меньше нуля, то приращение v всегда положительно при всякой
Фиг. 27. График безразмерной
скорости х снаряда по време¬
ни 0 при оптимальной про¬
грамме работы двигателя.
71
вариации А х. Отсюда следует, что выбранный первоначально закон-
изменения скорости по времени с постоянной скоростью до 0=|3 и
нулевой тягой от 0 =(3 до 02 действительно соответствует минимуму
запаса топлива при заданном х2.
Остается задача выбора значения х2, обеспечивающего абсолют¬
ный минимум запаса топлива. Для рассматриваемого класса режи¬
мов изменения скорости по времени это равносильно выбору соот¬
ветствующего значения (3. Для исследования влияния |3 на необходи¬
мый запас топлива в рассматриваемом случае можно рассчитать
г*
zt
0,8
0,7
0,6
0,5
О А
0,3
0,2
0,1
I>--2,0
1.5
1,0
0,8
0,7
0,6
0,5
ОА
о,з
0,2
0,1
О
V-1,5
1,0
0,5
-0,25-
/
■ 1
^
1
С??.
О 0,2 ОА 0,6 0,8 1ft
У К
V?
Фиг. 28. Зависимость безразмерной средней скорости х* от отно¬
шения Чк/Лг при оптимальной тяге двигателя.
02 Ofi 0,6 0,8 1,0
Ъ-
изменение х* в зависимости от (3 или т|к при постоянных значениях v
Так как в данном случае
ТП,
В = —
и из
уравнения (20) при лг0 = 0 следует
Чк =
(у 4-1) е *к — 1
слОхк
(23)
(24)
то можно рассчитать значения я* как функцию г\к по формуле (7).
На фиг. 28, 29, 30 показаны графики зависимости средней скорости
от активной дальности при различных значениях v и безразмер¬
ной дальности т]2, равной 1, 2, 3, 4, 5 и 6. Эти кривые построены для
оптимальной программы работы двигателя в соответствии с диа¬
граммой изменения скорости, показанной на фиг. 27.
Указанные кривые очень похожи по форме на кривые фиг. 22, 23
и 24, полученные для постоянной тяги двигателя. Следует отметить,
72
V?
0,8
0,7
0,6
0,5
OS
0.3
0,2
0.1
c?;f/3
1,0
05
0,2 OS 0,6 0,8 fJO
Ь.
Ог
Фиг. 29. Зависимость безразмерной средней скорости х* от отно¬
шения TjK/T)2 при оптимальной тяге двигателя.
h
Фиг. 30. Зависимость безразмерной средней скорости х* от отно¬
шения г|к/г|2 при оптимальной тяге двигателя.
73
что потребный запас топлива действительно уменьшается при зна¬
чениях т]к/р2, меньших единицы, что соответствует Действи¬
тельно, при малых значениях полной дальности оптимальная дли¬
тельность работы двигателя равна-нулю, как и в случае постоянной
тяги. Значения х* и v, соответствующие этим условиям, должны со
гла-соваться с соответствующими величинами, вычисленными для
постоянной тяги двигателя. Оптимальная длительность работы дви¬
гателя становится конечной при меньших
дальностях, чем в случае постоянной тя¬
ги, и, как правило, бывает больше, чем в
этом последнем случае.
Условия, при которых оптимальная
длительность работы двигателя точно рав¬
на нулю, можно определить аналогично
тому, как это было сделано в предыдущем
случае. Интегрируя уравнение (20) в пре
делах активного участка полета, находим
(\+'>)ex° = ex* + $cXl>xlex«. (25)
Кроме того, при оптимальной програм¬
ме работы двигателя дальность и время
работы двигателя связаны с через инте¬
грал уравнения (21):
Ч8 = ^кР+ — 1П{1+*КС*„(°2 — р)}. (26)
Сл-0
Н-а основании этих двух уравнений на
ходим, что v имеет экстремумы, определи
емые условием
= О-г'.-р (с,0 (дй + ж,)--!-} .
(27)
Это уравнение имеет решение при конечном (3 только при условии
т]2>1п(хк-[-2)/(хк-{-1) ; в этом случае v обнаруживает относитель¬
ный максимум при (3 = 0. При приближении этого решения к (3=0
критическая дальность выражается через среднюю скорость =
=г]2/0 путем исключения хк из уравнений (26) и (27). На фиг. 31
показана зависимость дальности Ц2, для которой оптимальное время
работы двигателя точно равно нулю, от я*. В этом случае критиче¬
ская дальность не зависит от Xq.
Сравнение фиг. 31 и 25 показывает, что эта дальность значитель¬
но меньше критической дальности при постоянном расходе топлива
и немного уменьшается с ростом х*.
V. выводы
Обеспечение наилучших летных данных снаряда малой дальности
сводится, по существу, к сопоставлению потери импульса, обуслов¬
ленной действием лобового сопротивления во время работы двига¬
Фиг. 31. Критическое
значение безразмерной
дальности при нулевом
оптимальном времени ра¬
боты двигателя и опти¬
мальной тяге.
74
теля, с потерей импульса, обусловленной действием того же сопро¬
тивления во время полета при неработающем двигателе, и к отыска¬
нию минимума суммы обеих потерь.
Если заданы только скорость в конце полета и дальность, то как
при постоянном расходе топлива, так и при оптимальной программе
работы двигателя выгодно выбирать возможно более низкую ско¬
рость снаряда на протяжении всего полета на заданную дальность и
затем разгонять снаряд до заданной скорости с помощью импульса
тяги двигателя в конце полета. Получаемый при этом оптимум
является бессмысленным с практической точки зрения и показывает,
что для получения практически пригодных летных данных снаряда
необходимо задаваться еще одной характеристикой.
Если задана средняя скорость полета, то оптимальные летные
данные при малых дальностях получаются при нулевой продолжи¬
тельности работы двигателя. Для больших дальностей имеется неко¬
торое конечное оптимальное время работы двигателя. Наилучшие
летные данные, можно было бы получить при двухрежимном двига¬
теле, обеспечивающем получение короткого начального импульса
тяги, разгоняющего снаряд до заданной скорости, с последующей
работой при малой постоянной тяге, поддерживающей скорость, сна¬
ряда в течение определенного времени строго постоянной. При боль¬
ших дальностях экономия топлива при таком режиме получается
довольно значительной. Так, например, при г|2=6 и ^=1/3 необхо¬
димый запас топлива при средней скорости х*=0,3 составляет около
170% пустого веса при нулевом времени работы двигателя и всего
только 90% пустого веса—при оптимальной программе работы дви¬
гателя.
При таких больших дальностях, по-видимому, играет существен¬
ную роль неучет силы тяжести; в расчетах следует учитывать индук¬
тивное сопротивление несущей поверхности при полете на постоян¬
ной высоте.
При описанном исследовании не учитывалось изменение веса
конструкции снаряда или двигателя, связанное с изменением про¬
граммы работы двигателя. Возможно, что увеличение продолжитель¬
ности работы двигателя с соответствующим уменьшением тяги поз¬
волило бы уменьшить вес двигателя при заданном количестве топ¬
лива, что сделало бы еще более выгодным увеличение продолжитель¬
ности работы двигателя.
В связи с этим обстоятельством, а также учитывая другие допу¬
щения, сделанные при исследовании, следует считать, что приведен¬
ные результаты расчетов показывают только общие закономерности
и свидетельствуют о существовании оптимальной программы работы
Двигателя, которая должна задаваться в каждом конкретном случае
на основании более точных расчетов.
Л. ГИББС
ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ ТЯГИ
ДВИГАТЕЛЯ ПРИ ГОРИЗОНТАЛЬНОМ ПОЛЕТЕ1
ВВЕДЕНИЕ
Постановка задачи об оптимальных характеристиках ракетною
самолета или снаряда зависит от того, какие конкретные характерь-'
стики движения должны быть обеспечены как экстремальные—высота,
горизонтальная дальность, максимальная скорость в заданной точке
или максимальная полезная нагрузка при заданных размерах сна-
ряда и заданной дальности полета. Исследования могут определять
также некоторые специальные требования.
Настоящая статья касается вопроса, связанного с проблемой мак¬
симальной горизонтальной дальности и максимальной скорости в за
данной точке.
В работе рассматривается только траектория горизонтального по
лета. Требование постоянства высоты полета приводит к -постоянной
скорости звука вдоль траектории, постоянной плотности воздуха и
постоянной скорости истечения газов из сопла двигателя.
Сделаем дальнейшие упрощающие предположения, а именно,
коэффициент лобового сопротивления при а=0 будем считать по
стоянным, а вертикальной составляющей тяги будем пренебрегать..
Можно показать, что принятие этих предположений вводит лишь
небольшие погрешности. Подобное исследование, в котором величи¬
на индуктивного сопротивления опускалась, как пренебрежимо ма¬
лая, было проведено Паккеттом и Эдвардсом [1]. Решение рассматри¬
ваемой задачи, в частности, может иметь применение к снарядам,
запуск которых производится в воздухе либо в виде второй (крыла¬
той) ступени составного самолета-снаряда, либо снаряда классе
«воздух—воздух». В первом случае вторая ступень запускается
обычно на большой высоте и с момента запуска на большей части
траектории дальнейшего полета изменения, связанные с изменением
высоты, будут малыми. Поэтому расчеты, основанные на предполо¬
жении постоянства высоты, не будут содержать в себе значительный
погрешностей. Во втором случае снаряд типа «воздух—воздух» бу¬
дет обладать небольшим радиусом действия, в связи с чем макси¬
мальная ошибка расчета также будет малой.
Независимо от этих соображений решение поставленной пробле¬
мы с принятыми ограничениями может быть найдено точно и резуль¬
таты, следовательно, могут рассматриваться как вполне определен¬
ные. Эги результаты показывают влияние различных переменных
величин на горизонтальный полет снаряда и относительную их зна¬
чимость. Помимо того, что эта работа может быть использована для
практических задач, приведенные в ней расчеты имеют ценность и в
том отношении, что они иллюстрируют возможность применения мс-
1 А. Н i b b s, Optimum Burning Program for Horizontal Flight, «Journal o!
the American Rocket Society >, 1У52, vol. 22, No. 4, pp. 204 — 212.
76
од о в вариационного исчисления к более общим задачам исследова-
ия траектории. Эти более общие задачи приводят к таким сложным
'езудьтатам, что для выяснения их математической сущности необ¬
ходимо проведение подробных исследований более простых случаев.
УРАВНЕНИЕ ДВИЖЕНИЯ
В соответствии с принятыми допущениями, уравнение горизон-
гадьного движения ракетного самолета может быть записано в виде
Mdv/dt=;P-Q,
где М — мгновенная масса снаряда;
dvjdt — ускорение;
Р — тяга;
Q — сопротивление воздуха.
Сопротивление может быть представлено в виде суммы сопротив¬
ления формы (вредного сопротивления) и индуктивного сопротив¬
ления.
Сопротивление формы может быть выражено как
Q»pM=!-{*,№
где сл — коэффициент сопротивления, который будем принимать по¬
стоянным;
р—плотность окружающего воздуха, также величина посто¬
янная;
F — некоторая характеристическая площадь снаряда, например
площадь поперечного сечения.
Индуктивное сопротивление записываем в виде
о = У2
^инд | *
где Y — общая аэродинамическая подъемная сила;
b—длина (принимаемая постоянной), которая при дозвуковых
скоростях равна размаху несущих поверхностей.
Требование горизонтального полета соответствует условию
Y=Mg, поскольку вертикальной составляющей тяги мы пренебре¬
гаем. Точность этого приближения будет увеличиваться со ско¬
ростью, т. е. при уменьшении угла атаки.
Используя это условие, получаем для индуктивного сопротивле¬
ния следующее выражение:
п -
^инд |
77
Выражение для тяги может быть записано как
р= - vr—,
r at
где Vr — эффективная скорость истечения (которая при неизменной
высоте также постоянна), a dM/dt — секундный расход топлива.
Тогда уравнение движения приобретает вид (путем деления на
Mv)
do у dM 1_ v 2g2M
ds r М Us 2 Р Х~М npbW 9
где s —расстояние (путь), проходимое самолетом-снарядом.
Переменные в этом выражении могут быть приведены к безраз¬
мерному виду.
Например,
М- .
V^fb / ncxF ’
— V
V — —г •
’
С —С ^ 1 у
f CXF
s SbViV
7t
Г- t-S-J
bVr V
Тогда уравнение движения может быть переписано в виде
do 1 dM v М
ds М ds М v3
Для того чтобы отметить специальные точки на траектории -вве¬
дем следующие обозначения:
( )о—начальные условия,
( )к—условия в конце горения,
( ) 2—условие, соответствующее окончанию горизонтального гю
лета.
ОПТИМАЛЬНЫЙ ЗАКОН СЖИГАНИЯ ТОПЛИВА
А. Применение вариационного исчисления
Путь ракетного снаряда, проходимый им за время работы дви¬
гателя, в течение которого масса снаряда изменяется от М\ до Мл,
может быть выражен в безразмерной форме следующим интегралом
Для решения этого интеграла может быть применен метод вариаци¬
онного исчисления.
Подынтегральную функцию можно представить в виде
х* + (М)-1
xfU+V= F,
х(М)-' + М(х)-3
где
xf *=dxjdM\
как £/, так и V не зависят от х'.
Для того чтобы интеграл давал экстремальное значение пути,
подынтегральная функция должна удовлетворять уравнению Эйлера:
Если F задано в форме F=x'U+V, то это условие примет вид
После подстановки значений U и V это выражение приобретает
вид
Выражение (1) является соотношением, которому должны удов¬
летворять переменная масса и скорость полета снаряда для того, что¬
бы интеграл пути имел экстремальное значение. Однако этот резуль¬
тат содержит в себе ограничение. Из самого уравнения видно, что
начальные величины массы и скорости не могут быть произвольны¬
ми. Поскольку переменные должны удовлетворять этому соотноше¬
нию во всех точках, то только одна из величин может быть выбрана
произвольно для точки, соответствующей началу движения. Поэтому
это уравнение не дает ответа на вопросы, возникающие в связи с
независимым и произвольным выбором начальных условий. Более
того, не имеется возможности применить другие строгие методы ва¬
риационного исчисления, такие как условие Лежандра, для того
чтобы определить, что исследуемый интеграл имеет максимум или
минимум.
Таким образом, необходимо специально рассмотреть вопросы,
связанные с начальными условиями, а также должен быть найден
какой-то метод для определения качества экстремума, вытекающего
из уравнения (1).
ду dU =р
дх дМ
ИЛИ
(1)
Если соотношение (1) переписать в виде
то его можно рассматривать как соотношение между индуктивным
сопротивлением М2/х2 и вредным сопротивлением х2. Как известно,
подобное соотношение получено для самолета [2], согласно которому
максимальная дальность полета получается, когда вредное сопро¬
тивление во все время полета равно индуктивному сопротивлению.
В случае движения самолета-снаряда с ракетным двигателем отно¬
шение индуктивного и вредного сопротивлений изменяется в преде¬
лах от единицы для бесконечно большой скорости до 1/3 для ско¬
рости, равной нулю.
Б. Проблема начальных условий
Задачи, вытекающие из произвольного выбора начальных величин
массы и скорости, могут быть разделены на три типа.
Предположим, что начальная масса задана; тогда ее величина
вместе с выражением (1) определяет оптимальную начальную ско¬
рость. Но если предположить, что начальная скорость также задана,
тогда каждая из трех задач будет решаться в зависимости от того,
больше, равна или меньше заданная скорость по сравнению с опти¬
мальной.
Должны быть рассмотрены только первый и третий случаи, так
как во втором случае, когда начальная скорость равна скорости,
соответствующей оптимальному соотношению, программу оптималь¬
ного сжигания топлива можно осуществлять немедленно.
Первая задача имеет только небольшое практическое значение,
поскольку большинство самолетов-снарядов будет начинать гори¬
зонтальный полет с относительно небольшой горизонтальной ско¬
ростью.
В любом случае, если скорость снаряда в любой момент времени
больше скорости, определяемой уравнением (1), то за некоторое вре¬
мя до этого момента скорость снаряда или ускорителя была равна
оптимальной, а еще ранее была меньше, чем оптимальная.
Постулируем следующую программу сжигания топлива:
Для того чтобы увеличить скорость и уменьшить массу до вели¬
чин, которые бы удовлетворяли соотношению (1), мгновенно ежи
гается необходимое количество топлива, а с этого момента и далее
строго соблюдается оптимальное условие (1). Предполагаем, что
эта программа должна обеспечить максимальную дальность само¬
лета-снаряда.
Справедливость этого предположения может быть подтвержде¬
на сравнением дальностей, полученных данным способом, с дально¬
стями, полученными другими возможными способами. Изменение
скорости в результате мгновенного сжигания части топлива (т. е. при
dMjdt = —оо) может удовлетворить уравнению движения только в
30
том случае, если* положить путь равным нулю. Скорость хи после
т0го как количество топлива Л40—М\ сгорит, будет
II
Х.=Хг)+\П-=±-.
1 0 мх
Исходя из того условия, что Mi и xi должны удовлетворять соот¬
ношению (1), можно получить их в зависимости от начальных значе¬
ний массы и скорости. С этой точки, где s=0, снаряд может начать
движение уже в соответствии с оптимальным законом (1).
Рассмотрим теперь любое малое отклонение от этой программы,
характеризующееся тем, что небольшие количества топлива Д М бу¬
дут сжигаться не мгновенно. Поскольку dM/dt =—м>—сю, то масса
Д42 и скорость х2 будут удовлетворять неравенствам
М0>Л*2> Л^,
х0<С*2 < хг.
(2)
За время сжигания этой части топлива снаряд пройдет путь Д s',
который может__быть рассчитан по начальным величинам массы и
скорости М0 и Xq и величине массы М2 в той точке, где произошло
отступление от заданного закона мгновенного сжигания массы.
После этого малого отклонения режим мгновенного расходования
массы восстанавливается и продолжается до тех пор, пока не будут
достигнуты оптимальные условии Для_величин массы и скорости в
3Tofi_j04Ke_ введем ^обозначения М/ и х/. Может быть показано [4],
что и Поэтому с целью сравнения рассмотрим полет
самолета-снаряда, следующего точно постулированной оптималь¬
ной программе без отклонений, до тех пор пока его масса и ско¬
рость не станут равными также М/ и х/, т. е. такими же, как и у
снаряда, нарушившего эту программу.
Путь Д s, соответствующий этому отрезку полета, может быть
рассчитан.
Можно составить отношение дальностей, соответствующих этим
Двум программам, которое будет функцией М0, х0 и k, где
1.
мх
Это отношение -может быть записано так:
Х=-=/(Ч» *о> *)•
Когда k равно 1, это отношение равно 1. Может быть показано,
что при всех величинах k, больших 1, производная от этого отноше¬
ния по k всегда положительна.
6 394 81
Поэтому это отношение представляет собой никогда не убываю,
щую функцию k и равно 1, когда k=\. Поскольку любая программа
с конечной скоростью сжигания топлива может быть аппроксими¬
рована е желаемой степенью точности конечным числом таких ма¬
лых отклонений от программы с мгновенным сжиганием топлива, т0
этим доказывается сделанное допущение.
Таким образом, если начальная масса и скорость таковы, что
мента создания оптимальных условий, будет всегда обеспечивать
большую дальность, чем любая другая программа расходования
того же количества топлива. Конечно, мгновенное сжигание
большого количества топлива практически осуществить невоз¬
можно, но начальный импульс, подобный орудийному выстрелу
или разгону при большом ускорении, может оказаться пригодным
для этих целей.
Случай, когда начальная скорость больше необходимой, соответ¬
ствующей начальной массе и удовлетворяющей уравнению (1), мо¬
жет быть рассмотрен подобным же образом. Можно показать, что
максимальная дальность полета будет соответствовать режиму поле¬
та с выключенным двигателем, при котором скорость должна будет
уменьшаться до тех пор, пока не достигнет оптимальной величины,
и в дальнейшем будет изменяться в соответствии с уравнением (!).
Эти подробности в настоящей статье не рассматриваются.
Полученные результаты приводят к следующим выводам.
Сжигание топлива по любому закону, отличающемуся от закона,
определяемого уравнением (1), будет приводить к уменьшению мак¬
симально возможной дальности горизонтального полета.
Если начальные скорости слишком высоки, снаряд должен иметь
возможность двигаться без расхода топлива до установления уело
вий оптимального движения.
Если начальная скорость слишком низка, топливо должно сжи¬
гаться с бесконечно большой скоростью, пока не установятся опти¬
мальные условия.
В. Четыре проблемы, связанные с маршевым режимом
работы двигателя
Общее рассмотрение участка траектории полета снаряда при ра¬
ботающем двигателе уже произведено методами вариационного исчи¬
сления. Но некоторые вопросы, связанные с начальной и конечной
точками активного участка, не могут быть адекватно разрешены
этими методами и должны быть рассмотрены специально. Ниже при-
ведены четыре вопроса, на которые должны быть найдены ответы.
1. Было доказано, что когда начальная скорость меньше опти¬
мальной, то в начальный момент расходование топлива должно быть
бесконечно быстрым. Этот режим должен продолжаться по крайней
мере до тех пор, пока не будут установлены оптимальные условия.
Возможно, что такой режим должен быть продолжен и после дости-
1/2
мгновенное расходование топлива, до мо-
82
жени я этой точки. Однако в предыдущих исследованиях не рассмат¬
ривался вопрос об обязательности этого условия. Вопрос заключает¬
ся в следующем: какова должна быть программа сжигания топлива
после того, как будут достигнуты оптимальные условия в результате
импульсного разгона?
2. Когда начальная скорость больше оптимальной, можно пока¬
зать, что полет с выключенным двигателем должен продолжаться до
тех пор, пока не установятся оптимальные условия. Вопрос заклю¬
чается в следующем: какая программа должна быть применена по¬
сле достижения оптимальных условий в результате полета с выклю¬
ченным двигателем?
3. Вариационные методы применялись только к моторному поле¬
ту. Общая же дальность включает в себя как активный участок, так
и последующий участок полета с выключенным, двигателем.
В предыдущих исследованиях не указывалось, что программа
сжигания топлива, обеспечивающая максимальную дальность актив¬
ного участка, одновременно с этим обеспечит и общую максималь¬
ную дальность.
Так как дальность полета с неработающим двигателем возрастает
с увеличением скорости в конце работы двигателя, то некоторая дру¬
гая программа сжигания топлива, обеспечивающая большие скоро¬
сти в конце горения, чем получающиеся при оптимальной программе,
может привести и к наибольшей общей дальности. Всякая програм¬
ма, отличная от оптимальной, конечно, будет приводить к меньшей
дальности активного участка полета, поэтому увеличение протяжен¬
ности свободного полета, связанное с новой программой, должно
быть больше, чем уменьшение дальности активного полета.
Вопрос заключается в том, существует ли какая-либо программа
сжигания, обеспечивающая выполнение этих требований?
4. Может потребоваться, чтобы при заданной дальности достига¬
лась максимально возможная скорость. Если дальность, заданная
в этих требованиях, больше чем максимально возможная дальность
активного полета, эта задача сведется к отысканию программы,
обеспечивающей наибольшую общую дальность.
Однако, если заданная дальность может быть достигнута до окон¬
чания моторного полета, то найденная выше оптимальная программа
сжигания топлива обеспечит достижение наибольшей возможной
скорости. Этот факт объясняется тем, что снаряд достигнет заданной
дальности в то время, когда еще не все топливо будет израсходовано.
Ясно, что остаток топлива можно было бы использовать для увели¬
чения скорости. Тогда вопрос может быть поставлен следующим об¬
разом: какая программа обеспечивает максимально возможную ско¬
рость при заданной дальности в предположении того, что эта задан¬
ная дальность может быть достигнута на оптимальной траектории,
определяемой уравнением (1), еще до того момента, как будет из¬
расходовано все топливо?
Отвечая на первый вопрос, можно показать, что как только
будут достигнуты оптимальные условия, режим бесконечно быстрого
сжигания топлива должен быть приостановлен и заменен оптималь¬
83
ным режимом, удовлетворяющим уравнению (1). Для подтвержде¬
ния этого обстоятельства необходимо рассмотреть единственную
возможную альтернативу, т. е. продолжение режима бесконечно
быстрого сжигания топлива.
Произвольный режим с конечным расходом массы, (Начинающийся
при значениях массы и скорости, удовлетворяющих соотношению
(1), исключается по самому существу вариационного метода решении
задачи.
Поэтому представим, что бесконечно быстрый режшч сжигания
топлива продолжается и посл_е точки, в которой масса АД и скорость
х1 станут удовлетворять соотношению
(1). Тогда скорость в рассматриваемый
момент будет больше, чем необходимая
для оптимального движения.
Предположим, что бесконечно бы¬
строе сжигание приостановилось в не¬
который произвольный момент, когда
масса стала равной АД. Скорость х2 в
этой точке может быть выражена как
функция АД, Xi и АД:
Уже отмечалось, что в таком случае наилучшим режимом тюлета
является полет с выключенным двигателем до тех пор, пока скорость
не упадет до оптимальной величины.
Ответ на первый вопрос должен тогда быть найден из сравнения
дальности, получающейся при мгновенном сжигании топлива с по¬
следующим полетом с выключенным двигателем (начало и конец
этого полета протекают при оптимальных условиях), и дальности,
получающейся в том случае, если движение будет происходить по
оптимальному режиму в тех же самых пределах изменения массы и
скорости.
На фиг. 32 представлен график скорости по пути, который дает
качественную картину этого сравнения. _
Разница дальностей является функцией xt (начальной скорости
для обоих случаев) и числа к, которое определяется как отношение
начальной и конечной скоростей.
Выражение этой разности представляется как
D=s0—5- =--D(xi, k)y
где s0—дальность, соответствующая оптимальной программе, а^-
дальность, соответствующая мгновенному сжиганию топлива с по¬
следующим полетом с выключенным двигателем до тех пор, пока
скорость не достигнет той же самой величины, что и в случае опти¬
мальной программы. Может быть показано, что эта разность равна
нулю, когда k=\y и что ее производная по k положительна при всех
величинах k, равных или больших 1.
Фиг. 32. Схема изменения без¬
размерной скорости в зависи¬
мости от безразмерной даль¬
ности полета (задача 1).
84
Поэтому дальность, 'получающаяся при расходовании любого за¬
паса топлива по оптимальной программе, будет больше дальности,
получающейся при мгновенном расходовании того же количества
топлива с последующим полетом с выключенным двигателем при
условии, что начальные и конечные значения массы и скорости в обо¬
их случаях одинаковы.
Во вто р о й задаче оптимальное соотношение (1) между массой
и скоростью достигается после полета с выключенным двигателем,
начинающегося со скоростью, большей оптимальной. Если после до¬
стижения этой точки должно быть продолжено сжигание, то его за¬
кон должен быть оптимальным. Бесконечно быстрый темп расходова¬
ния топлива уже был отвергнут при рассмотрении первой задачи.
Произвольный конечный закон, отличающийся от оптимального, ис¬
ключается самим существом вариационного исчисления. Следова¬
тельно, имеются только две возможности выбора. Одна из них пред¬
ставляет собой дальнейший полет с выключенным двигателем, дру¬
гая—возобновление сжигания топлива по оптимальному режиму. По
аналогии с первой задачей рассмотрим выражение для пути, про¬
ходимого снарядами при каждой из этих двух программ, и их раз¬
ность.
Предположим, что скорость в точке, где впервые устанавливаются
оптимальные условия, равна
В соответствии с «прерывисто-импульсной» программой от этой
точки снаряд будет совершать полет с выключенным двигателем до
тех пор, пока не будет достигнута скорость х2 . Эту скорость выберем
произвольно, требуя только, чтобы она не была настолько малой, что
на снаряде не окажется достаточно топлива для того, чтобы мгно¬
венным импульсом поднять скорость до оптимального значения.
Поскольку снаряд должен двигаться по горизонтальной траекто¬
рии, то единственной действующей силой на этом участке полета
является сила сопротивления воздуха.
Поэтому хС>х2'. Поскольку теперь скорость ниже оптимальной,
то, как показывают предыдущие расчеты, оптимум должен быть до¬
стигнут путем мгновенного сжигания достаточного количества топ¬
лива, если оно имеется, для того чтобы увеличить скорость и умень¬
шить массу до уровня оптимальных условий.
Предположим, что это требование выполнено. Тогда в конце этого
прерывисто-импульсного движения скорость вновь станет оптималь¬
ной. Альтернативой является оптимальная программа; При этом,
как только скорость х± будет достигнута, начнется сжигание топлива
по оптимальному режиму, который будет продолжаться до тех пор,
пока снаряд не достигнет старости агз.
Рассмотрим_теперь две возможные программы при одних и тех
же начальных Х\ и конечных х3 скоростях. Обе эти скорости удовлет¬
воряют соотношению (1). Поэтому при обеих программах начальная
масса равна Мх и конечная масса равна М3. Пути при этих двух про¬
граммах и их разность являются функцией Х\ и числа k\ которое
представляет собой отношение конечной скорости к начальной ско-
85
роста и поэтому всегда меньше или равно единице. Разность равна
нулю, когда k'=\. Параметр k' имеет физический смысл как мера:
а) .времени полета с выключенным двигателем при программе преры¬
висто-импульсного движения; б) импульса, необходимого для того,
чтобы увеличить скорость в конце полета с выключенным двигателем
до оптимальной величины. Поэтому время (или величина конечного
импульса) равно нулю, когда k'=\4 а начальная и конечные скоро¬
сти идентичны. Следовательно, время полета с выключенным дви¬
гателем увеличивается при уменьшении k'.
Можно показать, что производная рассматриваемой разности
пути по kJ всегда равна или меньше нуля, когда k'=\. Следовательно,
эта разность, равная нулю при kr-—\y с уменьшением к! может толь¬
ко возрастать. Таким образом, прерывисто-импульсная программа,
начинающаяся и заканчивающаяся при оптимальных условиях, ни¬
когда не будет приводить к повышению дальности сравнительно с
дальностью при полностью оптимальной программе.
Третья задача возникает в связи с окончанием моторного по¬
лета. Необходимо установить, будет ли при оптимальном движении
полная дальность наибольшей подобно тому, как это имеет место для
активного участка.
Для этого необходимо рассмотреть другие программы сжигания
топлива, которые позволят достаточно увеличить скорость в конце
активного участка с целью увеличения дальности полета с нерабо¬
тающим двигателем, для того чтобы компенсировать возможное
уменьшение дальности активного участка, являющееся результатом
отступления от оптимальной программы.
Рассмотрим импульсную программу с мгновенным сжиганием то¬
плива, при которой снаряд после выхода на оптимальный режим со¬
храняет его до некоторой точки, предшествующей окончанию горения,
а затем остаток топлива сжигается мгновенно. После того, как топли¬
во будет израсходовано, снаряд будет совершать полет с нерабо¬
тающим двигателем. Масса сжигаемого топлива в обоих рассматри¬
ваемых случаях одинакова. Но скорость в конце работы двигателя
при «прерывисто-импульсной» программе будет большей, чем
скорость х°"т,при оптимальной программе.
При «прерызисто-имнульсной» программе после окончания работы
двигателя скорость будет уменьшаться во время полета с неработаю¬
щим двигателем и в некоторый момент станет равна скорости в конце
работы двигателя снаряда, движущегося по оптимальной программе
(фиг. 33).
В этот момент скорости и массы с-наряда для обоих случаев дви¬
жения равны. Но дальности полета по этим двум траекториям могут
и не быть равными, так как, продолжая из этих точек полет с нера¬
ботающим двигателем, снаряд может пройти только один и тот же
дополнительный отрезок пути.
Таким образом, несмотря на то, что движение осуществлялось при
равных начальной скорости Х\ и массе Мх и конечной скорости хК и
массе Мк, пройденный путь не одинаков. Этот результат должен в
86
-точности соответствовать ответу на первую задачу, где было пока¬
зано, что оптимальная программа обеспечивает наибольшую даль¬
ность активного полета.
Любая программа, которая должна приводить к большей общей
дальности по сравнению с оптимальной, должна, по меньшей мере,
обеспечивать большую скорость в конце активного участка. Поэтому
скорость сжигания топлива при такой программе должна быть ка¬
кой-то промежуточной между оптимальной и бесконечно большой
(фиг. 34).
Снова рассматриваем две программы.
При первой, начинающейся при оптимальных условиях, характе-
гания количества топлива—Д Mt по оптимальному режиму снаряд
ство топлива—А М2, в результате чего увеличивается скорость до х3
бей изменения дальности s2.
В качестве второй программы выберем конечную программу с
ния запаса топлива A Afi—А М2 будет достигнута скорость, также
равная х3.
Расчеты показывают, что получающаяся при этом дальность ока¬
зывается меньшей, чем при первых двух программах. Очевидно, что
произвольная не импульсная программа может быть аппроксими¬
рована с любой точностью суммой малых участков с постоянным рас¬
ходом.
Таким образом, комбинация программы с бесконечно большим
расходом топлива с оптимальной программой обладает наибольшей
Дальностью по сравнению с любой другой программой при равных
Условиях.
Эта комбинация обладает также тем свойством, что при заданной
Дальности скорость в конечной точке будет наибольшей по сравне¬
нию с любой другой программой. Эти результаты показаны только
Для малых участков, но любой большой участок может быть пред¬
рй'зующихся массой Ми скоростью х1 и путем slf в результате ежи
I*
Оптимально - импульсная
программа
Оптимальная^
программа
Промежуточная
программа
Т
s
Фиг. 34. Схема трех возможных про¬
грамм (задача 3).
Фиг. 33. Схема протекания
оптимальной и оптимально¬
импульсной программы (за¬
дача 2).
проходит расстояние A s±. В этой точке снаряд характеризуется ве¬
личинами М2, х2 и s2. Затем мгновенно сжигается некоторое количе-
секундным расходом dMjdt=—М, при которой в результате сжига-
87
ставлен в виде суммы таких малых участков и три этом сделанные
выводы останутся справедливыми.
Уже было показано, что если топливо сжигать мгновенно в лю¬
бой момент после установления оптимальных условий перед оконча¬
нием работы двигателя, то результативная общая дальность будет
меньше, чем возможный максимум.
Только что рассмотренные в общих чертах соображения дают
также ответ и на четвертый вопрос, касающийся метода дости¬
жения максимально возможной скорости при любой заданной даль¬
ности. Программа работы двигателя, которой в данном случае нуж¬
но следовать, должна удовлетворять следующим двум требованиям:
во-первых, масса и скорость должны удовлетворять уравнению (i)
до тех пор, пока не будет достигнута заданная дальность, и, во-вто¬
рых, остающееся топливо должно быть сожжено при бесконечной
большой скорости (или насколько возможно близко к бесконечной
скорости).
Общее заключение, отмеченное раньше, может быть таким обра¬
зом подтверждено.
Если необходимо достигнуть максимальной дальности, то уста¬
новленное уравнением (1) оптимальное соотношение между массой
и скоростью должно сохраняться до тех пор, пока не выгорит все
топливо.
Если необходимо обеспечить максимальную скорость при некото¬
рой дальности, то оптимальное соотношение должно сохраняться до
момента, пока не будет достигнута заданная дальность, а остаток
топлива затем должен быть израсходован мгновенно й виде импульса.
СРАВНЕНИЕ ОПТИМАЛЬНОЙ ПРОГРАММЫ С ДРУГИМИ
ВОЗМОЖНЫМИ ПРОГРАММАМИ
Уже указывалось, что результаты решения вариационной задач;;
таковы, что к ним в дальнейшем нельзя применить известные вариа¬
ционные методы испытания с целью проверки действительного мак¬
симума, определяемого уравнением (1); можно лишь сказать, чтп
поскольку подынтегральная функция удовлетворяет условию Эйлера,
то величина интеграла дальности является, по крайней мере, -макси¬
мумом или минимумом или некоторой стационарной точкой. Метод
определения того, какая из этих возможностей является правильной,
состоит в том, чтобы сравнить дальность, полученную в соответствии
с требованиями уравнения (1), с дальностями, полученными при при¬
менении различных других программ работы двигателя. Для этой
цели можно задать ряд программ с постоянным секундным расходом
топлива. Если дальность оптимальной траектории превышает даль
ность, получающуюся при любом постоянном расходе, то, следова¬
тельно, возможность получения минимума должна быть отброшена.
Кроме того, благоприятные результаты этого сравнения вместе с
другими расчетами, рассмотренными в настоящей статье, могут точ¬
но указать, что найден действительный максимум.
Результаты этого сравнения показаны на фиг. 35—40. На фиг. 35
и 36 даны графики изменения скорости в зависимости от дальности
Фиг. 35. Кривые дальностей, получаемых при программах с различными
постоянными расходами и оптимальной программе при малой начальной
скорости.
Сплошная линия—GO?.;-ный запас топлива, пунктирная линия—70%-ный запас топлива.
Безразмерное время указано для кривых постоянного расхода.
Фиг. 36. Кривые дальностей, получаемых п,ри программах с различными
постоянными расходами и оптимальной программе при большой начальной
скорости.
Сплошная линия—60%-ный запас топлива, пунктирная линия—70%-ный запас топлива.
Безразмерное время указано для кривых постоянного расхода при 60% топлива.
89
для различных постоянных секундных расходов и при оптимальной
программе.
Представленные на этих двух фигурах графики отличаются вели¬
чинами начальных скоростей, но в обоих случаях начальная скорость
и масса удовлетворяют уравнению (I) для всех программ расходо¬
вания топлива. В каждом случае рассматриваются варианты с отно
сительным запасом топлива, равным 60 и 70%. Из графиков видно,
что во всех случаях при оптимальной программе достигается наи¬
большая дальность.
Рассматривался случай с очень малым секундным расходом
топлива,'при котором на траектории скорость полета снаряда умень-
\юо
ю
12
10
в
6
о-
2
0.7
0,6
1
1 ,
7/7
. _
1 1 1 и 0
Оптимум
1 г
^ ‘
i-i г
Пптиклшт /7 0
1 L
90 е/
\
\
0,3
0,2
Начапьная
безразмерная
спиристь х0
1 1 L. I
\ 1
0,1
0,1 0,2 0,3 0,0 0,5 L
Фиг. 37. Изменение дальности в зависи-
мости от величины постоянных расходов
при малой начальной скорости.
-
Оптимум
"г —
Оптимум
!
170%
s'
s'
>
90%
\
л
/•
/X
*
i
Ha4aj
I о
\
пьная
норос>
\
бвзра.
Ч1ЬХ0
|
змерь
>а я
1
- i
. i
О
0,1 0,2 0,3 0,0 0,5 0,6 0,7 L
Фиг. 38. Изменение дальности в за
висимости от величины постоянных
расходов при большой начальной
скорости.
шается до нуля еще до того момента, когда может быть израсходова¬
но все топливо. Если принять во ;знимание вертикальную составляю¬
щую тяги, это явление потери скорости при таком темпе расходова¬
ния топлива вряд ли могло наблюдаться, за исключением случаев
настолько малых расходов, при которых величина тяги могла быть
меньше, чем сила тяжести, действующая на снаряд. Однако при боль¬
ших скоростях (вызванных большими секундными расходами) пре¬
небрежение вертикальной составляющей тяги не приводит к суще¬
ственным погрешностям, так как индуктивное сопротивление при
этом мало.
Скорость при оптимальной программе изменяется в небольших
пределах, поэтому допущение о постоянстве коэффициента сопротив¬
ления также не приводит к значительным ошибкам.
На фиг. 37 и 38 даются графики общей дальности в зависимости
от времени горения для программ с различными постоянными се¬
кундными расходами. Из графиков видно, что полная максимальная
дальность достигается при одном из значений секундного расхода.
Этот расход будет не одинаковым для двух различных начальных
условий, но максимальная дальность во всех этих случаях меньше,
90
tjeM при оптимальной программе (показана на графиках прямой
Данией).
На графиках все переменные величины представлены в безраз¬
мерной форме, поэтому должны быть даны дополнительные пояснс-
дмя к графикам с различными начальными скоростями, соответствен¬
но представленным на фиг. 35, 37 и фиг. 36, 38. Установлено, что
начальная масса и скорость удовлетворяют уравнению (1). Поэтому
двум различным начальным условиям могут соответствовать две
различные скорости (и две различные высоты) для одного и того же
снаряда или одинаковые начальные скорости и высоты для двух сна-
0,20
010
0,10
0,05
О
- г
—
{
От
<
\ ЖП
Пкн
ая
7Ь
Шльпосп
от ofof6 tK
Фиг. 39. Сравнение дальностей, полу¬
ченных при оптимальной программе
и программах с постоянными расхо¬
дами при малой начальной скорости.
Начальная скорость меньше оптималь¬
ной. Относительный запас топлива 70%-
Безразмерное время указано для кри¬
вых постоянного расхода.
Фиг. 40. Изменение дально¬
сти в зависимости от вели¬
чины постоянных расходов
при малой начальной ско¬
рости
Относительный запас топли¬
ва 70%. Начальная безразмер¬
ная скорость равна 0,1. Началь¬
ная безразмерная масса рав¬
на 0,5.
рядов с различными массами, эффективной скоростью истечения пли
аэродинамическими характеристиками. Любое изменение безразмер¬
ной дальности, вносимое этими изменениями в физические параметры,
Должно быть, конечно, одинаковым, как для программы с постоян¬
ным расходом, так и для оптимальной программы.
На фит. 39 и 40 представлено сравнение оптимальной программы
с несколькими программами постоянного расхода для случая, когда
начальная скорость меньше, чем необходимая для оптимальной про-
^аммы. В этом случае в начале движения оказывается необходимым
сжечь некоторое количество топлива мгновенно для того, чтобы обе¬
спечить установление оптимальных условий. Преимущества опти¬
мальной программы здесь становятся еще более резко выраженными.
Значение опущенной вертикальной составляющей тяги в этих при¬
мерах оказывается весьма существенным, так как из-за низкой на¬
чальной скорости индуктивное сопротивление становится большим.
При малых расходах вскоре после запуска снаряда происходит по¬
теря скорости еще задолго до окончания сжигания всего топлива.
91
Влияние изменяющихся начальных условий .рассмотрено на чис~
ленном примере, результаты которого приведены на фит. 41. В это\г
примере задавались два значения начальной скорости и 1менялась
начальная масса. Подсчитывалась общая дальность, полученная при
оптимальной программе, и результаты фиксировались на график**
в функции значений начальной массы. Все переменные величины при
этом давались в их безразмерной форме. Построение кривых про¬
изведено от точки, названной «точкой равновесия», соответствующей
такому значению массы, которая вместе с заданной начальной ско¬
ростью удовлетворяет уравнению (1). Кривые проходят через так
1,2
1,0
0,8
0,6
0,4
0,2
О
ООО/ 0,0/ 0,1 1г0 10,0 100,0 мс
Фиг. 41. Влияние начальной безразмерной массы
на общую безразмерную дальность.
Относительный запас топлива 70% . Сплошная линия оп¬
тимальная программа, пунктирная линия—импульсная про¬
грамма с мгновенным сжиганием топлива.
называемую «критическую точку», соответствующую такому значе¬
нию начальной массы, при котором все топливо должно быть израс¬
ходовано в импульсе нулевой продолжительности, для того чтобы
привести снаряд к оптимальным условиям.
Понятно, что после достижения этих условий для дальнейшего
моторного полета топлива больше не остается. Для всех значений
массы выше этой критической точки все топливо должно выгорать
мгновенно, но оптимальные условия никогда не могут быть достиг¬
нуты. Как и можно было ожидать, каждая кривая имеет максимум
дальности при некоторой величине начальной массы. Величины
этих масс различны для каждой из двух кривых, но расположение
максимумов подобно. Для обеих кривых принимался относительный
запас топлива, равный 70%. Для одной кривой была выбрана на¬
чальная безразмерная скорость, равная 7ю, для другой кривой -
равная 1. Для кривой с начальной физической скоростью, равной
7ю эффективной скорости истечения, было найдено, что макси машин¬
ная дальность будет иметь место при начальной массе, соответст¬
вующей мгновенному начальному расходу 94,5% всего топлива. Для
другой кривой с начальной скоростью, равной эффективной скорости
истечения, максимальная дальность достигается при начальной ма ¬
сс, соответствующей мгновенному начальному расходу 92,2% все¬
го топлива.
Lf
\mli4
т
et
а
?ная
чна
1,0
ш
/
\
Го*
Ч№ у
oat
?НО(
деси
я-
}
N
г
-Нач
иы,
альныи
тулье
п
14h
и
*0
*
Критичес¬
кая точна
равновесия
1 m-dr:
Нашri
импу,
ы
пь
iblU
>с 1
92
С практической точки зрения, по-видимому, наиболее целесооб¬
разно в этом случае принять для таких снарядов наиболее простую
одноступенчатую программу, которая могла бы обеспечивать даль¬
ность полета снаряда, близко приближающуюся к максимальному
значению. Для того чтобы проиллюстрировать возможность такой
программы, на графики пунктирными линиями была нанесена общая
дальность, получающаяся в результате мгновенного сжигания всего
топлива (ем. фиг. 41). Из этого графика видно, что, хотя дальность
при такой программе и получается значительно ниже оптимальной
дальности для малых значений начальной массы, максимальная ве¬
личина незначительно отличается от соответствующего максималь¬
ного значения дальности при оптимальном режиме. Расчеты пока¬
зывают, что эта разница составляет менее 1%. Значения начальной
массы при этих максимумах примерно одинаковы как для програм¬
мы с бесконечно быстрым расходом топлива, так и для оптимальной
программы.
Поскольку начальная масса выражена в безразмерной форме, то
при изменении этой величины не обязательно производить изменение
действительной массы снаряда, а могут изменяться высота полета,
размер снаряда, ето аэродинамические формы или эффективная ско¬
рость истечения.
ЗАКЛЮЧЕНИЕ
А. Общие правила
Найдены две программы расходования топлива самолетом-сна¬
рядом, осуществляющим полет по горизонтальной траектории на
Любой высоте при произвольных начальных массе и скорости. Первая
из этих программ обеспечивает наибольшую возможную общую
дальность для данных начальных условий. Вторая программа обе¬
спечивает наибольшую возможную скорость при заданной дальности
и данных начальных условиях.
Произведено предварительное исследование влияния начальных
условий на характеристики снарядов, результаты которого представ¬
лены в виде графика (см. фиг. 41), которые сводятся к следующим
трем положениям:
1. Снаряд при данной стартовой скорости только на одной высоте
Может достичь своей наибольшей возможной горизонтальной даль¬
ности, следуя оптимальной программе работы двигателя. Этот же
снаряд будет достигать дальности, незначительно отличающейся от
этого максимального значения, если в начале движения все топливо
будет сожжено мгновенно. При любой высоте выше или ниже этой
оптимальной высоты общая достижимая дальность даже при опти¬
мальной программе работы двигателя будет меньше максимального
значения.
2. Для данной стартовой скорости и данной высоты имеется неко¬
торый определенный размер (для снаряда данной схемы и эффек¬
тивной скорости истечения), при котором будет достигаться наиболь¬
шая возможная дальность, если полет осуществляется при оптималь¬
93
ной программе работы двигателя. Здесь будут справедливы также ц
другие положения пункта «1», если термин «высота» заменить теп.
мин ом «размер».
3. Подобные результаты были также получены при изменявшихся
значениях эффективных скоростей истечения и различных аэродина¬
мических характеристиках, но при фиксированных значениях началу
ной скорости, высоты полета и веса снаряда.
Б. Расчетный пример
Для иллюстрации этих положений приводится численный пример^
в котором в качестве исходных данных взяты характеристики второй
ступени гипотетического двухступенчатого снаряда. Плотность ат¬
мосферы принята стандартная [5]. В рассмотренном примере скоро¬
сти полета—сверхзвуковые, поэтому число Ь2 в выражении индук-
1 дс
тивного сопротивления будет иметь вид b2=— — F, г/а
iz до.
- принимается постоянной величиной.
Приняты следующие характеристики снаряда:
Общая начальная масса
32,8 кг сек2/м
Масса пустого снаряда
9,85 кг сск^/м.
Относительный запас топлива •
70%
Лобовая площадь
, 0,09 м2
дсу/дя
7
. 0,2
Эффективная скорость истечения
1980 м/сек
Начальная скорость
1980 м/сек
Тогда постоянная величина Ь будет равна 0,45 м. Начальная бе
размерная скорость хо равна 1. Начальная безразмерная масса как
функция плотности воздуха будет иметь вгл
^ _ mQg = 4,8-10—4
0 Vfro У rw cxF р
Общая дальность может быть выражена
как функция безразмерной общей дально¬
сти:
bV2 -
s2 = =52=2,4* 103s2 км.
Максимально возможная общая даль¬
ность для любой высоты полета представле¬
на на фиг. 41.
Результаты расчета обобщены в табл. 1-
Наибольшая из возможных значений даль¬
ности равна 2360 км и может быть достиг^
нута на высоте полета 44,4 км.
94
Таблица 1
Максимальная возмож¬
ная дальность второй
ступени гипотетиче¬
ского двухступенча¬
того самолета-снаряда
Высота
км
Даль¬
ность
км
30
1540
35
2100
42
2330
44,4
2360
48
2210
54
1685
60
1080
Данные в таблице приведены для случая горизонтальной траекто¬
рии при v0 =Vr.
Если бы стартовая скорость была равна 0,lVr, то наибольшая
достижимая дальность для того же снаряда была бы равна 666 км
на оптимальной высоте, равной 39 км.
В. Рекомендации
Следует сделать две рекомендации для дальнейших Исследова¬
ний: во-первых, постановку задачи следует расширить. Установлено,
что при соблюдении оптимальных условий, выраженных уравнением
(1), происходит небольшое изменение скорости. Отсюда, следова¬
тельно, допущение о постоянстве коэффициента лобового сопротив¬
ления не приводит к большой неточности для этой части траектории.
Однако, если начальная скорость существенно меньше ее оптималь¬
ного значения, то в начале полета будет иметь место значительное
изменение скорости. В результате этого изменения постоянный коэф¬
фициент сопротивления уже не может считаться достаточно точным.
Кроме того, в конце траектории во время фазы полета с неработаю¬
щим двигателем скорость будет также сильно изменяться, что также
не позволяет считать коэффициент сопротивления постоянным. По¬
этому при рассмотрении полной траектории в дальнейшем представ¬
ляется целесообразным исследовать влияние переменного коэффи¬
циента лобового сопротивления. Подобно изложенному выше, пло¬
щадь 62, определяющая индуктивное сопротивление и предполагав¬
шаяся постоянной величиной, в действительности является функцией
числа М полета. Должны быть рассмотрены более реальные, не го¬
ризонтальные траектории. Решение проблемы обеспечения макси¬
мальной дальности на траектории с изменяющейся высотой могло
бы найти большее практическое применение.
Во-вторых, показано, что в начальные условия, определяющие
максимально возможную дальность, входят и конструктивные харак¬
теристики самолета-снаряда. Дальнейшее исследование влияния
этих характеристик могло бы помочь определению различных крите¬
риев оценки эффективности снарядов на различных высотах при
различных начальных скоростях полета.
ЛИТЕРАТУРА
1. Паккетт А. и Эдвардс Р., Оптимальные характеристики ракетных
снарядов малой дальности.
Puckett A. and Edwards R., The Optimum Performance of Short-Range
Rocket Powered Missiles, Institute of the Aeronautical Sciences, Preprint, No. 279.
2. M и л л и к e н С., Аэродинамика самолета.
Millikan С., Aerodynamics of the Airplane, John Wiley and Sons, New
York, 1941.
3. Форсайт А., Вариационное исчисление.
Forsyth A., Calculus of Variations, Cambridge University Press, New York,
1927.
4. Гиббс А., Оптимальная программа изменения тяги двигателя ракетного
снаряда при горизонтальном полете.
Hibbs A., Optimum Burning Program for Rocket-Propelled Missile щ
Horizontal Flight, Memorandum No. 4—62, Jet Propulsion Laboratory, Pasadena,
1951.
5. У a p ф и л д С., Опытные таблицы свойств верхней атмосферы.
Warfield C.t Tentative Tables for Properties of Upper Atmosphere, NAC^
Technical Note, No. 1200, 1947.
А. МИЕЛЕ.
ОПТИМАЛЬНАЯ ПРОГРАММА ПОДЪЕМА САМОЛЕТА
С РАКЕТНЫМ ДВИГАТЕЛЕМ 1
Принятые обозначения
sa—площадь выходного сечения сопла ракетного двигателя
сх — коэффициент лобового сопротивления
Схо—коэффициент лобового сопротивления при нулевой подъемной
силе
Q — лобовое сопротивление
Qo — лобовое сопротивление при нулевой подъемной силе
е — аэродинамическое качество самолета
g — ускорение силы тяжести
h — высота
v^
ле = h-\- — энергетический уровень
Y — почъемпля сила
М — мгновенная масса самолета
секундный расход массы топлива
М — число М
р} — атмосферное давление
Ра — стати mi с кое лав..сине в вылолпом сечении сопла
р. — местII* е статическое давление в точке на внешней стенке
самолета
Re — число Рейнольдса
5кр—площадь крыла
I — время
Р — тяга
v — абсолютная скорость самолета
G—вес самолета
Vr — средняя величина осевой составляющей относительной скорости
газ,.в в реактивном сопле ракеты (г. е. скорость относительно'
самолета)
Gs — секундный расход топлива воздушно-реактивного двигателя
са.моле га
а — произв.-дпая температуры воздуха п > высоте
г.- показатель политропы, -/„=1,4 для воздуха
£ — удельная энерт ия
0 — у,ол цак:в па 1раектории полета по отношению к горизонталь¬
ной плоскости (положи 1ельный для полета с набором высоты)
1 А. М i е I е, Optimum Climbing Technique for a Rocket-Powered Aircraft,
Jet Propulsion, 1955, August, vol. 25, No. 8, pp. 38o—891, 399.
96
к— удлинение крыла
р — плотность воздуха
1 — начальное условие (момент времени t{)
2 — конечное условие (момент времени t2)
О — условие, соответствующее моменту времени t = 0 или условию
нулевой подъемной силы
(') —знак производной по высоте
( )н.сж — условие обтекания несжимаемым потоком
( )у.м — условие уровня моря.
За последнее время уделяется значительное внимание изучению
оптимальных траекторий нестационарного полета самолетов, обла¬
дающих большой скоростью. Рассматриваются следующие, типичные
проблемы: полет с набором высоты за 'минимальное время [1—4,
6—8], полет с набором высоты с минимальным расходом топлива
[1, 4, 7, 8] и наиболее крутой подъем [4, 8]. Для частного случая са¬
молета с ТРД систематическое применение теории изложено в рабо¬
тах [5] и [91.
Из-за аналитических трудностей, связанных с проблемой, ранние
исследования основывались на некоторых упрощающих предполо¬
жениях, касающихся уравнений движения, в частности: а) масса
самолета считалась постоянной; б) предполагалось, что движение
осуществляется таким образом, что Y = Q. Эти две гипотезы, эквива¬
лентные выражению функции лобового сопротивления в виде
Q = Q{v, /г), приводили к упрощенной форме проблемы минимума,
решение которой дано в работах [1, 2, 4].
В работе [1] показано, что проблема перемещения самолета с по¬
стоянной массой из точки, где скорость равна V\ и высота hb к точке
со скоростью v2 и высотой h2 в 'минимальное время или с минималь¬
ным расходом топлива, или же с кратчайшим участком горизонталь¬
ного пути в общем случае приводится к определению специальной
траектории, состоящей из трех кривых: а—начального участка вер¬
тикальной кривой, начинающейся у точки 1\ b—конечного участка
вертикальной кривой, заканчивающейся у точки 2\ с—связующей
Центральной кривой, описываемой ура1внением:
где F — (P— Q) v — для минимального времени;
F=(P— Q) vjGs — для минимального расхода топлива;
F = (Р— Q) — для самого крутого подъема.
Для случая самолета с ракетным двигателем приведенные выше
Проблемы минимума усложняются необходимостью учета изменения
Массы самолета по времени. Автору настоящей статьи неизвестны
Какие-либо опубликованные исследования, кроме ранней попытки,
сделанной Липпишем [10], который получил решение задачи Эйлера,
вносящееся ко всем возможным траекториям полета, удовлетворяю¬
щим условию Cjj=const.
7 394 97
ВВЕДЕНИЕ
(1)
Однако Литшиш получил неполное решение, поскольку оно щ
удовлетворяет граничным условиям как задачи с подвижными гра¬
ницами, так и задачи с фиксированными границами. Необходимо
отметить, что Липпиш установил «неэкстремальный характер» сво¬
его решения путем численного сравнения траектории, полученной по
методу Эйлера, с двумя произвольными траекториями полета, 15-
расчете одной из которых был принят постоянным скоростной напор,
а в другой — принималась постоянной скорость полета.
Целью настоящей работы является выбор программы набора вьь
соты за минимальное время для самолета с ракетным двигателем:
т. е. такое изменение скорости по высоте v=v(h), которое сокращает
время, необходимое для полета от точки с данными начальными
условиями (h\y vt) к точке с заданными конечными условиями (/ь,
и2). Главная идея работы заключается в приближении математиче¬
ской формы проблемы минимума к форме задачи, уже решенной для
самолета с постоянной массой, путем соответствующего преобразо¬
вания уравнений движения.
В работе сделаны следующие допущения:
а) самолет с ракетным двигателем рассматривается как частица
переменной массы;
б) рассматриваются лишь плоские траектории полета в верти¬
кальной плоскости;
в) угол между вектором силы тяги и вектором скорости считается
пренебрежимо малым;
г) движение топлива в системе подачи, камере сгорания и в сопле
по отношению к корпусу самолета считается установившимся;
д) неустановившийся аэродинамический режим не рассматри¬
вается, т. е. подъемная сила и сила лобового сопротивления опреде¬
ляются как бы при установившемся полете.
Вследствие допущений «а», «б» и «в» уравнения движения по ка¬
сательной и по нормали к траектории полета записываются в сле¬
дующем виде [1, 11, 121:
Как следствие допущения «г» масса самолета представляется з
виде линейной функции времени
ПРЕДМЕТ НАСТОЯЩЕГО ИССЛЕДОВАНИЯ
ОСНОВНЫЕ УРАВНЕНИЯ
Р — Q — М (g + vv') sin 0 = 0,
Y— M (g cos 6 + н20' sin 0) = 0.
(Л
(3)
M=Mq—12 AfT,
(4)
98
где М0—масса в произвольно выбранный момент времени ^=0. Знак
суммы 2 распространяется на все двигатели самолета в общем слу¬
чае самолета с несколькими ракетными двигателями.
Для случая параллельных сопел вектор тяги определяется как
По определению термина скороподъемности, а также из уравне¬
ний (2) и (4) получаем интервал времени, необходимый для полета
от начальной высоты h\ до конечной высоты h2:
жуток времени A t представляет собой монотонно возрастающую
функцию интеграла / [см. уравнение (6)]. Следовательно, проблема
минимума A t по существу идентична с проблемой минимума инте¬
грала (7).
В уравнениях (8) и (9) переменные величины Png зависят
только от высоты. Лобовое сопротивление Q согласно предположе¬
нию «д» определяется функцией Q = Q(h, v, У). Подъемная сила
представляет собой У=У (/г, v, О, 0', t) и может быть определена из
уравнения (3). Следовательно, две функции Фиф приводятся к виду
Решение проблемы минимума затруднено в основном тем, что
Интеграл (7) зависит от трех функций: v(ft), 0 (ft) и t(h). Поэтому
следует упростить уравнения движения, приняв предположение о
том, что так называемое «индуктивное лобовое сопротивление» не¬
значительно по отношению к лобовому сопротивлению самолета при
нулевой подъемной силе. Основанием для этого предположения слу¬
(5)
(6)
где
(7)
(8)
тр _- S
v(P-Q)’
(9)
Необходимо отметить, что для данных величин Mt и 2Мт проме-
Ф = ф (ft, v, 6, 6', t) и ф = ф(А, vy б, 6', t).
РЕШЕНИЕ ПРОБЛЕМЫ МИНИМУМА
7*
9§
жит то обстоятельство, что самолет с ракетным двигателем в режиме
набора высоты имеет относительно малые углы атаки, особенно па
малых высотах. Математически это предположение эквивалентно
замене уравнения (-3) уравнением
Для данного самолета коэффициент лобового сопротивления при
нулевой подъемной силе с^о является функцией числа М и числа
Рейнольдса. Для стандартной атмосферы М=М(а, A), Re=Re(y, А)
и, следовательно, Cxo = Cxo(v, А). Лобовое сопротивление самолета,
следовательно, приводится к функции, зависящей лишь от скорости и
высоты, а выражения (8) и (9) упрощаются к виду Ф=Ф(у, А);
ф = А). Отсюда следует, что интеграл (7) принимает форму
и приводится к хорошо известному виду, уже рассмотренному в ра¬
ботах [1, 2, 4] для самолета с постоянной массой.
Поскольку существует математическая аналогия между рассмат¬
риваемой упрощенной минимальной проблемой и проблемой, рас¬
смотренной в работах [1, 2, 4], то выкладки здесь опущены и читатель
должен обратиться к библиографии.1
Функция скорости от высоты v = v(h), дающая интегралу (И)
минимум и удовлетворяющая граничным условиям (Аь v{) и (А2, v2),
состоит из трех кривых:
1—центральной кривой, определенной уравнением, не зависящим
от граничных условий проблемы:
2 и 3—начальной кривой 1М и конечной привой N2, зависящих от
граничных условий проблемы [1, 4].
Возможны четыре типа граничных условий в соответствии с отно¬
сительным положением точек 1 и 2 относительно кривой со = 0 [1].
Четыре различных решения соответственно найдены для конечных
отрезков 1М и N2.
Эти решения указаны в табл. 1 и на фиг. 42, где А ((о<0) обозна¬
чает область плоскости (v, А), расположенной слева от кривой со = О,
а £((о>0) обозначает область плоскости, расположенной справа от
этой же кривой.
1 Для частного случая hi < h < h2 доказательство минимального характера
траектории 1MN2 изложено в приложении А.
Q^Qo=jcxopSKpv2.
(10)
(П)
(12)
100
Таблица 1
ОПТИМАЛЬНЫЕ СООТНОШЕНИЯ высоты И СКОРОСТИ
—
Полет¬
ный
случай
Область
точки 1
Область
точки 2
Кривая
1М
Кривая
MN
Кривая
N2
Примечание
I
А
В
п
о
О) = 0
б п
11
III
А
В
А
А
71
==~~~ 2
®-+Т
О) = 0
03 = 0
2
7С
е=+-
тс
е=+т
Никаких ог¬
раничений на
траекторию не
налагается
IV
В
В
п
0= + Т
03 = 0
7С
0=-~~2~
I
А
В
h=hx
03 = 0
7С
0=
—
II
А
А
h=.hx
03 = 0
7С
0=+т
h^-hi
III
В
А
71
0= + т
03 = 0
7С
0= + —
—
IV
В
В
7С
0= + т
03 = 0
7С
0=-Т
—
I
А
В
h=hx
03 = 0
h=h2
—
II
А
А
h=hx
03 = 0
тс
6= + —
h>hx
III
В
А
г.
0= + Т
03 = 0
0=+Т
h<h2
IV
В
В
тс
0=+Т
03=0
h—h2
—
Случай 1
Фиг. 42. Оптимальное соотношение высоты и скорости полета для общего
случая движения.
101
Кроме проблем абсолютного экстремума методом, приведенным
в работах [1, 4], могут быть решены проблемы условного экстремума.
Приведенная таблица и фиг. 43, 44 содержат решение пробле¬
мы минимального времени подъема при ограничениях h>h\ и
h1<h<h2. Первое ограничение представляет интерес в случаях, ког¬
да высота hi есть уровень земли, что исключает возможность полета
n--ht i
Случаи!
Случай Е
Случай Ш
Случай N
Фиг. 43. Оптимальные соотношения высоты и скорости для случая h> hi.
па меньших высотах. Второе ограничение означает, что определение
наилучших условий полета должно производиться среди семейства
траекторий, находящихся внутри области, ограниченной горизон¬
тальными плоскостями, соответствующими конечным высотам.
Случай Е
Случай Ш
Фиг. 44. Оптимальное соотношение высоты и скорости для случая
hi < h < Л2.
Преобразованием координат плоскости (у, h) к плоскости (о, е)
уравнение (12) можно привести к эквивалентному виду
е)
dv
=о,
где
>-т+1 *м-
(13)
(14)
102
(?) “О-
\ dv //,
Для частного случая £=const уравнение (13) можно предста-
цИТЬ В ВИДС
(15)
"е
у2
где he=h-\-- так называемый энергетический уровень [2]. Пере-
менная е представляет собой у дельную энергию. Она имеет размер¬
ность энергии на единицу массы и ее введение удобно при решении
задач, в которых ускорение силы тяжести рассматривается .как функ¬
ция высоты.
ОПТИМАЛЬНЫЕ ЗНАЧЕНИЯ ЧИСЕЛ М
Центральная кривая MN оптимального распределения скоростей
не зависит от граничных условий и определяется эквивалентными
выражениями (12) или (13). Из уравнений (8), (9), (10) и (12) по¬
дучаем следующую формулу для оптимального соотношения скоро¬
сти и высоты:
д (Ру — Q0v)
dv
__ 2!1Г
^ g L
d(P-Qo)
dh
= 0.
(16)
Выражение (16) можно привести к удобной для применения фор¬
ме, если пренебречь зависимостью с& от числа Рейнольдса и исполь¬
зовать уравнения (5) и (10), а также выражения для скорости звука,
для производных плотности, давления и температуры воздуха по вы¬
соте и ввести вместо скорости в качестве независимой переменной
число М. Получаем следующий результат:
Ph.S кр
- = хМ2
3 I М dcxо
2 х0 2 дМ
hsa
кр
+
*2М4
, т — 1 дсхо
тс,п Н М ——
л0 2 дМ
:где
т=1 +
aR
g
(17)
(18)
R — газовая постоянная воздуха.
В общем случае уравнение (17) должно решаться графически.
Аналитическое решение возможно лишь в отдельных частных слу-
. чаях. Например, если производная минимального коэффициента ло¬
бового сопротивления относительно числа М может быть опущена,
уравнение (17) упрощается и получаем следующее решение:
М
1+?Г
схоР1г$к\>
где
К = -
Sa
CxqS
(19)
(20)
Кр
103
Уравнение (19) можно применить для исследования режима по¬
лета на малых высотах для случаев, когда скорость оптимального
подъема все еще находится в области, где можно пренебречь сжи¬
маемостью потока. Численный анализ, однако, показывает, что ре¬
жим полета, определенный уравнением (19) при различных высотах,
характеризуется в первом приближении постоянством динамического
напора, но в тех случаях, когда высота возрастает и скорость, и чи¬
сла М увеличиваются с такой быстротой, что гипотеза dcxJdN[=--(j
больше не удовлетворяется, расчет оптимального распределения ско¬
ростей должен производиться с помощью уравнения (17).
Интересно сравнить центральную кривую MN приведенного
выше решения с хорошо известным «квазистационарным» решением
проблемы оптимального подъема. При «квазистационарном» подхо¬
де оптимальное распределение скоростей определяется соотношением
-^-(Pv — Qv)
dv
= 0. (21)
При малых высотах гипотеза Q = Qo может быть введена в урав¬
нение (21), что дает
£[(P«-Q0tf)]A=0. (22)
Из уравнений (22), (5) и (10), а также из определения числа №
получаем следующие соотношения для «квазиетационарной» опти¬
мальной зависимости скорости от высоты подъема:
Р %М2
Ph$ кр 2
Зсх0 + М —^
дМ
(23)
Члены, содержащие дс^о/дRe, опущены в уравнении (23). Число
М, удовлетворяющее уравнению (23), обозначим М«. В частности,
когда соблюдается условие дсх0/(?М=0:
М-“/зТ7^- <24>
На фиг. 45 представлен график отношения М/Мв между
числами М, соответственно определяемыми уравнениями (19)
и (24), по параметрам (——-—^ и ——) для несжимаемого
V / V-eJ С^о^кр/
потока при полете в тропосфере. Оптимальная программа подъема
при неустановившемся движении характеризуется скоростями,
меньшими на 2 — 10% скоростей, полученных в предположении
„квазистационарного" движения.
На фиг. 46 представлены результат типового расчета, выполненно¬
го для ракетного самолета, со следующими характеристиками!:
Х = 5, ^ = 275 кгсек2[м, Ру м = 2000 кг,
е)н.сж = 0.8. SKp=25,0 м2, 2 sa=0,045 м2,
(сх0)н.сж = 0,018, 2^т = 0>48 кгсек1м.
104
Расчет силы лобового сопротивления в сжимаемом воздушном по¬
токе произведен по формулам работы [13]:
1. Кривая А получена из уравнения (16) с учетом инерционных
сил, действующих по касательной, и без учета индуктивного сопро¬
тивления.
// м
гюоо
18000
15000
12000
9000
6000
3000
1
\
С'
1
1
1 ,
\
J~B
1
О
тог
туза
---
/1
г
—
у.
У
А
у
/
4
у
V.
ft .
Фиг. 45. Оптимальная ско¬
рость полета в тропосфере
(несжимаемый лоток).
Фиг.
вые
Ш 5*5 610 675 7*0 805 870 935
v мм/час
46. Сравнительные кри-
изменения скорости по
высоте.
у2 Г
g L
[
]v= const
dh
кривая В —
d(Pv-Q0v) 1
dv \h= const
кривая С —
d (Pv — Qv)
= 0;
2. Кривая В определена из уравне¬
ния (22) без учета инерционных сил,
действующих по касательной, и индук- L dv
тивного сопротивления. v2 \д(Р— Qp)
3. Кривая С определена из уравне¬
ния (21) без учета инерционных сил,
но с учетом индуктивного сопротивле¬
ния исходя из условия Y=Mg COS0.
В выполненном частном примере гипо¬
теза (10) относительно лобового сопро¬
тивления самолета приближенно удов¬
летворяется до высот около 12 000 м. I ' : =0-
До этой высоты наилучшее распреде¬
ление скоростей v = v(h) дает уравнение (16), так как ошибка при
этом не превышает 2,0/о.
На больших высотах ввиду меньшей плотности воздуха и влия¬
ния сжимаемости на лобовое сопротивление коэффициент подъемной
силы для наивыгоднейшего набора высоты изменяется уже таким
образом, что индуктивное сопротивление не является более прене-
брежимым по сравнению с минимальным лобовым сопротивлением.
Примечания. 1. Уравнение (6) является общим и может быть
использовано в частном случае применительно к самолету с обычными
поршневыми или турбокомпрессорными двигателями. Для самолета с идеаль¬
но постоянной массой (2МТ -» 0) уравнение (6) приводится к виду
At=M 11.
кривая А —
д(Рг>—<?о*]
J Л— const,
105
2. Для самолета с реактивным двигателем, работающим при постоянных
условиях в камере сгорания, 2Мг — величина постоянная и расход топлива
пропорционален времени полета. Вследствие этого траектория минимального
времени полета идентична траектории минимального расхода топлива.
Подобная идентичность не имеет места для самолета с поршневым или
воздушно-реактивным двигателем. Для турбореактивного самолета, напри¬
мер, кривые минимального времени и минимального расхода топлива весьма
'различаются между собой, ибо в первом случае самолет должен) лететь со
сравнительно большими, чем во втором случае скоростями [4].
3. Установленная выше зависимость скорости от высоты v = v(fi) (с уче¬
том сил инерции) отличается от распределения скоростей в «квазистацио-
нарной» задаче (не учитывающей сил инерции) в сторону меньших скоро¬
стей движения. Для самолета с ТРД, напротив, учет сил инерции сдвигает
оптимальное распределение скоростей в область больших значений [4].
4. Особо важным является допущение [10], касающееся силы лобового
сопротивления. Проверка подобной гипотезы показывает, что она вводит
относительно небольшую ошибку при малых высотах для участка MN опти¬
мальной траектории полета. Однако по мере возрастания высоты точность
в определении оптимальной зависимости скорости от высоты снижается.
Из-за отсутствия общей аналитической зависимости между сх, су и М трудно
определить точные границы применимости настоящей теории.
Для больших высот, однако, точность уравнения (16) может быть повы¬
шена, если подставить в него Q вместо Q0.
5. Числовой пример приведен для условий
гч = 480 км/час, hi = 0 м, tb=928 км/час, /г2 = 15 ООО м, hi<h < h->.
Время At подсчитано для трех кривых распределений скорости А, В, С
(см. фиг. 46) согласно уравнениям (6), (7), (8), (9), причем во всех трех
случаях принималось Q = Qo- Результаты расчетов подтверждают экстремаль¬
ную природу оптимального решения А.
6. Оптимальная зависимость между скоростью и высотой v = v(h) имеет
угловые точки М и N, где кривая 0 = 0 пересекает две вертикальные кривые,
из которых одна начинается в точке 1, вторая заканчивается в точке 2 (см.
фиг. 42). Подобный разрыв кривой является следствием допущения, что
Q = Qo, и его можно было бы избежать, если бы проблема минимума реша¬
лась по более точным уравнениям движения.
7. Основное преимущество приведенного выше решения заключается в
его простоте и легкости расчета. Результаты, однако, должны рассматри¬
ваться с осторожностью. С точки зрения практического полета оптимальная
ломаная разрывная кривая 1MN2 должна быть заменена возможной плав¬
ной кривой, без угловых точек М и <V; для этого между экстремальной кри¬
вой 0 = 0 (MN) и двумя концевыми участками (1М и N2) приходится ввести
соответствующие переходные кривые. Очевидно, что указанные выше пере¬
ходные кривые должны быть согласованы с прочностными ограничениями,
налагаемыми конструкцией самолета, физиологической способностью лет¬
чика выдерживать возникающие ускорения, устойчивостью самолета при
больших углах атаки и располагаемым отношением тяги к силе лобового
сопротивления самолета.
В настоящее время автором статьи совместно с профессором Чи¬
кала (Туринский политехнический институт, Италия) решается ми¬
нимальная проблема при более общих допущениях. Предваритель¬
ный анализ [14] указывает, что если уравнение движения по нормали
к кривой полета записать как Y—Mg=0, то все решения, указанные
в табл. 1, остаются формально правильными при условии подстанов¬
ки Q вместо Qo в аналитических выражениях для кривых 1М, MN и
N2. Если же уравнение движения по нормали к траектории полети
применено в его точной форме (3), то Эйлеровекая траектория опре¬
деляется системой из шести нелинейных дифференциальных урав-
106
^еший, интегрируемых обычно лишь приближенными методами. Ре¬
зультаты подобного исследования будут сообщены в скором
будущем.
Приложение А
ДОКАЗАТЕЛЬСТВО МИНИМАЛЬНОГО ХАРАКТЕРА КРИВОЙ 1MN2
I. Введение
Результаты, приведенные в табл. 1 (см. стр. 101) и на фиг. 42—
44, могут быть доказаны двумя путями: а) посредством косвенных
вариационных методов [16], т. е. формулировкой минимальной про¬
блемы, как проблемы типа Майера, и решением ее при помощи урав¬
нений Эйлера и неопределенных множителей Лагранжа;-б) посред¬
ством теоремы Грина с учетом особых свойств функции
, , v dlIr дФ / л 1 \
ю(®, /г) = - —. (А-1)
до oh
где Ф и х¥ определены уравнениями (8) и (9).
Методы «а» и «б» дают идентичные результаты. Второй метод,
применялся автором статьи в работах [1] и [4] для случая самолета,
масса которого постоянна.
Теорема Грина ведет к прямому доказательству минимальной
природы траектории 1MN2, и ее применение бывает особенно удоб¬
ным в случаях рассмотрения класса задач по отысканию кривых
внутри некоторой области, ограниченной двумя плоскостями, как это
имело место в рассмотренной выше задаче, где h1<h<fi2.
II. Свойства функции со(vf h)
Вследствие допущения Q = Qo и имея в виду зависимости
= VJ-2 А /Qv ~ Pv N (Д-2)
dv dv\ g ) 4 ’
£_,.± (Q-P), <A"3)
Уравнение (А-1) можно представить в виде
, ,v ф'2 Г «2 д {Р — Q0) , д п .1
А) = — ——+ — (Q0v — Pv) . (А-4)
g L g dh dv J
Представляет особый интерес определить геометрические места
точек плоскости (v, h), где со=0. Такие геометрические места точек
определяются уравнением
J-(Q0v-Pv) +^Яу(?о), = а (А.5)
dv g dh
Уравнение (А-5) в общем допускает более чем одно решение
v{ti) в зависимости от вида функции лобового сопротивления
с*о = /(М). Решение, соответствующее малой скорости, обозна¬
107
чается здесь V\(ti). Последующие решения (если они существуют)
обозначаются vu (Л); vni (Л) и т. д. При этом v, (Л) < vn (h) < vm (м
и т. д.
Плоскость (V, h) поэтому МОЖц0
разделить на следующие области:
А — область, ограниченную .щ.
ниями о = 0 и Vi(h);
0 / @ В — область между г», (А) и
ю<о / / и»о г>п(Л):
/ / А' — область между 'Оц(^) и
(Л);
В'— область между vm (/г)
и
ц1У (Л) и т. д.
(фиг. 47).
Численный анализ показывает,
"р" что функция со отрицательна в рано-
Л ~ не Л, положительна в районе В,
Фиг. 47. Оптимальное измене- »л/
ние скорости для случая I опять отрицательна в районе Л и
(ht<h<h2). положительна в районе В\
III. Допустимые перемещения
Рассмотрим самолет, положение которого в момент времени t
задается координатами (v, h), и допустим, что P>Qo, т. е. рассмот¬
рим случай полета с набором высоты.
К моменту времени t^ = t + dt самолет может достигнуть нового
положения полета, определяемого
координатами (v*, к*). Не все пере¬
мещения РР* возможны физически.
Из уравнения движения по каса¬
тельной к траектории полета
dh v - (А-6)
dv
(P-Qo)
М sin 0
- g
Фиг. 48. Допустимые переме¬
щения в плоскости (v, h).
видно, что для данных величин h, v
и М производная dhjdv является
функцией sin 0. Вследствие этого все
возможные перемещения РР* при¬
надлежат району С, ограниченному
двумя предельными перемещениями PF и РУ, соответствующими
sin 0 =!+ 1 и sin 0 =■—1 (фиг. 48).
Если ищутся реальные решения, то в любой точке траектории
полета должно удовлетворяться неравенство —l<sin0<l. Если-
кроме того, на траекторию полета наложить ограничение hi<h<hb
то необходимо в точках 1 и 2 рассмотреть также неравенство
0<sin 0 <1.
108
IV. Доказательство минимума
Оптимальные зависимости между скоростью и высотой 1MN2
приведены в табл. 1 для двенадцати возможных случаев полета.
Здесь дается доказательство минимума для одного из этих двенад¬
цати случаев. Техника исследования одиннадцати других случаев
аналогична и должна быть основана на соображениях, изложенных
в разд. II и III, и на применении теоремы Грина.
Предложенная здесь иллюстрация относится к первому случаю
(hi<h<h2) у т. е. к разгону самолета с ракетным двигателем и набо¬
ру высоты от малой скорости и малой высоты к большой скорости и
большой высоте. Кроме того, заметим, что здесь рассматриваются
внутренние траектории по отношению к областям, обозначенным А
и В.
Оптимальная траектория состоит из трех кривых: начального
участка 1М (прямая h = h1)1 центральной кривой MN (кривая со=0)
и конечного участка N2 (прямая h = h2). Можно показать, что при
сравнении специальной траектории 1MN2 с произвольной, но физи¬
чески возможной траекторией 1К2 имеет место следующее неравен¬
ство (ем. фиг. 48):
(At)lK2— (At)iMN2 'I> 0. (А-7)
Так как время At является монотонно возрастающей функцией
интеграла I, то из этого следует, что неравенство (А-7) эквивалентно
другому:
д/= j (Ф®' + Ф)<*Л — j (Фг>' + !Г)<й>0» (А-8)
1К2 1MN2
т. е,
Д/=* ф (d>dv + Wdh)>0. (А-9)
1K2NKM1
Для доказательства неравенства (А-9) разобьем этот криволи¬
нейный интеграл на два криволинейных интеграла по контурам
K2NK и К1МК:
д/= (j5 (Ocfo + 'Frf/z)- (j) (Ф dv + '¥dh). (А-10)
K2NK К1МК
Применяя теорему Грина, превращаем криволинейные интегралы
® Два двойных интеграла по площадям 5Л и SB, охватываемым кон¬
турами К1МК и K2NK:
<А‘П)
SB SA
т. е.
д/= f ш dv dh — j ^ to dv dh. (A-12)
109
Так как функция со положительна в области В и отрицательна в
области А (разд. II настоящего приложения), то из (А-12) вытекает,
что
что и доказывает неравенство (А-9) и, следовательно, минимальный
характер кривой 1MN2.
Этот же метод может быть легко применен к другим случаям дви¬
жения. Например, если ограничение h1<h<h2 снять, то оптимальная
программа движения изменится в том смысле, что горизонтальные
участки 1М и N2 превратятся в две траектории пикирования. Подоб¬
ный случай рассмотрен в работе [1], где, как и выше, применена тео¬
рема Грина с учетом соображений, изложенных в разд. III настояще¬
го приложения и касающихся возможных перемещений самолета в
плоскости (v, h).
РАЗВИТИЕ АНАЛИЗА, СВЯЗАННОГО С УРАВНЕНИЕМ (6)
После подстановки выражений (8) и (9) в уравнение проекций
сил на касательную к траектории полета (2) можно получить
Отсюда получаем зависимость между скороподъемностью, ско¬
ростью и углом наклона траектории dhldt=v sin 0 и, следовательно,
Если уравнение (В-2) проинтегрировать с учетом уравнения (4),
то получим следующий результат:
Необходимо отметить, что интеграл (В-4) зависит от характера
движения, т. е. от трех функций v(h)\ 0(/i); t(h). В случае, когда
условие (3) может быть аппроксимировано выражением Y=mgfI не
зависит от 0 (h). Для другого частного случая Q = Qo I зависит лишь
от распределения скорости v (h).
А />0,
(А-13)
Приложение В
(В-1)
(В-2)
1 inmQ-~
2 Мт т0 — tx 2дИх
(В-3)
где
(В-4)
л.
Из уравнений (4) и (В-3) следует
(В-5)
110
Приложение С
СВЕРХЗВУКОВОЙ ПОДЪЕМ
Приложение А содержит доказательство минимального характера
траектории 1MN2 при различных ограничениях, наиболее важным
из которых является то, что исследование относится к кривым, внут¬
ренним по отношению к областям А и В.
Если это ограничение снять, то доказательство, приведенное в
приложении А, теряет силу. Наиболее удобным способом решения
проблемы минимума является способ, основанный на применении
непрямых методов вариационного исчисления, как это сделано в
работах [14], [15] и [16]. В работе [16] показано, что если на геометрию
траектории полета не наложены ограничения, решение определяется
уравнением типа со cos 0=0, которое представляет собой произве¬
дение 1 уравнения вертикальной траектории cos 9 =0 и кривой поле¬
та е набором высоты, описываемой уравнением со=0.
Если уравнение со = 0 допускает одно единственное решение v1 (h),.
то оптимальные траектории являются кривыми типа, показанного
на фиг. 42, 43 и 4-4 настоящей работы. Если же уравнение со=0 до¬
пускает различные решения V\(h)\ vu{h)\ Vm (h) . . . ., положение
изменяется: V\(h) есть кривая минимального времени, vn(h)—кри¬
вая максимального времени, vU\{h)—другая кривая минимального
времени и т. д.
Численный анализ показывает, что в общем случае vx(h) являет¬
ся кривой дозвукового—звукового полета, тогда как vU\(h) соответ¬
ствует кривой сверхзвукового полета. Довольно часто скороподъем¬
ности вдоль Vm (h) отрицательны. Для больших значений параметра
P/phSKр, однако, скороподъемности вдоль vm(h) могут стать поло¬
жительными, так что сверхзвуковой подъем физически возможен.
Необходимо также определить, правильно ли будет совершать
набор высоты по закону vl{h) или по закону ^Ш(А), или же
набирать высоту по комбинированной кривой, состоящей из
участка полета по ^i(A) и участка полета по %i(A).
В случае, когда третья альтернатива представляет технический
интерес, необходимо установить высоту, по достижении которой це¬
лесообразно прекратить дозвуковой подъем по Vi(h) и перейти на
пикирование с переходом на сверхзвуковые скорости.
Для уяснения изложенной проблемы автором проведены предвари¬
тельные вычисления для самолета, характеризующегося относитель¬
ной тягой Р/5кр = 240 кг/ж2, и исследован диапазон высот от уровня
моря и до h= 18 ООО м при следующих граничных условиях: Mi=0,5;
hi = 0 м\ М2=2,8; /12=18 000 м.
Результаты этих исследований указывают, что дозвуковой набор
высоты по кривой Vi (h) имеет преимущества по сравнению со сверх¬
звуковым набором высоты по кривой vU\{h). Автор, однако, не скло¬
нен выводить общее заключение из отдельных частных расчетов и
полагает, что изложенный вопрос требует дальнейших исследований.
1 Приведенный результат можно также получить путем видоизменения до¬
казательства, изложенного в приложении А, основанного на теореме Грина.
111
ЛИТЕРАТУРА
1. Миеле А., Задачи о минимальной продолжительности нестационарного
полета самолета.
Miele A., Problemi di Mimino Tempo nel Volo Non-Stazionario degli Aero-
plani, «Atti della Accademia delle Scienze di Torino. Classe di Scienze, Fisiche,
Matematiche e Naturali», 1950—1951, vol. 85, pp. 41—52.
2. JI а ш К., Обзор проблемы выбора программы подъема скоростных само¬
летов с предложением новой программы.
Lush К., A Review of the Problem of Choosing a Climb Technique with
Proposals for a New Climb Technique for High Performance Aircraft, «Aeronau¬
tical Research Council Rep. Mem», 2557, 1951.
3. Кайзер, Набор высоты реактивным самолетом, ч. I «Скорость на траек¬
тории оптимального подъема».
Kaiser, The Climb of Jet Propelled Aircraft P. I., „Speed Along the Path
in Optimum Climb“, Ministry of Supply, RTP/T1B Translation GDC (15) 148T
(April, 1944).
4. Миеле А., Общие решения задач по определению оптимальных режи¬
мов нестационарного полета.
Miele A., Soluzioni Generali di Problemi di Ottimo in Volo Non-Stazio¬
nario, «L’Aerotecnica», 1952, vol. 32, No. 3, pp. 135—142.
5. M и e л e А, Оптимальная траектория полета самолетов с ТРД.
Miele A., Traiettorie Ottime di Volo degli Aeroplani Azionati da Turbo-
reattori, «L’Aerotecnica», 1952, vol. 32, No. 4, pp. 206—219.
6. К e л л и JI., Оптимальная программа подъема реактивного самолета.
Kelly L., Optimum Climb Technique for a Jet-Propelled Aircraft, The Col¬
lege of Aeronautics, Cranfield, Report No. 57, April, 1952.
7. Рутов с кий E., Энергетический подход к общей проблеме летных ха
рактеристик самолета.
Rutowski Е., Energy Approach to the General Aircraft Performance Pro¬
blem, „Journal of the Aeronautical Sciences", 1954, vol. 21, March, pp. 187—195.
8. Гарбелл М., Оптимальная программа подъема скоростных самолетов.
Gar be 11 М., Optimum Climbing Techniques for High-Performance Aircraft
«Garbell Aeronautical Series», 1953, No. 8.
9. M и e л e А., О неустановившемся режиме подъема самолета с ТРД.
Miele A., On the Non-Steady Climb of Turbo-Jet Aircraft, «Journal oi
the Aeronautical Sciences», 1954, vol. 21, November, pp. 781—783.
10. Липпи.ш А., Механика полета самолета с ТРД.
Lippi sch A., Flugmechanische Beziehungen der Flugzeuge rnit Strah 1 -
antrieb, Headquarters Air Material Command, Wright Field, Dayton, Ohio. Trans¬
lation Report N F-TS-685-RE, October, 1946.
11. Бэркли, Россер Дж., Ньютон Р. Р. и Г p о с с Г. Л., Математи¬
ческая теория полета ракеты.
Barkley, Rosser Y., Newton R. R. and Gross G. L., Mathematical
Theory of the Rocket Flight, McGraw-Hill Book Company, Inc., New York, 1947.
12. Г антмахер Ф. P. и Левин Л. М., Уравнения движения ракеты.
Gantmacher F. R. and Levin L. М., Equations of Motion of a Rocket.
NACA TM 1255, 1950.
13. Перки нз К. Д. и X е й д ж Р. Е., Летные данные, устойчивость и
управление самолета.
Perkins ::С. D. and Hage R. Е., Aeroplane Performans, Stability and
Control, John Wiley and Sons, Inc. New York, 1949.
14. Ч и к а л а П. и Миеле А., Брахистохронные маневры самолета.
Cicala P. and М i е 1 е A., Evoluzioni Brachistocrone di un Aereo <Atn
della Accademia delle Scienze di Torino, Classe di Scienze Fisiche, Matematiche
e Naturali», 1954—1955, vol. 89.
15. Чикала П. и M и е л е А., Брахистохронный маневр самолета с посто¬
янной массой в вертикальной плоскости.
112
Cicala P. and M i e 1 e A., Brachistocronic Manoeuvres of a Constant Mass
Aircraft in a Vertical Plane, «Journal of the Aeronautical Sciences», 1955, vol. 22,
дрпЬ pp. 286—288.
16. Чикала П. и Ми еле А., Брахистохронный маневр самолета с пере¬
менной массой в вертикальной плоскости.
Cicala P. and М i е 1 е A,, Brachistocronic Manoeuvres of a Variable Mass
дщгаП in a Vertical Plane, «Journal of the Aeronautical Sciences». 1955, vol. 22,
Mo. PP- 577—578.
17. Доммаш Д. О., Аналитическое развитие уравнений оптимальной
траектории полета.
Dommasch D. О., Analytic Development of the Optimum Flight Path
Equations, Princeton University, Initial Report, 1955, March 16.
П. ЧИКАЛА и /1. МИЕЛЕ
БРАХИСТОХРОННЫЕ МАНЕВРЫ САМОЛЕТА
С ПЕРЕМЕННОЙ МАССОЙ В ВЕРТИКАЛЬНОЙ
ПЛОСКОСТИ 1
ВВЕДЕНИЕ
В предыдущей работе авторов [4] была рассмотрена задача бра-
хиетохронного маневра самолета с постоянной массой и силовой
установкой, тяга которой зависит только от скорости и высоты.
В настоящей статье авторы распространяют свои предыдущие
выводы на случай самолета, масса которого M=M(t) является про¬
извольной функцией времени, а тяга P=P(h, v, t) в общем случае
есть функция скорости, высоты и времени.
Здесь исследуется более общий случай задачи, включающий в
себя как определение горизонтального пути, проходимого самолетом,
так и определение характеристик движения самолета при перехвате.
Кроме того, ускорение силы тяжести принимается зависящим от
высоты g=g{h), что позволит применить данную теорию к летатель¬
ным аппаратам, предназначенным для полета в верхних слоях атмо¬
сферы.
При решении задачи принимаются следующие допущения:
1) угол между векторами скорости и силы тяги считается пре¬
небрежимо малым;
2) полет самолета предполагается плоским и происходящим в вер¬
тикальной плоскости;
3) аэродинамическое запаздывание не учитывается, т. е. подъ¬
емная сила и сила лобового сопротивления вычисляются как для
Установившегося полета. Последнее допущение эквивалентно допу¬
щению, что сила сопротивления является функцией вида Q = Q (/?,
Щ У), где, однако, учитывается влияние чисел М и Re на аэродина¬
мические характеристики.
1 Placido Cicala and Angelo M i e 1 e, Brachistocronic Maneuvers
Щ a Variable Mass Aircraft in a Vertical Plane, «Journal of the Aeronautical
Sciences», 1955, vol. 22, No. 8, pp. 577 — 578.
8 394
113
Выражение для составляющих скорости (х, К) и уравнения дви¬
жения по касательной и по нормали записываются в следующем виде:
Ji х — v cos 0 = 0; (1)
J2 = h — v sin 9 = 0; (2)
■/3 = t>4-gsin6 + Q~P =0; (Й)
Y—M (g-cos0 + ^6) = O, (4)
где x — горизонтальная дальность;
0 — угол наклона траектории к горизонту;
знак (*) —относится к производной (полной) по времени.
НЕОБХОДИМОЕ УСЛОВИЕ СУЩЕСТВОВАНИЯ ЭКСТРЕМУМА
Задача определения траектории с минимальным полетным време¬
нем, начинающейся в точке с начальными условиями 1 и заканчи¬
вающейся в точке с конечными условиями 2, в общем случае пред¬
ставляет собой вариационную задачу Майера [6]. Очевидно, так а и
траектория будет определяться системой уравнений (1)—(4)1 при
условии, что полетное время будет минимальным.
Принимая t в качестве независимой переменной, рассматривае¬
мую брахистохронную задачу можно сформулировать следующий
образом: «определить четыре неизвестные функции v(t)y 0(/), h(i\
и x(t), которые дают интегралу j dt экстремальное значение при
1
вспомогательных условиях (1), (2), (3)».
Вводя три множителя Лагранжа М(0> и А,3(0> можно по¬
лучить для определения оптимальной траектории следующие необ¬
ходимые условия 2:
хз + хз Pv~^Qv — W + х2sin6 + Х1 cos0=0; (5)
— Q.3vQy) + ^3g(Qr sin 0 —cos 0) + ® (X2cos 0 —Xt sin 0) = O; (6)
dt
Ч + Хз {РЦ77~ ®— — хзS' (sin 0 + Qy cos 0) = 0; (7)
M
X, = 0, (8)
1 Если подъемную силу Y исключить из уравнения (3), используя уравнение
(4), то получим выражение типа /3(/, h, 6 , 0, v, v)=Q.
2 Уравнения с (5) по (8) получаются как выражение Эйлера для
2 / 3 V
j (tlh Л-j dt.
114
Уравнения (1) — (8) образуют систему дифференциальных урав¬
нений, общее решение которых включает восемь постоянных интег¬
рирования, определяемых из граничных условий задачи.
Необходимо отметить, что уравнения (5) — (8) являются однород¬
ными относительно К\, Х2, Как следствие этого, один из этих трех
множителей может быть принят произвольной величиной (но не рав¬
ной нулю), например Л2=1, в связи с тем, что это условие никак не
повлияет на все остальные неизвестные функции h(t), v(t), x(t) и
g(^). Дополнительно к указанному свободному условию на траекто¬
рию полета могут быть наложены семь условий, например началь¬
ные значения для h, t, v, 0 и х и конечные значения для h, v, 0, х.
Следует иметь в виду следующие важные замечания:
1. Приведенная выше система дифференциальных уравнений при¬
менима также для нахождения экстремумов и в других аналогичных
задачах, таких как отыскание условий, обеспечивающих максималь¬
ную дальность, максимальную высоту или максимальную скорость.
В каждом случае должны быть определены пределы изменения
остальных переменных и их значения в крайних точках.
2. С помощью обычных граничных условий (условий трансвер¬
сальности) приведенные выше уравнения могут быть применены
для решения задачи перехвата, т. е. для определения брахистохрон-
ной траектории самолета Л, который должен настигнуть самолет В,
совершающий произвольный маневр xB(t), hB(t) в той же верти¬
кальной плоскости, что и самолет А. Кроме того, с помощью этих
уравнений могут быть исследованы также задачи с некоторыми
дополнительными условиями, например очень важный случай, ког¬
да h>hi, т. е. когда маневр самолета ограничен нижней высотой —
поверхностью земли.
3. Уравнение (1) может быть заменено эквивалентными изопери-
метри'ческими условиями путем задания определенного значения ин-
2
теграла /= j v cos 0 dt. В этом случае решение системы дифферен-
1
циальных уравнений будет зависеть ог семи постоянных интегриро¬
вания. Например, в точке 1 могут быть заданы (h, t, vy 0), а точке 2—
{h, vf 9 ) дополнительно к свободным условиям и значению I. Однако
Уравнению (1) авторы отдали предпочтение в основном потому, что
в такой форме более удобно исследовать реальную вариационную
задачу в пределах общей схемы решения Майера.
ЧАСТНЫЕ СЛУЧАИ
Интегрирование приведенной выше системы дифференциальных
Уравнений для большинства общих случаев должно производиться с
помощью приближенных методов. Для некоторых частных случаев
эта задача может быть упрощена.
А. Неограниченная горизонтальная дальность
Если на величины Х\ и л:2 не наложены никакие условия, то урав¬
нения (1) и (8) пропадают.
8*
115
Новая форма системы уравнений Эйлера (5), (6), (7) и (8) по¬
лучается при подстановке в исходные уравнения значения 7i = 0.
Число постоянных интегрирования уменьшается до шести при
одном свободном условии в произвольной точке траектории .полета.
В точке 1 могут быть заданы к, v, 0, t, а в точке 2—h, v, 0. В случае
исключения множителей Лагранжа число уравнений системы
уменьшится до 5, причем свободное условие исчезает.
Б. Постоянная масса, тяга не зависит от времени
Гипотеза М = 0 и dP/dt = 0 приводит систему дифференциальной
уравнений (5), (6), (7) и (8) к первому интегралу
~Ь 0 у п 0) Ч- (7^2 sin 0 —|— X-1 cos b) = О. (9)
Путем замены одного из указанных уравнений уравнением (9)
получаем новую систему уравнений, однородных относительно л;,,
Аз и С. Отсюда следует, что альтернативной формой свободного усло¬
вия может быть С= 1.
Если исключить время путем использования уравнения (2), то
число постоянных интегрирования системы уменьшится до семи.
Шесть других условий получаются путем задания значения для (//,
v, 0, х) в точках 1 и 2.
Для частного случая Р = 0=0 число дифференциальных уравне¬
ний системы уменьшается до трех путем исключения .переменной
времени и множителей Лагранжа, и решение сводится к хороню
известной брахистохронной траектории в гравитационном поле, т. о.
в циклоиде.
В. Неограниченная горизонтальная дальность,
постоянная масса, тяга не зависит от времени
При Х[=0 М = 0 и dP/dt = 0 исключение переменной времени л
множителей Лагранжа сводит число уравнений системы до четырех
Эта задача рассмотрена авторами в работе [4].
Г. Неограниченная горизонтальная дальность,
центробежные силы не принимаются во внимание
При У = Mg cos 0 уравнения Эйлера (5) и (6) изменяются, по¬
скольку члены 73ОГ 0 и d(KzQY v) jclt исчезают. Кроме того, при
Я1 = 0 исключение множителей Лагранжа Хг и из уравнений (5),
(6) и (7) приводит к следующему результату:
Gu + (QP — Pv) gu + Ggu2 sin 0 + Qh — Ph + MQy = 0, (10)
COS 0
где
u — (Qy tg 0— 1)A; (П)
G—вес самолета.
116
Уравнения (2), (3) и (10) образуют систему дифференциальных
уравнений, для которых могут быть заданы значения (h, v, t) в точ¬
ке 1 и (h, v) в точке 2. Следует отметить, что для параболической
поляры с коэффициентами, зависящими от чисел М и Re, найдено
дополнительное к уравнению (10) решение cos 0=0.
Д. Неограниченная горизонтальная дальность.
Требуемая подъемная сила не зависит от центростремительного
ускорения и кривизны траектории
При Л.1 = 0, Y=Mg уравнения (5), (6) и (7) приводят к решению,
которое составляется из дуг вида
cos 0=0 (12)
я дуг вида
P—Q + {Qk—Ph) — + (Pv~ Qv) * + ^Qy = о. (13)
g g
Уравнение (13) можно переписать в следующем виде:
±(Pv-Qv)-^-^-(P-Q)=0. (14)
dv g dh
Последнее выражение является зависимостью вида f(h, v, t)= 0.
Для частного случая М = 0, dP/dt = 0 уравнение (14) превращается
в конечное соотношение между h и v (ом. работы [1, 2, 4]).
Е. Неограниченная горизонтальная дальность,
индуктивное сопротивление не принимается во внимание
При ^i=0, Qr = 0 уравнения (12), (13) и (14) упрощаются
(Q = Qo). Для частного случая dP/dt=0 уравнение (14) сводится к
конечному соотношению, как показано в работе одного из
авторов [5].
ЛИТЕРАТУРА
1. Ми еле А., Задачи о минимальной продолжительности нестационарного
полета самолета.
Miele A., Problemi di Minimo Tempo nel Volo Non-Stazionario degli
Aeroplani, «Atti della Accademia delle Scienze di Torino. Classe di Scienze
Matematiche, Fisiche e Naturali», 1950—1951, vol. 85, pp. 41 —52.
2. M и e л e А., Общие решения задач по определению оптимальных режи¬
мов нестационарного полета.
Miele A., Soluzioni Generali di Problemi di Ottimo in Volo Non-Stazio¬
nario, «L/ Aerotecnica», 1952, vol. 32, No. 3, pp. 135—142.
3. Чикала П. и M и e л e А., Брахистохронные маневры самолета.
Cicala P. and Miele A., Hvoluzioni Brachistocrone di un Aereo, «Atti
della Accademia delle Scienze di Torino. Classe di Scienze Matematiche, Fisiche
e Naturali».
4. Ч и к а л а П. и M и e л e А., Брахистохронные маневры самолета постоян¬
ной массы в вертикальной плоскости.
Cicala P. and Miele A., Brachistocronic Manoeuvres of a Constant Mass,
Aircraft in a Vertical Plane, Readers Forum, «Journal of the Aeronautical Sciences»,
1955, vol. 22, No. 4.
117
5. Миеле А., Оптимальная программа подъема самолета с ракетным двщ
ггтелем.
Miele A., Optimum Climbing Technique for a Rocket-Powered Aircraft, «Jet
Propulsion*, 1955, vol. 25, No. 8, pp. 385—391.
6. Паскаль E., Справочник по высшему анализу.
Pascal E., Repertorium der Hoheren Analysis, 1927, vol. 1, B. G. Teubner,
Leipzig.
Я. ЧИКАЛА и А. МИЕЛЕ
ОБОБЩЕННАЯ ТЕОРИЯ ОПТИМАЛЬНОГО
ПРОГРАММИРОВАНИЯ ТЯГИ ПРИ ГОРИЗОНТАЛЬНОМ
ПОЛЕТЕ САМОЛЕТА С РАКЕТНЫМ ДВИГАТЕЛЕМ1
Принятые обозначения
я— скорость звука
с*/—коэффициент индуктивного сопротивления
коэффициент подъемной силы
су £— коэффициент подъемной силы, соответствующий максимальному кач
ству
су шах'— максимальный коэффициент подъемной силы
Q —сила лобового сопротивления
Qy— частная производная силы лобового сопротивления по подъемной силе.
вычисленная при постоянных высоте и скорости полета
Qv—частная производная силы лобового сопротивления по скорости, вычис¬
ленная при полете на постоянной высоте при постоянной подъемной силе
g— ускорение силы тяжести
h— высота полета
k=cJCilc2y —отношение коэффициента индуктивного сопротивления к квадратv
коэффициента подъемной силы
У—подъемная сила
М—текущее значение массы самолета
V
M*=MeVr— приведенная масса
М - —
а
Ра— атмосферное давление
р— характеристика
Re— число Рейнольдса
5—характерная поверхность
t— время
Р— тяга
v— абсолютная скорость самолета как твердого тела, т. е. скорость, отне¬
сенная к системе координат, неподвижной относительно Земли
1 P. Cicala and A. Miele, Generalized Theory of the Optimum Thrust Program¬
ming for the Level Flight of a Rocket-Powered Aircraft, „Jet Propulsion", 1956, vol.
26, No. 6, June, pp. 443—473.
118
Гг — эквивалентная относительная скорость истечения газов, т. е. скорость,
отнесенная к системе координат, жестко связанной с конструкцией
самолета (эффективная скорость истечения)
^кр— критическая скорость
G— текущее значение веса самолета
X— горизонтальная дальность
—М— текущее значение расхода топлива
отношение удельной теплоемкости при постоянном давлении к удельной
теплоемкости при постоянном объеме (для воздуха %=1,4)
X— множитель Лагранжа
v
= -т~—отношение скорости полета к эффективной скорости истечении газов
»'г
И-— множитель Лагранжа
М
и. = — безразмерная масса
Мг
м*
р.* = 77"— безразмерная приведенная масса
Мт
р— плотность воздуха
Индексы
к— конечное состояние
/— начальное состояние, также переменный номер
г— исходное состояние
Значки над буквенными обозначениями
* (точка)— дифференцирование по времени;
/ (штрих)—дифференцирование по массе.
ВВЕДЕНИЕ
Расчет оптимального программирования расхода топлива -при по¬
лете самолета или снаряда с ракетным двигателем в последние годы
привлекает внимание многих исследователей. Частный случай вер¬
тикальной траектории был исследован Гамелем [1] и позже—Тзяном
и Эвансом [2]. Другой случай—случай горизонтальной траектории
был исследован Гиббсом [3].
Задача, решением которой занимался Гиббс, может быть сформу¬
лирована следующим образом: «требуется определить зависимость
между массой и скоростью летательного аппарата, при которой по¬
лучается максимальная дальность при горизонтальном полете по
прямой при заданных удельном расходе топлива и конечной скоро¬
сти». При этом рассматривалась поляра самолета в виде параболы
с постоянными коэффициентами; эквивалентная скорость истечения
газов Vr считалась не зависящей от расхода топлива (р = —М).
119
По теории Гиббса сформулированная выше вариационная задача
сводится к отысканию экстремалей интеграла вида
где М — текущее значение массы самолета и и — скорость -поступа¬
тельного движения самолета.
Так как подынтегральное выражение является линейной функцией
v', то соответствующее интегралу (1) решение Эйлера и-меет нулевой
порядок. Иными словами, решение Эйлера вырождается в уравнение
в конечной форме
дБ q Л)\
до дМ ’ W
которое в общем случае не удовлетворяет граничным условиям за¬
дачи с заданными начальными и конечными значениями (заданы М;,
viy Мк, vk). Более того, в данном особом случае принятые в вариа¬
ционном исчислении классические критерии достаточности условий
(например, критерий Лежандра) не доказывают наличия максимума
при изменении массы и скорости в соответствии с решением Эйлера,
даже в простейшем случае граничных условий, удовлетворяющих
уравнению (2).
Зная об этих трудностях, Гиббс постулировал решение с наруше¬
нием непрерывности, в общем случае состоящее из системы импуль-
полета в соответствии с уравнением (2). Интуитивно найденное та¬
ким образом правильное решение подтверждалось физическими со¬
ображениями [3], причем доказательство носило характер исследова¬
ния этапов полета без последовательного применения одной какой-
либо техники исследования.
В настоящее время можно исследовать задачу в общем виде,
пользуясь математическими методами, разработанными авторами
настоящей статьи в работах [7] и [4, 5].
В работе [7] приводятся общие уравнения и методы расчета опти¬
мального закона изменения тяги двигателя самолета.
В работах [4, 5] разработан, а в работах [6, 14] продемонстри¬
рован на конкретных примерах метод решения широкого класса
важных вариационных задач динамики полета. Этот метод расчета
удобно применять во всех случаях, когда требуется отыскать макси¬
мум или минимум интеграла вида (1) при наличии ряда неравенств,
ограничивающих изменение переменных под знаком интеграла и их
производных.
Так, например, условие, что самолет не заправляется топливом
в полете, формулируется в виде неравенства
лг
к
(!)
ЛИ¬
СОВ тяги (М = —оо), участков пассивного полета (М = 0) и режимов,
(31
из которого следует
(41
120
ПРЕДМЕТ ИССЛЕДОВАНИЯ
В настоящей статье ‘излагаются две теории обобщенного расчета
оптимального .закона расходования топлива при горизонтальном
полете самолета.
Первая теория основана на теореме Грина [4, 5] и на специальных
свойствах функции со [уравнение (13)] и приводит к простому и ло¬
гичному доказательству необходимых и достаточных условий суще¬
ствования максимума интеграла. Как и в работе Гиббса [3], принято
постоянное значение эффективной скорости истечения Vr.
Задача решена в более общем виде, в частности: а) устранены
все ограничения в отношении формы поляры самолета; б) учтено
ограничение максимального расхода топлива (Ртах); с) учтено ко¬
нечное значение максимального коэффициента подъемной силы
(С// max) •
Как показано в части I настоящей статьи, условие «а» равносиль¬
но учету лобового сопротивления как функции вида Q = Q(v, М).
Условие «б» сводится к замене неравенства (3) другим неравенством:
0<Р ртал-, (5)
где Pun* — конечное значение максимального расхода топлива. Усло¬
вие «в» эквивалентно исключению из рассмотрения всех точек в пло¬
скости (v, М) (см. фиг. 49 и 50), принадлежащих к запрещенной
области, ограниченной осью М и кривой по уравнению с/у = с,/тах.
Вторая теория основана на уравнениях Эйлера—Лагранжа [7]
для вариационной задачи, сформулированной как задача типа зада¬
чи Майера. В порядке дальнейшего обобщения теории рассматри¬
вается произвольная однозначная зависимость тяги от расхода то¬
плива. Особое внимание уделяется зависимости Р (р) в виде лома¬
ной линии, позволяющей отобразить с любой степенью точности дей¬
ствительную характеристику двигателя. При решении рассматри¬
ваемой задачи используется понятие характеристики, введенное ра¬
нее одним из авторов [7]. Использование этой величины, сходной с
множителями Лагранжа, оказывается очень полезным при опреде¬
лении оптимального закона расхода топлива в случае разрывных ре¬
шений Эйлера.
Часть I
А. Миеле
РЕШЕНИЕ С ИСПОЛЬЗОВАНИЕМ ТЕОРЕМЫ ГРИНА
ДЛЯ СЛУЧАЯ ЛИНЕЙНОЙ ХАРАКТЕРИСТИКИ ТЯГИ
В настоящем разделе статьи рассматривается приложение метода
решения, изложенного в работах [4, 5]. Рассматривается прямоли¬
нейный полет на постоянной высоте, и в дополнение к перечисленным
выше допущениям принимается, что аэродинамическое запаздывание
не имеет места, т. е. что значения подъемной силы У и лобового
сопротивления Q могут быть вычислены, как для установившегося
режима полета. Самолет с ракетным двигателем упрощенно рассмат¬
ривается как точка переменной массы.
121
1.1. ОСНОВНЫЕ УРАВНЕНИЯ
Уравнения движения самолета с ракетным двигателем при гори¬
зонтальном прямолинейном полете имеют вид [15, 16]:
Q+М (Vr-\-Mv') =0; (6)
Y—Mg = 0, (7)
где g—ускорение силы тяжести; M = dM/dt\ v' = dvjdM и Vr—эффек¬
тивная скорость истечения газов из сопла ракетного двигателя,
принимаемая в настоящем исследовании постоянной.
Если пренебречь аэродинамическим запаздыванием, то силу ло¬
бового сопротивления можно рассматривать как функцию высоты,
скорости полета и подъемной силы Q(h, v, Y) даже при учете влия¬
ния вязкости и сжимаемости воздуха. Принимая во внимание усло¬
вие полета на постоянной высоте и исключив подъемную силу с по¬
мощью уравнения (7), можно представить лобовое сопротивление в
виде функции только скорости и массы Q(v, М). После этого урав¬
нение (6) может быть переписано в виде
где
Ф = У?—=шф(М,ъ) (9)
Q (М, v) V ’ •
И
w= v). (10)
Q(M,v) V ' V ;
Расстояние, пролетаемое самолетом при горизонтальном полете,
определяется как интеграл вида
Л1К мк
X— - | jdM= J (Фъ' + У)с1М. (11)
Mj Mi
Задача заключается в отыскании специальной функции v = v(M),
при которой получается максимальное значение X при заданных
начальных и конечных условиях Miy viy МКу vRy причем класс иссле¬
дуемых зависимостей подчинен дополнительным условиям в виде
неравенств (4) и (5) и условию
М_ <_fS_
V2 ^ 2g
где Су max= f (М, Re). При заданной высоте полета cum&x=f(v).
^<±ГСуш ах, 02)
1.2. ДОПУСТИМЫЕ ПЕРЕМЕЩЕНИЯ
Рассмотрим самолет, условия полета которого в некоторый мо¬
мент времени t характеризуются значениями скорости и массы (о,
М), и примем, что это состояние самолета изображается точкой Р
122
{фиг. 49) на плоскости (v, М). По истечении промежутка времени
—t новое значение массы самолета будет новое
значение скорости v# =v-\-dv и_новый радиус-вектор самолета на
плоскости (v, М)—ОР*=ОР + РР*.
Класс допустимых перемещений
РР* определяется неравенством (5)
я ограничен двумя предельными
случаями [см. уравнение (8) и фиг.
49]: перемещением PC ((3 = 0), соот¬
ветствующим полету при неработаю-
щем двигателе, и перемещением PD
(Р=[3шах), соответствующим макси¬
мальному расходу топлива.
Перемещения типа РЕ физически
возможны, перемещения же типа PQ
физически невозможны, так как
масса самолета не мо_жет увеличи¬
ваться. Перемещение PG также фи¬
зически невозможно, так как сохра¬
нение постоянной массы самолета
соответствует нулевой тяге двигателя, и, значит, отрицательному
ускорению dvjdt. Таким образом линии (3 = 0 и |3 = |3тах разделяют пло¬
скость (v, М) на две области, связанные с точкой Р: область Н, в ко¬
торой может находиться самолет, совершающий горизонтальный по¬
лет, и запрещенную область L, в которую самолет не может попасть
в связи с физическими законами движения.
1.3. СВОЙСТВА ФУНКЦИИ со(и, М)
Рассмотрим теперь функцию переменных v и М, определяемую
уравнением
(13)
Воспользовавшись уравнениями (9) и (10), можно переписать
уравнение (13) в виде
(D = — !vVr— — f-^Л] . (14)
Q2 1 ;dv\vj дМ\М)\ К '
В частном случае параболической поляры, коэффициенты которой
зависят от чисел М и Re, т. е. в случае, когда аэродинамическое со¬
противление выражается формулой
Q = A (v, h)v2 + B (<!/, А)-^-, (15)
Уравнение (14) принимает вид
m==AVr^_i 1+_i_ + jlA±\-^X^L[s (i6)
Q2 \ Vr A dv J Q2i)2 \ Vr В dv J 4
Фиг. 49. Перемещения изобража¬
ющей точки самолета на плоско¬
сти (v, М).
123
Особый интерес представляет геометрическое место точек, в кото¬
рых о равно нулю (фиг. 50). Это геометрическое место в общем слу¬
чае определяется уравнением
д /Q\ Л/12 д / Q
-М2-
дМ
(17)
В частном случае поляры самолета, определяемой формулой (1;>)
уравнение геометрического места (со=0) имеет вид
M = v2
У
Г л^+^ + ^Ог)
/дВ
B(v + 3Vr)~vVr
V dv
(18)
В случае, когда коэффициенты параболической поляры не зави-
' сят ни от числа М, ни от числа Re,
указанное уравнение принимает
вид [3]
М
A i-f 1
~В х + 3
(19)
Дальнейшие исследования вы¬
полнены в предположении, что
уравнение (17) имеет единствен¬
ное решение, причем функция с»
принимает отрицательные значе¬
ния в области А, влево от кривой
со = 0, и положительные значения в
области В, вправо от этой кривой
(см. фиг. 50). Справедливость
этих допущений легко проверить в
частном случае параболической поляры с постоянными коэффициен¬
тами. Однако результаты исследований нетрудно распространить
также и на случай, когда уравнение со = 0 имеет более одного реше¬
ния v = v (М) (см. работу [6]).
Фиг. 50. Области на
(v, М).
плоскости
1.4. ЛЕММА I
Рассмотрим два допустимых перемещения изображающей точке
между точками С и D, соответствующими началу и концу полета, по
кривым CPD и CQD, лежащим в области А (со<0) и ограничиваю
щим площадь а. Тогда кривая CQD, при движении по которой огра¬
ничиваемая площадь а остается справа, соответствует большей даль¬
ности полета.
Это положение можно доказать, показав, что разность дальностей
AX=Xcqd-Xcpd= j' (Фv' + xY)dM—§ №v' + 'Y)dM (20)
CQD CPD
положительна.
124
Эта разность может быть -представлена в виде криволинейного
интеграла
A A'— (j) (Ф dv + 4'dM), (21)
CQDPC
который может быть затем преобразован в соответствии с теоремой
Грина в двойной интеграл по площади а:
^X=~$(^~'m)dvdM,= — \^mdvdM- (22)*
а а
Так как функция ю в области а отрицательна, то из формулы (22)
следует
Д А>0, (23)
что и доказывает сформулированную выше лемму.
1.5. ЛЕММА II
Рассмотрим две допустимые кривые GKH и GLH, лежащие в
области В (со>>0), соединяющие те же точки начала и конца полета
G и Н и ограничивающие площадь [3. Тогда кривая GKH, при пере¬
мещении вдоль которой ограничиваемая площадь (3 остается слева,
соответствует большей дальности полета.
Доказательство этой леммы не приводится, так как оно аналогич¬
но доказательству леммы I в предыдущем разделе.
1.6. ГРАНИЧНЫЕ УСЛОВИЯ
В зависимости от положения точек / и F относительно кривой
оз=0 (см. фиг. 50) могут иметь место граничные условия четырех
типов [4, 5, 6]. В соответствии с этим необходимо исследовать четыре
типа условий полета, перечисленные ниже в табл. 1.
Таблица 1
Случай полета
Область, в которой
находится точка /
Область, в которой
находится точка F
I
А
В
11
А
А
III
В
А
IV
В
В
* Знак «минус», появляющийся п-ри замене криволинейного интеграла (21)
Двойным интегралом (22), связан с тем, что обход по контуру CQDPC совер¬
шается по часовой стрелке.
125
1.7. ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ
Как следствие лемм I и II можно сформулировать следующее?
правило, определяющее геометрию экстремальной траектории на
плоскости (v, М): при перемещении вдоль идеальной оптимальной
траектории в области А необходимо стремиться к крайнему левому
расположению траектории, насколько это позволяют граничные ус¬
ловия задачи. В области В необходимо держаться возможно правее
Отсюда следует, что при расположении точек / и F на кривой
(о=0 оптимальная траектория совпадает с кривой со = 0.
со=0 М
со -О
Случай П
Случай Ш
Фиг. 51. Оптимальные траектории при различных типах граничных условий.
Если концевые точки I \\ F не лежат на кривой со = 0, то опти¬
мальная траектория имеет изломы и обычно состоит из трех отрез¬
ков: начального отрезка IM, среднего отрезка MN по уравнению
(о = 0 и последнего отрезка NF (табл. 2 и фиг. 51). Начальный отре¬
зок IN соответствует полету при максимальной тяге двигателя, если
точка I расположена в области А, или полету при неработающее
двигателе, если точка / находится в области В. Последний отре¬
зок NF соответствует полету при неработающем двигателе, если
точка F расположена в области А, или полету при максимальной тя¬
ге двигателя, если точка F находится в области В.
Таблица-2
Случай полета
Отрезок 1М
Отрезок MN
Отрезок NF
I
Р — Ртах
(0=0
Р = Ртах
II
Р = Ртах
СО —0
(3=0
III
Р=о
со=0
з=о
IV
Р=о
со—0
Р—Ртах
1.8. ДОКАЗАТЕЛЬСТВО
Ниже приведено аналитическое доказательство для одного ю
четырех типов граничных условий, перечисленных в табл. 1, а имен¬
но, для условий полета, обозначенных как случай II, т. е. для случая
горизонтального полета самолета с ракетным двигателем при отно¬
сительно низких скоростях в начале и конце полета. Доказательств я
126
для случаев I, III и IV строятся аналогичным образом и основы
раются на .положениях разделов I. 2, I. 3, 1.4 и 1.5, касающихся
класса допустимых перемещений, свойств функции со и использова¬
ния теоремы Грина.
В случае II оптимальная траектория состоит из начального от¬
резка IM, соответствующего полету при максимальной тяге двига¬
теля, отрезка MN, соответствующего полету при умеренной тяге
двигателя (со = 0) и последнего отрезка NF, соответствующего по¬
лету при неработающем двигателе.
Это положение можно доказать, показав, что дальность полета
по программе, соответствующей
траектории IMNF' всегда боль¬
ше дальности полета по про¬
грамме, соответствующей лю¬
бой допустимой траектории,
проведенной между теми же
начальной и конечной точками
/ и F (фиг. 52).
Если такая контрольная тра¬
ектория, выбранная для целей
сравнения, не пересекает кри¬
вой со = 0 (например, траекто¬
рия ISF), то неравенство
Ximnf ^ XISF (24)
непосредственно следует из
леммы I.
Если контрольная траектория пересекает кривую со = 0 (например
траектория IPQRF), то требуется доказать справедливость нера¬
венства
XlMNF > ^IPQRF» (25)
эквивалентного неравенству
Xjmp
+xPR +
XrnF > XlP + XpQR + XRF. (26)
Справедливость неравенства (26) следует из того обстоятельст¬
ва, что первый, второй и третий члены в левой части этого неравен¬
ства больше соответствующих членов в правой части неравенства.
Действительно,
Х1МР > Х/р —■* в соответствии с леммой I;
XPR^> XPQR — в соответствии с леммой II;
XRNF^>XRF — в соответствии с леммой I.
Следует подчеркнуть, что главным преимуществом описанного
выше математического аппарата является возможность учета лю¬
бого числа неравенств в условиях вариационной задачи. Кроме то¬
го, при описанном методе решения удается избегнуть трудностей,
связанных с условиями Лежандра, Вейерштрасса и Якоби.
Основное ограничение описанного метода связано с тем обстоя¬
тельством, что теорема Грина применима только к линейным интег¬
Фиг. 52. Сравнение оптимальной тра¬
ектории и произвольной траектории
(граничные условия типа II).
127
ралам К Тем не менее описанный метод представляет большую
ценность при решении различных задач в области динамики полета,
так как там часто встречаются линейные интегралы. Так, например’
линейные интегралы получаются при решении задачи о минималь¬
ном времени набора высоты [4, 5, 6], о наборе высоты с минималь¬
ным расходом топлива [5, 6] и о наиболее крутом подъеме. Кроме
того, при соответствующем преобразовании координат даже про¬
блема оптимального программирования тяги двигателя при верти¬
кальном полете [1, 2] может решаться по методу, в общих чертах
напоминающему метод решения линейных задач.
1.9. СООБРАЖЕНИЯ ОБ ИНТЕГРАЛЕ, ВЫРАЖАЮЩЕМ
ДАЛЬНОСТЬ ПОЛЕТА
Выражение для интеграла, определяющего дальность полета
[формула (11)], может быть значительно упрощено -при замене си¬
стемы координат (М, v) системой координат (М*, v), где М*—при¬
веденная масса, определяемая выражением
V
М*--=Меу'. (27)
После введения новой переменной А'1* уравнение (11) прини¬
мает вид
X=Vr ^ (28)
В частном случае полета при неработающем двигателе (Л4 =
= const) уравнения (11) или. (28) преобразуются к виду
Х= f Ф dv. (29)
Ч
В другом частном случае [3] идеальной импульсной работы дви¬
гателя (р = оо), М* постоянно, как это следует из уравнения (8).
При этом из уравнения (28) получается
Х = 0. (30)
1.10. ЗАМЕЧАНИЯ ПО СОСТАВУ ЭКСТРЕМАЛЬНОЙ ТРАЕКТОРИИ
Экстремальные траектории, перечисленные в табл. 2 и изобра¬
женные на фиг. 51, соответствуют наиболее обычным типам гра¬
ничных условий, встречающихся в полете. Следует заметить, одна¬
ко, что при некоторых типах граничных условий в состав экстре¬
мальной траектории может не входить кривая со = 0.
1 Теорема Г.рина не применима при решении нелинейной задачи, рассматри¬
ваемой в части II.
128
Рассмотрим, например, случай II, т. е. случай, когда начальная
точка / и конечная точка F находятся в области А (фит. 53), соот¬
ветствующей малым скоростям полета.
При заданных значениях Mif viy vK со¬
став экстремальной траектории являет¬
ся функцией конечной массы Мк.
При М*<^Ми кривая со = 0 является
частью экстремальной траектории. При
Л1к]>Мм (например, при F=F") опти¬
мальная траектория состоит всего толь¬
ко из отрезка IG, соответствующего по¬
лету при максимальной тяге двигателя,
и отрезка GF", соответствующего по¬
следующему полету при неработающем
двигателе.
В предельном случае, когда точка
F оказывается на кривой про¬
веденной через точку I (F=F'")y уча¬
сток полета -при неработающем двига¬
теле исчезает и оптимальная траекто¬
рия состоит из одного только отрезка
IF'", соответствующего полету при ма¬
ксимальной тяге двигателя.
Аналогичные положения могут иметь место также и при усло¬
виях полета, обозначенных как случай IV.
1.11. СВОБОДНЫЕ И НЕСВОБОДНЫЕ ВАРИАЦИИ
Интересная интерпретация результатов, полученных с использо¬
ванием теоремы Грина, может быть получена по методу свободных
и несвободных вариаций,
описанному в работе Воль¬
ца [13].
Рассмотрим, например,
граничные условия типа I
(фиг. 54). Экстремальная
траектория IMNF состоит из
двух отрезков IM и NF, со¬
ответствующих полету при
максимальной тяге двигате¬
ля, и отрезка MNy соответ¬
ствующего полету при уме¬
ренной тяге двигателя по
уравнению со = 0. Замкнутая
линия IHKNFGMI ограничи¬
вает область R, содержащую
все допустимые кривые (см.
разд. I. 2).
Нетрудно заметить, что отрезок MN оптимальной траектории
’Находится внутри области R, тогда как остальные два отрезка IM и
MF принадлежат к границе области R—кривой IHKNFGMI.
Фиг. 54. Свободные и несвободные ва¬
риации при граничных условиях типа I.
Фиг. 53. Влияние конечной мас¬
сы Мк на состав экстремальной
траектории при граничных ус¬
ловиях типа II.
9 394
129
На основании этого -при данном значении М в пределах от¬
резка MN необходимо рассматривать вариации типа Sv t о.
В пределах отрезка IM необходимо рассматривать односторон¬
нюю вариацию 8v<0, а в пределах отрезка NF—одностороннюю ва¬
риацию 8v^0.
В соответствии с выводами работы [13] приведенные соображе¬
ния позволяют сформулировать следующие условия, которые долж¬
ны быть удовлетворены для получения максимальной дальности по¬
лета при граничных условиях типа I:
где F = 0 v'+УР.
После несложных преобразований из формул (31) получается
где со—функция, определяемая уравнением (13).
Таким образом, метод свободных и несвободных (вариаций по¬
зволяет определить условия, которым должна быть подчинена фун¬
кция со (у, М) для получения максимальной дальности полета. Сле¬
дует заметить, что полученные здесь результаты соответствуют ги¬
потезам разд. I. 3 в отношении свойств функции со, определяемых
физикой движения.
Теорема Грина с успехам может применяться также при решении
вариационных задач с подвижными границами, что можно показать
на следующем примере.
Примем, что начальная точка (Mi, щ) является фиксированной
и находится, наоример, в области А. Примем, что конечная масса
Мк задана (фиг. 55), а конечную скорость vK можно выбирать про¬
извольно.
В этом случае траектория, соответствующая максимальной даль-
ности полета, состоит из отрезка IM, соответствующего полету пр1*
максимальной тяге двигателя, отрезка MN, соответствующего полету
при умеренной тяге двигателя при выполнении условия со = 0, и п°'
dF d д f* / л т»ж
— -<0 —в пределах отрезка IM,
dv дм _dv\ F
пределах отрезка NF, |
о)<0-в пределах отрезка IM,
о)=-0 — в пределах отрезка MN,
о)>0 —в пределах отрезка NF,
(32)
1.12. ЗАДАЧИ С ПОДВИЖНЫМИ ГРАНИЦАМИ
130
следнего отрезка NF, соответствующего
двигателе, в конце которого достигается
ная критической скорости икр при мас¬
се М=МК.
Для доказательства того, что траек¬
тория IMNF соответствует максимуму
дальности полета, рассмотрим для срав¬
нения произвольную контрольную тра¬
екторию IRG с началом в точке / и кон¬
цом в точке G линии М=МК.
Разность дальностей, соответствую¬
щих этим двум траекториям,
АХ= Xjmnf Xirg (33)
может быть представлена в виде
ах=(xJMNq X!RG) + XGF. (34)
Величина (XIMNG — XJRG) положи¬
тельна в соответствии с леммой I (см.
разд. 1.4). Величина XGF также поло¬
жительна, так как она представляет
собой расстояние, проходимое самоле¬
том при полете с неработающим двига¬
телем и соответствующее перемещению
из точки G в точку F. Отсюда следует,
что A^O>0.
полету при неработающем
конечная скорость vSt рав-
Фиг. 55. Оптимальная тра¬
ектория при заданных зна¬
чениях v^ Mi, Мк . Конеч¬
ная скорость vK может быть
выбрана произвольно (зада¬
ча с переменной конечной
точкой).
1.13. МЕТОД РЕШЕНИЯ УРАВНЕНИЯ w (v, Af)=0
Из табл. 2 и фиг. 51 видно, что кривая со = 0 играет важную роль
при решении задачи о максимуме дальности полета. Действительно,
кривая 0 = 0 всегда является частью экстремальной траектории во
всех случаях за исключением специального случая, рассмотренного
в -разд. I. 10. Важным свойством кривой (о=0 является то, что урав¬
нение ее зависит только от характеристик самолета и двигателя. При
известных данных самолета и двигателя кривая со = 0 может быть
вычислена независимо от граничных условий задачи.
Следует отметить, что в тех случаях, когда необходимо учитывать
влияние сжимаемости воздуха на характеристики самолета, решение
уравнения
(35)
.(«, л()=[«-1 -\Щ =0
v ' L dv \м [dM\v
представляет значительные трудности. Можно, однако, существенно
упростить задачу при решении ее в координатах (Af*, v) вместо ко¬
ординат (М, v), причем переменная М* определяется уравнением
(27). После такого преобразования координат получается уравнение
[£к-°- <зб)
где Ф(М#, v)—функция, определяемая уравнением (9).
9*
131
Таким образом, задача отыскания решения уравнения со = 0 ма¬
тематически однозначна с определением минимума Ф как функции v
при постоянных значениях М*.
При специальных формах поляры самолета возможно дальней¬
шее упрощение решения. Так, например, при параболической поляре
с коэффициентами, зависящими только от числа М, т. е. при аэроди¬
намическом сопротивлении, определяемом формулой
сх=сх0(М) + к(Щс1, (37)
уравнение (36) может быть приведено к виду
=0 (38)
Щ =(
дМ}*
путем замены координат (v, М%, Ф) координатами (М, a, rj),
где
ч(м’ a)==<m=a?F°(м)+/г' (39>
М а
F0(M) = Mc,0(M)A, (40)
^•(М) = ^Л (41)
%pS
2
Мд
У7
(42)
Р* = ре г, (43)
? = (44)
МГ
После этого отыскание решения уравнения со = 0 при поляре са¬
молета, удовлетворяющей уравнению (37), равнозначно определе¬
нию минимума rj как функции М, при постоянных значениях а.
Другой метод решения заключается в использовании уравнения
(18). Если не учитывать влияния числа Рейнольдса на аэродинами¬
ческие характеристики самолета, то на основании уравнения (18)
можно непосредственно определить функцию р(М). Однако это пре¬
имущество покупается ценой необходимости определения угловых
коэффициентов кривых сх0(Щ и /ДМ).
1.14. ЗАКОН ПОДОБИЯ ДЛЯ УСЛОВИЙ ПОЛЕТА В СТРАТОСФЕРЕ
Ниже сформулирована задача, имеющая большое практическое
значение. Пусть дана функция рДМ*), представляющая собой реше¬
ние уравнения со = 0 при высоте полета h = h\. Требуется определить
132
другую функцию ц2(М2), являющуюся решением уравнения со = 0
при высоте полета h = h2.
При полете в стратосфере dajdh = 0. При этих условиях уравне¬
ния (38)ч-(44) показывают, что одно и то же значение а(а =а2) на
двух различных высотах (Ь1фк2)
определяет одно и то же решение
Mi— М2. Из уравнения (42) следует
±L=:i2-. (45)
Hi Pi
Таким образом, при известном ре¬
шении уравнения со = 0 для высоты
полета h=h1 новое решение для вы-
соты h=ht получается путем умно- фиг т 3акон ПОДобия для
жения ординат кривой ц (М) на по- полета в стратосфере,
стоянный множитель p2/pi (фиг. 56).
Следует заметить, что, как видно
из уравнения (19), этот простой закон подобия остается в силе и в
случае полетов в тропосфере, где da|dhф0 при условии, что поляра
самолета представляет собой параболу с постоянными коэффициен¬
тами.
1.15. ПОТРЕБНАЯ ТЯГА ПРИ ПОЛЕТЕ НА РЕЖИМЕ со=0
Интересно определить величину тяги, необходимой для полета
самолета на режиме, обеспечивающем максимальную дальность.
На основании уравнения (6) и определения тяги (Р = р Vr) полу¬
чаем следующее выражение:
£ = 1 +м£. (46)
Так как при полете на режиме оо=0 величина v' положительна,
то двигатель должен быть отрегулирован таким образом, чтобы тяга
его во всех точках кривой со = 0 была меньше лобового сопротивле¬
ния самолета.
В частном случае параболической поляры с постоянными коэф¬
фициентами схо и k из уравнений (19) и (46) получается
Р х 4- 2 (х -[- 1) (х -|~ 3) (А7}
Q х + (х -f 1) (х + 2) (х + 3) ’
где x = v/Vr.
Строго говоря, эта формула справедлива только в случае несжи¬
маемого потока. Тем не менее, формула позволяет получить пра¬
вильное качественное представление о величине потребной тяш при
сжимаемом потоке при условии, что производные dcxo/dN[ и dk/dM
достаточно малы, что как раз и имеет место при сверхзвуковых ско¬
ростях полета. Здесь следует указать на то, что тяга, необходимая
Для полета на режиме оз = 0 при сверхзвуковой скорости полета, мо¬
жет быть значительно меньше силы лобового сопротивления.
133
При околозвуковых скоростях уравнение (47) дает неправильные
результаты, так как занижает отношение потребной тяги к силе ло¬
бового сопротивления. При околозвуковых скоростях это отношение
близко к единице.
1.16. ЧИСЛОВОЙ ПРИМЕР
Значение описанного выше метода для технических расчетов
можно показать на следующем примерном расчете, выполненном
применительно к гипотетическому самолету, подобному по форме
аэродинамической модели AGARD № 2, описанной в работе [17].
Эта модель имеет фюзеляж с удлинением 8,5, треугольное крыло с
чечевицеобразным профилем с относительной толщиной в 4% и не¬
большие кили для обеспечения путевой устойчивости.
М
•м
ос,
i
S'
1
!
.§
CJTJi
ь
— м
да*
III.
m
ь
-Mi
m
:и.
м да>
IbhOCt
Jib'
i
01 0,5 ГР 5 Ю 50 100 от
Фиг. 57. Решение уравнения со=0 при полете
в стратосфере.
Примем, что поляра самолета описывается уравнением (37).
Функция Сго(М) известна из данных летных испытаний [17].
Функцию А(М), описывающую индуктивное сопротивление, опреде¬
ляем на основании имеющихся теоретических и экспериментальных
данных.
Принимаем следующие основные данные самолета:
G = 6000 кг,
5 = 25 м\
Vr = 20l0 м/сек.
Принимаем, что воздух является двухатомным газом с х = 1,4-
Скорость звука в воздухе считаем равной 295 м/сек (предполагается
полет в стратосфере).
На фиг. 57 показан график функции М(а), являющейся решени¬
ем уравнения со = 0 для условий полета в стратосфере, в соответст¬
вии с уравнениями (38) — (44).
134
0,3
о
При больших значениях а уравнение (38) имеет единственное
решение; при малых значениях а существует несколько значений
числа М, соответствующих стационарным значениям тр При внима¬
тельном анализе фиг. 57 можно установить наличие трех решений
уравнения при а<^3: а) решение, соответствующее максимальной
дальности при дозвуковых-околозвуковых скоростях (нижняя кри¬
вая) ; б) решение, соответствующее минимальной дальности при око¬
лозвуковых скоростях, не имеющее практического значения (средняя
кривая, проведенная пунктиром), и в) решение, соответствующее
максимальной дальности при сверхзвуковых скоростях (верхняя
кривая). ju
Следует отметить, что ^
Гиббс [3] установил наличие
одной только области скоро¬
стей, в пределах которой по¬
лучается максимальная даль¬
ность, так как он рассматри¬
вал параболическую поляру
с коэффициентами, не зави¬
сящими от числа М. Изло¬
женная выше теория, напро¬
тив, учитывает влияние -сжи¬
маемости воздуха и позво¬
ляет установить наличие двух
областей максимальной даль¬
ности: дозвуковой-околозвуковой
ласти.
Этот результат представляет интерес, но не должен вызывать
удивления, так как при решении аналогичной в математическом от¬
ношении проблемы определения оптимального режима набора высо¬
ты самолета с жидкостным реактивным двигателем [6] автор также
установил наличие двух областей наивыгоднейшего набора высоты:
одной—дозвуковой-околозвуковой и другой—сверхзвуковой.
На фиг. 58 показаны данные фиг. 57, перестроенные из системы
координат (М, а) в более наглядную систему координат (М, jli) для
одного значения высоты h = 21350 м. Аналогичное решение для лю¬
бой другой высоты в пределах стратосферы легко может быть най¬
дено с помощью закона подобия, сформулированного в разд. I. 14.
М Мин им. 1 /
1 дальность /
со<
0
1
|
(W-
О) .
си
>0
\
Е><0
Максим.
дальность
\
у
1 Максим,
бальное пи
ь
( ш
J
>0
(СО
*и)
У
0.8
1.6
2,4 3У2 М
Фиг. 58. Решение уравнения 0=0 для
высоты h=21350 м.
области и сверхзвуковой об-
I. 17. СЛУЧАЙ НАЛИЧИЯ БЕСКОНЕЧНО БОЛЬШОГО ЧИСЛА
ЭКСТРЕМАЛЕЙ
Оптимальные траектории, показанные на фиг. 51, и доказатель¬
ство в разд. I. 8 основаны на допущении наличия единственного ре¬
шения уравнения оз = 0. Как показывает уравнение (19), это допуще¬
ние полностью оправдывается в случае несжимаемого потока.
В случае комбинации фюзеляжа и треугольного крыла, описанной
в работе [17], влияние сжимаемости воздуха обусловило наличие
Двух имеющих практическое значение решений уравнения со = 0.
135
Это обстоятельство заслуживает более подробного исследования.
Рассмотрим, например, случай, когда в начальной точке / имеет ме¬
сто сверхзвуковая скорость и в конечной точке F—дозвуковая ско¬
рость (фиг. 59).
В соответствии с теоремой Грина траектория типа ICDBGF яв¬
ляется экстремалью. На том же основании траектория (ICAEGF)
также является экстремалью. Более того, комбинированная траекто¬
рия ICAKBGF также является экстремалью 1 по отношению к классу
траекторий, проходящих через три фиксированные точки I, F и Ку
где точка К является точкой пересечения кривой М = МЛ = МВ с
V
И и ним. х Мане им.
дальность дальность
и
Фиг. 59. Семейство экстремалей при
наличии двух решений уравнения
0 = 0, соответствующих максимальной
дальности.
Фиг. 60. Изменение дальности, соот¬
ветствующей семейству экстремалей
IABF.
Pi = 1,2; Mi = 2,35;
Рк = 9,4; Мк = 0,87;
h = 21 350 м;
— отношение масс, при котором
осуществляется полет при
неработающем двигателе из
точки А в точку В.
кривой со = 0, соответствующей ми¬
нимальной дальности.
Таким образом, рассматривае- ^
мая вариационная задача имеет
специальную математическую
структуру, так как наличие двух
кривых о) = 0 допускает бесконечно большое число экстремалей,
удовлетворяющих одним и тем же граничным условиям.
Далее следует определить, какую из этого бесчисленного множе¬
ства экстремалей следует выбрать для того, чтобы обеспечить полу¬
чение максимальной дальности полета. Эта часть задачи, очевидно,
не относится к области вариационного исчисления и представляет
собой скорее задачу обычной теории максимумов и минимумов.
Действительно для определенного, как указано выше, семейства
экстремалей дальность полета от состояния / до состояния F зависит
только от значения отношения масс рл, при котором начинается /пе¬
реход от сверхзвукового решения к дозвуковому. Результаты некото¬
рых типичных расчетов из этой области показаны на фиг. 60.
Эти расчеты выполнены для следующих граничных условий: на¬
чальная точка /(pi= 1,2; М; = 2,35) расположена на кривой решения
уравнения оз = 0, соответствующего высоким скоростям. Конечная
1 Экстремальный характер обобщенной траектории ICAKBGF может быть
доказан как с помощью теоремы Грина, так и по методу частных вариаций [13].
136
точка /7(|1к = 0,4; Мк = 0,87) расположена на кривой решения уравне¬
ния о)=0, соответствующего малым скоростям. Кривая IABF при¬
надлежит к семейству экстремалей рассматриваемой задачи, каждый
из членов которого характеризуется своим значением \хА. Масса то¬
плива составляет 2/з начальной массы самолета. Высота полета
равна 21350 м.
График дальности полета X, соответствующий указанному семей¬
ству экстремалей, как функции рл, показан на фиг. 60. Из этого гра¬
фика видно, что при рассматриваемых граничных условиях имеет
место максимум дальности при рл=0,6. Иными словами, для полу¬
чения максимальной дальности
следует строить программу по¬
лета следующим образом: а) ис¬
пользовать решение уравнения
о)=0, соответствующее сверхзву¬
ковым скоростям, до момента,
когда масса самолета будет
равна приблизительно 50% на¬
чальной массы; б) совершить
переход в дозвуковую область
и в) использовать решение
уравнения оз = 0, соответствую¬
щее дозвуковым скоростям.
Результаты расчета в силь¬
нейшей степени зависят от гра¬
ничных условий, как это пока¬
зано на фиг. 61, где представ¬
лены результаты расчета при
новых граничных условиях.
Начальная точка / (pi = 1,2; ЛК = 0,91) расположена на кривой
решения уравнения о) = 0, соответствующего малым скоростям поле¬
та. Конечная точка F (щг=0,4; Мк=1,31) расположена на кривой
решения уравнения со = 0, соответствующего высоким скоростям по¬
лета. Кривая IABF принадлежит к семейству экстремалей рассмат¬
риваемой проблемы, каждый элемент которого определяется своим
значением отношения масс \хА , при котором самолет прекращает
полет в соответствии с решением уравнения со = 0 для дозвуковых
скоростей и начинает разгон для перехода в сверхзвуковую область.
Отрезок А В соответствует режиму полета при (3= ртах. Ввиду качест¬
венного характера примера и в целях упрощения вычислений этот
отрезок траектории заменен участком импульсной работы двигателя
р * = const.
Зависимость дальности полета X, соответствующей этому семей¬
ству экстремалей, от рл показана на фиг. 61. Из этой фигуры видно,
что при рассматриваемых граничных условиях выгодно про¬
ходить возможно большую часть пути при сверхзвуковой ско¬
рости, полностью исключив из программы полета участок, соот¬
ветствующий решению уравнения со=0 для дозвуковых ско¬
ростей.
XJ
а2
32
28
уДь-СОПЯ
0,4 0,8 1,2 мй
Фиг. 61. Изменение дальности, соответ¬
ствующей семейству экстремалей IABF.
II/ = 1,2; М/ = 0,91;
р.к = 0,4; Мк = 1,31;
}лЛ—отношение масс, при котором на¬
чинается режим импульсной работы дви¬
гателя АВ.
137
1.18. КРИТЕРИИ ДЛЯ ВЫБОРА НАИВЫГОДНЕИШЕЙ ЭКСТРЕМАЛИ
На основании теоремы Грина можно получить интересный каче¬
ственный критерий для выбора наивыгоднейшей экстремали в том
случае, когда уравнение со = 0 имеет два решения.
Рассмотрим, например, условия полета, исследованные на фиг. 60,
и обратим внимание на семейство экстремалей IABF, для которого
X=f(MA ). Оптимальная экстремаль должна удовлетворять очевид¬
ному условию
Применяя теоремы Грина, можно вычислить бесконечно малое
изменение дальности полета при переходе от траектории IABF к
смежной траектории IA'B'F:
Интегрирование выполняется вдоль линии М = МА= Мв. Из
уравнений (48) и (49) получается следующее окончательное выра¬
жение:
Интегрирование в левой части уравнения (50) также выполняет¬
ся вдоль линии М = МА = Мв. Уравнение (50) определяет (M^)opt
и таким образом указывает наивыгоднейшую экстремаль.
Аналогичные критерии могут быть получены и для других гра¬
ничных условий.
1.19. ОГРАНИЧЕНИЯ, СВЯЗАННЫЕ С КОЭФФИЦИЕНТОМ
ПОДЪЕМНОЙ СИЛЫ
Для проверки ограничений, связанных в соответствии с работой
[12] с коэффициентом подъемной силы, вычислим величину су в точ¬
ках кривой (о = 0. В частном случае поляры в виде параболы с посто¬
янными коэффициентами получается следующее выражение:
Из формулы (51) вытекает неравенство су<суЕ, где суе —
значение коэффициента подъемной силы, соответствующее мак¬
симальному аэродинамическому качеству самолета. Отсюда сле¬
дует, что неравенство удовлетворяется во всех точ¬
ках кривой ш = 0.
dX= Xja’B’f — XiABF = dMA (У——(49)
J \дг; дМ/
(50)
—=гД*+1)(х+з),
(51)
138
Приведенный вывод, однако, может потребовать пересмотра в
случае использования поляры, описываемой уравнением (37), ис¬
пользованной, например, в числовом примере разд. I. 16 (см. фиг. 58).
Действительно, при больших значениях отношения масс р. = М/Мг
кривая Cy = cVma.x может пересекать ветвь кривой о = 0, соответствую¬
щую малым скоростям.
В этом случае решение вариационной задачи изменяется. Пусть
координаты предполагаемой точки пересечения кривой со=0 с кри¬
вой Су = Су шах
будут t%_M, тогда, применяя теорему Грина, можно по¬
казать, что при М^>М вместо экстремали со = 0 должна быть исполь¬
зована кривая си = Су шах. Мы не останавливаемся на доказательстве
этого положения, не представляющем никаких трудностей.
1.20. ЗАКЛЮЧЕНИЕ
В работе рассмотрено применение теоремы Грина при решении
вариационной задачи, связанной с определением оптимальной про¬
граммы работы двигателя при горизонтальном полете самолета.
Разработан метод непосредственного определения экстремальных
траекторий при различных типах граничных условий.
Программа полета на максимальную дальность представляет со¬
бой комбинацию участков полета при неработающем двигателе,
участков полета при максимальной тяге двигателя и участков поле¬
та при умеренной тяге двигателя в соответствии с уравнением (17).
Основным результатом работы с 'математической точки зрения
является получение полного доказательства необходимых и доста¬
точных условий получения максимальной дальности полета и обна¬
ружение возможности существования бесконечно большого числа
экстремалей, удовлетворяющих одним и тем же дифференциальным
уравнениям при одних и тех же граничных условиях.
С технической точки зрения основным результатом является рас¬
пространение предыдущих исследований на случай, когда учитывает¬
ся влияние сжимаемости воздуха, и доказательство существования
двух областей, где может быть достигнута максимальная дальность—
дозвуковой-околозвуковой и сверхзвуковой.
Часть II
Я. Чикала
РЕШЕНИЕ ПО МЕТОДУ МНОЖИТЕЛЕЙ ЛАГРАНЖА
ДЛЯ СЛУЧАЯ ПРОИЗВОЛЬНОЙ ХАРАКТЕРИСТИКИ
ДВИГАТЕЛЯ
В предыдущей работе автора [7] были приведены общие уравне¬
ния для определения оптимального режима полета. В настоящей
статье эти результаты используются для решения рассмотренных
н части I задач при более общих предположениях в отношении ха¬
рактеристики двигательной установки, именно, в предположении
139
произвольной однозначной зависимости тяги Р от расхода топлива р.
Остальные допущения остаются теми же, что и в части I статьи.
Основные уравнения имеют вид
В рассматриваемом случае уравнения Эйлера>—Лагранжа (см.
работу [8], стр. 203) имеют следующий вид1:
где X = X(t), (л = fx(^)—множители Лагранжа и p = \iM/%.
Тан как время не входит в явном виде в дифференциальные урав-
ения, то первый интеграл имеет вид2
При использовании этого уравнения уравнение (59) может быть
опущено. Уравнения (52)(56), (58), (60) и (61) составляют си¬
стему дифференциальных уравнений третьего порядка 3; начальные
значения v, М, t и конечные значения v и М могут быть заданы. По¬
сле этого дальность определяется путем интегрирования уравнения
На практике обычно бывает неудобно решать задачу при задан¬
ных граничных условиях. Систему дифференциальных уравнений
1 См. работу [7], формулы (13), (14) и (17). В работе [7] величины ц и %
обозначены соответственно X5/Xi и %s/Xi. Кроме того, лобовое сопротивление Q
рассматривается как функция скорости, высоты и угла атаки. В связи с этим
смысл частной производной Qv в работе [7] отличается от принятого в настоящей
статье.
2 См. работу [71, формулу (15). Здесь используется естественное условие
С=0.
3 Если выбрать в качестве независимой переменной массу и исключить вре¬
мя путем .подстановки dt= — (*Ш/|3), то порядок системы дифференциальных
уравнений был бы снижен до второго, однако при этом нельзя было бы рас¬
сматривать полет при неработающем двигателе (Р = 0).
Mv-\-Q—Р = 0;
Р = Р(Р);
Р = — М;
Q=Q(v, У);
Y=Mg;
X=v.
(52)
(53)
(54)
(55)
(56)
(57)
11.1. НЕОБХОДИМЫЕ УСЛОВИЯ ОПТИМУМА
X_^i-+1=0.
м
(58)
(59)
(60)
(61)
(57).
140
необходимо решать путем последовательного .интегрирования, что
требует знания всех данных в одной из концевых точек. В связи с
этим в тех случаях, когда заданы условия в обеих концевых точках,
необходимо решать уравнения путем подбора.
При исключении множителей Лагранжа1 из уравнений (58), (60)
л (61) получается уравнение, дополняющее систему уравнений
(52-f-57), что придает решению экстремальный характер. Такой ме¬
тод решения, однако, в общем случае не упрощает расчетов. В связи
с этим, а также ввиду физического смысла множителей и их исполь¬
зования в качестве контрольных характеристик при определении
состава оптимальной траектории исключать Я и р из уравнений не
имеет смысла. Важность множителей и величины р, именуемой ниже
«характеристикой», особенно отчетливо проявляется в приведенном
ниже анализе, связанном со сравнением двух смежных решений.
Допустим, что найдена экстремальная траектория, соединяющая на¬
чальное состояние Mi, viy при котором X — Xi, p = fii, и конечное со¬
стояние MR, vK, при котором Х = ХК, ^1 = ^. При рассмотрении беско¬
нечно малых изменений граничных условий множители позволяют
определить соответствующее изменение дальности полета по экстре¬
мальной траектории. Если рассматривать дальность X, соответст¬
вующую Эйлеровой траектории, как функцию граничных условий,
т. е. принять X = X(vi, vK, Mit Мк), то будут иметь место соотно-
(62)
(63)
1
дХ
дХ '
я/==
dvi ’
К—
dvK ’
дХ
_ дХ
сШ£9
дМк'
Это означает, например, что при изменении начальной скорости
на $ Vi при неизменных остальных граничных условиях дальность
полета по экстремальной траектории2 увеличивается на XiS Та¬
ким образом, уравнения (62) и (63) позволяют непосредственно по¬
лучить ответ на многие вопросы, касающиеся соотношений между
летными данными самолета и его проектными параметрами.
1 Эти свойства решения Эйлера могут быть выведены из уравнений возмож¬
ных перемещений концевых точек / и F экстремальной траектории. В обозначе¬
ниях работы [7] эти уравнения имеют вид: 5 * (/) = 5 * (F). В несколько иной фор¬
ме этот принцип положен в основу теоремы 2 : 1 работы [9].
2 Величина Я, очевидно, не может быть отрицательной. Если изменить про¬
грамму полета, соответствующую решению Эйлера, путем введения кратковре¬
менного начального этапа полета при неработающем двигателе, снижающего
Начальную скорость на о vL , дальность увеличилась бы на величину
(MvjQ—Я) /о Vi. Эта величина не может быть положительной не только для кон-
Цевых точек, но и для любой другой точки экстремали, так как каждый отрезок
экстремали представляет собой местное решение задачи определения максималь¬
ной дальности по сравнению е любой смежной траекторией. Отсюда следует, что
*>Mv/Q во всех точках
141
II. 2. УСЛОВИЯ ЛЕЖАНДРД, ВЕИЕРШТРАССА И ЯКОБИ
В соответствий с работой [7] условия Вейерштрасса и Лежандра—.
Клебша удовлетворяются в их усиленной форме при выпуклой
характеристике тяги *, т. е. при d2P!d [32<^0 на всем протяжении ха¬
рактеристики. В работе [7] показано также, что в том случае, когда
указанное неравенство не соблюдается во всех точках характеристи¬
ки двигателя, оптимальная программа полета должна строиться по
несколько измененной характеристи¬
ке, имеющей конфигурацию нити, на¬
тянутой на жесткий шаблон, контур
которого соответствует исходной ха¬
рактеристике. На фиг. 62 показана
такая гипотетическая характеристика
двигателя (заштрихованный контур).
При расчете программы полета па
максимальную дальность часть ха-
р а ктер исти к и зам ен яется отр езк a a i и
прямой (показаны пунктиром) пере¬
крывающими вогнутые участки ха¬
рактеристики 2.
Исследование условия Якоби—Майера значительно сложнее.
Форма его зависит от граничных условий задачи, в частности от того,
являются ли условия в концевых точках фиксированными или пере¬
менными. Практически удобно исследовать это условие геометриче¬
ским методом, построив поле, в котором находится решение, подле¬
жащее проверке3. В этом поле должны быть проведены экстремали
вблизи кривой рассматриваемого решения. Таким образом -получает¬
ся достаточное семейство условий для определения оптимума.
II. 3. ХАРАКТЕРИСТИКА В ВИДЕ ЛОМАНОЙ ЛИНИИ
Примем теперь, что характеристика двигательной установки имеет
вид ломаной линии с прямыми сторонами. Обозначим вершины ло¬
маной линии буквами Аи А2 Ап (фиг. 63) с координатами
Pi и Pi, (*‘=1, 2 /г). Расположим начало координат ((Зо —
= 0 = Ро) в начальной точке характеристики.
1 Общее уравнение (24) в работе [7] содержит множитель, который в соот¬
ветствии с предыдущим примечанием должен быть положительным при макси¬
мальной дальности.
2 Теоретически двигательная установка может работать на любой точке
режима, соответствующего пунктирному отрезку АС при попеременном переходе
с высокой частотой от режима А к режиму С и обратно. Так, например, для
работы в средней точке отрезка АС двигатель должен работать равные проме¬
жутки времени на режимах А и С. Такая гипотеза, естественно, предполагает
безынерционность системы управления двигателем.
3 Для выполнения такого построения можно исключить время t. В соответ¬
ствии с предложением Блисса и Гестенса поле должно быть построено как трех¬
мерное в координатах (у, М, X). По данным работы [10] во всех случаях, когда
это возможно, удобнее использовать двухмерную проекцию (например, на пло¬
скость v, XI).
Фиг. 62. Гипотетическая зави¬
симость тяги двигателя от рас¬
хода топлива.
142
Уравнение стороны A^Ai ломаной линии имеет вид
P = a,+bi 0, (64)
где
(Pz-jpz-P/p,-,)
(Р/-Р/-1)
* h -
* (?/—Р/-1) '
С эвристической точки зрения общие выводы работы [7], касакь
щиеся характера экстремальных траекторий \ в случае разрывной
характеристики двигателя допус¬
кают удобную интерпретацию, ес¬
ли рассматривать характеристику
двигателя -в виде ломаной линии
как предельный случай кривой с
непрерывным изменением углового
коэффициента. В связи с этим мо¬
жно утверждать, что для удовлет¬
ворения условия Вейерштраоса ло¬
маная линия должна быть выпук¬
лой, т. е. должна полностью распо¬
лагаться по одну сторону прямой,
совпадающей с одной из ее сторон.
Кроме того, обратив внимание на
характеристику р и уравнение
(60), можно прийти к следующим
выводам:
а) если изображающая точка состояния самолета в некоторый
момент времени полета на диаграмме ((3, Р) находится на стороне
Ai-tAi характеристики, то характеристика р равна p = bi\
б) если величина р находится между значениями угловых коэф¬
фициентов смежных сторон характеристики двигателя bi и bi+и то
изображающая точка находится в вершине А* характеристики.
Аналогично при р<^Ьп расход топлива (3 равен рл, а полет при нера¬
ботающем двигателе (|3 = 0) соответствует величине характеристики
Р>Ь1.
Из изложенного выше следует, что экстремальная траектория
может быть составлена из следующих элементов:
а) отрезков, на протяжении которых p = bi(i = 1, 2 п),
обозначенных в дальнейшем изложении «отрезки bi»;
б) отрезков, на протяжении которых (3 = |3;(/=1, 2 ... п), обо¬
значенных далее «отрезки |3г». В частности, отрезок, соответствующий
1 В соответствии с авторитетными источниками [8] разрывные решения вариа¬
ционной задачи нельзя называть «экстремалями». Равным образом здесь нельзя
применять термин «экстремалоиды» в связи со специальным характером рас¬
сматриваемой задачи. Учитывая это, полученные решения названы «экстремаль¬
ными траекториями».
Фиг. 63. Зависимость тяги двигателя
от расхода топлива в виде ломаной
линии.
143
полету при неработающем двигателе, обозначается далее как «отре¬
зок Ро».
Теперь исследуем конфигурацию этих отрезков сначала в плос¬
кости (v, М) для определения поведения множителей. В случае от¬
резков bi(p=bi, [i = ibi/M), из уравнения (61) получается
Х = (65)
Q—at
Из уравнений (58) и (65) имеем
(Q—cii) (bi—v)-\-MgvQy—bivQv=Q. (66)
Уравнение (66) представляет собой зависимость между v ,и М, в
конечной форме изображаемую одной кривой 1 для каждой пары
значений йг, Ьг. Из уравнения (66)
можно определить значения
dvjdM. После этого можно опреде¬
лить 'расход топлива из выраже¬
ния
Р
dv
dM
bi+MTT, =Q — a» (67)
полученного из уравнения (52).
Используемый отрезок кривой, со¬
ответствующий уравнению (66),
ограничен точками, в которых рас¬
ход топлива (3, определяемый из
уравнения (67), достигает значе¬
ний (3г—1 и Pi. В примере, рассмот¬
ренном в разд. II. 4, сторонам
А0Аи AiA2j А2А3 характеристики
двигателя (см. фиг. 63) соответст¬
вуют отрезки BiCi, В2С2у В3С3 на
фиг. 64.
Для определения отрезков [я
(т. е. линий постоянной тяги Р =
= Pi) необходимо проинтегриро¬
вать уравнение (52). Каждому
значению Pi соответствует семей¬
ство кривых с одним параметром,
каждая из которых заканчивается в точке на оси v, где сила лобового
сопротивления при нулевой подъемной силе равна Рг. Одна из этик
кривых показана на фиг. 64 и обозначена буквой С. Эта кривая
соответствует p = Pi (точка А\ на фиг. 63). Некоторые из этих кри¬
вых, в том числе и кривая С, обнаруживают уменьшение скорости в
верхней части и увеличение скорости в нижней части. Точка, в кото¬
рой касательная к кривой параллельна оси М, соответствует усло¬
вию Q = Pi. Пунктирная кривая / на фиг. 64 представляет собой гео¬
1 Здесь принято, что уравнение (66) выражает однозначную зависимость ^
от 714. Это допущение справедливо при поляре в виде параболы с постоянными
коэффициентами [см. уравнение (71)].
Фиг. 64. Основные кривые на пло¬
скости (v, 714) в случае характеристи¬
ки двигателя (тяга по расходу топ¬
лива) в виде ломаной линии.
144
метрическое место таких точек при P=Pt. Линии (3i, не попадающие
внутрь области, ограниченной контуром Q = Pi, обнаруживают
уменьшение скорости на всем протяжении.
Решение уравнения (58) выражается в виде
Пользуясь формулой (68), можно вычислить значения X вдоль
кривой (Зг, если известно значение % в одной точке t=to. Аналогич¬
ным образом вычисляется характеристика р по формуле (61), кото¬
рая может быть переписана в виде
Соотношение a = Mv/Q остается в силе1 и для линии (30 (полет
при неработающем двигателе), множитель ц может быть найден 2
путем интегрирования уравнения (59).
Следующий вопрос заключается в том, как скомбинировать эти
частные решения для получения экстремальной траектории. Для раз¬
решения этого вопроса используются условия Вейерштрасса—Эрд¬
мана для точек излома (см. работу [8], стр. 203). Эти условия тре¬
буют [7] непрерывности значений множителей X и, значит, р в точках
излома.
В свете этого основного требования рассмотрим два возможных
случая сопряжения кривых:
а) кривой (3 = с кривой р = Pi—i или |3=|3г+г,
б) кривой p — bi с кривой р = pi-i или р = Pi.
В первом случае переход наступает при достижении характери¬
стикой р на линии (3 предельных значений Ьь или bi+i.
Переход второго типа может быть в любой точке линии 6;. По¬
ложение точки излома и тип пересекающей кривой (Pi или 6 й-i) за¬
висят от положений обоих концов экстремальной траектории3. При
подстановке значения X в соответствии с формулой (65) в уравнение
1 Это значение X получается из уравнений (52) и (61) и согласуется с урав¬
нением (58).
2 По существу, уравнение (59) не может быть написано для линий M = const
без более подробного исследования, так как это уравнение получено путем варь¬
ирования М. Однако можно доказать справедливость уравнения (59) путем не¬
посредственного сравнения проварьированных экстремалей и с помощью урав¬
нения (63).
3 См., например, случай прямолинейной характеристики (часть I статьи).
Положение точек перехода на кривую со=0 (т. е. линию р = Ь) и точек перехода
с этой кривой определяется положением двух концевых точек экстремальной
траектории. В этом случае задача с начальными условиями является неопреде¬
ленной, тогда как та же задача с граничными условиями является определенной.
(68)
где
ср (t) =eto
(69)
Ю 394
145
(70) получается р=(Р—cii)/(3. Это уравнение удовлетворяется при
Р = ЬЧ P = Pi, p = pi, а также при p = bi9 Р = Р^и Р=р/_1- > В силу
этого могут иметь место оба этих типа 'Перехода без нарушения не¬
прерывности множителей.
II.4. ЧИСЛОВОЙ ПРИМЕР
Полученные выше зависимости использованы ниже для постро¬
ения диаграммы 1 экстремальных траекторий на плоскости (v, М) с
общей конечной фиксированной точкой О. При расчете принята ха¬
рактеристика двигателя в виде ломаной линии, состоящей из трех
отрезков прямой (см. фиг. 63).
Примем уравнение поляры в виде уравнения параболы
Q = Av*+B^- (71)
v2
с постоянными коэффициентами А и В. Основные данные для
фиг. 63, 64 и 65 и характеристики двигателя приведены ниже:
Vr=b{, А; РГ-АЬ\, t=Abi;
Pi = P,; Р2 = 2рг; Рз = 3,2р,;
Pi = Pa ^2=1.8Д; ^3=2,4 Я,.
Линии p = b±, p = b2 и р = 6з представлены соответственно кривы¬
ми ВхСи В2С2 и В3Сг на фиг. 64 и отрезками 1—2—3, 6—7—8 и
11—12 на фиг. 65. Концевые точки 3, 8, 12 на фиг. 65 соответствуют
точкам Сь С2 и С3 на фиг. 64.
Определим теперь экстремальную траекторию, начиная с точки
конца полета и выполняя интегрирование в направлении, обратном
полету.
Начнем с экстремальной траектории с характеристикой p = &i в
точках линии О—1 (линия (30), где X=MvjQ (см. фиг. 65). Переход
(Pi-^Po) происходит2 на линии О—1. Последующее интегрирование
вдоль линии (3 = (3i приводит к точке, в которой характеристика р
становится равной Ь2. В этой точке имеет место3 переход
(02-* Pi)- Пунктирная кривая 5—5* представляет собой линию
изломов [11], т. е. геометрическое место точек перехода 4 между кри¬
выми р = Pi и Р=р2-
1 В связи с особым характером задачи диаграмма не удовлетворяет некото¬
рым условиям построения поля Майера. Так, например, через точки линии p = bi
проходят бесконечные решения. Тем не менее, диаграмма может быть использо¬
вана для доказательства достаточных условий решения.
2 Переход от линии р/ к линии Р/—i обозначается символом (Р/-*- Р/—i)-
Переход от линии (3/к линии 6/обозначается символом (Р/-*&/).
3 После этого характеристика р еще раз достигает величины Ь2. Однако,
полученная при этом ветвь линии изломов, очевидно, должна быть отброшена
в связи с тем, что она не удовлетворяет условию, требующему, чтобы положи¬
тельные касательные к экстремальной траектории в точке излома располагались
по одну сторону линии изломоб (см. [11], разд. 10-е).
4 Цифра со звездочкой* является общим обозначением семейства точек.
Так, например, 13* является общим обозначением точек линии р = рз, проходя¬
щей через точку 9 (см. фиг. 65).
146
В другой класс траекторий входит часть кривой р = Ь1 (отрезок
]—5). В любую точку этого отрезка можно попасть либо по линии
(3 = 0о, либо по линии P=pi. Первый случай соответствует располо¬
жению начальной точки справа от отрезка 1—3 между линиями
и М = М3. Во втором случае особо важную роль играет отре¬
зок 2—6 с уравнением 0 = 01. При движении вдоль этого отрезка зна¬
чение характеристики изменяется от р = Ь± в точке 2 до р = Ь2 в точ¬
ке 6У т. е. .в точке пересечения с линией Ь2. При движении вдоль от¬
резков р = Pi, начинающихся
в точках линии 1—2 (p = bj),
характеристика р становится
равной Ь2 в точках линии из¬
ломов 5—6. Эта линия пред¬
ставляет собой геометриче¬
ское место точек излома
(02^ Pi)*
При движении вдоль от¬
резков P = Pi, оканчивающих¬
ся в точках линии 2—3, ха¬
рактеристика р никогда не
становится равной Ь2. Дейст¬
вительно, величина р сначала
уменьшается, но вскоре начи¬
нает расти и становится рав¬
ной p = b 1 в точках отрезка
3—4. В силу этого отрезок
3—4 является частью линии
изломов, на которой имеет
место переход (0i->0o). От¬
резок 2—6 (0 = 0i) в данном
случае называется «мости¬
ком», так как все траектории,
идущие от линии Ь2, проходят
через этот отрезок по пути к
линии Ьл.
Дальнейшее построение производится аналогичным образом. На¬
чинаем с линии изломов 5—6 и выполняем интегрирование вдоль
линии Р = р2- Новая линия изломов 9—10 представляет собой гео¬
метрическое место точек перехода (0з->02). Другие возможные тра¬
ектории имеют общий отрезок 6—8 (р = Ь2). Дальнейшее интегриро¬
вание выполняем, начиная с точек отрезка 6—8, вдоль линий 0 = 01
или 0 = 02. На линиях 0 = pi характеристика р достигает значения
P = &i в точках линии 4—4*, на которой имеет место переход (ро-*
-*0i). В случае линий 0 = 02 имеются две возможности: а) характе¬
ристика р достигает значения Ь3 в пределах линии 0=02; б) харак¬
теристика никогда не становится равной Ь3. В случае «а» можно оп¬
ределить отрезок 10—11 линии изломов, на которой имеет место
'Переход (рз-^Рг); этот отрезок оканчивается в точке 11 на линии
Р=63. В случае «б» можно построить отрезок 8—<5*, на котором
Фиг. 65. Экстремальные траектории
в случае характеристики двигателя (тяга
по- расходу топлива) в виде ломаной
линии.
10*
147
■имеет место переход ((3i->(32). Отрезок 11—7 (|3 = (32) представляет
собой «мостик» между отрезком 11—12 (р = Ь3) и отрезком 6—7
(Р = Ь2).
Описанное построение, очевидно, может быть выполнено анало¬
гичным образом также и в случае, когда ломаная линия характери¬
стики двигателя имеет большее число сторон.
Область диаграммы в окрестности концевой точки О представле¬
на в увеличенном масштабе в круге на фиг. 65. Линия pi (отрезок
5Г—О) прерывает линию изломов 5—5* и является геометрическим
местом точек перехода (|32->(3i). Аналогично отрезки (32, оканчи¬
вающиеся в точках отрезка О—5', определяют остальную часть пре¬
рванной линии изломов 9*—9—О для переходов ((33-*p2). Из этого
следует, что некоторые траектории оканчиваются в точке О без по¬
следнего участка полета при неработающем двигателе; у некоторых
траекторий не имеется даже отрезка (Зь Линия р = р3 и линия М = М.:„
проходящие через точку О, ограничивают часть плоскости (М, v),
из которой экстремальная траектория может проходить в точку О.
Эту часть плоскости (М, v) назовем «разрешенной зоной».
Состав экстремальных траекторий в разрешенной зоне отчетливо
определяется линиями изломов I, II и ///, т. е. линиями О—1—2-
3—4—4*, О—5'—5—6—7—8—8* и О—9'—9—10—11—12—12*
Эти линии подразделяют зону на четыре области:
а) область (Зз—выше линии ///;
в) область р2—между линиями III и //;
c) область Pi—между линиями II и /;
d) область Ро—между линией / и нижней границей зоны.
В каждой области Pi Эйлеровы траектории состоят из отрезков
Pi. При пересечении линии изломов экстремальная траектория пере¬
ходит в следующую область и в общем случае изменяет свой угловой
коэффициент. Исключение составляет случай, когда пересечение
имеет место в части линии изломов, принадлежащей к кривой Ь,.
В этом случае экстремальная траектория проходит вдоль последо¬
вательных отрезков Ьь и линий, обозначенных как «мостики» Л
Таким образом, при наличии сетки линий изломов, соответствую¬
щих данной концевой точке О, можно без всяких затруднений по¬
строить экстремальную траекторию, начинающуюся в любой точке
разрешенной зоны плоскости (М, v). Найденное таким образом ре¬
шение в каждом случае является единственным 2. Действительно,
1 Так, например, если начальная точка находится на линии Р = Рз, пересе¬
кающей отрезок 11—12, то последующей экстремальной траекторией (см. фиг. 65:
будет лишня 11—7—6—2—1—О. Соответствующие точки характеристики двига¬
теля (тяга по расходу топлива, фиг. 63) будут: Р3 (точка И), А-> (отрезок 11—7)
/?2 (точка 7), Р2 (точка 6), (отрезок 6—2), Pi (точка 2), Рi (точка Л
71 о (отрезок О—/).
- В каждую точку линии bi можно прийти по экстремальным траектория''
с трех различных направлений. Тем не менее, решение, начинающееся в любой
точке этой линии, является единственным. Множители 1 и ц являются однознач¬
ными функциями координат разрешенной зоны с единственным исключением
для [I вдоль отрезка О—1. Это ограничение не нарушает свойств интеграла Гиль¬
берта J (A clv-\-\i dM), остающегося не зависящим от пути интегрирования, как
это имеет место в поле Майера.
148
рассмотрим две точки А и В на одной из этих экстремалей, причем
примем, что точка В находится ближе к точке О, чем точка А. Обо¬
значим через Х(А, В) дальность полета, соответствующую экстре¬
мальной траектории АВ, и через Х'(А, В)—дальность, соответствую¬
щую любой неэкстремальной траектории, проведенной через те
же концевые точки А и В. Тогда можно показать, что во всех
случаях 1
Х(А, В)>Х'{А, В).
Конфигурация линий изломов, естественно, изменяется три из¬
менении положения концевой точки О. Следует, однако, отметить,
что изменение формы линий изломов наблюдается только в части
плоскости (М, v). Так, например, при уменьшении скорости в точ¬
ке О изменение линий изломов происходит только слева от линии
9'—5'—О. Уменьшение конечной массы вызывает изменение ли¬
ний изломов только слева от линии 13*—9—5—1. При увеличении
конечной массы2 остается без изменения часть диаграммы спра¬
ва от линии 10*—10—6—2 при условии, что М0<^М2.
Совершенно очевидно, что при уменьшении углов между смеж¬
ными сторонами характеристики двигателя линии изломов будут
сближаться, сливаясь в пределе в одну единственную кривую, имен¬
но в кривую со = 0, фигурирующую в части I статьи.
ЗАКЛЮЧЕНИЕ
Изложенный выше метод, основанный на понятии характеристи¬
ки, позволяет решить без существенных затруднений довольно слож¬
ную вариационную задачу. Эта характеристика служит непосред¬
ственным критерием состава экстремалей, терпящих разрыв, прямо
показывая точки сочленения отдельных отрезков траектории.
Линии изломов, на которых характеристика р достигает критиче¬
ских значений, соответствующих переходу от одного режима работы
1 Доказательство достаточности условий оптимума требует особого внима¬
ния в связи с тем, что рассматриваемая задача является специальной, тогда как
в литературе [11, 12] .рассматриваются обыкновенные задачи. Тем не менее,
в связи со свойством, отмеченным в предыдущем примечании, можно сформули¬
ровать теорему, аналогичную теореме 10:1 работы [11]. Более прямой путь
заключается в использовании интеграла Гильберта для доказательства того, что
разность X—X' равна интегралу по времени от величины
£= + а),
где X, ji, Р и р являются функциями вычисленных координат экстремальной
траектории, а (Г m РДР7) являются величинами, определяющими одну из воз¬
можных неэкстремальных' траекторий. Е является так называемой остаточной
функцией, обладающей следующими свойствами: Е=0 при р = р7 и на границе
областей Р/_2 и Р/ при условии, что Р*-] < р' < pt-+1; £>0 во всех остальных
точках при любых значениях р'. Таким путем можно доказать, что Х^>ХГ.
2 Положение «мостиков» не зависит от конкретных условий в концевых
точках.
149
двигателя -к другому, существенно облегчают .решение задачи с за¬
данными граничными условиями, в которой заданы обе концевые
точки экстремальной траектории. При практических расчетах, оче¬
видно, не требуется исследовать всю плоскость (М, v), как это было
сделано в настоящей работе для общего обзора всей проблемы. При
использовании простых и ясных результатов части I статьи доста¬
точно построить несколько экстремальных траекторий и на основа¬
нии их вычертить линии изломов для рассматриваемой задачи.
Дальнейшее, решение не представляет трудностей.
В примере в разд. II-4 был подробно рассмотрен случай малой
конечной скорости, имеющий большое практическое значение в связи
с тем, что при этих условиях получается максимальная дальность
при заданном весе топлива. Однако те же уравнения могут быть ис¬
пользованы также и при других граничных условиях.
Рассмотренный пример позволяет вывести и заключение о том,
что кривизна характеристики двигателя оказывает существенное
влияние на оптимальную программу изменения тяги по времени. На¬
личие кривизны характеристики уменьшает длительность периодов
работы двигателя на максимальной тяге 1 и таким образом увеличи¬
вает длительность периодов работы двигателя в области характери¬
стики, соответствующей более высоким значениям отношения Р/р.
ЛИТЕРАТУРА
1. Гамель Г., Об одной задаче вариационного исчисления, связанной
с движением ракеты.
Hamel G., Uber eine mit dem Problem der Rakete zusammenhangende
Aufgabe der Variationsrechnung, «ZAMM», vol. 7, 1927.
2. T з я н С. и Эванс P, Оптимальное программирование тяги высотной
ракеты.
Tsien Н. S., Evans R. С., Optimum Thrust Programming for a Sounding
Rocket, «Journal of the American Rocket Society», 1951, vol. 21, No. 5, pp. 99—107.
3. Гиббс А., Оптимальная программа изменения тяги двигателя при гори¬
зонтальном полете.
Hibbs A., Optimum Burning Program for Horizontal Flight, «Journal of the
American Rocket Society», 1952, vol. 22, No. 4, pp. 206—212.
4. Ми еле А., Задачи о минимальной продолжительности нестационарного
полета самолета.
Miele A., Problemi di Mimino Tempo nel Volo Non-Stazionario degli
Aeroplani, «Atti della Accademia delle Scienze di Torino. Classe di Scienze
Matematiche, Fisiche e Naturali», 1950—1951, vol. 85.
5. Ми еле А., Общие решения задач по определению оптимальных режи¬
мов нестационарного полета.
Miele A., Soluzioni Generali di Problemi di Ottimo in Volo Non-Stazio¬
nario, «L’Aerotecnica», 1952, vol. 32 (перевод издан как отчет NACA No. 1388,
1955).
1 Рассмотрим условия в начале полета, при (которых лобовое сопротивление
самолета меньше максимальной тяги двигателя. В случае, рассмотренном на
фиг. 65, это означает, что начальная точка экстремальной траектории лежит ниже
пунктирной линии I, соответствующей Q = Pa. Отсюда видно, что для .рассматри¬
ваемой кривизны характеристики двигателя полет на участке пути, соответствую¬
щем большей части экстремальной траектории, должен происходить при задрос-
селированном двигателе.
150
6. Ми еле А., Оптимальная программа подъема самолета с ракетным дви¬
гателем.
М i е 1 е A., Optimum Climbing Technique for a Rocket-Powered Aircraft,
<Jet Propulsion», 1955, vol. 25, No. 8, pp. 385—391.
7. Ч и к а л а П., Оптимальные эволюции самолета.
Cicala P., Le Evoluzioni Ottime di un Aereo, «Atti della Accademia delle
Scienze di Torino. Classe di Scienze Matematiche, Fisiche e Naturali», 1954—1955,
vol. 89.
8. Блисс Г., Лекции по вариационному исчислению.
Bliss G., Lectures on the Calculus of Variations, University of Chicago
press, 1945.
9. Блисс Г. и Г естнес М., Достаточные условия задачи Майера в ва¬
риационном исчислении.
Bliss G. and Н е s t е n е s М., Sufficient Conditions for a Problem of Mayer
in the Calculus of Variations, «Trans. American Math. Soc.», 1933, vol. 35,
pp. 305-326.
10. Лерю Г., Интеграл Гильберта и поля Майера в задаче Майера в ва¬
риационном исчислении.
La rew G., The Hilbert Integral and Mayer Fields for the Problem of Mayer
in the Calculus of Variations, «Trans. American Math. Soc.», 1924, vol. 26,
pp. 61—67.
И. Рид У., Разрывные решения непараметрической задачи Майера.
Reid W., Discontinuous Solutions in the Non-Parametric Problem of Mayer
«American Journal of Mathematics», 1935, vol. 57, pp. 69—93.
12. Фоллингер О., Разрывные решения вариационных задач с ограни¬
чением углового коэффициента.
Follinger О., Diskontinuierliche Losungen von Variationsproblemen mit
Gefallebeschrankung, «Mathem. Annalen», 1933, vol. 126.
13. Больца О., Лекции по вариационному исчислению.
Bolza О., Lectures on the Calculus of Variations, G. E. Stechert Company,
New York, 1946.
14. Миеле А., Оптимальные траектории полета самолетов с турбореактив¬
ными двигателями.
Miele A., Traiettorie Ottime di Volo degli Aeroplani Azionati da Turbo-
reattori, «L’Aerotecnica», 1952, No. 4 (переведена и издана как отчет NACA № 1389,
сентябрь, 1955).
15. Г а н т м а х е р Ф. и Л е в и н Л., Уравнения движения ракеты.
Gant та с her F. R. and Levin L. М., Equations of Motion of a Rocket,
NACA, Т. M. 1255, 1950.
16. Беркли И., Ньютон P. и Гросс Г., Математическая теория по¬
лета ракеты.
Barkley I., Newton R. and Gross G, Mathematical Theory of the
Rocket Flight, McGraw-Hill Book Co., Inc., New York, 1947.
17. Пилэнд P., Лобовое сопротивление при нулевой подъемной силе мо¬
дели самолета с 60°-ным треугольным крылом (AGARD Model 2), полученное при
свободных летных испытаниях при числах М от 0,8 до 1,7.
Piland R., The Zero-Lift Drag of a 60° Delta-Wing-Body Combination
(AGARD Model 2) Obtained from Free-Flight Tests Between Mach Numbers 0,8
and 1,7, NACA T. N. 3081, April 1954.
А. МИ ЕЛЕ
РАСШИРЕНИЕ ТЕОРИИ ОПТИМАЛЬНОЙ ПРОГРАММЫ
РАСХОДОВАНИЯ ТОПЛИВА РАКЕТНЫМ САМОЛЕТОМ
ПРИ ГОРИЗОНТАЛЬНОМ ПОЛЕТЕ1
В статье рассматривается и анализируется программа оптимального расхо¬
дования топлива самолетом с ракетным двигателем при горизонтальном полете.
Теоретические выводы предыдущих исследований распространяются на решение
общей проблемы минимума произвольной функции конечных значений времен и
массы, расстояния и скорости.
При помощи непрямых методов вариационного исчисления показано, что
общая экстремальная кривая состоит из участков нулевой тяги, участков макси¬
мально возможной тяги и участков переменной тяги. Для последних .получено
решение в замкнутой форме.
В общих рамках теории, изложенной в настоящей работе, рассматриваются
при различных типах граничных условий такие частные проблемы, как макси¬
мальная дальность, максимальная продолжительность, минимальный расход го¬
рючего, максимальное увеличение скорости.
Особое внимание уделено программированию тяги для обеспечения макси¬
мума дальности полета при заданной продолжительности полета. Дается метод
построения экстремальных траекторий в предположении, что тюраболическая
поляра лобового, сопротивления характеризуется постоянными коэффициентами
или коэффициентами, зависящими от числа М.
Главное затруднение, связанное с линейным характером рассматриваемой
задачи, заключается в том, что условие Лежандра—Клебша не может быть при¬
менено для решения вопроса о качестве экстремума, получающегося из реше¬
ния уравнения Эйлера. Более того, фуекция Вейерштра-сса оказывается равной
нулю во всех точках кривой переменной тяги. Эта трудность преодолена с по¬
мощью обобщения одного ранее разработанного автором метода, на оснопе
теоремы Грина.
Принятые обозначения
а — скорость звука.
А— лобовое сопротивление при нулевой подъемной силе.
В—отношение индуктивного сопротивления к квадрату массы.
С— постоянная интегрирования.
схо— коэффициент лобового сопротивления при нулевой подъемной силе.
Q—лобовое сопротивление.
Qv—частная производная лобового сопротивления по скорости.
Qm—частная производная лобового сопротивления по массе.
Е— максимальное аэродинамическое качество.
з
р = j ХК7К—основная функция.
к—\
g — ускорение силы тяжести.
GK— функция, экстремум которой отыскивается.
Н—постоянная, определяемая из уравнения (36).
Н— частное значение постоянной Н.
JK(k = 1, 2, 3)—левые части уравнений, описывающих вариационную задачу.
1 A. Miele, An Extension of the Theory of the Optimum Burning Program
for the Level Flight of a Rocket-Powered Aircraft, «Journal of the Aeronautical
Science», 1957, vol. 24, No. 12, pp. 874—884.
152
k— отношение коэффициента индуктивного сопротивления к квадрату ко эф
фициента подъемной силы.
У—подъемная сила.
т— масса в данный момент.
т\> т2—масса, соответствующая моменту времени 1 и 2.
М— число М.
р— атмосферное давление.
S— условная поверхность.
t— время.
Р— тяга.
X=vjVг—отношение скорости самолета к эффективной скорости истечения.
v— абсолютная скорость самолета.
Vr— эффективная скорость истечения.
X— горизонтальная дальность.
а—независимый параметр ракетного двигателя..
Р—секундный расход массы двигателя.
т.— отношение удельной теплоемкости при постоянном давлении к удельное
теплоемкости при постоянном объеме (v-= 1,4 для воздуха).
Ак(& = 1, 2, 3)—множители Лагранжа,
р— плотность воздуха.
Ф—функция из урдзнения (75).
(1}1— » » » (47).
Ф2— » » » (48).
'Г— » » » (76).
Wi— » » » (47).
W2— .ч> » » (48).
О)— » » » (63).
и>1— » » » (61).
о>2— » » » (62).
Подстрочные индексы
/— начальное условие,
к— конечное условие.
Надстрочные индексы
(•)— производная по в-ремени.
( )' — производная по числу М.
I. ВВЕДЕНИЕ
За последние годы большое внимание уделялось теории опти¬
мальных характеристик самолетов и управляемых снарядов. Клас¬
сический «квазистационарный» метод, широко используемый при
анализе характеристик работы обычного самолета, часто заменяет¬
ся все более современными и более специфическими методами, в ко¬
торых учитываются и инерционные члены.
Для того чтобы учесть влияние инерционных членов, в анализ
оптимальных траекторий необходимо ввести существенные измене¬
ния. В качестве первого приближения можно было бы сказать, что
вследствие учета инерционных сил существо проблемы оптимально-
153:
го режима «перемещается из области обычной теории максимума и
минимума в область вариационного исчисления. Это, в свою очередь,
приводит к увеличению трудности анализа, поскольку оптимальные
кривые уже больше не определяются конечными уравнениями, а ско¬
рее контролируются нелинейными системами дифференциальных
уравнений высшего порядка, интегрируемых (в общем) только при¬
ближенными методами.
В связи с применением вариационного исчисления к общей тео¬
рии характеристик самолета и управляемого снаряда, основная за¬
дача заключается в том, чтобы определить как геометрию полетной
траектории, так и режим работы двигателя, которые обеспечивают
оптимальное значение рассматриваемой характеристики. Хотя в ли¬
тературе и освещались общие уравнения, дающие решение этой за¬
дачи, тем не менее получить решение в замкнутой форме практиче¬
ски невозможно. Именно поэтому внимание большинства исследо¬
вателей сосредоточивалось на сравнительно более простых задачах.
В этой связи исследовались две основные группы вариационных
задач.
Первая группа (задачи программирования траектории)
посвящена определению геометрии оптимальной траектории полета
при заданном режиме работы двигателя. Типичными задачами здесь
являются: оптимальный способ набора высоты турбореактивным са¬
молетом с данной силовой установкой или оптимальный способ на¬
бора высоты самолетом с ракетным двигателем с заданным расхо¬
дом.
Вторая группа (задачи программирования тяги) посвяще¬
на определению оптимального режима работы двигателя, когда гео¬
метрия траектории полета или эквивалентное ей условие заданы.
Вариационная задача, анализируемая в этой статье, является част¬
ным случаем этой группы задач.1
I. 1. Состояние исследования в этой области
Исследования теории оптимальной программы расходования топ¬
лива для ракетного самолета проводились ранее Гамелем [1], Тзя-
ном и Эвансом [2] для вертикального полета и Гиббсом [3] и Чикала
и Миеле [4] для горизонтального полета. Работа последних рассмат¬
ривается ниже.
Изучение условий обеспечения максимальной дальности горизон¬
тального полета при данных конечной скорости и расходе топлива
и при произвольной продолжительности полета было начато Гиббсом.
Он рассматривал идеальный случай ракетного двигателя, способного
расходовать всю массу топлива с любой скоростью—от нулевой до
бесконечно большой,—и самолета с параболической полярой лобо¬
вого сопротивления с постоянными коэффициентами. Однако вари¬
ационное решение Гиббса не удовлетворяло граничным условиям
проблемы в фиксированных конечных точках.
1 Настоящая статья представляет собой краткое изложение' технического
отчета 56-302 Управления научных исследований ВВС США [7].
Как следствие из этого он постулировал существование двух ко¬
нечных кривых, вдоль которых движение должно определяться про¬
граммой движения с неработающим двигателем или программой пре-
рьго-и сто-импульсного расходования топлива, и успешно подтвердил
эТу свою догадку численным анализом.
Совсем недавно эта же проблема была подвергнута рассмотре¬
нию с точки зрения более общих гипотез [4]. При этом было снято
любое ограничение в отношении формы поляры сопротивления. Рас¬
сматривался более реальный случай двигателя с конечным макси¬
мальным секундным расходом топлива. Для случая, когда предпола¬
галось линейное соотношение между тягой и расходом массы, полное
доказательство необходимых и достаточных условий для достижения
максимальной дальности было получено Миеле путем использова¬
ния теоремы Грина.
Для более общего нелинейного случая доказательство дал Чика¬
ла с помощью непрямых методов вариационного исчисления и вве¬
дения нового понятия характеристики.
I. 2. Описание исследования
Управление научно-исследовательских работ ВВС США органи¬
зовало исследование широкого класса вариационных проблем, пред¬
ставляющих интерес для теории программы расходования топлива,
с конечной целью попытаться обобщить все существующие теории
программирования тяги.
В пределах этого исследования была вновь изучена программа
расходования топлива -при горизонтальном полете, и при этом была
поставлена следующая общая задача: «Ракетный двигатель, могу¬
щий создавать переменную тягу, придан летательному аппарату
данной конфигурации, двигающемуся вдоль прямолинейной гори¬
зонтальной траектории. Заданы: начальное, время масса miy абс¬
цисса Xi и скорость Vi\ но конечные параметры tK, mK, Хк и vK
заданы не все. Требуется определить, такую программу изменения
тяги, которая обеспечивает минимальное значение некоторой опреде¬
ленной, хотя произвольной функции GK(4, Як, ик), являющейся
функцией параметров конечной точки».
Частными случаями этой общей проблемы являются:
1) случай, когда GK=—Хк, приводящий к максимальной даль¬
ности;
2) случай, когда GK = —tKy приводящий к максимальному времени;
3) случай, когда G*=—mK, приводящий к минимальному расходу
топлива;
4) случай, когда GK = —vR% приводящий к максимальной конечной
скорости.
Наиболее интересным побочным результатом, вытекающим из
приведенного выше анализа, возможно, является исследование про¬
граммы расходования топлива, которая приводит к максимальной
Дальности Як, когда начальное и конечное значения скорости, массы
и времени заданы. На практическую важность этой задачи указывал
Н сентябре 1955 г. на конференции Американского ракетного общеет-
155
ва Дж. Лорелл (лаборатория ракетного движения Калифорнийского
технологического института). При обсуждении статьи П. Чикала и ап.
тора настоящей работы (см. [4]) Лорелл поставил вопрос о возмож¬
ности распространения техники анализа, разработанного в эгог,
статье на случай, когда исследуются условия, обеспечивающие до¬
стижение максимальной дальности при заданном времени полета.
Он указал, что траектория максимальной абсолютной дальности для
случая, когда время произвольно (см. работы [3] и [4]), относительно
плавная, так что изучение программы расходования топлива инк*,
реоно с .практической точки зрения для случая, когда общая продол
жительность полета задана.
II. ФИЗИЧЕСКИЙ СМЫСЛ ЗАДАЧИ
В дальнейших разделах статьи принимаются следующие допу¬
щения: а) ракетный самолет рассматривается как материальна1/!
точка с массой /л, переменной по времени t\ б) рассматривается пря¬
молинейная горизонтальная траектория; в) угол между векторам;!
тяги Р и скорости v пренебрежимо мал; г) эффективная скорость
истечения Vr ракетного двигателя рассматривается как постоянная
величина; д) двигатель может работать при любых секундных рас¬
ходах массы топлива (3, ограниченных значениями (3 = 0 и (3 = (3n:;w
е) аэродинамическое запаздывание не учитывается, т. е. подъемная
сила У и сила лобового сопротивления Q вычисляются, как для уста¬
новившегося полета.
В силу допущений «а», «б» и «в» уравнения движения по каса¬
тельной и по нормали к траектории полета примут вид:
Р—Q—mv = 0; (П
Y—mg = 0, (2)
где g — ускорение силы тяжести, a v — производная по времени.
II. 1. Функция силы лобового сопротивления
и ее производные
Исходя из гипотез «б» и «е» силу лобового сопротивления Ц
можно рассматривать как функцию Q(ty У) скорости и подъемное
силы даже при учете влияния на поляру чисел М и Re. Тогда с по¬
мощью уравнения (2) можно исключить подъемную силу, а силу ло¬
бового сопротивления свести к функции только скорости и массы.
В дальнейшем рассматривается два случая:
а) общий случай функции силы лобового сопротивления
156
Q = Q(v, т);
(•-/
б) частный случай параболической поляры силы сопротивления
Q — A-\-Bm.2, (4)
где
В =
pSi>2
(5)
(6)
В этих уравнениях схо есть коэффициент лобового сопротивления
при нулевой подъемной силе; k — отношение так называемого коэф¬
фициента индуктивного сопротивления к квадрату коэффициента
подъемной силы; S—условная поверхность и ?—плотность воздуха.
Из уравнения (4) можно вычислить частную производную сопротив¬
ления по массе:
dQ ]
Qm =
dtll J с,'—const
— 2 Вт.
(7)
Затем из уравнений (4) и (6) получают частную производную
силы лобового сопротивления по скорости:
Q
Г а<?~
v 1д»_
где
2 +
М
сд0
сд0 .
С л-
dcxo
х 0
</М
k'
dk
dNi
Вт 2
Г к'
[-2 + М —
(8)
(9)
(10)
Следует отметить, что уравнение (8) получено без учета зависи¬
мости силы лобового сопротивления от числа Re, т. е. считалось, что
сх0 и k суть функции только числа М.
II. 2. Функция тяги
В силу допущения «г» тяга Р должна быть представлена как ли¬
нейная функция секундного расхода массы (3:
P = $Vr. (11)
В свою очередь, допущение «д» означает, что неравенству
0<р<рш« (12)
Должен удовлетворять класс всех кривых, рассматриваемых в на¬
стоящей работе.
Ограничение (12), которое через расход массы топлива выра¬
жает ограничение размеров двигателя, имеет особое значение в опре¬
делении характера решения, как уже указывалось ранее (см. работы
13] и: [4]). В работе [4] задача с учетом 'Приведенного выше неравен¬
157
ства решалась путем введения понятия характеристики. Другой воз¬
можный путь решения задачи (несколько лучший с формальной
точки зрения) с учетом этого неравенства состоит в использовании
параметрического представления характеристик двигателя. Такой
метод решения использован в настоящей работе.
Секундный расход массы р представляют как функцию парамет¬
ра а, обладающего следующими
свойствами: а) для —со<а<сц
расход массы (3 = 0; б) для ct2<a '
<:+оо расход массы р Ртах И
в) для ап<а<(Х2 между р и а при¬
нимается некоторая однозначная
зависимость.
Таким образом, по этой схеме а
может рассматриваться как неза¬
висимый параметр ракетного дви¬
гателя, который может изменяться
от —со до +со. Секундный расход
массы Р становится зависимой ве¬
личиной, изменяющейся от 0 до
Ртах согласно схеме на фиг. 66.
В свою очередь, тяга ограничивается пределами 0 и Ртах согласно
уравнению (11) и фиг. 66.
Отметим, что условие dp/da=0 представляет или полет с нера¬
ботающим двигателем или полет на режиме максимальной тяги дви¬
гателя. С другой стороны, c/p/da-7^0 представляет любой рабочий-
режим двигателя, промежуточный между этими двумя граничными
состояниями. Отметим также, что а является только параметром и
что нет необходимости придавать ему какое-либо специальное физи¬
ческое значение.
III. ФОРМУЛИРОВКА ВАРИАЦИОННОЙ ЗАДАЧИ
Рассмотрим теперь следующую систему уравнений:
J\ = m + р (a) =0; (13)
J2 = X-v = 0; (14)
J3=v+ Q(^-OT)~ =0. (15)!)
m
Уравнение (13) является соотношением между изменениями мас¬
сы самолета по времени и секундным расходОхМ топлива р. В свою
очередь, р является известной функцией а согласно параметрическо¬
му представлению, показанному на фиг. 66. Уравнение (14) является
дифференциальным соотношением между положением и врехменем-
Уравнение (15) выведено из уравнения движения по касательной к
1 По терминологии вариационного исчисления уравнения (13)— (15) явля¬
ются неголономными или дифференциальными связями.
Фиг. 66. Параметрическое представ¬
ление характеристик двигателя.
158
-траектории полета путем подстановки аналитических выражений
тяги и лобового сопротивления.
Время t принимается как независимая переменная задачи. Зави¬
симыми переменными являются масса га, горизонтальный путь X,
скорость v и параметр двигателя а.
Если задать начальные координаты ^ = 0, /Нг = га(0), Х» = 0, Vi =
c^v(0), а также некоторые (не все) координаты конечной точки, то
вариационная задача будет формулироваться следующим образом:
«Среди всех семейств функций m(t), X(t), v(t), a(t)y удовлетворяю¬
щих уравнениям (13) и (14), (15) и заданным конечным условиям,
определить специальное семейство, которое даст минимум некоторой
функции GK(tKy гак, Хк, ок) координат конечной точки»1.
Следует заметить, что ни одно условие не может быть наложено
ка си и ак, т. е. на секундный расход массы (3* и (Зк. В свете аналити¬
ческой природы задачи граничные значения (3 определяются в ре¬
зультате решения семейства уравнений Эйлера, что показывается в
последующих разделах.
III. 1. Уравнения Эйлера
Введем семейство переменных множителей Лагранжа A,i(/),
Яз(0 и составим следующее выражение:
(16)
1
где Ju J2, h обозначают соответственно первые члены уравнений (13),
(14), (15). Поскольку неизвестных функций четыре, следует напи¬
сать четыре уравнения Эйлера. Записываем их так:
Hiybf <у='’2'3^ <|7>
где
Zi—m, г^=Х, z3 = v и z4 = a.
Из уравнений (13) — (17) получаем следующие уравнения Эйлера:
Xj —
(18)
\ т1 т )
*а='
0;
(19)
II
со
— x2-f Х3-5^- ;
(20)
т
0 =
da \ т )
(21)
1 Таким образом, рассматриваемая вариационная задача формулируется в
границах общей вариационной задачи типа Майера. Задача Майера известна
Как наиболее общая вариационная задача одномерного вариационного исчисле¬
ния [5], эквивалентная формулировкам Лагранжа и Больца.
159
III. 2. Первый интеграл
Так как время выражено в задаче не явно, то первый интеграл
•может быть записан в виде [5]:
±^С, (22)
У=1 J
тде С—постоянная интегрирования. В соответствии с уравнениями
(13) — (16) уравнение (22) перепишем так:
Х^/71 -f” ^2^
Последнее выражение является математическим следствием
уравнений (18) — (21), и поэтому его можно применять для замеще¬
ния одного из них, например уравнения (18). Следует подчеркнуть,
что семейство уравнений Эйлера—Лагранжа (18) — (21) и первый
интеграл (22) или (23) описывают все задачи, рассматриваемые н
этой работе, независимо от природы функции GK(tK, mKf Xk, vk) и от
конечных условий.
III. 3. Разрыв решения Эйлера
Уравнение Эйлера (21) особенно важно, так как оно показывает,
что экстремальная кривая не непрерывна, будучи в целом составле¬
на из участков кривых, описываемых уравнением
-^• = 0, (24)
da
и участков кривых, описываемых уравнением
Ь-Ч —=0. (25)
m
•
Согласно параметрическому представлению, показанному па
фиг. 66, уравнение (24) представляет или полет с неработающим дви¬
гателем или полет на режиме 'максимальной тяги двигателя. Уравне¬
ние же (25) описывает условие полета с непрерывной переменно]!
тягой, как показывается ниже.
III. 4. Условия Эрдмана—Вейерштрасса для угловых точек
В связи с разрывным характером решения рассматриваемой за¬
дачи следует применить условия Эрдмана—Вейерштрасса для углей
вых точек. Они являются условиями непрерывности, которые дол¬
жны удовлетворяться в каждой угловой точке разрывного экстре -
мального решения следующими пятью величинами:
ЗЛ (У =1,2, 3,4). <20
JmJ dz . dz т
У-1 J J
160
Так как F не зависит от а, то выражение dF/d а по своей природе
непрерывно во всех угловых точках. Аналогичное требование к
остающимся четырем величинам (26) приводит к
(Ч)- = (Ч)+ (*= 1.2,3); (27)
(С)_ = (С)+, (28)
где подстрочный индекс «—» показывает условие непосредственно
перед узлом, а индекс «-{-» условие сразу после узла. Поэтому усло¬
вия Эрдмана—Вейерштраоса требуют, чтобы:
а) множители %к (К= 1, 2, 3) были непрерывными в узлах;
б) значение постоянной интегрирования С было одним и тем же
для всех участков кривых разрывного экстремального решения [это
последнее условие означает также, что величина (А*—А3 Vr/m)
должна быть равна нулю в узле; таким образом угловая точка может
находиться на участке кривой переменной тяги, определяемой урав¬
нением (25)].
IV. РЕШЕНИЕ ЗАДАЧИ В ПЛОСКОСТИ «МАССА—СКОРОСТЬ»
В следующих разделах даются общие решения, определяющие
оптимальную программу расходования топлива в плоскости «мас¬
са—скорость».
Эти решения включают в общем случае постоянные интегрирова¬
ния, которые определяются в соответствии) с природой минимальной
задачи и граничными условиями.
IV. 1. Участки кривой постоянной тяги
Исходя из уравнения (13) ускорение v перепишем следующим
образом:
(29)
dm
так что уравнение (15) примет вид
dm
•—1—dv. (30)
т Q—$Vr V '
Уравнение (30) является дифференциальным уравнением первого
порядка, связующим величины v и т, и должно интегрироваться в
общем приближенным методом, если даже поляра сопротивления
имеет параболическую форму, представленную уравнением (4). Точ¬
ные решения возможны только в особых случаях, таких, например,
как полет с неработающим двигателем (нулевой расход массы),
когда
(3 = 0; т = const, (31)
или мгновенное сжигание запаса топлива (бесконечно большой рас¬
ход массы), когда
v
(3 = оо; meVr = const. (32)
11 394
161
IV. 2. Участки кривой переменной тяги
В уравнении (25) для участков кривой экстремального решения
множители Лагранжа Xt и Х2 можно исключить следующим образом.
Путем преобразования уравнений (13), (14), (15), (23) и (25) мож¬
но получить
Х1 = —— (Х2^ С); (33)
= (34)
Вычисляя производную по времени из уравнений (34) и из урав¬
нений (13), (15), (19) и (20), получаем следующий результат:
где
Н=——. (36)
Уравнение (35) представляет собой соотношение, связывающее
конечные величины массы и скорости, справедливое при любом виде
функции GK, для которой решается задача-минимум. Констан¬
та Н должна определяться для каждой частной задачи согласно G<
и конечным условиям.
Для специального случая параболической поляры сопротивления,
когда коэффициенты зависят от числа М, уравнения (4) — (10) и
(35) приводят к соотношению массы и скорости в такой форме:
где
т _ М2 f F\ ~ HF2
щ У f3 — HFь
(37)
_ xpS a
1 2 g ’
(38)
F 1 = £*оО ~\~x) + MCxo',
(39)
F^c^{l+Zr) + c'*o-T;
(40)
F3=*k(3 + x)-Mk'-,
(41)
(42)
В этих уравнениях —начальная масса; к—отношение удельной
теплоемкости при постоянном давлении к удельной теплоемкости при
постоянном объеме (воздуха); а—скорость звука; x = v/VT\ р—атмо¬
сферное давление. Для частного случая, когда коэффициенты пара-
162
боличеокой поляры постоянны, уравнение (37) упрощается и приоб¬
ретает вид
где т2 представляет собой конечную массу, определяемую равенством
Определение дальности и времени в (Плоскости (v, т) осущест¬
вляется с помощью следующих формул, выведенных из уравнении
В граничные условия изучаемой задачи входит ряд условий для
неподвижных конечных точек и ряд естественных условий. Послед¬
ние должны выводиться из следующего общего условия трансвер¬
сальности [5]:
Которое должно тождественно удовлетворять всем системам вари¬
аций, имеющих место при заданных конечных условиях. Принимая
во внимание уравнения (13) — (16) и выражение (22) для первого
интеграла и учитывая, что начальные координаты заданы, уравнение
(49) можно привести к виду
(43)
(44)
IV. 3. Определение дальности и времени
(13), (14) и (15):
(45)
К
(46)
где
(47)
(48)
V. ГРАНИЧНЫЕ УСЛОВИЯ
(49)
4" 4~ Ч^-^4- Kov — С5^]к=0.
(50)
11*
163
(51)
Так как GK зависит от mK, Хк tx0 vK, то уравнение (50) разбив ас те я
на следующие четыре вспомогательных условия:
(^-с)а«=°'
(^7+Ч8”>=0'
(ж+,»Ух‘=°-
VI. СПЕЦИАЛЬНЫЕ ЗАДАЧИ
При помощи общих решений, данных в разд. IV, и граничных ус¬
ловий, показанных в разд. V, теперь можно проанализировать ряд
частных задач.
VI. 1. Максимальная дальность, произвольное время, заданная
конечная скорость, заданная масса топлива *
Для случая задачи обеспечения максимальной дальности GK =
=—Хк, при заданной конечной скорости (8^ = 0), заданной конеч¬
ной массе (8тк=0), произвольной продолжительности полета (8 tK
произвольная) условие трансверсальности (51) дает С = 0;
Для функции лобового сопротивления вида Q = Q(v, m) программа
оптимального расходования топлива включает участки кривых по¬
стоянной тяги, определяемых уравнением (30), и участки кривых
переменной тяги, уравнения которых можно получить из уравне¬
ния (35):
v(Q+VrQv—tnQm)—VrQ==0. (г>2)
Для параболической поляры с коэффициентами схо и k, завися¬
щими только от числа М, уравнение (52) дает
м2 i/.^oc+M+Meo 53)
mi V k(3-\-x)—М£'
— уравнение, которое также может определяться как частный слу¬
чай уравнения (37) при Н — 0. Когда коэффициенты параболической
поляры постоянны, уравнение (53) упрощается [3] и принимает вид
ЛТ=хъл/1±±. (54)
т2 у 3 + *
Отметим, что метод сопряжения участков кривых постоянно]!
тяги ((3 = 0 или (3 = Ртах) с участками кривых переменной тяги (53)
* Задача обеспечения максимума дальности при заданном времени полета
рассматривается подробно в разд. IX настоящей статьи.
164
или (54), при котором заданные граничные условия удовлетворяют¬
ся, был подробно рассмотрен ранее Гиббсом [3] и Чикала и Мие-
ле [4].
VI. 2. Максимальная продолжительность, произвольная
горизонтальная дальность, заданная конечная скорость,
заданная масса топлива
Теперь рассмотрим задачу увеличения продолжительности полета
(GK=—4) до максимума при заданной конечной скорости (8^к = 0),
заданной конечной массе (8тк = 0) и произвольной горизонтальной
дальности (8ХК—произвольная величина). Хотя эта проблема с тех¬
нической точки зрения имеет меньшее значение, тем не менее инте¬
ресно отметить, что ее решение входит в общую теорию, излагаемую
здесь. Условие трансверсальности (51) дает С=—1; А,2К = 0, та-к что
уравнение (35) упрощается, принимает вид
Для параболической поляры лобового сопротивления с коэффи¬
циентами, зависящими только от числа М, уравнение (37) дает
если схо и k—константы. Поэтому решение состоит из участков кри¬
вой, удовлетворяющих уравнениям (56) и (57), участков кривой по¬
лета при неработающем двигателе и участков кривой полета на ре¬
жиме максимальной тяги двигателя (|3 = ртах). Чтобы удовлетворить
граничным условиям задачи, эти участки должны сопрягаться ана¬
логично тому, как это было рассмотрено в работе [4] для задачи
разд. VI. 1.
Следует подчеркнуть, что для обеих задач, рассмотренных в
разд. VI. 1 и VI. 2, оптимальную программу расходования топлива
можно предсказать в плоскости (v, т) независимо от дальности и
времени. Если только оптимальное соотношение массы и скорости
известно, значения Хк и 4 определяются путем вычисления интегра¬
лов (45) и (46).
VI. 3. Минимальный расход топлива, произвольное время,
заданная дальность, заданная конечная скорость
Теперь проанализируем задачу обеспечения минимума расхода
топлива (GK = —mR) при заданной конечной скорости (8ик = 0), за¬
данной дальности (8ХК = 0) и произвольной продолжительности по¬
лета (8 4—произвольная). Условие трансверсальности (51) дает
^1к=1, С = 0, так что выражение для участков кривой переменной
Q+ VrQv ftlQm — 0.
(55)
(56)
которое после упрощения приводится к виду
(57)
165
тяги сводится к уравнению (52). Поэтому заключаем, что задача уве¬
личения дальности до максимума при заданном расходе топлива и
задача сведения расхода топлива к минимуму для заданной даль¬
ности ведут к одной и той же экстремали. Это свойство является
следствием того, что система уравнений Эйлера (18) — (21) однород¬
на относительно множителей Лагранжа, В результате, два пропор¬
циональных семейства множителей можно связать с одним и тем же
решением m(t), X(t)y v(t), a(t) С
VI. 4. Максимальная конечная скорость, произвольное время,
заданная дальность, заданный расход топлива
Для случая задачи увеличения конечной скорости (GK =—t>K) до
максимума при заданной дальности (8ХК=0), заданной массе то¬
плива (S тк = 0) и произвольном времени (8tK—произвольная вели¬
чина) условие трансверсальности (51) дает ^зк=1, С=0. Поэтом,
эта задача приводит к одной и той же экстремали, что и для задач,
рассмотренных в разд. VI. 1 и VI. 3.
VI. 5. Максимальная конечная скорость, произвольное время,
произвольная дальность, заданный расход топлива
При заданном расходе массы (S тк = 0) и для задачи GK=—v,
($tK и Ь Хк—произвольные) условие (51) дает Я3к=1, С = О, А,2К = 0.
Участок кривой переменной тяги (35) исключается из решения, ко¬
торое состоит из кривых постоянной тяги. При помощи обычных фи¬
зических рассуждений освобождаемся от участка (3=0.
Кик вывод, экстремальная кривая для указанной задачи вы¬
рождается в простейшую траекторию полета на режиме максималь¬
ной тяги двигателя.
VII. УСЛОВИЕ ЛЕЖАНДРА—КЛЕБША И ВЕЙЕРШТРАССА
Необходимое условие по Лежандру—Клебшу в его усиленной
форме требует, чтобы во всех точках кривой Эйлера для функции Ск.
определяющей вариационную задачу, удовлетворялось следующее
неравенство [5]:
1 Это свойство можно рассматривать в качестве побочного вывода,* вытекаю¬
щего из общего закона Майера о взаимосвязи изопериметрических проблем [б].
4 4
,j.= 1 v=l
где тri = m, 7г2 == Xt тг3 = 1д тг4=а. Система вариаций должна согласовы¬
ваться с уравнениями движения, т. е. с
4
(59)
166
Развертывание уравнения (58) дает
Q = -yr (Ч2=(к (&*)2. (60)
да2 \ tn J da2
Для участков кривых постоянной тяги, определяемых уравнением
(24), вторая производная с/2 (З/d а2 равна нулю, так что Q = 0; кроме
того, для участка кривой переменной тяги также Q = 0, что следует
из уравнения (25). Поэтому заключаем, что условие Лежандра—
Клебша не может быть использовано в данном случае для выяснения
максимального или минимального характера траектории Эйлера.
Аналогичную трудность встречаем, когда применяем более жест¬
кое условие Вейерштрасса, так как функция Вейерштрасса [5] равна
нулю во всех точках участков кривой переменной тяги:
Указанные трудности проистекают вследствие того, что настоя¬
щая вариационная задача линейна относительно т, v, Ху (3. Эти
трудности, однако, можно преодолеть с помощью свойств трех функ¬
ций cot, 0)2 и со, определяемых в разд. VIII, и теоремы Грина, исполь¬
зованной в разд. IX этой статьи.
VIII. ОПРЕДЕЛЕНИЕ ФУНКЦИИ соь со, и ©
Введем следующие функции переменных v и т:
со (-D, 1и)=-^р-—-^1-; (61)
dv от
<о2 (V, т) = Jh_; (62)
dv dm
<s>(v, m, Я)=со1—HVr gl>2, (63)
где Фь i|h, Ф2, ф>2 определяются уравнениями (47) и (48), а Н—
уравнением (36).
После подстановки уравнений (47) и (48) в уравнения (61), (62),
(63) получим
u1Q2=v(Q+ VrQv-mQm)- VrQ\ (64)
(O 2Q2= Q + VrQv — mQm; (65)
<oQ’ = (Q + VrQv — mQm) (v О Vr) — VrQ. (66)
Для параболической поляры с коэффициентами сх0 и К, завися¬
щими только от числа М, уравнения (64), (65) и (66) вместе с урав¬
нениями (4) — (10) дают
“>iQ2CX1L=F _g3/_gl\a ; (67)
AVr М4 \ т\ )
<*2Q2Cx0 р ( т \2
К—); (68)
I4 \ mi /
А " 2 М4
о Q*Cx о / п /-(Р \ _|_ 4 — Лз ( ™ \2
+ , (69)
AVr М4 \ mi /
где Fly F2, Гз, Fa определяются уравнениями (39) — (42).
167
Если коэффициенты параболической поляры постоянны, уравне¬
ния (67), (68) и (69) ведут к
iQi
iVr
“2 Q2
AVr
3+*
X*
№
е+т)[4Ш:
oQ2
AVT
1 1 -f- X
"О+т)-3-'
x4
\ то /
(70)
(71)
(72)
Сравнение уравнений (35) и (66), (37) и (69), (43) и (72) пока-
зывает, что точки плоскости (vy т), где со=0, принадлежат участ¬
кам кривых переменной тяги, связанным со всеми задачами вида
GK(tK, тк, Хк, vK). Поэтому уравнения (35), (37) и (43) можно пред¬
ставить как
о)(т, v, Я) =0.
IX. АНАЛИЗ ЗАДАЧИ МАКСИМАЛЬНОЙ ДАЛЬНОСТИ
ПРИ ЗАДАННОЙ ПРОДОЛЖИТЕЛЬНОСТИ ПОЛЕТА
Для задачи обеспечения максимума дальности (GK =—^к) прз
заданной конечной скорости (8vK = 0), заданной конечной массе
(В тк = 0) и заданной продолжительности полета (8£к = 0) условие
трансверсальности (51) даетЛ2к=1.
Поэтому экстремальная кривая состоит из участков кривых поле¬
та с неработающим двигателем, участков кривых полета на режиме
максимальной тяги двигателя и участков кривых переменной тяге:
последние определяются уравнением (35) для случая, когда функ¬
ция силы лобового сопротивления имеет вид Q = Q(v, т). Далее сле¬
дует определить, как должны сопрягаться участки кривой 'постоянной
тяги с участками кривой переменной тяги, чтобы удовлетворить за¬
данным граничным условиям и установить, дает ли решение Эйлера
минимум или максимум дальности.
Эти вопросы можно выяснить в значительной степени, если иссле¬
дование разделить на две части: 1) случай, когда коэффициен л
схо, k параболической поляры—постоянные величины, и 2) случай,
когда схо, k являются функциями числа М. Для краткости тальке
первый из этих случаев рассматривается в данной статье. Обширный
анализ второго случая дан в работе автора [7].
IX. 1. Случай параболической поляры
с постоянными коэффициентами
Для этого весьма идеального случая экстремальная кривая со¬
ставляется из участков кривых постоянной тяги ((3 = 0 или |3 = (3тах>
участков кривых, удовлетворяющих уравнению (43). Можно пока¬
зать, что последние должны удовлетворять уравнению со\т, и, Н) -
(см. разд. VIII).
168
IX. 1. 1. Группа кривых переменной тяги
Уравнение (43), представляющее семейство участков кривых пе¬
ременной тяги, дано на графике фиг. 67 для различных значений
постоянной Я.
Для ЖО уравнение (43)
таково, что скорость v является
однозначной функцией массы
т. С другой стороны, для Я>0
скорость v является двузначной
функцией массы га; поэтому для
такого случая каждый участок
кривой переменной тяги разде¬
ляется на две ветви — ветвь
большой скорости (показа¬
на сплошной линией на
фиг. 67) и ветвь малой ско¬
рости (показана пунктирной
линией).
IX. 1.2. Минимальные или максимальные свойства участков кривых
переменной тяги
Как было указано в разд. VII, условие Лежандра—Клебша и
условие Вейерштрасса ничего не могут дать относительно макси¬
мальной или минимальной природы кривой Эйлера. Несмотря на это,
можно получить важный вывод, используя теорему Грина и особые
свойства функций coi, со2, о, определенных в разд. VIII. В этой связи
*важны следующие замечания:
а) участок кривой Я = 0 является геометрическим местом точек,
где (i)i (у, га) = 0. Функция соДу, га) положительна в области А
(фиг. 68), находящейся справа от ш = 0, и отрицательна в области В,
слева от coi = 0;
б) участок кривой Я= ±со устанавливается последовательностью
точек, где (о2(щ га) =0. Функция соДи, га) положительна в области А
(см. фиг. 68), справа от со2 = 0, и отрицательна в области В, слева от
со2 = 0;
в) для конечных значений /7 таких, когда Н</0, функция о (га, щ
Я) положительна в области А (фиг. 69) справа от (о = 0 и отрица¬
тельна в области В слева от со = 0;
г) для конечных положительных значений Я функция со (га, v, И)
положительна в области А (см. фиг. 69), справа от сплошной линии
(о = 0, и в области С, слева от пунктирной линии (о = 0, но функция со
отрицательна в промежуточной области В, между сплошной и пунк¬
тирной линиями фиг. 69. Чтобы установить, дают ли кривые фиг. 67
максимальные или минимальные решения, рассматривается частное
значение для Я (например, Я<Д0, см. фиг. 69) в связи со случаем,
когда обе конечные точки / и F помещаются на участке кривой пере¬
менной тяги, определяемой избранным значением для Я. Участок
/
/
h=oj
н=о,г\
Я-±°о,
у
'о/о\
/ /
У 0,2/
//
(/
/
/
i
/
//
д
У
/
/
\
/
^ <
у
/
0 0,10 0,20 0,30 0,40 0,50
Фиг. 67. Семейство участков кривых
со(т, v, Н) = 0 переменной тяги для
случая параболической поляры с посчо-
янными коэффициентами.
169
кривой Эйлера IQF сравнивается с контрольной кривой1 IPQRF, и
выводятся следующие разности:
(73)
(74)
[^к] IQF [X^ipQFtF,
А^к= [tK] iqf [tK ]lpQRf
После введения множителя HVr и определений
Ф(т, v, Н) =<Dl—HVrФ2; (75)
'Г (m, v, Н) = 4x—HVrV2 (76)
{<x>(mtv, н). о
Р f'/sl @
и>(т,цн)<0 /У]><7
т
V
OJ ~ О (JL) - О
© / ® /®
vtH) >О/ (i)(mtvfH)< 0 /и(тьгН)>0
Фиг. 68. Свойства функций
(Di(m, v) и (Os (т, v).
Фиг. 69. Свойства функций
со (т, v, Н).
получаем
д*к - НУг Мк = j [ Ф (т, V, Н) dv + W (т, ю, Н) dm] -
IQF
(77)
т. е.
— j* [Ф (т, v, H)dv + X¥ (m,v, Н) dm],
IPQRF
ДАГК — HVrMK= (j) [Ф (m, v, H) dv + W (my v, H) dm}-\-
IQPI
+ (j) [Ф (/w, ^,//) ^ + ^(/71, //) rfm], (78)
С помощью теоремы Грина два линейных интеграла в уравнении
(78) преобразуются в два интеграла по площадям, соответственно
1 Контрольная кривая IPQRF должна ограничиваться неравенством
О < Р< р,пн*.
связанным с областями SB внутри контура IQPI и SA внутри конту-
где функция со определяется уравнением (63). Знак «минус» перед
первым интегралом площади показывает направление обхода по ча¬
совой стрелке IQPI. Аналогично знак плюс перед вторым интегра¬
лом по площади SA показывает движение против часовой стрелки
QFRQ. Так как функция co(m, v, Н) для 0 отрицательна в обла¬
сти SB и положительна в области SA, получаем следующий вывод:
В случае, когда движение вдоль контрольной кривой IPQRF и по
участку кривой Эйлера IQF совершается за одно и то же время
(АК = 0), приращение ДХк>0. Это означает, что движение по кривой
Эйлера IQF обеспечивает достижение максимальной дальности при
заданной продолжительности полета. С другой стороны, если конт¬
рольная кривая берется такой, что А Хк = 0% то имеет место неравен¬
ство А ^к>0, так как И предполагалось отрицательным. Это значит,
что движение по кривой Эйлера IQF, представленной на фиг. 69.
обеспечивает максимальную продолжительность полета при задан¬
ной дальности.
Рассуждая подобным образом, можно показать далее, что:
а) участок кривой Н = 0 связан с решениями максимальной даль¬
ности, когда продолжительность полета произвольная (см. фиг. 68);
б) участок Я=±оо связан с решениями максимального времени
полета, когда дальность произвольная (см. фиг. 68);
в) участок кривой, на котором скорость наибольшая для всех
кривых, где #>0 (сплошная линия на фиг. 69), обеспечивает дости¬
жение максимальной дальности при заданном времени и, наоборот—
сводит к минимуму время при заданной дальности;
г) участок кривой, на котором скорость наименьшая для всех кри¬
вых, где Н^>0 (пунктирная линия на фиг. 69), сводит к минимуму
дальность при заданном времени и, наоборот, увеличивает до макси¬
мума время при заданной дальности.
IX. 1.3. Простой критерий распознавания характера участка кривой
переменной тяги
Когда время полета задано, из раздела IX. 1.2 можно получить
следующий критерий: «Участок кривой переменной тяги со(т, и,
Н) —0 связан с решением максимума дальности, если функция со от¬
рицательна вблизи со=0 при подходе слева и положительна вблизи
<*> = 0 при подходе справа; та же самая кривая дает решение мини¬
мума дальности, когда знаки функции а) обратные».
pa QFRQ:
—(Y \dvdm
dm) J J \ dv dm )
д
<b{m,ev, 'H)dvdmJr &{m,v, Н) dv dm, (79)
A XK—HVr A tK>0.
(80)
IX. 1.4. Сопряжение участков кривых
Рассмотрим один частный участок кривой семейства, определяе¬
мого уравнением (43), например участок Н = —0,2. Предположим
теперь, что начальная точка I и конечная точка F не находятся па
кривой о)(т, и, Н) = 0.
Задача заключается в
том, чтобы определить, как
должен сопрягаться этот уча¬
сток кривой переменной тяги
со = 0 с траекторией постоян¬
ной ТЯГИ ((3 = 0 ИЛИ (3=(3m,:j.
Ясно, что для того, чтобы
удовлетворить конечным ус¬
ловиям, связанным с задан¬
ными конечными величинами
для массы и скорости, кривая
Эйлера, соединяющая точки
/ и F, должна составляться
из трех ветвей (фиг. 70): на¬
чальной ветви IM, централь¬
ной ветви MN — полет вдоль
со (т, v, Н)= 0—и конечной
ветви NF.
На начальном участке / VI
д в и ж е и и е п р он сходит п р и
максимальном расходе топ¬
лива', если точка I находится
слева от со = 0, или при нера¬
ботающем двигателе, если
точка / находится справа от со = 0. На конечном участке NF полог
^происходит при неработающем двигателе, если точка F лежит с. с-
ва от со = 0, или с максимальным расходом топлива, если F лежат
справа от со = 0. Другими словами, в плоскости «масса—скоросы
могут существовать четыре вида граничных условий [4]. Они пока¬
заны на фиг. 70 цифрами I, II, III, IV.
IX. 1. 5. Решение проблемы граничных значений
Допустим, что заданы семь величин: miy Хч су, /к, тк vK и с-л
необходимо найти максимум дальности Хк.
Рассмотрим (фиг. 71) группу кривых IABF, ICDF, IEGF, IRJF.
IKLF, составленных из участков с [3 = const и кривых со (т, v, II) =
Каждая из этих кривых представляет собой решение семейства урав¬
нений Эйлера (18) — (21). Более того, все они удовлетворяют задан¬
ным исходным и конечным условиям относительно массы и скорости
и условиям Эрдмана—Вейерштрасса для угловых точек [7].
Последующий шаг заключается в определении интервала време¬
ни. По-видимому, прямое решение невозможно, поэтому йредлагаечея
следующее косвенное рассуждение.
Случай I Случай П
Фиг. 70. Пример сопряжения участков
кривых.
172
Интеграл времени, определяемый уравнением (46), вычисляется
(в общем, приближенными методами) вдоль кривых IABF, . .
IKLF. Так как каждая из
этих кривых связана с раз- Щ7&г
ными значениями постоянной
Я, интегрирование приводит
к результату следующего
вида:
к=А(Н).
(81]
Аналогичное интегриро¬
вание уравнения (45) приво¬
дит к выражению
О
QJ8 0,20
ХК = В(Н).
(82)
OfiO 0fi3
v
х = -л
Уравнение (81) дает зна¬
чение Я (а потому особую
кривую Эйлера), связанное
с требуемым значением вре¬
мени. В свою очередь урав¬
нение (82) определяет максимум
рую может пролететь самолет с
ленный интервал времени.
Фиг. 71. Семейство экстремальных кри¬
вых, соответствующих заданным исход¬
ным и конечным значениям массы и ско¬
рости (параболическая поляра с посто¬
янными коэффициентами).
(или минимум) дистанции, кото¬
ракетным двигателем в установ-
IX. 1. 6. Численный пример
Для иллюстрации предыдущих положений даются численные
расчеты для следующего ряда условий (фиг. 72):
= 0; -Х = 0;
-^- = 0,074; = 0,3;
т2 Vr
-^-=0,027; -^*-=0,38.
т2 Vr
Так как этот пример имеет качественный характер, для упроще¬
ния предполагается, что 13™* = оо. Время tK и дальность Хк представ¬
лены с помощью следующих безразмерных параметров:
gXK
EVr' EV2 ’
где
(83)
E=\Vkcx о (84)
представляет собой максимальное аэродинамическое качество са¬
молета.
Решение проблемы граничных значений дано на фиг. 72 в пара¬
метрической форме уравнениями (81) и (82). Для интервала времени
173
^k = 0,71Z: (lA/g) траектория, приводящая к максимуму дальносг;.
есть кривая IRJF, связанная с участком кривой переменной тяг]
Я = +0,1 (см. фиг. 71). Аналогично для интервала времени tK =
= 0y87EVr/g решение соответствует кривой Н = —0,1. Исключен и.
Ug
EVr
1,0
0,8
0,6
0,4
0,2
-0,2 -0,1
1
1
1 -
м
хкд I
xL = 0,30; хк=0,38
- WfOm-, If--0,027 Л-
Ml 1
0,26
0/24
0,22
0,20
0,18
*к9
EVi
О 0/ 0,2
"-Ъ
Фиг. 72. Пройденный путь и общее время
как функция параметра Я (параболическая
поляра с постоянными коэффициентами).
параметра Я приводит к выражению типа XK = C(tK)y которое пред¬
ставлено на фиг. 73. Этот график непосредственно дает максималь¬
ную дальность, возможную при заданном времени полета.
С инженерной точки зрения интересно заметить, что максималь¬
ная абсолютная дальность получается на кривой Я~0 [3 и 4]. При
полете вдоль участка кривой Я = -[-0,12, что соответствует скоростям
0,2k
0,22
Кя
О 18
’ 04 05 0,6 0,7 0,8 0,9
М
EVr
Фиг. 73. Максимальная дальность как
функция общего времени полета (парабо¬
лическая поляра с постоянными коэффи¬
циентами).
. —1
Н--й
Xi-0,30 , Х/0,38
н:°’2/
— --0,074 , ~/=0 027
т2 ’т2 '
I I
полета примерно на 20% выше, можно сэкономить около 20% вре¬
мени с потерей всего около 5% дальности. Аналогично, следуя по
кривой Я=+0,2, что соответствует скорости полета примерно на
30—60% выше, чем скорости, связанные с Я = 0, экономия во време¬
ни около 40% приведет к потере 20% дальности.
174
IX. 1.7. Доказательство достаточности решения
Предположим теперь, что особая 'Кривая Эйлера, удовлетворяю¬
щая граничным условиям, указанным в разд. IX. 1. 5, найдена. Пред¬
положим также, что И является частным значением Ня которое обес¬
печивает полет самолета от I
до F в заданное время /к. Су¬
ществуют две возможности:
случай^ когда Н<О, и случай,
когда Я>0.
Для Я<0 (фиг. 74) доказа¬
тельство максимального харак¬
тера дальности траектории
IMNF осуществляется путем
сравнения ее с контрольной
кривой IKF. При этом следует
воспользоваться свойствами
функции со и теоремой Грина,
как это показано в разд. IX. 1. 2.
Кроме того, следует иметь в виду неравенство (Зтах, так как
оно определяет класс допустимых перемещений для самолета в пло¬
скости (т, v) [4]. _
Аналогичный прием можно 'Применить для случая И>0. Можно
показать, что кривая Эйлера IMNF дает решение максимальной
дальности, если она полностью заключена в областях А и В (см.
фиг. 69). Наоборот, она дает решение минимальной дальности, если
она полностью заключена в областях В и С1.
3АКЛ ЮЧ ЕН И Е
В настоящей статье рассматривалась программа расходования
топлива, обеспечивающая достижения минимума произвольных фун¬
кций, зависящих от конечных величин'времени, массы, дальности и
скорости. Было показано, что экстремальные кривые состоят из уча¬
стков кривых нулевой тяги, кривых максимальной тяги двигателя и
кривых переменной тяги.
В общих рамках изложенного подхода исследовано программиро¬
вание тяги, приводящее к максимальной дальности при заданном
времени полета, и дан способ построения экстремальных кривых.2
Подбором подходящего режима расходования топлива можно
значительно уменьшить общее время полета в заданную точку по
сравнению со временем, связанным с решением, обеспечивающим до¬
стижение абсолютного максимума дальности. Численные примеры
1 Авгор не нашел удовлетворительного способа решения более общего слу¬
чая кривых, пролегающих в трех областях Л, В и С.
2 В 1958 г. А. Миеле опубликовал р-аботу, посвященную изучению изопери-
Метриче-ской задачи» движения ракеты в «изотермической атмосфере по прямолиней¬
ной траектории, наклоненной к горизонту.
A. Mielle, On the Brachistooronic Program for a Rocket Powered Missile Tra¬
veling in a Isotermal Medium, „Jet Propulsion", 1958, vol. 28, No. 10, pp. 675—684.
m
[ to (my H)- 0
О3*,.
©
N
Фиг. 74. Сравнение кривой Эйлера
IMNF и произвольной контрольной,
кривой IKF.
175
показывают, что время полета можно сократить до 20% за счет по¬
тери менее чем 5'°/о дальности К
ЛИТЕРАТУРА
1. Гамель Г., «Об одной задаче вариационного исчисления, связанной с
движением ракеты».
Hamel G., Uber eine mit dem Problem der Rakete zusammenhangende
Aufgabe der Variationsrechnung, ZAMM, 1927, vol. 7.
2. С. Тзян1 и P. Эванс, «Оптимальное программирование тяги высотоой
ракеты».
Tsien Н. S. and Evans R. С., Optimum Thrust Programming for a Soun¬
ding Rocket, «Journal of the American Rocket Society», 1951, vol. 21, No. 5
pp. 99—107.
3. А. Г и б с с, «Оптимальная программа изменения тяги двигателя при гори¬
зонтальном полете».
Hibbs A. R., Optimum Burning Program for Horizontal Flight, «Journal oi
the American Rocket Society», 1952, vol. 22, No. 4, pp. 206 —212.
4. П. Чикала и А. Миеле, «Обобщенная теория оптимального про¬
граммирования тяги при горизонтальном полете самолета с ракетным двигате¬
лем».
Cicala P. and Miele A., Generalized Theory of the Optimum Thrust
Programming for the Level Flight of a Rocket-Powered Aircraft, «Jet Propulsion»,
1956, vol. 2b, No. 6, pp. 443—455.
5. Г. Блисс, «Лекции по вариационному исчислению».
Bliss G. A., Lectures on the Calculus of Variations, The University of
Chicago Press, Chicago, 1946.
6. Вольца О., «Лекции по вариационному исчислению».
Bolza О., Lectures on the Calculus of Variations, G. E. Stechert and1 Co,
New York, 1946.
7. А. Миеле, «Расширение теории оптимальной программы расходования
топлива ракетным самолетом при горизонтальном полете».
Miele A., An Extension of the Theory of the Optimum Burning Program
for the Level Flight of a Rocket-Powered Aircraft, Purdue University, School of
Aeronautical Engineering, Report A-56-1, 1956 (AFOSR-TN-56-302).
1 Указанную выше точку зрения подтвердили обширные цифровые подсче¬
ты, проведенные для случая параболической поляры с коэффициентами, завися¬
щими от числа М [7].
РАЗДЕЛ III
ОПТИМАЛЬНОЕ НАПРАВЛЕНИЕ ТЯГИ И МЕТОДЫ
ПОДБОРА СТУПЕНЕЙ БАЛЛИСТИЧЕСКИХ РАКЕТ
Д. ЛОУДЕН
МАКСИМАЛЬНАЯ ДАЛЬНОСТЬ
МЕЖКОНТИНЕНТАЛЬНЫХ РАКЕТ1
ВВЕДЕНИЕ
В предыдущей статье автора [1] проблема программирования на¬
правления тяги двигателя ракеты для обеспечения максимальной
дальности была исследована в предположении, что влиянием кривиз¬
ны земной поверхности и вращения Земли, а также влиянием сопро¬
тивления воздуха и изменением силы тяжести с высотой можно пре¬
небречь. В случае межконтинентальных ракет сопротивление возду¬
ха всегда мало по сравнению с тягой двигателя и весом ракеты, бы¬
стро уменьшается по мере набора высоты и становится ничтожно
малым на высотах более 30 км. Однако влияние кривизны земной
поверхности и вращения Земли, а также изменение силы тяжести с
высотой необходимо учитывать, иначе возможны существенные по¬
грешности в расчетах. Целью настоящей статьи является выяснение
необходимых изменений методики предыдущего исследования для
учета всех этих факторов.
Принятые обозначения
а—Р/у.
Л, В, С—см. формулы (2)-^-(4)
/—составляющая ускорения снаряда, обусловленная тягой двигателя
^—ускорение силы тяжести на поверхности Земли
h=qilV
h' =h (для ракет малой дальности)
h' = h-\-w (для ракет большой дальности)
И—высота верхней точки траектории ракеты
k = q2IV
1 D. Law den, Maximum Ranges of Intercontinental Missiles, «Aeronautical
Quarterly», 1957, vol. VIII, No. 3, pp. 269 — 279.
12 394
177
h> h— направляющие косинусы линии тяги двигателя
т—относительная масса ракеты
М о— масса ракеты при старте
Р— тяга двигателя
<7i, q2—координаты ракеты в момент окончания работы двигателя
Яь Яч—составляющие скорости ракеты в момент окончания работы двигателя
г— расстояние от ракеты до центра Земли
R— радиус Земли
t— время с момента старта ракеты
Т—время полета до окончания работы двигателя
u=k —|—X/v
V—скорость, при которой ракета удерживается в пустоте на круговой орбите
на уровне поверхности Земли
w=* Wl V
W— скорость точки на экваторе при суточном вращении Земли
x=qi/R
xi> х2— координаты ракеты в момент времени t
X— см. формулу (31)
_v=?2/fl
а— разница значений долготы в точке падения ракеты и в момент окончания:
работы двигателя
г - угол поворота Земли за время полета ракеты
б—долгота ракеты, отсчитываемая от неподвижного меридиана ракеты
у, v— см. формулы (25) или (29)
Р — массовый секундный расход топлива
р—дальность ракеты в угловом измерении
х=ЛГ0/р
о— угол наклона тяги двигателя к горизонту
ПРЕДВАРИТЕЛЬНЫЕ ИССЛЕДОВАНИЯ
Для того чтобы иметь возможность ограничиться рассмотрением
двухмерной задачи примем, что ракета движется в плоскости эква¬
тора. Кроме того, не будем учитывать влияние кривизны земной по¬
верхности и вращения Земли, а также изменения силы тяжести на
начальном участке траектории ракеты, когда двигатель работает.
Выберем в плоскости движения горизонтальную и вертикальную осп
Ох и Ох2, образующие систему координат с началом в точке старта О.
вращающуюся вместе с Землей. Обозначим координаты ракеты п
'момент окончания работы двигателя через <7i и <72 и составляющие
скорости ракеты в тот же момент—через q\ и q2. Примем, что состав¬
ляющие скорости ракеты в момент окончания работы двигателя от¬
носительно неподвижной системы координат, совпадающей с мгно¬
венным положением осей Ох1 и Ох2 в этот момент времени, будут
равны qi-\-W—параллельно поверхности Земли и q2—перпендику¬
лярно поверхности Земли. Здесь через W обозначена скорость точки
на экваторе при суточном вращении Земли. В случае стрельбы про¬
тив вращения Земли знак W следует заменить обратным.
Рассмотрим дальнейшее движение ракеты в поле земного притя¬
жения и обозначим через г расстояние ракеты от центра Земли, вы¬
178
раженное в радиусах Земли R, и через 0—разницу значений долго¬
ты ракеты в рассматриваемый момент вращения и в момент оконча¬
ния работы двигателя. При этом будем рассматривать движение в
неподвижной системе координат и будем отсчитывать долготу от
меридиональной плоскости, сохраняющей неизменное положение в
пространстве. Тогда, обозначив через V скорость тела, движущегося
в пустоте под действием притяжения Земли по круговой орбите, ра¬
диус которой равен радиусу Земли, получим следующее уравнение
эллиптической траектории ракеты в полярных координатах:
Л- = В-\-(\—В) cos 0 — С sin 0, (1)
где
А = \ +у; (2)
£ = - ; (3)
<Л + «О2 (1 +V)
С=~Г7_— • (4)
h -f- w
В точке пересечения траектории с земной (поверхностью r= 1 и О
удовлетворяет уравнению
£_|_(1—Б)cos 0—С sin 0 =А. (5)
Если обозначить удовлетворяющее условиям задачи решение
этого уравнения через а, то можно показать, что
t « - С+/С* + (Л-1)(2В-Л-1) (6)
ё 2 2В— А — 1 ’ 1 '
где а—разность значений долготы ракеты в точке падения и в мо¬
мент окончания работы двигателя.
Из уравнения (1) следует, что расстояние от ракеты в верхней
точке траектории до центра Земли Я может быть найдено по формуле
Н= ■■ А (7)
В — /С* + (В - 1)2 v 7
Эффективная дальность ракеты в угловом измерении может быть
вычислена путем вычитания из угла а (значение которого известно)
угла поворота Земли е за время свободного полета ракеты и прибав¬
ления величины изменения долготы ракеты относительно Земли за
время работы двигателя. Эта последняя величина может быть найде¬
на по формуле
х=*±. (8)
R v ’
Так как за время баллистического полета ракеты момент коли¬
чества движения ее относительно центра Земли остается постоян¬
ным, то
r20 = const = —. (9)
R v '
12*
179
Отсюда следует, что (поскольку для оптимальных траекторий г
мало отличается от единицы и А ~ 1, то можно 'принять с вполне до¬
статочной степенью точности
i-<t±pz. „о,
Отсюда получаем приближенное выражение времени полета ра¬
кеты по баллистической части ее траектории
Так как угловая скорость вращения Земли равна W/R, то угол
поворота Земли за время е будет равен
= (12)
V(h-\-w) h-\-w
В соответствии с этим полная дальность ракеты в угловом изме¬
рении будет равна
Для ракеты относительно малой дальности упрощения, использо¬
ванные при вычислении е, не приводят к большим погрешностям.
Для ракеты большой дальности погрешность увеличивается, однако
тот член в формуле (13), в котором содержится погрешность, а имен¬
но w/(h-\-w), будет невелик, так как в этом случае w мало по срав¬
нению с к. Отсюда следует, что ошибка в величине ? в обоих случаях
получается незначительной.
В следующем разделе статьи проведено исследование программы
изменения направления тяги двигателя, при котором получается
максимальное значение ?.
ОПТИМАЛЬНАЯ ПРОГРАММА ИЗМЕНЕНИЯ НАПРАВЛЕНИЯ
ТЯГИ ДВИГАТЕЛЯ
Опыт предварительных исследований позволяет предполагать,
что максимальная дальность, которую можно получить от данной
ракеты, сравнительно мало зависит от программы изменения на¬
правления тяги двигателя. Поэтому можно с достаточным основани¬
ем до расчета оптимальной программы предварительно принять
относительно грубое приближенное значение величины ?. Так, в
уравнении (13) можно пренебречь величиной х, так как горизон¬
тальная дальность ракеты за время работы двигателя составляет
незначительную часть полной дальности (обычно меньше 10%)-
Величина у также ничтожно мала по сравнению с единицей. На ос¬
новании этого можно заменить уравнения (2)-4-(4) следующей си¬
стемой уравнений:
е
V(h+w)
(П)
(13)
Л= 1; В =
(h -f- w)2 * (h w)
(14)
180
После этого из уравнения (6) 'Получается
tgiL^ _?<* + ”> , (15)
8 2 1 — (h + wf v ;
В случае ракеты большой дальности величина w/(h-\-w) мала, и
поэтому уравнение (13) можно заменить приближенным соотноше¬
нием
?=а, (16)
после чего задача сводится к определению условий получения макси¬
мального значения а, а значит, и тангенса tg а/2, определяемого по
формуле (15).
При малой дальности ракеты величина wJ(h-\-w) не может счи¬
таться малой, однако в этом случае можно полностью пренебречь
вращением Земли, не внося существенной погрешности в определе¬
ние дальности и тем более в расчет оптимальной программы направ¬
ления тяги, и рассматривать всю траекторию ракеты в системе коор¬
динат, неподвижной относительно Земли. Положив в уравнении (15)
w=0, найдем следующее выражение для дальности в угловом вы¬
ражении относительно Земли, отсчитывая ее от точки окончания ра¬
боты двигателя:
tg- = -^. (17)
s 2 1 — Л2 v ’
Равным образом уравнение (13) в результате упрощений прини¬
мает вид ? = а-\-х и при возможности пренебречь величиной х задача
сводится к определению условий получения максимального значе¬
ния а, определяемого формулой (17).
Если обозначить через 1± и h направляющие косинусы линии тяги
двигателя в системе координат OxLx2, то, !как показано в работе [1],
условия получения максимума ? = p (qly q2t qь q2) без учета влияния
кривизны земной поверхности и вращения Земли, а также сопротив¬
ления воздуха и изменения ускорения силы тяжести с высотой за
время работы двигателя имеют вид
др до
Лл (18)
dq2 dq2
где Т—время полета ракеты при работающем двигателе.
В случае ракеты большой дальности, при котором требуется обе¬
спечить максимум величины а, определяемой формулой (15), при¬
веденное выше условие принимает вид
1Х _ k\\ +(h+w)*] (19)
(h -ф w) [1 — (h -\-w)2\
181
В случае ракеты малой дальности о определяется по форму,-ю
(17), и условие максимума а имеет вид
Л; (14-/г2)
/2 ~h( 1 — А2)
(20)
Таким образом как в первом, так и во втором случаях оптималь¬
ное направление тяги оказывается постоянным.
Аналогично тому, как это сделано в работе Ш, рассмотрим два
случая: 1) случай уменьшения тяги двигателя по экспоненциальному
закону, при котором обусловленная тягой составляющая ускоренна
ракеты / получается постоянной, и 2) случай постоянной тяги дви¬
гателя.
В первом случае, как показано в работе [1]:
На основании этого получаем, переходя к безразмерным величи¬
нам, следующие соотношения:
Величина /Г представляет собой приращение скорости, которое
получила бы ракета под действием одной только тяги двигателя. Ве¬
личина К показывает, какую часть составляет это приращение oi
скорости тела, описывающего в пустоте под действием земного при¬
тяжения круговую орбиту с радиусом, равным радиусу Земли. Если
бы К было равно единице и топливо было израсходовано в течешь1
ничтожно малого промежутка времени, то ракета получила бы ско¬
рость, достаточную для того, чтобы удержаться в пустоте на круговой
орбите, проходящей у поверхности Земли. Величина v означает отно¬
шение ускорения ракеты под действием тяги двигателя к ускорению
силы тяжести у поверхности Земли.
Во втором случае, обозначив постоянную тягу двигателя
через Р, массовый секундный расход топлива через ц и массу ракеты
при старте через Мо, найдем ускорение ракеты под действием тягп
двигателя в некоторый момент времени t по формуле
?1=Ы/Т <72=(4/-S')7”;
Я2=\(к/-g)T*.
(21)
(22)
(23)
(24)
где
'> = L и V^gR.
v g
(25)
а
(26)
Р
где а = — и х
V-
М0
182
При этом, как показано в работе [1], .параметры движения ракеты
В момент окончания работы двигателя определяются по формулам
qxz=.alx In -
q2 = al2\n-
т — т ’
<72 = a/2[7’-(x-7')ln-l7'
■gh
(27)
(28)
Безразмерные уравнения, соответствующие формулам (27), сов¬
падают с уравнениями (23) при условии, что параметры X и v опре¬
деляются в этом случае по формулам
\ л , т а |
Х==— In = — In m\
V z-T V
a , x
-In
gT z-T gT
In m, (29)
где m-
z—T
■относительная масса ракеты.
При этом безразмерные уравнения, соответствующие формулам
(28), имеют вид
X=2LilX; y=^-hi2x-l)y
v \ v I
где
Л=-
]n m m — 1
(30)
(31)
В конце настоящей статьи приведена таблица значений X. Не¬
трудно заметить, что уравнения (30) совпадают с уравнениями (24)
при подстановке в них значения Х=\/2. Таким образом при соответ¬
ствующем определении параметров X, v и X уравнения (23) и (30)
могут быть использованы в обоих случаях для определения парамет¬
ров движения ракеты в момент окончания работы двигателя.
После подстановки в уравнения (23) выражений для направляю¬
щих косинусов 1\ и /2, обеспечивающих максимальную дальность ра¬
кеты [в соответствии с формулой (19) для ракеты большой дально¬
сти и с формулой (20) для ракеты малой дальности], получаются сле¬
дующие соотношения:
А =
lk( 1 +/г/2)
k =
Vk2(\+h'2Y+h'2{\- /У2)2
\h' (1 — h'2)
Vk2(\ + h'2)2 + h'2(\-h'2)2 ''
(32)
(33)
183
где h' = h—для ракеты малой дальности и h' = h-\-w—для ракеты
большой дальности. Путем несложных (Преобразований можно пока¬
зать, что эти соотношения эквивалентны следующим зависимостям;
А + - = КХ2 —Л2,
N
hr
(34)
В случае h' = h из этих зависимостей можно исключить h. Не-
трудно показать, что при этом величина u — k-\ удовлетворяет
v
кубическому уравнению
а3 + v (|— х) н2 - (1 + X2) и - vX (1 - X2) = 0. (35)
Уравнения (34) и (35) были решены численным методом относи¬
тельно h и k при ряде значений параметров К и v. В каждом случае
по формулам (23) были вычислены значения U и /2 и был найден
угол Ф между направлением тяги и горизонтом. Эти значения Ф при¬
ведены в следующем разделе статьи. При известном Ф можно рас¬
считать по формулам (30) путь ракеты за время работы двигателя и
затем заново вычислить значения h и & по формулам (23). После
этого можно вычислить по формуле (13) дальность ракеты и по фор¬
муле (7)—высоту верхней точки траектории.
ЧИСЛОВЫЕ РЕЗУЛЬТАТЫ
Уравнения (32) и (33) были решены численным методом при
следующих значениях конструктивно-баллистических параметров:
Х=0; 0,2, 0,4, 0,6, 0,8; v = 1, 3, 5, 7, 9,оо. В каждом случае были вычи¬
слены два значения Ф: одно—для ракеты малой дальности и второе—
для ракеты большой дальности. Оказалось, что эти пары значений Ф
разнятся между собой во всех случаях не более чем на 10%, а при
средних дальностях, когда не так очевидно, к какой категории отне¬
сти ракету, не более чем на 1%. Поэтому правильный выбор опти¬
мального значения Ф для каждой пары значений к и v не вызывал
каких-либо трудностей. Найденное значение Ф проверялось путем
расчета изменения дальности при уменьшении и увеличении угла Ф
на 1°. Изменение дальности во всех случаях оказалось малым (по¬
рядка 2 дуговых минут), однако в тех случаях, когда это было необ¬
ходимо, на основании этих расчетов были введены поправки для по¬
лучения значений Ф в табл. 1 с точностью до 1°. Под каждым значе¬
нием Ф в таблице приведено соответствующее значение дальности
184
по экватору в градусах и, минутах дуги экватора. В правом крайнем
столбце таблицы приведено значение А,, необходимое для достижения
скорости ХСу при которой радиус орбиты ракеты в пустоте под дейст¬
вием земного притяжения был бы равен радиусу Земли для каж¬
дого из рассмотренных значений v. Величина определялась по
формуле.
Х-“73=Г <36>
При этих расчетах, а также и в других местах настоящего иссле¬
дования величина w была принята равной 0,0587. При расчете
дальности значения х и у определялись по формулам (24), а не по
формулам (30). Однако и в тех случаях, когда применялись бы фор¬
мулы (30), ошибка в результатах расчета не превышала бы несколь¬
ких дуговых минут.
Все расчеты были повторены при значении w = —0,0587, т. е. в
предположении запуска ракеты против направления вращения Зем¬
ли. Результаты этих расчетов сведены в табл. 2.
Нетрудно заметить, что при дальностях, превышающих 3200 км
(? >29°), разница в дальностях ракеты при стрельбе в направлениях
на восток и на запад—порядка 10%. При дальностях больше 6400 км
эта разница превышает 25%.
При приближении скорости в момент окончания работы двига¬
теля к значению, достаточному для удержания ракеты в пустоте на
круговой орбите на уровне поверхности Земли (т. е. при очень боль¬
ших дальностях), угол Ф становится малым и начальная часть тра¬
ектории ракеты проходит с небольшим углом наклона сквозь земную
атмосферу. В этих условиях сопротивление воздуха является важным
фактором, определяющим форму начального отрезка оптимальной
траектории и резко увеличивающим ее крутизну до момента выхода
за пределы атмосферы, после чего форма траектории определяется
уравнениями, выведенными в настоящей статье. Определение точной
формы начальной части траектории будет предметом дальнейшей
работы.
Из табл. 1 и 2 видно, что дальности, превышающие 6400 км, соот¬
ветствуют интервалу значений Ху не превышающему по своей протя¬
женности величины 0,2. Проектирование ракет с такой дальностью
представляется технической задачей одного порядка трудности с
проектированием искусственного спутника Земли.
Необходимо предостеречь читателя о том, что в тех случаях, ког¬
да оптимальный угол Ф мал и тяга двигателя постоянна, вертикаль¬
ная составляющая тяги может быть меньше стартового веса ракеты.
В этом случае начальная часть траектории ракеты пересекает поверх¬
ность Земли, и найденное решение является, очевидно, нереальным.
Этот недостаток решения не имеет места при учете сопротивления
воздуха.
185
Таблица l
Оптимальный угол наклона тяги двигателя к горизонту Ф и дальность
в угловом измерении р при стрельбе по направлению вращения Зем л и
A=0
0,2
0,4
0,6
0,8
X,
v=l
90°
0°0'
90°
0°0'
90°
0°0'
90°
0°0'
90°
0°0'
U>0
V = 3
53°
0°0'
50°
1°47'
49°
7° 36'
46°
19° 9'
42°
41°34'
0,998
v=5
49°
0°0'
49°
2° 2/
48°
8° 43'
45°
22°27'
37°
51°3'
0,961
v=7
48°
0°0'
47°
2°9'
45°
9° 14'
40°
23°54'
33°
55°4'
0,951
v=9
47°
0°0'
46°
2° 12'
44°
9°29'
40°
24°41'
32°
57°14'
0,947
\i = oo
45°
o°o'
44°
2°23'
42°
10°25'
37°
27° 14'
27°
64° 7'
0,941
Таблица 2
Оптимальный угол наклона тяги двигателя к горизонту Ф и дальность
в угловом измерении р при стрельбе против вращения Земли
X=0
0,2
0,4
0,6
0,8
1,0
V=1
90°
0°0'
90°
0°0'
90°
0°0'
90°
0°0'
90°
0°0'
90°
0°0'
ОО
v=3
53°
0°0'
51°
1°31'
50°
7°11'
47°
17°23'
Co 4^
С л
о о
ОО
О О
ОО о
oo
1,123
v=5
49°
0°0'
48°
2°1'
46°
8°14'
oo
о о
О
Tf* CM
39е
41°42'
30°
89°19'
1,081
v=7
48°
0°0'
47°
2°4'
45°
8° 38'
42°
21° 17'
38°
44° 24'
26°
97° 27'
1,07
■v = 9
47°
0°0'
46°
2° 8'
44°
8° 52'
41°
21°52'
37°
45° 54'
25°
101°43'
1,065
v = oo
45°
0°0'
45°
2° 20'
44°
9° 40'
39°
23°57'
СЯ СО
О СО
о о
о
18°
114о10'
1,059
Значения X по формуле (31)
т
1,0
1.5
2,0
2,5
3,0
3,5
4,0
4,5
5,0
5,5
X
0,5
0,4662
0,4427
0,4246
0,4101
0,3982
0,388
0,3792
0,3715
0,364[
т
6
6,5
7
7,5
8
8,5
9
9,5
10
10,5
X
0,3582
0,3524
0,3472
0,3425
0,338
0,334
0,3301
0,3265
0,3232
0,3199
ЛИТЕРАТУРА
1. Д. Ф. Лоуден, Проблемы динамики межпланетного полета.
D. F. Lowden, Dynamic Problems of Interplanetary Flight, „The Aeronautical
Quarterly-, 1955, vol. VI, August, p. 165.
186
Б. ФРИД и Дж. РИЧАРДСОН
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ РАКЕТ1
ВВЕДЕНИЕ
Несмотря на то, что изучению оптимальных траекторий ракеты
уделялось достаточное внимание, по-видимому, один простой резуль¬
тат еще недостаточно известен. Если массу ракеты М и тягу двигате¬
ля Р рассматривать как функцию времени и если пренебречь влияни¬
ем аэродинамических сил на ракету как материальную точку, а также
предположить, что гравитационное поле постоянно по величине и
направлению, то максимальной дальности полета ракеты будет соот¬
ветствовать неизменяемое в пространстве в течение всего активного
полета направление силы тяги. Справедливость этого вывода не
зависит от природы функций M(t) и P(t), хотя величина угла на¬
правления тяги будет, конечно, зависеть от этих функций. Из двух
главных допущений—пренебрежение аэродинамическими силами и
изменение интенсивности гравитационного поля—первое является
более трудным для учета, так как включение в рассмотрение подъем¬
ной силы и силы лобового сопротивления значительно усложняет
анализ. Однако получаемые при введении упрощений значения мак¬
симальной дальности представляют интерес даже для случая полета
в земной атмосфере, так как в тех случаях, когда рассматриваются
более реальные траектории, они дают представление о некоторой
теоретически возможной оптимальной величине.
Более того, допущение о постоянстве гравитационного поля мо¬
жет быть опущено без особой трудности. При замене постоянного
гравитационного поля центральным гравитационным полем, интен¬
сивность которого изменяется обратно пропорционально квадрату
расстояния до центра Земли (поле Кеплера), максимальная даль¬
ность не вполне точно соответствует условию постоянства направле¬
ния тяги, однако будет показано, что для наиболее интересных
случаев оптимальное направление линии тяги весьма близко к усло¬
вию постоянства направления.
В работе выводятся условия для оптимального направления ли¬
нии тяги при постоянном гравитационном поле и в поле Кеплера—
точные для первого и приближенные для второго.
ОБЩИЕ СООБРАЖЕНИЯ
Предположим, что ракета в течение периода времени 0<t<TK
движется под действием силы тяги (активный участок), а с момента
выключения двигателя Тк до момента падения на землю Гк+т она
следует по траектории свободного падения. В этих условиях полная
дальность ракеты определяется ее положением и скоростью в момент
■выключения двигателя, т. е. векторами гк и vK:
R=R(rK,vK).
1 В. Fried and J. Richardson, Optimum Rocket Trajectories, «Journal
of Applied Physics», 1956, vol. 27, No. 8, pp. 955 — 961.
187
Последние величины, в свою очередь, зависят от программы и >,
менения направления тяги, поскольку будем считать, что тяга Р и
масса ракеты М являются заданными, но произвольными 1 функция¬
ми времени. Для плоской траектории направление силы тяги опре¬
деляется углом ф(£) между вектором тяги в момент времени t и на¬
правлением горизонта в месте запуска (фиг. 75). Любому виду этой
функции соответствуют определенные величины радиус а-вектор а п
вектора скорости в момент выключения двигателя^ rK w_vK и даль¬
ность R, т. е. R, ик и гк являются
функционалами от функций ф(0-
Для определения функции ф(£),
определяющей максимальную даль¬
ность R, наиболее удобно применить
метод функциональной производной.
Если /?(ф) представляет собой даль¬
ность, соответствующую некоторой
выбранной функции б, то функцию
/?[б+ец], где т] есть произвольная!
функция времени, можно разложить
в ряд по степеням е:
Фит. 75. Схема типовой пло¬
ской траектории.
R И + «ч!=R Ж + з J z (t) -nWdt+Q и.
(i)
Функция х называется функциональной производной 2 R относи¬
тельно ф, которая в наиболее распространенной форме записывается
как
ья
об (t)
■lit).
Она даег, в сущности, изменение R при малом (соответственно
установленном) изменении ф в точке t. Более наглядно это видно
из другой формы записи этой производной:
ЪЯ
(t)
Him — /?[ф + е&,)>
£->0 da
(T)
где 8t—дельта-функция Дирака [2], характеризующаяся тем, что
8, (0 = 0 при V =f=t и +| dt'bt(t) = \.
1 Здесь и далее термин «произвольная функция» следует понимать скорее
в физическом, чем в математическом смысле. Под этим термином понимается
любая функция, удовлетворяющая таким ограничениям, как непрерывность,
дифференцируемость, положительность и т. п., а также соответствующая физи¬
ческому смыслу описываемых величин.
2 Если функционал R есть интеграл, то функциональная производная пре¬
вращается в известную из вариационного исчисления вариационную производ¬
ную. См. [1] и [2].
188
Так как согласно уравнению (Г) функциональная производная
может быть выражена в виде обычной производной, то большинство
правил дифференциального исчисления будет справедливо для функ¬
циональных производных. В частности, «цепное правило» (при диф¬
ференцировании функции от функции) дает
bR (2)
b^(t) r* 0^(t) L'K 5'HO ’
где VrKR — вектор с компонентами дЩдхк и dRjdyK и
VvKR— вектор с компонентами dRjdvХк и dR/dvyк.
Поскольку режим с очень малыми секундными расходами топли¬
ва для ракет неэкономичен, то расстояние, пройденное, во время ак¬
тивного полета, по сравнению с радиусом Земли может считаться
малым. Поэтому можно предположить с достаточным приближением,
что во время активного полета гравитационное силовое поле постоян¬
но по величине и направлению. Тогда уравнение движения ракеты
dv Р - /Qv
dt М ^
(где /—единичный вектор по оси у) может‘быть сведено к квадрату¬
рам, в результате чего для момента отсечки (t = TK) получаем
^=idt^m~gTj+i’' <4)
о
т
7К = J dt(TK-t)-^-±g7V+v0TK + 70, (5)
о
где v0 и г0—начальные значения векторов скорости и положения.
Из этих уравнений можно легко найти вариационные производ¬
ные, входящие в уравнение (2). Если ф(/) ->ф(0+£Т|(0> то> огра¬
ничиваясь только членом с первой степенью е, будем иметь
v С) ->V(t) + SY] (t) р (*) yv (£),
где N—единичный вектор, нормальный к F и
т
о
По определению Ъьк - есть коэффициент при sy] (^) в послед-
Ц (О
нем выражении, т. е.
-^-=^-yv(0. (6)
о ф(0 M(t) 4
189
Аналогично из уравнения (5) получаем
4V) 9
bv к
Уравнения (6) и (7) можно получить также исходя из простых
'физических соображений. Если мы будем изменять только направ¬
ление тяги, а не ее величину, тогда вектор SP должен быть направ¬
лен нормально к вектору Р. Этот дополнительный импульс произведет
за единицу времени приращение скорости
которое, очевидно, равно приращению скорости ик, так как силовое
поле постоянно. Это приводит сразу к уравнению (6). Уравнение (7)
выражает тот факт, что изменение координаты отсечки равно прира¬
щению скорости, умноженному на время до момента выключении
двигателя. Из уравнений (2), (3) и (4) получим
Условие максимума функционала R может быть записано в виде
Поскольку N нормален к тяге, то это означает, что вектор тяги i
момент времени t направлен вдоль вектора
Во всех задачах подобного рода бывает необходимо -проводить
специальные исследования для установления характера экстремума.
Мы же не будем проводить его, поскольку из самой физической при
роды задачи ясно, что в данной задаче экстремум является макси
мумом.
Следует отметить, что уравнения (8) и (9) носят общий характер
и поэтому они справедливы для любой формы функции дальности
R(rK, vK). Последняя зависит от наших допущений относительно ха
рактера внешнего силового поля, которое определяет участок пас-
сквного полета (постоянное, обратно квадратичное и т. д.), но в урав¬
нениях (8) и (9) содержится только допущение о том, что во время
активного полета внешнее силовое поле постоянно, а аэродинами¬
ческие силы пренебрежимо малы или вообще отсутствуют.
ov(t) = P(t) otyN (t)/M (t)
Для всего интервала времени полета, в котором Р(1)ф0, мы по
этому потребуем
M(t)[vVKR+(TK-t)vrJi)=0.
p(t) = vVKR + (TK-t)vrKR.
(9)
190
ПОСТОЯННОЕ СИЛОВОЕ ПОЛЕ
Рассмотрим вначале случай постоянного гравитационного сило¬
вого поля на участке пассивного полета ракеты. Это допущение
очень близко к действительности для ракеты с дальностью (от места
запуска до места падения), малой по сравнению с радиусом Земли.
Б этом случае мы видим, что
где т есть время свободного полета (от момента отсечки до момента
падения). Действительно ясно, что в постоянном силовом поле изме¬
нения ovK в скорости в момент отсечки и изменения &гк в положении
места отсечки, при условии SrK=xSvK, должны вызывать одинаковое
изменение в дальности R.
Тогда из уравнения (9) получаем
Так как VVk R представляет собой вектор, не зависящий от вре¬
мени t, то направление вектора р также не зависит от t, и поэтому
экстремальное решение характеризуется постоянным направлением
вектора тяги.
Для того чтобы определить величину угла направления вектора
тяги, необходимо составить явное выражение для R(rKy vK). Это вы¬
ражение можно записать очень просто:
Кроме того, если вектор тяги параллелен VvKR (и VrKR), то
VvKR=>^rKR,
(10)
R—Т* XVK
(11)
где х время свободного полета, определяемое уравнением
yK + vKy*-jg*2=0,
т. е.
Таким образом, имея в виду уравнение (10), получаем
1
(12)
(*2ку+2£Ук)2
191
Эта формула содержит ф в неявной форме, так как vK -и гк сами
суть функции ф. Последняя зависимость может быть выведена а-
уравнений (4) :и (5).
Поскольку ф есть постоянная величина, то можно получить сле¬
дующие соотношения:
-г = ^COS Ф + v0x,
vKy=>Ssln4? + v0y — gTK,
xK = D cos^ + Xq,
ук = D sin«1* +y0 + v0yTK—~gTl
(13)
Величины 5=1 dt и D— Г (71 — t) TD dt представляют
J M(t) У K M(t)
0 0
собой скорость и путь, которые были бы достигнуты ракетой
при полете по прямой линии без воздействия гравитационного
поля. Например, для одноступенчатой ракеты с постоянной
тягой Р= — MVr= const
in г
D=VrTK
1
1 —г
S=Vr\nr и
где г — отношение масс;
Vr — скорость истечения.
Тогда уравнение (12) можно записать в следующей форме:
tg <1» = [Scos+ Vx\ [(Ssin<l> + K )2н- 2^ (Z) sin 4» + К)]
(14)
где V,j=v0,—gTs и Y=y0+v0JK
gTf представляют ско¬
рость и высоту, которые должна была бы иметь ракета в момент от¬
сечки двигателя, если бы тяга была равна пулю. Поскольку S, D, VT,
V:y и У являются хорошо известными численными величинами, то
значение ф легко получается в численном виде.
Интересно отметить, что оптимальное 'направление тяги и каса¬
тельная к траектории в момент падения ракеты перпендикулярны
между собой.
В этом можно сразу убедиться, переписав уравнение (12) в сле¬
дующей форме:
Рх
■ Vlx
^ку — g^
V/y
или /уУ/;+/уУ/,,=0,
где индекс I относится к точке падения. Это соотношение является
частным случаем более общей задачи, рассмотренной ниже
(стр. 198).
192
В предельном случае при импульсном разгоне (п-*оо, D-+ О,
Гк->0) с нулевой начальной скоростью, уравнение (14) сводится к
известному баллистическому решению
tg<I> = Ctg<|>, +
ЦЕНТРАЛЬНОЕ СИЛОВОЕ ПОЛЕ КЕПЛЕРА
Свойство параллельности векторов VVkR и ^rKR> приводящее к
не зависимому от времени оптимальному направлению силы тяги,
является результатом допущения постоянства силового тюля.
Поэтому уравнение (10) непригодно для случая поля Кеплера,
но можно показать, что за исключе¬
нием некоторых единичных случаев,
\vVKR\--r-\VrM (15)
%
где Rз — радиус Земли.
Отсюда следует, что если
vKTк Лз> то направление
p=VVKR+(TK-t)vrKR (16)
будет почти параллельно постоянно¬
му направлению VVKR.
Таким образом, до тех пор пока
расстояние, проходимое ракетой во
время активного полета, остается
сравнимым с радиусом Земли, макси¬
мальная дальность будет еще дости¬
гаться при почти постоянном направ¬
лении ТЯГИ. Фиг. 76. Схема к выводу урав-
Для того, чтобы подтвердить эти нения максимальной дальности
положения, необходимо иметь выра- в полярной системе координат,
жение^ для функции дальности
R(rKj vK). Используя схему, представленную на фиг. 76, и имея в
виду, что
получим
где
Ф = 7Г
13 394
Я=/?3(ф + ек),
(17)
■sin"
1 — оХ sin2 у
— 1-чг' не»
(1 — 2Х sin2 7 -4- X2 sin2 7)2
X sin 7 cos 7
193
представляет собой дальность в угловом измерении от места отсечю
до места падения ракеты *.
Здесь у — угол между вектором скорости и местной вертикалью.
0К — угловое перемещение от места запуска до выключе¬
ния двигателя.
Эквивалентная форма уравнения (18) имеет вид
1 — cos 0 sin (7—Ф)
-3 = 0.
(Щ
X sin2 7 sin 7
Введем единичные векторы тип, направленные соответственно
параллельно и перпендикулярно скорости в момент отсечки, и еди¬
ничные векторы р и т, направленные вдоль мгновенной горизон¬
тали и вертикали (см. фиг. 76). Опуская индекс «к», получим
(20)
2з
sin 7
где
sin (7 — Ф)
sin 7
j+
i4 = ctgf+(3— l)ctg-|-,
B= — 2ctgTf|o-
sin (27 — Ф)
sin 27
За исключением нескольких единичных случаев, таких, как верти
кальный подъем (Х~0, jt) или полет спутника (Ф~2л). А, В, и о
будут иметь значение порядка 1. Тогда
1
R3
vA
что подтверждается также и уравнением (15).
Выкладки, связанные с нахождением аналогов уравнений (12-
или (14), определяющих оптимальное направление тяги, могут быть
упрощены, если в уравнениях (18) и (20) положить (7=1. Тогда
получим (фиг. 77)
Ф , _1 X sin 7 cos 7
=tg 1 ! L.
2 & 1 - X Sin2 7
(2Г
N2R,
/ • ф
/ sin —
Xu \ sin 7 cos 7
где N= (1 + 2X sin2 y cos 2 y + A,2 sin4 Y) V2-
sin 2yt -\-(X sin2 y -|- cos 2y) n
N
(22)
1 Параметр X по существу выражает собой удвоенное отношение кинетиче¬
ской энергии к потенциальной. Он также равен (&к/'/;спутн)2, где ^спу-гн —ск°"
рость обращения спутника на орбите радиусом г. Поэтому можно ограничиться
случаем, когда Х<1, так как к>\ означает, что ракета может стать спутником
на соответствующей орбите, и тогда вопрос о максимальной дальности теряем
смысл.
194
Таким образом, выражение, заключенное в квадратных скобках,
представляет собой единичный вектор.
Мы будем предполагать, что условие (16) удовлетворяется и
что оптимальное направление тяги определяется вектором
p=Vv Л
Если а|) есть угол между р и местной горизонталью в момент от¬
сечки, то согласно уравнению (22), будем иметь
cos<|> = -^- = yV_1 [sin 2 у/гет-{-(Х sin2 7 -fcos 2f) mn.] =
\p\
s=N-1 [sin2TfSinY-f-Csia2T-bcos2T) cos-f] = [(X sin2 7 + 1) cos if].
7-Д51Л У
ЛЯП у COS у
Фиг. 77. Треугольник, иллюстрирующий
соотношение между углами ср и 7.
Таким образом, аналог уравнения (12) для этого случая будет
иметь вид
(X sin2 7 -|- 1) cos 7
(1 —|— 2Х sin2 7 cos 27 -f- X2 sin4 7)
ИЛИ
tg 7 (1 — X sin2 7) v\
= \ = —±-9 (23)
(1 + X sin2 7) ' gRs V
Из этого уравнения видно, что оно отличается от уравнения (12)
для постоянного силового поля только множителем (1—К sin 2 7/(14-
+Я sin2 у) (при условии, что в уравнении (12) положено ук=0, соот¬
ветствующее нашему допущению <у=1 для рассматриваемого слу¬
чая). Таким образом, влияние переменного гравитационного поля
оказывается незначительным до тех пор, пока скорость остается
небольшой по сравнению со скоростью спутника (gRs)1/2-
Для получения аналога уравнения (14) необходимо объединить
уравнения (23) и (13), считая, что оси х и у являются теперь мест¬
ной горизонталью и вертикалью в месте отсечки. Таким образом,
tg Ф = 5 CQS ф + 1 - (s cos ,J; + Vo r)2/ff/?3 ^ /24\
S sin ф -j- vqу — gTK 1 + (S cos ^ -j- VQX)2/gR3
195
Для частного случая—импульсного разгона от нулевой началь¬
ной скорости
tg2,HkzlE^ (25)
5 Г 1+XCCS2^ У °}
(здесь X=S2/gR3), откуда
tgt|>=(l-М1/2. (26)
Как и должно быть при k=(uAWrH)2<l, получаем известный
результат <ф=тг/4.
СВЯЗЬ МАКСИМАЛЬНОЙ ДАЛЬНОСТИ С КЛАССИЧЕСКОЙ
БАЛЛИСТИЧЕСКОЙ ЗАДАЧЕЙ
Известная в элементарной баллистике задача состоит в том, что
по данной высоте и скорости в момент бросания определяется угол
бросания, дающий максимальную дальность (поскольку искомая
траектория удовлетворяет также решению другой сопряженной зада¬
чи—по данной высоте бросания и дальности найти угол бросания,
соответствующий наименьшей скорости бросания,—то эти траекто¬
рии иногда называют «траекториями минимальной энергии»).
В этом разделе рассматривается связь между исследуемой за¬
дачей максимальной дальности и классической баллистической за¬
дачей.
Начнем с 'последней задачи. Для постоянного внешнего силового
поля эта дальность равна vKsx, где т определяется уравнением (11).
Записывая d(v^^x)/da=0, где а=(тг/2—у)—угол, образуемый век¬
тором скорости с горизонталью, найдем
tga=—^~—щ- (27)
Ку + 2№)
В частности, если высота запуска уТ~0, уравнение (27) приводит
к хорошо известному результату tg2 a=l, a=45°. Для центрального
силового поля (задача Кеплера) эта дальность равна ЯФ, где Ф
определяется уравнениями (18) или (21). Пренебрегая высотой за¬
пуска (т. е. полагая, а=1) и приравнивая д(Я3Ф) /да = 0, получим
tga=(l—X)i/2. (28)
Теперь можно сравнить эти задачи. Основное различие состоит
в том, что в случае классической задачи, т. е. при импульсном разго¬
не, скорость является заданной величиной, тогда как при конечном
времени горения, как в случае обычной ракеты, скорость изменяет¬
ся в течение всего времени активного участка. -
Изменение направления силы тяги приводит не только к измене¬
нию направления вектора скорости в момент отсечки, но также и к
изменению его величины, поэтому траектория максимальной даль¬
ности при конечном времени горения в общем случае не является
«траекторией минимальной энергии», встречающейся в классической
задаче.
196
Приведем численный пример. Если пренебречь влиянием высоты
запуска, то в случае постоянного силового поля максимальная даль¬
ность для классической задачи будет всегда достигаться при угле
бросания а = 45°. С другой стороны, если найти величину ф из урав¬
нений (12) или (14) и затем определить а, то в общем случае мы не
получим а = 45°. Например, при 7" = 100 сек. и S = 3000 м/сек мы по¬
лучим ф = 52° и а = 38°. (В общей форме при ук=0 мы имеем
s.”!» ,
vKy S sin 4 — gT
Если решить это уравнение, то получим
sin4 = l/4[(a2 + 8)1/2 + a)],
где a=g77S)*.
Следует отметить одно положение формального подобия между
двумя этими задачами. При времени горения, равном нулю, и посто¬
янном силовом поле уравнение (27) можно совершенно правомерно
заменить уравнением
(29)
так как в этом случае а (направление вектора скорости) и ф (на¬
правление вектора тяги) идентичны. Сравнивая его с уравнением
(12), мы видим, что оно справедливо также для времени горения,
отличного от нуля. Конечно, уравнение (29) осталось неизменным
только по форме, так как предшествующий численный пример пока¬
зывает, что величины ф, а и vK зависят от времени горения. Кроме
того, полезно также отметить, что если классическое уравнение пред¬
ставить в форме уравнения (29), то оно также будет справедливо
для ракеты с произвольным временем горения.
Аналогичные замечания можно сделать и к задаче Кеплера, если
преобразовать классическую формулу (28) к более сложному, но
(для а>0) совершенно эквивалентному виду
, , 1 — X COS2 a /orv4
tg«=ctg. 1 + tco>ia . (30)
При Т—0 ф и а опять совпадают, поэтому можно записать
.,2
1
, , , 1 —XcOS2a vKX gR3 /01Ч
tg<b = ctga = —^ . (31)
1 -f- X COS2 a VK у v\
14
К Л'
£*3
Поскольку это уравнение эквивалентно уравнению (23), оно
справедливо также для времени горения, отличного от нуля (при
условии, как и ранее, что мы пренебрегаем влиянием высоты за¬
пуска) .
* Предполагается, что приГ>0 ф>я/4, и так как vKX/vKy=ctg а, то отсюда
следует, что а = к/2—ф<тс/4. Таким образом, если пренебречь влиянием высоты
запуска при конечном времени горения, а будет всегда меньше 45°.
197
ГЕОМЕТРИЧЕСКАЯ ИНТЕРПРЕТАЦИЯ
В этом разделе представлена геометрическая интерпретация оп¬
тимального характера программы постоянного направления тяги дли
случая постоянного силового поля. Проведем произвольную линию
через точку запуска, т. е. LA (фиг. 78). Найдем такую траекторию,
которая характеризуется максимальным перемещением в направле¬
нии LA, т. е. траекторию, которая имеет наибольшую проекцию па
LA. Назовем ее «траекторией, связанной с LA». Построим А'А", ка¬
сательную к этой траектории и перпендикулярную к линии LA. Обо¬
значим точку касания А'". Проделаем то же самое для других на¬
правлений LB, LC и т. д. В результате получим кривую Е точек /1"',
В'п, С'" и т. д.
По смыслу построения ни одна
точка на любой траектории не мо¬
жет лежать вне кривой Е (т. о.
быть дальше от точки L)1. Поэто¬
му, если точка I есть место пере¬
сечения кривой Е с поверхностью
Земли, то расстояние от L до /
есть максимальная дальность. Она
достигнута при такой траектории
которая имеет максимальное пере¬
мещение в некотором направле¬
нии LD (не показанном на черте¬
же). Так как соответствующая
нормаль D'Dn будет касательная
к траектории в точке I, то LD пер¬
пендикулярна к вектору скорости
в момент падения.
Этот результат, заключающийся в том, что максимальная даль¬
ность соответствует некоторому максимальному перемещению в не¬
котором фиксированном, хотя и предварительно неизвестном,
направлении, является совершенно общим результатом, не основан¬
ным на каком-либо допущении относительно характера силового по¬
ля на 'протяжении всего времени полета ракеты. (Конечно, следует
выделить случай движения спутника в центральном силовом поле,
при котором вопрос о максимальной дальности потеряет обычный
физический смысл).
Если силовое поле постоянно по направлению, то ясно, что мак¬
симальному перемещению по линии LD должно соответствовать по¬
стоянное направление тяги также вдоль LD, так как составляющая
силы тяжести, нормальная к LD, при этом не оказывает влияния
1 Предположим, что существует траектория, содержащая точку X, которая
лежит вне кривой Е, Пускай точка X' находится на пересечении линии LX
с кривой Е. Для некоторого направления LY траектория, связанная с LY и нор¬
малью Y'Y", будет иметь точку Хг, как точку касания (т. е. Y'" = X'). Проекция А
на линию LY будет тогда дальше от L, чем от точки Y'. Однако это невозмож¬
но, поскольку при построении траектория, связанная с LY} характеризуется
максимальным перемещением (т. е. LY') в направлении LY.
Фиг. 78. Графическое построение
траектории максимальной даль¬
ности.
198
на перемещение в данном направлении, а составляющая, действую¬
щая вдоль LD, остается неизменной но величине. Действительное
определение линии LD может основываться на свойстве перпендику¬
лярности ее к вектору скорости в момент падения. Этот факт мы от¬
мечали ранее для случая плоской поверхности Земли (см. разд.
«Центральное силовое поле»). Для центрального поля труднее
наглядно показать то, что максимальное перемещение в фиксирован¬
ном направлении достигается (хотя и приблизительно) при почти
неизменном направлении тяги, но это доказывается в предыдущих
разделах статьи.
ЗАКЛЮЧЕНИЕ
В статье показано, что траектории с максимальной дальностью
для данной ракеты (т. е. ракеты, масса и величина тяги которой яв¬
ляются произвольной функцией времени) соответствует неизменное
или почти неизменное направление тяги ф. При исследовании учи¬
тывались гравитационные силы и сила тяги и не учитывалось влия¬
ние аэродинамических сил. В случае постоянного гравитационного
поля оптимальной траектории соответствует точно постоянный угол
ф. При движении в центральном силовом поле Кеплера постоянный
угол ф обеспечивает с достаточным приближением оптимальную тра¬
екторию при условии, что расстояние, пройденное во время активно¬
го полета, мало по сравнению с радиусом Земли.
Выведены конечные выражения для определения оптимальной
величины ф—уравнение (14) для постоянного силового поля и урав¬
нение (24) для поля Кеплера. Эти уравнения совместно с уравне¬
ниями дальности (И) и (17) и формулами (4) и (5) для скорости
и положения ракеты в момент отсечки двигателя позволяют произ¬
вести вычисление предельной дальности.
В предельном случае импульсного разгона (когда время горения Т
стремится к нулю) формула для ф0пт сводится к хорошо известному
из классической баллистики результату. Выведенные в этой статье
формулы могут рассматриваться как обобщение этих результатов
для случая, когда Т конечно.
Поскольку исследования были проведены для произвольных на¬
чального положения и скорости, то уравнения для оптимального на¬
правления тяги могут быть применены для любого участка активно¬
го полета, в том числе и для участка полета за пределами атмосферы.
ЛИТЕРАТУРА
1. Вольтерр а В., Теория функционалов.
Vo Iter га V., Theory of Functionals, Blackie and Son, Limited, London,
1931, pp. 22—24.
2. К У P а н т—Г и л ь б е р т, Математическая физика, I.
Couran t—Н i 1 b е г t, Mathematische Physik, I. Julius Springer, Berlin, 1931,
second edition, p. 159.
3. Д и p а к П. А., Квантовая механика.
Dirac P., Quantum Mechanics, Clarendon Press, Oxford, England, 1947,
third edition, p. 58.
М. ФЕРТРЕГТ
К РАСЧЕТУ СОСТАВНЫХ РАКЕТ 1
Существуют самые разнообразные системы обозначения весов
основных частей составной ракеты и соотношений этих весов между
собой.
Американские [1], английские [2] и немецкие [3] авторы употреб¬
ляют самые разнообразные системы определения и обозначения
исходных величин, что делает их работы трудными для чтении и
затрудняет сравнение полученных результатов.
Так, например, немецкие авторы применяют тщательно разрабо¬
танную систему обозначений и определений, базирующуюся не ме¬
нее чем на восьми различных соотношениях.
Ниже предлагается разработанная автором методика расчета
составной ракеты, основанная на определении только четырех весов
составной ракеты и трех соотношений между ними, которые являют¬
ся достаточными для выполнения расчетов основных типов состав¬
ных ракет.
На фиг. 79 представлена предлагаемая для целей расчета упро¬
щенная схема составной ракеты и показаны обозначения ее принци¬
пиальных составных частей.
По этой схеме составная ракета разбивается на ступени и суб¬
ракеты.
Ступень ракеты состоит из топлива, расходуемого ракетой
в период действия данной ступени до ее отделения; емкостей (баков),
содержащих это топливо; двигателей, арматуры и приборов управ-
1 М. Vertregt, Calculation of Step-Rockets, «Journal of the British In¬
terplanetary Society», 1955, No, 1, vol 14, pp. 20—25; то же, 1955, № 3, vol.^14,
pp. 152— 153; A Method for Calculation the Mass Ratios of Step-Rockets; там же,
1956, No 2, vol. 15, pp, 94 — 97.
200
леиия, если они имеются в отделяющейся ступени, а также ив обо¬
лочки отсеков и их несущей силовой конструкции.
Суб ракет ой . называется такое сочетание полезного груза и
ступеней составной ракеты, в 'котором одна из ступеней является ра¬
бочей (действующей), а все остальные ступени, продолжающие по¬
лет вместе с полезным грузом составной ракеты, являются как бы
«полезным грузом» для данной субракеты.
Предложено нумеровать ступени и субракеты в восходящем по¬
рядке, начиная от вершины ракеты к ее основанию по схеме, пока¬
занной на фиг. 79.
Тогда для субракеты 1 рабочей ступенью будет ступень 1, а
«полезной нагрузкой» ее—полезный груз составной ракеты; для суб-
ракеты 2 1рабочей ступенью будет ступень 2, а «полезной нагрузкой»
ее—субракета 1, т. е. ступень 1 вместе с полезной нагрузкой состав¬
ной ракеты; для субракеты 3 рабочей ступенью будет ступень 3, а
«полезной нагрузкой»—субракета 2 и так далее. Полезная нагрузка
не входит в понятие ступени.
Такое разграничение определений и обозначений отдельных ос¬
новных частей составной ракеты—очень важно; оно просто, легко
запоминается и позволяет избежать целого ряда ошибок, которые
всегда возможны при отсутствии подобной четкой систематизации.
Четыре основных веса составной ракеты определяются так:
1. Спи—вес полезной нагрузки составной ракеты1.
Под этот ’вес’11р6ёктируется и строится ~вся ракета. Поэтому он
является наиболее важным весом в расчетах. Полезная нагрузка
состоит из аппаратуры или живых существ, помещаемых в ракету,
силовой конструкции, несущей их, и оболочки, предохраняющей их
в полете.
Для отдельных субракет, как указано выше, «полезной нагруз¬
кой» будет вес той субракеты, которую она несет, т. е. субракета 1
является как бы «полезной нагрузкой» субракеты 2—субракета 2—
нагрузкой субракеты 3 и т. д.
2. Gj^^ eec^Tonjiuea, расходуемого из ступени.
В этот вес, обычно состоящий в основном из веса горючего и оки¬
слителя, должны быть обязательно включены веса вспомогательных
компонентов, например перекиси водорода, используемой для рабо¬
ты тур бон ас оси ого агрегата, и ряда других химикалиев, расходуемых
из данной ступени во время ее работы в полете.
Qo —«сухой вес» ступени, т. е. суммарный вес порожних ба¬
ков, двигателей, турббнасбсТГы'х агрегатов, клапанов и трубопрово¬
дов, несущей конструкции, оболочки, механизмов управления и т. п.,
т. е. вес всего того, что имеется в данной ступени и вместе с нею
отделяется от остальных частей ракеты в полете.
4. G — полный начальный вес субракеты; Gn—полный начальный
вес ракеты, состоящей из п ступеней.
1 В оригинале весовые характеристики, обозначенные в переводе (как это
принято в советской литературе) буквами Gn.u, GT, Gc, G и Gn, обозначены бук¬
вами m и М с соответствующими индексами (mp, tnby mct Мп). Обозначения
введенных автором весовых соотношений р, г к s сохранены. (Примечание ред.)
201
В соответствии с обусловленной выше индексацией отдельных
составных частей ракеты Gx2 будет обозначать суммарный вес топли¬
ва, расходуемого из второй ступени; Gc3—«сухой вес» третьей сту¬
пени; G3—полный начальный вес третьей субракеты и т. д.
На основе этих определений получается, что
^1 = Gn н -f Gcl + GTl: (1)
Gn=Gn-l + Gcn+GT„• (2)
Кроме этих четырех определений весов наиболее существенных
частей составной ракеты, применяются три следующих их соотно¬
шения:
1. £—«относительный» вес субракеты,_т. е. отношение полного
начального'веса субракеты к весу ее «полезной нагрузки». Таким
образом,
(О
^п.н
Рп = т?2-. (4)
G/z-i
Тогда Р — будет полный «относительный» вес всей составной ра¬
кеты, т. е. отношение начального веса всей n-ступенчатой составной
ракеты к весу полезной нагрузки первой ступени:
► • 1
Оп \
ибо
откуда
Gn.H
0\ G2 G3 Gn Gn
(5)
Оп.н G, G4 Gn—i Gn.H
= P,
P^PiPtPs . . .pn. (6)
Величина P является одним из наиболее важных соотношений
составной ракеты. В практике проектирования численное значение
величины Р обычно не должно превосходить своего рационального
значения, которое зависит от целого ряда экономических и техниче¬
ских условий, но автор согласен с Краузе [3] в том, что с запасом
можно положить
Р<500.
2. 5 — «конструктивная характеристика» ступени, т. е. величина,
характеризующая собой отношение"пюлного начального веса данной
ступени с топливом к ее~«сухому весу».
Таким образом,
Si==g£1^gi2i (7)
Ucl
Sa=:.G**±.G?*. . (8)
Gc п
202
3^ г — «отношение масс». Это есть отношение начального веса
(или'м'ассы) .субракеты к весу (или массе) той же субракеты после
израсходования всего топлива, заключавшегося в данной ступени.
Таким образом,
(9)
(10)
G,
G\ — GT1
Gn
п Gn — GTn
«Конструктивная характеристика» 5 ступени по аналогии могла
бы называться также отношением масс или весов ступени, но лучше
этого не делать во избежание возможной путаницы в обозначениях.
«Отношение масс» г определяет собой идеальную скорость, кото¬
рую ракета может получить при отсутствии поля тяготения и сил со¬
противления среды в соответствии с уравнением
tW=Vrrlnr, (И)
где Vr — эффективная скорость истечения газов из сопла двигателя
ракеты.
В случае составной ракеты идеальная скорость для нее может
быть получена как сумма аналогичных скоростей для каждой суб¬
ракеты.
Тогда полная идеальная скорость для составной ракеты, имею¬
щей п ступеней, будет определяться равенством
S®na*=rrtlnr1 + Vrrtlnr2+V’rtlnr3+ • . • +Vrn\nr„. (12)
Если для всех ступеней приведенные скорости отброса одинаковы
и равны Vr, то
2‘0т.х=Гг1пГ1Г2Г8 . . Г„. (13)
Введя обозначение R как приведенное отношение масс составной
ракеты, будем иметь
R = r1r2r3. .. гп% (14)
и, следовательно,
откуда
Ztw=VVln/?, (15)
R = e vr , (16)
что справедливо только при условии, если скорость Vr для всех сту¬
пеней будет одинакова.
Отношения 5 и г, определенные таким путем, будут всегда иметь
численные значения больше единицы и будут соответствовать обыч¬
но применяемым понятиям отношения масс. На практике часто поль¬
зуются обратными величинами, что не является наглядным и есте¬
ственным. Преимущество предложенного автором определения ха¬
рактеристик 5 и г заключается в том, что, во-первых, численные
203
значения их всегда больше единицы и они дают более наглядное
представление о действующих соотношениях, чем десятичные дроби
и, во-вторых, они значительно легче запоминаются.
Более того, уравнения, полученные ив этих соотношений, симмет¬
ричны, если iBce соотношения построены по одному и тому же прин¬
ципу, и, нроме того, устраняется необходимость применять отрица¬
тельные показатели.
' Из равенства (9) получим
г\ — 1 С?т1
г 1 Oi
Из равенства (7)
Осг Т- Gti
si — 1 G,
l-l
cl
sl
Gci GTi
Gci
Gci + GTi
а из равенства (3)
0i -i
Gn.H
Pi -1 _
Gi — G„.h
Pi
G,
Gn.H
Oi
Подставив сюда из равенства (1)
— Gn.H = Gcl + GT„
получим
Pi — 1 _ Gci4~ G-ri
Pi Gi
Тогда
Si — 1 Pi — 1 Gt\ Gq1 -f- GTi ___ GTl = Г\ — 1
«1 Pi Ga +Gn Gx Gx n
Следовательно, три отношения p, s и г связаны 'между собой
уравнением
г — 1 = -у - 1 р - 1
Г S р
откуда может быть получено
(17)
s = (18)
р — г
• р — г ; (19)
S — г
Ps
, 1 <20)
Р + S — 1
Из этих трех равенств для одноступенчатой ракеты могут быть '
получены следующие уравнения для многоступенчатой ракеты.
204
S„— 1
Так, например, для ракеты с п ступенями будем иметь
Si — 1 So — 1
Р\ — Г\— , Л.= г2— , . . .
«1 — П «2 — Г2
Sn 1
л=Гл^глГ'
Учитывая-выражения (6) и (14), получим
Р=р1р2 . . .pn=--rxr2. . . r„ 51-1 *2~1 .
5i — n i’2--r2 — Гл
или окончательно
191-1 52-1 . . . 5п~1 . (21)
Si—ri s2 — r2 sn— rn
Из выражения (5) следует, что
Gn= Gn.HP.
Подставляя сюда вместо Р выражение (21), получим
Gn = GnHR^^-^^- . , . (22)
Sl — ri S2 Г 2 Sn Г п
Из выражения (10) получим, что
G =0 .
Т. п п
Г п
После подстановки -сюда Gn из выражения (22) получим
GTn=On JRr-^(23)
Гп «i— Г2 Sn—rn
Подобно предыдущему определив Gcn из выражения (8) после
подстановки равенства (23) для GT п, получим
= (24)
Гп Si —Г! S2—r2 Sn Г п
Если «конструктивная характеристика» s и «отношение масс» г
одинаковы для всех ступеней и субракет, то могут быть написаны
простые уравнения:
Р=рп; (25)
R = rn\ (26)
(27)
\s-Rn )
у. (28)
\рп +S-\)
205
С помощью этих уравнений легко могут быть получены также
другие соотношения.
Например, обозначая символом 2GC суммарный «сухой» вес весу
п ступеней ракеты, а символом 2Gt — суммарный вес топлива, за¬
ключенного в них, получим
£°С + И ог=ая - оп. н=(Р-1) оп.„.
Следовательно,
SGc + 2Gt GnM(P-l) 1
Gn Gn.HP Р
При одинаковом значении конструктивных характеристик для все
ступеней из формулы (8) получим
с* Gc-f-GT £ Сс + 2 Ст
Gc 20с 5
откуда
2gc ^ 2gc 2gc + 2Qt=z i р—1
Gn e2Gc + 2GT Gn s p
Аналогично
2GT = s — i P—\
Gn s P
(29)
(30)
(s и г одинаковы для всех ступеней и субракет).
Однако для проведения основных расчетов составной ракете
вполне достаточны лишь три первых соотношения.
Приведем некоторые простые примеры расчетов:
Пример 1. Одноступенчатая ракета с полным начальным весом Gи равным
500 т, имеет вес бп.и полезной нагрузки, равный 1 т. Таким образом, «полный отно¬
сительный вес» Р ракеты будет равен 500 т. Конструктивная характеристика s ее
ступени равна 5. Спрашивается, как велик будет вес двухступенчатой ракеты с
той же конечной идеальной скоростью полета, если конструктивная характери¬
стика ее ступеней будет такой же, как у одноступенчатой ракеты?
Ответ. Сухой вес Gc одноступенчатой ракеты будет
- G\ — Gn.H 500 - 1
G с —
а «отношение масс»
5
G\
500
Г\ = 5 = = 4,96,
еп.н+Ос 1 + 99,8
Следовательно,
V,
• =10/-! = 1,6014.
206
Для двухступенчатой ракеты будем иметь
5!!ш«=1пГ2 = 1,6014,
У” т
откуда
г=2,227,
а следовательно,
5—1 5—1
/> = г =2,227 — —— = 3,213
* 5 — /* 5 — 2,227
и
Р = ^2 = 3,2132= 10,32,
что соответствует примерно 1/50 веса одноступенчатой ракеты.
Пример 2. Четырехступенчатая ракета имеет следующие характеристики:
2^тах = 9,0 км!сек
(идеальная скорость, необходимая для того, чтобы тело могло свободно обра¬
щаться вокруг земного шара);
Vт == 2,4 км/сек, 5 = 4,7
(характеристики американской ракеты «Викинг»).
Характеристики s, г и скорости Vr одинаковы для всех ступеней.
Как велик должен быть полный начальный вес такой составной ракеты для
полезной нагрузки весом в 1 т?
Ответ. Приведенное отношение масс
R = е9'2,4 = е3,75 = 42,5.
Тогда
Р = R (-S~1—У = 42-5 ( 4,7-1 Л4 = 3?2-
\s—R п ) \4.7 — 42,54 J
Следовательно, полный начальный вес такой четырехступенчатой составной
ракеты будет равен
Gn = Gn.HP= 1-372 = 372 т.
Такой вес является приемлемым.
Пример 3. Для того, чтобы долететь с Земли до Луны, облететь вокруг нее
и вернуться на Землю, согласно Кларку [4], необходимо обеспечить скорость в
22,4 км/сек.
Как велик должен быть вес десятиступенчатой составной ракеты с теми же
характеристиками s, г и Vг, что и в предыдущем примере, и с тем же полезным
грузом?
Ответ.
/г = £22,4/2.4=е9.33=ц 270(
/ 4,7—1 \Ю
Я = 11 2701 ———„-г) =3 160000,
\4,7 — 11 270 ’ /
т. е. такая ракета должва весить перед стартом 3 160 000 т.
МЕТОД ПОДСЧЕТА КОЭФФИЦИЕНТА ОТНОШЕНИЯ МАСС г
Очевидно, что произведение R, определяемое равенством (14),
может состоять из неограниченного числа множителей#^, г2, г3. . . гп,
но ниже доказывается, что только при одной вполне определенной
комбинации этих множителей можно получить составную ракету ми¬
нимального общего веса.
207
Выше было показано, что
Рп = Гп
sn 1
Gc п бгт п
разности sn—rnt
Таким образом, рп пропорционален гп и обратно пропорционален
откуда ясно, что рп будет увеличиваться все быст¬
рее, по мере того как разность sn—~
—гп будет уменьшаться (фиг. 80).
Для того, чтобы «относительный
вес» ракеты р был возможно мень¬
шим (а следовательно, и общий вес
ракеты), необходимо соответствую¬
щим образом подбирать величины
«конструктивной характеристики»
х и «коэффициента отношения
масс» г.
В общем случае величины 5 для
различных ступеней составной раке¬
ты между собой не равны.
Нижняя ступень в большинстве
случаев бывает снабжена стабилизи¬
рующими поверхностями, которые
увеличивают вес конструкции и
уменьшают коэффициент «отноше¬
ния масс», а последняя ступень не¬
больших составных ракет, например
«Mouse», бывает настолько мала, что
оптимальные конструктивные соот¬
ношения для нее не могут быть реа¬
лизованы. Поэтому представляется
важным предложить метод расчета
величины наиболее выгодного «отно¬
шения масс» г, соответствующих из¬
менениям «конструктивной характе¬
ристики» 5.
Поскольку величина общего «коэффициента относительного веса»
0 12 3 4
$п~ гп
Фиг. 80. График изменения отно¬
сительных весов составной ракеты.
в соответствии с уравнением (21) равна
P = R
S1—1 6'2 — 1
Sn — 1
Si — Г\ S 2 — /*2
где
R=ru г2 .
г л’
то задача заключается в том, чтобы отыскать такое распределение
множителей гъ г2, .. . гп, при котором величина Я была бы минималь¬
ной, удовлетворяя одновременно дополнительному условию
X г'тах ( Vri In rx -f- Vr2 lnr2 -+•
4„lnrn)=0.
(31)
208
Для решения этой задачи воспользуемся методом неопределенных
множителей Лагранжа. Обозначим равенство (21) через f(ru г2, . . .
г„), а равенство (31)—через F(гъ г2, . . . . гп) и составим уравнение
ф(гиг2, . . . rn) = f(rv г2, . . . rn) + lF(ru г2 . . . г„),
где
Х = const.
(9 Ф 3 Ф д Ф
Полагая = 0, = 0 и =*0, мы можем получить п
дп дг2 дгп
уравнений, которые вместе с уравнением (31) определяют мини¬
мальную величину Р и величину неопределенного множителя X
Так как
дФ- = г2г3. . .гд^-l)
дг\ П 52— Г2 5Л—Г, 2 (-S'l — /Д2
\Vn
Г1
= 0,
Г ~ 1 52-1 . . Jaiii £} Wrl = 0.
— Г\ 52 — r2 6М— Гп Si — Г\
Поскольку
51 1 <S 2 1 & п 1 т~\
ГхГ/з . . . Г„-^ 2 . . .-2 =Р,
5]— ГХ S2—r2 *п—Гп
то, подставляя это выражение, окончательно получаем
О *1 .~хкг1 = 0. (32)
5l Г\
Аналогично можно получить
и р-41—^Л=о; (зз)
дг<2 s2—Г2
— = 0 и /Л/„, -0. (34)
<3^ л 5/2 г п
Используя уравнение (32), исключаем Я и X из уравнений (33) и
(34)1 в результате чего получаем равенства
^2=*2-—Ta-(s1-r>); <35)
5'i У г2
—(36)
5 1 У гп
Эти величины можно подставить в уравнение (31)
2 У тах~ {У Л 1пГ2+ • • • + У гп I*1 Г п) ~ 0
и численно определить значение гх.
14 394 209
Когда значения I7,- для всех ступеней одинаковы, то решение са¬
дани упрощается.
Действительно,
Выше мы предположили, что «коэффициент отношения масс» и
«конструктивная характеристика» не зависят друг от друга, но это
не всегда оказывается справедливым.
Увеличение «коэффициента отношения масс» имеет своим след¬
ствием увеличение ускорений, действующих на ракету, поэтому изме¬
нение г субракеты сопряжено с увеличением «конструктивной
характеристики» 5 соответствующей ступени. Однако выведенные
выше формулы могут быть полезными при предварительных рас¬
четах.
1. Малина Ф. и Саммерфилд М., Проблема преодоления силы тяго¬
тения Земли с помощью ракеты.
Mali па F. and S u rn m е г f i е 1 d М., The Problem of Escape from Earth
by Rocket, «Journal of the Aeronautical Sciences», 1947, vol. 14, No. 8, p. 471.
2. Кливер А.. Отношение масс.
И
'Xt'™*=l/'(lnri + ln~,'i+ • • • +ln —о)
\ Si sx I
— Vrltl\n — -j-lnSj + lnSj-f . . . +lri6’n) =
\ .c.
Обозначим
тогда
но
(я 1птг+1п5!
Поэтому
п In — + In S= In R
Si
и окончательно получаем
(37)
(38)
ЛИТЕРАТУРА
210
Cleaver A., Mass Ratios, «Journal of the British Interplanetary Society».
1949, vol. 8, p. 173.
3. К p а у з e Г., Общая теория составной ракеты.
Krause Н., Allgemeine Theorie der Stufenrakete, «Weltraumfahrt», 1953,
p. 52.
4. К л a p к e А., Межпланетный полет.
Clarke A., Interplanetary Flight, Temple Press Ltd., 1952, p. 68.
М. ВИЛЬЯМС
РАСЧЕТ РАСПРЕДЕЛЕНИЯ ТОПЛИВА
МЕЖДУ СТУПЕНЯМИ СОСТАВНЫХ РАКЕТ1
В (работах [1, 2] Фертрегтом проведены исследования характери¬
стик составных ракет при помощи метода, в котором использовались
совершенно необычные элементы и обозначения, более логичные,
однако, чем все другие 'применявшиеся до настоящего времени.
Цель этой статьи состоит в том, чтобы распространить метод
Фертрегта на случай исследования, когда принимается во внимание
взаимная связь между весом конструкции и весом топлива ступеней
ракеты.
ОБЩАЯ СХЕМА РЕШЕНИЯ
Задача, сформулированная и решенная Фертрегтом, может быть
рассмотрена как задача об отыскании условий, обеспечивающих мак¬
симальную полезную нагрузку ракете, состоящей из N ступеней, с
заданными стартовым весом и скоростью в момент выключения дви¬
гателя, для случая полета в пространстве, где нет сил тяготения и
среды, сопротивляющейся полету.
«Конструктивные характеристики» .рассматриваются как некото¬
рые параметры, так же как и скорости истечения, а отыскиваются
такие «коэффициенты отношения масс», которые обеспечивают мак¬
симальную полезную нагрузку.
Приведем наиболее важные характеристики и обозначения;
Gn — вес /2-й субракеты составной ракеты;
Gin — вес топлива п-й ступени составной ракеты;
Gc п — сухой вес /2-й ступени;
Gn.H — вес полезной нагрузки;
гп — коэффициент «отношения масс» /г-й субракеты:
R — общий коэффициент «отношения масс» составной ракеты,
состоящей из N ступеней:
R = i\r2. . . rN\ (2)
1 М. L. W i l 1 i a in s, The Calculation of Fuel Distribution in Step-Rockets,
«Journal of the British Interplanetary Society», 1957, vol. 16, No. 4, pp. 211—215.
14*
211
«ко негр укт-ив н а я х а р акт ер истика »:
_ Gc п “Ь GT п
(3)
рп — коэффициент (Полезной нагрузки («относительный вес»):
Рп-
Gn /„ _ G] __ G] \
П-1 ( 1 G0 Gn.H) ’
G,
s„ —1
-r
rtl
P — «общий относительный вес»:
Р — Р\РъРъ' • • Z7// = ~~с^= с N • (^)
^0 ап.н
Используя затем выражения для идеальной скорости составной
ступенчатой ракеты путем суммирования составляющих скоростей
ступеней в функции коэффициентов «отношения масс»
.v='Zvn = '^lVmlnrn, (6)
записываем следующую вариационную задачу, в которой исполь¬
зуется метод неопределенных множителей Лагранжа в виде:
ф (rn) = Р(r„) + X У (<0п - Vrn In rn) = min. (7)
Полагая дф/дгп=0 (/2=1, 2, можно получить N уравне¬
ний с (iV-f-l) -неизвестными, rn(n= 1, 2, N) и X, которые вместе с
уравнением (6) образуют систему уравнений, определяющую иско¬
мые значения коэффициентов отношения масс в виде
г\
Si
(«! —г i). (8)
Величина /у определяется путем совместного решения уравнений!
(6) и (8).
РАЗВИТИЕ РЕШЕНИЯ ФЕРТРЕГТА
В своем анализе Фертрегт отметил, что предположение о незави¬
симости коэффициента «отношения масс» от «конструктивной харак¬
теристики» ступеней не вполне справедливо и что здесь необходимы
дальнейшие исследования.
Конечно, если sn являются независимыми параметрами, тогда из
(3) можно получить
Ос» = (««-1)-1Отя, (9)
что свидетельствует о пропорциональности сухого веса весу топлива.
Необходимо, однако, отметить, что сухой вес ракеты включает в
себя несколько составляющих, причем не все они увеличиваются
212
прямо 'пропорционально весу топлива. Например, мы можем рас¬
смотреть сухой вес, как состоящий из веса двигателя, полезной
нагрузки, веса конструкции как несущей, так и не 'Несущей полезную
нагрузку, и других компонентов, не входящих в конструкцию ракеты,
таких как вес элементов аппаратуры управления, устройства отде¬
ления ступеней и т. п. По этой причине термин «конструктивный
коэффициент» не вполне соответствует существу дела и его было бы
более правильно наименовать — отношением масс ступени.
Ниже показано, как изменится решение поставленной задачи в
случае, если сухой вес рассматривать состоящим из трех основных
частей.
1. Вес конструкции, несущей полезную нагрузку, G^
Качественно можно показать, что вес конструкции, несущей по¬
лезную нагрузку, зависит главным образом от веса топлива. Напри¬
мер, если предположить, что топливные баки являются стенками ра¬
кеты, то эта часть конструкции может быть схематично представлена
в виде цилиндрического бака радиусом а и с толщиной стенок и пло¬
ских днищ — верхнего и нижнего — h. Средняя массовая удельная
плотность топлива будет равна GmhcPL, а продольная перегрузка
(Г+&), где k — действующее продольное ускорение, выраженное в
единицах g.
Стенки топливных баков должны быть способны противостоять
напряжениям сжатия, возникающим под действием инерционных
нагрузок, передающихся через ступени ракеты, и напряжениям рас¬
тяжения в стенках цилиндра, возникающим под действием гидроста¬
тического давления жидкого топлива. Предположим, что расчетным
случаем является второй.
В случае реального проектирования расчетные условия опреде¬
ляются при более полном анализе, когда учитывается отношение
длины бака к его диаметру, число ступеней и т. п.
Напряжение растяжения в стенках обечайки баков будет
Отсюда получаем отношение толщины стенки к радиусу баков:
которое, как мы видим, пропорционально весу топлива.
Подобным же образом получаем напряжение в днищах баков,
которые рассматриваем как круглые мехмбраны (см. Тимошенко [3]):
2
213
откуда 'получаем, что относительная толщина днищ также пропор¬
циональна весу топлива:
з
h l + k Grng
0,423 —
ао
а Е ка2
Поскольку вес баков линейно связан с относительной толщиной
стенок, то можно считать, что эта часть конструкции, несущая по¬
лезную нагрузку, пропорциональна весу топлива.
Имея это в виду, примем, что веса и других элементов, несущих
полезную нагрузку, линейно зависят от веса топлива, как это при¬
нимал Фертрегт:
g^ = t£Jgt„. (10)
2. Вес не несущих элементов GW
Предположим для простоты анализа, что вес но несущих элемен¬
тов G ^пропорционален весу несущей конструкции G(cl)n и поэтому,
имея в виду (10), можно принять
g<2>^t<2>gt„ (in
что находится также в соответствии с условием (9).
3. Вес двигательной установки G^
В отличие от допущений, сделанных выше, предположим, как
это обычно и делается, что вес двигателя пропорционален развивае¬
мой тяге. Но тяга пропорциональна произведению веса на продоль¬
ную перегрузку, т. е.
Р (1 -f- k) Gnff.
Тогда в отличие от условия (9) получим
Gfn^[Ce{\ + k)g)Gn^^nGn. (12)
Таким образом, метод Фартрегта, при котором сухой вес прини¬
мался пропорциональным только весу топлива, можно расширить и
на случай, когда сухой вес представлен в виде составляющих, зави¬
сящих как от веса топлива, так и от общего веса:
Gcn= Ис1* + Tc2n] GT„ + 7с3л£„• (13)
МИНИМАЛЬНАЯ ЗАДАЧА
Сформулируем теперь вариационную задачу с применением по¬
лученного выше результата
(14)
Рп =
| Ос п От
G„ Gn
После подстановки выражений (10) — (12) получаем:
Отл I-1
/»я=[(1-^)-(1+т^ + т^)-57
214
Обозначая
A,=i—f(3).
п • с п
-х n = ^JL,
п а ’
(15)
(16)
(17)
получаем
Рп = [Лп-Вп^п]-\ (18)
Отметим еще, что коэффициент «отношения масс» (1) можно
записать в виде
'■* = (1-|‘л)-1- (19)
Используя (18) и (19), запишем условия нашей вариационной
задачи в виде
Ф (l\,) = Р GO + Ф + £ ^ 1п (1 - IS,)) = min (20)
N
*+Е Vrn In И — Рл) = 0 (21)
как условие связи.
Легко показать, что решение в этом случае будет иметь вид
1
п 1
1 — \>-п
1 --
Ап
-Hi
Vn
и
i — —V
Вп .
1
Vrn
1 в,)
Величины [xt или г\ могут быть определены путем совместного
решения уравнений (21) и (22).
ЧАСТНЫЙ СЛУЧАЙ РАВНЫХ СКОРОСТЕЙ ИСТЕЧЕНИЯ Vn=Vrn=Vr
В частном случае постоянства скоростей истечения Vr возможно
следующее формальное решение:
1
1 —
В1
Жг"
вп
(23)
L огда
N
V=I,Vn=Vrlnr1r2 . . . / дг =
= VM
А'
К X-1
(24)
215
Обозначим произведение последних членов через S:
N
(25)
Тогда г{ может быть определено по формуле, вытекающей из (2!,
Для случая, рассмотренного Фертрегтом, легко показать, что
В заключение необходимо указать, что константы пропорциональ¬
ности Yen должны быть определены в результате значительно более
подробного расчета, чем делалось в этой статье.
В тех случаях, когда эти константы представляется возможным
выбрать в качестве типичных, все приведенное исследование может
быть проведено в качестве предварительного расчета.
г V -1N
(26)
или в зависимости от общего «коэффициента масс» R
г' = \Д1п R, где 1— —1Л
(27)
и
(28)
£
при Ап= 1 и Вп== —- получаем
Sn— 1
R \Л
216
ЛИТЕРАТУРА
1. Vertregt М., «Journal of the British Interplanetary Society», 1955, 14,
20, 152.
2. Vertregt М., «Journal of the British Interplanetary Society», 1956, 15, 25,
3. T и м о ш e н к о С., Теория пластам и оболочек.
Timoshenko S., Theory of Plates and Shells, 1940, p. 337, New York, Me.
Graw-Hill Book Co.
4. Гольдсмит М., Выбор оптимальных весовых соотношений для двухсту¬
пенчатых ракет.
Goldsmith М., On the Optimization of Two-Stage Rockets, Rand Cor¬
poration Report, RM 1796, 1956.
Э. ШУРМАН
МЕТОД ОПТИМАЛЬНОГО ПОДБОРА СТУПЕНЕЙ
СОСТАВНОЙ РАКЕТЫ1
Принятые обозначения
ап—максимальная предельная перегрузка для л-ой ступени
Vr — скорость истечения
g — ускорение силы тяжести
Руд — удельная тяга
М — масса
N — число ступеней
t — время
btn — время работы двигателей л-ой ступени
Рп — тяга двигателей л-ой ступени
v — скорость
&vn — приращение скорости л-ой ступени
Goп — общий вес л-ой ступени
GT п — вес топлива л-ой ступени
Осп — сухой вес конструкции л-ой ступени
GI0—стартовый вес
Gnн— вес полезной нагрузки аппарата
Осп
еп = — относительный вес конструкции л-ои ступени
Ос п + От п
0-т п
1= — относительный вес топлива л-ои ступени
О0п
1п — — — коэффициент полезной нагрузки л-ой ступени
G0 (л + 1)
Лтл -- -т-безразмерное время работы двигателей л-ой ступени
Рул
т( — неопределенный множитель Лагранжа
1 Е. Schurmann, Optimum Staging Technique for Multistaged Rocket
Vehicles, „Jet Propulsion*, 1957, No. 8, vol. 27, pp. 863—865.
217
&хп — ~— — приращение безразмерной скорости л-ой ступени
gPyA
Хк — конечная безразмерная скорость
Осек п — секундный расход топлива л-ой ступени
ВВЕДЕНИЕ
При предварительных расчетах многоступенчатых ракетных
аппаратов приходится решать проблему оптимального подбора сту¬
пеней. Обычно при решении этой задачи определяется величина
стартового веса ракеты, обеспечивающая достижение заданной ко¬
нечной скорости при различных комбинациях времени работы сту¬
пеней. Вследствие этого возникает необходимость в разработке мето¬
да, пригодного для быстрого предварительного расчета оптимального
времени работы двигателей каждой ступени многоступенчатого ра¬
кетного аппарата.
Для выполнения проектных исследований обычно бывает необхо¬
димым иметь следующие исходные данные: (а) конечную скорость
последней ступени конструируемого аппарата; (б) удельные тяги
ракетных двигателей; (в) максимально допустимую перегрузку, на
которую рассчитывается конструкция и (г) вес полезной нагрузки.
По этим данным подсчитываются минимальный стартовый вес, по¬
требный запас топлива и вес конструкции. Для исследования влия¬
ния веса полезного груза, максимально допустимой перегрузки и т. и.
обычно производится очень большое количество расчетов. Автор
статьи предлагает метод быстрого подбора оптимальных ступеней
ракеты, с помощью которого все расчеты значительно упрощаются.
ДОПУЩЕНИЯ
Изложенное ниже исследование основано на следующих допу¬
щениях:
1. Во время работы любой ступени аппарата
тяга двигателя считается постоянной. Это предпо¬
ложение не является слишком ограничительным, поскольку ракет¬
ные двигатели проектируются обычно для работы на режиме мак¬
симальной тяги в течение всего времени действия ступени. Измене¬
ние тяги с высотой обычно невелико.
2. Удельная тяга двигателей ступени считает¬
ся постоянной. Удельная тяга зависит главным образом от
конструкции двигателя и типа используемых компонентов топлива.
Поэтому допущение постоянства удельной тяги весьма близко к дей¬
ствительности, за исключением малых высот, где она несколько
уменьшается.
3. Лобовое сопротивление считается равны м
нулю. В ряде работ уже показано, что в случае больших летатель¬
ных ракетных аппаратов влияние лобового сопротивления во время
работы двигателей очень мало [1].
4. Ускорение силы земного тяготения g счи¬
тается 'Постоянным. Изменение g оказывает небольшое
влияние на конечную скорость ракеты (например, разница в вели¬
чине g на высоте 91 500 м и на уровне моря составляет только 3%).
МЕТОДИКА ИССЛЕДОВАНИЯ
Если предположить, что подъем ракеты происходит по вертикаль¬
ной траектории, то уравнение движения можно записать следующим
образом:
-Mg=MjZ+V,%. (!)
Уравнение (1) после интегрирования может быть переписано
так:
+ gLtn = g Руд In . (2)
G0n — GT ,
Для упрощения уравнений и исключения удельной тяги как пара¬
метра из рассмотрения перейдем к безразмерным величинам скоро¬
сти и времени ^ ^
о УД Г уд
Тогда уравнение (2) может бытыперепиеано следующим образом:
А-*»+Атя = 1п—Цг, (4)
1 —
где =
Gon
Уравнение (4) представляет собой сумму приращения безраз¬
мерных скорости и времени работы двигателей ступени, выраженных
через относительный вес топлива для каждой ступени.
Один из результатов, полученных в работе [1], сводится к тому,
что
Gon 1 гп
^О(Л-И) 1 — гп
(5)
Здесь вп = — относительный вес конструкции сту-
Gcn+GTn
пени.
Принимая обозначения Geo — стартовый вес, (/п.н —вес полез¬
ной нагрузки конечной ступени, можно составить равенство
^20 G02 G0n , , , geo /£Ч
ТС-77- • . . — =V2- • -*'N=-pr • (6)
G02 G03 Gu H ^n.H
Уравнение (6) определяет отношение стартового веса аппарата
к весу полезной нагрузки через относительные веса топлива £ и отно¬
сительные веса конструкции в каждой ступени. Далее задача за¬
219
ключается в том, чтобы получить соотношение, связывающее коэф¬
фициент полезной нагрузки со временем работы двигателей.
Если выразить тягу двигателей каждой ступени как
п
или разделить обе части этого равенства на G0n получим
Рп _ Ся
Максимальная предельная перегрузка для ступени с постоянно)!
тягой будет иметь место в момент выгорания топлива ступени и мо¬
жет быть выражена следующим образом:
Pfl C/0,!
^0 (л*1) + п О0 (^1) + С?с П Ат/г
ИЛИ
Сп
(У)
e»^„=TJ:У- НО
Тогда можно показать, что
1п(1 + аЛДтя) = 1п—1— (11)
или из уравнения (4)
1п(1+алДтя) =Ахп-\-/±хп. (12)
Если безразмерная конечная скорость определяется как
Хк=~^~, (13)
к Py*g
тогда
= Е = S In (1 + ап\->п) - 2 д V (14)
Л—1 Л = 1 /2 = 1
Уравнения (6, 14), включающие в себя известные параметры aJit
Еп, ХКу дают возможность решить поставленную задачу, которая сво¬
дится к тому, чтобы определить такие Ат*, которые дадут минималь-
220
яое значение для Gso/Gn.H и одновременно будут удовлетворять урав¬
нению (14).
Решение задачи минимума должно удовлетворять следующей
системе уравнений [2]:
1 31' ЙФ =0; (15-1)
(15-2)
0; (15N)
оп.н
h
Ч =
1 dA-i
1
dl2
дЛт2
<ЭФ
— п-
^п.н
^2
— о,
<?Дт2
^Е0
1
dljy
дФ
=
где
'Л' дДтдс
Ф = 0, (15N+1)
Ф- 21п(1+аяДтя) -
П — 1 /2 = 1
т) — неопределенный множитель Лагранжа.
Решение уравнений (15)-(1) — (15JV) можно получить в форме
AV
1-с,
а1£1
А Я1 — 1
Ах,
ах
л- 1~£
Ах
А 1
Дтп-
—1. (16)
0/1 J
Таким образом, время работы двигателя любой ступени опреде¬
ляется уравнением (16) в зависимости от времени работы двигате¬
лей первой ступени. Решая совместно уравнения (15N+1) и (16),
можно определить оптимальное соотношение ступеней.
ВЫВОДЫ
Совместное решение уравнений (15N+1) и (16) (возможно только
методом последовательных приближений. Бели величина Ati выбра¬
на, то могут быть вычислены Дт2, <Дт3. .Дтп. Так как уравнение
(16) является уравнением второй степени относительно Дт^, то для
Дтп будет два решения; правильным решением будет меньший поло¬
жительный корень. После определения всех времен Дт может быть
вычислена величина если при этом полученное значение не будет
совпадать с заданной величиной то следует предпринять сле¬
дующую попытку и т. д. до тех пор, пока заданная и действительная
величины не совпадут с достаточной точностью. Типовой расчет пред¬
ставлен в табл. 1. Результаты выбранного варианта этого расчета
приведены в табл. 2.
На фиг. 81 показано решение задачи оптимального распределе¬
ния времени работы двигателей ступеней составной ракеты для ти¬
пового случая. Из графиков можно видеть, что оптимальное распре¬
деление имеет отчетливо выраженный характер. На фиг. 82 и 83
показано влияние различных параметров для случая, когда макси¬
мальное ускорение и относительный вес конструкции одинаковы для
всех ступеней аппарата.
221
Я >->
сх я
03 о
с Ч
X
Я
я
я
я
ч
СП
03
03
-
Я Н о
°-5
аз я
я
я ч
« о
я
4 £
ю §
О и
s 5 2
5 к
я § m
Oj я
С? &
2? Н »Я
£■ g га
& §к
t-J- V!
CL) л
М с Оо
СЯ I Со
Sg!
Pi
е я :
со Ч >» г
я
Ч
CQ
я
е
1
i
1 lo
,°°
Vr5
1
- 1
/
/
см*
и —
*
X
-Л
г
i
ГО
см
/
)
L—
<
-L-
j
1 V
1
А—
_ _
l-> СМ
<1
<
аЗ о
н га .
аз о g я
о \о га н
д с\3 S Qj
я сх н я
с- я
Я S ’Я О.
^ Я
к га га ®
га 2
я S
> 2
н 2
Я '■
О
оо s’!
га |
gSi
е §:
222
Таблица I
Типовой расчет
v—7625 м/сек руд=300 кг сек/кг ^=2,585
аг = 8 а2~Ю а3=8
£j=0,05 £2=0,05 £3=0,10
At,
At2
Дтз
*K. расч
0,15
0,160
0,0950
1,911
0,20
0,203
0,1320
2,269
0,25
0,257
0,1760
2,572
0,253
0,259
0,1785
2,585
Таблица 2
Окончательные результаты расчета
Вес полезной нагрузки Gn. н=453 кг
Ступени
Дтл
Gj п
кг
б?с п
кг
Go п
кг
Рп
кг
м/сек
1
0,253
3,39
76
12 280
646
18 337
48 500 :
2500
2
0,259
4,15
78
3 900
206
5411
15 020
5460
3
0,1785
2,88
54
767
85
1305
4 300
7570
ЛИТЕРАТУРА
1. Малина Ф. и Саммерфилд М., Проблема преодоления притяже¬
ния Земли при помощи ракет.
Mali па F. and Summerfield М., The Problem of Escape from the
Earth by Rocket, «Journal of the Aeron%itical Sciences», 1947, No. 8, vol. 14, pp.
471—480.
2. Г ильдебрант Ф., Методы прикладной математики.
Hildebrand F., Methods of Applied Mathematics, Prentice-Hall, New
York, 1952, pp. 120—122.
М. ГОЛДСМИТ
ВЫБОР ОПТИМАЛЬНЫХ ВЕСОВЫХ СООТНОШЕНИИ
ДЛЯ ДВУХСТУПЕНЧАТЫХ РАКЕТ1
ВВЕДЕНИЕ
При конструировании многоступенчатых ракет желательно рас¬
пределить вес конструкции, топлива и других элементов по ступеням
ракеты таким образом, чтобы достигнуть заданных характеристик
1 М. Goldsmith, On the Optimization of Two-Stage Rockets. «Jet Propul¬
sion», 1957, vol. 27, No. 4, pp. 415 — 416.
223
при минимальном ее общем весе. Эта задача рассматривалась в ра_
боте Малина и Сам(мерфилда [1] для случая ракетного аппарата с
произвольным количеством ступеней при том допущении, что кон¬
структивные характеристики всех ступеней были одинаковы. В ка¬
честве критерия для оценки ракеты принималось максимальное зна¬
чение скорости в конце работы двигателя последней ступени (ракеты
с заданным стартовым весом. Удельная тяга двигателей предпола¬
галась одинаковой для всех ступеней. Расчеты Малина и Саммер-
филда показали, что величина отношения веса топлива к общему
начальному весу должна быть одинаковой для каждой ступени.
Целью настоящего анализа является определение оптимального
распределения весов для двухступенчатой ракеты последовательной
схемы для случая, когда конструктивные характеристики и удельные
тяги двигателей обеих ступеней различны. Критерием для оценки ра¬
кеты здесь принимается 'минимальный общий вес ракеты при задан¬
ной конечной скорости, что эквивалентно критерию, использованно¬
му Малина и Саммерфилдом.
Вследствие принятых упрощений полученные решения не вполне
соответствуют результатам точного анализа, но они представляют
собой полезные отправные данные, необходимые для последователь¬
ных приближений, к которым обычно прибегают при более деталь¬
ном расчете оптимальных проектных соотношений.
ИССЛЕДОВАНИЕ
Скорость в конце работы двигателя в случае полета в условиях
отсутствия силы тяготения и силы сопротивления среды определяется
уравнением (1). Предполагается, что скорости истечения струи из
ракетных двигателей не одинаковы, но постоянны по времени:
(1)
о 4 иК2
Здесь .0*2 — скорость в конце работы двигателя второй ступени;
Vr — скорость истечения струи;
G0 — начальный вес ступени;
G*— вес в момент окончания работы двигателя.
Индексы «1» и «2» относятся к первой и второй ступеням соот¬
ветственно. Общий вес первой ступени включает в качестве полезно¬
го груза общий вес (второй ступени.
Предположим, что вес конструкции ступени пропорционален весу
топлива, а вес двигателя пропорционален общему весу ступени. Для
того, чтобы эти предположения были справедливы для больших ра¬
кет, постоянные коэффициенты пропорциональности должны быть
тщательно выбраны с учетом особенностей рассматриваемых систем
подачи топлива.
Таким образом принимается:
вес топлива 1-й CTyneHH = £1G0i; 2-й CTyneHH = &2G02; } (2)
вес конструкции 1-й ступени = f1Gn\ 2-й ступени = [2Gt2 , J
где GT — вес топлива.
Эти допущения приводят к следующим типовым соотношениям
0К1 = Оог + ЛОт1 + kx G0l,
Gk2 = °п.н + /2Gt2 + ЛаОда,
G01 = Gk1 + Gt1>
G02 = Gk2 + Gt2>
(3)
где Опн —полезная нагрузка второй ступени.
Для дальнейшего исследования весовые характеристики, входя¬
щие в уравнение (1) и (3), удобно выразить в следующей форме:
G,
1
кГ
к2 "
1 +/l
1
:1+/2
[G02 + (^i +/i) G01],
[Gn.H + (^2+ Л) G02]-
(4)
Используя выражение (4), уравнение максимальной скорости
можно теперь преобразовать к виду
Vr1 In G01 — Vл In
l
+ Vr2 In G02 —- V r2 In
l+/i
1
1+/2
[G02 + (&i + /1) G01] +
[Gn.H + (^2 + /2) G02].
(la)
Принимая теперь в качестве переменных G01 и G02, а в качестве
параметра vKj это уравнение можно продифференцировать, в резуль¬
тате чего получаем
Vrl(kl+fl)
+
’Vr2
*01
Vr 1
Gq2 + (^1 +/l) Goi
rfG01 +
G#2
откуда
G02 + (&1 +/l) Ooi
dG01
Угг(*2+/2)._1 rfOo2 = 0,
Gn.H + (^2 + /2)Go2J^
dGo2
]a
(5)
(6)
Экстремальное значение общего начального веса G01 можно най¬
ти, если приравнять это дифференциальное частное нулю, что озна¬
чает, что числитель должен равняться нулю, при условии, что зна¬
менатель отличен от нуля.
1 Уравнение (1а) может быть представлено в ©аде F (G02, G0i)=0, и тогда,
используя правило дифференцирования неявной функции, получаем G'0i —
=—f'o IF'gqi и> слеД°вательно, dGoi/dG0*=—•[ ]#/[ ]д (Примечание ред.)
15
394
225
Алгебраические выкладки показывают, что числитель превра¬
щается в нуль, когда
1
G„.„ Vn(k2+f2)
<Ул-ул)-
Gq\
O02
vm + Ь)
(7)
Легко показать, что знаменатель никогда не может быть равен
нулю (для случаев, когда G02T^O)> следовательно, отношение, задан¬
ное уравнением (7), является оптимальным критерием.
Фиг. 84. Номограмма уравнения (9).
Уравнение (1а) может быть переписано с учетом уравнения (7)
1 +/2
Ут\ (#2 +Л)
(Vr2- Vn)+-^vr2{kx+fx)
Ц)2
+ (^2 + /2)
(8)
Так как величины Vr\ и W2 различны, то решение этого уравне¬
ния должно быть численным Решение уравнения (8) упрощается,
если воспользоваться вспомогательным графиком.
На фиг. 84 Изображен график зависимости некоторого парамет¬
ра (обозначенного буквой А), состоящего из членов, представляю¬
щих собой только заданные числа задачи, от выражения (обозна¬
ченного буквой А), включающего заданные числа и искомое отно¬
шение G02/G01. На графике представлен ряд таких кривых, соответ¬
ствующих различным значениям Угг/Уп.
1 Анализ, подобный представленному здесь, был опубликован недавно
Фертрегтом [2]. Он показал, как может быть получено точное решение этой задачи
для случая равных скоростей истечения
226
Таким образом, эти новые переменные имеют вид
J^__6?Q2 1
Goi /1 + ki
а соотношение, отображенное на графиках фиг. 84, получается соот¬
ветствующим преобразованием уравнения (8), т. е.
Затем по найденной при помощи уравнения (7) величине G0i/G02
определяется отношение G02/Gn,н.
Таким образом, задавая желаемые величины Gn.H, все необходи¬
мые веса можно найти из соотношения (2) и (3).
Для того случая, когда можно считать, что весовые параметры
конструкции ракеты и двигателя и эффективные скорости истечения
не очень сильно различаются для разных ступеней ракеты, оптималь¬
ный критерий Малина—Саммерфилда соответствует первому при¬
ближению к оптимальной конструкции. Критерий Малина-Саммер-
филда может быть получен из уравнения (7), если положить Vr\ =
= Vr2> ki = k2 = 0 и /i = /2, так как в результате этого получаем следую¬
щую оптимальную характеристику G02/Gn.»= G0i/G02. Однако если
эти параметры сильно отличаются между собой, то оптимальное ус¬
ловие, выведенное выше в настоящей работе, будет также намного
отличаться от критерия Малина—Саммерфилда, как это показано на
следующем численном примере.
Используем уравнения (7, 8) для расчета оптимального распреде¬
ления веса в двухступенчатой ракете, которой должна быть сообщена
скорость к моменту отсечки двигателя, равная 7645 м/сек. Допустим,
что ракетный двигатель первой ступени работает на химических то¬
пливах, а вторая ступень представляет собой атомную ракету. В рас¬
сматриваемом примере параметры, входящие в расчет, выбраны про¬
извольно.
Используя график на фиг. 84, решаем уравнение (8), что дает
GqiIG02== 1,97. Подставляя это значение в уравнение (7), получим
G02/Gn.H=6,19.
Следовательно, в рассматриваемой конструкции на каждый кило¬
грамм полезного груза, разгоняемый до заданной максимальной
скорости, будет приходиться 6,19X1,97=12,19 кг общего стартового
веса ракеты.
Имея эти данные, можно приступить к исследованию конструк¬
ции, используя их и другие весовые характеристики (двигателей,
конструкции) в качестве удобных исходных данных при условии,
что конструктивные параметры (kif fi) с самого начала были выбра¬
(9)
Vri = 3050 м/сек-, П =0,15; £, = 0,05;
Кг2=7625 м/сек; f2 = 0,25; £2 = 0,15.
15*
227
ны хорошо. Полезно сопоставить полученные выше результаты с ре¬
зультатами вычисления исходных данных двухступенчатой ракеты с
двигателями на химическом и атомном топливе по методу Малина —
Саммерфилда. Тогда в результате решения уравнения (1а) можно
получить, что G01/G02=G02/Gn н = 3,79 и, следовательно, на каждый
килограмм полезного груза потребуется (3,79)2 = 14,4 кг общего стар¬
тового веса ракеты.
Преимущество предложенной методики расчета заключается в
том, что при ее использовании общий стартовый вес ракеты в резуль¬
тате оптимального распределения его между ступенями получается
меньшим.
ЛИТЕРАТУРА
1. Малин»а Ф. и Самме!рф«лд М., Проблема преодоления силы тяго¬
тения Земли с помощью ракеты.
Mali па F., and Sumrnerfield М., The Problem of Escaoe from the
Earth by Rocket, «Journal of theA eronautical Sciences», 1947, vol. 14, No. 8, p. 471.
2. Фертрегт М., Метод расчета весовых соотношений ступенчатых ракет.
Vertregt М., A. Method for Calculation the Mass Ratios of Step Rockets,
«Journal of the British Interplanetary Society», 1956, No. 2, vol. 15, p. 95.
РАЗДЕЛ IV
ОПТИМАЛЬНЫЕ РЕЖИМЫ ДВИЖЕНИЯ РАКЕТ
\Ъ МЕЖПЛАНЕТНОМ ПРОСТРАНСТВЕ
В. ФРИД
ОБ АКТИВНОМ УЧАСТКЕ ТРАЕКТОРИИ ПОЛЕТА
СПУТНИКА ЗЕМЛИ 1
В статье рассматривается проблема программирования активного
участка траектории спутника Земли с целью достижения максималь¬
ной высоты орбиты.
Оптимальная траектория для ракеты, представленной в виде ма¬
териальной точки, движущейся в однородном гравитационном поле,
в условиях, когда аэродинамические силы пренебрежимо малы, по¬
лучается в том случае, если тангенс угла Ф между вектором тяги и
горизонтом является линейной функцией времени.
Этот результат справедлив при любой зависимости массы и тяги
от времени, включая разрывы непрерывности, соответствующие отде¬
лению ступеней. Более того, если заменить высоту орбиты какой-
нибудь другой функцией высоты конца активного участка и вектора
конечной скорости, например высотой перигея эллиптической орбиты,
и отыскать стационарное решение, то снова будет получена линей¬
ная зависимость тангенса угла от времени. В статье даются нагляд¬
ные выражения для скорости и высоты, которые получаются при
применении такого типа программы изменения направления вектора
тяги для частного случая постоянной тяги и постоянного секундного
расхода массы.
ВВЕДЕНИЕ
Практический выбор траектории активного полета будущего
спутника Земли, который должен быть запущен в соответствии с
программой 2 Международного геофизического года, будет зависеть
от проектных параметров ракеты-носителя, от выбранной орбиты,
определяемой установленной аппаратурой и измеряемыми парамет¬
1 В. D. F г i е d, On the Powered Flight Trajectory of an Earth Satellite,
«Jet Propulsion», 1957, vol. 27, pp. 641.— 643.
2 H. E. Newell, Scientific Uses of an Artificial Earth Satellite, «Jet Propul¬
sion», 1955, vol. 25, No. 12, pp. 712 — 715.
229
рами. Однако независимо от этих соображений интересно знать,
какая траектория будет оптимальной с точки зрения эффективности
самой ракеты-носителя спутника. Для того чтобы решить этот во¬
прос, сначала необходимо выбрать некоторый надежный критерии
для сопоставления различных траекторий.
При выборе ракет класса «земля—земля» таким критерием яв¬
ляется дальность полета, однако не ясно, какая величина будет
эквивалентна этой характеристике в случае спутников. Одной и?,
важных характеристик спутника является полезное время нахожде¬
ния его на орбите. Слишком низкая орбита приведет к быстрому
замедлению движения спутника под действием сопротивления
атмосферы и к нежелательному сокращению времени его существо¬
вания. Это обстоятельство не имеет существенного значения, если
ускоритель достаточно мощный, поскольку на высотах свыше 480 км
время нахождения на орбите измеряется годами и, вероятно, опреде ¬
ляющим фактором будет срок существования источника энергии, а
не разрушение спутника вследствие сопротивления воздуха. Однако
если ракета-носитель спутника обладает только минимальными ха¬
рактеристиками без запаса, то высота орбиты будет играть решаю¬
щую роль и может служить определяющим критерием.
«Высота» орбиты является достаточно определенной величиной
только для круговых орбит. В 'случае эллиптической орбиты обычно
имеют дело с расстоянием наибольшего приближения (р. н. п.), т. е.
с высотой перигея. Высота перигея примерно согласуется со време¬
нем разрушения спутника под действием атмосферы, потому что
замедление спутника вследствие сопротивления атмосферы происхо¬
дит в основном вблизи перигея. Это соответствие не вполне точно,
поскольку из двух орбит с одинаковыми р. н. п. на орбите с большим
эксцентриситетом время существования спутника будет больше.
Однако приведенный ниже анализ не изменится сколько-нибудь зна¬
чительно, если р. н. п. заменить средним значением между высотой
перигея и высотой апогея или какой-нибудь другой функцией высоты
и вектора скорости в конце активного участка траектории. Для опре¬
деленности примем в качестве критерия именно расстояние наиболь¬
шего приближения (р. н. п.). Данные о траекториях в аналитическом
виде можно получить лишь при условии пренебрежения некоторыми
членами в уравнениях движения, так как, если включить в рассмот¬
рение влияние атмосферы, изменения силы гравитационного поля и
т. п., то решение дифференциальных уравнений можно будет полу¬
чить лишь путем численного интегрирования. Гораздо важнее уста¬
новить, что при нескольких целесообразно принятых допущениях мы
приходим к очень простому результату: тангенс угла направления
вектора тяги относительно Земли должен быть линейной функцией
времени 1.
1 Стационарный характер такой программы изменения наклона вектора тяги
для круговой орбиты был также показан Перкинсом.
F. М. Perkins, Flight Mechanics of Ascending Satellite Vehicles, «Jet
Propulsion», 1956, vol, 26, No. 5, pp. 352 — 358.
230
В следующем разделе -представлен вывод этого результата и дан
метод определения коэффициентов получающейся линейной функции.
Мы увидим, что хотя этот результат и является приближенным,
однако он при правильном использовании имеет практическое зна¬
чение.
При подходе к решению задачи мы будем предполагать, что ха¬
рактеристики ракеты-носителя, т. е. тяга и масса в функции времени
определены. В таком случае задача сводится к определению такого
активного участка траектории полета, при котором спутник будет
выведен на орбиту с максимальной высотой. Возможны и другие
формулировки задачи; например, для данного полезного груза (т. е.
того веса аппарата, который будет обращаться по орбите) и данной
орбиты найти траекторию, которая обеспечит минимальный старто¬
вый вес аппарата в целом. Решение проблем такого рода требует
довольно точных сведений о ракете-носителе, о принципе сопряжения
ступеней, конструктивных коэффициентах, коэффициентах емкости
баков и т. д., поэтому достаточно точное общее решение вряд ли
возможно получить.
Эти затруднения отпадают, если рассматривать, как это сделано
в настоящей работе, характеристики ракеты заданными.
Рассмотрим задачу определения активного участка траектории
ракеты, обеспечивающую максимальную высоту орбиты спутника,
если величины тяги и массы ракеты являются определенными, хотя
и .произвольными функциями времени.
Мы будем считать ракету материальной точкой, а Землю—не-
вращающимся шаром, а также будем пренебрегать влиянием сле¬
дующих факторов:
1) аэродинамическими силами — лобовым сопротивлением, подъ¬
емной силой и т. д.;
2) зависимостью тяги от высоты;
3) изменением величины направления силы тяжести в течение
активного участка траектории.
Если орбита должна быть круговой (эллиптические орбиты будут
рассмотрены дальше), тогда к моменту выгорания топлива ракеты-
носителя вертикальная составляющая скорости должна стать равной
нулю, а тангенциальная составляющая должна быть такой величи¬
ны, при которой центростремительная и гравитационная силы урав¬
новешивались бы:
где (их, щ)—составляющие скорости к моменту выгорания топлива;
R3 —радиус Земли; у—высота, на которой закончилось выгорание
топлива; g — ускорение силы тяжести на поверхности Земли.
Для плоских траекторий путь вполне определяется заданием угла
наклона тяги (скажем, относительно горизонта) ф(0- Поставим за-
АНАЛИЗ ТРАЕКТОРИЙ
(И
231
дачу определения такой функции которая увеличивает высоту
конца активного участка до максимального значения, удовлетворяя
одновременно равенству (1). Для 'простоты предположим сначала,
что и Исп*тн является заданной величиной, пренебрегая ее зависи¬
мостью от высоты (которая будет незначительна, по крайней мере,
для 'Случая высот, малых по сравнению с радиусом Земли). Дальше
мы увидим, что эту зависимость легко учесть.
Если 8у является изменением высоты конца активного участка,
соответствующим изменению ф(/) (£)+#ф(0> а Ьих и 8щ — по¬
добные же изменения составляющих скорости, то необходимым усло¬
вием для того, чтобы высота, определяемая уравнением (1), полу¬
чила максимальное значение, является следующее соотношение:
8y-\-X$Uy-\-\i8iiy=Qy (2)
где коэффициенты Лагранжа X и ц являются неизвестными посто¬
янными.
Если обозначить N(t) =P(t)/M(t)—отношение тяги к массе в
данный момент времени, то
х*
их = § dtN cos $+ и°л
о
т
иу = J dt N sin ty — gT— u°y,
о
T
y = j dt(T— t)Nsin —^gT^+y* + u°yT,
(3)
де Г—общая продолжительность активного участка. Если
т
Ф (0 Ф (0 + Ц (0» т0ГДа их~>их'~ j dtNsm ф 8ф (t) и, следова-
о
тельно,
т \
Ъих— — j* dtN sin ф 8ф,
оиу = j dt N cos ф 8ф,
о
т
by = ^dt(T—t)Ncos ф 8ф.
(4)
После подстановки этих выражений в равенство (2) убеждаемся,
что оно может быть удовлетворено произвольным значением
232 *
если только N[(T—/)cost|)—% sin ф+М- cos ф] = 0 для любых значе¬
ний t. Таким образом, когда Ыф О, необходимо, чтобы
f [(v- + T)-t]. (5)
Поскольку X и ц, являются неизвестными постоянными, можно
выразить полученный результат в следующей форме:
tg ty = a—bt, (6)
где а и Ь—постоянные, выбираемые так, чтобы они удовлетворяли
равенству (1).
Несмотря на то, что результат (6) справедлив для произвольных
значений P(t) и M(t), точные значения а я b будут, конечно, зави¬
сеть от этих функций. В частном случае, когда P(t) и M(t) являются
на определенных отрезках постоянными функциями, выражения (3)
для их и щ можно проинтегрировать в элементарных функциях.
Приращения их, щ и у вследствие срабатывания одной ступени
с коэффициентами отношения масс г, скоростью истечения газов Vr.
временем горения tt при условии, что tg яр является линейной функ¬
цией времени, равны
17 7 (t 1 Г1 —cos —ф) СОвф, 1) |
Лиг= Vrcos Ф In г — In —— ——±г — ,
I L1 —1— cos (ф: — ф) cos ф0 JJ [
Ду
где фо есть первоначальное значение ф; ф!—величина, соответст¬
вующая отрезку времени t±, а ф—величина в момент
^г
~ М " г — 1 ’
где Mq и М суть начальные значения массы и секундного расхода
массы для данной ступени К Суммируя приращения всех ступеней и
прибавив к (иу и у) гравитационные члены (—gT и — где
Т—общее время активного полета), получаем выражения для их, иу
к у. Положив их = испутнииу=0у можно использовать эти оба соотно¬
шения для определения коэффициентов а и b и затем подставить
полученные значения а и b в выражение для у с тем, чтобы найти
высоту орбиты.
До сих пор мы только показали, что уравнение (6) имеет стаци¬
онарное решение. Однако легко показать, что высота, получаемая
при такой программе наклона тяги, в действительности является
1 В членах а и Ь уравнения (6) tg фо = a, tg фi=a—btlt tg Ф ————.
233
= t
+ sin фо cos фт
+ sin ф! cos Фо .
COS ф} — cos ф0 Д Uy
Vrin |j
,[ю
(7)
sin (Фо — ФО
г-1
абсолютным максимумом. Доказательство этого обстоятельства, по¬
лученное Г. Галлером и К. Гоффманом, дано в приложении.
Процесс определения а и Ь прост, однако на практике несколько
громоздок вследствие того, что приходится совместно решать два
трансцендентных уравнения. Кроме того, в нашем решении мы пре¬
небрегли зависимостью испУтн от высоты. Обоих этих затруднений
можно избежать, если воспользоваться более общим методом подхо¬
да к решению задачи. Откажемся от принятого ранее ограничения
круговыми орбитами и просто предположим, что после выключения
двигателя достигнуты определенные величины их> ии и у. Они одно¬
значно определяют эллипс Кеплера, по которому движется спутник
и, в частности, р. н. п. (расстояние наибольшего приближения) этой
орбиты. Если Н является р. н. п. и D=R3-\-H, тогда в символах
энергии Е и кинетического момента L имеем
n_-k+(k* + 2 EL^>2
u Ye ’ (8)
где
E=^—k(R3+y)-\
(9)
L — ux(R3+y),
k = gRl-
Если i|)(f)—'функция, дающая максимум D, тогда потребуем,
чтобы
'JD=Dyr>y + Dubax + = 0, (10)
где Dy=dD/dy и т. д. Иопользуя (4), снова находим
tg ф = а—Ы,
где а и Ь определяются как
TDy+Duy 6==£l. (И)
D‘X
Эти формулы позволяют вычислить а и 6 методом итераций, на¬
пример, задаться величинами их, Uyj вычислить ЕиХу DUy, Dy из (8, 9),
вычислить а и b из (11), найти их, иу, у из (7) и т. д. Эта процедура
позволяет вычислить максимальную 1 возможную для ракеты вели¬
чину D с учетом условий «1», «2», «3». Наиболее важным из них яв¬
ляется первое условие, потому что программа, подобная (6), дала бы
недопустимо большие углы атаки. Следовательно, желательно при¬
менить программу изменения угла тангажа, обеспечивающую мини-
1 Р. н. п. стационарно при программе изменения направления вектора тяги
(6) с коэффициентами а и 6, определяемыми уравнением (11). Хотя и было дос¬
казано, что действительный максимум соответствует только случаю круговой
орбиты (см. приложение), некоторые соображения, вытекающие из физической
непрерывности решения, говорят о том, что уравнение (6) должно также приво¬
дить к максимальному значению р. н. п. и для эллиптических орбит, по крайней
мере для орбит с малым эксцентриситетом.
234
мальные углы атаки до тех пор, пока 'ракета не поднимется на до¬
статочно большую высоту для того, чтобы можно было пренебречь
аэродинамическими силами и переключиться на выполнение про¬
граммы (6). Пользуясь тем обстоятельством \ что модуль скорости в
конце обычной плавной программы тангажа является намного менее
чувствительной функцией первоначальных условий (угла тангажа и
т. д.), чем направление вектора скорости, легко показать, что плавная
программа должна быть выбрана так, чтобы в момент перехода к
режиму (6) функция ф не терпела бы разрыва.
При этой программе по-прежнему сохраняется условие «2», по¬
скольку мы следуем уравнению (6) только на больших высотах, где
тяга не зависит от высоты. Наконец, то обстоятельство, что актив¬
ный полет происходит в непостоянном гравитационном поле, не¬
сколько изменит наши результаты. Однако это влияние будет незна¬
чительным при условии, что длина активного участка траекторий
мала по сравнению с радиусом Земли.
ВЫВОДЫ И ОБСУЖДЕНИЕ РЕЗУЛЬТАТОВ
Показано, что для получения орбиты спутника с максимальной
высотой при использовании в качестве носителя заданной ракеты,
угол наклона вектора тяги ф должен зависеть от времени следующим
образом:
tg ф = а—bt (6)
на том участке активного полета, где аэродинамические силы и изме¬
нения силы тяжести могут не приниматься во внимание. Этот вывод
справедлив при любой зависимости тяги и массы от времени и, сле¬
довательно, для любых схем сопряжения ступеней. Более того, если
заменить высоту орбиты какой-нибудь другой функцией высоты и
вектора скорости в конце активного участка, например высотой пери¬
гея, и искать стационарное решение — будет снова получен результат
в форме (6). Для определения коэффициентов а и Ъ необходимо вы¬
числить скорость в конце активного участка с учетом значения ф,
взятого из уравнения (6). Для частного случая, когда тяга и секунд¬
ный расход массы постоянны, это решение можно получить в анали¬
тическом виде. Результат—уравнение (7) —является обобщением
известных формул Av = VT\n г, получаемых при постоянном ф. Про¬
грамма управления, подобная (6), физически возможна. Для полу¬
чения больших высот необходимо запускать ракету-носитель при
большом значении ф так, чтобы вертикальная составляющая скоро¬
сти с течением времени могла обеспечить необходимую высоту. Позд¬
нее в полете необходимо уменьшить угол ф для создания необходи¬
мой горизонтальной составляющей скорости, а также для того, что¬
бы любая возросшая вертикальная составляющая скорости могла
бы быть погашена силой тяжести.
Наилучший способ сочетания этих условий и дает программа (6).
Поскольку общая форма этой функции качественно похожа на ту,
1 G. Culler and D. В. Fried, Universal Gravity Turn Curves, «Journal of
Applied Physics» (в печати).
235
которая связана с плавной программой тангажа баллистической
ракеты, можно предполагать, что проигрьгш в результате использо¬
вания этой последней программы при полете в пределах атмосферы
будет невелик.
ПРИЛОЖЕНИЕ
Покажем теперь, что высота круговой орбиты не только является:
стационарной для данной программы наклона тяги (5), но в дейст¬
вительности является абсолютным максимумом, как это -впервые
отметили Г. Галлер и К. Гоффман (работа не публикована). Вычи¬
слим вторую вариацию величины
7(ф) = ,
первая вариация которой приводит -к уравнению (5). Имеем
-J!b-=_Af[(!i + 7’— t) sinфXcosф]. (A-l)
Допустим, что ф0(t)—программа наклона тяги, определяемая
уравнениями (5) или (6), т. е.
tg’VoC)=«-^=Y(li + 7’_^ °<*o<Y' (А'2)
тогда (А-1) дает
ЦЧ*)
— АД [cos ф + tg ф0 sin ф] = — А/Х sec ф0 cos (ф — ф0)- (А-3)
Видно, что при наличии физически допустимых условий
0<Ч[>оО/2 и Я>0 имеем 1
<0> (А'4)
&Ф2(0 Ф=Ф. (О
а это гарантирует, что J имеет относительный максимум при
ф = фо(/). Поскольку
т т
J = ^dtN {(Г + u — t) sin ф + X cos ф} = А/Х sec ф0 j dt cos (ф — ф0),
о о
то ф = фо в действительности обеспечивает абсолютный максимум
для /. Необходимо отметить, что
1. Поскольку фо(0 удовлетворяет ограничениям, заложенным в
уравнениях (1), то значения К и ц выбирают с таким расчетом, что¬
бы удовлетворить этим условиям. Будем предполагать, что общий
импульс v = Vr\n г ракеты должен быть достаточно большим по
сравнению с gT и исп>Тн, чтобы такие величины X и ц существовали.
2. фо(0 дает максимум J относительно всех остальных допусти¬
мых функций, независимо от того, удовлетворяют ли они ограниче¬
ниям.
1 >,>0 просто означает, что является монотонно уменьшающейся функ¬
цией t.
236
3. Отсюда следует, что tyo(t) даст максимум J для более ограни¬
ченного класса функций, удовлетворяющих этим ограничениям.
4. Для функций, удовлетворяющих уравнению (1), наличие мак¬
симума J равноценно наличию максимума у.
Таким образом можно прийти к выводу о том, что ф0 (0 даст мак¬
симум высоты орбиты то сравнению со всеми другими программами
наклона тяги, удовлетворяющими уравнению (1).
КОММЕНТАРИИ К СТАТЬЕ В. ФРИДА
«ОБ АКТИВНОМ УЧАСТКЕ ТРАЕКТОРИИ ПОЛЕТА
СПУТНИКА»
I
Т. ЭДЕЛЪБАУМ 1
ОБСУЖДЕНИЕ
В журнале «Jet Propulsion» [1, 2] приводилось два вида анализа
оптимального изменения угла тяги ракеты-носителя спутника. Оба
эти анализа показали, что тангенс угла между вектором тяги и гори¬
зонтом должен быть линейной функцией времени. Однако ни в одном
из этих анализов не рассматривалось действие центробежной силы,
влияние которой для ракеты-носителя значительно.
Значение центробежной силы было установлено Ф. М. Перкинсом
в работе [2]. Он исключает ее из своего рассуждения путем искусст¬
венного предположения о том, что сила тяжести на активном участке
полета имеет постоянное среднее направление. Это предположение
позволяет получить приближенное решение об оптимальной траек¬
тории в замкнутой форме.
Значение центробежной силы можно продемонстрировать, напи¬
сав уравнения движения спутника для случая сферической Земли и
отметив те допущения, которые необходимо принять для того, чтобы
эти уравнения можно было свести к уравнениям для плоской Земли,
приведенным в работах [1, 21.
Считая ракету материальной точкой, движущейся в вакууме во¬
круг сферической невращающейся Земли, можно записать уравне¬
ния движения в обозначениях, принятых в работе [1], в следующем
виде:
duv и\ ш R\
:iVsin^ — g
dt Яз+У (Яз+У)2
UXU
хиу
dt Я3 +У
dy
• N cos ф;
— = u v.
dt y
(i)
1 T. N. E d e I b a u m, Comments on the Powered Flight Trajectory of a Sa¬
tellite, «Jet Propulsions 1957, vol. 27, No. 12, pp. 1260—1261.
237
Эти уравнения можно упростить, предположив, что высота актив-
иого участка полета невелика по сравнению с радиусом Земли. Отсю¬
да следует, что R3 -]-// в уравнениях может быть заменено радиусом
Земли Д3> а второй член во втором из уравнений (1) опущен. По¬
следнее упрощение можно произвести путем подстановки третьего
уравнения во второе:
Ux R3
N cos ф
dt.
Ux
с
Поскольку высота обычно невелика по сравнению с 7?3, величину
dy/R3 можно считать бесконечно малой и опустить. В этом случае
уравнения (1) принимают вид
duy
dt
— -M = A/sin ty — g-,
Кз
—=N cos ф;
at
dy
dt
'y*
(3)
Уравнения движения (3) равноценны уравнениям, приведенным
в работах [1, 2], за исключением члена центробежной силы в первом
уравнении. Центробежное ускорение u2JR3 можно исключить
только в том случае, если оно невелико по сравнению с ускорением
силы тяжести g, или по сравнению с отношением вертикальной со¬
ставляющей скорости к массе N sin ф. Поскольку эти предположения
обычно несправедливы для ракет—носителей спутников, центробеж¬
ное ускорение необходимо учитывать в уравнениях движения. Ниже
дается вывод оптимальной траектории с учетом этого члена.
Оптимальную траекторию запуска спутника ддя уравнений дви¬
жения (3) можно определить с помощью методов вариационного ис¬
числения. Для удобства задача формулируется как задача опреде¬
ления минимального значения времени, требующегося для вывода
спутника на орбиту с заданным расстоянием наибольшего прибли¬
жения (р. н. п.). 3>та постановка задачи равноценна задаче обеспе¬
чения максимального значения р. н. п. при заданном времени работы
двигателей.
Минимум интеграла времени при заданной функциональной за¬
висимости между высотой, горизонтальной скоростью и вертикаль¬
ной скоростью в момент окончания работы двигателя принимает
следующий вид:
'=J*+b(v-;|-Wsl"t+s)+
+ *2 'N cos ф) + ( *Г_ “*)}dt- ' (4)
238
Уравнения Эйлера для этого интеграла имеют вид:
=0= — — — Х3>
By dt з.
“дг
^2
rtf /?з
(5)
еф = 0 = — XjN cos ф -f X2/V sin ф.
Отсюда можно получить следующие выражения:
^Ф = г-.
А2
Х1 = Х17,-|- Хзг (Г £),
л2 —
Лз
(6>
Значения ут, и ^ должны быть такими, чтобы результи¬
рующая орбита имела требуемую величину р. н. п.
Это можно обеспечить, предположив, что величины р. н. п. и соот¬
ветствующие неопределенные множители Лагранжа из уравнений
(6) трансверсальны. В данном случае условия трансверсальности
имеют вид условий (7), где D^=dD/dy1 и т. п.:
\]Т
^2 т
\зт
Du у
:дГ
hr Du
(7>
Решение уравнений (3) и (6) при .начальных и конечных гранич¬
ных условиях (7) являются решением данной проблемы для любого
закона изменения тяги и массы в зависимости от времени.
К сожалению обязательное включение в рассмотрение центро¬
бежной силы не позволяет получить приближенное решение опти¬
мальной траектории в простой замкнутой форме.
ЛИТЕРАТУРА
1. Фрид Б. Д., Об активном участке траектории полета спутника Земли.
Fried В. D., On the Powered Flight Trajectory of an Earth Satellite, «Jet
Propulsion», 1957, vol. 27, No. 6, pp. 641—643.
2. Перкинс Ф. М., Механика полета при подъеме !ракеты-носителя спутни¬
ка Земли.
Perkins F. М., Flight Mechanics of Ascending Satellite Vehicles, «Jet
Propulsion», 1956, vol. 26, No. 6, 352—358.
1 Выражение для p. н. п. можно найти в работе [1].
II
Д. ЛОУДЕН1
В. Д. Фрид показал [1], что если пренебречь действием силы со
противления атмосферы и изменением величины и направления силы
тяжести во время движения .ракеты-носителя искусственного спутни¬
ка Земли с работающим двигателем, то для получения оптимальных
характеристик подъема тангенс угла наклона вектора тяги двигателя
должен быть линейной функцией времени.
Этот результат может быть обобщен следующим образом: напра¬
вим горизонтальные и вертикальные оси координат Ох и Оу через
точку старта аппарата и предположим, что траектория лежит в пло¬
скости Оху, и будем считать, что (qu q2) являются координатами
точки окончания работы двигателя, a (qu q2)—составляющими ско¬
рости в этой точке. Тогда, если R есть какая-нибудь функция пере¬
менных (qly q2l qlf q2) (например, дальность ракеты, максимальная
высота или эксцентриситет орбиты), то R будет становиться экстре¬
мальной величиной (обычно максимумом), если направление векто¬
ра тяги двигателя будет изменяться в соответствии с уравнением
ilift t
dqi dq i
где ф — угол между направлением вектора тяги и осью Ох в момент
t, отсчитываемый с момента старта;
Т — общая продолжительность работы двигателя.
Таким образом, tgip всегда является дробнолинейной функцией
времени, т. е.:
tg+=^.
ST ct+d
Доказательство этого вывода приведено в работе [2].
Очевидно, что tg ф может быть линейной функцией t только в том
случае, если R не зависит от q±.
ЛИТЕРАТУРА
1. Фрид Б. Д., Об активном участке траектории полета спутника Земли.
Fried В. D., On the Powered Flight Trajectory of an Earth Satellite. «Jet
Propulsion», 1957, vol. 27, No. 6, pp. 641—643.
2. Лоуден Д. Ф., Динамические проблемы межпланетного полета.
Law den D. F., Dynamic Problems of Interplanetary Flight, «Aeronautical
Quarterly», 1955, vol. 6, pp. 165—180.
1 D. F. Low den, Optimal Rocket Trajectories, «Jet Propulsion», 1957, vol. 27,
No. 12, p. 1263.
Д. ЛОУДЕН
ОПТИМАЛЬНОЕ ПРОГРАММИРОВАНИЕ НАПРАВЛЕНИЯ
ТЯГИ ДВИГАТЕЛЯ РАКЕТЫ i
ВВЕДЕНИЕ
Полное решение задачи о 'перемещении ракеты между двумя точ¬
ками пространства с минимальным расходом топлива дано автором
в работах [1, 2]. В них показано, что оптимальная траектория движе¬
ния ракеты в вакууме может быть осуществлена только путем прило¬
жения нескольких импульсов тяги двигателя, а в интервалах между
ними ракета должна двигаться свободно, находясь только под дейст¬
вием сил тяготения.
Если на ракету воздействуют также силы атмосферного сопро¬
тивления, то оптимальное движение на участках траектории может
быть осуществлено при некоторых конечных тягах, однако приложе¬
ние мгновенных импульсов тяги в общем случае не исключается. При
использовании обычных двигателей отрезки времени работы двига¬
телей будут настолько малыми по сравнению со временем перемеще¬
ния ракеты между заданными конечными точками, что импульсы, со¬
ответствующие этим отрезкам, с достаточным приближением можно
рассматривать, как теоретически оптимальные импульсы. Когда же
для перехода с одной круговой орбиты вокруг одного тела на другую
орбиту вокруг другого тела должен использоваться двигатель с ми¬
кротягой, то, по заключению некоторых авторов [3, 4], уже никакая
аппроксимация теоретически строгой оптимальной траектории невоз¬
можна и условие минимального расхода топлива по существу сво¬
дится к требованию, чтобы тяга двигателя не превышала некоторой
величины.
Введение этого 'специфического условия существенно усложняет
теорию вопроса. Очевидно, что при этих условиях оптимальная тра¬
ектория должна состоять из
а) дуг нулевой тяги;
б) дуг конечной тяги, удовлетворяющих уравнениям первона¬
чальной теории;
в) дуг максимальной тяги.
Участок траектории нулевой тяги при всех условиях несомненно
является минимальной дугой благодаря тому, что любая близкая тра¬
ектория может быть осуществлена только при затрате топлива. Лю¬
бая дуга конечной тяги, определяемая уравнениями неизменной тео¬
рии и удовлетворяющая специфическому условию об ограничении
тяги, также является оптимальной дугой в силу тех же самых при¬
чин, что и в случае, когда специфические условия не накладываются.
Любая другая дуга С конечной тяги, на которой тяга не равна мак¬
симально возможной, не является оптимальной дугой, поскольку мо¬
гут существовать траектории, на которых расход топлива будет
1 D. Law den, Optimal Programming of Rocket Thrust Direction, «Astro-
nautica Acta», 1955, vol. 1, Fase 1, pp. 41—56.
16 394
241
меньше. Эти близкие траектории могут быть реализованы путем не-
значительной корректировки 'программы изменения тяги двигателя,
поскольку такие корректировки легко осуществимы даже в том слу-’
чае, когда используется двигатель ограниченной тяги при условии,
что он на дуге С не развивает предельной тяги. Единственным воз¬
можным другим типом оптимальной траектории является, поэтому,
дуга, соответствующая максимальной тяге.
Исследование условий сопряжения дуг различных типов и реше¬
ние уравнений, определяющих направление тяги на участках траек¬
тории, где тяга должна быть максимальной, весьма сложны,
В настоящей статье дается частное решение указанной за¬
дачи.
Предположим, что программа расходования топлива задана и
величина тяги может быть определена для любого момента времени
начала работы двигателя. В частности, эта программа может соот¬
ветствовать режиму максимальной тяги во все время работы двига¬
теля. Можно рассчитать такую программу изменения направ¬
ления тяги, в результате которой к заданному моменту времени
ракета получит максимум полной энергии (кинетической и потен¬
циальной) .
Результат решения такой задачи может оказаться особенно полез¬
ным при определении оптимальной траектории отрыва ракеты с ог¬
раниченной тягой от некоторой круговой орбиты. Допустим, что дви¬
гатель работает непрерывно; тогда из сказанного выше следует, что
тяга должна поддерживаться на максимальном уровне до тех пор,
пока энергия ракеты не станет достаточной для отрыва от круговой
орбиты (или превысит эту величину, если необходимо, чтобы скорость
в бесконечности не была равна нулю). В случае движения по опти¬
мальной программе, предложенной в этой статье, это требование в
отношении энергии будет удовлетворяться в наиболее ранний момент
времени и, следовательно, общий расход топлива при этом будет ми¬
нимальным.
Тзяном было проведено предварительное исследование задачи от¬
рыва от круговой орбиты ракеты с двигателями ограниченной тяги
[5]. Его методы являются приближенными и ограничены случаями,
когда тяга f, отнесенная к единице массы, во все время движении
постоянна и направлена:
а) по радиусу-вектору, соединяющему ракету с центром притяже¬
ния, или
б) по касательной к первоначальной круговой орбите.
По заключению Тзяна последний способ программирования на¬
правления тяги является более экономичным, чем первый. Он пока¬
зал, что для этого случая уменьшение f с 1# до 0,001 g приводит к
удвоению величины характеристической скорости итах. Дадим эле¬
ментарное доказательство этому выводу.
Обозначим скорость ракеты в момент времени t через v, а потен¬
циальную функцию гравитационного поля, в котором движется ра¬
кета, через Ф. Пусть скорость истечения газов из двигателя относи-
242
телыю ракеты будет Vг, а масса ракеты в момент «времени t будет М.
Тогда уравнение движения будет иметь вид
(1)
Умножая скалярно обе части равенства на v и подставляя
w=\n М, получим
где s представляет собой параметр длины дуги искомой траектории
и, таким образом, дФ/ds является производной от Ф по направле¬
нию движения. Так как v = ds/dt, то отсюда v d(i)/ds = dO/dt и урав¬
нение (2) можно представить его эквивалентной формой
массы ракеты. Уравнение (3) можно преобразовать к виду
из которого можно заключить, что темп возрастания Е относитель¬
но w (и, следовательно, М) будет наибольшим при совпадении на¬
правлений Vr и v, т. е. при совпадении направления тяги с касатель¬
ной к траектории. Поэтому, если программа расходования топлива
предопределена таким образом, чтобы тяга была постоянно направ¬
лена по касательной к круговой орбите, то при этом будет также
постоянно обеспечен максимальный темп увеличения Е от отрица¬
тельных значений до нуля или выше нулевого уровня и, следователь¬
но, условие для отрыва от круговой траектории будет создано наи¬
более быстро, т. е. будет осуществлена оптимальная программа взле¬
та. Отсюда ясно, почему вторая программа задачи Тзяна (случай
«б») более экономична, чем первая (случай «а»), так как по мере
удаления ракеты по спирали от круговой орбиты касательная к тра¬
ектории редко будет отклоняться от направления касательной к кру¬
говой орбите более чем на несколько градусов и, следовательно,
условия рассмотренной выше задачи будут приближенно все время
выполняться.
Приведенное выше исследование является лишь приближенным
решением задачи и, к сожалению, не дает решения об абсолютном
оптимуме. Поэтому может оказаться выгодным для некоторых объ¬
ектов с большой скоростью в течение начального периода разгона
направлять тягу по линии, заведомо не совпадающей с касательной
к орбите, с тем чтобы на конечных участках траектории разгона, ко¬
гда направления тяги и касательной совпадут, скорость v стала бы
большей по величине, чем в первом случае, и, следовательно, соглас¬
но уравнению (4) темп возрастания Е также бы возрос. Такое быст-
(2)
16*
2А 3
рое возрастание Е должно скомпенсировать уменьшение темпа воз¬
растания энергии на начальном участке, и «ниже будет доказана спра¬
ведливость этого утверждения. Однако в работе [6], касающейся
отрыва от круговой орбиты при импульсном режиме работы двигате¬
ля, показано, что при некоторых условиях неэкономично поддержи ¬
вать темп увеличения Е на максимальном уровне на всей траектория
отрыва. Действительно, если требуется произвести отрыв от круговой
орбиты таким образом, чтобы скорость в бесконечности превышала
некоторую величину, то оказывается выгодным вначале направит],
тягу даже против движения. В этом случае Е будет вначале умень¬
шаться и ракета станет двигаться со смещением к центру притяже¬
ния по эллиптической траектории. В точке наибольшего приближения
направление тяги двигателя может быть изменено на противополож¬
ное и, поскольку скорость теперь велика, Е начнет также возрастать
очень быстро и ракета устремится по гиперболической траектории в
бесконечность. Общий расход топлива в этом случае окажется мень¬
шим, чем в случае отрыва от круговой орбиты при тангенциальном
направлении тяги.
ОБЩАЯ ТЕОРИЯ
Обозначим через Охъ Ох2у Охз направление прямоугольных осей
декартовой системы координат. Эти оси могут быть неподвижными
или перемещающимися без вращения (инерциальная платформа).
Пусть <D(xi, х2, Хз, t) будет потенциальная функция гравитационного
поля, в котором помещены эти оси. Обозначим через х* (/=1, 2, 3)
координаты ракеты в момент времени t. Если Vr есть скорость исте¬
чения, а М—масса ракеты, то ускорение, обусловленное силой тяги,
будет равно—Vr!M dM/dt.
Обозначим эту величину через f, а направляющие косинусы тя¬
ги—через U; тогда составляющие ускорения от тяги двигателя будут
равны flu Предположим, что ракета, помимо гравитационных сил и
тяги двигателя, подвергается воздействию сил сопротивления среды,
в которой она движется. Этим силам соответствует ускорение, состав¬
ляющие которого обозначим через—Fu В общем случае величины
Fi будут зависеть от времени, места расположения ракеты в про¬
странстве, скорости и массы ракеты и ее ориентации относительно
направления движения. Допустим, что направление оси ракеты па¬
раллельно линии тяги. Следовательно, положение ракеты можно
определить, если U и Х\ известны, и поэтому можно записать
Е 1’==Е}{х^ х<2, Х3, Х2, Х3, /j, /2, /3, Л4, t). (5)
Тогда уравнение движения ракеты можно представить в следую¬
щем виде:
;1+fI+e._A. (6,
Функцию f=f(t) рассматриваем как заданную функцию, т! е. счи¬
таем, что программа расхода топлива предопределена. Функции
244
z=zli(t), определяющие программу направления тяги, должны удов¬
летворять равенству
/12 + /22 + /з2=1. (7)
Но сами эти величины могут быть соответствующим образом вы¬
браны. Предположим, что они выбраны таким образом, что за время
от t = 0 до t=T обеспечивается наибольшее возможное приращение
полной энергии, отнесенной к единице массы,
Е=±-{к\ + к\+'х*) + Ф. (8)
Допустим, что местоположение и скорость ракеты в момент вре¬
мени t='0 заданы.
Если E=Eq при t = 0, а Е = Е1 при t—T и поскольку Е0
является заданной величиной, то Lt (t) должны быть выбраны
таким образом, чтобы энергия Ех стала максимальной.
Допустим, что // = /;(0 определяют траекторию xi = xl(t) и
что Ех максимальна. Пусть li = li(t)-\-bli(t) соответствует близ¬
кой траектории xl = xi(t)-\-hxl{t), для которой при t=T
E=El + oEl. Поскольку Ег является максимальной величиной,
она является также стационарной величиной по отношению к
малым изменениям 8lt программы направления тяги, и, следо¬
вательно, с точностью до величины первого порядка малости
8^ = 0 при всех возможных малых вариациях о/.. Но только
две вариации функции 8/. являются независимыми, поскольку,
если продифференцировать уравнение (7), можно получить
условие
/j8/j -J- ^8/2 -}- /38/3 = 0. (9)
Первая вариация уравнений движения (6) будет иметь вид
” . dF 1 <s , dFi cs * , л 1 dFi <s 1 /1 r\\
ox I + —<- 0 Xj + -T- 8 Xj + —-— bxt = fol, — —L (ilj, (10)
dxj dxj J dxidxj dlj
где индекс j означает, что каждое из уравнений (10), соответствую¬
щих осям координат 1, 2, 3, должно быть составлено по отношению
к каждой составляющей /=/=1, 2, 3, т. е. всего может быть состав¬
лено 9 уравнений. Это правило сохраняется и для всех последующих
рассуждений.
Будем решать уравнение (10) относительно функций Sxi методом
вариации параметров [7, 8]. Рассмотрим систему однородных урав¬
нений относительно у, (/=1, 2, 3):
•• . dFi dFi • . с>2ф
У1 + Г~ + —yj=0'
dxj J dxj J dxi dxj J
соответствующих уравнению (10). Эти уравнения эквивалентны ше¬
сти уравнениям первого порядка:
• . dFi dFi д2ф
zi-\ ~У/ Ч У,-=0, (12)
дхj у dxj у dxi dxj J
yl = zi
245
с шестью неизвестными г,-. Предположим, что yi=yiky zi==zik
(i= 1, 2, 3; &=1, 2, 3, 4, 5, 6) ‘представляют фундаментальную систе¬
му шести решений этих однородных уравнений.
По аналогии уравнения (10) эквивалентны следующим шести
уравнениям первого порядка:
CN I д F i ts I dFi rs I (N Г Л / d Fi IN f /dr.,
°Pi+0Xj + JTj OJo=M- ~ ТД aJ' <13)
Ъх, = Ьр,
с шестью неизвестными Sxi, Spi. Для решения этой системы уравне¬
ний введем новые зависимые переменные Xi (i= 1, 2, 3, 4, 5, 6), опре¬
деляемые уравнениями
bxt=yikXk, oPi = zikXk. (14)
Подставляя (14) в уравнения (13) и имея в виду, что ут и zпо¬
являются решениями системы (12), получим
*А-/Ч-^Ч: I (16)
лА=о. I
Решая эту систему относительно X, найдем, что
= (16)
где А — определитель шестого порядка \ац\ (/=1, 2, 3, 4, 5, 6; /=
= 1, 2, 3, 4, 5 , 6), где
aij = zij (i = U 2, 3); (17)
=yt-3j (i = 4, 5, 6), (18)
a Aw — алгебраическое дополнение элемента ацс.
Так как начальное местоположение и скорость ракеты фиксиро¬
ваны, то при ^ = 0 $Хг=0, $Xi=$pi = 0. Поэтому в соответствии с урав¬
нением (14) Хъ = 0 при t = 0 для fe=l, 2, 6.
Интегрирование уравнения (16) при этих начальных условиях
дает
х*=1т(/8,'“^78'-')*- (|9)
о
Подставляя (19) в (14), получим
о
S* = ip,=j (0 (f М, - *-£- «/,) ds.
(20)
246
где величины, для -которых аргумент не указан, следует (понимать как
функции аргумента s.
yrk(t)Aik равно определителю, который можно образовать из
А путем замены его i-той строки строкой элементов yri(t),
Уг2^) • • • Угб(*)- Обозначим этот определитель через ari(t, s).
Аналогично zrk(t)Aik является определителем, полученным из А
путем замены элементов его i-той строки строкой элементов
2,1 (0. 2,2 (t) ■ ■ 2Л6 (/). Обозначим его через $rl(t, s). Тогда
уравнения (20) можно переписать в следующем виде:
0
^ = j (/ Ц) ds.
(21)
Возьмем первую вариацию уравнения (8)
CN Z7 ’ * * . дФ ъ
о Е = л:г Н охг
дхг
(22)
Подставляя (21), получим
ъ
оЕ = j JL (*) prf (t, s) + (t) ari (tt s) j (fbit - L 8/.) ds. (23)
0
Для произвольных функций 8U, удовлетворяющих уравнению (9),
при t = T SE = 0. Следовательно, для такой функции
т
j‘ Д- \к,(Т) р„. (Т, s) + -g- (Т) ari (Г, s)} (/ о/,. - 8/у) ds = 0. (24)
о
Если заменить переменную интегрирования s в уравнении (24)
переменной t, это уравнение можно переписать в виде
] (А 8/, + Р2 Ц + Р3 8/3) dt=0, (25)
где
Pj = Pj(T, t) = f£L\xr{T)$rj(T, t)+£-(T)arj(t, D}-
~^[Xr{T)h{t' т)+£;(т)аАТ, ф (26)
Уравнение (25) справедливо для произвольных функций 8U, удов¬
летворяющих уравнению (9) и условию
: Р2 : Pz=l\ ' h '• h
(27)
247
которому должны удовлетворять направляющие косинусы тяги вг
всех точках оптимальной траектории.
В частности, когда t = T, то определитель ан{Т, t) —0, так как дне
его строки будут идентичны. Точно так же при этом значении
t, jЗн(Т, £)=0, если гф i, ибо тогда две строки будут идентич¬
ными, и $н(Т, t)=A(T), если r=i. Поэтому из уравнения (26) мож¬
но заключить, что
Pj(T, T)=f(T)xJ(T)-xi(T)^i(T). (28)
01 j
Из уравнений (27) и (28) можно вычислить направление тяге
при t=T. В частности, если силы сопротивления отсутствуют, т. е
/ч = 0,
к'Л2:1г = х1{Т) :х2{Т) : х,{Т) (29)
и в (момент t=T тяга направлена по касательной к траектории.
Оптимальная траектория определяется уравнениями (6), (7),
(26) и (27). В общем случае эти уравнения могут быть решены толь¬
ко численными методами и, поскольку в уравнение (26) явно вхо¬
дит Т, следует задаться граничными условиями при t=T и интегри¬
ровать уравнение от этого момента в обратном порядке. Если по
достижении момента t=0 условия, вычисленные для этого момента.,
не будут удовлетворять исходным данным, то должна быть пред¬
принята вторая попытка при скорректированных данных для момен¬
та t=T, а также, если нужно, то и следующие попытки, пока не бу¬
дет получено удовлетворительное совпадение. Фундаментальная
система общих решений однородных уравнений (12) должна быть
также получена подобным же методом последовательного интегри¬
рования при тех же интервалах времени, что и основное интегриро¬
вание, и также в обратном порядке от t=T. Если выполнить это
интегрирование, начиная с величин, равных при t=T,
Zikz=Cji + з,(30)
где $1ъ= 1, если i=k, или $uc—0 в других случаях, то в результате
этого получим фундаментальную систему решений.
Следовательно, как это было показано, расчет оптимальной тра¬
ектории, характеризующейся максимальным приростом энергии, тео¬
ретически возможен. Однако ясно, что при отсутствии аналитиче¬
ского решения эта работа практически очень трудоемка. Задача не¬
сколько упрощается для плоской траектории и существенно
упрощается в случае отсутствия сил сопротивления среды. В общем
же следует считать, что расчеты целесообразно производить при по¬
мощи вычислительных машин.
ОПТИМАЛЬНЫЕ ТРАЕКТОРИИ В ОДНОРОДНОМ ПОЛЕ
ТЯГОТЕНИЯ
В этом разделе в виде примера рассмотрено применение общей
теории, рассмотренной в предыдущем разделе, к случаю, когда силы
сопротивления отсутствуют, гравитационное поле постоянно и на¬
248
правлено к центру оемли, а тяга двигателей поддерживает постоян¬
ное ускорение ракеты при отсутствии всех других сил. Движение
предполагается плоским.
Возьмем оси координат Охи Ох2 в плоскости движения, причем
Ох1 направим горизонтально, а Ох2—вертикально вверх. Допустим,
что в начале движения при t=0 составляющие скорости равны {иъ
и2)у в конце же движения при t=T в точке (Хи Х2)—равны (Uu U2).
Ускорение силы тяжести равно g и, следовательно, Ф—gx2. Направ¬
ляющие косинусы тяти будут /1, 12, а постоянная составляющая уско¬
рения от тяги будет f. Если масса ракеты в момент времени t равна
ЬЛ, а скорость истечения Vr, то
V7 __ ,
М dt J
(31)
и, следовательно, коэффициент отношения масс R в конце разгона
будет равен
Iт
R=evr. (32)
Уравнение движения (6) примет вид
•*1 = А» *2 + &=Дг-
(33)
Система однородных уравнений (12) будет теперь состоять из
следующих четырех уравнений:
z1 = z2 = 0, yx = zu y2=z2.
(34)
Условиями (30), которым должна удовлетворять фундаменталь¬
ная система четырех решений этих уравнений при t=T, являются:
а)
■Уп = 1.
^21 = 0.
г„ = 0,
«21 = °»
б)
ю
II
р
У 22 — Г
^2 = 0,
г22 = 0,
в)
^13 = 0.
_v23 = 0,
*13=1.
N
ю
со
II
о
г)
о
II
^24 = 0-
«14 = 0,
^24 — 1 *
(35)
Сама фундаментальная система этих решений, соответствующая
этим условиям, будет:
а) .У ц = 1, ^21 = 0»
б) У\2~®’ -У22== 1 ’
в) У\ъ= t ^ > У2 з~0’
г) ^14=0, У 24 Т,
zn = 0, z21 = О,'*
zl2 = 0, z22 — 0,
z13~ 1, ^23 = ® >
^i4 = 0, <С24 = 1 .
(36)
249
Полагая s аргументом А, можно записать следующий опреде¬
литель:
A(s) =
Отсюда следует, что
ап о=
и, следовательно, ссп (Г, t)=T—t.
Аналогично
0
0
1
0
0
0
0
1
1
0
s — T
0
0
1
0
s — T
1
0
t — T
0
0
0
0
1
1
0
s—T
0
0
1
0
s-T
1.
= t—s
«12 (7> О — О,
«21 (Г 0 = 0,
«22 (Г, О = T—t
М7’. 0 = 1. МГ 0=0, |
МО 0=0, 0=1- /
Уравнение (26) можно теперь записать в виде
Л=АЛ, P2=f{U2+g(T-i)},
тогда, используя уравнения (7) и (27), получим
, _ Ux 1
Vu\+{Ui + g{T-t)}*'
Uj + g{T-t) •
(37)
(38)
(39)
(40)
(41)
(42)
Подставляя (42) в (33), получим уравнения оптимальной траек¬
тории в виде
fUx 1
*2 + £ =
Vu\+{U2 + g(T-t))t'
f{U2 + g{T-t)}
Vu'i+{u2+g(T-t)}C
(43)
250
Первое интегрирование этих уравнений при условиях xl = Ul,
x2=>U2, t=T дает:
/
1 + — Jsh'
g
itf2._sh-i Ц» + г<7’-<>У
и, ux j.
xl=Ul
x2=U2 + g(T-t) + J-[/u\ + U\-
~~VU\ + {U2-\-g(T—t)}2 I .
(44)
Подставляя t=0, получим
/ Ли-1^2
"'=y'[,+7(sh"'57-
sh'
-lUt + gT
u.
u2=u2+gT+-t-{Yut+ui-Yu* + (u2+gTy
(45)
Интегрируя (44) при начальных условиях хг=х2=0 при t = 0, мы
получим уравнения, по которым можно построить оптимальную тра¬
екторию, т. е.
- (U2+gT) sh-1 Ы~- -Vui+Wi+S(T~t)V +
“1
+ У Uf + (U2 + gT)>};
x2=u2t4-±gr-yg(T-ty+^y U*+U*+
(46)
+ ^-
2^2
2. 2
Ч и, и i I
+ {t/2 + ^(7’-0}K^+(^2 + 5'(7-m2-
-Щ2 + вО/ Ut + (U2 + gTf
(47)
В качестве примера рассмотрим случай, когда f = g, Ui =
=7,900 • 105 см!сек, и2 = 0. Эти данные соответствуют ракете, которая
вначале движется горизонтально. Скорость движения выбрана с
таким расчетом, чтобы она соответствовала скорости ракеты, запу¬
щенной с искусственного спутника, двигающегося по круговой орби¬
те, расположенной сразу же за пределами земной атмосферы. Резуль¬
тирующая траектория поэтому будет приближаться к оптимальной,
с которой можно произвести переход на другую орбиту, пренебрегая
сходимостью земного поля. Примем время моторного полета, необхо¬
димое для сообщения ракете скорости отрыва, равным Г = 333 сек.
Решая численно уравнения (45), найдем, что Ut= 11,09 • 105 см/сек,
U2 = —3,920 - 105 см/сек, что соответствует полной скорости
251
11,77* 105 см/сек. Скорость отрыва на поверхности Земли составляет
11,19 • 105 см!сек.
Подставляя эти результаты в уравнение (46) и (47), можно гю
строить оптимальную траекторию (фиг. 85). Если ф—угол -между
направлением движения и осью хь то tgty=x2/x1. Значения углов ii-
по времени полета приведены i
табл. 1, где для сравнения даны так¬
же соответствующие значения ф-
угла между направлением тяги и го
ризонталью. Значения углов ф под
считаны по формуле
tgtt>= Uz + g{T-t) (48
ь • ^ V
Фиг. 85. График оптимальной
траектории. выведенной из уравнений (42).
Таблица 1
t
4
«Р
4—?
0
0°
—3°,4
3° ,4
0,2 Т
00
с
-sf
1
—6°, 7
1° ,9
0,4 Т
—9°,0
—10°,0
1°,0
0,67"
-12°,8
—13°,3
0° ,5
0,8 Т
—16°,3
—16°, 4
0°,1
Т
—19° ,5
—19°, 5
0°
Из таблицы видно, что направление тяги вначале смещается от¬
носительно касательной к траектории на угол более 3° в направлении
к центру притяжения, но затем в процессе разгона это смещение по¬
степенно уменьшается, причем совпадение направлений тяги и дви¬
жения наступает в момент выключения двигателя.
В работе автора [9] были получены уравнения движения ракеты,
движущейся в однородном поле тяготения при том же законе измене¬
ния тяги, что и в данном разделе статьи, но в предположении, что на¬
правление тяги все время совпадает с направлением касательной к
траектории. Для тех же самых начальных условий и при той же ве¬
личине тяги, как и в разобранном выше примере, можно вычислить
по уравнениям, приведенным в работе [9], полную энергию, отнесен¬
ную к единице массы, полученную ракетой, движущейся под дей¬
ствием тангенциальной тяги в течение 333 сек. Для этого случая
имеем £=6,304 • 1011 эрг/г масса. При движении же по оптимальной
траектории полная энергия, сообщаемая ракете, составляет Е =
= 6,307 • 1011 эрг/г масса.
Следовательно, при тангенциальной тяге приращение энергии,
сообщаемое ракете, близко к максимально возможному. В следую¬
щем разделе будет показано, что при меньших тягах программа
совмещения линии действия тяги с касательной заметно хуже опти¬
252
мальной. Однако для большинства случаев программа тангенциаль¬
ной тяги может считаться вполне удовлетворительным первым при¬
ближением.
ОТРЫВ ОТ КРУГОВОЙ ОРБИТЫ
Исследование, проведенное в предыдущем разделе, показывает,
что в том случае, когда ракета должна оторваться от круговой орби¬
ты, описанной вокруг некоторого центра притяжения, при помощи
двигателя, тяга которого в любой момент после начала движения
фиксирована, то экономичным режимом движения будет такой ре¬
жим, при котором тяга будет направлена по касательной к траекто¬
рии. Еще более экономичным, т. е. оптимальным режимом, будет
такой режим, когда направление тяги будет смещено от касатель¬
ной в сторону центра притяжения на не¬
которую величину, постепенно уменьшаю¬
щуюся до нуля в процессе осуществления
разгона. Оптимальная величина угла сме¬
щения в каждый момент может быть вы¬
числена точно только путем численного
интегрирования уравнений, выведенных в
разд. «Общая теория». Однако, если пред¬
положить линейное уменьшение угла сме¬
щения со временем от некоторой принятой
начальной величины до нуля в момент
окончания маневра, то можно надеяться
получить при помощи корректировки этой
начальной величины очень близкое при¬
ближение к оптимальной траектории, из¬
бежав необходимости решения сложных
точных уравнений. В настоящем разделе
дается методика такого расчета и сравнение траектории, вычислен¬
ной при помощи этого упрощенного метода, с траекториями танген¬
циальной и трансверсальной тяги (как предполагал Тзян в рабо¬
те [5]).
Пусть (г, 0) (фиг. 86) будут полярными координатами ракеты Р,
двигающейся в плоскости круговой орбиты, центр которой примем
за полюс полярной системы координат. Пусть р/r2 будет силой при¬
тяжения, отнесенной к единице массы ракеты, f—ускорение, обуслов¬
ленное силой тяги двигателя, ф—угол между направлением тяги и
перпендикуляром к ОР, ф—угол между направлением- движения и
этим перпендикуляром, ф—ф = е—угол смещения и а—радиус круго¬
вой орбиты.
Тогда величина полной энергии, отнесенной к единице массы ра¬
кеты Е, в любой момент времени будет равна
£=i(r2 + r2e2)-i. (49)
Если f—вектор ускорения, обусловленный тягой, то
7=Vr^ (50)
Фиг. 86. Схема траектории
взлета ракеты с круговой
орбиты в случае, (когда ъфО,
253
и, следовательно, уравнение (3) можно переписать в виде
E=vf = rf sin с? + r0/coscp.
Обозначив
(51)
h = r4,
(52)
напишем уравнение движения для случая трансверсального на¬
правления тяги (т. е. перпендикулярного к ОР) в виде
Уравнения (54), (56) и (57) представляют собой дифференци¬
альные уравнения первого порядка относительно величин г, Е и h.
Углы ф и е, которые входят в эти уравнения, вычисляются по фор¬
мулам
т. е. предполагается, что е уменьшается линейно от некоторой на¬
чальной величины Со до нуля в течение времени разгона Т.
Уравнения (54), (56) и (57) легко интегрируются численно в
любом частном случае, но прежде чем приступить к такому интег¬
рированию, желательно систему уравнений привести к безразмерно¬
му виду. Это можно сделать путем введения новых зависимых пере¬
менных р, е и k путем следующих подстановок:
(53)
Используя уравнение (49) и (52), исключим 0 и перепишем пер¬
вое уравнение в виде
Исключая 0 из уравнения (51) аналогичным путем и подставляй
ср = ф—е, получим
Ё = rf s'm (ф — г) + — cos(<b — в).
г
(55)
Подставляя (53) в (55), будем иметь
£' = г/ sin (ф — е) -J .
т-
(56)
Уравнение (53) можно переписать также в виде
h = rf cos (-ф—е).
(57,
(58)
(59)
г —ар, Е-—~е, h = Ypak
(60)
а
й новой независимой переменной т, определяемой подстановкой
_з_
J а2
t==~rT'
.. 2
(61)
Обозначая дифференцирование по т символом ('), приведем урав¬
нения (54), (56), (57), (58) и (59) к виду
е' — пр’ sin (ф — е) +
k’ — Щ COS (ф — е),
kk'
tg
рр
(62)
Фиг. 87. Сравни¬
тельная схема трех
возможных траек¬
торий взлета раке¬
ты с круговой
орбиты.
где n=a2fl\ 1 и Т= а2 ^/{П. Число п представ¬
ляет собой отношение ускорения от тяги к
ускорению от гравитации на круговой ор¬
бите.
Первоначально ракета двигается по круговой орбите и в этом
случае р = 1, е=—k=l и ф = 0. Эти величины и будут начальны¬
ми условиями, при которых должна интегрироваться система урав¬
нений (62). После выполнения интегрирования уравнений (62) мо¬
жет быть найдена координата 0 путем интегрирования уравнения
(52), преобразованного к виду
е'=4- <63>
р2
В табл. 2 приведены результаты численного интегрирования этих
уравнений, выполненного при я = 0,1 (т. е. тяга составляет одну
десятую силы тяжести) и начальном угле смещения ео = 5°. Ракета
оторвется и под действием своего момента количества движения
начнет удаляться в бесконечность при е = 0. Из опыта ранее выпол¬
ненных расчетов следует, что этому условию соответствует т = 5,
поэтому при численном интегрировании принималась ^ = 5.
На фиг. 87 построена траектория (кривая А) для вычисленного слу¬
чая. Путем обратной интерполяции по таблице найдено, что е = 0
при т = 5,1130.
Сравним полученные результаты с результатом, соответствующим
случаю, когда тяга направлена в траневерсальном направлении (про¬
грамма, принятая Тзяном), и случаю, когда тяга направлена по ка¬
сательной к траектории.
В случае трансверсальной тяги ф—6=0, вследствие чего первые
три уравнения системы (62) упрощаются:
p'-l/г *+--+
£ = ■
г
kk'
k' = пр.
(64)
J
Результаты численного интегрирования уравнений (64) при
п = 0,1 представлены в табл. 3. Траектория (кривая В) для данного
случая построена на фиг. 87.
Таблица 2
0,0
1,0000
0°0'
1,0000
—0,5000
0,4
1,0015
23°21/
1,0399
—0,4594
0,8
1,0144
47°20'
1,0801
-0,4173
1,2
1,0500
71 о7/
1,1213
-0,3745
1,6
1,1145
93°35'
1,1643
—0,3318
2,0
1,2086
113°51'
1,2100
-0,2898
2,4
1,3290
131°31'
1,2590
-0,2490
2,8
1,4717
146°35'
1,3120
-0,2096
3,2
1,6326
159°23'
1,3691
—0,1715
3,6
1,8093.
170°15'
1,4304
—0,1345
4,0
2,0001
т°зу
1,4959
—0,0983
4,4
2,2044
187°29'
1,5653
-0,0627
4,8
2,4216
194°2Г
1,6385
-0,0275
5,2
2,6522
200°21'
1,7149
+0,0076
Путем обратной интерполяции найдено, что е = 0 соответствует
г = 5,546. Величина fT представляет собой характеристическую ско¬
рость разгона, и, следовательно, т есть мера этой величины. Полу¬
ченные результаты показывают, что при использовании трансвер¬
сальной программы направления тяги характеристическая скорость
увеличивается на 8,5%.
Для случая тангенциальной тяги уравнение (51) принимает вид
E=fv, (65)
Скорость v имеет трансверсальную и радиальную составляющие
г0 и г и, следовательно, если использовать уравнение (52), получим
v2 = г2 + г282 = г2 + — . (66)
г2
256
Таблица 3
г
Р
0
k
в
0,0
1,0000
0°0'
1,0000
—0,5000
0,4
1,0021
23°21'
1,0400
—0,4592
0,8
1,0168
47°15'
1,0803
—0,4171
1,2
1,0539
70°54'
1,1217
—0,3745
1,6
1,1184
93°13'
1,1650
—0,3323
2,0
1,2099
113° 24'
1,2115
—0,2914
2,4
1,3247
131°7'
1,2621
—0,2533
2,8
1,4580
146°26'
1,3177
—0,2152
3,2
1,6058
159с38'
1,3789
-0,1800
3,6
1,7651
171°4/
1,4463
-0,1465
4,0
1,9340
181°1'
1,5203
—0,1144
4,4
2,1112
189°47'
1,6011
—0,0835
4,8
2,2962
197°33'
1,6893
-0,0536
5,2
2,4886
204° ЗГ
1,7849
—0,0246
5,6
2,6882
210°48'
1,8884
4-0,0038
Подставляя (66) в (65), получаем
e=j\f r!+f •
Приводим это уравнение к безразмерному виду
/,2 . k2
9 +V'
(67)
(68)
В рассматриваемом случае е = 0 и поэтому из уравнения (57)
имеем
h=rf cos ф.
Так как гб^исоэф, то из уравнений (52) и (65) следует, что
д^/г29 =р h
v Ё
Безразмерная форма уравнения (70) будет
(69)
(70)
к'-
П?рр'
(71)
Первое из уравнений (62) вместе с уравнениями (63), (68) и (71)
образуют систему уравнений первого порядка относительно искомых
переменных Р, 0, k, е. Результаты численного интегрирования этих
уравнений при п—0,1 приведены в табл. 4. Соответствующая траек¬
тория (кривая С) представлена на фиг. 87. Обратная интерполяция
17 354
257
дает, что е = 0 достигается при т = 5,135. Отсюда следует, что для
данного случая характеристическая скорость увеличивается на 0,4%
сверх той скорости, которая требуется для осуществления отрыва от
орбиты при первом способе.
Хотя этот первый способ и не дает абсолютного оптимума, нет
же можно предполагать, что разница между тангенциальной про¬
граммой тяги и оптимальной программой также не будет большой
Таблица 4
X
Р
0
k
е
0,0
1,0000
0°0'
1,0000
—0,5000
0,4
1,0022
23°21'
1,0400
—0,4592
0,8
1,0171
47°16'
1,0803
-0,4171
1,2
1,0553
70°52'
1,1215
—0,3743
1,6
1,1226
93° 4'
1,1644
-0,3317
2,0
1,2190
113°1'
1,2098
—0,2899
2,4
1,3414
130° 21'
1,2586
—0,2494
2,8
1,4852
145°9'
1,3111
—0,2102
3,2
1,6470
157°43'
1,3676
—0,1724
3,6
1,8241
168°23'
1,4284
—0,1356
4,0
2,0150
177°29'
1,4934
—0,0996
4,4
2,2191
185°19'
1,5625
—0,0642
4,8
2,4361
192°6'
1,6354
—0,0292
5,2
2,6660
198°0'
1,7121
+0,0057
ВЫВОДЫ И РЕКОМЕНДАЦИИ
Из рассмотрения результатов, полученных в данной работе, мо¬
жно сделать следующие выводы:
1. В тех случаях, когда ракете при ее движении в вакууме необхо¬
димо сообщить максимально возможное приращение энергии, на¬
правление тяги должно смещаться от направления движения в сто¬
рону гравитационного поля на некоторый угол, который в процессе
разгона должен уменьшаться до нуля к моменту окончания разгона.
2. Достаточное приближение к оптимальному программированию
направления тяги (упомянутому в п. 1) может быть достигнуто при
совмещении линии направления тяги с касательной к траектории
движения.
3. Если требуется осуществить отрыв от круговой орбиты, то
программирование тяги в трансверсальном направлении не является
более экономичной программой по сравнению с оптимальным разго¬
ном или тангенциальным разгоном.
4. Лучшее приближение к оптимальным условиям отрыва от кру¬
говой орбиты, чем в случае тангенциального разгона, может быть
258
достигнуто, если принять линейное уменьшение угла смещения по
времени. Выигрыш, однако, при этом невелик.
В отношении приближения к такому оптимальному переходу с
круговой орбиты необходимы дальнейшие исследования с целью оп¬
ределения рациональных величин начального угла смещения во для
различных значений п (величина ускорения от тяги, выраженная
в единицах гравитационного ускорения на орбите). Имея в виду эти
оптимальные величины ео, необходимо будет затем произвести рас¬
четы значений характеристических скоростей, соответствующих пе¬
реходу с орбиты в диапазоне изменений /г = 0,0001 — l,0g\ .Автор
предполагает представить эти исследования в последующей работе.
ЛИТЕРАТУРА
1. Л оуден Д., Минимальные траектории ракет.
Lawden D., Minimal Rocket Trajectories, «Journal of the American Rocket
Society», 1953, vol. 23, p. 360.
2. Лоуден Д., Стационарные траектории ракет
Lawden D., Stationary Rocket Trajectories, «Quarterly Journal of Mecha¬
nics».
3. Форбс Дж., Траектория ракетного полета в пространстве.
Forbes G., The Trajectory of a Powered Rocket in Space, «Journal of the
British Interplanetary Society», 1950, vol. 9, p. 75.
4. С п и т ц е р Л., Межпланетное путешествие между орбитами спутников.
Spitzer L., Interplanetary Travel between Satellite Orbits, «Journal of the
British Interplanetary Society», 1951, vol. 10, p. 249.
5. T з я н С., Взлет с орбиты спутника.
Tsien Н., Take-off from Satellite Orbit, «Journal of the American Rocket
Society, 1953, vol. 23, p. 233.
6. Л о у д e н Д., Уход в бесконечность с круговых орбит.
Lawden D., Escape to Infinity from Circular Orbits, «Journal ot the British Inter¬
planetary Society, 1953, vol. 12.
7. Пуул E., Теория линейных дифференциальных уравнений.
Poole Е., Theory of Linear Differential Equations, 1956, Oxford.
8. Айне E., Обыкновенные дифференциальные уравнения.
In се E., Ordinary Differential Equations, 1927, London, Longmans.
9. Лоуден Д., Начальная дуга траектории отрыва.
Lawden D., Initial Arc of the Trajectory of Departure, «Journal of the
British Interplanetary Society», 1948, vol. 7, p. 119.
Д. ЛОУДЕН
МИНИМАЛЬНЫЕ ТРАЕКТОРИИ РАКЕТ1
ВВЕДЕНИЕ
Настоящая работа посвящена решению в общем виде задачи о
наиболее экономичном перемещении ракеты в вакууме между двумя
1 D. Lawden, Minimal Rocket Trajectories, «Journal of the American Rocket
Society», 1953, vol. 23, No. 11—12, pp. 360—367, 382.
17* 259
конечными точками, скорость в которых задана. На гравитационное
поле, воздействующее на ракету, никаких ограничений не налагается.
Полученное решение поэтому применимо к задачам навигации меж¬
планетного корабля между двумя точками солнечной системы, ко¬
гда необходимо учитывать воздействие гравитационных полей раз¬
личных тел. Частные задачи этого типа исследовались автором ранее
в работах [1, 2, 3]. Задачи аналогичного характера, связанные с ис¬
следованием прямолинейных траекторий с учетом действия сил
сопротивления воздуха и постоянного гравитационного поля, рас¬
сматривались Тзяном и Эвансом [4] и Гиббсом [5].
Одним из общих результатов, полученных до настоящего вре¬
мени при решении всех задач об оптимальном движении ракет,
является необходимость применения кратковременных импульсов
тяги.
Для случая оптимального перемещения ракеты между двумя точ¬
ками однородного гравитационного поля без учета всех других сил
сопротивления автор показал [6] необходимость приложения им¬
пульса тяги в каждой из заданных точек, а также то, что во время
самого 'перемещения ракета должна находиться в состоянии свобод¬
ного полета. Обязательность приложения таких им'пульсов в общем
случае движения ракеты показана в работе [3]. Понятно, что на¬
личие импульсов в решении несомненно усложняет математический
анализ задачи. Другая еще большая трудность заключается в том,
что для решения рассматриваемой в работе оптимальной задачи'
нельзя непосредственно применить уравнение Эйлера в связи
с тем, что основные участки минимальных траекторий между
конечными точками представляют собой дуги нулевой
тяги.
В связи с этим возникает необходимость решения некоторых ви¬
доизменений математической задачи, в которой эта последняя ано¬
малия не возникает, но которая позволяет подойти к решению по¬
ставленной частной задачи предельным переходом.
ОБЩАЯ ТЕОРИЯ
Рассмотрим вначале задачу оптимального перемещения ракеты
между двумя точками, лежащими в одной плоскости, предполагая
при этом, что все гравитационные силы и сила тяги параллельны
этой плоскости и что сама траектория ракеты также заключена в
этой плоскости. Это ограничение задачи двумерным пространством
не является принципиальным и введено лишь для уменьшения про¬
межуточных выкладок. Полученный конечный результат может быть
очевидным образом распространен и на случай трехмерного прост¬
ранства.
Пусть Ох и Оу будут неподвижными осями прямоугольной систе¬
мы координат в плоскости движения, а I, т—■направляющие косину¬
сы силы тяги ракеты, находящейся в точке (х, у) в момент вре¬
мени t.
260
Обозначая скорость истечения Vг, а массу ракеты М, записываем
уравнения движения ракеты в следующем виде:
(и
где (—f, —g)—составляющие результирующей силы тяжести, отне¬
сенные к единице массы. Принимаем, что ■направление движения и
направления тяги не обязательно должны совпадать и что гравита¬
ционное поле непостоянно и, следовательно, зависит от t Примем,
что f и g зависят только от t, х и у.
Так как l2 + m2= 1, то из уравнения (1) следует, что
где Mq и Мх—массы ракеты в начале и в конце интервала соответ¬
ственно.
Если ракета должна переместиться из точки (х0у у0), скорость в
которой (и0у у0), в точку (хи ух)у скорость в которой должна быть
(и\у Vi), то рассматриваемая навигационная задача будет состоять
в (выборе функций x(t) и y(t), определяющих траекторию перемеще¬
ния и удовлетворяющих следующим граничным условиям:
Конечной целью задачи является нахождение среди всех возмож¬
ных функций, удовлетворяющих этим условиям, такой, которая бы
давала минимум интегралу (3).
Для того чтобы показать трудности, которые неизбежно возни¬
кают при анализе общей задачи, рассмотрим вначале частный слу¬
чай, когда f=g = 0.
В этом случае интеграл (3) при выполнении граничных условий
(4) приобретает вид
—~=[(X + /у + (у + gf] ^.
м at
(2)
Интегрируя уравнение (2) в интервале от 10 до tly получим
К1п = f [ (х + /)2 + (У + g)2]1/2 dt,
М\ J
(3)
x(tn) = x0, x(ta) = u0, X (tt) = xlt x(t1)=u1,
y(t0)=y0> y(t0) = vo, y(tl)=yi, y{tx) = vx.
(4)
(5)
Ищем минимум этого интеграла.
261
Предполагая, что время перемещения задано, можем получить
уравнения Эйлера для этой задачи в виде
d2
X
_ d*
Г у
dfl
L (*2 +У2)42 J
dt2
L^T?)1'2
или 1=т = 0.
Интегрирование последнего уравнения дает нам общее решение
l=A + Bt, tn = C-\~Dt. (7)
Но, так как l2 + m2 = 1, необходимо положить B^D = 0, а Л и С
выбрать таким образом, чтобы А2-\-С2= 1, т. е. направление тяги не
должно изменяться за все время перемещения ракеты. Следователь¬
но, остается только одна произвольная постоянная, и поэтому в об¬
щем случае при таком решении оказывается невозможным удовлет¬
ворить всем восьми граничным условиям (4). Это несоответствие
характеристических уравнений поставленной задаче (5) в общем
случае показывает, что необходимо искать минимум интеграла в виде
Л
I=\{(x + f? + G + g?+^dt, (8)
требуя, чтобы в конечном результате е->0. Характеристические урав¬
нения, соответствующие этому последнему интегралу, получаются
нетождественными и их общее решение содержит необходимое для
решения задачи число произвольных постоянных.
Если проинтегрировать уравнение (1) на коротком интервале,
где приложен импульс тяги, то получим
IVг In r= \x\i, mVr In r=\y\i, (9)
где \x\ i, \y\i—приращения составляющих скорости под действием
импульса, а г—отношение масс, соответствующее концу этого интер¬
вала.
При этом мы пренебрегаем интегралами ^ Jdt, ^ mgdt, поскольку
fug конечны на интервале i. Предполагается, что направление тяги
(/, т) в течение этого времени не изменяется.
Возводя в квадрат и складывая уравнения (9), получаем
Vrlnr = ]/ \хЦ + \у\2,. (10)
Это показывает, что введение такого импульса в интеграл (3)
равно по величине приращению вектора скорости, вызываемому этим
импульсом. Соответствующее введение подобного импульса в инте¬
грал (8) даст аналогичный результат, так как е также конечно, по¬
добно f и g, и, 'Следовательно, им можно пренебречь по сравнению
с х и у.
Теперь введем параметр К, от которого будет зависеть t и, следо¬
вательно, х в у. Этот параметр не имеет физического смысла, но он
таков, что при его монотонном увеличении от а до |3, t увеличивает -
262
ся от to до 11. Обозначая дифференцирование по t символом (') н
производя само дифференцирование, получаем
• v' trx,,—tnxr t'y—t'y' /11Ч
= * = т;з . У ==~ " з ^ ■ (II)
V " *
После этого интеграл / примет вид
£ .. .. Р
/== j Л(£, х,у, x,y)dt = j #(/, л,_у, ft х\у', t", л;",У')Л, (12)
*0 *
где Я{t, х, у, t\ xf, у', Г, х\ у") =t'h{t, *, у, ху у). (13)
Будем считать, что л*=л;(^), У=У(к), (при а<А,<(3) опре¬
деляют траекторию ракеты, которая удовлетворяет граничным усло¬
виям (4) и соответствует минимальному расходу топлива. Вначале
предположим, что прилагается только один импульс тяги в момент,
когда А,= у. После того как будут найдены условия, удовлетворяю¬
щиеся с каждой стороны такого импульса, можно будет снять эти
ограничения. Пусть V—приращение скорости, вызванное этим им¬
пульсом. Уравнение (12) можно тогда переписать в следующем виде:
т-о р
/= j Hdl+ j HdX+V. (14)
a T+0
Если a: = a;(X)-J-8a;(X), J>=.y (M+ &У 00»
t = t(l) + ot(l), (a<X<p)
определяют близкую траекторию ракеты, удовлетворяющую гранич¬
ным условиям (4) в моменты t = t0+Sto, t = t\-\-bt1 соответственно, а
импульс изменяется таким образом, что увеличивает приращение ско¬
рости, вызванное им на ЗУ, то из уравнения (14) получим
т-о р
~ ~дН , дН * , дН * , дН , дН
ы= Г + Г \—U + — bx + —by+-¥!-W+-¥Lbx' +
J J L dt дх dy У dt' дхг
dl + o I/.1 (15)
T+o
+ sy + <OL bf + — — lx" + Sv"
dy' * dt" dx" dy" J
Введем следующие обозначения.
Переменные со значениями, соответствующими Х=а, будем снаб¬
жать индексом «0», а переменные, соответствующие А, = (3,—индексом
1 В целях сокращения записи подынтегральное выражение для первого
интеграла опущено, так как оно аналогично подынтегральному выражению вто¬
рого интеграла [см. формулу (14)].
263
«1». Значение переменных в момент, непосредственно предшествую¬
щий импульсу, будем отмечать индексом «—», а сразу же после им¬
пульса—индексом « + ».
Тогда 8V = 8 {(х+ — х_)2 + (у+ — _у_)2}1,2 =
(х+ - х_) (5*+ — 5дт_) 4- (у+ —у-) (8у+ — 8у_)
{(.X+ -х-)* + (у+-у-У}
211/2
но х=
ох =
t'bx' — х'Ы'
(16)
(17)
и аналогичные уравнения можно написать и для у и $у. Подставляя
(17) в (16), получим
1 ;Х
81/=-
.2 .2
t+t_ {(X+t_ - X_t+)2 + (У+ -y_f + )2}
1/2
X [(-*Д'_ —x(_f+) (С (^'+8x'+ — Х+Ы\ ) —
— С— X_SC)} + (y'J'~ —y_t\) X
X {t’_ (t'Jy'+ —y'+W_. ) — С Ц'_8/_-y'jfj}].
(18)
Это выражение для 3*1/ можно теперь подставить в уравнение (15).
Интегрируя по частям, можно упростить интегралы, входящие в
уравнение (15):
ГЁ**-Ъ? dk = — M— Г — (—)udK
J dt' dt' J dk\dt' J
„«"sc-J./iiiM+fJL/w.w*
ar \ J j d\2 \ /
и Т. Д.
Отсюда 'следует, что уравнение (15) можно записать в следующей
форме:
8/ж — Aq0^0-j- A_ot_ -f* Е_Ьх_-f- С_oy_ — A+tt+ — E — C±oy+ -f-
+ Afitl — G0§tQ — J 08л;0 — К0ъу’0 + Lbt’_ + МЬх_ + Л/£у_ —
— P&t + — Qox+ — R^y + ^i°^i "b J i^i 4“ Klbyl -f-
T-0 P
+ j + j (nt + Xbx + Yby)dkt ' (20)
a T +0
поскольку 8x{i=8y0 = 8x\=8y1 = 0, что следует из граничных усло¬
вий (4).
264
Соотношения для коэффициентов Л, Б и т. д. перечисляются ниже:
а=и—). в-
dt> d\ \ dt” )
дН
дН d I дН
G =
dy' d\ \ ду
ОН /= дН
dt” ‘ ‘
дН
~dt
к*
dx'
дН
дИ
d\ I дх”
дх” ’ ду”
-*L {x'+t'_ — X-t'+) +у'_ (y'+t'_ —y'_t'+)
M = {—\
x’+t_ — x'_t[.
dx" J- t'_ {(x’+t'_ - x'J+V+(У’+ L-y'-t'+П1/2
dH\ y'+C-y'J+
N I dy" )- t’_ {(x’+t'_-x'_t'+) 2 H- (y+t'_ -y'_t'+) 2}1/2 '
I OH \ x’+ (x'+t_ — x'_t'+) -f y'+ (y'+t'_ —y'_t'+)
dt" )+ + t’2 {(Jf'+ t'_ -x'_ t'+ )2+ (/, t'_ -y'_ t + )2}
1/2
x, t —x t\
*+*--*-*+
t'+ {(yC-x_t’+y + (y'+t’_-y'_t'+)4ll2 ’
R--
T=
y'+t'_-yj+
x=
m\
X"/+~ t'+ {(x+t'_-x'_t'+)2 + (y'+t'_-y'_t'+yj1'
dP- / dH \ d I dH\ дН
dk2 \ dt" ) dk \ dt' J dt ’.
dP j dH \ d
1/2 ’
dX2 \ dx
Y— d2 / dM \ d I dH\
d\2 ^ dy” ) dX [ dy' j
dH \ dH
d\ \ dx' J dx
dH
dv
(21)
Так как x — x'/f и у ==y'/t' должны удовлетворять граничным
условиям в начальной и конечной точках, то величины
s • t'bx' — x'bt' * - t'by'—y'bt'
Ьх — л и оу — ——тг
t/ t'2
равны нулю при Я = а и Х=р. Отсюда следует, что© эти моменты
= oy = 2^_
(22)
265
Поэтому при Х=а и Х= 3
Уравнения (11) и (13) дают
дН / dh dx dh dy \ х' dh у’ dh
dt" \ дх dt" dy dt" ) t'2 dx t'2 dy
1 (dh ■ dh \
= ~(x7i+yw)'
(24)
dH ^ dh dx 1 dh
dx" dx dx" V dx
dH p dh dy 1 dh
dy" dy dy" tr dy
(25)
(26)
Подставляя эти значения в уравнение (23), можно убедиться в
том, что в начальной и конечной точках
Соответственно уравнение (20) сводится к ©иду
8/ = — ЛA_ot__ -J- В ^_бх_ -f- С__оу_ — —
— С+оу-|- Л^о^ Lot„ -j- Л^бХ— -j- Noy^ — Pot+ — Q8x+ —
Но так как Ы, Ьх в оу непрерывны при переходе через
импульс, то — ох_ = ох+ и 8у_ = 8у+. За исключением
этих величин, все другие величины 8/0, 8£_, ох_ и т. д. произ¬
вольны и, поскольку интеграл / варьируется относительно
своего минимума, первая вариация 8/ равна нулю для всех
произвольно малых вариаций траектории. Это условие может
иметь место только тогда, когда
Если моменты начала и окончания перемещения выбираются так,
что $t0=8ti = 0, то можно ограничиться условиями Л0=Л1 = 0. Если же
время перемещения задается так, что St0=Stu то в этом случае коэф¬
фициенты Л0=Л1 уже не обязательно равны нулю.
Последние три равенства (28) являются дифференциальными
уравнениями характеристических кривых. Известно [7], что только два
GU' + Joxf + Koyr=0.
т-0 Р
- RW+ +1 + 1 (nt+х*0Х + Ydy)8)'* (27)
а 7+0
А0 = А+ — А_ = В+ — В_ = С+ — С_ = А1 =0,
l=m=n=p=q=r=о,
Х^У=Т= 0.
(28)
266
(29)
из этих трех уравнений являются независимыми. Подставляя X = t
в уравнение X=Y=.О, получим два независимых уравнения для этих
кривых в форме
d2 / dh \ \dji_ q
dt2 \ ад: / дх ’
/ а/г \ , а/г q
fltf2 \ ду ) ду
Возвращаясь к уравнениям (11) и (13), получим
дН , / dh дх dh ду \ ,,
dt' ~ V~aT ay a?"~J _
, /ЗГ'х'-2t'x" \ dh , /3t"y' -2t'y")\ dh . /Qm
-*+(, 7 m+\—7—J^T' (30)
a// ,, dh dx t" dh /01 \
1 ~ 772” » V°>U
ад:' ад: dx' t' dx
dH _t, dh dy _ (32)
ay' ay ay" г2 ay
Уравнения (24) — (26) совместно с последними уравнениями
дают:
а/г -а/г , ■ а / аЛ \ . ' d / dh
<33)
* —^(&)i (34)
с=
дх
d
dt
dh
— (35)
Л V ду /
Условия (28) требуют, чтобы эти последние соотношения были
непрерывными при переходе через импульс. Кроме того, если на
моменты начала и окончания перемещения никаких условий не на¬
лагается, то соотношение (33) в обеих граничных точках пропадает.
Рассмотрим теперь условия M=Q = 0. Используя уравнение (25),
найдем, что они эквивалентны условию
/i*.\ = *+-*= : _=(i£-\ . (36)
\д*/- {(■*?+ -х_)2-Р(у+-у_)2}1'2 \дх )+
Аналогичным образом равенство N—R=0 дает условие
( dh \ = У+—У- = (^\ . (37)
\ду )- {(■*+ - *-)2 + (У+ —У-)2}112 \ дУ J+
Из уравнений (24) —(26) следует тождество
дН . , дН , ti, дН Л /Q54
Отсюда условия L=.P = 0 являются линеаризованными комбина¬
циями условий, выраженных уравнениями (36) и (37).
Поскольку h= {(x+f)2+ {y+g)2 + z2}1/2, то уравнения (36) и (371
можно -переписать в следующем виде:
Оба эти равенства должны удовлетворяться непосредственно пе¬
ред импульсом и после него. Это может быть только в том случае,
скольку корни квадратных уравнений (3) и (8) должны быть взяты
со знаком +, то из этого следует, что все образующиеся из них квад¬
ратные корни, также должны быть взяты с тем же знаком. В част-
Физичеекий смысл этих условий можно выяснить, если обратить¬
ся к уравнению (1). Направление тяги ракеты непосредственно перед
импульсом и непосредственно после него должно совпадать с направ¬
лением импульса, а сама величина этой тяги должна стремиться
к бесконечности при приближении к нему с любой стороны.
Вычислим теперь величины Л, б и С, заданные уравнениями
(33) — (35). Заменяя А, получим
Таким образом, мы получили условия, которые должны удовле¬
творяться вблизи любого импульса, приложенного в какой-то момент
времени между t0 и t\. Если импульс должен быть приложен в каж¬
дой из конечных точек, то аналогичное исследование показывает, что
{(* +/)2+СУ + g)2 + е2}1'2 Нх+ - х_)2 + (у+ ~ У-)2) 1/2 ’
(39)
У+g
У+—У-
{(*+f)2+(y+g)2 + *2}m
{(Х+-Х_)1 + (Д_у_)2}>/2 ‘
если в выражении для отношения (х+—х)/(у+—у~) по обеим сторонам
импульса (*+/) и (*/+£') обращаются в бесконечность. Далее, по-
ности, корни уравнения (39) положительны и, следовательно, x-\--j
и х+—х- имеют тот же знак, что и y+g и у+—г/-.
Принимая во внимание это обстоятельство, получим
(40)
(41)
x+f
(42)
dt L {(x + f)* + G + g)i + z2}1'2
dt [{(x+f)2-t(y + g)2+t2}m_ '
■V + g
(43)
268
направление тяги ракеты должно быть неизменным при переходе от
импульсного режима к режиму 'конечной тяги и что величины x-\-f
и У-^гё должны стремиться к бесконечности при приближении к
импульсу. Знаки этих величин также предопределяются вблизи
импульса, о чем указывалось выше. Никаких других условий, кото¬
рые должны удовлетворяться в этих точках, нет.
Возвращаясь теперь к характеристическим уравнениям, опреде¬
ляющим траекторию в интервале между импульсами, и заменив h
в уравнении (29), получим следующие уравнения:
dt*
x+f
{(x+f)2+G + g)2 + z2}112J
df dg \
(*+/)—+(y+s)jt
i(x+f)2 + G+g)2+s2}112 = *
(x +/) -T~+( у + g) 4^
(44)
d2 Г -V 1 _| dy dy_ _ q
dt2 [{(x+f)2+(y + g)2 + z2}ii2\ {(x+f)2 + 0 + g)2 + s2}112
Будем вначале искать решение в форме
x = X+el; У=У+Щ, (45)
где А" и Y — любые функции, удовлетворяющие уравнениям
x + f=y + g= о, (46)
т. е. найдем решение, близкое к траектории нулевой тяги, которое
стремится к этой траектории при в->0.
Заменяя л; и у значениями из равенств (45), получим
х + f = X + e'i + / (t, X + s£, Y + ет]) =
= X + f(t, X, К) + е('5+-^г6+-^гч) + 0(г*) =
= e/7 + 0(e2), (47)
где
где
‘4S>
Аналогичным путем получим
.У+£ = е<7 + 0(е2), (49)
^ + ^ + <50>
269
Подставляя значения x-\-f и y-\-g из последних равенств в (44;
найдем, что эти уравнения могут быть приведены к виду
" I df I дк п
u + u-^ + v—?- = Q,
дХ дХ
v + иv-^-== О,
дГ дУ
(51)
где
“ (р2+ч2 + 1)1/2 ! V (р2 + я2+^112 ' (52j
Член 0(e) опускается.
Из уравнений (52) получим
(1 — „2 _ v2)l/2 * ^ (1 __ и2 _ «2)1/2
(53)
Функции р и q полностью определяются этими уравнениями, за
исключением членов 0(e), которыми пренебрегли выше.
g и т] определяются уравнениями (48) и (50) с тем же самым по-
рядком точности, а уравнение (45) определяет (х, у) с точностью
до 0(e).
Сделаем допущение, что функции fug можно дифференцировать
любое число раз по всем своим переменным. Тогда X и Y также
должны быть дифференцируемыми функциями t любого порядка, так
же как и функции вида df/dX и dgjdY и т. п. Поэтому уравнение (51)
дает связь между и и v как между дифференцируемыми функциями t.
В частности, эти функции будут граничными для конечных величин t.
Обращаясь к уравнению (53), видим, что и в этом случае р и q явля¬
ются дифференцируемыми функциями t, но обе функции стремятся
к бесконечности при приближении (u2-\-v2) к единице. За исключе¬
нием областей, близких к этим значениям, g и тр заданные уравне¬
ниями (45) и (50), будут поэтому дифференцируемыми и ограничен¬
ными величинами. Однако при приближении к моменту, где
u2+v2=1, р и q стремятся к бесконечности, а уравнения (48) и (50)
показывают, что g->oo и т)->'оо хотя g и т\ остаются конечными.
Ввиду ограниченности этих последних величин произведения eg, гц
будут оставаться малыми величинами, подобно е, и поэтому допуще¬
ние, сделанное при выводе (51) из (44), остается справедливым
в таких соседних областях. Поэтому, если уравнения (47)—(53)
проинтегрировать с целью определения g и и подставить их в (45),
то конечное решение для х и у будет верным даже вблизи значения,
когда u2-\-v2 = 1. Однако при приближении к такому моменту х-+'оо
и у-+оо одновременно с g и т], хотя х и у будут оставаться конеч¬
ными.
Поэтому такой момент соответствует моменту приложения
импульса тяги.
Далее предположим, что минимум интеграла (8) при граничных
условиях (4) определяется траекторией, состоящей из дуг, описы-
270
ваемых уравнениями (45), 'причем эти дуги соединены узлами, в ко¬
торых u2-\-v2= 1 и в которых приложен импульс. Предположим, что
условия определенные нами, которые должны были удовлетворяться
в конечных точках и в таких узлах, действительно удовлетворяются.
Для того чтобы получить соответствующее решение нашей основной
задачи, потребуем, чтобы е->0. Поскольку £, rj суть величины по¬
всеместно ограниченные, то из уравнения (45) следует, что дуги
траектории стремятся к дугам нулевой тяги. Поэтому в пределе мы
получим ряд дуг нулевой тяги, разделенных узлами с приложенными
в них импульсами тяги. Остается рассмотреть предельные условия,
которые должны удовлетворяться в этих узлах и в двух конечных
точках.
Предположим, что х = Хи y=Yx и х = Х2, y=Y2 представляют две
части минимальной траектории ракеты, разделенные импульсом тяги,
когда е мало, но не равно нулю. Для первой дуги решение уравне¬
ния (51) дает и = их, v = vXy для второй дуги решение будет и = и2,
v=v2. В момент приложения импульса ul2Jrvl2 = u22-\-v22= 1.
Кроме того, в соответствии с уравнением (40) необходимо, чтобы
на каждой стороне импульса были справедливы следующие зависи¬
мости:
•*+ — •*-_ *+/_ £Р + °(£2) _ Р [0(c),
У+—У- y+g е^ + °(£2) Я
Если е->0, то это условие будет приближаться к предельному
значению
Физический смысл этих условий состоит в том, что на каждой
стороне импульса величины и, v должны представлять собой направ¬
ляющие косинусы направления тяги.
Уравнения (53) показывают, что если р и q должны быть дейст¬
вительными величинами во всех точках траектории, то необходимо,,
чтобы а2+^2<1.
Для траектории, определяемой уравнениями (45), величины А,
В, С [см. уравнение (41), (42) и (43)] могут быть представлены при
помощи равенств (47) и (49) в следующей форме:
При 8->0 эти величины приближаются к своим предельным зна¬
чениям
х+ — JC_ р и
У +—У- Я v
(54)
А = tif + vg + Xu + Yv + 0(e),
В=— tt-f-O(e),
С = — V -|- 0 (б).
А = uf + vg + Хи -{- Yv,
В= —ц,
C=-v.
(55)
271
Поэтому необходимо, чтобы эти три величины были бы непре¬
рывными при переходе через импульс, когда е = 0. Поскольку и и v
стремятся к направляющим косинусам тяги при -подходе к узлу
с каждой стороны, то они непрерывны и -при переходе через узел.
Составляющие гравитационного поля fug должны быть также
непрерывны -при переходе через узел и, следовательно, выражение
(uf-\-vg) непрерывно. Поэтому непрерывность А предполагает так¬
же и непрерывность (Xu-\-Yv), поскольку и и v непрерывны:
х+и+У+ъ = х_и
или
(х+ — х_)и + {y+—yj)v=0. (56)
Уравнение (54) убеждает нас в том, что это условие эквива¬
лентно
uu + vv = 0
или
-%т(» 2 + ^)=0. (57)
at
Величина (u2-\-v2) стационарна при значении, равном единице
с каждой стороны узла, и, поскольку (ы2-|-а2)<1, это стационарное
значение должно быть максимумом.
Суммируем условия, которые должны удовлетворяться в месте,
соединения дуг (в узлах):
а) и и v должны быть направляющими косинусами тяги,;
б) и и v должны быть непрерывны,
в) (u2+v2) должна быть максимумом, [ (58)
г) кроме того, лу у должны быть также непрерывны, что
очевидно.
Если моменты начала и конца перемещения переменны, то в ко¬
нечных точках А — 0. Если время перемещения задано, то значения А
должны быть взяты равными по своей величине в каждой конечной
точке.
Аналогичным образом можно показать, что в конечной точке тяга
может быть приложена также в виде импульса при условии, что и
и v в этот момент будут направляющими косинусами тяги.
Ясно, что в узле между двумя дугами нулевой тяги, в котором
импульс отсутствует, X, Y, X, Y будут непрерывны и поэтому X, У
будут непрерывно представлять одни и те же решения уравнения
(46), т. е. две соседние дуги не будут различаться и плавно перейдут
одна в другую. Далее, допуская наличие такого узла, мы получим
первую вариацию интеграла / в форме, представленной уравне¬
нием (20) с членами
(59)
•272
в предположении, что мы допускаем только те вариации, кото¬
рые не вводят импульс в узел. Для таких вариаций Ъх, не¬
прерывны при переходе через узел, т. е. (8х+=8л:_, 8у+=8у_),
и из уравнений (59) и (24) —(26) можно записать
L + М 3x1 + А/ 3_у’_ — Pot'+ — Q ох'+ — R 8у'+ —
/ t'bx' — х'Ы' \ / dh \ / t'bv' — y'bt' \ { dh \
\ t'2 )+\дх)+ \ t<2 )Лду1+~
( t'bx' —х'Ы' \ ( dh \ , / t'by' —y'bt' \ f dh\
”\ г* )- Ux )-+1 Y2 )-\Jy L~
[(£).-(& )J+[(■#•).-(f X] • (60>
откуда -сразу следует, что dhjdx и dh/dy непрерывны при переходе
через узел. В пределе е-*0, если эти две величины будут стремиться
к и и v соответственно, откуда следует, что и и v непрерывны при
переходе через узел. Но и и v непрерывны при переходе узла и и и v
удовлетворяют дифференциальному уравнению второго порядка.
Поэтому можно сделать заключение, что решения этих уравнений
на каждой стороне узла не различаются между собой. Поэтому узел,
в котором импульс не приложен, можно считать нереальным слу¬
чаем.
Этим мы заканчиваем рассмотрение доказательства условий ми¬
нимума интеграла /, которые сводятся к использованию дуг нулевой
тяги и импульсов тяги, приложенных в местах соединения дуг. Как
уже упоминалось, невозможность существования минимальных
траекторий с ненулевой тягой была установлена в работе [3]. Сле¬
довательно, никаких других возможных случаев, подлежащих рас¬
смотрению, не имеется.
ПЕРВЫЙ ИНТЕГРАЛ
Если f и g явно не зависят от ty т. е. гравитационное поле инва¬
риантно относительно времени, то первый интеграл уравнения (51)
легко получить. Действительно, дифференцируя уравнения
Х + /(Х9 Г) = 0, r+g(X, Y) = 0 (61)
по t, получаем
*+^•*+7^-°' ?+&*+1^-0 <62>
и далее, умножая уравнения (51) на X и Y соответственно и склады¬
вая их, получаем
Xu + Yv - Xtt - Yv » 0. (63)
18 394
273
Интегрируя это уравнение, сразу получаем
Ха + Yv — Xu — Yv = const.
(64)
Используя уравнение (61), этот первый интеграл можно пере¬
писать также в следующей форме:
Из уравнения (55) следует, что последнее равенство выполняет¬
ся при i4=const. Так как А непрерывно при переходе через каждый
узел между дугами нулевой тяги, то следует поэтому допустить, что
в случае поля, инвариантного по времени, А имеет постоянное значе¬
ние по всей траектории. Если мы ищем минимальное решение при
переменном времени перемещения, то в конечных точках А=0 и,
следовательно, везде равно тому же значению.
В этом разделе устанавливается форма функций (и, v) для слу¬
чая, когда гравитационное притяжение всегда направлено в некото¬
рую неподвижную точку О поля и по величине, отнесенной к единице
массы, равно р/r2, где г — радиус-вектор. В этом случае траектории
нулевой тяги будут коническими кривыми с фокусом в точке О.
Поместим прямоугольную систему координат с осями Ох, Оу в плос¬
кость такой траектории и пусть (г, 0) будут полярными координа¬
тами с полюсом в точке О и осью Ох как начальной линией отсчета.
Тогда
где р — фокальный параметр;
е — эксцентриситет;
Y — угол, определяющий ориентацию траектории в плоскости
Используя (68), это уравнение можно преобразовать к виду
uf + vg+ Xu + Yv = const.
(65)
ЦЕНТРАЛЬНОЕ ПОЛЕ КЕПЛЕРА
x=rcos 0, г/ = г sin 9,
а уравнение траектории примет вид
(66)
1=р {1 +ecos(0 + T))>
(67)
Дифференцируя уравнение (67) по t, получим
(68)
-^-=ре sin(6 + T)e.
r—\\pe sin(6 + T).
(69)
274
Величины f и g будут равны
J- [Л „ их их 1
/=— COS 0 = 4— = : S-, I
J Г2 /*3 3,1
(*2 + /2)
2
I
\ т
^г=_т sin6
Гг 4- ’ i
(*2+у2)2 >
откуда
д/ у2 — 2х2 1 — 3 cos2 о /71Ч
17"11 Г=11 ? ; (71)
(х*+у*)'2
df dg 3(jixy 3[x sin 0 cos
(72)
dy dx JL /-3
(-*2+У 2) 2
dg x2 — 2_y2 1—3sin20
^-=1Х —= У- ; • (73)
ду ±. гЗ
(*2+_У2)2
Эти величины, а также (67) (для замены г через 0) могут быть
теперь подставлены в (51).
Ясно, что для этого случая более удобно в качестве независимой
переменной принять 0 взамен t. Отмечая дифференцирование по 6
значком (') во всех выкладках этого раздела, получаем
v=v"b2 + v'ti. (74)
Из (68) имеем
1 • <75)
Далее, дифференцируя (75) по t и используя (69), получаем
«“-С)/ 7'=-'7Tsin (e+i)- (™)
Уравнение (74) можно теперь переписать в виде
v= v" — sin (0 -h -f)- (77)
Следовательно, второе уравнение (51) эквивалентно
{1 + е cos (0 + f)} v" — 2ev' sin (0 -f- f) — Зи sin 0 cos 0 +
+ t>(l —3sin20)=O. (78)
Упростить это выражение можно путем введения новых незави¬
симых переменных (w и г), связанных с переменными и и v следую¬
щими соотношениями:
w — (u cos 0 + v sin 0) {1 + е cos (0 + if)}; (79)
z—( — «sin 0 + ■у cos 0) {1 -f* в cos (0 +y)}. (80)
18* 275
При переменных до и z уравнение (78) упрощается и принимает
вид
z" + 2w'=0. (81)
После интегрирования сразу получаем
zr=Ee—2 до; (82)
здесь Е — произвольная постоянная.
Так как / и g явно не зависят от t, то мы воспользуемся уравне¬
нием (64).
Продифференцируем уравнение x=^r cos 0 по t и, используя (67)
и (69), получим
A; = rcos 0 — гб sin Ь = У^ре sin (9 + y) cos 0 —
— VvP {1 + £ cos (б + ?)} sin 0 = VV/? (е sin у — sin 6). (83)
Дифференцируя далее еще раз, получим
— yVpcos06. (84)
Аналогичным образом можно показать, что если y=r sin 0, то
y = Ypp(e cos у + cos б); (85)
y=— V"ja/7 sin 00. (86)
Уравнение (64) теперь примет следующую форму:
(е sin у — sin 0) a' + (£cos 7 + cos 6) v' + a cos 6 -\-v sin 6 = 0. (87)
Значение постоянной в правой части уравнения принимается
равным нулю для того, чтобы время перемещения было минималь¬
ным.
Производя подстановку до и 2: из уравнений (79) и (80) в (87),
получаем
е (1 -\-е cos ф) sin фдо' + (1 -\-е cos ф) 2z'-f
+ (e2+2+3e cos ф) до=0, (88)
где ф= 0 + Y-
Исключая zr из (82) и (88), получаем линейное уравнение пер¬
вого порядка относительно до, т. е.
(1 -\-е cos ф) sin фдо'+ (е—cos ф—2е cos2 ф) до =
= —Е( 1+^ cos ф)2. (89)
Интегрирующий множитель этого уравнения будет (1+е cos ф)~2Х
Х5т_2ф, и соответственно решение уравнения получаем в виде
до = (1 -\-в cos ф) (De sin ф-(-,£ созф), (90)
где D — вторая произвольная постоянная.
276
Подставляя (90) в (82), находим решение для г:
z = D (1-j-e cos ф)2—Е sin ф (2-\-е cos ф) +F, (91)
где F — третья постоянная интегрирования.
Введем новые независимые переменные U и V, определяемые
соотношениями
U=-
1 -\-е cos ф
—- и cos 0 + v sin 6;
V=■
— /г sin 0 + cos l
1 -f- e cos ф
Тогда уравнения (90) и (91) можно переписать так:
U = De sin у + Е COS
V = D( 1 -Н^соэф) — Е sin ф -
F — Е sin ф
(92)
(93)
(94)
1 -{- е cos ф
Пусть О'и и O'v будут оси прямоугольной системы координат
в плоскости траектории, в которой величины и, v -можно представить
в виде составляющих некоторого вектора
O'Р. Тогда величины U, V, определяемые
уравнениями (92), могут рассматриваться
как составляющие того же самого вектора
по осям O'U, O'V, образующие с осями O'U,
O'V угол 6, как указано на фиг. 88.
В узле и, v представляют собой направ¬
ляющие косинусы вектора тяги; следова¬
тельно, если О'и и О'у направлены по осям
Ох и Оу, то вектор О'Р будет единичным век¬
тором тяги. Аналогично O'U, O'V направлены
соответственно по радиусу-вектору и по пер¬
пендикуляру к нему. Соответственно U и V
будут составляющими единичного вектора тяги по радиальному и
трансверсальному направлениям. Таким образом, если угол между
направлением тяги и трансверсалью по ходу движения обозначить
через ф, то в узлах будут справедливы следующие соотношения:
Фиг. 88. Соотношения
систем координат (u, v)
И (и, V).
U= sincp, I/' = cos ср.
Дифференцируя уравнения (92) по t, получим
U=Vb + u cos 0 4- v sin 0, j
]/= — /70 — wsin0 + ^cos0 |
или, используя (75),
(95)
(96)
V
/
— (U' — V) = (и cos 6 -f v sin 0) r2,
P
-^(l//+f/) = (-USin0-|-'DCOS 0)Г2.
(97)
277
Но и, v, г и 0 непрерывны при переходе через узлы минимальной
траектории, и поэтому соотношения
-L-(U’-V), -У(V' + U) (98)
при переходе через узлы также непрерывны.
Теперь можно записать все условия, которые должны удовлетво¬
ряться на оптимальной траектории движения ракеты в центральном
поле тяготения. Полученные уравнения имеют практическое значе¬
ние, поскольку основная часть пути любой будущей межпланетной
ракеты будет проходить в таком поле.
ПЕРЕХОД МЕЖДУ ДВУМЯ ПОДОБНЫМИ ОРБИТАМИ
Задача оптимального перехода ракеты между двумя копланар-
ными орбитами, идентичными по размеру и форме и описанными
в одном и том же направлении, но различным образом ориентиро¬
ванными, рассмотрена в работе [1]. Используем это исследование для
проверки точности рассмотренной выше теории. Метод подхода,
использованный в работе [1], совершен¬
но отличен от метода, рассматриваемо¬
го в данном исследовании.
Выбирая параметры орбит (р, е, v)
и (р, е,— у) таким образом, чтобы на¬
чальная линия была линией симметрии,
сократим объем исследования, подобно
тому, как это сделано в работе [1], пред¬
полагая, что траектория перехода рас¬
полагается симметрично относительно
конечных траекторий (фиг. 89). Поэто¬
му параметрами переходной орбиты
будут (р\ е\ О). Для осуществления
перехода между орбитами прилагаем
импульсы в точках Р и Р'. Пусть точ¬
ка Р характеризуется полярными коор¬
динатами (г, 0). Тогда координатами
точки Р' будут (г,—0). В работе [3] показано, что изменение пара¬
метров (р, е, y) орбиты ракеты, в точке (г, 0) которой к ракете
приложен кратковременный импульс тяги, происходит в соответст¬
вии с уравнениями
ре cos (0 + y)— s — р\ (99)
ре sin (0 + y) =(5—р2 w)tg<p, (100)
где 5= l/r, ф — угол направления тяги, определяемый в предыдущем
разделе, и \i1/2W sin ф — составляющая скорости ракеты по нормали
к линии тяги. На эту составляющую тяга не влияет. Если ф, W соот-
Фиг. 89. Схема конечных эллип¬
тических орбит с параметрами
(Р> ±Т ) и траектории пере¬
мещения ракеты (//, е/, О).
278
ветст.вуют тяге в точке Р% то тогда можно записать следующие
равенства:
ре cos ф = s— р;
ре sin ф = (s — р'12Щ tg ср;
р'е' cos 0 = s —/7';
р'е' sin 0 = (s — p'h2W) tg ср,
(101)
(102)
(ЮЗ)
(104)
где ф = 0 + Y •
Пусть три произвольные величины, связанные с функциями U и V
уравнениями (93) и (94), принимают для эллиптической орбиты
ракеты (параметры р, е, у) значения D, Е, F, а для. траектории
перехода — значения D\ Е', F'. Покажем, что все наши условия
минимальности могут быть удовлетворены, если мы примем значе¬
ния этих величин для конечной орбиты равными —D, Е, —F, что
вытекает из условия симметрии.
Условия, удовлетворяющие уравнению типа (95), в этой задаче
в узлах Р и Р' могут быть записаны в виде
De sin ф -f-£cos ty = D'e' sin 0 + Я' cos 0 = sin cp,
F — E sin ф
D (1 + e cos ф) — E sin ф
= D' (1 +e' cos 0)—sin 0
1 e cos ф
F' —Er sin (
1 -f- ef cos 0
D'er sin 0 + Er cos 0 = sin cp,
= COS cp,
r~\f /1 i t л\ j-'f . л F ~j— E sin 0
— D(l+e cos 0) — E sin 0 — = cos cp.
1 ~\~ er cos 0
Отсюда видно, что должно удовлетворяться условие D'=F'=0,
и, следовательно, эти уравнения сводятся к
(105)
De sin <J> + Е cos 4 = Е' cos 9 = sin cp,
D (1 +ecos <10 —£ sin Ф + F~ £&|П ^~ =
1 -f- e COS ф
cv • л 2 -f- ef cos 0
= — E sin 0 —1 = cos cp.
\ e' cos 0
(106)
(107)
Поскольку величины, входящие в (98), непрерывны при переходе
через узел, то можно записать следующие уравнения:
Десять уравнений (101) — (104) и (106) — (109) достаточны для
определения десяти неизвестных D, Е, F, Е', ф, W, 0, s, р', е', и, сле¬
довательно, задача может быть решена.
Исключая F в уравнениях (108) и (109), получим
De sin ф + Е cos ф plj2 (er -f- cos 0) (1 -J- е cos ф) — e sin 0 sin ф ('1 -f- & cos 0)
E' cos 0 p'112 cos 0 (1 -j- e' cos 0)2
Из уравнения (106) следует, что это равенство эквивалентно
(er + cos 0) (1 +е cos б) — е sin 0 sin ф (1 +е' cos в) =
cos 0 (1 +е' cos б)2. (110)
Исключение Е' из уравнений (106) и (107) дает
1 , Л l+e'COS0 /111\
tgcptg6= L . (Ш)
S 2 -f- e' cos 0 V ’
В уравнениях (ПО) и (111), как мы видим, исключены величины
D, Е, F, Е'.
Используя уравнения (101) — (Ю4), можно преобразовать урав¬
нения (ПО) и (111) к виду, приведенному в работе [I].
Возводя в квадрат и складывая уравнения (ЮЗ) и (104), получим
/V2=(s-ру + (s-p,li2Wy- tg2cp. (М2)
При делении этих уравнений получим
. Л s—p'll2W , /11Q4
^9== , -tg<p. (113)
S — р
Уравнение (103) можно переписать в виде
l+e' cos 0 = — . (114)
р’
Уравнения (111), (ИЗ) и (114) дают
(115)
Подставляя значение tg2 ф в (112), найдем, что
,/2 (s-p')(Ws-p'312)
р, 3/2(s+y)
Из (114) и (116) получаем
^+e'cos»=i<£=("7)
Используя (102), (104), (114) и (115), можно также показать,
е>2=^-Ю\^-Р' :±. (116)
_/ о/2 / „ I _/ \ ' 7
что
s2(P' —S) (s—pll2W)
рр/2(р' +S)
280
sin 0 sin ф (1 -j- е' cos 0) = ———/2}\ (118)
Умножая (110) на е' и используя (114), можно представить
уравнение (110) в следующей форме:
(e'2+ef cos 0)~ ее' sin 6 sin.ф (1 + er cos 6)= s2\*2~~,[j2) . (119)
Р р Р
Уравнения (117) и (118) показывают, что последнее уравнение
эквивалентно равенству
(s+р’ + pni2W) (р’112-р^) = о
ИЛИ
s+p' +p,l2w=0. (120)
Это равенство является упрощенной формой уравнения (ПО).
Можно показать, что равенство (111) эквивалентно равенству
(115), которое в свою очередь в соответствии с уравнением (120)
эквивалентно уравнению
(l +P^)(s-p') + (s-p'll2W) tg*? = 0, (121)
Решение уравнений (101) — (104), (120), (121) дано в работе [1].
ЛИТЕРАТУРА
1. Лоуден Д., Определение минимальных орбит.
Law den D., The Determination of Minimal Orbits, «Journal of the British
Interplanetary Society», 1952, vol. 11, pp. 216—224.
2. JI о у д e и Д., Орбитальный переход по касательной к эллипсам.
Law den D., Orbital Transfer via Tangential Ellipses, «Journal of the
British Interplanetary Society», 1952, vol. 11, pp. 278—289.
3. JI о у д e н Д., Межорбитальное перемещение ракеты.
Lawden D., Inter-Orbital Transfer of a Rocket. Annual Report of the Bri¬
tish Interplanetary Society, 1951—1952, pp. 321—333.
4. T з я н С. и Эванс P., «Оптимальное программирование тяги высотной
ракеты-зонд а
Tsien Н. S. and Evans Р. С., Optimum Thrust Programming fora Sound¬
ing Rocket, «Journal of the American Rocket Society», 1951, vol. 21. pp. 99—107.
5. Гиббс А., Оптимальная программа изменения тяги двигателя при гори¬
зонтальном полете.
Hibbs A., Optimum Burning Program for Horizontal Flight, «Journal of the
American Rocket Society», 1952, vol. 22, No. 4, pp. 204—212.
6. JI о у д e н Д., Минимальные траектории.
L a w d e n D., Minimal Trajectories, «Journal of the British Interplanetary
Society», 1955, vol. 9, pp. 179—186.
7. Форсайт А., Вариадиюниное исчисление.
Forsyth A., Calculus of Variations, Cambridge University Press, New York,
1927.
394
Д. ЛОУДЕН
ПЕРЕМЕЩЕНИЕ РАКЕТЫ МЕЖДУ ДВУМЯ
КРУГОВЫМИ ОРБИТАМИ1
ПОСТАНОВКА ЗАДАЧИ
Метод расчета траектории, по которой ракета может перемес¬
титься с одной круговой орбиты вокруг некоторой планеты на дру¬
гую круговую орбиту вокруг второй планеты с минимальным расхо¬
дом топлива рассмотрен в работе автора [1]. Кроме определения
оптимальной траектории перемещения, в этой работе устанавлива¬
ются наиболее выгодные положения планет на своих орбитах вокруг
Солнца в момент старта ракеты.
В ряде случаев удобнее назначить старт ракеты именно на время
наиболее выгодного взаимного положения планет.
В тех случаях, когда старт ракеты не может быть отложен до
этого наиболее выгодного взаимного положения планет, а назначен
на определенное время, задача сводится к тому, чтобы подсчитать
наиболее удовлетворительную траекторию перемещения ракеты при
заданном таким образом положении планет. В настоящей работе
именно и будет рассмотрена такая задача.
РЕШЕНИЕ ЗАДАЧИ
Ограничимся рассмотрением двумерной задачи перемещения
ракеты между двумя планетами, двигающимися по копланарным
эллиптическим орбитам вокруг Солнца. Обозначим через Ох, Оу
неподвижные оси прямоугольной декартовой системы координат в
плоскости орбит. Рассматриваемый метод может быть обобщен и на
случай реального трехмерного пространства введением третьей
оси Ог. Очень высокая точность расчетов может быть достигнута
лишь в случае учета взаимного притяжения планет и притяжения
других тел солнечной системы. Но экономия в топливе, которая
могла бы быть достигнута в результате учета этих влияний, будет
пренебрежимо малой по сравнению с потерями, которые будут
неизбежным следствием ошибок навигации вдоль заданного пути.
Наиболее целесообразно незначительное влияние упомянутых фак¬
торов при определении оптимального пути не учитывать, а в про¬
цессе полета корректировать их, а также и накопившиеся погреш¬
ности навигации путем изменения тяги двигателя в различных
контрольных точках траектории перемещения. Метод расчета таких
коррекций дан в работе [2].
Как и в работе [1], предположим, что ракета отрывается от своей
круговой орбиты вокруг планеты отправления путем приложения
импульса тяги двигателя по касательной к этой орбите. Далее ракета
удаляется по гиперболической траектории, незаметно переходящей
в эллиптическую орбиту перемещения, по которой она движется под
1 D. L a w d е п, Transfer Between Circular Orbits, ,Jet Propulsion,® 1956, vol. 26.
No. 7, pp. 555—-558.
282
влиянием притяжения одного Солнца. После входа в сферу влияния
притяжения планеты прибытия ракета начнет двигаться по гипербо¬
лической кривой, вершина которой находится на круговой орбите.
При достижении этой точки ракета с гиперболической траектории
будет переведена на круговую путем приложения второго импульса,
направленного тангенциально к круговой орбите в сторону, противо¬
положную движению. Таким образом, за исключением двух корот¬
ких периодов приложения тяги, двигатель на траектории перехода
не работает.
Если (—f, —g) представляют собой составляющие интенсивности
гравитационного поля, воздействующего на ракету, когда последняя
находится в точке (х, у) в момент времени ty то / и g суть' функции
переменных (х, у, t). Пусть x = X(t)9 y=Y(t) определяют оптималь¬
ную траекторию ракеты. Вдоль этой траектории определим единич¬
ный направляющий вектор с составляющими и и vy удовлетворяю¬
щий уравнениям
и + и — + 1)^=0,
дХ дХ
v-\-u — -\-v —=0.
дГ дУ
(1)
В работах [1] и [3] показано, что на абсолютно оптимальной
траектории тяга прилагается только во вполне определенных точках
в виде кратковременных импульсов. Кроме того, на такой траектории
должны удовлетворяться следующие условия:
а) u2-\-v2< 1 во всех точках траектории;
б) (и, v) являются натравляющими косинусами векторов
импульса тяги, прилагаемых в каждой узловой переходной точке
траектории;
в) (и, v) непрерывны при переходе через такие узловые точки;
г) A = ufJrvg-\-Xu-\-Yv непрерывны в узлах;
д) А= 0 на участках орбиты перехода, где притяжение планет
пренебрежимо мало.
Эти условия были получены при допущении, что мы свободны в
выборе узловых переходных точек. В рассматриваемом случае дело
обстоит иначе.
Если обратиться к рассуждениям, приведенным в работе [1], то
можно убедиться, что условие «в» можно опустить, если положение
узла задано. Поэтому в данной задаче мы не будем требовать
удовлетворения этого условия в каждом из узлов.
В начале движения по гиперболической траектории взлета с на¬
чальной круговой орбиты пренебрегаем влиянием притяжения
Солнца. Пусть ро/б)2 будет сила притяжения, отнесенная к единице
массы планеты отправления на расстоянии г0 от ее центра. Обозна¬
чим соответственно через е0 и /0 эксцентриситет и фокальный пара-
метр гиперболической орбиты. Тогда уравнение гиперболической
траектории в полярных координатах будет иметь вид
-^ = \+е0 cos %, (2)
П)
где я|)0 — угол, отсчитываемый от направления на вершину.
Если Uo и Vo — проекции направляющего вектора соответствен¬
но на радиус-вектор и на перпендикуляр к нему, то решение урав¬
нений (1), приведенное в работе [4], имеет вид
Uq=Pocos -J- (Q0 + -^с/о) ео sin ^0> (3)
И0= — Р0 sin Ф0 + (Qo + Що) (l+eo cos to) +
, Rq Ppsintp-f-//pCtgфо
1 + COS to
где Po, Qo, Rq, Hq — постоянные интегрирования и
I — tg— ctg —•
0 2(e0 —1)2 6 2 2(<?0 + l)2. s 2
(4)
6eo 4,-1 U f eo— M , 4 sinto
"(eg-1)5/2 th VT e0+ltg 2/+ (^-1)2 l + eocost0‘ (5)
Импульс тяги прилагается В вершине гиперболы перпендикуляр¬
но к ради усу-вектор у по часовой стрелке. Следовательно, согласно
условию «б» при ^o = 0 Uo = 0, V=l, что приводит к следующим
условиям:
Р0 %—Я0=0; (6)
° («0+1)2 ° W
Qo(l+^o) + 7X-=b (7)
1 + ^0
Необходимо отметить, что при яр =0 выражение для /о становится
неопределенным. Поэтому мы должны будем считать, что в урав¬
нении (5) o|)o-*0.
Пусть сила притяжения Солнца, отнесенная к единице массы, на
расстоянии г от его центра равна р/г2. Напишем уравнение траек¬
тории перемещения в полярных координатах, на которой влиянием
притяжения планет можно пренебречь:
— =l+<?cosd>, (8)
г
где \р—угол, отсчитываемый от перигелия. Если U и V—проекции
направляющего вектора на радиус-вектор г и на перпендикуляр к
нему, то, поскольку А = 0, как это показано в работе [4] (условие «д»),
U—Pcos ф -f Qe sin ф; (9)
V = — Р sin t + Q (1 + e cos t) + v J-P-s^-, (10)
\ e cos ф
где P, Q, R—постоянные интегрирования, которые будут определены
ниже.
284
Эти уравнения должны быть идентичными уравнениям (3) и (4)
в точках перехода гиперболической траектории в траекторию пере¬
мещения.
Эти величины суть решения дифференциального уравнения вто¬
рого порядка (1), в чем можно убедиться, если произвести сравнение
величин Uо и Vq и их первых производных, полученных из уравнений
(3) и (4), с соответствующими величинами, полученными из уравне¬
ний (9) и (10).
Если обозначить через сро угол между направлением асимптоты
гиперболической траектории взлета и перпендикуляром к радиусу-
вектору г, отложенный в направлении увеличения ф, то составляю¬
щие производной направляющего вектора по времени, вычисленные
по уравнениям (9) и (10), как это показано в работе [1], будут равны
(vSsin ср0+ Г cos ср0) ф по асимптоте, (И)
(— S cos -Ь 7"sin ср0) ф перпендикулярно асимптоте, (12)
где
с Р sin ф — R
Q, (13)
(14)
1 -j-e cos ф
j. Re sin — Ре — P cos ф
(1 -ф e cos ф)2
Выясним теперь, какую форму примут уравнения (3) и (4)
для точек, находящихся на большом расстоянии от места взлета
вдоль асимптоты гиперболической орбиты. В таких точках г—>оо
и, следовательно, cos ф0= — \/е0 и sin ф0 = — 1 )^2je0. Таким
образом, ф0 = const и поэтому
U0 = HjQeQ sin %=H0(el-1 )W0. (15)
Первые два члена в уравнении (5) для /о являются постоянными
величинами и в выражении для /0 исчезают. Два же последних члена
велики и поэтому должны быть специально рассмотрены.
Дифференцируя эти два члена уравнения (5) по t, получим
е0 (е0 — 3 — 2е0 cos Фо) ;
*Т”2 1Ч9/1 , 1 )
(4 — 1) (1 + е0 cos 4/0)2
Имея в виду уравнение (2) и то, что cos%=—l/е, упрощаем вы¬
ражение (16):
„2
2 г
''оФо- (17)
Но г02фо является постоянным кинетическим моментом ракеты
относительно центра притяжения и соответственно равен (цо^о)1/2.
Тогда получаем
Л1/2
'•"тар- (18)
285
Отсюда следует, что при большом (расстоянии: от планеты отправ¬
ления
(19)
Рассмотрим далее уравнение (4). Можно показать, что, когда
cos ф -> ——, /0 (1 + £0 cos ф0) -> const,
откуда следует, что единственным числом, которое устраняет равен¬
ство нулю производной скорости К0, когда г0 велико, является
#о — Ро sin фр + Но ctg фр
1 + е0 cos фо
Используя равенство (2), это последнее соотношение можем за¬
писать в форме
1
— (Я0 - ро sin Фо + Я0 ctg Фо) г0 =
(20)
1
~h
Я0 Рй
(4- D1/2
ео
Н,
о<
где ф0=соз-1 (— 1/^о)-
Дифференцируя далее по ^ получим
С„=-
Я0 я0
(eg-l)1/2
И,
0 (е2-!)1'2
(21)
(22)
Но г0 —скорость удаления от планеты отправления. Следо¬
вательно, г0= [р-о (^0 — 1)/А>)1/2-
Тогда
„1/2
1/ — 0
0 /3/2
‘о
я0(^-1)1/2-я0
«0-1
«о
ял
(23)
Уравнения (19) и (23) определяют составляющие производной
по времени направляющего вектора вдоль асимптоты гиперболиче¬
ской орбиты и перпендикулярно ей на достаточно большом расстоя¬
нии ракеты от планеты отправления. Приравнивая эти величины со¬
ответствующим составляющим, определяемым уравнениями (11) и
(12), получим
ч н3'2
(.S sin «Ро + т cos <р0) —щ- —
Но'
( —5coscp0+ Гэтсро)
№
(«S-1)1P ’
el— 1
1/2.
«о
-я0.
(24)
(25)
Но Po1/2//f=(^o+l)-3/2, умноженному на угловую скорость дви¬
жения ракеты по круговой орбите вокруг планеты отправления, и,
286
следовательно, больше угловой скорости движения ракеты вокруг
Солнца в начале орбиты перемещения.
В таком случае равенства (24) и (25) можно аппроксимировать
следующим образом:
(e|^ipr = Ro~И0=0. (26)
Решая уравнение (26) совместно с (6) и (7), получим
Р0=/?0=Я0=0, Qo=rZ-- (27>
1+^0
Таким образом, мы установили, что на большом расстоянии от
планеты отправления
У»=/ЙТ' *-«•
(28)
Отсюда следует, что составляющие направляющего вектора
вдоль радиуса-вектора от Солнца и перпендикулярно ему в начале
траектории перемещения равны
‘,='/^+Tcos«>-
(29)
Идентичные результаты должно дать решение уравнений (9) и
(10) и, таким образом,
Pcos4 + Qesin<b = 1/ ——- sin ср0,
V е0 +1
(30)
— Psin4> + Q(l+<?cos^)+ R Psin^ =Т//Г jcoscp0, (31)
1 -j- £ COS ф У £0+l
где ip имеет значение, соответствующее 'началу траектории переме¬
щения.
Переход от траектории перемещения в гиперболическую траекто¬
рию приближения аналогичен рассмотренному случаю и характери¬
зуется следующими условиями:
|/ = i/ £i—I
Г V «1 + 1
Pcos<)/ + Qesitnp' = l/ — sin®!; (32)
— Psinf + Q(1 4-«cos-У) + у- = iX+TTcos(33)
1 + e cos <1/ \ £i + 1
где о|/—значение -ф, соответствующее концу траектории перемещения,
cpi—угол между асимптотой траектории приближения и перпендику¬
ляром к радиусу-вектору г и е1—эксцентриситет гиперболы прибли¬
жения.
Условие «г» может быть применено к каждой узловой переходной
точке, в результате чего получаются уравнения, в которые входят по¬
стоянные интегрирования, аналогичные случаю интегрирования урав¬
нений (1) для движения по круговым орбитам. Такие уравнения не
287
накладывают никаких новых условий на траекторию перемещения,
но оказываются 'полезными для определения новых постоянных ин¬
тегрирования.
Исключая Р, Q, R из равенств (30) — (33), получаем условие,
удовлетворяющее оптимальной траектории перемещения, а именно:
Е0 sin ср0 [(2 + е cos ф) cos (ф — ф') — (2 + е cos ф')] +
+ Ех sin <?г[(2 + е cos ф') cos (ф — ф') — (2 + е cos ф)] +
+ [Z?0 (1 +е cos ф) coscpQ — Ег (1 -f £cos ф') cos ©J sin (ф' — ф)=0, (34)
где
Обозначим через (г0, г{) соответствующие расстояния планет
отправления и прибытия от Солнца в моменты отправления или при¬
бытия ракеты, а через (0о, 0i)—соответствующие долготы планет в
эти моменты. Если у будет долготой перигелия на траектории пере¬
мещения, то тогда в конечных точках ее будут иметь место равен¬
ства
Используя последние соотношения, условие (34) можем записать
в форме
Если обозначить через w0 скорость ракеты на круговой орбите
вокруг планеты отправления относительно этой планеты, то скорость
ракеты в бесконечности на гиперболической траектории, по которой
она удаляется от планеты, будет w0= (е0—1)1/2. Эта величина долж¬
на быть равна векторной разности скоростей движения планеты по
ее орбите в момент старта ракеты и скорости ракеты относительно
Солнца в начале движения по траектории перемещения.
Если обозначить через Хо фокальный параметр, через е0—
эксцентриситет и через у о—долготу перигелия орбиты планеты от¬
правления, то можно показать, что это приводит к условиям
(35)
•Ф = Оо— y, ^'= 01—y;
подставляя эти значения в уравнение (8), получим
(36)
—=\+ecos (90—т);
(37)
—— = 1 “f"6 COS (6Х — у).
(38)
w0 (е0 -1 )’/2 cos ?0 = ^ (№ - kf) -L ; (40)
Щ (е0 ~ 1 )1/2 sin То = **1/2 [jj2 sin (6о ~ Y) “ sin (8о~ То)] • (41)
288
Отсюда, исключая <р0, получим
К (*о—l)el*
2<?с о
cos (f — То)-
-(тГ-ПгЛ1 +
2ll^\V2
го
(42)
Этот результат был получен ранее в работе [5].
Аналогичным образом можно получить условия, относящиеся к
моменту прибытия:
Щ (ei — 1 )1/2 cos 9i = p'l2 (Xf _ /i/2) _L.
r 1
(43)
^(^-lPsintp^^2 ^5 sin (6j -b)-±-2 sin (0, — T>]; (44)
2ee,
I ' Xj /1(2aJ/2
cos(T-Tl) —
^1/2 xi/2 ) ( 1 4
2/!'2X}/2 V
(45)
Используем соотношения (40), (41), (43) и (44) и исключим ф0
и ф! из уравнения (39), в результате чего получим
У
(46)
где
X
*i (ei +1) Li'
Lo=-jo {Iх12 - К12)sin (0> - ео) + [(1 + ^-) cos (0, - е0) -
_(1 + n”) ^sin(0o-Y)-|-2sin(Go-ro) ;
Li =-рг (Ч'2~ /1/2) sin (0i - 0о) - [(1 + -у) cos(01 - 0О) -(l + -Ь.)'
x[^sin(01-Tl)--^sm(01-T) .
Уравнения (37), (38) и (46) определяют пять неизвестных е0, еъ
U е, у и, следовательно, оптимальную траекторию перемещения. Эти
уравнения легко сводятся к одному условию, поскольку уравнения
(42) и (45) могут быть использованы для исключения е0 и ег из урав¬
нения (46), а. уравнения (37) и (38)—для исключения I я е.
Остается одно уравнение для у, которое можно решить численно.
19 394
289-
ПЕРЕМЕЩЕНИЕ МЕЖДУ КРУГОВЫМИ ОРБИТАМИ
Поскольку орбиты главных небесных тел солнечной системы очень
близки к круговым, полученные выше уравнения можно упростить,
предположив, что орбиты планет отправления и прибытия в точности
соответствуют круговым. В этом случае eo = ei = 0 и %о и М становят¬
ся радиусами орбит планет: г0 = Хо, П =
В этом случае уравнения (42) и (45) примут вид
wUeQ-l) = V-(e-J-
«н*!— О—р
Условие (46) примет вид
— 1,3
<?2 — 1
Го
3
гЗ/2
'о
2/1/2
*-3/2
Ч
(47)
(48)
/
з/ / / \3/2
е2_1 + __2 — -
Го \ Г0 /
2*о
Go
3/ / I \3/2 2да?
е2-1+—2 — +—/
Л \ Г! / к-
(49)
где
+
(l +—)cos(01 —0О) —1—-lesin(0o —т);
V г0/ Г\ _
Gi =
+
1 +—) cos(0o — 6i) — 1—— esm(0j — f).
r\ / Л) J
Уравнения (49), (37) и (38) определяют оптимальную траекто¬
рию перемещения.
Если ракета должна переместиться с круговой орбиты на границе
земной атмосферы на другую круговую орбиту, близкую к поверхно¬
сти Марса, то в уравнение (49) должны быть подставлены следую¬
щие численные значения известных величин:
г0 = 1,497 • 1013, Г! = 2,280 • 1013, ц= 1,33 • 1026, о>0=7,912 • 105,
= 3,557 • 105
(размерность дана в системе CGS).
Решение уравнения (49) относительно у для этого случая при
различных значениях (Oi—0О) показано в таблице, приведенной ни¬
же. Там же приведены соответствующие значения для I и е, истинной
характеристической скорости V (в км/сек) маневра и времени пере¬
мещения Т (в днях). В последней колонке дается величина Асо—раз¬
ница долгот Марса и Земли в момент отправления.
290
01—00
7
1
е
v в км/сек
Т в днях
Д а>
СЛ
о
—108,5°
1,259-1013
0,5010
18,58
80
3,2°
90°
-62,5°
1,696-1013
0,2889
9,61
136
18,7°
Co
СЛ
о
—30°
1,786-1013
0,2241
6,38
198
31,5°
180°
0е
1,807-1013
0,2076
5,75
259
44,4°
225°
30°
1,786-1013
0,2241
6,38
317
58,8°
to
“O
о
о
62,5°
1,696-1013
0,2889
9,61
366
78,2е
СО
СЛ
о
108,5°
1,259-1013
0,5010
18,58
354
129,5°
При 0i—0o=18Oo оптимальная траектория перемещения каса¬
тельно к орбитам обеих планет. Это хорошо известный случай Гома¬
на, соответствующий полному оптимуму.
Прн значениях Асо, больших и меньших, чем указанные в табли¬
це, характеристическая скорость становится большой и практически
недостижимой, в связи с чем траектория перемещения займет больше
чем один полный цикл и таким образом время совершения маневра
будет больше, чем время соответствующего ожидания до момента
прихода Марса в наиболее выгодное положение. Следовательно,
имеются периоды, во время которых перемещение между Марсом и
Землей практически нецелесообразно. Это явление рассмотрено в
работе [6] Престон-Томасом.
ЛИТЕРАТУРА
1. JI о у д е н Д., Оптимальное перемещение между круговыми орбитами двух
планет.
Law den D., Optimal Transfer Between Circular Orbits About Two Planets,
«Astronautica Acta», 1955, vol. 1, pp. 88—89.
2. Лоуден Д., Корректировка межпланетной траектории.
Law den D., Correction of Interplanetary Orbits, «Journal of the British
Interplanetary Society», vol. 13, pp. 215—223.
3. Лоуд ен Д., Минимальные траектории ракет.
Lawden D., Minimal Rocket Trajectories, «Journal of the American Rocket
Society», 1953, vol, 23, pp. 360—367.
4. Лоуден Д., Основы межпланетной навигации.
Lawden Г)., Fundamentals of Space Navigation, «Journal of the British
Interplanetary Society», 1954, vol. 13, p. 87—101.
5. Лоуден Д., Определение минимальных орбит.
Lawden D., The Determination of Minimal Orbits, «Journal of the British
Interplanetary Society», 1952, vol. 11, pp. 216—224.
6. Престон-Томас Г., Два аспекта элемента времени в межпланетном
полете.
Р г е s t о n-T h о m a s Н., Two Aspects of the Time Element in Interplane¬
tary Flight, «Proceedings of Fifth International Astronautical Congress», Inns¬
bruck, 1954, Springer-Verlag, Vienna.
19*
СОДЕРЖАНИЕ
Стр.
От редактора 3
Раздел I
Оптимальные режимы вертикального подъема ракет-зондов
Г. Гамель. Об одной задаче -вариационного исчисления, связанной с движе¬
нием ракеты 13
С. Тзян и Р. Эванс. Оптимальное программирование тяги высотной раке¬
ты-зонда 13
Г. Лейтманн. Оптимальное программирование тяги высотных ракет ... 34
Г. Лейтманн. Решение задачи Годдарда методами вариационного исчис¬
ления 42
Г. Лейтманн. Оптимальные траектории для высотной ракеты с отделяю¬
щимся ускорителем 52
Раздел II
Оптимальные режимы движения ракетных самолетов
и самолетов-снарядов
А. Паккетт и Р. Эдвардс. Оптимальные характеристики ракетных снарядов
малой дальности 60
А. Гиббс. Оптимальная -программа изменения тяги двигателя при горизон¬
тальном полете 76
А. Миеле. Оптимальная программа подъема самолета с ракетным двига¬
телем 96
П. Чикала и А. Миеле. Брахистохронные маневры самолета с переменной
массой в вертикальной плоскости 113
П. Чикала и А. Миеле. Обобщенная теория оптимального программирова¬
ния тяги при горизонтальном полете самолета с ракетным двигателем 118
А. Миеле. Решение с использованием теоремы Грина для случая линей¬
ной характеристики тяги 121
П. Чикала. Решение по методу множителей Лагранжа для случая произ¬
вольной характеристики двигателя 139
А, Миеле. Расширение теории оптимальной программы расходования топ¬
лива ракетным самолетом при горизо-нталыиом полете 152
Раздел III
Оптимальное направление тяги и методы подбора ступеней
баллистических ракет
Д. Лоуден. Максимальная дальность межконтинентальных ракет .... 177
Б. Фрид и Дж. Ричардсон. Оптимальные траектории ракет 187
М. Фертрегт. К расчету составных ракет 200
292
Стр.
М. Вильямс. Расчет (распределения топлива между ступенями составных
ракет 211
Э. IIIурман. Метод оптимального подбора ступеней составной ракеты . . . 217
М. Голдсмит. Выбор оптимальных весовых соотношений для двухступенча¬
тых ракет 223
Раздел IV
Оптимальные режимы движения ракет в межпланетном
пространстве
В. Фрид. Об активном участке траектории полета спутника Земли . . 229
Т. Эдельбаум и Д. Лоуден. Комментарии к статье В. Фрида «Об активном
участке траектории полета спутника» 237
Д. Лоуден. Оптимальное программирование направления тяги двигателя
ракеты 241
Л. Лоуден. Минимальные траектории ракет . . . . . 259
Д. Лоуден. Перемещение ракеты между двумя круговыми орбитами . . 282
ИССЛЕДОВАНИЕ ОПТИМАЛЬНЫХ РЕЖИМОВ
ДВИЖЕНИЯ РАКЕТ
Издат. редактор Ф. Г. Тубянская Техн. ред. В. П. Рожин
Т-03865 Подписано в печать 20/III 1939 г. Учетно-изд. л. 17,39
Формат бумаги 60х921/16. 9,19 бум. л.—18,38 печ. л.
Цена 13 р. 70 к. Тираж 6000 экз. Заказ 394/1655
Типография Оборонгиза
Цена 13 p. 70 и.