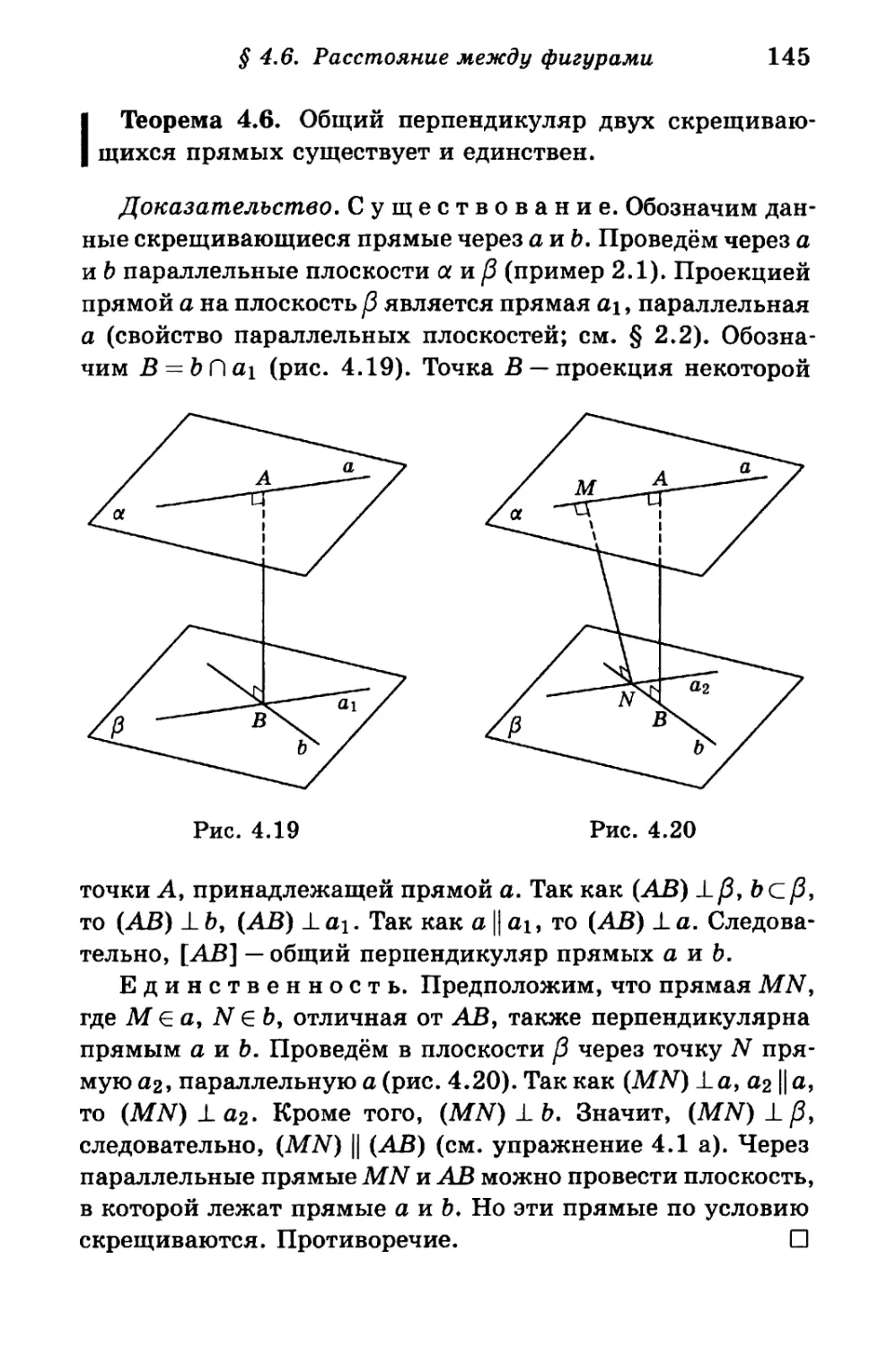
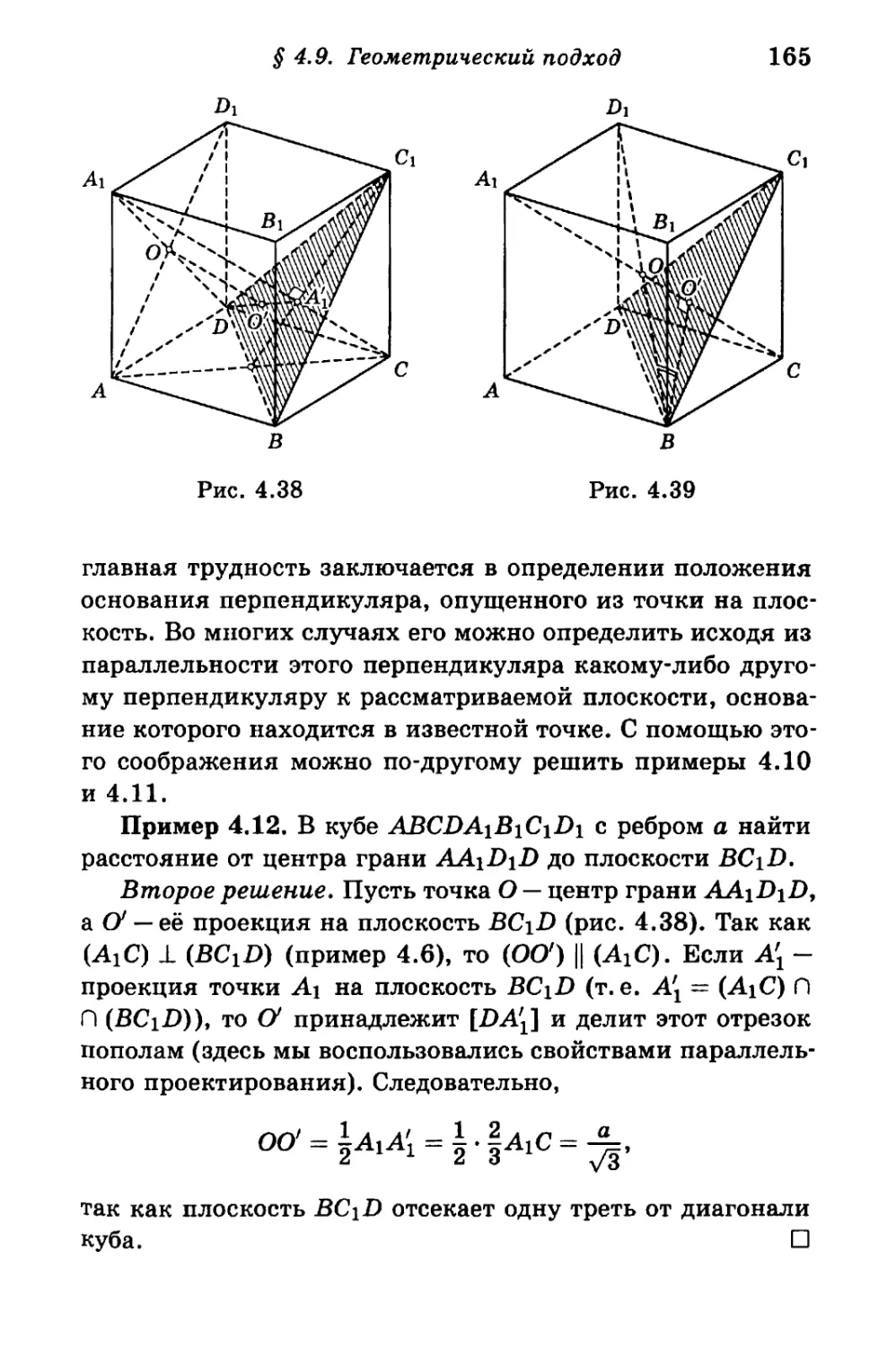
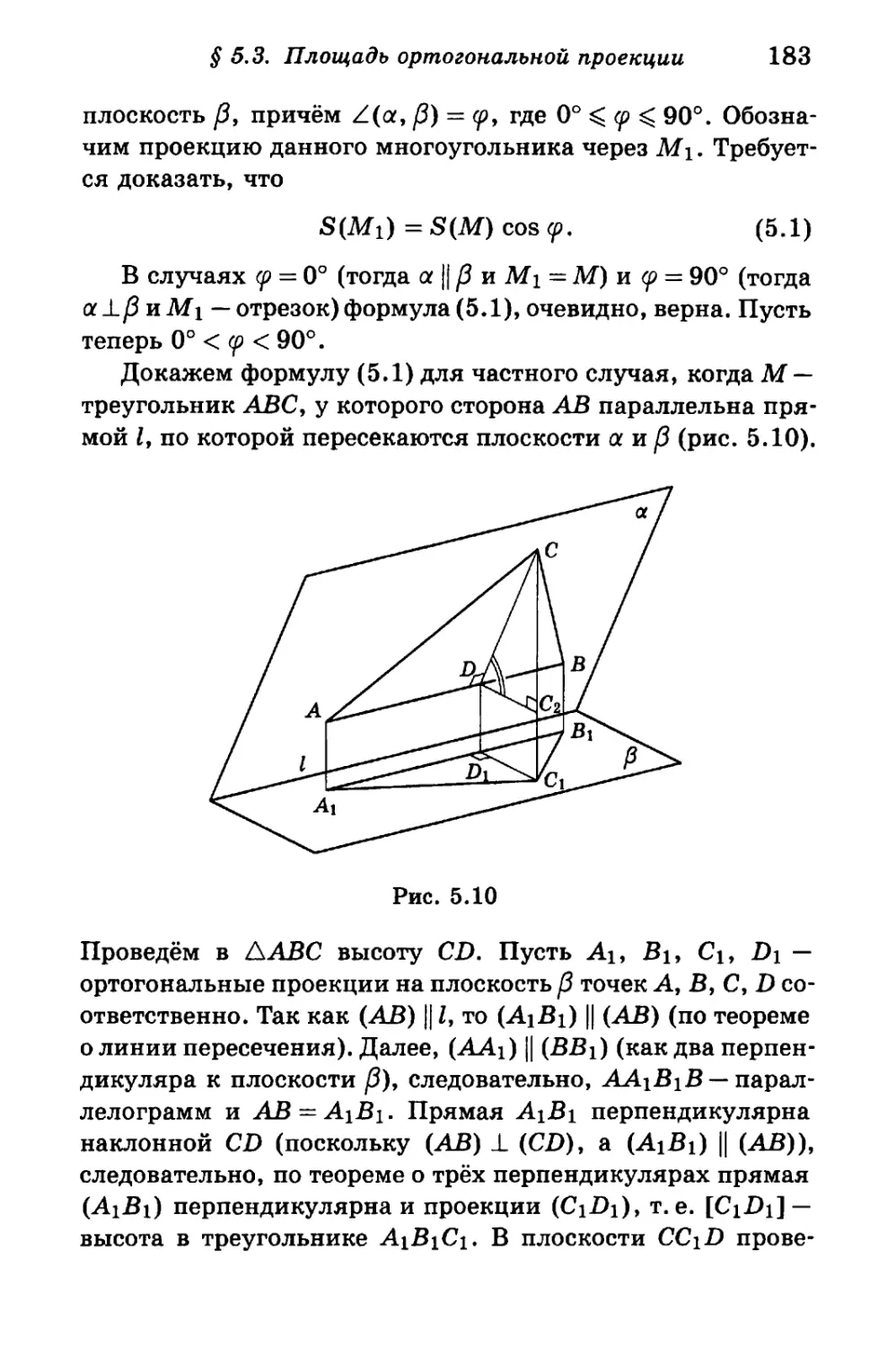
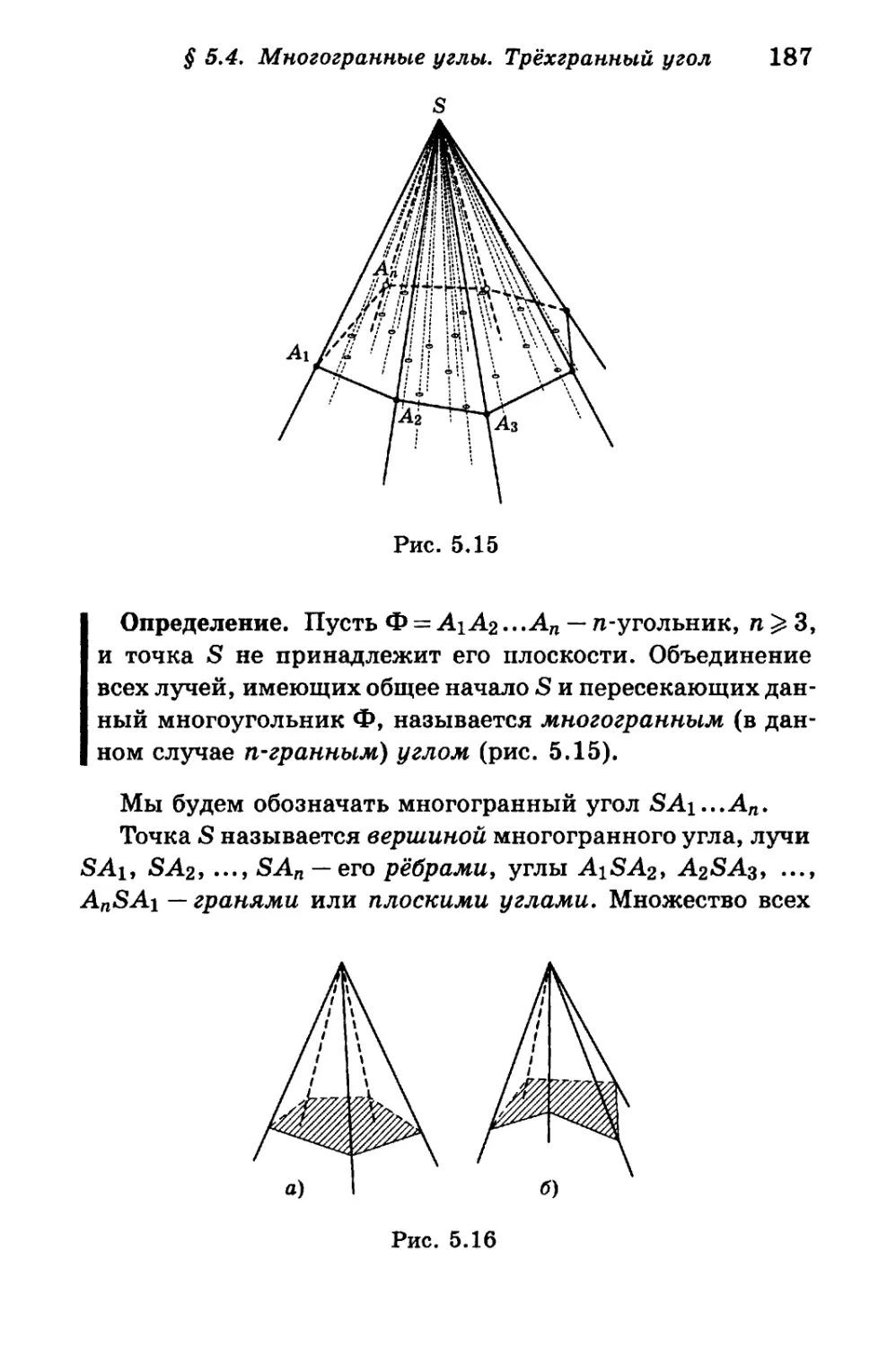
Author: Калинин А.Ю. Терёшин Д.А.
Tags: геометрия топология математика
ISBN: 978-5-94057-581-8
Year: 2011
Text
А. Ю. Калинин, Д. А. Терешин
Геометрия
10-11 классы
мцнмо
А. Ю. Калинин, Д. А. Терёшин
Геометрия
10—11 классы
Новое издание,
исправленное и дополненное
Учебник для общеобразовательных учреждений
Профильный уровень
Рекомендован Министерством образования
и науки Российской Федерации
Москва
Издательство МЦНМО
2011
УДК 514.1
ББК 22.151
К17
Калинин А. Ю., Терёшин Д. А.
К17 Геометрия. 10—11 классы,— Новое изд., испр. и доп.—
М.: МЦНМО, 2011.-640 с, ил.
ISBN 978-5-94057-581-8
В учебнике изложен курс геометрии для 10—11 классов
средней школы (профильный уровень). Подробно разобран
теоретический материал и многочисленные задачи. В каждой главе
приводятся задачи для самостоятельного решения, к которым
даны ответы и указания. Наряду со «стандартными» широко
представлены «нестандартные» задачи, в том числе задачи
математических олимпиад разного уровня и вступительных
экзаменов в ведущие российские вузы. В отдельную главу
выделено систематическое обсуждение некоторых важных идей
и методов решения задач.
Для учащихся школ с углубленным изучением математики
и абитуриентов.
ББК 22.151
Александр Юрьевич Калинин
Дмитрий Александрович Терёшин
ГЕОМЕТРИЯ
10-11 КЛАССЫ
Научный редактор С. В. Резниченко
Технический редактор Д. Е. Щербаков
Подписано в печать 11/IX 2010 г. Формат 60 х 90 Vie.
Бумага офсетная № 1. Печать офсетная. Объём 40 печ. л.
Гарнитура Школьная. Тираж 2000 экз. Заказ 3383
Издательство Московского центра
непрерывного математического образования.
119002, Москва, Большой Власьевский пер., 11.
Тел. (499) 241-74-83.
Отпечатано в ГУП «Типография „Наука"».
199034, Санкт-Петербург, В. О., 9 линия, 12
© А. Ю. Калинин,
Д. А. Терёшин, 20ll.
ISBN 978-5-94057-581-8 © Издательство МЦНМО, 2011.
Оглавление
Предисловие 7
Благодарности 13
10 класс
Глава 0. Вводная
§ 0.1. Игра в геометрию 17
§ 0.2. Элементы логики и теории множеств 22
§ 0.3. Основные обозначения 30
Глава 1. Введение в стереометрию
§1.1. Неопределяемые понятия и аксиомы 33
§ 1.2. Простейшие следствия из аксиом 37
§ 1.3. Взаимное расположение двух прямых 40
§1.4. О существовании объектов и построениях 43
Задачи 45
Глава 2. Параллельпость в пространстве
§2.1. Прямая и плоскость в пространстве 47
§ 2.2. Параллельность плоскостей. Транзитивность .... 50
§ 2.3. Параллельное и центральное проектирование ... 55
§ 2.4. Первоначальное понятие о многогранниках .... 59
§ 2.5. Изображение фигур в стереометрии 63
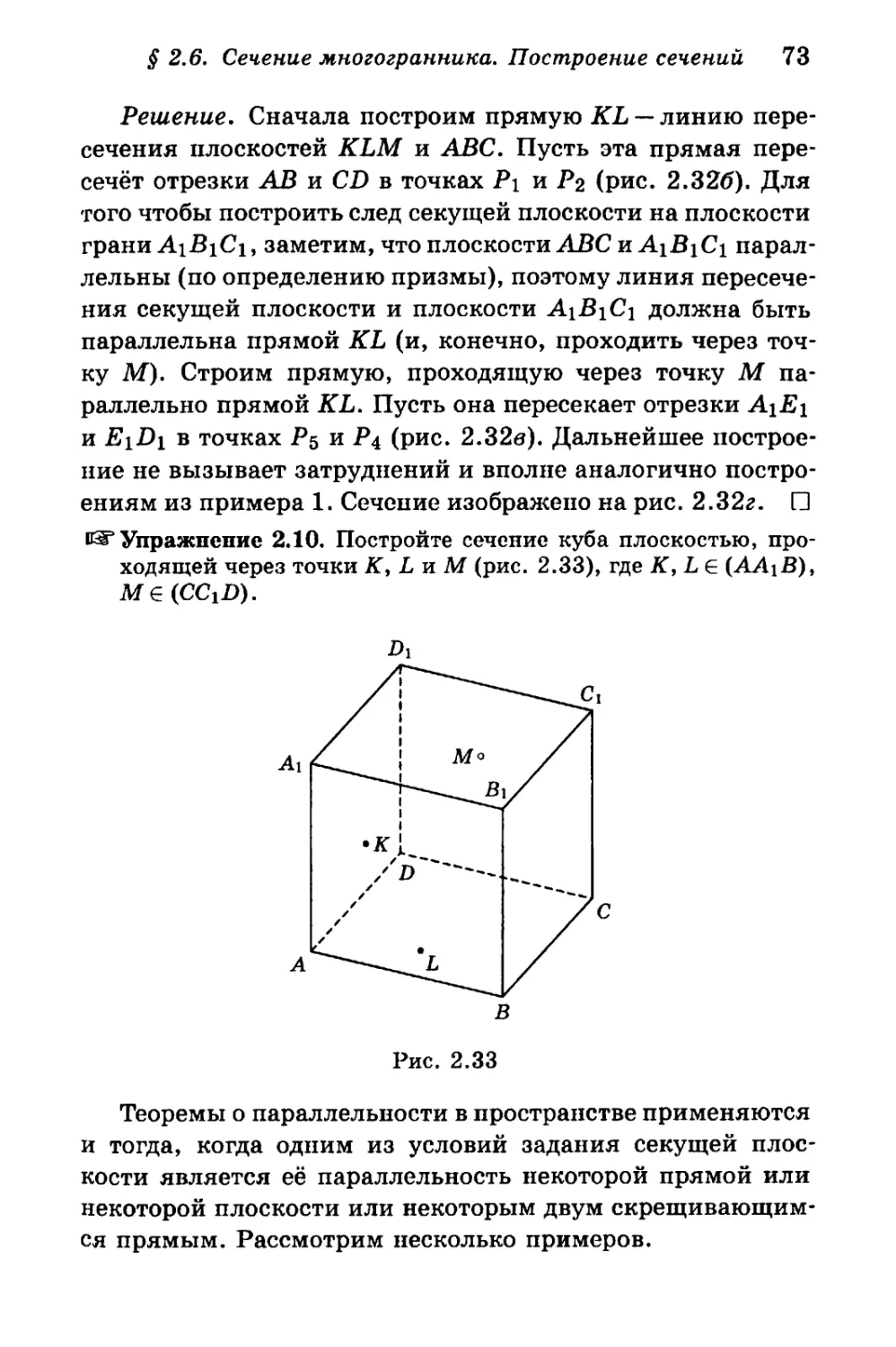
§ 2.6. Сечение многогранника. Построение сечений ... 67
§ 2.7. Применение проектирования 77
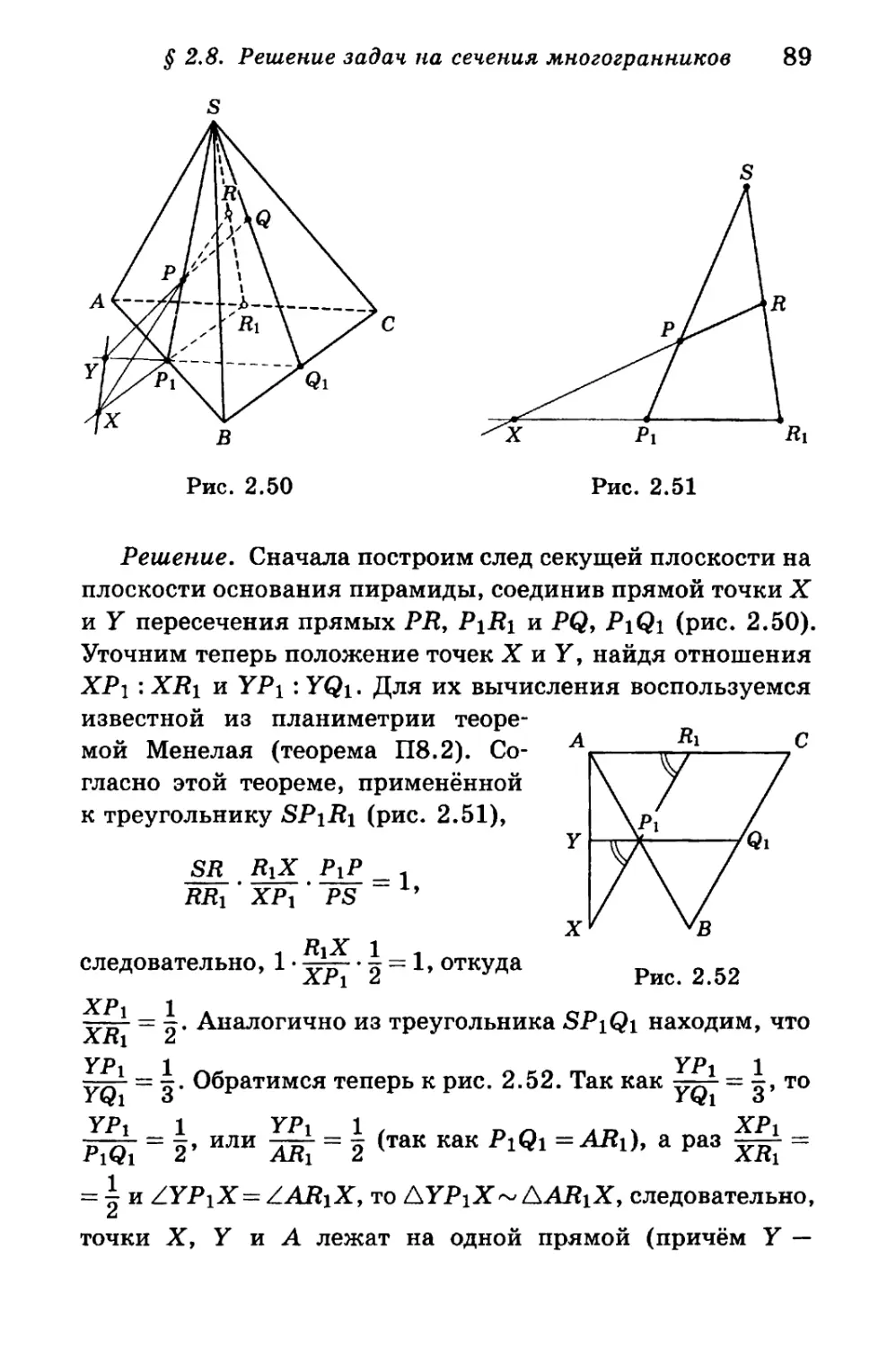
§ 2.8. Решепие задач на сечения многогранников 84
Задачи 93
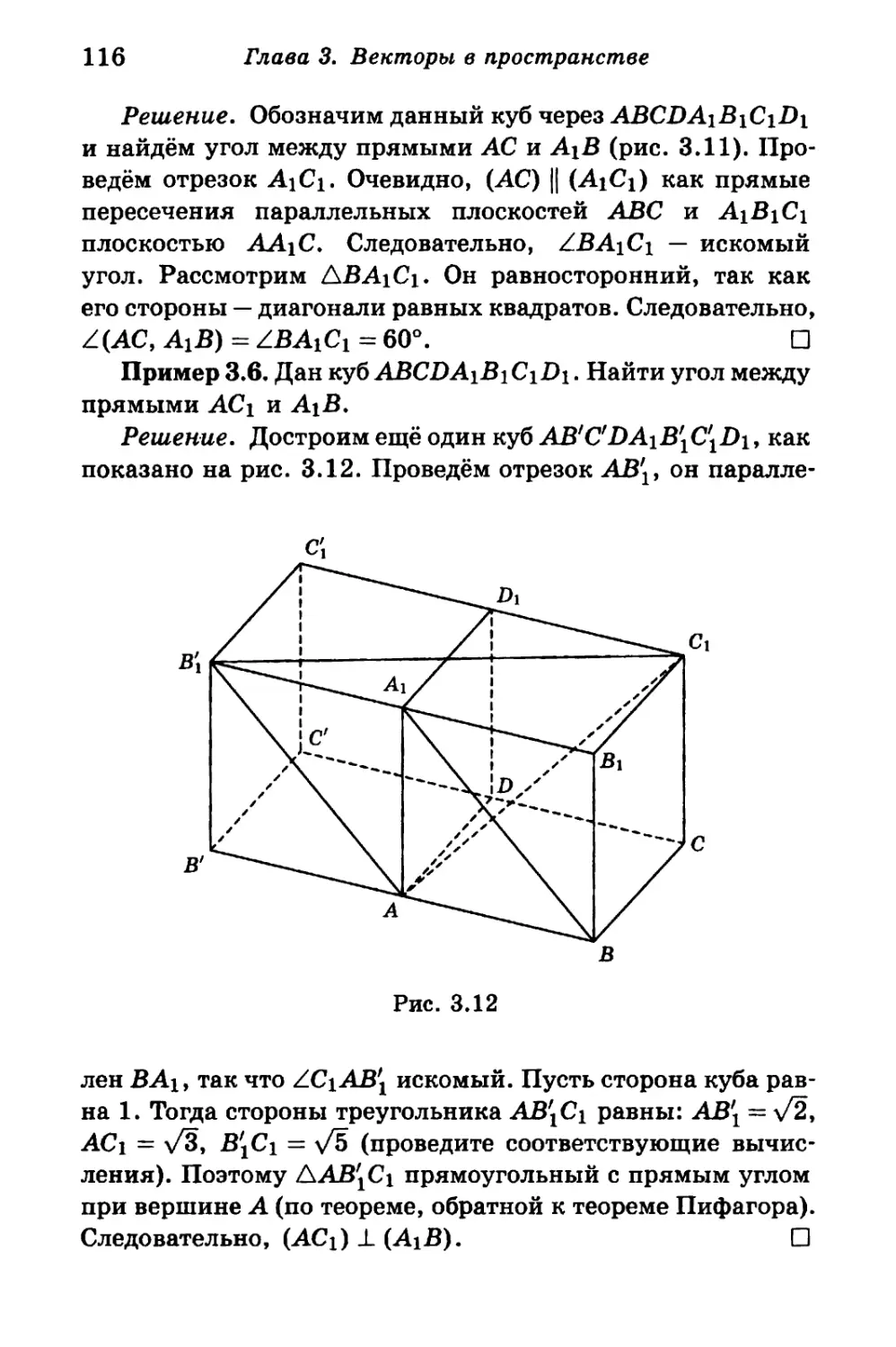
Глава 3. Векторы в пространстве
§ 3.1. Определение вектора. Линейные операции 101
§ 3.2. Компланарность векторов 107
§ 3.3. Угол между прямыми. Угол между векторами ... 112
§ 3.4. Скалярное произведение векторов 117
§ 3.5. Примеры решения задач 120
Задачи 125
4 Оглавление
Глава 4. Перпендикулярность в пространстве
§4.1. Перпендикулярность прямой и плоскости 129
§ 4.2. Связь параллельности и перпендикулярности . . . 132
§ 4.3. Теорема о трёх перпендикулярах 133
§ 4.4. Дальнейшие сведения о многогранниках 134
§ 4.5. Угол между прямой и плоскостью 141
§ 4.6. Расстояние между фигурами 143
§ 4.7. Применение теорем о перпендикулярности 147
§ 4.8. Нахождение расстояний и углов 155
§ 4.9. Геометрический подход 161
Задачи 168
Глава 5. Двугранные и многогранные углы
§ 5.1. Двугранный угол и его измерение. Биссектор ... 173
§ 5.2. Угол между двумя плоскостями 177
§ 5.3. Площадь ортогональной проекции 182
§ 5.4. Многогранные углы. Трёхгранный угол 186
§ 5.5. Расчёт трёхгранных углов 191
Задачи 197
Глава 6* Элементы теории многогранников
§ 6.1. Пространственная область 201
§ 6.2. Многогранники и их элементы 203
§ 6.3. Правильные многогранники 204
§ 6.4*. Теорема Эйлера 208
Задачи 211
Глава 7. Геометрические места точек пространства
§ 7.1. Основные геометрические места точек 213
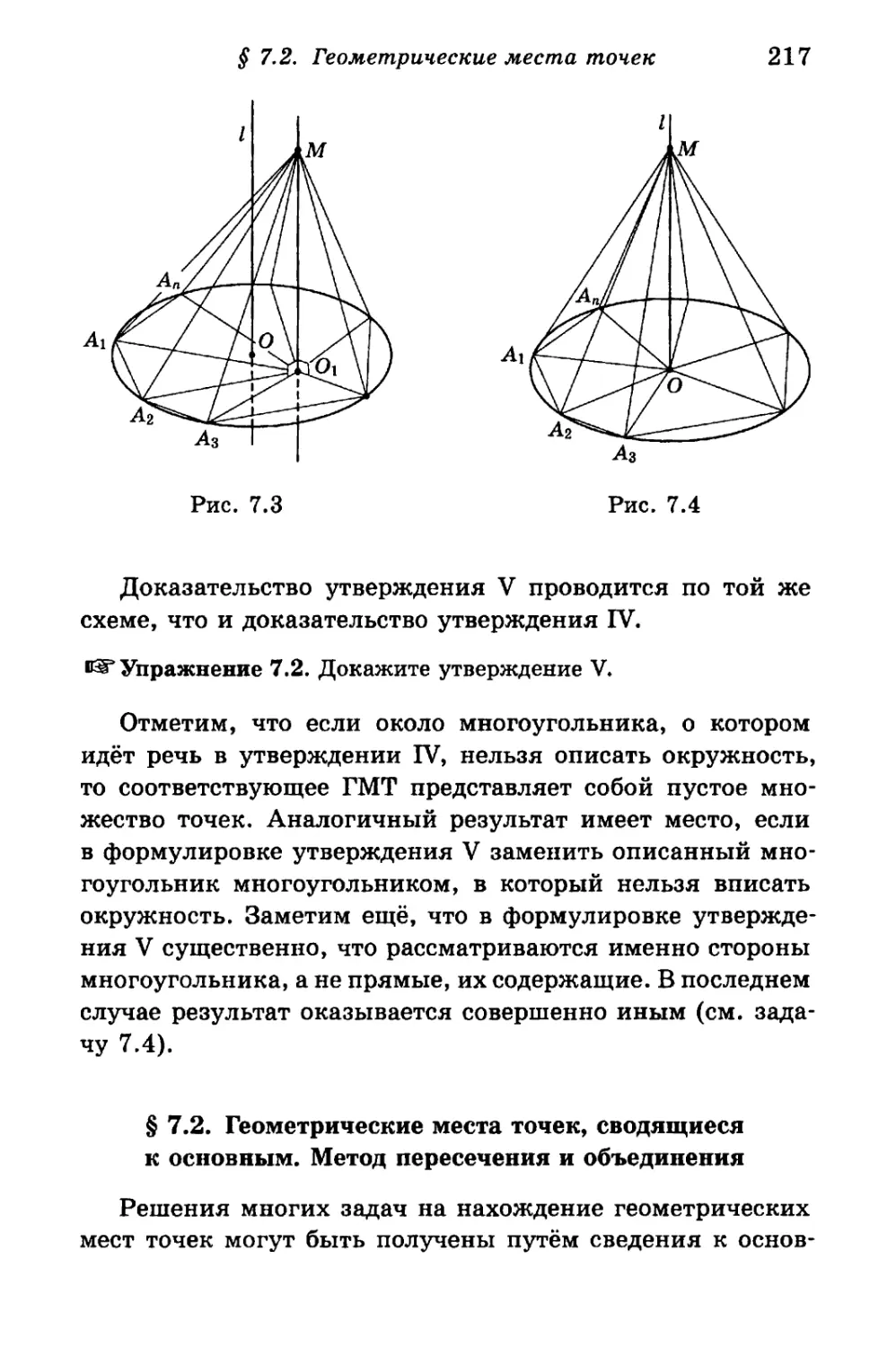
§ 7.2. Геометрические места точек 217
§ 7.3. Различные геометрические места точек 222
Задачи 226
Глава 8. Преобразования пространства
§ 8.1. Основные определения. Перемещения 229
§ 8.2. Параллельный перенос 237
§ 8.3. Поворот вокруг оси 240
§ 8.4. Центральная симметрия 245
§ 8.5. Преобразование подобия в пространстве 250
§ 8.6*. Равенство и подобие треугольников 254
§ 8.7*. Группы преобразований 256
Оглавление 5
§ 8.8*. Классификация перемещений 264
Задачи 268
Глава 9*. Решение задач
§ 9.1. Зависимость между углами в пирамиде 271
§ 9.2. Положение основания высоты пирамиды 276
§ 9.3. Метод вспомогательного объёма 282
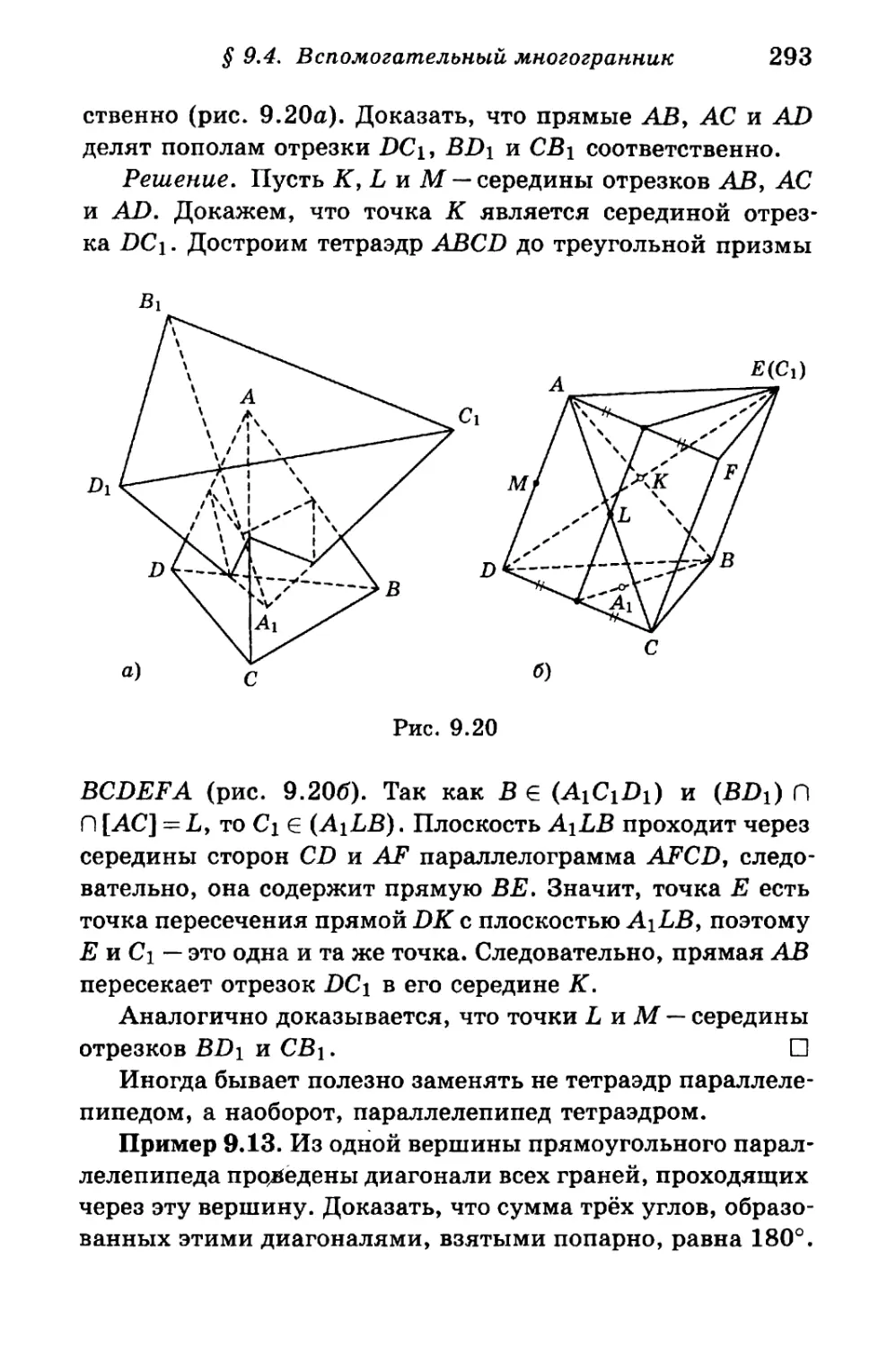
§ 9.4. Вспомогательный многогранник 287
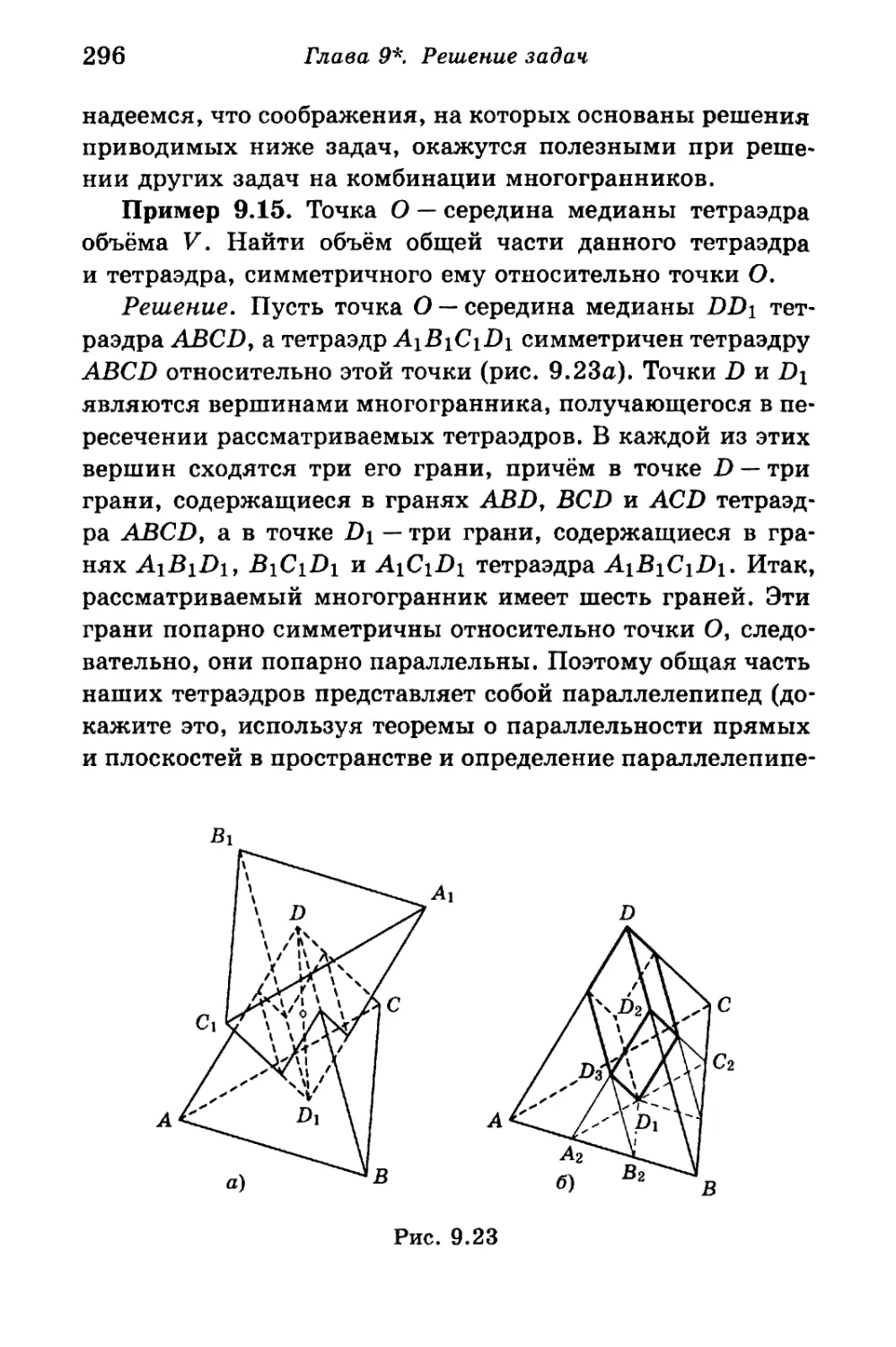
§ 9.5. Задачи на комбинации многогранников 295
Задачи 304
11 класс
Глава 10* Тела вращения
§ 10.1. Предварительные замечания 313
§ 10.2. Сфера и шар 326
§ 10.3. Части шара и сферы 330
§ 10.4. Комбинации шара с цилиндром, конусом 333
§ 10.5. Взаимное расположение двух сфер 338
§ 10.6. Комбинации с многогранниками 346
§ 10.7. Теоремы о касательных и секущих 358
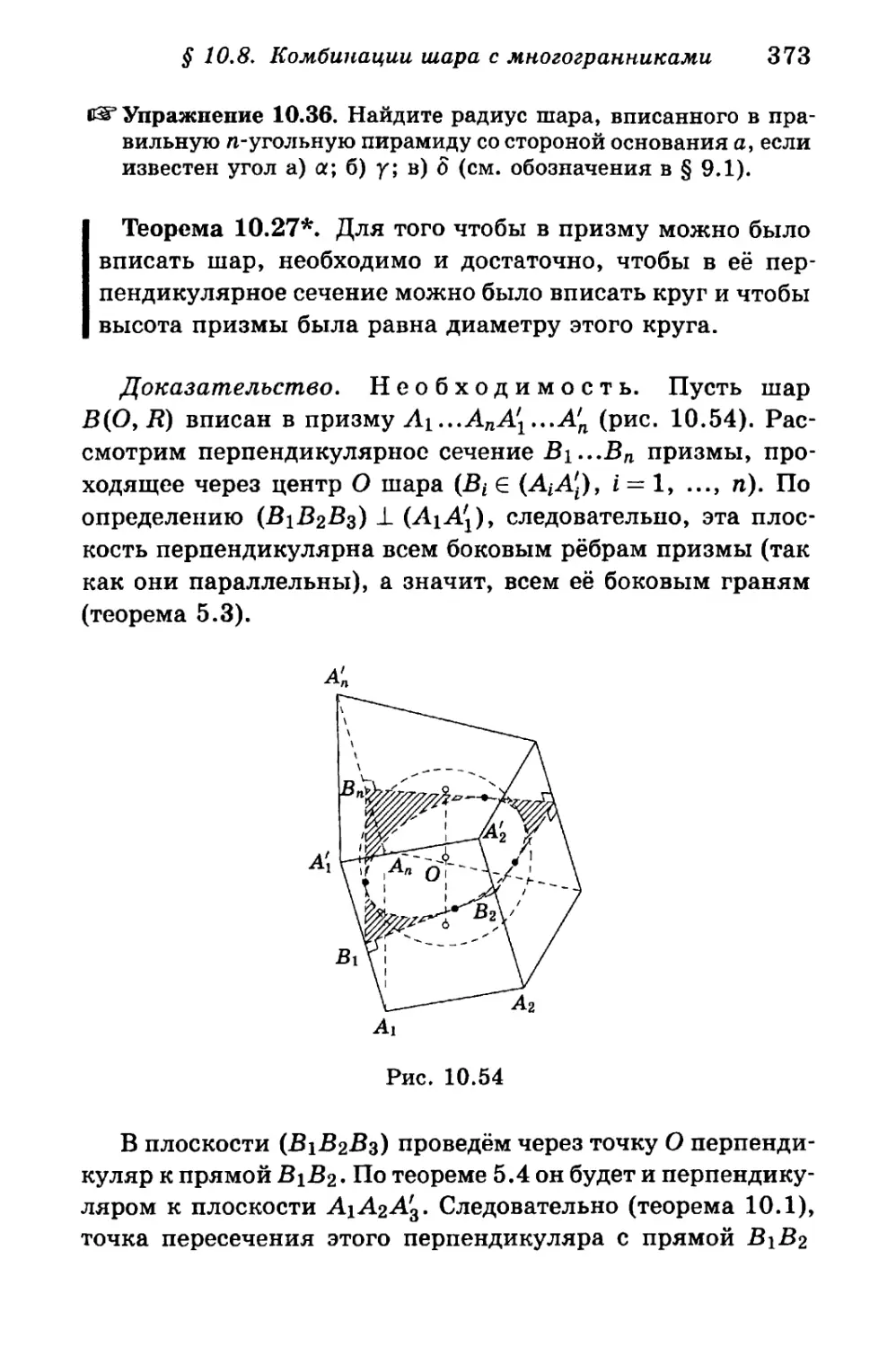
§ 10.8. Комбинации шара с многогранниками 364
§ 10.9*. Нестандартные комбинации 387
§ 10.10*. Конические сечения 402
Задачи 411
Глава 11. Векторы в пространстве (продолжение)
§ 11.1. Векторное и смешанное произведения 423
§ 11.2. Приложения произведений векторов 434
§ 11.3. Уравнение прямой в пространстве 440
§ 11.4. Уравнение плоскости 447
§ 11.5. Некоторые примеры 453
§ 11.6. Декартова система координат 459
§ 11.7. Уравнение сферы 467
§11.8. Примеры решения задач методом координат ... 474
Задачи 482
Глава 12. Задачи на максимум и минимум
§ 12.1. Предварительные замечания 489
§ 12.2. Примеры решения задач 493
6 Оглавление
§ 12.3. Геометрические неравенства 513
Задачи 520
Глава 13. Объём и площадь поверхности тела
§ 13.1. Определение объёма 525
§ 13.2. Объём прямоугольного параллелепипеда 528
§ 13.3. Методы вычисления объёма. Объём цилиндра . . 534
§ 13.4. Объём тетраэдра 540
§ 13.5. Объём пирамиды и конуса 545
§ 13.6. Объём шара и его частей 546
§ 13.7. Об определении площади поверхности 549
§ 13.8. Площадь поверхности по Минковскому 555
Задачи 567
Приложение
Избранные теоремы и методы планиметрии
§ 1. Свойство биссектрисы угла треугольника 573
§ 2. Решение треугольников 576
§ 3. Некоторые формулы площади треугольника 581
§ 4. Формулы, связывающие элементы треугольника . . . 585
§ 5. Следствия из теоремы о вписанном угле 589
§ 6. Вписанные и описанные многоугольники 594
§ 7. Геометрические места точек плоскости 599
§ 8. Теоремы Чевы и Менелая 607
Ответы и указания к задачам 614
Литература 636
Предисловие
Это не предисловие, а
преамбула. Она необходима, однако
я постараюсь быть кратким.
Р. Стаут. Резиновая лента
Этот учебник представляет собой курс геометрии для
старших классов профильной физико-математической
школы.
Книга написана на основе лекций, читавшихся
авторами с 1991 года учащимся физико-математических классов
при Московском физико-техническом институте,
созданных в конце восьмидесятых годов прошлого века на базе
средней школы № 5 (ныне — физико-математический лицей
№ 5) г. Долгопрудного, а также на основе опыта проведения
практических занятий по геометрии в этих классах.
Учебник обладает рядом особенностей, на которые нам
хотелось бы обратить внимание читателей. В ту его часть,
которая предлагается для изучения в десятом классе,
включены некоторые разделы стереометрии, которые ранее
традиционно относились к курсу одиннадцатого класса
(например, двугранные и многогранные углы, элементы теории
многогранников). Причин этому несколько.
Во-первых, отделение аффинных вопросов
стереометрии от метрических (десятый класс — параллельность
прямых и плоскостей в пространстве, одиннадцатый класс —
многогранники, тела вращения, теория площади
поверхности и объёма) представляется нам неестественным.
Интуитивные представления о геометрических телах и их объёме
формируются с самого детства. Этих представлений,
основанных на повседневном опыте, зачастую оказывается
достаточно для решения многих содержательных
метрических задач. Нам кажется совершенно необходимым как
можно раньше учиться решать задачи, ведь формулировки
8 Предисловие
многих из них понятны, даже если строгие определения
тела и его объёма ещё неизвестны.
Во-вторых, как нам кажется, изучение нового
материала в конце одиннадцатого класса вряд ли целесообразно. Не
секрет, что в это время у большинства учащихся на первый
план выходит решение чисто утилитарной задачи —
успешного поступления в вуз. На сегодняшний день это означает
подготовку к участию в олимпиадах и к сдаче экзаменов,
где задачи по геометрии традиционно являются одними из
самых сложных. Поэтому нам представляется, что второе
полугодие одиннадцатого класса лучше посвятить
повторению всего курса геометрии и хорошенько потренироваться
в решении задач.
Отметим ещё, что выбор тем, отнесённых к курсу
одиннадцатого класса, также не совсем обычен. Мы старались
включить в эту часть учебника те вопросы стереометрии,
которые требуют более серьёзной подготовки в области
алгебры и математического анализа, и уделить им серьёзное
внимание (что, на наш взгляд, трудно сделать в конце
последней четверти одиннадцатого класса). Например,
теорию площадей поверхностей и объёмов естественно
излагать в конце первого — начале второго полугодия
одиннадцатого класса, поскольку, с одной стороны, у учащихся к
этому моменту сложились достаточные интуитивные
представления об объёме и площади поверхности и, с другой
стороны, в курсе алгебры и математического анализа изучен
необходимый для изложения аппарат дифференциального
и интегрального исчисления.
В то же самое время, предложенное разделение
стереометрии на две части — 10 и 11 классы — не является
столь жёстким. В зависимости от интересов и подготовки
учащихся, преподаватель может решить вернуться к темам,
опущенным при изучении первой части курса.
Таким образом, в нашей модели из всего курса
стереометрии приблизительно две трети приходится на курс
десятого класса. Опыт авторов и многих учителей, рабо-
Предисловие 9
тавших по первым двум изданиям этой книги,
показывает, что такой путь изучения материала вполне реален.
Разумеется, он не является единственно возможным, и
авторам известны многочисленные примеры работы по
нашему курсу в рамках привычной большинству учителей
модели.
Ещё одной особенностью книги является
систематическое обсуждение важных идей и методов решения задач.
В каждой главе содержатся многочисленные примеры,
снабжённые подробными решениями. Более того, методам
решения задач посвящена отдельная глава (девятая).
Разумеется, все они не являются новыми и оригинальными, но
их изложение ранее можно было найти, пожалуй, в
разрозненных журнальных статьях. По-видимому, вместе и с
достаточной степенью подробности эти идеи и методы
изложены здесь впервые. (Заметим, что соответствующую
главу вовсе не обязательно изучать целиком в конце курса
десятого класса: с отдельными её параграфами можно
знакомиться и раньше.) Кроме того, в виде задач представлен
ряд «второстепенных» тем курса, которые можно сделать
темой отдельного занятия или предоставить школьникам
для самостоятельного изучения.
Основной текст учебника содержит лишь разделы,
относящиеся к стереометрии. Та часть курса, которая содержит
сведения по планиметрии, вынесена в приложение. Выбор
тем, вошедших в приложение, обусловлен действующим на
данный момент стандартом среднего (полного) образования
по математике (профильного уровня).
Отметим, что книга написана весьма сжато, и её
изучение потребует от читателя большого объёма
самостоятельной работы. Временами мы сознательно оставляли
небольшие пробелы в доказательствах, предоставляя читателю
их устранение. В таких случаях в скобках после
высказанного утверждения мы помещаем вопрос — почему? Мы
старались сделать так, чтобы восполнение упомянутых
пробелов не вызывало особых трудностей, помня меткое заме-
10 Предисловие
чание английского математика Дж. Литтлвуда: «две подряд
пропущенные тривиальности могут составлять
непреодолимое препятствие». Кроме того, изложение теории часто
прерывается упражнениями, самостоятельное выполнение
которых поможет лучше усвоить материал. Текст,
напечатанный мелким шрифтом, а также параграфы, отмеченные
звёздочкой, при первом прочтении можно пропустить (они
не являются обязательными).
Книга содержит много задач для самостоятельного
решения. Некоторые из них оригинальны и составлены
авторами специально для неё, но подавляющее большинство
из них известны и заимствованы, в частности, из книг:
[Делоне, Житомирский, 1959], [Шклярский и др., 1954],
[Шарыгин, 1984], [Шарыгин, Голубев, 1991], [Прасолов,
Шарыгин, 1989]. Многие задачи предлагались в различные
годы на вступительных экзаменах и олимпиадах в МГУ,
МФТИ, МИФИ, НГУ и других вузах и на различных
математических олимпиадах (Московской, Ленинградской,
Всесоюзной, Всероссийской и других). Перечислить всех авторов
этих задач, к сожалению, невозможно, но нам хотелось бы
отдать дань уважения всем задачным композиторам, чьи
задачи мы использовали в этой книге. Большинство из
приведённых в книге задач являются задачами повышенной
трудности.
Отметим особо, что читатель почти не найдёт здесь
стандартных упражнений по стереометрии вычислительного
характера. Исключение сделано лишь в тех немногих
случаях, когда упражнения некоторых типов оказывались
недостаточно представленными в распространённых
задачниках. Поэтому в дополнение к учебнику следует выбрать
какой-либо задачник, в изобилии содержащий стандартные
упражнения. Мы обычно используем в работе проверенные
временем, но не потерявшие своей актуальности книги
[Антонов и др., 1968], [Говоров и др., 1983], [Егерев и др.,
1988], [Киселёв, Рыбкин, 1995], неоднократно
переиздававшиеся.
Предисловие 11
Наиболее трудные (на наш взгляд) задачи отмечены
звёздочкой. Хотим предупредить читателя о том, что некоторые
из этих задач чрезвычайно трудны (например, задача 8.29),
но не требуют для своего решения никаких сведений,
выходящих за рамки школьной программы.
Структура учебника такова. Он состоит из
тринадцати глав и приложения. Каждая глава содержит
несколько параграфов. Нумерация параграфов, теорем, примеров,
упражнений, задач, рисунков и формул двойная. Число
слева от разделительной точки обозначает номер главы,
число справа от точки — соответственно номер параграфа,
теоремы и т.п. Например, упражнение 4.7 —это седьмое
упражнение из четвёртой главы. Приложение состоит из
восьми параграфов. Нумерация в приложении аналогична
нумерации в основном тексте учебника, но перед каждым
номером добавлена буква П. Например, задача П6.5 — это
пятая задача к шестому параграфу приложения.
Мы будем рады получить отзывы, критические
замечания и предложения по адресу: 141700, Московская область,
г. Долгопрудный, Институтский переулок, д. 9,
Московский физико-технический институт, кафедра высшей
математики. E-mail: stereolO-ll@mccme.ru.
Авторы
Благодарности
Книга — это большое кладбище,
ще на многих плитах уж не
прочесть стёршиеся имена.
М. Пруст. Обретённое время
Авторы глубоко благодарят всех тех, кто способствовал
появлению на свет этой книги:
научного редактора СВ. Резниченко, проделавшего
скрупулёзную работу по улучшению изложения многих
разделов книги;
Е. В. Малинникову, М. Я. Пратусевича, С. Е. Рукшина и
М. Г. Сонкина, прочитавших рукопись отдельных глав и
сделавших ряд полезных замечаний;
директора физико-математического лицея № 5 г.
Долгопрудного Е. Г. Ермачкову, всячески поддерживающую
благоприятные условия работы преподавателей МФТИ в
лицее;
наших коллег по кафедре высшей математики МФТИ и
лицею № 5 Н. X. Агаханова, И.И.Богданова, Р.Н. Карасё-
ва, П.А.Кожевникова, А.С.Кочерову, О. К. Подлипского,
Б. В. Трушина, И. А. Чубарова и В. М. Уроева, с которыми
мы обсуждали содержание курса математики для
физико-математических классов и различные аспекты его
преподавания;
всех наших учеников, без которых эта книга никогда не
была бы написана, а впоследствии улучшена;
[И. Ф. Шарыгина], чьи книги, статьи и оригинальные
задачи, а также многолетнее личное общение с которым
оказали большое влияние на наше геометрическое
мировоззрение и взгляды на преподавание геометрии;
наших коллег, в разные годы бывших вместе с нами
(некоторые из них являются ими до сих пор) членами жюри
Всероссийской (ранее Всесоюзной) олимпиады школьни-
14 Благодарности
ков по математике, особенно А. А» Берзиныыа, С.Л.Бер-
лова, В. Л. Дольникова, Л. А. Емельянова, Л. П.
Купцова, О.Р.Мусина, Н.Ю.Нецветаева, А.Б. Скопенкова,
М. В. Смурова , Д. Е. Тамаркина, Б. И. Чиника — авторов
красивых олимниадных задач по геометрии;
Н. М. Седракяна — мастера геометрической композиции;
И. В. Ященко, ставшего инициатором нового издания
книги, а также всех сотрудников издательства МЦНМО.
С особой теплотой и сердечной благодарностью авторы
вспоминают своих школьных учителей математики Е, А. Те-
рентьева и В. П. Филинову, а также профессоров МФТИ
А.А.Абрамова, |А. А. Дезина|, |В. Б. Лидского|, В. С.
Рябенького и А. М. Тер-Крикорова, чьи блестящие лекции
существенно повлияли на наше понимание математики
и послужили образцом педагогического мастерства.
А. Ю. Калинин, Д. А. Терёшин
10 класс
Глава О
Вводная
§ 0.1. Игра в геометрию
Все мои произведения — это игры.
Серьёзные игры.
М, К. Эшер
Изучая планиметрию, вы уже несколько лет играли в
увлекательную игру под названием «геометрия». Правила
этой игры вырабатывались тысячелетиями и окончательно
сложились лишь к концу прошлого века. Их обсуждение
естественно начать с вопроса: а что такое геометрия? Как
это, быть может, ни странно, на этот вопрос очень трудно
дать однозначный ответ. Геометрия многолика, и в школе
изучается лишь малая часть того, что в современной
математике принято называть геометрией. Но дело не только
в этом. Даже если мы ограничимся рассмотрением
планиметрии и стереометрии в традиционном их понимании,
наша задача вряд ли будет существенно облегчена. С одной
стороны, геометрия — это аксиоматическая теория,
которая изучает объекты абстрактной природы, находящиеся в
определённых отношениях друг с другом. С другой стороны,
геометрия изучает размеры и форму реальных тел. Для
того чтобы понять, как соотносятся между собой две эти
ипостаси геометрии, коротко проследим исторический путь
её развития.
Всякая естественная наука начинается с установления
некоторых фактов. Затем, по мере их накопления,
вырабатываются законы и теории, превращающие науку в
стройную систему. Так развивалась и геометрия. Ещё в древнем
Египте и Вавилоне были известны многие содержательные
факты, такие, как теорема Пифагора или формула для
вычисления объёма пирамиды. Эти результаты были
получены опытным путём, их справедливость подтверждалась
18 Глава 0. Вводная
множеством экспериментов. Количество подмеченных
геометрических закономерностей росло, и возникла задача
систематизации накопленных знаний.
К началу III в. до н.э. окончательно оформилась идея
построения научной теории, согласно которой отправным
пунктом теории должны служить положения, основанные
на опытных данных и поэтому не вызывающие сомнения.
Все остальные положения должны быть получены из них
логическим (дедуктивным) путём. Здание логики уже было
возведено, в основном благодаря работам
древнегреческого философа Аристотеля (384—322 гг. до н.э.). Им же
впервые была ясно сформулирована идея построения
научной теории. Применительно к геометрии её реализовал
Евклид (III в. до н.э.) в своих «Началах». Опираясь на
опыт своих предшественников, он сформулировал
несколько утверждений (аксиом, или постулатов), принимаемых
без доказательства. Из аксиом выводились их логические
следствия — теоремы. Так геометрия превратилась в
дедуктивную науку. Суть дедуктивного метода блестяще передал
Артур Конан Дойл словами своего излюбленного героя
Шерлока Холмса: «...человека, умеющего наблюдать и
анализировать, обмануть просто невозможно. Его выводы
будут безошибочны, как теоремы Евклида... По одной капле
воды... человек, умеющий мыслить логически, может
сделать вывод о возможности существования Атлантического
океана или Ниагарского водопада, даже если он не видел
ни того, ни другого и никогда о них не слышал. Всякая
жизнь — это огромная цепь причин и следствий, и природу
её мы можем познать по одному звену»1).
Система Евклида просуществовала больше двух
тысячелетий без сколько-нибудь существенных изменений.
Однако с современной точки зрения она уже не кажется
совершенной. В ней не выделены основные понятия, некоторые
аксиомы излишни, многие доказательства не ограничива-
!)А. Конан Дойл. Этюд в багровых тонах.
§ 0.1. Игра в геометрию 19
ются логическим выводом, а апеллируют к соображениям
наглядности.
На рубеже XIX и XX веков после кропотливых усилий
многих математиков, среди которых в первую очередь
следует назвать Феликса Клейна (1849—1925 гг.) и Давида
Гильберта (1862—1943 гг.), была построена геометрическая
система, свободная от указанных недостатков. В основу
этой системы был положен аксиоматический метод.
Суть этого метода построения научной теории
заключается в следующем. Перечисляются основные
(неопределяемые) понятия, или объекты. Все вновь возникающие
понятия должны быть определены через основные
понятия и понятия, определённые ранее. Формулируются
аксиомы — предложения, принимаемые без доказательства.
Все остальные предложения должны являться
логическими следствиями аксиом или ранее доказанных
предложений.
Отметим, что аксиомы вовсе не являются «очевидными
истинами». То, что очевидно для одного, вполне может
казаться абсурдным для другого. Так, зритель футбольного
матча, знающий правила игры, может получить огромное
удовольствие от разворачивающегося на поле
захватывающего действия. Тот же, кто не знаком с правилами, вполне
может считать происходящее на ноле нелепицей, не
заслуживающей внимания. Смысл аксиом в том, что они
являются соглашениями, которые мы заключаем,
приступая к созданию теории.
Основные понятия и аксиомы вовсе не обязательно
имеют отношение к окружающему нас реальному миру. Строя
абстрактную теорию, мы отвлекаемся от наглядного
смысла основных понятий (если он вообще существует).
Единственный смысл, который вкладывается в основные
понятия, таков: они обладают ровно теми свойствами, которые
описаны в аксиомах. Поэтому часто говорят, что аксиомы
являются «скрытыми определениями» основных понятий.
Подчеркнём ещё раз, что математик отнюдь не утверждает,
20 Глава 0. Вводная
что аксиомы верны. Он лишь строит систему утверждений,
с необходимостью вытекающую из них, оставляя за собой
свободу менять аксиомы (и соответственно получать
другую систему следствий).
Итак, понятия абстрактной теории лишены конкретного
смысла. Но если им можно придать этот смысл (т.е.
указать систему конкретных объектов и отношений между
ними) так, чтобы соблюдались установленные аксиомы, то
мы получим, как говорят, интерпретацию, или модель,
абстрактной теории. Одна и та же теория может иметь
множество различных моделей.
Теперь мы можем объяснить ту двойственность
геометрии, о которой говорили выше. Пока мы не конкретизируем
смысл основных геометрических понятий, т. е. не
прибегаем к наглядным представлениям о прямой, плоскости
и т.п., построенная нами геометрия — абстрактная теория.
Все выводы этой теории будут понятны воображаемому
существу, которое обладает нашей логикой и нашей
арифметикой, но ровным счётом ничего не знает об устройстве
окружающего нас мира (французский математик Жак Ада-
мар назвал это существо «Гомо Арифметикус»). Но как
только мы представим себе точку как идеализацию следа
остро отточенного карандаша на бумаге, прямую — как
идеализацию туго натянутой нити, а плоскость — как
идеализацию гладкой поверхности стола, наша геометрия
становится моделью абстрактной теории. Эта модель не
единственная из возможных, но именно её мы и изучаем в школьном
курсе геометрии, так как она с большой точностью
описывает геометрические свойства окружающих нас реальных тел.
Вернёмся теперь к вопросу о правилах нашей игры,
резюмируя сказанное выше. Предметом нашего изучения
является модель абстрактной теории, построенной на основе
аксиоматического метода. Эта модель отражает
геометрические свойства окружающей нас части пространства в том
виде, в каком оно воспринимается нашими органами чувств.
Все утверждения, относящиеся к этой модели, являются
§ 0.1. Игра в геометрию 21
логическими следствиями аксиом и ранее установленных
утверждений (т.е. доказываются). Все вновь возникающие
понятия определяются через основные и известные ранее.
В процессе доказательств мы прибегаем к чертежам,
которые помогают делать правильные логические выводы (но
отнюдь не заменяют их). Использование чертежей удобно
по той причине, что изучаемая модель является для нас
естественной и привычной, мы многое можем
«подсмотреть» на чертеже, догадаться с его помощью о правильной
формулировке утверждения, а затем уже доказать его (ясно,
что это — специфика нашего восприятия: для Гомо Арифме-
тикуса наши чертежи непонятны, а поэтому бесполезны).
Но нет правил без исключений. Отметим, что при
построении школьного курса геометрии идея
аксиоматического метода не выдерживается до конца. Вместо
последовательного изложения логических следствий из аксиом
с полными их доказательствами принят, выражаясь
шахматным языком, гамбитный стиль: логическая строгость
и стройность изложения местами сознательно приносятся
в жертву краткости и наглядности. Некоторые теоремы не
доказываются или доказываются лишь для простейших
частных случаев, не даются строгие определения
некоторых понятий и т.п. Это связано с тем, что все логически
строгие курсы геометрии довольно трудны для восприятия
и весьма объёмны.
В заключение мы обсудим весьма важный вопрос о
выборе аксиом. Требования, предъявляемые к системе аксиом,
которая кладётся в основу теории, таковы. Во-первых,
система аксиом должна быть непротиворечивой, т.е. из неё
не должно следовать какое-либо утверждение вместе с его
отрицанием. Это требование самое главное, оно является
абсолютно необходимым. Далее мы будем говорить только
о непротиворечивых системах аксиом. Во-вторых,
желательно, чтобы система аксиом была независимой, т. е.
чтобы ни одна из этих аксиом не следовала из других.
Выполнение этого требования не обязательно, но всё же естественно
22 Глава 0. Вводная
стремиться к тому, чтобы среди аксиом не было «лишних».
В-третьих, хотелось бы, чтобы система аксиом была полной,
т. е. чтобы к этой системе нельзя было добавить новую
аксиому так, чтобы она не следовала из уже имеющихся аксиом
и не противоречила им1* (имеется в виду, что множество
основных понятий остаётся при этом неизменным).
Заметим, что системы аксиом геометрии являются полными,
но это скорее исключение, чем правило: обычно в
математике системы аксиом оказываются неполными. Наконец,
в-четвёртых, можно потребовать от системы аксиом её
замкнутости^ т. е. чтобы в ней не использовались понятия
из другой теории. Системы аксиом геометрии, как
правило, незамкнуты, поскольку в них, например, используется
понятие числа, определяемое обычно в курсах
математического анализа.
§ 0.2. Элементы логики и теории множеств
— Так бы и сказала, — заметил Мартовский Заяц. —
Нужно всегда говорить то, что думаешь.
— Я так и делаю, — поспешила объяснить Алиса.—
По крайней мере... По крайней мере я всегда думаю
то, что говорю... а это одно и то же...
— Совсем не одно и то же,— возразил Болванщик.—
Так ты ещё чего доброго скажешь, будто «Я вижу то,
что ем» и «Я ем то, что вижу»,— одно и то же!
Л". Кэрролл. Приключения Алисы в стране чудес
В этом параграфе приводятся элементарные сведения
из логики и теории множеств. Возможно, вы уже знакомы
с изложенным здесь материалом, однако ввиду важности
обсуждаемых понятий лучше повторить их ещё раз. Мы
затрагиваем логику и теорию множеств настолько, насколь-
^Поясним смысл слова «следует» в этом определении: утверждение
следует из системы аксиом, если во всякой модели, где выполняются
эти аксиомы, верно и данное утверждение; если же существует такая
модель этой системы аксиом, где данное утверждение неверно, то
считается что оно не следует из этой системы аксиом.
§ 0.2. Элементы логики и теории множеств 23
ко это необходимо для нашего курса стереометрии. Более
подробное и строгое введение в эти разделы математики
можно найти, например, в книге [Кутасов и др., 1981].
Будем называть высказыванием любое утверждение, о
котором можно сказать, истинно оно или ложно.
Примерами высказываний могут служить следующие утверждения:
сборная Испании — чемпион мира по футболу 2010 г.;
число 100 чётное; сумма углов треугольника равна 90°. Первые
два из этих высказываний истинны, а последнее ложно. Не
является высказыванием, например, такое утверждение:
учиться в школе легко, так как нельзя наверняка сказать,
истинно оно или ложно. Многие теоремы (в частности,
большинство теорем геометрии) можно сформулировать в виде1*
p=>Q, где Р и Q — высказывания (читается: из Р следует
Q или если Р, то Q). Это означает, что если высказывание
Р истинно, то высказывание Q также истинно2*.
При этом высказывании Р называется условием
теоремы (посылкой), a Q — её заключением (следствием). Для
того чтобы доказать такую теорему, надо показать, что во
всех случаях, когда Р истинно, Q также истинно. Для того
же чтобы её опровергнуть (т.е. заключить, что теорема
неверна), достаточно привести один пример, когда Р
истинно, a Q ложно (т. е. привести контрпример).
Пусть дана теорема
P^Q. (1)
Теорему вида
Q^P (2)
будем называть теоремой, обратной к теореме (1) (саму
теорему (1) при этом будем называть прямой). Поскольку
1}В математической логике высказывание такого вида называется
импликацией от латинского implicare — тесно связывать).
2)Бсли Р ложно, то Q может быть как истинным, так и ложным.
При этом подразумевается, что теорема Р => Q верна. Точнее говоря,
импликация Р => Q — ложное высказывание лишь в том случае, когда
Р истинно, a Q ложно; во всех остальных случаях высказывание Р => Q
истинно.
24 Глава 0. Вводная
в таком случае теорема (1) является обратной к теореме (2),
говорят, что теоремы (1) и (2) взаимно обратит. Прямая
и обратная теоремы могут быть обе верными, обе
неверными, а может быть так, что из них одна верна, а другая нет.
Пример 0.1. Рассмотрим теорему: диагонали
параллелограмма точкой пересечения делятся пополам. Она, как
известно из планиметрии, верна. Для удобства
переформулируем её, выделив условие и заключение: если
четырёхугольник является параллелограммом, то его диагонали
точкой пересечения делятся пополам (Р => Q).
Сформулируем обратную теорему (Q => Р): если диагонали
четырёхугольника точкой пересечения делятся пополам, то этот
четырёхугольник является параллелограммом. Эта
теорема, как известно, также верна.
Пример 0.2. Рассмотрим следующую теорему (сразу
приведём удобную для нас формулировку): если
четырёхугольник является ромбом, то его диагонали перпендикулярны
(Р => Q). Эта теорема верна. Обратная
теорема: если диагонали четырёхугольника
перпендикулярны, то этот
четырёхугольник является ромбом (Q => Р). Эта
теорема неверна. Контрпример приведён
на рис. 0.1.
Если Р => Q, то говорят, что Р —
достаточное условие для Q, a Q —
необходимое условие для Р. Если же
Рис. 0.1 верны как теорема P^Q, так и обратная
к ней теорема Q => Р, то пишут Р <з> Q
и говорят, что Р — необходимое и достаточное условие
для Q (a Q — необходимое и достаточное условие для Р). При
этом говорят также, что высказывания Р и Q равносильны
или эквивалентны.
Пример 0.3. Для того чтобы диагонали
четырёхугольника были перпендикулярны, достаточно (но не необходимо),
чтобы он был ромбом. Для того чтобы четырёхугольник
был ромбом, необходимо (но не достаточно), чтобы его
§ 0.2. Элементы логики и теории множеств 25
диагонали были перпендикулярны. Для того чтобы
четырёхугольник был параллелограммом, необходимо и
достаточно, чтобы его диагонали в точке пересечения делились
пополам.
Часто вместо слов «необходимо и достаточно» говорят
«тогда и только тогда», «в том и только том случае» или
«если и только если». Эти термины —синонимы.
Рассмотрим некоторое множество1* М. Предположим,
что мы изучаем подмножество Ms этого множества,
состоящее из всех элементов т, удовлетворяющих определённому
условию S.
Пусть Р — высказывание: элемент т удовлетворяет
условию S; a Q — высказывание: элемент т удовлетворяет
условию R. Тогда если верна теорема Р => Q, то говорят,
что она выражает свойство элементов т из Ms* Если верна
теорема Q=>P, то она выражает признак принадлежности
элемента т множеству М$- Если же верны обе эти
теоремы, то теоремаP^Q выражает критерий принадлежности
элемента т множеству М$.
Пример 0*4. Пусть М — множество четырёхугольников,
a Ms — множество вписанных четырёхугольников. Тогда
теорема «если четырёхугольник вписанный, то сумма его
противоположных углов равна 180°» выражает свойство
вписанного четырёхугольника. Теорема — если сумма
противоположных углов четырёхугольника равна 180°, то он
вписанный — выражает признак вписанного
четырёхугольника, а теорема — четырёхугольник является вписанным
тогда и только тогда, когда сумма его противоположных
углов равна 180° — выражает критерий вписанности
четырёхугольника.
Мы видим, что существует следующая параллель:
необходимое условие — свойство, достаточное условие —
признак, необходимое и достаточное условие — критерий. Пусть
конечно, известны понятия «множество», «подмножество»,
«элемент множества». Впрочем, ниже мы обсудим их поподробнее.
26 Глава 0. Вводная
Р — некоторое высказывание. Наряду с ним будем
рассматривать высказывание Р (читается: не Р) — отрицание
высказывания Р. Высказывание Р истинно, когда Р ложно,
и наоборот. Для того чтобы сформулировать
высказывание Р, достаточно перед формулировкой высказывания Р
добавить слова «неверно, что».
Рассмотрим теорему Р => Q (прямую). Теорема Р => Q
называется противоположной к ней, а теорема Q => Р —
противоположной к обратной.
Пример 0.5. Сформулируем противоположную теорему
и теорему, противоположную к обратной, для теоремы из
примера 0.2, которая, как мы знаем, верна.
Противоположная теорема: если четырёхугольник не является ромбом, то
его диагонали не перпендикулярны (P=>Q). Теорема,
противоположная к обратной: если диагонали четырёхугольника
не перпендикулярны, то он не является ромбом (Q => Р).
Первая из этих теорем неверна (контрпример приведён на
рис. 0.1), а вторая верна.
Тот факт, что теорема, противоположная к обратной,
как и прямая теорема, оказалась верной, не случаен.
Рассмотрим четыре теоремы и для удобства расположим их
в виде схемы:
прямая Р => Q Q =ф Р обратная
противоположная Р => Q Q => Р противоположная к обратной
Теоремы, расположенные по диагоналям, равносильны
(т.е. одновременно либо верны, либо нетХ)).
Вспомните, например, как доказывается теорема P=>Q
методом от противного. Мы предполагаем, что
заключение Q ложно (т. е. Q истинно), и приходим к противоречию
с условием Р (т.е. доказываем, что Р истинно). Таким
Х)Для того чтобы доказать этот факт, нужно рассмотреть четыре
случая: 1) Р истинно, Q истинно; 2) Р истинно, Q ложно; 3) Р ложно,
Q истинно; 4) Р ложно, Q ложно — и убедиться, что в каждом из этих
случаев соответствующие высказывания (P=>Q n Q=>p9 а также
и Р => Q) одновременно либо истинны, либо ложны.
§ 0,2. Элементы логики и теории множеств 27
образом, мы фактически доказываем теорему,
противоположную к обратной. Отметим ещё, что для доказательства
теоремы Р <=> Q достаточно доказать любые две теоремы,
расположенные в одной строке или в одном столбце нашей
схемы.
^Упражнение 0.1. Для каждой из следующих теорем
сформулируйте обратную, противоположную и противоположную
к обратной. Укажите, какие из этих теорем верны, а какие —
нет:
а) величины вписанных углов, опирающихся на равные
дуги, равны;
б) сумма внутренних углов четырёхугольника равна 360°;
в) если параллелограмм является ромбом, то в него можно
вписать окружность;
г) если 2 х 2 = 5, то Париж — столица Франции.
Переформулируйте все теоремы, используя термины
«необходимо, но не достаточно», «достаточно, но не необходимо»,
«необходимо и достаточно».
Напомним теперь простейшие сведения из теории
множеств. Понятие множество является неопределяемым
(основным). Оно служит для описания совокупности
предметов или объектов. Эти объекты, или элементы
множества, считаются отличными друг от друга и от объектов, не
входящих в данное множество. Каждая из существующих
математических теорий занимается изучением
некоторого множества — основного множества теории. Например,
в геометрии основным множеством является множество
всех точек (пространство).
Элементы множества могут находится в некоторых
отношениях как между собой, так и с элементами других
множеств. Отношение считается заданным, если для любого
элемента (или множества) х и элемента (или множества) у
указано, связаны они этим отношением или нет.
Приведём примеры.
Отношение принадлежности. Тот факт, что
объект а является элементом множества А, словесно
выражается так: элемент а принадлежит множеству А. Обо-
28 Глава 0. Вводная
значение: аеА. Отрицание этого факта выражается другим
отношением: элемент а не принадлежит множеству А.
Обозначение: а $ А.
Отношение включения. Говорят, что
множество В включено в множество А, если каждый элемент
множества В принадлежит А. Обозначение: В С А.
Подмножеством множества А называется всякое множество В,
удовлетворяющее условию В С А. Множество, не
содержащее ни одного элемента, называется пустым множеством
и обозначается 0. Заметим, что для любого множества А
справедливо включение Ас А. Считается, что 0 С А для
любого множества А.
Отношение равенства множеств. Говорят,
что множества А и В равны, если Ас В и В С А, иными
словами, если множества А и В состоят из одних и тех же
элементов. Обозначение: А~В.
Обсудим теперь некоторые общие свойства отношений. Пусть
в множестве А задано отношение о. Говорят, что это отношение
рефлексивно у если для любого элемента а из множества А
выполнено а о а (т. е. любой элемент связан отношением о с самим
собой). Говорят, что отношение о симметрично, если а о Ь => Ь о а
для любых элементов а и Ь из множества А. Наконец,
отношение о называется транзитивныму если (аоЬиЬос)=>аос для
любых элементов а, Ь и с из множества А.
Не всякое отношение обладает этими свойствами. Но
может случиться так, что некоторое отношение о в множестве А
рефлексивно, симметрично и транзитивно. Тогда говорят, что
отношение о есть отношение эквивалентности.
Пример 0.6*. Отношение равенства множеств рефлексивно
(А = А), симметрично (А = В => В = А) и транзитивно ((А = В
и В = С) =» А = С); следовательно, оно является отношением
эквивалентности.
Импликация как отношение между высказываниями
рефлексивна (Р => Р), транзитивна ((Р => Q и Q =» R) =» (Р => Я)), но
не обязательно симметрична (из того, что Р => Q, вообще
говоря, не следует, что Q => Р). Значит, это отношение не является
отношением эквивалентности. Подчеркнём значение свойства
транзитивности импликации: оно обеспечивает возможность де-
§ 0,2. Элементы логики и теории множеств 29
дукции, так как логический вывод осуществляется цепочкой
импликаций.
и^ Упражнение 0.2*. Являются ли следующие отношения
отношениями эквивалентности:
а) отношение включения множеств;
б) отношение перпендикулярности прямых на плоскости;
в) отношение параллельности прямых на плоскости?
с^ Упражнение 0.3*. Пусть взвод солдат построен в шеренгу.
Рассмотрим следующее отношение: солдат А стоит в строю
правее солдата Б. Докажите, что это отношение не является
ни рефлексивным, пи симметричным, но является
транзитивным.
в^ Упражнение 0.4*. Пусть несколько теннисистов провели
между собой однокруговой турнир (т. е. каждый сыграл с каждым
один раз). Рассмотрим следующее отношение: теннисист А
выиграл матч у теннисиста В. Докажите, что это отношение
не является ни рефлексивным, ни симметричным, ни
транзитивным.
Всякое отношение эквивалентности ^ в множестве А
позволяет специальным образом различать элементы этого множества.
Обозначим через С(а) множество таких элементов х из А, что
х^а. Это множество является подмножеством множества А,
которое называется классом эквивалентности элемента а. Если Ь ~ а
(элемент Ь эквивалентен элементу а), то в силу симметричности
и транзитивности отношения ~ любой элемент х,
эквивалентный а, эквивалентен и Ь. Если же элемент Ь не эквивалентен а,
то С(а) и С(Ь) не имеют общих элементов. Действительно, если
существует такой элемент ху что х~аих~Ь, то в силу
симметричности и транзитивности а~ Ь, что противоречит условию. Итак,
множество А разбивается па непересекающиеся (т. е. не имеющие
общих элементов) классы, при этом каждый элемент попадает
в свой класс. Поэтому говорят, что отношение эквивалентности
задаёт разбиение множества на классы эквивалентности. С
подобной конструкцией вы уже сталкивались в алгебре: две дроби а/Ъ
и c/d назывались эквивалентными, если ad — bc. Нетрудно
проверить, что это отношение является отношением эквивалентности
в множестве дробей (чем и оправдывается название
эквивалентные дроби). Таким образом, множество дробей распадается на
классы эквивалентности, каждый из которых называется рацио
нальным числом.
Приведём другой важный пример. Рассмотрим множество Р
всех направленных отрезков плоскости. Из планиметрии вам из-
30 Глава 0. Вводная
вестно понятие равенства направленных отрезков (которые
считаются равными, если они имеют одинаковые длины и одинаковые
направления). Отношение равенства направленных отрезков
является отношением эквивалентности в множестве Р, поэтому
оно задаёт разбиение Р на классы эквивалентности, каждый из
которых называется вектором (сравните с определением вектора,
приведённым в гл. 3).
В заключение напомним определения основных
операций над множествами. Пусть U — некоторое множество
такое, что все рассматриваемые нами множества являются
его подмножествами (U — основное множество1^).
Множество, состоящее из тех и только тех элементов, которые
принадлежат и множеству А, и множеству В, называется
пересечением этих множеств и обозначается А Г) В.
Множество, состоящее из тех и только тех элементов, которые
принадлежат множеству А или множеству В, называется
их объединением и обозначается Аи В. Множество,
состоящее из тех и только тех элементов множества А, которые
не принадлежат множеству В, называется разностью
множеств А и В и обозначается А\В. Разность множеств U
и А называется дополнением множества А. Эти операции
обладают многими интересными свойствами, но мы не
будем пользоваться ими в нашем курсе, поэтому не станем
обсуждать здесь эти свойства»
§ 0.3. Основные обозначения
О книгах Жордана говорили, что если ему нужно
было ввести четыре аналогичные или родственные
величины (такие как, например, а, Ь, с, d), то они
у него получали обозначения а, М'3, £2, Щ 2.
Дж. Литтлеуд, Математическая смесь
Условимся всюду, если не оговорено противное,
использовать следующие обозначения.
геометрии основным множеством является пространство.
§ 0.3, Основные обозначения 31
Геометрические фигуры:
А, В, С, ♦.., X, У, Z- точки;
a, ft, с, ♦.,, jc, у, 2 — прямые;
(АВ) — прямая, проходящая через точки А и В;
[АВ) — луч (полупрямая) с началом в точке А,
проходящий через точку В;
[АВ] — отрезок с концами А и В;
а, /3, у, ..., ф, х> ^ —плоскости;
(ABC) — плоскость, проходящая через точки А, В и С;
ААВС — треугольник с вершинами А, В и С.
Величины:
АВ — расстояние между точками А и В (длина
отрезка АВ);
р(Ф\, Фг) —расстояние между фигурами <J>i и Ф2;
S — площадь (плоской фигуры, поверхности тела);
SAiA2...An —площадь многоугольника с вершинами А\,
А2, ..., Ап\
V — объём тела;
2...An —объём многогранника с вершинами Ai, A2,
Z(a, b) —величина угла между прямыми а и Ь\
Z(a, a) — величина угла между прямой а и плоскостью а;
Z(a, /3) — величина угла между плоскостями а и /3.
Отношения:
= — равенство;
~ — подобие;
|| — параллельность;
± — перпендикулярность;
6 — принадлежность элемента множеству;
С — включение одного множества в другое.
Например:
ААВС = ЛА1В1С1 — треугольник ABC равен
треугольнику AiBiCi;
ЛАВС~ ДА1В1С1 — треугольник ABC подобен
треугольнику AB
32 Глава 0. Вводная
a La — прямая а перпендикулярна плоскости а;
а || Р — плоскость а параллельна плоскости /3;
Аеа — точка А принадлежит прямой а, или прямая а
проходит через точку А;
аса — прямая а лежит в плоскости ау или плоскость а
проходит через прямую а.
Перечёркнутый знак отношения означает, что данные
объекты не связаны этим отношением. Например, а(/_а —
прямая а не лежит в плоскости а.
Прочие символы:
П, U — операции пересечения и объединения множеств;
например, а Па — прямая а пересекает плоскость а; запись
аП а = А означает, что прямая а пересекает плоскость а
в точке А;
\ — операция разности множеств;
=>, <=> — знаки следования и равносильности;
D — конец доказательства;
V —квантор всеобщности (читается: для любого);
3 —квантор существования (читается: существует).
Все остальные обозначения будут введены и пояснены
по мере изложения материала.
Глава 1
Введение в стереометрию
Ломиться в двери пошлых аксиом,
Где лгут слова и красноречье храмлет?..
О! весь Шекспир, быть может, только в том,
Что запросто болтает с тенью Гамлет.
Б. Пастернак. Брюсову
§ 1.1. Неопределяемые понятия и аксиомы стереометрии
Кто не согласится, что никакая наука не должна
бы начинаться с таких тёмных понятий, с каких,
повторяя Евклида, начинаем мы геометрию?
Н. И. Лобачевский
Итак, мы приступаем к изучению стереометрии. Следуя
идее аксиоматического метода, мы сначала перечислим
основные понятия, которым не даются определения. В нашем
курсе таких понятий четыре: точка, прямая, плоскость
и расстояние от точки до точки. Кроме того, мы будем
пользоваться понятиями, известными из других разделов
математики: множество, величина, число и др.
Прежде чем сформулировать аксиомы, сделаем
несколько замечаний, касающихся применения в стереометрии
теоретико-множественного подхода и некоторых
особенностей терминологии.
С точки зрения теории множеств стереометрия изучает
основное множество U (пространство), состоящее из всех
рассматриваемых точек, а также его подмножества —
геометрические фигуры. Прямые и плоскости также
считаются множествами точек. В соответствии с
теоретико-множественным определением равенства (§ 0.2) мы считаем две
фигуры, состоящие из одпих и тех же точек, одной и той же
фигурой (таким образом, мы не будем использовать термин
«совпадающие» для точек, прямых, плоскостей и т.д.; если,
2 Зак 3383
34 Глава 2. Введение в стереометрию
например, две прямые, а и Ь, «совпадают», т.е. состоят из
одних и тех же точек, то а и b — это одна прямая,
обозначенная двумя различными способами). Поэтому всюду
ниже, говоря «три точки», «две прямые» и т.п., мы будем
иметь в виду различные точки, прямые и т. д* Отметим ещё,
что понятия принадлежности, пересечения и объединения
всюду используются в теоретико-множественном смысле.
Так, говоря, что две плоскости пересекаются, мы имеем
в виду пересечение их как множеств точек. Наряду с
теоретико-множественными понятиями мы будем
использовать аналогичные понятия «геометрического языка».
Например, вместо прямая а является подмножеством
плоскости а будем писать прямая а лежит в плоскости а или
плоскость а проходит через прямую а.
А теперь перечислим аксиомы стереометрии.
Аксиома О. В пространстве существуют плоскости. В
каждой плоскости пространства выполняются все аксиомы
планиметрии.
Аксиома 1 (аксиома плоскости). Через любые три
точки, не лежащие на одной прямой, можно провести
плоскость, и притом только одну (рис. 1.1).
Рис. 1.1 Рис. 1.2
I Аксиома 2 (аксиома прямой и плоскости). Прямая, про-
I ходящая через две точки плоскости, лежит в этой плоско-
I сти (рис. 1.2).
§1.1* Неопределяемые понятия и аксиомы 35
I Аксиома 3 (аксиома пересечения плоскостей). Если
две плоскости имеют общую точку, то их пересечение есть
| прямая (рис. 1.3).
Рис. 1.3
Аксиома 4 (аксиома расстояния). Расстояние между
| любыми двумя точками пространства одно и то же на
любой плоскости, проходящей через эти точки.
Вторая часть аксиомы 0 позволяет применять в любой
плоскости пространства все теоремы, доказанные в
планиметрии. Из первой части этой аксиомы вытекает, что
для любой плоскости а в пространстве существуют не
принадлежащие ей точки. Действительно, если бы все
точки пространства принадлежали этой плоскости, то других
плоскостей в пространстве не было бы. Более того, точек, не
принадлежащих плоскости а, бесконечно много. В самом
деле, возьмём согласно первой части аксиомы 0 ещё одну
плоскость /3. Если плоскость /3 не имеет общих точек1*
с плоскостью а, то все точки плоскости /3 не принадлежат
плоскости а, а их, как известно из планиметрии,
бесконечно много. Если же плоскости а и [3 имеют общую точку, то
по аксиоме 3 их пересечение есть прямая. Все точки
плоскости /3, за исключением точек этой прямой, не принадлежат
плоскости а. Из планиметрии известно, что таких точек
также бесконечно много.
1)Здесь мы отнюдь не предполагаем, что плоскости, не имеющие
общих точек, существуют, а лишь рассматриваем один из логически
возможных случаев.
36 Глава 1. Введение в стереометрию
Из аксиомы 2 вытекает, что если прямая не лежит в
плоскости а, то она имеет с ней не более одной общей
точки. Такие прямые существуют. Действительно, возьмём
согласно первой части аксиомы 0 ещё одну плоскость (3
и выберем в ней две точки, не лежащие в плоскости а (выше
мы показали, что это возможно). Через эти точки проведём
прямую в плоскости /3. Эта прямая не лежит в плоскости а.
I Определение. Если прямая и плоскость имеют ровно
одну общую точку, то они называются пересекающимися.
Из аксиомы 3 вытекает, что фигура, которая является
прямой на одной плоскости, является прямой и на любой
другой плоскости, в которой она лежит. Поэтому прямую
в пространстве можно рассматривать саму по себе,
независимо от плоскостей, в которых она лежит.
В связи с аксиомой 3 дадим ещё одно определение.
I Определение* Две плоскости, имеющие общую точку,
называются пересекающимися.
Согласно второй части аксиомы 0 в каждой плоскости
определено расстояние между любыми двумя точками этой
плоскости. Значение аксиомы 4 состоит в том, что
расстояние между двумя точками пространства однозначно
определяется этой парой точек. Другими словами, единица
измерения расстояний во всех плоскостях пространства
одна и та же. Мы будем считать эту единицу выбранной
раз и навсегда. Более подробно понятие расстояния в
пространстве обсуждается в § 8.1.
Замечание. Приведённая система аксиом полна и
непротиворечива (см. соответствующие определения в § 0.1). Однако
она не является замкнутой (например, потому что планиметрия
предполагается известной) и независимой. Оказывается,
требование единственности плоскости, проходящей через три точки
(аксиома 1), излишне, а аксиома 2 следует из аксиом 1 и 3.
Доказательства этих фактов несложные, но они занимают довольно
мпого места. Тем самым введение в стереометрию оказывается
несколько затянутым, а в школьном курсе этого хотелось бы
§1.2. Простейшие следствия из аксиом 37
избежать. Поэтому недостатки рассматриваемой системы аксиом
можно рассматривать как сознательную жертву в пользу
краткости изложения.
§ 1.2. Простейшие следствия из аксиом
Я видел одни и те же следствия, которые
каждый год порождались другой причиной.
С. Е. Лец. Непричёсанные мысли
Здесь мы получим несколько следствий из аксиом,
которые будут широко использоваться в дальнейшем.
Следствие 1. Через любую прямую и не лежащую на
ней точку можно провести плоскость, и притом только
одну.
Доказательство. Пусть даны прямая а и точка М,
причём М £ а. Нужно доказать, что плоскость, проходящая
через а и М, существует и единственна.
Существование. Возьмём на прямой а две
точки: Р и Q (рис. 1.4). По аксиоме плоскости существует
Рис. 1.4
плоскость, проходящая через точки М, Р и Q.
Поскольку точки Р и Q принадлежат этой плоскости, по аксиоме
прямой и плоскости и прямая а принадлежит ей.
Существование искомой плоскости доказано.
Единственность. Искомая плоскость должна
проходить через три точки М, Р и Q, не лежащие на одной
прямой. Следовательно, по аксиоме плоскости такая
плоскость единственна. □
38 Глава 1. Введение в стереометрию
Дадим два определения, аналогичные соответствующим
определениям из планиметрии.
Определение. Две прямые в пространстве называются
пересекающимися, если они имеют хотя бы одну общую
точку.
■ Утверждение. Пересекающиеся прямые имеют ровно
одну общую точку.
Доказательство. Пусть пересекающиеся прямые а и Ъ
имеют по крайней мере две общие точки: Аи В. Проведём
через А и В произвольную плоскость. Согласно аксиоме
прямой и плоскости прямые а и Ъ лежат в этой плоскости
и проходят через Аи В, но, как известно из планиметрии,
через две точки в данной плоскости проходит единственная
прямая. D
Тот факт, что прямые а и Ъ пересекаются в точке О,
кратко записывают так: а П Ъ = О.
I Определение. Две прямые в пространстве называются
I параллельными, если они лежат в одной плоскости и не
I пересекаются.
Если прямые а иЪ параллельны, то пишут а || &,
I Следствие 2. Через две пересекающиеся прямые можно
провести плоскость, и притом только одну.
Доказательство. Пусть даны две прямые а и Ь,
пересекающиеся в точке О. Докажем, что плоскость, проходящая
через а и Ь, существует и единственна.
Существование. Возьмём на прямой а точку А,
не принадлежащую Ь, а на прямой Ъ — точку Б, не
принадлежащую а (рис. 1.5). Тогда в силу аксиомы плоскости
существует плоскость, проходящая через три точки А> В
и О, а в силу аксиомы прямой и плоскости такая плоскость
проходит через а и Ь.
§ 1.2. Простейшие следствия из аксиом 39
Рис. 1.5 Рис. 1.6
Единственность. Искомая плоскость должна
проходить через точки А, В и О; по аксиоме плоскости она
единственна. □
I Следствие 3. Через две параллельные прямые можно
провести плоскость, и притом только одну.
Доказательство. Существование искомой плоскости
следует из определения параллельных прямых.
Единственность доказывается точно так же, как и в двух предыдущих
следствиях (рис. 1,6)» □
^Упражнение 1.1. Докажите единственность этой плоскости.
Пример 1.1. Доказать, что через данную точку
пространства, не лежащую на данной прямой, можно провести
ровно одну прямую, параллельную этой прямой.
Решение. Обозначим данные прямую и точку
соответственно через а и А. Искомая прямая, параллельная а,
если она существует, лежит в одной плоскости с а (по
определению параллельных прямых) и проходит через точку А.
Но через а и А можно провести единственную плоскость.
Поэтому задача сводится к построению прямой,
проходящей через А и параллельной а, в плоскости. Эта задача,
как известно из планиметрии, разрешима единственным
образом. □
Пример 1.2. Доказать, что если плоскость пересекает
одну из двух параллельных прямых, то она пересекает
и вторую прямую.
40
Глава 1. Введение в стереометрию
Решение. Пусть даны параллельные прямые а и &, а
плоскость а пересекает а в точке L. Через а и Ъ проведём
плоскость у (рис. 1.7). Тогда у и а имеют общую точку L,
Рис. 1.7
принадлежащую а, следовательно, они пересекаются по
прямой» Обозначим эту прямую 1= у П а. Прямая /
пересекает одну из двух параллельных прямых, следовательно,
она пересекает и другую (этот факт известен из
планиметрии). Точка М = 1Г)Ь — единственная общая точка прямой Ъ
и плоскости а, т.е. Ь пересекает а. □
§ 1.3. Взаимное расположение двух прямых
в пространстве. Скрещивающиеся прямые
Пусть в пространстве даны две прямые, имеющие
хотя бы одну общую точку. Тогда они пересекаются ровно
в одной точке (см. утверждение, доказанное в § 1.2). Если
же две прямые не имеют общих точек, то возможны два
случая: они либо лежат в одной плоскости (и,
следовательно, параллельны), либо нет. Последний случай взаимного
расположения двух прямых является специфическим для
стереометрии.
I Определение. Две прямые, которые не имеют общих
точек и не параллельны, называются скрещивающимися.
Если прямые а и Ъ скрещиваются, то пишут а — Ь.
§1.3. Взаимное расположение двух прямых 41
Замечание. Скрещивающиеся прямые можно определить и
так: две прямые называются скрещивающимися, если через них
нельзя провести плоскость.
\® Упражнение 1.2. Докажите, что два приведённых
определения скрещивающихся прямых равносильны.
Теорема 1.1 (признак скрещивающихся прямых). Если
одна из двух прямых лежит в плоскости, а вторая
пересекает эту плоскость в точке, не принадлежащей первой
прямой, то эти прямые скрещиваются.
Доказательство. Пусть прямая а лежит в плоскости ау
а прямая Ъ пересекает плоскость а в точке М, не
принадлежащей прямой а (рис. 1.8).
Докажем, что а - Ь.
Предположим противное:
прямые а и Ь не скрещиваются.
Тогда они либо пересекаются,
либо параллельны. В обоих случаях
через них можно провести
плоскость /3 (следствия 2 и 3). Но 1 ft
через прямую а и точку М <£ а
молшо провести единственную плоскость (следствие 1). Это
означает, что прямая b лежит в плоскости а. Получили
противоречие. D
^ Упражнение 1.3. Докажите, что справедливо утверждение,
обратное к признаку скрещивающихся прямых.
Пример 1.3. Является ли необходимым, достаточным
или необходимым и достаточным для того, чтобы прямые
а и Ъ скрещивались, следующее условие:
За: а С а, ЬПа = М?
(Советуем вам перед тем как читать решение, ещё раз
внимательно прочитать § 0.2)
Решение. Обозначим Р — {3 а: а с ос, b Г\ а = М}, Q =
= {а - Ъ). В задаче спрашивается, следует ли из
утверждения Р утверждение Q, и наоборот.
42 Глава 1. Введение в стереометрию
1. Выясним, верно ли, что
Известно, что существует плоскость а, проходящая
через прямую а и пересекающаяся с прямой Ъ в точке М. Это
напоминает формулировку признака скрещивающихся
прямых. В чём разница? Вспомните признак; в нём требуется,
чтобы точка М не принадлежала прямой а, а утверждение
Р этого не требует. Но из этого сразу ещё ничего не следует.
Может быть, условие М £ а в признаке несущественно
(например, взято для упрощения доказательства)? Остаётся
внимательно проанализировать случай МGo. А это сразу
даёт контрпример к утверждению Q: прямые а и b
пересекаются, а не скрещиваются (рис. 1.9). Итак, из Р не следует Q.
2. Выясним, верно ли, что Q=>P.
Известно, что прямые а и Ъ скрещиваются. Нужно
выяснить, существует ли плоскость а, проходящая через
прямую а и пересекающая прямую Ь. Но это утверждение
следует из теоремы, обратной к признаку
скрещивающихся прямых, которая, как мы уже знаем, верна
(упражнение 1.3).
Действительно, возьмём на прямой Ъ произвольную
точку М и проведём плоскость ос через прямую а и точку М
(рис. 1.10). По построению аса. Прямая Ь имеет с
плоскостью а общую точку Мине может лежать в ней (через
скрещивающиеся прямые нельзя провести плоскость),
значит, Ь П а = М. Итак, из Q следует Р.
Итак, выполнение условия Р является необходимым, но
не достаточным для выполнения условия Q. □
Рис. 1.9 Рис. 1.10
§ 1.4. О существовании объектов и построениях 43
§ 1.4. О существовании объектов и построениях
в стереометрии
Я хочу вам доказать, что единорог существует. Для
этого, очевидно, достаточно доказать более сильное
утверждение о том, что существует существующий
единорог. Возможны два и только два случая:
существующий единорог существует и существующий
единорог не существует. Второй случай мы исключаем
из рассмотрения как противоречивый.
Р. Смаллиан. Как же называется эта книга?
Когда вы читали предыдущий параграф, у вас могло
возникнуть чувство некоторого неудовлетворения.
Действительно, существование параллельных и пересекающихся
прямых известно из планиметрии (через такие прямые
можно провести плоскость). Но откуда следует, что
существуют скрещивающиеся прямые? Ведь ясно, что не
обязательно существуют объекты, обладающие наперёд
заданными свойствами. Классические примеры так называемых
Рис. 1.11
44 Глава L Введение в стереометрию
невозможных объектов изображены на рис. 1.11. Если же
скрещивающиеся прямые не существуют, то теряют смысл
и все утверждения о них, поскольку о несуществующем
объекте можно сказать всё что угодно.
На самом деле скрещивающиеся прямые, конечно же,
существуют. Для того чтобы убедиться в этом, мало
наглядного представления о скрещивающихся прямых. Но
достаточно такие прямые построить. Для этого сначала
уточним, что мы понимаем здесь под построением в
пространстве.
Мы считаем, что в пространстве можно провести
плоскость через три точки, не лежащие на одной прямой (а
значит, и через прямую и не лежащую на ней точку, через
пересекающиеся прямые и т. д.). Кроме того, в каждой
плоскости можно выполнять обычные построения, например
с помощью циркуля и линейки.
Доказав признак скрещивающихся прямых, мы
фактически доказали, что если прямые а и Ъ удовлетворяют
условию этой теоремы, то они удовлетворяют и
определению скрещивающихся прямых. Мы воспользуемся этим
фактом.
Возьмём в пространстве произвольную плоскость а и
проведём в ней пересекающиеся прямые а и с, аПс = О.
Выберем точку А £ а. Проведём через точку А и прямую с
плоскость /3. Плоскости а и /3 пересекаются по прямой с
Рис. 1.12
Задачи 45
(рис. 1.12). Возьмём на прямой с точку В, отличную от О.
В плоскости (5 проведём прямую Ъ через точки А и В.
Очевидно, что построенные прямые а и b удовлетворяют
условию теоремы 1.1 и, следовательно, скрещиваются.
Аналогичным образом можно доказать существование
параллельных прямой и плоскости, параллельных
плоскостей (эти понятия вводятся позже) и т.д. Надеемся, что
всякий раз, когда мы не приводим соответствующее
построение, вы без труда его восстановите.
Задачи
Если вы хотите научиться плавать, то
смело входите в воду, а если хотите
научиться решать задачи — решайте их.
Д. Пойа. Математическое открытие
1.1. В пространстве дано несколько прямых, любые две
из которых пересекаются. Докажите, что либо все они
лежат в одной плоскости, либо все они проходят через одну
точку.
1.2. Даны две прямые а и Ь. Выясните, являются ли
сформулированные ниже условия необходимыми,
достаточными или необходимыми и достаточными для того, чтобы
а и Ъ скрещивались:
а) а и Ъ не имеют общих точек;
б) любая плоскость, проведённая через прямую а и
точку, принадлежащую прямой Ь, пересекает Ь.
1.3. Каждая из двух прямых скрещивается с третьей
прямой. Верно ли, что эти две прямые являются
скрещивающимися?
1.4. Докажите, что если любая плоскость, пересекающая
одну из двух данных прямых, пересекает и вторую, то эти
две прямые параллельны (ср. с примером 1.2).
Глава 2
Параллельность в пространстве
Ах, зачем у нас граф Пален
Так к присяжным параллелен!
Будь он боле вертикален,
Суд их боле был бы делен.
А, К. Толстой. Рондо
§ 2Л. Прямая и плоскость в пространстве.
Признак параллельности
— Но скажите мне, пожалуйста, была бы
у нас та геометрия, которой меня учили
в школе, если бы материи не было вообще,
и пересекались бы тогда параллельные?
— Параллельные не пересекались бы, —
подтвердил профессор,—но ни одно
материальное существо не могло бы проверить это.
Г. Гамов. Приключения мистера Томпкинса
Пусть в пространстве даны плоскость а и прямая а.
Если они имеют по крайней мере две общие точки, то по
аксиоме прямой и плоскости аса (прямая а лежит в
плоскости а). Если общая точка одна, то а Па = А (прямая а
пересекает плоскость а в точке А). Оказывается, возможен
и третий случай, когда прямая и плоскость не имеют общих
точек: аПа — 0.
(Определение. Прямая и плоскость называются
параллельными^ если они не имеют общих точек.
Теорема 2.1 (признак параллельности прямой и
плоскости). Если прямая, не лежащая в плоскости, параллельна
какой-либо прямой, лежащей в этой плоскости, то эти
прямая и плоскость параллельны.
Доказательство, Обозначим данные прямую и
плоскость через аи а соответственно. Пусть а || ft, где Ьсаиафа,
48
Глава 2. Параллельность в пространстве
Предположим, что прямая а и плоскость а не параллельны.
Тогда они имеют общую точку М (рис. 2.1). Следовательно,
по признаку скрещивающихся прямых а — Ь, что
противоречит условию теоремы. G
■^Упражнение 2.1. Сформулируйте и докажите теорему,
обратную к признаку параллельности прямой и плоскости.
и^ Упражнение 2.2. Докажите существование параллельных
прямой и плоскости, решив следующие задачи на
построение:
1) через данную точку, не лежащую в данной плоскости,
проведите прямую, параллельную этой плоскости;
2) через данную точку, не лежащую на данной прямой,
проведите плоскость, параллельную этой прямой.
Исследуйте единственность решения этих задач.
Теорема 2.2 (о линии пересечения двух плоскостей,
одна из которых проходит через прямую, параллельную
другой плоскости1*). Если плоскость проходит через
прямую, параллельную другой плоскости, и пересекает эту
плоскость, то линия пересечения плоскостей параллельна
данной прямой.
Доказательство. Пусть плоскость j3 пересекает
плоскость а по прямой Ъ и проходит через прямую а такую, что
Рис. 2.1 Рис. 2.2
а || а (рис. 2.2). Тогда прямые а и Ь лежат в плоскости /?,
!)В дальнейшем мы будем ссылаться на эту теорему как на теорему
о линии пересечения.
§2.1. Прямая и плоскость в пространстве
49
причём аПЬ = 0 (иначе точка их пересечения лежала бы
в плоскости а, что противоречит параллельности прямой а
и плоскости а). Следовательно, а\\Ъ. □
Следствие 4. Если через каждую из двух параллельных
прямых проведена плоскость, причём эти плоскости
пересекаются, то линия их пересечения параллельна каждой
из данных прямых.
Доказательство. Пусть а || Ь, где а С а, Ъ с /3, причём
а П /3 — с (рис. 2.3). Докажем, что с \\ а и с \\Ь.
Действительно, поскольку Ь С (3 и а \\ Ь9 то
а || (3 по признаку параллельности
прямой и плоскости. Далее, по
теореме о линии пересечения получим
с || а. Аналогично доказывается, что
с||&. □
Отношение параллельности
прямых в пространстве, так же как и на
плоскости, обладает свойством тран- рис 2.3
зитивности.
I Следствие 5. Если прямая а параллельна прямой b, a
прямая b параллельна прямой с, то а параллельна с.
Доказательство. Пусть а || b и
Ъ || с. Докажем, что а \\ с. Если прямые
a, b и с лежат в одной плоскости,
то а || с по соответствующей теореме
планиметрии. Предположим теперь,
что эти прямые не лежат в одной
плоскости. Возьмём на прямой а точку М.
Через с и М проведём плоскость <х>
а через Ъ и М — плоскость /3 (рис. 2.4)
(здесь мы пользуемся следствием 1
из аксиом § 1.2). Линия пересечения
плоскостей а и /3 согласно следствию 4 из теоремы о линии
пересечения параллельна прямым с и 6. Но через точ-
Рис. 2.4
50
Глава 2. Параллельность в пространстве
ку М можно провести только одну прямую, параллельную
прямой Ь (см. пример 1.1). Поэтому линия пересечения
плоскостей а и (5 и прямая а — это одна и та же прямая.
Следовательно, а\\с. □
Следствие 6. Если прямая параллельна каждой из двух
пересекающихся плоскостей, то она параллельна их
линии пересечения.
Доказательство. Пусть
плоскости а и /3 пересекаются по прямой а,
а прямая Ъ параллельна плоскостям а
и /3. Возьмём на прямой а точку М
и проведём плоскость у через
прямую b и точку М (рис. 2.5). Пусть
плоскость у пересекает плоскость а
по прямой п\у а плоскость j3 — по
прямой п2- Тогда по теореме о
линии пересечения получаем, что а\ || Ъ
и п2 || Ь. Но прямые а\ и п2
имеют общую точку М, следовательно
(пример 1.1), это одна и та же прямая — прямая а.
Поэтому а || b. D
§ 2.2. Параллельность плоскостей. Транзитивность
параллельности плоскостей
Что лучше: вечное блаженство или бутерброд с
ветчиной? На первый взгляд кажется, что вечное блаженство
лучше, но в действительности это не так! Судите
сами. Что лучше вечного блаженства? Ничто. А
бутерброд с ветчиной лучше, чем ничто. Следовательно,
бутерброд с ветчиной лучше, чем вечное блаженство.
(Пример рассуждения по транзитивности.)
Р. Смаллиан. Как же называется эта книга?
Рис. 2.5
Вы уже знаете, что если две плоскости имеют общую
точку, то они пересекаются по прямой, проходящей через
§ 2.2. Параллельность плоскостей. Транзитивность 51
эту точку (аксиома пересечения плоскостей). Оказывается,
две плоскости могут и не иметь общих точек.
(Определение. Две плоскости называются параллелъны-
миу если они не имеют общих точек.
Теорема 2.3 (признак параллельности плоскостей).
Бели две пересекающиеся прямые одной плоскости
параллельны соответственно двум прямым другой плоскости,
то эти плоскости параллельны.
Доказательство. Пусть а и Ъ — прямые в плоскости а,
а\ и Ъ\ — прямые в плоскости /3, причём аГ\Ъ — М, а || ах
и b || Ь\. Предположим, что а и /3 не параллельны; тогда они
пересекаются, пусть а П/3 = с (рис. 2.6). По следствию 4 из
Рис. 2.6
теоремы о линии пересечения имеем с \\ а и с || Ъ. Но тогда
в силу транзитивности (следствие 5 из той же теоремы) а \\ Ь.
Получили противоречие. □
Замечание. Обратите внимание на то, что в условии теоремы
не требуется, чтобы прямые а% и Ь\ пересекались.
Приведём основные свойства параллельных плоскостей.
I Теорема 2.4. Линии пересечения двух параллельных
плоскостей третьей плоскостью параллельны.
Доказательство. Обозначим данные параллельные
плоскости через а и (3. Пусть плоскость у пересекает их
по прямым а и & соответственно (рис. 2.7а). Предположим
52
Глава 2. Параллельность в пространстве
Рис. 2.7
противное: прямые а и Ь не параллельны» Тогда они
пересекаются (так как лежат в одной плоскости), пусть аГ\Ь = М.
Так как М G а, то М € а; аналогично Мер. Таким образом,
плоскости а и jS имеют общую точку М, что противоречит
условию. □
Теорема 2.5. Отрезки параллельных прямых,
заключённые между двумя параллельными плоскостями, равны по
| длине.
Доказательство. Пусть даны параллельные плоскости
а и /3, а параллельные прямые а и Ъ пересекают эти
плоскости в точках А и А\> В и В\ соответственно (рис. 2.76). По
следствию 3 из аксиом (§ 1.2) через а и Ъ можно провести
плоскость у. Она пересечёт плоскости а и /3 по прямым АВ
и Ai£i соответственно. В силу свойства 1 (АВ) || {A\Bi).
Кроме того, по условию (AAi) || (ВВ\). Значит, АА\В\В —
параллелограмм (в плоскости у), и по свойству
параллелограмма АА\ — ВВ\. □
Теорема 2.6. Через каждую точку пространства, не
лежащую в данной плоскости, можно провести плоскость,
параллельную этой плоскости, и притом только одну.
§ 2.2. Параллельность плоскостей. Транзитивность 53
Доказательство. Пусть требуется через данную точ-
ку А, не лежащую в данной плоскости ау провести
плоскость/3, параллельную плоскости а.
Существование плоскости (3. Возьмём в
плоскости ol произвольную точку В и проведём через неё в
плоскости а две прямые а и Ъ. Через точку А проведём
прямые а\ и bi9 параллельные прямым а и b соответственно
(см. пример 1.1). Проведём через а\ и bi плоскость (3. По
признаку параллельности двух плоскостей а || /?♦
Единственность плоскости /3. Предположим
противное: через точку А можно провести две плоскости (3
и (3\у параллельные плоскости а. Так как плоскости (3 и (3\
имеют общую точку А, то по аксиоме пересечения
плоскостей они пересекаются по прямой; обозначим т = (3 D/3i
Рис. 2.8
(рис. 2.8). Возьмём в плоскости а прямую 1У не
параллельную т и такую, что I - т. Через точку А и прямую I
проведём плоскость у. Плоскость у пересекает плоскости (3
и (3i (так как имеет с ними общую точку А) по прямым b и Ь\
соответственно. По свойству 1 параллельных плоскостей
b || I и Ь\ || I. Но через точку А может проходить только
54 Глава 2. Параллельность в пространстве
одна прямая, параллельная L Полученное противоречие
означает, что /3 и (5\ — это одна и та же плоскость. D
Следующее свойство параллельных плоскостей
аналогично соответствующему свойству параллельных прямых.
Теорема 2.7 (транзитивность параллельности
плоскостей). Если плоскость ос параллельна плоскости /3, а
плоскость (3 параллельна плоскости у, то а параллельна у.
Доказательство. Предположим противное: a$у. Тогда
плоскости any пересекаются; обозначим т = аПу.
Возьмём на прямой т точку А. Получаем, что через точку А
проведены две плоскости а и у, параллельные плоскости /3,
что противоречит предыдущей теореме. D
Пример 2.1. Доказать, что через каждую из двух
скрещивающихся прямых можно провести плоскость так, чтобы
эти плоскости были параллельны.
Решение. Пусть а — Ь. Возьмём на прямой а точку А
и проведём через неё прямую а\, параллельную прямой Ъ
(пример 1.1). Через прямые а и а\ проведём плоскость
а (следствие 2 из аксиом, § 1.2). Аналогично строим
плоскость/3 (рис. 2.9). По признаку параллельности плоскостей
а||/3. □
Рис. 2.9
|^ Упражнение 2.3. Выясните, единственное ли решение имеет
эта задача.
§ 2.3. Параллельное и центральное проектирование 55
§ 2.3. Параллельное и центральное проектирование
Ветреный летний день.
Прижавшееся к стене
дерево и его тень.
И тень интересней мне.
И. Бродский. Сидя в тени
В этом параграфе мы познакомимся с новым видом
отображения1* — проектированием.
Пусть в пространстве заданы
плоскость а и прямая Z,
пересекающая а. Возьмём в
пространстве произвольную точку М и
проведём через неё прямую т,
параллельную / (если Mel, то
в качестве т берётся сама
прямая /) (рис. 2.10). Точку
пересечения Mi прямой т с плоскостью а
назовём параллельной проекцией рис 2.10
точки М на эту плоскость. При
этом плоскость а называется плоскостью проектирования,
а прямая I —направлением проектирования.
Определение. Пусть в пространстве задана фигура2^ Ф.
Отображение, ставящее в соответствие каждой точке М е
6 Ф её параллельную проекцию М\ на плоскость а в
направлении 1> называется параллельным
проектированием (на плоскость а в направлении Z), а множество всех
точек Mi — параллельной проекцией фигуры Ф на
плоскость а в направлении L
Вы не раз встречались с параллельным
проектированием в жизни. Например, ваша тень в солнечный день на
^Напомним, что отображением множества X в множество У
называется закон» по которому каждому элементу х £Х ставится в соответствие
ровно один элемент у eY.
2)Непустая, но, возможно, совпадающая со всем пространством.
56 Глава 2, Параллельность в пространстве
ровном асфальте есть ваша параллельная проекция
(солнечные лучи приближённо можно считать параллельными
ввиду большой удалённости Солнца от Земли).
Параллельное проектирование позволяет получать
наглядные изображения пространственных (трёхмерных)
фигур на (двумерной) плоскости (рис. 2.11). Дело в том, что
Рис. 2.11
параллельное проектирование сохраняет ряд важных черт
изображаемой фигуры. Перечислим основные свойства
параллельного проектирования в предположении, что
направление проектирования не параллельно рассматриваемым
прямым и отрезкам (в противном случае их проекциями
являются точки).
1°. Проекция прямой есть прямая, проекция отрезка —
отрезок.
2°. Две параллельные прямые проектируются либо в две
параллельные прямые, либо в одну и ту же прямую.
Проекции параллельных отрезков лежат либо на
параллельных прямых, либо на одной прямой.
3°. Длины проекций параллельных отрезков или
отрезков, лежащих на одной прямой, пропорциональны
длинам этих отрезков.
в^" Упражнение 2.4. Докажите свойства 1° и 2°.
§ 2.3. Параллельное и центральное проектирование 57
В*
Рис. 2.12
Рис. 2.13
Доказательство свойства 3°. Пусть АВ и CD —
отрезки, не параллельные направлению проектирования I] А',
В', С", Df — проекции точек А, В, С, D соответственно на
плоскость а в направлении /. Если А!В1 и CD' — один и тот
же отрезок, то АВ = CD и доказываемое утверждение
очевидно. Пусть А!В* и CfDf различны. Рассмотрим
сначала случай, когда проектируемые отрезки лежат на одной
прямой (рис. 2.12). Тогда их проекции лежат на линии
пересечения плоскости а и плоскости, проходящей через
прямую АВ параллельно направлению проектирования /
(почему?). Применяя известную из планиметрии теорему
о пропорциональных отрезках, получим, что1* АВ : CD —
= A'B':C'D'.
Теперь рассмотрим случай, когда отрезки АВ и CD
параллельны, а их проекции различны (рис. 2.13). Возьмём
на продолжении отрезка CD за точку С такую точку Е, что
СЕ = АВ. Так как (СЕ) || (АВ), то четырёхугольник АВЕС-
параллелограмм в плоскости, проходящей через прямые
АВ и CD (по признаку параллелограмма), следовательно,
(АС) || (BE). Пусть Е1 — проекция точки Е на плоскость а
в направлении L По свойству 2° (А!С) \\ (В'Е1) и (AfBf) \\
1}На рис. 2.12 отрезки АВ и CD не пересекаются, но в наших
рассуждениях мы нигде не использовали этот факт.
58 Глава 2. Параллельность в пространстве
|| (СЕ1) (так как (AC) \\ (BE) и (АВ) || (СЕ)), но (А!В1) \\ (CD1),
значит, Е1 € (CD') у и, так как A!BfEfC — параллелограмм,
А!В! = С'Я\ Итак, равенство AB:CD = А!В1: C'Df
равносильно равенству СЕ : CD = А'В1: CD1 > и тем самым мы свели
рассматриваемый случай к разобранному выше. □
При построении сечений пирамид (§ 2.7) нам
понадобится ещё один вид проектирования — центральное
проектирование.
Пусть в пространстве даны
плоскость а и точка S £ а.
Возьмём в пространстве произвольную
точку М, не лежащую в плоскости,
проходящей через S параллельно
плоскости я, и проведём через
точки S иМ прямую т (рис. 2.14).
Точку пересечения М\ прямой т
с плоскостью а назовём централь- Рис g 14
ной проекцией точки М. При
этом плоскость а называется плоскостью проектирования,
а точка S — центром проектирования.
Определение. Пусть в пространстве задана фигура1^ Ф.
Отображение, ставящее в соответствие каждой точке М €
€ Ф её центральную проекцию М\ на плоскость а с
центром S, называется центральным проектированием (на
плоскость а с центром S), а множество всех точек М\ —
центральной проекцией2^ фигуры Ф на плоскость а с
центром S (рис. 2.15).
Замечание. Иногда говорят, что параллельное
проектирование есть частный случай центрального, в котором центр
проектирования «удалён в бесконечность».
^Непустая, но, возможно, совпадающая со всем пространством.
2)В силу данного определения точки плоскости /3, проходящей
через S параллельно плоскости а, не имеют образов в плоскости а.
Однако это несоответствие можно устранить, если формально пополнить
плоскость а «бесконечно удалённой точкой», которая по определению
является образом плоскости /5,
§ 2.4. Первоначальное понятие о многогранниках 59
S%
Рис. 2.15
§ 2.4. Первоначальное понятие о многогранниках
В этом параграфе мы определим некоторые виды
многогранников, наиболее часто встречающиеся в
стереометрических задачах. Под многогранником мы понимаем
тело1*, ограниченное конечным числом плоскостей. Эти
плоскости, пересекаясь, образуют грани многогранника —
многоугольники. Стороны этих многоугольников называются
рёбрами многогранника, а концы рёбер —его вершинами.
Отрезок, соединяющий вершины многогранника, не
принадлежащие одной грани, называется диагональю
многогранника.
Отметим, что наше знакомство с многогранниками
носит лишь предварительный характер. Мы ещё не раз
вернёмся к ним в нашем курсе.
Призма
Определение. Призма — это многогранник, две грани
которого — равные многоугольники, лежащие в
параллельных плоскостях, а все рёбра, не лежащие в этих
плоскостях, параллельны между собой (рис. 2.16).
1JMbi пока не даём строгого определения понятия «тело», а
опираемся здесь на интуитивное представление о теле, поверхности тела и т. п.
60 Глава 2. Параллельность в пространстве
Два равных многоугольника, лежащие в параллельных
плоскостях, называются основаниями призмы. Остальные
грани призмы (являющиеся параллелограммами —
докажите это) называются её боковыми гранями^ а их
объединение — боковой поверхностью призмы. Рёбра, не лежащие
в основании призмы, называются её боковыми рёбрами.
Если в основаниях призмы лежат д-угольники, то призма
называется п-угольной.
Частным случаем призмы является параллелепипед —
призма, основаниями которой служат параллелограммы
(рис. 2.17).
Укажем основные свойства параллелепипеда.
1°. Противоположные грани параллелепипеда попарно
параллельны.
2°. Все четыре диагонали параллелепипеда
пересекаются в одной точке и делятся ею пополам.
И* Упражнение 2.5. Докажите эти свойства.
Отметим ещё, что если все грани параллелепипеда
являются прямоугольниками, то параллелепипед
называется прямоугольным. Если же все грани параллелепипеда —
квадраты, то он называется кубом.
§ 2.4. Первоначальное понятие о многогранниках 61
Пирамида
Определение. Пирамида — это многогранник, одна из
граней которого — произвольный многоугольник1 \ а
остальные грани — треугольники с общей вершиной (рис. 2.18).
Этот многоугольник называется
основанием пирамидыу а остальные
(треугольные) грани — боковыми гранями.
Объединение боковых граней пирамиды
называется её боковой поверхностью.
Рёбра пирамиды, не принадлежащие
основанию, называются её боковыми
рёбрами. Общая вершина всех боковых граней
называется вершиной пирамиды.
Пирамида называется правильной, если в её основании
лежит правильный многоугольник, а все боковые грани —
равнобедренные треугольники с общей вершиной. Высота
боковой грани правильной пирамиды, проведённая из её
вершины, называется апофемой этой пирамиды (рис. 2.19).
Рис. 2.19
1}В дальнейшем, если не оговорено противное, мы будем
рассматривать только те пирамиды, в основании которых лежит выпуклый
многоугольник.
62
Глава 2. Параллельность в пространстве
Если в основании пирамиды
лежит я-угольник, то пирамида
называется м-угольной. Треугольная
пирамида называется тетраэдром
(рис. 2.20). Тетраэдр называется
правильным, если все его рёбра равны
(таким образом, все грани
правильного тетраэдра — равные правильные
треугольники).
Усечённая пирамида
Определение. Усечённой пирамидой называется часть
пирамиды, заключённая между плоскостью основания и
плоскостью, параллельной плоскости основания и
пересекающей все боковые рёбра пирамиды (рис. 2.21).
Основание исходной пирамиды и многоугольник,
полученный при пересечении её плоскостью, указанной в
определении, называются основаниями усечённой пирамиды.
Остальные её грани называются боковыми.
Усечённая пирамида называется правильной, если она
является частью правильной пирамиды. Боковые грани
Рис. 2.22
§ 2.5. Изображение фигур в стереометрии 63
правильной усечённой пирамиды — равные
равнобедренные трапеции. Высота каждой из этих трапеций называется
апофемой усечённой пирамиды (рис. 2.22).
§ 2.5. Изображение фигур в стереометрии
Рисовать — значит обманывать.
М. К Эшер
В стереометрии, хотя мы и имеем дело с
пространственными фигурами, для рассуждений используются плоские
чертежи, выполненные на листе бумаги. Только
благодаря пространственному воображению мы можем говорить
о трёхмерных фигурах, глядя на их плоские
изображения. Дадим определение изображения пространственной
фигуры.
Определение. Изображением фигуры называется
любая фигура, подобная параллельной проекции данной
фигуры на некоторую плоскость.
Далее мы рассмотрим некоторые правила, полезные при
изображении многогранников. Грани многогранников —
многоугольники, лежащие в различных плоскостях.
Поэтому для начала изучим, как изображаются (плоские)
многоугольники. При этом мы исключаем из рассмотрения
случаи, когда плоскость многоугольника параллельна
плоскости проектирования (в этом случае изображение
строится тривиально) или когда его плоскость параллельна
направлению проектирования (тогда изображением
многоугольника служит отрезок).
Треугольник
Справедливо следующее утверждение: для каждого
треугольника любой треугольник является некоторым его
изображением.
с^ Упражнение 2.6. Докажите это утверждение.
64 Глава 2. Параллельность в пространстве
Таким образом, параллельное проектирование, вообще
говоря, не сохраняет величин углов и отношений длин
непараллельных отрезков.
Пример 2.2. Пусть ААВС — изображение некоторого
правильного треугольника. Построить изображение центра
этого треугольника.
Решение. Вспомним, что центр правильного
треугольника является точкой пересечения его медиан. В силу
свойств 1° и 3° параллельного проектирования1*
изображениями медиан данного правильного треугольника
служат медианы его изображения (т.е. треугольника ABC).
Поэтому искомым изображением
центра является точка
пересечения медиан треугольника ABC
М (рис. 2.23). □
Обратите внимание на тот
факт, что медианы
треугольника-оригинала изображаются ме-
Рис. 2.Z3 дианами
треугольника-изображения, однако аналогичное
свойство, вообще говоря, не имеет места для высот и биссектрис
треугольника.
Параллелограмм
Для каждого параллелограмма (в частности,
прямоугольника, ромба, квадрата) любой параллелограмм
является некоторым его изображением. (Обоснуйте
самостоятельно это утверждение, используя соответствующий факт
для треугольника.)
ВЗР Упражнение 2.7. Постройте изображение равнобедренной
трапеции и её высоты.
^Заметим, что и преобразование подобия (на плоскости), как
известно из планиметрии, также переводит прямую в прямую,
параллельные прямые — в параллельные прямые и сохраняет отношение длин
параллельных отрезков.
§ 2.5. Изображение фигур в стереометрии
Правильный шестиугольник
65
На рис. 2.24а изображён оригинал — правильный
шестиугольник ABCDEF с центром О. В соответствии с
вышесказанным ромб АВСО изображается параллелограммом
Е
А!В'СО1 (рис. 2.246). Далее, в силу свойств 1° и 3°
параллельного проектирования точки оригинала, симметричные
относительно точки О, переходят
в точки изображения, симметричные
относительно точки О'. Поэтому,
отражая точки А! у В', С симметрично
относительно точки О', получаем
точки 2У, Е'у F1 соответственно.
Отметим без доказательства, что
изображением окружности является
эллипс — геометрическое место точек
М плоскости, сумма расстояний от которых до двух данных
точек F\ и F2 этой плоскости (фокусов) есть константа (при
условии, что 2a>-FiF2>0, где 2а — указанная константа).
Эллипс изображён па рис, 2*25*
Перейдём теперь к изображению некоторых
многогранников. На этих изображениях обычно сплошными линиями
показываются «видимые» рёбра многогранника, а
штриховыми — «невидимые».
Рис. 2.25
3 Зак
66 Глава 2. Параллельность в пространстве
Тетраэдр
Для каждого тетраэдра любой четырехугольник
(выпуклый или невыпуклый) с проведенными в нем диагоналями
является некоторым его изображением1* (рис. 2.26а, б).
а) б)
Рис. 2.26
В
Параллелепипед
Изобразим сначала три ребра, выходящие из одной
вершины А (это можно сделать произвольно, см. рис. 2.27а).
Дальнейшее построение осуществляется уже однозначно:
Х)Это утверждение называют теоремой Польке—Шварца. Его
доказательство можно найти, например, в [Веский, 1971].
§ 2.6. Сечение многогранника. Построение сечений 67
каждый из остальных отрезков параллелен и равен по
длине одному из уже построенных трёх отрезков (по свойствам
параллельного проектирования, см. рис. 2.276).
Изображения других пирамид и призм строятся
аналогично. Главное — не забывать о свойствах параллельного
проектирования.
$Ш* Упражнение 2.8. Постройте изображение правильной
четырёхугольной пирамиды, правильной четырёхугольной
усечённой пирамиды.
§ 2.6. Сечение мпогограппика.
Построение сечений методом следов
--Как милости вашей будет завгодно,
—отвечал на всё согласный Селифап,— коли посечь, то
и посечь; я ничуть не прочь от того... Оно нужно
посечь, потому что... порядок нужно наблюдать.
Н. Гоголь. Мёртвые души
Пусть в пространстве заданы многогранник М и
плоскость а. Эта плоскость может не пересекать многогранник,
иметь с ним ровно одну общую точку (вершину
многогранника), пересекать его по отрезку (ребру многогранника) и,
наконец, пересекать его по многоугольнику (рис. 2.28а—г
соответственно). В последнем случае говорят, что
многоугольник является сечением многогранника плоскостью,
а эту плоскость называют секущей плоскостью.
Определение. Если пересечением многогранника и
плоскости является многоугольник, то он называется
сечением многогранника указанной плоскостью.
В этом и в следующих параграфах мы будем
заниматься решением задач такого типа: на данном изображении
многогранника требуется построить изображение его
сечения данной плоскостью. Термину «построить» мы придаём
обычный планиметрический смысл (построения
проводятся циркулем и линейкой), поскольку построения на изоб-
ражепии многогранника осуществляются в плоскости.
68
Глава 2. Параллельность в пространстве
Рис. 2.28
По сложившейся традиции мы будем вместо слов «на
изображении многогранника построить изображение его
сечения» писать «построитьсечение многогранника»,
опуская слово «изображение». Кроме того, отметим, что раз
речь идёт об изображениях фигур, то мы, разумеется,
будем использовать свойства параллельного проектирования
(см. § 2.3). Те места в последующих рассуждениях, где
эти свойства используются, обычно легко обнаруживаются,
поэтому мы не будем делать ссылок на указанные свойства,
полагая, что вы уже приобрели некоторый опыт работы
с изображениями по мере изучения двух предыдущих
параграфов.
В формулировке поставленной задачи мы не указали
способ задания секущей плоскости. Это можно сделать по-
§ 2.6, Сечение многогранника. Построение сечений 69
разному, например тремя точками, не лежащими на одной
прямой (реже встречается задание секущей плоскости
точкой и прямой, не проходящей через неё, а также двумя
пересекающимися прямыми; эти способы, впрочем, легко
сводятся к первому), двумя точками и условием
параллельности некоторой прямой, точкой и условием
параллельности некоторой плоскости и т. п.
Рассмотрим сначала самый простой случай, когда
секущая плоскость задана тремя точками, две из которых
лежат в плоскости одной грани многогранника, а третья —
в плоскости грани, смежной с первой. В этом случае, как
правило (если не возникает параллельности некоторых
прямых, на чём мы ниже остановимся особо), для обоснования
построения не приходится выходить за рамки аксиом и,
быть может, простейших следствий из них.
Приведём характерный пример.
Пример 2.3. Построить сечение пирамиды SABC
плоскостью, проходящей через точки Ку L и М (рис. 2.29а;
Ке (ABC), Le (ABC), Me (ASQ).
Решение. Для решения поставленной задачи построим
линии пересечения секущей плоскости с гранями
пирамиды. Предположим, что плоскость KLM (которую мы
обозначим а) построена. Так как плоскости а и ABC имеют
общую точку К у то они пересекаются по прямой,
проходящей через К (согласно аксиоме пересечения плоскостей),
а так как эти плоскости имеют ещё одну общую точку —
точку L, то прямая KL является линией пересечения
плоскостей а и ABC. Отсюда вытекает следующее построение:
проведём прямую KL до пересечения с отрезками АВ и ВС
в точках Е и F (рис. 2.296). Пусть эта прямая пересечёт
прямую АС в точке X. Будем рассуждать аналогично: точки
X иМ лежат как в плоскости а, так и в плоскости ASC,
следовательно, прямая ХМ — их линия пересечения, поэтому
строим прямую ХМ до пересечения с отрезками SA и SC
в точках Н и G (рис. 2.29в). Повторяя рассуждения по той
же схеме, делаем вывод, что плоскости а. и ASB пересека-
70
Глава 2. Параллельность в пространстве
ются по прямой ЕН9 а плоскости а и BSC — по прямой FG.
Поэтому для завершения построения остаётся соединить
точку Е с точкой Н и точку F с точкой G (рис. 2.29г).
Единственность решения вытекает из аксиомы плоскости.
S
§2.6. Сечение многогранника. Построение сечений 71
$Ж Упражпепие 2.9. Постройте сечение параллелепипеда
ABCDA\B\C\Di плоскостью (KLM) (рис. 2.30), где К, Le
), а М е (ААХВ).
Что же изменится, если прямые KL и АС окажутся
параллельными? В этом случае придётся
воспользоваться теоремами о параллельности в пространстве. Так как
прямая KL параллельна прямой АС, лежащей в плоскости
ASC, то по признаку параллельности прямой и плоскости
прямая KL параллельна плоскости ASC. Но плоскость а
проходит через прямую KL> следовательно (по теореме о
линии пересечения), линия пересечения плоскостей ос и ASC
должна быть параллельна прямой KL. Проведём через
точку М прямую, параллельную KL. Пусть она пересекает
отрезки SA и SC в точках Н и G. Соединив точки Н и J5,
а также G и F, получим искомое сечение (рис. 2,31). □
Мы видим, что проведённое построение сечения в обоих
случаях было основано на нахождении линий пересечения
секущей плоскости с плоскостями граней многогранника —
так называемых следов секущей плоскости на плоскостях
граней. Отсюда и происходит название метода построения
сечений, который мы только что проиллюстрировали, —
метод следов.
72
Глава 2. Параллельность в пространстве
Приведём теперь пример использования для
обоснования построения сечения теоремы о линиях пересечения
двух параллельных плоскостей третьей плоскостью. Эту
теорему удобно использовать, когда речь идёт о сечениях
многогранников, имеющих параллельные грани: призм,
параллелепипедов, кубов и т. д.
Пример 2.4. Построить сечение призмы пятиугольной
ABCDEA\B\C\D\Ei плоскостью, проходящей через точки
К,ЬиМ (рис. 2.32а), где К, Le (ABC), Me (AxBiCx).
Рис. 2.32
§ 2.6. Сечение многогранника. Построение сечений 73
Решение. Сначала построим прямую KL — линию
пересечения плоскостей KLM и ABC. Пусть эта прямая
пересечёт отрезки АВ и CD в точках Pi и Рг (рис. 2.326). Для
того чтобы построить след секущей плоскости на плоскости
грани А\В\С\, заметим, что плоскости ABC и AiB\C\
параллельны (по определению призмы), поэтому линия
пересечения секущей плоскости и плоскости А\В\С\ должна быть
параллельна прямой KL (и, конечно, проходить через
точку М). Строим прямую, проходящую через точку М
параллельно прямой KL. Пусть она пересекает отрезки А\Е\
и E\D\ в точках Р$ и Р± (рис. 2.32в). Дальнейшее
построение не вызывает затруднений и вполне аналогично
построениям из примера 1. Сечение изображено на рис. 2.32г. П
и^ Упражнение 2.10, Постройте сечение куба плоскостью,
проходящей через точки К, L и М (рис. 2.33), где К, Le (АА\В),
Me(CCiD).
Рис. 2.33
Теоремы о параллельности в пространстве применяются
и тогда, когда одним из условий задания секущей
плоскости является её параллельность некоторой прямой или
некоторой плоскости или некоторым двум
скрещивающимся прямым. Рассмотрим несколько примеров.
74
Глава 2. Параллельность в пространстве
Пример 2.5. Построить сечение призмы АВСА\В\С\
плоскостью а у проходящей через точку К е (АА\С)
параллельно плоскости АВ\С (рис. 2.34а).
Решение. Допустим, что сечение данной плоскостью а
построено. Так как плоскости а и АВ\С параллельны, то
линии их пересечения плоскостью АА\С также
параллельны. Поэтому следом секущей плоскости на плоскости грани
АА\С является прямая, параллельная прямой АС и
проходящая через точку К. Построим эту прямую. Пусть она
пересечёт отрезки АА\ и СС\ в точках Pi и Рг (рис. 2.346).
Рассуждая аналогично, получаем, что линия пересечения
плоскостей а и АА\В проходит через точку Pi параллелыю
прямой ABi, а линия пересечения плоскостей а и ВВ\С —
через точку Рг параллельно прямой СВ\. Дальнейшее
очевидно (рис. 2.34в). Решение задачи единственно согласно
теореме 2 из § 2.2. □
и^ Упражнение 2.11. Постройте сечение куба ABCDA\B\C\D\
плоскостью, проходящей через середину отрезка A\D
параллельно плоскости BC\D.
Пример 2.6. Построить сечепие пирамиды SABCD
плоскостью а, проходящей через точки К и L параллельно ребру
SB, где К, L e (ABC) (рис. 2.35а).
§ 2,6. Сечение многогранника. Построение сечений 75
Решение, Строим прямую
KL — след секущей плоскости
на плоскости грани ABCD. Для
определённости будем считать,
что эта прямая пересекает
отрезки АВ и CD, а не их
продолжения, в точках Pi и Р%
(другие случаи
рассматриваются аналогично). Так как
прямая SB параллельна секущей
плоскости а, то линия
пересечения плоскостей а и ASB
параллельна прямой SB. Поэтому
проводим через точку Pi
прямую, параллельную прямой SB.
Пусть построенная прямая
пересекает отрезок AS в точке Р±
(рис. 2.356). Пусть прямая KL
пересекает отрезок BD в точке X.
Плоскость BSD проходит через
прямую, параллельную
плоскости а.у следовательно, линия
пересечения этих плоскостей
параллельна прямой SB.
Строим прямую, проходящую через
точку X параллельно прямой
SB,—линию пересечения
плоскостей а и BSD. Пусть эта
прямая пересекается с отрезком SD
в точке Рз. Для завершения
построения достаточно соединить
эту точку с точками Рг и Р±
(рис. 2.35в).
в^ Упражнение 2.12. Докажите,
что решение рассмотренной в
примере 2.6 задачи единственно.
Рис. 2.35
76
Глава 2. Параллельность в пространстве
I®*Упражнение 2.13. Постройте сечение призмы АВСА\В\С\
плоскостью, проходящей через середину ребра АВ и вершипу
С параллельно прямой ВС\.
Пример 2.7. Построить сечение пирамиды SABC
плоскостью, проходящей через точку К, лежащую внутри
SABCy параллельно скрещивающимся рёбрам АВ и SC
(рис. 2.36а).
Построение искомого сечения показано на рис. 2.366, б.
Для его обоснования используется теорема о линии
пересечения.
Рис. 2.36
§2.7. Применение проектирования 77
ti& Упражнение 2.14. Обоснуйте построение из последнего
примера и докажите, что решение поставленной задачи
единственно.
§ 2.7. Применение проектирования при построении
сечепий многогранников
В примерах, разобранных в предыдущем параграфе,
следы секущей плоскости находились достаточно легко, что
объясняется наличием двух точек в плоскости одной грани
многогранника, принадлежащих также и плоскости
сечения. Теперь мы рассмотрим более сложные ситуации.
Пример 2.8. Построить сечение призмы ABCAiB\C\
плоскостью KLMy где Ке (AAiB), L e (BBiC), M e (AAiC)
(рис. 2.37а).
Решение. Точки Ку L и М находятся по одной на каждой
из боковых граней призмы. Проблема заключается в
нахождении следа плоскости KLM на плоскости ABC (мы
предполагаем, что эти плоскости пересекаются). Для того
чтобы построить этот след, воспользуемся параллельным
проектированием. Пусть точки К\у L\ и М\ — проекции
точек К у L и М на плоскость ABC в направлении бокового
ребра призмы, а X и У — точки пересечения прямых KL
и K\L\y KM и К\М\ соответственно (рис. 2.376). Так как
(KLM) П (ABC)у то из трёх пар прямых KL и К\Ь\У КМ
и K\M\j LM и L\M\ есть по крайней мере две пары
пересекающихся прямых (докажите это самостоятельно). Пусть
это будут пары KL, K\L\ и КМ, К\М\. Тогда прямая XY —
искомый след (рис. 2.37в). Действительно, точка X лежит
на прямой KLy следовательно, она принадлежит плоскости
сечения. Но эта же точка лежит и в плоскости ABC, так
как она находится на прямой K\L\. Следовательно, точка X
принадлежит линии пересечения плоскостей KLM и ABC.
Аналогичный вывод делаем и относительно точки У.
Теперь, после того как нужный след построен, дальнейшее
построение без труда проводится методами предыдущего
параграфа (рис. 2.37г).
78 Глава 2. Параллельность в пространстве
Рис. 2.37
§ 2.7. Применение проектирования
79
В случае когда плоскости KLM и ABC параллельны,
достаточно через точки К, L и М провести прямые, парал-
В
Рис. 2.38
лельные прямым АВ> ВС и СА (рис. 2.38). Искомое сечение
тем самым будет построено (докажите это). □
Параллельное проектирование удобно использовать при
построении сечений призм (в частности, параллелепипедов
и кубов). При этом, как правило, в качестве плоскости
проектирования выбирают плоскость основания призмы,
а за направление проектирования принимают направление
бокового ребра призмы.
При построении сечений пирамид удобно пользоваться
центральным проектированием. За плоскость
проектирования принимается плоскость основания, а в качестве центра
проектирования берут вершину пирамиды. Приведём
соответствующий пример.
Пример 2.9. Построить сечение пирамиды SABC
плоскостью KLM, где К е (ASB)y L € (BSC), M e (CSA)
(рис. 2.39а).
Решение. Построим центральные проекции точек Ку L
и М на плоскость ABC. Пусть это будут точки К\> L\
и М\ (рис. 2.396). Построим точки пересечения прямых KL
80 Глава 2. Параллельность в пространстве
S S
Рис. 2.39
и K\L\ (точка Х)у LM и L\M\ (точка У). Тогда аналогично
тому, как это было сделано в примере 2.8, доказываем,
что прямая XY — линия пересечения секущей плоскости
и плоскости основания пирамиды. Дальнейшее построение
показано на рис. 2.39в. □
Проектирование помогает и при построении некоторых
сечений, заданных условием параллельности.
в^ Упражнение 2.15. Постройте сечение призмы ABCA\B\Ci
плоскостью, проходящей через точки К и L параллельно
прямой АВ, где Ке (ВВгС), Le (ААгС) (рис. 2.40).
§ 2.7. Применение проектирования
81
В
Рис. 2.40
В рассмотренных выше примерах проектирование
применялось, по существу, для некоторого
усовершенствования метода следов. Метод следов, как мы видели, довольно
универсален, но у него имеется, пожалуй, один серьёзный
недостаток: построения следов занимают довольно много
места на листе бумаги, а в некоторых случаях точки
пересечения прямых вообще выходят за его пределы. От этого
недостатка свободен другой метод — метод внутреннего
проектирования у который мы сейчас проиллюстрируем.
Пример 2.10. Построить сечение призмы ABCA\BiC\
плоскостью KLM (рис. 2.41а), где К € (АА\В), L е {АА\С),
Me [ВС].
Решение. Сначала построим проекции точек К и L на
плоскость ABC в направлении ребра АА\ — точки К\ и L\.
Отрезок K\L\ является проекцией отрезка KL. Пусть Xi —
точка пересечения отрезков AM и K\L\. Построим
точку X отрезка KL, проекцией которой является точка Xi
(рис. 2.416). Теперь найдём точку пересечения прямой А\А
с прямой MX — точку Р. Эта точка лежит в плоскости
сечения. Действительно, эта точка принадлежит прямой MX,
которая проходит через точки М и X, лежащие в плоскости
сечения (точка М по условию, а точка X — так как
принадлежит прямой KL, лежащей в плоскости сечения). Остаётся
82 Глава 2. Параллельность в пространстве
В
в
Б
построить прямые РК и PL, пусть они пересекают отрезки
АВ и СС\ в точках Q и N соответственно. Четырёхугольник
MNPQ — искомое сечение (рис. 2.41в). □
Пример 2.11. Построить сечение пирамиды SABC
плоскостью KLM (рис. 2.42а), где Ке (ASB), Le (ASC), Мб
е(ВС).
Этот пример решается аналогично предыдущему с той
лишь разницей, что вместо параллельного проектирования
используется центральное (рис. 2.426).
I®* Упражнение 2.16. Постройте сечения многогранников,
изображённых на рис. 2.43 и рис. 2.44, плоскостью KLM с
помощью метода внутреннего проектирования.
§ 2.7. Применение проектирования
83
а)
В
Рис. 2.42
В
Рис. 2.43
Рис. 2.44
Как видно из приведённых примеров, все построения
мы проводили, не выходя за пределы изображения данного
многогранника. Отсюда и происходит название описанного
метода.
В заключение этого параграфа отметим, что многие
задачи на построение сечений многогранников могут быть
решены и с помощью комбинации метода следов и метода
84 Глава 2. Параллельность в пространстве
внутреннего проектирования. Выбор того или иного
метода (или их комбинации) диктуется в каждом конкретном
случае соображениями удобства, а также личным вкусом
решающего.
§ 2,8. Решение задач на сечения многогранников
— Мой дорогой Уотсон, попробуйте
немного поанализировать сами,— сказал
он с лёгким раздражением,— Вы знаете
мой метод. Примените его, и будет
поучительно сравнить результаты.
А. Конан Дойл. Знак четырёх
В этом параграфе мы разберём решения некоторых
задач, связанных с определением вида сечения
многогранника, вычислением периметров, площадей сечений,
отношений, в которых секущая плоскость делит рёбра
многогранника (или другие отрезки) и т. п. При этом мы не будем
подробно описывать само построение сечения и проводить
обоснование построения, полагая, что после внимательного
изучения двух предыдущих параграфов вы без труда
сделаете это самостоятельно. Тем не менее, когда вы будете
решать задачи, подобные разбираемым в этом параграфе,
не забывайте проводить аккуратное построение сечения
и давать обоснование построения — без этого решение
нельзя признать полным.
Отметим, что зачастую в формулировках задач о
сечениях не содержится требования построить их. Однако
чертежи, на которых сечение построено «на глазок», в
большинстве случаев являются источниками ошибок при
дальнейшем решении. Поэтому даже если не сказано:
«построить сечение плоскостью PQR*y— не поленитесь выполнить
черновую работу и проведите построение, это поможет
правильно решить задачу.
Пример 2.12. Точки Р, Q и Л —середины рёбер AiB\,
В\С\ и CD куба ABCDA\BiC\D\. Какой многоугольник
§ 2Я. Решение задач на сечения многогранников 85
Вг
получится в сечении куба плоскостью PQR? Определить
площадь этого многоугольника, если известно, что ребро
куба равно а.
Решение. Построим сечение методом следов (рис. 2.45).
По теореме о линиях пересечения двух параллельных
плоскостей третьей плоскостью стороны сечения, лежащие на
параллельных гранях куба, параллельны. Треугольники
PB\Q и QC\X равны, поэтому С\Х= ^ а так как и RC = ^,
то точка К — середина [CCi]. Так как (PQ) \\ (А\С\) (средняя
линия AAxJBiCi), (RL) || (PQ), (Aid) || (АС), то (LR) \\ (АС),
следовательно, L — середина [AD]. Аналогично М
—середина [AAi]. Из равенства прямоугольных треугольников1^
MAiP, PBiQ, QCiK, KCR, RDL и LAM следует, что все
стороны шестиугольника PQKRLM равны. Из равенства
^Заметим, что мы ещё не доказали справедливость известных
из планиметрии признаков равенства для треугольников, лежащих
в разных плоскостях. Мы сделаем это в гл. 8, не опираясь на результаты
предыдущих глав, а пока будем пользоваться указанными признаками
без доказательства.
86
Глава 2. Параллельность в пространстве
прямоугольных треугольников QC\X> XC\K и KC\Q
следует, что треугольник QKX равносторонний. Тогда Z.PQR =
= ZQKR— 120°. Аналогично доказывается, что все углы
шестиугольника PQKRLM равны 120°. Поэтому
полученное сечение является правильным шестиугольником.
Сторона этого шестиугольника равна -—^ следовательно, его
площадь равна
□
Пример 2.13. Дан куб ABCDAiB\C\D\ с ребром длины 1,
Точка Р — середина ребра A\D\, точка Q делит отрезок
АВ\ в отношении 2 : 1, считая от вершины А\ Л —точка
пересечения отрезков ВС\ и В\С. Построить сечение куба
плоскостью PQR. Найти периметр сечения и отношение,
в котором плоскость сечения делит диагональ АС\ куба.
Решение. Построим след секущей плоскости на
плоскости верхнего основания куба, для чего спроектируем на эту
плоскость параллельно ребру АА\ точки Q и R. Если Q\
и Ri — проекции этих точек, а X — точка пересечения
прямых QR и Qii?i, то прямая ХР — искомый след (рис. 2.46).
Глядя на рис. 2.46, трудно определить, какую именно сторо-
Рис. 2.46
§ 2Я. Решение задач на сечения многогранников 87
ну верхнего основания, кроме AiD\, пересекает прямая ХР.
Поэтому, чтобы не сделать ошибку и правильно нарисовать
сечение, определим положение точки X вычислением.
Из подобия треугольников АА\В\ и QQ\B\ находим,
что QQi = 1/3. Кроме того, ясно, что ARi = 1/2.
Поэтому из подобия треугольников XQQi и XRR\ получаем
XQi = QQi = 2
следовательно,
= 2. Но и
RRi ~ Г
= 2, a ZAiQiX=Zi?iQiEi. Значит,
(рис. 2.47), следовательно, (AiX) || (i?iBi), а это означает,
Рис. 2.47
Рис. 2.48
что точка X лежит на прямой A\D\. Поэтому сечение
выглядит так, как показано на рис. 2.48 (сечение —
параллелограмм и даже прямоугольник; докажите это). Из
прямоугольного треугольника A\B\N находим длину
отрезка A\N = ¥р~. Периметр сечения равен
= 2(AXN + NM) =
88
Глава 2. Параллельность в пространстве
Построим теперь точку пересечения К секущей
плоскости с прямой АС\. Для этого достаточно найти точку
пересечения отрезков RD\ и АС\ (почему?). Теперь из подобия тре-
АК
угольников AD\K и C\RK находим, что
СгК
= 2. □
Ключевым моментом в решении этой задачи явилось
определение положения прямой ХР относительно сторон
верхнего основания куба. Ошибка в этом пункте привела
бы к изменению формы сечения (рис» 2.49). Поэтому при
"У С
Рис. 2.49
решении таких задач целесообразно одновременно с
построением сечения проводить вычисления, уточняющие
положение всех его вершин.
Приведём ещё один подобный пример»
Пример 2.14, В основании треугольной пирамиды SABC
лежит правильный треугольник ABC. Точки Р, Q и R взяты
на медианах SP\> SQi и SR\ граней SAB, SBC и SCA
соответственно так, что SP : PPi = 2:1, SQ : QQi =2:3,
а Л-середина отрезка SR\♦ Построить сечение пирамиды
плоскостью PQR и определить, в каком отношении эта
плоскость делит ребро SB.
§ 2.8. Решение задач на сечения многогранников 89
S
Pi Ri
Рис. 2.51
Решение. Сначала построим след секущей плоскости на
плоскости основания пирамиды, соединив прямой точки X
и У пересечения прямых PR, P\Ri и PQ, P\Q\ (рис. 2.50).
Уточним теперь положение точек X и У, найдя отношения
XPi : XR\ и УР1 : YQ\. Для их вычисления воспользуемся
известной из планиметрии
теоремой Менелая (теорема П8.2).
Согласно этой теореме, применённой
к треугольнику SP\R\ (рис. 2.51),
SR
RiX
ХРХ
PS
следовательно, 1 • ^=- • ~ = 1, откуда
ХРл 1
^г—- = ;г. Аналогично из треугольника
Arii ^
1
= ^. Обратимся теперь к рис. 2.52. Так как
6
УР1
УР1
1
== ^, то
6
= hили ж=\ <так как
a
= ^ и
^ , то AyPiX-AARiX, следовательно,
точки X, У и А лежат на одной прямой (причём У —
90 Глава 2. Параллельность в пространстве
S
Рис. 2.54
М
Б
середина отрезка АХ). Теперь уже легко достроить сечение
(рис. 2.53).
Чтобы найти SM: MB (М — точка пересечения АР и SB)>
обратимся к рис. 2.54. Как известно из планиметрии,
точка Р, делящая медиану SP\ в отношении 2:1, считая
от вершины S, является точкой пересечения медиан
треугольника ASB. Поэтому AM — медиана этого
треугольника и SM: MB = 1:1. (Здесь нам немного повезло. Если бы
отношения АР\ : Р\В и SP: РР\ были другими, то снова
нужно было бы воспользоваться теоремой Менелая,
применив её к треугольнику SBP\.) □
Рассмотренная задача интересна ещё и тем, что
приведённое нами решение иллюстрирует удобство
применения теоремы Менелая для вычисления отношений, в
которых плоскость сечения делит рёбра (или другие отрезки)
пирамиды. Ведь при построении сечения пирамиды
методом следов неизбежно возникают конфигурации, подобные
изображённым на рис. 2.51 и 2.52.
Приведём теперь пример, иллюстрирующий идею так
называемого вспомогательного сечения (решение ряда
задач существенно упрощается, если удачно провести
некоторое дополнительное сечение).
§ 2,8. Решение задач на сечения многогранников 91
Пример 2.15. Пусть на диагоналях АВ\ и ВС\ граней
куба ABCDA\B\C\D\ расположены точки М и N
соответственно так, что отрезок MN параллелен грани ABCD. Найти
отношения, в которых точки М и N делят отрезки АВ\
и ВСи если
о
Решение. Проведём через отрезок MN плоскость,
параллельную основаниям куба. (Как это сделать? Единственна
ли эта плоскость?) Сечение куба этой плоскостью является
квадратом, который равен грани куба (рис. 2.55). Пусть реб-
ро куба равно a, a AM: AB\ = х. Из подобия треугольников
MBiP2 и ABiB имеем MBi : ABi = МР2 : АВ = ВХР2 : BiB.
Так как МВ\ = (1 - х) АВг, то МР2 = (1 - х)а, ВХР2 = (1 - х)а>
ВР2 = ВВ\ — В\Р2 = ха. Из подобия треугольников BP2N
и BBiC находим, что P2N: BiCi = BN: БС1 = ВР2 : BBi = л\
Поэтому P2N — ха и ЛЛГ: BCi = AM : AB\ = х. По теореме
Пифагора из треугольника MP2N имеем МР\ + NP\ = MN2.
Следовательно, (1 - х)2а2 +х2а2 = (5/9)а2, откуда получаем
xi = 2/3 и JC2 = 1/3. Тем самым задача имеет два решения
(рис. 2.55 и рис. 2.56). □
92
Глава 2. Параллельность в пространстве
В заключение рассмотрим планиметрическую задачу,
которая легко решается, если данную плоскую
конфигурацию представить как проекцию пространственной (этот
приём часто называют выходом в пространство).
Пример 2.16, На плоскости даны три параллельные
прямые и три точки. Построить треугольник, вершины
которого лежат на данных прямых, а данные точки лежат
на прямых, содержащих его стороны (по одной на каждой
прямой).
Решение. Рассмотрим треугольную призму. Данные
прямые можно считать проекциями на данную плоскость
прямых, содержащих боковые рёбра этой призмы, а данные
точки — проекциями точек, лежащих в плоскостях боковых
граней призмы. Тогда искомый треугольник будет
проекцией сечения призмы, проходящего через эти точки (призму
нужно взять достаточно «длинной», чтобы в сечении
получился треугольник). Тем самым наша задача свелась
к построению сечения призмы по трём точкам в плоскостях
боковых граней; эта задача решена нами в предыдущем
параграфе. □
Задачи 93
Задачи
Если вы пе можете решить задачу, вы всегда можете
взглянуть на ответ. Но, пожалуйста, постарайтесь
решить её самостоятельно, тогда вы научитесь большему
и быстрее.
Д. Кнут. The
2.1. Даны скрещивающиеся прямые а и Ъ и точка М.
Постройте прямую, проходящую через М и пересекающую
а и Ъ. Найдите все точки М, для которых задача не имеет
решения.
2.2* В пространстве даны три попарпо
скрещивающиеся прямые. Постройте прямую, пересекающую каждую
из них. Всегда ли это возможно? Сколько таких прямых
существует? Через любую ли точку, взятую на одной из
данных прямых, можно провести искомую прямую?
2.3. Верно ли, что две плоскости параллельны тогда
и только тогда, когда всякая прямая, пересекающая одну
из них, пересекает и другую?
2.4. Скрещивающиеся прямые а и & проектируются на
плоскость а у пересекающую обе прямые, причём прямая а
проектируется параллельно прямой Ьу а прямая Ъ —
параллельно прямой а. Докажите, что проекции данных прямых
параллельны.
2.5. Может ли параллельная проекция тетраэдра на
плоскость быть:
а) трапецией;
б) параллелограммом;
в) пятиугольником?
Если может, то укажите явно плоскость проектирования
и направление проектирования.
2.6. Может ли параллельная проекция параллелепипеда
на плоскость быть:
а)трапецией;
б) пятиугольником;
в) шестиугольником?
94
Глава 2. Параллельность в пространстве
Если может, то укажите явно плоскость проектирования
и направление проектирования.
2.7. Постройте сечения многогранников (рис. 2.57)
плоскостью PQR.
D
Рис. 2.57
2.8. Постройте сечения многогранников (рис. 2.58)
плоскостью, проходящей через точки Р и Q параллельно
прямой /.
Рис. 2.58
Задачи
95
2.9. Постройте сечения многогранников (рис. 2.59)
плоскостью, проходящей через точку Р параллельно
плоскости а.
Рис. 2.59
2.10. Постройте сечения многогранников (рис. 2.60)
плоскостью, проходящей через точку Р параллельно
прямым 1\ и /г-
а)
в
Рис. 2.60
96 Глава 2. Параллельность в пространстве
D D
Na
М
М
в а) в б)
Рис. 2.61
2.11. Может ли четырёхугольник KLMN быть сечением
пирамиды ABCD (рис. 2.61)?
2.12. а) Какие многоугольники могут быть сечениями
куба плоскостью?
б) Какие правильные многоугольники могут быть
сечениями куба плоскостью?
2.13. Может ли сечение куба быть тупоугольным
треугольником?
2.14. В прямоугольном параллелепипеде одно из
сечений является правильным шестиугольником. Докажите,
что этот параллелепипед— куб.
2.15*. Сечение правильной четырёхугольной пирамиды
является правильным пятиугольником. Докажите, что
боковые грани этой пирамиды — правильные треугольники.
2.16*. В основании пирамиды
лежит правильный тг-угольник. При
каких п эта пирамида может иметь
сечение, являющееся правильным
(п + 1)-угольником?
2.17. На рис. 2.62 изображён
шестигранник ABCDA\B\CiD\> все
грани которого являются
четырёхугольниками. Постройте изображе-
Рис. 2.62 ние его вершины D\.
Задачи 97
2.18. а) Через точку на ребре тетраэдра проведите
плоскость а так, чтобы сечение тетраэдра было
параллелограммом.
б) Докажите, что сечение тетраэдра плоскостью /3 || а
также является параллелограммом.
2.19. Докажите, что каждый тетраэдр имеет сечение,
являющееся ромбом. Сколько таких сечений можно
построить?
2.20. Скрещивающиеся рёбра тетраэдра имеют длины а
и &. Сечение тетраэдра, параллельное этим рёбрам, —ромб.
В каких отношениях плоскость сечения делит рёбра
тетраэдра, которые она пересекает?
2.21. Докажите, что любую четырёхугольную пирамиду
можно пересечь плоскостью так, что в сечении получится
параллелограмм.
2.22*. Докажите, что периметр любого
четырёхугольного сечения правильного тетраэдра с ребром длины 1 не
меньше 2, но меньше 3.
2.23. Длина ребра куба ABCDA\B\C\Di равна а. На
рёбрах AD и В\С\ взяты соответственно точки М и Q, а на
ребре CD - точки Р и N так, что AM = CiQ = CP = DN = а/3.
Постройте сечение куба плоскостью, проходящей через
прямую МР параллельно прямой NQ, и найдите его
площадь.
2.24. Точки М, N и Р — середины рёбер АВ, CD и ВС
тетраэдра ABCD. Через точку Р проведена плоскость,
параллельная прямым DM и AN. В каком отношении она
делит ребро AD?
2.25. Через середины М и N рёбер AD и СС\
параллелепипеда ABCDA\B\C\D\ проведена плоскость,
параллельная его диагонали B\D. В каком отношении она делит
ребро ВВх?
2.26. Точки О и Oi -центры граней ABCD и A\BiC\Di
куба ABCDA\B\C\D\. На отрезке ОО\ взята точка S так,
что O\S : OS =1:3. Через эту точку проведено сечение
куба, параллельное его диагонали АС\ и диагонали BD
4 Зак. 3383
98 Глава 2. Параллельность в пространстве
основания. Найдите площадь сечения, если длина ребра
куба равна а.
2.27. Точка О — центр основания правильной
четырёхугольной пирамиды SABCD. Через середины отрезков АВУ
ВС и SO проведена плоскость а. Найдите площадь сечения
пирамиды этой плоскостью, если известно, что площадь
её сечения плоскостью, проходящей через точки А и С
параллельно ребру SB, равна q.
2.28. В правильной четырёхугольной пирамиде SABCD
через середины отрезков АВ и AD проведена плоскость,
параллельная ребру SA. Найдите площадь сечения, если
АВ = ау SA = b.
2.29. В правильной шестиугольной пирамиде SABCDEF
на диагонали основания AD взяты три точки, делящие её
на четыре равные части. Через эти точки проведены
сечения, параллельные плоскости SAB. Найдите отношения
площадей этих сечений.
2.30. Основанием пирамиды SABCD является
параллелограмм ABCD. Точка L лежит на ребре SD и делит его
в отношении SL : LD = 2 :1, а точка К — середина ребра SB.
Постройте сечение пирамиды плоскостью AKL и
определите, в каком отношении эта плоскость делит ребро SC.
2.31. В правильной четырёхугольной пирамиде SABCD
точка К — середина ребра AD, точка М — середина
ребра АВ, а точка N — середина ребра ВС. Точки Р, Q и R
лежат на отрезках SK, SM и SN соответственно, причём
SP : РК = 2 :1, SQ : QM = 4:7, аД- середина отрезка SN.
В каком отношении плоскость PQR делит рёбра пирамиды,
которые она пересекает?
2.32. Правильная пятиугольная пирамида SABCDE
пересечена плоскостью, проходящей через вершину А
основания и середины рёбер SD и SE. Найдите площадь сечения,
если сторона основания пирамиды равна а, а боковое ребро
равно Ь.
2.33*. Через точку, взятую внутри треугольной
пирамиды, параллельно её рёбрам проведены отрезки с концами на
Задачи 99
гранях пирамиды. Докажите, что сумма шести отношений
длин этих отрезков к длинам параллельных им рёбер не
зависит от выбора первоначальной точки. Чему равна эта
сумма?
2.34. а) Три прямые одной плоскости параллельны. На
первой из них взяты точки А\ и Аг, на второй — В\ и Бг, на
третьей — С\ и Сг- Пусть прямые А\В\ и А2Б2, В\С\ и Б2С2,
А\С\ и А2С2 пересекаются в точках X, Y и Z. Докажите,
что точки X, У и Z лежат на одной прямой.
б) В плоскости даны треугольники ABC и A\BiC\9
причём прямые АА\У ВВ\ и СС\ пересекаются в одной
точке. Докажите, что если прямые АВ и А\В\> ВС и В\С\,
СА и С\А\ попарно пересекаются, то точки их
пересечения лежат на одной прямой. (Частные случаи теоремы
Дезарга.)
2.36. На плоскости даны три луча с общим началом,
и внутри каждого из трёх углов, образованных этими
лучами, отмечено по точке. Постройте треугольник так, чтобы
его вершины лежали на данных лучах, а стороны (или
их продолжения) проходили через отмеченные точки (по
одной через каждую из точек).
2.36. В четырёхугольник ABCD вписаны два
прямоугольника с параллельными сторонами так, что на каждой из
сторон АВ, ВС, CD, DA лежит по одной вершине
каждого прямоугольника. Периметр каждого
прямоугольника равен 10. Найдите площадь четырёхугольника ABCD
и докажите, что для каждой точки на любой из сторон
четырёхугольника ABCD можно построить прямоугольник
с вершиной в этой точке, вписанный в ABCD, стороны
которого параллельны сторонам данных прямоугольников
и периметр которого также равен 10.
Глава 3
Векторы в пространстве
В некотором пространстве, в некотором
подпространстве жило-было-задано
нормализованное удобопорядоченное семейство векторов...
Адам Ар и Ева Клад, Как три вектора
один детерминант в нуль обратили
§ 3.1. Определение вектора.
Линейные операции над векторами
Особенность понятия вектор заключается в том, что все
определения и теоремы, связанные с векторами на
плоскости, дословно (кроме, быть может, замены слова
«плоскость» на слово «пространство») переносятся на
пространственный случай. Поэтому мы лишь напомним схему
введения этого понятия и подробно обсудим новые свойства,
возникающие в пространстве. Рекомендуем вам, прежде
чем продолжать изучение, освежить в памяти
соответствующий раздел планиметрии (см., например, [Гусятников,
Резниченко, 1985]).
Понятие вектора вводится так: сначала определяют
направленный отрезок (как упорядоченную пару точек
пространства) и понятия, связанные с ним (начало, конец,
длина, направление). Затем даётся определение равных
направленных отрезков (как имеющих одинаковую длину
и направление). После этого определяют вектор.
I
Определение. Вектором называется множество всех
равных между собой направленных отрезков.
Векторы обычно обозначают строчными латинскими
буквами со стрелкой сверху: 3, ft, ? и т.д. Направленные
отрезки обозначают, указывая их начало и конец, также
со стрелкой сверху: АВ.
102 Глава 3. Векторы в пространстве
Итак, вектор — это множество, состоящее из
бесконечного числа элементов. Напомним одно важное соглашение,
связанное с этим понятием: если АВ € #, то говорят, что
направленный отрезок АВ изображает вектор й\ при этом
на чертеже рисуется именно направленный отрезок АВ,
а говорят про него «вектор»1*. В частности, когда мы
говорим «отложим вектор а от точки О», то имеется в виду,
что строится направленный отрезок ОА, изображающий
вектор 3.
После того как дано определение вектора, все понятия,
связанные с направленными отрезками, переносятся на
векторы следующим образом: говорят, что векторы
обладают некоторым свойством, если этим свойством обладают
изображающие их направленные отрезки. Например,
векторы называются равными, если равны изображающие их
направленные отрезки.
Определённый выше объект часто называют свободным
вектором, чтобы подчеркнуть, что вектор в геометрии
характеризуется только длиной и направлением, в отличие
от связанного вектора, имеющего фиксированное начало
(таков, например, в физике «вектор силы», действующей
на упругое тело, который характеризуется ещё и точкой
приложения).
Под линейными операциями над векторами мы будем
понимать сложение и вычитание векторов, а также
умножение вектора на число (скаляр). Эти операции определяются
так же, как и для плоскости. В частности, произведением
вектора 3 на действительное число а называется вектор
длины \а\ • |а|, сонаправленный с а, если а ^ 0, и направленный
противоположно а, если а < 0.
Из планиметрии вам известны правило треугольника
(рис. 3.1), правило параллелограмма (рис. 3.2) и правило
ломаной сложения векторов (если А\9 А^ ..-, Ап — произ-
^Далее мы в тех случаях, когда не возникает двусмысленности,
будем обозначать вектор так же, как изображающий его направленный
отрезок, например Л5.
§3.1. Определение вектора. Линейные операции 103
Рис. 3.1
Рис. 3.2
вольные точки плоскости, то А1А2 + ... + Ап-\Ап = А\Ап).
Правила треугольника и параллелограмма сохраняются
и в пространстве, правило ломаной справедливо для
произвольных точек Аь A<iy .♦♦, Ап пространства; кроме того, в
пространстве справедливо правило параллелепипеда: если
ОА Е 3, ОВ е £, ОС е ?, то, построив на направленных
отрезках параллелепипед OAEBCFDG (рис. 3.3), можно
о
Рис. 3.3
найти направленный отрезок ОХ>, изображающий вектор
который является суммой векторов 3, Ь, ?.
Напомним основные свойства линейных операций
(которые доказываются точно так же, как и для плоскости).
Свойства сложения векторов
(Нулевой вектор б и противоположный вектор
деляются так же, как и в планиметрии.)
—а опре-
104 Глава 3. Векторы в пространстве
—♦ > ►
1°. V 3, b: cl + b = b + ct (коммутативность сложения).
2°. V 3, ft, ?: 3 + (& + ?) = (а + Ь) + ? (ассоциативность
сложения).
3°. V3: 3 + 6 = 3.
4°. V3:3+(-3)=6.
Свойства умножения вектора на число
1°, V3; Var, /ЗбК: (а/3)а= а(/33) (ассоциативность).
2°. V3; Va, /ЗеМ: (a+P)3=a2 + /33 (дистрибутивность
по отношению к сложению действительных чисел).
3°. V 3, Ь; V a e R: а (3 + Ь) = оси + аЬ (дистрибутивность
по отношению к сложению векторов).
4°. V3: 13=3.
о^ Упражнение 3.1. Докажите правило ломаной в пространстве
и правило параллелепипеда, используя правила
треугольника и параллелограмма.
Решим несколько задач, используя свойства линейных
операций над векторами в пространстве. Первые две из них
дословно повторяют соответствующие задачи из
планиметрии.
Пример 3.1. Доказать, что если М — середина отрезка
АВ, в. О — произвольная точка пространства, то
(3.1)
/и
Решение. По правилу треугольника AM = АО + ОМ =
= ~ОА + ОМ (рис. 3,4). Аналогично MB = -ОЙ + ОВ.
Поскольку AM = MB у то —ОА + ОМ = -ОМ + ОВ, откуда и
следует равенство (3.1). □
Замечание. Формула (3.1) — частный случай формулы
деления отрезка в данном отношении: если точка М делит
отрезок АВ в отношении А, т. е. AM : MB = А, а О — произвольная
точка пространства, то
Ъ^М (3-2)
§ 3.1. Определение вектора. Линейные операции 105
Рис. 3.5
с^ Упражнение 3.2. Докажите формулу (3.2).
Очевидно, при А = 1 формула (3,2) переходит в (3.1).
Формулу (3.2) можно и не запоминать, а в каждом конкретном случае
воспроизводить соответствующий вывод.
Пример 3.2. Доказать, что если М — точка пересечения
медиан треугольника ABC, а О — произвольная точка
пространства, то
ом = ±
(3.3)
Решение. Пусть АА\ — медиана треугольника ABC
(рис. 3.5). По свойству медиан треугольника AM = 2МА\.
Но AM = -ОА + ОМ, МА\ = -ОМ + ОА\. Следовательно,
ОМ=-2ОМ+ 20А\. По формуле (3.1) имеем OAi =
= л (ОВ + ОС). Подставляя это выражение для ОА\ в послед-
нее равенство, получаем, что ЗОМ = ОА + ОВ + ОС, откуда
следует равенство (3.3). □
Следующая задача представляет собой обобщение
свойства медиан треугольника на пространственный случай.
Конечно, оно может быть доказано и чисто геометрически,
см. [Кутасов и др., 1981], но мы приведём здесь векторное
доказательство.
106 Глава 3. Векторы в пространстве
Пример З.З, В тетраэдре ABCD каждая вершина
соединена с точкой пересечения медиан противолежащей грани.
Доказать, что все эти отрезки1* имеют общую точку,
которая делит каждый из них в отношении 3:1, считая от
вершины тетраэдра.
Решение. Обозначим точки пересечения медиан граней
BCD, ACD, ABD и ABC через Аь Вь С\ и D\
соответственно. Пусть точка X делит отрезок АА\ в отношении
3:1, считая от точки А, т.е. АХ = 3XAi, О —
произвольная точка пространства (рис. 3.6). Тогда АХ = —ОА
ХА\ = -ОХ + ОАь Следовательно, -ОА + ОХ = -ЗОХ +
+ ЗОАь откуда получаем ОХ = jOA + jOA\. Но в силу
равенства (3-3) имеем ЗОА\ = ОВ + ОС + OD. Окончательно
получаем Ш? = -г (ОА + ОВ + об + OD). Полученное
выражение симметрично относительно перестановок вершин А> В,
С и D. Следовательно, мы получим то же самое выражение
для векторов OY, OZ и OU, где точки Y, Z и U делят отрезки
СС\ и DD\ в отношении 3:1, считая соответственно
1>Их часто называют медианами тетраэдра.
§ 3,2, Компланарность векторов 107
от точек В, С и В. Это означает, что X, У, Z и U — одна
и та же точка, т.е. X — общая точка всех четырёх отрезков,
делящая каждый из них в отношении 3:1. □
§ 3.2. Комплапарность векторов.
Разложение вектора по базису
Перед чтением этого параграфа советуем вам вспомнить
понятие коллинеарности векторов и теорему о разложении
вектора по базису на плоскости. Если вы вдумчиво
изучили соответствующий раздел планиметрии, то всё, что
содержится в этом параграфе, покажется вам не более чем
тривиальным обобщением соответствующих понятий и
теорем для плоскости — двумерного пространства — на
трёхмерный случай.
Определение понятия коллинеарности в пространстве
дословно повторяет аналогичное определение в случае
плоскости.
Определение. Два вектора называются коллинеарными>
если изображающие их направленные отрезки
параллельны некоторой прямой. Нулевой вектор коллинеарен
любому вектору.
Если векторы 3 и ft коллинеарны, то мы будем
обозначать это так: 31| ft.
Напомним известный вам из планиметрии признак
коллинеарности векторов.
Если для векторов а и Ъ существует такое число х,
что ft = х39 то dub коллинеарны.
Это утверждение доказывается точно так же, как и в
планиметрии. Заметим, что обратное неверно: если а || ft,
то может и не найтись такое х, что Ъ — хЗ. Действительно,
если 3 = б, то а \\ Ъ для любого ft, а равенство ft = хЗ в этом
случае возможно лишь для ft = б. Если же а ф б, а || ft, то
— xd для некоторого х (докажите!).
108
Глава 3. Векторы в пространстве
Новое понятие, возникающее в пространстве и
играющее ту же роль, что и коллинеарность векторов на
плоскости,—компланарность векторов.
Определение. Векторы а, о и ? называются
компланарными, если изображающие их направленные отрезки
параллельны некоторой плоскости, в частности, если хотя
бы один из них нулевой1*.
Данные нами определения коллинеарных и
компланарных векторов корректны (т.е. параллельность, о которой
в них идёт речь, сохраняется при любом выборе
изображающих векторы направленных отрезков) в силу свойства
транзитивности параллельности прямых в пространстве
(следствие 5 из теоремы 2.2).
Докажем признак компланарности.
Теорема 3.1 (признак компланарности векторов). Если
для векторов а, Ъ и <? существуют такие числа х и г/, что
?= хй + уЬу то й, b и ? компланарны.
Доказательство. Рассмотрим два случая.
1. Пусть а || Ъ. Если 3 = 5, то векторы а, Ъ и с?
компланарны. Если а ф б, то Ь — za для некоторого г.
Следовательно, <?= xd + yb = xd + y(zfi) = (х + zy)a = йа, где k = х + zy,
и по признаку коллинеарности векторов ? коллинеарен 3.
Аналогично ? коллинеарен ft. Тогда
найдётся прямая I, параллельная 3,
Ъ и ?. Проведём через Z плоскость а.
Векторы 3, 6 и ? параллельны а и,
следовательно, компланарны.
2. Пусть З^Ь. Отложим данные
векторы от одной точки О (рис. 3.7):
ОА = 3, ОВ = Ь, об = ?. По условию
теоремы ОС — хй + у$. Предположим,
Рис. 3.7
^Нулевой вектор по определению считается параллельным любой
плоскости.
§ 3.2. Компланарность векторов 109
что 2, 6 и ? некомпланарны. Это означает, что точка С
не принадлежит плоскости АОВ. В плоскости АОВ можно
построить такую точку £>, что OD = xa + yb (см» рис. 3.7).
Следовательно, Ои = OD, поэтому С и D — одна и та же
точка. Полученное противоречие означает, что 3, b и ?
компланарны. П
US' Упражнение 3.3. Дан пространственный четырёхугольник
ABCDj где N я М — середины отрезков ВС и DA. Докажите,
что прямые АВ, CD и MiV параллельны некоторой плоскости.
Указание. Докажите равенство MN= -={AB-\-CD) и восполь-
зуйтесь признаком компланарности.
Подумайте, как обобщить задачу: в каких отношениях точки
М и N должны делить [ВС] и [AD], чтобы утверждение задачи
оставалось верным?
Замечание. Теорема, обратная признаку компланарности:
если а, Ь и *£ компланарны, то существуют такие числа хиу, что
(*=xfi-\-yb, неверна (приведите соответствующий контрпример).
Однако верно следующее утверждение.
Теорема 3.2. Пусть 3, b и ?—компланарные векторы,
причём 3 и b неколлинеарны. Тогда существует
единственная такая пара чисел х и у9 что ?= хй + yb.
Эта теорема сразу вытекает из теоремы о разложении
вектора по двум неколлинеарным векторам на плоскости.
(Напомним: говорят, что вектор b разложен по векторам
#2, •••» 2П, если указаны такие действительные числа
#2> •••> #л> что fr = ai3i + af232 + ... + an3n.) Аналогичная
теорема о разложении вектора имеет место в пространстве.
Теорема 3.3. Пусть 3, b и ?— некомпланарные векторы.
Тогда для любого вектора 3 существует единственная
тройка таких действительных чисел х, у и 2, что a = jc3 + t/fe + z2.
Доказательство. Существование. Рассмотрим
два случая.
110 Глава 3. Векторы в пространстве
1. Пусть Z || ?♦ Тогда, поскольку ?^ б (иначе 2, Ъ и ? были
бы комланарны), существует такое число z, что 5 = 2? =
2. Пусть З-lf?. Отложим векторы 3, Ь, ? и 3 от одной
точки О (рис. 3.8): ОА = й, ОВ = Ь, Об = ?, OD = d.
Рис. 3.8
Точки С, О и D не лежат на одной прямой (так как
проведём через них плоскость а. Точки А, О и В также
не лежат на одной прямой (cttyb; если а || ft, то a, ft и ?
компланарны), проведём через них плоскость/3. Поскольку
3,Ь и ? некомпланарны, построенные плоскости различны.
Они имеют общую точку О и, следовательно, пересекаются
по прямой /, проходящей через О (см. рис. 3.8). В плоскости
а проведём (DCi) ||Z, где Ci G (ОС^и (DDi) \\ (ОС), где Di б/.
По правилу параллелограмма OD — ОС\-\-OD\. Векторы
ОС\ и ОС = ? коллинеарны, ?^ 0 (иначе а, Ь и ? были бы
комланарны), следовательно, существует такое число 2, что
ОС\ = г?. Далее, вектор OD\ можно разложить по неколли-
неарным векторам ОА и ОВ в плоскости р: OD\ =xct + yb.
Окончательно получаем OD = d = xa + yb + z<*.
Единственность. Предположим, что требуемое
разложение неединственно, т.е. также 5 = x\U+ y\b + Z\S
для некоторых действительных чисел х\у у\ и z\. Без
ограничения общности можно считать, что хфх\. Вычитая
§3.2. Компланарность векторов 111
данные равенства одно из другого, получаем
(х - хх)П+ (у - ух)Ъ + (г - zi)? = б,
откуда, поскольку х - #i ф 0, имеем
X — Х\ Х-Х\
Значит, по признаку компланарности а, Ь и ? компланарны.
Получили противоречие. □
Базисом на плоскости называется упорядоченная пара
неколлинеарных векторов. Любой вектор на плоскости
может быть однозначно разложен по базисным. Аналогично
определяется базис в пространстве.
Определение. Базисом в пространстве называется
упорядоченная тройка некомпланарных векторов.
Базис из векторов 3, Ь и ? обозначают {3, Ь, ?}.
Только что доказанная теорема утверждает, что любой вектор
пространства однозначно раскладывается по базисным
векторам.
Пусть а, Ъ и ? — некоторый базис, а — произвольный
вектор пространства.
Определение. Коэффициенты а, б, у в разложении 3 =
= оса + (ЗЬ + у<* называют координатами вектора а в
базисе {3, Ь, ?}.
Координаты вектора в данном базисе определяются
однозначно, поэтому если нам каким-то способом удалось их
определить, то можно быть уверенными, что и любым
другим способом получится тот же самый результат. При этом,
конечно, если мы сменим базис, то координаты вектора,
вообще говоря, изменятся.
Пример 3.4. Дан параллелепипед ABCDAiB\C\D\. Точ-
ки М и N — середины рёбер ВС и C\D\. Разложить вектор
MN: _^ _^ ^
1) по векторам АВ, AD, АА\\
2) по векторам АВ, AD, АС\.
112 Глава 3. Векторы в пространстве
Решение. Для начала заметим, что векторы каждой из
троек некомпланарны, поэтому искомые разложения
существуют и единственны. Для удобства обозначим АВ = р,
AD = qy АА\ = /*, АС\ = s (рис. 3.9). По правилу ломаной
N
В
= — -=$• Окончательно имеем MN= — -кр+ ?>q + ?. Далее, по
правилу параллелепипеда s = р + $ + ?, откуда получаем
= 3-p-q. Следовательно, МЛ^= ~т>Р+ к? + 0*—р- Я) =
2
3^. 1
p 2 Говоря другими словами, вектор MN име
ет координаты ( —■«; к; 1) в базисе {j^; g; F} и координаты
(3 1 \
"2; ~2; 1J В базисе
§ 3.3. Угол между прямыми. Угол между векторами
Здесь и далее под углом мы понимаем не
геометрическую фигуру, а величину. Соответствующую фигуру,
образованную двумя лучами с общим началом и одной из плос-
§ 3.3. Угол между прямыми. Угол между векторами 113
ких областей, ограниченных ими, будем называть плоским
углом. Аксиомы измерения плоских углов считаются
известными из планиметрии. Напомним, что согласно этим
аксиомам каждый плоский угол имеет угловую величину,
которая неотрицательна, инвариантна относительно
перемещений (равные плоские углы имеют равные угловые
величины), аддитивна (если плоский угол является
объединением неперекрывающихся плоских углов с той же
вершиной, то его угловая величина равна сумме угловых
величин этих плоских углов) и определённым образом
нормирована (задана единица измерения величины плоского
угла). При этом предполагается, что единица измерения
плоских углов одинакова во всех плоскостях. Из
планиметрии известны две единицы измерения углов — градус и
радиан, которыми мы будем пользоваться и в дальнейшем.
Из планиметрии вам известно, что угол между
параллельными прямыми по определению полагается равным нулю,
а углом между пересекающими прямыми называется
величина наименьшего из плоских углов, образованных этими
прямыми. Эти определения сохраняются и в пространстве.
Нам остаётся только определить угол между
скрещивающимися прямыми.
Определение. Углом между двумя
скрещивающимися прямыми называется угол между пересекающимися
прямыми, параллельными данным скрещивающимся
прямым.
Угол между прямыми обозначается Z(a, Ь). Прямые а
и Ъ называются перпендикулярными, если /.(а, Ь) = тг/2.
Ясно, что пару пересекающихся прямых, о которых идёт
речь в этом определении, можно выбрать в пространстве
бесконечным числом способов. Поэтому нам необходимо
доказать корректность данного определения, т. е. показать,
что величина угла между двумя скрещивающимися
прямыми не зависит от выбора пары пересекающихся прямых,
параллельных им. Это следует из такой теоремы.
114
Глава 3. Векторы в пространстве
Теорема 3.4. Величины двух выпуклых плоских углов
с соответственно параллельными и одинаково
направленными сторонами равны.
Доказательство. Для развёрнутых углов теорема
очевидна. Пусть АОВ и А\О\В\ — плоские углы, не
являющиеся развёрнутыми. Возьмём на сторонах плоского угла
АОВ точки М и N, а на сторонах
плоского угла A\O\Bi — точки М\
и N\ так, что О\М\ = ОМ и O\N\ =
= ON (рис. 3.10).
Четырёхугольник 0ММ\0\ — параллелограмм,
так как его стороны ОМ и О\М\
равны и параллельны,
следовательно, (OOi) || (MMi) и OOi =
= ММ\. Аналогично
доказывается, что (OOi) || (NNi) и OOi =
= NN\. Следовательно, ММ\ =
= AWi, и ввиду транзитивности
параллельности прямых (ММ\) ||
|| (NN\). Поэтому
четырёхугольник NMM\N\ — параллелограмм,
а значит, MN = M\N\. Треугольники M0N и MiOiNi
равны по трём сторонам1^, следовательно, ZAOB =
= ZAiOiBi- П
В заключение этого параграфа мы введём понятие угла
между векторами в пространстве. Пусть даны два
направленных отрезка О А и ОВ с общим началом. Углом между
ними назовём угловую величину наименьшего из плоских
углов, образованных лучами О А и ОВ, если О А ф б и ОВ ф б.
Если же хотя бы один из этих направленных отрезков
нулевой, то угол между ними не определяется.
^Отметим ещё раз, что мы ещё не доказали справедливость
известных из планиметрии признаков равенства треугольников для
треугольников, лежащих в разных плоскостях. Мы сделаем это в главе 8,
не опираясь на результаты предыдущих глав, а пока будем пользоваться
указанными признаками без доказательства.
§ 3.3. Угол между прямыми. Угол между векторами 115
Определение. Углом между двумя векторами
называется угол между изображающими их направленными
отрезками, отложенными от одной точки пространства.
Корректность этого определения следует из теоремы 3.4.
Обращаем ваше внимание на разницу между понятиями
угла между прямыми и угла между векторами: угол между
прямыми не может быть тупым, в то время как угол между
векторами — может.
В дальнейшем мы будем обозначать через Z(a,b) угол
между прямыми а и 6, a Z(а, о) —угол между векторами
а и Ь. Если эти углы измерены в радианах, то Z(a, Ъ) Е
€ [0, тг/2], а /.{а, Ь) е [0, л:]. Ненулевые векторы
называются ортогональными, если угол между ними равен л/2.
Нулевой вектор по определению считается ортогональным
любому вектору.
Рассмотрим несколько задач, в которых угол между
скрещивающимися прямыми легко может быть найден
непосредственно но определению.
Пример 3.5. Найти угол между скрещивающимися
диагоналями двух соседних граней куба.
^9 С
116
Глава 3. Векторы в пространстве
Решение. Обозначим данный куб через ABCDA\B\C\D\
и найдём угол между прямыми АС и А\В (рис. 3.11).
Проведём отрезок А\С\. Очевидно, (AC) || (AiCi) как прямые
пересечения параллельных плоскостей ABC и А\В\С\
плоскостью AAiC. Следовательно, £ВА\С\ — искомый
угол. Рассмотрим АВА\С\. Он равносторонний, так как
его стороны — диагонали равных квадратов. Следовательно,
Z(AC, АХВ) = ZBAiCi = 60°. □
Пример 3.6, Дан куб ABCDA\B\C\D\. Найти угол между
прямыми ACi и А\В.
Решение. Достроим ещё один куб AB'CDAiB^C^Di, как
показано на рис. 3.12. Проведём отрезок АВ\, он паралле-
Рис. 3.12
лен ВА\9 так что /.С\АВ\ искомый. Пусть сторона куба
равна 1. Тогда стороны треугольника АВ\С\ равны: АВ[ = \/2,
АСу = \/3, В'ХС\ = у/5 (проведите соответствующие
вычисления). Поэтому ААВ^Сх прямоугольный с прямым углом
при вершине А (по теореме, обратной к теореме Пифагора).
Следовательно, (ACi) J_ (A\B). □
§ 3.4. Скалярное произведение векторов 117
§ 3.4. Скалярное произведение векторов
Известная вам из планиметрии операция скалярного
умножения векторов определяется в пространстве
аналогично.
Определение. Скалярным произведением двух
ненулевых векторов называется число, равное произведению их
длин на косинус угла между ними. Если хотя бы один
из векторов нулевой, то их скалярное произведение по
определению полагают равным нулю.
Скалярное произведение векторов 3 и Ъ обозначается
а • Ь или (3, Ь). Таким образом, 3 • Ъ = |3| • \Ь\ • cos (p, где <р —
= Z(3, fe), для аф~6 иЬ^б и 3-5 = 6-£=0-5 = 0.
Свойства скалярного произведения
1°. V3, Ь: й-Ь = Ь>а (коммутативность).
2°. V3: 3-3= |3|2; выражение ci-ct называется скалярным
квадратом вектора 3 и обозначается З2.
3°. Скалярное произведение равно нулю тогда и только
тогда, когда сомножители ортогональны.
—> —► —*
4°. V3, b, V&eM: (kU) -b = k(ct-b) (ассоциативность по
отношению к умножению вектора на число).
5°. V 3, ft, ?: 3 • (В + ?) = 3 • $ + 3 • ? (дистрибутивность).
Свойства 1°—3° вытекают непосредственно из
определения скалярного произведения.
Доказательство свойства 4°. Рассмотрим три
возможных случая.
1. Пусть k = 0. В этом случае, очевидно, обе части
доказываемого равенства обращаются в нуль.
2. Пусть k > 0. Тогда
(A3) - Ь = \Ы\ • |6| * cos Z(hd, b) =
|3| • |£| -cos Z(3, b) = й(3, Ь).
118 Глава 3. Векторы в пространстве
3. Пусть k < 0. Тогда
(ka) • Ь = |А£| • |b|. cos Z(№, Ь) =
= |ft| • |3| -1&| -cos(tt - Z(a, &)) - -ЩЩ • |&| - (- cos
= k\U\ ■ |b| • cos Z(3, fe) = *(3, &). □
Наименее тривиально доказательство дистрибутивности
скалярного произведения (свойство 5°). Докажем
предварительно несколько вспомогательных утверждений.
Лемма 3.1. Va, 6: (3 + 6)2 = й2 + 2Я-$+ Ь2.
Рис. 3.13
Доказательство. Отложим векторы Й и Ь так, как
показано на рис. 3.13. Тогда по теореме косинусов из
треугольника ABC имеем
d + b\2 = \Щ2 + \Ь\2 - 2\а\ • |&| -cos(tt - Z(a, b)) =
- |3|2 + |&|2 + 2|a| • \b\ -cos Z(a, b),
следовательно, (a + 6)2 = 32 + 23 • b + b2. П
| Лемма 3.2. Va, b: (a - b)2 = a2 - 23-b-f 62.
Доказательство. Имеем (a — 6)2 = (a+ (—b))2. По
лемме 3.1 получаем
(3+ (-b))2 = a2 + 2a- (-6) + (-b)2.
Пользуясь свойствами 1° и 4° скалярного произведения,
получаем
322 2 □
§ ЗА. Скалярное произведение векторов 119
Лемма 3.3. V3, Ъ: (а + Ь)2 = П2 + 2Ъ2 - (П~ $)2.
Для доказательства достаточно сложить равенства, по
лученные в леммах 3.1 и 3.2.
Доказательство свойства 5°. Подсчитаем (а + Ь 2
двумя способами. С одной стороны,
(а + Ь + с)2 = (3+ (Ь + ?))2 = Я2 + 2а>(Ь
= а2 + 2а • (Ь + ?) + Р + 26 - ?+ ?2
(здесь мы дважды воспользовались леммой ЗЛ). С другой
стороны, пользуясь леммами 3.3 и ЗЛ, запишем
Далее, в силу свойства 4° скалярного произведения и лем
мы 3.2 имеем
ft ?)2 2 b2 ?2 22&
Следовательно,
+ Ь2 + ?2 + 2Ь • ?+ 22
откуда получаем a • (Ь + ?) = a • Ь + U • ?. □
Выведем теперь выражение для скалярного
произведения векторов в координатной форме. Мы будем
рассматривать в пространстве базис специального вида. Пусть базис
{?ь ?2> ?з} таков, что ?i ± ?2> ?2 -L ^з и ?з -L ?ь кроме того,
|?i| = |?2| = |?з| = 1 (такой базис называется ортонормиро-
ванным). Рассмотрим векторы Зиб, заданные
координатами в ортонормированном базисе {ё\9 ?2» ?з}« 2= (л:а> уа, 2а),
120 Глава 3. Векторы в пространстве
Теорема 3,5. В ортонормированном базисе скалярное
произведение векторов равно сумме произведений их
соответствующих координат»
Доказательство. Действительно,
Ъ = (а1 + уа2 ah) (Ь1 + УЬ2 +
= ХаХь
так как ?1.?2 = ?2-?з = ?з*?11::0и^ = ^ = ?| = 1. □
Замечапие. В произвольном базисе (не в
ортонормированном) эта формула неверна.
0^ Упражнение 3.4. Пусть скалярное произведение любых двух
векторов равно сумме произведений их координат в
некотором базисе. Верно ли, что этот базис ортонормированный?
§ 3.5. Примеры решения задач
Поверь в то, что ты знаешь все
ответы, и ты их узнаешь.
Р. Бах. Иллюзии
В этом параграфе мы покажем, как применяются
признаки коллинеарности и компланарности векторов при
решении задач. Кроме того, мы решим задачу о нахождении
длины отрезка и угла между скрещивающими прямыми
с помощью скалярного произведения векторов (другие
применения скалярного произведения к вычислению
расстояний и углов обсуждаются в § 4.8).
Пример 3,7. Плоскость пересекает боковые рёбра SA,
SB, SC и SD правильной четырёхугольной пирамиды
SABCD в точках М, N, Р и Q соответственно (рис. 3.14).
Доказать, что
+ = +
SM^SP SN^SQ'
Решение. Положим, не ограничивая общности, SA =
= SB = SC = SD = 1. Пусть также SM = a, SN = b, SP = с,
SQ = d.
§ 3.5. Примеры решения задач 121
М
Векторы NM, NP и NQ компланарны и NMjfiNP,
поэтому существуют единственные такие числа х и у, что
NQ — xNM + yNP. Разложим обе части этого векторного
равенства по базису {SA, S5, SC}:
= cSC - bSB,
= dSD-bSE = d(Sl + AD) -bSE =
= d (Si - SE + Sd) - bSS = dSl ~(d + b)Sl!i + ds6.
Получаем
dSA - (d + b)SB + ds6 = axSA - b(x + y)SB
Отсюда в силу единственности разложения по базису
получаем d = ax, d + b — b(x + у) и d — су. Следовательно,
Пример 3.8. На диагоналях АВ\ и СА\ боковых граней
треугольной призмы АВСА\В\С\ расположены точки Е nF
соответственно так, что (EF) || (BCi). Найти отношение
длин отрезков EF и ВС\.
122
Глава 3. Векторы в пространстве
В
Рис. 3.15
Решение. Пусть СА = <$> СЁ = Ь, СС[ = ? (рис. ЗЛ5).
Разложим векторы ABi, CA\ и ВС\ по базису {3, &, ?},
используя правило ломаной. Имеем
СМ = СА +
= 2 + ?,
= -ъ
В силу коллинеарности векторов АЕ и
существует
такое число х, что АЕ = #ABi = jc(—3+ fc + ?). Аналогично
существует такое число у, что CF = yCA\ = y(S + ?). По
условию EFJjBCi, следовательно, существует такое число г, что
= zBC[ = z(—& + ?). По«шэавилуломаной, применённому
к ломаной CAEF, имеем АС = АБ + EF + FC, откуда следует,
что -а = х(-
, т.е.
(1 - # - у)а + (х - г)Ъ + (х + z - y)Z = б.
В силу единственности разложения по базису
последнее векторное равенство равносильно трём скалярным:
§ 3.5. Примеры решения задач 123
- х - у = 0, х - г = О и х -\- г - у — О. Отсюда следует,
1 2
что х — г— д, У=£-
Искомое отношение i£F : BCi = |z| = ~. П
о
Пример 3.9. На рёбрах SA и SB тетраэдра SABC
выбраны соответственно точки А\ и Вь причём известно,
что SB\ : SB = m. Точки М и N лежат на отрезках AiB
и СВ\ соответственно, причём CN: СВ\ =р, а отрезок МЛГ
параллелен плоскости ASC. Найти отношение ВМ: BAi.
Решение. Выберем базис в пространстве: SA = a, SB = b,
= ? (рис. 3.16). Обозначим SAi : SA= п и ВМ : BAi = q.
Рис. ЗЛ6
Тогда SAi = па, BAi = BS + SAi = -Ь + па, ВМ =
= —qb + qna. Аналогично SB\ = mb, СВл =CS + SBi = —c +
= =► ► ►
=► —=—► ► -> —►
+ mb и CN =pCB\ = —рд + pmb. По правилу ломаной ВМ +
4- MN + NC + С В = б, откуда следует, что
= -(-qb + qnU) + (-pc+pmb) + (?- b) =
= -nqa+ (q + mp- 1)S+ (1 -p)c.
С другой стороны, поскольку вектор MN параллелен плос
кости ASC, он раскладывается по базису {а, ?} в этой плос
кости: MN = aU+ 7?, где а и у — некоторые действительные
124 Глава 3. Векторы в пространстве
числа. Сравнивая два последних выражения, приходим
к выводу, что q + тр -1 = 0, откуда следует, что q = 1 - тр.
П
Пример 3.10. В правильном тетраэдре ABCD точки М
и N — середины рёбер АВ и CD.
1. Известно, что АВ = а. Найти: а) длину отрезка MN;
б) угол между прямыми MN и ВС.
2. Доказать, что (MN) 1 (АВ) и (MN) I (CD).
Рис. 3.17
Решение. Введём базис й—ВС^ b = BAy ?=BD (рис. 3.17).
1. а) Имеем
следовательно, MN =
д, ^
б) Нам нужно найти угол а между прямыми MN и ВС.
Найдём связь между а и Z (МЛГ, ВС). Из определения
скалярного произведения векторов вытекает, что
cos
Задачи 125
Но угол между прямыми не может быть тупым. Поэтому
если Z(W$9 вб) < J, то a = Z(MNy ВС), а если Z(MN, вб) >
^ ^, то а = 7Г - Z(MN, ВС). И в том, и в другом случае
cos a = I cos Z(MN, ВС)I, следовательно,
cos a =
mn-b6\
\MN\. \вб\ *
= а, то cos а = ^~-, т* е. а = ~.
2. Ясно, что достаточно доказать равенства MN>ВА = 0
и MiVCD = O. Имеем
CD = hs-b + d)-(d-u) =
Задачи
Решение задач является наиболее
характерной и специфической разновидностью
свободного мышления.
У. Джеймс
3.1. В пространстве даны четыре точки А, Б, С и D.
Точки М и N — середины отрезков АВ и CD. Докажите, что
126 Глава 3. Векторы в пространстве
3.2. Дан тетраэдр ABCD. Найдите все такие точки М
пространства, что
3.3. Докажите, что отрезки, соединяющие середины
скрещивающихся рёбер тетраэдра (иногда называемые би-
медианами тетраэдра), пересекаются в одной точке. В
каком отношении они делятся точкой пересечения?
Докажите, что точка пересечения бимедиан совпадает с точкой
пересечения медиан тетраэдра (см. пример 3.3).
3.4. Пусть G и G\ — точки пересечения медиан
тетраэдров ABCD и A\B\C\D\. Докажите, что
АА\
3,5*. На рёбрах АВ, АС и AD тетраэдра ABCD взяты
точки К, L и М так, что АВ = а АК, АС = (3AL и AD = у AM.
а) Рассмотрим всевозможные такие плоскости KLM, что
у = а +/3 + 1. Докажите, что все они проходят через
фиксированную точку.
б) Рассмотрим всевозможные такие плоскости KLM, что
j0 = а + 1 и у = а + 2. Докажите, что все они проходят через
фиксированную прямую.
3.6*. Даны два правильных пятиугольника OABCD и
OA\BiC\D\, не лежащие в одной плоскости. Докажите, что
прямые АА\У ВВ\У СС\ и DD\ параллельны одной
плоскости.
3.7. Через концы трёх рёбер ОАУ ОВ и ОС
параллелепипеда проведена плоскость ABC. Докажите, что точка
пересечения медиан треугольника ABC лежит на
диагонали параллелепипеда. В каком отношении эта точка делит
указанную диагональ?
3.8. Дан куб ABCDAiB\CiDi, точка К — середина его
ребра АА\ш Найдите угол между прямыми:
а) ВК и
Задачи 127
3.9. Точки М и N — соответственно середины рёбер ВС
й AD тетраэдра ABCD, в котором АС = BD, а угол между
прямыми АС и BD равен а. Найдите угол между прямыми
MN и АС.
3.10. Длины рёбер АВ и ВС прямоугольного
параллелепипеда ABCDA\B\C\D\ равны соответственно а и 2а.
Известно, что существует прямая, пересекающая прямые
АЛь ВС и CiDi и образующая с ними равные углы.
Найдите длину ребра АА\ ♦
3.11*. В тетраэдре ABCD длины рёбер АВ, ВС и CD
равны a, ZABC= J, ZBCD = Z(AB, CD) = arccos |. Найдите
длину ребра AD.
3.12. В треугольной пирамиде сумма квадратов длин
сторон основания равна а2, а сумма квадратов длин боковых
рёбер равна Ь2. Найдите длину отрезка, соединяющего
вершину пирамиды с точкой пересечения медиан основания.
3.13. Даны три некомиланарных вектора. Существует ли
ненулевой четвёртый вектор, ортогональный трём данным?
3.14. Четыре луча, выходящих из одной вершины,
образуют попарно углы величины а. Найдите а.
3.15. Даны точки А, В, С и D, не лежащие в одной
плоскости. Найдите точку М, для которой сумма MA2 + MB2 +
+ МС2 + MD2 принимает наименьшее значение.
3.16. Точка пересечения медиан тетраэдра ABCD
одинаково удалена от вершин А и В. Докажите, что
AC2+AD2 =
3.17. Докажите, что для любых четырёх точек простран
ства А, В, С и D справедливо равенство
ABCD
3.18. Докажите, что если две пары противоположных
рёбер тетраэдра перпендикулярны, то перпендикулярны
и два оставшихся противоположных ребра.
Глава 4
Перпендикулярность в пространстве
— Я думаю, Дон, что в моей голове это
просто не может уместиться. Я просто не
знаю, как мне удастся всё это выучить.
— Практикой. Немножко теории и
много практики,—сказал он. —На это уходит
примерно дней десять.
Р. Бах. Иллюзии
§ 4.1. Перпендикулярность прямой и плоскости
...возьми
перо и чистый лист бумаги
и перпендикуляр стоймя
восставь, как небесам опору.
И. Бродский. Пенье без музыки
Определение. Прямая называется перпендикулярной
плоскости, если она перпендикулярна любой прямой,
лежащей в этой плоскости.
То, что прямая а перпендикулярна плоскости а, кратко
записывают так: a J_ а (или а ±а).
Данное нами определение не очень удобно использовать
при проверке перпендикулярности прямой и плоскости.
Гораздо удобнее пользоваться следующей теоремой.
Теорема 4.1 (признак перпендикулярности прямой и
плоскости). Если прямая перпендикулярна двум
пересекающимся прямым, лежащим в плоскости, то она
перпендикулярна этой плоскости.
Доказательство. Пусть в плоскости а даны две
пересекающиеся прямые, Ь и с, а прямая а перпендикулярна этим
прямым. Возьмём в плоскости а произвольную прямую d,
отличную от Ъ и с. Мы должны показать, что прямая а
перпендикулярна прямой d.
5 3ак 3383
130 Глава 4. Перпендикулярность в пространстве
Рис. 4.1
Рис. 4.2
Выберем произвольно точки А и А\ на прямой а, В
и Bi - на прямой Ь, С и Ci - на прямой с, D и Di - на
прямой d (рис. 4Л). Введём векторы 3, Ь, ? и а, изобра-
► ► —► ►
жаемые направленными отрезками AAi, ВВ\9 СС\ и DD\
соответственно. Так как прямые Ь и с пересекаются, то
{£, ?} — базис в плоскости а. По теореме о разложении
вектора по базису существуют такие числа хну, что а = хЪ + yZ.
Умножим обе части этого равенства скалярно на вектор 3
и раскроем скобки, пользуясь дистрибутивностью
скалярного произведения. Получим # • с? = 3 • (xb + у?) = ха • Ъ + уй • ?.
Но так как а±Ь и aJ_c, то 3-Ь = 3*?=0, следовательно,
3-Я = 0, и, значит, aid. □
Ниже мы убедимся, что перпендикулярные прямая и
плоскость действительно существуют.
Пример 4.1. Даны прямая а и точка Л. Доказать, что
через точку А можно провести плоскость, перпендикулярную
прямой а, и притом только одну.
Решение. Приведём построение искомой плоскости и
тем самым докажем её существование. Проведём
плоскость /? через точку А и прямую а (если At а, то (3 —
произвольная плоскость, проходящая через а) и, кроме
того, проведём через а плоскость у, отличную от /3 (рис. 4.2).
Через точку А в плоскости /3 проведём прямую 6,
перпендикулярную прямой а. Пусть она пересекает прямую а
§ 4.L Перпендикулярность прямой и плоскости 131
Рис. 4.3
Рис. 4.4
в точке М. В плоскости у проведём через М прямую с La.
Наконец, через прямые b и с проведём плоскость а. По
построению а1Ьиа!с, где Ъ и с — пересекающиеся прямые,
лежащие в плоскости а. Следовательно, в силу признака
перпендикулярности прямой и плоскости a Lot.
Докажем единственность искомой плоскости.
Предположим, что через А можно провести две плоскости а и а\,
перпендикулярные прямой а. Обозначим через с линию
пересечения плоскостей а и <х\. Так как alaaccaf, то по
определению a L с. Поэтому либо а и с — скрещивающиеся
прямые, либо прямая а пересекается с прямой с в
некоторой точке О.
Рассмотрим первый случай (рис. 4.3). Проведём через
точку А и прямую а плоскость у. Она пересечёт плоскости а
и #i соответственно по прямым Ъ и Ь\9 проходящим через
точку А, Так как а 1 а и a _L с*ь то по определению а 1 Ъ
и а ± Ъ\. Это означает, что в плоскости у существуют две
различные прямые, проходящие через точку А и
перпендикулярные прямой а. Но из планиметрии известно, что это
невозможно.
Во втором случае (рис. 4.4) проведём через прямую а
плоскость у так, что c(/Ly\ Она пересечёт плоскости а и ot\
по прямым Ъ и Ъ\ соответственно, причём Ъ La и Ъ\ L а.
Таким образом, в плоскости через точку О проходят две
прямые, перпендикулярные а, что невозможно. □
132 Глава 4. Перпендикулярность в пространстве
Следующую задачу мы предлагаем вам решить
самостоятельно.
Пример 4.2. Даны плоскость а и точка А. Доказать, что
через точку А можно провести прямую, перпендикулярную
плоскости а у и притом только одну.
Определение. Прямая, перпендикулярная плоскости,
называется перпендикуляром к этой плоскости. Прямая,
не перпендикулярная плоскости и пересекающая её,
называется наклонной к этой плоскости.
§ 4.2. Связь между параллельностью
и перпендикулярностью
Палочки должпы быть попендикулярны.
В. Каверин. Два капитана
Теорема 4.2. Если одна из двух параллельных прямых
перпендикулярна данной плоскости, то и вторая прямая
перпендикулярна этой плоскости.
Доказательство. Пусть даны две параллельные
прямые а\ и п2 и плоскость а, причём известно, что а\ J_ a
(рис. 4.5). Докажем, что а^ -1 ос.
Рис. 4.5
Возьмём в плоскости а две пересекающиеся прямые
и &2- Поскольку а\ J_ а, по определению перпендикуляр
§ 4.3. Теорема о трёх перпендикулярах 133
ности прямой и плоскости а\ J_ 61 и а\ J_ &2- Но так как
то Z(a2, b\) =Z(ai, fei) = 90°. Аналогично/(02, &2) =
y 62) =90°. Значит, a2-L&i иа2-1-&2> и в силу признака
перпендикулярности прямой и плоскости аг -L а. □
Теорема 4.3. Если две плоскости перпендикулярны
одной прямой, то они параллельны.
Доказательство. Пусть даны две плоскости а и J5 и
прямая а, причём известно, что a La и a J_/3. Нужно доказать,
что плоскости а и/3 параллельны. Предположим противное:
а и J3 имеют общую точку М. Тогда через точку М
проходят две плоскости, перпендикулярные данной прямой,
что противоречит результату примера 4.1. Следовательно,
а ||/3. □
с^ Упражнение 4.1. Докажите, что: а) если две прямые
перпендикулярны плоскости, то они параллельны; б) если прямая
перпендикулярна одной из двух параллельных плоскостей,
то она перпендикулярна и другой плоскости.
§ 4.3. Теорема о трёх перпендикулярах
Нас мало. Нас может быть трое...
Б. Пастернак. Из цикла «Я их мог позабыть»
Определение. Параллельное проектирование, при
котором направление проектирования перпендикулярно
плоскости проектирования, называют ортогональным
проектированием.
В дальнейшем, говоря о проектировании, если не
оговорено противное, мы будем иметь в виду ортогональное
проектирование.
Теорема 4.4 (о трёх перпендикулярах). Прямая,
лежащая в плоскости, перпендикулярна наклонной тогда и
только тогда, когда она перпендикулярна проекции
наклонной на эту плоскость.
134 Глава 4. Перпендикулярность в пространстве
Доказательство. Пусть прямая т лежит в плоскости а,
а —наклонная, а\ —её проекция на плоскость а, (AAi) —
перпендикуляр к а (A G а, Aj 6 а\) (рис. 4.6). Так как
Рис. 4.6
± а, то (AAi) J_ т. Проведём через прямые а и а\
плоскость /3.
Пусть т±.а\. Тогда, поскольку m± (AAi), по признаку
перпендикулярности прямой и плоскости mJ_/3, и,
следовательно, т X. а.
Обратно, если т±а, то, поскольку т± (AAi), имеем
т±/3, следовательно, т 1 а\ ♦ □
§ 4.4. Дальнейшие сведения о многогранниках
...прячет с помощью пирамид
горизонтальность свою земля...
И, Бродский, В окрестностях Александрии
Теперь, когда вы познакомились с понятием
перпендикулярности прямой и плоскости, мы продолжим изучение
многогранников и их элементов, начатое в § 2.4. Здесь
мы выведем основные формулы для вычисления площадей
поверхностей многогранников и приведём (без
доказательства) формулы для вычисления их объёмов. При этом под
площадью поверхности многогранника мы понимаем сум-
§ 4Л. Дальнейшие сведения о многогранниках 135
му площадей его граней и полагаемся на интуицию при
использовании понятия объёма.
Отметим ещё раз, что наше знакомство с
многогранниками носит предварительный характер. Мы ещё вернёмся
к ним в гл. 6, где, в частности, будет дано общее
определение геометрического тела. Понятия площади поверхности
и объёма многогранника будут обсуждаться в курсе
стереометрии 11 класса в рамках общей теории площадей
поверхностей и объёмов тел. Там же будут выведены
формулы для объёмов многогранников.
Призма
Определим ещё один элемент призмы — её высоту.
Отрезок перпендикуляра к плоскостям оснований призмы,
заключённый между этими
плоскостями, называют высотой призмы.
Призма называется прямой, если её
боковые рёбра перпендикулярны
плоскостям оснований (рис. 4.7). Прямая
призма, основаниями которой
являются правильные многоугольники,
называется правильной призмой.
Пусть дана произвольная призма
AiA2^.AnAflAf2...Afn (рис. 4.8).
Проведём через точку А", принадлежащую
ребру A\Afly плоскость а,
перпендикулярную этому ребру. Пусть плоскость а
пересекает прямые, содержащие боковые рёбра призмы,
в точках Аг(, ...,А^. Многоугольник А![А!^ ..*А^ будем
называть перпендикулярным сечением призмы (он не
обязательно целиком лежит внутри призмы; см. рис. 4.9).
Пусть боковые рёбра призмы имеют длину I. Вычислим
площадь боковой грани А\А2А/2А!1 по формуле площади
параллелограмма; она равна A"A'J> • / (сторона А![А!2 — высота
параллелограмма). Складывая площади всех боковых гра-
Рис. 4.7
136 Глава 4. Перпендикулярность в пространстве
Рис. 4.8
Рис. 4.9
ней, получаем, что площадь боковой поверхности призмы
равна произведению периметра перпендикулярного
сечения на боковое ребро:
= -P.L
(здесь SfoK обозначает площадь боковой поверхности —
сумму площадей боковых граней, a Pi — периметр
перпендикулярного сечения). В частности, для прямой призмы
к — P*U где Р — периметр основания.
Объём (наклонной) призмы вычисляется по формуле
где S± — площадь перпендикулярного сечения, / — длина
бокового ребра, или по формуле
где SOch — площадь основания призмы, Н — длина её
высоты.
В § 2.4 мы определили частный вид призмы —
параллелепипед. Параллелепипед, боковые рёбра которого
перпендикулярны плоскости его основания, называется прямым.
§ 4.4. Дальнейшие сведения о многогранниках 137
Прямой параллелепипед, в основании которого лежит
прямоугольник, называется прямоугольным.
Замечание. В § 2.4 мы определили прямоугольный
параллелепипед как параллелепипед, все грани которого являются
прямоугольниками. Нетрудно видеть, что данные определения
эквивалентны.
t& Упражнение 4.2. Докажите это утверждение.
Объём прямоугольного параллелепипеда вычисляется
по формуле
V = аЪсу
где а, 6, с — длины трёх его рёбер, выходящих из одной
вершины (которые мы будем называть измерениями
прямоугольного параллелепипеда).
и^ Упражнение 4.3. Докажите, что диагональ d прямоугольного
параллелепипеда связана с его измерениями а, Ь, с
соотношением d2 = а2 + Ь2 + с2.
Прямоугольный параллелепипед, все рёбра которого
равны, называется кубом. Объём куба вычисляется по
формуле
где а — длина ребра куба.
Замечание. В § 2.4 мы определили куб как прямоугольный
параллелепипед, все грани которого — квадраты. Данные два
определения куба эквивалентны.
^ Упражнение 4.4. Докажите это утверждение.
Пирамида
Определим новый элемент пирамиды — её высоту.
Отрезок перпендикуляра, проведённого из вершины
пирамиды к плоскости основания, заключённый между
вершиной и плоскостью основания пирамиды, называется
высотой пирамиды. Основание высоты — общая точка высоты
138 Глава 4. Перпендикулярность в пространстве
и плоскости основания пирамиды — может лежать как
внутри основания пирамиды, так и на границе или вне его
(рис. 4.10).
Рис. 4.10
В § 2.4 мы определили правильную пирамиду как
пирамиду, у которой в основании лежит правильный
многоугольник, а все боковые грани — равнобедренные
треугольники с общей вершиной. Докажем, что основание
высоты правильной пирамиды является центром
правильного многоугольника, лежащего в её основании. Пусть
SА\А2.>.Ап — правильная n-угольная пирамида, SO — её
высота (рис. 4.11). Треугольники A1SA2, A2SA3, .-., AnSAi
равнобедренные, поэтому SAi = SA2 = ... = SAn. Значит,
А2
Рис. 4.11
§ 4.4. Дальнейшие сведения о многогранниках 139
прямоугольные треугольники SOAi, SOA2,..., SOAn имеют
общий катет SO и равные гипотенузы. Следовательно, эти
треугольники равны, и ОА\ = ОА% — ... = ОАп, т.е. О —
центр многоугольника
Замечание. Следующее определение правильной пирамиды:
пирамида называется правильной, если в её основании лежит
правильный многоугольник, а ортогональная проекция
вершины на плоскость основания — центр этого многоугольника,—
эквивалентно приведённому нами выше определению
(доказательство этого утверждения в одну сторону мы только что привели,
доказательство его в другую сторону предоставляется читателю).
Пример 4.3. Доказать, что скрещивающиеся рёбра
правильного тетраэдра перпендикулярны.
Решение. Пусть SABC — правильный тетраэдр, тогда
ААВС правильный, а вершина S проектируется в его
центр — точку О (рис. 4Л2). Рассмотрим наклонную SA
Рис. 4.12
к плоскости АВС и её проекцию АО на эту плоскость. Так
как О — центр правильного ДАВС, то (ВС) J_ (АО). По
теореме о трёх перпендикулярах отсюда следует, что (ВС) ± (AS).
D
Пусть SA\...An — правильная n-угольная пирамида
с апофемой h (рис. 4ЛЗ). Имеем S^saxa2 = -0А1А2 ■ h,
140 Глава 4. Перпендикулярность в пространстве
Рис. 4.13
Рис. 4.14
22* СклаДывая эти
равенства, получаем формулу для вычисления площади
боковой поверхности правильной пирамиды
где Роен — периметр основания.
Объём любой пирамиды вычисляется по формуле
где S0CH — площадь основания, Н — длина высоты
пирамиды.
Усечённая пирамида
Отрезок перпендикуляра к плоскостям оснований
усечённой пирамиды с концами в этих плоскостях называется
высотой усечённой пирамиды (рис. 4.14).
ВЗГ Упражнение 4.5. Докажите, что площадь боковой
поверхности правильной усечённой пирамиды можно вычислить по
§ 4.5. Угол между прямой и плоскостью 141
формуле
где Р и р — периметры оснований пирамиды, А — её апофема.
Объём любой усечённой пирамиды можно найти по
формуле
где S\ и S2 —площади оснований, if— высота пирамиды.
§ 4.5. Угол между прямой и плоскостью
...Итак, кому ж, как не
мне, катету, незриму, нему,
доказывать тебе вполне
обыденную теорему
обратную, где, муча глаз
доказанных обильем пугал,
жизнь требует найти от нас
то, чем располагаем: угол.
И. Бродский. Пенье без музыки
Определение. Углом между наклонной и плоскостью
называется угол между наклонной и её проекцией на эту
плоскость.
Если прямая параллельна плоскости или лежит в ней,
то угол между прямой и плоскостью по определению
считается нулевым. Если прямая перпендикулярна плоскости,
то угол между ними по определению считается равным ^.
Угол ср между прямой а и плоскостью а обозначается
через Z(a, а). Из определения вытекает, что 0 < ср ^ ^.
Теорема 4.5. Угол между наклонной к плоскости и её
проекцией на эту плоскость есть наименьший из углов
между наклонной и каждой прямой, лежащей в этой
плоскости.
142 Глава 4. Перпендикулярность в пространстве
Доказательство. Пусть А\ — проекция точки А на ^
скость of, (АВ) — наклонная к плоскости а, В € а (рис. 4.15);
Рис. 4.15
Пусть / — прямая в плоскости а. В силу определения угла
между скрещивающимися прямыми достаточно
рассмотреть только прямые, проходящие через точку В. Обозначим
угол между прямой АВ и плоскостью а через (р, тогда
ZABA\ = ср. Далее, пусть Z((AB), I) = у. Докажем, что
ср^у.
Если I и (BAi) —одна и та же прямая, то (р = у.
Если I А. (ВА\), то по теореме о трёх перпендикулярах
/ J_ (АВ) и у = £-♦ Теорема верна, поскольку ср < -~.
Во всех остальных случаях построим (АВ\) ±l> B\ e I.
Обозначим АВ — а. Из AABBi находим ABi = a sin у, из
ААВА\ находим AAi=asin<jp. Так как AAB\Ai
прямоугольный и АВ\ — его гипотенуза, то АА\ < АВ\
(перпендикуляр короче, чем наклонная). Следовательно, a sin (p <
< a sin у и sin (р < sin у. Функция у = sin x строго возрастает
, поэтому отсюда следует, что (р < у. О
на отрезке
к
О -
и' 2
§ 4.6. Расстояние между фигурами
143
§ 4.6. Расстояние между фигурами
Страус всегда находится на равном
расстоянии от своего клюва и своего хвоста.
Ж. Ренар
Определение. Если среди всех расстояний между
точками, одна из которых принадлежит фигуре Фх, а другая —
фигуре Фг (рис. 4.16), существует наименьшее, то его
называют расстоянием между фигурами Ф\ и
Рис. 4.16
Расстояние между фигурами Ф1 и Ф2 обозначается
через |О(Фь Фг)* Согласно определению
р(ФьФ2)= min M1M2.
М£Ф
Замечание. 1. Из определения следует, что если фигуры Ф1
и Фг имеют общую точку, то р(Фь Фг) =0.
о
Рис. 4.17
144 Глава 4. Перпендикулярность в пространстве
2. Расстояние между фигурами определено не для любых
фигур. Действительно, например, две ветви Ф\ и Фг графика
функции у = 7~г (Рис* 4.17) не имеют общих точек, но существуют
такие точки М\ € Ф\ и Мг € Фг, что расстояние между М\ и
сколь угодно мало.
3. Понятие расстояния от точки до фигуры — частный случай
введённого понятия расстояния между двумя фигурами.
Расстояние между точкой и плоскостью
Докажем, что расстояние от точки до плоскости
равно расстоянию от этой точки до её проекции на эту
плоскость.
Пусть даны точка М и плоскость а. Докажем, что
р(М, а) = ММь где М\ —проекция точки М на
плоскость а.
Если М е а, то р (Му а) = 0.
Пусть М £ а, и пусть Мг — произвольная точка
плоскости а у отличная от М\ (рис. 4.18). Поскольку в прямо-
Рис. 4.18
угольном треугольнике ММ\М2 гипотенуза ММ2 длиннее
катета ММ\У то ММ\ — искомое расстояние от М до а.
Расстояние между скрещивающимися прямыми
Определение. Общим перпендикуляром двух
скрещивающихся прямых называется отрезок, концы которого
лежат на данных прямых, перпендикулярный к ним.
§ 4,6, Расстояние между фигурами
145
Теорема 4.6. Общий перпендикуляр двух
скрещивающихся прямых существует и единствен.
Доказательство. Существование. Обозначим
данные скрещивающиеся прямые через а и Ъ. Проведём через а
и Ъ параллельные плоскости а и /3 (пример 2.1). Проекцией
прямой а на плоскость J3 является прямая а\, параллельная
а (свойство параллельных плоскостей; см. § 2.2).
Обозначим B = bDai (рис. 4.19). Точка В —проекция некоторой
Рис. 4.19
Рис. 4.20
точки А, принадлежащей прямой а. Так как (АВ) J_/3, bc/3,
то {АВ) _1_ Ь, (АВ) _L а\. Так как а \\ аи то (АВ) J_ а.
Следовательно, [АВ] — общий перпендикуляр прямых а и Ь.
Единственность. Предположим, что прямая MN,
где Мее, Neb, отличная от АВ9 также перпендикулярна
прямым а и Ь. Проведём в плоскости /3 через точку N
прямую аг, параллельную а (рис. 4.20). Так как (MN) ±а, аг || а,
то (MN) J_a2. Кроме того, (MN) Lb. Значит, (MN) 1/3,
следовательно, (MN) \\ (АВ) (см. упражнение 4.1 а). Через
параллельные прямые MN и АВ можно провести плоскость,
в которой лежат прямые а и &. Но эти прямые по условию
скрещиваются. Противоречие. □
146 Глава 4. Перпендикулярность в пространстве
Докажем, что расстояние между скрещивающимися
прямыми равно длине их общего перпендикуляра.
Действительно, пусть а и ft—две скрещивающиеся
прямые, [АВ] — их общий перпендикуляр, Аеа, Beb. Пусть М
и N — произвольные точки на прямых а и Ъ соответственно
(рис. 4.21). Пусть К — проекция точки М на плоскость /3.
Тогда MN ^ МК = АВ, т. е. АВ < MN, что и требовалось
доказать.
Рис. 4.21
Рис. 4.22
■^Упражнение 4.6. Докажите, что:
1) расстояние между прямой и параллельной ей
плоскостью равно расстоянию от произвольной точки прямой до
данной плоскости;
2) расстояние между двумя параллельными плоскостями
равно длине отрезка перпендикулярной к ним прямой, концы
которого принадлежат этим плоскостям.
Пример 4.4. Найти расстояние между
скрещивающимися рёбрами правильного тетраэдра с ребром длины а.
Решение. Пусть SABC — правильный тетраэдр, М
—середина [АВ], N — середина [SC] (рис. 4.22). Докажем, что
[MN] — общий перпендикуляр скрещивающихся прямых
АВ и SC. Действительно, SM = CM как высоты в равных
§ 4.7. Применение теорем о перпендикулярности 147
правильных треугольниках ABS и ABC. Значит, ASMC
равнобедренный, [MN] — его медиана, проведённая к
основанию, следовательно, (MN) J_ (SC). Аналогично (MN)
±АВ. Итак, р((АВ), (SC))=MN.
Из прямоугольного треугольника MNC находим
§ 4.7. Применение теорем о перпендикулярности
к решению задач
Хоть мне и хотелось бы принять все те
восхваления, которые ты мне столь
безмерно воздаёшь, я должен чистосердечно
признаться тебе: это очень просто,
Р. Бах. Иллюзии
Рассмотрим сначала две задачи, в решении которых
используется теорема о трёх перпендикулярах.
Пример 4.5. В тетраэдре SABC плоские углы ASB, BSC
и CSA прямые. Доказать, что ортогональной проекцией
вершины S на плоскость ABC является ортоцентр1*
треугольника ABC.
Решение. Из условия вытекает, что (AS) J_ (BS) и (AS) J_
-L(CS), следовательно, по признаку перпендикулярности
прямой и плоскости (AS) J_ (BSC). Прямая ВС лежит в
плоскости BSC, поэтому (AS) J_ (ВС). Пусть Я — ортогональная
проекция точки S на плоскость ABC (рис. 4.23). Тогда
(АЯ) — проекция прямой AS на эту плоскость. По теореме
о трёх перпендикулярах (АН) ± (ВС). Аналогично
доказывается, что (ВН) _L (AC) у следовательно, Я —ортоцентр
треугольника ABC. □
Пример 4.6. Дан куб ABCDA\B\C\Di. Доказать, что его
диагональ А\С перпендикулярна (BDC\) (рис. 4.24).
!)Точка пересечения высот.
148 Глава 4. Перпендикулярность в пространстве
и^у с
Рис. 4.23
Рис. 4.24
Решение. Прямая А\С — наклонная к плоскости ABC,
прямая АС — её проекция на эту плоскость, (BD) J_ (AC)
как диагональ квадрата ABCD. Следовательно, по теореме
о трёх перпендикулярах (BD) J. (AiC). Аналогично
доказывается, что (BCi) J_ (AiC) (при этом рассматривается
плоскость ВСВ\). Итак, прямая AiC перпендикулярна двум
пересекающимся прямым в плоскости BDC\. По признаку
перпендикулярности прямой и плоскости (AiC) ± (BDCi).
□
Замечание. Рассматриваемая плоскость делит диагональ
куба в отношении 2:1, считая от вершины А\ (этот факт нетрудно
доказать, используя рис. 4.24 и 4.25).
§4.7. Применение теорем о перпендикулярности 149
Прежде чем решать следующую задачу, сделаем
небольшое отступление. Некоторые теоремы планиметрии
допускают прямое обобщение на пространственный случай.
Например, утверждение о медианах тетраэдра (пример 3.3)
является трёхмерным аналогом теоремы о медианах
треугольника. Однако так бывает не всегда. Например, из
планиметрии известно, что высоты1* произвольного
треугольника пересекаются в одной точке. Оказывается,
аналогичное утверждение в пространстве, вообще говоря, не
имеет места: существуют тетраэдры, высоты2^ которых
не пересекаются. Действительно, рассмотрим
равнобедренный треугольник ABC (АВ = АС). На его основании ВС
возьмём точку D, не являющуюся серединой отрезка ВС,
и проведём через D перпендикуляр к плоскости ABC.
Возьмём на этом перпендикуляре точку S и соединим её с
точками А, В и С (рис. 4.26). В тетраэдре SABC высоты,
Рис. 4.26
проведённые из вершин А и S, не пересекаются.
Докажем это. Высота, проведённая из вершины S, —это прямая
SD. Так как (SD) 1 (ABC), то (SD) ± (AAi), где (AAi) -
высота треугольника ABC. Но (AAi) ± (ВС),
следовательно, по признаку перпендикулярности прямой и плоскости
высотами здесь понимаются не отрезки, а прямые.
2)См. предыдущее примечание.
150 Глава 4. Перпендикулярность в пространстве
(АА\) ± (SBC), т.е. прямая АА\ является высотой
тетраэдра. Но А\ — середина отрезка ВС, a D — нет, поэтому
(АА\) - (SD) согласно признаку скрещивающихся прямых.
Тем не менее существуют тетраэдры (например,
правильный), у которых высоты пересекаются в одной точке.
Точку пересечения высот тетраэдра, если она существует,
мы будем называть ортоцентром, а тетраэдры,
обладающие ортоцентром,— ортоцентрическими.
Пример 4.7. Доказать, что тетраэдр является ортоцен-
трическим тогда и только тогда, когда у него имеются две
пары скрещивающихся взаимно перпендикулярных рёбер.
Решение. Заметим сначала, что если две пары
противоположных рёбер тетраэдра перпендикулярны, то и
оставшиеся два ребра перпендикулярны (задача 3.18).
Докажем теперь, что если в тетраэдре ABCD (ВС) J_
± (AD), то высоты (BBi) и (СС\) пересекаются в точке Hi,
высоты (АА\) и (DD\) — в точке Яг, причём (Н1Н2) —
общий перпендикуляр к (ВС) и (AD) (рис. 4.27).
Рис. 4.27
Действительно, пусть I — общий перпендикуляр к (ВС)
и (AD). Проведём плоскость а через I и (ВС). Высоты
§4.7. Применение теорем о перпендикулярности 151
(ВВ\) и (CCi) перпендикулярны (AD), следовательно, они
лежат в плоскости а, а значит, пересекаются в
некоторой точке Hi (почему невозможна параллельность этих
высот?). Аналогично, рассматривая плоскость /?,
проходящую через I и (AD), получаем, что высоты (AAi) и (DD\)
пересекаются в некоторой точке if 2 • Поскольку Н\ — точка
пересечения двух высот треугольника ВСХ, она должна
лежать и на третьей его высоте, т. е. на прямой I. Аналогично
доказывается, что Нч 6 L
Из доказанного утверждения вытекает, что в
рассматриваемом тетраэдре все высоты попарно пересекаются,
следовательно (задача 1.1), они пересекаются в одной точке
(почему они не могут лежать в одной плоскости?). Итак,
в одну сторону требуемое утверждение доказано.
Для доказательства обратного утверждения установим
сначала, что если высоты (ВВ\) и (СС{) тетраэдра ABCD
пересекаются, то (AD) _]_ (ВС). Действительно, каждая из этих
высот перпендикулярна (AD), поэтому проходящая через
них плоскость перпендикулярна (AD), т.е. и (ВС) J_ (AD),
так как (ВС) лежит в указанной плоскости. Аналогично
доказывается, что если пересекаются высоты (AAi) и
(ВВ\)9 то (АВ) ± (DC)у а если пересекаются высоты (AAi)
и (CCi), то (AC) _L (BD). Тем самым утверждение задачи
полностью доказано. D
Отметим, что ортоцентрический тетраэдр обладает
рядом красивых свойств, на которых мы не имеем
возможности здесь останавливаться. Часть из них будет
сформулирована в виде задач к этой главе (задачи 4.12, 4.13; см. также
[Прасолов, Шарыгин, 1989, § 6.5]).
В заключение мы разберём задачу, в которой требуется
построить сечение, заданное условием
перпендикулярности некоторой прямой. Обращаем ваше внимание на то,
что на рисунках изображения двух взаимно
перпендикулярных прямых, вообще говоря, не обязательно должны быть
перпендикулярными (так как параллельное
проектирование может не сохранять величины углов)» Это обстоятель-
152 Глава 4. Перпендикулярность в пространстве
ство затрудняет построение сечений, заданных условием
перпендикулярности. Чтобы преодолеть это затруднение,
обычно на рисунке определяют положение основания
перпендикуляра по отношению к положению каких-либо точек,
расположенных уже известным образом» Это делается либо
прямым вычислением, либо из других соображений.
Поясним сказанное на примере.
Пример 4.8. Все рёбра правильной четырёхугольной
пирамиды SABCD имеют длину 2. Точки М и N —
середины рёбер AS и АВ соответственно. Построить сечение
пирамиды плоскостью, проходящей через точку М
перпендикулярно прямой CN, и найти площадь этого сечения.
Решение. Обозначим секущую плоскость через а и
предположим, что искомое сечение построено. Так как a J_ (CN),
то прямая CN перпендикулярна любой прямой, лежащей
в плоскости а, в частности линии пересечения плоскостей а
и ABC. Кроме того, плоскость а должна содержать
перпендикуляр, опущенный из точки М на плоскость ABC (этот
перпендикуляр параллелен высоте SO пирамиды).
Действительно, если точка М\ — основание перпендикуляра,
опущенного из точки М на плоскость ABC, а точка L —
основание перпендикуляра, опущенного из точки Mi на прямую
CN, то по теореме о трёх перпендикулярах (ML) ± (CN).
А так как (MiL) ± (CN), то (MMiL) _L (CN). Но через
точку М проходит единственная плоскость, перпендикулярная
прямой CN (пример 4.1), поэтому а и (MMiL) —одна и та
же плоскость.
Отсюда вытекает следующее построение (рис. 4.28).
Сначала строим изображение центра основания пирамиды —
точку О пересечения диагоналей АС и BD основания, затем
строим отрезок SO — изображение высоты пирамиды.
После этого через точку М проводим прямую, параллельную
прямой SO, до пересечения с отрезком АС в точке Mi. Тем
самым мы построим изображение перпендикуляра,
опущенного из точки М на плоскость ABC. Остаётся построить
изображение перпендикуляра к прямой CN> проходяще-
§4.7. Применение теорем о перпендикулярности 153
М
Рис. 4.29
го через точку М\. Пусть этот перпендикуляр пересекает
прямую CN в точке L. Уточним положение точки L
вычислением, обратившись к рис. 4.29. По теореме Пифагора
CN2 = BC2 + BN2 = 4 + 1 = 5, т. е. CN= л/Ь. Пусть К= (CN) П
П (BD). Так как К — точка пересечения медиан треугольни-
2 2\/5
ка ABC у то СК = |CiV = -jp. Заметим, что М\ —
середина [ОА], поскольку М — середина [AS], a (MMi) || (SO).
3 3\/2
Следовательно, CAfi = т^С= -^-. Теперь из подобия
прямоугольных треугольников CLM\ и С(Ж получаем, что
CL =
• ОС =
, т. е.
= ^. Тем самым положение
точки L определено. Для того чтобы её построить,
достаточно отложить на [CN] от точки N отрезок NL длины
jfiCN (задача деления отрезка на равные части известна
из планиметрии и решается с помощью теоремы Фалеса).
Пусть теперь (МгЬ) П (АВ) = Q, (MiL) П (AD) = Р.
Заметим, что Q € [АВ], а Р Е [AD]. Действительно, из подобия
треугольников LNQ и ВЛГС (рис. 4.30) следует, что
LN - CN 10
NB
154 Глава 4. Перпендикулярность в пространстве
N Q
Рис. 4.30
Поэтому NQ<NB, значит, Qe [АВ]. Из подобия
треугольников APQ и BNC следует, что
AQNB
ВС
NQ)NB
il-1
ВС
3
4'
поэтому Р € [AD]. Соединив точки Р и Q с точкой М,
получаем искомое сечение (рис. 4.28).
Действительно, по построению (ММ\) J_ (ABC), a (CN) с
С (ABC), следовательно, (ММ\) 1 (CN). Опять-таки по
построению (PQ) -L (CN), следовательно, по признаку
перпендикулярности прямой и плоскости (MPQ) J_ (CN).
Вычислим площадь сечения. Имеем
S
mpq =
PQ = | • (±
PQ.
Длину высоты пирамиды находим из прямоугольного тре
угольника ASO:
SO2 = SA2 - АО2 -4-2 = 2,
т. е. SO = \/2. Длину отрезка PQ находим из прямоугольно
го треугольника APQ:
^_ 9
16 + 4
45
16'
т. е. PQ
3v/5
. Итак,
3\/lO
16 #
П
§ 4.8. Нахождение расстояний и углов 155
§ 4.8. Нахождение расстояний и углов
с помощью векторов
— Не желаете ли, чтобы я помог
вам считать? — вызвался Швейк. —
Я в этих делах разбираюсь.
Я. Гашек. Похождения бравого солдата Швейка
В § 3.5 мы использовали векторы для вычисления
угла между скрещивающимися прямыми. Здесь мы
продемонстрируем, как векторный аппарат позволяет находить
расстояния и углы в различных геометрических
конфигурациях. Несомненным достоинством описываемого метода
является его универсальность и алгоритмичность. К
сожалению, это нередко «компенсируется» довольно большим
объёмом вычислений. Однако если простое и красивое
геометрическое решение не приходит в голову, векторы всё
же позволяют решить задачу.
Итак, перейдём к изложению метода.
Расстояние между скрещивающимися прямыми
Пусть в пространстве задана прямая 1\ с известным
направляющим вектором1* ai, прямая /г с известным
направляющим вектором #2 и точки А\ и Аг, лежащие соот-
ветственно на 1\ и h, кроме того, известен2* вектор А\ Аг =
Пусть [Р\Р2\ — общий перпендикуляр к 1\ и 1% {Р\ €
1*2 €.h\ см. рис. 4.31). Задача заключается в нахождении
►
►
длины этого отрезка. Представим вектор Р\Р2 в виде суммы
► ► У
Р\А\ + А\А2 + ^2^2- Затем, пользуясь коллинеарностью
векторов Р\А\ и d\, A2P2 и Зг, получим для вектора
представление Р\Р2 = х&1 + У&2 + ^> где х и у — неизвестные
пока числа. Эти числа можно найти из условия
перпендикулярности вектора Р1Р2 векторам й\ и Зг, т. е. из следующей
направляющим вектором прямой мы понимаем ненулевой
вектор, параллельный этой прямой.
2)Здесь и ниже, когда мы говорим, что вектор известен, мы
подразумеваем, что известны его координаты в некотором базисе.
156 Глава 4. Перпендикулярность в пространстве
Рис. 4.32
системы линейных уравнении:
=0,
=0.
После этого находим длину вектора Р1Р2:
Пример 4.9. Вычислить расстояние между
скрещивающимися диагоналями двух соседних граней куба с ребром а.
Решение. Пусть дан куб ABCDA\B\CiD\ с ребром а.
Найдём расстояние между прямыми AD\ и DC\ (рис. 4.32).
[
Введём базис {3, &, ?}, где a = ADy b = DC, ?= DD[. Для
удобства дальнейших вычислений составим «таблицу умно-
ъ
й
а2
0
0
ь
0
а2
0
д
0
0
а2
Таблица 4.1
§4,8. Нахождение расстояний и углов 157
жения» векторов базиса, в которую занесём попарные
скалярные произведения базисных векторов (таблица 4.1). За
направляющие векторы прямых AD\ и DC\ можно взять
► ► -►
AD\ = ? - а и DCi = Ъ + ?♦ Если [Р1Р2] — общий
перпендикуляр к рассматриваемым прямым, то Р\Р2 = х(?— 3) +
+1/ (ft + ?) + с?• Составим систему уравнений для нахождения
неизвестных чисел х и у:
' [*(?- 3) +у(£ + ?) +3] • (?- 2) = О,
С помощью «таблицы умножения» приведём эту
систему к равносильной:
' 2х + у-1 = 0,
<
2 1
Отсюда находим jc = ^, у = — ^. Тогда
о О
П
Расстояние от точки до плоскости.
Угол между прямой и плоскостью
Пусть в пространстве заданы плоскость а с известным
базисом {а, 6}, точка А, лежащая в этой плоскости, и
точка М вне её, причём вектор AM = ? предполагается
известным (в том же базисе, что и S и Ь). Пусть N — ортогональная
проекция точки М на плоскость а (рис. 4.33). Задача
заключается в нахождении длины отрезка MN, а также угла
между прямыми AM и AN.
Представим вектор MN в виде разности векторов А1ч
и AM, а затем, пользуясь компланарностью векторов
AN, й и by запишем его в виде MN = ха + уЬ — F, где х
и у — неизвестные пока числа. Эти числа можно найти из
158 Глава 4. Перпендикулярность в пространстве
Рис. 4.33
условия перпендикулярности вектора Mis' векторам S и &,
т.е. из следующей системы линейных уравнений:
' (xa + yb-?)•&= О,
Затем, зная х и j/, найдём MN~ J(ха + уЪ — ?)2. Угол
находится так: если AN = O, то, очевидно, прямая AM перпен
дикулярна плоскости а, если же AN ф б (т. е.
то
cos Z(AM, a) = cos
, A/V) =
Пример 4Л0. В кубе ABCDA\B\C\D\ с ребром а найти
расстояние от центра грани AA\D\D до плоскости BC\D.
Решение. Обозначим центр грани AA\D\D через О
(рис. 4.34). Введём базис {3, ft, с}, где а = DA, b = DC> ? =
= DD\. «Таблица умножения» векторов этого базиса такая
же, как и в примере 4.9 (таблица 4.1).
Векторы DB = а + Ъ и DC\ = b + ? образуют, очевидно,
базис в плоскости BC\Dy а в качестве вектора Р возьмём
вектор DO = ^ (2 + ?). Тогда если О\ — ортогональная
проекция точки О на (BCi-D), то
ООл = х/г* ' ^ч ' ""'*"' ' ^ч
§ 4.8. Нахождение расстояний и углов
159
Составим систему уравнений для нахождения неизвестных
чисел х и у:
Используя «таблицу умножения», приведём эту систему
к равносильной:
4у= 1.
Отсюда находим х = у = ^. Тогда
Об[ - i
п
Пример 4.11. В кубе ABCDAiBiCiDi найти угол между
прямой BD\ и плоскостью BC\D.
Решение. Пусть длина ребра куба равна а. Введём тот
же базис, что и в предыдущем примере. Обозначим через
160 Глава 4. Перпендикулярность в пространстве
ортогональную проекцию точки D\ на плоскость BC\D. To
гда
= x(3+b)+y(b £
Условия перпендикулярности вектора D1D2 векторам DB
и DC\ приводят к системе линейных уравнений
[ х (а + Ъ) + у (Ъ + ?) + а + Ъ - Z\ • (а + $) = 0,
[х (а + Ь) + у (Ъ + ?) + а + b - ?] • (Ъ + ?) = 0,
откуда получаем
Тем самым мы получили, что £1>2 — — ^ (а + Ь) + ^ (6 + ?) =
= —■53— о^+ о?- Теперь найдём косинус искомого угла ср:
о о о
=
\DtB\-\BD2
2л/2
Следовательно, Z(BDi, BCiD) — arccos —5—. □
о
В рассмотренных примерах «таблица умножения»
векторов выглядела достаточно просто. Это объясняется тем,
что при решении использовался прямоугольный базис.
Заметим, однако, что при решении многих задач
пользоваться прямоугольным базисом неудобно, а более естественно
работать в некотором косоугольном базисе (пример ЗЛО).
Чаще всего выбор базиса определяется видом данного в
§ 4.9. Геометрический подход 161
условии задачи многогранника, например, в качестве
базиса часто выбирают векторы, изображаемые тремя его
некомпланарными рёбрами, выходящими из одной
вершины (правда, может случиться, что и такой базис по тем или
иным причинам неудобен). Удачный выбор базиса довольно
важен, так как он позволяет свести к минимуму объём
проводимых вычислений. Наконец, бывают случаи, когда
условие задачи не позволяет выбрать базис с полностью
определённой «таблицей умножения». Тогда необходимо
получить дополнительные уравнения, связывающие
недостающие элементы. Примеры подобных задач вы найдёте
в конце этой главы.
§ 4.9. Геометрический подход к пахождепию
расстояний и углов
Генри снова кивнул, над его головой
поднялось облачко табачного дыма.
— В первых примерах тебе навязывалось
определённое однобокое
представление,—заметил он, — я подумал, что будет справедливо,
если будет представлена и противоположная
сторона, чтобы ты мог составить целостную
картину.
Р. Желязны. Одержимый волшебством
Задачи на вычисление расстояний и углов, которые
были решены нами в предыдущем параграфе с помощью
векторов, могут быть решены и чисто геометрически. Здесь
мы хотим познакомить вас с некоторыми полезными
геометрическими идеями.
Расстояние между скрещивающимися прямыми можно
находить с помощью ортогонального проектирования.
Основная идея этого метода заключена в следующей теореме.
бЗак 3383
162 Глава 4. Перпендикулярность в пространстве
Рис. 4.35
Теорема 4.7. Расстояние между двумя
скрещивающимися прямыми равно расстоянию от точки пересечения
одной из этих прямых с перпендикулярной ей плоскостью
до проекции другой прямой на эту плоскость.
Доказательство. Пусть а\ и а2 — данные прямые, а —
плоскость, перпендикулярная а\, А — точка пересечения а\
с плоскостью а, а'2 — проекция а2 на ту же плоскость,
[PiP2] — общий перпендикуляр к а\ и а2, Pi € аь Р2 € а2
(рис. 4.35). Докажем, что р(аь а2) = р(А, аг2).
Проекцией точки Pi на плоскость а является точка А,
а проекцией точки Р2 на эту плоскость — некоторая точка В.
Следовательно, проекцией отрезка Р1Р2 на плоскость а
является отрезок АВ. Так как а\ J_ a, a (P1P2) -1 аь то
(PiP2) || а либо (PiP2) С а (почему?). Поэтому [PiP2] || [AB]
или PiP2 и АВ — один и тот же отрезок, и, следовательно,
PiP2 = АВ. Остаётся показать, что (АВ) A.af2.
Пусть (PiP2) || ее. Если а2 || а, то а'2 || а2, a если а2 с а,
то а2 и а2 — это одна и та же прямая. В обоих случаях
^(PiP2> я2) = ^/2 (теорема 3.4). Если же прямая а2 и
плоскость а не параллельны, то (АВ) J_a2, так как (PiP2) J-a2,
а (АВ) || (PiP2). Следовательно, по теореме о трёх
перпендикулярах (АВ) 1 а'2.
Случай (PiP2) С ос рассматривается аналогично. □
§ 4.9. Геометрический подход
163
t /
Рис. 4.36
Покажем, например, как с помощью проектирования
можно решить пример 4.9. Пусть дан куб ABCDA\B\C\D\
с ребром а. Найдём расстояние между прямыми AD\
и jDCi. Для этого спроектируем куб на плоскость,
проходящую через вершину А и перпендикулярную прямой AD\
(рис. 4.36). Согласно доказанной теореме достаточно найти
расстояние от точки1* Аг до прямой D'C^. Так как плоскость
A\B\CD перпендикулярна прямой ADi, то прямоугольник
' равен прямоугольнику A\BiCD. Его стороны
равны а и а\/2, следовательно, А!В1 = a, A!Df = -^= и В7!)' = - _
V2 \/2
(из AA'B'D по теореме Пифагора). Искомое расстояние
получим, выразив площадь треугольника AlB!Df двумя
A'Df
способами: h — —
а
Заметим, что, обратившись к рис. 4.35, можно найти
и угол между скрещивающимися прямыми.
Действительно, если обозначить искомый угол Z(ai,a2) через ср, то,
очевидно, ср = т£ - Z(a2, a). Если на прямой аг дан отрезок
длины d, а di — длина его проекции на плоскость а, то
(рис. 4.35) cos Z(a2, ос) = -^-, следовательно, sin <p = -^-.
^Буквами со штрихами мы обозначаем проекции соответствующих
вершин куба.
164 Глава 4. Перпендикулярность в пространстве
Найдём таким способом угол между прямыми AD\ и DC
из предыдущего примера. Так как C\Df = B'D' = ^=-, а
DL\ = av А то sin ^ =
Другое соображение, полезное при вычислении
расстояния между скрещивающимися прямыми, состоит в
следующем: расстояние между скрещивающимися прямыми
равно расстоянию между параллельными плоскостями,
проведёнными через эти прямые. (Для доказательства
этого утверждения вспомните, как мы строили общий
перпендикуляр к скрещивающимся прямым; см. также
упражнение 4.6.)
Дадим теперь ещё одно (третье) решение примера 4.9.
Рассмотрим плоскости AB\D\ и BC\D> содержащие
прямые AD\ и DC\ (рис. 4.37). Они параллельны (почему?).
Согласно результату примера 4.6 (см. также замечание к
нему) эти плоскости перпендикулярны диагонали А\С куба
и делят её на три равные части. Поэтому искомое
расстояние равно одной трети диагонали куба, т.е. -~%
V3
При геометрическом способе нахождения расстояния от
точки до плоскости и угла между наклонной и плоскостью
§ 4.9. Геометрический подход
165
Рис. 4.38
главная трудность заключается в определении положения
основания перпендикуляра, опущенного из точки на
плоскость. Во многих случаях его можно определить исходя из
параллельности этого перпендикуляра какому-либо
другому перпендикуляру к рассматриваемой плоскости,
основание которого находится в известной точке. С помощью
этого соображения можно по-другому решить примеры 4.10
и 4.11.
Пример 4,12. В кубе ABCDA\B\C\D\ с ребром а найти
расстояние от центра грани AA\D\D до плоскости BC\D.
Второе решение. Пусть точка О — центр грани AA\D\Dy
а О7 — её проекция на плоскость BC\D (рис. 4.38). Так как
(AiC) 1 (BCiD) (пример 4.6), то (OOf) \\ (АХС). Если А[ -
проекция точки А\ на плоскость BC\D (т. е. А\ = (А\С) П
П (BCiD)), то <У принадлежит [DA'J и делит этот отрезок
пополам (здесь мы воспользовались свойствами
параллельного проектирования). Следовательно,
оо' =
2 3
%
так как плоскость BC\D отсекает одну треть от диагонали
куба. □
166 Глава 4. Перпендикулярность в пространстве
Пример 4.13. В кубе ABCDAiB\C\Di найти угол между
прямой BD\ и плоскостью BC\D.
Второе решение. Пусть длина ребра куба равна а,
точка О — центр куба (точка пересечения его диагоналей). Так
как (А\С) 1 (BCiD), то точка О7 пересечения (AiC) и (BC\D)
является проекцией точки О на плоскость BC\D (рис. 4.39).
Поэтому прямая ВО1 — проекция прямой BD\ на эту
плоскость. Искомый угол ср находим из прямоугольного
треугольника ОБО1:
ОО1
1
3'
т.е. ср = arcsin «♦ □
Разумеется, возможны и другие способы решения
разобранных задач. Например, расстояния можно находить с
помощью метода вспомогательного объёма, который будет
рассмотрен нами в § 9.3.
В заключение мы приведём пример ещё одной задачи,
которая просто решается с помощью проектирования, в то
время как её векторное решение требует проведения
большого числа выкладок.
Пример 4.14. В основании прямоугольного
параллелепипеда ABCDA\B\C\D\ лежит квадрат ABCD со стороной
rj-t /
/
р'
D' = Яху/'
С
В'
Рис. 4.40
§ 4.9, Геометрический подход 167
длины 2а. Боковое ребро имеет длину а.
Рассматриваются отрезки с концами на диагонали AD\ боковой грани
и диагонали B\D параллелепипеда, параллельные
плоскости АА\В\В. Один из этих отрезков проведён через такую
точку М диагонали AD\> что AM: AD\ = 2:3.
а) Найти его длину.
б) Найти наименьшую длину рассматриваемых
отрезков.
с^ Упражнение 4.7. Решите этот пример с помощью векторов.
Решение. Спроектируем параллелепипед параллельно
диагонали B\D на плоскость АВВ\А\ (рис. 4.40). Всякий
отрезок, параллельный этой плоскости, спроектируется в
отрезок той же длины. Поэтому рассматриваемые отрезки
равны своим проекциям. (Далее буквами со штрихами
будем обозначать проекции соответствующих точек.)
а) Рассматриваемый отрезок равен отрезку D'M'. Пусть
точка Р' — основание перпендикуляра, опущенного из
точки М' на прямую B'D\. Из подобия прямоугольных
треугольников M'P'D' и A'B'D' следует, что
MfPf = \а!В' = \а.
о
Поэтому
D'P' = D'D'i - P/D[ = a-la=\a.
о о
Из прямоугольного треугольника M'D'P' по теореме Пифа
гора находим длину отрезка D'M':
D'M' = л/UXP')2 + Ш'Р*)* = л/£ + 2£ = ^
б) Кратчайшая из рассматриваемых проекций —
перпендикуляр D'H'y опущенный из точки D' на (A'D'X). Так как
А'В' = B'D/1 = 2а, то Z.D'D'XH' = j, следовательно,
\/2 V2
168 Глава 4. Перпендикулярность в пространстве
Задачи
Что же мы видим, товарищи? Мы видим, что блондин
играет хорошо, а брюнет плохо. И никакие лекции не
изменят этого соотношения сил, если каждый индивидуум
не будет постоянно тренироваться.
И, Ильф, Е. Петров. Двенадцать стульев.
(Из лекции старшего мастера О. Бендера
«Плодотворная дебютная идея»,
прочитанной в г. Васюки.)
4.1. Докажите, что рёбра SA\ и АпАп+\ правильной
пирамиды SA\...A2n-\ перпендикулярны.
4.2. Ребро AD тетраэдра ABCD перпендикулярно
грани ABC. Докажите, что при проектировании на плоскость
BCD ортоцентр треугольника ABC переходит в ортоцентр
треугольника BCD.
4.3. Высота SO тетраэдра SABC проходит через
ортоцентр грани ABC. Известно, что ZBSC прямой, SB = m,
SC = п. Найдите отношение площадей граней SAB и SAC.
4Л. Точки Ait B\ и С\ лежат соответственно на рёбрах
SA, SB и SC тетраэдра SABC, причём SAi = aSA, SBi =/3SB
и SCi = ySC. Докажите, что отношение объёмов тетраэдров
SA\BiC\ и SABC равно ос(3у. Верна ли аналогичная
формула для четырёхугольных пирамид?
4.5. Объём тетраэдра ABCD равен V. Точки К> М, Р
и Т таковы, что АК = СА, СМ = ВС, DP = AD и DT = CD.
Найдите объём тетраэдра КМРТ.
4.6. В основании четырёхугольной пирамиды SABCD
лежит параллелограмм ABCD. Площадь грани SAB равна Q,
а расстояние от точки С до плоскости этой грани равно h.
Найдите объём пирамиды.
4.7. В основании пирамиды SABCD лежит
параллелограмм ABCD. Через середину ребра SA проведена
плоскость, параллельная грани SBC. В каком отношении эта
плоскость делит объём пирамиды?
4.8. Точки DnE лежат соответственно на рёбрах SA и SB
тетраэдра SABC, причём SD : DA = SE : ЕВ =1:2. Через
Задачи 169
эти точки проведена плоскость, параллельная ребру SC.
В каком отношении эта плоскость делит объём пирамиды?
4.9. В двух параллельных плоскостях взяты два
многоугольника. Их вершины соединены отрезками так, что
у полученного многогранника каждая боковая грань —
трапеция, треугольник или параллелограмм» Докажите, что
справедлива формула
где V — объём многогранника, h — его высота, Si и S2-
площади оснований, a S$ — площадь сечения плоскостью,
параллельной плоскостям оснований и равноудалённой от
них (формула Симпсона).
4.10. Рёбра АА\у ВВ\ и СС\ многогранника АВСА\В\С\
лежат на параллельных прямых Zi, /2 и Is
соответственно. Его треугольные грани ABC и А\В\С\ лежат, вообще
говоря, в непараллельных плоскостях. Докажите, что для
объёма V многогранника справедлива формула
V=hAA1+BBl+CC1)S,
где S — площадь треугольника, вершинами которого
являются точки пересечения прямых /i, I2 и Is с плоскостью,
им перпендикулярной.
4.11. Докажите, что если основание высоты тетраэдра
есть ортоцентр соответствующей грани, то этот тетраэдр
ортоцентрический.
4Л2* Докажите, что тетраэдр является ортоцентриче-
ским тогда и только тогда, когда:
а) отрезки, соединяющие середины противоположных
рёбер, равны;
б) суммы квадратов длин противоположных рёбер
равны.
4ЛЗ. Какие тетраэдры имеют три непараллельных
прямоугольных сечения?
170 Глава 4. Перпендикулярность в пространстве
4.14. Постройте сечение куба плоскостью, проходящей
через его центр перпендикулярно одной из его диагоналей.
4.15. Рассматриваются сечения куба плоскостями,
перпендикулярными одной из его диагоналей. Определите
наибольшую возможную площадь сечения, если ребро куба
равно 1.
4.16. Постройте сечение правильной треугольной
пирамиды SABC плоскостью, перпендикулярной высоте СС\
основания и проходящей через середину ребра AS.
4.17. Длина стороны основания правильной пирамиды
SABCD равна а, длина бокового ребра — I. Постройте
сечение пирамиды плоскостью, перпендикулярной ребру SC
и проходящей через его середину, и найдите площадь
сечения, если: a) l = aJт>; б) l = aJ•=.
4.18. Длина ребра куба ABCDA\B\C\Di равна 1. Точки
М и N — середины рёбер CD и CCi соответственно. Найдите
расстояние между прямыми AN и ВМ.
4.19. В правильном тетраэдре ABCD точки М и N —
середины рёбер АС и АВ соответственно, Е — центр грани
BCD. Найдите угол между прямыми MN и DE.
4.20. Основанием пирамиды SABC является
равносторонний треугольник ABC со стороной 4\/2. Боковое ребро
SC перпендикулярно основанию и имеет длину 2.
Найдите угол и расстояние между скрещивающимися прямыми,
одна из которых проходит через S и середину ребра ВС,
а другая — через С и середину ребра АВ.
4.21. В правильной четырёхугольной пирамиде SABCD
боковая грань — равносторонний треугольник со стороной 2.
Точка Q — центр грани SCD.
а) Найдите угол и расстояние между прямыми ВС и AQ.
б) Найдите расстояние от основания общего
перпендикуляра к этим прямым, лежащего на (AQ)> до плоскости
ABC.
4.22. В основании треугольной пирамиды SABC лежит
прямоугольный треугольник ABC с катетами АВ = \/2 и
Задачи 171
AC = 1. Боковое ребро SA длины 4 перпендикулярно
основанию; точка Q — середина ребра SC.
а) Найдите угол и расстояние между прямыми BQ и AS.
б) Найдите расстояние от основания общего
перпендикуляра к этим прямым, лежащего на (AS), до плоскости
BSC.
4.23. Всегда ли существует прямая, проходящая через
данную точку и образующая с данными двумя плоскостями
равные углы?
4.24. В правильной треугольной призме АВСА\В\С\
выполнено соотношение АА\ =АВ. Найдите угол между
прямой АВ\ и плоскостью АА\С.
4.25. Отношение длин бокового ребра и стороны
основания в правильной четырёхугольной призме ABCDA\B\CiD\
равно 2. Найдите угол между прямой BD\ и плоскостью
4.26. Длина стороны основания ABCD правильной
пирамиды SABCD равна а, длина бокового ребра — 2а.
Рассматриваются отрезки с концами на диагонали BD основания
и боковом ребре SC, параллельные (SAD). Найдите
наименьшую длину рассматриваемых отрезков.
4.27. а) Верно ли, что угол между двумя наклонными
меньше угла между их ортогональными проекциями на
плоскость?
б) Из точки Ау расположенной вне плоскости, проведены
перпендикуляр АО и наклонные АВ и АС к этой плоскости.
Известно, что ВО = 1, СО = 2у/2 и ZBOC-45°. Найдите
наибольшее возможное значение угла ВАС.
Глава 5
Двугранные и многогранные углы
— Надо же, как всё просто.
— Как научиться ходить. Потом ты
начинаешь удивляться, что в этом было такого
сложного.
Р. Бах. Иллюзии
§5.1. Двугранный угол и его измерение. Биссектор
В каждой ситуации обычно есть одна
фигура, чьё влияние ни в коем случае
нельзя недооценивать.
К, Кизи. Над кукушкиным гнездом
Определение. Две полуплоскости с общей
ограничивающей их прямой разбивают пространство на две части,
общей границей которых они являются. Объединение
рассматриваемых полуплоскостей с одной из этих частей
называется двугранным углом. Полуплоскости
называются гранями двугранного угла, а их общая прямая — его
ребром.
б)
Рис. 5Л
174 Глава 5. Двугранные и многогранные углы
Двугранный угол может быть как выпуклым (рис. 5.1а),
так и невыпуклым1* (рис. 5.16).
Двугранный угол с гранями а и /3 и ребром I мы будем
обозначать <x\f
Измерение двугранных углов
Определение. Пересечение двугранного угла и
плоскости, перпендикулярной его ребру, называют линейным
углом двугранного угла. Величиной двугранного угла
называют величину его линейного угла.
Корректность данного определения вытекает из
следующей теоремы.
I Теорема 5.1. Величина двугранного угла не зависит от
выбора его линейного угла.
Доказательство. Пусть АОВ и А\О\В\ — два линейных
угла данного двугранного угла (рис. 5.2). Их стороны па-
Рис. 5.2
раллельны (теорема 2.4; (АОВ) || (A\OiBi), так как обе
плоскости перпендикулярны ребру двугранного угла) и
одинаково направлены, следовательно (теорема 3.4), ZAOB =
О
и в планиметрии, множество точек называется выпуклым,
если оно вместе с любыми двумя своими точками целиком содержит
соединяющий их отрезок.
§ 5Л. Двугранный угол и его измерение. Биссектор 175
Величина двугранного угла (измеренная в градусах)
принадлежит промежутку (0°, 360°). Величина выпуклого
двугранного угла (измеренная в градусах) принадлежит
промежутку (0°, ISO0]1*.
В дальнейшем мы будем рассматривать только
выпуклые двугранные углы. Двугранный угол называется
острым, тупым, прямым или развёрнутым в зависимости
от того, каков его линейный угол (соответственно острый,
тупой, прямой или развёрнутый). Двугранные углы —
пространственные аналоги углов на плоскости. Так же, как
и на плоскости, определяются вертикальные и смежные
двугранные углы, остаются в силе и соответствующие
теоремы.
Биссектор двугранного угла
Определение. Полуплоскость, границей которой
является ребро двугранного угла, делящая его на два
двугранных угла равной величины, называется биссектором
двугранного угла (аналог биссектрисы плоского угла),
■^Упражнение 5.1. Докажите, что биссектриса любого
линейного угла данного двугранного угла принадлежит его биссекто-
РУ-
I
Теорема 5.2. Биссектор двугранного угла есть
множество точек этого угла, равноудалённых от его граней.
Доказательство. Все точки М, принадлежащие ребру
данного двугранного угла al(3 (рис. 5.3), очевидно,
принадлежат и биссектору, и искомому множеству. Поэтому далее
будем рассматривать только точки М £1.
I. Пусть М —любая точка искомого множества, т.е.
такая, что р{Му а) =р(Му /3). Докажем, что М принадлежит
биссектору двугранного угла al(3. Пусть М\ и Мг —
проекции точки М на грани а и В соответственно (рис. 5.4).
!)В радианах— соответственно (0, 2п) и (0, 7г].
176
Глава 5. Двугранные и многогранные углы
Рис. 5.3
Рис. 5.4
Проведём через точки М, Mi и Мг плоскость у. Так как
(MMi) J_ а, то (MMi) 11. Аналогично (ММ2) -L /.
Следовательно, I Ly по признаку перпендикулярности прямой
и плоскости. Поэтому угол М\ОМ2 — линейный угол
двугранного угла al/3 (О — точка пересечения прямой / и
плоскости у). Точка М равноудалена от сторон линейного
угла М\0М2, следовательно, она лежит на его биссектрисе,
а значит, и на биссекторе двугранного угла al(3
(упражнение 5.1).
II. Пусть теперь М — произвольная точка биссектора 8
двугранного угла al(3 (М £ I). Докажем, что она
принадлежит искомому множеству. Проведём через М плоскость
у _L /, получим линейный угол АОВ рассматриваемого дву-
в
Рис. 5.5
гранного угла (рис. 5.5). Кроме того, углы АОМ и ВОМ —
линейные углы двугранных углов <х18 и 5Z/3 соответственно.
По определению биссектора величины этих двугранных уг-
§ 5.2. Угол между двумя плоскостями 177
лов равны, следовательно, Z.AOM—ZBOM. Итак, точка М
лежит на биссектрисе получившегося линейного угла,
значит, она равноудалена от его сторон. Но перпендикуляры
к сторонам линейного угла являются и перпендикулярами
к граням двугранного угла (так как у J_ Z), следовательно,
р(М9а)=р(М,р). □
§ 5.2. Угол между двумя плоскостями.
Признак перпендикулярности
Скалы встали
Перпендикулярно
К плоскости залива.
Н. Рубцов. Утро перед экзаменом
Определение. Углом между двумя пересекающимися
плоскостями называется наименьшая из величин
двугранных углов, образованных при их пересечении. Угол
между параллельными плоскостями по определению
считается равным нулю.
Таким образом, угол между плоскостями (измеренный
в градусах) принадлежит промежутку [0°, 90°].
и^ Упражнение 5.2. Докажите, что угол между двумя
плоскостями равен углу между прямыми, перпендикулярными к ним.
I
Определение. Две плоскости называются
перпендикулярными, если угол между ними равен 90°.
Теорема 5.3 (признак перпендикулярности двух
плоскостей). Если плоскость проходит через перпендикуляр
к другой плоскости, то она перпендикулярна этой
плоскости.
Доказательство. Пусть прямая а перпендикулярна
плоскости а у а плоскость (5 проходит через а. Обозначим
основание перпендикуляра через М (М = аПа), а прямую
пересечения плоскостей а и /3 — через с (рис. 5.6; плоскости а
и /3 не могут быть параллельными, так как М — их общая
178
Глава 5. Двугранные и многогранные углы
Рис. 5.6
Рис. 5.7
точка). Через точку М в плоскости а проведём прямую ft,
перпендикулярную с. Пусть у — плоскость, проходящая
через а и ft. Так как с 1 а и с J_ ft, то по признаку
перпендикулярности прямой и плоскости у 1 с. Значит, угол между
а и /3 равен углу между а и ft, но а J_ ft (так как по условию
а _]_ а, a ft с ос по построению), следовательно, а 1(3. D
Теорема 5.4 (свойство перпендикулярных плоскостей).
Если две плоскости перпендикулярны, то прямая,
проведённая в одной плоскости перпендикулярно линии
пересечения плоскостей, перпендикулярна второй плоскости.
Доказательство. Пусть a_L/3, с = аГ)/39 плоскость а
проходит через прямую а, перпендикулярную с (рис. 5.7).
Докажем, что a_L/3.
Пусть аПс = М. В плоскости /3 через точку М проведём
прямую 6, перпендикулярную с. Тогда угол aMft
—линейный угол двугранного угла, образованного плоскостями а
и /3. Так как ос ±(3, то alb. Итак, a_Lc (по условию) и a_L&,
следовательно, а 1(3 (по признаку перпендикулярности
прямой и плоскости). □
Приведём пример построения сечения, заданного
условием перпендикулярности некоторой плоскости. Основная
§ 5.2. Угол между двумя плоскостями
179
идея решения подобных задач заключается в следующем:
секущая плоскость должна проходить через прямую,
перпендикулярную данной плоскости.
Пример 5.1. Построить сечение куба ABCDA\BiC\D\>
проходящее через диагональ AD\ грани AA\D\D и
перпендикулярное плоскости BCiD.
Решение. Построим сначала какую-нибудь прямую,
пересекающую прямую AD\ и перпендикулярную
плоскости BC\D. Для этого достаточно через середину О
диагонали AD\ провести прямую /, параллельную прямой А\С
Рис. 5.8
(рис. 5.8). Действительно, (А\С) J_ (BC\D) (пример 4.6),
следовательно, l± (BC\D). Прямая / лежит в плоскости (A\DC)
(почему?), параллельна {А\С) и проходит через середину О
отрезка AD\, поэтому она пересекает ребро DC куба в его
середине К. Соединив точку К с точками А и D\9 получим
искомое сечение: так как / С (AD\K) и I _L (BCiD), то по
признаку перпендикулярности плоскостей (AD\K) J_ (BC\D). □
В заключение этого параграфа обсудим способ
нахождения угла между плоскостями с помощью векторов. Так
как угол между плоскостями равен углу между
перпендикулярными к ним прямыми (см. упражнение 5.2), то
задача о вычислении угла между плоскостями сводится
180
Глава 5. Двугранные и многогранные углы
ъ
а ь г
3 0 0
° » 1
Таблица 5 Л
к уже решённой нами в § 3.3, 3.5 задаче о вычислении
угла между прямыми. Приведём пример.
Пример 5.2. В основании треугольной пирамиды SABC
лежит правильный треугольник ABC со стороной 1.
Ребро SA пирамиды перпендикулярно плоскости основания,
а его длина равна у/3. Плоскость а параллельна прямым
SB и АС у а плоскость (5 параллельна прямым SC и АВ.
Найти угол между этими плоскостями.
Решение. Выберем базис fi = AS, 6 = AB, (* = АС и
составим «таблицу умножения» базисных векторов
(таблица 5Л). Если т и Я —ненулевые векторы,
перпендикулярные плоскостям а и (3 соответственно, а ср — угол между а
и /3, то
\ffi-ft\
ooscp = ' '
В качестве А можно взять любой такой ненулевой
вектор, что fh • SB = rft - AC = 0, Пусть fh — хй + уЪ + г?. Тогда
—► —> —>•
(дч? + j/b + 2?) • (6 - 3) = 0 и (хЗ + уЬ + 2?) • ? = 0. Эта
система уравнений с помощью «таблицы умножения» базисных
векторов приводится к равносильной системе:
6x-2y-z = Q,
Выразим х и у через г: х = -|, у= -2г. Положив,
например, z = — 2, получим х — 1, у = 4. Итак, мы нашли один
из ненулевых векторов /й, перпендикулярных плоскости от:
§ 5,2. Угол между двумя плоскостями 181
fh — а + 46 — 2? (именно тем, что условие in J_ а не
определяет m однозначно, и объясняется то, что в полученной нами
системе неизвестных больше, чем уравнений).
Вектор ft, перпендикулярный плоскости/3, можно найти
аналогично. Но мы поступим по-другому. Заметим, что
условие, задающее плоскость /3, получается из условия,
задающего плоскость а, заменой точки В на точку С, а
точки С, наоборот, — на точку В. Поэтому чтобы получить Н±/3,
достаточно в выражении для т поменять местами векторы
Ъ и ?: Н = а - 2Ь + 4?, Вычисляя m-Й, \т\ и |Й|, находим,
Ml 1 1 г-.
что cos Ф = —==—== = -?> т. е. (р = arccos ^. u
Разобранный пример можно решить, не пользуясь
векторами, геометрически. Приведём это решение.
Ясно, что в качестве плоскости а можно выбрать
плоскость, проходящую через прямую SB параллельно прямой
АС (почему?). Тогда её линия пересечения с плоскостью
ABC будет параллельна прямой АС. Аналогично проведём
плоскость (5 через прямую SC параллельно прямой АВ.
Линия её пересечения с плоскостью ABC параллельна АВ.
Если ещё через точку А провести прямую, параллельную
прямой ВС, то три полученные прямые пересекутся в
точках Аи Bi и Си причём (AiBi) || (AB), (BiCi) || (ВС),
Рис. 5.9
182 Глава 5. Двугранные и многогранные углы
(AC), AAiB\Ci правильный, а его сторона равна 2
(рис. 5.9).
Искомый угол — угол между (SA\Ci) и (SA\Bi).
Рассмотрим ASAAi. Так как [AAi] —высота правильного
треугольника А\В\С\У то АА\ = \/3. Но ребро SA
перпендикулярно плоскости ABC и SA = \/3. Поэтому SАА\ —
равнобедренный прямоугольный треугольник. Проведя его высоту
AM к гипотенузе SAi, найдём, что AM = — = J-=.
Прямая BiCi перпендикулярна плоскости SAAi, так
как она перпендикулярна прямым SA и AAi этой
плоскости. Следовательно, (AM) является проекцией прямой
BiM на (SAAi), и так как (AM) ± (SAi), то (ВХМ) J_ (SAi)
(по теореме о трёх перпендикулярах). Аналогично (С\М) J_
_L (SAi), и, значит, угол С\МВ\ искомый. Обозначим его
через (р. Из равенства прямоугольных треугольников С\АМ
и В\АМ получаем, что ср — 2ZAMB\. В треугольнике В\АМ
имеем AM = w^> AB\ = 1, следовательно, tg /.AMB\ =
у/6 п . (р л/6
= -^-. Зная tg Tj- = -^г-, можно найти
COS (D = 1- = ■=-. П
§ 5.3. Площадь ортогональной проекции многоугольника
Иногда приходится говорить о трудных
вещах, но следует делать это как можно проще.
Г. Харди
Теорема 5.5. Площадь ортогональной проекции
выпуклого многоугольника на плоскость равна площади
проектируемого многоугольника, умноженной на косинус угла
между плоскостями многоугольника и его проекции.
Доказательство. Пусть выпуклый многоугольник М,
лежащий в плоскости а, спроектирован ортогонально на
§ 5.3. Площадь ортогональной проекции
183
плоскость /3, причём Z(a, /3) = ср, где 0° ^ ср < 90°.
Обозначим проекцию данного многоугольника через М\.
Требуется доказать, что
S(Mi) =S(M) cos ср.
(5.1)
В случаях ср = 0° (тогда а \\ /3 и Mi = М) и <р = 90° (тогда
а±/3 и Mi —отрезок) формула (5 Л), очевидно, верна. Пусть
теперь 0°<<р<90°.
Докажем формулу (5Л) для частного случая, когда М —
треугольник ABC, у которого сторона АВ параллельна
прямой I, по которой пересекаются плоскости а и /3 (рис. 5.10).
Рис. 5.10
Проведём в ДАВС высоту CD. Пусть Ai, B\9 C\, D\ —
ортогональные проекции на плоскость [3 точек А, В, С, D
соответственно. Так как (АВ) || Z, то (AiBi) || (АВ) (по теореме
о линии пересечения). Далее, (AAi) || (BB\) (как два
перпендикуляра к плоскости /3), следовательно, AAiBiB
—параллелограмм и AB = AiBi- Прямая AiBi перпендикулярна
наклонной CD (поскольку (АВ) J_ (CD), a (AiBi) || (АВ)),
следовательно, по теореме о трёх перпендикулярах прямая
(AiBi) перпендикулярна и проекции (CiZ>i), т.е. [CiDi] —
высота в треугольнике AiBiCi. В плоскости CC\D прове-
184
Глава 5. Двугранные и многогранные углы
дём (DC2) || (D\Ci) (где Сг € [СС\]). Из прямоугольного
треугольника CDC2 (где /ССг1> = 90°, ZCDC2 = <р) находим
C2D = CD cos ср. Поскольку C\D\ — C2-D, получаем C\D\ =
= CD cos cp. По формуле для площади треугольника
= \АВ ■ CD cos cp.
I
Следовательно, в рассмотренном случае формула (5.1)
верна.
Пусть теперь М — произвольный треугольник.
Проведём через его вершины прямые, параллельные /. Одна из
них разобьёт рассматриваемый
треугольник на два треугольника, у
каждого из которых одна сторона
параллельна I (рис. 5.11), Остаётся
для каждого из этих треугольников
воспользоваться формулой (5.1) и
сложить полученные равенства.
Рассмотрим теперь общий случай:
М — произвольный выпуклый
многоугольник. Возьмём одну из его
вершин и проведём все выходящие из
неё диагонали многоугольника. Они
разбивают исходный многоугольник
на неперекрывающиеся треугольники
(рис. 5.12). Применяя формулу (5.1)
к каждому из этих треугольников
и складывая полученные равенства,
приходим к тому, что формула (5Л)
верна для любого выпуклого
многоугольника. □
Рис. 5.11
Рис. 5.12
Замечания. 1. Представление многоугольника в виде
объединения конечного числа треугольников, внутренние области
которых попарно не пересекаются, называется триангуляцией.
С триангуляцией выпуклого многоугольника вы, наверное, уже
§ 5.3. Площадь ортогональной проекции 185
встречались в планиметрии при выводе формулы для суммы
внутренних углов многоугольника. Указанный нами в
доказательстве способ триангуляции, конечно, не единственный. Для
того чтобы строго доказать, что треугольники разбиения,
полученные таким способом, действительно не перекрываются, а их
объединением является исходный многоугольник, надо
воспользоваться методом математической индукции (рекомендуем вам
проделать это самостоятельно).
2. Формула (5.1) остаётся в силе и для невыпуклых
многоугольников. Для доказательства достаточно показать, что
невыпуклый многоугольник также можно триангулировать. Можно
доказать1*, что невыпуклый
многоугольник можно триангулировать
с помощью его диагоналей (не
обязательно исходящих из одной
вершины). Мы поступим проще.
Проведём все прямые,
содержащие стороны данного
(невыпуклого) многоугольника. Они
разобьют исходный многоугольник на
несколько частей-многоугольников рис g
(рис. 5.13). Каждая из этих частей,
будучи пересечением выпуклых
фигур —полуплоскостей, является выпуклым многоугольником.
Теперь остаётся только триангулировать каждый из них,
например способом, указанным на рис. 5.12.
3. С помощью предельного перехода формулу (5.1) можно
распространить на достаточно широкий класс измеримых фигур
(т. е. имеющих площадь).
■^ Упражнение 5.3. Используя тот факт, что эллипс является
ортогональной проекцией круга, докажите, что площадь
эллипса равна каЬ, где а и Ъ — его полуоси.
Пример 5.3. Пусть в пирамиде ABCD плоские углы при
вершине А прямые, а площади граней BCD, ABC, ABD
и ACD равны So, Si, S2 и S3 соответственно. Доказать, что
о2 q2 1 о2 i Cf2
Доказательство. Спроектируем пирамиду
ортогонально сначала на плоскости ABC, ABD и ACD, а затем на
г)См., например» [Прасолов, 1991, Ч. 2, задача 22.22].
186 Глава 5. Двугранные и многогранные углы
cos аз
S2 cos
S\ cos <Х\
Рис. 5.14
плоскость BCD (рис. 5.14). Обозначим углы, образуемые
гранями ABC, ABD и ACD с гранью BCD, через <Х\, #2 и аз.
Тогда по теореме о площади ортогональной проекции
многоугольника получаем Si — So cos oti, i= 1, 2, 3 (так как
плоские углы при вершине А прямые, то проекция основания
BCD на плоскость любой из трёх боковых граней
представляет собой эту боковую грань), и So = Si cos <X\ + S2 cos
+ S3 cos a3. Отсюда следует, что So = Si-^- + S2^ + Ss-J-,
00 00 00
т.е. Sl = Sl + S% + Sl. □
Замечание. Приведённое решение не использует того, что
проекция точки А лежит внутри ADBC (почему?). На самом
деле можно доказать, что эта проекция действительно находится
внутри указанного треугольника (см. задачу 5.18 и пример 4.5).
§ 5.4. Многогранные углы.
Трёхгранный угол и его свойства
Преподнося сюрприз
суммой своих углов,
вещь выпадает из
миропорядка слов.
И. Бродский. Натюрморт
Наряду с двугранными углами в стереометрии
рассматриваются трёхгранные и четырёхгранные углы, а также
углы с большим числом граней.
§ 5Л. Многогранные углы. Трёхгранный угол 187
Рис. 5Л5
Определение. Пусть Ф = А\А%...Ап — л-угольник, п ^ 3,
и точка S не принадлежит его плоскости. Объединение
всех лучей, имеющих общее начало S и пересекающих
данный многоугольник Ф, называется многогранным (в
данном случае п-гранным) углом (рис. 5.15).
Мы будем обозначать многогранный угол SA\...An.
Точка S называется вершиной многогранного угла, лучи
SAi, SA2, ..., SAn — его рёбрами, углы A1SA2, A2SA3, ...,
AnSA\ — гранями или плоскими углами. Множество всех
Рис. 5.16
188
Глава 5. Двугранные и многогранные углы
точек многогранного угла, не принадлежащих его граням,
называется его внутренней областью.
Многогранный угол может быть выпуклым (рис. 5.16а)
или невыпуклым (рис. 5.166) (в соответствии с общим
определением выпуклости). В дальнейшем мы ограничимся
изучением выпуклых многогранных углов, более того, в
основном будем иметь дело с трёхгранными углами.
Рассмотрим следующие два свойства плоских углов
трёхгранного угла.
Теорема 5.6. Величина каждого плоского угла
трёхгранного угла меньше суммы величин двух других его плоских
углов.
Доказательство. Пусть а ^ (5
^ у — величины плоских углов
трёхгранного угла SABC (а = /.BSC,
/3 = ZASC, r = Z.ASB\ см. рис. 5.17).
Достаточно доказать, что у < а + /3
(остальные неравенства, очевидно,
выполнены). Проведём в плоском
угле SAB луч SM так, что /,ASM=(3.
Пусть он пересекает [АВ] в точке N.
Отложим на луче SC отрезок SD>
равный по длине отрезку SN. Тогда
AASD = AASN (по двум сторонам
и углу между ними), следовательно,
AD — AN. В силу неравенства треугольника, записанного
для ДАВЯ, AD + DB > АВ. Но AD = AN, АВ = AN + NB,
следовательно, DB>NB. Применим теорему косинусов к
треугольнику BSD:
Рис. 5.17
DB2 = SB2 + SD2 - 2SB • SD cos a,
(5.2)
и к треугольнику BSN:
NB2 = SB2 + SN2 - 2SB • SN cos ZNSB.
(5.3)
§ 5.4. Многогранные углы. Трёхгранный угол 189
Из (5.2) и (5.3), учитывая, что SD = SN и DB > NB,
получаем cos a < cos ZNSB. Так как функция у = cos x
является строго убывающей на (0, 7г), отсюда следует,
что ZNSB < а. Значит, у = ZASN + Z.NSB < а + р, что и
требовалось доказать. □
I Следствие 7. Величина каждого плоского угла
трёхгранного угла больше разности величин двух других его
плоских углов.
Теорема 5.7. Сумма величин всех плоских углов трёх-
LHHoro угла меньше 360°.
Доказательство. Пусть дан трёхгранный угол SABC
с плоскими углами а, /3 и у (рис. 5.18). Пусть луч SAi —про-
I Т,
|rpai
Рис. 5.18
должение луча SA. Рассмотрим трёхгранный угол SA\BC.
Его плоские углы равны а, 180° — /? и 180° — у. По
теореме 5.6 имеем а < (180° - р) + (180° - у), т. е. а + р +
+ у< 360°. □
Замечания. 1. Теоремы 5.6 и 5.7 выражают свойства
трёхгранного угла, т.е. являются необходимыми условиями
существования трёхгранного угла. Оказывается, выполнение этих
условий является и достаточным (доказательство можно
найти, например, в книге [Клопский, Скопец, Ягодовский, 1977]).
Таким образом, трёхгранный угол с плоскими углами а ^ /3 < у
190 Глава 5. Двугранные и многогранные углы
существует тогда и только тогда, когда выполнены
неравенства
<x+p + Y <360°, (5.4)
Г <<*+/?. (5.5)
2. Аналогичные свойства имеют место и для n-гранных углов:
<х\ + ... + ап < 360°, <хп < an_i + ... + аи где а\ ^ а2 < ... ^ ап —
плоские углы (доказать это можно методом математической
индукции; утверждения теорем 5.6 и 5.7 составляют базу индукции
(п = 3), см., например, [Клопский, Скопец, Ягодовский, 1977]).
Справедливо и обратное утверждение.
ВЗГ Упражнение 5.4. Два плоских угла трёхгранного угла равны
70° и 80°. Какие значения может принимать третий угол?
Сформулируем свойство биссекторов двугранных углов
трёхгранного угла.
I Теорема 5.8. Биссекторы двугранных углов
трёхгранного угла пересекаются по одному лучу (рис. 5.19).
Рис. 5.19
Предлагаем вам самостоятельно доказать это
утверждение.
Указание. Вспомните, как доказывается, что
биссектрисы треугольника пересекаются в одной точке. Здесь мож-
§ 5.5. Расчёт трёхгранных углов 191
но применить тот же метод. Используйте результат
теоремы 5.2.
BS9 Упражнение 5.5. Докажите, что биссекторы двугранных
углов тетраэдра пересекаются в одной точке.
§ 5.5. Расчёт трёхгранных углов. Теорема о трёх синусах
И я выхожу из пространства
В запущенный сад величин
И мнимое рву постоянство
И самосознанье причин.
О. Мандельштам. Восьмистишия
Характеристиками трёхгранного угла SABC являются
величины трёх его плоских углов а, /3, у (а = ZBSC, /3 =
= ZASC, у = /-ASB)> и трёх его двугранных углов, А, В, С
(А — величина двугранного угла при ребре SA, В — при
ребре SB> С— при ребре SC)l\ Между этими величинами
существует ряд соотношений. Некоторые из них будут
получены в этом параграфе. Однако нет нужды запоминать
все соотношения (зачастую громоздкие), которые мы
выведем. Гораздо полезнее уяснить метод получения таких
соотношений и использовать его при решении конкретных
задач.
Пример 5*4. Заданы величины плоских углов
трёхгранного угла а, (3 и у. Найти величины его двугранных углов.
Решение. Найдём двугранный угол С, считая а и (3
острыми. Построим линейный угол двугранного угла при
ребре SC (см. рис. 5.20, где (DFE) 1 (SC), De [SA), Ее [SB),
Fe[SC), Z.DFE = C). Из AEFD по теореме косинусов
получаем
ED2 = FE2 + FD2 - 2FE - FD cos С. (5.6)
Из AESD по теореме косинусов получаем
ED2 = SE2 + SD2 - 2SE - SD cos у. (5.7)
мы будем обозначать таким образом плоские и двугранные
углы всех встречающихся трёхгранных углов SABC.
192 Глава 5. Двугранные и многогранные углы
С
Е В
Приравнивая правые части равенств (5.6) и (5.7), получаем
FE2 + FD2 - 2FE ♦ FD cos С = SE2 + SD2 - 2SE - SD cos у,
или
2 FE2) + (SD2 FD2
SD cos 7 - (S£2 - FE2) + (SD2 - FD2) + 2FE - J7) cos C.
Из прямоугольных треугольников SEF и SZXF по
теореме Пифагора имеем SE2 - FE2 = SF2, SD2 - FD2 =
поэтому
S£ • SD cos 7 = SF2 + FE-FD cos С.
Отсюда следует, что
С учётом того, что -щт; = cos а, -~= = sin а, -^ = cos/3,
-^=г = sin/3, последнее равенство принимает вид
cos у = cos a cos /3 + sin a sin j3 cos C, (5.8)
откуда следует, что
^ cos у - cos a cos /3
С = 4 . д г .
sin a sin p
cos 4.
sin a sin
Проверьте самостоятельно, что во всех оставшихся случаях
выражение для cos С будет таким же. Аналогично
находятся углы А и В. □
§ 5,5, Расчёт трёхгранных углов 193
Замечания. 1. Приведём идею другого решения этой задачи,
использующего векторный аппарат. Пусть Й, b и ? — единичные
векторы, направленные вдоль лучей SA, SB и SC. Вектор 2,
лежащий в плоскости SAC, можно представить в виде 8 = с cos /3 + ?j^
где ?i _L с, |?i | = sin (3 (рис. 5.21). Аналогично выражается вектор Ь.
В
Рис. 5.21
После этого надо вычислить скалярное произведение а • Ь. Оно
равно cos у у и оно же равно cos a cos/J + sin ос sin/? cos С.
2. Доказанное нами соотношение (5.8) часто называют первой
теоремой косинусов для трёхгранного угла.
Предлагаем вам самостоятельно решить обратную
задачу — найти величины плоских углов трёхгранного угла,
зная величины его двугранных углов.
и^ Упражнение 5.6. Докажите равенство
cos С = -cos A cos В + sin A sin В cos у (5.9)
(вторая теорема косинусов для трёхгранного угла).
Замечание. Укажем на одну красивую идею, помогающую
при решении ряда задач. Пусть SABC — трёхгранный угол, а,
/3, у — величины его плоских углов; А, Б, С — величины
двугранных углов. Возьмём внутри угла произвольную точку Si
и опустим из неё перпендикуляры S\Ai, S\B\t S\C\ на грани
BSCy ASCj ASB соответственно. Получим новый трёхгранный
угол SiA\B\C\ (рис. 5.22). Величины его плоских и
двугранных углов связаны с соответствующими величинами в исходном
трёхгранном угле равенствами а\ = п — А, /3\ = к — В, у\ — к — С;
А\ = к - а, В\ — к — (3, С\ = к - у (проверьте!). Угол S\A\B\C\
называют полярным к углу SABC. Рассмотрение полярного
трёхгранного угла позволяет свести утверждения о плоских углах
7 3ак 3383
194 Глава 5. Двугранные и многогранные углы
С
Рис. 5.22
к аналогичным утверждениям о двугранных углах, и наоборот.
Рассмотрим, например, как с помощью введения полярного угла
доказывается равенство (5.9). Запишем первую теорему
косинусов для полярного угла:
cos у 1 = cos <x\ cos /?i 4- sin a\ sin/?i cos C\,
или
cos(7r-C)=cos(7r-A) cos(7r-B)-fsin(7r-A) sin(7r-B) cos(n-y),
откуда в силу формул приведения сразу следует равенство (5.9).
Пример 5.5. Доказать, что справедливы равенства
sina = sin£ = sinr
sin A sin В sin С ' '
(теорема синусов для трёхгранного угла).
Решение. Для доказательства, например, второго из
равенств (5.10) возьмём на ребре SA точку М и спроектируем
её на плоскость SBC и прямые SB и SC (здесь возможно
много различных случаев; см., например, рис. 5.23а—в —
все они разбираются аналогично). Обозначим SM = a. Для
доказательства нужного равенства достаточно двумя спосо-
§ 5.5. Расчёт трёхгранных углов
195
Рис. 5.23
бами выразить МН. В случае, изображённом на рис. 5.23а,
МН = MN sin В = SM sin у sin В (из AMHN и AMSN);
MH = MKsinC = SMsinpsmC (из АМНК и ДМ&йГ),
. я . л . „ sin /3 sin у
следовательно, sin у sin р = sin p sin С, т. е. ——^ = -:—^.
Sin x5 Sin О
п
Рассмотрим теперь трёхгранный угол SABC, в котором
В= ^. Тогда из теоремы синусов для трёхгранного угла
вытекает, что
sin у = sin С sin р. (5.11)
Полученный результат можно сформулировать
следующим образом.
Теорема 5.9* Если в одной из граней двугранного угла
величины а проведена прямая /, пересекающаяся с его
ребром и образующая с ним угол /3, а с другой гранью —
угол у у то
sin у = sin a sin/3. (5.12)
Это утверждение часто называют теоремой о трёх
синусах (см., например, [Габович, 1989]). Приведём
доказательство этой теоремы, не использующее теорему синусов
для трёхгранного угла.
Доказательство. Возьмём на прямой I точку А,
отличную от точки D, в которой I пересекается с ребром дву-
196
Глава 5. Двугранные и многогранные углы
Рис. 5.24
Рис. 5.25
гранного угла (рис. 5.24). Построим линейный угол
данного двугранного угла. Для этого в грани, содержащей
прямую Z, проведём перпендикуляр АВ к ребру
двугранного угла и опустим из точки А перпендикуляр АС на
другую грань двугранного угла. Тогда /ABC — <х> /ADB — fi,
/.ADC— у. Из прямоугольного треугольника ACD находим
АС = AD sin у. Далее, из AABD находим АВ = AD sin /3,
а из ABAC находим АС — АВ sin a> следовательно, АС =
= AD sin a sin /3. Сравнивая два полученных выражения
для АС, приходим к выводу, что равенство (5.12)
выполнено. □
В следующем примере мы покажем, как применяется
теорема о трёх синусах.
Пример 5.6. Дан двугранный угол тао величиной 60°.
Правильный треугольник ABC лежит в грани т, причём
вершина А принадлежит ребру а двугранного угла. Сторона
АВ образует с гранью о угол 30°. Найти величину угла,
образуемого стороной АС с гранью а.
Решение. Обозначим: Z(r, а) = а = 60°, Z(AB, a) =
= /3 = 30°, /{АС, а) ~ у — искомый угол, Z(AB, а) = ср,
/(АС, а) = д (рис. 5.25). По теореме о трёх синусах имеем
sin /3 = sin a sin cp,
sin у — sin a sin i?.
(5.13)
(5.14)
Задачи 197
Поскольку /.ВАС = 60° (ЛАВС правильный), то $ =
^180° -60°-<р -120°-<р и
sin $ — sin(120° - (р) = ^г cos <р + ~ sin ср. (5.15)
Из соотношения (5.13) находим
Угол ср острый, поэтому cos (p = \/-=. Учитывая соотно-
л/б + 1
шение (5.15), находим sin v = —. Теперь из соотноше-
2\/3
/К1уйЧ . . . Q \/3 \/б+1 \/б+1
ния (5.14) получаем sin у = sin or sin v = -^-- -—7=- = -^—j—,
. \/6 + l ,-,
r = arcsin Z—A—. П
4
Задачи
Каждая проблема таит в себе бесценный дар.
И ты создаёшь себе проблемы — ведь эти дары
тебе крайне необходимы.
Р. Бах. Иллюзии
5.1. Докажите, что если две плоскости
перпендикулярны плоскости а и пересекаются, то их линия пересечения
перпендикулярна плоскости а.
5.2. Постройте сечение правильной четырёхугольной
пирамиды SABCD, все рёбра которой имеют одинаковую
длину, плоскостью, проходящей через середину её высоты,
вершину А основания и перпендикулярной грани SBC.
5.3. Постройте сечение куба ABCDA\B\C\Di
плоскостью, проходящей через центр грани AA\D\D> вершину В
и перпендикулярной плоскости C\NM, где М — середина
ребра ВС, а N — середина ребра CD. Найдите отношение
объёмов частей, на которые секущая плоскость делит куб.
198 Глава 5. Двугранные и многогранные углы
5.4. В правильной шестиугольной пирамиде SABCDEF
угол между апофемой и плоскостью основания равен 60°.
Постройте сечение пирамиды плоскостью, проходящей
через ребро АВ и перпендикулярной грани SCD> и определите,
в каком отношении секущая плоскость делит высоту
пирамиды*
5.5. Какие значения может принимать величина угла,
получающегося при пересечении двугранного угла
величины ср всевозможными плоскостями?
5.6* Двугранный угол вместе со своим биссектором /3
пересекается плоскостью а. В каких случаях луч,
являющийся пересечением плоскостей а и /3, будет биссектрисой
получающегося в пересечении угла?
5.7. На гранях двугранного угла расположены точки А
и Б. Докажите, что биссектор делит отрезок АВ в
отношении, равном отношению расстояний от точек А и В до ребра
двугранного угла.
5.8. В кубе ABCDA\B\C\Di точки Е> F и М — середины
рёбер ААь АВ и СС\ соответственно. Найдите угол между
плоскостями EFD и A\D\M.
5.9* В правильной шестиугольной пирамиде SABCDEF
отношение длины высоты к длине стороны основания равно
у/б : 4. Найдите угол между плоскостями SBC и SDE.
5* 10. В основании четырёхугольной пирамиды SABCD
лежит прямоугольник ABCD со сторонами АВ — 3 и ВС = 2.
Боковые рёбра пирамиды имеют одинаковую длину, а её
высота равна 3. Плоскость а параллельна прямым SB и АС>
а плоскость /3 — прямым SC и BD. Найдите угол между
этими плоскостями.
5.11. Дан куб ABCDAxB\C\D\. Плоскость а
перпендикулярна прямой А\С\, а плоскость (3 параллельна прямой CD\.
Найдите наименьший возможный угол между этими
плоскостями.
5.12. Дан куб ABCDAiB\C\D\ с ребром длины 1. На
рёбрах ААь ВВ\, DD\ взяты соответственно точки К> Р,
М так, что АК: АХК= 1:3, ВР: ВХР = 3:1, DM: DXM = 3 :1.
Задачи 199
Дайдите объём пирамиды, у которой основание — сечение
куба плоскостью КРМ, а вершина — точка А\.
5.13. Правильная треугольная пирамида с двугранным
углом а при ребре основания пересечена плоскостью,
параллельной основанию, так, что площадь полученного
сечения равна площади боковой поверхности образовавшейся
усечённой пирамиды. Определите отношение площади
основания к площади сечения.
5.14. В правильной четырёхугольной усечённой
пирамиде проведены два сечения: плоскостью, проходящей
через диагонали оснований, и плоскостью, проходящей через
сторону нижнего основания и противоположную сторону
верхнего основания. Угол между секущими плоскостями
равен а. Найдите отношение площадей сечений.
5.15. Найдите наибольшую площадь ортогональной
проекции правильного тетраэдра с ребром а на плоскость.
5.16*. Докажите, что площадь ортогональной проекции
куба с ребром 1 на плоскость численно равна длине его
проекции на прямую, перпендикулярную этой плоскости.
5.17*. Докажите, что плоскости, проходящие через
рёбра трёхгранного угла и биссектрисы противолежащих
плоских углов («медианы»), пересекаются по одной прямой.
5*18. Докажите, что плоскости, перпендикулярные
граням трёхгранного угла и проходящие через их биссектрисы
(«серединные перпендикуляры»), пересекаются по одной
прямой.
5.19. Любой ли трёхгранный угол имеет сечение,
являющееся правильным треугольником?
5.20. Существуют ли такие выпуклая л-угольная (п > 4)
и треугольная пирамиды, что четыре трёхгранных угла
/z-угольной пирамиды равны трёхгранным углам
треугольной пирамиды?
5.21. Угол между плоскостью квадрата ABCD и
некоторой плоскостью т равен or, а угол между стороной АВ и той
же плоскостью равен /5. Найдите угол между стороной AD
и плоскостью г.
200 Глава 5. Двугранные и многогранные углы
5.22. Стороны АВ и АС равностороннего треугольника
ABC расположены соответственно в гранях Р и Q острого
двугранного угла величины <р. Сторона АВ образует с
ребром двугранного угла острый угол а. Найдите величину
угла между плоскостью ABC и гранью Q.
5.23. Пусть а — угол между наклонной I и плоскостью т,
/3 — угол между проекцией наклонной на эту плоскость
и прямой а, проведённой через основание наклонной в
плоскости проекции, и у — угол между наклонной / и
прямой а. Докажите, что cos у = cos a cos /3 (теорема о трёх
косинусах).
5.24. Высота правильной треугольной призмы равна Н.
Через одно из рёбер нижнего основания и
противоположную ему вершину верхнего основания проведена плоскость.
Найдите площадь получившегося сечения, если его угол,
взятый при вершине верхнего основания призмы, равен а.
Найдите также допустимые значения а.
5.25. В плоскости г расположен правильный
треугольник ABC со стороной а. На перпендикуляре к плоскости т
в точке А отложен отрезок AD = а. Найдите угол между
прямыми АВ и CD.
5.26. Каждый двугранный угол трёхгранного угла имеет
величину а. Найдите величины его плоских углов. Укажите
также все возможные значения а.
5.27. Плоские углы ASB, BSC и CSA трёхгранного угла
SABC имеют величины ~, ^ и arccos —= соответственно.
3 6 у/%
Найдите величину двугранного угла при ребре SB.
5.28. Каждый плоский угол трёхгранного угла имеет
величину ~. Внутри него расположена точка, удалённая
о
от двух граней на расстояние а, а от третьей — на
расстояние За. Найдите расстояние от этой точки до вершины
трёхгранного угла.
Глава 6
Элементы теории многогранников
Геометр отправился в Египет
Посмотреть па параллелепипед.
И представьте вы его обиду,
Когда он увидел пирамиду.
Б. Берестов. Геометрия
§ 6.1. Пространственная область. Геометрическое тело
Там, за нигде, за его пределом —
чёрным, бесцветным, возможно, белым —
есть какая-то вещь, предмет.
Может быть, тело»
И. Бродский. Лагуна
В этом параграфе мы определим основной объект
изучения в стереометрии — (геометрическое) тело. Для этого нам
понадобится сначала дать ряд вспомогательных
определений. Определяемые ниже понятия играют важную роль не
только в геометрии, но и в других разделах математики.
Сферой с центром О и радиусом R>0 называется
множество всех точек пространства, удалённых от точки О на
расстояние R. Обозначение: S(0, R) (от английского sphere).
Шаром с центром О и радиусом R>0 называется
множество всех точек пространства, удалённых от точки О на
расстояние, не превосходящее R. Обозначение: В (О, R) (от
английского ball).
Фигура Ф называется ограниченной, если она целиком
лежит в некотором шаре, и неограниченной в противном
случае. Например, точка, отрезок, шар — ограниченные
фигуры, а прямая, плоскость и всё пространство —
неограниченные.
202 Глава 6. Элементы теории многогранников
Пространственной областью называется непустая
фигура Ф, обладающая следующими свойствами:
1) любые две точки фигуры Ф можно соединить
ломаной1*, целиком принадлежащей Ф;
2) вместе с любой своей точкой фигура Ф содержит хотя
бы один шар с центром в этой точке.
Первое из этих свойств называется связностью,
второе—открытостью. Поэтому говорят, что
пространственная область — это открытое связное множество точек
пространства.
Приведём примеры. Всё пространство является
пространственной областью (но эта область, очевидно,
неограниченная), а точка, прямая и плоскость — нет (так как
они не открыты). Пример ограниченной пространственной
области даёт фигура В (О, R) \S(O, R). Заметим, что шар
В (О, R) не открыт, следовательно, он не является
пространственной областью.
в^ Упражнение 6.1. Приведите пример открытой, но не связной
фигуры.
Границей пространственной области называется
непустое множество всех точек пространства, для каждой из
которых любой шар с центром в этой точке, содержит как
точки, принадлежащие данной области, так и не
принадлежащие ей.
Пространственная область может не иметь границы*
Единственным примером такой области служит всё
пространство. Все остальные пространственные области, в
частности ограниченные, всегда имеют границу2*. Обратное
неверно, т. е. пространственная область может иметь
границу, но не быть ограниченной. Например, этим свойством
обладает внутренность многогранного угла.
Наконец, сформулируем основное определение.
^Звенья этой ломаной не обязательно лежат в одной плоскости.
2)Доказательство этого утверждения выходит за рамки нашего курса.
Подобные вопросы обсуждаются в курсах топологии (см., например,
книгу [Стинрод, Чинн, 1967], рассчитанную на начинающих).
§ 6.2. Многогранники и их элементы 203
I Определение. Объединение ограниченной
пространственной области и её границы называется телом.
Из этого определения вытекает, что тело является
ограниченной фигурой.
Граница указанной пространственной области
называется поверхностью тела Т и обозначается дТ> а сама эта
пространственная область называется его внутренней
областью и обозначается int T (от английского interior).
Например, поверхностью тетраэдра является объединение всех
его граней, а поверхностью шара является сфера.
§ 6.2. Многогранники и их элементы
Проблемы нам создают не те вещи,
которых мы не знаем, а те, о которых
мы ошибочно полагаем, что знаем.
В. Роджерс
Важным классом геометрических тел являются
многогранники. Определение многогранника уже было дано в
§ 2.4. После того как мы придали точный смысл понятиям
«тело» и «поверхность тела», нам остаётся лишь напомнить
это определение.
Определение. Многогранником называется тело,
поверхность которого является объединением конечного числа
многоугольников.
В соответствии с общим определением выпуклого
множества многогранник называется выпуклым, если вместе
с любыми двумя своими точками он содержит
соединяющий их отрезок. На рис. 6.1а, б изображены соответственно
выпуклый и невыпуклый многогранники. В дальнейшем,
если не оговорено противное, мы всюду подразумеваем под
многогранником выпуклый многогранник1*.
обстоятельство следует иметь в виду, так как не все факты,
которые мы формулируем в этой главе, а также в задачах к ней, верны
для невыпуклых многогранников.
204
Глава б. Элементы теории многогранников
Рис. 6.1
Многоугольник, принадлежащий поверхности
многогранника, называется его гранью, если он не содержится
ни в каком другом многоугольнике, также принадлежащем
поверхности многогранника. Стороны граней называются
рёбрами многогранника, а вершины — вершинами
многогранника. Отрезки, соединяющие вершины многогранника,
не принадлежащие одной грани, называются диагоналями
этого многогранника.
Частные виды многогранников были определены и
изучены нами в § 2.4, 4.4.
§ 6.3. Правильные многогранники
Евклид вовсе и не собирался выпускать
систематический учебник геометрии. Он задался целью
написать сочинение о правильных многогранниках,
рассчитанное на начинающих, в силу чего ему
пришлось изложить все необходимые сведения.
Т.Д'Арси
Определение. Многогранник1* называется правильным,
если все его грани — равные правильные многоугольники
и из каждой его вершины выходит одинаковое число
рёбер.
^Какбыло отмечено в § 6.2, мы имеем в виду выпуклый
многогранник.
§ 6.3. Правильные многогранники
205
Как мы знаем, на плоскости существует бесконечно
много типов правильных многоугольников (для любого п ^ 3
существует правильный л-угольник). В пространстве дело
обстоит не так: существует всего пять типов правильных
многогранников, которые известны ещё с древних времён.
Это тетраэдр, гексаэдр (куб), октаэдр, додекаэдр и икосаэдр
(рис, 6.2-6.6).
Рис. 6.2
Рис. 6.3
Рис. 6.4
Рис. 6.5
Рис. 6.6
Действительно, пусть гранями правильного
многогранника являются правильные n-угольники, а в каждой его
вершине сходится т рёбер. Так как внутренний угол пра-
к(п-2)
вильного многоугольника равен , а для существова-
206
Глава 6. Элементы теории многогранников
п
т
3
3
3
4
3
5
4
3
5
3
Таблица 6.1
Тетраэдр
Куб
Октаэдр
Додекаэдр
Икосаэдр
Грани
4
6
8
12
20
Вершины
4
8
6
20
12
Рёбра
6
12
12
30
30
Таблица 6.2
ния m-гранного угла (при вершине многогранника)
необходимо1^, чтобы сумма всех его плоских углов была меньше
2 л;, то т
к(п-2)
< 2тг, откуда следует, что
т
!
2"
(6.1)
В соответствии с геометрическим смыслом тип —
натуральные числа, не меньшие 3. При таких ограничениях
неравенство (6.1) имеет лишь конечное число решений.
Действительно, при п > 6 решений нет, а все решения
при п = 3, 4, 5 приведены в таблице 6Л. Эти значения п
и т отвечают соответственно правильным тетраэдру,
октаэдру, икосаэдру, кубу и додекаэдру. Конечно, надо ещё
убедиться, что каждый из вышеназванных многогранников
существует. Мы не будем здесь доказывать их
существование, а ограничимся лишь констатацией этого факта. Более
подробное исследование содержится, например, в книгах
[Прасолов, Шарыгин, 1989], [Шклярский и др., 1954].
Названия правильных многогранников греческие, они
соответствуют числу граней, например, тетраэдр — четы-
. замечание 2 к теореме 5.7.
§ 6.3. Правильные многогранники
207
рёхгранник. В таблице 6.2 указано количество граней,
вершин и рёбер для каждого правильного многогранника.
Интересно отметить, что правильные гексаэдр и октаэдр
являются двойственными друг другу: центры граней
куба являются вершинами правильного октаэдра (рис. 6,7а),
Рис. 6.7
и наоборот: центры граней правильного октаэдра
являются вершинами куба (рис. 6.76). Аналогичным свойством
обладают правильные икосаэдр и додекаэдр (рис. 6.8а, б).
Рис. 6.8
208 Глава 6. Элементы теории многогранников
§ 6.4*. Теорема Эйлера
Читайте Эйлера, читайте Эйлера, он учитель
для всех нас.
/7. Лаплас
Оказывается, число граней, вершин и рёбер
многогранника не может быть произвольным. Например, не
существует многогранника с семью рёбрами. Действительно,
пусть такой многогранник существует и имеет k граней.
Если все его грани — треугольники, то (поскольку каждая
грань содержит три ребра, а каждое ребро принадлежит
двум соседним граням) у многогранника 3&/2 рёбер, т.е.
число рёбер делится на 3. Если же одна из граней имеет
по крайней мере четыре ребра, то всего рёбер не меньше
восьми (не менее четырёх рёбер в этой грани и ещё не менее
четырёх рёбер — по одному ребру, исходящему из каждой
её вершины).
Следующее важное соотношение между числом граней,
вершин и рёбер многогранника было установлено
Леонардом Эйлером в 1758 г.
Теорема 6.1. Для числа граней Г, числа вершин В и
числа рёбер Р любого выпуклого многогранника справедливо
соотношение
В-Р-2.
Доказательство. Ортогонально спроектируем
многогранник на плоскость, не перпендикулярную ни одной из
его граней. При этом проекцией каждой грани будет
некоторый выпуклый многоугольник, число сторон которого
равно числу рёбер этой грани. Проекцией многогранника
будет выпуклый многоугольник Q, граница которого
представляет собой проекцию некоторой замкнутой
(пространственной) ломаной М, состоящей из рёбер многогранника1*.
1}В случае невыпуклого многогранника это утверждение, вообще
говоря, неверно.
§ 6.4*. Теорема Эйлера 209
Эта ломаная делит поверхность многогранника на две
части. Пусть первая часть содержит Fi граней, вторая —
Гг граней. Далее, пусть Bi —число внутренних (т.е. не
принадлежащих М) вершин первой части, В2 — второй
части, В' — число вершин ломаной М,
Рис. 6.9
Рассмотрим проекцию только первой части (рис. 6.9).
Пусть грани первой части, а следовательно, и их проекции
имеют rii рёбер, i — 1, 2, ..., Fi. Вычислим двумя способами
сумму Si углов проекций всех граней первой части. С одной
стороны, так как сумма внутренних углов щ-угольника
равна к(щ — 2), то Si = YL к{щ — 2). С другой стороны,
эта сумма складывается из суммы углов многоугольника Q
и углов при внутренних вершинах: Si = ^(В' — 2) + 27rBi.
Сравнивая два полученных выражения для Si, получаем
^ — 2Г1 =B'-2 + 2Bi. (6.2)
Аналогично
г2
mi-2T2 = B' -2 + 2В2, (6.3)
210
Глава 6, Элементы теории многогранников
Рис. 6.10
где mi — количества рёбер у граней второй части, i = 1,
2, ..., Г2. Складывая равенства (6.2) и (6.3) и учитывая,
что каждое ребро принадлежит двум граням, получаем
2Р - 2(Гх + Г2) = 2(Bi + В2 + В') - 4,
или
2Р-2Г=2В-4,
т.е.
В-Р-2,
что и требовалось доказать.
□
Замечание. Доказанная теорема верна не только для
выпуклых, но и для некоторых невыпуклых многогранников, а
именно для многогранников, у которых нет «сквозных дыр» (для
так называемых односвязных многогранников). На рис. 6.10
приведён пример неодносвязного многогранника, для которого
Г + В-Р = 0(Г=12, В = 12, Р = 24).
о^ Упражнение 6.2. Используя теорему Эйлера, докажите, что
любой правильный многогранник принадлежит к одному из
пяти типов, перечисленных в § 6.3.
Задачи 211
Задачи
Я занимался до сих пор решением ряда задач,
ибо при изучении наук примеры полезнее правил.
И. Ньютон. Всеобщая арифметика
6.1. Докажите, что многогранник является выпуклым
тогда и только тогда, когда он целиком лежит по одну
сторону от каждой плоскости, содержащей его грань.
6.2. Докажите, что тело является выпуклым тогда и
только тогда, когда каждый луч, выходящий из произвольной
внутренней точки, пересекает поверхность тела ровно в
одной точке.
6.3. Найдите сумму двугранного угла правильного
тетраэдра и двугранного угла правильного октаэдра.
6.4. Докажите, что центры граней куба являются
вершинами правильного октаэдра, а центры граней правильного
октаэдра — вершинами куба.
6.5. Боковые грани правильной четырёхугольной
пирамиды и правильного тетраэдра равны. Эти многогранники
приложили друг к другу так, что боковая грань одного
из них совпала с боковой гранью другого. Сколько граней
у получившегося многогранника?
6.6. Обязательно ли является правильным
многогранник, у которого равны:
а) все рёбра и все двугранные углы;
б) все рёбра и все многогранные углы;
в) все грани и все многогранные углы?
6.7. Докажите, что у любого многогранника:
а) число граней с нечётным числом рёбер четно;
б) число вершин, в которых сходится нечётное число
рёбер, четно.
6.8. Докажите, что в любом многограннике найдётся
либо треугольная грань, либо трёхгранный угол.
6.9. Докажите, что в любом многограннике найдётся
грань, у которой менее шести сторон.
212 Глава б. Элементы теории многогранников
6Л0*. Существует ли семигранник, все грани которого
являются четырёхугольниками?
6.11*. При каких п существует многогранник, имеющий
п рёбер?
6.12*. Все рёбра многогранника с шестью вершинами
имеют одинаковую длину а, а расстояние между любыми
двумя несмежными вершинами равно а\/2. Верно ли, что
это правильный октаэдр? Если нет, то найдите все
многогранники, удовлетворяющие перечисленным условиям.
6ЛЗ*. У выпуклого многогранника внутренний
двугранный угол при каждом ребре острый. Сколько может быть
граней у этого многогранника?
6.14*. Докажите, что у всякого выпуклого
многогранника найдутся три ребра, из которых можно составить
треугольник.
Глава 7
Геометрические места точек пространства
— А ещё они рисовали... Всякую всячину...
Всё, что начинается на «М»... Они рисовали
мышеловки, месяц, математику, множество.♦.
Ты когда-нибудь видела, как рисуют
множество?
— Множество чего? — спросила Алиса.
— Ничего,— отвечала Соня.— Просто
множество!
Л. Кэрролл. Приключения Алисы в стране чудес
§ 7.1. Основные геометрические места
точек пространства
Предположим, что из всех точек пространства нам
нужно выделить точки, обладающие некоторым свойством S.
Множество этих точек в геометрии принято называть
геометрическим местом точек (сокращённо ГМТ),
обладающих свойством S. Тем самым термин «геометрическое
место точек» является синонимом термина «множество
точек», а так как понятие «множество» относится к
неопределяемым математическим понятиям, то давать определение
понятия «геометрическое место» не имеет смысла.
Геометрическое место точек, обладающих заданным
свойством,—это некоторая фигура Ф в пространстве.
Найти геометрическое место точек — значит описать эту фигуру.
Нужно также постараться (если это возможно) дать это
описание на геометрическом языке, т. е. сказать, как эта
фигура называется (например, три точки, пара прямых,
сфера и т.п.), и указать параметры, задающие её
положение в пространстве (например, центр и радиус сферы, три
точки, через которые проходит плоскость, и т. п.). При этом
необходимо установить справедливость двух утверждений:
1) если точка М обладает свойством S, то она
принадлежит фигуре Ф;
214 Глава 7. Геометрические места точек
2) если точка М принадлежит фигуре Ф, то она обладает
свойством S.
Доказательство этих двух утверждений равносильно
нахождению тех и только тех точек, которые обладают
свойством S. Условимся первое из них считать прямой
теоремой, тогда второе будет обратной теоремой и можно
сказать, что при нахождении ГМТ следует доказывать обе
теоремы: прямую и обратную (или прямую и
противоположную к прямой, которая равносильна обратной).
Подчеркнём, что если при нахождении ГМТ доказана только
прямая теорема и не доказана обратная, то нет никакой
гарантии, что найденная нами фигура не содержит точек,
не обладающих заданным свойством S. Поэтому такое
решение задачи нельзя признать полным, даже если получен
правильный ответ.
Ситуация, подобная описанной, уже встречалась в
алгебре, когда при решении уравнения или неравенства нужно,
с одной стороны, не потерять ни одного решения, а с другой
стороны, не приобрести ничего лишнего, т.е. убедиться,
что все найденные числа действительно являются
решениями. Эта аналогия более глубокая, чем кажется на первый
взгляд. Дело в том, что многие задачи на нахождение ГМТ
могут быть решены с помощью метода координат, который
позволяет свести их решение к решению уравнений и
неравенств. Подобные примеры будут рассматриваться в курсе
стереометрии 11-го класса, после того как будет изложен
метод координат в пространстве.
Полезно знать геометрические места точек
пространства, которые часто встречаются при решении задач.
Перечислим некоторые из них в виде следующих пяти
утверждений.
I. Геометрическим местом точек пространства,
удалённых от точки О на расстояние R > О, является сфера
S(0, R) с центром в точке О и радиусом R.
§ 7.L Основные геометрические места точек 215
IL Геометрическим местом точек пространства,
равноудалённых от двух точек А и В, является плоскость,
перпендикулярная отрезку АВ и проходящая через его
середину.
III. Геометрическим местом точек, равноудалённых от
двух пересекающихся плоскостей, является пара
взаимно перпендикулярных плоскостей, делящих пополам
двугранные углы, образованные данными плоскостями.
IV. Геометрическим местом точек, равноудалённых от
всех вершин плоского вписанного многоугольника,
является прямая, перпендикулярная плоскости этого
многоугольника и проходящая через центр описанной около
него окружности.
V. Геометрическим местом точек, равноудалённых от
всех сторон плоского описанного многоугольника,
является прямая, перпендикулярная плоскости этого
многоугольника и проходящая через центр вписанной в него
окружности.
Утверждение I является переформулировкой
определения сферы, данного в § 6.1. Остальные утверждения
нуждаются в доказательстве.
Доказательство утверждения П. Сначала покажем,
что если точка М такова, что МА = МВ, то М лежит в
плоскости а, проходящей через середину О отрезка АВ и
перпендикулярной ему. Достаточно проверить этот факт для
точек М, отличных от точки О. Проведём через точку М
плоскость /3, перпендикулярную прямой АВ (рис. 7.1). Пусть
Ох =(Зп(АВ). Прямоугольные треугольники АО\М и ВО\М
равны по гипотенузе и катету, следовательно, равны и их
оставшиеся катеты, т. е. АО\ —О\В. Поэтому О\ — середина
отрезка АВ и, следовательно, а и j3 — одна и та же
плоскость.
Теперь докажем обратное утверждение: если точка М
принадлежит плоскости ос, то MA — MB. Соединим
точку М с точками А, В и О (рис. 7.2). Так как (АВ) _L a,
216
Глава 7. Геометрические места точек
Рис. 7.1
Рис. 7.2
а (ОМ) G а, то (ОМ) ± (АВ). Прямоугольные треугольники
АОМ и ВОМ равны по двум катетам, следовательно, равны
и гипотенузы этих треугольников, т.е. МА — МВ. □
Утверждение III следует из теоремы 5.2 о биссекторе
двугранного угла.
DS3 Упражнение 7.1. Выведите утверждение III из теоремы о
биссекторе.
Доказательство утверждения IV. Пусть
плоский многоугольник, вписанный в окружность с
центром О, а I — прямая, проходящая через О и
перпендикулярная плоскости А1Л2А3. Докажем, что если МА\ = ... =МАп,
то Mel. Предположим противное, т. е. пусть М^ I. Опустим
из точки М перпендикуляр на плоскость A\AzA^ и
обозначим его основание через О\ (рис. 7.3). Прямоугольные
треугольники А\О\М, А2О1М, ..., АпО\М равны по
гипотенузе и катету, следовательно, О\А\ = О\А2 = ... = О\Ап.
Поэтому О\ и О — это одна и та же точка (как известно из
планиметрии, если около многоугольника можно описать
окружность, то эта окружность единственна), т. е. Me I.
Докажем обратное утверждение. Пусть Mel. Из
равенства прямоугольных треугольников А\ОМ> А2ОМ, ...,
АпОМ с общим катетом ОМ и равными (как радиусы
окружности) катетами OAi, ..., ОАп получаем, что МА\ = ...
...=МАп (рис. 7.4). □
§ 7.2. Геометрические места точек
217
м
м
Рис. 7.3
Доказательство утверждения V проводится по той же
схеме, что и доказательство утверждения IV.
вЗР Упражнение 7.2. Докажите утверждение V,
Отметим, что если около многоугольника, о котором
идёт речь в утверждении IV, нельзя описать окружность,
то соответствующее ГМТ представляет собой пустое
множество точек. Аналогичный результат имеет место, если
в формулировке утверждения V заменить описанный
многоугольник многоугольником, в который нельзя вписать
окружность. Заметим ещё, что в формулировке
утверждения V существенно, что рассматриваются именно стороны
многоугольника, а не прямые, их содержащие. В последнем
случае результат оказывается совершенно иным (см.
задачу 7.4).
§ 7.2. Геометрические места точек, сводящиеся
к основным. Метод пересечения и объединения
Решения многих задач на нахождение геометрических
мест точек могут быть получены путём сведения к основ-
218
Глава 7. Геометрические места точек
ным ГМТ, перечисленным в предыдущем параграфе.
Приведём несколько примеров.
Пример 7.1. Найти геометрическое место точек М
пространства, из которых данный отрезок АВ виден под
прямым углом (т. е. таких, что ZAMB — 90°).
Решение. Нужно найти геометрическое место таких
точек М, что треугольник АМВ прямоугольный с
гипотенузой АВ. Это равносильно тому, что точка М находится
от середины отрезка АВ на расстоянии, равном половине
длины этого отрезка, причём М отлична от А и В.
Следовательно, искомым геометрическим местом является сфера
с центром в середине отрезка АВ и радиусом АВ/2 без точек
А и В. D
Полученный результат полезно помнить, так как это
ГМТ наряду с основными часто используется при решении
задач.
Пример 7.2. Дан плоский четырёхугольник ABCD,
никакие две стороны которого не параллельны. Найти
геометрическое место таких точек М, что боковую поверхность
пирамиды MABCD можно пересечь плоскостью так, что
в сечении получится прямоугольник.
Решение. Пусть Р = (АВ) П (CD), a Q = (ВС) П (AD).
Тогда прямые МР и MQ — линии пересечения плоскостей,
Q
Рис. 7.5
§ 7.2. Геометрические жеста точек 219
содержащих противоположные боковые грани пирамиды
MABCD (рис. 7.5).
Пересечение плоскости а и пары плоскостей,
пересекающихся по прямой I, представляет собой две
параллельные прямые тогда и только тогда, когда плоскость а
параллельна I. Поэтому сечение пирамиды MABCD будет
параллелограммом тогда и только тогда, когда плоскость
сечения параллельна плоскости MPQ, и при этом стороны
сечения параллельны прямым МР и MQ. Этот
параллелограмм является прямоугольником тогда и только тогда,
когда ZPMQ = 90°. Из результата предыдущего примера
следует, что точка М принадлежит сфере с диаметром PQ,
из которой исключены точки Р и Q. Кроме того, ясно,
что точки этой сферы, лежащие в плоскости ABCD, не
принадлежат искомому ГМТ. □
ВЭ* Упражнение 7.3. Решите предыдущую задачу при условии,
что четырёхугольник ABCD является: а) трапецией; б)
параллелограммом.
Пример 7.3. Даны две пересекающиеся плоскости и
точка А. Найти геометрическое место таких точек М, что
прямая МА образует с этими плоскостями равные углы.
Рис. 7.6
220 Глава 7. Геометрические места точек
Решение. Рассмотрим сначала случай, когда точка А
лежит на линии пересечения данных плоскостей ос и /3.
Из определения угла между прямой и плоскостью
следует, что прямая МА образует с а и /3 равные углы тогда
и только тогда, когда точка М равноудалена от а и (5
и отлична от точки А (рис. 7.6). Следовательно, в
рассматриваемом случае искомым геометрическим местом
является пара плоскостей, делящих пополам двугранные углы,
образованные плоскостями а и /3, без точки А. Общий
случай сводится к разобранному путём проведения через
точку А плоскостей ос' и /?', параллельных плоскостям ос
и /3 соответственно. Действительно, прямая МА образует
с параллельными плоскостями равные углы. Поэтому
искомые ГМТ — пара плоскостей, делящих пополам двугранные
углы, образованные плоскостями ocf и /3', без точки А. □
До сих пор мы рассматривали задачи, в которых
требовалось найти геометрическое место точек, удовлетворяющих
одному условию. В том случае, когда в задаче нужно найти
геометрическое место точек, удовлетворяющих
одновременно нескольким условиям, достаточно найти геометрические
места точек, удовлетворяющих отдельно каждому из
условий, а затем взять их пересечение.
Пример 7.4, Найти геометрическое место точек М,
равноудалённых от четырёх данных точек пространства, А, В,
СиВ, не лежащих в одной плоскости.
Решение. Геометрическим местом точек,
равноудалённых от точек А, В и С, является прямая I,
перпендикулярная плоскости треугольника ABC и проходящая через
центр описанной около него окружности. Плоскость а,
перпендикулярная отрезку AD и проходящая через его
середину, есть геометрическое место точек, равноудалённых от А
и D. Следовательно, искомое ГМТ представляет собой точку
пересечения прямой I и плоскости а (почему эти прямая
и плоскость не могут оказаться параллельными?). D
Замечания. 1. Можно дать и другое описание полученного
ГМТ, например, представить его как пересечение трёх плоско-
§ 7.2. Геометрические места точек 221
стей, равноудалённых соответственно от точек А и В, А и С, А
и D, т.е. проходящих через середины отрезков АВ, АС и AD
и перпендикулярных к ним.
2. Из полученного результата вытекает, что через любые
четыре точки пространства, не лежащих в одной плоскости, можно
провести сферу, и притом только одну. Иными словами, около
любого тетраэдра можно описать единственную сферу. К
рассмотрению других многогранников, вписанных в сферу, мы
обратимся в курсе стереометрии одиннадцатого класса.
ИЗГ Упражнение 7.4. Докажите с помощью метода пересечения
утверждение IV из § 7.1.
Если в задаче требуется найти геометрическое место
точек, удовлетворяющих хотя бы одному из нескольких
условий, то достаточно найти геометрические места точек,
удовлетворяющих отдельно каждому из условий, а затем
взять их объединение.
Пример 7.5. Данный трёхгранный угол пересекается
плоскостями, проходящими через данную точку на одном
из его рёбер, так, что в сечении получаются
треугольники. Найти геометрическое место точек пересечения медиан
этих треугольников.
Решение. Пусть А — данная точка на ребре
трёхгранного угла, а АВС — треугольник, полученный в сечении
этого угла. Зафиксируем точку В и найдём геометрическое
место точек пересечения медиан треугольников АВС при
условии, что меняется только
положение точки С. Взяв затем
объединение таких
геометрических мест для всевозможных
положений точки В, мы найдём
ответ к нашей задаче.
Пусть D — середина отрезка
АВ (рис. 7.7), Q — точка
пересечения медиан треугольника
АВС, В — вершина данного
трёхгранного угла, Q\ — точка
пересечения медиан треугольника Рис. 7.7
222 Глава 7. Геометрические места точек
ASB. Так как |^ = ^ = |, то (QiQ) || (SC). Следовательно,
Q лежит на прямой, проходящей через точку Qi и
параллельной ребру SC. Ясно, что точки этой прямой, лежащие
вне трёхгранного угла, следует исключить. Остаётся луч I
с началом в точке Q\, параллельный прямой SC.
Все точки этого луча, кроме точки Qi, принадлежат
искомому множеству. Действительно, если Qel и Q
отлична от Qi, то проведём плоскость ABQ, которая пересечёт
третье ребро в некоторой точке С. Так как (QQi) || (SC),
то плоскость SQC пересечёт отрезок АВ в его середине D.
Следовательно, прямые CQ и SQi пересекаются в точке Z),
причём тг-к = тт^- Но -—^ = т> поэтому Q — точка пересе-
чения медиан треугольника ABC.
Теперь нужно взять объединение всех лучей /,
отвечающих всевозможным положениям точки В на
соответствующем ребре. Ясно, что при этом точки Qi будут лежать
на луче, параллельном этому ребру, с началом в точке (?2>
делящей отрезок SA в отношении 2:1, считая от точки А.
Объединение лучей / даёт пересечение данного угла с
плоскостью, проходящей через точку Q% параллельно его
рёбрам, по которым перемещаются точки В и С. Из указанного
множества ещё следует исключить луч, отвечающий
различным положениям точки Q\. □
с^3 Упражнение 7.5« Докажите с помощью метода объединения
утверждение II из предыдущего параграфа.
§ 7.3. Различные геометрические места точек
Здесь мы разберём несколько примеров, решения
которых не связаны какой-либо одной общей идеей. Тем не
менее, эти примеры иллюстрируют некоторые приёмы
(проекция, симметрия, вспомогательный объём), полезные при
нахождении геометрических мест.
§7.3. Различные геометрические места точек 223
Рис. 7.8
Пример 7.6. Найти
геометрическое место середин отрезков,
концы которых лежат на данных
скрещивающихся прямых.
Решение. Обозначим данные
прямые через 1\ и l2> a
длину общего перпендикуляра PQ —
через d. Построим плоскости
<Х\ и а2 так, что 1\ С <х\> 12 С
С <х2 и <х\ || а2 (рис. 7.8). Пусть
точка М принадлежит искомому
множеству, т.е. она является
серединой отрезка АВ, где Ае 1\9
а В € 12. Спроектируем точки В
и М на плоскость а\ и
обозначим проекции через В\ и Mi
соответственно. Так как ВВ\ —d>
а отрезок ММ\ — средняя линия
треугольника АВВ\> то MMi =
= d/2, т. е. р (МУ oti) = р (М, а2).
Следовательно, точка М
находится на равном расстоянии от
плоскостей «1 и #2 и, значит,
лежит в плоскости /3,
перпендикулярной отрезку PQ и
проходящей через его середину.
Докажем теперь, что если
М €/?, то М является серединой
некоторого отрезка АВ с
концами на прямых 1\ и 12. Спроектируем точку М на
плоскость (Х\. Через полученную точку М\ проведём
отрезок ABi так, что А £ l\9 a B\ e 1'2> где 1'2 — проекция
прямой 12 на плоскость tfi, причём A/Vfi =M\B\. Для этого
достаточно соединить точку пересечения прямых 1\ и V2
с точкой Mi, продолжить полученный отрезок за точку Mi
на такую же длину, а затем через полученную точку
Рис. 7.9
224 Глава 7. Геометрические места точек
провести прямые, параллельные 1\ и /'2, до пересечения
с ними (рис. 7.9) (докажите это). Спроектировав точку В\
на плоскость с*2, мы получим точку В. Отрезок АВ будет
содержать точку М (почему?), а из подобия треугольников
АМ\М и АВ\В следует, что AM = MB. О
Пример 7,7. На поверхности правильного тетраэдра
найти геометрическое место концов отрезков, которые делятся
пополам серединой данной высоты этого тетраэдра.
Решение. Пусть точка О — середина данной высоты
тетраэдра Т. Поставим в соответствие каждой точке X
тетраэдра Т такую точку У, отличную от X, что ОХ = ОУ,
причём точки Ху О и У лежат на одной прямой1*.
Ясно, что таким образом мы получим новый тетраэдр Т\у
причём рассматриваемая высота у тетраэдров Т и Т\ об-
Рис. 7.10
щая (рис. 7.10). Пусть точки Р и Q лежат на поверхности
тетраэдра Т, РО = OQ и точки Р, О и Q лежат на одной
прямой. Тогда точке Р согласно нашему определению
соответствует точка Q, и наоборот. Следовательно, точки Р и Q
1)Такое преобразование называется симметрией относительно
точки или центральной симметрией; оно будет подробно изучено нами
в §8.4
§7.3. Различные геометрические места точек 225
лежат также и на поверхности тетраэдра Т\. Верно и
обратное. Из этого следует, что искомое геометрическое место
есть пересечение поверхностей
тетраэдров Т и Т\. Это
замкнутая ломаная ABCDEF и
концы данной высоты тетраэдра Т
(рис. 7.11). □
Пример 7.8. Найти
геометрическое место точек данного
трёхгранного угла, сумма
расстояний от которых до его граней
равна данному положительному
числу а.
Решение. Пусть OXYZ —
данный трёхгранный угол. Возьмём
на его рёбрах OX, OY и OZ точки А, В и С соответственно
так, что расстояния от этих точек до противоположных им
граней равны а (рис. 7.12). Пусть точка М принадлежит
трёхгранному углу, а расстояния от неё до граней равны
п\у п2 и аз- Сумма объёмов пирамид с вершиной М
Рис. 7.11
и основаниями ОАВ, ОВС и ОСА равна ^S(ai + а>2
о
где S — площадь треугольников ОАВ, ОВС и ОСА (эти
треугольники равновелики, так как их площади равны
Рис. 7.12
8 Зак. 3383
226 Глава 7. Геометрические места точек
—, где V — объём тетраэдра О ABC). Следовательно, V =
= о£(ai + 02 + Дз) ± *>> где и — объём тетраэдра МАВС. Так
о
как V = xSa, то ai + аг + аз = а тогда и только тогда, когда
v = О, т. е. точка М принадлежит треугольнику ABC. П
Задачи
— Задай ещё вопрос. Какое же
наслаждение наблюдать за работой собственной
головы, решающей мировые проблемы!
Р. Бах, Иллюзии
7Л. Найдите геометрическое место точек пространства,
равноудалённых от вершин равнобедренной трапеции.
7.2. Найдите геометрическое место точек, делящих
отрезки с концами на данных скрещивающихся прямых в
отношении k.
7.3. Найдите геометрическое место точек,
а) сумма;
б) модуль разности
расстояний от которых до двух данных плоскостей
постоянна.
7.4. Найдите геометрическое место точек пространства,
равноудалённых от всех прямых, содержащих стороны
данного плоского выпуклого многоугольника. Рассмотрите
отдельно случаи треугольника и четырёхугольника.
7.5. Концы отрезков длины а лежат на двух данных
взаимно перпендикулярных скрещивающихся прямых.
Найдите геометрическое место середин этих отрезков.
7.6. Найдите геометрическое место точек пространства,
являющихся основаниями перпендикуляров, опущенных
из данной точки на прямые, лежащие в данной плоскости
и пересекающиеся в одной точке.
7.7. Найдите геометрическое место проекций данной
точки на плоскости, проходящие через другую данную точку.
Задачи 227
7.8. В треугольной пирамиде вершина S перемещается
так, что один из отрезков, соединяющих середины
противоположных рёбер пирамиды, не меняет своей длины.
Найдите геометрическое место точек S.
7.9. В тетраэдре ABCD точка О — точка пересечения
медиан треугольника ABC. Точка А перемещается так, что
длина отрезка OD постоянна. Найдите геометрическое
место точек А.
7.10. Дан треугольник ABC. Рассматриваются
всевозможные тетраэдры РАВС, у которых наименьшей из высот
является РН (Н — проекция точки Р на плоскость ABC).
Найдите геометрическое место точек Н.
7.11. Дан остроугольный треугольник ABC. Найдите
геометрическое место проекций на плоскость ABC всех
точек М, для которых треугольники ABM, BCM и САМ
остроугольные.
7.12. Дан плоский четырёхугольник ABCD, никакие две
стороны которого не параллельны. Найдите
геометрическое место таких точек М, что боковую поверхность
пирамиды MABCD можно пересечь плоскостью так, что в сечении
получится: а) ромб; б) квадрат.
7.13. Даны три попарно скрещивающиеся прямые и
плоскость. Найдите геометрическое место точек
пересечения медиан треугольников, параллельных данной
плоскости, вершины которых лежат на данных прямых. Как
изменится ответ, если отказаться от условия параллельности
плоскости?
7Л4. Паук сидит в одной из вершин куба, ребро
которого равно 1 см. Он может ползти по поверхности куба со
скоростью 1 см/с. Найдите геометрическое место точек на
поверхности куба, которых паук может достичь за 2 с.
7.15. Найдите геометрическое место таких точек М
внутри данного правильного тетраэдра, что расстояния от М
до граней тетраэдра служат длинами сторон некоторого
четырёхугольника.
Глава 8
Преобразования пространства
Господь с тобой, Моток!
Господь с тобой! Тебя преобразили!
В. Шекспир. Сон в летнюю ночь
§ 8.1. Основные определения. Перемещения.
Общие свойства перемещений
Четверг. Сегодня стул был не у дел.
Он не переместился. Ни на шаг.
И. Бродский. Посвящается стулу
Из планиметрии вам известно понятие преобразования
плоскости. В пространстве это понятие вводится
аналогичным образом. Приведём основные определения, связанные
с этим понятием.
Пусть X и У — два непустых множества. Если указано
правило, по которому каждому элементу х е X ставится
в соответствие ровно один элемент у £ У', то говорят, что
задано отображение множества X в множество У.
Мы будем обозначать отображения буквами /, g9 h, •..
и писать X—>Y. Элемент у£У, который ставится в
соответствие элементу х 6 X, называется образом элемента х
при отображении / и обозначается у — f{x). При этом х
называется прообразом элемента у.
Образом множества М С X называется множество М'
(обозначаемое /(М)), состоящее из образов всех элементов
множества М. Прообразом множества М1 С Y
называется множество М, состоящее из всевозможных прообразов
всех элементов множества М'.
Пусть задано отображение X —► У. Если для любых двух
различных элементов х\, х% <еХ их образы f(x\) и /(#2) так-
230 Глава 8. Преобразования пространства
же различны, то отображение / называется
обратимым.
Если каждый элемент j/бУ имеет хотя бы один прообраз,
то говорят, что / — это отображение X наУ.
Обратимое отображение / множества X на множество У
называется взаимно однозначным соответствием между
множествами X и Y или, короче, взаимно однозначным
отображением X наУ.
Для любого взаимно однозначного отображения /
существует обратное отображение /"*, при котором
каждому элементу у е Y ставится в соответствие (тот
единственный) элемент хеХ> для которого y = f(x). Таким образом,
x = f-l(f(x)) УхеХиу = НГ1(у)) Vz/ЕУ. Очевидно, что
если g = f~l* to f = g'1.
Если X—»Y, аУ = Х, то говорят, что задано
отображение множества X в себя.
Всякое взаимно однозначное отображение множества X
на себя называется преобразованием множества X.
Пусть Gx — множество всех преобразований непустого
множества X, / £ Gx и g e Gx- Поставим каждому
элементу х из X в соответствие элемент г из X по следующему
правилу: z = g{y)> где y — f{x), т.е. 2 = £(/(*)). Тем самым
мы получим преобразование множества X, которое
называется композицией преобразований f и g и обозначается
g о /\ (Обратите внимание на это обозначение:
преобразование /\ которое выполняется первым, стоит справа от
знака о.)
Пусть Ф —некоторая фигура в пространстве. Будем
говорить, что эта фигура переходит в себя при
преобразовании /, если ДФ) =Ф, и в фигуру Фь если /(Ф) =Фх.
В дальнейшем мы будем рассматривать только
преобразования пространства (т, е. в качестве множества X
выбирать множество всех точек пространства). Преобразование
пространства, вообще говоря, изменяет форму, размеры
и положение геометрических фигур в пространстве.
Выделим из множества всех преобразований пространства те
§ 8Л. Основные определения. Перемещения 231
преобразования, которые не изменяют ни форму, ни
размеры геометрических фигур.
Определение. Преобразование / пространства
называется перемещением1^, если оно сохраняет расстояния между
точками, т. е. если для любой пары точек Аи В
выполняется равенство А! В* = АВ, где А! = f(A), В' = f(B).
Данное определение нуждается в комментарии.
Действительно, как мы уже отмечали в § 1.1, расстояние между точками
определено пока лишь в каждой плоскости пространства, и априори
возможна ситуация, при которой единица измерения расстояния
изменяется при переходе от одной плоскости к другой. Но на
самом деле из аксиомы расстояния (аксиома 4 из § 1.1) следует,
что это невозможно. Для того чтобы доказать это утверждение,
рассмотрим два случая. Пусть плоскости а и /3 пересекаются по
прямой /. Из аксиомы расстояния следует, что на этой прямой
расстояние между точками А и В, измеренное в плоскости а,
совпадает с расстоянием между этими точками, измеренным
в плоскости /3. Задание единичного отрезка полностью
определяет расстояние во всей плоскости, поэтому, расположив
единичный отрезок на прямой Z, убеждаемся, что единица измерения
расстояния одна и та же в любых двух плоскостях,
пересекающихся по прямой /. Если же плоскости а и /? параллельны, то
пересечём их третьей плоскостью у и применим то же
рассуждение к парам плоскостей а и у, /3 и у.
Итак, расстояние между точками однозначно определено во
всём пространстве (т. е. единица измерения расстояния во всём
пространстве одна и та же), следовательно, данное нами
определение перемещения корректно.
Перейдём теперь к изучению общих свойств
перемещений.
Из данных выше определений непосредственно
вытекает, что перемещение взаимно однозначно и, в частности,
обратимо; преобразование, обратное к перемещению, —
перемещение; композиция перемещений — перемещение.
Другие свойства перемещений мы сформулируем в виде
теорем.
^Часто употребляется и термин движение.
232 Глава 8. Преобразования пространства
Теорема 8.1. Пусть точки А, X и В лежат на одной
прямой, причём точка X лежит между А и В. Тогда их
образы при перемещении А', Х! и Bf также лежат на одной
прямой, причём точка Xf лежит между Af и В'.
Доказательство. Из определения перемещения
вытекает, что A!Xf = АХ, Х'В* = ХВи А!В1 = АВ. Следовательно,
А!Х' + Х'ВГ =АХ + ХВ = АВ = А!В1. Итак,
А'Х' + Х'В' = А'В'. (8.1)
Проведём через точки А! у X1 и В! плоскость (если
указанные точки не лежат на одной прямой, то эта плоскость
единственна согласно аксиоме плоскости; если они лежат
на одной прямой, то таких плоскостей бесконечно много,—
мы выберем из них любую). Как известно из планиметрии,
в плоскости равенство (8Л) означает, что точки Af, Xf и В'
лежат на одной прямой, причём точка X1 лежит между А!
и В'. □
Теорема 8.2. Образом прямой при перемещении
является прямая, образом луча — луч, образом отрезка — отрезок
той же длины.
Эти свойства перемещений пространства доказываются
так же, как и аналогичные свойства перемещений
плоскости.
I®9 Упражнение 8.1. Используя определение перемещения и
теорему 8.1, докажите теорему 8.2.
I Теорема 8.3. Образом плоскости при перемещении
является плоскость.
Доказательство. Пусть / — перемещение, а—данная
плоскость. Выберем в плоскости а две пересекающиеся
прямые а и Ь. Обозначим a1 ~f{a) и У = f(b). Прямые а'
и Ь1 также пересекаются, причём а! фЪ* в силу взаимной
однозначности отображения /\ Проведём через эти прямые
плоскость а' и докажем, что а1 — f(oc).
§ 8.1. Основные определения. Перемещения 233
Рис. 8.1
Пусть М — произвольная точка плоскости а и М' = /(М).
Если М еа или М е 6, то М' е а'. Если жеМ^аиМ^,
то проведём через эту точку прямую с, пересекающую
прямую а в точке А, а прямую Ъ — в точке В (рис. 8.1) (почему
такая прямая найдётся?). Тогда Ml G f(c) ~c\ но прямая с'
лежит в плоскости а', так как она проходит через две точки,
А! и В' (образы точек А и В), лежащие в этой плоскости.
Следовательно, и в этом случае М' е ос*.
Итак, образ любой точки М € а принадлежит
плоскости а\ т.е. f(a) С а!. Аналогично доказывается, что
f~l (а') С <х, т. е. а' С f{a). Следовательно, а1 — f(a). □
Далее нам понадобится следующее вспомогательное
утверждение.
Лемма 8.1. Пусть А', В' и С — образы точек А, В и С
соответственно при перемещении /. Тогда /.СA!Bf = ZCAB.
Доказательство. Если точки А, В и С лежат на одной
прямой, то доказываемое утверждение следует из
теоремы 8.1.
Пусть теперь эти точки не лежат на одной прямой, АВ =
= с, ВС = а, CA = b, ZCAB = an ZC'A'Bf = a'. Из определения
перемещения следует, что А! В' = с, BfCf = а и С А1 = 6.
Проведём через точки А, В и С плоскость т, а через точки А',
В' и С — плоскость г' (возможно, т и т' — одна и та же
плоскость) (рис. 8.2). В этих плоскостях мы можем
применить известную из планиметрии теорему косинусов. Из
треугольника ABC находим cos а = (Ь2 + с2 — а2)/2Ьс, из
234
Глава 8. Преобразования пространства
Рис. 8.2
треугольника1* А'В'С находим cos af = (b2 + с2 - a2)/2bc.
Мы видим, что cos а' — cos а. Так как функция у = cos x
строго убывает на (0, 7г), а а', а. € (О, тг), то а'= а. D
I Теорема 8.4. Образом полуплоскости при перемещении
является полуплоскость.
Доказательство. Пусть f — перемещение, а Р —
полуплоскость, ограниченная прямой а. Дополним данную
полуплоскость до плоскости а. Обозначим <xr ~/(a), a! = f(a).
Пусть также А £ int P, А! = f(A), a P1 — та из двух
полуплоскостей плоскости <х\ в которой лежит точка А!.
Докажем, что Р; = /(Р). Пусть М — произвольная точка
полуплоскости Р, отличная от А, а М' = f(M). Если М € а> то
М1 е а! и М е Р. Если М £ а, то M'g P;, так как в
противном случае [М'А;] Па' = О' (рис. 8.3), следовательно,
Рис. 8.3
1)Точки А\ В' и С не лежат на одной прямой. Действительно, в
противном случае по теореме 8.1 точки А, В и С — их образы при
перемещении f'1 — также должны были бы лежать на одной прямой.
§ 8.1. Основные определения. Перемещения
235
r1([M'A'])C\f-1(a')=f-l(Of),T.e.[MA]na. Пришли к
противоречию. Итак, всякая точка полуплоскости Р имеет
образ на полуплоскости Р'. Аналогично доказывается, что
верно и обратное. Следовательно, Р' = f(P). □
Теорема 8.5. Образом выпуклого плоского угла при
перемещении является выпуклый плоский угол той же
величины.
Доказательство. Если данный плоский угол
развёрнутый, то доказываемое утверждение вытекает из
предыдущей теоремы.
Пусть данный угол не является развёрнутым. Всякий
выпуклый плоский угол, отличный от развёрнутого,
является пересечением двух полуплоскостей Pi и?2- Пусть
/ — перемещение, а образы полуплоскостей Р\ и Рг —
полуплоскости Р'х и Pf2 (теорема 8.4). Образом выпуклого
угла Pi Г1Р2 является пересечение полуплоскостей Р[ и Р'2,
т.е. выпуклый угол.
Докажем теперь, что величина плоского угла при этом
не изменяется. Пусть образом плоского угла с вершиной О
и сторонами а и 6 при перемещении / является плоский
угол с вершиной О' и сторонами af и Ь1 ((У = f(O), а! — f(a),
b' = f(b)). Выберем точку Аба и точку Beb (рис. 8.4). Тогда
А' = f(A) е а' и Bf = f(B) e &'. Согласно лемме 8.1 получаем
ZAOB = ZA'(yB'. □
Вспомним теперь, что величина угла между
скрещивающимися прямыми, между наклонной и плоскостью, пер-
Рис. 8.4
236 Глава 8. Преобразования пространства
пендикуляром и плоскостью, величина двугранного угла
и угла между плоскостями определяются через величину
соответствующего выпуклого плоского угла (см. определения
этих понятий). Поэтому из теоремы 8.5 вытекает
следующая теорема.
Теорема 8.6. Перемещение сохраняет величину угла
между прямыми, между прямой и плоскостью и между
плоскостями.
При изучении преобразования важно найти все его
неподвижные точки, неподвижные прямые и неподвижные
плоскости.
Определение. Неподвижной точкой (прямой,
плоскостью) преобразования называется такая точка (прямая,
плоскость) пространства, которая при этом
преобразовании переходит в себя.
Частным случаем неподвижной прямой (плоскости)
является прямая (плоскость) неподвижных точек, все
точки которой неподвижны.
В заключение этого параграфа обсудим понятие
равенства фигур, которое вводится в стереометрии точно так же,
как и в планиметрии.
Определение. Фигура Ф\ называется равной фигуре <Х>2,
| если существует перемещение пространства /, которое
переводит фигуру Ф\ в фигуру Фг, т.е. Фг = f(*&i)*
Из определения вытекает, что отношение равенства фигур
в пространстве является отношением эквивалентности.
Действительно, это отношение рефлексивно (всякая фигура равна самой
себе; чтобы это показать, достаточно взять в качестве f
преобразование, при котором каждая точка пространства переходит
в себя, т. е. остаётся неподвижной; такое преобразование
называется тождественным и обозначается £), симметрично (так как
f — перемещение, то f~x — также перемещение, и Ф\ = /"4^2))
и транзитивно (так как композиция перемещений —
перемещение).
§ 8.2, Параллельный перенос 237
§ 8.2. Параллельный перенос
Параллельный перенос пространства определяется
аналогично параллельному переносу плоскости.
Определение. Пусть в пространстве задан вектор 3.
Отображение, при котором каждой точке М пространства
ставится в соответствие такая точка М', что ММ' = й>
называется параллельным переносом на вектор а.
Из определения вытекает, что указанное отображение
является взаимно однозначным отображением
пространства на себя (почему?), т. е. преобразованием пространства.
Параллельный перенос на вектор а мы будем
обозначать Т$.
Заметим, что в определении параллельного переноса
возможно, что вектор 3 нулевой. В этом случае
параллельный перенос является тождественным преобразованием.
| Теорема 8.7. Параллельный перенос — перемещение.
Доказательство. Рассмотрим параллельный перенос
7V Возьмём две произвольные точки пространства X и Y
и обозначим их образы при параллельном переносе через X'
и У соответственно. Тог^а по определению параллельного
переноса XX1 = й и YY' = 5, т. е. XXf = YY'. Прибавляя
к обеим частям этого равенства X'Y, получаем XY =XfY'.
Следовательно, XY = X'Y'. □
Мы доказали, что параллельный перенос является
перемещением, следовательно, он обладает всеми общими
свойствами перемещений, перечисленными в предыдущем
параграфе. Теперь мы займёмся изучением специфических
свойств параллельного переноса.
Из определения параллельного переноса вытекает, что
параллельный перенос однозначно задаётся указанием
какой-нибудь одной точки и её образа и что преобразование,
обратное к параллельному переносу Т& есть параллель-
238 Глава S. Преобразования пространства
ный перенос Т-& а композиция параллельных переносов
Т$ и Tg есть параллельный перенос Т^.
о^ Упражнение 8.2. Докажите эти утверждения.
Под образом вектора а, изображаемого направленным
отрезком ХУ, при перемещении мы будем понимать
вектор 5', изображаемый направленным отрезком Х'У, где X'
и У — образы точек X и У соответственно.
с^3 Упражнение 8.3. Докажите корректность этого определения,
т. е. что образ вектора не зависит от выбора изображающего
этот вектор направленного отрезка.
Будем говорить, что перемещение / сохраняет
направления, если для любого вектора а выполняется равенство
№ = з.
Сформулируем и докажем теорему, выражающую
критерий того, что перемещение пространства является
параллельным переносом.
I Теорема 8.8. Перемещение пространства является
параллельным переносом тогда и только тогда, когда оно
сохраняет направления.
Доказательство. Необходимость данного условия по
сути дела уже была получена при доказательстве
предыдущей теоремы: мы показали, что для произвольных точек
X, У и их образов припараллельном переносе X', У
выполняется равенство ХУ = Х'У, а из него следует, что
параллельный перенос сохраняет направления.
Докажем достаточность. Пусть перемещение /
сохраняет направления. Тогда для любых точек пространства_Х,
У и их образов X', У выполняется равенство ХУ = Х'У.
Вычитая из обеих частей этого равенства Х'У, получаем
равенство XX'= УУ, следовательно, f = T$, гдеа = ХХг. D
Мы знаем, что при перемещении образом прямой
является прямая, образом плоскости — плоскость. В случае,
когда это перемещение — параллельный перенос, данный
результат можно усилить.
§ 8,2, Параллельный перенос
239
Теорема 8.9. Параллельный перенос переводит прямую
I в себя или в параллельную ей прямую, плоскость — в себя
| или в параллельную ей плоскость.
^Упражнение 8.4. Докажите теорему 8,9.
Далее нам понадобится следующее утверждение.
Теорема 8.10. Пусть в пространстве заданы две парал-
[ лельные плоскости. Тогда одну из них можно перевести
в другую параллельным переносом.
Доказательство. Пусть а и (5 — параллельные
плоскости. Возьмём на плоскости а точку А, а на плоскости /3 —
точку В. Покажем, что /3 = T^g(of). Допустим, что это не
так. Тогда Т^(а) =/3', причём по теореме 8.9 имеем а \\/3'
(рис. 8.5). Точка В принадлежит плоскости /3;, так как
Рис. 8*5
В = T^g(A). Следовательно, через точку В проходят две
плоскости (3 и /3\ параллельные плоскости а, что
невозможно. Полученное противоречие показывает, что /3 и /3' —
одна и та же плоскость. □
240 Глава 8. Преобразования пространства
В заключение укажем неподвижные точки, прямые и
плоскости параллельного переноса. Рассмотрим
параллельный перенос Т#. Если 3=0, то Т$ — тождественное
преобразование и, очевидно, всякая точка, всякая прямая
и всякая плоскость являются неподвижными. Если же 3^6,
то неподвижных точек нет, неподвижными являются все
прямые и все плоскости, параллельные вектору а, и только
такие прямые и плоскости.
§ 8.3. Поворот вокруг оси
«Правда, я... всячески вывёртывался,
но ведь так полагается»,— говорит всегда
адвокат Басе своим клиентам.
Я. Гашек. Похождения бравого солдата Швейка
Напомним, что на плоскости поворотом вокруг точки О
на угол а называется преобразование, при котором
точка О переходит в себя, а любая точка X, отличная от
точки О, переходит в такую точку X'> что OXf = OX и
Z.XOX' = а. При этом подразумевается, что а —
ориентированный угол, а б (-оо, +оо). Этот угол откладывается от
луча ОХ против часовой стрелки, если а > 0, и по часовой
стрелке в противном случае1*.
Рассмотрим прямую в пространстве. Всякий ненулевой
вектор, параллельный этой прямой, называется
направляющим вектором этой прямой. Совокупность прямой и её
направляющего вектора будем называть осью, а
направление указанного вектора — направлением оси. Таким
образом, ось —это ориентированная прямая, т.е. прямая, на
которой задано направление.
^Вообще-то задание ориентации с помощью часовой стрелки не
является строгим с математической точки зрения, поскольку понятие
«часовая стрелка» не имеет отношения к геометрии. Однако в нашем
курсе мы не будем обсуждать вопрос о строгом определении ориентации
плоскости или пространства, а ограничимся лишь указанным выше
наглядным истолкованием этого понятия.
§ 8.3. Поворот вокруг оси 241
Определение. Пусть в пространстве задана ось I.
Возьмём произвольную точку X пространства и проведём через
неё плоскость т, перпендикулярную I и пересекающую её
в точке О. Пусть X1 — образ точки X при повороте
плоскости г вокруг точки О на угол а (при этом предполагается,
что на плоскость г мы смотрим в направлении,
противоположном направлению оси). Отображение
пространства, при котором каждой точке X ставится в соответствие
так определённая точка X', называется поворотом вокруг
оси I на угол а.
Из определения вытекает, что указанное отображение
является взаимно однозначным отображением
пространства на себя (почему?), т. е. преобразованием пространства.
Таким образом, поворот вокруг оси состоит в том, что
в каждой плоскости, перпендикулярной оси, делается
поворот на один и тот же угол в одну и ту же сторону вокруг
точки пересечения этой плоскости с осью.
Поворот вокруг оси I на угол а мы будем обозначать Rf.
| Теорема 8.11. Поворот вокруг оси —перемещение.
Доказательство. Рассмотрим поворот Rf. Пусть X1 —
= Rf (X) и У = Rf (У). Докажем, что X'Y' = ХУ^Для этого,
очевидно, достаточно проверить, что |X'Y'| = \XY |. Рассмот-
рим_векторы 2 = X?f х' = XT*, а = хб, а' = XU Ъ = ОО1',
c = OfY и с' = (УТ (рис. 8.6а).
Тогда x — a + b + ?nxf — а! + Ь + ?'. Возведём эти
векторные равенства в квадрат, учитывая, что
Получим
g 2
Из определения поворота следует, что S2 = а'2 и ?2 = ?'2,
поэтому для доказательства равенства х2 = х'2 достаточно
242
Глава 8. Преобразования пространства
проверить, что Z(a, ?) — Z(af, ?')• Отложим векторы 3, й\
с, с1 от точки О в плоскости ХОХ1 (рис. 8.66). Равенство
указанных углов следует из того, что Z(a, ?) = а + Z(a', ?)
и Z(a', с') = а + Z(3', <?) (все углы предполагаются
ориентированными). □
Частными случаями поворота вокруг оси являются
симметрия относительно прямой (осевая симметрия) и
тождественное преобразование.
Симметрией относительно прямой Si называется
поворот вокруг оси I на угол а —к (при таком повороте
направление оси, очевидно, не имеет никакого значения, поэтому
говорят о симметрии относительно прямой, а не оси). Так
как поворот на угол a + 2nk (keZ) и поворот на угол а — это,
очевидно, одно и то же преобразование, то поворот вокруг
оси I на угол а = л + 2nh (k e Z) также является симметрией
относительно прямой I. Симметрию относительно прямой I
мы будем обозначать S/.
Поворот вокруг оси I на угол а = 2лk (keZ) является
тождественным преобразованием.
Рис, 8.6
§ 8.3. Поворот вокруг оси 243
Укажем неподвижные точки, неподвижные прямые и
неподвижные плоскости поворота вокруг оси. Если угол
поворота не равен Kk (k e Z), то множество неподвижных
точек поворота совпадает с его осью, ось поворота является
его неподвижной прямой (более того, прямой
неподвижных точек), а неподвижной плоскостью является всякая
плоскость, перпендикулярная оси. Если угол поворота
равен 27гАг (ke Z) (тождественное преобразование), то всякая
точка, всякая прямая и всякая плоскость являются
неподвижными. Наконец, если угол поворота равен к + 2nk
(k e Z) (симметрия относительно прямой), то множество
неподвижных точек поворота совпадает с его осью, ось
поворота является прямой неподвижных точек и, кроме того,
неподвижной является всякая прямая, перпендикулярная
оси, а неподвижной плоскостью является всякая плоскость,
перпендикулярная оси. Других неподвижных точек,
неподвижных прямых и неподвижных плоскостей у поворота
нет, что вытекает непосредственно из определения.
Наличие у перемещения пространства единственной
прямой неподвижных точек при отсутствии других
неподвижных точек является критерием того, что данное
перемещение — поворот вокруг оси (отличный от
тождественного преобразования).
Теорема 8*12. Множество неподвижных точек
перемещения является прямой I тогда и только тогда, когда
это перемещение — поворот вокруг оси /, отличный от
тождественного преобразования.
Доказательство. Необходимость условия
очевидна. Докажем достаточность. Пусть / —
перемещение, множество неподвижных точек которого есть прямая I.
Возьмём произвольную точку М пространства и построим
плоскость т, проходящую через эту точку и
перпендикулярную L Обозначим О = I П г (возможно, О и М — это
одна и та же точка) и М* = f(M) (рис. 8.7). Так как О —
неподвижная точка, (ОМ) J_ /, а перемещение сохраняет
244
Глава 8. Преобразования пространства
Рис. 8.7
угол между прямыми, то (OMf) _L U следовательно, М' е г,
причём ОМ' = ОМ. Возьмём в плоскости т произвольную
точку N9 отличную от точки М. Пусть N' = f(N). Тогда
аналогично Nf 6 г, причём точка N' отлична от Mf и N'Mf = NM.
Итак, если мы рассмотрим сужение отображения / на
плоскость г, то получим перемещение /т этой плоскости.
Перемещение /т имеет единственную неподвижную точку
(точку О), поэтому, как известно из планиметрии, fT —
поворот вокруг точки О.
Мы получили, что во всякой плоскости пространства,
перпендикулярной прямой /, данное перемещение
представляет собой поворот вокруг точки пересечения прямой I
с данной плоскостью. Осталось показать, что все эти
повороты происходят согласованно, т. е. на один и тот же угол.
Предположим, что это не так. Тогда, обозначая Xf = f(X),
Y' = f(Y) (рис. 8.6) и дословно повторяя рассуждения,
проведённые при доказательстве теоремы 8.11, получаем, что
X'Y'^XY, а это противоречит тому, что / —
перемещение. □
В заключение этого параграфа мы сформулируем одну
почти очевидную теорему, которая понадобится нам в
дальнейшем.
Теорема 8.13. Пусть в пространстве заданы две
плоскости, пересекающиеся по прямой I. Тогда одну из них
можно перевести в другую поворотом вокруг оси I.
fl^* Упражнение 8.5. Докажите теорему 8.13.
§ 8.4, Центральная симметрия 245
§ 8.4. Центральная симметрия и симметрия
относительно плоскости
Первое, что он увидел утром, проснувшись,—
это был Тигра, который сидел перед зеркалом,
уставившись на своё отражение.
— Доброе утро! — сказал Пух.
— Доброе утро! — сказал Тигра. — Смотри-ка,
тут есть кто-то, точь-в-точь как Я. А я — думал,
я только один такой.
А. Милн. Винни Пух и всевсе-все
В предыдущем параграфе мы познакомились с осевой
симметрией. В пространстве различают ещё два вида
симметрии — центральную симметрию и симметрию
относительно плоскости.
Определение. Пусть в пространстве задана точка О.
Отображение пространства, при котором точка О
переходит в себя, а произвольная точка М, отличная от О,—
в такую точку М', что точка О является серединой
отрезка ММ', называется симметрией относительно точки О
или центральной симметрией.
Точка О называется центром симметрии, а о точках
М и М' говорят, что они симметричны относительно
точки О.
Из определения вытекает, что указанное отображение
является взаимно однозначным отображением
пространства на себя (почему?), т. е. преобразованием пространства.
Центральную симметрию с центром О мы будем
обозначать Zq.
Также из определения непосредственно вытекает, что
центральная симметрия однозначно задаётся
указанием какой-нибудь точки, отличной от центра симметрии,
и её образа, а также что преобразование, обратное
центральной симметрии, есть та же центральная
симметрия,
и^ Упражнение 8.6. Докажите эти утверждения.
246 Глава 8. Преобразования пространства
| Теорема 8.14. Центральная симметрия — перемещение.
Доказательство. Рассмотрим центральную
симметрию Zq. Возьмём две произвольные точки пространства
X и У и обозначим их образы при центральной
симметрии через X' и У соответственно ♦ Из определения
симметрии Zo следует, что ОХ1 = -ОХ и OY' = -OY. Вычитая из
второго равенства первое, получаем, что Х'У = —ХУ,
следовательно, Х'У - ХУ. □
Будем говорить, что перемещение f изменяет
направления на противоположные, если для любого вектора 3
выполняется равенство f(a) = — 3.
Сформулируем и докажем теорему, выражающую
критерий того, что перемещение пространства является
центральной симметрией.
Теорема 8.15. Перемещение пространства является
центральной симметрией тогда и только тогда, когда оно
изменяет направления на противоположные.
Доказательство. Необходимость данного
условия по сути дела уже была получена при доказательстве
предыдущей теоремы: мы показали, что для произвольных
точек X, У и их образов X' и Y' при центральной симметрии
выполняется равенство Х'У = —ХУ, а из него следует, что
центральная симметрия изменяет направления на
противоположные.
Докажем достаточность. Пусть перемещение /
изменяет направления на противоположные. Тогда для
любых точек пространства X, У и их образов X' и У
выполняется равенство —хУ = Х'У. Вычитая из обеих ча-
стей этого равенства Х'У, получаем -(ХУ + ХГУ) =УУ,
т. е, YY' = Ylt + УХ', следовательно, середины отрезков
XX' и УУ —это одна и та же точка О (почему?). Поэтому
f = zo. a
§ 8.4. Центральная симметрия 247
Как и в случае параллельного переноса, для
центральной симметрии теорема об образах прямой и плоскости при
перемещении может быть усилена.
I Теорема 8.16. Центральная симметрия переводит
прямую в себя или в параллельную ей прямую, плоскость —
в себя или в параллельную ей плоскость.
^Упражнение 8.7. Докажите теорему 8.16.
Укажем неподвижные точки, неподвижные прямые и
неподвижные плоскости центральной симметрии.
Неподвижной точкой является только центр симметрии.
Неподвижной прямой является всякая прямая, проходящая
через центр симметрии, а неподвижной плоскостью —
всякая плоскость, проходящая через центр симметрии.
Перейдём теперь к изучению симметрии относительно
плоскости.
Определение. Пусть в пространстве задана плоскость а.
Отображение пространства, при котором каждая точка
плоскости а переходит в себя, а произвольная точка М,
не лежащая в плоскости а,—в такую точку М1, что
прямая ММ1 перпендикулярна ос и точка пересечения этой
прямой с плоскостью а является серединой отрезка ММ',
называется симметрией относительно плоскости а.
Плоскость а называется плоскостью симметрии, а о
точках М и Mf говорят, что они симметричны
относительно плоскости <х.
Из определения вытекает, что указанное отображение
является взаимно однозначным отображением
пространства на себя (почему?), т. е. преобразованием пространства.
Симметрию относительно плоскости а мы будем
обозначать Sa.
Из определения непосредственно вытекает, что
симметрия относительно плоскости однозначно задаётся
указанием какой-нибудь точки, не лежащей в плоскости ос, и её
образа, а также что преобразование, обратное симметрии
248
Глава 8, Преобразования пространства
относительно плоскости, есть та же симметрия
относительно плоскости.
и^ Упражнение 8.8. Докажите эти утверждения.
I Теорема 8.17. Симметрия относительно плоскости — пе-
I ремещеиие.
Доказательство. Рассмотрим симметрию
относительно плоскости а. Возьмём две произвольные точки
пространства X и У и обозначим их образы через X1 и Y1
соответственно. Пусть а = ХОу Ь = ОО\ d=OfY (рис. 8.8). Тогда из
определения симметрии относительно плоскости следует,
что ХЮ = -a, O'Y' = -с и $.Ь = Ь-с = О. Выразим Х? = х
и ХНГ = $ через 2, Ъ и ?: £ = 3+Ь + ?, х' = -U + Ъ - ?.
Следовательно, х2 = а2 + Ь2 Л-с2 + 2с1-(*=х'2, откуда вытекает,
что XY = X'Yr. □
Укажем неподвижные точки, неподвижные прямые и
неподвижные плоскости симметрии Sa. Неподвижными
являются те и только те точки, которые лежат в плоскости а.
Неподвижными являются все прямые, лежащие в этой
плоскости (более того, прямые, лежащие в плоскости or,
являются прямыми неподвижных точек), а также все прямые,
перпендикулярные плоскости а. Неподвижной является
плоскость а (которая является плоскостью неподвижных
точек), а также всякая плоскость, перпендикулярная
плоскости а.
§ 8.4. Центральная симметрия
249
Наличие у перемещения пространства единственной
плоскости неподвижных точек при отсутствии других
неподвижных точек является критерием того, что данное
перемещение—симметрия относительно плоскости.
Теорема 8.18. Множество неподвижных точек
перемещения является плоскостью тогда и только тогда, когда
это перемещение — симметрия относительно указанной
плоскости.
Доказательство. Необходимость условия
очевидна. Докажем достаточность. Возьмём
произвольную точку пространства X, не лежащую в данной
плоскости а, и опустим из неё перпендикуляр I на эту плоскость
(рис. 8.9). Пусть точка X' — образ точки X при данном
перемещении /. Заметим, что X1 е L Действительно,
при перемещении / прямая / должна перейти в прямую,
перпендикулярную плоскости а и проходящую через
точку О пересечения прямой / с этой плоскостью (почему?),
т. е. в себя. Так как / — перемещение, то ОХГ = ОХ, причём
точки X и X* различны. Следовательно, точки X и X1
симметричны относительно а. □
В заключение отметим, что в геометрии слово
«симметрия» часто употребляется в несколько ином смысле,
а именно как характеристика фигуры. Придадим
сказанному точный смысл.
I X
250 Глава 8. Преобразования пространства
Определение. Фигура называется симметричной
относительно точки (прямой или плоскости), если существует
симметрия относительно некоторой точки (прямой или
плоскости), при которой эта фигура переходит в себя.
Соответствующая точка (прямая, плоскость) называется
центром (осью, плоскостью) симметрии этой фигуры.
Некоторые свойства симметричных фигур
сформулированы в задачах 8.8—8.12.
§ 8.5. Преобразование подобия в пространстве
— Может объяснишь? Как это получается,
что я подобен вашей высокочтимой персоне?
Или под словом «подобное» ты имел в виду,
что наши самолёты похожи, да?
Р. Бах, Иллюзии
Преобразование подобия в пространстве определяется
точно так же, как и на плоскости.
Определение. Отображение пространства называется
преобразованием подобия, если для любых точек
пространства X, Y и их образов X', У выполняется
соотношение XfY' — k • XY, где k — некоторое фиксированное
положительное число (называемое коэффициентом
подобия).
Из определения вытекает, что указанное отображение
является взаимно однозначным отображением
пространства на себя (почему?), т. е. преобразованием пространства.
Говоря иными словами, преобразование подобия — это
преобразование, которое изменяет все расстояния в
одинаковое число раз.
Преобразование подобия с коэффициентом k мы будем
обозначать Pk.
Очевидно, что всякое перемещение пространства
является преобразованием подобия (с коэффициентом подобия,
равным единице).
§ 8.5. Преобразование подобия в пространстве 251
Менее тривиальный пример преобразования подобия
даёт гомотетия пространства, определяемая аналогично
гомотетии плоскости.
Определение. Гомотетией с центром О и
коэффициентом k ф 0 называется преобразование пространства, при
котором образом каждой точки X является такая точка X',
Гомотетию с центром О и коэффициентом k мы будем
обозначать Hq.
Из определения непосредственно вытекает, что при k =
= ~1 гомотетия является центральной симметрией, при
k=l — тождественным преобразованием, а также что
преобразование, обратное гомотетии Hq, является
гомотетией Hq . Заметим ещё, что гомотетия однозначно
задаётся указанием её центра, произвольной точки, отличной
от центра, и её образа.
I Теорема 8.19. Гомотетия с коэффициентом k является
I преобразованием подобия с коэффициентом |ft|.
Доказательство. Пусть X и У — произвольные точки
пространства, X' — Hq (X), У = Hq (У). По определению
гомотетии ОХ' = k • ОХ и OY1 = k-OY. Вычитая из второго
равенства первое, получаем, что X'Y' = k -ХУ,
следовательно, X'Y' = \k\ XY. □
Многие свойства гомотетии в пространстве аналогичны
свойствам гомотетии на плоскости. Сформулируем
некоторые из этих свойств в виде теоремы.
Теорема 8.20. Гомотетия переводит прямую, не
проходящую через центр гомотетии, в параллельную ей
прямую, а прямую, проходящую через центр гомотетии,—
в себя. Гомотетия сохраняет угол между прямыми.
Доказываются эти свойства точно так же, как и в
планиметрии (правда, при доказательстве второго из них придёт-
252 Глава 8. Преобразования пространства
ся ещё воспользоваться определением угла между прямыми
в пространстве).
о^ Упражнение 8.9. Докажите теорему 8.20.
Специфической для гомотетии в пространстве является
теорема об образе плоскости.
Теорема 8.21. Гомотетия переводит плоскость, не
проходящую через центр гомотетии, в параллельную ей
плоскость, а плоскость, проходящую через центр гомотетии,—
в себя.
Доказательство. Утверждение второй части теоремы
очевидно, поэтому будем считать, что плоскость а не
проходит через центр гомотетии Hq.
Выберем в плоскости а прямые а и Ь, пересекающиеся
в точке С. Пусть а\ —Н^(а), Ъ\ = #£(&). Прямые а\ и Ъ\
пересекаются в такой точке Си чт0 С\ = Hq(C) (почему?),
и, следовательно, определяют плоскость аи Докажем, что
ai=H*(or).
Возьмём произвольную точку Me a> не лежащую на
прямых а и by и проведём через неё прямую с, пересекающую
прямые а и Ъ в точках В и А соответственно (рис. 8.10).
Пусть Аг = Hk0 (А), Вг = Hk0 (В) и с\ = Hk0 (с). Так как А € &,
а Ъ\ = Hq (b), то А\ € Ь\. Аналогично Bi е п\. Следовательно,
точки А\ и Si принадлежат плоскости ai, поэтому (аксиома
прямой и плоскости) С\ с а\. Точка М\ =Hq(M)
принадлежит прямой с\ — образу прямой с при гомотетии Hq, но
с\ С ai, следовательно, М\ € а\.
Итак, образ всякой точки М 6 а принадлежит
плоскости а\ш Аналогично доказывается, что справедливо и
обратное: всякая точка М\ имеет прообраз на плоскости а.
Поэтому а\ = Hq (a). D
Укажем неподвижные точки, неподвижные прямые и
неподвижные плоскости гомотетии. Пусть коэффициент
гомотетии не равен единице, т.е. гомотетия не является
тождественным преобразованием. Тогда неподвижной точ-
§ 8,5. Преобразование подобия в пространстве 253
Рис. 8.10
кой гомотетии является только её центр. Неподвижной
прямой является любая прямая, проходящая через центр
гомотетии, а неподвижной плоскостью — любая плоскость,
проходящая через центр гомотетии.
Вернёмся теперь к произвольным преобразованиям
подобия. Из определения преобразования подобия вытекает
следующее свойство.
Теорема 8.22. Композиция преобразований подобия с
коэффициентами к\ и кг является преобразованием
подобия с коэффициентом
и^ Упражнение 8.10. Докажите теорему 8.22.
Дальнейшие свойства преобразований подобия
обсуждаются в § 8.8.
В заключение этого параграфа дадим определение
подобных фигур в пространстве.
Определение. Фигура Ф\ называется подобной
фигуре Фг, если существует преобразование подобия, которое
| переводит Ф Ф
254
Глава 8. Преобразования пространства
§ 8.6*. Признаки равенства и подобия
треугольников в пространстве
При изучении стереометрии мы неоднократно
пользовались известными из планиметрии признаками равенства
треугольников, применяя их к треугольникам, лежащим
в различных плоскостях. Теперь мы можем доказать
признаки равенства треугольников в пространстве, используя
свойства перемещений.
Теорема 8.23. Если длины трёх сторон одного
треугольника соответственно равны длинам трёх сторон другого
треугольника, то эти треугольники равны.
Доказательство. Пусть даны треугольники ABC и
AiBiCi, у которых AB = Ai£b ВС = В\СХ и CA = CiA\. Если
эти треугольники лежат в одной плоскости, то
доказываемое утверждение известно из планиметрии.
Предположим, что плоскости ABC и А\В\С\ различны.
Обозначим их через а и а\ соответственно. Возможны два
случая: а П ос\ = I (рис. 8.11) и а \\ а\ (рис. 8.12). В первом
Рис. 8.11
Рис. 8.12
случае согласно теореме 8.13 существует такой поворот
вокруг оси U что #1 —Ri(а). Пусть образом треугольника ABC
при этом повороте является треугольник А2В2С2 (равный
§ 8,6*. Равенство и подобие треугольников 255
треугольнику ABC). Треугольники А2В2С2 и А\В\С\ лежат
в одной плоскости of 1, и длины их сторон соответственно
равны, следовательно, ДА2В2С2 = АА\В\С\. В силу
транзитивности отношения равенства фигур ААВС = АА\В\С\.
Во втором случае согласно теореме 8.10 существует
такой параллельный перенос, что <Х\ = Т^(а). Рассуждая
аналогично первому случаю, получаем, что ААВС = AA\BiC\.
□
Замечание. Разумеется, можно явно указать перемещение
пространства, переводящее ААВС в АА\В\С\. Если
треугольники лежат в одной плоскости а, то существует такое
перемещение fa этой плоскости, что АА\В\С\ = /(ААВС). Это
перемещение можно распространить на всё пространство, считая,
что в каждой плоскости /?, параллельной а, определено
перемещение fp аналогично перемещению fa (давая выше определение
поворота пространства вокруг оси, мы фактически
распространили поворот плоскости вокруг точки на всё пространство). Таким
образом, мы получаем такое перемещение пространства /, что
AA\B\C\ = f(AABC). Если плоскости ABC и AiBiCx
пересекаются по прямой U то искомое перемещение, переводящее ААВС
в ДА\В\С\, есть g о Rh где /?* —поворот вокруг линии
пересечения этих плоскостей, a g — распространение перемещения
плоскости ol\ переводящего АА2В2С2 в АА\В\С\, на всё
пространство (см. доказательство теоремы). Аналогично если плоскости
ABC и А\В\С\ параллельны, то искомое перемещение есть g о 7^,
где <Х\ = Г#(а), a g определяется аналогично предыдущему
случаю.
Из доказанного признака равенства треугольников по
трём сторонам вытекает справедливость признаков
равенства по двум сторонам и углу между ними и по стороне
и двум прилежащим к ней углам.
в^3 Упражнение 8.11. Докажите эти признаки равенства
треугольников.
Признаки подобия треугольников по трём
соответственно пропорциональным сторонам, по двум соответственно
пропорциональным сторонам и углу между ними, а также
по двум углам, известные из планиметрии, справедливы
256 Глава 8. Преобразования пространства
и в пространстве. Докажем, например, первый из этих
признаков.
Теорема 8.24. Если длины трёх сторон одного
треугольника соответственно пропорциональны длинам трёх
сторон другого треугольника, то эти треугольники подобны.
Доказательство. Пусть даны такие треугольники ABC
л т> ту/^1 О А
и А\Е\С\У что . D = -z^-pr = уг-т- = k. Рассмотрим гомо-
Air>\ ХЗ1С1 Ь\А\
тетию Hq с произвольным центром О. Пусть АА2В2С2 =
= Я* (ДАЛО. Тогда |ig = Mi = |£ = *, еледо»,-
тельно, АВ — А2В2, ВС = В2С2 и СА-С2А2. У
треугольников ABC и А2В2С2 соответственно равны длины трёх
сторон, поэтому (теорема 8.23) эти треугольники равны,
и, следовательно, существует такое перемещение /, что
ААВС - /(ДА2В2С2) (в замечании к теореме 8.23 это
перемещение указано явно). Итак, ААВС= (/ oHq)(AA\BiCi).
Композиция / о Hq является в силу теорем 8.19 и 8.22
преобразованием подобия с коэффициентом ft, следовательно,
D
с^ Упражнение 8.12. Докажите остальные признаки подобия
треугольников.
§ 8.7*. Группы преобразований
В этом параграфе вы познакомитесь с одним из
фундаментальных понятий современной математики — понятием
группы.
Рассмотрим произвольное непустое множество.
Элементами этого множества могут быть объекты любой
природы—числа, преобразования или что угодно другое. Пусть
в силу некоторого правила любым двум элементам данного
множества сопоставлен некоторый элемент этого же
множества. Тогда говорят, что на рассматриваемом множестве
задана операция*
§ 8.7* Группы преобразований 257
Примерами операций могут служить известные вам из
курса алгебры сложение и умножение, определённые на
множестве действительных чисел* Композиция
преобразований, определённая, например, на множестве всех
преобразований пространства, также является примером
операции.
Вы знаете, что сложение действительных чисел
подчиняется переместительному и сочетательному законам, т. е.
для любых чисел а,Ьис справедливы равенства a + b = b + a
и (а + Ь) + с = а + (Ь + с). В современной алгебре эти свойства
принято называть соответственно коммутативностью и
ассоциативностью.
Будем говорить, что операция *, определённая на
некотором множестве X, коммутативна, если для любых
элементов а, Ь е X справедливо равенство а * Ъ = Ъ * а. Если
ясе для любых элементов а, Ь, с 6 X справедливо равенство
(а * Ъ) * с = а * {Ь * с), то будем говорить, что эта операция
гссоциативна.
Дадим теперь определение группы.
I Определение. Непустое множество G, на котором
определена операция *, называется группой (относительно
этой операции), если выполнены следующие условия:
1) для любых элементов а, Ъ и с из G справедливо
равенство (а*Ь) *с = а* (Ь*с) (т.е. операция * ассоциативна);
2) существует такой элемент eeG, что для любого
элемента а е G справедливы равенства а*е = е*а = а (такой
элемент е называется единицей или нейтральным
элементом);
3) для любого элемента aeG существует такой элемент
а"1 € G, что справедливы равенства а* а"1 = а"1 * а = е
(такой элемент а"1 называется обратным к элементу а).
Замечапие. Подчеркнём два обстоятельства, связанные с дан-
:ым определением, которые необходимо иметь в виду. Во-пер-
ых, так как операция * определена на множестве G, то это
значает, что для любых элементов а и b из G элемент (а * Ь)
ринадлежит G, т. е. применение операции * не выводит из
Зак. 3383
258 Глава 8, Преобразования пространства
множества G. Во-вторых, в определении группы отнюдь не
предполагается, что операция * коммутативна. Если же операция
* коммутативна, то группа называется коммутативной (или
абелевой).
Приведём примеры групп. Множество целых чисел Ъ
является группой относительно сложения. Действительно,
сложение целых чисел ассоциативно, роль единицы играет
число 0, а роль обратного элемента для числа п
играет число —п.
Множество рациональных чисел Q образует группу
относительно сложения.
Множество положительных рациональных чисел Q+
образует группу относительно умножения, так как
умножение ассоциативно, единицей является число 1, а обратным
для элемента q является элемент 1/д.
Заметим, что все эти группы коммутативные.
Множество натуральных чисел N не образует группу ни
относительно сложения, ни относительно умножения, так
как и в том, и в другом случае не выполняется условие 3,
а в случае сложения — ещё и условие 2.
Множества целых чисел Z, рациональных чисел Q и
действительных чисел R не являются группами относительно
умножения, так как не выполняется условие 3.
я^9 Упражнение 8.13. Образует ли группу множество всех
многочленов одного переменного относительно: а) сложения;
б) умножения? Является ли эта группа коммутативной?
ч^ Упражнение 8.14. Докажите, что единица группы
единственна1).
Понятие группы было введено французским
математиком Эваристом Галуа (1811—1832 гг.), который применил
его при доказательстве неразрешимости в радикалах
алгебраического уравнения степени выше четвёртой. Сейчас
теория групп является одним из самых важных и богатых
интересными результатами разделов современной алгебры.
^Можно доказать также, что каждый элемент группы имеет
единственный обратный.
§ 8.7'К Группы преобразований 259
Группы играют важную роль и в геометрии. В § 1.1 мы
говорили, что с точки зрения теории множеств геометрия
изучает основное множество — пространство. Это не совсем
точно. В геометрии изучаются два основных множества:
пространство и группа некоторых его преобразований, с
помощью которой в пространстве вводится понятие равенства
фигур.
На множестве преобразований пространства нами уже
была определена операция — композиция преобразований.
Относительно этой операции множество всех
преобразований пространства образует группу.
Докажем это утверждение. Во-первых, необходимо
проверить ассоциативность композиции, т. е. что для любых
преобразований пространства f, g и h справедливо
равенство h о (g о f) = (h о g) о f. Действительно, если X —
произвольная точка пространства, Х\ — /(X), X2 = g(Xi),
а Хз = h(X2), то, с одной стороны, Хз = Л(Хг) =h(g(Xi)) =
= (hog) (Xi ) = (hog){f(X)) = ((hog)o f) (X). С другой
стороны, Х2 = g{X\) = g(f(X)) = (gof)(X), следовательно, Х3 =
= h(X2) = h((g о f) (X)) = (h о (g о f)) (X). Сравнивая
полученные выражения для Хз, заключаем, что (h о g) о f =
= ho(gof). □
Во-вторых, единицей является тождественное
преобразование Е, так как для любого преобразования / имеем
foE = Eof = f.
Наконец, в-третьих, всякое преобразование /, будучи
взаимно однозначным, имеет обратное преобразование Z"1,
удовлетворяющее условию / о f~l = f~l of = E.
Изучать действие всевозможных преобразований
пространства на геометрические фигуры — задача непосильная,
результат этого действия априори непредсказуем. В этом
смысле группа всех преобразований пространства с точки
зрения геометрии неинтересна. Она слишком широка и в
связи с этим лишена сколько-нибудь конкретных свойств.
Поэтому рассматриваются более узкие группы
преобразований, например группа перемещений.
260 Глава 8, Преобразования пространства
ВЭ* Упражнение 8.15. Проверьте, что множество всех
перемещений пространства является группой относительно их
композиции1*.
Группа перемещений пространства является самой
важной группой в геометрии, так как с помощью перемещения
вводится понятие равных фигур. Равные фигуры
обладают одинаковыми геометрическими свойствами, которые не
изменяются под действием перемещений. Говоря иными
словами, геометрия, которую мы изучаем, в основном
рассматривает свойства фигур, неизменные (инвариантные)
относительно группы перемещений.
Кроме группы перемещений есть и другие группы
преобразований, например группа преобразований подобия
(докажите самостоятельно, что всевозможные
преобразования подобия образуют группу). Можно считать, что
каждая группа преобразований задаёт свою геометрию, в
которой изучаются свойства фигур, инвариантные
относительно данной группы преобразований. Эта идея была
высказана в 1872 г. немецким математиком Феликсом
Клейном (1849—1925 гг.). Групповой подход к геометрии,
предложенный Клейном, оказался весьма плодотворным и
способствовал как появлению новых разделов геометрии, так
и переосмыслению старых.
Обсудим теперь интересный вопрос о симметрии
правильных многогранников, который тесно связан с
понятием группы. С древних времён правильные
многогранники притягивали к себе внимание людей. Возможно, это
связано с тем, что из всех многогранников правильные
многогранники «самые симметричные», точнее говоря,
существует довольно много перемещений пространства,
которые переводят правильные многогранники в себя. Ниже
1}Если множество G — группа относительно операции *, а его
подмножество Н также образует группу относительно этой же операции, то
говорят, что Н — подгруппа группы G. Выполнив это упражнение, вы
докажете, что перемещения пространства образуют подгруппу группы
преобразований пространства.
§ 8.7*. Группы преобразований
261
мы опишем все эти перемещения, а пока дадим некоторые
вспомогательные определения.
Будем называть перемещение, переводящее данную
фигуру в себя, самосовмещением этой фигуры. Рассмотрим
всевозможные самосовмещения правильного
многогранника. Они, очевидно, образуют группу, которая является
подгруппой группы перемещений пространства. Эту группу
принято называть группой самосовмещений или группой
симметрии правильного многогранника.
Перечислим элементы групп симметрии правильных
многогранников. Заметим, что всякое самосовмещение
данного правильного многогранника является одновременно
и самосовмещением двойственного ему правильного
многогранника, и наоборот. Поэтому достаточно рассмотреть
только группы симметрии тетраэдра, куба и додекаэдра.
Рис. 8.13
Группа симметрии тетраэдра состоит из следующих
преобразований: тождественное преобразование; по два
поворота вокруг каждой из высот (на 120° и 240°, рис. 8.13а) —
всего восемь поворотов; шесть симметрии относительно
плоскостей, проходящих через каждую из высот и
соответствующее ребро (рис. 8.136); три поворота вокруг
прямых, проходящих через середины скрещивающихся рёбер
(рис. 8.13в); наконец, по две композиции поворота вокруг
этих прямых (на 90° и 270°) и симметрии относительно
плоскости, перпендикулярной им и проходящей через
262
Глава 8. Преобразования пространства
центр тетраэдра (рис. 8.13г). Такая композиция называется
поворотным отражением. Всего, таким образом, указано
24 различных самосовмещения. Ими исчерпывается
группа симметрии тетраэдра.
В группу симметрии куба (октаэдра) входят:
тождественное преобразование; по три поворота вокруг каждой из
прямых, соединяющих центры противоположных граней
(на 90°, 180° и 270°, рис. 8.14а) —всего девять
поворотов; по два поворота вокруг диагоналей (на 120° и 240°,
рис. 8.146) —всего восемь поворотов; шесть поворотов
вокруг прямых, соединяющих середины противоположных
рёбер (рис. 8.14в); три симметрии относительно
плоскостей, проходящих через центр куба параллельно его
граням (рис. 8.14г); шесть симметрии относительно
диагональных плоскостей (рис. 8.145); по два поворотных отражения
вокруг прямых, соединяющих центры противоположных
граней (на 90° и 270°, рис. 8.14е) — всего шесть; по два
поворотных отражения вокруг диагоналей (на 60° и 300°,
рис. 8.14ж) —всего восемь; наконец, центральная
симметрия относительно центра куба. Всего, таким образом, ука-
§ 8.7*. Группы преобразований
263
зано 48 самосовмещений. Ими исчерпывается группа
симметрии куба.
Группа симметрии додекаэдра (икосаэдра) содержит 120
самосовмещений. Попробуйте перечислить их
самостоятельно, пользуясь рис. 8.15а—е.
Заметим теперь, что число плоских углов тетраэдра
равно 12, куба —24, додекаэдра —60, т.е. оно равно половине
числа преобразований в группе симметрии
соответствующего многогранника. Это не случайно. Оказывается,
справедлива следующая теорема, которую можно доказать, не
перечисляя всех элементов группы симметрии.
Теорема 8.25. Число элементов группы симметрии
правильного многогранника равно удвоенному числу его
плоских углов.
На этом мы заканчиваем знакомство с группами.
Дальнейшие сведения о них можно найти, например, в книгах
[Александров, 1980], [Калужнин, Сущанский, 1985],
[Алексеев, 1976].
264
Глава 8. Преобразования пространства
■^Упражнение 8.16. Образует ли группу множество:
а) параллельных переносов;
б) поворотов вокруг всевозможных осей;
в) поворотов вокруг осей, пересекающихся в одной точке;
г) симметрии относительно всевозможных плоскостей?
Коммутативна ли эта группа?
§ 8.8*. Классификация перемещений
и преобразований подобия в пространстве
В этом параграфе мы опишем все возможные
перемещения и преобразования подобия в пространстве.
Предварительно обсудим вопрос об ориентации пространства.
Пусть в пространстве задан базис {а, &, ?}.
Предположим, что векторы базиса отложены от одной точки О. Если
для наблюдателя, находящегося на конце вектора ?,
кратчайший поворот вокруг точки О от вектора 3 к вектору Ъ
виден против часовой стрелки (рис. 8.16а), то базис {а, £, ?}
называется правым, в противном случае, т.е. когда этот
поворот виден по часовой стрелке (рис. 8.166), — левым.
а)
Рис. 8.16
Если в пространстве задан правый базис, то говорят,
что оно ориентировано положительно, а если задан левый
базис, то ориентировано отрицательно.
§ 8.8*, Классификация перемещений
265
Данные нами определения не являются математически
строгими, так как понятия «против часовой стрелки»,
«кратчайший поворот виден наблюдателю» и т.п. не были
строго определены (см. замечание в § 8.3). Разумеется,
существует математически строгое определение понятия
ориентации пространства, но мы не будем обсуждать его
в нашем курсе, так как для понимания дальнейшего
материала этого параграфа вполне достаточно приведённых
наглядных соображений. Заметим, что в курсе физики вы
уже встречались с подобным подходом к введению понятия
ориентации пространства (вспомните правило буравчика
и правило левой руки; правый буравчик и правая рука
задают положительную ориентацию пространства (рис. 8.17
и 8.18)).
Мы примем без доказательства следующий
фундаментальный факт: всякое перемещение пространства либо
сохраняет его ориентацию, либо изменяет её на
противоположную. Точнее, если перемещение переводит
некоторый правый базис в правый базис, то оно переводит
любой правый базис в правый базис (сохраняет
ориентацию), а если перемещение переводит некоторый правый
базис в левый базис, то оно переводит любой правый базис
в левый базис (изменяет ориентацию); то же самое
справедливо и для левых базисов.
Перемещения пространства, сохраняющие ориентацию,
называются перемещениями первого рода, а изменяющие
ориентацию — перемещениями второго рода.
левый правый
у
Рис. 8.17
Рис. 8.18
266 Глава 8. Преобразования пространства
Из рассмотренных нами перемещений перемещениями
первого рода являются параллельный перенос и поворот
вокруг оси (в частности, осевая симметрия), а
перемещениями второго рода — центральная симметрия и симметрия
относительно плоскости. Прежде чем сформулировать
основную теорему о классификации перемещений
пространства, мы рассмотрим ещё три вида перемещений.
Композиция поворота вокруг оси и параллельного
переноса на вектор, параллельный этой оси, называется
винтовым перемещением. Проверьте самостоятельно, что
результат этой композиции не зависит от того, какое из двух
перемещений — поворот или перенос — выполняется первым.
Частными случаями винтового перемещения являются
поворот вокруг оси и параллельный перенос.
Композиция поворота вокруг оси и симметрии
относительно плоскости, перпендикулярной оси поворота,
называется поворотным отражением. Результат этой
композиции также не зависит от порядка выполнения поворота
и симметрии. Частным случаем поворотного отражения
является центральная симметрия. Она соответствует
повороту на угол к.
Композиция симметрии относительно плоскости и
параллельного переноса на вектор, параллельный этой
плоскости, называется скользящим отражением. Результат
этой композиции также не зависит от порядка выполнения
симметрии и параллельного переноса. Симметрию
относительно плоскости можно рассматривать и как частный
случай поворотного отражения (угол поворота равен 0°),
и как частный случай скользящего отражения (вектор
переноса равен б).
Сформулируем теперь теорему о классификации
перемещений.
Теорема 8.26. Всякое перемещение пространства есть
либо винтовое перемещение, либо поворотное отражение,
либо скользящее отражение.
§ 8.8*. Классификация перемещений 267
Точнее говоря, всякое перемещение первого рода
является винтовым перемещением (в частности, поворотом вокруг
оси или параллельным переносом), а всякое перемещение
второго рода является либо поворотным отражением, либо
скользящим отражением (в частности, центральной
симметрией или симметрией относительно плоскости).
Мы не будем доказывать здесь эту теорему, поскольку
её доказательство довольно сложно, а этот параграф
носит чисто ознакомительный характер, и его результаты
не используются в дальнейшем. Доказательство теоремы
о классификации перемещений можно найти, например,
в книгах [Александров и др., 1992], [Болтянский, 1985].
Сформулируем и докажем теорему о классификации
преобразований подобия.
I Теорема 8.27. Всякое преобразование подобия является
композицией гомотетии и перемещения.
Доказательство. Пусть Pk — произвольное
преобразование подобия. Рассмотрим гомотетию Hkn с тем же коэф-
1 / Ь
фициентом и с произвольным центром О и гомотетию Но' ,
обратную к ней. Преобразование Pk о Н^ в силу теорем
8.19 и 8.22 является преобразованием подобия с
коэффициентом ft.- = l, т.е. перемещением. Обозначим это
перемещение через f. Тогда / о Н% = {Pk о H)Jk) о Hho = Pk о
о (Hq**oHq) =Pk oE = Pk (мы воспользовались
ассоциативностью композиции преобразований, Доказанной в
предыдущем параграфе), т. е. Pk = / о Hq. О
Из доказанной теоремы сразу вытекают многие свойства
преобразований подобия. В частности, вспоминая свойства
перемещений и гомотетии, заключаем, что преобразование
подобия переводит прямую в прямую, плоскость в
плоскость, а также сохраняет угол между прямыми (а
следовательно, угол между прямой и плоскостью и угол между
плоскостями).
268 Глава 8. Преобразования пространства
Задачи
Что означает владение математикой? Это есть умение
решать задачи, притом не только стандартные, но
и требующие известной независимости мышления,
здравого смысла, оригинальности, изобретательности.
Д. Пойа. Математическое открытие
8.1. Пусть / — перемещение пространства. Докажите,
что для любых векторов а и Ь и для любого числа k
справедливы равенства f(a + b) = f(a) + /(ft), f(M) = kf{a) и
f(<i).f(b)=a-b.
8.2. Может ли перемещение пространства иметь ровно
две неподвижные точки?
8.3. Докажите, что если перемещение пространства
имеет три неподвижные точки, не лежащие на одной прямой,
то плоскость, проходящая через эти точки, является
неподвижной. Обязательно ли эта плоскость будет плоскостью
неподвижных точек?
8.4. Докажите, что если перемещение пространства
имеет четыре неподвижные точки, не лежащие в одной
плоскости, то оно является тождественным преобразованием.
8.5. При некотором перемещении шар перешёл в себя.
Докажите, что у этого перемещения есть неподвижная точка.
8.6. В пространстве даны прямая I и точки А и В, причём
прямые I и (АВ) скрещивающиеся. Найдите на прямой I
такую точку М, чтобы сумма расстояний AM + MB была
наименьшей.
8.7. Пусть А!г и А![ (i = l, 2, 3, 4) —проекции вершин
тетраэдра А1А2А3А4 на плоскости а и (3 соответственно.
Докажите, что существует перемещение пространства,
переводящее точки А[ в такие точки А°> что прямые А°А![
попарно параллельны.
8.8. Фигура Ф имеет две пересекающиеся
перпендикулярные оси симметрии. Докажите, что Ф имеет ещё одну
ось симметрии.
Задачи 269
8.9. Докажите, что никакое тело не может иметь чётное
(ненулевое) число осей симметрии.
8.10. Тело имеет центр симметрии и плоскость
симметрии. Докажите, что центр симметрии лежит в плоскости
симметрии.
8.11. Тело имеет несколько плоскостей симметрии.
Докажите, что все эти плоскости имеют общую точку.
8.12*. Каждая грань выпуклого многогранника
центрально-симметрична. Докажите, что этот многогранник
центрально-симметричен.
8.13*. Даны тетраэдр и точка N внутри него. Через
каждое ребро тетраэдра проведена плоскость, параллельная
отрезку, соединяющему точку N с серединой
скрещивающегося с ним ребра. Докажите, что все шесть этих плоскостей
пересекаются в одной точке,
8.14*, Через середину каждого ребра тетраэдра
проведена плоскость, перпендикулярная противоположному ребру.
Докажите, что все шесть этих плоскостей пересекаются
в одной точке.
8.15. По одну сторону от плоскости а расположены
точки А и В. Найдите на плоскости а такую точку М, чтобы
сумма расстояний AM + MB была наименьшей.
8.16. Даны острый двугранный угол с гранями а и (5
и точка С внутри него. Найдите такие точки Ае а и В е /3,
чтобы треугольник ABC имел наименьший периметр.
8.17. Какое наибольшее число плоскостей симметрии
может иметь пространственная фигура, состоящая из трёх
попарно непараллельных прямых?
8.18. Докажите, что каждая плоскость, проведённая
через прямую, соединяющую середины скрещивающихся
рёбер правильного тетраэдра, делит этот тетраэдр на две
равные части.
8.19. Докажите, что каждая плоскость, проведённая
через диагональ куба, делит этот куб на две равные части.
8.20. В пятиугольной пирамиде соответственно равны
между собой боковые рёбра и все двугранные углы при
270 Глава 8. Преобразования пространства
боковых рёбрах. Докажите, что эта пирамида
правильная.
8.21. а) Докажите, что композиция двух симметрии
относительно пересекающихся плоскостей есть поворот вокруг
их линии пересечения.
б) Докажите, что любой поворот пространства
относительно оси можно представить в виде композиции двух
симметрии относительно двух плоскостей.
8.22. Докажите, что композиция двух поворотов, оси
которых пересекаются, есть поворот вокруг оси.
8.23*. Докажите, что любое перемещение пространства
можно представить в виде композиции не более чем
четырёх симметрии относительно плоскостей.
8.24. Докажите, что любые два равных треугольника,
лежащие в разных плоскостях и имеющие общую вершину,
можно перевести друг в друга поворотом вокруг оси.
8.25. Докажите, что любые две сферы гомотетичны друг
другу.
8.26. Докажите, что преобразование подобия с
коэффициентом k ф 1, переводящее каждую плоскость в себя или
в параллельную ей плоскость, является гомотетией.
8.27. Докажите, что два подобных, но не равных
треугольника можно перевести друг в друга композицией
гомотетии и поворота вокруг оси.
8.28*. В плоскости боковой грани правильной
четырёхугольной пирамиды взята фигура Ф. Пусть Ф\ — проекция
фигуры Ф на плоскость основания пирамиды, аФг-
проекция фигуры Ф на плоскость смежной с ней боковой грани.
Докажите, что фигуры Фх и Фг подобны.
8.29*. Преобразование пространства переводит любые
две точки, находящиеся на расстоянии 1, в две точки,
также находящиеся на расстоянии 1. Докажите, что это
преобразование является перемещением.
Глава 9*
Решение задач
Ты спросишь, кто велит? —
Всесильный бог деталей...
Б. Пастернак. Давай ронять слова.,,
§ 9.1. Зависимость между основными углами
в правильной пирамиде
Ещё столетия пройдут,
Пока Осирисы-Исиды
Нам в руки мудрость отдадут
Всех элементов пирамиды.
А. Чижевский. Пирамиды
Правильная пирамида — один из наиболее часто
встречающихся в стереометрических задачах многогранников.
В этом параграфе мы установим некоторые соотношения
между углами в правильной пирамиде, которые позволяют,
зная величину одного из этих углов, определить величины
остальных. Заметим, что нет необходимости запоминать
все эти формулы. Гораздо полезнее уяснить себе метод
их получения (который, в принципе, весьма прост), с тем
чтобы применять его при решении конкретных задач.
Итак, рассмотрим правильную д-угольную пирамиду
SAiAz.'.An (рис. 9.1). Под основными углами в этой
пирамиде мы будем понимать:
• угол наклона бокового ребра к плоскости основания (а);
• двугранный угол при основании ((3);
• плоский угол при вершине (у);
• двугранный угол при боковом ребре (б).
Пусть О — центр основания пирамиды, В — середина
ребра А\Аъ, D — точка пересечения отрезков А\А% и ОА2,
С —такая точка на боковом ребре SA2, что (AiC) _L (SA2),
Ег— точка пересечения отрезков SB и А\С> К — точка пе-
272
Глава 9*. Решение задач
Рис. 9.1
ресечения отрезков А\А% и ОВ. Пусть также /.А\ОА^ = (р
(очевидно, (р~2п/п).
в^ Упражнение 9.1. Докажите, что ZSA\O = a, ZSBO = /?,
ZCA = 5, АА2АХА3 = tp/2.
Обозначим высоту пирамиды через Ну апофему —
через т, боковое ребро — через I, сторону основания — через а,
а через г и R — радиусы окружностей, вписанной в
основание и описанной около него.
1. Связь между а и /3:
tga = cos ^
(9.1)
Доказательство. Из ASA\O находим, что Н = Rtga.
Из ASBO находим, что Н — г tg /3. Следовательно, Л tg a =
= r tg /3. Остаётся заметить, что r = Rcos -^ (из АА\ОВ). □
§ 9.1. Зависимость между углами в пирамиде 273
2. Связь между а и у:
sin у/2
cosa=-—Ц-. (9.2)
sin 7г/гГ
Доказательство. Из
а из ASA\O получаем 1=
находим, что / =
2 sin у/2'
. Остаётся заметить, что
R=
(из АА\ОВ), и приравнять правые части по-
□
2 sin <p/2
лученных выражений для I.
3, Связь между а и 8:
(9.3)
Доказательство. Из треугольников CDA\ и CDA2
получаем, что CD — A\DB ctg тг и CD = A2D sin а. Но AiD =
= a cos -£, A2D = а sin ^. Приравнивая правые части выра-
жений для CD, получим требуемую формулу. □
4. Связь между /3 и у:
Доказательство. Из треугольников SBO и
(9.4)
найдём т: т =
и т =
2 tg(r72)
' СлеД°вательН0>
= a cos (3. Остаётся заметить, что 2г = a ctg ^ (из AA\OB).
2
5. Связь между у и 8:
Y _ cos к/п
C0S ^ ~
sin 5/2 ■
(9.5)
274 Глава 9*. Решение задач
У
Доказательство. Так как ZCA1A2 = тс, то из
треугольников СА\ А2 и CA\D получаем СА\ — a cos 7: и СА\ = —~т^ •
Z sin 0/2
Следовательно, a cos 77 = . V /f>» Остаётся заметить, что
^ sin 0/2
(О
A\D = a cos -5-» П
6. Связь между (3 и 8:
sin/З =
cos 5/2
sin тг/n'
(9.6)
Доказательство. Поскольку плоскости А1СА3 и SBO
перпендикулярны плоскости SA1A2 (почему?), прямая их
пересечения КЕ также перпендикулярна плоскости
Далее, ZA^KE=^ - ZKAXE= f - (f -
= -z • Из АКЕВ находим sin /3 = ^^. Подставляя в эту
формулу выражения КЕ = КА\ cos ^ (из AiiT^Ai) и KB =
= КА\ sin -£ (из AJiTBAi), получаем формулу (9.6). D
Замечание. Формулу (9.6) можно получить ещё тремя
способами:
1) исключить из формул (9.4) и (9.5) угол у;
2) записать двумя способами площадь треугольника SA1A2
(2SsaiA2 — а' т — А\С -1), а затем подставить выражения для /п,
А\С и I через а и тригонометрические функции углов /?, 5 и (р\
3) применить теорему о трёх синусах (теорема 5,9) к
двугранному углу с ребром А\А2 (приведённое выше доказательство
фактически повторяет её вывод в данном конкретном случае).
Пример 9.1. Сторона основания правильной
четырёхугольной пирамиды SABCD (S — вершина) равна а, а дву-
§9.1. Зависимость между углами в пирамиде 27Г5
гранный угол при боковом ребре равен а. Найти площадь
боковой поверхности пирамиды.
Решение. Пусть О — центр основания, F — середина
ребра CD, Е — такая точка на ребре SC, что (DE) 1 (SC)
(рис. 9.2).
Рис. 9.2
Докажем, что ZBED = a. Действительно, &DEC =
(по двум сторонам и углу между ними), поэтому (BE) J_ (SC),
следовательно, по признаку перпендикулярности прямой
и плоскости (SC) I (BED), т.е. /.BED — линейный угол
двугранного угла при боковом ребре пирамиды, значит,
ABED = а.
Искомая площадь боковой поверхности пирамиды
равна SfoK = 4 • ^а • m, где т = SF — длина апофемы пирамиды.
Найдём т. Пусть /SFO = f5. Тогда по формуле (9.6) имеем
sin В = \/2 cos ~. Из треугольника SOF находим т = ъ —
' & cos р
2cos/J
, следовательно,
т2 =
4 cos2/? 4(1-sin2 /3) 4(1 - 2 cos2 a/2) -4cos a*
276 Глава 9*, Решение задач
а значит, т = — а (подкоренное выражение положи-
2у/- cos a
тельно, так как п/2 < а < п). Окончательно получаем, что
а2
Замечание. Разумеется, прямой ссылки на формулу (9.6)
можно было бы избежать, например, повторив её вывод в случае
п = 4. Но проще, по-видимому, поступить по-другому — записать
двумя способами площадь треугольника SDC (см. предыдущее
I 2~
замечание): 2Ssdc — а- т — DE • SC — • \ т2 + ^-. Из
V2 sin a/2 V 4
этого соотношения находим т =
§ 9.2. Определение положения основания высоты
пирамиды или призмы
Я чувствую непобедимый страх
В присутствии таинственных высот.
О. Мандельштам» Пешеход
При решении задач часто бывает необходимо
определить положение основания высоты пирамиды или призмы
по отношению к элементам основания• Из-за
неправильного изображения высоты возникают ошибки при
вычислении углов наклона прямых и плоскостей к плоскости
основания и т. п.
Приведём некоторые теоремы, полезные при
нахождении положения основания высоты. Большинство из них
является переформулировкой полученных нами ранее
результатов, поэтому доказательство этих теорем мы
предоставляем вам в качестве полезного упражнения.
Теорема 9.1. Если в пирамиде равны длины всех
боковых рёбер или все боковые рёбра образуют с
плоскостью основания равные углы, то около основания можно
описать окружность, а вершина пирамиды проектируется
в центр этой окружности.
§ 9.2. Положение основания высоты пирамиды 277
(Сравните с утверждением IV из § 7.1.)
Теорема 9.2. Если все двугранные углы при
основании пирамиды равны, то в основание пирамиды можно
вписать окружность, а вершина пирамиды проектируется
в центр этой окружности.
(Сравните с утверждением V из § 7.1.)
Заметим, что в формулировке этой теоремы
существенно, что рассматриваются именно двугранные углы, а не
углы между плоскостями боковых граней и плоскостью
основания. Если же плоскости всех граней пирамиды
образуют с плоскостью основания равные углы, то вершина
пирамиды не обязательно проектируется в центр
вписанной окружности, а может проектироваться и в центр одной
из вневписанных в основание окружностей1*.
Это обстоятельство следует учитывать при решении
задачи, обращая особое внимание на то, о каких углах идёт
речь в её формулировке. (Мы рекомендуем сравнить это
замечание с замечанием, сделанным в конце § 7.1; см. также
задачу 7.4.)
Теорема 9.3. Если в трёхгранном угле два плоских угла
равны, то проекция их общего ребра на плоскость третьего
плоского угла принадлежит прямой, содержащей
биссектрису этого угла.
Следствие 8. Пусть AiA2..-AnBiB2.~Bn — наклонная
призма, в которой боковое ребро А\В\ образует равные
углы со сторонами А\А2 и А\Ап основания. Тогда
вершина В\ проектируется в точку на прямой, содержащей
биссектрису угла А*ьА\Ап.
^Окружность называется вневписанной в многоугольник, если её
центр равноудалён от всех прямых, содержащих его стороны, и лежит
вне многоугольника. Можно доказать, что у всякого треугольника
существуют три вневписанные окружности, а у четырёхугольника — не
более одной. У выпуклого многоугольника с числом сторон, большим
четырёх, вневписанных окружностей нет.
278
Глава 9* Решение задач
Теорема 9.4. Если в треугольной пирамиде все плоские
углы при вершине прямые или если имеются две пары
скрещивающихся перпендикулярных рёбер, то вершина
проектируется в ортоцентр основания пирамиды.
(См. примеры 4.5 и 4.7.)
Приведём теперь несколько примеров, в которых
используются эти теоремы.
Пример 9.2. Основание пирамиды SABC — треугольник
ABC, в котором АС = ВС = а, АВ = Ь. Все боковые рёбра
пирамиды наклонены к плоскости основания под углом 60°.
Найти объём пирамиды.
Решение. По теореме 9.1 основанием высоты пирамиды
служит центр О окружности, описанной около
треугольника ABC. Найдём радиус R этой окружности. По теореме
/ ft2 1
Пифагора из ABCCi находим СС\ = da2 - -j = -^J^a2 -b2.
Из подобия треугольников ОА\С и CBCi (рис. 9.3 и 9.4;
в случае, когда ААВС прямоугольный, О и С\ — это одна
= . (Подкоренное
и та же точка) получаем, что R= ——
v 4а2 — &2
выражение положительно, так как в силу неравенства
треугольника 2а > Ь.)
Рис. 9.4
§ 9.2, Положение основания высоты пирамиды 279
Далее находим высоту пирамиды:
SO = R tg 60° =
и площадь основания:
Sabc = \ЛВ • CCi = ±Ь\/4а2-Ь2.
Для объёма получаем выражение V = ^ \/За2&. П
Пример 9.3. Квадрат ABCD со стороной а является
основанием параллелепипеда ABCDA\B\CiDi. Ребро АА\
образует с рёбрами АВ и AD углы величины а (45° < а <
< 90°). Найти объём параллелепипеда, если известно, что
проекция вершины А\ на плоскость основания лежит на
прямой BD.
Решение. Так как ZA\AB = Z.A\AD, проекция О
точки А\ на плоскость ABC лежит на прямой АС. Но по
условию О€ (BD). Следовательно, точка О — центр
квадрата ABCD (рис. 9.5), и, значит, АА\ —A\D. Из равно-
Di
В
Рис, 9.5
бедренного треугольника AA\D найдём длину ребра АА\\
АА\ — а/(2 cos а). Найдём высоту параллелепипеда Н =
280
Глава 9* Решение задач
~ А\О. Из AAAiO по теореме Пифагора получаем
Н = JaA*- АО* =
V 1
2 cos a
2 2 cos
/-cos 2а
(подкоренное выражение положительно, так как 45° < а <
< 90°). Стало быть, объём равен V = а3\/- cos 2а/(2 cos a).
□
Пример 9.4. В основании четырёхугольной пирамиды
SABCD лежит выпуклый четырёхугольник, длины двух
сторон которого равны 6, а длины двух других 10.
Высота SO пирамиды равна 7. Найти объём пирамиды, если
плоскости всех её боковых граней образуют с плоскостью
основания углы величиной 60°.
Решение. Из условия следует, что точка О (основание
высоты) равноудалена от всех прямых, содержащих
стороны основания пирамиды. Предположим, что две
противоположные стороны четырёхугольника ABCD равны 6, а две
другие равны 10. Тогда ABCD — параллелограмм,
отличный от ромба. Для такого параллелограмма точки О,
обладающей указанным свойством, не существует (почему?).
Поэтому две соседние стороны четырёхугольника ABCD
Рис. 9.6
§ 9,2. Положение основания высоты пирамиды 281
(например, АВ и ВС) равны 6, а две другие 10. При этом О —
либо центр вписанной в него окружности, либо центр внев-
писанной окружности (рис. 9.6а, б). Рассмотрим отдельно
оба эти случая.
Пусть О — центр вписанной окружности, ОЕ — её радиус,
проведённый к стороне АВ (рис. 9.7). Из треугольника
SOE находим, что г = ОЕ = SO ctg 60° = -р. Площадь че-
v3
тырёхугольника ABCD равна Sabcd = Saob + &вос + Scod +
+ SD0A = \{AB + BC + CD + DA)r = ^1. Пусть углы Аи С
равны а. Тогда площадь Sabcd равна 6 10- sin а, следова-
112
тельно, S0CH ^ 60, Но —=- > 60, значит, рассматриваемый
v3
случай невозможен.
Пусть теперь О —центр вневписанной окружности. Ра-
диус её равен г = — (аналогично первому случаю). Пло-
v3
щадь основания равна Sabcd = Scod + Sdoa — Saob - Sboc =
1 9Я
= | (CD + DA -АВ- ВС) • r = -=- < 60. Следовательно, объём
пирамиды равен ^ • —г= • 7 = ——.
«* v3 ЗуЗ
П
282 Глава 9*. Решение задач
§ 9.3. Метод вспомогательного объёма
В § 4.8, 4.9 мы рассмотрели некоторые способы
нахождения расстояний. Здесь мы укажем ещё один способ
(метод вспомогательного объёма), идея которого
заключается в следующем. Известно, что объём пирамиды V,
площадь её основания S и длина высоты h связаны
формулой
Но длина высоты пирамиды есть не что иное, как
расстояние от её вершины до плоскости основания.
Следовательно, для вычисления расстояния от точки до плоскости
достаточно найти объём и площадь основания
какой-нибудь пирамиды с вершиной в этой точке и с основанием,
лежащим в данной плоскости.
Приведём несколько примеров, иллюстрирующих
применение этой идеи.
Пример 9.5. Длина ребра АА\ прямоугольного
параллелепипеда ABCDA\B\C\Di равна а, угол В\АВ равен а,
а угол С\ВС равен /3. Найти:
а) расстояние от точки А\ до плоскости BDC\;
б) расстояние между прямыми AD\ и DC\.
Решение, а) Рассмотрим тетраэдр A\BDC\ (рис. 9.8).
Искомое расстояние h есть длина высоты этого тетраэдра,
опущенной из вершины Ai. Для её нахождения достаточно
знать объём V тетраэдра A\BDC\ и площадь S
треугольника BDCi. Вычислим их. Пусть объём данного
параллелепипеда равен Vn, а объём тетраэдра A\ABD равен v.
Тогда v = т? • Sabd • я — z^n- Аналогично объёмы тетраэдров
о о
ВА\В\С\, C\BCD и DA\C\D\ равны ^Vn> следовательно,
V = Vn-4.±Vn = ±Vn.Ho
Vn = AB - ВС • а = (a ctg ос) • (а ctg /3) • а,
§ 9.3. Метод вспомогательного объёма
283
поэтому V — ^а3 ctg a ctg/З. Далее,
S = \
2
sin
2 sin a sin /3
sin
Чтобы вычислить ZBC\D = (py воспользуемся теоремой
косинусов, а затем теоремой Пифагора:
_ DC\ + BC\ -BD2 _ РС\+ВС\-{ВС2+СР2) _
C0S ^ " 2DClBCi " 2-DdBCi "
_ (DC2 - CD2) + (ВС2 - ВС2) _ CCl + CCl _ 2СС2
~ 2-DCi-BCi " 2'DCx-BCi ~ 2-DCi-BCi
сс\
= sin oc sin/3.
sin of sin
Следовательно, sin cp = yl - sin2 a sin2 j3 и
1 a2 \/l — sin2 a sin2 /3
2 sin a sin /3
284
Глава 9*. Решение задач
Теперь мы можем найти искомое расстояние:
3V
a3 ctg a ctg /3
2a cos a cos /?
S S a Vl - sin2 or sin2 /3 \/l - sin2 a sin2 /J
2 sin a sin /3
Замечание. Соотношение V — -^Vn совершенно аналогично
о
доказывается в случае, когда параллелепипед не является
прямоугольным. Оно понадобится нам в следующем параграфе.
б) Проведём через скрещивающиеся прямые AD\ и DC\
параллельные плоскости AD\Bi и BD\C (почему эти
плоскости параллельны?). Проведём через точку А\ прямую,
перпендикулярную этим плоскостям. Пусть прямая /
пересекает плоскость BDC\ в точке О, а плоскость AD\B\ —
точке О\ (рис. 9.9). Тогда искомое расстояние р равно
расстоянию между плоскостями ADiBi и BDC\, т. е. длине
отрезка ОО\. Но ОО\ = А\О - А\О\. Длину отрезка А\О
мы нашли в п. а): А\О = h. Осталось найти А\О\. Для
этого вычислим двумя способами объём тетраэдра A\AB\D\.
С одной стороны, аналогично п, а) находим, что Fa1ab1Di =
= QVn- С другой стороны, VAlABlDl = ^ . А\О\ -S (так как
§ 9,3. Метод вспомогательного объёма 285
треугольники ADiBi и BDC\ равны), откуда получаем, что
1 V 1
А\О\ = 77 • -£ = oh. Следовательно,
п
i^ Упражнение 9.2. Решите пример 9.5 методами, изложенными
в § 4.8, 4.9.
Пример 9.6. Доказать, что сумма расстояний от
произвольной точки, взятой внутри правильного тетраэдра, до
его граней есть величина постоянная.
Решение. Пусть М — произвольная точка внутри
правильного тетраэдра ABCD. Соединим её с вершинами
тетраэдра (рис. 9.10). Обозначим через S площадь грани
Рис. 9.10
тетраэдра ABCD, через Н — его высоту, а через Hi, H%y
Нз и #4 — расстояния от точки М до граней ABC, BCD,
ACD и ABD соответственно. Так как объём тетраэдра ABCD
равен сумме объёмов тетраэдров МАВС, MBCD, MACD
и MABD, то
следовательно, Н\ + Hz Л- Нз + Н^ — Н — const, что и
требовалось доказать. □
286
Глава 0* Решение задач
^Упражнение 9.3. Верно ли, что если сумма расстояний от
произвольной точки, взятой внутри тетраэдра, до его граней
постоянна, то этот тетраэдр правильный?
Утверждение следующего примера является
пространственным аналогом свойства биссектрисы внутреннего угла
треугольника.
Пример 9.7. Доказать, что биссектор двугранного угла
при ребре тетраэдра делит противоположное ребро на части,
пропорциональные площадям граней тетраэдра, лежащих
на гранях этого угла.
Решение. Пусть биссектор двугранного угла при
ребре АВ тетраэдра ABCD пересекает ребро CD в точке Е
(рис. 9.11). Обозначим длины высот тетраэдров ABED и
АВСЕ, опущенных из точек D и С, через h\ и h<i
соответственно. Тогда -=п — j~ (почему?). По теореме 5.2 о бис-
секторе двугранного угла расстояния от точки Е до граней
§ 9.4. Вспомогательный многогранник 287
двугранного угла равны. Обозначим их через h. Тогда
DE = /ц = Sabe = У abed = 3^ABD'a = Злю п
EC h2 Wabce Vabce ISabc-H s^bc'
Sabe 3
§ 9.4. Вспомогательный многогранник
Рассмотрим же фигуру ту,
которая в другую пору
заставила бы нас в поту
холодном пробуждаться. ♦♦
И. Бродский. Пенье без музыки
Из курса алгебры вам известен метод замены
переменных при решении уравнений и систем. Удачная замена
позволяет решить задачу красиво и коротко, однако её выбор —
это своего рода искусство. Правда, существует несколько
стандартных замен переменных, помогающих решать
целые классы алгебраических задач.
Сходная ситуация имеет место и в геометрии. Один
из эффективных приёмов решения геометрических задач
состоит в том, что изучаемая конфигурация заменяется
другой, более удобной. В этом параграфе мы обсудим
несколько стандартных геометрических замен.
При решении задач на прямые и плоскости в
пространстве, если заданная в условии конфигурация не связана
с конкретным телом, бывает полезно (в том числе,
чтобы представить конфигурацию) связать её с каким-нибудь
многогранником. Часто в качестве такого многогранника
выбирается куб.
Пример 9.8. Угол между двумя скрещивающимися
прямыми равен 60°. Точка М лежит на одной прямой,
точка N — на другой, причём расстояния от этих точек до
общего перпендикуляра данных прямых одинаковы и
равны расстоянию между этими прямыми. Найти угол между
общим перпендикуляром и прямой MN.
288
Глава 0*. Решение задач
Решение. Рассмотрим куб ABCDAiB\C\D\. Пусть одна
из данных прямых проходит через его вершины АиДа
вторая лежит в плоскости грани A\B\C\D\ и проходит через
вершину Ai под углом 60° к ребру A\D\ (рис. 9.12). Тогда
Ci
M(D)
Рис. 9.12
общим перпендикуляром к этим прямым служит ребро АА\.
Пусть его длина равна а. Поместим точку М в вершину D
куба. Тогда точка N лежит либо справа, либо слева от
точки А\ (см. рис. 9.12) и удалена от неё на расстояние а.
Рассмотрим оба этих случая.
Если точка N лежит правее точки Аь то AAiND\
равносторонний, следовательно, ND\ = a. Искомый угол а между
прямыми АА\ и MN равен углу NMDi, так как (AAi) ||
|| (MDi). Треугольник ND\M прямоугольный и
равнобедренный (ZMDiN = 90°, NDX = MDi = а), поэтому а = 45°.
Если точка N лежит левее точки А\9 то AA\ND\
равнобедренный (A\N = A\D\ =a) с углом 120° при вершине Аи
следовательно, ND\ = a\/3. Искомый угол а равен углу
NMD\. Его мы находим из AND\M:
tga =
следовательно, а = 60°.
пД
MD\
□
§ 9Л. Вспомогательный многогранник
289
С помощью куба удобно изображать трёхгранные углы,
две грани которых перпендикулярны.
Пример 9.9. Плоские углы трёхгранного угла равны 45°,
45° и 60°. Через его вершину проведена прямая,
перпендикулярная одной из граней, плоский угол которой равен 45°.
Найти угол между этой прямой и ребром трёхгранного угла,
не лежащим в указанной грани.
Решение. Рассмотрим куб ABCDAiB\C\Di. Заданный
в условии трёхгранный угол —это угол АВСВ\ (рис. 9ЛЗ),
так как ZBAC = ZB) АВ = 45°, а АВ\АС = 60° как угол
равностороннего треугольника АСВ\. Прямая АА\
перпендикулярна грани ABC, следовательно, искомый угол — это угол
. Он равен 45°. □
Рис. 9.13
Из планиметрии вам известно, что иногда треугольник
бывает полезно достроить до параллелограмма (вспомните,
как таким способом можно вычислить длину медианы
треугольника по трём его сторонам, используя теорему о сумме
квадратов диагоналей параллелограмма). Подобно этому
некоторые стереометрические задачи легко решаются,
если тетраэдр достроить до параллелепипеда (или, образно
говоря, «уложить тетраэдр в коробку»).
3483
290
Глава 0* Решение задач
Обычно используют два способа достраивания. Первый
способ заключается в том, что три грани тетраэдра А\ ABC,
имеющие общую вершину А, достраиваются до
параллелограммов (рис. 9.14). Затем проводятся плоскости A\BiCit
B\BD и C\CD, пересекающиеся в точке D\. Получается
параллелепипед ABDCA\B\D\C\ (рис. 9.15). Тем самым
наш тетраэдр оказывается «уложенным в угол коробки».
Рис. 9.16
Другой способ состоит в проведении через каждое ребро
тетраэдра плоскости, параллельной противоположному
ребру (рис. 9.16). Получается параллелепипед, для которого
рёбра нашего тетраэдра являются диагоналями граней.
Назовём этот способ «укладыванием в коробку по диагонали».
Заметим, что укладывать тетраэдр в угол коробки
удобно, если известны плоские углы при одной из его вершин,
а укладывание по диагонали предпочтительнее в задачах,
где речь идёт о скрещивающихся рёбрах тетраэдра.
Пример 9.10. В тетраэдре ABCD плоские углы при
вершине А прямые. Точка О удалена от всех вершин тетраэдра
на одинаковое расстояние. Доказать, что это расстояние
равно длине отрезка, соединяющего середины
скрещивающихся рёбер данного тетраэдра.
§ 9.4. Вспомогательный многогранник
291
Решение. Уложим тетраэдр в угол параллелепипеда
ABKCDLMN (рис. 9 Л 7). Этот параллелепипед
прямоугольный (так как плоские углы при его вершине А прямые),
следовательно, его диагонали равны, а точка О их
пересечения равноудалена от всех вершин параллелепипеда (на
расстояние, равное половине его диагонали).
Рис. 9.17
Пусть отрезок PQ соединяет середины скрещивающихся
рёбер тетраэдра ABCD, скажем, рёбер ВС и AD. Тогда
этот отрезок — средняя линия треугольника AKD, поэтому
PQ— 7>KD, т.е. длина этого отрезка также равна половине
диагонали параллелепипеда. □
Замечание. Попутно мы установили, что длины отрезков,
соединяющих середины скрещивающихся рёбер тетраэдра с
прямыми плоскими углами при вершине, равны.
Пример 9.11. Длины двух скрещивающихся рёбер
тетраэдра равны а и Ь, расстояние между ними равно d> а угол
между прямыми, содержащими эти рёбра, равен (р.
Доказать, что объём тетраэдра V равен -^abd sin ср.
Решение. Уложим данный тетраэдр в коробку по
диагонали (рис. 9.18). Пусть Vn — объём коробки
(параллелепипеда). Тогда V = ^Vn (см. решение задачи из п. а)
о
292
Глава 9*, Решение задач
Рис. 9.18
примера 9.5, а также замечание к нему). Величина Vn
легко вычисляется через данные задачи. Действительно,
d — это длина высоты параллелепипеда; его грань —
параллелограмм с диагоналями а и & и углом <р между ними.
Следовательно, Vn = (^ab sin (pyd, V = -^abd sin (p. □
В некоторых задачах тетраэдр удобно заменять не
параллелепипедом, а треугольной призмой (рис. 9.19).
Рис. 9.19
Пример 9.12*. Тетраэдры ABCD и A\B\CiD\
расположены так, что А\ — точка пересечения медиан треугольника
BCD, Bi e (ACD), Сг € (ABD), Dx e (ABC), A e (BiCiDi),
Be (A1C1D1), Се (AiBiDi), De (ABiCi), а прямые BDi,
CB\ и DC\ делят пополам отрезки AC, AD и АВ соответ-
§ 9.4. Вспомогательный многогранник
293
ственно (рис. 9.20а). Доказать, что прямые АВ, АС и AD
делят пополам отрезки DC\, BD\ и СВ\ соответственно.
Решение. Пусть К, L и М — середины отрезков АВ, АС
и AD. Докажем, что точка К является серединой
отрезка DC\. Достроим тетраэдр ABCD до треугольной призмы
Е(Сг)
б)
Рис. 9.20
BCDEFA (рис. 9.206). Так как В е (AiCiDi) и (BZ>i) П
П [АС] = L, то С\ е (А\ЬВ). Плоскость A\LB проходит через
середины сторон CD и AF параллелограмма AFCD,
следовательно, она содержит прямую BE. Значит, точка Е есть
точка пересечения прямой DK с плоскостью А\ЬВ, поэтому
Е и С\ — это одна и та же точка. Следовательно, прямая АВ
пересекает отрезок DC\ в его середине К.
Аналогично доказывается, что точки L и М — середины
отрезков BD\ и СВ\. □
Иногда бывает полезно заменять не тетраэдр
параллелепипедом, а наоборот, параллелепипед тетраэдром.
Пример 9.13. Из одной вершины прямоугольного
параллелепипеда проведены диагонали всех граней, проходящих
через эту вершину. Доказать, что сумма трёх углов,
образованных этими диагоналями, взятыми попарно, равна 180°.
294
Глава 9*. Решение задач
Решение. Пусть из вершины В\ прямоугольного парал-
лелепипеда ABCDA\B\C\D\ проведены диагонали граней,
сходящихся в этой вершине. Соединив концы этих
диагоналей, получим тетраэдр ACB\D\ (рис. 9.21).
Рис. 9.21
Заменим параллелепипед этим тетраэдром. Достаточно
доказать, что сумма плоских углов при вершине
тетраэдра равна 180°. Заметим, что ДАВХС = AADiC ACBiDx =
= ACADi и AABiDi = AACDi, следовательно, ZABiC =
= Z.AD\Cy ZCBiDi = ZCADi и ZABiDi = ZACDi. Но
поскольку ZADiC + ZCADt + ZACDi = 180°, мы получаем ZABiC +
+ ZCBiDi + ZABiDi = 180°. П
В заключение приведём пример нестандартной замены
(рассматриваемая ниже задача очень похожа на
предыдущую, но идея её решения совершенно другая).
Пример 9.14. Диагональ прямоугольного
параллелепипеда образует с его рёбрами, выходящими из той же
вершины, что и диагональ, углы а, /3 и у. Доказать, что
oc + P+y <180°.
Решение. Расположим четыре равных прямоугольных
параллелепипеда так, как показано на рис. 9.22. Тогда
ZBOC = 2а, ZAOC = 2/3, /LAOB = 2у. Точка О не лежит
в плоскости ABC (почему?), следовательно, по теореме о
§ 9.5. Задачи на комбинации многогранников
А
295
Рис. 9.22
сумме плоских углов трёхгранного угла (теорема 5.7) 2а+
3 т.е. а + /3+у<180°. D
§ 9.5. Задачи на комбинации многогранников
И от того, что что-то очень сложно,
ты не пытаешься это сделать? Научиться
ходить вначале тоже было тяжело, но ты
позанимался, и теперь, глядя на тебя,
может показаться, что это всё не трудно.
Р. Бах, Иллюзии
В этом параграфе мы приведём примеры решения задач,
в которых фигурируют сразу несколько многогранников.
Обычно эти задачи нестандартны, каждая из них требует
индивидуального подхода к своему решению и
предъявляет высокие требования к пространственному воображению
решающего.
Трудно дать какие-то общие рекомендации, которые во
всех случаях могли бы облегчить решение подобных задач,
но кое-что посоветовать можно. Прежде всего, начинать
решение такой задачи нужно с изготовления хорошего
чертежа, на ковром отчётливо видны все детали заданной
в условии задачи конструкции. Особенно это необходимо
в задачах на пересечение многогранников. Кроме того, мы
296
Глава 0*. Решение задач
надеемся, что соображения, на которых основаны решения
приводимых ниже задач, окажутся полезными при
решении других задач на комбинации многогранников.
Пример 9.15. Точка О — середина медианы тетраэдра
объёма V. Найти объём общей части данного тетраэдра
и тетраэдра, симметричного ему относительно точки О.
Решение. Пусть точка О — середина медианы DD\
тетраэдра ABCDy а тетраэдр A\B\CiDi симметричен тетраэдру
ABCD относительно этой точки (рис. 9.23а). Точки D и D\
являются вершинами многогранника, получающегося в
пересечении рассматриваемых тетраэдров. В каждой из этих
вершин сходятся три его грани, причём в точке D — три
грани, содержащиеся в гранях ABD, BCD и ACD
тетраэдра ABCD, а в точке D\ — три грани, содержащиеся в
гранях AiB\D\y B1C1D1 и A\C\D\ тетраэдра A\BiC\D\. Итак,
рассматриваемый многогранник имеет шесть граней. Эти
грани попарно симметричны относительно точки О,
следовательно, они попарно параллельны. Поэтому общая часть
наших тетраэдров представляет собой параллелепипед
(докажите это, используя теоремы о параллельности прямых
и плоскостей в пространстве и определение параллелепипе-
D
Рис. 9.23
§ 9.5. Задачи на комбинации многогранников 297
да). Он получается из тетраэдра ABCD отсечением трёх тет-
2
раэдров, подобных ему с коэффициентом ^ (один из них —
тетраэдр A2BC2D2 — показан на рис. 9.236). Заметим, что
три этих тетраэдра попарно пересекаются по тетраэдрам,
подобным исходному с коэффициентом ^ (один из этих трёх
о
тетраэдров — A2B2D1D3 — показан на рис. 9.236). Поэтому
искомый объём равен V- 3-(§) 'v + s'(l) V = \V- D
Пример 9.16. Через середины двух параллельных рёбер
куба, не лежащих в одной грани, проведена прямая, и куб
повёрнут на 90° вокруг неё. Найти объём общей части
исходного куба и повёрнутого, если ребро куба имеет длину а.
Решение. Разрежем куб пополам диагональной
плоскостью, перпендикулярной оси вращения. Получим две
одинаковые призмы. Рассмотрим одну из них и повернём её
на 90° вокруг данной оси. Общая часть призмы и её образа
(рис. 9.24) будет состоять из прямоугольного
параллелепипеда, в основании которого находится квадрат со
стороной а, и правильной четырёхугольной пирамиды с тем же
основанием (докажите это, используя тот факт, что при
поворотах на углы, кратные 90°, многогранник, являющийся
пересечением призм, должен переходить в себя).
Рис. 9.25
298
Глава 9*. Решение задач
Найдём высоту h параллелепипеда и высоту Н
пирамиды, обратившись к рис. 9.25: h = АА\ = А\Т = fl ^~a,
Я = ^ h = §. Искомый объём равен
Пример 9.17. Дана пирамида ABCD, в которой ZABC =
= ZBCD = ZDAB = 90°, АВ = а. Вершины правильного
тетраэдра расположены на рёбрах этой пирамиды так, что одно
из рёбер тетраэдра лежит в грани ABD, а противоположное
ему ребро лежит в грани ABC и параллельно ребру АВ.
Найти длину ребра этого тетраэдра.
Решение. Рассмотрим высоту DE пирамиды ABCD
(рис. 9.26). Тогда (АЕ) 1 (АВ) и (ЕС) 1 (ВС) (теорема о трёх
перпендикулярах), следовательно, АЕСВ —
прямоугольник. Обозначим рассматриваемый правильный тетраэдр
через MNPQy а длину его ребра — через х> Обратимся к
\
м
/
/
у.
N
A R р В
Рис. 9.27
§ 9.5. Задачи на комбинации многогранников 299
рис. 9.27. (На этом рисунке (MR) _L (AB), AMNP
правильный, Qi — его центр, лежащий на диагонали ЕВ
прямоугольника АЕСВ.) Тогда MR =
= Ц*,РВ = %,
о &
RB = х и AR = а — х. Обозначим величину равных углов
ЕВА и CAB через а. Из APQiB и AMAR найдём, что
l
РВ
откуда получаем
c\/3
и
MR хУЗ
AR 2(а~х)у
—~—, следовательно, х= -=а.
о 7
□
2(a~x)
Рассмотрим более сложный пример, иллюстрирующий
(как и пример 9 Л 7) алгебраический метод решения задачи
на комбинацию многогранников.
Пример 9.18*. Точка D —середина ребра А\С\ правиль
ной треугольной призмы ABCAiB\C\. Правильная треу
гольная пирамида SMNP расположена так, что её осно
вание MNP лежит в плоскости ABC, точка М лежит на
продолжении отрезка АС, причём СМ = -кАС, ребро SN
проходит через точку D, а ребро SP пересекает отрезок
ВВ\ в точке К. В каком отношении отрезок ВВ\ делится
точкой К?
Рис. 9.28
Рис. 9.29
300 Глава 9*. Решение задач
Решение. Пусть О — проекция вершины пирамиды S на
плоскость ABC. Тогда отрезок ON проходит через
середину Е отрезка АС, & отрезок ОР — через точку В (рис. 9.28).
Обозначим АВ = а, ОЕ = х, ОМ = у и ОВ = г. Рассмотрим
прямоугольный треугольник ВЕМ (рис. 9.29). Точка О
обладает тем свойством, что все стороны этого треугольника
видны из неё под одинаковыми углами в 120°. Используя этот
факт, а также то, что ВЕ~ —х-* ЕМ —а (и, следовательно,
ВМ= ^—), запишем уравнения, получаемые применением
теоремы косинусов к АЕОМ и АВОМ:
а2 = х2 + у2 + ху, (9.7)
\a2 = y2 + z2 + yz. (9.8)
Применим теорему синусов к АЕОМ:
а = У
УЗ/2 sin /.OEM'
следовательно,
У^-у = a sin /.OEM. (9.9)
Теперь применим теорему синусов к АЕОВ:
пуД/2 _ z
УЗ/2 " sin /OEBy
но
sin /LOEB = sin (90° - /OEM) = cos /OEM,
следовательно,
z = acos/OEM. (9.10)
Возведём обе части уравнений (9.9) и (9.10) в квадрат
и сложим получившиеся уравнения:
!«/2 + г2 = а2. (9.11)
§ 9.5. Задачи на комбинации многогранников 301
Исключив а из уравнений (9.11) и (9.8), получим
16 4
или
Разделив обе части полученного уравнения на у2 ф 0 и введя
переменную t = -, приведём его к виду
1 5
Решениями последнего уравнения являются t\ = т> и ^2 = * •
Z О
Рассмотрим отдельно оба этих случая.
Пусть - = «г. Тогда из уравнения (9.8) находим, что i/ = a,
У *
и уравнение (9.7) примет вид х = -а. Так как по смыслу
задачи я > 0, то этот случай невозможен.
z 5
Пусть - = д- Тогда из уравнения (9.8) получаем, что
о 5 3 5
у = а. Следовательно, z = -= • —=а — —=а. Из уравне-
6 у1з 2ТЗ
ния (9.7) находим, что х~ —=а. Обозначив SO = H и
vl3
= Л, из подобия треугольников NDE и iVSO имеем дгрг = -=^,
т.е. = 77- Подставив найденные значения х и у в по-
о
следнее уравнение, получим, что Н= „h. Теперь из подобия
треугольников КВР и SOP имеем -^ = т^, т. е. -==- = >
откуда получаем KB = (l - -ЧЯ= ^11= jA. Следовательно,
1 3
#Bi = BBi — .ЙГВ — h — jh=jh. Окончательно получаем, что
вк № 1 п
квх
В заключение приведём пример использования
векторного метода в задачах на комбинации многогранников.
302
Глава 9*. Решение задач
Пример 9Л9*. Дана прямая призма ABCDA\B\C\D\, в
основании которой лежит ромб ABCD с углом при
вершине А9 равным 60°. Все рёбра призмы имеют длину а.
Точка К является ортогональной проекцией точки Bi на
плоскость DA\C\, а точка L — ортогональной проекцией
точки К на плоскость DD\C\. Найти объём пирамиды DCLK.
Рис. 9.30
Решение. Примем за основание пирамиды DCLK
треугольник CDLy лежащий в плоскости DD\C\ (рис. 9.30).
Тогда отрезок KL — высота этой пирамиды, так как (KL) _L
_L (DD\C\). Объём пирамиды DCLK равен V = -^Scdl 'KL =
о
= -r • 77 • CD • LM • KL, где точка М — ортогональная проекция
точки L на прямую DC. Найдём длины отрезков CD, LM
и KL с помощью векторов. Выберем в качестве базиса
векторы fh = C\B\y ft = C\Di ир=С\д (см. рис. 9.30). Составим
«таблицу умножения» векторов этого базиса (таблица 9.1).
Имеем
= х(т
= x • CiА[ + у •
+ у(П +р) -М=(х-
§ 9.5. Задачи на комбинации многогранников 303
Так как (BtK) ±
ш
я
р
л
а2
а2
2
0
Я
а2
2
а2
0
Р
0
0
а2
Таблица 9.1
и (ВХК) ±
, то
С помощью найденного разложения вектора В\К по базису
{fh, ft,p) и «таблицы умножения» базисных векторов
приведём эту систему уравнений к равносильной:
3 1
Отсюда х = g, i/ = - -g. Следовательно,
Аналогично
Из условий KL• ft = Kl-p=0 находим, что г=тт
Поэтому KZ = ~r (-2/71 + Л) и
KL = ^у/(-
= ^\/4/Й2 - 4Й • Я + Я2 =
За\/3
10 '
304 Глава 9*. Решение задач
Наконец,
Так как LM - ft = 0, то и—^-^ и LM — ~р, следовательно,
LM = -^а. Искомый объём равен
v_l 6a W3_3oV3 _
6 5 ' 10 ~ 50 '
Задачи
Го тс п ер
...Не нахожу забавы в травле зайцев:
Достойнее охотиться на львов.
Нортумберленд
Чуть услыхал про трудную задачу,
Воображенье так уж и кипит.
В. Шекспир. Король Генрих четвёртый
9.1. В правильной треугольной пирамиде угол наклона
бокового ребра к плоскости основания равен плоскому углу
при вершине пирамиды. Найдите объём пирамиды, если
длина ребра её основания равна а.
9.2. Линейный угол двугранного угла при боковом ребре
правильной четырёхугольной пирамиды в два раза больше
плоского угла при вершине пирамиды. Найдите этот
плоский угол.
9.3. В правильной четырёхугольной пирамиде угол
между боковым ребром и плоскостью основания равен углу
между боковым ребром и плоскостью боковой грани, не
содержащей это ребро. Найдите этот угол.
9.4. Длина стороны основания правильной треугольной
пирамиды равна а. Пусть а — плоский угол при вершине
пирамиды, j3 — двугранный угол при основании, у— угол
Задачи 305
наклона бокового ребра к плоскости основания, 8 —
двугранный угол при боковом ребре пирамиды. Найдите объём
пирамиды в каждом из следующих случаев:
i; 6)tg/? = 2; B)tgy = l; г) cos 8 = ±.
9.5. В пирамиде SABC равны длины рёбер SA, SB и SC,
ZASB = ZASC = 60°, ZBSC = 90°. Докажите, что вершина S
проектируется в середину отрезка ВС.
9.6. В пирамиде SABC известно, что ZACB = 90° и (АС) ±
I. (BS). Докажите, что вершина S проектируется в точку,
лежащую на прямой ВС.
9.7. Боковые рёбра треугольной пирамиды имеют
одинаковую длину /. Два плоских угла при вершине пирамиды
равны а, а третий — (5. Найдите объём пирамиды.
9.8. В основании пирамиды SABC лежит треугольник,
у которого АВ = ВС = 20, АС = 32. Боковые грани пирамиды
наклонены к плоскости основания под углом 45°. Найдите
объём пирамиды.
9.9. Основанием пирамиды SABC служит треугольник
ABC, у которого АВ = а, ВС = Ъ. Боковая грань, содержащая
сторону АСУ перпендикулярна плоскости основания, а две
другие боковые грани образуют с плоскостью основания
равные углы. Найдите отношение объёмов пирамид SABC
и SOBC, где О —основание высоты пирамиды SABC.
9.10. Дана правильная призма ABCDAiBiCiDi, в
которой АВ = а, АА\ = 2а. Найдите:
а) р(Оь BDCi), где О\ —точка пересечения диагоналей
основания A\B\C\D\\
6)p(ABbBCi).
9.11. В основании пирамиды лежит выпуклый
многоугольник, а площади её боковых граней равны.
Докажите, что сумма расстояний от любой точки основания до
плоскостей боковых граней пирамиды есть величина
постоянная.
9.12. Докажите, что если #ь *2> #з и Х4 —расстояния от
произвольной/точки тетраэдра до его граней, a Ai, Л2» Л3
306 Глава 0* Решение задач
и h± — длины соответствующих высот тетраэдра, то
fl\ 1%2 Лз "4
9.13. На грани ABC тетраэдра ABCD взята точка О и
через неё проведены отрезки ОА\, ОВ\ и ОС\, параллельные
рёбрам DA, DB и DC, до пересечения с гранями тетраэдра.
Докажите, что
ОАг ОВг
1
DC
9.14. В тетраэдре ABCD плоские углы при вершине D
прямые. Пусть Л — длина высоты тетраэдра, опущенной
из вершины D, а а, Ь и с — длины рёбер, выходящих из
этой вершины. Докажите, что
h2 ~a2 + b2 + c2-
9.15. Угол между двумя гранями трёхгранного угла
прямой, а величина каждого плоского угла этих граней равна а.
Найдите величину плоского угла третьей грани.
9.16. Вершины В и С треугольника ABC лежат на
разных гранях двугранного угла величины 45° с ребром I.
Сторона АС перпендикулярна одной из граней и
пересекает её в своей середине. Проекция отрезка ВС на другую
грань параллельна ребру / и по длине равна расстоянию от
точки С до L Найдите углы треугольника ABC.
9.17. Угол между двумя скрещивающимися прямыми
равен 45°. Точка М лежит на одной из них, точка N —
на другой. Длина общего перпендикуляра к этим прямым
вдвое больше расстояния от точки М до него и втрое меньше
расстояния от точки N до него. Найдите угол между общим
перпендикуляром и прямой MN.
9.18. Дан треугольник LMN, в котором Z.LNM — 90°,
Z.MLN = 30°. Через точку L проведена прямая Z,
перпендикулярная отрезку LN и не лежащая в плоскости LMN. На
прямой I взята точка F так, что LF = MN. Двугранный угол,
Задачи 307
гранями которого являются треугольники LMN и LNF,
равен 60°. Найдите угол между прямыми LM и NF.
9.19. Сечение тетраэдра плоскостью, параллельной двум
его скрещивающимся рёбрам и равноудалённой от них,
имеет площадь S. Расстояние между этими рёбрами равно Л.
Найдите объём тетраэдра.
9.20*. В тетраэдре площади двух граней равны Si и S2,
а двугранный угол между ними равен а; площади двух
других граней равны Qi и (?2> а двугранный угол между
ними равен /3. Докажите, что
si + S2 - 2SiS2 cos a = Q? + Q\ - 2QXQ2 cos /3.
9.21. Длины двух скрещивающихся рёбер тетраэдра
равны а, двух других скрещивающихся Ь, двух оставшихся с.
Найдите объём тетраэдра.
9.22. Даны прямая а и точки А и В, находящиеся на
равных расстояниях от неё и такие, что ABjfa. Точки С и
D симметричны точкам Аи В относительно а. Длины
отрезков, соединяющих середины скрещивающихся рёбер
тетраэдра ABCDy равны х, у и г. Найдите объём тетраэдра ABCD.
9.23. Пусть Ль /*2> Лз и /ц — высоты тетраэдра, a d\9 c?2
и с?з —расстояния между его скрещивающимися рёбрами.
Докажите, что
9.24. Докажите, что сумма квадратов длин рёбер
тетраэдра в четыре раза больше суммы квадратов расстояний
между серединами его скрещивающихся рёбер.
9.25. Прямая I проходит через середины рёбер АВ и CD
тетраэдра ABCD. Плоскость а, содержащая I, пересекает
рёбра ВС и AD в точках М и N. Докажите, что прямая I
делит отрезок MN пополам.
9.26. Докажите, что все грани тетраэдра равны1* тогда
и только тогда, когда:
Х)Такие тетраэдры называются равногранными.
308 Глава 9*. Решение задач
а) отрезки, соединяющие середины скрещивающихся
рёбер, попарно перпендикулярны;
б) площади всех граней равны.
9.27. Сколько осей симметрии имеет правильный
тетраэдр?
9.28. Дан куб с ребром а. Найдите объём общей части
трёх четырёхугольных призм, у которых вершины
расположены в серединах сторон двух противоположных граней
куба.
9.29. Точка О — центроид тетраэдра ABCD объёма V.
Тетраэдр AiBiCiDi симметричен тетраэдру ABCD
относительно точки О. Найдите объём общей части этих тетраэдров.
9.30*. Тетраэдры ABCD и A\B\C\Di расположены так,
что у каждого из них все вершины лежат в плоскостях
соответствующих граней другого тетраэдра (т.е. Ае (BiCiDi),
Be (A\C\Di) и т.д.). Кроме того, А\ —точка пересечения
медиан треугольника BCD, а прямые BZ>i, CB\ и DC\ делят
пополам отрезки АСУ AD и АВ соответственно. Найдите
объём общей части тетраэдров, если объём тетраэдра ABCD
равен V.
9.31*. Правильный тетраэдр объёма V повёрнут вокруг
прямой, проходящей через середины его скрещивающихся
рёбер, на угол а (0 < а < п). Найдите объём общей части
исходного тетраэдра и повёрнутого.
9.32*. Ребро куба равно а. Куб повёрнут вокруг своей
диагонали на угол а (0 < а < к). Найдите объём общей части
исходного куба и повёрнутого.
9.33. Объём правильной четырёхугольной пирамиды
SABCD равен V. Высота SR пирамиды является ребром
правильного тетраэдра SPQR, плоскость грани PQR
которого перпендикулярна ребру SC. Найдите объём общей части
этих пирамид.
9.34*. Объём правильной призмы АВСА\В\С\ равен V.
Точка N — центр грани ВВ\СС\. Объём общей части двух
призм: АВСА\В\С\ и призмы, симметричной ей
относительно прямой AiN, где N — центр грани ВВ\С\СУ— равен
Задачи 309
~V. Найдите отношение АА\ :АВ, если известно, что оно
о
меньше \/3.
9.35. В тетраэдре два скрещивающихся ребра
перпендикулярны, их длины равны а и Ь, а расстояние между ними
равно с, В тетраэдр вписан куб так, что его четыре ребра
перпендикулярны этим двум рёбрам тетраэдра и на каждой
грани тетраэдра лежат ровно две его вершины. Найдите
длину ребра этого куба.
9.36*. В тетраэдре ABCD рёбра АВ и CD
перпендикулярны, АВ — a, CD = b. Отрезок, соединяющий середины
рёбер АВ и CD, перпендикулярен им, а его длина равна с.
Вершины правильного тетраэдра A\B\CiDi лежат на
поверхности тетраэдра ABCD, одно из его рёбер параллельно
ребру АВ, другое — ребру CD. Найдите длину ребра
тетраэдра A\B\CiDi.
9.37*. Все вершины правильной пирамиды SABCD (S —
вершина) расположены на рёбрах правильной пирамиды
QMNP с основанием MNP. Известно, что плоскость ABC
перпендикулярна плоскости QMN. Найдите отношение
объёмов этих пирамид.
9.38*. Длина ребра куба ABCDA\B\C\D\ равна а. Точка
£ — середина ребра AD. Одно ребро правильного тетраэдра
лежит на прямой EDi, другое —на прямой, проходящей
через точку А\ и пересекающей прямую ВС в точке R.
Найдите длину ребра тетраэдра и длину отрезка BR.
9.39*. Докажите, что в деревянном кубе можно вырезать
отверстие, через которое может пройти точно такой же куб.
9.40*. Можно ли из деревянного куба с единичным
ребром вырезать:
а) два;
б) три
правильных тетраэдра с единичным ребром?
11 класс
Глава 10
Тела вращения
А карусель уже вертелась полным
ходом. Уже нельзя было различить
лошадей, стоек — всё слилось в один
блестящий, сверкающий круг.
П. Треверс. Мэри Поплине
§ 10.1. Предварительные замечания. Цилиндр. Конус.
Усечённый конус
— Посмотри-ка, что мы нашли, —
с гордостью сказал Муми-Тролль.
— Мировецкий чёрный цилиндр, как
раз для тебя!
Т. Янссон. Шляпа Волшебника,
В курсе стереометрии десятого класса мы уделили
основное внимание изучению многогранников. В этой главе
мы расширим класс рассматриваемых тел и приступим
к изучению цилиндра, конуса, усечённого конуса и шара,
которые относятся к так называемым телам вращения.
Определение. Фигура называется фигурой вращения,
если в пространстве существует такая ось, что при любом
повороте вокруг этой оси фигура переходит в себя1*.
Указанная ось называется осью вращения фигуры. В
случае, если фигура вращения является телом, это тело
называют телом вращения, а его поверхность — поверхностью
вращения (рис. 10.1).
Апеллируя к наглядным представлениям, мы можем
сказать, что тело вращения получается в результате
(непрерывного) вращения плоской фигуры вокруг некоторой оси.
^Вспомните соответствующие определения (см. § 8.1 и § 8.3).
314
Глава 10. Тела вращения
Такой подход является общепринятым в
элементарной геометрии, поэтому далее мы,
согласно традиции, будем говорить о телах
вращения как о телах, полученных
вращением плоской фигуры вокруг оси.
Аналогично поверхность вращения
можно представлять как результат вращения
(конечного куска) плоской непрерывной
кривой1* вокруг некоторой оси. Указанную
кривую называют образующей поверхности
вращения.
Исходя из этих наглядных
представлений ясно, что всякая плоскость,
перпендикулярная оси и пересекающая поверхность вращения,
даёт в сечении окружность с центром на оси (возможно,
вырождающуюся в точку).
В школьном курсе геометрии изучают простейшие тела
вращения — прямые круговые цилиндр, конус и усечённый
конус; шар и его части.
Рис. 10.1
Цилиндр
Пусть в пространстве заданы плоскость а, прямая /,
пересекающая её, и кривая L, лежащая в плоскости а.
Рассмотрим множество всех прямых, параллельных I и
пересекающих кривую L. Это множество называется
цилиндрической поверхностью (рис. 10.2). Кривая L называется
направляющей цилиндрической поверхности, а прямые,
параллельные I и пересекающие L, — образующими
цилиндрической поверхности. В случае если кривая L замкнутая
и не самопересекающаяся, то соответствующая
цилиндрическая поверхность называется замкнутой (рис. 10.3).
^Строгое определение этого понятия находится далеко за рамками
курса элементарной геометрии. Здесь нам вполне достаточно под
конечным куском плоской непрерывной кривой понимать линию,
которую можно начертить на плоскости, не отрывая от неё карандаша.
§10.1. Предварительные замечания
315
Рис. 10.2
Рис. 10.3
Определение. Цилиндром называется тело,
ограниченное замкнутой цилиндрической поверхностью и двумя
параллельными плоскостями, которые не параллельны
образующей этой цилиндрической поверхности1*.
Цилиндр изображён на рис. 10.4. Часть
цилиндрической поверхности, заключённая между указанными
параллельными плоскостями, называется боковой поверхностью
цилиндра, а части плоскостей, отсекаемые цилиндрической
поверхностью, — основаниями цилиндра. Отрезки
образующих цилиндрической поверхности, заключённые между
основаниями цилиндра, называются образующими
цилиндра2* .
Цилиндр называется прямым, если его образующие
перпендикулярны плоскостям оснований. Цилиндр
называется круговым, если его основания — круги.
^Заметим, что согласно данному определению частным случаем
цилиндра является призма.
2)Следует обратить внимание на то, что на протяжении всего этого
параграфа словом «образующая» будут названы различные объекты.
Чтобы избежать путаницы, необходимо следить, к какой именно фигуре
(цилиндрической поверхности, цилиндру, конусу и т.п.) относится это
понятие. Сказанное имеет место и для терминов «высота», «основание»,
«боковая поверхность» и т.д.
316
Глава 10. Тела вращения
Рис. 10.4
Рис. 10.5
Далее в нашем курсе будут рассматриваться только
прямые круговые цилиндры, которые мы для краткости будем
называть просто цилиндрами.
Соответствующую цилиндрическую поверхность будем
называть прямой круговой.
Радиусом цилиндра называется радиус его основания.
Осью цилиндра называется прямая, проходящая через
центры его оснований. Высотой цилиндра называется отрезок
оси, заключённый между основаниями.
и^ Упражнение 10.1. Докажите, что а) основания цилиндра
равны; б) образующие цилиндра равны; в) высота цилиндра
равна его образующей.
Цилиндр изображён на рис. 10.5 (напомним, что
изображением окружности является эллипс).
Сечение цилиндра, проходящее через его ось,
называется осевым сечением цилиндра.
в^3 Упражнение 10.2. Докажите, что всякое осевое сечение
цилиндра радиуса R и высоты Н является прямоугольником
со сторонами 2R и Н. (Указание: тот факт, что секущая
плоскость пересечёт боковую поверхность цилиндра по его
образующим, нуждается в обосновании; для этого можно
воспользоваться признаком перпендикулярности плоскостей
и определением цилиндра.)
в^3 Упражнение 10.3. На изображении цилиндра постройте
изображение двух его взаимно перпендикулярных осевых
сечений. (Указание: воспользуйтесь тем, что прямая, проходя-
§10,1. Предварительные замечания
317
щая через середины двух параллельных хорд, проходит через
центр окружности и перпендикулярна этим хордам, а затем —
свойствами параллельного проектирования,)
Цилиндр может быть получен вращением
прямоугольника вокруг оси, проходящей через его сторону. Поэтому
цилиндр является телом вращения.
Вкратце обсудим вопрос о сечениях цилиндра. Рассуждая
так же, как при выполнении упражнения 10.1 а), вы
можете получить следующий результат: сечения цилиндра плоско
стями, перпендикулярными образующей, являются кругами,
равными основаниям цилиндра. Нетрудно доказать также, что
всякое сечение цилиндра, параллельное его оси, является
прямоугольником. Действительно, пусть плоскость а,
параллельная оси О\С>2 цилиндра, пересекает одно из его оснований по
отрезку ВС. Построим плоскости О1О2В и О1О2С, Пусть они
пересекают плоскость а по прямым Ьис соответственно. Так как
(O1O2) || а, то Ь || (О\Ог) и с || (O1O2). Следовательно, прямые Ь
и с перпендикулярны основаниям цилиндра и, значит, проходят
через его образующие ВВ\ и СС\ (рис. 10.6). Четырёхугольник
ВСС\В\ -прямоугольник, так как (ВС) || (BiCi), (ВВ\) || (CC\) и
Гораздо сложнее ответить на такой вопрос: какая фигура
является сечением цилиндра плоскостью, пересекающей все его
образующие и не перпендикулярной им? Оказывается, такое
сечение — эллипс, рассматриваемый вместе со своей
внутренностью (рис. 10.7). Ясно, что поставленная задача эквивалентна
Рис. 10.7
318 Глава 10. Тела вращения
нахождению параллельной проекции круга на плоскость, не
параллельную плоскости этого круга. Ответ к этой задаче нам
известен, но обоснуем мы его позднее, в § 10Л0.
Конус
Пусть в пространстве заданы плоскость а, точка S, не
лежащая в этой плоскости, и кривая L, лежащая в а.
Рассмотрим множество всех прямых, проходящих через S и
пересекающих кривую L. Это множество называется
конической поверхностью (рис. 10.8). Точка S называется
вершиной конической поверхности, кривая L — её направляющей,
а прямые, проходящие через S и пересекающие L,—
образующими конической поверхности. В случае, если кривая L
замкнутая и не самопересекающаяся, соответствующая
коническая поверхность называется замкнутой (рис. 10.9).
Обратите внимание на то, что коническая поверхность
состоит из двух частей (каждая из которых называется
полостью)^ расположенных по разные стороны от её вершины.
Рис. 10.8 Рис. 10.9
Определение. Конусом называется тело, ограниченное
частью замкнутой конической поверхности, расположен-
§10.1. Предварительные замечания 319
|ной по одну сторону от её вершины, и плоскостью,
пересекающей все образующие по ту же сторону от вершины1*.
Иными словами, конус ограничен одной полостью
замкнутой конической поверхности и плоскостью,
пересекающей все образующие этой полости.
Конус изображён на рис. 10.10. Часть конической
поверхности, заключённая между вершиной и указанной пло-
Рис, 10.10
скостью, называется боковой поверхностью конуса, а часть
плоскости, отсекаемая этой поверхностью, — основанием
конуса. Вершина конической поверхности,
ограничивающей конус, называется вершиной этого конуса. Отрезки
образующих конической поверхности, заключённые между
вершиной и основанием конуса, называются образующими
конуса. Перпендикуляр, опущенный из вершины конуса на
плоскость его основания, называется высотой конуса.
Конус называется круговым, если его основание — круг.
Круговой конус называется прямым, если его высота
проходит через центр основания.
Далее в нашем курсе будут рассматриваться только
прямые круговые конусы, которые мы для краткости будем
называть просто конусами.
Соответствующую коническую поверхность будем
называть прямой круговой.
^Заметим, что согласно данному определению частным случаем
конуса является пирамида.
320
Глава 10. Тела вращения
Для того чтобы изобразить конус, сначала рисуют
эллипс, являющийся изображением основания конуса
(разумеется, это невозможно сделать с помощью циркуля и
линейки, поэтому на практике его рисуют от руки,
пользуются шаблоном или, как это делается в черчении, заменяют
эллипс овалом, составленным из дуг окружностей). Эллипс
удобно расположить так, чтобы его большая ось (т. е.
отрезок, соединяющий две наиболее удалённые точки эллипса)
была горизонтальна. Затем строят вертикальный отрезок
OS, являющийся изображением высоты конуса (центр
симметрии О эллипса считаем заданным). Далее проводятся
касательные SA и SB к эллипсу. Это делается
приближённо, прикладыванием линейки1*. Заметим, что точки
А и В не симметричны относительно центра эллипса. Что-
])На самом деле эти касательные можно построить точно, используя
циркуль и линейку. Пусть дан эллипс с центром симметрии О и малой
осью MN (рис. 10.11); ОМ = b, OS = h (точка S лежит на продолжении
малой оси). Обозначим через у расстояние от искомой точки касания до
большой оси эллипса. Можно доказать, что y = b2/h. Поэтому отрезок у,
как известно из планиметрии, легко строится циркулем и линейкой.
Отложив его на отрезке ОМ от точки О и проведя через его конец прямую,
параллельную большой оси, мы получим в пересечении с эллипсом
искомые точки касания.
§10.1. Предварительные замечания
321
бы подчеркнуть это, обычно строят точку С,
симметричную точке А относительно О, и проводят образующую SC
(рис. 10.12а). Из сказанного следует, что фигура,
показанная на рис. 10.126, не является изображением конуса.
а)
б)
Рис. 10.12
Прямая, содержащая высоту конуса, называется его
осью. Сечение конуса, проходящее через его ось,
называется осевым сечением конуса.
в^ Упражнение 10.4. Докажите, что всякое осевое сечение
конуса высоты Н и с радиусом основания R является
равнобедренным треугольником с основанием 2R и высотой Н.
Конус может быть получен вращением прямоугольного
треугольника вокруг катета. Поэтому конус является телом
вращения.
Нетрудно доказать, что всякое сечение конуса, проходящее
через его вершину, является равнобедренным треугольником.
в^ Упражнение 10.5. Докажите это утверждение.
Сечение конуса плоскостью, параллельной основанию, есть
круг, подобный основанию с коэффициентом, равным
отношению расстояния от вершины конуса до секущей плоскости
к высоте конуса.
Действительно, пусть дан конус с основанием К и вершиной S,
а плоскость а пересекает конус по некоторой фигуре Ф и
параллельна основанию. Каждой точке М € К поставим в соответствие
11 Зак 3383
322
Глава 10. Тела вращения
Рис. 10.13
её центральную проекцию с центром S на плоскость а — точку М\.
Пусть О — центр основания конуса, а О\ — её образ при
указанном отображении; X и У — произвольные точки основания,
Х\ и Y\ — их образы (рис. 10.13). Из подобия треугольников
SO\X\ и SOX (почему эти треугольники подобны?) получаем,
что
хо ~
и SOY, находим, что
' Аналогично, рассматривая треугольники SO\Y\
= -~рр Из этих равенств и равен-
ства ZXiO\Yi =ZXOY (теоремы 2.4 и 3.4) следует подобие тре-
угольников Х1О1У1 и ХОУ с коэффициентом -^тг- В частности,
J:^1 = -577 • ^ силу произвольности выбора точек X и У тем
самым доказано, что рассматриваемое отображение является
подобием.
Следовательно, фигура Ф — круг, подобный^ К с
коэффициентом SOi/SO. □
Возникает естественный вопрос о форме сечения конуса
плоскостью, не проходящей через вершину и не параллельной
основанию. Ответ на этот вопрос мы отложим до § 10.10.
^Строго говоря, для того чтобы сделать этот вывод, необходимо
указать преобразование подобия пространства, переводящее К в Ф
(см. § 8.5). Для этого достаточно распространить наше отображение
на всё пространство, положив X\Y\/XY = SOi/SO для любых точек
пространства X и У и их образов. Легко понять, что полученное
преобразование подобия является гомотетией с центром S и коэффициентом
SOi/SO.
§10,1. Предварительные замечания 323
Усечённый конус
Определение. Часть конуса, заключённая между его
основанием и секущей плоскостью, параллельной
основанию, называется усечённым конусом.
Усечённый конус изображён на
рис. 10.14. Усечённый конус имеет два
основания, которые являются
гомотетичными кругами. Понятия боковой
поверхности, образующей и высоты
усечённого конуса вводятся по одной
и той же схеме: это часть
одноимённого объекта конуса, из которого
получен усечённый конус,
заключённая между основаниями усечённого Рис. 10.14
конуса. Ось усечённого конуса — это
ось конуса, из которого получен усечённый, а осевое
сечение — сечение, проходящее через ось.
и^ Упражнение 10.6. Докажите, что всякое осевое сечение
усечённого конуса высоты Н и с радиусами оснований Лиг
есть равнобедренная трапеция с высотой Н и основаниями
2R и 2г.
Усечённый конус — тело вращения. Он может быть
получен вращением прямоугольной трапеции вокруг боковой
стороны, перпендикулярной основаниям.
и^ Упражнение 10.7. Докажите, что сечение усечённого конуса
плоскостью, проходящей через вершину конуса, из которого
он получен, является равнобедренной трапецией.
Приведём формулы для вычисления площадей
поверхностей и объёмов рассмотренных нами тел вращения. При
этом, как и в случае с многогранниками, мы будем
использовать наглядно-интуитивные представления о площади
поверхности и об объёме. Строгие определения и
доказательства приводимых ниже утверждений будут даны в
главе 13.
324
Глава 10, Тела вращения
Рассмотрим цилиндр радиуса R и высоты Н. Площадь
его боковой поверхности можно вычислить так:
= 2kRH.
(10.1)
Для того чтобы найти площадь полной поверхности
цилиндра, необходимо прибавить к площади его боковой
поверхности удвоенную площадь основания, т. е.
(10.2)
Объём цилиндра равен произведению площади основания
на длину его высоты:
'ц. = kR2H.
(10.3)
Справедливость формулы (10.1) подтверждается
следующими наглядными соображениями. Представим себе, что
боковая поверхность цилиндра сделана из бумаги.
Разрежем её по образующей и «развернём» так, чтобы
получилась плоская фигура. Эта фигура является
прямоугольником со сторонами 2л\К и Н, который называется
развёрткой боковой поверхности цилиндра (рис. 10.15).
Представляется довольно естественным принять за площадь боковой
поверхности площадь её развёртки1*. Тогда Яб.ц. = 2kRH.
2kR
Рис. 10.15
^Недостатки такого подхода к определению площади боковой
поверхности будут обсуждены в главе 13.
§10.1. Предварительные замечания
325
Пусть теперь дан конус с радиусом основания R,
образующей L и высотой1* Н.
Тогда площадь его боковой поверхности, площадь
полной поверхности и объём можно найти так:
1 Sq, k.
Sn.K. =
vK.=
= nRL,
kR(R + L]
\kR*H.
(10.4)
1, (10.5)
(10.6)
Если разрезать боковую поверхность конуса по
образующей и «развернуть» сё на плоскость, то получится круговой
сектор (рис. 10.16) радиуса L и с длиной дуги 2тгД. Угол при
вершине этого сектора легко вычислить: а = —=—. Площадь
L
сектора равна оа-^2' т'е- Равна тгДЬ. Таким образом, мы
получили наглядное подтверждение справедливости
формулы (10.4).
Рассмотрим усечённый конус с радиусами оснований R
и г, образующей L и высотой2* Н. Площадь его боковой
поверхности, полной поверхности и объём можно вычислить,
зная, что усечённый конус получается отрезанием от
конуса меньшего конуса, и используя формулы (10.4)—(10.6).
В результате получается, что
(Ю.7)
(10.8)
(10.9)
I®3 Упражнение 10.8. Выведите эти формулы из (10.4)—(10.6).
S6.y.K. = n(R + r)L,
5п.у.к. = 7гД2 + 7ГГ2 + 7Г(Д-
fr)L,
у. . g
J)3th параметры не являются независимыми: они связаны, согласно
теореме Пифагора, соотношением L2 = R2 + Н2. Конус однозначно
определяется заданием двух из этих трёх параметров.
2>См. предыдущее примечание. В этом случае Н2 + (R— г)2 = L2.
326 Глава 10. Тела вращения
Развёртка усечённого конуса представляет собой часть
кругового кольца (рис. 10.17) с дугами длин 2nR и 2кг
и отрезками радиусов длины L.
§ 10.2. Сфера и шар
Определения сферы и шара были даны в § 6.1. Шар
можно получить вращением полукруга вокруг его диаметра,
поэтому шар относится к телам вращения. Сфера
(поверхность шара) является поверхностью вращения. Она
получается в результате вращения полуокружности вокруг её
диаметра.
Аналогично тому, как это делалось в планиметрии в
случае окружности, определим понятие касательной
плоскости к сфере.
I Определение. Плоскость называется касательной к
сфере (шару), если она имеет с ней (с ним) ровно одну
общую точку.
Указанная точка называется точкой касания плоскости
со сферой (шаром).
I Теорема 10.1. Плоскость является касательной к сфере
(шару) тогда и только тогда, когда она перпендикулярна
радиусу, проведённому в точку касания.
Доказательство. Необходимость. Пусть
плоскость а касается сферы S(O, R) (шара В (О, В)) в точке А.
Возьмём произвольную точку X плоскости ос у отличную от
§ 10.2. Сфера и шар 327
А. По определению касательной плоскости точка X не
принадлежит сфере (шару), более того, она лежит вне сферы
(шара) (почему?). Итак, ОХ>ОА для всех X,
следовательно, ОА — расстояние от точки О до плоскости а. Поэтому
(см. утверждение из § 4.6) (ОА) ± а.
Достаточность. Пусть [ОА] — радиус сферы
(шара), а плоскость а проходит через точку А и
перпендикулярна прямой ОА. Возьмём в плоскости а произвольную
точку X, отличную от А. Расстояние от точки X до
центра сферы (шара) больше, чем ОА (перпендикуляр короче
наклонной), поэтому точка X лежит вне сферы (шара).
Следовательно, А — единственная общая точка сферы (шара)
и плоскости а. Значит, плоскость а —касательная. □
Определение. Прямая называется касательной к сфере
(шару), если она имеет с ней (с ним) ровно одну общую
точку. Указанная точка называется точкой касания прямой
и сферы (шара).
Очевидно, что существует бесконечно много
касательных к сфере (шару), проходящих через данную точку сферы
(поверхности шара).
в^ Упражнение 10.9. 1) Докажите, что если прямая является
касательной к сфере (шару), то она лежит в касательной
плоскости, проходящей через точку касания прямой и сферы
(шара).
2) Докажите, что если прямая является касательной к
сфере (шару), то она перпендикулярна радиусу, проведённому
в точку касания.
Из теоремы 10.1 вытекает, что если расстояние от
центра сферы (шара) до плоскости равно радиусу сферы (шара),
то плоскость и сфера (шар) имеют единственную общую
точку. Ясно также, что если расстояние от центра
сферы (шара) до плоскости больше радиуса сферы (шара), то
плоскость и сфера (шар) не имеют общих точек. Чтобы до
конца ответить на вопрос о взаимном расположении сферы
(шара) и плоскости, осталось рассмотреть случай, когда
328
Глава 10. Тела вращения
расстояние от центра сферы (шара) до плоскости меньше
радиуса сферы (шара).
Теорема 10.2. Если расстояние от центра сферы (шара)
до плоскости меньше радиуса сферы (шара), то
пересечение сферы и плоскости (сечение шара плоскостью) есть
окружность (круг).
Доказательство. Пусть плоскость а пересекает сферу
S(O,R) по множеству L; М — произвольная точка из L
Рис. 10.18
(рис. 10.18). Спроектируем центр сферы О на плоскость а.
Пусть О\ —полученная проекция, a d = ОО^К Тогда из
А00\М находим О\М = \/Д2 - d2 = const = г. Итак, все
точки L лежат в плоскости а и равноудалены от точки О\.
Осталось доказать, что L содержит все точки М
плоскости а, для которых О\М = г. Возьмём в плоскости а
точку N такую, что O\N = г. Тогда из AOO\N получаем
ON = VV2 + d2 —R, т. е. N лежит на сфере, следовательно,
N лежит на линии пересечения S и а, т.е. на L. Итак,
L — геометрическое место точек плоскости ос, удалённых
от точки О\ на расстояние г. Поэтому L — окружность.
Утверждение теоремы в случае шара доказывается
аналогично. □
^Возможно, d = 0. Тогда AOOiM и AOOiN будут вырожденными, но
все написанные ниже равенства остаются справедливыми.
§ 10.2. Сфера и шар 329
Следствие 1. Сечения шара равны тогда и только тогда,
когда они равноудалены от центра шара.
Следствие 2. Из двух неравных сечений шара больший
радиус имеет то, которое ближе к центру; верно и
обратное.
Следствие 3. Диаметр шара, перпендикулярный
плоскости сечения, проходит через центр сечения; верно и
обратное.
I Следствие 4. Среди всех сечений шара наибольший
радиус имеет сечение, проходящее через его центр.
к^3 Упражнение 10.10. Докажите эти утверждения.
Сечение, проходящее через центр шара, называется
большим кругом, а граница этого круга — окружностью
большого круга.
с^ Упражнение 10.11. а) Докажите, что через две точки сферы,
не являющиеся концами её диаметра, можно провести
единственную окружность большого круга.
б) Докажите, что окружности двух больших кругов при
пересечении делятся пополам.
в*) Докажите, что длина меньшей из двух дуг
окружности большого круга, проходящей через две данные точки
сферы, меньше длины любой другой кривой, лежащей на
сфере и соединяющей эти точки. (Указание: воспользуйтесь
теоремой 5.6.)
Сделаем несколько замечаний, касающихся
изображения сферы (и, соответственно, шара). По традиции сферу
принято изображать в ортогональной проекции.
Нетрудно доказать (проведите доказательство самостоятельно),
что ортогональной проекцией сферы на плоскость
является круг того же радиуса. Поэтому изображением сферы
(в указанной проекции) является круг. Чтобы подчеркнуть,
что изображена именно сфера, а, скажем, не окружность
или круг, на изображении рисуют ещё изображение
какой-нибудь окружности большого круга, которую называют
330
Глава 10, Тела вращения
экватором (рис. 10.19). Концы диаметра,
перпендикулярного плоскости экватора, называют полюсами. Их тоже
часто указывают на изображении сферы.
Рис. 10.19
Рис. 10.20
DS* Упражнение 10.12. На рис. 10.20 дано изображение сферы
и её экватора. С помощью циркуля и линейки постройте
изображение полюсов сферы.
Приведём формулы для вычисления площади
поверхности и объёма шара радиуса Я, которые будут доказаны
в главе 13:
. = 4тгД2,
v -i
У т.- з
(10.10)
(10.11)
§ 10.3. Части шара и сферы
Но у холма нет вершины — он
круглый, как эта Земля.
И. Кормильцев. Люди на холме
Сегмент
■ Определение. Шаровым сегментом называется часть
шара, отсекаемая от него плоскостью.
Круг, являющийся сечением шара этой плоскостью,
называется основанием сегмента, а отрезок диаметра шара,
§10.3. Части шара и сферы
331
Рис, 10.21
перпендикулярного этой плоскости, принадлежащий
сегменту,— высотой сегмента. Секущая плоскость делит шар
на два сегмента с общим основанием (рис. 10.21). Сегмент,
основанием которого является большой круг, называется
полу шаром. Его высота равна радиусу шара. Шаровой
сегмент является телом вращения. Он получается вращением
половины кругового сегмента вокруг его оси симметрии.
Определение. Сегментной поверхностью {сферическим
сегментом) называется часть сферы, отсекаемая от неё
плоскостью.
Основание и высота сегментной поверхности
определяются аналогично основанию и высоте шарового сегмента.
Рассмотрим шаровой сегмент высоты Н> полученный
из шара радиуса R. Тогда площадь соответствующей
сегментной поверхности и объём сегмента можно вычислить
так:
. = 2kRH,
(10.12)
(10.13)
Слой
Определение. Шаровым слоем называется часть
шара, заключённая между двумя секущими параллельными
плоскостями.
332 Глава 10. Тела вращения
Круги, получаемые в сечении шара этими плоскостями,
называются основаниями слоя, а расстояние между
секущими плоскостями — высотой слоя.
I Определение. Часть сферы, заключённая между двумя
секущими параллельными плоскостями, называется
сферическим поясом.
Основания и высота сферического пояса определяются
аналогично основаниям и высоте слоя.
Сферический пояс — боковая поверхность шарового
слоя.
Шаровой слой — тело вращения. Он получается
вращением части круга, заключённой между двумя
параллельными хордами, вокруг её оси симметрии.
Две параллельные секущие плоскости разбивают шар
на три части —два сегмента и слой. На этом замечании
основано вычисление площади боковой поверхности и объёма
шарового слоя, ведь формулы для площадей поверхностей
и объёмов шара и сегмента уже известны.
^ Упражнение 10.13. Докажите, что площадь сферического
пояса высоты Я можно найти по формуле (10.12). Можно ли
найти объём шарового слоя высоты Н по формуле (10.13)?
Сектор
Определение. Одна полость (прямой круговой)
конической поверхности с вершиной в центре шара делит шар на
две части. Каждая из этих частей называется шаровым
сектором.
Шаровой сектор — тело вращения. Он получается
вращением кругового сектора вокруг его оси симметрии.
Шаровой сектор можно получить также из шарового сегмента
и конуса, основание которого является основанием
сегмента, а вершина находится в центре шара. Если
рассматриваемый сектор меньше полушара, то он получается из
шарового сегмента дополнением указанного конуса. Если
§ 10.4. Комбинации шара с цилиндром, конусом 333
же сектор больше полушара, то этот конус следует удалить
из сегмента.
На этом замечании основан способ вычисления объёма
и площади поверхности шарового сектора.
Объём шарового сектора равен
мсект. — 77 Я"R И,
3
(10.14)
где R — радиус шара, а Н — высота соответствующего
шарового сегмента.
i№ Упражнение 10.14. Выведите эту формулу из формул (10.6)
и (10.13).
§ 10.4. Комбинации шара с цилиндром, конусом
и усечённым конусом
Он — член... как он это назвал?
Триады, кажется? Он в триаде с этим
пузырём, которого зовёт Смоки.
К. Саймак. Проект «Ватикан»
Описанный шар
Определение. Шар (сфера) называется описанным око-
\ ло цилиндра, если окружности оснований цилиндра
лежат на поверхности шара (на сфере).
Ниже мы будем формулировать и доказывать все
утверждения лишь для шара, так как в случае сферы они
аналогичны.
Если шар описан около цилиндра, то говорят, что
цилиндр вписан в шар.
Теорема 10.3. Около всякого цилиндра можно описать
шар. Центр описанного шара находится в середине
высоты цилиндра, а радиус равен радиусу круга, описанного
около осевого сечения цилиндра.
334
Глава 10. Тела вращения
Доказательство. Рассмотрим цилиндр радиуса г и
высоты Л. Пусть А и В — центры его оснований. Выберем
на окружности основания с центром А произвольную
точку X. Построим осевое сечение цилиндра, проходящее
через X. Это сечение — прямоугольник со сторонами 2г и h
(упражнение 10.2). Как известно из планиметрии, около
прямоугольника можно описать
окружность, а её центр находится
в середине отрезка, соединяющего
середины противоположных сторон.
В рассматриваемом случае центр О
описанной окружности — середина
отрезка АВ, т.е. середина высоты
цилиндра (рис. 10.22). Из ААОХ
находим ОХ = у/г2 + Л2/4 = const = R.
В силу произвольности выбора
точки X заключаем, что
рассматриваемая окружность основания цилиндра лежит на
поверхности шара с центром О и радиусом R. Аналогично
доказывается, что окружность другого основания также
лежит на поверхности этого шара. □
Замечание. Метод, использованный при доказательстве этой
теоремы, заключается в сведении пространственной задачи о
фигурах вращения к плоской задаче путём рассмотрения осевого
сечения. Этим методом доказываются и все остальные теоремы
этого параграфа.
Определение. Шар называется описанным около
конуса, если вершина конуса и окружность его основания
лежат на поверхности шара.
Если шар описан около конуса, то говорят, что конус
вписан в шар.
Теорема 10.4. Около всякого конуса можно описать шар.
Центр описанного шара есть центр круга, описанного
около осевого сечения конуса, а радиус шара равен радиусу
этого круга.
§ 10,4, Комбинации шара с цилиндром, конусом 335
Доказательство в точности аналогично доказательству
теоремы 10.3.
Определение. Шар называется описанным около
усечённого коцуса, если окружности оснований усечённого
конуса лежат на поверхности шара.
Если шар описан около усечённого конуса, то говорят,
что усечённый конус вписан в шар.
Теорема 10.5. Около всякого усечённого конуса можно
описать шар. Центр описанного шара есть центр круга,
описанного около осевого сечения усечённого конуса, а
радиус шара равен радиусу этого круга.
Доказательство в точности аналогично доказательству
теоремы 10.3.
с^Упражнение 10.15. Докажите теоремы 10.4 и 10.5.
Вписанный шар
Определение. Шар называется вписанным в цилиндр,
если он касается всех образующих цилиндра и его
оснований.
Если шар вписан в цилиндр, то говорят, что цилиндр
описан около шара.
Теорема 10.6. Для того чтобы в цилиндр можно было
вписать шар, необходимо и достаточно, чтобы высота
цилиндра была равна диаметру его основания.
Доказательство. Необходимость. Пусть в
цилиндр вписан шар. Рассмотрим произвольное осевое
сечение цилиндра плоскостью а. Это сечение — прямоугольник,
стороны которого равны высоте и диаметру основания
цилиндра (упражнение 10.2). Сечение шара плоскостью а —
круг (теорема 10.2), причём из определения вписанного
шара вытекает, что этот круг вписан в осевое сечение
цилиндра. Как известно из планиметрии, в прямоугольник
336 Глава 10. Тела вращения
можно вписать круг тогда и только тогда, когда он является
квадратом. Поэтому у рассматриваемого цилиндра высота
равна диаметру основания.
Достаточность. Пусть дан цилиндр, у которого
высота равна диаметру основания. Рассмотрим
произвольное осевое сечение цилиндра. Это квадрат, сдедовательно,
в него можно вписать круг. Докажем, что шар с центром
в центре этого круга и радиусом, равным радиусу круга,
вписан в цилиндр. Действительно, в силу
произвольности выбора осевого сечения указанный шар касается всех
образующих цилиндра и плоскостей его оснований в их
центрах. □
Если высота цилиндра равна диаметру его основания,
то цилиндр называется равносторонним.
Следствие. Центр шара, вписанного в равносторонний
цилиндр, есть середина высоты цилиндра, а радиус шара
равен радиусу цилиндра.
Определение. Шар называется вписанным в конус,
если он касается всех образующих конуса и его основания.
При этом говорят, что конус описан около шара.
Теорема 10.7. Во всякий конус можно вписать шар.
Центр вписанного шара есть центр круга, вписанного
в осевое сечение конуса, а радиус шара равен радиусу
этого круга.
Определение. Шар называется вписанным в усечённый
конус, если он касается всех образующих конуса и его
оснований. При этом говорят, что усечённый конус описан
около шара.
I Теорема 10.8. Для того чтобы в усечённый конус можно
I было вписать шар, необходимо и достаточно, чтобы его
I образующая равнялась сумме радиусов оснований.
§ 10.4. Комбинации шара с цилиндром, конусом 337
I Следствие. Центр шара, вписанного в усечённый конус,
есть середина высоты усечённого конуса, а радиус шара
равен её половине.
^Упражнение 10.16. Докажите теоремы 10.7 и 10.8.
Пример 10.1. Вычислить радиусы оснований усечённого
конуса, описанного около шара радиуса i?, зная, что
отношение площади полной поверхности усечённого конуса
к площади поверхности шара равно т.
Решение. Пусть SK. — площадь полной поверхности
усечённого конуса, г и г\ — радиусы его нижнего и
верхнего1^ оснований (г\ < г), I — длина образующей; 5Ш. —
площадь поверхности шара (т.е. сферы). Рассмотрим осевое
сечение усечённого конуса некоторой плоскостью а и
сечение вписанного в него шара той же плоскостью.
Получим равнобедренную трапецию ABCD со вписанным в неё
D
Рис. 10.23
кругом (рис. 10.23). Воспользовавшись равенствами (10.8)
и (10.10), перепишем условие задачи в виде
Sv nlr -f к1г\ + кг2 + кг?
Ж^.= 4^ = т'
названия для оснований усечённого конуса (а также цилиндра)
общеприняты. Однако их условность очевидна: молчаливо
предполагается, что плоскости оснований горизонтальны.
338 Глава 10. Тела вращения
Преобразуем это равенство, вспомнив, что / = г + т\
(теорема 10.8):
(г + п)2 + г2 + r\ = AmR2. (10.15)
Из прямоугольного треугольника СОВ находим, что
rn=R2. (10.16)
Из равенств (10.15) и (10.16) следует, что
г2 + г? = R2(2m - 1). (10.17)
Наконец, решая систему (10.16)—(10.17), находим ответ:
Q
Заметим, что задача имеет решение, если m > ■=, так как
Г2 + Г2 1
из равенств (10.15) и (10.16) следует, что m = -5—- + н ^
13 3
> 1 + ^ = т> (при m = 7) усечённый конус вырождается в
цилиндр). □
§ 10.5. Взаимное расположение двух сфер.
Задачи о касающихся сферах
Попробуй-ка сообразить: когда ядра
уложены на земле в кучу, со
сколькими ядрами соприкасается каждое ядро,
лежащее внутри кучи?
— Я где-то видел такую кучу, —
припомнил Илюша,—кажется, во
фруктовом магазине...
С. Бобров. Волшебный двурог
Рассмотрим две сферы S\(Oi9 R\) и 5г(0г, i?2)« Пусть
расстояние между их центрами равно d. Аналогично
соответствующим планиметрическим утверждениям о
взаимном расположении двух окружностей легко получить
следующие результаты.
§ 10,5. Взаимное расположение двух сфер 339
1. Если d>R\ + i?2> то сферы не пересекаются (т.е. не
имеют общих точек) и расположены одна вне другой.
2. Если d = R\ + i?2> то сферы имеют единственную
общую точку (касаются). Касательная плоскость к
сфере Si, проведённая через эту точку, является
одновременно касательной плоскостью к сфере S2- При этом сферы
расположены по разные стороны от указанной плоскости
(касаются внешним образом).
3. Если \R\-R2\<d<Ri + #2, то сферы пересекаются,
т. е. имеют более одной общей точки.
4. Если d= \R\ - i?2|> то сферы касаются и расположены
по одну сторону от общей касательной плоскости
(касаются внутренним образом) при R\^R2. В случае R\ = R2
сферы Si и S2 — это одна и та же сфера.
5. Если d < \R\ - .R2I и R\ ^J?2> то сферы не пересекаются
и расположены одна внутри другой. При d = О их центры —
это одна и та же точка (сферы концентричны).
и^ Упражнение 10.17. Докажите эти утверждения.
Заменим сферы шарами Bi(Oi>R\) и £2(О2,/?г) и по"
смотрим, изменится ли что-нибудь в формулировках
приведённых выше утверждений. Утверждения 1—3 остаются
в силе. Следует лишь заменить слово «сферы» на слово
«шары». Утверждение 4, формально говоря, также останется
справедливым, если под касанием шаров в данном случае
понимать касание ограничивающих их сфер. В
утверждении 5 перестанет быть верной первая часть (что шары не
пересекаются).
В связи с утверждением 3 возникает естественный
вопрос: что является пересечением двух сфер?
| Теорема 10.9. Пересечение двух сфер есть окружность.
Доказательство. Рассмотрим две сферы S\(O\,R\) и
S2(C>2, Лг)- Пусть X — их общая точка (Хе S\ ПЯг). В силу
определения пересекающихся сфер найдётся точка Y e S\ П
HS2, отличная от X. Треугольники О1УО2 и О1ХО2 равны
340
Глава 10. Тела вращения
(по трём сторонам). Следовательно, у этих треугольников
равны высоты, опущенные на общую сторону O1O2. Более
того, основания этих высот — одна и та же точка О
(почему?).
Всякая прямая, проходящая через точку О
перпендикулярно прямой O1O2, лежит в плоскости а, проходящей
через О перпендикулярно O1O2. Поэтому Si nS2 — плоская
фигура. Кроме того, как мы показали выше, все точки из
Si HS2 равноудалены от точки О. Следовательно, Si HS2 —
подмножество окружности с центром О и радиусом ОХ = г.
Докажем теперь обратное утверждение: если точка У
принадлежит указанной окружности, то она
принадлежит обеим сферам. Действительно, ЛО1УО2 = AO1XO2 (по
двум катетам), следовательно, O\Y — O\X — Ri. Аналогично
Итак, пересечением сфер Si и S2 является окружность.
□
Вычисление радиуса окружности, являющейся
пересечением двух сфер, сводится к решению планиметрической
задачи. Достаточно рассмотреть сечение сфер, проходящее
через линию их центров (рис. 10.24).
■®* Упражнение 10.18. Найдите радиус окружности, по которой
пересекаются две сферы, если расстояние между их центрами
равно d, а радиусы равны Rx и R2 (|#i - Дг| < d < R\ + R2).
Рис. 10.24
§ 10.5, Взаимное расположение двух сфер 341
Сделаем теперь одно общее замечание, относящееся к
задачам о комбинациях шаров друг с другом, с цилиндрами,
конусами, многогранниками. Обычно решение задачи
начинают с построения чертежа. В случае, когда в условии речь
идёт о сферах (шарах), особенно в комбинации с другими
фигурами, построить наглядный чертёж нелегко. Однако
для того чтобы решить задачу, чаще всего не обязательно
изображать шары или сферы. Обычно достаточно
нарисовать их центры, радиусы, проведённые в точки касания,
касательные плоскости и прямые, осевые сечения,
проекции на касательные плоскости и т. п.1* Приведём несколько
примеров применения этих приёмов в задачах о
касающихся шарах и сферах.
Пример 10.2. В сферу S радиуса R вписаны восемь
одинаковых сфер меньшего радиуса, каждая из которых
касается двух соседних, а все вместе касаются сферы S по
окружности большого круга. Сфера Si касается всех восьми
сфер и сферы S. Найти радиус сферы S\.
Рис. 10.25
Решение. Рассмотрим сечение сферы S и данных
восьми сфер плоскостью, содержащей указанную в условии
окружность большого круга (см. рис. 10.25 и обозначения
Х)В предыдущем параграфе вы уже видели, как «работает» осевое
сечение.
342
Глава 10. Тела вращения
Рис. 10.26
на нём). Из ААОВ найдём радиус г каждой из восьми сфер:
АВ _ г
поэтому
sin|
Теперь рассмотрим сечение, проходящее через центр О
сферы S, центр О\ сферы Si и центр А одной из восьми
сфер (рис. 10.26). Из AAOOi находим, что АО\ = АО2 + ОО\У
т.е.
(r + p)2 = (R-r)2 + (R-p)2,
где р — радиус сферы Si. Отсюда
Подставляя найденное значение г, получаем
R
Р =
1 + 2 sin |'
Вычислим sin £:
о
sin£ =
1 - cos 4
I _ у/2-\/2
Итак,
§ 10.5. Взаимное расположение двух сфер
R
343
D
Пример 10.3. На плоскости лежат три равных шара
радиуса R> попарно касающиеся друг друга. Четвёртый шар
касается плоскости и каждого из первых трёх шаров. Найти
радиус четвёртого шара.
Решение. Пусть А, В, С —центры шаров радиуса R; Аь
Ви С\ — проекции этих центров на данную плоскость; О —
центр четвёртого шара, радиус г которого нужно найти.
Из условия задачи следует, что АВСА\В\С\ — правильная
треугольная призма со стороной основания 2R и боковым
ребром R, а ОАВС — правильная треугольная пирамида
с боковым ребром R + r (рис. 10.27)1*.
Рис. 10.27
Спроектируем точку О на плоскость ABC. Получим
точку Q, являющуюся центром треугольника ABC. Ясно, что
OQ = R-r, a AQ = — (как радиус окружности, описанной
v3
около правильного треугольника со стороной 2R). Из AAOQ
находим, что
так называемый «скелетный чертёж», на котором
изображаются только центры шаров и радиусы, проведённые в точки касания
344
т. е.
откуда
Глава 10. Тела вращения
□
Пример 10.4. На плоскости лежат четыре равных шара,
причём три из них попарно касаются друг друга, а
четвёртый касается двух из этих трёх. На эти шары сверху
положены два равных шара меньшего радиуса, касающиеся друг
друга, причём каждый из них касается трёх больших шаров.
Найти отношение радиусов большого и малого шаров.
Рис. 10.28
Решение. Пусть А, В, С и D — центры больших шаров.
Рассмотрим проекцию всех шаров на плоскость ABCD
(почему эти точки лежат в одной плоскости?). Так как центры
малых шаров равноудалены от центров соответствующих
больших шаров, они спроектируются в точки пересечения
медиан треугольников ABC и BCD (рис. 10.28). Радиусы
малых шаров равны, следовательно, отрезок, соединяющий
их центры, параллелен плоскости ABC и делится точкой
касания шаров пополам. Поэтому проекция точки касания
попадает на отрезок ВС. Из сказанного вытекает, что малые
§ 10,5. Взаимное расположение двух сфер
345
шары спроектируются в круги, вписанные в треугольники
ЛВС и BCD. Следовательно,
г =
АВУЗ 2Д\/3
6 6
где Диг- радиусы большого и малого шаров. Итак, — = \/3.
□
Пример 10.5. Три шара радиуса г лежат на нижнем
основании цилиндра, причём каждый из них касается двух
других и боковой поверхности цилиндра. Четвёртый шар
лежит на этих трёх шарах, касаясь
боковой поверхности цилиндра и его
верхнего основания. Найти высоту
цилиндра.
Решение. Пусть А, В и С — центры
первых трёх шаров, а В- центр
четвёртого шара. Рассмотрим сечение
заданной конфигурации плоскостью ABC.
Это круг с центром О и радиусом R,
равный основаниям цилиндра, внутри
которого расположены три равных
круга, касающиеся друг друга (рис. 10.29).
Заметив, что ZAOB = 120°, находим
r = (R- r) sin 60°,
откуда
Рис. 10.29
Из условия задачи вытекает, что
ABCD — правильная треугольная
пирамида со стороной основания 2г и боко- Рис. 10.30
вым ребром R + г. Кроме того, если Л —
высота этой пирамиды, то искомая высота Н цилиндра
равна r + h + R (рис. 10.30). Из AAOD находим
346
Глава 10. Тела вращения
т. е. h = 2г. —= + 1. Следовательно,
V /5
10.6. Комбинации цилиндра, конуса и усечённого
конуса с многогранниками
Порас-с-скинуть мозгами, пус-с-скай
дас-с-ст нам время порас-с-скинуть,
моя прелес-с-сть.
Дж. Р. Р. Толкин. Хоббит, или Туда и обратно
Вписанные многогранники
Определение. Призма называется вписанной в цилиндр
(а цилиндр, соответственно, описанным около призмы),
если её основания вписаны в основания цилиндра
(рис. 10.31).
Рис. 10.31
Боковые рёбра призмы, вписанной в цилиндр, являются
образующими этого цилиндра.
§10.6. Комбинации с многогранниками 347
с^ Упражнение 10.19. Докажите это утверждение. (Указание:
рассмотрите параллельный перенос, переводящий одно
основание призмы в другое.)
Теорема 10.10. Для того чтобы призму можно было
вписать в цилиндр, необходимо и достаточно, чтобы призма
была прямая, а около её основания можно было описать
окружность.
Доказательство. Необходимость. Если призма
вписана в цилиндр, то её основания по определению
вписанные многоугольники. Кроме того, боковые рёбра призмы —
образующие цилиндра (упражнение 10.19). Образующие
цилиндра перпендикулярны плоскостям оснований,
следовательно, рассматриваемая призма прямая.
Достаточность. Пусть дана прямая призма, около
одного из оснований которой можно описать окружность.
Так как одно основание призмы переводится в другое
параллельным переносом на вектор, перпендикулярный этим
основаниям, окружность, описанная около одного основания,
переходит при этом параллельном переносе в окружность,
описанную около другого основания. Из этого следует, что
существует цилиндр, основания которого —
рассматриваемые круги, а образующая — боковое ребро призмы. Этот
цилиндр по определению описан около призмы. □
Из доказанной теоремы сразу следует, что около любой
прямой треугольной призмы можно описать цилиндр и что
около любой правильной призмы можно описать цилиндр.
Определение. Пирамида называется вписанной в конус
(а конус, соответственно, описанным около пирамиды),
если вершина пирамиды является вершиной конуса, а
основание пирамиды вписано в основание конуса (рис. 10.32).
Боковые рёбра пирамиды, вписанной в конус, являются
его образующими; в отличие от соответствующего
утверждения для призмы, вписанной в цилиндр, это утверждение
совершенно очевидно.
348
Глава 10. Тела вращения
Рис. 10.32
Рис. 10.33
Теорема 10.11. Для того чтобы пирамиду можно было
вписать в конус, необходимо и достаточно, чтобы боковые
рёбра пирамиды были равны.
Доказательство. Необходимость сразу следует
из того, что образующие конуса, являющиеся
одновременно боковыми рёбрами вписанной пирамиды, равны.
Достаточность. Если боковые рёбра пирамиды
равны, то около её основания можно описать окружность,
а вершина проектируется в центр этой окружности
(теорема 9Л). Конус, основание которого ограничено этой
окружностью, а вершина является вершиной пирамиды, описан
около пирамиды по определению. □
В частности, около любой правильной пирамиды можно
описать конус.
Определение. Усечённая пирамида называется
вписанной в усечённый конус (а усечённый конус,
соответственно, описанным около усечённой пирамиды), если её
основания вписаны в основания усечённого конуса.
Усечённая пирамида, вписанная в усечённый конус,
изображена на рис. 10.33.
№ Упражнение 10.20. По аналогии с теоремой 10.11
сформулируйте и докажите необходимое и достаточное условие
вписанности усечённой пирамиды в усечённый конус.
§ 10.6. Комбинации с многогранниками
349
fj® Упражнение 10.21. Является ли следующее условие
необходимым, достаточным или необходимым и достаточным для
того, чтобы в усечённый конус можно было вписать
усечённую пирамиду: около основания усечённой пирамиды можно
описать окружность?
Описанные многогранники
Определение. Плоскость называется касательной к ци-
| линдру, если она проходит через образующую и не имеет
с цилиндром других общих точек.
Теорема 10.12. Плоскость, проходящая через
образующую цилиндра, является касательной к нему тогда и
только тогда, когда она перпендикулярна осевому сечению
цилиндра, проведённому через эту образующую.
Рис. 10.34
Доказательство. Необходимость. Пусть
плоскость а проходит через образующую I цилиндра и не имеет
с цилиндром других общих точек, а [3 — плоскость осевого
сечения цилиндра, проходящая через /. Рассмотрим линию
пересечения а плоскости а с плоскостью любого основания
цилиндра и линию пересечения Ъ плоскости (3 с плоскостью
этого же основания (рис. 10.34). Ясно, что прямая а —
касательная к окружности рассматриваемого основания,
350
Глава 10. Тела вращения
так как она лежит в плоскости основания и имеет с
окружностью ровно одну общую точку — точку пересечения М
образующей I с этой окружностью. Прямая Ъ содержит
диаметр основания цилиндра, одним из концов которого
является точка М. Тогда, как известно из планиметрии,
ЪJL а. Кроме того, Ъ J_/ (так как образующая цилиндра
перпендикулярна плоскости его основания). Следовательно,
Ь _1_ а по признаку перпендикулярности прямой и плоскости
(теорема 4.1), а /3 ± а по признаку перпендикулярности
плоскостей (теорема 5.3).
Достаточность. Пусть плоскость а проходит через
образующую / цилиндра перпендикулярно плоскости (5
осевого сечения, содержащего I. Докажем, что а не имеет с
цилиндром других общих точек, кроме точек образующей L
Пусть у — плоскость, перпендикулярная прямой / и
пересекающая цилиндр. Сечением цилиндра плоскостью у
является круг, равный основаниям цилиндра (или одно
из оснований). Линия пересечения у и /3 — прямая с,
содержащая диаметр этого круга, а линия пересечения у
и а — прямая d, перпендикулярная прямой с (почему?)
и проходящая через точку окружности, ограничивающей
этот круг (рис. 10.35). Как известно из планиметрии, пря-
Рис. 10.35
Рис. 10.36
§10.6, Комбинации с многогранниками 351
мая d является касательной к окружности, т. е. имеет с ней
(и с ограниченным ею кругом) ровно одну общую точку. Из
произвольности выбора плоскости у вытекает, что
плоскость а не имеет с цилиндром общих точек, не лежащих
на /. □
Определение. Призма называется описанной около
цилиндра (а цилиндр, соответственно, вписанным в призму),
если её основания описаны около оснований цилиндра
(рис. 10.36).
Плоскости боковых граней призмы, описанной около
цилиндра, касаются цилиндра.
и^ Упражнение 10.22. Докажите это утверждение. (См. указание
к упражнению 10.19.)
Теорема 10.13. Для того чтобы призму можно было
описать около цилиндра, необходимо и достаточно,
чтобы призма была прямая, а в её основание можно было
вписать окружность.
Доказательство этой теоремы проводится аналогично
доказательству теоремы 10.10.
в^ Упражнение 10.23. Докажите теорему 10.13
В частности, во всякую прямую треугольную призму
и во всякую правильную призму можно вписать цилиндр.
Определение. Плоскость называется касательной к
конусу, если она проходит через его образующую и не имеет
с конусом других общих точек.
Теорема 10.14. Плоскость, проходящая через
образующую конуса, является касательной к нему тогда и только
тогда, когда она перпендикулярна осевому сечению
конуса, проведённому через эту образующую.
Доказательство. Необходимость. Введём
обозначения так же, как при доказательстве первой части
теоремы 10.12 (рис. 10.37). Аналогично тому, как это было
352
Глава 10. Тела вращения
Рис. 10.37
Рис. 10.38
сделано при доказательстве указанной теоремы, получаем,
что Ъ JL а. Прямая Ъ — проекция наклонной, содержащей
образующую конуса /. По теореме о трёх перпендикулярах
(теорема 4.4) / JL а. Согласно признаку перпендикулярности
прямой и плоскости (теорема 4.1) a.L/3, тогда aJ_/3 по
признаку перпендикулярности плоскостей (теорема 5.3).
Достаточность. Доказательство аналогично
доказательству второй части теоремы 10.12 (рис. 10.38).
Проведите его самостоятельно. □
Определение. Пирамида называется описанной около
конуса (а конус, соответственно, вписанным в
пирамиду), если вершина пирамиды является вершиной конуса,
а основание пирамиды описано около основания конуса
(рис. 10.39).
Плоскости боковых граней пирамиды, описанной около
конуса, являются касательными к конусу.
в®* Упражнение 10.24. Докажите это утверждение.
Теорема 10.15. Для того чтобы пирамиду можно было
описать около конуса, необходимо и достаточно, чтобы
| двугранные углы при основании пирамиды были равны.
§ 10.6. Комбинации с многогранниками 353
Рис. 10.39 Рис. 10.40
Доказательство. Необходимость. Пусть
пирамида SA\...An описана около конуса. Тогда основание
конуса — круг с центром О — вписано в основание
пирамиды. Обозначим точки касания этого круга со сторонами
А\А2у ..., АпА\ основания пирамиды через В\,...уВп
соответственно. Прямоугольные треугольники SOB\, SOB2,
..., SOBn равны по двум катетам, следовательно, ZSB\O —
= ZSB2O — ... = ZSBnO. Указанные углы являются
линейными углами двугранных углов при основании пирамиды
(почему?), они равны, т. е. равны и двугранные углы при
основании.
Достаточность. Если двугранные углы при
основании пирамиды равны, то в её основание можно вписать
окружность, а вершина проектируется в центр этой
окружности (теорема 9.2). Конус, основание которого ограничено
указанной окружностью, а вершина является вершиной
пирамиды, по определению вписан в пирамиду. □
В частности, всякую правильную пирамиду можно
описать около конуса.
На рис. 10.40 изображена усечённая пирамида,
описанная около усечённого конуса.
*®* Упражнение 10.25. Дайте определение усечённой пирамиды,
описанной около усечённого конуса, а затем сформулируйте
и докажите необходимое и достаточное условие вписанности
Усечённого конуса в усечённую пирамиду.
12 3ак 3383
354 Глава 10. Тела вращения
Теперь мы обсудим одну красивую идею, которая
помогает при решении задач о касающихся конусах (т. е.
конусах, имеющих общую образующую и не имеющих других
общих точек). В подобных задачах, как и вообще в задачах
на комбинации тел, существенная трудность заключается
в том, чтобы представить себе взаимное расположение
данных тел в пространстве и нарисовать «осязаемый» чертёж.
Часто пространственное восприятие конусов облегчается,
если поместить их в многогранники специального вида
(которые мы, следуя традиции, будем называть каркасами).
После этого о конусах можно «забыть» и рассматривать
лишь конструкцию из многогранников. Наиболее
употребительным каркасом для конуса является пирамида.
Теорема 10.16. Около всякого конуса, угол при
вершине осевого сечения которого острый, можно описать
пирамиду, в основании которой лежит равнобедренный
треугольник, а боковое ребро, проходящее через вершину
этого треугольника, перпендикулярно противоположной
боковой грани (рис, 10.41).
ВЗР Упражнение 10.26. Докажите теорему 10.16.
Указанную пирамиду мы будем называть каркасной
пирамидой для конуса.
ВЗР Упражнение 10.27. а) Докажите, что каркасные пирамиды,
построенные для двух равных конусов, равны.
б) Пусть SABC — каркасная пирамида для конуса (АС =
= ВС, (SC) 1 (ASB)). Докажите, что AS = BS.
Теорема 10.17. Пусть SABC — каркасная пирамида, в
которой АС = ВС у (SC) -L (ASB), а — угол наклона ребра
ВС к плоскости ASB, /3 —двугранный угол при ребре АВ.
Тогда
cos a = ctg/3.
Доказательство. Обратимся к рис. 10.42. Так как
прямая ВС касается основания конуса, (ВС) ± (ОЕ). Прямая
§ 10.6, Комбинации с многогранниками
355
Рис. 10.41
ОЕ — проекция прямой SE на плоскость основания конуса,
следовательно, по теореме о трёх перпендикулярах
(теорема 4.4) {ВС) 1 (SE). Угол BSC прямой, поэтому ZESC =
= ZSBC= ос. Чтобы построить линейный угол двугранного
угла при ребре АВ, достаточно соединить середину D этого
ребра с точками S и С: Z.SDC — (5 (почему?). Из прямо-
ES
угольного треугольника SEC находим, что cos a = -$„. Но
сп
ES = SD как образующие конуса. Поэтому cos a = -577- Из
ctn
прямоугольного треугольника SDC получаем ctg /3 = -^,
следовательно, cos a = ctg /3. □
Приведём несколько примеров использования
каркасной пирамиды в задачах о касающихся конусах.
Пример 10.6. На плоскости лежат три равных конуса
с общей вершиной, каждый из которых касается двух
других. Найти угол при вершине осевого сечения каждого из
этих конусов.
Решение. Опишем около каждого из данных конусов
каркасную пирамиду. Все эти пирамиды равны и в объ-
356
Глава 10. Тела вращения
единении дают правильную треугольную пирамиду. Общая
вершина S каркасных пирамид является центром
основания этой правильной треугольной пирамиды.
Рис. 10.43
Рассмотрим одну из каркасных пирамид — пирамиду
SABX (рис. 10.43) и вписанный в неё конус. Заметим,
что ABSE = ABSD (по гипотенузе и катету), следовательно,
ZXBS = ZDBS = \ZABC= 30°. По теореме 10.17 ctg ZODS =
л/3
= cos 30° = ^-. Угол OSD — половина искомого угла при
вершине осевого сечения конуса. Из AOSD находим, что
ZOSD = 90° - ZODS. Следовательно, tg ZOSD = ^y ZOSD =
= arctg ^тр, а искомый угол равен 2 arctg ^p. □
Пример 10.7. Два равных конуса имеют общую вершину
и касаются по образующей. Угол при вершине осевого
сечения конуса равен 2а (а < j). Найти величину угла между
двумя плоскостями, каждая из которых касается конусов,
но не проходит через их общую образующую.
§ 10.6. Комбинации с многогранниками
357
Решение. Опишем около конусов каркасные
пирамиды так, чтобы их общая грань касалась обоих конусов
(рис. 10.44).
Высоты этих пирамид ZO vlZ\O лежат на одной прямой,
перпендикулярной плоскости их общей грани OCD. Грани
ZOC и Z\OC лежат в одной плоскости, также в одной
плоскости лежат грани ZOD и ZiOD. Эти плоскости пересекаются
по прямой ZZ\.
Искомой является величина угла COD (почему?). По
условию АЛОВ = а. Пусть ZAOC = х. Тогда 1ВАО = | - а,
a Z.ECO = £ - х (см- решение предыдущего примера). По
Рис. 10.44
358 Глава 10. Тела вращения
теореме 10.17 ctg /В АО = cos /ECO, т. е.
ctg(f-a)=coe(f-*)f
откуда х = arcsin(tg a), a /.COD — 2x — 2 arcsin(tg a).
Попробуйте сами ответить на такой вопрос: где в
приведённом решении использовано условие а < j и имеет ли
решение задача, если а ^ j? □
В некоторых задачах в качестве каркаса для конуса
удобно выбирать описанную около него правильную пирамиду.
Пример 10.8*. Шесть равных конусов имеют общую
вершину, причём каждый из них имеет с четырьмя
другими по одной общей образующей. Найти отношение суммы
объёмов конусов к объёму шара, касающегося оснований
всех конусов.
Решение. Опишем около каждого из данных конусов
правильную четырёхугольную пирамиду. Объединением
этих пирамид является куб (почему?). В центре этого куба
находится общая вершина конусов, а основания конусов
вписаны в грани куба. Указанный в условии шар должен
касаться всех граней куба. Если ребро куба равно 2а, то
центр куба удалён от всех его граней на расстояние а,
поэтому шар с центром в центре куба и радиусом а касается
всех граней куба1).
Объём шара равен ^тга3, а суммарный объём конусов
равен 6-~тга2-а, т.е. 2яа3. Следовательно, искомое
отношение равно 3:2. □
§ 10.7. Теоремы о касательных и секущих для сферы
В § 10.2 мы определили касательную к сфере как
прямую, имеющую со сферой ровно одну общую точку.
^Такой шар называется вписанным в куб. Мы подробно изучим
вписанные шары в § 10.8
§ 10.7. Теоремы о касательных и секущих 359
Из теоремы 10.2 непосредственно вытекает, что прямая
имеет со сферой две общие точки тогда и только тогда,
когда расстояние от центра сферы до этой прямой меньше
радиуса сферы. Такая прямая называется секущей.
Отрезок секущей, соединяющий две точки сферы, называется
хордой.
Две теоремы о касательных вы доказали, выполняя
упражнение 10.9.
Сформулируем ещё несколько утверждений, которые
являются аналогами планиметрических свойств касательных,
секущих и хорд окружности.
Мы не будем доказывать эти теоремы, так как они сразу
вытекают из теоремы 10.2 и соответствующих
планиметрических фактов.
I Теорема 10.18. Отрезки касательных, проведённых к
сфере из одной точки1*, равны.
I
Теорема 10.19. Если хорды АВ и CD сферы
пересекаются в точке X, то АХ ХВ = СХ- XD.
Теорема 10.20. Если из точки X, лежащей вне сферы,
проведены две секущие, пересекающие сферу в точках А
и В, С и D соответственно, то АХ • ХВ = СХ • XD.
Теорема 10,21. Если из точки X, лежащей вне сферы,
проведены касательная, пересекающая сферу в точке А,
и секущая, пересекающая сферу в точках С и D, то АХ2 =
= CXXD.
Как и в планиметрии, теоремы 10.19, 10.20 и 10.21
называются теоремами о пересекающихся хордах, о двух
секущих и о касательной и секущей соответственно.
Приведём примеры, в которых используются эти
теоремы.
^Измеренные, как и в планиметрии, от данной точки до точек
касания.
360 Глава 10. Тела вращения
Пример 10.9. В тетраэдре ABCD АВ = 2, CD = 4, а
остальные рёбра равны 6. На отрезке MN, соединяющем
середины рёбер АВ и CD, как на диаметре построена сфера,
которая пересекает ребро ВС в точках Р и Q. Найти длину
отрезка PQ.
м
Решение. Заметим, что отрезок MN перпендикулярен
рёбрам АВ и CD (рис. 10.45). Действительно, DM = MC
как медианы в равных по трём сторонам треугольниках
ABC и ABD. Следовательно, (MN) I (CD), так как MN-
медиана в равнобедренном треугольнике CMD.
Аналогично (MN)±(AB).
Так как МN — диаметр сферы, прямые АВ и CD —
касательные к сфере.
Пусть ВР = х, a CQ = у. По теореме о касательной и
секущей (теорема 10.21) ВМ2 =BPBQh NC2 = QC • PC, откуда
получаем систему уравнений
Г*(б-у) = 1,
\у(6-*) = 4.
Эта система имеет два решения:
11-\/Т05 13-\/1б5
§ 10.7. Теоремы о касательных и секущих
361
и
4
У2 =
VTQ5
Первое решение даёт PQ = 6 - Х\ — j/i =
\/105
. Второе
решение отбрасываем, так как 6 — %2 — у г < 0- □
Пример 10.10. Дан прямоугольный параллелепипед
ABCDAiBiCiDly у которого АВ:ВС = 2:3. Точки F и Л -
середины рёбер ВС и BiCi соответственно. Сфера касается
всех звеньев ломаной AFDD\A\ и пересекает отрезок FF\
о
в точках Fi и Е. Известно, что F\E = ^. Найти объём
параллелепипеда.
В
Рис. 10.46
Решение. Пусть О —центр сферы, Ki, K2, АГ3, К4
—точки, в которых сфера касается звеньев ломаной AFDD\A\,
G —середина ребра AD (рис. 10.46).
Ясно, что точка О лежит в плоскости GFF\K±, а так как
она равноудалена от точек F\ и £, она лежит и в
плоскости а, проходящей через середину М отрезка F\E и
перпендикулярной ему (утверждение И, § 7.1). Так как сфера
362 Глава 10. Тела вращения
касается прямойDD\, имеем (ОК3) I (DD\), следовательно,
1 3
Кз € а. Это означает, что K3D1 =MF\ = -rEFi = j. По
теореме 10.18 DiK* = DiKs, поэтому DxAi = 2DiK4 = |. Тогда
g ^
ВС = ~, т. е. АВ = 1. Из AFCD по теореме Пифагора находим,
5
что ^7) = j. Осталось найти длину ребра DD\. По теореме
о касательной и секущей (теорема 10.21) FK\ =FF\ -FE.
Пусть DKz = х. Тогда FM = DK3 = ху FFX = DDi = x + |,
= jc - |, Dif2 = D^ = x, FK2 = I - x. Таким образом,
2)
мый объём равен АВ-ВС-DDX = 1 -1 ■ | = ^. П
Наконец, приведём пример использования векторного
метода для решения задач о касательных к сферам.
Пример 10.11. Сферы с центрами в точках О\ и 0%
радиусов 3 и 1 соответственно касаются друг друга. Через
точку М, удалённую от О2 на расстояние 3, проведены
две прямые, каждая из которых касается обеих сфер,
причём точки касания лежат на прямых по одну сторону от
точки М. Найти угол между этими касательными, если
известно, что одна из них образует с прямой O1O2 угол 45°.
Рис. 10.47
Решение. Пусть первая прямая касается сфер в
точках А и Б, а вторая — в точках Си/), О\ и <У2 —
центры сечений сфер плоскостью АМС (рис. 10.47). Так как
§ 10.7. Теоремы о касательных и секущих
363
(02D) -L (MD), DM = yjQ2M2 - O2D2 = 2л/2. Умножив ска-
лярно обе части равенства CD = СО\ + О\О2 + O2D на CD,
получим CD2 = CD -OiO2'-j=, так как CD COl=CDO2D = 0.
Отсюда CD = 2\/2. Пусть ZAMO[ = a.
Тогда DOf2 = 2л/2 tg а, С0'2 = 4л/2 tg ос и
Далее,
020' =
2-O;C2 = N/9-32tg2a,
* = л/Г- 8 tg2 a.
cos
Рис. 10.48
Отрезки О\О2 и ЩЩ либо пересекаются (рис. 10.486),
либо нет (рис. 10.48а). Не зная пока, каково их
действительное расположение, мы можем составить два уравнения
ОХО\ = (OiOi ± О2О2)2
т. е.
16 = (\/9 - 32 tg2 а ± л/1 - 8 tg2 a)2 +
cos2 a'
Решая это уравнение, находим, что tg2 а = ^. Сделав
проверку, получаем, что внутри скобки должен стоять знак
плюс, т.е. отрезки О\О2 и О[О;2 пересекаются. Итак, а =
= arctg ^, а искомый угол равен 2 arctg ^. □
о о
364 Глава 10. Тела вращения
§ 10.8. Комбинации шара с многогранниками
Он принял пирамидальную форму —
состояние неприкосновенного бытия — и упрятал
себя под сферу непроницаемости.
К. Саймак. Принцип оборотня
Вписанные многогранники
Определение. Многогранник называется вписанным в
сферу (шар), если все его вершины лежат на этой сфере
(на поверхности шара).
Если многогранник вписан в сферу (шар), то говорят,
что эта сфера (шар) описана (описан) около многогранника.
Далее мы будем формулировать и доказывать
утверждения, относящиеся к описанному шару, а не к описанной
сфере. Соответствующие утверждения для сферы
получаются автоматически.
Из данного нами определения вытекает, что если
многогранник можно вписать в шар, то центр этого шара
равноудалён от всех его вершин. Обратно, если существует
точка, равноудалённая от всех вершин многогранника, то
около многогранника можно описать шар с центром в этой
точке1*.
Заметим, что если около многогранника можно описать
шар, то этот шар единственный (см. пример 7.4).
Теорема 10.22. Для того чтобы около пирамиды можно
было описать шар, необходимо и достаточно, чтобы в
основании пирамиды лежал вписанный многоугольник.
Доказательство. Необходимость. Если около
пирамиды описан шар, то сечение шара плоскостью
основания—круг (теорема 10.2). Этот круг описан около
основания пирамиды.
!)См. также замечание 2 к примеру 7.4.
§ 10.8. Комбинации шара с многогранниками 365
Достаточность. Пусть в основании пирамиды
SA\ ■•• Ап лежит вписанный многоугольник А\...Ап.
Геометрическим местом точек, равноудалённых от всех вершин
основания, является перпендикуляр / к плоскости А1А2А3,
проходящий через центр описанного около
многоугольника Ai...An круга (утверждение IV, § 7.1). Геометрическим
местом точек, равноудалённых от точек S и А\, является
плоскость а, перпендикулярная отрезку SA\ и проходящая
через его середину (утверждение II, § 7.1). Пусть 1Пос = 0
(почему эти прямая и плоскость пересекаются?), тогда
точка О равноудалена от всех вершин пирамиды.
Следовательно, около данной пирамиды можно описать шар. Очевидно,
что этот шар единственный. □
Из доказанной теоремы, в частности, вытекает, что
около любого тетраэдра можно описать единственный шар
(иными словами, через любые четыре точки
пространства, не лежащие в одной плоскости, можно провести
сферу, и притом только одну) и около любой правильной
пирамиды можно описать единственный шар. При
доказательстве теоремы мы попутно установили положение
центра шара, описанного около пирамиды.
и^ Упражнение 10.28. Обязательно ли центр шара, описанного
около пирамиды, лежит внутри пирамиды?
Пример 10.12. В правильной /i-угольной пирамиде
сторона основания равна а, а угол наклона бокового ребра
к плоскости основания равен а. Найти радиус шара,
описанного около пирамиды.
Решение. Пусть дана правильная пирамида SAi...An
с центром основания О\. Чтобы определить положение
центра описанного шара, достаточно найти точку
пересечения высоты SOi пирамиды с серединным
перпендикуляром к ребру SA\y проведённым в плоскости SA\O\
(почему?). Полученная точка О и есть центр описанного шара
(рис. 10.49). Радиус R шара находим из ABOS (рис. 10.50):
366
Глава 10. Тела вращения
S
Ant-
BS
sin a
. Ho
(из AAiSOi). Осталось заметить, что А\О\ = ——=-. Итак,
2sin£
R =
2 sin £ sin 2a
П
Из решения примера 10.12, в частности, следует, что
радиус шара, описанного около правильного тетраэдра с
ребром а, равен1*
а ау/6
2 sin ~ sin (2 arccos -j=)
Аналогично находится радиус описанного шара, если
заданы другие параметры правильной пирамиды (при этом
в случае необходимости можно воспользоваться
формулами из § 9.1 и результатом примера 10.12).
1}Радиус шара, описанного около правильного тетраэдра, можно
(и нужно) вычислить проще, воспользовавшись тем, что центр шара
является центром тетраэдра и поэтому делит его высоту в отношении
3:1, считая от вершины.
§ 10.8. Комбинации шара с многогранниками
S
О
Ах
а)
О,
А,
б)
Рис.
О
10,
,о
.50
в)
V& Упражнение 10.29. Найдите радиус шара, описанного около
правильной n-угольной пирамиды со стороной основания а,
если известен угол а) /?; б) у; в) 5 (см. обозначения в § 9.1).
Теорема 10.23. Для того чтобы около призмы можно
было описать шар, необходимо и достаточно, чтобы призма
была прямая, а в её основании лежал вписанный
многоугольник.
Доказательство. Необходимость. Если около
призмы описан шар, то её основания вписаны в круги,
являющиеся сечениями шара плоскостями оснований, а
боковые грани вписаны в круги, являющиеся сечениями
шара плоскостями этих граней. Боковые грани призмы
—параллелограммы. Как известно из планиметрии,
параллелограмм можно вписать в круг тогда и только тогда, когда
он является прямоугольником. Итак, все боковые грани
призмы — прямоугольники. Следовательно, призма прямая
(см. определение прямой призмы и теорему 4.1).
Достаточность. Пусть имеется прямая призма
А\...АпА\... А'п, основания которой А\...Ап и А[...А!п —
вписанные многоугольники с центрами описанных кругов О\
и О[ соответственно (ясно, что если одно из оснований
призмы — вписанный многоугольник, то этим свойством
368 Глава 10, Тела вращения
обладает и другое основание, причём радиусы описанных
кругов равны).
Пусть О —середина ОхО^. Докажем, что эта точка
равноудалена от всех вершин призмы. Действительно,
= ОА2 = ... = ОАп =
оа[ = оа!2 =... = оа!п =
где R — радиус круга, описанного около основания
призмы, а ОО\ = ОО'Х. Итак, около призмы можно описать шар
с центром в точке О. □
В частности, мы установили, что около любой прямой
треугольной призмы можно описать шар и что около любой
правильной призмы можно описать шар. Шар можно
описать также около любого прямоугольного параллелепипеда,
в частности куба. Кроме того, при доказательстве теоремы
мы показали, что центр шара, описанного около призмы,
есть середина отрезка, соединяющего центры кругов,
описанных около оснований призмы.
в^ Упражнение 10.30. Докажите, что центр шара, описанного
около прямоугольного параллелепипеда, есть точка
пересечения его диагоналей.
^Упражнение 10.31. Докажите, что если призму вписать в
цилиндр, а затем описать около цилиндра шар, то этот шар
будет описан около призмы, и обратно. Получите отсюда и из
теоремы 10.10 другое доказательство теоремы 10.23.
Теорема 10.24. Для того чтобы около усечённой
пирамиды можно было описать шар, необходимо и достаточно,
чтобы её основаниями были вписанные многоугольники1*,
а прямая, проходящая через центры кругов, описанных
около оснований, была перпендикулярна плоскостям
оснований.
^Основания усечённой пирамиды подобны, поэтому если одно из
них вписано в круг, то и другое вписано в круг.
§ 10.8. Комбинации шара с многогранниками 369
ffS* Упражнение 10.32. Докажите теорему 10.24, используя метод
пересечения ГМТ. Укажите положение центра описанного
шара (если он существует).
Пример 10.13. Стороны оснований правильной л-уголь-
ной усечённой пирамиды равны а и Ь. Угол наклона
бокового ребра к плоскости основания равен а. Найти радиус
шара, описанного около усечённой пирамиды.
Ох
Рис. 10.52
Решение. Пусть дана правильная усечённая пирамида
Ai...AnA\...A'n с центрами оснований О\ и О'г (рис. 10.51).
Центр О описанного шара есть точка пересечения
серединного перпендикуляра к ребру A\A!l9 проведённого в
плоскости A\A!xOi, и прямой О\О\ (почему?). Тем самым задача
свелась к планиметрической: найти расстояние R от
точки О до точек Ai и А[ прямоугольной трапеции A\O\OfxAl
(рис. 10.52) с углом а при большем основании и длинами
^=г и Ъ\ = =■ (см. пример 10.12).
оснований а\ =
2sinf
lsin£
Решая эту задачу1*, получаем, что
_ \/а\ -f b\ + 2a\b\ cos 2a
~~ sin 2a
Х)На рис. 10.52 изображён случай, когда Об [OiO\]. Проверьте, что
в остальных случаях ответ не изменится (ср. с примером 10.12).
370 Глава 10, Тела вращения
Искомый радиус шара равен
D Va2 + Ь2 + 2ab cos 2a —
К — = . U
2 sin \ sin 2a
Описанные многогранники
Определение. Многогранник называется описанным
около сферы {шара), если эта сфера (шар) касается всех
граней1* многогранника.
При этом указанная сфера (шар) называется вписанной
в многогранник.
Далее мы, как и в первой части этого параграфа, будем
говорить только о вписанном шаре (утверждения о
вписанной сфере совершенно аналогичны).
Из определения следует, что если многогранник описан
около шара, то центр шара равноудалён от всех граней
многогранника. Верно и обратное: если существует точка,
равноудалённая от всех граней многогранника, то в него
можно вписать шар с центром в этой точке. Вспоминая
теорему 5.2, мы можем сказать, что в многогранник можно
вписать шар тогда и только тогда, когда биссекторы
всех его двугранных углов пересекаются в одной точке.
Исходя из этого переформулируем результат, который вы
получили, выполняя упражнение 5.5.
I Теорема 10.25. Во всякий тетраэдр можно вписать шар
и притом только один.
с^3 Упражнение 10.33. Докажите, что если в многогранник
можно вписать шар, то этот шар единственный.
ч^ Упражнение 10.34. Докажите, что а) для того чтобы в
пирамиду можно было вписать шар, необходимо и достаточно, чтобы
биссекторы всех двугранных углов при её боковых рёбрах
пересекались по одной прямой; б) для того чтобы в пирамиду
можно было вписать шар, необходимо и достаточно, чтобы все
^Обратите внимание: именно граней, а не плоскостей граней.
§ 10.8. Комбинации шара с многогранниками 371
биссекторы двугранных углов при основании пересекались
в одной точке.
Приведём достаточное условие описанности пирамиды,
которого часто хватает для решения конкретных задач.
I Теорема 10.26. Если все двугранные углы при
основании пирамиды равны, то в неё можно вписать шар.
Доказательство, Согласно теореме 10.15 в данную
пирамиду можно вписать конус, а в этот конус можно вписать
шар (теорема 10.7). Докажем, что этот шар вписан в
пирамиду.
Действительно, этот шар касается основания
пирамиды, так как он касается основания конуса, а оно вписано
в основание пирамиды. Шар касается каждой образующей
конуса, а в каждой боковой грани пирамиды лежит
ровно одна образующая конуса (которая является апофемой
этой грани). Следовательно, шар касается и каждой грани
пирамиды. D
Замечание 1* Приведённое условие описанности пирамиды,
очевидно, не является необходимым. В качестве примера можно
взять любой тетраэдр, у которого не равны двугранные углы.
Замечание 2. Теорему можно доказать и не пользуясь
вписанным конусом, а показав непосредственно, что все биссекторы
двугранных углов при основании пересекаются в одной точке
(для этого нужно воспользоваться теоремой 9.2, а затем
доказать, что точка пересечения высоты пирамиды с биссектрисой
линейного угла какого-нибудь двугранного угла при основании
принадлежит всем указанным биссекторам, т.е. является
центром вписанного шара).
о^ Упражнение 10.35. Докажите теорему 10.26, используя план,
изложенный в замечании 2.
Из доказанной теоремы следует, что во всякую
правильную пирамиду можно вписать шар. Радиус этого шара
нетрудно найти, зная сторону основания пирамиды и
двугранный угол при основании.
372
Глава 10. Тела вращения
Пример 10.14. Пусть а — сторона основания правильной
пирамиды SA\ ...Ал, а/3 — двугранный угол при основании
пирамиды. Найти радиус вписанного в эту пирамиду шара.
Рис. 10.53
Решение. Пусть О\ — центр основания пирамиды, а В —
середина ребра А\А2> В треугольнике SBO\ проведём
биссектрису угла В до пересечения со стороной SO\ в точке О.
Эта точка и есть центр вписанного шара (почему?).
Искомый радиус находим из АВОО\ (рис. 10.53):
Остаётся заметить, что ВО\ = § ctg — (из £±А\ВО\). Итак,
= !■*•:*§•
□
Отсюда, в частности, следует, что радиус шара, вписан-
ного в правильный тетраэдр с ребром а, равен -т=-. Но
проще воспользоваться тем, что центр шара, вписанного
в тетраэдр, является центром тетраэдра, а значит, делит
высоту длины h в отношении 3:1, считая от вершины:
1. 1 а\/б а\/б
Г=4Л=4в"Т"=="1Г'
Используя формулы из § 9.1, можно найти радиус шара,
вписанного в правильную пирамиду, если заданы другие
её параметры.
§ 10,8. Комбинации шара с многогранниками 373
с& Упражнение 10.36. Найдите радиус шара, вписанного в
правильную л-угольную пирамиду со стороной основания а, если
известен угол а) а; б) у; в) 5 (см. обозначения в § 9.1).
Теорема 10.27*. Для того чтобы в призму можно было
вписать шар, необходимо и достаточно, чтобы в её
перпендикулярное сечение можно было вписать круг и чтобы
высота призмы была равна диаметру этого круга.
Доказательство. Необходимость. Пусть шар
В(О,К) вписан в призму Ai...AnAi*.*A'n (рис. 10.54).
Рассмотрим перпендикулярное сечение Bi...Bn призмы,
проходящее через центр О шара (В* Е (А/Aj), / = 1, ..., п). По
определению (В1В2В3) -L {А\А!1)У следовательно, эта
плоскость перпендикулярна всем боковым рёбрам призмы (так
как они параллельны), а значит, всем её боковым граням
(теорема 5.3).
В плоскости (В1В2В3) проведём через точку О
перпендикуляр к прямой В1В2. По теореме 5.4 он будет и
перпендикуляром к плоскости А1А2А3. Следовательно (теорема 10.1),
точка пересечения этого перпендикуляра с прямой В1В2
374 Глава 10. Тела вращения
является точкой касания шара с плоскостью А1А2А3. Из
определения вписанного шара вытекает, что указанная
точка лежит на отрезке В1В2. Аналогично доказывается, что
все остальные точки касания шара с боковыми гранями
призмы лежат по одной на соответствующих сторонах
рассматриваемого перпендикулярного сечения. Отсюда
следует, что большой круг, являющийся сечением шара
плоскостью В1В2В3, вписан в многоугольник В\...Вп. Диаметр
этого круга равен диаметру шара.
Основания призмы параллельны, а вписанный шар
касается каждого из них. Поэтому расстояние между
плоскостями оснований равно диаметру шара. Следовательно,
высота призмы равна диаметру круга, вписанного в её
перпендикулярное сечение.
Достаточность. Пусть дана призма, в
перпендикулярное сечение которой можно вписать круг, а
высота призмы равна диаметру 2R этого круга. Центр круга
равноудалён от всех сторон перпендикулярного сечения,
следовательно, он равноудалён и от всех боковых граней
призмы (теорема 5.4). Это означает, что биссекторы всех
двугранных углов при боковых рёбрах призмы
пересекаются по прямой, проходящей через центр круга (теорема 5.2
и аксиома пересечения плоскостей). Все точки этой прямой
удалены от плоскостей боковых граней призмы на
расстояние Я. Пусть биссектор какого-нибудь двугранного угла при
основании призмы пересекает указанную прямую в точке О
(почему эти прямая и полуплоскость пересекаются, причём
внутри призмы?). Эта точка удалена от всех боковых граней
и одного из оснований призмы на расстояние Я. По
условию основания призмы находятся на расстоянии 2R друг от
друга, следовательно, точка О находится на расстоянии R
и от другого основания. Осталось доказать, что проекции
точки О на плоскости оснований призмы попадут именно
на сами основания. Допустим, что это не так. Тогда
перпендикуляр, опущенный из точки О на плоскость одного
из оснований, пересечёт какую-то боковую грань призмы.
§ 10.8. Комбинации шара с многогранниками 375
Следовательно, расстояние от точки О до этой грани
меньше Я, что невозможно.
Итак, шар с центром О и радиусом R вписан в призму.
□
В частности, в правильную призму можно вписать шар
тогда и только тогда, когда высота призмы равна диаметру
круга, вписанного в основание. Центр шара, вписанного
в такую призму, есть середина высоты, соединяющей
центры кругов, вписанных в основания призмы.
Произвольная усечённая пирамида, описанная около
шара, редко встречается в задачах. Поэтому мы
сформулируем необходимое и достаточное условие описанности
только для правильной усечённой пирамиды.
Теорема 10.28. Для того чтобы в правильную
усечённую пирамиду можно было вписать шар, необходимо и
достаточно, чтобы её апофема была равна сумме апофем
оснований1*.
^Упражнение 10.37. Докажите теорему 10.28. Укажите
положение центра вписанного шара.
В заключение отметим, что у всех правильных
многогранников существуют описанные и вписанные шары,
центры которых находятся в центрах этих многогранников.
Вневписанный шар
Определение. Шар называется вневписанным в
многограннику если он касается одной из его граней и
продолжений всех остальных граней.
В нашем курсе мы не будем подробно обсуждать внев-
писанные шары, отметим только, что у всякого тетраэдра
есть четыре таких шара. Это утверждение будет доказано
ниже (см. пример 10.21).
^Напомним, что в планиметрии апофемой правильного
многоугольника называют радиус вписанного в него круга, проведённый в точку
касания со стороной.
376
Глава 10. Тела вращения
D
Q
Ox
0
/
v.
к
о2
Пример 10.15. Найти радиус шара,
вневписанного в правильный тетраэдр
с ребром а.
Решение. Пусть шар В(О, R) вневпи-
сан в правильный тетраэдр ABCD с
ребром а так, что он касается грани ABC
в точке О\. Проведём плоскость,
параллельную плоскости ABC, касающуюся
шара в точке О2 и пересекающую
продолжения рёбер DA, DBy DC в точках
А\у В\у С\ соответственно. Мы получим
правильную усечённую треугольную
пирамиду А\В\С\АВС, в которую вписан
шар В (О, R). Центр О шара находится
в середине отрезка O1O2, где О\ и Ог — центры правильных
треугольников ABC и А\В\С\ (упражнение 10.37). При
этом точка касания шара с гранью АА\В\В лежит на
апофеме XY этой грани. Сечение рассматриваемой
конфигурации изображено на рис. 10.55 (Q — центр вписанного
в тетраэдр ABCD шара). Проведём радиусы ОМ и QN
в точки касания шаров с плоскостью ABD. Получим
прямоугольную трапецию MOQN. Искомый радиус находим,
применяя свойство высоты прямоугольного треугольника
к AOXQ:
т.е.
Рис. 10.55
(здесь мы воспользовались тем, что длина отрезка ХО\
равна одной трети высоты правильного треугольника, а
QO\ — радиус вписанного в тетраэдр ABCD шара, который
был вычислен нами ранее — см. замечание после приме-
ау/6
ра 10.14). Итак, R =
6
□
В некоторых задачах речь идёт о шарах, касающихся
плоскостей всех граней многогранника. Такой шар может
§ 10.8, Комбинации шара с многогранниками 377
быть вписанным в многогранник, вневписанным в
многогранник и не быть ни тем, ни другим (т.е. касаться
продолжений всех граней многогранника). Решая
подобные задачи, важно в первую очередь исходя из условия
определить, каких граней (и, соответственно, продолжений
каких граней) касается шар, о котором идёт речь.
Пример 10.16. В основании четырёхугольной пирамиды
SABCD лежит ромб ABCD с острым углом при вершине
А. Высота ромба равна 4, точка пересечения его
диагоналей Н — основание высоты данной пирамиды. Шар радиуса
2 касается плоскостей всех граней пирамиды. Найти объём
пирамиды, если расстояние от центра шара до прямой АС
2\/2
равно
-АВ.
Решение. Сначала найдём геометрическое место точек,
равноудалённых от плоскостей ASB, DSC и ABC. Это ГМТ
является пересечением биссекторов всех двугранных углов,
образованных указанными плоскостями. Чтобы
представить себе, как устроено это пересечение, проведём через
апофемы SK и SN граней ASB и DSC плоскость а.
Используя известные теоремы о перпендикулярности, нетрудно
доказать, что плоскость ос перпендикулярна плоскостям ASB,
DSC и ABC (сделайте это самостоятельно). Поэтому упомя-
Рис. 10.56
378
Глава 10. Тела вращения
нутые выше биссекторы пересекают а по биссектрисам всех
внутренних и внешних углов равнобедренного
треугольника KSN. Эти биссектрисы, как известно из планиметрии,
пересекаются по три в четырёх точках — центрах О\, Ог, Оз
вневписанных окружностей треугольника и центре О4 его
вписанной окружности (рис. 10.56). Заметим ещё, что из
равнобедренности треугольника KSN следуют
параллельность прямых О\С>2 и KN и равенства SO2 = SN = SK = SOi
(почему?).
Из сказанного вытекает, что искомое ГМТ состоит из
прямых 1\у /г» hy h> проходящих соответственно через
точки О\у О2, Оз, О а перпендикулярно плоскости KSN (а
следовательно, параллельно рёбрам АВ и CD пирамиды).
Центр рассматриваемого шара должен лежать на одной
из этих прямых. Заметим сразу, что точки прямых £з и U
не удовлетворяют условию задачи. Действительно, если
О±Н = 2, то О±Н = HN (Н — середина отрезка KN),
следовательно, /.HNS— ^, что невозможно. Аналогично получаем
противоречие, если ОзН=2.
Итак, центр шара может лежать только на прямых,
проходящих через точки О\ и О2 и параллельных прямым АВ
§ 10.8. Комбинации шара с многогранниками 379
и CD. При этом высота пирамиды равна радиусу шара, т. е.
Stf=2.
Аналогичные рассуждения, применённые к плоскостям
граней SBC, SAD и ABCD, показывают, что центр
шара может находиться лишь в вершинах ромба A\B\C\D\
((AiDi) || CB1C1) || (AD), см. рис. 10.57), а вершина S
пирамиды является центром этого ромба. Ромб A\B\C\D\
подобен основанию ABCD пирамиды с коэффициентом j^j = >/2.
Заметим, что точки А\ и Ci не подходят, так как иначе
2\/2АВ
3 =2, т.е.
АВ = 4= < 4 = KN,
V2
что невозможно. Для точек В\ и Di получаем, что, с одной
стороны,
ВН2 = \bxS2 = \ (ВХН2 - SH2) = |ЛВ2 - 2,
а с другой стороны,
ВН2 = jBD2 = J (BM2 + DM2) = i ((АВ - AM)2 + DM2) =
= \((AB - VAD2-DM2)2 + DM2) =
= \((AB - VAB2 - 16)2 + 16) = |(AB2 - ABVAB2 - 16),
где М — основание высоты ромба, опущенной из
вершины D на сторону AJ3.
Приравнивая правые части полученных равенств,
находим АВ — 3\/2, а следовательно,
Vsabcd - \АВ.#ЛГ. Stf = 8>/2.
Проверьте самостоятельно, что шар с центром Bi (или Di)
радиуса 2 действительно касается плоскостей всех граней
данной пирамиды. □
380
Глава 10. Тела вращения
Полувписанный шар
I Определение. Шар называется полувписанным в мно-
гограннику если он касается всех рёбер этого
многогранника.
В задачах обычно встречается шар, полувписанный в
пирамиду (чаще всего в треугольную), поэтому мы подробно
остановимся на случае шара, полувписанного в тетраэдр.
I Теорема 10.29*. Для того чтобы существовал шар, по-
I лувписанный в тетраэдр, необходимо и достаточно, чтобы
I суммы длин его скрещивающихся рёбер были равны.
Доказательство. Необходимость. Пусть шар
касается рёбер АВу ВСу САу AD, BD и CD тетраэдра ABCD
в точках К у L, M, N9 P и Q соответственно. Из равенства
отрезков касательных, проведённых к шару из одной точки
(теорема 10.18), получаем, что
AN = AM = АК, ВР = ВК = BLy
CQ = CL = CM и DN = DP = DQ.
Следовательно, AB + CD = BC + AD = AC + BD.
M
§ 10.8. Комбинации шара с многогранниками 381
Достаточность. Пусть дан тетраэдр ABCD, в
котором AB + CD = BC + AD = AC + BD.
Впишем в грани ABC и BCD окружности. Пусть эти
окружности касаются рёбер АВ, ВС, АС и ВС, CD, DB в
точках К, L, М и L\, Q, Р соответственно (рис. 10.58). Так как
а АК — AM, QD = PD (как отрезки касательных,
проведённых к окружности из одной точки), то из равенства
АВ + CD = АС + BD вытекает, что KB + CQ = МС + ВР.
Заменив отрезки KB, CQ, МС и ВР на соответственно равные им
отрезки BL, CL\, CL и BL\, получаем, что BL + CL\ -CL +
+ BLi, следовательно, L и L\ — это одна и та же точка.
Обозначив через О\ и 0% центры рассматриваемых
окружностей, построим в плоскости О\ЬОч перпендикуляры
О\Х и O2Y к прямым O\L и O2L соответственно. Так как
(OiL) 1 (ВС) и (O2L) 1 (ВС), то (OiLO2) ± (ВС) (по
признаку). Поэтому О\Х и O2Y перпендикулярны прямой ВС,
а следовательно, перпендикулярны и плоскостям ABC и
BCD соответственно (теорема 4.1).
Согласно утверждению V из § 7.1 точка О пересечения
прямых О\Х и O2Y (почему они пересекаются?) удалена
от всех рёбер тетраэдра ABCD, кроме ребра AD, на
расстояние г. Тогда шар В (О, г) касается всех рёбер тетраэдра,
кроме, быть может, ребра AD.
Проводя аналогичные рассуждения для окружностей,
вписанных в грани ABC и ABD, мы получим шар ВГ(О', г1),
касающийся всех рёбер тетраэдра, кроме CD. Заметим
теперь, что сферы, ограничивающие шары В(О, г) иВ'((У, г'),
имеют общую окружность (вписанную в грань ABC) и
общую точку Р вне этой окружности.
Следовательно, В(О, г) и В*(О*, rf) —это один и тот же
шар. Он касается всех рёбер тетраэдра. □
Заметим, что если существует шар, полувписанный в
тетраэдр, то его центр есть точка пересечения
перпендикуляров к граням, проходящих через центры вписанных
в грани окружностей.
382
Глава 10, Тела вращения
Пример 10.17. Сторона основания правильной
треугольной пирамиды равна а, боковое ребро пирамиды равно Ь.
Найти радиус полувписанного шара.
м
Решение. Заметим сначала, что указанный шар
существует в силу теоремы 10.29.
Пусть SABC — данная пирамида, О — центр
полувписанного шара, SK — высота пирамиды, (ОМ) 1 (BS), (OD) 1
1 (АВ), ОМ = OD = г — искомый радиус шара (рис. 10.59).
По теореме 10.18 BM = BD= ^. Из подобия
треугольников SOM и SBK находим, что
г =
SMBK
SK
а(2Ь-а)
□
В частности, радиус шара, полувписанного в правиль-
г а\/2 т^
ныи тетраэдр с ребром а, равен —j—. Впрочем, этот
результат можно получить значительно проще. Например,
заметив, что искомый радиус равен половине расстояния
между скрещивающимися рёбрами тетраэдра, и
воспользовавшись результатом примера 4.41).
!)См. также ниже пример 10.19.
§ 10.8. Комбинации шара с многогранниками 383
Приведём теперь несколько примеров,
иллюстрирующих использование укладывания тетраэдра в коробку и
метода вспомогательного объёма1* для вычисления радиусов
описанных, вписанных, вневписанных и полувписанных
шаров.
Пример 10.18. Рёбра АВ, АС и AD тетраэдра ABCD
попарно перпендикулярны, а их длины равны а, & и с
соответственно. Найти радиус шара, описанного около этого
тетраэдра.
Решение. Уложим тетраэдр в угол параллелепипеда
ABKCDLMN. Тогда шар, описанный около тетраэдра ABCD,
является описанным около параллелепипеда, а его радиус
равен половине диагонали параллелепипеда (см. решение
примера 9.10). Следовательно,
R=±Va2 + b2 + c2. □
Пример 10.19. Найти радиус шара, полувписанного в
правильный тетраэдр с ребром а.
Решение. Уложим данный тетраэдр в параллелепипед
по диагонали (см. § 9.4). Легко доказать, что этот
параллелепипед будет кубом с ребром -у=, а шар, вписанный в куб,
/2
полувписан в тетраэдр. Следовательно, г = ^т—• □
Пример 10.20. Пусть V — объём, a S —площадь полной
поверхности многогранника, описанного около шара
радиуса г. Доказать, что
Г» Y Г
(10.18)
г =
3V
Решение. Разобьём данный многогранник на
пирамиды, соединив центр шара со всеми его вершинами. Пусть
Si, ..., Sn — площади граней многогранника. Тогда
V = |Sir + ±S2r + ... + ±Snr = ±
откуда и следует доказываемое равенство. □
г)См. § 9.3 и 9.4.
384 Глава 10, Тела вращения
Формулу (10.18) иногда удобно использовать для
вычисления радиуса шара, вписанного в многогранник.
■^ Упражнение 10.38. Вычислите с помощью формулы (10.18)
радиус шара, вписанного в правильную треугольную
пирамиду со стороной основания а и боковым ребром Ь.
и^ Упражнение 10.39» а) Используя метод вспомогательного
объёма, докажите аналог формулы (10.18) для вневписанного
шара: радиус Го шара, вневписанного в многогранник и
касающегося грани площади So, равен
Г°~ S-2S0'
где V — объём, a S — площадь полной поверхности
многогранника.
б) Используя полученную формулу, найдите радиус шара,
вневписанного в правильный тетраэдр с ребром а (ср. с
результатом примера 10.15).
Пример 10.21*. Доказать, что для всякого тетраэдра
существует не менее пяти и не более восьми шаров,
касающихся плоскостей всех его граней.
Решение. Пусть дан тетраэдр объёма V. Пронумеруем
его грани от первой до четвёртой и обозначим площади
этих граней через Si, S2, S3 и S4 соответственно. Для
произвольной точки О пространства обозначим расстояние
от неё до плоскости £-й грани тетраэдра через Л/ (i = 1, ..., 4).
Тогда
eiftiSi + s2h2S2 + sshsS3 + s4h4S4 = 3F, (10.19)
где Si = ±1, причём знак « + » берётся тогда и только тогда,
когда точка О лежит вместе с данным тетраэдром по одну
сторону от плоскости его i-й грани. Для доказательства
этого равенства достаточно заметить, что если соединить
точку О с вершинами тетраэдра, то, комбинируя объёмы
четырёх полученных тетраэдров, выбирая знаки « + » или
« —» по указанному выше правилу, мы получим объём
исходного тетраэдра.
§ 10.8. Комбинации шара с многогранниками 385
Пусть О — центр, а г — радиус шара, касающегося
плоскостей всех граней тетраэдра. Тогда ft* = r (i = 1, ..., 4) и
s2S2 + S3S3 + £4S4 = ^г > О-
Верно и обратное: если для данного набора (е\9 е2у £з> £а)
сумма S\S\ -Ь £2^2 + ^з^з + ^4^4 положительна, то
существует шар, касающийся плоскостей всех граней тетраэдра.
Действительно, рассмотрим точку 1\ для которой
h _ и _ h _ 3V;
tii - п2 - ns - г - ^iSi + s^ + ^Sg + ^S4.
Подставляя эти значения hi, h2 и hs в равенство (10.19),
получаем, что и h± = г.
Плоскости граней тетраэдра делят пространство на 15
частей четырёх типов: одна часть типа I, внутренняя
относительно тетраэдра, для точек которой все Si = 1; четыре
части типа II (рис. 10.60а), для точек которых ровно одно
из чисел Si равно —1; четыре части типа III (рис. 10.606),
для точек которых ровно одно из чисел €i равно +1; шесть
частей типа IV (рис. Ю.бОв), для точек которых два числа
из Si положительны, а два отрицательны.
В области I всегда есть точка, равноудалённая от граней
(центр вписанного шара), так как Si + S2 + S3 + S4 > 0.
В области типа II также всегда есть точка,
равноудалённая от плоскостей граней (центр вневписанного шара), так
как сумма площадей любых трёх граней тетраэдра больше
площади четвёртой (это легко доказать, спроектировав три
грани ортогонально на плоскость четвёртой и заметив, что
проекции покроют четвёртую грань независимо от того,
куда попадёт проекция вершины, в которой сходятся
проектируемые грани).
Внимательный читатель может спросить: «А почему такая точка
существует?» Существование этой точки доказывается построением.
Искомой является точка пересечения трёх плоскостей, соответственно
параллельных граням 1, 2 и 3, удалённых от них на расстояние г и
расположенных в соответствии со знаками ei, £2 и ег в соответствующих
полупространствах относительно этих граней.
13 Зак 3183
386
Глава 10. Тела вращения
а)
б)
е)
г)
Рис. 10.60
Тем самым, мы уже указали пять шаров, касающихся
плоскостей всех граней тетраэдра. Заметим теперь, что
если для некоторого набора (е±9 £2» £з> £4) сумма S\Si + S2S2 +
+ SsSs + €484 положительна, то для набора с
противоположными знаками эта сумма отрицательна. Так как всего
наборов 16, не более половины из них дают положительную
сумму £TiSi + C2S2 + £3^3 + ^4^4. Значит, существует не
более восьми шаров, касающихся плоскостей всех граней
тетраэдра.
В принципе мы полностью решили поставленную
задачу, однако интересно выяснить, при каких условиях
существуют ещё три шара и где они расположены.
§ 10.9*. Нестандартные комбинации 387
Заметим, что они не могут лежать в областях типа III,
так как st = Sj• = Sk = -1, a si — 1. В областях типа IV, если
Si + Sj > Sk + Si и Si = Sj = 1, sk = si = -1, выполняется
неравенство
s2S2 + s3S3 + S4S4 > 0,
поэтому существует нужный нам шар (рис. Ю.бОг).
Понятно, что при этом в области типа IV, относящейся к
противоположному ребру, это неравенство не выполняется. Оно
не выполняется также при условии St + Sj = S^ + Si.
Итак, если сумма площадей любых двух граней
тетраэдра не равна сумме площадей двух оставшихся граней, то
шаров, удовлетворяющих условию задачи, существует
ровно 8. В случае, когда площади всех граней тетраэдра равны
(а следовательно, равны и сами грани —см. задачу 9.26),
таких шаров ровно 5. Их может быть и 7, и 6. При этом
равенство Si + Sj = Sk + Si выполнено соответственно ровно
для одного и ровно для двух различных наборов индексов
(i, ], ky I) (i<j, Ь<1)из множества {(1, 2, 3, 4); (1, 3, 2, 4);
(1,4,2,3)}. □
§ 10.9*. Нестандартные комбинации тел вращения
с многогранниками
Теперь вы знаете достаточно, и
можно продолжать.
Дж. Р. Р. Толкин. Хоббит, или Туда и обратно
В этом параграфе мы приведём примеры решения задач
о комбинациях тел вращения и многогранников, отличных
от рассмотренных выше. К подобным задачам в полной
мере относится всё, что было сказано в начале § 9.5. Здесь мы
лишь подчеркнём ещё раз, что умение решать
нестандартные задачи приходит с опытом, и предложим для начала
подробно разобрать приведённые ниже примеры.
Пример 10.22. Пусть ABCA\B\C\ — правильная призма.
Вершина А является вершиной конуса, вершины В и С
388
Глава 10. Тела вращения
лежат на боковой поверхности этого конуса, а вершины
В\ и С\ — на окружности его основания. Найти отношение
объёмов конуса и призмы, если АВ\ : АВ = 5:1.
Рис. 10.61
Решение. Без ограничения общности можно считать,
что АВ = 1. Тогда АВ\ = 5. Введём базис а = АВ, Ь- АС, ? =
= АА\ (рис. 10.61) и составим таблицу умножения векторов
этого базиса (таблица 10.1). Скалярный квадрат вектора ?
находится по теореме Пифагора из /\AA\B\:
= АВ\ -
= 25-1-24.
Пусть О — центр основания конуса, а АО = xcl + yb + zc, где
х, у и z — неизвестные пока числа. Всякая образующая
конуса составляет один и тот же угол а с его высотой АО,
следовательно,
АВ[а6 а-АО Ь-АО
\ - \АО\ \Щ'\Аб\ \Ь\ • \АО\
= cos a.
Эти равенства дадут нам связь между х, у и z (почему их
недостаточно для однозначного определения этих чисел?).
Из первого равенства получаем, что
т.е.
= {a>AO)\ABi\,
(а + ?) (ха + уЬ + г?) = 5а(ха + yb + г?).
§ 10.9*. Нестандартные комбинации
389
а
Ь
с
п
1
1/2
0
Ь
1/2
1
0
г
0
0
24
Таблица 10.1
С помощью таблицы умножения это равенство приводится
к равенству
2x + v = 12г.
Из равенства
а Ад
\Щ-\а5\ \ь\-\ао\
с учётом того, что \а\ — \Ь\ = 1, вытекает, что
т. е.
а(ха + yb
= Ь (ха
г?),
откуда х — у (впрочем, это можно было получить и без
вычислений, воспользовавшись соображениями симметрии).
Подставляя х = у в найденное выше соотношение между х,
у и г, находим, что * = у = 4г. Итак,
Так как ZAOB\ = ^, мы получаем АО • OBi = 0, т. е.
Подставляя в это равенство АО = г (43 + 4Ь + ?) и АВ\ =2
с помощью таблицы умножения приводим его к виду 12z
= 5, откуда г = Yo. Теперь легко найти АО:
2 '
390 Глава 10. Тела вращения
т.е.
A0=~k'
Радиус основания конуса находим из ААОВ\ по теореме
Пифагора:
Объём конуса равен
а объём призмы —
Искомое отношение объёмов равно *. П
1о
Пример 10.23. Длина ребра основания правильной
треугольной пирамиды SABC (S — вершина) равна 8. Точки К
и L расположены на рёбрах АВ и АС соответственно,
причём АК = 7, AL = 4. Известно, что для данной пирамиды
существует единственный конус, вершина которого
находится в точке К, центр основания лежит на прямой SC,
а отрезок KL является одной из образующих. Найти объём
этого конуса.
Решение. Пусть D — середина ребра АВ, SH = h —
высота пирамиды, О— центр основания конуса (рис. 10.62),
Введём ортонормированный базис
Таблица умножения для этого базиса выглядит очень
просто (единицы по диагонали, остальные элементы —нули).
§ 10.9*. Нестандартные комбинации
S
391
Пусть Об = хСЁ, где х — неизвестное пока число.
Разложим по базису {?i, ?2> ?з} векторы ЛГО и LO:
Кб = #£> + Ы + Сб = -3?i +
= -3?i + 4\/3?2
= -3?i + 4v/3?2 "
id=
+
2л/3?2) =
Так как высота конуса перпендикулярна плоскости его
основания, получаем КО • LO = 0, т. е.
-б+(4\/3-
x2h2 = 0.
392 Глава 10. Тела вращения
После преобразований получаем равносильное уравнение
относительно х:
~2/
(ft2+ 51)-48*+18 = 0.
Условие единственности конуса означает, что это
квадратное уравнение имеет один корень, значит, его
дискриминант D равен нулю, т. е.
откуда h = 4л/«. При этом х= -т. Поэтому
КО = -3?i + 2х/3е2 + 3 уДё3
следовательно, \КО\ — 3\/3, \LO\ = VTO, а искомый объём
конуса равен
^д25 / П
Пример 10.24. Основанием четырёхугольной пирамиды
SABCD является трапеция ABCD (ВС \\ AD), ВС = |AD,
ZASD — ZCDS = ~. Все вершины пирамиды лежат на окруж-
ностях оснований цилиндра высоты 2, радиус которого
равен ^. Найти объём пирамиды.
о
Решение. Заметим сначала, что если гипотенуза
прямоугольного треугольника является хордой круга радиуса R,
то расстояние р от вершины прямого угла этого
треугольника до плоскости круга не больше чем R> Действительно,
р ^h^l^Rj где h — расстояние от вершины прямого угла
до гипотенузы, а 21 — длина гипотенузы.
По условию задачи AASD прямоугольный, а
расстояние между основаниями цилиндра, равное двум, больше
§ 10.9*. Нестандартные комбинации
С
393
в
с,
Рис. 10.64
радиуса основания, равного ^. Поэтому либо вершины
о
А и D находятся на разных основаниях цилиндра, либо
AASD лежит в плоскости одного из оснований. Первый
случай невозможен, так как тогда (АВ) \\ (CD) (теорема 2.4)
и ABCD — параллелограмм, а не трапеция. Следовательно,
AASD вписан в окружность одного из оснований цилиндра
(причём AD — диаметр), а точки ВиС лежат на окружности
другого основания (рис. 10.63).
Пусть В\ и С\ — проекции точек В и С на плоскость ASD
(рис. 10.64). Точки В\ и D различны, так как иначе из
условия (ВС) || (AD) следует, что ВС = AD, а это противоречит
условию задачи.
Так как ZCSD= ^, по теореме о трёх перпендикулярах
(теорема 4.4) (C\D) I (SD). Но тогда ASDC\
—прямоугольник и AS = C\D. Трапеция AB\C\D вписана в окружность,
следовательно, АВ\ — C\D. Таким образом, АВ\ = AS и
(BiS) ± (AD). Пусть К = (AD) П (SBi). Тогда ВХК - SK. По
условию
Из AB\OCi находим
\ - LC\ =
394 Глава 10. Тела вращения
Поскольку (ВВ\) _L (ASD), мы получаем, что (SBBi) 1
± (ASD), а так как (AD) I (SBX), то (AD) _L (KB).
Следовательно, [JSTB] — высота трапеции ABCD, a ZBKBi —
угол между плоскостями ABC и ASD. Если i/ — высота
пирамиды, то её объём равен
= J (AD + ВС)ВК. Slf sin Z.BKBX =
о
±(AD + BC)SKBBi = 2. П
Пример 10.25. Боковое ребро правильной пирамиды
SABC имеет длину -=- и составляет с плоскостью основания
5
ABC угол, равный arctg ——. Цилиндр расположен так, что
окружность одного из его оснований проходит через
середину ребра АС и не пересекает грань SAB. Ортогональные
проекции цилиндра на плоскости SAB и SBC —
прямоугольники с общей вершиной S. Найти объём цилиндра.
Решение. Пусть К — точка, в которой плоскость т,
проходящая через точку А и перпендикулярная ребру SB,
пересекает это ребро (рис. 10.65а). Обозначим через О центр
основания пирамиды, а через а — угол SBO. По условию
следовательно,
cos a = 2^Х,
ВО = SB cos a = |\/тг,
5 V о
5
Пусть Т — середина ребра АС. Тогда Сет, Т е т,
поэтому ТК — высота треугольника TSB, в котором SB = —,
= ^л/66, а высота SO равна \/-я-- Записывая двумя спо-
0 V о
собами удвоенную площадь треугольника TSB9 находим,
§ 10.9*. Нестандартные комбинации
S
395
а)
б)
Рис. 10.65
что ТК = у/2. Пусть
/3 = ZAfiTT =
Тогда из ПАКТ имеем
Следовательно,
' 6
\lAKC.
5 *
cos б 5
Определим теперь расположение цилиндра. Если
проекция цилиндра на некоторую плоскость является
прямоугольником, то его ось параллельна этой плоскости. Таким
образом, ось цилиндра параллельна плоскостям SAB и SBC,
396 Глава 10, Тела вращения
следовательно, она параллельна их общей прямой SB
(теорема 2,2). Кроме того, точки Т и S принадлежат плоскостям
оснований цилиндра, поэтому его высота Н равна SK, т. е.
и
Далее, проекции цилиндра на плоскости SAB и SCB —
прямоугольники с общей стороной SK, поэтому проекции
нижнего основания цилиндра на эти плоскости — отрезки
с общим концом К. Это значит, что окружность нижнего
основания цилиндра вписана в угол EKF, где (ЕК) ± (СК),
(FK) ± (АК) (рис. 10.656). Отметим, что угол АКС острый,
так как
cos /.АКС = cos 2(5 = 2 cos2 (3 - 1 = 2 - f |) - 1 > 0.
Итак, окружность нижнего основания цилиндра — либо
окружность o)i (Оь R\), вписанная в AEKF, либо окружность
6)2(02, jF?2)> вневписанная в угол К этого треугольника. Но
цилиндр с основанием, ограниченным окружностью 6Ji,
пересекает грань SAB, поэтому основание — круг,
ограниченный окружностью о>2- Из АО2РК (см. рис. 10.656) находим,
что
Д2 = О2К • sin ZTKF = (Д2 + ТК) sin(| - /3) = (Д2 + V2)|,
т. е. Д2 = 5\/2. Искомый объём цилиндра равен пЩ = 70п.
□
Пример 10.26. В правильной треугольной пирамиде
SABC (S — вершина) точка Р — середина апофемы SD грани
SBC. На ребре АВ взята точка М так, что MB : АВ = 2:7.
Сфера, центр которой лежит на отрезке МР> проходит через
точки А и С и пересекает прямую ВС в точке Q так, что
CQ = m. Найти объём пирамиды SABC, если радиус сферы
равен -Ijz.
v3
Решение. Пусть О — центр данной сферы, а О', S' и Р' —
проекции точек О, S, Р соответственно на плоскость ABC
м
§ 10.9*. Нестандартные комбинации 397
А N С
D
Рис. 10.66
В
Рис. 10.67
(рис. 10.66). Отметим, что S' — центр треугольника ABC,
Р* — середина отрезка S'D, а О' лежит на (BSf) (так как она
равноудалена от точек А и С).
Опустим из точки О1 перпендикуляр на прямую ВС
и обозначим его основание через F (рис. 10.67). Для того
чтобы найти сторону а основания пирамиды, вычислим
двумя способами длину отрезка BF. Так как сфера проходит
через точки А, С и Q, то (У — центр окружности, описанной
около AACQ, поэтому, с одной стороны,
а с другой стороны, по теореме о пропорциональных
отрезках EF^BD во*
' BS''
Длины отрезков BD и BSf равны ^ и ^—соответственно.
Z о
Найдём длину отрезка ВС/, для чего проведём через точку
S' прямую, параллельную (Р'М), до пересечения с (ВС)
в точке М\. Дважды применяя теорему о пропорциональ-
398 Глава 10. Тела вращения
ных отрезках, находим
AS>
АР' AS' + ±
fly/3
— n 5a 3 _ _ 4a _ 3a
12
и
_2a
Rn/ _ dq/БМ _ ал/3 7 _ 2ал/3
7
следовательно,
2fl\/3
a 9 — a
Итак,
откуда
3m
Высота SSf пирамиды вдвое больше длины отрезка PPf.
Из подобия треугольников МРР1 и МОСУ находим
РР' - nnfMEL - по1 (л 4- °'р'\
Поскольку
o's' = bs'-bo> = ^ -
ZO'S'P' = 60°,
по теореме косинусов для АСУР'Я' вычисляем длину
отрезка О'Р':
О'?2 = O'S'2 + P'S'2 - 2 • O'S' • P'S' • cos
§ 10.9*. Нестандартные комбинации 399
откуда
_ а /Т3~_ т /Ш
-T2VT~T6VT-
Длину отрезка ОО1 находим из прямоугольных
треугольников ОО'С и CO'F:
ОС/2 = ОС2 - О'С2 = ОС2 - (O'F2 + FC2) =
f
откуда
Поскольку
о /Л 0
ОО' =
АМХ = ±
лы а\/3
Зт
~ 7 '
ту/3
т2
3
13т2
48 "
т2
16
' = 30°,
по теореме косинусов для AAM\S' вычисляем длину
отрезка
'2 = AMf + AS'2 - 2 • AMi -AS' -cos
откуда
Я1
\/39
"28"'
Из подобия треугольников МВО1 и MiBS' получаем
Итак,
т
рр' _ т | 1 , 16 V 3 \ _ 15т
14
следовательно,
15m
400
Глава 10. Тела вращения
Искомый объём пирамиды равен
п
U
Пример 10.27. Сфера, касающаяся нижнего основания
цилиндра, имеет единственную общую точку с
окружностью его верхнего основания и делит ось цилиндра в
отношении 1:6:2, считая от центра одного из оснований.
Найти объём цилиндра, если известно, что сфера касается
двух его образующих, находящихся на расстоянии 8 друг
от друга.
Q
Рис. 10.68
Решение. Пусть г — радиус цилиндра, h — его высота,
р — радиус сферы, А — общая точка сферы и окружности
верхнего основания цилиндра, KN — ось цилиндра, О —
центр сферы, Е — точка касания сферы и нижнего
основания цилиндра. Точки А и Е лежат в плоскости а = (OKN),
сечение цилиндра плоскостью а — прямоугольник ABCD со
§ 10.9*. Нестандартные комбинации 401
сторонами AD = h, AB = г; сечение сферы плоскостью а —
окружность большого круга (радиуса р), проходящая через
точку А, касающаяся стороны CD в точке Е и пересекающая
отрезок KN в точках L и М. На рис. 10.68 изображены
проекции заданной в условиях задачи конфигурации на
плоскость а и плоскость основания цилиндра/3. Проекции
сферы и цилиндра на плоскость /3 — круги, окружности
которых пересекаются в точках R и Q, где RQ = 8, а
расстояние между центрами О; и Oi кругов равно UN = ОР>
где Р — середина отрезка LM. Пусть F — точка пересечения
прямых ОЕ и АВ.
Заметим, что PN = OE = OA>OF = KP. Так как PN =
= РМ + МЛГ, KP = KL + LP и РМ = LP, из полученного
неравенства вытекает, что MN > KL, Поэтому
KL:LM:MN=1 : 6 : 2,
следовательно, FO : ОЕ - 4 : 5, т. е. FO = ^р.
Найдём высоту и радиус цилиндра:
h = FE = FO + OE=^t
о
= л/АО2 - FO2 + VOL2 - PL2 = Jp2 - (|р)2+
Искомый объём V цилиндра равен тгг2Л, т.е. ур^7ф3. Для
того чтобы найти р, запишем двумя способами площадь S
треугольника O\ROf. С одной стороны,
С другой стороны, по формуле Герона
S=y/p(p-O1O')(p-OiR)(p-RO'),
402 Глава 10. Тела вращения
где
RO' = p,
Следовательно,
Приравнивая правые части найденных выражений
для S, получаем, что р = —.
V6
О
§ 10.10*. Конические сечения
Вы узнаете всё, что знаю я. Но
я бы предпочёл, чтобы вы добрались
до правды своими силами, чтобы мне
не надо было вести вас за ручку.
А Кристи. Убийство на поле для гольфа.
В § 2.5 мы дали определение эллипса. Напомним его.
Определение. Эллипсом называется геометрическое
место точек М плоскости, сумма расстояний от которых до
двух данных точек F\ и J^ этой плоскости постоянна, т. е.
+ MF2 = 2а, где а = const, 2а > FiF2, а > 0.
Точки F\ и F2 называются фокусами эллипса. Ниже нам
понадобятся ещё две плоские кривые, которые мы сейчас
определим.
§10.10*. Конические сечения 403
Определение. Гиперболой называется геометрическое
место точек М плоскости, модуль разности расстояний от
которых до двух данных точек F\ и ¥% этой плоскости
постоянен, т. е. \MF\ - MF2I = 2а, где а — const, 2а < F\F2,
а>0.
Точки F\ и F2 называются фокусами гиперболы. Заме-
k
тим, что кривая, заданная уравнением у =-, k — const, кфО>
которая называлась гиперболой в курсе алгебры, является
гиперболой и в смысле данного нами сейчас определения1*.
DS3 Упражнение 10.40. Докажите, что кривая у = ^ (k ф 0) есть
геометрическое место точек плоскости, модуль разности
расстояний от которых до точек с координатами (V2&, y/2k)
и (—\/2fc, —y/2k) при k > 0 и до точек с координатами
(—y/-2k, V—2k) и (у/—2ky — у/—2k) при k < 0 есть величина
постоянная, равная 2>/2|fe|.
Определение. Параболой называется геометрическое
место точек М плоскости, расстояния от которых до
данной точки F и до данной прямой d, лежащих в этой
плоскости, равны, т. е. MF = р (М, d).
Точка F называется фокусом параболы, а прямая d —
директрисой параболы.
Кривая, заданная уравнением у — ах2> а = const, а фО,
которая называлась параболой в курсе алгебры, является
параболой и в смысле только что данного определения2*.
^Следовательно, гиперболой является и кривая
_ ах + Ъ
У~~ cx + d
фО> а<1ф be)у которая получается из кривой
be -ad
параллельным переносом, что вытекает из тождества
ах + Ь _ be — ad a
cx + d ~~ с2(х + die) с"
^Следовательно, параболой является и кривая у — ах2 4- Ьх 4- с
(а/0), получающаяся из кривой у —ах2 параллельным переносом, что
404 Глава 10. Тела вращения
и^ Упражнение 10.41. Докажите, что кривая у — ах2 (а Ф 0) есть
геометрическое место точек плоскости, расстояние от
которых до точки (0; j-) равно расстоянию до прямой у — - —.
Теперь всё готово для того, чтобы исследовать вопрос
о форме сечения конуса (точнее говоря, прямой круговой
конической поверхности, состоящей, напомним, из двух
полостей— см. § 10.1).
Теорема 10.30. Если плоскость пересекает все
образующие прямой круговой конической поверхности и не
проходит через её вершину, то линия пересечения плоскости
с этой конической поверхностью является эллипсом.
Доказательство. Пусть плоскость а пересекает все
образующие конической поверхности1* с вершиной S.
Заметим, что поскольку плоскость а не проходит через S, она
пересекает только одну из двух полостей конической
поверхности (почему?).
Впишем в коническую поверхность две сферы,
касающиеся плоскости а с разных сторон (рис. 10.69а, б). Пусть
F\ и F% — точки касания сфер с плоскостью а. Возьмём на
линии пересечения плоскости а и конической поверхности
произвольную точку М, а на образующей, проходящей
через М, — точки Pi и Р2, лежащие на окружностях 0)\ и 0)2,
по которым сферы касаются конической поверхности. По
теореме 10.18 MF\ = МР\ и MF2 = MP2. Следовательно,
MF\ + MF2 = MP\ + МР2=Р\Р2. Длина отрезка Р\Р2 одна
и та же для всех точек М: этот отрезок является
образующей усечённого конуса, ограниченного параллельными
плоскостями, в которых лежат окружности coi и а>2>
Поэтому точка М принадлежит эллипсу с фокусами F\ и F2,
вытекает из тождества
2 / b \2 Ь2 — 4ас
ах +Ьх + с = а[х+ — ) .
V 2а/ 4а
^Здесь и далее мы опускаем слова «прямая круговая», относящиеся
к рассматриваемой конической поверхности.
§ ЮЛОК Конические сечения
S
405
Рис. 10.69
406 Глава 10. Тела вращения
лежащему в плоскости а. Нетрудно показать, что верно
и обратное утверждение, т. е. если точка М принадлежит
этому эллипсу, то он лежит на линии пересечения
плоскости а с конической поверхностью. Действительно, пусть
М — произвольная точка эллипса с фокусами F\ и F2, для
которого MF\ + MF2 = Р1Р2 = 2а, a M\ — точка
пересечения луча F\M с конической поверхностью.
Существование точки М\ вытекает из того, что фокус F\ находится
внутри конической поверхности. Как мы доказали выше,
M\F\ + M1F2 = 2а. Из этого следует, что М и М\ — это
одна и та же точка, так как иначе луч F\M пересекал
бы эллипс в двух точках, что невозможно
(действительно, из равенства MF\ + MF2 = M\F\ + M\F2 следует, что
\MF2 - M1F2I =ММ\, а. это противоречит неравенству
треугольника). □
Замечание. Если плоскость а перпендикулярна оси
конической поверхности, то F\ и F2 — это одна и та же точка. Поэтому
эллипс, являющийся сечением, вырождается в окружность.
Теорема 10.31. Если плоскость параллельна двум
образующим конической поверхности, то линия пересечения
плоскости с этой конической поверхностью является
гиперболой.
Эта теорема доказывается аналогично предыдущей.
Сделайте это самостоятельно, используя рис. 10.70а, б.
Обратите внимание на то, что плоскость, параллельная двум
образующим конической поверхности, не может проходить
через её вершину и пересекает обе полости этой
поверхности (почему?).
Теорема 10.32. Если плоскость параллельна ровно
одной образующей конической поверхности, то линия
пересечения плоскости с этой конической поверхностью
является параболой.
Доказательство. Пусть плоскость а параллельна
ровно одной образующей I конической поверхности с верши-
§ 10.10*. Конические сечения
407
а)
Рис. 10.70
408 Глава 10. Тела вращения
ной S. Тогда а не проходит через S и пересекает только
одну полость конической поверхности (почему?).
Впишем в коническую поверхность сферу, касающуюся
плоскости а (рис. 10.71а, б). Пусть F — точка касания
сферы и плоскости, со — окружность, по которой касаются
сфера и коническая поверхность. Обозначим через d
линию пересечения плоскости а и плоскости /3, содержащей
окружность со. Возьмём на линии пересечения плоскости а
с конической поверхностью произвольную точку М и
проведём через М плоскость у, параллельную /3. Она пересечёт
коническую поверхность по окружности со\. Опустим из М
перпендикуляр MD на прямую d. Ясно, что он параллелен
образующей /. Если Е и В — точки пересечения I с со и со\, то
MDEB — параллелограмм, следовательно, BE = MD. Если
Н — точка пересечения образующей, содержащей точку М,
с со, то MF — МН (теорема 10.18) и МН — BE (как две
образующие усечённого конуса с основаниями,
ограниченными окружностями со и со\). Из полученных равенств
вытекает, что MF — MD, т.е. точка М лежит на параболе
с фокусом F и директрисой d, принадлежащей плоскости а.
Аналогично тому, как это было сделано при доказательстве
теоремы 10.30, показывается, что справедливо и обратное
утверждение: всякая точка М указанной параболы
принадлежит линии пересечения плоскости а с конической
поверхностью (сделайте это самостоятельно). □
Приведённые здесь доказательства теорем 10.30—10.32
были предложены в 1822 г. бельгийским инженером Дан-
деленом, в честь которого названы сферы, использованные
при доказательстве.
Ответим теперь на вопрос, поставленный в § 10.1, о
форме сечения цилиндра наклонной плоскостью.
Теорема 10.33. Сечение цилиндрической поверхности1*
плоскостью, не параллельной её образующим, является
эллипсом.
§ 10.10*. Конические сечения
409
(d,D)
Рис. 10.71
410
Глава 10. Тела вращения
О
0
Рис. 10.72
Доказательство этой теоремы проводится по той же
схеме, что и доказательство теоремы 10.30.
и^ Упражнение 10.42. Докажите теорему 10.33.
На рис. 10.72 изображены все возможные виды
сечений конической и цилиндрической поверхностей, в том
числе точка и пустое множество. Все их принято называть
коническими сечениями. Это собирательное название не
1}Мы
снова опускаем слова «прямая круговая».
Задачи 411
должно вызвать недоумения, поскольку можно считать
цилиндрическую поверхность частным случаем конической,
полагая, что вершина этой конической поверхности
находится в бесконечно удалённой точке (вспомните, как в § 2.3
мы отождествили параллельное и центральное
проектирование).
Эллипс, гиперболу и параболу называют
невырожденными коническими сечениями. Они обладают многими
красивыми свойствами, на которых мы, к сожалению, не
можем здесь останавливаться. Дальнейшие сведения об этих
кривых вы найдёте, например, в статье [Скопец, 1966],
содержащейся в пятом томе «Энциклопедии элементарной
математики».
Задачи
— О! Задачка!
— Да. И к тому же трудная, —
продолжала Джейн Уилкинсон. — А вы,
я знаю, трудностей не боитесь.
А. Кристи, Смерть лорда Эдвера
10.1. Из бумажного прямоугольника со сторонами а и &
склеивают боковую поверхность цилиндра. Какие стороны
следует склеить между собой, чтобы цилиндр с такой
боковой поверхностью имел наибольший объём?
10.2. Развёртка конуса представляет собой сектор круга
радиуса R с углом а при вершине. Чему равен объём этого
конуса?
10.3. Докажите, что плоскость, пересекающая боковую
поверхность цилиндра, но не пересекающая его основания,
делит ось цилиндра, боковую поверхность и объём в
одинаковом отношении.
10.4. Цилиндр пересекается плоскостью, не
перпендикулярной его образующей и не пересекающей его
основания. Какая кривая получится, если развернуть линию
412 Глава 10. Тела вращения
пересечения вместе с боковой поверхностью цилиндра на
плоскость?
10.5. Можно ли внутри куба с ребром 1 разместить три
иилиндра высоты 1 и диаметра ^ так> чтобы они не могли
перемещаться внутри куба?
10.6. С помощью циркуля и линейки постройте на
плоскости отрезок, равный радиусу данного деревянного шара.
10.7. Планета получена вращением квадрата со
стороной а вокруг его диагонали. Маршрут по поверхности этой
планеты называется кругосветным, если он замкнут и
симметричен относительно центра квадрата. Найдите длину
кратчайшего кругосветного маршрута.
10.8. Найдите геометрическое место центров кругов,
образуемых при сечении данного шара плоскостями,
проходящими
а) через данную прямую а;
б) через данную точку Н.
10.9. а) Докажите, что если все сечения тела
плоскостями являются кругами, то это тело — шар.
б*) Докажите, что если все сечения тела плоскостями,
проходящими через данную точку, являются кругами, то
это тело —шар.
10.10. а) Можно ли четырьмя шарами закрыть
точечный источник света? (Источник считается закрытым, если
любой выходящий из него луч пересекает хотя бы один из
шаров.)
б*) Каким наименьшим числом шаров одинакового
радиуса можно закрыть точечный источник света?
10.11. В деревянном шаре просверлен цилиндрический
канал длины h (т. е. высота соответствующего цилиндра
равна h)y осью которого является диаметр шара. Найдите
объём оставшейся части шара.
10.12*. В пространстве заданы тридцать ненулевых
векторов. Докажите, что среди них найдутся два, угол между
которыми меньше 45°.
Задачи 413
10.13. Докажите, что отношение объёмов шара и
описанного около него усечённого конуса равно отношению
площадей их полных поверхностей.
10.14. Найдите отношение объёмов цилиндра и конуса,
вписанных в один и тот же шар, если высота и цилиндра,
и конуса равна радиусу шара.
10.15. Плоскость касается двух касающихся шаров
радиусов йигв точках А и В. Найдите длину отрезка АВ.
10.16. Три шара попарно касаются, а плоскость касается
этих шаров в точках А, В и С. Найдите радиусы шаров, если
стороны треугольника ABC равны а, & и с.
10.17. Два шара одного радиуса и два другого
расположены так, что каждый шар касается трёх других и данной
плоскости. Найдите отношение радиусов шаров.
10.18. Центры трёх сфер радиусов 3, 4 и 6
расположены в вершинах правильного треугольника со стороной 11.
Сколько существует плоскостей, касающихся
одновременно этих сфер?
10.19. Внутри конуса находятся четыре шара равного
радиуса. Три шара касаются его основания, каждый шар
касается боковой поверхности конуса, кроме того, каждый
шар касается трёх других. Найдите угол при вершине
осевого сечения конуса.
10.20. Радиус основания и высота конуса равны 1.
Внутри конуса находятся три шара равного радиуса. Каждый
шар касается двух других, основания конуса и боковой
поверхности конуса. Найдите радиус каждого из этих
шаров.
10.21. В пространстве расположены четыре шара так,
что каждый касается трёх других. Докажите, что шесть
точек касания принадлежат одной сфере или одной
плоскости.
10.22. В пространстве расположены четыре конуса с
общей вершиной и одинаковой образующей (но, вообще
говоря, с разными радиусами оснований). Каждый из этих
конусов касается двух других. Докажите, что четыре точки
414 Глава 10. Тела вращения
касания окружностей оснований конусов лежат на одной
окружности.
10.23. В правильную шестиугольную пирамиду вписан
конус, и около неё описан конус. Найдите разность объёмов
этих конусов, если высота пирамиды равна Н9 а радиус
основания описанного конуса равен R.
10.24. Докажите, что четырёхгранный угол можно
вписать в конус тогда и только тогда, когда суммы его
противоположных двугранных углов равны.
10.25. Радиус основания цилиндра равен г, а его
высота равна 5г. Около цилиндра описан параллелепипед,
отношение объёма которого к объёму цилиндра равно 5 : к.
Найдите длину отрезка большей диагонали
параллелепипеда, лежащего внутри цилиндра.
10.26. Два равных конуса с общей вершиной S,
высотой h и радиусом основания R (R<h) касаются друг друга
и плоскости Р, находясь по одну сторону от этой
плоскости. Пусть / — прямая, по которой пересекаются плоскости
оснований конусов. Найдите угол между прямой I и
плоскостью Р.
10.27. Два конуса, осевое сечение каждого из которых
является правильным треугольником со стороной а, лежат
на горизонтальной плоскости, касаясь друг друга и имея
общую вершину. На какой высоте над этой плоскостью
находится точка касания оснований этих конусов?
10.28. Четыре равных конуса имеют общую вершину,
причём каждый конус имеет с тремя другими по одной
общей образующей. Найдите отношение суммы объёмов
конусов к объёму шара, касающегося оснований конусов.
10.29. На плоскости лежат п равных конусов с общей
вершиной (п ^ 3). Каждый конус касается двух других
конусов. Найдите угол при вершине осевого сечения конуса.
10.30. Оси трёх равных попарно касающихся
цилиндрических поверхностей взаимно перпендикулярны. Найдите
радиус наименьшего шара, касающегося всех трёх
поверхностей, если радиус каждой из них равен г.
Задачи 415
10.31. Оси трёх равных попарно касающихся
цилиндрических поверхностей взаимно перпендикулярны. Найдите
радиус наибольшей цилиндрической поверхности, которая
может пройти между данными, если их радиус равен г.
10.32. Радиусы двух непересекающихся шаров равны R
и г, расстояние между их центрами равно а. В каких
пределах может изменяться длина общей касательной к этим
шарам?
10.33. Сфера с диаметром СЕ касается плоскости ABC
в точке С, AD — касательная к этой сфере. Докажите, что
если точка В лежит на прямой DE, то АВ = АС.
10.34. АВ и CD — различные касательные к двум
данным шарам (А и С принадлежат поверхности одного шара,
В и D — другого). Докажите, что проекции отрезков АС
и BD на линию центров шаров равны.
10.35. Три сферы имеют общую хорду. Через точку этой
хорды проведены три хорды, принадлежащие различным
сферам. Докажите, что концы этих трёх хорд лежат на
одной сфере или в одной плоскости.
10.36. а) Две окружности, не лежащие в одной
плоскости, пересекаются в двух точках А и Б. Докажите, что
существует единственная сфера, содержащая эти
окружности.
б) Докажите справедливость утверждения предыдущего
пункта в случае, когда обе окружности касаются прямой I
в точке А.
10.37. Докажите, что если две боковые грани усечённой
треугольной пирамиды — вписанные четырёхугольники, то
и третья боковая грань — вписанный четырёхугольник.
10.38. а) В пространстве расположены несколько
окружностей, причём любые две из них имеют пару общих точек.
Докажите, что либо все эти окружности имеют две общие
точки, либо все они лежат на одной сфере (или в одной
плоскости).
б) Три окружности попарно касаются друг друга (т.е.
имеют общие точки и общие касательные в этих точках),
416 Глава 10. Тела вращения
причём все точки касания различны. Докажите, что эти
окружности лежат на одной сфере (или в одной
плоскости).
10.39. На сфере радиуса 2 расположены три попарно
касающиеся окружности радиуса 1. Найдите радиус
наименьшей окружности, расположенной на этой сфере и
касающейся всех трёх окружностей.
10.40. Докажите, что в четырёхгранный угол можно
вписать сферу тогда и только тогда, когда суммы его
противоположных плоских углов равны.
10.41. В правильную усечённую четырёхугольную
пирамиду с апофемой а вписан шар. Найдите площадь её
боковой поверхности.
10.42. Призма с площадью основания S описана около
шара. Найдите площадь её полной поверхности.
10.43. Докажите, что все грани тетраэдра равны тогда
и только тогда, когда центры вписанного и описанного
шаров совпадают.
10.44. На рёбрах A\Di и CiDx куба ABCDA\BiCiDi
выбраны точки К и М так, что плоскость KDM касается
вписанного в куб шара. Докажите, что
а) сумма KD\ + D\M\
б) величина двугранного угла при ребре B\D тетраэдра
B\DKM не зависят от выбора точек К и М.
10.45. Рассмотрим все тетраэдры ABXY, описанные
около данного шара. Докажите, что при фиксированных
точках А и В сумма углов четырёхугольника АХ BY, т. е.
ZAXB + ZXBY + ZBYA + Z.YAX,
не зависит от выбора точек X и У.
10.46. В правильной четырёхугольной пирамиде центр
описанного шара лежит на поверхности вписанного.
Найдите плоский угол при вершине пирамиды.
10.47. Найдите радиус шара, вписанного в тетраэдр,
пять рёбер которого равны 2, а шестое ребро равно 1.
Задачи 417
10.48. Радиус шара, описанного около правильной
четырёхугольной пирамиды, равен 1, а радиус вписанного
шара равен —^—. Найдите объём пирамиды.
10.49*. Докажите, что каждые три плоскости граней
тетраэдра пересекают касательную плоскость к
описанному шару в вершине, в которой сходятся эти три грани,
по трём прямым, образующим при этой вершине шесть
углов по 60°, тогда и только тогда, когда произведения
противоположных рёбер этого тетраэдра равны.
10.50*. Докажите, что отрезки, соединяющие вершины
тетраэдра с противоположными им точками касания
вписанного шара с гранями тетраэдра, пересекаются в одной
точке тогда и только тогда, когда точки касания являются
точками Торичелли граней (т. е. все стороны грани видны
из точки касания под одинаковыми углами).
10.51*. Докажите, что многогранник, описанный
около сферы радиуса 10 и целиком лежащий внутри сферы
радиуса 11, имеет более двадцати двух граней.
10.52. Докажите, что если все грани многогранника
являются вписанными многоугольниками, а в каждой его
вершине сходятся три ребра, то этот многогранник можно
вписать в шар.
10.53*. У белого многогранника некоторые грани
покрашены чёрной краской так, что никакие две чёрные грани не
имеют общего ребра. Докажите, что если выполнено хотя
бы одно из условий:
а) чёрных граней больше половины;
б) площадь чёрных граней больше половины площади
поверхности многогранника, то в этот многогранник
нельзя вписать шар.
10.54*. У белого многогранника некоторые вершины
покрашены чёрной краской так, что никакие две чёрные
вершины не соединены ребром и чёрных вершин больше
половины. Докажите, что этот многогранник нельзя
вписать в шар.
14 Зак Я383
418
Глава 10. Тела вращения
Рис. 10.73
Рис. 10.74
10.55. а) Можно ли описать около
шара многогранник, получаемый из куба
отрезанием всех его вершин (рис. 10.73)?
б) Можно ли вписать в шар
многогранник, получаемый из куба отрезанием
одной вершины (рис. 10.74)?
10.56. Известно, что все рёбра
многогранника М равны и касаются некоторого
шара.
а) Докажите, что если одна из граней
М имеет нечётное число сторон, то
существует шар, описанный около М.
б) Обязательно ли в условиях пункта а)
существует вписанный в М шар?
в) Докажите, что если все грани М
имеют одинаковое число сторон, то
существует шар, вписанный в М.
г) Обязательно ли в условиях пункта в) существует
описанный около М шар?
10.57. Докажите, что шар, полувписанный в призму,
существует тогда и только тогда, когда призма правильная
и все её рёбра равны.
10.58. Докажите, что если центр шара, полувписанного
в пирамиду (усечённую пирамиду), лежит на её высоте, то
эта пирамида (усечённая пирамида) правильная.
10.59. В л-угольную призму вписан шар и полувписан
шар. Какая это призма?
10.60. В правильную тг-угольную усечённую пирамиду
вписан шар и полувписан шар. Найдите п.
10.61. Сторона основания правильной четырёхугольной
пирамиды равна а, а двугранный угол при боковом ребре
равен ср. Докажите, что существует шар, полувписанный
в эту пирамиду, и найдите его радиус.
10.62. Сторона основания правильной я-угольной
пирамиды равна а, а боковое ребро образует с плоскостью
основания угол а. На каком расстоянии от плоскости осно-
Задачи 419
вания находится центр шара, полувписанного в эту
пирамиду?
10.63. Шар касается рёбер АВ, ВС, CD и AD
тетраэдра ABCD в точках, являющихся вершинами квадрата.
Докажите, что если этот шар касается и ребра АС> то он
полувписан в тетраэдр.
10.64*. Сколько существует шаров, касающихся всех
сторон данного пространственного четырёхугольника или
их продолжений?
10.65*. Сколько существует шаров, касающихся всех
рёбер данного тетраэдра или их продолжений?
10.66. Длины двух противоположных рёбер тетраэдра
равны а, длины двух других противоположных рёбер
равны 6, оставшихся двух —с. Найдите радиус шара,
описанного около этого тетраэдра.
10.67. Для тетраэдра из предыдущей задачи найдите
расстояния от центра вписанного шара до центров вневпи-
санных шаров.
10.68. В тетраэдре ABCD грани ABC и ABD имеют
площади р и q и образуют между собой угол а. Найдите
площадь сечения, проходящего через ребро АВ и центр
вписанного в тетраэдр шара.
10.69. Найдите радиус шара, вписанного в тетраэдр,
если радиусы вневписанных шаров равны г\, Г2, гз и г\.
10.70. Боковые грани треугольной пирамиды
равновелики и образуют с основанием углы а, /3 и у, Найдите
отношение радиуса шара, вписанного в эту пирамиду, к
радиусу вневписанного шара, касающегося её основания.
10.71. Сторона KL прямоугольника KLMN служит
высотой конуса с вершиной L. Радиус основания этого конуса
в три раза больше отрезка NK. Шар касается плоскости
KLM в точке М и имеет единственную общую точку с
конусом. Найдите радиус шара, если KL = 6.
10.72. Три одинаковых конуса, радиусы оснований
которых равны г и составляют 3/4 от их высоты, расположены
по одну сторону от плоскости Р, а их основания лежат
420 Глава 10. Тела вращения
в этой плоскости. Окружности оснований каждых двух из
этих конусов касаются. Найдите радиус шара, лежащего
между конусами и касающегося как плоскости Р, так и всех
трёх конусов.
10.73. Два равных конуса с общей вершиной А
расположены по разные стороны от плоскости Р так, что только
одна образующая каждого конуса (АВ для одного конуса
и АС для другого) лежит в плоскости Р. Известно, что
/.ВАС = (3, а угол между высотой и образующей каждого
конуса равен ср. Найдите угол между линией пересечения
плоскостей оснований конусов и плоскостью Р.
10.74. Высота конуса равна диаметру его основания. В
конус вписан куб так, что его четыре вершины
расположены на основании, а оставшиеся четыре — на боковой
поверхности конуса. Найдите отношение объёмов куба и конуса.
10.75. Две противоположные вершины куба являются
центрами оснований цилиндра, а остальные вершины
лежат на его боковой поверхности. Найдите отношение
объёмов цилиндра и куба.
10.76. Сфера проходит через вершины одной грани куба и
касается сторон противоположной грани куба. Найдите
отношение объёмов шара, ограниченного этой сферой, и куба.
10.77*. Основанием пирамиды ABCD является
правильный треугольник ABC со стороной 12. Ребро BD
перпендикулярно плоскости основания и равно 10\/3. Все вершины
этой пирамиды лежат на боковой поверхности цилиндра,
ось которого пересекает ребро BD и плоскость ABC.
Найдите радиус цилиндра.
10.78*. Основанием пирамиды служит квадрат ABCD со
стороной а, боковое ребро SC перпендикулярно плоскости
основания и равно Ь\ М — точка на ребре AS. Точки М, В
и D лежат на боковой поверхности конуса с вершиной А,
а точка С — в плоскости основания этого конуса.
Определите площадь боковой поверхности конуса.
10.79*. Дан правильный тетраэдр ABCD с ребром 1.
Точка М — середина ребра CD, N — середина ребра ВС, Р ле-
Задачи 421
ясит на ребре АВ, причём АР = ЗВР. Сфера касается
плоскостей ABC и ACD, при этом точки касания лежат на
прямых PN и AM соответственно. Найдите радиус сферы.
10.80*. В плоскости Р дан равнобедренный треугольник
ABC такой, что АВ = ВС — /, АС = 2а. Шар радиуса г
касается плоскости Р в точке В. Две скрещивающиеся прямые
проходят через точки А и С и касаются шара. Угол между
каждой из этих прямых и плоскостью Р равен а. Найдите
расстояние между этими прямыми.
Глава 11
Векторы в пространстве (продолжение)
«Координаты»,—сказал Экайер, но
что такое «координаты»? Какие я могу
найти координаты, чтобы заставить их
поверить?
К. Саймак. Проект «Ватикан»
§ 11.1. Векторное и смешанное произведения векторов
О ты, очаровательный отрок,
постигший таинства умножения!
Ну-ка, давай умножать.
С. Бобров. Волшебный двурог
В этом параграфе мы определим две новые операции
над векторами и изучим их свойства. Всюду далее будем
считать, что единица длины фиксирована раз и навсегда.
Определение. Векторным произведением ненулевых
векторов а иЬ называется такой вектор ?, что
1°. ||S|£
2°.
3°. если векторы а и & не коллинеарны, то
упорядоченная тройка {а, &, ?} правая1*.
В случае, когда хотя бы один из векторов U или b
нулевой, их векторное произведение ? по определению полагают
равным 0.
Итак, если векторы a, b не коллинеарны, то вектор ?,
очевидно, однозначно определён условиями 1°—3°. Если
векторы Зиб коллинеарны, но оба они ненулевые, то из
условия 1° следует, что |?| = 0 (так как sin Z(2, b) = 0), т. е.
?=б. Условие 2° при этом выполняется автоматически,
^Напомним, что определение правой тройки некомпланарных
векторов было дано в начале § 8.8.
424 Глава 11. Векторы в пространстве {продолжение)
так как ранее мы договорились считать нулевой вектор
ортогональным любому другому.
Векторное произведение мы будем обозначать косым
крестом: ?=# х Ь.
Свойства векторного произведения
1°. Va, Ь: ахЬ — —Ъха (антикоммутативность).
2°. Векторное произведение равно нулю тогда и только
тогда, когда сомножители коллинеарны1*.
3°. Модуль векторного произведения неколлинеарных
векторов численно равен площади параллелограмма,
построенного на сомножителях.
4°. Va, £, ?, Vft, meR: (ka+mb) x ?=fe(ax ?) + m(bx ?)
(линейность по первому сомножителю) и
a x (kb + тс) =k(axo) + m(ax(*) (линейность по второму
сомножителю).
Свойства 1°—3° вытекают непосредственно из
определения векторного произведения, а свойство 4° мы докажем
ниже.
пЗГУпражнение 11.1. Докажите свойства 1°—3°.
в^ Упражнение 11.2. Докажите, что если {е*\9 ё*2, ?з} — правый ор-
тонормированный базис, то е\ х ?2 = ?з> ^2 х ?з = ?1 > ?з х ^1 = ^2•
Как следует изменить эти равенства для левого ортонормиро-
ванного базиса?
(Определение. Число 3 • (b x ?) называется смешанным
произведением векторов 3, & и ?.
Таким образом, чтобы вычислить смешанное
произведение, необходимо первый сомножитель скалярно умножить
на векторное произведение второго и третьего
сомножителей (взятых в указанном порядке).
Смешанное произведение мы будем обозначать
следующим образом: (3, &, ?).
Х)В § 3.2 мы договорились считать нулевой вектор коллинеарным
любому другому.
§ 11.1. Векторное и смешанное произведения 425
Свойства смешанного произведения
1°. Смешанное произведение равно нулю тогда и только
тогда, когда сомножители компланарны.
2°. Модуль смешанного произведения некомпланарных
векторов численно равен объёму параллелепипеда,
построенного на сомножителях. Если {3, &, ?} — правая тройка,
то (а, &, ?) > 0; в противном случае (т. е. когда эта тройка
левая) (3, Ь, ?) < 0.
3°. V3, b, ?: (3, $, с) = (?, 3, Ъ) = (&, ?, 3) =
- -(&, а, ?) = -(?, Ь, 3) = -(3, ?, &).
4°. V3b 32, &,^?, Vfe, mGR:
(fe3i +jnU2y &, ?) = Л(аь b9 ?) + /п(а2, Ь, ?);
Va, ^ь &2, ?, Vft, mel:
(a, fe&i +тпЬ2,?) =й(а, &i, ?) + m(5, b2» ?);
V3, b,Jl9 ?2, Vfe, /nGR: ^
(3, &, ft?i + /n?2) = й(а, Ь, ?i) + m(a, 6, ?2) (линейность
по первому, второму и третьему сомножителям).
Доказательство свойства 1°. Пусть (а, &, с) = 0, т.е.
3- (6 х ?) = 0. Тогда либо хотя бы один из векторов a, b x ?
нулевой, либо |3| • |Ь х с| cos <р = 0, где (р — угол между
векторами а и & х б.
В первом случае если 3=6, то 3, £ и ? компланарны,
а если афб, но & х ?= б, то по свойству 2° векторного
произведения & и ? коллинеарны, поэтому 3, b и с компланарны.
Во втором случае cos ср = 0 (сомножители — ненулевые
векторы, поэтому |3| ф 0 и |^ х ?| ^ 0), следовательно, 3 ±
J. (& х ?), значит, 3, & и ? компланарны.
Доказательство обратного утверждения проводится
аналогично. Сделайте это самостоятельно. □
Доказательство свойства 2°. Отложим векторы 3, b
и ? от одной точки О и построим на них параллелепипед
OBDCAB\DiC\. Пусть <р — угол между 3 и b х ?, Л' —
проекция точки А на плоскость ОВС. Тогда Z.OAA' равен либо (р
(рис. 11.1а), либо к — ср (рис. 11.16). В обоих случаях из
426 Глава 11. Векторы в пространстве (продолжение)
Сх
Ьх?
Рис. 11.1
ДОАА' находим, что АА! = \3\ • |cos cp\. По свойству 3°
векторного произведения Sobdc = |& х ?|. Следовательно, объём
параллелепипеда равен Sobdc • АА' = \Щ • |Ь х ?| • |cos <p\ =
= |(3,Ь,?)|.^
Знак (3, £, ?) определяется знаком cos ср. Ясно, что если
{3, $, ?} — правая тройка (как на рис. 11.1а), то cos <p > О,
а если {3, Ь, ?} — левая тройка (как на рис. 11.16), то cos cp <
<0. П
Свойство 3° следует из свойств 1° и 2°, поскольку модуль
смешанного произведения при перестановке сомножителей
§ ILL Векторное и смешанное произведения 427
останется тем же, а знак, если сомножители ненулевые,
определяется ориентацией тройки сомножителей.
Доказательство свойства 4°. Объединяя свойства 4°
и 5° скалярного произведения векторов (см. § 3.4), которые
в совокупности выражают линейность скалярного
произведения по первому сомножителю, мы получим, что V й, теШ
И
та2) • (Ь х ?) =
т(П2 • (Ь х ?)) = Л(2Ь Ь,
Переставляя теперь сомножители согласно свойству 3°,
получим оставшиеся два из доказываемых равенств. □
D^"Упражнение 11.3. Докажите, что если {?i, ё*2, ?з} — правый
ортонормированный базис, то (?ь ?2* ?з) = 1* Как изменится
это равенство в случае левого ортонормированного базиса?
Докажем теперь линейность векторного произведения.
Доказательство свойства 4° векторного произведения.
Выберем ортонормированный базис {?ь ?2> ?з}* В силу
линейности смешанного произведения по второму
сомножителю Va, b, ?и\/й, тп€М справедливы равенства
(ih kU+mb, ?) = k(e*h 3, ?) + m(gl9 b, ?) (i = 1, 2, 3),
т.е.
т?) x?) =?r(ft(2x?) + m(&x?)) (i = 1,2,3)
(здесь мы воспользовались определением смешанного
произведения и линейностью скалярного произведения).
Полученные равенства означают, что в базисе {?ь ?2> ?з} равны
координаты векторов (kd + mb) х ? и k(d х ?) + m(b x ?).
Действительно, если H = d\e\ +d2?2 + ^з?з» т0> умножая это
равенство скалярно сначала на ?i, затем на ?2 и, наконец,
на ?з> мы получим, что dt = it -5 (/= 1, 2, 3).
Из единственности разложения по базису (теорема 3.3)
вытекает, что векторы (kct+ mb) x ? и k(S х ?) + m(& x ?)
равны. □
428 Глава 11. Векторы в пространстве (продолжение)
Подобно тому как это было сделано в конце § 3.4 для
скалярного произведения, можно получить выражения для
векторного и смешанного произведений векторов через их
координаты в заданном базисе. Для этого нужно записать
разложения векторов по базису и перемножить их,
пользуясь доказанными свойствами векторного и смешанного
произведений. Мы сделаем это ниже, однако уже сейчас
ясно, что получатся весьма громоздкие выражения. Чтобы
записать их в компактной и удобной для запоминания
форме, нам потребуется понятие определителя.
Рассмотрим четыре числа: a, ft, с и d. Из них можно
составить таблицу размера 2x2:
с
которая называется матрицей второго порядка.
Числа a, ft, с и d называются элементами матрицы.
Элементы а и ft образуют первую строку матрицы, элементы
cud — вторую строку; элементы а и с образуют первый
столбец матрицы, элементы ft и d — второй столбец.
Определение. Число ad — be называется определителем
(или детерминантом) матрицы
(а Ъ\
\е d) •
Определитель матрицы будем обозначать так:
а Ь
с d
Аналогично таблица
составленная из девяти чисел, называется матрицей
третьего порядка.
§ ILL Векторное и смешанное произведения 429
Как и в случае матрицы второго порядка, вводятся
понятия элементов матрицы, её строк и столбцов. Строки
по-прежнему нумеруются сверху вниз, а столбцы — слева
направо.
Определение. Число
Ь2
ах
-а2
с\ с3
Ь\ Ь2
с\ с2
Ь\
с\
«2
ь2
С2
as
Ьз
сз
называется определителем (или детерминантом)
матрицы
и обозначается
На первый взгляд, данное нами определение
детерминанта представляется странным. К сожалению, в нашем
курсе мы не сможем в полной мере проиллюстрировать
естественность и важность этого понятия, в частности
применение детерминантов в теории систем линейных уравнений.
Вы познакомитесь с этим материалом в курсе линейной
алгебры в высшей школе.
Существует несложное правило для запоминания
определения детерминанта матрицы третьего порядка, которое
в данных нами выше обозначениях состоит в следующем.
Рассмотрим число а\ и мысленно вычеркнем в матрице
строку и столбец, на пересечении которых стоит это число
(т. е. первую строку и первый столбец). При этом
получается матрица второго порядка
(Ъ2 Ьз\
с2 сз)
Умножим число а\ на определитель этой матрицы.
Получим число . ,
сз
430 Глава 1L Векторы в пространстве (продолжение)
Проделав аналогичную процедуру с числами аг и as (при
этом следует мысленно вычеркнуть первую строку и
соответственно второй и третий столбцы), мы получим числа
и
Ь\
с3
с2
Остаётся написать перед
знак «минус», а затем сложить все полученные числа. Эта
процедура схематически изображена на рис. 11.2.
п\
bx
С\
а\
bx
ах
bx
С\
а2
Ьо,
С2
а2
ll
а2
ъ2
сч
аз
Сз
йг
с!
а3
&з
Сз
ь2
с2
А
->а2-
^i
в
^1
/»,
Ьз
сз
сз
2
Рис. 11.2
А-В + С
Пример 11.1. Вычислить
12 3
4 5 6
7 8 9
Решение. По определению детерминанта матрицы
третьего порядка
12 3
4 5 6
7 8 9
= 1-
5 6
8 9
-2-
4 6
7 9
+ 3-
4 5
7 8
= 1-(5-9-6-8)-2-(4-9-6-7)+ 3-(4-8-5-7) =
= (45 - 48) - 2 • (36 - 42) + 3 ■ (32 - 35) = -3 + 12 - 9 = О
§ ILL Векторное и смешанное произведения 431
(в процессе вычисления мы воспользовались и
определением детерминанта матрицы второго порядка). □
Сделаем одно важное замечание, которое понадобится
нам в дальнейшем. Нетрудно видеть, что данные выше
определения детерминантов будут иметь смысл, если в первой
строке матрицы второго или третьего порядка записаны
векторы, а остальные строки состоят из чисел, поскольку
мы умеем умножать вектор на число и складывать векторы.
Например,
3 $ ?
1 2 3
4 5 6
= 3-
2 3
5 6
—
а
1
ь.
b
2
1
4
3
6
23-
+ ?
ь,
1 2
4 5
Теперь всё готово для того, чтобы получить компактные
выражения для векторного и смешанного произведений
векторов через их координаты.
Теорема 11.1. Пусть {?i, t2, Зз} — правый ортонормиро-
ванный базис и в этом базисе й= (аи &г> #з)> Ь = (&ь &2> &з)«
Тогда
(11.1)
Зх£ =
п\ CL2 Us
Ъ\ Ъ2 bs
•
Доказательство. Действительно,
Uxb= (fli?i + а2?2 + яз^з)
- a2bi) (?i х ё2
(a\b2 —
а2 а3
Ъ2 Ь3
аз
а\
Ьх
а2
Ьг
Ьх
а2 as
b2 bs
432 Глава 11. Векторы в пространстве (продолжение)
Мы воспользовались линейностью векторного
произведения, результатом упражнения 11.2 и определением
детерминанта. □
Замечание. В случае левого ортонормированного базиса в
правой части формулы (11.1) появится знак «минус». В неорто-
нормированном базисе эта формула неверна.
с^ Упражнение 11.4. Пусть в некотором базисе выражение век-
торногр произведения через координаты сомножителей для
любых двух векторов даётся формулой (11.1). Верно ли, что
этот базис правый ортонормированный?
Теорема 11.2. Пусть {g\, £2> ^з} — произвольный базис
и в этом базисе а = (а\> п2, аз); 6=(Ьь &2> &з); ?= (съ ^2, сз).
Тогда
U,?) =
Ь\ Ь2 &3
(Ё1>ё2>ёг)-
(11.2)
Доказательство. Действительно,
(3, Ь, ?) =
- Ъ2сг) (g\ x g2)
+ (Ь2с3 - bsc2) (g2 x £3) + (bad - hcs) (ga x
- b2ci)(gi, Mi, Mz) + a2(bic2 - b2ci)(g2, g\,
- b2ci) (§3, Mu i2) + 01 (Ь2с3 - b3c2) {Mi, Мг,
g2, Мг, Мг) +а3(Ь2Сз - Ь3с2)(М3, Мг, Мз)
- Ь\с%)(Mi, Мз, Mi) +
- &ic3)(Мз, Мз, Mi) =
+ а\(Ьгсз - ЬзС2)(Ми Мг, Мз) +
ь2
Ьз
-a2
b\ b$
Cl C3
4- аз
bi
сг\
a\
h
Cl
)«
a2
b2
c2
аз
Ьз
сз
,M3,Mi) +
-Ь2С1)(М1,Мг,Мз) +
-Ь1Сз)(М1,Мг,Мз) =
,Мг,Мз) =
§ ILL Векторное и смешанное произведения 433
Здесь мы сначала воспользовались определением
смешанного произведения векторов, затем преобразовали
векторное произведение
аналогично тому, как это было сделано в доказательстве
предыдущей теоремы, после чего использовали линейность
скалярного произведения и снова применили определение
смешанного произведения. Далее, согласно свойству 1°
смешанного произведения были опущены шесть из девяти
слагаемых, которые равны нулю. И наконец, мы
воспользовались определением детерминанта. □
Из доказанной теоремы, в частности, вытекает, что в ор-
тонормированном базисе
id, $,г) = ±
п\ Q-2 &3
Ь\ &2 ^3
C\ C2 C3
9
где знак «плюс» выбирается в случае правого базиса, а знак
«минус» — в случае левого (см. упражнение 11.3).
В качестве ещё одного следствия формулы (11.2)
сформулируем и докажем критерий компланарности векторов.
ах
с\
аз
Ъз
Теорема 11.3. Векторы а = (аь ^2» яз)> b = (&ь Ьг
— (d, C2, сз)1^ компланарны тогда и только тогда, когда
= 0.
Доказательство. Согласно свойству 1° смешанного
произведения векторов векторы а, Ъ и ? компланарны тогда
и только тогда, когда (а, 6, ?) =0. Доказываемое
утверждение вытекает из формулы (11.2), так как смешанное
произведение базисных векторов не равно нулю. □
На практике данным критерием компланарности
векторов зачастую удобнее пользоваться, чем теоремой 3.1.
^Координаты векторов заданы в произвольном базисе.
434 Глава 11. Векторы в пространстве (продолжение)
§ 11.2. Геометрические приложения векторного
и смешанного произведений векторов
Мы пришли в отличное настроение
и начали разбирать новую задачу Хунты,
и очень скоро он сказал, что и раньше
считал себя побрекито, а в том, что
я математически невежествен, убедился
при первой же встрече.
А. и Б. Стругацкие, Понедельник начинается в субботу
С помощью векторного произведения удобно находить
площадь S параллелограмма, построенного на векторах 2
и b: S= \U х Ь|. Воспользовавшись тем, что диагональ
параллелограмма делит его на два равных треугольника, мы
сразу получаем, что площадь треугольника, построенного
на векторах а и Ъ, равна -^\S х Ъ\.
Пример 11.2. Доказать, что площадь треугольника,
составленного из медиан треугольника1* площади S,
равна ?S.
4
Решение. Пусть дан треугольник ABC площади S, АА\9
ВВ\ и СС\ —его медианы; й = СА9 Ь = СВ. Тогда (см.
пример 3.1)
Найдём CCi x BiB:
f (2 + Ь) х (S-|з) =
1}Из медиан всякого треугольника можно составить новый
треугольник. Более того, это можно сделать, параллельно перенося медианы.
Это вытекает из того, что сумма векторов-медиан равна 0 (проверьте
это).
§ 11.2. Приложения произведений векторов 435
Следовательно,
т. е. Si = jS, где Si — площадь треугольника, составленного
из медиан АА\, ВВ\ и СС\. □
Применение смешанного произведения векторов часто
связано с вычислением объёмов. Согласно свойству 2°
смешанного произведения объём параллелепипеда,
построенного на векторах а, Ь и ?, равен | (а, Ь, ?) |. Используя тот
факт, что диагональная плоскость делит параллелепипед
на две треугольные призмы равного объёма, мы сразу
получаем, что объём треугольной призмы, построенной на
векторах а, Ь, ?, равен ^ | (Й, Ь, ?) |.
Рассмотрим теперь тетраэдр ABCD, в котором U = ДА,
b = DB и ?=5С. Уложив этот тетраэдр в угол
параллелепипеда (рис. 11.3), мы найдём, что
где Л — высота, опущенная из вершины С на плоскость ABD,
а V — объём параллелепипеда.
Итак, объём тетраэдра, построенного на векторах а,
b и ?, равен тг | (5, К, ?) |.
436 Глава 11. Векторы в пространстве (продолжение)
Оказывается, справедливо более общее утверждение.
Теорема 11.4. Объём тетраэдра равен одной шестой
модуля смешанного произведения любых трёх
некомпланарных векторов, изображаемых рёбрами тетраэдра.
Доказательство. Пусть дан тетраэдр ABCD. Мы
только что доказали, что VXbqd = 7t\(DA, DB, DC)\. Осталось
7t
проверить справедливость равенств
(DA, DB, DC) = (ВА, DB, DC) = (СА, DB, DC).
Так как BA = DA- DB, slCA = DA- DC, то
(BA, DB, DC) = (DA - DB, DB, D$) =
= (DA, DB, Ш) - (DB, DB, DC) = (Ш, Шу DC)
и
(CA, DB, DC) = (DA - DC, DB, DC) =
= (Ш, M, D6) - (DC, DB, уШ) = (Ш, DB,Dd). D
Пример 11.3. На боковых рёбрах AAi, BB\ и СС\
призмы ABCA\B\C\ взяты точки М, N и К соответственно
так, что сумма длин отрезков AM, BN и СК равна длине
бокового ребра призмы. Точка Q —точка пересечения
медиан треугольника ABC. Найти отношение объёма призмы
к объёму тетраэдра QMNK.
Решение, Введём базис Ш, Ъ, ?}, где а = АВ, Ь = АС, ? =
= AAi (рис. 11.4). Пусть АМ=а?, В^ = /3?, СК = у?, где
а, /3, у — некоторые неотрицательные числа, причём по
условию а + /3 + у — 1. Тогда
MN = АВ + BN - AM = П + (5?- aZ= a + ((3 - а)д,
§ 11.2. Приложения произведений векторов
437
Рис. 11.4
(см. пример 3.2). Итак, в базисе {а, 6, ?}: MN= (1, О, /3 - а),
Ш= (О, 1, у - а), Щ= (|, J, -а).
Вычислим (MN, MK, MQ). Пользуясь формулой (11.2),
получаем
(MN, MK, MQ) =
1 0 р-а
О 1 у-а
1/3 1/3 -а
, 6, ?) =
Поскольку а + [3 + у = 1, находим отсюда, что
(Ш, Ш, MQ) - -|(а, Ь, ?).
Объём призмы равен т>|(5, Ь, ?)|, а объём тетраэдра QMNK
равен -^о I (3> &> ?) |» поэтому искомое отношение равно 9. □
С помощью векторного и смешанного произведений
можно вычислять расстояние от точки до плоскости и
расстояние между скрещивающимися прямыми.
Пусть в пространстве заданы плоскость а с известным
базисом {3, Ь}, точка А, лежащая в этой плоскости, и
точка М вне её, причём вектор АМ—И предполагается
известным (в том же базисе, что и а и Ъ). Отложим векторы ct и Ъ
от точки А (рис. 11.5).
438 Глава 11. Векторы в пространстве (продолжение)
М
Рис. 11.5
Рис. 11.6
Расстояние от точки М до плоскости а равно высоте
MMi параллелепипеда, построенного на векторах 3, Ь и ?,
следовательно,
р(М,сс) =
(11.3)
Пусть в пространстве заданы прямая I с направляющим
вектором 3, прямая т с направляющим вектором ft, точки
А и В9 лежащие на прямых I и т соответственно. Вектор
? = АВ предполагается известным (в том же базисе, что и
Зи ft), Отложим векторы а и ft от точек А и В
соответственно (рис. 11.6). Рассмотрим тетраэдр ABCD (D — конец
вектора 3, С — конец вектора ft). Воспользуемся результатом
примера 9.11, согласно которому Vabcd = -zobd sin (p, где
= BC, d = p(AD,BC), cp = Z(AD,BC). Это
равенство можно переписать в виде Vabcd = «^1^ х ^|* С другой
стороны, Vabcd — лК^> ^> *01- Приравнивая правые части
полученных равенств, мы найдём d. Итак,
p(l,m) =
\Sxb\
(Н.4)
Покажем, как с помощью выведенных нами формул
можно иначе решить примеры 4.10 и 4.9.
§ 11.2. Приложения произведений векторов
439
Ci|(r
Пример 11.4. В кубе ABCDA\BiC\D\ с ребром а найти
расстояние от центра О грани AA\D\D до плоскости BC\D.
Решение. Введём (правый ортонормированный) базис
{?ь ?2> ?зЬ где векторы ?i, ?2 и ?з сонаправлены с
векторами DA, DC и DDi соответственно (рис. 11.7). Поскольку
^ 9 в этом
базисе DB = (а, а, 0), 5сГ== (0, а, а), 1)5= (|»°» §)• Вы"
числим (DB, DC\, DO), пользуясь формулой (11.2):
(DB,DCi,DO) =
а а О
О а а
a/2 0 a/2
С помощью формулы (11.1) найдём DB x DC\:
а а О
О а а
Теперь для нахождения искомого расстояния можно
воспользоваться формулой (11.3):
а* а2у/3 >/з"
П
Пример 11.5. Вычислить расстояние между
диагоналями AD\ и DCi граней куба ABCDA\B\CiD\ с ребром а.
440 Глава 11. Векторы в пространстве (продолжение)
Решение. Рассмотрим тот же самый базис {?ъ ?2> 2з}>
что и в предыдущем примере (рис. 11.8). Мы уже знаем,
что в этом базисе DC\ - (0, а, а). Вычислим координаты
векторов AD[ и DDj: РР[= (0, 0, a), AD\ = (-а, 0, а) (так
как ADi = -DA + DDi). Найдём теперь (DD[9 DCi, AD[) и
l
(DDu DCU ADi) =
0 0a
0 a a
-a 0 a
= a-a2 = a3:
DCi x
в\ е2 #з
0 a a
-a 0 a
= a e\ — a
Для нахождения искомого расстояния воспользуемся
формулой (11.4):
p(ADuDC1) =
\РС[х
= -т=. п
с^3 Упражнение 11.5. Решите пример 9.5, используя формулы
(11.3) и (11.4).
§ 11.3. Уравнение прямой в пространстве
Малыш взял ещё один сандвич.
— Я прошу у вас прощенья,— сказал он,— но вас
там сколько?
— Сколько... нас?!
— Да, вас. Так сколько вас там?
— То есть как это... —оторопело соображая,
произнёс Блейк.—Один я и есть. Кто же ещё может
быть?
К. Саймак. Принцип оборотня
В этом параграфе мы начинаем изложение метода
координат в пространстве. Предварительно введём несколько
новых понятий, которые будут использоваться в
дальнейшем.
Пусть в пространстве зафиксирована некоторая точка О.
Тогда между точками М пространства и направленными
§ 11.3. Уравнение прямой в пространстве 441
отрезками ОМ есть, очевидно, взаимно однозначное
соответствие (т. е. каждой точке М соответствует
единственный направленный отрезок ОМ и наоборот). Вектор Гм,
изображаемый направленным отрезком ОМ, называется
радиусом-вектором точки М относительно точки О.
Если в пространстве кроме точки О выбран некоторый
базис {g\y g2> £з}> то каждой точке М пространства можно
сопоставить единственную упорядоченную тройку чисел —
координаты её радиуса-вектора в данном базисе. Верно
и обратное: каждая упорядоченная тройка чисел задаёт
единственную точку М пространства.
■ Определение. Аффинной системой координат в
пространстве называется совокупность точки и базиса.
Мы будем обозначать аффинную систему координат так:
{О, £i> g2, is}- Точка О называется началом координат,
прямые, проходящие через начало координат и
параллельные соответственно векторам|ь|2И?з> называются осями
координат и обозначаются Ох, Оу и Oz1^. Три плоскости,
определяемые осями координат, взятыми попарно,
называются координатными плоскостями. Они обозначаются
Оху, Оуг и Ozx в соответствии с тем, через какие оси
проходит рассматриваемая плоскость (Оху — через Ох и Оу
и т.д.).
В системе координат {О, jfi, i?2> £з} координатами точ-
киМ называются координаты (х, у, г) её радиуса-вектора
ОМ в базисе {^ь #2, is}-
Тот факт, что точка М имеет координаты2* (х, у, z), мы
будем обозначать так: М(х, у, z).
в^Упражнение 11.6. Докажите, что М(х, у, z) nMi(x\, y\, Z\) —
это одна и та же точка тогда и только тогда, когда х = х\, у = у\,
г = zi.
!)Ось Ох называется осью абсцисс, Оу — осью ординат, Ог — осью
аппликат.
2)Называемые соответственно абсциссой, ординатой и аппликатой
точки М.
442 Глава 11. Векторы в пространстве (продолжение)
Сформулируем одно важное утверждение, которым мы
часто будем пользоваться.
Теорема 11.5. Пусть в аффинной системе координат
{О, gi,g2, Из} заданы точки А(хиуи г\) и В(х2,У2>22).
Тогда в базисе {£ь#2>£з} вектор АВ имеет координаты
(х2 -
Доказательство. Очевидно, что АВ = ОВ — ОА. По
определению координат точки ОВ= (Х2, У2> *2) и ОА= (xi, z/i, 2\),
т. е. ОВ = x2g\ + У2ё2 + *2ёг и ОА = xigi + y\g2 + z\gz.
Поэтому
угёг + *2ёг) - (*iffi + У1Й2
(Уг - Уг)Й2
Следовательно, АВ = (Х2 — хи у2 — !/ь ^2 —
Итак, для того чтобы найти координаты вектора,
нужно из координат его конца вычесть координаты его
начала.
Пример 11.6. В некоторой аффинной системе координат
заданы точки А(х\, уь 2\) и В(х2, У2> *2)- Найти
координаты середины отрезка АВ.
Решение. Пусть М — середина отрезка АВ, О —начало
координат. Согласно формуле (3.1) ОМ— ^(ОА + ОВ), т.е.
ОМ = | (xigi + yi$2 + ziis + x2gi + J/2I2 + Z2I3) =
Если {хму Ум^ 2м) — координаты точки М, то
ОЙ = xMg\ + уме 2 +
Из единственности разложения вектора по базису вытекает,
что
Х\+Х2 „ У1+У2 „
Хм— о » УМ = о ' 2М=
§ 1L3. Уравнение прямой в пространстве 443
Замечание. Аналогично, используя формулу (3.2), можно
доказать, что если AM: MB = А, то
_ х\ + Хх2 „ __ У\ + Az/2 _ 2?i + Аг2
Пример 11.7. Лежат ли в одной плоскости точки А,
В, Си Д если они заданы в некоторой аффинной
системе координат следующим образом: А(1, 0, -2), В(-3, 4, 2),
С(0, 1,3),Д(2,-1,1)?
Решение. Из теоремы 11.5 имеем А§= (—4, 4, 4), А<5 =
= (-1, 1, 5) и AD= (1, -1, 3). Точки А, В, С и D лежат
в одной плоскости тогда и только тогда, когда эти векторы
компланарны. Так как
= -4 • (3 + 5) - 4 • (-3 - 5) + 4 ■ (1 - 1) -
-4 4 4
-115
1-13
= -32 + 32 = 0,
по теореме 11.3 векторы АВ, АС и AD компланарны, т.е.
ответ на заданный вопрос утвердительный. D
Обсудим теперь вопрос о задании пространственной
фигуры Ф способами, принятыми в методе координат.
Пусть в пространстве зафиксирована точка О. Будем
говорить, что фигура Ф задана векторным соотношением,
если точка М принадлежит фигуре Ф тогда и только
тогда, когда радиус-вектор точки М относительно точки О
удовлетворяет этому соотношению. Термин «соотношение»
понимается здесь в широком смысле: это любое условие,
о котором можно однозначно сказать, удовлетворяет ему
радиус-вектор ?м или нет. В частности, это может быть
алгебраическое уравнение (в смысле векторной алгебры),
например f=a или ?-а = 0, где а —известный
радиус-вектор. Это может быть неравенство, например \?\ ^ а, где а —
данное число.
Пусть теперь задана аффинная система координат.
Будем говорить, что фигура Ф задана в этой системе
координат некоторым соотношением, если точка М принадлежит
444 Глава 11. Векторы в пространстве (продолжение)
фигуре Ф тогда и только тогда, когда координаты точки М
удовлетворяют этому соотношению. Здесь снова под
соотношением понимается любое условие, о котором можно
однозначно сказать, удовлетворяют ему координаты
точки М или нет. Этим условием может быть и алгебраическое
уравнение, как, например, x2+y2 = z2, и неравенство,
скажем \х\ + \у\ + \г\ ^ 1, но это вовсе не обязательно.
Ниже мы будем иметь дело преимущественно с теми
фигурами, которые задаются алгебраическими (векторными
или скалярными) уравнениями или неравенствами.
Теперь всё готово для вывода уравнения прямой в
пространстве в различных формах.
Прямая однозначно задаётся указанием какой-либо
точки, лежащей на ней, и направляющего вектора этой
прямой. Разумеется, и направляющий вектор, и эту точку
можно выбрать бесконечным числом способов, но мы пока
будем считать, что они фиксированы.
Итак, пусть в пространстве фиксирована точка О и
задана прямая /, для которой известны направляющий вектор 3
и радиус-вектор го некоторой точки Мо Е I. Через ?
обозначим радиус-вектор произвольной точки Mel.
Точка М лежит на прямой / тогда и только тогда, когда
векторы f - ?о и а коллинеарны. Это имеет место в том
и только в том случае, когда существует действительное
число t такое, что ? - ?о — tft, или
(11.5)
Мы доказали, что прямую / можно задать
уравнением (11.5). Оно называется векторным параметрическим
уравнением прямой (параметром называется число t;
отметим, что параметр зависит от М, от ?о и от 3). Справедливо
и обратное утверждение: уравнение (11.5) при 3^5 задаёт
в пространстве прямую с направляющим вектором 3,
проходящую через точку с радиусом-вектором г*о- Для
доказательства достаточно провести рассуждения, доказывающие
прямое утверждение, в обратном порядке.
§ 11.3. Уравнение прямой в пространстве
445
Для вывода векторного уравнения прямой условие
коллинеарности векторов ? — ?о и а можно использовать и по-другому,
а именно, сославшись на свойство 2° векторного произведения
векторов. Тогда мы получим ещё одно векторное уравнение,
задающее прямую /:
(?-?<,) х 2= 5. (11.6)
ti& Упражнение 11.7. Докажите, что всякое уравнение вида (11.6)
при а ф 0 задаёт в пространстве прямую с направляющим
вектором а, проходящую через точку с радиусом-вектором ?о-
с^ Упражнение 11.8. Докажите, что прямую с направляющим
вектором 3 можно задать уравнением ?х а — Ь, где а-Ь = 0.
Докажите справедливость обратного утверждения.
и^ Упражнение 11.9. Докажите, что прямую, проходящую
через две точки с радиусами-векторами ?i и т*2> можно задать
уравнением 7 — ?\ +1{?2 — ^0-
Теперь мы выведем координатные уравнения прямой,
равносильные векторному параметрическому уравнению.
Пусть в пространстве задана аффинная система
координат. Сохраняя обозначения, введённые ранее, и полагая,
что точка Мо имеет координаты (яо, Уо> ^о), точка М —
координаты (х, у, г)у а вектор а — координаты (ах, ауу а2), мы
можем записать уравнение (11.5) в координатной форме:
(П.7)
Уравнения (11.7) называются параметрическими
уравнениями прямой в пространстве.
Пусть ах ф О, ау ф 0 и az ф О. Тогда, исключая параметр t
из уравнений (11.7), мы получим уравнения прямой в виде
X - Xp _ У - У0 _ 2-ZQ
ах ~ ац ~ az '
(11.8)
Уравнения (11.8) называются каноническими
уравнениями прямой в пространстве.
446 Глава 11. Векторы в пространстве (продолжение)
В случае, когда одна из координат вектора 2 равна нулю,
скажем ах = О, а две другие отличны от нуля, исключение
параметра t из уравнений (11.7) приводит нас к
каноническим уравнениям прямой в виде
х =
(аналогичные уравнения при ау = О или аг = О напишите
самостоятельно).
Если какие-то две координаты вектора а, например ах
и ауу равны нулю, то параметрические уравнения (11.7)
имеют вид
х = х0, у = Уо> 2 = 20 + a2t.
Задаваемая ими прямая параллельна оси аппликат, и
«исключение» параметра t из этих уравнений сводится к
утверждению о произвольности г. Поэтому в указанном случае
канонические уравнения прямой записывают в виде
х = х0, I/ = г/о-
Аналогично при ах = а2 = 0 получаем х = #0, 2 = го, а при
ау = аг = 0 имеем у = уо, г — 2$. Случай ах = ау = а2 = О
невозможен, так как вектор а ненулевой.
При решении конкретных задач необходимо уметь
переходить от одной формы записи уравнения прямой к другой
форме. Выше мы показали, как перейти от векторного
параметрического уравнения к параметрическим
уравнениям, а затем — к каноническим уравнениям. Обратный
переход осуществляется так: пусть прямая задана
уравнениями (11.8); положим
Х-Хр __ У-УО _ 2-2р = {
ах ау аг '
тогда
х = х0 + axt, y = yo + ciyt, 2 = 20 + a2t;
теперь если положить ? = (х, у, г), ?о = (лго, уо> 2о), 2 =
= (аХ9 ау, а2)у то ?=?
§11.4. Уравнение плоскости 447
Для удобства мы договоримся записывать канонические
уравнения прямой в виде (11.8), даже если одна или две
координаты направляющего вектора равны нулю. При этом,
если знаменатель какой-то дроби в (11.8) равен нулю, мы
будем полагать равным нулю и её числитель. Например,
запись 0
Х- 1 У + * 2
2 " 0 " 1
х — 1 z
означает, что —^— = у и у = -2.
Пусть даны точки A(xi,yi9zi) и В(#2, J/2» 2г)* Тогда
можно в качестве направляющего вектора прямой АВ взять
вектор (Х2 - Х1,У2-У1> 22- г{) и уравнения (11.8)
переписать в виде
х-хг _ у-уг _ 2-,
Х2 -Xi у2- У\
(11.9)
Эти уравнения называются уравнениями прямой,
проходящей через две данные точки. Здесь по-прежнему считается,
что если знаменатель какой-либо дроби равен нулю, то
равен нулю и её числитель.
В заключение отметим, что прямую в пространстве
можно задать и как линию пересечения непараллельных
плоскостей. Оказывается, уравнения (11.8) и (11.9) как раз
и соответствуют такому способу задания прямой. Но чтобы
понять это, надо научиться задавать уравнением плоскость.
Различным видам уравнения плоскости посвящен
следующий параграф.
§ 11.4. Уравнение плоскости
Теннисону снился математический мир. На этот
раз одно из уравнений показалось ему знакомым.
Да нет, не одно, а больше...
К. Саймак. Проект «Ватикан»
Пусть в пространстве с фиксированной точкой О
задана плоскость а. Любой ненулевой вектор, параллельный
448 Глава 11. Векторы в пространстве (продолжение)
этой плоскости, мы будем называть её направляющим
вектором. Плоскость однозначно задаётся двумя неколлине-
арными направляющими векторами и точкой (почему?).
Договоримся, что когда ниже речь будет идти о двух
направляющих векторах плоскости, они всегда будут
подразумеваться неколлинеарными.
Пусть известны направляющие векторы а и Ъ
плоскости а и радиус-вектор ?о точки Mq e ос. Через Р обозначим
радиус-вектор произвольной точки М еос.
Точка М лежит в плоскости а тогда и только тогда, когда
векторы г - ?о, а и Ь компланарны, т. е. в том и только в том
случае, когда существуют числа А и у такие, что Р — р0 =
= A3 + ytb (теоремы 3.1 и 3.2), или
(11.10)
Итак, мы задали плоскость а векторным уравнением
(11.10), которое называется векторным параметрическим
уравнением плоскости (числа А и fjt называются
параметрами; они зависят от М, ?$у 3, и Ь).
Как и в случае прямой, легко проверяется, что
справедливо и обратное утверждение: всякое уравнение вида
(11.10) при alftb задаёт плоскость с направляющими
векторами а и Ъ, проходящую через точку с
радиусом-вектором Fq.
Условие компланарности векторов ? — ?о> аиЬ, согласно
свойству 1° смешанного произведения, равносильно
равенству нулю смешанного произведения этих векторов. Тем
самым мы получаем ещё одно векторное уравнение
плоскости а:
(Г-Го,а,Ь)=О. (11.11)
Всякое уравнение такого вида при ctftb задаёт плоскость
с направляющими векторами й и Ь, проходящую через
точку с радиусом-вектором ?о-
§11,4. Уравнение плоскости 449
^Упражнение 11.10. Докажите, что плоскость, проходящую
через три точки, не лежащие на одной прямой, с
радиусами-векторами ?о> ?1 и ?2> можно задать уравнением
Пусть ненулевой вектор Я перпендикулярен плоскости а.
Такой вектор называется нормальным вектором этой
плоскости. Разумеется, нормальный вектор определён
неоднозначно (как по длине, так и по направлению). Тем не менее,
плоскость однозначно задаётся указанием какой-либо её
точки и какого-либо её нормального вектора (почему?).
Сохранив введённые ранее обозначения, отметим, что
точка М лежит в плоскости а тогда и только тогда, когда векторы
Т — ?о и ft ортогональны. Следовательно, плоскость а можно
задать уравнением
которое называется нормальным векторным уравнением
плоскости. Раскрывая скобки и обозначая известное число ?о • Я
через D, можно переписать уравнение (11.12) в виде
\Г-Я = Р.\ (11.13)
в^ Упражнение 11.11. Докажите, что всякое уравнение вида
(11.12) или (11.13) при Кф б задаёт плоскость,
перпендикулярную вектору Н, которая проходит через точку с
радиусом-вектором ?о в случае уравнения (11.12) и через точку
с радиусом-вектором -г-^ ■ Н в случае уравнения (11.13).
Пусть в пространстве заданы аффинная система
координат и точки Мо(хо, уъ> Zo), M(x, у, z). Пусть также заданы
векторы а— (ах, ау, аг),Ь=(Ьх,Ьу,Ьг) в базисе,
соответствующем данной системе координат.
Тогда мы можем переписать уравнение (11.10) в
координатной форме:
(11.14)
15 Зак 338Я
450 Глава 11. Векторы в пространстве (продолжение)
Эти уравнения, равносильные уравнению (11.10),
называются параметрическими уравнениями плоскости.
Уравнение (11.11) в координатной форме принимает вид
(11.16)
(см. теоремы 11.5 и 11.2). В силу отмеченной только что
равносильности уравнений (11.10) и (11.11) всякое
уравнение вида (11.14) или (11.15) задаёт плоскость.
о^ Упражнение 11.12. Докажите, что уравнение плоскости,
проходящей через три данные точки (см. упражнение 11.8), в
координатной форме можно записать так:
X —
— Хо Х2~ Хо
у-уо Уг-Уо У2- Уо
Z — Zq Z\ — Zq Z2 — Zq
= 0,
где (х, у у z) — координаты произвольной точки плоскости, а
(*ь Уь *i) — координаты данных точек (i = 0, 1, 2).
Выведем теперь уравнение плоскости, которое принято
называть общим уравнением.
Теорема 11.6. Всякая плоскость в пространстве может
быть задана в аффинной системе координат линейным
уравнением Ах + By + Cz + D = Q,B котором коэффициенты
А, В и С не равны нулю одновременно; и обратно, всякое
уравнение такого вида, в котором А2 + В2 + С2 Ф 0, задаёт
в аффинной системе координат в пространстве плоскость.
Доказательство. Первая часть утверждения теоремы
следует из того, что уравнение плоскости (11.15) можно
записать в виде Ах + By + Cz + D = 0 (А2+В2 + С2Ф 0).
Действительно, раскрывая определитель, стоящий в левой
части указанного уравнения, получаем
(х - х0)
- (у - уо)
ах а2
Ьх Ьг
~ 20)
ах ау
Ьх Ьу
= 0.
§ 11.4. Уравнение плоскости
451
Обозначив через А, Б, С и D числа
ау
by
аг
Ьг
ах
ьх
аг
bz
»
ах
ъх
ау
by
и -
- Byq - Czq
соответственно, приходим к линейному уравнению Ах +
+ By + Cz + D = О, в котором А2 + В2 + С2 ф 0, так как
в противном случае уравнению (11.15) удовлетворяет
любая точка (х, у, z) пространства, что невозможно.
Докажем вторую часть утверждения теоремы. Пусть
дано уравнение Ах + Ву + Cz + D = 0, причём А2 +В2 + С2 ф 0.
Без ограничения общности можно считать, что АфО.
Рассмотрим плоскость, проходящую через точку ( —-р
с направляющими векторами (-£, А, 0) и (-С, 0, А)
(почему эти векторы неколлинеарны?). Такая плоскость
существует и единственна. Запишем уравнение этой плоскости
в виде (11Л5):
x + D/A у z
-В АО
-С 0 А
т. е.
=0,
Деля обе части этого уравнения на А Ф 0 и раскрывая
скобки, получаем, что Ах + By + Cz + D — 0. Тем самым
мы указали плоскость, которая задаётся данным линейным
уравнением. □
Доказательство второй части теоремы 11.6 порождает
естественный вопрос: каким образом были угаданы
направляющие векторы плоскости? Мы сейчас дадим ответ на
более общий вопрос: при каком необходимом и достаточном
условии вектор (ах, ау, аг) является направляющим
вектором плоскости, заданной уравнением1*
^Ниже мы будем опускать слова «заданной уравнением * и писать
«плоскость Ах + By 4- Cz + D = 0».
452 Глава 11. Векторы в пространстве (продолжение)
Теорема 11.7. Ненулевой вектор (ах, ау, а2) является
направляющим вектором плоскости Ах + By + Cz + D = О
(А2 + В2 + С2 ф 0) тогда и только тогда, когда Аах + Вау +
+ Са2 = 0.
Доказательство. Вектор (аХ9 ау, аг) параллелен
плоскости тогда и только тогда, когда вместе с произвольной
точкой Мо(хо,уо, zo) данной плоскости в этой плоскости
лежит также точка М\ (хо + ах, у о + ау, zo + аг).
Следовательно,
ах) + В(у0 + ау) + C(z0 + az)+D = O,
т.е.
(Ах0 + By о + Czo + D) + (Аах + Вау + Саг) = 0.
Так как точка Мо лежит в данной плоскости, Ахо + By о +
+ Czo +D = 0. Значит, Аах + Вау + Са2 = 0. Остаётся
вспомнить, что направляющий вектор плоскости должен быть
ненулевым. □
Теперь уже нетрудно проверить, что каждый из
векторов (—Б, А, 0) и (—С, 0, А) при А ф 0 ненулевой и
может быть взят в качестве направляющего для плоскости
= 0: А • (-Б) +БА + С0 = 0иА. (-C) +
Используя общее уравнение плоскости
—1 (иле)
и предполагая дополнительно, что все числа А, Б, С, D
отличны от нуля, получим ещё одно уравнение, равносильное
уравнению (11.16):
(11.17)
где а — —-ту Ь = — ■=, с = — 77- Это уравнение называется
А. 15 G
уравнением плоскости в отрезках. Происхождение этого
названия будет пояснено ниже.
§11.5. Некоторые примеры 453
Отметим, что в конкретных задачах часто приходится
задавать уравнением плоскость, проходящую через три точки
с известными координатами (см. упражнение 11.12). Это
уравнение после раскрытия определителя, стоящего в его
левой части, превращается в общее уравнение плоскости.
Ниже мы в основном будем иметь дело с плоскостями,
заданными общими уравнениями.
В заключение вернёмся к уравнению прямой. Как было
сказано выше, прямую можно задать как линию
пересечения двух непараллельных плоскостей. В частности,
система двух общих уравнений плоскости А\х + В\у -\-C\z + D\ =
= О, А^х + В^у + С22 +1>2 = 0 (при условии, что
коэффициенты при одноимённых переменных не пропорциональны —
см. ниже пример 11.11 и замечание к нему) задаёт в
пространстве прямую. Нетрудно видеть, что уравнения (11.18)
и (11.19) по сути дела задают прямую именно в таком виде.
§ 11.5. Некоторые примеры
Поясняю для прессы на доступном
ей примере.
А. и Б. Стругацкие. Понедельник начинается в субботу
В этом параграфе мы приведём примеры решения
типовых задач о прямых и плоскостях в пространстве.
Начнём с задач, связанных с векторными уравнениями.
Пример 11.8*. Записать уравнение: а) прямой ? х а = Ь
в виде f*=J*o + at; б) плоскости ? =?о + Ла + цЬ в виде ?-Й = £>.
Решение, а) Вектор а в уравнении г х а = & —
направляющий вектор прямой. Нам остаётся найти радиус-вектор т*о
какой-либо точки этой прямой, зная векторы а и Ь.
Вектор г*о удовлетворяет уравнению ? х а = Ь, т.е. ?о х а = Ъ.
Следовательно, ?о -LЬ, т. е. ?о *b = 0. Будем искать вектор ?о>
перпендикулярный также и вектору 3: Го -5 = 0. Значит,
?о || 2 х 6, или Fo = Я • (ct х $) ♦ Итак,
454 Глава 11. Векторы в пространстве (продолжение)
Следовательно, .... -> ... .-.
|Л| ■ \а\ • \о\ • \а\ = \Ъ\
(углы между ?о> Зиб прямые), т.е.
Поэтому мы можем взять А = г^ и Fo = ,^2 - Отсюда сразу
получаем ответ:
б) Нормальный вектор плоскости можно взять в виде
Я = U х Ъ. Умножая обе части уравнения ? = ?$ -\- Х& + уЪ
скалярно на Я, получаем, что
т. е.
Пример 11.9*. Найти радиус-вектор точки пересечения
прямой Т — ?о + 2* с плоскостью ?-ft = D, если 3, • Я ^ 0.
Решение. Условие 3-Я^О означает, что направляющий
вектор прямой и нормальный вектор плоскости не
ортогональны, т. е. прямая не параллельна плоскости и не лежит
в ней. Поэтому прямая и плоскость действительно имеют
единственную общую точку. Пусть т*\ — радиус-вектор этой
точки. Тогда ?i = Fq + ctti и f\ - ft = D. Подставляя ?i из
первого уравнения во второе, находим
Следовательно,
Пример 11.10*. Даны точка М\ (?\) и плоскость ?-H~D.
Найти радиус-вектор: а) проекции Mq точки Mi на
плоскость; б) точки Мг, симметричной точке М\ относительно
плоскости.
§11.5. Некоторые примеры 455
Решение, а) Пусть ?р — радиус-вектор точки Мо- Тогда
MoMi = f*i — т*о» Вектор MoMi коллинеарен нормальному
вектору ft плоскости, т.е. существует число А такое, что
MoMi = Xft. Итак, ?i — т*о = Xft. Умножим это равенство
скалярно на ft:
Так как точка Мо лежит в плоскости, ?о - Н = D.
Следовательно,
т. е.
и, значит,
б) Пусть т*2 — радиус-вектор точки М2. Так как
M2Mi = 2ЩМ[ = 2ХЙ = 2fl'*~D • Я
и
М2М\ = 7*1 — ?2>
мы получаем
Другие примеры подобных задач вы найдёте в конце
этой главы, а мы перейдём к задачам, связанным с
координатными уравнениями.
Пример 11.11. Доказать, что вектор
А\ В\ С\
А2 В2 С2
является направляющим вектором прямой
= 0, А2х + В2у + C2z + D2 = 0.
456 Глава 11. Векторы в пространстве (продолжение)
Вх Сх
в2 с2
-Bt
А2 С2
+ ct
А2 В2
Решение. Нетрудно проверить, что при i= 1, 2
выполняются равенства
Л Г* Л Т>
= 0.
Согласно теореме 11.7 это означает, что вектор а является
направляющим вектором плоскостей AiX + Bty + CiZ + Dt = 0,
i = 1, 2, а следовательно, и направляющим вектором их
линии пересечения (следствие 3 из теоремы 2.2), если этот
вектор ненулевой.
Покажем, что если а = б, то рассматриваемые плоскости
параллельны или это одна и та же плоскость.
Действительно, условие 3 = 6 равносильно тому, что
Вх d
В2 Со
=
At d
А2 С,
=
АХ Вх
А2 В2
т.е.
- A2Ci =
-О,
- A2Bi = 0,
следовательно, числа А2 и А\, В2 и Ви С2 и С\
пропорциональны, т.е. существует такое число Л^О, что А2 = \А\У
В2 = ХВ\ иС2 = ЛС\. Если к тому же D2 = AZ>i, то уравнения
AiX + Biy + C\z + D\ = 0 и А2х + В2у + C2z + D2 = 0
равносильны, т.е. задают одну и ту же плоскость. Заметим также,
что координаты (а, (5, у) направляющих векторов обеих
плоскостей удовлетворяют одному и тому же уравнению
(теорема 11.7). Это означает, что одна и та же пара
векторов может быть принята за направляющие векторы обеих
плоскостей. Если D2^XD\, то плоскости различны и
параллельны. □
Отметим, что попутно мы доказали достаточное
условие параллельности плоскостей, заданных в аффинной
системе координат общими уравнениями: если А2 = ААь
В2 = \В\ и С2 = ACi, D2 ф XD\, то плоскости A\x + B\y + C\z +
+ D\ = 0 и А2х + В2у + C2z + D2 = 0 параллельны (если же
§ 11.5. Некоторые примеры 457
и 1>2 = ^Оъ то эти уравнения задают одну и ту же
плоскость). Оказывается, это условие является и необходимым.
Однако доказательство этого факта несколько громоздко,
и мы проведём его в следующем параграфе лишь в одном
важном частном случае.
Пример 11.12. Записать канонические уравнения
прямой x-i/ + 2z + 4 = 0, 2x-y-z-3 = 0.
Решение. Направляющий вектор а найдём,
воспользовавшись результатом примера 11.11:
Ё\ $2 ёг
1-12
2 -1 -1
= (3,5,1).
Координаты точки, лежащей на прямой, найдём,
положив zq = 0: хо - уо + 4 = 0, 2#о - Уо - 3 = 0, откуда х0 = 7,
i/o = ll- Искомое каноническое уравнение выглядит так:
х-7 У-П z
3 5 1
(см. уравнение (11.8)). D
Пример 11.13. Найти координаты точки пересечения
прямой
х-1 __ l __ г
1 " 2 3
и плоскости 2х + у + z — 9 = 0.
Решение. Запишем параметрические уравнения данной
прямой: положим
х-1 _ У _ z
~Т~ " 2 ~ 3 "" Г'
откуда х = 1 +1> у = 2t, z = 3t. Подставив х, у и z в уравнение
плоскости, найдём значение параметра to,
соответствующее искомой точке пересечения:
2 + 2*о + 2*о + 3*о-9 = О, т.е. to = 1.
Тогда координаты точки пересечения суть хо = 1 + *о = 2,
3. □
458 Глава 11. Векторы в пространстве (продолжение)
Пример 11.14. Написать уравнение плоскости,
проходящей через точку (3, 7, 2) и параллельной прямым
х-1 _ У + 2 2~4
4 ~ 1 2
И *-3 = У-2 г
=
5 3 1 '
Решение. Искомая плоскость параллельна
направляющим векторам (4, 1,2) и (5, 3, 1) данных прямых.
Следовательно, эти векторы могут быть взяты за
направляющие векторы этой плоскости. Воспользовавшись
уравнением (11.15), получаем, что
х-3 у~1 z-2
4 1 2
5 3 1
= 0,
т. е. 5* - 6у - lz + 41 = 0. □
Различные примеры подобного рода вы найдёте среди
задач в конце этой главы. Мы же в качестве резюме
отметим, что при решении задач, связанных с координатными
уравнениями прямых и плоскостей, часто удобно
проводить рассуждения в терминах направляющих и
нормальных векторов. Например, «прямая параллельна плоскости,
следовательно, её направляющий вектор ортогонален
нормальному вектору плоскости», «прямая перпендикулярна
плоскости, следовательно, её направляющий вектор
ортогонален направляющим векторам плоскости (коллинеарен
нормальному вектору плоскости)» и т.п. Следует также
иметь в виду, что произвол, связанный с выбором
нормальных и направляющих векторов, а также точек,
принадлежащих прямым и плоскостям, приводит к отличающимся друг
от друга внешне, но равносильным уравнениям и
системам уравнений. Поэтому далеко не всегда следует искать
ошибку в решении, если полученные вами уравнения не
совпадают с уравнениями, приведёнными в задачнике в
качестве ответа. Достаточно убедиться, что эти уравнения
задают одно и то же множество точек.
§ 11.6. Декартова система координат 459
§ 11.6. Декартова система координат
Что такое полярный медведь? — Это
прямоугольный медведь после замены координат.
Б. Уайт
В § 11.3 мы назвали аффинной системой координат
совокупность точки и базиса. Если этот базис ортонормирован-
ный, то соответствующая система координат называется
декартовой (или прямоугольной). Для удобства
дальнейшего изложения договоримся всюду ниже, если не оговорено
обратное, считать ортонормированный базис правым.
Разумеется, всё, что было ранее доказано для
произвольной аффинной системы координат, остаётся в силе и для
декартовой. Однако декартова система координат обладает
рядом специфических особенностей, которые мы сейчас
и обсудим.
Теорема 11.8. В декартовой системе координат
расстояние между двумя точками равно квадратному корню из
суммы квадратов разностей их одноимённых координат.
Доказательство. Пусть точки Аи В имеют кординаты
(*Ау Уа> %а) и (хв> Ув> ?в) соответственно. По теореме 11.5
А& = (хВ - ХАу уВ - уА, 2В - 2А),
а по теореме 3.5
АВ2 = (хв - хА)2 + (ув - уА)2 + (zB - zA)2.
Следовательно,
АВ = у/Ж2 = у/(хв - хА)2 + (г/в - Уа)2 + (гв - *А)*. □
Теорема 11.9. Пусть в декартовой системе координат
плоскость а имеет уравнение Ах + By + Cz + D = 0. Тогда
вектор Я= (А, Б, С) является нормальным вектором этой
плоскости.
Доказательство. Пусть U= (ax, ayjaz) nb=(bx,by,b2)
суть направляющие векторы плоскости а. По теореме 11.7
460 Глава 11. Векторы в пространстве (продолжение)
Аах + Вау + Саг = 0 и АЬХ + ВЪу + СЪг = 0. Следовательно,
ft • а = 0 и Я • b = О, т. е. ft ±3 и ft ±b. Значит, по
теореме 4.1 Н±а. Заметим, наконец, что Я^б, так как иначе
А2 + В2 + С2 = 0, что невозможно (уравнение Ах + By + Cz +
+ D = 0 не задаёт плоскость). □
В декартовой системе координат легко доказывается
критерий параллельности плоскостей, сформулированный
в предыдущем параграфе. Действительно, плоскости А\х +
+ В\у + C\z + D\ = 0 и A<lx + В2У + C2Z + D2 = 0 параллельны
или являются одной и той же плоскостью тогда и только
тогда, когда их нормальные векторы коллинеарны, т. е.
когда существует такое число А ф 0, что А2 = AAi, В2 = А-Вь
Если и £>2 = ADi, то плоскости А\х + В\у + C\z + D\ = 0 и
А2Х + В2У + C2Z + Z>2 = 0 — это одна и та же плоскость
(уравнения равносильны, так как А ф 0). Если же 1>2 ф А£>ь то
данные плоскости не имеют общих точек и, следовательно,
параллельны.
Столь же несложно доказывается и критерий
перпендикулярности двух плоскостей.
ЧЗГ Упражнение 11.13. Докажите, что плоскости А\х + В\у + С\2 +
+ D\ = 0 и Аг* + В2У + Сг2 +1>2 = 0 перпендикулярны тогда
и только тогда, когда А\Аг + В\Вч + С1С2 = 0.
Вернёмся к примеру 11.11. Его результат в декартовой
системе координат нисколько не удивителен:
направляющий вектор линии пересечения двух плоскостей можно
взять в виде векторного произведения нормальных
векторов этих плоскостей. Если плоскости имеют уравнения
А[Х + Bty + Ctz + Dt = 0, i = 1, 2, то согласно теоремам 11.1
и 11.9 направляющий вектор их линии пересечения имеет
вид
А2 B2 С2
В аффинной системе координат это выражение для
направляющего вектора прямой не имеет ничего общего с вектор-
§ 11.6. Декартова система координат 461
ным произведением векторов (Ai,Bi,Ci)9 i=l, 2, кроме
внешнего вида (так как теорема 11.1 неверна в
произвольном базисе).
Теперь мы выведем некоторые формулы для
вычисления углов и расстояний между прямыми и плоскостями,
заданными своими уравнениями в декартовой системе
координат.
Пусть прямые 1\ и h заданы уравнениями
х - хо у-Уо z-zq
и
х — Х\ У — У\ 2 —;
Ъх by Ьг
Тогда угол ср между этими прямыми либо равен углу между
их направляющими векторами, либо дополняет его до 180°,
следовательно,
(11.18)
так как по теореме 3.5
й'Ъ = ахЬх + йуЬу + о2&г,
U2 = 0,1 + 0,1 + 0,*,
Р = Ь2х + Ь2у+Ъ2г.
Угол $ между прямой
Х- Хр _ У - У 0 __ Z-2Q
ах ау а2
и плоскостью
Ах + By + Cz + D = 0
удовлетворяет соотношению $ — 90° - ср, где ср — угол
между данной прямой и перпендикуляром к плоскости.
Следовательно, sin # = cos <p, a cos ср вычисляется по
формуле (11.18), в которой вектор £= (Ьх, Ъуу Ьг) заменяется
вектором Н= (А, Ву С) (так как нормальный вектор плоскости
462 Глава 11. Векторы в пространстве (продолжение)
является направляющим вектором перпендикуляра к ней).
Окончательно получаем
(11.19)
Угол у между плоскостями А\х + В\у + C\z + D\ — 0 и
А2Х + В2У + C%z + Z>2 = 0 равен углу между нормальными
векторами Н\ = (А\9 В\, С\) и Яг = (Аг, Вг> Сг) этих
плоскостей или дополняет его до 180°. Следовательно,
(11.20)
Расстояние от точки Mq(jco, уо> 2о) до плоскости а,
заданной уравнением Ах + By + Cz + D = 0, можно вычислить
следующим образом. Если Я — единичный нормальный
вектор плоскости, a Mifoi, у\, z{) — проекция точки Мо на
плоскость, то р(Мо, ее) — \Н - М\Мо\. В качестве Я можно
взять вектор
ABC
-21). Итак,
+B(y0 -
p + Bi/o + Сг0 -
+ Вуг + C2?i) |
. =
Так как точкаМх лежит в плоскости a, Axri +By\+Cz\ +D =
= 0, т.е. — (Ах\ + Byi +Cz\) =D. Окончательно получаем,
что
(11.21)
§ 11.6. Декартова система координат 463
Расстояние между прямыми
х-хо У~Уо _ z-zq
И
ax ciy
x-xi У-У\
bx by
аг
2-21
ьг
ставив в формулу (11.4)
а= (аХУ ау, а
Ь= {bx> by, b,
(xi - *о, У\ - Уо
г),
г),
hZi-Zo)
(почему?), но раскрывать получающиеся определители мы
не будем, поскольку окончательная формула в общем виде
выглядит весьма громоздко.
С помощью полученных формул можно иначе оформить
решения примеров 4.9, 4.10 и 4.111*.
Пример 11.15. В кубе ABCDA\B\C\D\ с ребром а найти:
а) угол и расстояние между прямыми AD\ и DC\; б)
расстояние от центра грани AA\D\D до плоскости BC\D\ в) угол
между прямой BD\ и плоскостью BC\D; г) угол между
плоскостями AA\D\ и BC\D.
Решение. Введём декартову систему координат с
началом в точке D и базисом {?ь ?2> ?з}> гДе векторы t\% ?2> ?з
имеют единичные длины и сонаправлены соответственно
с векторами ДА, D& и DD\ (см. рис. 11.8). В этой
системе координат вершины куба имеют координаты: А (а, 0, 0),
В(а, а, 0), С(0, а, 0), D(0,0,0), Аг(а, 0,а), Bi(a,a,a),
Ci (0, а, а) и Di (0, 0, а).
а) Направляющий вектор прямой АР\ — вектор AD\ =
= (-a, 0, а), а прямой £>Ci — вектор DC[ = (0, a, a). Эти
прямые проходят через точки А и D соответственно, поэто-
1}Хотя этот способ в данном случае и не является самым коротким,
мы приводим его в качестве иллюстрации метода координат и для
сравнения с другими методами решения, которые были изучены ранее.
464 Глава 11. Векторы в пространстве (продолжение)
му канонические уравнения этих прямых имеют вид
. х~а - У. - *
: -а " 0 ~ а'
• - = ^ = -
" 0 ~~ а "" а*
Угол между прямыми найдём по формуле (11.18):
21 Л2 1
cos ср =
2'
следовательно, ^> = 60о.
Для нахождения расстояния между прямыми
воспользуемся формулой (11.4), где нужно положить 3— (—а, 0, а),
&- (0, а, а), ?=DA= (а, 0, 0).
Имеем
-а
0
0
а
(а
а
а
—.
?) =
-а
0
а
+ а
0
а
0
,2г
а
а
0
2 "
?3 = (-а2,а2,-а2),
|(3, Ь,?)| = а3, |3 х Ь| = v/(-o2)2 + (а2)2 + (-а2)2 = а2^,
з Л
следовательно, p(AD\y DC\) = — = -=.
а2у/3 \/3
б) Координаты точки О — центра грани AA\D\D (см.
рис. 11.7) равны (§, 0, § ); уравнение плоскости BC\D име-
ет вид (см. упражнение 11.10; эта плоскость проходит через
три точки: (0, 0, 0), (а, а, 0) и (0, а, а))
= 0,
т.е. а2х-а2у + а22 = 09 илих~у + г = 0. По формуле (11.21)
X
а
0
У
а
а
2
0
а
§ 11.6. Декартова система координат 465
в) Направляющий вектор прямой BD\ — вектор BD\ =
= (-а, -а, а). Искомый угол $ находим по формуле (11.19):
sin $ =
т.е. # = arcsin «.
г) Уравнение плоскости AA\D\\ y = 0. По формуле (11.20)
находим искомый угол у:
'
y/S
т.е. r = arccos-7=. П
V3
Рассмотрим плоскость а и зафиксируем какой-нибудь её
нормальный вектор Я. Отложим его от точки, лежащей в плоскости.
Назовём ориентированным расстоянием от точки Mq до
плоскости а расстояние от неё до этой плоскости, взятое со знаком « + »,
если точка Мо лежит в том же полупространстве относительно
плоскости а, что и конец вектора Я, и со знаком «-» в противном
случае. Если плоскость а имеет уравнение Ах + By + Сг + D — 0,
ft = (At В, С), а точка Мо имеет координаты (дго, #<ъ 2о)> то
ориентированное расстояние р(Мо, ос) равно
Ахо + Вур + Czp + D
VA2+B2 + C2
(это сразу следует из формулы (11.21)).
Для любых двух точек М\ £ а и М2 £ а знаки чисел р (Mi, a)
и р (Мг, ос) одинаковы тогда и только тогда, когда точки М\ и Мг
лежат по одну сторону от плоскости а. Кроме того, р(М, а) > 0
тогда и только тогда, когда точка М лежит в том же
полупространстве, что и конец вектора Я= (А, Б, С), если он отложен от
точки, лежащей в плоскости ос.
Приведённые только что соображения помогают при решении
задач о нахождении уравнений биссекторных плоскостей1*.
!)В § 5.1 мы определили биссектор двугранного угла (как
полуплоскость). Две пересекающиеся плоскости образуют две пары
вертикальных двугранных углов. Под биссекторной плоскостью пары
вертикальных двугранных углов мы будем понимать плоскость, деля-
466 Глава 11. Векторы в пространстве (продолжение)
Пример 11.16*. Написать уравнение биссекторной плоскости
пары вертикальных двугранных углов, образованных
плоскостями 8л: + 4i/ + 2-1-1 = 0 и 2х - 2у + z + 1 = 0, если известно, что
точка (1, 1, 1) лежит в одном из углов этой пары.
Решение. Из теоремы 5*2 о биссекторе двугранного угла
вытекает, что пара взаимно перпендикулярных биссекторных
плоскостей вертикальных двугранных углов, образованных двумя
пересекающимися плоскостями, есть геометрическое место точек,
равноудалённых от этих плоскостей. Согласно формуле (11.21)
это ГМТ задаётся уравнением
|2*2y + z + l|
' (11-22)
Раскрывая модули, легко убедиться, что это уравнение задаёт
две плоскости, но нам необходимо выбрать одну из них.
Отложим нормальные векторы /?i = (8, 4, 1) и п*ъ = (2, —2,1)
данных плоскостей от точек, лежащих в этих плоскостях.
Заметим, что
И
• 2-1-2-1 + 1 + 1 ^п
Это означает, что точка (1, 1, 1) лежит в том двугранном угле,
который является пересечением полупространств, ограниченных
данными плоскостями, в которых лежат концы векторов Н\ и Яг.
В этом же двугранном угле и в угле, вертикальном ему, по
условию должна лежать искомая биссекторная плоскость.
Следовательно, в уравнении (11.22) нужно раскрыть модули, взяв
одинаковые знаки в левой и правой частях, тогда мы получим
уравнение нужной плоскости:
8* + 4# 4- г + 1 _ 2x-2y + z+l
9 ~ 3 '
т.е.
х + Ьу -2-1 = 0. □
Иногда возникает необходимость определить, является ли
данный двугранный угол острым или тупым. Это можно сделать
на основании следующего утверждения.
щую каждый из этих углов на два равных двугранных угла (или, что
то же самое, объединение биссекторов каждого из двугранных углов,
образующих эту пару).
§11.7. Уравнение сферы 467
Теорема 11.10. Двугранный угол, образованный
пересекающимися и не перпендикулярными плоскостями А\х + В\у +
+ С\г + D\ = 0 и Агл: + Вгу + Сг-г + £>2 = О, содержащий точку
(#<ь Уо> zo), является острым (тупым) тогда и только тогда,
когда число
(АхА2
x (A2x0 4- B2f/o + C2z0
отрицательно (положительно).
в^ Упражнение 11.14*. Докажите теорему 11.10.
Пример 11.17*. Написать уравнение биссекторной плоскости
пары острых вертикальных углов, образованных плоскостями из
примера 11.16.
Решение. Так как
(8 • 2 + 4(-2) + 1-1)(8-1 + 4-1 + 1 + 1)(2-1-2.1 + 1 + 1)>0,
по теореме 11.10 тот двугранный угол, который содержит точку
(1, 1, 1), является тупым. Поэтому мы должны написать
уравнение биссекторной плоскости пары двугранных углов, смежных
с теми, уравнение биссекторной плоскости которых мы нашли
в примере 11.16. Для этого достаточно раскрыть модули в
уравнении (11.22), взяв различные знаки в левой и в правой частях:
8х + 4у + г + 1 _ 2х - 2у + z + 1
9 " 3
7x-y+2z + 2 = 0. □
§ 11.7. Уравнение сферы
Пусть в пространстве задана сфера S(O, if). По
определению точка М принадлежит этой сфере тогда и только
тогда, когда 0M = R. Если в декартовой системе координат
центр О сферы имеет координаты (#o, Уо> 2о), а точка М —
координаты (x,y,z)y то по теореме 11.8 условие OM — R
равносильно условию
или
' " = = ^ (11.23)
Это и есть уравнение, задающее сферу S.
468 Глава 11. Векторы в пространстве (продолжение)
ю^ Упражнение 11.15. При каком необходимом и достаточном?
условии уравнение
Ах2
является уравнением сферы?
в^ Упражнение 11.16. Докажите, что неравенство
(* - *о)2 + (У - Ы2 -И* ~ 20)4 Я*
задаёт шар с центром в точке (хо, Уо> zo) и радиусом R.
Используя уравнение сферы, можно дать другие
доказательства теоремы 10.2 (о сечении сферы плоскостью)
и теоремы 10.9 (о пересечении двух сфер). Изложим идеи
этих доказательств. Пусть d — расстояние от центра О
сферы S(O,R) до плоскости а. Выберем декартову систему
координат так, чтобы точка О имела координаты (0, 0, d),
а плоскость а — уравнение z = 0 (как это сделать?). Тогда
сфера имеет уравнение х2 + у2 + (z - d)2 = i?2, а пересечение
сферы и плоскости задаётся системой уравнений
В случае d < R уравнение х2 + у2 = R2 - d2 задаёт окружность
в плоскости z = 0. Это доказывает теорему 10.2. Если даны
две пересекающиеся сферы Si(Oi,JRi) и S2(O2,i?2)>
Центры которых имеют координаты (а, 0, 0) и (Ь, 0, 0), а ф Ь,
соответственно (как для этого нужно выбрать систему
координат?), то пересечение этих сфер задаётся системой
уравнений
Точки, координаты которых удовлетворяют этой системе,
таковы, что их координаты удовлетворяют и разности
уравнений системы, т.е. уравнению
2(& - а)х = Д? - Д| - а2 + Ь2,
§11.7. Уравнение сферы 469
которое является уравнением плоскости. Тем самым мы
свели утверждение теоремы 10.9 к утверждению теоремы 10.2.
В связи с теоремой 10.2 представляет интерес задача об
определении центра и радиуса окружности, которая
является пересечением плоскости и сферы. Покажем, как эта
задача решается методом координат.
Пусть плоскость
Ах + By + Cz + D = 0
пересекает сферу
(х - х0)2 +(у- г/о)2 + (* - 20)2 = R2.
Центр Oi(#i, i/i, z\) окружности, являющейся их
пересечением, есть точка пересечения с плоскостью
перпендикуляра U проведённого к ней через центр О сферы. В качестве
направляющего вектора прямой I можно взять нормальный
вектор Н = (А, В, С) плоскости. Удобно записать
уравнения прямой / в параметрической форме (11.7): х — хо +At,
y = yo + Bt, z — Zo + Ct, а затем подставить эти выражения
для х, у и z в уравнение плоскости. Тем самым мы
найдём значение параметра *ь соответствующее точке О\ 6 I
(см. пример 11.13):
_ Ахр + By о + Cz0 + D
Тогда х\ = х0 + Atu У1=Уо + Btu г\ = z0 + Ct\. Радиус г
окружности легко найти по теореме Пифагора:
где
4-Bj/o
(по формуле (11.21). Разумеется, мы предполагаем, что
В случае, когда i?=ОО\, плоскость касается сферы (г = 0,
(#ь i/i, z\) — координаты точки касания).
470 Глава 11. Векторы в пространстве (продолжение)
Поставим теперь задачу написать уравнение плоскости,
касающейся сферы
(х- х0)2 + (у-уо)2 + (г- г0)2 = R2
в точке (#i, J/1, z\). Согласно теореме ЮЛ в качестве
нормального вектора искомой плоскости можно взять вектор
Я = (XI - Х0, У1-УО,21- 20).
В силу того, что плоскость проходит через точку (х\, yi, z\),
её уравнение имеет вид
(у\ - уо) (У - Уг) + (*1 - 20) (г - z\) = 0 &
i - х0) ((х - х0) - (*i - х0)) + (j/i - уо) ((у - уо) -
У1 - Уо)) + (zi - zo) ((z - z0) - (zi - zo)) = 0 <£>
- x0) (x - x0) + (j/i - уо) (У - Уо) + (zi - zo) (z - 20) =
- (X! - X0)2 + (У1
Так как точка (jci, j/i, 21) лежит на сфере, правая часть
последнего уравнения равна i?2. Итак, касательная плоскость
имеет уравнение
- хо)(х - х0) + (у\ - у о) (У - Уо) + (zi - zo)(z - zo) = R2.
(11.24)
Если координаты точки касания заранее неизвестны, то
следует воспользоваться определением касательной
плоскости к сфере. Будучи переведённым на алгебраический язык,
оно означает, что система, составленная из уравнения
плоскости и уравнения сферы, имеет единственное решение.
Пример 11.18. Написать уравнение плоскости,
касательной к сфере
если известно, что она проходит через ось апплцкат. Найти
также координаты точки касания.
§11.7. Уравнение сферы 471
Решение. Заметим сначала, что искомая плоскость не
может иметь уравнения у = О, так как система уравнений
не имеет решений. Поэтому уравнение искомой плоскости
имеет вид х = ау. Параметр а определим из условия
единственности решения системы уравнений
\х = ау.
Подставляя х = ау в первое уравнение и группируя
слагаемые, получим уравнение, квадратное относительно у:
Оно имеет единственное решение тогда и только тогда,
когда его дискриминант равен нулю, т. е.
или, что равносильно
2 _ 2а(УЗ-а)
2 " а* + 1 *
Последнее уравнение определяет единственное z, если а = О
или а= \/3. Следовательно, искомая плоскость имеет
уравнение х = 0 или х = у\/3. Координаты точек касания
находим, подставляя найденные значения а в систему и решая
её при этих а.
Если а = 0, то
jc = О
Х = 0
472 Глава 11, Векторы в пространстве {продолжение)
Если а = \/3, то
х =
f(V3y-l)s
\х=у/Ву
«■
= 0,
х=у/3у
У- 2 »
В заключение выведем общее уравнение поверхности
вращения. Напомним, что в начале § 10.1 мы
договорились представлять поверхность вращения как результат
вращения некоторого конечного куска плоской
непрерывной кривой вокруг оси. Сейчас нам будет удобнее несколько
расширить понятие поверхности вращения, полагая, что
кусок кривой, который мы вращаем вокруг оси, может
быть и бесконечным. Например, вращая прямую вокруг
параллельной ей оси, мы получим прямую круговую
цилиндрическую поверхность. Аналогично, вращая прямую
вокруг пересекающей её оси, получим прямую круговую
коническую поверхность.
Пусть поверхность S получена вращением плоской
непрерывной кривой L вокруг оси dy лежащей в плоскости
кривой. Введём декартову систему координат {О, ?i, ?2> ?з}>
поместив начало координат на ось d, направив вектор ё?з
по направлению1) оси d, а вектор ?i поместив в
плоскости а кривой L (рис. 11.9). Таким образом, {0, ?ь?з}~~
^Напомним, что ось — это ориентированная прямая, т. е.
совокупность прямой и её направляющего вектора.
§ 11.7. Уравнение сферы
473
декартова система координат в плоскости ос. Пусть в этой
системе координат кривая L имеет уравнение f(x> г) = 0.
Рассмотрим точку М(х, у9 z). Она лежит на поверхности S
тогда и только тогда, когда на окружности с центром на
оси d, лежащей в плоскости, перпендикулярной этой оси
и проходящей через М, найдётся точка М\ е L. Радиус
этой окружности равен
Координаты точки Mi
легко находятся: у\ = 0, z\ = z, х\ — ±у/х2 + у2 (хотя бы для
одного из знаков перед корнем); при этом х\ и z\ обязаны
удовлетворять уравнению L. Итак, М £ S тогда и только
тогда, когда
(11.25)
Это и есть уравнение поверхности S. Его можно записать
в виде g(x2 + у2у z) = 0, если кривая L задана уравнением
D^3 Упражнение 11.17. Выведите уравнение сферы с центром в
начале координат и радиусом R, используя уравнение (11.25).
Пример 11.19. Написать уравнение прямой круговой
конической поверхности с вершиной в начале координат,
осью которой является ось аппликат, а образующая
наклонена к оси под углом (р = arctg ft.
474 Глава 11. Векторы в пространстве (продолжение)
Решение. Указанную в условии поверхность можно
получить, вращая прямую, имеющую в плоскости Oxz
уравнение х = kz, k > О, вокруг оси Oz. Записав уравнение прямой
в виде х — kz = 0n воспользовавшись формулой (11.25),
найдём уравнение конической поверхности ±у/х2 + у2 — kz = O,
которое можно записать в равносильной форме х2 + у2 =
= *V. □
в^ Упражнение 11.18. Докажите, что прямую круговую
цилиндрическую поверхность радиуса г с осью Oz можно задать
уравнением х2 + у2 = г2.
§ 11.8. Примеры решения задач методом координат
— Теперь формулирую задачу, —
сказал он, как говаривал когда-то, читая
лекции.—Повесьте уши на гвоздь
внимания.
Е. Войскунский, И. Лукодъянов. Экипаж «Меконга»
В этом параграфе мы решим несколько задач, в которых
система координат изначально не фигурирует, а вводится
по мере надобности в процессе решения (упрощённо говоря,
в этом и заключается суть метода координат). В целом
приводимые ниже задачи значительно сложнее задач, которые
встречались на протяжении этой главы.
Пример 11.20. В основании призмы ABCDA\BiC\Di
лежит трапеция ABCD, в которой (АВ) \\ (CD) и CD: АВ = А < 1.
Плоскость, проходящая через точку В, пересекает рёбра
АА\, СС\ и прямую DD\ в точках М, N и Р
соответственно, причём AM : АА\ — т, CN : СС\ = л. Найти отношение
DP:DDi. у
Решение. Обозначим jfi = dA9 ^2 = D6 и gs = DD\ и
введём аффинную систему координат {£>, £ь j?2,1?з}- в эт°й
системе (рис. 11.10) вершины призмы имеют
координаты А(1, 0, 0), В(хв, ув, 0), С(0, 1, 0), D(0, 0, 0), Ai(l, 0, 1),
В\(хв,Ув^ 1), Ci(0, 1, 1), Di(0, 0, I), где хв, У в —
неизвестные пока абсцисса и ордината точки В (эта точка лежит
§ 11.8. Примеры решения задач методом координат 475
г
Рис. 11.10
в плоскости DAC, поэтому её аппликата г в равна нулю).
По условию DC — ЛАВ, т. е.
Й2 = Ц(ХВ - 1)ё1+Увё2+0-ёз).
Отсюда находим, что Х(хв - 1) = 0, Хув = 1» следовательно,
Хв = 1, у в — т- Далее, по условию
ЛМ = {хм - 1, Ум, 2М) = тААи
где AAi = (0, 0, 1). Значит, Хм — 1 = тп * 0 = 0, ум = тп • 0 = 0,
гм = ^-1=:^» т. е. точка М имеет координаты (1, 0, /п).
Аналогично N(0, 1, л). Напишем уравнение плоскости BMN:
х-1 у-1/Х 2-0
1-1 0-1/А т-0
0-1 1-1/Л п-0
= 0
т-п — Хт
Точка Р(0, 0,
Поэтому
лежит на оси аппликат, и Р 6 (BMN).
/71 — л — Хт /Гь 1ч
т. е. 2р = n + Am. Тогда DP: DDi = \zP§9\: Цз\ = \zp\ = п + Хт.
П
476 Глава 11. Векторы в пространстве (продолжение)
Пример 11.21. Дан параллелепипед ABCDAiBiC\Di.
Через вершину Су проведена плоскость, пересекающая
продолжения рёбер АВУ AD и АА\ за точки В, D и А\ в точках
Во, Do и Ао соответственно так, что АВо : АВ = ADo : AD =
= 3 • ААо: АА\. Найти отношение объёмов параллелепипеда
и тетраэдра AAqBqDq -
Рис. 11.11
Решение. Пусть j?i = AAi, §2 =А&, g$ = AD, и введём
аффинную систему координат {А, £ь#2»1Гз} (рис. 11.11).
По условию -Ао(^, 0, 6\9 В0(0, А, 0), D0(0, О, А), А>0.
Напишем уравнение плоскости
х-Л/3 у-0 2-0
О-А/3 А-0 0-0
О-А/3 0-0 А-0
= 0
Точка С\ (1, 1, 1) лежит в этой плоскости, поэтому 3 • 1 + 1 +
+ 1-А = 0, т.е. А = 5.
§ 11.8. Примеры решения задач методом координат 477
Объём параллелепипеда равен V = \(gi, g2, Йз)\, а объём
тетраэдра —
±* Ж £ = || (£iu \g2,
итак, Fj - 125- u
Как видно из приведённых примеров, аффинную
систему координат целесообразно использовать в задачах о
нахождении отношений длин отрезков, площадей, объёмов.
Подобные задачи, как правило, относятся к
многогранникам достаточно общего вида: произвольным призмам,
пирамидам и т.п., для которых удобно ввести систему
координат, связав её с тремя рёбрами данного
многогранника, выходящими из одной вершины. Решать такие задачи
в декартовой системе координат весьма затруднительно, да
и неестественно.
Декартовы координаты удобны при решении задач о
вычислении длин отрезков и величин углов, особенно если
они относятся к многогранникам, имеющим три
попарно перпендикулярных ребра, — прямоугольным тетраэдрам,
прямоугольным параллелепипедам и т.д. Примеры
подобных задач мы уже приводили выше, а сейчас рассмотрим
несколько более сложные ситуации.
Пример 11.22. В правильной пирамиде SABCD (S —
вершина) величина двугранного угла при основании равна 30°.
Точки Му N, Р, Q — середины рёбер АВУ ВС, CD и DA
соответственно. Точка Е лежит на ребре АВ, точка F — на
ребре SC. Известно, что углы, образованные прямой EF
с плоскостями SMP и SBA, а также прямой DF с
плоскостью SNQ, равны. Найти величину а этих углов.
Решение, Пусть О — центр основания данной пирамиды.
Возьмём за единицу длины половину длины отрезка АВ
и введём декартову систему координат <О, ОМ, ON, -=- \
478 Глава 11. Векторы в пространстве (продолжение)
Рис. 11.12
(рис. 11.12). Тогда в этой системе М(1, 0, 0), Р(-1, 0, 0),
N(0, 1, 0), Q(0, -1, 0), А(1, -1, 0), В(1, 1, 0), С(-1, 1, 0),
D(-l, -1,0), S(0, О, Л), £(1, да, 0), F(-A, Л, (1 - Л)А), где
пока неизвестны). Запишем
уравнения плоскостей ABC, SMP, SNQ и SAB:
(ABC): z = 0,
(SMP):y = 0,
(SNQ): x = 0,
(SAB):
jc-0 j/-0 z-h
1-0 1-0 0-h
1-0 -1-0 0-Л
= 0
Нормальные векторы этих плоскостей имеют вид Н\ =
= (0, 0, 1), Я2 = (0, 1, 0), Я3 = (1, 0, 0) и Я4 = (h, 0,1), а
направляющие векторы прямых EF и DF таковы:
П=Ш=(-\-\,\-т, (1-Я)А)
и
= 5?= (-Я+1.Я + 1, (1-Д)А).
§ 11.8. Примеры решения задач методом координат 479
Согласно формулам (11.19) и (11.20) и в соответствии с
условием задачи
л/5
2
— с
1*1
о
•Я2|
•|Й2|
|Й1-Я4
КГ
121-1Й41
/(А + 1)2
*iV(A + ]
| 1
\Л — TYt\
+ (A-m)2 + (l
|2ЛА|
1)2 + (А-тп)2 +
- A)2ft2
(1-А)2Л2
-А)2 + (А + 1)2 + (1-А)2Л2
\Х — щ\ — А,
<^ < А 1-А
Следовательно, либо А - m = А, т. e. m = 0, либо m = 2A,
причём А в обоих случаях находится из уравнения
т. е. А= ^. Итак, либо т = 0, Х=^, h= —, либо ш= 1, А = ^,
4 I j§ 6
h = —=.. В обоих случаях
3
Г5Г
т.е. а = arcsin у от- □
Пример 11.23. Сторона основания правильной
треугольной пирамиды равна 2\/б, а высота — 3. Вершина А куба
480 Глава 11. Векторы в пространстве (продолжение)
ABCDA\B\CiDi находится в центре основания пирамиды,
вершина С\ — на высоте пирамиды, а ребро CD — в
плоскости одной из боковых граней пирамиды. Найти длину
ребра куба.
Рис. 11.13
Решение. Обозначим данную пирамиду через SMNP
(S — вершина). Без ограничения общности можно считать,
что ребро CD куба лежит в плоскости SMP. Введём декарто-
ву систему координат {А, ?ь ?2> ?зЬ гДе единичные векторы
?ь ?2 и ?з направлены по рёбрам АВ, AD и АА\ куба
(рис. 11.13). Пусть АВ = т.ТогдаС(т, т, 0),S(\/3, y/3y i/3),
D(0, m, 0). Так как плоскость SMP проходит через точки
S, С и D, её уравнение имеет вид
у/Зу +(т- \/Z)z - тл/З = 0.
Найдём расстояние от точки А(0, 0, 0) до этой плоскости
по формуле (11.21):
jc-0
m-0
v/3-0
У
m
v/j
-m
— m
\-m
z-0
0-0
v/3-0
p(A,SMP) =
\/m2-2mv/3 + 6
Это же расстояние можно найти по-другому. Проведём
в грани SMP апофему SK и соединим точки А и К. В тре-
§ 11.8. Примеры решения задач методом координат 481
угольнике SAK опустим высоту AL на гипотенузу. Тогда
AL — искомое расстояние от А до (SMP) (почему?). Теперь
уже нетрудно найти, что AL = —^— = ^~^. Итак,
ьл VII
/иа/3 _ Зл/2
откуда
m =. U
5
Разобранная только что задача представляет собой
пример «умного» использования метода координат (т.е. в
совокупности с чисто геометрическими методами).
В заключение покажем, как применяется метод
координат в задачах на ГМТ.
Пример 11.24. Даны две точки А и В и положительное
число ft. Найти геометрическое место таких точек М, что
AM:BM = k.
Решение. Введём декартову систему координат так,
чтобы точки А и В имели координаты (—а, 0, 0) и (а, 0, 0)
соответственно, а > 0. Тогда условие AM: BM—k
равносильно такому: (х + а)2 + у2 + г2 = k2(x - а)2 + k2y2 + k2z29 где
(х, у, г) — координаты точки М (мы воспользовались
теоремой 11.8). Если k = 1, то полученное уравнение приводится
равносильными преобразованиями к виду л; = 0, т.е.
задаёт координатную плоскость Oyz, которая проходит через
середину отрезка АВ и перпендикулярна ему. Тем самым
мы дали другое доказательство утверждения II из § 7.1.
Пусть теперь кф 1. Тогда наше уравнение
равносильными преобразованиями может быть приведено к виду
(1 -I- £>2 \
— 2а, 0, О) и радиусом
R —
Этот результат можно сформулировать, не ис-
16 3ак 3383
482 Глава 11. Векторы в пространстве (продолжение)
пользуя координаты: если АВ = 2а, то искомым ГМТ (при
кф1) является сфера с центром на прямой АВ (укажите
самостоятельно, в какой точке по отношению к А и В он
находится) и радиусом R. Эта сфера называется сферой
Аполлония. □
Задачи
— Пуаро,— сказал я. — Я только что
думал...
— Очаровательное занятие, мой друг.
Не гнушайтесь им и впредь.
А. Кристи. Загадка Эндхауза
11.1. Известно, что для ненулевых векторов 3, Ъ и ?
справедливы равенства 3=Ь х ?, Ь = ? х 3 и ?= axb. Найдите
длины векторов 3, Ъ и ? и углы между ними.
11.2. Докажите, что для трёх попарно неколлинеарных
векторов равенство ЙхЬ = Ьх?=?хЗ выполняется тогда
и только тогда, когда 3 + Ъ + ?= б.
11.3. Докажите, что |3 х Ь|2 = а ^ aJ
#• b Ь
11.4. Докажите, что если векторы 3 х Ь9 &х?и ?хЗ
компланарны, то
а) векторы 3, & и ? компланарны;
б) векторы ЗхЬ, &х?и?ха коллинеарны.
11.5. Векторы 3, & и ? некомпланарны. При каких Л
компланарны векторы 3 + 2Ъ + А?, 43 + 5& + 6? и 73 + 8& + Л2??
11.6. На векторах 3(2, 3, 1) и Ь(—1, 1, 2) построен
треугольник. Найдите его площадь и длины высот.
11.7. Даны точки
а) А(2, 1, -1), В(3, 0, 2), С(0, -1, 3), D(5, 1, 1);
б) А(0, 0, 2), В(3, 0, 5), С(1, 1, 0), £>(4, 1, 2),
являющиеся вершинами тетраэдра. Найдите его объём и
длину высоты, опущенной из вершины D.
11.8. В тетраэдре ABCD точки М, N, Р и Q лежат на
рёбрах ВС, AD, АВ, CD соответственно, причём АР = РВ,
Задачи 483
AN = ND, CQ = QD, MC = 2BM. Пары точек Аь Bi и Сь
D\ выбраны на отрезках NM и PQ соответственно так, что
NAi = А\В\ — В\М и РС\ = C\D\ = D\Q. Найдите отношение
объёмов тетраэдров ABCD и A\B\C\Di.
11.9*. В параллелепипеде ABCDAiB\C\D\ длины всех
рёбер равны 1, a /.DAB = /LDAA\ — Z3AA\. Найдите
величину этих углов, если объём параллелепипеда равен —=.
у/2
11.10. Дан тетраэдр ABCD. На рёбрах АВ, CD и
продолжении ребра АС за точку С выбраны точки М, N и Р
соответственно так, что AM: АВ = Л, CN: CD = [ииРС: С А = v ♦
Определите объём той части тетраэдра, отсекаемой плоскостью
MNPy которая содержит точку А, если объём тетраэдра
ABCD равен V. Рассмотрите отдельно случай Л = и = ^
и дайте ему геометрическую интерпретацию.
11.11*. Пусть грани выпуклого многогранника
пронумерованы числами 1, 2, ..., л, a Sj —вектор,
перпендикулярный i-й грани, отложенный от неё во внешнюю
сторону и численно равный по длине площади этой грани
(i = l, 2, ..., п). Докажите, что^х +§2 + ... + Sn = 6 (теорема
Минковского о еже).
11.12*. Даны точка М$ (?о) и прямая f= f*i +ctt. Найдите
а) радиус-вектор проекции точки Мо на прямую; б)
радиус-вектор точки, симметричной точке Мо относительно
прямой.
11.13*. Составьте уравнения а) проекции прямой ? =
= ?о + at на плоскость 7*-H = D; б) перпендикуляра,
опущенного из точки Мо(а*о) на прямую ?=?i+ Ш\ в) общего
перпендикуляра к прямым ?= Т\ + a\t и ?= ?2 + $2*-
11.14*. Найдите расстояние а) от точки Мо(?о) Д°
плоскости j*-H = D\ б) между прямыми ?=?г + а^ и г*=?2 + Й2*;
в) между прямыми ? х а\ = Ъ\ и ? х Иг = ^2-
В задачах 11.15—11.18 система координат аффинная.
11.15. При каких а плоскости
484 Глава 11. Векторы в пространстве (продолжение)
и
ах + 9у + у z + 3 = О
а) пересекаются; б) параллельны; в) являются одной и той
же плоскостью?
11.16. Определите взаимное расположение прямой
aj 5 " 4 "" 7 '
б) х - у + 2г = 0, х + у - Зг + 2 = 0;
в) х = 2, г/ = 5 + t, z = 4 + 3t;
r)x = 2 + 3t,y = 7 + t,2 = l + t
и плоскости х — 3i/-bz-fl = 0.
11.17. Три грани параллелепипеда лежат в плоскостях
из его вершин имеет координаты (—1, 3, 1). Составьте
уравнения остальных граней параллелепипеда и его диагонали,
проходящей через указанную вершину.
11.18. Точки Л(1, 0, 3) и Б(-1, 2, 1) - вершины
тетраэдра ABCD, точка К(—1, 5, 2) — середина ребра ВС, а точка
М(0, 1,4)— точка пересечения медиан грани BCD.
Составьте уравнения плоскостей, в которых лежат грани тетраэдра.
В задачах 11.19—11.29 система координат декартова.
11.19. Найдите координаты точки прямой
jc-1 j/-3
1 " 3 "~ -5 '
равноудалённой от точки (0, 1, 1) и от плоскости 2х — у +
+ 22+1 = 0.
11.20. Дана точка А(3, —1, 1). Найдите координаты
проекции точки А на плоскость х + 2у + 2г + 6 = 0и координаты
точки, симметричной А относительно этой плоскости.
11.21. Составьте уравнение прямой, симметричной
прямой
х-2 У + 1 2-2
3 1 4
относительно плоскости 5jc — у + 2 — 4 = 0.
Задачи 485
11.22. Точки А(-1,-3, 1), В(5, 3, 8), С(-1, -3, 5) и
D(2, 1 — 4) являются вершинами тетраэдра. Найдите угол
и расстояние между прямыми AD и ВС, а также угол между
прямой AD и плоскостью ABC.
11.23. Грани ABCDy ABBiA\ и ADD\A\
параллелепипеда ABCDA\B\C\D\ лежат в плоскостях 2х + Зу + 4z + 8 = О,
х + Зу — 6 = 0 и z + 5 = 0 соответственно, вершина С\ имеет
координаты (6, -5, 1). Найдите а) расстояние от точки А\
до плоскости B\BD\ б) расстояние от точки D до прямой
АВ; в) расстояние между прямыми АС и А\С\, АА\ и ВС;
г) угол между прямыми АС и C\D\j между плоскостями
BDD\ и АСС\> а также угол между прямой АуС и
плоскостью DCCi.
11.24*. Напишите уравнение биссекторной плоскости
пары вертикальных двугранных углов, образованных
плоскостями х — z — 5 = 0 и Зх + 5у + 4:2 = 0, если известно, что
а) точка (1, 1, 1) лежит в одном из углов этой пары; б) эти
двугранные углы острые.
11.25*. Вершинами тетраэдра являются точки А(1, 2, 3),
В(-2, 8, 9), С(5, 0, 7) и D(3, 4, 2). Найдите радиусы и
координаты центров вписанной и описанной сфер этого
тетраэдра.
11.26*. Дан треугольник ABC с вершинами А(1, 2, 3),
В(1, 5,-1) и С(5, 3, -5). Найдите радиусы и координаты
центров вписанной и описанной окружностей этого
треугольника.
11.27. Найдите радиус и координаты центра сферы,
проходящей через точку (0,1,0) и касающейся плоскостей
х-\-у — 09 х — у = 0 и х + у + 4г = 0.
11.28. Определите взаимное расположение сферы и
плоскости. Если они пересекаются, укажите центр и радиус
окружности, являющейся пересечением:
а) (х + 2)2 + у2 + (2 - 1)2 = 1 и 2х + у - 2г + 3 = 0;
б) х2 + (у - I)2 + (г + I)2 = 4 и 4х + 2у + 2г + 3 = 0.
11.29. Докажите, что указанные уравнения задают
сферы. Определите взаимное расположение этих сфер. Если
486 Глава 11. Векторы в пространстве (продолжение)
они пересекаются, укажите центр и радиус окружности,
являющейся их пересечением:
а) х2 + у2 + 22 + 4х-22 + 4 = 0 и x2+y2 + z2
2 22 2
11.30*. Составьте векторное уравнение
а) сферы с центром Мо(?о) и радиусом R\
б) прямой круговой цилиндрической поверхности с осью
? = /*о + ctt и радиусом R;
в) прямой круговой конической поверхности с вершиной
в точке Мо(а*о) и осью ?=r*o + Bt, зная, что угол между
образующей и осью равен а.
11.31*. Напишите уравнение прямой круговой
конической поверхности
а) полученной вращением прямой х = —t, у = z = 2t
вокруг прямой x — y — z\
б) полученной вращением прямой я = 0, у — г + 1 = 0
вокруг оси аппликат.
11.32. В основании треугольной пирамиды SABC лежит
прямоугольный треугольник, катеты АВ и АС которого
равны За и 4а соответственно. Ребро SA пирамиды
перпендикулярно плоскости основания и имеет длину а. Через
середины рёбер АВ, SC и точку, лежащую на ребре АС
и удалённую от точки А на расстояние а, проведена
плоскость. Найдите угол между этой плоскостью и плоскостью
основания.
11.33. В основании треугольной пирамиды SABC лежит
правильный треугольник ABC. Грань SAB
перпендикулярна плоскости основания, ZASB = ZASC = 45°. Найдите углы
треугольника SAC.
11.34. В правильной треугольной пирамиде SABC длина
ребра основания ABC равна а, а угол между апофемой
грани ASC и гранью BSC равен 45°. Найдите длину высоты
пирамиды.
11.35. Дан куб ABCDAiBxCiDi с ребром 1. Найдите
радиус сферы, проходящей через вершину А, середины
рёбер DC и ВВ\ и центр грани AiB\C\D\.
Задачи 487
11.36. Дан наклонный параллелепипед ABCDA\B\CiD\>
в основании которого лежит прямоугольник ABCD. Длина
стороны АВ равна длине высоты параллелепипеда. Сфера
с центром в точке О проходит через вершину В и касается
рёбер -AiBi и DD\ соответственно в точках А\ и D\.
Найдите отношение объёма параллелепипеда к объёму шара,
ограниченного этой сферой, если /.А\ОВ = /LD\OB = 120°.
11.37. Внутри тетраэдра ABCD взята точка О. Точки А\,
Si, Ci и D\ —точки пересечения прямых АО, ВО, СО и
DO с плоскостями BCD, ACD, ABD и ABC соответственно.
Вычислите
D\O
ААХ + ВВг + ССг
11.38. Докажите, что пересечение трёх цилиндров
радиуса 1, оси которых попарно перпендикулярны (но не
обязательно пересекаются), содержится в некотором шаре
радиуса ^g-
11.39. Оси двух прямых круговых конических
поверхностей параллельны. Углы между осью и образующей у этих
поверхностей равны. Докажите, что все точки их
пересечения лежат в одной плоскости.
11.40. Дан куб с ребром 1. Найдите геометрическое
место точек пространства, сумма квадратов расстояний от
которых до вершин куба равна: а) 8; б) 12.
11.41. Рассматриваются всевозможные положения
окружности постоянного радиуса, при которых она касается
трёх различных граней прямого трёхгранного угла.
Докажите, что в каждом из таких положений центр окружности
лежит на одной и той же сфере.
11.42. Дана сфера с центром О и радиусом R. Точка М
удалена от точки О на расстояние d. Число d2 — R2
называется степенью точки М относительно этой сферы.
Докажите, что геометрическим местом точек, степени
которых относительно двух данных неконцентрических сфер
488 Глава 11. Векторы в пространстве (продолжение)
равны, является плоскость (радикальная плоскость двух
сфер).
11.43. Найдите геометрическое место середин общих
касательных к двум данным сферам, расположенным одна
вне другой.
Глава 12
Задачи на максимум и минимум
Минимум и максимум».♦ Путаю я их
чертей!
М. Булгаков
§ 12.1. Предварительные замечания
А теперь немного сведений из
«Справочника по восьмой галактической
зоне» Лиги, которые тоже правда.
У. Ле Руин. Мир Роканнона
Эта глава посвящена методам решения геометрических
задач на экстремумы, т. е. задач, в которых требуется найти
наибольшее и (или) наименьшее возможное значение
некоторой геометрической величины, например длины отрезка,
площади фигуры, объёма тела и т. п. Мы не ставим себе
целью подробную классификацию таких задач по способам
решения, а хотим продемонстрировать несколько идей,
полезных для их решения.
Возможные подходы к решению указанных задач можно
условно разделить на два класса: геометрический и
аналитический. Аналитическим мы будем называть метод,
основанный на составлении функции и исследовании её на
экстремум либо с помощью производной, либо
алгебраическими методами (с помощью неравенств). Суть его
заключается в следующем. Выбирается переменная дг, через неё
выражается величина у, которую необходимо исследовать
на максимум и минимум, и определяется область
изменения переменной х (разумеется, всё это делается с учётом
геометрической сущности задачи, поэтому, как было
отмечено выше, деление методов решения экстремальных
задач на геометрические и аналитические весьма условно).
490 Глава 12. Задачи на максимум и минимум
Тем самым на некотором подмножестве S множества
действительных чисел оказывается заданной функция у = f{x),
которая подлежит исследованию.
Чаще всего на практике встречается случай, когда S
представляет собой отрезок [a, b], a функция / непрерывна
на этом отрезке. Из курса алгебры и начал анализа вам
известно правило нахождения наибольшего и наименьшего
значений функции в этом случае. Напомним его.
Сначала следует найти все точки внутри [а, &], в
которых производная функции у = f(x) равна нулю или не
существует (критические точки), затем вычислить
значения функции в этих точках и в точках а и Ъ. Наконец, из
полученных чисел необходимо выбрать наибольшее и
наименьшее — они и будут являться наибольшим и
наименьшим значениями данной функции на [а, Ь].
Как вы знаете, функция, непрерывная на отрезке,
всегда принимает на нём наибольшее и наименьшее значения.
Если же заменить отрезок полуинтервалом или интервалом,
то это утверждение перестаёт быть справедливым. Поэтому
в этих случаях исследование на экстремум требует большой
аккуратности. Кроме вычисления значений функции в
критических точках, необходимо изучить её поведение в
окрестностях концов интервала или полуинтервала, а уже затем
на основании полученной информации судить о наличии
или отсутствии экстремальных значений. Ввиду важности
сказанного мы приведём простые примеры,
иллюстрирующие возможные ситуации.
Пример 12.1. Найти наибольшее и наименьшее
значения функции у = хг - 6х2 + 9х + 1 на следующих
промежутках: а) (-1, 5); б) (0, 4); в) (-1, 4]; г) [0, +оо).
Решение. Найдём критические точки данной функции:
у1 = Зх2 - 12* + 9 = 3(* - 1) (х - 3) = 0,
откуда х\ = 1, Х2 = 3. Эти точки принадлежат всем
указанным в условии задачи промежуткам; у(1) = 5, у(3) = 1.
§12.1. Предварительные замечания 491
Заметим теперь, что в точках х = -1,х = 0,х = 4их = 5
можно считать (если промежуток, на котором рассматривается
функция, не содержит указанные точки), что у(-1) = -15,
у(0) = 1, j/(4) = 5 и у(5) = 21. В случаях а)—в) мы заменим
промежутки (-1,5), (0,4) и (-1,4] на отрезки [-1,5],
[0, 4] и [—1, 4], исследуем функцию на этих отрезках, а
затем сделаем соответствующие выводы о поведении
функции на заданных в условии промежутках.
а) На [—1, 5] наибольшее и наименьшее значения
данной функции следует искать среди чисел j/(-l), 1/(1), 1/(3),
z/(5). Наименьшее значение равно z/(-l) = -15, а
наибольшее— у(5) = 21. На (—1, 5) наша функция принимает
значения, сколь угодно близкие к -15 и 21 (при х, достаточно
близких к -1 и 5), но не достигает их, так как точки х= — 1
и х = 5 исключены из области определения. Следовательно,
на (—1, 5) у функции нет ни наименьшего, ни наибольшего
значения.
б) На [0, 4] наибольшее значение равно 5 (оно
достигается при х = 1 и х = 4), а наименьшее равно 1 (оно достигается
при х = 0 и х — 3). Поэтому, несмотря на то что,
рассматривая нашу функцию на (0,4), мы исключаем из области
определения точки х = 0 и я = 4, её наибольшее и
наименьшее значения остаются теми же, что и на [0, 4] (но
достигаются они только при х = 1 и х = 3 соответственно).
в) Рассуждая аналогично пунктам а) и б), мы
получаем, что на полуинтервале (-1,4] функция принимает
значения, сколь угодно близкие к -15 (при х, достаточно
близких к -1), но не достигает его, т.е. наименьшего
значения у неё нет. Наибольшее значение такое же, как на
отрезке [-1, 4]. Оно равно 5.
г) На луче [0, +оо) рассматриваемая функция
принимает сколь угодно большие положительные значения (при
достаточно больших положительных х), поэтому
наибольшего значения у неё нет. Наименьшее значение ищем среди
её значений в критических точках и у(0). Оно равно 1
и достигается при jc = 0 и л: = 3. □
492 Глава 12. Задачи на максимум и минимум
Мы рассмотрели пример, в котором заданная функция
оказалась непрерывной на более широком множестве
(конкретно в этом примере — на всей оси), чем то, на котором
следовало изучить её экстремальные значения. На
практике это могло случиться, например, потому, что значения
функции вне данного множества не имеют геометрического
смысла или не удовлетворяют условию зада ш. В
описанной ситуации исследование поведения функции на концах
промежутка проводится несложно именно из-за
возможности доопределить функцию в этих точках так, чтобы она
оказалась непрерывной на отрезке. Разумеется, подобное
возможно далеко не всегда. Мы сейчас приведём пример
исследования функции, которая определена на интервале
(а, Ь), но не является непрерывной на более широком
множестве.
Пример 12.2. Найти наибольшее и наименьшее значе-
х2 1
ния функции у = — + - на промежутке (0, +оо).
и X
Решение. Найдём критические точки данной функции
на (0, +оо): у1 = х ^ = О, т. е. х = 1 (точка х = О, в которой
у1 не существует, не принадлежит указанному интервалу).
Ясно, что при малых положительных х наша функция
принимает сколь угодно большие значения, как, впрочем,
и при больших положительных х. Значит, наибольшего
значения у неё нет. Наименьшее значение следует искать
в критической точке. Оно равно у(1) = ^. D
Аналитический метод решения экстремальных задач
обладает достаточной универсальностью и алгоритмичностью,
но его применение часто приводит к довольно трудоёмким
вычислениям. Впрочем, главная трудность обычно лежит
не в области анализа, а в области геометрии: далеко не
всегда просто задать функцию, которую предстоит
исследовать на экстремум (примеры таких задач вы встретите
ниже).
§12.2, Примеры решения задач 493
Геометрический подход к экстремальным задачам
обычно приводит к кратким и изящным решениям. Зачастую
эти решения опираются на нестандартную идею,
придумать которую довольно трудно.
В следующем параграфе вы познакомитесь с
некоторыми из этих идей, а также найдёте примеры задач, решённых
и геометрически, и аналитически.
§ 12.2. Примеры решения задач
Ну-с, вторая задача — дело ещё
далёкое, а вот первая... Впрочем, смотрите
сами.
Е. Войскунский, И. Лукодъянов. Экипаж «Меконга»
Мы начнём с задач, которые можно решить
аналитическим методом без привлечения производной, используя
свойства квадратного трёхчлена или простые
алгебраические неравенства1*.
Пример 12.3. В правильную четырёхугольную
пирамиду с ребром основания а и высотой h вписана правильная
четырёхугольная призма так, что её нижнее основание
лежит внутри основания пирамиды, а вершины верхнего
основания — на боковых рёбрах пирамиды. Найти
наибольшую площадь боковой поверхности таких призм.
Решение. Введём обозначения так, как показано на
рис. 12.1. Пусть —!- = х. Ясно, что хе (0, 1). Из подобия
треугольников SO А и Е\ЕА получаем, что ЕЕу = Л(1 - х) и
ЕО = х • АО. Так как ЕО = ^, АО = -^=, то EF = ах. Тогда
>/2 у/2
площадь боковой поверхности равна
= 4-EF-EE1 =4ahx(l-x).
^Отметим ещё, что ранее нам уже встречались задачи на нахождение
наименьших и наибольших значений, которые можно решить без
применения производной: 3.15, 5.15, 8.6, 8.15, 8.16, \0Л9 10.7, 10.10,
10.30-10.32.
494 Глава 12, Задачи на максимум и минимум
S
Рис. 12.1
Поскольку 4аЛ — величина постоянная, достаточно найти
наибольшее значение функции у(х) — х(1 — х) на (0, 1).
Напомним, что квадратный трёхчлен ах2 + Ьх + с при а < О
Ь
достигает своего наибольшего значения в точке xq = —
2а'
если он рассматривается на промежутке, содержащем эту
точку. В нашем случае xq = -= 6 (0, 1), и наибольшее значе-
ние функции у{х) на (0, 1) равно j. Следовательно,
наибольшее значение функции S(x) равно 4аЛ • -т = ah. □
Замечание. Функцию у(х) =х{1 — х) можно исследовать на
наибольшее значение по-другому. Так как х€ (0, 1), то и (1 — х) £
€ (0, 1). В силу неравенства y/ab
о среднем геометри-
Li
ческом и среднем арифметическом двух положительных чисел
имеем
4'
Равенство в этом неравенстве достигается в точке дго,
удовлетворяющей условию хо — 1
о, т.е. в точке хо = ^. Значит,
наибольшее значение функции у(х) на (0, 1) равно -.
§ 12.2, Примеры решения задач 495
Отметим, что неравенство
удобно использовать при нахождении наибольшего значения
функции вида f(x)(A - f(x))> где 0 ^ f(x) ^A, A = const, или при
нахождении наименьшего значения функции вида f(x) + тг-г>
где f(x) > О, А = const, А > 0. Г{х)
Аналогично можно использовать и другие неравенства о
средних:
а -\-о
где а > О, Ъ > 0. Равенства в этих неравенствах достигаются тогда
и только тогда, когда а = Ь.
Пример 12.4. Образующая конуса имеет
фиксированную длину и составляет с высотой конуса угол а. В конус
вписана правильная шестиугольная призма с равными
рёбрами (одно основание призмы лежит внутри основания
конуса, а вершины другого основания лежат на боковой
поверхности конуса). При каком значении а площадь
боковой поверхности призмы будет наибольшей?
Решение. Введём обозначения так, как показано на
рис. 12.2а, б. Из условия вытекает, что ОА = О\А\ =АВ =
= АА\. Обозначим длины этих отрезков через а. Из
треугольника АА\К находим, что АК = a tg a, a из
треугольника OSK получаем ОК = / sin а, где I = SK — образующая
конуса. Равенство ОК = ОА + АК принимает вид
/ sin a = a + a tg a,
следовательно,
Zsin a _ I sin a cos a
1 + tg a sin a + cos a'
Тогда площадь боковой поверхности призмы равна
ч _ ~,2 sin2 a cos2 a
(sin a + cos а)2 '
496 Глава 12. Задачи на максимум и минимум
Ах
/
/а
/
/
J
п
У
/
а
А
L
а
Г
К
а)
б)
Рис. 12.2
Ясно, что при этом а € (О, ^ j. На указанном промежутке
sin a > 0 и cos a > 0. Согласно неравенству о среднем
гармоническом и среднем квадратическом двух положительных
чисел
2аЬ
а + Ь
имеем
2 sin a cos a
sin a -f cos a
Следовательно,
sin2 a + cos2
л/2'
Наибольшее значение функция S(a) принимает тогда и
только тогда, когда в использованном неравенстве имеет
место равенство, т. е. при sin ао = cos «о- Так как а Е (0, ~ j,
ТО ОСп = т. U
§ 12.2. Примеры решения задач
497
Пример 12.5. Площадь основания правильной
треугольной призмы ABCA\B\C\ равна S. Точки D и Е —
середины рёбер ВС и А\В\ соответственно. Рассматриваются
треугольники, вершинами которых служат точки пересечения
плоскостей, параллельных основаниям призмы, с
отрезками А\ВУ АС\ и DE. Найти наименьшее значение площади
рассматриваемых треугольников.
Решение. Проведём плоскость а, параллельную
плоскостям оснований призмы. Пусть она пересекает прямые AAi,
ВВи ССЬ А\В, АСг и DE в точках А2, В2, С2, К, N и М
соответственно (рис. 12.3). Положим
АгА2
= х. Из условия
задачи следует, что 0 < х < 1.
Пусть F — середина отрезка BiCi, a G — середина
отрезка АВ. Очевидно, что точки Е, F, D и G лежат в одной
плоскости. В этой же плоскости лежит точка М.
Следовательно, М лежит на средней линии PQ треугольника
А2Б2С2 (рис. 12.4), равного основаниям призмы. При этом
из подобия треугольников А\А^К и ВВ^К, AA2N и C1C2N,
498 Глава 12. Задачи на максимум и минимум
РМЕ и MQD находим, что
А2К _ NC2 PM_
А2В2 " А2С2 PQ х'
Найдём теперь площадь треугольника KMN:
= Sa2c2qp ~
По свойству средней линии треугольника Spb2q = jS9 поэто-
g
му Sa2c2QP — т5* Для вычисления площадей треугольников,
входящих в выражение для Skmn, мы воспользуемся тем,
что отношение площадей треугольников, имеющих общий
угол, равно отношению произведений их сторон, между
которыми заключён этот угол (что сразу вытекает из формулы
5д = о ab sin у). Итак,
A2K-A2N o n vo
= S = x(1-x)S
PK-PMp п о v 1q
Sq = (1 *) S
NC2-C2Q o ^ 1
= S = X-
Следовательно,
= f S- x(l - x)S- \x(l - 2x)S- \(1 -
Рассмотрим функцию j/(x) = 3x2 —3jc + 1, x€[0, 1].
Квадратный трёхчлен Зх2 — Sx + 1 принимает своё наименьшее
значение на указанном отрезке в точке хо = т>.
Следовательно, наименьшее возможное значение площади треугольни-
1 S
ка KMN достигается также при xq = ^ и равно ^. D
§ 12.2. Примеры решения задач 499
US* Упражнение 12.1. Решите пример 12.5, вычислив площадь
треугольника KMN с помощью векторного произведения
векторов.
Приведённые примеры показывают, что иногда
экстремумы функции легко найти без применения производной.
Впрочем, часто без производной обойтись трудно.
Пример 12.6. Из круга радиуса R вырезан сектор, из
которого склеена боковая поверхность конуса. Каков
наибольший объём получившейся конической воронки?
Решение. Если а — центральный угол данного сектора,
то объём конической воронки равен (см. задачу 10.2)
Рассмотрим функцию у (а) = а2\/4ь.к2 — а2, а 6 (0, 2к),
и исследуем её на наибольшее и наименьшее значения.
Найдём критические точки этой функции на (0, 2к):
при а = 2nJ-=. Если мы рассмотрим у(а) на [0, 2л:], то её
наибольшее и наименьшее значения следует искать среди
чисел z/(0), у(2кх-=) и у(2л:). Получаем, что у(0) =у(2к) =
\ v о/
2/rWr ) = —— — наиболь-
• о / 3 V 3
шее. Следовательно, на (0, 2л:) рассматриваемая функция
не имеет наименьшего значения, а её наибольшее значение
равно 1б7г3
Итак, наибольший возможный объём воронки равен
R3 16тг3 = 2тгД3 п
24л:2 3\/3 9\/3 '
Пример 12.7. Стороны оснований правильной
четырёхугольной усечённой пирамиды равны а и & (а > Ъ).
Рассматриваются конусы, вершины которых находятся в центре
500
Глава 12. Задачи на максимум и минимум
нижнего основания усеченной пирамиды, а основания
вписаны в сечения пирамиды плоскостями, параллельными её
основаниям. Найти наибольший объём рассматриваемых
конусов, если угол наклона боковой грани усечённой
пирамиды к плоскости её нижнего основания равен у.
Рис. 12.5
Решение, Введём обозначения так, как показано на
рис. 12.5. Пусть ОС>2 = х. Из условия вытекает, что 0 < х ^
< ООь где ОО\ — высота усечённой пирамиды. Из
прямоугольной трапеции ОО\Е\Е находим, что
00, = ^tgy.
Итак, х е (О, а~ tg у . Из другой прямоугольной
трапеции ОО2Е2Е найдём радиус основания конуса:
= ! -xctgy.
Тогда объём конуса равен
• оо2 - !
§ 12,2. Примеры решения задач 501
Рассмотрим функцию
у{х) = x(|-
и вычислим её производную:
у'(х) = (%-х ctg г) (| ~ Зх ctg у).
Производная обращается в нуль при х\ = ~ tg у и Х2 = % tg у.
Заметим, что
следовательно, х^ £ (о, а-=— tg уч. Выясним теперь, когда
этому промежутку принадлежит х\. Очевидно, что xi > 0.
Решая относительно Ь неравенство
получаем, что Ь<-!^. Итак, х\ £ (0, ^— tg у J при условии
Ь < -^. Рассмотрим в этом предположении функцию i/(x) на
0, fl~ tg у , её экстремальные значения на этом отрезке
L ^ J
следует искать среди чисел у(0), у(х\) и у(а tg у j.
Наименьшее значение равно у(0) =0, а наибольшее — у(х\) =
а3 / а-Ь 1
= -гт tg у. Следовательно, на (0, 9 tg у наименьшего
значения нет, а наибольшее равно ^-т tg у.
Пусть теперь Ь > -^. Тогда jci £ [О, g~ tg у j и
экстремальные значения у(х) на 0, а~ tg у следует искать на
концах этого отрезка. Наибольшее значение достигается
(а-Ь)Ъ2 .
на правом конце и равно -—^—tgy, наименьшее — на
о
левом конце и равно 0. Следовательно, на (0, а~ tgy
502
Глава 12. Задачи на максимум и минимум
наименьшего значения у функции у(х) нет, а наибольшее
(a-b)b2 ,
равно -—^— tg у.
8
2а
Итак, если Ъ < -^-, то наибольшее значение объёма рас-
сматриваемых конусов равно
п(а~Ь)Ъ2 .
равно 24 *ff >"•
У> а если Ь ^ -^-, то оно
о
Теперь приведём несколько примеров задач, которые мы
решим как аналитически, так и геометрически. В каждой
из этих задач геометрический подход представляется нам
более эффектным и поучительным.
Пример 12.8. Дан куб ABCDAiB\C\Di с ребром а;
точка О — центр грани ABCD. Найти наименьшее значение
суммы ОЕ + ЕА\, если точка Е лежит на отрезке АВ.
ЛЕ
Первое решение. Пусть — = х. По условию х е [0, 1].
АЛ
Из треугольника АОЕ (рис. 12.6) по теореме косинусов
найдём длину отрезка ОЕ:
ОЕ2 =ОА2+АЕ2-2-ОА-АЕcos 1= (-$=
4 Vv/2
-Z=ax-±=
Рис. 12.6
§12.2, Примеры решения задач 503
т.е.
ОЕ = -j=V2x2 - 2х + 1 = -£= v7*2 + (1 - х)2.
Из треугольника AiAE по теореме Пифагора найдём
f = AE2+AA\ = (ах)2 + а2 - а2(я2 + 1),
т. е. EAi — а\/л:2 + 1.
Итак,
Исследуем функцию
2
на наименьшее значение на [0, 1]. Вычисляя производную
и решая уравнение yf(x) =0, находим единственную
критическую точку хо = я (производная, очевидно, всюду
существует). Так как
^-А.
1+ 1 < 8
ч/2 У2
(проверьте!), наименьшее значение функции i/(x) на [0, 1]
/5"
равно л/т>, следовательно, наименьшее значение суммы
равно
Второе решение. Развернём грань АВВ\А\ на плоскость
ABC (рис. 12.7). Применяя теперь неравенство
треугольника к АОЕА\, мы получаем, что ОЕ + ЕА\ ^ ОА\. Равенство,
504 Глава 12, Задачи на максимум и минимум
D A Ai
очевидно, достигается в том и только в том случае, когда
точка Е лежит на отрезке А^О. Итак, наименьшее
возможное значение суммы OE + EA!V а следовательно, и суммы
ОЕ + ЕА\, равно длине отрезка ОА!г, которая легко
находится по теореме Пифагора:
□
Замечание. С применением развёртки к нахождению
кратчайших расстояний мы уже встречались в задаче 10.7. Эту идею
следует запомнить, так как она очень полезна при решении задач
о путях на поверхности тела.
Пример 12.9. Длина ребра куба ABCDAiB\C\Di равна 4.
На ребре АА\ взята точка Е, а на ребре ВВ\ — точка F так,
что АЕ = B\F = 1. Точки G и Я" — середины рёбер А\В\ и
C\D\ соответственно. Найти наименьшее значение суммы
СР + PQ, где точка Р принадлежит отрезку GH, а точка Q —
отрезку EF.
Первое решение. На первый взгляд, задача является
двухпараметрической, т. е. положения точек Р и Q
задаются числами р и q, которые выбираются независимо друг
от друга. Например, можно взять р = РН, q = EQ, и тогда
сумма СР + PQ представляет собой функцию, зависящую
и от /7, и от q. Правила нахождения экстремальных
значений таких функций не входят в школьную программу.
§ 12.2. Примеры решения задач
505
Таким образом, самый очевидный и естественный подход
к решению задачи завёл нас в тупик1*.
Но оказывается, от одного параметра можно избавиться.
Действительно, зафиксируем точку Р на отрезке GH. Тогда
кратчайшим расстоянием от точки Р до точек отрезка EF
является перпендикуляр РО, проведённый в плоскости PEF
к прямой EF, если, конечно, его основание О принадлежит
отрезку EF. Покажем, что для любой точки Р е [GH]
точка О принадлежит отрезку EF, более того, она одна и та
же для всех точек Р. Обратимся к рис. 12.8. Пусть О — осно-
Рис. 12.8
вание перпендикуляра, опущенного из точки G на отрезок
EF (в плоскости грани АВВ\А\). Тогда точка О является
и основанием перпендикуляра, опущенного из точки Р на
прямую EF, какова бы ни была точка Р на отрезке GH
(по теореме о трёх перпендикулярах). Восставим в
плоскости АВВ\ перпендикуляр к прямой EF в точке F. Пусть
он пересечёт ребро А\В\ в точке М. Длину отрезка МВ\
несложно найти из подобия треугольников MB\F и FKE,
^Строго говоря, этот путь оказался тупиковым лишь в рамках
школьной программы. В высшей школе вы познакомитесь со способами
нахождения экстремумов функций многих переменных, которые столь
же алгоритмичны и универсальны, как и в случае функций одного
переменного.
506
Глава 12. Задачи на максимум и минимум
где К — такая точка на ребре ВВ\, что (ЕК) || (АВ): МВ\ = •=.
Но тогда B\G> МВ\, т.е. точка G лежит на [AiBi] левее
точки М9 следовательно, точка О лежит на [EF], а не на
его продолжении.
Итак, сумма СР + PQ минимальна, когда точки Q и о —
это одна и та же точка. Пусть GP = х. Тогда
РН = 4 - *, СР = у/РН2 + СН2 = V(4 - х)2 + 20
(из прямоугольных треугольников СРН и
РО = VGP2 + GO2 = yjx2 + GO2
(из AGPO). Чтобы найти длину отрезка GO, обратимся
к рис. 12.9. Из подобия прямоугольных треугольников
и A\EN находим, что B\N = 2, затем из подобия
треугольников GON и EA\N получаем, что GO= —. Зна-
V5
чит, нам необходимо исследовать на наименьшее значение
функцию
у(х) = ^х2 + ^
, х е [0, 4].
Вычисляя производную этой функции, получаем, что
единственной критической точкой на (0, 4) является точка хо =
= §, при этом z/f|) =2л/^, у(0) =6 + -i,
Рис. 12.9
§ 12.2. Примеры решения задач 507
Наименьшим из этих чисел является у( -=). Итак, наимень-
шее возможное значение суммы СР + PQ равно 2л/^-.
В
Рис. 12.10
Второе решение. Поставим сверху на данный куб
равный ему куб A1B1C1D1A2B2C2D2 (рис. 12.10). Пусть Qi —
точка пересечения отрезков BG и EF. Докажем, что
искомый минимум реализует длина отрезка D2Q1•
Заметим, что прямые BG и EF перпендикулярны.
Действительно, если М — середина отрезка АА\ (рис. 12.11), то
перпендикулярны прямые BG и В\М (они переходят друг
в друга при повороте на 90° относительно центра квадрата
АВВ\А\), но прямые EF и В\М параллельны.
508
Глава 12. Задачи на максимум и минимум
Прямые ВС и EF также перпендикулярны. Это следует
из того, что (ВС) ± (ABBi), a (EF) С {АВВг).
Из сказанного вытекает, что прямая EF
перпендикулярна плоскости ВСАг, а следовательно, и прямой I>2Qi- Итак,
Qi — основание перпендикуляра, опущенного из точки £>2
на прямую EF, причём Qi лежит на отрезке EF, а прямая
D2Q1 пересекает отрезок GH в некоторой точке Pi. Это
означает, что для любых точек Р е [GH] и Q € [EF] справедливо
неравенство D2P + PQ ^ D2Q1 • Осталось заметить, что точка
1>2 симметрична точке С относительно прямой GH, поэтому
Найдём длину отрезка DzQi* Из треугольника D2A2Q1
по теореме Пифагора получаем D2Q1 =^2^1 +^2©1- Из
подобия треугольников A2Q\E и BQ\F находим, что A2Q\ =
определяем из треугольника
= 16 + 64 = 80.
= -^гА^В. Длину отрезка
АВА2:
А2В2 = АВ2
Итак, A2Qi = ^p, a D2Q
Пример 12.10. Найти наименьшую площадь сечения
куба с ребром а плоскостью, проходящей через его диагональ.
Рис. 12.12
§12,2. Примеры решения задач 509
Первое решение. Пусть дан куб ABCDA\B\C\D\ с
ребром а. Если сечением является прямоугольник,
проходящий через диагональ и два ребра куба, выходящие из её
концов, то площадь этого сечения равна So = а2у/2. В
остальных случаях без ограничения общности можно считать, что
секущая плоскость пересекает ребро АА\. Согласно
теореме 2.4 сечением куба является параллелограмм. Мы
обозначим его через KBLD\ (рис. 12.12). Пусть также AiK = х,
хе[0, а].
По теореме Пифагора легко находятся стороны сечения:
ВК = \](а - х)2 + a2, KD\ — \Jx2 + a2. Будем
минимизировать половину площади сечения — площадь треугольника
BKD\, все стороны которого известны (BDi = aVS —
диагональ куба). Из ABKDi по теореме косинусов найдём
cos
«ZHhJi."'-™'-™1
следовательно,
sin
Площадь треугольника BKD\ равна
S = \KDi -BDi sin ZKDxB - -^Va2 - ax + x2.
Рассмотрим функцию у(х) = Va2 - ax + x2 на [О, a].
Исследуя её на наименьшее значение (для этого не
обязательно вычислять производную — достаточно исследовать
функцию у2(х) =а2 — ах + х2 (почему?)), получим, что оно
достигается при х — ^и равно —=—. Следовательно,
наименьшая возможная площадь треугольника BKD\ равна
5>д2 V 29 а соответствУюЩая площадь сечения Smin = a2 J ^ •
Осталось заметить, что Smin < So-
510 Глава 12. Задачи на максимум и минимум
Второе решение. Сохраним обозначения, введённые в
первом решении. Для вычисления площади сечения
воспользуемся следующим утверждением (которое
представляет и самостоятельный интерес):
квадрат площади плоского многоугольника равен
сумме квадратов площадей его проекций на три взаимно
перпендикулярные плоскости.
Докажем это утверждение. Пусть а — площадь
многоугольника, Oi — площадь его проекций на указанные
плоскости (i= 1, 2, 3), CLi — углы, которые образует плоскость
многоугольника с этими плоскостями. Заметим сначала,
что если плоскость многоугольника параллельна одной из
указанных плоскостей, то доказываемое утверждение
очевидно. Поэтому далее будем считать, что oct^O, i= I, 2, 3.
По теореме о площади ортогональной проекции
многоугольника (теорема 5.5) а* = a cos а,, i = 1, 2, 3, откуда
°\ + °2 + °\ = <72(cos2 <*i + cos2 а2 + cos2 or3).
Вспомним теперь решение примера 5.3. Мы получили,
что Si = So cos (Xt (в обозначениях примера 5.3),
следовательно,
S\ + S\ + sl = S(j(cos2 <*i
а затем доказали, что S2 + S| + S| = S%. Это означает, что
cos2 <x\ + cos2 a2 + cos2 as = 1.
Следовательно,
что и требовалось доказать.
Вернёмся к нашей задаче. Проекции сечения на
плоскости ABC, ABB\ и ADDi изображены на рис. 12.13.
Площади этих проекций легко вычисляются: они равны а2, ах
и а (а - х) соответственно. Тогда квадрат площади сечения
равен 2а2(х2 — ах + а2). Дальнейшее ясно.
Третье решение. Пусть М — основание
перпендикуляра, опущенного из точки К на прямую BD\ (см. рис. 12.12).
§ 12.2. Примеры решения задач
511
в)
Площадь параллелограмма KBLD\ вычислим по формуле
Следовательно, S принимает своё наименьшее значение
тогда, когда наименьшее значение принимает длина
отрезка КМ у т. е. когда КМ — расстояние между прямыми
АА\ и BD\. Находя это расстояние любым из известных
методов, получаем, что оно равно -~=. Поэтому наименьшее
у/ Z
значение S равно Smin = -^= • aVS = а2 \/-=.
/2 V 2
□
В заключение мы приведём пример задачи, которую
довольно сложно решить аналитически (попробуйте это
сделать), а её геометрическое решение изящно и коротко1*.
Пример 12.11*. Рассматриваются отрезки, один конец
которых расположен на окружности, вписанной в грань
ABCD куба ABCDAiBiC\Di с ребром 1, а другой конец —
на окружности, проходящей через вершины А\, В и D
этого куба. Найти наименьшую длину рассматриваемых
отрезков.
Решение. Рассмотрим две концентрические сферы:
касающуюся всех рёбер куба и описанную около куба. Ра-
у/2 у/3
диусы этих сфер равны ~~ и ^г соответственно, а их
центры находятся в центре куба. Окружности, о которых
!)Это не означает, что рассматриваемая задача является простой. В её
сложности вы сможете убедиться, попытавшись решить её
самостоятельно, перед тем как читать приведённое ниже решение.
512
Глава 12. Задачи на максимум и минимум
Рис. 12.14
идёт речь в условии, лежат на этих сферах. Следовательно,
длины рассматриваемых отрезков не меньше, чем
расстояние между сферами, равное разности их радиусов. Остаётся
показать, что среди этих отрезков найдётся отрезок длины
у/В-у/2
2
Пусть О — центр куба, 0)\ —окружность, вписанная в
грань ABCD, &>2 — окружность, описанная около AAyBD.
Рассмотрим гомотетию Н$ ' , переводящую меньшую из
сфер в большую. Если окружность сд\ = ^о (<*>i)
пересечёт окружность со 2 в точке М, а N — прообраз М при
указанной гомотетии, то MN = ^ • Для доказательства
существования точки М рассмотрим проекцию нашей
конфигурации на плоскость АА\С (рис. 12.14; на этом рисунке
§ 12,3. Геометрические неравенства 513
буквами со штрихами обозначены проекции
соответствующих точек). Нам достаточно показать, что проекции E\Fi
и А\Х окружностей а>\и 0)2(Е и F — точки пересечения о)\
с отрезком АС, Е\ и F\ — их образы при рассматриваемой
гомотетии) пересекаются в некоторой точке М', тогда любой
из двух возможных прообразов этой точки при
проектировании и есть искомая точка М. Эти отрезки пересекаются, так
как они являются хордами одного круга (проекции большей
сферы), а точки Е\ и F\ лежат по разные стороны от прямой
AiBf (почему?). □
§ 12.3. Геометрические неравенства
Половину из вас я знаю вполовину хуже,
чем хотел бы, а другую половину люблю
вполовину меньше, чем она того заслуживает.
Дж. Р. Р. Толкин. Властелин Колец
Задачи на нахождение наибольших и наименьших
значений тесно связаны с неравенствами. Действительно, всякая
задача об определении наибольшего (М) и наименьшего
(т) значений функции / на множестве G может быть
сформулирована так: доказать, что на множестве G справедливо
неравенство m^f^M.
Из сказанного вытекает один из способов
доказательства неравенств — сведение к эквивалентным
экстремальным задачам. Мы не станем приводить здесь примеры
применения производной к доказательству геометрических
неравенств, а займёмся обсуждением геометрических
методов.
Напомним, что ранее мы уже доказали два важных
неравенства, выражающие свойства плоских углов
трёхгранного угла (см. теоремы 5.6 и 5.7, а также пример 9.14).
Эти неравенства часто используются при доказательстве
других неравенств, в которых фигурируют углы.
17 3ак 3383
514 Глава 12. Задачи на максимум и минимум
Пример 12.12. Доказать, что сумма углов, под которыми
видны рёбра тетраэдра из произвольной его внутренней
точки, больше Згс.
Решение. Пусть О — точка внутри тетраэдра ABCD; а,
/3 и у — углы, под которыми из неё видны рёбра AD, BD
и CD; (р, (р и 1? —углы, под которыми видны рёбра ВС, С А
и АВ; Р — точка пересечения прямой OD с гранью ABC; К —
точка пересечения прямой АР с ребром ВС (рис. 12.15).
Применим неравенство из теоремы 5.6 к трёхгранным
углам ОВКР и ОАКС:
/РОК + ZKOB > ZBOP,
Сложим эти неравенства и учтём, что
ZKOB + /.СОК = /ВОС.
Получаем
/РОК + /АОС + /ВОС > /ВОР + /АОК.
§12.3. Геометрические неравенства 515
Перенося /.РОК в правую часть и заменяя разность /АОК —
- /РОК на /АОР, получим, что1*
/АОС + /ВОС > /ВОР + /АОР,
т.е. ф + ср > (к - а) + (к - (3)- Поэтому сс+{3 + (р + ф> 2к.
Аналогично доказываются неравенства /3 + у + ф + $ >
> 2п и у + а + 'д + (р>2л. Складывая три последних
неравенства, получаем неравенство
2(а+р + у + ср + ф + Ф) >6тг,
т.е. а+р + у + ср + ф + дуЗк. П
При доказательстве геометрических неравенств часто
используются следующие идеи: сведение к
алгебраическому неравенству, применение неравенства треугольника,
проектирование, симметрия, построение развёртки,
использование векторов и координат. Весьма плодотворными
являются и комбинации этих идей. Приведём примеры,
иллюстрирующие сказанное.
Пример 12.13. Пусть а, Ъ и с — длины рёбер
параллелепипеда, выходящих из одной вершины, ad — длина
диагонали параллелепипеда. Доказать, что
Решение. Для всякой диагонали параллелепипеда
справедливо неравенство d < а + Ъ + с. Действительно, пусть
в параллелепипеде ABCDAiB\C\D\ AB = a, AD = fe, AA\ = с,
АС\ = d. Применяя неравенство треугольника к
треугольникам АСС\ и ABC, мы получаем
d < АС + CCi <AB
промежуточный результат можно сформулировать так: пусть
луч ОР лежит внутри трёхгранного угла О ABC (с вершиной О), тогда
сумма плоских углов трёхгранного угла ОАВС больше, чем сумма
плоских углов трёхгранного угла ОАВР.
516 Глава 12. Задачи на максимум и минимум
что и утверждалось. Из этого неравенства вытекает, что
d2 < (а + Ь + с)2 = а2 + Ь2 + с2 + 2аЬ + 2Ьс + 2са <
<^а2 + Ь2 + с2 + (а2 + Ъ2) + (Ъ2 + с2) + (с2 + а2) =
т. е. а2 + Ь2 + с2 > ^d2. Мы воспользовались неравенством
2аЪ < а2 + Ь2, которое равносильно очевидному: (а — Ъ)2 ^ 0.
П
Пример 12.14. Пусть р —сумма длин рёбер выпуклого
многогранника, ad — наибольшее из расстояний между его
вершинами. Доказать, что р > 3d.
Решение. Обозначим наиболее удалённые друг от друга
вершины многогранника через Аи В (если таких вершин
более двух, то А и В — любые из них). Рассмотрим проекцию
многогранника на прямую АВ. Если некоторая точка С
проектируется на продолжение отрезка АВ, например за
точку В, то АС > АВ, что противоречит выбору точек А и В.
Значит, все точки многогранника проектируются в точки
отрезка АВ. Так как длина проекции отрезка на прямую
не больше длины самого отрезка, достаточно доказать, что
в каждую внутреннюю точку отрезка АВ проектируются
точки по крайней мере трёх различных рёбер (т. е. отрезок
АВ покрыт проекциями не менее чем в три слоя). Это
действительно имеет место, так как сечение многогранника
плоскостью, проходящей через произвольную внутреннюю
точку отрезка АВ и перпендикулярной ему, является
многоугольником, т.е. секущая плоскость пересекает хотя бы
три ребра. □
Пример использования проекции не на прямую, а на
плоскость при доказательстве неравенств даёт решение уже
встречавшейся нам ранее задачи: доказать, что площадь
любой грани тетраэдра меньше суммы площадей трёх
остальных его граней (см. решение задачи из примера 10.21).
§12.3. Геометрические неравенства
517
Пример 12.15. В тетраэдре ABCD плоские углы при
вершине А равны 60°. Доказать, что
AD^BC
+ DB.
Рис. 12.16
Решение. Пусть В\ и С\ — точки, симметричные
точкам В и С относительно биссектрисы угла А (рис. 12.16).
Заметим, что ВС + В\С\ ^СС\ +ВВ\ (достаточно сложить
неравенства треугольника, применённые к треугольникам
BOBi иСОСЬ гдеО= (ВС)n(BiCi)). НоB1Ci=BC,CC1 = АС
и BBi = АВ, следовательно, АВ + AC ^ 2BC. Аналогично
доказывается, что АС + AD ^ 2CD и AD + АВ ^ 2DB. Остаётся
сложить все три полученные неравенства:
2(AB
AD)
т.е. AB + AC + AD^BC + CD + DB.
Отметим, что равенство в последнем неравенстве
достигается тогда и только тогда, когда ABCD — правильный
тетраэдр (почему?). D
518
Глава 12. Задачи на максимум и минимум
Пример 12Л6. Доказать, что если сумма плоских углов
при вершине пирамиды больше 180°, то каждое её боковое
ребро меньше полу периметра основания.
Решение. Пусть SA\... Ап — данная пирамида. Разрежем
её боковую поверхность по ребру SA\ и развернём на
плоскость (рис. 12.17). Из условия задачи следует, что точка S
Рис. 12.17
лежит внутри многоугольника А\...АпА[. Пусть В —точка
пересечения прямой A\S со стороной этого
многоугольника, отличная от точки А\. Если а и b — длины ломаных
AiA2.-.B и B...AnA'v то AiS + SB<a
следовательно, 2A\S <a + b, т. е.
Ь) = \
А2А3 + ...+АпАх).
Осталось заметить, что ребро SA\ было выбрано
произвольно. □
Пример 12.17. Доказать, что сумма косинусов
двугранных углов произвольного тетраэдра не превосходит 2.
Решение. Пусть ?*, / = 1, 2, 3, 4,—единичный вектор,
перпендикулярный г-й грани тетраэдра, направленный во
внешнюю по отношению к тетраэдру сторону;, (рц —
двугранный угол, образованный i-й и ;-й гранями тетраэдра
§ 12,3. Геометрические неравенства 519
(i < ]\ iy 7 = If 2, 3, 4). Углы между рассматриваемыми
векторами дополняют до 180° соответствующие
двугранные углы тетраэдра, поэтому их скалярные произведения
противоположны косинусам этих двугранных углов.
ВЫЧИСЛИМ (ё\ + $2 + ?3 + ?4)2*
?2 + ... + ?3 '*4) = 4 - 2S,
где S — сумма косинусов углов срц. Так как скалярный
квадрат любого вектора неотрицателен, S ^ 2.
Заметим, что S = 2 тогда и только тогда, когда тетраэдр
является равногранным (попробуйте доказать это
самостоятельно). □
Пример 12.18. Дан куб ABCDA\B\C\D\ с ребром а.
Доказать, что расстояние от произвольной точки пространства
до одной из прямых AAi, B\C\, CD не меньше -^=.
у/ Z
Решение. Пусть ?i, ?2> Зз — ортонормированный базис,
векторы которого сонаправлены с векторами АВ, AD и АА\
соответственно. В системе координат {А, ?ь ?2> ?з} прямая
АА\ задаётся уравнениями д: = 0, г/ = 0; прямая CD —
уравнениями у = а, 2 = 0; прямая В\С\ — уравнениями х = а, 2 = а.
Квадраты расстояний от произвольной точки с
координатами (х, z/, г) до этих прямых равны х2 + у2, (у — а)2 + z2 и
(х — а)2 — (г — а)2 соответственно, а их сумма S равна
х2 + у2 + (у- а)2 + z2 + (х - a)2 + (z- a)2.
В силу легко проверяемого неравенства t2 + (t — а)2 ^ ^-г-
имеем
Это означает, что числа
х2 + у\ (у-а)2 + г2 и(х-а)2-(г-а)
2
не могут быть одновременно меньше ^-. Отсюда вытекает
доказываемое утверждение. □
520 Глава 12. Задачи на максимум и минимум
Задачи
Они могут и просто говорить, но чаще
всего решают задачи. Большой нужды
разговаривать попусту у них нет.
К. Саймак. Проект «Ватикан»
12.1. Найдите наибольший объём цилиндра, вписанного
в конус с высотой h и радиусом основания г так, что одно
из оснований цилиндра лежит внутри основания конуса,
а окружность другого его основания принадлежит боковой
поверхности конуса.
12.2. Дана правильная треугольная пирамида объёма V.
В эту пирамиду вписан цилиндр так, что одно из его
оснований принадлежит основанию пирамиды, а другое
основание вписано в сечение пирамиды плоскостью,
параллельной основанию. Найдите наибольший объём такого
цилиндра.
12.3. Найдите наименьший объём конуса, описанного
около шара радиуса 1.
12.4. Чему равно наименьшее значение отношения
объёмов конуса и цилиндра, описанных около одного шара?
12.5. Площадь поверхности сферического сегмента
равна S (имеется в виду только сферическая часть его полной
поверхности). Каков наибольший объём такого сегмента?
12.6. В треугольной пирамиде проведено сечение
плоскостью, параллельной одной из граней и касающейся
вписанного в пирамиду шара. Найдите наибольшее значение
площади такого сечения, если площадь полной
поверхности пирамиды равна S.
12.7. Внутри конуса расположены два шара, центры
которых лежат на его высоте. Радиус первого шара равен 1,
а второго — а. Первый шар касается боковой поверхности
конуса, второй касается первого и основания конуса.
Найдите высоту конуса, при которой его объём будет
наименьшим.
Задачи 521
12.8. В правильной треугольной пирамиде SABC угол
наклона бокового ребра к плоскости основания равен а,
длина бокового ребра SA равна I; О — центр основания,
точки Ai, Bi и С\ —середины рёбер ВС, С А и АВ
соответственно, Si e [SO]. Найдите объём пирамиды SiAiBiCi,
если известно, что сумма SiS + S\A\ + S\Bi + S\Ci имеет
наименьшее значение.
12.9. Угол между боковым ребром и высотой правильной
треугольной пирамиды равен а, длина высоты равна ft.
Найдите наименьшую площадь сечения этой пирамиды,
проходящего через ребро основания.
12.10. Дан куб ABCDA\BiC\D\ с ребром а. Концы
отрезка, образующего угол 60° с плоскостью грани ABCD, лежат
на прямых АВ\ и ВС\. Какую наименьшую длину может
иметь этот отрезок?
12.11. Сторона основания правильной треугольной
призмы АВСА\В\С\ имеет длину 4, а боковое ребро — 3. На
ребре ВВ\ взята точка F, а на ребре СС\ — точка G так,
что B\F — 1, a CG — 2/3. Точки Е и D — середины рёбер
АС и В\С\ соответственно. Найдите наименьшее значение
суммы ЕР + PQj где точка Р принадлежит отрезку A\D,
а точка Q — отрезку FG.
12.12*. В тетраэдре SABC ZASB = ZBSC = ZCSA = 90°,
а сумма длин всех его рёбер равна а. Найдите наибольший
объём такого тетраэдра.
12.13. Точки А, В, С и В пространства таковы, что не
более чем одно из расстояний АВ, AC, AD, ВС, BD, CD
больше 1. Определите наибольшее значение суммы этих
шести расстояний.
12.14. Чему равна наибольшая площадь проекции на
плоскость
а) правильного тетраэдра с ребром а;
б) прямоугольного параллелепипеда с измерениями а,
Ъ и с?
12.15. Внутри правильного тетраэдра найдите точку,
сумма расстояний от которой до его вершин минимальна.
522 Глава 12. Задачи на максимум и минимум
12.16*. Найдите точку, сумма квадратов расстояний от
которой до граней произвольного тетраэдра минимальна.
12.17*. Дан куб ABCDAiBiCiDi с ребром а. На лучах
А\А, А\В\ и A\D\ взяты соответственно точки Е, F и G
так, что А\Е = A\F = A\G = b. Пусть М — точка
окружности, вписанной в квадрат ABCD, a N — точка окружности,
проходящей через £, F и G. Каково наименьшее значение
длины отрезка MN1
12.18. В усечённом конусе угол между осью и
образующей равен 30°, радиус большего основания равен R.
Найдите длину кратчайшего пути по поверхности усечённого
конуса, соединяющего точку окружности одного основания
с диаметрально противоположной точкой окружности
другого основания.
12.19. а) Докажите, что сумма двугранных углов
трёхгранного угла больше п.
б) Докажите, что сумма двугранных углов л-гранного
угла больше (п - 2) к.
12.20. Докажите, что сумма двугранных углов тетраэдра
заключена между 2к и Зтг.
12.21. Докажите, что сумма расстояний от
произвольной точки до всех вершин единичного куба не меньше 4\/3.
12.22. Внутри куба с ребром 1 расположено несколько
отрезков так, что любая плоскость, параллельная одной из
граней куба, пересекает не более одного из них. Докажите,
что сумма длин этих отрезков не больше 3.
12.23. Замкнутая ломаная проходит по поверхности
куба с ребром 1 и имеет общие точки со всеми его гранями.
Докажите, что её длина не меньше Зл/2.
12.24*. Вершины тетраэдра KLMN лежат внутри или на
поверхности тетраэдра ABCD. Докажите, что сумма длин
всех рёбер тетраэдра KLMN меньше, чем 4/3 суммы длин
всех рёбер тетраэдра ABCD.
12.25. Докажите, что для любого тетраэдра найдутся
две такие плоскости, что отношение площадей проекций
тетраэдра на них не меньше \/2.
Задачи 523
12.26. Докажите, что площадь любого сечения тетраэдра
не превосходит площади одной из его граней.
12.27. Докажите, что любое сечение куба, проходящее
через его центр, имеет площадь, не меньшую площади
грани куба.
12.28. Длины пяти рёбер тетраэдра не превосходят 1.
Докажите, что его объём не превосходит ^.
12.29. На гранях BCD, CD A, BDA, ABC тетраэдра ABCD
выбраны точки Аи Ви Си -Di соответственно так, что
отрезки АА\, ВВ\, СС\ и DD\ пересекаются в одной точке.
Докажите, что VAiBxCidx ^ 97vabcd*
12.30*. На рёбрах SA, SB и SC тетраэдра SABC объёма V
взяты точки А\у В\у Си а на сторонах В\С\У С\А\, А\В\
полученного треугольника А\В\С\ —точки Аг, Вг> ^2
соответственно. Пусть Vu V2, V% — объёмы тетраэдров АА1В2С2,
ВВ1С2А2, СС\А2В2- Докажите, что
12.31. Докажите, что радиус вписанной окружности
любой грани тетраэдра больше радиуса его вписанной сферы.
12.32. Пусть А, В, С и D — произвольные точки
пространства. Докажите, что
АС2 + BD2 + AD2 + ВС2 > АВ2 + CD2.
12.33. Внутри единичной сферы расположены п точек.
Докажите, что сумма квадратов попарных расстояний
между ними не превосходит п2.
Глава 13
Объём и площадь поверхности тела
Просто мне некогда было рассказать
об этом раньше. И сейчас тоже некогда.
Дж. Р. Р. Толкин. Хоббипг, или Туда и обратно
§ 13.1. Определение объёма
Я много раз обращался к этой задаче
и снова её откладывал, а вот сегодня
добил-таки. Получилось очень изящно,
А. и Б. Стругацкие. Понедельник начинается в субботу
В предыдущих главах нашего курса мы опирались на
интуитивные представления об объёме тела и площади его
поверхности. Ниже мы дадим определения этих понятий
и докажем формулы для вычисления объёмов и площадей
поверхностей многогранников и тел вращения, которыми
мы ранее пользовались без доказательства.
Отметим, что построение логически безупречной
теории измерения длин, площадей или объёмов, или, как
принято говорить в математике, теории меры,
неэлементарно, в частности требует привлечения тонких методов
математического анализа. Находясь в рамках школьного
курса, мы лишь наметим основные этапы такого
построения, оставив без доказательства многие фундаментальные
факты. Более полное изложение вопросов, касающихся
теории объёмов и площадей поверхностей, вы сможете найти,
например, в статьях [Болтянский, 1964] и [Рохлин, 1964],
опубликованных в пятом томе «Энциклопедии
элементарной математики».
526 Глава 13. Объём и площадь поверхности тела
Всюду ниже, говоря об объёме и площади поверхности
фигуры, мы будем предполагать, что эта фигура является
телом1*. Кроме того, зафиксируем раз и навсегда единицу
длины»
Определение. Пусть на некотором множестве Dy,
являющемся подмножеством множества всех тел, определена
функция V такая, что
1°. VTeDv: V(T) >0;
2°. если Т = Т\ U Т2, причём int Ti П int T2 = 0, то2)
V(T)=V(T1) + V(T2);
3°. если Тх = Г2> то V(Ti)=V(T2);
4°. если К —куб с ребром длины 1, KeDy, то V(K) = 1.
Объёмом тела Т е Dy называется значение этой функции
для 7\ т.е. число V(T).
Подобный подход, когда объект определяется путём
перечисления свойств, которым он должен удовлетворять,
называется аксиоматическим определением, а сами эти
свойства — аксиомами.
Итак, объём — это функция с областью определения Dy>
удовлетворяющая аксиомам 1°—4°. Аксиома 1° утверждает,
что эта функция положительна на своей области
определения. Смысл аксиомы 2° заключается в том, что как бы мы
ни разбили тело Т на неперекрывающиеся тела Ti и Тг,
объём тела Т равен сумме объёмов тел Т\ и Тг (при этом Т,
Ti, 7*2 должны, разумеется, принадлежать множеству Dy).
Это аксиома аддитивности3^ объёма. Аксиома 3° гласит,
2)Тем самым мы не распространяем эти понятия, например, на
объединения тел, не имеющих общих точек (будучи несвязными, такие
фигуры не являются телами). Это делается лишь для упрощения
изложения и не является принципиальным.
2)Отсюда по индукции вытекает, что если Т— Т\ U Тг U... U Тп и Vi ф}
int Тх Hint Т2 = 0 (i, j = 1, 2, .... п), то V(T) - V{Ti) + V(T2) + ... + V(Ta).
3)От латинского слова additivus — прибавляемый.
§13.1. Определение объёма 527
что объёмы равных тел равны, или что объём не
изменяется при перемещениях. Это аксиома инвариантности1^
объёма относительно перемещений. Наконец, аксиомой 4°
задаётся единица объёма, или, как принято говорить, его
нормировка. Поэтому объём часто коротко определяют как
положительную, аддитивную, инвариантную относительно
перемещений нормированную функцию, определённую на
некотором подмножестве множества всех тел.
Дав аксиоматическое определение, следует ответить на
два вопроса: существует ли объект, обладающий
перечисленными свойствами; если существует, то однозначно ли
он этими свойствами определён. Оказывается, на всём
множестве тел функции, удовлетворяющей аксиомам 1°—4°,
не существует. Иными словами, существуют тела, не
имеющие объёма. Поэтому построение теории объёма
проводится следующим образом. Сначала в качестве области
определения функции V рассматривается множество
многогранных тел, т. е. тел, которые можно разбить на конечное
число неперекрывающихся тетраэдров2*. Далее
доказывается, что объём, определённый на множестве многогранных
тел аксиомами 1°—4°, существует и единственен. Затем
определяется кубируемое или измеримое тело К как тело,
для которого Ve > 0 существуют многогранные тела А и
В такие, что А с К С В и V(B) — V(A) < е. Оказывается,
такое определение позволяет рассматривать объём,
определённый аксиомами 1°—4° на множестве всех измеримых
тел, и доказать, что он существует и единственен.
Мы не будем заниматься реализацией намеченного
плана построения теории объёма, а лишь примем выделенные
выше утверждения о его существовании и единственности
без доказательства. В дальнейшем нам будет важно лишь
то, что многогранники и тела вращения измеримы.
J)Ot латинского invariant — неизменный.
2)Выпуклые многогранники являются многогранными телами
(почему?).
528 Глава 13. Объём и площадь поверхности тела
§ 13.2. Объём прямоугольного параллелепипеда.
Объём призмы
— Значит, так,—сказал он.—Первый ящичек, «ля прев» —
это «доказательство». «Лясуре» означает «источник». «Клеф
де мистэр» — «ключ тайны».
— Ишь ты, ключ тайны! — Юра взял штангенциркуль
и измерил длину, ширину и высоту железной коробки.
Е. Войскунский, И, Лукодъянов. Экипаж «Меконга»
В этом параграфе мы приступаем к вычислению
объёмов конкретных тел.
I Теорема 13.1. Объём прямоугольного параллелепипеда
равен произведению его измерений.
Прежде чем доказывать эту теорему, сформулируем и
докажем два вспомогательных утверждения.
I Лемма 13.1 (монотонность объёма). Если тела Т\ и Г2
измеримы и Ti С Г2, то V{T{) ^ F(T2).
Доказательство. В случае, когда Т\ и Г2 — это одно
и то же тело, V(T\) = У{Т2) по аксиоме 3°. В противном
случае утверждение вытекает из аксиом 1° и 2°. □
Лемма 13.2. Объёмы двух прямоугольных
параллелепипедов с равными основаниями относятся как длины их
боковых рёбер.
Доказательство. Расположим параллелепипеды так,
как показано на рис. 13.1, совместив их равные
основания. Обозначим параллелепипеды через ABCBAiB\C\D\ и
ABCDA2B2C2D2, а их объёмы —через Vi и F2
соответственно. Без ограничения общности рассуждений можно считать,
что F2 ^ V\.
Докажем, что -ту- = -т-т* Предположим, что это не так
У\ АА\
И
=Д —-jr— = е > 0. Возьмём натуральное число п >
У\ АА\
§ 13,2. Объём прямоугольного параллелепипеда 529
(например, п— - + 1, где - —наибольшее целое число,
не превосходящее 1/е) и разделим отрезок АА\ на п
равных частей. Пусть на отрезке АА2 укладывается т полных
отрезков разбиения. Это означает, что
п
откуда
т +1
(13.1)
Проведём через точки, разбивающие отрезок АА\>
плоскости, параллельные плоскости ABCD. Они разобьют
параллелепипед ABCBAiBiCiDi на п равных прямоугольных
параллелепипедов (рис. 13.2). Из аксиом 2° и 3° следует,
что объём каждого из этих параллелепипедов равен —.
Параллелепипед ABCBA2B2C2D2 содержит т полных
параллелепипедов разбиения, поэтому по лемме 13.1
530 Глава 13. Объём и площадь поверхности тела
откуда
m ^ V2 m +
п ^ Vi n
(13.2)
Из неравенств (13.1) и (13.2) следует, что
V2 АА2 ^ 1
Полученное противоречие доказывает требуемое
утверждение. D
Доказательство теоремы 13.1. Рассмотрим четыре
прямоугольных параллелепипеда с измерениями а, Ь, с;
1, Ь, с; 1, 1, с и 1, 1, 1, объёмы которых равны V, V\, V2
Рис. 13.3
и 1 соответственно (рис. 13.3). Пользуясь утверждениями
леммы 13.2, последовательно получаем
а
1'
b
1'
l
£
1'
откуда V = abc.
§ 13.2. Объём прямоугольного параллелепипеда 531
Теорема 13.2. Объём прямой призмы равен
произведению площади основания на высоту призмы.
а)
б)
Рис. 13.4
Доказательство. Разберём сначала случай
треугольной призмы. Пользуясь тем, что в любом треугольнике
найдётся сторона, внутри которой лежит основание опущенной
на неё высоты (почему?), достроим основания призмы до
прямоугольников (рис. 13.4а), а саму призму —до
прямоугольного параллелепипеда (рис. 13.46). Объём
достроенной части призмы, очевидно, равен объёму первоначальной
призмы. То же самое верно и для площади достроенной
части основания. Таким образом, если V и Vq — объёмы, а
S и So — площади оснований призмы и параллелепипеда,
соответственно, a if— их общая высота, то
Для доказательства теоремы в случае n-угольной (л > 3)
призмы достаточно разбить её на треугольные призмы,
используя триангуляцию оснований (см. рис. 13.5). □
532 Глава 13. Объём и площадь поверхности тела
Рис. 13.5
Рис. 13.6
Теорема 13.3. Объём наклонной призмы равен
произведению площади перпендикулярного сечения на боковое
ребро.
Доказательство. Пусть AiA2...AnB\B2...Bn — данная
наклонная призма. Продолжим рёбра призмы в одну
сторону (например, за точки В/). Проведём плоскость,
перпендикулярную боковым рёбрам и пересекающую их
продолжения в точках А[, А2, ..., А!п (рис. 13.6). Пусть при
параллельном переносе на вектор А\В\ точки А[, А!2, ..., А!п
перейдут в точки B'l9 В2, ...,£^. При этом переносе
многогранник AiA2...AnA!lA!2...Afn перейдёт в многогранник
BiB2.>.BnB'1Br2...B/n, следовательно, данные
многогранники имеют равные объёмы. Заметим, что многогранник
BiB2-..BnA!lA!2...A!n — пересечение упомянутых
многогранников, поэтому объём данной в условии наклонной призмы
равен объёму прямой призмы А!1А!2.ш.А'пВ'1В12..-В'н. Высота
последней призмы равна (по построению) боковому ребру
§ 13.2. Объём прямоугольного параллелепипеда 533
исходной призмы, а площадь основания — площади
перпендикулярного сечения исходной призмы. Ссылка на
теорему 13.2 завершает доказательство. □
I Следствие. Объём наклонной призмы равен
произведению площади основания на высоту.
Доказательство. Пусть угол между плоскостью
основания и плоскостью перпендикулярного сечения призмы
равен ср. Заметим, что при ортогональном проектировании
на плоскость перпендикулярного сечения основание
призмы переходит в её перпендикулярное сечение, поэтому по
теореме о площади ортогональной проекции (теорема 5.5)
Sj. = S0CH. cos (р, где S0CH. — площадь основания, S± —
площадь перпендикулярного сечения.
Боковое ребро и высота призмы перпендикулярны
соответственно плоскостям перпендикулярного сечения и
основания, поэтому угол между ними равен ср (упражнение 5.2).
ТТ
Следовательно (рис. 13.7), I— , где I — длина бокового
COS (I/
Рис. 13.7
ребра, if— длина высоты призмы. По теореме 13.3 объём
ТТ
призмы равен V — S± • / = SOCH. cos cp — SOCH, • Н. □
534 Глава 13. Объём и площадь поверхности тела
Итак, объём любой призмы может быть найден по
формуле
где Sqch. — площадь основания призмы, Н — длина её
высоты.
§ 13.3. Методы вычисления объёма. Объём цилиндра
Сегодня нам предстоит о многом
услышать и многое решить.
Дж. Р. Р. Толкин. Властелин Колец
Методы вычисления объёма аналогичны известным из
планиметрии методам вычисления площади. Наиболее
простой метод — метод разрезания и складывания
(называемый также методом разложения). Он заключается в
разбиении данного тела на конечное число частей, объёмы
которых уже известны, либо на части, из которых можно
сложить одно или несколько тел известного объёма. Этот
метод часто заменяют другим способом вычисления
объёма, являющимся в некотором смысле обратным: вместо
того чтобы разрезать тела на равные части, их дополняют
равными частями так, чтобы получившиеся после такого
дополнения тела были равны (метод дополнения).
Описанные методы мы применили в предыдущем параграфе при
вычислении объёма призмы.
В более сложных случаях объём может быть вычислен
с помощью предельного перехода (называемого также
методом исчерпывания). Оказывается, если для данного тела Т
существуют такие последовательности измеримых тел
Fn и Gn, что для любого натурального п тело Т
содержится в теле Fn и содержит тело Gn> причём
lim V(Fn) = lim V(Gn) = V,
ГС—ЮО П—КХ>
то тело Т измеримо и V(T) = V. Доказательство этого
утверждения выходит за рамки нашего курса.
§ 13.3. Методы вычисления объёма. Объём цилиндра 535
Предельный переход (хотя и в весьма завуалированной
форме) был использован нами при доказательстве формулы
для объёма прямоугольного параллелепипеда.
В точности описанный выше метод предельного
перехода может быть реализован, например, при выводе формулы
для объёма цилиндра.
I Теорема 13.4. Объём (прямого кругового) цилиндра
равен произведению площади его основания на высоту.
Доказательство. Пусть Т — данный цилиндр с
основанием площади S и высотой Н. Рассмотрим
последовательность Fn (п > 3) правильных гс-угольных призм,
описанных около цилиндра Т. Высота призмы Fn равна Н,
площадь её основания обозначим через Sn. По теореме 13.2
V{Fn) — Sn • Н. Как известно из планиметрии,
последовательность площадей правильных многоугольников,
описанных около круга, при неограниченном увеличении числа
их сторон имеет предел, равный площади этого круга.
Следовательно,
lim V(Fn) = lim (Sn.H)=H- lim Sn=S-H.
Аналогично если Gn (n ^ 3) — последовательность
правильных д-угольных призм, вписанных в цилиндр Т, то
lim V(Gn) = \im(sn-H)=H. lim sn = S-H
П-+ОС П—►ОС П-+ОО
(здесь sn — площадь правильного я-угольника, вписанного
в основание цилиндра; lim sn = S).
Итак, цилиндр Т содержится в призме Fn и содержит
призму Gn (n = 3, 4, 5, ...), причём
lim V(Fn) = lim V(Gn) =S>H.
Л-ЮО П—ЮО
Следовательно, V(T) =SH. □
Метод предельного перехода позволяет свести
нахождение объёма измеримого тела к вычислению интеграла.
536 Глава 13. Объём и площадь поверхности тела
Теорема 13.5. Пусть измеримое тело Т содержится
между плоскостями, имеющими в некоторой декартовой
системе координат уравнения х = а и х = Ъ {а < fc), a S(c) —
площадь сечения этого тела плоскостью х — с (а^с ^Ь).
Тогда объём тела Т может быть найден по формуле
(13.3)
Доказательство этой теоремы можно найти в курсах
математического анализа.
Сделаем несколько замечаний по поводу теоремы 13.5.
Во-первых, в её формулировке на первый взгляд
отсутствуют требования существования площади S(x) для всех
х е [а, Ь] и интеграла, стоящего в правой части
формулы (13.3). Но оказывается, их существование
автоматически следует из измеримости тела Т. Во-вторых,
доказательство теоремы основано на формуле объёма цилиндра
(теорема 13.4), поэтому не следует применять формулу (13.3)
к вычислению объёма цилиндра.
Отметим важный частный случай формулы (13.3).
Теорема 13.6. Пусть f(x) — непрерывная
неотрицательная функция, определённая на [a, b], a тело Т получено
вращением криволинейной трапеции, ограниченной
графиком у = f{x) и прямыми х — а, х = Ь, у = 0 (рис. 13.8).
Тогда объём тела вращения Т вычисляется по формуле
(13.4)
Доказательство. Тело Т измеримо согласно замечанию,
сделанному в конце § 13.1. Сечение тела Т плоскостью
х — с (а^с^Ь) является кругом площади л:/2(с) (возможно,
что этот jcpyr вырожден и его площадь нулевая).-Остаётся
применить теорему 13.5. □
§ 13.3. Методы вычисления объёма. Объём цилиндра 537
О
а)
б)
Рис. 13.8
Приведём примеры использования формул (13.3), (13.4).
Пример 13.1. Найти объём тела, полученного
вращением вокруг оси Ох фигуры, ограниченной графиком
функции у = sin х, О ^ х ^ я, и прямой у = 0.
Решение. Согласно формуле (13.4),
V = nlsin2xdx=nl i-™*2*
о о 2
dx =
так как, очевидно,
cos
= 0.
□
Пример 13.2. Дан цилиндр, у которого радиус
основания равен г, а высота — Н. Пусть О — центр нижнего
основания, АВ — его диаметр. Пусть L —точка на боковой
поверхности цилиндра, лежащая в плоскости, проходящей
через точку О перпендикулярно прямой АВ. Обозначим
через h расстояние от точки L до плоскости нижнего
основания. Назовём цилиндрическим сегментом радиуса г
и высоты h (h < Н) тело, отсекаемое от цилиндра
плоскостью ABL и не содержащее точек верхнего основания
(рис. 13.9). Найти объём цилиндрического сегмента.
538 Глава 13. Объём и площадь поверхности тела
Р
L
Решение. Введём декартову систему координат, как
показано на рис. 13.9 (ось Ог не изображена). Пусть угол
между плоскостью ABL и плоскостью нижнего основания
цилиндра равен а.
Будем рассматривать сечения цилиндрического
сегмента всевозможными плоскостями, перпендикулярными оси
Ох. Сечение данного сегмента, пересекающее ось Ох в точке
М(лг, 0, 0), есть прямоугольный треугольник MNP,
площадь которого равна
S(x) = SAMNP = \MN. NP = \MN2 tg a - \ (r2 - x2) tg a,
поскольку из прямоугольного AMNO имеем
По формуле (13.3) находим искомый объём:
г г
V = 5 S(x) dx = | tg a ^ (r2 - x2) dx =
—r —r
поскольку из треугольника KLO имеем KL = h — r tg a.
§ 13.3. Методы вычисления объёма. Объём цилиндра 539
Рис. 13.10
Заметим, что тот же результат можно получить,
рассматривая сечения цилиндрического сегмента
плоскостями, перпендикулярными оси Оу. Сечение, проходящее
через точку с ординатой у, — это некоторый прямоугольник
EGFH (рис. 13.10) площади
Q(y) =EGGF = 2y/r2-y2y tg a.
Объём сегмента равен
y2d(y2) =
□
CS* Упражнение 13Л, Найдите объём цилиндрического сегмента,
рассматривая его сечения плоскостями, перпендикулярными
оси Oz.
Наконец, ещё один метод вычисления объёмов связан
с одним важным следствием из формулы (13.3).
540 Глава 13. Объём и площадь поверхности тела
Теорема 13.7 (принцип Кавальери1)). Пусть в
пространстве заданы измеримые тела Т\9 Т2 и плоскость а.
Если любая плоскость, параллельная а и пересекающая
тело Ть пересекает и тело Тг, причём сечения имеют
одинаковые площади (рис. 13.11), то объёмы тел Т\ и Т%
равны.
Рис. 13.11
Эта теорема сразу следует из теоремы 13.5. Применение
принципа Кавальери к вычислению объёма заключается
в том, что для данного тела, объём которого подлежит
вычислению, подбирается тело известного объёма, имеющее
такие же по площади сечения, что и данное тело.
Конкретные примеры применения этого метода мы приведём
в следующих параграфах.
§ 13.4. Объём тетраэдра
В этом параграфе мы дадим несколько доказательств
формулы для объёма тетраэдра.
I Теорема 13.8. Объём тетраэдра равен одной трети
произведения площади его основания на высоту.
^Назван в честь итальянского математика Франческо Бонавентура
Кавальери (1598-1647).
§ 13Л. Объём тетраэдра
541
Первое доказательство.
Рассмотрим тетраэдр 7\ у которого в
основании лежит треугольник Л площади S,
а высота, опущенная на основание,
равна Н. Разделим одно из
боковых рёбер тетраэдра на п равных
частей и проведём через точки деления
плоскости, параллельные основанию.
Обозначим треугольники,
получившиеся в сечениях, через Дь Дг, ...,
Дл-ь ^п = Д> считая от вершины
тетраэдра к его основанию. Каждый из
треугольников Ль А2, ..., Ап подобен
треугольнику Д, причём коэффициент подобия
k
равен -. Поэтому 9
Рис. 13.12
и Д
Для каждого слоя построим призму, содержащуюся в
нём, и призму, содержащую его (см. рис. 13.12; основания
призм — треугольники Ль ..., Дл, боковые рёбра
параллельны выбранному ребру тетраэдра, высоты призм равны
Н/п). Пусть Fn — объединение всех призм, содержащих
в себе соответствующие слои тетраэдра, a Gn — объединение
всех призм, заключённых в этих слоях. Тогда
GncTcFn.
Объёмы тел Fn и Gn соответственно равны
V(Fn) =
£ + S(A2)f
22
' п
и
V(Gn) = ^fl
Найдём пределы последовательностей объёмов V{Fn) и
V(Gn) при п —►оо, используя известную из алгебры формулу
542 Глава 13. Объём и площадь поверхности тела
для суммирования квадратов1*:
lim V(Fn)= lim Щ±n(n
п-+ос П-+ОО П° О
и аналогично
Ша V(Gn) = §j* lim
Следовательно, 7(Г) = |sH. □
Второе доказательство. Сначала сформулируем и
докажем вспомогательное утверждение.
I Лемма 13.3. Объёмы тетраэдров с основаниями равной
площади и равными высотами равны.
Доказательство. Расположим основания данных
тетраэдров в одной полуплоскости, как показано на рис. 13.13.
Рис. 13.13
Рассмотрим плоскость, параллельную основаниям и
пересекающую оба тетраэдра. Сечения тетраэдров —
треугольники, подобные соответствующим основаниям с
коэффициентом ~, где h — расстояние от вершин тетраэдров до
м
1)Цля любого натурального п справедливо равенство I2 + 22 + ...
... 4- п2 = п(п + 1)(2п 4- 1)/6, которое легко доказывается (например,
методом математической индукции)
§ 13.4. Объём тетраэдра 543
построенной плоскости, Я —высота тетраэдров. Поскольку
площади оснований тетраэдров равны, то площади сечений
тоже равны. Следовательно, по принципу Кавальери
(теорема 13.7) объёмы тетраэдров равны. □
Пусть дан тетраэдр ABCD с основанием ABC
площади S и высотой Ну опущенной на это основание.
Проведём через вершину D плоскость, параллельную ABC, и
достроим тетраэдр ABCD до призмы ABCDEF (рис. 13.14).
Рис. 13.14
Данную призму можно разрезать на три тетраэдра: ABCD,
DEFB и DFCB. Тетраэдры ABCD и DEFB имеют основания
ABC и DEF равной площади и равные высоты,
проведённые к этим основаниям. Следовательно, по лемме 13.3
V(ABCD) = V(DEFB). Аналогично основания ADC и DFC
тетраэдров ABCD и DFCB равновелики, а высоты,
опущенные из точки В, равны, откуда V(ABCD) ^V(DFCB). Итак,
V(ABCD) = |v(ABCDEF). Но по следствию из теоремы 13.3
объём призмы ABCDEF равен SH, откуда V(ABCD) = hsH.
□
в§* Упражнение 13.2. Докажите теорему 13.8, используя
интеграл ьную формулу (13.3).
Все упомянутые нами доказательства формулы для объёма
тетраэдра имеют одну общую черту — они, явно или неявно,
544 Глава 13. Объём и площадь поверхности тела
используют предельный переход. В то же время в
планиметрии, после того как (также с помощью предельного перехода)
выведена формула площади прямоугольника1*, площадь любого
многоугольника может быть найдена элементарно методом
разрезания и складывания.
Таким образом, возникает естественный вопрос: можно ли
получить формулу для объёма тетраэдра, зная формулу для
объёма параллелепипеда, методом разрезания и складывания (или
дополнения), т. е. без предельного перехода?
Прежде чем ответить на этот вопрос, напомним, что две
фигуры на плоскости (в пространстве) называются равновеликими у
если они имеют равные площади (объёмы). Две фигуры (на
плоскости или в пространстве) называются равносоставленными,
если одну из них можно разрезать на конечное число частей
так, что из полученных частей можно сложить вторую фигуру.
Очевидно, что в силу аксиом площади и объёма две равносо-
ставленные фигуры равновелики. Оказывается, на плоскости
любые два равновеликих многоугольника равносоставлены. Это
утверждение было независимо доказано в 1832 г. венгерским
математиком Ф. Бойяи и немецким офицером (и
математиком-любителем) П. Гервином. Доказательство теоремы Бойяи—Гервина
можно найти, например, в книгах [Александров и др., 1991],
[Болтянский, 1956]. Аналогичный вопрос для пространства был
включён Д. Гильбертом в число важных нерешённых проблем
математики, сформулированных им в 1900 г.
Третьей проблеме Гильберта можно придать такую
формулировку: всякий ли тетраэдр равносоставлен с некоторым
прямоугольным параллелепипедом того же объёма?
я& Упражнение 13.3. Приведите пример тетраэдра, равносостав-
ленного с прямоугольным параллелепипедом.
В общем случае решение третьей проблемы Гильберта
оказалось отрицательным. В 1901 г. немецкий математик М. Ден
доказал2*, что куб и правильный тетраэдр равного объёма не
равносоставлены и не могут быть дополнены равными
частями до равносоставленных многогранников. Оказалось также,
^Здесь возникает следующий вопрос: можно ли вывести формулу
площади прямоугольника и формулу объёма прямоугольного
параллелепипеда элементарно, т. е. не используя предельный переход?
Оказывается, этого сделать нельзя (см., например. [Болтянский, 1964]).
^Доказательство теоремы Дена можно найти в упомянутой книге
[Болтянский, 1956].
§ 13.5. Объём пирамиды и конуса 545
что существуют два не равносоставленных тетраэдра с
равными основаниями и высотами.
Тем самым дан ответ на поставленный выше вопрос: доказать
формулу для объёма тетраэдра методом разрезания и
складывания (или методом дополнения) невозможно.
§ 13.5. Объём пирамиды и конуса
I Теорема 13.9. Объём пирамиды равен одной трети
произведения площади её основания на высоту.
Для доказательства достаточно выполнить
триангуляцию основания и разбить пирамиду на тетраэдры,
основаниями которых служат треугольники разбиения, а
вершина находится в вершине данной пирамиды (рис. 13.15).
Затем следует воспользоваться доказанной формулой для
объёма тетраэдра.
Рис. 13.15
^Упражнение 13.4. Докажите теорему 13.9.
I Теорема 13.10. Объём конуса равен одной трети
произведения площади его основания на высоту.
и^3 Упражнение 13.5. Докажите теорему 13.10, используя
а) предельный переход (приближая конус
последовательностями правильных вписанных в него и описанных около
него пирамид);
б) интегральную формулу (13.3);
18 3ак 3383
546 Глава 13. Объём и площадь поверхности тела
в) принцип Кавальери (взяв в качестве второго тела
пирамиду с той же площадью основания и высотой, что и у
конуса).
и^г1 Упражнение 13.6. Докажите, что объём усечённой пирамиды
и усечённого конуса можно вычислить по формуле
где Si и S2 — площади оснований, а Н — высота. (См. также
упражнение 10.8.)
§ 13.6. Объём шара и его частей
— А вы не могли бы вычислить
диаметр земного шара?
— Извиняюсь, не смог бы, — сказал
Швейк. — Однако мне тоже хочется,
господа, задать вам одну загадку...
Я. Гашек. Похождения бравого солдата Швейка
Теорема 13.11. Объём шара радиуса R вычисляется по
формуле
Первое доказательство. Рассмотрим шар как
результат вращения полукруга вокруг прямой, содержащей его
диаметр, и воспользуемся формулой (13.4). Выберем
систему координат, как показано на рис. 13.16. Искомый
-R
Рис. 13.16
§ 13.6. Объём шара и его частей
547
полукруг ограничен дугой окружности, задаваемой
уравнением у — VR2 - х2, -R ^x^R7 и отрезком оси Ох. По
формуле (13.4) объём тела вращения равен
IX IX
V = п 5 (VR2 - х2)2 dx=K J (R2 - х2) dx =
Второе доказательство. Расположим на плоскости а
данный шар радиуса R и цилиндр, радиус основания
которого равен R, а высота — 2R (рис. 13.17). Удалим из
Рис. 13.17
цилиндра два конуса, у которых вершина есть середина оси
цилиндра, а основаниями являются соответственно нижнее
и верхнее основания цилиндра. Докажем с помощью
принципа Кавальери, что объём тела, оставшегося от цилиндра,
равен объёму шара. Проведём плоскость, параллельную а,
пересекающую оба тела и отстоящую от центра шара на
расстояние d. Сечение шара этой плоскостью есть круг радиуса
г = VR2 — d2 и соответственно площади кг2 = k(R2 — d2),
сечение второго тела есть кольцо, у которого радиус внешнего
круга равен Я, а радиус внутреннего круга — d (почему?).
Площадь этого кольца равна k(R2 — d2). Таким образом,
в силу принципа Кавальери объём шара равен объёму тела,
оставшегося от цилиндра, т. е.
D * 3 ' 3
548 Глава 13. Объём и площадь поверхности тела
(здесь Vuj., F4. и VKm обозначают соответственно объёмы
шара, цилиндра и конуса). □
Замечание. В ходе второго доказательства мы установили
знаменитый результат Архимеда: объём шара в полтора раза
меньше объёма описанного цилиндра.
в^ Упражнение 13.7. Выведите формулу для объёма шара
методом предельного перехода, приближая его «ступенчатыми»
телами, состоящими из цилиндров (рис. 13.18).
Рис. 13.18
BS* Упражнение 13.8. Выведите формулу для объёма шара с
помощью принципа Кавальери, используя в качестве второго тела
тетраэдр (с определёнными параметрами и определённым
образом расположенный в пространстве).
Теорема 13.12. Объём шарового сегмента вычисляется
по формуле
где R — радиус шара, Н — высота сегмента.
Доказательство отличается от первого доказательства
теоремы 13.11 только выбором пределов интегрирования
(см. рис. 13.19):
R-H
R-H
§ 13.7. Об определении площади поверхности
R
549
-R О
Рис. 13.19
Теорема 13.13. Объём шарового сектора вычисляется
по формуле
где R — радиус шара, Н — высота соответствующего
сегмента.
Эту теорему вы уже доказали при выполнении
упражнения 10.13.
§ 13.7. Об определении площади поверхности
Дело не в том, что они не видят решения,
а в том, что они не видят проблемы.
Г. К. Честертон. Остриё иглы
В этом параграфе мы обсудим различные подходы к
определению площади поверхности тела, имея перед собой
две задачи: вычисление площадей поверхностей
многогранников и тел вращения, а также формулировку
достаточно универсального определения, пригодного для широкого
класса поверхностей.
В § 10.1 были приведены формулы, по которым можно
вычислить площадь боковой поверхности цилиндра,
конуса и усечённого конуса. Наглядным подтверждением
справедливости этих формул служат соображения,
связанные с возможностью «развернуть» указанные поверхности
550 Глава 13. Объём и площадь поверхности тела
Н
Н
а)
2kR
2kR
б)
Рис. 13.20
(рис. 13.20). К сожалению, в школьном курсе мы не можем
дать точного определения развёртывающихся
поверхностей, и поэтому свойства развёртки не могут послужить для
строгого вывода полученных формул. Скажем лишь, что
развёртывающиеся поверхности — это те, которые могут
быть «развёрнуты» на плоскость без деформаций, т.е. без
сжатий и растяжений. К ним относятся поверхности
выпуклых многогранников, конусов, цилиндров, но, оказывается,
сфера не является развёртываемой поверхностью. Поэтому
даже при наличии строгого определения развёртки подход
к определению площади поверхности через площадь её
развёртки применим не ко всем поверхностям,
встречающимся в курсе геометрии, и для наших целей заведомо
непригоден.
По аналогии с тем, как в планиметрии определялась
длина окружности, можно попытаться найти площадь
криволинейной поверхности как предел «приближающихся к
ней многогранных поверхностей». Например, определим
площадь боковой поверхности цилиндра как предел
последовательности площадей боковых поверхностей
правильных призм, вписанных в цилиндр (или описанных
около него), при неограниченном увеличении числа сторон
§ 13.7. Об определении площади поверхности 551
многоугольников, лежащих в основаниях призм. Площадь
боковой поверхности каждой такой призмы равна
произведению высоты (призмы и цилиндра) на периметр
основания. При рассматриваемом предельном переходе
периметры оснований стремятся к длине окружности основания
цилиндра; следовательно, S = 2nRH> что, как мы уже знаем,
верно.
Аналогичное построение можно провести и для
конуса, рассматривая вписанные в него (или описанные около
него) правильные пирамиды. Это построение приводит нас
к верному результату.
В случае сферы рассмотрение многогранных
поверхностей, подобных изображённым на рис. 13.21, также приво-
Рис. 13.21
дит нас к цели, хотя соответствующее рассуждение
довольно громоздкое.
Недостатки указанного подхода не так очевидны.
Немецкий математик Г. Шварц показал в 1890 году, что попытка
определить площадь криволинейной поверхности как
предел последовательности площадей поверхностей
многогранников, вписанных в эту поверхность, при неограниченном
измельчении их граней обречена на неудачу. С этой целью
он привёл следующий пример.
Пусть дан цилиндр радиуса R и высоты Н. Впишем
в него многогранник таким образом.
552 Глава 13. Объём и площадь поверхности тела
1° Разделим высоту цилиндра на т равных частей и
проведём через точки деления плоскости, параллельные
основаниям; на боковой поверхности цилиндра образуется
(т+ 1) окружностей, считая и окружности его оснований;
пронумеруем их, начиная с окружности нижнего
основания.
2° Каждую из этих окружностей разделим на п равных
частей так, чтобы точки деления (*+ 1)-й окружности
находились над серединами дуг t-й окружности, i = 1, 2, ..., т.
3° Соединим точки деления, как показано на рис. 13.22.
Рис. 13.22
Две грани полученного многогранника1^ являются
правильными n-угольниками, вписанными в окружности ос-
6
Рис.
13.
/ 1
Е
23
В
н
с
^Этот многогранник называют «сапогом Шварца».
§ 13.7. Об определении площади поверхности 553
нований цилиндра. Остальные его грани (назовём их
боковыми) — равные равнобедренные треугольники, вершины
которых лежат на боковой поверхности цилиндра.
Найдём площадь о каждого из этих треугольников,
обратившись к рис. 13.23:
ав = Vac2 + вс2 = ^(ос - оа)2 + вс2 =
Боковые грани рассматриваемого многогранника
образуют его боковую поверхность, площадь которой Smn равна
2тпа. Следовательно,
Smn = 2mnRsin J
Перепишем полученное выражение в следующем виде:
sinf
л / ^._ к \ 4
j£—*
/
4Я2 n4 I JL
\ 2д
+ 1.
Теперь, задавая т как функцию от я, будем получать
различные последовательности многогранников, боковые
поверхности которых «стремятся» к боковой поверхности
цилиндра с ростом п.
Используя известный из курса алгебры и начал анализа
первый замечательный предел lim smx = 1, мы получаем,
0 х
sin £ sin £
что lim —=-£■ = 1 и lim —==^- = 1. Теперь уже нетрудно
л—►схэ — п—юс -^~
л 2д
найти lim Smn при различных т(п).
554 Глава 13. Объём и площадь поверхности тела
Если т = 1 (что соответствует последовательности
боковых поверхностей правильных призм, вписанных в
цилиндр, которую мы уже рассматривали выше), то lim Smn —
п—*-оо
= 2 л:RH. Такое же предельное значение получается для
т — п (проверьте!). Если же т = л2, то
lim Smn =
л-юо
а при m — v? вообще получается неограниченная
последовательность (которая, следовательно, не имеет предела).
Разумеется, можно привести ещё множество примеров
более сложной зависимости между т и л, но и приведённые
примеры достаточно красноречивы.
Заметим, что в первом примере мы получили
правильный результат для площади боковой поверхности цилиндра,
а второй и третий примеры оказались «плохими». Причина
состоит в том, что боковая грань соответствующего сапога
Шварца близка к боковой поверхности цилиндра по
расстоянию, но далека по направлению. Оказывается, тангенс
угла между гранью сапога Шварца и касательной
плоскостью к цилиндру в вершине этой грани пропорционален
отношению Щ: ♦ В случае т = 1 этот тангенс, а следовательно,
п2
и сам угол, стремится к нулю при п —► оо и обе плоскости
стремятся совпасть. Если т = п2, то указанный угол
стремится к конечному, но ненулевому пределу, а если т = п3,
то сапог настолько быстро «складывается по вертикали»,
что его грань стремится стать перпендикулярной
касательной плоскости.
Пример Шварца показывает, что измельчение граней
многогранной поверхности, вписанной в криволинейную
поверхность, не гарантирует стремления площади её
поверхности к площади криволинейной поверхности.
Описанный подход, тем не менее, может быть развит путём
уточнения понятия «близости» многогранной поверхности к кри-
§ 13.8. Площадь поверхности по Минковскому 555
волинейной, однако соответствующее построение
неэлементарно и выходит за рамки школьного курса.
Отметим, что вопрос об измерении площади
поверхности является очень трудным и даже в курсах
математического анализа для высшей школы не рассматривается до
конца.
В следующем параграфе мы изучим ещё один подход
к определению площади поверхности, который
оказывается универсальным для тел, рассматриваемых в курсе
элементарной геометрии, — многогранников и тел
вращения.
§ 13.8. Площадь поверхности по Минковскому
Кстати о теориях, у нас тут есть одна,
которая не сработает сама по себе без
большого нажима с нашей стороны.
Р. Асприн. Корпорация М. И. Ф. в действии
В этом параграфе мы дадим определение площади
поверхности, предложенное немецким математиком и
физиком Г. Минковским, и с его помощью найдём площадь
сферы и сферического сегмента, площадь боковой
поверхности цилиндра и конуса.
Идея Минковского проста и наглядна. «Раздуем»
поверхность в обе стороны так, чтобы получился слой
толщины 2Л, «окутывающий» данную поверхность. Тогда объём V
этого слоя приближённо равен S • 2Л, где S — площадь
поверхности, следовательно, S« V/2h, причём чем меньше Л,
тем точнее формула.
Теперь переведём эту идею на математический язык.
Роль «окутывающего» слоя будет играть А-окрестность
поверхности.
(Определение. Пусть даны поверхность F и
положительное число Л. Назовём h-окрестностыо Fn поверхности F
556 Глава 13. Объём и площадь поверхности тела
I множество всех точек М пространства, для каждой из
которых найдётся точка А е F такая, что AM ^ Л.
и^г1 Упражнение 13.9. Найдите Л-окрестность отрезка длины d
и окружности радиуса R> h. Докажите, что их объёмы равны
соответственно nh2d-\- —7гЛ3 и 2n2Rh2.
о
I Определение. Площадью поверхности F называется
предел отношения Vh/2h при Л -►(), где Vh — объём
окрестности Fh.
ю^ Упражнение 13.10. Докажите, что объём Л-окрестности
выпуклого n-угольника равен Vh — 2h • S + nh2p + ^ тгЛ3, где S —
его площадь, ар —полупериметр.
Из результата предыдущего упражнения вытекает, что
lim ттт — S9 т. е. определение площади по Минковскому даёт
правильное значение площади плоского многоугольника.
Оказывается, это определение согласуется и с данным
нами ранее определением площади поверхности выпуклого
многогранника как суммы площадей всех его граней.
Доказательство этого утверждения требует преодоления
определённых технических трудностей, поэтому мы приведём
его в конце параграфа.
Вычисление площадей криволинейных поверхностей с
помощью определения Минковского в большинстве случаев
требует изощрённых оценок объёма Л-окрестности.
Исключениями являются вычисление площади сферы и площади
поверхности тора (см. задачу 13.15).
Теорема 13.14. Площадь сферы радиуса R вычисляется
по формуле
Доказательство. Заметим, что ft-окрестность сферы
ограничена концентрическими с ней сферами радиусов R — h
ий-fft (рис. 13.24). Объём Л-окрестности равен разности
§ 13.8, Площадь поверхности по Минковскому 557
Рис. 13.24
объёмов шаров, ограниченных указанными сферами:
Vh = |тг(Д + А)3 -|тг(Д- Л)3 = |тг • 2Л(ЗД2 + Л2).
Площадь S сферы по определению равна
lim ^ - lim |тг(ЗД2 + А2) = 4тгЯ2. П
Замечание. Если S(r) и V(r) —соответственно площадь
сферы и объём шара как функции их радиуса г, то поскольку
площадь сферы радиуса R равна производной функции V(r) в
точке г = R. Значит,
S(R) = (|
Часто нахождение объёма Л-окрестности поверхности
непросто. Чтобы упростить вычисления, воспользуемся
следующим приёмом. Вместо «настоящей» Л-окрестности
объёма Vh, возьмём «подправленную» окрестность, объём
которой V'h легко вычисляется. Этот объём мы используем для
558 Глава 13. Объём и площадь поверхности тела
у/
у
вычисления площади поверхности по формуле S = lim ттг
л—о *п
Найденное так значение S совпадает с lim -£, если объём
«подправленной» окрестности не сильно отличается от
объёма «настоящей», т. е. тогда и только тогда, когда
Л—О
2Л
Теорема 13.15. Площадь боковой поверхности цилин-
I дра радиуса R и высоты Н вычисляется по формуле
= 2nRH.
н
2h
2ft
а)
б)
Рис. 13.25
Доказательство. На рис. 13.25а, б изображены
половины осевых сечений «настоящей» и «подправленной»
Л-окрестностей боковой поверхности цилиндра
соответственно. Объём V'h последней равен разности объёмов
цилиндров с радиусами R+h и R-h и одинаковой высотой Н:
(13.5)
§ 13.8. Площадь поверхности по Минковскому 559
Следовательно,
Величина v(h) = \V^ — V'h\ заведомо не превосходит
объёмов тел, получаемых при вращении прямоугольников И\
и Пг, изображённых на рис. 13.26, вокруг оси цилиндра.
п2
Рис. 13.26
Пользуясь формулой (13.5), находим
v(h) < 2
откуда
v[h) ^
следовательно,
2Л
lim
= 0,
что доказывает законность «подправления» Л-окрестности.
D
Теорема 13.16. Площадь боковой поверхности конуса
с радиусом основания R и образующей L вычисляется по
формуле
S = nRL.
560 Глава 13. Объём и площадь поверхности тела
а)
h/ cos a
б)
Рис. 13.27
Доказательство. На рис. 13.27а, б изображены
половины осевых сечений «настоящей» и «подправленной»
Л-окрестностей. Объём V'h последней равен разности объ-
Л
ёмов конусов с радиусами оснований R\ = R +
cos a
и R2 =
cos ос
, где а — угол между образующей и осью конуса,
и с высотами Hi = Ri ctg or и if 2 =
<*• Следовательно,
-I*
cos
Переходя к пределу, получаем
sin a
h2
3cos2
__\ _ kR2
a / sin a'
§ 13.8. Площадь поверхности по Минковскому 561
Поскольку L = — , получаем S = kRL.
Законность «подправления» й-окрестности
обосновывается так же, как и в предыдущей теореме:
где V(Hi) и Т^(П2) —объёмы тел, полученных вращением
прямоугольников III и Пг, изображённых на рис. 13.28,
Рис. 13.28
вокруг оси конуса. Первое из этих тел — цилиндр радиуса h
2h
и высоты
sin a
, следовательно,
2h
sin a'
562 Глава 13. Объём и площадь поверхности тела
Объём второго тела можно найти, воспользовавшись
формулой (13.5):
V(U2) =
2ft
cos a
2nR2h.
Итак,
sin a cos oc /'
следовательно, hm -^г = 0, что и завершает доказатель-
л—о 2п
СТВО. U
^Упражнение 13.11. Докажите, что площадь боковой
поверхности усечённого конуса с радиусами оснований Лиги
образующей L вычисляется по формуле
S = k(R + r)L.\
Теорема 13Л7, Площадь сферического сегмента
вычисляется по формуле
= 2nRH,
где R — радиус сферы, a if —высота сегмента.
R
а)
H + h
R + h
б)
Рис. 13.29
Доказательство. На рис. 13.29а и б изображены
половины осевых сечений «настоящей» и «подправленной»
§ 13.8. Площадь поверхности по Минковскому 563
Л-окрестностей сегментной поверхности. Объём
«подправленной» окрестности равен разности объёмов сегмента
высоты Н + h шара радиуса R + h и сегмента высоты Н — h
шара радиуса R — h.
Используя формулу для объёма шарового сегмента
(теорема 13.12), находим
= ~(H + h)2(3R-H+2h)-^(H-h)2(3R-H-2h) =
= | • 2h • (6ДЯ + 2ft2) = 2Л • (2nRH +
следовательно,
S = lim ^ = 2nRH.
A-o 2Л
Обоснуем законность замены Л-окрестности. Величина
v(h) = |F& — V'h\ не превосходит объёма тела, полученного
Рис. 13.30
564 Глава 13, Объём и площадь поверхности тела
вращением прямоугольника П вокруг оси симметрии
сегментной поверхности (рис. 13.30).
Пользуясь формулой (13.5), находим
v(h) < -Э-. 2тг- R sin a -2h = 8KRh2,
sin a
откуда lim -^— = 0, и теорема доказана. □
I Теорема 13.18. Площадь поверхности выпуклого
многогранника равна сумме площадей всех его граней.
Доказательство. Пусть М — выпуклый многогранник
с гранями F\, ..., Fn; Si, ..., Sn — площади этих граней.
На каждой грани как на основании построим две прямые
призмы высоты Л, лежащие по разные стороны от
плоскости данной грани. Для грани Ft объединение
указанных призм — призма Pi высоты 2Л. Будем считать, что
0 < h < 1. Пусть 7^ — объединение призм Pi9 V® — объём Т£;
Th — Л-окрестность Му Vh — её объём, а^- сумма объёмов
призм Рь. Ясно, что Vh ^ Гл° и7[) v£.
Поскольку
lim -^г = lim ^т
для завершения доказательства теоремы достаточно
убедиться, что
Vh~, =0.
Сделаем это. Заключим многогранник М в шар с
центром О и радиусом R - 1, а через В обозначим шар с
центром О и радиусом R. Для каждых двух граней рассмотрим
линию I пересечения их плоскостей (пока будем считать,
что параллельных граней нет1)) и построим бесконечный
прямой круговой цилиндр с осью I и радиусом, равным
13Если они есть, то соответствующего цилиндра нет, но он нам и не
нужен.
§ 13,8. Площадь поверхности по Минковскому 565
h
-, где а — угол между плоскостями этих граней. Нас
интересует пересечение этого цилиндра с шаром В. Ясно,
что его объём не превосходит —5 . Поэтому если V —
sin2 (а/2)
объём объединения G всех таких пересечений, то V ^ Ch2,
где С — некоторая положительная константа.
Нам понадобятся два вспомогательных утверждения.
| Лемма 13.4. Пусть X е Th \ T°h. Тогда X е G.
Доказательство. Все точки окрестности Т^ лежат в Б;
значит, осталось доказать, что X лежит в одном из
цилиндров* Это очевидно (даже для цилиндров радиуса К). □
| Лемма 13.5. Пусть XePiOPj. Тогда XеG.
Доказательство. Опять же, ХеВ. Кроме того, X лежит
в пересечении двух слоев высоты Л, пересекающихся под
углом а. А такое пересечение, как легко понять, лежит
в соответствующем цилиндре. □
Теперь заметим, что
Согласно лемме 13.4,
Vh-V°<V^Ch2.
Чтобы оценить Vfh — V^9 применим лемму 13.5. Согласно ей
при любом £, i = l, 2, ..., л, множество P^ — Pt \7не лежит
в остальных Pt (но, разумеется, лежит в 7^). Обозначим
через V[ объём Pt. Тогда V°^V[ + ... + Vfn>Vfh- nV, т.е.
vh ~ vh < nV ^ лСЛ2. Следовательно,
0 ^ \Vh - V'h\ < Ch2 + nCh2 = 2С1Л2, 0 ^ lVh2^ < Cxh.
Значит, \vh-V\
lim \1^ZA = 0,
Л0 2h
что и требовалось.
566 Глава 13. Объём и площадь поверхности тела
Осталось разобраться со случаем, когда у
многогранника есть параллельные грани. Наличие таких граней может
сделать неверным утверждение леммы 13.5 (и,
следовательно, оценку для \Vfh - V®\). Чтобы этого избежать, достаточно
рассматривать ft, меньшие половины минимального
расстояния между парами параллельных граней. □
В связи с только что изложенным доказательством
может возникнуть вопрос: а нельзя ли было просто,
сославшись на результат упражнения 13.10, сложить площади
граней многогранника? Так можно было бы поступить,
если бы мы предварительно доказали, что площадь
поверхности в смысле определения Минковского обладает свойством
аддитивности, т.е. S(FiUF2) =S(Fi) +£(^2), где
поверхности F\ и F2 могут пересекаться разве лишь по своей границе.
К сожалению, это утверждение, вообще говоря, неверно.
^Упражнение 13.12. Пусть К — квадрат, лежащий на
координатной плоскости Оху, Q — множество всех его точек, обе
координаты которых рациональны, Р — множество остальных
его точек. Докажите, что все эти множества имеют площадь
по Минковскому, причём S(K) =S(Q) —S(P) (таким образом,
Разумеется, для всех «хороших» поверхностей
аддитивность площади по Минковскому имеет место, но доказать
это непросто.
Наличие «патологических» примеров, подобных
приведённому в упражнении 13.12, показывает, что с
определением площади по Минковскому следует обращаться
аккуратно. Это определение интересно тем, что оно
значительно увеличивает класс множеств (эти множества могут
и не быть поверхностями в общепринятом смысле),
которым можно приписать «площадь поверхности».
В заключение отметим, что в более сложных, чем
рассмотренные выше, случаях площадь поверхности может
быть вычислена с помощью различных интегральных
формул, доказываемых в курсах математического анализа.
Приведём (без доказательства) одну из них.
Задачи 567
Теорема 13.19. Пусть функция у = f(x) непрерывно
дифференцируема на [а, 6]. Площадь поверхности,
образованной при вращении графика этой функции вокруг оси Ох,
вычисляется по формуле
Задачи
— Думайте, мой друг, — ободряюще
сказал Пуаро. —Приведите в порядок
мысли. Будьте методичны. Будьте
последовательны. В этом секрет успеха.
А. Кристи» Убийство на поле для гольфа
13.1. Докажите, что отношение объёмов двух подобных
измеримых тел равно кубу коэффициента подобия.
13.2. Круг радиуса г вращается вокруг оси, лежащей
в его плоскости и удалённой от центра круга на
расстояние а, а>г. Найдите объём полученного тела (рис. 13.31;
это тело называется тором).
Рис. 13.31
13.3. Оси двух бесконечных прямых круговых
цилиндров, каждый из которых имеет радиус г, пересекаются
под углом а. Найдите объём пересечения цилиндров.
13.4*. Оси трёх бесконечных прямых круговых
цилиндров (каждый радиуса г) взаимно перпендикулярны и про-
568 Глава 13. Объём и площадь поверхности тела
ходят через одну точку. Найдите объём пересечения этих
цилиндров.
13.5. Серёжа насыпал в цилиндрическую кастрюлю
немного пшена и спросил соседку тётю Люду: «Сколько
нужно налить воды, чтобы получилась вкусная каша?» — «Это
очень просто, —отвечала соседка. — Наклони кастрюлю-—
вот так; постучи, чтобы крупа пересыпалась и закрыла
ровно половину дна. Теперь заметь точку на стенке
кастрюли, ближайшую к краю, до которой поднялась крупа,—
и зажми её пальцем. До этого уровня и надо налить воду» .—
«Так ведь пшена можно насыпать побольше и поменьше,
да и кастрюли бывают разные — широкие и узкие»,
—усомнился Серёжа.— «Всё равно мой способ годится в любом
случае!» — гордо ответила тётя Люда.
Докажите, что тётя Люда права: отношение объёмов
воды и пшена по её рецепту всегда одинаково, — и
вычислите это отношение. (Считайте, что пшено заполняет часть
кастрюли без пустот, наподобие жидкости.)
13.6*. Через центр основания прямого кругового
конуса проведена плоскость, параллельная образующей конуса.
Найдите отношение объёмов частей, на которые рассечён
конус.
13.7. Тело, имеющее объём, расположено между
плоскостями z — Q и z — h. Известно, что площадь сечения тела
плоскостью z = const есть функция вида
S(z) = az2 + bz + c, О ^ z ^ Л.
Докажите, что объём тела равен
(Формула Симпсона; ср. с задачей 4.9.) Вычислите с
помощью этой формулы объёмы конуса и шара.
13.8. Объём куба равен V. Найдите объём тела,
получающегося при вращении этого куба вокруг
а) его диагонали;
б) диагонали его грани.
Задачи
569
13.9. Докажите, что объём тела, полученного при
вращении сегмента круга относительно не пересекающего его
диаметра, равен
каЧ
6
, где а — длина хорды этого сегмента,
Рис. 13.32
Л —длина проекции этой хорды на диаметр.
13.10. Золотое колечко имеет форму тела,
ограниченного поверхностью шара и цилиндра (рис. 13.32). Сколько
золота нужно добавить, чтобы
увеличить диаметр d в два раза, а
высоту h оставить прежней?
13.11. Дуга окружности
радиуса г, имеющая угловую
величину 2а, вращается вокруг своей
хорды. Найдите объём тела
вращения.
13.12. Через высоту
правильного треугольника со стороной а
проведена плоскость,
перпендикулярная плоскости этого
треугольника, и в этой плоскости
проведена прямая /, параллельная высоте треугольника. Найдите
объём тела, образованного вращением треугольника вокруг
прямой I.
13.13. Объём треугольной призмы АВСА\В\С\ равен V.
Рассмотрим всевозможные треугольники, лежащие в
плоскостях, параллельных основаниям призмы, с вершинами
на диагоналях АВ\, ВС\ и СА\ боковых граней призмы.
Найдите объём тела, образованного этими треугольниками.
13.14*. Назовём два тела равными по Кавальеры, если
их можно расположить в пространстве так, что любая
горизонтальная плоскость, пересекающая одно из них,
пересекает и другое, причём площади сечений равны. Докажите,
что два прямоугольных параллелепипеда равного объёма
равны по Кавальери.
13.15. Найдите площадь поверхности тора, пользуясь
результатом задачи 13.2.
570 Глава 13. Объём и площадь поверхности тела
13.16. Докажите, что отношение площадей
поверхностей двух подобных тел (если известно, что эти площади
существуют) равно квадрату коэффициента подобия.
13.17. Сферический пояс высоты Н является частью
сферы радиуса R. Найдите площадь его поверхности.
13.18. Дуга окружности радиуса R, имеющая угловую
величину 2а, вращается вокруг своей хорды. Найдите
площадь поверхности вращения.
13.19*. Найдите площади поверхностей тел,
являющихся пересечениями цилиндров из задач 13.3 и 13.4.
13.20. Треугольник ABC вращается вокруг оси,
проходящей через вершину А, но не пересекающей сторону ВС.
Докажите, что объём тела, получаемого при таком вращении,
равен произведению площади поверхности, образуемой
вращением стороны ВС, на одну треть высоты, опущенной на
эту сторону (ось вращения и ВС лежат в одной плоскости).
13.21. Плоская ломаная состоит из п равных отрезков,
имеющих длину а и соединённых в виде зигзага под углом а
друг к другу. Найдите площадь поверхности, образуемой
вращением этой ломаной вокруг оси, которая проходит
через один из её концов параллельно биссектрисе угла а.
13.22. Прямоугольник вращается около оси,
проходящей через его вершину параллельно диагонали. Найдите
объём и площадь поверхности тела вращения, если длина
диагонали равна d, а угол между диагоналями равен ср.
13.23*. Тело образовано вращением куба с ребром а
вокруг его диагонали. Найдите площадь поверхности этого
тела.
13.24. Центр сферы Si принадлежит сфере S2. Площадь
части сферы S2, лежащей внутри сферы Si, равна одной
пятой площади сферы Si. Найдите отношение радиусов
этих сфер.
13.25*. Площади проекций тела на три взаимно
перпендикулярные плоскости равны Si, S2 и S3. Докажите, что
его объём не превосходит /Щ^Щ
Приложение
Избранные теоремы и методы планиметрии
Плюнь тому в глаза, кто скажет,
что можно обнять необъятное!
К. Прутков.
§ 1. Свойство биссектрисы угла треугольника
Теорема П1.1. Биссектриса внутреннего угла
треугольника делит его сторону на отрезки, пропорциональные
двум другим сторонам.
Приведём два доказательства этой теоремы.
Первое доказательство. Пусть в треугольнике ABC
отрезок АА\ — биссектриса внутреннего угла А; АВ = с, АС = Ь,
ВА\ = т, А\С — п. Докажем, что
т
п
с
Ь'
(П1.1)
Проведём через точку В прямую,
параллельную прямой ААь до пересечения
с прямой АС в точке D (рис. Ш).
Заметим, что /.DBA = /ВАА\ (как
внутренние накрест лежащие при
параллельных BD и АА\ и секущей АВ),
/BDA = /,А\АС (как соответственные
при параллельных BD и AAi и
секущей CD). По определению биссектрисы
ZBAA\ = /A\AC. Из полученных
равенств вытекает, что /DBA = /BDA,
поэтому треугольник ABD
равнобедренный (АВ — AD = с). По теореме о пропорциональных
В
т
Ах
Рис. П1
отрезках
— -т^, а это в наших обозначениях и есть
АО
равенство (П1.1). □
Второе доказательство. В дополнение к
обозначениям из первого доказательства положим /А— 2а, AAi = I
574 Избранные теоремы и методы планиметрии
А
А
В т Ах л С
Рис. П2
т
Рис. ПЗ
(рис. П2). Так как у треугольников АВА\ и АА\С общая
высота, опущенная из вершины А, их площади относятся
как т: п\ Sabax = «с' sin a, SaaiC—2^ s*n a» следовательно,
m
n
}jd sin a
Ь/sina
П
c^* Упражнение П1.1. Пусть в A ABC ZB Ф ZC, отрезок АА\ —
биссектриса внешнего угла А (рис. ПЗ); АВ — с, АС = Ь, ВА\ — т,
А\С = п. Докажите справедливость равенства (П1.1).
■^Упражнение П1.2. Сформулируйте и докажите теорему,
обратную к теореме П1.1, а также утверждение, обратное к
утверждению из предыдущего упражнения.
Задачи к § 1
П1.1. Пусть в треугольнике ABC ВС = а, АС = 6, АВ = с,
/ — центр вписанной окружности, АА\ — биссектриса
угла А. Докажите, что AI: 1А\ = (Ь + с) :а.
П1.2. В прямоугольном треугольнике биссектриса
острого угла делит катет на отрезки тип. Найдите другой катет
и гипотенузу.
П1.3. Дан треугольник со сторонами 12, 15 и 18.
Проведена окружность, касающаяся обеих меньших сторон и
имеющая центр на большей стороне. Найдите отрезки, на
которые центр окружности делит большую сторону
треугольника.
§ 1. Свойство биссектрисы угла треугольника 575
П1.4. Биссектриса треугольника делит одну из его
сторон на отрезки с длинами 3 и 5. В каких границах может
изменяться периметр треугольника?
П1.5. На гипотенузе АВ прямоугольного треугольника
ABC во внешнюю сторону построен квадрат ABDE. В каком
отношении делит сторону DE биссектриса угла С, если
АС=1, ВС=3?
П1.6. В выпуклом четырёхугольнике ABCD
биссектрисы углов CAD и CBD пересекаются на стороне CD.
Докажите, что биссектрисы углов АСВ и ADB пересекаются на
стороне АВ.
П1.7. В треугольнике со сторонами а, Ь и с проведены
биссектрисы, точки пересечения которых с
противолежащими сторонами служат вершинами второго треугольника.
Найдите отношение площадей этих треугольников.
Ш.8. В треугольнике ABC биссектрисы AD и BE
пересекаются в точке О. Найдите отношение площади
треугольника ABC к площади четырёхугольника ODCE, зная, что
ВС = а, АС = Ь, АВ = с.
П1.9. В параллелограмме ABCD на сторонах АВ и ВС
выбраны точки М и N соответственно так, что AM = CN.
Пусть Q — точка пересечения отрезков AN и СМ. Докажите,
что DQ — биссектриса угла D.
П1.10. Длины сторон треугольника различны и
образуют арифметическую прогрессию. Докажите, что прямая,
проходящая через точку пересечения медиан и центр
вписанной окружности, параллельна одной из сторон треугольника.
П1.11. Длины сторон треугольника образуют
арифметическую прогрессию. Докажите, что радиус вписанной
в него окружности втрое меньше одной из высот
треугольника.
Ш.12. Медиана ВК и биссектриса CL треугольника ABC
PC AC
пересекаются в точке Р. Докажите, что -=г=- — -577 = 1-
П1.13. Две стороны треугольника равны 10 и 15.
Докажите, что биссектриса угла между ними не больше 12.
576 Избранные теоремы и методы планиметрии
П1.14. Две окружности пересекаются в точках А и В.
Прямая, проходящая через точку А, вторично пересекает
эти окружности в точках С и D, причём точка А лежит
между С и D, а хорды АС и AD пропорциональны радиусам
своих окружностей. Докажите, что биссектрисы углов ADB
и АСВ пересекаются на отрезке АВ.
П1.15. В треугольнике ABC точка D лежит на стороне
АС, углы ABD и BCD равны, АВ = CD, AE — биссектриса
угла А. Докажите, что отрезки CD и АВ параллельны.
§ 2. Решение треугольников
Пусть дан треугольник ABC. Всюду ниже мы будем
использовать следующие обозначения для его сторон и углов:
ВС = ау CA = b, AB = c, ZBAC = cc, ZABC = (3, ZACB=y.
■ Определение. Стороны и углы треугольника
называются его основными элементами.
Под «решением треугольника» мы будем понимать
вычисление по трём данным его независимым основным
элементам трёх остальных основных элементов1*. Эта задача
важна, так как является одной из опорных задач при
вычислении элементов более сложных фигур (как плоских,
так и пространственных).
Решение прямоугольных треугольников
В прямоугольном треугольнике известен один из его
основных элементов у = -£, поэтому в задачах на решение
прямоугольных треугольников задаются два основных
элемента, один из которых является его стороной. Заметим,
!)Как известно, углы треугольника не являются независимыми
элементами, так как они связаны соотношением а + /3 + у = п. Если
заданы три угла, удовлетворяющие этому условию, то треугольник
определён с точностью до подобия.
§ 2. Решение треугольников 577
что в рассматриваемом частном случае вычисление
неизвестных элементов выполняется непосредственно на
основании определений тригонометрических функций острого
угла и теоремы Пифагора. Рассмотрим задачи,
возникающие в случае прямоугольного треугольника.
1. Даны гипотенуза с и острый угол а. Найти а, Ъ и /3.
Решение, а —с sin а, Ъ = с cos а, (3 = ■£ — а.
2. Даны катет а и острый угол а. Найти 6, с и /3.
Решение. b = a ctg а, с = .а , /3 = ■£ — а.
sin ос с*
3. Даны катет а и гипотенуза с. Найти 6, а и /?.
Решение. Ъ — у/с2 -а2, а = arcsin -, /3 = ■£ — а.
4. Даны катеты а и &. Найти с, а и /3.
Решение, с = у/а2 +&2, а = arctg ^, /3 = ■£ - а.
Очевидно, что все остальные возникающие здесь задачи
простыми переобозначениями элементов сводятся к
задачам 1, 2 и 3.
Решение косоугольных треугольников
Возникающие здесь задачи решаются с помощью
теоремы косинусов, теоремы синусов и теоремы о сумме углов
треугольника.
1. Даны1* а, & и с. Найти а, /3 и у.
Решение. По теореме косинусов
а2 = Ъ2 + с2 -2bccosa7
следовательно,
~ 2Ьс '
откуда
a = arccos—t— ;
1)Разумеется, данные должны удовлетворять неравенству
треугольника (наибольшее из чисел а, Ь, с меньше суммы остальных), иначе
поставленная задача не имеет решения.
19 Зак 3383
578 Избранные теоремы и методы планиметрии
выражения для /3 и у получаются из выражения для а
круговой перестановкой букв.
2. Даны a, b и у. Найти с, а и /3.
Решение. Имеем
с = \/а2 + b2 - 2abcos у,
Ь2 + с2-а2
а — arccos —-^гг ,
6ОС
/3 = л: - а — у.
3. Даны а, /3 и у. Найти Ь9 с и а.
Решение, а = п — /3 - у; по теореме синусов
а _ Ь _ с
sin a sin /3 sin у *
откуда
sin /3 sin r
b = а--т—1-', с —а-— .
sin a sin а
Сделаем несколько замечаний к решениям задач 1—3.
Решение задачи 1 (если оно существует — см. сноску к
задаче 1) единственно в силу равенства треугольников по трём
сторонам. Очевидно, что задача 2 решается аналогично,
если заданы другие две стороны и угол между ними.
Решение этой задачи существует для любых положительных
а и b и любого у из интервала (0; к). Решение единственно
в силу равенства треугольников по двум сторонам и углу
между ними. Задача 3 решается аналогично, если задана
любая другая сторона и два прилежащих к ней угла; более
того, могут быть заданы любые два угла, так как третий
угол сразу находится с помощью теоремы о сумме углов
треугольника. Решение этой задачи существует при любом
а > 0 и любых /3 и у таких, что /3>0, у >0 к /3 + у < к.
При этих условиях решение единственно в силу равенства
треугольников по стороне и двум углам.
Заметим ещё, что в случае равнобедренного
треугольника решения рассмотренных задач упрощаются, так как
он разбивается высотой (она же медиана и биссектриса) на
§ 2. Решение треугольников
С А
579
А В В С
Рис. П4 Рис. П5
два прямоугольных треугольника. Пусть в задаче 1 а = Ь,
тогда (рис. П4)
а = (3 = arccos jr, у = к - 2а.
Равенство а — Ъ в задаче 2 даёт решение
7Г — У V
а = (3 = —^—, с = 2а sin —.
Наконец, в задаче 3 при /? = у (рис. П5) получаем
а
OL — TZ-
Ь = с =
2 cos /?'
Самой непростой для решения оказывается задача, в которой
по двум сторонам и углу, лежащему напротив одной из них,
требуется найти остальные основные элементы. Не ограничивая
общности рассуждений, рассмотрим следующую задачу.
4. Даны а, Ь и а. Найти с, /3 и у.
Решение. Из теоремы синусов следует, что sin/3 = sln a.
Если Ь sin a > а, то решения не существует, так как sin (3 не может
быть больше единицы. Если Ъ sin а = а, то sin/З = 1, т. е*
с = Ьсоз а,
при этом а < g-, и решением (единственным) служит
прямоугольный треугольник. Если а > ^, то задача не имеет решения. Пусть
frsin a < а. Тогда существует, вообще говоря, два угла, синусы
которых равны sina. Один из этих углов острый, а второй
тупой. Заметим, что а >/3 при а > Ь, а так как у треугольника не
580 Избранные теоремы и методы планиметрии
может быть двух тупых углов, /3 — острый угол. В этом случае
решение единственно:
п . / ft . \ п a sin у
р = arcsin [- sin а , у = гс — а— р, с — —: .
г \а ) r sin а
При а — Ь имеем
п Л а sin у
В = а, у = тг-2а, с=——-;
г > i ' sin а
при а < т£ единственным решением служит равнобедренный
треугольник, а при а ^ у задача не имеет решения. Наконец, при
а < Ь задача имеет два решения:
a sin у\
о • (Ь . \
Pi = arcsin - sin а ,
= 7Г — а — pi,
sin a
и
a sin у г
(32 = 7r-arcsin(^- sin orJ,
При этом а < -^ (так как а </3 при а < ft), a при а ^ -^ задача не
имеет решения.
Ответ: 1) при ft sin a > а решений нет;
2) при ft sin of = а и а ^ -х- решений нет;
3) если ft sin а = аиа<^,то/? = ^, у — ^ — а, c = ft cos а;
4) при ft sin а<а, a = b и ос^ ^ решений нет;
, . , 7Г л я sin у
5) если ft sma<a, а = &иа<77,тор = а, у = тг-2а,с=^ ;
Z ' Sin OL
6) если ft sin af < а, а > ft, то /3 = arcsin( - sin см, у — к — а —/3,
_ а sin у ш
sin а '
7) при ft sin а<а, а<&иа^^ решений нет;
/у. ч
8) если ft sin а<а, a<ft и а<^-, то [i\ — arcsin f - sin см,
2 = 7Г — arcsinf - sin a J, уг = тг — а —
= 7г - а
ь i ;
sin а
a sin Г2
§ 3. Некоторые формулы площади треугольника 581
^ Упражнение П2.1. Дайте геометрическую интерпретацию
задачи 4, решив следующую задачу: построить треугольник по
a, ft и а.
Таким образом, мы рассмотрели все возможные случаи
решения треугольников. В связи с тем, что эти задачи
полностью решены нами в общем виде, задачи для
самостоятельного решения к этому параграфу не приводятся.
Отметим ещё, что формулы, которые мы получили
выше, ни в коем случае не следует заучивать наизусть. Важно
запомнить метод решения каждой из рассмотренных задач
и научиться применять его на практике в каждом
конкретном случае.
§ 3. Некоторые формулы площади треугольника
Мы будем предполагать известным, что площадь любого
треугольника есть полупроизведение любой его стороны на
высоту, проведённую к этой стороне, а также
полупроизведение двух любых его сторон на синус угла между ними.
Таким образом, в стандартных обозначениях
s=h
и
= т>я& sin у.
(П3.1)
(П3.2)
Докажем ещё три формулы, по которым можно
вычислить площадь треугольника.
Теорема П3.1. Пусть S —площадь треугольника со
сторонами а, Ь, с; R — радиус описанной около этого
треугольника окружности. Тогда
аЬс
(ПЗ.З)
Доказательство. По теореме синусов -А— = 2R, т. е.
Д
sin у = ~=. Подставляя это выражение для sin у в форму-
582 Избранные теоремы и методы планиметрии
лу (П3.2), получаем
Q 1 . с abc
S=ab =
П
Теорема П3.2. Пусть S — площадь треугольника с
полупериметром р, г — радиус вписанной в этот треугольник
окружности. Тогда
(П3.4)
S=pr.
Доказательство. Соединим
центр вписанной окружности с
вершинами треугольника и
проведём радиусы в точки касания
вписанной окружности со
сторонами (рис. П6). Согласно
свойству касательной проведённые
радиусы перпендикулярны
соответствующим сторонам
треугольника, следовательно, они являются
высотами трёх треугольников,
на которые разбился исходный треугольник в результате
соединения центра вписанной окружности с вершинами.
Складывая площади трёх указанных треугольников и
используя формулу (П3.1), получаем
В
Рис. П6
□
Замечание. Аналогично доказывается, что площадь S
любого описанного около окружности радиуса г
многоугольника с полупериметром р может быть вычислена по
формуле (П3.4).
Теорема ПЗ.З (формула Герона). Пусть S — площадь
еугольника со
периметр. Тогда
треугольника со сторонами а, Ь, с; р— —его
полу(П3.5)
§ 3. Некоторые формулы площади треугольника 583
Доказательство. Используя теорему косинусов
с2 = а2 + Ь2 - 2аЪ cos у,
найдём cos у, затем sin у и подставим получившееся
выражение в формулу (П3.2). После алгебраических
преобразований мы получим нужный результат.
Итак,
COS у = ^г-т , Sill у = V 1 — COS'2 у
/Lao
(перед радикалом взят знак « + », так как синус угла
треугольника всегда положителен),
cz-(a2-2ab + b2) (а2 + 2аЬ + Ъ2) - с2
2аЬ '
2аЬ '
(с - а + 6) (с + а - 6) (а + Ь - с) (а + Ь + с)
2{р
4
=> sin у -
=> S =
-а)-
4c2b2
2{p-b)-
4a2b2
Ур(р — a
sin r =
2(p-
«,,
)(P-
c)-2p
b) (p — с) =Ф-
-a)(v- b) (v - c)
Существует также доказательство формулы Герона,
которое в гораздо меньшей степени опирается на
алгебраическую технику, но требует некоторых дополнительных
584 Избранные теоремы и методы планиметрии
геометрических знаний. Это доказательство вы получите
самостоятельно, решив задачу П3.10.
Задачи к § 3
П3.1. В прямоугольном треугольнике известны отрезки
а и by на которые точка касания вписанной окружности
делит гипотенузу. Найдите площадь треугольника.
П3.2. В равносторонний треугольник со стороной а
вписана окружность. К окружности проведена касательная так,
что её отрезок внутри треугольника равен Ь. Найдите
площадь треугольника, отсечённого касательной.
ПЗ.З. Радиус вписанной окружности треугольника
равен 1. Докажите, что наименьшая высота этого
треугольника не превосходит 3.
П3.4. Докажите, что если стороны треугольника
образуют арифметическую прогрессию, то радиус его вписанной
окружности втрое меньше одной из высот.
П3.5. Докажите, что прямая делит треугольник на два
многоугольника, отношение площадей которых равно
отношению их периметров, тогда и только тогда, когда она
проходит через центр его вписанной окружности.
П3.6. В треугольнике каждую сторону увеличили на 1.
Обязательно ли при этом увеличится его площадь?
П3.7. а) Докажите, что из всех треугольников данной
площади наименьший периметр имеет равносторонний
треугольник.
б) Докажите, что из всех треугольников данного
периметра наибольшую площадь имеет равносторонний
треугольник.
П3.8. Найдите площадь треугольника, зная три его
высоты hi у /*2 и Аз-
П3.9. Найдите площадь треугольника, зная три его
медианы mi, /П2 и т^.
П3.10. а) Докажите, что для любого треугольника
существуют три окружности, каждая из которых касается
§ 4. Формулы, связывающие элементы треугольника 585
одной из его сторон и продолжений двух других сторон
(вневписанные окружности).
б) Докажите, что для площади S треугольника
справедлива формула S = {р - а)гп9 где га — радиус вневписанной
окружности, касающейся стороны а.
в) Докажите, что в любом треугольнике rra=(p — b)(p-c).
г) Выведите формулу Герона, используя пункты б) и в).
§ 4. Некоторые формулы,
связывающие элементы треугольника
В этом параграфе мы докажем несколько соотношений,
позволяющих вычислять некоторые не основные элементы
треугольника: медианы, биссектрисы, высоты и т. п.
Сначала договоримся об обозначениях. Пусть дан
треугольник ABC. Будем считать, что а,Ь, с — это длины его
сторон ВС, С А, АВ; а, /3> у — величины его углов CAB, ABC,
ВСА\ р = а+ +с — полупериметр; S — площадь; R —
радиус описанной окружности; г — радиус вписанной
окружности; ha, Ь,ъ<> hc — высоты, выходящие из вершин А, В, С;
та, ттц, тс — медианы, a Za, /&> lc — биссектрисы, выходящие
из тех же вершин.
Нам понадобится одно важное следствие из теоремы
косинусов.
I Теорема П4.1 (о сумме квадратов диагоналей паралле-
I лограмма). Сумма квадратов диагоналей параллелограм-
I ма равна сумме квадратов всех его сторон.
Доказательство. Обозначим непараллельные стороны
параллелограмма через а и Ь, а его диагонали — через тип
(рис. П7). Применяя теорему косинусов к треугольникам
ABD и ABC, получим
п2 = а2 + Ь2 - 2аЪ cos ZA, (П4.1)
т2 = а2 + Ъ2 - 2аЪ cos ZB. (П4.2)
586 Избранные теоремы и методы планиметрии
С
D
т
А а В
Рис. П7
Так как ZB = к - ZA, cos(n - ZA) = - cos ZA, то
равенство (П4.2) можно переписать в виде
т2 - а2 + Ъ2 + 2аЪ cos ZA. (П4.3)
Складывая равенства (П4.1) и (П4.3), получаем, что
п2 + т2 = 2а2 + 2Ь2,
что и требовалось. □
Покажем, как с помощью этой теоремы можно найти
длину медианы треугольника, зная длины всех его сторон.
Пусть С\ — середина стороны АВ треугольника ABC,
afl- точка, симметричная С относительно С\ (рис. П8).
Тогда четырёхугольник ADBC — параллелограмм,
следовательно,
откуда
тс = ±
(П4.4)
Высоту треугольника проще всего найти по формуле
(П4.5)
к = —,
которая следует из известной формулы для площади
треугольника.
§ 4. Формулы, связывающие элементы треугольника 587
С
A d В
Рис. П9
о^3 Упражнение П4.1. Докажите, что ha = ^.
АН
Рассмотрение вспомогательной площади позволяет
получить и формулу для вычисления длины биссектрисы
внутреннего угла треугольника. В самом деле (см. рис. П9),
Sabc = SAdC + Sbccx <& \ab sin у = |b/c sin ^ + ^alc sin £ &
Y Y Y
4Ф 2ab sin g- cos -~ = lc(a + b) sin -^ <»
(П4.6)
lc =
2
Метод вспомогательной площади, очевидно, даёт
возможность вычислить радиусы вписанной и описанной
окружностей треугольника:
и
аЪс
(П4.7)
(П4.8)
Впрочем, в последнем случае удобнее использовать теорему
синусов:
2Д =
sin a sin /3 sin у'
(П4.9)
588 Избранные теоремы и методы планиметрии
Задачи к § 4
П4.1. Найдите угол между диагоналями
параллелограмма, если известно, что квадрат их произведения равен
сумме четвёртых степеней двух его смежных сторон.
П4.2. Найдите отношение суммы квадратов медиан
треугольника к сумме квадратов его сторон.
П4.3. Докажите, что медианы та и ть треугольника
ABC перпендикулярны тогда и только тогда, когда
П4.4. Докажите, что в любом треугольнике
П4.5. Высоты треугольника равны Ла, А&, hc, a радиус
описанной окружности равен R. Найдите площадь
треугольника.
114.6. Найдите угол у треугольника, если известно, что
1 = 1 + 1
lc a ^ Ь'
П4.7. а) Пусть точка А\ лежит на стороне ВС
треугольника ABC; ВА\ = т, СА\ — п, АА\ = х. Докажите, что
а(х2 + тп) = Ь2т + с2п
(теорема Стюарта).
б) Докажите, что
ll = bc — ran,
где тип — длины отрезков, на которые биссектриса угла А
треугольника ABC делит сторону ВС.
в) Докажите, что
П4.8*. Докажите, что если для некоторого треугольника
р= 2R+ г у то он прямоугольный.
§ 5. Следствия из теоремы о вписанном угле 589
П4.9*. Докажите, что в любом треугольнике 2r ^ R.
П4.10*. Докажите, что если в треугольнике равны
длины двух биссектрис внутренних углов, то он
равнобедренный.
§ 5. Некоторые следствия из теоремы о вписанном угле
Мы будем предполагать известной из курса
планиметрии 8 класса следующую теорему.
Теорема П5.1 (о вписанном угле). Величина вписанного
угла равна половине угловой величины дуги, на которую
| он опирается.
Важнейшим (и чаще всего используемым) следствием
этой теоремы является то, что величины вписанных углов,
опирающихся на равные дуги, равны, а величины углов,
опирающихся на равные хорды, либо равны, либо
составляют в сумме 180°.
Извлечём из теоремы о вписанном угле ещё несколько
следствий.
Теорема П5.2 (об угле с вершиной внутри круга).
Величина угла с вершиной внутри круга равна полусумме
угловых величин двух дуг, одна из которых находится
внутри этого угла, а другая — внутри угла, вертикального
с ним.
Доказательство. Пусть вершина В угла ABC лежит
внутри круга (точки Аи С лежат на окружности со,
ограничивающей этот круг), прямые АВ и СВ вторично
пересекают &> в точках А\ и С\ соответственно (рис. П10). Соединим
точки А и С\. По теореме о внешнем угле треугольника
ZABC = ZACiC + ZA\AC\. По теореме о вписанном угле
величина каждого из углов в правой части этого равенства
равна половине угловой величины соответствующей дуги.
Поэтому ААВС = \ (^АС + wAiCi). □
590 Избранные теоремы и методы планиметрии
В
Рис. П10 Рис. ПИ
Теорема П5.3 (об угле с вершиной вне круга). Величина
угла с вершиной вне круга равна модулю полуразности
угловых величин двух дуг, находящихся внутри этого
угла.
Доказательство проводится аналогично
доказательству теоремы П5.2 (см. рис. ПИ).
с^ Упражнение П5Л. Докажите теорему П5.3.
Теорема П5.4 (об угле между касательной и хордой).
Величина угла между касательной к окружности и
хордой, проведённой через точку касания, равна половине
угловой величины дуги, находящейся внутри этого угла.
Доказательство. Пусть /.ABC — меньший из углов,
образованных касательной и хордой АВ (рис. П12). Если
АВ — диаметр окружности, то /ABC = 90° по свойству
касательной и равен половине угловой величины дуги АВ
(равной 180°). Если /ABC < 90°, то проведём диаметр BD.
Тогда по теореме о вписанном угле /BAD = 90°; кроме того,
/CBD = 90°. Следовательно, /ABC = 90° - /ABD = 90° -
- (90° - /ADB) = /ADB = ~wAB. Больший из углов, об-
Li
разованных касательной и хордой АВ (/АВС\), дополняет
§ 5. Следствия из теоремы о вписанном угле 591
Рис. П12
Рис. П13
/ABC до 180°, следовательно, измеряется половиной
угловой величины большей дуги, стягиваемой хордой АВ. □
Теорема П5.5 (о пересекающихся хордах). Если хорды
АВ и CD окружности пересекаются в точке X, то АХ-ХВ =
= CXXD.
Доказательство. По теореме о вписанном угле /ВАС =
= /BDC, а /АХС = /BXD как вертикальные (рис. П13).
a у СУ
Поэтому ААХС ~ ADXB, следовательно, ^ = ^, т.е.
AXXB = CXXD. П
с^ Упражнение П5.2. Пусть дополнительно к условию
теоремы П5.5 R — радиус окружности, a d — расстояние от центра
окружности до точки X. Докажите, что АХ • ХВ = Л2 — d2.
Теорема П5.6 (о двух секущих). Если из точки X,
лежащей вне круга, проведены две секущие, пересекающие
окружность этого круга в точках А и В, С и D
соответственно, то АХ ХВ = СХ- XD.
^Упражнение П5.3. Докажите эту теорему. Вычислите
произведение АХ и ХВ> если радиус круга равен R> а расстояние
от центра круга до точки X равно d.
Теорема П5.7 (о касательной и секущей). Если из
точки X, лежащей вне круга, проведены прямая, касающаяся
окружности этого круга в точке А, и секущая,
пересекающая эту окружность в точках С и D, то АХ2 = СХ • XD.
592 Избранные теоремы и методы планиметрии
X
Рис. П14
Рис. П15
Доказательство. По теореме об угле между
касательной и хордой ZDAX= ZACX (рис. П14). Поэтому AAXD ~
АХ СХ
АСХА (ZX — общий). Следовательно, ^г= = -гт?, т. е.
= CXXD.
Задачи к § 5
П5Л. Две окружности пересекаются в точках М и N.
Через эти точки проведены прямые АВ и CD соответственно,
пересекающие первую окружность в точках А и С, а
вторую — в точках В и D. Докажите, что AC || BD (теорема
EL И. Фусса).
П5.2. На стороне АВ равнобедренного треугольника ABC
(АВ = ВС) взята точка D, и вокруг треугольников ADC и
BDC описаны окружности о)\ и 0)2 соответственно.
Касательная, проведённая к о)\ в точке Dy вторично
пересекает (02 в точке М. Докажите, что ВМ || АС.
П5.3. Две окружности пересекаются в точках Р и Q.
Прямая пересекает эти окружности в точках А, В, С, Dy
как показано на рис. П15. Докажите, что ZAP В = ZCQD.
П5.4. Две окружности касаются прямой в точках А и В
и пересекаются в точках С и D.
а) Найдите сумму углов АСВ и ADB.
§ 5. Следствия из теоремы о вписанном угле 593
б) Докажите, что прямая CD делит отрезок АВ пополам.
в) Докажите, что радиус окружности, описанной около
ААВС, не зависит от длины отрезка АВ, если считать
радиусы окружностей заданными.
П5.5. На окружностях даны точки А, В, С, D в
указанном порядке; А\, В\, С\, D\ —середины дуг АВ, ВС, CD,
DA. Докажите, что А\С\ LB\D\.
П5,6. На окружности взяты точки А, С\, В, А\, С, В\
в указанном порядке.
а) Докажите, что если прямые АА\, ВВ\ и СС\ являются
биссектрисами углов треугольника ABC, то они являются
высотами треугольника А\В\С\.
б) Докажите, что если прямые AAi, BBi и СС\ являются
высотами треугольника ABC, то они являются
биссектрисами углов треугольника А\В\С\.
П5.7. В треугольнике ABC через вершину А проведена
прямая U касающаяся описанной около этого треугольника
окружности. Найдите высоту треугольника, проведённую
к стороне ВС у если расстояния от В и С до I равны а и 6.
П5.8. К окружности проведены две касательные (А и В —
точки касания). Пусть М — произвольная точка на
окружности* Найдите расстояние от М до АВ, если расстояния
от М до касательных равны а и ft.
П5.9. Две окружности со i и со 2 пересекаются в точках М
и N. Докажите, что если вершины А и С прямоугольника
ABCD лежат на&>ь а В и D — на. со2> то точка пересечения
его диагоналей лежит на прямой MN.
П5.10. Из центра симметрии двух равных
пересекающихся окружностей проведены два луча, пересекающие
окружности в четырёх точках, не лежащих на одной
прямой. Докажите, что эти точки лежат на одной окружности.
П5.11. Внутри круга расположен пятиугольник ABCDE
с равными сторонами (не обязательно выпуклый). Каждая
сторона продолжена до пересечения с окружностью,
ограничивающей круг. Продолжения сторон АВ, ВС, CD, DE, ЕА
за точки В, С, D, Е, А соответственно окрашены в красный
594 Избранные теоремы и методы планиметрии
цвет, а продолжения этих же сторон за точки А, В, С, D,
Е окрашены в синий цвет. Докажите, что сумма длин всех
красных отрезков равна сумме длин всех синих отрезков.
§ 6. Вписанные и описанные многоугольники
Напомним, что многоугольник1* называется вписанным,
если существует окружность, на которой лежат все его
вершины. Эта окружность называется описанной около
многоугольника. Известно, что около любого треугольника
можно описать окружность. Легко привести и пример
вписанного многоугольника с большим числом вершин — квадрат
(и вообще любой правильный многоугольник). Нетрудно
понять, что около ромба, отличного от квадрата, описать
окружность невозможно.
■&1 Упражнение П6.1. Докажите, что многоугольник является
вписанным тогда и только тогда, когда серединные
перпендикуляры ко всем его сторонам пересекаются в одной точке.
Пользуясь этим утверждением, покажите, что ромб,
отличный от квадрата, невозможно вписать в окружность.
Имеется простой критерий, позволяющий определить,
является ли данный четырёхугольник вписанным.
Теорема П6.1. Для того чтобы четырёхугольник был
вписанным, необходимо и достаточно, чтобы сумма двух2*
его противоположных углов была равна 180°.
Доказательство. Необходимость указанного
условия вытекает из теоремы о вписанном угле. Дуги, на
которые опираются два противоположных угла вписанного
четырёхугольника, в объединении дают всю окружность.
1}Здесь и далее мы, если не оговорено противное, рассматриваем
только выпуклые многоугольники.
2)Сумма углов четырёхугольника равна 360°, поэтому если сумма
двух его противоположных углов равна 180°, то сумма двух оставшихся
противоположных углов также равна 180°.
§ 6. Вписанные и описанные многоугольники 595
С
Е / \Е
а)
В
б)
Рис. П16
Сумма этих углов равна половине угловой величины
окружности, т.е. |. 360° = 180°.
Докажем достаточность. Пусть в
четырёхугольнике ABCD выполнено равенство /DAB + /DCB — 180°.
Опишем окружность около треугольника ABD и покажем,
что точка С также будет лежать на этой окружности.
Предположим, что это не так. Тогда она либо лежит вне круга,
ограниченного этой окружностью (рис. П16а), либо лежит
внутри него (рис. П166). Заметим, что в обоих случаях
/.BED = /BCD, что противоречит теореме о внешнем угле
треугольника (применённой к ACED). □
Вписанный четырёхугольник обладает рядом
интересных свойств. Мы остановимся на одном из них, а некоторые
другие вы найдёте среди задач к этому параграфу.
Теорема П6.2 (теорема Птолемея). Произведение
диагоналей вписанного четырёхугольника равно сумме
произведений его противоположных сторон.
Доказательство. Пусть четырёхугольник ABCD
вписан в окружность.
Возьмём на диагонали BD точку М такую, что Z.MCD =
= /ВСА (рис. П17). Тогда ACDM ~ ACAB (ZBAC=/BDC
как вписанные, опирающиеся на одну дугу), следовательно,
596 Избранные теоремы и методы планиметрии
АВ • CD = АС • MD. Аналогично ДВСМ ~ AACD, откуда
ВС • AD = АС • ВМ. Складывая эти равенства, получим
требуемое. □
Перейдём к обсуждению описанных многоугольников.
Многоугольник называется описанным, если существует
окружность, касающаяся всех его
сторон. Эта окружность
называется вписанной в многоугольник.
Известно, что во всякий треугольник
можно вписать окружность и что
в любой правильный многоугольник
также можно вписать окружность.
Ясно, что не всякий многоугольник
является описанным: в
прямоугольник, отличный от квадрата, вписать
окружность нельзя.
в^ Упражнение П6.2. Докажите, что многоугольник является
описанным тогда и только тогда, когда биссектрисы всех его
внутренних углов пересекаются в одной точке.
Пользуясь этим утверждением, покажите, что
прямоугольник, отличный от квадрата, нельзя описать около
окружности.
Теорема П6.3. Для того чтобы четырёхугольник1* был
описанным, необходимо и достаточно, чтобы суммы его
противоположных сторон были равны.
Доказательство. Необходимость указанного
условия следует из теоремы о равенстве отрезков
касательных, проведённых к окружности из одной точки.
Обратившись к рис. П18, получаем, что АВ + CD = BC + AD~
Докажем достаточность. Пусть в
четырёхугольнике ABCD АВ + CD = ВС + AD. Если все стороны
четырёхугольника равны, то он ромб, а у ромба диагонали
^Напомним, мы рассматриваем только выпуклые многоугольники.
§ 6. Вписанные и описанные многоугольники
А
597
М
N
являются биссектрисами внутренних углов. Следовательно,
точка пересечения диагоналей ромба равноудалена от всех
его сторон, т. е. существует окружность с центром в этой
точке, касающаяся всех сторон ромба. Если
четырёхугольник отличен от ромба, то у него есть две неравные смежные
стороны (почему?). Для определённости будем считать, что
это стороны АВ и ВС, причём АВ > ВС (если это не так, то
просто поменяем обозначения вершин). Тогда из равенства
АВ + CD = ВС + AD следует, что CD < AD. Возьмём на
сторонах АВ и AD точки М и N соответственно так, что
ВМ = ВС и DN = CD (рис. П19). Тогда
(AM + MB) +CD = ВС + (AN + ND),
откуда AM = AN. Проведём биссектрисы внутренних углов
А, В и D четырёхугольника. Так как треугольники AMNy
ВСМ и CDN равнобедренные, эти биссектрисы являются
серединными перпендикулярами к сторонам треугольника
CMNy следовательно, они пересекаются в одной точке /.
Эта точка равноудалена от всех сторон четырёхугольника,
значит, он описанный. D
Аналогично можно доказать следующее утверждение.
598 Избранные теоремы и методы планиметрии
Теорема П6.4. Пусть продолжения противоположных
сторон четырёхугольника ABCD пересекаются в точках Е
и F (рис. П20). Для того чтобы четырёхугольник ABCD
был описанным, необходимо и достаточно, чтобы
выполнялось одно из равенств:
2) АЕ + AF = CE + CF.
В
Рис. П20
я& Упражнение П6.3. Докажите эту теорему.
Задачи к § 6
П6.1. Докажите, что для того, чтобы выпуклый
четырёхугольник ABCD был вписанным, необходимо и достаточно,
чтобы ZABD=^ACD.
П6.2. На сторонах АВ, J3C, С А треугольника ABC взяты
соответственно точки С\, А\, В\. Докажите, что
окружности, описанные около треугольников АВ\С\> А\ВС\ и
А\В\СУ пересекаются в одной точке (точка Микеля).
П6.3. Докажите, что основания перпендикуляров,
опущенных из произвольной точки описанной окружности
треугольника на прямые, содержащие его стороны, лежат на
одной прямой (прямая Симпсона).
П6.4. Диагонали вписанного четырёхугольника
перпендикулярны.
§ 7. Геометрические места точек плоскости 599
а) Докажите, что прямая, проходящая через точку их
пересечения и перпендикулярная одной из сторон, делит
противоположную сторону пополам.
б) Докажите, что расстояние от центра описанной
окружности до любой из сторон равно половине противоположной
стороны.
П6.5. Докажите, что площадь вписанного
четырёхугольника со сторонами а, &, с, d может быть вычислена по
формуле
полупериметр {формула Врахмагупты);
б) S = j5 ч/(а& + cd) (be + ad) (ca + bd), где Я — радиус
описанной окружности.
П6.6. На дуге CD окружности, описанной около
квадрата ABCD, взята точка X. Докажите, что ХА + ХС = ХВ • \/2.
П6.7. Докажите, что четырёхугольник ABCD
описанный тогда и только тогда, когда окружности, вписанные
в треугольники ABC и ACDy касаются.
П6.8. Докажите, что если четырёхугольник со
сторонами a, by су d вписанный и описанный одновременно, то его
площадь может быть вычислена по формуле S = Vabed.
П6.9. Докажите, что если в четырёхугольник можно
вписать окружность, то её центр лежит на одной прямой
с серединами диагоналей (теорема Ньютона).
П6.10. Через точки пересечения продолжений сторон
выпуклого четырёхугольника ABCD проведены две
прямые, делящие его на четыре четырёхугольника. Докажите,
что если четырёхугольники, примыкающие к вершинам В
и D, описанные, то четырёхугольник ABCD также
описанный.
§ 7. Геометрические места точек плоскости
Если из всех точек плоскости нам нужно выделить те
и только те точки, которые обладают некоторым свойст-
600 Избранные теоремы и методы планиметрии
вом S, то нужное множество точек принято называть
геометрическим местом точек (сокращённо ГМТ),
Геометрическое место точек — это некоторая фигура Ф
на плоскости. Найти ГМТ — значит описать эту фигуру.
Принято давать это описание «на геометрическом языке»,
т. е. назвать эту фигуру (например, окружность, пара
прямых и т. п.) и указать параметры, задающие эту фигуру
(например, центр и радиус окружности, точки, через
которые проходит прямая, и т. п.). При этом необходимо
установить справедливость двух утверждений:
1) если точка М обладает свойством S, то она
принадлежит фигуре Ф;
2) если точка М принадлежит фигуре Ф, то она обладает
свойством S,
Полезно знать геометрические места точек плоскости,
которые часто встречаются при решении задач.
Перечислим некоторые из них в виде следующих утверждений.
I. Геометрическим местом точек плоскости, удалённых
от точки О на расстояние R > 0, является окружность
со (О, R) (с центром в точке О и радиусом R).
П. Геометрическим местом точек, равноудалённых от
концов отрезка, является серединный перпендикуляр к
этому отрезку.
III. Геометрическим местом точек, равноудалённых от
сторон угла, является биссектриса этого угла.
IV. Геометрическим местом точек плоскости, из которых
данный отрезок АВ виден под данным углом, меньшим
180°, является объединение двух дуг окружностей,
симметричных относительно прямой АВ, за исключением
точек А и В.
Утверждение I — это переформулировка определения
окружности (оно не нуждается в доказательстве).
Утверждения II и III известны из курса геометрии 8—9 классов.
Прежде чем доказывать утверждение IV, решим
следующую задачу.
§ 7. Геометрические места точек плоскости 601
Задача. На плоскости задан отрезок АВ. Найти
геометрическое место точек М, лежащих в заданной
полуплоскости с границей АВ и таких, что Z.AMB = ос (это и означает,
что из точки М отрезок АВ виден под углом а).
м
а)
б)
Решение. Построим угол ВАС> равный а, так, чтобы
точка С не лежала в заданной полуплоскости. Пусть О —
точка пересечения серединного перпендикуляра к отрезку
АВ и перпендикуляра к прямой АС, восставленного в
точке А (при а = 90° в качестве О возьмём середину АВ).
Построим окружность со (О, ОА) (рис. П21а—в) и
рассмотрим дугу АВ этой окружности, лежащую в заданной
полуплоскости (в той, в которой не лежит точка С). Из теорем
о вписанном угле и об угле между касательной и хордой
следует, что для любой точки М этой дуги, кроме точек А
и J3, ZAMB = а. Обратно, если точки М и С лежат по разные
602 Избранные теоремы и методы планиметрии
стороны от прямой АВ и /AMВ = а, то точка М лежит на
указанной дуге. Действительно, если М лежит вне круга,
ограниченного oj, to из теоремы об угле с вершиной вне
круга следует, что /AMВ < а. Если же М лежит внутри
этого круга (и по-прежнему в нужной полуплоскости с
границей АВ), то по теореме об угле с вершиной внутри круга
/АМВ > а. В обоих случаях мы получили противоречие
с условием /АМВ = а. Итак, искомым ГМТ является
дуга АВ окружности а), из которой удалены точки А и В,
лежащая в данной полуплоскости. □
а)
б)
Рис. П22
Доказательство утверждения IV. Мы только что
нашли нужное геометрическое место точек в предположении,
что эти точки лежат в заданной полуплоскости. Очевидно,
что достаточно найти геометрическое место точек М,
лежащих в полуплоскости, дополняющей данную до плоскости,
а затем взять объединение этих двух геометрических мест.
Повторяя проведённые в решении рассмотренной выше
задачи рассуждения, мы получим дугу, симметричную уже
найденной, относительно прямой АВ. Искомое ГМТ
изображено на рис. П22а—в. □
§ 7, Геометрические места точек плоскости 603
Отметим, что мы воспользовались так называемым
методом объединения, который состоит в следующем.
Если требуется найти геометрическое место точек,
удовлетворяющих хотя бы одному из нескольких условий, то
достаточно найти геометрические места точек,
удовлетворяющих отдельно каждому из условий, а затем взять их
объединение.
■^Упражнение П7.1. Найдите геометрическое место точек,
равноудалённых от двух пересекающихся прямых.
Если в задаче требуется найти геометрическое место
точек, удовлетворяющих одновременно нескольким
условиям, то достаточно найти геометрические места точек,
удовлетворяющих отдельно каждому из условий, а затем
взять их пересечение. В этом заключается метод
пересечения.
я& Упражнение П7.2. Найдите геометрическое место точек,
равноудалённых
а) от вершин данного треугольника;
б) от прямых, содержащих стороны данного
треугольника.
Сейчас мы докажем один важный факт, который
применяется не только в геометрии, но и в физике (точнее,
в электростатике в методе изображений).
Теорема П7.1. Пусть даны отрезок АВ и положительное
число Хф1\ М\ — точка на отрезке АВ, M<i — точка на его
продолжении, причём АМ\ : М\В — AM% : М^В = А.
Геометрическим местом точек, удовлетворяющих условию
AM: MB = А, является окружность со, построенная на
отрезке М1М2 как на диаметре. (Эта окружность называется
окружностью Аполлония.)
Доказательство. Очевидно, что на прямой АВ есть
только две точки такие, что AM : MB = А, — это точки М\
и М2. Пусть М — какая-то другая точка, удовлетворяющая
данному условию. Тогда ММ\ — биссектриса угла АМВ,
604 Избранные теоремы и методы планиметрии
С
а ММ2 — биссектриса угла ВМС (рис. П23). Это вытекает
из результатов, сформулированных в упражнении П1.2.
Указанные биссектрисы являются биссектрисами смежных
углов, следовательно, из точки М отрезок М\М2 виден под
прямым углом и, значит, Me о.
Обратно, если М е (о, то AM : MB = А. Для точек М\
и Мг это так. Пусть М — какая-то другая точка
окружности Аполлония. Проведём через точку В прямую,
параллельную AM. Обозначим точки пересечения этой
прямой с прямыми ММ\ и ММ% через К и L
соответственно (рис. П24). Из подобия (по двум углам) треугольников
м2
Рис. П24
АМ\М и ВМ\К следует, что AM: KB = AM\: М\В = А.
Аналогично AM: LB = AM2 : М2В = А из подобия треугольников
АМ2М и BM2L. Тогда AM : KB = AM : LB, т. e. KB = LB.
Угол М\ММ2 прямой, так как он вписанный,
опирающийся на диаметр. Точка В — середина гипотенузы KL пря-
§ 7, Геометрические места точек плоскости 605
моугольного треугольника К ML, поэтому KB — MB. Из
равенства AM: KB = А тогда получаем, что AM: MB = A. □
№ Упражнение П7.3. Докажите теорему П7.1 методом
координат.
В заключение этого параграфа мы дополним список
основных ГМТ тремя новыми.
Рис. П25 Рис. П26 Рис. П27
Эллипсом называется геометрическое место точек М
плоскости, сумма расстояний от которых до двух данных
точек Fi и F2 постоянна, т.е. MF\+MF2:=2aJ где а = const,
2a>FiF2, a>0.
Точки F\ и 2^2 называются фокусами эллипса. Эллипс
изображён на рис. П25.
Гиперболой называется геометрическое место точек М
плоскости, модуль разности расстояний от которых до
двух данных точек F\ и F^ постоянен, т. е. \MF\ - MF?\ =
= 2а, где а = const, 2а < F1F2, а > 0.
Точки Fi и F2 называются фокусами гиперболы.
Гипербола изображена на рис. П26.
Параболой называется геометрическое место точек М
плоскости, расстояния от которых до данной точки F и до
данной прямой d равны, т.е. MF — p{M, d).
Точка F называется фокусом параболы, а прямая d —
директрисой параболы. Парабола изображена на рис. П27.
606 Избранные теоремы и методы планиметрии
Эллипс, гиперболу и параболу часто можно встретить
в классической механике. Так, согласно первому закону
Кеплера траекториями планет являются эллипсы, в одном
из фокусов которых находится Солнце. Траекториями
комет могут быть и эллипсы, и гиперболы, и параболы.
Эти кривые относятся к коническим сечениям (§ 10.10).
Они обладают красивыми геометрическими свойствами,
которые изложены, например, в книге [Акопян, Заславский,
2007].
Задачи к § 7
П7.1. Дан прямоугольник ABCD. Найдите
геометрическое место точек М таких, что
а) AM + ВМ = СМ + DM;
б) AM2 + СМ2 = ВМ2 + DM2.
П7.2. Сколько существует окружностей, касающихся
всех прямых, содержащих стороны данного треугольника?
П7.3. Найдите геометрическое место середин хорд
данной окружности, проходящих через данную точку.
П7.4. На окружности заданы точки А и В, а точка С
перемещается по этой окружности. Найдите геометрическое
место точек пересечения а) высот; б*) биссектрис
треугольников ABC.
П7.5. а) На плоскости даны точки Аи В. Найдите
геометрическое место точек М, для которых разность квадратов
длин отрезков МА и MB постоянна.
б) Докажите, что для того, чтобы диагонали
четырёхугольника были перпендикулярны, необходимо и
достаточно, чтобы суммы квадратов его противоположных сторон
были равны (четырёхугольник не обязательно выпуклый).
в*) (Теорема Карно) Докажите, что перпендикуляры,
опущенные из точек Аи В\> С\ на стороны ВС, СА9 АВ
треугольника ABC, пересекаются в одной точке тогда и только
тогда, когда
2 + CiA2 + BiC2 = ВгА2 + AiC2 + СХВ2.
§ 8. Теоремы Чевы и Менелая 607
П7.6. На плоскости дан отрезок ВС. Найдите
геометрическое место точек А таких, что медиана СС\ треугольника
ABC равна стороне АВ.
П7.7*. а) Степенью точки М относительно
окружности со (О, R) назовём число d2 -Я2, где d = OM1\ Докажите,
что геометрическим местом точек, для которых степени
относительно двух данных неконцентрических окружностей
равны, является прямая, перпендикулярная линии
центров этих окружностей (радикальная ось двух
окружностей).
б) Пусть центры трёх окружностей образуют
треугольник. Докажите, что существует единственная точка,
степени которой относительно этих трёх окружностей равны
(радикальный центр трёх окружностей).
П7.8*. Точка А находится вне эллипса с фокусами F\
и F2- Отрезки AF\ и AF2 пересекают эллипс в точках В и D
соответственно, отрезки F\D и F2B пересекаются в точке С.
Докажите, что в четырёхугольник ABCD можно вписать
окружность.
§ 8. Теоремы Чевы и Менелая
Теорема П8.1 (теорема Чевы). Пусть точки А\9 Вь С\
лежат соответственно на сторонах ВС, СА, АВ
треугольника ABC. Отрезки АА\> ВВ\ и СС\ пересекаются в одной
точке тогда и только тогда, когда
АС\ ВА\ СВ\ Л тй 1v
Доказательство. Необходимость. Пусть отрезки
АА\У ВВ\ и СС\ пересекаются в точке Р (рис. П28). Тогда
АС\ &АСС\ ^АРС\ &АСС\ ~~ ^АРС\ ^АСР
C\B Sbcc} Sbpci ^bcCi - SbpCi Sbcp
Действительно, первые два из этих равенств следуют из
того, что треугольники АСС\ и ВСС\ имеют общую высоту,
. упражнения П5.2 и П5.3.
608 Избранные теоремы и методы планиметрии
С С
Сх В А Сх В
Рис. П28 Рис. П29
проведённую из вершины Р, поэтому отношение их
площадей равно отношению оснований. Если j- — ^, то, как легко
проверить, j- = ?~^- Из этого вытекает третье равенство.
Итак, ^ = £*£. Аналогично BAl - Sbaf CBl - Sbcp
ЬвСР А\С &APC x>iA &BAP
Осталось перемножить эти три пропорции.
Достаточность. Пусть точки А\, В\, С\ лежат на
соответствующих сторонах треугольника ABC и
выполняется равенство (П8.1), Р — точка пересечения отрезков ВВ\
и CCi, а прямая АР пересекает сторону ВС в точке А2
(рис. П29). Тогда, как мы уже доказали,
CBl=l. (П8.2)
СгВ А2С
Из равенств (П8.1) и (П8.2) следует, что -j-Д = -т-77. На
A2\s A\Lj
отрезке ВС есть ровно одна точка, делящая его в данном
отношении, считая от точки В. Поэтому А\ и А% — это одна
и та же точка. D
Отрезок, соединяющий вершину треугольника с точкой
на противоположной стороне, называется чевианой
треугольника.
в^ Упражнение П8Л. Докажите, что в любом треугольнике еле
дующие тройки чевиан пересекаются в одной точке: а) меди
§ 8. Теоремы Чевы и Менелая 609
аны; б) биссектрисы внутренних углов; в) отрезки,
соединяющие вершины с точками касания противоположных сторон
с вписанной окружностью.
Теорема П8.2 (теорема Менелая). Пусть точки А\ и В\
лежат соответственно на сторонах ВС и С А треугольника
ABC у а точка С\ — на продолжении стороны АВ за точку В.
Точки А\9 В\ и С\ лежат на одной прямой тогда и только
тогда, когда
АСг ВАг СВХ
С\В А\С
= 1. (П8.3)
А В Ci
Рис. ПЗО
Доказательство. Необходимость. Пусть точки
А\, В\ и С\ лежат на одной прямой (рис. ПЗО). Опустим на
неё перпендикуляры АА\У ВВ\ и СС\ из вершин
треугольника. Из подобия (по двум углам) треугольников АС\А!
и BC\Bf следует, что ^^ = -^т. Аналогично /SBA\Bf
и ACBlC> ~ AABlA>, ^ = Щ и
Перемножая эти три пропорции, получим равенство (П8.3).
Достаточность. Пусть точки Ai, В\, С\
расположены так, как сказано в условии теоремы, выполнено
равенство (П8.3) и прямая В\С\ пересекает сторону ВС в точке Аг
20 Зак 3383
610 Избранные теоремы и методы планиметрии
С
А В
Рис. П31
(рис. П31). Тогда
ВА2 СВХ
СгВ ' А2С ' ВХА
= 1. (П8.4)
Из равенств (П8.3) и (П8.4) следует, что -гг— = -т-я,
поэтому А\ и Аг — это одна и та же точка. D
i^* Упражнение П8.2. Докажите, что биссектрисы двух
внутренних углов равностороннего треугольника и биссектриса
внешнего угла при третьей вершине пересекают прямые,
содержащие стороны треугольника, в трёх точках, лежащих на одной
прямой.
Приведём идеи доказательств теорем П8.1 и П8.2,
использующих выход в пространство (см. пример 2.16, а также
задачи 2.34-2.36).
Восставим из вершин А, Б и С треугольника ABC
перпендикуляры к его плоскости. Отложим от точек А, В и С отрезки
АА'', ВВ1 и СС так, чтобы точки А1 и В! находились по одну
сторону от плоскости ABC, а точка С — по другую (рис. П32).
Пусть (АВ) П (А'В') = СЬ (ВС) П (В'С) = Аь (АС) П (А'С)=Вг.
Точки Ai,Bi и С\ при этом таковы, что
АС\
СхВ
АА1
ВВ"
ВАХ
АгС
ВВ'
СС '
СВх
ВхА
СС
АА"
следовательно, выполнено равенство (П8.1). Кроме того, эти
точки лежат в плоскостях ABC и А1 В С', значит, принадлежат
и линии их пересечения, которая является прямой.
■^Упражнение П8.3. Используя приведённые соображения,
докажите теорему Менелая.
§ £. Теоремы Чевы и Менелая
611
Пусть теперь (А'В) П (ABf) — D, а С\ — проекция точки D
на плоскость ABC (рис. ПЗЗ). Из подобия соответствующих
треугольников снова получаются равенства
ACi
AA!
BB"
BAi
AXC
BBf
CC"
CBx
BXA
cc
612 Избранные теоремы и методы планиметрии
т. е. и равенство (П8.1). При этом точка Р1 пересечения отрезков
А!А\ и В'В\ принадлежит линии пересечения плоскостей А1 ВС1
и В1 АС у т.е. прямой CD. Итак, прямые А(А\У В'В\ и CD
пересекаются в точке Р'. Проекция Р' на плоскость ABC будет точкой Р
пересечения отрезков АА\, ВВ\ и СС\.
0^ Упражнение П8.4. Используя приведённые соображения,
докажите теорему Чевы.
Задачи к § 8
П8.1. На сторонах ВСУ С А и АВ треугольника ABC взяты
точки Ль Bi и С\ соответственно. Докажите, что отрезки
АА\, ВВ\ и СС\ пересекаются в одной точке тогда и только
тогда, когда
sin ZACCi sin ZBAAi sin ZCBBi _ 1
sin ZCiCB ' sin ZAiAC ' sin /_B\BA ~
(тригонометрическая формулировка теоремы Чевы).
П8.2. Пусть чевианы ЛЛь ВВ\ и СС\ треугольника
ABC пересекаются в одной точке. Докажите, что прямые,
симметричные прямым ЛЛь ВВь СС\ относительно
биссектрис внутренних углов ВАСУ ABC, BCA соответственно,
пересекаются в одной точке.
П8.3. Противоположные стороны выпуклого
шестиугольника попарно параллельны. Докажите, что прямые,
соединяющие середины противоположных сторон,
пересекаются в одной точке.
П8.4. Треугольники А\В\С\ и Л2В2С2 таковы, что
прямые Л1Л2, B1B2, С\С% имеют общую точку, прямые В\С\
и В%Сг пересекаются в точке Л, прямые А\С\ и Л2С2 —
в точке В, а прямые Л1В1 и Л2В2 — в точке С. Докажите, что
точки Л, В и С лежат на одной прямой (теорема Дезарга).
П8.5. На одной из двух пересекающихся прямых взяты
точки Ль Вь Сь на другой — точки Лг, ^2> Сг. Прямые
Л1В2 и Л2В1, B1C2 и В2С1, С1Л2 и Сч* .пересекаются
в точках С, Л и В соответственно. Дока ^, что точки
Л, В и С лежат на одной прямой (теорема
§ 8. Теоремы Чевы и Менелая 613
П8.6. Пусть общие внешние касательные, проведённые
к каждой паре из трёх данных окружностей, пересекаются
в точках А, В и С соответственно. Докажите, что точки А,
В и С лежат на одной прямой (теорема о трёх колпаках).
II8.7. Докажите, что основания перпендикуляров,
опущенных из точки описанной окружности треугольника на
прямые, содержащие его стороны, лежат на одной прямой
(прямая Симпсона).
П8.8. Докажите, что если шестиугольник вписан в
окружность, а три пары прямых, содержащих его
противоположные стороны, пересекаются, то эти три точки
пересечения лежат на одной прямой (теорема Паскаля).
Ответы и указания к задачам
Глава 1
1.1. Указание: примените метод математической индукции.
1.2. а) Необходимое, но не достаточное; б) необходимое и
достаточное.
1.3. Неверно.
Глава 2
2.1. Задача не имеет решения, если точка М лежит в одной
из двух параллельных плоскостей, проходящих через данные
прямые, но не лежит на данных прямых.
2.2. Всегда. Бесконечно много. Не через любую.
2.3. Верно.
2.5. а) Может; б) может; в) не может.
2.6. а) Не может; б) не может; в) может. Указание*, проекция
должна иметь центр симметрии.
2.11. Не может.
2.12. а) Треугольник, четырёхугольник, пятиугольник,
шестиугольник; б) правильный треугольник, квадрат, правильный
шестиугольник. Указание: у куба шесть граней, которые попарно
параллельны.
2.13. Не может. Указание: воспользуйтесь теоремой
Пифагора и теоремой косинусов.
2.14. Указание: достройте правильный шестиугольник до
правильного треугольника.
2.15*. Указание: пусть SABCD — данная четырёхугольная
пирамида, a KLMNO — данное сечение (К е [АВ], L € [ВС], М €
G [SC]> Ne[SD]y Oe[SA]); спроектируйте пирамиду на плоскость,
проходящую через точку S и середины рёбер AD и ВС.
2.16*. л = 3, 4. Указание: при п = 3 примером служит
правильный тетраэдр ABCD и его сечение, проходящее через середины
рёбер ВС, AC, AD и BD; при п = 4 см. задачу 2.15; при п ^ 5
спроектируйте сечение на плоскость основания пирамиды, взяв
в качестве центра проектирования вершину пирамиды.
2.17. Указание: если Р= (АВ) П (AiBi), Q= (ВС) П (BiCi),
М = (AD) П (PQ), N = (CD) П (PQ), то D^ = (АгМ) П (dN).
2.18. Указание: достаточно через точку М н£ мебре АВ
тетраэдра ABCD провести плоскость, параллельную рёбрам АС
hBD.
2.19. 3.
Ответы и указания к задачам 615
2.20. Если в тетраэдре ABCD имеем AD = а, ВС = fe, a MNPQ -
ромб (М G [АБ], N е [BD]y Р £ [CD], Q е [АС]); тогда АМ:МВ =
2.21. Указание: искомая плоскость параллельна линиям
пересечения противоположных боковых граней пирамиды.
2.22*. Указание: для доказательства неравенства р ^ 2
рассмотрите развёртку тетраэдра; для доказательства неравенства
р < 3 покажите, что если параллельно перемещать плоскость
сечения, то его периметр будет линейной функцией.
2.23. Щ^-а2. 2.24. 1:1. 2.25. 5:1, считая от вершины В.
1о
2.26. ^а2. 2.27. f <?. 2.28. ^-аЪ. 2.29. 25 : 20 : 9.
16 4^ 16
2.30. 2:3, считая от вершины S.
2.31. Ребро SA делится в отношении 3:2, считая от точки А;
ребро SB — в отношении 2:1, считая от точки В; ребро AD —
в отношении 3:1, считая от точки А. Указание: см. пример 2.14;
сечение проходит через точку С.
2.32. ^(\/5 + 2)\/4&2 + 3а2. Указание: сечение — трапеция;
2.33*. 3. Указание: проведите через два из данных отрезков,
параллельных двум скрещивающимся рёбрам тетраэдра,
плоскость и докажите, что сечение тетраэдра этой плоскостью —
параллелограмм.
2.34. Указание: представьте данную в условии задачи
конфигурацию как изображение треугольной призмы (пирамиды) и её
треугольного сечения.
2.35. Указание: см. пример 2.16.
2.36. =£. Указание: представьте данную в условии задачи
конфигурацию как изображение тетраэдра и двух его сечений.
Глава 3
3.2. М — точка пересечения медиан тетраэдра ABCD.
Указание: воспользуйтесь векторным равенством, полученным в
примере 3.3.
3.3. Указание: докажите, что ON = ^
где N — середина произвольной бимедианы.
3.4. См. указание к задаче 3.2.
616 Ответы и указания к задачам
3.5*. Указание: введите базис а — АВ9 b = AC, c* = AD и
получите необходимое и достаточное условия^ для того, чтобы
произвольная такая точка X, что АХ = A3 + yib + v?, принадлежала
плоскости KLM.
3.6*. Указание: воспользуйтесь тем, что правильные
пятиугольники OABCD и O\A\B\C\D\ подобны, а также признаком
компланарности.
3.7. 1:2. 3.8. a) arccos -^; б) arccos -p=.
ч/ТО vT6
3.9. Два решения: Щ и к ~ а. 3.10. Два решения: а и За.
3.11*. Такого тетраэдра не существует. Указание: если
получились значения AD — а\/3 или AD = -j=9 убедитесь, что при
этом не все условия выполнены.
3.12. i\/3&2 -а2. Указание: воспользуйтесь формулой (3.3).
о
3.13. Не существует. Указание: разложите четвёртый вектор
по первым трём и воспользуйтесь условием
перпендикулярности.
3.14. к - arccos ^.
о
3.15. Середина отрезка PQ, где Р и Q — середины отрезков
АВ и CD (если Р и Q совпадают, это и есть искомая точка).
3.16. См. указание к задаче 3.2.
3.17. Указание: пусть AB = S, вб = Ь, CD = <*. Выразите все
векторы, входящие в доказываемое равенство, через а, Ь и ?.
3.18. Указание: воспользуйтесь результатом задачи 3.17.
Глава 4
4.1. Указание: воспользуйтесь теоремой о трёх
перпендикулярах (см. также пример 4.3).
4.2. Указание: воспользуйтесь признаком
перпендикулярности прямой и плоскости, а затем теоремой о трёх
перпендикулярах.
4.3. т : п. 4.4. Вообще говоря, неверна.
4.5. 2V. Указание: докажите, что объёмы тетраэдров МКТР
и МАКР равны и вдвое больше объёма тетраэдра MCAD.
4.6. |QA. 4.7.11:5. 4.8.7:20.
4.9. Указание: разбейте поверхность многогранника на
треугольники с вершинами в вершинах многогранника, а затем
разбейте многогранник на две пирамиды и не \^ько тетраэдров,
соединив точку, равноудалённую от его основ V с вершинами.
Ответы и указания к задачам 617
4.10. Указание: если АА\ =ВВ\ —СС\, то данный
многогранник — треугольная призма, для которой формула справедлива;
общий случай сводится к этому частному с помощью
дополнительного построения.
4.11. Указание: воспользуйтесь теоремой о трёх
перпендикулярах и результатом примера 4.7.
4.12. а) Указание: пусть К, L, М и N — середины рёбер АВ,
ВС, CD и DA; докажите, что (АС) 1 (BD) & КМ = LN, а затем
воспользуйтесь результатом примера 4.7. б) Указание: с
помощью векторов докажите, что в тетраэдре суммы квадратов двух
пар скрещивающихся рёбер равны тогда и только тогда, когда
третья пара скрещивающихся рёбер перпендикулярна.
4.13. Ортоцентрические (и только они).
4.14. Указание: сечение — правильный шестиугольник.
4.15. ^х^» 4.16. Указание: см. пример 4.8.
л м mr \ V 6 9 ^-ч 5v5 9
4.17. а) -Ч~а , сечение — пятиугольник; б) а , сечение —
четырёхугольник.
4.18. -|=. 4.19. £. 4.20. £, 4=-
\/4Т 2 4 уз
4.21. a) arccos |, 2л/£; б)
О V 11 хх
4.22. a) arccos |, ^; б) |. 4.23. Всегда.
4.24. arcsin ^-. 4.25. arcsin —-.
4 9
4.26. у|тя. Указание: см. пример 4.14.
4.27. а) Вообще говоря, неверно; б) arccos —~- (> 45°!).
Указала *2 + 2 2у^6 6(х2
«ие: если АО = х, tocos ф = - —
2 -h 8 7
Глава 5
5.2. См. пример 5.1.
5.3. 1 : 3. Указание: если К — середина ребра АА\, то (СК) _1_
±(CiMN).
5.4. 1:2, считая от S.
5.5. Независимо от (р указанная величина угла изменяется
от 0 до к.
618 Ответы и указания к задачам
5.6. В двух случаях: если a _L/3 или а _1_ Ь, где Ь — прямая,
параллельная биссектору /3 и перпендикулярная ребру двугранного
угла.
5.7. Указание: искомое отношение равно отношению высот,
опущенных из концов отрезка на биссекторную плоскость.
5.8. arccos -§=• 5.9. f.
V5 d
5.10. arccos pr. Указание: см. пример 5.2.
5.11. ^. Указание: наименьшим из углов между прямой А\С\
и прямыми, лежащими в плоскости, перпендикулярной прямой
CDi, является угол между А\С\ и её проекцией на эту плоскость.
п
5.12. ^~. Указание: введите в рассмотрение угол между (AAi)
и перпендикуляром к плоскости сечения и воспользуйтесь
результатом упражнения 5.2 и формулой (5.1).
5.13. 1 +cos а. Указание: примените формулу (5.1).
5.14. 2 cos а.
о
5.15. —-. Указание: рассмотрите отдельно случаи, когда про-
z
екция — треугольник и четырёхугольник.
5.16*. Указание: Пусть ABCDA\BiC\D\ — данный куб;
убедитесь, что площадь его проекции на искомую плоскость равна
удвоенной площади проекции треугольника ACD\, а длина его
проекции на искомую прямую совпадает с проекцией диагонали
B\D на эту прямую.
5.17*. Указание: возьмите на рёбрах трёхгранного угла по
точке так, чтобы рассматриваемые плоскости пересекали
выбранный треугольник по его медианам.
5.18. Указание: воспользуйтесь тем, что рассматриваемые
плоскости есть геометрические места точек, равноудалённых от
пар сторон плоских углов данного трёхгранного угла.
5.19. Нет, не любой.
5.20. Не существуют. Указание: воспользуйтесь теоремой 5.6.
5.21. arcsin \/sin(a +/?) sin(a — /3).
5.22. arcsin( ~~= sin cp sin a].
5.24. ' . H2sina 0 < a < f.
8sin(| + f)sin(f-f)
Ответы и указания к задачам 619
5.25. arctg \/7. 5.26. 2 arccos —i-=-, %<а<к.
2sinf 3
5.27. arccos ~. 5.28. 3\/3а.
Глава 6
6.3. тг. Указание: если SABCD и PBEFC — правильные
четырёхугольные пирамиды, все рёбра которых равны, а основания
ABCD и BEFC лежат в одной плоскости, то BCSP — правильный
тетраэдр.
6.5. 5. Указание: см. задачу 6.3.
6.6. Не обязательно.
6.7. а) Указание: если просуммировать количества рёбер по
всем граням, то получится удвоенное количество рёбер
многогранника, б) Указание: если просуммировать количества рёбер
по всем вершинам, то получится удвоенное количество рёбер
многогранника.
6.8. Указание: пусть Г* — число ft-угольных граней
многогранника, a Bk — число его вершин, в которых сходится k рёбер;
докажите, что 2Р = ЗБ3 + 4В4 4- 5Б5 + ... = ЗГ3 + 4Г4 4- 5Г5 + ...,
а затем воспользуйтесь теоремой Эйлера.
6.9. См. задачу 6.8.
6.10*. Нет. Указание: докажите сначала, что в некоторой
вершине такого многогранника, если он существует, должно
сходиться не менее четырёх граней.
6.11*. п = 6, 8, 9, ... (п > 5, п ф 7).
6.12*. Неверно. Кроме правильного октаэдра условию
удовлетворяет правильная треугольная призма, все рёбра которой
имеют одинаковую длину.
6.13*. 4.
Глава 7
7.1. Прямая, перпендикулярная плоскости трапеции и
проходящая через центр описанной около неё окружности (ср. с
утверждением IV).
7.2. Плоскость, параллельная данным прямым и делящая их
общий перпендикуляр в отношении k (ср. с примером 7.6).
7.3. Указание: рассмотрите два случая взаимного
расположения данных плоскостей; в каждом из этих случаев решите
соответствующую плоскую задачу (заменив в формулировке
плоскости прямыми).
7.4. Если п — число сторон данного многоугольника, то при
п = 3 искомое ГМТ состоит из четырёх прямых, перпендикуляр-
620 Ответы и указания к задачам
ных плоскости треугольника и проходящих через центры
вписанной и вневписанной в него окружностей. При п = 4 искомое ГМТ
состоит из прямых, перпендикулярных плоскости
четырёхугольника и проходящих через центры вписанной и вневписанной
в него окружностей (если обе эти окружности существуют; если
существует только одна из них, то в ГМТ входит только одна из
указанных прямых; в противном случае искомое ГМТ — пустое
множество). Если п ^ 5 и в /г-угольник можно вписать
окружность, то искомое ГМТ — прямая, перпендикулярная плоскости
л-угольника и проходящая через центр вписанной окружности.
В противном случае искомое ГМТ — пустое множество.
7.5. Окружность, лежащая в плоскости, параллельной обеим
данным прямым и проходящей через середину О их общего
перпендикуляра длины А. Центр окружности лежит в точке О,
а радиус равен ^\fa2 - A2.
7.6. Если А — данная точка, В — её проекция на данную
плоскость, С — точка пересечения рассматриваемых прямых, то
искомым ГМТ является окружность с диаметром ВС
(вырождающаяся в точку, если В = С).
7.7. Если А и В — данные точки, то искомым ГМТ является
сфера с диаметром АВ.
7.8. Если SABC — рассматриваемая пирамида, К — середина
ребра ВСУ L — середина ребра AD, а отрезок KL не меняет своей
длины, то искомым ГМТ является сфера с центром в точке О,
симметричной точке А относительно точки Ку и радиусом 2Kb
(исключая точки этой сферы, лежащие в плоскости ABC).
7.9. Если точка К — середина отрезка ВС, а точка D\ такова,
что D\K~3DKy то искомым ГМТ является сфера с центром в
точке D\ и радиусом 30D (исключая точки этой сферы, лежащие
в плоскости D\BC).
7.10. Внутренность треугольника А1Б1С1, у которого точки
А, В и С являются серединами сторон.
7.11. Внутренность шестиугольника, стороны которого
проходят через вершины треугольника ABC перпендикулярно его
сторонам.
7.12. Пусть Р и Q — точки пересечения противоположных
сторон четырёхугольника ABCD, а К и L — точки пересечения
его диагоналей с прямой PQ. Тогда искомым ГМТ будут а) сфера
с диаметром KL; б) пересечение сфер с диаметрами PQ и KL.
Указание: см. пример 7.2.
7.13. Прямая. Если отказаться от условия параллельности
плоскости, то получится всё пространство.
7.14. Указание: сделайте развёртку куба.
Ответы и указания к задачам 621
7.15. Внутренность правильного октаэдра с вершинами в
серединах рёбер данного тетраэдра.
Глава 8
8.2. Нет. Более того, если А и В — неподвижные точки
перемещения, то (АВ) —прямая неподвижных точек.
8.3. Обязательно.
8.4. Указание: три сферы с радиусами ХА, ХВУ ХС и
центрами А, В, С пересекаются, вообще говоря, в двух точках,
симметричных относительно плоскости ABC, из которых ровно
одна удалена от точки D на расстояние XD.
8.5. Указание: докажите, что центр шара — неподвижная
точка.
8.6. Указание: поворотом около оси I переведите точку В
в плоскость, проходящую через точку А и прямую /, так, чтобы
точка А и образ точки В были по разные стороны от /.
8.7. Указание: если а ||/3, искомое перемещение —
параллельный перенос, если a jf/? — поворот.
8.8. Указание: докажите, что фигура Ф симметрична
относительно прямой, проходящей через точку пересечения данных
осей симметрии и перпендикулярной к ним.
8.9. Указание: зафиксируйте какую-нибудь ось симметрии I
и докажите, что при симметрии относительно I ось симметрии
переходит в ось симметрии.
8.12*. Указание: докажите, что для любой грани найдётся
центрально симметричная ей грань, а затем докажите, что все
центры симметрии пар граней совпадают.
8.13*. Указание: докажите, что все шесть плоскостей
проходят через точку, симметричную точке N относительно точки
пересечения медиан тетраэдра.
8.14*. Указание: пусть О — точка, равноудалённая от всех
вершин тетраэдра, М — точка пересечения его медиан, О' —
точка, симметричная О относительно М. Докажите, что все шесть
плоскостей проходят через точку О'.
8.15. Указание: отразите точку В симметрично
относительно а.
8.16. Указание: отразите точку С симметрично относительно
а и/3.
8.17. 9. Указание: если а — плоскость симметрии данной
фигуры, то либо все три прямые симметричны относительно а,
либо одна прямая симметрична относительно а, а две другие
симметричны друг другу.
622 Ответы и указания к задачам
8.18. Указание: докажите, что рассматриваемые части осе-
симметричны.
8.19. См. задачу 8.18.
8.21. а) Указание: рассмотрите сечение плоскостью,
перпендикулярной линии пересечения, и воспользуйтесь
соответствующим планиметрическим утверждением, б) Указание: искомые
плоскости проходят через ось поворота и образуют друг с другом
угол, вдвое меньший угла поворота.
8.23*. Указание: пусть Р — данное перемещение, и пусть
At (i = 1, ..., 4) — образы четырёх точек, не лежащих в одной
плоскости, при перемещении Р. Укажите k ^ 4 таких симметрии
относительно плоскостей S*, что преобразование Si о ... о Sk о Р
оставляет точки At неподвижными.
8.24. Указание: воспользуйтесь композицией двух симметрии
относительно плоскостей.
8.25. Как и в случае двух окружностей на плоскости, центров
гомотетии два —внешний и внутренний.
8.29*. Указание: «замостите» пространство правильными
тетраэдрами и правильными октаэдрами; докажите, что если
преобразование пространства сохраняет расстояние г, то оно
сохраняет правильный тетраэдр и правильный октаэдр с ребром г.
Глава 9
9.1. eVy^ 9.2.arccos4pL 9.3. arctg ^f.
о
9.4. Yo BO BCex случаях.
9*5. Указание: покажите, что /.ВАС = ZBSC = 90°, и
воспользуйтесь теоремой 9.1.
9.6. Указание: докажите, что высота пирамиды лежит в
плоскости BSC.
9.7. ^/3 sin £\/cos2 £ -cos2 а. Указание: рассмотрите три
о 2 у б
случая — основание высоты лежит внутри основания пирамиды,
вне основания пирамиды, принадлежит ребру основания
пирамиды.
9.8. ±^, 768 или 3072.
о
9.9. 2, если а = Ь; а~1 или аТ , если а> Ь\ ^-г— или 7 а,
0 0 0 0
если а < Ь.
9.10. ^~. Указание: см. пример 9.5.
о
Ответы и указания к задачам 623
9.11. Указание: см. пример 9.6.
9.12. Указание: разрежьте тетраэдр на четыре пирамиды,
общей вершиной которых является данная точка; указанная сумма
есть сумма отношений объёмов этих пирамид к объёму тетраэдра.
9.13. Указание: докажите, что ^ = ^, ^ = ^ и
DA Vabcd vB Vabcd
ОС i _ Vqabd
DC " VABcd '
9.14. Указание: выразите объём тетраэдра двумя способами
и воспользуйтесь результатом примера 5.3.
9.15. arccos (cos2 а). Указание: расположите данный
трёхгранный угол на кубе.
9.16. Все углы по 60°. Указание: нарисуйте вспомогательный
куб.
9.17. arctg — 5— • Указание: см. пример 9.8.
9.18. arccos \. Указание: разместите треугольник LMN на
о
вспомогательном кубе, поместив точку L в вершину А\9 а
точку N — в вершину А.
9.19. |SA. Указание: уложите тетраэдр в коробку по
диагонали.
9.20*. Указание: достройте тетраэдр до треугольной призмы.
9.21. iyj2{a2 + b2 - с2)(а2 +с2- Ь2)(Ь2 +с2 - а2). Указание:
уложите тетраэдр в коробку по диагонали.
9.22. ^хуг. Указание: уложите тетраэдр в коробку по
диагонали.
9.23. Указание: пусть площади граней тетраэдра равны Si, S2,
S3 и S4. Уложим его по диагонали в параллелепипед с площадями
граней Р\у Рг и Рз- Докажите сначала, что
затем разделите обе части этого равенства на 9V2, где V — объём
тетраэдра.
9.24. Указание: уложите тетраэдр в коробку по диагонали
и воспользуйтесь теоремой о сумме квадратов диагоналей
параллелограмма.
9.25. Указание: уложите тетраэдр в коробку по диагонали.
9.26. Указание: докажите сначала, что тетраэдр является
равногранным тогда и только тогда, когда параллелепипед, в
который он уложен по диагонали, прямоугольный.
624 Ответы и указания к задачам
9.27. 3. Указание: уложите правильный тетраэдр в куб по
диагонали и воспользуйтесь тем, что из девяти осевых симметрии,
переводящих куб в себя, лишь три переводят в себя тетраэдр.
9.28. jfl3. Указание: общая часть двух из трёх указанных
призм — октаэдр.
9.29. ^V. Указание: общая часть — октаэдр.
о
9.30*. §7. Указание: воспользуйтесь результатом, получен-
о
ным в примере 9.12.
9.31*. ^—Ц—. 9.32*. ^ г. 9.33. —!рГ
1+sina 4 sin2 (|+|) 21
9.34*. \/2:1. 9.35. -
>0.
V2c
9.37*. (20 - 14\/2): 1. 9.38*. -|=а и 2а.
v 15
9.39*. Указание: рассмотрите проекцию куба на плоскость,
перпендикулярную его диагонали.
9.40*. Можно.
Глава 10
10.1. Меньшие по длине стороны (если а = Ь, то всё равно
какие).
24тг2
10.4. Часть синусоиды. Указание: если А — произвольная
точка линии пересечения, О — точка пересечения оси цилиндра с
секущей плоскостью, Р — плоскость, проходящая через О
параллельно основанию цилиндра, В — проекция А на плоскость Р,
М и N — точки линии пересечения, лежащие в плоскости Р,
ZMOB = Ху OR= г, а угол между секущей плоскостью и Р равен а,
то АВ = (г tg a) sin jc.
10.5. Можно.
10.6. Указание: постройте сначала на , ^ом шаре
окружность, отметьте на ней три точки, а затем по< \те на плоскости
треугольник, равный треугольнику с верши в этих точках.
10.7. 4а sin -~г—. Указание: сделайте раз
Ответы и указания к задачам 625
10.8. а) Пусть О — центр шара, (ОМ) ± а, плоскость а
перпендикулярна а и проходит через М (М е а). Искомое ГМТ
представляет собой заключённую внутри шара часть окружности,
лежащей в а, с диаметром ОМ. б) Часть сферы с диаметром
ОН, заключённая внутри шара.
10.9. б*) Указание: докажите сначала, что если окружности
0)\ и со2 пересекаются в двух точках, Р — точка на прямой,
проходящей через их общую хорду, а точка М не лежит в плоскостях
окружностей o>i и о>2> то найдётся плоскость а, проходящая
через прямую МР и имеющая с со\ и 6^2 не менее трёх общих
точек.
10.10. а) Можно, б*) 6. 10.11. ^.
о
10.12*. Указание: отложите все векторы от одной точки и
окружите их сферой радиуса 1 с центром в этой точке, затем
каждую точку пересечения вектора (или его продолжения) со сферой
окружите сферическим сегментом с «угловым раствором» в 45°;
сравните площадь сферы с суммой площадей этих сегментов.
10.14. 9:4. 10.15. 2\/йг.
10.16. §£, §- и ~^. Указание: воспользуйтесь результатом
задачи 10.15.
10.17. 2 + \/3* Указание: воспользуйтесь результатом
задачи 10.15.
10.18. 6. 10.19. arccos \. 10.20. ^? _.
10.23. ±kR2H. 10.25. Зг.
10.26. arccos ^. Указание: воспользуйтесь теоремой 10.17.
10.27. -~=. Указание: заключите конусы в каркасные пира-
V3
МИДЫ.
10.28. 2:1. Указание: см. пример 10.8.
10.29. 2arctg(sin ~J. Указание: см. пример 10.6.
10.30. г(уД- 1). Указание: рассмотрите куб ABCDAxBxCiD\
с ребром 2г и докажите, что если оси цилиндрических
поверхностей суть прямые АА\9 CD и В\С\, то центр искомого шара
является центром куба.
10.31. г(у/2 - 1). Указание: см. задачу 10.30.
10.32. От V^-CR + r)2 до y/a2-(R-r)2.
626 Ответы и указания к задачам
10.34. Указание: эти проекции равны —^—, где АВ = I,
CD=^m, расстояние между центрами шаров равно d.
10.35* Указание: воспользуйтесь теоремой 10.19.
10.36. Указание: если О\, 0<l — центры окружностей, а М —
середина [АВ] в задаче а) или точка А в задаче б), то центр искомой
сферы — точка пересечения перпендикуляров, восставленных в
(О1О2М) из точек О\ и Ог к прямым О\М и О2М.
10.37. Указание: воспользуйтесь результатом задачи 10.36 а)
и теоремой 10.2.
10.38. Указание: если окружности не лежат в одной
плоскости, то воспользуйтесь результатом задачи 10.36.
10.39. 1 - л/|. 10.41. 4а2. 10.42. 6S.
10.43. Указание: докажите, что суммы плоских углов при
каждой вершине тетраэдра равны, а затем сделайте развёртку
тетраэдра.
10.44. Указание: a) KD\ + D\M = а, где а — длина ребра куба;
б) эта величина равна 60°.
10.45. Указание: если Х\, Y\ — точки касания шара с гранями
YAB и ХАВ, то рассматриваемая сумма углов равна ZAX\B +
+
10.46. Щ или £. 10.47. У11^. 10.48. | или 4 - 2\/3.
3 6 4/3 + VT5 3
10.49*. Указание: докажите, что сечение, параллельное
касательной плоскости, является правильным треугольником тогда и
только тогда, когда произведения скрещивающихся рёбер равны
(используя подобие треугольников).
10.50*. Указание: воспользуйтесь симметрией относительно
биссекторов двугранных углов тетраэдра.
10.51*. Указание: плоскость каждой грани отрезает от
внешней сферы сегмент высоты 1; все такие сегменты должны
покрыть внешнюю сферу целиком.
10.52. Указание: для каждой вершины многогранника
постройте сферу, проходящую через неё и концы трёх выходящих
из неё рёбер; затем воспользуйтесь результатом задачи 10.36.
10.53*. Указание: если О\ и Ог — точки к Чсании с шаром
граней с общим ребром АВ, то AABOi = Л А V»
воспользуйтесь этим для доказательства исходных утвержу ^ методом от
противного. \
10.54*. Указание: проведём в каждой верп писанного
многогранника плоскость, касательную к описах \ару; тем
самым построено такое обратимое отображение _>ва впи-
Ответы и указания к задачам 627
санных многогранников в множество описанных, что каждой
вершине, ребру, грани вписанного многогранника
сопоставляется соответственно грань, ребро, вершина описанного; теперь
воспользуйтесь утверждением задачи 10.53 а).
10.55. а), б) Нет. Указание: воспользуйтесь результатами двух
предыдущих задач.
10.56. б), г) Не обязательно. 10.59. Эта призма —куб.
10.60. 3. 10.61. а
10.62.
у/2 sin (р 4- 2 cos % >/- cos tp
afsin £ -cos a)
2 sin ^ sin or
10.64*. 8, если сумма любых двух сторон не равна сумме
оставшихся двух сторон, и бесконечно много в остальных
случаях.
10.65*. О, 1, 2, 4 или 5. Указание: см. доказательство
теоремы 10.29.
I 2 2 2
10.66. \\ а о • Указание: уложите тетраэдр в коробку
по диагонали.
10.67. \\ а "*" 0 +С . Указание: уложите тетраэдр в коробку
по диагонали.
2pq cos |
10.68. . Указание: воспользуйтесь методом
вспомогательного объёма, доказав предварительно, что объём тетраэдра
равен —1 J sin a, где Si,S2 —площади двух граней с общим
ребром а, а —угол между этими гранями.
10.69. -л 2 г. Указание: сложите равенства вида
Г1 Г2 ^ Гз ^ Г4
(10.19), записанные для вневписанных шаров.
*гч«Л 3 — cos a — cos б — cos у __ .
10.70. т; • Указание: воспользуйтесь фор-
3 + cos af + cos p + cos у
мулой (10.18), её аналогом для радиуса вневписанного шара и
теоремой 5.5.
10.71. 2. Указание: пусть LP — образующая конуса, Q —
основание перпендикуляра, опущенного из точки К на (LP), к —
плоскость, проходящая через LP перпендикулярно KQ\ тогда п —
касательная плоскость к конусу; кроме того, если шар имеет
лишь одну общую точку с поверхностью конуса и расположен вне
628 Ответы и указания к задачам
его, то в сечении шара плоскостью, проходящей через ось конуса
и центр шара, получится круг, касающийся стороны осевого
сечения конуса.
2\/3 — 3
10.72. 2г —^-5 . Указание: точка касания шара с плоско-
о
стью Р находится в центре правильного треугольника,
образованного центрами оснований конусов.
12<5>/2-7)
10.73. arctgf ctg (p sin | V 10.74.
10.75. 1|. 10.76
10.77*. -~- или 20 J —г. Указание: ось цилиндра проходит
^ v 1 (
через середину отрезка BD и лежит в плоскости BDL, где L —
середина ребра АС,
1ЛРТО. 4уДпа(у/2а2 + Ь2-а)
10.78*. — такая точка на ребре
(2а2 + b2) w • (3\/2а2 + Ь2 - 4а)^2
AS, что АК" = а. Тогда В, D и К принадлежат сечению конуса
плоскостью, параллельной его основанию и делящей пополам
его высоту.
10.79*. ^5~. Указание: так как прямые PN и AM образуют
о
равные углы с прямой АС, искомая сфера единственна.
1ЛОЛ, 2а tg «v/2W sin а - (г2 + /2) sin2 а
1U.OU*. .
VI2 — а2 cos2 а
Глава 11
11 Л. Векторы образуют правый ортонормированный базис.
11.5. А = 3, А = -4. 11.6. S = Ц1, h1=h2 = Ь\1т1> hs = -|=.
11.7. а) I -±=; б) ± 1
3 V30 2
11.8. 216. Указание: см. пример 11.3.
/Щ — 1
11.9*. ^ или тг - arccos —к—»
О и
11.10. А^ц( —-—т)^; ПРИ ^~ независимо
от v объём равен ^; это обобщает результг \i 8.18 на
случай произвольного тетраэдра: всякая плоскость, проходящая
Ответы и указания к задачам 629
через середины скрещивающихся рёбер тетраэдра, делит его на
равновеликие части.
11Л1*. Указание: при гс = 4 утверждение следует из
линейности векторного произведения векторов; при п > 4 разбейте
многогранник на тетраэдры.
11.13*. а) (?-?о,2, tf)=0, ?>H = D; б) (?- /*0, ?\ - ?о, а) = О,
ц.14* а) |я| ; б) ^^ ; в) ^^
11.15. а) а ф ±3; б) а = 3; в) а = -3.
11.16. а) Прямая лежит в плоскости; б) пересекаются в точке
(~~f' ly l); B^ пРямая параллельна плоскости; г) пересекаются
в точке (53, 24,18).
11.17. х - Ъг Л- 4 = 0, 2х - 4j/ + 5г + 9 = 0, 6* + у -f z + 2 = 0;
2 1 3 '
11.18. 4x + y-3z
- 29 = 0 и х - 2у - 32 + 8 = 0.
11.19. (0, 0, 1) или (-А, _1|, 12Г).
11.20. (2, -3, -1), (1, -5, -3). 11.21. £±б = У-^ = ^.
О. /О о -I
11.22.
11.23. а) Ж. б) 1^; в) ^, 6; г) arccos lg, arccos A
1 S
и arcsin —1^=.
19\/Т0
11.24*. a)8x + 5i/ —г —25 = 0; б)2х — 5у — 92 — 25 = 0. Указание:
см. примеры 11.16* и 11.17*.
Q /i А
11.25*. Радиусы: 1 и —■=—; координаты центров: (2, 3, 4) и
1>5'т)-
11.26*. Радиусы: v2 и —^—; координаты центров: (2, ^~, -|
/31 6 _29\
И1в'5' 40Г
630 Ответы и указания к задачам
11.27. у/2, (0, 2, 1) или ^, (О, §, \).
О \ О О /
11.28, 11.29. а) Касаются в точке (-^, i 4 ); б) пересекаются
\ О О О /
по окружности с центром ("о' 4' 4) и РаДиУсом \у %•
11.30*. а) |?-?о|=Д; б) |(?-?о) хЗ|=Д|2|; в) |(?-?0).г| =
|||||
11.31*. a) jci/ + i/2 + zx = 0. Указание: воспользуйтесь
результатом задачи 11.30 в); б) х2 + у2 - (г - I)2 = 0.
11.32. arccos |.
11.33. 45°, 45°, 90° или 45°, arctg2, arctg3.
1t ni a rjrTTTr a ii qk V371 11 ос 27y3
11.34. — или ^. 11.35.-^3-. 11.36.
— или ^. 11.35.^3
11.37. 1. Указание: введите аффинную систему координат
{А, АВ, АИ, AD).
11.38. Указание: введите систему координат так: постройте
прямоугольный параллелепипед, три ребра которого идут по
осям цилиндров; начало координат — центр параллелепипеда,
оси координат параллельны его рёбрам.
11.39. Указание: разность уравнений
и
является линейным уравнением.
11.40. а) Сфера, вписанная в куб; б) сфера, описанная около
куба.
11.42. Указание: введите систему координат с началом в
центре первой сферы и осью Ох, проходящей через центр второй
сферы.
11.43. Кольцо, расположенное в радикг ной плоскости
данных сфер (см. задачу 11.42).
Глава 12
12.1. ±nhr2. 12.2. Щ±У. 12.3. Щ-.
12.4.|. 12.5. S^. 12.6. £S.
Ответы и указания к задачам 631
12.7. Если 0 < а ^ ^"1, то h = 4а + 2 + 2Va2+a + l; если
12.8. Если 0 < а < arcctg 4\/2, то V — -^-l3 sin 2a cos ос; если
arcctg 4>/2 ^ а < тт, то К = jxqI3 cos3 a.
12.9. Если 0 < а < arctg v2, то S = -~- sin а tg а; если
arctff у/2 ^ of < —, то S = ^-— Л2 \/4 + tg"2 а tc а.
bv\ g' 4VI& &
12.10. 2а(\/3 - \/2). 12.11. y^. Указание: см. пример 12.9.
12.12*. —т^г—а3. Указание: используйте неравенства
12.13. 5 + \/3. 12.14. а) ^; б) Va2b2 + Ь2с2 + с2а2.
12.15. Центр данного тетраэдра.
12.16*. Точка, расстояния от которой до граней тетраэдра
соответственно пропорциональны площадям этих граней.
12.17*. Если b < a^tl, то
MNmin - |
если 6 ^ а - , то
3a2 - a\/2).
Указание: см. пример 12.11.
12.18. 2#. Указание: сделайте развёртку.
12.19. а) Указание: примените теорему 5.7 к углу, полярному
к данному (см. замечание после упражнения 5.6). б) Указание:
разрежьте данный угол на п — 2 трёхгранных угла и
воспользуйтесь задачей а).
12.20. Указание: воспользуйтесь результатом задачи 2.20 а),
теоремой Минковского о еже и теоремой 5.6.
12.21. Указание: воспользуйтесь неравенством треугольника.
12.22. Указание: рассмотрите проекции на рёбра куба.
632 Ответы и указания к задачам
12.23. Указание: рассмотрите проекции на три
непараллельных ребра куба.
12.24*. Указание: докажите сначала, что если Н Е [#i#2],
то для любых трёх точек Е, F и G либо Pefgh ^Pefgh^
либо Pefgh ^ Pefgh2> гДе Р — периметр (т.е. сумма длин всех
рёбер); с помощью этого утверждения доказательство неравенства
Pklmh < o^abcd сводится к его проверке в случае, когда точки К,
о
L, М и N (возможно, какие-то из них «совпадают») расположены
в вершинах тетраэдра ABCD.
12.25. Указание: такую плоскость можно найти среди
плоскостей, перпендикулярных плоскости, параллельной двум
скрещивающимся рёбрам тетраэдра.
12.26. Указание: рассмотрите два случая — сечение,
являющееся треугольником, и сечение, являющееся четырёхугольником.
12.27* Указание: рассмотрите два случая — сечение,
являющееся параллелограммом, и сечение, являющееся
шестиугольником.
12.28. Указание: докажите, что V ^ ^а (1 - ~ J, где а — длина
ребра, скрещивающегося с ребром, длина которого может быть
больше 1.
12.29. Указание: пусть О — точка пересечения указанных
отрезков; V\9 V2, Vs, V4 — объёмы тетраэдров OBCD, OCDA, ODAB,
ОАВС: докажите сначала, что
где
^ =
(Vabcd — Vi)(Vabcd — V2) (Vabcd — Уъ)(Vabcd — Va) f
а затем воспользуйтесь неравенством a ~ ^ fyabc.
12.30*. Указание: пусть SA\ :SA = x, SB\ :SB = y, SCi :SC = 2y
B\A2 : B\C\ = a, C\B2 : C\A\ — b, A\C2 : A\B\ ~c\ г\>гда требуется
доказать, что
- b)c(l - x)yzA- У(1 - c)a(l -y)xz+ ^/(1 -a).
k + m + n
воспользуйтесь неравенством
12.31. Указание: рассмотрите сечение тетраэдра
параллельной его грани и проходящей через центр вписанной
сферы.
12.32, 12.33. Указание: используйте векторы.
Ответы и указания к задачам 633
Глава 13
13.2. 2тг2г2а. 13.3. j-jfj-^- 13-4*- 8(2 ~ ^)г3.
13.5. (Зя — 2) : 2. Указание: см. пример 13.2.
13.6*. (3/г-4):(Зтг + 4).
13.7. Указание: воспользуйтесь формулой (13.3).
13.8. а) —; б) _j_.
13.10. Нисколько, так как объёмы старого и нового колец
равны (ср. с задачей 10.11).
13.11. 2кг3 (sin а - a cos а - | sin3 а).
ка'
13.12. ка' д . Указание: докажите, что искомый объём не
зависит от положения прямой U и проведите её так, чтобы объём
легко вычислялся.
13.13. %.
13.14*. Указание: докажите сначала, что если два
прямоугольника равновелики, то они (в плоском смысле) равны по
Кавальери; затем рассмотрите вспомогательный третий
параллелепипед, имеющий общее ребро как с первым, так и со вторым
из данных параллелепипедов и тот же объём; первый и третий
параллелепипеды можно расположить так, что прямые,
параллельные некоторой прямой 1\, будут пересекать их по отрезкам
равной длины; аналогично для второго и третьего
параллелепипедов найдите прямую /г» обладающую тем же свойством;
остаётся взять плоскость, параллельную 1\ и /2» в качестве
горизонтальной плоскости.
13.15. 4тг2га. 13.17. 2kRH. 13.18. 4^2(sin а - а cos а).
13.19*. Д^- и 24(2 - \/2)г2.
sin a v '
13.20. Указание: не забудьте рассмотреть все возможные
случаи взаимного расположения треугольника и оси вращения.
13.21. ка2 п2 sin |.
13.22. F = i
13.23* fffl24
634
Ответы и указания к задачам
13.24. -—=. Указание: если бы сферы пересекались, то отно-
шение площадей, о которых идёт речь в условии задачи, было
бы равно j; следовательно, одна сфера лежит внутри другой.
13.25*. Указание: воспользуйтесь формулой (13.3) и
неравенством
f(x)g(x) dx
Гь
dx-Л g2(x) dx,
V
вытекающим из того, что квадратный трёхчлен
= К g2(x) dxYx2-(2 I f(x)g(x) dxY\+l f2(x) dx
принимает при всех А неотрицательные значения,
следовательно, его дискриминант неположителен; вам понадобится также
плоский аналог формулы (13.3):
где 1(х) — длина отрезка, по которому прямая,
перпендикулярная оси Ох, пересекает плоскую фигуру площади S,
заключённую между прямыми х — а и х — Ъ\ проверьте, что
V =
dx=
dx
dx
h(x) dx*
h(x) dr,=
Избранные теоремы и методы планиметрии
Ш.2. пх№Щ, mJp±JL П1.3. 8 и 10.
у \т - п\ у \т - п\
П1.4. Больше 16, но меньше 40. П1.5. 1 : 3.
Ответы и указания к задачам 635
п1 7 2аЬс П1 о
(а + Ь)(Ь + с)(с + а)'
П3.1. ab. П3.2. flv5(f ~ 2Ь). П3.6. Обязательно.
П3.8.
1
hi h2 Лз/Ui Л2 АзАА2 Лз
пз.э!
П4.1. J. П4.2. |. П4.5. ^±Rhahbhc. П4.6. ^.
П5.7. Vab. П5.8. \/а&.
П7.1. а) Прямая, проходящая через середины ВС и AD. б) Вся
плоскость.
П7.2. 4.
П7.3. Окружность, построенная как на диаметре на отрезке,
соединяющем данную точку с центром данной окружности.
П7.5. а) Прямая, перпендикулярная АВ.
П7.6. Окружность Аполлония для отрезка BD и Л = 2, где D —
точка, симметричная В относительно С.
Литература
Данный список довольно обширен, хотя и не претендует на
полноту. Приведённые здесь книги и статьи оказали влияние на
авторов при написании этого пособия. В тексте книги имеются
ссылки лишь на некоторые из них. Во многих из
перечисленных ниже источников содержатся дополнительные сведения по
некоторым разделам курса.
Как правило мы указываем только одно издание книги,
необязательно самое последнее. Некоторые книги выложены в
электронном виде в Интернете; в тех случаях, когда нам известна
ссылка, мы её приводим.
Учебники и учебные пособия
[1] Адамар Ж. Элементарная геометрия. Ч. П. Стереометрия,—
М.: Учпедгиз, 1951. (http://math.ru/lib/14)
[2] Александров А. Д. 9 Нецветаев Н. Ю. Геометрия. —М.:
Наука, 1990.
[3] Александров А.Д., Вернер А.Л.У Рыжик В, И. Геометрия
для 8—9 классов. Учеб. пособие. —М.: Просвещение, 1991.
[4] Александров А. Д., Вернер А.Л.У Рыжик В. И. Геометрия
для 10—11 классов. Учеб. пособие. — М.: Просвещение,
1992.
[5] Атанасян Л. С, Бутузов В. Ф., Кадомцев С. Б. и др.
Геометрия. Учебник для 7—9 кл. ср. шк.—М.: Просвещение,
1991.
[6] Бескин Л.Н. Стереометрия.—М.: Просвещение, 1971.
[7] Болтянский В, Г., Сидоров Ю. В., Шабунин М. И. Лекции
и задачи по элементарной математике.—М.: Наука, 1971.
[8] Болтянский В. Г. Элементарная геометрия. Книга для
учителя.— М.: Просвещение, 1985.
[9] Дорофеев Г. В., Потапов М. К, Розов Я. X. Пос ^ по
математике для поступающих в вузы. —М.: Наука, ^.
[10] Киселёв А. Я., Рыбкин Я. А. Стереометрия 10—11. 3 ч
и задачник.—М.: Дрофа, 1995.
[11] Клопский В, М., Скопец 3. А, Ягодовский М. И. Геоа -^л:
Учеб. пособие для 9 и 10 кл. ср. шк. Под ред. З.А. Скопеца.—
М.: Просвещение, 1977.
[12] Кутасов А. Д., Пиголкина Т. С, Чехлов В. И,,
Яковлева Т. X. Пособие по математике для поступающих в вузы.
Под ред. Г. Я. Яковлева.- М.: Наука, 1981.
Литература 637
[13] Лурье М.И., Александров Б, И. Пособие по геометрии.—
М.: Изд-воМГУ, 1984.
[14] Погорелое А. В, Геометрия. Учебник для 7—11 кл. ср. шк.—
М.: Просвещение, 1992.
[15] Ткачу к В. В. Математика — абитуриенту. Т. I, II. — М.: Теис,
1994. Последнее издание: М.: МЦНМО, 2008.
[16] Шарыгин И.Ф., Голубев В. И. Факультативный курс по
математике. Решение задач. Учебное пособие для 11 кл. ср.
шк.—М.: Просвещение, 1991.
Сборники задач
[17] Антонов Н.П., Выгодский М.Я., Никитин В. В,, Сан-
кин А. И. Сборник задач по элементарной математике. —
М.: Наука, 1968.
[18] Белоносов B.C., Фокин М. В. Задачи вступительных
экзаменов по математике в НГУ. — Новосибирск: изд-во НГУ,
1992.
[19] Говоров В. М., Дыбов /7. Т., Мирошин Н. В., Смирнова С. Ф.
Сборник конкурсных задач по математике. Под ред.
А. И. Прилепко.-М.: Наука, 1983.
[20] Делоне Б. Н., Житомирский О. К. Задачник по геометрии.—
М.: Физматгиз, 1959. (http://math.ru/lib/23)
[21] Дятлов В.Н.у Дятлов Г В. Стереометрические задачи.—
Новосибирск: изд-во НГУ, 1991.
[22] Егерев В. i£., Кордемский Б. А., Зайцев В. В. и др. Сборник
задач по математике для поступающих во втузы. Под ред.
М.И. Сканави.— М.: Высш. шк., 1988.
[23] Куштр I.A. Трикутник i тетраедр у задачах. — Киев: Рад.
шк., 1991.
[24] Лидский В. Б., Овсянников Л. В., Тулайков А.Н., Шабу-
иин М. И., Федосов Б. В. Задачи по элементарной
математике.—М.: Наука, 1973.
[25] Лоповок Л. М. Сборник геометрических задач для 10
класса.—Киев: Рад. шк., 1979.
[26] Лоповок Л. М. Факультативные задания по геометрии для
7—11 классов. — Киев: Рад. шк., 1990.
[27] Нестеренко Ю.В.У Олехник С.Н., Потапов М. К.
Задачи вступительных экзаменов по математике.—М.: Наука,
1983.
[28] Прасолов В. В. Задачи по планиметрии. Ч. 1.—М.: Наука,
1991.
638 Литература
[29] Прасолов В. В. Задачи по планиметрии. Ч. 2.—М.: Наука,
1991.
Задачник В. В. Прасолова неоднократно переиздавался; последнее
издание: Прасолов В. В. Задачи по планиметрии.—М.: МЦНМО,
2007. (http://math.ru/lib/426)
[30] Прасолов В. В., Шарыгин И. Ф. Задачи по стереометрии.—
М.: Наука, 1989. (http://math.ru/lib/bib-mat-kr/19)
[31] Фетисов А. И. Геометрия в задачах. — М.: Просвещение,
1977.(http://math.ru/lib/35)
[32] Шарыгин И.Ф. Задачи по геометрии. Стереометрия,—М.:
Наука, 1984. (http://math.ru/lib/bmkvant/31)
[33] Шахно К. У. Сборник задач по элементарной математике
повышенной трудности.—Минск: Вышэйш. шк., 1969.
[34] Шклярский Д. О., Чепцов Н.Н., Яглом И.М. Избранные
задачи и теоремы элементарной математики. Ч. 3.
Геометрия (стереометрия).—М.: Гостехиздат, 1954.
(http://math.rU/lib/bib-mat-kr/3)
Литература к отдельным главам курса
[35] Акопян А. В. у Заславский А. А. Геометрические свойства
кривых второго порядка. —М.: МЦНМО, 2007.
(http: //math. ru/lib/452)
[36] Александров П. С. Введение в теорию групп.—М.: Наука,
1980.
[37] Алексеев В. Б. Теорема Абеля в примерах и задачах. —
М.: Наука, 1976. Последнее издание: М.: МЦНМО, 2001.
(http: //math. ru/lib/270)
[38] Бескин Л.Н., Бескин В. Л, Многогранники, —Киев: Вища
шк., 1984.
[39] Бескин Н. М. Изображения пространственных фигур.—М.:
Наука, 1971. (http://math.ru/lib/plm/51)
[40] Васильев Я. Б., Гутенмахер В,Л. Прямые и цвые.—
М.: Наука, 1970. Последнее издание: М.: МЦВ 2010.
(http: //math.ru/lib/zaochn/4)
[41] Габович И. Г. Алгоритмический подход к решен*. *ет-
рических задач.—Киев: Рад. шк., 1989.
[42] Гольдберг Я. Е. С чего начинается решение
стереометрической задачи.—Киев: Рад. шк., 1990.
[43] Готман Э.Г., Скопец 3. А. Решение геометрических задач
аналитическим методом.—М.: Просвещение, 1979.
[44] Гусятников П. Б., Резниченко СВ. Векторная алгебра
в примерах и задачах.—М.: Высш. шк., 1985.
Литература 639
[45] Калужнин Л. А., Сущанский В. И, Преобразования и
перестановки,— М.: Наука, 1985.
[46] Литвиненко В. Я. Задачи на развитие пространственных
представлений. —М.: Просвещение, 1991.
[47] Скопец З.А. Геометрические миниатюры.—М.:
Просвещение, 1990.
[48] Стинрод Н., Чинн У. Первые понятия топологии. — М.: Мир,
1967.
Олимпиадные задачники
[49] Васильев Я. Б., Гутенмахер В. Л., Раббот Ж.М., То-
ом А. Л. Заочные математические олимпиады.—М.: Наука,
1986. (http://math.ru/lib/96)
[50] Васильев //.Б., Егоров А. А. Задачи Всесоюзных
математических олимпиад. —М.: Наука, 1988.
(http://math.ru/lib/bib-mat-kr/18)
[51] Гальперин Г. А, Толпыго А, К Московские математические
олимпиады. Под ред. А. Н. Колмогорова, —Ж»:
Просвещение, 1986. (http://math.ru/lib/95)
[52] Конягин СВ., Тоноян Г. А., Шарыгин Я. Ф. и др.
Зарубежные математические олимпиады. Под ред. И. Н. Сергеева.—
М.: Наука, 1987. (http://math.ru/lib/bib-mat-kr/17)
[53] Кюршак #., Нейкомм Д., Хайоги Д., Шурани Я.
Венгерские математические олимпиады,—М.: Мир, 1976.
(http: //math. ru/lib/93)
[54] Морозова Е. А., Петраков И. С., Скворцов Б. А.
Международные математические олимпиады.—М.: Просвещение,
1976. (http://math.ru/lib/92)
[55] Страшевич С, Бровкин Е. Польские математические
олимпиады.-М.: Мир, 1978. (http://math.ru/lib/94)
[56] Фомин Д. В. Санкт-Петербургские математические
олимпиады.—С.-Пб.: Политехника, 1994.
[57] Яковлев Г.Н., Купцов Л. П., Резниченко СВ.,
Гусятников П. Б. Всероссийские математические олимпиады
школьников,—М.: Просвещение, 1992.
Статьи
[58] Вавилов Б. В, Сечения многогранников // Квант.— 1979.—
№ 1.
[59] Вагутен В. Н. Правильные многогранники и повороты //
Квант.-1989.-№ 10.
640 Литература
[60] Габович И. Г Векторы помогают на экзамене // Квант. —
1979. -№ 1.
[61] Габович И. Г. Основные углы в правильной пирамиде //
Квант.-1986.-№ 1.
[62] Габович И. Г Теорема о трёх синусах // Квант.— 1989.—
№ 9.
[63] Габович И. Г, Горнштейн /7. if. Скалярное умножение
векторов // Квант.- 1978.-№ 1.
[64] Дубровский Б. Н. Неожиданный ракурс // Квант.— 1980.—
№ 2.
[65] Дубровский Б. Н. Что скрывается за превращениями
тетраэдра // Квант.- 1983.- № 7.
[66] Дубровский В. Я., Шарыгин И.Ф. Геометрический
стереоскоп // Квант.- 1993.-№ 1/2.
[67] Егерев В. К., Мордкович А. Г Правильная пирамида //
Квант.-1975.-№ 3.
[68] Ионии Ю. И., Некрасов Б. Б. Вычисление расстояний и
углов // Квант.- 1987.-№ 1.
[69] Кострикии А И. Простые группы // Квант,— 1987. —№ 2.
[70] Крайзман М. Заменим фигуру // Квант,— 1979. —№ 5.
[71] Либерзон М.Р. Вспомогательный куб // Квант.— 1986.—
№ 5.
[72] Матизен Б. Э. Равногранные и каркасные тетраэдры //
Квант.-1983.-№ 7.
[73] Матизен В. Э., Дубровский Б. Н. Из геометрии тетраэдра //
Квант.- 1988.-№ 9.
[74] Мельник И. Где расположено основание высоты? // Квант.—
1980.-№4.
[75] Сосинский А. Б. Перемещения пространства // Квант.—
1980.-№8.
[76] Сосинский А. Б. Конечные группы // Ki \— 1987. — № 2.
[77] Суконник Я, у Горнштейн П. Задачи на \ яци и
двугранные углы // Квант.- 1977.-№ 12.
[78] Чехлов В, И. Эти «коварные» векторы , \— 1980.—
№ 12.
[79] Шарыгин И.Ф. Выход в пространство // Квант.— 1975.—
№ 5.
[80] Шарыгин Я. Ф. Достраивание тетраэдра // Квант,— 1976.—
№ 1.
"[81] Шарыгин И.Ф. Чертёж в стереометрической задаче //
Квант.-1991.-№ 5.
В учебнике изложен курс геометрии
для 10-11 классов средней школы
(профильный уровень). Подробно
разобран теоретический материал
и многочисленные задачи. В каждой
главе приводятся многочисленные
задачи для самостоятельного решения,
к которым даны ответы и указания.
Наряду со «стандартными» широко
представлены «нестандартные» задачи,
в том числе задачи математических
олимпиад разного уровня
и вступительных экзаменов в ведущие
российские вузы. В отдельную главу
выделено систематическое обсуждение
некоторых важных идей и методов
решения задач.
Для учащихся школ с углубленным
изучением математики и абитуриентов.
ISBN 978-5-94057-581-8
biblio.mccme.ru