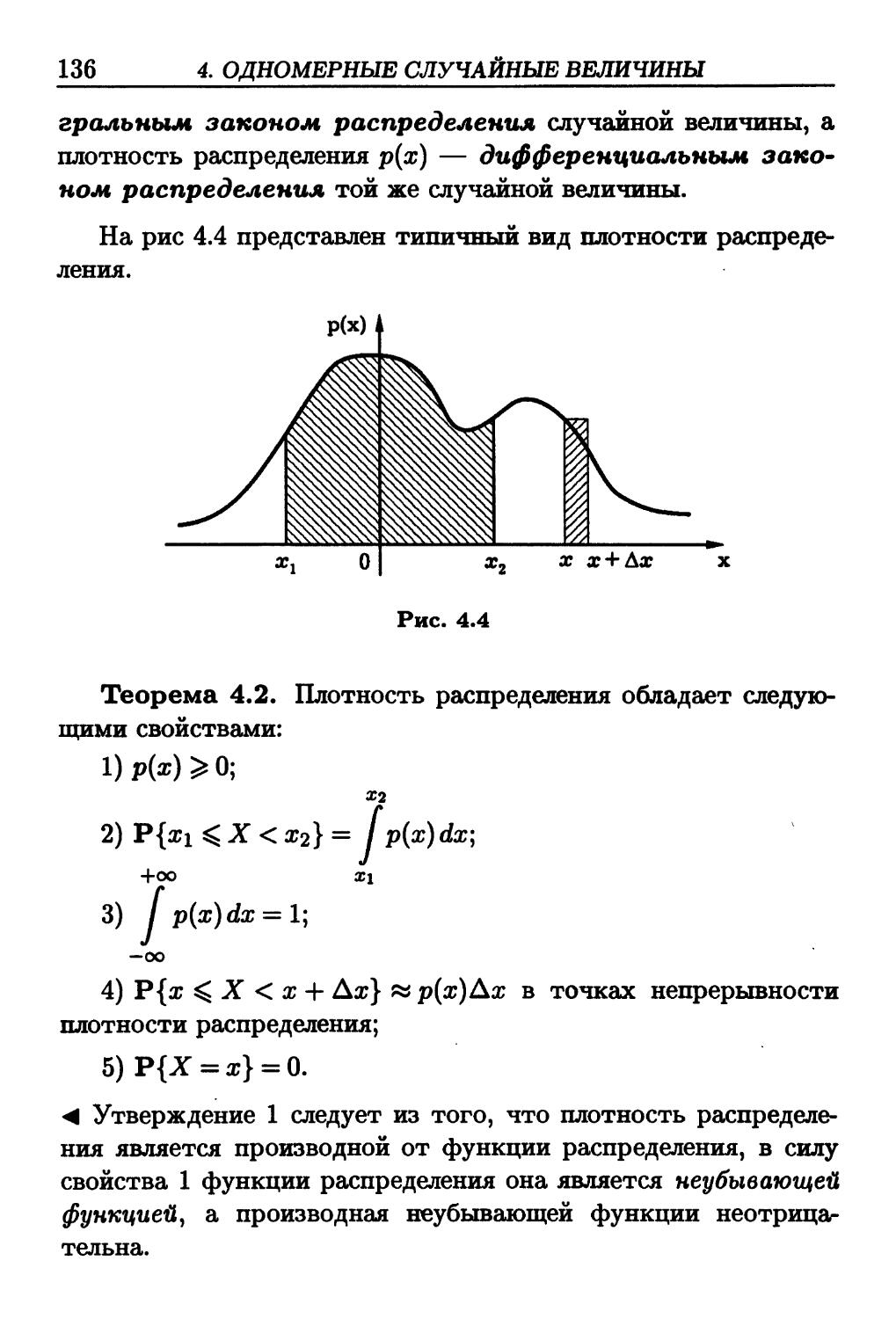
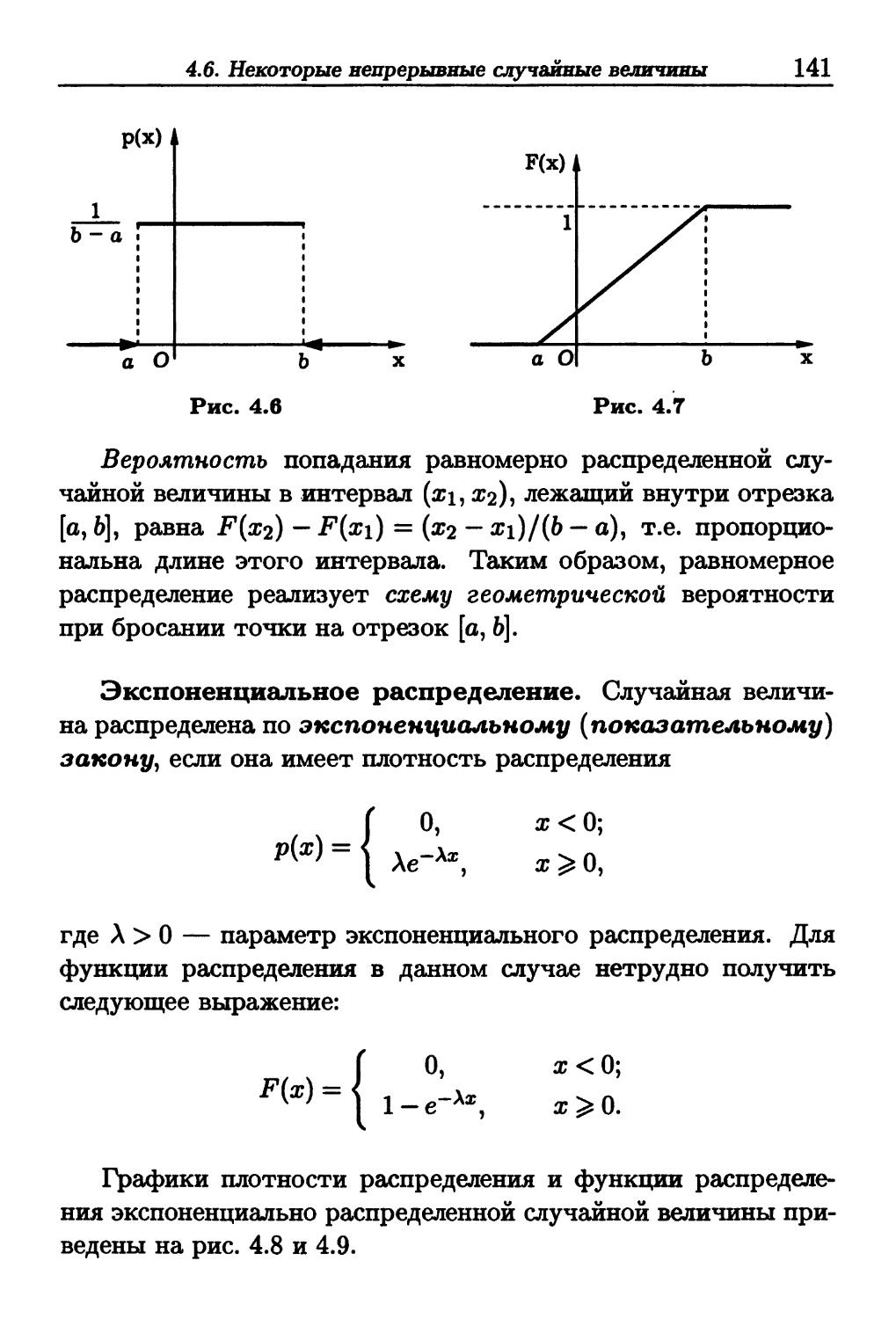
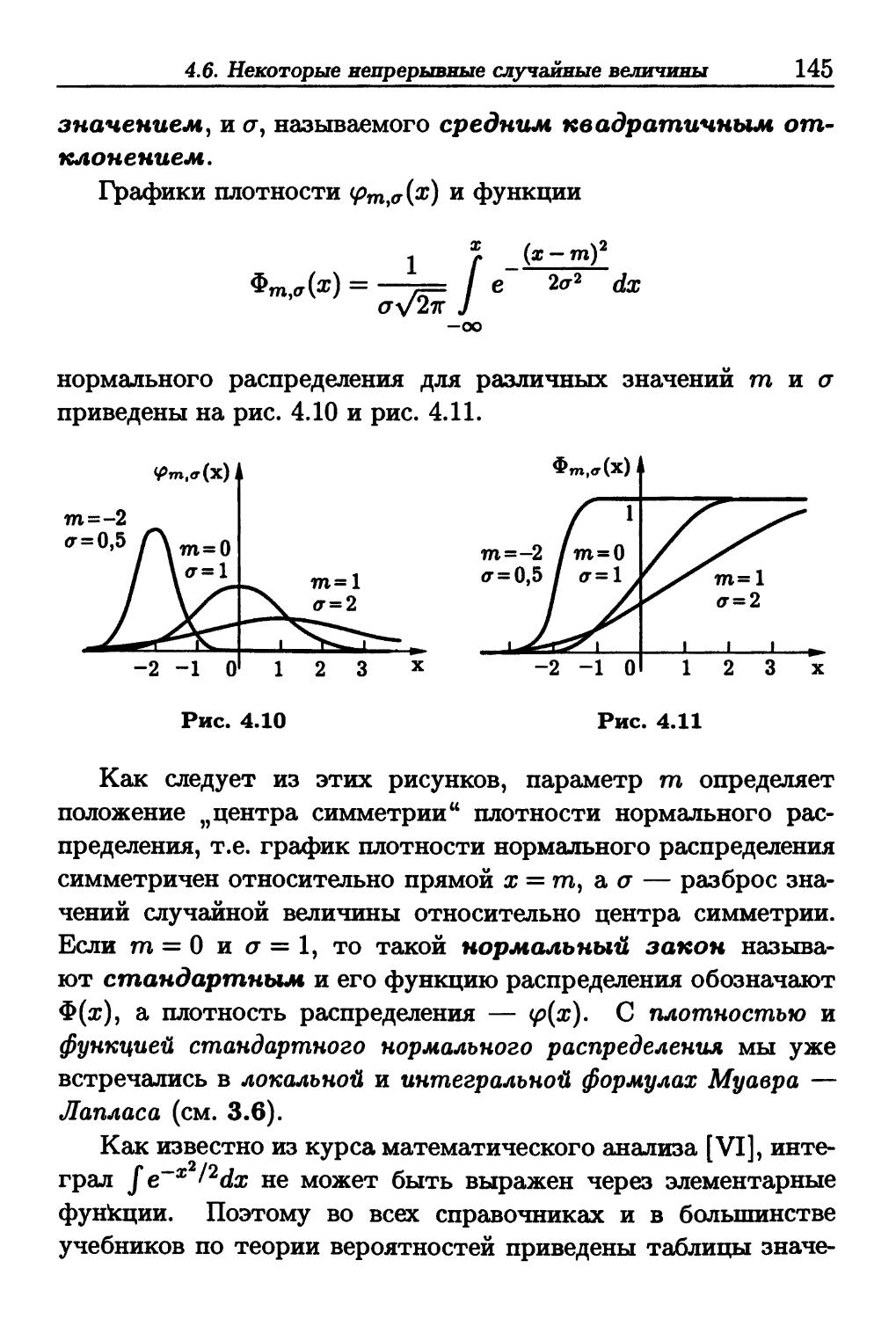
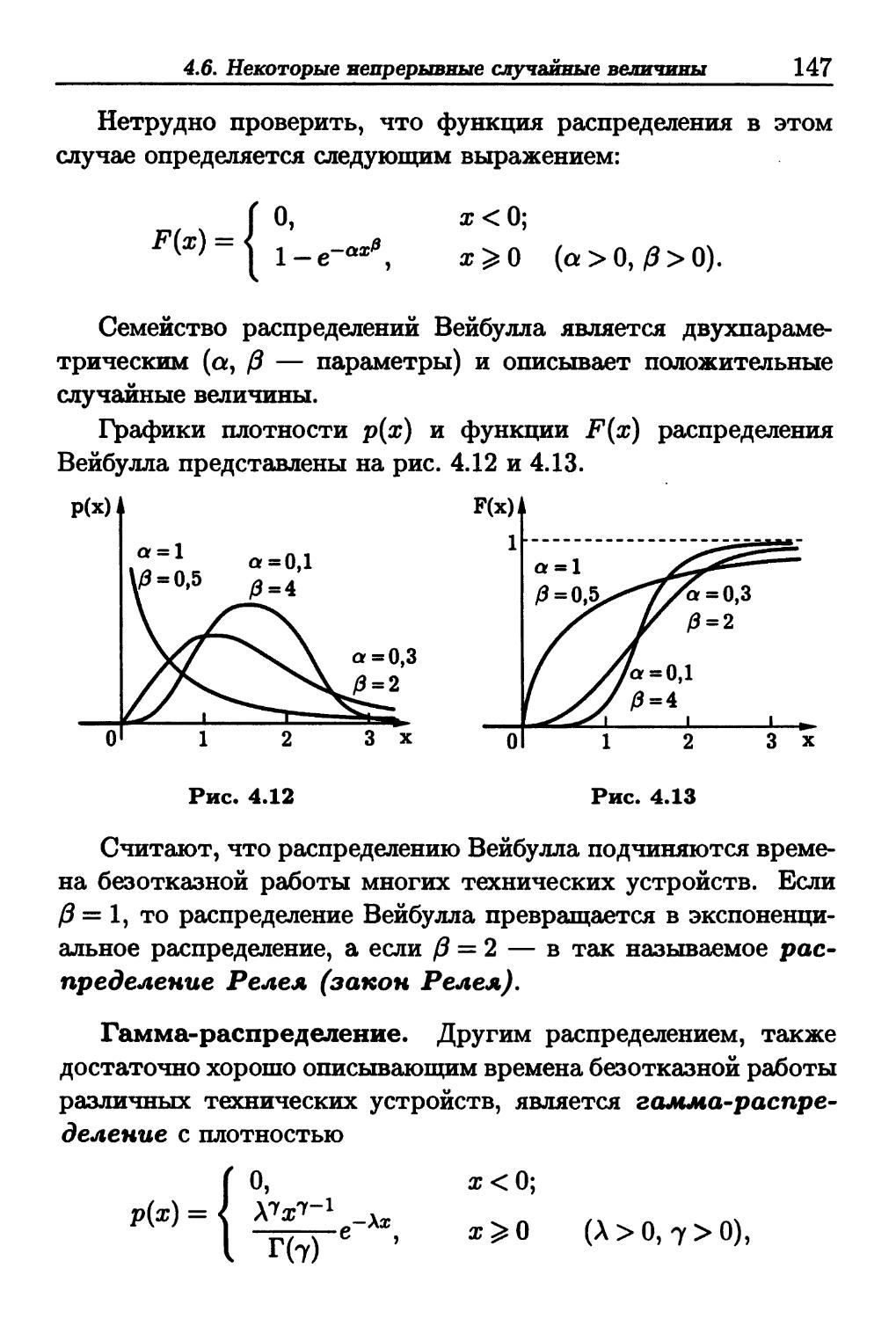
Author: Зарубин В.С. Крищенко А.П.
Tags: теория вероятностей и математическая статистика теория вероятностей математическая статистика комбинаторный анализ теория графов математика
ISBN: 5-7038-2485-0
Year: 2004
Text
Комплекс учебников из 21 выпуска
Под редакцией В. С. Зарубина и А. П. Крищенко
I. Введение в анализ
П. Дифференциальное исчисление функций
одного переменного
III. Аналитическая геометрия
IV. Линейная алгебра
V. Дифференциальное исчисление функций
многих переменных
VI. Интегральное исчисление функций
одного переменного
VII. Кратные и криволинейные интегралы.
Элементы теории поля
VIII. Дифференциальные уравнения
IX. Ряды
X. Теория функций комплексного переменного
XI. Интегральные преобразования
и операционное исчисление
XII. Дифференциальные уравнения
математической физики
XIII. Приближенные методы математической физики
XIV. Методы оптимизации
XV. Вариационное исчисление и оптимальное управление
XVI. Теория вероятностей
XVII. Математическая статистика
XVIII. Случайные процессы
XIX. Дискретная математика
XX. Исследование операций
XXI. Математическое моделирование в технике
ТЕОРИЯ
ВЕРОЯТНОСТЕЙ
Под редакцией
д-ра техн. наук, профессора B.C. Зарубина
и д-ра физ.-мат. наук, профессора А.П. Крищенко
Рекомендовано
Министерством образования
Российской Федерации
в качестве учебника для студентов
высших технических учебных заведений
Издание третье, исправленное
Москва
Издательство МГТУ им. Н.Э. Баумана
2П04
УДК 519.2.21@75.8)
ББК 22.17
Т34
Рецензенты: проф. А.Д. Соловьев, проф. В.В. Рыков
Т34 Теория вероятностей: Учеб. для вузов. - 3-е изд., испр. /
А.В. Печинкин, О.И. Тескин, Г.М. Цветкова и др.; Под ред.
B.C. Зарубина, А.П. Крищенко. - М.: Изд-во МГТУ им. Н.Э. Бау-
Баумана, 2004. -456 с. (Сер. Математика в техническом универси-
университете; Вып. XVI).
ISBN 5-7038-2485-0 (Вып. XVI)
ISBN 5-7038-2484-2
Несмотря на большое количество учебных руководств по теории веро-
вероятностей, в том числе появившихся и в последние годы, в настоящее время
отсутствует учебник, предназначенный для технических университетов
с усиленной математической подготовкой. Отличительной особенностью
данной книги является взвешенное сочетание математической строгости
изложения основ теории вероятностей с прикладной направленностью за-
задач и примеров, иллюстрирующих теоретические положения. Каждую
главу книги завершает набор большого числа контрольных вопросов, ти-
типовых примеров и задач для самостоятельного решения.
Содержание учебника соответствует курсу лекций, который авторы
читают в МГТУ им. Н.Э. Баумана.
Для студентов технических университетов. Может быть полезен
преподавателям и аспирантам.
Ил. 68. Табл. 76. Библиогр. 29 назв.
УДК 519.2.21@75.8)
ББК 22.17
© А.В. Печинкин, О.И. Тескин,
Г.М. Цветкова, П.П. Бочаров,
Н.Е. Козлов, 1998; 2004,
с изменениями,
© Московский государственный
технический университет
им. Н.Э. Баумана, 1998; 2004,
с изменениями
ISBN 5-7038-2485-0 (Вып. XVI) © Издательство МГТУ
ISBN 5-7038-2484-2 им на БаУмана>1998; 2004>
с изменениями
К 175-летию
МГТУ им. Н.Э. Баумана
ПРЕДИСЛОВИЕ
Предлагаемая читателю книга является одним из выпусков
полного курса математики для студентов высших технических
заведений и учитывает специфику математической подготовки
этих студентов.
В основе выпуска лежит курс лекций по теории вероятно-
вероятностей, читавшийся на протяжении ряда лет студентам различ-
различных специальностей МГТУ им. Н.Э. Баумана, а также опыт
проведения семинарских занятий по этому курсу.
Построение книги имеет так называемую „блочную" струк-
структуру. После изложения теоретического материала в конце
каждой главы представлены типовые примеры с решениями,
а также контрольные вопросы и задачи для самостоятельного
решения. Наличие большого количества примеров и задач по-
позволяет использовать данную книгу не только как учебник, но
и как задачник при проведении семинарских занятий.
Естественно, что ограничения на объем привели и к жест-
жесткому отбору включаемого материала.
Содержание материала и стиль его изложения определялись
под углом зрения их практических приложений в различных
областях инженерной практики. Более того, ряд приведенных
задач и примеров ориентирован на дальнейшее изучение веро-
вероятностных дисциплин, таких, как математическая статистика,
теория случайных процессов, математическая теория надежно-
надежности и т.д.
Авторы старались расположить излагаемый материал та-
таким образом, чтобы на основе данной книги можно было стро-
строить курсы теории вероятностей различного уровня сложности.
Так, при изложении стандартного 34-часового курса рекомен-
ПРЕДИСЛОВИЕ
дуется пропустить главу 8, параграфы 6.5, 6.6, 7.5 и 9.3, в
параграфе 5.5 ограничиться только двумерным нормальным
законом, а центральную предельную теорему из параграфа 9.4
приводить без доказательства, останавливаясь только на ее
смысле.
Применяемый в книге математический аппарат основан на
втузовском курсе высшей математики и не использует сложных
понятий функционального анализа, теории меры, интеграла
Лебега. Тем не менее принят современный способ изложения
теории вероятностей на основе введения пространства элемен-
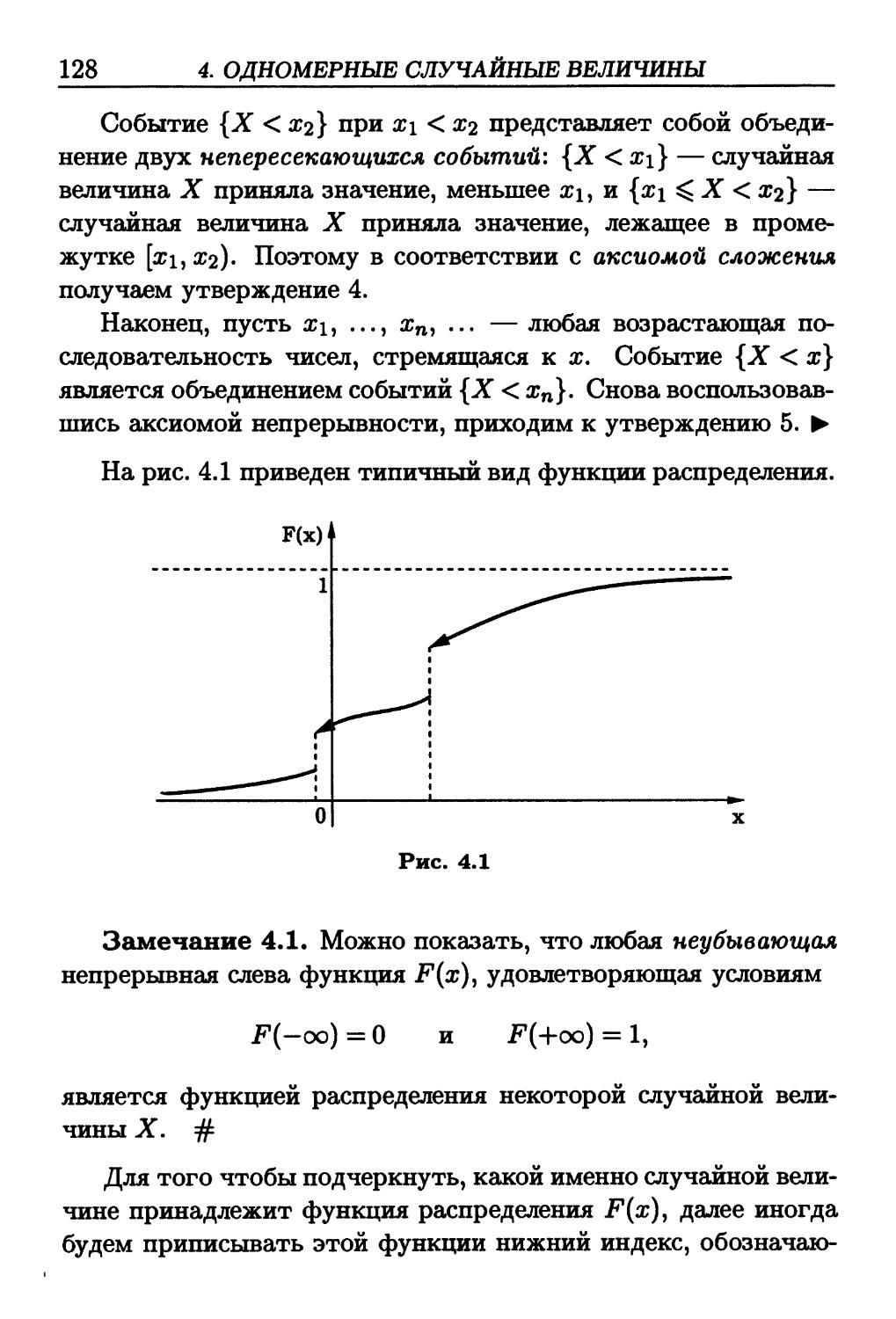
элементарных событий и системы аксиом А.Н. Колмогорова. Однако
аксиомы вводятся лишь после рассмотрения классического, гео-
геометрического и статистического определений как естествен-
естественное распространение получающихся при таких определениях
свойств вероятностей случайных событий.
Основное внимание авторы уделяют не строгим формаль-
формальным доказательствам, а единству методического подхода, ил-
иллюстрируемого многочисленными приложениями. Именно та-
такой подход к изучению теории вероятностей более всего по-
полезен тем, кто ставит перед собой цель решение конкретных
инженерных задач.
Авторы предполагают, что читатель знаком с основными
понятиями линейной алгебры, математического анализа, диф-
дифференциального и интегрального исчисления, теории рядов,
теории функций комплексного переменного и преобразований
Фурье.
С целью уточнения того, что обязательно нужно знать из
перечисленных разделов математики, в начале книги сформу-
сформулированы вопросы для самопроверки. При этом в вопросах
понятия и термины, которые нужно знать, выделены прямым
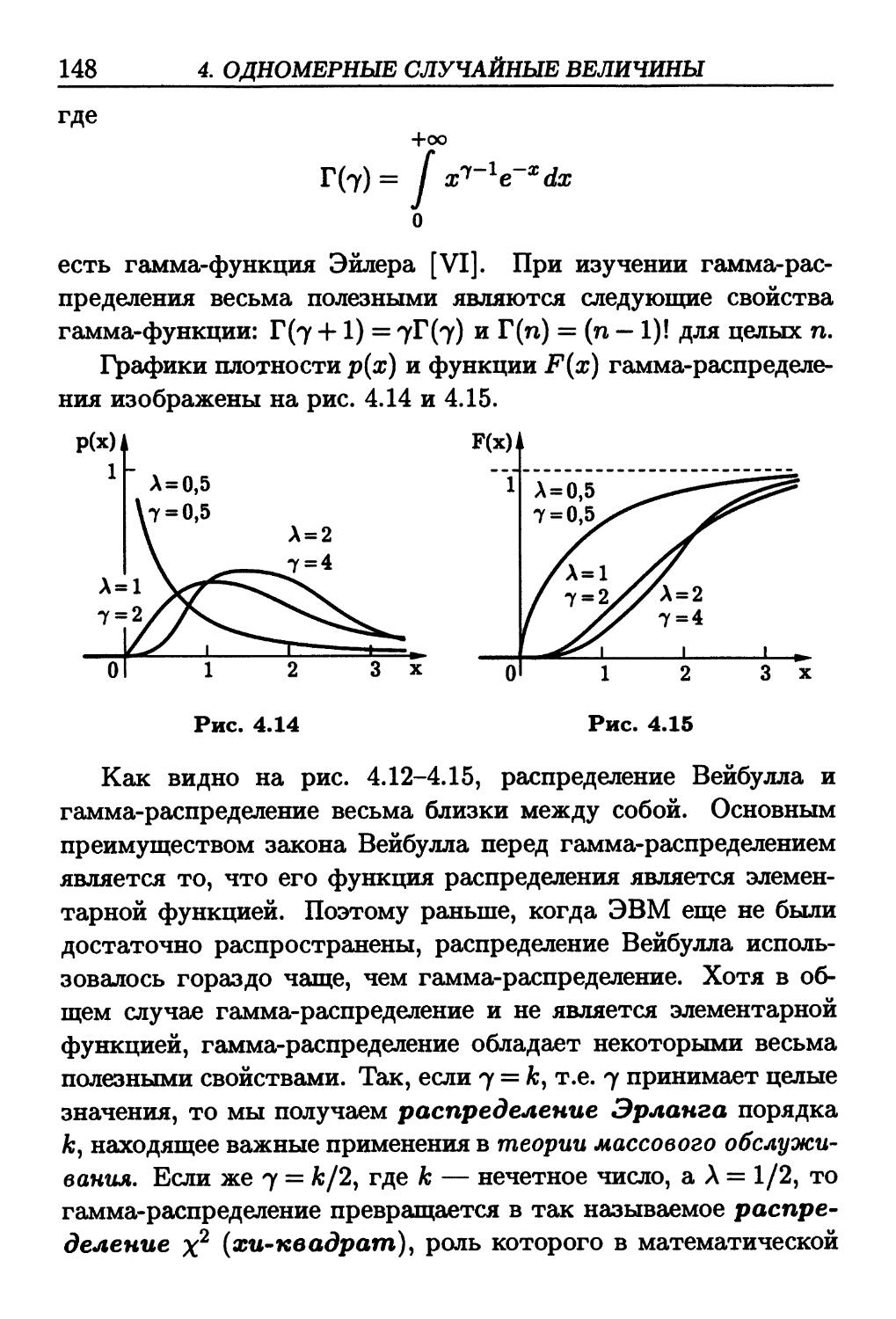
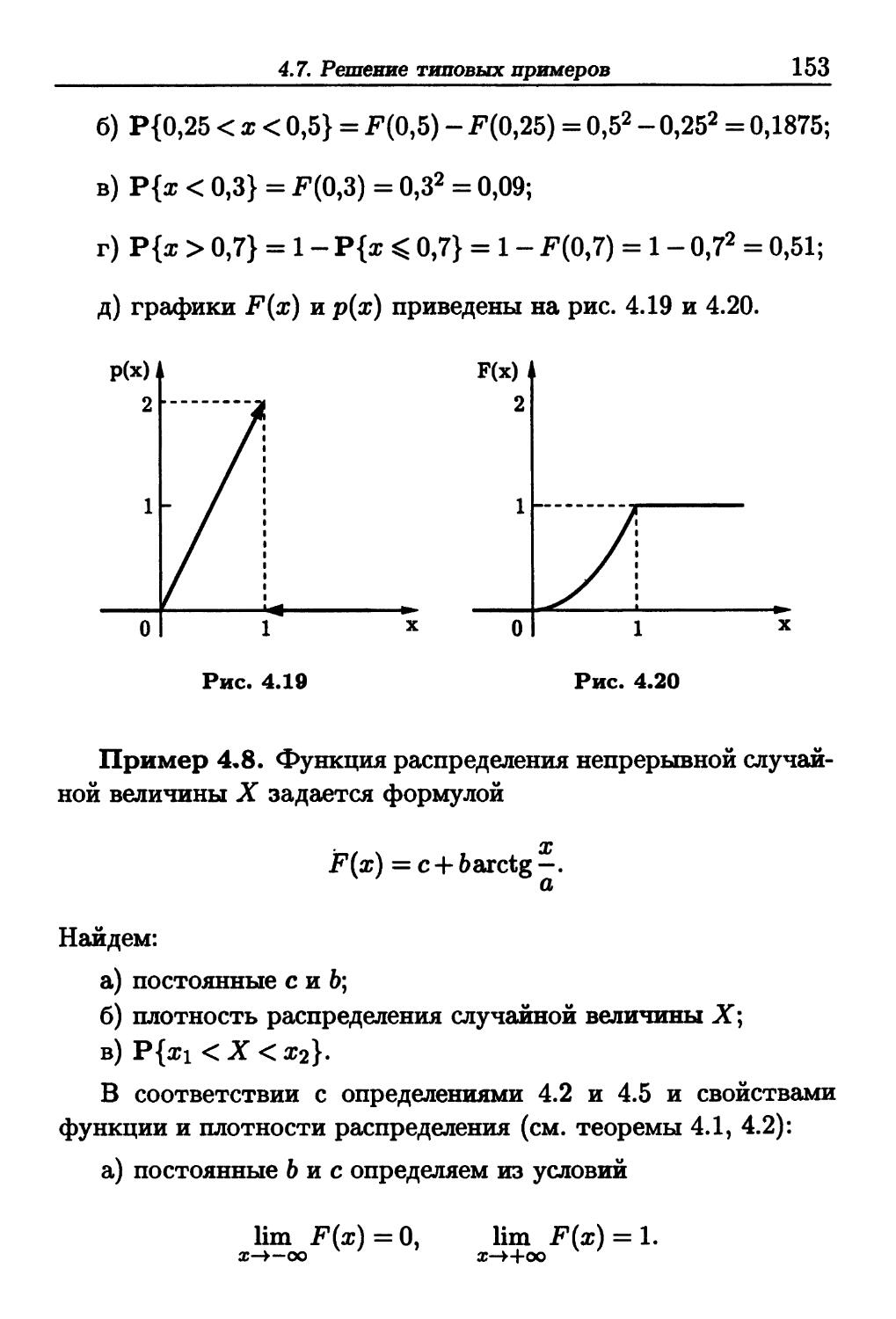
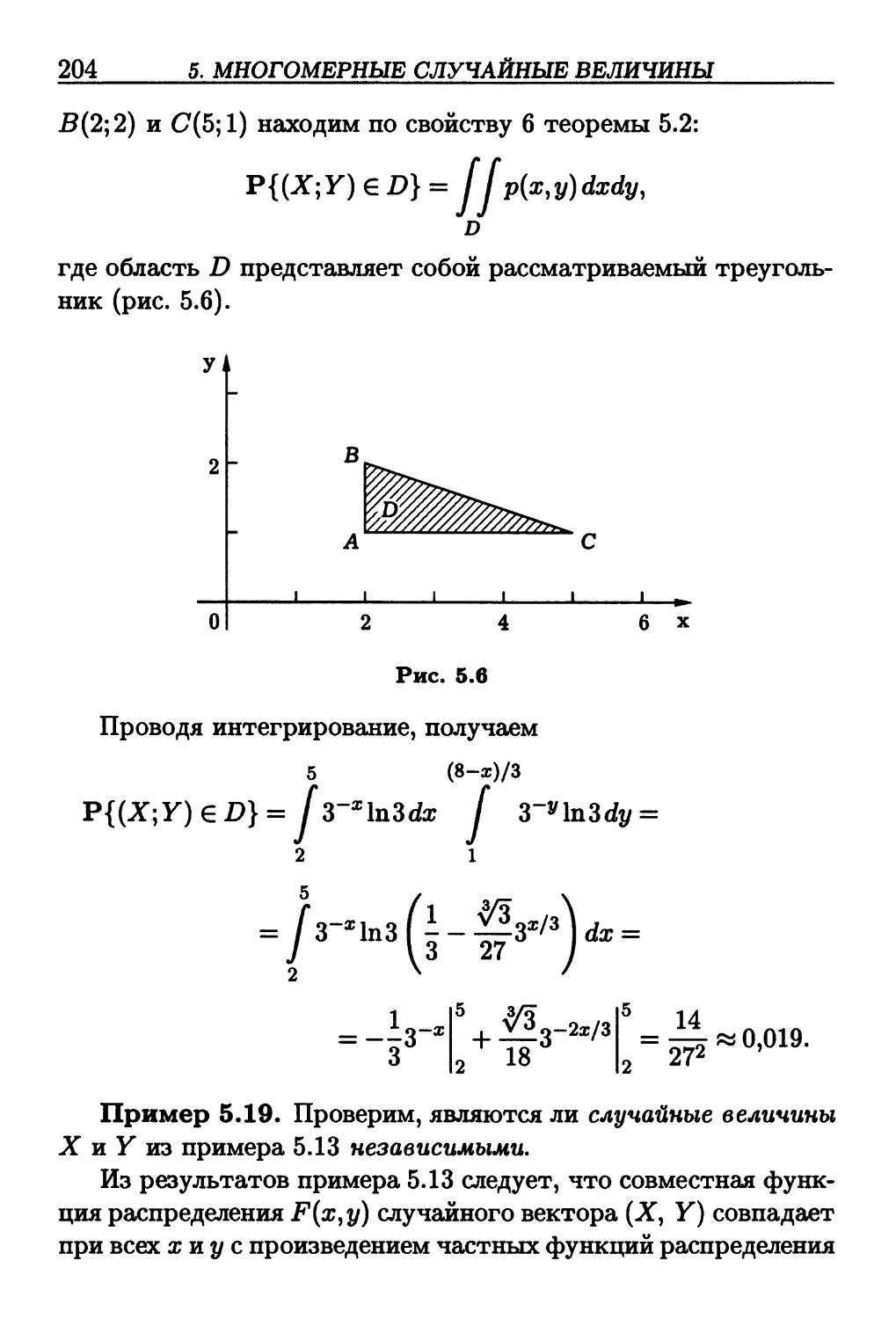
полужирным шрифтом. Далее помещен список основных
обозначений, содержащий часто встречающиеся в тексте сим-
символы и их расшифровку.
В конце книги приведены таблицы некоторых распределе-
распределений, список рекомендуемой литературы и предметный указа-
тель, в который входят в алфавитном порядке (по существи-
существительному в именительном падеже) все выделенные в тексте
полужирным курсивом термины с указанием страниц, на
которых они строго определены или описаны. Выделение тер-
термина светлым курсивом означает, что в данном параграфе он
является одним из ключевых слов и читателю должно быть
известно значение термина. Читатель может уточнить это зна-
значение, найдя при помощи предметного указателя необходимую
страницу:
Ссылки в тексте на номера формул и рисунков набраны
обычным шрифтом (например, A.5) — формула A.5) в главе 1,
рис. 3.2 — рис. 3.2 в главе 3), а на параграфы и таблицы при-
приложений — полужирным (например, 1.3 — третий параграф в
главе 1, табл. П.2 — таблица приложения 2). В квадратных
скобках даны ссылки на другие выпуски данной серии, напри-
например [X] — на десятый выпуск.
Работа над книгой между авторами распределилась следую-
следующим образом. Основной текст книги был написан А.В. Печин-
киным и О.И. Тескиным, фактический материал подготовлен
Г.М. Цветковой при участии Н.Е. Козлова. Над обсуждением
структуры книги и формы подачи материала работали П.П. Бо-
Бочаров, А.В. Печинкин, О.И. Тескин, Г.М. Цветкова.
Авторы выражают благодарность Елене Беляковой за по-
помощь, которую она оказала при подготовке рукописи к печати.
Задания для самопроверки
1. Что такое множество? подмножество? Какие множе-
множества называют конечными? счетными? Какие операдии над
множествами и подмножествами Вы знаете? Какими свойства-
свойствами обладают эти операции? Что называют окрестностью
точки? [I]
2. Какие величины называют биномиальными коэффи-
коэффициентами? [I]
игидпилииии
3. Дайте определение числовой последовательности. Ка-
Какую последовательность называют возрастающей? убыва-
убывающей? Что называют пределом последовательности? [I]
4. Дайте определение отображения. Дайте определение
действительной функции действительного переменно-
переменного. Какую функцию называют монотонной? возраста-
возрастающей? убывающей? неубывающей? четной? нечет-
нечетной? Какую функцию называют обратной к данной? Какие
функции называют элементарными? [I]
5. Что называют пределом функции f(x) при ж, стре-
стремящемся к жо? к +оо? к — оо? Какую функцию называют
непрерывной в точке? непрерывной слева в точке? в
интервале? на отрезке? [I]
6. Дайте определение производной действительной функ-
функции действительного переменного. Дайте определение про-
производной n-го порядка. Запишите формулы Тейлора и
Маклорена. [II]
7. Запишите зависимость между декартовыми прямо-
прямоугольными и полярными координатами точки на плоско-
плоскости. Какие кривые называют кривыми второго порядка?
Запишите каноническое уравнение эллипса в декартовой
прямоугольной системе координат. [III]
8. Какие поверхности называют поверхностями второго
порядка. Запишите каноническое уравнение эллипсоида
в декартовой прямоугольной системе координат. [III]
9. Что такое матрица? Какую матрицу называют транс-
транспонированной по отношению к данной? диагональной? еди-
единичной? симметрической? Что называют определителем
квадратной матрицы? Дайте определение произведения
двух матриц. Какую квадратную матрицу называют не-
невырожденной? вырожденной? Опишите процедуру приве-
приведения невырожденной квадратной матрицы к диагональному
виду. Какую квадратную матрицу называют обратной по
отношению к данной? Как связаны между собой определите-
определители взаимообратных матриц? Сформулируйте необходимое и
достаточное условие существования обратной матрицы. Что
называют рангом матрицы? Какую матрицу называют по-
положительно определенной? [III], [IV]
10. Что называют базисом линейного пространства?
Какие векторы линейного пространства называют нормиро-
нормированными? Какое линейное пространство называют ариф-
арифметическим? [IV]
11. Дайте определение собственного значения и собст-
собственного вектора квадратной матрицы. Как их можно вычис-
вычислить? [IV]
12. Что такое квадратичная форма? Какую квадратич-
квадратичную форму называют положительно определенной? неот-
неотрицательно определенной? Что называют матрицей ква-
квадратичной формы? Запишите формулу преобразования
квадратичной формы при линейной замене переменных.
Какие способы приведения квадратичной формы к канониче-
каноническому виду Вы знаете? В чем состоит метод Лагранжа приве-
приведения квадратичной формы к каноническому виду? [IV]
13. Дайте определение скалярной функции векторного аргу-
аргумента (функции многих переменных). Что называют частной
производной функции? Что такое смешанная производ-
производная? [V]
14. Какую функцию называют дифференцируемой в точ-
точке? Сформулируйте правило дифференцирования сложной
функции. Что такое якобиан? [II], [V]
15. Дайте определение векторной функции векторного ар-
аргумента. Дайте определение экстремума функции. Сформу-
Сформулируйте необходимое и достаточное условия экстремума функ-
ции. [II], [V]
16. Что такое определенный интеграл? Сформулируйте
теорему о производной интеграла с переменным верхним
пределом. Сформулируйте условия и правило замены пере-
переменного в определенном интеграле. В чем состоит метод
интегрирования по частям? [VI]
10 ПРЕДИСЛОВИЕ
17. Дайте определение несобственного интеграла. Ка-
Какой несобственный интеграл называют абсолютно сходя-
сходящимся? [VI]
18. Что называют двойным, тройным, кратным ин-
интегралом? Какой интеграл называют повторным? Как
вычисляют кратные интегралы? Сформулируйте условия и
правило замены переменных в кратном интеграле. Чему равно
значение интеграла Пуассона? [VII]
19. Какой числовой ряд называют сходящимся? абсо-
абсолютно сходящимся? Сформулируйте свойства абсолютно
сходящихся рядов. [IX]
20. Дайте определение комплексного числа. Что называ-
называют мнимой единицей? [I]
21. Что называют функцией комплексного переменно-
переменного? Какую функцию называют аналитической? Что называ-
называют изолированной особой точкой аналитической функции?
Какие типы особых точек Вы знаете? Что такое вычет? За-
Запишите интеграл Коши. [X]
22. Что называют композицией (сверткой) двух функ-
функций? [XI]
23. Запишите прямое и обратное преобразования Фу-
Фурье. Что называют интегральным преобразованием Лапла-
Лапласа? [XI]
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
< и > — начало и окончание доказательства
# — окончание примера или замечания
« — знак равенства, задаваемого приближенной форму-
формулой
= — знак тождественного равенства
п — пространство элементарных исходов, достоверное
событие 1.1, 1.2
ш — элементарный исход 1.1
А, В, С, ... — случайные события 1.2
0 — невозможное событие 1.2
ш Е А — элементарный исход и принадлежит событию А
1.2
А С 2?, В D А — событие А включено в событие В 1.2
AflJS, А-В, АВ — пересечение событий Аи В 1.2
Аи В — объединение событий А и В 1.2
А + В — объединение непересекающихся событий А и В 1.2
А — событие, противоположное событию А 1.2
А \ В — разность событий Аи В 1.2
93 — сигма-алгебра (а-алгебра) событий 1.3
Р(А) — вероятность события А 2.1
N — число элементарных исходов в пространстве элемен-
элементарных исходов 2.1
— число элементарных исходов, благоприятствующих
событию А 2.1
— число размещений (без повторений) из п элементов
по т 2.2
12 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
С™ — число сочетаний (без повторений) из п элементов
по га 2.2
Рп — число перестановок из п элементов 2.2
А™ — число размещений (с повторениями) из п элементов
по га 2.2
С™ — число сочетаний (с повторениями) из п элементов
по т 2.2
C(ni,..., пт) — полиномиальный коэффициент 2.2
P(ni, ...,nm) — вероятность, определяемая гипергеометриче-
гипергеометрическим распределением 2.2
ц(А) — мера множества А 2.3
п — число испытаний (опытов) 2.4
па — число появлений события А в п испытаниях 2.4
га — относительная частота появления события А 2.4
Р(А\В) — условная вероятность события А при условии собы-
события В 3.1
Рп(к) — биномиальная вероятность 3.6
Р(к\ Л) — вероятность, определяемая распределением Пуассо-
Пуассона 3.6, 4.4
Ф(х) — функция стандартного нормального (гауссова) рас-
распределения 3.6, 4.6
(р(х) — плотность стандартного нормального (гауссова) рас-
распределения 3.6, 4.6
Фо(ж) — функция Лапласа 4.6
Г(х) — гамма-функция Эйлера 4.6, XI
В(я,у) — бета-функция Эйлера 6.4
X, У, Z, ... — случайные величины 4.1
"Р{Х < ж}, Р{Х ^ #}, P{#i < X < Х2} — вероятности событий
{X < х}, {X > ж}, {х\ < X <#2} соответственно 4.2
F(x), Fx{x) — функция распределения (вероятностей) случай-
случайной величины X 4.2
13
Pi, pxi — вероятность события {X = X{} для дискретной слу-
случайной величины X 4.3
р(#), рх{х) — плотность распределения (вероятностей) непре-
непрерывной случайной величины X 4.5
ФШ)(Т(а:) — функция нормального (гауссова) распределения с
параметрами га и а 4.6
?>т,а(#) — плотность нормального (гауссова) распределения с
параметрами т и а 4.6
Rn — n-мерное линейное арифметическое пространство,
n^l 5.1,IV
(X, У), (Xi, X2) — двумерный случайный вектор 5.1
(X, У, Z), (Xi, Х2, Х3) — трехмерный случайный вектор 5.1
X = (Jf 1, ..., Хп) — многомерный (n-мерный) случайный век-
вектор 5.1
F(xi, • • •, хп), Fxlv..,xn(xu • • • >хп) — функция распределения
n-мерного случайного вектора (Х\, ..., Хп) 5.1
Pij — вероятность совместного осуществления событий
{X = Х{} и {У = yj} для двумерного дискретного
случайного вектора (X, У) 5.2
р(гг, у), рх,у(я> у) — плотность распределения непрерывного
двумерного случайного вектора (X, У) 5.3
Е, Е^ — ковариационная матрица случайного вектора X
5.5, 7.4
S, S^ — матрица, обратная ковариационной матрице слу-
случайного вектора X 5.5, 7.4
р = р(Х,У) — коэффициент корреляции случайных величин X
и У 5.5, 7.4
У(Х) — функция от случайной величины 6.2
Рх *Ру — свертка (композиция) плотностей распределения слу-
случайных величин X и У 6.4
MX — математическое ожидание случайной величины X
7.1
14 ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
DX — дисперсия случайной величины X 7.3
га* — начальный момент fc-ro порядка 7.3
о
га* — центральный момент fc-го порядка 7.3
Р = Pg — корреляционная матрица случайного вектора X
7.4
cov(X,Y) — ковариация случайных величин X и К 7.4
71 — асимметрия случайной величины 7.5
72 — эксцесс случайной величины 7.5
Qa — а-квантиль случайной величины 7.5
Н(Х) — энтропия случайной величины X 7.5
Fx(x\y), Fx{x\Y = у) — условная функция распределения слу-
случайной величины X при условии У = у 8.1
TTij, тг^ — условные вероятности события {X = а^} при усло-
условии события {У = yj} и события {У = yj} при усло-
условии события {X = Xi} для двумерного случайного
вектора (X, У) соответственно 8.1
Рх(х\у), Px(x\Y=y) — условная плотность распределения слу-
случайной величины X при условии У = у 8.1
М(Х|у), М(Х|У = у) — значение условного математического
ожидания случайной величины X при условии У = у
8.1
М(Х|У) — условное математическое ожидалие случайной ве-
величины X при условии У 8.2
, h(x) — регрессии X на У и У на X 8.2
— значение условной дисперсии случайной величины
X при условии Y = у 8.2
D(X|y) — условная дисперсия случайной величины X при
условии У 8.2
— корреляционное отношение 8.2
Хп —^> 0 — сходимость последовательности случайных вели-
чин к нулю с вероятностью 1 (почти наверное) 9.1
15
__ р _
Хп —> О — сходимость последовательности случайных вели-
n-юо л ч
чин к нулю по вероятности 9.1
Хп -^ 0 — сходимость последовательности случайных вели-
чин к нулю в среднем квадратичном 9.1
Fn(x) ==> F(x) — слабая сходимость последовательности функ-
функций распределения 9.1
/(*)> fx(t) — характеристическая функция случайной величи-
величины X 9.3
f(s) — преобразование Лапласа — Стилтьеса 9.3
f*(z) — производящая функция 9.3
[о, Ь] — замкнутый промежуток (отрезок) I
(а, Ь) — открытый промежуток (интервал) I
[а, 6), (а, Ь] — полуинтервалы I
% = 1,п — число г принимает последовательно все натуральные
значения от 1 до п включительно I
п! — произведение всех натуральных чисел от 1 до п
включительно I, 2.2
16
ОСНОВНЫЕ ОБОЗНАЧЕНИЯ
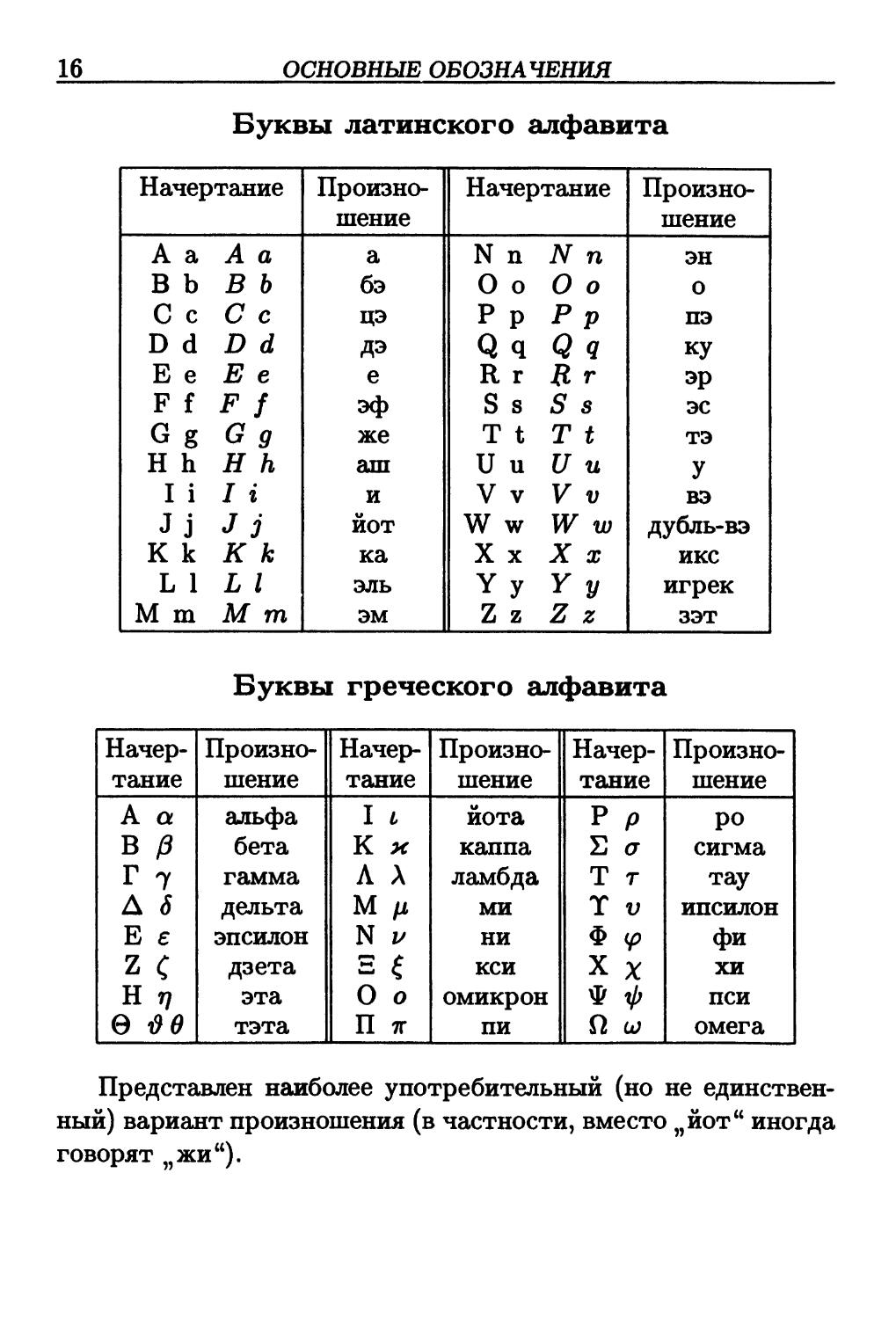
Буквы латинского алфавита
Начертание
А а
В b
С с
D d
Е е
F f
Gg
Н h
I i
Jj
К к
L 1
M m
A a
В b
С с
D d
E e
F f
G g
H h
I i
J 3
К к
L I
M m
Произно-
Произношение
a
бэ
цэ
ДЭ
e
эф
же
аш
и
йот
ка
эль
эм
Начертание
N п
О о
Рр
Qq
R г
S s
Т t
U u
V v
W w
X х
Yy
Z z
N п
О о
Рр
Qq
R г
S s
Т t
U и
V v
W w
X х
Y у
Z z
Произно-
Произношение
эн
о
пэ
ку
эр
эс
тэ
У
вэ
дубль-вэ
икс
игрек
зэт
Буквы греческого алфавита
Начер-
Начертание
А а
в р
Г 7
A S
Е е
z С
Н г,
6 <дв
Произно-
Произношение
альфа
бета
гамма
дельта
эпсилон
дзета
эта
тэта
Начер-
Начертание
I i
К и
Л Л
М /х
N v
Е f
О о
П 7Г
Произно-
Произношение
йота
каппа
ламбда
ми
ни
кси
омикрон
пи
Начер-
Начертание
р р
Е а
Т т
Т v
Ф <р
х х
ф ф
U и)
Произно-
Произношение
ро
сигма
тау
ипсилон
фи
хи
пси
омега
Представлен наиболее употребительный (но не единствен-
единственный) вариант произношения (в частности, вместо „йот" иногда
говорят „жи").
ВВЕДЕНИЕ
Теория вероятностей является разделом математики, в ко-
котором изучают математические модели случайных экспери-
экспериментов, т.е. экспериментов, исходы которых нельзя опреде-
определить однозначно условиями проведения опыта. При этом пред-
предполагается, что сам эксперимент может быть повторен (хотя
бы в принципе) любое число раз при неизменном комплексе
условий, а исходы эксперимента обладают статистической
устойчив остью.
Приведем простейшие примеры таких экспериментов.
1. Однократное подбрасывание монеты. Возможными ис-
исходами в этом опыте будут: падение монеты пгербом" вверх
(или просто выпадение „герба") или выпадение „цифры". В ре-
результате проведения опыта возникает лишь один исход, однако
установить до проведения опыта, какой именно, невозможно.
2. Бросание игральной кости. В данном случае возможны
шесть исходов: выпадение 1, 2, 3, 4, 5 и 6 очков на верхней
грани бросаемой кости.
3. Работа телефонной станции. Предположим, что нас ин-
интересует число вызовов, которое поступит за определенный
промежуток времени на телефонную станцию. Как и в преды-
предыдущих примерах, интересующую нас величину до проведения
эксперимента определить невозможно, хотя очевидно, что ре-
результатом будет целое неотрицательное число.
4. Измерение времени безотказной работы электрической
лампочки. Время безотказной работы лампочки, которое в
принципе может быть любым неотрицательным числом, для
конкретного образца предсказать невозможно.
5. Стрельба по плоской мишени с большого расстояния.
Введем в плоскости мишени прямоугольную систему координат
Оху, в которой начало координат (точка О) является точкой
18 ВВЕДЕНИЕ
прицеливания. Возможные исходы в этом опыте можно описать
координатами (#; у) точки падения снаряда. Случайные воз-
воздействия на траекторию движения снаряда приводят к тому,
что установить координаты (ж; у) можно только после выст-
выстрела.
Примеров такого рода можно привести сколь угодно мно-
много. Принято говорить, что исходы опытов (экспериментов),
подобных перечисленным выше, являются случайными.
В чем же состоит общность опытов со случайными исхода-
исходами? Оказывается, несмотря на то что результат каждого из
перечисленных выше экспериментов предсказать невозможно,
на практике для них уже давно была замечена закономерность
определенного вида, а именно: при проведении большого ко-
количества испытаний наблюденные частоты появления каждого
случайного события (наблюденной частотой случайного
события называют отношение числа его появлений к общему
числу испытаний) стабилизируются, т.е. все меньше отличают-
отличаются от некоторого числа, называемого вероятностью события.
Так, при многократном бросании игральной кости „шестерка"
выпадает в среднем в каждом шестом случае.
Такое свойство устойчивости частоты позволяет, не
имея возможности предсказать исход отдельного опыта, до-
достаточно точно прогнозировать свойства явлений, связанных с
рассматриваемым опытом. Поэтому методы теории вероятно-
вероятностей в современной жизни проникли во все сферы деятельности
человека, причем не только в естественно-научные, экономиче-
экономические, но и гуманитарные, такие, как история, лингвистика и
т.д.
Практическое применение методов теории вероятностей за-
заключается в пересчете вероятностей „простых" случайных со-
событий в вероятности „сложных" событий. Например, веро-
вероятность выпадения „герба" при однократном подбрасывании
обычной монеты равна 1/2. Спрашивается, как часто выпа-
выпадают два „герба" при трех подбрасываниях монеты? Решение
19
данной задачи дает формула Бернулли, которую мы получим в
третьей главе.
Однако определение вероятности через частоту не является
удовлетворительным для теории вероятностей как математи-
математической науки. Поэтому А.Н. Колмогоров предложил аксио-
аксиоматическое определение вероятности. Именно оно и является
общепринятым в настоящее время. В частности, на его основе
изложен курс теории вероятностей в предлагаемом учебнике.
Характерной особенностью современной теории вероятно-
вероятностей является тот факт, что, несмотря на свою практическую
направленность, в ней используют новейшие разделы почти
всех разделов математики, а значит, для ее изучения на высо-
высоком уровне требуются математические знания, в объеме суще-
существенно превосходящем возможности технического вуза. В свя-
связи с этим даже при подготовке специалистов в области теории
вероятностей принят многоуровневый подход, в соответствии
с которым изложение ведется сначала на первом (простейшем)
уровне, затем на втором (более сложном) и т.д. Настоящий
учебник соответствует первому уровню изложения, скоррек-
скорректированному с учетом математической подготовки студентов
технического университета. Впрочем, этого уровня вполне
достаточно для того, чтобы научиться решать многие прак-
практические задачи.
Приведем краткую историческую справку о становлении
теории вероятностей как раздела математики.
Исторически теория вероятностей возникла как теория
азартных игр (рулетка, игральные кости, карты и т.д.) в конце
XVII в. Начало ее развития связано с именами Б. Паскаля,
Я. Бернулли, А. Муавра, П. Лапласа, а позднее (начало
XIX в.) — К. Гаусса, С. Пуассона.
Первые исследования по теории вероятностей в России от-
относятся к середине XIX в. и связаны с именами таких вы-
выдающихся математиков, как Н.И. Лобачевский A792-1856),
М.В. Остроградский A801-1861), В.Я. Буняковский A804-1889).
В частности, В.Я. Буняковский издал в 1846 г. один из первых
ZV ВВЕДЕНИЕ
учебников по теории вероятностей (с приложениями в страхо-
страховом деле, демографии и др.).
Дальнейшее развитие теории вероятностей (конец XIX в.
и 20-е гг. XX в.) в основном связано с именами русских уче-
ученых П.Л. Чебышева A821-1894) и его учеников A.M. Ляпунова
A857-1918) и А.А. Маркова A856-1922). С 30-х гг. XX в. этот
раздел математики переживает период расцвета, находя при-
приложения в различных областях науки и техники. И в это время
российские ученые С.Н. Бернштейн A880-1968), А.Я. Хинчин
A894-1959), А.Н. Колмогоров A903-1987) и многие другие
вносят существенный вклад в развитие теории вероятностей.
Именно А.Н. Колмогоров в 1933 г. предложил аксиоматическое
построение теории вероятностей, установив ее связь с други-
другими разделами математики (теорией множеств, теорией меры,
функциональным анализом).
1. СЛУЧАЙНЫЕ СОБЫТИЯ
Любая современная математическая дисциплина основыва-
основывается на некоторых исходных понятиях (аксиомах). В теории
вероятностей такой аксиоматический подход был введен срав-
сравнительно недавно (в 30-х гг.) А.Н. Колмогоровым.
Аксиомы, лежащие в основе этого подхода, отражают и
обобщают те свойства понятия вероятности случайных собы-
событий, которые использовались на интуитивном уровне с давних
времен — с момента зарождения теории вероятностей как те-
теории wазартных игр".
В этой и следующих главах будет показано, что основные
понятия и аксиомы теории вероятностей представляют собой
математические отражения понятий, хорошо известных любо-
любому человеку, наблюдавшему опыты со случайными исходами.
Одним из таких понятий является пространство элементар-
элементарных исходов, введение которого позволяет при решении кон-
конкретных практических задач оперировать общим для современ-
современной математики аппаратом теории множеств.
1.1. Пространство элементарных исходов
Определение 1.1. Элементарным исходом (или эле-
элементарным событием) называют любой простейший (т.е.
неделимый в рамках данного опыта) исход опыта. Множество
всех элементарных исходов будем называть пространством
элементарных исходов.
Другими словами, множество исходов опыта образует про-
пространство элементарных исходов, если выполнены следующие
требования:
22 1. СЛУЧАЙНЫЕ СОБЫТИЯ
- в результате опыта один из исходов обязательно происхо-
происходит;
- появление одного из исходов опыта исключает появление
остальных;
- в рамках данного опыта нельзя разделить элементарный
исход на более мелкие составляющие.
В дальнейшем пространство элементарных исходов будем
обозначать прописной буквой ?2, а сами элементарные исхо-
исходы — строчной буквой о;, снабженной, при необходимости,
индексами. То, что элемент ш принадлежит ?2, записывают в
виде ш Е п, а тот факт, что множество ?2 состоит из элементов
a?i, CJ2, ..., ь;п, ..., и только из них, записывают в виде
или в виде
В частности, ?2 может содержать конечное число элементарных
исходов.
Рассмотрим примеры, поясняющие понятие пространства
элементарных исходов.
Пример 1.1. Пусть опыт состоит в однократном подбра-
подбрасывании монеты. При математическом описании этого опыта
естественно отвлечься от несущественных возможностей (на-
(например, монета встанет на ребро) и ограничиться только двумя
элементарными исходами: выпадением „герба" (можно обозна-
обозначить этот исход Г, шг или и\) и выпадением „цифры" (Ц, шц или
и>2). Таким образом, П = {Г, Ц}, ?2 = {иг, <*>ц} или U = {cji, о^}-
При двукратном подбрасывании монеты (или однократном
подбрасывании двух монет) пространство элементарных исхо-
исходов будет, очевидно, содержать четыре элемента, т.е.
где, например, ыгг — появление „герба" и при первом, и при
втором подбрасываниях.
1.1. Пространство элементарных исходов 23
Пример 1.2. При однократном бросании игральной кости
возможен любой из шести элементарных исходов cji, ..., (Je, где
о;», г = 1, 6, означает появление % очков на верхней грани кости,
т.е.
О = {о;*, г = 1, 6}.
При двукратном бросании игральной кости каждый из ше-
шести возможных исходов при первом бросании может сочетаться
с каждым из шести исходов при втором бросании, т.е.
где u>ij — исход опыта, при котором сначала выпало г, а затем
j очков.
Нетрудно подсчитать, что пространство элементарных ис-
исходов ?1 содержит 36 элементарных исходов.
Пример 1.3. Пусть опыт заключается в определении числа
вызовов, поступивших на телефонную станцию в течение за-
заданного промежутка времени. Разумеется, реально это число
не превышает некоторого значения (определяемого, в частно-
частности, пропускной способностью линий связи), но, поскольку это
значение может быть достаточно большим, в качестве про-
пространства элементарных исходов можно принять множество
целых неотрицательных чисел, т.е.
Пример 1.4. Предположим, что стрелок производит един-
единственный выстрел по плоской мишени. В этом случае ?2 есте-
естественно отождествить с множеством точек на плоскости или
множеством пар (х;у) действительных чисел, где х — абсцис-
абсцисса, а у — ордината точки попадания пули в мишень в некоторой
системе координат. Таким образом,
?1 = {(х;у): —оо < х < +оо, —оо < у < +оо}.
24 1. СЛУЧАЙНЫЕ СОБЫТИЯ
1.2. События, действия над ними
Введем понятие случайного события. Поскольку в даль-
дальнейшем будем рассматривать только случайные события, то,
начиная с этого момента, будем называть их, как правило, про-
просто событиями.
Определение 1.2. Любой набор элементарных исходов,
или, иными словами, произвольное подмножество простран-
пространства элементарных исходов, называют событием.
Элементарные исходы, которые являются элементами рас-
рассматриваемого подмножества (события), называют элемен-
элементарными исходами, благоприятствующими данному
событию, или образующими это событие.
События будем обозначать прописными латинскими бу-
буквами, снабжая их при необходимости индексами, например:
i4,JBi,C3 и т.д.
Сразу же оговоримся, что определение 1.2 события будет
уточнено в следующем параграфе в том случае, когда fi не явля-
является счетным множеством. Здесь же мы вводим определение 1.2
по двум причинам.
Во-первых, основная цель настоящего параграфа — нагляд-
наглядно показать, как физическое понятие случайного события фор-
формализуется в математических понятиях теории множеств, и
описать операции над событиями.
Во-вторых, определение 1.2 вполне удовлетворительно мож-
можно применять для решения практических задач, в то время
как строгое определение события служит лишь для построе-
построения теории вероятностей как раздела современной математики,
оперирующей логически безупречными, но сложными для не-
неподготовленного читателя понятиями.
Часто используется следующая терминология: говорят, что
событие А произошло (или наступило), если в результате опыта
появился какой-либо из элементарных исходов ш 6 А.
1.2. События, действия над ними 25
Замечание 1.1. Во многих учебниках по теории веро-
вероятностей (и в данной книге тоже) для удобства изложения
материала, особенно при решении задач, термин псобытие"
как подмножество пространства элементарных событий п ото-
отождествляется с термином „событие произошло в результате
опыта", или „событие заключается в появлении таких-то эле-
элементарных исходов".
Так, в примере 1.2, где ?1 = {с^, г = 1, 6}, событием А явля-
является подмножество {o;i, из, ujs}- Но мы будем также говорить,
что событие А — это появление любого из элементарных исхо-
исходов u>u г = 1,3,5.
Пример 1.5. В примере 1.2 было показано, что при одно-
однократном бросании игральной кости
П = {ши г =176},
где щ — элементарный исход, заключающийся в выпадении
% очков. Рассмотрим следующие события: А — выпадение
четного числа очков; В — выпадение нечетного числа очков;
С — выпадение числа очков, кратного трем. Очевидно, что
А = {а;2, о>4, ^б}, В = {cjb (j3, с*;5} и С = {а;3, ^б}.
Определение 1.3. Событие, состоящее из всех элементар-
элементарных исходов, т.е. событие, которое обязательно происходит в
данном опыте, называют достоверным событием.
Достоверное событие, как и пространство элементарных
исходов, обозначают буквой П.
Определение 1.4. Событие, не содержащее ни одного эле-
элементарного исхода, т.е. событие, которое никогда не происходит
в данном опыте, называют невозможным событием.
Невозможное событие будем обозначать символом 0.
Пример 1.6. При бросании игральной кости достоверное
событие можно описать, например, как выпадение хотя бы
одного очка, а невозможное — как выпадение 7 очков. #
26 1. СЛУЧАЙНЫЕ СОБЫТИЯ
Часто бывает полезно наглядно представить события в
виде диаграммы Эйлера — Венна. Изобразим все про-
пространство элементарных исходов прямоугольником (рис. 1.1).
При этом каждый элементарный исход и) соответствует точке
внутри прямоугольника, а каждое событие А — некоторо-
некоторому подмножеству точек этого прямоугольника. Трактовкой
диаграммы Эйлера — Венна
может служить опыт с броса-
бросанием случайным образом ча-
частицы в прямоугольник. То-
Тогда элементарный исход и> —
это попадание частицы в точ-
точку и прямоугольника, а собы-
событие А — в часть прямоуголь-
ника, задаваемую подмноже-
ством А.
Рассмотрим теперь операции (действия) над событи-
событиями, которые, по существу, совпадают с операциями над под-
подмножествами [I]. Эти операции будем иллюстрировать на диа-
диаграммах Эйлера — Венна. На рис. 1.2 заштрихованы области,
которые соответствуют событиям, являющимся результатами
таких операций.
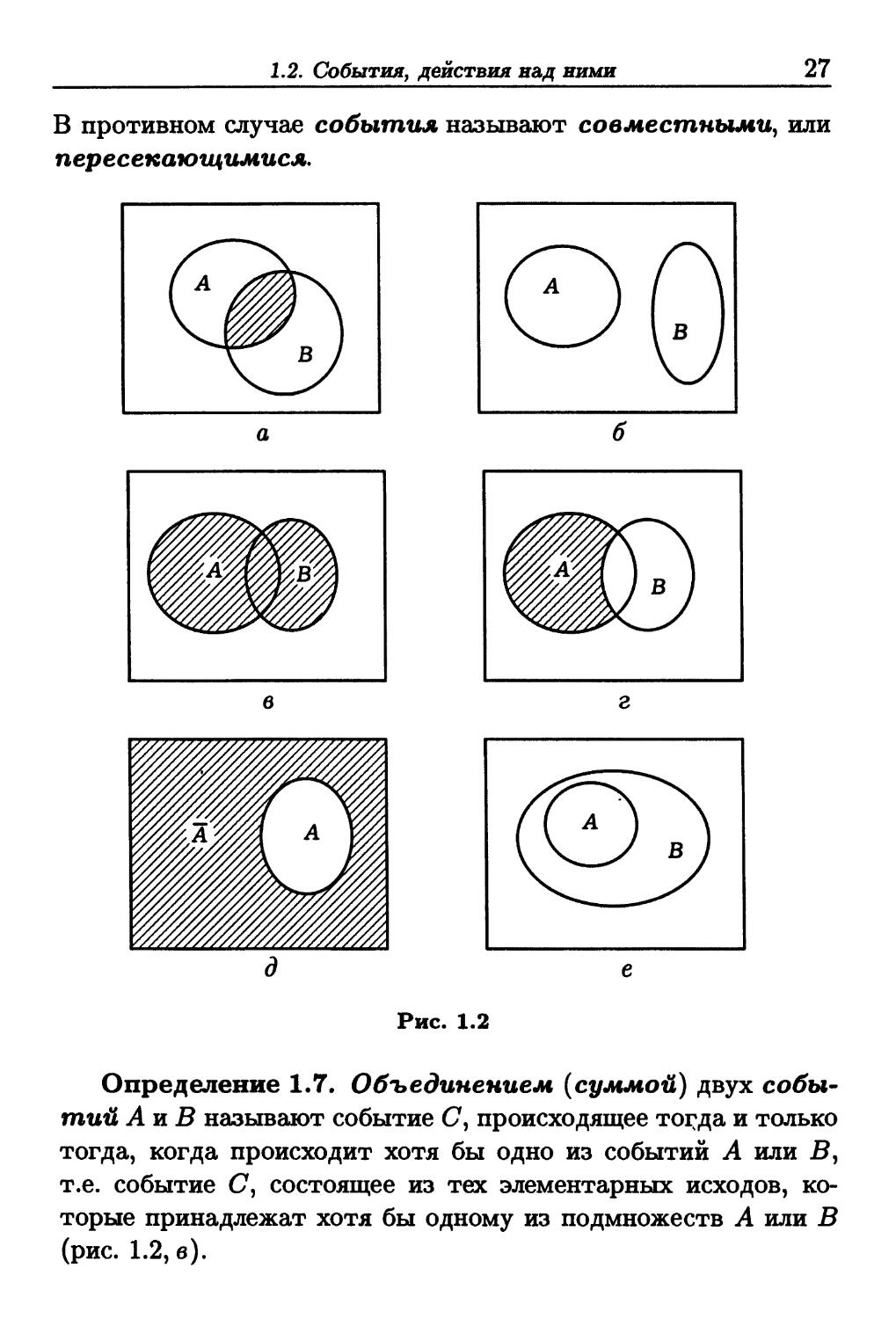
Определение 1.5. Пересечением (произведением) двух
событий А и В называют событие С, происходящее тогда и
только тогда, когда одновременно происходят оба события А
и В, т.е. событие, состоящее из тех и только тех элементарных
исходов, которые принадлежат и событию А, и событию В
(рис. 1.2, а).
Пересечение событий А и В записывают следующим об-
образом:
С = АГ)В, или С = АВ.
Определение 1.6. События Аи В называют несовмест-
несовместными, или непересекающимися, если их пересечение явля-
является невозможным событием, т.е. если АПВ = 0 (рис. 1.2,б).
1.2. События, действия над ними
27
В противном случае события называют совместными, или
пересекающимися.
Рис. 1.2
Определение 1.7, Объединением (суммой) двух собы-
событий Аи В называют событие С, происходящее тогда и только
тогда, когда происходит хотя бы одно из событий А или Б,
т.е. событие С, состоящее из тех элементарных исходов, ко-
которые принадлежат хотя бы одному из подмножеств А или В
(рис. 1.2, в).
28 1. СЛУЧАЙНЫЕ СОБЫТИЯ
Объединение событий А и В записывают в виде
Бели события А и В несовместны, наряду со знаком „U"
для их объединения употребляют знак „+". Обычно знак п+а
применяют в том случае, если заведомо известно, что А и
В несовместны, и это особо хотят подчеркнуть. Например,
поскольку невозможное событие 0 несовместно с любым собы-
событием А, то
Аналогично определяют понятия произведения и суммы
событий для любого конечного числа событий и даже для
бесконечных последовательностей событий. Так, событие
оо
AiA2...An...= П Ап
п=1
состоит из элементарных исходов, принадлежащих всем собы-
событиям Ап, п G N, а событие
i4iUi42U...UAnU...= U Ап
п=1
состоит из элементарных исходов, принадлежащих хотя бы од-
одному из событий Ап, п Е N. В частности, события Аи А2,...,
Ап называют попарно несовместными (непересекающи-
(непересекающимися), если
AiAj = 0
для любых ij = 1,п, г Ф j, и несовместными (непересека-
(непересекающимися) в совокупности, если
Определение 1.8. Разностью двух событий А и В
называют событие С, происходящее тогда и только тогда,
когда происходит событие А, но не происходит событие В, т.е.
1.2. События, действия над ними 29
событие С, состоящее из тех элементарных исходов, которые
принадлежат А, но не принадлежат В (рис. 1.2, г).
Разность событий А и В записывают в виде:
С = А\В.
Определение 1.9. Дополнением события А (обычно
обозначают А) называют событие, происходящее тогда и толь-
только тогда, когда не происходит событие А (рис. 1.2, <?). Другими
словами,
Событие А называют также событием, противополож-
противоположным событию А,
Если некоторое событие записано в виде нескольких дей-
действий над различными событиями, то сначала переходят к
дополнениям, а затем умножают и, наконец, складывают и вы-
вычитают (слева направо) события. Так, формула
С = A{A2BXU A3B2\B3
эквивалентна формуле
С = {[АгШВг] U [Аг(В2)]}\В3.
Следует отметить, что все действия над событиями можно
получить с помощью только двух действий — объединения
и дополнения (или пересечения и дополнения). Основанием
для этого утверждения служат законы де Моргана, а также
соотношение
А\В = АВ.
Кроме перечисленных выше действий над событиями нам в
дальнейшем понадобится понятие включения.
Определение 1.10. Событие А включено в событие В,
что записывают А С В, если появление события А обязательно
30
1. СЛУЧАЙНЫЕ СОБЫТИЯ
влечет за собой наступление события В (рис. 1.2, е), или
каждый элементарный исход ш, принадлежащий А, обязательно
принадлежит и событию В.
Ясно, что включение АсВ эквивалентно равенству АВ = А.
Используют и обратное понятие: событие В включает со-
событие А (В D А), если А С В.
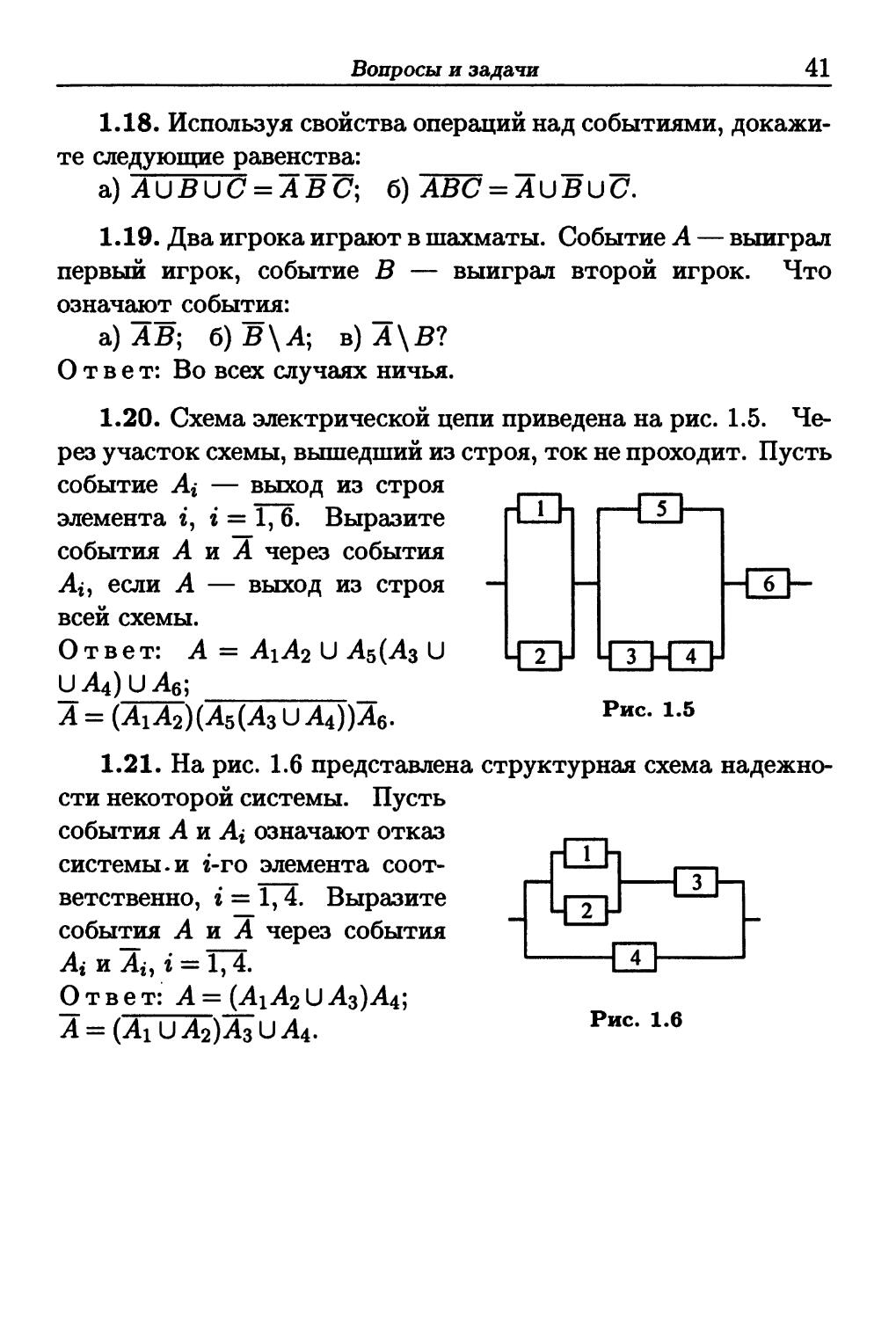
Пример 1.7. Рассмотрим техническое устройство (ТУ),
состоящее из т элементов. В теории надежности принято
говорить, что элементы соединены последовательно, если ТУ
прекращает функционировать при отказе любого элемента, и
соединены параллельно, если прекращение функционирования
ТУ наступает только при отказе всех т элементов. Условное
изображение последовательного и параллельного соединений
представлено на рис. 1.3, а и б соответственно.
Обозначим А событие, означающее отказ ТУ, a Ai —
событие, означающее отказ г-го элемента (г = 1,т). Тогда
события А и А{ связаны соотношениями:
для рис. 1.3, а А = А\ U... U Ату
для рис. 1.3, б А = А\ П... П Ат.
Рис. 1.3
Очевидно, что при параллельном соединении элементов со-
событие А включено в каждое событие Ai, % = 1, m, а при последо-
последовательном соединении, наоборот, любое событие A», t = 1, т,
включено в событие А. #
1.2. События, действия над ними 31
Приведем основные свойства операций над событиями, спра-
справедливость которых нетрудно проверить с помощью диаграмм
Эйлера — Венна (проделайте это самостоятельно).
1. Коммутативность суммы и произведения:
, АВ = ВА.
2. Ассоциативность суммы и произведения:
A\JBUC = AU{BUC), (АВ)С = А(ВС).
3. Дистрибутивность относительно сложения:
(A\JB)C = ACUBC.
4. Дистрибутивность относительно умножения (новое свой-
свойство, не выполняющееся для чисел):
AB\JC=(AuC)(B\JC).
5. Включение А в В, т.е. А С J5, влечет за собой включение
Вв1, т.е. А Э В.
6. Совпадение двойного дополнения с исходным событием:
7. Совпадение суммы и произведения одинаковых событий
с самим событием
8. Законы де Моргана:
Замечание 1.2. Законы де Моргана верны для любого
конечного числа событий:
32 1. СЛУЧАЙНЫЕ СОБЫТИЯ
1.3. Сигма-алгебра событий
Настоящий параграф носит ознакомительный характер и ни
в коем случае не претендует на строгость изложения*. Необ-
Необходимость его введения обусловлена тем, что современная те-
теория вероятностей основывается на понятии вероятностного
пространства, одним из трех компонентов которого является
сигма-алгебра событий.
В предыдущем параграфе мы назвали событием любое под-
подмножество пространства элементарных исходов fi. Такое
определение допустимо, если ft является конечным или счет-
счетным множеством. Оказывается, однако, что в случае несчет-
несчетного множества элементарных исходов уже нельзя построить
логически непротиворечивую теорию, называя событием про-
произвольное подмножество множества ?}. Поэтому событиями в
этом случае называют не любые подмножества элементарных
исходов, а только подмножества из ft, принадлежащие неко-
некоторому классу 03. Этот класс в теории множеств принято
называть сигма-алгеброй событий (пишут сг-алгебра).
С точки зрения здравого смысла событие — это то, что
мы наблюдаем после проведения опыта. В частности, если
можно после опыта установить, произошли или нет события
А и В, то можно также сказать, произошли или нет собы-
события А и В, объединение, пересечение и разность событий А
и В. Таким образом, сг- алгебра событий обязана быть классом
подмножеств, замкнутым относительно приведенных операций
над подмножествами, т.е. указанные операции над элементами
(подмножествами) данного класса приводят к элементам (под-
(подмножествам) того же класса.
Дадим теперь строгое определение сг-алгебры событий.
* Строгое обоснование основ теории вероятностей можно найти в спе-
специальной математической литературе (см., например: Колмогоров А.Н.
Основные понятия теории вероятностей. М.: Наука, 1974).
1.3. Сигма-алгебра событий 33
Определение 1.11. Сигма-алгеброй (а-алгеброй) 05
называют непустую систему подмножеств некоторого множе-
множества J, удовлетворяющую следующим двум условиям.
1. Если подмножество А принадлежит 05, то дополнение А
принадлежит 05.
2. Если подмножества Ai, Л2,..., -An,... принадлежат 05,
то их объединение А\ U A2 U ... U An U ... и их пересечение
А\ А2 ... Ап ... принадлежит 05.
Поскольку J = Аи А и 0 = J, то множество J и пустое
множество 0 принадлежат 05.
Рассмотрим пространство элементарных исходов f2. Эле-
Элементы некоторой ет-алгебры 05, заданной на 12, будем называть
событиями. В этом случае а-алгебру 05 принято называть
сигма-алгеброй (а-алгеброй) событий.
Любая а-алгебра событий содержит достоверное событие
п и невозможное событие 0.
В случае конечного или счетного пространства элементар-
элементарных исходов ft в качестве ст-алгебры событий обычно рассма-
рассматривают множество всех подмножеств Л.
Замечание 1.3. Если в условии 2 счетное множество собы-
событий заменить на конечное, то получим определение алгебры
событий. Любая сг-алгебра событий обязательно является ал-
алгеброй событий. Обратное утверждение, вообще говоря, не
верно.
Пример 1.8. Пусть опыт состоит в подбрасывании один
раз тетраэдра, каждая грань которого помечена одним из чисел
1, 2, 3 и 4.
Очевидно, что пространство элементарных исходов ?1 в
этом опыте имеет вид
где щ — падение тетраэдра на грань с числом г, г = 1,4.
2 - 10047
34 1. СЛУЧАЙНЫЕ СОБЫТИЯ
Поскольку в рассматриваемом опыте может происходить
одно из следующих событий:
то алгебра событий будет содержать все подмножества fi,
включая fi (достоверное событие) и 0 (невозможное событие).
Пример 1,9. Пусть опыт состоит в случайном бросании
точки на числовую прямую R1 = (—оо,+оо), которая в данном
случае будет представлять собой пространство элементарных
исходов Q. Ясно, что, зная результат опыта, всегда можно
установить, попала или нет точка в любой из промежутков
[а, 6], [а, Ь), (а, 6], (а, Ь). Поэтому относительно а-алгебры собы-
событий 53 предполагают, что она содержит все эти промежутки.
В принципе могут существовать различные а-алгебры, удо-
удовлетворяющие этому требованию. Но среди них есть одна
(Т-алгебра, элементы которой принадлежат всем остальным. Ее
называют минимальной, или бор елее ской, а-алгеброй на
числовой прямой.
Аналогично определяют борелевскую а-алгебру и в Rn,
п>1. #
В заключение заметим, что с точки зрения повседневной
практики подмножества пространства п элементарных исхо-
исходов, не являющиеся событиями, представляют собой чистую
математическую абстракцию и в практических задачах ни-
никогда не встречаются. Даже само доказательство их суще-
существования представляет весьма сложную задачу. Поэтому мы
предлагаем при первоначальном знакомстве с теорией веро-
1.4. Решение типовых примеров 35
ятностей под событием понимать произвольное подмножество
пространства п элементарных исходов, а под сг-алгеброй собы-
событий — совокупность всех подмножеств множества п.
1.4. Решение типовых примеров
Пример 1.10. Опыт состоит в однократном бросании
игральной кости. Опишем пространство элементарных исходов
п и укажем состав подмножеств, соответствующих следующим
событиям:
а) А — число очков, выпавших на верхней грани игральной
кости, кратно трем;
б) В — на верхней грани игральной кости выпало нечетное
число очков;
в) С — число очков, выпавших на верхней грани игральной
кости, больше трех;
г) D — число очков, выпавших на верхней грани игральной
кости, меньше семи;
д) Е — число очков, выпавших на верхней грани игральной
кости, не является целым числом;
е) F — число очков, выпавших на верхней грани игральной
кости, заключено в пределах от 0,5 до 1,5.
Установим пары совместных событий.
Пространство элементарных исходов в данном опыте имеет
вид
п = {UU LJ, CJ3,
где uji — выпадение на верхней грани игральной кости % очков.
а. Очевидно, что событие А происходит тогда и только
тогда, когда выпадает либо 3, либо 6 очков, т.е. А = {из, ш^}.
Аналогично получаем следующие выражения для остальных
описанных событий.
б. -В =
в. С
г. D = {wi, о;2,
36 1. СЛУЧАЙНЫЕ СОБЫТИЯ
д. Е = 0.
е. F = {"i}-
Сопоставляя попарно события и проверяя наличие общих
элементов, находим пары совместных событий: А и В; А и С;
А и D; В и С; В и D; В та. F; С и D; D и F.
Пример 1.11. Игральную кость бросают один раз. Со-
События A, B,CjD,E и F определены в примере 1.10. Опишем
следующие события:
a) Gi = B;
6)G2 = C;
в) G3 = АВ;
г) G4 =
е) G6 =
ж) G7 = EF.
а. Событием, противоположным событию В, является вы-
выпадение четного числа очков, т.е. G\ = {u;2> <*>4? ^б}-
Аналогичные рассуждения приводят нас к следующим ре-
результатам.
б. G2 = {c^i, с^2, о;з} — выпало не более 3 очков.
в. Сгз = {<*>з} — выпавшее число очков нечетно и кратно
трем, т.е. равно трем.
г. G± = {wi, и>ъ, с^б) ^б} — выпавшее число очков или нечет-
нечетно, или кратно трем.
Д- {^б} — выпавшее число очков четно и кратно трем, т.е.
равно 6.
е. G6
ж. G7
Пример 1.12. Из множества супружеских пар наугад
выбирают одну пару. Событие А — мужу больше 30 лет,
событие В — муж старше жены, событие С — жене больше
30 лет. Выясним смысл событий:
а) АВС;
1.4. Решение типовых примеров
37
б) А\АВ;
в) ABC.
Покажем, что АС С В.
а. АВС — оба супруга старше 30 лет, причем муж старше
жены.
б. А\АВ — мужу больше 30 лет, но он не старше своей
жены.
в. АВС — оба супруга старше 30 лет, причем муж не стар-
старше своей жены.
АС — пересечение событий; мужу больше 30 лет, а жене не
больше 30 лет. Следовательно, муж старше жены, т.е. АС С В.
Пример 1.13. Пусть А, В — произвольные события. До-
Докажем следующие равенства:
а) (AUS)(AUB) = A;
б) {AUB)(AUB)(AUB) = AB.
Используя свойства операций над событиями, получаем:
a.
б.
Пример 1.14. Выясним, в каких случаях совместны (в со-
совокупности) события Аи В, Аи В и Аи В?
_ Так как__(А U B)(A U В){A UB) = АВ, то события A U J5,
A\J В и Аи В совместны тогда и только тогда, когда совместны
события А и В.
Пример 1.15. Схема элек-
электрической цепи приведена на
рис. 1.4. Выход из строя эле-
элемента г — событие А^ г = 1, 4.
Запишем выражения для собы-
событий А и А, если А означает
разрыв цепи.
Разрыв цепи произойдет,
если выйдет из строя элемент Рис«
38 1. СЛУЧАЙНЫЕ СОБЫТИЯ
1 или все три элемента 2, 3, 4, т.е. произойдут событие А\ или
событие А2А^А^. Поэтому
В соответствии с законами де Моргала находим
А = Ai U А2АгА^ = Ai (А2 U Л3 U А4).
Вопросы и задачи
1.1. Что понимают под пространством элементарных исхо-
исходов?
1.2. Что называют случайным событием?
1.3. Какое событие называют достоверным? Какое событие
называют невозможным?
1.4. Какие действия над событиями Вы знаете?
1.5. Какие два события называют несовместными? Какие
события называют совместными?
1.6. Какие п событий (п > 2) называют несовместными
попарно? в совокупности?
1.7. Какие события называют противоположными?
1.8. Перечислите свойства операций над событиями.
1.9. В каком случае говорят, что событие А включено в
событие В?
1.10. Какими свойствами должна обладать некоторая си-
система подмножеств пространства элементарных исходов п для
того, чтобы быть сг-алгеброй событий? алгеброй событий?
1.11. Что называют борелевской ст-алгеброй на числовой
прямой?
Вопросы и задачи 39
1.12. Случайным образом выбирают одну из 28 костей до-
домино. Опишите пространство элементарных исходов п. Пере-
Перечислите все элементарные исходы, из которых состоят следую-
следующие события:
а.) А — на выбранной кости очки совпадают;
б) В — сумма очков на выбранной кости равна 6;
в) С — произведение числа очков на кости нечетно;
г)В\А; д)АВ; е) АС; ж) АВ\С; з) (АиВ)С.
Ответ: U = {(i,j), i,j = 0, 6, t <j};
аМ = {'@,0), A,1), ...,F,6)};
б) В = {@,6), A,5), B,4), C,3)};
в) С = {A,1), A,3), A,5), C,3), C,5), E,5)};
г) В\А = {@,6), A,5), B,4)}; д) ЛЯ = {C,3)};
е)АС = {A,1), C,3), E,5)}; ж)АВ\С = 0;
з) (AUВ)С = {A,1), A,5), C,3), E,5)}.
1.13. Производят обследование случайным образом выбран-
выбранной семьи, имеющей четырех детей, с целью определения пола
этих детей. Пол каждого ребенка отмечают в порядке стар-
старшинства. Определите:
а) из какого числа элементарных исходов состоит простран-
пространство элементарных исходов;
б) сколько элементарных исходов соответствуют семьям, в
которых первый ребенок — девочка;
в) сколько элементарных исходов соответствуют семьям, в
которых есть дети обоего пола.
Ответ: а) 16; б) 8; в) 14.
1.14. По мишени производят три выстрела. Пусть событие
A», i = 1, 2,3, — попадание при г-м выстреле. Представьте в
виде объединения и пересечения событий Аг или А{ следующие
события:
а) А — три попадания в мишень;
б) В — три промаха;
в) С — хотя бы одно попадание;
г) D — хотя бы один промах;
40 1. СЛУЧАЙНЫЕ СОБЫТИЯ
д) Е — не менее двух попаданий;
е) F — не больше одного попадания;
ж) G — попадание в мишень не раньше, чем при третьем
выстреле.
Ответ:
а) А = AiA2AS] б) В =
в) С = АгиА2иАз; г) D =
д) Е = АгА2А3 UAiA2A3 UAXA2A3 U МА2АЪ;
е) F = AiA2j43 U >liА2А3 U AxA2A3 U АгА2А$\ ж) G = Ax A2.
1.15. Монету подбрасывают три раза. Опишите простран-
пространство элементарных исходов п и определите подмножества, со-
соответствующие следующим событиям:
а) А — „герб" выпал ровно один раз;
б) В — ни разу не выпала „цифра";
в) С — выпало больше „гербов", чем „цифр";
г) D — „герб" выпал не менее двух раз подряд.
Ответ: П = {(Г|Г,Г)| (Ц,Г,Г), (Г,Ц,Г), (Г,Г,Ц), (Г,Ц,Ц),
(Ц,Г,Ц),(Ц,Ц,Г),(Ц,Ц,Ц)};
а) А = {(Г,Ц,Ц), (Ц,Г,Ц),
в) С = {(Г,Г,Г), (Ц,Г,Г), (Г,Ц,Г), (Г,
г)Р = {(Г,Г,Г),(Ц,Г,Г),(Г,Г,Ц)}.
1.16. Пусть А, В, С — случайные события. Выясните смысл
неравенств: а) А В С = Л; б) A U В U С = А.
Ответ:
а) А С БС, т.е. событие ВС происходит всегда, когда
происходит событие А;
б) В С А, С С А, т.е. всякий раз, когда происходит В или С,
происходит также и А.
1.17. Пусть Ас В. Упростите выражения:
а) АВ\ б) A U J5; в) ABC; г) A U В U С.
Ответ:
=Л; 6)AUB=B; в) ABC=АС; г) AUBUC=B\JC.
Вопросы и задачи
41
1.18. Используя свойства операций над событиями, докажи-
докажите следующие равенства:
a) AUBUC = ABC; 6)A13C = AUB\JC.
1.19. Два игрока играют в шахматы. Событие А — выиграл
первый игрок, событие В — выиграл второй игрок. Что
означают события:
а)АВ; б)В\А; в)А\В?
Ответ: Во всех случаях ничья.
1.20. Схема электрической цепи приведена на рис. 1.5. Че-
Через участок схемы, вышедший из строя, ток не проходит. Пусть
событие Ai — выход из строя
элемента г, г = 1, 6. Выразите
события А и А через события
А», если А — выход из строя
всей схемы.
Ответ: А = АХА2 U А5(Л3 U
Рис. 1.5
1.21. На рис. 1.6 представлена структурная схема надежно-
надежности некоторой системы. Пусть
события Аи Ai означают отказ
системы.и г-го элемента соот-
соответственно, г = 1,4. Выразите
события А и А через события
Ответ: А= (A1A2VА$)А±;
Рис. 1.6
2. ВЕРОЯТНОСТЬ
Говоря о событиях, мы с различной степенью уверенности
относимся к возможности их наступления. Так, с большей уве-
уверенностью можно утверждать, что при однократном подбрасы-
подбрасывании монеты выпадет „герб", чем при однократном бросании
игральной кости — 6 очков. Говорят, что первое событие более
вероятно, чем второе.
Что же такое вероятность события? Возникает мысль по-
поставить каждому событию А в соответствие некоторое число
Р(-А), которое характеризует меру возможности появления это-
этого события. Если принять, что P(ft) = 1 и Р@) = 0 (хотя воз-
возможны и другие допущения), то естественно ожидать, что для
любого события А выполняется условие 0 < Р(А) ^ 1.
Определение вероятности как меры возможности появле-
появления события в современной математике вводится на основании
аксиом. Но, прежде чем перейти к аксиоматическому определе-
определению, остановимся на нескольких других определениях, которые
исторически возникли раньше. Они, с одной стороны, позво-
позволяют лучше понять смысл аксиоматического определения, а с
другой — во многих случаях являются рабочим инструментом
для решения практических задач. Приведем их, следуя хроно-
хронологическому порядку появления.
2.1. Классическое определение вероятности
В классическом определении вероятности исходят из того,
что пространство элементарных исходов п содержит конечное
число элементарных исходов, причем все они равновозможны.
Понятие равновозможности поясним следующим образом.
Элементарные исходы в некотором опыте называют
равное озможнъши, если в силу условий проведения опыта
2.1. Классическое определение вероятности 43
можно считать, что ни один из них не является объективно
более возможным, чем другие. Опыт, удовлетворяющий усло-
условию равновозможности элементарных исходов, часто называют
также „ классической схемой11.
Пусть N — общее число равновозможных элементарных ис-
исходов в ft, a Na — число элементарных исходов, образующих
событие А (или, как говорят, благоприятствующих собы-
событию А.
Определение 2.1. Вероятностью события А назы-
называют отношение числа Na благоприятствующих событию А
элементарных исходов к общему числу N равновозможных эле-
элементарных исходов, т.е.
Данное определение вероятности события принято назы-
называть классическим определением вероятности.
Заметим, что наряду с названием „классическая схема"
используют также названия „случайный выбор", „равновероят-
„равновероятный выбор" и т.д.
Пример 2.1. Из урны, содержащей к = 10 белых и / =
= 20 черных шаров (шары отличаются лишь цветом), наугад
вынимают один шар. Требуется найти вероятность Р(А)
события А, заключающегося в том, что из урны извлечен белый
шар.
Для решения поставленной задачи заметим, что число эле-
элементарных исходов в данном опыте совпадает с общим числом
шаров в урне
причем все исходы равновозможны, а число благоприятствую-
благоприятствующих событию А исходов
= k = 10.
44 2. ВЕРОЯТНОСТЬ
Поэтому в соответствии с определением классической вероят-
вероятности
р<Л>=ш4 *
Используя классическое определение вероятности события,
докажем следующие свойства.
Свойство 2.1. Для любого события А вероятность удовле-
удовлетворяет неравенству
Свойство очевидно, так как отношение Na/N не может быть
отрицательным.
Свойство 2.2. Для достоверного события ?1 (которое
содержит все N элементарных исходов)
Р(П) = 1.
Свойство 2.3. Бели события Аи В несовместны (АВ = 0),
то
Действительно, если событию А благоприятствуют N\ ис-
исходов, а событию В — JV2 исходов, то в силу несовместности А
и В событию А + В благоприятствуют N\ + N2 исходов. Сле-
Следовательно,
Оказывается, что эти три свойства являются основными.
Из них как следствия можно получить другие полезные свой-
свойства (подробнее они будут рассмотрены ниже), например:
A Р@) = О;
Р(А)<Р(В), если АС В.
Недостаток классического определения заключается в том,
что оно применимо только к пространствам элементарных ис-
исходов, состоящим из конечного числа равновозможных исходов.
2.2. Вычисление вероятностей с помощью формул комбинаторики 45
Этим определением нельзя воспользоваться даже в тех случаях,
когда пространство элементарных исходов конечно, но среди
исходов есть более предпочтительные или менее предпочти-
предпочтительные.
2.2. Вычисление вероятностей
с помощью формул комбинаторики
При решении задач, заключающихся в определении вероят-
вероятности, наибольшую трудность представляет подсчет общего
числа элементарных исходов, благоприятствующих данному
событию. В этом случае полезно обратиться к формулам ком-
комбинаторики.
Теорема 2.1. Пусть даны т групп элементов, причем г-я
группа состоит из щ элементов. Общее число N способов,
с помощью которых можно осуществить указанный выбор,
определяется равенством
Это выражение называют основной формулой комбинато-
комбинаторики.
<4 Воспользуемся методом математической индукции по числу
групп т.
Очевидно, что основная формула комбинаторики справед-
справедлива для т = 1. Предполагая ее справедливость для т ^ 1,
покажем, что она выполняется также для т +1. Действитель-
Действительно, поскольку первые т элементов можно выбрать п\П2*..пт
способами, а (т + 1)-й элемент можно выбрать nm+i способа-
способами, то все т +1 элементов можно выбрать (п\П2.. .nm)nm+i =
... nm+i способами. >
Пример 2.2. В трех ящиках находятся радиодетали трех
типов с различными значениями параметров. В первом ящике
46 2. ВЕРОЯТНОСТЬ
ящике находится п\ = 20 резисторов, во втором — П2 = 15
конденсаторов и в третьем — щ = 10 транзисторов.
Найдем вероятность Р(А) того, что схема, собранная из вы-
выбранных наугад трех элементов разного типа, будет содержать
элементы с минимальными значениями параметров. Согласно
определению 2.1 классической вероятности,
где N — общее число элементарных исходов; Na — число
исходов, благоприятствующих событию А. Очевидно, что
а в силу основной формулы комбинаторики
N = nin2n3 = 3000.
Поэтому искомая вероятность
- #
Предположим теперь, что имеется группа из п различных
элементов и из этой группы нужно выбрать га элементов.
Определение 2.2. Результат выбора т элементов из
группы, содержащей п элементов, будем называть выборкой
из п элементов по т. Бели при этом элемент после выбора
снова возвращается в группу, то выборку называют выборкой
с возвращением. Бели же выбранный элемент не участвует
в дальнейшем выборе, то выборку называют выборкой без
возвращения.
Заметим, что в любом случае результат выбора т эле-
элементов из группы, содержащей п элементов, будем называть
выборкой.
2.2. Вычисление вероятностей с помощью формул комбинаторики 47
Определение 2.3* Выборку, в которой не учитывают по-
порядок выбора элементов, называют сочетанием, а выборку, в
которой учитывают порядок выбора элементов, — размеще-
размещением. При этом если рассматривгиют выборку с возвращением,
то сочетание (размещение) называют сочетанием (разме-
(размещением) с повторениями, а если рассматривают выборку
без возвращения, то сочетание (размещение) называют соче-
сочетанием (размещением) без повторений, или просто со-
сочетанием (размещением).
Замечание 2.1. Размещение без повторений из п элемен-
элементов по п элементов называют перестановкой из п элементов.
Теорема 2.2. Число размещений (без повторений) из п
элементов по т определяется формулой
n!
(n - m) (n - m - 1)... 2 • 1 (n-m)V
< Число А™ размещений (без повторений) подсчитаем следу-
следующим образом: первым можно выбрать любой из п элемен-
элементов, вторым — любой из п — 1 оставшихся,..., m-м — любой
из п — т + 1 элементов. Воспользовавшись основной форму-
формулой комбинаторики (выбор осуществляется из групп размером
n, n — l,...,n — m + 1), приходим к утверждению теоремы. >
Замечание 2.2. Из этой теоремы, в частности, следует,
что число Рп перстановок из п элементов равно п!
Пример 2.3. Из шести карточек, образующих слово
„МАСТЕР", наудачу выбирают четыре и выкладывают слева
направо. Найдем вероятность Р(-А) того, что в результате
получится слово „ТЕМА".
Элементарным исходом в данном опыте является любая че-
четверка карточек с учетом порядка их выбора, т.е. размещение
48 2. ВЕРОЯТНОСТЬ
из п = 6 элементов по m = 4 элементов. Поэтому число этих ис-
исходов равно числу размещений из шести элементов по четыре
элемента, т.е.
N = А\ = 360.
Очевидно, что число исходов, благоприятствующих событию А,
Следовательно,
P(i4) = =
( ] N 360'
Пример 2.4. К Новому году четырем детям были приго-
приготовлены подарки. Дед Мороз перепутал подарки и вручил их
детям случайным образом.
Найдем вероятность Р(-А) того, что каждый ребенок по-
получил свой подарок. В данном случае число элементарных
исходов равно числу перестановок из п = 4 элементов, т.е.
N = P4 = 24.
Поскольку число благоприятствующих событию А исходов
то
Теорема 2.3. Число С™ сочетаний (без повторений) из п
элементов по т определяется формулой
n m\(n-m)V
< Для нахождения числа сочетаний (без повторений) заметим,
что сочетание от размещения отличается только тем, что
2.2. Вычисление вероятностей с помощью формул комбинаторики 49
входящие в него элементы не упорядочены, т.е. могут быть
выбраны в любой последовательности. Но число способов,
которыми можно упорядочить m элементов, совпадает с числом
парестановок из m элементов, т.е. равно т! Значит, каждое
сочетание соответствует т! размещениям и
Am
Отсюда получаем утверждение теоремы. >
Замечание 2.3. Число С™ называют также биномиальным
коэффициентом [1-2.6].
Пример 2.5. Группа состоит из п = 20 студентов. Для
дежурства по институту наудачу выбирают т = 3 студента.
Требуется найти вероятность Р(А) того, что будут выбраны
первые три студента по списку.
Для решения поставленной задачи достаточно заметить,
что, поскольку порядок выбора студентов не существен, общее
число элементарных исходов равно числу сочетаний из п = 20
по т = 3, т.е.
Учитывая, что число благоприятствующих событию А исходов
получаем
Теорема 2.4. Число А™ размещений с повторениями из п
элементов по т определяется формулой
™ = nm.
<4 Поскольку выбор осуществляется из одной и той же группы,
причем элемент после возвращения каждый раз снова возвра-
возвращается в группу, то в силу основной формулы комбинаторики
50 2. ВЕРОЯТНОСТЬ
число всех выборок с возвращением из п элементов по т рав-
равно nw. >
Пример 2.6. Замок камеры хранения открывается при
наборе определенной комбинации из четырех цифр от 0 до 9.
Пассажир забыл свой номер и набирает комбинацию наугад.
Найдем вероятность Р(А) того, что он откроет замок с пер-
первого раза. Элементарным исходом является появление любой
четверки из цифр 0, 9, т.е. любое размещение с повторением из
п = 10 элементов по т = 4 элемента. Значит,
NA = Ajo = 104 = 10000.
Поскольку благоприятствующий событию А исход один, то
Теорема 2.5. Число С™ сочетаний с повторениями из п
элементов по т определяется формулой
- B-1)
Рассмотрим разность
Подставляя в нее вместо С™*^ и СЦ^^ их значения (см.
теорему 2.3), имеем
fim+1 _ fjm+l _ (п + m)! (n + m-1)!
n+m n+m~1 (m+l)!(n-l)! (m + l)!(n-2)!
_ (n + m)(n + m-l)! (n + m-1)!
I
= Cm
(т + 1)!(п - 1)(п - 2)! (т + 1)!(п - 2)!
-1)\ (n + m-1)!
2.2. Вычисление вероятностей с помощью формул комбинаторики 51
Воспользуемся теперь методом математической индукции
по переменной т.
Поскольку число выборок из п элементов по одному элемен-
элементу равно п = С„ = С*, то формула B.1) справедлива при га = 1.
Пусть теперь формула B.1) справедлива для некоторого
га ^ 1. Покажем, что она справедлива и для га +1. Для этого
разобьем все выборки с повторениями из п элементов по га +1
элементов на п типов. К первому типу отнесем те выборки,
в которых хотя бы один раз встречается первый элемент, ко
второму — выборки, в которых отсутствует первый элемент,
но при этом хотя бы один раз встречается второй элемент, к
третьему — выборки, в которых отсутствуют первый и второй
элементы, но хотя бы один раз встречается третий элемент и
т.д. Наконец, в выборке n-го типа (единственной!) встречается
только n-й элемент. Число выборок г-го типа равно CJJL^+1, так
как выбор га элементов производится из группы, содержащей
п — i +1 элементов. Поэтому
n+m-2 т • • •
Используя теперь доказанное равенство
при к = n, n — 1,..., 1, получаем
лт+1 __ //orm+1 /n»m+l \ ¦ //nrm+1
Формулы для числа размещений и сочетаний можно при-
применять и при решении задач комбинаторики, описываемых в
несколько отличных от приведенных выше постановках.
В частности, при распределении частиц по ячейкам:
- число способов, с помощью которых можно заполнить п
разных ячеек га различимыми частицами, причем в каждой
52 2. ВЕРОЯТНОСТЬ
ячейке может находиться не более одной частицы, равно числу
А™ размещений из п элементов по т элементов, А™ = -—'—^;
- число способов, с помощью которых можно заполнить
п различных ячеек т неразличимыми частицами, причем в
каждой ячейке может находиться не более одной частицы,
равно числу С™ сочетаний из п элементов по т элементов,
m\{n-m)V
- число способов, с помощью которых можно заполнить п
различных ячеек т различимыми частицами без ограничения
на число попавших в каждую ячейку частиц, равно числу А™
размещений с повторениями из п элементов по т элементов,
- число способов, с помощью которых можно заполнить п
различных ячеек m неразличимыми частицами без ограничения
на число попавших в каждую ячейку частиц, равно числу С™
сочетаний с повторениями из п элементов по т элементов,
Рассмотрим еще одну часто встречающуюся на практике
задачу комбинаторики. Требуется найти число размещений
с повторениями из п элементов по т элементов, в которых
первый элемент встречается ровно mi раз, второй элемент
встречается ровно тг раз, ..., го-й элемент встречается ровно
тп раз (mi + т^ + ...тп = т). Число таких размещений
обозначим С (mi,..., тп).
Теорема 2.6. Число C(mi,...,mn) определяется формулой
т\
< Для нахождения C(mi,...,mn) вычислим сначала число раз-
различных способов, с помощью которых можно выбрать первый
элемент. Это число равно CJJJ1. После определения места, на
котором появился первый элемент, вычислим число способов,
2.2. Вычисление вероятностей с помощью формул комбинаторики 53
с помощью которых можно выбрать второй элемент. Посколь-
Поскольку число мест теперь равно m — mi, to число таких способов
равно C™imi. Число способов выбора третьего элемента равно
^m~mi-m2 и Т-Д- Используя теперь основную формулу комби-
комбинаторики, получаем
т\(т — mi)!... (m — mi — ... — mn_i)!
mi!(m — mi)!m2!(m — mi — 7712)!... mn!0!
m!
Число C(mi,...,mn) совпадает с числом способов, с помо-
помощью которых можно заполнить m разных ячеек п различимыми
частицами без ограничения на число попавших в каждую ячей-
ячейку частиц таким образом, чтобы в первой ячейке находилось
mi частиц, во второй — rri2 частиц и т.д., в п-й — mn частиц.
Замечание 2.4. Число C(mi,...,mn) называют также по-
линомиальным (мультиномиальным) коэффициентом,
поскольку оно появляется как коэффициент при х™1... х™п в
разложении функции
по степеням x\, ..., xn.
Пример 2.7. Из цифр 1, 2 и 3 случайным образом состав-
составляют шестизначное число. Требуется найти вероятность Р(А)
того, что в этом числе цифра 1 будут встречаться один раз,
цифра 2 — два раза и цифра 3 — три раза.
Элементарными исходами опыта являются всевозможные
размещения с повторениями из трех элементов по шесть эле-
элементов, т.е.
N = А\ = З6 = 729.
54 2. ВЕРОЯТНОСТЬ
Число исходов, благоприятствующих данному событию, равно
NA = СA, 2, 3) = 60.
Поэтому
^ 0,082. #
В заключение приведем решение часто встречающейся в
приложениях вероятностной задачи, которую формулируют в
рамках классической схемы.
Пусть имеется п = п\ +... + п^ различных элементов, причем
из них п\ элементов первого типа, n<i — второго типа,..., п^ —
fc-го типа. Случайным образом из этих элементов выбираются
т элементов. Вероятность события А, состоящего в том, что
среди выбранных элементов окажется ровно mi ^ п\ элементов
первого типа, Ш2 ^ П2 второго типа,..., т* ^ п^ элементов fc-ro
типа, т\ +... + rrik = m, обозначают P(mi,... ,mfc).
Определение 2.4. Рассмотренный способ выбора элемен-
элементов называют гипергеометрической схемой, а совокуп-
совокупность вероятностей P(mi,... ,mk) в гипергеометрической схеме
при фиксированных n, m, щ, г = 1, fc, и различных ш^, г = 1, А;,
mi +... + rrik = ш, называют гипергеометрическим распре-
распределением.
Теорема 2.7. Вероятности P(mi,... ,m^) в гипергеометри-
ческой схеме определяют по формуле
< Поскольку порядок выбора элементов не существен, то при
определении общего числа элементарных исходов и числа бла-
благоприятствующих исходов будем пользоваться формулой для
числа сочетаний (см. теорему 2.3). Общее число элементарных
исходов есть число сочетаний из п элементов по т, т.е. С?\ Да-
Далее mi элементов первого типа можно выбрать C^J1 способами,
2.3. Геометрическое определение вероятности 55
Ш2 элементов второго типа — С™2 способами,..., т* элементов
fc-ro типа — C™kk способами. При этом любой способ выбора
элементов определенного типа можно комбинировать с любыми
способами выбора элементов остальных типов. Значит, в силу
основной формулы комбинаторики (см. теорему 2.1) число бла-
благоприятствующих событию А исходов равно С™ХХС™22...C™kk.
Поэтому
rjrni ПГП2 Г}ГПк
что и доказывает теорему. >
Пример 2.8. Из колоды в 36 карт наудачу извлекают 10
карт. Найдем вероятность Р{А) того, что среди выбранных
карт окажутся четыре карты пиковой масти, три — трефовой,
две — бубновой и одна — червовой. Для этого воспользуемся
гипергеометрической схемой, в которой п = 36, п\ = п<ъ = пз = 9,
т\ = 4, Ш2 = 3 тз = 2, 7714 = 1- Следовательно,
«о,ОО91. #
36
Во многих случаях вычисление вероятности по схеме клас-
классической вероятности удобно проводить с помощью условной
вероятности, которую мы введем в следующей главе.
2.3. Геометрическое определение вероятности
Геометрическое определение вероятности обобщает класси-
классическое на случай бесконечного множества элементарных ис-
исходов П тогда, когда п представляет собой подмножество про-
пространства R (числовой прямой), R2 (плоскости), Rn (п-мерного
евклидова пространства).
В пространстве R в качестве подмножеств будем рассма-
рассматривать лишь промежутки или их объединения, т.е. подмно-
подмножества, которые имеют длину. В пространстве R2 — те под-
подмножества, которые имеют площадь, и т.д.
56 2. ВЕРОЯТНОСТЬ
Под мерой ц(А) подмножества А будем понимать его длину,
площадь или объем (обобщенный объем) в зависимости от того,
какому пространству принадлежит ?2: в R, в Е2 или в R3 (Rn).
Будем также считать, что пространство элементарных исходов
?2 имеет конечную меру, а вероятность попадания „ случайно
брошенной" точки в любое подмножество ft пропорциональна
мере этого подмножества и не зависит от его расположения и
формы. В этом случае говорят, что рассматривается „геоме-
„геометрическая схема" или „точку наудачу бросают в область пи.
Определение 2.5. Вероятностью события А называ-
называют число P(j4), равное отношению меры множества А к мере
множества П:
где ц{А) — мера множества А.
Данное определение вероятности события принято назы-
называть геометрическим определением вероятности.
Заметим, что в литературе вероятность события А, опре-
определенную выше, на основе геометрической схемы, часто
называют геометрической вероятностью.
Геометрическая вероятность, очевидно, сохраняет отмечен-
отмеченные ранее свойства вероятности Т?(А) в условиях классической
схемы.
Замечание 2.5. Приведенное определение геометриче-
геометрической вероятности с математической точки зрения не является
корректным, поскольку в n-мерном пространстве существуют
подмножества, не имеющие меры. Поэтому для строгости необ-
необходимо в качестве событий А рассматривать только элементы
борелевской а-алгебры 93 (см. 1.3), что, впрочем, более чем до-
достаточно для практических потребностей.
Пример 2.9. Ромео и Джульетта договорились встретить-
встретиться в определенном месте между двенадцатью часами и часом
2.3. Геометрическое определение вероятности
57
дня. Необходимо найти вероятность встречи, если приход ка-
каждого из них в течение указанного часа происходит наудачу,
причем известно, что Ромео ждет Джульетту ровно 20 минут,
а Джульетта Ромео — 5 минут.
Для решения задачи вос-
воспользуемся геометрической схе-
схемой вероятности. Обозначим
момент прихода Ромео через
ж, а Джульетты через у. Тогда
любой элементарный исход и
в данной задаче можно ото-
отождествить с некоторой точкой
(х; у) на плоскости хОу. Вы- рис# 2.1
берем за начало отсчета 12 ча-
часов, а за единицу измерения 1 минуту и построим на плоскости
хОу пространство элементарных исходов п. Очевидно, что это
будет квадрат со стороной 60 (рис. 2.1). Событие А (Ромео и
Джульетта встретятся) произойдет тогда, когда разность у — х
не превысит t\ = 20, а разность х — у не превысит <2 == 5, т.е.
условие встречи определяет систему неравенств
х-у
Область А элементарных исходов, благоприятствующих этому
событию, на рис. 2.1 заштрихована. Бе площадь Sa равна
площади квадрата без двух угловых треугольников, т.е.
= 1287,5.
Тогда, согласно определению 2.5, находим
_ gA _ 1287,5 _
n~ 3600 ~°'36-
58 2. ВЕРОЯТНОСТЬ
2.4. Статистическое определение вероятности
В основе статистического определения вероятности лежит
общий принцип, в соответствии с которым методы теории
вероятностей применимы только к таким испытаниям, кото-
которые могут быть, по крайней мере теоретически, повторены
бесконечное число раз, и при этом имеет место свойство устой-
устойчивости частот появления связанных с этими испытаниями
событий (см. Введение).
Пусть произведено п повторений опыта, причем в па из
них появилось событие А. Обозначим га = пл/п наблюденную
частоту события А. Практика показывает, что в тех экспери-
экспериментах, для которых применимы методы теории вероятностей,
частота события А с увеличением числа опытов п стабилизиру-
стабилизируется, т.е. стремится к некоторому пределу (допуская некоторую
вольность речи).
Определение 2.6. Вероятностью события А на-
называют (эмпирический) предел Р(-А), к которому стремится
частота га события А при неограниченном увеличении числа п
опытов.
Данное определение вероятности события принято назы-
называть статистическим определением вероятности.
Можно показать, что при статистическом определении ве-
вероятности события сохраняются свойства вероятности собы-
события, справедливые в условиях классической схемы, т.е.
2) Р(П) = 1;
3) Р(А + В) = Р(А) + Р(Б), если АВ = 0.
С практической точки зрения статистическое определение
вероятности является наиболее разумным. Однако с позиции
теории вероятностей как раздела современной математики не-
недостаток статистического определения очевиден: нельзя прове-
провести бесконечное число повторений опыта, а при конечном числе
2.5. Аксиоматическое определение вероятности 59
повторений наблюденная частота, естественно, будет разной
при различном числе повторений.
Заметим, что связь между классическим и статистическим
определениями была выявлена еще в период становления теории
вероятностей как теории азартных игр. Было установлено,
что при корректном использовании классического определения
вероятность событий практически совпадает с их частотами
при большом числе повторений эксперимента.
И хотя игроков интересовала частота определенных собы-
событий, решение задач, полученное на основе классического опре-
определения вероятности, их вполне устраивало. Иными словами,
даже игроки азартных игр знали о совпадении статистическо-
статистического определения с другими (классическим и его обобщением —
геометрическим).
Собственно говоря, задача определения связи вероятности
с частотой не потеряла актуальности и в наши дни, когда в те-
теории вероятностей повсеместно используется аксиоматическое
определение вероятностей Колмогорова (см. 2.5). Это приве-
привело к появлению и широкому внедрению в практику обширного
раздела теории вероятностей — математической статистики.
2.5. Аксиоматическое определение вероятности
Для того чтобы понять смысл аксиоматического опре-
определения вероятности, рассмотрим классическую схему.
В этом случае вероятность любого элементарного исхода
1
Вероятность любого события А при этом равна Р(А) =
= Na/N, где Na — число исходов, благоприятствующих собы-
событию А.
Вероятность P(j4) можно записать также в следующем виде
Р(А) =
60 2. ВЕРОЯТНОСТЬ
где суммирование ведется по всем значениям индекса г, при
которых элементарные исходы cj» образуют событие А.
Однако задать вероятность события по такому принципу
уже в случае геометрической схемы нельзя, так как при этом
вероятность любого элементарного события равна нулю.
Поэтому следует дать определение вероятности события
для любого пространства элементарных исходов п, не связан-
связанное с вероятностями элементарных исходов, а учитывающее
те свойства вероятностей событий, которые имеют место для
всех предыдущих определений (классического, геометрическо-
геометрического, статистического).
Напомним, что этими свойствами являются следующие:
2) Р(П) = 1;
3) Р(Аг + ... + Ат) = P(Ai) + ... + Р(Ат), если события
ill, •••> Am попарно несовместны.
Именно эти три свойства лежат в основе аксиоматического
определения вероятности. При этом свойство 3 постулиру-
постулируется для суммы счетного множества попарно несовместных
событий.
Определение 2.7. Пусть каждому событию А (т.е. под-
подмножеству А пространства элементарных исходов ft, принад-
принадлежащему а-алгебре 95) поставлено в соответствие число Т?(А).
Числовую функцию Р (заданную на а-алгебре 95) называют
вероятностью (иливероятностной мерой), если она удо-
удовлетворяет следующим аксиомам:
Аксиома 1 (аксиома неотрицательности): Р(А) ^0;
Аксиома 2 (аксиома нормированности): P(ft) = 1;
Аксиома 3 (расширенная аксиома сложения): для лю-
любых попарно несовместных событий А\,..., Апу ... справедливо
равенство
Значение Р(А) называют вероятностью события А.
2.5. Аксиоматическое определение вероятности 61
Замечание 2.6. Если пространство элементарных исходов
п является конечным или счетным множеством, то каждому
элементарному исходу ^Gfi, i = 1,2,..., можно поставить в
соответствие число P(u>i) =Pi ^ 0 так, что
М = f> = 1.
г=1
Тогда для любого события А С ft в силу аксиомы 3 вероят-
вероятность Р(А) равна сумме вероятностей P(ui) всех тех элемен-
элементарных исходов, которые входят в событие А, т.е.
Таким образом, мы определили вероятность любого собы-
события, используя вероятности элементарных исходов. Заметим,
что вероятности элементарных исходов можно задавать совер-
совершенно произвольно, лишь бы они были неотрицательными и в
сумме составляли единицу. Именно в этом и состоит идея ак-
аксиоматического определения вероятности. #
В следующей теореме докажем утверждения, описывающие
ряд полезных свойств вероятности.
Теорема 2.8. Вероятность удовлетворяет следующим свой-
свойствам.
1. Вероятность противоположного события
2. Вероятность невозможного события
Р@) = О.
3. Если А С В, то
(„большему" события соответствует большая вероятность).
62 2. ВЕРОЯТНОСТЬ
4. Вероятность заключена между 0 и 1:
5. Вероятность объединения двух событий
6. Вероятность объединения любого конечного числа собы-
событий
-... - Р(Ап-г Ап) +
+ Р(А1А2А3) + ... + (-l)n+lP(Al A2 ...An).
•4 Поскольку
то, согласно расширенной аксиоме сложения,
Р(П)=Р(Л) + РA),
откуда с учетом аксиомы нормированности получаем утвер-
утверждение 1.
Утверждение 2 вытекает из равенства
и расширенной аксиомы сложения.
Пусть А С В. Тогда
В = А + (В\А).
В соответствии с расширенной аксиомой сложения
2.5. Аксиоматическое определение вероятности 63
Отсюда и из аксиомы неотрицательности приходим к утвер-
утверждению 3.
В частности, так как всегда А С ft, то с учетом аксиомы
неотрицательности получаем утверждение 4.
Поскольку
то, используя расширенную аксиому сложения, находим
P(AUB)=
и
Р(В)=Р(В\А)+Р(АВ).
Подставляя в первое из последних двух равенств вероятность
Р(В \ А), выраженную из второго равенства, приходим к
утверждению 5.
Утверждение 6 можно доказать с помощью метода матема-
математической индукции по п. Так, для трех событий А, В и С
= P(A)+P{BUC)-P(A(BUC)) =
= Р(А) + Р(В) + Р(С) - Р(ВС) - Р(АВ U АС) =
= Р(А) + Р(В)+Р(С)-Р(ВС)-Р(АВ)-
Для четырех и более событий это утверждение проверьте
самостоятельно. >
Замечание 2.7. Утверждения 5 и 6 называют теоремами
сложения вероятностей для двух и для п событий соответ-
соответственно.
Приведем пример, показывающий, что без учета того,
что события совместные, можно прийти к неправильному
результату.
64 2. ВЕРОЯТНОСТЬ
Пример 2.10. Опыт состоит в двукратном подбрасывании
симметричной монеты. Найдем вероятность события А, озна-
означающего появление „герба" хотя бы один раз. Обозначим А{
появление „герба" при i-м подбрасывании, г = 1,2. Ясно, что
и в соответствии с классической схемой вероятности
Если не учитывать, что А\ и А2 — совместные события, то
можно получить „результат"
= + = l,
противоречащий здравому смыслу, поскольку ясно, что собы-
событие А не является достоверным. Применяя теорему сложения
для двух совместных событий и учитывая равенство
Р(А1А2) = \,
находим
Р(А) = P(A0 + Р(А2) - Р(АгА2) = I + i-I = | #
Иногда вместо аксиомы 3 удобно использовать две другие
аксиомы.
Аксиома 3; (аксиома сложения): для любых попарно
непересекающихся событий А\, ..., Ап справедливо равенство
Аксиома 4 (аксиома непрерывности): если последо-
последовательность событий j4i, ..., Ап, ... такова, что AncAn+i,
neN, и
А\ U... U An U... = А,
2.5. Аксиоматическое определение вероятности 65
то
Можно доказать, что аксиомы 3' и 4 в совокупности равно-
равносильны аксиоме 3.
Покажем, как конструктивно можно задать вероятность
для некоторых наиболее часто встречающихся на практике
пространств элементарных исходов, содержащих бесконечное
число элементарных исходов.
Пусть п содержит счетное множество элементарных исхо-
исходов их, ..., u;n, ... В этом случае любую вероятностную меру Р
можно получить, задав вероятности
элементарных исходов, где последовательность pi, ..., рп,
должна удовлетворять только условиям неотрицательности
Pi > О, г е N,
и нормированности
оо
т.е. J2 Pi является знакоположительным числовым рядом, сум-
г=1
ма которого равна единице. Вероятность любого события А
равна сумме Х^Рг вероятностей всех входящих в А элементар-
элементарных ИСХОДОВ Ш{.
Предположим теперь, что пространство элементарных ис-
исходов Q представляет собой числовую прямую (—оо, +оо) с
борелевской a-алгеброй на ней. Для задания вероятностной
меры на числовой прямой можно взять произвольную неубы-
неубывающую для любого жЕК непрерывную слева функцию F(x),
удовлетворяющую условиям
F(-oo)= lim F(z) = 0, F(+oo)= lim F{x) = 1,
3 - 10047
66 2. ВЕРОЯТНОСТЬ
и каждому событию Ах = (—оо, х) поставить в соответствие
вероятность
а событию А = [х\, жг) — вероятность
Найденная таким образом для всех событий А = [я^зд)
числовая функция Р(А) будет удовлетворять аксиомам в опре-
определении 2.7. Для других событий из борелевской а-алгебры
на числовой прямой, вероятность определяется единственным
образом с помощью так называемой теоремы о продолжении
меры, формулировку и доказательство которой можно найти в
специальной литературе*.
Определение 2.8. Тройку (ft, 2$, Р), состоящую из про-
пространства элементарных исходов ?2, с а-алгеброй событий 93
и определенной на 93 вероятности Р, называют вероятност-
вероятностным пространством.
Таким образом, понятие вероятностного пространства объ-
объединяет хорошо известные физические понятия: исход опыта,
событие, вероятность события.
2.6. Решение типовых примеров
Пример 2.11. Куб с окрашенными гранями распилен на
27 одинаковых кубиков. Найдем вероятность того, что у
выбранного наудачу кубика будет окрашена одна грань (две
грани, три грани).
Общее число элементарных исходов в данном опыте N =
= 27. Обозначим: А — событие, заключающееся в том, что у
выбранного кубика окрашена одна грань; В — две грани и С —
*См., например, Лоэв М. Теория вероятностей. М.: Изд-во иностр. лит.,
1962.
2.6. Решение типовых примеров 67
три грани. Событию А благоприятствует Na = 6 элементарных
исходов (число граней у исходного куба), событию В — Nb = 12
исходов (число ребер у исходного куба), а событию С — 8
исходов (число вершин у исходного куба). Поэтому
Пример 2.12. Из 33 карточек с написанными на них раз-
различными буквами русского алфавита наугад извлекаются пять
карточек и располагаются слева направо в порядке извлечения.
Найдем вероятность появления слова „РАДИО" (событие А).
Поскольку карточки обратно не возвращаются и порядок
выбора существен, то общее число элементарных исходов равно
числу размещений без повторений из 33 элементов по пять
элементов:
N = А1г = 28480320.
Событию А благоприятствует только один элементарный исход
(Na = 1). Значит,
3510"8
Пример 2.13. Из колоды в 52 игральные карты выбирают
наудачу три карты. Найдем вероятность того, что среди этих
карт будут тройка „пик", семерка „пик", туз „пик".
Поскольку порядок выбора в данном случае не существен
и карты обратно в колоду не возвращаются, то число элемен-
элементарных исходов равно числу сочетаний без повторений из 52
элементов по три элемента, т.е.
N = С|2 = 22100.
Рассматриваемому событию А благоприятствует единствен-
единственный исход (Na = 1). Поэтому
68 2. ВЕРОЯТНОСТЬ
Пример 2.14. Группа, состоящая из восьми человек, зани-
занимает место за круглым столом. Найдем вероятность того, что
два определенных человека окажутся сидящими рядом.
Так как упорядочивается все множество из восьми элемен-
элементов, то мы имеем дело с перестановкой из восьми элементов.
Поэтому
N = Р8 = 8!
Рассматриваемому событию А благоприятствуют такие пере-
перестановки, когда два отмеченных лица садятся рядом: всего
восемь различных пар мест за столом и за каждую пару мест
данные лица могут сесть двумя способами. При этом осталь-
остальные шесть человек могут разместиться на оставшихся местах
произвольно. Значит,
и
~«0,29.
Для сравнения приведем еще одно решение поставленной за-
задачи. Заметим, что поскольку нас интересуют только два опре-
определенных лица, то порядок размещения остальных не играет
роли. В свою очередь, если первый человек сел на определенное
место, то второй может сесть на оставшиеся семь мест. При
этом в двух случаях оба лица окажутся рядом и
\
Пример 2.15. Из десяти первых букв русского алфави-
алфавита составлены всевозможные трехбуквенные „слова". Найдем
вероятность того, что случайно выбранное „слово" окажется
„словом" „ИИИ".
2.6. Решение типовых примеров 69
Число различных „слов" равно числу размещений с повто-
повторениями из 10 элементов по три элемента, т.е.
Поскольку благоприятствующий исход только один, то
Р(А)= 0,001.
Пример 2.16. Опыт состоит в четырехкратном случайном
выборе С возвращением одной буквы из букв алфавита „А",
„Б", „К", „О" и „М" и записывании результата выбора слева
направо в порядке поступления букв. Найдем вероятность того,
что в результате будет записано слово „МАМА".
Число элементарных исходов равно числу размещений с
повторениями из пяти элементов по четыре элемента, т.е.
ЛГ = Л| = б4.
Слову „МАМА" соответствует лишь один исход. Поэтому
Пример 2.17. В урне имеются четыре шара различного
цвета. Наудачу из урны извлекают шар и после определения
его цвета возвращают обратно. Найдем вероятность того, что
среди восьми выбранных шаров будут только шары одного
цвета (событие А)? будет по два шара разного цвета (собы-
(событие В).
Число элементарных исходов равно числу размещений
с повторениями из четырех элементов по восемь элементов.
Для того чтобы найти число исходов, благоприятствующих
событию А, предположим сначала, что вынимают только шары
70 2. ВЕРОЯТНОСТЬ
первого цвета. Это можно сделать только одним способом.
Аналогично только одним способом можно выбрать шары
второго, третьего и четвертого цветов. Поэтому Na = 4 и
Р(А) = ^ «0,00061.
Число исходов, благоприятствующих событию В, равно числу
тех сочетаний с повторениями из четырех элементов по восемь
элементов, в которых каждый элемент повторяется по два раза,
т.е.
NB = СB,2,2,2) = 2520.
Значит,
?р° «0,0385.
Пример 2Л8. Первенство по баскетболу оспаривают
18 команд, которые путем жеребьевки распределены на две
подгруппы по девять команд в каждой. Пять команд обычно
занимают первые места. Найдем вероятность попадания всех
лидирующих команд в одну подгруппу (событие А); трех
лидирующих команд в одну подгруппу, а двух — в другую
(событие J5).
Пространство элементарных исходов в данном случае со-
состоит из всевозможных способов выбрать из 18 команд, среди
которых пять лидирующих, девять команд в первую подгруппу
(тогда вторую подгруппу будут составлять оставшиеся девять
команд), причем события А и В происходят тогда, когда в
первую подгруппу попадет определенное число лидирующих
команд и команд аутсайдеров. Значит, мы имеем дело с гипер-
гипергеометрической схемой, в которой А; = 2, п = 18, п\ = 5, т = 9.
Событие А происходит тогда, когда в первую подгруппу
попадают или пять лидирующих команд и четыре команды-
аутсайдера (mi =5, Ш2 = 4), или девять команд-аутсайдеров
(mi = 0, гиг = 9). Значит,
Р(А) = Р(б, 4) + Р@, 9) = C|C*3CV^3 = ^ * °'029'
2.6. Решение типовых примеров
71
Аналогично событие В происходит тогда, когда в первую
подгруппу попадут или три лидирующие команды и шесть
команд-аутсайдеров (mi =3, Ш2 = 6) или две лидирующие
команды и семь команд-аутсайдеров (mi =2, rri2 = 7). Таким
образом,
Р(В) = РC,6) + РB, 7) =
'18
а-г —
Пример 2.19. На бесконечную шахматную доску со сто-
стороной квадрата а наудачу бросают монету радиуса г, г < а/2.
Найдем вероятность того, что монета попадет целиком внутрь
одного квадрата.
Пусть (х;у) — координаты
центра упавшей монеты. В силу
бесконечности шахматной дос-
доски можно считать, что элемен-
элементарные исходы данного экспери-
эксперимента полностью определяются
положением центра упавшей мо-
монеты относительно вершин ква-
квадрата, содержащего этот центр.
Помещая начало координат в од-
одну из вершин указанного квад-
квадрата (рис. 2.2), можно записать множество элементарных исхо-
исходов в виде
ft = {(х;у): О^х^а, О^у^а}.
Область А, соответствующая рассматриваемому событию, име-
имеет вид
А = {(х;у): г ^х ^а-r, г^у^а-г},
т.е. является квадратом со стороной а — 2г. В соответствии с
формулой геометрической вероятности находим
(а-2гJ
a-r r
Рис. 2.2
М(П)
72
2. ВЕРОЯТНОСТЬ
Пример 2.20, В любые моменты интервала времени Т
равновозможны поступления в приемник двух независимых сиг-
сигналов. Сигналы искажаются, если разность между моментами
их поступления меньше т. Опре-
Определим вероятность того, что сиг-
сигналы будут искажены.
Изобразим случайные момен-
моменты t\ и <2 поступления сигналов в
приемник в виде точки на плоско-
плоскости с координатами (ж; у). Обла-
Областью возможных значений явля-
является квадрат площадью /х(ГХ) =
= Т2 (рис. 2.3). Сигналы будут
искажены, если \t\ — *г| ^ т. Эта
область лежит между прямыми
Рис. 2.3
*2 ~ *1 = т и t\ — *2 = —т. Площадь ее равна
ц(А)=Т2-(Т-тJ.
Следовательно,
Р(А) =
Г2
Т2
Вопросы и задачи
2.1. Приведите классическое определение вероятности.
2.2. Напишите основную формулу комбинаторики.
2.3. Что называют выбором с возвращением? без возвра-
возвращения?
2.4. Что называют сочетанием? размещением? переста-
перестановкой?
Вопросы и задачи 73
2.5. Приведите формулы для числа сочетаний и размещений
из п элементов по т элементов с поторениями и без повторений
и для числа перестановок из п элементов.
2.6. Чему равно число размещений с повторениями из п эле-
элементов по га элементов, в которых первый элемент встречается
ровно mi раз, второй элемент — m*i раз, ..., гс-й элемент —
тп раз?
2.7. Что называют гипергеометрической схемой? Напиши-
Напишите формулу, используя которую можно вычислить вероятности
событий в гипергеометрической схеме.
2.8. Приведите геометрическое определение вероятности.
2.9. Приведите статистическое определение вероятности.
2.10. Дайте аксиоматическое определение вероятности.
2.11. Перечислите основные свойства вероятности.
2.12. Как можно задать вероятность в случае конечного
пространства элементарных исходов? счетного пространства
элементарных исходов?
2.13. Как можно задать вероятность на числовой прямой?
2.14. Что называют вероятностным пространством?
2.15. У человека имеется N ключей, из которых только
один подходит к его двери. Он последовательно испытывает
их, выбирая случайным образом (без возвращения). Найдите
вероятность того, что этот процесс закончится на fc-м испыта-
испытании k^N.
Ответ: Р = 1/ЛГ.
2.16. Из десяти первых букв русского алфавита выбирают
наудачу без возвращения четыре буквы и записывают в порядке
поступления слева направо. Какова вероятность того, что
составленное „слово" будет оканчиваться на букву „А"?
Ответ: Р = 1/10.
74 2. ВЕРОЯТНОСТЬ
2.17. Из шести карточек с буквами „Л", „И", „Т", „Е",
„Р", „А" выбирают наугад в определенном порядке четыре.
Найдите вероятность того, что при этом получится слово
„ТИРЕ".
О т в е т: Р = \/А\ « 0,0028.
2.18. Набирая номер телефона, абонент забыл две последние
цифры и, помня лишь то, что эти цифры различны, набрал их
наугад. Определите вероятность того, что набраны нужные
цифры.
Ответ: Р = 1/А?0 «0,011.
2.19. При наборе телефонного номера абонент забыл две
последние цифры и набрал их наудачу, помня только, что эти
цифры нечетные и разные. Найдите вероятность того, что
номер набран правильно.
Ответ: Р = 1/А§ = 0,05.
2.20. Среди 25 экзаменационных билетов пять „хороших".
Три студента по очереди берут по одному билету. Найдите
вероятности следующих событий: А — третий студент взял
„хороший" билет; В — все три студента взяли „хороший"
билет.
О т в е т: Р(А) = 5/25; Р(В) = 1/230 « 0,0044.
2.21. В урне пять белых и четыре черных шара. Из урны
в случайном порядке извлекают все находящиеся в ней шары.
Найдите вероятность того; что вторым по порядку будет вынут
белый шар.
Ответ: Р = 5/9«0,56.
2.22. Кодовые комбинации содержат пять различных цифр
от 1 до 5. Какова вероятность того, что цифры в случайным
образом выбранной кодовой комбинации образуют последова-
последовательность 1, 2, 3, 4, 5?
Ответ: Р = 1/5! и0,0083.
2.23. Из урны, содержащей 10 перенумерованных шаров,
наугад выбирают один за другим все находящиеся в ней шары.
Вопросы и задачи 75
Найдите вероятность того, что все номера вынутых шаров
будут идти по порядку.
О т в е т: Р = 1/10! « 2,8 • НГ7.
2.24. В шкафу находятся 10 пар ботинок. Из них наугад
выбирают четыре ботинка. Найдите вероятность того, что
среди выбранных ботинок отсутствуют парные.
О т в е т: Р = 24С?0/С|0 « 0,69.
2.25. Из урны, содержащей шары с номерами 1, 2, ..., 9,
пять раз наугад вынимают шар и каждый раз возвращают
обратно. Найдите вероятность того, что из номеров шаров
можно составить возрастающую последовательность.
О т в е т: Р = С|/95 « 0,0021.
2.26. В лифт семиэтажного дома на первом этаже вошли
три человека. Каждый из них случайным образом может выйти
на любом из этажей, начиная со второго. Найдите вероятности
следующих событий: А — все пассажиры выйдут на четвертом
этаже; В — все пассажиры выйдут на одном и том же этаже;
С — все пассажиры выйдут на разных этажах.
Ответ: Р(А) = 1/63 « 0,0046; Р(В) = 6/63 « 0,028; Р(С) =
= А3/63«0,56.
2.27. Какова вероятность того, что в группе изп(п< 365)
случайно отобранных студентов хотя бы у двоих окажется один
и тот же день рождения?
Ответ: Р = 1-Л?65/365П.
2.28. Найдите вероятность того, что дни рождения 12
случайным образом выбранных человек придутся на разные
месяцы года.
О твет: Р = 12I/1212 « 5,4 -НГ6.
2.29. Десять студентов договорились о поездке за город, но
не договорились о вагоне. Любой из студентов наугад может
сесть в любой из десяти вагонов поезда. Какова вероятность
того, что они все попадут в разные вагоны?
Ответ: Р = 10I/1010 «0,00036.
76 2. ВЕРОЯТНОСТЬ
2.30. В отделение связи поступило шесть телеграмм. Те-
Телеграммы случайным образом распределяют по четырем ка-
каналам, причем каждая телеграмма может быть передана по
любому из четырех каналов. Найдите вероятность того, что
на первый канал попадут три телеграммы, на второй — две
телеграммы, на третий — одна телеграмма и четвертый канал
не будет загружен.
Ответ: Р = СC,2,1,0)/44 «0,23.
2.31. Чему равна вероятность того,что дни рождения шести
наугад выбранных человек придутся в точности на два месяца?
О т в е т: Р = С?2 [(A/6N - 2A/12N] « 0,000092.
2.32. В партии из 50 изделий четыре нестандартных. Опре-
Определите вероятность того, что среди выбранных наугад 10 из-
изделий есть хотя бы одно нестандартное.
Ответ: Р = 1 -С%С$/С$ «0,60.
2.33. На стелаже в библиотеке стоят 15 учебников, причем
пять из них в переплете. Библиотекарь берет наудачу три
учебника. Найдите вероятность того, что хотя бы один из
взятых учебников окажется в переплете.
Ответ: Р = 1 -<ВД0/С?5 «0,74.
2.34. Колоду из 52 карт случайным образом делят пополам.
Найдите вероятность того, что в каждой половине будет по два
„туза".
Ответ: Р = CjCg/Cgf «0,39.
2.35. Какова вероятность того, что среди выбранных нау-
наудачу четырех карт из колоды в 52 карты ровно две окажутся
трефовой масти?
Ответ: Р = С$3С$9/С?2 «0,39.
2.36. Некто купил карточку „Спортлото 6 из 49" и отметил
в ней шесть из имеющихся 49 номеров. В тираже разыгры-
разыгрываются шесть „выигрышных" номеров. Найдите вероятности
Вопросы и задачи 77
следующих событий: А$ — угадано три номера; А\ — угада-
угадано четыре номера; А*> — угадано пять номеров; Aq — угадано
шесть номеров.
Ответ:
Р(А3) = С63С433/С469 »0,018; Р(А4) = С64С423/С469 а0,00097;
5165 6068
2,37, Из колоды в 32 карты наугад выбирают четыре карты.
Найдите вероятности того, что среди них окажется: один „туз"
(событие А); хотя бы один „туз" (событие В); хотя бы один
„туз" и обязательно „туз пик" (событие С).
О т в е т: Р(А) = С\СЫС& » 0,36; Р(В) = 1 - <^С|8/С342 « 0,43;
С342« 0,125.
2.38. Стержень длиной / ломают на три части, причем
точки разлома выбирают наудачу. Найдите вероятность того,
что из получившихся частей можно составить треугольник.
Ответ: Р = 1/4 = 0,25;
2.39. Два приятеля условились встретиться в определенном
месте между двумя и тремя часами дня. Пришедший первым
ждет другого в течение 10 минут, после чего уходит. Чему
равна вероятность встречи приятелей, если приход каждого из
них в течение указанного часа может произойти в любое время?
Ответ: Р= 11/36 «0,31.
3. УСЛОВНАЯ ВЕРОЯТНОСТЬ.
СХЕМА БЕРНУЛЛИ
Рассмотрим события А и Б, связанные с одним и тем же
опытом. Пусть из каких-то источников нам стало известно,
что событие В наступило, но не известно, какой конкретно из
элементарных исходов, составляющих событие В, произошел.
Что можно сказать в этом случае о вероятности события А?
Вероятность события А, вычисленную в предположении,
что событие В произошло, принято называть условной веро-
вероятностью и обозначать Т*(А\В).
Понятие условной вероятности играет важнейшую роль в
современной теории вероятностей. Условная вероятность по-
позволяет учитывать дополнительную информацию при определе-
определении вероятности события. В ряде случаев при помощи условной
вероятности можно существенно упростить вычисление вероят-
вероятности. Понятию условной вероятности и посвящена настоящая
глава.
3.1. Определение условной вероятности
Предположим сначала, что мы находимся в рамках класси-
классической схемы. Пусть событиям Аи В благоприятствуют Na
и Nb элементарных исходов соответственно. Посмотрим, что
дает нам имеющаяся информация о событии В. Поскольку со-
событие В произошло, то достоверно известно, что в результате
опыта появился один из Nb элементарных исходов, составля-
составляющих событие В. Значит, теперь уже при определении сте-
степени возможности события А необходимо выбирать только из
Nb возможных исходов, причем событию А благоприятствуют
Nab исходов, при которых происходят и событие А, и собы-
3.1. Определение условной вероятности 79
тие В, или, другими словами, происходит событие АВ. При
этом по-прежнему будем считать все Nb входящих в событие В
исходов равновероятными. Поэтому условную вероятность
Р(А\В) события А при условии события В в рамках классиче-
классической схемы вероятности естественно определить как отношение
числа Nab исходов, благоприятствующих совместному осуще-
осуществлению событии А и В, к числу Nb исходов, благоприятству-
благоприятствующих событию В, т.е.
Бели теперь поделить числитель и знаменатель полученного
выражения на общее число N элементарных исходов, то придем
к формуле
Обратимся теперь к статистическому определению вероят-
вероятности.
Пусть п — общее число экспериментов; па — число экс-
экспериментов, в которых наблюдалось событие А; пв — число
экспериментов, в котрых наблюдалось событие В, пав — число
экспериментов, в которых наблюдалось событие АВ. Напо-
Напомним, что частота события А — это отношение
пА
Условной частотой события А при условии, что В про-
произошло (будем обозначать ее га\в) естественно назвать частоту
события Ау но только не среди всех повторений опыта п, а лишь
среди тех, в которых наблюдалось событие В, т.е.
пав
1 пв
Последнее выражение можно представить в виде
пв/п
80 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
При п -? оо, согласно определению 2.6 статистической веро-
вероятности, tab ->• P(-AU), г в -* Р(-В) и, следовательно, условная
частота
т.е. условной вероятностью события А при условии события В
естественно назвать число Р(А\В) = P(AB)/P(J3).
Таким образом, мы пришли к тому же самому выражению,
что и в случае классической схемы.
На основании изложенного выше можно дать следующее
определение.
Определение 3.1. Условной вероятностью события
А при условии (наступлении) события В называют отношение
вероятности пересечения событий А и В к вероятности собы-
события В:
Ц^± C.1)
При этом предполагают, что Р(В) ф 0.
В связи с появлением термина „условная вероятность" будем
вероятность события называть также безусловной вероят-
вероятностью события.
Рассмотрим теперь условную вероятность P(j4|B) как функ-
функцию события А.
Теорема 3.1. Условная вероятность Р(А\В) обладает
всеми свойствами безусловной вероятности Р(-А).
< Для доказательства достаточно показать, что условная веро-
вероятность P(j4l|J3) удовлетворяет аксиомам 1, 2 и 3 (см. 2.5).
Из определения 3.1 следует, что условная вероятность, удо-
удовлетворяет аксиоме неотрицательности, так как числитель дро-
дроби является неотрицательным числом, а знаменатель — поло-
положительным числом.
3.1. Определение условной вероятности 81
Поскольку пВ = JB, то
Р(ад = ?№ = Ш = 1,
т.е. условная вероятность удовлетворяет аксиоме нормирован-
ности.
Наконец, пусть А\,..., Лп,... — попарно непересекающиеся
события. Тогда
и
где в последнем равенстве использовано свойство умножения
сходящегося ряда на постоянную. Следовательно, условная ве-
вероятность удовлетворяет расширенной аксиоме сложения 3. >
Смысл теоремы 3.1 заключается в том, что условная вероят-
вероятность представляет собой безусловную вероятность, заданную
на новом пространстве п\ элементарных исходов, совпадаю-
совпадающем с событием В.
Пример 3.1. Рассмотрим опыт с однократным бросанием
игральной кости, но не обычной, а с раскрашенными гранями:
грани с цифрами 1, 3 и 6 окрашены красным, а грани с
цифрами 2, 4 и 5 — белым цветом. Введем события: А\ —
выпадение нечетного числа числа очков; A<i — выпадение
четного числа очков; В — появление грани красного цвета.
82 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Интуитивно ясно, что если произошло событие J3, то условная
вероятность события А\ больше, чем условная вероятность
события Лг, поскольку на красных гранях нечетных чисел
в два раза больше, чем четных. Заметим, что безусловные
вероятности событий А\ и A*i при этом одинаковы и равны,
очевидно, 1/2.
Найдем условные вероятности событий А\ и Ач при условии
события В. Очевидно, что
)
Р<*В>-
Следовательно, в силу определения 3.1 условной вероятности
имеем
что подтверждает наше предположение.
Геометрическая интерпретация условной вероятно-
вероятности. При практическом вычислении условной вероятности со-
события А при условии, что событие В произошло, часто удобно
трактовать условную вероятность как безусловную, но задан-
заданную не на исходном пространстве п элементарных исходов, а
на новом пространстве Q\ = В элементарных исходов. Дей-
Действительно, используя геометрическое определение вероятно-
вероятности, получаем для безусловной и условной вероятностей со-
события А (на рис. 3.1 заштрихованная область соответствует
3.1. Определение условной вероятности
83
событию АВ):
Р(А\В) =
Sb
Здесь Sai Sn и т.д. обознача-
обозначают соответственно площади «А,
п и т.д. Таким образом, выра-
выражение для Р(А\В) будет совпа-
совпадать с выражением для Р(А),
вычисленным в соответствии со
схемой геометрической вероят-
вероятности, если исходное простран-
пространство п элементарных исходов
заменить новым пространством
Рис. 3.1
Пример 3.2. Из урны, в которой а = 7 белых и Ь = 3
черных шаров, наугад без возвращения извлекают два шара.
Пусть событие А\ состоит в том, что первый извлеченный из
урны шар является белым, а Аг — белым является второй шар.
Требуется найти P(-A2|Ai).
Приведем решение этой задачи двумя способами.
Первый способ. В соответствии с определением услов-
условной вероятности имеем (опуская пояснения):
Второй способ. Перейдем к новому пространству п\
элементарных исходов. Так как событие А\ произошло, то
это означает, что в новом пространстве элементарных исходов
всего равновозможных исходов
84 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
а событию A<i благоприятствует при этом
исходов. Следовательно,
Пример 3.3. Пусть событие В — выпадение 4 или б очков
на игральной кости, событие А\ — выпадение четного числа
очков, событие А2 — выпадение 3, 4 или 5 очков, событие А$ —
выпадение нечетного числа очков.
Найдем условные вероятности событий А\, А2 и А$ при
условии события В.
Так как событие В принадлежит событию А\^ то при
наступлении события В событие А\ обязательно произойдет,
т.е. событие А\ имеет условную вероятность
Поскольку события Аз и В несовместные, то при наступ-
наступлении события В событие As уже не может произойти и его
условная вероятность
Наконец, в соответствии с классической схемой вероятно-
вероятности приходим к следующему значению условной вероятности
события А2 при условии события В:
\.
Заметим, что условная вероятность события А2 при условии В
совпадает с безусловной вероятностью события А2.
3.2. Формула, умножения вероятностей 85
3.2. Формула умножения вероятностей
При решении различных задач вероятностного характера
часто интересующее нас событие А можно достаточно просто
выразить через некоторые события А\,А2^..., Ап с помощью
операций объединения или пересечения. Если А = А\А2...Ап,
то для нахождения вероятности Р(А) события А обычно
удобно использовать следующую теорему.
Теорема 3.2 (теорема умножения вероятностей). Бели
А = А\А2... Ап (т.е. А — пересечение событий А\^ Лг, ..., Ап)
и Р(А) > 0, то справедливо равенство
Р(А)=Р(А1)Р(А2\А1)Р(Аг\А1А2)...Р(Ап\А1А2...Ап-1),
называемое формулой умножения вероятностей.
< Поскольку Р(А) = P(AiА2... Ап) > 0, а
..Ak 2МА2...Ап (к = 1,п~1),
то и Р(-А) = P(Aii42...Afc) > 0. Учитывая это неравенство,
согласно определению 3.1 условной вероятности, имеем
Умножая обе части этого равенства на P(AiA2...An-i), полу-
получаем
Р(А1А2... Ап) =
Аналогично находим
P(i4iA2... Ап-х) = Р(АгА2... А„_2
Тогда
ЛЛ) Р(АЛЛ)Р(А|АА...АП_2) х
86 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Продолжая эту процедуру, получаем формулу умножения веро-
вероятностей. >
Замечание 3.1. Из свойства коммутативности пересече-
пересечения событий следует, что правая часть формулы умножения
для пересечения одних и тех же событий может быть записала
по-разному. Например, как
Р(А1А2)^Р(А1)Р(А2\А1),
так и в виде
Р(АХА2) = Р(А2Аг) = Р(А2)РША2).
Обычно выбирают тот вариант формулы, который приводит к
более простым вычислениям.
Пример 3.4. На семи карточках написаны буквы, образу-
образующие слово „СОЛОВЕЙ". Карточки перемешивают и из них
наугад последовательно извлекают и выкладывают слева на-
направо три карточки. Найдем вероятность того, что получится
слово „ВОЛ" (событие А).
Введем события: А\ — на первой выбранной карточке
написана буква „В"; А2 — на второй карточке — буква „О";
А$ — на третьей карточке — буква „Л". Тогда событие
А есть пересечение событий А\, A*i и А$. Следовательно, в
соответствии с формулой умножения вероятностей
= P(Al)P(A2\A1)P(A3\AlA2).
Согласно классическому определению 2.1 вероятности, имеем
p(^i)=\-
Бели событие А\ произошло, то на шести оставшихся кар-
карточках буква „О" встречается два раза, поэтому условная ве-
вероятность
Р(А2\Аг) = Н в 1.
3.3. Независимые и зависимые события 87
Аналогично определяем
Окончательно получаем
Р(А) = Р(АгА2Аг) = I ¦ 1 ¦ 7 = J^r « 0,0095.
3.3. Независимые и зависимые события
Из рассмотренных выше примеров видно, что условная ве-
вероятность Р(А\В) события А при условии, что событие В
произошло, может как совпадать с безусловной вероятностью
Р(Л), так и не совпадать, т.е. наступление события В может
влиять или не влиять на вероятность события А. Поэтому
естественно степень связи (или степень зависимости) событий
А и В оценивать путем сопоставления их условных вероятно-
вероятностей P(A|J3), P(B\A) с безусловными.
Определение 3.2. События Аи В, имеющие ненулевую
вероятность, называют независимыми, если условная вероят-
вероятность А при условии В совпадает с безусловной вероятностью
А или если условная вероятность В при условии А совпадает с
безусловной вероятностью В, т.е.
C.2)
или
Р(В|Л)=Р(В), C.3)
в противном случае события Аи В называют зависимыми.
Теорема 3*3. События А и В, имеющие ненулевую вероят-
вероятность, являются независимыми тогда и только тогда, когда
Р(АВ)=Р(А)Р(В). C.4)
88 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Ч Пусть выполнено равенство C.3). Воспользовавшись форму-
формулой умножения вероятностей для двух событий, получим
Р(АВ) = Р(А)Р{В\А) = Р(А)Р(В).
К аналогичному выводу приходим и в случае выполнения равен-
равенства C.2), т.е. из условия независимости событий следует C.4).
Обратно, пусть выполнено равенство C.4). Тогда, согласно
определению 3.1 условной вероятности,
т.е. в силу определения 3.2 события А и В независимы. >
Таким образом, в качестве эквивалентного определения не-
независимости двух событий, имеющих ненулевую вероятность,
может служить следующее определение.
Определение 3.3. События Am В называют независимы-
независимыми, если выполняется равенство C.4).
Отметим, что последним определением можно пользоваться
даже в том случае, когда вероятности событий А или В равны
нулю.
Замечание 3.2. Из теоремы 3.3 следует, что если в опре-
определении 3.2 независимости выполняется одно из равенств C.2)
или C.3), то выполняется автоматически и другое, т.е. в опре-
определении 3.2 достаточно потребовать выполнения любого одного
из них.
Пример 3.5. Из колоды карт, содержащей п = 36 карт,
наугад извлекают одну карту. Обозначим через А событие,
соответствующее тому, что извлеченная карта будет пиковой
3.3. Независимые и зависимые события 89
масти, а -В — событие, соответствующее появлению „дамы".
Определим, являются ли зависимыми события А и В.
После вычислений получаем
т.е. события А и В независимы. Как отмечалось в замеча-
замечании 3.2, имеет место и равенство
- *
Следовательно, события Аи В независимы.
Изменим теперь условия опыта, дополнительно добавив
в колоду, допустим, N = 100 „пустых" карт (без рисунка).
Изменится ли ответ? Имеем
т.е. безусловная вероятность события В уменьшилась. Однако
условная вероятность
Р(А) 9/136 9
не изменилась, т.е события Аи В стали зависимыми.
Теорема 3.4. Если события А и В независимые, то неза-
независимыми также являются пары событий А и В, Аи В, А и В,
если вероятности соответствующих событий ненулевые.
Ч В силу теоремы 3.1 и независимости событий Аи В имеем:
90 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
что означает независимость событий А и В. Независимость
остальных пар событий можно доказать аналогично. >
Определение 3.4. События А\, A<i, ..., Ап называют
независимыми в совокупности, если вероятность пересе-
пересечения любых двух различных событий равна произведению
вероятностей этих событий; вероятность пересечения любых
трех событий равна произведению их вероятностей; ...; ве-
вероятность- пересечения всех событий равна произведению их
вероятностей.
Для событий А\, -А2, ..., Ап, независимых в совокупности,
имеет место утверждение, аналогичное утверждению теоре-
теоремы 3.4.
Теорема 3.5, Если события А\, ^2, ..., Ап независимы
в совокупности, то и события А\, A2, ..., Ап независимы в
совокупности. #
Если только любые два события из данной совокупности
являются независимыми, то говорят о попарной независи-
независимости событий из этой совокупности.
Так же как и в случае двух событий, можно показать, что на
вероятность каждого из независимых в совокупности событий
не оказывает влияние появление или непоявление остальных
событий.
Замечание 3.3. В силу определения независимости собы-
событий в совокупности формула умножения вероятностей для не-
независимых в совокупности событий имеет вид
Р(А1А2...АП) = Р(Л1)Р(А2)...Р(АП). #
Из независимости событий с ненулевыми вероятностями в
совокупности, согласно теореме 3.3, следует их попарная неза-
независимость. Однако из попарной независимости, вообще говоря,
3.3. Независимые и зависимые события
независимость в совокупности не следует, что демонстрирует
следующий пример.
Пример 3.6. Опыт состоит в однократном подбрасывании
тетраэдра, грани которого „пронумерованы" следующим обра-
образом: на трех гранях стоят цифры 1, 2 и 3 соответственно (одна
цифра на каждой из них), а на четвертой присутствуют все
цифры 1, 2 и 3.
Введем события Аг — падение тетраэдра на грань, на
которой присутствует цифра г, г = 1,3. Покажем, что события
ill, Аг и As попарно независимы, но зависимы в совокупности.
Согласно классическому определению вероятности, полу-
получаем
1/4 1
2/4 = 2'
Аналогично
при любых г, j = 1,3, г ф j, т.е. события А\, Аг и As являются
попарно независимыми.
Однако, например,
т.е. события Ai, A<i и Аз зависимы в совокупности. #
Заметим, что, когда говорят о независимости событий
Ai, ..., Ап, подразумевают именно независимость событий в
совокупности, в отличие от попарной независимости событий
A\j ..., АЛ.
Запишем формулу для вероятности объединения независи-
независимых событий. Пусть
A = AiU...UAn.
92 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Тогда в соответствии с законом де Моргана
Если события Ai,..., Ап независимые, то, согласно теореме 3.5,
события «Ai, ..., Ап также независимые и, значит,
Отсюда окончательно получаем формулу для вероятности
объединения независимых событий:
Замечание 3.4 (о связи между совместными и зави-
зависимыми событиями). Между понятиями „несовместные" и
„независимые" события имеется следующая связь:
1) если А и В — несовместные события (и Р{А) ф О, и
P(J5) ф 0), то они обязательно зависимые (убедитесь самостоя-
самостоятельно);
2) если А и В — совместные события, то они могут быть
и зависимыми, и независимыми;
3) если А и В — зависимые события, то они могут быть
и совместными, и несовместными. #
Следует помнить, что при использовании теоремы сложе-
сложения вероятностей нужно проверять несовместность со-
событий, а при использовании теоремы умножения — не-
независимость событий.
В заключение отметим, что понятие независимости явля-
является очень важным в теории вероятностей. При этом следует
различать формальное понятие независимости событий, опре-
определяемое свойствами вероятностной модели, и понятие незави-
независимости событий, возникающее в прикладных задачах и озна-
означающее, что события не связаны причинно. При корректном
построении вероятностной модели второе трансформируется в
первое, но это может быть не всегда.
3.4. Формула полной вероятности 93
3.4. Формула полной вероятности
Предположим, что в результате опыта может произойти
одно из п событий Н\, H2, ..., Нп, которые удовлетворяют
следующим двум условиям:
1) они являются попарно несовместными, т.е.
HiHj = 0
при г ф j\
2) хотя бы одно из них обязательно должно произойти
в результате опыта, другими словами, их объединение есть
достоверное событие, т.е.
Определение 3.5. События Н\, #2? ..., Нп удовлетворяю-
удовлетворяющие условиям 1 и 2, называют гипотезами.
Заметим, что если события удовлетворяют второму из двух
указанных требований, то их совокупность называют полной
группой событий. Таким образом, гипотезы — это попарно
несовместные события, образующие полную группу событий.
Пусть также имеется некоторое событие А и известны веро-
вероятности гипотез P(i?i), ..., Р(#п), которые предполагаются
ненулевыми, и условные вероятности Т?(А\Н\), ..., ?(А\Нп)
события А при выполнении этих гипотез. Задача состоит в
вычислении безусловной вероятности события А. Для реше-
решения этой задачи используют следующую теорему.
Теорема 3.6. Пусть для некоторого события А и гипотез
-Hi,..., Нп известны P(H\),..., Р(ЯП), которые положительны,
и P(A|#i), ..., Р(А\Нп). Тогда безусловную вероятность
определяют по формуле
= Р(Ях) Р(Л|#!) +... + Р(ЯП) Р(А\Нп), C.5)
которую называют формулой полной вероятности.
94 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
А Представим событие А в виде
(на рис. 3.2, область, соответствующая событию А, заштрихо-
заштрихована).
С учетом того, что события АЩ, г = 1,п, несовместны,
имеем
Р(А)=Р(АН1) + ... + Р(АНп).
В соответствии с формулой умножения вероятностей полу-
получаем
Р(АН1)=Р(Н1)Р(А\Н1), ..., Р(АНп) = Р(Нп)Р(А\Нп).
Поэтому
= Р(Н1)Р(А\Н1) + ... + Р(Нп)Р(А\Нп). >
Рис. 3.2
Формула полной вероятности при всей своей простоте игра-
играет весьма существенную роль в теории вероятностей.
3.4. Формула полной вероятности 95
Пример 3.7. Путник должен попасть из пункта В в пункт
А в соответствии со схемой дорог изображенной на рис. 3.3.
Выбор любой дороги в любом пункте равновозможен. Найдем
вероятность события А — достижения путником намеченной
цели.
Для того чтобы попасть в пункт А, путник должен пройти
один из промежуточных пунктов Н\, Н*ъ или Н$. Введем
гипотезы Щ, где Щ означает, что путник выбрал в пункте В
путь, ведущий в пункт Щ, i = 1,2,3. Ясно, что события Щ
несовместные и одно из них обязательно происходит, причем в
силу равновозможности выбора дорог из В в Щ
Остается вычислить условные вероятности P(A\Hi), кото-
которые легко найти, если рассматривать новое пространство эле-
элементарных исходов, соответствующее выбранной гипотезе Щ.
Например, появление Н\ означает, что есть два равновоз-
можных исхода (из пункта Н\
выходят две дороги), из ко-
которых лишь один благоприят-
благоприятствует событию А, т.е. yS * '—^>А
Р(А\Нг) = \.
Аналогично находим, что
Р(А|#2) = \
Рис. 3.3
И
Р(Л|Я3) = 0.
Согласно формуле 3.5 полной вероятности, получаем
р(л)=г(}+1+0)=0'25- *
96 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Заметим, что данная задача может иметь техническую
интерпретацию: сеть дорог — это сеть каналов передачи
информации, а Р{А) — вероятность предачи сообщения по
такой сети.
Пример 3.8. Студент Иванов выучил все N = 30 экзаме-
экзаменационных билетов, но из них на „пять" — лишь N\ = 6. Опре-
Определим, зависит или нет вероятность извлечения „счастливого"
билета (событие А) от того, первым или вторым выбирает Ива-
Иванов свой билет.
Рассмотрим две ситуации.
Иванов выбирает билет первым. Тогда
Иванов выбирает билет вторым. Введем гипотезы: Н\ —
первый извлеченный билет оказался „счастливым", #2 — „не-
„несчастливым". Ясно, что
В силу формулы C.5) полной вероятности
5 29 + 5 29 " 5 " N*
что совпадает с первой ситуацией.
Изменится ли ответ, если Иванов будет выбирать билет
третьим, четвертым, ..., последним?
3.5. Формула Байеса
Пусть по-прежнему некоторое событие А может произой-
произойти с одним из событий #i,..., Яп, образующих полную группу
3.5. Формула Байеса 97
попарно несовместных событий, называемых, как уже отмеча-
отмечалось, гипотезами. Предположим, что известны вероятности
гипотез P(#i),..., Р(#п) (Р{Щ) > О, г = Т~п) и что в резуль-
результате опыта событие А произошло, т.е. получена дополнитель-
дополнительная информация. Спрашивается, как „изменятся" вероятно-
вероятности гипотез, т.е. чему будут равны условные вероятности
P(#i|j4), ...,Р(#п|л4), если известны также условные вероят-
вероятности P(A|#i), ...,Р(А|#П) события А? Для ответа на этот
вопрос используют следующую теорему.
Теорема 3.7. Пусть для некоторого события А, Р(А) > О,
и гипотез #i,...,ffn известны P(#i), ...,P(#n) (P(#i) >0,
i = 1,п) и P(A|lfi),..., P(i4|#n). Тогда условная вероятность
P(Hi\A), i = 1, п, гипотезы Д» при условии события А опреде-
определяется формулой Байеса
< Согласно определению 3.1 условной вероятности,
ГША) = Щ&.
Выражая теперь по формуле умножения вероятностей Р(АЩ)
через Р(А\Н{) и P(#i), получаем
Поэтому
Подставляя вместо вероятности Р(А) ее значение, вычи-
вычисленное в соответствии с формулой C.5) полной вероятности,
приходим к утверждению теоремы. >
4 - 10047
98 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Формула Байеса находит широкое применение в математи-
математической статистике, теории принятия решений и их приложе-
приложениях. Заметим, что вероятности Р(Ях), ...,Р(ЯЛ) обыч-
обычно называют априорными (т.е. полученными „до опыта"), а
условные вероятности Р(Нх\А),..., Т?(Нп\А) — апостери-
апостериорными (т.е. полученными „после опыта").
Пример 3.9. Врач после осмотра больного считает, что
возможно одно из двух заболеваний, которые мы зашифруем но-
номерами 1 и 2, причем степень своей уверенности в отношении
правильности диагноза он оцениваниет как 40 % и 60 % соот-
соответственно. Для уточнения диагноза больного направляют на
анализ, исход которого дает положительную реакцию при забо-
заболевании 1 в 90 % случаев и при заболевании 2 — в 20 % случаев.
Анализ дал положительную реакцию. Как изменится мнение
врача после этого?
Обозначим через А событие, означающее, что анализ дал
положительную реакцию. Естественно ввести следующие ги-
гипотезы: Н\ — имеет место заболевание 1; Яг — имеет место
заболевание 2. Из условий задачи ясно, что априорные вероят-
вероятности гипотез равны:
Р(Ях)=0,4 и Р(Я2)=0,6,
а условные вероятности события А при наличии гипотез Н\ и
Яг равны 0,9 и 0,2 соответственно. Используя формулу Байеса,
находим
Итак, врач с большей уверенностью признает наличие заболе-
заболевания 1.
Пример 3.10. Рассмотрим случай, когда
Р(А\Щ) = const = С, i = 1, n,
3.6. Схема Бернулли 99
т.е. на вероятность появления события А все гипотезы влияют
одинаково. Тогда, согласно формуле Байеса, получаем
т.е. дополнительная информация о появлении события А не
имеет никакой ценности, поскольку не меняет наших предста-
представлений об априорных вероятностях гипотез.
3.6. Схема Бернулли
Повторные испытания — это последовательное проведение
п раз одного и того же опыта или одновременное проведение п
одинаковых опытов. Например, при контроле уровня надежно-
надежности прибора могут либо проводить п испытаний с одним и тем
же прибором, если после отказа полностью восстанавливают
его исходные свойства, либо ставить на испытания п опытных
образцов этого прибора, которые считают идентичными.
Определение 3.6. Схемой Бернулли (или последова-
последовательностью независимых одинаковых испытаний, или
биномиальной схемой испытаний) называют последователь-
последовательность испытаний, удовлетворяющую следующим условиям:
1) при каждом испытании различают лишь два исхода:
появление некоторого события А, называемого „успехом", либо
появление его дополнения А, называемого „неудачей";
2) испытания являются независимыми, т.е. вероятность
успеха в fc-м испытании не зависит от исходов всех испытаний
до fc-ro;
3) вероятность успеха во всех испытаниях постоянна и
равна
Вероятность неудачи в каждом испытании обозначим q, т.е.
100 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Приведем примеры реальных испытаний, которые в той
или иной степени „вписываются" в рамки сформулированной
модели испытаний по схеме Бернулли.
1. Последовательное подбрасывание п раз симметричной
монеты (здесь успехом является появление „герба" с вероятно-
вероятностью р = 1/2) или последовательное бросание п раз игральной
кости (здесь успехом можно считать, например, появление ше-
шестерки с вероятностью р = 1/6). Эти две реальные схемы
испытаний являются примером идеального соответствия схеме
испытаний Бернулли.
2. Последовательность п выстрелов стрелка по мишени
можно лишь приближенно рассматривать как схему испытаний
Бернулли, так как независимость результатов стрельбы может
нарушаться либо из-за „пристрелки" спортсмена, либо вслед-
ствии его утомляемости.
3. Испытания п изделий в течение заданного срока при кон-
контроле уровня их надежности, как правило, хорошо согласуются
с моделью испытаний по схеме Бернулли, если на испытания
поставлены идентичные образцы.
При рассмотрении схемы испытаний Бернулли основной за-
задачей является нахождение вероятности события Ak, состоя-
состоящего в том, что в п испытаниях успех наступит ровно к раз,
к = 0, п. Для решения этой задачи используют следующую тео-
теорему, обозначая вероятность P{Ak) через Рп{к).
Теорема 3.8. Вероятность Рп(к) того, что в п испытаниях
по схеме Бернулли произойдет ровно к успехов, определяется
формулой Бернулли
Рп(к) = С*ркдп~к, fc = 0^. C.7)
< Результат каждого опыта можно записать в виде последо-
последовательности УНН...У, состоящей из п букв „У" и „Н", причем
буква „У" на г-м месте означает, что в г-м испытании про-
произошел успех, а „Н" — неудача. Пространство элементарных
исходов Q состоит из 2п исходов, каждый из которых ото-
отождествляется с определенной последовательностью УНН...У.
3.6, Схема Бернулли 101
Каждому элементарному исходу ш =УНН...У можно поставить
в соответствие вероятность
РЦ = Р(УНН...У).
В силу независимости испытаний события У,Н,Н,...,У явля-
являются независимыми в совокупности, и потому по теореме умно-
умножения вероятностей имеем
если в п испытаниях успех „У" имел место г раз, а неуспех „Н",
следовательно, п — i раз.
Событие Ak происходит всякий раз, когда реализуется
элементарный исход о;, в котором г = к. Вероятность любого
такого элементарного исхода равна pkqn"~k.
Число таких исходов совпадает с числом способов, которы-
которыми можно расставить к букв „У" на п местах, не учитывая
порядок, в котором их расставляют. Число таких способов рав-
но С*.
Так как Ak есть объединение (сумма) всех указанных эле-
элементарных исходов, то окончательно получаем для вероятности
Р(Ак) = Рп{к) формулу C.7). >
Формулу C.7) называют также биномиальной, так как
ее правая часть представляет собой (к + 1)-й член формулы
бинома Ньютона [I].
Набор вероятностей Рп(к), к = 0, п, называют биномиальным
распределением вероятностей.
Из формулы Бернулли вытекают два следствия.
1. Вероятность появления успеха (события А) в п испыта-
испытаниях не более к\ раз и не менее кч раз равна:
^ к < к2} = J2 СпРк<1п~к- C-8)
102 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Это следует из того, что события Аь при разных к являются
несовместными.
2. В частном случае при к\ = 1 и &2 = п из C.8) получаем
формулу для вычисления вероятности хотя бы одного успеха в
п испытаниях:
Р{А;^1} = 1-<Л C.9)
Пример 3.11. Монету (симметричную) подбрасывают п =
= 10 раз. Определим вероятность выпадения „герба":
а) ровно пять раз;
б) не более пяти раз;
в) хотя бы один раз.
В соответствии с формулой C.7) Бернулли имеем:
A \ 10
У =
1024
¦ч f
6)
C10 + C10 + C10 -f Ciq
1024
/1\
= l~ l-J
/1\
в) P{fc^l} = l~ l-J «0,999.
Пример 3.12. Вероятность выигрыша на один лотерейный
билет равна 0,01. Определим, сколько билетов нужно купить,
чтобы вероятность хотя бы одного выигрыша в лотерее была
не менее заданного значения Р3 == 0,9.
Пусть куплено п билетов. Предположим, что общее чи-
число билетов, разыгрывающихся в лотерее велико (во много раз
больше купленных билетов). При этом можно считать, что
каждый билет выигрывает независимо от остальных с вероят-
вероятностью р = 0,01. Тогда вероятность получить к выигрышных
билетов можно определить, используя формулу Бернулли. В
частности, согласно C.9), имеем при q = 1 — р:
Р{к > 1} = 1 - qn = 1 - A - р)п ^ Рз,
3.6. Схема Бернулли 103
откуда получаем
1пA-Р3) _ 1п0,1
П> ln(l-p) -1О99
Таким образом, нужно купить не менее 230 лотерейных биле-
билетов. #
При больших значениях числа испытаний п использование
формулы Бернулли затруднительно в вычислительном плане.
Здесь существенную помощь могут оказать приближенные
формулы.
Пусть число испытаний п по схеме Бернулли „велико",
а вероятность успеха р в одном испытании „мала", причем
„мало" также произведение А = пр. Тогда Рп(к) определяют
по приближенной формуле
д*
Рп(к) « -?|-е-\ к = 0, п,
называемой формулой Пуассона. Совокупность вероятно-
вероятностей Р(к\ А) = \ке~х/к\, к = 0,1,..., называют распределени-
распределением Пуассона.
Значения функции Р(к; А) для некоторых А приведены в
табл. П.1.
Формула Пуассона справедлива также для числа неудач, но
только в том случае, когда „мало" А; = nq.
Замечание 3.5. Слова „мало" и „велико" здесь и далее
носят относительный характер. Рекомендации по выбору чи-
численных значений соответствующих величин будут приведены
ниже.
Пример 3.13. Вероятность выпуска бракованного сверла
равна 0,015. Сверла укладывают в коробки по 100 штук. Най-
Найдем вероятность того, что в коробке, выбранной наудачу, не
окажется ни одного бракованного сверла.
104 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Очевидно, что мы имеем дело со схемой Бернулли, причем
п = 100, р = 0,015 и fc = 0, Поскольку число п испытаний
„велико", а вероятность успеха р в каждом испытании „мала",
воспользуемся приближенной формулой Пуассона, в которой
А = пр= 100-0,015 = 1,5.
Тогда искомая вероятность
По табл. П.1 находим
Р@; 1,5) =0,22313.
Локальная формула Муавра — Лапласа. Бели в схеме
Бернулли число испытаний п „велико", причем „велики" также
вероятности р успеха и q неудачи, то для всех к справедлива
приближенная формула
называемая локальной формулой Муавра — Лапласа, где
к — пр
Функцию (р называют плотностью стандартного нор-
нормального (или гауссова) распределения.
Значения функции <р для некоторых х приведены в табл. П.2.
Поскольку функция ср является четной, то при определении (р
для отрицательных х нужно воспользоваться равенством
3.6. Схема Бернулли 105
Пример 3.14. Вероятность попадания в цель при одном
выстреле равна 0,8. Определим вероятность того, что при 400
выстрелах произойдет ровно 300 попаданий.
В данном случае „велики" и число п = 400 испытаний, и
вероятности р = 0,8 успеха и q = 1 — р = 0,2 неудачи в одном
испытании, поэтому воспользуемся локальной формулой Муа-
Муавра — Лапласа при к = 300. Получим:
к-пр 300-320
Jb —— — — *t*O
y/npq 8
Отсюда, учитывая четность функции <р(ж), с помощью табл. П.2
окончательно получаем
ШВ «0,0022.
Интегральная формула Муавра — Лапласа. Бели чи-
число п испытаний по схеме Бернулли „велико", причем „велики"
также вероятности р успеха и q неудачи, то для вероятности
P{fci ^ к ^ Аъ} того, что число успехов к заключено в пределах
от к\ до /с2, справедливо приближенное соотношение
называемое интегральной формулой Муавра — Лапласа,
где
к\ —пр А?2 — пр
-ОО
106 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Функцию Ф(х) называют функцией стандартного нор-
нормального (или гауссова) распределения.
Определение 3.7. Функцию
о
называют интегралом Лапласа.
В табл. П.З приведены значения Фо(я) для положительных х.
В силу четности (р(х) интеграл Лапласа Фо(я) является нечет-
нечетной функцией, т.е.
(-я) = -Фо(я),
и, кроме того,
Ф(я) = Ф0(а;) + ~.
Используя интеграл Лапласа, интегральную формулу Муа-
вра — Лапласа можно записать в виде
P{fci < к < к2} « Ф0(х2) - Ф0(«1).
Пример 3.15. Найдем вероятность того, что при 600 бро-
бросаниях игральной кости выпадет от 90 до 120 „шестерок".
Воспользуемся интегральной формулой Муавра — Лапласа,
в которой нужно положить
600-1/6
-1,10
120-600-1/6 О1О
х2 = , —-— « 2,19.
^/600-1/6-5/6
Тогда искомая вероятность приближенно равна:
Р«ФоB,19)-Фо(-1,1О).
3.6. Схема Бернулли 107
В соответствии с табл. П.З имеем
Р » 0,48574 + 0,36433 = 0,85007. #
Дадим некоторые рекомендации (носящие, вообще говоря,
условный характер) по применению приближенных формул.
Бели число испытаний п = 10, 20, то приближенные форму-
формулы используют для грубых прикидочных расчетов. При этом
формулу Пуассона применяют в том случае, когда А = пр или
Л; = nq изменяются в пределах от 0 до 2 (при п = 10) и от 0 до
3 (при п = 20); в противном случае необходимо пользоваться
формулами Муавра — Лапласа.
При п = 20,100 приближенные формулы уже можно исполь-
использовать для прикладных инженерных расчетов. Формулу Пуас-
Пуассона рекомендуется применять, когда Л или Л' заключены в
пределах от 0 до 3 (при п = 20) и от 0 до 7 (при п = 100).
Бели п = 100,1000, то практически в любых инженерных
расчетах можно обойтись приближенными формулами. Фор-
Формулу Пуассона используют в случае, когда Л или Л; изменяются
в пределах от 0 до 7 (при п = 100) и от 0 до 15 (при п = 1000).
Наконец, при п > 1000 даже специальные таблицы рассчи-
рассчитывают с помощью приближенных формул (правда, для уве-
увеличения точности используют специальные поправки). В этом
случае для применения формулы Пуассона необходимо, чтобы
Л или Л' лежали в пределах от 0 до а, где а = 15 при п = 1000 и
увеличивается с ростом п.
Во многих задачах рассматривают такие независимые оди-
одинаковые испытания, в каждом из которых может произойти не
одно из двух несовместных событий (успех и неудача), как в
схеме Бернулли, а одно из т таких событий.
Определение 3.8, Опыт, состоящий в n-кратном повто-
повторении одинаковых независимых испытаний, в каждом из кото-
которых может произойти одно и только одно из т несовместных
событий Ai, ..., Ат, причем событие А{ наступает с вероят-
108 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
ностью pi, называют полиномиальной (мультиноминаль-
ной) схемой.
Теорема 3.9, Вероятность P(ni,...,nm) того, что в п
испытаниях событие А\ произойдет ровно п\ раз, событие А2
произойдет ровно n<i раз,..., событие Ат произойдет ровно пт
раз {п\ + n<i +... + пт = п), равна:
< По аналогии со схемой Бернулли в полиномиальной схеме
исход каждого опыта можно записать в виде набора чисел
к\, &2> • ••> кп, hi = l,m, где число к{ на i-м месте означает,
что в г-м испытании произошло событие Akr Поскольку
испытания являются независимыми, то исходу fci, &2, •••> кп
соответствует вероятность р^ .. .pkn, которую можно записать
в виде p^.-.pj^, где п*, к = 1,т, — число испытаний, в
которых произошло событие А^.
Теперь, для того чтобы найти вероятность P(ni,...,nm),
необходимо подсчитать число способов, которыми щ символов
А\9 П2 символов А2, ..., пт символов Ат можно расставить на
п местах (см. также 2.2). Поскольку порядок расстановки
не существенен, то щ символов А\ можно расставить на п
местах CJJ1 способами. Затем n<i символов A<i можно расставить
на оставшихся п — п\ местах C?ini способами. Продолжая
эту процедуру и используя основную формулу комбинаторики,
получаем, что общее число способов равно:
(n-ni-...-nm_i)! n!
" nm!0!
Отсюда приходим к утверждению теоремы. >
Набор вероятностей P(ni,..., пт) также называют полино-
полиномиальным распределением.
3.7. Решение типовых примеров 109
Вероятность P(ni,...,nm) можно получить кале коэффици-
коэффициент при х™1... х^1 в разложении полинома
по степеням х\у ..., хт.
Пример 3,16. В некотором государстве живут 60% блон-
блондинов, 25% брюнетов и 15% шатенов. Найдем вероятность
того, что среди восьми наудачу отобранных подданных этого
государства окажутся четыре блондина, три брюнета и один
шатен.
В данном случае мы имеем дело с полиномиальной схемой, в
которой га = 3, р\ = 0,6, Р2 = 0,25, рз = 0,15, п = 8, п\ = 4, n<i = 3
и пз = 1. Тогда
8!0^;°-15^ 0,085.
Замечание 3.6. Иногда в практических приложениях рас-
рассматривают обобщенную схему Бернулли или обобщен-
ную полиномиальную (мулътиноминалъную) схему, для
которой третье условие в определениях схемы Бернулли или
полиномиальной схемы заменяют следующим: вероятность р
успеха или вероятность pk появления события А^ в г-м ис-
испытании могут меняться с изменением номера г = 1, п. Для
обобщенных схем также можно указать соответствующие фор-
формулы для вероятностей сложных событий, рассматривавшихся
выше*.
3.7. Решение типовых примеров
Пример 3.17. Одновременно бросают две игральные кости
(белую и черную). Рассмотрим следующие события: А — на
белой кости выпало более двух очков; В — в сумме выпало
четное число очков; С — в сумме выпало менее десяти очков.
*Вентцелъ E.G. Теория вероятностей. М.: Наука, 1969.
110 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Вычислим условные вероятности P(j4|J3), Т?(В\А), P(j4|C),
Р(С|А), Р(В\С) и Р(С\В) и определим, какие из событий А,
В иС являются независимыми.
Нетрудно подсчитать в соответствии с классическим опре-
определением вероятности, что
|, Р(В) = ±, р(О = J,
"з' *^~>-2'
Поэтому
Отсюда, в частности, следует, что независимыми являются
события А и В. События А и С, В и С зависимые. Поэтому
события А, В и С не являются независимыми в совокупности.
Пример 3.18. Каждая буква слова „МАТЕМАТИКА" на-
написана на отдельной карточке. Карточки тщательно переме-
перемешаны. Последовательно извлекают четыре карточки. Найдем
вероятность события А — получить слово „ТЕМА"?
Пусть А\, А2, Аз и А± — события, состоящие в последова-
последовательном извлечении букв „Т", „Е", „М", „А". Тогда соответ-
соответствующие вероятности равны:
P(Ai) = |, \
Р(А3\А1А2) = \, P(A4\AiMA3) .
Отсюда, согласно формуле умножения вероятностей, полу-
получаем
3.7. Решение типовых примеров 111
Пример 3.19. Обнаружение воздушной цели проводит-
проводится независимо двумя радиолокационными станциями. Веро-
Вероятность Р(А) обнаружения цели первой станцией равна 0,7.
Вероятность Р(В) обнаружения цели второй станцией равна
0,8. Определим вероятность Р(С) того, что цель будет обнару-
обнаружена хотя бы одной станцией.
По условию события А и В являются независимыми, по-
поэтому по формуле умножения вероятностей для независимых
событий вероятность события АВ (цель обнаружена обеими
станциями) равна:
Р(АВ) = Р(А)Р(В) = 0,7 - 0,8 = 0,56.
Значит, в силу теоремы сложения вероятностей
Р(С) = Р(А U В) = Р(А) + Р(В) - Р(АВ) = 0,94.
Так как события Аи В независимые, то Р{С) можно найти
путем перехода к противоположным событиям А и В, В этом
случае, используя закон де Моргана и теорему 3.4, имеем
Р(С) = Р(А В) = 1 - Р(АВ) = 1 - Р(А)Р(В) =
Пример 3.20. Система управления состоит из четырех уз-
узлов с номерами 1, 2, 3 и 4 (рис. 3.4). Вероятности Pi безотказной
работы узлов равны Pi = 0,7,
Р2 = 0,6, Р3 = 0,8 и Р4 = 0,9 со-
со1
н
ответственно. Вычислим ве-
вероятность безотказной рабо-
работы всей системы управления,
считая отказы узлов незави-
независимыми событиями.
Вероятность Р\2 работы
участка 1-2 цепи, состоящего
из двух соединенных последо-
112 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
вательно элементов 1 и 2, равна: P\*i = Р\Р2 = 0,42. Вероятность
Рз4 работы участка 3-4 цепи, состоящего из двух соединенных
последовательно элементов 3 и 4, равна:
Поскольку вся система состоит из параллельно соединенных
участков 1-2 и 3-4, то вероятность ее безотказной работы
равна:
Р = 1 - A - Pi2)(l - Р34) = 1 - A -0,42)A - 0,98) и 0,99.
Пример 3,21. Партия транзисторов, среди которых 10%
дефектных, поступила на проверку. Схема проверки такова,
что с вероятностью 0,95 обнаруживается дефект, если он есть,
и существует ненулевая вероятность 0,03 того, что исправный
транзистор будет признан негодным. Найдем вероятность то-
того, что проверяемый транзистор будет признан негодным.
Пусть А — событие, состоящее в том, что проверяемый
транзистор признан негодным. С этим событием связаны две
гипотезы: Н\ — проверяемый транзистор дефектный и H<i —
проверяемый транзистор исправный. По условию
= 0,1, Р(Я2)=0,9,
P(A|#i) = 0,95, Р{А\Н2) = 0,03.
Тогда в силу формулы полной вероятности
Р(А) = 0,1 • 0,95 + 0,9 • 0,03 = 0,122.
Пример 3.22. В поступивших на склад трех партиях де-
деталей годные составляют 89%, 92% и 97% соответственно, а
количества деталей в партиях относятся как 1:2:3. Ответим
на два вопроса.
1. Чему равна вероятность того, что случайно выбранная
со склада деталь окажется негодной?
3.7. Решение типовых примеров 113
2. Пусть известно, что случайно выбранная деталь оказа-
оказалась негодной. Найдем вероятности того, что она принадлежит
первой, второй и третьей партиям.
Обозначим #i, #2 и #з события, состоящие в том, что
деталь принадлежит первой, второй и третьей партиям соот-
соответственно. Поскольку эти события попарно несовместные и
образуют полную группу событий, то они являются гипотеза-
гипотезами, причем, как нетрудно подсчитать,
Р(я8) = |.
Событие А — выбранная деталь является негодной. Услов-
Условные вероятности события А равны:
P(A\Hi) = 0,11, Р(А\Н2) = 0,08, Р(А\Н3) = 0,03.
Согласно формуле полной вероятности, найдем
Р(А) = \ • 0,11 + \ • 0,08 + | • 0,03 = 0,06.
6 6 6
Вероятности того, что негодная деталь принадлежит пер-
первой, второй и третьей партиям, определям, используя формулу
Байеса:
Пример 3.23. По каналу связи, подверженному воздей-
воздействию помех, передают одну из двух команд управления в виде
114 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
кодовых комбинаций 11111 или 00000, причем априорные веро-
вероятности передачи этих команд равны 0,7 и 0,3 соответствен-
соответственно. За счет помех вероятности правильного приема каждого
из символов 1 и 0 уменьшаются до 0,6. Предполагается, что
символы кодовых комбинаций искажаются независимо один от
другого. На выходе зарегисрирована комбинация 10110. Опре-
Определим, какая из команд наиболее вероятно была передана.
Пусть А — событие, состоящее в приеме комбинации 10110.
К этому событию ведут две гипотезы: #i — была передана
комбинация 11111; #2 — была передана комбинация 00000. По
условию задачи P(#i) = 0,7 и Р(#2) = 0,3.
Определим условные вероятности Р(А\Нх) и Р(А|#2)- В
силу независимости искажения символов имеем:
Р(А\Нг) = 0,6 • 0,4 - 0,6 • 0,6 - 0,4 « 0,035;
Р(А|#2) .= 0,4 • 0,6 • 0,4 • 0,4 • 0,6 « 0,023.
Воспользовавшись теперь формулой Байеса, получим:
л\ 0,7-0,035 ЛМ
-0,023 ~°'22-
Сравнивая найденные вероятности, заключаем, что при
появлении комбинации 10110 с большей вероятностью 0,78
была передана команда 11111.
Пример 3.24. По цели производят шесть независимых
выстрелов. Вероятность попадания при каждом выстреле р =
= 0,75. Вычислим:
а) вероятность ровно пяти попаданий (событие А);
б) вероятность не менее пяти попаданий (событие В)\
в) вероятность менее трех попаданий (событие С).
3.7. Решение типовых примеров 115
Очевидно, мы имеем дело со схемой Бернулли, в которой п =
= 6, р = 0,75 и q = 0,25. Воспользовавшись формулой Бернулли,
будем иметь:
а) Р(Л) = Р6E) = С|0,7б50,2б1 « 0,356;
б) Р(В) = Р{Л ^ 5} = Cf 0,7550,25х + С|0,7560,25° * 0,534;
в) Р(С) = Р{Л < 2} = С?0,75°0,256 + С^0,7510|255+
+ С|0,7520,254« 0,0376.
Пример 3.25. В коробке лежит 200 конденсаторов, причем
два из них нужной емкости. Случайным образом из коробки
вынимают один конденсатор и после определения его емкости
возвращают обратно в коробку. Выясним, сколько раз нуж-
нужно осуществить указанную операцию, чтобы вероятность хотя
бы один встретить конденсатор нужной емкости была не ме-
менее 0,95.
Поскольку выбор осуществляется с возвращением, мы име-
имеем дело со схемой Бернулли, в которой
и 9 = 1-Р = 0,99.
Пусть А — интересующее нас событие. Тогда А — событие,
состоящее в том, что при п испытаниях ни разу не появился
конденсатор нужной емкости. Из условия задачи следует:
Р(А) = 0,99п ^ 1 - 0,95 = 0,05.
Поэтому
1п0,05
Итак, указанную операцию необходимо осуществить, по край-
крайней мере, 296 раз.
116 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Пример 3.26. Вероятность искажения одного символа при
передаче сообщения по линии связи равна 0,001. Сообщение
считают принятым, если в нем отсутствуют искажения. Най-
Найдем вероятность того, что будет принято сообщение, состоящее
из 20 слов по 100 символов каждое.
Передаваемое сообщение содержит 2000 символов. Пред-
Предполагая, что символы искажаются независимо, имеем дело со
схемой Бернулли, в которой п = 2000, р = 0,001, к = 0. Посколь-
Поскольку п „велико", причем
Л = пр = 2
„мало" (см. с. 107), то для вычисления интересующей нас ве-
вероятности применим приближенную формулу Пуассона. Тогда,
используя табл. П.1, получаем
Р«Р@; 2) = 0,13534.
Пример 3.27. На факультете обучаются 300 студентов.
Предполагая, что вероятность родиться в каждый день года
одинакова, найдем вероятность того, что ровно 80 студентов
факультета будут праздновать дни рождения летом.
Вероятность того, что ровно к студентов будут отмечать
летом день рождения, определяется по формуле Бернулли, в
которой п = 300, р = 1/4 и q = 3/4. Так как n, p и q „велики" и
Л = пр = 75 и \* = щ = 225,
то для вычисления искомой вероятности необходимо применить
одну из формул Муавра — Лапласа. Поскольку в задаче нужно
найти вероятность наступления ровно к успехов, то применим
локальную формулу Муавра — Лапласа, в которой
-е к-пр 80-75 _„
3,7. Решение типовых примеров 117
Воспользовавшись табл. П.2, имеем
7,5 7,5
Пример 3.28. Определим вероятность того, что при 900
бросаниях игральной кости „шестерка" выпадет от 130 до 300
раз.
Поскольку в данном примере „велики" п = 800,
Л = пр = 150 и У = nq = 750,
то, согласно интегральной формуле Муавра — Лапласа, имеем:
fci - пр 130 - 150
^800-1/6-5/6
«-1,90,
fc2-np 300-150
#2 = —. = —j ~ 14,zo.
Так как в табл. П.З значение ФоA4,23) отсутствует, заменим
его на 0,5. Тогда
Р « ФоA4,23) - Ф0(-1,90) = 0,5 + 0,47128 = 0,97128.
Пример 3.29. Игральную кость бросают 10 раз. Требуется
найти вероятность того, что пшестерка" выпадет два раза, а
япятерка" — 3 раза.
В данном опыте имеем дело с 10 независимыми испытания-
испытаниями, причем в каждом испытании с вероятностью 1/6 происхо-
происходит событие А\ (выпадает „шестерка"), с той же вероятностью
1/6 происходит событие А2 (выпадает „пятерка") и, наконец,
с вероятностью 4/6 происходит событие Аз (выпадает любое
другое число очков). Искомую вероятность можно вычислить,
используя теорему 3.9:
= РB,3,5) = «?№>! ,„,043.
118 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Вопросы и задачи
3.1. Дайте определение условной вероятности.
3.2. Сформулируйте теорему умножения вероятностей и
объясните ее геометрический смысл для двух событий.
3.3. Какие два события называют независимыми? зависи-
зависимыми?
3.4. Какие п событий называют независимыми в совокуп-
совокупности? попарно?
3.5. Какая связь существует между совместными и зависи-
зависимыми событиями?
3.6. Какие события называют гипотезами?
3.7. Напишите формулу полной вероятности.
3.8. Напишите формулу Байеса.
3.9. Что называют схемой Бернулли?
3.10. Напишите формулу Бернулли.
3.11. Напишите формулу для вероятности того, что в п
испытаниях по схеме Бернулли число успехов будет заключено
в пределах от fci до fo.
3.12. Напишите формулу для вероятности того, что в п
испытаниях по схеме Бернулли произойдет, по крайней мере,
один успех.
3.13. Напишите формулу Пуассона.
3.14. Напишите локальную формулу Муавра — Лапласа.
3.15. Напишите интегральную формулу Муавра — Лапласа.
3.16. В каких случаях можно применять формулу Пуассона?
3.17. В каких случаях можно применять локальную форму-
формулу Муавра — Лапласа?
Вопросы и задачи 119
3.18. В каких случаях можно применять интегральную
формулу Муавра — Лапласа?
3*19. Что называют полиномиальной схемой?
3.20. Напишите формулу для вероятности того, что в
полиномиальной схеме событие А\ произойдет ровно п\ раз,...,
событие Ат произойдет ровно пт раз.
3.21. Подбрасывают наудачу три игральные кости. Наблю-
Наблюдаемые события: А — на трех костях выпадут разные числа
очков, В — хотя бы на одной из костей выпадет „шестерка".
Вычислите Р(А|В) и Р(В\А).
Ответ: Р(А\В) = 60/91, Р(В\А) = 1/2.
3.22. В шкаф поставили девять новых однотипных прибо-
приборов. Для проведения опыта берут наугад три прибора, после
работы их возвращают в шкаф. На вид прибор, бывший в упо-
употреблении, не отличается от нового. Определите вероятность
того, что после проведения трех опытов в шкафу не останется
новых приборов.
О т в е т: Р = 1 - F/9 - 5/8 • 4/7) • C/9 • 2/8 • 1/7) « 0,0028.
3.23. На карточках разрезной азбуки написаны 32 буквы
русского алфавита. Пять карточек вынимают наудачу одна за
другой р укладывают на стол в порядке появления. Найдите
вероятность того, что получится слово „КОНЕЦ".
Ответ: Р = 1/32-1/31 -1/30-1/29-1/28 «4,14-10"8.
3.24. Студент пришел на зачет, зная из 30 вопросов только
24. Если студент не отвечает на один вопрос, преподаватель
задает другой. Найти вероятность того, что студент сдаст
зачет.
Ответ: Р = 1 -1/29 « 0,966.
3.25. Два стрелка стреляют в цель, причем каждый делает
по одному выстрелу. Для первого стрелка вероятность попада-
попадания в цель равна 0,7, для второго — 0,8. Какова вероятность
попасть в цель хотя бы одному стрелку?
Ответ: Р = 0,94.
120
3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
Г2 "
L з -
- 4
Ответ:
Рис. 3.5
' = Pl[l-(l-
3.26. Система состоит из
четырех узлов (рис. 3.5). Веро-
Вероятности Р{ безотказной рабо-
работы узлов равны соответствен-
соответственно Pi, Р2, Рз и Р*. Вычислите
вероятность безотказной рабо-
ты всей системы.
3.27. При одном цикле обзора радиолокационной станции,
следящей за космическим объектом, объект обнаруживают
с вероятностью р. Обнаружение объекта в каждом цикле
происходит независимо от других. Найдите вероятность того,
что при п циклах объект будет обнаружен.
Ответ: Р = 1-A-р)п.
3.28. В первой урне лежат 10 шаров, из них восемь белых,
во второй — 20 шаров, из них четыре белых. Из каждой
урны наудачу извлекают по одному шару, а затем из этих двух
наудачу берется один шар. Найдите вероятность того, что это
будет белый шар.
Ответ: Р = 0,5.
3.29. На шахматную доску ставят двух слонов: белого и
черного. Какова вероятность того, что при первом ходе один
слон может побить другого?
Ответ: Р = 5/36 «0,139.
3.30. В продажу поступают телевизоры трех заводов. Про-
Продукция первого завода содержит 20 % телевизоров со скрытым
дефектом, второго — 10 % и третьего — 5 %. Определите ве-
вероятность приобрести исправный телевизор, если в магазин
поступило 30 телевизоров с первого завода, 20 — со второго
и 50 — с третьего.
Ответ: Р = 0,895.
Вопросы и задачи 121
3.31* На заводе, изготавливающем болты, на первом стан-
станке производят 25%, на втором 35% и на третьем 40% всех
изделий. В продукции брак составляет 5 %, 4 % и 2 % соответ-
соответственно.
а) Найдите вероятность того, что случайно выбранный
болт будет дефектным.
б) Пусть случайно выбранный болт оказался дефектным.
Найдите вероятности Pi, Рг и Рз того, что болт был произведен
на первом, втором, третьем станке.
Ответ: а) Р = 0,0345; б) Рх = 125/345 » 0,36, Р2 = 140/345 «
« 0,406, Рз = 80/345 « 0,23.
3.32. Два стрелка стреляют по одной мишени, делая каждый
по одному выстрелу. Вероятность попадания в мишень для
первого стрелка равна 0,8, для второго — 0,4. После стрельбы
в мишени обнаружена одна пробоина. Определите вероятность
того, что в цель попал первый стрелок.
Ответ: Р = 6/7«0,857.
3.33. Три стрелка производят по одному выстрелу в одну
и ту же мишень. Вероятности попадания в мишень при одном
выстреле для каждого из стрелков равны Pi, P2 и Рз соответ-
соответственно. Какова вероятность того, что второй стрелок промах-
промахнулся, если после стрельбы в мишени оказались две пробоины?
Ответ:
р=_ ад-ад»
3.34. Наудачу подбрасывают три монеты. Найдите вероят-
вероятность того, что выпадут ровно два „герба".
Ответ: Р = 3/8«0,375.
3.35. Бросают пять игральных костей. Вычислите вероят-
вероятность того, что на трех из них выпадет пятерка.
Ответ: Р = С|A/6KE/6J «0,032.
122 3. УСЛОВНАЯ ВЕРОЯТНОСТЬ. СХЕМА БЕРНУЛЛИ
3.36. Бросают 10 одинаковых игральных костей. Определи-
Определите вероятность того, что ни на одной из них не выпадет шесть
очков.
Ответ: Р= E/6I0 «0,16.
3.37. Оптовая база снабжает 10 магазинов, от каждого
из которых может поступить заявка на очередной день с
вероятностью 0,4 независимо от заявок других магазинов.
Найдите вероятность того, что в день поступит четыре заявки.
Ответ: Р«0,251.
3.38. Вероятность рождения мальчика равна 0,515, девоч-
девочки — 0,485. В некоторой семье шестеро детей. Какова вероят-
вероятность того, что среди них не более двух девочек?
Ответ: Р«0,3723.
3.39. Что вероятнее: выиграть у равносильного противни-
противника (ничейный исход исключается) три партии из четырех или
пять из восьми?
Ответ: Вероятнее выиграть три партии из четырех.
3.40. Сколько нужно параллельно соединить элементов, ве-
вероятность безотказной работы каждого из которых за время t
равна 0,9, чтобы вероятность безотказной работы всей систе-
системы за время t была не менее 0,999?
Ответ: не менее трех.
3.41. Известно, что на выпечку 1000 булочек с изюмом
нужно израсходовать 10000 изюмин. Найдите вероятность
того, что:
а) наудачу выбранная булочка не будет содержать изюма;
б) среди пяти выбранных наудачу булочек две не будут
содержать изюма, а в остальных будет хотя бы по одной
изюмине.
Ответ:
а) Р = е-10 « 0,0000468;
б) Р « С|(е-10JA - е~10K « 2,19 • ИГ8.
Вопросы и задачи 123
3.42. Телефонная станция обслуживает 1000 абонентов.
Вероятность того, что в течение минуты какому-либо абоненту
понадобится соединение, равна 0,0007. Вычислите вероятность
того, что за минуту на телефонную станцию поступит не менее
трех вызовов.
Ответ: Р «1 -Р@; 0,7) -РA; 0,7) -РB; 0,7) = 0,03414.
3.43. Известно, что 40% автомобилей, следующих по шоссе,
у развилки поворачивают направо и 60% — налево. Какова
вероятность того, что из 400 автомобилей, проехавших по
шоссе, ровно 250 повернули налево?
Ответ: Р«(рA,02)/у/Ш¦ 0,4• 0,6и0,024.
3.44. Симметричную монету подбрасывают 10000 раз. Най-
Найдите вероятность того, что наблюденная частота выпадения
„герба" будет отличаться от 1/2 не более чем на 2%.
Ответ: Р»Ф0B) -Фо(-2) =0,9545.
3.45. Найдите вероятность того, что среди 10 случайным
образом выбранных человек у четырех дни рождения будут в
первом квартале, у трех — во втором, у двух — в третьем и у
одного — в четвертом.
О т в е т: Р = 10! - 0,2510/D! 3! 2! 1!) и 0,012.
4. ОДНОМЕРНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В предыдущих главах мы изучали случайные события, что
позволяло нам исследовать вероятностные свойства (законо-
(закономерности) случайных экспериментов на качественном уровне
(„да" — „нет"): попадание в цель — промах, отказал прибор
за время t — не отказал и т.д.
Однако с момента возникновения теории вероятностей ее
основной задачей было изучение не вероятностных свойств экс-
экспериментов со случайными исходами, а связанных с этими экс-
экспериментами числовых величин, которые естественно назвать
случайными величинами. Начиная с настоящей главы и до кон-
конца книги мы будем изучать именно случайные величины.
4.1. Определение случайной величины
Для того чтобы лучше осознать связь, существующую меж-
между случайными величинами и случайными событиями, начнем
с пояснения понятия случайной величины.
Случайной величиной естественно называть числовую ве-
величину, значение которой зависит от того, какой именно эле-
элементарный исход произошел в результате эксперимента со
случайным исходом. Множество всех значений, которые слу-
случайная величина может принимать, называют множеством
возможных значений этой случайной величины.
Следовательно, для задания случайной величины необходи-
необходимо каждому элементарному исходу поставить в соответствие
число — значение, которое примет случайная величина, если в
результате испытания произойдет именно этот исход.
4.1. Определение случайной величины 125
Случайные величины будем обозначать прописными латин-
латинскими буквами, снабжая их при необходимости индексами:
X, Yi, Zi и т.д., а их возможные значения — соответствующими
строчными буквами: жз> Ум, Щ- В русскоязычной литературе
принято также обозначение случайных величин греческими бу-
буквами: f, ГЦ, [ii И Т.Д.
Рассмотрим примеры.
Пример 4Л. В опыте с однократным бросанием игральной
кости случайной величиной является число X выпавших очков.
Множество возможных значений случайной величины X имеет
вид
Бели вспомнить, как выглядит пространство элементарных
исходов в этом опыте, то будет очевидно следующее соответ-
соответствие между элементарными исходами ш и значениями случай-
случайной величины X:
I I ... i
X = 1 2 ... 6.
Иными словами, каждому элементарному исходу и*, i = 1,6,
ставится в соответствие число г.
Пример 4.2. Монету подбрасывают до первого появле-
появления „герба". В этом опыте можно ввести, например, такие
случайные величины: X — число бросаний до первого появле-
появления „герба" с множеством возможных значений {1, 2, 3, ...} и
у — число )?цифр", выпавших до первого появления „герба", с
множеством возможных значений {0, 1, 2, ...} (ясно, что X =
= Y +1). В данном опыте пространство элементарных исходов
?1 можно отождествить с множеством
{Г, ЦГ, ЦЦГ, ...,Ц...ЦГ, ...},
126 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
причем элементарному исходу Ц... ЦГ ставится в соответствие
число т +1 или ш, где т — число повторений буквы „Ц".
Пример 4.3. На плоский экран падает частица. Будем
считать, что нам известна вероятность попадания частицы
в любое (измеримое, т.е. имеющее площадь) множество на
экране. Случайными величинами в данном случае будут,
например, расстояние X от центра экрана до точки падения,
квадрат этого расстояния У = -X, угол Z в полярной системе
координат и т.д. #
Теперь мы можем дать определение случайной величины.
Определение 4.1. Скалярную функцию Х(и), заданную
на пространстве элементарных исходов, называют случайной
величиной, если для любого х ER множество {ш: Х(ш) < х}
элементарных исходов, удовлетворяющих условию Х(и) < х,
является событием.
Для краткости условимся в дальнейшем вместо записи
{и: Х(ш) < х) использовать запись {Х(ш) < х}, если необхо-
необходимо подчеркнуть связь случайной величины с пространством
элементарных исходов п, или даже запись {X < х}, если не ак-
акцентируется внимание на этой связи.
4.2. Функция распределения
случайной величины
Для исследования вероятностных свойств случайной вели-
величины необходимо знать правило, позволяющее находить веро-
вероятность того, что случайная величина примет значение из
подмножества ее значений. Любое такое правило называют
законом распределения вероятностей, или распределе-
распределением (вероятностей) случайной величины. При этом слово
„вероятностей" обычно опускают.
Общим законом распределения, присущим всем случайным
величинам, является функция распределения.
4.2. Функция распределения случайной величины 127
Определение 4.2. Функцией распределения (вероят-
(вероятностей) случайной величины X называют функцию F(x), зна-
значение которой в точке х равно вероятности события {X < #},
т.е. события, состоящего из тех и только тех элементарных
исходов о;, для которых X(ш) < х:
F(x)=P{X<x}.
Обычно говорят, что значение функции распределения в
точке х равно вероятности того, что случайная величина X
примет значение, меньшее х.
Теорема 4.1. Функция распределения обладает следующи-
следующими свойствами:
2) F(x\) < F(x2) при xi < Х2 (т.е. F(x) — неубывающая
функция);
3)\F(-oo)= lim F(x)=0, F(+oo) = lim F(x) = l;
4) P{x! < X < x2} = F(x2) - F(xi)i
5) F(x) = F(x - 0), где F(x - 0) = lim F(y) (т.е. F(x) —
непрерывная слева функция).
< При доказательстве будем использовать свойства вероятно-
вероятностей событий, доказанные в теореме 2.8.
Поскольку значение функции распределения в любой точке х
является вероятностью, то из свойства 4 вероятности вытекает
утверждение 1.
Бели х\ < а?2, то событие {X < х\} включено в событие
{X < #2} и, согласно свойству 3, Р{Х < х\} < Т?{Х < жг}, т.е. в
соответствии с определением 4.2 выполнено утверждение 2.
Пусть a?i, ..., жп, ... — любая возрастающая последователь-
последовательность чисел, стремящаяся к +оо. Событие {X < +оо}, с одной
стороны, является достоверным, а с другой стороны, предста-
представляет собой объединение событий {X < хп}. Отсюда в силу
аксиомы непрерывности следует второе равенство в утвержде-
утверждении 3. Аналогично доказывается и первое равенство.
128
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Событие {X < #2} при х\ < Х2 представляет собой объеди-
объединение двух непересекающихся событий: {X <х\} — случайная
величина X приняла значение, меньшее xi, и {х\ ^ X < Х2} —
случайная величина X приняла значение, лежащее в проме-
промежутке [х\уХ2). Поэтому в соответствии с аксиомой сложения
получаем утверждение 4.
Наконец, пусть хц ..., жп, ... — любая возрастающая по-
последовательность чисел, стремящаяся к х. Событие {X < х)
является объединением событий {X < хп}. Снова воспользовав-
воспользовавшись аксиомой непрерывности, приходим к утверждению 5. >
На рис. 4.1 приведен типичный вид функции распределения.
Рис. 4.1
Замечание 4.1. Можно показать, что любая неубывающая
непрерывная слева функция F(x), удовлетворяющая условиям
F(-oo)=0 и
является функцией распределения некоторой случайной вели-
величины X. #
Для того чтобы подчеркнуть, какой именно случайной вели-
величине принадлежит функция распределения F(x), далее иногда
будем приписывать этой функции нижний индекс, обозначаю-
4.3. Дискретные случайные величины 129
щий конкретную случайную величину. Например, для случай-
случайной величины X
В некоторых учебниках функцией распределения называют
функцию, значение которой в точке х равно вероятности
события {-X" ^ х). Такое определение ничего не меняет во
всех наших рассуждениях. Единственное изменение касается
свойства 5: функция F(x) будет непрерывна справа.
Чтобы избежать сложных математических конструкций,
обычно при первоначальном изучении теории вероятностей
ограничиваются только дискретными и непрерывными случай-
случайными величинами. Не давая пока строгие определения, приве-
приведем примеры:
- дискретных случайных величин (число очков, выпавших
при бросании игральной кости; число бросаний монеты до
первого появления „герба"; оценка студента на экзамене и т.д.);
- непрерывных случайных величин (погрешность измере-
измерений; время до отказа прибора; время опоздания студента на
лекцию и т.п).
4.3. Дискретные случайные величины
Определение 4.3. Случайную величину X называют дис-
дискретной, если множество ее возможных значений конечно или
счетно.
Распределение дискретной случайной величины удобно опи-
описывать с помощью ряда распределения.
Определение 4.4. Рядом распределения (вероятно-
(вероятностей) дискретной случайной величины X называют та-
таблицу (табл. 4.1), состоящую из двух строк: в верхней строке
перечислены все возможные значения случайной величины, а в
5- 10047
130
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
нижней — вероятности pi = P{X = Х{} того, что случайная
величина примет эти значения.
Таблица 4-1
X
р
Х\
Pi
Х2
Р2
...
...
Xi
Pi
...
...
хп
Рп
Чтобы подчеркнуть, что
ряд распределения относится
именно к случайной величи-
величине X, будем наряду с обозна-
обозначением pi употреблять также
обозначение рх%-
Для проверки правильности составления табл. 4.1 рекомен-
рекомендуется просуммировать вероятности р». В силу аксиомы нор-
мированности эта сумма должна быть равна единице:
Покажем теперь, как по ряду распределения дискретной слу-
случайной величины построить ее функцию распределения F(x).
Пусть X — дискретная случайная величина, заданная своим
рядом распределения, причем значения #i, Ж2, ..., хп располо-
расположены в порядке возрастания. Тогда для всех х < х\ событие
{X < х\ является невозможным и поэтому в соответствии с
определением 4.2 F(x) = 0 (рис. 4.2). Бели х\ < х ^ #2, то собы-
F(x),
1
Pi+Рг+Рз
i
i
i" i
xx x2 о
Pi
• • •
r4
Pl+P2
^Л _ „.
x3 xn x
Рис. 4.2
4.3. Дискретные случайные величины 131
тие {X < х) состоит из тех и только тех элементарных исходов
о;, для которых Х(ш) = х\, и, следовательно,
Аналогично при x*i < х < х$ событие {X < х] состоит из
элементарных исходов о;, для которых либо X(ш) = ?i, либо
Х(ш) =^2, т.е.
а следовательно,
и т.д. Наконец, при х > хп событие {X < х} достоверно и
F(x) = 1.
Таким образом, функция распределения дискретной случай-
случайной величины является кусочно постоянной функцией, прини-
принимающей на промежутке (—оо, х\] значение 0, на промежутках
(ж»,&t+i]> I ^ t < n, — значение р\ +... +pi и на промежутке
(жп, +оо) — значение 1.
Для задания закона распределения дискретной случайной
величины, наряду с рядом распределения и функцией распре-
распределения используют другие способы. Так, его можно задать
аналитически в виде некоторой формулы или графически. На-
Например, распределение игральной кости (см. пример 4.1) опи-
описывают формулой
Графическое изображение этого распределения приведено
на рис. 4.3.
132
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
0,2
0,1
1 2 3 4 5 6 х
Рис. 4.3
4.4. Некоторые дискретные случайные величины
В этом параграфе рассмотрим некоторые наиболее часто
встречаюпщеся на практике распределения дискретных случай-
случайных величин.
Биномиальное распределение. Дискретная случайная
величина X распределена по биномиальному закону, если
она принимает значения 0,1, 2,... ,п в соответствии с распреде-
распределением, заданным формулой
г =
или, что тоже самое, рядом распределения, представленным в
табл. 4.2, где 0<p,g< 1
X
р
0
1
...
Таблице
%
...
г 12
п
рп
Проверим корректность определения биномиального рас-
распределения. Действительно,
4.4. Некоторые дискретные случайные величины
133
t=0 t=0
Биномиальное распределение является не чем иным, как
распределением числа успехов X в п испытаниях по схеме
Бернулли с вероятностью успеха р и неудачи g = 1 — р (см. 3.6).
Распределение Пуссона. Дискретная случайная величи-
величина X распределена по закону Пуассона, если она принимает
целые неотрицательные значения с вероятностями
или, по-другому, с вероятностями, представленными рядом
распределения в табл. 4.3, где Л > 0 — параметр распределения
Пуассона.
Таблица 4-3
X
р
0
е"Л
1
Ле"А
2
...
...
п
...
...
Убедимся в том, что распределение Пуассона определено
корректно:
00
00
00
i=0
i=0
i=0
С распределением Пуссона мы тоже уже встречались в фор-
формуле Пуассона (см. 3.6). Распределение Пуассона также на-
называют законом редких событий, поскольку оно всегда
проявляется там, где производится большое число испытаний, в
каждом из которых с малой вероятностью происходит „ редкоеu
событие. В соответствии с законом Пуассона распределены,
например, число вызовов, поступивших в течение суток на те-
телефонную станцию; число метеоритов, упавших в определенном
134
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
районе; число распавшихся частиц при радиоактивном распаде
вещества.
Геометрическое распределение. Снова рассмотрим схе-
схему Бернулли. Пусть X — число испытаний, которое необходи-
необходимо провести, прежде чем появится первый успех. Тогда X —
дискретная случайная величина, принимающая значения 0, 1,
2, ..., п, ... Определим вероятность события {X = п}. Очевид-
Очевидно, что X = 0, если в первом же испытании произойдет успех.
Поэтому
Далее, X = 1 в том случае, когда в первом испытании произо-
произошла неудача, а во втором — успех. Но вероятность такого
события (см. теорему 3.8), равна др, т.е.
Аналогично X = 2, если в первых двух испытаниях произошли
неудачи, а в третьем — успех, и, значит,
Продолжая эту процедуру, получаем
Таким образом, случайная величина X имеет ряд распределе-
распределения, представленный в табл. 4.4.
Таблица 4-4
X
р
0
р
1
ЯР
2
Я2Р
• • •
...
П
ЯпР
...
Случайную величину с таким рядом распределения называ-
называют распределенной согласно геометрическому закону.
Правильность составления табл. 4.4 вытекает из равенства
00 00 ОО
г=0
t=0
i=0
4.5. Непрерывные случайные величины 135
4.5. Непрерывные случайные величины
Определение 4.5* Непрерывной называют случайную
величину Ху функцию распределения которой F(x) можно
представить в виде
>(*)= JpWv- D-1)
—оо
Функцию р(х) называют плотностью распределения (ве-
(вероятностей) случайной величины X.
Предполагают, что несобственный интеграл в представле-
представлении D.1) сходится.
Как и прежде, для того чтобы подчеркнуть принадлеж-
принадлежность плотности распределения случайной величине X, будем
наряду с записью р(х) употреблять запись рх(х)>
Все реально встречающиеся плотности распределения слу-
случайных величин являются непрерывными (за исключением,
быть может, конечного числа точек) функциями. Следова-
Следовательно, функция распределения для непрерывной случайной
величины является непрерывной на всей числовой оси и в точ-
точках непрерывности плотности распределения р(х) имеет место
равенство
p(x) = F'(x), D.2)
что следует из свойств интеграла с переменным верхним пре-
пределом [VI].
Только такие случайные величины мы и будем рассматри-
рассматривать в дальнейшем.
Замечание 4.2. Соотношения D.1) и D.2), связываю-
связывающие между собой функцию и плотность распределения, дела-
делают понятной следующую терминологию, часто употребляемую
на практике. Функцию распределения F(x) называют инте-
136
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
гральным законом распределения случайной величины, а
плотность распределения р(х) — дифференциальным зако-
законом распределения той же случайной величины.
На рис 4.4 представлен типичный вид плотности распреде-
распределения.
Р(х)
Теорема 4.2. Плотность распределения обладает следую-
следующими свойствами:
Х2
+00
f
3)
XI
4) Т?{х < X < х + Ах} « р(х) Ах в точках непрерывности
плотности распределения;
<4 Утверждение 1 следует из того, что плотность распределе-
распределения является производной от функции распределения, в силу
свойства 1 функции распределения она является неубывающей
функцией, а производная неубывающей функции неотрица-
неотрицательна.
4.5. Непрерывные случайные величины 137
Согласно свойству 2 функции распределения,
X < х2} = F(a?2) ~
Отсюда в соответствии с определением непрерывной случайной
величины и свойством аддитивности сходящегося несобствен-
несобственного интеграла [VI] имеем
Х2 Х\ Х2
= / p(x)dx- / p(x)dx = p(x)dx,
—OO X\
что и доказывает утверждение 2.
В частности, прих\ = —оо, х2 = +оо событие {х\ ^Х <
является достоверным, и поэтому справедливо утверждение 3.
Согласно свойству 4 (см. теорему 4.1),
= F(x + Ах) - F{x) = AF{x).
Бели Аж „мало" (см. рис. 4.4), то имеем
AF{x) и rfF(rc) = F'(x)Ax=p{x)Ax,
что и доказывает утверждение 4.
Наконец, поскольку в силу определения 4.5 функция распре-
распределения случайной величины есть несобственный интеграл от
плотности, то она является непрерывной, что приводит нас к
утверждению 5. >
Замечание 4.3. В силу свойства 2 плотности распределе-
распределения вероятность попадания непрерывной случайной величины
в промежуток [х\,Х2) численно равна площади криволинейной
трапеции, заштрихованной на рис. 4.4.
Согласно свойству 3 площадь, заключенная под всей кривой,
изображающей плотность распределения, равна единице.
В соответствии со свойством 4 вероятность попадания
случайной величины X в некоторый „малый" промежуток
138 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
(я, х + Ах) практически пропорциональна Ах с коэффициентом
пропорциональности, равным значению плотности распределе-
распределения в точке х. Поэтому выражение р(х)Ах или p(x)dx на-
называют иногда элементом вероятности. Можно также
сказать, что непрерывная случайная величина реализует геоме-
геометрическую схему с коэффициентом пропорциональности р(х),
но только в „малой" окрестности точки х.
Наконец, согласно свойству 5, вероятность попадания в
любую (заданную до опыта) точку для непрерывной случайной
величины равна нулю. #
В заключение отметим, что на практике иногда встречают-
встречаются случайные величины, которые нельзя отнести ни к дискрет-
дискретным, ни к непрерывным случайным величинам, как показывает
следующий пример.
Пример 4.4. На перекрестке стоит автоматический свето-
светофор, в котором Т\ = 1 мин горит зеленый свет, Т2 = 0,5 мин —
красный, снова 1 мин — зеленый, 0,5 мин — красный и т.д. В
случайный момент времени, не связанный с работой светофора,
к перекрестку подъезжает автомобиль.
Пусть X — время ожидания у перекрестка. Покажем,
что X не является ни дискретной, ни непрерывной случайной
величиной.
Обозначим г = т\ + тъ = 1,5 мин цикл работы светофора.
Естественно считать, что автомобиль подъезжает к перекрест-
перекрестку в случайный момент времени по отношению к циклу работы
светофора. Тогда, с одной стороны, с вероятностью т\/т = 2/3
автомобиль проедет перекресток не останавливаясь, т.е. X при-
принимает значение 0 с вероятностью 2/3 > 0. Поэтому X не может
быть непрерывной случайной величиной. С другой стороны,
на второй 0,5-минутной части цикла работы светофора время
ожидания X может принять любое значение от 0 до 0,5. Зна-
Значит, X не может быть также дискретной случайной величиной.
Для того чтобы лучше понять существо дела, построим
функцию распределения F(x) случайной величины X. Посколь-
4.5. Непрерывные случайные величины 139
ку время ожидания не может принять отрицательное значе-
значение, то
F(x)=Q
для всех х < 0. Далее если 0 < х < 0,5, то событие {X < х}
происходит в том случае, когда автомобиль либо попадет на
первую часть цикла работы светофора (зеленый свет), либо
подъедет к светофору при красном свете, но до включения
зеленого света останется время, меньшее х. В соответствии
с определением геометрической вероятности
Наконец, поскольку автомобиль в любом случае проведет у
перекрестка не более 0,5 мин, то
F{x) = 1, х > 0,5.
Таким образом,
0, х < 0;
ь 1, х> 0,5.
График функции распределения F(x) приведен на рис. 4.5.
Отметим, что в рассмотренном примере случайная величи-
величина X представляла собой ясмесь" дискретной и непрерывной
случайных величин, причем Р{Х = 0} = F(+0) — F@) — скачку
функции распределения в точке х = 0. Можно привести и бо-
более сложные примеры, в которых случайные величины уже не
являются „смесью" дискретной и непрерывной составляющих,
однако эти примеры нужно отнести к разряду математических
абстракций.
140
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
F(x)
4.6. Некоторые непрерывные случайные величины
Приведем примеры некоторых наиболее важных распреде-
распределений непрерывных случайных величин. То, что приводимые
функции F(x) являются функциями распределения, следует из
замечания 4.1 и проверяться не будет.
Равномерное распределение. Случайная величина име-
имеет равномерное распределение на отрезке [а, 6], если ее
плотность распределения
р(х) =
0,
х < а или х > Ь.
Легко видеть, что функция распределения в этом случае
определяется выражением
0,
ж —а
1,
х<а\
а ^ х ^ 6;
х>Ъ.
Графики плотности распределения р(х) и функции распре-
распределения F(x) приведены на рис. 4.6 и 4.7.
4.6. Некоторые непрерывные случайные величины 141
а О
Рис. 4.6
Рис. 4.7
Вероятность попадания равномерно распределенной слу-
случайной величины в интервал (х\, Х2), лежащий внутри отрезка
[a, ft], равна Ffa) — F(x\) = (#2 — x\)/(b — а), т.е. пропорцио-
пропорциональна длине этого интервала. Таким образом, равномерное
распределение реализует схему геометрической вероятности
при бросании точки на отрезок [а, Ь].
Экспоненциальное распределение. Случайная величи-
величина распределена по экспоненциальному (показательному)
закону, если она имеет плотность распределения
о,
где А > 0 — параметр экспоненциального распределения. Для
функции распределения в данном случае нетрудно получить
следующее выражение:
F(x) =
х<0;
Графики плотности распределения и функции распределе-
распределения экспоненциально распределенной случайной величины при-
приведены на рис. 4.8 и 4.9.
142
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
P(x)i
A
A
2
<5
To T
Рис. 4.8
F(x)j
1
1
2
x О
^
/fl
/ 1 i
1 То Г x
Рис. 4.9
Экспоненциально распределенная случайная величина мо-
может принимать только положительные значения.
Примером случайной величины, имеющей экспоненциальное
распределение, является время распада радиоактивных элемен-
элементов. При этом число
называют средним временем распада. Кроме того, употребля-
употребляют также число
называемое периодом полураспада.
Название „период полураспада" основано на следующем фи-
физическом соображении. Пусть у нас первоначально имелось п
атомов вещества. Тогда спустя время То каждый атом распа-
распадется с вероятностью
le = l =
Поэтому в силу независимости отдельных распадов число рас-
распавшихся за время То атомов имеет биномиальное распределе-
распределение с р = q = 1/2. Но, как мы увидим далее, согласно закону
больших чисел (см. 9.2), при больших п это число будет пример-
примерно равно п/2, т.е. период полураспада То представляет собой
4.6. Некоторые непрерывные случайные величины 143
время, в течение которого распадается половина имеющегося
вещества.
Экспоненциально распределенная случайная величина X об-
обладает весьма важным свойством, которое естественно наз-
назвать отсутствием последействия. Трактуя X как время
распада атома, рассмотрим событие
А = {х\ < X < Х\ + Х2}
и найдем условную вероятность этого события при условии
выполнения события В = {X >х\}. В соответствии с определе-
определением условной вероятности
Но событие АВ, как нетрудно понять, совпадает с событием
А. Поэтому
Далее, используя свойство 4 функции распределения (см. тео-
теорему 4.1), имеем:
Р(А) = Р{ж1 < X < xi + х2} =
= l-P{X<xi} = e-Aa;i.
Значит,
— 1 _ р-Лж2
Таким образом, вероятность распада атома за время х-i при
условии, что перед этим он уже прожил время х\, совпадает
с безусловной вероятностью распада того же самого атома за
144 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
время Х2- Именно это свойство и представляет собой отсут-
отсутствие последействия. Допуская некоторую вольность речи, от-
отсутствие последействия можно трактовать как независимость
остаточного времени жизни атома от того времени, которое он
уже прожил. Можно показать и обратное: если случайная вели-
величина X обладает свойством отсутствия последействия, то она
обязательно должна быть распределена по экспоненциальному
закону. Таким образом, отсутствие последействия является ха-
характеристическим свойством экспоненциально распределенных
случайных величин.
Практика показывает, что экспоненциальное распределе-
распределение имеют и другие физические величины, например: времена
между падениями метеоритов в определенный район, времена
между соседними поступлениями вызовов на телефонную стан-
станцию и т.д. Экспоненциальное распределение тесно связано с
распределением Пуассона, а именно: если времена между после-
последовательными наступлениями некоторого события представля-
представляют собой независимые (определение независимости случайных
величин будет дано в 5.4) экспоненциально распределенные (с
одним и тем же параметром Л) случайные величины, то чи-
число наступлений этого события за время t распределено по
закону Пуассона с параметром At. Отметим также, что дис-
дискретным аналогом экспоненциального распределения является
геометрическое распределение.
Нормальное распределение. Случайная величина рас-
распределена по нормальному (или гауссову) закону, или
имеет нормальное (гауссово) распределение, если ее плот-
плотность
m
Нормальное распределение зависит от двух параметров: т,
называемого математическим ожиданием или средним
4.6. Некоторые непрерывные случайные величины
145
значением, и сг, называемого средним квадратичным от-
отклонением.
Графики плотности <pmi(T(x) и функции
1 } (*-™J
[х) = —= \ е 2<т* dx
нормального распределения для различных значении m и а
приведены на рис. 4.10 и рис. 4.11.
Фт,<г(х)
-2-10 12 3
Рис. 4.10
-2 -1 0
1 2 3 х
Рис. 4.11
Как следует из этих рисунков, параметр т определяет
положение „центра симметрии" плотности нормального рас-
распределения, т.е. график плотности нормального распределения
симметричен относительно прямой х = m, a a — разброс зна-
значений случайной величины относительно центра симметрии.
Бели т = 0 и а — \, то такой нормальный закон называ-
называют стандартным и его функцию распределения обозначают
Ф(#), а плотность распределения — <р{х). С плотностью и
функцией стандартного нормального распределения мы уже
встречались в локальной и интегральной формулах Муавра —
Лапласа (см. 3.6).
Как известно из курса математического анализа [VI], инте-
интеграл fe~~x l2dx не может быть выражен через элементарные
функции. Поэтому во всех справочниках и в большинстве
учебников по теории вероятностей приведены таблицы значе-
146 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ний функции стандартного нормального распределения. На-
Напомним, что в табл. П.З даны значения интеграла Лапласа
X
Фо(гг) = J(p(y)dy. Покажем, как, используя эту таблицу, найти
о
вероятность попадания случайной величины, распределенной
по нормальному закону с произвольными параметрами т и а,
в интервал (а, 6).
В соответствии со свойством 2 плотности распределения
(см. теорему 4.2) вероятность попадания случайной величины
X, распределенной по нормальному закону с параметрами т и
сг, в интервал (а, Ь) задается формулой
о о
{« < X < Ь) ш J<pm><r(y)dy = /^e"(v
Проводя замену х = (у — т)/а, этот интеграл можно записать
в виде
(Ь—т)/а F—т)/а
f f
()/ ()/
Р{а<Х<Ъ}= f -j=:e-x2ftdx= f (p{x)dx.
(a—m)/or
Таким образом, окончательно получаем
—— )-фо(—— J- D.3)
Распределение Вейбулла. Случайная величина распреде-
распределена по закону Вейбулла, если она имеет плотность распре-
распределения
{О, х < 0;
аРх*-хе-«х*, х > 0 (а > 0, 0 > 0).
4.6. Некоторые непрерывные случайные величины
147
Нетрудно проверить, что функция распределения в этом
случае определяется следующим выражением:
F(x)
-1°'
"\ 1-е—',
(а>0,
Семейство распределений Веибулла является двухпараме-
трическим (а, /3 — параметры) и описывает положительные
случайные величины.
Графики плотности р(х) и функции F(x) распределения
Веибулла представлены на рис. 4.12 и 4.13.
F(x)i
1
а = 0,3
Рис. 4.13
Считают, что распределению Веибулла подчиняются време-
времена безотказной работы многих технических устройств. Бели
/3=1, то распределение Веибулла превращается в экспоненци-
экспоненциальное распределение, а если /3 = 2 — в так называемое рас-
распределение Релел (закон Релел).
Гамма-распределение. Другим распределением, также
достаточно хорошо описывающим времена безотказной работы
различных технических устройств, является гамма-распре-
гамма-распределение с плотностью
(
(
о,
ГG)
-Ах
е
(Л > 0, 7 > 0),
148
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
где
+оо
/
ГG) =
есть гамма-функция Эйлера [VI]. При изучении гамма-рас-
гамма-распределения весьма полезными являются следующие свойства
гамма-функции: ГG +1) = 7Г(т) и Г(п) = (п — 1)! для целых п.
Графики плотности р(х) и функции F(x) гамма-распределе-
гамма-распределения изображены на рис. 4.14 и 4.15.
Р(х),
1
1
А =
7 =
0
" А = 0,5
\7 = 0,5
Г 1
Рис.
"—г
2
4.14
= 2
= 4
3 х
F(X);
1
0
А
/
/
= 0,5
1
Рис.
7=4
2 3 х
4.15
Как видно на рис. 4.12-4.15, распределение Веибулла и
гамма-распределение весьма близки между собой. Основным
преимуществом закона Веибулла перед гамма-распределением
является то, что его функция распределения является элемен-
элементарной функцией. Поэтому раньше, когда ЭВМ еще не были
достаточно распространены, распределение Веибулла исполь-
использовалось гораздо чаще, чем гамма-распределение. Хотя в об-
общем случае гамма-распределение и не является элементарной
функцией, гамма-распределение обладает некоторыми весьма
полезными свойствами. Так, если 7 = &> т.е. у принимает целые
значения, то мы получаем распределение Эрланга порядка
к, находящее важные применения в теории массового обслужи-
обслуживания. Бели же 7 = &/2, где А; — нечетное число, а А = 1/2, то
гамма-распределение превращается в так называемое распре-
распределение х2 (хи-квадрат), роль которого в математической
4.7. Решение типовых примеров 149
статистике невозможно переоценить. Параметр к называют в
этом случае числом степеней свободы распределения х2>
а само распределение — распределением х2 (хи-квадрат)
с к степенями свободы. Наконец, при 7 = 1 мы имеем де-
дело все с тем же экспоненциальным распределением. Гамма-
распределение обладает и другими интересными свойствами,
которые мы здесь не будем рассматривать.
4.7. Решение типовых примеров
Пример 4.5, Игральную кость бросают один раз. Бели
выпадает четное число очков, игрок выигрывает 8 рублей,
если нечетное, но больше одного — проигрывает 1 рубль,
если выпадает одно очко — проигрывает 10 рублей. Найдем
распределение случайной величины X — величины выигрыша
в данной игре.
Пространство элементарных исходов в данном случае име-
имеет вид
где Ш{ — выпадение г очков. Считая, что игральная кость
симметричная, имеем
Случайная величина X может принять всего три значения:
a?i=8, %2 = — 1 и хз = —10 (является дискретной), причем
каждому из этих значений соответствуют события
{X = 8} = {и: Х(ш) = 8} = {ш2, щ, о;6},
{X = -1} = {w: Х(ш) = -1} = {о>з, о>5},
{X = -10} = {ш: Х(ш) = -10} =
150
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
с вероятностями
Р1=Р{Х = 8} =
Р2=Р{Х = -1} =
= Р(о*) + Р(с*
X
р
-10
1/6
-1
1/3
8
1/2
Таблица 4-5 Таким образом, ряд рас-
распределения случайной величи-
величины X можно представить в
виде табл. 4.5.
Графическое изображение распределения случайной величи-
величины X приведено на рис. 4.16.
Найдем теперь функцию распределения F(x) случайной ве-
величины X. В соответствии с определением функции распреде-
распределения
F(x)=P{X<x} =
0,
х < -10;
График функции распределения F(x) изображен на рис. 4.17.
.1...
-10
р,
1
0,5
....1
1
0 10 х
Рис
. 4.16
-10
F(x),
1
0,5 ,
1
|
1
0 10 х
Рис
. 4.17
Пример 4.6. Производят четыре независимых опыта, в
каждом из которых некоторое событие А появляется с веро-
вероятностью р = 0,8. Построим ряд распределения и функцию
4.7. Решение типовых примеров
151
распределения случайной величины X — числа появлений со-
события А в четырех опытах.
В соответствии с условием задачи мы имеем дело со схемой
Бернулли, т.е. число появлений события А распределено по
биномиальному закону с параметрами п = 4, р = 0,8ид = 1—р =
= 0,2. Значит, случайная величина X может принимать только
значения г, г = 0,4.
Согласно формуле Бернулли
определим вероятности возможных значений случайной вели-
величины X:
Р{Х = 0} = C$p°q4 = 0,0016, Р{Х = 1} = С\р1<р = 0,0256,
Р{Х = 2} = С|рУ = 0,1536, Р{Х = 3} = С|рУ = 0,4096,
Р{Х = 4} = С|рУ = 0,4096.
Ряд распределения рассматриваемой случайной величины
представлен в табл. 4.6.
Таблица 4-6
X
р
0
0,0016
1
0,0256
2
0,1536
3
0,4096
4
0,4096
Функция распределения случайной величины X имеет вид
0, х < 0;
0,0016, 0 < х ^ 1;
0,0272, К х < 2;
0,1808, 2 < х < 3;
0,5904, 3 < х < 4;
1, ж > 4.
= <
152
4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
График функции распределения F(x) изображен на рис. 4.18.
F(x)
Пример 4.7. Функция распределения непрерывной случай-
случайной величины X задана выражением
F(x) =
Найдем:
а) плотность распределения р(х) случайной величины Х\
б) вероятность попадания случайной величины X в интер-
интервал от 0,25 до 0,5;
в) вероятность того, что случайная величина X примет
значение меньшее 0,3;
г) вероятность того, что случайная величина X примет
значение большее 0,7;
д) графики F(x) и р(х).
Воспользовавшись определением 4.5 и свойствами плотно-
плотности распределения и функции распределения, (см. теоремы 4.1
и 4.2, имеем:
а) р(х) =
(
{
1
О х ^ 0#
= {2х, 0<х<
О, х > 1;
АЛ. Решение типовых примеров
153
б) Р{0,25 < х < 0,5} = F@,5) - F@,25) = 0,52 - 0,252 = 0,1875;
в) Р{х < 0,3} = F@,3) = 0,32 = 0,09;
г) Р{х > 0,7} = 1 - Р{ж < 0,7} = 1 - F@,7) = 1 - 0,72 = 0,51;
д) графики F(x) и р(х) приведены на рис. 4.19 и 4.20.
F(x)
Рис. 4.19
Рис. 4.20
Пример 4,8. Функция распределения непрерывной случай-
случайной величины X задается формулой
х
F(x) = c + barctg-.
а
Найдем:
а) постоянные с и 6;
б) плотность распределения случайной величины Х\
в) P{si < X < х2}.
В соответствии с определениями 4.2 и 4.5 и свойствами
функции и плотности распределения (см. теоремы 4.1, 4.2):
а) постоянные бис определяем из условий
lim
x-»-oo
lim
х-ч+оо
154 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Имеем:
lim F(x) = lim [c + barctg —) = c — 6— =0,
X-+
/ X \ 7Г
lim F(x) = lim (c + 6arctg-) = c + 6—
Из системы уравнений
с-6§=0|
находим, что с=-иЬ=-и поэтому F(rr) = - + - arctg -;
2 тг 2 тг а
б) плотность распределения равна
в) вероятность попадания X в интервал (х\, х2) равна:
P{xi < X < х2} = F{x2) ~ -^(^l) =
11 Х2 1 1 Я?1 1 / 2?2 Д?1 \
= 2 + ^arCtg^-2-^arCtgT = ^(arCtgT-arCtST)'
Пример 4.9. Непрерывная случайная величина X имеет
следующую плотность распределения:
у а/х , х > 1.
Определим:
а) коэффициент а;
б) функцию распределения F(x);
в) графики р(ж) и F(x);
г) вероятность Р{2 < X < 3} попадания случайной величи-
величины Л" в интервал B, 3);
д) вероятность того, что при четырех независимых испы-
испытаниях случайная величина X ни разу не попадет в интервал
B, 3).
4.7. Решение типовых примеров
155
а. Для нахождения коэффициента а воспользуемся свой-
свойством 3 плотности распределения. Тогда
+оо
—оо
-foo
p(x)dx= J±dx = -1
-00
+оо
откуда получаем а = 1.
б. В соответствии с определением 4.5 плотности распреде-
распределения
F(x) =
X
I
—оо
X
dy x-l
[dy_
J У2"
1
в. Графики функций р(х) и F(x) изображены на рис. 4.21
и 4.22.
г.
|
д. Вероятность того, что X не попадет в интервал B,3)
при одном испытании равна 1 — 1/6 = 5/6, та же вероятность
при четырех испытаниях равна E/6L « 0,48.
F(x)
1 2 3 х
Рис. 4.22
156 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Пример 4.10. Случайное отклонение размера детали от
номинала имеет нормальное распределение со средним значени-
значением m = 1мм и средним квадратичным отклонением а = 2мм.
Найдем:
а) вероятность того, что отклонение от номинала будет
отрицательным;
б) процент деталей, размер которых будет иметь отклоне-
отклонение от номинала не более 5 мм;
в) верхнюю границу отклонения от номинала, обеспечивае-
обеспечиваемую с вероятностью 0,9.
Обозначим через X отклонение от номинала. Случайная
величина X имеет нормальное распределение с параметрами
т = 1мм и о = 2мм.
а. Используя формулу D.3) и данные из табл. П.З, содержа-
содержащей значения интеграла Лапласа, находим:
= Фо (^) - Фо(-оо) = -0,19146 - (-0,5) = 0,30854.
б. Аналогично
= Ф0B) - Фо(-З) = 0,47725 - (-0,49865) = 0,9759.
Таким образом, в пределах допуска ±5 мм находится 97,59%
деталей.
в. Для ответа на третий вопрос нужно найти такое число
ж+, при котором Т?{Х < х+} = 0,9. Поскольку
4.7. Решение типовых примеров 157
ТО
2 -,-~
их+ = 3,56. Значит, с вероятностью 0,9 отклонение от номина-
номинала будет меньше 3,56.
Цример 4.11. Случайная величина X распределена по
нормальному закону с параметрами т = 0 и а. При каком
значении среднего квадратичного отклонения а вероятность
попадания случайной величины X в заданный интервал (а, 6),
0 < а < Ь < оо, будет наибольшей?
Вероятность попадания случайной величины X в интервал
(а, Ъ) можно определить по формуле D.3):
Поскольку Фо(Ь/а) и Фо(а/сг) — дифференцируемые по о функ-
функции, то необходимым условием экстремума является равенство
нулю производной (Р{а < X < b})'G. Отсюда, согласно опреде-
определению интеграла Лапласа, имеем
где
есть плотность стандартного нормального распределения. Про-
Производя элементарные арифметические преобразования, прихо-
приходим к уравнению
относительно а > 0. Его решение имеет вид
¦/
!-а2
2Aп6-1по)'
158 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Нетрудно проверить, что при фиксированных значениях а
и 6, в силу условия 0 < а < Ь < +оо справедливы соотношения
a
Поэтому вероятность Р{а < X < 6} при
¦/.
(Ь2-а2)
2Aп6-1па)
принимает максимальное значение.
Вопросы и задачи
4.1. Дайте определение случайной величины.
4.2. Что называют законом распределения (вероятностей)
случайной величины?
4.3. Дайте определение функции распределения (вероятно-
(вероятностей). Перечислите и докажите свойства функции распределе-
распределения.
4.4. Как, зная функцию распределения, найти вероятность
попадания случайной величины в заданный интервал?
4.5. Какие свойства должна иметь некоторая функция для
того, чтобы она могла быть функцией распределения?
4.6. Какую случайную величину называют дискретной?
Приведите примеры дискретных случайных величин.
4.7. Что называют рядом распределения дискретной слу-
случайной величины? Как еще можно задать закон распределения
дискретной случайной величины?
Вопросы и задачи 159
4.8. Какой вид имеет функция распределения дискретной
случайной величины?
4.9. Какое распределение называют биномиальным?
4.10. Какое распределение называют распределением Пуас-
Пуассона?
4.11. Какое распределение называют геометрическим рас-
распределением?
4.12. Какую случайную величину называют непрерывной?
Приведите примеры непрерывный случайных величин.
4.13. Дайте определение плотности распределения (вероят-
(вероятностей). Перечислите и докажите свойства плотности распре-
распределения. Существует ли плотность распределения у дискретной
случайной величины?
4.14. Как, зная плотность распределения, найти вероят-
вероятность попадания случайной величины в заданный интервал?
4.15. Чем различаются графики функций распределения
дискретной и непрерывной случайных величин?
4.16. Какое распределение называют равномерным?
4.17. Какое распределение называют экспоненциальным
(показательным) ?
4.18. Какое распределение называют нормальным?
4.19. Как выглядит график плотности нормального распре-
распределения?
4.20. Что называют интегралом Лапласа? Как, пользуясь
таблицей значений интеграла Лапласа, вычислить вероятность
попадания нормально распределенной случайной величины в
некоторый интервал?
4.21. Какое распределение называют распределением Вей-
булла?
160 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
4.22. Какое распределение называют гамма-распределением?
4.23. Из партии в 10 деталей, среди которых две бракован-
бракованные, наудачу выбирают три детали. Найдите закон распределе-
распределения числа бракованных деталей среди выбранных. Постройте
функцию распределения.
Ответ:
0 х ^ 0*
ш, 7/15, * 6@,1];
К } S 14/15, х 6A, 2];
1, х > 2.
4.24. Вероятность приема самолетом радиосигнала при ка-
каждой передаче равна 0,7. Найдите ряд распределения и функ-
функцию распределения числа X принятых сигналов при шестикрат-
шестикратной передаче.
Ответ: Ряд распределения и функцию распределения слу-
случайной величины X легко построить, зная, что Р{Х = г} =
4.25. Найдите закон распределения случайной величины
X — числа таких бросаний трех игральных костей, в каждом из
которых ровно на двух костях появится по 2 очка, если общее
число бросаний равно 15.
Ответ: Т>{Х=1} = С\ър^1Ъ-\ * = 0Д5, гдер=С32A/6JE/6I =
= 5/72 «0,0694.
4.26. В течение часа на станцию скорой помощи поступает
случайное число X вызовов, распределенное по закону Пуассона
с параметром А = 5. Найдите вероятность того, что в течение
часа поступит:
а) ровно два вызова;
б) не более двух вызовов;
в) не менее двух вызовов.
Вопросы и задачи 161
О т в е т: а) Р{Х = 2} = Ь2е~ъ/2\ » 0,086;
б) Р{Х ^ 2} = E°/0! + 51/!! + 52/2!)е~5 « 0,127;
в) Р{Х > 2} = 1 -Р{Х < 2} = 1 - E°/0! + 5Vl!)e «0,041.
4.27. Число вызовов, поступающих на АТС (автоматиче-
(автоматическая телефонная станция) каждую минуту, распределено по
закону Пуассона с параметром А = 1,5. Найдите вероятность
того, что за минуту поступит:
а) ровно три вызова;
б) хотя бы один вызов;
в) менее пяти вызовов.
О т в е т: а) 0,12551; б) 0,77687; в) 0,98143.
4.28. В приборный отсек космического корабля за время
полета попадает случайное число частиц, распределенное по за-
закону Пуассона с параметром Л, причем вероятность попасть в
блок управления, расположенный в отсеке космического кора-
корабля, для каждой из этих частиц равна р. Определите вероят-
вероятность попадания в блок:
а) ровно к частиц; б) хотя бы одной частицы.
О т в е т: а) (\р)ке~хР/к\) б) 1 - e~A*\
4.29. По цели производят серию независимых выстрелов
до первого попадания. Даны вероятность р попадания в цель
при одном выстреле и запас патронов п. Найдите ряд распре-
распределения и функцию распределения числа X израсходованных
патронов.
п тугг л Jw*~\ t = 0,n-l (g = l-p);
Ответ: Р{Х-.} = |^ . = п
4.30. Летательный аппарат, по которому ведется стрельба,
состоит из двух различных по уязвимости частей. Аппарат вы-
выходит из строя при одном попадании в первую часть или трех
попаданиях во вторую. Стрельба ведется до поражения лета-
летательного аппарата. Постройте ряд распределения и функцию
6 - 10047
162 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
распределения числа попаданий X в летательный аппарат, ко-
которое понадобится для его поражения, если каждый попавший
в аппарат снаряд с вероятностью 0,3 поражает первую часть и
с вероятностью 0,7 — вторую.
Ответ: Р{Х = 1} = 0,3; Р{Х = 2} = 0,21; Р{Х = 3} = 0,49.
4.31. Непрерывная случайная величина X распределена по
экспоненциальному закону с параметром Л = 0,2. Найдите
вероятность попадания этой случайной величины в интервал
@,2).
Ответ: 1 -е'4 «0,33.
4.32. Длительность времени X безотказной работы элемен-
элемента имеет экспоненциальное распределение с параметром Л =
= 0,02 ч". Вычислите вероятность того, что за время t = 100 ч
элемент: а) выйдет из строя; б) будет исправно работать.
О т в е т: а) 1 - е « 0,865; б) е « 0,135.
4.33. Случайная величина X имеет нормальное распреде-
распределение с параметрами га = 2 и а = 1. Определите вероятность
попадания случайной величины в интервал A, 5).
Ответ: 0,83999.
4.34. Случайная величина X распределена по нормальному
закону с параметрами т = 4 и а = 1. Определите вероятность
попадания случайной величины X в интервал F, 8).
Ответ: 0,0227.
4.35. Случайная величина X имеет нормальное распределе-
распределение с параметрами т и а. Вычислите вероятность попадания
случайной величины в интервал (ш — 4сг, т).
Ответ: 0,499971.
4.36. Случайная величина X подчинена нормальному закону
распределения с т = 0. Вероятность попадания случайной
величины в интервал (—0,3, 0,3) равна 0,5. Найдите среднее
квадратичное отклонение а.
Ответ: а«0,44.
Вопросы и задачи 163
4.37. Измерительный прибор имеет систематическую по-
погрепшость 5 м. Случайные погрешности подчиняются нормаль-
нормальному закону со средним квадратическим отклонением, равным
10 м. Какова вероятность того, что погрешность измерения не
превзойдет по абсолютному значению 5 м?
Отрет: 0,3413.
4.38. Измерение дальности до объекта сопровождается слу-
случайными погрешностями, подчиняющимися нормальному за-
закону со средним квадратичным отклонением, равным 50 м.
Систематическая погрешность отсутствует. Найдите:
а) вероятность измерения дальности с погрешностью, не
превосходящей по абсолютному значению 100 м;
б) вероятность того, что измеренная дальность не превзой-
превзойдет истинной.
Ответ: а) 0,9545; б) 0,5.
4.39. Высотомер имеет случайную и систематическую по-
погрешности. Систематическая погрешность равна 20 м. Слу-
Случайная погрешность распределена по нормальному закону. Ка-
Какую среднюю квадратичную погрешность должен иметь при-
прибор, чтобы с вероятностью 0,9452 погрепшость измерения вы-
высоты была меньше 10 м?
Ответ: 50 м.
4.40. Случайная величина X распределена по нормальному
закону с математическим ожиданием т и средним квадратич-
квадратичным отклонением ст. Определите абсциссы и ординаты точек
перегиба кривой плотности распределения.
Ответ: т±а\ е~^2/(а\Дп).
4.41. Нормально распределенная случайная величина X име-
имеет математическое ожидание, равное нулю. Найдите среднее
квадратичное отклонение <т, при котором вероятность попада-
попадания случайной величины в интервал E,10) была бы наибольшей.
Ответ: <т= ^7Ь/BЫ2).
164 4. ОДНОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
4.42. Время X (в часах) безотказной работы электрической
лампочки имеет распределение Вейбулла с параматрами а —
= 0,02 и C = 0,5. Определите вероятность того, что лампочка
проработает не менее 10000 ч.
Ответ: Р{Х > 10000} = е-0,02.100001/2 « 0,14.
4.43. Время X (в месяцах) безотказной работы некоторой
системы, состоящей из одного основного и двух резервных
элементов, имеет гамма-распределение с параматрами 7 = 3и
Л = 0,05. Найдите вероятность того, что система проработает
не менее 5 лет.
Ответ: Р{Х > 60} = е-3A + 3 = 32/2) « 0,42.
5. МНОГОМЕРНЫЕ
СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
В прикладных задачах обычно приходится рассматривать
не одну случайную величину, а несколько случайных величин,
одновременно измеряемых (наблюдаемых) в эксперименте. При
этом с каждым элементарным исходом wGfi бывает связан на-
набор числовых значений некоторых количественных параметров.
В этой главе мы обобщим ранее полученные результаты на
совокупность из нескольких случайных величин, заданных на
одном и том же вероятностном пространстве.
5.1. Многомерная случайная величина.
Совместная функция распределения
Определение 5.1. Совокупность случайных величин
заданных на одном и том же вероятностном пространстве
(?2,9$,Р), называют многомерной (п-мерной) случайной
величиной, или п-мерным случайным вектором. При
этом сами случайные величины Xi,X2,...,Xn называют коор-
координатами случайного вектора. В частности, при п — 1
говорят об одномерной, при п = 2 — двумерной случайной
величине (или двумерном случайном векторе).
Для n-мерного случайного вектора воспользуемся обозначе-
обозначениями (Xi, ..., Хп) иХ = (Xi, ..., Хп). В случае двумерных
и трехмерных случайных векторов наряду с обозначениями
(Xi, X2) и (Xi, Хг, -Хз) будем использовать также обозначе-
обозначения (X, Y) и (X, Y, Z).
166 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Множество значений n-мерного случайного вектора можно
отждествить с точками п-мерного линейного арифметического
пространства Шп [IV].
Замечание 5.1. Обратим внимание, что в данном выпуске
в отличие от предыдущих [IV] вектор пространства Rn будем
обозначать матрицей-строкой.
Приведем примеры случайных векторов.
Пример 5.1. Отклонение точки разрыва снаряда от точки
прицеливания при стрельбе по плоской цели можно задать
двумерной случайной величиной (X, У), где X — отклонение
по дальности, а У — отклонение в боковом направлении.
При стрельбе по воздушной цели необходимо рассматривать
трехмерный случайный вектор (X, У, Z), где X, У, Z —
координаты отклонения точки разрьгаа зенитного снаряда от
точки прицеливания в некоторой пространственной системе
координат [III].
Пример 5.2. При испытании прибора на надежность со-
совокупность внешних воздействий в некоторый момент време-
времени можно описать случайным вектором (X, У, Z, ...). Здесь,
например, X — температура окружающей среды, У — атмо-
атмосферное давление, Z — амплитуда вибрации платформы, на
которой установлен прибор и т.д. Размерность этого вектора
зависит от количества учитываемых факторов и может быть
достаточно большой. #
Свойства многомерных случайных векторов мы будем в
основном изучать на примере двумерного случайного вектора,
делая, если это потребуется, пояснения для случайного вектора
произвольной размерности.
Напомним, что рассмотрение одномерной случайной вели-
величины начиналось с обсуждения способа задания ее закона рас-
распределения. В частности, закон распределения одномерной
случайной величины можно задать с помощью функции распре-
распределения. То же можно сказать и по отношению к п-мерному
5.1. Совместная функция распределения
167
случайному вектору. Отметим, что в дальнейшем для пересе-
пересечения событий {Х\ < х\},..., {Хп < хп} вместо записи
{X1<xi}n...n{Xn<xn}
будем использовать запись
Определение 5.2. Функцией распределения (вероят-
(вероятностей)
(n-мерного) случайного вектора (Х\, • •> Хп) назьшают
функцию, значение которой в точке (#i, ..., хп) € Rn равно ве-
вероятности совместного осуществления (пересечения) событий
{Хх < хг},..., {Хп < хп}, т.е.
Функцию распределения F(x\,...,хп) называют также со-
совместной (п-мерной) функцией распределения случай-
случайных величин Xi,..., Хп. В частности, при п = 1 будем гово-
говорить об одномерной, при п = 2 —
о двумерной функции распреде-
распределения.
Значение двумерной функции
распределения в точке (ai;a2), со-
согласно определению 5.2, предста-
представляет собой не что иное, как ве-
вероятность попадания точки с ко-
координатами {X\\X*i) в квадрант
с вершиной в точке {a\\a<i), за-
заштрихованный на рис. 5.1.
Свойства двумерной функции распределения, аналогичные
свойствам функции распределения одномерной случайной вели-
величины, доказываются в следующей теореме.
Рис. 5.1
168
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Теорема 5.1. Двумерная функция распределения удовле-
удовлетворяет следующим свойствам.
2. F(x\,x2) — неубывающая функция [V] по каждому из
аргументов х\ ихг-
3. F(-oo,x2) = F(xb-oo) =0.
4. F(+oo,+oo) = l.
5. P{ai < Хг ^ 6Ь a2 ^ X2 < 62} = FFb 62) - F(bu a2) -
6. F(x\,X2) — непрерывная слева в любой точке (#i,a;2) G
по каждому из аргументов х\ и ж2 функция.
^ Утверждения 1 и 2 доказываются точно так же, как и в
одномерном случае (см. теорему 4.1).
События {Х\ < —оо} и {Х2 < —оо} являются невозможны-
невозможными, а пересечение невозможного события с любым событием,
как известно, также невозможное событие, вероятность кото-
которого равна нулю. Отсюда с учетом определения 5.2 вытекает
утверждение 3.
Аналогично из того, что события {Xi < +00} и {Х2 < +оо}
так же, как и их пересечение, являются достоверными, веро-
вероятность которых равна единице, вытекает утверждение 4.
Рис. 5.2
Чтобы найти вероятность попадания двумерной случайной
величины (Х\,Х2) в прямоугольник {ai^xi<6i, а2^ж2<62} (на
5.1. Совместная функция распределения 169
рис. 5.2 заштрихован), сначала определим вероятность попа-
попадания в полуполосу {х\ < oi, а2 ^ Х2 < Ьг} (отмечена двойной
штриховкой). Но эта вероятность представляет собой веро-
вероятность попадания в квадрант {х\ < 6i, Х2 < Ь2} за вычетом
вероятности попадания в квадрант {х\ < bi, Х2 < а2}, т.е.
Теперь осталось заметить, что вероятность попадания в пря-
прямоугольник {ai^#i<bi, 0,2^X2<b2} совпадает с вероятностью
попадания в полуполосу {#i<bi, а2^ж2<Ь2} из которой вычи-
вычитается вероятность попадания в полуполосу {х\ <ai, a2 ^ж2 <6г},
равная F(ai,b2) — ^(^i,a2). Окончательно получим утвержде-
утверждение 5.
Подобно одномерному случаю доказывается и утвержде-
утверждение 6.
Наконец, событие {Х2 < +оо} является достоверным, по-
поэтому
{Хг < хг} П {Х2 < +оо} = {Xi < xi}.
Аналогично
{Xi < +00} П {Х2 < х2} = {Х2 < х2}.
Отсюда приходим к утверждению 7, которое устанавливает
естественную связь между двумерной функцией распределения
Fxi,x2 случайного вектора (Xi, X2) и функциями Fxx и Fx2, ко-
которые называют одномерными (говорят также частными,
или маргинальными) функциями распределения случай-
случайных величин Х\ и JC2. >
Пример 5,3. Некоторое техническое устройство состоит
из двух различных по надежности элементов, причем время
безотказной работы первого элемента можно задать случайной
величиной X\j а второго — случайной величиной Х2. То-
Тогда надежность всего устройства можно описать двумерным
случайным вектором (Ai, X2), имеющим неотрицательные ко-
координаты Х\ и Х2.
170 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Пусть известно, что для любых х\ ^ 0 и х2 ^ 0 вероятность
события {Х\ ^х\,Х2^ х2} определяется формулой
Р{Хг > XU Х2 > Х2} = е^1^-^2-Л12тах{а:1,х2})
где А* > 0, г = 1,2, и Ai2 > 0. Найдем совместную функцию
распределения FXl>X2(xi,x2) и одномерные функции распреде-
распределения FXl(x) hFX2(x).
В силу неотрицательности Х\ и Х2 событие {Х\ ^ х)
совпадает с событием {Х\ ^х,Х2^0}1 а событие {Х2 ^ х) —
с событием {Х\ ^ 0, Х2 ^ х). Подставляя 0 вместо х\ и х2 в
выражение для P{-Xi ^ rci, X2 ^ жг}, получаем:
х} = Р{ХХ ^ Ж,Х2 > 0} = е-(Л^Л")^, х > 0;
а; ^ 0.
Отсюда находим одномерные функции распределения Fxx (x) и
FXl (х) = 1 - P{Xi ^ ж} = 1 - e-(Al+Al2)*, ж ^ 0;
^ о;} = 1 - е-<Аа+А»>*, я: > 0.
Естественно, поскольку случайные величины Xi и -Хг неотри-
неотрицательные, то
Так как событие {Х\ < х\, Х2 < х2} совпадает с событием
ft \ ({Х\ ^x\}U {X2 ^ х2}), то совместная функция распределе-
распределения Jjfi^^b^li согласно свойствам 1 и 5 (см. теорему 2.8),
при х\,х2 ^ 0 имеет вид
FXux2{xux2) = l-P({Xi ^ xi}U{X2 >x2}) =
_ e-(A2+Ai2)x2 ^_e~Aia;i-A2a;2-
5.2. Дискретные двумерные случайные величины 171
Очевидно, что значение совместной функции распределения
при х\ < О или Х2 < О задается равенством
Полученная функция распределения задает двумерное экс-
экспоненциальное распределение. Заметим, что это распре-
распределение моделирует простейший случай зависимых отказов,
при котором могут одновременно отказать оба элемента. При
этом в теории надежности Ai называют интенсивностью отка-
отказа только первого элемента, Х2 — только второго элемента и
Ai2 — одновременно и первого, и второго элементов.
5.2. Дискретные двумерные
случайные величины
Определение 5.3. Двумерную случайную величину
(X, У) называют дискретной, если каждая из случайных
величин X и У является дискретной.
Как и в одномерном случае, распределение двумерной дис-
дискретной случайной величины естественно описать с помощью
перечисления всевозможных пар (xi, yj) значений координат
случайного вектора (X, У) и соответствующих вероятностей,
с которыми эти пары значений принимают случайные величи-
величины X и У.
Для простоты ограничимся конечным множеством воз-
можных значений, когда случайная величина X может прини-
принимать только значения х\, ..., хп, У — значения у\, ..., ут,
а координаты двумерного случайного вектора (X, У) — пары
значений (xi, yj), г = l,n, j = l,m. Такое перечисление удобно
представить в виде таблицы (табл. 5.1). В этой таблице в верх-
верхней строке перечислены все возможные значения у\, ..., yj, ...,
Ут случайной величины У, а в левом столбце — значения х\,...,
xi,..., хп случайной величины X. На пересечении столбца „у/с
со строкой nXiu находится вероятность pij = Т?{Х = X{,Y = yj}
совместного осуществления событий {X = ж$} и {Y = yj).
172
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Таблица 5.1
X
XI
хп
Ру
Y
У\
Рп
Р21
Рп\
PY1
У2
Р\2
Р22
...
Рп2
PY2
...
Ут
Р\т
Р2т
Рпт
PYm
Рх
Рхг
РХ2
РХп
В этой таблице обычно добавляют еще одну строку „Ру" и
столбец „Рх"-
На пересечении столбца „Рх" со строкой „ж$" записывают
число
Но pxi представляет собой не что иное, как вероятность того,
что случайная величина X примет значение Х{, т.е.
Таким образом, первый и последний столбцы таблицы дают нам
ряд распределения случайной величины X.
Аналогично, в последней строке „Ру" помещены значения
а первая и последняя строки дают ряд распределения случайной
величины У. Для контроля правильности составления таблицы
рекомендуется просуммировать элементы последней строки и
последнего столбца. Если хотя бы одна из этих сумм не будет
равна единице, то при составлении таблицы была допущена
ошибка.
Используя табл. 5.1, нетрудно определить совместную функ-
функцию распределения Fxy{x,y)- Ясно, что для этого необходимо
5.2, Дискретные двумерные случайные величины
173
просуммировать Pij по всем тем значениям г и j, для которых
х% < ж, yj < у, т.е.
i: Xi<x
Г- Уз<У
Пример 5.4. В соответствии со схемой Вернулли (см. 3.6)
с вероятностью успеха р и вероятностью неудачи q = 1 — р про-
проводятся два испытания. Выпишем распределение двумерного
случайного вектора (Х\, Х2), где Х^ % = 1,2, — число успехов в
г-м испытании. Каждая из случайных величин Х\ и Х2 может
принимать два значения: 0 или 1. Числа успехов в обоих испы-
испытаниях равны нулю тогда, когда произойдут две неудачи, а это
в силу независимости испытаний происходит с вероятностью
qq. Поэтому
и на пересечении столбца „О" со строкой „О" нужно записать
q2 (табл. 5.2).
Далее, Х\ = 1 и X*i = 0, если в первом испытании произошел
успех, а во втором — неудача, и,
значит> Таблица 5.2
Xi
0
1
Рх2
х2
0
92
РЯ
я
1
ЯР
Р2
р
Рхх
Я
р
Аналогично заполняем второй стол-
столбец:
= 1} = qp,
Наконец, на пересечении столбца „Pxi" и строки „О" должно
стоять
= 0} = q2 +pq = q(q+p) = q,
а на пересечении столбца „Pxi" и строки „1" —
= 1} =pq+p2 =p(p + q) =p.
174 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Проверим правильность составления таблицы. Сумма эле-
элементов последнего столбца р+q = 1, последней строки р + g == 1.
Так и должно быть.
Построим теперь совместную функцию распределения слу-
случайных величин Х\ и Х2:
F(xux2) = P{Xi < хиХ2 < х2}.
Поскольку при х\ < 0 или х2 < 0 нет ни одного элементар-
элементарного исхода ш, для которого или Х2(ш) < Х2, то для таких х\ и
х2 событие {Х\ < х\>Х2 < х2} невозможное, и, значит
F(xux2)=0
при х\ < 0 или х2 ^ 0.
Далее, еслиО<Ж1^1иО<а:2^1, то событие {-X"i<?i,-X2<#2}
эквивалентно событию {Х\ = 0, Х2 = 0}, которое, как видно из
табл. 5.2, происходит с вероятностью д2, и
Если же 0 < дгх < 1, а х2 > 1, то событие {Х\ < х\, Х2 < х2}
совпадает с объединением непересекающихся событий
=0,Х2 = 0} и
Тогда F(rci,x2) = q2 + qp = q. Аналогично
при х\ > 1 и 0 < х2 < 1.
Наконец, если х\ > 1 и х2 > 1, то событие {-Xi < жх, Х2 < х2}
достоверно, и, следовательно,
F{xux2) = 1.
Совместная функция распределения F(x\,x2) задает поверх-
поверхность в трехмерном пространстве, и ее не очень удобно изо-
5.2. Дискретные двумерные случайные величины
175
бражать графически. Тем не менее такая попытка предпринята
на рис. 5.3.
Рис. 5.3
Пример 5.5. Игральная кость размечена таким образом,
что сумма очков на противоположных гранях равна 7
(т.е. 1 — 6, 2 — 5, 3 — 4). Случайная величина X —
число очков, выпавших на верхней грани, случайная величина
У — то же на нижней грани. И случайная величина Х} и
случайная величина Y могут принимать любые значения от 1
до 6 с одинаковой вероятностью 1/6. Однако если случайная
величина X приняла значение 1(на верхней грани выпало 1
очко), то единственным значением случайной величины Y
может быть только 6 (на нижней грани обязательно вьшадет 6
очков). Значит, строка „1" табл. 5.3 будет состоять из нулей,
за исключением пересечения со столбцом „6": на этом месте
должна стоять вероятность 1/6. Аналогично строка „2" будет
иметь единственный отличный от нуля элемент на пересечении
со столбцом „5 й, также равный 1/6 (на верхней грани выпало
2 очка, на нижней — 5), и т.д. Столбец „Рх" и строку „Ру"
находим, суммируя соответствующие строки и столбцы; как и
должно было быть, мы получаем в них одинаковые значения
1/6, соответствующие классической схеме.
176
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Таблица 5.3
X
1
2
3
4
5
6
Ру
У
1
0
0
0
0
0
1/6
1/6
2
0
0
0
0
1/6
0
1/6
3
0
0
0
1/6
0
0
1/6
4
0
0
1/6
0
0
0
1/6
5
0
1/6
0
0
0
0
1/6
6
1/6
0
0
0
0
0
1/6
1/6
1/6
1/6
1/6
1/6
1/6
Предоставляем возможность интересующемуся читателю
самостоятельно построить совместную функцию распределе-
распределения случайных величин X ylY.
5.3. Непрерывные случайные величины
Определение 5.4. Непрерывной двумерной случай-
случайной величиной (X, Y) называют такую двумерную случай-
случайную величину (X, У), совместную функцию распределения ко-
которой
F(xux2) =
xuY < х2)
можно представить в виде сходящегося несобственного инте-
интеграла:
Xl X2
F(xux2)= I I p{yuV2)dyidy2.
Функцию
р(х\,х2) =
5.3, Непрерывные случайные величины 177
называют совместной двумерной плотностью распре-
распределения случайных величин X и У, или плотностью распреде-
распределения случайного вектора (X, У). Область интегрирования в
двойном интеграле представляет собой квадрант {у\ <а?ьУ2 <^г}
с вершиной в точке (xi;#2)« Как известно [VII], двойной инте-
интеграл можно представить в виде повторного, причем в любом
порядке, следовательно,
Х\ Х2 Х2 XI
/Г Г Г
dy\ / p(yi,Jtt)dltt= / dy2
J J J
—oo —oo —oo —oo
Так же как и в одномерном случае, будем предполагать, что
р(яъ#2) непрерывная (или непрерывная за исключением от-
отдельных точек или линий) функция по обоим аргументам.
Тогда в соответствии с определением непрерывной случайной
величины и теоремой о дифференцировании интеграла с пе-
переменным верхним пределом [VI] совместная плотность рас-
распределения представляет собой (в точках ее непрерывности)
вторую смешанную производную [V] совместной функции рас-
распределения:
p(Xl,X2) = ^frb^) = d2F{Xl,x2)
Заметим, что аналогичный смысл имеет совместная
п-мерная плотность распределения случайных величин
-^ъ •••? -Хп? или плотность распределения случайного
вектора (Хи ...,Хп):
d"F(xu...,xn)
р(хи...,хп)-
Нетрудно доказать следующие свойства двумерной плотно-
плотности распределения.
178 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Теорема 5*2. Двумерная плотность распределения облада-
обладает следующими свойствами: J
2) P{ai
+OO+OO
i <X <bua2<Y <h}= / dx\ p(xu
++OO °1 a2
3) / / p(xux2)dxidx2 = 1;
-00-00
4) P{si <X <x\ + Да?!,X2 <Y<X2+АГС2}
6) Р{(Х;У) € D} = Jjp(xux2)dxldx2;
+oo ^
7)px(^)= / Px,Y(x,y)dy;
—oo
+oo
8) py(y) = / PxtY(xiV)dx-
—oo
М Свойства 1 — 5 аналогичны свойствам одномерной плот-
плотности распределения. Свойство 6 является обобщением свой-
свойства 2.
Докажем утверждения 7 и 8. Из свойства 7 двумерной
функции распределения (см. 5.1) и определения 5.4 двумерной
плотности распределения вытекает:
X +00
+
= FXyY(x,+oo)= I I pxiY{y
—oo— oo
+oo у
,y)= I I Рх,
5.3. Непрерывные случайные величины 179
откуда, дифференцируя интегралы по переменному верхнему
пределу и учитывая формулу D.2), получаем утверждение 7 для
одномерных (частных, маргинальных) плотностей распределе-
распределения рх(х) и ру(у) случайных величин X и У. >
Пример 5.6. Рассмотрим двумерную случайную величину,
плотность распределения которой имеет вид
f
Для определения коэффициента А воспользуемся свойством 3
двумерной плотности распределения. Поскольку p(xi,#2) =0
при х\ + х\ > Я2, то
+ОО+ОО
/ / p{x\,X2)dx\dx2 = / / Adx\dx2 = ttAR2 = 1,
и, значит, А = —^т. Таким образом,
Нетрудно найти одномерную плотность распределения случай-
случайной величины Х\:
+оо
ж) = / Р(ж,у)dj/ = / ^jdy =
О, |г| > Д;
180
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Аналогичное выражение можно получить и для рх2 (у) •
Совместная функция распределения F{x\,x2) в СИЛУ опреде-
определения двумерной плотности распределения равна
= ^дг / I
Рис. 5.4
D
где область D представляет
собой пересечение квадранта
{у\ < х\) 2/2 < х2} и круга х\ +
+ х2 < Я2, т.е. F(x\iX2) с точ-
точностью до множителя —^ со-
совпадает с площадью области
D, имеющей двойную штри-
штриховку на рис. 5.4.
Предлагаем самостоятель-
самостоятельно определить площадь области D для различных значений
Х\ И Х2. #
В заключение рассмотрим пример, показывающий, что да-
даже на практике реально могут встретиться двумерные случай-
случайные величины, не являющиеся ни дискретными, ни непрерыв-
непрерывными.
Пример 5.7. Рассмотрим двумерный случайный вектор
(Xi, X2) из примера 5.3. Результаты этого примера, в частно-
частности, показывают, что случайные величины Х\ и Х2 являются
непрерывными и распределенными по экспоненциальному зако-
закону с параметрами Ai + A12 и \2 + Х\2 соответственно.
Функция распределения двумерного случайного вектора
(Хи Х2)
5.4. Независимые случайные величины 181
непрерывна во всех точках. Бе смешанная производная
A2(Ai + A12)e-(Al+Al2)Xl-A2X2, xi > х2 > 0;
Ai(A2 + Ai2)e"AlXl"(A2+Al2)X2, х2>хх> 0;
0, Х\ < 0 ИЛИ Х2 < 0
непрерывна во всех точках, кроме точек прямых х\ = 0; ж2 = 0
и х\ = х2.
Убедимся, что функция p(xi,#2) не является плотностью
распределения двумерного случайного вектора (Х\, Х2). Дей-
Действительно,
+ОО+ОО +ОО+ОО
/ p(xux2)dxidx2= p{xux2)dxidx2 =
~оо-оо О О
+ОО Х\
= Г (f\2(Xi + А12)
о о
+оо
j
Adxx =
XI
что противоречит свойству 3 (см. теорему 5.2).
5.4. Независимые случайные величины
Определение 5.5. Случайные величины X и Y называ-
называют независимыми, если совместная функция распределения
FxtY(x,y) является произведением одномерных функций распре-
182 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
деления Fx(x) и Fy(y):
В противном случае случайные величины называют Зави-
Зависимыми.
Пример 5.8. Снова обратимся к примеру 5.3 и определим,
в каком случае компоненты Х\ и Х2 двумерного случайного
вектора (Ai, Х2) будут независимыми. Заметим, что при х\ < О
ИЛИ ГГ2 < О
FXl {x)FX2{x2) = 0 = Fx,y{xi,x2).
Бели же #i, х2 > 0, то
FXl{x)FX2{x2) = 1 -e
Нетрудно видеть, что произведение ^1(^)^X2(^2) совпада-
совпадает при всех х\х2 с совместной функцией распределения (см.
пример 5.3)
и
или
только в том случае, когда Ai2 = 0. Таким образом, условие
Л12 = 0 является необходимым и достаточным, чтобы времена
безотказной работы элементов были независмыми. Как следует
из результатов примера 5.7, это условие соответствует тому,
что одновременно два отказа произойти не могут. #
Из определения 5.5 вытекает, что для независимых слу-
случайных величин X и Y события {-X" < ж} и {Y < у} являются
независимыми. Покажем, что независимыми являются и все
события {ж1 < X < х2} и {j/i < У < у2}. Действительно, в силу
5.4. Независимые случайные величины 183
независимости X и Y, свойства 5 двумерной функции распре-
распределения (см. теорему 5.1) и свойства 4 одномерной функции
распределения (см. теорему 4.1) имеем
Р{Ж1 < X < Х2, у! < У < у2} =
= F(x2,y2)-F(xuy2)-F(x2,yl) + F(x1,yi) =
= Fx(x2)FY(y2) - Fx{x{)FY{y2) - Fx(x2)FY(yi) +
+ Fx(xi)FY{yi) = [Fx(x2)-Fx{xl)][FY(y2)-FY(yi)} =
= Р{ж1 < X < х2}Р{У1 < Y < уз},
что и означает независимость двух событий {х\ ^ X < хг} и
Замечание 5.2. Можно доказать и более сильное утвер-
утверждение, состоящее в следующем. Для того чтобы случайные
величины X и У были независимыми, необходимо и достаточно,
чтобы были независимыми любые события {X Е А} и Y G J5},
где А и 2? — промежутки или объединения промежутков.
Теорема 5.3. Для того чтобы непрерывные случайные ве-
величины X и Y были независимыми, необходимо и достаточно,
чтобы для всех х и у
PXyY (Я, У) = РХ (х)
Ч Пусть случайные величины X и У независимые. Тогда, со-
согласно определению 5.5,
С учетом формул E.1) и D.2) имеем
d2Fx,Y(x,y)
fdFx(x)\ fdFY(y)\
Тем самым необходимость утверждения доказана.
¦{
184 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Для доказательства достаточности следует воспользоваться
определением 5.4 двумерной плотности распределения и опре-
определением 4.1. л
Fx7y(x,y)= // px,Y(v,w)dvdw =
—oo<w<y
= 1 J Px{v)dv\ I J pY(w)dw\ =Fx(x)FY{y). >
Пример 5.9. а. Рассмотрим двумерный вектор (Ai, -X2),
совместная плотность распределения которого имеет вид
1, a?iG[0,l] игг2Е[0,1];
О, xi 0[О,1] или ж2?[0,1].
Нетрудно показать, что одномерные плотности распределения
{г (х) и рх2 (х) случайных величин Х\ и X<i задаются формулой
1, * е[0,1];
0, а; 0 [0,1].
Очевидно, что в данном случае совместная плотность рас-
распределения p{x\,x*i) для всех #i, X2 является произведением
одномерных плотностей pxi(#i) и Рх2{х\). Значит, случайные
величины Х\ и X*i являются независимыми.
б. Также нетрудно показать, что случайные величины Х\
и Х2 из примера 5.6 являются зависимыми. #
Отметим, что если независимые случайные величины X и
У являются непрерывными, то двумерная случайная величина
(X, У) непрерывна.
Теорема 5.4. Дискретные случайные величины X и У
являются независимыми тогда и только тогда, когда для всех
возможных значений Х{ и yj
= xi}P{y = yj}=j
Г
[
5.4. Независимые случайные величины 185
Мы предоставляем возможность читателю доказать эту
теорему самостоятельно.
Пример 5.10. В схеме Бернулли с двумя испытаниями
(см. пример 5.4)
Р{Хг = 0,Х2 = 0} = q2 = P{Jti = 0}Р{Х2 = 0},
Р{ХХ = 0,Х2 = 1} = qp = Р{Хг = 0}Р{Х2 = 1},
= 0} =pg = P{X1 = 1}Р{Х2 = 0},
2 = 1}.
Таким образом, числа успехов Х\ и Х2 в первом и втором испы-
испытаниях представляют собой независимые случайные величины.
Впрочем, в силу определения схемы Бернулли иного нельзя было
ожидать. Убедитесь самостоятельно в том, что независимы-
независимыми в совокупности являются случайные величины Xi,..., Хп —
числа успехов в первом, втором, ..., n-м испытаниях по схеме
Бернулли. #
В заключение заметим, что в 8.1 будут приведены другие
необходимые и достаточные условия независимости случайных
величин, выраженные в терминах условных распределений.
Определение 5.6. Случайные величины Х\, ..., Хп,
заданные на одном и том же вероятностном пространстве,
называют независимыми в совокупности, если
Замечание 5.3. Теоремы 5.3 и 5.4 распространяются на
любое число случайных величин.
Разумеется, как и для событий, из попарной независимости
не следует независимость случайных величин в совокупности.
Пример 5.11. Свяжем с бросанием тетраэдра из при-
примера 3.6 три случайные величины: Х\,Х2 и Х$, каждая из
186 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
которых может принимать значения 0 или 1, причем -XV = 1,
если тетраэдр упал на грань, на которой присутствует цифра
1, и Х\ = 0 в противном случае. Аналогично Х2 характеризует
наличие цифры 2, а Х$ — цифры 3. Покажем, что случайные
величины Х\, Х2 и Х$ будут попарно независимыми, но не явля-
являются независимыми в совокупности.
Действительно, Р{Х{ = 1} = Р{Х{ = 0} = |, ъ = 1,2,3, и
P{Xj = l,-Xj = l} = -=P{Xi = l}P{X7==l}, %Фз, т.е. Xi попарно
независимы. Однако, например, P{Xi = 1, -Х2 = 1, Хз = 1} =
= \ ф Р{Хг = 1}Р{Х2 = 1}Р{Х3 = 1} = |, т.е. Хь t = 1,2,3, не
являются независимыми в совокупности.
5.5. Многомерное нормальное распределение
Нормальное распределение одномерной случайной величины
рассмотрено выше (см. 4.6). Обратимся к многомерному слу-
случаю. При этом сначала введем двумерное нормальное рас-
распределение случайного вектора X = (Х\, Х2), а затем обоб-
обобщим полученные результаты на случайный вектор X произ-
произвольной размерности п > 2.
Пусть координаты Х\ и Х2 случайного вектора J?=(Jf i, X2)
являются случайными величинами, распределенными по нор-
нормальному закону, т.е. имеют плотности распределения
Напомним, что параметры mi и &{ > 0, г = 1,2, этих распре-
распределений называют математическими ожиданиями и средними
квадратическими отклонениями случайных величин Xi и J^.
5.5. Многомерное нормальное распределение 187
Бели Х\ и Х2 являются независимыми случайными величи-
величинами, то, согласно результатам предыдущего параграфа (см.
теорему 5.3),
и в этом случае плотность двумерного нормального распреде-
распределения имеет вид
В общем случае вектор X = (Xi, -Х2) имеет (невыроасден-
ное) двумерное нормальное распределение, если его плот-
плотность распределения определяется формулой
где функция двух переменных
E.2)
у^ = Х{ — т», г = 1, 2, есть положительно определенная квадра-
квадратичная форма [IV] (т.е. Q(yi,j/2) > 0 для любых (yi, у2) Е М,
(УЫ*) 940,0)).
Двумерное нормальное распределение зависит от пяти па-
параметров:
-координат mi и т2 вектора m = (mi,m2), называемо-
называемого вектором математических ожиданий вектора X —
- координат а\ и а2 вектора о = (ai, аг), называемого
вектором средних квадратичных отклонений вектора
Х = (ХиХ2);
- числа р, \р\ < 1, называемого коэффицитентом корре-
корреляции случайных величин Х\ и Х2-
188 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Последние три параметра запишем для дальнейшего обоб-
обобщения на случай п > 2 в виде матрицы ковариаций (кова-
(ковариационной матрицы) S вектора X = (Xi
@И 012 \
^21 ^22 / '
где аи = а?, г = 1, 2, a <ri2j= a2i =
Бели ввести матрицу Е, обратную матрице S, т.е.
и вектор
г7=(уы/2)>
то квадратичную форму E.3) можно записать в матричной
форме в виде
Q(y) = yS/, E.4)
где знак „т" означает транспонирование. Действительно, если
учитывать, что
то, подставляя ? в E.4), приходим к выражению E.3).
Далее, если заметить, что множитель o\o*i у/1 — р2 = л/det S,
где detS — определитель матрицы S, то выражение E.2)
можно записать в виде
А*2)Т. E.5)
Теперь можно записать плотность (невырожденного) нор-
нормального распределения для случайного вектора Х=(Х\У..., Хп)
произвольной размерности п > 2.
5.5. Многомерное нормальное распределение 189
Как и в двумерном случае, многомерное нормальное
распределение (многомерный нормальный закон) опре-
определяется вектором средних значений
m = (mi, ..., тп)
и матрицей ковариаций (ковариационной матрицей)
причем Е является положительно определенной симметриче-
симметрической матрицей [IV].
Диагональный элемент оц матрицы Е называют диспер-
дисперсией случайной величины Х{, а сг^ = у/aU — средним ква-
квадратичным отклонением Х{. Недиагональный элемент a%j
называют ковариацией случайных величин Х\ и Xj (a%j за-
записывают также в виде оц = PijOiOj, и тогда pij называют
коэффициентом корреляции Х{ и Xj).
Обозначив, как и прежде, S матрицу, обратную к матрице
Е, и использовав матричную запись, плотность многомер-
многомерного (п-мерного) нормального распределения определим
следующим выражением, аналогичным E.2):
р$(х) =
Бели матрица S (а значит, и матрица Е = Е 1) совпадает с
единичной матрицей J, а вектор т = @, ..., 0), то
.,xn(^i,...,xn) = в*?.
Такую плотность по аналогии с одномерным случаем называют
плотностью стандартного многомерного (п-мерного)
нормального распределения.
Дадим геометрическую интерпретацию плотности нормаль-
нормального распределения.
190 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Начнем с двумерного случая. При этом (Xi,^) будем
трактовать как координаты брошенной случайным образом на
плоскость точки.
Функция pxi,X2(xiix2) задает некоторую поверхность в
трехмерном пространстве. Линии уровня этой поверхности
имеют уравнение
которое с учетом E.2) можно записать в виде
Q(xi - mi, x2 - m2) = Ь, E.6)
где Ь= —21n{27ra(detSJ}, а Q(x\ — rai,a:2 — тг) определяется
формулой E.3).
Последнее уравнение представляет собой уравнение эллипса
(точнее говоря, семейства эллипсов при разных значениях Ь).
Оси симметрии Ofx\ и О'хг этого эллипса (рис. 5.5) проходят
через точку 0;(mi;m2), а их направления совпадают с напра-
направлениями собственных векторов матрицы S. В свою очередь,
собственные векторы ei, г = 1,2, матрицы S определяются из
уравнений [IV]
где А$ — собственные значения матрицы Е, т.е. решения
характеристического уравнения
det(S-A/) = O, ;
или
\2<j\gI{1 - р2) - А(а? + а\) +1 = 0.
Углы a», i = 1,2, между осями симметрии эллипса и осью
Ох\ можно выразить через параметры ai,G2 и р по формуле
E.7)
5.5. Многомерное нормальное распределение
191
Оси
рассеивания
Эллипсы
рассеивания
Рис. 5.5
Оси симметрии эллипса E.6) называют осями рассе-
рассеивания, сам эллипс — эллипсом рассеивания (или элли-
эллипсом равной вероятности), а центр эллипса — точку
01[т\;т2) — центром рассеивания.
Из формулы E.7), в частности, следует, что при р = О,
ах фо<1 оси рассеивания параллельны координатным, при о\ =
G2 = а эллипс рассеивания представляет собой окружность
радиуса айв качестве осей рассеивания можно взять любые
две перпендикулярные прямые, проходящие через точку О'.
Вводя новую (прямоугольную) систему координат, оси ко-
которой совпадают с осями рассеивания, т.е. каноническую систе-
систему координат для эллипса рассеивания, можно показать, что в
этой системе координаты (Х[, Х2) случайной точки имеют нор-
нормальное распределение с нулевым вектором средних значений
т' = @;0) и матрицей ковариаций Е' = [ а* /2 ), где а[ = —=,
Бели изменить масштабы на осях канонической системы ко-
координат, взяв за единицы отсчета а[ и аг2 соответственно, то в
такой системе координат координаты случайной точки будут
иметь нормальное распределение с нулевым вектором средних
192 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
и единичной матрицей ковариаций, т.е. иметь двумерное стан-
стандартное нормальное распределение.
Аналогично в случае п > 2 уравнение
или эквивалентное ему уравнение
(?-га)?(?-га)т = Ь, Ь =-
в силу положительной определенности матрицы S представляет
собой уравнение n-мерного эллипсоида, называемого эллипсо-
эллипсоидом рассеивания, его оси симметрии по-прежнему называ-
называются осями рассеивания.
Будем трактовать n-мерный случайный вектор X как ко-
координаты случайной точки в n-мерном пространстве. Пусть
xv • • • >жп — каноническая система координат эллипсоидов рас-
рассеивания, тогда новые координаты (Х{,..., Х'п) случайной точ-
точки снова будут описываться n-мерным нормальным законом,
имеющим нулевой вектор средних га' и диагональную матрицу
ковариаций Е', причем ее диагональные элементы а!? = l/A*,
где А$, % — 1, п, — собственные значения матрицы Е с учетом
их кратностей. Еще раз вводя новые координаты у{ = а\х\ (т.е
изменяя масштабы на осях канонической системы координат),
получаем, что в последней системе координат yi,...,yn коор-
координаты случайной точки будут распределены по стандартному
нормальному закону.
Таким образом, делая обратные преобразования, можно
трактовать (невырожденный) нормально распределенный век-
вектор X с произвольным вектором средних га и матрицей ковари-
ковариаций Е как координаты случайной точки в некоторой (вообще
говоря, не ортонормированной, но ортогональной) прямолиней-
прямолинейной системе координат, причем эта точка имеет стандартное
нормальное распределение.
Пример 5.12. Известно, что при стрельбе по плоской
цели отклонение точки разрыва снаряда от точки прицеливания
хорошо описывается двумерным нормальным распределением.
5.5. Многомерное нормальное распределение 193
При испытании гаубицы было обнаружено, что в некоторой
прямоугольной системе координат с центром в точке О прице-
прицеливания вектор X = (Х\, X2) отклонений (в метрах) от точки
О имеет вектор средних т = B, 3) и матрицу ковариации (в
ч ^ /300 140 \
квадратных метрах) S = I ш ш 1.
Найдем уравнения осей рассеивания двумерной случайной
величины pfi,^). Центр рассеивания находится в точке
О'B, 3). Матрица Е = S" имеет вид
а / 0,005 -0,0035 \
\ -0,0035 0,0075 ) '
Определим собственные значения и собственные векторы
матрицы 2. Собственные значения находим из уравнения
40400Л2-500А + 1=0,
они равны Ai « 0,0025, А2 « 0,01.
Решая уравнения
/ 0,005 ,0035 \_
61 V -0,0035 0,0075 J-0'0025eb
/ 0,005 -0,0035\
62 { -0,0035 0,0075 J=0'01e2'
находим собственные векторы
ei«G, 5), е2«(-5, 7).
Тогда уравнения осей рассеивания принимают вид
х\ — 2 Х2 ~~ 3 Х\ — 2 Х2 — 3
7 = 5 ' -5 = 7 '
а матрица ковариации в канонических координатах
1 /400 0
1 0 V1 /
o х2) ш{
О 100
7 - 10047
194 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Плотность распределения случайного вектора (Х^Х^),
представляющего собой координаты отклонения точки разрыва
от точки О', вычисленные в ортонормированной системе коор-
координат, связанной с осями рассеивания, имеет вид
__*> 2l400 + 100
Для того чтобы получить стандартное нормальное распределе-
распределение, мы должны за единицу масштаба по большей оси эллипса
рассеивания принять 20 м, а по меньшей — 10 м.
Предположим теперь, что цель поражается в том случае,
когда точка разрыва снаряда находится от нее не далее чем в
10 м. Вычислим вероятность поражения цели одним снарядом.
В соответствии с формулой E.5) двумерная плотность рас-
распределения вектора X = (Ai, X2) имеет вид (см. вид матри-
матрицы ?)
1 _
\ [0,005(*i -2)? -0,007(*i -2)(х2 -3)+0,0075(х2 -ЗJ]
400тг
Искомая вероятность равна вероятности попадания снаряда
в область х\ + х\ < 100 и в силу свойства 6 двумерной плотности
распределения определяется выражением
Г Г
Для вычисления последнего интеграла необходимо применить
численные методы, поэтому окончательный ответ мы не при-
приводим. #
Рассмотрим основные свойства многомерного нормального
распределения.
5.5. Многомерное нормальное распределение 195
1. Закон распределения каждой из координат случайного
вектора X, имеющего n-мерное нормальное распределение с
вектором средних т = (mi, ..., тп) и матрицей ковариаций
? = <Jij, является нормальным с параметрами т» и а*.
<4 Докажем это утверждение для случая п = 2 (общий случай
требует более громоздких преобразований).
Определим плотность распределенияpxi(%i) в случае, когда
РХ1,х2(х1)х2) определяется формулами E.2) и E.3). Используя
свойство 7 двумерной плотности распределения, находим
+00
где
_2
Делая замену
У 1-р2
после преобразований получаем
-оо
Поскольку с учетом значения интеграла Пуассона [VII]
+ОО +00
f e-*2l2dy = л/2 / е-'2Л =
-ОО —ОО
приходим к окончательному ответу
196
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
что и доказывает требуемое утверждение. Аналогично можно
показать, что
(ж2 - т2J
-е 2<Т2 . *
2. Если ковариационная матрица Е случайного вектора
Ху распределенного по нормальному закону (невырожденному),
является диагональной [III], то координаты вектора Х\,..., Хп
являются независимыми случайными величинами.
< Действительно, матрица S = S" также является диагональ-
диагональной и имеет вид
/ 1
О
о Дг ...
о
о
о о ... 4
и, следовательно, формула E.2) для совместной (п-мерной)
плотности распределения имеет вид
1
хе
2а?
(хп - тпп)
2о*
т.е. случайные величины Xi,...,Xn являются независимыми
(см. замечание 5.3). >
Заметим, что если Oi j = 0 для некоторых inj или, что то же
самое, коэффициент корреляции р% j = 0, то говорят, что слу-
случайные величины Х{ и Xj являются некоррелированными.
Таким образом, из некоррелированности координат случай-
случайного вектора, распределенного по нормальному закону, следует
(в силу теоремы 5.3) их независимость. Легко показать и
обратное: независимые нормально распределенные случайные
5.6. Решение типовых примеров 197
величины являются некоррелированными (в 7.4 будет показа-
показано, что для произвольно распределенных случайных векторов
некоррелированность координат есть лишь необходимое усло-
условие независимости).
3. Если вектор X = (Jfi, ..., Хп) имеет нормальный за-
закон распределения с вектором средних m = (mi, ..., mn) и ма-
матрицей ковариаций Е, то вектор X1 = (Xi, ..., Xn_i) также
распределен по нормальному закону с вектором средних fh! =
= (mi, ..., mn_i) и матрицей ковариаций S', полученной из
матрицы S вычеркиванием последних строки и столбца.
< Это свойство доказывается так же, как и свойство 1, но в
силу громоздкости вывода оно здесь не приводится. >
Из свойства 3 методом математической индукции можно
показать, что любой набор координат n-мерного случайного
вектора X = (Xi, ..., Хп), распределенного по нормальному за-
закону, снова имеет нормальное распределение. В частности,
двумерный случайный вектор (Xi, X*i) распределен по нормаль-
нормальному закону с вектором средних (mi, тг) и матрицей ковариа-
тттжи v (ап
ции 1/ = I
5.6. Решение типовых примеров
Пример 5.13. Двумерная случайная величина (X, У) име-
имеет совместную функцию распределения
Г 0, х<0илиу<0;
^^У^|1.е-^е~2У + е^-2У? а;>0иу>0.
Найдем:
а) вероятности событий
{-2 < X < 2, 1 < У < 3}, {X > О, У ^ 1} и {X < 1, У ^ 2};
б) частные функции распределения случайных величин X
и У.
198 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
а. В соответствии со свойством 5 двумерной функции рас-
распределения имеем
- F(-2,3) + F(-2,1) = 1 - е~4 - е + е~10 -
- A - е-4 - е-2 + е) - 0 + 0 = е~2 - 2e~6 + е0.
Событие {X ^ О, У ^ 1} представляет собой попадание дву-
двумерной случайной величины (X, У) в квадрант {х ^ 0,у ^ 1}.
Поэтому
0, У ^ 1} = F(+oo, +оо) - F(+oo, 1) -
-.F@, +oo) + F@,1) = 1 - A - е) - 0 +.0 = е.
Аналогично
1, У > 2} = F(l, +оо) - F(l,2) - F(-oo, +oo) +
б. В соответствии со свойством 7 двумерной функции рас-
распределения частные распределения случайных величин X и У
задаются формулами
Пример 5.14. Двумерная случайная величина (X, У)
имеет совместную функцию распределения
F(x,y) =
0, х < 0 или у ^ 0;
sin х sin у, 0 < х ^ тг/2 и 0 < у ^ тг/2;
sins, 0 < х < тг/2 и у > тг/2;
siny, ж > тг/2 и 0 < у < тг/2;
1, ж > 7г/2 и у > тг/2.
5.6. Решение типовых примеров
199
Найдем:
а) вероятности событий
б) частные функции распределения случайных величин X
и Г.
Действуя таким же образом, как в примере 5.13, получаем:
4'4/ ~~2 2~ + T~2~2 '
б)
=
0,
sinx,
1,
X
0
X
<
<
>
0;
f;
7Г
2'
FY(v) = ^
0,
sinj/,
1,
У
0
У
<
>
0;
У^
¦к
2'
;2'
Пример 5,15. Распределение
вероятностей дискретной двумер-
двумерной случайной величины (X, У) за-
задано табл. 5.4. Найдем:
а) ряды распределения случай-
случайных величин X hlY\
Таблица 5.4
X
3
5
У
3
0,17
0,10
8
0,13
0,30
12
0,25
0,05
200
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
б) значения совместной функции распределения F(x,y) в
точках D,5; 8) и (9; 11), а также вероятность события {4^Х<9,
а. Поскольку событие {X = 3} совпадает с объединением
непересекающихся событий {X = 3, У = 3}, {-X" = 3, У = 8} и
{X = 3, У = 12}, то
= 3} = Р{Х = 3, У = 3} + Р{Х = 3, У = 8} +
= 3, У = 12} =0,55.
, У = 8} +
= 3, У = 12} = 0,45.
Рл<? распределения случайной величины X приведен в табл. 5.5.
Таблица 5.5 Таблица 5.6
Аналогично
X
р
3
0,55
5
0,45
Y
Р
3
0,27
8
0,43
12
0,30
Суммируя вероятности по столбцам (см. табл. 5.4), находим:
5, У = 3}=0,27,
= 5, У = 8}=0,43,
Р{У = 12} = Р{Х = 3, У = 12} + Р{Х = 5, У = 12} = 0,30.
Ряд распределения случайной величины У представлен в
табл. 5.6.
б. Используя определение 5.3 совместной функции распреде-
распределения и то, что событие {X < 4,5, У < 8} совпадает с событием
{X = 3, У = 3}, получаем
FD,5, 8) = Р{Х < 4,5, У < 8} = Р{Х = 3, У = 3} = 0,17.
5.6. Решение типовых примеров 201
Аналогично событие {X < 9, У < 11} совпадает с объедине-
объединением непересекающихся событий {X = 3,У = 3}, {X = 3,У = 8},
{X = 5,У = 3} и {X = 5,У = 8}, и, значит,
+ Р{Х = 5,У = 3} + Р{Х = 5, У = 8} = 0,70.
Наконец,
Р{4 < X < 9,8 ^ У < 11} = Р{Х = 5,У = 8} = 0,30.
Пример 5.16. Совместная функция распределения непре-
непрерывной двумерной случайной величины (X, У) имеет вид
F(x,y) = ± (arctg5 +1) (arctg V- +1) (а > 0,6 > 0).
Найдем совместную плотность распределения.
Воспользовавшись равенством
получим
Пример 5.17. Совместная плотность распределения непре-
непрерывной случайной величины (X, Y) имеет вид
Найдем:
а) постоянную С;
б) частные плотности распределения случайных величин X
и У.
202 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
а. Постоянную С находим согласно свойству 3 совместной
плотности распределения
+ОО+ОО
I I p{x,y)dxdy = l.
Вычисления интеграла с помощью перехода к полярным коор-
координатам [VII] дают:
+оо +оо 2тг +оо
Cdxdy _„/\ [ Pdp _
+ + +
Г Г Cdxdy f f
-oo-oo 0 0
Поэтому С = 1.
б. Частные плотности распределения случайных величин
X mY вычисляются в соответствии со свойством 7 совместной
плотности распределения:
+ОО +ОО
dy тг
—00 —ОО
+ОО +ОО
ру(у) =
-оо -оо
Пример 5.18. Совместная плотность распределения не-
непрерывной двумерной случайной величины (X, Y) имеет вид
J0, х ^ 0 или у < 0;
р^'у)~ 1 3"х^1п23, ж>0иу>0.
5.6. Решение типовых примеров 203
Найдем:
а) совместную функцию распределения;
б) частные плотности распределения случайных величин
ХиУ;
в) вероятность попадания случайного вектора (X, У) в
треугольник с вершинами в точках АB, 1), 2?B, 2) и СE, 1).
а. Совместная функция распределения
при х^О или у < 0, а при х > 0 и у > 0, согласно определению 5.4,
х у х у
F(x,y)= f [3-u-v\n23dudv= fdu /Vu
0 0 0 0
= ( /Vuln3du J И 3-"ln3*i) =(l-3-x)(l-3-y).
\o / \o /
б. Частная плотность распределения случайной величины X
равна 0 при х <0, а при х>0 имеет вид
+00
рх()
+00
(х) = /
Аналогично частная функция распределения случайной величи-
величины У равна 0 при у ^ 0, а при у > 0 определяется выражением
+оо
ру(у) = I
о
в. В соответствии со свойством 6 (см. теорему 5.2) совмест-
совместной плотности распределения вероятность попадания случайно-
случайного вектора (X, У) в треугольник с вершинами в точках АB; 1),
204
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
ВB;2) и СE;1) находим по свойству 6 теоремы 5.2:
D
где область D представляет собой рассматриваемый треуголь-
треугольник (рис. 5.6).
В
0 2 4 6 х
Рис. 5.6
Проводя интегрирование, получаем
(8-х)/3
f
()/
;У) G D} = /Vxln3dx f 3'y\n3dy =
= ^«0,019.
Пример 5.19. Проверим, являются ли случайные величины
X и Y из примера 5.13 независимыми.
Из результатов примера 5.13 следует, что совместная функ-
функция распределения F(x,y) случайного вектора (X, У) совпадает
при всех хиус произведением частных функций распределения
5.6. Решение типовых примеров
205
Fx{x) и Fy{y) случайных величин X и У. Поэтому случайные
величины X и У являются независимыми согласно определе-
определению 5.5.
Пример 5.20. Распределение вероятностей двумерной слу-
случайной величины (X, У) задано табл. 5.7. Проверим, являются
ли случайные величины X иУ независимыми.
Таблица 5.7
X
-1
1
У
2
0,08
0,12
4
0,12
0,18
6
0,20
0,30
Ряды распределения случайных величин X и У представле-
представлены в табл. 5.8 и 5.9.
Таблица 5.8
Таблица 5.9
X
р
-1
0,4
1
0,6
У
р
2
0,2
4
0,3
6
0,5
Из табл. 5.7-5.9 следует, что вероятность события {X =
= — 1, У = 2} совпадает с произведением вероятностей событий
{X = — 1} и {У = 2}. Это же свойство верно и для всех
остальных возможных пар значений случайных величин X и У.
Поэтому случайные величины X и У являются независимыми
согласно теореме 5.4.
Пример 5.21. Проверим, являются ли случайные величины
X и У из примера 5.15 независимыми.
Поскольку вероятность события {X = 3, У = 3} не равна
произведению вероятностей событий {X = 3} и {У = 3}, то,
согласно теореме 5.3, случайные величины X и У являются
зависимыми.
Пример 5.22. Проверим, являются ли случайные величины
X и У из примера 5.17 независимыми.
206 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Из результатов примера 5.17 видно, что совместная плот-
плотность распределения р(ж, у) случайного вектора (X, У) не равна
тождественно произведению частных плотностей распределе-
распределения рх(х) и ру(у) случайных величин X и У. Поэтому, согласно
теореме 5.3, случайные величины X nY являются зависимыми.
Пример 5*23. Проверим, являются ли случайные величины
ХиУиз примера 5.18 независимыми.
В данном случае совместная плотность распределения р(ж, у)
случайного вектора (X, У) тождественно равна произведению
частных плотностей распределения рх(%) и ру{у) случайных
величин X и У. Значит, согласно теореме 5.4, случайные
величины X и У являются независимыми.
Пример 5.24. Известно, что рост Х\ til вес Х*ь взрослого
мужчины (и женщины), проживающего в одном регионе, до-
достаточно хорошо описывается двумерным нормальным законом
распределения. В частности, рост (в сантиметрах) и вес (в
килограммах) мужчин некоторой страны Нормалии подчинены
нормальному закону с вектором средних значений т = A72, 74)
ч_ /45 28 \
и матрицей ковариаций Е = ( ).
Найдем вероятности следующих событий:
а) рост случайно встретившегося нормальца больше средне-
среднего;,
б) его вес меньше среднего;
в) его рост больше среднего, а вес меньше среднего.
а. Одномерное распределение случайной величины Х\ явля-
является нормальным со средним значением т\ = 172 и дисперсией
а\ = 45. Поэтому вероятность того, что рост случайно встре-
встретившегося нормальца будет больше среднего, равна:
Р{Х! > 172} = 1 - Ф172>^45A72) = 1 - фо(О) = 0,5.
б. Действуя, как и в предыдущем пункте, приходим к следу-
следующему результату: вероятность того, что вес случайно встре-
встретившегося нормальца будет меньше среднего, также равна 0,5.
5.6. Решение типовых примеров
207
в. Для того чтобы найти вероятность P{-X"i > 172, Х2 < 74}
того, что рост случайно встретившегося нормальца будет боль-
больше среднего, а его вес меньше среднего, выпишем совместную
плотность распределения случайных величин X и Y. Вычислив
коэффициент корреляции
имеем
«0.66,
-iQ(xi-172,x2-74)
40-A-0,66я)
где
Q(*i-172,*2-74) =
l-0,662 L 45
Тогда
2-0,
(х2-74J
40
1
2яУ45-40-A-0,662)
xi > 172
х2<74
Проводя замену
xi -172 =
вычисляя якобиан [VII]
0X2
~дг
= л/45^40.A-0,662)г
208 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
и учитывая, что область интегрирования {х\ > 172, x*i < 74}
при этом переходит в область {г > 0, Зтг/2 < <р < 2тг}, получаем
2тг +оо
2тг +оо
х d(p rexp< --(r2cos2<p—2-0,66r2cos?>siny?+r2sin2<p) >dr=
Зтг/2 О
Таким образом, искомая вероятность равна примерно 0,11.
Отметим, что если бы рост и вес были независимыми величи-
величинами, то эта вероятность равнялась бы 0,5 • 0,5 = 0,25, т.е. была
бы в два с липшим раза больше.
Пример 5.25. Трехмфньшсмучаиныйвектор J?=(Xi, X2, Х3)
распределен по нормальному закону с вектором средних значе-
значений т = B,5, 1, 2) и матрицей ковариаций
Найдем:
а) совместную плотность распределения случайного век-
вектора Х\
б) одномерные плотности распределения случайных величин
X2 и Х$.
5.6. Решение типовых примеров 209
а. Вычислим определитель матрицы S и матрицу Е, обрат-
обратную к матрице S [II]:
/ 2 1 0,5\
detS = det 13 2 =13,25,
\0,5 2 4 / ¦
8-3 0,5
?'75 >
\0,5 -3,5 5
Тогда
(x-m)S(x-m)T = (xi-2,5 х2-1 х3-2)х
/8-3 0,5\/xi-2,5
ХТ?9^ 7'75 'Ч Ж2
"'25 \0,5 -3,5 5 / V х3-2
= j^g [8(xi - 2,5J - 6(Х! - 2,5)(х2 -1) + 7,75(х2 -1J +
+ (X! - 2,5)(х3 - 2) - 7(х2 - 1)(х3 - 2) + 5(х3 - 2J],
и совместная плотность распределения случайного вектора X,
согласно E.5), имеет вид
х exp [-^L (8(хг-2,5J - 6(х1-2,5)(х2-1) + 7,75(х2-1J +
+ (xi - 2,5)(х3 - 2) - 7(х2 - 1)(х3 - 2) + 5(х3 - 2J)].
б. Случайные величины Х\, Хъ и Х% распределены по
нормальному закону с параметрами mi = 2,5 и о\ = л/2, т2 = 1
210 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
и 0*2 = л/3, тз = 2 и аз = л/2. Поэтому
ни
\
4=
V07T
Пример 5.26. Двумерная случайная величина {Х\,
представляющая собой координаты падения случайной точки
на плоскость, распределена по нормальному закону с вектором
средних значений rhg = A, 2) и матрицей ковариаций
= L( 8 -2
36^-2 Ъ
Найдем:
а) оси рассеивания двумерной случайной величины (Х\, Х2);
б) вероятность попадания случайной величины Х\ в интер-
интервал A/3, 1);
в) вероятность попадания двумерной случайной величины
X2) в область D, ограниченную эллипсом [III],
5x1 + 4a?ia;2 + 8^2 - 18a?i - 36аг2 + 41 = 0.
а. Направление осей рассеивания совпадает с направлением
собственных векторов матрицы [IV]
D
Собственные значения матрицы Е^ определим из уравнения
=А2- 13Л + 36 = 0.
2 g^
Они равны Ai = 4, А2 = 9. Решая систему
5.6. Решение типовых примеров
211
находим нормированные собственные векторы
г' ( 2 • 1\ г' ( 1 ¦ 2
Поскольку оси рассеивания проходят через точку О'A;2), то
уравнения осей рассеивания имеют вид
Х\ — 1 Х2 ~ 2 Х\ — 1 _ Х2 — 2
И
В частности, в системе координат x'jO'x!^ с центром в точке
О1 и базисными векторами [IV] ё\ и SJ координаты (XJ;^)
случайной точки имеют нормальное распределение с вектором
средних mg, = @; 0) и матрицей ковариаций
0
1/4 0
о
Наконец, если ввести систему координат
в той же точке О1 и базисными векторами
с центром
1 "
то в этой последней системе координаты (Ух,!^) случайной
точки будут иметь стандартное нормальное распределение.
б. Случайная величина Xi имеет нормальное распределение
со средним значением тхх = 1 и средним квадратичным от-
отклонением axi = л/2/3. Поэтому
в. Матрица квадратичной формы Ъх\ + Ах\Х2 + 8х^ которая
представляет собой многочлен второй степени, определяющий
212 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
рассматриваемый эллипс, совпадает с матрицей Е^. Поэтому
оси симметрии эллипса параллельны осям рассеивания случай-
случайной величины (Х\, Х2)> Более того, проводя вычисления, по-
получаем, что центр эллипса совпадает с центром рассеивания
О'. Значит, в системе координат, образованной осями рас-
рассеивания, т.е. в системе координат с центром в точке О1 и
базисными векторами ё\ и е2, эллипс имеет каноническое урав-
уравнение. Поскольку матрица квадратичной формы в уравнении
рассматриваемого эллипса совпадает с матрицей Е^, видим,
что этот эллипс является одновременно эллипсом рассеивания,
и в системе координат У\Оу2 он превращается в окружность
Ух + у\ = 4- Поэтому вероятность попадания двумерной случай-
случайной величины (Xi, Х2) в область D равна вероятности попада-
попадания двумерной случайной величины (Yi, Y2), распределенной по
стандартному нормальному закону, в круг радиуса 2 и опреде-
определяется формулой
Ял У1+У2
2^е 2 dyidy2.
Переходя к полярным координатам, получаем
2тг 2 р2
P{{XuX2)eD}= fdip /^e~Tpdp= 1-е-2 «0,14.
о о
Таким образом, искомая вероятность приближенно равна 0,14.
Вопросы и задачи
5.1. Что называют n-мерной случайной величиной (п-мер-
ным случайным вектором)?
5.2. Дайте определение совместной функции распределения
(вероятностей) n-мерной случайной величины (п-мерного слу-
случайного вектора).
Вопросы и задачи 213
5.3. Какими свойствами обладает функция распределения
n-мерного случайного вектора?
5.4. Как найти вероятность попадания двумерной случай-
случайной величины (X, Y) в прямоугольник (а\ ^ х < аг, Ь\ ^ у < Ьг)
с помощью совместной функции распределения -Fxr (#>!/)?
5.5. Какую двумерную случайную величину называют дис-
дискретной?
5.6. Каким образом можно задать распределение двумерной
случайной величины?
5.7. Какую двумерную случайную величину называют не-
непрерывной?
5.8. Дайте определение совместной (n-мерной) плотности
распределения (вероятностей).
5.9. Какими свойствами обладает двумерная плотность
распределения?
5.10. Как найти одномерные плотности распределения по
двумерной плотности распределения?
5.11. Как найти вероятность попадания в некоторую область
с помощью плотности распределения?
5.12. Как найти совместную плотность распределения, ес-
если известна совместная функция распределения непрерывной
случайной величины?
5.13. Как найти совместную функцию распределения п-
мерной непрерывной случайной величины, если известна ее
совместная плотность распределения?
5.14. Какие случайные величины называют независимыми?
5.15. Могут ли случайные величины быть независимыми
попарно, но зависимыми в совокупности?
5.16. Как проверить независимость двух дискретных слу-
случайных величин?
214 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
5.17. Как проверить независимость двух непрерывных слу-
случайных величин?
5.18. Запишите выражение совместной плотности распре-
распределения для двух нормально распределенных независимых слу-
случайных величин.
5.19. Запишите выражение совместной плотности распре-
распределения двумерного нормального закона (в общем случае).
5*20. Что называют вектором средних и матрицей ковари-
аций двумерного случайного вектора, имеющего нормальное
распределение? Чему равен коэффициент корреляции коор-
координат двумерного случайного вектора, имеющего нормальный
закон распределения?
5.21* Запишите выражение плотности n-мерного нормаль-
нормального распределения.
5.22. Что называют вектором средних значений и матрицей
ковариаций многомерного нормального распределения? Чему
равен коэффициент корреляции координат n-мерного случайно-
случайного вектора, имеющего многомерное нормальное распределение?
5.23. Какой нормальный закон называют стандартным?
5.24. Что называют эллипсом рассеивания двумерного нор-
нормального закона? Как определить угол поворота осей сим-
симметрии эллипса рассеивания двумерного закона относительно
осей координат?
5.25. Что называют эллипсоидом рассеивания многомерно-
многомерного нормального закона? Как можно получить n-мерный случай-
случайный вектор, распределенный по произвольному нормальному
закону, с помощью n-мерного случайного вектора, распреде-
распределенного по стандартному нормальному закону?
5.26. Какие свойства многомерного нормального распреде-
распределения Вы знаете?
Вопросы и задачи 215
5.27. Двумерная случайная величина (X, У) имеет совмест-
совместную функцию распределения
F(x,y) = —J Darctgxarctg2/ + 27rarctga; + 27rarctgj/ + 7r2).
Вычислите: а) вероятности событий {—1<Х<1,1^У< л/3}
/
б) частные функции распределения случайных величин X
и У;
в) проверьте, являются ли случайные величины X и Y
независимыми.
Ответ:
д\т>г 1 < Y" <^ 1 1 < V <^ \/5\ = 1 /24 P-f X > 1 У > \/S\ =
= 1/24;
б) Fx\X) ^ —Barctgx -Ь тг), J*y(y)== —Barctgy-t-7r);
в) да, являются.
5.28. Двумерная случайная величина (X, У) имеет совмест-
совместную функцию распределения
О, х < 0 или у ^ 0;
sin ж + sin у — sin(x ¦
F{x,y) =
~иу> тг/2;
2 ' ~ ^
sing-cosа: 4-1 л ^
2 '
siny — cosy + 1 тг л <; 7Г.
2 ' 2^ ^^2^'
1 ъ- w ъ. п
Найдите:
а) вероятности событий {тг/12 < X < тг/4, {тг/12 ^ У < тг/4},
{X ^ тг/4, У ^ тг/4} и {X < тг/3, У ^ тг/6};
б) частные функции распределения случайных величин X
и У;
в) проверьте, являются ли случайные величины X и У
независимыми.
216
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Ответ: а) Р{тг/12 < X < тг/4, тг/12 < У < тг/4} = Bл/3 - 3)/4,
Р{Х > тг/4, У > тг/4} =
б)
- 1)/2, Р{Х < тг/3,
= 1/2;
О,
sins — cosa; + l
2
1,
О,
Жг/) =
1,
в) нет, не являются.
О < х ^ 7г/2;
ж > тг/2;
0<у<тг/2;
У > тг/2;
5.29. Распределение вероятностей дискретной двумерной
случайной величины (X, Y) задано табл. 5.10. Найдите:
а) ряды распределения случайных величин X иУ;
б) значения совместной функции распределения F(x,y) слу-
случайных величин X и У в точках B,5; 25) и (9; 11), а также
вероятность события {2 < X < 9,10 < Y < 30};
в) проверьте, являются ли случайные величины X и Y
независимыми.
Таблица 5.10
X
0,5
2,5
У
10
0,05
0,09
20
0,12
0,30
30
0,08
0,11
40
0,04
0,21
Ответ:
а) ряды распределения случайных величин X и Y приведены
в табл. 5.11 и 5.12;
б) FB,5,25) = 0,17, F(9,11) = 0,14,
Р{2 ^ X < 9, 10 < У < 30} = 0,50;
в) нет, не являются.
Вопросы и задачи
217
Таблица 5.11
X
Р
0,5
0,29
2,5
0,71
Y
Р
10
0,14
Таблица 5.12
20
0,42
30
0,19
40
0,25
5.30. Найдите совместную плотность распределения для
непрерывной двумерной случайной величины (X, У) из зада-
задачи 5.28.
Ответ:
0,
5.31. Совместная плотность распределения непрерывной
двумерной случайной величины (X, У) имеет вид
, Г 0, (*-3J + (у-2J>4;
-2J), Ог-
Найдите:
а) постоянную С; ^
б) частные плотности распределения случайных величин X
и У;
в) вероятность попадания случайного вектора (JC, У) в круг
(я-3J + (у-2J<1;
г) проверьте, являются ли случайные величины X и У
независимыми.
Ответ:
а)С = 3/(8тг);
0, .
б) Рх(х) =
218 5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
О, У*[0,4];
Му) = | ^(У4-(^2>2-
в) Р = 1/2; г) нет, не являются.
5.32* Совместная плотность распределения непрерывной
двумерной случайной величины (X, У) имеет вид
, ч Г 0, я^0илиу<0;
Р(гГ'У) = \Се-4^, *>0иу>0.
Найдите:
а) постоянную С;
б) совместную функцию распределения;
в) частные плотности распределения случайных величин X
и У;
г) вероятность попадания случайного вектора (X, У) в
область, ограниченную прямыми у = ж, ж + у = 2иж = 0;
д) проверьте, являются ли случайные величины X и У
независимыми.
Ответ: *
а)С = 8;
Г 0, х^Оилиу^О;
б)^М = (A_е-4,)A_е-Ч ж>0иу>0;
Г 0, ж<0; Г 0, у<0;
= |4е_4Ж) ж>0; Pv(y) = |2e-2yj y>0.
г) Р = 2A - Зе~4 + 2е"~6)/3; д) да, являются.
5.33. Непрерывная двумерная случайная величина (X, У)
распределена равномерно в квадрате с вершинами @,0), @,1),
A,0) и A,1). Найдите:
а) совместную плотность распределения;
Вопросы и задачи 219
б) совместную функцию распределения;
в) частные плотности распределения случайных величин X
и У;
г) вероятность попадания случайного вектора (X, У) в круг
д) проверьте, являются ли случайные величины X и У
независимыми.
Ответ:
О, х < 0 или у ^ 0;
h 1, ж>1 иу> 1;
{0, х & [0,1]; Го, у 0 [0,1];
1, а: €[0,1]; Py(j/) = 11, уЕ[0,1];
г) Р = тг/8; д) да, являются.
5*34. Непрерывная двумерная случайная величина (X, У)
имеет совместную плотность распределения
, v С
Найдите:
а) постоянную С;
б) совместную функцию распределения;
в) частные плотности распределения случайных величин X
и У;
г) вероятность попадания случайного вектора (X, У) в
треугольник с вершинами в точках (—1; 1), A; 1) и @; 0);
д) проверьте, являются ли случайные величины X и У
независ дмыми.
220
5. МНОГОМЕРНЫЕ СЛУЧАЙНЫЕ ВЕЛИЧИНЫ
Ответ:
а) С=1/тг; б) F(a:,y) = (i
iy, РУ(У) =
г) Р = ~; д) да, являются.
5.35. Распределение вероятностей дискретной двумерной
случайной величины (X, Y) задано в табл. 5.13. Проверьте,
являются ли случайные величины X nY независимыми.
Таблица 5.13
X
-1
0
1
-3
0,06
0,15
0,09
У
-1
0,02
0,005
0,03
1
0,04
0,10
0,06
3
0,08
0,20
0,12
Ответ: да, являются.
5.36. Двумерная случайная величина (Xi, Х2) распределена
по нормальному закону с вектором средних m = B,0) и матри-
1 /25 7 \ „ u
цеи ковариации S = — I 7 2g J. Найдите:
а) оси рассеивания двумерной случайной величины (Х\, Хг);
б) вероятности события {Х\ > 2,28} и {-0,2 <Х2< 0,2};
в) вероятность попадания двумерной случайной величины
(Xi, X2) внутрь эллипса 25х* - 14Ж1Ж2 + 25гг2 - ЮОжх + 28а?2 +
+ 98 = 0.
Ответ: а) х\ — х2 = 2 и х\ + Х2 = 2;
б) P{Xi > 2,28} w 0,159, Р{~0,2 < Х2 < 0,2} « 0,711;
в) Р = 1-е «0,63.
5.37. Трехмерный случайный вектор X = (Xi, X2, -Х*з) рас-
распределен по нормальному закону с вектором средних значений
Вопросы и задачи 221
m = (—2, О, 1) и матрицей ковариаций
г /13 5 2
S = — 5 35/2 7
81 \ 2 7 19,
Найдите: а) плотность распределения случайного вектора X;
б) одномерные плотности распределения случайных величин
Х\, Х2 и Хз-
Ответ:
а) р*{в)=щ^Д ехр{"зк К+2J -
-1J] }•
26
81s2
9
рхЛх) = , г— е 38
5.38. Независимые случайные величины Х\ и X<i имеют
нормальное распределение с математическими ожиданиями
х = 3 и тх2 = 2 и средними квадратичными отклонениями
= ^х2 = 0,5. Найдите радиус R круга с центром в точке
C; 2), вероятность попадания в который равна 0,997.
Ответ: Д«0,45.
6. ФУНКЦИИ
ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
На практике очень часто встречается случаи, когда рассма-
рассматриваемая числовая величина У является функцией от одной X
или нескольких Х\, ..., Хп числовых величин, т.е., как говорят,
связана с этой или этими величинами функциональной зависи-
зависимостью У = Y(X) или Y = Y(Xi,... ,Хп). Очевидно, что если
величина X или величины Х\, ..., Хп, через которые выража-
выражается У, являются случайными, то и У также будет случайной
величиной. Таким образом, мы приходим к понятию функ-
функции от случайной величины X или от случайного вектора
(Xi, ..., Хп)у которое будет рассмотрено в настоящей главе.
6.1. Примеры функциональной зависимости
между случайными величинами
Прежде чем переходить к строгому математическому опре-
определению функции от случайной величины и выводу формул,
связывающих законы распределения аргумента и самой функ-
функции, остановимся несколько подробнее на описании функцио-
функциональной связи между случайными величинами и приведем по-
поясняющие примеры.
В предыдущей главе были рассмотрены многомерные слу-
случайные величины, или случайные векторы. Было показано,
что полное вероятностное описание многомерного, в частности
двумерного, случайного вектора состоит в задании совместной
функции распределения. Бели же нам известно, какое значение
приняла одна из координат двумерного случайного вектора,
то вероятностные свойства второй координаты определяются
6.1. Примеры функциональной зависимости 223
условным законом распределения, который будет рассмотрен
ниже в 8.1.
Однако условная функция распределения отражает только
вероятностную, или стохастическую, связь между случайными
величинами, а предсказать точное значение одной случайной
величины по значению другой, вообще говоря, невозможно. Бо-
Более того, как мы теперь знаем, для весьма часто встречающихся
в реальной жизни независимых случайных величин по значению
одной случайной величины нельзя судить о значении другой, и
в этом плане независимость нужно признать крайним случаем
стохастической связи.
Еще один крайний случай стохастической связи между слу-
случайными величинами, также постоянно используемый на прак-
практике, заключается в том, что по значению одной случайной
величины можно однозначно определить значение другой; его
называют функциональной зависимостью между случайными
величинами. При этом говорят также, что вторая случайная
величина является функцией от первой случайной величины.
Аналогично вводят скалярную и векторную функции от слу-
случайного вектора.
Рассмотрим примеры.
Пример 6.1. Для измерения недоступного предмета, на-
например высоты Н трубы, с помощью угломера используют
функциональную зависимость (рис. 6.1) Н = atga, где а —
размер „базы"; а — угол, под
которым видна труба. Одна-
Однако если размер а можно из-
измерить практически точно, то
вследствие погрешностей из-
измерений, присущих угломеру,
а необходимо считать случай-
случайной величиной. Таким обра-
образом, приведенная выше фор-
, Рис. 6.1
мула задает функциональную
224 б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
связь между измеренным значением угла а и полученной по
этой формуле высотой Н трубы.
Пример 6.2. Пусть X и У — измеренные (с погрешно-
погрешностями) длины катетов прямоугольного треугольника. Тогда
функциями от двух случайных аргументов X и У будут:
L = VX2 + У2 — найденная по теореме Пифагора длина
гипотенузы;
S = XY/2 — вычисленная площадь этого треугольника.
Пример 6.3. Предположим, что на плоскость в соответ-
соответствии с некоторым вероятностным законом случайным образом
бросают точку и измеряют ее полярные координаты р и (р. То-
Тогда формулы X = рсоз<р и Y = psirnp перехода от полярных
координат р и <р к декартовым X и У [III] определяют век-
векторную функцию от векторного аргумента.
6.2. Функции от одномерной случайной величины
Пусть на вероятностном пространстве (S7,95,P) задана
случайная величина X = X(ш). Рассмотрим действительную
функцию
y = Y(x)
действительного аргумента х (область определения которой
включает в себя множество возможных значений случайной
величины X).
Определение 6.1. Случайную величину У, которая каждо-
каждому элементарному исходу ш ставит в соответствие число
называют функцией Y(X) (скалярной) от скалярной слу-
случайной величины X.
Функция У = У (X) от дискретной случайной величины так-
также является дискретной случайной величиной, поскольку она
6.2. Функции от одномерной случайной величины
225
не может принимать больше значений, чем случайная величи-
величина X. Очевидно, что если случайная величина X имеет ряд
распределения, представленный в табл. 6.1, то ряд распределе-
распределения случайной величины Y = Y(X) определяется табл. 6.2.
X
р
Р\
Таблица 6.1
х2
Р2
...
...
хп
Рп
Y
Р
Y{xi)
Pi
УЫ
Рг
Таблица 6.2
...
Y(xn)
Рп
При этом, если в верхней строке табл. 6.2 появляются
одинаковые значения Y(xi), соответствующие столбцы нужно
объединить в один, приписав им суммарную вероятность.
Пример 6.4. Рассмотрим игру „ Спортлото 6 из 49". По-
Поставив на некоторые фиксированные номера, мы в результате
розыгрыша получим случайную величину X — число угадан-
угаданных номеров. Число угаданных номеров имеет гипергеометри-
гипергеометрическое распределение (см. 2.2, а также задачу 2.36), в котором
к = 2, п = 49, п\ = 6, П2 = 43 и т = 6, а значит, вероятность
угадать г, г = 0,6, номеров определяется формулой
Р(г,6 - г) = Р{Х = г} =
Проводя вычисления, получаем ряд распределения случайной
величины X, представленный в табл. 6.3.
Таблица 6.3
X
р
0
0,4360
1
0,4130
2
0,1324
3
0,0176
4
0,00097
5
1,8 10-®
6
7 10"8.8
Однако случайная величина X нас не интересует, для нас
важен выигрыш, связанный с числом угаданных номеров X.
Рассмотрим идеализированный вариант игры, при котором,
не угадав ни одного или угадав один или два номера, мы
проигрываем (с учетом платы за билет) 0,3 р., угадав три
8 - 10047
226
б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
номера, получаем выигрыш 2,7 р., угадав четыре номера —
54,7 р., пять номеров — 699,7 р. и шесть номеров — 9999,7 р.
Выигрыш У зависит только лишь от числа угаданных номеров,
т.е. представляет собой функцию от случайной величины X:
Y = Y(X).
При этом числовая функция У (х) определена формулами:
У@)=УA)=УB) = -0,3, УC)=2,7,
У D) = 54,7, У E) = 699,7, У F) = 9999,7.
Ряд распределения случайной величины У получаем из ряда
распределения X (см. табл. 6.3) заменой в верхней строке чисел
г = 0,6 на соответствующие значения У (г) (табл. 6.4).
Таблица 6.4
Y
Р
-0,3
0,4360
-0,3
0,4130
-0,3
0,1324
2,7
0,0176
54,7
0,00097
699,7
1,8 Ю
9999,7
7-10-"
Осталось заметить, что в табл. 6.4 три первых столбца
имеют одинаковые значения У, равные —0,3. Объединяя их
в один, окончательно получаем ряд распределения случайной
величины У, представленный в табл. 6.5.
Таблица 6.5
Y
Р
-0,3
0,9814
2,7
0,0176
54,7
0,00097
699,7
1,8 Ю
9999,7
7 10"8
Реально при игре в „Спортлото" выигрыш У зависит от чи-
числа играющих, поставивших на ту или иную комбинацию, и в
этом случае его нельзя считать функцией от числа угаданных
номеров X, а необходимо рассматривать более сложную модель,
учитывающую вероятности (частоты) использования различ-
различных комбинаций номеров. В частности, нельзя (без обращения
к „потусторонним" силам) изменить вероятность угадывания
определенного числа номеров, но можно увеличить выигрыш,
6.2. Функции от одномерной случайной величины 227
ставя на „ непопулярные" комбинации, которые, хотя и появля-
появляются с той же частотой, что и остальные, но приносят больший
выигрыш. Однако риск от „ непопулярных" комбинаций отно-
относится к сфере психологии, а не к теории вероятностей. #
Функция У = Y(X) от непрерывной случайной величины
X может быть как непрерывной, так и дискретной (если,
например, множество значений функции Y(X) конечное или
счетное).
Сформулируем правило определения функции распределения
Fy(y) по заданной плотности распределения рх(х), пояснив
идею вывода (при строгом выводе необходимо использовать
понятие интеграла Лебега).
В силу определения Fy(y) представляет собой вероятность
события {Y < у}, состоящую из тех элементарных исходов а;,
для которых Y(X(uj)) < у. Для этих же элементарных исходов
ш случайная величина Х(и) будет принимать свои возможные
значения на некоторой совокупности {A*}, fc = 1,2,..., непере-
непересекающихся промежутков числовой прямой R. Иными словами,
событие [Y(X(u)) < у} эквивалентно событию и{Х(ш) € А*},
и, следовательно, по расширенной аксиоме сложения вероят-
вероятностей
FY(y) = *{Y(X(u>)) <y} = ^P{X(uk) € A*}.
к
Зная плотность распределения рх(я) случайной величины
Г, имеем
а следовательно, учитывая свойство аддитивности определен-
определенного интеграла, получаем
j)dx, A =
где сумма может быть и бесконечной.
228 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Поскольку совокупность промежутков {Д&} определена как
множество тех значений случайной величины Х(ш), для кото-
которых Y(X(u)) < у, то для множества Д = U Д*, по которому
ведется интегрирование, принято обозначение: У (х) < у. Окон-
Окончательно получаем
FY(y)= I px(x)dx. F.1)
Y(x)<y
Последняя запись означает, что интегрирование проводит-
проводится по всем тем значениям #, для которых У(х) < у. Множество
таких значений может представлять собой совокупность про-
промежутков, и тогда нужно использовать свойство аддитивности
интеграла, а пределы интегрирования по отдельным промежут-
промежуткам определяются их границами.
Таким образом, формула F.1) позволяет вычислять функ-
функцию распределения Fy(y) случайной величины У (X) через плот-
плотность рх{%) распределения случайной величины X. В случаях,
когда функция У = Y(X) является монотонной или кусочно
монотонной, формула F.1) далее будет записана в более про-
простом виде.
Пример 6.5. Случайная величина X имеет стандартное
нормальное распределение. Найдем распределение случайной
величины У = X2. В данном случае У(х) = ж2, поэтому
FY(y)= J px{x)dx = -j= J
x2<y x2<y
Поскольку при у ^ 0 нет ни одного значения х, для которого
х2 < у, то не существует ни одного о;, для которого Y(X(u)) =
2
FY(y) = 0 при
6.2. Функции от одномерной случайной величины 229
Если же у > О, то область {х2 < у} совпадает с областью
{-у/у <х< у/у}, и, значит,
или в силу четности <р(х)
у/у
J
О
Делая в последнем интеграле замену z = x2 при у > 0, получаем
о
Следовательно (см. 4.1),
}
= I PY(y)dy,
где
f 0, y<0;
Так как 0г = Г(-1, где Т(х) — гамма-функция Эйлера
[XI], то плотность распределения ру(у) случайной величины Y
совпадает с плотностью гамма-распределения с параметрами
Л = 1/2 и 7 = 1/2.
Замечание 6.1. Напомним (см. 4.6), что эту плотность
распределения также называют плотностью ^-распределения
230
б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
с одной степенью свободы. Таким образом, х2"РаспРеДеление
с одной степенью свободы является распределением квадрата
случайной величины, имеющей стандартное нормальное рас-
распределение.
В общем случае в математической статистике используют
Х2-распределение с п степенями свободы, которое, по опреде-
определению, есть распределение суммы квадратов п независимых
случайных величин, распределенных по стандартному нормаль-
нормальному закону. #.
Бели функция Y(х) является монотонной или кусочно мо-
монотонной, что обычно бывает в прикладных задачах, то закон
распределения случайной величины Y = Y(x) в виде функции
распределения или плотности распределения можно получить
без интегрирования через функцию распределения или плот-
плотность распределения случайной величины X.
Действительно, предположим сначала, что функция Y (х)
является непрерывной возрастающей (рис. 6.2) или убывающей
функцией. В этом случае существует обратная функция [I]
х=ф(у) х
Рис. 6.2
6.2. Функции от одномерной случайной величины 231
и событие {У(Х(ш)) < у} эквивалентно событию Х(ш) < ф(у)}
(в случае возрастающей функции Y(x)) или событию {Х(ш) >
>ф(у)} (в случае убывающей Y(х)). Значит, для возрастающей
функции Y (х)
P{Y(X) < у} = Р{Х < ф(у)}, F.2)
для убывающей Y(x)
Р{У(Х)<у} = Р{Х>^(у)}. F.3)
Поскольку, согласно определению D.2) функции распределения,
FY(y)=P{Y<y},
окончательно получаем:
для возрастающей функции Y(x)
F.4)
для убывающей функции Y(x)
FY(y) = l-Fx(<<l>(y)). F.5)
Напомним, что ф(х) = Y(y) — функция, обратная к Y(x).
Пример 6.6. Пусть случайная величина X имеет непре-
непрерывную функцию распределения F(x), которая является воз-
возрастающей функцией. Рассмотрим случайную величину Y =
= F(X). Она принимает значение только на промежутке [0,1].
Обратная функция для функции F
при у G [0,1], очевидно, удовлетворяет тождеству
Р(Ф(у))=у,
и, следовательно, в соответствии с формулой F.4) имеем для
уе[о,1]:
FY(y)=F(F-1(y)) = y.
232 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
В случае у < О событие {У < у} является невозможным. По-
Поэтому, если у < О, то
В случае у > 1 co^wmwe {У < у} является достоверным. Поэто-
Поэтому, если у > 1, то
Итак,
Fy(y)
{О, у<0;
У, 0<у<1;
и случайная величина У имеет равномерное распределение на
отрезке [0,1].
Переходя к обратной функции, видим, что случайная вели-
величина
X = F(y) F.6)
имеет функцию распределения -Р(ж), если случайная величина
У имеет равномерное распределение на отрезке [0,1].
Полученный результат широко применяют при моделиро-
моделировании случайных величин с заданной функцией распределения
F(x). Действительно* если нужно смоделировать такую случай-
случайную величину, то достаточно иметь датчик случайных чисел У,
распределенных равномерно на отрезке [0,1], и каждое такое
число преобразовать по формуле F.6).
Например, пусть нужно смоделировать реализацию случай-
случайной величины X с экспоненциальной функцией распределения
F(x) = 1 — еЛа\ х ^ 0, при известном параметре Л. Тогда, учи-
учитывая, что
h
реализацию X можно получить по формуле
6.2. Функции от одномерной случайной величины 233
где У — случайное число с равномерным в интервале @,1)
законом распределения. #
Используя формулы F.4) и F.5), легко найти связь меж-
между плотностью распределения рх(х) случайной величины X и
плотностью распределения ру(у) случайной величины У = У (X)
в том случае, когда функция Y(x) не только монотонна, но и
дифференцируема. Действительно, согласно правилу диффе-
дифференцирования сложной функции [II], имеем:
в случае возрастающей функции У (ж)
ру(у) = F*Y(y) = fe(*)Y у (у) =
в случае убывающей функции Y(x)
PY(y) = F*Y(y) = -(fx(x))'\ У (у) = -рх(Ф(у))Ф'(у).
Оба эти случая можно записать в виде
F-7)
Пример 6.7. Пусть случайная величина У получена из
случайной величины X линейным пребразованием
Y = aX + b (а ?*0),
где а и 6 — неслучайные числа. Поскольку линейная функция
является монотонной, то, учитывая, что
и
согласно F.7), имеем
234 б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Применим полученный результат к случайной величине
X, распределенной по нормальному закону распределения с
параметрами тх и ах- Тогда случайная величина Y = аХ + Ъ в
соответствии с формулой F.8) имеет плотность распределения
т.е. также распределена по нормальному закону с параметрами
ту = атпх + Ь и ay = |a|ax.
В частности, с помощью линейного преобразования
v_X-mx _ I Y тх { _ 1 ,_ тх\
ох ох ох \ ох ох)
из случайной величины X, распределенной по нормальному
закону с параметрами тх и ах, получаем случайную величину
У, имеющую стандартное нормальное распределение, так как
ту = атх + Ь = 0, оу = \a\cx = 1- И наоборот, с помощью
линейного преобразования
из случайной величины У, имеющей стандартное нормаль-
нормальное распределение, получаем случайную величину X, имею-
имеющую нормальное распределение с произвольными параметрами
ах • 0 + тх = тх и ах • 1 = ох- #
Пусть теперь Y(x) является непрерывной кусочно моно-
монотонной функцией [I], имеющей п интервалов монотонности
(рис. 6.3). Для любого у все решения уравнения
Y(x) = y
6.2. Функции от одномерной случайной величины
235
обозначим х\ = #i(y), ..., Xk = ж* (у) (в силу кусочной монотон-
монотонности Y(x) таких решений не более п, причем каждое решение
соответствует определенному интервалу монотонности). Пусть
для определенности х\ соответствует интервалу возрастания, а
Xk — интервалу убывания функции Y(x). Тогда событие Y < у
представляет собой (см. рис. 6.3) объединение несовместных
событий {X е (-oo,xi)}, {X е (х2,жз)}, •••» {-*" 6 (xki+oo)}, и,
значит, согласно определению 4.2 функции распределения и ак-
аксиоме 3; сложения,
хк} =
-^хЫ. F.9)
+ Р{ж2 < X
Рис. 6.3
Из формулы F.9) можно получить выражение для плотно-
плотности распределения случайной величины Y в том случае, когда
Y(х) является дифференцируемой функцией. Действительно,
пусть /i, ..., Ik — интервалы монотонности У, которым при-
принадлежат a?i, ..., х^ Тогда в этих интервалах существуют
обратные к Y{x) дифференцируемые функции, которые обо-
обозначим ф\{у), ..., ^fc(y) соответственно. Учитывая, что х\ =
= V>i(y)? • • ¦» s* = Vb(y)> перепишем F.9) в виде
FY(y) =
236 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Дифференцируя обе части последнего равенства, получаем
к
ру(у) =
г=1
Пример 6.8. Снова обратимся к задаче, рассмотренной
в примере 6.5, однако теперь для ее решения воспользуемся
формулой F.10).
Заметим, что функция Y(х) = х2 принимает только не-
неотрицательные значения и, следовательно, при у < 0 уравнение
Y (х) = у не имеет решений. Поэтому случайная величина
Y = Y(X) = X2
не может принимать отрицательные значения и, следовательно
функция распределения Fy(y) = 0 при у < 0. Отсюда диффе-
дифференцированием получаем
у) = 0, у<0.
Далее, при у > 0 уравнение у = ж2 имеет два решения:
И х
причем первое решение принадлежит интервалу (—оо,0) убыва-
убывания функции У(х) =#2, а второе — интервалу @,+оо) возра-
возрастания этой функции. Подставляя if>i(y), Ф2(у) и плотность
стандартного нормального распределения в формулу F.10),
получаем
РК(У) =
1 ""/2, у>0.
Таким образом, пришли к тому же выражению для плотно-
плотности распределения, что и в примере 6.5.
6.3. Скалярные функции от случайного векторного аргумента 237
\
6.3. Скалярные функции
от случайного векторного аргумента
Скалярную функцию от случайного векторного аргумента
определяют так же, как и функцию от одномерной случайной
величины. Для простоты изложения ограничимся рассмотрени-
рассмотрением функции от двух случайных аргументов, хотя приведенные
ниже выводы можно полностью перенести на случай любого
числа аргументов.
Рассмотрим на вероятностном пространстве A7,9$,Р)
двумерный случайный вектор X = (Xi, X2) и числовую функ-
функцию Y(x\,X2) числовых аргументов х\ и Х2-
Определение 6.2. Случайную величину
У = Y(XUX2) = y(XiM,X2M)
называют функцией (скалярной) от двумерной случайной
величины (двумерного случайного вектора) (Х\,
Ясно, что функция Y(Xi,X2) от двумерной дискретной
случайной величины (Xi, X2) является дискретной случайной
величиной, принимающей значения Y(xu,X2j) с вероятностью
Pij =
где хц и X2j — значения случайных величин Х\ и Х2 соответ-
соответственно.
Чтобы построить ряд распределения дискретной случайной
величины Y = Y(X\1X2)J необходимо, во-первых, не учитывать
все те значения Y{x\i,X2j)i вероятность принять которые слу-
случайной величине Y равна нулю, а во-вторых, объединить в один
столбец все одинакоые значения Y(xu,X2j) случайной величины
У, приписав этому столбцу суммарную вероятность.
Пример 6.9. Пусть У — случайная величина, равная сум-
суммарному числу успехов в двух испытаниях по схеме Бернулли,
238
б. ФУНКЦИИ ОТ СЛУЧА
ВЕЛИЧИН
число успехов в i-м испытании,/г = 1,2. Тогда
У = Х\ + Х2 И У(хцХ2) = Х\ + Х2-
Поскольку Xi могут принимать только значения 0 или 1, то
случайная величина У может принимать четыре значения:
У@,0) =0 + 0 = 0, УA,0) = 1 + 0 = 1,
У@,1) = 0 +1 = 1, У A,1) = 1 +1 = 2
с вероятностями g2, pqy qp и р2 соответственно, где р —
вероятность успеха в одном испытании, q = 1 — р (табл. 6.6,
см. также пример 5.4 и табл. 5.2).
Y
Рк
У@,0) = 0
я2
УA,0) = 1
РЯ
У@,1)
ЯР
Таблица
= 1
YQ.,1)
Р2
6.6
= 2
Заметим, что двум средним столбцам соответствует одно и
то же значение 1 случайной величины У, и их необходимо объ-
объединить. Окончательно получаем ряд распределения случайной
Таблица 6.7 величины У, представленный в табл. 6.7.
Как и следовало ожидать, суммарное
число успехов У в двух испытаниях име-
имеет биномиальное распределение. #
В том случае, когда (Х^ Х2) — двумерная непрерывная
случайная величинас плотностью распределенияpxx,x<Sp\<>
функцию распределения случайной величины У =
можно найти по формуле, аналогичной F.1):
F.11)
Y
Рк
0
Я2
1
2pq
2
Р2
Fy(v)= If Pxux2{xux2)dxldx2,
Y(xi>x2)<y
где область интегрирования состоит из всех значений х\ и а?2,
для которых У(жх,Х2) < у.
рункции
6.3. Скалярные функции от случайного векторного аргумента 239
Поясним геометрически вывод формулы F.11). Пусть
поверхность, определенная функцией у = Y(x\,x2), имеет вид
„чаши" (рис. 6.4) и у ±- произвольное значение случайной
величины У = Y(X\,X2). Проведем плоскость тг, проходящую
через точку @;0;у) и ортогональную оси 0у. Обозначим через
L линию пересечения плоскости 7г и поверхности у = Y(xi,x2);
V — ее проекцию на плоскость х\Ох2; D(y) — ту часть
плоскости xi 0x2, попадание в которую случайного вектора
(Х\, Х2) ведет к реализации события {Y < у}. Поскольку
Y = Y(XuX2),to
D(y) = {(m, ^2): Y(xux2) < у} = {Y{xux2) < у}.
События {У < у) и {(J^i, X2) G D(y)} совпадают, и в соответ-
соответствии со свойством 6 двумерной плотности распределения
Р{У < у} = P{(XU X2) e D(y)} = JJ рх
Учитывая равенство Р{У < у) = iV(y), приходим к форму-
формуле F.11).
Пример 6.10, Пусть (JCi, X2) — двумерный случай-
случайный вектор, имеюпщй стандартное нормальное распределение.
Найдем распределение случайной величины
В этом случае
Очевидно, что
О, у<0;
И ±-e-te\+A)dxtdxi, у>0.
240
б. ФУНКЦИИ ОТ СЛУЧА
йнцх
ВЕЛИЧИН
I/
Рис. 6.4
Переходя к полярным координатам р и <р, имеем
у 2тг у
FY(y) = jdpj ^e-*2l2pd<p = jpe-'2l2dp = 1 - е-*2/2? у > 0.
0 0 0
Это известное нам распределение Релел (см. 4,6).
Полученный результат допускает многочисленные физиче-
физические трактовки. Приведем одну из них. Бели движущаяся в
плоскости частица имеет случайные составляющие скорости,
распределенные по двумерному стандартному нормальному за-
закону, то абсолютное значение скорости распределено по закону
Релея. Трехмерным аналогом распределения Релея (абсолют-
(абсолютное значение скорости частицы, движущейся в трехмерном
пространстве, причем составляющие скорости распределены
по трехмерному стандартному нормальному закону) является
распределение Максвелла, представляющее собой распре-
распределение случайной величины Y = у/Х, где X — случайная вели-
величина, распределенная по закону х2 с числом степеней свободы,
равным трем.
6.4. Формула свертки 241
6.4. Формула свертки
Важную роль в теории вероятностей и ее применениях игра-
играет тот случай, когда Х\ и Х2 являются независимыми случай-
случайными величинами, т.е. их двумерная плотность распределения
(мы ограничиваемся здесь только случаем непрерывных случай-
случайных величин), а случайная величина Y является их суммой:
и, согласно формуле F.11),
Г Г
х\+х2<у
Ж1+Х2<У
+00
= / pxx(xi;
-оо
находим:
(Xl)PX2(X2)dXldx2 =
y-xi
)dxi / px2(x2)dx2 =
-oo
+OO
= [FX2(y-X]
Дифференцируя последнюю формулу по у под знаком инте-
интеграла (см. [VI]), получаем (с учетом переобозначения х\ = х)
выражение для плотностиру (у) распределения суммы Х\ и Х2:
+00
Рг{у) = / РХ2 (У - Фхг (х) dx. F.12)
242 0. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
В этом случае говорят, что плотность распределения ру(у)
случайной величины Y является сверткой (композицией)
плотностей распределения рхх (х) и рх2 (х) слагаемых Х\ и
^2 или что закон распределения суммы двух независимых слу-
случайных величин является сверткой (композицией) законов
распределения слагаемых. Соотношение F.12) условно запи-
записывают в виде
PY = Рх2*Рхг-
Формулу F.12) называют формулой свертки для плот-
плотностей распределения случайных величин Х\ и X<i, она хорошо
известна из теории преобразований Фурье [XI].
Пример 6.11. Пусть X\ и X*i — независимые случайные
величины, распределенные по нормальному закону со средними
значениями mi и Ш2 и средними квадратичными отклонениями
0*1 и 02- Найдем плотность распределения суммы У = Х\ +Х2»
Воспользовавшись формулой свертки, имеем
+00
_Т_1
-J ^л^
-оо
(x-m2J
я
J _
+оо
ехр —* 9 ?[х о о —) \dx.
Делая теперь замену
Z — | ju о~ о I ?
6.4. Формула свертки 243
получаем
+00
(у-"»1-ш2J
Таким образом, случайная величина У также распределена
по нормальному закону с параметрами тп\ + Ш2 и V^T+^2»
т.е. композиция плотностей нормальных законов распределения
является плотностью нормального закона распределения.
Замечание 6.2. Выведенное свойство справедливо для
суммы любого числа слагаемых, распределенных по нормаль-
нормальному закону, т.е. если Х\,..., Хп — независимые случайные
величины, распределенные по нормальному закону со средними
значениями mi,..., mn и средними квадратичными отклонени-
отклонениями ах,..., <тп, то их сумма У = Х\ + ... + Хп также распре-
делена по нормальному закону с параметрами mi +... + mn и
Замечание 6.3. В условиях примера 6.11 случайная вели-
величина —X*i имеет нормальное распределение с параметрами — rri2
и o*i (см. пример 6.7), случайные величины Х\ и —Хг являют-
являются независимыми (см. далее лемму 1, с. 251). Поэтому, согласно
результату примера 6.11, разность Z = Х\ — Х2 распределена по
нормальному закону с параметрами mi — 7712 и \Jo\ + a|. #
Рассмотрим независимые случайные величины Х\ и -Х2,
имеющие гамма-распределения с параметрами Л и 7ъ А и 72
соответственно. Найдем плотность распределения суммы
Поскольку Х\ и Х2 — положительные случайные величи-
величины, то случайная величина У также положительна и поэтому
при у < О
244 б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
В случае у > О, учитывая, что рхх {х) = 0 при х < О и
рх2 (у — х) = О при х > у, имеем, согласно формуле свертки,
+00
PY (У) = I РХ2 (У - Фхг (х) dx =
гG2)гG1)
где ГG) — гамма-функция.
Делая замену х = yz, получим
Интеграл, стоящий в последнем выражении, представляет
собой так назьгоаемую бета-функцию ВG1,72)- Согласно свой-
свойству бета-функции, имеем
О
Следовательно,
Д71+72у71+72~1е-Л2/
ГG1+72)
т.е. случайная величина У также имеет гамма-распределение с
параметрами Л и 71 +72-
Полученный результат можно обобщить на любое число не-
независимых слагаемых, имеющих гамма-распределение. Ввиду
6.5. Векторные функции от случайного векторного аргумента 245
важности полученного результата сформулируем его в виде
следующей теоремы.
Теорема 6.1. Бели случайные величины Х\,Х2т--,Хп
являются независимыми и имеют гамма-распределения с пара-
параметрами Л и 7ь i = 1? Щ соответственно, то их сумма
имеет гамма-распределение с параметрами А и ]Г^7ь т-е-
композиция гамма-распределений с одинаковым параметром А
и различными параметрами 7» является также гамма-распреде-
п
лением с параметрами А и ^7г- #
Поскольку распределение Эрланга и х2-распределение явля-
являются частным случаем гамма-распределения (см. 4.6), то ком-
композиция любого конечного числа распределений Эрланга с
одним и тем же параметром А или х2-распределений снова явля-
является распределением того же типа.
В частности, учитывая, что х2-распределение с одной сте-
степенью свободы есть распределение квадрата случайной величи-
величины, распределенной по стандартному нормальному закону (см.
пример 6.5), распределение х2 с п степенями свободы можно
трактовать как распределение суммы квадратов п независимых
случайных величин, имеющих стандартное нормальное распре-
распределение.
6.5. Векторные функции
от случайного векторного аргумента
Пусть теперь с двумерным случайным вектором (Х\, Х2)
связала не одна, а две (можно рассматривать и большее коли-
количество) случайные величины
246 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Тогда мы можем определить совместную функцию распределе-
распределения случайных величин Y\ vlY2. Можно доказать, что в случае
непрерывной двумерной случайной величины (Х\, Х2) двумер-
двумерная функция распределения вектора (Yi, I2) будет иметь вид
= / / PXuX2{xi,X2)dxidX2, F.13)
ь Х2) — совместная плотность распределения слу-
случайных величин Xi и Хг. Эта формула является обобщени-
обобщением F.11) на случай двух функций. Но в отличие от форму-
формулы F.11), область интегрирования в формуле F.13) задана дву-
двумя неравенствами
Yi(xi,x2) < 2/1 и Y2{xi,x2) < 2/2-
Пример 6.12. Пусть случайный вектор (Х\, X2) имеет
двумерное стандартное нормальное распределение. Случай-
Случайные величины Y\ = Y\(Xi,X2) и Y2 = Y2(X\,X2) определяются
функциями Y\(xi,x2) и Y2(xijX2), заданными неявно уравне-
уравнениями
х\ = yi cosy2, х2 = yi siny2,
О ^ у\ < +оо, 0 < J/2 < 2тг,
относительно yi, y2. Нетрудно видеть, что если трактовать
{х\\х2) как прямоугольные декартовы координаты случайной
точки на плоскости, то (у\\у2) представляют собой полярные
координаты этой же точки [III].
Найдем двумерную функцию распределения вектора (Yi, Y2).
Поскольку полярный радиус Y\ и полярный угол Y2 не могут
быть отрицательными, то при у\ ^ 0 или 2/2^0
Уь Y2 < у2} = 0.
6.5. Векторные функции от случайного векторного аргумента 247
Пусть теперь j/i > 0 и О < у\
формулой F.13)
2тг. Тогда в соответствии с
где область интегрирования D представляет собой сектор,
ограниченный окружностью радиуса j/i, осью Ох\ и лучом,
исходящим из начала координат и составляющим с осью Ох\
угол у2 (на рис. 6.5 этот сектор заштрихован). Переходя к
полярным координатам р и </?, получаем
е
x2i
Рис. 6-5
Наконец, пусть yi > 0 и j/2 > 2тг. Тогда событие {Ух < yi
совпадает с событием {Ух < yi, Уг < 2тг} и, значит,
= FYuY2(yi,2n) = (l - е-^/2) ^ =
248 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Согласно теореме 5.1,
{О, 3/1 < 0;
1 -1/2/2
1-е *i/2, j/i>0;
{0, 3/2^0;
2/2/2тг, 0 < у2 < 2тг;
1, 2/2 > 2тг.
Таким образом, для любых у\ и у2
Следовательно, случайные величины Y\ и 3^ являются незави-
независимыми, причем Y\ имеет распределение Релел, &Y2 — равно-
равномерное распределение в промежутке [0,27г).
Полученный результат обычно используют для моделиро-
моделирования случайных величин, распределенных по нормальному за-
закону. Действительно, пусть Y\ и Y2 — независимые случай-
случайные величины, имеющие соответственно распределение Релея
и равномерное распределение на промежутке [0,2тг) (их моде-
моделирование с учетом изложенного в примере 6.6 не вызывает
затруднения). Тогда случайный вектор (jfi
Хг = Yi совУ2, X2 = Yi sinY2
имеет двумерное стандартное нормальное распределение. #
В заключение отметим, что если функции Yi(zi,#2) и
УгС^ъЯг) задают преобразование плоскости или некоторой ее
области G, причем обратное преобразование х\ = V>i(yi>!/2)?
х2 = V*2(yi»!ti) имеет непрерывные частные производные по у\ и
2/2? то плотности распределения случайных векторов (Х\, Х2)
и (Yi, Y2) связаны между собой соотношением
PYuY2(VUV2) =PXi,Xa(^l(yii!tt)i^(yiiIte))l^li F.14)
6.5. Векторные функции от случайного векторного аргумента 249
где
дух
ду2
дух ду2
представляет собой якобиан преобразования W>i (у ь У2) > V>2 (у ъ У2)) •
Формула F.14) вытекает из правила замены переменных в
двойном интеграле [VII].
Пример б, 13. Найдем совместную плотность распределе-
распределения случайного вектора (Ух, Уг) из примера 6.12. Воспользуем-
Воспользуемся формулой F.14). Поскольку в данном случае
У2) = yisiny2,
(К yi < +оо, (К у2 < 2тг,
то J = yi, Рхих2(ФЛУиУ2),ЫУиУ2)) = ^е~у*/2> и> соглас-
согласно F.14), получаем, что при у\ ^ 0, 0 ^ у2 < 2тг
Так как все значения случайного вектора (Yi, У2) содержатся
в множестве {(ух, у2)- Ух ^ 0, 0 < у2 < 2тг} (см. пример 6.12), то
в остальных случаях
Таким образом, мы пришли к тому же результату, что и
в примере 6.12, но только в терминах плотности распределе-
распределения. #
Покажем, как будет выглядеть формула F.14) в случае
линейного преобразования
или в матричной записи
У2), ж =
= (сь с2),
250 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
где В = (b{j) — невырожденная матрица. Обратное преобразсн
вание
Ф(У) = Ш-с)В, У = (Уь Ы>
также будет линейным, причем матрица
является обратной к 5, а якобиан J равен определителю
~ _ 1
Gt ^detS'
где deti? — определитель матрицы В.
Поэтому формула F.14) принимает вид
pyiMv) =
Пример 6.14. Пусть двумерная случайная величина [Х
имеет равномерное внутри треугольника D с вершинами в
точках @, 0), @, 1) и A, 0) распределение. Найдем плотность
распределения двумерного случайного вектора Y = ХВ + с, где
( )
( )
Нетрудно видеть, что совместная плотность распределе-
распределения
если точка (#i, ж2) принадлежит треугольнику D, в противном
случае
=0.
При рассматриваемом линейном преобразовании треуголь-
треугольник D переходит в треугольник D1 с вершинами в точках
(~1;2), B;3) и @;3), a deti? = -2. Поэтому в соответствии
с формулой F.15)
6.5. Векторные функции от случайного векторного аргумента 251
если точка (j/i, 2/2) принадлежит треугольнику D', в противном
случае
У2) = 0. #
В заключение приведем простой, но важный для дальнейше-
дальнейшего результат, устанавливающий достаточное условие независи-
независимости функций от независимых случайных величин.
Лемма 1. Пусть случайные величины Х\ и Х2 являются
независимыми, а функции Y\{x\,x<i) и Y*i{x\,Х2) таковы, что
т.е. Yi(#i,#2) зависит только от х\, а
т.е. 12(^1^2) зависит только от х2. Тогда случайные величины
и Y2
также являются независимыми.
< Действительно (ограничиваясь непрерывными случайными
величинами Х\ и Х2), в соответствии с F.13) и теоремой 5.3
имеем:
Yi ,у2 (Уь Уг) = / /
= II РхЛх1)рх2(х2)Aх1Aх2= ( / PXi
Vi(xi)<yi ^Vi(a:i)<yi
x( J
^Y2(x2)
Y2(x2)<y2
252 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Замечание 6.4. Утверждение леммы 1 обобщается на
случай п случайных величин Х\,..., Хп.
Пример 6.15, Пусть Х\,..., Хп — независимые случайные
величины, имеющие стандартное нормальное распределение.
Тогда случайные величины Х\,...,Х\ также являются незави-
независимыми и распределены по закону х2 с одной степенью свободы
(см. пример 6.5), и, как следует из теоремы 6.1, случайная ве-
величина
имеет распределение %2 с п степенями свободы. Извлекая ква-
квадратный корень из У, получаем при п = 2ип = 3 распределения
Релея и Максвелла (см. пример 6.10). #
Отметим еще раз, что приведенные в настоящей главе
результаты сформулированы для векторов размерности п = 2
лишь для краткости и наглядности изложения. Нетрудно
показать, что они остаются справедливыми для случайных
векторов, имеющих произвольную размерность п ^ 2.
6.6. Линейные преобразования
нормально распределенных случайных
величин. Метод линеаризации
В силу особой важности для практических применений в
этом параграфе мы подробно остановимся на линейных пре-
преобразованиях многомерных случайных величин, распределен-
распределенных по нормальному закону.
Пусть X = (Xi, ..., Хп) — n-мерный случайный вектор,
распределенный по нормальному закону с матрицей ковариации
Е^ и вектором средних значений т%. Рассмотрим новый
случайный вектор Y = (Yi, ..., Уп), полученный из вектора X
с помощью линейного преобразования
F.16)
6.6. Линейные преобразования гауссовых величин 253
где В — невырожденная квадратная матрица порядка n [III], a
с — n-мерный вектор. Тогда в соответствии с формулой F.15)
случайный вектор Y имеет плотность распределения
|detJ5|
где В = В — матрица, обратная к матрице В; Е^ = Е"^1 —
матрица, обратная к матрице Е^;
Е? = 5ГЕ^5; F.17)
Е^ = Е^1 — матрица, обратная к матрице Е^;
F.18)
Таким образом, случайный вектор Y также распределен по нор-
нормальному закону с вектором средних значений га^ и матрицей
ковариаций Е^, определяемыми формулами F.18) и F.17).
Пример 6.16. Предположим, что двумерный случайный
вектор X = (X\j X2) имеет нормальное распределение с век-
вектором средних значений т^ = A, 2) и матрицей ковариаций
„ / 1 -1 \ „ w
2j^ =1 1. Найдем вектор средних значении т^ и
матрицу ковариаций Е^ случайного вектора У = ХВ + с, где
254 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
В соответствии с формулами F.17) и F.18) имеем:
_} 2 До l) = (o l)'
J J) +(-1,-3) = @,0).
Значит, вектор У имеет двумерное стандартное нормаль-
нормальное распределение. #
Пусть n-мерный случайный вектор X имеет многомерное
нормальное распределение с матрицей ковариадии S^ и векто-
вектором средних значений rhg. Формула F.17) является формулой
преобразования матрицы квадратичной формы. Поскольку
матрица S^ является положительно определенной, то всегда
можно подобрать невырожденное линейное преобразование В
таким образом (например, используя метод Лагранжа [IV]),
чтобы матрица Е^, определенная формулой F.17), была еди-
единичной. Полагая теперь
с = — mg В,
из формулы F.18) заключаем, что т^ есть нулевой вектор.
Таким образом, приходим к выводу, что вектор Y имеет
многомерное стандартное нормальное распределение.
Выражая теперь вектор X через вектор Y по формуле
Х = УВ-1+т^, F.19)
приходим к следующему результату (ср. с результатом в 5.4):
n-мерный случайный вектор X, распределенный по нормально-
нормальному закону с произвольными вектором средних значений mg и
матрицей ковариадии ?^, может быть получен с помощью пре-
преобразования F.19), где вектор У распределен по стандартному
нормальному закону.
6.6. Линейные преобразования гауссовых величин 255
Пример 6.17. Пусть X = (Х\, Х2) имеет нормальное рас-
распределение с вектором средних значений га = (—2, 4) и матри-
„ - /0,04 0,04 \ ы „
цеи ковариации ?^ = ( ' I. Найдем вектор с и мат-
матрицу В линейного преобразования, переводящего вектор X в
вектор У, имеющий стандартное нормальное распределение.
Запишем квадратичную форму, соответствующую матрице
И^ и преобразуем ее методом Лагранжа [IV] к каноническому
виду, являющемуся суммой квадратов:
0,04s2 + 0,08zy + 0,2у2 = @,2а; + 0,2уJ + @,4J = z\ + z\,
где
fzi=0,2o: + 0,2y;
Поэтому матрица В~1 имеет вид
а матрица В — вид
я (Ъ ~2Л
B=Z\0 2,5 )'
Вектор с задается равенством
КЧ =A0,-15).
Отметим, что к стандартному нормальному распределению
приводят и другие линейные преобразования, например пре-
преобразование с матрицей:
1=(Ъ -2,
\о 2,
2,5\/ 0,6 0,8\ f 5 2,5\
,5; v-0,8 o,e; V-2 1.5;*
256 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Общий нормальный закон. Как известно (см. 5.5), не-
невырожденный n-мерный закон вполне определяется вектором
средних значений т и матрицей ковариации Е, которая являет-
является положительно определенной. Для общего n-мерного нормаль-
нормального закона условие положительной определенности матрицы
ковариации I! заменяется условием неотрицательной опреде-
определенности этой матрицы [IV]. В частности, если detE = 0, то
нормальное распределение называют вырожденным.
Оказывается, что вырожденное нормальное распределение
не является распределением непрерывного случайного вектора.
Определим общий нормальный закон, исходя из формулы F.16).
Скажем, что вектор Y распределен по общему п-мерному
нормальному закону, если он может быть получен из нор-
нормально распределенного случайного вектора X с помощью ли-
линейного преобразования F.16). При этом матрица В может
быть и вырожденной [III]. Более того, матрица В не обязатель-
обязательно должна быть квадратной, а может иметь размерность п х fc,
и тогда из n-мерного нормально распределенного вектора X с
помощью линейного преобразования получается fc-мерный нор-
нормально распределенный вектор У. Бели матрица ковариации Е
имеет ранг к [III], то n-мерный вектор Y может быть выражен
с помощью линейного преобразования F.16) через Л-мерный
вектор X, имеющий стандартное нормальное распределение.
В частности, если матрица S нулевая, т.е. ее ранг равен ну-
нулю, то вектор Y состоит из неслучайных координат YJ = с»,
т.е. вектор с неслучайными координатами представляет собой
частный случай нормально распределенного вектора.
Формулы F.17) и F.18), выведенные нами для матриц ко-
ковариации и векторов средних невырожденных нормальных рас-
распределений, полностью сохраняются и для общих нормальных
распределений (напомним, что матрица В может быть не ква-
квадратной). Более того, в следующей главе будет показано, что
эти формулы имеют место для произвольно распределенных
случайных векторов.
6.6. Линейные преобразования гауссовых величин 257
Пример 6.18. Пусть двумерный случайный вектор X =
= (X\j X2) распределен по стандартному нормальному закону.
Рассмотрим трехмерный случайный вектор Y = (Yi, Y2, Уз)? по-
полученный из вектора X с помощью линейного преобразования
У ЛГ
И *= A,0,-1).
Следовательно, вектор У имеет нормальный трехмерный закон
с матрицей ковариаций
и вектором средних значений
= A,0,-1).
Матрица Е^> является вырожденной, причем ее ранг равен
единице, собственные значения Ai = 6, А2 = A3 = 0 и собствен-
собственный вектор, соответствующий ненулевому собственному зна-
значению Ai, имеет вид е\ = A, 1, 1). Последнее означает, что
трехмерный случайный вектор У может принимать только знаг
чения j/i = z + 1, j/2 = 2> 2/з = ^ — 1? т.е. множество всех его
значений лежит на прямой у\ = z +1, j/2 = ^, j/з = z — 1. Иными
словами, зная, например, значения координаты У2 случайного
вектора У, можно однозначно определить значения остальных
координат по формулам
Ух=У2 + 1 и У3 = У2-1,
что следует и непосредственно из определения вектора У.
Метод линеаризации. Пусть X = (Хх, ..., Хп) — п-мер-
ный случайный вектор, распределенный по нормальному (не-
(невырожденному) закону с матрицей ковариаций Е^ и вектором
9 - 10047
258 б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
средних значений rhg. Вернемся к общему случаю и предпо-
предположим, что Y = Y(X) — векторная функция от случайного
вектора X.
В ряде практических задач функция Y(x) хотя и не является
линейной, но тем не менее хорошо аппроксимируется линейной
в области реального изменения случайного вектора X. Тогда
можно воспользоваться методом линеаризации, который
мы сейчас опишем.
Положим
fh9 = Y(mx). F.20)
Кроме того, считая, что функция Y(x) дифференцируема в
точке т^, введем матрицу
В окрестности точки т^ функцию Y(x) можно приближен-
приближенно заменить линейной [V]:
Y(х) « т? + (х - т
Поэтому
и, значит, случайный вектор Y распределен приближенно по
нормальному закону с вектором средних т^, определяемым
формулой F.20), и матрицей ковариаций Е^, задаваемой фор-
формулой F.17), в которой матрица В вычисляется по форму-
формуле F.21).
Пример 6.19. Для определения плотности минерала был
взят образец цилиндрической формы с неизвестными радиусом
основания mi, высотой т2 и массой т3. Измерения проводи-
проводились со случайными погрешностями и дали следующие резуль-
результаты: радиус основания Х\) высота Хг и масса Х$. Плотность
6.6. Линейные преобразования гауссовых величии 259
минерала У была вычислена по формуле
Считая, что результаты измерений Xi, X2, Х$ являются не-
независимыми случайными величинами, имеющими совместное
нормальное распределение с вектором средних (mi, 7712, газ) (в
этом случае говорят, что отсутствуют систематические по-
погрешности измерений) и средними квадратичными отклонения-
отклонениями (ох, G2, CJ3) (которые предполагаются малыми по сравнению
с истинными значениями радиуса mi, высоты т^ и массы газ),
найдем распределение полученной плотности У минерала.
Из условия задачи следует, что измеренные параметры
представляют собой трехмерный случайный вектор
J? = (Xi, Х2, Х3),
распределенный по нормальному закону с вектором средних
значений
и матрицей ковариаций
а полученное значение плотности минерала У является скаляр-
скалярной функцией вектора X:
Для нахождения распределения У воспользуемся методом
линеаризации. В соответствии с формулами F.20) и F.21)
260
б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
положим:
F.22)
/ д хз
=mtf
д хз
д
Далее, воспользовавшись формулой F.17), имеем:
'a\ О О
x | 0 a\ 0
0 0 <j|
F.23)
Таким образом, полученное значение плотности У распре-
распределено приближенно по нормальному закону со средним значе-
значением и дисперсией, определяемыми формулами F.22) и F.23).
6.7. Решение типовых примеров
Пример 6.20* Дискретная случайная величина X имеет
Таблица 6.8 ряд Ряспределекш*, представ-
представленный в табл. 6.8. Найдем
ряд распределения случайной
величины У = 2Х2 +1.
X
р
-2
0,2
-1
ОД
0
0,1
1
0,2
2
0,4
6.7. Решение типовых примеров
261
Значениям — 2, — 1, 0, 1и2 случайной величины X соответ-
соответствуют значения 9, 3, 1, 3 и 9 случайной величины У. Вос-
Воспользовавшись табл. 6.8, получим ряд распределения случайной
величины У, представленный в табл. 6.9. Теперь, для того что-
чтобы получить окончательный ответ, нужно объединить столбцы
с одинаковыми значениями У (табл. 6.10).
Таблица 6.9 Таблица 6.10
Y
Р
9
0,2
3
0,1
1
0,1
3
0,2
9
0,4
Y
Р
1
ОД
3
0,3
9
0,6
Пример 6.21. Случайная величина X имеет экспоненци-
экспоненциальное распределение с параметром Л = 1. Найдем функцию
распределения случайной величины У = (X — 2J.
Случайная величина У может принимать только неотрица-
неотрицательные значения. Поэтому при у < 0
При у > 0 функцию распределения Fy(y) определяем по
формуле
Fy(v)= I Px(x)dx.
Y(x)<y
Поскольку в данном примере
то область интегрирования представляет собой интервал
B — у/у, 2 + у/у). Согласно определению плотности распреде-
распределения экспоненциального закона, получаем:
при у < 4
2+у/У
FY{y)= f
262 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
при у > 4
2+y/V
Пример 6.22. Случайная величина X имеет равномерный
закон распределения в интервале @, тг). Найдем плотность
распределения случайной величины У = cosX.
Функция Y(x) = cos ж является непрерывной убывающей в
интервале @, тг) и отображает этот интервал в интервал (—1,1).
Обратная функция
ф(у) = Y~l(y) = arccosj/
имеет производную
ФЪ) = -
Поскольку плотность распределения случайной величины X
Рх1*'-\1/ж, «6@,»),
ТО
Пример 6.23* Случайная величина X равномерно распре-
распределена в интервале @,2тг). Найдем плотность распределения
случайной величины Y = cosX.
6.7. Решение типовых примеров
263
Эта задача отличается от предыдущей только тем, что те-
теперь функция У (х) = cos ж не является монотонной в интервале
(О, 2тг). Однако она является непрерывной функцией, имею-
имеющей два интервала монотонности: @, тг) и (тг, 2тг). Обозначая
для любого у, — 1 < у < 1, решения уравнения у = cos ж в ин-
интервалах @, тг) и (тг, 2тг) через фг{у) и гр2(у) соответственно
= arccosy, Ф2 (у) = 2тг — arccosy), находим
ру(у) =
О,
-у*), у 6 (-1,1).
Таким образом, мы получили тот же ответ, что и в предыдущем
примере.
Пример 6.24. Распределение Таблица 6.11
дискретной случайной величины
(Х\, Х2) задается табл. 6.11. Най-
Найдем ряд распределения случайной
величины У = Xl + Х\ - 1.
Табл. 6.11 представим в виде
табл. 6.12, состоящей из двух строк, причем в верхней строке
перечислены все значения случайной величины У, а в нижней —
соответствующие вероятности.
Таблица 6.12 Таблица 6.13
Х2
1
Xi
-1
0,07
0,20
0
0,10
0,23
1
0,13
0,27
Y
Р
1
0,07
0
0,10
1
0,13
1
0,20
0
0,23
1
0,27
Y
Р
0
0,33
1
0,67
Объединяя теперь столбцы с одинаковыми значениями У,
получаем окончательно ряд распределения случайной величины
У (табл. 6.13).
Пример 6.25. Двумерная случайная величина (-Xi, X2)
распределена равномерно в круге х\ + х\ ^ 1. Найдем функцию
распределения случайной величины Y = Х1Х2.
Значение функции распределения Fy(y) случайной величи-
величины У равно вероятности попадания двумерного случайного
264
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
вектора (Xi, X2) в область х\Х2 < у- Эта вероятность, в свою
очередь, равна площади Sd области ?), состоящей из точек кру-
круга, координаты которых удовлетворяют неравенству х\х% < у
(на рис. 6.6 и рис. 6.7 область D заштрихована), поделенной на
площадь круга 7г. Это следует из того, что случайная величина
(Ai, X2) равномерно распределена.
Х2
Рис. 6.7
При у ^ —1/2 область D пуста, а при у > 1/2 эта область
совпадает с кругом. Поэтому
Fy(y) =
0,
Пусть теперь —1/2 < у ^ 0. Тогда пересечение гиперболы
2 = уа окружности х\ + х\ = 1 происходит в четырех точках
(см. рис. 6.6):
Ах(-^1/2+^1/4-у2; y/l/2-y/l/A-^Fj,
6.7. Решение типовых примеров 265
координаты которых находятся из системы уравнений
\ xix2 = у.
Значит,
SD =
и поэтому при —1/2 < j/ ^ О
Аналогично при 0 < у ^ 1/2 имеем (см. рис. 6.7):
Fy(y) = | + f
Полученные формулы задают значения функции распреде-
распределения Fy(y) при всех значениях аргумента у.
Пример 6.26. Независимые случайные величины Х\ и Хъ
имеют стандартное нормальное распределение и распределение
X2 с к степенями свободы соответственно (см. 4.6). Найдем
плотность распределения случайной величины Y = Хх/у/Х^/к.
Поскольку случайные величины Х\ и X*i являются независи-
независимыми, двумерная случайная величина (Xi, X2) имеет совмест-
совместную плотность распределения:
{О, я2<0;
_
266
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Значение функции распределения Fy(y) равно вероятности
попадания двумерного случайного вектора (Х\, X2) в область
D (на рис. 6.8 эта область заштрихована), определяемую нера-
неравенствами
< У, Х2 > О,
т.е.
(хф
Сделаем замену z = у/х^. Тогда
где область интегрирования D9 (рис. 6.9) представляет собой
угол между лучами х\ = —<, z = 0 (t ^ 0) и х\ = yt, z =
= \/fc< (t ^ 0). Переходя теперь к полярным координатам
Х\ =
получаем
+ОО
/
6.7. Решение типовых примеров 267
Снова делая замену и = р2/2 и учитывая, что
+00
находим
f
2/arctg(>/ib/y)
Так как нам необходимо определить плотность распределе-
распределения случайной величины У, мы не будем вычислять интеграл в
последней формуле, а воспользуемся формулой дифференциро-
дифференцирования интеграла:
7Г
* l
sin* lcpd<p | =
Учитывая, наконец, соотношение
х
sin(arctga;) = ,
Vl + ж2
приходим к окончательному ответу:
fc + 1
268 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Распределение случайной величины У называют распреде-
распределением Стпъюдента (t-распределением). Распределение
Стьюдента, наряду с распределением х2> играет важную роль
в математической статистике.
Пример 6.27. Случайная величина Х\ распределена равно-
равномерно на отрезке [1, 2], а случайная величина X*i имеет показа-
показательное (экспоненциальное) с параметром Л = 2 распределение.
Предполагая, что случайные величины Х\ и Х2 являются не-
независимыми, и воспользовавшись формулой свертки, найдем
функцию распределения и плотность распределения случайной
величины У = Х\ + Х2.
Запишем формулу свертки:
+00
= I РхЛу)рх2(х-у)Aу.
-оо
Поскольку рхх (х) = 0 при ж<1 и рх2 (х) = 0 при х < О,
то при х < 1 подынтегральное выражение тождественно равно
нулю, и, значит,
ру(ж)=О, х < 1.
При х > 1 формула свертки принимает вид
х
pY(x) = I pXl (y)px2 (x - у) dy,
1
причем, поскольку
РхЛх)=°
также при х > 2, то при х > 2 формулу свертки можно записать
в виде
Py (х) = I рхх (у) Рх2 (з -y)dy.
6.7. Решение типовых примеров
269
Подставляя в полученные формулы выражения для рав-
равномерной и экспоненциальной плотностей распределения, на-
находим
х
ру(х) = 2 /
1
2
ру(х) = 2
= 1 - е-2**-1), 1 < х < 2;
), х > 2.
Таким образом,
о,
е-2(а:-2)_е-2(х-1))
ж<1;
Пример 6.28. Задано распределение вероятностей дис-
дискретной двумерной случайной величины (Х\^ Х2) (табл. 6.14).
Найдем распределение вероятнос-
вероятностей двумерной случайной величи- Таблица 6.14
ны (Уь У2), где
0
1
-1
0,15
0,20
0
0,25
0,05
1
0,10
0,25
Для того чтобы определить совместное распределения слу-
случайных величин Yi и 1г? удобно сначала выписать общую табли-
таблицу, в которой в первой строке и первом столбце перечислены
значения случайных величин Yi и 12? соответствующие всем
парам значений случайных величин Х\ и J^2? на главной диаго-
диагонали записаны вероятности, а на остальных метах стоят нули
(табл. 6.15).
270
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Таблица 6.15
Y2
1
0
0
1
1
0
Yi
1
0,15
0
0,25
1
0,10
0
0,20
1
0,05
0
0,25
Объединяя строки с одинаковыми значениями Y2, приходим
к табл. 6.16.
Таблица 6.16
Таблица 6.17
Y2
0
1
1
0,15
0
0,25
1
0,10
0
0,20
1
0,05
0
0,25
Y2
0
1
Yi
0
0,50
0,20
1
0,10
0,20
Наконец, объединяя столбцы с одинаковыми значениями
Yi, получаем табл. 6.17, окончательно задающую совместное
распределение вероятностей случайных величин Yi и Y2.
Пример 6.29. Двумерная случайная величина (Х\, -Хг)
распределена равномерно в квадрате с вершинами в точках
;4i@; -1), А2@; 1), А3B; 1) и Л4B; -1). Найдем совместную
функцию распределения случайных величин
Y\ = Х2 и Y<i = X1 + Х2.
Очевидно, что случайная величина Yi может принимать
только значения от 0 до 1, а случайная величина У2 — от — 1
до 3. Поэтому Fyuy2(vuV2) = °> если Vi ^ О ™H У2 < -1? и
^КьУ2(УьУ2) = 1, если j/i > 1 и у2 > 3. Пусть теперь 0 < j/i < 1
и -1 < у2 ^ 3. Тогда значение -Руьу2(у1,*у2) равно четверти
6.7. Решение типовых примеров
271
площади части D квадрата, ограниченной прямыми у\ = —х\,
ух = х\ и у2 = х\ + Х2. Область D при различных соотношениях
между ух и J/2 на рис. 6.10-6.14 отмечена штриховкой. Проводя
вычисления, получаем
ГО, у2<
= <
8
У2у/У1
2 '
Далее, если 0 < у\ < 1, а уг > 3, то ^.^(уьуг) совпадает с
функцией распределения Fyx (yi), которая, как нетрудно видеть,
равна
Наконец, при j/i > 1 и - 1<уг^3 совместная функция рас-
распределения -РуьУ-ДУьУг) совпадает с функцией распределения
(У2 + 1J
8 '
-C-у2)
8
-, У2>1.
Рис. 6.10
Рис. 6.11
Рис. 6.12
272
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Х2
1
0
//у/у/////
V
\
2 х
Рис. 6.13
Рис. 6.14
Полученные формулы определяют значения совместной
функции распределения Руиу2 (УъЗ/2) при всех значениях j/i
Пример 6.30. Двумерная случайная величина (Хи Х2)
имеет совместную плотность распределения
1
Найдем совместную плотность распределения случайных вели-
величин
Yi = eXl + е*2 и У2 = eXl - ех\
С помощью преобразования
осуществим взаимооднозначное преобразование плоскости в
область D\ задаваемую неравенствами уг+У2> 0, у\—у2> О,
причем обратное преобразование
= In
6.7. Решение типовых примеров
273
имеет непрерывные частные производные
д . , v 1 д . .
и якобиан
1
У1+У2
1
У1-У2
1
У1+У2
1
У1-У2
2
9 9 *
У1-У2
Поэтому
о,
,(,
(УЬ
-» (Уь
Пример 6.31. Двумерная случайная величина (JCi, JC2)
распределена равномерно в круге Z), определяемом неравен-
неравенством х\ + (#2 — IJ < 1 (рис. 6.15). Найдем совместную плот-
плотность распределения случайных величин
и
Совместная плотность распределения двумерного случайно-
случайного вектора (Ai, X2) имеет вид
о, (жь
Линейное преобразование
Yi(xi,X2) =X
=Xi -2Ж2+3,
274
б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
в матричной форме имеет вид
с=(о, з),
где В — невырожденная матрица. Это преобразование осуще-
осуществляет отображение круга D в множество D' (рис. 6.16) точек
внутри эллипса с центром в точке 0A; 1), задаваемого уравне-
уравнением
| - 12yi - буг = 0.
Рис. 6.15 Рис. 6.16
Нетрудно подсчитать, что
Обозначая В = В~х обратную к В матрицу, получаем
1 Г О,
|detB| \ 1/C*),
(уь уз) е D'.
Пример 6.32. Пусть X = (A"i, Х2, Х3) — трежлсерныв
случайный вектор, распределенный по нормальному закону
6.7. Решение типовых примеров 275
с вектором средних значений т% — B, — 1, 0) и матрицей
ковариации
C/2 1/2 1/2 \
1/2 3/2 -1/2 .
1/2 -1/2 1 /
Найдем вектор средних значений fh-f и матрицу ковариации
случайного вектора Y = ХВ + с, где
и с = (-3, -2, 0).
\2 -1 0/
Имеем
/10 2 \ /3/2 1/2 1/2
f = BTS^B =2 1 -11/2 3/2 -1/2
\1 0 0 / \1/2 -1/2 1
15/2 2 5/2'
2 19/2 3
5/2 3 3/2,
+ (-3,-2,0) = (-1,1, 2).
Пример 6.33. Пусть X = (Xi, X2, Хз) — трехмерный слу-
случайный вектор — имеет нормальное распределение с вектором
средних значений т% = C, 1, 2) и матрицей ковариации
276 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Найдем вектор с и матрицу В линейного преобразования,
переводящего вектор X в вектор У, имеющий стандартное
нормальное распределение.
Запишем квадратичную форму S^(x), соответствующую
матрице ?^:
= х\ — 2x1^2 + 2x1^3 + 5а?2
?^ (х) = х\ — 2x1^2 + 2x1^3 + 5а?2 4-
Воспользовавшись методом Лагранжа выделения полных ква-
квадратов, получим
= (xi -Х2
где
< Z2 = 2Ж2
Значит,
+ 4x1 + 4ж2Яз + 2х\ =
1 1/2 -3/2 \
В = I 0 1/2 -1/2
\О О 1 /
Вектор с задается равенством
1 1/2 -3/2ч
с = -C, 1, 2)| 0 1/2 -1/2 j= (-3,-2,3).
.0 0 1
Пример 6.34. Для определения абсолютного значения ско-
скорости движущейся в пространстве частицы были замерены ее
составляющие (получены значения Х\, Хч и Хз). Абсолютное
6.7. Решение типовых примеров 277
значение скорости У вычислялось по формуле
Считая, что результаты измерений представляют собой не-
независимые нормально распределенные случайные величины и
отсутствуют систематические погрешности, причем средние
квадратичные отклонения <ti, 0*1 и а% малы по сравнению с
истинными значениями составляющих mi, Ш2 и газ, найдем рас-
распределение полученного абсолютного значения скорости У.
Из условия задачи следует, что измеренные параметры
представляют собой трехмерный случайный вектор X =
= (Х\, Лг, Хз), распределенный по нормальному закону с век-
вектором средних значений
— (mi,
и матрицей ковариаций
а полученное абсолютное значение скорости Y является (ска-
(скалярной) функцией
от вектора X.
Для нахождения распределения У воспользуемся методом
линеаризации. Тогда полученное абсолютное значение скоро-
скорости У распределено приближенно по нормальному закону со
средним значением
ту = У (™>х) = у т\ + 7П2 + т\.
278
б. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Для определения дисперсии нормального закона вычислим ма-
матрицу частных производных
/ д
dxi
д
дх2
xi
7П2
Имеем
\Jm\
ТП2
Перемножая матрицы, находим, что дисперсия нормального за-
закона, приближенно описывающего распределение полученного
абсолютного значения скорости У, определятся формулой
тЗ
Вопросы и задачи 279
Вопросы и задачи
6.1. Как могут быть связаны между собой случайные вели-
величины?
6.2. Что называют функцией от одномерной случайной
величины?
6.3. Как найти ряд распределения функции от дискретной
случайной величины?
6.4. Как найти функцию распределения функции от непре-
непрерывной случайной величины?
6.5. Как найти плотность распределения монотонной функ-
функции от непрерывной случайной величины?
6.6. Как найти плотность распределения кусочно монотон-
монотонной функции от непрерывной случайной величины?
6.7. Как найти плотность распределения линейной функции
от непрерывной случайной величины?
6.8. Как найти ряд распределения скалярной функции от
дискретного случайного вектора?
6.9. Как найти функцию распределения скалярной функции
от случайного вектора?
6.10. Что называют сверткой (композицией) плотностей
распределения случайных величин?
6.11. Как найти функцию распределения векторной функ-
функции от случайного вектора?
6.12. Как изменится плотность распределения векторной
функции от случайного вектора при линейном преобразовании?
6.13. Какое распределение имеет случайный вектор, полу-
полученный из нормально распределенного случайного вектора с
помощью линейного преобразования?
280
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
6.14. Как изменяются вектор средних и матрица коварна-
ций нормально распределенного случайного вектора при линей-
линейном преобразовании?
6.15. Какими параметрами определяется общий нормаль-
нормальный закон? В каком случае нормальный закон называют выро-
вырожденным?
6.16. Какими свойствами обладает ковариационная матри-
матрица общего нормального закона?
6.17. Какая связь существует между нормально распреде-
распределенным случайным вектором и случайным вектором, распреде-
распределенным по стандартному нормальному закону?
6.18. В чем заключается метод линеаризации? Когда его
можно применять?
6.19. Как вычислить параметры нормального распределе-
распределения, приближенно описывающего распределение функции от
случайного вектора в соответствии с методом линеаризации?
6.20. Дискретная случайная величина X имеет ряд распре-
распределения, представленный в табл. 6.18. Найдите ряд распреде-
распределения случайной величины У, если:
a) У = 10Х - 1; б) У = -X2; в) У = 2х.
X
р
-0,5
0,1
0
0,4
Таблица
0,5
0,1
1
0,3
6.18
1,5
0,1
Ответ: ряд распределения случайной величины У предста-
представлен:
а) в табл. 6.19; б) в табл. 6.20; в) в табл. 6.21.
У
р
-6
0,1
-1
0,4
Таблица
4
0,1
9
0,3
6.19
14
0,1
У
Р
-2,25
0,1
Таблица
-1
0,3
-0,25
0,2
6.20
0
0,4
Вопросы и задачи
281
Таблица 6.21
У
Р
1Л/2
од
1
0,4
л/2
од
2
0,3
2>/2
од
6.21. Случайная величина X распределена равномерно в
интервале @, 3). Найдите функцию распределения случайной
величины У = X2 +1.
Ответ:
Г 0, у<1;
, У>Ю.
6.22. Случайная величина X имеет экспоненциальное рас-
распределение с параметром Л. Найдите плотность распределения
случайной величины У, если:
Ответ:
„Л-1
О, У * @,1);
У €@,1);
0,
в) Ру(у) =
0,
у < 0;
у>0;
г) ру(у)
¦{
0,
У<0;
У>0.
6.23. Случайная величина X распределена по нормальному
закону со средним значением т и дисперсией а2. Найдите
плотность распределения случайной величины У, если:
а) У = |Х|; б) У = arctgX; в) У = X2; r)Y = ex (плот-
(плотность логарифмически нормального, или логнормалъно-
го, распределения).
282
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
Ответ:
а) ру(у) =
О, у < О,
+ e-(y+m)VB<r2)
л/2тг<т
-, У>0;
О,
б) РУ{У) = { e-(tg»-m)VB<72)
2y/2nacos2y
, уе(-7г/2,тг/2);
О,
в)
О, у<0;
Г) РУ(У) = •{ e-(lny-m)VB<r2)
—, у>о.
У<0;
, У>0;
6.24. Распределение двумерной случайной величины (Х\, Х2)
Таблица 6.22 задается табл. 6.22. Найдите ряд
распределения случайной величи-
величины Y, если:
a) Y = Xi - ЧХ2 - 8;
х2
1
2
10
0,08
0,32
12
0,02
0,08
14
0,10
0,40
b)Y = (X1-12)/X2.
Ответ: ряд распределения случайной величины Y предста-
представлен:
а) в табл. 6.23; б) в табл. 6.24; в) в табл. 6.25.
Таблица 6.23
Таблица 6.24
Y
Р
2
0,32
0
0,16
2
0,42
4
0,10
У
Р
0
0,02
3
0,08
4
0,18
7
0,72
Вопросы и задачи
283
Таблица 6.25
Y
Р
-2
0,08
-1
0,32
0
0,10
1
0,40
2
0,10
6.25. Двумерная случайная величина (Xi, X2) распределена
равномерно в прямоугольнике с вершинами в точках Ai@; 0),
-Аг(О; 2), АзC; 2) и -А^З; 0). Найдите функцию распределения
случайной величины У, если: а) У = Х\ + Хц б) Y =
Ответ:
0, у < 0;
у2/12, 0 < у < 2;
2<у<3;
6)FY(y) =
у < 0;
0<у<3/2;
у>3/2.
6.26. Независимые случайные величины Х\ и X*i имеют
стандартное нормальное распределение. Найдите плотности
распределения случайной величины Y =
Ответ:
6.27. Независимые случайные величины Х\ и Х^ имеют
распределение х2 с к и п степенями свободы соответствен-
соответственно. Найдите плотность распределения случайной величины У =
= nXi/(kX2) (плотность F-распределения, или распределе-
распределения Фишера — Снедекора).
Ответ:
0,
)f29 у>0.
284
6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
6.28. Независимые случайные величины Х\ и Хч имеют экс-
экспоненциальное распределение с параметрами Ах = 1 и Аг = 2
соответственно. Воспользовавшись формулой свертки, найди-
найдите плотность распределения случайной величины Y = Х\ + -Х^.
Ответ:
/ 0, у<0;
2(е-^еЛ у>0.
6.29. Независимые случайные величины Х\ и Х2 имеют рав-
равномерное распределение на отрезках [0,1] и [0, 2] соответствен-
соответственно. Воспользовавшись формулой свертки, найдите плотность
распределения случайной величины Y = Х\ + Хъ-
Ответ:
О, У 2 @,3);
у/2, 0 < у < 1;
1/2, Ку<2;
C-у)/2, 2<у<3.
6.30. Распределение вероятностей дискретной двумерной
случайной величины (Х\, Х2) задается табл. 6.26. Найдите
распределение вероятностей двумерной случайной величины
(Уь У2), где П = XiX2, Y2 = (Xt - Х2J.
Pv(y) =
Хг
-1
0
2
Таблица 6.26
Х\
0
0,15
0,25
0,10
1
0,20
0,10
0,20
У*
-1
0
2
Таблица 6.27
п
0
0
0
0
1
0,25
0,25
0,20
4
0,20
0,10
0
Ответ: Совместное распределение вероятностей двумерной
случайной величины (Yi, У2) представлено в табл. 6.27.
6.31. Двумерная случайная величина (Xi, X2) распределена
равномерно в прямоугольнике с вершинами в точках А\A; —1),
А2(—1; 1), Аз@; 2) и AjB; 0). Найдите совместную функ-
функцию распределения случайных величин Y\ = (Х\ — Х2J и Y2 =
. 285
Ответ:
О, у\ ^ 0 или уг < 0;
2;
Вопросы
г о,
Угу/уЦЬ,
л/уГ/2,
Уг/2,
i 1,
и задачи
0<yi
0<yi
У\ >4
У1>4
ИЛИ 3/2 ^
<4 и 0<
<4 и у2
И 0<У2
и уг > 2.
0;
:У2
>2;
^2;
6.32. Двумерная случайная величина (<Xi, X2) имеет сов-
совместную плотность распределения
0, (a?i
где ?> — треугольник с вершинами в точках Ai@; 0), ^(l; 1)
и Аз B; 0). Найдите совместную плотность распределения слу-
случайных величин Y\ = X2KX1 + 1) и У2 =
Ответ:
Ч
где D; — область, ограниченная линиями yi = 0, j/2 = 0 и
6.33. Двумерная случайная величина (Х\^ Х2) распреде-
распределена равномерно в параллелограмме с вершинами в точках
А\{—1; —1), A2{—1; 3), -АзD; 5) и -^4D; 1). Найдите плотность
распределения случайных величин Y\ = 2Х\ + Х2 — 1 и 12 =
= Xi-3
Ответ:
где ?>' — параллелограмм, ограниченный прямыми 3yi + уг —
- 27 = 0, 3yi + у2 + 8 = 0, ух + 12у2 + 96 = 0 и ух + 12у2 - 44 = 0.
286 6. ФУНКЦИИ ОТ СЛУЧАЙНЫХ ВЕЛИЧИН
6.34. Пусть X = (Л*!, -Хг, Х$) — трехмерный случайный
вектор, распределенный по нормальному закону с вектором
средних значений rhg = A, 2, 1) и матрицей ковариаций
Найдите вектор средних значений т^ и матрицу ковариаций
Еу> случайного вектора Y = ХВ + с, где
В= 1 1 и с=A, 3).
0твет:т? = B, -l),Ef
6.35. Пусть X == (A"i, Л2) — двумерный случайный вектор,
распределенный по нормальному закону с вектором средних
B 1\
)•
Найдите вектор с и матрицу В линейного преобразования
Y = X В + с, переводящего вектор X в вектор У, имеющий
стандартное нормальное распределение.
Одним из возможных ответов является:
М.
\-%/15/15 л/3/3
6.36. Трехмерный случайный вектор Х=(Х\, Х2, Х$) имеет
нормальное распределение с вектором средних значений т —
— A0, 5, 3) и матрицей ковариаций
/ 0,01 0,0042 -0,0024'
Е^ = 0,0042 0,0036 0,00288
V-0,0024 0,00288 0,0064
Вопросы и задачи 287
Воспользовавшись методом линеаризации, найдите параметры
нормального закона, приближенно описывающего распределе-
распределение величины У = (ЗХ? + 1)/(Х| + 2X1).
Ответ: ту = 7, <7у«0,26.
6.37- Независимые случайные величины Х\ и Х<± распреде-
распределены по нормальному закону с математическими ожиданиями
тхх = ™>х2 = 900 и средними квадратическими отклонения-
отклонениями ох\ — &х2 = 3. Воспользовавшись методом линеаризации,
найдите приближецное распределение случайного вектора Y =
Ответ: Случайный вектор У имеет распределение, близкое
к нормальному закону с вектором средних значений
= D50, 810) и матрицей ковариаций
= /1Д25 0,405 \
у \ 0,405 16,544 у '
7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ВЕЛИЧИН
Из результатов предыдущих глав следует, что вероятности
любых событий, связанных с каждой случайной величиной (в
том числе многомерной), полностью определяются ее законом
распределения, причем закон распределения дискретной слу-
случайной величины удобно задавать в виде ряда распределения, а
непрерывной — в виде плотности распределения.
Однако при решении многих задач нет необходимости ука-
указывать закон распределения случайной величины, а достаточно
характеризовать ее лишь некоторыми (неслучайными) числа-
числами. Такие числа (в теории вероятностей их называют числовы-
числовыми характеристиками случайной величины) будут рассмотрены
в настоящей главе. Отметим, что основную роль на практике
играют математическое ожидание, задающее „центральное"
значение случайной величины, и дисперсия, характеризующая
wразброс" значений случайной величины вокруг ее математи-
математического ожидания. В математической статистике [XVII] для
построения доверительных интервалов и проверки статистиче-
статистических гипотез широко используются квантили.
7.1. Математическое ожидание
случайной величины
Как уже отмечалось выше, наиболее употребляемой на
практике числовой характеристикой является математическое
ожидание, или, по-другому, среднее значение случайной вели-
величины. Роль математического ожидания более подробно будет
выяснена ниже (см. 9).
7Л. Математическое ожидание случайной величины 289
Определение 7.1. Математическим ожиданием
(средним значением) Ъ/LX дискретной случайной величины
X называют сумму произведений значений Х{ случайной вели-
величины и вероятностей pi = Р{Х = #j}, с которыми случайная
величина принимает эти значения: Ъ/LX = YlixtPi- При этом,
если множество возможных значений случайной величины X
счетно, предполагается, что
00
т.е. ряд, определяющий математическое ожидание, сходится аб-
абсолютно [IX]; в противном случае говорят, что математическое
ожидание случайной величины X не существует.
Математическое ожидание дискретной случайной величины
имеет аналог в теоретической механике. Пусть на прямой
расположена система материальных точек с массами pi ( Y^Pi=
г
= 1) и пусть Х{ — координата г-й точки. Тогда центр масс
системы будет иметь координату
rv
совпадающую с математическим ожиданием MX случайной
величины X.
Пример 7.1. Пусть X — число угаданных номеров в
„Спортлото 6 из 49" (см. пример 6.4). В соответствии с рядом
распределения в табл. 6.3 имеем
+ 6-рб« 0-0,436 +1-0,413 + 2-0,1324 +3-0,0176+
+ 4-0,00097 + 5-1,8-10~5 + 6• 7-10~8 «0,735.
Таким образом, среднее число угаданных номеров равно 0,735.
10 - 10047
290 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 7.2. Найдем математическое ожидание случайной
величины X, распределенной по биномиальному закону (число
успехов в п испытаниях по схеме Бернулли с вероятностью
успеха р):
п п п ,
iPn{%) = j ^iCfjp q = у А~/ л?Р 9 ==:
i=0 г=0 г=0
t=i v '*v r j=o
n-l
i=o
Пример 7.3. Пусть случайная величина X имеет распре-
распределение Пуассона. Тогда
00 \t °° \t—1
ljrv v ^ .А \ г v ^ А \
IVI-Л .— > 2-7Гв — А > _т. ГТТб —
ОО
j=0
Пример 7.4. Найдем математическое ожидание случайной
величины X, имеющей геолсетрическое распределение:
7.2. Математическое ожидание случайной величины 291
Пример 7.5. Положительная целочисленная случайная ве-
величина X имеет закон распределения, задаваемый выражением
«> <1А
Тогда
ОО
Vs # —
и, значит, математическое ожидание случайной величины X не
существует.
Определение 7.2. Математическим ожиданием
{средним значением) MX непрерывной случайной величины
называют интеграл
+00
MX
-ОО
При этом предполагается, что
+ОО
\x\p{x)dx<+oo,
-ОО
+оо
= / xp{x)dx.
+ос
т.е. несобственный интеграл [VI], определяющий математиче-
математическое ожидание, сходится абсолютно.
Заметим, что определение 7.2 является естественным обоб-
обобщением определения 7.1, так как для непрерывной случайной
величины с плотностью распределения р(х)
Р{х < X < х + Ах) « p{x)dx.
Так же как и в дискретном случае, математическое ожи-
ожидание непрерывной случайной величины можно интерпрети-
интерпретировать как центр масс стержня, плотность массы которого в
точке х равна р{х).
ю*
292 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 7.6. Найдем математическое ожидание равно-
равномерно распределенной на отрезке [а, Ь] случайной величины X.
Поскольку в этом случае р(х) = 0 при х < а и х > 6, то
+оо
/
Как и следовало ожидать, ЫХ совпадает с серединой отрезка
[о, Ч-
Пример 7.7. Найдем математическое ожидание случайной
величины X, распределенной по нормальному закону с параме-
параметрами т и а:
+ОО +00
[ [
—00 —ОО
Делая замену у = (х — га)/а, получаем
+ОО +ОО
2тг j у2тг
-00 -ОО
+О0 +ОО +ОО
+ т I -j=e~y2/2dy=-jL I ye"y2/2dy + m J <p(y)dy.
—00
Первый интеграл равен нулю в силу нечетности подынтеграль-
подынтегральной функции, а второй равен единице как интеграл от стан-
стандартной нормальной плотности. Таким образом,
MX = m,
т.е. параметр т имеет смысл математического ожидания слу-
случайной величины X (см. 4.6).
7Л. Математическое ожидание случайной величины 293
Пример 7.8* Пусть X — случайная величина, имеющая
распределение Вейбулла (см. 4.6). Тогда, поскольку
при х < О, то
+00 +ОО
МХ= f xp(x)dx= i
О
О
Делая замену у = аж^, получаем
+оо
МХ
о
+
= f ye-"a-WyW-1dy =
± + Л
Пример 7.9. Математическое ожидание случайной вели-
величины X, имеющей гамма-распределение, задается вьфажением
+оо
~~ J ГG)
о
Делая замену у = Аж, получаем
+00
АГG) Л'
что следует из свойства гамма-функции Эйлера: ГG + 1) =
= 7ГG).
294 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 7.10. Случайная величина X имеет распределе-
распределение Коши, т.е. распределение с плотностью
р(х) =
Тогда
+00
\x\dx
Т5=
1
поскольку подынтегральная функция эквивалентна 1/(тгх) при
х -> Н-оо. Поэтому математическое ожидание случайной вели-
величины X не существует.
Замечание 7.1. В общем случае математическое ожидание
случайной величины задается выражением
+оо
MX
= JxdF(x),
где F(x) — функция распределения случайной величины X, а
интеграл понимают в смысле Римана — Стилтьеса [XI]. По-
Поскольку мы рассматриваем только дискретные и непрерывные
случайные величины, последнее выражение можно трактовать
как обобщенную запись формул для математических ожиданий
дискретной и непрерывной случайных величин.
7.2. Математическое ожидание
функции от случайной величины.
Свойства математического ожидания
Прежде чем переходить к описанию свойств математиче-
математического ожидания случайной величины, позволяющих, как будет
видно из примеров, в ряде случаев существенно упростить
7.2. Математическое ожидание функции от случайной величины 295
его вычисление, определим математическое ожидание функции
случайной величины (случайного вектора). Итак, пусть
У = У (X)
является функцией от случайной величины. Для определения
МУ = MY(X) можно было бы сначала по формулам из 6.2
найти распределение случайной величины У и затем уже,
воспользовавшись определением 7.1 или 7.2, вычислить МУ.
Однако мы применим другой, более удобный подход.
Рассмотрим сначала дискретную случайную величину X,
принимающую значения х\)...,хп. Тогда случайная величина
У = Y(X), как мы уже знаем, принимает значения У(жх), ...,
Y(xn) с вероятностями
и ее математическое ожидание определяется формулой
МУ = MY(X) =
t=i
Если же величина X принимает счетное число значений, то
математическое ожидание У определяется формулой
МУ = MY(X) = fV(*<)pi, G.2)
г=1
но при этом для существования математического ожидания
требуется абсолютная сходимость соответствующего ряда [IX],
т.е. выполнение условия
G.3)
Пример 7.11. Определим математическое ожидание вы-
выигрыша У в „Спортлото 6 из 49" (см. пример 6.4). Поскольку
296 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
У является функцией от случайной величины X — числа уга-
угаданных номеров, то, воспользовавшись формулой для матема-
математического ожидания функции от случайной величины и рядом
распределения (см. табл. 6.3), получим
MY = М(Х) = У @)Р{Х = 0} + YA)P{X = 1} +
+ У B)Р{Х = 2} + У C)Р{Х = 3} + У D)Р{Х = 4} +
+ УE)Р{Х = 5} + УF)Р{Х = 6} «
» -0,3 • @,436 + 0,413 + 0,1324) + 2,7 • 0,0176 +
+ 54,7 • 0,00097 + 699,7 ¦ 2 ¦ 10 + 9999,7 - 7 • 10~8 » -0,179.
Таким образом, математическое ожидание выигрыша отри-
отрицательно и равно примерно 18 к., а это означает, что играющий
в среднем проигрывает больше половины стоимости билета
C0 к.). Естественно, мы получим то же значение МУ, ес-
если воспользуемся рядом распределения случайной величины У,
представленным в табл. 6.5. #
Для непрерывной случайной величины X, имеющей плот-
плотность распределения р(х), математическое ожидание случай-
случайной величины У = Y(X) можно найти, используя аналогич-
аналогичную G.3) формулу
+00
М = МУ(Х)= IY(x)p(x)dx, G.4)
-оо
причем и здесь требуется выполнение условия
+ОО
\Y(x)\p{x)dx <+oo.
1-ос
В дальнейшем, чтобы каждый раз не оговаривать условие
существования математического ожидания, будем предпола-
предполагать, что соответствующие сумма или интеграл сходятся аб-
абсолютно.
7.2. Математическое ожидание функции от случайной величины 297
Аналогично можно вычислить математическое ожидание
функции от многомерной случайной величины. Так, матема-
математическое ожидание МУ функции Y = Y(X\,X2) от дискретной
двумерной случайной величины (Xi, X2) можно найти, восполь-
воспользовавшись формулой
MY = MY(XUX2) =
где pij = P{Xi = Xi, X2 = j/j}, а функции Y = У(ХЬХ2) от дву-
двумерной непрерывной случайной величины (Х\, Х2) — формулой
4+
МУ = MY(XUX2) = J I Y(x,y)pXl,x2(x,y)dxdy, G.5)
— ОО—ОО
где pxi9x2(xiV) — совместная плотность распределения случай-
случайных величин Х\ и Х2.
Докажем теперь теорему о свойствах математического ожи-
ожидания.
Теорема 7.1. Математическое ожидание удовлетворяет
следующим свойствам.
1. Если случайная величина X принимает всего одно значе-
значение С с вероятностью единица (т.е., по сути дела, не является
случайной величиной), то МС = С.
2. М(аХ + Ь) = аЫХ + Ь, где а, 6 — постоянные.
3. М(Хг + Х2) = МХХ + МХ2.
4. M(Xi-X2) = Ъ/LXi • ЫХ2 для независимых случайных вели-
величин Х\ ъ Х2.
М Если случайная величина X принимает всего одно значение
С с вероятностью единица, то
откуда следует утверждение 1.
Доказательство свойств 2 и 4 проведем для непрерывных
случайных величин (для дискретных случайных величин пред-
298 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
латаем читателю провести самостоятельно), а свойство 3 дока-
докажем для дискретных случайных величин (для непрерывных —
доказать самостоятельно).
Найдем математическое ожидание случайной величины Y —
= I {ax + b)px{x)dx =
—OO
+OO +00
= 0 / xpx{x)dx + b / px{x)dx =
—00 —00
т.е. приходим к утверждению 2.
Пусть теперь У = Х\ + Х2 (У(#ьх2) = х\ + х2). Тогда
МУ = М(ХХ+Х2) =
и, значит, утверждение З доказано.
Наконец, если Х\ и Хъ независимые случайные величины,
то для математического ожидания их произведения Y = X\X*i
(воспользовавшись формулой 7.5 и теоремой 5.3) имеем:
+ОО+ОО
MY =
++
= I I
—00—OO
+OO+OO
++
= / /
+oo \ / +oo
f+ +
/ xipXl(xi)dxi 1 I / x2px2(x2)dx2 I =MXiMX2.
7.2. Математическое ожидание функции от случайной величины 299
Замечание 7.2. В соответствии с ранее принятым со-
соглашением в теореме 7.1 предполагается, что математические
ожидания случайных величин X, Х\ и Х2 существуют. Однако
математическое ожидание суммы случайных величин может су-
существовать даже тогда, когда математические ожидания обоих
слагаемых не существуют. Так,
несмотря на то, что MX может и не существовать.
Очевидно также, что свойство 3 можно обобщить на случаи
произвольного числа слагаемых, т.е.
Замечание 7.3. Свойство 4 также допускает обобщение на
произведение конечного числа независисмых (в совокупности)
случайных величин:
Пример 7.12. Математическое ожидание случайной вели-
величины X, распределенной по стандартному нормальному зако-
закону, имеет вид
+00 +ОО
МХ
-ОО
+
= [ хф)<1х= Г x-^=e-x2
-ОО -ОО
В примере 6.7 было показано, что случайная величина
распределена по нормальному закону с параметрами тиа. Та-
Таким образом, согласно свойству 2 математического ожидания,
300 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
и, следовательно, параметр т нормального распределения явля-
является математическим ожиданием. Этот результат был получен
непосредственным вычислением в примере 7.7.
Пример 7.13. Представим число успехов X вп испытаниях
по схеме Бернулли в виде
где Х{ — число успехов в г-м испытании. Нетрудно видеть, что
Значит, в силу свойства 3
MX = МХХ +... + МХп = пр,
что совпадает с результатами примера 7.2, но получено с
минимальными вычислениями. #
Перейдем теперь к многомерному случаю и рассмотрим п-
мерный случайный вектор X = (Xi, ..., Хп).
Определение 7.3. Вектор m = (MAi, ..., МХп) называют
вектором математических ожиданий (средних значе-
значений) случайного вектора X.
Из замечания 7.2 и свойства 2 математического ожидания
следует, что если случайный вектор Y связан со случайным
вектором X линейной зависисмостью
то
(покажите это самостоятельно). В частном случае нормально
распределенного вектора X этот результат был получен в 6.6.
7.3. Дисперсия. Моменты высших порядков 301
7.3. Дисперсия. Моменты высших порядков
Две случайные величины могут иметь одинаковые средние
значения, но их возможные значения будут по-разному рассеи-
рассеиваться вокруг этого среднего. Например, средний балл на экза-
экзамене в двух группах равен „4", но в первой группе почти все
студенты получили „4", а во второй группе „четверочников"
нет вообще, но есть как „пятерочники", так и „троечники".
Поэтому, наряду со средним значением, хотелось бы иметь
и число, характеризующее „разброс" случайной величины от-
относительно своего среднего значения. Такой характеристикой
обычно служит дисперсия.
Кроме дисперсии можно предложить и другие меры разбро-
разброса, например центральные моменты любого четного порядка,
которые также будут определены в этом параграфе. Однако
именно использование дисперсии и других характеристик вто-
второго порядка (ковариаций) позволяет применить в теории веро-
вероятностей сильно развитый аппарат гильбертовых пространств
[IX]. Особо важную роль этот аппарат играет в теории так
называемых стационарных в широком смысле случайных про-
процессов, которые, в свою очередь, являются основной математи-
математической моделью в ряде практических приложений [XVIII].
Определение 7.4. Вторым начальным моментом
(обычно опускают слово „начальный") m<i случайной величины
X называют математическое ожидание квадрата X (У (х) = ж2):
i
для дискретной случайной величины X и
+оо
f
+
= f x2p(x)dx
для непрерывной.
302 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Определение 7.5. Дисперсией ИХ случайной величины
X называют математическое ожидание квадрата отклонения
случайной величины X от ее среднего значения, т.е.
Используя формулы G.1)-G.4), в которых положено
легко написать расчетные формулы для дисперсий дискретной
и непрерывной случайных величин соответственно:
i G.6)
и
+00
f
+
DX= f (x-MXJp(x)dx. G.7)
—00
Замечание 7.4. Из определения непосредственно следует,
что дисперсия любой случайной величины является неотрица-
неотрицательным числом.
Дисперсия ИХ представляет собой второй момент цен-
центрированной (имеющей нулевое математическое ожидание)
случайной величины
Х = Х-МХ.
Поэтому иногда дисперсию называют вторым централь-
центральным моментом случайной величины.
Дисперсия имеет аналог в теоретической механике — цен-
центральный (относительно центра масс) момент инерции массы,
распределенной на оси с линейной плотностью р(х).
Выведем некоторые свойства дисперсии.
\ 7.3. Дисперсия. Моменты высших порядков 303
Теорема 7.2. Дисперсия удовлетворяет следующим свой-
свойствам.
1. Бели случайная величина X принимает всего одно значе-
значение С с вероятностью единица, то DC = 0.
2. D{aX + b) = a2BX.
3. DX = MX2-(MXJ.
4. D(X + У) = DX + Dy для независимых случайных вели-
величин X и У.
Ч Бели случайная величина X с вероятностью единица прини-
принимает всего одно значение С, то в силу свойства 1 математиче-
математического ожидания (М.Х = С) получаем
откуда вытекает утверждение 1.
Определим дисперсию случайной величины
Используя свойство 2 математического ожидания, имеем
BY = М(У - MY) = М(аХ + Ь - М(аХ + Ь)J =
= М(аХ + Ь-аМХ ~ЬJ = М(а(Х -MX)J =
= М(а2(Х - MXJ) = а2М(Х - MXJ.
Поэтому справедливо утверждение 2.
Далее, согласно свойствам 2 и 3 математического ожидания,
получаем
Т>Х = М(Х - MXJ = М(Х2 - 2ХМХ + (MXJ) =
= MX2 ~ 2(MXJ + (MXJ = MX2 - (MXJ,
т.е. приходим к утверждению 3.
304 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Наконец, пусть X и У — независимые случайные величи-
величины. Тогда, используя независимость случайных величин (см.
лемму 1)
Х=Х-МХ и У = У-МУ,
а также свойства 2-4 математического ожидания, получаем
D(X + У) = М(Х + Y -М(Х + У)J =
= М((Х - MX) + (У - МУ)J = М(Х - MXJ +
+ 2М((Х - МХ)(У - MY)) + М(У - MYJ =
= DX + 2(МХ • MY) + DY = 1>Х + DY,
О О
поскольку ЫХ = 0 и MY = 0. Значит, имеет место утверж-
утверждение 4. >
Замечание 7.5. Можно показать, что справедливо и
свойство, обратное свойству 1, а следовательно, имеет место
утверждение: дисперсия случайной величины X равна нулю
тогда и только тогда, когда X с вероятностью 1 принимает
всего одно значение.
Замечание 7.6. Свойство 3 дает весьма удобную формулу
для расчета дисперсии случайной величины с помощью ЭВМ
или микрокалькулятора. Действительно, если вычислять дис-
дисперсию по первоначальной формуле G.6), то необходимо два
раза суммировать по г: первый раз при подсчете математиче-
математического ожидания и второй — дисперсии. Свойство 3 позволяет
обходиться одним циклом: можно одновременно суммировать
с коэффициентами pi и сами значения случайной величины, и
их квадраты.
Замечание 7.7. Очевидно, что свойство 4 справедливо
для суммы не только двух, но и любого числа п попарно
независимых случайных величин
7.3. Дисперсия. Моменты высших порядков 305
Замечание 7.8. В 7.4 будет приведена формула для диспе-
дисперсии суммы любых (а не только независимых) слагаемых. #
Нетрудно видеть, что дисперсия DX имеет размерность
квадрата размерности случайной величины X. Для практи-
практических же целей удобно иметь величину, характеризующую
разброс значений случайной величины вокруг ее математиче-
математического ожидания, размерность которой совпадает с размерно-
размерностью X. В качестве такой величины естественно использовать
а = \/DX, которую называют средним квадратичным от-
отклонением случайной величины X (иногда также стандартом,
или стандартным отклонением).
Пример 7.14. Найдем дисперсию случайной величины X,
распределенной по закону Пуассона. Для этого воспользуемся
свойством 3 дисперсии. Математическое ожидание Ъ/LX = Л
было найдено в примере 7.3. Определим второй момент:
г-1
MX2 = У\2^е-Л =
i=o
Таким образом,
и, значит, дисперсия X, так же как и математическое ожида-
ожидание, совпадает с параметром А.
Пример 7.15. Пусть X — число успехов в п испытаниях
по схеме Бернулли. Дисперсию X можно подсчитать так же,
как в примере 7.2 было подсчитано математическое ожидание,
а именно непосредственно воспользоваться определением 7.5
306 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
дисперсии. Однако мы поступим другим образом. Для этого
снова (см. пример 7.13) представим X в виде суммы
Дисперсия каждого слагаемого равна:
i = @ - MXiJq + A - MXtfp =
~ Р?Р = 2
Учитывая, что случайные величины Х{ являются независимы-
независимыми, в силу свойства 4 дисперсии получаем
ВХ = BXi +... + DXn = npq.
Пример 7.16. Дисперсия равномерно распределенной на
отрезке [а, Ь] случайной величины X определяется формулой
Ь-а
1 // Ь + а\3 / Ь + а\3\_ (b^QK
3F-a)Vv 2 / Г 2 ij"l2(l-a)"
12
Пример 7.17. Дисперсия случайной величины X, распре-
распределенной по нормальному закону с параметрами т и а, имеет
вид
° 7^2 (*-™J
W dx.
7 77т-г^
= / (*-тJ»^(*)Лр= / l J
J J ау2тг
-оо —с»
Делая замену у = (х — га)/а, получаем
+00 Л
-оо
7.3. Дисперсия. Моменты высших порядков 307
Полагая и = у/%/2тг, dv = уе~у l2dy и интегрируя по частям,
находим
+00 +ОО
-]=e-v^dy = a>J<p(y)dy = cT*.
—оо —оо
Таким образом, дисперсия нормально распределенной случай-
случайной величины совпадает с квадратом второго параметра. Это-
Этого и следовало ожидать, поскольку а носит название среднего
квадратичного отклонения.
Пример 7.18. Для определения дисперсии случайной ве-
величины X, имеющей гамма-распределение, воспользуемся свой-
свойством 3 дисперсии. Имеем
+оо
О
или после замены у = Хх
+ОО
-^ЛХ* — * 1 */у+1~""~*/ л- — * w ¦ -/ __ 7G"
Л2Г(А) J У
Учитывая, что MX = *у/\ (см. пример 7.9), окончательно
получаем
Пример 7.19. Пусть X — случайная величина, имеющая
дисперсию DX. Введем новую случайную
308 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Найдем число а, при котором достигается минимум МУ2.
Согласно свойствам 2 и 3 дисперсии, имеем
МУ2 = БУ + (МУJ = ВХ + (MX - aJ.
Первое слагаемое от а не зависит, а второе принимает мини-
минимальное значение, равное 0, при а = Ъ/LX. Таким образом, в
качестве а нужно взять MX, а само минимальное значение
МУ2 совпадает с дисперсией ИХ. #
В некоторых теоретических исследованиях встречаются
моменты высших порядков.
Определение 7.6. Моментом k-го порядка т* (k-м
моментом) случайной величины X называют математиче-
математическое ожидание fc-й степени случайной величины X:
г
если X — дискретная случайная величина, и
+ОО
+
= f xkp{x)dx,
если X — непрерывная случайная величина.
Иногда k-и момент называют также начальным момен-
моментом к-го порядка.
Определение 7.7. Центральнглм моментом к-го по-
порядка гпь (k-м центральным моментом) случайной ве-
величины X называют математическое ожидание fc-й степени
о
случайной величины X = X — MX:
тк = М(Х - МХ)к = Y^i^i - MX)kPi
7.4. Ковариация и коэффициент корреляции случайных величин 309
И
+оо
mk = М(Х - MX)k = f (х -
-00
для дискретной и непрерывной случайных величин X соответ-
соответственно.
Момент первого порядка совпадает с математическим ожи-
ожиданием, центральный момент первого порядка равен нулю, цен-
центральный момент второго порядка является дисперсией. От-
Отметим также, что в теоретических изысканиях рассматривают
моменты не обязательно целого порядка к.
7.4. Ковариация и коэффициент
корреляции случайных величин
Пусть (Xi, X2) — двумерный случайный вектор.
Определение 7.8. Ковариацией (корреляционным мо-
моментом) cov(-X"i, X2) случайных величин Х\ и Х2 называют
математическое ожидание произведения случайных величин
X1 = Хг - МХХ иХ2 = Х2- МХ2:
cov(Xb Х2) = М(ХгХ2) = М((Хг - МХг)(Х2 - МХ2)).
Запишем формулы, определяющие ковариацию.
Для дискретных случайных величин Х\ и Х2
cov(Xb Х2) = J2(Xi - MXi)(tfi - MX2)Pij,
для непрерывных случайных величин Х\ и Х2
+ОО+ОО
= / / (xi-MXi)(x2-MX2)pXux2(xux2)dxidx2.
-00-00
310 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Заметим, что введение понятия ковариации позволяет запи-
записать выражение для дисперсии суммы случайных величин и к
уже имеющимся свойствам дисперсии добавить еще одно:
ЩХ + Y) = DX + DY + 2cov(JT,Y)
(свойство 5 дисперсии), справедливое для произвольных, а не
только независимых случайных величин X и Y. Действительно,
D(X + Y) = М((Х + Y) -М(Х + Y)J =
= М(Х - MXJ + 2Ы((Х - MX)(Y - MY)) + M{Y - MYJ =
+ BY + 2cov(X,Y).
Свойство 5 дисперсии допускает обобщение на произволь-
произвольное число слагаемых:
Следующая теорема устанавливает основные свойства кова-
ковариации.
Теорема 7.3. Ковариация имеет следующие свойства.
2. cov(Xi,Jf2) =0 для независимых случайных величин Х\
3. Если Yi = aiXi +Ьг и У2 = «2^2 + &2, то cov(YuY2) =
4. -
5. Равенство
|cov(Xi, Х2) | = л/Б^БХз G.8)
верно тогда и только тогда, когда случайные величины Х\ и Х2
связаны линейной зависимостью, т.е. существуют такие числа
а и Ь, при которых
X2 = aXi-6. G.9)
6. cov(XuX2) =
7.4. Ковариация и коэффициент корреляции случайных величин 311
Утверждение 1 вытекает из очевидного соотношения
Бели случайные величины Х\ и Х2 являются независимыми
(и имеют математические ожидания), то
cov(XbX2) = M((Xi - MXi)(X2 - МХ2)) =
- МХг)) {М(Х2 -
откуда приходим к утверждению 2.
Пусть Yi = aiXi + 6Ь Y2 = a2X2 + Ь2. Тогда
соу(УьУ2) = М((Ух - МУх)(У2 -МУ2)) =
- 6i)(a2X2 + Ь2 - a2MX2 - Ы) =
- МХг)(Х2 - MX2)).
Поэтому справедливо утверждение 3.
Рассмотрим дисперсию случайной величины
где х — произвольное число. В силу свойств дисперсии и
свойства 3 ковариации
BYX =
Дисперсия DYX, как функции от ж, представляет собой ква-
квадратный трехчлен. Но дисперсия любой случайной величины
не может быть меньше нуля, а это означает, что дискриминант
D = Bcov(XuX2)J -4DXiDX2 G.10)
квадратного трехчлена DY^ является неположительным, т.е.
имеет место утверждение 4.
312 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Далее, пусть выполнено равенство G.8). Значит, дискрими-
дискриминант G.10) равен нулю, и уравнение
имеет решение, которое обозначим а. Тогда в соответствии с
замечанием 7.5 случайная величина Ya = аХ\ — Х2 принимает
всего одно значение (допустим, 6), и, следовательно,
Х2 = аХ\ — 6,
т.е. из G.8) вытекает G.9).
Наоборот, пусть выполнено G.9). Тогда в соответствии со
свойством 1 дисперсии DYa = 0, а значит, дискриминант G.10)
является неотрицательным. Поскольку при доказательстве
утверждения 4 было показано, что этот дискриминант непо-
неположителен, то он равен нулю, откуда следует, что
\cov(XuX2)\ =
Таким образом, из G.9) вытекает G.8). Утверждение 5 полно-
полностью доказано.
Наконец, раскрывая скобки в формуле, определяющей ко-
вариацию, и используя свойства математического ожидания,
получаем утверждение 6, которое часто бывает полезным при
численном подсчете ковариации. >
Замечание 7.9. Если случайные величины Х\ и Х2 связаны
линейной зависимостью Х2 = аХ\ — Ь, а ф 0, то в соответствии
со свойствами 3 и 1
Поэтому знак ковариадии совпадает со знаком коэффициента а
и свойство 5 допускает следующее уточнение:
a>0;
o<Q.
7.4. Ковариация и коэффициент корреляции случайных величин 313
Замечание 7.10. Из свойств дисперсии и ковариации
можно получить еще одно полезное при расчетах свойство
дисперсии
+ a2X2 + b) = a2{DXi + а2ВХ2 + 2aia2cov(Xi,X2).
Докажите это свойство самостоятельно.
Замечание 7.11. Как следует из свойства 2, ковариация
независимых случайных величин равна нулю. Однако обрат-
обратное, вообще говоря, неверно. Существуют зависимые и даже
функционально зависимые случайные величины, ковариация
которых равна нулю, что демонстрирует следующий пример.
Пример 7.20. Пусть случайная величина X имеет равно-
равномерное в интервале (—1,1) распределение, а случайная величина
У связана со случайной величиной X функциональной зависи-
зависимостью У = X2 (см. 6.1). Покажем, что cov(X,y) = 0, несмо-
несмотря на функциональную зависимость X и У.
Действительно, учитывая равенство MX = 0 и свойство 6
ковариации, имеем
cov(X,F) = М(Х • У) - MX • MY =
+ОО
= f xsp{x)dx = ^ f
Определение 7.9. Случайные величины X и У назы-
называют некоррелированными, если их ковариация равна ну-
нулю, т.е.
Приведенный выше пример показывает, что из некоррели-
некоррелированности случайных величин не следует их независимость.
Можно сказать, что ковариация случайных величин отражает,
насколько их зависимость близка к линейной.
314 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Рассмотрим теперь n-мерный случайный вектор
X — (Jfi, ..., Хп).
Определение 7.10* Матрицей ко вариаций (ковариа-
(ковариационной матрицей) случайного вектора X называют мат-
матрицу
состоящую из ковариаций случайных величин Х{ и Xj,
Пример 7.21. Рассмотрим двумерную случайную величи-
величину (X, У), распределенную по нормальному закону. Тогда
+ОО+ОО
2p(x-mi)(y-m2) , (y-m2J
+
Делая замену и = (ж — mi)/cri, v = (у — тп2)/(Т2, получаем
cov(X,F) =
Н-оо+оо
-00-00
+ОО +00
/ 1
Внутренний интеграл равен ри. Поэтому
2
cov(X,y) =
7Л. Ковариация и коэффициент корреляции случайных величин 315
Поскольку DX = af, DY = о^, то матрица S представляет
собой матрицу ковариации (в данном случае понятие „ковариа-
„ковариационная матрица" мы ввели раньше, нежели выяснили смысл
этого понятия).
Аналогично в общем случае n-мерного нормального случай-
случайного вектора
X = (Х\, ..., Хп)
элементы atj ковариационной матрицы I! являются ковариаци-
ями случайных величин Х{ и Xj. #
Основные свойства матрицы ковариации определяются сле-
следующей теоремой.
Теорема 7.4. 1. Матрица ковариации S является симме-
симметрической.
2. Пусть га-мерный случайный вектор У = (Ух, ..., Ym) по-
получен из n-мерного случайного вектора X = (Ai, ..., Хп) с
помощью линейного преобразования В, т.е.
Тогда матрица ковариации S^ случайного вектора У связана с
матрицей ковариации Е^ случайного вектора X соотношением
Sy? == В YjgB.
3. Матрица ковариации Е является неотрицательно опреде-
определенной, т.е. ЬИо ^ 0 для всех векторов Ь.
< Утверждение 1 следует непосредственно из определения
матрицы ковариации.
Пусть матрица В линейного преобразования У = ХВ + с
имеет вид В = {bij). Вычислим ковариациюслучайных величин
316 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
?{ и Yy.
k,l=l к,1=1
Записывая последнее равенство в матричной форме, получаем
утверждение 2.
Для доказательства утверждения 3 рассмотрим скалярную
случайную величину
В случае скалярной случайной величины У ее дисперсия DV =
= ?у, и поэтому в соответствии утверждением 2 теоремы
имеем
откуда в силу неотрицательности дисперсии получаем утвер-
утверждение 3. >
Замечание 7.12. Для многомерного случайного вектора,
распределенного по нормальному закону, свойства 1-3 ковари-
ковариационной матрицы уже были получены ранее (см. 5.5).
Замечание 7.13. В том случае, когда ранг т ковариа-
ковариационной матрицы S строго меньше размерности п вектора X,
можно доказать, что среди п случайных величин Х\,..., Хп име-
имеется ровно т таких, что остальные п — т случайных величин
являются их линейной комбинацией [IV]. Это свойство так-
также отмечалось нами для нормально распределенных случайных
векторов. #
Существенным недостатком ковариации является то, что ее
размерность совпадает с произведением размерностей случай-
случайных величин. Естественно, хотелось бы иметь безразмерную
7.4. Ковариация и коэффициент корреляции случайных величин 317
характеристику степени линейной зависимости. Но это очень
просто сделать — достаточно поделить ковариацию случайных
величин на произведение их средних квадратичных отклонений.
Определение 7.11. Коэффициентом корреляции слу-
случайных величин X и У называют число р = р(Х,У), определяе-
определяемое равенством (предполагается, что ВХ > 0 и BY > 0)
y/BX BY
Теорема 7.5. Коэффициент корреляции имеет следующие
свойства.
2. Бели случайные величины X и Y являются независимыми
(и существуют ВХ > 0 и BY > 0), то p(X,Y) = 0.
3. p{a\X\ + 6i, a^Xi + 62) = ±p(X\,X2)' При этом знак плюс
нужно брать в том случае, когда а\ и a*i имеют одинаковые
знаки, и минус — в противном случае.
5. |р(Х,У)| = 1 тогда и только тогда, когда случайные ве-
величины X и У связаны линейной зависимостью.
< Доказательство теоремы следует из свойств ковариации, и
мы предлагаем провести его самостоятельно. >
Пример 7.22. Найдем коэффициент корреляции случай-
случайных величин X — числа очков, выпавших на верхней грани
игральной кости, и У — на нижней (см. пример 5.5). Для этого
сначала вычислим MX, МУ, DX, BY и cov(X,y). Воспользо-
Воспользовавшись табл. 5.3, получим
318 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
3,5H + B-3,5)A-3,5)-0 +
5)-i + (l-3,5)B-3,5)-0 + ...+
о
3,5)- + C
1 1 Я*>
B-3,5)E-3,5)-- + ... + A-3,5)F-3,5)-- = --.
Таким образом,
-35/12
Р 35/12
Впрочем, это мы могли бы установить и без всяких вычислений
в силу свойства 5 коэффициента корреляции, если бы вспомни-
вспомнили, что сумма чисел очков на противоположных гранях равна
семи и, значит, X = 7 — Y (X иУ связаны линейной зависимо-
зависимостью с отрицательным коэффициентом пропорциональности).
Пример 7.23* Температура воздуха Х\ и Х2 в два по-
последовательных дня представляет собой двумерную случайную
величину с вектором средних (mi, 7712), дисперсиями а\ > О и
а2 > 0 и коэффициентом корреляции р. Рассмотрим новую слу-
случайную величину
G.11)
где я, Ь — некоторые числа. Назовем Х2 линейным прогнозом
температуры воздуха на следующий день при известной тем-
температуре воздуха в предыдущий день. Подберем числа х и Ь
таким образом, чтобы математическое ожидание
М(Х2-Х2J
приняло минимальное значение. В этом случае Х2 называют
наилучшим в средне квадратичном линейным прогнозом. В
7.4. Ковариащия и коэффициент корреляции случайных величин 319
соответствии со свойствами математического ожидания и дис-
дисперсии находим
М(Х2 - Х2J = В(Х2 - Х2) + [М(Х2 - Х2)]2 =
- 2cov(X2, Х2) + Т>Х2 + (МХ2 - МХ2J =
= (х2 с\ — 2хро\о2 + a2) + {xm\ + b — m2J.
Заметим, что первое слагаемое х2о\ — 2xpa\a2 + о\ в по-
последнем выражении зависит только от х. Второе слагаемое
(#mi + Ь — гагJ является неотрицательным, причем при любом
фиксированном х его минимальное значение, равное нулю, до-
достигается при
Ъ = тп2 — xrai.
Минимум первого слагаемого достигается при
х = р—. G.12)
Следовательно, минимальное значение математического ожи-
ожидания М(А — Х2J достигается при х = po2jo\ и Ь = га2 —
— mipa2/ai и равно:
= ра2 - 2р2о\ + о\ = A -
Поэтому М(Х2 - Х2J = 0, т.е. Х2 = Х2 в случае |р| = 1,
и наилучший линейный прогноз является абсолютно точным.
Качество прогноза ухудшается с уменьшением |р|. При /9 = 0
наилучший линейный прогноз Х2 = b = ra2, состоит в указании
средней температуры на следующий день и не зависит от
температуры в предыдущий день. #
Примеры 7.22 и 7.23 показывают, что коэффициент корре-
корреляции (также как и ковариация) отражают „степень линейной
близости" случайных величин. При этом, если р > 0, то ко-
коэффициент пропорциональности G.12) в наилучшем линейном
приближении G.11) одной случайной величины другой является
положительным, а в случае р < 0 — отрицательным.
320 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Поэтому при р > 0 говорят о положительной корреляци-
корреляционной зависимости X и У, при р < 0 — об отрицательной.
Например, рост и вес человека связаны положительной корре-
корреляционной зависимостью, а температура и время сохранности
продукта — отрицательной.
Однако, коэффициент корреляции (ковариация) может не
улавливать „степень нелинейной близости" случайных величин.
Для этой цели служат другие характеристики, например, кор-
корреляционное отношение, которое будет рассмотрено в 8*2.
По аналогии с ковариационной матрицей для случайного
вектора X = (Xi, ..., Хп) можно ввести корреляционную ма-
матрицу.
Определение 7* 12. Корреляционной {нормированной
ковариационной) матрицей случайного вектора X называ-
называют матрицу
состоящую из коэффициентов корреляций случайных величин
Л. i И Л. j •
Корреляционная матрица Р порядка п имеет вид
1 pi2 ... Pin
Р21 1 ... Р2п
я Рп\ Рп2
7.5. Другие числовые
характеристики случайных величин
В этом параграфе мы дадим краткое описание некоторых
других применяемых на практике числовых характеристик
случайных величин. Отметим, что эти характеристики, как
и все остальные, рассматриваемые в настоящей главе, по
7.5. Другие числовые характеристики случайных величин 321
сути дела, являются характеристиками законов распределений
случайных величин.
Поэтому в дальнейшем вместо слов „характеристика случай-
случайной величины, имеющей некоторое распределение (закон рас-
распределения)" будем говорить „характеристика распределения".
Случайную величину X называют симметрично распреде-
распределенной относительно математического ожидания, если
?{Х < MX - х} = Р{Х > MX + х}
для любого х. В частности, непрерывная случайная величина
X является симметричной тогда и только тогда, когда график
ее плотности распределения симметричен относительно прямой
х = MX.
Определение 7.13. Асимметрией А случайной величи-
величины X называют отношение третьего центрального момента
шз к кубу среднего квадратичного отклонения а:
Нетрудно видеть, что (при условии существования третьего
момента) для симметрично распределенной относительно ма-
математического ожидания случайной величины X асимметрия
равна нулю.
Определение 7.14. Эксцессом Е случайной величины X
о
называют отношение четвертого центрального момента т\ к
квадрату дисперсии за вычетом числа 3:
Ясно, что асимметрия и эксцесс — безразмерные величины.
Пример 7.24. Вычислим асимметрию и эксцесс случайной
величины, имеющей нормальное распределение. Согласно опре-
11 - 10047
322 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
делению,
+00 +ОО
ау2тг
—00 —ОО
+ОО +00
ay/Zn
-oo —oo
Делая замену у = x —• m, имеем
+00
—oo
откуда в силу нечетности подынтегральной функции следует,
что тз = 0 и асимметрия 71 = 0.
Для того чтобы найти ттц, применим формулу интегриро-
интегрирования по частям. Полагая
(х — тK . х — т -(Т-.гп
имеем
+00
-oo
Воспользовавшись теперь результатом примера 7.17, оконча-
окончательно получим, что Ш4 = За4, и, следовательно, эксцесс Е = 0.
Таким образом, для нормального распределения асимметрия
и эксцесс равны нулю.
Определение 7.15. Квантпилыо уровня а, или а-кван-
Ш1хлыо, @ < а < 1) случайной величины X (распределения
случайной величины X) называют число Qa, удовлетворяющее
неравенствам
<Qa}^a и
7.5. Другие числовые характеристики случайных величин 323
1/2-квантиль называют также медианой М случайной вели-
величины X.
Для непрерывной случайной величины X а-квантиль Qa
является решением уравнения
где F(x) — функция распределения случайной величины X.
Таким образом, для непрерывной случайной величины X кван-
квантиль Qa — это такое число, меньше которого X принимает
значение с вероятностью а.
Бели известна плотность распределения р(х) случайной ве-
величины X, то, учитывая связь между функцией распределения
и плотностью распределения, уравнение для определения а-
квантили можно записать в виде
Qa
р(х) dx = a.
Пример 7.25. Найдем a-квантиль и медиану экспоненци-
экспоненциального распределения. В этом случае Qa представляет собой
решение уравнения (рис. 7.1)
Поэтому
_
Qa-
Ясно, что медиана экспоненциального распределения
Бели трактовать экспоненциальное распределение как рас-
распределение времени распада атома (см. 4.6), то медиана будет
соответствовать периоду полураспада.
324 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
F(x)i
Пример 7*26. Пусть случайная величина X представляет
собой число успехов в одном испытании по схеме Бернулли с
вероятностью успеха р. Тогда,
как видно на рис. 7.2,
1
я
Рис. 7.2
Qol = 0 при 0 < а < д,
Qa — 1 при д<а< 1,
a g-квантиль может быть лю-
любым числом от 0 до 1 включи-
включительно. Этот пример показы-
показывает, что, во-первых, квантили
могут совпадать для разных а,
а, во-вторых, для некоторых а квантили могут определяться
неоднозначно.
Определение 7.16. Модой непрерывной случайной
величины называют точку максимума (локального) плотно-
плотности распределения р{х). Различают унимодальные (имеющие
одну моду), бимодальные (имеющие две моды) и мулътимо-
дальные (имеющие несколько мод) распределения.
Для определения моды дискретной случайной величины
предположим сначала, что ее значения #1,...,жп расположены
в порядке возрастания.
7.5. Другие числовые характеристики случайных величин 325
Определение 7.17. Модой дискретной случайной
величины называют такое значение ж*, при котором для
вероятностей выполняются неравенства
Pi_i < pi и pi+i < р^
В случае дискретных случайных величин распределения
также могут быть унимодальными, бимодальными и мульти-
мо дальними.
Наивероятнейшим значением называют моду, при ко-
которой достигается глобальный максимум вероятности (дис-
(дискретной случайной величины) или плотности распределения
(непрерывной случайной величины).
Если распределение унимодальное, то мода также будет
наивероятнейшим значением.
Мода и наивероятнейшее значение введены, скорее, для
наглядности, чем для практических целей.
Пример 7.27. Плотность нормального распределения
имеет единственный максимум в точке т (см. 5.6). Поэтому
мода нормального закона совпадает с математическим ожида-
ожиданием. Она же является наивероятнейшим значением и медиа-
медианой.
Пример 7.28. Найдем моду биномиального распределения.
Для этого заметим, что
Рп(г)
Pn{i + 1) Сгп+ V+V-(i+i) (n - Op'
Отсюда нетрудно вьюести, что отношение Pn(i)/Pn{i +1) мень-
меньше единицы при г <np — q и больше единицы при i> np — q.
Таким образом, если np — q не является целым числом, то ми-
минимальное г, для которого % > np — g, является модой и наи-
наивероятнейшим значением. Бели же np — q — целое число, то
326 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
биномиальный закон имеет две моды и два наивероятнейших
значения: пр — q и пр — q +1. #
Последнюю числовую характеристику, которую мы здесь
рассмотрим, называют энтропией. Эта характеристика играет
одну из основных ролей в теории информации*. Мы ограни-
ограничимся здесь лишь определением энтропии и перечислением ее
основных свойств.
Определение 7.18. Энтропией Н = Н(Х) дискретной
случайной величины X называют число, равное
1=1
(здесь и далее в определениях энтропии принято соглашение
О • log 0 = 0, a logpi обычно означает log2Pi).
Отметим, что энтропия не зависит от значений Х{ слу-
случайной величины X, а определяется только вероятностями зд,
с которыми эти значения принимаются. Энтропия является
мерой неопределенности случайной величины. Максимальное
значение НтпХ = logn энтропия дискретной случайной величи-
величины достигает тогда, когда все п возможных значений случайная
величина принимает с одной и той же вероятностью Pi = 1/п,
минимальное Нт{п =0 — когда случайная величина принимает
единственное значение с вероятностью 1.
Определение 7.19. Энтропией H(XyY) двумерной
дискретной случайной величины {X,Y) называют число,
равное
"См., например: Кульбак С. Теория информации и статистика. М.:
Наука, 1967. 407 с.
7.5. Другие числовые характеристики случайных величин 327
Поскольку для независимых случайных величин X и У
Pij = PXiPYj И logpi, = logpxi + \0gpYj,
то
т.е. энтропия случайной величины (Х,У), если ХиУ — не-
независимые случайные величины, представляет собой сумму эн-
энтропии. Показано*, что в случае зависимости X и У энтропия
#(-Х",У) всегда меньше суммы H(X) + H(Y).
Энтропия в некотором смысле представляет собой мини-
минимальный объем памяти, необходимый для записи информации,
содержащейся в случайной величине. Поскольку информация
записывается обычно в двоичной системе, то основанием лога-
логарифма берется число 2.
Определение 7.20. Энтропией Н = Н(Х) непрерыв-
непрерывной случайной величины X и энтропией H(X,Y) дву-
двумерной случайной величины (Х,У) называют числа, равные
соответственно
+00
Я = Н(Х) = - Ipx(x)\ogpx(x)dx,
—оо
+ОО+ОО
++
#(Х,У) = -ll pxty(o;y
—оо— оо
*См.: Вентцель Е.С. Теория вероятностей: Учеб. М.: Наука, 1969.
с.
328 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Для непрерывных, так же как и для дискретных, случайных
величин X и У энтропия H(X,Y) двумерной случайной величи-
величины совпадает с суммой Н(Х) + H(Y) энтропии координат тогда
и только тогда, когда X и У являются независимыми случай-
случайными величинами; иначе H(X,Y) < H(X) + H(Y) (см. учебник
Е.С. Вентцель). Отметим также, что при заданной дисперсии
а2 максимальную энтропию log л/2тгеа2 имеет нормально рас-
распределенная случайная величина.
7.6. Решение типовых примеров
Таблица 7.1
X
р
0
0,41
1
0,43
2
0,11
3
0,05
Пример 7.29. Найдем математическое ожидание, диспе-
дисперсию и среднее квадратичное
отклонение дискретной слу-
случайной величины X, ряд рас-
распределения которой предста-
представлен в табл. 7.1.
В соответствии с определением математического ожидания
дискретной случайной величины X
п
MX = ]Г хгрг = 0 • 0,41 +1 • 0,43 + 2 • 0,11 + 3 • 0,05 = 0,8.
Дисперсию находим по формуле DX = MX2 — (MXJ.
Математическое ожидание квадрата X равно
п
MX2 = ^2хЬг = О2 • 0,41 +12 • 0,43 + 22 • 0,11 + З2 - 0,05 = 1,32.
г=0
Поэтому DX = 1,32 - 0,82 = 0,68.
Наконец, среднее квадратичное отклонение
Пример 7.30. Вероятность того, что в течение часа
на станцию скорой помощи не поступит ни одного вызова,
7.6. Решение типовых примеров 329
равна 0,00248. Считая, что число вызовов X, поступающих
в течение часа на станцию, имеет распределение Пуассона,
найдем математическое ожидание и дисперсию X.
Поскольку случайная величина X имеет распределение
Пуассона, то
где А — параметр распределения Пуассона. В свою очередь, из
условия задачи следует, что
Р{Х = 0} = е~А = 0,00248.
Решая последнее уравнение относительно А с помощью табл. П.1,
получаем А = 6. Так как параметр А является одновременно
математическим ожиданием и дисперсией случайной величины
X (см. примеры 7.3 и 7.14), то MX = 6 и DX = 6.
Пример 7.31. Найдем математическое ожидание, диспе-
дисперсию и среднее квадратичное отклонение непрерывной случай-
случайной величины X, плотность распределения которой имеет вид
cos ж/2, \х\ ^ тг/2.
В соответствии с определением математического ожидания
непрерывной случайной величины X
+оо тг/2
МХ= f xp{x)dx= I \
-оо -тг/2
Вычислим теперь дисперсию X:
+ОО 7Г/2
DX= j (x-MXJp{x)dx =
-оо -тг/2
Наконец, а = у/DX = у/(Щ8 « 0,684.
330 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 7.32. Найдем математическое ожидание, диспе-
дисперсию и среднее квадратичное отклонение случайной величины
-X", имеющей логнормальное распределение (см. задачу 6.23),
т.е. случайной величины с плотностью распределения
о,
е
х ^ 0;
Найдем математическое ожидание X:
+00
/
Для вычисления интеграла в последней формуле сделаем замену
х = еу. Тогда
+00
-00
+оо
-оо
Делая теперь замену t = (у - а - /?2)//3, получаем
+оо
Аналогично находим математическое ожидание X2:
+оо
7.6. Решение типовых примеров 331
Тогда
DX = MX2 - (MXJ = e2«+W2 - е2а+Р = е2а+^(е* - 1).
Наконец,
а =
Пример 7.33. Случайная величина X распределена по
равномерному закону на отрезке [а, 6], причем а и & не известны,
a MX = 4 и DX = 3. Найдем а и Ь.
Для равномерно распределенной случайной величины
(см. примеры 7.6 и 7.16). Поэтому
Ь_ (Ь-аJ
4
Решая полученную систему и учитывая, что 6 > а, находим:
а = 1, 6 = 7.
Пример 7.34. Из хорошо перетасованной колоды карт
слева направо последовательно выкладывают карты лицевой
стороной наверх. На карты первой колоды таким же образом
кладут карты второй колоды. Найдем среднее число совпаде-
совпадений верхней и нижней карт.
Пусть число карт в каждой колоде равно п. Число совпаде-
совпадений X можно записать в виде
где Х{ = 1, если i-я пара карт совпала, и Х{ = 0 в противном слу-
случае. Воспользовавшись свойством математического ожидания,
получаем
332 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Далее, вероятность совпадения верхней и нижней карт в ка-
каждой паре в соответствии с принципом классической вероят-
вероятности равна 1/п. Поэтому
П
П
П
Окончательно имеем
п
Интересно отметить, что ответ не зависит от числа п карт в
колодах.
Пример 7.35, Независимые случайные величины Х\ и
Х2 имеют нормальное распределение со средними значениями
mi и Ш2 и дисперсиями а\ и а\ соответственно. Найдем
математическое ожидание случайной величины У = X\X<i.
Поскольку случайные величины Х\ и X*i являются неза-
независимыми, то в соответствии со свойством математического
ожидания
MY =
Таблица 7.2
Пример 7.36. Дискретная случайная величина X имеет
ряд распределения, представленный
в табл 7.2. Найдем математическое
ожидание и дисперсию случайной
величины Y = 1пХ.
Поскольку математическое ожи-
ожидание MY(X) и второй момент ШУ2(Х) функции Y(X) от
дискретной случайной величины X можно вычислить по фор-
формулам
X
p
1
0,2
e
0,1
e2
0,5
e3
0,2
MY(X) =
MY2(X) =
t=i
7.6. Решение типовых примеров
333
то
Значит,
и БУ = МУ2 -(МУJ = 3,9 -A,7J = 1,01.
Пример 7.37. Случайная величина X имеет экспоненци-
экспоненциальное распределение с параметром А = 3. Найдем математи-
математическое ожидание и дисперсию случайной величины У = ех.
Поскольку математическое ожидание ЪЛУ(Х) и второй мо-
момент ЪЛУ2(Х) функции Y(X) от непрерывной случайной вели-
величины X можно вычислить, используя формулы
+00 +ОО
MY(X)= f Y(x)p{x)dx, МУ2(Х)= f Y2{x)p(x)dx,
то
+ОО +ОО
MY= Г ex3e~3xdx = |, MY2 = f e2xZe~3xdx = 3.
Значит,
3
2'
-&-i
Пример 7.38. Закон распределения вероятностей двумер-
двумерной дискретной случайной ве-
величины (Xi, X2) представлен в
табл. 7.3. Найдем математиче-
математическое ожидание и дисперсию слу-
случайной величины
Y = log2(Xl/X2).
Таблица 7.3
1
2
Хх
0,5
0,1
0,2
1
0,4
0
2
0,2
од
334 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
В соответствии с формулой для вычисления математиче-
математического ожидания функции от двумерной дискретной случайной
величины
MY = log2 М . 0,1 + log2 i ¦ 0,4 + log21 • 0,2 +
My2=(log2^J.0,l+(log2iJ-0,4+(log2|J.0,2 +
^J-0,2+ (log2iJ.0+ (log2|J0,l = 1,2
DY = 1,2 -(-0,2J = 1,16.
Пример 7.39. Совместная плотность распределения дву-
двумерной непрерывной случайной величины (Xi,X2) имеет вид
х\ + х\
Найдем математическое ожидание и дисперсию случайной ве-
величины Y = Х\Х2.
Используя формулу для вычисления математического ожи-
ожидания функции от двумерной непрерывной случайной величи-
величины, получаем
MY
7.6. Решение типовых примеров 335
БУ=МУ2-(МУJ= И Yx\x%\lx
2тг 1
_ 3 / 2 • 2 ^4
о о
2тг
J A - cosDy?)) Ар = ^ w 0,05.
1127Г
о
Пример 7.40. Плотность распределения непрерывной слу-
случайной величины X имеет вид
— "\2х, х6@,1).
Найдем начальные и центральные моменты первого, второго,
третьего и четвертого порядков, а также асимметрию и экс-
эксцесс случайной величины X.
В соответствии с формулой
+00
= f xkp(x)dx
-оо
вычислим начальные моменты:
Шз
О
1 1
= / x2xdx = -, т2 = / x22xdx = -,
У 3' У 2'
о о
1 1
= у я 2х х = -, т,4 = J х 2xdx = ~.
336 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Для нахождения центральных моментов выведем формулы,
выражающие центральные моменты через начальные:
+3X(MXJ-(MXK)=m3-3m2mi
МХ)А = М(ХА-4Х3МХ+6Х2{МХJ-
-4Х(МХK + (MXL) =m4 -4m3mi+6m2mf -Ът\.
Подставляя в эти формулы найденные значения начальных
моментов, получаем
mi=0,
1
i35'
2 1
Т2
2 2
Наконец, в соответствии с определениями асимметрии
7i = гпз/ст и эксцесса 72 = тп^/g — 3
2>/2 __3
5 ' 5
Таблица 7.4
Пример 7.41, Распределение вероятностей двумерной слу-
случайной величины pfi, X2) задано
табл. 7.4. Найдем математические
ожидания, дисперсии, ковариацию,
коэффициент корреляции, а так-
также ковариационную и коррелл^м-
онную матрицы случайных вели-
величин Х\ и ^2-
*2
0
1
Хх
-1
0,10
0,15
0
0,15
0,25
1
0,20
0,15
7.6. Решение типовых примеров 337
Вычислим математические ожидания и дисперсии случай-
случайных величин Xi иХг:
MXi=(-l)@,10+0,15)+0@,15+0,25)+l@,20+0,15)=0,10,
МХ2 = 0- @,10 + 0,15 + 0,20) +1 • @,15 + 0,25 + 0,15) = 0,55,
DXi = MX2 - (MXiJ = (-1J • @,10 + 0,15) +
+ О2 • @,15 + 0,25) +12 • @,20 + 0,15) - @,10J = 0,59,
DX2 = МХ| - (МХ2J = О2 • @,10 + 0,15 + 0,20) +
+12 • @,15 + 0,25 + 0,15) - @,55J = 0,2475.
Для определения cov(Xi,X2) воспользуемся формулой
cov(XbX2) = M(XiX2) - МХХМХ2.
Тогда
М(ХхХ2) = (-1) • 0 • 0,10 + (-1) • 1 • 0,15 + 0 • 0 • 0,15 +
+ 01-0,25 +10 0,20 + 1-1-0,15) = 0,
cov(XbX2) = 0 - 0,10 • 0,55 = -0,055
= соу№,Х2) = 0,055
г /f-ч \г Т\ V /С\ КЛ (\ ЪЛТК '
/\JX\JX и5Уи^40
Ковариационная и корреляционная матрицы имеют вид
/ 0,59 -0,055 \ / 1 -0,144 \
V ~0,055 0,2475 )' \ -0,144 1 )'
Пример 7.42. Совместная плотность распределения дву
мерной случайной величины (Xi, X2) имеет вид
f о,
338 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Найдем математические ожидания, дисперсии, ковариацию, ко-
коэффициент корреляции, а также ковариационную и корреляци-
корреляционную матрицы случайных величин Х\ и X<i.
Имеем
тг/2 тг/2 тг/2
i=- / x\dx\ I sm(xi+X2)dx2:=:'z I #i(si
oo о
тг/2 тг/2
/ /
= о / Ж2^2 / sin(a;i + X2) dx\ = p
tt/2 tt/2
1 f
1 f
о о
- (MX2J =
тг/2 тг/2
/ j
/
f sm(xx + x2)dx2-^ = 7г2
о
Далее,
тг/2 тг/2
X) = -z I x\dx\ I ff2si
0
7Г/2
= - / a:i(~sina;i H-cos^i — sinxi)da:i = j
0
J
7.6. Решение типовых примеров 339
Наконец, ковариационная и корреляционная матрицы имеют
вид
Чвтг-зг
i —
S =
16
*D-у)
р _ I тг2 + 8тг-32
5 + 8тг-32
Пример 7.43. Совместная плотность распределения дву-
двумерной непрерывной случайной величины (Х\, X2) имеет вид
Проверим, являются ли случайные величины Х\ иХ2 некорре-
некоррелированными.
Найдем
+00+00 +00 +00
[ f 2dd f f xxdxx
++ +
[ f 2xidxidx2 f
-OO-OO
Здесь внутренний интеграл равен нулю, поскольку подынте-
подынтегральная функция нечетная, а пределы интегрирования симме-
симметричны относительно начала координат. Поэтому ЪАХ\ = 0.
Аналогично получаем, что TS/LX2 = 0.
Вычислим теперь ковариацию Х\ и Х2:
солг{ХъХ2) = М(ХгХ2) - MXiMX2 =
+ОО+ОО +ОО +ОО
2Xldx! f X2dX2
++ +
_ [ [ 2xix2dxidx2 _ Г
" J J 1г(х?+^ + 1K"У
оо оо оо
—оо— оо
Поскольку cov(-X"i,X2) = 0, случайные величины Х\ и Х2
являются некоррелированными.
340 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 7.44. Случайные величины Х\ и Х2 имеют мате-
математические ожидания MXi = 2, МХ2 = —1, дисперсии DXi = 3,
DX2 = 4 и ковариацию covpfi, X2) = — 1- Найдем математичес-
математическое ожидание и дисперсию случайной величины
В соответствии со свойствами 2 и 3 математического ожи-
ожидания
MY = 2MXi + (-3)MX2 -5 = 2,
а, согласно свойствам 2 и 5 дисперсии,
DY = 22ВХг + 2 ¦ 2 • (-3)cov(Xb X2) + (-3JDX2 = 60.
Пример 7.45. Трехмерный случайный вектор X имеет век-
вектор средних значений rhg = (—1, 0, 2) и матрицу ковариации
Найдем вектор средних значений и матрицу ковариации слу-
случайного вектора Y = ХВ + с, где
с =A,13).
Используя правило изменения вектора средних значений при
линейном преобразовании случайного вектора, получаем
, 13) = A, 2).
с={-\, 0, 2) 1 5
7.6. Решение типовых примеров 341
Аналогично в силу утверждения 2 теоремы 7.4 имеем
'"-(iii)(-i:)G3-e*>-
Пример 7.46. Для случайной величины X, имеющей
распределение Релел с параметром 71 > найдем а-квантиль,
медиану, моды и наиверолтпнейшее значение.
Функция распределения Релея имеет вид
^ 1 е , х ^ и.
Поэтому а-квантиль Qa определяется из уравнения
т.е.
QaV
Поскольку медиана М является 1/2-квантилью, то
7
Плотность распределения Релея
О, х < 0;
= Г
является дифференцируемой функцией (кроме точки х = 0)
причем
342 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Значение х = 0 не является модой, так как р@) = 0. Поэтому
любая мода удовлетворяет уравнению
Решая это уравнение, имеем
При хо достигается как локальный, так и глобальный максимум
плотности распределения Релея, а значит, хо является как един-
единственной модой, так и наивероятнейшим значением случайной
величины X.
Таблица 7.5
Пример 7.47. Распределение вероятностей двумерной дис-
дискретной случайной величины (Хх, Х2)
задано табл. 7.5. Найдем энтропии
скалярных случайных величин Х\ и
X<i, а также энтропию двумерной слу-
случайной величины (-Xi, X*i). Являются
ли случайные величины Х\ и X2 неза-
независимыми?
Случайные величины Х\ и Х^ имеют ряды распределения,
представленные в табл. 7.6 и 7.7.
х2
-2
-1
Хх
-2
од
0,2
-1
0,2
од
0
0,3
0,1
p
Таблица 7.6
-2
0,3
-1
0,3
0
0,4
Таблица 7.7
x2
P
-2
0,6
-1
0,4
В соответствии с определением энтропии дискретной слу-
случайной величины
Н(Хх) = -X^PXxilogpxxt = -@,31ogO,3 +
г
+ 0,3 log 0,3 + 0,4 log 0,4) = log 5 + 0,2 log 2 -0,6 log 3,
= Iog5 - 0,41og2 - 0,61og3.
7.6. Решение типовых примеров 343
Энтропия двумерного случайного вектора (Х\9 Х2) равна:
H(XUX2) = -
- @,1 logO,l + 0,21ogO,2 + 0,31ogO,3 + 0,21ogO,2 +
Производя простые арифметические подсчеты, получаем
Поскольку энтропия Н(Х\,Х2) меньше суммы энтропии Н{Х\)
и Н(Х2), то случайные величины Х\ и Х2 являются зависи-
зависимыми.
Пример 7.48. Двумерная случайная величина (Xi, X2)
имеет нормальное распределение со средними значениями т\
и ГП2, дисперсиями aj и а! и коэффициентом корреляции р, т.е.
т|
/J
Найдем энтропии случайных величин Xi и Хг, а также
энтропию случайного вектора (Xiy X2)- В каком случае
энтропия случайного вектора (Xi, X2) совпадает с суммой
энтропии случайных величин Х\ и Х21
Поскольку случайная величина Х\ имеет нормальное рас-
распределение со средним значением mi и дисперсией <т2, т.е.
344 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
то, согласно определению энтропии непрерывной случайной
величины,
+00
H(Xi) = - / pXl(x)logpXl(x)dx =
—00
+ОО +00
= logJ2ira% / <pmu*1(x)dx + —T / {x-miJ<pmuai(x)dx.
v J *°l J
—00 — OO
В записанной формуле первый интеграл равен единице как
интеграл от плотности распределения, а второй — дисперсии
случайной величины Х\. Значит,
Н(Хг) = log yj 2ъа\ + -|- = log yj 2-кеа\.
Аналогично
Н(Х2) = log у2тгесг|.
Энтропия двумерного случайного вектора (J\Ti, X2) равна:
+ОО
H(Xi,X2) = - / рх1у
—оо
= log ( 2па\ С2 л/l — р2) \
+00
loge Г
+ 2а?A~^)У [Xl
+00
-00
+00
—00
+00
/9 log e /*
— г- / (д?! — 77li)(iE?2—^2)^X1 Х2\X\4X2)dx\ С?Х2 +
<71СГ2A — /9Z) У
+00
(lg~p2) J ^"
-00
Вопросы и задачи 345
Здесь первый интеграл равен единице, второй и четвертый —
дисперсиям случайных величин Х\ и Хъ соответственно, а
третий — ковариации Х\ иХг- Таким образом,
H(XuX2) = \og
p2loge
Нетрудно видеть, что энтропия Н(Х\,Х2) равна сумме
энтропии Н(Х\) и Н{Х2) тогда и только тогда, когда р = 0.
Значит, из условия некоррелированности случайных величин
Xi и А*2 вытекает их независимость. Этот результат нам уже
известен из 5.5.
Вопросы и задачи
7.1. Что называют математическим ожиданием дискретной
случайной величины? В каком случае существует математиче-
математическое ожидание дискретной случайной величины, принимающей
счетное число значений?
7.2. Что называют математическим ожиданием непрерыв-
непрерывной случайной величины? В каком случае существует матема-
математическое ожидание непрерывной случайной величины?
7*3. Как можно вычислить математическое ожидание функ-
функции от скалярной случайной величины?
7Л. Как можно вычислить математическое ожидание функ-
функции от многомерного случайного вектора?
7.5. Перечислите свойства математического ожидания слу-
случайной величины.
7.6. В каком случае математическое ожидание суммы слу-
случайных величин равно сумме математических ожиданий слага-
слагаемых?
346 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
7.7. В каком случае математическое ожидание произведе-
произведения случайных величин равно произведению математических
ожиданий сомножителей? Является ли независимость случай-
случайных величин необходимым условием для того, чтобы матема-
математическое ожидание произведения случайных величин равнялось
произведению математических ожиданий?
7.8. Что называют вектором средних значений (вектором
математических ожиданий) случайного вектора? Как изменя-
изменяется вектор средних значений при линейном преобразовании
случайного вектора?
7.9. Что называют вторым (начальным) моментом случай-
случайной величины?
7.10. Что называют дисперсией случайной величины?
7.11. Что называют средним квадратичным отклонением
случайной величины?
7.12. Перечислите свойства дисперсии случайной величины.
7.13. В каком случае дисперсия суммы случайных величин
равна сумме дисперсий слагаемых?
7.14. Что называют начальным моментом Л-го порядка
случайной величины?
7.15. Что называют центральным моментом fc-ro порядка
случайной величины?
7.16. Что называют ковариацией случайных величин?
7.17. Перечислите свойства ковариации случайных вели-
величин?
7.18. Как называют случайные величины, ковариация кото-
которых равна нулю?
7.19. Напишите формулу для дисперсии суммы произволь-
произвольных случайных величин.
Вопросы и задачи 347
7.20. Что называют ковариационной матрицей случайного
вектора? Перечислите свойства ковариационной матрицы.
7.21. Приведите достаточное условие, при котором слу-
случайные величины являются некоррелированными. Можно ли
сказать, что если случайные величины являются некоррелиро-
некоррелированными, то они также являются независимыми?
7.22. Что называют коэффициентом корреляции случайных
величин?
7.23. Перечислите свойства коэффициента корреляции слу-
случайных величин.
7.24. В каких пределах может изменяться коэффициент
корреляции случайных величин?
7.25. Приведите условие, необходимое и достаточное для
равенства коэффициента корреляции случайных величин ±1.
7.26. Что называют матрицей корреляций случайного век-
вектора?
7.27. Что называют асимметрией случайной величины?
7.28. Что называют эксцессом случайной величины?
7.29. Что называют а-квантилью случайной величины?
7.30. Что называют модой дискретной случайной величи-
величины? Какую дискретную случайную величину называют унимо-
унимодальной? бимодальной? мультимодальной?
7.31. Что называют наивероятнейшим значением дискрет-
дискретной случайной величины?
7.32. Что называют модой непрерывной случайной вели-
величины? Какую непрерывную случайную величину называют
унимодальной? бимодальной? мультимодальной?
7.33. Что называют наивероятнейшим значением непрерыв-
непрерывной случайной величины?
X
р
1
0,30
2
0,21
3
0,49
348 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
7.34* Что называют энтропией дискретной скалярной слу-
случайной величины?
7.35. Что называют энтропией дискретной двумерной слу-
случайной величины? В каком случае энтропия дискретной дву-
двумерной случайной величины равна сумме энтропии координат?
7.36. Что называют энтропией непрерывной случайной
величины?
7.37. Что называют энтропией непрерывной двумерной слу-
случайной величины? В каком случае энтропия непрерывной дву-
двумерной случайной величины равна сумме энтропии координат?
_ _, „ о 7.38. Найдите математическое ожи-
Таблица 7.8
дание, дисперсию и среднее квадратич-
квадратичное отклонение дискретной случайной
величины X, ряд распределения кото-
которой представлен в табл. 7.8.
Ответ: MX = 2,19, DX = 5,55, а « 2,35.
7.39. Вероятность того, что при трех выстрелах стрелок
попадет в цель хотя бы один раз, равна 0,992. Найдите
математическое ожидание и дисперсию числа X попаданий при
двадцати выстрелах.
Ответ: MX = 16, DX = 3,2.
7.40. Время X безотказной работы станка имеет экспонен-
экспоненциальное распределение. Известно, что вероятность отказа
станка за 5 ч равна 0,39347. Найдите математическое ожи-
ожидание, дисперсию и среднее квадратичное отклонение времени
безотказной работы станка.
Ответ: MX = 10 ч, DX = 100 ч2, а = 10 ч.
7.41. Найдите математическое ожидание, дисперсию, сред-
среднее квадратичное отклонение, асимметрию, эксцесс, а-квантиль,
медиану, моды и наивероятнейшее значение случайной величи-
величины X, имеющей плотность распределения р(х) = е"'х"''2.
Ответ: МХ = 3, DX = 2, a = y/2,<yl =0,72 = 3, Qa = 3 + lnBa),
если а ^ 1/2 и Qa = 3 - lnB(l - а)), если а > 1/2, М = 3.
Вопросы и задачи
349
Случайная величина имеет единственную моду и наивероятней-
шее значение xq = 3.
7.42. Непрерывная случайная величина X имеет плотность
распределения
О, х ? (о, Ь);
Р(х) = 4 2 4
х —
х е (о, 6),
причем а и Ь не известны, но Ь > a, a TAX = 5 и "DX = 6. Найдите
а и Ь.
Ответ: а = —1, Ь= 11.
7.43. Каждый из 25 студентов группы выучил 80% экзаме-
экзаменационных билетов. Найдите среднее число студентов, сдавших
экзамен.
Ответ: 20.
7.44. Независимые случайные величины Х\ и Хч имеют
экспоненциальное распределение с параметрами Ai и Л2 со-
соответственно. Найдите математическое ожидание случайной
величины У = X\X*i-
Ответ: MY = l/(AiA2).
7.45. Дискретная случайная величина X имеет ряд распре-
распределения, представленный в табл. 7.9.
Найдите математическое ожидание
и дисперсию случайной величины
Таблица 7.9
X
р
1
0,1
2
0,4
3
0,3
4
0,2
Ответ: MY = 2,6, DY = 0,84.
7.46. Площадь круга вычисляют по измеренному диаметру
круга X, используя формулу 5 = тсХ2/А. Считая, что измерен-
измеренный диаметр круга X распределен равномерно на отрезке [о, Ь],
найдите математическое ожидание и дисперсию случайной ве-
величины S»
Ответ: MS = тг(о2 + ab + 62)/12, D5 = тг2F - аJDа2 + lab +
+ 462)/720.
350 7, ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Таблица 7.10
0
1
Хх
-1
од
0,2
0
0,2
0,3
1
0
0,20
7.47, Закон распределения ве-
вероятностей двумерной дискретной
случайной величины (Xi, Х2) пред-
представлен табл. 7.10. Найдите мате-
математическое ожидание и дисперсию
случайной величины У = Х^ + 2X2*
Ответ: MY = 1,9, BY = 1,29.
7.48. Двумерная случайная величина (Ai, X2) распределена
равномерно в квадрате {0 < х\ < 1, 0 < Х2 < 1}. Найдите мате-
математическое ожидание и дисперсию площади У прямоугольника
со сторонами Х\ и Х^-
Ответ: MY = 1/4, BY = 7/144.
7.49. Плотность распределения непрерывной случайной ве-
величины X имеет вид
а; $< (-М);
* 6 (-1,1).
Найдите начальные и центральные моменты первого, второго,
третьего и четвертого порядка, а также асимметрию и эксцесс
случайной величины X.
Ответ: т\ = т\ = 0, гп2 = Ш2 = DX = 1/5, шз = тз = 0, 7714 =
= т4 = 3/35, 71=0, 72 = ~
7.50. Изготавливаемые в цехе втулки сортируют по откло-
отклонению их внутреннего диаметра от номинального размера на
четыре группы со значениями 0,01, 0,02, 0,03 и 0,04 мм и по
овальности на четыре группы со значениями 0,002, 0,004, 0,006
и 0,008 мм. Совместное распределение вероятностей откло-
отклонения диаметра Х\ и овальности Х2 представлено табл. 7.11.
Найдите математические ожидания, дисперсии, ковариацию,
коэффициент корреляции, а также ковариационную и корре-
корреляционную матрицы случайных величин Х\ иХг-
Вопросы и задачи
351
Таблица 7.11
0,002
0,004
0,006
0,008
Х\
0,01
0,01
0,03
0,04
0,02
0,02
0,02
0,24
0,10
0,04
0,03
0,04
0,15
0,08
0,03
0,04
0,4
0,06
0,08
0,02
Ответ: MXi = 0,026 мм, МХ2 = 0,005 мм, BXi = 81 х
х 10~5 мм2, ШГ2 = 4 • Ю-6 мм2, cov(XuX2) = 254 • 10~5 мм2,
-5 254-10~5
0-ь 4.10-б
(XuX2) = 254 10
_ / 1 0,41 \
'Р=[о,41 1 J'
7.51. Совместная плотность распределения двумерной не-
непрерывной случайной величины (Х\, Х2) имеет вид
0, х\ ^ 0 или Х2 < 0;
(x*+x*\ xi > 0 и х2 > 0.
у
Г
\
Найдите математические ожидания, дисперсии, ковариацию,
коэффициент корреляции, а также ковариационную и корре-
корреляционную матрицы случайных величин Х\ и Х2-
Ответ:
= МХ2 =
= D - тг)/4,
\ О D-ir)/4y \О 1/
7.52. Совместная плотность распределения двумерной не-
непрерывной случайной величины (Х\, Х2) имеет вид
х\ ^ 0 или х2 ^ 0;
Х\ > 0 И Ж2 > 0,
352 7. ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Проверьте, являются ли случайные величины Х\ и X<i
некоррелированными.
Ответ: да, являются.
7*53. Случайные величины Х\ и X*i имеют математические
ожидания У1Х\ = —5, М-Х2 = 2, дисперсии ТЬХ\ = 0,5, D-Хг =
= 0,4 и ковариацию cov(Xi,X2) = 0,2. Найдите математическое
ожидание и дисперсию случайной величины Y = \Х\ — ЬХ% + 25.
Ответ: MY = -5, DY = 10.
7.54. Найдите математические ожидания, дисперсии и ко-
ковариацию случайных величин Y\ и Y2, где Yi = 3Xi — 2X2,
I2 = 5X2 — -Xi, а случайные величины Х\ и X*i имеют следую-
следующие числовые характеристики: ЪИХ\ = —0,5, ЪАХг = 1, DXi = 3,
DX2 = 2,9, cov(JfbX2) = 2.
Ответ: MYi =-3,5, MY2 = 5,5, DYi = 14,6, DY2 = 50,5,
cov(YbY2) = -4.
7.55. Двумерный случайный вектор X имеет вектор сред-
средних значений rhg = @,06, 0,08) и матрицу ковариаций S^ =
/0,2 0,3\ „ u
= I n q пс • Найдите вектор средних значении и матрицу ко-
вариаций случайного вектора Y = XВ + с, где В = I J,
а с = @, -0,1, -0,2).
/1,0 1,1 1,2>
Ответ: mf = @,10, 0,04, -0,02), Е? = 1,1 1,3 1,5
\1,2 1,5 1,8,
7.56. Для непрерывной случайной величины X, имеющей
плотность распределения
найдите а-квантиль, медиану, моду и ее наивероятнейшее
значение.
Вопросы и задачи
353
Ответ: Qa = 2tg(?rBa - 1)/2) + 3, М = 3. Случайная величи-
величина X имеет единственную моду и наивероятнейшее значение
-0,19
12,24
Xi
-0,5
0,08
0,12
0,34
0,12
0,18
1,48
0,20
0,30
7.57. Распределение вероятностей двумерной дискретной
случайной величины (Xi, X2)
задано табл. 7.12. Найдите эн- Таблица 7.12
тропии скалярных случайных
величин Х\ и Х2, а также эн-
энтропию двумерного случайно-
случайного вектора (Xi, X2). Являют-
Являются ли случайные величины Х\
и Х2 независимыми?
Ответ: Н(Хг) = 0,5log5 + 0,8log2-0,3log3, #(X2) = log5-
-0,41og2-0,61og3, #(ХЬХ2) = 1,5 log 5+ 0,4 log 2-0,9 log 3.
Случайные величины Х\ и Х2 являются независимыми.
7.58. Двумерная непрерывная случайная величина (Xi, X2)
имеет совместную плотность распределения
0, х\ ^ 0 или Х2 ^ 0;
ГЛ1Ж1"Л2Х2, Ж1>0их2>0.
Найдите энтропии скалярных случайных величин Х\ и Х2,
а также энтропию двумерного случайного вектора (Xi, X2).
Являются ли случайные величины Х\ и Х2 независимыми?
Ответ: #(Xi) = lqg(e/Ai), #(Х2) = log(e/A2), Я(ХьХ2) =
= log(e2/(AiA2)). Случайные величины Х\ и Х2 являются
независимыми.
У212 - 10047
8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ
СЛУЧАЙНЫХ ВЕЛИЧИН
Одним из основных понятий теории вероятностей является
понятие условной вероятности, введенное в гл. 3. Там же
было показано, что условная вероятность "Р(А\В) обладает
всеми свойствами безусловной вероятности и так же, как и
безусловная вероятность, представляет собой численную меру
наступления события -А, но только при условии, что событие
В произошло.
Аналогом понятия условной вероятности для двух случай-
случайных величин X и Y является условный закон распределения
одной из них, допустим, X при условии, что вторая случайная
величина Y приняла определенное значение. С помощью услов-
условного закона распределения вводят условные числовые характе-
характеристики. Именно эти понятия и рассматриваются в настоящей
главе.
8.1. Условные распределения
Понятие условного распределения, как обычно, введем толь-
только для случаев дискретных и непрерывных случайных величин.
В случае двумерной дискретной случайной величины (X, Y)
будем предполагать для простоты изложения, что множества
возможных значений случайных величин X и Y являются
конечными, т.е. координаты X и Y принимают значения ж»,
г = 1, гс, и yj, j = l,m, соответственно. В этом случае, как
мы знаем, закон распределения двумерного случайного вектора
(X, Y) удобно задавать набором вероятностей
8.1. Условные распределения 355
для всех значений г и j. Напомним, что, зная вероятности
Pij, нетрудно найти (см. 5*2) законы распределений каждой из
координат по формулам
т
pXi = P{X = Xi} =
Определение 8.1. Для двумерной дискретной случайной
величины (Xj У) условной вероятностью эту, г = 1, n, j =
= 1, ш, того, что случайная величина -X* примет значение Х{
при условии У = j/j, называют условную вероятность события
= х*} при условии события {У = j/j}, т.е.
)^ (в..)
При каждом j, j = l,m, набор вероятностей тт^-, г = 1,п,
определяет, с какими вероятностями случайная величина X
принимает различные значения х^ если известно, что случай-
случайная величина У приняла значение у у Иными словами, набор
вероятностей 7Гу, t = 1, п, характеризует условное распреде-
распределение дискретной случайной величины X при условии У = j/j.
Обычно условное распределение дискретной случайной ве-
величины X при условии, что дискретная случайная величина У
примет все возможные значения, задают с помощью табл. 8.1.
Элементы щ$ табл. 8.1 получают из элементов табл. 5.1, исполь-
используя формулу
Pij
Очевидно, что, наоборот, элементы табл. 5.1 можно выразить
через элементы табл. 8.1 с помощью соотношения
Pij =
У212*
356 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Для проверки правильности составления табл. 8.1 рекомен-
рекомендуется просуммировать 7Г^ по столбцам. Сумма элементов
последней строки должна быть равна 1.
Таблица 8.1
X
XI
х2
хп
Ру
Y
2/1
7Гц
7Г21
7ГП1
PY1
2/2
7Г12
7Г22
7Гп2
PY2
...
...
Ут
Kim
К2т
Кпт
PYm
Рх
Рхг
РХ2
РХп
Аналогично определяют условную вероятность тг*«- того, что
случайная величина У примет значение yj при условии X = ж»:
Таблица 8.2
0
1
Рх2
0
Я
р
я
1
я
р
р
р*
Р
Пример 8.1. Условное распре-
распределение числа Х\ успехов в первом
испытании по схеме Бернулли (см.
пример 5.4) при условии, что чи-
число успехов во втором испытании
Х2 = j, j = 0,1, задается табл. 8.2.
Из этой таблицы следует, что, не-
независимо от числа успехов во вто-
втором испытании, 0 или 1 успех в первом испытании происходит с
одними и теми же вероятностями puq. Это очевидно, посколь-
поскольку испытания по схеме Бернулли являются независимыми.
Пример 8.2. Условное распределение случайной величины
X (числа очков, выпавших на верхней грани игральной кости,
см. пример 5.5) при условии Y = yj (числа очков, выпавших
на нижней грани игральной кости), j = 1, 6, представлено в
табл. 8.3. Действительно, если, например, на нижней грани
8.1. Условные распределения
357
выпало одно очко, то на верхней грани может выпасть только
шесть очков (тгб1 = 1). #
Таблица 8.3
X
1
2
3
4
5
6
Ру
Y
1
0
0
0
0
0
1
1/6
2
0
0
0
0
1
0
1/6
3
0
0
0
1
0
0
1/6
4
0
0
1
0
0
0
1/6
5
0
1
0
0
0
0
1/6
6
1
0
0
0
0
0
1/6
Рх
1/6
1/6
1/6
1/6
1/6
1/6
В общем случае (т.е. когда 1иУне обязательно дискрет-
дискретные случайные величины) хотелось бы ввести условную функ-
функцию распределения случайной величины X при условии У = у
по формуле
P{X<x,Y = ;
(8.2)
Однако это не всегда возможно (например, для непрерывной
случайной величины У событие {У = у} имеет нулевую веро-
вероятность, т.е. Р{У = у} = 0). Поэтому воспользуемся предель-
предельным переходом, рассматривая вместо события {У = у} событие
{у ^ У < у + Д} и устремляя Д к нулю.
Ограничимся случаем, когда двумерный случайный вектор
(X, У) имеет непрерывную совместную плотность распреде-
распределения р(ж,у), а следовательно (см. 5.3), и маргинальные плот-
плотности распределения
+ОО +00
Рх(х) = I p(x,y)dy и pY(y) = I p(x,y)dx,
-00
которые также будем считать непрерывными.
12- 10047
358 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Определим условную вероятность события {X < х} при
условии события {у ^ Y < у + Ау}:
у+Ау х
Г dv f p(u,v)du
У
Можно показать, что в силу сделанных предположений
х
функция f p(u,v)du является непрерывной. Поэтому, соглас-
—оо
но теореме о среднем значении [VI],
у+Ау х х
I dv I p(u,v)du = Ay I p{u,?)du,
у -оо -оо
/ PY(v)dv=pY{rj)Ay
У
и, следовательно,
PY(V) '
где ? и т/ — некоторые числа, заключенные между у и у + Ау.
Устремляя теперь Ау к нулю, получаем следующие выраже-
выражения для условной функции распределения Fx(x\Y = y):
х
I P(u,y)du
Fx(x\Y = у) = lim P{X < х\у < У < у + Ау} = -г
8.1. Условные распределения 359
Таким образом, по определению, имеем
X
Fx(x\Y = у) = ^ Ip(u,y)du. (8.3)
При сделалных предположениях о непрерывности случайно-
случайного вектора (X, У) условная функция распределения Fx(x\Y = у)
имеет производную по #, т.е. существует условная плотность
распределения случайной величины X при условии У = у:
Аналогично определяют условную функцию распределения
Fy(y\X = х) и условную плотность распределения ру(у\Х = х)
случайной величины Y при условии X = х:
у
FY(y\X = х) = ^у | p(*,<;)di;, (8.4)
Для краткости далее вместо рх (я|У = у) и ру (у\Х = х) будем
писать рх(х\у) ъру(у\х).
Итак, для непрерывного случайного вектора (X, Y) мы при-
пришли к следующему определению условной плотности распреде-
распределения.
Определение 8*2. Условной плотностью распреде-
распределения случайной величины X, являющейся координатой дву-
двумерного случайного вектора (X, У), при условии, что другая
его координата приняла некоторое фиксированное значение у,
т.е. Y = у, называют функцию Рх{х\у), определяемую соотно-
соотношением
Ш
360 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Аналогично определяют условную плотность распределения
PY(у\х) координаты Y при условии X = х:
Введенные понятия — условное распределение (дискретной
случайной величины), условная функция распределения и услов-
условная плотность распределения (для непрерывных случайных ве-
величин) — называют условными законами распределения.
Смысл введенных понятий поясним на примерах.
Пример 8.3. Пусть двумерный случайный вектор (X, Y)
имеет нормальное распределение с вектором средних значений
(mi, ГП2) и матрицей ковариаций
/ а{ рага2
V рохо2 <т2
\
J
Найдем условную плотность распределения случайной величи-
величины X при условии У = у.
Как известно (см. 5.5), совместная двумерная плотность
распределения случайных величин X и Y
Рх,г(х,у) =
== х
y/l — P
ч,^/ 1 ((х-miJ 2p(s-mi)(y-m2) . (y-m2J
ХеХР\ 2(l-p»)V о\ *х*2 ^ *\
а маргинальная плотность распределения случайной величины Y
8.1. Условные распределения 361
Значит,
Таким образом, условное распределение X при условии Y = у
также является нормальным со средним значением (которое
обозначим д{у))
^ (8.7)
и средним квадратичным отклонением (обозначим его &х\у)
(8.8)
Аналогично условное рапределение Y при условии X = х
является нормальным со средним значением (которое обозна-
обозначим h(x))
h(x) = га2 + р—(ж - mi) (8.9)
и средним квадратичным отклонением (обозначим его сгу|х)
aY\x = (J2\/l-p2- (8.10)
Для того чтобы дать наглядную интерпретацию получен-
полученного результата, обратимся к примеру 5.24, в котором ко-
координаты Х\ и Х2 двумерного случайного вектора (Xi, X2)
представляют собой рост и вес жителя страны Нормалии.
Пусть известно, что вес случайно встреченного нормальца
равен Х2. Тогда его рост будет иметь нормальное распределе-
распределение со средним значением (в см)
. ,„ +
V40
362 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
и средним квадратичным отклонением
-0,662 « 5,0.
= 1 _c-fei -120-0 Jxa)a/50>
Таким образом,
В частности, весу 70 кг соответствует среднее значение роста
169 см, весу 75 кг — около 173 см и т.д.
Отметим, что в отличие от среднего роста д(х2), завися-
зависящего линейно от #2, среднее квадратичное отклонение роста
аХ\\х2 является постоянным, т.е. не зависит от х2.
Графическое изображение зависимости роста от веса при-
приведено на рис. 8.1. Здесь по оси абсцисс отложены значения
роста нормальца, а по оси ординат — его веса. Прямая ли-
линия х\ = д(х2) показывает зависимость среднего роста от веса.
Условная плотность распределения pxi(x\\x2) роста, как функ-
функции от веса х2, изображена в виде „срезов".
х2, кг
xlf см
190
180
170
160
0 160 170 180 190 xltCM 0 60 70 80 90 х2, кг
Рис. 8.1 Рис. 8.2
Аналогичные вычисления показывают, что условная плот-
плотность распределения px2(x2\xi) веса нормальца Х2 в зависимо-
зависимости от его роста х\ является плотностью нормального распре-
распределения с параметрами
h{xx) « 0,62zi - 33 и аХ2\Х1 « 4,8,
8.1. Условные распределения 363
т.е. имеет вид
Графическое изображение зависимости веса от роста при-
приведено на рис. 8.2.
Пример 8.4. Пусть случайные величины Х\ и Хч предста-
представляют собой координаты точки падения частицы, случайным
образом брошенной в круг радиуса R с центром в начале ко-
координат (см. пример 5.6). Случайный вектор (Х\, Хч) имеет
плотность распределения
=Ц
Найдем условную плотность распределения абсциссы Х\
точки падения частицы при условии, что ордината Хч приняла
значение хч- Поскольку маргинальная плотность распределения
Рх2(х2) случайной величины Хч имеет вид
¦{
О, \х2\ > Л;
получаем при \хч\ < R:
Ш
Таким образом, случайная величина Х\ при условии Х% = Х2
равномерно распределена на отрезке [— y/R2 — х\, y/R2 — х\].
Если |#21 > -R, то условная плотность распределения рх\{х\\хг)
не определена; но это нас не должно волновать, поскольку
случайная величина Хч не может принимать значения, по
абсолютной величине большие R. #
364 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Для проверки независимости случайных величин часто
удобно пользоваться следующим критерием.
Критерий независимости случайных величин X и Y.
Случайные величины X и Y являются независимыми тогда и
только тогда, когда условное распределение (функция распре-
распределения, плотность распределения) случайной величины X при
условии Y = у совпадает с безусловным распределением (функ-
(функцией распределения, плотностью распределения) случайной ве-
величины X.
В частности, дискретные величины X и Y являются незави-
независимыми тогда и только тогда, когда все условные вероятности
совпадают с безусловными вероятностями
т.е. все столбцы табл. 8.1 совпадают с последним.
Пример 8.5. В двух испытаниях по схеме Бернулли
(см. пример 8.1) числа успехов Х\ и X<i в первом и втором
испытаниях являются независимыми случайными величинами,
поскольку в табл. 8.2 все три столбца совпадают. Этот факт
нами уже был установлен другим способом в примере 5.9.
Пример 8.6. Число очков X, выпавших на верхней гра-
грани игральной кости, и число очков У — на нижней грани (см.
пример 8.2) — зависимые случайные величины, поскольку во-
вообще ни один из первых шести столбцов табл. 8.3 не совпадает
с последним.
Пример 8.7. Условная плотность распределения случайной
величины Х\ (абсциссы точки падения при равномерном бро-
бросании частицы в круг, см. пример 8.4) при условии Х2 = #2
(ординаты точки падения) равномерна, в то время как без-
безусловная плотность Х\ таковой не является. И в этом примере
Х\ и X2 зависимые случайные величины.
8.2. Условные числовые характеристики 365
8.2. Условные числовые характеристики
Рассмотрим двумерную случайную величину (X, У). В со-
соответствии с результатами предыдущего параграфа можно
определить условное распределение случайной величины X при
условии, что случайная величина У приняла определенное зна-
значение у. Поскольку условное распределение обладает всеми
свойствами обычного (безусловного) распределения, то по не-
нему можно определить математическое ожидание, дисперсию и
другие числовые характеристики, которые естественно назвать
условными.
Начнем со случая дискретной случайной величины (X, У).
Пусть случайная величина X принимает значения Я1,...,жп, а
случайная величина У — значения yi,... ,ym и пусть
условные вероятности случайной величине X принять значение
Xi При УСЛОВИИ Y = yj.
Определение 8.3, Для дискретной двумерной случайной
величины (JC, У) значением М(Х|У = yj) условного мате-
математического ожидания дискретной случайной величины X
при условии У = j/j, называют число
г=1
Далее для краткости будем писать M(X\yj) вместо
По аналогии с (безусловным) математическим ожиданием
случайной величины X значение b/l(X\yj) условного ма-
математического ожидания при условии У = yj задает „среднее"
366 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
значение случайной величины X, но при условии, что случайная
величина У приняла значение у у
Таким же образом интерпретируют значение М(У|а^) =
= M(Y\X = Х{) условного математического ожидания случай-
случайной величины Y при условии X = х%.
Согласно определению 8.3, значение M(X|j/j) условного
математического ожидания зависит от значения yj случайной
величины У, и только от него. Вспоминая понятие функции
от случайной величины, приходим к следующему определению
условного математического ожидания.
Определение 8.4. Условным математическим ожи-
ожиданием M(X\Y) дискретной случайной величины X относи-
относительно дискретной случайной величины У называют функцию
M(X\Y)=g(Y)
от случайной величины У, где область определения функции
д(у) совпадает с множеством значений j/i, ..., ут случайной
величины У, а каждому значению yj аргумента у поставлено в
соответствие число
g(yj) = M(X\yj).
Подчеркнем еще раз, что условное математическое ожида-
ожидание М(Х|У) является функцией от случайной величины, т.е.
также случайной величиной.
Приведем примеры.
Пример 8.8. Пусть Х\ и Х2 — числа успехов в первом и
втором испытаниях по схеме Бернулли с вероятностью успеха
р. Найдем M(-X"i|-X2). Используя табл. 8.2, получаем:
8.2. Условные числовые характеристики 367
Таким образом, значения M(Xi|0) и M(A"i|l) условного
математического ожидания совпадают для обоих значений О
и 1 случайной величины Х2 и равны р. Поэтому
М(Х1\Х2)=р.
Пример 8.9. Найдем условное математическое ожидание
M(X\Y) случайной величины X — числа очков, выпавших
на верхней грани игральной кости, относительно случайной
величины У — числа очков, выпавших на нижней грани (см.
пример 8.2). В соответствии с табл. 8.3
= 1-0 + 2.0 + 3 -0 + 4- 0 + 5 -0 + 6-1 = 6,
М(Х|2) = 1-0 + 2.0 + 3.0 + 4.0 + 5-1 + 6.0 = 5,
1.1 + 2.0 + 3.0 + 4.0 + 5.0 + 6.0 = 1.
Полученный результат в терминах условного математиче-
математического ожидания можно записать в виде
Теорема 8.1. Условное математическое ожидание М(Х|У)
обладает следующими свойствами.
1. М(с|У) = с.
2.
3.
4. Пусть случайные величины Х\ и Х2 являются независи-
независимыми при условии, что случайная величина У приняла любое
конкретное значение. Тогда M(XiX2\Y) = M(Xi\Y)M(X2\Y)
(это утверждение мы приводим без доказательства).
5. МХ = М(М(Х|У)).
6. Пусть и(Х) и v(Y) — функции от случайных величин X
и У. Тогда M(u(X)v(Y)\Y) = v(Y)M(u(X)\Y).
368 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
7. Если X и Y — независимые случайные величины, то
M(X\Y) = MX.
< Утверждения 1-3 доказываются совершенно аналогично
тому, как это делалось для безусловного математического ожи-
ожидания (разумеется, арифметические действия нужно понимать
уже не как действия над числами, а как действия над функция-
функциями, определенными для всех значений случайной величины Y).
Докажем последние три утверждения.
Действительно, в силу определений математического ожи-
ожидания и условного математического имеем
M(M(X\Y)) =f
m n n m
что доказывает утверждение 5.
Далее, случайная величина u(X)v(Y) принимает значение
u(xi)v(yj)j когда X принимает значение Х{ и Y — значение у^,
и, следовательно, для каждого j
*
M{u(X)-v(Y)\yj) =
г=1
откуда вытекает утверждение 6.
Наконец, используя условие независимости случайных вели-
величин X и У, выраженное в терминах условного распределения
(см. 8.1), находим
откуда следует справедливость утверждения 7.
8.2. Условные числовые характеристики 369
Пример 8.10. Еще раз вычислим Ъ/1(Х\\Х2) (см. при-
пример 8.8), но теперь уже воспользуемся свойством 7 условного
математического ожидания. Тогда, поскольку Х\ и X*i — не-
независимые случайные величины, то
Пример 8.11. Снова обратимся к примеру 8.9. Так
как сумма очков на противоположных гранях игральной кости
равна 7, то X = 7 — У. Представим X в виде
Используя теперь свойство 6, в котором положено и(х) = 1,
v(у) = 7 — у, и свойство 1, получим
т.е. мы пришли к тому же результату, что и раньше, но
практически без вычислений. #
Перейдем теперь к двумерной непрерывной случайной вели-
величине.
Определение 8.5. Для непрерывной двумерной случайной
величины (X, У) значением Ы(Х\у) = М(Х|У =s у) условно-
го математического ожидания непрерывной случайной
величины X при условии У = у называют число
+оо
ЪЛ{Х\у)= jxpx(x\y)dx,
где
является условной плотностью распределения случайной вели-
величины X при условии Y = у.
370 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Определение 8.6. Для непрерывной двумерной случайной
величины (X, У) условным математическим ожиданием
M(X\Y) непрерывной случайной величины X относительно
случайной величины У называют функцию g(Y) = М(Х|У) от
случайной величины У, принимающую значение д(у) = М(Х\у)
при Y = у.
Проверьте самостоятельно, что свойства условного мате-
математического ожидания, выведенные для дискретного случая,
справедливы и для непрерывного (исключение составляет свой-
свойство 1, поскольку непрерывная случайная величина не может
принимать всего одно значение).
Резюмируя изложенное выше, можно сказать, что зависи-
зависимость поведения „в среднем" случайной величины X от значе-
значения случайной величины Y характеризуется функцией д(у) =
= М(Х\у).
Определение 8.7. Функцию д(у) называют функцией
регрессии, или просто регрессией, случайной величины X
на случайную величину У, а ее график — линией регрессии
случайной величины X на случайную величину У, или просто
X на У.
Линия регрессии графически изображает зависимость
„в среднем" случайной величины X от значения случайной
величины У.
Совершенно аналогично определяют значение М(У \х) услов-
условного математического ожидания случайной величины У при
условии X = х и условное математическое ожидание М(У \Х) =
= h(X). При этом функцию h(x) называют функцией регрес-
регрессии, или просто регрессией, случайной величины У на случай-
случайную величину X, а ее график — линией регрессии У на X.
Линия регрессии У на X графически изображает зависимость
„в среднем" случайной величины У от значения случайной ве-
величины X.
8.2. Условные числовые характеристики 371
Пример 8.12. Пусть (X, Y) — двумерная случайная вели-
величина, имеющая нормальное распределение. Как было показано
в примере 8.3, условное распределение X при условии Y = у
является нормальным со средним значением
Следовательно, согласно определению математического ожида-
ожидания, имеем
•K/r(Y\v\ ™ , p<Ti(Y-m2)
М(ЛГ) = 7711 Н ?
02
т.е. линия регрессии случайной величины X на случайную
величину Y в этом случае представляет собой прямую линию
Очевидно, что аналогичный вид имеет в рассматриваемом случае
и линия регрессии h(x) координаты У на координату X.
В частности, регрессия роста жителя страны Нормалии на
его вес определяется формулой
а веса на рост — формулой
h(xi) =0,62si-33.
Линии регрессии роста на вес и веса на рост приведены на
рис. 8.1 и рис. 8.2. #
Условное математическое ожидание, как обычное (безуслов-
(безусловное) математическое ожидание, характеризует центр рассеи-
рассеивания случайной величины. Однако оно не дает никакой ин-
информации о степени рассеивания случайной величины относи-
относительно среднего значения.
372 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Поскольку степень рассеивания случайной величины X мож-
можно оценить с помощью дисперсии, то в качестве меры рассеи-
рассеивания случайной величины X относительно У можно принять
условную дисперсию, которую естественно определить анало-
аналогично обычной дисперсии, но используя условное распределение
случайной величины X при условии Y = у.
Определение 8.8. Условной дисперсией D(X\Y) слу-
случайной величины X относительно (случайной величины) У на-
называют случайную величину, задаваемую формулой
Б(Х|У) = М([Х - М(Х|У)]2|У).
Приведенное определение применимо как для двумерной
дискретной случайной величины, так и для непрерывной.
Для двумерной дискретной случайной величины (X, У)
значение "D(X\yj) условной дисперсии X при условии У = yj
определяется формулой
Б(ВД = M{[X-M(X\yj)J\yj) =^Г[х{-М(Х\у1)]\ф
г=1
а для двумерной непрерывной случайной величины (Л", У)
значение 1Э(Х\у) условной дисперсии X при условии У = у
задается формулой
+00
ЩХ\у) = М{[Х-М(Х\у)]2\у) = I [x-M(X\y)]2Px(x\y)dx.
-оо
Условная дисперсия случайной величины X так же, как и
условное математическое ожидание этой случайной величины,
зависит от того значения, которое приняла случайная величина
У. Поэтому условная дисперсия D(X|y) является функцией от
случайной величины У, область определения которой совпадает
с множеством возможных значений случайной величины У.
8.2. Условные числовые характеристики 373
Наряду с условной дисперсией D(X|y) (или ее значением
D(X\y)) используют условное среднее квадратичное отклоне-
отклонение <Jx\Y =: у/^НЩУ) (или его значение &х\у == у/ЩЩу))-
Все сказанное выше относительно условной дисперсии
D(-X"|y) справедливо и для условной дисперсии D(Y\X) случай-
случайной величины У относительно X.
Свойства условной дисперсии определяются следующей те-
теоремой.
Теорема 8.2. Условная дисперсия D(X|y) обладает следу-
следующими свойствами.
1. Б(с|У)=0.
2. D(aX +
3. B{X\Y) =
4. Пусть случайные величины Х\ и Хч являются независимыми
при условии, что случайная величина У приняла любое конкрет-
конкретное значение. Тогда В(Хг + X2\Y) = D(Xi\Y) + B(X2\Y) (это
утверждение мы приводим без доказательства).
5. Пусть и(Х) и v(Y) — функции от случайных величин X
и У. TorflaD(u(Y).v(y)|y)=i;2(y)D(u(Z)|y).
6. Если X и У — независимые случайные величины, то
7. DX = M(T>(X\Y))+M(M(X\Y)-MXJ.
< Первые два утверждения мы предлагаем доказать самостоя-
самостоятельно.
Докажем оставшиеся четыре утверждения.
Согласно определению условной дисперсии,
-2XM(X\Y) + [М(Х|У)]2)|у).
Воспользовавшись свойством 2 условного математического
ожидания, имеем
D(X\Y) = М(Х2|У) - 2M(XM(X\Y)\Y) + М((М(Х|У)J|У).
374 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Поскольку М(-Х"|У) и (М(Х|У)) являются функциями от
случайной величины У, то в соответствии со свойством 6
условного математического ожидания
ЩХ\У) = М(Х2|У) - 2(М(Х|У)) (М(Х|У)) + (М(Х|У)J.
Отсюда вытекает утверждение 3.
В силу определения условной дисперсии и свойства 6 услов-
условного математического ожидания имеем
D{u(X)-v(Y)\Y) =
= М((«(Х) • v(Y) - М(«(Х) • *,(У)|У)J|у) =
= m({v(Y)-u(X)-v(Y)M(u(X)\Y)J\y) = ^
= M(y2(Y)(u(X)-M(u(X)\Y)J\Y) =
= v2(Y)m({u(X)-M(u(X)\Y)J\y) =
= v\Y)B(u(X)\Y).
Поэтому справедливо утверждение 5.
Далее, если случайные величины X и Y являются неза-
независимыми, то в силу свойства 7 условного математического
ожидания
B{X\Y) = М((Х - M(X\Y)J\Y) = М((Х - MXJ\Y).
Поскольку (X — MXJ и У также независимые случайные
величины, то, вновь воспользовавшись свойством 7 условного
математического ожидания, получим утверждение 6 теоремы.
Наконец, согласно свойству 3 условной дисперсии, имеем
М(Х2|У) = B(X\Y) + {M(X\Y))\
Беря от обеих частей этого равенства математическое ожида-
ожидание, согласно свойству 5 условного математического ожидания,
8.2. Условные числовые характеристики 375
находим
MX2 = M(M(X2\Y)) = М(Б(Х|У)) + M(M(X\Y)J.
Вычитая из обеих частей последнего равенства (MXJ, полу-
получаем
DX = MX2 - (MXJ = М(Б(Х|У)) + М(М(Х|У)J - (MXJ.
Осталось заметить, что в соответствии со свойствами 2 и 5
условного математического ожидания
М(М(Х|У) - MXJ = М(М(Х|У)J-
- 2(МХ)М(М(Х|У)) + (MXJ = М(М(Х|У)J-
- 2(МХ)(МХ) + (MXJ = М(М(Х|У)J - (MXJ.
Подставляя полученное равенство в предыдущую формулу,
приходим к утверждению 7. >
Пример 8.13. Пусть (X, У) — двумерная случайная ве-
величина, имеющая нормальное распределение (см. примеры 8.3,
8.12). Из результатов этих примеров следует, что
B(X\y)=al(l-p2) и V{X\Y)=o\{l-p\
Таким образом, значение D(X|y) условной дисперсии D(X|y)
не зависит от значения у случайной величины У (естественно,
что для произвольного двумерного случайного вектора (X, У)
это, вообще говоря, не так). Отметим также, что при фикси-
фиксированной дисперсии DX = а2 условная дисперсия Ю(Х|У) тем
меньше, чем больше абсолютное значение коэффициента корре-
корреляции р.
При р = ±1 условная дисперсия D(X|y) = 0. Этот факт ста-
становится очевидным (причем для произвольно распределенных
случайных векторов (X, У)), если вспомнить (см. 7.4), что при
р = ±1 существует линейная зависимость
376 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
между X и У, а значит, в силу свойств 2, 5 и 1 условной
дисперсии
B(X\Y) = B(aY + b\Y) = a2D{Y \Y) = а2У2БA|У) = 0.
Вычислим теперь дисперсию DX с помощью условной дис-
дисперсии "D(X\Y). Воспользовавшись свойством 7 условной дис-
дисперсии и подставляя вместо условного математического ожида-
ожидания М(Х|У) его значение, вычисленное в примере 8.12, имеем
02
Естественно, мы получили хорошо известный нам результат
(см. пример 7.17 и 5.5).
Пример 8.14. Рассмотрим двумерный случайный вектор
(X, У), где X*— случайная величина, равномерно распределен-
распределенная на отрезке [^1,1], а У = X2 (см. пример 7.20). Найдем
условные дисперсии "D(X\Y) и D(y|X) и с их помощью вычи-
вычислим ВХ и БУ.
Определим сначала D(y|X) и DY. В соответствии со
свойствами 6 и 1 условного математического ожидания имеем
M{Y\X) = М(Х2\Х) = Х2МA|Х) = X2.
Тогда, согласно свойствам 5 и 1 условной дисперсии,
T>(Y\X) = D{X2\X) = ХАЩ1\Х) = 0.
Полученный результат очевиден, поскольку если случайная
величина X приняла конкретное значение х, то вследствие
8.2. Условные числовые характеристики 377
наличия функциональной зависимости Y = X2 значение у = х2
случайной величины Y определяется однозначно.
Так как
-1
то, согласно свойствам 1 и 7 условной дисперсии, получаем
1
/
-1
Вычислим теперь D(X|y) и DX. Для этого заметим, что
если случайная величина Y приняла конкретное значение у
(лежащее на отрезке [0,1]), то случайная величина X может
принять только одно из двух значений:
и
причем, поскольку X равномерно распределена на отрезке
[—1,1], оба эти значения равновероятны. Иными словами,
значению у случайной величины Y соответствуют значения
х\ = —у/у и #2 = у/У случайной величины X, принимаемые с
вероятностью 1/2. Значит,
И
Таким образом,
М(Х|У) = 0 и D{X\Y) = Y.
Наконец, поскольку
1
= i fxdx = 0,
378 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
то в силу свойства 7 условной дисперсии с учетом равенства
B(X\Y) = Y получаем
-0J = \. #
О
В заключение отметим, что для характеристики нелинейной
связи случайных величин X и У часто используют корреляци-
корреляционные отношения tjx\y и Vy\x-
Определение 8.9. Корреляционными отношениями
случайных величин X и Y называют числа г/х\у и Vy\Xi которые
задаются выражениями
Vx\Y =
И
(8.11)
(8.12)
Корреляционное отношение г)Х\у вычисляют для дискрет-
дискретной и непрерывной случайных величин (X, Y) в соответствии
с формулами
VX\Y =
\
И
r)x\Y =
+оо
T>(X\y)pY(y)dy.
(8.14)
Заметим, что, в отличие от коэффициента корреляции
р, корреляционное отношение зависит от порядка следования
случайных величин X и У, т.е. г/х|у, вообще говоря, не
совпадает с
8.2. Условные числовые характеристики 379
Свойства корреляционного отношения tjx\y определяются
следующей теоремой.
Теорема 8.3, 1. Корреляционное отношение tjx\y можно
записать в виде
VX\Y =
2. Корреляционное отношение t)x\y удовлетворяет неравен-
неравенству
О ^ Vx\Y < 1-
3. Корреляционное отношение
Vx\Y = 1
тогда и только тогда, когда случайная величина X функцио-
функционально (не обязательно линейно) зависит от У.
4. Корреляционное отношение
Vx\Y = О
тогда и только тогда, когда
т.е. линия регрессии X на Y представляет собой горизонталь-
горизонтальную прямую.
5. Коэффициент корреляции р и корреляционное отношение
rjx\Y связаны неравенством
6. Модуль |р| коэффициента корреляции совпадает с корре-
корреляционным отношением t)x\y тогда и только тогда, когда линия
регрессии X на Y является прямой.
< Первое утверждение теоремы вытекает из свойства 7 услов-
условной дисперсии. Действительно,
2 _ DX-M(B(X\Y)) _ М(М(Х|У) - MXJ
x\Y" пх " вх •
380 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Правая часть неравенства утверждения 2 следует из опре-
определения корреляционного отношения, поскольку
B(X\Y) ^ 0 и M(B(X\Y)) ^ 0.
При этом равенство M(D(X|y)) = 0, эквивалентное равенству
Vx\Y = 1? имеет место тогда и только тогда, когда D(X|y) = 0.
В свою очередь, это тождество означает, что при каждом зна-
значении случайной величины У случайная величина X принимает
всего одно значение, т.е. X является функцией от У, что дока-
доказывает утверждение 3.
Аналогично левая часть неравенства утверждения 2 следует
из утверждения 1 теоремы, так как
при этом тождество (М(Х|У) — MX) = 0, эквивалентное то-
тождеству М(Х|У) = MX, имеет место тогда и только тогда,
когда t)x\y == 0? чт0 доказывает утверждение 4.
Для доказательства утверждения 5 рассмотрим случайную
величину
где х — произвольное число, и вычислим ее дисперсию:
BZX = x2BY - 2xcov(Y,M(X\Y)) +B(M(X\Y)).
Дисперсия DZX, как функция от ж, представляет собой ква-
квадратный трехчлен. Поскольку дисперсия любой случайной ве-
величины является неотрицательной, то дискриминант
Bсоу(У,М(Х|У))J -4DyD(M(X|y)) ^ 0. (8.15)
Найдем для соу(У,М(Х|У)) и T)(M(X\Y)) другие выраже-
выражения. Воспользовавшись свойством 5 условного математическо-
математического ожидания и утверждением 1 теоремы, заметим, что
М(М(Х|У))J =
= М(М(Х|У) - MXJ =
8.2, Условные числовые характеристики 381
По определению 7.8 ковариации, имеем
= м((У - MY) (M(X\Y) - М(М(Х|У)))). (8.16)
Выражение под знаком математического ожидания в правой
части равенства можно преобразовать, используя свойства 6
и 3 условного математического ожидания, следующим образом:
(у - my) (m(x\y) - м(м(х|у))) =
= м[(у-му)*|у] -м[((у-му)мх)|у] =
= m((xy - xmy -ymx + mxmy)\y) =
- MX) (У - МУ)|У).
Подставляя найденные значения И(М(Х\У)) и cov(Y,M(X\Y))
в (8.15), имеем
^ rJxlYBYDX,
откуда после деления на DYDX получаем утверждение 5.
Наконец, для того чтобы доказать утверждение 6, доста-
достаточно заметить, что, согласно свойству 5 ковариации (см.
с. 310), неравенство (8.15) превращается в равенство тогда и
только тогда, когда
b + x0Y-M(X\Y)=0
для некоторых хо и Ь, или
что эквивалентно утверждению 6. >
382 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 8.15. Вычислим корреляционное отношение г)Х\у
для случайного вектора (X, У), распределенного по нормаль-
нормальному закону. Как следует из формулы (8.16) и примера 8.13,
Значение корреляционного отношения в данном случае совпа-
совпадает с модулем коэффициента корреляции. Это становится оче-
очевидным, если вспомнить (см. пример 8.12), что линия регрессии
X на У является прямой, и воспользоваться утверждением 6 те-
теоремы 8.3.
Пример 8.16. Найдем корреляционные отношения цх\у и
г)у\х для случайного вектора (X, У) из примера 8.14:
t)x\y = V1-ZMY = 0, r)Ylx = Jl-—MO =
Итак, мы получили, что tjx\y == 0> что соответствует утвер-
утверждению 4 теоремы 8.3, поскольку
M(X\Y)=0 = MX.
В свою очередь, равенство
Vy\x = 1
соответствует утверждению 3 той же теоремы, так как слу-
случайная величина У связана со случайной величиной X функци-
функциональной зависимостью
8.3. Решение типовых примеров
Пример 8.17. Распределение двумерного случайного век-
вектора (JC, У) задано табл. 8.4. Найдем условное распределение
случайной величины X при условии, что случайная величина У
8.3. Решение типовых примеров
383
приняла значение j/j, j = 1, 2, и условное распределение слу-
слуТаблица 84
чайной величины Y при условии,
что случайная величина X приня-
приняла значение Х{, г = 1,2,3. Исполь-
Используя найденные условные распреде-
распределения, проверим, являются ли слу-
случайные величины X и Y независи-
независимыми.
Распределения случайных величин Y и X приведены в
табл. 8.5 и 8.6.
X
0,04
0,08
У
0,2
0,15
0,05
0,5
0,30
0,12
0,8
0,35
0,03
У
Р
0,2
0,20
Таблица 8.5
0,5
0,42
0,8
0,38
X
Р
Таблица 8.6
0,04
0,8
0,08
0,2
Воспользовавшись определением условных вероятностей
имеем:
7гц = Р{Х = 0,04|У = 0,2} = 0,15/0,20 = 0,750,
7Г21 = Р{Х = 0,08|У = 0,2} = 0,05/0,20 = 0,250,
тг12 = Р{Х = 0,04|У = 0,5} = 0,15/0,42 » 0,714,
7Г22 = Р{* = 0,08|У = 0,5} = 0,12/0,42 и 0,286,
7Г13 = Р{Х = 0,04|У = 0,8} = 0,35/0,38 » 0,921,
7Г23 = Р{Х = 0,08|У = 0,8} = 0,03/0,38 « 0,079.
Таким образом, для условного закона распределения случай-
случайной величины X при условии У
получаем табл. 8.7. Аналогично Таблица 8.1
находим условные вероятности
представленные в табл. 8.8.
X
0,04
0,08
У
0,2
0,750
0,250
0,5
0,714
0,286
0,8
0,921
0,079
384 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Поскольку, например, строки в табл. 8.8 не совпадают, то
случайные величины X и Y являются независимыми.
Таблица 8.8
Y
0,2
0,5
0,8
X
0,04
0,1875
0,3750
0,4375
0,08
0,2500
0,6000
0,1500
Пример 8.18. Будем говорить, что случайный вектор
(X, Y) имеет равномерное распределение в области D (с
площадью 5), если его плотность распределения
I
(я, y)eD\
о,
Пусть случайный вектор (X, Y) имеет равномерное распре-
распределение в треугольнике с вершинами в точках @; 0), @; 2), A; 0).
Найдем условную плотность распределения случайной величи-
величины X при условии, что случайная величина Y приняла значение
у, и условную плотность распределения случайной величины Y
при условии, что случайная величина X приняла значение х.
Используя найденные условные плотности распределения, про-
проверим, являются ли случайные величины ХиУ независимыми.
Поскольку двумерный случайный вектор (X, Y) распределен
равномерно в области ?>, представляющей собой треугольник
с вершинами в точках @;0), @;2), A;0), то его плотность
распределения имеет вид
I 1» Кх> У) с ил
PX,Y(X,y) = <
{ 0, (х, у) & D.
8.3. Решение типовых примеров 385
Отсюда нетрудно найти частные плотности распределения
случайных величин X и Y:
0,
У 6 [0, 2];
0, у* [0,2].
Воспользовавшись теперь определением условной плотно-
плотности распределения, получаем
у)-РХ'у{х'у) = [ 2^' *б[0,1-у/2]«уе[0,2];
руШ = РхА**) = ( Щ=7у У 6 [О-
Px(s) \ 0, у * [0,
= [ 2^
РУ(У) \ О, а;ё[0,1-у/2]иу€[0,2];
2A - х)] и х 6 [0,1];
2A -х)]жхе [0,1].
При у ^ [0, 2] и х 0 [0,1] условные плотности распределения
Рх(#|у) и ру(у\х) не определяются, поскольку случайная ве-
величина Y не может попасть вне отрезка [0, 2], а случайная
величина X — вне отрезка [0,1].
Так как, например, условная плотность распределения
рх(х\у) зависит от у, а плотность распределения рх(х) от у
не зависит, случайные величины X и Y являются зависимыми.
Пример 8.19. В условиях примера 8.17 найдем условные
математические ожидания Ы(Х\У) и М(У|Х), условные дис-
дисперсии D(X|y) и D(y|X) и корреляционные отношения rjX\Y и
Используя определение условного математического ожида-
ожидания для двумерной дискретной случайной величины и результа-
результаты примера 8.17, находим значения TS/L(X\yj) и M(Y\xi) услов-
386 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
ных математических ожиданий М(-Х"|У) и М(У|Х):
М(Х|0,2) = 0,04 • 0,75 + 0,08 • 0,25 = 0,05,
М(Х|0,5) = 0,04 • 0,714 + 0,08 • 0,286 = 0,05144,
М(Х|0,8) = 0,04 • 0,921 + 0,08 • 0,079 = 0,04316,
М(У |0,04) = 0,2 • 0,1875 + 0,5 • 0,375 + 0,8 • 0,4375 = 0,575,
М(У |0,08) = 0,2 • 0,25 + 0,5 • 0,6 + 0,8 • 0,15 = 0,47.
Таким образом, условное математическое ожидание М(Х|У)
является функцией д(у) от случайной величины У, причем
область определения функции д(у) состоит из трех точек
0,2, 0,5, 0,8 и
р@,2) = 0,05, д@,5) = 0,05144, 5@,8) = 0,04316.
Аналогично условное математическое ожидание М(У|Х) явля-
является функцией h(X) от случайной величины X, причем область
определения функции h(x) состоит из двух точек 0,04, 0,08 и
Л@,04) = 0,575, Л@,08) = 0,47.
Вычислим, теперь значения D(X\yj) и D(y|a;i) условных
дисперсий B(X\Y) и B(Y\X):
D(X|0,2) = M(X2|0,2) - (М(Х|0,2)J =
= 0,042 • 0,75 + 0,082 • 0,25 - 0,052 = 0,0003,
D(*|0,5) = М(Х2|0,5) - (М(Х|0,5)J =
= 0,042 • 0,714 + 0,082 • 0,286 - 0,051442 = 0,00033,
D(X|0,8) = М(Х2|0,8) - (М(Х|0,8)J =
= 0,042 • 0,921 + 0,082 • 0,079 - 0,043162 » 0,00012,
Б(У|0,04) = М(У2|0,04) - (М(У|0,04)J =
= 0,22 • 0,1875 + 0,52 • 0,375 + 0,82 • 0,4375 - 0.5752 и 0,051,
8.3. Решение типовых примеров 387
D(y|0,08) = М(У2|0,08) - (М(У|0,08)J =
= 0,22 • 0,25 + 0,52 • 0,6 + 0,82 • 0,15 - 0,472 « 0,035.
Условная дисперсия D(-X"|y) является функцией от случайной
величины У с областью определения, состоящей из точек
0,2, 0,5, 0,8, и
D(X|0,2)=0,0003, D(X|0,5)=0,00033, D(X|0,8)=0,00012.
Условная дисперсия D(y|X) является функцией от случайной
величины X с областью определения, состоящей из точек
0,04, 0,8, и
Б(У|0,04) = 0,051, D(y|0,08) = 0,035.
Наконец, найдем корреляционные отношения t]x\Y и Vy\x-
Для этого вычислим сначала ИХ и BY. Имеем
MX = 0,04 • 0,8 + 0,08 • 0,2 = 0,048,
ВХ = 0,042 • 0,8 + 0,082 • 0,2 - 0.0482 = 0,000256,
МУ = 0,2 • 0,2 + 0,5 • 0,42 + 0,8 • 0,38 = 0,554,
BY = 0,22 • 0,2 + 0,52 • 0,42 + 0,82 • 0,38 - 0,5542 = 0,04928.
Далее вычисляем
MD(X|y) = 0,0003 • 0,2 + 0,0003308 • 0,42+
+ 0,0001164 • 0,38 = 0,000243,
MD(y \X) = 0,0508 • 0,8 + 0,0351 • 0,2 = 0,0475.
Окончательно получаем
MB(X\Y) I 0,000243
I 0,
= V 0
^00256
=0'225'
MD(y|X)
388 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
Пример 8.20. В условиях примера 8.18 найдем условные
математические ожидания М(Х|У) и М(У|Х), условные дис-
дисперсии D(X|y) и D(y|X) и корреляционные отношения r)x\Y
и tjy\x* Найдем регрессии случайных величин X на У и У на
X и построим линии регрессии. Не проводя дополнительных
вычислений, определим, чему равен коэффициент корреляции
случайных величин X и У.
Поскольку случайная величина У принимает значения толь-
только из отрезка [0, 2], а случайная величина X — из отрезка
[0,1], то значения М(Х\у) условного математического ожида-
ожидания М(Х|У) и значение D(X\y) условной дисперсии D(X|y)
заданы только для у из отрезка [0, 2], а значения М(У \х) дис-
дисперсии D(y|X) заданы только для х из отрезка [0,1]. Поэто-
Поэтому далее будем предполагать, не оговаривая этого особо, что
у е [0, 2], а х е [0,1].
Воспользовавшись определением 8.6 условного математи-
математического ожидания и условной дисперсии 8.8 для непрерывной
случайной величины и результатами примера 8.18, найдем:
+оо l-y/2
2-у
М{Х\у)= jxpx{x\y)dx =
+00
= I ypr(y\x)dy= I 2П~л =l-«i
-оо О
+00
I 2
= / {x-M(X\y)Ypx(x\y)dx =
B-УJ
48 '
8.3. Решение типовых примеров 389
+оо
Щ?\х) = j (x-M(Y\x)JpY(y\x)dy =
-OO
2A-
¦/
0
Таким образом, условное математическое ожидание
2{l~X\y-(l-x)Jdy = (l-
2A-ж) 3
о
условное математическое ожидание
условная дисперсия
условная дисперсия
В частности, регрессия случайной величины X на У зада-
задается формулой
а регрессия случайной величины У на Jf — формулой
Графики линий регрессии X на У и У на X приведены на
рис. 8.3 и 8.4.
390 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
lx 0 1 х
Рис. 8.3 Рис. 8.4
Найдем корреляционные отношения т)х\у и Vy\x- Имеем:
+ОО
MX
-оо О
-foo 2
+оо 1
/f *
У 3
-оо О
+oo » 1
= f (x-MXJpx(x)dx =
-оо О
H-oo 2
= J(y-MYJPY(y)dy =
-оо О
+00 2
—00
+00
МБ(У|Х) = I D(Y\x)px(x)dx = j
96 24'
2(l-xKdx
Вопросы и задачи 391
Отсюда получаем
Г MD(X\Y) / 1/24 Лг
"У1 5JL-2 = V1-I7i8=0'5'
/, MD(Y\X) I 1/6
Поскольку, например, линия регрессии X на Y прямая,
то абсолютное значение \р\ коэффициента корреляции равно
корреляционному отношению tjx\y- Кроме того, так как
с ростом X случайная величина Y в среднем убывает, то
коэффициент корреляции отрицателен и
1
P = -Vx\y = -«•
Вопросы и задачи
8.1. Дайте определение условного распределения одной ко-
координаты двумерного дискретного случайного вектора при
условии, что вторая координата приняла определенное значе-
значение.
8.2. Дайте определение условной плотности распределения
одной координаты двумерного непрерывного случайного век-
вектора при условии, что вторая координата приняла определенное
значение.
8.3. Сформулируйте условия независимости координат дис-
дискретного и непрерывного случайных векторов в терминах
условных распределений.
8.4. Как определяют значение условного математического
ожидания одной координаты двумерного дискретного случай-
случайного вектора при условии, что другая координата приняла
392 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
определенное значение? Что называют условным математиче-
математическим ожиданием одной координаты двумерного дискретного
случайного вектора относительно другой?
8.5. Как определяют значение условного математического
ожидания одной координаты двумерного непрерывного слу-
случайного вектора при условии, что другая координата приняла
определенное значение? Что называют условным математиче-
математическим ожиданием одной координаты двумерного непрерывного
случайного вектора относительно другой?
8.6. Перечислите свойства условного математического ожи-
ожидания.
8.7. Что называют регрессией одной координаты двумерно-
двумерного случайного вектора на другую? Что такое линия регрессии?
8.8. Что называют условной дисперсией одной координа-
координаты двумерного случайного вектора относительно другой? Как
определяется значение условной дисперсии одной координаты
двумерного случайного вектора при условии, что другая коор-
координата приняла соответствующее значение?
8.9. Перечислите свойства условной дисперсии.
8.10. Что называют корреляционным отношением 7/х|у?
Как вычислить корреляционное отношение для дискретных и
непрерывных случайных векторов?
8.11. Перечислите свойства корреляционного отношения.
8.12. Распределение двумерного случайного вектора (X, У)
задано табл. 8.9. Найдите условное распределение случайной
величины X при условии, что случайная величина У приня-
приняла значение yj, j = 1,2, и условное распределение случайной
величины У при условии, что случайная величина X приняла
значение х^ г = 1,2,3. Используя найденные условные распре-
распределения, проверьте, являются ли случайные величины X и У
независимыми.
Вопросы и задачи
393
Таблица 8.9
Таблица 8.10
X
0,3
0,6
Y
0,10
0,25
0,10
0,15
0,15
0,05
0,20
0,32
0,13
X
0,3
0,6
Y
0,10
5/7
2/7
0,15
3/4
1/4
0,20
32/45
13/45
Y
0,10
0,15
0,20
X
0,3
25/72
5/24
4/9
0,6
5/14
5/28
13/28
Ответ: Условные распределения Таблица 8.11
случайной величины X при усло-
условии У и случайной величины У
при условии X представлены в
табл. 8.10 и 8.11 соответственно.
Случайные величины X и У явля-
являются зависимыми.
8.13. Двумерный случайный вектор (X, У) распределен
равномерно в прямоугольнике с вершинами в точках (—3; —10),
(—3; 10), C; 10) и C;—10). Найдите условную плотность рас-
распределения случайной величины X при условии, что случайная
величина У приняла значение у и условную плотность распре-
распределения случайной величины У при условии, что случайная ве-
величина X приняла значение х. Используя найденные условные
плотности распределения, проверьте, являются ли случайные
величины X и У независимыми.
Ответ:
Рх(х\у) =
ру(у\х) =
1
б'
0,
2_
20'
о,
N < 3 и \у\ < 10;
|ж| > 3 и \у\ < 10;
\у\ < 10 и \х\ < 3;
\у\ > 10 и \х\ < 3.
Случайные величины X и Y являются независимыми.
8.14. Непрерывный двумерный случайный вектор (X, У)
имеет плотность распределения
Су, (x,y)eD;
0, (я, у
13-10047
Г
394 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
где D — область, ограниченная линиями у = х2 и у = 1.
Найдите постоянную С, условную плотность распределения
случайной величины X при условии, что случайная величина
У приняла значение у, и условную плотность распределения
случайной величины У при условии, что случайная величина X
приняла значение х. Используя найденные условные плотности
распределения, проверьте, являются ли случайные величины X
и У независимыми.
Ответ:
С = 5/4;
О, х & [—д/у, у/у\ и у е (О,1];
^У л. ?- Г~.2 11 „ я. с /_1 1\.
Условная плотность рх(^|у) не определяется при у ^ @,1],
условная плотность ру(у\х) — при х $ (—1,1). Случайные
величины X и У являются зависимыми.
8.15. Двумерный случайный вектор (X, У) имеет нормаль-
нормальное распределение с плотностью распределения
У)
/Г
Найдите условную плотность распределения случайной величи-
величины X при условии, что случайная величина Y приняла значение
у, и условную плотность распределения случайной величины Y
при условии, что случайная величина X приняла значение х.
Используя найденные условные плотности распределения, про-
проверьте, являются ли случайные величины X и У независимыми.
Ответ:
РхШ = -е-D*+*>2/4, pY(y\x) = Ie-(^
7Г 7Г
Случайные величины X и У являются зависимыми.
Вопросы и задачи 395
8.16. В условиях задачи 8.12 найдите условные математиче-
математические ожидания M(X\Y) и М(У |Х), условные дисперсии D(X\Y)
и В(У|Х), корреляционные отношения tix\y и Vy\x-
Ответ:
М(Х|0,10) « 0,39, М(Х|0,15) = 0,375, М(Х|0,20) и 0,39,
М(У|0,3)«0,16, М(У|0,6)«0,55, D(X|0,10)« 0,018,
D(Jf|0,15) « 0,17, D(X|0,20) и 0,17, D(Y|0,3) « 0,0019,
Б(У |0,6) « 0,0020, rjX|y « 0,59, r/yj* » 0,52.
8.17. В условиях задачи 8.13 найдите условные математиче-
математические ожидания М(Х| У) и М(У 1-Х"), условные дисперсии D(J?|y)
и D(y|X), корреляционные отношения rjx\Y и Vy\x- Определи-
Определите регрессии случайных величин X на У и У на X и постройте
линии регрессии. Не проводя дополнительных вычислений, ска-
скажите, чему равен коэффициент корреляции случайных величин
XvlY.
Ответ: М(Х|У) = MX = 0, М(У|Х) = МУ = 0,
Б(Х|У) s DX = 3, D(y|Х) = БУ = 100/3, 5Ы = 0,
= Vy\x = р = 0.
8.18. В условиях задачи 8.14 найдите условные математиче-
математические ожидания М(-Х"|У) и М(У 1-Х"), условные дисперсии D(A"|y)
и D(y|X), корреляционные отношения tjx\y и VyIX* Определи-
Определите регрессии случайных величин X на У и У на X и постройте
линии регрессии. Не проводя дополнительных вычислений, ска-
скажите, чему равен коэффициент корреляции случайных величин
XhY.
Ответ: М(Х|У)=0, M(Y\X) =
I, Б(У|Х) = A'^++Д2 + Х), 5Ы = 0,
= P = Of
396 8. УСЛОВНЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ ВЕЛИЧИН
8.19. В условиях задачи 8.15 найдите условные математиче-
математические ожидания М(-ХГ|У) и М(У 1-Х"), условные дисперсии D(X\Y)
и D(y \Х) и корреляционные отношения rfx\Y и Vy\x- Определи-
Определите регрессии случайных величин X на У и У на X и постройте
линии регрессии.
Ответ: M(X\Y) = -У/4, М(У|Х) = -X, D(X|Y) = 1/8,
U^j |Aj = 1/-*, 3^2/j == —У/4, ti(x) = —ж, ^7х|У ==: ^7у|Л" == А/л.
8.20. Случайная величина X имеет плотность распределе-
распределения
f 1 — Irl Ы < 1-
I J- р|> \х\ ^ 1,
а случайная величина У связана со случайной величиной X
функциональной зависимостью У = X4. Найдите условные ма-
математические ожидания М(Х|У) и M(y|JC), условные диспе-
дисперсии D(X|Y) и D(Y|Jf) и корреляционные отношения rjx\y и
Vy\x- Определите регрессии случайных величин X на У и У
на X и постройте линии регрессии. Не проводя дополнитель-
дополнительных вычислений, скажите, чему равен коэффициент корреляции
случайных величин X и У.
Ответ: М(Х|У) = О, М(У|JC) = X4, D(X|У) = л/У,
= 0, з(у) = 0, h(x) = х4, ffciy = p = 0,
9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ
ТЕОРИИ ВЕРОЯТНОСТЕЙ
С самого начала изучения курса теории вероятностей мы
говорили о том, что практическое применение методов этой
математической дисциплины основывается на законе предель-
предельного постоянства частоты события.
Закон предельного постоянства частоты события устано-
установлен эмпирически. В соответствии с этим законом повторе-
повторение одного и того же опыта приводит к тому, что частота
появления конкретного случайного события теряет свойства
случайности и приближается к некоторому пределу, который в
соответствии со статистическим определением вероятности
(см. 2.4) и называют вероятностью.
Однако для того чтобы теория согласовывалась с практи-
практикой, при аксиоматическом определении вероятности, которое
мы использовали, этот закон предельного постоянства часто-
частоты должен быть обоснован теоретически. Иначе говоря, он
должен быть сформулирован и доказан в виде одной или не-
нескольких теорем. В теории вероятностей теоремы такого типа
обычно называют различными формами закона больших чисел.
В настоящей главе мы докажем некоторые формы этого закона,
которые, в частности, поясняют смысл математического ожи-
ожидания случайной величины, и то, почему его называют также
средним значением.
Далее (см. 9.4) доказывается простейший вариант цен-
центральной предельной теоремы, уточняющей закон больших чи-
чисел. Центральная предельная теорема, в свою очередь, объясня-
объясняет то широкое распространение, которое получило на практике
нормальное распределение.
398 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
9.1. Сходимость последовательности
случайных величин
Пусть
представляет собой последовательность случайных величин,
заданных на одном и том же вероятностном пространстве.
Опишем типы сходимости последовательности Х\, X<i,..., Хп,...
к некоторой случайной величине X.
Сразу же отметим, что естественно все определения сходи-
сходимости вводить таким образом, чтобы сходимость последова-
последовательности случайных величин Х\, -Хг, ..., Хп, ... к случайной
величине X была эквивалентна сходимости последовательности
Y\ = Х\ - X, Уг = Х2 - -X", ..., Yn = Хп - X, ...
случайных величин к нулю, т.е. к случайной величине, принима-
принимающей всего одно значение 0. Поэтому далее мы будем говорить
только о сходимости последовательности Х\,Х2, ...Дп» ••• к
нулю.
Поскольку каждая из случайных величин Х{ представля-
представляет собой фуйкцию, заданную на пространстве элементарных
исходов ft, и существуют разные определения сходимости функ-
функций, то можно ввести и различные определения сходимости
последовательности случайных величин.
Казалось бы, наиболее разумно понимать сходимость по-
последовательности X\j -Х2,..., Хпу... случайных величин следу-
следующим образом. Для каждого элементарного исхода ш Eft по-
последовательность -Xi(u;), X2(w), •.., Хп(ш),... представляет со-
собой обычную числовую последовательность, и можно опреде-
определить сходимость последовательности Х\, Хг,..., Хп,... случай-
случайных величин как сходимость числовых последовательностей
Xi(u>), -^2@;),..., Хп(ш),... при всех ш ? ft.
К сожалению, такая сходимость (ее называют сходимо-
сходимостью всюду) редко встречается на практике.
9.1. Сходимость последовательности случайных величин 399
Введем некоторые типы сходимости случайных величин.
Рассмотрим все элементарные исходы а;, для которых после-
последовательности Xi(u;), ^2@;),..., Хп(ш),... сходятся к нулю, и
обозначим через А событие, состоящее из этих исходов, т.е.
А = \ ш: lim Хп(ш) = 0 \.
I п-юо J
Определение 9,1. Бели последовательность Х\, Хг, ...,
Хп, ... случайных величин удовлетворяет условию
то говорят о сходимости этой последовательности к нулю с
вероятностью 1, или почти наверное.
Сходимость к нулю с вероятностью 1 записывается в виде
п
п-юо
В дальнейшем мы в основном будем использовать сходи-
сходимость по вероятности.
Определение 9.2. Бели последовательность Х\, Х^, ...,
ХП1 ... случайных величин для любого е > 0 удовлетворяет
условию
то говорят о сходимости этой последовательности к нулю по
вероятности. Сходимость к нулю по вероятности записыва-
записывается в виде
хп Ло.
п-юо
Смысл сходимости по вероятности заключается в том, что
вероятность нарушения неравенства |Хп| < е при увеличении п
становится сколь угодно малой.
Наконец, во многих приложениях теории вероятностей важ-
важную роль играет сходимость в среднем квадратичном.
400 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Определение 9.3* Бели последовательность Х\, X*i, ...,
Хп, ... случайных величин удовлетворяет условию
lim MXl = 0,
П->ОО
то говорят о сходимости этой последовательности к нулю
в среднем квадратичном.
Сходимость к нулю в среднем квадратичном записывается
в виде
п
п-юо
При доказательстве центральной предельной теоремы нам
понадобится понятие слабой сходимости последовательности
функций распределения.
Определение 9.4. Последовательность функций распреде-
распределения Fi(x),...,Fn(x),... сходится к предельной функции рас-
распределения F(x), если
для любых ж, являющихся точками непрерывности F(x). Такую
сходимость называют слабой сходимостью последователь-
последовательности функций распределения и обозначают
Приведем пример последовательности случайных величин,
для которой не имеет место сходимость всюду.
Пример 9.1. Рассмотрим бесконечное число испытаний
по схеме Бернулли с равными вероятностями успеха и неудачи
р = q = 1/2. Последовательность Х\, X<i,..., Хп,..., где Х{ —
число успехов в i-м испытании, будет представлять собой по-
последовательность независимых одинаково распределенных слу-
случайных величин.
9.1. Сходимость последовательности случайных величин 401
Рассмотрим последовательность УъУг?---
представляет собой вычисленную по первым п испытаниям
частоту успеха.
Далее будет показано (см. теорему 9.4), что последователь-
последовательность Yi, У2,..., Yn,... сходится по вероятности к 1/2. Более
того, имеет место так называемый усиленный закон больших
чисел, согласно которому эта последовательность будет схо-
сходиться к 1/2 с вероятностью 1.
Установим существование таких элементарных исходов и, для
которых числовые последовательности Yi(u;), УгО^)? • • • > Yn(u))y • • •
не сходятся к 1/2. Это означает, что для последовательности
Уъ ^2> • • • ? ^п? • • • случайных величин сходимость всюду не имеет
места.
Пространство элементарных исходов О, состоит из всевозмож-
всевозможных (бесконечных) последовательностей УНН... УН... (см. 3.6).
В отличие от случая конечного числа испытаний, П уже не
будет дискретным (более того, П „почти" эквивалентно от-
отрезку [0,1] с равномерной вероятностью на нем; для доказа-
доказательства этого достаточно отождествить последовательность
-Хь-Х>... ,ХП... с двоичным представлением некоторого числа,
заключенного между нулем и единицей). При этом каждый эле-
элементарный исход ш имеет вероятность
Рассмотрим элементарный исход
Для него
) ХЫ = ... = 1 и
402 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
т.е. средние арифметические значения равны единице. Таким
образом, для элементарного исхода ио = УУ... У... последова-
последовательность Y\, Y2, • • • ,Ini • • • случайных величин сходится к 1, а не
к 1/2.
Читатель без труда может привести примеры и других
элементарных исходов, для которых последовательность Yi,
*2> • ••> In, ••• либо будет сходиться к некоторому отличному
от 1/2 числу из промежутка [0,1], либо вообще не будет
сходиться. #
К определению слабой сходимости можно сделать несколько
замечаний.
Замечание 9.1. Из слабой сходимости последовательности
функций распределения еще нельзя сделать вывод о какой-либо
сходимости последовательности самих случайных величин, так
как даже одинаково распределенные случайные величины мо-
могут быть заданы на совершенно разных вероятностных про-
пространствах.
Замечание 9.2. Требование сходимости в любой точке не-
непрерывности F(x) нельзя заменить более сильным требованием
сходимости во всех точках х. Это подтверждает следующий
пример.
Пример 9.2. Пусть на одном и том же вероятностном
пространстве задана последовательность случайных величин
Х\л Х2,..., Хп,..., причем каждая случайная величина Хп при-
принимает всего одно значение 1/п. Тогда последовательность
Х\у Х2,..., -Хп,... будет сходиться к случайной величине X = 0
для любого элементарного исхода и (причем даже равномерно).
Тем не менее
при всех п, но
9.1. Сходимость последовательности случайных величин 403
Приведенный пример показывает, что Fxn @) не стремится
к Fx@)j хотя естественно было бы ожидать сходимости Fxn{x)
к Fx(x) в любой точке х, поскольку
при всех элементарных исходах ш. Разгадка этого парадокса
заключается в том, что 0 является точкой разрыва Fx(x)y a
при определении слабой сходимости функций распределения
сходимости в таких точках мы не требовали.
Замечание 9.3. Бели последовательность F\ (х), 2*2 (х),...,
Fn (#),... функций распределения сходится к некоторой функ-
функции F(x) в каждой точке непрерывности последней, то это не
гарантирует слабой сходимости, поскольку F(x) может вообще
не быть функцией распределения.
Пример 9.3. Пусть Хп = п для всех ш. Тогда
при каждом х. Но F(x) не является функцией распределения,
так как
Значит, при определении слабой сходимости обязательно
нужно требовать, чтобы предельная функция являлась функ-
функцией распределения. #
Можно показать, что из сходимости с вероятностью 1 и
из сходимости в среднем квадратичном следует сходимость по
вероятности, а из сходимости по вероятности вытекает слабая
сходимость функций распределения*.
*См., например: Вентцель Е.С. Теория вероятностей, 1969.
404 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
9.2. Неравенства Чебышева. Закон больших чисел
Прежде чем приступить к рассмотрению закона больших
чисел, докажем два неравенства Чебышева. Заметим, что
неравенства Чебышева представляют и самостоятельный ин-
интерес, поскольку в современной теории вероятностей широко
используются неравенства такого типа.
Теорема 9.1. Для каждой неотрицательной случайной ее-
личины X, имеющей математическое ожидание Ъ/LX, при лю-
любом е > 0 справедливо соотношение
+оо
= / хр(х) dx.
называемое первым неравенством Чебышева.
М Доказательство проведем для непрерывной случайной вели-
величины X с плотностью распределения р(х) (для геометриче-
геометрической интерпретации доказательства удобно воспользоваться
рис. 9.1). Поскольку случайная величина X является неотри-
неотрицательной, то
+оо
MX
о
Так как подынтегральное выражение неотрицательное, то
при уменьшении области интегрирования интеграл может лишь
уменьшиться. Поэтому
е +оо +оо
Ъ/1Х = I xp(x)dx+ / xp(x)dx^ / xp(x)dx.
О е е
Заменяя в подынтегральном выражении сомножитель х на ?,
имеем
+ОО +00
+ +
/ xp(x)dx^e / p(x)dx.
9.2. Неравенства Чебышева. Закон больших чисел
405
Остается заметить, что последний интеграл (равный пло-
площади области, заштрихованной на рис. 9.1) представляет собой
вероятность события X ^ ?, и, значит,
откуда и вытекает первое не-
неравенство Чебышева. Анало-
Аналогично первое неравенство Че-
Чебышева доказывается и для
дискретной случайной вели-
величины, при этом нужно только
заменить интеграл суммой. >
О
Рис. 9.1
Ясно, что применять первое неравенство Чебышева имеет
смысл только тогда, когда е > MX; в противном случае оно
дает тривиальную оценку.
Пример 9.4. Пусть X — время опоздания студента на
лекцию, причем известно, что Ъ/LX = 1 мин. Воспользовавшись
первым неравенством Чебышева, оценим вероятность Р{Х ^ 5}
того, что студент опоздает не менее, чем на 5 мин.
Имеем
Таким образом, искомая вероятность не более 0,2, т.е. в среднем
из каждых пяти студентов опаздывает, по крайней мере, на
5 мин не более чем один студент. #
Рассмотрим теперь случайную величину X, имеющую дис-
дисперсию DX = а2. Мы уже говорили, что дисперсия является по-
показателем разброса X вокруг математического ожидания М-Х".
Однако с точки зрения исследователя разброс естественнее
характеризовать вероятностью Р{|-Х" — ЫХ\ ^ е} отклонения
случайной величины X от MX на величину, большую некото-
некоторого заданного е. Следующее неравенство позволяет оценить
эту вероятность с помощью дисперсии а2.
406 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Теорема 9.2. Для каждой случайной величины X, имею-
имеющей дисперсию DX = а2, при любом е > 0 справедливо второе
неравенство Чебышева
<4 Для доказательства воспользуемся утверждением первого
неравенства Чебышева. Применяя к случайной величине
это неравенство, в котором е заменено на ?2, получаем
- МХ\
- MXJ ^ е2} =
МГ DX a2
что и доказывает второе неравенство Чебышева. >
Геометрический смысл второго неравенства Чебышева по-
понятен из рис. 9.2.
У i
9.2. Неравенства Чебышева. Закон больших чисел 407
Второе неравенство Чебышева имеет содержательный смысл
лишь при е > а.
Пример 9.5. Пусть в условиях предыдущего примера из-
известно дополнительно, что а = y/DX = 1. Оценим минимальное
значение хо, при котором вероятность опоздания студента на
время не менее хо не превышает заданного значения Р3 = 0,1.
Для решения поставленной задачи воспользуемся вторым
неравенством Чебышева. Тогда
Р3 < Р{Х ^ х0} = Р{Х - MX ^ хо - MX} <
^ Р{\Х - МХ\ >х0- MX} ^-r— "
Значит,
Подставляя конкретные значения, имеем
Таким образом, вероятность опоздания студента на время
более 4,16 мин не более 0,1.
Сравнивая полученный результат с результатом приме-
примера 9.4, видим, что дополнительная информация о дисперсии
времени опоздания позволяет дать более точную оценку иско-
искомой вероятности.
Пример 9.6. Пусть случайная величина X имеет плотность
распределения
р(х) = ie-W.
408 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Тогда
+00 . .
—00
+00 . ,
2
—оо
Воспользовавшись вторым неравенством Чебышева, оценим
для е = 2, 5,10. В результате получим
Р2 ^ 0,5, р5 ^ 0,08, рю ^ 0,02.
Сравним полученные оценки с точными значениями. По-
Поскольку
Pe = l-F(e)+ F(-c)= е-,
имеем:
р2 = ~2 « 0^1353, р5 = ~5 « 0,0067, рю = -jo « 0,000045.
Таким образом, в этом примере второе неравенство Чебы-
Чебышева дает очень грубую оценку вероятности р?.
Пример 9.7, Предположим, что случайная величина X
принимает только значения 1 и —1 с одинаковыми вероятно-
вероятностями 1/2. Тогда
= (l) + l l.
Применяя второе неравенство Чебышева, получаем, что
9.2. Неравенства Чебышева. Закон больших чисел 409
Найдем точное значение вероятности р\ = P{|J\T| ^ 1}. По-
Поскольку оба возможных значения X равны по модулю единице,
то р\ = 1.
Этот пример указывает на тот факт, что по дисперсии
ТУХ нельзя оценить ре более точно, чем с помощью второго
неравенства Чебышева. #
Рассмотрим некоторые формы закона больших чисел.
Пусть Xi,X2,...,Xn,... — последовательность случайных
величин, имеющих математические ожидания mi = MX;.
Определение 9.5. Последовательность Xi, Х2, ..., Х„, ...
случайных величин удовлетворяет закону больших чисел
(слабому), если для любого е > 0
{' п л п
г=1 г=1
п-^оо
Иными словами, выполнение закона больших чисел отража-
отражает предельную устойчивость средних арифметических случай-
случайных величин: при большом числе испытаний они практически
перестают быть случайными и совпадают со своими средними
значениями.
Очевидно, что последовательность «Xi, X*i, ..., Xm ...
удовлетворяет закону больших чисел тогда и только тогда,
кбгда среднее арифметическое случайных величин Х\— mi,
-Х2 — Ш2, ..., Xn — mn сходится по вероятности к нулю при
п-»оо.
Теорема 9.3. Если последовательность Х\, X*i, ..., Хп, ...
независимых случайных величин такова, что существуют
Ъ/LXi = тп{ и DXi = of, причем дисперсии а\ ограничены в
совокупности (т.е. о\ < С < +сх>), то для последовательности
Х\, Х2, ..., Хп, ... выполнен закон больших чисел.
При этом говорят также, что к последовательности Xi,
Х2, ..., Хп, ... случайных величин применим закон больших
чисел в форме Чебышева.
410 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
< Теорема является элементарным следствием второго нера-
неравенства Чебышева. Действительно, в силу свойств математи-
математического ожидания и дисперсии
"(=?*)¦=?-
Применяя теперь второе неравенство Чебышева к случайным
величинам
получаем для любого е > О
п? п">0°
0.
Таким образом, мы показали, что для последовательности
Х\, Хг,..., Хп,*.. выполняется закон больших чисел. >
Следствие 9.1. Если случайные величины Xi, г = 1,2,...,
в условиях теоремы 9.3 являются также одинаково распреде-
распределенными (в этом случае mi = m и о\ = а2), то последователь-
последовательность Х\, Х2,..., -Уп > • • • случайных величин удовлетворяет зако-
закону больших чисел в следующей форме:
— > Ai ^ Ш.
П ^-^ п-»оо
г=1
«^ Доказательство проведите самостоятельно. >
Теорема 9.4. Пусть проводится п испытаний по схеме
Бернулли и Yn — общее число успехов в п испытаниях. Тогда
9.2. Неравенства Чебышева. Закон больших чисел
411
наблюденная частота успехов
п
сходится по вероятности к вероятности р успеха в одном
испытании, т.е. для любого е > О
Р{|гп-р|
fl—>ОО
< Обозначим Xi число успехов в t-м испытании Бернулли.
Тогда частоту успехов в п испытаниях можно определить в виде
П
причем
Ъ/LXi = р и i pg
Значит, выполняются все условия следствия 9.1, из которого
вытекает утверждение теоремы. >
Теорему 9.4 называют также теоремой Бернулли, или
законом больших чисел в форме Бернулли. Из хода дока-
доказательства теоремы 9.4 видно, что закон больших чисел в
форме Бернулли является частным случаем закона больших
чисел в форме Чебышева.
Пример 9.8. Пусть дана последовательность -Xi, -Х2, ...,
Хп, ... независимых случайных величин, причем ряд распреде-
распределения случайной величины Хп пред-
представлен в табл. 9.1. Покажем, что к
этой последовательности применим
закон больших чисел в форме Че-
Чебышева. Для этого вычислим дис-
дисперсию ИХп. Имеем
Таблица 9Л
Хп
р
-5п
1
2п2
0
>-?
5п
1
2п2
412 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
пхп = мх1 - (мхпJ =
Итак, дисперсии ИХп ограничены в совокупности, и к
последовательности Х\, -Х*2,..., Хп,... применим закон больших
чисел в форме Чебышева.
Замечание 9.4. В специальных курсах теории вероятно-
вероятностей рассматривают также усиленный закон больших чисел, в
котором сходимость по вероятности заменяется сходимостью с
вероятностью 1.
9.3. Характеристическая функция
Для дальнейших исследований нам понадобится понятие
характеристической функции.
Определение 9.6. Характеристической функцией
f(t) = fx(t) случайной величины X называют математическое
ожидание случайной величины eitx, где г — мнимая единица, а
t — произвольное? (действительное) число.
В определении математического ожидания фигурирует ком-
плекснозначная случайная величина, которая определяется так
же, как и скалярная, с той лишь разницей, что каждому элемен-
элементарному исходу ставится в соответствие комплексное число, а
не действительное.
Используя общее правило вычисления математического
ожидания и формулу Эйлера [X], получаем:
для дискретной случайной величины А", принимающей зна-
значения Xj, j = 1,2,...,
f(t) =
9.3, Характеристическая функция 413
для непрерывной случайной величины с плотностью распре-
распределения р(х)
+00
= Meitx = I eitxp(x)dx =
+оо
= / cos(tx)p(x) dx + i I sin(tx)p(x)dx.
—oo
Поскольку |eite| = 1, то
—oo
+oo +oo
~oo
-boo +oo
—00
+
Следовательно, Y^eltXjPj и / ettxp{x)dx сходятся при всех *
j -oo
(действительных), т.е. характеристическая функция существу-
существует при всех t для каждой случайной величины. Отметим, что
характеристическая функция определяется не собственно слу-
случайной величиной, а ее функцией распределения, т.е., по суще-
существу, она характеризует именно распределение случайной вели-
величины. Читатель, знакомый с преобразованием Фурье, сразу же
заметит, что характеристическая функция непрерывной слу-
случайной величины отличается от преобразования Фурье плот-
плотности распределения этой случайной величины только лишь
отсутствием множителя 1/\/27г, что, как будет видно из даль-
дальнейшего, представляет определенное удобство при действиях
над случайными величинами.
Пример 9.9. Найдем характеристическую функцию слу-
случайной величины X, распределенной по биномиальному закону.
Поскольку X — дискретная случайная величина, принимающая
414 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
значения 0, п, то
j=0
Пример 9.10. Характеристическая функция случайной
величины X, распределенной по экспоненциальному закону,
имеет вид
+ОО -1-00
Л
= Г J^Xe-^dx = A I
X-it'
Пример 9.11. Пусть случайная величина X распределена
по стандартному нормальному закону. Тогда
+00 +ОО
= f jtx(p(x)dx =
-оо -оо
Делая замену у = х — it, получаем
+00—it +оо—it
—oo-it -oo-it
Из теории функций комплексного переменного [X] известно,
что
—оо—it
Окончательно получаем f(t) = е~~* '2. #
Выведем некоторые свойства характеристических функций.
9.3. Характеристическая функция 415
Теорема 9.5. Характеристическая функция удовлетворяет
следующим свойствам.
1. f(t) — непрерывная функция, причем абсолютное значе-
значение f(t) ограничено единицей, т.е. |/(*)| < 1 и /@) = 1.
2. Если У = аХ + Ь, то fY(t) = fx(at)eibt.
3. Бели Х\ и Хъ — независимые случайные величины и
Y = Хх+Х2, то fy(t) = fXl(t)fxM
4. Бели случайная величина X имеет момент п-го порядка
тЛ, то характеристическая функция X дифференцируема п
раз, причем для к ^ п
Ч 1. Утверждение 1 докажем для дискретной случайной вели-
величины. Тогда
/@) = ]>>«<% = Х> = 1.
3 3
Из неравенства
вытекает ограниченность функции по абсолютной величине
единицей.
Непрерывность /(?) следует из непрерывности функции ег1х'
и абсолютной сходимости ряда ]Г)pj [X].
з
2. В силу определения характеристической функции и свой-
свойства 2 математического ожидания (см. 7.2)
= M(eietAVw) = е^Ме*** = eMfx{at).
3. Поскольку Х\ и Хч. независимые, то независимыми явля-
являются также случайные величины ettXl и еаХг. Поэтому в соот-
416 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
ветствии со свойством 4 математического ожидания (см. 7.2)
4. Формальное fc-кратное (А; ^ п) дифференцирование харак-
характеристической функции дает
+00
= ik f xkJtxp{x)dx.
—00
Законность дифференцирования определяется тем фактом, что
+00 +ОО
! xkeitxp(x)dx < f \xk\p(x)dx,
-00
—ОО
и существованием момента n-го порядка. Заметим, что при
четном п справедливо и обратное: если характеристическая
функция имеет производную f^n\O)j то существуют моменты
всех порядков к до n-го включительно, и
Заметим, что свойство 3 является основным свойством, бла-
благодаря которому характеристические функции нашли пшрокое
применение в теории вероятностей. При суммировании неза-
независимых случайных величин их плотности распределения пре-
преобразуются по формуле свертки. Но формула свертки весьма
неудобна для исследования, гораздо проще заменить ее про-
простым перемножением характеристических функций.
Пример 9.12. Как мы знаем, если случайная величина X
распределена по стандартному нормальному закону, то слу-
случайная величина
9.3. Характеристическая функция 417
распределена по нормальному закону с параметрами тп и а.
Согласно свойству 2 характеристические функции /ш,(г(*) и f(t)
случайных величин У и X связаны соотношением
или, с учетом результата примера 9.11,
Пример 9.13. Вычислим момент n-го порядка случайной
величины X, распределенной по экспоненциальному закону.
Воспользовавшись свойством 4 и результатом примера 9.10,
получим
t=o
An! nl
Лп+1 Ап
Пример 9.14. Найдем еще раз характеристическую функ-
функцию числа успехов X вп испытаниях по схеме Бернулли, одна-
однако, в отличие от примере 9.9, воспользуемся равенством
где Xj — число успехов в j-м испытании. Тогда
fxj(t)=qeito+peitl=q+peit
и в силу свойства 3
Важнейшей особенностью характеристической функции f(t)
является тот факт, что она однозначно определяет функцию
распределения F(x) с помощью формулы обращения [XI].
418 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Формула обращения. Для любых точек непрерывности
х\ и Х2 функции распределения F(x)
-т
Отметим, что формула обращения справедлива и в точках
разрыва F(x), если предположить, что в этих точках
v ' 2
Бели характеристическая функция /(*) является абсолютно
интегрируемой на (—оо, +оо) [IX], то существует непрерывная
плотность распределения р(х), задаваемая выражением
+00
Последнее соотношение называют формулой обращения для
плотности распределения случайной величины.
Формула обращения для плотности распределения р(х) хо-
хорошо известна из курса математического анализа как формула
обратного преобразования Фурье.
Не давая строго математического доказательства, пока-
покажем, что по своей сути формула обращения представляет собой
разновидность обратного преобразования Фурье. Действи-
Действительно, формально применяя обратное преобразование Фурье
+00
e-itxf(t)dt
—оо
к характеристической функции f(t) и вспоминая соотношение
между плотностью распределения р(х) и функцией распределе-
9.3. Характеристическая функция 419
ния F(x), имеем
Х2 Х2 +00
F(x2)-F(Xl) = jp{x)dx = ±Jdx J e-itxf(t)dt.
XI XI -00
Формально проводя еще одну операцию — перестановку инте-
интегралов, получаем
+00 Х2
F{x2) -F(xx) = ±J f(t)dtje-itxdx =
-OO X\
+oo
1 Г e-%tXl _ e-ltX2
—OO
Хотя каждая из формально проведенных операций, вообще го-
говоря, математически не обоснована (в частности, дискретные
случайные величины вообще не имеют плотности распределе-
распределения), конечный результат верен, если только понимать послед-
последний интеграл в том смысле, как написано в формуле обращения
(в смысле главного значения) [XI].
Из определения характеристической функции и формулы
обращения следует существование взаимно однозначного соот-
соответствия между плотностью распределения и характеристиче-
характеристической функцией, а следовательно, и между функцией распреде-
распределения и характеристической функцией.
Пример 9.15. Пусть Х\ и Х2 — независимые случайные
величины, распределенные по нормальному закону с параметра-
параметрами т\ и (Ji, 7П2 и G2 соответственно. Рассмотрим случайную
величину
Тогда, как показано в примере 9.12,
420 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
и в соответствии со свойством 3 характеристических функций
получаем, что
Но характеристическую функцию /y(t) имеет случайная ве-
величина, распределенная по нормальному закону с параметра-
параметрами mi+rri2 и \Jo\ + o\. Следовательно, случайная величина
У также распределена нормально (с параметрами mi + rri2 и
у/а\ + 02).
Таким образом, с помощью характеристических функций
получили хорошо известный нам результат (см. пример 6.11):
сумма независимых случайных величин, имеющих нормальное
распределение, также является распределенной по нормальному
закону — и вычислили параметры этого распределения. За-
Заметим, что использование многомерных характеристических
функций позволяет весьма просто установить аналогичный ре-
результат для суммы любого конечного числа случайных вели-
величин, распределенных по нормальному закону (ср. с результата-
результатами 6.6).
Пример 9.16. Рассмотрим независимые случайные величи-
величины Х\ и -Хг, распределенные по закону Пуассона с параметрами
Ai и Лг- Их характеристические функции задаются формулами
n=0 ' n=0
Пусть
Тогда
и в силу взаимно однозначного соответствия между функци-
функцией распределения и характеристической функцией случайная
9.3. Характеристическая функция 421
величина У распределена по закону Пуассона с параметром
Ai + A2. #
Основную роль при доказательстве центральной предельной
теоремы играет теорема о связи слабой сходимости последо-
последовательности функций распределения со сходимостью последо-
последовательности соответствующих характеристических функций,
или теорема непрерывности. Приведем без доказательства
формулировку этой теоремы.
Теорема 9,6 (теорема непрерывности). Для того что-
чтобы последовательность Fi(ж), ^(я), ..., Fn(x), ... функций
распределения слабо сходилась к функции распределения F(x),
необходимо и достаточно, чтобы последовательность /i(?),
/г(*)? •••> /п(?)> ••• характеристических функций сходилась к
характеристической функции f(t) в любой точке *.
Теорема непрерывности позволяет свести задачу изучения
предельного поведения распределений сумм независимых слу-
случайных величин к задаче изучения предельного поведения ха-
характеристических функций этих сумм. В разных учебниках
приведены различные формулировки теоремы непрерывности;
данная здесь формулировка наиболее естественна для наших
дальнейших рассуждений.
В заключение отметим, что наряду с характеристической
функцией в теории вероятностей используют также:
- для неотрицательной случайной величины X преобразо-
преобразование Лапласа — Стилтьеса
- для неотрицательной целочисленной случайной величины
X производящую функцию
Ясно, что преобразование Лапласа — Стилтьеса f(s) и
производящая функция f*(z) связаны с характеристической
422 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
функцией той же самой случайной величины соотношениями
Преобразование Лапласа — Стилтьеса и производящая
функция, по сути дела, имеют те же самые свойства, что и
характеристическая функция, но их существенно проще исполь-
использовать уже хотя бы потому, что они являются действительными
функциями.
9.4. Центральная предельная теорема
Рассмотрим последовательность Ai, X*i,..., Хп,... незави-
независимых одинаково распределенных случайных величин, имеющих
математическое ожидание МХП = га. Предположим также,
что существует дисперсия ЛХп = о2. Закон больших чисел
(слабый) для этой последовательности можно представить в
следующей форме:
где
суммарное значение первых п случайных величин последова-
последовательности, а сходимость можно понимать как в смысле сходи-
мости по вероятности (слабый закон больших чисел), так и в
смысле сходимости с вероятностью 1 (усиленный закон больших
чисел).
Однако сразу возникает вопрос: поскольку случайные ве-
величины Хп имеют не только математическое ожидание, но и
дисперсию, то нельзя ли доказать более „тонкую" предельную
теорему, позволяющую точнее описать предельное поведение
9.4. Центральная предельная теорема 423
распределений величин Sn — тьтп? Такая теорема существует,
ее называют центральной предельной теоремой.
Теорема 9.7 (центральная предельная теорема).
Пусть Х\, Х21 ..., Хп, ... — последовательность независи-
независимых одинаково распределенных случайных величин, МХп = т,
Т)Хп = а2. Тогда
п—юо
где Ф(х) — функция стандартного нормального распределения.
<4 Прежде всего заметим, что поскольку функция стандарт-
стандартного нормального распределения Ф(х) является непрерывной
функцией, то сходимость к ней последовательности функций
распределения в каждой точке представляет собой слабую схо-
сходимость, и, значит, для доказательства центральной предель-
предельной теоремы можно воспользоваться теоремой непрерывности.
Обозначим fi(t) характеристическую функцию случайных
величин Хп, a gn(t) — характеристическую функцию случайной
величины (Sn — nm)/Vna2. Воспользовавшись свойствами 2 и
3 характеристических функций, найдем
Поскольку /i(t) имеет производные первых двух порядков
(свойство 4 характеристических функций), то \nfi{t/y/na2)
можно в любой точке t представить первыми тремя слагаемыми
формулы Маклорена:
Л=1п/1@) + -Д=.^ +
*' у/па2 fi(v)
*2 //Г(о) (Л(о)J
424 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
или,
im\t a2t2
¦ + o
2na2
если учесть (см. теорему 9.5), что
/i@) = l, Л(О)=гшь /{'@)=г2ш2
Поэтому
(=).
]ngn{t)=n\]nfi[
9n(t) -> е-"*
t \ imt 1 t2
2
и, значит,
n—^oo
Для завершения доказательства теоремы осталось заметить,
что е~*2/2 — характеристическая функция /(?) стандартного
нормального распределения (см. пример 9.11). >
Центральная предельная теорема выявляет ту особую роль,
которую играет нормальное распределение на практике. Нор-
Нормальный закон всегда имеет место в тех ситуациях, когда
случайная величина порождена большим количеством случай-
случайных факторов, действующих независимо друг от друга. Уже
само название пнормальный закон" объясняется тем широким
распространением, которое он находит в самых различных
областях научных исследований.
Следствием из центральной предельной теоремы является
интегральная теорема Муавра — Лапласа (см. 3.6, интеграль-
интегральная формула Муавра — Лапласа).
Теорема 9.8 (интегральная теорема Муавра — Ла-
Лапласа). Обозначим Sn суммарное число успехов в п испытани-
испытаниях по схеме Бернулли с вероятностью успеха р и вероятностью
неудачи q = 1 — р. Тогда с ростом п последовательность функ-
функций распределения случайных величин (Sn — np)/^npq сходится
к функции стандартного нормального распределения, т.е.
9.4. Центральная предельная теорема 425
«* Пусть Х{ — число успехов в г-ы испытании. Тогда
MXi=p, T>Xi=pq.
Представляя Sn в виде
и используя центральную предельную теорему, приходим к
утверждению теоремы. >
Пример 9.17. Для определения скорости v движения объ-
объекта делают п измерений vi,..., vn, причем г-е измерение прово-
проводят с погрешностью Х{ (т.е. V{ = v + X;), при этом погрешности
измерений являются независимыми и одинаково распределен-
распределенными случайными величинами с математическим ожиданием
ЪАХ{ = 0 (отсутствуют систематические погрешности наблю-
наблюдений) и дисперсии DXi = a2.
Оценим вероятность того, что средняя наблюденная ско-
скорость
и
будет отличаться от истинной скорости v не более чем на е.
Имеем
Считая теперь, что число п измерений велико, воспользу-
воспользуемся центральной предельной теоремой, согласно которой слу-
случайная величина
VI + ... + Vn - TIV
426 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
приближенно распределена по стандартному нормальному за-
закону. Значит,
Значения интеграла Лапласа Фо(х) приведены в табл. П.З.
9.5. Решение типовых примеров
Пример 9.18* По многолетним наблюдениям, средняя
скорость ветра в некотором пункте равна 16 км/ч. Оценим
с помощью первого неравенства Чебышева вероятность того,
что в случайный момент времени скорость ветра в этом пункте
превысит 80 км/ч.
Обозначим через X скорость ветра при наблюдении в слу-
случайный момент времени и, воспользовавшись первым неравен-
неравенством Чебышева, получим
Пример 9.1$. Используя второе неравенство Чебышева,
оценим вероятность того, что случайная величина отклонится
от своего среднего значения т более чем на 3<т, где а — среднее
квадратичное отклонение случайной величины X.
В соответствии со вторым неравенством Чебышева
Пример 9.20. Пусть Х\, Х2,..., Хп,... — последователь-
последовательность независимых случайных величин, причем случайная вели-
величина Хп имеет гамма-распределение с параметрами 7n = n vl
\п = у/п. Покажем, что последовательность Х\, Хъ,..., Хп,...
удовлетворяет закону больших чисел в форме Чебышева.
9.5. Решение типовых примеров
427
Дисперсия случайной величины Хп равна
Поскольку дисперсии DXn ограничены 1, то к последователь-
последовательности Х\,Х2)... ,-^п,... применим закои больших чисел в форме
Чебышева.
Пример 9.21, Пусть Xi,X2,^.,Xn,... — последователь-
последовательность случайных величин, удовлетворяющих условиям
lim cov(Xi,Xj)=0.
Докажем, что к этой последовательности применим закон
больших чисел.
Согласно второму неравенству Чебьппева,
Поэтому для решения поставленной задачи достаточно пока-
показать, что
Действительно, в соответствии со свойствами
г=1
г=1
14*
428 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Из условия задачи следует существование для любого е > О
такого ЛГ, что
cov{Xi,Xj) <e
при всех i,j, для которых ъ — j > N. Поэтому сумма ковариаций
содержит не более nN слагаемых, больших е. Поскольку
всего слагаемых в этой сумме п(п — 1)/2 и в соответствии со
свойством 4 ковариаций
|cov(XbX,-)|
получаем
Значит,
г=1
1=1
п2
п
что в силу произвольности е доказывает утверждение.
Пример 9.22. Найдем характеристическую функцию слу-
случайной величины X, ряд распре-
1аолица 9.2 деления которой представлен в
табл. 9.2.
В соответствии с определени-
определением характеристической функции
X
р
-2
0,2
-1
0,1
0
0,4
1
0,1
2
0,2
** + еи) + 0,4e0i* = 0,4cosBt) + 0,2cost + 0,4 =
= 0,8 cos21 + 0,2 cost = 0,2 cos t D cos t +1).
Пример 9.23. Найдем характеристическую функцию слу-
случайной величины X, имеющей геометрическое распределение с
параметром р.
9.5. Решение типовых примеров 429
Используя ряд распределения случайной величины, имею-
имеющей геометрическое распределение с параметром р, получаем
/w = fvsa p)j =рЕИ1 р)У =
j=0 j=0 v r'
Пример 9.24. Найдем характеристическую функцию слу-
случайной величины X, имеющей равномерное на интервале (а, Ь)
распределение.
Вспоминая определение плотности распределения равно-
равномерно распределенной на интервале (а, Ь) случайной величины,
имеем
ь
eitxdx eitb-eita
[
-J
ъ-а " «*(Ь-а)'
Пример 9.25. Найдем характеристическую функцию не-
непрерывной случайной величины X, имеющей плотность распре-
распределения
Характеристическая функция случайной величины X равна:
2 7 2
~оо О
2(г* -
Пример 9.26. Найдем характеристическую функцию не-
непрерывной случайной величины X, имеющей плотность распре-
распределения Коти
р{х)=Ь
430 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Имеем
+00
eitxdx
-00
Для вычисления интеграла воспользуемся методом контурного
интегрирования [X]. При этом рассмотрим отдельно два слу-
случая: t > О и t < 0.
В первом случае выберем замкнутый контур L, состоящий
из полуокружности V большого радиуса R с центром в точ-
точке 0, лежащей в верхней части комплексной плоскости, и части
V1 действительной оси, представляющей собой диаметр этой
полуокружности (рис. 9.3). Поскольку подынтегральная функ-
функция является аналитической внутри рассматриваемого контура
за исключением простого полюса в точке z = г, то интеграл
по контуру L будет равен вычету в точке г, умноженному на
2ттг, т.е.
Г eitzdz Г
J лТГ+г2) =27Г*?=г?1тг
В свою очередь,
Atz \ Atz JXz
Оценим
У
при Л > у/2. Поскольку
9.5. Решение типовых примеров
431
при О 0 в верхней полуплоскости Imz >0и, кроме того,
на окружности \z\ = R при R > л/2, то
eitzdz
Г eltzdz f 2\dz\ _ 2тгД = 2
У тгA + г2) ^У тгД2 ~ тгД2 " Л'
Устремляя теперь R к бесконечности, видим, что интеграл по
полуокружности V стремится к нулю, а интеграл по диаметру
L" — к характеристической функции. Значит,
/(*) =
_--*
при
t>0.
L'
-R О
L"
R х
R
Рис. 9.3
Рис. 9.4
Во втором случае поступим точно так же, только вместо
полуокружности, лежащей в верхней части комплексной плос-
плоскости, возьмем полуокружность, лежащую в нижней части этой
плоскости (рис. 9.4). Аналогичные выкладки дают:
f(t) = е* при * < 0.
Объединяя оба случая, получаем
432 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Пример 9.27. Выясним, может ли функция
f(t) = sin*
являться характеристической функцией некоторой случайной
величины.
Не может, так как
что противоречит свойству 1 характеристической функции.
Пример 9.28. Ответим на вопрос: может ли функция
являться характеристической функцией некоторой случайной
величины?
Не может, так как f(t) не является ограниченной, что
противоречит свойству 1 характеристической функции.
Пример 9.29. Выясним, может ли функция
являться характеристической функцией некоторой случайной
величины.
Оказывается, что не может, так как функция f(t) терпит
разрыв в точках t = — 1 и< = 1, что противоречит свойству 1
характеристической функции.
Пример 9.30. Найдем характеристическую функцию слу-
случайной величины
Y = aX + b, a>0,
где X — случайная величина, определенная в примере 9.26.
Используя свойство 2 характеристической функции и ре-
результаты примера 9.25, имеем
9.5. Решение типовых примеров 433
Пример 9.31. Независимые случайные величины Х\ и Х2
распределены по экспоненциальному закону с параметрами Ах и
\2. Найдем характеристическую функцию случайной величины
Поскольку случайные величины Х\ и Х2 независимы и
имеют характеристические функции
(см. пример 9.10), то в соответствии со свойством 3 характе-
характеристической функции
Пример 9.32. Найдем математическое ожидание и дис-
дисперсию случайной величины X, имеющей характеристическую
функцию
Нетрудно видеть, что характеристическая функция /(<)
имеет производные всех порядков в любой точке t, причем
, <cost~sint ;// -
при t ^ 0, а /;@) и //;@) определяются из условия непрерывно-
непрерывности. Воспользовавшись правилом Лопиталя, имеем
Отсюда в силу свойства 4 характеристической функции
434 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Пример 9.33. Найдем закон распределения случайной
величины, характеристическая функция которой равна
Мы не будем пользоваться формулой обращения, а пред-
представим характеристическую функцию f(t) в соответствии с
формулой Эйлера в виде
Таблица 9.3
Отсюда видно, что /(<) является ха-
характеристической функцией дискрет-
дискретной случайной величины X, имеющей
ряд распределения, представленный в
табл. 9.3.
Пример 9.34. Найдем закон распределения случайной
величины X, характеристическая функция которой равна
X
р
-1
0,25
0
0,5
1
0,25
В данном случае характеристическая функция f(t) является
абсолютно .интегрируемой, а значит, случайная величина X
имеет плотность*распределения
+оо
Р(х) = -^
Производя интегрирование, получаем
+оо 0
р(х)=±-
2тг
2тг J
+оо
f
2/к
—оо
1
2ir(-ix +1) 2тг(-»ж -
9.5. Решение типовых примеров 435
Таким образом, случайная величина X имеет плотность рас-
распределения
р{х)=^П)
(см. также пример 9.25).
Пример 9.35. Случайная величина X является средним
арифметическим из 3200 независимых одинаково распределен-
распределенных случайных величин, причем каждое слагаемое имеет ма-
математическое ожидание 3 и дисперсию 2. Воспользовавшись
центральной предельной теоремой, оценим вероятность того,
что X попадет в интервал B,925, 3,075).
Случайная величина X имеет математическое ожидание
**„ о ^v 2 1
Мл =3 и дисперсию Da =
3200 1600
Тогда в силу центральной предельной теоремы случайная вели-
величина
имеет приближенно стандартное нормальное распределение, а
значит,
Р{2,925<Х<3,075} =
= Р{B,925 - 3)VT600 < У < C,075 - 3)л/Ш0} «
«ФоC)-Фо(-3).
Воспользовавшись табл. П.З, в которой приведены значения
функции Лапласа, имеем
Р{2,925 < X < 3,075} » 2 • 0,49865 = 0,9973.
Пример 9.36. Найдем вероятность того, что при 720
бросаниях игральной кости „шестерка" выпадает от 100 до 130
раз.
436 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
Обозначим через X суммарное число выпавших „шестерок"
при п = 720 бросаниях игральной кости. Поскольку вероят-
вероятность выпадения „шестерки" при одном бросании р = 1/6, то
в силу интегральной теоремы Муавра — Лапласа случайная
величина
Х-пр Х-120
y/npq 10
приближенно распределена по стандартному нормальному за-
закону. Значит,
Используя таблицу значений функции Лапласа (см. табл. П.З),
находим:
Р{100 < X < 130} и 0,34134 - (-0,47725) = 0,81859.
Отметим, что задачи такого рода уже рассматривались
нами (см. 3.6).
Вопросы и задачи
9.1. Какие тины сходимости случайных величин Вы знаете?
Как связаны между собой различные типы сходимости?
9.2. Дайте определение слабой сходимости последователь-
последовательности функций распределения.
9.3. Напишите первое неравенство Чебышева.
9.4. Напишите второе неравенство Чебышева.
9.5. В каком случае говорят, что последовательность неза-
независимых одинаково распределенных случайных величин удовле-
удовлетворяет закону больших чисел? В чем заключается физический
смысл закона больших чисел?
9.6. Докажите закон больших чисел в форме Чебышева.
Вопросы и задачи 437
9.7. Докажите закон больших чисел в форме Бернулли.
9.8. Дайте определение характеристической функции.
9.9. Перечислите основные свойства характеристической
функции.
9.10. Напишите формулу обращения.
9.11. Как связаны между собой слабая сходимость последо-
последовательности функций распределения и сходимость последова-
последовательности соответствующих им характеристических функций
(теорема непрерывности)?
9.12. Докажите центральную предельную теорему. В чем
заключается физический смысл этой теоремы?
9.13. Докажите интегральную теорему Муавра — Лапласа.
9.14. Средний ежедневный расход воды в некотором насе-
населенном пункте составляет 50000 л. Оцените с помощью первого
неравенства Чебышева вероятность того, что в произвольно
выбранный день расход воды в этом пункте превысит 150000 л.
Ответ: Р{Х > 150000} < 1/3.
9.15. Среднее потребление электроэнергии в мае в некото-
некотором населенном пункте составляет 360000 кВт-ч.
а) Оцените с помощью первого неравенства Чебышева веро-
вероятность того, что потребление электроэнергии в мае текущего
года в этом населенном пункте превысит 1000000 кВт-ч.
б) Оцените с помощью второго неравенства Чебышева ту
же вероятность, если известно, что среднее квадратичное от-
отклонение потребления электроэнергии в мае равно 40000 кВт-ч.
Ответ: а) Р{Х > 1000000} < 0,36; б) Р{Х > 1000000} < -^-.
9.16. Среднее квадратичное отклонение погрешности из-
измерения курса самолета равно 2°. Считая математическое
ожидание погрешности измерения равным нулю, оцените с по-
помощью второго неравенства Чебышева вероятность того, что
погрешность одного измерения курса самолета превысит 5°.
Ответ: Р{\Х\ > 5°} < 0,16.
438 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
9.17. Вероятность появления некоторого события в каждом
из 800 независимых испытаний равна 1/4. Воспользовавшись
вторым неравенством Чебышева, оцените вероятность того,
что число X появлений этого события заключено в пределах
от 150 до 250.
Ответ: Р{150 < X < 250} ^ 0,94.
9.18. Пусть дана последовательность Ai, X*i, ..., Ап, ...
независимых дискретных случайных величин, причем ряд рас-
_ _, л . пределения случайной величины Хп
Таблица 94 л л ,. тт
представлен в табл. 9.4. Проверьте,
применим ли к этой последователь-
последовательности закон больших чисел в форме
Чебышева.
Ответ: да, применим.
9.19. Пусть Ai, %2, •••? Хп, ••• — последовательность
независимых случайных величин, причем случайная величина
Хп имеет плотность распределения
Хп
р
-у/п
1
2п
0
1-1
п
1
2п
Проверьте, удовлетворяет ли последовательность Х\ ,X*i,... ,Хп,...
закону больших чисел в форме Чебышева.
Ответ: да, удовлетворяет.
9.20. Пусть последовательность Ai, A2, ..., Хпу ... некор-
некоррелированных случайных величин удовлетворяет условию
1 п
lim — У^ D Xi = 0.
п—юо ТЬ *—^
г=1
Проверьте, применим ли к этой последовательности закон
больших чисел.
Ответ: да, применим.
Вопросы и задачи
439
9.21. Найдите характеристичес-
характеристическую функцию случайной величины
X, ряд распределения которой пред-
представлен в табл. 9.5.
Ответ: /(*) = l/2 + ett(l + eftJ/8.
Таблица 9.5
X
р
0
1/2
1
1/8
2
1/4
3
1/8
Таблица 9.6
X
Р
-2
1/4
0
1/2
2
1/4
9.22. Найдите характеристиче-
характеристическую функцию случайной величины
X, ряд распределения которой пред-
представлен в табл. 9.6.
Ответ: /(i) = cos2*.
9.23. Найдите характеристическую функцию неотрицатель-
неотрицательной целочисленной случайной величины X, распределение кото-
которой задается вероятностями
Ответ: /(t) =p2/(l - A ~р)е^J.
9.24. Найдите характеристическую функцию непрерывной
случайной величины X, имеющей плотность распределения
0,
\х\ > 1;
Ответ:
Г l,
/(*) = \ 3(sint-tcost)
9.25. Найдите характеристическую функцию случайной
величины X, имеющей гамма-распределение с параметрами 7
и Л.
Ответ: /(*) =
440 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
9.26. Найдите характеристическую функцию непрерывной
случайной величины X, имеющей плотность распределения
Ответ: f(t) =
9.27. Может ли функция
являться характеристической функцией некоторой случайной
величины?
Ответ: не может.
9.28. Может ли функция
являться характеристической функцией некоторой случайной
величины?
Ответ: не может.
9.29. Может ли функция
где [t] — целая часть числа ?, являться характеристической
функцией некоторой случайной величины?
Ответ: не может.
9.30. Найдите характеристическую функцию случайной ве-
величины Y = аХ + Ь, где X — случайная величина, определенная
в задаче 9.26.
Ответ: f(t) = v/2e-la*l/^+ibtsinGr/4+ \at\/y/2).
9.31. Случайная величина Х\ распределена равномерно в
интервале @,1), а случайная величина Х2 имеет стандарт-
стандартное нормальное распределение. Найдите характеристическую
Вопросы и задачи
441
функцию случайной величины У = Х\ + Х2, если известно, что
Х\ и Xi являются независимыми.
Ответ: /у(*) = ~ -Д
2б
9.32. Найдите математическое ожидание и дисперсию слу-
случайной величины -Y, имеющей характеристическую функцию
/(*)= 1
Ответ: Ъ/LX = — 2,
9.33. Найдите математическое ожидание и дисперсию слу-
случайной величины X, имеющей характеристическую функцию
Ответ:
= 0, ВХ =
1 + 2>/2
9.34. Найдите закон распределения случайной величины,
характеристическая функция которой равна
cos*Bcos* + l)
Таблица 9.7
/(<) =
Ответ: /(*) является характе-
характеристической функцией дискрет-
дискретной случайной величины X, име-
имеющей ряд распределения, пред-
представленный в табл. 9.7.
9.35. Найдите плотность распределения случайной величи-
величины, имеющей характеристическую функцию
X
р
-2
1/6
J
1/6
0
1/3
1
1/6
2
1/6
/(*)=
-i*i, i*i <i-
Ответ: р(х) = —jsin21.
442 9. ПРЕДЕЛЬНЫЕ ТЕОРЕМЫ ТЕОРИИ ВЕРОЯТНОСТЕЙ
9.36. Проводится выборочное обследование большой партии
электрических лампочек для определения среднего времени их
горения. Среднее квадратичное отклонение времени горения
лампочки равно а = 80 ч. Из всей партии наудачу выбирается
400 лампочек. Воспользовавшись центральной предельной тео-
теоремой, оцените вероятность того, что среднее (математическое
ожидание) время горения лампочки будет отличаться от наблю-
наблюденного среднего времени горения выбранных 400 лампочек не
более чем на 10 ч.
Ответ: 0,98738.
9.37* Случайная величина X является средним арифметиче-
арифметическим из п независимых одинаково распределенных случайных
величин, дисперсия каждой из которых равна 5. Воспользовав-
Воспользовавшись центральной предельной теоремой, оцените, какое число
слагаемых п нужно взять для того, чтобы с вероятностью не
менее 0,9973 случайная величина X отклонялась от своего сред-
среднего не более чем на 0,01.
Ответ: п^450000.
9.38. Решите задачу 9.17, воспользовавшись для прибли-
приближенной оценки искомой вероятности интегральной теоремой
Муавра — Лапласа. Сравните полученные результаты.
Ответ: Р{150 ^X < 250} « 0,9999366. Сравнивая полученные
результаты, видим, что интегральная теорема Муавра —
Лапласа дает гораздо более точный ответ.
ПРИЛОЖЕНИЕ
Таблица ПЛ
Значения функции Р(га; А) =
т\
т
0
1
2
3
4
5
6
7
8
л
0,1
0,90484
09048
00452
00015
0,2
81873
16375
01637
00109
00005
0,3
74082
22225
03334
00333
00025
00002
0,4
67032
26813
05363
00715
00072
00006
0,5
60653
30327
07582
01264
00158
00016
00001
0,6
54881
32929
09879
01976
00296
00036
00004
0,7
49659
34761
12166
02839
00497
00070
00008
00001
0,8
44933
35946
14379
03834
00767
00123
00016
00002
0,9
40657
36591
16466
04940
01111
00200
00030
00004
1,0
36788
36788
18394
06131
01533
00307
00051
00007
00001
т
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
л
1,5
0,22313
33470
25102
12551
04707
01412
00353
00076
00014
00002
2,0
13534
27067
27067
18045
09022
03609
01203
00344
00086
00019
00004
00001
2,5
08208
20521
25652
21376
13360
06680
02783
00994
00311
00086
00022
00005
00001
3,0
04979
14936
22404
22404
16803
10082
05041
02160
00810
00270
00081
00022
00006
00001
3,5
03020
10569
18496
21579
18881
13217
07710
03855
01687
00656
00230
00073
00021
00006
00001
4,0
01832
07326
14653
19537
19537
15629
10420
05954
02977
01323
00529
00192
00064
00020
00006
00002
4,5
01111
04999
11248
16872
18981
17083
12812
08236
04633
02316
01042
00426
00160
00055
00018
00005
00002
5,0
00674
03369
08422
14037
17547
17547
14622
10444
06528
03627
01813
00824
00343
00132
00047
00016
00005
00001
5,5
00409
02248
06181
11332
15582
17140
15712
12345
08487
05187
02853
01426
00654
00277
00109
00040
00014
00004
00001
6,0
00248
01487
04462
08924
13385
16062
16062
13768
10326
06884
04130
02253
01126
00520
00223
00089
00033
00012
00004
00001
444
ПРИЛОЖЕНИЕ
Таблица П.2
Значения функции (р(х) =
е 2
X
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1.1
1.2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
X
3,0
4,0
Сотые доли х
0
0,39894
39695
39104
38139
36827
35207
33322
31225
28969
26609
24197
21785
19419
17137
14973
12952
11092
09405
07895
06562
05399
04398
03547
02833
02239
01753
01358
01042
00792
00595
1
39892
39654
39024
38023
36678
35029
33121
31006
28737
26369
23955
21546
19186
16915
14764
12758
10915
09246
07754
06438
05292
04307
03470
02768
02186
01709
01323
01014
00770
00578
2
39886
39608
38940
37903
36526
34849
32918
30785
28504
26129
23713
21307
18954
16694
14556
12566
10741
09089
07614
.06316
05186
04217
03394
02705
02134
01667
01289
00987
00748
00562
3
39876
39559
38853
37780
36371
34667
32713
30563
28269
25888
23471
21069
18724
16474
14350
12376
10567
08933
07477
06195
05082
04128
03319
02643
02083
01625
01256
00961
00727
00545
4
39862
39505
38762
37654
36213
34482
32506
30339
28034
25647
23230
20831
18494
16256
14146
12188
10396
08780
07341
06077
04980
04041
03246
02582
02033
01585
01223
00935
00707
00530
5
39844
39448
38667
37524
36053
34294
32297
30114
27798
25406
22988
20594
18265
16038
13943
12001
10226
08628
07206
05959
04879
03955
03174
02522
01984
01545
01191
00909
00687
00514
6
39822
39387
38568
37391
35889
34105
32086
29887
27562
25164
22747
20357
18037
15822
13742
11816
10059
08478
07074
05844
04780
03871
03103
02463
01936
01506
01160
00885
00668
00499
7
39797
39322
38466
37255
35723
33912
31874
29659
27324
24923
22506
20121
17810
15608
13542
11632
09893
08329
06943
05730
04682
03788
03034
02406
01888
01468
01130
00861
00649
00485
8
39767
39253
38361
37115
35553
33718
31659
29431
27086
24681
22265
19886
17585
15395
13344
11450
09728
08183
06814
05618
04586
03706
02965
02349
01842
01431
01100
00837
00631
00470
9
39733
39181
38251
36973
35381
33521
31443
29200
26848
24439
22025
19652
17360
15183
13147
11270
09566
08038
06687
05508
04491
03626
02898
02294
01797
01394
01071
00814
00613
00457
Десятые доли х
0
0,00443
00013
2
00238
00006
4
00123
00002
6
00061
00001
8
00029
445
Таблица П.З
Значения интеграла Лапласа Фо(я) =
1 } ?.
—т= / е 2 dt
у2тгУ
0,0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1,0
1,1
1,2
1,3
1,4
1,5
1,6
1,7
1,8
1,9
2,0
2,1
2,2
2,3
2,4
2,5
2,6
2,7
2,8
2,9
X
3,0
4,0
Сотые доли х
0
0,00000
03983
07926
11791
15542
19146
22575
25804
28814
31594
34134
36433
38493
40320
41924
43319
44520
45543
46407
47128
47725
48214
48610
48928
49180
49379
49534
49653
49744
49813
1
00399
04380
08317
12172
15910
19497
22907
26115
29103
31859
34375
36650
38686
40490
42073
43448
44630
45637
46485
47193
47778
48257
48645
48956
49202
49396
49547
49664
49752
49819
2
00798
04776
08706
12552
16276
19847
23237
26424
29389
32121
34614
36864
38877
40658
42220
43574
44738
45728
46562
47257
47831
48300
48679
48983
49224
49413
49560
49674
49760
49825
3
01197
05172
09095
12930
16640
20194
23565
26730
29673
32381
34850
37076
39065
40824
42364
43699
44845
45818
46638
47320
47882
48341
48713
49010
49245
49430
49573
49683
49767
49831
4
01595
05567
09483
13307
17003
20540
23891
27035
29955
32639
35083
37286
39251
40988
42507
43822
44950
45907
46712
47381
47932
48382
48745
49036
49266
49446
49585
49693
49774
49836
5
01994
05962
09871
13683
17364
20884
24215
27337
30234
32894
35314
37493
39435
41149
42647
43943
45053
45994
46784
47441
47982
48422
48778
49061
49286
49461
49598
49702
49781
49841
6
02392
06356
10257
14058
17724
21226
24537
27637
30511
33147
35543
37698
39617
41308
42786
44062
45154
46080
46856
47500
48030
48461
48809
49086
49305
49477
49609
49711
49788
49846
7
02790
06749
10642
14431
18082
21566
24857
27935
30785
33398
35769
37900
39796
41466
42922
44179
45254
46164
46926
47558
48077
48500
48840
49111
49324
49492
49621
49720
49795
49851
8
03188
07142
11026
14803
18439
21904
25175
28230
31057
33646
35993
38100
39973
41621
43056
44295
45352
46246
46995
47615
48124
48537
48870
49134
49343
49506
49632
49728
49801
49856
9
03586
07535
11409
15173
18793
22240
25490
28524
31327
33891
36214
38298
40147
41774
43189
44408
45449
46327
47062
47670
48169
48574
48899
49158
49361
49520
49643
49736
49807
49861
Десятые доли х
0
0,49865
49997
2
49931
49999
4
49966
6
49984
8
49993
СПИСОК РЕКОМЕНДУЕМОЙ
ЛИТЕРАТУРЫ
Учебники и учебные пособил
Боровков А. А. Курс теории вероятностей: Учеб. пособ. М.: Наука,
1972. 288 с.
Бочаров П.П., Печинкин А.В. Теория вероятностей. Математическая
статистика. М.: Гардарика, 1998. 328 с.
Вентцелъ Е.С. Теория вероятностей: Учеб. М.: Наука, 1969. 564 с.
Вентцель Е.С., Овчаров Л.А. Прикладные задачи теории вероятно-
вероятностей. М.: Радио и связь, 1973. 415 с.
Гмурман В.Е. Теория вероятностей и математическая статистика. М.:
Высш. ж., 1972. 477 с.
Гнеденко Б.В. Курс теории вероятностей: Учеб. М.: Наука, 1988.
447 с.
Карташов Т.Д. Теория вероятностей. Вероятностные модели: Учеб.
пособ. М.: Изд-во МГТУ, 1990. 63 с.
Климов Г. П. Теория вероятностей и математическая статистика. М.:
Изд-во МГУ, 1983. 328 с.
Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука,
1974. 120 с.
Лоэв М. Теория вероятностей / Пер. с англ. М.: Изд-во иностр. лит.,
1962. 719 с.
Неве Ж. Математические основы теории вероятностей / Пер. с франц.
М.: Мир, 1969. 310 с.
Прохоров Ю.В.} Розанов Ю.А. Теория вероятностей. М.: Наука, 1973.
494 с.
Пугачев B.C. Теория вероятностей и математическая статистика:
Учеб. пособ. М.: Наука, 1979. 495 с.
Розанов Ю.А. Лекции по теории вероятностей. М.: Наука, 1986. 213 с.
Севастьянов Б.А. Курс теории вероятностей и математической ста-
статистики. М.: Наука, 1982. 257 с.
Смирнов Н.В., Дунин-Барковский И.В. Курс теории вероятностей и
математической статистики для технических приложений: Учеб. пособ.
М.: Наука, 1965. 511 с.
447
Феллер В. Введение в теорию вероятностей и ее приложения / Пер. с
англ.: В 2 т. Т.1. М.: Мир, 1984. 498 с; Т.2. М.: Мир, 1984. 752 с.
Четыркин Е.М., Калихман И. Л. Вероятность и статистика. М.:
Финансы и статистика, 1982. 319 с.
Чистяков В.П. Курс теории вероятностей: Учеб. М.: Наука, 1987.
240 с.
Задачники
Агапов Г.И. Задачник по теории вероятностей. М.: Высш. шк., 1986.
80 с.
Вентцель Е.С., Овчаров Л. А. Теория вероятностей: Задачник. М.:
Наука, 1973. 172 с.
Гмурман В.Е. Руководство к решению задач по теории вероятностей
и математической статистике. М.: Высш. шк., 1975. 334 с.
Емельянов Г.В., Скитович В.П. Задачник по теории вероятностей и
математической статистике. Л.: Изд-во ЛГУ, 1967. 330 с.
Мешалкин Л.Д. Сборник задач по теории вероятностей. М.: Иэд-во
МГУ, 1963. 143 с.
Сборник задач по теории вероятностей, математической статистике и
теории случайных функций / Под ред А.А. Свешникова, М.: Наука, 1970.
632 с.
Тескин О.И., Тверитпинов Д.И., Северцев Н.А. Методические указания
к выполнению домашнего задания по теории вероятностей и математиче-
математической статистике. М.: Изд-во МВТУ, 1981. 58 с.
Сборник задач по математике для втузов. Ч. 3. Теория вероятностей
и математическая статистика: Учеб. пособ. / Под ред. А.В. Ефимова. М.:
Наука, 1990. 428 с.
Вспомогательная литература
Ежов И.И., Скороход А.В., Ядренко М.И. Элементы комбинаторики.
М.: Наука, 1977. 80 с.
Кофман А. Введение в прикладную комбинаторику / Пер. с англ. М.:
Наука, 1975. 479 с.
Кулъбак С. Теория информации и статистика / Пер. с англ. М.: Наука,
1967. 409 с.
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Аксиома неотрицательности 60
- непрерывности 64
- нормированное™ 60
- сложения 64
-- расширенная 60
Алгебра событий 33
Асимметрия 321
Вектор математических ожиданий
187, 300
- случайный двумерный 165
- п-мерный 165
- средних значений 300
-- квадратичных отклонений 187
Величина случайная 126
- двумерная 165
дискретная 171
непрерывная 176»
- дискретная 129
-- многомерная (п-мерная) 165
- непрерывная 135
-- одномерная 165
- центрированная 302
Величины случайные зависимые 182
-- независимые 181
в совокупности 185
-- некоррелированные 196, 313
Вероятности апостериорные 98
- априорные 98
Вероятность безусловная 80
- геометрическая 56
Вероятность события 43, 56, 58, 60
- условная 79, 80, 355
Выборка 46
- без возвращения 46
- с возвращением 46
Гипотезы 93
Группа событий полная 93
Диаграммы Эйлера — Венна 26
Дисперсия (второй центральный
момент) 189, 302
- условная 372
Дополнение события 29
Задача о встрече 56
Закон биномиальный 132
- больших чисел в форме Бернулли
411
Чебышева 409
слабый 409
- геометрический 134
- нормальный многомерный 189
- стандартный 145
- n-мерный общий 256
- Пуассона 133
- распределения Вейбулла 146
- вероятностей 126
- дифференциальный 136
- интегральный 135
-- Релея 147
449
Закон распределения
экспоненциальный
(показательный) 141
- X2 (хи-квадрат) 148
- редких событий 133
Законы де Моргана 31
- распределения условные 360
Значение наивероятнейшее 325
- среднее 144
- условного математического
ожидания 365, 369
- условной дисперсии 372
Интеграл Лапласа 106
Интерпретация геометрическая
вероятности условной 82
Исходы элементарные
равновоэможные 42
Исход элементарный 21
- благоприятствующий событию
24
- образующий событие 24
Квантиль уровня а (а-квантиль)
322
Ковариация 189, 309
Координаты случайного вектора
165
Коэффициент корреляции 187, 189,
317
- полиномиальный
(мультиномиальный) 53
Критерий независимости
случайных величин 364
Линия регрессии 370
Матрица ковариаций
(ковариационная матрица) 188,
189, 314
- корреляционная (нормированная
ковариационная) 320
Медиана 323
Мера вероятностная 60
Метод линеаризации 258
- математической индукции 1-63
Множество возможных значений
случайной величины 124
Мода случайной величины
дискретной 325
непрерывной 324
Момент второй начальный 301
- центральный 302
- корреляционный 309
- k-го порядка 308
начальный 308
центральный 308
Независимость событий попарная
90
Неравенство Чебышева второе 406
- первое 404
Объединение (сумма) событий 27
Ожидание математическое 144
- - (среднее значение) случайной
величины дискретной 289
непрерывной 291
-- условное 366, 370
Операции (действия) над
событиями 26
Определение вероятности
аксиоматическое 59
- геометрическое 56
- классическое 43
450
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Определение вероятности
статистическое 58
Оси рассеивания 191
Отклонение среднее квадратичное
145, 189, 305
Отношение корреляционное 378
Отсутствие последействия 143
Пересечение (произведение)
событий 26
Перестановка 47
Плотность распределения
(вероятностей) 135
- нормального многомерного 189
- случайного вектора 177
- совместная 208
двумерная 177
п-мерная 177
-- условная 359
Последовательность независимых
одинаковых испытаний 99
Преобразование Лапласа —
Стилтьеса 421
Пространство вероятностное 66
- элементарных исходов 21
Размещение 47
- без повторений 47
- с повторениями 47
Разность событий 28
Распределение бимодальное 324
- биномиальное 132
- (вероятностей) 126
- вероятностей биномиальное 101
- гамма 147
- гауссово 144
- геометрическое 134
- гипергеометрическое 54
Распределение Коши 294
- логарифмически нормальное
(логнормальное) 282
- Максвелла 240
- мультимодальное 324
- нормальное 144
- вырожденное 256
-- двумерное 186
невырожденное 187
-- многомерное 189
стандартное 189
- стандартное 104
- полиномиальное 108
- Пуассона 103, 133
- равномерное 140
-- в области 384
- Релея 147
- Стьюдента (^распределение) 268
- унимодальное 324
- условное 355
- Фишера — Снедекора
(F-распределение) 284
- экспоненциальное двумерное 171
- Эрланга 148
- X2 (хи-квадрат) 149
Регрессия 370
Ряд распределения (вероятностей)
дискретной случайной величины
129
Свертка (композиция) законов
распределения 242
-- плотностей распределения 242
Сигма-алгебра (а-алгебра) 33
- борелевская (минимальная) 34
- событий 33
Событие 24, 33
451
Событие достоверное 25, 168
- невозможное 25
- противоположное 29
- элементарное 21
События зависимые 87
- независимые 87
- - в совокупности 90
- несовместные
(непересекающиеся) 26
в совокупности 28
попарно 28
- совместные (пересекающиеся) 27
Сочетание 47
- без повторений 47
- с повторениями 47
Схема Бернулли 99
-- обобщенная 109
- биномиальная 99
- геометрическая 56
- гипергеометрическая 54
- классическая 43
- полиномиальная
(мультиноминальная) 108, 109
Сходимость в среднем
квадратичном 400
- всюду 398
- по вероятности 399
- с вероятностью 1 (почти
наверное) 399
- функций распределения слабая
400
Теорема Бернулли 411
- Муавра — Лапласа интегральная
424
Теорема непрерывности 421
- сложения вероятностей 63
- центральная предельная 423
Устойчивость статистическая 17
Формула Байеса 97
- Бернулли 100
- биномиальная 101
- вероятности объединения
независимых событий 92
- комбинаторики основная 45
- Муавра — Лапласа интегральная
105
- Муавра — Лапласа локальная 104
- обращения 418
- полной вероятности 93
- Пуассона 103
- свертки 242
- умножения вероятностей 85
Функция от случайной величины
двумерной 237
скалярной 224
- производящая 421
* распределения (вероятностей) 127
случайного вектора п-мерного
167
совместная 167
- нормального стандартного 106
- одномерная частная или
маргинальная 169
- условная 358
- регрессии 370
- характеристическая 412
Центр рассеивания 191
452
ПРЕДМЕТНЫЙ УКАЗАТЕЛЬ
Частота события случайного
наблюденная 18
— условная 79
Число степеней свободы
распределения \2 149
Эксперимент случайный 17
Эксцесс 321
Элемент вероятности 138
Эллипсоид рассеивания 192
Эллипс равной вероятности 191
- рассеивания 191
Энтропия случайной величины
дискретной 326
двумерной 326
непрерывной 327
двумерной 327
Якобиан VII, 207
ОГЛАВЛЕНИЕ
Предисловие 5
Основные обозначения 11
Введение 17
1. Случайные события 21
1.1. Пространство элементарных исходов 21
1.2. События, действия над ними 24
1.3. Сигма-алгебра событий 32
1.4. Решение типовых примеров 35
Вопросы и задачи 38
2. Вероятность 42
2.1. Классическое определение вероятности 42
2.2. Вычисление вероятностей с помощью формул комбина-
комбинаторики 45
2.3. Геометрическое определение вероятности 55
2.4. Статистическое определение вероятности 58
2.5. Аксиоматическое определение вероятности 59
2.6. Решение типовых примеров 66
Вопросы и задачи 72
3. Условная вероятность. Схема Бернулли 78
3.1. Определение условной вероятности 78
3.2. Формула умножения вероятностей 85
3.3. Независимые и зависимые события 87
3.4. Формула полной вероятности 93
3.5. Формула Байеса 96
3.6. Схема Бернулли 99
3.7. Решение типовых примеров . 109
Вопросы и задачи 118
454 ОГЛАВЛЕНИЕ
4. Одномерные случайные величины 124
4.1. Определение случайной величины 124
4.2. Функция распределения случайной величины 126
4.3. Дискретные случайные величины 129
4.4. Некоторые дискретные случайные величины 132
4.5. Непрерывные случайные величины 135
4.6. Некоторые непрерывные случайные величины .... 140
4.7. Решение типовых примеров 149
Вопросы и задачи 158
5. Многомерные случайные величины 165
5.1. Многомерная случайная величина. Совместная функ-
функция распределения 165
5.2. Дискретные двумерные случайные величины 171
5.3. Непрерывные случайные величины 176
5.4. Независимые случайные величины 181
5.5. Многомерное нормальное распределение 186
5.6. Решение типовых примеров 197
Вопросы и задачи 212
6. Функции от случайных величин 222
6.1. Примеры функциональной зависимости между случай-
случайными величинами 222
6.2. Функции от одномерной случайной величины .... 224
6.3. Скалярные функции от случайного векторного аргу-
аргумента 237
6.4. Формула^вертки 241
6.5. Векторные функции от случайного векторного аргу-
аргумента 245
6.6. Линейные преобразования нормально распределенных
случайных величин. Метод линеаризации 252
6.7. Решение типовых примеров 260
Вопросы и задачи 279
7. Числовые характеристики случайных величин 288
7.1. Математическое ожидание случайной величины . . . 288
7.2. Математическое ожидание функции от случайной ве-
величины. Свойства математического ожидания .... 294
7.3. Дисперсия. Моменты высших порядков 301
7.4. Ковариация и коэффициент корреляции случайных ве-
величин 309
455
7.5. Другие числовые характеристики случайных величин 320
7.6. Решение типовых примеров 328
Вопросы и задачи 345
8. Условные характеристики случайных величин 354
8.1. Условные распределения 354
8.2. Условные числовые характеристики 365
8.3. Решение типовых примеров 382
Вопросы и задачи 391
9. Предельные теоремы теории вероятностей 397
9.1. Сходимость последовательности случайных величин 398
9.2. Неравенства Чебышева. Закон больших чисел .... 404
9.3. Характеристическая функция 412
9.4. Центральная предельная теорема 422
9.5. Решение типовых примеров 426
Вопросы и задачи 436
Приложение 443
Список рекомендуемой литературы 446
Предметный указатель 448
Учебное издание
Математика в техническом университете
Выпуск XVI
Печинкин Александр Владимирович
Тескин Олег Иванович
Цветкова Галина Михайловна
Бочаров Павел Петрович
Козлов Николай Ефимович
ТЕОРИЯ ВЕРОЯТНОСТЕЙ
Редактор Г.А. Нилова
Художник С. С Водчиц
Корректор Е.В. Авалова
Компьютерная верстка В.Н. Подобрлев
Оригинал-макет подготовлен в Издательстве
МГТУ им. Н.Э. Баумана
под руководством А.Н. Калашникова
Подписано в печать 02.04.2004. Формат 60x88 1/16.
Печать офсетная Бумага офсетная.
Усл. печ. л. 28,5. Уч. изд. л. 29,12.
» Тираж 3000 экз. Заказ № 10047
Издательство МГТУ им. Н.Э. Баумана,
105005, Москва, 2-я Бауманская, 5.
Отпечатано в ГУП ППП «Типография «Наука».
121099, г. Москва, Шубинский пер., 6.
ISBN 5-7038-2485-0
985703"82
856